Текст
Т.И.Трофимова
ЗТЛавлова
СБОРНИК
задач по курсу
физики
с решениями
Рекомендовано
Министерством общего
и профессионального образования
Российской Федерации
в качестве учебного пособия
для студентов вузов
Москва
«Высшая школа»
1999
УДК 53
ББК 22.3
Т70
Оглавление
Р с ц е II з е и т: В. А. Касьянов
Трофимова Т. И., Павлова 3. Г.
Т 70 Сборник задач по курсу физик» с решениями: Учеб. пособие
для ну зов.— М.: Высш. шк., 1999.— 591 с: ил.
ISBN 5-06-003534-4
Предлагаемый задачник с решениями составляет единый методический
комплект с «Курсом физики» и «Сборником задач но курсу физики» Т. И.
1рофимо1юй (М., 1?1>гсш. школа). Ол состоит из семи разделав, полностью
соотвегствуюших jjpoipaw.Mc курсп физики для вузов.
Основное назначение пособия — научить студента решать задачи, показать
им рациональную зашгеь услопщг, решения, расчета, отпета. Решение задач дается
без каких-либо пояснений, что потребует от студента, п случае необходимости,
обратиться к теоретическому материалу, вникнуть в суть рассматриваемых
явлении и процессов.
JJjik студентов и преподавателей вузов и техникумов. Может быть полезен
учащимся лицеев и ко.меджей, а также абитуриентам, готовящимся к поступлению
и технические институты.
ISBN 5-06-003534-4
© Издательство «Высшая школа», 1999
. — s s s
Оригинал-макет данного издания является собственностью издательства «Высшая
школа» и CJo репродуцирование (воспроизведение) любым способом 6cj согласия
излателмлва запрещается.
'Предисловие 5
Методические указания 5
fl. Физические основы механики
1.1. Элементы кинематики 6
1.2. Динамика материальной точки и поступательного движения
твердого тела 29
1.3. Работа и энергия 48
1.4. Механика твердого тела 72
1.5. Тяготение. Элементы теории поля 94
1.6. Элементы механики жидкостей 114
1.7. Элементы специальной (частной) теории относительности 131
2. Основы молекулярной физики и термодинамики
2.1. Молекулярно-кинетическая теория идеальных газов 145
2.2. Основы термодинамики 166
, 2.3. Реальные газы, жидкости и твердые тела 186
3. Электричество и магнетизм
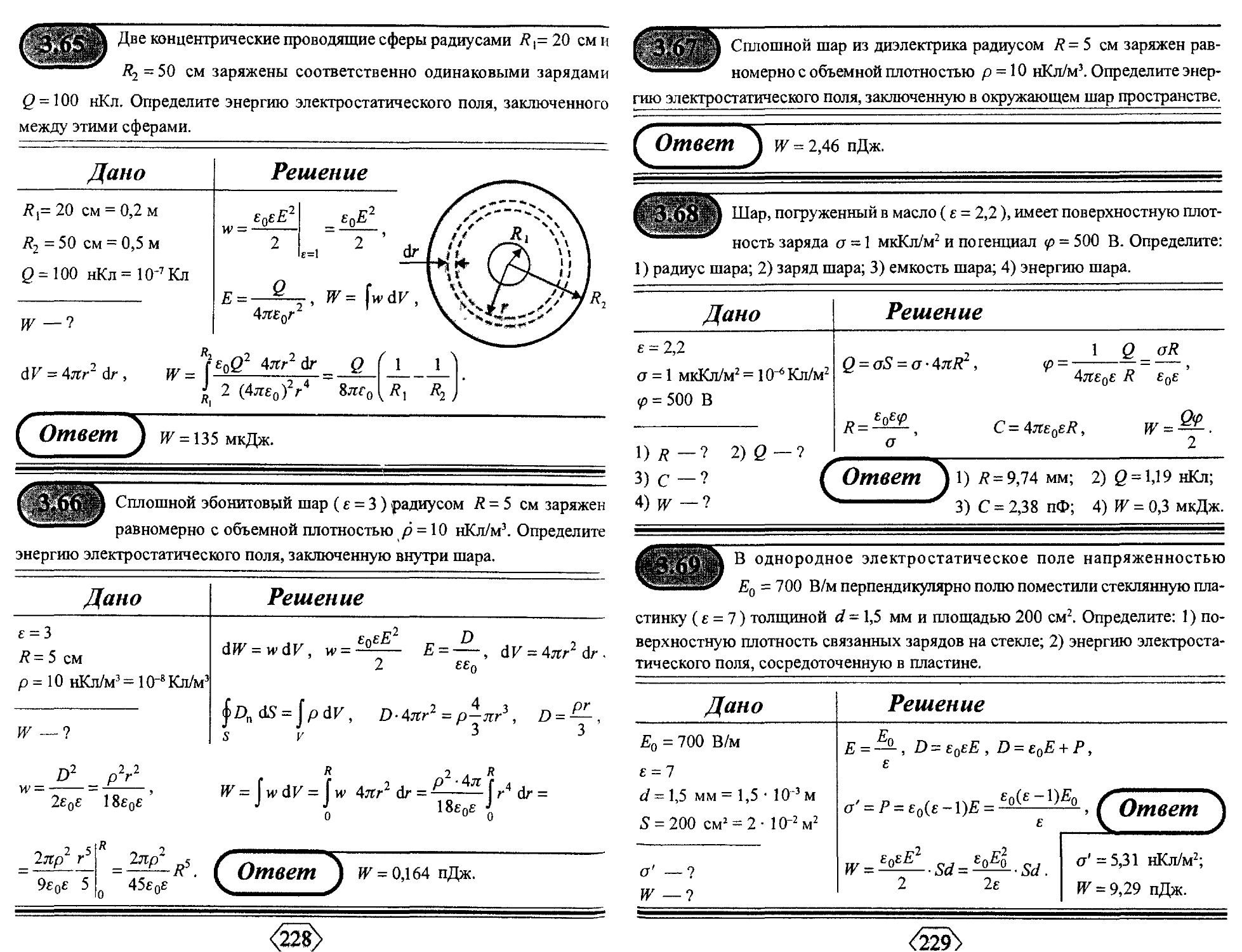
3.1. Электростатика 199
3.2. Постоянный электрический ток 233
3.3. Электрический ток в металлах, в вакууме и газах 247
3.4. Магнитное поле 251
3.5. Электромагнитная индукция 279
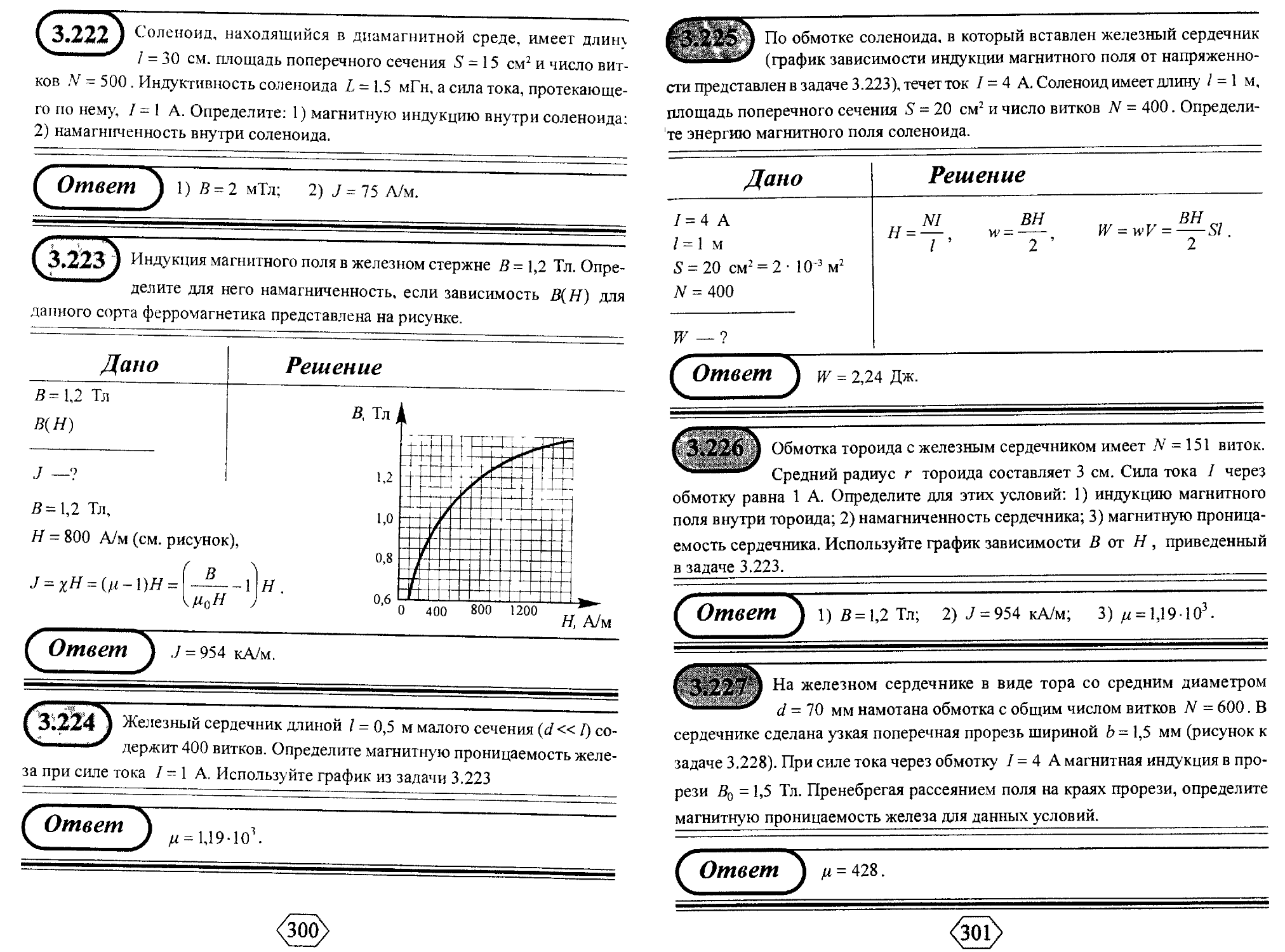
3.6. Магнитные свойства вещества...: 297
3.7. Основы теории Максвелла для электромагнитного поля 303
4. Колебания и волны
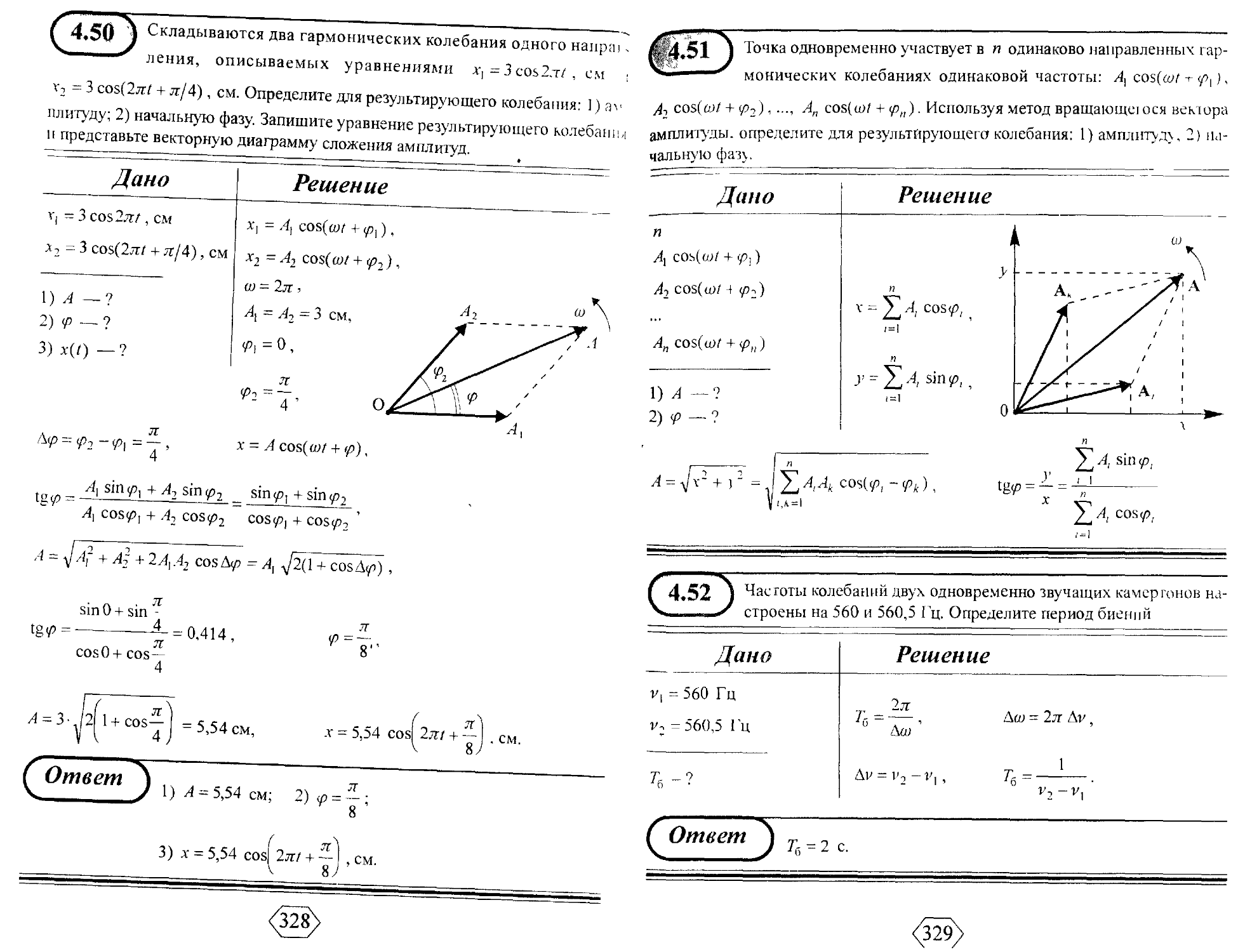
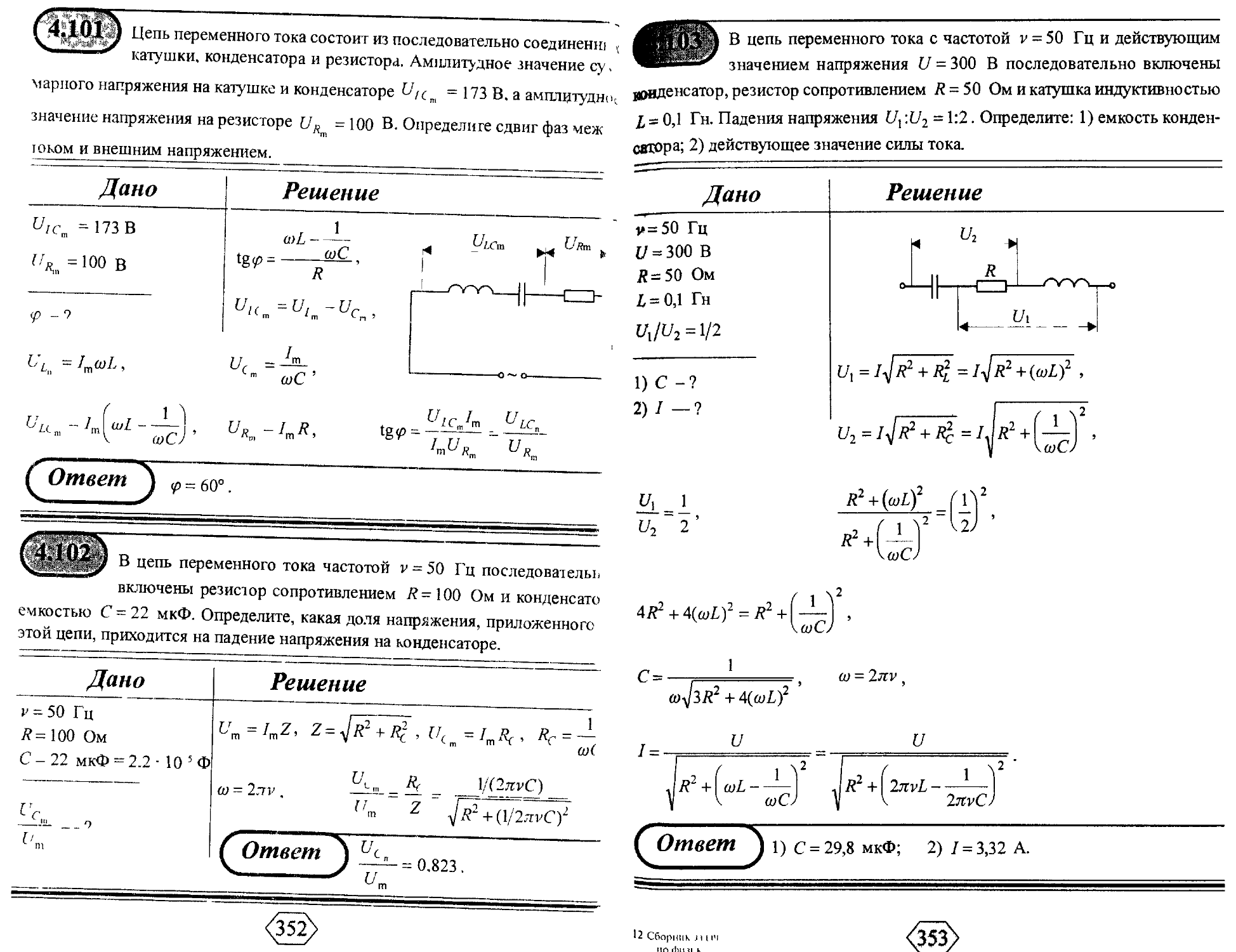
4.1. Механические и электромагнитные колебания 307
4.2. Упругие волны 360
4.3. Электромагнитные волны 377
5. Оптика. Квантовая природа излучения
5.1. Элементы геометрической и электронной оптики 385
5.2. Интерференция света 401
5.3. Дифракция света 413
5.4. Взаимодействие электромагнитных волн с веществом 431
5.5. Поляризация света 441
5.6. Квантовая природа излучения 452
6. Элементы квантовой физики атомов, молекул и твердых тел
6.1 1еоркя аюма водорода по Бору 47^
6.2. Элементы квантовой механики 491
6.3. Элементы современной физики атомов и молекул 526
6 4. Элементы квантовой статистики 539
6.5. Элементы физики твердого тела 542
7. Элементы физики атомного ядра и элементарных частиц
7 1. Элементы физики атомного ядра 547
7 2. Элементы физики элементарных частиц 572
Важнейшие формулы, используемые в задачнике 580
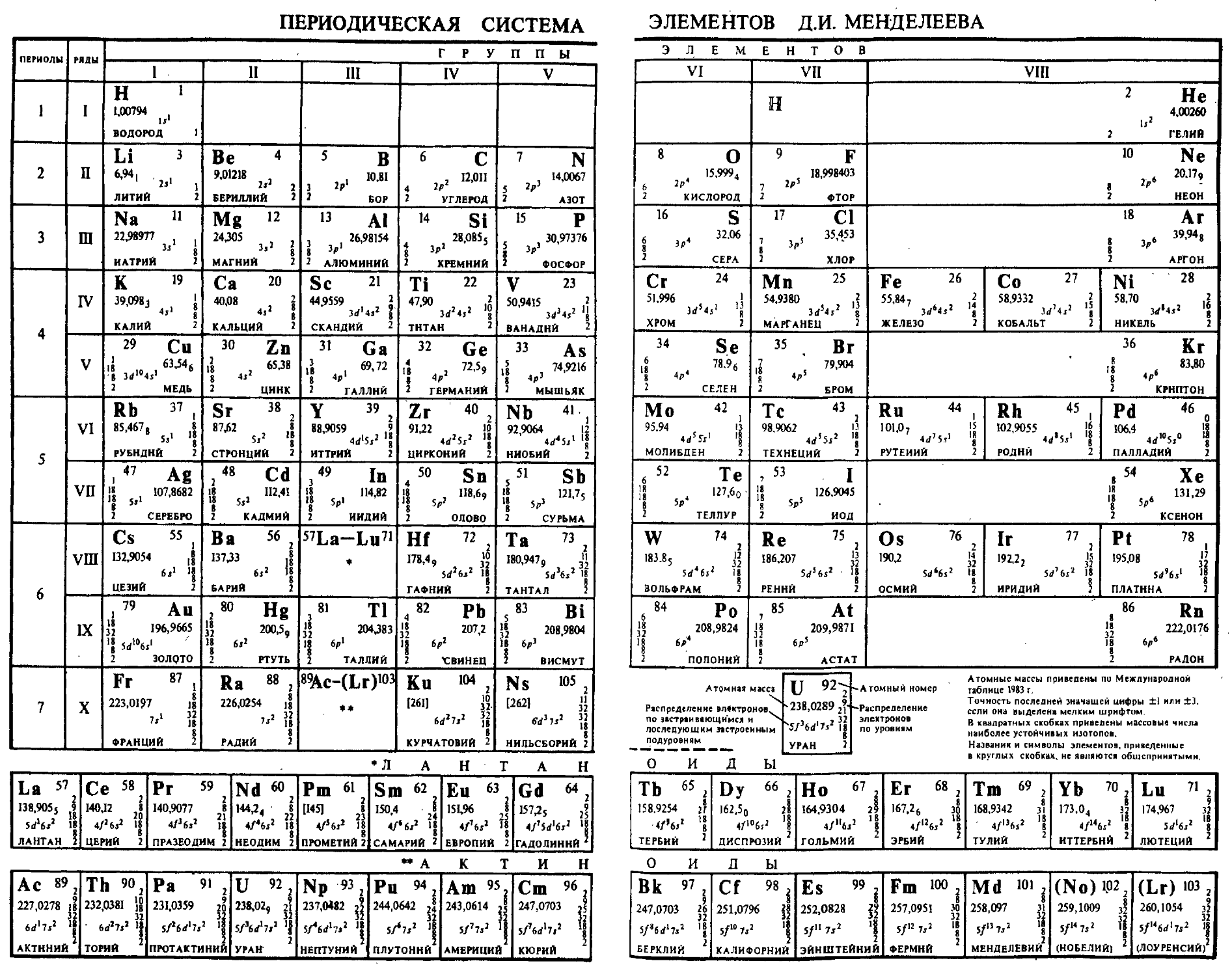
Периодическая система элементов Менделеева 590
Предисловие
При изучении курса физики во втузе большое значение имеет практичес-
кое применение теоретических знаний, главное из которых — умение решать
задачи. Данное учебное пособие полностью соответствует "Курсу физики"
X И. Трофимовой (издательство "'Высшая школа", 5-е изд., 1998) и "Сборнику
Задач по курсу физики" Т. И. Трофимовой (издательство "Высшая школа", 1996).
йбразуя, таким образом, с ними единый методический комплект.
Для формирования навыков работы над задачами все решения оформле-
ны однотипно: запись условия, перевод данных в СИ, запись необходимых урав-
нений, их решение в общем виде, подстановка числовых значений в конечную
'формулу, запись ответа. Решение задач приводится без каких-либо пояснений,
поскольку сначала следует тщательно изучить теоретический материал по дан-
'вой теме, затем провести собственный анализ задачи, решить ее и только тогда
Чдля сравнения результатов обратиться к готовому решению, которое, кета i и, не
всегда является единственным.
IJ, Все задачи снабжены ответами, которые даны с точностью до трех знача-
1 fUHx цифр. Таким же числом значащих цифр выражены величины в условиях
'Задач и справочных таблицах, приведенных по мере представления материала
.Значащие цифры — нули, стоящие в конце чисел, — для упрощения записи
'опускаются. В условиях задач и в ответах используются кратные и дольные
единицы, образованные от единиц СИ. В конце сборника приведен перечень
] зажнейших используемых формул.
А
Авторы
Методические указания
Решая задачи, целесообразно использовать следующие методические указания.
Ц] Вникнув в условие задачи, сделать краткую запись условия, выразить все
данные в СИ и, где это только возможно, дать схематический чертеж, по-
ясняющий содержание задачи.
ЩВыяснив, какие физические законы лежат в основе данной задачи, решить
ее в общем виде, т. е. выразить искомую физическую величину через за-
данные в задаче величины (в буквенных обозначениях, без подстановки
числовых значений в промежуточные формулы).
[3J Проверив правильность общего решения, подставить числа в окончатель-
ную формулу и указать единицу искомой физической величины, проверив
правильность ее размерности.
s
5
1. Физические основы механики
1.1. Элементы кинематики
f .'lilfsfM Скорость течения реки v = 3 км/ч, а скорость движения лодки
относительно воды у, = 6 км/ч. Определите, под каким углом от-
носительно берега должна двигаться лодка, чтобы проплыть поперек реки.
V
a
= 3
= 6
r
Дано
км/ч = 0,833
км/ч= 1,67
м/с
м/с
V
а-
Решение
- cosa,
V
arccos
Л
\
С Ответ) а =
60°
| т2 ~\ Капля дождя при скорости ветра и, = 11 м/с падает под углом
а = 30° к вертикали. Определите, при какой скорости ветра v2
ьапля воды будет падать под углом /? = 45°
Дано
м/с
а = 30°
Решение
м, = и2 = i
wl
— = tga,
и
tga tg/?
M / ^
tga' (Ответ j
= 19m/c.
t.. "]|[.3 ^y Два автомобиля, выехав одновременно из одного пункта, движут-
ся прямолинейно в одном направлении. Зависимость пройденно-
го ими пути задается уравнениями 5, = At + Bt" и s2 = Ct + Dt" + Ft* Опреде-
лите относительн> ю скорость автомобилей
Дано
- At + Bf
s-, -- Ct + Dt + Ft3
Решение
и = и, - v2,
dt
d/
Ответ J u = a-c+ 2{B-D)t-3Ft2.
% Велосипедист проехал первую половину времени своего движения
Д1** со скоростью у, =16 км/ч, вторую половину времени — со ско-
ростью и, = 12 км/ч Определите среднюю скорость движения велосипедиста.
г'|
<«;
=^2=
=16
= 12
Дано
t
км/ч = 4,44 м/с
км/ч = 3,33 м/с
Решение
(v> = -» * = «|
S2 = ^'2'2 » t\~t'
S = W[ — + W, — = (l>[ +
¦ = 2'
Д, =4,/,,
("I
ГОтвет j (v) =
14 км/ч
"S^fc) Велосипедист проехал первую половину пути со скоростью
v| = 16 км/ч, вторую половину пути—со скоростью v2 = 12 км/ч
Определите среднюю скорость движения велосипедиста.
Ответ } (v) = 13,7 м/с.
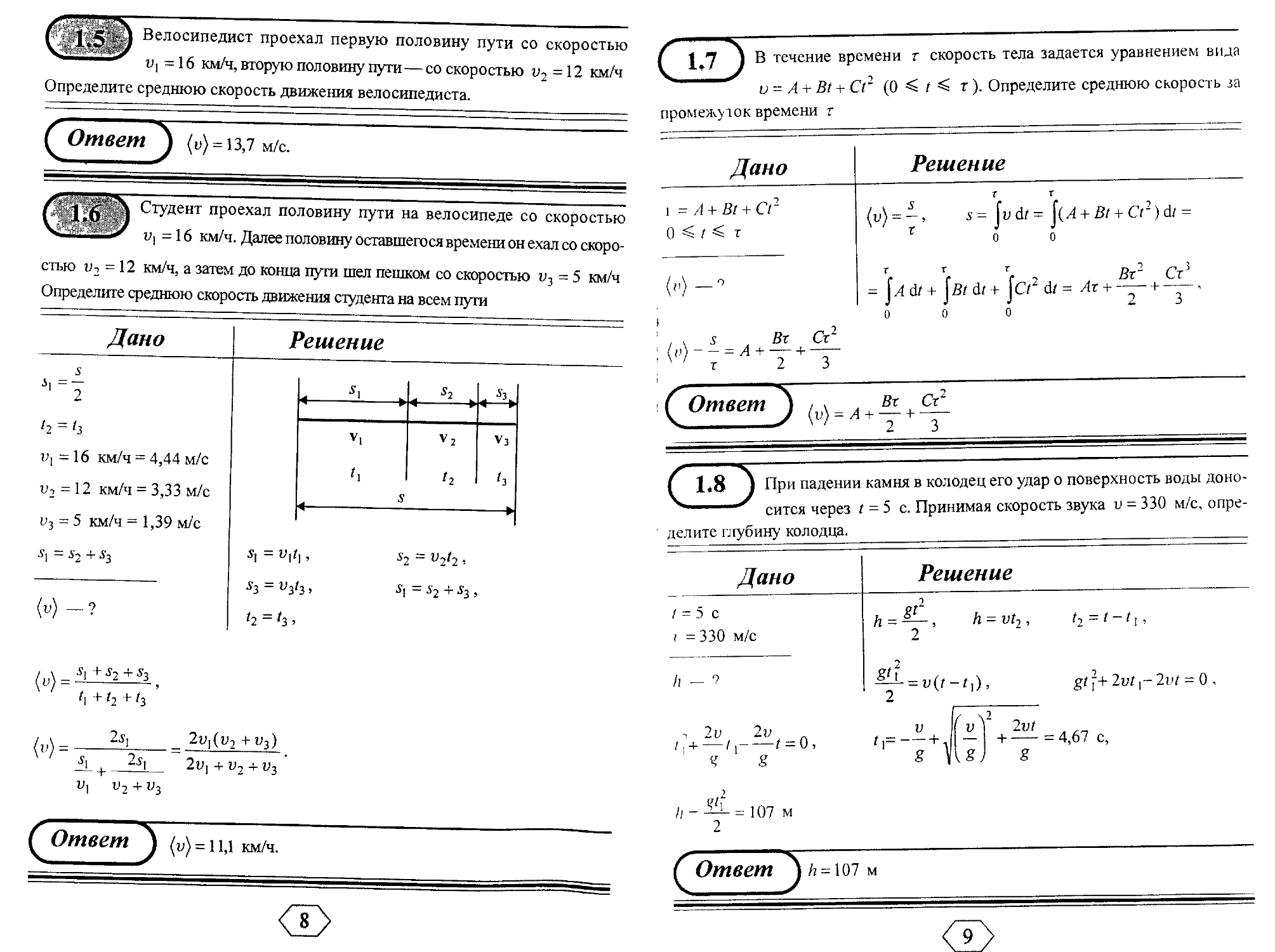
Г * 1 <?*' ^ Студент проехал половину пути на велосипеде со скоростью
У. ц i \У v ] = 16 км/ч. Далее половину оставшегося времени он ехал со скоро-
стью v2 = \2 км/ч, а затем до конца пути шел пешком со скоростью v3 = 5 км/ч
Определите среднюю скорость движения студента на всем пути
Дано
S
^ = 2
h = h
Uj =16 км/ч = 4,44 м/с
v2 = 12 км/ч = 3,33 м/с
и3 =5 км/ч = 1,39 м/с
.s, =s2+s3
Решение
4 ¦ fc
v,
?!
*3 = v3t
h = h>
3> s]
v2
/2
Hi
v3
^3
= U2'2 .
= s2 + s3 ,
•S] + ^2 + 53
'l + ^2 + ^3
i + __ffL. 2У]+у2+"з
COmeemj (v) = i ц км/ч.
В течение времени г скорость тела задается уравнением вида
и = А + Bt + Ct @ < / < г). Определите среднюю скорость за
промежуток времени г
1 = Ал
0 </
/¦Л
V7
Дано
v Bt + О2
< т
о
W-
Решение
Т
—, s = | v dt =
0
г г
d/ + f Bt dt + JO2
X
\{A
0
dt =
+ Bt
Ax +
+ Cr)
Br2
2
d/ =
Cr3
3
о о
COmeem J
Bx Cxl
2 3
f 1*8 } При падении камня в колодец его удар о поверхность воды доно-
сится через t = 5 с. Принимая скорость звука v = 330 м/с, опре-
делите глубину колодца.
Дано
t = 5 с
f = 330 м/с
/i — ¦>
Решение
st2
h = 2—, h = vt2, t2 = t-t1,
2 и
ri + —'r
g VV^/ я
у If w 1 2u/
i=— + J - + =4'67 c'
/, -
1L
{Ответ j /1 = 107
Тело падает с высоты h = \ км с нулевой начальной скоростью
Пренебрегая сопротивлением воздуха, определите, какой п\1ь
пройдет тело- 1) за первую секунду падения; 2) за последнюю сек>нду падения
Дано
h --1 км = 103 м
»\,=0
/, - 1 с
л, = 1 с
Решение
II-
t =
2h
o'l
h
t
К
1
1 hj.
л
\
•h
г
s, -¦
I.IV^ Тело падаете высоты h=\ км с нулевой начальной скоростью
Пренебрегая сопротивлением воздуха, определите, какое вре-
мя понадобится гелу для прохождения: П первых 10 м ими; 2) последних
10 мими
С Ответ J
1) /, --1,43 с; 2) /,=0,1 с
Первое тело брошено вертикально вверх с начальной скоростью
v0 = 5 м/с. В тот же момент времени вертикально вниз с той же
начальной скоростью из точки, соответствующей максимальной верхней точке
полета /^ первого тела, брошено второе тело. Определите: 1) в какой мо-
. мент времени / тела встретятся; 2) на какой высоте h от поверхности Земли
произойдет эта встреча; 3) скорость vx первого тела в момент встречи; 4) ско-
рость v2 второго тела в момент встречи.
Дано
Vq = 5 м/с
/ —?
h — ?
и,-?
«2-?
Umax
v\~
V2 =
Решение
,,2
2g'
vo-gt, йтх
"о + gt.
h
s, =vnt--
S2~
gt
r t-
!
gvj Ivl
= V0 - gt = V0-
Ag 4
g 4
i С Ответ Л i) г = 127 мс; 2) ft = 56 смГ
3) и, = 3,75 м/с; w2 = 6,25 м/с.
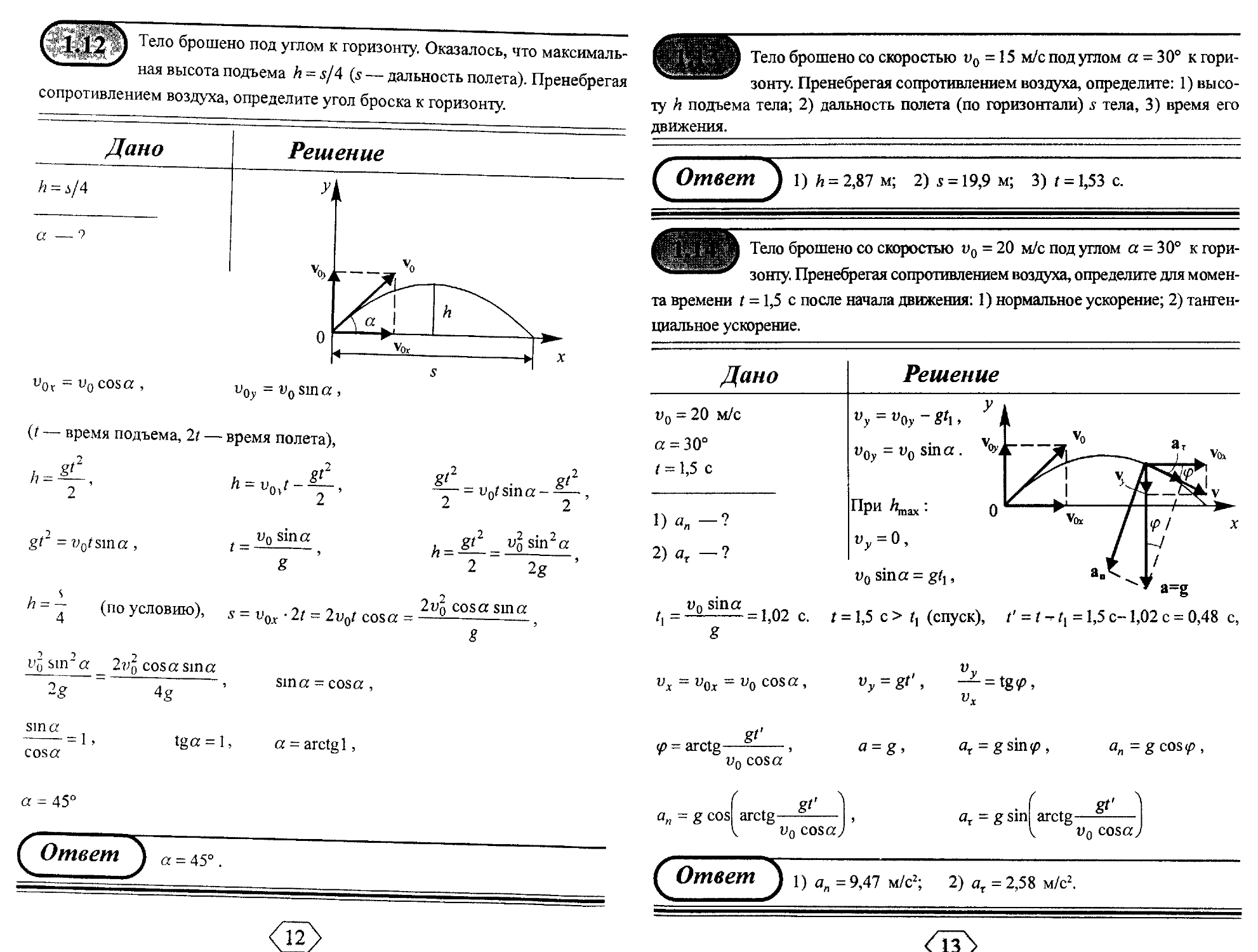
gfj Тело брошено под углом к горизонту. Оказалось, что максималь- ЦЦШ Тело брошено со скоростью v0 = 15 м/с под углом а = 30° кгори-
ная высота подъема h = s/4 (s — дальность полета). Пренебрегая ^™"^ зонту. Пренебрегая сопротивлением воздуха, определите: 1) высо-
сопротивлением воздуха, определите угол броска к горизонту. ту h подъема тела; 2) дальность полета (по горизонтали) s тела, 3) время его
движения.
Дано
h = i/4
а — 9
Решение
у
0
А а \
—>'
*
X
voy - vo sin a ,
(t — время подъема, It — время полета),
2
gt' =?;0/sina ,
_ v0 sin a
g
условию),
gt2
С Ответ J 1) h = 2,87 м; 2) s = 19,9 м; 3) t = 1,53 с.
Тело брошено со скоростью v0 = 20 м/с под углом а - 30° к гори-
зонту. Пренебрегая сопротивлением воздуха, определите для момен-
та времени t -1,5 с после начала движения: 1) нормальное ускорение; 2) танген-
циальное ускорение.
а -
t =
2)
= 20
= 30°
1,5 с
ar —
Дано
м/с
7
Решение
у
vy ~ v0y ~ 8h> i
V
V — V SU1СС ЧУл
При hnn: о
v, = 0,
i
v0
^ ; ь
-/
V
X
sina
v0 sina = gtx,
¦¦ 1,5 О ?, (спуск),
ап'
= 1,5 с-1,02 с = 0,48 с,
sina
cosa
a = 45°
Г Ответ
sina = cosa
tga = l, a = arctgl,
a = 45°.
vx = Vox = y0 cosa,
) = arctg-
cosa
vy = gf',
Vy
= gsm<p, an=gcostp.
( gt' }
an = g cos arctg—5
V v0 cosaj
at = g sin arctg—
V v0 cosa
Ответ J \) an= 9,47 м/с2; 2) aT = 2,58 м/с2.
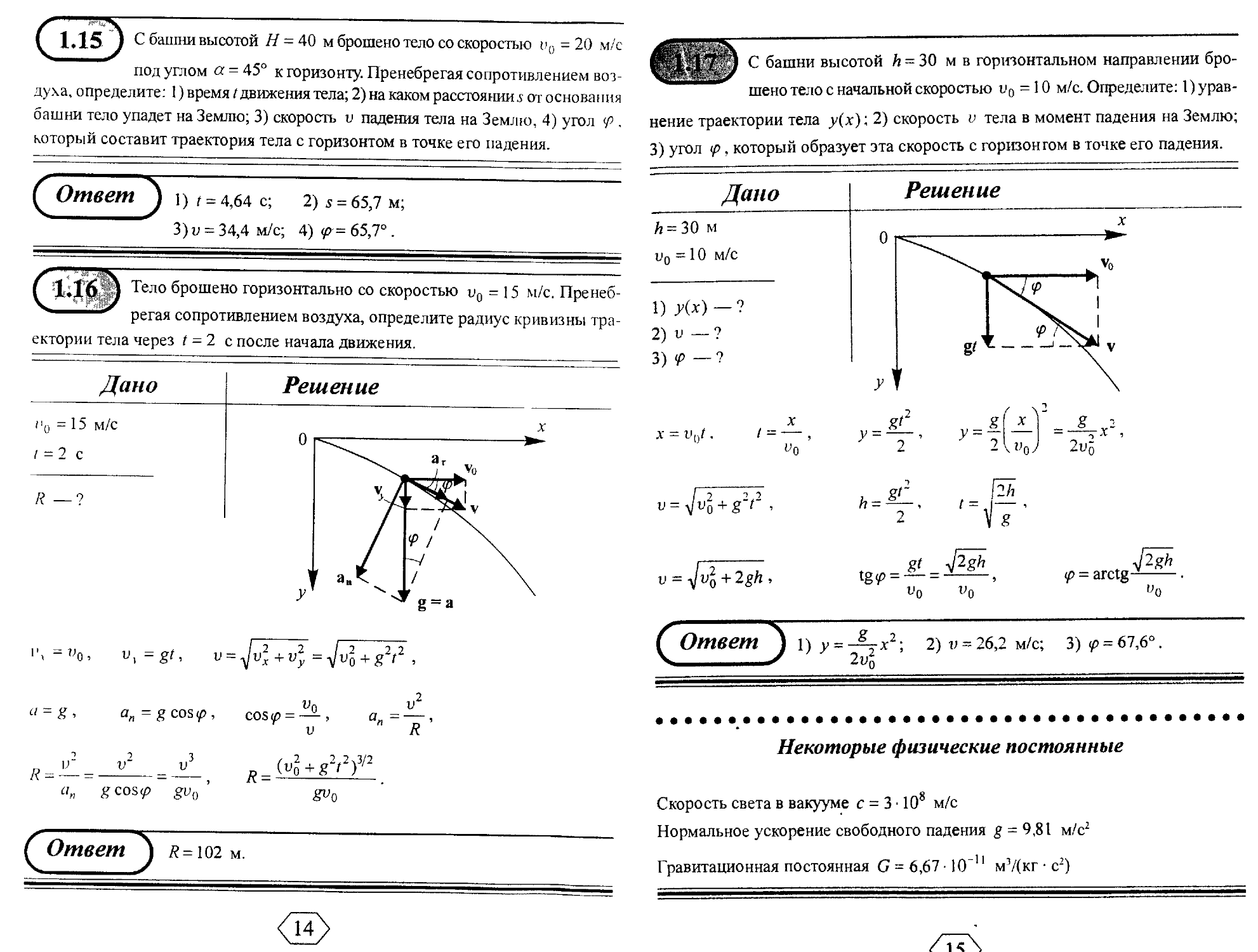
1.15 ) С башни высотой // = 40 м брошено тело со скоростью v0 = 20 м/с
под углом а = 45° к горизонту. Пренебрегая сопротивлением воз-
духа, определите: 1) время /движения тела; 2) на каком расстоянии .$ от основания
башни тело упадет на Землю; 3) скорость v падения тела на Землю, 4) угол f ,
который составит траектория тела с горизонтом в точке его падения.
С Ответ J ]) t = 4,64 с; 2) 5 = 65,7 м;
3)у = 34,4 м/с; 4) ^=65,7°.
Тело брошено горизонтально со скоростью ип = 15 м/с. Пренеб-
регая сопротивлением воздуха, определите радиус кривизны тра-
ектории тела через / -2 с после начала движения.
Дано
''о =15 м/с
1 = 2 с
R — ?
Решение
¦\=»о
= g, а„= g cos ip..
v
а„ gcosp gvQ
С Ответ ) R =
= 102 м.
^ ^ашни высотой й = 30 мв горизонтальном направлении бро-
шено тело с начальной скоростью vQ = 10 м/с. Определите: 1) урав-
нение траектории тела у(х); 2) скорость v тела в момент падения на Землю;
3) угол <р, который образует эта скорость с горшонгом в точке его падения.
Дано
й = 30 м
v0 = 10 м/с
1) У(х)— ?
2) и — ?
3) IP —?
0
Решение
X
^
А" = V,,t . I = ,
- ~ - , X ,
ML
2
t =
= arctg
2gh
(Ответ ) l) у =-2-х2, 2) и = 26,2 м/с; 3)^ = 67,6°.
Некоторые физические постоянные
Скорость света в вакууме с = 3 ¦ 108 м/с
Нормальное ускорение свободного падения g = 9,81 м/с2
Гравитационная постоянная G = 6,67 ¦ 10~!| м3/(кг ¦ с2)
Зависимость пройденного телом пути от времени задается урав-
нением 5 = A-Bt + Ct2 + Dp (Л = 6 м, В=3 м/с; С =2 м/с2,
D = 1 м/с3). Определите для тела в интервале времени от /, = 1 с до t2 = 4 с
1) среднюю скорость, 2) среднее ускорение
s =
A
Л —
в=
c=
D =
l\ =
h ~
D(
2)<<
A
0
3
2
1
1
4
Дано
~Bt + a2 + Dt3
M
м/с
м/с2
м/с3
с
с
?
9
s2
V -
1
\a,
V2
Решение
\ S2~S\
}'t2-tr
= S
J1=5I
-- — = -B + 2Ct + 3Dr,
Л t
Of
v2 - u,
— -
— J
'2-'l
ГОтеет
i) (w) = 28 м/с, 2) (a) = 19 м/с2.
Зависимость пройденного телом пути от времени задается урав-
нением s = А + Bt + О2 + Dt3 (С = 0,1 м/с2, D = 0,03 м/с3). Опре-
делите. 1) через сколько времени после начала движения ускорение а тела бу-
дет равно 2 м/с2; 2) среднее ускорение (а) тела за этот промежуток времени.
Г Ответ J
1) / = 10 с;
2) (а) = 1,1 м/с2.
Объясните, может ли изменяться направление вектора скорости,
ft _J в то время как его ускорение по модулю остается постоянным
jb^i !j Тело движется равноускоренно с начальной скоростью v0. Опре-
* * делите ускорение тела, если за время 1 = 2 с оно прошло путь
= 16 м и его скорост ь v = 3v0.
Дано
t = 2 с
5 = 16 M
w = 3w0
a —?
a/2
a = const, г1 = c0 + at, л = iy + ,
2t>n
v = 3v0, 3v0 = vo + at, a = .
A-1V+ ^^ -2u0/, «0=7--
a = ¦
2a __ s
2/ / Г
f Ответ j
« = 4 м/с2
1" 22 J Материальная точка движется вдоль прямой так, что ее ускорение
«Т-'У »/ линейно растет и за первые 10 с достигает значения 5 м/с2 Опре-
делите в конце десятой секунды 1) скорость точки, 2) пройденный точкой пу гь
Дано
а :
<i
«1
1)
2)
= kt
= 10
= 5
ui -
$\ ~
с
м/с2
_ 9
_ 9
Решение
а = kt,
w =
, = Ji'd/ =
kr_
2
— dt = —,
2 6
v, =¦
2 2
6 6
[Ответ j
1) u, =25 м/с, 2)s, =83,3 м
Jg| Кинематические уравнения движения двух материальных точек
имеют вид xx=Axt+$t2+Cf и х2 = A2t + B2t2 + С/, где
5, = 4 м/с2, С, = -3 м/с3, В2 = -2 м/с2, С2 = 1 м/с3. Определите момент време-
ни, для которого ускорения этих точек будут равны.
Q Ответ
, = 0>5 с.
'г- ненид движения двух материальных точек
имеют вид х, = Л, + 5,/ + С,?2 и х2 = А2 + B2t + C2t2, где 5, = Щ,
С, = -2 м/с2, С2 = 1 м/с2. Определите: 1) момент времени, для которого ско-
рости этих точек будут равны; 2) ускорения а, и а2 для этого момента.
Дано
Решение
х, =
= А2 + B2t + C2t2
С, = -2 м/с2
С2 = 1 м/с2
"|=»2
3) а, — ?
dx,
L
B,=
Bl+2Clt = B2+2C2t,
2(C2-C.)
17
С Ответ J
I) ? = О ;' 2) а, = -4 м/с2, 3) a2 = 2 м/с2.
Нормальное ускорение точки, движущейся по окружности радиу-
сом г = 4 м, задается уравнением а„ = А + Bt + Ct~ (A = \ м/с2,
В = 6 м/с1, С = 9 м/с4). Определите: 1) тангенциальное ускорение точки; 2) путь,
пройденный точкой за время ?, =5 с после начала движения; 3) полное ускоре-
ние для момента времени /2 = 1 с.
Дано
а„ = Л + 5/ + С/2
/4 = 1 м/с2
Л=6 м/с3
С = 9 м/с4
/,=5 с
1) аТ — ?
2L, ~'>
3) а2 — ?
Решение
В(+СГ,
V
г
и = yJr(A + Bt + а2) = -^4A + 6/ + 9t2) =
= 2A + 3/) = 2 + 6/, аг= — = — B + 6/),
d/ d/
5, = jv d/
'i
= JB + 6/) dt = 2/, + 3/2,
ar2 = ar ,
_ v2 _B + б/2)
г г
6/2L
С Ответ J 1) а, = 6 м/с2; 2) лг, = 85 м; 3) a2 = 17,1 м/с2.
Ш Зависимость пройденного телом пути j от времени / выражается
уравнением j = At - Bt2 + С/3 (А = 2 м/с, В = 3 м/с2, С = 4 м/с3).
Запишите выражения для скорости и ускорения. Определите для момента времени
I - 2 с после начала движения 1) пройденный путь; 2) скорость; 3) ускорение
2)?; = 38 м/с, 3) а = 42 м/с1
Cj\ <2fl$*l Зависимость пройденного телом пути по окружности радиу-
сом г = 3 м задается уравнением s - At + Bt (А = 0,4 м/с:,
В - 0.1 м/с) Определите для момента времени ( = 1 с после начала движе-
ния ускорение: 1) нормальное, 2) тангенциальное; 3) полное.
С
Ответ J \) ап = 0,27 м/с2; 2) ах = 0,8 м/с2;
3) я = 0,84 м/с2
,.р| Точка движется в плоскости ху из положения с координатами
х\ = >i = 0 с0 скоростью v = ai + bxj (a, b — постоянные, i, j —
орты осей а и у). Определите: 1) уравнение траектории точки у(х); 2) форму
траектории.
[Ответ
X, = V,
v = ai 4
Дано
= 0
focj
7
v =
w,
dx
Решение
ai + bxj,
= a , v
= vxdt, dj
' = vy dt,
dx = a dt,
¦ bx
dy = — dx
a
dy = fee d/,
[bx be, b
- —dx = — \xdx- —
-t/-
x ; 2) парабола.
2a
Радиус-вектор материальной точки изменяется со временем по
закону г = Н + Згj, где i, j — орты осей х иу. Определите для
момента времени / = 1 с: 1) модуль скорости; 2) модуль ускорения.
r = /3i
t = \ с
1) v -
2) я -
Дано
+ 3rj
_ 7
_ 9
v =
a =
Решение
dr d , 3. „7.
= —= —(^4-3/2j
d^ d/
dv
: — = 6ri + 6j,
d^
= зг2,
) = 3?2i + 6
w = x
vy =
6t,
яд = 6/,
= 6,
и =
a = VFO2 +
Ответ J I) t> = 6,7 м/с; 2) я = 8,48 м/с2.
Радиус-вектор материальной точки изменяется со временем по
закону г = 4t2i + 3t j + 2k . Определите: 1) скорость v; 2) ускоре-
ние а; 3) модуль скорости в момент времени t = 2 с.
г =
t =
1)
2)
3)
4/2i
2с
V —
а
v\ -
Дано
+ 3/j + 2k
9
9
_ 7
Решение
dr
v = — =8ri + 3j,
d/
dv «•
а = — = 8i,
df
"i = V(8O2 + 32 .
2)a = 8i; 3) u,= 16,3 м/с.
Щ/? Движение материальной точки в плоскости ху описывается зако-деВЯ
ном х- At, y = At(\ + Bt),TntAviB — положительные постоян- «Н^Ш Материальная точка начинает двигаться по окружности радиусом
ные. пределите: 1) уравнение траектории материальной точкиХх); 2) радиус- ^ПпГ"">' ''" г - 12,5 см с постоянным тангенциальным ускорением ат = 0,5 см/сг.
от воеме™-1^ В Зависимости от вРемени; 3) скорость v точки в зависимости Определите: 1) момент времени, при котором вектор ускорения а образует с
от времени; 4) ускорение а точки в зависимости от времени.
a =
+(A + lABtf = ^V1 + 0
a = 2Л2? = const.
Некоторые математические формулы
sin(a ±fi) = sina coS
cos(a±y3) = cos a coSjS + sina sin/?
= 12,5 см = 0,125 м
= 5-1O-3m/c2
вектором скорости v угол а = 45° ; 2) путь, пройденный за это время движу-
щейся точкой.
Решение
и' а'Г а.Г
tg« = =_!_^-?—
/¦ аТ г а. г
«г
dv
а= — = const.
dt
v- \aT dt = aTt ,
t= Ftga
я„ =¦
аг
s - \v dt - \art
= 5 c; 2) s = 6,25 см.
Линейная скорость v{ точки, находящейся на ободе вращающе-
гося диска, в три раза больше, чем линейная скорость и2 точки,
находящейся на 6 см ближе к его оси. Определите радиус диска.
Г Ответ J R^
9 см.
Колесо вращается с постоянным угловым ускорением е = 3 пал/с Ш*$6 ) К°ЛеС° автомашины вРаЩается равнозамедленно За время / - 2 мин
Определите радиус к _ ' оно изменило частоту вращения от 240 до 60 мин ' Определите
, ерез -1 с после начала движе л угловое ускорение колеса, 2) число полных оборотов, сделанных колесом за
'Скопение vnnem л ^- 7 <; »,/„2 •/-' j r / г
jjX) время
ния полное ускорение колеса а = 7,5 м/с2
Дано
? = 3 рад/с2
f = l с
а = 7,5 м/с2
/г —9
Решение
Дано
aT=sR,
V
~R
2 мин = 120 с
= 240 мин"' = 4 с'1
L = 60 мин = 1 с '
п __
С Ответ j /?=79
см
Якорь электродвигателя, имеющий частоту вращения и = 50 с
' после выключения тока, сделав N = 628 оборотов, остановился 1
Определите угловое ускорение г якоря
Решение
, = 2ли2,
2л:л2 =
? = -
2nN = 2
- п2 )t,
= n,t-~
Ответ J I) ? = 0,157 рад/с1, 2) N = 300
Дано
п = 50 с
# = 628
?
Точка движется по окружности радиусом Л = 15 см с постоян-
ным тангенциальным ускорением аТ К концу четвертого оборо-
гта после начала движения линейная скорость точки и, = 15 см/с Определите
[нормальное ускорение а„2 точки через t2 =16 с после начала движения
Решение
Дано
(oQ = 2лп,
= 2nnt -
0 =
2nN - Inn
2лп ?
2?2
? = •
пп
(jOmeem
--12,5 рад/с2.
R
*1
v\
12
(
= 15 см = О,
= const
= 4
= 15 см/с =
= 16 с
9
Ответ
15 м
0,15 м/с
Решение
)~
an=a)~R = (et) R, aT = — = eR- const, l{ =
и
Е = -
iR
гП R,
1.38 J Диск радиусом Л = 10 см вращается вокруг неподвижной оси так.
что зависимость угла поворота диска от времени задается уравне-
нием ip=A + Bt + Cr+Dt3 (B = \ рад/с, С=\ рад/с2, D = \ рад/с3). Опреде-
лите для точек на ободе диска к концу второй секунды после начала движения
1) тангенциальное ускорение ат; 2) нормальное ускорение а„; 3) полное уско-
рение а.
1.40 ) Диск вращается вокруг неподвижной оси так, что зависимость
угла поворота радиуса диска от времени задается уравнением
о = At2 (А = 0,1 рад/с2). Определите полное ускорение а точки на ободе дис-
а к концу второй секунды после начала движения, если линейная скорость
той точки в этот момент равна 0,4 м/с.
Q Ответ J i)flr = i,
Дано
.4 м/с2; 2) ап = 28,9 м/с2; 3) о = 28,9 м/с2.
Диск вращается вокруг неподвижной оси так, что зависимость угла
поворота радиуса диска от времени задается уравнением <р- At2
(А = 0,5 рад/с2). Определите к концу второй секунды после начала движения-
1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находя-
щейся на расстоянии 80 см от оси вращения, тангенциальное аТ, нормальное
ап и полное а ускорения.
Дано
<р= At2
А-0,5 рад/с2
1 = 2 с
г = 80 см = 0,8 м
1) @ —?
2) е —-?
3) вт — ?
я„ -?
я —-?
? =
«г
«г
Решение
-At2, w =
d(O
-- — = 2А = const,
dt
dv
= —, v =
dl
= 2Ar, an
.
d<f> 4At
dt
v2 , i -,
= — = ftTr = AA'rf ,
r
• a =
f Ответ J l) ш = 2 рад/с; 2) e-\ рад/с:;
^ -^ 3) ar = 0,8 м/с2; an = 3,2 м/с2; a = 3,3 м/с:.
p = АГ
A = ОД рад/с2
(, =2 с
и, =0,4 м/с
Решение
= 2А,
v,
n
i = 2At,
l=wR=2AtlR,
v2 v2-2At,
2At
=2Av[t1,
a, =
a, = 0,256 м/с2.
*И Диск радиусом R -10 см вращается так, что зависимость линей-
ной скорости точек, лежащих на ободе диска, от времени задается
уравнением v- At + Bt ( А = 0,3 м/с2, В = 0,1 м/с3). Определите угол а, ко-
торый образует вектор полного ускорения а с радиусом колеса через 2 с от
начала движения.
Дано
Л = 10 см = 0,1 м
v= At + Bt2
А = 0,3 м/с2
В = 0,1 м/с3
г = 2 с
a —?
Решение
a
tga = —,
a
dv
ar = — = /1 + 2Bt,
d/
i>2 (At + Bt2J
R R
(A+2Bt)R
Г Ответ j a =
4°.
*J Диск радиусом Л = 10 см вращается так, что зависимость угла
поворота радиуса диска от времени задается уравнением
<р= А + Bt (A = 2 рад, В = 4 рад/с3). Определите для точек на ободе колеса
1) нормальное ускорение ап в момент времени 1 = 2 с; 2) тангенциальное ус-
корение для этого же момента; 3) угол поворота <р, при котором полное уско-
рение составляет с радиусом колеса угол а - 45°.
R
<P
A
В
/ -
a
1)
2)
3)
С
Г-
M
к —
Дано
-10 см-0,1 м
= А + ВР
= 2 рад
= 4 рад/с3
= 2 с
= 45°
«„-?
<р — 9
Десятичные
-тераA012)
-гига A0")
— мегаA06)
-килоA03)
tg
C
Р
230
Решение
= А + Вр,
= 6Bt,
= eR= 6BtR,
a = —L,
BrJR = 6BtR,
= 3S'
м/с2; 2) aT =
a) = ЗВГ
an=orR
tga = l,
aT = an,
9B2t4R =
<p= A + B
4,8 м/с2;
' приставки к названиям
д —
с —
м —
мк-
дециA0 ')
сантиA0 2)
-милли A0 3)
-микро A0 6)
u
П —
Ф-
n
= {3Bt2fR,
6BtR,
2 2
3) <p - 2,67 рад.
единиц
нано(Ю')
пико A0 |2)
фемто A0 |5)
агтоA0~18)
1.2. Динамика материальной точки
и поступательного движения твердого тела
Ч
чЛ Тело массой ш=2кг движется прямолинейно по закону
s = А - Bt + Ct2 - Dp (С = 2 м/с2, D = 0,4 м/с3). Определите силу,
действующую на тело в конце первой секунды движения.
Дано
от = 2кг
С = 2 м/с2
D - 0,4 м/с3
( = 1 с
F —->
Решение
dv
F = та= т— >
„ = ^ = -5 + 20-3^,
d^
d^
F = mBC-6Dt).
Г Ответ j f = 3,2 h.
rJ1 44^ Тело массой т движется так, что зависимость пройденного пути
от времени описывается уравнением s = A cos<y/, где А и w —
постоянные Запишите закон изменения силы от времени.
Г Ответ j
F- -тАш
К нити подвешен груз массой т = 500 г. Определите силу натя-
жения нити, если нить с грузом: 1) поднимать с ускорением 2 м/с2;
2) опускать с ускорением 2 м/с2.
QOmeemj
г = 5,9
2) г = з,9 н.
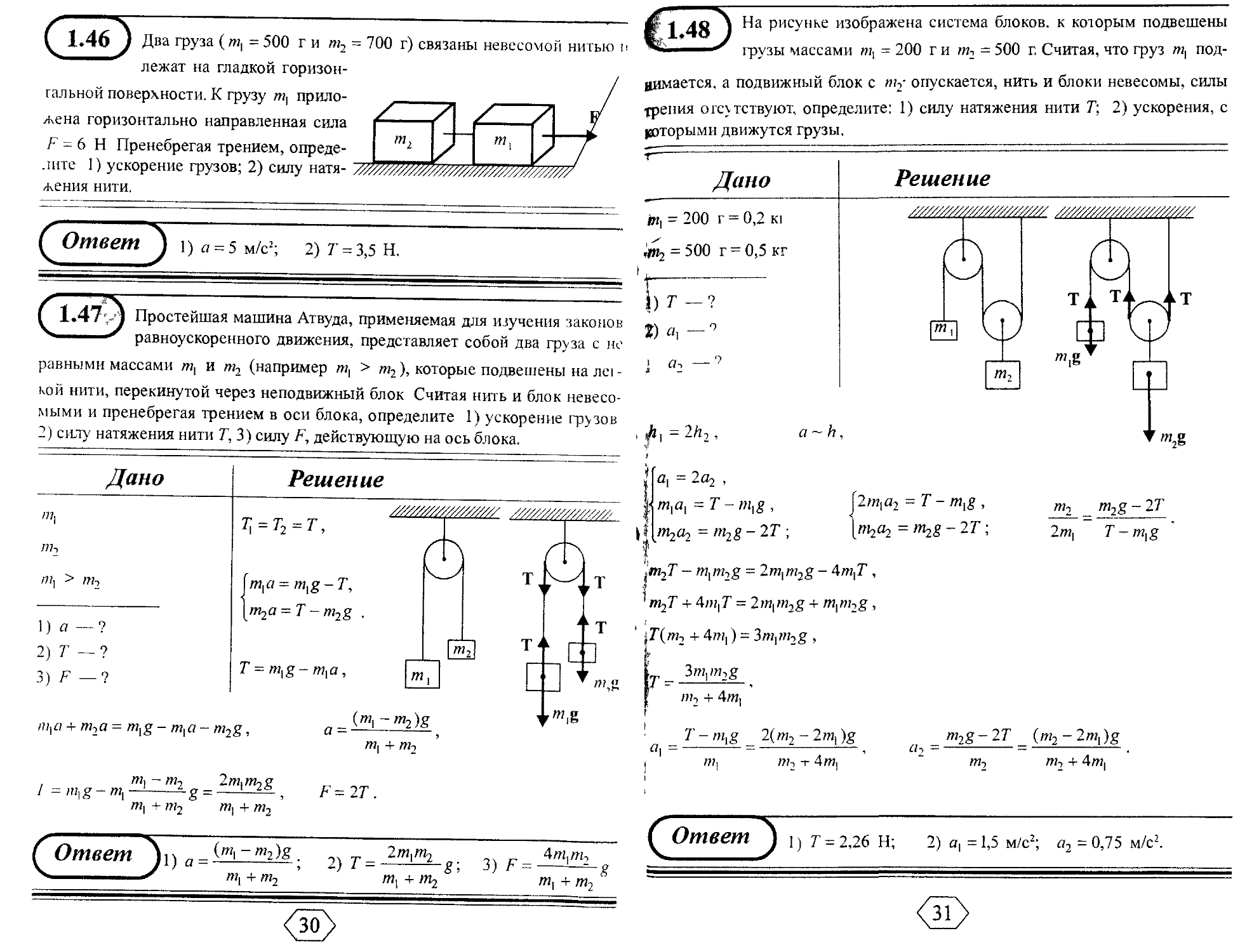
1.46 ) Два груза (m, = 500 г и т2 = 700 г) связаны невесомой нитью п
лежат на гладкой горизон-
тальной поверхности. К грузу /и, прило-
жена горизонтально направленная сила
F-6 Н Пренебрегая трением, опреде-
лите 1) ускорение грузов; 2) силу натя-
жения нити.
Г Ответ J
1) а = 5 м/с2; 2O' = 3,5Н.
1.47;-*1 Простейшая машина Атвуда, применяемая для изучения законов
равноускоренного движения, представляет собой два груза с но
равными массами т, и т-, (например т, > т2), которые подвешены на ле1 -
кой нити, перекинутой через неподвижный блок Считая нить и блок невесо-
мыми и пренебрегая трением в оси блока, определите 1) ускорение грузов
2) силу натяжения нити Г, 3) силу F, действующую на ось блока.
Дано
т2
»i > т-,
Решение
1) а —-?
2) Т — ?
3) F —?
цп + т-,а = mxg - т^а- m2g,
/и, - m2 2mlm2g
щ g =
/И, + W2 W| + «2
= T-m2g .
T*
m.
a —
F=2T.
W Ц
Ответ \} a = ("h-mi)8.
1 4K 1 ^a РисУнке изображена система блоков, к которым подвешены
грузы массами щ - 200 г и т2 = 500 г. Считая, что груз тх под-
нимается, а подвижный блок с т2 опускается, нить и блоки невесомы, силы
Трения отсутствуют, определите: 1) силу натяжения нити Т; 2) ускорения, с
раоторыми движутся грузы.
Дано
Ли, = 200 г = 0,2 Ki
^ = 500 г = 0,5 кг
1) т — ?
t) а, — 9
=2h2,
Решение
/У///////////////////////// //////////////////////////У
Т1 Т4^~4
/и,
J2m{a2 = T -
=m2g-2T;
m2
- 27'
2m, T-mxg
' т2Т + 4т(Г = 2m[m-,g +1
liT(m2 + 4пц) = 3m\in2g ,
3m]m2g
m-, + 4m,
T -
a, =-
2{m2-2m{)g
m-, -r 4 m,
m2g-2T _ (w2-2m,)g
m-, + 4/H|
m-,
С Ответ J
1) Г = 2,26 Н; 2) a, =1,5 м/с2; a2 = 0,75 м/с2.
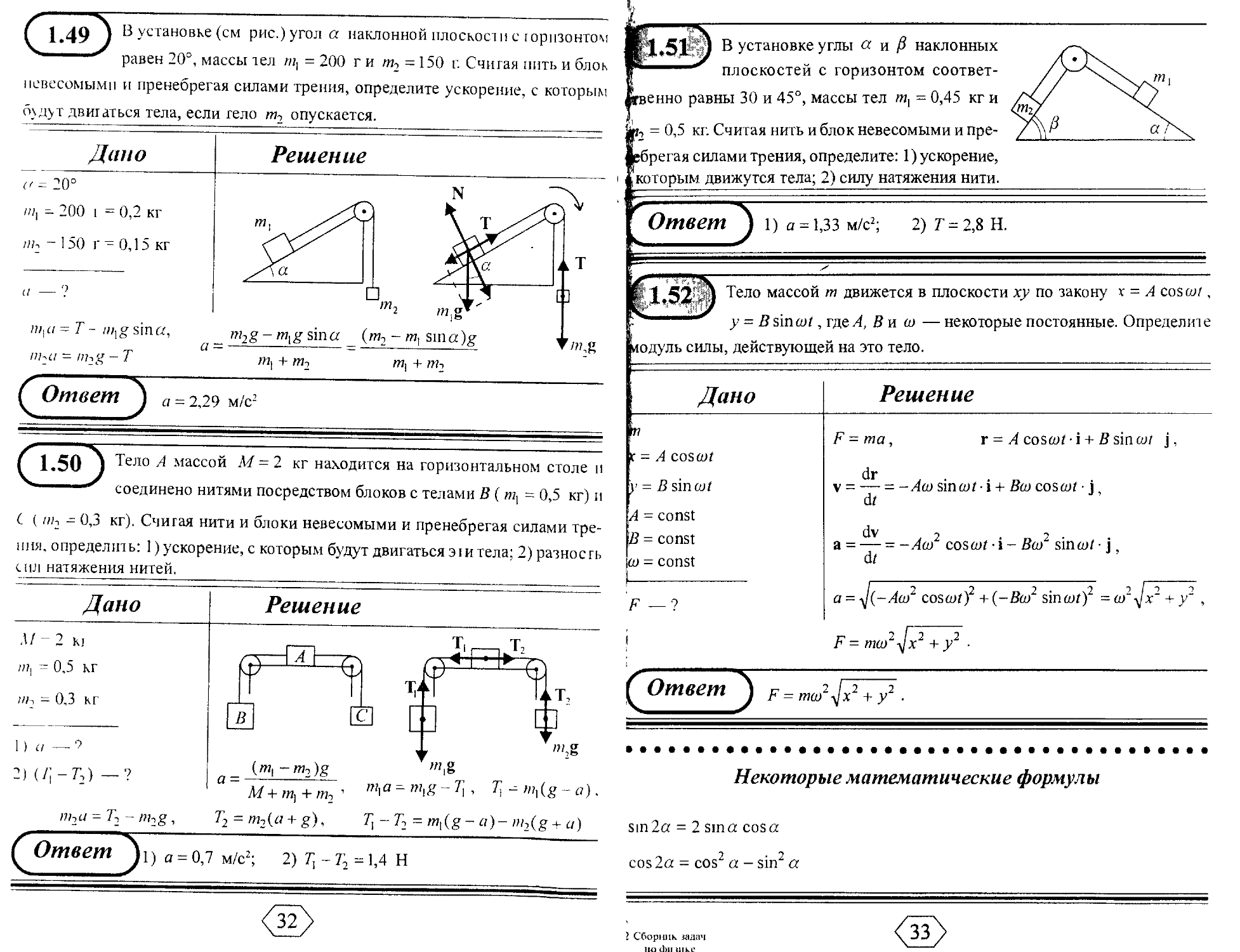
( 1.49 J B Устан°вке (см рис.) угол or наклонной плоскости с горизонтом
равен 20°, массы тел пц = 200 г и т2 = 150 г. Считая пить и блок
невесомыми и пренебрегая силами трения, определите ускорение, с которым
о\д>т двигаться тела, если гело т~, опускается.
Дано
с = 20°
ш, =- 200 1 = 0,2 кг
>п2 - 150 г - 0,15 кг
Решение
m,a = Т -
n^gsma,
2g-mlgsina (/я2-/я, smapg
т\ + т2 ~ От| + пи
"Kg
С Ответ j
а = 2,29 м/с2
С 1.50 ) Тело А массой М = 2 кг находится на горизонтальном столе и
соединено нитями посредством блоков с телами В ( т, = 0,5 кг) и
С ( ш2 - 0,3 кг). Считая нити и блоки невесомыми и пренебрегая силами тре-
ния, определить: 1) ускорение, с которым будут двигаться эш тела; 2) разность
сил натяжения нитей.
Дано
Д/-2 hi
;»i = 0,5 кг
»h - 0,3 кг
\) a —">
Решение
a =
llhU = T-, - lihg ,
С Ответ \} fl:
м/с2; 2OJ-r2=l,4H
В установке углы « и /8 наклонных
плоскостей с горизонтом соответ-
>енно равны 30 и 45°, массы тел тх = 0,45 кг и
ь = 0,5 кг. Считая нить и блок невесомыми и пре-
ебрегая силами трения, определите: 1) ускорение,
которым движутся тела; 2) силу натяжения нити.
Ответ J 1) о = 1,33 м/с2; 2) Г =2,8 Н.
Тело массой от движется в плоскости ху по закону х = ^ cosw/,
>> = .В sinw^, где Д В и ш — некоторые постоянные. Определите
лодуль силы, действующей на это тело.
Дано
I
- А
= В s,mwt
4 = const
3 = const
= const
F —?
Решение
r = A coswM + Ssinw/ j,
F = ma,
v = — = -Aw sin<y?-i + Ba) coswt- j
dv 2 i ¦
a = — = -Аш coscjt-\- Bcj sinw/j,
d/
a = ^(-Aw2 coswtf + (-Bw2 sinwtf = ar^jx2 + y2
F=mcj2Jx2 +y2 ¦
С Ответ j
F = mw2Jx2 + у2 .
Некоторые математические формулы
sin2a = 2 sina cosa
cos 2a - cos2 a - sin a
Частица массой т движется под действием силы F - Fo cosa>/
где Fo и (о — некоторые постоянные. Определите положение
частицы, т. е. выразите ее радиус-вектор г как функцию времени, если в на-
чальный момент времени t = 0 , г@) = 0 и v@) = 0.
v@) = 0,
v(O = —^sina»/,
met)
r(f) - r@) = -2- \s\na)t dt = V cos<yf
тш
nva
mco
= —T-O-cosa*). r@)=0, КО = -^5-0-cosa»/).
met) met)
С Ответ j
С Ответ Л 1) о = 4,П м/с2; 2) tf = 89,4 Н.
Тело массой т = 2 кг падает вертикально с ускорением а = 5 м/с2
Определите силу сопротивления при движении этого тела.
Ответ
Дано
m
F = Fo cosa>/
r = 0
r@) = 0
v@)=0
r(/)-?
Решение
F = F0 cosa>/,
dv „
m—=F0 cosa^,
dt
F 't
ml
F =
dv =
i, F"
dt —
met)
ma
Ei
m
sin
dv
= /»—-,
dt
coseDt dt,
tot
' Fo .
= —^sinotf,
0 rmo
С вершины клина, длина которого / = 2 м и высота h — 1 м, начинает
скользить небольшое тело Коэффициент трения между телом и кли-
ом / = 0,15. Определите: 1) ускорение, с которым движется тело, 2) время про-
ождения тела вдоль клина; 3) скорость тела у основания клина.
=-^sina>f, к
пил
Ответ
i) а = з,б3 м/с2, 2) f = i,05 c;
3) ?; = 3,81 м/с
tS?1 ) По наклонной плоскости с углом а наклона к горизонту, равным
*' """^ 30°, скользит тело. Определите скорость тела в конце второй се-
унды от начала скольжения, если коэффициент трения / = 0,15
Г Ответ j
v = 7,26 м/с.
154*J На тело массой от =10 кг, лежащее на наклон-
ной плоскости (угол а равен 20°), действует
горизонтально направленная сила F = 8 Н. Пренебрегая
трением, определите: 1) ускорение тела; 2) силу, с которой
тело давит на плоскость.
Вагон массой т=\ т спускается по канатной железной дороге с
уклоном а = 15° к горизонту. При- Vo
цимая коэффициент трения / = 0,05, определи-
Ге силу натяжения каната при торможении ваго-
на в конце спуска, если скорость вагона перед
торможением и0 = 2,5 м/с, а время торможения
( = 6 с
f Ответ j
Т = 2,48 кН.
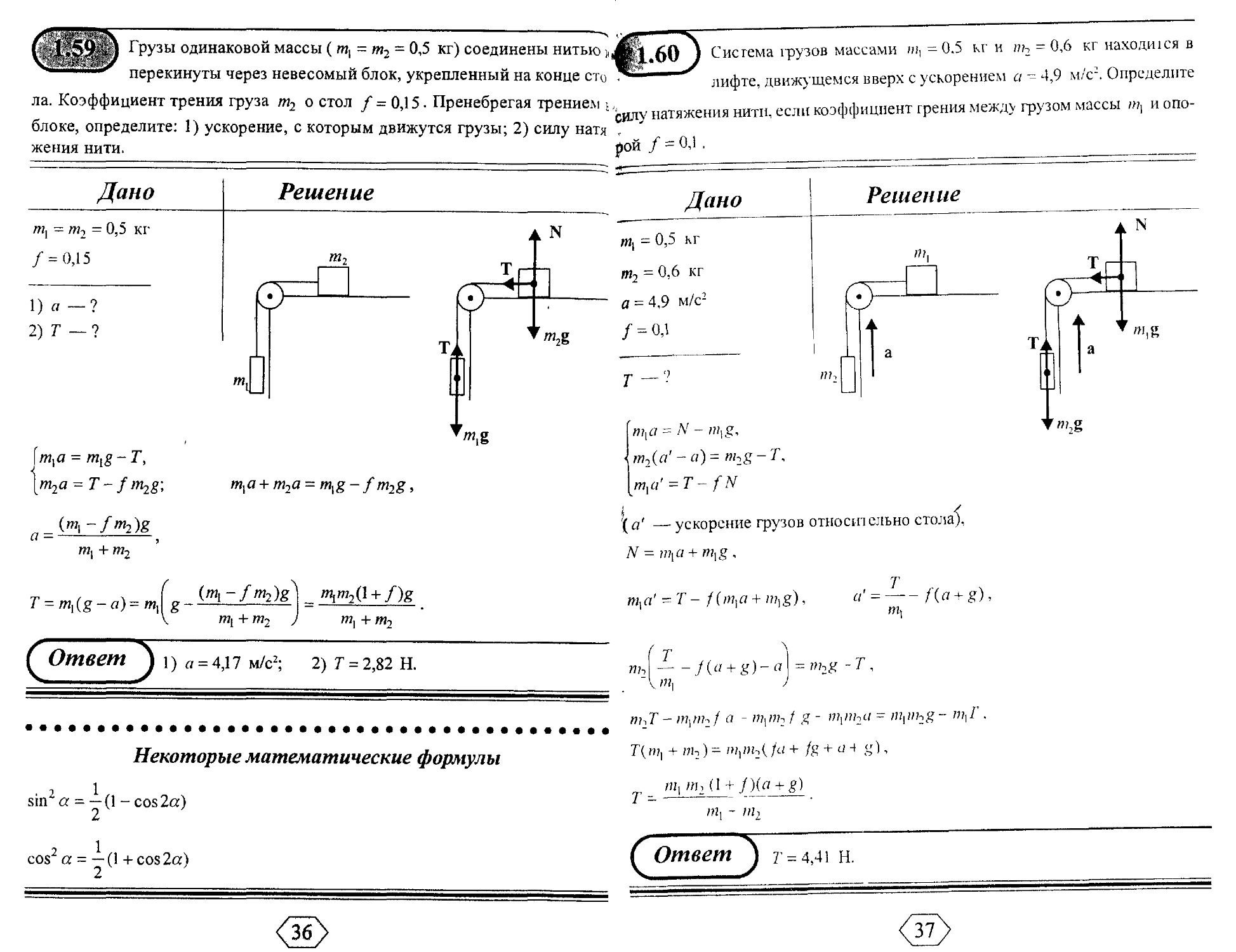
Грузы одинаковой массы ( т, = т2 = 0,5 кг) соединены нитью ъШ^ 60 J Система 1рузов массами ш, = 0.5 кг и »ь = 0,6 кг находшся в
перекинуты через невесомый блок, укрепленный на конце сто Щ~"--—^ лифте, движущемся вверх с ускорением а ¦= 4,9 м/с:. Определите
ла. Коэффициент трения груза т2 о стол /= 0,15. Пренебрегая трением ь,, атяжеНия нити, если коэффициент грениямежд> грузом массы пц иопо-
блоке, определите: 1) ускорение, с которым движутся грузы; 2) силу натя ,
жения нити. рой / = 0,1 .
Дано
тх—т2 = 0,5 кг
/ = 0,15
1) а — ?
2) Т — ?
Решение
/и,
Т
-Ч
«¦В
[т2а = Г -
/и2а = m,g -fm2g,
а — -
Ш\ + т2
g~-
m2
+m2
(Omeent\ l) а = 4,17 м/с2; 2) Г = 2,82 H.
Некоторые математические формулы
sin2 а = —A- cos 2а)
cos2 а = —A + cos 2а)
Дано
m, = 0,5 кг
т2 = 0,6 кг
а = 4,9 м/с2
/ = 0,1
а = Л' - /
Решение
1
{а' — ускорение грузов относительно стола),
N = 1ща + m^g ,
Г
" V '«I
-а\- rthg - Т ,
ihT - mYnuf a - пцпъ f g - щпии =
r{m] + >п2) - 1щт2( fa + /g + см g),
Г- »'i ^2 П + /)(я+ g)
m, - иь
( Ответ j
T = 4,41 H.
T
--Ч
1-
N
На гладкой горизонтальной поверхности находится доска массой
щ, на которой лежит брусок массой т], Коэффициент трения
бруска о поверхность доски равен / . К доске приложена горизонтальная сила F,
зависящая от времени по закону F - At, где А — некоторая постоянная. Опре-
делите: 1) момент времени t0, когда доска начнет выскальзывать из-под брус-
ка; 2) ускорения бруска а, и доски а2 в процессе движения.
В установке угол а наклона плоскости с горизонтом равен 30°
массы тел одинаковы (т -1 кг). Считая нить
^ блок невесомыми и пренебрегая трением в оси блока, т
Определите силу давления на ось, если коэффициент тре- ^
рия между наклонной плоскостью и лежащим на ней те-
jiom / = 0,1.
in.
m2
f
F
A-
n
2)
= At
Дано
= const
tr.
«1 —
a2 -
?
7
- 7
m2a2
^*тр m
a2 5
Решение
- p
= F -
их -J
«2
At
у/////////////-
At - Fw
-fr»u
m2
mx
— >
У////////Л
max
"i
~ > fg-
X
Ftp
F
V//////////////
t = 1
m-,
^=/g,
' < /n
= a-, =¦
At
ni] + m2
a}=fg = const,
a-, =
A
_ At-fm^g
С Ответ ~) 1} t = (m\ + mi)fg.
2) при t > t0 a{=fg = const; a2 =
lg
m2
С Ответ J
F = mg(\ + f cosa + since) cosl =13,5 H.
* 4 2)
1.63*1) ^a наклоннУю плоскость с углом наклона к горизонту а = 35°
положена доска массой т2 = 2 кг, а на доску — брусок массой
mi = 1 Ki. Коэффициент трения между бруском и доской _/j = 0,1, а между дос-
коп и плоскостью /2 = 0,2 . Определите: 1) ускорение бруска; 2) ускорение дос-
ки, 3) коэффициент трения f{ , при котором доска не будет двигаться.
Г Ответ Л \) Q} = g(sina- Д cosa) = 4,82 м/с2;
2) a, = J sin a + /B. cosa _ / <"¦ + ™i) cos Л = 3>62 м/с:;
V щ m2 J
Некоторые внесистемные единицы
1 сут = 86400 с 1" = 4,85 • 10 рад
1 год = 365,25 сут = 3,16- 107с 1 рад = 57,3°
1° =1,75- 10 2 рад 1 мм рт. ст. = 133,3 Па
Г = 2,91 • 10 4 рад 1эВ=1,6-10-19Дж
54tfiNBi§ Снаряд массой т = 5 кг, вылетевший из орудия, в верхней
траектории имеет скорость v = 300 м/с. В этой точке он разорвал
ся на два осколка, причем больший осколок массой т{ = 3 кг полетел в обрат
ном направлении со скоростью vx =100 м/с. Определите скорость v2 второго
меньшего, осколка.
$7< v Платформа с песком общей массой М = 2 т стоит на рельсах
—-¦"""^ на горизонтальном участке пути. В песок попадает снаряд мае-
Дано
т-5 кг
w = 300 м/с
от, = 3 кг
w, =100 м/с
v2~?
Решение
т\= ffj|V, + m2v2,
my = -т,?;, + m2v2,
m2- m-ni\,
mv + m, v,
v-, = i-L.
m2
?ой т = 8 кг и застревает в нем. Пренебрегая трением, определите, с какой
Скоростью будет двигаться платформа, если в момент попадания скорость
^наряда v = 450 м/с, а ее направление — сверху вниз под углом а = 30° к
^ризонту.
С Ответ
v2 = 900 м/с.
Лодка массой М = 150 кг и длиной / = 2,8 м стоит неподвижно в
стоячей воде. Рыбак массой т = 90 кг в лодке переходит с носа на
корму. Пренебрегая сопротивлением воды, определите, на какое расстояние s
при этом сдвинется лодка.
1,»(Ш; 1 Снаряд, вылетевший из орудия со скоростью v0 , разрывается на
* два одинаковых осколка в верхней точке траектории на расстоя-
нии / (по горизонтали). Один из осколков полетел в обратном направлении со
скоростью движения снаряда до разрыва. Пренебрегая сопротивлением возду-
ха, определите, на каком расстоянии (по горизонтали) от орудия упадет второй
осколок.
(Ответ j 5 = 4/.
f Ответ j v = i,.
,55 м/с.
$рщ На железнодорожной платформе, движущейся по инерции со ско-
ростью v0 = 3 км/ч, укреплено орудие. Масса платформы с ору-
дием М = 10 т. Ствол орудия направлен в сторону движения njiai формы. Сна-
ряд массой т = 10 кг вылетает из ствола под углом а = 60° к горизонту. Опре-
делите скорость v снаряда (относительно Земли), если после выстрела ско-
рость платформы уменьшилась в п = 2 раза.
Дано
vo=3 км/ч = 0,833 м/с
М = 10 т=104кг
т = 10 кг
а = 60°
v — ?
Решение
(т + M)vu = mv cos a +
Mv
о
mv cosa = mv0 + Mv0 -
n
Mv
о
mv cosa= mv0
Mvn
mcosa
f Ответ j v =
= 835 м/с.
Две легкие тележки (массы соответственно щ п т2 = 2тх) со.
единены между собой сжатой, связанной нитью пружиной. Пере,
жигая нить, пружина распрямляется и тележки разъезжаются в разные сторо.
ны. Считая коэффициент трения для обеих тележек одинаковым, определите
1) V\IV2 —отношение скоростей движения тележек; 2) t{/t2 —отношение
времени, в течение которого тележки движутся; 3) st/s2 — отношение путей,
пройденных тележками.
Определите положение центра масс системы, состоящей из че-
тырех шаров, массы которых равны соответственно т, 2т, Ът
лцт,о следующих случаях: а) шары расположены на одной прямой; б) шары
расположены по вершинам квадрата; в) шары расположены по четырем смеж-
Я$1М вершинам куба. Во всех случаях расстояние между соседними шарами
15 см. Направление координатных осей показано на рисунке.
t
m 2m 3m 4m
9—•—•—•
Ответ J а) хс = 30 см;
б) хс = 7,5 см, ус = 4,5 см;
в) хс = 1,5 см, ус = 4,5 см, zc = 3 см.
Две одинаковые тележки массой М каждая движутся по инерции
(без трения) друг за другом с одинаковой скоростью v0. В какой-
то момент времени человек массой т, находящийся на задней тележке, прыг- Щ
нул на переднюю тележку со скоростью и относительно своей тележки. Опре- f
делите скорость vt передней тележки. &
Определите положение центра масс половины круглого диска ра-
диусом R, считая его однородным.
\Ответ ) 4 л
Г ' Х(-=^
от центра.
Определите координаты центра у
масс системы, состоящей из че-
тырех шаров массами 2т, Ът, 4т и т, ко-
торые расположены в вершинах и в центре
равностороннего треугольника со стороной
а - 20 см. Направление координатных осей
показано на рисунке.
Зт
^ На катере массой т = 4,5 т находится водомет, выбрасывающий
со скоростью и = 6 м/с относительно катера назад ц = 25 кг/с
^>ды. Пренебрегая сопротивлением движению катера, определите: 1) скорость
Итера через t = 3 мин после начала движения; 2) предельно возможную ско-
|рсть катера.
Ответ
J 1) v = 3,
= 3,8 м/с; 2) wmax = 6 м/с.
Г Ответ j
xc = l2 см; _уг = 5,77 см.
Нагруженная песком железнодорожная платформа с начальной
массой щ начинает движение из состояния покоя под воздействи-
ем постоянной силы тяги F. Через отверстие в дне платформы высыпается пе-
сок с постоянной скоростью ft (кг/с). Определите v(f), т. е. зависимость ско-
рости платформы от времени.
Ракета, масса которой в начальный момент времени М - 2 кг,
запущена вертикально вверх. Относительная скорость выхода про-
ектов сгорания и = 150 м/с, расход горючего Ц = 0,2 кг/с. Пренебрегая со-
противлением воздуха, определите ускорение а ракеты через ( = 3 с после нача-
|а ее движения. Поле силы тяжести считать однородным.
Дано
/«о
F
/*
v(O
Дано
«а
т =
а =
Решение
= F + Fp,
т0- /ut < F
F
а
от0 - /г/
р = 0'
_ dv
)М = 2
f =0,2
» = 9,81
'V
(
КГ
м/с
кг/с
[ м/с2
а —?
Решение
= Fp-mg,
= /*".
= M- fit,
ци
M-
v@)=0,
v@= fad/
Ответ) a =
= 11,6 м/с2.
Некоторые математические формулы
С Ответ)
ГЩ-fXt
sin2a = 2 sina cosa
1
2
sin2 a = — A -cos 2a)
cos 2a = cos a - sin2 a
cos2 a = —A + cos 2a)
<44>
Пакета, масса Мкоторой в начальный момент времени равна 3001
начинает выбрасывать продукты сгорания с относительной ско
ростью и - 200 м/с. Расход горючего fi = 100 г/с. Пренебрегая сопротивлени
ем воздуха и внешним силовым полем, определите: 1) за какой промежуток
времени скорость ракеты станет равной и, = 50 м/с; 2) скорость v2, которое
достигнет ракета, если масса заряда т0 = 0,2 кг.
Ракета поднимается с нулевой начальной скоростью вертикально
вверх. Начальная масса ракеты щ, скорость истечения газа отно-
сительно ракеты постоянна и равна и. Пренебрегая сопротивлением воздуха,
азнте скорость ракеты v в зависимости от т и t (т — масса ракеты; t —
:мя ее подъема). Поле силы тяжести считайте однородным.
м
и -
М
v\
Щ
1)
2)
Дано
= 300 г = 0,3 кг
= 200 м/с
= 100 г/с = 0,1 кг/с
= 50 м/с
= 0,2 кг
'¦-?
-?
Решение
та = Fp , w =
Fp ци, а
dv
V(t)- fiU I -Ull
1 М-fit
M-fit,
dv
dt '
M
M-fit'
V, = и1п-
М
М-fit,
ln-
М
м
М
=-A-е-/"),
fi v '
fi
М - fit\ и
м
v2 = и In
M-,
QОтвет J l)t] = Q66 м/с; 2) Vi =
220 м/с.
Ракета с начальной массой щ, начиная движение из состояния
покоя, к некоторому моменту времени / израсходовав топливо
массой т, развивает скорость v. Пренебрегая сопротивлением воздуха и вне-
шним силовым полем, определите зависимость w mm, если скорость истече-
ния топлива относительно ракеты равна и.
Ответ J у = и
Ракета с начальной массой щ = 1,5 кг, начиная движение из со-
стояния покоя вертикально вверх, выбрасывает непрерывную
рую газов с постоянной относительно нее скоростью и = 600 м/с. Расход газа
[ = 0,3 кг/с. Определите, какую скорость приобретет ракета через 1 с после
чала движения, если она движется: 1) при отсутствии внешних сил; 2) в одно-
аом поле силы тяжести. Оцените относительную погрешность, сделанную
[ данных условий задачи при пренебрежении внешним силовьш полем.
Дано
, = 1,5 кг
1=600 м/с
[ = 0,3 кг/с
=1с
D У 2 — ?
Решение
dv
—
= 0,
d/
= и1п-
a/
щ- fit
щ-lit
— gt
v2 = win-
OTq
«In-
Г Ответ J I) «, = 134 м/с; 2) u2 = 124 м/с; 3) e = 7,3 %.
1.3. Работа и энергия
Тело массой т = 5 кг поднимают с ускорением а = 2 м/с2. Опре-
делите работу силы в течение первых пяти секунд.
Дано
m = 5 кг
a - 2 м/с2
t = 5 с
Решение
ma-F-mg, F- та+ mg — m(a+ g),
= Fh,
,2
—
2
QОтвет j A = i,48 кДж.
Автомашина массой т = 1,8 т движется в гору, уклон которой со-
ставляет 3 м на каждые 100 м пути. Определите: 1) работу, совер-
шаемую двигателем автомашины на пути 5 км, если коэффициент трения ра-
вен 0,1; 2) развиваемую двигателем мощность, если известно, что этот путь
был преодолен за 5 мин.
h = 3 м
/=100
/=0,1
t =
1)
2)
Дано
т= 1,8- 103кг
м
= 5 мин - 300 с
А —
р
.?
7
Решение
A^F^s + F^s, px =
F^ = fN = f mg cosa,
h
sin a = —,
/
cosa = vl-sin2a ,
A = mgi(sina + /cosa),
mg sin a
\ *т«гн
»\
r
С Ответ Л
1) /4 = 11,5 МДж; 2) P = 38,3 кВт.
Щ Определите работу, совершаемую при подъеме груза массой
т = 50 кг по наклонной плоскости с углом наклона а = 30° к го-
ризонту на расстояние 5 = 4 м, если время подъема / = 2 с, а коэффициент
трения / = 0,06.
Ответ J а = 1,48 кДж.
ffiSO
Тело скользит с наклонной плоскости высотой h и углом наклона а
к горизонту и движется далее по горизонтальному участку. При-
нимая коэффициент трения на всем пути постоянным и равным / , определите
расстояние 5 , пройденное телом на горизонтальном участке, до полной оста-
новки.
Дано
h
а
f
Решение
7 _
= fmg cosa,
h
FW2 =
sin a
- fmgcosa + f mgs ,
sin a
= -(l-/ctga).
= -(i-/ctga).
|Щ Насос мощностью N используют для откачки нефти с глубины h
Определите массу жидкости, поднятой за время /, если КПД на-
соса равен г].
Дано
N
h
I
V
т
Решение
Лолой _ mSh
4„™ Nt
т —
TjNt
(Ответ) m = H^L
v / gh
gh
Поезд массой m = 600 т движется под гору с уклоном а = 0,3° и
за время / = 1 мин развивает скорость « = 18 км/ч. Коэффициент
трения / = 0,01. Определите среднюю мощность {#) локомотива
Дано
= 6- 105кг
а = 0,3°
I = 1 мин = 60 с
г = 18 км/ч = 5 м/с
/ = 0,01
Решение
N
FTp = fmgcosa
v i \ nw I v
^«ш = '»-+ /«g cosa-mg sina, (/V; = —I—+ /gcosa-gsma
Автомобиль массой т = 1,8 т спускается при выключенном дви-
гателе с постоянной скоростью v = 54 км/ч по уклону дороги (угол
к горизонту a = 3°). Определите, какой должна быть мощность двигателя ав-
томобиля, чтобы он смог подниматься на такой же подъем с той же скоростью
[Ответ j w=27,7kBt.
Материальная точка массой т = 1 кг двигалась под действием неко-
торой силы согласно уравнению s = A- Bt + Ct~ - Dt (S = 3 м/с,
С - 5 м/с2, D = 1 м/с3) Определите мощность /V, затрачиваемую на движение
точки за время, равное 1 с.
т-
N -
Дано
1 кг
4-Bt + Ct2 -Dt3
3 м/с
5 м/с2
1 м/с3
1 с
_9
Решение
N=7i'
Т mv2
2 '
- d^l
3D^2,
wu ] dv
, 2 ; d^
— = 2C-6Dt,
dt
N = m(-B+2Ct-3Dt2)BC-6Dt)
Г Ответ j
TV = 16 Вт.
Некоторые математические формулы
sin2a = 2 sina cosa
cos 2a = cos2 a - sin2 a
Ветер действует на парус площадью 5 с силой F = ASp(v0 - vJ J2,
где А — некоторая постоянная; р — плотность воздуха; v0 —
скорость ветра; v — скорость лодки. Определите скорость лодки при макси-
мальной мгновенной мощности ветра.
Дано
F = ASp(vo-vJ/2
N = Nmm
v —-?
Решение
N = Fv, F=ASp(vo-vJ/2,
N - Oow 2vov +v ),
dN
dv
- = 0.
dv 2
v\ - Avov + 3v2 = 0 ,
3v2 - 4v0v + v2q = 0,
±
-\2v\ _ 4v0 ± 2v0
u, = v0 (не удовл.),
y, =¦
f Ответ j v -¦
d" 90 ~Щ ^ело масс°й '" поднимается без начальной скорости с поверхно-
сти Земли под действием силы F, изменяющейся с высотой подъе-
ма^ по закону F = -2mg(l - Ay) (где А — некоторая положительная постоян-
ная), и силы тяжести т% . Определите: 1) весь путь подъема; 2) работу силы F
на первой трети пути подъема. Поле силы тяжести считать однородным.
С Ответ j
2)AF=5mg/(?A).
i n< \ Тело массой in начинает двшаться под дейсчвпем силы
F = 2i i + 3rj, где i и j — соответственно единичные векторы ко-
ордннатныч осей х и v. Определите мощность Л*(/), развиваемую силой в мо-
MCHi времени I.
Дано
Решение
У - Fv ,
F =
1 -,. dv
а --B/1 кЗп) = — ,
т at
v=
j= тъ
1 2.
in
1 т. з.
n;
(Ответ Y
V(o--(^3+3/s)
f 1.92 J Тело массой т - 5 кгпадае! с высоты /; - 20 м Определите с\м-
^———^ м\ поюпциалмюй и кинетической энергий тела в точке, находя-
щсГкя от поверхпосш Земли на высоте /?, = 5 м Трением тела о воздчх пре-
небречь Сравнше эт\ энергию с первоначальной энергиен тела
Дано Решение
III 3 К1
// - 20 м
/;, 5 м
Е =- II = mgh ,
Е] = П, + У,,
11, =
,, ,
lllV-
А, - ///?/?,+
т 2
-1 = mgh
Ответ
дж
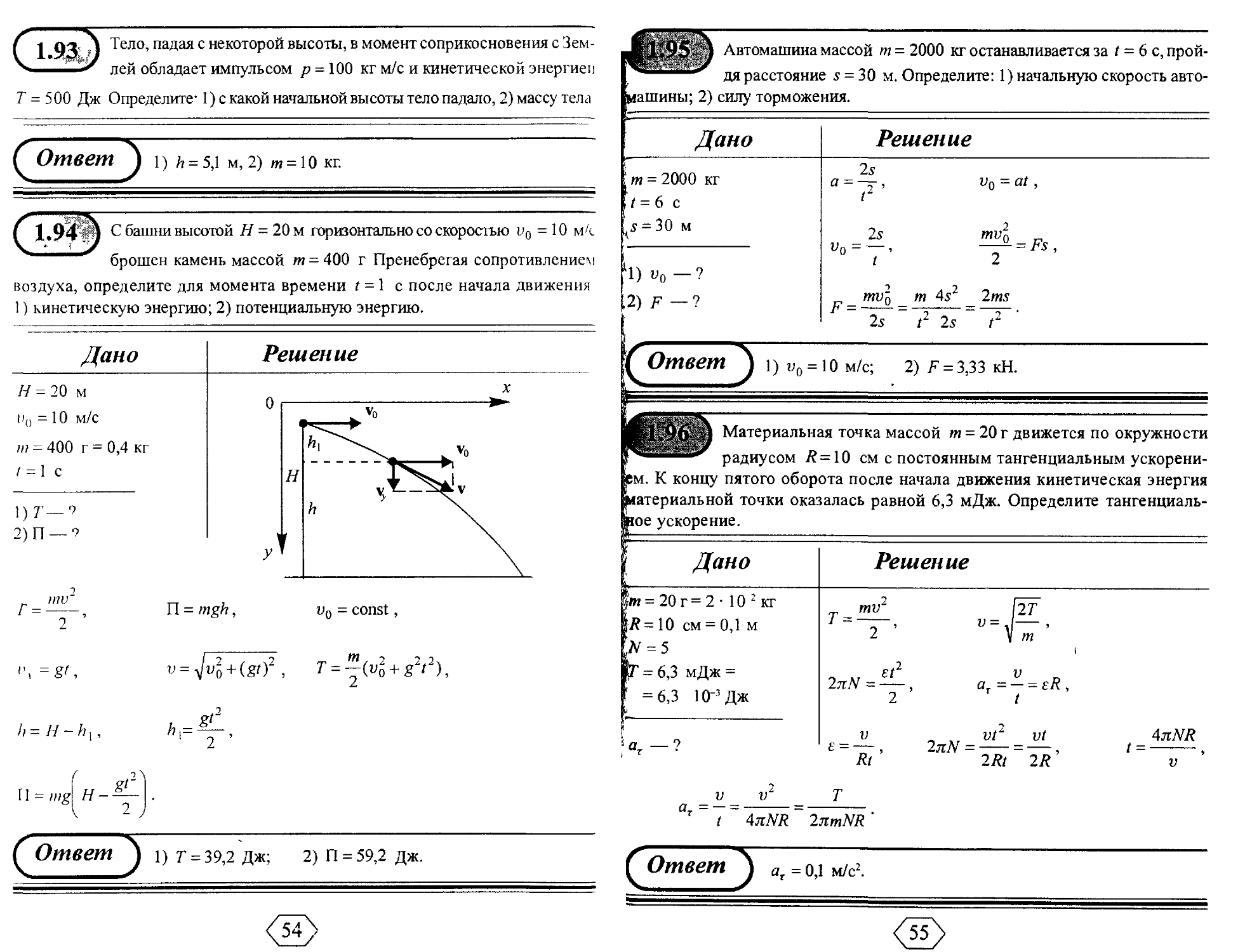
i, j Тело, падая с некоторой высоты, в момент соприкосновения с Зем-
лей обладает импульсом р = 100 кг м/с и кинетической энергиеп
Т = 5 00 Дж Определите' 1) с какой начальной высоты тело падало, 2) массу телл
С Ответ J
1) ft=5,l м, 2) от = 10 кг.
С
С башни высотой Я - 20 м горизонтально со скоростью v0 = 10 мА.
брошен камень массой т = 400 г Пренебрегая сопротивлением
воздуха, определите для момента времени t -\ с после начала движения
1) кинетическую энергию; 2) потенциальную энергию.
Дано
Я = 20 м
|»() =10 м/с
„? = 400 г = 0,4 кг
/ = 1 с
—¦>
2)П
Решение
г =
ню'
'', =g',
П =
v =
»,=v
w0 = const,
Н--
Г Ответ j
i) г = 39,2 дж; 2) п = 59,2 дж.
<54>
L.95 J Автомашина массой m = 2000 кг останавливается за / = 6 с, прой-
"¦""" дя расстояние 5 = 30 м. Определите: 1) начальную скорость авто-
ашины; 2) силу торможения.
Дано
т = 2000 кг
/ = 6 с
5 = 30 М
Решение
а = -
25
уо = а/,
Уп =¦
25
mvl
= Fs,
• - mvo _ m ^2 _ ^ms
~^7 = ~Гъ=~
Ответ Л i) «„ = i о м/с; 2) f = з,зз кн.
Материальная точка массой т - 20 г движется по окружности
радиусом /?=10 см с постоянным тангенциальным ускорени-
ем. К концу пятого оборота после начала движения кинетическая энергия
териальной точки оказалась равной 6,3 мДж. Определите тангенциаль-
ное ускорение.
Дано
= 20г=2- 102кг
= 10 см = 0,1 м
= 5
Г = 6,3 мДж =
= 6,3 10-3Дж
Решение
mv
2 '
v =
v vr vt
? = — , 2nN = = —,
Rt 2Rt 2R
t = -
v v
t 4nNR 2nmNR
С
Ответ
at = 0,1 м/с2.
массой от = 5 кг бросают под углом а = 60° к горизонту,
совершая при этом работу 500 Дж. Пренебрегая сопротивлением
воздуха, определите: 1) через какое время ядро упадет на землю; 2) какое рас-
стояние по горизонтали оно пролетит.
Дано
т- 5 кг
« = 60°
А = 500 Дж
1) t — ?
2) s — ?
s = vOxt,
Решение
vn =.
vux = v0 cosa ,
v0 sina
g
\2A sina
g
„uosina v0 .
¦> - v0 cosa-2— = —^ sin2a ,
g g
2A .
s - — sin 2a.
mg
Ответ J i> t = 2,5 C; 2) s = 17,6 M.
Тело массой от = 0,5 кг бросают со скоростью у0 = 10 м/с под
углом a = 30° к горизонту. Пренебрегая сопротивлением возду-
ха, определите кинетическую Т, пдтенциальную Пи полную ? энергии тела:
1) через t = 0,4 с после начала движения; 2) в высшей точке траектории.
С Ответ Л l) Г = 19 Дж; П-5,9Дж; ? = 24,9 Дж;
^ ^ 2) Г = 18,7 Дж; П = 6,2 Дж; ? = 24,9 Дж.
Тележка проходит расстояние s = 300 м под гору с уклоном a = 5°
и продолжает двигаться в гору с тем же уклоном. Принимая коэф-
фициент трения/постоянным и равным 0.05, определите расстояние х, на ко-
торое поднимается тележка.
Дано
5 = 300 м
a = 5°
/ = 0,05
x —?
Решение
1* х
a -4-—.
— ! .—i oi
mgh-FTp(s+x)=mghl
h = s sina , A, - x sina ,
mgs sina - /OTg cosaE + x) = mgx sina ,
x = ¦
sina+ /cosa
fOmeemj x = 8i,
= 81,8 м.
.100 j К нижнему концу пружины жесткостью кх присоединена другая
пружина жесткостью к2, к концу которой прикреплена гиря. Пренеб-
регая массой пружины, определите отношение потенциальных энергий пружин.
k2
mg
П,
i
n? ~
Дано
X,
x2
n,
n2
Решение
= *2^2 .
^ ГТ
it ' '
>t,x,2 *,А|
" -t2x22 " *2*,2 "
^,x2
2 '
*2
*i
П *2X2
U2 - - '
С Ответ j ni _ ^
Тело массой т = 0,4 кг скользит с наклонной плоскости высо-
той /г = 10 см и длиной 1 = 1 м, Коэффициент трения тела на
всем пути / = 0,04. Определите: 1) кинетическую энергию тела у основа-
ния плоскости; 2) путь, пройденный телом на горизонтальном участке до
остановки.
Й 1.104 ) Подвешенный на нити шарик массой « = 200 г отклоняют на угол
~"^^^~" а = 45° . Определите силу натяжения нити в момент прохождения
шариком положения равновесия
С Ответ J
= 0,24Дж; 2) s = l,53 м.
1*102 j Тело брошено вертикально вверх со скоростью ио=2О м/с
Пренебрегая сопротивлением воздуха, определите, на какой высо-
те h кинетическая энергия тела будет равна его потенциальной энергии
[Ответ J
= \0,2 м.
.103 j§ Тело массой т = 70 кг движется под действием постоянной силы
F = 63 Н. Определите, на каком пути s скорость этого тела воз-
растает в п = 3 раза по сравнению с моментом времени, когда скорость тела
была равна v0 = 1,5 м/с.
Дано
т= 70 кг
F = 63 Н
у0 = 1,5 м/с
п = Ъ
s —?
Решение
то2 mvl
л о — •
2 2
и = nv0,
Л = ^(«2-1),
Ответ Л s =
10 м.
f Ответ J fh3t = mgC- 2 cosa) = 3,11 н.
Щ При абсолютно упругом ударе шаров одинаковой массы всегда
отскакивает столько шаров, сколько налетает Докажите этот ре-
зультат.
Дано
Решение
//////////////////////////у/
Nlmvl = N2mv2 ,
mv-,
v2
Nj _ N2
v-2 N]
N
? N,
С Ответ j
Тело брошено под углом а = 45° к горизонту со скоростью
v0 = 15 м/с Используя закон сохранения энергии, определите ско-
рость v тела в высшей точке его траектории.
Г
Ответ
v = v0 cosa = 10,6 м/с.
1.107 ) Шайба массой w скользит без трения с высоты/ию желобу, пере Щл,-1У^Ш Пренебрегая трением, определите наименьшую высоту Некоторой
ходящему в пеглю радиусом R. Определите 1) силу давления / ^* '<>*-S должна скатываться тележка с человеком по желобу, переходяще-
шайбы на опору в точке, определяемой углом а (см. рис.); 2) уюл а , при щ в петлю радиусом R = 6 м, и не оторваться от него в верхней точке петли,
котором произойдет отрыв шайбы. ___^ :
Дано
т
h
R
\\ F ?
2) а — ?
т\Г
Решение
mv~
- R{\ + sina),
mgh + mgR{\ + sin a),
mir = 2mgh - 2mgR(\ + sina),
mv
F mg sin a ,
R
F =
R
2(/;-/?(l + siiltt)) 1
- mg sin a = mg\ — - sum ,
л J
sin« =
о
2
_ —
3
(h
\R
---2-3sina = 0,
R
a- arcsin — 11 |.
(Ответ ) Гi(h- R(\ + sma))
J I) F = mg\ -± > - sin a
R
Дано
R=6 м
Решение
mgh\ ,
h,=2R- mg =
mv
R '
mv~ = mgR,
mgR
mgh + mg 2 R,
\ = -r. С Ответ j
h=15 м.
Спортсмен с высоты h — 12 м падает на упругую сетку. Пренебре-
гая массой сетки, определите, во сколько раз наибольшая сила
давления спортсмена на сетку больше его силы тяжести, если прогиб сетки под
действием только силы тяжести спортсмена х0 = 15 см.
Дано
'А=12 м
х0 = 15 см = 0,15 м
Решение
F
, \F\ = kx,
mg
M\np = ДПГЯ, (в точках, где AT = 0),
Р*) С вершины идеально гладкой сферы радиусом R = 1,2 м соскаль-
зывает небольшое тело. Определите высоту h (от вершины сфе-
ры), с которой тело со сферы сорвется.
Дано
=1,2 м
h — ?
Решение
.2
mv\
-mgh,
mv
= mgcosa-N, NB = 0,
mV
R
2-=
=mgcosa,
muB - mgR cos a,
R— h
2h = R cos a = Я =R-h,
2mgh- mgR cos a,
3h=R,
R-h
cosa = -
*.f
Ответ
J
= o,4 м.
i цилиндра массами т{ -150 г и т^ = 300 г, соединенные сжа-
той пружиной, разошлись при внезапном освобождении пружины
в разные стороны. Пренебрегая силами сопротивления и учитывая, что кинети-
ческая энергия Т упругой деформации пружины составляет 1,8 Дж, определите
1) скорость и, движения первого цилиндра;
2) скорость v2 движения второго цилиндра.
т.
]¦
Ответ
J \) щ =
м/с; 2) v2 = 2 м/с.
Гиря массой т = 10 кг падает с высоты h = 0,5 м на подставку,
скрепленную с пружиной жесткостью it = 30 Н/см. Определите
при этом смещение д: пружины.
Дано
m = 10 кг
h = 0,5 м
к = 30 Н/см = 3
х —?
Решение
mg(h
Ах2
——mgx-mgh =
т
i
h
X
QOmeem ) х = 21,6 см.
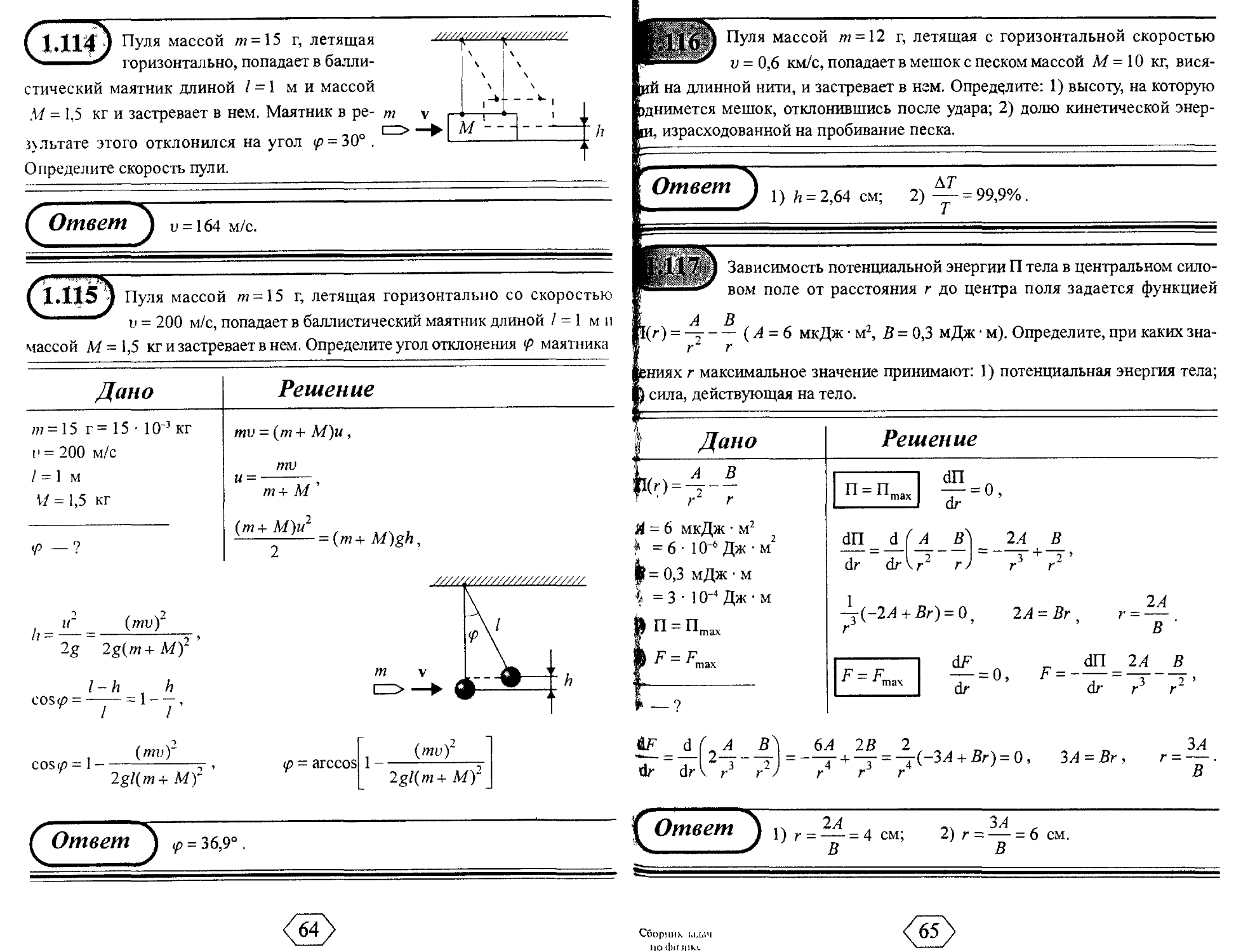
Пуля массой т = 15 г, летящая с горизонтальной скоростью
v - 0,5 км/с, попадает в баллистический маятник М = 6 кг и за-
стревает в нем. Определите высоту й, на которую поднимется маятник, откач-
нувшись после удара.
Дано
= 15 г= 15 ¦ 10~3кг
= 0,5 км/с = 500 м/с
= 6 кг
Решение
/////У////////////////////
M)u,
и =
mv
т+ М
т v
М)и2
M)gh,
(mvJ
2g 2g(m + M)
2 '
Пуля массой m = 15 г, летящая
горизонтально, попадает в балли-
стический маятник длиной 1 = \ ми массой
М - 1,5 кг и застревает в нем. Маятник в ре- т v
i—> —
з\льтате этого отклонился на угол <р = 30° .
Определите скорость пули.
М ---
1 ,.
Q Ответ J w =
м/с.
1.115 у Пуля массой т = 15 г, летящая горизонтально со скоростью
v = 200 м/с, попадает в баллистический маятник длиной / = 1 м и
массой М=\,5 кг и застревает в нем. Определите угол отклонения <р маятника
Дано
w = 15 г =15 ¦ 10'3 кг
с = 200 м/с
/ = 1 м
М = 1,5 кг
Решение
M)u,
т+ М '
(т+М)и2
/? =
и (mv)~
2g 2g(m+M\
l-h _ h
(mv)-
cos./5= 1 T ,
2gl(m+My
m v
> = arccos
2gl(m+ My
Пуля массой m = 12 г, летящая с горизонтальной скоростью
v = 0,6 км/с, попадает в мешок с песком массой М = 10 кг, вися-
на длинной нити, и застревает в нгм. Определите: 1) высоту, на которую
щнимется мешок, отклонившись после удара; 2) долю кинетической энер-
н, израсходованной на пробивание песка.
Ответ J 1) h = 2,64 см; 2) ^ = 99,9%.
Зависимость потенциальной энергии П тела в центральном сило-
вом поле от расстояния г до центра поля задается функцией
А В
) = -у-— (А = 6 мкДж • м2, В = 0,3 мДж • м). Определите, при каких зна-
г г
Ениях г максимальное значение принимают: 1) потенциальная энергия тела;
) сила, действующая на тело.
Дано
XD-4-"
14 = 6 мкДж • м2
* =6- 10-*Дж-м2
4=3- 10~4Дж-м
F = F
' m
Решение
= п„
йг
dr
г2 г
= 0,
2А В
= —г+—'
dF
—— = 0,
dr
&F _ d
Ш- dr
' з
г г
—т + —г
г г
_2А_
г~ в '
dn = Z?__S
dr ~ r" г2
= Br, r = —.
В
= 36,9°
СдтветЛ 1)г = Ц_ = 4 см; 2)г = Н = 6см.
В
5
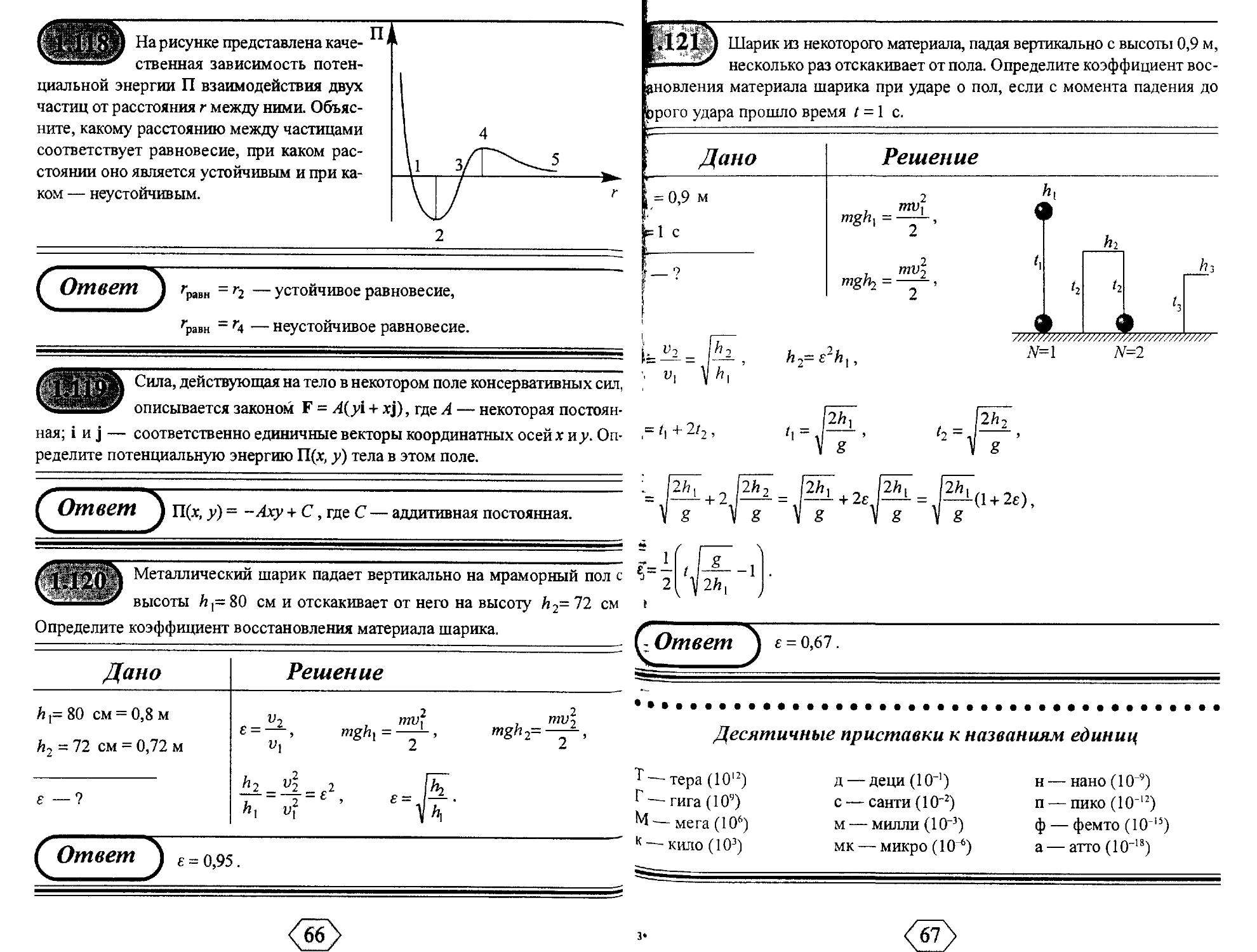
На рисунке представлена каче-
ственная зависимость потен-
циальной энергии П взаимодействия двух
частиц от расстояния г между ними. Объяс-
ните, какому расстоянию между частицами
соответствует равновесие, при каком рас-
стоянии оно является устойчивым и при ка-
ком — неустойчивым.
( Ответ j r^^ = r2 —устойчивое равновесие,
гравн = Г4 — неустойчивое равновесие.
Сила, действующая на тело в некотором поле консервативных сил, ,'
описывается законом F = A(yi + х\), где А — некоторая постоян-
ная; i и j — соответственно единичные векторы координатных осей хиу. Оп- .=
ределите потенциальную энергию Щх, у) тела в этом поле.
Шарик из некоторого материала, падая вертикально с высоты 0,9 м,
несколько раз отскакивает от пола. Определите коэффициент вос-
новления материала шарика при ударе о пол, если с момента падения до
эрого удара прошло время t = 1 с.
Решение
mv.
mgh1=-
N=l
N=2
2t2 .
f Ответ J Щх, у) = -Аху + С, где С — аддитивная
постоянная.
Металлический шарик падает вертикально на мраморный пол с v
высоты й,= 80 см и отскакивает от него на высоту h2=72 cm i
Определите коэффициент восстановления материала шарика.
Дано
й,= 80 см = 0,8 м
h2 = 72 см = 0,72 м
Решение
С Ответ j
е = 0,67.
? = ¦
Г Ответ Л е = о,95.
—тераA012)
— гига A09)
№ — мегаA06)
— килоA03)
д — деци(Ю')
с — сантиA0)
м — милли A0~3)
мк — MHKpo(lO^)
/?з
Десятичные приставки к названиям единиц
н — наноA09)
п — пикоA02)
ф — фемтоA0~'5)
а — аттоA0-18)
При центральном упругом ударе движущееся тело массой /и, уда
ряется в покоящееся тело массой т2, в результате чего скорое i ь
первого тела уменьшается в 2 раза Определите: 1) во сколько раз масса перве
го тела больше массы второго тела; 2) кинетическую энергию Т2 второго те п
непосредственно после удара, если первоначальная кинетическая энергия /
первого тела равна 800 Дж
Дано
7", - 800 Дж
1) /) — 9
2) /v — ?
Решение
от, и, - mxv\ + m2v'2,
mxv\ mxv'{ ( m2u22
2 2 2
i /'Г з
4 4 '
/ ' _ T T"
7; з
Л'- у; --L = -
- ' 4 4
Ответ
"' + v'
2 2'
2
,2
w2
и
3
4
f
8 2
2
1\ — Щ1),
1 ' '
2 4 4
2) 77 = 600 Дж
v.
T
123 i Определите'
во сколько раз уменьшится скорость шара,
движ> -
<* щегося со скоростью vi, при его соударении с покоящимся ша-
ом, масса ко юрою в п раз больше массы налетающего шара Удар
ен 1 ральным абсолютно упругим
7 =
>±
'i
'i -
)t2
Дано
/Hi
"'I
9
1) - (/
п
Решение
mfv{ — ni\v\ + m2v2 ,
,i ,¦>
m,uj" Wi?j|~ OTtWi"
2 2 ' 2
r, = uf + «i>2,
"> /2 /2
1>1 = W| + «W2 ,
считать
i
A
/7
x-1
Л
/7X + П - X - 1 ,
*•= --
/7+ 1 _ 1+ П
/1-1 ~ 1-Й
С Ответ j
Тело массой тх = 3 кг движется со скоростью и, = 2 м/с и ударя
ется о неподвижное тело такой же массы. Считая удар централь.
ным и неупругим, определите количество теплоты, выделившееся при ударе
= 3 д*.
Два шара массами тх =9 кги щ=12 кг подвешены на нитя\
длиной / = 1,5 м. Первоначально шары соприкасаются между со-
бой, затем меньший шар отклонили на угол а = 30° и отпустили. Считая удар
неупругим, определите высоту h, на которую поднимутся оба шара после удара
Дано
'«1
т2
/ =
а -
= 9 кг
= 12 кг
1,5 м
= 30°
h — ?
Решение
Два шара массами тх = 3 кг и щ = 2 кг подвешены на нитях дли-
ной 1 = 1 м. Первоначально шары соприкасаются между собой,
ем больший шар отклонили от положения равновесия на угол а = 60° и от-
стили. Считая удар упругим, определите скорость второго шара после удара.
i
Дано
h{=l~l cosa = /A-cosa), vx
mxvl = (mx
-cos a)
v = •
V -
/////У/////////
mx+ m2
v~ -t
2g (mx+m2)
2g/(l-cosa) — =
«1
2g \mx+m-
/A-cosa).
С Ответ j и = ъ,7
см.
|=ЗКГ
|г = 2кг
fp\ M
*-60°
Решение
mxgh =
2 '
h = l-l cosa = /A-cosa), vx = ^2gl(\- cosa)
ОТ,!), _ ffl^f
тх+щ
щ+щ
- cosa).
С Ответ Л
= 3,76 м/с.
Два шара массами я», = 200 г и »?2 = 400 г подвешены на нитях
длиной / = 67,5 см. Первоначально шары соприкасаются между
собой, затем первый шар отклонили от положения равновесия на угол a = 60°
И отпустили. Считая удар упругим, определите, на какую высоту h поднимет-
ся второй шар после удара.
С Ответ J h =
Атх /A - cosa)
= 15 см.
Шар сталкивается с другим покоящимся шаром такой же массы.
Докажите, что в случае упругого, но не центрального удара угол
между направлениями скоростей после удара составляет л/2 .
С Ответ j <р = —-
1.4. Механика твердого тела
Выведите формулу для момента инерции полого шара относитель-
но оси, проходящей через его центр. Масса шара равна т, внут-
ренний радиус г, внешний R.
Выведите формулу для момента инерции тонкого кольца ради>
com R и массой т относительно оси симметрии
С Ответ j J =
mRl
fl.jG3(M# Выведите формулу для момента инерции тонкого стержня мас-
сой т и длиной / относительно оси, проходящей через центр масс
перпендикулярно его длине.
т
г
R
J
Дано
Решение
2 j 2 j
J = -mlR ~-m2r ,
4 з
тг - —лрг , т =
' 3 '
4
ml-m2 -—лрA
1
Выведите формулу для момента инерции сплошного шара радиу-
y com R и массой т относительно оси, проходящей через центр масс
шара.
2 4
2 4
:5 Т
2_ 4
5 V
з 2 2 4 5 2 4 5
г = npR лрг =
5 Ъ И 5 3 И
f Ответ ) 2 л5-?-5
m
R
Дано
Решение
1
1 Ik
Vr \ "l
Выведите формулу для момента инерции цилиндрической муфты
относительно оси, совпадающей с ее осью симметрии. Масса
фты равна т, внутренний радиус г, внешний R.
,т mr2 pnr2dhr2 рлгА ,,
aJ = = — = аи ,
2 2 2
r2 = R2-h2,
j=\±J = 2\^{R2-h2JAh =
Дано
*
8 „5
TsR'
J— ?
Решение
= pdV = p-2jirhdr
R Я
J-\p 2лгък Ar - Inph fr3 dr - 2nph—
4
= p —tcR ,
i=ml-m2 = лрИ(Я2 -г2),
QOmeem
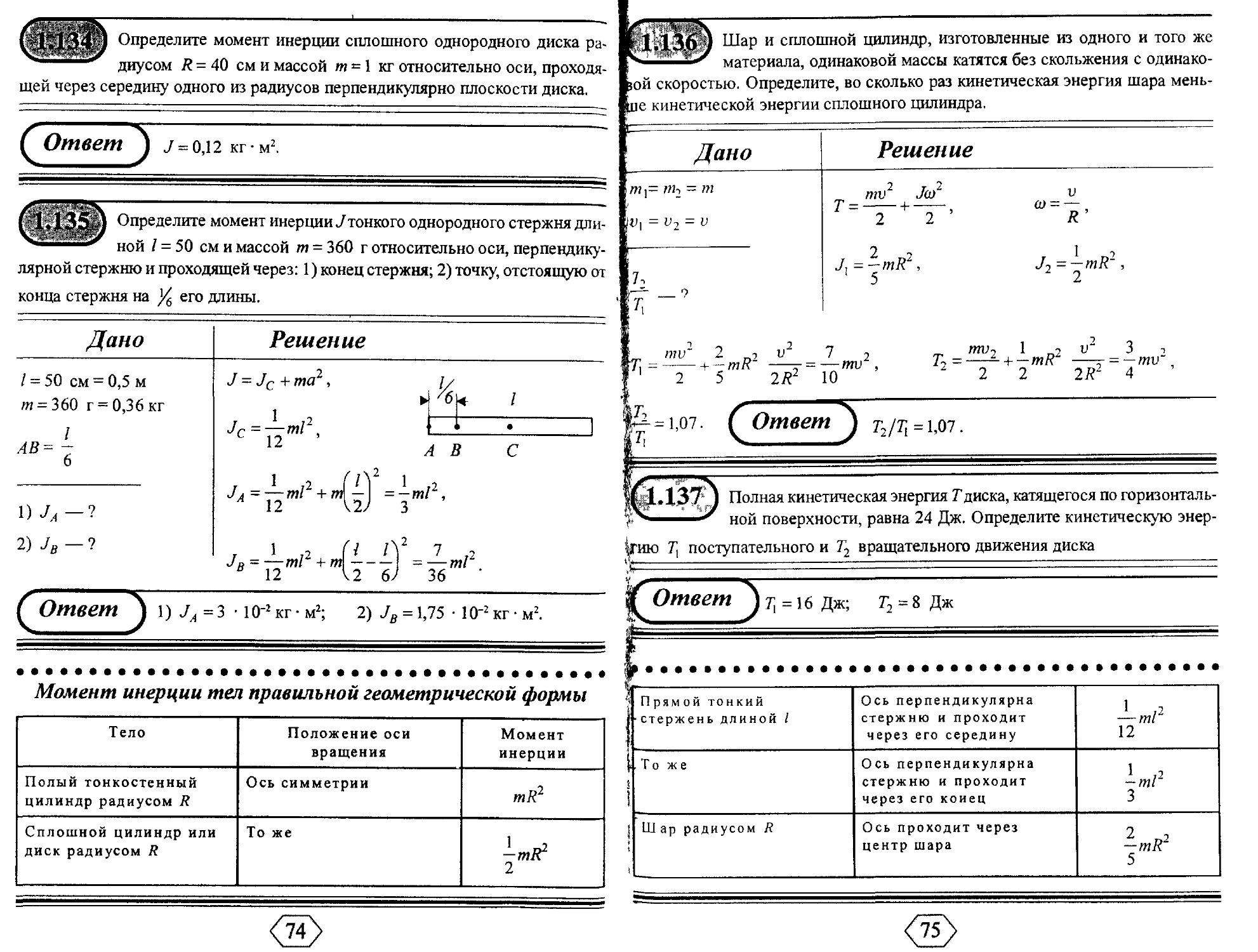
Определите момент инерции сплошного однородного диска ра-
диусом R = 40 см и массой т = 1 кг относительно оси, проходя-
щей через середину одного из радиусов перпендикулярно плоскости диска.
COmeemJ
кг • м .
ОпРеДелите момент инерции ./тонкого однородного стержня дли-
ной / = 50 см и массой т - 360 г относительно оси, перпендику-
лярной стержню и проходящей через: 1) конец стержня; 2) точку, отстоящую от
конца стержня на ]/6 его длины.
Дано
/ = 50 см = 0,5 м
т = 360 г = 0,36 кг
1) J,-?
2)JB—f
Решение
J -Jc л-та ,
Jc=— ml2,
с 12
А В
J ,2._//У_1_,2
7 *• Г^
—
12
U 6У 36
fOmeemj i)
= з
кг•
2) J. = 1,75 • io*кг•
Шар и сплошной цилиндр, изготовленные из одного и того же
материала, одинаковой массы катятся без скольжения с одинако-
юй скоростью. Определите, во сколько раз кинетическая энергия шара мень-
ие кинетической энергии сплошного цилиндра.
Дано
т<= m-i - т
V, = v-, - v
-=- 9
т - mv~ 1
?1= 2 V
Решение
Jt=~mR2,
v
2
2R2
7
—
10
'-mR2^
2 2R
__3_
¦2~4;
- = i,07. Comeem) T.
'2/21=l,07.
Полная кинетическая энергия Тдиска, катящегося по горизонталь-
ной поверхности, равна 24 Дж. Определите кинетическую энер-
гию 71 поступательного и Т2 вращательного движения диска
Момент инерции тел правильной геометрической формы
Тело
Полый тонкостенный
цилиндр радиусом Л
Сплошной цилиндр или
диск радиусом R
Положение оси
вращения
Ось симметрии
То же
Момент
инерции
mR2
\тВ?
Прямой тонкий
стержень длиной /
Тоже
Ш ар радиусом R
Ось перпендикулярна
стержню и проходит
через его середину
Ось перпендикулярна
стержню и проходит
через его конец
Ось проходит через
центр шара
12
-mR2
( -1Д38' J Полый тонкостенный цилиндр массой т = 0,5 кг, катящийся без
""^~""~' скольжения, ударяется о стену и откатывается от нее. Скорое ib
цилиндра до удара о стену и, = 1,4 м/с, после удара v\ = 1 м/с. Определите
выделившееся при ударе количество геплоты.
РаДиУсом Л = 10 см и массой w = 5 кг вращается вокруг оси
етрии согласно уравнению <р = А + B
С = -0,5 рад/с3). Определите момент сил Мдля Г = 3 с.
симметрии согласно уравнению <р = А + Bt2 + О3 (В = 2 рад/с2,
Дано
т = 0,5 кг
и, = 1,4 м/с
wj = 1 м/с
е-?
Решение
mv2 Jw2 mv'2 Jcj\2
i] — "I < о — + ,
1 2 2 2 2 2
со = —, J = mR2, Q = T:-T2,
R
Дано
= 10 см = 0,1 м
= 5 кг
mu2 Ja>2
.,'2
j|5=2 рад/с2
С = -0,5 рад/с3
= 3 с
е=
2 J_ 2
1 2 !
2
i )
Ответ J Q = o,48 дж.
К ободу однородного сплошного диска массой т = 10 кг, насажен-
ного на ось, приложена постоянная касательная сила F = 30 Н. Оп-
ределите кинетическую энергию через время t = 4 с после начала действия силы
Решение
co =
= Je,
dtp
d/ '
r = -mR2,
_ бы
;~~d7'
¦ = 2B+6Q ,
= -mR2{2B+6Ct).
Вентилятор вращается с частотой п = 600 об/мин. После вык-
лючения он начал вращаться равнозамедленно и, сделав
if = 50 оборотов, остановился. Работа А сил торможения равна 31,4 Дж. Оп-
рделите: 1) момент сил М торможения; 2) момент инерции J вентилятора.
Дано
Дано
m = 10 кг
F = 30 H
^ = 4 с
Тер"?
Решение
Т^М\ M=FR=Je, J=mR2
2 2
FT? 2F 2F
г= = , a) = ?t = 1,
J mR mR
if =600 об/мин =10 об/с
= 31,4 Дж
X) M — 1
t) J — ?
Решение
A = M<p,
= m?_ 2F Y 1 =
Bp 2 [mR ) 2
2tcN
aH 2л п
_2<p _ 2-2xN _ 2N
(On 2icn n
<p = 2jiN ,
M=Je,
= 2icn,
et
2
J
wot
2
M
?
MN
n,i2 '
С Ответ
rBp = 1,44 кдж
[Ответ
1)M = 0,1H-m; 2) J = l,5910 кг • м2.
Маховик в виде сплошного диска, момент инерции которого
= 150 кг • м2, вращается с частотой и = 240 обТмин. Через t-\ мин
после начала действия сил торможения он остановился. Определите: 1) мо-
мент Мсил торможения; 2) число оборотов маховика от начала торможения до
полной остановки.
[Ответ Л i) м=62,8 н • м; 2) n = 120.
Сплошной однородный диск скатывается без скольжения с наклон-
ной плоскости, образующей угол а с горизонтом. Определите
линейное ускорение а центра диска.
a
a
— ?
Дано
та
j
Решение
= mgsina-FTf,
mR2
R=Je,
a
141
R
Je mR2a ma , ma
rm= — = _ _-, = —, ma = mgsma- —,
—a=gsma,
= —gsma.
[Ответ ja=1
gsina.
Кинетическая энергия тела, катящегося по плоскости
без скольжения
2 С 2
где т — масса тела; vc — скорость центра масс тела; Jc — момент инерции
тела относительно оси, проходящей через его центр масс; (о — угловая ско-
рость тела.
К ободу однородного сплошного диска радиусом R = 0,5 м при-
ложена постоянная касательная сила F = \00 H. При вращении
иска на него действует момент сил трения М^ = 2 Н • м Определите массу т
а, если известно, что его угловое ускорение е постоянно и равно 16 рад/с2.
Дано
R = 0,5 м
F = \QO H
Mrp = 2 H • м
? = 16 рад/с2
m —?
Решение
M=FR-
miT
M=Je,
= FR-M
rp,
mi?2
= FR-Mtp,
m-
2(FR-M1V)
Ответ
Частота вращения п0 маховика, момент инерции J которого ра-
вен 120 кг • м2, составляет 240 об/мин. После прекращения дей-
ствия на него вращающего момента маховик под действием сил трения в под-
шипниках остановился за время t = л мин. Считая трение в подшипниках по-
стоянным, определите момент М сил трения.
Дано
n0 = 240 об/мин = 4 об/с
J = 120 кг-м2
t-л мин = 60л: с
А/—?
Решение
= Мр , М — ¦——,
2 2^>
2 °
м =
(Ответ
= \б н -м.
{ 1.1*мЩ Маховик в виде сплошного диска, момент инерции которого
тУ J -1,5 кг ¦ м2, вращаясь при торможении равнозамедленно, за
время (= 1 мин уменьшил частоту своего вращения с п0 = 240 об/мин до
л, =120 об/мин. Определите: 1) угловое ускорение ? маховика; 2) момент Л/
силы торможения; 3) работу торможения А.
J =
t-\
n\ =
Дано
1,5 кг • м2
мин = 60 с
240 об/мин =
120 об/мин =
= 4 об/с
2 об/с
а> =
? —
Решение
OJ0-?t ,
t ~ t ("°
2 2 2
а>0 = 2л:л0,
"),
0
а) =
М
2лп,
= Je,
2) М — ?
3) А — ?
С Ответ "V) ? = 0,21 рад/с2;
^ ^2) М = 0,315Н-м;
' J Колесо радиусом i? = 30 см и массой ш=3 кг скатывается без
трения по наклонной плоскости длиной 1 = 5 ми углом наклона
а = 25° . Определите момент инерции колеса, если его скорость v в конце дви-
жения составляла 4,6 м/с.
Дано
R =30 см = 0,3 м
ш = 3 кг
/ = 5 м
а = 25°
v - 4,6 м/с
J — ?
mg/i
Решение
2
mv
sina ,
mw
2
JoJ /V
1 5
w~~r'
Ju?
т >
2
J = \ mg/sina--
.^^fM^,!
r = 0,259 кг ¦ m2.
С наклонной плоскости, составляющей угол а = 30° с горизон-
том, скатывается без скольжения шарик. Пренебрегая трением,
определите время движения шарика по наклонной плоскости, если известно,
что его центр масс при скатывании понизился на 30 см.
Дано
а = 30°
A = 0,3 м
/ —?
Решение
mgh =
mv Ju)
= -mR2,
v
mgh =
mv2 2mR2 v2
5 2R2 '
mgh = —mu ,
v =
l_ar__vt_
2 ~ 2 '
21
/ = ¦
7 2A
sin а
2 I fh
и sina ylOg/г sina sinaylOg
QOmeemj , = 0,585 c.
Полый тонкостенный цилиндр катится вдоль горизонтального
участка дороги со скоростью v = 1,5 м/с. Определите путь, кото-
рый он пройдет в гору за счет кинетической энергии, если уклон горы равен 5 м
на каждые 100 м пути.
Г Ответ j s = 4,
= 4,59 м.
На однородный сплошной цилиндрический вал радиусом R = 50 см
намотана легкая нить, к концу которой прикреплен груз массой
т = 6,4 кг. Груз, разматывая нить, опускается с ускорением а = 2 м/с2. Опре-
делите: 1) момент инерции J вала; 2) массу т1 вала.
Дано
Л =50 см = 0,5 м
т - 6,4 кг
о = 2 м/с2
1) J —?
2) и, -?
Решение
та- mg-T,
T=m(g-a),
M=TR=m(g-a)R,
M=Js,
a
? — — *
a
J =
2J_
R2
С
Ответ
j l) j = 6,25 кг • м2; 2) и, = 50 кг.
На однородный сплошной цилиндрический вал радиусом R=5 см
и массой М = 10 кг намотана легкая нить, к концу которой при-
креплен груз массой т -1 кг. Определите: 1) зависимость s{t), согласно кото-
рой движется груз; 2) силу натяжения нити Т; 3) зависимость <p(t), согласно
которой вращается вал; 4) угловую скорость со вала через ( = 1 с после начала
движения; 5) тангенциальное (ах) и нормальное (ап) ускорения точек, находя-
щихся на поверхности вала.
С Ответ Л 1) s=0,82r2; 2)Г = 8,2Н;
2
3) р = 16,4г2; 4) со = 32,8 рад/с;
5) ах = 1,64 м/с2, а„ = 53,8 м/с2.
На однородный сплошной цилиндрический вал радиусом R=2Q см,
момент инерции которого J = 0,15 кг ¦ м2, намотана легкая нить, к
концу которой прикреплен груз массой т = 0,5 кг. До начала вращения бараба-
на высота h груза над полом составляла 2,3 м. Определите: 1) время опуска-
ния груза до пола; 2) силу натяжения нити; 3) кинетическую энергию груза в
момент удара о пол.
Дано
R
J
m
h
1)
2)
= 20
см = 0,2 м
= 0,15 кг-м2
= 0,5
= 2,3
t —
T —
кг
M
?
- ?
Решение
mo2 Jw2
~2~ + ~2~'
h = -
v = at,
at2 a2t2 f J
**"—rv
a = ¦
mg
J '
= л — > TR = Je,
R
T =
Ja
R
J'
w =
mv
ma2t2
[OmeemJ
= 2 c;
mg
Некоторые математические формулы
¦ + /J) = sin a cos fi ± cos a sin ft
cos(a±jg) = cos a cos fi + sin a sin /?
Через неподвижный блок в виде однородного сплошного цилинд-
ра массой т = 0,2 кг перекинута невесомая нить, к концам кото-
рой прикреплены тела массами тх = 0,35 кг н т2 = 0,55 кг. Пренебрегая тре-
нием в осн блока, определите: 1) ускорение груза; 2) отношение Т2/Тх сил на-
тяжения нити.
Дано
т = 0,2 кг
от, = 0,35 кг
т2 - 0,55 кг
1) а — ?
2) Т2/Тх — ?
Решение
тхах = 7j - mxg,
ща = n^g - Т2,
(T2-Tx)R=Je,
m
•R2
J =
Т2-Тх=-
? =
/г'
2 '
Т2-Тх= m2g - m2a - mxa - mxg,
ma + 2m2a + 2mxa = 2m2g - 2mxg,
a = ¦
m
, = OT2(g-a),
T2 ^ m2(g-a)
(
mx(g + a
Ответ
)¦
)
1) a
= 1,96
м/с2;
2)
A
= 1,05.
Некоторые внесистемные единицы
1 сут = 86400 с 1" = 4,85 • 10 рад
1 год = 365,25 сут = 3,16- 107с 1 рад = 57,3°
1° = 1,75 • К) рад 1 мм рт. ст. = 133,3 Па
Г = 2,91 • Ю-4 рад 1 эВ = 1,6 • 10|9Дж
JPIp Тело массой тх- 0,25 кг, соединенное невесомой нитью посред-
ством блока (в виде полого тонкостенного цилиндра) с телом мас-
сой т-> = 0,2 кг, скользит по поверхности горизонтального стола. Масса блока
от = 0,15 кг Коэффнциент трения / тела о поверхность равен 0,2. Пренебре-
гая трением в подшипниках, определите: 1) ускорение а, с которым будут дви-
гаться эти тела; 2) силы натяжения 7j н Т2 нити по обе стороны блока.
Дано
wp 0.25 кг
m-, - 0,2 кг
m = 0,15 кг
/ = 0,2
1) a — ?
2) Tx —•>
% —?
Решение
(T2-Tx)R=Je,
J — n\R~,
R
D >
к
-72 = m2a,
T2-Tx = ma ,
mx+m2 + m
"A
T, T,
a = 2,45 м/с2; 2) 7J = 1,1 H; T2 = 1,47 H
<85>
Для демонстрации законов сохранения применяется маятник Мак-
свелла, представляющий собой массивный диск радиусом R и
массой т, туго насаженный на ось радиусом г, которая подвешивается на двух
предварительно намотанных на нее нитях. Когда маятник отпускают, то он со-
вершает возвратно-поступательное движение в вертикальной плоскости при
одновременном движении диска вокруг оси. Не учитывая силы сопротивления
и момент инерции оси, определите: 1) ускорение поступательного движения
маятника; 2) силу натяжения нити.
Однородный шар радиусом г = 20 см скатывается без скольже-
ния с вершины сферы радиусом R — 50 см. Определите угловую
скорость со шара после отрыва от поверхности сферы.
Дано
R
т
г
1)а—?
2) Г—?
Решение
то2 М2
~ + ~2~'
v
—
J —
mR1
v2 mR2v2
mv2 m
at2 аЬ2(л R2
1 +
\ 2г'
а = -
g
h = -
27V = Js,
= at.
a
? — i
r
2Tr =
mR1
mgR2
2r (l + R2/Br2))'
2Br2 + R2)
2)
\+R2lBr2)
2Brl
Т —тераA012)
Г —гигаA09)
М —мегаA06)
к — кило A03)
д —дециA0-')
с —сантиA0)
м — милли A0)
мк — микро A0)
н — наноA0~9)
п — пикоA0'2)
ф —фемтоA0~'5)
а —аттоA0~18)
r =
R-
w -
20
50
Дано
см = 0,2 м
см - 0,5 м
mv2
R+r
cosa
Решение
= mg cosa .
v2
g(R+r)
^-~. r
mv Ja)
i = (R + r)-(R + r) cosa,
~
mw2r2 2 mr2a>2
mg(R + r)(\ - cosa) = ^^— + —
2 5 2'
1
g(R + r)j 10
g(R+r)-@2r2=—aJr2,
r)J-l@2r2,
(O
-1 ill
VT?
g(R+r).
ГОтвет J ш = ю рад/с.
Десятичные приставки к названиям единиц
Wl 157': i Маховик начинает вращаться из состояния покоя с постоянным
™""* "^ угловым ускорением ? = 0,4 рад/с2. Определите кинетическую
Жергию маховика через время t2 = 25 с после начала движения, если через
'i =10 с после начала движения момент импульса X, маховика составлял
>0 кг • м2/с.
Горизонтальная платформа массой т-25 кг и радиусом R = 0,8 м
вращается с частотой «,= 18 мин '. В центре стоит человек и дер-
жит в расставленных руках гири. Считая платформу диском, определите часто-
ту вращения платформы, если человек, опустив руки, уменьшит свой момент
инерции от J] = 3,5 кг • м2 до J2 -1 кг • м2.
Дано
т = 25 кг
R = 0,8 м
«,= 18 мин = 0,3 с"
J, =3,5 кг • м2
J2-\ кг ¦ м2
Лт •
L--
L--
(J
Решение
= const, __^-Q
0 л
2 Lj i
= 2лг«,, со2~2жп2,
,= л +
mRl
2J, + mR2
= 21 +„,/?2 "'
Ответ
= 23 МИН
Человек, стоящий на скамье Жуковского, держит в руках стержень
длиной / = 2,5 ми массой от = 8 кг, расположенный вертикально
вдоль оси вращения скамейки. Эта система (скамья и человек) обладает мо-
ментом инерции J = 10 кг • м2 и вращается с частотой «, = 12 мин"'. Опреде-
лите частоту «j вращения системы, если стержень повернуть в горизонталь-
ное положение.
ГдтветЛ Из = 85
МИН
Человек массой т - 60 кг, сто-
ящий на краю горизонтальной
платформы массой М=120 кг.
фащающсися но инерции вокруг неподииж-
юй вер шкальной оси с частотой пх - 10 мил ',
юреходт к ее цетру. Счшая платформу круг-
шм однородным диском, а человека — точеч-
юй массой, определи ic, с какой частотой п^
5удет тогда вращаться платформа.
Ответ )
СУ п.
(М + 2т)
М
w,= 20 мин".
Платформа, имеющая форму сплошного однородного диска, мо-
жет вращаться по инерции вокруг неподвижной вертикальной оси
1а краю платформы стоит человек, масса которого в 3 раза меньше массы плат-
)ормы. Определите, как и во сколько раз изменится угловая скорость враще-
:ия платформы, если человек перейдет ближе к центру на расстояние, равное
:оловине радиуса платформы.
Дано
W
R
Решение
L = const,
L =
= J2w2,
(о
2 _
со.
J2 =
2 3l2J 12
w.
-^ = 1,43.
Человек массой т = 60 кг, стоящий на краю горизонтальной плат-
формы радиусом R = 1 м и массой М = 120 кг, вращающейся по
инерции вокруг неподвижной вертикальной оси с частотой и( =10 мин ~', пере-
ходит к ее центру Считая платформу круглым однородным диском, а чело-
века — точечной массой, определите работу, совершаемую человеком при пе-
реходе от края платформы к ее центру.
К проволоке из углеродистой стали длиной / = 1,5 ми диаметром
d = 2,1 мм подвешен груз массой «=110 кг. Принимая для ста-
ли модуль Юнга Е = 216 ГПа и предел пропорциональности оп = 330 МПа,
определите: 1) какую долю первоначальной длины составляет удлинение про-
волоки при этом грузе; 2) превышает приложенное напряжение или нет предел
пропорциональности.
Дано
m = 60 кг
V/ = 120 кг
R=\ м
п,= 10 мин ' = 0,17 с
А —?
Решение
Л = -fo>2
2
./,=
ct>, =
MR2
MR2
J,w, [ МЛ" _, ] 2 _ M + 2m
<у, = ——-= ь mR~ г--2лт7|= 4лги
' Л 2 М/?2 А/
,_ MR2((M+2mJ
2 ( М2
MR1
+ mR2 [BnnxJ
2m)z (M
2M
QOmeem J a = 65,8 дж.
d
Дайте определение и объяснение гироскопического эффекта.
Дано
= 1,5 м
= 2,1 мм = 2,1 ¦ 10~3м
и=110 кг
= 216ГПа = 216-109Па
г=ЗЗОМПа=33-1О'Па
Решение
= mg,
_ F _ 4mg
S = -nd2,
4
Д/ 4mg
1 ~ nd2E
{Ответ ) t) а/ = 0>
0,14 %;
2) ст = 312 МПа, а<оп.
Медная проволока сечением 5 = 8 мм2 под действием растягиваю-
щей силы удлинилась на столько, на сколько она удлиняется при на-
ревании на 30 К. Принимая для меди модуль Юнга ? = 118 ГПа и коэффициент
инейного расширения а = 1,7 ¦ 10~ К, определите числовое значение этой силы.
Дано
= о ММ —' б ' 10 М
\Т=30 К
= 118 ГПа=118-109Па
= 1,7 10 К1
F 9
Решение
F
о = —,
S
Д/ =
ES
Д/ о F 1
' = alAT, F=aESAT
Ответ j f =
Н.
Резиновый шнур длиной 40 см и внутренним диаметром 8 мм на-
тянут так, что удлинился на 8 см. Принимая коэффициент Пуассо-
на для резины равным 0,5, определите внутренний диаметр натянутого шнура.
d =
Д/
Ц
dx
Дано
40 см = 0,4 м
= 8 мм = 8- 10'
= 8 см = 8 10
= 0.5
— ?
м
м
? =
Ad
d
Решение
А/
, ?
д/
=d-Ad=d
_Ad_
d '
Ad
( ^At
I1 /
?' = jUE ,
fid Al
J ¦
Г Ответ j dt = 7,2 мм.
J Определите работу, которую необходимо затратить, чтобы сжать
^ пружину на 15 см, если известно, что сила пропорциональна де-
формации и под действием силы 20 Н пружина сжимается на 1 см.
Г Ответ Л а = 22,5 Дж.
ОпРеДелите относительное удлинение алюминиевого стержня
если при его растяжении затрачена работа А = 6,9 Дж. Длина стер
жня / = 1 м, площадь поперечного сечения 5 = 1 мм2, модуль Юнга для алю-
миния Е = 69 ГПа.
Дано
А = 6,9 Дж
1 = 1 м
S = \ мм2= 10 6м2
? = 69 ГПа = 69- 109Па
t —
Решение
_ Д/
/ '
,=1^12=1
2 W ) 2
ESle2,
Г Ответ j
:= 0,014
Определите объемную плотность потенциальной энергии упруго-
растянутого медного стержня, если относительное изменение дли-
ны стержня е = 0,01 и для меди модуль Юнга ? = 118 ГПа.
[Ответ
' = 5,9 МДж/м3.
Двава'°на (масса каждого т = 15 т) движутся навстречу др\ г
другу со скоростью и = 3 м/с и сталкиваются между собой. Оп-
[ределите сжатие пружины буферов вагонов, если известно, что сила про-
порциональна деформации, и под действием силы F - 50 кН пружина сжи-
(мается на А/ = 1 см.
Дано
от = 15 т= 15- 103кг
v = 3 м/с
F = 50 кН = 5- 10" Н
Д/ = 1 см = 10 2м
/
Решение
2кГ
F_
Д/
с Ответ
= ц,6см.
Рекомендуемая литература
Трофимова Т И. Курс физики, М, 1998.
Трофимова Т. И. Сборник задач по курсу физики, М, 1996.
Трофимова Т. И Физика. 500 основных законов и формул. Справочник, М., 1997
Трофимова Т. И. Оптика и атомная физика: законы, проблемы, задачи (спра-
вочник для студентов вузов), М., 1998.
1.5. Тяготение. Элементы теории поля
Считая орбиту Земли круговой, определите линейную скорость v
движения Земли вокруг Солнца.
Определите период обращения вокруг Солнца искусственной
планеты, если известно, что большая полуось ее эллиптической
орбиты больше на 107 км большой полуоси земной орбиты.
Дано
030
Дано
#,= R2 + R
#,=1,49-10" м
#=107 км= 10|0м
Тг =12 мес
Т, — ?
Решение
M=l,98 10JU кг
# = 1,4910" м
G = 6,67 -10"" м3/(кг-с2)
г- »J
Вычисления:
Т, = 12 мес-
Т -Т —L
'" 2л'/?3 '
Решение
wiJ „mM
= G—г-
# #2
Г Ответ
v = 29,8 юл/с.
1,49-101 м + 1010 м
1,49-10" м
= 13,2 мес.
(
Период обращения искусственного спутника Земли составляет 3 ч.
Считая его орбиту круговой, определите, на какой высоте от по-
!ерхности Земли находится спутник.
)meem
Дано
= 3 ч=1,08- 10" с
Период обращения кометы Галлея вокруг Солнца Т = 76 лет.
Минимальное расстояние, на котором она проходит от Солнца,
составляет 180 Гм. Определите максимальное расстояние, на которое коме!а
Галлея удаляется от Солнца. Радиус орбиты Земли принять равным Rq = 150 Гм.
#=6,37106
,24
[А/= 5,98-10^ кг
G = 6,67 -10"" м3/(кг-с2)
Дано
Т = 76 лет
Rmm =180 Гм=1,8-10"м
#0 = 150 Гм= 1,5- 10" м
Решение
Решение
mv2 _ mM
= G—=—
v = <
.-3
(О = -
2л
2 '
-#.
А=-
{.
Ответ
) h = 4,
\9 Мм.
Некоторые астрономические величины
L)
Т )
2П
Ответ
км.
Радиус Земли
Иасса Земли
Радиус Солнца
Солнца
6,37-106 м
5,98-1024 кг
6,95-108 м
1,98-1030 кг
f 1.175 j Планета массой М движется по окружности вокруг Солнца со ско-
"¦"¦¦~- ростью v (относительно гелиоцентрической системы отсчета)
Определите период обращения этой планеты вокруг Солнца
м
V
т—:
Дано
Решение
2nR
V
GMC
К- , >
V'
Mv2 MMC
Ля2'
2nGMc
Две материальные ючки массами «, и щ расположены друг oi
друга на расстоянии R . Определите угловую скорость вращения,
с которой они должны вращаться вокруг общего центра масс, чтобы расстоя-
ние между ними осталось постоянным.
(Ответ )
•
1 -
тх
тг
R =
а) -
Дано
const
_ ?
Решение
л R2 '
щь2
Г2
г\+г2
с
— (J
w,m2
я2
ИГ| Ся2 '
Определите, во сколько раз сила притяжения на Земле больше силы
притяжения на Марсе, если радиус Марса составляет 0,53 радиу-
са Земли, а масса Марса — 0,11 массы Земли.
,щ
R2
К
3
ЦТ Ответ ) [g
G^
Л3
QОтвет J „ = 2,55.
Определите среднюю плотность Земли, считая известными гра-
витационную постоянную, радиус Земли и ускорение свободног о
падения на Земле
Два одинаковых однородных шара из одинакового материала, со-
прикасаясь друг с другом, притягиваются. Определите, как изме-
'Нится сила притяжения, если массу шаров увеличить в п - 3 раза за счет уве-
личения их размеров.
G = 6,67
я = 6,37
g = 9,81
р—?
Дано
10"" м7(кг-
106 м
м/с2
с2)
mg-
М =
Решение
тМ
R2 '
- 3^
М gi?2 3 3g
V G
AnGR
ГОтвет) р = 5,.
•р\=
•л/ =
~F '
т2
R2-
Pi =
пт
)
-'
Дано
= т
--Р
Решение
тхт2
г
Y3m~
\Апр
4i
(ЗптJ п
Gm2
AR2 ' "
М2
г2 ' ГЗ~2Л
2/3 F П F»
4 з
3
/за/
\ Ажр '
F3 4/3
F П '
= 5,51 г/см3.
С Ответ
<1^_
р^ Сборник задач
Определите высоту, на которой ускорение свободного падения
составляет 25% от ускорения свободного падения на поверхности
Земли
г = R, R — радиус Земли
Считая плотность Земли постоянной, определите глубину, на ко-
торой ускорение свободного падения составляет 25% от ускоре-
ния свободного падения на поверхности Земли
f Ответ J h=0,15R, R — радиус Земли.
На какой высоте h ускорение свободного падения вдвое меньше
его значения на поверхности Земли
g'
R
1,
Дано
= g/2
= 6,37 106 м
mg
8 .
g'
Решение
_ тМ
R2
(R + hJ
R2 '
mg' --
g
я'
с тМ
(R+hJ'
2,
'+2Rh-R2 = 0, /,= #G2-1)
QOmeemj h=
Мм
Некоторые астрономические величины
Радиус Луны 1,74 106 м
Масса Луны 7,33 1022 кг
Расстояние от центра Земли до центра Солнца 1,49 ю" м
Расстояние от центра Земли до центра Луны 3,84 108 м
Стационарным искусственным спутником Земли называется спут-
ник, находящийся постоянно над одной и той же точкой экватора.
Определите расстояние такого спутника до центра Земли
Т —
R ~~
г ~
Дано
Т = 24 ч = 86400 с
6,37 106 м
-?
mg =
д
g\
Решение
тМ
G R2 '
г2
Л2'
mgi
g\ =
тМ
г2 '
gR2
2 '
g,= — =
г
Ъг
г- 2 ,
= 4,22Ю4км
1*.1а4^ ^а экватоРе некоторой планеты (плотность планеты р = 3 г/см3)
тела весят в два раза меньше, чем на полюсе Определите период
обращения планеты вокруг собственной оси
р
7"
Дано
= 3 г/см1=3 108
2 "
9
кг/м3
М =
Решение
mg, ^э =
--JtpR3, g =
mg-
GM
R2
mv2
R '
4
= —npGR,
mg =
V
G
mM
R1 '
inR
T '
mg = 2\mg-
mv
~R
8лг2 R
-TtpGR- ¦---,
3 И T2
1
-
2 _
3 6л
4npGR pG
R ' 8 t2r
T =
f Ответ j t = 2,7 ч
**1ИЧ®1 Принимая, что радиус Земли известен, определите, на какой вы-
l соте ^ над поверхностью Земли напряженность поля тяготения
равна 4,9 Н/кг.
Дано
g, = 4,9 Н/кг
g = 9,81 Н/кг
Л = 6,37 106 м
/j 9
Решение
Fx GM
R + h Fg~
R Vft '
GM
S R2
ft
g (R + hJ
ft Л2
Г Ответ
i = 2,64 Mm.
Определите, в какой точке (считая от Земли) на прямой, соединяю-
щей центры Земли и Луны, напряженность поля тяготения равна
нулю. Расстояние между центрами Земли и Луны равно R, масса Земли в 81 раз
больше массы Луны.
Дано
R
Решение
ft = #2 '
m
7
R
x"
x2=81(/?-xJ,
A=0,9i?
M
M
Si =
81(Л-хJ
= 9(R-x)
Q
dmeem
Имеется тонкий однородный стержень массой т и длиной /. Для
точки, находящейся на одной прямой со стержнем на расстоянии а
от его ближайшего конца, определите: 1) потенциал гравитационного поля стер-
жня, 2) напряженность его гравитационного поля.
Дано
т
I
а
1) <Р —
2)g —
А т А
йт = — ах,
Решение
m
dx
dm
-ч4"
dm mdx
а<р = — G— = —О ,
х / х
m t ax
-о'!
<Р
g = —— - G— In
dV /
I a
i = G-
аа
a)a
1.
Ответ
-i.
Связь между потенциалом поля тяготения
и его напряженностью
(дф. д(О дф
или g = - -r.i + _r.j + -r.
Э 9 3
где i, j, k — единичные векторы координатных осей.
Тонкий однородный диск радиусом R имеет массу т. Опреде-
лите в точке А, расположенной на оси диска на расстоянии А от
него: 1) потенциал гравитационного поля; 2) напряженность гравитационного
поля.
R
m
A
2)8
Дано
— ?
Решение
ЕЙ
\ \
%
1
г
т _ , 2тх 4с
dm = —1г2лх 4с = z—
dm
dip = -G— ,
г
2т xdx
= -G-^\jh2 + R2 -h\,
R2l J
(Ответ) „2mr rr~j л
V V i) y) = -G—j- л/А' + Л2-А •
/г L J'
1.
Для тела массой т, находящегося в гравитационном поле Земли
над ее поверхностью, выведите зависимость потенциальной энер-
гии тела от расстояния до центра Земли. Считать известными радиус Земли Rq H
ускорение свободного падения g на поверхности Земли.
Дано
т
8
П (R) — ?
П= J
со
Решение
Fdr, F
mM \—y — —Gmh
г
~G r2 '
Ноо Л
, mAf
GmAf =
П = —
QOmeemJ
Как известно, искусственный спутник Земли движется вокруг нее
по круговой орбите. Определите, во сколько раз гравитационная
потенциальная энергия спутника больше его кинетической энергии.
Дано
R
П
7
WU2
Решение
тМ
R2
Т
то1
2 '
|П| _ GmM 2 R _
~Т~ R "mj2"^'
СОтвет\\ щ
л
Два алюминиевых шарика (р = 2,7 г/см3) радиусами г, = 3 см и
г2 = 5 см соприкасаются друг с другом. Определите потенциаль-
ную энергию их гравитационного взаимодействия.
1.193 } Принимая, что атмосфера на Луне отсутствует, определите ско-
рость падения метеорита на ее поверхность. Скорость метеорита
вдали от Луны считать малой.
Дано
р = 2,7 г/см3 =
= 2,7- Ю'кг/м3
'•, =3 см = 3 ¦ 10~2м
г2 = 5 см = 5 • 10 г м
П—?
Решение
Л = <
Qdmeemj п = - о,зб нДж.
Два одинаковых однородных щара из одинакового материала со-
прикасаются друг с другом. Определите, как изменится потенци-
альная энергия их гравитационного взаимодействия, если массу шаров увели-
чить в 3 раза.
От] - т2
1 =Г2 =
Pl=P2 :
Л/ = пт
п = 3
п, ¦
Дано
- т
г
--Р
П,=
м =
Л3
г3"
п2
п,
Решение
тхт2 т
rt+r2 2r
4 з
М Л ,г
— -и, ~-Ып,
т г
М\ 2 1 5/3
гт гМ"
П2 --G ,
2 2/?
M = p--nR\
¦
Ответ j v = 2,
37 км/с.
Спутник поднимают на высоту h = 6370 км и запускают его по
круговой орбнте на той же высоте. Определите отношенне работ
на поднятие ( Ах) и на запуск (А2) спутника.
Дано
h = 6370 км = 6,37- 106м
06 м
R = Я3 + h
-2L
^2
Решение
АГТ ^
= ДП = -G
R3+h
[
-1 ~ G
/иМ
= GmM\
«г;
mv
/?3
GmM?
= G
GmM _ GmM Ax _h 2(R3 + h) _2h
2R ~ 2(R3 + h)' Л, ~ Л3(Л3 + Л) ~ Л3 '
(Ответ j A _
X ^ -
Определите числовое значение первой космической скорости, т. е.
горизонтально направленной минимальной скорости, которую
надо сообщить телу, чтобы его орбита в поле тяготения Земли стала круговой
(тело могло превратиться в искусственный спутник Земли).
ГЪтветЛ щ = 7.
= 7,9 км/с.
Определите числовое значение второй космической скорости, т. е.
1 наименьшей скорости, которую надо сообщить телу, чтобы его
орбита в поле тяготения Земли стала параболической (тело могло превратить-
ся в спутник Солнца).
С Ответ Л 7. _
у у уг -
= 11,2 км/с.
Определите числовое значение второй космической скорости для
Луны
v Ответ
v2 = 2,37 км/с.
Искусственный спутник Земли движется по круговой орбите на
высоте h — 500 км. Определите скорость его движения.
Дано
/7 = 500 км = 5- 105м
Л = 6,37 10б м
Л/= 5,98 Ю24 кг
и — f
Решение
то' тМ
Г Г
С Ответ j v
R+h,
= 7,62
/ga
" = V r
км/с.
/ /GA/
\R + h
Два спутника с одинаковой массой движутся вокруг Земли по круго-
j/ вым орбитам разных радиусов Rx и R2 (R2 > Л,). Определите
1) отношение кинетической энергии второго спутника к первому, 2) как зави-
сят от радиуса орбиты потенциальная и полная энергия спутников.
(Ottxeettx I I \
J 1) — = —;
7Г - "r5"; 2) П и ? возрастают с удалением от Земли
h K2
Я52(Ш1^ Определите работу, которую необходимо совершить, чтобы тело
14 ¦" "'¦ ^ массой т = 1000 кг, находящееся на Земле, смогло превратиться
в спутник Солнца (при отсутствии сопротивления среды).
Г Ответ j л = б2,бЩж.
( 1.201 .-j К потолку вагона, движущегося в горизонтальном направлении с
" ^^У ускорением а = 9,81 м/с2, подвешен на нити шарик массой
т = 200 г. Определите для установившегося движения: 1) силу натяжения нити Т,
2) угол <р отклонения нити от вертикали.
Дано
а = 9,81 м/с2
g = 9,81 м/с2
т = 200 г = 0,2 кг
1)Г—?
2) Ч> — ?
Решение
я
W
«g
F
и
К=-
\FU\ = та,
FK + mg = F ,
ma a
= —
mg g
= arctg—.
g
f Ответ Л i) г = 2,77 H; 2)^=45°
Силы инерции
^ин = Ри + Fu + FK ,
где FH — силы инерции, проявляющиеся при поступательном движении сис-
темы отсчета с ускорением а0 : Fa = -та0; Fu — центробежные силы инер-
ции (силы инерции, действующие во вращающейся системе отсчета на тела,
удаленные от оси вращения на конечное расстояние R). Fu = -mo?R; FK —
кориолисова сила инерции (силы инерции, действующие на тело, движущееся
со скоростью v' во вращающейся системе отсчета): FK = 2m[v'a>].
A.202 1 Вагон под действием силы тяжести катится вдоль дороги, состав-
|ГТ"^ ляющей угол « = 30° с горизонтом. Сила трения составляет
г) = 10% от веса вагона. К потолку вагона на нити подвешен шарик массой
т = 15 г. Определите: 1) силу F, действующую на нить; 2) угол <р отклонения
нити от вертикали
Дано
а = 30°
г] =10%
т=15 г= 15- 103кг
1) F-l
2) <Р — ?
Решение
Ma = Mg sin a - Frp,
Fjp - t]Mg, Ma = Mg sin a - rjMg ,
a = g(sina~t]), F = Fu+mg, F =-ma,
F =
cos(90°-a)
in a-?;)] +(mgJ-2(mgJ(sina-?7)cos(90D-a) =
m a - r]f +1 - 2(sin a - tj) sin a ,
F
F,
sin<p sin(90°-a)
. mg(sina -w)cosa
^) = arcsin —s
sm(p = -
u sin(90°-a)
{Ътвет
h, 2) ^> = 23,5°.
Вагон под действием силы тяжести катится вдоль дороги, состав-
ляющей с горизонтом угол а = 30°, а затем переходящей в гори-
зонтальный участок. Силы трения на обоих участках составляют 10% от веса
вагона. К потолку вагона на нити подвешен шарик массой т = 15 г. Определи-
те силу F, действующую на нить, и угол <р отклонения нити от вертикали на.
1) наклонном; 2) горизонтальном участках дороги.
\) F = 0,128 Н; f = 23,5°; 2) F = 0,148 Н; <р = 5,7°.
у На наклонной плоскости с углом наклона а = 30° лежит тело.
/ Коэффициент трения между телом и наклонной плоскостью
/ = 0,2. Определите наименьшее горизонтально направленное ускорение а,
с юторым должна двигаться наклонная плоскость, чтобы тело, лежащее на ней,
поднималось по наклонной плоскости.
Дано
а = 30°
/ = 0,2
а — ?
Решение
Fu =ma,
а=ашт, mgsma + FTV-Fucosa = 0,
F™ - fN = f(mgcosa + Fu sina),
mg
mg sina + f(mg cose + ma sina)- ma cosa = 0 ,
ma cosa - fma sina = mg sina + jmg cosa ,
g(sina + / cosa)
a — ¦
cosa- / sina
С Ответ J a = 8,
62 м/с2.
Самолет, летящий со скоростью v = 360 км/ч, описывает верти-
кальную петлю Нестерова радиусом R = 360 м. Определите силу,
прижимающую летчика (т = 80 кг) к сиденью: 1) в нижней точке этой петли;
2) в верхней точке этой петли.
V ~
R =
т =
1 ^ i
2) /
360
360
80
Дано
км/ч = 100
м
кг
м/с
Решение
mv
R
тГ
... 2
Ответ J
i) /г, = з кН; 2) f2 = 1,44 кн.
Модель центробежного регулятора враща-
ется с частотой п - 2 с. Учитывая только
массу шаров, определите угол отклонения стержней,
несущих шары. Длина стержней / = 15 см.
Некоторые внесистемные единицы
1 сут = 86400 с 1" = 4,85 ¦ 10 рад
1 год= 365,25 сут =3,16- 107с 1 рад = 57,3°
1° = 1,75 • 10~2 рад 1 мм рт. ст. = 133,3 Па
Г = 2,91 ¦ Ю^рад 1эВ = 1,6-10|9Дж
J2071 Определите, во сколько раз ускорение а,, обусловленное центро-
бежной силой на экваторе Земли, меньше ускорения а2, вызыва-
силой тяготения на поверхности Земли.
Т--
м
El
а,
^24 ч
= 6,37
= 5,98
?
Дано
= 86400 с
10"" м3/(кг • с2)
•10б м
¦10 кг
а,
а\
а2
а\
Решение
= mcj2R-i,
GmMT2
R2m-4jt2Rz
2ж
а> = —
Т
GMT2
4ж2 Rl '
mM
R2 '
(Ответ j^- = 292.
У а.
Мотоциклист в цирке едет вдоль внутренней поверхности верти-
кального цилиндра радиусом г - 15 м. Центр масс мотоцикла с
человеком отстоит на h = 1 м от места соприкосновения колес со стенкой. Ко-
эффициент трения шин о стенки / = 0,5 , Определите: 1) минимальную ско-
рость wmm , с которой должен ехать мотоциклист; 2) угол а наклона мотоцик-
листа к горизонтальной поверхности при данной минимальной скорости.
Г Ответ j
l)umin= 17,1 м/с; 2) а = 26,6°.
Некоторые математические формулы
-(хя)=ихя-
±1
и+1
Тело массой т = \ кг, падая свободно в течение / = 4 с, попадает
на Землю в точку с географической широтой <р = 45° . Учитывая
вращение Земли, определите и нарисуйте все силы, действующие на тело в
момент его падения на Землю.
Дано
111 = 1 КГ
t -4 с
<р = 45°
G = 6,67-10"" м7(кг-с2)
/?з = 6,37-106 м
М = 5,98-1024 кг
F — ?
Решение
1. Сила тяготения Север Fk
2. Центробежная сила инерции
гц = -тси'г , /•ц = т<у-?-,
2л;
-y cos<p
3. Сила Кориолиса
Fk = 2w[v' ш], FK= 2mv'w sin(v', CO),
" =J
sin(v', CO) =
K=2nn,'f
С Ответ J
l) F = 9,83 H; 2) Fu =23,8 mH; 3) FK =4,04 мН.
¦Mm
щ Тело массой т = \
ш
** на Землю в точку
кг, падая свободно в течение г = 6
с географической широтой <р = 30'
ращение Земли, определите отклонение тела при его падении от
J= 1 КГ
= 6 с
1 = 30°
'=24 ч
?
t
; L
к - J «1
0
г
= |%
0
Дано
= 86400 с
Fk
Fk
v'
„ 2л
= 2gt—cosip,
4ngcos<p'r
i at T }tat
0
2ngcostpTc2
T I
Ответ M = 4,45
dt =
CM.
Решение
= 2m[v'co],
= 2mv'a) sin(v', со) = 2mv'w cosip ,
2л
2ngt2 cos<p
T
2ngr3 cos<p
ЪТ
с, попадает
5. Учитывая
вертикали.
Некоторые математические формулы
—-(sinx) = cosx
-(cosx) = -sinx
V
cos x
1.6. Элементы механики жидкостей
^ Полый медный шар (р = 8,93 г/см3) весит в возд>хе 3 Н, а в воде
(р' = 1 i/см3) — 2Н Пренебрегая выталкивающей силой воздуха
определите объем внутренней полости шара
1*2 j31'1 По трубе радиусом г = 1,5 см гечетуглекислый газ (р = 7,5 кг/м')
Определите скорость его течения, если за t - 20 мин через попе-
речное сечение трубы протекает т = 950 г газа.
ГОтвет
\(Р-1" р)
- __1=б8 см3.
g Р Р)
Па столе стоит цилиндрический сосуд, наполненный водой до уров-
ня Я = 20 см от дна. Если в воду (р = 1 г/см3) опустить плавать
тонкостей!' гй никелевый стакан (рг = 8,8 г/см3), то уровень воды подымается
на h = 2,2 см. Определив уровень Я, воды в сосуде, если стакан утопить.
Дано
Н=20 см = 0,2 м
А = 2,2 см = 2,2' 10 2м
р-1 г/см3 - 103 кг/м3
= 8,8 103ki/m1
Я,-?
Решение
А
я
S
А
ч
S
\
У
N
1
S
FA =
S,x = AS ,
С
Ответ
Я, = 20,2 см
Г Ответ J w = 0,15 м/с.
f 1
В бочку заливается вода со скоростью 200 см3/с На дне бочки
образовалось отверстие площадью поперечного сечения 0,8 см
Пренебрегая вязкостью воды, определите уровень воды в бочке
7=
А -
Дано
200 см3 = 2- Ю^м3
с
0,8 см2 = 0,8- Ю^м2
_ 9
Решение
V
vS = —, v —
t
2
V V2
St ' ' 2gS2r
[Ответ j a =
= 31,9 см.
В сосуд заливается вода со скоростью 0,5 л/с Пренебрегая вязко-
стью воды, определите диаметр отверстия в сосуде, при котором
вода поддерживалась бы в нем на постоянном уровне А = 20 см
Ответ J d = \,
8 см.
Формула Торричелли
v = jlgh,
(Где А — глубина, на которой находится отверстие относительно уровня жидко-
сти в сосуде.
1.216 ) Бак Цилиндрической формы площадью основания 10 м2 и объе-
"" S мом 1 оо м1 заполнен водой. Пренебрегая вязкостью воды, опреде-
лите время, необходимое для полного опустошения бака, если на дне бака об-
разовалось круглое отверстие площадью 8 см2.
Дано
5 = 10 м2
V = 100 м3
5, =-8 см2 = 8- Ю^м2
г —?
Решение
dh
H=V-, r
S чг
dF = -5,ud/,
h
v ~ J2gh ,
S
_—_ — - —
i
dV
H
dV S
T =
S
(
Ответ
= 1,78 1O4 c.
Сосуд в виде полусферы радиусом
R = 10 см до краев наполнен водой.
На дне сосуда имеется отверстие площадью по-
перечного сечения 5 = 4 мм2. Определите время,
за которое через это отверстие выльется столько
воды, чтобы ее уровень в сосуде понизился на 5 см.
С
Ответ
) t =
10 мин.
f 1 218^ Определите работу, которая затрачивается на преодоление трения
>¦ " ' S при перемещении воды объемом V = 1,5 м3 в горизонтальной трубе
эт сечения с давлением рх = 40 кПа до сечения с давлением р-, = 20 кПа
V
Р\
Pi
4
= 1,5
= 40
-20
0
Дано
м1
кПа = 4-
кПа = 2-
ю4
ю4
Па
Па
А =
Решение
Г Ответ Л л = зо кДж.
В дне сосуда имеется отверстие диаметром dx. В сосуде вода под-
держивается на постоянном уровне, равном h. Считая, что стр>я
не разбрызгивается, и пренебрегая силами трения в жидкости, определите ди-
аметр струи, вытекающей из сосуда на расстоянии й,= 2й от его дна.
Дано
hx=2h
Решение
S,u, = S2v2,
v2 =
у, = yjlgh ,
nd}
5, =
2g(h + h,) Sh л/3
С Ответ Л d2 = o,76rf,
Площадь поршня, вставленного в горизонтально расположенный на-
литый водой цилиндр, 5, = 1,5 см2, а площадь отверстия S2 = 0,8 мм2
Пренебрегая трением и вязкостью, определите время /, за которое вытечет вода из
цилиндра, если на поршень действовать постоянной силой F - 5 Н, а ход пор-
шня 1 = 5 см. Плотность воды р = 1000 кг/м3.
Дано
5, =1,5 см2 =1,5- \0г*м2
S2 = 0,8 мм2 = 0,8- Ю-'м2
F = 5 H
1 = 5 см = 5- 10~2м
р = 1000 кг/м3
/ —?
Решение
S,ui = S2v2,
pv\ pv\
2 ' И 2 '
/
F
Для измерения статического дав-
ления р используется зонд, для
измерения динамического давления pv /2 ис-
пользуется трубка Пито. Нарисуйте, как дол-
жен выглядеть прибор, который измеряет гид-
ростатическое давление.
Зонд
Трубка Пито
Объясните, почему легкий шарик, помещенный в
струю воздуха, выходящую с большой скоростью из
рубы с узким отверстием, свободно парит в этой струе.
Объясните, почему бумажный конус А втягивается в
воронку, а не выталкивается из нее при продувании
дерез воронку воздуха в направлении, указанном стрелкой.
Для точного измерения малых разностей давле-
ния служат U-образные манометры, которые за-
полнены двумя различными жидкостями. В одном из них при
Использовании нитробензола ( р = 1,203 г/см3) и воды
(р' = 1,000 г/см3) получили разность уровней Ah-26 мм.
Определите разность давлений.
Т
По горизонтальной трубе в направлении, указанном на рисунке
стрелкой, течет жидкость. Разность уровней Ah жидкости в мано-
метрических трубках 1 а 2 одинакового диаметра составляет 8 см. Определите
скорость течения жидкости по трубе.
Дано
dx = d2
Д/г = 8 см = 8 ¦ 10~2м
V ?
Решение
Ey = pgM,
v = J2g Ah . — -
-
Д/г
ж__.
А :
— _~~ __ ~ — А
2
)
COmeemJ „ = 1,25
м/с.
По горизонтальной трубе переменного сечения течет вода. Пло-
щади поперечных сечений трубы на разных ее участках соответ-
ственно равны S, = 10 см2 и S2 = 20 см2. Разность уровней ДА воды в верти-
кальных трубках одинакового сечения составляет 20 см. Определите объем воды,
проходящей за 1 с через сечение трубы.
Определите разность давлений в широком и узком (dx = 9 см,
d2 = 6 см) коленах горизонтальной трубы, если в широком колене
юздух (р = 1,29 кг/м3) продувается со скоростью у, = 6 м/с.
S2 =
ЛА =
V —
10
20
20
с
Дано
см =10
см2 = 2 ¦
см = 0,2
м2
10-3м2
м
Решение
pv] pv\
2 2 Р2'
V2 — Dj
52
ДА
— /
Рг~Р\=
V =
2gAA
l-5,2/522
1-5,75;
Ответ
= 2,29 103 см3.
L2'2.T;-y Определите, на какую высоту А поднимется вода в вертикальнон
трубке, впаянной в узкую часть горизонтальной трубы диаметром
d2 = 3 см, если в широкой части трубы диаметром d{ = 9 см скорость газа
и, = 25 см/с.
dt =
d2 =
Дано
9 см = 9- 10-2м
3 см = 3- 10-2м
25 см/с = 0,25 м/с
?
Решение
11 2 2' i 4
py, pw2
2 +A 2 'ftl
яс/2
4
Л Л 2
г;
f А Л
Ц4 т
Ответ J ap = 94,3 Па.
Вдоль оси горизонтальной трубки диаметром 3 см, по которой
течет углекислый газ (р = 7,5 кг/м3), установлена трубка Пито.
1ренебрегая вязкостью, определите объем газа, проходящего за 1 с через сечение
фубы, если разность уровней в жидкостном манометре составляет Ah = 0,5 см.
1лотность жидкости принять равной р' = 1000 кг/м3.
Дано
э = 7,5 кг/м3
о' = 1000 кг/м3
= 3 см = 3- 10м
* = 0,5 см = 5- 10~3м
f = l с
V _9
Решение
Ар =
pv
Ap = p'g ДА ,
.2
pv
= p'g AA,
,P1
р
= Svt,
я./2
Через трубку сечением
5,= 100 см2 продувается ^т
воздух со скоростью 2 м3/мин. В трубке . .
имеется короткий участок с меньшим по- 1 ''
перечным сечением S2 = 20 см2. Опре-
делите 1) скорость и, воздуха в широ-
кой части трубки, 2) разность уровней
Ah воды, используемой в подсоединен-
ном к данной системе манометре Плотность воздуха р = 1,3 кг/м\ во ил
р' = 1000 кг/м3
Г Ответ j
1) и, =3,33 м/с; 2) Ah = 1,8 см.
123Д1р) Пренебрегая вязкостью жидкости, определите скорость истечения
^ "" жидкости из малого отверстия в стенке сосуда, если высота h уров-
ня жидкости над отверстием составляет 1,5 м.
Дано
h = 1,5 м
is —
Решение
2
S, »52,
и, « v2,
f
Ў
— — -
~~ z. ——Z.
/г
боковой поверхности цилиндрического сосуда, стоящего на го-
ризонтальной поверхности, имеется отверстие, поперечное сече-
которого значительно меньше поперечного сечения самого сосуда. Отвер-
ие расположено на расстоянии \ = 49 см от уровня воды в сосуде, который
одерживается постоянным, и на расстоянии /^ = 25 см от дна сосуда. Пре-
брегая вязкостью воды, определите расстояние по горизонтали от отверстия
места, куда попадает струя воды.
Ответ J
= 70 см.
S ^a столе стоит наполненный водой широкий цилиндрический сосуд
высотой h = 40 см. Пренебрегая вязкостью, определите, на какой
соте от дна сосуда должно располагаться небольшое отверстие, чтобы расстоя-
ie по горизонтали от отверстия до места, куда попадает струя воды, было макси-
альным.
Ответ
г =20 см.
Для вытекания струи жидкости из сосуда с постоянной скорос-
тью применяют устройство, приведенное на рисунке (сосуд Ма-
отта). Определите скорость истечения струи.
Дано
///////////////////////////////¦'////77//
н
\h
u,S, = v2S2,
Решение
H
/?,, pg^l=Pg^2+ —
2 2
H
v2 =
v =
= const.
К
Ў Ў
Ответ
= 5,42 м/с
Ответ )
С 1.235 у Площадь соприкосновения слоев текущей жидкости 5 = 10 см1, ко
эффициент динамической вязкости жидкости г] = 1(Г3 Па с, а во,
пикающая сила трения между слоями F = 0,1 мН. Определите градиент скорости
S1 = 10
^ = 0,1
giad v
Дано
ш'= 10 3
3 Па с
мН= 10"
?
м2
Н
grad
6и =
ах
Решение
dx
?_
dv
dx
S,
Смесь свинцовых дробинок (плотность р = 11,3 г/см3) диамет-
ром 4 мм и 2 мм одновременно опускают в широкий сосуд глуби-
ной h - 1,5 м с глицерином (плотность р = 1,26 г/см3, динамическая вязкость
т^ = 1,48 Па • с). Определите, на сколько больше времени потребуется дробин-
кам меньшего размера, чтобы достичь дна сосуда.
С Ответ j gradv =
100 с1.
( 1,236|) Шарик всплываете постоянной скоростью в жидкости, плотность
^ ^ которой в три раза больше плотности материала шарика Опреде
ли! е отношение силы трения, действующей на всплывающий шарик, к его вес\
Дано
!' =
l>' ~-
Лр
P
const
-ъР
9
Решение
v_2gr2(p-p')^gd2(p-p')
9t] Щ
P=mg,
P=pgV,
тр
p
i
Ш
1
v, =•
v2~ v
v-, =
1 1
gd\{p-p')
Щ
\Щ f 1 1
g(p-p'){4
f Ответ
= 76,i с.
mg
^ p'gv-pgv__p'-p_ip-p_„
pg^ p p
Дано
p = 11,3 г/см3 =
= 11,3 • 103кг/м3
с/, =4 мм = 4 • 10 Зм
d2 = 2 мм = 2- 10~3м
h - 1,5 м
р' = 1,26 г/см3 =
= 1,26- 103кг/м3
г] = 1,48 Па • с
At —1
Решение
v ~ const
mg=FAi
Fa = P'gl
4 з
3Pg^ :
) t — 5
У
'-- r3
3
4 ' 3
4 ,
= 3 P'gnr + влг,
d
— — С —
С Ответ j Fip _
Некоторые математические формулы
— = lnx — = —
J V i X X
В широком сосуде, наполненном глицерином (плотность р = 1,26 г/см\
динамическая вязкость rj = 1,48 Па • с), падает свинцовый шарик
(плотность р = 11,3 г/см3). Считая, что при числе Рейнольдса Re < 0,5 выпол-
няется закон Стокса (при вычислении Re в качестве характерного размера бе-
рется диаметр шарика), определите предельный диаметр шарика.
С Ответ j ^ = 5,
41 мм.
Стальной шарик (плотность р = 9 г/см3) диаметром d = 0,8 см
падает с постоянной скоростью в касторовом масле (плотность
р' = 0,96 г/см3, динамическая вязкость г/ - 0,99 Па • с). Учитывая, что крити-
ческое значение числа Рейнольдса Re^ = 0,5, определите характер движения
масла, обусловленный падением в нем шарика.
Дано
р = 9 г/см3 = 9- 103 кг/м3
d = 0,8 см = 8 • 10 3 м
v - const
р' = 0,96 г/см3 = 960 кг/м3
т? = 0,99 Па ¦ с
кр
Re — ?
mg
FA
Решение
= FA+F,
,4 з
3
4 , з
3
= вжг/rv,
щ
h
V=
2(p-p')gr (p-p')gd2
!
9rj
Re =
p'vd p'(p-p')gd*
rj
( Ответ j Re = 2,2 , Re > Re , движение жидкости турбулентное.
Пробковый шарик (плотность р = 0,2 г/см3) диаметром d = 6 мм
всплывает в сосуде, наполненном касторовым маслом (плотность
р' = 0,96 г/ см3), с постоянной скоростью v = 1,5 см/с. Определите для касто-
рового масла: 1) динамическую вязкость rj; 2) кинематическую вязкость v .
Дано
р = 0,2 г/см3 = 2-102кг/м3
d = 6 мм = 6 • 10м
р' = 0,96 г/см3 = 960 кг/м3
w = l,5 см/с =1,5- 10м/с
1) rj — ?
jJ) v — ?
Решение
4 , з 4 j
—яр г =—жрг +6яг/т,
2gr2(p-pl)=gd2(p-p')
9v 18v
-1
p'
Ответ
J 1} ^ = o,99 Па • с; 2) v = 1,03 • 10'3 M2/c.
В боковую поверхность сосуда вставлен горизонтальный капил-
ляр с внутренним диаметром d = 2 мм и длиной / = 1,2 см. Через
капилляр вытекает касторовое масло (плотность р = 0,96 г/см3, динамическая
аязкость rj = 0,99 Па ¦ с), уровень которого в сосуде поддерживается постоян-
ным на высоте h - 30 см выше капилляра. Определите время, которое требует-
ся для протекания через капилляр 10 см3 масла.
ГотвепГ) (=
xd4pgh
Некоторые математические формулы
jsinx dx = -cosx fcosxdx = sinx
Je* ck =.
f J.242 ) ^ боковую поверхность цилиндрического сосуда D вставлен ка-
^* ^ пилляр с внутренним диаметром d и длиной /. В сосуд налита
жидкость с динамической вязкостью У]. Определите зависимость скорости v
понижения уровня жидкости в сосуде от высоты h этого уровня над капилляром
^44^ Определите наибольшую скорость, которую может приобрести
свободно падающий в воздухе (р = 1,29 кг/м3) свинцовый шарик
(р' = 11,3 г/ см3) массой т-\2 г. Коэффициент сопротивления Сх принять
эавным 0,5.
Дано
D
d
I
Г)
h
v(h) —
лг pght
Решение
v =
лг Apt
Ц1
= лг2,
v = s
v, =
r2pgh
S D2'
Ap = pgh,
S = лR2 ,
u,5, = vS,
v =
_ d2pgh-d2 pghd4
4 8?;/ D2 ~ 32^/D2
(Ответ")
4 ^
22r]lD2
^ боковую поверхность цилиндрического сосуда, установленного
на столе, вставлен на высоте h, = 10 см от его дна капилляр с
внутренним диаметром d = 2 мм и длиной / = 1 см. В сосуде поддерживается
постоянный уровень машинного масла (плотность р = 0,9 г/см3, динамичес-
кая вязкость г\ = 0,1 Па • с) на высоте /ь = 70 см выше капилляра. Определите
расстояние по горизонтали от конца капилляра до места, куда попадает струя
масла.
С Ответ j <, =
11 см.
Дано
р = 1,29 кг/м3
р' = 11,3 г/см3 =
= 11,3- 103kt/mj
/и = 12 г= 12 ¦ Ю-1 кг
Cv = 0,5
к —?
Решение
4 з
P'g -яг ,
3m
Алр'
FA « mg, p « p\ mg=Rx, Rx =
pu
С Ответ j
wmax = 53,9 м/с
;. «Й45»1 Парашют (m, = 32 кг) пилота (т2 = 65 кг) в раскрытом состоя-
нии имеет форму полусферы диаметром d = 12 м, обладая коэф-
фициентом сопротивления С, = 1,3 . Определите максимальную скорость, раз-
виваемую пилотом, при плотности воздуха 1,29 кг/м3.
Дано
тх - 32 кг
т2 = 65 кг
с/ = 12 м
С, =13
р = 1,29 кг/м3
Решение
m2)g = Rx + FA ,
Ответ j
Umax =3,17 М/С.
i Сборник ii iti
Автомобиль с площадью миделя (наибольшая площадь сечения в
направлении, перпендикулярном скорости) S = 2,2 м2, коэффици-
ентом лобового сопротивления Сх = 0,4 и максимальной мощностью Р = 45 кВт
может на горизонтальных участках дороги развивать скорость до 140 км/ч При
реконструкции автомобиля уменьшают площадь миделя до 5, = 2 м2, оставляя Сх
прежним. Принимая силу трения о поверхность дороги постоянной, определи-
те, какую максимальную мощность должен иметь автомобиль, чтобы он разви-
вал на горизонтальных участках дороги скорость до 160 км/ч. Плотность воз-
духа принять равной 1,29 кг/м3.
Дано
5 = 2,2 м2
С, =0,4
Р = 45 кВт = 45- 103Вт
у = 140 км/ч = 38,9 м/с
S, = 2 м2
Fw = const
у, = 160 км/ч = 44,4 м/с
р = 1,29 кг/м1
Р,~1
Решение
P = Fv, F=RX + FW,
b^c^s, p = \cx~s+f\v,
F p с Р»\ PJr PyK , F \,
Объясните, зависит ли разность давлений на нижнюю и верхнюю
поверхность крыла самолета от высоты его подъема.
AP--L.
н
1.7. Элементы специальной (частной) теории
относительности
Покажите, что события, происходящие одновременно в различ-
ных точках в одной инерциальной системе отсчета, не одновре-
менны в другой инерциальной системе отсчета.
В лабораторной системе отсчета в точках с координатами х, и
х2 = х, + /0 одновременно происходят события 1 и 2, причем
/0 = 1,4 км. Определите: 1) расстояние /', фиксируемое наблюдателем в систе-
ме отсчета, связанной с ракетой, которая движется со скоростью v = 0,6с в
отрицательном направлении оси х; 2) время между этими событиями, фикси-
руемое наблюдателем в системе отсчета, связанной с ракетой.
Дано
х2 = х, + /„
/0 = 1,4 км =1,4- 10»м
у = -0,6с
1) IL ~ ?
2) д/' _ ?
|._-г .., X2-Vt- X,
Решение
,! х,, х2 = х, + /„,
'1 > '2 ¦
Х2 =
l-u2/c2
Х2 - X,
t, t-vx2/c
2 "
С Ответ J
1) /' = 1,75 км; 2) ДГ = 3,5 мкс.
1.250 ) Две нестабильные частицы движутся в системе отсчета К вод-
ном направлении вдоль одной прямой с одинаковой скоростьк:
v = 0,6с . Расстояние между частицами в системе К равно 64 м. Обе частицы
распались одновременно в системе К', которая связана с ними. Определите
промежуток времени между распадом частиц в системе К .
Собственное время жизни частицы отличается на 1% от времени
жизни по неподвижным часам. Определите /? = v/c.
!—
jt= 0,01
>-?
Дано
к —
Решение
At - AtQ
At
At~-
At0
Jl-v2
1 ¦> ' с '
/с" c
Ш Докажите, что длительность события, происходящего в некото-
рой точке, наименьшая в той инерциальной системе отсчета, от-
носительно которой эта точка неподвижна.
Космический корабль движется со скоростью v = 0,8с по направ-
лению к Земле. Определите расстояние, пройденное им в системе
Ьтсчета, связанной с Землей (системе ?), за t0 = 0,5с, отсчитанное по часам в
рюсмическом корабле (системе К') ¦
j
Ответ j / = 200 Мм.
Определите, во сколько раз увеличивается время жизни нестабиль-
ной частицы (по часам неподвижного наблюдателя), если она на-
чинает двигаться со скоростью 0,9с .
v = 0,9с
At
Д/о
Дано
Решение
Д/о At 1
Jl-v2/c2 ' Д'о J\-v2/c2 '
Мюоны, рождаясь в верхних слоях атмосферы, при скорости
v = 0,995с пролетают до распада / = 6 км. Определите: 1) соб-
ственную длину пути, пройденную ими до распада; 2) время жизни мюона для
наблюдателя на Земле; 3) собственное время жизни мюона.
Дано
v = 0,995с
/ = 6 км
Решение
исо,
, Д/о; ИСО2 /, At;
Г Ответ Л д/
Д'п
2,29.
2) Дг — ? Г Ответ J 1) /0 =
3) Ал, — ? > *
599 м; 2) At = 20,1 мке;
3) ДГ0 = 2 мкс.
Докажите, что линейные размеры тела наибольшие в той инерци-
альной системе отсчета, относительно которой тело покоится.
Определите относительную скорость движения, при которой реля-
тивистское сокращение линейных размеров тела составляет 10%.
¦105 км/с.
С
1.253 J В системе К' покоится стержень (собственная длина /0 = 1,5 м),
~~^^~" ориентированный под углом #' = 30° к оси Ох'. Система К'
движется относительно системы К со скоростью v = 0,6с . Определите в сис-
теме К : 1) длину стержня / ; 2) соответствующий угол # .
Дано
'о
V
1)
2)
= 1,5.
' = 30°
= 0,6с
/ —
¦& —
м
?
?
Решение
К'
у'
о1
1Ох = /0
Iу - hy '
I = -J/O2(cos#'J0 - v2/c2) + /02 (sintf1J ,
l0y
tgd'
Г Ответ Л i> / = 1,28 м; 2) д = 35,8°.
Определите собственную длину стержня, если в лабораторной
системе его скорость v - 0,6с , длина / = 1,5 ми угол между ним
и направлением движения 9 = 30° .
Сотвегп\ /0 = 1,79 м.
Пользуясь преобразованиями Лоренца, выведите релятивистский
закон сложения скоростей, если переход происходит от системы К
к системе К' .
Дано
К-+К'
и'(и)-?
с
Решение
, x~vt
fl^ Д2
4с
и, = —,
dz
M^ = d7'
, 4c'
M* = -d7'
, dy'
Uy dt' '
dx-vdt
dz' = dz.
4c'
d/'
yi - fl2 _ dx-vdt I'd/
dt-vdxjc2 ~ dt-vdxjc2 Vdt
y~ dt' dt-vdx/c2 \-vuJc'
-, 14=-^
1-шх/с2
6X'n Космический корабль удаляется от Земли с относительной скоро-
стью vt = 0,8с , а затем с него стартует ракета (в направлении от
Земли) со скоростью v2 = 0,8с относительно корабля. Определите скорость и
ракеты относительно Земли.
Г
Ответ
и = о,97вс
Ионизированный атом, вылетев из ускорителя со скоростью 0,8с ,
испустил фотон в направлении своего движения. Определите ско-
рость фотона относительно ускорителя.
Дано
и' = 0,8с
Решение
1 + и'vie
0,8с + с
и= — = с.
V = С,
1 +0,8с-с/с2
С Ответ j u = c.
mi, - l1"
1.263 J Две ракеты движутся навстречу друг другу относительно непод-
вижного наблюдателя с одинаковой скоростью, равной 0,5с Оп-
ределите скорость сближения ракет, исходя из закона сложения скоростей
1) в классической механике; 2) в специальной теории относительности.
1)
2)
= v:
"кл
"рел
Дано
> = 0,5с
— ?
7
Ц» =
"рел -
Решение
vx + v2 = 0,5c + 0,5с = с,
V +U, С
1 + у,у2/с2 1 + 0,25 'UL"
ГдтветЛ
= с; 2)Црел=0,8с
кЩ.264) Релятивистская частица движется в системе К со скоростью и
^¦' ' * под углом # к 0СИ х определите соответствующий угол в систе-
ме К' , движущейся со скоростью v относительно системы К в положитель-
ном направлении оси х, если оси х и х' обеих систем совпадают.
Дано
и
.9
v
Решение
К' К
X X
\-vuJc2
l-WMr/cz
= w sin d
' = arctg-
sin ft -Jl - u2/c2
cos^-w/u
Г Ответ J s^
= arctg-
- v/u
Докажите, что интервал между двумя событиями является вели-
чиной инвариантной, т. е. имеет одно и то же значение во всех
инерциальных системах отсчета.
Воспользовавшись тем, что интервал является инвариантной ве-
личиной по отношению к преобразованиям координат, определи-
те расстояние, которое пролетел я-мезон с момента рождения до распада, если
время его жизни в этой системе отсчета At = 4,4 мкс, а собственное время жизни
Д/о = 2,2 мкс.
Дано
/о = о
At = 4,4 мкс = 4,4
А?0 = 2,2 мкс = 2,2-10-* с
/ —?
Решение
sn = ctn-1B = inv ,
с2 At2 = с2 At2-!2,
I = c^JAt2 - At2 .
[Ответ ^ / = i,i4km.
Частица движется со скоростью v ~ 0,8с. Определите отношение
полной энергии релятивистской частицы к ее энергии покоя.
( Ответ Л Е
1,67.
Определите, на сколько процентов полная энергия релятивистс-
кой элементарной частицы, вылетающей из ускорителя со скоро-
стью v = 0,75с, больше ее энергии покоя.
С Ответ J на 51,2%.
Определите скорость движения релятивистской частицы, если ее
полная энергия в два раза больше энергии покоя.
Qpmeem
Определите релятивистский импульс протона, если скорость его
движения v = 0,8с.
COmeemj р = 6,б9 ¦ i о49 н • с.
Определите скорость, при которой релятивистский импульс час-
тицы превышает ее ньютоновский импульс в 3 раза.
(Ответ)
/ v =
—f= 0,943c.
n
Определите зависимость скорости частицы (масса частицы т) от
времени, если движение одномерное, сила постоянна и уравне-
ние движения релятивистское.
m
F =
v{t)
Дано
const
— ?
F
P
Решение
dp
' dt'
= [Fdt = Ft,
dp = Fdt,
mv
P U ..21 Л9
mv
= Ft,
mv =.
m2v2 = F2t2(\ - v2/c2), m2v2 = F2t2 - F2t2v2/c2,
FW/c2 + W2W2 = F2^2 , ^2(f2/2/c2 + m2) = F2t2 ,
Ft Ft/m
2_ f?
U ~ 2.2/2
F2t2/
yj(Ft/mcf+l
С Ответ j
v(t) =
Ft/m
1.2"?3 J Полная энергия релятивистской частицы в 8 раз превышает ее
энергию покоя. Определите скорость этой частицы.
С Ответ j v =
= 298 Мм/с.
Кинетическая энергия частицы оказалась равной ее энергии по-
коя. Определите скорость частицы.
Дано
Ео = тс
v — ?
Решение
тс
Т=Е-Е0, Е =
T=mc2\-TJ—l\,
т г- 2
т, 1 = ?0 = тс
* = 2, 1-и2/с2=-, v2/c2=-,
V/? 4 4
k-v2/c2
v = cJ- = 0,866c.
V 4
Г Ответ
и = 260 Мм/с.
Определите релятивистский импульс р и кинетическую энергию /
ш1шИШВ* протона, движущегося со скоростью v = 0,75с.
Дано
/ир = 1,67-107 кг
у = 0,75с
Р —?
Г —?
Т =
Решение
mpv
mpc2 2
Il-v2/c2 '"^ '
QOmeem
н-с;
"п Дж-
ка Определите кинетическую энергию электрона, если полная энер-
гия движущегося электрона втрое больше его энергии покоя. От-
вет выразите в электрон-вольтах.
Е
Т
Дано
= 9,11-Ю1 кг
Решение
2
Ео = тес ,
С Ответ j
Ео = 2Е0,
Т=2тес2.
Т = 1,02 МэВ.
JL^73/S Определите, какую ускоряющую разность потенциалов должен
i!s - -'- iJ пройти протон, чтобы его скорость составила 90% скорости света.
Дано
= 1,67-107 кг
Кл
v = 0,9с
f/ —?
Решение
T=eU,
С Ответ j
|Wa4 Определите, какую ускоряющую разность потенциалов должен прой-
ти электрон, чтобы его продольные размеры уменьшились в два раза.
Дано
/иг=9,11-101 кг
Кл
= /0/2
Решение
= /0/2,
T=eU,
Т =
ее
С Ответ j u = sn кв.
^'(j Определите работу, которую необходимо совершить, чтобы уве-
личить скорость частицы от 0,5с до 0,7с '
v2
A
Дано
= 0,5c
= 0,7c
__7
A =
Решение
тс2 2
г, тс2 -,
A = mcL
{
Ответ ) А = 0;245тс1.
Выведите в общем виде зависимость между релятивистским им-
пульсом, кинетической энергией релятивистской частицы и ее
массой.
Определите релятивистский импульс электрона, кинетическая
энергия которого Т = 1 ГэВ.
те-
Т =
—
Р -
Дано
= 1,6-109 Кл
1 ГэВ =
ю9
_ ?
1,6 ¦ Ю9
Дж
^(Г + гот^е2)
Р
с
(Ответ j р = 534 ю19 н с.
Докажите, что выражение релятивистского импульса
р =
при v « с переходит в соответствующее вы-
ражение классической механики.
Дано
V «С
p = mv —'
Решение
тс
т
с2\
2тс2
с2
1 me 2 \\ тс 2 1
г-оте^ , +тсг\-
тс
= те.
- отсЧ =
1 ;
-и2А2
mv
«e
=1,
С Ответ j p = nw-
72 _2„
( 1.283 J Докажите, что для релятивистской частицы величина Е - р с
ViTiiii—X является инвариантной, т. е. имеет одно и то же значение во всех
инерциальных системах отсчета
E =
P
E2
Дано
= mc2
me
¦)J\- V /С
mv
^v2/c2
- p2c - inv
Решение
E2 p2c2
( me
J\-v
m2c4 m
~ 1 - v2/c2 1 -
m2cA-m2v2c2
\-v2/c2
2 П
^) I
2^2c2
y2/c2
m2c2(c
(c2-
mv
V1-»2/
2-y2)
^2)/c2
)\.
C2J
m2c4
¦ p2c2 = m2cA - mv ,
Ш
«284 Л Определите энергию, которую необходимо затратить, чтобы раз-
делить ядро дейтрона на протон и нейтрон. Массу ядра дейтрона
принять равной 3,343 • 10 27 кг. Ответ выразите в электрон-вольтах.
Дано
md = 3,343 10~27 кг
mp = 1,672 107 кг
т„ = 1,675 .Ю7 кг
Д? — ?
Решен ие
1 эВ = 1,6- 10 "Дж
QOmeemj д? = 2,25 МэВ.
ei Ц5*85^ Определите энергию связи ядра 'iN. Примите массу ядра азота
равной 2,325 • 10~26 кг. Ответ выразите в электрон-вольтах.
Ответ
J
= юомэв.
Основы молекулярной физики
и термодинамики
2.1. Молекулярно-кинетическая теория
идеальных газов
fe.lt J Начертите графики изотермического, изобарного и изохорного
ШшЛУ процессов в координатах р иУ,риТ,Ти?.
/Т я WJt\ Определите число N атомов в 1 кг водорода и массу одного атома
*¦ в**3- 4* водорода.
т--
М
NA
N
Щ
Дано
= 1 кг
= 2 • 10~ кг/моль
= 6,02-1023 моль1
— ?
, 9
Решение
т
'Na=~~mNa-
т
N '
Г Ответ j N = 3j
01 1026,
3,32 10 27 кг.
Основные физические постоянные
Постоянная Авогадро NA =6,02 1023 моль '
Молярная газовая постоянная R = 8,31 Дж/(К • моль)
Постоянная Больцмана >t = ],38 10~23 Дж/К
В закрытом сосуде вместимостью 20 л находятся водород массой 6 г
и гелий массой 12 г. Определите: 1) давление; 2) молярную массу
газовой смеси в сосуде, если температура смеси Т = 300 К.
V
m
M
= 20 J
= 6 г
г,=2-
m2 = \2
М-, =4-
Т
R
1)
2)
= 300
= 8,31
р
м —
Дано
[1 = 2- 10~2м3
= 6- 10кг
10~3 кг/моль
г= 12 ¦ 103кг
10~3 кг/моль
К
Дж/(К • моль)
?
?
Решение
Р = Р]+Р2
от, ЛГ
Pi =— >
RT(m\ + «2^1
F^M, M2J'
С Ответ ) 1)
2)
от2 ЛГ
/> = 0,75 МПа;
М= 3-1О кг/моль.
Определите плотность смеси газов водорода массой от,= 8 г и
кислорода массой щ = 64 г при температуре Т = 290 К и при
давлении 0,1 МПа. Газы считать идеальными.
Дано
/я,= 8 г = 8- 103кг
М = 2-10 кг/моль
,и2 = 64 г =64- 10~3кг
М2 = 32-10~3 кг/моль
Т = 290 К
р=0,1 МПа= 105Па
/? =8,31 Дж/(К-моль)
Р —?
Решение
m
V'
m-mx-vm2,
(mx mART
[Mx M2) p
(mx+m2)p
Гот, bij) '
\mx + м2 jRT
С Ответ ) D = 0,498 КГ/м3.
В баллоне вместимостью 15л находится азот под давлением 100 кПа
при температуре tx = 27 °С. После того как из баллона выпустили
i
азот массой 14 г, температура газа стала равной t2 = 17 °С. Определите давле-
ние азота, оставшегося в баллоне.
(Ответ
Баллон вместимостью V - 20 л содержит смесь водорода и азота
при температуре 290 К и давлении 1 МПа. Определите массу во-
дорода, если масса смеси равна 150 г.
С Ответ j »,н = 6,3 г.
Азот массой 7 г находится под давлением р - 0,1 МПа и темпера-
туре 7J = 290 К. Вследствие изобарного нагревания азот занял
объем К2 = Ю л. Определите: 1) объем F, газа до расширения; 2) темпера-
туру Т2 газа после расширения; 3) плотность газа до и после расширения
Дано
M=28-10 кг/моль
от=7 г=7- 103кг
^ = 0,1 МПа= 105Па
Tx = 290 К
F, =10 л=102м3
R = 8,31 Дж/(К ¦ моль)
1) F, —?
2) Г, — ?
Р2
-?
Решение
Г Ответ Л i) f, = 6,02-1 о м3;
2) Г2 = 481 К;
3) р, =1,16 кг/м3;
р2 = 0,7 кг/м3.
Г 2.8 i ® сосуде вместимостью 1 л находится кислород массой 1 г. Опре-
^ ¦* делите концентрацию молекул кислорода в сосуде.
Дано
= \ л= 10 Зм
-3
М = 32 10 кг/моль
т = \ г=101кг
Решение
p = nkT,
m
P ~ M
mR
п — -
RT,
кТ '
р _ m R
Т~ MV'
Mkv'
QOmeem
р| В сосуде вместимостью 5 л при нормальных условиях находится
азот. Определите: 1) количество вещества v ; 2) массу азота;
3) концентрацию п его молекул в сосуде.
Г Ответ J 1) г=0,233 моль; 2) ш=6,24 г; 3) п = 2,69-1025 м~3.
&»lv* j Средняя квадратичная скорость некоторого газа при нормальных
условиях равна 480 м/с. Сколько молекул содержит 1 г этого газа?
К
T =
m =
N-
Дано
) = 480 м/с
273 К
1 г=103кг
8,31 Дж/(моль К)
_?
Решение
[3RT
М у м '
mNA
N -,
М
3RT
N - m a\Vki><
3RT
Ответ
ю
22
В сосуде вместимостью V = 0,3 л при температуре Т = 290 К на-
ходится некоторый газ. На сколько понизится давление газа в со-
суде, если из него из-за утечки выйдет N = 1019 молекул?
V
т
N
Д/
= 0,3
= 290
= 10!
7 —1
Дано
л=3 10-" м3
К
Р{1
,
Am
Решение
т,
~ М
/V
2) /гг_
-W2«
AmRT
NRT
NkT
NAV
Г Ответ Л
па.
Определите давление, оказываемое газом на стенки сосуда, если
его плотность равна 0,01 кг/м3, а средняя квадратичная скорость
молекул газа составляет 480 м/с.
p =
p -
Дано
0,01 кг/м3
} = 480 м/с
о
(".
pF
Решение
N |злг
BM м '
А/ М
р = —— = р , = ±-щ
VMM М 3
р =
{Ответ) Р = 768 ш.
Определите наиболее вероятную скорость молекул газа, плотность
которого при давлении 40 кПа составляет 0,35 кг/м3.
Дано
о = 0,35 кг/м3
/? = 40 кПа = 4' 10" Па
9
*
Решение
т
pV = — RT
V И М '
яг
С Ответ Л Ut =
478 м/с.
Определите среднюю кинетическую энергию (е0) поступатель-
ного движения молекул газа, находящегося под давлением 0,1 Па.
Концентрация молекул газа равна 1013 см~3.
Дано
р = 0,1 Па
и = 1013 см-3 = 10" м~3
<*о)-?
Решение
р'п ' ~^*'
2 2 nk 2n'
QOmeem
дж.
Определите: 1) наиболее вероятную vt; 2) среднюю арифмети-
ческую (у); 3) среднюю квадратичную (^в) скорость молекул
азота (N2) при 27 °С.
Ub = 422 м/с; 2) (и) = 476 м/с; 3) (vKB) = 517 м/с.
При какой температуре средняя квадратичная скорость молекул
кислорода больше их наиболее вероятной скорости на 100 м/с.
Дано
{vm)-va = 100 м/с
М = 32 • 10 кг/моль
Г—?
Решение
Исоользуя закон распределения молекул идеального газа по ско-
-^" ростям, найдите формулу наиболее вероятной скорости vt.
Дано
/(и)-4л: —^— и е 2*г
Решение
/(у)-4лг у е -*г .
J \2лкТ)
/(у) = max
du
dv \2якТ)
-"•о"
Av. \2лкТ)
PUT
.2we
2кТ
.U2 =o,
2кТ
С Ответ j _ Уж
V щ
2.18 J Используя закон распределения молек>ч идеального газа по ско-
ростям, найдите закон, выражающий распределение молекул по
относительным скоростям и (и= и/ив).
Дано
V 2пкТ
2A/
и = -
N
y2 -^w
Решение
v.-J-
I2kf
V '"о
i - ! ..и , di» = d_
N
)
—
72 2кТ , ="шг~ \2кТ 4 2 _„,
тщ
?и е
Г Ответ Л
Используя закон распределения молекул идеального газа по скоро-
стям, найдите среднюю арифметическую скорость (у) молекул
Указание: средняя арифметическая скорость определяется по формуле
со
v= \v f(v)dv
С Ответ
V
Используя закон распределения молекул идеального газа по ско-
ростям, найдите среднюю квадратичную скорость (укв) .
Дано
( п, \У>
f( Л Л.тг
Ья^
-fflov2
е 2*?"
Решение
0
3/со 2
я о
x-v
a =
Щ
2kT
4
8 12лШ
u)=
Г Ответ j , v
Используя функцию распределения молекул идеального газа по
энергиям, найдите среднюю кинетическую энергию (е) молекул
Дано
л/я
(е)-?
Решение
Ответ ) {^^l
Используя функцию распределения молекул идеального газа по
энергиям, найдите наиболее вероятное значение энергии ее мо-
лекул.
Дано
2
л/я
Решение
df{e) d f
de ' de'
л/я
^ л
{2? ~~кт)=°'
e> = 2kT-
Используя функцию распределения молекул идеального газа по энер-
гиям, найдите для данной температуры отношение средней кинети-
ческой энергии (е) молекул к их наиболее вероятному значению энергии ев.
Дано
/(?)= 2 (jfc7TV2tV2e-*/CW)
л/я
7' = const
м_,
«в
Решение
00
(е)= Je/(e)de =
0
= -L(jfc7')-V2V2e-'/<tr)de = -*?-.
л/я 0J 2
Используя результат задачи 2.22, находим
•^- = 3.
Г Ответ j
? 2.24 J Закон распределения молекул газа по скоростям в некотором мо-
лекулярном пучке имеет вид f(v) = Av e~m°'' tr*. Определите:
1) наиболее вероятную скорость vB; 2) наиболее вероятное значение энергии
ев молекул в этом пучке.
Дано
1) w.
2) ?в
— ?
Решение
if (у)
dv
= 0
du
Ve 2кТ \=а\ 3v2e 2кт --3- 2v
-me''
...
= 3,
у =
v =
-
3/2 -t
±[™s\=™
2A d( t^
, e e
2А_ ^
ml
кТ
1- — = 0,
кТ
С Ответ
-кТ.
С 2.2§Й1 На какой высоте давление воздуха составляет 60% от давления
V ' VS на уровне моря? Считайте, что температура воздуха везде оди-
накова и равна 10 °С.
Дано
P = 0.6^0
/ = 1O°C
M =29 1O кг/моль
h — ?
Решение
p=poe
RT
Ро
RT
Mgh
1пА
Mg p0
СОтвет j /, = 4,22 км.
Каково давление воздуха в шахте на глубине 1 км, если считать,
что температура по всей высоте постоянная и равна 22 °С, а уско-
рение свободного падения не зависит от высоты? Давление воздуха у поверх-
ности Земли примите равным р0.
h =
t =
M
8 =
Po
Дано
1 км= 1О3 м
22 °C; T = 295 К
= 29 10~ кг/моль
: const
P=l
P l
Решение
-maghli.kT) _ -Mgk/(KT)
Определите отношение давления воздуха на высоте 1 км к давле-
нию на дне скважины глубиной 1 км. Воздух у поверхности Земли
находится при нормальных условиях, и его температура не зависит от высоты
71 ~
A
Дано
-1 км = 103 м
= -1 км = 10 3 м
273 К
-7
Решение
Mghx
jjj-
Z7! e~ «Г ~l «T^J
ft
p2=poe «• ,
ft
На какой высоте плотность воздуха в е раз (е — основание нату-
ральных логарифмов) меньше по сравнению с его плотностью на
уровне моря? Температуру воздуха и ускорение свободного падения считайте
не зависящими от высоты.
С Ответ j h = 7;
7,98 км.
Распределение Больцмана во внешнем потенциальном поле
или
»-П/(*Г)
где и и и0 — концентрация молекул на высоте /г и /г = 0; П = m^gh —
потенциальная энергия молекулы в поле тяготения.
Используя идею установки Перрена для определения постоянной
Авогадро и применив к частицам краски, взвешенным в воде, боль-
цмановское распределение, найдите объем частиц, если при расстоянии между
двумя слоями 80 мкм число взвешенных частиц в одном слое вдвое больше,
чем в другом. Плотность растворенной краски 1700 кг/м3, а температура окру-
жающей среды 300 К.
P =
Pi
*A
V
Дано
= 80 мкм = 8 • 10~5м
:1700 кг/м3
= 1000 кг/м3
:300 К
= 6,02-1023 моль
?
и, .
¦
к =
Решение
-(«-«, )g ДА
.... *г
ЗЛПп —
4лг3(р-р,Ж'
Ж
2 -
(
4 з
3
R1
V vg{p
Ответ
щ =
R
'
«2
— pj)
)
4 з
ДА
11
NAgbKp-p\)
V = 5,22-10! м3.
Определите среднюю длину свободного пробега (/) молекул кисло-
рода, находящегося при температуре 0 °С, если среднее число (г)
столкновений, испытываемых молекулой в 1 с, равно 3,7 ¦ 109.
Дано
¦10 3 кг/моль
Г = 273 К
(z) = 3,7-109c-
Решение
8ЛГ J_
'^гл7' (z)
С Ответ j (/) =
115 им.
При каком давлении средняя длина свободного пробега молекул
водорода равна 2,5 см, если температура газа равна 67 °С? Диа-
нетр молекулы водорода примите равным 0,28 им.
Дано
{/) = 2,5 см = 2,5 • 10"
/ = 67 °С, Т = 340 К
с? = 0,28 нм = 2,8- 10"
Р— ?
Решение
= пкт
/» = •
кТ
\Omeemj р = о,539 па.
Определите среднюю продолжительность (г) свободного пробе-
га молекул водорода при температуре 27 °С и давлении 0,5 кПа.
Диаметр молекулы водорода примите равным 0,28 нм.
Дано
М = 2-Ю кг/моль
Г= 27 °С, Т = 300 К
р = 0,5 кПа = 5- 102Па
rf = 0,28 нм = 2,8-10Ч0м
(г)-?
Решение
<«>=
лМ '
кТ'
к4Ш
Ответ
) (г) = 13,знс.
Средняя длина свободного пробега (/,} молекул водорода при нор-
мальных условиях составляет 0,1 мкм. Определите среднюю дли
ну их свободного пробега при давлении 0,1 мПа, если температура газа остае i -
ся постоянной.
Дано
{/i) = 0,l мкм= 10 7м
р2 =0,1 мПа= 10Па
/? i=l,01 105 Па
Т = const
Решение
(') =
jlnd'n
ft
С Ответ )<
м.
2ЛЛ^Л При температуре 300 К и некотором давлении средняя длина свобо t
ного пробега (/) молекул кислорода равна 0,1 мкм. Чему равно сред-
нее число (z) столкновений, испытываемых молекулами в 1 с, если сосуд откачан,
до 0,1 первоначального давления? Температуру газа считайте постояшюи.
Дано
Т = 300 К
(/) = 0,1 мкм = 10 7 м
Л/= 32-10 кг/моль
А = 0,1/?
Решение
Л
Q
Определите: 1) плотность р воздуха в сосуде; 2) концентрацию и
его молекул; 3) среднюю длину свободного пробега (/) молекул,
ели сосуд откачан до давления 0,13 Па. Диаметр молекул воздуха примите
вным 0,27 нм. Температура воздуха 300 К.
Дано
/7 = 0,13 Па
</ = 0,27 нм = 2,7- 10~10м
Г=300 К
0~3
= 29 10 кг/моль
1)Р—?
3)(/)-?
Решение
т
рМ
'~ RT
кТ
pV = —i
М
, = пкТ.
('К
Ответ j
1) р = 1,51-10"в кг/м3; 2) и = 3,14-1019 м-3; 3)(/) = 0,1
м.
Определите коэффициент теплопроводности Я азота, находяще-
гося в некотором объеме при температуре 280 К. Эффективный
Лиаметр молекул азота примите равным 0,38 нм.
т-
У =
¦Я -
= 28^
280
0,38
- 9
Дано
10" кг/моль
К
нм = 3,8- 10~10м
Решение
m рМ
nV РТ О ~~
М RT
, | г = 5 р=™,
1 ._
г- , р-пкТ,
-J2jid n
Р
я =l { R
~ 32
kT
3 2 М RT 42nd2р\ лМ 2nd2\nM-
pmeem
(г,) = 4,45 10s с1.
QOmeem J я = 8,25 мВт/(м • к).
> Сборник заллч
Кислород находится при нормальных условиях. Определите ко-
эффициент теплопроводности Я кислорода, если эффективный
диаметр его молекул равен 0,36 нм.
Ответ ) я = 8,49 мВт/(м • К).
С»
Пространство между двумя параллельными пластинами площа-
дью 150 см2 каждая, находящимися на расстоянии 5 мм друг от
друга, заполнено кислородом. Одна пластина поддерживается при температу-
ре 17 °С, другая — при температуре 27 °С. Определите количество теплоты,
прошедшее за 5 мин посредством теплопроводности от одной пластины к дру-
гой. Кислород находится при нормальных условиях. Эффективный диаметр
молекул кислорода считать равным 0,36 нм.
Дано
М = 32-10 кг/моль
5 = 150 см2 =15' 10-3м2
Ад: = 5 мм = 5 • 10~эм
/, =17 °С
/2 = 27 °С
t = 5 мин = 300 с
Т = 273 К
d = 0,36 нм = 3,6- 10"'° м
Решение
Ах
i к iRT
ДГ =?,-?.,
i к [RT(t2-h)St
ЪлсР-\лМ Ах
Г Ответ JQ = 76,4 д«.
Зависимость между коэффициентами теплопроводности,
диффузии и внутреннего трения
г] = pD, Xjr]cv = 1.
J 2.39 J Определите коэффициент диффузии D кислорода при нормаль-
ных условиях. Эффективный диаметр молекул кислорода прими-
fre равным 0,36 нм.
Дано
М = 32 10 3 кг/моль
Г = 273 К
р = 1,013-105 Па
d = 0,36 нм = 3,6 • 10"
D —?
Решение
p=nkT,
п =
кТ'
D = -.
8ДГ кТ
3V лМ
Ответ
= 9,i8io м2/с
Определите массу азота, прошедшего вследствие диффузии че-
""^"""" '-^ рез площадку 50 см2 за 20 с, если градиент плотности в направле-
1ии, перпендикулярном площадке, равен 1 кг/м4. Температура азота 290 К, а
федняя длина свободного пробега его молекул равна 1 мкм.
Дано
5 = 50 см2 = 5- 10 м2
М = 28 ¦ 10~3 кг/моль
dp
dx
Т = 290 К
{/) = 1 мкм = 10 м
m — ?
Решение
УП-
W-
|8ЯГ 1 I&RT , xdp
V яМ ' 3 V лМ dx
С Ответ j m = 15,6 мг.
2.41 «¦$) Определите, во сколько раз отличаются коэффициенты динами-
ческой вязкости У] углекислого газа и азота, если оба газа нахо
дятся при одинаковой температуре и одном и том же давлении. Эффективные
диаметры молекул этих газов равны.
Азот находится под давлением 100 кПа при температуре 290 К.
Определите коэффициенты диффузии D и внутреннего трения rj.
ективный диаметр молекул азота принять равным 0,38 нм.
Дано
,V/, =44-10 3 кг/моль
M2 =28-10 кг/моль
P\=Pi
Hi. _?
„ _IpzMi
Решение
(I)-
р = пкТ,
J D-9j4.l0-* M2/c; 77 = 1ДЗ-10~5 кг/(м-с).
Ниже какого давления можно говорить о вакууме между стенка-
ми сосуда Дьюара, если расстояние между стенками сосуда рав-
IIO 8 мм, а температура 17 °С? Эффективный диаметр молекул воздуха при-
нять равным 0,27 нм.
М
m _ pM
T~~RT'
Дано
г, J-
1 3
8 мм = 8- 10~3м
17 °С, Г=290 К
= 0,27 нм = 2,7- 10
г-• rOmeemj ^ = i25.
Решение
Рвак
Определите коэффициент теплопроводности Я азота, если коэф-
фициент динамической вязкости t] для него при тех же условиях
равен 10 мкПа • с.
Давление разреженного газа в рентгеновской трубке при температуре
17 °С равно 130 мкПа. Можно ли вести разговор о высоком вакууме,
если характерный размер 10 (расстояние между катодом и анодом трубки) составля-
нет 50 мм? Эффекшвный диаметр молекул воздуха примите равным 0,27 нм.
Дано
?; = 10мкПа-с=10-5Па-с
M = 28 ¦ 10" кг/моль
X —?
Решение
Я = — cFp(y){/), r/ = —p(v){l)? X = cvt],
j 3
' Л , ' Л
2 М 2Mf
Р-
О
Дано
13ОмкПа=13-
50 мм = 5- 10
0,27 нм = 2,7
7 °С, Г - 290
10-5Па
-2м
10-'° м
К
@
(
Решение
-~г=—j~» p-nkl , V/
Ответ J (/) = 95,1 м, </) »
Вакуум высокий.
кТ
¦find2p '
'к-
2.2. Основы термодинамики
В закрытом сосуде находится смесь азота массой тх - 56 г и кис-
лорода массой тг = 64 г. Определите изменение внутренней энер-
Азот массой т = 10 г находится при температуре Т = 290 К. Оп- г,ии этой смеси, если ее охладили на 20 °С.
ределите: 1) среднюю кинетическую энергию одной молекулы
азота; 2) среднюю кинетическую энергию вращательного движения всех моле- ^ Ответ
кул азота. Газ считайте идеальным.
' = pL + J^L .-ЯД7- = 1,66кДж.
\МХ М2) 2
Дано
ю = 10 г=10-2кг
Т = 290 К
М = 28 ¦ 10 кг/моль
2)(Е )-•>
Решение
(е) = -кТ, 1 = 5,
/е*\_/о\дГ / \ " т ^
\ 'вр/ \ вр/ ) \^вр/~ 'вр * ВР *" *
1 / ' \ "'"'Вр / *Вр — 1/ •
Я Считая азот идеальным газом, определите его удельную теплоем-
кость: 1) для изохорного процесса; 2) для изобарного процесса
С Ответ J
1)су= 742 Дж/(кг • К); 2) ср = 1,04 кДж/(кг • К).
( Ответ )
{е) = l0
-»
2)
= 860
Определите удельные теплоемкости су и ср, если известно, что
некоторый газ при нормальных условиях имеет удельный объем
, v = 0,7 м3/кг. Что это за газ?
Кислород массой т = \ кг находится при температуре Т = 320 К
Определите: 1) внутреннюю энергию молекул кислорода; 2) сред-
нюю кинетическую энергию вращательного движения молекул кислорода. Газ
считайте идеальным.
Дано
Дано
tfl = l КГ
Т = 320 К
М = 32 10~3 кг/моль
Решение
-"вр) 'вр _ ' ,, >
' 2 Л/
S i ? \ ~ /с \. ^^
\ вр / \ вр / '
'.р=2-
^ = 0,7 М3/кг
* = 273 К
? = 1,013 '105 Па
Решение
м =
у_
m
RT
pv '
i-JL
2 M
¦ =—лг,
м
R
2 М
Ответ J 1} v = 208 кДж; 2) (?Bp> = 83,1 кдж.
С Ответ Л кислород; cv = 649 Дж/(кг • К); ср = 909 Дж/(кг • К).
Связь между молярной Ст и удельной с теплоемкостями газа
Ст=сМ,
где М — молярная масса газа.
Определите удельные теплоемкости cv и ср смеси углекислого
газа массой т{ = 3 г и азота массой щ = 4 г.
Дано
/и,= 3 г = 3 ¦ 10~3кг
Л/, =44-10^3 кг/моль
от, =4 г = 4 • 10~3кг
Л/, = 28-10 кг/моль
су-!
ср -?
Решение
т- ml+m2,
Щ ~ Cv\m\ AT ,
AQ2 = cV2m2 AT ,
с^от AT = с,/,»», AT+cV2m2 AT ,
_
cv -
щ + т2
/, = 5
Cv = —
2 ^ М, М2 j mx+m2
_г,+ 2
2 Л/, '
l; + 2 jj
2 М2 '
с„ = —
2 М,
М2 J
Г Ответ
Cj- = 667 Дж/(кг -К); ср = 917 Дж/(кг • К).
Молярная теплоемкость
при постоянном объеме и постоянном давлении
Cn='-^-R. C. = C,, + R.
Определите показатель адиабаты у для смеси газов, содержащей
гелий массой т{ = 8 г и водород массой ш2 = 2 г.
¦к,= 8 г = 8 - 10-3кг
д/, =4-10~3 кг/моль
«2 = 2 г = 2- 10-3кг
-10~3 кг/моль
Г
у-?
Решение
ср -
(см. задачу 2.51)
'I'l -
2 M,
2 М2
'1=3
'2=5
2 М2
2 М,
!+2 R
2 М,'"'" 2 M2'"^J/ 1^2 Л/,' 2 М:
?2+2 R
My
, 7
'г— +h
1М, М2
Г Ответ
= i,55.
Применяя первое начало термодинамики и уравнение состояния
идеального газа, покажите, что разность удельных теплоемкостеи
( 2.54 J Кислород массой 32 г находится в закрытом сосуде под давлени-
^ ^ ем 0,1 МПа при температуре 290 К. После нагревания давление в
сосуде повысилось в 4 раза. Определите: 1) объем сосуда; 2) температуру, до
которой газ нагрели; 3) количество теплоты, сообщенное газом.
С
Ответ
1) F = 2,4110 м3; 2)Г = 1,16кК; 3) Q = 18,1 кДж. %
' * jJS^I Определите количество теплоты, сообщенное газу, если в процес-
се изохорного нагревания кислорода объемом V = 20 л его давле-
ние изменилось на Ар = 100 кПа.
Ар =
Q-
Дано
!0л = 2- 10
100 кПа=10
?
м3
5 Па
Решение
Q=AU+A,
А
А
U-—-RAT
Ml
= 0,
m
м
= — RAT,
M
—
м
= —-RAT = -VAp-
Ml 2
С Ответ j
> = 5 кДж.
Двухатомный идеальный газ ( v = 2 моль) нагревают при постоян-
ном объеме до температуры 289 К. Определите количество теплоты,
которое необходимо сообщить газу, чтобы увеличить его давление в п - 3 раза.
С Ответ j
кДж.
При изобарном нагревании некоторого идеального газа (v = 2 моль)
на Д7" = 90 К ему было сообщено количество теплоты 5,25 кДж.
Определите: 1) работу, совершаемую газом; 2) изменение внутренней энергии
газа; 3) величину у = cpjcv .
С Ответ J l) A = 1,5 кДж; 1) AU = 0,6 кДж; 3) у = 1,4 .
Азот массой т = 280 г расширяется в результате изобарного про-
цесса при давлении р = 1 МПа. Определите: 1) работу расшире-
ния; 2) конечный объем газа, если на расширение затрачена теплота Q = 5 кДж,
к начальная температура азота 7J = 290 К.
Дано
т = 280 г = 0,28 кг
М = 28-10 кг/моль
р = const
р = \ МПа=106Па
Q = 5 кДж=5- 103Дж
Г, = 290 К
1) А —?
Решение
М
т
QR-2 = 1Q
i+l'
м
т
~~м'
С Ответ j i) л = 1,43 кДж; i) v2 = 0,026 м3.
Кислород объемом 1 л находится под давлением 1 МПа. Опреде-
лите, какое количество теплоты необходимо сообщить газу, что-
бы: 1) увеличить его объем вдвое в результате изобарного процесса; 2) увели-
чить его давление вдвое в результате изохорного процесса.
1
i'Vj
P\
1)
2)
D
2)
-1
Pi
V\
Pi
p.
ft
Дано
л= 10M3
32-10 кг/моль
МПа= 106Па
= const
= 2^
= const
-2р,
9
— ?
/Л'
Pi
1
1 ; =
Решение
= const
/ _m RT
1 M ''
M
_ Pi &V p.
—
ill
= const
R
A 2 mj
AF = F2-f
(г + 2)Л (г
2
- м '
ДГ,
+ 2) ,
2 Pl
AT,
I, Ap = — RAT
1 M
> = Pl~ P\
ГдтветЛX
Ql = 3,5 кдж; 2) g2 = 2,5 кДж.
Некоторый газ массой т = 5 г расширяется изотермически от
объема Fj до объема V2 = 2VX. Работа расширения А = 1 кДж
Определите среднюю квадратичную скорость молекул газа.
(Ответ Л (икв) = 9зо м/с.
Азот массой m = 14 r сжимают изотермически при температуре
Г = 300 К от давления рх = 100 кПа до давления р2 = 500 кПа.
Определите: 1) изменение внутренней энергии газа; 2) работу сжатия; 3) коли-
чество выделившейся теплоты.
Ответ j
1) AU = 0; 2) ,4 = -2,01 кДж; 3) 6 = 2,01 кДж.
^^Жа Некоторый газ массой 1 кг находится при температуре Г = 300 К и
под давлением рх - 0,5 МПа В результате изотермического сжатия дав-
юние газа увеличилось в два раза Работа, затраченная на сжатие, А = -432 кДж.
Определите: 1) какой это газ; 2) первоначальный удельный объем газа.
Дано
т = 1 кг
Т = 300 К
р, = 0,5 МПа = 5 ¦ 105 Па
Pi - 2Pi
Л = -432 кДж =
= -4,32- 105Дж
1)газ —?
2) и, -?
Решение
dA = pdV, p\
М-тШ dV A
м~ mv ' А
P\V\ — р^У2 > А
mRT P|
Jvl — 1П , U|
м
hfmRT
1 м
M
г
dV
V
Pi
mRT ,
_
M
V\'
p2
m
Mpx
. С Ответ j
1) гелий; 2) и, = 1,25 м3/кг.
Азот массой т = 50 г находится при температуре 7j = 280 К.
В результате изохорного охлаждения его давление уменьшилось
в п = 2 раза, а затем в результате изобарного расширения температура газа
в конечном состоянии стала равной первоначальной. Определите: 1) работу,
совершенную газом; 2) изменение внутренней энергии газа.
1) а = 2,08 кДж; 2) AU = 0.
Работа расширения некоторого двухатомного идеального газа со-
ставляет А - 2 кДж. Определите количество подведенной к
теплоты, если процесс протекал: 1) изотермически; 2) изобарно.
Дано
А = 2 кДж = 2' 103Дж
1O" = const
2) р - const
па—?
' М
Q2=AU + A = -
Решение р
АТ =
Т = const,
дс/=о,
р = const, A = pAV,
pAV=—RAT
М
MA
mR
+Л _ Г Ответ
2 J'4"
При адиабатном расширении кислорода ( v = 2 моль), находящегося
при нормальных условиях, его объем увеличился в л = 3 раза.Опре-
делите: 1) изменение внутренней энергии газа; 2) работу расширения газа.
Азот массой m = 1 кг занимает при температуре 7J = 300 К объем
Vx - 0,5 м3. В результате адиабатного сжатия давление газаувели-
ось в 3 раза. Определите: 1) конечный объем газа; 2) его конечную темпера-
jj'py; 3) изменение внутренней энергии газа.
hi
1) y2 =| —Г =0,228 m3; 2)Г2=|^-Г =411 К;
Pi'
3) AU = ~^-R{T2-T{)=nA кДж.
M 2
Азот, находившийся при температуре 400 К, подвергли адиабатно-
му расширению, в результате которого его объем увеличился в п = 5
аз, а внутренняя энергия уменьшилась на 4 кДж. Определите массу азота.
Дано
ч-З
= 28 10 J кг/моль
Й=5
Дано
v = 2 моль
Г, = 273 К
1) AU — ?
2) Л —7
Решение
= AU+A
0=0,
/?,
НИН
Решение
A = -AU.
Y-l~
*-
Y-\
f1-
Q Ответ J
l) дс/ = -4,03 кДж;
= 4,03кДж.
ГОтвет j
ДвУхатомный идеальный газ занимает объем V\ = 1 л и находится п0
давлением />, = 0,1 МПа. После адиабатного сжатия газ характерна
Кислород, занимающий при давлении р{ = 1 МПа объем Vx = 5 л,
расширяется в п = 3 раза. Определите конечное давление и рабо-
ется объемом V2 и давлением р2. В результате последующего изохорного процесс (^совершенную газом. Рассмотрите следующие процессы: 1) изобарный;
газ охлаждается до первоначальной температуры, а его давление р3 = 0,2 МПа.О,,
ределите: 1) объем У2; 2) давление р2. Начертите график этих процессов.
Дано
V\=\ л=10-3м3
/=5
р, =0,1 МПа= 105Па
/?з = 0,2 МПа=2- 105Па
1) V2— ?
2) р2 - ?
Решение
F, =
Р\Ух
Ръ
V2 = 0,5 л; 2) р2 = 264 кПа.
т
i
М
или
у-1 М
у-1
у-\
у-1
изотермический; 3) адиабатный.
Дано
Работа в случае адиабатного процесса
где 7j, Т2 и Vx, V2 — соответственно начальные и конечные температура и
объем газа.
= 32-10 3 кг/моль
= 5
>,=1 МПа=106Па
Г, = 5 л -5- 10-3м3
= «К,
= 3
) р = const
) Т- const
и
м
Ответ
Решение
Q=AU+A,
= pAV,
p = const
P\
T = const
P-
V '
V
A = -AU,
i + 2
pVY = const,
M 2
P=
\) р = \ мпа, ^ =
2) p= 0,33 МПа, ^ = 5,5 кДж;
3) /7=0,21 МПа, /1 = 4,63 кДж.
f 2.70 ) Кислород массой 10 г, находящийся при температуре 370 К, прд*.
———- вергли адиабатному расширению, в результате которого его дав-
ление уменьшилось в п = 4 раза. В результате последующего изотермического
процесса газ сжимается до первоначального давления. Определите' 1) темпе-
ратуру газа в конце процесса; 2) количество теплоты, отданное газом; 3) прира-
щение внутренней энергии газа; 4) работу, совершенную газом.
Дано
т = \0 г= 10кг
М = 32 10~3 кг/моль
=370 К
Pi
= п
i) т2 — ? 2) e—'
3) ДС/ — ? 4) Л -?
Решение Уп з i
02=0
М
п
Ml
Q='Qn 03 = 02 + 023,
М
^-Ап+А2Ъ, А]2--1
К; 2) 0 = 896 Дж;
3) Д?/ = -786 Дж; 4) А = -\ 10 Дж.
?*) Идеальный двухатомный газ, занимающий объем Vx = 2 л, под-
вергли адиабатному расширению. При этом его объем возрос в 5
раз. Затем газ подвергли изобарному сжатию до начального объема В резуль^
тате изохорного нагревания он бьш возвращен в первоначальное состояние
Постройте график цикла и определите термический КПД цикла.
Г Ответ J v
= 34,1%.
Идеальный двухатомный газ (v = 3 моль), занимающий объем
V{ = 5 ли находящийся под давлением р\ = 1 МПа, подвергли
изохорному нагреванию до Т2 = 500 К. После этого газ подвергли изотерми-
ческому расширению до начального давления, а затем он в результате изобар-
ного сжатия возвращен в первоначальное состояние. Постройте график цикла
и определите термический КПД цикла.
Дано
v = 3 моль
/ = 5
F, =5 л = 5- 10мэ
р] =1 МПа=106Па
Т2 = 500 К
П—1
2~>3
Т2 = const
3-»l
Рх = const
С Ответ j n =
Решение
Vx = const
Л12=0
AU23 = 0
A Pi
a,=
13,3%.
Рг
On = ^23
<179>
Му Рабочее тело — идеальный газ — теплового двигателя совершает
&#J г
цикл, состоящий из последовательных процессов изобарного
адиабатного и изотермического. В результате изобарного процесса газ нагре-
вается от Тх - 300 К до Т2 = 600 К. Определите термический КПД теплового
двигателя
Дано
7] = 300 К
Т-> = 600 К
Решение
ч -
а
Qn '
р - const
Vx Tx>
V, V2 к
Qn = vCpR(T2 -Tx)=
a, = v«7; in-i = vrt,
31 ' p: '
in
Г, r-i Г,
2 T,
7? = -
Ответ j 77 = зо,
= 30,7%.
Азот массой 500 г, находящийся под давлением д = 1 МПа при
температуре f, = 127 °С, подвергли изотермическому расширению,
в результате которого давление газа уменьшилось в п = 3 раза. После этого газ
подвергли адиабатному сжатию до начального давления, а затем он был изо-
барно сжат до начального объема. Постройте график цикла и определите рабо-
ту, совершенную газом за цикл.
С Ответ J а = -\\,5 кДж.
Идеальный газ, совершающий цикл Карно, 70% количества теп-
лоты, полученного от нагревателя, отдает холодильнику. Количе-
ство теплоты, получаемое от нагревателя, равно 5 кДж. Определите: 1) терми-
ческий КПД цикла; 2) работу, совершенную при полном цикле.
Дано
0, =5 кДж = 5 • 103 Дж
2) A —1
Решение
С Ответ J i > ?? = зо%; 2) л = i,5
Идеальный газ совершает цикл Карно. Газ получил от нагревате-
ля количество теплоты 5,5 кДж и совершил работу 1,1 кДж. Опре-
делите: 1) термический КПД цикла; 2) отношение температур нагревателя и
холодильника.
(Ответ }
т,
\\ п = 20%: 2) -L = 1,25.
т
Идеальный газ совершает цикл Карно, термический КПД которо-
го равен 0,4. Определите работу изотермического сжатия газа, если
работа изотермического расширения составляет 400 Дж.
Дано
Л,2 = 400 Дж
Решение
»? = 7Г =
а а
Л =
Ап
Q Ответ j а34 = -240 дж.
Идеальный газ совершает цикл Карно. Температура нагревателя
Jj = 500 К, холодильника Г2 = 300 К. Работа изотермического
расширения газа составляет 2 кДж. Определите: 1) термический КПД цикла;
2) количество теплоты, отданное газом при изотермическом сжатии холодильнику.
Дано
7] =500 К
Т2 = 300 К
А12 -2 кДж = 2- 103 Дж
2) ft-?
Решетше
fl-ft г,-:
'"""а"-"
а
Многоатомный идеальный газ совершает цикл Карно, при этом в
процессе адиабатного расширения объем газа увеличивается в
; 4 раза. Определите термический КПД цикла.
Дано
Решение
y-l
у zz
i = 6
Y =
y-l
= 1-1^-1 =1-1-
y-1
Omeetnj n = 3i%.
Во сколько раз необходимо увеличить объем (у = 5 моль) идеаль-
ного газа при изотермическом расширении, если его энтропия
увеличилась на AS = 57,6 Дж/К?
[
Ответ
1O = 40%; 2) ft = 1.2
При нагревании двухатомного идеального газа (v = 2 моль) его
термодинамическая температура увеличилась в и = 2 раза. Опре-
делите изменение энтропии, если нагревание происходит: 1) изохорно; 2) нзо-
барно.
Дано
/ = 5
v = 2 моль
1) V = const
2) ?> = const
AS, — ?
Решение
V - const
dg = vQ d7",
2 h
1 Г,
г Г, i
AS, -v-йш-- r—/?lnn ,
1 2 7] 2
V 2 '
AS,
= const
Ответ J l) AS, = 28,8 Дж/К; 2) AS2 = 40,3 Дж/К.
Азот массой 28 г адиабатно расширили в п = 2 раза, а затем нзо-
барно сжали до начального объема. Определите изменение энт-
>пни газа в ходе указанных процессов.
Дано
= 28 10 3 кг/моль
i = 28 r=28- 10~экг
= 5
—?
Решение
-S = AS,2 + AS23,
AS12 = 0,
m^pai _m tdT _ m h
м г м р* т м p т2
'2
p - const
t, v, v,
M 2
i
Идеальный газ (v - 2 моль) сначала изобарно нагрели, так что
объем газа увеличился в И] = 2 раза, а затем изохорно охладили,
так что давление его уменьшилось в п - 2 раза. Определите приращение энт-
ропии в ходе указанных процессов.
ijDmeem ^ as = -20,2
Изменение энтропии при равновесном переходе
из состояния 1 в состояние 2
Г Ответ j as = 11,5 Дж/к.
2.3. Реальные газы, жидкости
и твердые тела
Г 2*84 Л Кислород (г = 10 моль) находится в сосуде объемом V-S л. Оп-
ределите: 1) внутреннее давление газа; 2) собственный объем мо-
лекул. Поправки а и Ь принять равными соответственно 0,136 Н • м4/моль2'И
3,17- 10-5м3/моль.
Углекислый газ массой 2,2 кг находится при температуре 290 К в
сосуде вместимостью 30 л. Определите давление газа, если: 1) газ
[реальный; 2) газ идеальный. Поправки а и Ъ примите равными соответственно
>,361 Н ¦ м"/моль2 и 4,28 • 10~3 м3/моль.
Ответ J I) Pl = 3,32 МПа; 2) р2 = 4,02 МПа.
Дано
v = \Q моль
V = 5 л = 5- 10м3
а = 0,136 Н- м"/моль2
Ь = 3,17-10 м3/моль
\) р' — ?
Решение
4
Плотность азота р -140 кг/мэ, его давление /7 = 10 МПа. Определи-
те температуру газа, если: 1) газ реальный; 2) газ идеальный. Поправ-
ки а и Ъ примите равными соответственно 0,135 Н • м"/моль2 и 3,86 ¦ 10~5 м3/моль.
QОтвет j l)T{ = 2бо К; 2) т2 = 241 к.
2) V — ?
J 1) р' = 544 кПа; 2) V = 79,3 см3.
Анализируя уравнение состояния реальных газов, определите ве-
личины поправок а и Ъ для азота. Критические давление и темпе-
ратура азота соответственно равны 3,39 МПа и 126 К.
Углекислый газ массой 6,6 кг при давлении 0,1 МПа занимает объем
3,75 м3. Определите температуру газа, если: 1) газ реальный; 2) газ
идеальный. Поправки аиЬ примите равными соответственно 0,361 Н • м4/моль*
и 4,28- 10-5м7моль.
Дано
М = 44-10 кг/моль
т = 6,6 кг
/7 = 0,1 МПа=105Па
F = 3,75 м3
а = 0,361 Н-м4/моль2
Ь= 4,28-10 м3/моль
От; —?
Т —
1\
т
Решение
М{р' mV2J
mi?
MpV
mR
RTU
rv-^b)
\ M )
m
nK- m RT
у м 2'
fc
; Дано
*7-K=126 К
}.pK = 3,39 МПа =
= 3,39- 106Па
a —?
b —?
Решение
[P+V^){V-vb) = vRT,
pV3-(vRT + pvb)V2 + v2aV- угаЪ = 0,
Vx,V2,Vt, — корни уравнения.
p = Pk,t = tk,v]=v2 = v3 = vk
P«(V-VKf^0,
= о,
3 - (vRTK + pKvb)V2 +v2aV- v^ab = 0, 3pKVK = vRTK + pKvb,
3vbf = v2a , a = 27pKb2
3pK ¦ 3vb = vRTK + pKvb,
> = vRTK, b = -
21R2T2
2) Т2 - ?
; = 302 K; 2) T2 = 301 K,
j
a = 0,136 н• м4/моль2; ь = з,8б¦ iо м3/моль.
Кислород массой 100 г расширяется от объема 5 л до объема 10 л.
Определите работу межмолекулярных сил притяжения при этом
расширении Поправку а примите равной 0,136 Н • м"/моль2.
м
т
v2
а
А
Дано
' = 32 10~3 кг/моль
= 100 г =0,1 кг
= 5 л = 5- 10м3
= 10 л = 10~2m3
= 0,136 Н-м4/моль2
о
Решение
(/" V2 Jvv J ' М' V2
V\m2 dV m2 ( 1 \Л
Л~ ^M2°v2 ~ M2a{v,~vJ'
ГЪтвет J л = 133 Дж.
Некоторый газ (v = 0,25 кмоль) занимает объем Vx = 1 м3. При
расширении газа до объема V2 = 1»2 м3 была совершена работа
против сил межмолекулярного притяжения, равная 1,42 кДж. Определите по-
правку а, входящую в уравнение Ван-дер-Ваальса.
ГОтвегп\ а = o,i 36 н
м4/моль2.
Азот (v = 3 моль) расширяется в вакуум, в результате чего объем
газа увеличивается от Fj = 1 л до V2 - 5 л. Какое количество теп-
лоты Q необходимо сообщить газу, чтобы его температура осталась неизмен-
ной? Поправку а примите равной 0,135 Н • м4/моль2.
Дано
V - 3 МОЛЬ
К,-1л-10м3
V2=5 л = 5- 103м3
о = 0,135 Н'М4/моль2
Q 7
Решение
2
dQ = dU + dA, dU = 0 dA = p'dV = ^-dV ,
V\v2a 2 ( 1 1 1
Q= \-^-dV = v2a\ — ¦
lv2 щ v2)
С Ответ Л q=972 д«.
Углекислый газ массой 88 г занимает при температуре 290 К объем
1000 см3. Определите внутреннюю энергию газа, если: 1) газ иде-
альный; 2) газ реальный. Поправку а примите равной 0,361 Н м4/моль2.
Дано
т = 88 г=88- 10~3 кг
М-44 10~3 кг/моль
Г=290 К
F = 1000 см3= 103м3
а = 0,361 Н-м4/моль2
/ = 6
1) С/, — ?
2) U2 - ?
Решение
т
1~ м v '
и =ЛЦс т —I,
м{ v vm)'
u2-Ut m2a
M V
(Omeemj
=14j5
2) щ = 13 кДж_
Кислород (v = 2 моль) занимает объем Vx -1 л. Определите изме-
нение температуры кислорода, если он адиабатно расширяется в
вакуум до объема V2 -10 л. Поправку а примите равной 0,136 Н • м"/моль2.
Дано
v = 2 моль
'^ =1 л=103м3
К2=10 л=10-2м3
a = 0,136 Н • м4/моль2
r2-2;-¦
Решение
, 0 = 0, Л = 0 AU = U2-Ul =
СуТ,- — =<
уТ,
;~1, ^2=v|cKr2-^i
:-2i=-
2m/fj 1_
)
r2-7; =-11,8 к.
Азот ( v = 2 моль) адиабатно расширяется в вакуум. Температура
газа при этом уменьшается на 1 К. Определите работу, совершае-
мую газом против межмолекулярных сил притяжения.
Дано
v = 2 моль
i = 5
ДГ=-1 К
Решение
Л = 0
с/,=
2
Ответ Л
'
4=83,1 Дж.
Кислород (v = 1 моль) (реальный газ), занимавший при 7] = 400 К
объем Vx - 1 л, расширяется изотермически до V2 = 2Fj. Опреде-
лите: 1) работу при расширении; 2) изменение внутренней энергии газа. Поправ-
ки а и Ь примите равными соответственно 0,136 Н • м4/моль2 и 3,17 • 10~5 мэ/моль.
Дано
г = 1 моль
Г = 400 К = const
К,=1 л=10-'м5
V2 = 2К,
д = 0,136 Нм"/моль2
fe = 3,17 10 м'/моль
1) А —?
Решение
\Р+ V2JV vb)-vRl
Vl v
г
С/
vRT
P~ V-vb
?Viv2-yJ'
v2a
V1'
1.
2) AU —1
Г Ответ Л 1) ^ = 2,29 кДж; 2) AC/ = 68 кДж.
L
Покажите, что эффект Джоуля — Томсона будет всегда отрица-
тельным, если дросселируется газ, для которого силами притяже-
ния молекул можно пренебречь.
-=
д = 0
G-2-7;
Дано
)>0 —?
Решение
Ux + PxVx =U2 + PlV2,
\U{ = vCvTx -
av
U¦ =vCyT2-
U,=vCvTx,
U2 = vCvT2,
px Vx=vRTx+pxvb, p2V2 =vRT2+p2vb,
vRTx + pxvb = vCvT2 + vRT2 + p2vb,
TX(CV + R) + Plvb=vT2(CV2 + R) + p2vb,
P\ » Pi
(T2-T])>0.
Ответ \ (Г2 - 7] )>0, эффект Джоуля — Томсона отрицательный.
Покажите, что эффект Джоуля — Томсона будет всегда положи-
тельным, если дросселируется газ, для которого можно пренеб-
речь собственным объемом молекул.
[Ответ)
Т2-Тх=-
<--
<0 (V2»VX).
При определении силы поверхностного натяжения капельным
методом число капель глицерина, вытекающего из капилляра, со-
ставляет п = 50. Общая масса глицерина т = 1 г, а диаметр шейки капли в мо-
мент отрыва d = 1 мм. Определите поверхностное натяжение о глицерина
Дано
и = 50
т = \ г=10~3кг
d = 1 мм = 10 м
о —?
Решение
F т ,
а = -Т> F = -g, l = nd,
1 п
rmd f Ответ j 0 = 62,5 мн/м.
Определите радиус Л капли спирта, вытекающей из узкой вертикаль-
ной трубки радиусом г = 1 мм. Считайте, что в момент отрыва капля
сферическая. Поверхностное натяжение спирта о = 22 мН/м, а его плотность
р = 0,8 г/см3.
Ответ j R = 1,61 мм.
Считая процесс образования мыльного пузыря изотермическим,
определите работу А , которую надо совершить, чтобы увеличить
его размер с dx = 6 мм до d2 = 60 мм. Поверхностное натяжение мыльного
раствора примите равным 40 мН/м.
Дано
Т = const
с?, = 6 мм = 6 • 10 м
t/2 = 60мм = 6 ¦ 10~2м
сг = 40 мН/м = 4-10Н/м
Решение
Д?
АЕ = А,
5, = nd\ ,
' = 2S2 - 25,
7" = const
о = const. A = o ¦
С Ответ j a = %96 мкДж.
Две капли воды радиусом г = 1 мм каждая слились в одну боль-
шую каплю. Считая процесс изотермическим, определите умень-
©ние поверхностной энергии при этом слиянии, если поверхностное натяже-
ие воды о = 73 мН/м.
Дано
= 1 мм = 10~3м
7 = 73 мН/м =
Г =73-103Н/м
Г = const
Решение
\Т = const 1 о = const,
5,=4яг2, ?i=:
' = 25, - S =
R=42-r, S
•г2 = 4яг2B-^4),
Ответ J д? = з78 нДж.
Давление воздуха внутри мыльного пузыря на Ар = 200 Па боль-
ше атмосферного. Определите диаметр d пузыря. Поверхност-
ное натяжение мыльного раствора о = 40 мН/м.
^ —
Дано
200 Па
?
ю-2
Н/м
Решение
2а %а
Ар- ~"Т'
~Ар'
f Ответ J d = 1,
6 мм.
7 Сборищ- задач
Воздушный пузырек диаметром d = 0,02 мм находится на глуби-
не h = 25 см под поверхностью воды. Определите давление воз-
духа в этом пузырьке. Атмосферное давление примите нормальным. Поверх-
ностное натяжение воды о = 73 мН/м, а ее плотность р = 1 г/см3.
Дано
d = 0,02 мм = 2- 10'5м
h = 25 см = 0,25 м
А,=1,01105 Па
о = 73 мН/м =
= 73- 10~3Н/м
р = 1 г/см3= 103кг/м3
/>—?
р
(
Решение
2а 4а
г d
= ро + pgh н
Ответ
V? > А = pg^.
4сг
d
) ^118 «Па.
Ртуть массой 3 г помещена между двумя параллельными стеклян-
ными пластинками. Определите силу, которую необходимо прило-
жить, чтобы расплющить каплю до толщины d = 0,1 мм. Ртуть стекло не смачи-
вает. Плотность ртути р = 13,6 г/см3, а ее поверхностное натяжение а - 0,5 Н/м.
COmeemj f = 2,2
Вертикальный стеклянный капилляр погружен в воду. Определи-
те радиус кривизны мениска, если высота столба воды в трубке
h = 20 мм. Плотность воды р = 1 г/см3, поверхностное натяжение о = 12 мН/м.
Дано
h=20 мм = 2- 10-2м
р = 1 г/см3=103кг/м3
о = 13 мН/м =
= 73- 10'3 Н/м
Решение
г» _.
2g
pgh
Г Ответ ) r=
744 мкм.
Капилляр, внутренний радиус которого 0,5 мм, опущен в жидкость.
Определите массу жидкости, поднявшейся в капилляре, если ее
¦оверхностное натяжение равно
] Дано
i=0,5 мм = 5 • \0г*м
п —?
т =
Ответ ) 10- 1П-5
? =
60 мН/м.
Решение
F, P=mg,
ol, I = 2лг,
2ягсг
g
кг.
В стеклянном капилляре диаметром d -100 мкм вода поднима-
ется на высоту h = 30 см. Определите поверхностное натяжение о
оды, если ее плотность р = 1 г/см3.
Дано
= 100 мкм=
= 30 см = 0,3 м
р = 1 г/см3= 103кг/м3
о —?
Решение
2G COS ^
о =
pgrh
о =
pghd
Поверхностное натяжение
a = F/l или o = AE/AS,
где F — сила поверхностного натяжения, действующая на контур /, ограничи-
вающий поверхность жидкости; Д? — поверхностная энергия, связанная с
площадью AS поверхности пленки.
Широкое колено U-образного манометра имеет диаметр dx-2 мм,
узкое — d2 = 1 мм. Определите разность Ah уровней ртути в обо-
их коленах, если поверхностное натяжение ртути а = 0,5 Н/м, плотность рту! и
р = 13,6 г/см3, а краевой угол 9 - 138°.
Дано
rf, =2 мм = 2- 10*3м
d2 =1 мм = 10 3 м
сг = 0,5 Н/м
р = 13,6 г/см3 =
= 13,6- 103кг/м3
5 = 138°
А/7 — ?
Решение
2ст cos 5
А|= ,
Р8П
2ст cos 5
k2~ PS4 '
dx d2
AA = |A2|-|A,|,
4G COS 5
pg
JJ
= 5>6 MM.
Изобразите элементарную ячейку ионной кубической объемноцен-
трнрованной решетки хлористого цезия (CsCl) и определите соот-
ветствующее этой решетке координационное число.
( ОшвеШ j Координационное число равно 8.
Изобразите элементарную ячейку ионной кубической решетки
поваренной соли (NaCl) и определите соответствующее этой ре-
шетке координационное число.
( Ответ j Координационное число равно 6.
Определите наименьшее расстояние между центрами ионов на-
трия и хлора в кристаллах NaCl (две одинаковые гранецентриро-
ванные кубические решетки, вложенные одна в другую). Плотность поварен-
ной соли р = 2,2 г/см3.
Дано
p = 2,2 г/см1 =
= 2,2- Ю'кг/м1
Л/= 58,5-10 кг/моль
Решение
т г л it r г
V -г?
У\-а ,
г/
Vm
п —
и —
м
р
1 м
pNAp'
С Ответ J а = о,28 нм.
Используя закон Дюлонга и Пти, определите удельную теплоем-
кость: 1) натрия; 2) алюминия.
Дано
1) MNa= 23-1 (Г3 кг/моль
-3
2) MAI=27-10"J кг/моль
сРМ -7
Решение
Су =
м'
3R.
М'
CV=3R,
(Ответ
= 1,08 кДж/(кг ¦ К); 2) сУМ = 0,924 кДж/(кг • К).
Пользуясь законом Дюлонга и Пти, определите, во сколько раз
удельная теплоемкость железа больше удельной теплоемкости
золота.
Ътвет
С
Дня нагревания металлического шарика массой 10 г от 20 до 50 °С
затратили количество теплоты, равное 62,8 Дж. Пользуясь зако-
ном Дюлонга и Пти, определите материал шарика.
Дано
m = 10 г=10-2кг
?, = 20 °С
t2 = 50 °С
2=62,8 Дж
Л = 8,31 Дж/(моль-К)
М — ?
Решение
Cv -3R, с,/ = ¦
Q = cvm{t2-tx), t
м
» = —mAt, M =
M
_3Rm{t2-tx)
Q
Г Ответ j м = o,i 19 кг/моль, олово.
Изменение энтропии при плавлении 1 моль льда составило 25 Дж/К.
Определите, на сколько изменится температура плавления льда
при увеличении внешнего давления на 1 МПа? Плотность льда р, = 0,9 г/см3,
плотность воды р2 = 1 г/см3.
v =
M
AS
bp
P\
Pi
\T
Дано
-1 моль
= 18-10~3 кг/моль
= 25 Дж/К
= 1 МПа=106Па
= 0,9 г/см3 =
= 9- 102кг/м3
= 1 г/см3 = 103кг/м3
Решение
Ар L
at W2-v^y
V - — i/ m
[~ о ' F2=^T'
Р\ Рг
L{Vl l)AP ASv
rMAefl П
AS U, oJ
л^. г А??
Дб = ^, AS=^,
P2 Pi > '
QOmeem J
= _008 K
3. Электричество и магнетизм
3.1. Электростатика
* J ^ш1а гравитационного притяжения двух водяных одинаково заря-
женных капель радиусами 0,1 мм уравновешивается кулоновской
силой отталкивания. Определите заряд капель Плотность воды равна 1 г/см3.
С Ответ j ?> = о,3б аКл.
Два заряженных шарика, подвешенных на нитях одинаковой дли-
ны, опускаются в керосин плотностью 0,8 г/см3. Какой должна быть
плотность материала шариков, чтобы угол расхождения нитей в воздухе и в
керосине был один и тот же? Диэлектрическая проницаемость керосина е - 2.
Дано
к =0,8г/см3 = 8-102кг/м:
а
? = 2
p—?
F. =¦
Решение
F=mgtga/2,
Q2
FK=(mg-FA)tga/2,
р =
4же0г
2 '
F.
mg mg-FA
?-1
С Ответ j p = i,
6 г/см3.
В вершинах равностороннего треугольника находятся одинаковые
положительные заряды 2 = 2 нКл. Какой отрицательный заряд Q]
необходимо поместить в центр треугольника, чтобы сила притяжения с его сто-
роны уравновесила силы отталкивания положительных зарядов?
Дано
2 = 2 нКл = 2-10">Кл
2,-?
Решение
F2 + F3 = 0,
4лг?0 r-
— = cosa,
2Л
cosa
= -F
3,
= -ръ. Q] = ^ . [Ответ
2 cosa Ч__
f''" %'А* "~\ Свинцовый шарик (р = 11,3 г/см1) диаметром 0,5 см помещен в гли-
^ ""^ церин (р = 1,26 г/см3). Определите заряд шарика, если в однородном
электростатическом поле шарик оказался взвешенным в глицерине. Электростати-
ческое поле направлено вертикально вверх, и его напряженность Е - 4 кВ/см.
Дано
р = П,3 г/см3 =
= 11,3- 103кг/м3
^ = 0,5 см = 5- 10м
/О, = 1,26 г/см3 =
= 1,26- 103кг/м3
? = 4 кВ/см = 4- 105В/м
2-?
Решение
Ответ)
= 161 нКл.
-
11 ' - 1 1
-
. F
L
i
- i
A
E
:
—
Два точечных заряда Qx = 4 нКл и Q2 = ~2 нКл находятся друг от
друга на расстоянии 60 см. Определите напряженность Е поля в
точке, лежащей посередине между зарядами. Чему равна напряженность, если
второй заряд положительный?
Дано
Q, = 4 нКл
Q2 = -2 нКл
/ = 60 см
E, —?
E2 — ?
Решение
E, = E++E_,
Ex = E+ + E_,
e - l lal ,
+ 4да0 (//2J
- 1 10.1
2,
a
e,
ЧГ "
Г
E+
?*-"
E.
22
9
Ь 2
(Omeemj Ei = 06 ^^. ?2 = 0>2
Определите напряженность поля, создаваемого диполем с элект-
рическим моментом р = 1 нКл • м на расстоянии г = 25 см от цен-
тра диполя в направлении, перпендикулярном оси диполя.
Дано
г = 25 см = 0,25 м
Решение
4ЛГ?О[ 2 /2
4Я?О г2
2'
4ЛГ?П Г 4ЛГ?О Г
(Ответ
f^ 2*7 ] Определите напряженность электростатического поля в точке А,
' расположенной вдоль прямой, соединяющей заряды $=10 нКл
и 02 = -8 нКл и находящейся на расстоянии г = 8 см от отрицательного заря-
да. Расстояние между зарядами / = 20 см.
Дано
Q, = 108Кл
& =-8 нКл = -8-10'Кл
г = 8 см = 8- 10~2м
/ = 20 см = 0,2 м
Е—?
Решение
1) е,
Е
= Е1+Е2,
E}=
4лг?0(/ -
„2 "
; = 10,1 кВ/м; 2) ? = 17,5 кВ/м.
На некотором расстоянии от бесконечной равномерно заряжен-
ной плоскости с поверхностной плотностью о = 0,1 нКл/см2 рас-
положена круглая пластинка. Плоскость пластинки составляет с линиями на-
пряженности угол 30°. Определите поток Ф? вектора напряженности через
эту пластинку, если ее радиус г равен 15 см.
Дано
о = 0,1 нКл/см2
/9 = 30°
г = 0,15 м
Решение
о
Or = ?5cosa, ? = ,
2?0
н
a ,
Фр = яг cosa *
S = яг2,
2?0
Ответ у Фе = 3,46 кв • м.
j Определите поток ФЕ вектора напряженности электростатичес-
кого поля через сферическую поверхность, охватывающую точеч-
ные заряды Q, = 5 нКл и Q2 = -2 нКл.
Г
Ответ
= 339 В • м.
Расстояние / между зарядами Q = ±2 нКл равно 20 см. Опреде-
лите напряженность ? поля, созданного этими зарядами в точке,
находящейся на расстоянии г, = 15 см от первого и г = 10 см от второго заряда.
Г Ответ j ? = 2,14 кв/м.
В вершинах квадрата со стороной 5 см находятся одинаковые поло-
жительные заряды Q = 2 нКл. Определите напряженность элект-
ростатического поля: 1) в центре квадрата; 2) в середине одной из сторон квадрата.
Дано
а = 5 см = 5-102м
2 = 2 нКл = 2- Ю-'Кл
1) ?, — ?
2) ?2 — ?
Решение
Q
Г
1) 3 = 0;
2) ?2 = 2? cosa ,
E\jV/«H
Q
Q
4яе,
2 а
а + —
5яеоа
Е.Г
а-
Е,
cosa -
g 2 = 4g
т?0д2 V? 5^леоа2 '
С Ответ j
1)?,=0; 2) ?2=1О,3 кВ/м.
С 3.12 ) Кольцо радиусом г = 5 см из тонкой проволоки равномерно заря-
жено с линейной плотностью г = 14 нКл/м. Определите напря-
женность поля на оси, проходящей через центр кольца, в точке, удаленной на
расстоянии а = 10 см от центра кольца.
Дано
/• = 5 см = 5 ¦ 10~2 м
г = 14 нКл/м =
= 1,4- 108Кл/м
а = 10 см = 0.1 м
ЕА -?
Решение
d?, = d? cosa ,
а
cosa = —
adQ
2 = d?sina
2лгсп
{Ответ ^ еа = 2,83 кв/м
Под действием электростатического поля равномерно заряженной
бесконечной плоскости точечный заряд Q = 1 нКл переместился
в^оль силовой линии на расстояние г = 1 см; при этом совершена работа 5 мкДж.
Определите поверхностную плотность заряда на плоскости.
{
Ответ
= 8,85 мкКл/м2
Электростатическое поле создается двумя бесконечными парал-
лельными плоскостями, заряженными равномерно одноименны-
ми зарядами с поверхностной плотностью соответственно о1 = 2 нКл/м2 и
о2 - 4 нКл/м2. Определите напряженность электростатического поля: 1) меж-
ду плоскостями; 2) за пределами плоскостей. Постройте график изменения
напряженности вдоль линии, перпендикулярной плоскостям.
J
1) ИЗ В/м; 2) 339 В/м.
Основные физические постоянные
,-19
Элементарный заряд е = 1,6-10" Кл
f^ Определите поверхностную плотность заряда, создающего вбли-
зи поверхности Земли напряженность Е = 200 В/м.
-31
Дано
Е = 200 В/м
? = 1
а —?
Решение
г. О
??0 °
{Ответ Л a = i,
,77 нКл/м2.
Масса покоя электрона те = 9,11 • 10 кг
Удельный заряд электрона е/те = 1,76 • 10" Кл/кг
Электрическая постоянная ?0 = 8,85 1О~12 Ф/м
1/Dл?0) = 9-109 м/Ф
Магнитная постоянная /i0 = 4я • 10~7 Гн/м
Электростатическое поле создается двумя бесконечными парал-
лельными плоскостями, заряженными равномерно разноименны ¦
ми зарядами с поверхностной плотностью ст, = 1 нКл/м2 и а2 = 2 нКл/м2, Оп-
ределите напряженность электростатического поля: 1) между плоскостями,
2) за пределами плоскостей. Постройте график изменения напряженности поля
вдоль линии, перпендикулярной плоскостям.
Ответ
?¦, =169 В/м; 2) Е2 = 56,5 В/м.
На металлической сфере радиусом 15 см находится заряд 0 = 2 нКл.
Определите напряженность Е электростатического поля: 1) на
расстоянии г, = 10 см от центра сферы; 2) на поверхности сферы; 3) на рассто-
янии г2 = 20 см от центра сферы. Постройте график зависимости Е(г).
Дано
R = 15 см = 0,15м
0 = 2 нКл = 2- 10-" Кл
г, =10 см = 0,1 м
г2 = 20 см = 0,2 м
Е(г) - ¦
Решение
?, В/м
?,=0,
800
^—
0
/
1
¦ з
L
1 х^
- !^
\ / IR •
А. /
1
~ п
г, м
r = R
0
Q Ответ
= о,
= 8оо в/м,
= 450 в/м.
Поле создано двумя равномерно заряженными концентрически-
ми сферами радиусами Щ = 5 см и R2 = 8 см. Заряды сфер соот-
ветственно равны 0! =2 нКли Q2--\ нКл. Определите напряженность элект-
ростатического поля в точках, лежащих от центра сфер на расстояниях:
1) г, = 3 см; 2) г2 = 6 см; 3) гъ = 10 см. Постройте график зависимости ?(г).
Rx--
Ri
0.
02
r\ =
ri =
Ex
= 5
= 8
= 2
= -
3
= 6
-10
?
?(r)-
Дано
см = 5 • 10м
см = 8 • 10'2 м
нКл = 2- 10-9Кл
1 нКл = -10-9Кл
:м = 3 • 10м
см = 6 ¦ 10 2 м
см = 0,1 м
2 , ?3 — ?
_ ?
|?
J "
s
?,=
/i2-
г*
ьъ =
Решение
?0
0,
01
4ЛГЕ0/22 '
01 + 02
4гг?0/з2 '
?,
кВ
^ —
У
/
/
/ >
/ /'
1 1
1 1
1 \
\ r;>
ч
¦s.
' J L
'мм
6
4
2
о1_
....
\
\ i
v , ' Г, СМ
Ч --'
С Ответ J
= о, Е2 = 5 кв/м,
Шар радиусом Л = 10 см заря-
жен равномерно с объемной
плотностью р -10 нКл/м3. Определите на-
пряженность электростатического поля: 1) на
расстоянии /} = 5 см от центра шара; 2) на рас-
стоянии /2 = 15 см от центра шара. Построй-
те зависимость Е(г).
СОтвет J щ = is,8 в/м, ?2 = 16,7 в/м.
Фарфоровый шар радиусом Л = 10 см заряжен равномерно с
объемной плотностью р = 15 нКл/м3. Определите напряженность
электростатического поля: 1) на расстоянии гх = 5 см от центра шара; 2) на
поверхности шара; 3) на расстоянии г2 = 15 см от центра шара. Постройте гра-
фик зависимости Е{г). Диэлектрическая проницаемость фарфора е = 5 .
Дано
R = 10 см = 0,1 м
р = 15 нКл/м3 =
= 1,5- 10"8Кл/м3
? = 5
г, =5 см = 5 • 10~2 м
г2 =15 см = 0,15 м
2)?я-?
3) Е2— ?
4)?(г)-?
Решение
Dnd5 = -
=JY
?>,=?<,??,,
EQE 3?0?
Г =
Ъе0г2
D2 = Е0Е2,
К см
Ответ j i) ?, =5,65 в/м;
2) ?я = 11,3 В/м (для г < Л); ER = 56,5 В/м (для г > R);
3) ?2 = 25,1 В/м; 4) см. рисунок.
Длинный прямой провод, расположенный в вакууме, несет заряд,
равномерно распределенный по всей длине провода с линейной
плотностью 2 нКл/м. Определите напряженность Е электростатического поля
на расстоянии г = 1 м от провода.
Г
Ответ
E = -
= 36 В/м.
Внутренний цилиндрический проводник длинного прямолиней-
ного коаксиального провода радиусом /?, = 1,5 мм заряжен с линей-
ной плотностью rt = 0,20 нКл/м. Внешний цилиндрический проводник этого про-
вода радиусом R2 = 3 мм заряжен с линейной плотностью г2 = -0,15 нКл/м.
Пространство между проводниками заполнено резиной (? = 3 ). Определите
напряженность электростатического поля в точках, лежащих от оси провода на
расстояниях: 1) г, = 1 мм; 2) г2 = 2 мм; 3) гъ = 5 мм.
я,
Г|
r2
?:
h
?
i)
2)
3)
Дано
= 1,5 мм =1,5- IO-'m
= 3 mm = 3 • 10'3 м
= 0,2 нКл/м =
= 2' 10 10Кл/м
= -0,15 нКл/м =
= -1,5' 1О'°Кл/м
= 3
= 1 мм = 10~3 м
= 2 мм = 2- 10м
= 5 мм = 5 • 10m
?, -?
Е2 — ?
?3-?
Решение
?i=0,
г - 1
Г, +Г2 ^1+^2
3 2яе0ег3[=1 2jr?0r3
С Ответ "^ i) ?,
2) ?2
3) ?3
= 0;
= 800 В/м;
= 180 В/м.
Электростатическое поле создается положительно заряженной с
постоянной поверхностной плотностью G = 10 нКл/м2 бесконеч-
ной плоскостью. Какую работу надо совершить для того, чтобы перенести элек-
трон вдоль линии напряженности с расстояния г, = 2 см до г2 = 1 см?
Дано
а = 10нКл/м2 = 108Кл/м:
г, = 2 см = 2- 10 2м
г2 = 1 см = 10~2 м
е = 1,6-10~ Кл
А —?
А
Решение
Г*
о
2еп
Е
2 1
-• •->
= h dr = - ^- fdr =~(Г] - г2).
Дж.
Электростатическое поле создается положительно заряженном
бесконечной нитью с постоянной линейной плотностью г = 1 нКл/см.
Какую скорость приобретет электрон, приблизившись под действием поля к
нити вдоль линии напряженности с расстояния г, = 1,5 см до г2 = 1 см?
Дано
г = 1 нКл/см= 10Кл/м
е = 1,6-1(Г19 Кл
те = 9,11-1(Г31 кг
г, =1,5 см =1,5- 10м
г2 = 1 см = 10~2 м
Решение
mv
v =.
F=-eE = —
2ле0г
2леог
= Fdr,
v — ?
ет fdr ex
V -
Ответ J v = 16 Мм/с.
Одинаковые заряды 6 = 100 нКл расположены в вершинах квад-
рата со стороной а = 10 см. Определите потенциальную энергию
)той системы.
Дано
6 = 100 нКл=10'7Кл
а = 10 см = 0,1 м
с/-?
Решение
: + и13 + ин+и2) + и24
1 О2 1
4ле0 а
1 Q1
24 = ип,
4яс0 а Апе0 ал
Г Ответ j и = 4,87 мДж.
В боровской модели атома водорода электрон движется по круго-
вой орбите радиусом г = 52,8 пм, в центре которой находится
протон. Определите: 1) скорость электрона на орбите; 2) потенциальную энер-
гию электрона в поле ядра, выразив ее в электрон-вольтах.
г = 52,8
е = 1,6-1
/я = 9,11
V —?
и —?
Дано
пм = 5,28
О9 Кл
¦1(Г31 кг
10"" м
mv
г
v =
Решение
1 е2
4ле0 г2 '
Г^ и-
Апеотг '
1 е2
4гг?0 г
Г Ответ ^ w = 2,19 мм/с, и = -27,з эв.
Кольцо радиусом г = 5 см из тонкой проволоки несет равномер-
но распределенный заряд 2 = 10 нКл. Определите потенциал <р
электростатического поля: 1) в центре кольца; 2) на оси, проходящей через центр
кольца, в точке, удаленной на расстояние а = 10 см от центра кольца.
Полый шар несет на себе равномерно распределенный заряд. Оп-
ределите радиус шара, если потенциал в центре шара равен
= 200 В, а в точке, лежащей от его центра на расстоянии г = 50 см, <р2 - 40 В.
Дано
г = :
Q =
а -
<Ро ¦
<Ра
5 см:
10
10
—
= 5- 10
нКл=108
с\
?
?
1 — 0,1 м
м
Кл
Решение
dtp =
1 dg
47Г?0 Г
Q
d/,dg
= !¦
о
Q
<Ра = J"
о
dg
Дано
ipx - 200 В
ip2 = 40 В
г = 50 см = 0,5 м
Решение
Q
Q /
Y2 ~ ' /
0
{
-ZT V 1
R
Q
<Р\
4жео\г2 + а2
'2 + а2
Ответ
Г Ответ J л=ю см.
в,
в.
На кольце с внутренним радиусом 80 см и внешним — 1м равно-
мерно распределен заряд 10 нКл. Определите потенциал в центре
кольца.
Электростатическое поле создается положительным точечным
зарядом. Определите числовое значение и направление градиента
(ютенциала этого поля, если на расстоянии г -10 см от заряда потенциал ра-
н у> = 100 В.
С
Ответ
Металлический шар радиусом 5 см несет заряд 2 = 10 нКл. Оп-
ределите потенциал <р электростатического поля: 1) на поверхно-
сти шара; 2) на расстоянии а - 2 см от его поверхности. Постройте график
зависимости <р(г).
СОтветЛ Х) ^ = i,8 кв; 2) <р2 = 1,29 кв.
Дано
г = 10 см = 0,1 м
у» =100 В
Решение
E = -grad^, i
, , д
L
grady?
А
Е = -
Q
Е = ?-,
Е
|gradp| = -^.
I Ответ \ grady5 = 1 кВ/м, направлен к заряду.
Г 2 32 J Электростатическое поле создается бесконечной плоскостью, за-
ряженной равномерно с поверхностной плотностью о = 5 нКл/м2
Определите числовое значение и направление градиента потенциала этого поля
Дано
ст = 5 нКл/м2 =
= 5- 109Кл/м2
grad (p — ">
Решение
/Т (У
2е0 ' ь п 2е0
С Ответ Л &*d<f> ш в/м
Электростатическое поле создается положительно заряженной
бесконечной нитью Протон, двигаясь от нити под действием поля
рдоль линии напряженности с расстояния г, = 1 см до г2 = 5 см, изменил свою
ркорость от 1 до 10 Мм/с Определите линейную плотность заряда нити
Г Ответ J r = i7,8
мкКл/м
В
Электростатическое поле создается бесконечной прямой нитью
заряженной равномерно с линейной плотностью г = 50 пКл/см
Определите числовое значение и направление градиента потенциала в точке на
расстоянии г = 0,5 м от нити
С Ответ } gradp = 180 В/м, направлен к нити
f \3 лЖ!?1 Определите линейную плотность бесконечно длинной заряженной
нити, если работа сил поля по перемещению заряда Q - 1 нКл <-
расстояния г, = 5 см до г2 = 2 см в направлении, перпендикулярном нити, рав-
на 50 мкДж
-\ Электростатическое поле создается бесконечной плоскостью, рав-
, номерно заряженной с поверхностной плотностью а = 1 нКл/м2
Определите разность потенциалов между двумя точками этого поля, лежащи-
ми на расстоянии х, = 20 см и х2 = 50 см от плоскости
Дано
0 = 1 нКл/м2= 10"9Кл/м2
'х, = 20 см = 0,2 м
|дгт = 50 см = 0,5 м
Решение
tpx-tp2 =
*Р\ ~~ ф">
2еп
о
2еп
Г Ответ j
-^2 = 16,9 В
Дано
Q = \ нКл=10-9Кл
г, =5 см = 5 10 2 м
г2 = 2 см = 2 10-2м
А =50 мкДж = 5 105Дж
Решение
АА =
р _
Определите поверхностную плотность зарядов на пластинах плос-
кого слюдяного (е = 7) конденсатора, заряженного до разности по-
тенциалов U - 200 В, если расстояние между его пластинами равно d = 0,5 мм
2ле0г '
А = -(
г =
2же0А
} 2ле0г 2ле0 J г 2яе0 г-,
1 г\
QOmeem
¦ = 3,03 мкКл/м
Дано
? = 7
U = 200 В
d=0,5 мм = 0,5 10 'м
о —">
Решение
D-eoeE, D-o, E- — , o-?q?U
d d
С Ответ Л а = 24,8 мккл/м2
<2Й>
Электростатическое поле создается равномерно заряженной сфе-
рической поверхностью радиусом /? = 10 см с общим зарядом
Q = 15 нКл. Определите разность потенциалов между двумя точками этого поля.
лежащими на расстояниях гх = 5 см и г2 = 15 см от поверхности сферы.
Электростатическое поле создается шаром радиусом R = 8 см,
равномерно заряженным с объемной плотностью р = 10 нКл/м1
Определите разность потенциалов между двумя точками этого поля, лежащи-
и на расстоянии гх = 10 см и г2 = 15 см от центра шара.
ГОтвет j д^ = збо в.
Г
Ътвет
= o,64 в.
$ Электростатическое поле создается сферой радиусом /? = 5 см.
равномерно заряженной с поверхностной плотностью о = 1 нКл/м1
Определите разность потенциалов между двумя точками поля, лежащими на
расстояниях г{ = 10 см и г2 = 15 см от центра сферы.
Электростатическое поле создается шаром радиусом Л =10 см,
равномерно заряженным с объемной плотностью р = 20 нКл/м3
Определите разность потенциалов между точками, лежащими внутри шара на
«сстояниях г, = 2 см и г2 - 8 см от его центра.
Дано
R=5 см = 5 • 10м
а = 1 нКл/м2=10-9Кл/м2
г, =10 см = 0,1 м
г2 =15 см = 0,15 м
<Р\~<Р2 —7
Решение
•2
I - <P2 = }
Edr.
4лге
0 г2
<P\-<P2 =
oR2
oRl( 1 __1_
r2
в.
_.
Pl-
Дано
10 см = 0,1 м
20 нКл/м3 =
2-10-8Кл/м3
2 см = 2- 10 2м
8 см = 8- 10 2м
-,2-1
JE
s
r<
E 4
r»
Решение
2_ p 4 з
? 3 '
PL
3?n
Электростатическое поле создается равномерно заряженным ша-
ром радиусом R = 1 м с общим зарядом Q = 50 нКл. Определите
разность потенциалов для точек, лежащих от центра шара на расстояниях
1) г, = 1,5 м и г2 = 2 м; 2) г{= 0,3 м и г{ = 0,8 м.
Г Ответ J 1) Л^, =75 В; 2) Д^2 = 124 В.
<Pi
¦2
Ответ
<P\-<p2= 2,26 B.
3.43V J Электростатическое поле создается бесконечным цилиндром ра-
диусом 8 мм, равномерно заряженным с линейной плотностью
т = 10 нКл/м. Определите разность потенциалов между двумя точками этого
поля, лежащими на расстоянии ц = 2 мм и г2 = 1 мм от поверхности этого
цилиндра.
Дано
R=8 мм = 8 ¦ 10м
г = 10 нКл/м=10'8Кл/м
/, =2 мм = 2 ¦ 10 Зм
г-, = 7 мм = 7 • 10~3м
Решение
Е = -
1 г
R+h
J 7ягр„ J r
7?+/;
0 /?+/•,
ln:
R+i\
x .R + r-,
In
2ле0
С Ответ j
В однородное электростатическое поле напряженностью
Ео - 700 В/м перпендикулярно полю помещается бесконечная
плоскопараллельная стеклянная пластина (? = 7). Определите: 1) напряжен-
ность электростатического поля внутри пластины; 2) электрическое смеще-
ние внутри пластины; 3) поляризованность стекла; 4) поверхностную плот-
ность связанных зарядов на стекле.
Дано
Ео = 700 В/м
? = 7
?-? ¦
D -?
Решение
? = —, D=??0?,
?
D=eqE + P, P=D-e0E,
о' = Р.
р-1
о' — ?
Г
Ответ
\) е = \оо в/м;
3) Р= 5,31 нКл/м:;
2) ?> = 6,19 нКл/м2;
4) о' = 5,31 нКл/м2.
Пространство между пластинами плоского конденсатора заполне-
но парафином (? = 2). Расстояние между пластинами d - 8,85 мм.
Какую разность потенциалов необходимо подать на пластины, чтобы поверх-
'ностная плотность связанных зарядов на парафине составляла 0,1 нКл/см2?
С Ответ
Др = 1 кВ.
Расстояние между пластинами плоского конденсатора составляет
d = 5 мм. После зарядки конденсатора до разности потенциалов
U = 500 В между пластинами конденсатора вдвинули стеклянную пластинку
(е = 7). Определите: 1) диэлектрическую восприимчивость стекла; 2) поверх-
ностную плотность связанных зарядов на стеклянной пластинке.
Дано
d = 5 мм = 5
U = 500 В
? = 7
1) X — ?
I) О' — ?
Решение
Х=?-1,
E° U
— = —
? ?Д
U_
d
сос --
Ed
2) ст'= 759 нКл/м2.
Определите поверхностную плотность связанных зарядов на слю-
дяной пластинке (? = 7) толщиной d = 1 мм, служащей изолято-
ром плоского конденсатора, если разность потенциалов между пластинами кон-
денсатора и - зоо в.
С
Ответ
ст = 15,9 мкКл/м2.
<?
Между пластинами плоского конденсатора помещено два слоя
диэлектрика — слюдяная пластинка (^ = 7) толщиной d] = 1 мм
и парафин (е2 = 2) толщиной d2 = 0,5 мм. Определите: 1) напряженность элек-
тростатических полей в слоях диэлектрика; 2) электрическое смещение, если
разность потенциалов между пластинами конденсатора U = 500 В.
Дано
dx=\ мм= 10м
?,=7
d-, =0,5 мм = 0,5- 10м
?2=2
U = 500 В
\) Е Е ">
2) D — ?
Решение
= ЕдЕ]^ = EQE2E2 ,
= Eldl + E2d2,
?2
С Ответ j \) j
^2
51=182
- ?0?,?, .
кВ/м, ?2 = 637 кВ/м
2) ?> = 11,3 мкКл/м2.
Расстояние между пластинами плоского конденсатора составляе i
d = 1 см, разность потенциалов U = 200 В. Определите поверх-
ностную плотность о' связанных зарядов эбонитовой пластинки (? = 3 ), по-
мещенной на нижнюю пластину конденсатора. Толщина пластины d2 = 8 мм
Дано
^ = 1 см
гу = 200 в
rf, = 8 мм
? = 3
п' —1
Решение
d,=d-d2,
U
E(d-d2) + d2
Свободные заряды равномерно распределены с объемной плот-
ностью р = 5 нКл/м3 по шару радиусом R = 10 см из однородно-
го изотропного диэлектрика с проницаемостью е- 5 Определите напряжен-
i ность электростатического поля на расстояниях гх - 5 см и г2 = 15 см от цент-
ра шара.
Дано
p-S нКл/м3
Л=10 см
? = 5
Г| = 5 см
г2 = 15 см
Решение
r,<R
2 4
D, = Е0еЕ{, ?, =
Ph
3??п
R
D2 =
D2 = е0Е
0Е2,
__?
•R3
(
Ответ
5, = 1,88 В/м; ?2 = 8,37 В/м.
Расстояние между пластинами плоского конденсатора d = 5 мм,
разность потенциалов U = 1,2 кВ. Определите: 1) поверхностную
плотность заряда на пластинах конденсатора; 2) поверхностную плотность свя-
занных зарядов на диэлектрике, если известно, что диэлектрическая воспри-
имчивость диэлектрика, заполняющего пространство между пластинами, х = 1.
(е-1)ео1/
e{d-d2)+d2
¦ (ОтветЛ а< = 253 нКл/м2 (Ответ \) о = 4,24 мкКл/м2; 2) а' = 2,12 мкКл/м2.
Пространство между пластинами плоского конденсатора запол-
нено стеклом (е = 7). Расстояние между пластинами d = 5 мм,
разность потенциалов U = 1 кВ. Определите: 1) напряженность поля в стекле;
2) поверхностную плотность заряда на пластинах конденсатора; 3) поверхнос-
тную плотность связанных зарядов на стекле.
Дано
? = 7
d = 5 мм = 5- 10m
G = 1 кВ = 103В
1)?—7
2)о — ?
3) а' — ?
Решение
G = JErf, Е = —,
d
о
Е = , СТ = ??П?,
??0
o' = P=D-eQE = ее0Е-?0Е = (е- 1)ео? .
Г Ответ Л 1) ? = 200 кВ/м; 2) а = 12,4 мкКл/м2;
3) о' = 10,6 мкКл/м2.
Определите расстояние между пластинами плоского конденсатора,
если между ними приложена разность потенциалов 17 = 150 В,
причем площадь каждой пластины S = 100 см2, ее заряд 6 = 10 нКл. Диэлект-
риком служит слюда (? = 7).
и
S
Q
Е
d
= 150
= 100
= 10
= 7
?
Дано
в
см2 = 1О
нКл=10-8
м2
Кл
eneS
d
Решение
qeS
d '
Q
~u'
с
d
Q
u'
eoeSU
Q
С Ответ j d = 9,29
MM.
К пластинам плоского воздушного конденсатора приложена раз-
ность потенциалов Ux = 500 В. Площадь пластин S = 200 см2,
расстояние между ними d = 1,5 мм. После отключения конденсатора от источ-
ника напряжения в пространство между пластинами внесли парафин (? = 2).
Определите разность потенциалов U2 между пластинами после внесения диэ-
лектрика. Определите также емкости конденсатора Сх и С2 до и после внесе-
ния диэлектрика.
s =
d =
? =
P2
b
Дано
= 500 В
200 см2 = 2 •
1,5 мм= 1,5-
2
?
— 9
10
ю-3
м2
м
Q\
Е2
с,
Решение
- у2 - {J - const, о
о
= —, ?/,=?,<*•
?0?
?05 ??05
" rf ' Cl~ d -
Q F _o
— — consl "i
5 ' ?о
и,
U2 = E2d, U2=^-,
-?С,.
__? ^ Ответ J t/2 = 250B,
= П8пФ,
= 236пФ.
Решите предыдущую задачу для случая, когда парафин вносится
в пространство между пластинами при включенном источнике
питания.
It-
Дано
= 500 В
200 см2 = 2 •
1,5 мм= 1,5 ¦
2
7
ю-2
10
м2
м
Решение
UX = U2 = U = const,
r ?qS г «о5
С, —?
Г Ответ j
= 500B, С, = 118пФ, С2=236пФ.
Определите емкость коаксиального кабеля длиной 10 м, если ра-
диус его центральной жилы г, = 1 см, радиус оболочки г2 = 1,5 см,
а изоляционным материалом служит резина (е = 2,5).
Дано
/ = 10 м
Г;=1 см=102м
г2 = 1,5 см = 1,5- 10~2м
? = 2,5
С ?
Решение
с — ш , >/ ,/
2Я??0 Г[ Z~^^^ /
с 2Я??0/ Л( Щ)/
Г2
—
С Ответ j с = з,43 нф.
Определите напряженность электростатического поля на рассто-
янии d = 1 см от оси коаксиального кабеля, если радиус его цент-
ральной жилы Г] = 0,5 см, а радиус оболочки г2 = 1,5 см. Разность потенциа-
лов между центральной жилой и оболочкой U = 1 кВ.
Дано
d = \ см=10м
Г[ =0,5 см = 0,5 • 10м
г7 = 1,5 см= 1,5 •
U = \ кВ = 103В
Е —?
Решение
Е = -
х = -
1 Q_tl _2ле0е1
' U~U~ г ч
2jie0eU
? = ¦
2jie0eU
?/
lnR
Ответ ) е = 9\ кв/м.
Сферический конденсатор состоит из двух концентрических сфер
радиусами rt = 5 см и г2 = 5,5 см. Пространство между обкладка-
ми конденсатора заполнено маслом (е = 2,2). Определите: 1) емкость этого
(сонденсатора; 2) шар какого радиуса, помещенный в масло, обладает такой же
1) С = 135 пФ; 2) г = 0,55 м.
Определите напряженность электростатического поля на рассто-
янии х = 2 см от центра воздушного сферического конденсатора,
[образованного двумя шарами (внутренний радиус rt = 1 см, внешний— г2 = 3 см),
[между которыми приложена разность потенциалов U = 1 кВ.
Дано
х = 2 см = 2 • 10 2м
rt = 1 см = 10 м
г2 = 3 см = 3 ¦ 10 2 м
Ь = \ кВ = 103В
Е —?
Решение
Q=CU,
r2-rx
2
х х" r2 ~ г\
Е = 37,5 кВ/м.
Два плоских воздушных конденсатора одинаковой емкости соеди-
нены параллельно и заряжены до разности потенциалов U = 300 В.
Определите разность потенциалов этой системы, если пространство между
пластинами одного из конденсаторов заполнено слюдой (е = 7).
Г Ответ
I/, = 75 В.
Сборник п мм
Разность потенциалов между точками А и В U = 9 В. Емкость
конденсаторов соответственно равна С\=Ъ мкФ и С2 - 6 мкФ
Определите емкость С батареи конденсаторов, изображенной на
рисунке. Емкость каждого конденсатора С, = 1 мкФ.
Определите: 1) заряды Q, и Q2; 2) разность потенциалов U\ и U2 на обкладках
каждого конденсатора.
Дано
Дано
U = 9 В
С, =3 мкФ = 3
Ф
С, = 6 мкФ = 6- 10"* Ф
а>
Решение
с, с2
\С,=1 мкФ
с-?
Решение
а = 02 = 0 -const -
I/,
uc,
{ Ответ Л с = 0,286 мкФ
Г Ответ j их = 6 в,
Уединенная металлическая сфера электроемкостью С = 4 пФ за-
ряжена до потенциала р = 1 кВ. Определите энергию поля, зак-
люченную в сферическом слое между сферой и концентрической с ней сфери-
Иеской поверхностью, радиус которой в 4 раза больше радиуса уединенной
|сферы.
= g2 = 18
Емкость батареи конденсаторов, образованной двумя последова-
тельно соединенными конденсаторами, С = 100 пФ, а заряд
Q = 20 нКл. Определите емкость второго конденсатора, а также разность по-
тенциалов на обкладках каждого конденсатора, если С, = 200 пФ.
Дано
С = 4 пФ = 4- 10~12Ф
р = 1 кВ=103В
Rl=4R
w — ?
Решение
с
C-4xe0R, R- ,
4яе0
4ле0гг
c=
Q =
c, -
100
20 i
200
9
-?
Дано
пФ = 10"
Жл = 2'
пФ = 2-
10 ф
10"8Кл
ю-10ф
Решение
Q\ = Q2 = Q = const,
Г Ответ J c2 =
0
с,'
200 пФ,
1 1 1
и Q
2 <V
С/, =100 В,
—
= 4лгг2 dr ,
?=1
W=
J DяJг02И 2 8я?о{г2
8лг?0 4С 8
?/, — ?
t/2 = 100 В.
{Ответ Л w = 1,5 мкдж.
Две концентрические проводящие сферы радиусами Л,= 20 см и
&> = 50 см заряжены соответственно одинаковыми зарядами
g = 100 нКл. Определите энергию электростатического поля, заключенного
между этими сферами.
Сплошной шар из диэлектрика радиусом R = 5 см заряжен рав-
номерно с объемной плотностью р = 10 нКл/м3. Определите энер-
гию электростатического поля, заключенную в окружающем шар пространстве.
Дано
Л,= 20 см = 0,2 м
R2 = 50 см = 0,5 м
2 = 100 нКл=10-7Кл
W —'
Решение
vv =
е0еЕ2
е0Е2
= h
Е = —^-т, W= LdV ,
4лг?0г2 '
;082 4лгг2 dr б f 1 1
R2
Q Ответ j ж = 135мкДж.
Сплошной эбонитовый шар (? = 3) радиусом R = 5 см заряжен
равномерно с объемной плотностью р• = 10 нКл/м3. Определите
энергию электростатического поля, заключенную внутри шара.
? = 3
#=ь
W —
см
)н!
?
Дано
d^ =
s
Решение
- -ui Л V и, ?(
do —-Ip dV
V
2
2
L>-4
D
??0 '
4
3
dF
ir '
= 4лгг2 dr
D2 = p2r2
2?0? 18?0?
w-
r4 dr =
2 „5
2жр г
9s0e 5
2жр2
Г Ответ J ^ = о,1б4пДж.
f~Omeemj w = 2,46 пДж.
|j§j§ Шар, погруженный в масло ( е = 2,2), имеет поверхностную плот-
ность заряда о -1 мкКл/м2 и потенциал <р - 500 В. Определите:
1) радиус шара; 2) заряд шара; 3) емкость шара; 4) энергию шара.
? = 2,2
р = 500
1) R-
Дано
в
9 2J-?
R =
Решение
= oS-o- 4жЯ2,
?0?<Р г
о
1
4Я?0?
R
oR
?0?
2
3)С-?
4) ж—?
С Ответ Л 1) Л = 9,74 мм; 2) 6 = 1,19 нКл;
3) С = 2,38 пФ; 4) Ж = 0,3 мкДж.
В однородное электростатическое поле напряженностью
Ео = 700 В/м перпендикулярно полю поместили стеклянную пла-
стинку (? = 7) толщиной d — 1,5 мм и площадью 200 см2. Определите: 1) по-
верхностную плотность связанных зарядов на стекле; 2) энергию электроста-
тического поля, сосредоточенную в пластине.
и -
S =
О
W
Дано
= 700 В/м
7
= 1,5 мм- 1,5 • 10~3м
= 200 см2 = 2- 1Ом2
— ?
Решение
Е — — ) L) ~ EqEei у х
Е
о-Р-е0(е 1УБ-
2 2е
Е0(Е-1)Е0
Е
о'
W
СОтвет
= 5,31 нКл/м2;
= 9,29 пДж.
)
Плоский воздушный конденсатор емкостью С = 10 пФ заряжен
до разности потенциалов ?/, = 500 В. После отключения конден-
сатора от источника напряжения расстояние между пластинами конденсатора
было увеличено в 3 раза. Определите: 1) разность потенциалов на обкладках
конденсатора после их раздвижения; 2) работу внешних сил по раздвижению
пластин.
С
Ответ
J 1) t/2=l,5 кВ; 2) Л = 2,5
мкДж.
К пластинам плоского воздушного конденсатора приложена раз-
ность потенциалов ?/, = 500 В. Площадь пластин S = 200 см2,
расстояние между ними dx -1,5 мм. Пластины раздвинули до расстояния
^2=15 мм. Найдите энергию W{ и W2 конденсатора до и после раздвижения
пластин, если источник напряжения перед раздвижением: 1) отключался; 2) не
отключался.
s
d\
d2
1)
2)
1)
2)
Дано
= 500 В
= 200 см2
f
= 1,5 мм =
= 15 мм =
Q = const
U = const
Щ; W2 -
Щ-.Щ —
= 2-
= 1,5
= 1,5
?
7
ю-2
•10-
¦10-
м2
JM
2м
1)
W
^2
2)
Решение
_?0S c
Q - const
C,t/,2 EoSt/,2
2 2rf, '
C2U2 e0Sd2U2
2 2d2d2
U = const
Q\
JX = C2U2,
-Wd2.
d\
= С|Ц. Qi = С2Щ,
w,=
Id,
2d2dx
Г Ответ J \) wx = 14,8 мкДж, W2 = 148 мкДж;
2) Wx = 14,8 мкДж, ^2 = 1,48 мкДж.
Разность потенциалов между пластинами плоского конденсатора
?/ = 100 В. Площадь каждой пластины S = 200 см2, расстояние
между пластинами d - 0,5 мм, пространство между ними заполнено парафи-
ном (е = 2). Определите силу притяжения пластин друг к другу.
d =
E -
F -
100
200
0,5
2
Дано
в
см2-2- 10 2м2
мм = 0,5 • 10 м
Решение
\F\~ Ql i
2e0eS '
C" d ' ^
"I d
/V 1 ?0?5t/2
J 2?0?5 2t/
Г Ответ Л f = 7,08 мн.
Пространство между пластинами плоского конденсатора запол-
нено слюдой (? = 7). Площадь пластин конденсатора составляет
50 см2. Определите поверхностную плотность связанных зарядов на слюде, если
пластины конденсатора притягивают друг друга с силой 1 мН.
Дано
e = 7
S = 50 см2 = 5- 10 Зм2
F = l mH= 10 3H
a' — ?
cr =
Решение
--aS,
l2e0eF
'i s '
2?0eS
a
?„? A|
a25
2?0?'
[2F
eoeS '
СГ' = ?0(?-1)? = (?-
Qpmeem ^ a =4,27
мкКл/м2.
Пространство между пластинами плоского конденсатора запол-
нено стеклом (е - 7). Когда конденсатор присоединили к источ-
нику напряжения, давление пластин на стекло оказалось равным 1 Па. Опреде-
лите: 1) поверхностную плотность зарядов на пластинах конденсатора; 2) элект-
рическое смещение; 3) напряженность электростатического поля в стекле,
4) поверхностную плотность связанных зарядов на стекле; 5) объемную плог-
ность энергии электростатического поля в стекле.
Дано
?
P
1)
2)
3)
4)
5)
= 7
= i
о
D
E
a'
w
H/m2
— ?
_?
_?
_?
— ?
Решение
\F\-
2?0?5 2?0?
1) о = л]2е0ер ,
2)D = a,
?п?
4) о' =
5) w =
е0еЕ2
Ответ
1) а = 11,1 мкКл/м2;
2) D = l 1,1 мкКл/м2;
3) ? = 179 кВ/м;
4) о' = 9,5 мкКл/м2;
5) w = 0,992 Дж/м3.
2Е0Е
Сила притяжения между двумя разноименно заряженными
обкладками конденсатора
Q _o2S _ eoeE2S
2e0eS 2e0? 2
3.2. Постоянный электрический ток
Сила тока в проводнике равномерно нарастает от /0 = 0 до / = 2 А
в течение времени т = 5 с. Определите заряд, прошедший по про-
воднику.
Дано
/0 = 0
/ = 2 A
т = 5 с
Q
Решение
dQ = / dr,
/=*/
kt dt,
т т
r ;_2
0
2~~T"
Г Ответ
»= 5 Кл.
РЗй^ЙРЙ Определите плотность тока, если за 2 с через проводник сечением
i .yjfg/ i;6 мм2 прошло 2 ¦ 1019 электронов.
Дано
f = 2 с
5 = 1,6 мм2 =1,6- 10л
Л^ = 2-1019
Решение
е
5'
Q = Ne,
;' =
Л
[Ответ ) j =
= 1 А/мм2.
Плотность тока в проводнике
\=пе{\),
где (v) — скорость упорядоченного движения зарядов в проводнике; п — кон-
центрация зарядов.
? 3?^fiy По медному проводнику сечением 0,8 мм2 течет ток 80 мА. Най-
дите среднюю скорость упорядоченного движения электронов
вдоль проводника, предполагая, что на каждый атом меди приходится один сво-
бодный электрон. Плотность меди р = 8,9 г/см3.
Дано
5 = 0,8 мм2 = 0,8- Ю-'м2
7 = 80 мА = 8- 102А
п = п'
р = 8,9 г/см3 =
= 8,9- 103кг/м3
М = 63,5-10 кг/моль
е = 1,6-1(Г19 Кл
Л^Л = 6,02 1023 моль-1
/ —
п =
I
S
Решение
j
5> j = ne(v),
п, ^а NAp
NAP I \
м ^и''
Ml
NApeS -
С Ответ J
(v) - 7,4 мкм/с.
суммарный импульс электронов в прямом проводе
длиной / = 500 м, по которому течет ток / = 20 А.
Дано
/ = 500 м
7 = 20 А
от = 9,11-10~31 кг
е = 1,6-1(Г19Кл
Р — ?
Решение
p-Nm(v), j = ne(v), n = — ,
. I IN,,
J = ~, V = Sl, - = —e(v),
/ V II xr / \ mH
(v) = —, p = Nm(v) =
Ne e
> = 5,69 10 8 кг • м/с.
C 79 1 Определите общее сопротивление между
^ У представленной на рисунке, если Щ
Л3 = ^ = щ = 2 Ом, /^ = 4 Ом.
точками
= 1 Ом,
А и
*2 =
В
= з
цепи,
Ом,
Дано
Л, = 1 Ом
R2 = 3 Ом
Я3 = #, = /^ = 2 Ом
&; = 4 Ом
Л —?
Решение
Рисунок б) — эквивалентная схема.
а) 1
Лз
^2365 =
^2365 '
б)
^12365^4
^12365 + ^
С Ответ Л r = \,2Om.
Определите сопротивление проволочного каркаса, имеющего фор-
му куба, если он включен в цепь между точками А и В. Сопротив-
ление каждого ребра каркаса г - 3 Ом.
Дано
= 3 Ом
Решение
а)
А
Л—7
Рисунок б) — эквивалентная схема.
г г г _Ъг
~3+6 + ^~ 6 '
QOmeem
А
о—
В
-о
б).
Вольтметр, включенный в сеть последовательно с сопротивлени-
ем Rl, показал напряжение t/j = 198 В, а при включении после-
довательно с сопротивлением R2 - 2R] показал t/2 = 180 В. Определите со-
противление Ri и напряжение в сети, если сопротивление вольтметра г = 900 Ом.
I/,
r =
*2
и
Дано
= 198 В
= 180 В
900 Ом
= 2Л,
?
9
<7-
с-
/? — -
Я1
Решение
const
2СЛ-1/, '
J.
Ji
t/2
t/ =
<7
R^+r
r
C/r
Л2 + г
+ r) =
+ r)
r
U2BR
(R
Л ^
t/
?2+r '
l + r)>
l , |
Цепи на рисунке амперметр показывает силу тока / = 1,5 А.Сила
тока через сопротивление R, равна /j = 0,5 А. Сопротивление
Л2 = 2 Ом, Л3 = 6 Ом. Определите сопротивление Л,, а также силу токов 12
и /3, протекающих через сопротивление R2 и R$.
Дано
/ = 1,5 А
/, = 0,5 А
Л2 = 2 Ом
Л3 = 6 Ом
R, —?
Решение
/ = /, + /2 + /3, [/ = const,
Rx = {I~h)R*R\ 72= — = Mia 73 = A^L.
/ " ( Ome^W ^ Л, = з Ом, А = 0,75 A, 73 = 0,25 A.
Через лампу накаливания течет ток, равный 0,6 А. Температура воль-
фрамовой нити диаметром 0,1 мм равна 2200 °С. Ток подводится
медным проводом сечением 6 мм2. Определите напряженность электрического поля:
1) в вольфраме (удельное сопротивление при 0 °С ро = 55 нОм ¦ м, температур-
ный коэффициент сопротивления а = 0,0045 °С~'); 2) в меди (р = 17 нОм • м).
Дано
7 = 0,6 A
rf = 0,l mm=10-1m
/ = 2200 °C
5 = 6 мм2
p0 = 55 нОм • м =
— 5510"8 Ом • м
a = 0,0045 °C-'
p = 17 нОм ¦ м =
= 1,7- 10-8Om-m
!)?,—? 2) E2 — ?
1)
Ji
2)
(
Решение
E
P
j\=YE\= — > P\
p\
I I
5, nd2l^ "'
?2
2 P '
Ответ j i) e
/
~5'
i = 45,8
47
7p
?2-P72-5-
B/m;2) ?2 = 1,7mB/m
По алюминиевому проводу сечением 5 = 0,2 мм2 течет ток
/ = 0,2 А. Определите силу, действующую на отдельные свобод-
ные электроны со стороны электрического поля. Удельное сопротивление алю-
миния р - 26 нОм ¦ м.
5 = 0,2
7 = 0,2
p = 26
= 2,6
e = \,6
F —?
Дано
мм2 = 0,2 • 10 m2
A
нОм•м =
¦ 10"8Om-m
Ю-19 Кл
F
I
5
(
Решение
= eE,
E
P
j = yE =
E-If>
E~ 5'
Ответ ^ F =
P
4,16 -101 H.
7
5
Ip
Электрическая плитка мощностью 1 кВт с нихромовой спиралью
предназначена для включения в сеть с напряжением 220 В. Сколь-
ко метров проволоки диаметром 0,5 мм надо взять для изготовления спирали,
если температура нити равна 900 °С? Удельное сопротивление нихрома при 0 °С
р0 = 1 мкОм • м, а температурный коэффициент сопротивления а - 0,4 • 10~3 К4.
Дано
Р=\ кВт=103Вт
U = 220 В
</ = 0,5 мм = 0,5- 10м
? = 900 °С
р0 = 1 мкОм • м =
= 10Om-m
а = 0,4-10 К-1
/ — ?
Р =
С -
Решение
и2
R '
7id2
4 '
Г Ответ Л /
г U2S U2nd2
Pp 4Ppn(l + at)"
= 6,99 м.
Два цилиндрических проводника одинаковой длины и одинаково-
го сечения, один из меди, а другой из железа, соединены парал-
лельно. Определить отношение мощностей токов для этих проводников. Удель-
ные сопротивления меди и железа равны соответственно 17 и 98 нОм • м.
Дано
5, = S2 = S
Pi = 17 нОм • м =
= 1,7- Ю^Ом-м
р2 = 98 нОм • м =
= 9,8- 10-8Омм
Решение
U - const
U2S
Pi/'
Р —
U2S
P2r
Pi
(Ответ
Сила тока в проводнике сопротивлением R = 120 Ом равномерно
возрастает от /0 = 0 до /тах = 5 А за время г = 15 с. Определите
^делившееся за это время в проводнике количество теплоты.
Дано
Я = 120 Ом
r = 15c
Решение
dQ=I2Rdt,
/ = ,
> = jd6 = j^i?/2df = -/
Ответ j 2 = 15 кДж.
Сила тока в проводнике сопротивлением Л =100 Ом равномерно
убывает от /0 = 10 А до / = 0 за время т = 30 с. Определите вы-
делившееся за это время в проводнике количество теплоты.
С Ответ j Q = 100 кДж.
Определите напряженность электрического поля в алюминиевом
проводнике объемом V -10 см3, если при прохождении по нему
постоянного тока за время t = 5 мин выделилоськоличество теплоты Q = 2,3 кДж.
Удельное сопротивление алюминия р = 26 нОм • м.
/ =
Q
p
F,
Дано
= 10 см3=10-5
= 5 мин = 300 с
= 2,ЗкДж = 2,3
= 26 нОм ¦ м =
= 2,6- 10-8Ом
м3
•103Дж
м
Решение
Vt
?2 ,—
w = — E-Jw)
Р
QOmeem^ e = o,\a\ в/м.
- \Qp
V Vt
Ш Плотность электрического тока в медном проводе равна 10 А/см2.
Определите удельную тепловую мощность тока, если удельное
сопротивление меди р = 17 нОм ¦ м.
С Ответ j w =
170 Дж/(м3-с).
Определите ток короткого замыкания источника ЭДС, если при
внешнем сопротивлении R х = 50 Ом ток в цепи 1Х = 0,2 А, а при
#,=110 Ом— /2 = 0,1 А.
я.
h =
R2
h =
4з
Дано
= 50 Ом
0,2 А
= 110 Ом
= 0,1 А
?
Решение
j *
JK3 '
J f
J2 R2+r'
I2R2-I,RX
j -
h /
с
+ г)=/2(Я2+г),
12R2-I\RX
Г Ответ j
1Ю = 1,2 А.
3.92SI) В цепь, состоящую из батареи и резистора сопротивлением R = 8 Ом,
включают вольтметр, сопротивление которого Лг=800 Ом, один
раз последовательно резистору, другой раз — параллельно Определите внут-
реннее сопротивление батареи, если показания вольтметра в обоих случаях
одинаковы.
Г Ответ j r = 0,
= 0,08 Ом.
На рисунке Л,= Л2 = Лз = 100 Ом. Вольтметр показывает
Uv = 200 В, сопротивление вольтметра Rv= 800 Ом. Определи-
те ЭДС батареи, пренебрегая ее сопротивлением.
Дано
Ом
Uу = 200 В
Rv= S00 Ом
Решение
/, = I у + I2 ,
На рисунке сопротивление потенциометра Л = 2000 Ом, внутрен-
нее сопротивление вольтметра Ry-5000 Ом, 1/0 = 220 В. Опре-
делите показание вольтметра, если подвижный контакт находится посередине
потенциометра.
Дано
R =2000 Ом
Як=5000 Ом
Uo = 220 В
/,=/2=//2
Решение
_
Я/2-/0
Я/2+Я/
Ответ j uv=ioo в.
Определите ЭДС # и внутреннее сопротивление г источника
тока, если во внешней цепи при силе тока 4 А развивается мощ-
ность 10 Вт, а при силе тока 2 А мощность 8 Вт.
Дано
/,=4 А
7? =10 Вт
/2 = 2 А
Р2 = 8 Вт
& — ?
г —?
Решение
#=I(R+r),
г =
{Ответ )^=5,5В; г = 0,75 Ом.
Даны четыре элемента с ЭДС &= 1,5 В и внутренним сопротивле-
нием г = 0,2 Ом. Как нужно соединить эти элементы, чтобы по-
лучить от собранной батареи наибольшую силу тока во внешней цепи, имею-
щей сопротивление R = 0,2 Ом? Определите максимальную силу тока.
Дано
#¦=1,5 В
г = 0,2 Ом
R = 0,2 Ом
Решение
Р=п&1-1 —г [пит —
т
соответственно число
последовательно и параллельно соединенных элемен-
тов]> f = 4n«>
дР дР
— =0, — =
д! dl
п
• —г
т
-
m
-
m
т
mR= nr
т + п = к
ц/{Ответ ) /тах = 7,5А~
ЭДЁИИ На рисунке Я,=Я2=50 Ом, Л3=100 Ом' С = 50 нФ. Определи-
те ЭДС источника, пренебрегая его внутренним сопротивлением,
если заряд на конденсаторе Q = 2,2 мкКл.
С
Дано
R{=R2= 50 Ом
R з=100 Ом
С = 50 нФ = 5- 10s Ф
Q = 2,2 мкКл =
= 2,2- 10~* Кл
Л —?
Решение
с с
u = i R^ ,
R, + R2
П( R + R 1
CRXR2
А
в
CRlR2
R
. {Ответ
На рисунке Ry=R, R2=2R, R3=3R, R4= 4Л. Определите за-
ряд на конденсаторе.
Дано
R2=2R
Q-i
Решение
/?23Д, 20/?
= =
С
Лэ
/?2 +-I
ип
29 Л
29
¦-иос.
29 °
т
B плоек™ конденсатор, расстояние между пластинами которого
d = 5 мм, вдвигают стеклянную пластину (е = 7) с постоянной ско-
ростью v = 50 мм/с. Ширина пластины Ъ = 4,5 мм, ЭДС батареи F = 220 В. Оп-
ределите силу тока в цепи батареи, подключенной к конденсатору.
d
E
V
b
I
Дано
-5 мм- 5 • 10
= 7
- 50 мм/с - 5 ¦
- 4,5 мм - 4,5
.- 220 В
9
3M
io-2
io-J
м/с
M
/-
dp
a'--
Решение
~d7'
- o'vb dt,
?-1, E =
&
7'
? d% V/////////////////A
dP=?0(?-
[)vb dt,
= eo(e-l)--vb.
d
Два источника тока с ЭДС <*,=2Ви«?, = 1,5Ви внутренними
сопротивлениями г, = 0,5 Омиг2 = 0,4 Ом включены параллель-
но сопротивлению R = 2 Ом. Определите силу тока через это сопротивление
Дано
/,=2B
<*2 = 1.5 В
r, = 0,5 Ом
r2 = 0,4 Ом
Л-2 Ом
Решение
i-i+i
ml?'*; ^
t
Г ^r2 + &2r\ 1 \
Rrx + rxr2 + Rr2 "
1
1
?2
R
1 1 1 1
^/=.0,
775 а.
На рисунке 8{ = ^1=3i, -Rj=48 Ом,
R2 = 24 Ом, падение напряжения U2 на
сопротивлении R2 равно 12 В. Пренебрегая внутрен-
ним сопротивлением элементов, определите: 1) силу т ^ j g.
тока во всех участках цепи; 2) сопротивление Л3. т т т
Q Ответ J \) /, = 0,25 А, /2 = 0,5 А, /3 = 0,75 А; 2) Я3 = 16 Ом.
На рисунке <* = 2 В, ^=60 Ом, Л2 = 40 Ом, Я3 = Д) = 20 Оми
^ = 100 Ом. Определите силу тока /G через гальванометр.
Дано
ё =2 В
/^ = 60 Ом
Л2 = 40 Ом
Я3 = д, = 20 Ом
Rq = 100 Ом.
Решение
/3 + /с=/4;
т п | т О in У
а)
4 = 0,2,
4/4-2/G = 0,2 -> /4=-i
6/,+10/с
l,2+24/G
10
= 2, 134/G=-0,2, IG = -1,49-10 A
( Ответ | ^c = Ь49 мА, направлен в сторону, противоположную пер-
^ ^ воначально выбранной.
На рисунке Щ = Ю В, <% = 20 В, ^ = 40 В, а сопротивления
Rt = R2 = R3 = R = IO Ом. Определите силу токов, протекающих
через сопротивления G) и через источники ЭДС (/'). Внутреннее сопротивле-
ние источников ЭДС не учитывать.
Дано
<*j=10 В
<«, = 20 В
<% = 40 В
R] = R2 = R3 = R=W Ом
Решение
Выберем направления а)
токов (рисунок б).
«2
ь-
/3 • 10 = 20,
/3 = 2 А,
/2.10 = 30 ,
/2 = 3 А,
/,-10+3-10=40;
/,=1 А;
/З'=3 А, 7^ = 0, /,' = -2 А,
/,' направлен в сторону, противоположную первоначально выбранной.
ГЬтвет Л /, = 1 а, /2 = з а, /3 = 2 а,
/,' = 2 А, /^ = 0, Ц = 3 А.
3.3. Электрический ток в металлах,
в вакууме и газах
Определите минимальную скорость электрона, необходимую для
ионизации атома водорода, если потенциал ионизации атома во-
дорода U, = 13,6 В.
Дано
?/,=13,6 В
е = 1,6 109 Кл
т~ 9?1110~31 кг
ft __ о
Решение
eU> 2 ' Vmn V « "
СЪтвет J wmin = 2,19 мм/с.
Отношение работ выхода электронов из платины и цезия
^Pt/^Cs ~ '>58 ¦ Определите отношение минимальных скоростей
теплового движения электронов, вылетающих из этих металлов.
QOmeemj
Работа выхода электрона из металла А - 2,5 эВ. Определите ско-
рость вылетающего из металла электрона, если он обладает энер-
гией ^ = 108 Дж.
Дано
А = 2,5 эВ = 4- 10-19Дж
^ = 108 Дж
Решение
mv
= W-A, v =
-А)/т .
Г Ответ J и = 1,15
Мм/с.
Термопара железо — константан, постоянная котором
а = 5,3' 10 В/К и сопротивление R = 15 Ом, замкнута на галь-
ванометр. Один спай термопары находится в сосуде с тающим льдом, а второй
помещен в среду, температура которой не известна. Определите эту темперах) -
ру, если ток, протекающий через гальванометр, / = 0,2 мА, а внутреннее со-
противление гальванометра г = 150 Ом.
С Ответ Л т = 896 к.
Термопара <*. железо—константан и соединенный с нею после-
довательно гальванометр включены, как показано на рисунке, где
<*" — батарея с ЭДС, равной 1,5 В. Полное сопротивление потенциометра равно
15 кОм. Холодный спай термопары находится в сосуде с тающим льдом. По-
стоянная термопары а = 5,3 1О~5 В/К. Определите температуру горячего спая
термопары, если при сопротивлении RAB = 150 Ом сила тока в цепи гальвано-
метра равна нулю. Внутренним сопротивлением батареи пренебречь.
Дано
if =1,5 В
RAC =15 кОм =
= 1,5- 104Ом
а-5,3-Ю 5 В/К
То = 273 К
RAB = l50 Ом
/с = 0
Г —?
Решение
(I - сила тока в потенциометре),
G ft
RAB RAC .
1
7
R.<c a °-
i .
с
. i—¦
в
Г Ответ ) T =
556 К.
Определите работу выхода электронов из металла, если плотность
тока насыщения двухэлектродной лампы при температуре 7j рав-
на у,, а при температуре Т2 равна j2.
Дано
h
h
Решение
h - cyi e
-А/(кТ)
А —?
А = -
С Ответ j
Ш
Выведите зависимость скорости изменения плотности термоэлек-
тронного тока насыщения от температуры.
С
Ответ j э/н
¦ = С\2Т + -\е-А/(кТ)
дТ { к
Ток насыщения при несамостоятельном разряде /нас = 6,4 пА. Най-
дите число пар ионов, создаваемых за 1 с внешним ионизатором.
^нас
Г = 1
N -
Дано
= 6,4 пА = 6,4
с
-?
10-12А
Решение
Q~2Ne,
2е
нас
Q
t
2Ne
t
QOmeem
N = 2.
Потенциал ионизации атома водорода U, = 13,6 В. Определите
температуру, при которой атомы имеют среднюю кинетическ> ю
энергию поступательного движения, достаточную для ионизации.
т
Дано
= 13,6 В
7
eU,
Решение
Зкт
Т =
2eU,
Ък
Qprneem )г = ю5кк.
Определите температуру, соответствующую средней кинетичес-
кой энергии поступательного движения электронов, равной рабо-
те выхода из вольфрама, если поверхностный скачок потенциала для вольфра-
ма 4,5 В.
Дано
= 4,5 В
Решение
= е<р,
т — ?
Ж
Ответ
3.4. Магнитное поле
В однородное магнитное поле с индукцией В = 0,1 Тл помещена
квадратная рамка площадью 5 = 25 см2. Нормаль к плоскости
амки составляет с направлением магнитного поля угол 60°. Определите вра-
цающий момент, действующий на рамку, если по ней течет ток 7=1 А.
в-
о
I-
м
0,1
25
60°
1 А
г
Дано
Тл
см2 = 25 10-4м2
р
Решение
М = [рга,В],
М- /)m5sina,
М- ISBsina.
ч
1' ,
\У" ,«
Г Ответ
'=217 мкН-м.
В однородном магнитном поле с индукцией В = 0,5 Тл находится
прямоугольная рамка длиной а = 8 см и шириной Ь = 5 см, со-
держащая N = 100 витков тонкой проволоки. Ток в рамке / = 1 А, а плоскость
рамки параллельна линиям магнитной индукции. Определите. 1) магнитный
момент рамки; 2) вращающий момент, действующий на рамку
С Ответ j
/?m=0,4 А-м:;
= 0,2Н-м.
Основные физические постоянные
Постоянная Больцмана к = 1,38-10~23 Дж/К
-19
Элементарный заряд е = 1,6 10 Кл
Масса покоя электрона те = 9,11 ¦ 10 кг
Основные физические постоянные
Электрическая постоянная е0 = 8,85 10~12 Ф/м
Магнитная постоянная ц0 = 4л 10~7 Гн/м
Масса покоя протона тр = 1,627 107 кг
V 31Йщ9 ^ однородном магнитном поле с индукцией В = 1 Тл находится
' квадратная рамка со стороной а - 10 см, по которой течет ток
/ = 4 А. Плоскость рамки перпендикулярна линиям магнитной индукции. Оп-
ределите работу А, которую необходимо затратить для поворота рамки относи-
тельно оси, проходящей через середину ее противоположных сторон: 1) на 90°;
2) на 180°; 3) на 360°.
Ответ J \) ах = 0,
04 Дж; 2) А2 = 0,08 Дж; 3) Аъ = 0.
1 3 Д ХЩ*} Тонкое кольцо массой 10 г и радиусом R = 8 см несет заряд, рав-
номерно распределенный с линейной плотностью г = 10 нКл/м.
Кольцо равномерно вращается с частотой и = 15 с4 относительно оси, пер-
пендикулярной плоскости кольца и проходящей через ее центр. Определите:
1) магнитный момент рт кругового тока, создаваемого кольцом; 2) отноше-
ние магнитного момента к моменту импульса кольца.
Дано
т = Ю г =
R = 8 см = 0,08 м
г = 10 нКл/м
и = 15 с4
1) Ал -?
2)pjL-1
Решение
О г ¦ 2лгД
/ = — = -innxR, An
Т Т ™ w
S = лЯ2 , т = 1/я ,
рт = 2лп xR ¦ rtR2 = 2л2пгЯъ,
L - mvR, v = (oR - 2nnR >
pm/L = 2n2
y^Omeem j
Pm_ 1>52 ha• M2;2)
= 251 нКл/кг.
Принимая, что электрон в атоме водорода движется по круговой
орбите, определите отношение магнитного момента рт эквивален-
тного кругового тока к моменту импульса L орбитального движения электрона.
Q
pmeem
^=
=87,8 гкл/кг.
Определите магнитную индукцию В поля, создаваемого отрез-
ком бесконечно длинного провода, в точке, равноудаленной от
концов отрезка и находящейся на расстоянии R = 4 см от его середины. Длина
отрезка провода / = 20 см, а сила тока в проводе / = 10 А.
Дано
tf=4 см =4- 10'2м
/ = 20 см = 0,2 м
7 = 10 А
8 —?
Решение
В = J-^— (cosa, - cosa2),
1/2
a2 = 180° -a,.
Г Ответ j в = 46,4 мкТл.
Определите индукцию магнитного поля в центре проволочной
квадратной рамки со стороной а = 15 см, если по рамке течет ток
7=5 А.
Дано
а = 15 см = 0,15 м
' = 5 А
Решение
В,= ——¦—(cosa, -cosa2),
1 4л:(а/2Г ' 2''
В=4-— 2-cosa,.
4л (а/2)
,1
{Ответ j 5 = 37,7 мкТл.
По двум бесконечно длинным прямым параллельным проводам,
находящимся на расстоянии R-10 см друг от друга в вакууме,
текут токи /j = 20 А и 12 = 30 А одинакового направления. Определите маг-
нитную индукцию В поля, создаваемого токами в точках, лежащих на прямой,
соединяющей оба провода, если: 1) точка С лежит на расстоянии ц = 2 см ле-
вее левого провода; 2) точка D лежит на расстоянии г2 = 3 см правее правого
провода; 3) точка G лежит на расстоянии гъ = 4 см правее левого провода.
Дано
/, = 20 A
I2 = 30 A
R = lO см = 0,1 м
r, = 2 см = 0,02 м
r2 - 3 см = 0,03 м
r3 = 4 см = 0,04 м
2)^-?
Решение
2/,
2/,
4лг
2/2
Q Ответ J 1) в,= 0,25 мТл; 2) 5г = 0,23 мТл;
3) Щ = 0 .
По двум бесконечно длинным прямым параллельным проводни-
кам, расстояние между которыми d = 20 см, текут токи /, = 40 А
и 12 = 80 А в одном направлении. Определите магнитную индукцию В в точке А,
удаленной от первого проводника на гх = \2 см и от второго — на г2 = 16 см.
<S54>
А 123) По двум бесконечно длинным прямым параллельным проводникам,
V ' У расстояние между которыми d -15 см, текут токи /, = 70 А и
/2 = 50 А в противоположных направлениях. Определите магнитную индукцию В
в точке А, удаленной на г, = 20 см от первого и г2 = 30 см от второго проводника.
d =
h =
B-
Дано
15 см = 0,15 м
70 A
50 A
20 см = 0,2 м
30 см = 0,3 м
_?
Решение
Г2яг,' ,^4
/^—-
n *^0 2 1Э
2лгг2
В = В, + B2,
B = ^B2+B22+2BiB2 cos^
v\
/. 0 © 1г
d2 = i
2г,г7
4?2
r2 rxr2
С Ответ j 5 = 42,8 мкТл.
Напряженность Н магнитного поля в центре кругового витка с
магнитным моментом рт =1,5 А • м2 равна 150 А/м. Определите:
1) радиус витка; 2) силу тока в витке.
Дано
Я = 150 А/м
An = 1,5 А • м2
1) R —?
2) / — ?
Решение
R=l
= 2RH,
{Ответ)
1) Я = 11,7 см; 2) 7 = 35,1 А.
3.125 J Определите магнитную индукцию в центре кругового проволоч-
ного витка радиусом R = IO см, по которому течет ток 1 = 1 А.
С Ответ J s=6,28
икТл.
Определите магнитную индукцию на оси тонкого проволочного
кольца радиусом /? = 5 см, по которому течет ток / = 10 А, в точ-
ке А, расположенной на расстоянии d = 10 см от центра кольца.
Дано
R = 5 см = 0,05 м
/ = 10 А
^ = 10 см = 0,1 м
В —?
2nR
В, = —iL-
Решение
d5 = ifo.1^ = ftp / d/
4л: г2 4гг'(/г2 + ^2)'
dS ( = dS sin <p,'
sin^> = ¦
R
dl
dB2
, =0,
в
V
Qpmeem
мкТл.
j Определите магнитную индукцию В4 на оси тонкого проволоч-
ного кольца радиусом R = 10 см, в точке, расположенной на рас-
стоянии d =20 см от центра кольца, если при протекании тока по кольцу в
центре кольца 5=50 мкТл.
Ответ
вА = 4,47
Круговой виток радиусом R = 15 см расположен относительно
бесконечно длинного провода так, что его плоскость параллельна
проводу. Перпендикуляр, восставленный на провод из центра витка, является
нормалью к плоскости витка. Сила тока в проводе 1Х=\ А, сила тока в витке
12 - 5 А. Расстояние от центра витка до провода d = 20 см. Определите маг-
нитную индукцию в центре витка.
Дано
/?= 15 см = 0,15м
/,=1 А
I2=5 A
d = 20 см = 0,2 м
В
Решение
\ B7tdf BRJ
[Ответ j 5 = 21,2 мкТл.
В однородном магнитном поле с индукцией В = 0,2 Тл находится
прямой проводник длиной / = 15 см, по которому течет ток / = 5 А.
На проводник действует сила F = 0,13 H. Определите угол а между направле-
ниями тока и вектором магнитной индукции.
Дано
В = 0,2 Тл
/ = 15 см = 0,15м
/=5 А
>F = 0,13 H
•а — ?
Решение
F = /[dl,B], F=//5sina,
F . F
sina= , a - arcsin .
IIB' IIВ
Г Ответ j a =
60°
Сборник uuv\
C 130 J ^° прямому горизонтально расположенному проводу пропускают ток
/j = 10 А. Под ним на расстоянии R = 1,5 см находится параллель-
ный ему алюминиевый провод, по которому пропускают ток /2 = 1,5 А. Опреде-
лите, какой должна быть площадь поперечного сечения алюминиевого провода,
чтобы он удерживался незакрепленным. Плотность алюминия р = 2,7 г/см3,
/l =
R =
h =
P =
=
10
1,5
1,5
2,7
2,7
Дано
A
см= 1,5- 10 2м
A
г/см3 =
• 103кг/м3
F
I
Г —
s-
Решение
2kR
Hohh
,,=\ lnR
">g' 2nR
mg
I
pbg,
pVg
I
—?
2nRpg
Ответ ^ 5 = 7,55 io9m2.
Два бесконечных прямолинейных параллельных проводника с оди-
наковыми токами, текущими в одном направлении, находятся друг от
друга на расстоянии R. Чтобы их раздвинуть до расстояния 2R, на каждый санти-
метр длины проводника затрачивается работа А = 138 нДж. Определите силу тока в
проводниках.
Дано
R
2R
Л = 138 нДж =
= 1,38- 10-7Дж
/ = 1 см=10м
/, = /, = /
Решение
2лх
2лх
2R
-2, 2R
-2, 2R , .1,
2л { x 2
2л { х 2л
R
Г Ответ
г=10 А.
Контур из провода, изогнутого в форме квадрата со стороной
а = 0,5 м, расположен в одной плоскости с бесконечным прямо-
линейным проводом с током / = 5 А так, что две его стороны параллельны
проводу. Сила тока в контуре /, = 1 А. Определите силу, действующую на контур,
если ближайшая к проводу сторона контура находится на расстоянии 6 = 10 см.
Направления токов указаны на рисунке.
Дано
а = 0,5 м
/,=1 А
6 = 10 см = 0,1 м
F — ?
Решение
F2=-F4,
2л
b b+aj 2ж(а+Ь)Ь
{Ответ j
F=4,17 mkH.
2л(Ь+а)
Десятичные приставки к названиям единиц
Т —тераA012)
Г —гига A09)
М —мегаA06)
к — кило A03)
д—дециA0-')
с — сантиA0)
м — миллиA0)
мк — микро A0**)
н — нано A0~9)
п —пикоA02)
ф—фемтоA045)
а —атгоA018)
Прямоугольная рамка со сторонами а = 40 см и Ъ - 30 см распо-
ложена в одной плоскости с бесконечным прямолинейным прово-
дом с током / = 6 А так, что длинные стороны рамки параллельны провод\
Сила тока в рамке /, = 1 А. Определите силы, действующие на каждую из сто-
рон рамки, если ближайшая к проводу сторона рамки находится на расстоянии
По тонкому проволочному полукольцу радиусом R = 50 см течет
ток / = 1 А. Перпендикулярно плоскости полукольца возбуждено
однородное магнитное поле с индукцией В= 0,01 Тл. Найдите силу, растяги-
вающую полукольцо. Действие на полукольцо магнитного поля подводящих
проводов и взаимодействие отдельных элементов полукольца не учитывать.
с = 10 см, а ток в
Дано
а = 40 см = 0,4 м
Ъ = 30 см = 0,3 м
/ = 6 А
/, = 1 А
с = 10 см = 0,1 м
F2 — ?
F3-'>
ней сонаправлен току /
решение
dF = /[dl,B],
ип1
~ 2лг'
[*»]-f.
F = jdF = jlBdl,
а а
С f Г R Al f 7 ^°
F,
^
1 Л1 Цо
с 2
с
ч>
л:с
»F,
a
1,
a
Дано
Л=50 см = 0,5 м
/=1 А
5=0,01 Тл
F — ?
Решение
dF = /[dl, B],
л , x
(dl, В) = л/2 , та
о
dF=IBdl, /
dl=Rda, f
dF - IBR da,
X
dFx = dF cosa , dF, = dF sina,
я
Fx = j IBR cosa da = M(sina)|" = 0,
0
У1
X
X
X
X dF,
s\a
X
X dFx
- - 5f,
/\a '
\X dF, X
1 *.*
X X
Fy = jlBRsina da = /ЯД-cos a) |* = 2IBR
2л:/
2лг
= Fy = 2IBR.
Ответ
= 4,8 mkH,
, = 1,2 mkH,
F2 = l,66 mkH,
F4 = 1,66 mkH.
QOmeem^ f = 0,01 н.
Применяя закон Ампера для силы взаимодействия двух параллель-
ных токов, выведите числовое значение магнитной постоянной ц0.
Закон Ампера
где dF — сила, действующая на элемент dl проводника с током /, помещен-
ный в магнитное поле с индукцией В.
4л: R
= /,= 1 А,
=1 м,
dF
dl
= 2 10"' Н/м,
dF
d/
4л:
2I2
10 H/A2= 4л: 10 Гн/м.
Электрон движется прямолинейно с постоянной скоростью
v = 0,2 Мм/с. Определите магнитную индукцию В поля, созда.
ваемого электроном в точке, находящейся на расстоянии г = 2 нм от электрона
и лежащей на прямой, проходящей через мгновенное положение электрона ц
составляющей угол а = 45° со скоростью движения электрона.
V-
r =
a-
B-
0,2
Дано
Мм/с = 0,2
2 нм = 2- 10-9
45°
_?
•106м/с
м
Решение
HQfiQ[\r]
В~ 4жг> '
_ unev . -
5 = ir°-_-sina. /*
4лгг2 f
0
Ответ
1
1,
)
У-е,
В = 566 мкТл
Определите напряженность Н поля, создаваемого прямолиней-
но равномерно движущимся со скоростью v = 5000 км/с элект-
роном, в точке, находящейся от него на расстоянии г = 10 нм и лежащей на
перпендикуляре к v, проходящем через мгновенное положение электрона.
(
Ответ
= б37А/м.
Согласно теории Бора, электрон в атоме водорода движется вокр> г
ядра по круговой орбите радиусом г = 52,8 пм. Определите маг-
нитную индукцию В поля, создаваемого электроном в центре круговой орбите
Дано
г = 52,8 пм = 5,28-10-"м
В —?
Решение«
(v;r)=|.
0o.fi
4л: г2
mv
1 g
4яе0 г:
Г Ответ j
В = 1,25 10'" Тл
\о
Электрон движется в однородном магнитном поле с индукцией
В = 0,1 Тл по окружности. Определите угловую скорость враще-
[ электрона.
Решение
?л = д[хВ), |е| = е,
•2 егВ
mv
= evB,
v--
т
2жг 2жт
2лг еВ
@ = =
еВ Т т
fOmee^Jw = ll6^o рад/с
Электрон, обладая скоростью v = 10 Мм/с, влетел в однородное
магнитное поле перпендикулярно линиям магнитной индукции.
Индукция магнитного поля В = 0,1 мТл. Определите нормальное и тангенци-
альное ускорения электрона.
С Ответ Л ап = const = 1,76 • l О14 м/с2; ах = 0.
В однородном магнитном поле перпендикулярно линиям магнит-
ной индукции движется прямой проводник длиной 40 см. Опре-
делите силу Лоренца, действующую на свободный электрон проводника, если
возникающая на его концах разность потенциалов составляет 10 мкВ.
Модуль силы Ампера
dF = IBdlsma,
где а — угол между векторами dl и В.
f 3.142 } Электрон, ускоренный разностью потенциалов U = 0,5 кВ, дви-
~~—^— жется параллельно прямолинейному длинному проводнику на
расстоянии г = 1 см от него. Определите силу, действующую на электрон, если
через проводник пропускать ток 7 = 10 А.
Дано
U = 0,5 кВ = 500
г = 1 см = 10м
7=10 А
F — ?
В
eU =
v = .l
Решение
mv'
2 '
от 2пг
F = evB =
nr
COmeemj f = 4,24io16h.
f 3.143 1 Протон, ускоренный разностью потенциалов U = 0,5 кВ, влетая в
однородное магнитное поле с магнитной индукцией 5 = 2 мТл,
движется но окружности. Определите радиус этой окружности.
U = 0,5
Q = \,6-
от =1,67
5=2 м
R —?
Дано
кВ = 500 В
109 Кл
¦Ю-27 кг
Тл = 2- 10'Тл
QU =
QvB-
Решение
mv"
2 '
myl R-
R '
v =
mv
QB
[2QU
V от '
JbnQU
QB '
Г Ответ
(=1,61 M.
3i 144 I Электрон, влетев в однородное магнитное поле с магнитной индук-
цией В = 2 мТл, движется по круговой орбите радиусом R = 15 см.
Определите магнитный момент рт эквивалентного кругового тока.
B =
R =
Pm
Дано
2 мТл = 2- 10-3Тл
15 см = 0,15 м
_ 9
Pm
Решение
2tzR
V
S = tzR2,
mv
evB- ,
7 =
v =
e
-,
e5/?
m '
Pm =
2т
ГОтветЛ Pm = o,632 па м2.
Электрон, обладая скоростью v -1 Мм/с, влетает в однородное
магнитное поле под углом а = 60° к направлению поля и начина-
ет двигаться по спирали. Напряженность магнитного поля Я = 1,5 кА/м. Опре-
делите: 1) шаг спирали; 2) радиус витка спирали.
Дано
u = l Mm/c= 106m/c
a = 60°
Я = 1,5 кА/м =
= 1,5- 103A/m
1) /7 —?
v =
v\ =
v2 =
T =
Решение
vt + v2, z J > x „
и cosa,
v >^
wsina, ,A у
IttR 2itR г' ' /' -Жн
v2 v sin a
2) R —1
, 2тг7?
/7 = v{T = v cosa =
v sina
2nvm cosa
mv2
~R
R =
v2m _ usma-w
Г Ответ J\) h = 9,49 мм; 2) R = 2,62 мм.
Электрон движется в однородном магнитном поле с магнитной
индукцией В - 0,2 мТл по винтовой линии. Определите скорость i
электрона, если радиус винтовой линии R = 3 см, а шаг h = 9 см.
Г
Ответ
) = 1,17 Мм/с.
Pfl Определите, при какой скорости пучок заряженных частиц, дви-
гаясь перпендикулярно скрещенным под прямым углом однород-
ным электрическому (Е = 100 кВ/м) и магнитному (В = 50 мТл) полям, не от-
клоняется
Дано
? = 100 кВ/м= 105
5 = 50 мТл = 5 • 10
v —?
В/м
2Тл
Решение
F, = 6E, F
?>?=?>иВ, v
л = е[
Е
~ В'
v,B],
~Fn-
Г
бтвет
> = 2 Мм/с.
В однородное магнитное поле с магнитной индукцией 0,2 Тл пер-
пендикулярно линиям магнитной индукции с постоянной скорос-
тью влетает заряженная частица. В течение 5 мкс включается электрическое
поле напряженностью 0,5 кВ/м в направлении, параллельном магнитному полю
Определите шаг винтовой траектории заряженной частицы.
Дано
5=0,2 Тл
t -5 мкс = 5 - 10 6 с
Е = 0,5 кВ/м = 500 В/м
А —?
QvB
Решение
mv2 rl
~ R '
mv], tJ, =
2л:/?
г;
^_
w
2nm
~ QB ' e"
QEt ,
w
ли
Qh,
T 2nEt
В
С Ответ) h = 7,S5cu.
Ионы двух изотопов с массами т] = 6,5 10 26 кги щ = 6,8-10 26 кг,
ускоренные разностью потенциалов U = 0,5 кВ, влетают в одно-
родное магнитное поле с индукцией В = 0,5 Тл перпендикулярно линиям ин-
[укции Принимая заряд каждого иона равным элементарному электрическо-
iy заряду, определите, на сколько будут отличаться радиусы траекторий ионов
[зотопов в магнитном поле.
Дано
m, = 6,5 106 кг
/^2 = 6,8 10~26 кг
t/ = 0,5 кВ
5=0,5 Тл
Л2-Д-?
Решение
evB=mv2 , Л
r то;2
/е- ! |2m?/ /¦
^~5V « ' ^
/иг)
= ^5'
\2eU
i m '
B\ e ^ ^ i
QOmeem
,-Я, =0,917 мм.
Циклотроны позволяют ускорять протоны до энергий 20 МэВ.
Определите радиус дуантов циклотрона, если магнитная индук-
ция 5 = 2 Тл.
Дано
Т = 20 МэВ =
= 3,2- 10ч2Дж
/я = 1,67 10~27 кг
5=2 Тл
R
Решение
mu
Ш
f = .
ew5 = -
mv
R
R =
mvz _ -j2Tm
evB eB
COmeemJ r > 32,3 см.
Определите удельный заряд частиц, ускоренных в циклотроне в
однородном магнитном поле с индукцией В = 1,7 Тл при частоте
ускоряющего напряжения v = 25,9 МГц.
Дано
В=],1 Тл
v = 25,9 МГц =
= 2,59- 107Гц
Решение
2nR 1 , ,
= — (условие синхронизма),
V V
mv
R
= QvB,
v = 2tzvR .
т
Q _ v 2nvR __ 2nv
m~ RB~ RB ' В
Ответ
^ = 9,57 107 Кл/кг.
m
Протоны ускоряются в циклотроне в однородном магнитном поле
с индукцией В = 1,2 Тл. Максимальный радиус кривизны траек-
тории протонов составляет R= 40 см. Определите: 1) кинетическую энергию
протонов в конце ускорения; 2) минимальную частоту ускоряющего напряже-
ния, при которой протоны ускоряются до энергий Т = 20 МэВ.
Дано
В =1,2 Тл
R = 40 см = 0,4 м
7] = 20 МэВ =
= 3,2' 1012Дж
т-f
Решение
evB =
mv
R
eBR
m
Т =
mv2 e2B2R2
2m
v, =¦
m
1 /27]
2nR\ m
С Ответ j
Г = 11 МэВ, г1=24,6 МГц.
В случае эффекта Холла для натриевого проводника при плотнос-
ти тока j = 150 А/см2 и магнитной индукции В - 2 Тл напряжен-
ность поперечного электрического поля Ев - 0,75 мВ/м. Определите концент-
|ацию электронов проводимости, а также ее отношение к концентрации ато-
:ов в этом проводнике. Плотность натрия р = 0,97 г/см3.
Дано
/ = 150 А/см2 =
= 1,5- 10бА/м2
В =2 Тл
?в - 0,75 мВ/м =
= 0,75- 103В/м
р = 0,97 г/см3 = 970 кг/м1
M=23-1O кг/моль
п —?
и
— 9
и'
«Я*
7^
и' =
и
Решение
- evB,
#А ^А
jBM
eEBNA p
С Ответ j
В '
и- j ;В
ew eEB
NAP
М '
и = 2,5 1028 м-3, п/п' = 0,984
Определите постоянную Холла для натрия, если для него отноше-
ние концентрации электронов проводимости к концентрации ато-
мов составляет 0,984. Плотность натрия р = 0,97 г/см3.
Дано
njri = 0,984
р = 0,97 г/см3 = 970 кг/м3
М=23 10 кг/моль
R -?
Решение
еп
п = 0,984л' ,
Л'а Л'а"
1
0,984ел' 0,S
Л'аР
М '
hi
»84еЛ^А р
(
Ответ
.Ю0 м3/(А-с).
?ЙШ Определите, во сколько раз постоянная Холла у меди больше, чем
' * у алюминия, если известно, что в алюминии на один атом в сред-
нем приходится два свободных электрона, а в меди — 0,8 свободных электро-
нов. Плотности меди и алюминия соответственно равны 8,93 и 2,7 г/см].
(Ответ
Дано
рСи = 8,93 г/см3 =
= 8,93- 103кг/м3
рм = 2,7 г/см3 =
= 2,7- 103кг/м3
МСи = 63,5-10 кг/моль
Л/А1 = 27-10~3 кг/моль
(А-
ЯА|
Решение
^Cu ~ > ЛА, -
епса епм
"си=0-8иСи. иа,=0,8и;,,
„' = ^РСи _^РА1
Л*си МА1
^Си _ ИА1 2"А|
Лд| "си 0,8/^и '
Лси _ 2рмМСи
ra\ 0,SpCuMM
Холловская поперечная разность потенциалов
d
где В — магнитная индукция; / — сила тока; d — толщина пластинки;
1
R = — — постоянная Холла (п — концентрация электронов).
р.п
Через сечение медной пластинки толщиной d = 0,2 мм пропус-
кается ток / = 6 А. Пластинка помещается в однородное магнит-
ное поле с индукцией 5 = 1 Тл, перпендикулярное ребру пластинки и направ-
лению тока. Считая концентрацию электронов проводимости равной концент-
рации атомов, определите возникающую в пластинке поперечную (холловс-
кую) разность потенциалов. Плотность меди р = 8,93 г/см3.
Дано
d = 0,2 мм = 2- КГ'м
1=6 А
В=\ Тл
р = 8,93 г/см3 =
= 8930 кг/м3
п = п
-3
М = 63,5 10 кг/моль
9
Решение
Aip
еЕв = е--*- = evB,
а
А<р = vBa,
I = jS = nev ¦ ad ,
S = ad,
IBa _ 1 IB
en d
1
Л//Д
= n =
vm м
QOmeemj
Определите циркуляцию вектора магнитной индукции по окруж-
ности, через центр которой перпендикулярно ее плоскости прохо-
дит бесконечно длинный прямолинейный провод, по которому течет ток / = 5 А.
1 = 5 A
^Bdl -
L
Дано
-?
Решение
^д\ = ^В,А1 = ^1,
L L
(Ответ ") г
у — j фВсИ =6,
,28 мкТл • м.
I 3.158 J Определите циркуляцию векто-
^>> S ра магнитной индукции для
замкнутых контуров, изобра-
женных на рисунке, если сила тока в обоих
проводниках I = 2 А.
( Ответг ) ,. <¦
у J 1) Ф
В dl = 2,51 мкТл ¦ м;
2) <j)Bdl =5,02мкТл-м;
L
3) <j>Bdl =0.
i 15*) } По прямому бесконечно длинному проводнику течет ток / = 10 А
Определите, пользуясь теоремой о циркуляции вектора В , ма) -
нитную индукцшо В в точке, расположенной на расстоянии г - 10 см от про-
водника.
Дано
/=10 А
г - 10 см = 0,1 м
В — ?
Решение
Ъсг
Г Ответ j в =
20 мкТл.
(*Ж 160J Используя теорему о циркуляции вектора В, рассчитайте магнит-
ен НУ10 индукцию поля внутри соленоида (в вакууме), если число
витков соленоида равно N и длина соленоида равна / .
UHHIp Соленоид длиной / = 0,5 м содержит N = 1000 витков. Опреде-
лите магнитную индукцию В поля внутри соленоида, если со-
противление его обмотки R = 120 Ом, а напряжение на ее концах U = 60 В.
Дано
I = 0,5 м
Л =120 Ом
U = 60 В
В—?
Решение
ту
Rl
Qpmeem
В соленоиде длиной / = 0,4 м и диаметром D = 5 см создается
магнитное поле, напряженность которого Н - 1,5 кА/м. Опреде-
лите: 1) магнитодвижущую силу Fm ; 2) разность потенциалов U на концах
обмотки, если для нее используется алюминиевая проволока (р - 26 нОм ¦ м)
диаметром d = 1 мм.
Дано
/ = 0,4 м
Z) = 5 см = 5- 10м
Я = 1,5кА/м=1,5-103А/м
р = 26 нОм • м =
= 26- 10 " Ом- м
d = 1 мм = 10 3 м
2) U — ?
Решение
L L
l,=2n—-N = ;
1_
4pDl
S = -
/ = i
Я/ = /
4pDHl
~1Г
Qpmeem J 1} Fm = 600 A. 2)U = 312 B.
Определите, пользуясь теоремой о циркуляции вектора В, индук-
цию и напряженность магнитного поля на оси тороида без сер-
дечника, по обмотке которого, содержащей 200 витков, протекает ток 2 А. Вне-
шний диаметр тороида равен 60 см, внутренний — 40 см.
Дано
N = 200
1=2 А
?>, = 60 см = 0,6 ь
D2 = 40 см = 0,4 м
Я — ?
Решение
N1
[ОтветЛ в = 0,32 мТл; Я = 255 А/и.
Определите магнитный поток сквозь площадь поперечного сече-
ния катушки (без сердечника), имеющей на каждом сантиметре
длины п = 8 витков. Радиус соленоида г = 2 см, сила тока в нем / = 2 А.
Дано
я = 8 см = 800 м
г = 2 см = 2' 10 2м
1=2 А
Ф; — ?
Решение
Ф, = 55 , 5 = лг2,
В = цоп1, Фх= цйп1лг2 .
Ответ J ф, = 2,53 мквб.
Внутри соленоида с числом витков N = 200 с никелевым сердеч-
ником (/i = 200) напряженность однородного магнитного поля
Я = 10 кА/м. Площадь поперечного сечения сердечника 5 = 10 см2. Опреде-
лите: 1) магнитную индукцию поля внутри соленоида; 2) потокосцепление.
Дано
N = 200
/г = 200
Я = 10 кА/м=10'А/м
5 = 10 см2 =103м2
1) В — ?
2) Ф — ?
Решение
В- ипиН
Ф = BSN.
1) 5 = 2,51 Тл; 2) Ф = 0,502 Вб.
В однородное магнитное поле напряженностью Я = 100 кА/м
помещена квадратная рамка со стороной а = 10 см. Плоскость
рамки составляет с направлением магнитного поля угол а = 60°. Определите
магнитный поток, пронизывающий рамку.
Дано
Я = 100 кА/м
а = 10 см = 0,1 м
а = 60°
Ф —?
Решение
Ф = BS cosa,
Ф = цоа' Н cosa.
С Ответ) ф = 628 мквб.
( 3.167 ^ Поток магнитной индукции через площадь поперечного сечения
-—-- соленоида (без сердечника) равен Ф = 1 мкВб. Длина соленоида
/ = 12,5 см. Определите магнитный момент рт этого соленоида.
ф =
/ =
Рт
Дано
= 1 мкВб=10~*Вб
12,5 см =0,125 м
В =
г
Решение
My,
Ф/
fi0NS'
Ф = 55
Рт ~IS
= Му5,
лг Ф/
/V .
Ответ ) Рт = 0,1А м1
В одной плоскости с бесконечным прямолинейным проводом с
током / = 20 А расположена квадратная рамка со стороной, дли-
на которой а = 10 см, причем две стороны рамки параллельны проводу, а рас-
стояние d от провода до ближайшей стороны рамки равно 5 см. Определите
магнитный поток Ф , пронизывающий рамку.
Дано
/=20 А
а = 10 см = 0,1 м
d=5 см = 0,05м
Ф — ?
Решение
в=
2жг'
<f+a
ф=
2лг
2лг
j г 2лг " а
(d+a)
' = 0,44 мкВб.
Прямой провод длиной / = 20 см с током / = 5 А, находящийся в
однородном магнитном поле с индукцией В = 0,1 Тл, расположен
перпендикулярно линиям магнитной индукции. Определите работу сил поля,
под действием которых проводник переместился на 2 см.
{Ответ j Azz
2 мДж.
Квадратный проводящий контур со стороной / = 20 см и током
/ = 10 А свободно подвешен в однородном магнитном поле с маг-
нитной индукцией В = 0,2 Тл. Определите работу, которую необходимо совер-
шить, чтобы повернуть контур на 180° вокруг оси, перпендикулярной направ-
лению магнитного поля.
Дано
1 = 20 см = 0,2 м
7 = 10 А
8 = 0,2 Тл
а = 180°
л —?
Решение
= [pm,B],
М= ртВsince,
А = J М йа = JIBI2 sina da = -IBl2 cosa|* = 2IB12
= 0,16 Дж.
В однородном магнитном поле с магнитной индукцией В = 0,2 Тл
находится квадратный проводящий контур со стороной / = 20 см
и током / = 10 А. Плоскость квадрата составляет с направлением поля угол в
30°. Определите работу удаления контура за пределы поля.
{
Ответ
а = о,О4 Дж.
Круговой проводящий контур радиусом г = 5 см и током / = 1 А
находится в магнитном поле, причем плоскость контура перпен-
дикулярна направлению поля. Напряженность поля равна 10 кА/м. Определите
работу, которую необходимо совершить, чтобы повернуть контур на 90° вокруг
оси, совпадающей с диаметром контура.
Дано
г = 5 см = 5 • 10~2 м
1 = 1 А
Я = 10 кА/м=104А/м
ж
а = —
2
А -?
Решение
M=Mda
M=PmBsina,
я/2 ж/2
A- J Mda = Inr2pi^H [sina dcr = цйл1г2Н.
о о
С Ответ Л а = 98,
= 98,7 мкДж.
..._ЯВ
3.173 j В однородном магнитном поле с магнитной индукцией В = 1 Тл
находится плоская катушка из 100 витков радиусом г = 10 см,
плоскость которой с направлением поля составляет угол уЗ = 60°. По катушке
течет ток 7 = 10 А. Определите: 1) вращающий момент, действующий на ка-
тушку; 2) работу для удаления этой катушки из магнитного поля.
(
Ответ
l) М = 15,7 Н-м; 2)Л = 27,2Дж.
Круглая рамка с током E = 15 см2) закреплена параллельно маг-
нитному полю ( В = 0,1 Тл), и на нее действует вращающий мо-
мент М = 0,45 мН • м. Определите силу тока, текущего по рамке.
С Ответ Л / =
3 А.
3.5. Электромагнитная индукция
Соленоид диаметром d = 4 см, имеющий N = 500 витков, поме-
щен в магнитное поле, индукция которого изменяется со скорос-
тью 1 мТл/с. Ось соленоида составляет с вектором магнитной индукции угол
а = 45° • Определите ЭДС индукции, возникающую в соленоиде.
Дано
d = 4 см = 4- 10м
W = 500
— = 1 мТл/с=10-3Тл/с
а = 45°
? 9
с( •
Решение
%=-—, <& = NBScosa, 5 = ^4~'
, | d nd2 6B
\Щ\= (NBScosa)-N — cosa.
Г Ответ Л 9i =444мкв
3.176 J в магнитное поле, изменяющееся по закону В = В0 coswl
(Во = 0,1 Тл, @ = 4 с'), помещена квадратная рамка со стороной
а = 50 см, причем нормаль к рамке образует с направлением поля угол а = 45°.
Определите ЭДС индукции, возникающую в рамке в момент времени ( = 5 с.
Дано
B= Bo cosw/
Во = 0,1 Тл
ш = 4 с '
а = 50 см = 0,5 м
а = 45°
/ = 5 с
Решение
ср
Ф = BS cosa ,
d ,
^ = (Воа coscut cosa) -
df
= -В0а2 cosa—(coswt)= Bq^w cosa-sinwt.
dt
— ?
Ответ J % =64
= 64 mB.
Кольцо из алюминиевого провода (р = 26 нОм • м) помещено в
магнитное поле перпендикулярно линиям магнитной индукции
Диаметр кольца D= 30 см, диаметр провода d = 2 мм. Определите скорость
изменения магнитного поля, если ток в кольце / = 1 А.
p =
D =
1 =
dB
dl
26
2,6
30
1 A
—
Дано
нОм•м =
¦ IO-'Om'm
cm = 0,3 м
tM-2- 10~3м
?
v -
vi -
dB
dt
Решение
i
do d
dt dtK"UJ
«jdB
dt
16/p
<j ndl * - w
s- 4 , », /л.
4 dr '
С
Ответ
dB
— =0,11 Tji/c.
at
Г 3
Плоскость проволочного витка площадью 5 = 100 см2 и сопро-
тивлением /? = 5 Ом, находящегося в однородном магнитном поле
напряженностью Я = 10 кА/м, перпендикулярна линиям магнитной индукции.
При повороте витка в магнитном поле отсчет гальванометра, замкнутого на
виток, составляет 12,6 мкКл. Определите угол поворота витка.
О
я=
Дано
100 см2=10м2
5 Ом
10 кА/м=104А/м
= 12,6 мкКл =
= 1,26- 10~5Кл
RdQ
Ф7 =
Решение
? =t
dr ' ' '
dФ
d/
^0Я5 cos a,
IR-RdQ
dt
Ф, - ^Я^ ,
а —?
cosa =
RdQ
Г Ответ
a = 60°.
В однородное магнитное поле с индукцией В = 0,3 Тл помещена
прямоугольная рамка с подвижной стороной, длина которой
/ = 15 см. Определите ЭДС индукции, возникающей в рамке, если ее подвиж-
ная сторона перемещается перпендикулярно линиям магнитной индукции со
скоростью v = 10 м/с.
Дано
В = 0,3 Тл
/ = 15 см = 0,15м
и = 10 м/с
Решение 0
®
0 I
dt
ф = В5 = в/х, 0 л 0 0 в
dx , ,
dt~ V' ''''"
if, =-—
Г Ответ ") щ = o,45 в.
Две гладкие замкнутые металлические шины, расстояние между
которыми равно 30 см, со скользящей перемычкой, которая мо-
жет двигаться без трения, находятся в однородном магнитном поле с индукци-
ей В = 0,1 Тл, перпендикулярном плоскости контура. Перемычка массой т = 5 г
скользит вниз с постоянной скоростью v = 0,5 м/с. Определите сопротивление
перемычки, пренебрегая самоиндукцией контура и сопротивлением остальной
части контура.
Дано
а = 30 см = 0,3 м
В = 0,1 Тл
w = 5 r = 5- 10-3кг
v = 0,5 м/с
R —?
_ BavBa B2a2v
Решение
t
BS Bavt п
= = Bav,
t t
А
ч
.Рл
' V
' mg
mg=FA=IBa, 1 = Ж,
Ва
mg
mg
Г Ответ
mOm.
В катушке длиной / = 0,5 м, диаметром d - 5 см и числом витков
N = 1500 ток равномерно увеличивается на 0,2 А за одну секунду,
На катушку надето кольцо из медной проволоки (р = 17 нОм • м) площадью
сечения SK - 3 мм2. Определите силу тока в кольце.
/ =
d =
N
d/
d7
P =
I*
Дано
0,5 м
= 5 см = 0,05 м
= 1500
= 0,2 A/c
= 17 нОм•м =
1,7- 10-8Om/m
= 3 мм2 = 3- 10м2
9
vis
T -
J -
Решение
- L^
"dt'
N2nd2 61
-^ 4/ dt'
K\ R_?k
R sK'
NSKddI
4//Э d/ j
r MOW
Ответ
v2s
" ?
Л&сс/2 d/
-^ 4/ «J/1
npd
J IK = 1,66 mA.
Катушка диаметром d = 2 см, содержащая один слой плотно при-
легающих друг к другу N = 500 витков алюминиевого провода
сечением S = 1 мм2, помещена в магнитное поле. Ось катушки параллельна
линиям индукции. Магнитная индукция поля равномерно изменяется со скоро-
стью 1 мТл/с. Определите тепловую мощность, выделяющуюся в катушке, если
ее концы замкнуты накоротко. Удельное сопротивление алюминия р = 26 нОм/м.
ДГ -
5 =
dB
~d7
P =
P -
Дано
2 см = 2- 10м
Sflrt
1 мм2 = 10-" m2
= 1 mTji/c= 10-3Tji/c
26 нОм • м =
26 • 10^9 Ом • м
_ 9
K
/ =
с
Решение
ifl - ДГИС
d/
- ТТЙЫ P '
Ответ j p=
s-*d2 R-ol
' S- 4 ' *-"s,'
4d/J 5l ^Af^2
/Эл:^ 16p idJ
0,302 mkBt.
В однородном магнитном поле (В = 0,1 Тл) вращается с постоян-
ной угловой скоростью со = 50 с вокруг вертикальной оси стер-
жень длиной / = 0,4 м. Определите ЭДС индукции, возникающей в стержне,
если ось вращения проходит через конец стержня параллельно линиям магнит-
ной индукции.
(Ответ
В однородном магнитном поле с индукцией В = 0,02 Тл равно-
мерно вращается вокруг вертикальной оси горизонтальный стер-
жень длиной / = 0,5 м. Ось вращения проходит через конец стержня парал-
лельно линиям магнитной индукции. Определите число оборотов в секунду,
при котором на концах стержня возникает разность потенциалов U = 0,1 В.
Дано
В = 0,02 Тл
/ = 0,5 м
t/ = 0,1 В
и —?
%
Ф
а
Решение
dO>
d/ '
= В5 cosa,
= 0,
X
х /
/
1
X
X
s
/
X
X
0*
X
/x
^x
X
в
^ X
\
1
X
d/'
я/2 ... 2лг
d<p = o) dt,
I2
dS = — d«> = —o) dt,
dS d(p\ 2 2
d/ dA2 J 2
си = Inn -
2U
Bl
2 >
U
лВ12
Г Ответ J „ =
= 6,37 с.
В однородном магнитном поле (В = 0,2 Тл) равномерно с часто-
той и = 600 мин"' вращается рамка, содержащая N = 1200 вит-
ков, плотно прилегающих друг к другу. Площадь рамки S = 100 см2. Ось вра-
щения лежит в плоскости рамки и перпендикулярна линиям магнитной индук-
ции. Определите максимальную ЭДС, индуцируемую в рамке.
Дано
В =0,2 Тл
и = 600 мин4 = 10 с
N = 1200
5 = 100 см2=10~2м2
Решение
1 d/
Ф = NBS cosa ,
= a)t- 2nnt,
?, = -NBS—(cos2nnt) = NBS ¦ 2nn-sin2nnt,
at
= 2nnNBS.
Ответ
= 151 B
Магнитная индукция В поля между полюсами двухполюсного
генератора равна 1 Тл. Ротор имеет 140 витков (площадь каждого
витка S = 500 см2). Определите частоту вращения якоря, если максимальное
значение ЭДС индукции равно 220 В.
С Ответ )
п = 5 с
В однородном магнитном поле (В = 0,2 Тл) равномерно вращает-
ся прямоугольная рамка, содержащая N = 200 витков, плотно
прилегающих друг к другу. Площадь рамки S -100 см2. Определите частот)
вращения рамки, если максимальная ЭДС, индуцируемая в ней, %1шк =12,6 В
Г Ответ
1= 5 с"
В однородном магнитном поле равномерно вращается прямоуголь-
ная рамка с частотой и= 600 мшг1. Амплитуда индуцируемой ЭДС
= 3 В. Определите максимальный магнитный поток через рамку.
СОтвет Л фтах = 47,7 мВб.
Катушка длиной / = 50 см и диаметром d = 5 см содержит
= 200 витков. По катушке течет ток / = 1 А. Определите:
1) индуктивность катушки; 2) магнитный поток, пронизывающий площадь ее
поперечного сечения.
Дано
/ =
d
N
I
1)
2)
= 50 см
= 5 см
= 200
= 1 A
I—?
ф — ¦;
= 0,5m
= 0,05 м
)
Решение
N2S
N2 nd1
I 4 '
ndl
* LI
Ф = —
N
С Ответ J 1) Z = 197 мкГн; 2) Ф =985нВб.
Длинный соленоид индуктивностью Z, = 4 мГн содержит
N = 600 витков. Площадь поперечного сечения соленоида
S = 20 см2. Определите магнитную индукцию поля внутри соленоида, если
сила тока, протекающего по его обмотке, равна 6 А.
Дано
L = 4 мГн = 4- 10-3Гн
N = 600
5 = 20 см2 = 2- 1Ом2
1=6 А.
В—?
Решение
ф п
Ф = LI, Ф = NBS , в-—- = -—.
NS NS
Г Ответ ^ в = о,о2 Тл.
Две длинные катушки намотаны на общий сердечник, причем ин-
дуктивности этих катушек Ц = 0,64 Гн и 1^ = 0,04 Гн. Опреде-
лите, во сколько раз число витков первой катушки больше, чем второй.
к
N
Дано
= 0,64 Гн
= 0,04 Гн
- 9
2
L-
Решение
N2S
к N2
ki N2'
С Ответ j
N.
¦ = 4.
Определите, сколько витков проволоки, вплотную прилегающих
друг к другу, диаметром d = 0,5 мм с изоляцией ничтожной тол-
щины надо намотать на картонный цилиндр диаметром D = 1,5 см, чтобы по-
лучить однослойную катушку индуктивностью Z = 100 мкГн?
Дано
d = 0,5 мм = 5' 10м
D=l,5 см =1,5- 10м
1 = 100 мкГн=10-4Гн
N —?
Решение
L=
= Nd,
N2S
S = -
4 '
Ad
AdL
Ответ
f 3.193.) Определите индуктивность соленоида длиной / и сопротивлени-
— ем R, если обмоткой соленоида является проволока массой т
(принять плотность проволоки и ее удельное сопротивление соответственно за
Р и р').
/
R
Р
Р'
т
L
Дано
— ?
Решение
N2S
L /ло/л
S-яг2 J
о — —
Bя
Л^25
J / '
/ J Л
Р'1' }
/>= 1™Л l= n2 я^ = i"° mR С Ответ j L_ ^0 mR
~\рр'' Ц° I BяЮ2 Ая1 рр' ' ^ ' 4я1 рр<
Сверхпроводящий соленоид длиной / = 10 см и площадью попе-
речного сечения 5 = 3 см2, содержащий N = 1000 витков, может
быть подключен к источнику ЭДС if = 12 В. Определите силу тока через 0,01 с
после замыкания ключа.
Дано
/ = 10 см = 0,1 м
5 = 3 см2 = 3
TV = 1000
«?=12 В
/ = 0,01 с
Решение
L = цоц
R = Q,
N2S
N2S
? + ?=№,
И =—#=—!-
61
d7
if =
/ = •
Kit
Ответ
= 31M.
( 3.195 ) Через катушку, индуктивность L которой равна 200 мГн, проте-
кает ток, изменяющийся по закону / = 2cos3/. Определите: 1) за-
кон изменения ЭДС самоиндукции; 2) максимальное значение ЭДС самоин-
дукции.
(
Ответ
= 1,2 В.
В соленоиде без сердечника, содержащем N = 1000 витков, при
увеличении силы тока магнитный поток увеличился на 1 мВб.
Определите среднюю ЭДС самоиндукции {$,), возникающую в соленоиде, если
изменение силы тока произошло за 1 с.
Дано
ЛГ = 1000
ДФ = 1 мВб=10-3Вб
&t = l с
Решение
W At
(Ответ ) (,) = 1В
Имеется катушка индуктивностью L = 0,1 Гн и сопротивлением
R = 0,8 Ом. Определите, во сколько раз уменьшится сила тока в
катушке через / = 30 мс, если источник тока отключить и катушку замкнуть
накоротко.
Дано
1 = 0,1 Гн
R = 0,8 Ом
/ = 30 мс = 30- 10'с
-У- 7
Решение
/=/ое''\
Г Ответ J
= 1,27.
Определите, через сколько времени сила тока замыкания достиг-
нет 0,95 предельного значения, если источник тока замыкают на
катушку сопротивлением Л = 12 Ом и индуктивностью 0,5 Гн.
С
Ответ
= 125мс.
Катушку индуктивностью L = 0,6 Гн подключают к источнику
тока. Определите сопротивление катушки, если за время ( = 3 с
сила тока через катушку достигает 80% предельного значения.
Дано
L = 0,6 Гн
1 = 3 с
/=80%/0
R —?
/=/0
R
Решение
и-
0,8/0
R
L In 0,2
- — Г = In 0,2,
л= —
С Ответ J л=322
мОм.
Бесконечно длинный соленоид длиной / = 0,8 м имеет од-
нослойную обмотку из алюминиевого провода массой
т = 400 г. Определите время релаксации г для этого соленоида. Плотность
и удельное сопротивление алюминия равны соответственно р = 2,7 г/см] и
р' = 26 нОм ¦ м.
С Ответ j г = 712мкс.
<288>
С OQpllllk J.I U'
Соленоид диаметром d = 3 см имеет однослойную обмотку из
плотно прилегающих друг к другу витков алюминиевого провода
(р = 26 нОм ¦ м) диаметром dx - 0,3 мм. По соленоиду течет ток /0 = 0,5 А
Определите количество электричества Q, протекающее по соленоиду, если его
концы закоротить.
d
P
'о
Q
Дано
= 3 см = 3
= 26
= 2,6
= 0,3
= 0,5
«Ом •
•ю-8
MM =
A
• 10
M =
Ом
3-
2M
• м
10-4м
/ = /o
e-J
0
I — a
Решение
R
e l ,
°° R
/d/ = /0Je"t'
0
#2S
u-l
dt
0N
I
2S
= Nd,,
*=д,
S =
nd1
/, = JtdN,
Q =
4d]P 4dN 16p
4 '
/n
Г Ответ Л 2 = 42,7 мкКл.
при размыкании и замыкании цепи
Катушка индуктивностью L = 1,5 Гн и сопротивлением R, = 15 Ом
и резистор сопротивлением Л2 = 150 Ом соединены параллельно
и подключены к источнику, электродвижущая сила которого Р = 60 В, через
ключ К. Определите напряжение на зажимах катушки через /, = 0,01 с и t2 = 0,1 с
после размыкания цепи.
Дано
L = 1,5 Гн
/г! = is Ом
Я, =150 Ом
«^ = 60 В
/, =0,01 с
t2 = 0,1 с
С/,-?
Решение
/o=v p^^-i
/ = /ое t ,
ДЛ,
^ШШ?—
U = IR2, f л
l/,=—Я2е L , f/2 = —Я2е L~ .
Rx 2 Л,
ГОтвет j
Ux = 200 В, t/2 = 0,01 В.
Две катушки намотаны на один общий сердечник. Определите их
взаимную индуктивность, если при скорости изменения силы тока
в первой катушке dlx /dt = 3 А/с во второй катушке индуцируется ЭДС ?, 2 = 0,3 В.
d/,
?.2
Дано
/dt = 3 A/c
= 0,3 В
9
Решение
hi = ^2i >
dO21
-.2- d, - ^2.
d/,
d/'
Ф21 =
Г
i21-
^2
d/,
d/
где r = L/R — время релаксации (Z, — индуктивность, R—сопротивление). С Ответ ) Ц2 = 0,1 Гн.
10*
( 3.204 Ц Два соленоида (Ц = 0,64 Гн, Z2 = 1 Гн) одинаковой длины и прак-
"'"" тически равных сечений вставлены один в другой. Определите
взаимную индуктивность соленоидов.
Дано
Z, = 0,64 Гн
1г = 1 Гн
S, = S2 = 5
Решение
N,=
(Ответ
Две катушки намотаны на один сердечник. Индуктивность первой
катушки L, = 0,12 Гн, второй — I2 = 3 Гн. Сопротивление второй
катушки R2 = 300 Ом. Определите силу тока 12 во второй катушке, если за вре-
мя At = 0,01 с силу тока в первой катушке уменьшить от 1Х = 0,5 А до нуля.
Трансформатор с коэффициентом трансформации 0,15 понижает
напряжение с 220 В до 6 В. При этом сила тока во вторичной об-
мотке равна 6 А. Пренебрегая потерями энергии в первичной обмотке, опреде-
лите сопротивление вторичной обмотки трансформатора.
Дано
N2/Nt= 0,15
Ux = 220 В
U 2 = 6 В
/2 = 6 А
R2 — ?
р
Л2
(
Решение
= UU ? = :&, *=^С/„ t2 = I2R2 + U2,
?2-и2 Ш/щ-щ
Ответ ^Rj = 4,5 Ом.
3.207
Автотрансформатор, понижающий напряжение с t/, = 6 кВ до
U2 = 220 В, содержит в первичной обмотке N] = 2000 витков. Со-
противление вторичной обмотки R2 -1 Ом. Сопротивление внешней цепи (в сети
пониженного напряжения) R = 12 Ом. Пренебрегая сопротивлением первичной
обмотки, определите число витков во вторичной обмотке трансформатора.
и2
R2
R =
N2
Дано
= 6 кВ = 6 • Ю3 В
= 220 В
= 2000
= 1 Ом
12 Ом
7
Решение
?2 = [2R2+U2,
">-№^)\
С Ответ j 7
/2
~ N. ' 2~ U, '
_и2
R '
с/, Ч л ;
= 79.
Трансформатор, понижающий напряжение с 220 В до 12 В, со-
держит в первичной обмотке ЛГ, = 2000 витков. Сопротивление
вторичной обмотки R2 =0,15 Ом. Пренебрегая сопротивлением первичной
обмотки, определите число витков во вторичной обмотке, если во внешнюю
цепь (в сети пониженного напряжения) передают мощность Р = 20 Вт.
^2
^1
Л2
Р =
^2
Дано
= 220 В
= 12 В
= 2000
= 0,15 Ом
20 Вт
9
#2
Я
С
Решение
?2NX
-h*2 + V2- и_
Ответ j
р--
2 ,
^2
= ^2>
U2, N2-^^+U2j^.
= 111.
Сила тока / в обмотке соленоида, содержащего N = 1500 вит-
ков, равна 5 А. Магнитный поток Ф через поперечное сечение
соленоида составляет 200 мкВб. Определите энергию магнитного поля в соле-
ноиде.
Дано
1=5 А
N = 1500
Ф = 200 мкВб =
= 2- 10-^Вб
W —?
W
L--
Решение
и2
/
/ '
ф =
W-
MD,=Z/,
N<t>xI
2 '
С Ответ Л ^ = 0,75 Дж.
Обмотка электромагнита, находясь под постоянным напряжени-
ем, имеет сопротивление Л = 15 Ом и индуктивность Z = 0,3 Гн.
Определите время, за которое в обмотке выделится количество теплоты, рав-
ное энергии магнитного поля в сердечнике.
Дано
Л = 15 Ом
Z = 0,3 Гн
t —?
Решение
Q = W,
U = const >
~ = I2Rt.
W = -
_L_
2R
Qpmeem
Объемная плотность энергии однородного магнитного поля
длинного соленоида
щ Соленоид без сердечника с однослойной обмоткой из проволоки
диаметром d = 0,5 мм имеет длину / = 0,4 ми поперечное сече-
ние 5 = 50 см2. Какой ток течет по обмотке при напряжении U = 10 В, если за
время t = 0,5 мс в обмотке выделяется количество теплоты, равное энергии
поля внутри соленоида? Поле считайте однородным.
d = 0,5
/ = 0,4
5 = 50
[/ = 10
f = 0,5
Q = W
I 9
Дано
мм = 5 • lO^1
M
см2 = 5- 10
В
мс = 5 • 10м (
Г Ответ J I
M
M2
= 995
IUt
mA.
Решение
W, Q-IUt ,
5/, / = ЛИ ,
M /
u° i A(V
~ 2rf2 '
w.
N
W
I-
J/
If
— У ,
_ i
~ d'
H2I2Sl MoI2Sl
d2-2n, 2d2 '
2Utd2
HoSl
Индуктивность соленоида при длине 1 м и площади поперечного
сечения 20 см2 равна 0,4 мГн. Определите силу тока в соленоиде,
при которой объемная плотность энергии магнитного поля внутри соленоида
равна 0,1 Дж/м3.
Дано
1 = 1 м
5 = 20 см2 = 2- 10м2
1 = 0,4 мГн = 4- КГТн
w = 0,l Дж/м3
Решение
_w_
w~ v'
1Z/2
w — ,
2 5/
i = Pf-- СОтветЛ / = 1А.
Объемная плотность энергии магнитного поля внутри соленоида
длиной 50 см и малого диаметра равна 0,7 Дж/м3. Определите
магнитодвижущую силу этого соленоида.
Дано
w - 0,7 Дж/м3
/ = 50 см = 0,5 м
9
Решение
w — -
тт
Mi = М ,
-l\
Ответ J Fm= 528 а.
Тороид с воздушным сердечником содержит 20 витков на 1 см.
Определите объемную плотность энергии в тороиде, если по ею
обмотке протекает ток 3 А.
N
1
1 =
w
= 20
3 А
?
Дано
см ' = 2 •
103м '
w =
{в,
Решение
w
У'
dl = /i0NI,
W =
Bl =
В2
2ц0ц
fioNl
Л=1
В2
2ц0 '
W —
— 1
2\l)
(
122ц0 2\l
С Ответ j
w = 22,6 Дж/м3.
3.6. Магнитные свойства вещества
Докажите, что отношение числового значения орбитального маг-
нитного момента рт электрона к числовому значению его орби-
тального механического момента Le (гиромагнитное отношение орбитальных
моментов) одинаково для любой орбиты, по которой движется электрон.
(Ответ ) g = —.
_^/ 2т
Принимая, что электрон в невозбужденном атоме водорода движет-
ся по круговой орбите радиусом г = 52,8 пм, определите: 1) магнит-
ный момент рт эквивалентного кругового тока; 2) орбитальный механичес-
кий момент Le электрона; 3) исходя из полученных числовых значений, гиро-
магнитное отношение орбитальных моментов, доказав, что оно совпадает со
значением, определяемым универсальными постоянными.
Дано
г = 52,8 пм = 52,8- 1041 м
т = 9,11-101 кг
1) An"?
2L-?
3) g — ?
Решение
mv2 e2
г 4лепг
evr e
2 4| 7ze0m
Le = mvr = —J '
е | mr
Le 2m
ГОтвет
i) Pm= 9,25¦ io~24 a ¦ м2;
2) Ie=l,05-10-34 кг-м2/с;
3) g=87,8 ГКл/кг.
( 3.217 J В пространство между полюсами электромагнита подвешиваюг-
ся поочередно висмутовый и алюминиевый стержни. Оказалось,
что при включении электромагнита алюминиевый стержень располагается вдоль
магнитного поля, а висмутовый — поперек магнитного поля. Объясните разли-
чие в их поведении.
( % 21 иС\ ® однородное магнитное поле вносится длинный вольфрамовый
^ *" стержень (магнитная проницаемость вольфрама ft = 1,0176) Оп-
ределите, какая доля суммарного магнитного поля в эгом стержне определяет-
ся молекулярными токами.
В'
в
Дано
1,0176
?
Решение
B = /iofiH, B' = p0J,
J = xH, x = /*-U
В1 = цй{р-\)Н,
В'
В
= 0,0173.
Напряженность однородного магнитного поля в платине равна
5 А/м. Определите магнитную индукцию поля, создаваемого мо-
лекулярными токами, если магнитная восприимчивость платины равна 3,6 • 10 4
Я=5
Х = 3,6
Я' -9
Дано
А/м
¦ ю-4
to to
и и
Решение
U0J ,
иохН
J = xh,
С Ответ) в'= 2,26 нТл.
По круговому контуру радиусом г = 40 см, погруженному в жид-
кий кислород, течет ток / = 1 А. Определите намагниченность в
центре этого контура Магнитная восприимчивость жидкого кислорода
у=3,4-Ю-3.
Дано
r = 40 см = 0,4 м
/ = 1 A
10
~3
Решение
2r
С Ответ J
' = 4,25 mA/m.
||Р По обмотке соленоида индуктивностью 1 = 3 мГн, находящегося
в диамагнитной среде, течет ток / = 0,4 А. Соленоид имеет длину
/ = 45 см, площадь поперечного сечения 5 = 10 см2 и число витков N = 1000.
Определите внутри соленоида: 1) магнитную индукцию; 2) намагниченность
Дано
1 = 3 мГн = 3' 103Гн
/ = 0,4 A
/ = 45 см = 0,45 м
S = 10 см2=10м2
TV = 1000
5 — ?
./ — ?
Решение
N2S
я = —,
L/ /V/ I/
~ N2S I NS '
I/
tv2^0-
В = ЦфН,
I/ . W
С Ответ j 5 = 1,
= 1,2 мТл, J = 66 А/м.
(. 3.222 ] Соленоид, находящийся в диамагнитной среде, имеет длит
/ = 30 см. площадь поперечного сечения S = 15 см2 и число вит-
ков .V = 500 . Индуктивность соленоида L = 1.5 мГн, а сила тока, протекающе-
го по нему, / = 1 А. Определите: 1) магнитную индукцию внутри соленоида:
2) намагниченность внутри соленоида.
Ответ
Л 1) В = 2 мТл; 2) 7 = 75 А/м.
Г 3.223 J Индукция магнитного поля в железном стержне В = 1,2 Тл. Опре-
делите для него намагниченность, если зависимость 5(Я) для
данного сорта ферромагнетика представлена на рисунке.
Дано
5=1,2 Тл
В(Н)
J О
В = 1,2 Тл,
Я = 800 А/м (см. рисунок),
Решение
Д Тл
С Ответ j
"'" 0 400 800 Г200 ""**,
Я А/м
./ = 954
Железный сердечник длиной / = 0,5 м малого сечения (d « Г) со-
держит 400 витков. Определите магнитную проницаемость желе-
за при силе тока /=1 А. Используйте график из задачи 3.223
С Ответ)
По обмотке соленоида, в который вставлен железный сердечник
(график зависимости индукции магнитного поля от напряженно-
сти представлен в задаче 3.223), течетток /=4 А. Соленоид имеет длину / = 1 м,
площадь поперечного сечения S = 20 см2 и число витков N = 400. Определи-
те энергию магнитного поля соленоида.
Дано
1=4 А
/ = 1 м
5 = 20 см2 = 2- 10-3м2
JV = 400
W — ?
Решение
я = ^, W = M w = wv = ™s,.
I 2 2
С Ответ j
W = 2,24 Дж.
Обмотка тороида с железным сердечником имеет Л' = 151 виток.
Средний радиус г тороида составляет 3 см. Сила тока / через
обмотку равна 1 А. Определите для этих условий: 1) индукцию магнитного
поля внутри тороида; 2) намагниченность сердечника; 3) магнитную проница-
емость сердечника. Используйте график зависимости В от Я , приведенный
в задаче 3.223.
Г Ответ J 1) В = 1,2 Тл; 2) 7 = 954 кА/м; 3) ^ = 1,19103.
%'2Т J На железном сердечнике в виде тора со средним диаметром
d = 70 мм намотана обмотка с общим числом витков N = 600. В
сердечнике сделана узкая поперечная прорезь шириной b = 1,5 мм (рисунок к
задаче 3.228). При силе тока через обмотку / = 4 А магнитная индукция в про-
рези Во = 1,5 Тл. Пренебрегая рассеянием поля на краях прорези, определите
магнитную проницаемость железа для данных условий.
СОтвет j ц =
428.
На железном сердечнике в виде тора со средним диаметром
d = 70 мм намотана обмотка с общим числом витков N = 600
В сердечнике сделана узкая поперечная прорезь шириной Ъ - 1,5 мм. Магнит-
ная проницаемость железа для данных условий fi = 500. Определите при силе
тока через обмотку 1-4 А: 1) напряженность Я магнитного поля в железе,
2) напряженность Яо магнитного поля в прорези.
Дано
d = 10MM = l 10 2м
W = 600
6=1,5 мм = 1,5- 10 Зм
/1 = 500
/=4 А
1) Я — ?
2) Яо - ?
i
н,
Решение
Ш
7 \'Л
d Ж1^
ь
HGCd-b)+H0b = NI,
flQflH = flQH0 ,
N1
-b) + fib'
В=В0,
Яо =
- Ь)Н + ЬцН = N1,
{nd-b)+ fib
С Ответ J l) Я =
2,48 kA/m, 2) Яо = 1,24 МА/м
На рисунке качествен-
но представлены гис-
терезисные петли для
двух ферромагнетиков. Объясните,
какой из приведенных ферромагне-
тиков применяется для изготовле-
ния сердечников трансформаторов
и какой—для изготовления посто-
ЯННЫ.Х магнитов.
3.7. Основы теории Максвелла
для электромагнитного поля
Длинный цилиндрический конденсатор заряжается от источника
ЭДС. Пренебрегая краевыми эффектами, докажите, что ток сме-
щения в диэлектрике, заполняющем пространство между обкладками конден-
сатора, равен току в цепи источника ЭДС.
Дано
I » d
f = U
E
Решение
s
ly
' У/
D =
D =
2xr '
g
2яг/'
ТлгЮ = xl,
ЭД 1 dQ
dt ~ 2nrl dt '
CM J 2nd dt
dQ _ dQ
dt ~ dt
Inrl dt
S = 2лг1,
s dQ
2nd dt
2nrl dQ dQ
CM ~ 2nrl dt ~ dt ~
(
Ответ ) /c
Запишите полную систему уравнений Максвелла в интегральной
и дифференциальной формах и объясните физический смысл каж-
дого из уравнений. Зачем вообще необходима дифференциальная форма урав-
нений9
Запишите полную систему уравнений Максвелла для стационар-
ных полей (Е = const и В = const) в интегральной и дифферен-
циальной формах и объясните физический смысл каждого из уравнений.
Запишите уравнения Максвелла через поток вектора электричес-
кого смещения Фо, поток вектора магнитной индукции Фя , за-
ряд Q и силу тока /.
Докажите с помощью одного из уравнений Максвелла, что пере-
менное во времени магнитное поле не может существовать без
электрического поля.
B = I
rotE
Дано
КО
9
Решение
в-B(t) aB*o
dt
rotE =
dt
, rotE^O.
( Ответ J Есть вихревое электрическое поле.
™'ЩЙйВ Докажите' что уравнения Максвелла rotE =-dB/dt и divB = 0
совместимы, т. е. первое из них не противоречит второму.
Дано
ев
1) rotE = - —
; dt
2) divB=0
Совместимы 1) и 2) ¦— ?
Решение
dt
divrotE= div (-— ]=-—(divB),
\ dtJ dt
div rotE = 0;
2) divB = 0;
div В = const,
1) div В = const
С ОтвепГЛ 1)и
2) совместимы.
<304>
Ток, проходящий по обмотке длинного прямого соленоида радиу-
сом R, изменяют так, что магнитное поле внутри соленоида рас-
тет со временем по закону В = At2, где А — некоторая постоянная. Определи-
те плотность тока смещения как функцию расстояния г от оси соленоида.
Постройте график зависимости /СМ(У).
Дано
R
B=At2
А = const
Решение
JCM
dD
dt
Edl = -| — dS,
dt
r<R,
r>R,
-2At,
2лгЕ = uR- -2At,
= Atr,
Jcm - ~?0
E =
R'At
Jcm
= R, E=AtR,
./cm = ?0AR ¦
С
Omeem
e0AR2
*l*3^B!Pl) ® физике известно так называемое уравнение непрерывности
Ф j dS = , выражающее закон сохранения заряда Докажите,
что уравнения Максвелла содержат это уравнение. Выведите дифференциаль-
ную форму уравнения непрерывности.
Дано
at
Вывести из уравнений
Максвелла, записать
дифференциальную фор-
му уравнения непрерыв-
ности.
Решение
3D
4. Колебания и волны
4.1. Механические и электромагнитные колебания
tflyk Гармонические колебания величины i описываются уравнением
SEf
= 0,02 cos 6ж1 н— , м. Определите: 1) амплитуду колебаний;
ФЯ/с1/=[ у'н 6S (S —любая поверх- 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний.
ность, опирающаяся на замкнутый контур L),
jn dS = Ф Н, d/ - [ — dS . Рассмотрим бесконеч-
i i s д1
но малый контур, стянув его в точку, а поверхность
оставим конечной. Тогда | Я, d/ = 0.
Поверхность замкнута, поэтому можем записать: <р jn dS = -ф —- &S .
s s Э'
Используем III уравнение Максвелла и продифференцируем его по времени:
Ф j dS = —уравнение непрерывности в интегральной форме
Ы
v
С
) Определите силу тока смещения между квадратными пластинами
y конденсатора со стороной 5 см, если напряженность электричес-
кого поля изменяется со скоростью 4,52 МВ/(м • с).
Ответ ) /CM = 0,1 m^a.
Дано
л = 0,02 cos 6л7 + — 1, м
1) А — ?
2) ш0 - ?
3) г —?
4) Г — ?
Решение
s = A cos(oHl + <р),
Л = 0,02 м,
с.
Г Ответ J \) а = 0,02 м; 2) ы0 = 6я с-1; 3) v = 3 Гц; 4) Т = 0,33 с.
С
Запишите уравнение гармонического колебательного движения
точки, совершающей колебания с амплитудой /4 = 8 см, если за
= 1 мин совершается п = 120 колебаний и начальная фаза колебаний равна 45°.
Дано
А = 8 см = 8- 10 2м
/ = 1 мин = 60 с
и = 120
« = 45°
Решение
п
2л
(On = ,
х = A cos(w0/ + tp).
С Ответ) х =
8 cos
л
, см.
Материальная точка совершает гармонические колебания с амп-
литудой А = 4 см и периодом Т = 2 с Напишите уравнение дви-
жения точки, если ее движение начинается из положения х0 = 2 см
Дано
см = 4- 10м
с
см = 2 • 10-2м
Решение
= Acos(w0t
л
x0 = A coscp,
2я
'o=— я с-',
дг = 0,04 cos. л7 + — I м.
(Ответ )
J х = 0,
,04 cos ягн—
, м.
Точка совершает гармонические колебания с периодом Т — 6 с и
начальной фазой, равной нулю. Определите, за какое время, счи-
тая от начала движения, точка сместится от положения равновесия на полови-
ну амплитуды.
С Ответ j t = \ с.
вВННН! Напишите уравнение гармонического колебания точки, если его
W™™™T™W амплитуда А = 15 см, максимальная скорость колеблющейся точ-
ки vmm = 30 см/с, начальная фаза <р = 10°.
Дано
А = \Ъ см = 0,15м
wmax = 30 см/с = 0,3 м/с
x(t) _?
Решение
х = A cos(oy
С Omeemj
0,15cos|2/
Точка совершает гармонические колебания по закон>
х = 3 cos — ? + — , м. Определите: 1) период Г колебаний, 2) мак-
I 2 8 j
симальную скорость \>тяк точки; 3) максимальное ускорение дтах точки.
Л
\) т = А с, 2) vт„ =4,71 м/с; 3) атах = 7,4 м/с2.
4,^*4 } Точка совершает гармонические колебания с амплитудой ^4 = 10 см
и периодом Т = 5 с. Определите для точки: 1) максимальную ско-
рость; 2) максимальное ускорение.
Дано
Л = 10 см = 0,1 м
Т=5 с
2) <W -
Решение
х- A cos(ty0/ +
а - -Awq
V = -/
<ыо=
Г
u0b
Awl
. Q Ответ
d Wmax =12,6 см/с;
2) агаах = ! 5>8
Скорость материальной точки, совершающей гармонические ко-
лебания, задается уравнением v(t)= -6sin2л:?. Запишите зави-
симость смещения этой точки от времени.
С Ответ j
л
Материальная точка совершает колебания согласно уравнению
х = A sin wl. В какой-то моментвремени смещение точки х, =15 см
При возрастании фазы колебания в два раза смещение х-, оказалось равным 24 см
Определите амготитуду А колебания
Г Ответ J А = 25 см.
МатеРиальная точка совершает гармонические колебания соглас-
но уравнению х = 0,02 cos л/ + - ,м. Определите: 1) ампли 1>д\
колебаний; 2) период колебаний; 3) начальную фазу колебаний; 4) максималь-
ную скорость точки; 5) максимальное ускорение точки; 6) через сколько време-
ни после начала отсчета точка будет проходить через положение равновесия
Дано
х = 0,02 cos л7 + — I, м
1) А —?
2) 7--?
3) <Р — ?
6) / — ?
При х = О О,
Решение
х = A cos(u>0t + <р),
Т = 2с,
v = -0,02л sin л/ + —
А = 0,02 м,
ш0 = л ,
л
2 '
''mj\ = 0,02л м/с.
а = -0,02л" cos[ jit + — j, ama4 = 0,02л2 м V'
+ 1)— (ш = 0. 1,2, 3,. .)
~j = 0
-
тел-
= т.
л
Ответ ^ 1)^ = 2 см; 2)Г = 2с; 3)^> = |; 4) „пт = 6,28 см/с.
«
5) атах =19,7 см/с2; 6) / = т с, где ш = 0, 1, 2, 3,...
.3Щ1) Определите максимальные значения скорости и ускорения точки.
совершающей гармонические колебания с амплитудой А - 3 см
и периодом Г = 4с.
„mdx = 4,71 см/с; 2) атач = 7,4 см/с2.
Материальная точка, совершающая гармонические колебания с
частотой v = 1 Гц, в момент времени / = 0 проходит положение,
определяемое координатой х0 = 5 см, со скоростью v0 = 15 см/с. Определите
амплитуду колебаний.
ГОтвет j а = 5,54 см.
^ело масс°й w = 10 г совершает гармонические колебания по за-
кону х - 0,1 совDл7 + л/4), м. Определите максимальные значе-
ния: 1) возвращающей силы; 2) кинетической энергии.
Дано
/и =10 г=10кг
х = 0,1 созDл? + л/4) м
1)Ы —?
А/ J max
Решение
х- A cos(aHt + (р),
А = 0,1 м,
v — —Аа>0 sin(ty? + (р
ятяч = -Awl,
x = 0,1 cos 4л:? + —
V 4
с,
a = -Awl
^max "
Г =
mv2
7 =-
Jmax
тА2ш\
Г Ответ Л \) |Fmax| = O,1S8 H; 2) Гтах = 7,89 мДж.
Материальная точка массой т = 50 г совершает гармонические
колебания согласно уравнению х = 0,1 cos—/, м. Определите:
1) возвращающую силу F для момента времени t = 0,5 с; 2) полную энергию Е
точки.
С Ответ J I) F = 78,5 mH; 2) ? = 5,55 мДж.
Материальная точка массой т = 20 г совершает гармонические
колебания по закону л 0,1 созDтп г г/\) м Oiijkhc ime потную
энергию Е этой точки
Дано
те =20 г = 2 102кг
х = 0,1 cosDjt/ + я/4), м
Решение
Е=Т 111,
/=
mv"
-ып (<о0/
_
П =
1 ,2 2
тел со
cos"(ay +<p), E =
Q Ответ ^ e = \s,% мДж
ТГ^1»ЭЙИ /f Полная энергия Е гармонически колеблющейся точки равна
10 мкДж, а максимальная сила Fma4. действующая на точку, рав-
на -0,5 мН Напишите уравнение движения этой точки, если период Т колеба-
ний равен 4 с, а начальная фаза <р = ж/6
Дано
? = 10 мкДж= 10 5 Дж
Fmax=-0,5MH
1 max
' = 4 с
я
'" 6
Решение
Е =
тА со0
? _ тА2а?й _ А
2тАа>п 2
2л_
Т
Вычисления
2 10 10 Дж
А =
0,5 10Н
= 0,04 м,
2л л
= — = — с
4с 2
х = A cos(co0/ + <р)
х - 0,04 cos \—t + — , м
B 6)
(Ответ ) ппл (л л
J х = 0,04 cos —/ + —
[2 6
4.17 J Onpt it Miv. hid н ! ii п пои JFiepnin 7 точки соверша
ющей ифмоническпс ко юопшя к ее потенциальной знергии П
если известна фаза кочебания
Дано
(O0t + lp
Решение
п
- \<)"{) cos(o),)t 4
wir mA'w'r,
П = -I F dx = J mwqX dx = =
2 2
тА
¦ cos~
T sin'(wot
П cos (wot
= (
Г Ответ
Определите полную энергию материальной точки массой те, ко-
леблющейся по закону х = A cos(cu0/ + <р)
Дано
х = A cos(cu0? + <р)
Е
Решение
?=Г+П,
T =
mv2 mA2wi
П = — = —^ cos (ш0/ + <р),
тА2ш\
h, —
( Ответ j Е_ тА2<4
( 4Д9' г у Груз, подвешенный к спиральной пружине, колеблется по вертика-
ли с амплитудой /4 = 8 см. Определите жесткость к пружины, если
известно, что максимальная кинетическая энергия Ттах груза составляет 0,8 Дж
A = i
т
к
Дано
см = 8 • 10 2 м
= 0,8 Дж
?
Решение
F — П - 7
^ xma\ 'max >
п —
п-
*=
/Ь2
2 '
27тах
Л2
н/м
Материальная точка колеблется согласно уравнению х = A coscot.
где А = 5 см и <у = л/12 с. Когда возвращающая сила F в пер-
вый раз достигает значения -12 мН, потенциальная энергия П точки оказыва
ется равной 0,15 мДж. Определите: 1) этот момент времени t; 2) соответствую-
щую этому моменту фазу cut.
А
w
П
1)
2)
= А
= 5
Дано
coscot
см = 5 10 2м
= яг/12 с '
= 0
= 1
, -
cot
12 мН = -1,2-10Н
15 мДж =
,5- КГ'Дж
_ 9
?
F = -
к
П = -
П_
/г ~
_ 1
СУ
Решение
кх- -Ак coscot,
¦х2 кА2 2
— = cos cot,
2 2
А
— cos cot,
2
( 2ГП
arccos ,
I AF)
cot = arccos -
2П
AF
= 4 c; 2) cot = — рад.
Груз, подвешенный к спиральной пружине, колеблется по верти-
кали с амплитудой А = 6 см. Определите полную энергию Е ко-
лебаний груза, если жесткость к пружины составляет 500 Н/м.
; = —= 0,9 дж.
Спиральная пружина обладает жесткостью к = 25 Н/м. Опреде-
лите, тело какой массой т должно быть подвешено к пружине,
чтобы за / = 1 мин совершалось 25 колебаний.
Дано
к = 25 Н/м
/ = 1 мин = 60 с
iV = 25
m —?
Решение
Т--
N
Г = 2л\ —
С Ответ j т=ъ,в5 кг
к-.) Если увеличить массу груза, подвешенного к спиральной пружи-
—- не, на 600 г, то период колебаний груза возрастает в 2 раза. Опре-
делите массу первоначально подвешенного груза.
Дано
Am =600 г = 0,6 кг
72 = 27]
т —?
7i
Решение
| от + Дот ^
V m ~^"
Т2-2я^-
Am = m +
n+Am
к '
Am
Ответ ) m = 200 г
При подвешивании грузов массами /и, = 600 г и щ = 400 г к сво-
бодным пружинам последние удлинились одинаково (/ = 10 см).
Пренебрегая массой пружин, определите: 1) периоды колебаний грузов; 2) ка-
кой из грузов при одинаковых амплитудах обладает большей энергией и во сколь-
ко раз.
(Ответ ) , 7Л Т т _п~ „.^ е] _ т,
J 1,2) 7, = Т2 = 0,63 с, 3) —- = — = 1,5.
' Ег тг
На горизонтальной пружине жесткостью к = 900 Н/м укреплен
шар массой М = 4 кг, лежащий на гладком столе, по которому он
может скользить без трения. Пуля массой т= 10 г, летящая с горизонтальной
скоростью vQ - 600 м/с и имеющая в момент удара скорость, направленную
вдоль оси пружины, попала в шар и застряла в нем. Пренебрегая массой пру-
жины и сопротивлением воздуха, определите: 1) амплитуду колебаний шара;
2) период колебаний шара.
Дано
к = 900 Н/м
М =
т = \
Щ =
1) А
2) Т
4 кг
10 г=10кг
600 м/с
7
9
Решение
mv0 = (М + m)v ,
mv0
v-
М + т'
v0 m
(M+m)v2 kA7
2, .2
т v
о _.
{М+т)к
2ш2
(М+т)А2ш2 _ кА2
2 2
w
Г Ответ J
1) Л = 10 см; 2) Г = 0,419 с.
На чашку весов массой М, подвешенную на пружине жесткос-
тью к, с высоты h падает небольшой груз массой т. Удар груза
о дно чашки является абсолютно неупругим. Чашка в результате падения груза
начинает совершать колебания. Определите амплитуду А этих колебаний.
V = ¦
m+ to
При ненагруженной чашке:
Mg I
к ' 2
M)v2
Решаем уравнение относительно дг0:
_ те + to \m2g2 2m2gh
*о- Г"Я±У *2 +(те+М)Л '
При нагруженной чашке:
к
m2g2 + 2m2gh
к2
М)к '
Г Ответ Л
_
А —
2n?gh
m+ M)k
м
к
h
m
д
Дано
7
mv2
2
v\ =
Решение
= mgh,
>&
= (w+ to)v,
m ПГТ.
w
у
о!
1
1
^0
-/)= \kxix,
Физический маятник представляет собой тонкий однородный стер-
жень длиной 35 см. Определите, на каком расстоянии от центра
масс должна быть точка подвеса, чтобы частота колебаний была максимальной.
Дано
/ = 35 см = 0,35 м
x — ?
, "й2 2
J = + тх .
12
Решение
= 2ж
а> =
\2х2)
= 0,
mgx
2л _ I mgx
mgx
ml2 2 ~
\-mx
12
l2-\2x2 = \
О
1/2
\2gx
12 + I2x2) '
X =
2V3-
Ответ
Однородный диск радиусом R - 20 см колеблется около горизон-
тальной оси, проходящей на расстоянии / = 15 см от центра диска.
Определите период Т колебаний диска относительно этой оси.
Дано
R = 20 см = 0,2 м
/ = 15 см = 0,15 м
Решение
mR
mgl '
mR2 + 2ml2
2mgl
= 2л.
R2 + 2l2
С Ответ j t = i,07 с.
Тонкий обруч радиусом R - 50 см подвешен на вбитый в стену
гвоздь и колеблется в плоскости, параллельной стене. Определи-
те период Т колебаний обруча.
[Ответ j т =
с.
Тонкий однородный стержень длиной / = 60 см может свободно
вращаться вокруг горизонтальной оси, проходящей через верх-
ний конец стержня. Стержень отклонили на угол а0 = 0,01 рад и в момент
времени t0 - 0 отпустили. Считая колебания малыми, определите период ко-
лебаний стержня и запишите функцию а(().
Г Ответ j r = 1).
27 с; a(t) = 0,01 cos 1,51 at рад.
Тонкий однородный стержень длиной 1-60 см может свободно
вращаться вокруг горизонтальной оси, отстоящей на расстоянии
х = 15 см от его середины. Определите период колебаний стержня, если он
совершает малые колебания.
Дано
¦/ = 60 см = 0,6 м
х = \5 см = 0,15 м
Т —?
Решение
mgx '
г ™1 2
J = + mx
12
О
mgx
2 + l2x2
I2gx
С Ответ
= i,i9 с.
f 4.32 1 Маятник состоит из стержня (/ = 30 см, да = 50 г), на верхнем
-^^^—- конце которого укреплен маленький шарик (материальная точка
массой да' = 40 г), на нижнем — шарик (R= 5 см, М = 100 г). Определите
период колебания этого маятника около горизонтальной оси. проходящей че-
рез точку О в центре стержня.
Дано
I = 30 см = 0,3 м
да =50 г =0,05 кг
от'= 40 г = 0,04 кг
R=5 см = 0,05 м
М=100 г = 0,1 кг
?
Решение
12
2) +7
даобщ = да+да'+М, d=OC,
m+m+M
С
Т = 2л
да/2
12 "
ют'
g
I
2
Г
L
\2 2
J +5
/'
1-/ -¦+
V 2
->
M7?2
\
R —
+ /
да'
/
I
/
2
/ V
2+ J
1
J /
м
Ответ j
Т = 1,24 с.
Математический маятник, состоящий из нити длиной / = 1 м и
свинцового шарика радиусом г = 2 см, совершает гармоничес-
кие колебания с амплитудой А = 6 см. Определите: 1) скорость шарика при
прохождении им положения равновесия; 2) максимальное значение возвраща-
ющей силы. Плотность свинца р = 11,3 г/см3.
Г
Ответ
= 0,186 м/с;
Два математических маятника имеют одинаковую массу, длин>.
отличающиеся в п = 1,5 раза, и колеблются с одинаковой угловой
амплшудои Определите, какой маятник обладает большей энергией и во сколько
Дано
Решение
т] — тг — т
а, = с/, - а
/, -1,5/,
А _,
F - U
/У////,//////////////,,////,/////////////////////
Г
да «в — —
Пп
^ "I,
= /(l -COSO"),
= »jg/,(l-cosa),
fOmeem j
= 1,5.
r 4 3S i Два лигемагичсских маятника, длины которых отличаются па
Л/ - 16 см, с оеершаюг ja одно и то же время один н, = 10 колеба-
ний, др>1 ой— /ь -6 колебании Определите длины маятников /, и U
С
Ответ
J /, = 9 см; /2 = 25 см.
Математический маятник длиной / = 50 см подвешен в кабине
самолета. Определите период Г колебаний маятника, если само-
лет движется: 1) равномерно; 2) горизонтально с ускорением а = 2,5 м/с2.
С Ответ J i) 1,42 с; 2) 1,4 с.
Математический маятник длиной / = 1 м подвешен к потолку ка-
бины, которая начинает опускаться вертикально вниз с ускорени-
ем flj = g/4. Спустя время tx = 3 с после начала движения кабина начинает
двигаться равномерно, а затем в течение 3 с тормозится до остановки. Опреде-
лите: 1) периоды 7j, Т2, Г3 гармонических колебаний маятника на каждом из
участников пути; 2) период ТА гармонических колебаний маятника при движе-
нии точки подвеса в горизонтальном направлении с ускорением а4 = g/4.
Колебательный контур состоит из катушки индуктивностью
L = 0,2 мГн и конденсатора площадью пластин 5 = 155 см2, рас-
стояние между которыми d = 1,5 мм. Зная, что контур резонирует на длину
волны Я = 630 м, определите диэлектрическую проницаемость среды, запол-
няющей пространство между пластинами конденсатора.
Дано
1 = 1 м
°\ = g/4
/j =3 с
1>2 = const
1) Тх, Т2, Тг— ?
2) ТА—1
Решение
Тг = 2л,
С
Ответ
1) 7J = 2,32 с, Т2 = 2,01 с, Тг = 1,79 с ; 2) Г4 = 1,97 с.
Колебательный контур состоит из катушки индуктивностью Z = 1 мГн
и конденсатора емкостью С = 2 нФ. Пренебрегая сопротивлени-
ем контура, определите, на какую длину волны этот контур настроен.
Дано
1 = 1 мГн=10-3Гн
С = 2 нФ = 2- 10-«Ф
Л=0
Я —?
Решение
Х = сТ, Т = 2я41с,
Х = 2жс-[Ес'.
QOmeem } я = 2,67™
Дано
? = 0,2 мГн = 2- Ю^Гн
5 = 155 см2=1,55'10-2м2
^=1,5 мм= 1,5 ¦ 10м
Я = 630 м
Е — 7
Решение
Q-
E0eS
е =
2жс
Г Ответ
= б,п.
Колебательный контур содержит соленоид (длина / = 5 см, пло-
щадь поперечного сечения 5, = 1,5 см2, число витков N = 500) и
плоский конденсатор (расстояние между пластинами d = 1,5 мм, площадь пла-
стин 52 = 100 см2). Определите частоту w0 собственных колебаний контура.
Дано
1 = 5 см = 0,05 м
5, =1,5 см2 =1,5- 10г*м2
N = 500
«/=1,5 мм= 1,5 • 10~3м
5, =100 см2 = 1О-"м2
<о0-
Решение
1 N2S{
"Vic' Z = /^ /
Л^25,
1 Ы
^EnM0N2S,S2 '
—?
С =
с W
(On -¦
N \ 5,5-
(Ответ j
суо=4,24 1О рад/с.
Колебательный контур состоит из катушки индуктивностью
L = 0,1 Гн и конденсатора емкостью С = 39,5 мкФ. Заряд конден-
сатора 2т=3 мкКл. Пренебрегая сопротивлением контура, запишите уравне-
ние: 1) изменения силы тока в цепи в зависимости от времени; 2) изменения
напряжения на конденсаторе в зависимости от времени.
[*43 ) Энергия свободных незатухающих колебаний, происходящих в
колебательном контуре, составляет 0,2 мДж. При медленном раз-
двигании пластин конденсатора частота колебаний увеличилась в п ~ 2 раза.
Определите работу, совершенную против сил электрического поля.
Дано
L = 0,1 Гн
С = 39,5мкФ=3,95-10-5Ф
Qm=3 мкКл = 3- 10Кл
R=0
1) /(/)—?
Решение
1
Q=Qm cos ay,
'=*?=-<
Qm<°0 SbWot = ~Qm<0° cosш°' + T
(Ответ}
- -— /
2) Uc = 76cosA60^),mB.
Сила тока в колебательном контуре, содержащем катушку индук-
тивностью L = 0,1 Гн и конденсатор, со временем изменяется
согласно уравнению / = -0,1 sin 200тг/, А. Определите: 1) период колебаний;
2) емкость конденсатора; 3) максимальное напряжение на обкладках конденса-
тора; 4) максимальную энергию магнитного поля; 5) максимальную энергию
электрического поля.
СОтвет
1)Г = — = 10 мс;
3)
2) С=
¦л'Ь
it
мкФ;
3,5 мДж;
Дано
А —?
_
Решение
l
v = —,
T
T = 2л- Vic ,
x
= const.
ГОтвет j
А = 0,6 мДж.
Ч$»'-J Конденсатор емкостью С зарядили до напряжения Um и замкнули
на катушку индуктивностью L . Пренебрегая сопротивлением кон-
тура, определите амплитудное значение силы тока в данном колебательном контуре.
Дано
С
L —
Решение
Q = Q
Qm=cum,
= -w0Qm sin(wot
С Ответ )
= !/„,-.
( 4.45 j Колебательный контур содержит катушку с общим числом витков
~"~"^~~^ N = 100 индуктивностью L-10 мкГн и конденсатор емкостью
С = 1 нФ. Максимальное напряжение Um на обкладках конденсатора состав-
ляет 100 В. Определите максимальный магнитный поток, пронизывающий ка-
тушку.
Амплитуда результирующего колебания, получающегося при сло-
жении двух одинаково направленных гармонических колебаний
одинаковой частоты, обладающих разностью фаз 60°, равна А = 6 см. Опреде-
лите амплитуду А 2 второго колебания, если A j= 5 см.
Дано
N = 100
1 = 10 мкГн=105Гн
С = \ нФ=10~9Ф
ит =юов
Решение
•=ет
(On =¦
1
ie
1 = -<»oQm МЩ1 + <Р), /m = O)QQm ,
N N
_ (QQLCUm __ Um^
N
N
Ответ
Фт = од мкВб.
PJI Два одинаково направленных гармонических колебания одинако-
вого периода с амплитудами А , = 4 см и А-, = 8 см имеют раз-
ность фаз <р = 45°. Определите амплитуду результирующего колебания.
Дано
A{ = 4 см = 4' 10м
A2=8 см = 8- 102м
V5=45°
A -?
Решение
X\ = A | cos(<y/ + ^>|),
X, = A-, COS((W/ + ^5, ) ,
<P2 - <Pt = <P .
A2 = A2 + A2+2A \A2 cosp ,
А =
С Ответ "\
/4 = 11,2 см.
Г Ответ j a2=i,65 cm.
Определите разность фаз двух одинаково направленных гармони-
ческих колебаний одинаковой частоты и амплитуды, если амплиту-
да их результирующего колебания равна амплитудам складываемых колебаний.
Разность фаз двух одинаково направленных гармонических колеба-
ний одинакового периода Т = 4 с и одинаковой амплитуды /4 = 5 см
составляет я/4 . Напишите уравнение движения, получающегося в результате
сложения этих колебаний, если начальная фаза одного из них равна нулю.
Дано
Г = 4 с
Л , = Л2 = 5 см = 5 •
л Л
Vi-0
10-2м
Решение
Хх = /4 j COSCO/ ,
x2 = ^2cos(w/ + y52)
4
А=^А2 + А2+2Аи
¦>, со
42 cosy?
2лг
"У
= ^ ! -^2A +COS Др) ,
= 0,414,
х = у4 cos(cof-
С
Ответ
х = 9,24 cos h — , см.
С4.50 1 Складываются два гармонических колебания одного напргп
^ "^ ления, описываемых уравнениями дг, = 3 cos2.т/ , см
х-, = 3 cosBjtC + лг/4), см. Определите для результирующего колебания: I) av
плитуду; 2) начальную фазу. Запишите уравнение результирующего колебанн,
и представьте векторную диаграмму сложения амплитуд.
= 3 cosB,t/ + я/4), см
= At cos(wt + <о,),
х2 =А2 cos(wt + <р2),
1) А —?
2) <Р ~?
3) х@ —
ж
' = <Pl -<Р]=Т
4
4 cosp,
4j + 24.4,
sin 0 + sin -
cosO+ cos—
= 0,414.
1) Л = 5,54 см; 2)<р = --
3) л-= 5,54 cos 2л:/+-)
, см.
|?4«5! | Точка одновременно участвует в п одинаково направленных гар-
монических колебаниях одинаковой частоты: 4 cos(&>/ -г <ру),
А-, cos(a>/ + <р2),..., А„ cos(to/ + ipn). Используя метод вращающе! ося вектора
амплитуды, определите для результирующего колебания: 1) амплитуду, 2) на-
чальную фаз\.
Дано
Ах соь(ш/ + <р])
А2 cos(co/ -\ tp2)
Ап cos(wt + <рп)
\) А — ?
2) <р — ?
Решение
ш
t cosy?,
4.52 1 Частоты колебаний двух одновременно звучащих камертонов на-
строены на 560 и 560,5 Гц. Определите период биений
Дано
v, = 560 Гц
v2 -560,5 Гц
Т, _?
Решение
Аш "
1 = 1'т - V, ,
) = 2л Av.
v2-v,
f
Ответ
?; = 2 с.
4 ЙЙР^ ® результате сложения двух колебаний, период одного из которых
7] = 0,02 с, получают биения с периодом Т& = 0,2 с. Определите
период Т2 второго складываемого колебания.
Г Ответ j 7;
= 18,2 мс
l^JfrTj Складываются два гармонических колебания одного направления,
. * л у имеющие одинаковые амплитуды и одинаковые начальные фазы,
с периодами 7] = 2 с и Т2 = 2,05 с. Определите: 1) период результирующего
колебания; 2) период биения.
Г Ответ j
1) Т = 2,02 с; 2) Гб = 82 с.
Результирующее колебание, получающееся при сложении двух
гармонических колебаний одного направления, описывается урав-
нением вида х = A cost cos45c (с — в секундах). Определите: 1) циклические
частоты складываемых, колебаний; 2) период биений результирующего колебания.
Дано
х- A cos/ cos45с
1) СУ, — 1 СУ2 — ?
2) Г6-?
Решение
X = X, + Х-, ,
су, - су-, (су, + су, "\
х = 2Л cos—¦ -t cos — Ч + Ф\,
— 1)
2су,=92,
су, -су2= 2,
<ы, = 46 с ',
СУ, +СУ2
= 45, су,+су,= 90,
су2 = 44 с"',
2.т 2л:
Асу 2 с
Г Ответ J
су, =46 с, су2 = 44с';
= 3,14с.
Точка участвует одновременно в двух гармонических колебаниях,
происходящих во взаимно перпендикулярных направлениях и опи-
сываемых уравнениями х = 3 coswt, см и у = 4 cosco/, см. Определите урав-
нение траектории точки и вычертите ее с нанесением масштаба.
Г Ответ ) 4х
Точка участвует одновременно в двух гармонических колебаниях,
происходящих во взаимно перпендикулярных направлениях и опи-
сываемых уравнениями х = 3 cos2co/, см и у = 4 cosBco? + л), см. Определите
уравнение траектории точки и вычертите ее с нанесением масштаба.
Дано
, см
у = 4 cosBcy/ + я), см
Решение
= А cosBcot + л) = -4 cos2co/,
cos2co/ = -—,
4
3 4
cos2«w? = —,
4
у = —х.
У 3
¦ = 0
{— —
х = 3 см, у - -4 см;
х = -3 см, у = 4 см;
х = 3 см, у = -4 см;
х = 0 см, у = О см.
, см
QOmeem
Точка участвует одновременно в двух гармонических колебаниях,
происходящих во взаимно перпендикулярных направлениях и опи-
сываемых уравнениями х = A sinwt и у = В cos cot, где А, В и (о — положи-
тельные постоянные. Определите уравнение траектории точки, вычертите ее с
нанесением масштаба, указав направление ее движения по этой траектории.
Точка участвует в двух гармонических колебаниях, происходящих
во взаимно перпендикулярных направлениях и описываемых урав-
рниями л: = cos 2л7 и у - cos nt. Определите уравнение траектории точки и
вычертите ее с нанесением масштаба.
Дано
х = A sincot
у = Bcoscut
А, В, со > О
Решение
х
—
А
У
— = coscot,
X У ¦ 2
—г + —г = siir cot + cos
A1 Bz
x = A, y = 0.
(Ответах2 у^_
у + "y = 1, по часовой стрелке.
Точка участвует одновременно в двух гармонических колебаниях
одинаковой частоты, происходящих во взаимно перпендикулярных
направлениях и описываемых уравнениями х = A sin(<u/ + л/2) и у - A sin cut
Определите уравнение траектории точки и вычертите ее с нанесением масшта-
ба, указав направление ее движения по этой траектории.
Дано
x = A sin(u)t + nj2)
y = A sin со/
У(х)~
/ = 0
_ T
'~ 2
?
x= A,
Решение
x = A sin (at + — = A coscot,
v 2;
у = A siruot,
t
t
T
~ —
4
УГ
4
= 0, y= A;
Ответ
против часовой стрелки.
С Ответ.)
2у2-х = 1.
Точка участвует одновременно в двух гармонических колебаниях,
происходящих во взаимно перпендикулярных направлениях и опи-
сываемых уравнениями х = Asinwt и у- A sin2«w/. Определите уравнение
траектории точки и вычертите ее с нанесением масштаба.
х = Л
Дано
sin со/
sin2«u/
— ?
Решение
x = Asin(ot, y =
X 1 X
у 2 cos to/' л
Л sin2co/
= sin со/,
= 2A sin to/
COS CO/ = ,
cosco/,
1 2~
1-—
A2 "
х . 1 1
y2 4 i^x-
,.
t
¦ t
t
t
= 0
T
=
12
T
8
T
=
6
x = 0,5A, j =
x = 0,707/i, у = A ;
x = 0,ША , у = 0,866^ .
(Ответ
Период затухающих колебаний Т - 1 с, логарифмический декре-
мент затухания 0 = 0,3, начальная фаза равна нулю. Смещение точ-
ки при t = IT составляет 5 см. Запишите уравнение движения этого колебания.
Дано
Т = \ с
0 = 0,3
х, = 5 см = 0,05 м
х@—?
Решение
Аое~ ' cos cot, (o = —,
Т
т
А Т' 2ЛГ
х- Аг. е ' cos—?.
Т
Г Ответ)
= 9,le °'3'cos2л*, см.
Докажите, что для затухающих колебаний, описываемых уравнени-
ем x(t) = Aq s~6' cosa)t, выполняется условие x(t + T) = x{t)t~6T .
Амплитуда затухающих колебаний маятника за t = 2 мин умень-
шилась в 2 раза. Определите коэффициент затухания д.
t = 2
Al-
A2
д —
Дано
мин= 120 с
2
9
Решение
х = Aq е~д< cos(<y? + p),
1 А] ~
8=Т1пТ2' С Ответ
А2
J = 5,78 ¦
А]
А2
10 с '.
Логарифмический декремент колебаний 0 маятника равен 0,01.
Определите число N полных колебаний маятника до уменьше-
ния его амплитуды в 3 раза.
Г Ответ)
N = 110 •
Амплитуда затухающих колебаний математического маятника
за 1 мин уменьшилась в 3 раза. Определите, во сколько раз она
леныгштся за 4 мин.
Ответ ) А
J л.
= 81.
Начальная амплитуда затухающих колебаний маятника А§ = 3 см.
По истечении г, =10 с А ,= 1 см. Определите, через сколько вре-
мени амплитуда колебаний станет равной А2 = 0,3 см.
Ответ
j t =
21 с.
Тело массой т = 0,6 кг, подвешенное к спиральной пружине же-
сткостью к-20 Н/м, совершает в некоторой среде упругие коле-
бания. Логарифмический декремент колебаний 0 = 0,01. Определите: 1) вре-
1«я, за которое амплитуда колебаний уменьшится в 3 раза; 2) число полных ко-
лебаний, которые должна совершить гиря, чтобы произошло подобное умень-
шение амплитуды.
Дано
т = 0,6 кг
.к=30 Н/м
© = 0,01
2) N} - ?
Решение
х = An е й/ cos(w/ + у?), —- =
А-,
?
2ж \т , А,
t, -—J— In—1-,
1 &\ к А-,
д А2
2лг .
: =2Л
О)
Т 0 А,
Ответ
1)/,= 97,6 с; 2) TV, =110.
^Докажите, что выражения для коэффициента загухания д = г/B
т)
циклической частоты w = -^Юд - о" - J — > 0 следуют из решения диф-
у т V 2т)
ференциального уравнения для загущающих колебаний тх f- rx + fa- = 0 ( т
масса тела, г —коэффициент сопротивления, к —кшффиниентупр}гости>
Дано
мх + rx -t kx - 0
2ff7
2) ш = ^и>1 -д2 =
'--I I >0
от v 2wy
Решение
йг
cos(wt
ix = ^e-*'<
x = -Aod e"
х=4N2е"л
t -V е Ar
sin(w? + p) ¦
- i0 e ^ si
- л{) е
¦<P)] ~
cos(wt
cos(cot + <p)=Q,
(md~ - mw —rd + k) cos(col + <p) + Bmd - r)w s\n(wt t- <p) = 0,
2/ий - ?¦ = 0 , <5 = —
2) /w<5" - отш" -гй +
2m
m
к
V m
(Ответ )
' т \ 2 т
При наблюдении затухающих колебаний выяснилось, что для двух
последовагельных колебаний амплитуда второго меньше ампли-
1ды первого на 60%. Период затухающих колебаний Т = 0,5 с Определите:
l| коэффициент затухания д : 2) для тех же условий частоту v0 незатухающих
Крлебании
Дано
Решение
A2 = OAA,
Г = 0,5 с
1)<J —?
2) v0 - ¦?
А2 - 0,4
Я ,,
2 о2
\-0
2л: 2л-\l Г
А2 ) 2жТ
Ответ Л i) й = i,83 с •; 2) v0 = 2,02 гц.
Тело массой от = 100 г, совершая затухающие колебания, за т = 1 мим
потеряло 40% своей энергии. Определите коэффициент сопротив-
ления г .
Дано
m=\QQ г = 0,1 кг
т = 1 мин = 60 с
г —?
Решение
тА'ш
ДО
E(t + x
0,6
1
0^6
i= —In ,
2г 0,6
e
2m
'2Ait+r)
=
2дт
.... ,1 от 1
Л In = — 111
2r 0,6 г 0,6
Г Ответ j
г -8,51 10 4 кг/с.
Дифференциальное уравнение для заряда в электрическом колеба
d2Q &Q О
тельном контуре задается в виде L—г + R— + — = 0. Найдите решение
dr dt С
го уравнения. Определите: 1) собственную частоту контура; 2) циклическую
стоту ш; 3) коэффициент затухания д.
Дано
это-
ча-
Решение
t-Q RdQ Q
, ще и =
После нахождения производных и подстановки
|| J За время, в течение которого система совершает N = 50 полных
¦^ колебаний, амплитуда уменьшается в 2 раза. Определите доброт-
ность Q системы.
S9St*A Частота свободных колебаний некоторой системы <ы = 65 рад/с, а
ее добротность 2 = 2. Определите собственную частоту <ы0 ко-
лебаний этой системы.
Дано
су = 65 рад/с
Решение
—
0
2л:
0 лг
(Ы0 =
Иц Колебательный контур состоит из катушки индуктивностью
^^ ? = 10 мГн, конденсатора емкостью С = 0,1 мкФ и резистора со-
L, — 1 v Ml и, кипдсщ-aiujja cmiujtaonj \_ — u,i тл*** п ^vjnviupu^u
противлением Л = 20 Ом. Определите, через сколько полных колебаний амп-
литуда тока в контуре уменьшится в е раз.
Дано
? = 10 мГн=10-2Гн
С =0,1 мкФ = 107Ф
Л=20 Ом
¦'то
Лп/V
N —?
Решение
AnO „At
^тЛ'
2я 2л:
" ® ~ Jo>l-d2
/т0 - с1 i i
/ с . (Зг = 1,
/тЛг
1 2?
t=- = —, t = NT,
[Т
J4
лR\LC U2
1С 4Z,2
{Ответ j
N = 5.
Колебательный контур содержит катушку индуктивностью
1-25 мГн, конденсатор емкостью С = 10 мкФ и резистор со-
противлением Л = 1 Ом. Конденсатор заряжен количеством электричества
Qm -1 мКл. Определите: 1) период колебаний контура; 2) логарифмический
декремент затухания колебаний; 3) уравнение зависимости изменения напря-
жения на обкладках конденсатора от времени Р
Дано
1 = 25 мГн = 2,5- 10Гн
С = 10 мкФ=10~5Ф
Я = 1 Ом
бт=1 мКл=10~3Кл
Решение
21'
шо=-
Ответ Ц)г=з,14мс;
3) t/@ = 100e-20'cos637^,B.
Определите логарифмический декремент, при котором энергия
колебательного контураза ^ = 5 полных колебаний уменьшается
П И = S nil
в п = 8 раз.
Колебательный контур содержит катушку индуктивностью
1 = 6 мкГн, конденсатор емкостью С = 10 нФ и резистор сопро-
¦щвлением Л = 10 Ом. Определите для случая максимума тока отношение энер-
гии магнитного поля катушки к энергии электрического поля.
Ответ
W ~ '
"О Определите добротность Q колебательного контура, состоящего
из катушки индуктивностью 1 = 2 мГн, конденсатора емкостью
С = 0,2 мкФ и резистора сопротивлением R = 1 Ом.
Г Ответ J
1=100.
Частота v затухающих колебаний в колебательном контуре с доб-
ротностью Q = 2500 равна 550 кГц. Определите время, за кото-
рое амплитуда силы тока в этом контуре уменьшится в 4 раза.
Дано
кГц =5,5- 105Гц
Q = 2500
Jm0
= 4
t —9
Решение
т0 _
t =
In 4
д '
nv
Ж Я ЯУ
t-
71V
С Ответ j t =
2 mc.
Определите закон убывания заряда конденсатора со временем при
его разряде в апериодическом режиме, т. е. когда д = а>0.
С Ответ Л
С 4.82 J Определите минимальное активное сопротивление при разрядке
^ *^ лейденской банки, при котором разряд будет апериодическим.
Емкость С лейденской банки равна 1,2 нФ, а индуктивность проводов состав-
ляет 3 мкГн.
c=
L —
R -
Дано
1,2 нФ= 1,2- 10
3 мкГн = 3- 10-6
_ ?
Гн
Т->
и> = \
(Оп =
Решение
°0 1 ft)
1
/о»о - <52 , си
1
->о,
_ R
2L'
R
VZc
QOmeem ^ я=юоом.
Щ Объясните, в чем заключается различие автоколебаний и вынуж-
денных колебаний.
Определите резонансную частоту колебательной системы, если
собственная частота колебаний v0 = 300 Гц, а логарифмический
декремент 0 = 0,2 .
Дано
v0 = 300 Гц
0 = 0,2
V3
Vn,, =
Решение
д _ ® = €to0
Г 2л:
%« = ujo_ L_ ©z
2л: 2л:
= vn,ll-
Vpei = 299,7 Гц
'¦^ Собственная частота v0 колебаний некоторой системы составля-
ет 500 Гц. Определите частоту v затухающих колебаний этой си-
стемы, если резонансная частота v = 499 Гц.
Дано
v0 = 500 Гц
vpe3 = 499 Гц
V-?
Решение
ш = ^ш\ - E2 ,
^рез = ^о-2E2,
w2 + E2 = w2 +2<52,
а>о = со2 + д2,
^0=<Урез+2<52,
,52 = а,2-а,2ез,
«у2 = w2 +<52 = w2 + ш2 - ш2ез = 2ш2-ш2ре
'рез
СОтвегп\ v = 499,5 Гц.
Период затухающих колебаний системы составляет 0,2 с, а отно-
шение амплитуд первого и шестого колебаний равно 13. Опреде-
лите резонансную частоту данной колебательной системы.
Г =0,2
V3-?
Дано
с
5<5Г =
ш = ^
Решение
4,e-dr, Дб
= 1п13, E =
/ft>o - <52 , су
1п13
5Г '
2л:
">рез = V^o
2 Г2ЯУ
г = 13,
-2<52,
<ЫРез=-
'рез '
2л\\ Т
5Г
2жТ
25
Гиря массой т - 0,5 кг, подвешенная на спиральной пружине
жесткостью к = 50 Н/м, совершает колебания в вязкой среде с
коэффициентом сопротивления г = 0,5 кг/с. На верхний конец пружины дей-
ствует вынуждающая сила, изменяющаяся по закону F = 0,1 cosco/, Н. Опреде-
лите для данной колебательной системы: 1) коэффициент затухания <5; 2) резо-
нансную амплитуду
Дано
те = 0,5 кг
к = 50 Н/м
г = 0,5 кг/с
F = ОД cosco/, Н
1) д — ?
Решение
тех = —foe - rx + Fo
г*
х + 2дх + щх - —
те
26^1-5
coswt,
coscot,
т „
те
/и 4те"
Qdmeem
2) Лрез = 2 см.
Гиря массой те = 400 г, подвешенная на спиральной пружине же-
сткостью к = 40 Н/м, опущена в масло. Коэффициент сопротив-
ления г для этой системы составляет 0.5 кг/с. На верхний конец пружины дей-
ствует вынуждающая сила, изменяющаяся по закону F = coscot, H. Определи-
те: 1) амплитуду вынужденных колебаний, если частота вынуждающей силы
вдвое меньше собственной частоты колебаний; 2) частоту вынуждающей силы,
при которой амплитуда вынужденных колебаний максимальна; 3) резонансную
амплитуду.
Ответ
2)а>рез=9,96с-'; 3)^=20
см.
Гиря массой т = 200 г, подвешенная на спиральной пружине же-
сткостью к — 50 Н/м, совершает колебания в вязкой среде с коэф-
фициентом сопротивления г = 0,2 кг/с. На верхний конец пружины действует
вынуждающая сила, изменяющаяся по закону F = 0,2 cos cot, Н. Определите:
1) частоту v0 собственных колебаний; 2) резонансную частоту rpe3; 3) резо-
нансную амплитуду Лрез; 4) статическое отклонение.
Ответ J
I) Vq = 7,96 Гц; 2) vpe3 = 7,88 Гц; 3) ^e3 = 2 см; 4) 4 мм.
vpe3
Амплитуды двух вынужденных колебаний системы с одинаковы-
ми собственными частотами при всех значениях частоты вынуж-
дающей силы различаются вдвое. Определите, какой одной (и только одной) из
величин (массой, коэффициентом сопротивления среды, коэффициентом упру-
гости, амплитудой вынуждающей силы) отличаются эти системы.
Дано
= со.
02
А,2
/н, г, *, Fo — ?
Решение
«
рез
= ^а>1 - 2<52 ,
т
к г2
m 2rrt
2 '
— = 2 для всех со, значит, и для сорез :
- д
' 2г,--
т Am
Должна меняться только одна из величин: ни /t, ни т (со0] = I— = со02 = |— ),
ни г (г входит в ^ез дважды в знаменателе)', изменяется Fo, причем F0] = 2F02.
СОтветЛ
^o,=2FO2.
В цепь колебательного контура, содержащего последовательно
соединенные резистор сопротивлением R = 40 Ом, катушку ин-
дуктивностью L = 0,36 Гн и конденсатор емкостью С = 28 мкФ, подключено
внешнее переменное напряжение с амплитудным значением Um = 180 В и ча-
стотой (о = 314 рад/с. Определите: 1) амплитудное значение силы тока /т в
цепи; 2) сдвиг <р по фазе между током и внешним напряжением.
Дано
Л=40 Ом
/, = 0,36 Гн
С = 28 мкФ =28
ит=тв
<ы = 314 рад/с
О А* -?
2) <Р —¦?
Вычисления:
Решение
a)L-
соС
R
L=-
180 В
402 Ом2 +314рад/ с-0,36Гн-
1
314рад/с-28-10~6Ф
= 4,5А;
314 рад/с-0,36 Гн-
1
314рад/с-2810"°Ф
40 Ом
= -Г . Ток опережает напряжение.
= -0,0175.
QOmeem
/m=4,5A;
В цепь колебательного контура, содержащего катушку индуктив-
ностью L = 0,2 Гни активным сопротивлением Л = 9,7 Ом, а так-
же конденсатор емкостью С - 40 мкФ, подключено внешнее переменное на-
пряжение с амплитудным значением Um =180 В и частотой w = 314 рад/с.
Определите: 1) амплитудное значение силы тока 1т в цепи; 2) разность фаз <р
между током и внешним напряжением; 3) амплитудное значение напряжения
UL на катушке; 4) амплитудное значение Uc^ на конденсаторе.
Дано
L = 0,2 Гн
Л = 9,7 Ом
С=40 мкФ = 4 ¦ 10~5 Ф
t/m=180B
<ы = 314
рад/с
— ?
'.-
При
При
Решение
m
jR2+{(vL-
С->оо U =
1->0, Л->(
¦V
-iJr2
) c/Cm =
+ (o)LJ ¦
\( ]
wL-
R
c)=1
i
шС
г 1
Ответ Л !) 7m = 927 A^ 2) ^ = -60°, ток опережает напряжение;
3) UL = 589 В; 4) Uc = 738 В.
Последовательно соединенные резистор с сопротивлением
R= 110 Ом и конденсатор подключены к внешнему переменно-
му напряжению с амплитудным значением Um =110 В. Оказалось, что ампли-
тудное значение установившегося тока в цепи /т = 0,5 А. Определите разность
фаз между током и внешним напряжением.
( Ответ j yj = -60°, ток опережает напряжение.
В колебательный контур, содержащий последовательно соединен-
ные конденсатор и катушку с активным сопротивлением, под-
ключено внешнее переменное напряжение, частоту которого можно менять
не меняя его амплитуды. При частотах внешнего напряжения су, = 400 рад/с
и щ - 600 рад/с амплитуды силы тока в цепи оказались одинаковыми. Опре-
делите резонансную частоту тока.
Колебательный контур содержит катушку индуктивностью
L - 0,1 мГн, резистор сопротивлением R = 3 Ом, а также конден-
сатор емкостью С = 10 нФ. Определите среднюю мощность, потребляемую
контуром, необходимую для поддержания в нем незатухающих колебаний с ам-
плитудным значением напряжения на конденсаторе Um = 2 В.
Дано
су, = 400 рад/с
оJ = 600 рад/с
Um - const
¦'ml = Лп2
<»рез ~
Решение
1=1т при су =
Vic
и„
су2С
7ml = 42
cy,Z-
су.С
(V2L-
ш2С
cy.iC
W-,-
су, -
СУ-,
СУ,
1
СУ,
1
а>2
Дано
1=0,1 мГн= 104Гн
Л=3 Ом
Решение
С =
I=dQ =
dt
= CUm
VZc'
2Q2mR_C2U2mR_\CU2mR
2LC 2 L
Г Ответ j
(P) = 0,6 мВт.
В цепь переменного тока напряжением 220 В и частотой 50 Гц пос-
ледовательно включены резистор сопротивлением R = 100 Ом, ка-
тушка индуктивностью L = 0,5 Гн и конденсатор емкостью С = 10 мкФ. Опре-
делите амплитудное значение: 1) силы тока в цепи; 2) падения напряжения на
активном сопротивлении; 3) падения напряжения на конденсаторе; 4) падения
напряжения на катушке.
С Ответ
i) /m=U6 а; 2) иКя = иб в;
3) ис =369 В; 4) UL =182 В.
|1Д1111§ В цепь переменного тока частотой v = 50 Гц включена катушка
длиной / = 20 см и диаметром d = 5 см, содержащая N - 500
витков медного провода площадью поперечного сечения 5 = 0,6 мм2. Опреде-
лите, какая доля полного сопротивления катушки приходится на реактивное
сопротивление. Удельное сопротивление меди р = П нОм • м.
В цепь переменного тока частотой v = 50 Гц включена катушка
длиной / = 30 см и площадью поперечного сечения 5 = 10 см2,
содержащая N = 1000 витков. Определите активное сопротивление катушки,
(сяи известно, что сдвиг фаз у между напряжением и током составляет 30°.
Дано
v = 50 Гц
/ = 20 см = 0,2 м
d = 5 см = 0,05 м
# = 500
5 = 0,6 мм2 = 6- 10м2
р = 17 нОм • м =
= 1,7-10-* Ом-м
X
су
Решение
RL=wL,
'
рлШ
(о = 2лр ,
4
Х=ЛЛ =
X
X
= 0,401.
^
= 0,97 Ом; R = 2,22 Ом;
( Ответ ) ?sQAOi.
Полное сопротивление Z цепи переменного тока,
содержащей последовательно включенные резистор сопротивлением R, катушку
индуктивностью L и конденсатор емкостью С, на концы которой подается пе-
ременное напряжение U = Um cos cut,
Дано
V = 50 Гц
"l = 30 см = 0,3 м
# = 1000
р = 30°
Я—?
(пТ.
R = -
Решение
(vL-
1
R
Rr= = 0,
X cuL
= -^ = ^Г> L = HaH-
tgv
СОтвет J л = 2,28 Ом.
К зажимам генератора присоединен конденсатор емкостью
С = 0,15 мкФ. Определите амплитудное напряжения на зажимах,
если амплитудное значение силы тока равно 3,3 А, а частота тока составляет 5 кГц.
ГОтвет j
Um = 0,7 кВ.
Определите в случае переменного тока (v = 50 Гц) полное сопро-
тивление участка цепи, состоящего из параллельно включенного
конденсатора емкостью С = 10 мкФ и резистора сопротивлением R = 50 Ом.
С Ответ j я
^ = 49,4 Ом.
\^N$||8gy цепь переменного тока состоит из последовательно соединенш ¦ЕИЕИР ® цепь пеРеменного тока с частотой v = 50 Гц и действующим
катушки, конденсатора и резистора. Амплитудное значение су, ЩВВЁР' значением напряжения U = 300 В последовательно включены
маркого напряжения на катушке и конденсаторе Ulc ^ = 173 В, а амплитудно яоиДенсатоР> резистор сопротивлением R = 50 Ом и катушка индуктивностью
значение напряжения на резисторе UR =100 В. Определите сдвиг фаз меж l = 0>1 Гн' Падения напряжения t/, :U2 = 1:2. Определите: 1) емкость конден-
юком и внешним напряжением. "" «пора; 2) действующее значение силы тока.
Дано
uicm =173 В
fV=100 в
<р -9
Решение
ct)L
шС
R
т шС
I/,
(j)meem
В цепь переменного тока частотой v - 50 Гц последователь!)
включены резистор сопротивлением R =100 Ом и конденсате»
емкостью С = 22 мкФ. Определите, какая доля напряжения, приложенного
этой цепи, приходится на падение напряжения на конденсаторе.
Дано
v =¦ 50 Гц
Я=Ю0 Ом
С-22 мкФ = 2.2- 10 5 Ф]
Решение
un=inz,
ш = 2.tv
С Ответ
U,
— = 0,823.
Дано
v=50 Гц
м ^™ „ {/ = 300 В
i
1)
2)
_ f
С
I
),1 Гн
/2 = l/2
-?
9
c=
/ = .
Решение
R
—]
(i)CJ
cy = 2jtv .
Л2+[2яг1-
l) с = 29,8 мкФ; 2) / = 3,32 A.
12 Сборник лц|
Генератор, частота которого составляет 32 кГц и амплитудное зна-
чение напряжения 120 В, включен в резонирующую цепь, емкость
которой С = 1 нФ. Определите амплитудное значение напряжения на конден-
саторе, если активное сопротивление цепи R - 5 Ом.
В цепи переменного тока (см. рисунок к задаче 4.105) с частотой
v = 50 Гц вольтметр показывает нуль при значении С = 20 мкФ.
Определите индуктивность катушки.
v = 32 кГц = 3,2- 10Тц
С/т = 120 В
С = \ нФ=10-9Ф
Л=5 Ом
ГОтвет
\Z~R (в случае резонанса),
R '
В приведенной на рисунке цепи переменного тока с частотой
v = 50 Гц сила тока внешней (неразветвленной) цепи равна нулю.
Определите емкость С конденсатора, если индуктивность L катушки равна 1 Гн.
Решение
Ответ ) с=Юмкф.
Zy=O,
(ОС
-<oL
с=
Активное сопротивление колебательного контура R = 0,4 Ом.
Определите среднюю мощность (Р), потребляемую колебатель-
ным контуром, при поддержании в нем незатухающих гармонических колеба-
ний с амплитудным значением силы тока /т = 30 мА.
Как и какими индуктивностью L и емкостью С надо подключи rt
катушку и конденсатор к резистору сопротивлением R = 10 кО,\,
чтооы ток через катушку и конденсатор был в 10 раз больше общего тока? Ча-
стота переменного напряжения v = 50 Гц.
Дано
Я =10 кОм= 104Ом
v = 50 Гц
IL = Ic=l0I
L — ?
С -?
Решение
Резонанс токов. Параллельное включение:
II. = Л/_ = г/ , U „ U
Rl
с
10
cuR
R
L =
R
су =
- = 3,18 Гн; С = 3,18 мкФ
Колебательный контур содержит конденсатор емкостью С = 5 нФ
и катушку индуктивностью L = 5 мкГн и активным сопротивлени-
ем R =0,1 Ом. Определите среднюю мощность (р), потребляемую колеба-
тельным контуром, при подцержании в нем незатухающих гармонических ко-
лебаний с амплитудным значением напряжения на конденсаторе Um =10 В
Дано
С = 5 нФ = 5 • 1О9 Ф
1 = 5 мкГн = 5 • 10-6Vh
R =0,1 Ом
ит =ю в
Решение
шС
RCU2m
[OmeemJ
) = 5 мВт.
Колебательный контур содержит катушку индуктивностью
L = 6 мкГн и конденсатор емкостью С = 1,2 нФ. Для поддержа-
дая в колебательном контуре незатухающих гармонических колебаний с амп-
лигудным значением напряжения на конденсаторе Um = 2 В необходимо под-
водить среднюю мощность (Р) = 0,2 мВт. Считая затухание в контуре доста-
точно малым, определите добротность данного контура.
Дано
1=6 мкГн = 61
С = 1,2 нФ=1,2-
Umc=2 В
(Р) = 0,2 мВт = 2-
Q — ?
3"*Гн
10~9Ф
Ю^Вт
Решение
~2д'
1
Rq~ шС* т'
21'
U A
/m( Rc '
1
ш° VZc'
;2 _С 2
mf ? mc,
С Ответ j e = i4i.
В сеть переменного тока с действующим значением напряжения
120 В последовательно включены проводник с активным сопро-
тивлением 10 Ом и катушка индуктивностью 0,1 Гн. Определите частоту v
Тока, если амплитудное значение силы тока в цепи равно 5 А.
Дано
?/=120 В
Д = 10 Ом
? = 0,1 Гн
^=5 А
v,— ?
Решение
t/™
' t/m =
-Л2=51,6Гц.
Г Ответ j у
= 51,6 Гц.
Диэлектрик, диэлектрическая проницаемость которого равна 2,8.
используется в конденсаторе в качестве изолятора. Конденсатор, нахо-
дясь под напряжением, погаощает некоторую мощность, причем при v = 50 Гц
коэффициент мощности cos<p = 0,1. Определите удельное сопротивление ди-
электрика.
Цепь, состоящая из последовательно соединенных безындукци-
^ онного резистора сопротивлением R = 100 Ом и катушки с ак-
¦ярным сопротивлением, включена в сеть с действующим напряжением
17 = 300 В. Воспользовавшись векторной диаграммой, определите тепловую
мощность, выделяемую на катушке, если действующее значение напряжения
на сопротивлении и катушке соответственно равно U R -150 В и UL = 250 В.
2nveeo-Jl - cos2 tp
= 12,9 МОм-м.
В цепь переменного тока напряжением Um - 220 В и частотой
50 Гц включена катушка с активным сопротивлением. Сдвиг фаз
между напряжением и током составляет л/6. Определите индуктивность
тушки, если известно, что она поглощает мощность 445 Вт.
ка-
Дано
Л = 100 Ом
$ = 300 В
{^ = 150 В
UL = 250 В
Решение
PL = IULcoS<pL, 1 = ^,
к
U2 = U2R + Ul-2URULcos<pL,
U2-U2R-U2L
cosip, = & -,
*L 2URUL
R 4 2URUL
QOmeem )^ =
U.
f4
Vtg>
ul
Ответ Л i = 0,i5rH.
Десятичные приставки к названиям единиц
Т —тераA012) д —дециСЮ-1) н —наноA0-9)
Г —гига A09) с — санти A0) п —пико A02)
М —мегаA06) м —миллиA0-3) ф —фемто A045)
к — килоA03) мк — микроСЮ) а —аттоA0-1В)
4.2. Упругие ВОЛНЫ ^IBl Волна Распространяется в упругой среде со скоростью v -150 м/с.
^ВИР^ Определите частоту v колебаний, если минимальное расстояние Дх
(-116^ Определите разность фаз Д„ колебаний двух точек, лежащих^ ^^^ WфаЗЫ ЮПСб>ЯИЙ ^^ "Р0™0™ раВ"° °'?5 *
луче и друг от друга на расстоянии Д/ = 1 м, если
/1 = 0,5 м.
™aB0J1Hbl fbmeem ) v = iooru.
Дано
Д/ = 1 м
Я = 0,5 м
Ар — ?
Решение
Ьр^Ы.
Вычисления:
Определите длину волны Я, если числовое значение волнового
^ вектора к равно 0,02512 см.
Qpmeem
0,5 м
точки колеблются в фазе.
>j Звуковые колебания с частотой v = 450 Гц и амплитудой Л = 0,3 мм
распространяются в упругой среде. Длина волны Я = 80 см. Оп-
ределите: 1) скорость распространения волн; 2) максимальную скорость час-
тиц среды.
Две точки лежат на луче и находятся от источника колебаний на
расстоянии х, = 4 м и х2 = 7 м. Период колебаний Т = 20 мс и
скорость v распространения волны равна 300 м/с. Определите разность фаз v= ^ ц
колебаний этих точек.
Дано
- лг, точки колеблются в противофазе.
Дано
v=450 Гц
Л = 0,3 мм = 3 ¦ Ю^м
Я = 80 см = 0,8 м
1) v —?
Решение
§ = /icosco Г — ,
V
v~kv,
Я = vT,
су = 2яг,
<% , ¦ ( *}
— = -Aw sin су t ,
А(о\ = 2nvA.
С Ответ J
i; = 360 м/с; 2)
=0,848 м/с.
УИ^^^Р Плоская синусоидальная волна распространяется вдоль прямой,
*cmmmmmS>r совпадающей с положительным направлением оси х в среде, не
поглощающей энергию, со скоростью v = 10 м/с. Две точки, находящиеся на
этой прямой на расстоянии х, = 7 ми х2 = 10 м от источника колебаний, ко-
леблются с разностью фаз Ар = Зл/5 . Амплитуда волны А - 5 см. Определи-
те: 1) длину волны X; 2) уравнение волны; 3) смещение ?2 второй точки в
момент времени t2 — 2 с.
Поперечная волна распространяется вдоль упругого шнура со ско-
ростью v = 10 м/с. Амплитуда колебаний точек шнура А = 5 см, а
период колебаний Г = 1 с, Запишите уравнение волны и определите: 1) длину
волны; 2) фазу колебаний, смещение, скорость и ускорение точки, расположен-
ной на расстоянии х, =9 м от источника колебаний в момент времени /, = 2,5 с.
Дано
Решение
2л;
т :
2лг
2лг . 2лг
2л: ( х,
С Ответ
Уравнение плоской волны,
распространяющейся вдоль положительного направления оси х,
^(х, 0 = 5 cos 2лг/ х , см; 1)Я = 10м;
2) р, = 3,2л:, f, = -4 см, ?, =18,5 см/с, f, = -160 см/с2
где ?(х, 0 — смещение точек среды с координатой х в момент времени t;A —
амплитуда волны; си — циклическая частота; к = 2л/Л = 2u/{vT) = w/v — вол-
новое число (X — длина волны; v — фазовая скорость; Т — период колеба-
ний); <р0 — начальная фаза колебаний.
Э? 1 Э^
Убедитесь, что волновому уравнению —т = ~Т—7 УД0ВлетВ0Ря-
dx v дг
ет плоская волна ?(х, t) = A cos[to{/ - х/и)+ (р0].
Выведите связь между групповой и фазовой
скоростями.
Два когерентных источника колеблются в одинаковых фазах с ча-
стотой v = 400 Гц. Скорость распространения колебаний в среде
У = 1 км/с. Определите, при какой наименьшей разности хода, не равной нулю,
будет наблюдаться: 1) максимальное усиление колебаний; 2) максимальное ос-
лабление колебаний.
Дано
v = 400 Гц
v = l км/с
Arnin"?
Решение
V
^max = 2w—
)-
7 = 1,
7=0.
Я v
2 ~ 2v
Докажите, что в недиспергирующей
скорости равны.
{.Ответ ) лтах = 2,5м,
Amin = 1,25 м.
среде групповая и фазовая
28 ^ Два когеРентнь1Х источника посылают поперечные волны в одина-
ковых фазах. Периоды колебаний Т = 0,2 с, скорость распростране-
ао=24 м-с-з/2, Ь =
Определите групповую скорость для частоты v = 800 Гц ее ния волн в сРеде v ~ ^00 м^с> ОпРеДелите' при какой разности хода в случае нало-
фазовая скорость задается выражен - // ~' жения волн будет наблюдаться: 1) ослабление колебаний; 2) усиление колебаний.
/v + b , где
а0 = 24 м • с -3/2
6 = 100 Гц
С Ответ J i) a = ±80Bw+i),m (w = 0,1,2,...);
2) Д = ±160те,м (от = 0,1,2,...).
1 7
dv,
По поверхности воды распространяются две волны, возбуждае-
мые двумя точечными когерентными источниками. Какую форму
имеют линии, на которых лежат точки, имеющие одну и ту же постоянную
разность хода?
Уравнение сферической волны
где г — расстояние от центра волны до рассматриваемой точки среды.
=
Образование стоячих волн обычно наблюдают при интерферен-
ции бегущей и отраженной волны. Объясните, когда и почему на
Два динамика расположены на расстоянии d = 0,5 м друг от др^
= 1500 г п И В°СПРОИЗВОДЯТ один и тот же музыкальный тон на частоте IUb—T ции оегущеи и отраженной видны, wv
Ппин™! Ц' РИСМНИК нах°Дится "а расстоянии / = 4 м от центра динамиков шанице Отражения получается узел или пучность.
Принимая скорость звука v = 340 м/с, определите, на какое расстояние от цен' — : =====
тральной линии параллельно динамикам надо отодвинуть приеГик ЧТобы о„ \
зафиксировал первый интерференционный минимум "'ШШ^ Z
— ^-1- минимум. ^ШШШт Объясните, где человек слышит более громкий звук: в пучности
или в узле стоячей волны.
Два динамика расположены на расстоянии d = 2,5 м друг от др> -
га и воспроизводят один и тот же музыкальный тон на определен-
ной частоте, который регистрируется приемником, находящимся
на расстоя-
нии / = 3,5 м от центра динамиков. Если приемник передвинуть от централь-
ной линии параллельно динамикам на расстояние х = 1,55 м, то он фиксирует
первый интерференционный минимум. Скорость звука и = 340 м/с. Определи-
те частоту звука.
ГОтвет j v = ns Гц.
Определите длину волны Я, если расстояние А/ между первым и
четвертым узлами стоячей волны равно 30 см.
i -
д/,
If
А-
Дано
, = 30 см = 0,3 м
_9
Решение
А; 3 .
at л, - — Я > /
•' 2
2
Д'4,1
3
[Ответ j я =
20 см.
СВЧ-генератор излучает в положительном направлении оси х
плоские электромагнитные волны, которые затем отражаются об-
ратно. Точки Мх и М2 соответствуют положениям двух соседних минимумов
интенсивности и отстоят друг от друга на расстоянии / = 5 см. Определите
частоту микроволнового генератора.
Дано
1 = 5 см = 5- 10м
с = 31О8 м/с
V —9
Решение
, Я ее
/ = -, v = — = —.
2 Я 2/
С Ответ
v = 3 гтц.
( 4.136 J Один конец упругого стержня соединен с источником гармони-
~ ческих колебаний, подчиняющихся закону ? = A cos со/, а другой
его конец жестко закреплен. Учитывая, что отражение в месте за
жня происходит от
жня происходит от менее плотной среды, определите характер колебаний
любой точке стержня.
Один конец упругого стержня соединен с источником гармони-
ческих колебаний, подчиняющихся закону ? = A cos cot, а другой
крепления стер. «» коне^ жестко закреплен. Учитывая, что отражение в месте закрепления стер-
0&я происходит от более плотной среды, определите характер колебаний в
любой то^ке стержня.
? = A cosa)t
Среда менее плотная
?(*, 0 — ?
§1= A COSCO| /
V
?2=^coscoI/ + — ,
I V
(ox Л
= 1А cos cosco?,
V
. (OX
sin—
V
%- A coscuf
Среда более плотная
Решение
Г ^1
?,= ^ cosco r— ,
= у4 COS Ш / + —
j
= -A coscy ? + —
[ V
g(x,t) = §,+^2 = A cos со? A cos cy/ + — =
V V J V V J
I СУХ . . COX COX .. COX
= A I coscy? cos— + sincu?-sin cosco?-cos— + smсо? sin— 1 =
V V V
V
-, A ¦ ШХ ¦
= 2A sin s
2ж
0 - 1A cosTx • zosm _
стоячей волны.
= ±т- (/и = 0,1, 2,...)-пучности.
Уравнение стоячей волны
@ =
c, ?) = 2A si
2tz
cox _ 2n T _2jt
— X — ' X,
v T Я Я
¦ sin со? — уравнение стоячей волны.
При х = ±w- (от = 0, 1, 2,. .) — узлы.
ПА
При х = ±1 ти + -г!т- (от = 0, 1, 2,...) — пучности.
Выведите условие для координат пучностей и узлов стоячей волны.
Для определения скорости звука в воздухе методом акустическо-
го резонанса используется груба с поршнем и звуковой мембра-
ной, закрывающей один из ее торцов. Расстояние между соседними положени-
ями поршня, при котором наблюдается резонанс на частоте v = 2500 Гц, со-
ставляет / = 6,8 см. Определите скпппг™ iD^«
Определите скорость звука в воздухе.
v = 2500 Гц
/ = 6,8 см = 6,8 10 2 м
v = 2lv.
Стержень с закрепленными концами имеет длину / = 70 см. При
трении стержень издает звук, основная частота (наименьшая час-
тота, при которой может возникать стоячая волна) которого vQ = 1 кГц. Опре-
делите: 1) скорость звука v в стержне; 2) какие обертоны (волны с кратными
основным частотами) может иметь звук, издаваемый стержнем.
Ответ
v = l,4 км/с; 2) v, = *v0 (*= 2, 3, 4,...).
Труба, длина которой /-1 м, заполнена
одного конца. Принимая скорость
воздухом и открыта с
Человеческое ухо может воспринимать звуки, соответствующие гра-
ничным частотам v, = 16 Гц и v2 = 20 кГц. Принимая скорость
зйука в воздухе равной 343 м/с, определите область слышимости звуковых волн.
ГОтветЛ пм+ 21,4 м.
Определите интенсивность звука (Вт/м2), уровень интенсивности
L которого составляет 67 дБ. Интенсивность звука на пороге слы-
шимости /0 = 10~12 Вт/м2.
Дано
„L = 67 дБ = 6,7 Б
/0 = 10-12 Вт/м2
I —?
Решение
Z = Igf, -^- = 10*,
/=/0-10Л.
QOmeem
Определите отношение интенсивностей звуков, если они отлича-
ются по уровню громкости на 2 фон.
Г = 2
h
h
Дано
фон
?
Решение
Г = 1 фон — единица уровня громкости.
| v = 1000 Гц| Г = 1 фон, если L = 1 дБ.
Г = 2 фон L = 2 дБ = 0,2 Б.
Разговор в соседней комнате громкостью 40 фон слышен
как шепот громкостью 20 фон. Определите
сивностей этих звуков.
отношение интен-
Г, = 40 фон
Г2 = 20 фон
~ 40 дБ = 4 Б;
= 20 дБ = 2 Б.
Средняя квадратичная скорость (vKR) молекул двухатомного газа
при некоторых условиях составляет 480 м/с. Определите скорость v
эостранения звука в газе при тех же условиях.
Определите, на сколько фонов увеличился уровень громкости
1 ~ звука, если интенсивность звука увеличилась: 1) в 1000 раз,
2) в 10 000 раз.
1) на 30 фон; 2) на 40 фон.
Скорость распространения звуковой волны в газе с молярной массой
М = 2,9 • 10 кг/моль при / = 20 °с гл-™.-.» о -->.-<- -
М = 2,9 • 10- кг/моль при / = 20 °С составляет 343 м/с Определи
моляоных теплл™»,™»". ^иредели-
_,. - - ш ,raU/u> п^и / = zu "С составляет 343 м/с. Определи
те отношение молярных теплоемкостей газа при постоянных давлении и объеме.
М= 2,9-10 кг/моль
= 20 °С, Г=293 К
и = 343 м/с
С,
Дано
„) = 480 м/с
— ?
Решение
y = -Z- = -
С Ответ j v =
м/с.
Докажите, что формула w -
, выражающая скорость звука
\УР
Я газе, может быть представлена в виде v ~ J , где у — отношение моляр-
ных теплоемкостей при постоянных давлении и объеме; р — давление газа;
р — его плотность.
Дано
Решение
v =
М '
M
\УР
m=pV ,
M т
\УР
v = — , что и требовалось доказать.
V Р
Плотность р некоторого двухатомного газа
при нормальном дав-
ШЩ Движущийся по реке теплоход дает свисток частотой vn = 400 Гц
д д систок частотой v0 = 400 Гц.
Наблюдатель, стоящий на берегу, воспринимает звук свистка час-
Гц Принимая с
щ а берегу, воспринимает звук свистка час-
тотой v = 395 Гц. Принимая скорость звука v - 340 м/с, определите скорость
движения теплохода. Приближается или уда
— г »ужм. 1/-JW М/С, ОП
движения теплохода. Приближается или удаляется теплоход?
Решение
ний знак — удаление.
' веРхний знак — сближение; ниж-
vmr = 4,3 м/с, теплоход удаляется.
В реке, скорость течения которой равна v, установлен неподвижный
источник колебаний, создающий в воде колебания
частотой vQ. По
разные стороны на равных расстояниях от источника установлены неподвиж-
ные приемники колебаний П, и П2. Определите частоты,
этими приемниками.
регистрируемые
Наблюдатель, стоящий на станции; слышит гудок проходящего
электровоза. Когда электровоз приближается, частота звуковых
иолебаний гудка равна vx, а когда удаляется — v2 ¦ Принимая, что скорость v
звука известна, определите: 1) скорость иист электровоза; 2) собственную час-
xoiy v0 колебаний гудка.
Г2
1L-
Дано
¦>
.?
Решение
(v±v )v0
V = , ^пр U .
w0 ^ wo
"' V-VHCT' ^ + ^ист
Wo Vo(Vl+V2
"'" V\~V2 2V2
vx-v2
1! ! U
v,+v2
) v -.2V\V*
vx + v2
Г Ответ J
v,-
2v,v2
Электропоезд проходит со скоростью 72 км/ч мимо неподвижно-
го приемника и дает гудок, частота которого 300 Гц. Принимая
скорость звука равной 340 м/с, определите скачок частоты, воспринимаемый
приемником.
Дано
уи„ = 72 км/ч = 20 м/с
v0 = 300 Гц
v = 340 м/с
Дг — ?
Решение
V V + VKUT v иист
v wo Дг_(. _„ - 2v**r°
f Ответ Л д^-зм Гц.
Поезд проходит со скоростью 54 км/ч мимо неподвижного при-
емника и подает звуковой сигнал. Приемник воспринимает ска-
чок частотой Av = 53 Гц. Принимая скорость звука равной 340 м/с, определите
частоту тона звукового сигнала гудка поезда.
4.3. Электромагнитные волны
Скорость распространения электромагнитных волн в некоторой
среде составляет v - 250 Мм/с. Определите длину волны элект-
ромагнитных волн в этой среде, если их частота в вакууме v0 = 1 МГц.
y-
v0
A
Дано
= 250Мм/с=2,5-108м/с
= 1 МГц=1ОбГц
— ?
Решение
f Ответ Л
X = vT
A = 250
V V
v vQ ¦
M.
Два катера движутся навстречу друг другу. С первого катера, дви-
жущегося со скоростью и, =10 м/с, посылается ультразвуковой
сигнал частотой v, = 50 кГц, который распространяется в воде. После отраже- "~%~
ния от второго катера сигнал принят первым катером с частотой v2 = 52 кГц. При- у J '
нимая скорость распространения звуковых колебаний в воде равной 1,54 км/с, оп-
ределите скорость движения второго катера.
Для демонстрации преломления электромагнитных волн Герц при-
менял призму, изготовленную из парафина. Определите показа-
тель преломления парафина, если его диэлектрическая проницаемость е = 2 и
магнитная проницаемость ц = 1.
г, =50 кГц = 5- 104Гц
v2 = 52 кГц = 5,2' 104Гц
v = 1,54 км/с = 1540 м/с
Электромагнитная волна с частотой v = 5 МГц переходит из не-
магнитной среды с диэлектрической проницаемостью е = 2 в ва-
куум. Определите приращение ее длины волны.
Дано
v =
v-v2 v-v{
= 5 МГц = 5- 106Гц
АЯ —?
Решение
v nv
с
v
(j)meem
Радиолокатор обнаружил в море подводную лодку, отраженны^
сигнал от которой дошел до него за t = 36 мкс. Учитывая, что
диэлектрическая проницаемость воды е = 81, определите расстоя
тора до подводной лодки.
эяние от лока-
После того как между внутренним и внешним проводниками ка-
беля поместили диэлектрик, скорость распространения электро-
магнитных волн в кабеле уменьшилась на 63%. Определите диэлектрическую
восприимчивость вещества прослойки.
Колебательный контур содержит конденсатор емкостью С = 0,5 нФ
и катушку индуктивностью L = 0,4 мГн. Определите длину вол-
ны излучения, генерируемого контуром.
Определите длину электромагнитной волны в вакууме, на кото-
(- р рую настроен колебательный контур, если максимальный заряд
#Г обкладках конденсатора Qm = 50 нКл, а максимальная сила тока в контуре
/ = 1,5 А. Активным сопротивлением контура пренебречь.
Дано
=1.5 А
я—'
Решение
do
Q=Qmcosajt, I = — = -cuQm sincut.
at
UQ
d/
ш = 2nv,
с _ 2жс __ 2ncQn
V Ш
Длина Я электромагнитной волны в вакууме, на которую настро-
ен колебательный контур, равна 12 м. Пренебрегая активным со-
противлением контура, определите максимальный заряд Qm на обкладках кон-
денсатора, если максимальная сила тока в контуре /т = 1 А.
я=
г
а.
Дано
12 м
= 1 А
9
Решение
Х = сТ , Т = 2яЛс ,
1С = Щ-, Т = 2л^-,
2С
2 '
/т
Ms*.
2лс '
СОтветЛ Qm = 6,37 нКл.
Два тонких изолированных стержня погружены в трансформатор.
ное масло и индуктивно соединены с генератором электромагнит-
ных колебаний. При частоте колебаний 505 МГц в системе возникают стоячие
волны, расстояние между соседними пучностями которых равно 20 см. Прини-
мая магнитную проницаемость масла равной единице, определите его диэлек-
трическую проницаемость.
В вакууме вдоль оси х распространяется плоская электромагнит-
ная волна. Амплитуда напряженности электрического поля волны
10 В/м. Определите амплитуду напряженности магнитного поля волны.
Дано
Решение
Е = Ео cos(cot - be), Н= Но cos(cot- he),
При е = 1 и ц =
Ео =
Qpmeem ^ я0 = 26,5 мА/м.
В вакууме вдоль осих распространяется плоская электромагнит-
ная волна. Амплитуда напряженности магнитного поля волны рав-
на 1 мА/м. Определите амплитуду напряженности электрического поля волны.
(Два параллельных провода, одни концы которых изолированы, a (f)nitteni\ F =0
вторые индуктивно соединены с генератором электромагнитных \^ V m
колебаний, погружены в спирт. При соответствующем подборе частоты коле-
баний в системе возникают стоячие волны. Расстояние между двумя узлами
стоячих волн на проводах равно 40 см. Принимая диэлектрическую проницае-
мость спирта е = 26, а его магнитную проницаемость ц = \, определите час
тоту колебаний генератора.
377 В/м.
Г Ответ j v = 73,5 мгц.
^И^^® Покажите, что плоская монохромная волна ? = Eq zos{ajt -bc + <p)
В вакууме вдоль оси х распространяется плоская монохромати-
ческая электромагнитная волна, описываемая уравнениями
Е = Ео cos(wt - be) и Н = Но cos(w? - be). Эта волна отражается от плоско-
сти, перпендикулярной оси х. Запишите уравнения, описывающие отраженную
волну, а также объясните их физический смысл.
удовлетворяет волновому уравнению
рость электромагнитных волн.
дх2 ~ v2 Ы2 '
V — Фазовая
Уравнение плоской электромагнитной волны
Е = Ео cos(w? - be + (р); Н = Но cos(w? - he + <р),
где ЕоиНд — соответственно амплитуды напряженностей электрического и
магнитного полей волны; со — круговая частота; k - cojv — волновое число;
V — начальные фазы колебаний в точках с координатой х = 0 .
Рассмотрите суперпозицию двух плоских монохроматических
электромагнитных волн с одинаковыми амплитудами Ео и Н„ (
распространяющихся вдоль оси х в противоположных направлениях. Началь-
ную фазу прямой и обратной волн примите равной нулю. Определите коорди-
наты пучностей и узлов для: 1) электрического вектора Е; 2) магнитного век-
тора Н стоячей волны.
1) Е, - Ео cos(tt^ - be) — прямая волна
Е2 = Ео cos(a>f + be) — отраженная волна
Хп — ? г _ ?
Е - Е, +Е2= E0[cos(wr - kx)+cos(ajt + be)] = 2Е0 cos—
coscut.
Пучности
2лх
¦ = ±тл
Узлы
2лх
2) Н, - Но cos(<w -be)— прямая волна
Н2 = Но сов(ш + Ь + л)~ отраженная волна
H - H, +H2= H0[cos(<w/ -bc) + cos(a)t +
Пучности I ^L
1 1 к
В вакууме вдоль оси х распространяется плоская электромагнитная
волна и падает по нормали на поверхность тела, полностью ее по-
0!01дающего. Амплитуда напряженности магнитного поля волны равна 0,15 А/м.
Определите давление, оказываемое волной на тело. Воспользуйтесь результа-
трц выводов теории Максвелла о том, что если тело полностью поглощает па-
дающую на него энергию, то давление равно среднему значению объемной
платности энергии в падающей электромагнитной волне.
Дано
Я0 = О,15 А/м
P=(w)
р—1
Решение
¦Jee^E = ,]цц0Н,
Е = Ео cos(wt - fa),
Я = #0 cos((ot - fa),
еоеЕ2 ц0цН2
Нэ 2 ' 2 '
w = w3 + wM= 2w3 = 2wM , w = 2wM = цоцН2 = цоцНц cos2(ty/ - foe),
(w) = (цоцН1 zos2{wt - fa)), (cos2(w/ - foe)) = -,
[ОтветЛ p =
В вакууме вдоль оси х распространяется плоская электромагнит-
ная волна и падает по нормали на поверхность тела, полностью ее
поглощающего. Амплитуда напряженности электрического поля волны равна
2 В/м. Определите давление, оказываемое волной на тело.
Г Ответ j
пПа.
^^^^^В Плоская монохроматическая электромагнитная волна распроср
^«ЯВШ»' раняется вдоль оси х. Амплитуда напряженности электрического
поля волны ?0 = 5 мВ/м, амплитуда напряженности магнитного поля волны
Но = 1 мА/м. Определите энергию, перенесенную волной за время t = 10 мин
через площадку, расположенную перпендикулярно осих, площадью поверхно-
сти 5 = 15 см2. Период волны Т « t.
Дано
В вакууме вдоль оси х распространяется плоская электромагнит-
ная волна. Амплитуда напряженности электпичяптпп ™™
и ьакууме вдоль оси х распространяется плоская электромагнит-
ная волна. Амплитуда напряженности электрического поля волны
3 мВ/м. Определите интенсивное, попит, т -- — -
.F,, .wnuiu ииля волнь:
Определите интенсивность волны /, т. е. среднюю энер-
рез единицу повеихногти п ("пи.™
«^едышю интенсивность волны /, т. е. cpi
гию, проходящую через единицу поверхности в единицу времени
5, Оптика. Квантовая природа излучения
5.1. Элементы геометрической
и электронной оптики
На горизонтальном дне бассейна глубиной h = 1,5 м лежит плоское
зеркало. Луч света входит в воду под углом ц = 45°. Определите
расстояние s от места вхождения луча в воду до места выхода его на поверх-
ность воды после отражения от зеркала. Показатель преломления воды п = 1,33.
Решение
= 2htgi2,
sin /t
¦= п,
sim-,
sin;,
sin i2 = ¦
sin i2
cos и
sin i j
Sin2!,
2-^2h Г Ответ } s = 1,88 м.
Луч света падает на плоскую границу раздела двух сред, частично
отражается и частично преломляется. Определите угол падения, при
Котором отраженный луч перпендикулярен преломленному лучу.
В вакууме вдоль оси х распространяется плоская электромагнит
ная волна. Амплитуда напряженности магнитного поля составля-
ет 5 мА/м. Определите интенсивность волны.
Дано
«21
;; + i2 = 90°
ч~ ?
Решение
- — Tit |
sin/2 ' '
i'\ = 'i.
'/,
¦У/
i2 = 90°- j[ = 90°- ix, sin i2 = sin(90°- /;) = cos /;,
sin»',
cos Ц
r = tg h = «21. '1 =
( Ответ ) ;, = arctg j^, .
13 Сборник з<
по фишке
На плоскопараллельную стеклянную (п = 1,5) пластинку
ной d = 5 ш падает под углом / = 30° луч света. Определите
ковое смещение луча, прошедшего сквозь эту пластинку.
Дано
Человек с лодки рассматривает предмет, лежащий на дне водо-
ема (п = 1,33). Определите его глубину, если при определении "на
по вертикальному направлению глубина водоема кажется равной 1,5 м.
п = 1,5
= 5 см = 5- Ю-2м
= 30°
С Ответ j н = г м.
Ответ Л х = 9>69 мм
Между двумя стеклянными пластинками с показателями прелом-
ления и, и п2 находится тонкий слой жидкости. Луч света, рас-
пространяющийся в первой пластинке под углом ц (меньше предельного),
выходя из слоя жидкости, входит во вторую пластинку под углом /2. Докажите,
что в данном случае выполняется закон преломления sin /,/sin i2 = п2)щ
:ости между пластинами.
Дано
Человек с лодки рассматривает предмет, лежащий на дне. Глуби-
на водоема везде одинакова и равна Я , показатель преломления
воды равен и. Определите зависимость кажущейся глубины я предмета от угла i,
образуемого лучом зрения с нормалью к поверхности воды.
Нп2 cos3 i
^ ^
{г? -sin2 03/2
Л Предельный угол полного отражения на границе стекло—жид-
I
кость /пр = 65°. Определите показатель преломления жидкости,
если показатель преломления стекла п = 1,5.
'l < 'пред
h
( sin i,
I sin ^2
sin a
sin a
sim2
n2
n
че
h-
smi\
sm i2 n2 и.
sin i.
\__n2
w = 65°
и = 1,5
Дано
sin
(
Решение
• _Цж
'HP" „ '
Ответ Л
"ж
пж -
= "sin»np-
= 1,36.
СВ6Та ВЫХ0ДИТ Ю СТеКЛа В ВаКуум- Недельный угол /„„
Определите скорость света в стекле.
J;;* j Длинное тонкое волокно, выполненное из прозрачного материа-
•—«"^ ла с показателем преломления п = 1,35, образует световод. Опре-
делите максимальный угол а к оси световода, под которым световой луч еще
может падать на торец, чтобы пройти световод с минимальным ослаблением.
Дано
п = 1,35
a —
Решение
У = 'пр ,
n
На дне сосуда, наполненного водой (п = 1,33) до высоты h = 25 см,
находится точечный источник света. На поверхности воды плава-
ет непрозрачная пластинка так, что центр пластинки находится над источни-
ком света. Определите минимальный диаметр пластинки, при котором свет не
пройдет сквозь поверхность воды.
= п, sin /3= cosy,
sina
cosy
-=п,
siny = —,
п
sina = n cosy
= n^\-sm2y = nil - — = 4n2-\ , a = arcsin л/и2 -1
/7=25 см = 0,25 м
и = 1,33
d — ?
С Ответ j a =
65 .
Расстояние а от предмета до вогнутого сферического зеркала
равно двум радиусам кривизны. Определите положение изобра-
жения предмета и постройте это изображение.
Дано
Sin; > _
n'
R2n2 > h2
sin / = ¦
R
a = 2R
R2(n2~\)
R
b —?
J_ l - 2
2R+~b~ R'
-!•¦
Решение
а + b R /'
На рисунке показаны поло-
жения главной оптической
оси MN сферического зеркала, светя-
щейся точки S и ее изображения S'.
Определите построением положение цен-
тра сферического зеркала и его фокуса.
Укажите вид использованного зеркала.
S
SS'->C,
ab = bd
(а — любая
точка на SS'),
Sd-> P (зеркало),
MN, KS'-*F.
На рисунке показаны поло-
жения главной оптической
оси MN сферического зеркала, светя-
щейся точки S и ее изображения S'. М_
Определите построением положение цен-
тра сферического зеркала и его фокуса.
Укажите вид использованного зеркала.
S
Выпуклое сферическое зеркало имеет радиус кривизны 60 см. На
расстоянии 10 см от зеркала поставлен предмет высотой 2 см.
Определите: 1) положение изображения; 2) высоту изображения. Постройте
чертеж.
S'
Дано
J?= 60 см = 0,6 м
д=10 см = 0,1 м
/j=2 см = 0,02 м
Решение
bR
1-2 I
b~ R a
aR
С, F, зеркало вогнутое.
S'
Вогнутое сферическое зеркало дает действительное изображение.
шгг которое в три раза больше предмета. Определите фокусное рассто-
яние зеркала, если расстояние между предметом и изображением равно 20 см
R-b
H = h
2a+R
R-b
R + a
\)b = l,5 см; 2) H = 1,5 см.
Постройте изображение произ-
вольной точки S , которая ле-
жит на главной оптической оси собираю-
щей линзы.
Постройте изображение про-
извольной точки S , которая
лежит на главной оптической оси рассеи-
вающей линзы.
Фокальная
| плоскость
Определите построением ход луча после преломления его собираю.
щей (рис. а) и рассеивающей (рис. б) линзами. На рисунках MN
ЛаВНОЙ ОПТИЧйгкпн пг*и- Л ~—
На рисунке показаны положения главной оптической оси MN
тонкой линзы, светящейся точки S и ее изображения 5' Опре-
- г U"A»«' Vjjjm*. wj JIUHJ
положение главной оптической оси; О—оптический цен ' "~~~г? ^ \!ш тонкой линзы, светящейся точки а и ее изооражени* о клас-
сы линзы. Среды по обе стороны линзы одинаковы линзы; b ~ фок>. j. ^ посгрОением оптический центр линзы и ее фокусы. Укажите вид линзы.
= — ЙЬеды по обе стороны линзы одинаковы.
На рисунке показаны положение главной оптической оси MS
w тонкой собирающей линзы и ход одного луча ABC через эту лин-
зу Постройте ход произвольного луча DE. Среды по обе стороны линзы оди-
наковы.
На рисунке показаны положение главной оптической оси MN
тонкой рассеивающей линзы, ход луча /, падающего на линзу, и
преломленного луча 2. Определите построением оптический центр и фокус-
ное расстояние линзы Среды по обе стороны линзы одинаковы.
М
N
N
S
*
S'
На рисунке показаны положения
главной оптической оси MN
тонкой линзы, светящейся точки S и ее изоб-
ражения S'. Определите построением поло-
жения оптического центра линзы и ее фокусов. Укажите вид линзы Среды по
обе стороны линзы одинаковы.
М
N
S'
S
*
На рисунке показаны положения
главной оптической оси MN
тонкой лиюы, светящейся точки S и ее изоб-
ражения S'. Определите построением поло- М
жения оптического центра линзы и ее фоку-
сов. Укажите вид линзы Среди по обе стороны линзы одинаковы.
N
Двояковыпуклая тонкая линза (показатель преломления п) с ради-
усами кривизны /?i и R2 находится в однородной среде с показате-
лем преломления щ . Выведите формулу этой линзы, используя принцип Ферма.
Выпукло-вогнутая тонкая линза (показатель преломления п) с
радиусами кривизны R\ (передняя поверхность) и R2 (задняя
, / .л 1^2 Кла
поверхность) находится в однородной среде с показателем преломления
Выведите Aonvn/nv тгг.» гг„ —
г _„..„« v^vmi, ^ показателем преломления ^
Выведите формулу этой линзы, рассматривая последовательное преломлени
света на двух сферических пакртип^т™.
Необходимо изготовить плосковыпуклую линзу с оптической си-
лой Ф = 4 ТТТТТП Лт»г.»п
v.w«_yiw лиллу с оптической си-
лой Ф = 4 дптр. Определите радиус кривизны выпуклой поверх-
, если показатель тйтгпидав»»
± ,,»„—««w радиус крИВИЗНЫ ВЫПУКЛОЙ 1
ности линзы, если показатель преломления материала линзы равен 1,6.
Определите расстояние а от двояковыпуклой линзы до предме-
та, при котором расстояние от предмета до действительного изоб-
кения будет минимальным.
Тонкая линза с показателем прелом-
ления и и радиусами кривизны R]
и R2 находится на границе раздела двух сред с
показателями преломления и, и и2 • Пусть а и
b — соответственно расстояния от предмета до
линзы и от изображения до линзы; fx и /2 —
соответствующие фокусные расстояния. Докажи-
те справедливость соотношения А + А _ j
д —
jiii i —
ab
Дано
in
?
- = 1, b = !-a,
l = t
i
lf =
Решение
7 + Ь,
1 1
al - a1,
L
i
F
a >
1
F
< b
J
d/
•, — = 0 (условие min): — = — —j-
da da (a-/)
= 0.
С Ответ Л a =
Двояковыпуклая линза с показателем преломления и = 1,5 имеет
одинаковые радиусы кривизны поверхностей, равные 10 см. Изоб-
ражение предмета с помощью этой линзы оказывается в 5 раз больше предме-
та. Определите расстояние от предмета до изображения.
Дано
л = 1,5
Л =10 см = 0,1 м
(а + Ь) —
Решение
a
6
= т]а,
a + b = ab{n-\) —
R
1-1—, a =
К
2гЦп-1)
Щп-\)
Г Ответ j (a
м.
Из тонкой плоскопараллельной стеклянной пластинки изготов^
ны три линзы. Фокусное расстояние линз / и 2, сложенных
ное расстояние каждой из линз.
Докажите, что освещенность, создаваемая изотропным (сила све-
та источника не зависит от направления) точечным источником
свега / на бесконечно малой площадке, удаленной на расстояние г от источ-
,, равна Е = — cos /, где i — угол падения луча на площадку.
Дано
Е = — cos г
Решение
Двояковыпуклая линза из стекла (и = 1,5) обладает оптической
силой Ф = 4 дптр. При ее погружении в жидкость (и, = 1,7) лиша
действует как рассеивающая. Определите: 1) оптическую силу линзы в жидко-
сти; 2) фокусное расстояние линзы в жидкости; 3) положение изображения точ-
ки, находящейся на главной оптической оси на расстоянии трех фокусов or
линзы (а = 3/ ) для собирающей линзы и рассеивающей линзы. Постройте
изображение точки для обоих случаев.
COS!
= r2d
Е- — cos;,
dS
с!Ф
г' ck>
cos;,
с!Ф
Ha какую высоту над чертежной доской необходимо повесить лам-
почку мощностью Р = 300 Вт, чтобы освещенность доски под
лампочкой была равна Е = 60 лк. Наклон доски составляет 30°, а световая от-
дача лампочки равна 15 лм/Вт. Примите, что полный световой поток, испуска-
емый изотропным точечным источником света, Фо = 4ж1.
Ф
/ =
ф'
*¦=¦
.я, )R «V a + b~f'b = ^~J
J>meem j i) ф, =-0,94
2) у| =-1,06 м;
Дано
Р=Ш Вт
? = 60 лк
; = 30°
1 = 15 лм/Вт
Фо = 4тг/
А—?
Фо
А =
Решение
= LP, Ф0 = 4ж1,
LP „ I . LP .
, с, — -, COS/— -, COS!,
Ал h2 4яА2
| IP cos г
V 4лг?
f Ответ
м.
изображения одного и довательном применении получить дв ШШШШ Отверстие в корпусе фонаря закрыто идеально матовым стеклом
зываются равными - 5 Т0Г° ^ ПреДМета' пРтем увеличения о^ ЩЩВ^ (т. е. яркость источника не зависит от направления) размером
вещенность изображений ^ ~ пРеДелите> как при этом изменяется Ос 7,5 *1 ° с**- Сила света 7 ФонаРя в направлении, составляющем угол <р = 30°,
12 кД. Определите яркость В стекла.
Решение
Ф, = /ш,
= 1,85 ккд/м2.
и S{ — площади предмета и изображения.
Светильник в виде равномерно светящегося шара радиусом
г = 10 см имеет силу света / = 100 кд. Определите для:
тальника: 1) полный световой поток Фо; 2) светимость R.
[ этого све-
Докажите, что в том случае, когда яркость источника не зави-
сит от направления, светимость R и яркость В связаны соот-
ношением R = лВ.
Дано
В*В(а)
дФ
Решение
Ф п
= BaS cosa dw, j^X
«Jft = sina dad(p,
<p — азимутальный угол,
f> -> 0 до 2лг, a -> 0 до л/2,
Ф = f с!Ф = S [ й<р \ Ba sin a cosa da =
о о
я/2 t
[sin a cosa da = 2яВ5 • — = я
sm a cos a da =
Д. = B
Ф = лгВ5,1
Ф = Л5, ]
С Ответ j я = жв.
pi? 5 38 I ^a лист белой бумаги размером 10 X 25 см нормально к поверх^
^ —г-—* сти падает световой поток Ф = 50 лм. Принимая коэффициец-
рассеяния бумажного листа р = 0,7 , определите для него: 1) освещенное-] ь
2) светимость; 3) яркость.
5.2. Интерференция света
ж
Ответ
^ 2) Л = 1,4 клк/м2; 3M =
Объясните, чем отличаются просвечивающие и отражательные
SSSSr электронные микроскопы.
Р Объясните, почему в электронно-оптических преобразователях
можно получить увеличенное изображение предмета большей
интенсивности, чем интенсивность го>
Некоторые математические формулы
о a
Определите длину отрезка /], на котором укладывается столько
же длин волн монохроматического света в вакууме, сколько их
укладывается на отрезке /2 = 5 мм в стекле. Показатель преломления стекла
я = 1,5.
446 кд/м2. А = А.
h
h
я,
h
= 1
= 1,5
Дано
= 5 мм = 5 • 10 3 м
h
Я2
9
V-
Я =
h =
Решение
Яу,
с
/А
2я2'
V =
h
я,
с
h
"я2'
/
¦'2 •
[
Ответ
= 7,5 мм.
Два параллельных световых пучка, отстоящих друг от друга на
расстоянии d = 5 см, падают на кварцевую призму (п = 1,49) с
Преломляющим углом а = 25° . Определите оптическую разность хода Д этих
Пучков на выходе их из призмы.
Дано
rf = 5 см = 5 ¦ 10 2м
п = 1,49
а = 25°
А —?
С Ответ) д = 3}.
Решение
д = (/2 -/,)л = ВС п,
BC-dtga,
А = ndiga.
= 3,47 см.
В опыте Юнга расстояние между щелями d = 1 мм, а расстояние /
от щелей до экрана равно 3 м. Определите: 1) положение перво|
светлой полосы; 2) положение третьей темной полосы, если щели освещац
монохроматическим светом с длиной волны Я = 0,5
мм = 5- КГ'м
Д = 0,6 мкм = 6 ¦ 10 7 м
де=1,2 мм=1,2- 10м
Расстояние между двумя щелями в опыте Юнга d - 0,5 мм
(Я = 0,6 мкм). Определите расстояние / от щелей до экрана, если
Ах интерференционных полос равна 1,2 м.
Решение
Imaxl д =
(и = 0,1, 2,...),
-А,
С Ответ j / = 1 м.
ЩЩШЩ В опыте с зеркалами Френеля расстояние d между мнимыми изоб-
ражениями источника света равно 0,5 мм, расстояние / от них
экрана равно 5 м. В желтом свете ширина интерференционных
Определите длину волны желтого света.
В опыте Юнга расстояние / от щелей до экрана равно 3 м. Опре-
делите угловое расстояние между соседними светлыми полоса-
ми, если третья световая полоса на экране отстоит от центра интерференцион-
ной картины на 4,5 мм.
до
полос равна 6 мм
Дано
/=3 м
7И-3
х = 4,5 мм = 4,5- 10~3м
Да —?
Решение
|max| А = ±тХ,
л xd SU-~-
яй = ^ 52А
(« = 0,1,2,...),
1
h
\х
х ml
7 = _
пй. (т-1)Х Я х
d ~ d ~ d~ ml
= 5 104рад
Если в опыте Юнга на пути одного из интерферирующих лучей
"^ поместить перпендикулярно этому лучу тонкую стеклянную пла.
станку (п = 1,5), то центральная светлая полоса смятяетш г, л«~
'¦'" *" ^«ч^ьная светлая полоса смещается в положение п
воначально занимаемое пятой светлой пол " $* = !'5) с преломл^Щ™ Углом # = 20' ¦ Определите длину волны света, если
Определите толщину пнягтт™, П°Л С°И' *1Ина волны Х = °>5 мкм Ширина интерференционных полос Дх = 0,65 мм.
Расстояние от бипризмы Френеля до узкой щели и экрана соот-
ветственно равно а = 30 см и Ь = 1,5 м. Бипризма стеклянная
и =1,5
т = 5
Я = 0,5 мкм = 5 • 10~7м
d —?
Ответ Л d = 5^
d = -
и-1
ных
изменится:
на экране в опыте i
интерференцион-
если фиолето-
Дано
= 0,4 мкм
2 = 0,7 мкм
t
Дано
|^=30 см = 0,3 м
5=1,5 м
^, = 1,5
0 = 20'
Дзс = 0,65 мм = 6,5-10^м
Я—?
Решение
Я —
Axd
I
- Ъщ> = 2а(п -
Я = -
a + b
гч-3
Ь = 20' = 20 2,91 10~4 рад = 5,82- 1(ГЛ рад;
2-30-10 м-0,5-5,82 10 рад -0,65-10"
'Я =
A,5+ 0,3) м
= о, 5 -10 М.
мкм.
Расстояние от бипризмы Френеля до узкой щели и экрана соот-
ветственно равно а = 48 см и Ь = 6 м. Бипризма стеклянная
(и= 1,5) с преломляющим углом 9 = 10'. Определите максимальное число
полос, наблюдаемых на экране, если Я = 600 нм.
Г Ответ j т_АаЪ<<п
-лу
= 6.
ныи
Р На плоскопараллельную пленку с показателем
фаллельный пу
--г-„^„14ч,, 11ри *.акои наименьшей толщине пнет™ ,«, "" ~" кий свет (л = ovs нм). ипределите угол между поверхностями
-W..14. luitnjui зеркально отоажри а
свет наиболее сильно окрасится в желтый цвет (Я - П Л кяЙ*18' еСЛИ Расстояние межлУ Двумя соседними интерференционными мини-
. ^ ~ ' мкм). ..«ми r птажринпм мете павно 2 мм.
Дано
maxj A = mX, /и = 0,1,2,...
= (АВ+ВС)п- АЕ--1,
2
На стеклянный клин (л = 1,5) нормально падает монохроматичес-
кий свет (Я = 698 нм). Определите угол между поверхностями
>асстояние между двумя сое
и в отраженном свете равно 2 мм.
Я"
Я*
Ьх
а
= 1,5
= 698
= 2
о
—— {
Дано
нм = 6,98
мм = 2- 10
• 10м
эм
а
Д
Решение
у
«tga = -f-, -
Ах
т
Г с
Ах
г
7W+1
У
I
(т = 0, 1,2,...),
Я
v = ¦
а = ¦
2иАх
а = 24" .
cosr
2dncosr = —
2'
Я
4и cosr '
На стеклянный клин (л = 1,5) нормально падает монохроматичес-
кий свет. Угол клина равен 4' , Определите длину световой вол-
ны, если расстояние между двумя соседними интерференционными максиму-
Ийми в отраженном свете равно 0,2 мм.
\OmeemJ
- sin
2 /
На тонкую мыльную пленку (л = 1,33) под углом / = 30° падает
монохроматический свет с длиной волны Д = 0,6 мкм. Определи-
те угол между поверхностями пленки, если расстояние b между интерферен-
ционными полосами в отраженном свете равно 4 мм.
Г Ответ Л
а = 12,5" .
Монохроматический свет падает нормально на поверхность а0
душного клина, причем расстояние между интерференционны^,
полосами Дх, = 0,4 мм. Определите расстояние Лх2 между интерференциой|'
ными полосами, если пространство между пластинками, образующими клщ
заполнить прозрачной жидкостью с показателем преломления п = 1,33.
Дано
Установка для наблюдения колец Ньютона освещается монохро-
матическим светом с длиной волны Я = 0,6 мкм, падающим нор-
о. Пространство между линзой и стеклянной пластинкой заполнено жид-
о, и наблюдение ведется в проходящем свете. Радиус кривизны линзы
м. Определите показатель преломления жидкости, если радиус второго
го кольца г - 1,8 мм.
Решение
п-
А = тХ , 2dn - rrik,
Плосковыпуклая линза радиусом кривизны 4 м выпуклой сторо
ной лежит на стеклянной пластинке. Определите длину волш
падающего монохроматического света, если радиус пятого светлого кольца i
отраженном свете равен 3 мм.
п =
Wmeem j « = i,48.
mX-2R mXR
2r2
1 2
ИВя Плосковыпуклая линза с показателем преломления п = 1,6 выпук-
¦¦"^ лой стороной лежит на стеклянной пластинке. Радиус третьего
тлого кольца в отраженном свете (Я = 0,6 мкм) равен 0,9 мм. Определите
|Кусное расстояние линзы.
\0твет) f = 0,9 м.
Установка для наблюдения колец Ньютона освещается монохро-
матическим светом с длиной волны Я = 0,55 мкм, падающим нор-
мально. Определите толщину воздушного зазора, образованного плоскопарал-
лельной пластинкой и соприкасающейся с ней плосковыпуклой линзой в том
месте, где в отраженном свете наблюдается четвертое темное кольцо.
Плосковыпуклая линза с радиусом сферической поверхности
лУ R = 12,5 см прижата к стеклянной пластинке. Диаметр десятого
(Jsmhoio кольца Ньюгона в отраженном свете равен 1 мм. Определите длину
дх света.
Ответ
)я =
4mR
= 0,2
мкм.
<409>
Установка для наблюдения колец Ньютона освещается монохро
матическим светом, падающим нормально. При заполнении про.
странства между линзой и стеклянной пластинкой прозрачной жидкостью ра.
диусы темных колец в отраженном свете уменьшились в 1,21 раза. Определите
показатель преломления жидкости.
Ответ } Й = 1}46
Для уменьшения потерь света из-за отражения от поверхностей
стекла осуществляют "просветление оптики": на свободную по-
верхность линз наносят тонкую пленку с показателем преломления п = ^/й~~. В
этом случае амплитуда отраженных волн от обеих поверхностей такой пленки
одинакова. Определите толщину слоя, при которой отражение для света с дли-
ной волны Я от стекла в направлении нормали равно нулю.
На линзу с показателем преломления п = 1,58 нормально падает
монохроматический свет с длиной волны Я = 0,55 мкм. Для уст-
ения потерь света в результате отражения на линзу наносится тонкая плен-
, Определите: 1) оптимальный показатель преломления для пленки; 2) тол-
пленки.
ШтветЛ
2) с/= 109 нм.
Определите длину волны света в опыте с интерферометром Май-
кельсона, если для смещения интерференционной картины на 112
юс зеркало пришлось переместить на расстояние / = 33 мкм.
Ответ
= 589 нм.
Для измерения показателя преломления аммиака в одно из плеч
интерферометра Майкельсона помещена закрытая с обеих сторон
сачанная до высокого вакуума стеклянная трубка длиной / = 15 см. При за-
шении трубки аммиаком интерференционная картина для длины волны
589 нм сместилась на 192 полосы. Определите показатель преломления
шиака.
Дано
= 15 см = 0,15 м
= 589 нм = 5,89- 10 7м
= 192
я-?
Решение
Д = 1п-1щ = 1(п-\
Я
Д = /и-,
тк .
п = — + 1.
2/
1(п~\)=т~,
»ычисления:
* 1
п
-9
192.589.10
2-15.10м
3?7
С Ответ J п = \,
000377.
«Ship На рисунке показана схема интерференционного рефрактометра,
применяемого для измерения показателя преломления прозрач-
ных веществ. S —узкая щель, освещаемая монохроматическим светом с дли
ной волны А = 589 им; 1 и 2 — кюветы длиной / = 10 см, которые заполнены
воздухом (п0 = 1,000277 ). При замене в одной из кювет воздуха на аммиак ин-
терференционная картина на экране сместилась на т=П полос. Определите
показатель преломления аммиака.
Дано
Я = 589 нм = 5,89- 10 7м
/ = 10 см = 0,1 м
«о = 1,000277
»;=17
п —¦?
Решение
<
i—
1 4
1 > [
-. *
2
>
Э
Д = In-!по = 1{п- п0), Д = тЯ ,
Вычисления:
17-589'10~9'м
-+«п.
0,1м
- +1,000277 = 1,000377.
С Ответ Л
« = 1,000377.
рВ На пути лучей интерференционного рефрактометра помещаются
™* трубки длиной 1 = 2 см с плоскопараллельными стеклянными ос-
нованиями, наполненные воздухом (п0 = 1,000277). Одну трубку заполнили
хлором, и при этом интерференционная картина сместилась на т=20 полос
Определите показатель преломления хлора, если наблюдения производятся с
монохроматическим светом с длиной волны Я = 589 нм.
« = i,ooo866.
5.3. Дифракция света
Точечный источник света (А = 0,5 мкм) расположен на расстоя-
нии а = 1 м перед диафрагмой с круглым отверстием диаметра
(= 2 мм. Определите расстояние Ь от диафрагмы до точки наблюдения, если
верстие открывает три зоны Френеля.
Дано
= 0,5 мкм = 5 • 10 м
= 1 м
=2 мм = 2- 10м
Решение
Г2 = а2_(а_хJ
t2.
-тк — -
a + b 4(a + by
b ab ,
f a +1
Г Ответ Л
and-г
4(a+by
d
г = —,
2
-пР'Х2 —пренебрежимо мало,
Ъ = -
ad2
4amX-d
,2 •
= 2 м.
S'^SfS'' ) ОпРеДелите радиус третьей зоны Френеля, если расстояние от
S точечного источника света (Я = 0,6 мкм) до волновой поверхнос-
ти и от волновой поверхности до точки наблюдения равно 1,5 м.
I
J Г3 = 1,16 ММ.
_ i^^^H На диафрагму с круглым отверстием диаметром d = 5 мм падает
нормально параллельный пучок света с длиной волны Я = 0,6 мкм.
Определите расстояние от точки наблюдения до отверстия, если отверстие от-
крывает: 1) две зоны Френеля; 2) три зоны Френеля.
Г Ответ j i) 5,21м; 2) з,47м.
'•™ *J$ Определите радиус третьей зоны Френеля для случая плоской вол-
ны. Расстояние от волновой поверхности до точки наблюдения
равно 1,5 м. Длина волны Я = 0,6 мкм.
A =
я=
г —
1,5
0,6
_ ?
Дано
м
мкм = 6 •
10-7м
Решение
г1 + Ъ2 = \Ъ + т~ , *.
1 2) -*.
4 /*
X «Ь, г =
Г Ответ Л г = 1,64 мм.
М
Определите радиус четвертой зоны Френеля, если радиус второй
зоны Френеля для плоского волнового фронта равен 2 мм.
Дано
тх =2
щ =4
г, = 2 мм = 2
Ъ — ?
Решение
¦ = -JbmX (см. задачу 5.71),
'=1
(j)meem
Определите радиус первой зоны Френеля, если расстояние от то-
чечного источника света (Я = 0,5 мкм) до зонной пластинки и от
пластинки до места наблюдения а-Ь~\ м.
(Ответ Л г, = о,5 мм.
|^ИНнН| На зонную пластинку падает плоская монохроматическая волна
ШВшШШг (д = о,5 мкм). Определите радиус первой зоны Френеля, если рас-
гояние от зонной пластинки до места наблюдения b -1 м.
Ответ j Г] =
707 мкм.
Зонная пластинка дает изображение источника, удаленного от нее
на 2 м, на расстоянии 1 м от своей поверхности. Где получится
эбражение источника, если его удалить в бесконечность?
Дано
(а = 2 м
А, — ?
Решение
а + Ь
ab
тк (см. задачу 5.68),
(см. задачу 5.71),
С Ответ Л ^, =
= 6,67 см.
Дифракция наблюдается на расстоянии 1 м от точечного источни-
ка монохроматического света (Я = 0,5 мкм). Посередине между
источником света и экраном находится диафрагма с круглым отверстием. Оп-
ределите радиус отверстия, при котором центр дифракционных колец на экра-
не является наиболее темным.
Дано
а+Ъ=\ м
Я = 0,5 мкм = 5- 10м
Решение
2 аЬ 1
г = ml
a+b
(см. задачу 5.68).
Центр наиболее темный при т=2.
а+Ь
аЪ \2аЪ .
-тк -А Я .
С Ответ j r =
= 0,5 мм.
Сферическая волна, распространяющаяся из точечного монохро-
матического источника света (Я = 0,6 мкм), встречает на своем
пути экран с круглым отверстием радиусом г = 0,4 мм. Расстояние а от ис-
точника до экрана равно 1 м. Определите расстояние от отверстия до точки
экрана, лежащей на линии, соединяющей источник с центром отверстия, где
наблюдается максимум освещенности.
см.
На экран с круглым отверстием радиусом г = 1,5 мм нормально
падает параллельный пучок монохроматического света с длиной
волны Я = 0,5 мкм. Точка наблюдения находится на оси отверстия на расстоя-
нии Ъ - 1,5 м от него. Определите: 1) число зон Френеля, укладывающихся в
отверстии; 2) темное или светлое кольцо наблюдается в центре дифракцион-
ной картины, если в месте наблюдения помещен экран.
Дано
г = 1,5 мм = 1,5 ¦ 10 ' м
Я = 0,5 мкм = 5 ¦ 10~7 м
5 = 1,5 м
1) т -?
2) min, max — ?
Решение
= jbmA (см. рисунок к задаче 5.71), т = — .
Ък
Если т — четное — min.
Если т — нечетное — max.
Вычисления:
т =
A,5-10'3Jм2
Л-6
= 3;
1,5 м 0,5'10"- м
2) т — нечетное, светлое кольцо.
С Ответ J 1) т = 3; 2) светлое кольцо.
На экран с круглым отверстием радиусом г = 1,2 мм нормально
падает параллельный пучок монохроматического света с длиной
волны Я = 0,6 мкм. Определите максимальное расстояние от отверстия на его
оси, где еще можно наблюдать наиболее темное пятно.
{Ответ j
/ = 1,2 м.
Покажите, что за круглым экраном С в точке В,
лежащей на линии, соединяющей точечный источ-
гк с центром экрана, будет наблюдаться светлое пятно. Разме-
экрана примите достаточно малыми.
С
Дифракция наблюдается на расстоянии / от то- ///////////////////
чечного источника монохроматического света q
\ Я = 0,5 мкм). Посередине между источником света и экраном
находится непрозрачный диск диаметром 5 мм. Определите расстояние / ,если
1иск закрывает только центральную зону Френеля.
Дано
Я = 0,5 мкм = 5- 10~7м
d = 5 мм = 5 • 10 м
от = 1
/ — ?
Решение
\
а ^-—"
--—~~~~^ г
S
1
1 b м
\
а' = {а - х) + г~,
b+m—\ -{h + xJ+r2\
а =а -2ах+х~ + г~,
2,2
Ь~ + Ъткл = о + 2Ьх + х~ +г~
2 тЧ2
х , пренебрежимо малы
2'
= 2Ьх + г2,
, .d2
г2 d2
2а
—,
2a 4/ '
bmX = 2r~,
m = 1,
I =.
С Ответ j
/ = 50 м.
14 Сборник эалач
На узкую щель шириной а = 0,05 мм падает нормально монохро-
матический свет с длиной волны Я = 694 нм. Определите направ-
ление света на вторую дифракционную полосу (по отношению к первоначаль-
ному направлению света).
Дано
а = 0,05 мм = 5 ¦ 10~5м
Я = 694 нм = 6,94- 10 7м
т = 2
<Р — ?
Решение
2а
5Я
2а
С Ответ J <р = 2°.
т=2
На щель шириной а = 0,1 мм падает нормально монохроматичес-
кий свет (Я = 0,6 мкм). Экран, на котором наблюдается дифрак-
:онная картина, расположен параллельно щели на расстоянии / = 1 м. Опре-
глите расстояние Ь между первыми дифракционными минимумами, распо-
оженными по обе стороны центрального фраунгоферова максимума.
Дано
1= 0,6 мкм = 6 ¦ 10м
= 1 м
77=1
= 0,1 мм=
к
Решение
См. рисунок к задаче 5.85,
min
я
sm<p = —.
а
m = \,
sin<p~ tg<p,
= \,2 см.
На узкую щель падает нормально монохроматический свет. Его
направление на четвертую темную дифракционную полосу состав-
ляет 2°12' . Определите, сколько длин волн укладывается на ширине щели.
Дано
ip = 2°\2'
т = 4
min
а
г/
Решение
asin<p = ±nu (т = 0, 1, 2,...),
а т
Я sinp
Вычисления:
На щель шириной а = 0,1 мм падает нормально монохроматичес-
кий свет с длиной волны X = 0,5 мкм. Дифракционная картина
наблюдается на экране, расположенном параллельно щели. Определите рас-
стояние / от щели до экрана, если ширина центрального дифракционного мак-
симума Ъ = 1 см.
Решение
Я sin 2,2°
= 104.
Я = 0,5 мкм = 5 • 10м
9
6 = 2/ tgp, / =
С Ответ j ±
= 104.
f Ответ
/ = i м.
Монохроматический свет с длиной волны Я = 0,6 мкм падает на
длинную прямоугольную щель шириной а = 12 мкм под углом
«0 - 45° к ее нормали. Определите угловое положение первых минимумов
расположенных по обе стороны центрального фраунгоферова максимума.
Я —
а -
а0
а+1
«-1
0,6
Дано
мкм = 6
12 мкм =12•
= 45
г
с
)
10
10
7М
Решение
Га
Z)
Д- AB-CD, A
| min | А = ±тХ (т = 1, 2, 3,...).
a(sina+,-sinao)= Я ,
sina+1 =sina0 + —
«+1 =arcsin sinao+— .
v a)
a(sina_, -sinao) = -Я ,
sina_! = sma0 —,
Я.
а
a , = arcsm sinan — ¦
Вычисления-
a+l = arcsin
V
о ¦
a
-^ ~
12 10м
= 49 2°= 49°12' ¦
_, = arcsinl sin45°—; —— I = 411°= 41°6'
12-10м '
QOmeem Jg~=
:49°12', а, =.
Монохроматический свет падает на длинную прямоугольную щель
шириной а = 12 мкм под углом а = 30° к ее нормали. Определи-
шну волны Я света, если направление <р на первый минимум (т = 1) от
рального фраунгоферова минимума составляет 33°.
Ответ J A = a(sin^-sina)=536 нм.
На дифракционную решетку нормально падает монохроматический
свет с длиной волны Я = 600 нм. Определите наибольший порядок
||1ектра, полученный с помощью этой решетки, если ее постоянная d - 2 мкм.
f
J
Дано
нм = 6- 10~7м
мкм = 2- 10-* м
Решение
с/sin уз = тк,
d_
Т'
С Ответ
mmax ~ ¦* •
На дифракционную решетку длиной / = 15 мм, содержащую
N = 3000 штрихов, падает нормально монохроматический свет с
Дяинойволны Я = 550 нм. Определите: 1) число максимумов, наблюдаемых в спек-
!ре дифракционной решетки; 2) угол, соответствующий последнему максимуму.
Дано
/ = 15 мм =1,5- Ю-2м
N = 3000
Л = 550 нм = 5,5- 10-7м
Решение
dsvnip- ±mX
| = 0,1,2,...),
N'
mmax = "Г ПРИ Sin ^) = 1
smVmax
u?sin^max = '
Vmax "
n = i8; 2)
{ fflfisH ¦! Определите число штрихов на 1 мм дифракционной решетки, если
Vi и, ifay уГЛу (р = 30° соответствует максимум четвертого порядка для
монохроматического света с длиной волны Я = 0,5 мкм.
<p
m
Я
n
= 30°
= 4
= 0,5
?
Дано
мкм = 5 •
10-7м
|max
d =
Решение
J c/sin^> = ±mk
mk I
simp' ~ N '
0 = 0,
JV
и —
1,2,
1
s\n<p
mk
f Ответ Л и=250мм-'.
На дифракционную решетку нормально падает монохроматичес-
кий свет с длиной волны Я = 0,5 мкм. На экран, находящийся от
решетки на расстоянии 1 = 1 м, с помощью линзы, расположенной вблизи ре-
шетки, проецируется дифракционная картина, причем первый главный макси-
мум наблюдается на расстоянии / = 15 см от центрального. Определите число
штрихов на 1 см дифракционной решетки.
Дано
Решение
Я = 0,5 мкм = 5 ¦ W'7 м
1 = 1 м
/ = 15 см = 0,15 м
п —?
max | d sin ip = mk, m = \
(Offlggw ) w=31O3clvr,
Монохроматический свет нормально падает на дифракционную
решетку. Определите угол дифракции, соответствующий макси-
i четвертого порядка, если максимум третьего порядка отклонен на <рх = 18°.
r*-
pi = 18'
»2 = 4
Дано
>
Решение
min | d sin <p} = mxk,
m2 .
sinp2 =— suip,,
^ Ответ j $
asin^2~m2^, ——^ = — ,
«2 = arcsin -^- sin уз, .
>2 = 24°20'.
На дифракционную решетку нормально падает монохроматичес-
кий свет. Определите угол дифракции для линии 0,55 мкм в четвер-
том порядке, если этот угол для линии 0,6 мкм в третьем порядке составляет 30°.
Г Ответ J <р =
37-42'.
На дифракционную решетку нормально падает монохроматичес-
кий свет. В спектре, полученном с помощью этой дифракционной
решетки, некоторая спектральная линия наблюдается в первом порядке под
углом (р = 11°. Определите наивысший порядок спектра, в котором может на-
блюдаться эта линия.
Дано
т = \
Решение
d sin tp = mk,
d sin ip^^
= 0,1,2,...,
sinp _ m
С Ответ j
'«max -
-Щ Определите длину волны монохроматического света, падающего
** нормально на дифракционную решетку, имеющую 300 штрихов
на 1 мм. если угол между направлениями на максимумы первого и второго
порядка составляет 12°
Дано
« = 300 мм ' =3 ¦ 105м
пц = 1
т-,-2
— ?
Решение
1
n
Sinyj,=—
d
d sin уз, = ю,Л,
d sin ^2 = т2Д;
_2Д
тх = 1, т1 = 2,
уз2 = уз, + A<p, sin(y3, + Ауз) = 2si
sin уз, cos A<p + cos ^>, sin Ауз = 2 sin уз,
sin <P]B~ cosA^)= cosy3, sinAy3,
_ sin^, _ sinAy3
cosy3, 2-cosA^'
m 1
ni-2
уз, = arctg -
sinAyj
A= d sii\(pl = —sin
arct
sin Ay?
2-cosA^
Г Ответ) х =
664 нм.
Какой должна была бы быть толщина шюскопараллельной стек-
лянной пластинки (« = 1,55), чтобы в отраженном свете макси-
мум второго порядка для Я = 0,65 мкм наблюдался под тем же углом, что и >
дифракционной решетки с постоянной d = 1 мкм.
Г Ответ)
х= 577 нм.
дифракционную решетку с постоянной d - 5 мкм под углом
Ь = 30° падает монохроматический свет с длиной волны А = 0,5 мкм.
еделите угол <р дифракции для главного максимума третьего порядка
Решение
f-?
Д = АВ - CD = d sin уз - d sin Ь ,
d sin уз - d sin ft = mk,
+3
sm<p =
mX
COmeemj y,
5,98 } ^a дифракционную решетку под углом Ь падает монохрома-
тический свет с длиной волны А . Найдите условие, определя-
ющее направления на главные максимумы, если d » тк (т — порядок
спектра).
С Ответ j
Узкий параллельный пучок рентгеновского излучения с длиной вол-
ны А = 245 пм падает на естественную грань монокристалла ка-
менной соли. Определите расстояние d между атомными плоскостями моно-
кристалла, если дифракционный максимум второго порядка наблюдается при
падении излучения к поверхности монокристалла под углом скольжения Ь = Ы°.
{Ответ j d = о,28 нм.
5«100*J Узкий параллельный пучок монохроматического рентгеновского
^* ¦ ^ излучения падает на грань кристалла с расстоянием между ei 0
атомными плоскостями d = 0,3 нм. Определите длину волны рентгеновскою
излучения, если под углом 9 = 30° к плоскости грани наблюдается дифракци-
онный максимум первого порядка.
Дано
с/= 0,3 нм = 3- 10-'°м
# = 30°
т = \
Я —?
Решение
2а sin v = тл, Я = .
т
Г Ответ Л д = зоо „„.
Узкий пучок рентгеновского излучения с длиной волны Я = 245 пм
падает под некоторым углом скольжения на естественную грань
монокристалла NaCl( М- 58,5-10~3 кг/моль), плотность которого р = 2,16 г/см1
Определите угол скольжения, если при зеркальном отражении от этой грани
наблюдается максимум второго порядка.
Дано
Я = 245 пм = 2,45-10 |Ом
М = 58,5 10 кг/моль
р = 2,16 г/см3 =
= 2,16- 103кг/м3
т = 2
д — ?
Решение
2dsind=mX,
= arcsin
i —
2</
В ячейке NaCl 4 Na+ и 4 Cl . Каждый ион входит в
8 ячеек. Число ячеек равно числу ионов.
В 1 моль — 2NA ячеек.
d =
ft = arcsin
V =
2NA
М
р ''
Узкий пучок монохроматического рентгеновского излучения па-
дает под углом скольжения f> = 60° на естественную грань моно-
рсталла NaCl ( М = 58,5-10 кг/моль), плотность которого р = 2,16 г/см3,
ределите длину волны излучения, если при зеркальном отражении от этой
ни наблюдается максимум третьего порядка.
Ответ
Я = 163 пм.
Диаметр D объектива телескопа равен 10 см. Определите наи-
меньшее угловое расстояние <р между двумя звездами, при кото-
ром в фокальной плоскости объектива получатся их разрешимые дифракцион-
ные изображения. Считайте, что длина волны света Я = 0,55 мкм.
D =
Я =
<р -
Дано
10 см = 0,1 м
0,55 мкм = 5,5
_ 9
107м
Решение
р = 1,22-.
Г D
Г Ответ Л у, = 1,
Определите наименьшее угловое разрешение радиоинтерферомет-
ра, установленного на Земле, при работе на длине волны Я = 10 м.
я =
*з
dip
Дано
10 м
= 6,37-106 м
d<p
dip
Решение
я
2Щ
10 м
= 0,785-
10
рад
= 0
,2".
Г^Ответ
dip = 0,2".
<426>
р% На дифракционную решетку нормально падает монохроматичес-
кий свет с длиной волны Я = 0,6 мкм. Угол дифракции для пятого
максимума равен 30°, а минимальная разрешаемая решеткой разность длин
волн составляет дХ = 0,2 нм. Определите: 1) постоянную дифракционной ре-
шетки; 2) длину дифракционной решетки.
Дано
Я =0,6 мкм = 6- 10м
т = 5
<р = 30°
«ЗА = 0,2 нм = 2- 10'° м
1) d —?
2) / — ?
Решение
dsin<p = mX, d = , R = — - mN,
sm<p дХ
N = , / = dN = = .
дХ т sin <р оХ т 6Х sin <p
QОтвет j i) d = 6 мкм; 2) / = з,б мм.
Щ Сравните наибольшую разрешающую способность для красной
линии кадмия (Я = 644 нм) двух дифракционных решеток одина-
ковой длины (/ = 5 мм), но разных периодов (dl - 4 мкм, d2 = 8 мкм).
Дано
Я = 644 нм = 6,44- 10 7м
1 = 5 мм = 5 ¦ 10 Зм
d] = 4 мкм = 4 • 10~6м
d-, = 8 мкм = 8 ¦ 10м
Решение
d] sm<p -
/2 sin#> =
т, =
Щ=
Я
т2 — целые числа.
\ max =
4-Ю м
5 Юм
410-6м~1250' ^-625; Л,тах = 61250 = 7500, Л2тах=7500
С Ответ) R
= 7500.
Покажите, что для данной Я максимальная разрешающая спо-
собность дифракционных решеток, имеющих разные периоды, но
знаковую длину, имеет одно и то же значение.
Определите постоянную дифракционной решетки, если она в пер-
вом порядке разрешает две спектральные линии калия (Я, = 578 нм
я Я2 = 580 нм). Длина решетки / = 1 см.
т
я,
1-
d
= 1
= 578
= 580
= 1 см
— ?
Дано
нм = 5,78-
нм = 5,8 •
= 1О-2м
10 7м
10м
Решение
J-N~
дХт 2 '
1дХт
я,
С Ответ
' = 34,6 мкм.
Постоянная d дифракционной решетки длиной / = 2,5 см равна
5 мкм. Определите разность длин волн, разрешаемую этой ре-
шеткой, для света с длиной волны Я = 0,5 мкм в спектре второго порядка.
Дано
1 = 2,5 см = 2,5 • К) м
d = 5 мкм = 5 • Ю^м
Я = 0,5 мкм = 0,5- 10"* м
т=2
дХ — ?
Решение
1 м 1 Я 1
йГ^' N=l' Tx = m~d'
6Х-^
ml
Q Ответ j ex = 50 пм.
Дифракционная решетка имеет N -1000 штрихов и постоянную
^/ = 10 мкм. Определите угловую дисперсию для угла дифракции
<р = 30° в спектре третьего порядка. Найдите разрешающую способность диф-
ракционной решетки в спектре пятого порядка.
Дано
N = 1000
d = !0 мкм = 10~5м
у = 30°
т{ =3
т2=5
Dу — ? К — ?
Решение
61 «|
dtp d cosy?
С Ответ Л d
R
1
p = 3,46
= 5000.
¦ 105 рад/м;
ЯНЯЯ Определите длину волны, для которой дифракционная решетка с
^^^^ постоянной d = 3 мкм в спектре второго порядка имеет угловую
дисперсию Оф = 7 105 рад/м.
Угловая дисперсия дифракционной решетки для Я = 500 нм в спек-
тре второго порядка равна 4,08 • 105 рад/м. Определите постоян-
ную дифракционной решетки.
я =
rf -
:500
= 2
= 4,С
Дано
нм = 0,5- Ю^м
)8 105 рад/м
Решение
D 6(f> m с
v 6Я dcos<p'
тХ
smip--—, tg
d
т л*- i
osy> = , a s\mp = тл,
sin (О mXD.d
cosy? a m v
mk
siny?
. ( Ответ
f = 5 мкм.
5.4. Взаимодействие электромагнитных волн
с веществом
Докажите, что если монохроматический пучок света падает на
грань призмы с показателем преломления п под малым углом, то
i малом преломляющем угле А призмы угол отклонения у лучей не зави-
• от угла падения и равен А(п -1).
«i
Дано
— мал
: А(П-Х) — ?
A
Решение
sinal
sin A
ft
«2
-« >
1
И
/
/A
sinj82 1
sina2 и'
-a]-A = А{п -
a,
Г
Ответ
У
На стеклянную призму с преломляющим углом А = 55° падает
луч света под углом а, = 30°, Определите угол отклонения у луча
призмой, если показатель преломления ц стекла равен 1,5.
С
Ответ
На грань стеклянной призмь< (п = 1,5) нормально падает луч све-
та. Определите угол отклонения у> луча призмой, если ее прелом-
ляющий угол А - 30°.
С Ответ
, - 1 Q°1?'
36'.
На рисунке представлен симметрич-
ный ход луча в равнобедренной при-
зме с преломляющим углом А = 40° (внутри при-
змы луч распространяется параллельно основа-
нию). Определите угол отклонения <р луча при-
змой, если показатель преломления п материла
линзы равен 1,75.
Определите максимальную скорость вынужденных колебаний сво-
бодного электрона, если в точке его нахождения радиопередат-
, работающий на частоте 500 кГц, создает поле электромагнитного излуче-
?0=10 мВ/см.
кг
кГц=5- Ю5Гц
мВ/см = 1 В/м
Lt A-J Луч света выходит из стеклянной призмы (и= 1,5) под тем же
углом, что и входит в нее. Определите угол отклонения <р луча
призмой, если ее преломляющий угол А = 60°.
Г Ответ j v
'max = 55,9 KM/C.
Дано
и = 1,5
а\ ~ а2 ~ а
Л = 60°
<р —?
Решение
A = ft = /* = f,
sin a
sin/3
Электромагнитная волна с частотой ш распространяется в разре-
женной плазме. Концентрация свободных электронов в плазме
равна и0. Определите зависимость диэлектрической проницаемости ? плаз-
мы от .частоты а>. Взаимодействием волны с ионами плазмы пренебречь.
sina = и sin/3 = и sin I — j,
= arcsin «sinf —j I,
= 2a - A = 2 arcsinl и sin— - A
v г)
"о
@
е(со) -
Дано
-?
? =
Е
Решение
?0?
= Ео coscot, х
-А
Р - поех
cos cot,
?
А--
?QE
еЕ0
т
? =
и>0 — и>
? = 1--
QOmeemj ^ =
еотш
г ¦
С Ответ) . _, п^
Еота>
Определите концентрацию свободных электронов ионосферы,
если для радиоволн с частотой v = 97 МГц ее показатель прелом-
ления « = 0,91.
Дано
v = 97 МГц = 97- 106Гц
«=0,91
Кл
31 кг
Решение
? = 1 + X,
Р=хе0Е0, Р=
«о —?
B" = t = 1+X=1+7F=1+7F*™»'
я2=(я2-1)-о_?о ! ей
ех,
max
л: + юох = cosw/,
т
При прохождении в некотором веществе пути х интенсивность
света уменьшилась в 3 раза. Определите, во сколько раз умень-
шится интенсивность света при прохождении пути 2х.
X
А-з
/,
2х
'о
Дано
Решение
« = 1пЗ, /2 = /ое-2^ = /ое-21п3, i^=e2In3.
/2
Г Ответ j i±_9
Коэффициент поглощения некоторого вещества для монохрома-
тического света определенной длины волны а = 0,1 см"'.Опреде-
кте толщину слоя вещества, которая необходима для ослабления света в 2 раза
и в 5 раз. Потери на отражение света не учитывать.
Qdmeemj d] = 6)9з см; d2 = 16,1 см.
Плоская монохроматическая световая волна распространяется в
некоторой среде. Коэффициент поглощения среды для данной
длины волны а = 1,2 м. Определите, на сколько процентов уменьшится ин-
тенсивность света при прохождении данной волной пути: 1) 10 мм; 2) 1 м.
Дано
а = 1,2 м-1
1) х = 10 мм = 10 2м
2) дс = 1 м
Решение
1-1
1 - io
/o-/_/o-/oe-gJ[_
Г Ответ Л i) 1,2%;
; 2) 70%.
Свет падает нормально поочередно на две пластинки, изготовлен-
ные из одного и того же вещества, имеющие соответственно тол-
щины Xj = 5 мм и х2 = Ю мм. Определите коэффициент поглощения этого
вещества, если интенсивность прошедшего света через первую пластинку со-
ставляет 82%, а через вгорую — 67% от начальной интенсивности.
Дано
лг, = 5 мм = 5 • 10 м
д:2 =10 мм = 10м
/,=0,82/0
12 = О,67/О
а —?
А
h
(
Решение
- io с ,
Ответ Л а
/2 - /о е"^ ,
,_Ь(/,//2)
дс2-дс,
= 0,404 см.
Источник монохроматического света с длиной волны Яо = 0,5 мкм
движется по направлению к наблюдателю со скоростью 0,15с (с —
скорость света в вакууме). Определите длину волны, которую зарегистрирует
приемник наблюдателя.
Дано
Яо = 0,5 мкм = 5 • 10 7 м
v = 0,15с
— ?
Решение
V-
l) QOmeem ) я =
430 нм.
При какой скорости красный свет F90 нм) будет казаться зеле-
ным E30 нм)?
{
Ответ
Мм/с.
В спектральных линиях, излучаемых астрономическими объекта-
ми — квазарами, наблюдалось красное смещение, отвечающее
трехкратному уменьшению частоты. Определите, с какой скоростью при этом
должен был бы удаляться квазар.
"-т
# = 0
и —?
Дано
Решение
i +
ч
— cos#
с
), cos ¦& - 1,
v-v0
1-
1 +
и
6*
V '
с
-1-1
vo~3
с
10—= 8, v = 0,8c.
с
COmeernS v = o,8C.
Известно, что при удалении от нас некоторой туманности линия
излучения водорода (Я = 656,3 нм) в ее спектре смещена в крае-
вую сторону на ДА = 2,5 нм. Определите скорость удаления туманности.
fOmeemj v = и 4 мм/с.
Выведите выражение для уширения ДА/А спектрал ьных линий в
случае продольного эффекта Доплера при v « с.
Исходя из общей формулы, описывающей эффект Доплера для
электромагнитных волн в вакууме, выведите формулу для попе-
речного эффекта Доплера. Почему поперечный эффект Доплера является чис-
то релятивистским эффектом?
Выведите выражение для уширения ДА/А спектрал ьных линий в
случае поперечного эффекта Доплера.
Дано
# = л/2
ДА
А ~"
Решение
1 +
(Г?
, cosu = cos— = Q, Я = —,
^cos^ 2
с
с V
А' = 7,Т = Ц-^
-Уг
2V/2
-Уг
ДА у1
А " 2с2
8U4
f Ответ Л да_ d2
4 ' А = 2с2
- . ^ {;. ':W i"
Определите доплеровское смещение ДА для спектральной линии
атомарного водорода (Я = 486,1 нм), если ее наблюдать под пря-
мым углом к пучку атомов водорода с кинетической энергией Т = 100 кэВ.
Дано
= 486,1нм=486,Ы0-*м
A _
V -
T--
m-
c =
ДЯ
Я'
я ¦
л
" 2"
= 100 кэВ =
= 1,6-
= 1,67 -
3-Ю8
— ?
-1 + —
2
10 м
ю-27
м/с
Дж
кг
Решение
V = V-
Я" Я "I* "-2
•-if
' = Я + ДЯ.
Я + ДЯ
1(V
с"
2> -2
дя = я-
m
2 •
Определите скорость электронов, при которой черенковское из-
лучение происходит в среде с показателем преломления п = 1,54
под углом # = 30° к направлению их движения. Скорость выразите в долях
скорости света.
и =
0 =
V -
1,54
30°
-?
Дано
Решение
„с ' с
cosv = —, v = .
m> n cos v
С Ответ Ju = o,75c.
Определите кинетическую энергию протонов, которые в среде с
показателем преломления п = 1,6 излучают свет под углом Ь = 20°
к направлению своего движения. Ответ выразите в электрон-вольтах.
от = 1,67
и = 1,6
# = 20°
Г(эВ) -
Дано
10~27 кг
-?
Решение
Q
cos# = —,
т>
/ 1
V \
с wcosft'
т- 2
Т = тс
1-
fOmeemj г = о,319Гэв.
Определите минимальный импульс, которым должен обладать
электрон, чтобы эффект Вавилова^—Черенкова наблюдался в сре-
де с показателем преломления п = 1,5.
мл О 1
и =1,5
Дано
МО1 кг
. ?
Решение
с
пи
п
и =
(СО!
С
п cos & '
!# = !),
тс
тс
тс
Рглт ~ I 1
V«2-i
(Ответ
2
„,„=2,44-10"'" кг -м/с.
Определите минимальную кинетическую энергию, которой дол-
жен обладать электрон, чтобы в среде с показателем преломления
п = 1,5 возникло черенковское излучение. Ответ выразите в МэВ.
С Ответ j
= тс2 , " -1 = 0,175 МэВ.
W«2-l
ОпРеделите минимальную ускоряющую разность потенциалон
Umm > которую должен пройти электрон, чтобы в среде с показа-
телем преломления п - 1,5 возникло черенковское излучение.
Дано
кг
и =1,5
Решение
с
пи
с
п
v =
ncosv
7Lin = me
/и2-1
In'-l
5.5. Поляризация света
Опишите поведение светового вектора Е в данной точке простран-
ства в случае эллиптически поляризованного света.
Определите степень поляризации частично поляризованного све-
та, если амплитуда светового вектора, соответствующая макси-
мальной интенсивности света, в 3 раза больше амплитуды, соответствующей
его минимальной интенсивности.
EKv
Р —
Дано
/ЕОт=3
?
Решение
п _ max mm
max "•" •'mm
1 Eq ,
О _
El -El (El /El J-l
"max "irun _ V ¦' ' """ /
Г Ответ
» = о,8.
Степень поляризации частично поляризованного света составля-
ет 0,75. Определите отношение максимальной интенсивности све-
та, пропускаемого анализатором, к минимальной.
Дано
P=0,75
¦'max rj
mm
p =
Решение
max ~ mm
p
max
¦'mm
max
Лит
-1
_i_ i
СОтвет j 4т_ = 7
Определите степень поляризации Р света, который представляе
собой смесь естественного света с плоскополяризованным, есл]
интенсивность поляризованного света равна интенсивности естественного
Определите степень поляризации Р света, который представляет
собой смесь естественного света с плоскополяризованным, если
интенсивность поляризованного света в 5 раз больше интенсивности ест
ного
стествен-
Ответ ) Р=0,т.
Угол между главными плоскостями поляризатора и анализатора
составляет 30°. Определите изменение интенсивности прошедшего
через них света, если угол между главными плоскостями равен 45е
а,, /2 = /0cos2a2,
]i__ cos2 a,
h cos2a2
Ответ
Интенсивность естественного света, прошедшего через два нико-
ля, уменьшилась в 8 раз. Пренебрегая поглощением света, опре-
ните угол между главными плоскостями николей.
a = 60° •
Определите, во сколько раз ослабится интенсивность света, про-
шедшего через два николя, расположенные так, что угол между
; главными плоскостями a = 60°, а в каждом из николей теряется 8% интен-
вности падающего на него света
а =
к =
h
h
Дано
60°
0,08
— ?
h
Решение
= ~'оA-*),
= -/0(l~JtJcos2a,
h
h
h
= /, A - к) cos
2
A - кJ cos2
"a,
a
Г Ответ Л h. = 945
> J Определите, во сколько раз уменьшится интенсивность естествен-
ного света, прошедшего через два николя, главные плоскости ко-
торых образуют угол в 60°, если каждый из николей как поглощает, так и отра-
жает 5% падающего на них света.
a-
*,=
h
h
60
k2
Дано
о
= 0,05
?
Решение
1{Л(\-{кх+к2)I
I2 = I\ 0,9 cos2 a =
/л
1
э = 2
2 /о
2
0,9 1
0,92
0,
cos2 а ,
ГдтветЛ к =
0,92 cos2 а '
Естественный свет проходит через поляризатор и анализатор, угол
между главными плоскостями которых равен а. Поляризатор и
анализатор как поглощают, так и отражают 10% падающего на них света. Оп-
ределите угол а, если интенсивность света, вышедшего из анализатора, равна
12% интенсивности света, падающего на поляризатор.
Дано
k,=k2 = 0,1
/2=0,12/0
а —?
Решение
/1=|A-(*1 + *2))/0=^-0,8-/0>
12 = /, -0,8 cos2 a , I2 = -I00,82 cos2 a ,
cosa =
'2-0,12
—-—у - 0,612, а = arccosO,612 = 52,24°= 52°14'
Естественный свет интенсивностью 10 проходит через поляриза-
тор и анализатор, угол между главными плоскостями которых со-
ставляет а . После прохождения света через эту систему он падает на зеркало
и, отразившись, проходит вновь через нее. Пренебрегая поглощением света,
определите интенсивность / света после его обратного прохождения.
Дано
'о
/ —?
/2=^^0cos2a,
/ = Л COS2G = —/„
Решение
1 О '
I2 = I] cos2a,
П
cosV (Om**n) /Л/о^~
Докажите, что при падении света на границу раздела двух сред
под углом Брюстера отраженный и преломленный лучи взаимно
рпендикулярны.
Известно, что при падении света на прозрачный диэлектрик под
углом Брюстера отраженный свет является плоскополяризован-
i. Чем необходимо воспользоваться, чтобы получить преломленный свет
гически полностью поляризованным?
Пучок естественного света падает на стеклянную призму с углом
а = 30°. Определите показатель преломления стекла, если отра-
женный луч является шюскополяризованным.
Дано
а = 30°
п —?
Решение
ГОтветij « = 1,73.
Ч:.-»
Определите показатель преломления стекла, если при отражении
от него света отраженный луч полностью поляризован при угле
преломления 35°.
V —
и -
35°
_?
Дано
sin a
sin у
Решение
-п, а = /в,
/в = 90°-у,
и =
sin(90°-y)
sin у
Г Ответ J п = 1,43.
Определите, под каким углом к горизонту должно находиться Сол
нце, чтобы лучи, отраженные от поверхности озера (п = 1,33)
были максимально поляризованы.
Предельный угол полного отражения для пучка света на границе
кристалла каменной соли с воздухом равен 40,5°. Определите угол
Брюстера при падении света из воздуха на поверхность этого кристалла.
Свет, проходя через жидкость, налитую в стеклянный сосуд
(п = 1,5), отражается от дна, причем отраженный свет плоскопо-
ляризован при падении его на дно сосуда под углом 41°. Определите: 1) показа-
. тель преломления жидкости; 2) угол падения света на дно сосуда, чтобы на-
блюдалось полное отражение.
1) и =1,73; 2) / = 60°7'.
Параллельный пучок света падает нормально на пластинку из ис-
ландского шпата толщиной 50 мкм, вырезанную параллельно оп-
гической оси. Принимая показатели преломления исландского шпата для обык-
новенного и необыкновенного лучей соответственно п0 - 1,66 и пе = 1,49, оп-
ределите разность хода этих лучей, прошедших через пластинку.
Дано
= 50 мкм = 5- 10-5м
«о = 1>66
4 = 1,49
А —?
Решение
С Ответ j а = 8,5 мкм.
и
,о
Плоскополяризованный свет, длина волны которого в вакууме
Я = 589 нм, падает на пластинку исландского шпата перпендику-
лярно его оптической оси. Принимая показатели преломления исландского
шпата для обыкновенного и необыкновенного лучей соответственно п0 = 1,66
Дано
Я = 589 нм = 5,89- К
по = 1,66
пе = 1,49
К-ч
А. -7
С Ответ j яо
)-7м
Решение
1=сТ, Яо
Хе = — (См. рисунок
= 355 нм, Хе = 395 нм.
= ^0Г, Я? = иеГ,
пе «о
к задаче 5.156).
Плоскополяризованный свет, длина волны которого в вакууме
Я = 530 им, падает на пластинку из кварца перпендикулярно ее
оптической оси. Определите показатели преломления кварца для обыкновен-
ного (по) и необыкновенного (пе) лучей, если длины волн этих лучей в крис-
талле соответственно равны ЯО = 344 нми Яе=341 нм.
С Ответ Л Яо = 1,54, и, = 1,55.
Определите наименьшую толщину кристаллической пластинки в
четверть волны для Я = 530 нм, если разность показателей пре-
ломления обыкновенного и необыкновенного лучей для данной длины волны
пе-по- 0,01. Пластинкой в четверть волны называется кристаллическая пла-
стинка, вырезанная параллельно оптической оси, при прохождении через кото-
рую в направлении, перпендикулярном оптической оси, обыкновенный и нео-
быкновенный лучи, не изменяя своего направления, приобретают разность хода,
равную Я/4.
Дано
Я = 530 нм = 5,3'
пе - по = 0,01
Д = Я/4
d — ?
10м
Д
d
Решение
= d(ne-n0), Д = -,
4
Я
4<Л-ио)"
QOmeemj
мкм.
Кристаллическая пластинка из исландского шпата с наименьшей
толщиной d — 0,86 мкм служит пластинкой в четверть волны (см
задачу 5.159) для Я = 0,59 мкм. Определите разность Ди показателей прелом-
ления обыкновенного и необыкновенного лучей.
Г Ответ ^ дя = о,171
Используя задачу 5.159, дайте определение кристаллической пла-
стинки в полволны и определите ее наименьшую толщину для
|S= 530 нм, если разность показателей преломления необыкновенного и обык-
венного лучей для данной длины волны пе-п0 = 0,01
ХОтвет j dmm = 26,5 мкм.
Используя задачу 5 159, дайте определение кристаллической пла-
стинки "в целую волну" и определите ее наименьшую толщину
Я - 530 нм, если разность показателей преломления необыкновенного и
(Обыкновенного лучей для данной длины волны пе — п0 = 0,01
Д = 530
пе-п0--
А = Х
d —
Дано
нм =5,3 ¦
= 0,01
10м
Решение
A = uLnK-"o)>
д = я
"mm ~
(при т - 0),
Я
пе~п0
{
Ответ
=53 мкм.
Объясните, изменится ли наблюдаемая оптическая картина в слу-
чае эффекта Керра, если направление напряженности электричес-
кого поля изменить на противоположное.
Определите толщину кварцевой пластинки, для которой угол по-
ворота плоскости поляризации монохроматического света опре-
деленной длины волны <р = 180° . Удельное вращение в кварце для данной дли-
ны волны а = 0,52 рад/мм.
Г Ответ j d = 6,
04 мм
Пластинка кварца толщиной dx = 2 мм, вырезанная перпендику-
лярно оптической оси кристалла, поворачивает плоскость поля-
ризации монохроматического света определенной длины волны на угол
р, - 30°. Определите толщину d2 кварцевой пластинки, помещенной между
параллельными николями, чтобы данный монохроматический свет гасился
полностью.
<P\
<Рг
d2
Дано
= 2 мм =2- 10 Зм
= 30°
= 90°
-7
С
Решение
1 d
— ;
Ответ j ^ =
= arf2,
t/,^2
6 мм.
Определите массовую концентрацию С сахарного раствора, если
при прохождении света через трубку длиной / = 20 см с этим ра-
створом плоскость поляризации света поворачивается на угол ip = 10° . Удель-
ное вращение [а] сахара равно 1,17- 10 рад ¦ м2/кг.
/ =
<р =
и
С -
Дано
20 см = 0,2 м
10°
= 1,17-10-2рад-м7кг
-7
1
с
Решение
= [а]С1,
°=1,75 10 рад.
Ответ j с
C = j
= 74,8
<Р
з:]/
кг/м3.
Некоторые внесистемные величины
1 сут = 86400с 1°=1,75 10 рЗД
1 год = 3,16-107 с Г = 2,9110 рад
1" = 4,85 10 рад
Раствор глюкозы с массовой концентрацией С, = 0,21 г/см3, на-
ходящийся в стеклянной трубке, поворачивает плоскость поляри-
щии монохроматического света, проходящего через раствор, на угол tpx = 24°.
пределите массовую концентрацию С2 глюкозы в другом растворе в трубке
^кой же длины, если он поворачивает плоскость поляризации на угол ip2 = 18° .
Ответ J с2 = о,
,157 г/см3.
Плоскополяризованный монохроматический свет, прошедший че-
рез поляроид, оказывается полностью погашенным. Если же на пути
i поместить кварцевую пластинку, то интенсивность прошедшего через поля-
роид света уменьшается в 3 раза (по сравнению с интенсивностью света, падаю-
щего на поляроид). Принимая удельное вращение в кварце [а] = 0,52 рад/мм и
^енебрегая потерями света, определите минимальную толщину кварцевой
астинки.
Дано
[а] = 0,52 рад/мм =
= 520рад/м
d —? '
Решение
(p = [a]d,
I = I0 cos2 у,
ж
cos — -
ж
= arcco
^J , [a]d = ~ arccosj^ j ,
и
(Ответ)
5.6. Квантовая природа излучения
Объясните, почему в неотапливаемом помещении температура
всех тел одинакова.
Объясните, почему открытые окна домов со стороны улиц кажут-
ся черными.
Чайная фарфоровая чашка на светлом фоне имеет темный рису-
нок. Если эту чашку быстро вынуть из печи, где она нагревалась
до высокой температуры, и рассматривать в темноте, то наблюдается светлый
рисунок на темном фоне. Объясните почему.
Имеются два одинаковых алюминиевых чайника, в которых до
одной и той же температуры нагрето одинаковое количество воды.
Один чайник закопчен, а другой чистый. Объясните, какой из чайников осты-
нет быстрее и почему.
Определите, во сколько раз необходимо уменьшить термодина-
мическую температуру черного тела, чтобы его энергетическая
светимость Re ослабилась в 16 раз.
Кг
ZL
7;
Дано
= 16
— ?
Решение
Re] = gT\ , Re2 = 0T2 >
ZL-Ж
r2 H2
Г Ответ Л ]\_ = 2
Температура внутренней поверхности муфельной печи при откры-
том отверстии площадью 30 см2 равна 1,3 кК. Принимая, что от-
верстие печи излучает как черное тело, определите, какая часть мощности рас-
сеивается стенками, если потребляемая печью мощность составляет 1,5 кВт.
5 = 30
T = l,3
P = \,5
^pac
Дано
см2 = 3- 10м2
kK = 1,3- 103K
кВт =1,5- 103Вт
_ ?
Решение
Pmn ~ KS = °
^pac аГ^
P P
С Ответ
гГ45,
5
) 5=
p = p- p
J рас 1 ' ии
= 0,676.
^P-oT'S,
Энергетическая светимость черного тела Re = lQ кВт/м2. Опреде-
лите длину волны, соответствующую максимуму спектральной
плотности энергетической светимости этого тела.
Г Ответ ^ я = 4,47 мкм.
Определите, как и во сколько раз изменится мощность излучения
черного тела, если длина волны, соответствующая максимуму его
спектральной плотности энергетической светимости, сместилась с Я, = 720 нм
до Я2 = 400 нм.
я,
я2
^1
Дано
= 720 нм = 7,2
= 400 нм = 4 ¦
— 9
• 10
107
-7м
м
(
Решение
ъ
1' Я2='
= йе25 = стГ2 5,
Ответ j
ъ
Рг
Л
Рх = <
Рг _
Л
= 10,5.
^,5 = ст7;45,
7 _ Я]
г4 ;4
il Л2
Черное тело находится при температуре 7j = 3 кК. При остыва-
нии тела длина волны, соответствующая максимуму спектраль-
ной плотности энергетической светимости, изменилась на ДА = 8 мкм. Опре-
делите температуру Т2 , до которой тело охладилось.
Черное тело нагрели от температуры Г] = 600 К до Т2 = 2400 К.
Определите: 1) во сколько раз увеличилась его энергетическая
светимость; 2) как изменилась длина волны, соответствующая максимуму спек-
тральной плотности энергетической светимости.
С Ответ J l)w = 256; 2) уменьшилась на 3,62 мкм.
Площадь, ограниченная графиком спектральной плотности энер-
гетической светимости гХт черного тела, при переходе от термо-
динамической температуры 7j к температуре Т2 увеличилась в 5 раз. Опреде-
лите, как изменится при этом длина волны Ятах , соответствующая максимуму
спектральной плотности энергетической светимости черного тела.
Дано
52 -5
max!
— ?
Решение iTf
00
= \
гХ,Тг
Т
В результате нагревания черного тела длина волны, соответству-
ющая максимуму спектральной плотности энергетической свети-
мости, сместилась с Я| = 2,7 мкм до Я2 = 0,9 мкм. Определите, во сколько раз
увеличилась: 1) энергетическая светимость тела; 2) максимальная спектраль-
ная плотность энергетической светимости тела. Максимальная спектральная
плотность энергетической светимости черного тела возрастает по закону
Ытах = СТ$ ' ГДе С = М-10 ВТ/(М3 • К5).
я,
я2
У*
с
1)
21
*•)
= 2,7
= 0,9
т)
•Т)тп<
= 1,3-
Кх
Кг
D,7
Li,.7
Дано
мкм = 2,7 •
мкм = 0,9 •
= СТ5
\0~5 Вт/(м3
— ?
1 max
10"* М
10-* м
•К5).
к=
Кх
Кг
f
\%.
Li,.J
Решение
_т}_х\
У, Я2
1 т 1
Г, \ Т7 А
г¦ ) 1Х А
1 max
{Ответ )
А =
(г
1
I
5 "
2
Кг
Ъ
_
т
\ -ГТ5
-1 — СУ ,
/max
Ч-ъЫ) 243
= 81; 2) =243.
Основные физические постоянные
уменьшится в 1,49 раза.
Постоянная Стефана—Больцмана
Постоянная Вина
Постоянная Планка
Постоянная в законе, связывающем
максимальную спектральную
плотность энергетической светимости
черного тела с термодинамической
температурой
а = 5,67-10"8 Вт/(м2-К4)
2>=2,90-10~3 м-К
Л = 6,63 10-34 Дж-с
С = 1,3 \0~5 Вт/(м3-К5)
Определите, какая длина волны соответствует максимальной спек-
тральной плотности энергетической светимости v>i,r)m , равной
1,3" Ю"Вт/м3.
Дано
С = 1,3-10s Вт/См3-К1)
Решение
г) — ^^ ,
'max
"max
с
[Ответ j
мкм-
Считая никель черным телом, определите мощность, необходи-
мую для поддержания температуры расплавленного никеля
1453 °С неизменной, если площадь его поверхности равна 0,5 см2. Потерями
энергии пренебречь.
t-
s
p
= 1453
= 0,5
9
Дано
°C; T —
см2 = 5 ¦
1726 К
10 5м2
p
(
Решение
= ReS = стГ45 .
Ответ j p = 25,2 вт.
Металлическая поверхность площадью 5 = 15 см2, нагретая до
температуры Т = 3 кК, излучает в одну минуту 100 кДж. Опреде-
лите: 1) энергию, излучаемую этой поверхностью, считая ее черной; 2) отно-
шение энергетических светимостеи этой поверхности и черного тела при дан-
ной температуре.
Г Ответ Л
кДж; 2) — = 0,242.
Принимая Солнце за черное тело и учитывая, что его максималь-
ной спектральной плотности энергетической светимости соот-
ветствует длина волны 500 нм, определите: 1) температуру поверхности Солнца;
2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин;
3) массу, теряемую Солнцем за это время за счет излучения.
Amax —
/ = 10
^ = 6
mc = 1
t\ T
U '
2) fF -
3) m -
Дано
500 нм = 5-
мин = 600 с
,95 108 м
,98 1030 кг
О
-?
_ 7
10-7м
Решение
г.
С Ответ
4 4Tff
)"
2)
3)
Ъ
^•тах
Г = 5,8
W = 2,3
т = 2,6
кК,
4-Ю29 Дж;
•1012 кг.
'5.185^ Определите температуру тела, при которой оно при температуре
окружающей среды t0 = 23 °С излучало энергии в 10 раз больше,
чем поглощало.
'о = 23
Кул
"погл
Т ?
Дано
°С; Го = 280 К
10
Решение
Wmn ATaT"St
Wnorn ATaT*St
Г Ответ j -j
г4
г = 533Ъ
T~T0
Vw
л\ HiJI
V погл
Некоторые астрономические величины
Радиус Земли 6,37 ¦ 106 м
Масса Земли 5,98 ¦ Ю24 кг
Радиус Солнца 6,95 • 108 м
Масса Солнца 1,98 • 1030 кг
<456>
Считая, что тепловые потери обусловлены только излучением,
определите, какую мощность необходимо подводить к медному
шарику диаметром d = 2 см, чтобы при температуре окружающей среды
г0 = —13 °С поддерживать его температуру равной t = 17 °С. Примите погло-
щательную способность меди Ат = 0,6.
Дано
d = 2 см = 2- 10м
г0 = —13 °С; Г0 = 260 К
г = 17 °С; Г = 290 К
Ат = 0,6
р <?
Решение
Р —А ггТ^ V Р — Л ггТ1^ С*
гизл - ^Г^ ° ' гпогл - ЛтО10 Ы ,
2
4
COmeemj /> = о,Ю7Вт.
Определите силу тока, протекающего по вольфрамовой проволо-
ке диаметром d - 0,8 мм, температура которой в вакууме поддер-
живается постоянной и равной t = 2800 °С. Поверхность проволоки считать
серой с поглощательной способностью Ат = 0,343. Удельное сопротивление
проволоки при данной температуре р = 0,92 • 10~4 Ом • см. Температура окру-
жающей проволоку среды t0 = 17 °С.
Дано
с/= 0,8 мм = 8
/ = 2800 °С; Г = 3073 К
Ат = 0,343
р = 0,9210~4 Ом-см =
= 9,2- 10Ом-м
К
Решение
' = /2Л, Р= Аго(Т* - Г04M (см. задачу 5.186),
I —?
Г Ответ j i = 48,8 а.
Преобразуйте формулу Планка для спектральной плотности энер-
гетической светимости черного тела от переменной v к перемен-
ной Я.
„„ 2nv hv
Пользуясь формулой Планка rvT- —j Ы(кТ)—' Докажите> что
С С "~ 1
в области малых частот (hv « кТ) она совпадает с формулой Рэлея—Джинса.
Inv hv
Пользуясь формулой Планка rvT= —5 ыЩ)—' выведите из
с е А -1
нее закон Стефана — Больцмана.
2nv2 hv
Пользуясь формулой Планка rv т = —5—ыпРп— > выведите из
с е п '—\
нее закон смещения Вина.
Используя формулу Планка, определите спектральную плотность
потока излучения единицы поверхности черного тела, приходя-
щегося на узкий интервал длин волн ДЯ = 5 нм около максимума спектраль-
ной плотности энергетической светимости, если температура черного тела
Г = 2500 К.
Дано
Т= 2500 К
ДЯ = 5 нм = 5- 10"м
Решение
2лИс2
дя) =
• дя.
Объясните: 1) происхождение радиационной, цветовой и ярко-
стной температур; 2) может ли радиационная температура быть
больше истинной.
щ-- J Для вольфрамовой нити при температуре Т - 3500 К поглощатель-
ная способность Ат = 0,35. Определите радиационную темпера-
туру нити.
Дано
Т = 3500 К
Ат = 0,35
Решение
RT = AToT\
АтоТ = oTp ,
Rr-,
COmeem Jtp = 2,69 кк.
Отношение энергетической светимости Я? серого тела к энерге-
тической светимости /^ черного тела равно АТ . Выведите связь
между истинной и радиационной температурами.
Определите максимальную скорость фотоэлектронов, вырываемых
с поверхности металла, если фототок прекращается при приложе-
нии задерживающего напряжения Uo = 3,7 В.
Дано
Uo = 3,7 В
e = l,6-109 Кл
m = 9,1110~31 кг
Umax ?
Решение
mi)L rT! .. l2eUo
'"Г - et70 . "max д
2 V m
Г Ответ ^) Vmax = 1,14 мм/с.
Освещая поочередно фотока-
тод двумя разными монохрома-
тическими источниками, находящимися на
'Ьдинаковых расстояниях от катода, получи-
ли две зависимости G и 2) фототока от на-
(Яряжения между катодом и анодом. Объяс-
•ните, в чем отличие этих источников.
U
Красная граница фотоэффекта для некоторого металла равна
500 нм. Определите минимальное значение энергии фотона, вы-
зывающего фотоэффект.
Дано
, = 500 нм = 5- 10-7м
Решение
vn=-
На рисунке схематически пред-
ставлены вольт-амперные ха-
рактеристики (кривые 1,2иЗ) фотоэффекта
Для одного и того же металла. Объясните
причину отличия этих кривых.
U
Фотоэлектроны, вырываемые с поверхности металла, полностью
задерживаются при приложении обратного напряжения Uo = 3 В
Фотоэффект для этого металла начинается при частоте падающего монохрома-
тического света v0 = 61014 с. Определите: 1) работу выхода электронов из
этого металла; 2) частоту применяемого излучения.
2) v = 1,32-1015 с.
Определите работу выходаЛ электронов из вольфрама, если '"крас-
ная граница" фотоэффекта для него Яо = 275 нм.
Дано
Яо = 275 нм =
= 2,75- 10 7м
7
Решение
vo=-
hc_
Яп
(Ответ Ла = 4,52эв
Калий освещается монохроматическим светом с длиной волны
400 нм. Определите наименьшее задерживающее напряжение, при
котором фототок прекратится. Работа выхода электронов из калия равна 2,2 эВ.
Дано
Я =400 нм = 4- 10 7м
А = 2,2 эВ =
= 3,52- 10-|9Дж
е = 1,6 -10~19 Кл
й = 6,63-10~34 Джс
Uo-7
Решение
2
hv Л, 2 ,
mvlax r r С
~ eU0' v~ . '
;-> А
he I ~
— -A + eU0, Uo--± .
Я е
ГОтвет Juo = 0,91 в.
Красная граница фотоэффекта для некоторого металла равна
500 нм. Определите: 1) работу выхода электронов из этого метал-
ла; 2) максимальную скорость электронов, вырываемых из этого металла све-
том с длиной волны 400 нм.
Яо
Я =
1)
2)
(
Дано
= 500 нм = 5 • 10
= 400 нм = 4- 10
л о
Ответ j
1)
7М
м
А--
hc
Я
А = 2,49
Решение
he
- hv0 - ,
Яо
he , ти2тт
— 1" )
"о 2
эВ; 2)итах = 468
/zv = ^ +
^тах-.
2
2
2йс
км/с.
ах
U к)
Выбиваемые светом при фотоэффекте электроны при облучении
фотокатода видимым светом полностью задерживаются обратным
напряжением Uo -1,2 В. Специальные измерения показали, что длина волны
падающего света Я = 400 нм. Определите красную границу фотоэффекта.
С Ответ ~\ я0 = 652 нм.
Задерживающее напряжение для платиновой пластинки (работа
выхода 6,3 эВ) составляет 3,7 В. При тех же условиях для друтй
пластинки задерживающее напряжение равно 5,3 В. Определите работу выхо-
да электронов из этой пластинки.
Дано
А ,= 6,3 эВ
С/, = 3,7 В
U2 = 5,3 В
Решение
hv - А,+ eUx, hv-A2+eU2,
Ах+ eV{ - А2 + eU2, А2 = Ах+ eUx - eU2.
Г Ответ ^ а2 = 4,7 эв.
Определите, до какого потенциала зарядится уединенный сереб-
ряный шарик при облучении его ультрафиолетовым светом дли-
ной волны Я = 208 нм. Работа выхода электронов из серебра А = 4,7 эВ
A
Я
У
= 4,7
= 7,52
= 208
7
Дано
эВ =
• 10 19 Дж
нм = 2,08 ¦
Ю'м
hv
<PZ
Решение
, с
= А + еср , v = —,
К
he А
Яе е Г Ответ J
he
т~
уз = 1,28
А + е<р,
В
При освещении вакуумного фотоэлемента монохроматическим све-
том с длиной волны Я, = 0,4 мкм он заряжается до разности потен-
циалов уз, = 2 В Определите, до какой разности потенциалов зарядится фотоэле-
мент при освещении его монохроматическим светом с длиной волны Я2 = 0,3 мкм
Q Ответ ^ ^ = 3,р4 в
~ *>ficf 1 Плоский серебряный электрод освещается монохроматическим
излучением с длиной волны Я = 83 нм Определите, на какое мак-
симальное расстояние от поверхности электрода может удалиться фотоэлектрон,
если вне электрода имеется задерживающее электрическое поле напряженнос-
тью ? = 10 В/см, Красная граница фотоэффекта для серебра Яо = 264 нм
Дано
Я = 83 нм = 8,3 • 10 8м
Я0 = 264 нм = 2,64 10 7м
? = 10 В/см= 1(ГВ/м
е = 1,6 Ю9 Кл
Решение
he he
— = — + eEs ,
Я Ап
_hc_(\_ 1_
S ~ еЕ Я ~ Хп
С Ответ j s =
1,03 см.
Фотоны с энергией е = 5 эВ вырывают фотоэлектроны из метал-
ла с работой выхода А = 4,7 эВ Определите максимальный им-
пульс, передаваемый поверхности этого металла
Дано
е = 5 эВ = 8- 10 |9Дж
А = 4,7 эВ =
= 7,52 10 "Дж
Ртах
Решение
Ртах = mV max'
1 7
итач = д— (Е-А),
при вылете
?= А +
Ртах
электрона
mwLx
2 '
lim(F АЛ
QOmeem
кг м/с.
При освещении катода вакуумного фотоэлемента монохромати-
ческим светом с длиной волны Я = 310 нм фототок прекращается
при некотором задерживающем напряжении При увеличении длины волны на
25% задерживающее напряжение оказывается меньше на 0,8 В. Определите по
этим экспериментальным данным постоянную Планка.
я,=
Я2 =
U2 =
AU
h -
Дано
310 нм = 3,1 Ю'м
1,25 А,
-L\~AU
= 0,8 В
_7
he
Я,
he
hr
— J
Решение
he
4 + eU, —= A + eU-,
A2
--Lj-Ci/,-^).
l—} = eAU,
V A, 1.25A,
, 5еЯ, AU
h = !
h =6,61 10 34 Дж с
<465>
Определите максимальную скорость итах фотоэлектронов, вы-
рываемых с поверхности цинка (работа выхода А = 4 эВ), при
облучении У -излучением с длиной волны Я = 2,47 пм.
Дано
A = 4 эВ =
= 4-1,6- 10">Дж
Я = 2,47 пм =
= 2,47- 10 :N-
Решение
= 0,503 106эВ = 0,503 МэВ.
е » А = 4 эВ.
¦тс -тс
(?+тс2J
= 259 Мм/с.
Определите для фотона с длиной волны Я = 0,5 мкм 1) его энер-
гию; 2) импульс; 3) массу.
Г Ответ j 1) ? = 2,48 эв;
-27
2) р = 1,33-10^' кг-м/с,
3) m = 4,43 106 кг.
Определите энергию фотона, при которой его эквивалентная масса
равна массе покоя электрона. Ответ выразите в электрон-вольтах
? = тес2
? (эВ)-
Дано
¦у
Решение
е = тес2, ?(эВ)-
?(Дж)
1,6 109 -
Определите, с какой скоростью должен двигаться электрон, что-
бы его импульс был равен импульсу фотона, длина волны которо-
го Я = 0,5 мкм.
Дано
Рс=Р
Я = 0,5 мкм = 5 • 10 7 м
ve — ?
Решение
Ре h
Ve - , Ре — Р — ~Г >
те л
h
Ате
С Ответ Л
v = 1,46 км/с.
ЯЙ:г | Определите длину волны фотона, импульс которого равен импуль-
|Л|**^ су электрона, прошедшего разность потенциалов U = 9,8 В.
Дано
e = l,6 109 Кл
U = 9,8 В
Ре = Р
я —->
Решение
2 \ те
р~-, Р = Ре, Я = , .
QOmeem ^ я = 392 нм
Определите температуру, при которой средняя энергия молек>л
трехатомного газа равна энергии фотонов, соответствующих ич-
лучению Я = 600 нм.
Г
Ответ
= 8 кк.
Определите, с какой скоростью должен двигаться электрон, что-
бы его кинетическая энергия была равна энергии фотона, длина
волны которого Я = 0,5 мкм.
СОтвегп\ v =
км/с.
Определите, с какой скоростью должен двигаться электрон, что-
бы его импульс был равен импульсу фотона, длина волны ко-
торого Я = 2 пм.
Ре
v -
= р
2 пм
Дано
= 2- 10-
12 м
he
с — —
д
Решение
-, е^
- тс'.
6,63 104 Дж.с -3 108м/с ,4
t = ——р = 9,9 104 Дж = 0,62 МэВ ;
2-10 ~ м
?0=9,П 10~31 кг C 108 м/сJ=8,2 10 |4 Дж = 0,51 МэВ;
h mv
Р--
mv
— тр2/ с-2
, , h2
т
' + h2), v = -
ch
Г Ответ j v = о,
77с.
Докажите, что световое давление, оказываемое на поверхность
тела потоком монохроматического излучения, падающего перпен-
дикулярно поверхности, в случае идеального зеркала равно 2w, а в случае
полностью поглощающей поверхности равно w , где w — объемная плот-
ность энергии излучения.
Давление монохроматического света с длиной волны Я = 500 нм
на зачерненную поверхность, расположенную перпендикулярно
падающим лучам, равно 0,12 мкПа. Определите число фотонов, падающих
ежесекундно на 1 м2 поверхности.
Дано
Я = 500 нм = 5- 10-7м
р = 0
р = 0,12 мкПа =
= 1,2-10Па
/ = 1 с
S = l м2
N —?
Решение
A
Nhc
N =
plSt
( Ответ
На идеально отражающую поверхность площадью S = 5 см2 за
время / = 3 мин нормально падает монохроматический свет, энер-
гия которого W-9 Дж. Определите: 1) облученность поверхности; 2) свето-
вое давление, оказываемое на поверхность.
Дано
= 5 см
2 =
t = 3 мин = 180 с
W = 9 Дж
2)
Решение
e~St'
= 24
Г Ответ j i) ?e = ioo вт/м2;
2) р = 667 нПа.
Определите давление света на стенки электрической 150-ваттной
лампочки, принимая, что вся потребляемая мощность идет на из-
лучение и стенки лампочки отражают 15% падающего на них света. Считайте
лампочку сферическим сосудом радиуса 4 см.
Дано
Р=\50 Вт
Р=Фе
р = 0,15
R = 4 см = 0,04 м
Р —?
Решение
Ееп ч „ W Фе Р
P~(Up), Ee=-r~ = ~,
S = 4nR2, p = ——r(l + p).
4nR с
[Ответ
> = 28,6 мкПа.
f 5.223 } Давление монохроматического света с длиной волны Я = 500 нм
-^— на зачерненную поверхность, расположенную перпендикулярно
падающему излучению, равно 0,15 мкПа. Определите число фотонов, падаю-
щих на поверхность площадью 40 см2 за одну секунду.
Дано
Я = 500 нм = 5- 10-7м
р = 0,\5 мкПа =
= 1,5-Ю-7 Па
р = 0
5 = 40 см2 = 4- 10~3m2
/ = 1 с
N —?
Решение
с
= pStc,
N _ Ш _ PStc
~ hc~ h
= 0,
= eN = — N,
Г Ответ j
N = 4,52.1017.
Давление р монохроматического света с длиной волны Я = 600 нм
на зачерненную поверхность, расположенную перпендикулярно
падающему излучению, составляет 0,1 мкПа. Определите: 1) концентрацию п
фотонов в световом пучке; 2) число vV фотонов, падающих ежесекундно на 1 м2
поверхности.
р
я
р
!
S
1)
2)
= 01
= 600
= 0
= 1 с
= 1 м
п —
N -
Дано
мкПа= 10"
нм = 6- 10
2
9
_ 7
'Па
М
Р-
? =
N =
Решение
A+ р)- w{
с
he
рс
0 + Р)
ncSt.
1 1 л\
1 + р)>
Яр
/7СA + р) '
E^Stk
he
w
?
W = ?,S/ -
pcStX
0 + p)hc
P
Up'
hc и
- x л>
/?5/Я
Ответ j 1} „ = ^02-10" м-'; 2) лг = 9,об-ю19.
На идеально отражающую поверхность нормально падает моно-
хроматический свет с длиной волны Я = 0,55 мкм. Поток излучения
Фе составляет 0,45 Вт. Определите: 1) число фотонов N, падающих на поверх-
ность за время / = 3 с; 2) силу давления, испытываемую этой поверхностью.
Я
P
Ф
/ =
1)
2)
Дано
= 0,55 мкм = 5,5 ¦
= 1
е = 0,45 Вт
= 3 с
N -
F -
_?
-?
107м
W
\Г
/V
(
Решение
= ?N = ^N, с
Л
Ответ j ^
?й - U + PJ
с
Л^ = 3,73-1018;
Ф
е П i ^'^
U ! Р).
с
2) F = 3 нН.
5.226 f Плоская световая волна интенсивностью /= 0,1 Вт/см2 падает под
углом а = 30° на плоскую отражающую поверхность с коэффи-
циентом отражения р = 0,7 . Используя квантовые представления, определите
нормальное давление, оказываемое светом на эту поверхность.
QОтвет
' a = 4,25 мкПа.
Рассматривая особенности механизма комптоновского рассеяния,
объясните: 1)почему длина волны рассеянного излучения боль-
ше, чем длина волны падающего излучения; 2) наличие в составе рассеянного
излучения "несмещенной" линии.
Определите длину волны рентгеновского излучения, если при ком-
птоновском рассеянии этого излучения под углом #=60° длина
волны рассеянного излучения оказалась равной 57 пм.
пм.
Фотон с энергией е = 1,025 МэВ рассеялся на первоначально по-
коившемся свободном электроне. Определите угол рассеяния фо-
тона, если длина волны рассеянного фотона оказалась равной комптоновской
длине волны Яс = 2,43 пм.
Дано
? = 1,025 МэВ =
= 1,64- 10 пДж
Х' = ХС
Яс = 2,43 пм =
= 2,43- 10 12м
# —?
Решение
he
? = hv = ^, Я
Я
Яс = — + ЯсA-со
hf
_ пс у -
е
s#), cos^
Г Ответ
А+ A^(l-cos#),
}_ he
Хс? '
J # = 60°.
Узкий пучок монохроматического рентгеновского излучения па-
дает на рассеивающее вещество. Оказывается, что длины волн
рассеянного под углами #, = 60° и #2 =120° излучения отличаются в 1,5 раза.
Определите длину волны падающего излучения, предполагая, что рассеяние
происходит на свободных электронах.
я,
#2
К
Дано
= 60°
= 120°
= 1,5
Решение
Х\ = Х + Ac(l-cos#,), Х'2 = Х + Ac(l-cos#-,),
Х\ Х + Ac(l-cos#2)
Х\ Я + ЯсA -cos^,)
А + Яс - Ас cos д2 = 1,5А + 1,5ЯС - 1,5АС cos #,.
А= ЯсC cos#] -2 cos#t -1).
ГОтвет j
Я = 3,64 пм.
/ Фотон с длиной волны Я = 5 пм испытал комптоновское рассея-
ние под углом д = 90° на первоначально покоившемся свобод-
ном электроне. Определите: 1) изменение длины волны при рассеянии; 2) энер-
гию электрона отдачи; 3) импульс электрона отдачи.
Дано
Я = 5 пм = 5 • 10 '-м
# = 90°
1) ЛЯ —?
2) WL - ?
3) А - ?
Решение
= Ac (cos?) = 0),
Р = Ре + Р' ,
(Ре) = Т
Я + АЯ
Г Ответ j
1)АЯ = 2,43пм; 2) We =81,3 кэВ; 3) ре = 1,6-10 " кг- м/с.
<473>
Фотон с энергией е = 0,25 МэВ рассеялся на первоначально поко-
ившемся свободном электроне. Определите кинетическую энергию
электрона отдачи, если длина волны рассеянного фотона изменилась на 20%.
Дано
е = 0,25 МэВ =
= 4- 10-мДж
Я' = 1,2Я
Т. — ?
Решение
т > he I he
le — Е — Е , Е— , Л — ,
Я ?
, he he e ? ?
? Я' 1,2Я 1,2' е Е U б'
ГдтветЛ
Фотон с энергией 0,3 МэВ рассеялся под углом 9 - 180° на сво-
бодном электроне. Определите долю энергии фотона, приходя-
щуюся на рассеянный фотон.
Фотон с энергией 100 кэВ в результате комптоновского эффекта
рассеялся при соударении со свободным электроном на угол
¦& = я/2. Определите энергию фотона после рассеяния.
(OmeernJ e =83,7кэв
Фотон с энергией ь = 0,25 МэВ рассеялся под углом Ь -120° на
первоначально покоившемся электроне. Определите кинетичес-
кую энергию электрона отдачи.
{Ответ J т; =
6. Элементы квантовой физики
атомов, молекул и твердых тел
6.1. Теория атома водорода по Бору
Определите энергию фотона, испускаемого при переходе электро-
на в атоме водорода с третьего энергетического уровня на второй.
II II 1
N ? s
Е
Дано
2
3,29-1015 г1
Решение
\т2 п2 )
F - ит>\ _
-f)-
С Ответ j еХ2 = 1,89 эв.
Определите максимальную и минимальную энергии фотона в ви-
димой серии спектра водорода (серии Бальмера).
z =
m =
2
Дано
?
?
v-Л
и = 3,
Решение
М-
4,5,...,
00 /llllll/1/il/n/lil,
^¦inin ?> max
Ответ
= 3,41эв,
НИ Определите длину волны Я. соответствующую второй спектраль-
ной линии в серии Пашена.
Ответ) я = 1,28 мкм.
Максимальная длина волны спектральной водородной линии се-
рии Лаймана равна 0,12 мкм. Предполагая, что постоянная Ридбер-
га неизвестна, определите максимальную длину волны линии серии Бальмера
z-
Щ
h
Дано
= 1
= 0,12 мкм=1,2'
1
= 2
7
1(Г7
м
X-R
Я
1
Ял""
1
Решение
1 2 ~ 2 J >
и
nn ////////У//////////////////////////////
1 ....
^ , .... 4
1 ' 1
' 1 ' ^
i ; 1
! | ! °ЯБ
1 ]
^ Определите длину волны спектральной линии, соответствующей
переходу электрона в атоме водорода с шестой боровской орбиты
на вторую К какой серии относится эта линия и какая она по счету?
Дано
и=6
Я — ?
Решение
А4
т п
С Ответ
^*
Я= 0,41 мкм, четвертая
линия серии Бальмера.
У l) Определите длины волн, соответствующие: 1) границе серии Лай-
мана, 2) границе серии Бальмера; 3) границе серии Пашена. Про-
анализируйте результаты.
Дано
1) серия Лаймана
2) серия Бальмера
3) серия Пашена
2)Я2-?
Решение
т = \, и = 2, 3,..., оо I — =Л'[ — - —
Л'= 1,1 107 м ', — =R' 1, и=оо,
Я
1
7 ..-1
R' 1,1 10' м
= 91нм.
т = 2, и = 3,4,..., оо | — =.
Я
и = со , Я2 = -^- = 364 нм.
т = 3, и = 4, 5,..., оо
22 n1
я = со , Я2 = — = 820 нм
Г Ответ J 1) Я,=91 нм, область ультрафиолета,
2) Я2 = 364 нм, вблизи видимого фиолетового излучения,
3) Я3 = 820 нм, область инфракрасного излучения.
Обобщенная формула Бальмера
где v — частота спектральных линий в спектре атома водорода; R — постоян-
ная Ридберга; т определяет серию (т = 1, 2, 3, ...), п определяет отдельные
линии соответствующей серии (и = т + 1, т + 2,...): т = 1 (серия Лаймана),
т = 2 (серия Бальмера), m = 3 (серия Пашена), m = 4 (серия Брэкета), т = 5
(серия Пфунда), m = 6 (серия Хэмфри).
Шт Атом водорода находится в возбужденном состоянии, характери-
зуемом главным квантовым числом и = 4. Определите возмож-
ные спектральные линии в спектре водорода, появляющиеся при переходе ато-
ма из возбужденного состояния в основное.
Дано
Я' = 1,Ы07 м-1
Я —?
Решение
А V 1 О* / D'
16 1
¦
15 Л'
м
Й-
.
36
'" 5
16
~ 3 '
1
Я7'
1
3
2
144 1
42J'
4 5
1 2 3
Я,=1,2110м; А2 = 1,02-Ю-7м; Я3 = 0,97-10 м;
Я4 = 6,54-10 м; Я5 = 4,85-10 м; Я6 = 18,7-10 м.
Основные физические постоянные
Постоянная Ридберга
Постоянная Планка
. = 3,29 1015 с
Л'= 1,10 107 м
й = 6,63-КГ34 Дж-с
А = 1,05 Ю-34 Дж-с
В инфракрасной области спектра излучения водорода обнаруже-
но четыре серии — Пашена, Брэкета, Пфунда и Хэмфри. Запиши-
те спектральные формулы для них и определите самую длинноволновую ли-
нию: 1) в серии Пашена; 2) в серии Хэмфри.
т = 3, 4
и 1,1 1
1) Яз.тах
2) Я6 тах
Дано
5,6
Ю7 м-'
— ?
Решение
Я ч/и и /
Серия Пашена
хг~ 1з2 »2J-
и
7б
4—р-
3
..I.
Лб.тах
Лз.пих
2
Серия Брэкета — = R' —г- —-
л4 ^4 и
Серия Пфунда
Серия Хэмфри
4Л
З2 42
О ^3,max = I.»7 МКМ; 2) Я6,тах = 12,3 МКМ.
Определите число спектральных линий, испускаемых атомарным
водородом, возбужденным на и-й энергетический уровень.
Г Ответ J N = n(n-l)/2.
На дифракционную решетку с периодом d нормально падает пу-
чок света от разрядной трубки, наполненной атомарным водоро-
дом. Оказалось, что в спектре дифракционный максимум к -щ порядка, на-
блюдаемый под углом <р, соответствовал одной из линий серии-Лаймана. Оп-
ределите главное квантовое число, соответствующее энергетическому уровню,
с которого произошел переход.
Дано
d
к
<Р
т=\
Решение
d sin ip = -
kc
4
r?) Rdsin<p'
и= 1-
ck \ 2
Rdsm<p)
Ответ
и= 1-
ск у 2
Rd sin ipj
Используя теорию Бора для атома водорода, определите: 1) ради-
ус ближайшей к ядру орбиты (первый боровский радиус), 2) ско-
рость движения электрона по этой орбите.
я
1)
= 1
-1
г\ —
Дано
•>
mv2
г
Z=\
Решение
Ze2
4же0г
я = 1,
mvr - rih ,
h = hjln.
2) и,—?
mv, e
4же0г2
,= h
me
П
mr
пм;
2) и, = 2,19 Мм/с.
<480>
Определите, на сколько изменилась энергия электрона в атоме во-
дорода при излучении атомом фотона с длиной волны
Я = 4,86 10 м.
Дано
|Я = 4,86 10 м
Решение
A? =
с
АЯ=т-
Ответ Л д? = 2,56 эв.
Определите длину волны Я спектральной линии, излучаемой при
переходе электрона с более высокого уровня энергии на более
низкий уровень, если при этом энергия атома уменьшилась на АЕ = 10 эВ.
Используя теорию Бора, определите орбитальный магнитный мо-
мент электрона, движущегося по третьей орбите атома водорода
h = 1,05
рт —7
Дано
10~34 Дж ¦ с
Рт
т-
Решение
Ь-яг ,
V
/Я
evr
2
= ~, pm =
enh
—
2m
Ответ
= 2,8 ю 23 а м*
Определите изменение орбитального механического момента элек-
трона при переходе его из возбужденного состояния в основное с
испусканием фотона с длиной волны Я = 1,02-10~7 м.
Предполагая, что в опыте Франка и Герца вакуумная трубка на-
полнена не парами ртути, а разреженным атомарным водородом,
определите, через какие интервалы ускоряющего потенциала <р возникнут
максимумы на графике зависимости силы анодного тока от ускоряющего по-
тенциала.
Дано
= 1,02-10~7 м
AZ, —?
Решение
mevr -rih , L = rih, AL = nh- mh = (n- m)fr .
Omeem j <p = 10,2 в.
m~
J_ J 1_
и2 ~ m2 XR '
n =
m
2XR'
ЛД'-/и2 '
AL = \
m
2XR
XR-i
¦mvh,
6,63.10
-^
1? ..-I i2
ГдтветЛ
Используя постоянную Планка h, электрическую постоянную ?о,
массу т и заряд е электрона, составьте формулу для величины,
характеризующей атом водорода по Бору и имеющей размерность длины. Ука-
жите, что это за величина.
Докажите, что энергетические уровни атома водорода могут быть
описаны выражением Еп = г- R, где R — постоянная Ридберга.
Позитроний — атомоподобная система, состоящая из позитрона
и электрона, вращающегося относительно общего центра масс.
Применяя теорию Бора, определите минимальные размеры подобной системы.
Дано
Дано
e~
e+
dmm — ?
Решение
(mvr)+ + {mvr)_ = nh,
2mvr = ий
m>2 г2
г 4жеоBгJ
E=-
2nh
Решение
mevr = nh,
2 h ¦ 4лге0 '
mev
r
2
4
1
e2
¦ЛГ?0,
e
2
1 m.
ree2 ' " 2 4лг?0гя и2 8ft2
4m2v2r2 = n2h2,
v = -
1 1
m
2h
n m
r =
4лг?отг12 ¦ 4r = e2,
, _,__2?0ft2
n=l
ne2m
лте
2 '
С Omeentj
dmm=l06 пм.
mee
2л:й _ 2nh mee4
т~ л *~ ~ т L.i T"
т„е
СОтвет j E
l7lh
R
6 20 ^ Определите скорость v электрона на третьей орбите атома во
Jr адрода
z =
n-
v3
~-\
3
—
?
Дано
mv"
r
mvr
Решение
e~
4Л?0! "
= иЙ,
e"
r ,
4n?0mv
mve
- = nh .
Определите 1) частоту /вращения электрона, находящегося на
первой боровской орбите, 2) эквивалентный ток
1 e"
v =
n
1 e"
Дано
n = \
r, = 52,8 пм
Решение
h
mvr = nh, n = \ i»i = >
r 27ГИ f I v} A
' J t' J ~~ -> ~ ** •> '
(jJmeem
; = 0,731 Мм/с
^^^ШК^ Электрон находится на первой боровской орбите атома водорода
Определите для электрона 1) потенциальную энергию Еп, 2) ки
нетическую энергию Ек. 3) полную энергию Е
Ответ
J
= 658 10is Гц> 2) 7 = 10
СОтветЛ \) еп =
-27,2 эВ 2) ?к =
ft^^^^H Определите частоту / вращения
XrfiT iSt*-!!»^ атома водорода в теории Бора
Дано
z = \
и = 1
/-9
и„ we4
2л-г„ 32л-3^Л3«3 <
Г Ответ ) у = 2,42
Решение
2 л 2
mv I e
г 4ль0 г2
2 4л:?0й
те'
те*
left3»3
1014 Гц
13,6 эВ,
электрона
mvr
'•„ =
3) ?=-13,6
по третьей
= nh,
1 е2
П 4ЛГ?ОЙ
эВ
орбите
Определите частоту света, излучаемого атомом водорода, при пе-
реходе электрона на уровень с главным квантовым числом п = 2,
если радиус орбиты электрона изменился в к - 9 раз
Дано
и=2
v —
Решение
J
n _ 1
m2 к
«2
fOmeem j
,15
v = 0,731 10" Гц
|Щ^№М Пользуясь теорией Бора, найдите числовое значение постоянной
(Ответ ) о те4 _
27 1015 с
Определите потенциал ионизации атома водорода.
Дано
z = \
Д = 3,29 1015 с-1
Решение
\\ °° )
hR
е
Основываясь на том, что энергия ионизации атома водорода
Е, =13,6 эВ, определите в электрон-вольтах энергию фотона, со-
>тветствуюигую самой длинноволновой линии серии Бальмера.
Дано
?,=13,6 эВ
COmaemj ,Pl = 13,6 в.
Решение
1 ив
^Ш=^ = ^3,2 = ^Ь-^'
2* У
Основываясь на том, что энергия ионизации атома водорода
Е, = 13,6 эВ, определите первый потенциал возбуждения tpl это-
го атома.
Дано
?,=13,6 эВ
<Р\ —'
Решение
^ГО1Х
?, = ,
1_J-
l2 22
<Pi =
1А
4 e "
Вычисления:
= 10,2B.
QpmeemJ) Еб х =1,89эв.
Основываясь на том, что первый потенциал возбуждения атома
водорода <рх ~ 10,2 В, определите в электрон-вольтах энергию
фотона, соответствующую второй линии серии Бальмера.
Дано
Определите первый потенциал возбуждения атома водорода.
р,=10,2 В
ЕА,—1
Решение
fOmeem Л ^, =ю,2 в.
Первый потенциал возбуждения
Первый потенциал возбуждения р, — это ускоряющее напряжение, соответ-
ствующее переходу невозбужденного атома в первое возбужденное состояние.
65 Ч
2
1
Г 1
^ /
V4,2
16
QOmeemj е4Л = 2,55 эв
Определите работу, которую необходимо совершить, чтобы уда-
лить электрон со второй боровской орбиты атома водорода за пре-
делы притяжения его ядром.
Определите, какие спектральные линии появятся в видимой обла-
сти спектра излучения атомарного водорода под действием ульт-
(афиолетового излучения с длиной волны Я = 95 нм.
A = 5А5Л0
-i9
Электрон выбит из атома водорода, находящегося в основном со-
стоянии, фотоном, энергия которого е = 17,7 эВ. Определите ско- i
рость v электрона за пределами атома.
Я =
К
1
95
Дано
нм = 9,5- 10 8м
7
Решение
he
?=Т'
?, =-13,6 эВ,
Ег
Ег
= ?,+?,
1
Дано
и=1
е = 17,7 эВ =
= 28,3- 10" Дж
v —?
Решение
п-.
е = Е,
mv2
?,=13,6 эВ = 21,8- 10-" Дж,
п= п, и-1,..., 3.
т
Вычисления:
6,63-10~34-3-108
С~95-10"9 1,6 1049
= 13,1эВ;
Г Ответ Л v = 1,2
?, = -13,6 эВ + 13,1 эВ = -0,5 эВ;
Мм/с
п =
Фотон с энергией е = 12,12 эВ, поглощенный атомом водорода,
находящимся в основном состоянии, переводит атом в возбужден-
ное состояние. Определите главное квантовое число этого состояния.
3 108 м/с
Дано
= 12,12 эВ
п —?
Решение
? = Е2 - Е{ (см. рисунок к задаче 5.34),
?,=-13,6 эВ,
3,29-1015 с
= 0,434-10 м;
Я4 = -
3 10 м/с
3-Ю8 м/с
Е, +? '
-Ю15 с'1(- -
= 0,486 -10~6 м;
= 0,656-10 м.
е
1
Л$ Я4 Л 3
Я
СОтвегп\ „ = з.
Г Ответ Л хп = 0,434 мкм; 0,486 мкм; 0,656
мкм.
6.35
В излучении звезды обнаружен водородоподобный спектр,
дли-
' ны волн которого в 9 раз меньше, чем у атомарного водорода
Определите элемент, которому принадлежит данный гпргт
которому принадлежит данный спектр.
Применяя теорию Бора к мезоатому водорода (в мезоатоме водо-
рода электрон заменен мюоном, заряд которого равен заряду элек-
трона, а масса в 207 раз больше массы электрона), определите: 1) радиус пер-
вой орбиты мезоатома; 2) энергию ионизации мезоатома.
= 0,254пм; 2) Е. = 2,8 кэВ.
Определите, какая энергия требуется для полного отрыва элект-
рона от ядра однократно ионизованного атома гелия, если: 1) элек-
трон находится в основном состоянии; 2) электрон находится в состоянии, со-
ответствующем главному квантовому числу п = 3 .
1) ?„=54,2 эВ;2) ?,, = 6,02 эВ.
6.2. Элементы квантовой механики
Определите импульс и энергию: 1) рентгеновского фотона; 2) элек-
трона, если длина волны того и другого равна 10~10 м.
Я = 1
У
е = \,
1) Ру
2) Ре
Дано
Э-'°м
6-Ю9 Кл
,^-?
Решение
h _.
Py=J> Ey=PYc,
Ре=Т=Ру, E< = ^t-
Я 2т
с
1
2)
Ру = 6,63
А = 6,63
-10-24кг-
•Ю-24 кг-
м/с, Еу = 12,4 кэВ;
м/с, ?, = 151 эВ.
iiiiiiiiiijiiib
§1§|||§1§| Определите длину волны де Бройля для электрона, находящегося
тВНРУ в атоме водорода на третьей боровской орбите.
Дано
е=1,6-109 Кл
и = 3
Я —?
Решение
h
р
= — = —, ffwr = nh,
mv
h_
mv
2
4же0г
2 '
1 г'
i» = — -
n 2e0h
X =
2h2ne0
me
[
Ответ
= i нм.
Щ Определите длину волны де Бройля для нейтрона, движущегося
со средней квадратичной скоростью при Т = 290 К.
Дано
w = 1,675 107 кг
Т = 290 К
Jt=l,38 10~23 Дж/К
Я —?
Решение
(v \ Wf
я л h h
ЦП Протон движется в однородном магнитном поле с индукцией
5=15 мТл по окружности радиусом R = 1,4 м. Определите дли-
ну волны де Бройля для протона.
COmeemS
Я = 0,197 пм
?Щ||Й1Щ Определите, какую ускоряющую разность потенциалов должен
" * * пройти протон, чтобы длина волны де Бройля Я для него была
равна 1 нм.
Дано
А = 1 нм=10"м
тп = 1,675 10~27 м
U 1
х-
Решение
р2
Ьп'
h
2meU '
р = -j2meU ,
L, *
2meX2 '
яЛ,
p
Заряженная частица, ускоренная разностью потенциалов U = 500 В,
имеет длину волны де Бройля Я = 1,282 пм. Принимая заряд этой
частицы равным заряду электрона, определите ее массу.
Дано
f/ = 500 В
Я = 1,282 пм =
= 1,282- 1012м
е = 1,6 Ю9 Кл
Решение
2m
x-h - h
p ы2тпги
p = yl2meU ,
h2
2eX2U
m
Г Ответ)
= 1,672-107 кг.
Выведите зависимость между длиной волны де Бройля Я реляти-
вистской частицы и ее кинетической энергией.
X{T)
Дано
. 9
2
P =
Решение
h I r
> pc - iJT(T + 2mc ) j
¦JT{T + 2mc2) he
c ' JT(T + 2mc2)'
Выведите зависимость между длиной волны де Бройля Я реляти-
вистского электрона и ускоряющим потенциалом U.
fOmeemj я =
he
eU)
Кинетическая энергия электрона равна 1 кэВ. Определите длину
волны де Бройля.
Дано
Т = \ кэВ =1,6- 10
и = 9,11 10~31 кг
Я — ?
16 Дж
Я -
А =
Решение
h h
р mv
h
42mT
т-
mv2
2 '
f Ответ
J2T
v U '
J Я = 38,8 пм.
Кинетическая энергия электрона равна 0,6 МэВ. Определите дли-
ну волны де Бройля.
Г = 0,6
= 9,6
m = 9,11
Я —?
Дано
МэВ =
1014Дж
¦Ю-31 кг
А =
Р-
Решение
h 2 :
Р
¦)]Т(Т + 2тс )
с
= Т(Т + 2тс2),
1 Ас
Ответ
= 1,2бпм
Определите, при каком числовом значении скорости длина волны
де Бройля для электрона равна его комптоновской длине волны.
и = 2,12-10е м/с.
Определите, при каком числовом значении кинетической энергии
Т длина волны де Бройля электрона равна его комптоновской дли-
не волны.
Г
Ответ
= о,212 мэв.
ц Выведите связь между длиной круговой электронной орбиты и
длиной волны де Бройля.
(Ответ Л
2лг = пХ ¦
Определите, как изменится длина волны де Бройля электрона в
атоме водорода при переходе его с четвертой боровской орбиты
на вторую.
Дано
и = 4
Решение
2жг = пк , 2лгг4 = 4Я4, 2лгг2 = 2Я2, г4 = 4 г,,
^2 ^4 2лгг4 2 г4 42г, л
'2 "" М' Я2 4 2лгг2 2г2 2 22г,
{Ответ j K_ = 2
В опыте Дэвиссона и Джермера, обнаруживших дифракцио1шую кар-
тину при отражении пучка электронов от естественной дифракцион-
ной решетки — монокристалла никеля, оказалось, что в направлении, составляю-
щем угол а = 55° с направлением падающих электронов, наблюдается максимум
отражения четвертого порядка при кинетической энергии электронов Т = 180 эВ.
Определите расстояние между кристаллофафическими плоскостями никеля.
а
Jt
Г
(
= 9,11
= 55°
= 4
= 180
= 2,88
7
Дано
10~31
эВ =
¦ 10'
Ответ
кг
Дж
\
Решение
г = А Р = ^
2от
., а И
/И рпч— ~ к
2 42тТ '
= 0,206 нм
= 90-|,
й —
' а\_
ч ° 2i"
kh
а
2 cos \
2
р
а
- cos—,
2
1ЪпТ
<495>
Моноэнергетический пучок нейтронов, получаемый в результате
ядерной реакции, падает на кристалл с периодом d = 0,15 нм
Определите скорость нейтронов, если брэгговское отражение первого порядка
наблюдается, когда угол скольжения ft = 30° .
Дано
с/= 0,15 нм=1,5- 10 10м
т = 1,675 107 кг
? = 1
# = 30°
v —?
2
С
Решение
i sin # = Ы,
Ответ j ,
kh
2 dm sin ft
= 2,64 км/с.
ЙГ! Параллельный пучок моноэнергетических электронов направлен
нормально на узкую щель шириной а- 1 мкм. Определите скорость
этих электронов, если на экране, отстоящем на расстоянии / = 20 см от щели,
ширина центрального дифракционного максимума составляет Ах - 48 мкм.
Дано
кг
а = 1 мкм = 10 м
/ = 20 см = 0,2 м
Ах = 48 мкм = 4,8- 10'5м
v —?
Решение
= +kX , k = \, s\ntp = — ,
= 2ltg<p, tg(p*sm<p (угол <р мал),
2/
am Ax
{Omeemj „ = 6>
06 Mm/c.
<496>
Параллельный пучок электронов, ускоренный разностью потен-
циалов U = 50 В. направлен нормально на две параллельные, ле-
жащие в одной плоскости щели, расстояние d между которыми равно 10 мкм
Определите расстояние между центральным и первым максимумом дифракци-
онной картины на экране, который расположен от щелей на расстоянии / = 0,6 м
Г Ответ j
мкм.
6 56 ) Исходя из общей формулы для фазовой скорости ( «(|ш = ш/к ),
определите фазовую скорость волны де Бройля свободно движу-
щейся с постоянной скоростью v частицы в нерелятивистском и релятивист-
ском случаях.
Дано
"фаз = Чк
1) V « С
2) v« с
Решение
со -
и«с, Е = ^—, уфаз1
2т
v « с,
Е-тс,
tm _E_
~Ьк~ р'
р mv v
~ 2т ~ 2т 2
Е _ тс" _ с"
р mv v
(Ответ)
с
v
Можно вывести, что для релятивистского случая фазовая скорость
"фаз = С7" (см. задачу 6.56), т.е. фазовая скорость волн де Бройля
больше скорости света в вакууме Объясните правомерность этого результата.
Объясните, почему представление о боровских орбитах не совме-
стимо с принципом неопределенности.
^ Докажите, что групповая скорость волн де Бройля равна скоросп
^ свободно движ> шейся частицы. Рассмотрите нерелятивистский v
релятивистский случаи
Докажите, что для свободно движущейся с постоянной скорос-
тью v частицы выполняется соотношение ^^и = с
повая скорость).
; и — фуп-
ГОтвет
Выведите закон дисперсии волн де Бройля, т.е. зависимость фазо-
вой скорости волн де Бройля от их длины волны Рассмотрите
нерелятивистский и релятивистский случаи.
ЁИЙ^ ШиРина следа электрона (обладающего кинетической энергией
Т = 1,5 кэВ) на фотопластинке, полученного с помощью камеры
Вильсона, составляет Ах = 1 мкм. Определите, можно ли по данному следу об-
наружить отклонение в движении электрона от законов классической механики.
Дано
и = 9ДЫ0~31 кг
Т = 1,5 кэВ = 2,4-10 16Дж
Ах - 1 мкм =10 " м
Решение
2 2т
Ах Арх = h ¦
Дх
h
Ах
С Omeemj
«1.
Электронный пучок ускоряется в электронно-лучевой трубке раз-
ностью потенциалов U = 1 кВ. Известно, что неопределенность
скорости составляет 0,1% от ее числового значения. Определите неопределен-
ность координаты электрона. Являются ли электроны в данных условиях кван-
товой или классической частицей?
Дано
/и = 9,11Ю~31 кг
е = 1,6-109 Кл
V = l кВ = 103В
^ = 0,001
v
Ах —?
Решение
v =
2eU
m
Ах Ар > h,
h h
Ар Av
=?- = — «1,
P v
Ах
Ар mAv 0,00\yl2meU '
f Ответ j
Ax =38,8hm.
ки
Ц Определите отношение неопределенностей скорости электрона,
если его координата установлена с точностью до 10 5 м, и пылин-
массой т -10~12 кг, если ее координата установлена с такой же точностью.
те = 9,1
Дх, = 1<
тп = \0
Ахп=\
Ave
Avn
Дано
МО1 кг
)-5 м
-2кг
О м
-9
Дх
т„
(
Решение
Арх > h,
Avn Axn=h,
Ответ )
Axemt
Avf
Avn
Ave_
Ave =
hme
1,1 10
--h,
ten
Axe
18
me
Avn
IM>5 J Электронный i
i пучок выходит из электронной пушки под действи
ем разности потенциалов U = 200 В. Определите, можно ли ол
новременно измерить траекторию электрона с точностью до 100 пм (с точное
тью порядка диаметра атома) и его скорость с точностью до 10%
Дано
U = 200 В
Ах = 100 пм = 10
Av = 0,Ь
Ах те Av — ?
Ответ
Решение
mev
2
Av =
- =
0,1
eU,
[2eU
v =
Axme Av = OjJbrLeU Ax
Ax me Av = 7,64 • 10 35 Дж • с < h.
MjO8" J Электрон движется в атоме водорода но первой боровской орбите
'"'"'""^ Принимая, что допускаемая неопределенность скорости составля-
ет 10% от ее числового значения, определит е неопределенное гь координаты элек-
трона Применимо ли в данном случае для электрона понятие траектории?
Да- — ?
AxmAux=h, Дх = __
т Av,
Применяя соотношение неопределенностей, покажите, что для
движущейся частицы, неопределенность координаты которой рав-
на длине волны де Бройля, неопределенность скорости равна по порядку вели-
чины самой скорости частицы
S«Do' j Используя соотношение неопределенностей в форме Аде Ар, > h ,
оцените минимально возможную полную энергию электрона в
атоме водорода. Примите неопределенность координаты равной радиусу ато-
ма. Сравните полученный результат с теорией Бора.
Дано
Ах Арх > Ь
Ах - г
и=1
Z = \
Етт -?
Решение
Ах Арх > h, -&-«1, рх = Арх = — = —,
Рх Ах г
Е = Т + П=(+{-/ ). Е= Ь\- ^ ,
2т \ 4ле0г] 2тг 4ле0г
2
me
d?
dr
Г1
те
h1
т? ' А
ГГ
-mrmm
те4
%h2el
-13.6 :
е~
\лг&г
е"
4яг0гт1П
mr)
me
Объясните физический смысл соотношения неопределенности для
энергии Е и времени t : АЕ А/ > И.
Основные физические постоянные
Постоянная Планка
ft = 6,63 104 Дж-с
й = 1,05 10~34 Дж'С
-12
Электрическая постоянная ?0 = 8,85 10~12 Ф/м
Воспользовавшись соотношением неопределенностей, оцените раз-
мытость энергетического уровня в атоме водорода 1) для основно-
го состояния; 2) для возбужденного состояния (время его жизни равно 10 s с)
Дано |. Решение
&f*t?Ч Длина волны ^ излучаемого атомом фотона составляет 0,6
Принимая время жизни возбужденного состояния At = 10~8 с,
определите отношение естественной ширины энергетического уровня,
торый был возбужден электрон, к энергии, излученной атомом.
мкм.
на ко-
= — > E = hv- —,
At Я
jtS"*! j Принимая, что электрон находится внутри атома диаметром 0,3 нм,
чишДинУ определите (в электрон-вольтах) неопределенность энергии дан-
ного электрона.
Объясните, почему физический смысл имеет не сама ? -функ-
ция, а квадрат ее модуля
Объясните, почему волновая функция должна быть конечной, од-
нозначной и непрерывной.
Запишите выражение для вероятности W обнаружения частицы
в конечном объеме V , если известна координатная пси-функция
частицы гр(х,у,г).
Волновая функция, описывающая некоторую частицу, может быть
- El
представлена в виде Ч*(х, t) = ip(x) e ь Покажите, что плотность вероятно-
сти нахождения частицы определяется только координатной Ц> -функцией.
Дано
W
Решение
w =
, г) |2,
\4>(x, t) f =
ip\x)
f '
Ответ
= \xp(xf
Некоторые математические формулы
sin(a + /J) = sir
cos(a ± /J) = cosa i
sin 2a = 2sin a cosa
sin2 a = —A - cos2a)
cos2a = cos2 a - sin2 a
cos2 a = — A + cos 2a)
V> -Функция некоторой частицы имеет вид if> = — е Г1а , где г —
г
расстояние этой частицы до силового центра; а — некоторая постоянная.
Используя условие нормировки вероятностей, определите нормировочный
коэффициент А.
Дано
г
а = const
А —?
Решение
= 2тгА a,
2лА2а = 1,
A =
Г Ответ
A =
Используя условие нормировки вероятностей, определите норми-
ровочный коэффициент А волновой функции \р = А е~г?а , опи-
сывающей основное состояние электрона в атоме водорода, где г — расстоя-
ние электрона от ядра, а — первый боровский радиус.
Дано
ip(r)=Ae-r'a
A -?
V
00
0
Решение
dV=\, dV = 4n
f2rla-4nr2dr = 4
r2dr,
00
жА2\г
0
\гр(г
2 е-2
)f
rja
= A2e-2r'°,
dr = l,
2! a3
2У 4
a,
4лА2- — = \,
Г Ответ Л
Используя условие нормировки вероятностей, определите норми-
ровочный коэффициент волновой функции гр(г)= Ае~г /Bа"',
вписывающей поведение некоторой частицы, где г — расстояние частицы от
силового центра; а — некоторая постоянная.
С Ответ Л А =
f> | Волновая функция Ц> = A sinBjrx//) определена только в области
О < х < / . Используя условие нормировки, определите норми-
ровочный множитель А .
Дано
. ¦ 2тгх
V(x)= A sin
0< х ^ 1
А -?
Решение
J|y(x)|2<k = l,
0
1 , ч,2 ,2-2 27ГХ
\гр(х)\ =Alsml-y,
.,2. Г.251П2 2ЯХ
1 2ТГХ
0
0
2 V А2 г
-[l - cos
4лх\ , А2 V, А2 г 4л:х
—J dx = — fdx - T f cos—
4тгх
2 4л:
-sin-
(Ответ ) (Y
-/ ^ =, - .
-Функция некоторой частицы имеет вид ip = — е г^а , где г —
расстояние этой частицы до силового центра; а — некоторая постоянная. Оп-
ределите среднее расстояние (г) частицы до силового центра.
Дано
г
a - const
Решение
(г) = jr\tp\2 dV = jr^np" dV,
A =
(см. задачу 6.77),
00
(r) = f —
2ла
- t~2rla ¦ 4лг
2 dr = - [r t-2rla dr = -
2 _1
2
a
2~2
СОтвет Л (Л = ?.
Волновая функция, описывающая некоторую частицу, имеет вид
гр = А е~г'( " , где г — расстояние этой частицы до силового
центра; а — некоторая постоянная. Определите среднее расстояние (г) час-
тицы до силового центра.
Дано
a = const
(r)~-
Решение
A = ¦ (см. задачу 6.79), dV = 4лт2 dr ,
VttV
W =
-i
bUe-^'dr =
3 -г2/а2 ,
e ^=
4 1 2a
х
Волновая функция, описывающая основное состояние электрона
в атоме водорода, имеет вид ip = А е~Г//" , где г —расстояние элек-
трона от ядра, а — первый боровский радиус. Определите среднее значение
квадрата расстояния (г j электрона до ядра в основном состоянии.
Дано
ip= Ae '
a - const
Решение
Jna
(rf dV, dV = 4nr2 dr ,
(см. задачу 6.78),
ГОтвет
ip(
Волновая функция, описывающая некоторую частицу, имеет вид
r) = — е"г Iй , где А — нормировочный множитель, равный / ; г —
у1жау12л
расстояние частицы от силового центра; а — некоторая постоянная. Опреде-
лите среднее значение квадрата расстояния \г ) частицы до силового центра.
Дано
а = const
Решение
(r2)= jr2\ip(rfdV ,
' = 4nr2 dr
4жА2]
r2e-2
л A2SH | 2f2 a2
= 4жА—— — | =-r.
4 U
И-т-
Волновая функция, описывающая основное состояние электрона
в атоме водорода, имеет вид \р~ A t'na, где г —расстояние элек-
трона от ядра, а — первый боровский радиус. Определите наиболее вероят-
ное расстояние гв электрона до ядра.
Дано
у = Ае-г/а
а = const
г.-?
Решение
dW = \ip(rfdV. dV = Anr2Ar,
dW - 4лЛ V e-2r'a dr, w-dW - 4лЛ V e''"
dr
dw
~dr
= 0
а
Волновая функция, описывающая некоторую частицу, имеет вид
\р = А е~г' " , где г — расстояние частицы от силового цент-
ра; а — некоторая постоянная. Определите наиболее вероятное расстояние ги
частицы до силового центра.
Ответ
Гв = а.
те"\ Запишите уравнение Шредингера для стационарных состоянии
электрона, находящегося в атоме водорода.
? оо Л Запишите одномерное уравнение Шредингера (для стационарных
"' состоянии) для частицы, движущейся под действием квазиупру-
гои силы
Запишите общее уравнение Шредингера для свободной частицы,
движущейся вдоль оси х, и решите это уравнение.
гЗ Исходя из принципа классического детерминизма и причинности
в квантовой механике, объясните толкование причинности в клас-
сической и квантовой теориях
f % Известно, что свободная квантовая частица описывается плоской
монохроматической волной де Бройля. Плотность вероятности
(вероятность, отнесенная к единице объема) обнаружения свободной частицы
" = |/)|" = const Объясните, что означает постоянсгво этой величины
Запишите уравнение Шредингера для стационарных состояний для
свободной частицы, движущейся вдоль оси х, а также определите
посредством его решения собственные значения энергии. Что можно сказать
об энергетическом спектре свободной частицы?
Ответ Л Е = ь2к2
^ 2т
спектр непрерывный
Волновая функция, описывающая частицу в момент времени 1 = 0,
имеет вид Ч*(х, 0) = А е~* '" +lla , где а и к — некоторые поло-
жительные постоянные Определите 1) нормировочный коэффициент А ,
2) область, в которой частица локализована.
С Ответ j
А =
2) 0 < х < а .
Л Частица находится в одномерной прямоугольной "потенциальной
яме" шириной / с бесконечно высокими "стенками". Запишите
уравнение Шредингера в пределах "ямы" @ < х < Г) и решите его.
Дано
О < дс </, {7 =
х <0, U->-<х>
х>1, U-too
тр(х) — ?
,2 2тпЕ
к = ~
тр(х) - A sin kx + В cos kx ,
y>(l)=Asinkl = Q,
Решение
/, U = 0,
2m
G=0
С/-» 00
= 0, 5=0,
' = — , ip(x)=Asm—x
QOmeem
Частица находится в одномерной "потенциальной яме" шириной /
с бесконечно высокими "стенками". Выведите выражение для соб-
ственных значений энергии Еп.
0 *
U-
En
; X
--0
—
Дано
?
Решение
dx
rm
к = — (см. задачу 6.94),
2mE
й2 '
п2л2 2тЕ
« = 1,2,3,...
СОтвет
2ml
2 '
« = 1,2,3,...
Волновая функция, описывающая состояние частицы в одномер-
ной прямоугольной "потенциальной яме" с бесконечно высокими
"стенками", имеет вид т/Ч*) = Asmkx . Определите: 1) вид собственной волно-
вой функции ipn(x); 2) коэффициент А , исходя из условия нормировки веро-
ятностей.
V(*) =
1) V»(<
2) A-
Дано
Asinkx
0—?
-?
kl =
i
Решение
) = /(
sin/fc/
(дс) =
= 0,
. wr
^sin—x,
/
(Ответ }
J
=А sin—x\
Известно, что нормированная собственная волновая функция, описы-
вающая состояние электрона в одномерной прямоугольной "потенци-
альной яме" с бесконечно высокими "стенками", имеет вид
y>n(x) = J— sin—х, где / — ширина "ямы". Определите среднее значение
координаты (х) электрона.
Дано
2 . лги
Решение
2лп
2г 1(, 2лп \
— дс — 1 - cos д: ох =
1{ 2{ I )
С Ответ j
Докажите, что собственные волновые функции, описывающие со-
стояние частицы в одномерной "потенциальной яме" с бесконечно
высокими "стенками", являются ортогональными, т. е. удовлетворяют условию
/
Ггрп(х)трт(х) дх - 0, если пФт. Здесь / - ширина "ямы"; пит — целые
о
числа.
Частица в одномерной прямоугольной "потенциальной яме" шири-
ной / с бесконечно высокими "стенками" находится в основном
состоянии. Определите вероятность обнаружения частицы в левой трети "ямы'".
Дано
II
1
I
3
tm
I
W —?
'/з
Решение
2 . л
= л/у SillyX,
'/3.
s—x dx =
l'f3 , l'r3 2лг . 11/. 2л:
= у dx-y ^„ix^ — ^x
1/3
3 2л:
^.o,195
3
Г Ответ j
W = 0,\95.
Частица в одномерной прямоугольной " потенциальной яме" ши-
риной / с бесконечно высокими "стенками" находится в возбуж-
денном состоянии (п = 2). Определите вероятность обнаружения частицы в
области %/ < х < %/.
С Ответ
W = 0,091.
Электрон находится в одномерной прямоугольной "потенциаль-
ной яме" шириной / с бесконечно высокими "стенками". Опре-
делите вероятность W обнаружения электрона в средней трети "ямы", если
электрон находится в возбужденном состоянии (п = 3 ). Поясните физический
смысл полученного результата, изобразив графически плотность вероятности
обнаружения электрона в данном состоянии.
Фп(х)
п = Ъ
V-
W —
Дано
[У . гт
= J7sinTx
7
Решение
[2 . Ъл
Ых) = ^-[ sm~x,
0
гр 2
ЛДЛ
1, 2,
3' 3'
п
1
л=3
/ X
w =
1/3
21/3
//3
'/3
= - dx-- cos—xdx=-;
/ j. / L i l
/{з
3 6л\ / 3
//3
16л
6л
-sin — x|
2//3
'/3
3 6я
ГОтвет J
Частица в одномерной прямоугольной "потенциальной яме" ши-
риной / с бесконечно высокими "стенками" находится в возбуж-
денном состоянии (п = 3). Определите, в каких точках "ямы" @ < х < /)
плотность вероятности обнаружения частицы: 1) максимальна; 2) минималь-
на. Поясните полученный результат графически.
I I 51
I I 51 .
при * = -,-,— ; 2) w = mm при
J
х --
2/
,
17 Сборник задп'|
Частица находится в одномерной прямоугольной "потенциальной
Определите, при какой ширине одномерной прямоугольной "по-
тенциальной ямы" с бесконечно высокими "стенками" дискрет ^БЛШ' Яме" с бесконечно высокими "стенками". Определите, во сколько
ность энергетического спектра электрона сравнима с его средней кинетичес- раз изменяется отношение разности соседних энергетических уровней
кой энергией при температуре Т. i Д?„+1 „/?„ частицы при переходе от п = 3 к п' = 8 . Объясните физическую
С Ответ Л
АЕ„ = 1
Т
1 —?
Дано
Решение
^п B« + 1) 2 >
2ml
Е.=-кТ,
h 2
2ml2 2
2n+l
ЪткТ
рущность
п = 3
\"'=«
Е„
полученного
Дано
— ? п -» п'
результата.
Решение
F 27rV *F F
tn ~ П л "¦ ,2 ' °^п+\,п ~ Лп+
2ml
АЕп+и 2n + l A
Еп п1 '
Е„.+1У 2п' +
Еп- («')'
2
Л
2п
1
h2
Вычисления:
6.104 J Докажите, что энергия свободных электронов в металле не квангу-
ется. Примите, что ширина / прямоугольной "потенциальной ямы"
с бесконечно высокими " стенками" для электрона в металле составляет 10 см.
Дано
m = 9,111031 кг
/ = 10 см = 0,1 м
АЕ„ — ?
Решение
? л2Н2
2ml2 '
2ml2
= Bи +
х п-
л2Ь2
2m/2 ml2
Ответ
АЕп К оЛ5»-ю-'6 эВ.
п = <
64
Г Ответ J Уменьшается в 3 раза.
Частица с энергией Е движется в положительном направлении
оси х и встречает на своем пути прямоугольный потенциальный
барьер высотой U и конечной шириной /, причем Е <U¦ Запишите уравне-
1)
2)
3)
дх2 '
дх2 '
a2V3 ,
Or2
1' 'ч
У Y2 — u ,
t2 - 2m F
Я2 = ^(Е~1
n
k2 - 2m F
') E<U
1
0
2
3
/ *
Для условия задачи 6 106 запишите решения уравнений Шредин-
гера для областей 1 2 иЗ Ц> -Функция обычно нормируется так,
что А | = 1 Представьте графически качественный вид V -функций.
1) V, = e'*'* + 3e-'*1*.
2) гр2 = А2 е"* + 52 е* .
3) V3 = ^e'M-
А,=1,
Электрон с энергией Е = 5 эВ движется в положительном направ-
лении оси х, встречая на своем пути прямоугольный потенциаль-
ный барьер высотой U = 10 эВ и шириной / = 0,1 нм. Определите коэффици-
ент D прозрачности потенциального барьера.
Дано
м = 9,1Ы0 34 кг
Е = 5 эВ = 8 10"" Дж
С/= 10 эВ = 1,6- 10-|8Дж
/ = 0,1 нм = 10-'°м
D —?
Решение
D=exJ-jj2m(U-E)\.
Ответ j
= o,\.
Прямоугольный потенциальный барьер имеет ширину / = ОД нм.
Определите в электрон-вольтах разность энергий U - Е , при ко-
торой вероятность прохождения электрона сквозь барьер составит 0,5.
Г Ответ j
Протон с энергией Е = 5 эВ движется в положительном направ-
лении оси х, встречая на своем пути прямоугольный потенциаль-
ный барьер высотой U = 10 эВ и шириной / = 0,1 нм. Определите вероятность
прохождения протоном этого барьера. Во сколько раз надо сузить барьер, что-
бы вероятность прохождения его протоном была такой же, как для электрона
При вышеприведенных условиях.
= 8-10|9Дж
= 10 эВ=1,6-1018Дж
Прямоугольный потенциальный барьер имеет ширину / = 0,1 нм.
** Разность между высотой потенциального барьера и энергией дви-
жущегося в положительном направлении оси х электрона U — Е-Ь эВ. Опре-
делите, во сколько раз изменится коэффициент прозрачности D потенциаль-
ного барьера для электрона, если разность U - Е возрастает в 4 раза.
(U-E) =0,454 эВ.
<5П>
Частица с энергией Е движется в положительном направлении
оси л: и встречает на своем пути бесконечно широкий прямоуголь-
ный потенциальный барьер высотой U, причем E>U. Запишите уравнение
Шредингера для областей / и 2.
-> _ 2т
1 = Vе
и
Т
Е
1
А
и
2 т ,.
Si Для условия задачи 6.112 запишите решение уравнений Шредин-
'<* гера для областей / и 2 V -Функция обычно нормируется так,
что А\=\. Представьте графически качественный вид Ц> -функций.
Кб. 114 J Частица с энергией ? = 10 эВ движется в положительном направ-
лении оси х. встречая на своем пути бесконечно широкий прямо-
угольный потенциальный барьер высотой U = 5 эВ. Определите коэффициент
Преломления п волн де Бройля на границе потенциального барьера.
Дано
? = 10 эВ
U = 5 эВ
и — V
Решение
дх
к, =¦
12тЕ
E-U
е С Ответ j и = о,7О7.
Электрон с длиной волны де Бройля Я, = 100 пм, двигаясь в поло-
жительном направлении оси х, встречает на своем пути бесконеч-
но широкий прямоугольный потенциальный барьер высотой U = 100 эВ. Оп-
ределите длину волны де Бройля после прохождения барьера
ГОтвет j
Я-, =
= 172 пм.
Частица с энергией Е = 50 эВ, двигаясь в положительном направ-
лении оси х, встречает на своем пути бесконечно широкий прямо-
угольный потенциальный барьер высотой U = 20 эВ. Определите вероятность
отражения частицы от этого барьера.
Е
и
W
Дано
= 50 эВ
= 20 эВ
__ 7
W -
Е>!
Решение
О —
J ,
кх-к2
к^ + к2
к,
2
t
, *,-
>*¦,,
42тЁ
42m{E-U)
ft
Ответ j
= 0,016.
Частица массой т - 10 кг, двигаясь в положительном направ-
лении оси х со скоростью v = 20 м/с, встречает на своем пути
бесконечно широкий прямоугольный потенциальный барьер высотой U = 100 эВ.
Определите коэффициент отражения R волн де Бройля на границе потенци-
ального барьера.
m
V
Г!
R
Дано
= 10-19кг
= 20 м/с
-100 эВ
7
F -
к\
Решение
mv2
Т= 2 '
*j2mE , yJ2m(E-U)
h ' - ft
R =
\k + k2]
Вычисления:
Ю~|9-B0 м/с
E = -
V125-V25
Дж =125 эВ.
V125 + V25
= 0'146- {ОтвепгЛ R=0M6.
^Й^^Я Частица с энергией Е движется в положительном направлении
' оси х и встречает на своем пути бесконечно широкий прямоуголь-
ный потенциальный барьер высотой U, причем Е <U. Запишите уравнение
Шредингера для областей / и 2. ^
д'г
дХ
*.=¦
/2тЕ
E<U
E<U
и
Для условия задачи 6.118 запишите решение уравнений Шредин-
гера для областей / и 2. Ц> -Функция обычно нормируется так,
го Ах = 1. Представьте графически качественный вид Ц) -функций.
i; W\ e toie '
e pm(U-E)
ft,
^2
-j2mE
~ ft '
= 0
v
V/
v,
V
V/
l
\
2
¦—.
%
X
Электрон с длиной волны Я де Бройля, равной 120 пм, движется в
положительном направлении оси х и встречает на своем пути бес-
энечно широкий прямоугольный потенциальный барьер высотой U = 200 эВ.
)пределите коэффициент отражения R волн де Бройля на границе потенци-
ШЬНОГО
« = 9,11
1 = 120
t/ = 200
R —?
барьера.
Дано
¦10 кг
пм= 1,2 ¦
эВ
10 1Ом
R —
Е =
Решение
к,-к2
кх + к2
р2
2т 2
2
У?
,2 (СМ-
Р
рисунок
h
Я '
к задаче 6.118),
*,=¦
\2тЕ
42m(E-U)
Ь
вычисления:
-^
F,63-10- Джс) -„
2-9Д1-101 кгA,2 10Ч0мJ
100-V100-200
V100+Vl00-200
— 1
Г Ответ j j? =
Частица с энергией Е движется в положительном направлении
оси х и встречает на своем пути бесконечно широкий прямоуголь-
ный барьер высотой U, причем Е <U. Принимая А{=\ (как это обычно де-
лается) и используя условия непрерывности волновой функции и ее первой
производной на границе областей / и 2, определите плотность вероятности
U2@)| обнаружения частицы в точке х = О области 2.
-?
ip[(O)=ikl-iklB], V2
1 + 5, = 4,
E
A
Ч>
<U
,=1
i@) =
i@) =
Дано
V2@)
Решение
,k,x -,ktx
,k2x
гр'(х) -к^+Ч ik
г.
kl
,)e-*'
¦JbnE
Л '
_pm(E-U)
h
ul
E<U
c/
Частица с энергией Е движется в положительном направлении
оси х и встречает на своем пути бесконечно широкий прямоуголь-
ный потенциальный барьер высотой U, причем Е <U. Принимая А ,= 1 (как
Вто обычно делается) и используя условия непрерывности волновой функ-
ции и ее первой производной на границе областей / и 2, определите плот-
Ьость вероятности обнаружения частицы на расстоянии х от потенциально-
Vi@)=V2@)
го
+ jfc.
го и
f—
Е<
4=
арье
и
1
г)|2
ра.
Дано
1р'2@)
«7
Решение
д\ 2т а
——•
^2(х)~4е
V2 2m
j2m(E-U)
5,= 4,
2
4е'^
2
/ft|
кх + кг
e2ik2x
1
E<U
_ ь
1
А
и
2 т
2
2*,
if i if
I 2
2
-Je+Je-u
AE
+ /W - ?
AE
AE
-E-i^U-E+ U- E U
AE
<522>
/?=
. Ответ j
Ы42 =
2k,
к1+ф
j2m(U-E)
Докажите, что волновая функция ip(x) = Ах e 2Л может быть
решением уравнения Шредингера для гармонического осциллятора, масса ко-
торого т и постоянная квазиупругой силы к . Определите собственное значе-
ние полной энергии осциллятора.
Дано
¦Jmk 2
ip(x) = Ах е 2Л
[к
т, к, <о0 = J—
V т
Е — ?
Решение
aV 2«Г mw2x2V V^
Эх2 ft i. 2 j ' 2ft
-at2 ^V -or2 2 ax2
j/'lxj^^xe , —=ле — 2a4x e
дх
8н5г1 Объясните физический смысл существования энергии нулевых
колебаний для квантового гармонического осциллятора. Зависит
t наличие нулевых колебаний от формы "потенциальной ямы"?
Математический маятник можно рассматривать в качестве гармо-
нического осциллятора. Определите в электрон-вольтах энергию
певых колебаний для маятника длиной / = 1 м, находящегося в поле тяготе-
[ Земли.
д2гр
3 -я
=-^ = -2аАх е" - АаАх е"" + Ас?Ах* е'т' = -баЛх е" + 4а2Ах3 fT"
дх'
. . 2-1 2тЕАх т2ю1Ахъ
- баАх + 4а2 Ах3 + ~2 \ = 0 ,
2тк ¦> тЕ т2к -,
+ тгХ~ +—г -X' = 0
2h 4h2 Ь2 т 2ft2
Решение
Е0=-ко0,
= 2яА-
mE Ъытк
Г Ответ Л
= i,o3io5 эв.
2ft
З.Гк 3
Ц
2т 2 Iffl 2
QOmeem
Частица массой m движется в одномерном потенциальном поле
С/(х) = Ьг2/2 (гармонический осциллятор). Волновая функция,
описывающая поведение частицы в основном состоянии, имеет вид
ip{x)= Az'ax , где А —нормировочный коэффициент; а —положительная
постоянная. Используя уравнение Шредингера, определите: 1) постоянную а ,
2) энергию частицы в этом состоянии.
Рассматривая математический маятник массой т = 100 г и дли-
ной / = 0,5 мв виде гармонического осциллятора, определите
нассическую амплитуду А маятника, соответствующую энергии нулевых ко-
лебаний этого маятника.
Ответ
8 =1,54-КГ17 м.
т
(Ответ
2) ? =
6.3. Элементы современной физики
атомов и молекул
f% Представьте: 1) уравнение Шредингера для стационарных состо-
^ яний электрона, находящегося в атоме водорода; 2) собственные
значения энергии, удовлетворяющие уравнению; 3) график потенциальной энер-
гии взаимодействия электрона с ядром; 4) возможные дискретные значения
энергии на этом графике.
{Ответ
h1"
1 me4
' n ~ ~~ 2 о 7 2 2 '
3), 4) см. рисунок.
U =
4ж0г
n = 1,2,3,...
Как известно, уравнению Шредингера, описывающему атом во-
дорода, удовлетворяют собственные функции \рп1т {г, #, <р), оп-
ределяемые тремя квантовыми числами: главным п, орбитальным / има1-
нитным т1. Объясните физический смысл указанных квантовых чисел и запи-
шите их возможные значения.
Волновая функция ^п/Щ[(г,й,^), описывающая атом водорода,
определяется главным квантовым числом п, орбитальным кван-
товым числом / и магнитным квантовым числом т1. Определите, чему равно
число различных состояний, соответствующих данному п.
С Ответ j n2
Запишите возможные значения орбитального квантового числа / и
магнитного квантового числа гп/ для главного квантового числа п = 4.
Ответ Jn=4, 1 = 0, т,=0. / = l,m, = 0,±l.
/ = 2 , т, = 0, ±1, ±2. / = 3 , т, = 0, ±1, ±2, ±3
Определите, сколько различных волновых функций соответству-
ет главному квантовому числу п = 3 .
Ответ
J и = 3;
9 различных волновых функций (без учета спина).
Учитывая число возможных состояний, соответствующих данно-
му главному квантовому числу п, а также правила отбора, пред-
вьте на энергетической диаграмме спектральные линии атома водорода,
разующие серии Лаймана и Бальмера.
Покажите возможные энергетические уровни атома с электроном
в состоянии с главным квантовым числом п - 6, если атом поме-
цен во внешнее магнитное поле.
Постройте и объясните диаграмму, иллюстрирующую расщепле-
ние энергетических уровней и спектральных линий (с учетом пра-
1ИЛ отбора) при переходах между состояниями с 1=2 и / = 1.
Ответ
т.
W--состояние / = 1, от, = 0, ±1.
4 -состояние I 1 = 2 , т, = 0, ±1, ±2.
1=2 '>
+2
+ 1
О
-1
_2
Постройте и объясните диаграмму, иллюстрирующую расщепле-
ние энергетических уровней и спектральных линий при перехо-
дах между состояниями с / = 1 и / = 0 .
Волновая функция, описывающая 1 j-состояние электрона в атоме
водорода, имеет вид у>(г) = С еГг1", где г — расстояние электро-
на от ядра, а — первый боровский радиус. Определите нормированную вол-
новую функцию, отвечающую этому состоянию.
Нормированная волновая функция, описывающая Ь-состояние
электрона в атоме водорода, имеет вид ViooCO -'
1
¦ е г " , где
\а —первый боровский радиус. Определите: 1) вероятность dW обнаружения
^электрона на расстоянии от г до r + dr от ядра; 2) расстояния от ядра, на
(которых электрон может быть обнаружен с наибольшей верояжостью.
гр(г) = С
а - const
ViooC'") -
Дано
_ ?
V
dV
Решение
= 4тгг2 dr ,
J |,/,|2 dV = JC2 s'2r/a 4лг2 dr = 4лС2 jr2 e~2'/a dr = 4лС2
4лС2-2аг
,-r/a
Ответ
7ГД
J Предполагая, что нормированная волновая функция, описываю-
щая 15-состояние электрона в атоме водорода, известна (см. зада-
чу 6.137), определите среднее значение функции \/г, принимая
во внимание, что
—)= f—vV
r/ f r
С Ответ j
Ответ
I) dW = ~r2 e-2r'la dr- 2)r = a.
a
Щ Нормированная волновая функция, описывающая l.s-состояние
1
электрона в атоме водорода, имеет вид
, где
а — первый боровский радиус. Определите среднюю потенциальную энер-
гию электрона в поле ядра.
Дано
Vioo('") = 7=7e ''"
V7TCI
a = const
(С/)-?
= f (-
Решение
(U) = jlfy'ip dV
dV = 4ттг2 dr ,
e2 4 1!
e2 4
e2 1
4тг?0 a f2
3 /-\2
0 a 4
4тг?0 д
С Ответ\\
1
Д
^^И^Ш Нормированная волновая функция, описывающая Is -состояние н
1
атоме водорода, имеет вид
, где а — первый
Определите, во сколько раз орбитальный момент импульса Ц
электрона, находящегося в /состоянии, больше, чем для элект-
зона в р-состоянии.
боровский радиус. Определите среднее значение модуля кулоновской силы,
действующей на электрон.
С Ответ j
Ф^к Электрон в атоме находится в /состоянии. Определите возмож-
ные значения (в единицах h) проекции момента импульса Lk
орбитального движения электрона в атоме на направление внешнего магнит-
ного поля.
QOmeem
:/z = о, ±п, ±ih, ±зй .
<»Л Электрон в атоме находится в ^/-состоянии. Определите: 1) мо-
мент импульса (орбитальный) Lt электрона; 2) максимальное зна-
чение проекции момента импульса (lfe) на направление внешнего магнит-
ного поля.
d
1
П
2)
Дано
-состояние
= 2
ч —?
4z max — ?
ч
ч
т,
Чг
Решение
= Й-Уб,
ma\ ~ ч
тач = 2^ ¦
/ =
т,
4z
2,
= 0, ±1, +2,
= hm, ,
Lf
—L
Ч
Дано
1 = 3
i = i
(о
Решение
^10 + 1) = ft V2 ,
meemj l[__
L{
ц
2,45.
Й>/3C
4п
V2
+1) = йТГг ,
Is электрон атома водорода, поглотив фотон с энергией Е = 12,1 эВ,
перешел в возбужденное состояние с максимально возможным ор-
битальным квантовым числом. Определите изменение момента импульса AZ-,
орбитального движения электрона.
? =
'2=
/, = 0
12,1
1,94
'max
Дано
эВ =
¦ 10"'8Дж
Vs
Е
1 =
0
Решение
/, = о, I, = h^Ki +1),
?^i2 «2J 1
,1,2,...,(«-1), /2=/
L,, = 0,
I ЙЛ
ihR-E'
max = "'
?, =i
'max
ГОтвет J
2,57-Ю4 Дж-с.
Объясните, почему в опыте Штерна и Герлаха по обнаружению соб-
ственного механического момента импульса (спина) электрона ис-
пользовался пучок атомов водорода, заведомо находящихся в ^-состоянии.
m 6.147 J Объясните, почему в опыте Штерна и Герлаха по обнаружению
собственного механического момента импульса (спина) электро-
на использовалось неоднородное магнитное поле.
Определите числовое значение: 1) собственного механического
момента импульса (спина) Ls; 2) проекции спина LS2 на направ-
ление внешнего магнитного поля.
1L=
2) 1„ = tim,,
Дж
0~35
- = ±5,25 10~35 Дж • с.
Объясните, что лежит в основе классификации частиц на фермио-
ны и бозоны, а также которые из них описываются симметричны-
ми волновыми функциями.
|ВО Исходя из принципа неразличимости тождественных частиц, дай-
а*^ те определение симметричной и антисимметричной волновой
функций. Объясните, почему изменение знака волновой функции не влечет за
собой изменение состояния.
|ЙО Учитывая принцип Паули, определите максимальное число элек-
тронов, находящихся в состояниях, определяемых данным глав-
ным квантовым числом
Ответ
/ = о,1,2,з,...,(»-1),
и,=0, ±1, ±2, ±3,..., ±/,
п-\
/=о
Заполненной электронной оболочке соответствует главное кван-
товое число п = 3 . Определите число электронов на этой оболоч-
е, которые имеют одинаковые квантовые числа: 1) ms = -1/2 ; 2) от, = 0 ;
, =-\, ms =1/2 .
p
p
2)
3)
•}
от,
m,
N
Дано
= -1/2, # — ?
= 0, N —?
= -1, m, = l/2,
7
/ = 0
/ = 1
/ = 2
Решение
, /и, = 0,
, от, =0, ±1,
, от, = 0, ±1, ±2,
от,=+-:
2
1
2
1
2
Ответ
2)
3)
2
), Л^ = 6;
Гд Заполненной электронной оболочке соответствует главное кван-
товое число п = 4. Определите число электронов на этой оболоч-
ке, которые имеют одинаковые квантовые числа. 1) и, =-3, 2) ms = 1/2,
/ = 2;3) /и, =-1/2, т,=1.
ГОтвет
2; 2M; 3K.
Определите суммарное максимальное число 5 -, р -, d -, f - и g -
электронов, которые могут находиться на N- и О-оболочках атома.
Ответ
Л
82.
Запишите квантовые числа, определяющие внешний, или валент-
ный, электрон в основном состоянии атома натрия.
ГЪтвет
| \s2 ъ2 2Р6 3s.
Валентный электрон: и = 3, 1 = 0, mt-0, ms = ±—
vl Пользуясь периодической системой элементов Д. И. Менделеева,
* запишите символически электронную конфигурацию следующих
атомов в основном состоянии: 1) неон; 2) аргон; 3) криптон.
Пользуясь периодической системой элементов Д. И. Менделеева,
запишите символически электронную конфигурацию атома меди
в основном состоянии.
Пользуясь периодической системой элементов Д. И. Менделеева,
запишите символически электронную конфигурацию атома цезия
в основном состоянии.
Электронная конфигурация некоторого элемента
15 2s 2p 3s' Зр . Определите, что это за элемент.
Электронная конфигурация некоторого элемента
Is2 2s2 2р6 3s2 Зр6 3d10 4s . Определите, что это за элемент
Определите в периодической системе элементов Д. И. Менделее-
ва порядковый номер, у которого заполнены К , L , М -оболоч-
ки, а также 4,5-подоболочка.
Объясните: 1) почему тормозной рентгеновский спектр является
сплошным, 2) почему сплошной рентгеновский спектр имеет рез-
кую фаницу со стороны коротких волн и чем определяется ее положение.
HM,VSf I ОпРеДелите наименьшую длину волны рентгеновского излучения,
" '"-у если рентгеновская трубка работает при напряжении U = 150 кВ
Дано
= 150 кВ=1,5 Ю5В
Решение
Ятач = ^тах = & ,
с ch
Ответ ) ят,п = 8,29 пм.
-VI Минимальная длина волны рентгеновских лучей, полученных от
трубки, работающей при напряжении U = 60 кВ, равна 20,7 пм.
Определите по этим данным постоянную Планка.
Q
Omeem
= 6fi2 10-34 Дж.с
Определите длину волны коротковолновой фаницы сплошного
рентгеновского спектра, если скорость v электронов, бомбарди-
рующих анод рентгеновской трубки, составляет 0,8с
Дано
v = 0,8с
Ото = 9,11 .Ю-31 кг
eU
eU
Решение
= Т,
he
= me
= тс i . г~* >
he
me
me
-и /с
1
С Ответ Л
Km = 3'64 ПМ-
'W-HBwp Определите длину волны коротковолновой границы сплошного
рентгеновского спектра, если при увеличении напряжения на рен-
тгеновской трубке в два раза она изменилась на 50 пм.
u2
АЯ
i
/li
= 2E/,
= 50
о
Дано
пм = 5' 10 '
м
h
U2
Решение
= Я,-АЯ,
= 2С/,,
е
Я,
^.=
йс
-АЯ
he
К
2hc
я, '
eU2 =
he
2(Я,-ДЯ) =
Я, = 2 АЯ .
Г Ответ
Я, =100 пм.
Определите порядковый номер элемента в периодической систе-
ме элементов Д. И. Менделеева, если граничная частота АГ-серии
характеристического рентгеновского излучения составляет 5,55 • 1018 Гц.
Дано
vo==5,55-1018 Гц
А"-серия
ст = 1
Z —?
Решение
v=R(Z-of{\
vx = R{Z-\J^j
т
, и = оо, т = \,
= R{Z-\f, Z = J^+1.
т~\
Г Ответ j z = 42,
молибден.
6.168 } Определите длину волны самой длинноволновой линии А"-серии
характеристического рентгеновского спектра, если анод рентге-
новской трубки изготовлен из платины. Постоянную экранирова-
ния принять равной единице.
Г Ответ j
Я =20,4 пм.
ш^^^^ш Определите порядковый номер элемента в периодической систе-
ме элементов Д. И. Менделеева, если длина волны Я линии Кп
характеристического рентгеновского излучения составляет 72 пм.
Дано
Ка -линия
G = 1
Я = 72 пм =7,2- 10 "м
Z —?
Решение
т п
7 ,, i
Л'= 1,1-10' м
т=\, и=2,
4
2 =
+ 1.
Q Ответ J z = 42, молибден.
W Определите постоянную экранирования о для I-серии рентгено-
^^ вского излучения, если при переходе электрона в атоме вольфра-
ма с А/-оболочки на L-оболочку длина волны Я испущенного фотона составля-
ет 140 пм.
Дано
Z=74
4
Я = 140пм =1,4-10-'°м
La -линия
Решение
м-
La -линия:
т=2, п=Ъ,
к-
3
¦2
2Z У
ГОтвет j а = 5,63.
В атоме вольфрама электрон перешел с М-оболочки на /,-оболоч
ку Принимая постоянную экранирования о = 5,63, определите
энергию испущенного фотона
Г Ответ ) Е = 88
f,' } Известно, что в спектре комбинационного рассеяния помимо не
смещенной спектральной линии возникают стоксовы (или крас-
ные) и антистоксовы (или фиолетовые) спутники Объясните механизм их воз
никновения и их свойства
rf*i;&y% объясните механизм возникновения, свойства и особенности вы-
..<*?
нужденного (индуцированного) излучения
Объясните, почему для создания состояний с инверсией населен^
ностей необходима накачка
Объясните, почему активные среды, используемые в оптических
квантовых генераторах, рассматриваются в качестве сред с отри
цательным коэффициентом поглощения
Объясните, какие три компонента обязательно содержит оптичес-
кий квантовый генератор (лазер) и каково их назначение
|||цЦЩ Перечислите и прокомментируйте основные свойства лазерного
излучения
6.4. Элементы квантовой статистики
j Объясните отличие бозе-газа от ферми-газа, а также обоих этих
газов от классического газа
Покажите, что при очень малом параметре вырождения распре-
деления Бозе—Эйнштейна и Ферми—Дирака переходят в распре-
деление Максвелла—Больцмана
Г Ответ j a =
1
-= Ае
Е /(«")
6.180 J Пользуясь распределениями Бозе—Эйнштейна и Ферми—Дира-
ка, получите распределение Максвелла—Больцмана
Объясните, при каких условиях к электронам в металле примени-
ма 1) классическая статистика, 2) квантовая статистика
Объясните, при каких условиях можно применять статистику
Максвелла—Больцмана к электронам в металле Пользуясь рас-
пределением Ферми—Дирака, получите распределение Максвелла—Больцмана
Г
Ответ
кТ
(Е ,1I(кГ) »
_ А е-Е 1(кТ)
Определите функцию распределения для электронов, находящих-
ся на энергетическом уровне Е для случая Е- EF « кТ, пользу-
ясь : 1) статистикой Ферми — Дирака; 2) статистикой Максвелла — Болышана
E-EF
(N(E))
Дано
« кТ
?
Решение
Статистика Ферми—Дирака
/ vc F\\ —
\М?); sE-Er/(kr)+l
(Е-Ег)«кТ
1
2
Статистика Максвелла—Больцмана
Jlzizl
=е
= 1,
(E-Ef)«kT
Определите функцию распределения Ферми—Дирака при Т * О К
для электронов, находящихся на уровне Ферми. Объясните полу-
ченный результат.
С Ответ Л
(N(E)) = -
1 1
Объясните физический смысл энергии Ферми.
Объясните, почему работа выхода электрона из металла следует
отсчитывать от уровня Ферми, а не от дна "потенциальной ямы",
как это делается в классической теории.
ЙЦ Определите число свободных электронов, занимающих в среднем
»?'<ft'i3r уровень энергии, равной энергии Ферми.
С Ответ J „ = j
Объясните на основе квантовой теории отсутствие заметного от-
личия в теплоемкостях металлов и диэлектриков.
Объясните целесообразность введения фононов, а также перечис-
лите их свойства.
Какая статистика описывает фононный газ? Почему?
Определите в электрон-вольтах максимальную энергию Е фоно-
на, который может возбуждаться в кристалле Nad, характеризуе-
мом температурой Дебая TD = 320 К. Фотон какой длины волны Я обладал
бы такой энергией?
Дано
NaCl
Го=320 К
Е —?
Я —?
Решение
E = kTD,
E=hv = ~,
Я = ^
j
Ответ ) е = 0,028 эв, я = 45 мкм.
Сравните выражения для удельной электрической проводимости
металла по классической и квантовой теории и объясните, чем
отличаются они по физическому содержанию.
Объясните причину электрического сопротивления металлов с
точки зрения квантовой теории электропроводности металлов.
6.5. Элементы физики твердого тела
Объясните различие энергетических состояний электронов в кри-
сталле и в изолированном атоме.
Объясните образование зонного энергетического спектра в крис-
талле, показав, что этот эффект — квантово-механический и вы-
текает из соотношения неопределенности Гейзенберга.
Объясните, как изменится энергетический спектр валентных элек-
тронов, если число образующих кристалл атомов увеличить в 3 раза.
Объясните различие в электрических свойствах металлов, ди-
электриков и полупроводников с точки зрения зонной теории
твердого тела.
Объясните различие между диэлектриками и полупроводниками
с точки зрения зонной теории твердого тела.
Объясните различие между металлами и диэлектриками с точки
зрения зонной теории твердого тела.
Объясните механизм дырочной проводимости собственных по-
лупроводников.
Объясните электрические свойства полупроводников с точки зре-
ния зонной теории твердого тела. Как меняется с температурой
сопротивление полупроводника — увеличивается или уменьшается? Почему?
Докажите, что уровень Ферми в собственном полупроводнике дей-
ствительно расположен в середине запрещенной зоны.
Ответ ) F _^_
Германиевый образец нагревают от 0 до 17 °С. Принимая ширину
запрещенной зоны германия Д? = 0,72 эВ, определите, во сколь-
ю раз возрастает его удельная проводимость.
Г Ответ ) у г _7d<
k Л
Определите ширину запрещенной зоны собственного полупровод-
ника, если при температуре 7] и Т2 (Т2 > 7J) его сопротивление
соответственно равно
Т2>Т1
Щ, R2
jfe = 1,38
Д? —
Дано
• 1(Г23 Дж/К
Я,,
л R2.
У~
у-
Решение
1
R'
Р
ехр[-
__J_
2к{ 7] Т2
6.205 ) ' '^Рисуйте зонные схемы полупроводников и-типа и р-типа v.
-оъясните механизм их проводимости
0^ЩШ& В чистый германий введена небольшая примесь мышьяка Польз\
Sttubи 1йш»г ясь периодической системой этементов Д И Менделеева, опре
делите и объясните тип проводимости примесного германия
L'tHU^Kfjp В чистый кремний введена небольшая примесь бора Пользуясь
<ЖЙЬ* периодической системой элементов Д И Менделеева, определи-
те и объясните тип проводимости примесного кремния
ЬШ^ЩШЯ Объясните и нарисуйте на зонной схеме положение уровня Фер-
Xiiii- ЛиидУ ми для электронного и дырочного полупроводников 1) при 0 К
2) при повышении температуры
6,209 J Пользуясь периодической системой элементов Д И Менделеева,
Km '•?(••%У объясните, какой проводимостью будет обладать германий,
в него ввести небольшую примесь 1) алюминий, 2) фосфор
если
$Шу Объясните с помощью зонной теории механизмы собственной и
примесной фотопроводимости
Какие признаки лежат в основе деления люминесцентного излу-
чения на разные его виды17
Объясните с помощью зонной теории механизм возникновения
флуоресценции и фосфоресценции
Объясните на основе зонной теории контакт двух металлов с раз-
личными работами выхода
Чем объясняется при контакте двух металлов 1) возникнове-
ние внешней контактной разности потенциалов7 2) возникнове-
ние внутренней контактной разности потенциалов17
Используя зонную схему объясните механизм физических про-
цессов, происходящих при контакте металла с полупроводником
и-типа для случаев I) Ам> А,2) 4М < А ( Ам — работа выхода из металла,
А — работа выхода из полупроводника)
Используя зонную схем}, объясните механизм физических про-
цессов происходящих при контакте металта с полупроводником
р-типа для случаев 1) 4М > А , 2) Ам < А ( Аи — работа выхода из металла
А — работа выхода из полупроводника)
Объясните, каким образом удалось установить, что люминесцен-
тное излучение не является тепловым
Объясните, по какому признаку удалось установить, что излуче-
ние Вавилова—Черенкова не является люминесценцией
Объясните, почему возникает запирающий контактный слой при
контакте 1) донорного полупроводника с металлом, если А< Ам,
2) акцепторного полупроводника с металтом, если А> Ам (Av — работа вы-
хода из металла, А — работа выхода из полупроводника)
6 220 I Объясните механизм возникновения для контакта металл—полу-
проводник проп> скного и запорного направлений (для тока)
<54?>
Какое направление (и почему) при контакте металл—полупровод-
ник является для тока пропускным, если: 1) внешнее и контактное
поля по направлению совпадают; 2) внешнее и контактное поля по направле-
нию противоположны?
Используя зонную схему, объясните механизм физических про-
цессов, происходящих в /?-и-переходе.
Какое направление (и почему) в/?-и-переходе является для тока про-
пускным, если: 1) внешнее и контактное поля противоположны по
направлению; 2) внешнее и контактное поля по направлению совпадают?
k$fi?#^* J Объясните, в каком направлении не могут проходить через запи-
рающий слой контакта полупроводников п- и р-типа: 1) свобод-
ные электроны; 2) дырки.
Объясните механизм односторонней (вентильной) проводимости
/?-и-перехода.
Объясните принцип устройства и действия полупроводниково-
го триода (транзистора). Сравните работу транзистора и лам-
пового триода.
7. Элементы физики атомного ядра
и элементарных частиц
7.1. Элементы физики атомного ядра
54,
Определите массу нейтрального атома 24 Сг.
ГдтветЛ ,„ = 8,64
Ю~26 кг.
Объясните отличие изотопов и изобаров.
]|
Определите, какую часть массы нейтрального атома ]|с
(т -19,9272 • 10~27 кг) составляет масса его электронной оболочки.
I26c
m =
me~-
Дано
19,9272 107 кг
= 9,1110 3I кг
Zme
m
Решение
6-9,11-101
19,9272-107
кг
КГ
= 2,74-
10.
т
-? COmeemjZmjL = 274_l0-
^ m
^ Определите число протонов и нейтронов, входящих в состав ядер
трех изотопов бора 1) ?В ; 2) '°В ; 3) '^В.
Определите число протонов и нейтронов, входящих в состав ядер
трех изотопов кислорода: 1) '^0 ; 2) 17,0 ; 3) 'gO .
Определите, пользуясь таблицей Менделеева, число нейтронов и
протонов в атомах платины и урана.
Pt
и
N —
Дано
?
?
195 р.
78 П
238 п
92 U
Решение
Z=78, N =
Z = 92, N =
A-Z = \\l.
146.
Определите зарядовые числа ядер, массовые числа и символы ядер.
которые получатся, если в ядрах ^Ве, ^N, ,]Na нейтроны заме-
нить протонами, а протоны — нейтронами.
[:1%$В^Щ Определите плотность ядерного вещества, выражаемую числом
¦"¦¦¦ нуклонов в 1 см5, если в ядре с массовым числом А все нуклоны
плотно упакованы в пределах его радиуса.
А
V = l
N —
Дано
cmj=10m3
1,4-10 15 м
9
Решение
и п л 1/3
К- KqA ,
V
N
4
~ з3
4
А
nF^A
3
4лВ>'
ГОтвет Л
ю37 см3.
Объясните, почему плотность ядерного вещества примерно оди-
накова для всех ядер.
Определите, что больше — масса атомного ядра или масса сво-
бодных нуклонов (протонов и нейтронов), входящих в его состав
Определите, какая энергия в электрон-вольтах соответствует де-
фекту массы Am - 3 ¦ 10~20 мг.
COmeemj
Определите энергию связи ядра атома гелия
рального атома гелия равна 6,6467 ¦ 10 27 кг.
. Масса нейт-
тн
тн
т„
К,
Дано
е = 6,6467 -107 кг
= 1,6736-107 кг
= 1,675-10~27 кг
?
Z =
с
Решение
= [ZmH+(A-Z)mn
2, А = 4,
Ответ ) Е
у Лсв
-т]с2
А-
= 28,4
Z=2.
МэВ.
Определите удельную энергию связи дЕсв (эцергию связи, отнесен-
ную к одному нуклону) для ядер: 1) \ Не; 2)' \ С. Массы нейтральных
атомов гелия и углерода соответственно равны 6,6467 • 10 27 и 19,9272 ¦ 10~27 кг.
Дано
2I2С
9
Решение
*?„ =
= Атс ,
= [ZmH +(A- Z)mn - т]с2,
[ZmH+(A-Z)mn-m]c2
07
т)Не = 6,6467 107 кг.
»»„=: 1,675-107 кг.
,-27
тх1с= 19,9272-10"" кг.
-27
тн= 1,6736-10"'" кг.
С Ответ J I) 6ECB = 7,1 МэВ/нуклон; 2) й?св = 7,7 МэВ/нуклон.
Используя данные задачи 7.13, определите, какая необходима энер-
гия, чтобы разделить ядро 'gС на три альфа-частицы.
С Ответ J е = 7,26 мэв.
Определите массу изотопа '*N, если изменение массы при обра-
зовании ядра '*N составляет 0,2058 • 10~27кг.
Дано
Д/и = 0,2058-107 кг
т — ?
Ат =
т—2
тп-
Решение
Zmn + (А — Z)mn — т,
'тн +(А- Z)mn - Am,
1,675 ¦ 107 кг, тн -1,6736 • 10~27 кг,
QOmeem ^ m = 2,49O9-io-26 кг.
При отрьше нейтрона от ядра гелия \ Не образуется ядро \ Не. Оп-
ределите энергию связи, которую необходимо для этого затратить
Масса нейтральных атомов jHe и jHe соответственно равна 6,6467 • 1О~27кг и
5,0084-КГ27 кг.
т
т
Ес
(
Дано
1е
Не = 6,6467
Не = 5,0084
В '
Ответ
ю-27
ю-27
)*¦
кг
кг
4.
„ = 0,3303
Решение
= Атс2 =
/йзт. + т* — tn* .
JHe " JHe
с2.
•10"" Дж = 20,64 МэВ.
Энергия связи ?св ядра, состоящего из трех протонов и четырех
нейтронов, равна 39,3 МэВ. Определите массу т нейтрального
1тома, обладающего этим ядром.
Дано
Есъ = 39,3 МэВ =
= 6,288 10'2Дж
„ = 1,675-107 кг
н = 1,6736-10"7 кг
Решение
св = [ZmH
- = ZmH +(A- Z)mn - т,
т = ZmH +(A- Z)mn f- ¦
с
т
COmeemj
= i,i65 ю6 кг.
Определите, какую долю кинетической энергии теряет нейтрон
при упругом столкновении с покоящимся ядром углерода Х2ЬС, если
после столкновения частицы движутся вдоль одной прямой. Массу нейтраль-
ного атома углерода принять равной 19,9272 • 10~27 кг.
п
|2С
тп
тс
AT
Т
Дано
= 1,675 -10~27 кг
= 19,9272-107 кг
— ?
mnvn
mnv\
2
удар
ЛГ =
Решение
1 (V f
2
упругий|и;
(mcv'cf
2 '
mc(v'c
2
mn
2
-mc)vn , 2mnvn
+ m^ mn + ШB
2 '
AT
,\2 ( -
mn{mn
(mn + mc)
fOmeemj ^L = 0,286.
55©>
^ШВЙ ОпРеделите число нуклонов, кегорыс могут находиться в ядре щ Г <ч 25' J Определите постоянную радиоактивного распада Я для изотопов:
ь/ зХЗЯагу низшем квантовом уровне. I " J
1) тория ~90lh , 2) урана 2f2\J ; 3) иода „1. Период полураспада
этих изотопов соответственно равен 1) 7 ¦ 103 лет; 2) 4,5 • 109 лет; 3) 8 сут.
С Ответ) n = 4.
Определите, во сколь:, раз .. гнтоь -"ра (единица магнитною
момеша элеьл(> jhs) болььх ядерно!о Mai (илона (единицамагннi-
ного момента ядра).
Дано
Решение
eh
2те
eh
2т „
те
— =1835.
Охарактеризуйте свойства и особенности сил, действующих меж-
ду составляющими ядро нуклонами.
в
Объясните принципы построения капельной и оболочечной мо-
делей ядра.
Объясните, почему радиоактивные свойства элементов обуслов-
лены только структурой их ядер.
СОтвегп\
^2=Х;
я'
J 1) Я - 3,П не; 2) Я -- 4,87 ас; 3) 1
МКС.
Определите, что (и во сколько раз) продолжительнее — три пери-
ода полураспада или два средних времени жизни радиоактивного
ядра.
37]/2
2г
Дано
Решение
3 In 2 > 2, следовательно,
371/2 >
31п2 ^_2
х ' ~r i
7.27 Щ Определите, во сколько раз начальное количество ядер радиоак-
тивного изотопа уменьшится за три года, если за один год оно
уменьшилось в 4 раза.
Дано
/, = 1 год
t2 = 3 год
7.24 1 Считая постоянную Я радиоактивного распада известной и ис-
1 пользуя закон радиоактивного распада, выведите выражение:
1) для периода полураспада 7],2 радиоактивного ядра; 2) для среднего времени —5- ?
жизни г радиоактивного ядра. 2
Решение
Я =
In 4
N,
1П4<;
. = е^=е '¦ =е31
[ Ответ ) n0
\. J —-=64.
Определите, какая часть (%) начального количества ядер радио
активного изотопа останется нераспавшейся по истечении врем,,
ни /, равного двум средним временам жизни г радиоактивного ядра
Дано
t = 2r
—(%) — ?
Решение
N = Noe-M, т = - / = 2г = 2- = -
Л А Я
N = Noe Л=Л^ое, —= е"" =0,135.
^0
Ответ ) *1 =
ШЙГОза Определите, какая часть начального количества ядер радиоактив-
ного изотопа распадется за время t , равное двум периодам полу-
распада Ту2.
N
Определите период полураспада радиоактивного изотопа, если 5/8
начального количества ядер этого изотопа распалось за время
t = 849 с.
Дано
AN _ 5
No ~8
t = 849 с
Решение
-?
1п-
1п2_ In2-t
Я ~7~8~'
Ответ ) т]/2 = ю мин.
2|
Период полураспада радиоактивного изотопа актиния 2g|Ac со-
ставляет 10 сут. Определите время, за которое распадется 1/3 на-
чального количества ядер актиния.
Г Ответ j t = 5,85 сут.
Постоянная радиоактивного распада изотопа ^РЬ равна 10 9 с '.
Определите время, в течение которого распадется 2/5 начального
количества ядер этого радиоактивного изотопа.
Дано
Я = 10-9с-'
82™
&N _2
No ~ 5
( — ?
Решение
-Xt = \n-, Я? = 1п-, t = ~T-
5 3 Л
Г Ответ Л t = i6,2 год
Выведите формулу для скорости (активности) радиоактивного
—?^ распада через период полураспада Ту2 и начальное число No
радиоактивных атомов.
т
А —?
Дано
Решение
dN = -XN dt,
In 2
Л — >
А =
А =
dN
dt
In 2
т
= XN , N = N0 e~h,
( Ответ
(In 2) г
Первоначальная масса радиоактивного изотопа иода '^I (период
полураспада 7J/2 = 8 сут) равна 1 г. Определите: 1) начальную ак-
тивность изотопа, 2) его активность через 3 сут
Дано
А/ = 131-10 кг/моль
т -
Ту:
t =
1)
-\ г= 103кг
= 8 сут = 6,91 • 105с
3 сут = 2,59- 105с
Л-?
А О
Решение
v т"л
"°- м '
1 -
л
А}
А--
1п2
In 2
TV
In 2
Т,„
mNA
М
mNA -Я/
м с •
Бк; 2) л = 3,
Бк.
Активность некоторого радиоактивного изотопа в начальный мо-
мент времени составляла 100 Бк. Определите активность этого
изогопа по истечении промежутка времени, равного половине периода полу-
распада.
Дано
Aq -100 Бк
' = ^Л/2
А 9
Решение
. , -и , In 2
Л/2
1п2 /
^-Ае^" —--
Л/2 2
In 2
Л = Ае 2
Ответ
Вет^Ш Начальная активность 1 г изотопа радия 2Ц Ra равна 1 Ки Опре-
делите период полураспада 7}/2 этого изотопа.
Дано
3
М = 226 10 3 кг/моль
т = 1 г= 103кг
4 = 1 Ки = 3,7 10|0Бк
Решение
и М
, In 2
'1/2
In 2
С Ответ J Ty2 = 1582 год:
К З^ШзЙзд Принимая, что все атомы изотопа иода n5\l G],2 = 8 сут) массой
т = 1 мкг радиоактивны, определите: 1) начальную активность
этого изотопа; 2) его активность А через 3 сут.
Г Ответ J 1) Aq = 4,61 ТБк; 2) А = 3,55 ТБк.
Определите период полураспада 7]м некоторого радиоактивного
изотопа, если его активность за 5 суток уменьшилась в 2,2 раза
Дано
-^ = 2,2
А
/ = 5 сут
Решение
1п2
1п2
С Ответ j ту2 = 4,
А сут.
Определите удельную активность а (число распадов в 1 с на 1 кг
вещества) изотопа ^U, если период его полураспада
232-
= 4,5 • 109 лет.
Ядра радиоактивного изотопа тория ^Th претерпевают после-
довательно а -распад, два /Г -распада и а -распад. Определите
конечный продукт деления.
( Ответ
К
1 = 12,3 МБк/кг.
Г Ответ ) 224 R_
Объясните, как изменится положение химического элемента в таб-
лице Менделеева после a-nf} -распадов ядер его атомов.
Пользуясь таблицей Менделеева и правилами смещения, опреде-
лите, в какой элемент превращается ^U после трех а - и двух
-распадов.
Дано
238 п
92 U
За
2/Г
X—?
Решение
238 т, " 234-т^ " 23Ор ° 226R *\ 226Fr \, 226Р
92 U -> 90ln~* 88Ка~» 86*^"* 87" ~> 88Ка ¦
/ / / / /
торий радий радон франций радий
QOmeem
Пользуясь таблицей Менделеева и правилами смещения, опреде-
лите, в какой элемент превращается 2^ U после шести а - и трех
/Г -распадов.
Ответ
Определите, сколько /3 - и а -частиц выбрасывается при превра-
щении ядра таллия 21g°,Tl в ядро свинца 20? РЬ.
Ответ
J
Радиоактивный изотоп радия 2^Ra претерпевает четыре а-рас-
пада и два (}~ - распада. Определите для конечного ядра: 1) заря-
довое число Z; 2) массовое число А .
f Ответ Л i) z = 82;
2) А = 209 .
Запишите а - распад радия
226,
ИИИЩ Определите высоту кулоновского потенциального барьера для
а - частицы в ядре свинца 2g2 Pb.
Дано
T2Pb
<Не
i?b = 1,4 10 15 м
TJ '•)
и *.ул ¦
Решение
"""-teeo R ' QPb = ZPb\e\, Qa = Z(!e,
R=RPh + Ru , RPb = i?o4b3, Ru = R^Af,
i zDhz el2 Г Ответ Л
' 4^0 ^(ДЧД1/3); с/к>л= 22,5 МэВ.
I Покоившееся ядро радона 22jRn испускает а-частицу, имеющую
скорость 16 Мм/с. Зная, что масса дочернего ядра составляет
3,62 ¦ 10~25 кг, определите: 1) импульс а-частицы; 2) кинетическую энергию
а -частицы; 3) импульс отдачи дочернего ядра; 4) кинетическую энергию от-
дачи дочернего ядра.
СОтвет Л 1) 1,07¦ ю-19кг• м/с, 2M,35Мэв;
> ' 3) 1,07 • 10 "> кг ¦ м/с; 4) 9,89 кэВ.
Покоившееся ядро полония 2^Ро испускает а - частицу с кине-
тической энергией Та = 5,77 МэВ. Определите: 1) скорость отда-
чи дочернего ядра; 2) какую долю кинетической энергии а -частицы составля-
ет энергия отдачи дочернего ядра.
Дано
2°°Po-V*>Pb+^He
Та = 5,77 МэВ =
= 9,23- 10"|5Дж
1)ид-?
Т
Решение
mava = mava , Ta - m"V'x ,
у _maVa fb"Ja T rnAvl mja
Д ma mR ' a 2 mR
COmeetnS
1) ил = 339 км/с; 2) ^ = 0,02.
Правила смещения
для а - распада
для /Г - распада z
для /}+ - распада Az
JX -» А?_42У +
?_2
pWlSPift Определите энергию, выделяющуюся в результате реакции
pMg —» 2|Na + \e + qV . Массы нейтральных атомов магния и на-
трия соответственно равны 3,8184 ¦ 106 кг и 3,8177 • 1026кг
ft
те
Q
Дано
vlg —» 2|Na + fe ч
, = 3,8184 Ю-26
а = 3,8177 10~26
= 9,1 МО1 кг
9
-°Ov
кг
кг
Решение
Шщс - mNac + iNa +
т =т =т
e=7-Na + r++rv=(ir
т^с + -1е* +',,
м8 - «N. - »«,* )с2 ,
+ llme -me)c2,
f Ответ Л 2 = 2,91Мэв.
Запишите E - распад магния
{Ответ J
\ 7 *Щ§, IS Известно, что ft - активные ядра обладают до распада и после
^ него вполне определенными энергиями, в то же время энергети-
ческий спектр j(}~ - частиц является непрерывным. Объясните непрерывность
энергетического спектра испускаемых электронов.
Объясните, почему существование антинейтрино полностью по-
зволяет объяснить все особенности /Г - распада.
<5бГ>
С 7*54 I Запишите превращение нейтрона в протон с указанием частиц,
которые при этом испускаются. Объясните, почему этот процесс
является энергетически возможным.
Объясните, почему при а- распаде одинаковых ядер энергии
а - частиц одинаковы, а при fi~ - распаде одинаковых ядер энер-
гии электронов различны.
Применяя понятия квантовой статистики, объясните, почему не-
возможно принципиально создать "нейтринный лазер''.
Опишите основные процессы, происходящие при взаимодействии
У - излучения с веществом.
Свободное покоившееся ядро '^Ir (m = 3l7,10953 10 27 кг) с
энергией возбуждения Е = 129 кэВ перешло в основное состоя-
ние, испустив У - квант. Определите изменение энергии у - кванта, возникаю-
щее в результате отдачи ядра.
Дано
191
77
Ir
i = 317,10953-107 кг
; = 129кэВ=2,06-10-|4Дж
tSE—1
Решение
mv= т
Чу С ,
гтГ__Р__ Е
2 2т 2тс2
Ее Е
С Ответ j
Де = 0,047 эВ.
Назовите два важных механизма, которыми можно объяснить ос-
лабление потока фотонов с энергией Е = 500 кэВ при его про-
хождении через вещество.
Объясните, почему треки а - частиц представляют сплошную тол-
стую линию, а треки /Г - частиц — тонкую пунктирную линию.
Объясните, где и почему лучше использовать длинные цепи рож-
дений и распадов частиц высоких энергий — в камере Вильсона
или в пузырьковой камере.
Щ J Определите, является ли реакция ]hi+ |Н-> 4Ве+ \п экзотерми-
ЧкВЬ* чесКой или эндотермической. Определите энергию ядерной реакции.
™и =
«н =
»'Вс =
т„ =
\Е -
Дано
11.65079 10~27 кг
1,6736 10~27 Ki
= 11,65231 10~27 кг
1,675 10~27 кг
А?
(
Решение
v 7 I
+ |Н-> 4Ве+ о«.
= (ти + тн - тВе - т„ )с" •
Ответ j A? = -i,64 мэв,
т Определите, поглощается или выделяется энергия при ядерной
и»
реакции 2,Н + ]Н -» 42Яе + о" . Определите эту энергию
С Ответ Л ае = 17,6 мэв.
Определите, выделяется или поглощается энергия при ядерной
реакции ^Са + ]Н -4 ^К + гНе . Массы ядер, участвующих в ре-
7
07
акции:
= 7,2992-Ю6 кг, 1я,н =1,6736 Ю7 кг, т;,к = 6,8021 107 кг,
~27
4,Ie = 6,6467 10~27 кг.
Определите, выделяется или поглощается энергия при ядерной
реакции 14,N + 2Не -> |н + 'gO . Массы ядер, участвующих в ре-
акции:
-,-26
: т„ы =2,3253-10 *° кг, miu =6,646710 кг, m,u =1,6736-10"*7 кг
7 Гч 2 НС I H
г„ = 2,8229 -10~27 кг.
Определите зарядовое число Z и массовое число А части-
цы, обозначенной буквой х, в символической записи реакции:
( Ответ
17
0+
2) *
3) ^
Запишите недостающие обозначения х в следующих ядерных ре-
акциях: 1) '°В(и, а)х; 2) tgАг(а, и)дс; 3) х(р, п)]]Ах;
4) 23He(x, Р)]Н; 5) ж(и, а)]Н.
Символическая запись ядерной реакции
или
AzX(a,b)Az.Y,
A
где ^Х и AZY - исходное и конечное ядра с зарядовыми числами Z и Z' и
массовыми числами АиА';аиЬ — соответственно бомбардирующая и испус-
каемая (или испускаемые) в ядерной реакции частицы.
Г 7.68 J В ядерной реакции 2,Н + 2Н—> liie+ оп выделяется энергия
Д? = 3,27 МэВ. Определите массу атома 32Не, если масса атома 2 Н
равна 3,34461 ¦ Ю~27 кг.
Дано
1 ") "\ 1
АЕ = 3,27 МэВ =
= 1,0032- 1(Г18Дж
т,н=3,3446Ы0~27 кг
Решение
Q Ответ J т^ = 5,oo84i ¦ ю7 кг.
Первая в истории искусственная ядерная реакция осуществлена
Резерфордом. Запишите эту реакцию и объясните ее огромное
значение для развития ядерной физики.
Ответ
uN + 4Не
п
0+{р.
Жолио-Кюри облучали алюминий 2jAl ее - частицами, в резуль-
тате чего испускался нейтрон и образовывалось искусственно-
радиоактивное ядро, испытывающее /Г - распад. Запишите эту реакцию.
С Ответ j ]]а\
?5?+ 10п,
( 7.71 J Жолио-Кюри облучали магний ^ Mg a - частицами, в результате
"~"~~"^ чего испускался нейтрон и образовывалось искусственно-радио-
активное ядро, испытывающее /3+ - распад. Запишите эту реакцию.
^^^^В Запишите превращение протона в нейтрон с указанием частиц,
>QmmmmMlr которые при этом испускаются. Объясните, почему это превраще-
ние энергетически возможно только для протона, связанного в ядре.
процессе осуществления реакции у —> й{е + +°{е энергия Ео фо-
тона составляла 2,02 МэВ. Определите полную кинетическую
энергию позитрона и электрона в момент их возникновения.
Дано
Ео = 2,02 МэВ =
= 3,23 • 1019эВ
Т — ?
Решение
Ео = 2тс2 + Т,
Т= Ео- 2тс2 .
Ответ J т = \ МэВ.
7.74
При столкновении позитрона и электрона происходит их анниги-
ляция, в процессе которой электронно-позитронная пара превра-
щается в два у - кванта, а энергия пары переходит в энергию фотонов. Опреде-
лите энергию каждого из возникших фотонов, принимая, что кинетическая
энергия электрона и позитрона до их столкновения пренебрежимо мала.
Дано
т = о
т = 9,11101 кг
Еа—1
Решение
_?е++?е = 2у, 2тс2 + Т = 2Е0,
Т = 0, Е0 = тс2.
Ответ
= о,51Мэв
Запишите схему электронного захвата (е-захвата) и объясните его
отличия от jS* - распадов. Приведите пример электронного захвата.
Ответ J е.захват: *Х+ _?е-> Z*XY+ \ve, вылетает °ve.
При jg* - распаде вылетают две частицы: (_°{е + qV ) или (+°{е + qV ).
Дополните недостающие обозначения х в следующих ядерных
реакциях:
rbi-»9?Zr+ !35xTe + д:0!п ;
НШП Под действием каких частиц — нейтронов или а - частиц—ядер-
щ|^^ ные реакции осуществляются более эффективно? Объясните ответ.
Объясните, почему на медленных нейтронах в основном идут ре-
акции типа (и, п) и (и, у ), а на быстрых нейтронах — реакции
типа (и, р) и (п, а ).
Для обнаружения нейтрона используются реакции захвата тепло-
вых нейтронов легкими ядрами (?,Не, 'зВе), в результате кото-
рых испускаются заряженные частицы. Запишите возможные реакции.
( Ответ) зНе + .„_> зн+ ^
10<B+n'n->4Li+ ^Не.
При энергии нейтронов х\0 МэВ становится возможной на ядре
урана 2%2 U ядерная реакция типа (п, 2и), в результате чего обра-
зуется искусственно-радиоактивное ядро, испытывающее /Г - распад. Запи-
шите эту реакцию.
Ответ
,!n ^2?u
92 l
237,
92 I
237»
С ?«SJt • J Ядро урана 2^U, захватывая быстрый нейтрон, превращается в
радиоактивный изотоп урана, который претерпевает f}~ -распад,
и превращается в трансурановый элемент, который в свою очередь также пре-
терпевает fF -распад, в результате чего образуется плутоний. Запишите все эти
процессы в виде ядерной реакции.
23|
и
239^
Определите кинетическую энергию Е и скорость v теплового ней-
трона при температуре окружающей среды, равной 17 °С.
mn
I —
E
v -
Дано
= 1,675 107 кг
17 °C; Г = 290 К
9
_7
Е =
v =
Решение
~~\кт' Е
щ.
mnv2
2 '
СОтвет J Е = 6 Ю1 Дж; и = 2,68 км/с.
Ядро урана 2^U , захватывая тепловой нейтрон, делится на изо-
топы стронция и ксенона с массовыми числами 95 и 139, второй
из которых, являясь радиоактивным, претерпевает три /Г - распада. Запишите
реакцию деления, а также цепочку /}~ - распадов.
fOmeem j
95 <
*** При захвате теплового нейтрона ядром урана 2^U образуются
два осколка деления и два нейтрона. Определите порядковый но-
мер Z и массовое число А одного из осколков, если другим осколком являет-
95с
ся ядро стронция 3gSr
7.85}
Объясните, почему деление ядер должно сопровождаться выде-
лением большого количества энергии.
?gf|j||||||j|| Определите энергию (в электрон-вольтах), которую можно полу-
чить при расщеплении 1 г урана 2^ U , если при расщеплении каж-
дого ядра урана выделяется энергия 200 МэВ.
Q
pmeem
ю
23
• •VVVVWWWWWW-. --------
Скорость нарастания цепной реакции
dN N(k-\) ,. ,.,,_
— = ^~, откуда N=N0 e(*-Wr,
где No — число нейтронов в начальный момент времени; N— число нейтро-
нов в момент времени t\ Т— среднее время жизни одного поколения; к— коэф-
фициент размножения нейтронов.
Определите суточный расход чистого урана 2^U атомной элект-
ростанцией тепловой мощностью Р - 300 МВт, если энергия Е .
выделяющаяся при одном акте деления, составляет 200 МэВ.
Дано
235 п
92
Р = 300 МВт = 3- 108Вт
? = 200 МэВ =
= 3,2- 10"" Дж
/ = 24 ч = 86400 с
М = 235-10 кг/моль
т ?
Решение
ы Pt
Е
NM PtM
NA ENA
Г Ответ Л m = 3i6 г.
Определите, во сколько раз увеличится число нейтронов в цепной ядер-
ной реакции за время / = 10 с, если среднее время жизни Т одного
поколения составляет 80 мс, а коэффициент размножения нейтронов к = 1,002 .
Дано
/ = 10 с
Г = 80 мс=8' Ю-2 с
к = 1,002
^-?
s s.—~
Решение
d/= г ' Л Лие '
Л^о е •
С Ответ) JL = i,284
Объясните, какой характер носит цепная реакция деления, если
коэффициент размножения: 1) ? > 1; 2) ? = 1; 3) it < 1.
В ядерном реакторе на тепловых нейтронах среднее время жизни Т
одного поколения нейтронов составляет 90 мс. Принимая коэф-
фициент размножения нейтронов к = 1,002 , определите период т реактора,
т.е. время, в течение которого поток тепловых нейтронов в реакторе возрастает
в ераз.
т = 45 с.
Определите число нейтронов, возникающих за 1 с в ядерном ре-
акторе тепловой мощностью Р = 200 МВт, если известно, что при
одном акте деления выделяется энергия Е = 200 МэВ, а среднее число нейтро-
нов на один акт деления составляет 2,5.
C
Omeem
1019 с'.
Объясните особенности реактора-размножителя и запишите ядер-
ные реакции, за счет которых может в них идти процесс воспро-
изводства ядерного горючего.
В водородной бомбе вместо реакции 2[Н + 2[Н —>
пользуется реакция \я+ ]Н-^> %Н& + о
+ In ис-
п • Объясните почему.
Объясните, почему реакция синтеза атомных ядер — образование
из легких ядер более тяжелых — является колоссальным источ-
ником энергии.
*7_Ф*[ 1 Объясните, почему для протекания термоядерной реакции необ-
ходима очень высокая температура.
<571>
7.2. Элементы физики элементарных частиц
}Ж) Известно, что в углеродно-азотном, или углеродном, цикле число
^ "' ядер углерода остается неизменным. В результате этого цикла че-
тыре ядра водорода JH (протона) превращаются в ядро гелия 2Не, а также
образ) ются три у -кванта, два позитрона и два нейтрино. Записав эту реакцию
определите выделяющуюся в этом процессе энергию.
Дано
m,H =1,6736 107 кг
miHc= 6,6467 107 кг
me, =9,11 1O1 кг
Решение
4|Н
= Атс2
QOmeem
Дайте определение и объясните происхождение первичного и вто-
ричного космического излучения.
Объясните происхождение мягкого и жесткого компонентов вто-
ричного космического излучения.
^Ш Представьте схематически и объясните происхождение электрон-
' ""*" * но-позитронно-фотонного, или каскадного, ливня
Запишите схемы распада положительного и отрицательного мюо-
!*• нов.
Ответ ^ И+ -> > + gve + gv~,
При соударении высокоэнергетического положительного мюона
и электрона образуются два нейтрино. Запишите эту реакцию и
объясните, какой тип нейтрино образуется.
С Ответ J
При захвате протоном отрицательного мюона образуется нейтрон
и еще одна частица. Запишите эту реакцию и определите, что это
за частица.
ГОтвет j ц- +
\ 7 103 ) Принимая, что энергия релятивистских мюонов в космическом
Ч. '• J излучении составляет 3 ГэВ, определите расстояние, проходимое
мюонами за время их жизни, если собственное время жизни мюона
/0 = 2,2 мкс, а энергия покоя Ео = 100 МэВ.
Дано
Е = 3 ГэВ = 3- 109эВ
^0 = 2,2 мкс = 2,2 ¦ 10"* с
?„ = 100 МэВ=108эВ
Решение
к
_
COmeemj / = 19,8 км.
Известно, что продукты распада заряженных пионов испытыва-
ют дальнейший распад. Запишите цепочку реакций для лг+ - и л~ -
мезонов.
( Ответ
о- _
л:
Г7.105 } л - мезон распадается в состоянии покоя на два у - кванта. При-
; нимая массу покоя пиона равной 264,\те, определите энергию
каждого из возникших у -квантов.
Дано
тп = 264,\те
те=9,1Ы01 кг
Решение
ж0 ->2у, Еп = тжс2,
г. Еж тлс2
Еу ~ 2 ~ 2 ¦
(^Ответ ") ?у = 67,7 Мэв.
Известно, что распад нейтрального короткоживущего каона про-
исходит по схеме К® -> лг+ + п'. Принимая, что до момента рас-
пада каон покоился и его масса покоя составляет 914те, определите массу
покоя образовавшихся заряженных ж - мезонов, если известно, что масса каж-
дого образовавшегося пиона в 1,783 раза больше его массы покоя.
К+ - мезон распадается (в состоянии покоя) на два пиона. Прини-
мая массу покоя каона равной 966,2те и пренебрегая разностью
масс заряженного и нейтрального пионов, определите энергию каждого из воз-
никших пионов.
Ответ Л ? = 247,5 Мэв.
Назовите и охарактеризуйте четыре типа фундаментальных взаи-
модействий, а также сравните радиусы их действия. Какое из вза-
имодействий является универсальным.
Что называется изотопическим мультиплетом и изотопическим
спином?
Возможно ли вынужденное излучение, если фотоны были бы фер-
мионами? Дайте объяснение.
Объясните, в чем заключается принцип зарядового сопряжения.
Запишите продукты распада антинейтрона.
При столкновении нейтрона и антинейтрона происходит их анни-
гиляция, в результате чего возникают два У - кванта, а энергия
частиц переходит в энергию у - квантов. Определите энергию каждого из воз-
никших у - квантов, принимая, что кинетическая энергия нейтрона и позитро-
на до их столкновения пренебрежимо мала.
ЕУ
Дано
= 1,675-10'21 кг
9
Решение
on + (}л~-> 2у,
?-2/?гяс2,
= тяс2.
Г Ответ ~\ еу = 942 Мэв.
Перечислите основные свойства нейтрино и антинейтрино и
объясните, чем они отличаются по современным представлени-
ям-друг от друга.
jjjjjlP Выбрав из четырех типов нейтрино (ve, ve, v^ , v^ ) правильное,
напишите недостающие обозначения (х) в каждой из приведен-
ных реакции:
х+
2) х+о'я-» \р + ц~;
3) х + \р -> {Qn + +°е ¦
QOmeem
2) о%+"> P
^^^^» Назовите элементарную частицу, обладающую наименьшей мас-
%ЩЗШг сой покоя. Чему равен электрический заряд этой частицы?
ffijj Элементарным частицам приписывают квантово-механическую
величину — четность. Что она характеризует? В чем заключается
закон сохранения четности и при каких взаимодействиях он выполняется?
Объясните, какая характеристика элементарных частиц положена
в основу деления адронов на мезоны и барионы.
С Ответ ) Барионноечисло В:
^ S мезоны: В = 0 ;
барионы: 5=1.
^'jf,t 119} Объясните, к какой группе элементарных частиц и почему отно-
сится: 1) Л° - гиперон; 2) протон; 3) тау-лептон; 4)тг°-мезон.
Объясните, к какой группе элементарных частиц и почему отно-
сится. 1) мюонное нейтрино; 2) нейтрон; 3) фотон; 4) К0 -мезон.
Перечислите, какие величины сохраняются для процессов взаи-
мопревращаемости элементарных частиц, обусловленных слабым
и сильным взаимодействиями.
Ответ
1. Энергия.
2. Импульс.
3. Момент импульса.
4. Зарядовое число.
5. Массовое число.
6. Спин.
7. Лептонное число.
8. Барионное число.
9. Изотопический спин (только сильное взаимодействие).
10. Странность (только сильное взаимодействие).
11. Четность (только сильное взаимодействие).
12. Очарование (только сильное взаимодействие).
7 122) Определите, какие из приведенных ниже процессов разреше-
нызаконом сохранения лептонного числа: 1 )/?->« + е+ +ve;
2) К~
е~ + е+ ; 4) К+ -> е
QОтвет J i) p^n+e+ +ve;
@) = @) + (-1) + (+1) разрешен;
2) К~ -> ц~ + v^ ;
@) = (+1) + (-1) разрешен;
3) л+ -> fi+ + е~ + е+ ;
@)*(-1) + (+1) + (-1) запрещен;
4) К+ -+е+ +nd + ve;
@) = (-1)+@) + (+1) разрешен.
,П?Щ$\ Определите, какие из приведенных ниже процессов запре-
щены законом сохранения странности: 1) р + л" -> Л° + К0 ¦
2) Р + л--+Ъ+ + КГ;3)
+п.
@) + @) = (-1
разрешен;
2)
@) + @) * (-1) + (-1), запрещен;
3) р + п-+ Л° + 1+;
@) + @)^(-1) + (-1), запрещен;
4) р + л~ ->¦ К' + К+ + п,
@) + @) = (-1) + (+1) + @), разрешен.
7.124 ) Ниже приведены запрещенные способы распада. Перечислите для
45 каждого из них законы сохранения, которые он нарушает:
1) л' -> fi' + v^; 2) КГ + п -> ?Г + К* + К0; 3) р + п -> Л° + Е+.
С Ответ
\)п -*ц +vfi;лептонноечисло: )
2) K~ + n-+Q~ + K+ +К°; зарядовое число: (-1) + @) * (-1) + (+1) + @);
3) р + и->Л° + ?+; странность: @) + @)*(-1)+(-1).
5'} Ниже приведены запрещенные способы распада. Перечисли-
те для каждого из них законы сохранения, которые в нем на-
рушаются: 1) р + р-^р + л*', 2) л~ + /?-» К~ + Е+ ; 3) п~ + и-> Л° +К~ ;
4) я
Исследование взаимопревращаемости элементарных частиц при-
вело к открытию нового свойства симметрии ¦— операции зарядо-
вого сопряжения, заключающееся в том, что при замене частицы на античасти-
цу в уравнении данной реакции получается новая реакция. Примените опе-
рацию зарядового сопряжения к следующим процессам: 1) Е+ —> р + л° ',
2) p + p-±Z.- + A° + K° + K- .
Illll Примените операцию зарядового сопряжения (см. задачу 7.126) к
следующим процессам: 1) л° ->2у; 2) р+ К~ -> ?° + ж+ +л~ .
С Ответ J 1) л° -> 2у ¦,
Охарактеризуйте основные свойства кварков (антикварков) — за-
рядовые числа (электронное и барионное), спин, странность, цвет,
очарование, прелесть.
Объясните, почему понадобилось введение внутренних характе-
ристик кварков — цвета и очарования.
Запишите, какие комбинации известных в настоящее время квар-
ков воспроизводят свойства: 1) нейтрона; 2) протона; 3) эт+ - ме-
зона; 4) л~ - мезона; 5) ? - гиперона.
С Ответ J 1) п- нейтрон (исИ);
2) р - протон (uud);
3) эт+ - мезон (ud );
4) л' - мезон (ud);
5) ?°- гиперон (uds ).
Важнейшие формулы, используемые в задачнике
1. Физические основы
механики
Средняя скорость и среднее ускоре-
ние
(v) = —; (а) = —.
w At w At p = wv.
Мгновенная скорость и мгновенное Второй закон Ньютона
ускорение
Связь между линейными и угловыми
величинами при вращательном дви-
жении
s = R<p; v= R(o;
at = Re; an = w2R.
Импульс (количество движения)
v =
Дг
—
A/
а =
Ду
dt
Сила трения скольжения
Тангенциальная и нормальная состав- F - f\r
ляющая ускорения ^
_ du _ v Закон сохранения импульса (для замк-
а* ~~4~( ' а" ~ ~' нутой системы)
л
Полное ускорение
а = аг + а„; а
Работа переменной силы на участке
Кинематические уравнения равнопе- траектории / 2
ременного поступательного движения
\v = v0 ± at,
л
р = ^щ\, = const
1=1
А= \Fcosa ds
t = vot±
at"
Мгновенная мощность
л, dA «,
Угловая скорость и угловое ускорение N = —— = Fv.
- _ dip ,_ da>
°)~~di' ?~~dt' Кинетическая энергия
nw2
Кинематические уравнения равнопе-
р
ременного вращательного движения
\<p--a)Qt±—.
Т = -
2
Потенциальная энергия тела, подня-
того над поверхностью Земли
П = mgh.
Потенциальная энергия упругодефор-
мированного тела
Полная механическая энергия системы
Е=Т+П.
Закон сохранения механической энер-
гии (для консервативной системы)
[ = Е — const.
Скорость шаров массами тпх и щ
после абсолютно упругого централь-
ного удара
„' - (r"i
vi
стержню и проходящей через его
середину
J = -ml2.
12
Момент инерции тонкого стержня
относительно оси, перпендикулярной
стержню и проходящей через его
конец
Теорема Штейнера
J=JC + ma2.
Кинетическая энергия вращающегося
тела относительно неподвижной оси
v2 —
Скорость шаров после абсолютно
неупругого удара
ГП\ГП2
Момент инерции системы (тела)
1=1
Моменты инерции полого и сплош-
ного цилиндров (или диска) относи-
1 ельно оси симметрии
J = mR2;
f = -mR2.
2
т — *¦
р 2 '
Момент силы относительно непод-
вижной точки
М = [rF].
Момент силы относительно непод-
вижной оси
M = [rF]z.
Момент импульса материальной
точки относительно неподвижной
точки
Момент импульса твердого тела от-
носительно неподвижной оси
Момент инерции шара относительно
оси, проходящей через центр шара
Момент инерции тонкого стержня
относительно оси, перпендикулярной
1=1
Уравнение динамики вращательного
движения твердого тела
Mz = Jze; M = —
Закон сохранения момента импульса
L = const.
Закон всемирного тяготения
Сила тяжести
P = mg.
Напряженность поля тяготения
g = ?/т.
Потенциал поля тяготения
П М
<р = — = -G—.
т R
Взаимосвязь между потенциалом
поля тяготения и его напряженно-
стью
g = -gradp.
Уравнение неразрывности
Sv = const.
Уравнение Бернулли
pv2 ,
-— + pgh + p = const.
Релятивистское замедление хода часов
Релятивистское (лоренцово) сокра-
щение длины стержня
Релятивистский закон сложения ско-
ростей
и' + v . u-v
и = -
\ + vu
'/с2' l-vu/c2
Релятивистский импульс
т
Закон взаимосвязи массы и энергии
„2
Е = -
тс
Связь между полной энергией и им-
пульсом релятивистской частицы
2. Основы молекулярной
физики и термодинамики
Закон Бойля—Мариотта
pV = const при Т,т = const.
Законы Гей-Люссака
V = КоA + at) при р,т- const,
р = ро(\ + at) при V, т - const.
Закон Дальтона
Уравнение Клапейрона — Менде-
леева для произвольной массы газа
pV = ^
Основное уравнение молекулярно-
кинетической теории
1 / \2
Средняя квадратичная скорость мо-
лекулы
1 Urt
(«-К
Средняя арифметическая скорость
молекулы
UT \8RT
лМ
Наиболее вероятная скорость молекулы
ШТ _ \2RT
v*~i щ ~\ м ¦
Барометрическая формула
Первое начало термодинамики
Средняя длина свободного побега
молекул
М
Среднее число столкновений моле-
кулы за 1 с
(г) = 42лс12п(у).
Закон теплопроводности Фурье
AT1 1
Закон диффузии Фика
Закон Ньютона для внутреннего тре-
ния (вязкости)
Средняя энергия молекулы
Внутренняя энергия произвольной
массы газа
U = viRT = ^lRT.
2 Ml
Молярная теплоемкость газа при посто-
янном объеме и постоянном давлении
Lv=—R\ l_= R
Работа газа при изменении его объема
Работа газа при изобарном расишрении
m
'~ М
Работа газа при изотермическом
расширении
М Vx М р2
Уравнения адиабатного процесса
(уравнение Пуассона)
pVr = const; TV7' - const,
'y = const.
Работа газа при адиабатном расши-
рении
A = ^CATl-T2).
Термический КПД для кругового
процесса
Термический КПД цикла Карно
Тх
Уравнение Ван-дер-Ваальса для
ля реального газа
3. Электричество
и электромагнетизм
Закон Кулонч
F = -
laal
4ле0 г
Напряженность электростатического
поля
Поток вектора напряженности элек-
тростатического поля сквозь замкну-
тую поверхность S
s s
Принцип суперпозиции
Электрический момент диполя
Теорема Гаусса для электростатиче-
ского поля в вакууме
?° '=1
Объемная, поверхностная и линейная
плотности заряда
dQ dQ dQ
р = —; о = — ; г = —.
dF dS d/
Напряженность поля, создаваемого
равномерно заряженной бесконечной
плоскостью,
о
Напряженность поля, создаваемого
двумя бесконечными параллельными
разноименно заряженными плоско-
стями,
Напряженность поля, создаваемого
равномерно заряженной сфериче-
ской поверхностью,
Е = -Г—% ir>R);
4л?0 г1
? = О (r<R).
Потенциал электростатического поля
U А„
Ф- — = —.
а а
Связь между потенциалом электро-
статического поля и его напряжен-
ностью
Е = — grady?.
Связь между векторами Р и Е
Связь между е и х
? = 1 + х.
Связь между векторами электриче-
ского смещения и напряженностью
электростатического поля
D = ?0еЕ.
Электрическая емкость уединенного
проводника
с=Я-.
<р
Электрическая емкость шара
Электрическая емкость плоского кон-
денсатора
Электрическая емкость цилиндриче-
ского конденсатора
с= 2л?0/
\п(г2/п)'
Электрическая емкость сферическо-
го конденсатора
Электрическая емкость параллельно
и последовательно соединенных
конденсаторов
i=i "- 1=1 ^-i
Энергия заряженного уединенного
проводника
Г,п2 П,п П2
W = -
2 2 2С
Энергия заряженного конденсатора
= Q4> = Q2
2 2 2С'
W =
Объемная плотность энергии элек-
тростатического поля
_ W _ ефЕ1 _ ED
F 2 2
Сила тока
Плотность тока
d?
d/
Электродвижущая сила, действ> ю-
щая в цепи
Закон Ома для однородного участка
цепи
I = U/R.
Закон Ома в дифференциальной форме
Мощность тока
dt
Закон Джоуля — Ленца
dt.
R
Закон Джоуля—Ленца в дифферен-
циальной форме
о) = jE = уЕ2.
Закон Ома для неоднородного участ-
ка цепи (обобщенный закон Ома)
j
R
Магнитный момент рамки с током
Рт = ISn .
Связь между индукцией и напряжен-
ностью магнитного поля
Закон Био — Савара — Лапласа для
элемента проводника с током
4л гъ
Магнитная индукция поля прямого гока
4л R
Магнитная индукция поля в центре
круглого проводника с током
Закон Ампера
Магнитное поле свободно движущего-
ся заряда
Сила Лоренца
ЭДС самоиндукции
dt
Индуктивность бесконечно длинпогс
соленоида, имеющего N витков,
N2S
4л:
„з •
F = e[vB].
Холловская поперечная разность
потенциалов
1 IB IB
/Sip = = R—.
en d d
Закон полного тока для магнитного
поля в вакууме (теорема о циркуля-
ции вектора В)
/
Ток при размыкании цепи
/=/ое-'/\
Ток при замыкании цепи
/=/0(l-e-'/r).
Энергия магнитного поля, связанно-
го с контуром,
W = Ы2/2.
Объемная плотность энергии маг-
нитного поля
_ W _ ц0цН2 _ ВН
W~T~~T~'~2-
Намагниченность
Магнитная индукция поля внутри
соленоида (в вакууме), имеющего N
витков,
N1
B=fi0~.
Поток вектора магнитной индукции
(магнитный поток) сквозь произ-
вольную поверхность
Связь между векторами J и Н
Связь между ц и %
Закон полного тока для магнитного
поля в веществе (теорема о циркуля-
ции вектора В)
Закон Фарадея
Теорема о циркуляции вектора Н
j>Hdl=/.
4. Колебания и волны
Уравнение гармонического колебания
юо-2л:/Т =
Период колебаний физического ма-
ятника
Т =
Период колебаний математического
маятника
Формула Томсона
Т=2жл/1С .
Логарифмический декремент затухания
A(t+T)
Индуктивное сопротивление
RL = (oL.
Емкостное сопротивление
RC=±-.
Полное сопротивление цепи
Длина волны
= vT.
Уравнение плоской волны
?(х,/)= Acos(eot-
Уравнение сферической волны
А
?(r,t) = —cos(cot -
г
Фазовая и групповая скорости
о) da>
V = T' U = ~dk'
Уравнение стоячей волны
* -> . 2*х
Е, - 2А cos cosw^.
Аи
Эффект Доплера в акустике
(v±v )v0
v- -z-^- •
v + vHCT
Скорость распространения электро
магнитных волн в среде
с
V -
5. Оптика. Квантовая
природа излучения
Закон отражения света
;; = /,.
Закон преломления света
sin I,
T-L=«2I-
sin/2
Формула тонкой линзы
U
R2) a b
Показатель преломления света
v
п = —.
с
Оптическая длина пути
L = ns.
Оптическая разность хода
Условия интерференционных мак-
симумов и минимумов
Л = ±тЛ0 (т = 0,1,2,...);
Л = ±Bи+1)^ (т = 0,1,2,...).
Оптическая разность хода в тонких
пленках в отраженном свете
Степень поляризации
р_ -"max ~ '
Закон Малюса
/ = /0 cos2 a .
Закон Брюстера
Условия дифракционных максиму-
мов и минимумов от одной щели
)— {m= 1, 2, 3,...);
asin(p = ±2m— (т = 1, 2, 3,...).
Условие главных максимумов ди-
фракционной решетки
dsin<p = ±nd (т» = 0, 1, 2,...).
Условие дополнительных миниму-
мов дифракционной решетки
dsm<p = ±— {tri* 0,N,2N,...).
N
Формула Вульфа — Брэггов
2dsind = тА. (т = 1, 2, 3,...).
Разрешающая способность спек-
трального прибора и дифракционной
решетки
Д = —; R = mN.
О/.
Продольный эффект Доплера
M-v/c
VI + v/c
Поперечный эффект Доплера
Угол вращения плоскости поляриза-
ции в кристаллах и растворах
(p = ad; <p = [a]Cd.
Закон Стефана — Больцмана
Закон смещения Вина
Формула Планка
hv
Уравнение Эйнштейна для внешнего
фотоэффекта
Энергия и импульс фотона
hv_
с
Давление света при нормальном па-
дении на поверхность
Изменение длины волны при эффек-
те Комптона
ДД =
щс
2h . 2в
sin —,
щс 2
6. Элементы квантовой Закон Мозли
физики атомов, молекул
и твердых тел
v=R(Z-oY\— j .
т п
Обобщенная формула Бальмера
т п
Энергия электрона в водородопо-
добном атоме
_ _L ?т?_ л.., 2 3 Л
^п - ~ 2 „,2 5 \П *' Z> J' —>
Длина волны де Бройля
Соотношение неопределенностей
ЛхДр^ > h,
¦ Axbpy > h, \EAt > h.
AxApz > h,
Общее уравнение Шредингера
—
2т
= ih
—
dt
Уравнение Шредингера для стацио-
нарных состояний
7. Элементы физики
атомного ядра
и элементарных частиц
Энергия связи нуклонов в ядре
Еа = [Zmp + (А - Z)mn - ms] с2 .
Дефект массы ядра
Am = \Zmp +(A-Z)mn\-тя .
Закон радиоактивного распада
Период полураспада
- 1п2
Среднее время жизни радиоактивно-
го ядра
_ 1
Правило смещения для а -распада
Правило смещения для /3~ -распада
v О
Коэффициент прозрачности прямо-
угольного потенциального барьера
D
Г 2 1
=D0 exp j2m(U-E)l .
Правило смещения для /3+ -распада
Энергия квантового осциллятора
Е„=\ п+-
ПЕРИОДИЧЕСКАЯ СИСТЕМА
ш
IV
VI
VD
vin
IX
ГРУППЫ
Н
..00794 if,
ВОДОРОД
Li
6,94,
2,' ,
ЛИТИЙ 2
Na
ИАТРИЙ
К
39,098,
КАЛИЙ
29
Си
МЕДЬ
Rb 37
85,467,
Ss1
РУБНДНЙ
, Ag
it SJ, «"*«
2 СЕРЕБРО
CS 55 j
132,9054 ,|
ЦЕЗИЙ 2
79
Аи
\\ 196,9665
2 ЗОЛрТО
Fr 87 ,
223,0197 18
5
7.'
ФРАНЦИЙ
Be
9,01218
2.1
БЕРИЛЛИЙ
Mg
24,305
12
з," J
МАГНИЙ 2
Ca
40,08
КАЛЬЦИЙ
20
30
Zn
65,38
ЦИНК
Sr
38
СТРОНЦИЙ
,« Cd
2 КАДМИЙ
Ba
13733
БАРИЙ
56
80
li
32
1J 6s'
2
Hg
200,5,
Ra 88
226,0254
РАДИЙ
III
If1
В
10.81
БОР
13 Al
26,98154
АЛЮМИНИЙ
21
Sc
44,9559
3rf'4.J
СКАНДИЙ
31 Ga
it , m'n
ft ^P
2 ГАЛЛНЙ
Y 39
88,9059 »
«Л.1 'j
ИТТРИЙ 2
49
5.1
In
114,82
ИИДИЙ
"La-Lii71
204.383
таллий
IV
С
12,011
14
Si
28.085s
КРЕМНИЙ
Ti
47,90
22
3if'4s
ТИТАН
' i
32
Ge
ГЕРМАНИЙ
Zr
91,22
40
ЦИРКОНИЙ
4 50 Sn
f 1186
ОЛОВО
Hf
178,4,
ГАФНИЙ
72
82
Pb
207,2
•P1
СВИНЕЦ
Ku
B61)
КУРЧАТОВИЙ 2
N
14,0067
15 p
, 30,97376
V
50,9415
23
ВАНАДИЙ -
33
As
Л 74,9216
I МЫШЬЯК
Nb
41.
92,9064 4 ( 12
НИОБИЙ 2
51
Sb
121,75
P
СУРЬМА
Та
180,947, .'I
ТАНТАЛ !
83
Bi
К 208,9804
II б,'
2 ВИСМУТ
Ns
[2621
105
и
32
з:
НИЛЬСБОРИЙ 2
Sd'
• Л
H
H
La 57
138.9O55
idW
ЛАНТАН
Се 58
140,12 8
4j4s> 18
ЦЕРИЙ 2
Рг
59
140,9077 8
it'б,1 Ig
ПРАЗЕОДИМ 2
Nd
M4,2<
2
8
4/46,! 18
НЕОДИМ 2
Pm 6.
11451 2!
«/'б,1 18
ПРОМЕТИЙ 2
Sm 62
150,4 J
«/'Si1 11
САМАРИЙ 2
Eu
151,96
g
ЕВРОПИЙ 2
Gd 64
ГАДОЛИНИЙ
и
H
AC 89 2
227,0278 il.
6d4S 4
АКТННИЙ
Th 'О 2
232,0381 ig
¦ 6<f'7,' >}
ТОРИЙ
U « }
238,02, 2]
srt/7»1 'j
Np 93
237,04S2 Л
нептуний'
PU «2
244,0642 2J
ПЛУТОНИЙ
Am 95
243,0614 j
if1!,' 1
АМЕРИЦИЙ"
Cm
247,0703 Л
s/Vt,2 'j
КЮРИЙ
ЭЛЕМЕНТОВ Д.И. МЕНДЕЛЕЕВА
э
8
Л Е М
VI
О
15,999.
6 2""
2
16
« 3
2
Сг
51.996
ХРОМ
34
6
Мо
95.94
КИСЛОРОД
S
4 32.06
СЕРА
24
}dUs> »
2
Se
78.96
СЕЛЕН
42
, , ]1
МОЛИБДЕН 2
52
Те
11 |27'6° ¦
в 5р
5
W
183.8;
ТЕЛЛУР
74
id'ts' II
ВОЛЬФРАМ 5
84
18
32
18
Ро
208,9824
р4
ПОЛОНИЙ
Е Н
н
9
7 *PS
2
17
7 Зр
2
Мп
54,9380
т о в
VII
F
18,998403
ФТОР
С1
35,453
ХЛОР
25
5 1 13
МАРГАНЕЦ I
35
18
1
Тс
98.9062
Вг
79,904
БРОМ
43
13
..!5,г 18
ТЕХНЕЦИЙ 2
, 53
it
'« 5"
2
Re
I86JO7
РЕННЙ
,85
а
2
I
126.9045
ИОД
75
13
2
At
209,9871
АСТАТ
Fe
55,847
id
ЖЕЛЕЗО
Ru
101JB,
id
РУТЕНИЙ
Os
190-2 sd
осмий
26
2
2
44
15
s,< Ч
2
76
2
VIII
Со
58,9332
3</7
КОБАЛЬТ
Rh
102,9055
РОДНИ
Ir
192,22
Я
ИРИДИЙ
27
45
77
2
IS
2
1
16
2
7
IS
Я
5
2
2
10
я ^
2
18
8 3,
2
Ni
58,70
Не
4,00260
ГЕЛИЙ
Ne
20.П9
¦
НЕОН
Аг
6 39,94,
АРГОН
28
,4j! 16
НИКЕЛЬ 2
36
8
18
2
Pd
106.4 ^
Кг
83,80
КРИПТОН
46
о
ПАЛЛАДИЙ 2
» 54
18
2
Pt
195,08
Хе
131,29
КСЕНОН
78
17
ПЛАТИНА 2
86
II
?| 6,
2
Rn
222,0176
»
РАЛОН
Атомная масс!
Распределение
-Атомный номер
-Распределение
и
Атомные массы приведены пи Международной
таблице 1983 г,
Точность последней значащей цифры ±1 или ±3.
если она выделен» мелким шрифтом.
В квадратных скобках прнвеаены массовые числа
наиболее устойчивых изотопов.
Названии и символы элементов, приведенные
в круглых скобках, не являются общепринятыми,
ТЬ 652
158.9254 г!
¦</'«»' 1
ТЕРБИЙ !
Dy
66
162,50 2
4/'6.1
ДИСПРОЗИЙ
НО 67
164,9304 2?
4/"б,! '!
ГОЛЬМИЙ '
ЕГ 68
167.26 з
ЭРБИЙ
Тш
69
168,9342 31
4/l)«!J 'I
ТУЛИЙ 2
Yb 70 2
173,04 з|
tfub,' 1
ИТТЕРБИЙ 2
Lu
174,967
32
! 8
ЛЮТЕЦИЙ
О
Вк '•
247,0703
ifhdh,1
ЕЕРКЛИЙ
и
г
к
18
1
а
Cf
251,0796
if 7,'
ы
98
S
КАЛИФОРНИЙ
Es
252,0828
S/" 7,2
99 ,
1
ЭЙНШТЕЙНИЙ
Fm 10(
257,0951
S/12 7»2
ФЕРМНЙ
3 з
IB
Md 1
258,097
if"!,1
01 8
\
менделевий'
(No) юг2
259,1009 32
if4!,1 И
(НОБЕЛИЙ1 2
(Lr) 'оз 2
260,1054 з?
32
(ЛОУРЕНСИЙ)
Учебное издание
Трофимова Таисия Ивановна
Павлова Зоя Григорьевна
Сборник задач по курсу физики
с решениями
Редактор /. Н. Чернышева
Художественный редактор Ю. Э. Иванова
Корректор Г. Н. Петрова
Компьютерная верстка С. Ч. Соколовский
ЛР № 010146 от 25.12.96. Изд. № ФМ-179. Сдано в набор 17.03.98. Подп. в печать
12.10.98. Формат 60x88/16. Бумага газетная. Гарнитура «Тайме». Печать офсетная
Объем: 36,26 усл.печ.л.; 36,51 усл. кр.-отт.; 23,49 уч.-изд. л. Тираж 10000 экз. Зак. №1718
Издательство «Высшая школа», 101430, Москва, ГСП-4. Неглинная ул., д. 29/14
Огаечатано в ГУП ИПК «Ульяновский Дом печати»,
432601, г. Ульяновск, ул. Гончарова, 14