Теория гидравлических цепей - Меренков А.П.

Автор: Меренков А.П.

Теги: машиностроение механика гидравлика гидравлические расчеты академия наук ссср издательство наука

Год: 1985

Похожие

Справочник по гидравлическим сопротивлениям

Справочник по гидравлическим расчетам

Таблицы для гидравлического расчета стальных, чугунных, асбестоцементных, пластмассовых и стеклянных труб

Таблицы для гидравлического расчета канализационных сетей и дюкеров по формуле Павловского Н. Н.,

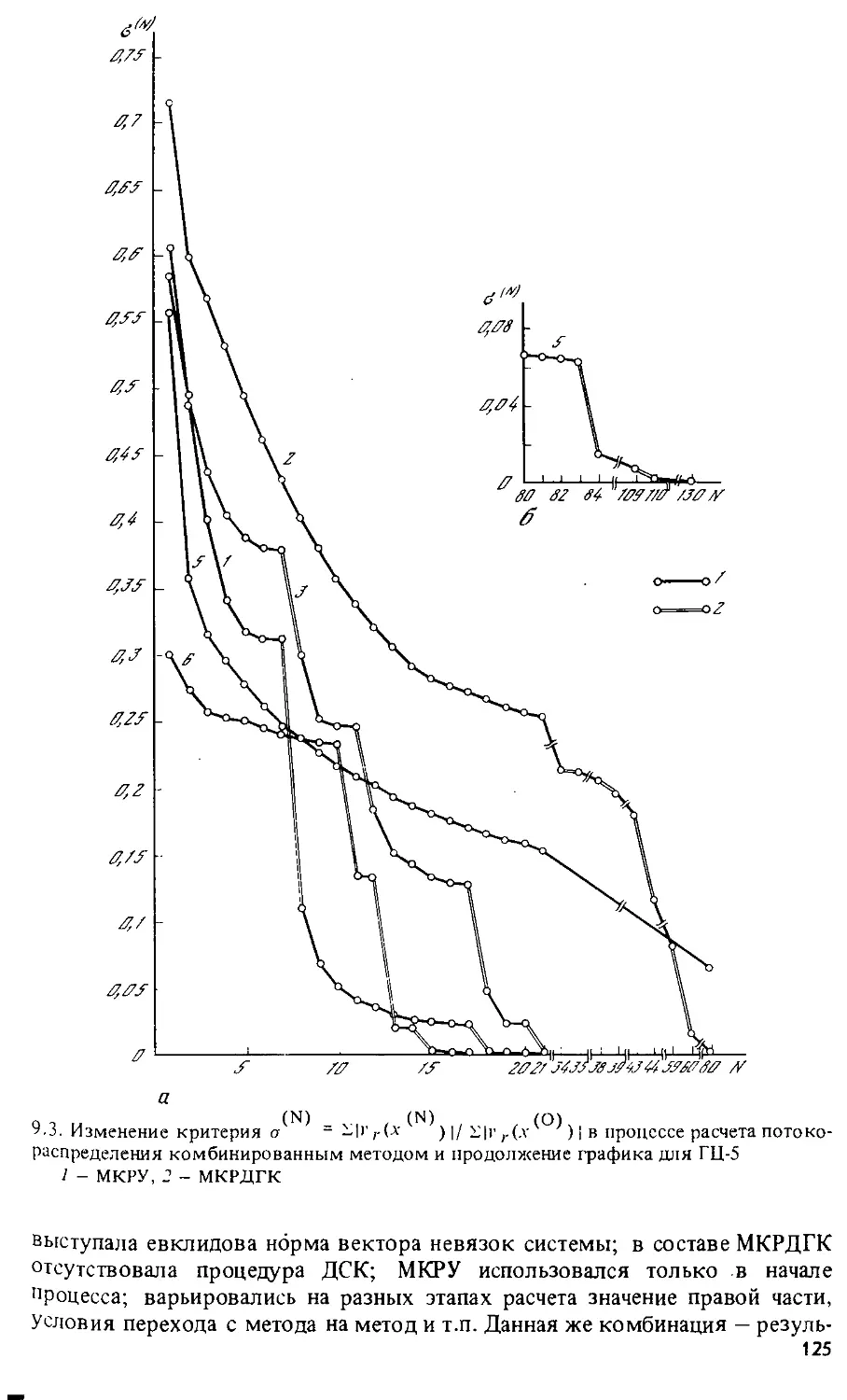
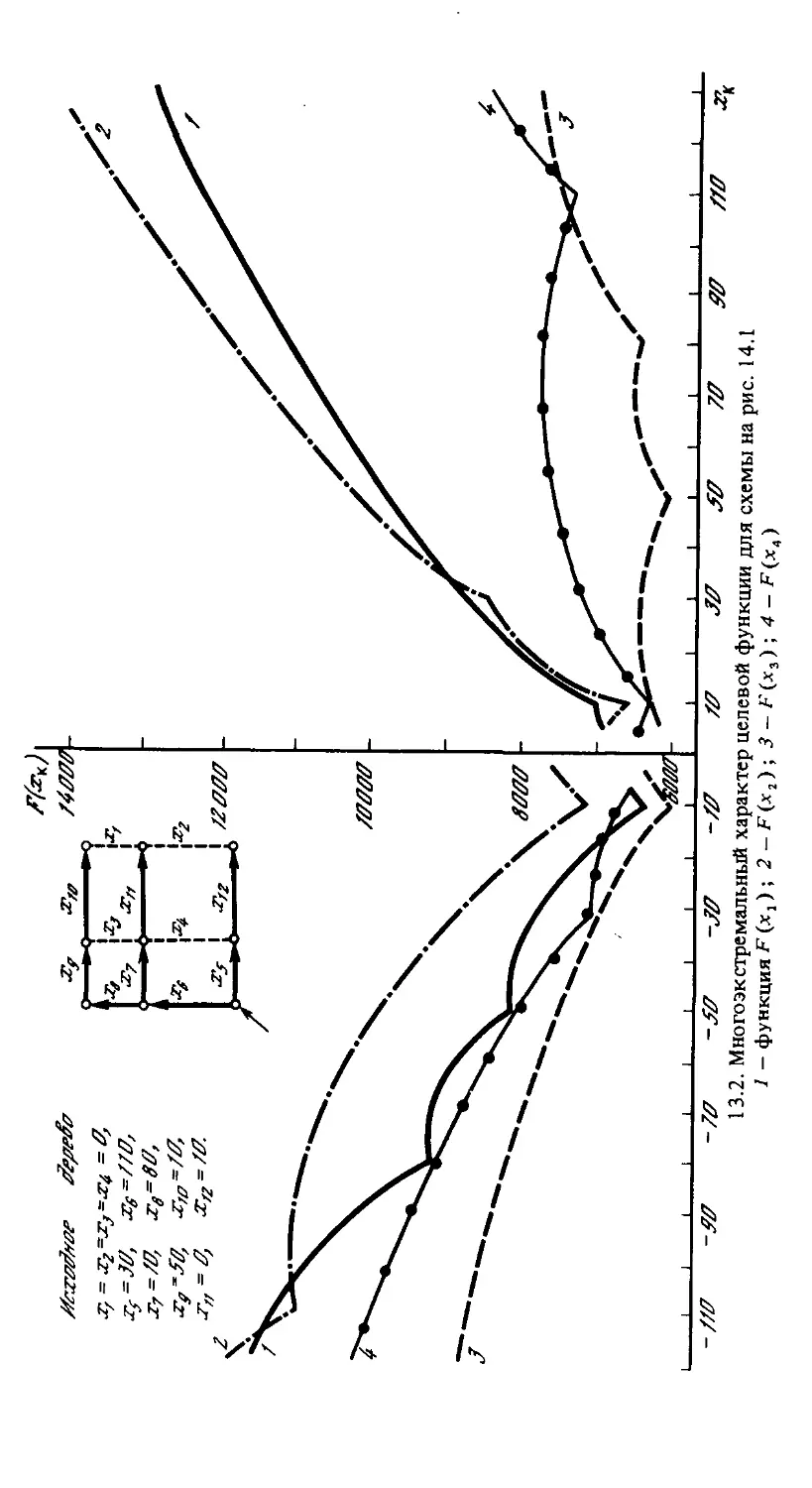
Текст

АКАДЕМИЯ НАУК СССР
ОРДЕНА ЛЕНИНА СИБИРСКОЕ ОТДЕЛЕНИЕ
Сибирский энергетический институт
АПМеренков, ВЯХасилев
ТЕОРИЯ
гидравлических
ЦЕПЕЙ
Ответственный редактор
доктор технических наук М.Г. Сухарев
МОСКВА
"НАУКА"
1985

УДК E19.9 +518.5) :532.54
Меренков АЛ., X а с и л е в В.Я. Теория гидравлических це-
цепей. М.: Наука, 1985.
В монографии излагаются основные положения, математический
аппарат и приложения теории гидравлических цепей - научно-методи-
научно-методической базы для моделирования, оптимального проектирования и
функционирования трубопроводных и других гидравлических сис-
систем. Показывается преемственная связь данной теории с теорией
электрических цепей и ее межотраслевое значение как синтезирую-
синтезирующей научно-технической дисциплины.
Для научных работников и преподавателей вузов, математиков
и инженеров, занимающихся применением математических методов
и ЭВМ в области трубопроводных систем тепло-, водо-, нефте- и га-
газоснабжения, вентиляции и других гидравлических систем.
Табл. 11, ил. 62, список лит. 294.
Рецензенты:
О.Ф. Васильев, А.З. Гамм
Научная библиотека ХГТУ
0483970
М
2305020000-382
042 @2)-85
© Издательство "Наука", 1985 г.

ПРЕДИСЛОВИЕ ,
Физико-технические системы, осуществляющие централизованное снабже-
снабжение рассредоточенных потребителей электрической и тепловой энергией,
топливом, водой или ка.кой-нибудь другой транспортируемой средой,
приобретают всевозрастающее значение в энергетике, коммунальном и
водном хозяйствах и в других отраслях. Они представлены весьма широ-
широким спектром объектов, различающихся назначением, масштабностью,
принципами построения, физической сущностью процессов функциони-
функционирования и т.д. К ним относятся: глобальные системы, такие, как электро-
электроэнергетическая и газоснабжающая системы страны; межрегиональные
(объединенные энергосистемы, магистральные нефте- и газопроводы, си-
системы каналов и групповые водопроводы для переброски вод и обводне-
обводнения больших территорий); системы электро-, тепло-, водо- и газоснаб-
газоснабжения городов и промышленных центров; системы отопления, вентиля-
вентиляции и другие.
Все они имеют довольно четкую ведомственную принадлежность, ко-
которая диктуется главным образом видом транспортируемой среды, а так-
также технологией ее добьии (или производства), переработки, транспорти-
транспортировки и потребления. И именно отраслевые факторы определяют основную
массу публикаций, научно-методических и алгоритмических разработок.
Вместе с тем все более актуальными становятся межотраслевые аспекты,
которые требуют совместного рассмотрения такого рода систем на том или
ином уровне абстрагирования от их специфических особенностей и свойств.
В этой связи можно указать на экономические, энергетические или эколо-
экологические проблемы, при решении которых данные объекты выступают
уже как подсистемы. Иллюстрацией правомочности и полезности такого
подхода могут служить общеэнергетические исследования.
Так, в работах Сибирского энергетического института (СЭИ) СО АН
СССР [5, 22, 111, 121, 122, 172, 208] с позиций общей энергетики дана
развернутая классификация систем энергетики и задач их планирования,
проектирования и эксплуатации, а также сформулированы основные прин-
принципы создания для них автоматизированных систем: плановых расчетов
(АСПР), проектирования (АСП или САПР) и диспетчерского управления
(АСДУ). Межотраслевой аспект оказывается целесообразным и при изу-
изучении отдельных общих проблем, например надежности сложных физико-
технических систем [165, 170, 172, 192 и др.].
Наряду с этим не менее важными и продуктивными оказываются иссле-
исследования, связанные с физико-математической общностью задач расчета,
оптимизации и управления для какого-либо класса систем, поскольку
во многих случаях это дает возможность существенно повысить уровень
3

и практическую эффективность применения математических методов и
ЭВМ.
Данная книга посвящена подобному межотраслевому научному направ-
направлению, которое сформулировано и развивается в СЭИ с 1961 г., — теории
гидравлических цепей (ТГЦ). Предметом ТГЦ являются общие вопросы
математического и алгоритмического обеспечения задач функциониро-
функционирования и оптимального проктирования трубопроводных и других гидравли-
гидравлических систем, характеризующихся произвольными схемами с течением
жидкости и газа. Отправной точкой для разработки этой теории служит
тот факт, что данные объекты обладают топологической общностью своих
расчетных схем, а движение транспортируемой среды в них подчиня-
подчиняется единым законам течения и сетевым законам сохранения массы и
энергии.
Выше говорилось о значении систем централизованного снабжения вооб-
вообще. Однако гидравлические, и в частности трубопроводные, системы (ТПС)
сами играют весьма существенную роль в экономике страны и отдельных
регионов. Достаточно сказать, что одних только стальных труб в СССР
ежегодно используется (с учетом импорта труб большого диаметра) более
20 млн. т. При этом наряду с бурным ростом магистрального трубопровод-
трубопроводного транспорта нефти, газа и воды на расстоянии в сотни и тысячи кило-
километров основное место здесь по-прежнему занимают ТПС коммунального
и промышленного назначения. Это видно из значения среднего диаметра
труб, которое при общей длине производимых за год труб порядка мил-
миллионов км имеет величину примерно 100 мм.
Данные факторы, а именно: народнохозяйственная важность гидравли-
гидравлических систем и их многообразие, с одной стороны, а также принципиаль-
принципиальная общность математических моделей и алгоритмов для их расчета и оп-
оптимизации, с другой - вызвали огромный поток математических и отрас-
отраслевых работ-, во многом дублирующих друг друга. Свидетельством такого
положения является и множество наименований этих объектов, фигури-
фигурирующих в литературе: "энергетические сети [188]^"гидравлические сети"
[71, 103, 145, 206, 259], "сетевые системы" [53], "инженерные сети"
[60-62], "производственные сети и системы" [107], "потоковые графы"
[84], "системы сетевой структуры" и другие.
Ни в коей мере не отрицая правомочность различных подходов, уровней
формализации и тем более терминологий (вопросы терминологии и обозна-
обозначений подробнее рассматриваются ниже, во Введении),отметим,что слово-
словосочетание "гидравлические цепи" [242] имеет с точки зрения правильно-
правильного отражения основных черт рассматриваемого ниже научного направления
два решающих преимущества: 1) оно подчеркивает его органическую связь
с теорией электрических цепей и 2) отмечает равную важность как мате-
математического, так и физического ("гидравлического") аспектов иссле-
исследований.
Для проведения теоретических, методических и алгоритмических разра-
разработок по ТГЦ и ее приложениям в СЭИ при его организации В.Я. Хасиле-
вым была создана специальная лаборатория, состоящая из математиков-
прикладников и инженеров - специалистов по отдельным типам гидравли-
гидравлических систем. Все эти годы лаборатория работала (и продолжает работать)
в рамках данной тематики, и основная задача монографии как раз и заклю-
4

чается в том, чтобы систематизировать и компактно представить результа-
результаты исследований.
Монография состоит из двух частей. Изложение основных положений
ТГ1Д начинается с главы 4, содержащей описание алгебры гидравлических
цепей. Так что те из читателей, кто захочет пропустить вводный материал
и обзор литературы, могут обратиться сразу к этой главе. Далее в первой
части даются математические описания гидравлических цепей с сосредото-
сосредоточенными, переменными и распределенными параметрами и общих методов
их расчета как основных инструментов для математического моделирова-
моделирования (с разной степенью точности) реальных гидравлических систем. Спе-
Специальные главы посвящены вопросам практической реализации методов
гидравлического расчета на ЭВМ и способам повышения их вычислитель-
вычислительной эффективности (глава 9) , а также обратным задачам потокораспреде-
ления и связанной с этим проблеме идентификации ТПС — на уровне гид-
гидравлических цепей с сосредоточенными и переменными параметрами (гла-
(глава 11).
Вторая часть (главы 12—19) отведена проблеме математизации, алго-
алгоритмизации и автоматизации оптимального проектирования разветвленных
и многоконтурных систем.
В целом же данная книга преследует в известной степени противоречи-
противоречивые цели. Во-первых, хотелось бы, обратившись к первоисточникам, лучше
разобраться в некоторых-изначальных вопросах (которые нередко считают-
считаются очевидными, но ссылки на них носят зачастую путаный характер или
отсутствуют вовсе). Во-вторых, показать на этом фоне преемственность
и взаимосвязь принципиальных методических положений и в связной фор-
форме представить основные результаты работ, выполненных в СЭИ по теории
и методам расчета и оптимизации гидравлических цепей. В-третьих, изло-
изложить материал на таком уровне, который позволил бы инженерам, имею-
имеющим вузовскую подготовку по высшей математике, в систематизированном
виде ознакомиться с основами математического моделирования и алгорит-
алгоритмизации при постановке и численном решении задач анализа и проектиро-
проектирования гидравлических систем. И в-четвертых, дать возможность математи-
математикам, которые хотели бы заняться приложениями в данной области, полу-
получить общее представление о проблематике и типах возникающих здесь
задач.
Книга содержит описание основных алгоритмов и характеристику разра-
разработанных программ для ЭВМ. Изложение иллюстрируется примерами
построения и преобразования математических моделей, а также расчетов
условных и реальных объектов. В то же время число возможных приме-
примеров сознательно сокращено, чтобы не загромождать основной материал,
тем более что они в достаточной степени представлены в других публика-
публикациях лаборатории [77, 147, 223].
Очевидно, что многие вопросы, обсуждаемые в монографии, неизбежно
носят постановочный и дискуссионный характер. Тем не менее хочется
надеяться, что попытка связного изложения основных результатов иссле-
исследований по ТГЦ окажется успешной и книга заинтересует широкий круг
читателей.
Вопрос об издании обобщающей монографии по ТГЦ обсуждался неодно-
неоднократно, и В.Я. Хасилев все последние годы своей жизни считал написание
5

такой книги своим главным делом. Он не хотел превращать ее в простую
компиляцию из отчетов, статей и диссертаций, а стремился к анализу перво-
первоисточников и переосмыслению исходных положений, раскрытию взаимо-
взаимосвязи различных вопросов. К сожалению, по болезни и другим причинам
он так и не смог приступить к ней. И после его неожиданной кончины в
апреле 1980 г. остались лишь некоторые наметки по поводу возможного
содержания книги, а также его публикации и докторская диссертация.
Вместе с тем коллектив лаборатории СЭИ считает В.Я. Хасилева основопо-
основоположником ТГЦ и одним из основных авторов данной монографии.
Исходный вариант текста книги написан автором этих строк. При этом
использовались статьи и диссертационные работы, выполненные в лабора-
лаборатории за минувшие годы. Соавторами отдельных глав являются: В.Г. Сид-
лер (главы 8, 9, 11 и 17), Е.В. Сеннова (главы 1, 16, 18 и 19), СВ. Сума-
Сумароков (главы 1 и 15), М.К. Такайшвили (главы 5,9), К.С. Светлов (гла-
(глава 5), Н.Н. Меренкова (глава 13), Т.Б. Ощепкова (главы 14 и 15),
А.В. Храмов (главы 16, 18 и 19).
Авторы благодарны академику Л.А. Мелентьеву, членам-корреспонден-
членам-корреспондентам АН СССР Ю.Н. Руденко и О.Ф. Васильеву за постоянное внимание к
работам лаборатории и ценные советы. Кроме того, большую техническую
помощь в подготовке рукописи оказали Л.Е. Сидлер и И.М- Серобабенко.
А.П. Меренков

ВВЕДЕНИЕ
О ТЕОРИИ ГИДРАВЛИЧЕСКИХ ЦЕПЕЙ
КАК НАУЧНО-ТЕХНИЧЕСКОЙ ДИСЦИПЛИНЕ
Вопросы математического описания и расчета электротехнических и гид-
гидравлических систем имеют несомненную общность ряда исходных физико-
математических положений. Вместе с тем теория электрических цепей су-
существует уже более 150 лет, начиная с работ Ома A827 г.), Кирхгофа
A847 г.), Гельмгольца A853 г.) и Максвелла A873 г.), и уже давно оп-
определилась как самостоятельная дисциплина, результаты которой исполь-
используются в теоретической и прикладной электротехнике, радиотехнике,
теории автоматического регулирования и математическом программиро-
программировании. Что же касается гидравлических систем, то работы обобщающего
характера начали интенсивно проводиться здесь лишь с появлением ЭВМ,
хотя можно отметить и отдельные более ранние публикации (см. об этом
ниже).
Теория электрических цепей, очевидно, ведет свое начало с работ Г. Ома,
который первым поставил изучение электротехнических объектов на ма-
математическую основу. Дело не только в том, что ему принадлежит извест-
известный закон, устанавливающий пропорциональную зависимость между си-
силой постоянного тока и разностью потенциалов (напряжением). Он ввел
и уточнил такие фундаментальные понятия, как сила тока, электродвижу-
электродвижущая сила (эд.с), напряжение, сопротивление [96], а также, по-видимому,
и сам термин "цепь", поскольку название его работы [292], упоминание
о которой имеется в БСЭ [29], в переводе на русский звучит как "Галь-
"Гальваническая цепь, обработанная математически".
Следующей по времени и по значению является статья Г. Кирхгофа "О
решении уравнений, описывающих линейное распределение гальваническо-
гальванического тока", опубликованная в 1847 г. [288]. Поскольку в отечественной
литературе удалось обнаружить лишь ссылки на нее (например, в моно-
монографиях В.П. Сигорского [203] и Л.А. Крумма [99]) без описания ее
содержания, то имеет смысл привести здесь перевод начальной части этой
статьи, в которой, собственно, и формулируются знаменитые законы
Кирхгофа.
Без какого-либо вступления и ссылок на других авторов Г. Кирхгоф
сразу формулирует основные результаты: "Пусть задана система из п про-
проводников 1,2,..., л, которые произвольным образом соединены между со-
собой и в каждом из которых имеется своя электродвижущая сила, тогда
Для определения силы токов h,h, ..., /« в проводниках можно построить
необходимое число линейных уравнений на основе использования следую-
следующих двух правил:
7

1. Если проводники &i, к2, ... образуют замкнутую фигуру и wk озна-
означает сопротивление проводника к, а Ек — электродвижущую силу, имею-
имеющую положительную величину в случае ее действия в направлении течения
тока /fc, то /fcj, /fcj, ..., взятые положительными в соответствующем направ-
направлении, удовлетворяют уравнению:
wk Ik + wk Ik + ••• = Ek + -fife + ••• •
2. Если проводники Xt, X2, — соединяются в одной точке и те из /\,,
1\г, ..., которые отвечают токам, направленным к этой точке, берутся по-
положительными, то 4х +1\г + ... = 0.
Теперь я хочу доказать, что решение уравнений, которые можно выпи-
выписать для 1\, /г, ..., 1п на основе этих правил, при условии, что система про-
проводников не распадается на несколько независимых друг от друга под-
подсистем, в общем случае может быть выполнено следующим образом.
Пусть т — число имеющихся точек пересечения, т.е. точек, в которых
соединены два или более проводников, и ц = п - т + 1, тогда общий зна-
знаменатель каждой из величин представляет собой комбинации тех ц эле-
элементов wk , wfcj, ..., wk из w i, vv2, ..., wn, которые соответствуют про-
проводникам ki, кг, ...Дд,обладающим свойством - в случае их удаления -
превращать систему проводников в разомкнутую.
Числитель для /х представляет собой комбинацию тех ju— 1 элементов
wk1> w.k2 у ¦¦¦, wkn_t из и>ь w2, ..., и>„, которые соответствуют проводни-
проводникам fcj, k2, ..., &д_1, обладающим свойством - в случае их удаления -
оставлять единственную замкнутую фигуру, в которую входит данный
проводник X. Каждая такая комбинация умножается на сумму электро-
электродвижущих сил, действующих в данной замкнутой фигуре".
Далее в статье доказывается, что "ju — это минимальное число провод-
проводников, которое следует удалить из системы, чтобы разорвать все ее замкну-
замкнутые фигуры, тогда д будет также и числом независимых уравнений, со-
составляемых на основе правила 1", и выводятся формулы для искомых сил
токов.
Очевидно, приведенные правила составления уравнений и стали называть-
называться законами (или постулатами) Кирхгофа, причем интересно отметить,
что во всей литературе первым законом почему-то считается тот, который
соответствует второму приведенному правилу.
В этой же статье Г. Кирхгоф по существу впервые предложил и переход
к системе независимых переменных в форме контурных токов (аналогич-
(аналогичный вывод делается в монографиях Ф. Реза и С. Сили [191], Л.А. Крумма
[99]) и фактически ввел в обращение понятие о главных ветвях (хордах),
удаление которых превращает исходную схему в разомкнутую, т.е. в
"дерево".
В 1857 г. Г. Кирхгоф опубликовал новую статью, посвященную некото-
некоторым топологическим представлениям в теории цепей (изложение данной
статьи дано в качестве приложения к уже упомянутой книге [191]) ,в ко-
которой, в частности, предлагается метод установления соответствия между
схемой цепи и прямоугольной таблицей чисел 0, +1, —1, т.е. вводится матри-
матрица соединений (инциденций) ее узлов и ветвей.
Здесь нет ни намерения, ни возможности давать обзор дальнейших пуб-
публикаций по теории электрических цепей. Из последующих работ выделим
8

тотько (что важно с точки зрения дальнейшего изложения) теорему
д к Максвелла о принципе наименьшего теплового действия для электри-
электрических цепей. В "Трактате об электричестве и магнетизме" [290] доказа-
доказано что "в любой системе проводников, где нет источников э.д.с. и токи
отвечают закону Ома, тепло, генерируемое установившимся токораспреде-
лением, всегда меньше, чем токами, распределенными любым другим
образом, но согласующимися с условиями притекания и вытекания".
Эта теорема стала объектом пристального внимания относительно недавно,
в связи с попытками обобщения результатов теории электрических цепей
на нелинейные системы [263, 278, 283]. Кроме того, она лежит в основе
физической аналогии и взаимосвязи между задачами математического
программирования и токораспределением в электрической цепи [58],
а также экстремального подхода к описанию и расчету потокораспределения
в различных системах (см. об этом ниже, в гл. 7).
Отметим, что именно Максвеллом предложено также и сведение исход-
исходной системы уравнений Кирхгофа к уравнениям относительно узловых
напряжений (указание на это содержится в книге [99]).
Таким образом, теория электрических цепей имеет уже довольно длин-
длинную и богатую историю. Несомненно, что широкое использование матема-
математических методов в этой области и вообще в теоретической электротехнике
в значительной мере было связано с бурным развитием физики и большим
практическим значением электрической энергии. Но очевидно и то, что са-
сама возможность их эффективного применения определялась также и линей-
линейностью исходных элементов, использовавшихся в то время при построении
электрических цепей. Поэтому данная теория развивалась (и имела прак-
практические приложения даже в условиях ручного счета) прежде всего как ли-
линейная теория.
Известно, что такие результаты этой теории, являющиеся ее стержнем,
как методы контурных токов и узловых напряжений, принцип суперпо-
суперпозиции и взаимности отдельных решений, теорема об эквивалентном гене-
генераторе, преобразование "звезды" в многоугольник, а также обратное его
преобразование и другие, которые стали мощным инструментом для иссле-
исследований и расчетов, это в конечном итоге следствие и сетевая интерпрета-
интерпретация основных положений линейной алгебры.
В современной теории электрических цепей используются, конечно,
не только линейная алгебра, но и: гармонический анализ, операционное
исчисление, интегральные преобразования, теория графов, математическое
программирование, вероятностные методы и другие дисциплины. Являясь
областью приложений для многих математических результатов, она сама
оказывала серьезное влияние на их развитие и даже на возникновение ряда
новых математических методов, приобретавших впоследствии более широ-
широкое значение. В качестве примера можно указать, что упомянутые работы
Кирхгофа стимулировали создание топологии, изучающей наиболее общие
геометрические свойства тел и фигур, а также теории графов. То же самое
имело место при создании операционного исчисления в связи с возникно-
возникновением задач по расчету электромагнитных колебаний в контурах.
В области расчетов гидравлических систем сложилось качественно
иное положение. Такой общей физико-математической базы, какую пред-
представляет для электротехники теория электрических цепей, здесь не было.
9

И одно из главных объяснений заключалось в существенной нелинейности
гидравлических систем, которая в условиях ручного счета лишала практи-
практического смысла разработку их общих математических описаний и методов
расчета.
Вместе с тем отдельным вопросам расчета гидравлических систем посвя-
посвящались сотни работ, публикуемых в научно-технической литературе с кон-
конца 19-го столетия. Среди них немало таких, которые и до сего дня сохраня-
сохраняют свое значение. Одними из первых здесь можно считать работы фран-
французских и русских горных инженеров по расчету рудничной вентиляции
[291, 185 и др.] и работы русских, немецких и американских инженеров-
гидравликов по системам водоснабжения [271, 224, 113 и др.].
Потребность в обобщении имеющихся разработок и их распростране-
распространении на другие типы систем стала осознаваться лишь с 30-х годов, когда стали
активно вестись исследования по разработке и применению различных
аналоговых устройств в виде электрических и,в меньшей мере,гидравличес-
мере,гидравлических моделей. С появлением ЭВМ необходимость в систематизации извест-
известных и использовании новых методов, а также в различных обобщениях
стала особенно острой и вызвала множество статей и монографий.
Так, Е. Черри и У. Миллар [263], а также Г. Биркгоф и Д.Б. Диаз [278]
рассмотрели некоторые идеи и общие теоремы, относящиеся к "нелиней-
"нелинейным энергетическим и механическим системам", и "новые вариационные
принципы" для нелинейных систем, которые должны, по их мнению, прий-
прийти на смену приведенного выше принципа наименьшего теплового действия,
сформулированного Максвеллом для линейного случая (см. об этом
в гл. 7).
Книга Г. Кёнига и В. Блекуэлла "Теория электромеханических систем"
[86] посвящена "объединению в целях теоретического анализа и синтеза
весьма различных по своим свойствам и назначению элементов (электри-
(электрические машины, электронные, магнитные и другие усилители, гидропреоб-
гидропреобразователи, гироскопы)", которое авторы основывают "не на применении
известного метода аналогий, а на использовании одной из ветвей тополо-
топологии — теории графов". Речь идет о стремлении выявить "глубокую общ-
общность в математическом описании элементов различной физической при-
природы", чтобы обеспечить применение строгих методов и их обоснованное
упрощение.
Став на путь формализации и систематизации, Г. Кёниг и В. Блекуэлл
упорядочивают исходные понятия, обозначения и методические приемы.
Они разбивают все основные величины по способу их измерения на две
группы: 1) "продольные" (параллельные) переменные (напряжения, пе-
перемещения, углы поворота, изменения давления и температуры), измере-
измерение которых требует одновременного подсоединения прибора в двух точ-
точках, и 2) "поперечные^' (последовательные) -переменные (ток, сила, мо-
момент, расход жидкости), которые можно измерить последовательным
включением прибора с каждым из элементов системы. Далее ими вводится
понятие графа электромеханической системы и обобщаются законы Кирх-
(гофа в виде двух следующих постулатов для контуров и вершин: 1) сумма
продольной переменной вдоль контура и 2) сумма поперечной переменной
в вершине равняются нулю. И все содержание книги в методическом плане
фактически сводится к рассмотрению (на довольно абстрактном уровне)
10

уравнений ветвей и отсечений, хорд и фундаментальных контуров. Подоб-
Подобная терминология стала применяться и в отечественной литературе [60, 83].
Разработкой и применением математических методов и ЭВМ для расчета
и оптимизации электроэнергетических, трубопроводных и других систем
сетевой структуры занимались и занимаются очень много авторов. (Обзору
этих работ посвящены гл. 3 и 12.) Однако в большинстве из них превали-
превалирует или формальная (математическая) сторона, когда физическая сущ-
ность и принципиальные особенности рассматриваемых задач отходят на
второй план, или сугубо отраслевой аспект. И в том и в другом случае
имеет место известный ущерб как для самих исследований, так и для
практики.
На этом фоне теория гидравлических цепей (ТГЦ) выделялась именно
тем, что она с самого начала строилась и развивалась [242, 243, 247, 128,
132, 140 и др.] как научно-техническая дисциплина, смежная с теорией
электрических цепей и синтезирующая — на некотором межотраслевом
и в известном смысле оптимальном "физико-математическом" уровне —
общие результаты, справедливые в принципе для любых трубопроводных
и гидравлических систем.
Подобный подход, ориентированный на гидравлические системы в це-
целом, и построение общей для них теории обеспечивают: единый язык для
постановки задач и достаточно строгую" базу для применения современных
достижений смежных математических и других дисциплин; обоснованную
классификацию задач, а также дифференциацию методов их решения в
зависимости от целей исследования, типа системы, параметров исполь-
используемой ЭВМ, качества и количества исходных данных; комплексное ре-
решение вопросов математического и алгоритмического обеспечения опти-
оптимального проектирования и управления этими системами.
Следует отметить существенное различие между теорией цепей и теорией
графов. Если предметом последней является изучение произвольного мно-
множества точек и отношений между ними как абстрактного математического
объекта, то ТГЦ занимается математическим моделированием и изучением
реальных физико-технических систем. Теория графов используется при
этом как один из вспомогательных инструментов, позволяющих компакт-
компактно учитывать топологические свойства рассматриваемых объектов.
Сочетание математического и вычислительного аспектов с понимани-
пониманием и учетом физической, инженерной и сетевой сущности рассматриваемых
задач позволило получить ряд результатов, выходящих за рамки односто-
односторонних (по типам систем) исследований. Собственно, одна из основных
Целей данной монографии как раз и состоит в показе целесообразности,
а также научно-методической и практической значимости такого научного
направления.
Основные разделы и приложения ТГЦ, составляющие содержание кни-
книги, показаны на рис. В.1.
ТЕРМИНОЛОГИЯ, ИСХОДНЫЕ ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
Понятие "цепь" и словосочетания с ним: "электрическая цепь", "магнит-
"магнитная цепь", "радиоэлектронная цепь" и др. - 'широко используются в раз-
различных областях науки и техники. В теории графов [25, 97, 175, 234]
11

Экстремальный
подход
Численные
методы
Изучение
стационарных
процессов
Автоматизация
гидравлических
расчетов'
¦е-g

простой цепью понимается маршрут, составленный из конечной после-
вательности ребер графа и проходящий через различные его вершины.
для ориентированного графа (орграфа) это соответственно путь из после-
последовательности дуГ) в КОТОрОИ ни одна вершина не встречается дважды.
Замкнутая же цепь называется циклом (контуром).
С учетом этого электрической или гидравлической цепью естественно
считать заданную совокупность "маршрутов" (или "путей") для движения
электрического тока, жидкости или газа. Более строго электрическая
цепь определяется [30, 210] как "совокупность различных устройств и
соединяющих их проводников (или элементов электропроводящей среды),
по которым может протекать электрический ток". Соответственно гидрав-
гидравлической цепью (г. ц.) будем считать "совокупность устройств и соеди-
соединяющих их трубопроводов, закрытых или открытых каналов, осуществля-
осуществляющих транспортировку сжимаемых и несжимаемых жидкостей (воды,
нефти, газа, воздуха и других) ".
Таким образом, г. ц. должна рассматриваться прежде всего как физи-
физическая модель реальной гидравлической системы и, следовательно, как
самостоятельный объект, который можно собрать или мысленно себе
представить. Однако чаще всего под г. ц. будем понимать и собственно
математическую модель, включающую две составные части: расчетную
схему цепи, геометрически отображающую конфигурацию (структуру)
изучаемой системы и картину возможных направлений, смешения и раз-
разделения потоков транспортируемой среды; совокупность математических
соотношений, описывающих взаимозависимость количественных характе-
характеристик элементов данной схемы, а также законы течения и распределения
расходов, давлений и температур (в неизотермическом случае) транспорти-
транспортируемой среды по всем этим элементам и их изменения во времени (при
изучении динамических процессов).
Подобная многозначность этого термина не вызовет трудностей, по-
поскольку из текста будет ясным, что имеется в виду. Зато это позволяет
более экономно излагать материал. Например, вместо "математического
описания гидравлической системы в виде модели с сосредоточенными
параметрами" можно просто говорить о "г. ц. с сосредоточенными па-
параметрами" и т.п.
В любой гидравлической системе различают три ее основные состав-
составляющие (подсистемы): 1) источники давления или расхода (например,
насосные или компрессорные станции, аккумулирующие емкости и др.),
обеспечивающие притоки транспортируемой среды и привносящие энергию
в систему; 2) трубопроводную или гидравлическую сеть (в виде совокуп-
совокупности взаимосвязанных трубопроводов, воздуховодов и открытых кана-
каналов) , соединяющую источники со множеством потребителей и доставляю-
доставляющую эту среду; 3) абонентские подсистемы (или просто потребители).
Такое деление, в общем-то, довольно условно и зависит от целей изу-
изучения реальной системы и характера решаемых задач, степени детали-
детализации, а также и от режимов ее работы. Например, в качестве потреби-
потребителей могут рассматриваться как отдельные установки, так и здания или,
скажем, кварталы города или даже город в целом. Сеть в одних случаях
включает лишь основные магистрали между источниками и укрупненными
потребителями, а в других она может отображать и конкретизировать
13

эта связи вплоть до разводящих линий и фактических потребителей. Точно
так же и источники могут задаваться вместе со своей "начинкой" (обору-
(оборудованием) или лишь выходными параметрами. Одни и те же аккумули-
аккумулирующие емкости в системе в режимах их заполнения являются потребите-
потребителями, а в режимах опорожнения — источниками и т.п.
При математическом моделировании все эти подсистемы находят соот-
соответствующее отражение в расчетной схеме цепи: участки сети, включаю-
включающие арматуру и другие местные сопротивления, — в виде ветвей; места
расположения источников расхода (притоков) и потребителей (стоков),
а также соединений ветвей — в виде узлов (вершин); источники напора
(а иногда и расхода) могут относиться как к узлам, так и к ветвям.
Среди параметров узлов и ветвей г. ц. будем различать: технические
характеристики (диаметры трубопроводов, размеры сечений каналов,
длины и гидравлические сопротивления ьетвей); гидравлические пара-
параметры (расходы жидкости на ветвях или в узлах, давления в узлах, из-
изменения давления и температуры на ветвях), описывающие состояние
системы в любом из ее режимов работы; граничные условия — варьи-
варьируемые входные данные (величины притоков и нагрузок, допустимые
диапазоны в значениях гидравлических параметров).
Гидравлическая цепь удовлетворяет всем основным требованиям,
предъявляемым к моделям [157]: 1) она способна замещать исследу-
исследуемый и управляемый объект, т.е. реальную гидравлическую систему, и
2) ее изучение и реализация (с помощью ЭВМ) повышают наши знания
о системе и позволяют управлять ее структурой и режимами работы.
Математическое моделирование всегда является приближенным, и
степень его точносги должна согласовываться с целями исследования
или управления, количеством и качеством исходных данных, парамет-
параметрами используемой ЭВМ. В связи с этим точность как физического, так
и математического моделирования любой гидравлической системы бу-
будет определяться в основном выбором для ее отображения и изучения
г. ц. одного из следующих трех типов:
1) с сосредоточенными параметрами, когда все технические характе-
характеристики узлов и ветвей, а также граничные условия считаются констан-
константами, не зависящими от того или иного потокораспределения (такие це-
цепи моделируют реальные системы как системы с изотермическим тече-
течением несжимаемой жидкости);
2) с переменными параметрами, когда хотя бы часть технических и
гидравлических параметров или граничных условий задается в виде функ-
функций от искомых величин, так что их фактические значения являются пере-
переменными и определяются ("регулируются") самим потокораспределе-
нием;
3) с распределенными параметрами - в случае наиболее строгого описа-
описания совместного изменения гидравлических параметров вдоль элементов
расчетной схемы.
С математической точки зрения это приводит для установившихся ре-
режимов к системам уравнений специальной структуры:
1) из линейных (сетевых) и нелинейных (замыкающих) алгебраических
уравнений с постоянными коэффициентами; 2) из уравнений общего
характера с переменными коэффициентами и правыми частями и 3) сме-
14

иных систем, содержащих подсистемы уравнений в дифференциальной
ши интегральной форме.
Тчудности с терминологией и выбором обозначений, особенно для сты-
стыковых научных направлений, общеизвестны. В качестве посильной цели
будем руководствоваться лишь стремлением отбора и упорядочения не-
необходимого "рабочего" минимума понятий и символики, используемых
й смежных дисциплинах: теории электрических цепей, линейной алгебре,
теории графов и гидравлике. При этом будем отдавать предпочтение тех-
техническим терминам как более наглядным и привычным для теории эле-
электрических цепей и отраслевой литературы и говорить: "ветвь" и "уча-
"участок" (сети), а не "'ребро" или "дуга", "узел" вместо "вершины" и т.п.
Ниже дается сводка исходных понятий и обозначений, используемых
в дальнейшем (начиная с гл. 4).
Схема цепи - графическое изображение моделируемой системы,
совокупность трех упорядоченных множеств: множества узлов
у = { / : } = 1, ..., т}, состоящего из подмножеств (потребителей J\, ис-
источников Л и простых точек разветвления на схеме У3)| множества вет-
ветвей / = {i '¦ ' = 1, •••, п), отображающих заданные попарные связи (сое-
(соединения) 'между узлами; множества условных знаков, характеризующих
тип и специфические особенности элементов. С точки зрения теории гра-
графов схема г. ц. - конечный ориентированных граф (орграф), дополнен-
дополненный специальными поясняющими знаками, если это требуется. Числа
т и п называются параметрами г. ц.
Простой контур — конечная и замкнутая последовательность ориенти-
ориентированных ветвей, у которой совпадают только начальный и конечный
узлы. (В дальнейшем рассматриваются именно такие контуры.) Число
с линейно-независимых контуров в любой выбранной на схеме ба-
базисной системе контуров однозначно определяется параметрами г. ц.:
с = п ~ т + 1. Текущий номер базисного контура будем обозначать через
г: >¦= 1,...,с.
Источники (притоки) и потребители (стоки) - узлы, в которых за-
задано поступление или отбор транспортируемой среды.
Активная (пассивная) ветвь — связь между узлами, содержащая (не
содержащая) источник подводимой среды или энергии.
Базисный (опорный) узел - точка на схеме с фиксированным значе-
значением потенциала (чаще всего это узел, в котором поддерживается извне
атмосферное давление).
Циклическая схема - расширенная связная схема г. ц. без притоков
и стоков, полностью отображающая "круговорот" при движении среды
в системе. Она может быть получена из исходной схемы соединением
всех ее источников и потребителей дополнительными условными ветвя-
ветвями с одним и тем же опорным узлом.
Остовное дерево (каркас, или просто дерево) - подсхема без контуров
Vможет совпадать с исходной схемой), соединяющая все узлы и имеющая
т - 1 ветвей.
Хорды - главные ветви, не вошедшие в выбранное остовное дерево и
Дополняющие его до полной схемы.
Движение транспортируемой среды будем считать одномерным, усред-
1ЯЯ по сечению трубы или канала скорость, плотность, давление и темпе-
15

ратуру потока. При этом, как правило, будет рассматриваться стационар-
стационарный гидравлический режим, отвечающий некоторому установившемуся
в системе процессу течения.
Параметры узла: Q,- - расход среды в узле/, т.е. количество жидкости
(воды, нефти, газа, воздуха, смеси) в единицах объема или массы, при-
притекающей к нему или вытекающей из него за единицу времени (при этом
Q,- > 0 в случае источника (притока), Q/ < 0 для потребителя и Q,- = О,
если у?ел/-простая точка разветвления на схеме); 2х =2 Q/ =- Б Q,--
суммарная производительность источников, которая должна совпадать с
общим расходом (нагрузкой) у потребителей; Pj — значение потенциала
(гидростатического давления) в узле /; 7) — температура (смешанного)
в узле потока жидкости (если этот узел является общим для нескольких
ветвей); Щ - действующий (развиваемый) в источнике / е J2 напор,
задаваемый в виде потенциала, подводимого в точку / источником пита-
питания или циркуляции (насосом), аналог электродвижущей силы (э.д.с.)
в электрической цепи; Э = 2 #/(?/ - величина, пропорциональная общей
/е/2
энергии системы, создаваемой ее источниками; t';c/ — заданные темпера-
температура и теплоемкость жидкости, притекающей к узлу/.
В случае г.ц. с переменными параметрами (см. гл 8) данные величины
могут задаваться функционально связанными, например: Qj (Pj), ///(&•)
и т.д.
Параметры, характеризующие ветвь с номером / и номерами его конце-
концевых узлов /, /+ 1 (/=[/',/+ 1 ]):
X; - установившийся на ветви / расход транспортируемой среды, т.е.
количество жидкости, проходящей через поперечное сечение трубы или
канала за единицу времени (аналог силы электрического тока); при этом
Xj > 0, если направление течения совпадает с ориентацией ветви /, и xt < О
в противном случае;
у{ = Pj - Р/+1 (или yi = Pf - Pj+ j, например, для газопроводов среднего
и высокого давлений) — разность потенциалов, перепад давлений на ветви;
Hi — действующий напор, задаваемый в виде подводимой к ветви разно-
разности потенциалов (будем считать, что он измеряется в тех же единицах,
что и величины Pj), для пассивной ветви Щ = 0;
hi ~ Уг + Hi — потеря давления на ветви, связанная с преодолением
трения (мера удельной кинетической энергии потока), для пассивной
ветви hj = yt;
dj — внутренний диаметр трубы;
Lj — длина ветви;
s,- (dj, Li) — коэффициент гидравлического сопротивления (или просто
сопротивление) ветви - при одночленной зависимости между /г,- и xt.
В случае распределенных параметров необходимо вводить в рассмотре-
рассмотрение кривые Pi (/,-), f/(/,-), с,(/,), описывающие изменение давления, темпера-
температуры и изобарной теплоемкости вдоль ветви и соответствующие подсисте-
подсистемы дифференциальных или интегральных уравнений (см. гл. 10). Здесь
/ ,• — переменная, характеризующая расстояние от начального узла ветви
до любой ее точки @< /,< Lt); 2— суммирование по всем ветвям, имею-
/
16

ним общий узел /; Б -- суммирование по всем ветвям, составляющим кон-
контур г.
Векторные обозначения:
/, = (/,),..., Uif - вектор из длин ветвей;
/ = (/,,. . . , 1„У — вектор переменных/,@ < / </,);
.V, d, s - векторы расходов xjt диаметров dj труб и гидравлических сопро-
сопротивлений Sjl
yt h, H - векторы перепадов у{, потерь /г,- и действующих напоров //,• на
ветвях;
хк = (*,,..., хс)т, ук = (у, усУ, hK = (hi /г„)т - векторы
расходов, перепадов и потерь давлений на хордах, т.е. векторы "контур-
"контурных переменных";
хд = (xc+i, .... хп)т, уа = (ус+1> . . . ,у„У, /гд = (hc+u. . . ,И„)Т -векто-
-векторы расходов, перепадов и потерь давлений на ветвях дерева;
Р = (Pi,. . . , Рт-\, Р'т)Т - вектор узловых давлений (или их квадра-
квадратов) , где Р',„ — заданное значение (в качестве опорного узла, как пра-
правило, будет выбираться узел m)\ m
Q - (Qi, ¦ ¦ ¦, Qmf - полный вектор расходов в узлах, 2 Qj = 0;
Р = (Л Рт 1 )]Q - (Q\. • • • , Qm- l )T - векторы расходов и давле-
давлений в линейно-независимых узлах;
Т = G*! ТтУ — вектор узловых температур смешанных потоков:
р (/), t(l), c(l) - вектор-функции кривых изменения давления p,-Gi)>
температуры /,• (/,•) и изобарной теплоемкости с,- (/,¦) на ветвях;
р@), p(L); t@), t(L); c@), c(L) - векторы граничных значений этих вели-
величин соответственно в начальных и конечных узлах ветвей;
т — знак транспонирования.
Матричные обозначения:
А = { dji} - полная т X п - матрица соединений узлов и ветвей, она
однозначно описывает структуру схемы цепи и ориентацию ее ветвей;
здесь aji = 1, если узел / является начальным для ветви i
(т.е. ветвь i исходит из узла/), я,-,- = -1, если узел / является конечным для
ветви /' (т.е. ветвь / ориентирована в направлении к узлу/), иа;-,- = 0, когда
узел/ не принадлежит ветви /;
А - (т — 1) х и — матрица соединений для линейно-независимых уз-
узлов;
Ли А2; Ait А2 - матрицы ориентирования ветвей, получаемые из А
или А заменой всех их элементов, равных соответственно (-1) или (+1),
нулями, они фиксируют отдельно все начальные или конечные узлы ветвей;
очевидно, что Л! +А2 = А к Ах +А2 = А;
В ={bri} - с х п — матрица контуров, она описывает совпадение выбран-
выбранной базисной системы контуров и ветвей; здесь bri = 1, если ветвь / при-
принадлежит контуру г и ее ориентация совпадает с направлением обхода
контура; ЬГ( = — 1, когда ориентация входящей в контур г ветви/ противо-
2- Зак. 384 17

лоложна направлению его обхода, и brj = О, если ветвь / не входит в контур
П
S, X, С (I) — диагональные матрицы порядка п, составленные из вели-
величину, \х( \®~1 и с,-(/,-)д}., где/3 — заданный показатель степени.
Некоторые сокращения:
ЭЭС и ТПС - электроэнергетическая и трубопроводная системы; ТСС,
ВСС, НСС и ГСС - тепло-, водо-, нефте-и газоснабжающие системы:
НС и КС - насосная и компрессорная станции;
РР и РД - регуляторы расхода и давления;
PC — разветвленная система, схема которой представляет собой граф
в виде дерева;
МКС — многоконтурная система, описываемая произвольной схемой,
содержащей контуры, так что для всех или части ее потребителей может
быть осуществлено двух- и многостороннее снабжение от источников;
МКР - метод контурных расходов;
МД - метод узловых давлений;
МКО — многоконтурная оптимизация;
ПВК — программно-вычислительный комплекс.

Часть первая
ОСНОВЫ ТЕОРИИ И МЕТОДЫ РАСЧЕТА
[лава 1
ГИДРАВЛИЧЕСКИЕ СИСТЕМЫ
И ИХ ГИДРАВЛИЧЕСКИЕ ЦЕПИ
1.1. ПРИМЕРЫ ГИДРАВЛИЧЕСКИХ ЦЕПЕЙ
Трубопроводные и другие гидравлические системы при всем разнообразии
их назначения и физико-технических особенностей имеют, как отмечалось
выше, геометрически аналогичные конфигурации, подчиняются одним и
гем же "сетевым постулатам" Кирхгофа и однотипным законам гидравли-
гидравлического сопротивления. Эта общность отчетливо проявляется при моде-
моделировании данных систем с помощью г.ц. и переходе к математическим
формулировкам и численным методам решения задач их расчета, оптими-
оптимизации и управления.
Рассмотрим несколько примеров представления различных систем в
тис 1.Ц., отмечая при этом их существенные для моделирования особен-
особенности. Заметим сразу, что г.ц., моделирующие рдин и тот же объект, будут
рачличными в зависимости от целей расчета и характера решаемых задач.
Среди ТПС уникальными во многих отношениях являются теплоснаб-
теплоснабжающие системы (ТСС) E4. 147]. В отличие от во до-, газо-и нефтеснаб-
жаюших систем (ВСС, ГСС и НСС) они имеют двухлинейную сеть трубо-
пронодов: подающую — от источников до потребителей — и обратную -
от потребителей до источников, т.е. являются системами с замкнутой
циркуляцией. При этом свойство саморегулирования у потребителей здесь,
как правило, отсутствует, поскольку распределение теплоносителя произ-
производится не авторегуляторами, а предварительной установкой специально
рассчитанных (на о/дан из режимов) постоянных гидравлических сопротив-
сопротивлений.
Увеличение единичной мощности источников до 2500 мВт и более, и их
совместное использование для покрытия общей тепловой нагрузки привело
к образованию крупных многоконтурных ТСС с несколькими источника-
источниками, весьма сложной конфигурацией тепловых сетей, тысячами потребите-
потребителей и диаметрами магистральных трубопроводов 1200—1400 мм.
На рис. 1.1 и 1.2 даны варианты г.ц. для ТСС левобережной части г. Ново-
Новосибирска. Схема на рис. 1.1 отображает трубопроводную сеть системы в
однолинейном" представлении и содержит 61 узел, 90 ветвей и 30 неза-
нисимых контуров. Потребители представлены здесь отборами воды из
' (• С, а источники — притоками в нее. Подобными г.ц. ТСС моделируются
при решении проектных задач. В задачах же гидравлического расчета (осо-
(особенно при анализе послеаварийных ситуаций) и управления режимами эти
19

1.1. Схема теплоснабжающей системы в "однолинейном" изображении
1 — существующие участки; 2 — вновь проектируемые участки; 3 — ТЭЦ; 4 -
требители; 5 — насосные подстанции
системы должны моделироваться более сложными г.ц., отображающими
как подающие, так и обратные трубопроводы тепловых сетей, а также
теплоподготовительные установки источников и установки потребителей
(рис. 1.2). Параметры "двухлинейной" схемы существенно больше (т=
= 122, п- 221 и с = 100), причем источники и потребители в ней уже должны
моделироваться в виде специально вводимых ветвей.
Современные городские ВСС [2,223] являются не менее сложными
инженерными сооружениями с несколькими источниками водоснабжения,
множеством насосных станций (НС) и регулирующих емкостей. К ним
подключается большое число потребителей, потребляющих воду в раз-
различных количествах в соответствии с переменными суточными и годо-
годовыми графиками. На рис. 1.3 показана схема ВСС одного из районов
г. Иркутска, имеющая четыре источника поступления воды (притоки),
две НС подкачки и три аккумулирующих емкости (резервуары).
Наряду с крупными городскими ВСС получили развитие системы груп-
групповых водопроводов [222, 223] для централизованного водоснабжения
многочисленных населенных пунктов и сельскохозяйственных объектов
в пределах района, области или более обширного региона. На рис. 1.4
приведена схема центральной части Пресновского группового водопровода
20

1.2. Схема теплоснабжающей системы в "двухлинейном" изображении
1,2 — участки подающих и обратных трубопроводов; 3 — ТЭЦ", 4 — узлы под-
подключения потребителей
1-3. Схема водоснабжающей системы
1 - насосная станция подкачки (НС) ; 2 — резервуар; 3 — потребитель воды;
- приток (поступление) воды

1.5. Схема Ростовско-Краснодарской системы магистральных каналов
КЗС — водозаборное сооружение; НС — насосная станция; 1 — сопрягающее со-
сооружение (для гашения избыточной энергии потока воды)
с тремя источниками подачи воды из рек Ишим и Тобол, который охва-
охватывает площадь в 45 тыс. км2.
Важными транспортными гидравлическими системами водного хозяй-
хозяйства страны стали каналы различного типа (оросительные, осушительные,
энергетические, судоходные, для переброски вод и пр.), предназначенные
Для подащ, распределения, подвода и отвода больших количеств воды.
Их можно выделить [143, 221, 264] в отдельный класс объектов — системы
многопрофильных каналов, имеющие общие отличительные особенности
(характерные профили и поперечные сечения, однотипные аналитические
нависи мости, описывающие течение воды и т.д.). На рис. 1.5 представлена
схема Ростовско-Краснодарской системы магистральных каналов для
череброски воды из р. Дон с общей длиной трасс порядка 1500 км.
Мощными и сложными системами трубопроводного транспорта стали
магистральные нефтепроводы страны [137, 155]. Они имеют трубопрово-
трубопроводы большого диаметра (до 1200 мм) протяженностью в тысячи километ-
километров, проложенные в несколько ниток с множеством лупингов и перемычек
между ними со значительным числом НС, суммарная мощность электро-
23

1.6. Фрагмент двухниточного нефтепровода (а) и схемы его гидравлических цепей
(б, в)
1 — расчетный узел; 2 — подпорный насос; 3 — нефтеперекачивающая станция
(НПС)-; 4 — регулятор давления (РД) ; 5 — промежуточный приток нефти; 6 — основ-
основная нитка; 7 — перемычка; 8 - фиктивная (условная) ветвь; 9 — регулятор рас-
расхода (РР) ; 10 — фиктивный действующий напор; 11 — фиктивный узел; 12 — на-
направление потока
приводов которых измеряется миллионами киловатт, а также сложную
автоматику для управления режимами их работы.
На рис. 1.6, а представлен типичный фрагмент двухниточного нефте-
нефтепровода, а на рис. 1.6,6 - схема его г.ц. для задачи анализа потокораспре-
деления. Здесь регуляторы на перемычках (РД) являются условными и
моделируют работу задвижек в случае различных значений давления нефти
на параллельных нитках. На рис. 1.6, в показана г.ц. рассматриваемого
фрагмента в более сложных задачах определения допустимых объемов
притоков и максимальной производительности всей системы. В данном
случае потребовался переход к циклической схеме, которая получается
введением дополнительного узла 11 и соединения его фиктивными ветвями
со всеми узлами, имеющими притоки или отборы нефти. На этих ветвях
вводятся условные РР для учета ограничений на максимально допустимые
24

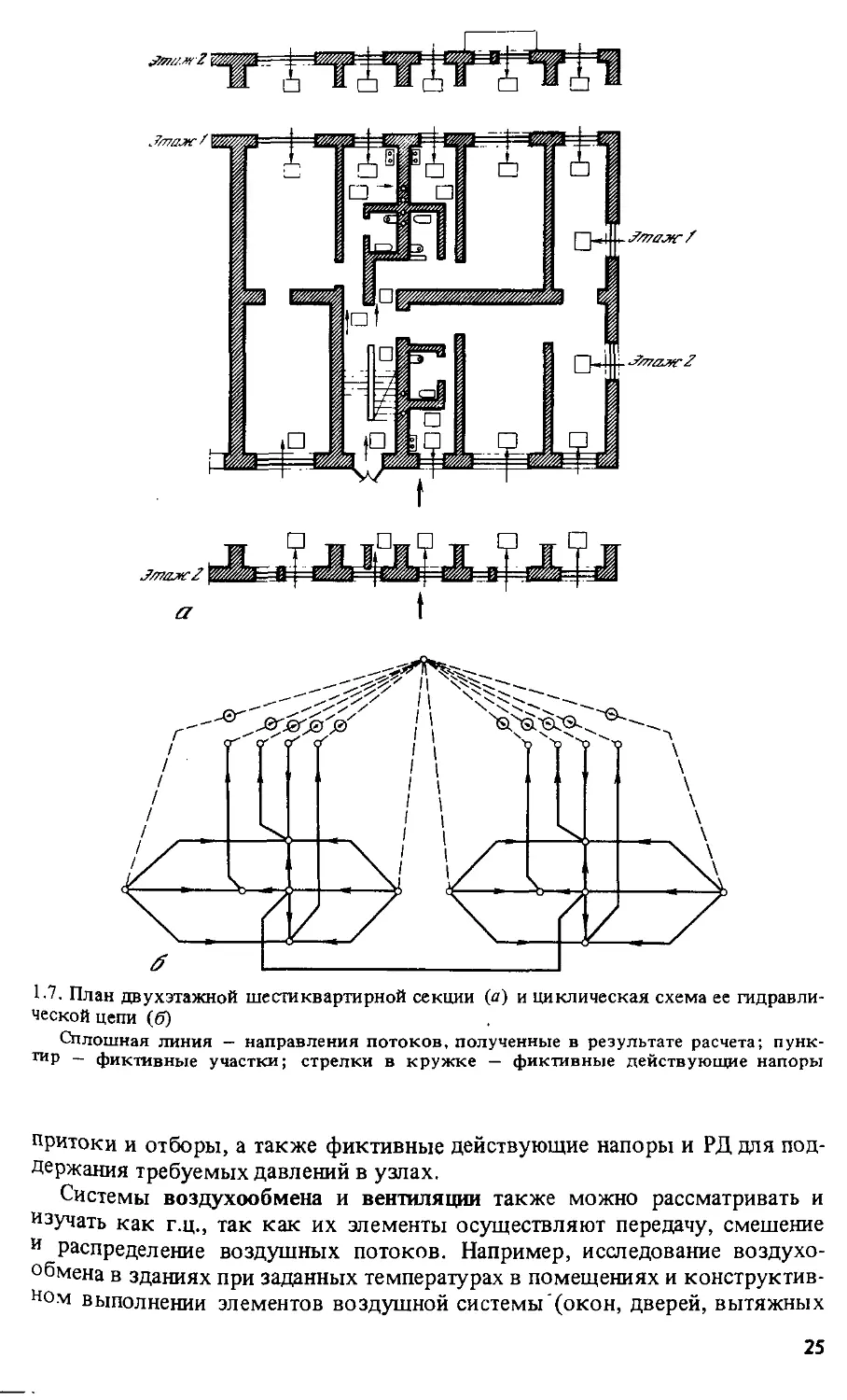
1.7. План двухэтажной шестиквартирной секции (а) и циклическая схема ее гидравли-
гидравлической цепи (б)
Сплошная линия — направления потоков, полученные в результате расчета; пунк-
ТИР — фиктивные участки; стрелки в кружке — фиктивные действующие напоры
притоки и отборы, а также фиктивные действующие напоры и РД для под-
Держания требуемых давлений в узлах.
Системы воздухообмена и вентиляции также можно рассматривать и
изучать как г.ц., так как их элементы осуществляют передачу, смешение
и распределение воздушных потоков. Например, исследование воздухо-
воздухообмена в зданиях при заданных температурах в помещениях и конструктив-
конструктивном выполнении элементов воздушной системы (окон, дверей, вытяжных
25

каналов, открытых проемов и т.д.) может быть сведено к задачам потоко-
распределения в кольцевых гидравлических цепях [195—197]. Специфика
данных систем заключается в том, что они представляются неплоскими
схемами с большим числом элементов и неоднородной зависимостью
потерь напора от расхода.
На рис. 1.7, а показан план двухэтажной шестиквартирной секции жило-
жилого дома, а на рис. 1.7, б - циклическая схема г.ц., моделирующей воздущ.
ную сеть данной секции. Элементы системы на плане и соответствующие им
элементы цепи пронумерованы одинаковыми цифрами. (При составлении
схемы окна одной квартиры, выходящие на одну сторону, заменены одним
элементом, два вытяжных канала одной квартиры объединены в один по
правилу суммирования проводимостей). Напор фиктивных источников
равен разности давлений между соединенными точками.
Многие гидравлические системы используются для вертикального тран-
транспорта тепловой энергии. Теплоносителем в них является сама движущаяся
среда, как и в ТСС, но ее распределение по ветвям существенно зависит
от тепловых потоков и температур. Это связано с тем, что плотности
жидкости на отдельных ветвях, где происходит активный теплообмен
с окружающей средой, заметно изменяются. А так как эти ветви расположе-
расположены в различных горизонтальных плоскостях, то возникают неуравновешен-
неуравновешенные силы тяжести, которые действуют как дополнительные источники
напора и влияют на распределение потоков. Такие системы должны моде-
моделироваться гравитационными г.ц. [246] .
На рис. 1.8 представлены фрагменты отопительных систем различных
типов (с непосредственным водозабором) и их г.ц. Показанные при этом
действующие напоры являются гравитационными и вычисляются как
произведение разности средних плотностей теплоносителя (до и после
прибора) на соответствующий перепад высот.
Примером компактной гидравлической системы могут служить жидко-
жидкостные системы охлаждения автодвигателей [68], которые постоянно услож-
усложняются в связи со все усиливающейся тенденцией повышения их абсолют-
абсолютной и удельной мощности. Кроме того, на большегрузных автомобилях,
мощных самосвалах и междугородных автобусах наряду с обеспечением
нормального теплового режима работы двигателя требуется обеспечивать
необходимый тепловой режим агрегатов трансмиссии и температурный
уровень в кабине автомобиля или салоне автобуса. В связи с этим системы
охлаждения представляют собой сложное сочетание целого ряда узлов и
элементов (теплообменных аппаратов, насосов, терморегулирующих
устройств и трубопроводов), т.е. особый вид гидравлических систем.
Их особенностью является то, что они состоят почти из одних местных
сопротивлений, а ограниченное пространство, в котором они размещаются,
обусловливает их многообразие для различных автомобилей. На рис. 1.9
показана схема системы охлаждения грузового двигателя (т = 27,и =42,
с = 16).
Особый класс гидравлических систем составляют газотранспортные и
газоснабжающие системы, а также смешанные (с точки зрения состава
элементов, осуществляющих транспортировку среды) системы типа
"пласт — скважины — газосборная сеть", которые можно изучать с по-
26

1.8. Фрагмент отопительной системы (с) и схема ее гидравлической цепи (б)
1 — источник гравитационного напора
1.9. Схема системы охлаждения грузового автомобиля
мощью методов ТГЦ [225, 226, 128, 131, 3]. Принципиальные особен-
особенности такого рода систем (в плане их математического моделирования)
заключаются в сжимаемости транспортируемой среды и в наличии мно-
множества специальных "активных элементов" - КС, которые дискретно
и по сложным правилам изменяют параметры газа.
27

Эти системы, за некоторым исключением (см. гл. 8), не рассматривают-
рассматриваются в настоящей монографии, иначе это привело бы к неоправданному в
данном случае усложнению материала и увеличению объема книги. К тому
же вопросы применения математических методов и ЭВМ для расчета, опти-
оптимального проектирования и развития газотранспортных систем уже нашли
развернутое изложение, например, в монографиях [226-228].
Для всех приведенных примеров реальных объектов в СЭИ проводились
многовариантные расчеты, связанные с оптимизацией их конфигурации
и параметров элементов или анализом режимов их работы (результаты
этих расчетов частично будут даны ниже).
Данные примеры на "объектном" уровне показывают правомочность
постановки проблемы межотраслевого изучения гидравлических систем.
Этот тезис развивается в следующем разделе применительно к законам
течения различных сред.
1.2. О ЗАКОНАХ ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ1
В связи с качественно новыми возможностями, которые открыло приме-
применение ЭВМ для математического моделирования гидравлических систем,
возникла необходимость в некотором _ анализе, а в ряде случаев -
и пересмотре исходных аналитических зависимостей между основными
величинами, характеризующими движение жидкостей в трубе или канале.
Сделаем, однако, ряд оговорок.
Во-первых, будем использовать термин "жидкость" в широком смысле
(как это и принято в гидромеханике), имея в виду не только собственно
капельные жидкости, но и газы, различая их лишь по сжимаемости.
Во-вторых, речь будет идти главным образом об установившемся (стацио-
(стационарном) изотермическом движении. И, кроме того, это движение рассмат-
рассматривается в трубе или канале с постоянным по длине сечением.
Как известно ([186] и др.), основной формулой, связывающей потерю
давления h, Па,с осредненной по сечению трубы скоростью потока жидко-
жидкости v, м/с, является формула Дарси:
v2 I
h=\—-p, A.1)
2 d
где X — коэффициент гидравлического трения (сопротивления); d — диа-
диаметр трубы, м; / — ее длина, м; р — плотность жидкости, кг/м3.
Эта формула считается универсальной, а все разнообразие гидродина-
гидродинамических состояний потока и соответственно режимов движения жидкости
сводится к изучению различных закономерностей изменения функции
X = / (v), отвечающих ламинарному, переходному или турбулентному ре-
режимам. Так, в соответствии с формулами Шевелева [266] для металличес-
металлических водопроводов, работающих в квадратичной области при v > 1,2 м/с,
X = 0,021 Id0 '3 ; A.2)
1 В этом разделе все обозначения используются без индексов узлов и ветвей.
28

тех же труб при v < 1,2 м/с, что соответствует переходному режиму,
A.3)
Такой подход во многом объясняется стремлением получить в конце
или иную одночленную формулу, удобную для аналитических преобра-
ований и позволяющую относительно легко организовать ручной счет.
С того момента, когда появились одночленные формулы, описывающие
движение жидкостей в трубах, вес развитие трубопроводной гидравлики
было связано в основном с отысканием формул для X. Ранние исследо-
исследователи считали его постоянным, но различным для разных жидкостей.
Первые выражения для X в зависимости от d были получены Дарси и Базе-
нрм на основе наблюдений над опытными трубопроводами и каналами из
различного материала. Затем Блазиус (также на основании опытных дан-
данных) получил X в виде функции не только d, но и v. (Подробно история
этого вопроса рассматривается в монографии А.Д. Альтшуля [8].)
В общем случае все множество формул X характеризует и уточняет
связь X =f(k3ld, Re), где кэ — эквивалентная шероховатость, Re - кри-
критерий Рейнольдса. В частности, рекомендованная для использования при
расчетах водопроводных сетей формула Кольбрука имеет вид
1/ VT = -2 lg B,51 /Re y/\ + d/.k3). A.4)
Преимущество ее перед другими формулами в том, что она охватывает
все три режима движения воды. Однако это выражение фактически пред-
представляет собой неявное трансцендентное уравнение относительно X и по-
потому весьма трудоемко для вычислений даже с учетом применения ЭВМ.
Для расчета газопроводов низкого давления и теплопроводов применяет-
применяется более простая формула Альтшуля
X = 0,11 {kjd + 68,5 /ReH'25, A.5)
полученная в результате аппроксимации A.4).
В различных отраслях трубопроводного транспорта (водо-, тепло-,
газо- и нефтеснабжения) используются формулы Абрамова [2], Андрияше-
ва [9], Шифринсона [269], Шевелева [266] и многих других авторов-,
которые так или иначе сводят все дело к одночленной зависимости между
h и расходом х,
h = s(K.t)xl>, A.6)
где s - гидравлическое сопротивление, а 0 - показатель степени, принимае-
принимаемый различным в зависимости от типа системы и режима течения. При
этом A.6) в упрощенном виде квадратичного закона h = sx2 с высокой
точностью описывает движение жидкости в зоне так называемого "вполне
шероховатого трения" при хорошо развитой турбулентности потока.
Например, практически все режимы работы водяных тепловых сетей (а
также паропроводов) полностью соответствуют этим условиям. Что каса-
касается газопроводов среднего и высокого давления, то для их расчетов в
качестве h используют не потерю давления, а разность квадратов давле-
давлений на концах трубопроводного участка [266].
29

Тем не менее точность подобных соотношений в реальных задачах не-
нередко оказывается недостаточной. К тому же многообразие их для раз-
различных условий представляет известную трудность и неудобства при реали-
реализации общих методов расчета потокораспределения в гидравлических
системах. Вместе с тем еще в прошлом веке Прони, Арсон и другие ис-
исследователи предлагали использовать двучленную формулу
h = av + bv2 A.7)
с коэффициентами а и Ь, зависящими от диаметра трубопровода. Воз-
Возвращаясь к этой идее и используя тот факт, что, как показывают опытные
данные, зависимость h = f(x) для ньютоновских жидкостей всегда явля-
является строго возрастающей и выпуклой функцией, можно в принципе в
основу расчетов положить двучленное выражение
h = Six + s2x2. (lj?)
Коэффициенты x j a s2 здесь определяются по имеющимся эксперименталь-
экспериментальным и табличным данным, например, с помощью метода наименьших
квадратов.
Результаты расчетов показали, что для водопроводных труб и газо-
газопроводов низкого давления данная формула с достаточной степенью точно-
точности может представлять зависимость потери давления от расхода в доволь-
довольно широком диапазоне изменения последнего. Например, обработка таблиц
Ф.А. Шевелева [266] дает при d =0,125 м: sx = 3,77 • 10; s2 =7,69 • 10~3
(для х в м3/ч). При этом результаты отличаются от табличных данных не
более чем на 2% в диапазоне изменения расходов от 9 до 135 м3/ч, что
соответствует интервалу значений скорости и = 0,2—3,1 м/с.
В основе расчета открытых каналов с безнапорным движением жидко-
жидкости лежит формула Шези, связывающая среднюю скорость потока и, м/с,
с гидравлическим радиусом R, м, и уклоном /:
v = Су/Ш, A.9)
где коэффициент С, носящий название скоростного множителя, или коэф-
коэффициента Шези, — величина размерная и зависящая от рода жидкости,
гидравлического радиуса и шероховатости стенок. Между С и Л существу-
существует зависимость, имеющая вид X = 8g/C2.
Несмотря на все достоинства формулы Дарси (в частности, безразмер-
ность X), формула Шези является более подходящей для каналов, так как
соответствует многообразию их профилей, учитываемому через гидравли-
гидравлические радиусы. Более подробно вопросы гидравлики открытых каналов
рассмотрены в монографии [7], посвященной выводу различных формул
для описания движения воды в их руслах.
Особым вопросом является математическое описание активных эле-
элементов, содержащих источники действующего напора (Я), т.е. удельной
энергии, подводимой к системе источником питания или циркуляции.
Исходя из аналогии с электродвижущей силой (э.д.с.) в электрических
цепях, будем на первом этапе (на уровне г.ц. с сосредоточенными пара-
параметрами) считать, что Я — независимый параметр активного элемента
(такой же, например, как диаметр или длина трубы, коэффициент гидрав-
30

1.10. Характеристики насосов и других нагнетателей
лического сопротивления) и что в отличие от потери давления на трение
(/;) он не меняется с изменением расхода.
Такой методический подход позволяет упорядочить и упростить общее
математическое описание и расчеты потокораспределения в гидравли-
гидравлической системе, тем более что учет фактических характеристик насосов
или других нагнетателей может быть при этом полностью обеспечен следую-
следующим образом.
Как известно, "падающий" характер таких характеристик (рис. 1.10, я)
объясняется наличием внутреннего сопротивления источника и соответ-
соответственно внутренней потери давления /гвн, которая может быть просумми-
просуммирована с изменением давления на всем участке системы, содержащем
данный источник (рис. 1.10,5). В результате Н можно считать постоянной
величиной. К тому же для сложных систем изменение характеристики груп-
группы параллельно соединенных насосов по сравнению с падением давления'
в сети пренебрежимо мало и потому часто вообще может не учитываться.
Если все-таки падение давления на выходе из источника и в сети соизмери-
соизмеримо, то это легко может быть учтено суммированием коэффициентов
внутреннего гидравлического сопротивления источника и соответствующе-
соответствующего участка сети (при одинаковых законах гидравлического сопротивления)
или введением дополнительного участка со своим законом изменения
hBH в зависимости от расхода.
Рассмотрение Н в качестве независимого параметра является особенно
очевидным при расчете систем без искусственного побуждения, например
систем воздухообмена в зданиях. Здесь роль действующих напоров вы-
выполняют так называемые "ветровой" и "тепловой" напоры, которые не
зависят от количества воздуха, поступающего в помещение.
Методические и вычислительные проблемы математического описания
элементов рассчитываемой гидравлической системы и режимов их функ-
'шонирования заключаются здесь в следующем. Во-первых, оно должно
выть "равноточным", т.е. необходимо согласовывать допустимую погреш-
погрешность результатов с выбором расчетной схемы системы и степенью учета
ес активных, пассивных элементов и регулирующих устройств. Одним
Из вспомогательных методических способов для решения такого вопроса
ж служить четкое представление о том, на каком уровне строгости
31

будет осуществляться моделирование системы: как г.ц. с сосредоточенны-
сосредоточенными, переменными или распределенными параметрами (см. гл. 5, 8, 10)?
Во-вторых, выбор формул должен увязываться также и с назначением
расчетов. Если на стадии проектирования системы вполне правомочным
будет использование упрощенных гидравлических зависимостей, то при
наладке и управлении эксплуатацией такого рода объектов, когда нужно
обеспечить необходимую адекватность математической модели конкрет-
конкретной управляемой системе, требования к точности описания ее фактиче-
фактической структуры, параметров элементов, а также режимов течения среды
становятся более серьезными. В принципе с данной проблемой можно
справиться лишь в условиях автоматизированного управления с обеспе-
обеспечением постоянного слежения за действительными параметрами элементов
системы - на базе совместного решения прямых и обратных задач потоко-
распределения (см. гл. 11).
И в-третьих, эти формулы должны удовлетворять требованию макси-
максимального быстродействия при их численной реализации, поскольку машин-
машинное время для анализа сложных систем большой размерности может ока-
оказаться чрезмерным даже на мощных ЭВМ. Оно в значительной степени
определяется именно способом описания и преодоления нелинейного
характера гидравлических зависимостей.
С этой точки зрения линейно-квадратичная зависимость A.8) имеет
преимущества перед другими, так как позволяет относительно легко
учитывать меняющийся (от элемента к элементу и от итерации к итера-
итерации) закон гидравлического сопротивления для всех режимов соответ-
соответствующим варьированием величинами коэффициентов 5] их2 или выбором
формул для них (в случае гидравлической цепи с переменными пара-
параметрами) . Кроме того, она хорошо согласуется и с экстремальным под-
подходом к потокораспределению.
Вместе с тем при изложении материала в последующих главах будет
использоваться в основном одночленная формула A.6), так как это су-
существенно упрощает выкладки, тем более что основные методические
результаты и алгоритмы, в общем-то, инварианты относительно того,
какие конкретно из этих формул включаются в математические модели.
Глава 2
МЕТОДЫ РУЧНОГО РАСЧЕТА ГИДРАВЛИЧЕСКИХ СИСТЕМ
В настоящей главе рассматриваются известные методы ручного расчета
гидравлических систем и дается их анализ с точки зрения методик расчета,
отличающихся между собой не столько областями приложений, сколько
своей сущностью. Это имеет целью, во-первых, показать общее состояние
вопроса и связь результатов, накопленных в различных областях, с со-
содержанием данной книги и, во-вторых, выяснить, в какой мере эти методы
могут (или не могут) сохранить свое значение при использовании ЭВМ
Последнее представляется весьма важным. Здесь, как и во многих
других областях, на первом этапе применения ЭВМ обращаются, как пра-
32

к известным и уже привычным инженерным методам расчета. В
дальнейшем выясняется, что эти методы, создававшиеся применительно
к ограниченным возможностям ручного счета, использовать непосредствен-
непосредственно без переосмысливания и переработки невозможно или нецелесообраз-
нецелесообразно' При этом ни в коем случае не следует пренебрегать принципиальными
преимуществами некоторых из известных инженерных методов, не
разобравшись в их математической сущности. Стремление к применению
самых современных математических методов также не может быть само-
самоцелью, поскольку такая крайность может привести лишь к неоправданно
сложным алгоритмам для ЭВМ.
2.1. ГРАФИЧЕСКИЕ И АНАЛИТИЧЕСКИЕ МЕТОДЫ
Графические и графоаналитические методы всегда занимали большое
место в литературе, они разрабатывались начиная с прошлого века для
расчета прежде всего еистем водоснабжения. Помимо работ иностранных
авторов, этим методам посвящены работы Ф.Е. Максименко [113],
М.С. Ясюковича, Е.Б. Батурина и других авторов. Обобщение и развитие
графических методов применительно к системам этого рода дано в книге
Н.Н. Абрамова [1].
Для расчета напорных конденсатопроводов графический метод использо-
использовался в работе БЛ. Шифринсона. В монографиях С.Ф. Копьева, Л.А. Ме-
лентьева [120], Л.Г. Скрицкого, Е.Я. Соколова, Н.К. Громова и А.П. Са-
Сафонова, Е.П. Шубина и других этот же метод применялся для иллюстрации
переменных режимов в тепловых сетях. Имеются работы, в которых графо-
графоаналитическая методика используется для расчета систем воздухообмена
в зданиях, газовых сетей.
Ограниченные возможности графических методов для получения числен-
численных результатов, относящихся к сложным системам, очевидны. Однако
они приносят большую пользу благодаря своей иллюстративности, способ-
способности показать на простых примерах качественный характер изменения
режимов в гидравлических системах.
Среди графических методов следует различать две группы построений.
Первая имеет своей непосредственной целью выполнение расчетов потоко-
распределения, и ее отличительной особенностью является построение
сопрягающихся кривых в системе координат "напоры - расходы". Прин-
Принципиальная выполнимость таких построений определяется возможностью
оценивать сопротивления отдельных ветвей и общее сопротивление гидрав-
гидравлической системы, отнесенное к тому или иному источнику действующего
напора.
Вторая группа используется как в области водоснабжения, так и (осо-
(особенно широко) теплоснабжения. Это - построения так называемых "пьезо-
"пьезометрических графиков", которые выполняются в системе координат
'напоры - длины участков сети". Методическая и иллюстративная роль
таких графиков несомненна. Во многих статьях, монографиях и учебниках
пьезометры" мастерски применяются для характеристики установив-
установившихся и динамических режимов сетей. Можно сказать, что несколько
поколений специалистов воспитывалось, усваивая методику построения
3- Зак. 384 33

и анализ этих графиков. Однако по мере усложнения схем и режимов
систем их полезность явно снизилась.
Для многих гидравлических систем особенно важны были наиболее
простые схемы с последовательно-параллельным соединением ветвей
при одном источнике питания. Поэтому в большинстве ранних работ пред-
предлагались и использовались методы расчета именно таких схем. К ним
относятся: метод "эквивалентных отверстий", предложенный в 1873 г.
Д. Мюргом [291] и развитый В. Блессом; метод "перемещения единиц
объема", описанный П.Н. Каменевым [79]; метод суммирования сопротив-
сопротивлений и проводимостей, использованный Б.Л. Шифринсоном [269].
С.Ф. Копьевым, Е.Я. Соколовым и многими другими авторами для расчета
переменных режимов в тепловых сетях, а Н.Н. Гениевым [49] - для
простых водопроводов.
В алгебраическом отношении указанные методы эквивалентны и основа-
основаны на специальном свойстве матрицы соединений такого рода схем, ко-
которое позволяет в результате элементарных преобразований (см. гл. 4)
свертывать ее к единичной строке (или контуру). Это формальное свойство
матриц специального вида, справедливо для электрических и гидравли-
гидравлических цепей, определяет линейную природу методов расчета и оптимиза-
оптимизации любых систем, имеющих подобные схемы соединений.
Метод, основанный на суммировании сопротивлений и проводимостей,
удобен не только для ручных, но и для машинных расчетов потокораспре-
деления, связанного с отключением и включением отдельных ветвей раз-
разветвленной (разомкнутой) сети. Например, он также использовался ав-
авторами [124] для анализа гидравлической устойчивости тепловых сетей.
Описываемый в данной книге (см. разд. 6) метод линеаризованных пре-
преобразований "гидравлического треугольника в звезду" [243] расширяет
использование данного метода на более сложные схемы нелинейных систем.
Другие аналитические методы связаны со стремлением получить неко-
некоторую формулу, которая выражала бы зависимость ^ежду техническими
параметрами системы и характеристиками ее режима, гидравлического
и теплового; они также весьма широко использовались, особенно в об-
области теплофикации и централизованного теплоснабжения. В этой связи
следует указать на работы С.Ф. Копьева, С.А. Чистовича, Н.М. Зингера
[73] и других. Располагая подобной формулой и варьируя значениями
входящих в нее величин, можно исследовать характер изменения режима
и получать необходимые выводы.
Такого рода формулы, получаемые в результате зачастую весьма гро-
громоздких, но простых по существу алгебраических преобразований, выра-
выражали решение задачи в радикалах и поэтому требовали так или иначе све-
сведения схемы к единичному контуру. Как показано ниже (см. разд. 4.2),
этот подход возможен при условии, что г.ц. содержит не более двух неза-
независимых контуров.
Специальное место в литературе по аналитическим методам расчета
занимают системы центрального водяного отопления из-за особых трудно-
трудностей, которые связаны с тем, что это - вертикальные гидравлические
системы, работающие в условиях теплообмена с окружающей средой.
Их необходимо рассматривать уже как гравитационные цепи специаль-
специального вида [246]. К такого же рода системам могут быть отнесены, на-
34

имер. циркуляционные контуры водогрейных котлов, а также и систе-
системы воздушного отопления.
Таким образом, графические и аналитические методы сохраняют свое
начение как вспомогательные и иллюстративные методы при расчете
равлических систем простой структуры. Однако их ограниченность
очевидна, и единственным способом ее преодоления является обращение
к более общим и современным методам математического моделирования
с применением ЭВМ.
2.2. МЕТОДЫ ПОКОНТУРНОЙ И ПОУЗЛОВОЙ УВЯЗКИ
В научно-технической и учебной литературе хорошо известны и до настоя-
настоящего времени широко применяются на практике (в том числе и в 'каче-
'качестве расчетных методов для ЭВМ) относительно простые методы последо-
последовательных приближений для расчета потокораспределения в кольцевых
многоконтурных трубопроводных сетях. Эти методы органически учиты-
учитывают сетевой характер задачи гидравлического расчета и сводятся к после-
последовательному уравновешиванию (балансированию, или, как уже обще-
общепринято называть в отечественной инженерной практике и литературе,
увязке) перепадов давлений на ветвях контуров или расходов в узлах
сети, исходя из законов Кирхгофа.
Метод поконтурной увязки перепадов давлений (потерь напора) обычно
связывают у нас с именами В.Г. Лобачева [108, 109], X. Кросса [281]
и в меньшей степени М.М. Андрияшева [9, 10], а в зарубежных публика-
публикациях данный метод и метод поузловой увязки расходов однозначно назы-
называются методами X. Кросса. Вместе с тем, несмотря на огромное число
статей и монографий, посвященных этим методам и их модификациям
[2, 6, 20, 26, 36, 37, 71, 106, 188,212,231 и др.], в них нелегко найти стро-
строгай и объективный анализ первоисточников, а ссылки часто носят непра-
неправильный характер. Поэтому целесообразно дать здесь хронологически выдер-
выдержанное и достаточно четкое представление о первых публикациях, связан-
связанных с увязочными методами (с сохранением стиля изложения и обозна-
обозначений авторов).
Исходной публикацией по методу поконтурной увязки перепадов дав-
давлений (потерь) следует считать вышедшую в 1932 г. небольшую моно-
монографию М.М. Андрияшева [9], в которой впервые зафиксированы основ-
основные положения данного метода и предложена формула для увязочного
контурного расхода. Приведем несколько выдержек из этой работы:
"Самый процесс работы по нахождению правильного распределения рас-
расходов, называемый иногда увязкой потерь напора или увязкой сети, со-
состоит из ряда перемещений расходов, при помощи которых невязки по-
постепенно уменьшаются . . . Остается определить, какова же должна быть
величина увязочного расхода. Теоретически этот вопрос может быть раз-
разрешен следующим образом. Сумма потерь в участках ячейки или — что
то же - невязка . . . запишется так:
h =
Найдем первую производную h no Q:
dh/dQ = Z2gQ,
35

отсюда
dQ = dh/Z TgQ.
Переходя с некоторым приближением от бесконечно малых величин
к весьма малым конечным величинам, имеем выражение
AQ = ДЛ/2 2gQ, B.1)
при помощи которого можно найти величину изменения расхода AQ,
необходимую для изменения невязки на величину ДА".
В 1934 г. В.Г. Лобачев [108] предлагает метод, который "основан на
применении математического анализа и позволяет решение квадратичных
уравнений . . . свести к решению линейных уравнений". При этом он делает
следующую ссылку на упомянутую выше книгу М.М. Андрияшева: "Обыч-
"Обычно расчет сети приводится к расчету отдельных колец. Имеющиеся в сети
расходы определяют тем или иным способом, разбрасывания их путем
интуиции по отдельным линиям сети". По отношению к М.М. Андрияшеву,
который применительно к отдельным кольцам фактически первым пере-
перешел от интуиции к основной (для всей последующей литературы по дан-
данному вопросу) формуле B.1), такое заявление, конечно, некорректно.
Приоритет В.Г. Лобачева заключается не в получении данной формулы,
которая дается им в виде
Д<7 - AhllHsq, B.2)
что по форме и существу совпадает с B.1), а в переходе к системному
рассмотрению совокупности колец. (Попутно отметим, что он, по-видимо-
по-видимому, первый отметил здесь аналогию с расчетом электрических сетей и ввел
понятие о "сопротивлении линий сети".) Основное содержание его статьи
сводится к построению и решению на примере "двухколечной сети" систе-
системы из двух линейных уравнений относительно " добавочных перекидных
расходов" для этих колец, а также к обобщающему выводу: "Продолжая
применение указанного метода к расчету многоколечных систем, мы
будем каждый раз получать столько добавочных перекидных расходов,
сколько колец".
Наибольшее число ссылок, особенно в зарубежной литературе, имеет
изданная в США в 1936 г. статья X. Кросса "Анализ течений в сетях из
трубопроводов или проводников" [281], о которой сам автор говорит,
что она не является предметом его основных научных интересов, а пред-
представляет побочный продукт исследований в области структурного анализа
(Действительно, ранее, в 1932 г., он предложил широко известный в строи-
строительной механике математически идентичный метод моментов в рамных
конструкциях.) Значение этой работы состоит в том, что в ней впервые
в общем виде сформулированы основные положения для описания потоко-
распределения в сетях (но без введения векторых и матричных обозначе-
обозначений) и его расчета на базе идей поконтурной и поузловой увязки потерь
давления и расходов.
Обсуждая данный тип задач, Кросс отмечает, что потокораспределение
в сети определяется "двумя группами достаточно простых и очевидных
условий: а) общий расход, притекающий к любому узлу, равен общему
расходу, покидающему его (непрерывность течения); б) общее изменение
потенциала вдоль любого замкнутого пути равно нулю (непрерывность
36

потенциала)", эти группы условий совместно с соотношением между
расходом и падением потенциала приводят в зависимости от того, какие
переменные являются неизвестными, к той или иной системе уравнений.
Закон, определяющий потерю давления в трубе, рассматривается им в
вИде одночленной зависимости
h=rQ", . B.3)
где г _ "потеря давления в трубе для потока единичной величины".
Далее автором предлагаются два метода для расчета потокораспределе-
ния. Один исходит из того, что "потоки в трубах или проводниках сети
всегда удовлетворяют условию равенства нулю их общего баланса в каж-
каждом узле и они последовательно корректируются с тем, чтобы удовлетво-
удовлетворить условию равенства нулю общего изменения давления вдоль каждого
контура". Другой основан на том, что "общее изменение давления вдоль
каждого контура всегда равно нулю, а потоки в трубах контура последо-
последовательно подбираются так, чтобы общий их баланс в каждом узле в конце
концов, приблизительно или точно, стал равным нулю". Первый метод
назван им методом "балансирования (уравноэ вшивания) давлений",
а второй — методом "балансирования потоков" (расходов). (Поскольку
в отечественной литературе об этих методах принято говорить как об
"увязочных", в дальнейшем будем придерживаться этой терминологии.)
Для поконтурной увязки потерь давлений X. Кросс выводит формулу
Б А 2 rQ о (с учетом направления потока)
А = = : , B.4)
2 7? 2 wQ" "' (без учета направления потока)
где Д - увязочный расход, Qo - предыдущее приближение в значении
расхода на каждом трубопроводе в данном контуре. Она получена из
условия
" ^ 2г@о +Д)" = О,
которое после отбрасывания нелинейных относительно Д членов переходит
в приближенное равенство
XrQg * -AZnrQS-1, B.5)
откуда и следует B.4).
Что касается второго метода (поузловой увязки расходов), то он ха-
характеризуется им следующим образом (без каких-либо формул и четкого
алгоритма): "Мы можем задаться значениями давлений в системе и вы-
вычислить расход в каждой трубе, соответствующий разностям давления.
Отсюда находится общий расход в каждом узле, исключая входы и выходы.
Распределим этот расход по трубам, сходящимся в данном узле, обратно
пропорционально их сопротивлениям (R = nrQ* ~l). Это, конечно, вызовет
избыток (или недостаток) расхода в последующих узлах, но путем после-
последовательного распределения избыточные расходы в конце концов должны
вытесниться через входы и выходы системы". (Более подробно алгоритмы
и первого, и второго увязочных методов приводятся в следующей главе.).
В статье оба метода иллюстрируются многочисленными примерами
расчета, но не дается анализа их сходимости. В конце автор рассматрива-
рассматривает общий случай зависимости между потерей давления и расходом в виде
37

h = f(Q) и Дает соответствующую формулу для увязочного контурного
расхода:
ДС = -2/B)/2/'@. B.6)
Отметим, что статья Кросса не имеет ссылок на какие-либо источники.
Таким образом, проведенный анализ фактического содержания первых
публикаций по методам "гидравлической увязки" сети позволяет сделать
следующие выводы:
1. Метод поконтурной увязки перепадов давлений впервые предложен
М.М. Андрияшевым и независимо X. Кроссом, поэтому должен считаться
методом Андрияшева-Кросса, а не методом Лобачева-Кросса, как он
называется во многих работах, и прежде всего в области систем водо-
водоснабжения [2].
2. Что касается В.Г. Лобачева, то ему принадлежит идея совместной
многоконтурной увязки перепадов давления путем построения и решения
системы линейных уравнений относительно увязочных расходов. По су-
существу, он предвосхитил ряд положений метода контурных расходов
(см. гл. 5), однако не формализовал их в полной мере.
3. X. Кроссом в общем виде сформулированы основные принципы
как поконтурного, так и поузлового уравновешивания (увязки) пере-
переменных, описывающих потокораспределение, и потому справедливо дан-
данные методы носят его имя.
В следующей главе обсуждаются вычислительные возможности увязоч-
увязочных методов и дается краткий аналитический обзор других работ по при-
применению различных подходов, математических методов и ЭВМ для расчета
трубопроводных систем различного типа и назначения.
Глава 3
О ПРИМЕНЕНИИ МАТЕМАТИЧЕСКИХ МЕТОДОВ И ЭВМ
ДЛЯ РАСЧЕТА ГИДРАВЛИЧЕСКИХ СИСТЕМ
3.1. ВЫЧИСЛИТЕЛЬНЫЕ ВОЗМОЖНОСТИ УВЯЗОЧНЫХ МЕТОДОВ
Методы поконтурной увязки перепадов давлений и поузловой увязки
расходов предназначены для нахождения таких взаимосвязанных расходов
на ветвях и давлений в узлах, которые с наперед заданной точностью в
отношении расходов и (или) давлений удовлетворяли бы первому и вто-
второму законам Кирхгофа.
Поконтурная увязка перепадов давлений состоит из следующих этапов:
1. По данным о нагрузках у потребителей выбирается какое-либо на-
начальное приближение для расходов на всех ветвях расчетной многоконтур-
многоконтурной схемы, но такое, чтобы во всех узлах соблюдался первый закон Кирх-
Кирхгофа.
2. Для полученных расходов с учетом данных о коэффициентах гидрав-
гидравлического сопротивления вычисляются потери давления на всех ветвях
и их суммарные "невязки" во всех независимых контурах. Эти невязки
в соответствии со вторым законом Кирхгофа должны быть сведены до
нулевых значений.
38

3 По выявленным невязкам тем или иным образом определяются
еличины так называемых контурных "увязочных расходов".
4. Каждый увязочный расход "проводится" по всем ветвям своего
контура алгебраическим суммированием с расходами, принятыми по
начальному приближению. (Как будет видно из дальнейшего, фактиче-
фактически на этом этапе решается система однородных (с нулевой правой частью)
линейных уравнений первого закона Кирхгофа.)
Расходы, полученные на последнем этапе, используются в качестве
очередного приближения для начала следующей итерации (п. 2-4) и т.д.
вплоть до приближенного (в пределах заданной погрешности) совпадения
последовательных значений всех или части искомых величин.
Скорость сходимости алгоритмов данного типа зависит от: начального
приближения; степени преобладания коэффициентов, относящихся к
контурным расходам, над коэффициентами для остальных ветвей и, сле-
следовательно, от выбора системы независимых контуров. При этом следует
учитывать два важных обстоятельства, вытекающих из бесконечности
итерационного процесса для нелинейных цепей:
1) по невязке потерь давления в контурах невозможно судить о погреш-
погрешности расходов на ветвях и 2) одна и та же невязка потерь давления для
различных систем контуров приводит к различным значениям расходов
на ветвях.
Второй увязочный метод - метод поузловой увязки расходов (в таком
виде, как он предложен Кроссом [281]) - сводится к следующим опе-
операциям:
1) задаются наряду с заранее фиксированными давлениями давления
во всех узлах схемы;
2) исходя из них, определяются потери давления и отвечающие им
расходы на всех ветвях;
3) для каждого из узлов подсчитывается алгебраическая сумма рас-
расходов на примыкающих к нему ветвях, включая нагрузку или приток
в данном узле (если они имеются), и в результате выявляются небалансы
(невязки) расходов во всех узлах;
4) каждый из этих небалансов делится в каком-то отношении (напри-
(например, обратно пропорционально гидравлическим сопротивлениям) между
ветвями, сходящимися в данном узле, и прибавляется (с соответствующим
знаком) к их расходам.
Это перераспределяет расходы во всех смежных узлах, что требует
нового последовательного обхода всех узлов схемы и выполнения для
них п. 3 и 4 до тех пор, пока узловые небалансы расходов не станут меньше
заданной погрешности.
Исходя из основной идеи данного метода, на этапе 4 должно корректи-
корректироваться (по соответствующей формуле, использующей полученные не-
небалансы узловых расходов) давление в каждом из узлов, а далее должны
повторяться п. 2—4 и т.д. (см. общую схему метода узловых давлений
в гл. 5). Приведенный же алгоритм выглядит не очень четким в этом от-
отношении, но, главное, он не гарантирует сходимости вычислительного
процесса даже для плоских схем.
Что касается метода поконтурной увязки потерь давления Андрияше-
Ва-Кросса, то он, благодаря своей относительной строгости, наглядности
39

и относительно быстрой сходимости, получил самое широкое распростра-
распространение и стал основным инструментом гидравлических расчетов и на ЭВМ
как за рубежом [284,286,293], так и в нашей стране.
В СССР в самом начале 60-х годов практически одновременно появилось
несколько программ, реализующих этот метод. Так, в ВЦ АН СССР и
Мосинжпроекте Я.И. Алихашкиным и А.Р. Юшкиным была составлена
программа для расчета водопроводных сетей на машине "Стрела" [6],
при этом основная формула для определения приращения расходов назва-
названа формулой Андрияшева. К.П. Вишневским в институте ВОДГЕО была
разработана соответствующая программа для ЭВМ "Урал-1" [37], но при
этом говорится, что речь идет о методе Лобачева. Дня расчета кольцевых
тепловых сетей в ВТИ им. Ф.Э. Дзержинского были составлены программы:
Н.М. Зингером, К.С. Андреевой и Ф.А. Вульманомдля "Урала-1" [71]
и Н.М. Зингером и М.А. Маханьковой — для "Урала-2".
Кроме того, аналогичные программы для расчета газовых и газосбор-
газосборных сетей описаны в работах А.М. Левина, В.А. Смирнова и А.Я. Черкасо-
Черкасовой [106], Е.Р. Ставровского и М.Г. Сухарева [212] и других авторов.
В СЭИ оба увязочных метода были реализованы в ряде программ для
БЭСМ-2м с целью сопоставления с другими численными методами и все-
всесторонней опытной проверки их сходимости [209,231].
Сходимость метода поконтурной увязки потерь давления для плоских
схем была доказана, исходя из различных положений, Б.Н. Пшеничным
[188], М.Г. Сухаревым [225] (эти работы подробнее обсуждаются ниже)
и В.Я. Хасилевым [247,248].
Вместе с тем опытным расчетчикам давно было известно, что иногда
данный увязочный метод "почему-то" не работает. С началом использо-
использования ЭВМ такие случаи, естественно, стали выявляться все чаще, особен-
особенно когда рассчитывались сложные схемы, в которых сопротивления от-
отдельных ветвей отличались друг от друга на несколько порядков (напри-
(например, в двухтрубных тепловых сетях) и к тому же имелись источники с
заданными у них напорами, а не производительностями. Общая характери-
характеристика сложившегося положения была дана Ш. Дюбеном [282] на Между-
Международном конгрессе по водоснабжению в 1964 г. Он отметил, что со време-
времени появления (обсуждавшейся выше) работы X. Кросса не достигнуто
существенного прогресса в методах расчета кольцевых сетей и что оба
увязочных метода имеют одинаковые недостатки, но второй представ-
представляется еще менее надежным, чем первый. В этой связи Ш. Дюбен указыва-
указывает на три существенных момента: 1) очевидную связь увязочных методов
с методом Ньютона для решения систем нелинейных уравнений; 2) пред-
предпочтительность "последовательной коррекции" (т.е. метода Зейделя)
перед "одновременной коррекцией" и 3) целесообразность выбора колец,
исходя из минимума гидравлического сопротивления трубопроводов.
(Аналогичные выводы были одновременно сделаны и В.Я. Хасилевым при
разработке и реализации общих методов расчета гидравлических цепей с
сосредоточенными параметрами [242,247]).
В эти же годы число публикаций по поводу увязочных методов не умень-
уменьшилось, только центр тяжести переместился на их модификации. Н.У. Кой-
да в работе [91] высказывает как новую, идею о том, что возможен другой
метод расчета, противоположный увязке потерь напора, когда "должен
40

облюдаться баланс потерь напора по кольцам, что же касается расходов
узлам, то расчетчик должен стремиться получить такое распределение
потерь напора по участкам сети, чтобы и он имел место". Ясно, что речь
идет о втором методе Кросса.
Метод увязки расходов предлагается также и Ю.И. Максимовым [148,
149]: для каждого узла записывается уравнение баланса, неизвестные
расходы газа при этом выражаются через узловые давления и в результа-
результате получается система нелинейных уравнений относительно квадратов
давлений, которую предлагается решать методом последовательных при-
приближений (без дополнительных разъяснений).
МЛ. Васильченко в работе [36] обычный поправочный расход для
кольца заменяет полным, равным сумме поправочных расходов всех
смежных колец, взятых с "коэффициентами влияния", - это позволяет
учитывать взаимное .влияние колец.
А.Е. Белан [20], описывая как универсальный метод гидравлическо-
гидравлического увязочного расчета с помощью введения "итерационных напоров",
одновременно предлагает находить поправочный расход не с помощью
линеаризованной формулы Андрияшева, а путем точного решения для
каждого контура соответствующего квадратного уравнения. Позже такая
же рекомендация была дана С. Цоем и Г.К. Рязанцевым [259]. Эта моди-
модификация метода поконтурной увязки потерь давления в настоящее время
широко и эффективно используется в различных программах для ЭВМ.
Подводя некоторые итоги истории возникновения, развития и приме-
применения увязочных методов, можно прямо сказать, что это замечательные
и удивительные по своей простоте и эффективности методы, которые
вобрали в себя три основные идеи упрощения и уменьшения трудоемко-
трудоемкости вычислительных процессов: линеаризации нелинейных зависимостей;
декомпозиции задачи, т.е. сведения ее к более простым "сетевым" опера-
операциям, и покомпонентной релаксации, когда уменьшение невязок сетевых
уравнений производится их последовательной обработкой по отдельным
уравнениям и переменным. Такое сочетание являлось в свое время опти-
оптимальным, так как давало, быть может, единственную возможность выпол-
выполнять расчеты потокораспределения даже вручную.
Вместе с тем именно в излишней простоте увязочных методов и в "тор-
"торможении" ньютоновского процесса (из-за нестрогого решения системы
линеаризованных уравнений на каждом его шаге) заключается их ограни-
ограниченность и недостатки, которые проявляются, конечно, не всегда, но во
все более расширяющемся числе случаев. Несмотря на огромное число работ,
посвященных этим методам и их модификациям (часть их которых оха-
охарактеризована выше), большинство их авторов не ставили своей целью
раскрыть основное математическое содержание данных методов, их связь
с известными методами вычислительной математики и теории электри-
электрических цепей.
Одно из объяснений такого положения состоит в том, что подобный
математический анализ инженерных (по существу) методов может и дол-
должен проводиться с некоторых более общих и формальных позиций, обес-
обеспечивающих строгую математическую формулировку и классификацию
Решаемых задач, а также обоснованное применение общих математиче-
х методов. Рассмотрим работы, относящиеся к данной проблеме.
41

3.2. РАБОТЫ ОБЩЕГО ХАРАКТЕРА
Среди различных методических приемов описания и расчета потокорас-
пределения с математической точки зрения можно (несколько условно)
выделить два основных подхода: алгебраический и экстремальный. Первый
так или иначе сводится к построению и решению замкнутой системы урав-
уравнений, которой должны удовлетворять искомые расходы и давления для
всех элементов расчетной схемы.
Наряду с этим имеется довольно большое число работ, посвященных
теоретическим и вычислительным аспектам другого подхода к данной
задаче, который можно назвать экстремальным. Речь идет об одном из
следующих способов, опирающихся на физическую или математическую
сущность задачи о потокораспределении в произвольной системе:
1) минимизации (или максимизации) специальной функции, отвечаю-
отвечающей тому или иному вариационному принципу, с учетом связей, налагае-
налагаемых уравнениями лишь первого (или второго) законов Кирхгофа, т.е.
с помощью перехода к задачам на условный экстремум;
2) построения особым образом подбираемых функций с последую-
последующим применением методов их безусловной минимизации;
3) перехода к задачам нелинейного программирования, и прежде всего
к нелинейной сетевой транспортной задаче.
Исходными для работ первой группы стали приведенная во введении
теорема Максвелла о принципе наименьшего теплового действия для пас-
пассивной электрической цепи, а также и другие (в основном чисто формаль-
формальные) представления о том, какой экстремальной задаче на условный экст-
экстремум должно отвечать искомое установившееся потокораспределение.
В работах Е. Черри и У. Миллара [263], Г. Биркгофа и Д.Б. Диаза [278],
опубликованных в 1951-1956 гг., на довольно асбтрактном уровне излага-
излагаются новые понятия и теоремы в области нелинейных систем. По поводу
причин такого рода исследований в работе [263] говорится: "В настоящее
время наблюдается всевозрастающий интерес к системам, в которых в
значительной степени проявляются нелинейные эффекты . . . При этом
может появиться стремление к чрезмерному распространению понятий и
теорем линейной теории на нелинейные системы". Считая неправомочным
использование "энергетического функционала" и соответственно теоремы
Максвелла для постановки экстремальной задачи расчета нелинейных
цепей, они вводят понятия полного объема
G = 2/uctf C.1)
и кообъема
J = Zfidv C.2)
цепи, где и - напряжения на зажимах элементов цепи, a i — сила проходя-
проходящего через них тока, и формулируют теорему о стационарных точках.
Из нее следует, что распределение токов или напряжений в любой много-
многоконтурной цепи, совместимого с первым (вторым) законом Кирхгофа,
отвечает минимуму полного объема (кообъема) цепи и что только в линей-
линейном случае эта теорема сводится к утверждению Максвелла о принципе наи-
наименьшего теплового действия. Фактически функционалы C.1) и C.2)
подобраны исходя из формальных требований, связанных с возможно-
42

стью произвольных нелинейных соотношений между и и /, а не привне-
привнесены извне, опираясь на какие-либо физические соображения и экстре-
мапьные принципы механики.
Работа Г. Биркгофа и Д.Б. Диаза посвящена аналогичным вопросам
для нелинейных сетевых задач. В ней вначале рассматривается функция
рассеивания энергии
D = 2 i(ak)te(ak), C.3)
к е L
где L — множество ак ветвей сети, i(ak) ~ поток, а Аи(ак) - разность
потенциалов на ветви и аналогичная функция энергии притоков (источ-
(источников). Затем утверждается,, что только в линейном случае имеет место
классический результат, связанный с этой функцией и соответствующий
теореме Максвелла. Для общего же (нелинейного) случая ими формули-
формулируется "новый вариационный принцип", заключающийся в минимизации
функционалов, совпадающих по математическому смыслу с полным объ-
объемом C.1) и кообъемом C.2) сети.
Ю. Картерон [280], 1956 г., также вводит в рассмотрение функцию,
частные производные от которой дают уравнения первого закона Кирхго-
Кирхгофа, и затем интерпретирует процедуру поконтурной увязки как процесс
минимизации этой функции. Затем строит аналогичную функцию по отно-
отношению к уравнениям второго закона Кирхгофа.
В отечественной литературе экстремальный подход в области нелиней-
нелинейных сетей представлен не менее широко. Большое значение имела опубли-
опубликованная в 1962г. уже упоминавшаяся статья Б.Н. Пшеничного [188].
Сформулировав ряд общих положений по применению теории графов к
"энергетическим сетям", а также задачу их "гидравлического решения",
автор затем оперирует с общим решением системы уравнений первого за-
закона Кирхгофа
q = q° + ? caqa, C.4)
а= 1
где q° - частное решение исходной системы, а - индекс линейно незави-
независимых колец, qa - решения однородной системы уравнений, а са — неза-
независимые параметры. Зафиксировав математические свойства (нечетность
и строгое возрастание) функций в замыкающих соотношениях h ap =
= fap (Яар). он вводит в рассмотрение функцию
ф=2; fa0{z)dz, (з.5)
точка минимума которой дает решение задачи"и определяется из решения
системы уравнений для частных производных по са. Поскольку параметры
са аналогичны контурным расходам, то им по существу доказана (на базе
экстремального описания потокораспределения) сходимость поконтурно-
го увязочного метода для плоских схем.
Отметим, что в этой работе не дается матричной формы записи уравне-
уравнений законов Кирхгофа (они задаются перечислением), нет никаких ссы-
ссылок и упоминаний о методе Андрияшева—Кросса, а функция C.5) вводит-
вводится формально, без каких-либо комментариев.
43

В 1929 г. ЛД. Шевяков [267] показал, что известные формулы рас-
распределения воздуха в горных выработках для различного типа соединений,
полученные "исходя из соображения, что при растекании воздуха между
двумя какими-либо пунктами по разным путям депрессия h по всем
направлениям должна быть одна и та же", могут быть выведены "из начала
наименьшей работы", т.е. в результате минимизации величины общей ра-
работы, необходимой для движения данного количества воздуха. Очевидно,
что речь идет о принципе наименьшего действия.
А.В. Курман и В.М. Каганер [103] используют данное утверждение
ЛД. Шевякова в качестве "принципа экстремальности" для постановки
общей задачи о естественном распределении воздуха по ветвям вентиля-
вентиляционной сети. При этом рассматриваются сети с однородными квадратич-
квадратичными характеристиками ветвей при отсутствии внутри них вентиляторов.
А в основу итерационного процесса для решения задачи ими берется про-
процедура поконтурной минимизации функции, выражающей "суммарную
мощность, теряемую в сети потоком".
Повышенный интерес к экстремальному подходу и виду миними-
минимизируемого функционала объясняется еще и тем, что задачу расчета потоко-
распределения можно тогда трактовать и как нелинейную сетевую транс-
транспортную задачу. Такая интерпретация имеет теоретическое и практическое
значение. Первое заключается в том, что формальное применение теоремы
о потенциалах позволяет установить двойственный характер гидравли-
гидравлических параметров (расходов на ветвях и давлений в узлах) и соответст-
ственно систем уравнений первого и второго законов Кирхгофа, а также
и вид функционала. Подобное рассмотрение проведено КШ. Ермольевым
и И.М. Мельником [66]. Подробный содержательный и математический
анализ применимости теории нелинейных сетевых транспортных задач
к "сетям физической природы" дан в книге ЕД1. Васильевой, Б.Ю. Левита
и В Л. Лившица [35]. Прикладная сторона здесь заключается в возможнос-
возможности применения методов и стандартных программ для решения сетевых
транспортных задач или даже общих методов нелинейного программирова-
программирования, например методов возможных направлений [74,211].
Помимо отмеченных выше, имеется еще целый ряд, по-видимому,
независимых друг от друга работ, посвященных применению теории гра-
графов, аппарата линейной и нелинейной алгебры и минимизации функций
для математического моделирования и расчета систем трубопроводного
транспорта и вентиляции. Так, АД. Багриновский [16], 1964 г., говорит
о необходимости "новой математической теории сетей".
Широкий спектр вопросов математического описания, расчета и опти-
оптимизации систем транспорта газа с упором на разработку общих алгоритмов
и доведение их до машинных программ представлен в монографиях
М.Г. Сухарева и ЕР. Ставровского [226-228]. Ранее A965 г.) в статье
[225] М.Г. Сухарев дал матричную форму записи системы уравнений
законов Кирхгофа (на примере газосборных сетей), а также общее дока-
доказательство сходимости для нее (в случае плоских схем) метода простой
итерации. Причем в отличие от других авторов [188, 247] сделано это
подстановкой общего решения подсистемы уравнений первого закона
Кирхгофа непосредственно в уравнения второго закона. Монография
[226] содержит уже общие исходные положения, математические модели,
44

оды и алгоритмы для изучения и расчета газосборных и газораспреде-
ельнь1Х сетей и магистральных газопроводов. В ней, в частности,
обсужда10™ вопросы экстремального подхода к расчету потокораспреде-
ения, двойственности систем уравнений первого и второго законов Кирхго-
Кирхгофа и области применения различных методов.
Из других работ можно указать на статью [283] Р. Даффина A947 г.),
где рассматриваются квазилинейные цепи, в которых "ток, идущий через
проводник, и соответствующее ему падение напряжения не уменьшают
значений друг Друга", и доказывается единственность токораспределения
для таких цепей. Кроме того, в ней устанавливается взаимно однозначное
соответствие узловых и контурных уравнений для планарных схем и пред-
предлагается один из механических аналогов квазилинейных цепей — "эластич-
"эластичные цепи" (совокупности связанных между собой пружин).
Специальным, но весьма перспективным направлением работ в данной
области является применение методов гибридного моделирования [187].
Этот подход сочетает в себе преимущества автоматизированной обработки
данных на ЭВМ и сверхбыстродействие аналоговых сетевых устройств.
Назначение данного обзора литературы (который в известной мере бу-
будет продолжен и ниже, при изложении отдельных вопросов) состоит в
том, чтобы дать представление о проблематике исследований, имеющих
отношение к предмету данной монографии, и показать общий фон теорети-
теоретических, математических и отраслевых работ в этой области. Нетрудно
увидеть, что отмеченные работы, имея несомненное научно-методическое и
практическое значение, весьма многоплановы, различны по уровню изло-
изложения и вместе с тем во многом дублируют друг друга, поскольку не
имеют четкого объединяющего стержня и ограничивающих рамок. Это еще
раз показывает актуальность и полезность ТГЦ как самостоятельного
научно-технического направления. Систематическое изложение ее основных
положений, математических моделей и методов начинается со следующей
главы.
Глава 4
АЛГЕБРА И ТОПОЛОГИЯ ГИДРАВЛИЧЕСКИХ ЦЕПЕЙ
4.1. УРАВНЕНИЯ ГИДРАВЛИЧЕСКОЙ ЦЕПИ
И ФОРМЫ ИХ ПРЕДСТАВЛЕНИЯ
Распределение расходов и напоров в г.ц. с сосредоточенными постоянными
при установившемся движении несжимаемой жидкости описывается, во-
первых, линейными соотношениями, аналогичными законам Кирхгофа
Для электрической цепи, и, во-вторых, нелинейными уравнениями связи
между расходами и потерями давления на ветвях, которые будем назы-
называть замыкающими соотношениями.
Итак, рассматривается г.ц. с произвольной схемой соединений, состоя-
состоящей из т узлов, и ветвей и*с линейно-независимых контуров (т — 1 + с =
~п)- Будем считать, что для каждой ветви i = [/, /+ 1], где / и / + 1 -
ее начальный и конечный узлы, задан закон гидравлического сопротивле-
сопротивления, связывающий общую потерю А,- давления на трение, перепад у{
45

/ /¦'/
4.1. Изменение давления вдоль активной
ветви
У1 — разность (перепад) давлений;
И( — потеря давления; Я,- — действующий
напор; sj — сопротивление ветви; х{ _
установившийся расход среды; L/ —
длина
4.2. Возможные зависимости между
потерей давления и расходом
(V-V"):hj = SjXf B'-2'"):'i,- =
= SjXj\Xj\;
B'-2") :/!,• = i/xj. C) :hj= /,-(jc,-)
давления, действующий напор Я,- и установившийся расход X; (рис. 4.1):
hi=yt+H, = fi(xt); i =l,...,n, D.1)
где
yi = Pi-Pi+i- D-2)
Для пассивной ветви Яг- = 0 и, следовательно, йг- =^;-. Поскольку знак
величины х{ должен характеризовать направление потока на ветви (точнее
его совпадение с ее ориентацией) и одновременно отвечать знаку /г,-, то
одночленную зависимость между ними представим в виде
где S/ ~ коэффициент гидравлического сопротивления, /3 — заданный пока-
показатель степени.
Возможные графики зависимости между потерей давления и расходом
приведены на рис. 4.2. Для линейных электрических цепей /3 = 1 и имеет
место закон Ома:
/}(*,) = stxt. D.4)
В случае г.ц. довольно часто берется квадратичный закон @ = 2), являю-
являющийся для круглых труб следствием известной в гидравлике формулы
Дарси -Вейсбаха:
D.5)
46

Коэффициенты гидравлического сопротивления (или просто "сопротив-
ения") s,- в D.3) ч svj отличаются друг от друга размерностью, опреде-
яемой в соответствии с принятыми единицами измерения расхода -
массовым, объемным или весовым.
Формулы Дарси, как и закон Ома, получена обработкой опытных дан-
данных и достаточно хорошо, но не абсолютно точно отражает действительные
соотношения. Поэтому в общем случае, когда это необходимо, замыкаю-
замыкающее уравнение D.1) может быть представлено в форме алгебраического
многочлека (для л:,. > 0)
и, = *;*, + *;'*? +«Г*?+ ¦•¦. D.6)
который (при соответствующем выборе коэффициентов) хорошо ¦ ап-
аппроксимирует любую функцию/J (*,•).
Число членов и наибольший показатель степени здесь определяются
требованиями к точности расчета, с одной стороны, и емкостью памяти
ЭВМ - с другой, поскольку с увеличением числа членов растет и объем
информации о расчетной схеме цепи. Как отмечалось в разд. 1.2, в боль-
большинстве практических случаев можно ограничиться двучленной (линей-
(линейно-квадратичной) зависимостью
Л, = *',*,- + Чх]. D-7)
Что касается минимально необходимых формальных требований к
виду J} (Xj), отвечающих наиболее общим физическим свойствам устано-
установившегося течения жидкости, а также, исходным положениям математи-
математического моделирования гидравлических систем, то они сводятся к усло-
условиям:
1) непрерывности и гладкости, т.е. существования непрерывных произ-
производных/) (л:,-) на всей числовой прямой — °° < х{ < +°°;
2) нечетности, т.е. ft {-х) = -ft (х(), причем f{ (*,•) > 0 для х,- > 0 и
fi(Xj) =0прих,- =0;
3) строгого возрастания — для случая течения несжимаемой жидкости,
™. л (*;).</;¦(*,") при *;<*;'.
Из второго условия следует, к примеру, что для любых хг f;(Xj)x{>
> 0, т.е. энергетические затраты на преодоление трения всегда положитель-
положительны независимо от знака х,-, что отвечает физической сущности течения.
В то же время третье условие не соблюдается, например,, при течении
Двухфазных жидкостей (парожидкостньгх смесей, гидровзвесей и др. —
см. кривую 3 на рис. 4.2). Возможная неопределенность (неоднозначность)
в определении расхода таких жидкостей объясняется тем, что одному зна-
значению напора может отвечать не одно, а три значения расхода. При этом
падающий участок кривой 3 не противоречит принципу возрастания потери
Давления с увеличением скорости, так как массовый (или объемный) рас-
расход эквивалентен осредненной скорости потока, что, однако, теряет смысл
при расслоении двухфазной среды.
Однозначность потокораспределения в г.ц. с сосредоточенными параметра-
1411 следует из даваемого ниже (в гл. 7) обобщения теоремы Максвелла о
принципе наименьшего теплового действия на нелинейные цепи.
47

Введением векторных обозначений х, у, Н и f(x) = (ft (*! ),...,/„ (хп))т,
а также диагональных матриц
о u,^-1 о
О
X =
О
!-1
соотношения D.1) и D.3) приобретают компактный вид, относящийся
сразу ко всем ветвям цепи:
h = у + Н = f(x) = SXx. ; D.8)
Перейдем теперь от замыкающих соотношений к схемным (сетевым)
законам Кирхгофа, которые должны выполняться для любого потоко-
потокораспределения. Во-первых, в каждом узле / должен соблюдаться материаль-
материальный баланс, отвечающий принципу сплошности потока, т.е.
2 Xi = Qj, j = 1.....1Я, D.9)
i
где слева стоит алгебраическая сумма расходов по всем ветвям, имеющим
общий (независимо от того, конечный это или начальный) узел /, а справа -
расход в этом узле: нагрузка Qj < 0, если это потребитель, приток Qj > О,
если речь идет об источнике, и Q/ = 0 в случае, когда узел / является прос-
простой точкой разветвления на схеме.
Значения Qj должны быть заданы (или определяться — в более сложных
задачах расчета потокораспределения, см. об этом ниже, в гл. 8) таким
образом, чтобы имел место их общий нулевой баланс по всем от узлам
схемы:
т- 1
Ь = 0, т.е. Qm =-
Qy
D.10)
В связи с этим условием одно (любое) из уравнений D.9) можно отбро-
отбросить. (Как правило, будем исключать уравнение для узла от.)
Второй закон Кирхгофа требует суммарного нулевого изменения пере-
перепадов У\ давления (разностей потенциала) в любом контуре схемы; для
этого необходимо и достаточно, чтобы равенство
2yt = 0, , D.11)
г
где суммирование ведется по всем ветвям /, входящим в контур г, выпол-
выполнялось для любого из линейно-независимых контуров (г = 1,..., с).
Поскольку уравнения D.11) не описывают изменения давлений по
ответвлениям схемы, находящимся вне ее "контурной" части, то в таком
общем случае следует обратиться к связям D.2) между У{ и узловыми
давлениями Ру. Так как одно из давлений (например, Р'т в узле т) должно
быть обязательно задано (в качестве точки отсчета для их значений в ос-
остальных узлах), что физически очевидно и для электрических, и для гидрав-
гидравлических систем, то неизвестными могут быть не более от — 1 значений Р/.
48

рассмотренных соотношений и сетевых условий достаточно для построе-
построения ДВУ4 эквивалентных систем уравнений, описывающих потокораспре-
еяение в произвольной г.ц. с сосредоточенными параметрами. В первом
случае объединение п замыкающих соотношений D.1), т — 1 линейно-не-
линейно-независимых уравнений вида D.9) и с уравнений D.11) приведет к общей
система из п + т — I + с = 2п уравнений относительно 2и неизвестных х{
Kyjt если\будут заданы все s{ и Щ. Вторую систему можно получить, если
использовать п соотношений D.1) и т — 1 уравнений из D.9) с п уравне-
уравнениями D.12), тогда получим систему из 2и + т — 1 уравнений относительно
Хи yt и rh — 1 значений Р/.
Подобное выписывание уравнений для каждой рассчитываемой схемы
является довольно утомительным занятием, не говоря уже о возможных
при этом ошибках. Но самое главное: игнорирование компактных и доста-
достаточно формальных средств — речь идет о математическом аппарате вектор-
векторной и матричной алгебры — для обозримой записи и преобразований мате-
математической формулировки задач не дает возможности в полной мере клас-
классифицировать получаемые системы уравнений и оперировать с ними, а
также эффективно применять численные методы линейной и нелинейной
алгебры.
Алгебра векторов и матриц уже давно получила широкое распростране-
распространение в различных областях естественных наук и техники. Весьма успешно
применялась она и в теории электрических цепей, что (как уже отмечалось
во введении) позволило дать наиболее общее описание и обоснова-
обоснование многим расчетным методам и приемам, используемым в электро-
электротехнике.
В специальной литературе по инженерным методам расчета гидравличес-
гидравлических систем водо- и теплоснабжения, вентиляции и других матричная алгеб-
алгебра до появления и активного применения ЭВМ, в общем-то, не использо-
использовалась. Американский математик Л.А. Пайпс, перечисляя в своей обзорной
статье [181] области применения матриц в технике, поставил на второе
место -(после электрических цепей) "распределение скоростей потоков
воды в сложных гидравлических системах".
Ниже вводятся основные матрицы гидравлической цепи и рассматри-
рассматриваются их линейные преобразования [242,243].
4.2. МАТРИЦЫ ЦЕПИ И ИХ ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
Введем полную матрицу А соединений т узлов и и ветвей цепи, однозначно
описывающую ее конфигурацию, безотносительно к конкретным длинам
ветвей и фактическому месторасположению узлов. В этой матрице на пере-
пересечении строки /, отвечающей узлу/,и столбца i, соответствующего ветви г,
помещается элемент
10, если ветвь i не соединена с узлом /;
+1, когда ветвь z исходит из узла/ и
—1, если узел / является для ветви i конечным.
Приведем пример такой матрицы для схемы, состоящей из четырех узлов
и шести ветвей (рис. 4.3):
4- Зак. 384 49

1
2
3
4
1
- 1
1
2
1
- 1 -
3
1
1
1
4
_
1
- 1
5
1
1
6
1
- 1
D.12)
В каждом столбце матрицы только два ненулевых элемента: 1 и - 1, поэто-
поэтому сумма всех ее строк дает нулевую строку, что означает их линейную
зависимость. Таким образом, ранг матрицы ЛГ, т.е. максимальное число ее
линейно-независимых строк (или столбцов), составляет т - 1. В дальней-
дальнейшем здесь чаще всего будет использоваться неполная матрица соединений
с размерами (т — 1) Хп, имеющая только линейно-независимые строки,
которую будем обозначать через А. Ее можно получить из А вычеркиванием
любой из строк (как правило, это будет строка т).
4.3. Пример расчетной схемы г.ц.
Цифрами указаны номера уз-
узлов, цифры в кружках — номера
ветвей, кружок со стрелкой -
источник напора, цифры в центре
контуров обозначают их номера,
а стрелки вокруг — направления
обхода
Матрица соединений выполняет ряд взаимосвязанных между собой
функций. Во-первых, как уже говорилось, она отображает и представляет
схему рассматриваемой цепи. Можно считать, что схема цепи задана, если
известна ее полная матрица соединений, и наоборот. Таким образом, ис-
использование этой матрицы в том или ином математическом описании и
в его алгебраическом преобразовании автоматически учитывает конкрет-
конкретные особенности схемы.
Во-вторых, она позволяет дать алгебраическое описание материального
баланса .сразу во всех узлах, т.е. для схемы в целом. Это следует из того,
что каждое из уравнений материального баланса D.9) для любого из узлов
можно представить в виде скалярного произведения строки матрицы А,
соответствующей этому узлу, на один и тот же вектор - столбец х расхо-
расходов на всех ветвях. Например, для узла 2 схемы рис. 4.3 имеем
_ 1
-1
1
X
хг
Хт,
х6
= о,
50

то после выполнения скалярного произведения дает - х2 - х3 + х6 = 0.
Лля всех узлов этой схемы материальные балансы могут быть представле-
ы в виде произведения уже всех строк матрицы на вектор х:
или
-1 1
-1
1
кратко
— 1
1
1
-1
1
1
-
X
Х\ '
х2
Хъ
*4
х$
=
¦ о ¦
0
0
.0 .
Ах = 0. D.13)
В большинстве случаев при расчете потокораспределения отдельные
расходы в узлах или на ветвях задаются. Последние тогда должны быть
также отнесены и к соответствующим узлам. При этом каждый фиксиро-
фиксированный на ветви расход суммируется с известным (или нулевым) расходом
в начальном ее узле и вычитается из расхода в конечном узле, а отвечающие
ему столбец матрицы А и компонента векторах исключаются. Все получен-
полученные таким образом (с учетом алгебраического суммирования) расходы в уз-
узлах составят вектор правых частей Q. Покажем это для схемы на рис. 4.3,
когда, к примеру, известны расходы на ветвях 2 и 4. Тогда искомая (но
теперь уже неоднородная) система уравнений материального баланса в уз-
узлах примет вид
1
- 1
1
3
-1
1
5
-1
-1
6
1
-1
х2
х6
С помощью полной матрицы соединений А можно в общем виде записать
также и связь между давлениями Р/ во всех узлах схемы и их перепадами
Ух на ветвях. Действительно, /-ый столбец А,- этой матрицы содержит инфор-
информацию (в виду двух чисел: 1 и - 1 на соответствующих местах /, и / 2)
не только о концевых узлах данной ветви / = \j\ , j2 ], но и о ее ориентации,
поэтому
где справа стоит скалярное произведение столбца А,-, записанного как век-
вектор-строка, на вектор-столбец Р. По отношению ко всем ветвям схемы
одновременно это даст
У=Атр. D.14)
51

Для схемы на рис. 4.3 D.14) будет выглядеть следующим образом:
У1
Уг
Уз
Уа
У$
=
-1
1
-1
-1
-1
1
1
1
-1
1
1
-1
-Pi +ра
Pi Pi - Рг
- Рг + Ра
Рз-Ра
-Pi+Рз
Рг-Рз]
Матрица соединений называется также матрицей инциденций вершин и
дуг ориентированного графа. Она обладает свойством унимодулярности
[25], заключающимся в том, что определитель любой ее квадратней под-
подматрицы равен 0, + 1 или - 1.
Другой основной матрицей цепи является матрица В контуров, которая
фиксирует выбранную на схеме систему контуров. В ней на пересечении
строки г, соответствующей контуру г, и столбца i задается элемент
0, если ветвь г не принадлежит контуру г; •
1, если ветвь г входит в контур г и ее ориентация совпадает
с направлением его обхода;
— 1, если ветвь / входит в контур г, но ее ориентация противо-
противоположна направлению его обхода.
В качестве примера рассмотрим систему из трех контуров для схемы
на рис. 4.3 (они пронумерованы цифрами с круговыми стрелками, пока-
показывающими заданные направления их обхода). Соответствующая матрица
имеет вид
В =
1
2
3
1
1
2
1
3
1
4
1
1
Ь
-1
1
-6
1
1
D.15)
Уравнение второго закона Кирхгофа для отдельно взятого контура
может быть записано как скалярное произведение вектора-строки матрицы
В, отвечающей этому контуру, и вектора-столбца у перепадов давлений.
Для всех контуров одновременно эти уравнения представляются уже в мат-
матричной форме
1 -1
1 1
1 1
Уг
Уг
Уз
Ул
Уа
Уб
=
о'
0
.0.
или кратко
52
D.16)

4-
©
а
Of/
J
и
1
1
/
4.4. Примеры преобразований схемы на рис. 4.3.
а - объединение узлов 1 и 2;б~г исходная и преобразованные системы контуров,
отвечающие матрицам В, В', В".
Перейдем к рассмотрению известных в алгебре элементарных преобразо-
преобразований матриц, которые имеют практическое значение при составлении и
преобразовании расчетных схем электрических и гидравлических цепей.
1. Перестановка (транспозиция) любых двух строк равносильна измене-
изменению нумерации узлов (для матрицы А) или контуров (для матрицы В).
Перестановка столбцов фактически изменяет нумерацию ветвей. Эти опера-
операции позволяют упорядочить (сгруппировать) расположение нулевых эле-
элементов в матрицах и приводить их (если это возможно) к тому или иному
(например, диагональному) виду.
2. Умножение столбца i на - 1 меняет ориентацию ветви i на противопо-
противоположную. Для изменения направлений потоков, притекающих или вытекаю-
вытекающих из узла /, или направления обхода контура г следует умножить на
-1 строку/ матрицы А или строку г матрицы В.
3. Сложение (вычитание) строк в матрицей приводит к новой линейной
комбинации узлов, а сложение строк в В - к новой системе контуров. При-
Прибавим, к примеру, в матрице соединений D.12) первую строку ко второй.
Получим новую матрицу и схему соединений (рис. 4.4, а), в которой узел
1+2" соответствует области, ограниченной пунктирной кривой, т.е.
K_J_2 3 4 5 6
1
А'= 1 + 2
3
аким образом, уравнение D.13) для узла 2 изменится на
*i +х3+х$ -Хб =о.
53
-1
1
-1
1
-1
-1
-1
1
-1

Матрица В в D.16) отвечает системе контуров, представленной на
рис. 4.4, б. Вычтем, например, из третьей строки вторую, получим матрицу
, "Ч 1 2 3 4 5 6
1
1
-1
1
1
1
-1
1
-1
1
1
1
1
2
1
-1
1
4
1
1
1
Ь
-1
-1
6
1
В'= 2
3- 2
что соответствует системе контуров, изображенной на рис. 4.4, в. Прибав-
Прибавляя теперь ко второй строке первую, получим
1
В" = 2 + 1
3-2
и соответственно еще одну систему контуров (рис. 4.4, г).
Очевидно, что число таких линейных комбинаций векторов-строк матри-
матрицы В и связанных с ними вариантов систем контуров будет очень большим
даже для относительно простых схем. Вместе с тем среди них можно выде-
выделить такие, которые принципиально отличаются от всех прочих и, как будет
видно из дальнейшего, являются предпочтительными. Прежде всего заме-
заметим, что число выбранных контуров, проходящих через одну ветвь, в точ-
точности совпадает с числом ненулевых элементов в соответствующем столбце
в матрицах В, В' и В". При этом в вариантах В я В' в каждом из трех конту-
контуров имеется одна ветвь, не принадлежащая никакому другому контуру,
а в случае В" такие ветви содержатся лишь в двух контурах. Соответствен-
Соответственно в матрицах В к В' можно выделить по три столбца с единственным нену-
ненулевым элементом, причем перестановкой второго и шестого столбцов в В'
можно добиться такого же диагонального расположения этих элементов
в первых трех столбцах, как ив В.
С помощью данных преобразований строго описывается процесс исклю-
исключения из схемы цепи зависимых ветвей, узлов и контуров, т.е. тех из них,
решения для которых тривиально определяются исходя из элементов
получаемой сокращенной расчетной схемы. Речь идет, в частности, о широ-
широко используемых при расчетах потокораспределения приемах суммирова-
суммирования коэффициентов сопротивления ветвей, соединенных последовательно,
и проводимостей ветвей, соединенных параллельно.
Исходя из этого, получаем очевидные выводы: 1) независимый узел
(не имеющий стока, т.е. потребителя) должен быть общим не менее чем
для трех ветвей и 2) независимый контур должен состоять не менее чем
их трех ветвей, т.е. проходить по трем и более узлам. Отсюда вытекают
простые правила приведения исходной схемы цепи к ее расчетному эквива-
эквиваленту с исключением тривиально зависимых узлов и ветвей.
54

4 3. ДЕКОМПОЗИЦИЯ ВЕКТОРОВ И МАТРИЦ ЦЕПИ
Одним из самых важных вопросов, относящихся к векторам и матрицам
цепи и вообще к математическому описанию и методам расчета потокорас-
еделения, является их рациональная декомпозиция (разложение, расщеп-
расщепление) на части с выделением тех или иных групп переменных и блоков
в матрицах. Именно с этим прежде всего и связаны такие теоретически и
практически важные вопросы, как строгое математическое описание преоб-
преобразований основных переменных к контурным или узловым величинам,
сокращение размерности задач о потокораспределении и анализ общих
свойств их решений, получение замечательных соотношений между матри-
матрицами и векторами, учет специфических особенностей сетевых задач при
применении численных методов линейной и нелинейной алгебры и др.
Известно, что в работах знаменитых физиков прошлого века (Кирх-
(Кирхгофа, Максвелла, Гельмгольца) такого рода преобразования лежали в осно-
основе предложенных ими методов для нахождения распределения токов, на-
напряжений и мощностей в линейных цепях. Эти же вопросы возникают при
описании и расчете гидравлических цепей на ЭВМ, но уже в рамках аппарата
нелинейной алгебры.
Практическая эффективность декомпозиции здесь тесно связана с уче-
учетом топологической структуры цепи, для чего требуется привлечение и
использование таких понятий, как граф в виде дерева, ветви-хорды, систе-
система главных контуров и др.
Дерево, по определению [25], - конечный связный граф без циклов,
имеющий не менее двух вершин. Дерево, связывающее все вершины графа,
называют остовным деревом, или каркасом. Применительно к схеме цепи,
которая представляется ориентированным графом из узлов и ветвей, дере-
дерево - это конечный связный орграф без контуров, имеющий не менее двух
узлов.
Поскольку висячий узел - это узел, присоединенный к схеме с помощью
только одной ветви, т.е. имеющий лишь одну общую с ней ветвь, то всякое
дерево имеет по крайней мере два висячих узла.
Число уУд различных деревьев, которое можно выделить в полном графе,
имеющем т узлов (т.е. в графе, в котором каждая пара узлов соединена
ветвью), выражается астрономическим числом тт ~ 2 (теорема Кэли
[234]). Так, например, даже для простейшего полного графа с четырьмя
вершинами это число равно 16, а при~т= 5 оно сразу возрастает до 125
И 1.Д.
Именно с выделением в схеме цепи того или иного остовного дерева
(или каркаса), соединяющего все его т узлов (будем называть его просто
Деревом), связаны в основном процедуры разбиения переменных на от-
отдельные группы, матриц - на блоки, а также и выбора системы линейно-
независимых (т.е. несводимых друг к другу посредством их линейных
комбинаций) контуров.
Для плоских схем одной из систем независимых контуров может слу-
служить система граней, где под гранью понимается часть плоскости, ограни-
ограниченная ветвями и не содержащая внутри себя никаких других ветвей.
Например, такая система показана на рис. 4.4, б. Все прочие системы конту-
Р°в для этой схемы могут рассматриваться как ее линейные комбинации.
4"неплоских схем такой подход уже неосуществим. Однако среди мно-
55

а
j J j
4.5. Переход от контуров-граней (я) к главной системе контуров (б) с выделе-
выделением отвечающего ей дерева (в)
жества систем независимых контуров для произвольной схемы соединений,
плоской или неплоской, можно выделить системы так называемых главных
контуров, понятие о которых, по существу, было введено еще Кирхгофом
[288] и используется практически во всех работах по теории цепей.
Системой главных контуров называется такая их совокупность, в каж-
каждом контуре которой имеется по меньшей мере одна ветвь, не принадлежа-
принадлежащая никакому другому контуру, — такие ветви называются хордами.
Из этого следует, что удаление всех хорд из исходной схемы превращает
ее в полностью разомкнутую схему, т.е. в дерево. Таким образом, каждому
дереву схемы отвечает своя система главных контуров, и наоборот.
Не каждая система независимых контуров, в том числе и контуров-гра-
контуров-граней, является главной. Например, для схемы на рис. 4.5, а (т = 6, и= 10,
с = 5) система граней не будет системой главных контуров из-за наличия
одной внутренней грани (она заштрихована) . Однако с помощью линейной
комбинации первой и пятой строк матрицы контуров можно получить
новую систему главных контуров и соответствующее ей дерево (рис. 4.5,
б, в).
Выбор одной из возможных систем главных контуров для схемы, в ко-
которой с помощью элементарных преобразований, описанных выше, уже
исключены все зависимые узлы и ветви, а затем удалены также и все вися-
висячие узлы, обычно осуществляется следующим образом:
1) на схеме выделяется некоторое дерево, связывающее ее т узлов,
в результате множество / всех ветвей разобьется на те — 1 ветвей (подмно-
(подмножество /п), составивших дерево, и с = п — (т — 1) ветвей (/к), не вошед-
вошедших в него, т.е. хорд;
2) поскольку каждая хорда замыкает некоторую последовательность
ветвей дерева, то тем самым ею однозначно определяется контур, который
и фиксируется соответствующей строкой в матрице В, в результате обра-
образуется система из с главных контуров;
3) векторы и матрицы цепи "расщепляются" на векторы и матрицы
хорд (хк, yK,hK, Нк, Ак,Вк)к дерева (хд,уп, йд, Яд, Ал, Яд).
56

Если при этом нумерацию ветвей провести так, что первые номера
присвоить хордам,т.е.хк = (*,,..., хс)т, хд = (хс+ ,,..., х„)т, аномера кон-
контуров и направления их обхода сделать совпадающими с номерами и ориен-
ориентацией хорд, то тогда матрицы А и В приобретут следующую структуру:
/7
Л*
ч
D.17)
/!7-/
Ч>
D.18)
Таким образом, А = (Ак, Аа) и В = (?', Ва), где ?" - единичная матрица
(составленная из единиц по главной диагонали) порядка с. -
Исходя из этого, декомпозиция систем уравнений первого и второго
законов Кирхгофа дает
Акхк +Ааха = Q, ук+Вауя = 0. D.19)
Из изложенного нетрудно, в частности, прийти к выводу о том, что значе-
значения расходов на всех хордах, т.е. вектор хк и вектор Q узловых расходов
однозначно определяют расходы на ветвях дерева, т.е. хд. Действительно,
из D.19) имеем
*д=^д1(б-^к*к), D-20)
причем матрица Лд1, обратная к Ал, здесь всегда существует, поскольку
в случае графа-дерева его матрица соединений (без последней строки)
обязательно будет иметь определитель, отличный от нуля, т.е. будет неосо-
неособенной [25,56].
4.4. ЦИКЛИЧЕСКАЯ СХЕМА ЦЕПИ
Исходная г.ц. отвечает некоторой реальной системе с течением жидкости
или газа. Однако во многих случаях требуется переход к некоторому ее
условному расширению до циклической (полностью замкнутой) схемы,
отображающей "кругооборот" в движении транспортируемой среды. Эта
схема, как правило, имеет вспомогательноее (методическое и практичес-
практическое) значение: она позволяет провести анализ всей картины потокораспре-
Деления, расширить и усложнить постановку задачи, а затем обоснованно
вернуться, если это целесообразно, к исходной схеме цепи [132, 140].
Такая схема может быть получена из любой первоначальной схемы сое-
соединением всех ее m узлов условными (фиктивными) ветвями с дополни-
дополнительным опорным узлом m + 1, имеющим фиксированный потенциал (дав-
(давление) . в частности, в качестве подобного узла можно взять один из исход-
исходных, что сократит дополнительные построения.
57

4. 6. Пример перехода к циклической схеме гидравлической цепи
»л = 4, л = 6, с = 3 , m '= т + 1 =5, л'=n + m = 10, с' = с + т — 1=6
Будем рассматривать общий случай и от схемы, имеющей т узлов, п вет-
ветвей и с контуров (для дерева п = т - 1, с = 0), перейдем к циклической
схеме (см. пример на рис. 4.6) с т + 1 узлами, п + т ветвями и с + т - 1
контурами. Предположим, что Рт + i = 0. Замыкающее соотношение для
любой новой ветви может быть записано, например, в следующей линейной
форме:
h, = yt = Pj Pm + l=P,= StQj + Hi, D.21)
S{ - 0, Hi'=Pj, если задано Р,¦ ;
где Si = Pjl\ Qj |, //,- = 0, если задано Qj ;
Si = °°, Ht = 0, если Qj = 0.
Дополним теперь систему из с главных контуров исходной схемы сле-
следующим образом. С каждой условной ветвью [},т+ 1 ], ведущей из любо-
любого линейно-независимого узла / = 1, ..., т - 1 в новый узел т + 1, можно
однозначно связать контур, проходящий по данной ветви, далее всегда по
одной и той же ветви [т + 1, т], а затем — по ветвям дерева от узла т
до узла /. В результате ветви i = п + / ( / = 1, ..., т — 1) дополнят число
хорд и определят контуры г = с + 1,..., с + m — 1 (см. рис. 4.6).
Ориентацию новых хорд и, следовательно, направления обхода дополни-
дополнительных контуров выберем одинаково, например от узла / к узлу т + 1.
Рассмотрение будем вести применительно к типовой задаче гидравлическо-
гидравлического расчета, когда заданы все узловые расходы Qj и давление^.
Структура матриц и векторов цепи, расширенных в результате добавле-
добавления фиктивных ветвей и узла т + 1, показана на рис. 4.7. В новой матрице
А, как и в любой полной матрице соединений узлов и ветвей, ее строки
линейно зависимы. В качестве лишней будем считать строку т, тогда систе-
система уравнений в "расщепленном" виде применительно к циклической схеме
запишется следующим образом:
58

4
ff
4.7. Структура матриц и векторов для циклической схемы цепи
Акхк +Аахя - Q = 0,
т -- 1
ук + ваУл = о,
D.22)
D.23)
D.24)
+ Р I Р' - Г) (A ~>*Л
у + Н = SXx, D.26)
глеЛд -- квадратная матрица (порядка т - 1) путей (радиусов) снабжения
по ветвям дерева от опорного узла т до любого другого; / ^т _ i) — век-
вектор, составленный из т— 1 единиц.
Это система из (т — 1) + 1 + с + т -¦ 1 + п = т + 2w уравнений относи-
относительно л:, у, Р и 2т- Примечательно, что в ней присутствуют величины,
относящиеся лишь к исходной схеме. Однако в отличие от первоначальной
системы уравнений D.13), D.16) и D.8) здесь имеется уравнение D.25),
связывающее векторы уп и Р, и в таком виде эта система уравнений спра-
справедлива для не полностью "закольцованных" схем с "висячими" ответвле-
ответвлениями и вершинами. В частности, для дерева, когда с = 0 и уравнение D.24)
вообще отсутствует, D.25) полностью описывает распределение узловых
Давлений и их перепадов по всем ветвям.
Переход к циклической схеме используется как основной прием при
расчете цепей с переменными параметрами (см. гл. 8), когда притоки и
потребление в узлах не фиксируются, а задаются в виде тех или иных
аналитических выражений. В этом случае дополнительным ветвям цикли-
циклической схемы присваиваются именно эти зависимости, которые описывают
правила "взаимного регулирования" расходов и давлений в узлах. И в ито-
итоге задачу о потокораспределении приходится решать для расширенной та-
таким образом г.ц.
59

4.5. СВЯЗИ МЕЖДУ МАТРИЦАМИ И ВЕКТОРАМИ ЦЕПИ
Между матрицами и векторами цепи существуют замечательные соотноше-
соотношения, которые являются математическим отражением сетевого характера
изучаемых объектов и служат основным инструментом для преобразова-
преобразований к контурным или узловым величинам [132, 133, 140]. Прежде всего
выявим связь между матрицами соединений и контуров, т.е. А к В.
Рассмотрим однородную систему уравнений первого закона Кирхгофа
Ах = 0 D.27)
и покажем, что любая строка матрицы В является ее решением. Действи-
Действительно, пусть aj = (д;1, ... , а,п) - /-я строка A (j = 1 т - 1), а Ь? =
= (br ь..., Ъг п) - г-л строка В (г = 1,. .. , с), где элементы а;-,- и br,- (/ =
= 1,. . ., и) принимают значения 0, 1 и -1 (как это описано выше).
В случае, когда контур г не проходит через узел/, ненулевые элементы
uji и br i имеют обязательно различные номера i и потому скалярное произ-
произведение ajbr = 0. Если же простой контур г проходит через узел/, то ему
могут принадлежать лишь две ветви: z'i и /2, инцидентные данному узлу,
и только для них одновременно не равны нулю соответствующие элементы
пц и bri, так что скалярное произведение фактически будет сводиться к
сумме двух слагаемых:
ajbr = al-ii brii + а/!г brii. D.28)
Как видно из рис. 4.8, в любом случае прохождения контура через узел/
произведения в правой части D.28) обязательно имеют разные знаки, так
что их сумма равна нулю и потому всегда aj br = 0.
Так как это справедливо для любых / и г, то, во-первых,
Abr = 0; r=\,...,c, D.29)
т.е. любая строка матрицы В (берущаяся здесь как вектор-столбец) удов-
удовлетворяет системе D.27), во-вторых, это может быть записано сразу для
всех строк, что приведет к искомому произведению матриц
АВТ = 0. D.30)
Применяя D.30) поблочно для матриц циклической схемы (см.
рис. 4.7), будем иметь
0(сХ>
(Ак,Аъ,-с ч1 "ЧЧ " Лд((т-1)Х(«-1))
Тем самым получены следующие равенства, которые существенным обра-
образом используются в дальнейшем:
Ак+АаВ1.-0, т.е. 5д = — Ад1Ак, D.32)
AaR* = E, т.е. Rl=A^. D.33)
60

4.8. Различные случаи прохождения контура г через узел j
Эти выражения, связывающие матрицы Ва и Ra с Ак и Аа, отражают,
в частности, тот факт, что матрица соединений А и выбранное на схеме
цепи дерево однозначно определяют матрицу контуров В, что может быть
использовано для ее автоматического построения при расчетах на ЭВМ.
Практически более эффективным, однако, является выбор системы глав-
главных контуров и построение их матрицы В непосредственно по информации
о схеме цепи.
Перейдем теперь к виду общего решения системы уравнений первого
закона Кирхгофа и соответственно к связи между векторами хп и л:к.
Из предыдущего ясно, что ранг матрицы А равен т - 1 и поэтому фунда-
фундаментальная система решений приведенной системы уравнений Ах - 0 состо-
состоит из п — (т — 1) = с специально подобранных наборов чисел. В качестве
таковых можно взять, как это следует из D.29) и D.30), систему из с
строк матрицы В, построенной для главной (хордовой) системы контуров.
Любая линейная комбинация этих строк с произвольными постоянными
коэффициентами х'к = (х[, ..., х'с)Т также будет решением приведенной
системы, так что
АВтх'к = 0. D.34)
Нетрудно заметить, что вектор @(с), R^Q) может служить частным ре-
решением исходной неоднородной системы Ах = Q, поскольку в силу D.33)
\ RIQ
Таким образом, общее решение системы может быть записано в виде
т.е.
X ~ х х — R1*' х + R1* О (A ^S^
С другой стороны, систему уравнений первого закона Кирхгофа, пред-
представленную в блочном виде D.22), можно непосредственно разрешить
относительно лгд:
хя =Ад1(-Акхк + Q)= - А^Акхк+ A^Q, D.36)
ГДе Ац обязательно существует, так как. определитель квадратной матри-
Чы Аа, как отмечалось в разд. 4.3, отличен от нуля.
Из сравнения D.35) и D.36) видна их эквивалентность, так что элемен-
ты общего решения получают ясную схемную интерпретацию:
О частное решение хк = 0, ха = R^Q отвечает потокораспределению в
выбранном дереве и может быть получено простым суммированием узло-
61

вых расходов Qj с учетом их знаков вдоль ветвей дерева, т.е. без обраще-
обращения матрицы Лд (что и делается на практике);
2) в качестве произвольных постоянных могут браться расходы на хор-
хордах, т.е. "контурные расходы", составляющие вектор хк, что позволяет
любой вычислительный процесс относительно расходов сводить к рас-
рассмотрению контуров.
Гидравлический расчет, который связан с определением перепадов yi
давления на ветвях, завершается обьино "откладыванием" этих значений от
заданной величины Р'т для получения искомых давлений во всех узлах
схемы. Для этой процедуры достаточно использовать значения у( только
для ветвей дерева (их значения для хорд будут автоматически подтвержде-
подтверждены в силу второго закона Кирхгофа). В связи с этим дадим в общем виде
связь между векторами Р, уа и значением Р'т.
Ранее уже приводилась система уравнений D.14), связывающая у и Р.
Если выделить отдельные блоки Ак и Аа матрицы А, относящиеся к дереву
и хордам схемы, а также ее т-ю строку а?, = (am,i> • • • . ат,с\ ^т,с + \. • ¦ •
• ••.Чл) = (ди,к.вт,д).та D-14) примет вид
(У). ( + *•-¦¦*-¦•) (М. D36)
Выполняя здесь поблочно скалярные произведения, получим
аР'т,
так что из второго векторного уравнения в D.37)
Р = (А1У1(уа-ат,дР^),
а с учетом D.33) окончательно имеем
Р = Ял{Уъ-ат,пР'т). ' D.38)
Уравнение D38) описывает процесс определения давления Pj в любом уз-
узле/, исходя из заданного Р'т, через "цепочку" значений у1 но ветвям дере-
дерева, соединяющим узлы ми/.
Глава 5
ГИДРАВЛИЧЕСКИЕ ЦЕПИ
С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
5.1. ИСХОДНЫЕ СИСТЕМЫ УРАВНЕНИЙ
В данном разделе рассматриваются в матричной форме две основные систе-
системы уравнений (или, как говорят,математические модели), которым долж-
должны удовлетворять искомые гидравлические параметры, описывающие рас-
распределение расходов и давлений по всем элементам цепи с сосредоточен-
сосредоточенными параметрами для некоторого установившегося течения [242, 247,
248, 132]. В каждой из них фигурируют уравнения законов Кирхгофа и
'замыкающие соотношения, которые по отдельности уже приводились
62

в гл. 4. Отличаются же они составом векторов цепи, которые привлекаются
для описания потокораспределения, способом отражения второго закона
Кирхгофа, а также числом уравнений и неизвестных.
Замыкающие уравнения, как уже отмечалось, зависят от типа системы
и характера течения и в компактной форме, относящейся сразу ко всем
ветвям расчетной схемы цепи, имеют вид
E.1)
где в случае квадратичной зависимости между потерей давления ht и расхо-
расходом х,- (которая берется лишь для упрощения изложения)
hi = si\xi \Xj, i= 1,.. . ,п.
Для пассивной ветви действующий напор Я, = 0 и, следовательно, h; совпа-
совпадает с перепадом (разностью) yt давлений в ее концевых узлах.
Введением диагональных матриц S и X, составленных из элементов s,- и
\Xj\, выражение E.1) запишется как
у = SXx - Н. E.2)
Первая ("контурная") система уравнений включает три группы урав-
уравнений:
Ах = Q, By = 0, у + Н = SXx,
E.3)
где Q, Н и S заданы, а А и В отвечают расчетной схеме цепи. Она может
быть представлена в виде следующей блочной структуры (с указанием
размерности всех составляющих):
1
I
/7
-V
777-/
E.4)
Ух
E5)
/7
0
•
X
•
E.6)
Это система из т - 1 + с + п = 2и уравнений относительно неизвестных
xi и .V/.
63

В ней можно исключить вектор у подстановкой E.2) во вторую под-
подсистему уравнений E3):
Ax = Q, BSXx=BH, E.7)
что понизит ее порядок с 2л до п. Кроме того, порядок системы уменьшит-
уменьшится еще более, до с, если общее решение подсистемы E.4) в виде D.35)
или D.36) подставить во вторую группу уравнений E.7). Именно это
и делается в методе контурных расходов (см. ниже), но только для
линеаризованных уравнений E.7).
Решение данной системы уравнений даст представление о потокорас-
пределении в виде значений (для всех ветвей) расходов и перепадов
давления, "увязанных" в соответствии с требованиями законов Кирх-
Кирхгофа по всей закольцованной части цепи, но без определения значений уз-
узловых давлений Pj. Их подсчет, исходя из заданного Р'т, обычно произво-
производится уже после решения системы E.7). Однако соответствующая груп-
группа уравнений D.38),связывающая вектор Р с перепадами давлений на
ветвях дерева, формально для полноты картины может быть добавлена
к E.3), и тогда в целом будем иметь систему из 2п + т —1 уравнений
относительно х, у и т - 1 значений Pj.
Вторая ("узловая") система уравнений, приводящая к тем же числен-
численным решениям, опирается на использование полного вектора Р и поэтому
не требует обращения к контурам, так как при любом Р уравнения второго
закона Крихгофа обращаются в тождества. Однако вместо этого в системе
уравнений должна быть представлена связь D.14) между векторами Р и
у, так что общий вид этой системы следующий:
Ax = Q, у=^4ТР, y+H = SXx. E.8)
Она имеет m — 1 + 2л уравнений относительно векторов*, у и тп — 1 значе-
значений Pj в линейно-независимых узлах. Здесь также может быть исключен
вектор у, что сократит E.8) до
Ax = Q, ATP = H + SXx, ' E.9)
где уже m - 1 + и уравнений.
С целью более удобной и компактной записи отдельных подсистем урав-
уравнений в E.7) и E.9), а также операций над ними (различных подстановок,
взятия производных и др.) введем следующие обозначения:
u(x) = Ax-Q = {ui(x)=I,xi-Qj = aJx-Qj}, j = 1,. . . ,m - I; E.10)
v(x) = BSX -BH={vr(x)=T, bri(Sj| xt | Xi -#,) =bJ (SHx - H) },
r=l,...,c;_ E.11)
w(x, P) = ArP + H- SHx = {Wj(x, P) = Pfi - PJ2 + Hi - Si | xt \x/),
/=1,...,«, E.12)
где ?и ^означают суммирование по всем ветвям /, инцидентным соответ-
ственно узлу / и контуру г; aj и bj — строки/ иг соответственно матриц
А и В; ветвь / = \jx, j2 ].
64

В результате системы E.7) и E.9) могут быть записаны также и следую-
следующим образом:
u(x) = 0, v(x) = O; E.13)
и(лг) = О, w(x,P) = 0. E.14)
Корректность постановки задач гидравлического расчета. Решение этого
вопроса связано прежде всего с пониманием физической сущности задачи
и в конечном итоге зависит от правильности соотношения заданных и иско-
искомых величин, от соразмерности степени детализации и агрегирования схе-
схемы качеству и количеству имеющихся исходных данных и от разброса
в их значениях.
Системы уравнений, представленные выше, рассчитаны на один важный,
но все-таки частный случай, когда задаются все расходы Q в т - 1 узлах
и давление Р,- в одном из узлов расчетной схемы. Тогда имеем замкнутую
систему уравнений, для разрешимости которой необходим баланс между
общим притоком в цепь и суммарным расходом у потребителей:
т
2 Qj+ 2 Q,-= 2 Qj = 0, E.15)
где для /e/i Qj<0-
Доказательство этого факта легко следует из линейной зависимости
строк полной матрицы А , так как по построению их сумма дает нули во
всех столбцах. Таким образом, материальный баланс в узле т автомати-
автоматически должен иметь место, если он соблюден вт-1 линейно-независимых
узлах, что и приводит к условию E.10).
Для этих же систем уравнений недопустимо фиксировать (при заданном
Q) два значения и более узловых давлений, так как тогда она становится
переопределенной, что может привести к ее несовместности. В общем же
случае правило корректной постановки задачи может быть сформулирова-
сформулировано следующим образом: если хотя бы в одном из узлов расход является
неизвестной величиной, то в систему уравнений необходимо включить
уравнение E.15) общего баланса узловых расходов, а количество заданных
значений Qj должно при этом совпадать с числом неизвестных Р,-.
Пример составления системы уравнений. Рассмотрим прежний пример
цепи, схема которой дана на рис. 4.3 (для нее т = 4,и = 6ис=3). Стрелки
на ветвях показывают выбранные направления потоков для начального
приближения. Дополнительно предположим, что в узлах 1 и4 расположены
потребители с нагрузками ??i < 0 и Q4 < 0, в узле 2 - источник с произво-
производительностью Qi = - ((?, + Qn), а в узле 3 Q?, = 0. Кроме того, ветви / и 6
будем считать активными, с действующими напорами Н{ и Нь. Таким обра-
образом, заданы векторы узловых расходов Q = (Qlt Q2, 0, Q4)T и действую-
действующих на ветвях напоров Н = (НХ, 0,0, 0,0,Я6)т.
Базисная система из трех контуров, показанная на рисунке, является
одной из возможных — она отвечает выбранному дереву, состоящему из
ветвей i = 4, 5, 6. Ветви / = 1, 2, 3 считаются хордами, так что они опре-
определяют контуры г = 1, 2, 3 и направления их обхода. В качестве линей-
линейно-независимых приняты первые три узла/ = 1, 2, 3. Матрицы соединений
и контуров были приведены ранее в виде таблиц D.12) и D.15).
s- Зак. 384 65

Si
1
1*11
s2
2
1*2 1
«3
3 i
1 i
1
1*3 1 I
4
4l*4l
54*4
5
- S5 |*s |
ssi*sl
6
S6 1*6 I
S6 1*6 1
Первую группу уравнений материального баланса в узлах можно по-
получить посредством скалярного произведения первых трех строк матри-
матрицы А D.12) на вектор х и вычитанием соответствующих Qj :
ul(x)=-x1 +x2 -xs -Qy =0,
и2(х)=-х2 -x3 +x6 -Qi =0, E,16)
= x4 +xs - x6 =0.
Запишем теперь произведение трех матриц:
r/i
1
BSX= 2
3
Элементы этой матрицы являются коэффициентами при х{ (i = 1,..., 6)
в уравнениях второго закона Кирхгофа
4 -Ss*l -Н1=0,
= s2xl +ssx2s+s6xl -Я6=0, E.17)
з +s4xj +s6xj -H6=0.
Уравнения E,16) и E.17) представляют искомую систему относительно
расходов *i,..., х6,
5.2. МЕТОДЫ КОНТУРНЫХ РАСХОДОВ И УЗЛОВЫХ ДАВЛЕНИЙ
Данные методы предназначены для численного решения систем E.7) и
E.8). Они являются аналогом и обобщением известных электротехни-
электротехнических методов контурных токов и узловых напряжений для расчета ли-
линейных электрических цепей в сочетании с методом Ньютона для решения
системы нелинейных алгебраических уравнений [242, 247, 248, 132, 140]
Как известно [57, 177 и др.], при решении системы нелинейных урав-
иений g (x) = (?i (*),..., ga (х)У = 0 относительно векторного аргумента
х по методу Ньютона осуществляется процесс последовательных прибли-
приближений
E.18)
где N - порядковый номер итерации. Для определения Дх^ на каждом
шаге проводится линеаризация вектор-функции g (х) в точке л: W с целью
получения и решения системы линейных уравнений:
^W+A^))«^W))+g'(*W)A*(iV) = 0. E.19)
Здесь g (x W ) — вектор невязок уравнений при подстановке в них прибли-
приближенного решения х^, a g'ix^)- матрица Якоби, составленная из
частных производных:
g'(xW)=bg.(x)ldx.; x = x<N\ E.20)
66

Определение начального приближения х(°) составляет самостоятельную
проблему.
Проведение линеаризации E.19) в данном случае (см. E.7) и E.13)),
Но отдельно для подсистем уравнений первого и второго законов Кирх-
Кирхгофа дает
U(X(N)+ Ax{N)) = AxW - Q +AAxW = 0, E.21)
N) = 0. E.22)
Процесс Ньютона в методе контурных расходов (МКР) реализуется
не в общем виде, а с некоторыми особенностями, существенно учитываю-
учитывающими сетевую специфику задачи расчета потокораспределения и связь
между матрицами А и В. Во-первых, все приближения х W берутся строго
удовлетворяющими уравнениям первого закона Кирхгофа. Это будет
обеспечено, если данное условие соблюдено для начального прибли-
приближения т.е.
u(x°) = Ax<o)-Q = 0, E.23)
а все приращения (поправки) Дх = (Ах^ A*n)T K расходам на вет-
ветвях будут характеризоваться нулевыми балансами в узлах: ААх^ =
= А Ax(N) +A AxiN) = 0. Отсюда с учетом D.32)
К К Д Д
Ах^^-(А-аЫк)Ах^=В1Ах^\ E.24)
т.е. в качестве независимых переменных можно взять поправки к расхо-
расходам на хордах. При этом не потребуется обращать матрицу Аа, так что
TK,Axl)T = (EAx(kn\ В* Ax{kN) ) = Вт Ax{kN\ E.25)
Что касается Д х ^, то этот вектор можно определить путем решения
системы E.22), где каждая из невязок vr в силу физического смысла
второго закона Кирхгофа совпадает с "небалансом" ЬНГ при подсчете
суммарного изменения потери давления в контуре г (по данным N-vo
приближения в значениях расходов на всех его ветвях):
ЬНг = 2 {h.{x\N>)-//.), г = 1, . . . , с. E.26)
Тогда
и(*(лг)) = вЯ^),' E.27)
где справа стоит вектор, составленный из этих поконтурных "небалансов".
В результате E.22) после подстановки в него E.25) и E.27) сведется
к искомой системе линейных уравнений
E.28)
Квадратную матрицу этой системы (имеющую порядок с)
K(x(n>) = kW = 2BSX(n)Bt E.29)
назовем матрицей Кирхгофа, впервые рассмотревшего переход к контур-
контурным уравнениям (об этом говорилось в разд В.1). Нетрудно увидеть,
67

что данная матрица является симметрической, поскольку при транспо-
транспонировании (т.е. при перемене местами ее строк и столбцов с сохранением
их номеров) она не изменится, так как S и X - диагональные. Таким
образом, элементы kr t (г, t = 1, . . . , с) этой матрицы удовлетворяют
условию kr t = ktr при г Ф t.
Посредством обращения этой матрицы или решения системы E.28)
каким-либо из численных методов линейной алгебры [235, 239] опре-
определяются поправки Ах^ к расходам на хордах, затем с помощью E.24)
или непосредственней "проводкой" этих увязочных расходов по конту-
контурам вычисляются приращения Дх^ к расходам на ветвях дерева и в
целом новое приближение x^N + ^ для вектора расходов по формуле
E.18). Далее выполняется анализ сходимости вычислительного процесса:
Здесь 6 - вектор допустимых погрешностей в значениях расходов.
В соответствии с очередным приближением *(w+1) опять формируется
и решается система уравнений E.28) и т.д.
В зависимости от выбора метода решения E.28) получим тот или иной
вариант МКР. В частности, при использовании метода простой итерации —
с отбрасыванием всех внедиагональных-элементов матриц К*-^ — имеет
место известный метод Андрияшева-Кросса поконтурной увязки потерь
давления. Покажем это.
Предварительно выведем формулы, связывающие элементы krtмат-
krtматрицы Кирхгофа с коэффициентами уравнений E.11) и E.25).
Поскольку вектор-градиент, составленный из частных производ-
производных от каждой из функций v r (х) в E.11), имеет вид
(bvr(x)}
vr(x) = — = {2brisi\xi\ = 2siXi},i = 1 и; г = 1 с,
{ Эх,- J E.30)
to с X «-матрица из этих частных производных сведется к выражению
и'(*) = [Эи, (хIдх, ] = 2BSX, E.31)
а транспонированная к ней п X с-матрица к виду
(v\x)Y = 2XrSTBT = 2SXBT. E.32)
Поэтому, исходя из E.29) , получим (без указания номера приближе-
приближения)
krt = brr\v't(x) = 22 bribttSi\xt\, E.33)
где v t (x) — вектор-столбец с номером t в матрице E.32).
Таким образом, для диагональных элементов
krr= 22 sf- |x,|, E-34)
г
поскольку произведение bnbri всегда равно 0 или 1.
68

В случае плоских схем, для которых можно выбрать такую систему
главных контуров, что каждая ветвь будет входить не более чем в два
контура, скалярное произведение двух различных строк br и Ь, матрицы
В будет равно 0, 1 или-1:'
bjbt = 2 Ьгри — \ -1, если ветвь / является общей длядвух контуров,
' ~~ ' 1 Ов противном случае.
Поэтому для каждой такой пары смежных контуров
krt = ±2s,\Xi\, E.35)
где берется знак "минус", если при обходе этих контуров общая для них
ветвь / "проходится" в противоположных направлениях.
Таким образом, подобная система контуров характеризуется следую-
следующей существенной особенностью отвечающей ей матрицы Кирхгофа: ее диа-
диагональные элементы кгг всегда превосходят (по абсолютной величине)
сумму остальных элементов соответствующих им строк, т.е.
с
кгг > 2 \кп |, г = 1,..., с, E.36)
где штрих у знака суммы означает пропуск значения при t = г . Строгое
неравенство здесь объясняется тем, что в сумме E.34) содержатся не толь-
только все элементы E.35),но и слагаемое 2sr\xr\, относящееся к хорде г ,
которая (по условию) входит только в данный контур и, следовательно,
не может принадлежать какому-либо смежному контуру.
Если теперь в системе E.28) разрешить каждое из уравнений относи-
относительно Дх> ', то получим следующую систему, приведенную к виду,
удобному для метода итерации:
— 6#^ -к
ДлДЛО = 1— + ? -——Ax(N) ,537)
к„ t Фг кгг ' v
где справа - сумма всех коэффициентов при Дх^ меньше единицы
в силу E.36). А это является достаточным условием сходимости метода
в данном случае [57].
Для того чтобы прийти к формулам поконтурного увязочного метода,
необходимо в E.37) положить все krt = 0(r Ф t), тогда с учетом E. 26)
получим известную формулу Андрияшева—Кросса
г г
Пример применения МКР. Рассмотрим один (jV-й) шаг МКР для цепи,
схема которой приведена на рис. 4.3, а исходная система уравнений запи-
записана в виде E.16) и E.17). Введем для удобства дальнейшего изложения
69

матрицу, транспонированную к заданной матрице контуров D.15):
/12 3
Вт=
1
2
3
4
5
6
1
1
-1
1
1
1
1
1
1
E. 39)
К
С помощью подматрицы #д в E.39) можно выписать уравнения E.24),
связывающие приращения к расходам на ветвях i =4, 5,6 дерева с при-
приращениями на хордах i = 1,2,3:
Y(N)
E.40)
Матрица Кирхгофа E.29) в соответствии с формулами E.34) и
E.35) для ее элементов примет вид
к,,
= (S,|X,
= -ss |х.
= s4 |х4 I
1 +s4 |х4| +
,(Л0
(N)
к1 г — s5
*22 = (Ы
i" — ? 1 X
л 3 2 6 '
глл
х51 v
х,| +
б! (л°
/Л')
13 Х4
fc2 3 = «6
-V4
IX,
(ЛО
1
(Л') 1
1 +
E.41)
Ввдно, что в ней диагональные элементы превышают сумму абсолютных
величин всех остальных элементов в своей строке (или столбце), т.е. мат-
матрица имеет "диагональное преобладание".
Данная матрица представляет таблицу коэффициентов при искомых
Дх^, Дх|^ в системе линейных уравнений E.28) со сле-
следующим вектором правых частей:
E.42)
Метод узловых давлений (МД) обобщает известный электротехнический
метод узловых напряжений и сочетает преобразования Максвелла к узло-
узловым величинам с методом Ньютона. Исходной здесь является система
уравнений E.9), опирающаяся на использование вектора узловых давле-
давлений.
70

Если в МКР процесс последовательных приближений осуществляется
для расходов на ветвях, то МД сводится к последовательным поправ-
поправкам узловых давлений, определяемых через невязки (небалансы) расхо-
расходов в узлах. Для математического описания этого процесса необходимо
иметь взаимосвязь двух векторов приращений: АР и Ах. С этой целью
проведем линеаризацию уравнений E.9), записанных в форме E.14):
и(х + Ах) = и(х) + А Ах = 0, E.43)
w(x+ Ах,Р + АР) <*w(x,P) - ISXAx + А1 АР = 0, E. 44)
где АР = (Д/»1,..., АРт-\У\Рт задано и потому АР'т= 0.
Поскольку для любого Р^ всегда можно подсчитать такие х^ , что
будут удовлетворяться все замыкающие уравнения E.. 12)
w (*w ,PW) = A*pW + Н- SX^x<"> = 0 E.45)
то E.44) сведется к линейной системе -2SXW Ax(N) + АТ АР w =0,
откуда
Axw = й [SXW)~lATAPw. E.46)
Подставим E.46) в E.43) .считая, что
u(xW) = AxW_q = AGW) E47)
тогда придем к искомой системе линейных уравнений относительно m — 1
неизвестных APj (j = 1,..., m-\):
A [SX(N)] ~1ATAP^N) = -2AQ(N> . E.48)
Квадратную матрицу (имеющую порядок m— 1):
M(Jc(Af)) = Ww = Л[5Х^]-'^Т E.49)
будем называть матрицей Максвелла.
Таким образом, общая схема МД сводится к выполнению следующих
операций:
1) задается начальное приближение для вектора />@) = (Л(о), • • ¦ ,
Р„Х'-\У', которое вообще говоря, может быть произвольным;
2) определяются расходы лг0) = (х[°\ . . . , х^)т, соответствую-
соответствующие этим узловым давлениям и заданному Р'т с помощью уравнений
E.50)
3) подсчитываются (см. E.47)) небалансы расходов AQJ0^ в узлах
и из них составляется вектор AQ ^°\
4) вычисляются элементы матрицы Ар0' исходя из ее выражения
E.49);
5) составляется и решается система уравнений E.48) для определе-
определения Д/><°).
6) производится подправка вектора Р:Р^1^ = />(°) ¦+д/> (°) и ана-
анализируется сходимость вычислительного процесса;
7) повторяются, если это требуется, п. 2-6, только вместо N= 0 берет-
берется W= 1,2 и т.д.
Матрица М(х), как и К(х), симметрическая, однако диагональное
преобладание для нее не имеет места даже в случае плоских схем. Дейст-
71

вительно, ее элементы в соответствии с E.49) должны вычисляться по
следующей формуле:
" ! E 5П
щ, = I aiflu — ; /, t = 1,..., т 1. ;
/••¦ 1 S,- | X,- |
Для диагональных элементов
1 1
[хи = 2 e>Ja/,- = 2 —¦ -, E.52)
поскольку суммирование в данном случае ведется лишь по ветвям /
имеющим общий узел / , а для них а^ац = 1.
Для пары различных узлов jut, связанных единственной ветвью /
в сумме E.51) будет фигурировать лишь одно Слагаемое, для которого
ajiari = — 1> так как здесь один из сомножителей равен — 1, а другой +1,
так что при / Ф i
W/ = " 1/s/ \x/\ , E.53)
если нет другой (устранимой) ветви, связывающей эти же узлы.
Таким образом, для всех узлов, не связанных непосредственно с базис-
базисным узлом / = т, справедливо строгое равенство каждого из диагональ-
диагональных элементов сумме (по модулю) остальных элементов в соответствую-
соответствующей строке матрицы М{х):
цЦ = -'?'"' njt, E.54)
t=\
где штрих означает пропуск при суммировании слагаемого с f = / .
Такие условия для М(х) в отличие от E.36) для К(х) объясняют, в част-
частности, почему метод поузловой увязки расходов, когда отбрасываются
все внедиагональные элементы и система E.48) тривиально разрешается
относительно APJN^'-
-2AO(N)
= !LL. = _2AG/W) 2 s,\x,\ , <5.55)
сходится в меньшем числе случаев, чем метод поконтурной увязки потерь
давления.
Вопроосы сходимости МКР и МД более подробно обсуждаются в гл. 7.
Приведем пример построения матрицы М(х) для схемы на рис. 4.3. От-
Отвечающая ей матрица соединений D.12) после вычеркивания последней
строки примет вид
__/__ 12 3 4 5 6
'1
А ¦= 2
3
Обращаясь к этой матрице, можно с помощью формул E.52) и E.53)
получить конкретные выражения для элементов матрицы Максвелла
E.49):
72
-1
1
-1
1
1
-1
1
1

/1 1 1 \(Л0
1
M?i (Л0
1
М31 с IV |W
1
i ^
i
M32 "~ •- '" (ту)
s«l-f6l
¦
1
*5|*,|(Л1) ;
i
-( ' +
\S4|JC4I
1 1 МЛ')
1 ~г* I
1
E.56)
Поскольку в рассматриваемой схеме все линейно-независимые узлы
/ = .1, 2. 3 соединены ветвями с опорным узлом/ = 4, то диагональные
элементы матрицы Лт-^ превышают (по абсолютной величине) сумму
остальных элементов своих строк (или столбцов).
Глава 6
ГЕОМЕТРИЧЕСКИЕ ИНТЕРПРЕТАЦИИ
И ЛИНЕАРИЗАЦИЯ ГИДРАВЛИЧЕСКИХ ЦЕПЕЙ
6.1. ИСХОДНЫЕ ПОЛОЖЕНИЯ И КЛАССИФИКАЦИЯ ЗАДАЧ
Практически во всех областях применения математических методов весьма
полезными оказываются геометрические интерпретации. Они не могут,
конечно, дать всестороннего описания задач, тем более что невозможно
переносить выводы, получаемые из построений на плоскости и в трехмер-
трехмерном пространстве, на пространство многих измерений. Однако такие пост-
построения позволяют уловить ряд общих, чисто качественных моментов, ко-
которые без этого ускользают от внимания.
В данном случае речь пойдет не о графических методах расчета и не о
построениях вида "изменение давления (напор) - расход" (характеристи-
(характеристических кривых) или "изменение давления - длина" (пьезометрических
графиков), а о представлении потокораспределения в г.ц. с помощью
вектора расходов на ветвях в пространстве п или с измерений (будем
говорить об и-или опространствах) , т.е. в пространствах переменных
*= (*i,..., х„O или хк= (*,,..., хс)т.
Положение рассматриваемых точек будет определяться пересечением
множества поверхностей (гиперповерхностей). Среди них — плоскости
(гиперплоскости), отвечающие узловым уравнениям материального балан-
баланса (Ах = 0 г а также поверхности второго порядка (при /3 = 2), соот-
соответствующие подсистеме контурных уравнений (BSXx = ВН). Очевидно,
Чт° нахождение общей точки пересечения указанных поверхностей равно-
73

сильно расчету потокораспределения в цепи. Отсюда следует полезность
изучения вида и расположения этих поверхностей, а также их деформаций
в зависимости or а) особенностей расчетной схемы; б) ее параметров;
в) соотношения между известными и неизвестными величинами; г) выб-
выбранных систем независимых узлов и контуров (что отражается на виде
матриц Л к В).
Прежде чем перейти к геометрическим построениям и их анализу, оста-
остановимся на элементах классификации задач расчета потокораспределения
применительно к цепи с циклической схемой соединений (см. разд. 4.4).
Задачи
С известным распре
делением расходов
с
k
С неизвестными рас
ходами на всех ветвях
Смешанные
о
г
о"
1
у
-Р
Линейные 1^"—
V
О
с
о
*
Нелинейные
6.1. Классификация задач расчета г.ц.
пд — число ветвей с заданными рас-
расходами; cs - число контуров с задан-
заданными сопротивлениями
Введем обозначения: ns — число ветвей с заданными коэффициентами
Sj сопротивлений и неизвестными расходами xt (на схемах эти ветви
изображаются сплошными линиями); пд — число ветвей с заданными
расходами Qt и неизвестными сопротивлениями (эти ветви обозна-
обозначаются пунктиром); cs — число контуров, состоящих из ветвей с извест-
известными сопротивлениями.
Будем считать, что в цепи нет ветвей, для которых одновременно не
известны ни сопротивления, ни расходы (это особого рода задачи, которые
в известной мере обсуждаются в гл. 8), так что п = ns + пд = т- 1 + с.
Тогда по мере уменьшения числа ветвей с заданными расходами (от пд =
= с до пд =0) математическая сложность задач о потокораспределении
будет расти следующим образом (рис. 6.1):
а) при пд г* с - будем иметь группу линейных (в отношении расхо-
расходов) задач, поскольку нелинейных контурных уравнений здесь не потре-
потребуется (так как в качестве хорд можно выбрать ветви с заданными расхо-
расходами);
б) при пд = 0 придем к нелинейным задачам наибольшей степени слож-
сложности (они описывались в гл. 5);
в) при 0 < пд <с получим смешанные задачи с уменьшенным числом
независимых контуров и соответственно сокращенным числом нелинейных
алгебраических уравнений второго закона Кирхгофа.
Наиболее характерным примером простейшей линейной задачи является
расчет потокораспределения в разветвленной цепи (имеющей схему в виде
дерева) с одним или многими источниками питания при заданных нагрузках
у всех потребителей и производительностях источников.
Легко видеть, что ранг матрицы соединений здесь равен единице, по-
поскольку элементарными преобразованиями (последовательным вычита-
вычитанием столбцов) она может быть сведена к одной ненулевой строке. Это и
74

обусловливает возможность расчета таких цепей (при одном источнике
и заданном у него давлении) методами суммирования сопротивлений и
проводимостей (в частности, методами "эквивалентных отверстий" и
"перемещения единицы объема"), о которых говорилось в гл. 2. Однако
и более сложные (многоконтурные) схемы, для которых пд = с, оказыва-
оказываются в расчетном отношении линейными, если удаление из них ветвей
с известными расходами превращает их в разомкнутые схемы (деревья).
Геометрическая интерпретация подобных линейных задач наиболее
проста: их решение определяется пересечением в и-мерном пространстве
т-\ гиперплоскостей D.9) - по числу независимых узлов. Поскольку
определитель квадратной (в таких случаях) матрицы А отличен от нуля,
система линейных уравнений первого закона Кирхгофа обязательно име-
имеет ненулевое решение, если она является неоднородной (с ненулевой пра-
правой частью). Это означает, в частности, что при одном источнике питания
должен существовать по меньшей мере один узел с присоединенной к нему
известной нагрузкой, чтобы соответствующая гиперплоскость не проходила
через начало координат, а отсекала бы отрезки на осях.
Геометрические интерпретации в общем случае нелинейных задач су-
существенно сложнее даже в с-пространстве контурных расходов, хотя,
как правило, с много меньше п. Если для линейных электрических цепей
переход к контурным величинам сохраняет линейность системы уравне-
уравнений, то в случае г.ц. такое понижение порядка исходной системы уравне-
уравнений с и до с осложняется появлением попарных произведений переменных
Xj (/ = 1,..., с) с соответствующими коэффициентами. Наличие таких
произведений математически отражает главную особенность г.ц., не под-
подчиняющихся принципу суперпозиции (наложения) и симметричности
(относительно знаков при переменных) отдельных решений. Рассмотре-
Рассмотрение этих вопросов [243, 247] и составляет основное содержание следую-
следующего раздела.
6.2. КВАДРАТИЧНЫЕ ФОРМЫ ГИДРАВЛИЧЕСКОЙ ЦЕПИ
И АСИММЕТРИЯ РЕШЕНИЙ
Уравнения второго закона Кирхгофа, как в их исходной записи относи-
относительно вектора л:, так и после перехода к контурным переменным, пред-
представляют совокупность положительно и отрицательно определенных квад-
квадратичных форм [67], отвечающих некоторым поверхностям в многомер-
многомерных п- или с-пространствах.
Наглядное представление о виде этих поверхностей, их взаимном поло-
положении в пространстве и характере их деформации при изменении сопро-
сопротивлений s{, расходов х; и действующих напоров Я,- можно получить
с помощью геометрической интерпретации, лишь когда и<Зис<З.В свя-
связи с этим предварительно рассмотрим две г.ц. (рис. 6.2), циклические
схемы которых состоят из двух или трех независимых контуров.
Схема "а" соответствует, например, случаю параллельной работы двух
ТЭЦ на общую разветвленную тепловую сеть с помощью длинных фиде-
Р°в 1 и 2 и центрального пункта смешения. В схеме "б" параллельная
Работа двух ТЭЦ на две группы потребителей 4 и 5 обеспечивается с по-
помощью перемычки 3. (Очевидно, что подобные схемы могут характери-
характеризовать и другие гидравлические системы).
75

J
J
0\/0
/
6.2. Циклические схемы двухконтурной (а) и трехконтурной (б) цепей
1 - схема гидравлической системы; 2 — расчетная схема; 3 — варианты деревьев
схемы; 4 — система независимых контуров для вариантов дерева
Каждой из схем соединений отвечает свое множество деревьев и каждо-
каждому из них своя система главных контуров. Для двухконтурной схемы име-
имеем три варианта, а для трехконтурной -восемь вариантов деревьев и соот-
соответственно систем независимых контуров.
76

Для двухконтурной схемы выберем первый вариант дерева и рассмот-
рассмотрим полную систему уравнений Кирхгофа:
•Х\ + *2 - Х3 = 0. FЛ)
Slxl+s3-xl'Hlt F.2)
s2xl+ s3x\ = H2. F.3)
Для контура Я/ имели бы (при Ht < Н2)
s2x\-iix\= Нг-Hi. F.4)
Однородное уравнение F.1) материального баланса в узле соответ-
соответствует плоскости, проходящей через начало координат. Нетрудно увидеть
далее, что левые части F.2) и F.3) представляют простейшие положи-
положительные квадратичные формы, а их линейная комбинация F.4) - отрица-
отрицательно определенную форму. Таким образом, контурам I и II отвечают
эллипсы, уравнения которых в канонической форме имеют вид
i, F.5)
Для контура /// получаем уравнение гиперболы
= I- F-7)
Важно подчеркнуть следующее важное свойство этих квадратичных
форм, которое справедливо здесь для и-пространства при любом числе
переменных: в уравнениях эллипсов и гипербол отсутствуют, во-первых,
члены с неизвестными в первой степени и, во-вторых, с их попарными про-
произведениями. Поэтому главные направления (оси) этих эллипсов и ги-
гипербол совпадают с осями координат.
Соответствующее графическое построение выполнено на рис. 6.3, а, б,
где показано решение х' = (х{, х2, х\У, одинаковое для двух вариантов
дерева и систем контуров (/—//и / -III). Соответствующая ему точка
находится на пересечении двух эллиптических цилиндров или эллипти-
эллиптического и гиперболического цилиндров с плоскостью IV, заданной урав-
уравнением F.1) и проходящей через начало координат. Аналогичные иллю-
иллюстрации даны на рис. 6.4, но уже не для параллельного, а последователь-
последовательного включения насосов. Характерно, что каждая из поверхностей авто-
автономна, т.е. сохраняет неизменным свое положение в пространстве при
другом варианте дерева и системы контуров.
Переход в с-пространство осуществляется теперь посредством разре-
разрешения F.1) относительно х3 и подстановки его в F.2) и F.4) :
A +щ)х\ + 2x^2 = vi, F.2а)
х\ + A+ы2)х!+ 2ххх2= v2, F.3а)
«2*2 - щх\ = и2 -ui,- F.4а)
где
ui=sils3, u2=s2ls3, Ui=#i/s3, v2=H2ls3. F.8)
" Дальнейшем, если дерево состоит более чем из одной ветви, исполь-
используются обозначения: urt = srjst — относительные сопротивления, vrt =
77

«
о
SB
л
1
g
§
s
p.
e
ж
о
X
a,
>
2
п.
ft

- Hr/s t — относительные действующие напоры, г = 1,... , С/ — номера
хорд; t =с+ I,... , и - номера ветвей дерева.
Уравнения F.2а) и F.3а) для контуров / и II, как и в и-лространстве,
являются уравнениями эллипсов, так как дискриминанты соответствую-
соответствующих квадратичных форм удовлетворяют неравенствам
1+«! 1 1
8i = ' > 0, 52 = > 0. F.9)
11 1 1+м2
Здесь важно подчеркнуть, что гидравлические режимы, которые возни-
возникают при изменении направления потоков жидкости на отдельных ветвях,
никоим образом не могут уже описываться и иллюстрироваться уравнения-
уравнениями, составленными для иной картины направлений. В этом отношении не-
нелинейные г.ц. существенно отличаются от линейных электрических цепей.
Указанное еще более очевидно для трехконтурной цепи (рис. 6.2), в ко-
которой среди хорд имеется одна пассивная ветвь 3 с неизвестным заранее
направлением потока. В сложных системах пассивные ветви, не содержа-
содержащие источников, составляют основную часть схемы, что повышает неопре-
неопределенность общей картины фактического потокораспределения.
Графическая интерпретация распределения расходов для данного при-
примера с и = 5 и с = Ъ возможна лишь в трехмерном пространстве. Главную
систему контуров выберем, исходя из второго варианта дерева. При этом,
однако, контур /// будет описываться вырожденной квадратичной формой,
так как он не содержит источника давления. Поэтому будем рассматривать
линейную комбинацию контуров / й III, что соответствует первому вариан-
варианту дерева. После преобразований к контурным расходам получим систему
независимых уравнений соответственно для контуров /-///:
A + Мм)*! + Х% — 2*1*з = 1*14, F.10)
A+ M2s)*2 + *3+ 2X2X3 = U25. F-11)
«15*1 + *2 + О + «3$)*3 + 2*2*3 = "IS- F.12)
Здесь контуры I к II представляются эллиптическими цилиндрами (по-
(поскольку в первом случае нет переменной*2, а во втором — хх), а контур
/// —эллипсоидом. Пересечение этих поверхностей в восьми точках дает
формальные (математические) решения данной системы уравнений. Исходя
из симметрии такого рода гиперповерхностей в с-пространстве относитель-
относительно начала координат, можно утверждать, что в каждом квадранте (октанте
и т.д.) этого пространства имеется по единственной точке их пересечения.
Таким образом, общее число формальных решений системы контурных
уравнений составляет 2е = 2"~т +1.
Известно, однако, что с физической точки зрения при движении одно-
однофазной жидкости в гидравлической системе потокораспределение одно-
однозначно (о математическом доказательстве этого факта см. в следующей
главе). Противоречие между однозначностью потокораспределения и
математической многозначностью решений является кажущимся. Нали-
Наличие множества формальных решений объясняется параболической (в об-
общем случае - многочленной) зависимостью между потерей давления и
расходом. В данном случае это А,- = s,-*?, так что здесь каждому нену-
80

6.5. Симметрия системы решений для линейной (а) и асимметрия - для гидравли-
гидравлической (б) цепи
левому значению потери давлешя соответствует не одно, а два решения
х(, из которых лишь одно отвечает истинному.
С учетом этой существенной особенности сравним математическую
и физическую сущности решений для электрических и гидравлических
цепей. Рассмотрим снова двухконтурную цепь (рис. 6.2), но в предпо-
предположении, что действителен линейный закон /г,- = s,-x,- (закон Ома). Тогда
для контуров / и II имеем систему уравнений
A+ «Ox, + х2 = 1л, F.13)
хх + A + и2)х2 = v2, F.14)
решение которой является точкой пересечения двух прямых F.13) и
F.14) в первом квадранте (рис. 6.5).
Если при составлении линейных уравнений законов Кирхгофа для элек-
электрической цепи направление тока в какой-либо из ветвей было принято
неправильным, то решение все равно будет получено, но в другом квадран-
квадранте. Существенно, однако, то, что этому множеству возможных решений
отвечает система точек пересечения (рис. 6.5,а), которая обладает сим-
симметрией не только относительно диагоналей а-а nb-b, но и относительно
осей координат. Поэтому любая ошибка в направлении тока для каждой
отдельной ветви приводит к изменению знака решения, но оставляет его
истинным по модулю (что также отвечает принципу суперпозиции реше-
решений). На этом основано фундаментальное для линейных электрических
Цепей "правило знаков".
В целом здесь для электрической цепи имеем систему из четырех реше-
решений, представленных заштрихованным прямоугольником; аналогично
Для трехконтурной схемы — прямоугольным параллелепипедом и т.д.
Гидравлические цепи существенно отличаются от линейных асимметрией
системы решений (рис. 6,5,6), которая является следствием наличия
попарных произведений в расчетных контурных уравнениях и поворота
6- Зак. 384 8t

главных осей квадратичных форм вокруг начала координат. Поэтому,
как видно из рисунка, прямоугольник деформируется в параллелограмм
с непрямыми углами. '
Подобная асимметрия решений показывает, что каждой ветви схемы
отвечает не один, а множество вещественных корней, отличающихся друг
от друга не только по знаку, но и по модулю. Поэтому изменение направ-
направления потока на одной из ветвей приводит к тому, что на других ветвях
изменятся не только направления, но и абсолютные значения их расходов.
Это связано с тем, что при смене знака у какого-либо расхода изменится
положение соответствующей гиперповерхности в с-пространстве и ее вид,
так что ее пересечение с поверхностями других независимых контуров
произойдет в других (несимметричных) точках.
6.3. ЛИНЕАРИЗАЦИЯ ГИДРАВЛИЧЕСКИХ ЦЕПЕЙ
Определение всех компонент вектора расходов, требующее численного
решения системы нелинейных уравнений, связано в принципе с беско-
бесконечным итерационным процессом, и потому речь может идти лишь о том
или ином приближении к истинному решению. В то же время для линейных
систем может быть получено практически точное решение и за конечное
число шагов. Отсюда, а также из других известных преимуществ линейных
систем становится понятной важная роль, во-первых, выбора начального
приближения, во-вторых, линеаризации самой г.ц.
Линеаризация г.ц. может выполняться различным образом. Собственно,
основные численные методы нелинейной алгебры уже используют линеари-
линеаризацию (в той или иной форме) на каждом шаге последовательных прибли-
приближений. При этом бесконечная вычислительная процедура состоит из цепоч-
цепочки операции, в каждом "звене" которой реализуется некоторый линейный
метод. Это в полной мере относится к методу Ньютона и его модификаци-
модификациям, а также к градиентным и другим методам.
Другой способ линеаризации может заключаться в линейной или кусоч-
кусочно-линейной аппроксимации нелинейных замыкающих уравнений А,- =
= fi(xi) Для всех ветвей схемы. Подобный прием является естественным
и успешно применялся, например, при построении нелинейных электри-
электрических моделей трубопроводных систем [182]. В литературе предлагалась
также и простая линейная аппроксимация парабол А,- = s,-x? некоторыми
прямыми, что имело известный практический смысл в условиях ручного
счета.
Предлагаемый здесь метод линеаризации имеет целью получить такую
эквивалентную систему линейных уравнений, решение которой окажется
достаточно близким к истинному решению для нелинейной г.ц. в целом.
Таким образом, речь идет о методе отыскания точки х^°\ близкой к
искомому решению х, которая может быть использована в качестве на-
начального приближения, уточняемого рядом последующих итераций, а
также и вообще в качестве приближенного линеаризованного решения
для нелинейной цепи. Он основан на замене квадратичных форм в п- и
с-мерном пространствах некоторыми линейными гиперплоскостями, ко-
которые в зависимости от выбранной системы контуров отсекают отрезки
на осях или проходят через начало координат.
82

Рассмотрим в связи с этим общую систему уравнений относительно
вектора х для\циклической схемы цепи:
Ах = 0, ВЗХх = ВН. F.15)
Если во второй группе уравнений диагональную матрицу X принять равной
единичной, то получим систему линейных уравнений
Az = 0, BSz=BH. F.16)
?е решение, являющееся точкой пересечения и гиперплоскостей, будет
значительно отличаться от решения исходной системы F.15). Однако
попробуем сблизить эти два решения корректировкой коэффициентов
5(- и правых частей Н. в F.16), исходя из условия совпадения точек пе-
пересечения соответствующих гиперповерхностей и гиперплоскостей с поло-
положительными полуосями координат.
Прежде всего, в системе уравнений F.15) и F.16) перейдем (см.
разд. 4.5) к контурным переменным:
BSXBTxK = ВН, F.17)
BSBrzK=BH. F.18)
Далее предположим (для упрощения изложения), что в схеме цепи
подобрана такая система независимых контуров, каждый из которых,
во-первых, будет содержать по меньшей мере активную ветвь и, во-вто-
во-вторых, состоять из ветвей, ориентированных в одном направлении с направ-
направлением его обхода. Тогда все уравнения в F.17) будут неоднородными
(с нулевой правой частью), а их левые части будут представлять положи-
положительно определенные (эллиптические) квадратичные формы.
Определим теперь точки пересечения гиперповерхностей F.17) и ги-
гиперплоскостей F.18) с осями координат, для чего выделим поочередно
каждую из с компонент хг и zr (г = 1,. .., с) векторов хк и zK (т.е. рас-
расход в одной из хорд), полагая остальные с — 1 их компонент равными
нулю.
Тогда в выражении F.17) будут обращаться в нуль все попарные про-
произведения переменных и мы последовательно получим из г-го уравнения
xr = y/Hr/Zs,; xt = sjHr/st (r,t=l,...,c; гФг). F.19)
При решении линейных уравнений F.18) соответственно имеем
zr=HrfLs,; zt=Hr/st. F.20)
Сопоставляя эти величины, которые определяют длины отрезков, отсе-
отсекаемых от положительных полуосей гиперповерхностями F.17) и ги-
гиперплоскостями F.18), видим, что между ними существует точное со-
соответствие, которое может быть выражено следующим образом:
xr=y/Tr, xt= \pz~T (r,t=l,...,c;t?r). F.21)
Для обеспечения такого соответствия можно, однако, поступить и по-
Другому, а именно: в F.18) вместо диагональной матрицы S и вектора Я
взять матрицу S', составленную из элементов s[- = Vs7 по диагонали, и
83

вектор #', составленный из Н\ = \/Щ (/ = 1,..., и), что обеспечит
совпадение хг с zr.
В общем случае для произвольной цепи с циклической схемой соеди-
соединений система линеаризованных уравнений представляется в матричной
форме следующим образом:
Ах = 0, BS'x=BH', F.22)
где
//' =
\fH~n
О
F.23)
Эту систему можно решать непосредственно относительно и-мерного век-
вектора х или после перехода к контурным переменным как систему пони-
пониженного порядка относительно с-мерного вектора хк. Матрица К' - {krt}
коэффициентов данной системы уравнений обладает следующими общими
свойствами:
1) по диагонали располагаются корни квадратные из сумм сопротив-
сопротивлений ветвей, входящих в соответствующий контур, т.е.
*rr = 2V^ r=l,...,c; F.24)
2) недиагональными (г Ф t) элементами являются корни квадратные
из сопротивлений ветвей дерева, смежных данному контуру.
В качестве иллюстрации такого перехода к линейным уравнениям рас-
рассмотрим квадратичные формы F.2а) —F3а) двухконтурной цепи, схема
которой приведена на рис. 6.3, и заменим их уравнениями вида F.18),
но с учетом F.21) :
+S3 =
Что касается отрицательно определенной квадратичной формы F.4а),
то ей будет отвечать уравнение асимптоты, проходящей через начало ко-
координат:
= 0.
F.26)
Это уравнение может заменить любое из уравнений в F25).
Решению системы F.25) соответствует точка "с" на рис. 6.6, а, другим
двум решениям после замены каждого из уравнений в F.25) на F.26)
отвечают точки "а" и "ft". Любая из вершин треугольника аЪс, как не-
нетрудно увидеть, дает хорошее начальное приближение к истинному ре-
решению х. По крайней мере, по знакам компонент этого начального при-
приближения можно правильно наметить направления потоков на ветвях
схемы.
Уравнения асимптот, как это видно из F26), содержат в качестве
коэффициентов только сопротивления S/, в них не входят действующие
напоры Hf, влияющие на форму гиперболы, или, в общем случае, гипер-
гиперболической поверхности. Поэтому при линеаризации достаточно большого
84

6.6. Линеаризация двухконтурной цепи в с-и «-пространствах
числа контурных уравнений с отрицательно определенными квадратич-
квадратичными формами в левой части решение получается более удаленным от
истинного, чем при линеаризации одних только эллиптических форм.
Аналогичным образом линеаризуется система уравнений в и-простран-
стве (рис. 6.6, б). При этом уравнение F.1) "узловой" плоскости оста-
остается неизменным, а уравнения F.2) и F.3) "следов" эллиптических
цилиндров на координатных плоскостях (для контуров I и И) заменяются
аппроксимирующими хордами, лежащими на прямых:
В данном случае система линеаризованных уравнений по своей струк-
структуре совпадает с системой линейных уравнений законов Кирхгофа, только
вместо независимых параметров s{ и Н{ принимаются корни квадратные
из них. Такая замена в совокупности с линейным законом /г,- = y/s^х{
превращает г.ц. в линеаризованную, по отношению к которой можно при-
применять известные методы теории электрических цепей, использующие
принцип суперпозиции.
Решения систем уравнений, линеаризованных в и- и с-пространствах,
не будут совпадать. С точки зрения близости к истинному потокорас-
пределению, а также времени счета линеаризация в с-пространстве пред-
предпочтительнее, хотя и несколько более трудоемка из-за необходимости
преобразования к контурным переменным.
Таким образом, общая схема линеаризации г д. с целью получения
начального приближения потокораспределения сводится к выполнению
следующих основных операций:
1. Предварительно схема г д. приводится к циклической. Эта опера-
операция может не потребоваться для систем, обладающих естественной цик-
цикличностью, таких, как закрытые двухтрубные тепловые сети, системы
отопления и другие циркуляционные системы.
2. Намечаются произвольные направления потоков на ветвях схемы.
Дня ветвей с фиксированным направлением течения оно таким и при-
принимается .
3. Составляется система линеаризованных уравнений F.22), которая
преобразуется к контурному виду и решается каким-либо из стандартных
методов линейной алгебры. 85

4. Меняются на противоположные направления потоков на тех ветвях,
для которых значения расходов получились со знаком "минус".
Полученное с учетом исправления знаков решение используется в даль-
дальнейшем как начальное приближение для расчета потокораспределения.
6.4. ЛИНЕЙНЫЕ И ЛИНЕАРИЗОВАННЫЕ ПРЕОБРАЗОВАНИЯ
СХЕМ ГИДРАВЛИЧЕСКИХ ЦЕПЕЙ
При расчете потокораспределения в сложных гидравлических системах,
даже в случае применения современных ЭВМ, весьма актуальным явля-
является построение их упрощенных эквивалентных схем, состоящих из мень-
меньшего, чем в оригинале, числа ветвей и узлов, по возможности плоских
и поддающихся (хотя бы частично) расчету, основанному на суммиро-
суммировании сопротивлений и проводимостей. Последнее возможно, когда от-
отдельные фрагменты схемы представлены в виде последовательно-парал-
последовательно-параллельных соединений.
Из-за нелинейности г.ц. их системы уравнений не обладают аддитив-
аддитивными свойствами, в силу которых для линейных систем можно, прирав-
приравнивая расходы на отдельных ветвях нулю, получать частные решения,
а общее решение представлять как их сумму. Однако некоторые возмож-
возможности для упрощения схем здесь имеются, и они должны использоваться
при описании и расчете гидравлических систем на ЭВМ. В данном разделе
рассматриваются два вида преобразования схем цепей: 1) точные линейные
преобразования, которые не затрагивают нелинейной связи между рас-
расходом и потерей давления; 2) приближенные преобразования, основан-
основанные на использовании метода линеаризации г д., описанного выше.
Линейные преобразования. Ряд трудностей при моделировании и рас-
расчете гидравлических систем можно устранить, используя топологические
особенности конкретных систем и условия решаемых задач. Так, при
определенном сочетании ветвей с фиксированными и неизвестными рас-
расходами, а также узлов с фиксированными и неизвестными давлениями
можно значительно сократить число ветвей и независимых контуров и в
результате даже неплоские схемы представить в плоском изображении.
Основой для такого эквивалентирования являются элементарные пре-
преобразования матриц соединения А и контуров В, описанные в разд. 4.2.
Исходя из этого, для удаления лишних ветвей и узлов из схемы можно
сформулировать следующие правила: "Если ветвь с фиксированным рас-
расходом присоединена хотя бы к одному узлу, в котором фиксировано
давление, то такая ветвь в расчетном отношении является лишней и может
быть устранена из схемы. Одновременно должен быть исключен один из
независимых контуров. Сам узел с фиксированным давлением исключа-
исключается только в том случае, когда в нем сходится не более двух ветвей с не-
неизвестными расходами.
В практических задачах фиксирование расходов может иметь различ-
различный смысл. В одних случаях жестко регламентируются расходы воды,
газа, воздуха и т.д., которые должны получать потребители. В других пред-
предполагается установка регуляторов постоянства расходов на магистраль-
магистральных участках сети, в циркуляционных системах охлаждения и пр. Фикса-
Фиксация давления обычно имеет место, когда отдельные узлы цепи связаны
86

6.7а,б. Проекция многогранника на сферу (а) и плоскость (б)
с внешней средой (чаще всего с атмосферой), в которой поддерживается
постоянное давление, а также когда подключаются расширительные со-
сосуды или водонапорные баки с регуляторами постоянного уровня, под-
питочные насосы и т.п.
Аналогично эквивалентируются схемы для систем охлаждения различ-
различных агрегатов, возврата конденсата на промышленных предприятиях,
воздушного отопления и многие другие. При расчете некоторых систем,
например систем воздухообмена в зданиях, возможна такая формулиров-
формулировка задачи, при которой ни для одной ветви циклической схемы расход
воздуха заранее не известен. В таких случаях линейные преобразования
за счет устранения ветвей невозможны.
Проективные преобразования. Наиболее трудными для расчета явля-
являются системы с неплоской схемой соединений, когда имеются самопере-
самопересечения ветвей без образования узлов. Превращение ее в плоскую с по-
помощью линейных преобразований в принципе возможно лишь за счет
устранения лишних ветвей, когда это удается по условиям постановки
задачи. Однако иногда решение вопроса о том, является ли вообще схе-
схема неплоской, осложняется ее внешним видом и потому приводит к не-
недоразумениям. Известное упрощение данного вопроса дают топологи-
топологические преобразования схем, которые при сохранении прямолинейности
ветвей являются проективными.
Любая связная и циклическая цепь (как плоская, так и неплоская)
имеет свое пространственное изображение. Во всяком случае, ее можно
представить стереографической проекцией некоторого односвязного пра-
правильного или неправильного многогранника, перенесенной на плоскость
с произвольной деформацией ребер. При таком топологическом преоб-
преобразовании закономерность соединений ребер с вершинами (или, что то
87

6.8а,б. Построение плоской расчетной схемы для двухтрубной тепловой сети
же, ветвей с узлами) сохраняется, а одна из граней исчезает. Отсюда, между
прочим, следует, что так как согласно теореме Эйлера между числом гра-
граней (Г), ребер (Р) и вершин (В) существует связь Г = Р-В + 2, то соот-
соотношение между числами независимых, контуров с = Г - 1 ветвей п = Р и
узлов т = В представляется известным выражением: с = п - т + 1.
Рассмотрим теперь преобразование многогранника, состоящего из
24 граней (рис. 6.7, а). Его проекция на.окружающую сферу из ее центра
преобразуется внутрь себя на одну из граней, например ABC. В результате
получаем плоский граф без самопересечения ребер, в котором одна из
граней А'В'С'имеет края, уходящие в бесконечность (рис. 6.7, б). Из
сопоставления рис. 6.7, а и б видно, что каждая новая линия, соединяю-
соединяющая вершины многогранника, оставит граф плоским при условии, что
88

она сама лежит в плоскости любой из граней. Так, например, соединения
?)._Ff C-G, F-N, C-N, С-М и т.д. не создадут самопересечений ветвей
на плоском графе. В то же время такие соединения, как D—N, М—Е, К- G,
R—В и т.п., которые проходят внутри многогранника, делают граф не-
неплоским.
Рассмотрим, например, к примеру схему двухтрубной тепловой сети
с двумя источниками питания (рис. 6.8, а). Примененное здесь кольце-
кольцевание и наличие двух магистральных перемычек создают ложное впечат-
впечатление о том, что в схеме есть ряд самопересечений и она является нешюс-
кой. В действительности же, если пространственное изображение этой
схемы, исключая потребитель А, подвергнуть проективному преобразо-
преобразованию на произвольную грань, например на грань 13-15-16-14, то по-
получим плоскую схему (рис. 6.8, б). Она станет неплоской в том случае,
когда потребители типа А будут подключены к магистральным перемыч-
перемычкам, как и показано на рисунке. При этом ветвь А не лежит в плоскости
граней, что приводит к самопересечениям. Устранить такую ветвь и сделать
схему плоской можно только в том случае, если задать на ней расход и
давление в одной из ее конечных узлов.
Линеаризованные преобразования. В расчетной практике часто возни-
возникает необходимость определить в г.ц. некоторое новое потокораспреде-
ление, которое возникает после полного отключения одной или группы
ветвей. Это нетрудно делать для цепи, схема которой представляется как
совокупность последовательно-параллельных соединений с одним источ-
источником питания, поскольку тогда можно вычислить величину нового о'5-
щего гидравлического сопротивления изменившейся схемы.
В различных областях встречаются, однако, такие г.ц., общее сопротив-
сопротивление которых невозможно определить какими-либо точными методами,
так как их матрицы соединений и контуров не свертываются к единичной
строке или контуру. Для таких цепей ниже предлагаются два приближен-
приближенных метода линеаризованных преобразований нелинейных цепей с по-
помощью известного в электротехнике приема замещения треугольника
эквивалентной трехлучевой звездой. Оба метода основаны на методе ли-
линеаризации г.ц., описанном выше.
Первый метод рассматривает линеаризованную гидравлическую цепь,
У которой s't = yjsf и Н\ - \ГЩ, как некоторую электрическую цепь,
Для которой справедливо эквивалентное преобразование треугольника
в звезду согласно рис. 6.9. Исходя из того, что линеаризованные сопротив-
сопротивления между любой парой вершин треугольника и звезды должны быть
одинаковыми, получаем для вершин J и 2 (с учетом параллельного соеди-
соединения в треугольнике стороны b и двух сторон а - с):
Аналогично для вершин 2 и 3
Vs7+ у/ц = V?(Vs7+ v/^)/(v/57+ V^T+ Vx7) F.28)
и для вершин 3 и 1
7Г 7V7 " ^7 F.29)
89

а
V'
А
ь-Х
6.9а,б. Преобразование треугольника (а) в трехлучевую звезду (б)
Решая систему уравнений F.27) —F.29) относительно линеаризованных
сопротивлений звезды, получаем
F.30)
Второй метод основан на том, что в соответствии с принципом супер-
суперпозиции каждый контур в линеаризованной цепи может рассматриваться
отдельно в отрыве от всей цепи в целом. Тогда проводимость каждой пары
лучей звезды должна быть равна общей проводимости соответственных сто-
сторон треугольника. Исходя из этого, получаем
для вершин 1 и 2
или
90
+ sbJ;
F.31)

для вершин 2 и 3
ь^ =sAsa +^)(v^7+V^ +sftJ: F.32)
для вершин 7 и i
^V^T^J. (б.зз)
С другой стороны, очевидно, что
Sail = Sa + S0. s?7 = Х/3 + Ь' *<*7 = Х« + Х7 • F.34)
Решая систему F.34) относительно- сопротивлений отдельных лучей
звезды, имеем
-Say)/2, F.35)
Определив предварительно по формулам F.31)-F.33) сопротивления
лучевых пар sap, Spy и say, получим затем из F.35) значения сопротивле-
сопротивлений эквивалентной схемы.
Применение первого и второго методов линеаризованных преобразова-
преобразований иллюстрируется на схеме рис. 6.9, б, которая соответствует, например,
системе теплоснабжения или центрального отопления с попутным движе-
движением воды, а также применяется и в системах вентиляции. Оригинал схе-
схемы, показанный сплошными линиями, заменяется эквивалентной схемой,
намеченной пунктиром.
Для данного перехода к новой схеме по первому методу применяется
следующий порядок вычислений:
l.-По сопротивлениям первого треугольника 4-8-7, используя форму-
формулы F.30),определяютi'aj, s'^, x'7l ¦
2. Рассматривается второй треугольник 3-4-6 с сопротивлениями сто-
сторон х34 + s'y , s'p+'s76 и 53б, по которым с помощью формулF.30)вычис-
ляютs'a,,*'/?,'иs'7j.
3. По сопротивлениям сторон л2з + s'y , s'p + ^es ИХ25 третьего треу-
треугольника 2-3-5 находят s'O}, s'pt hs'7j.
4. Для двух параллельных ветвей между точками 1 и 2, имеющих сопро-
сопротивления s12 + s'y} и s'рг + s5i, определяют эквивалентное сопротивле-
сопротивление s'a<.
Для эквивалентирования схемы по второму методу последовательность
преобразования контуров в звезды сохраняется той же, что и по первому
методу. Однако при этом на каждом этапе по формулам F.31)—F.33)
предварительно вычисляются сопротивления лучевых пар и затем уже по
формулам F.35) линеаризованные сопротивления отдельных лучей звезды.
В результате получаем общее сопротивление исходной схемы как сопротив-
сопротивление эквивалентного контура:
Очевидно, что второй метод связан с более трудоемкими вычислениями,
вместе с тем он обеспечивает значительно более высокую точность резуль-
результатов, поэтому несомненно предпочтительнее, особенно при использова-
использовании ЭВМ.
91

Глава 7
ЭКСТРЕМАЛЬНЫЙ ПОДХОД К ОПИСАНИЮ
И РАСЧЕТУ ПОТОКОРАСПРЕДЕЛЕНИЯ
Данная глава посвящена физико-математическим и вычислительным ас-
аспектам экстремального подхода к потокораспределению в г.ц. с сосредо-
сосредоточенными параметрами [132, 133, 140]. Такой подход, как уже отмеча-
отмечалось в разд. 3.2, характеризуется тем, что рассматриваемая задача может
ставиться и решаться (исходя из физических принципов или формальных
соображений) как задача на условный или безусловный экстремум, а также
и нелинейного программирования.
Представляется целесообразным и интересным изложить основные поло-
положения и формы экстремального подхода, а также сравнить его в методи-
методическом и вычислительном отношениях с алгебраическим описанием потоко-
распределения в виде замкнутой системы уравнений Кирхгофа. При этом
возникают такие вопросы, как: условия эквивалентности данных подхо-
подходов, "системные" требования к виду замыкающих соотношений, взаимо-
взаимосвязь прямой и двойственной экстремальных задач, практическая эффек-
эффективность тех или иных численных методов и др. Многие из приводимых
ниже результатов уже известны. Однако речь идет о систематическом и
компактном изложении данного круга вопросов на базе алгебры и методов
ТГЦ с целью более строгого описания, анализа и дифференциации различ-
различных подходов и методов.
7.1. ОБОБЩЕНИЕ ТЕОРЕМЫ МАКСВЕЛЛА
О ПРИНЦИПЕ НАИМЕНЬШЕГО ТЕПЛОВОГО ДЕЙСТВИЯ
НА ГИДРАВЛИЧЕСКИЕ ЦЕПИ
Из теоремы Максвелла (см. разд. В.1) следует, что токораспределение в
пассивной электрической цепи является решением следующей задачи на
условный экстремум (в наших обозначениях) :
lthiXj= 2 stxj ->min G.1)
/= i /= i
при
Ах = Q, ht = SiXi (i = 1,.. ., n). G.2)
Возьмем за отправной пункт рассуждений аналогичную постановку, толь-
только не будем фиксировать конкретный вид функций fy =//(*,), т.е.
рассмотрим задачу I:
п т
F(x)= 2 hiXj = h x ->-min G.3)
при
Ax = Q, h=f(x) = (f1(x1),...Jn(xn))T. G.4)
Таким образом, речь идет об описании установившегося потокораспреде-
ления в произвольной пассивной цепи (все Я,- = 0) в виде задачи на мини-
минимум суммарной кинетической энергии, затрачиваемой на движение жидкос-
жидкости в изолированной системе, при соблюдении условий материального балан-
баланса в узлах. Предположим лишь для функций/,¦ (х,-), составляющих век-
92

тор-фУнкцию /М > выполнение следующих (физически очевидных) условий
(о них уже говорилось выше, в разд. 4.1):
1) монотонного возрастания, т.е. /,- 1х") >/,• (х|-) прих|.' >xj;
2) нечетности, т.е. /,(-х,) = --/}(х,-), где/;(х,) >° Для х,->0;
3) гладкости, т.е. существования непрерывных производных f\ (х,-)
на всей числовой прямой.
Отсюда следует, что независимо от знака х,- Xjfj (х,) > О, а так как
при Q - 0 любое допустимое решение системы уравнений первого закона
Кирхгофа будет нетривиальным (т.е. х Ф 0), то, следовательно, всегда
F(x) > 0, что также отвечает физическому смыслу энергетических потерь.
Следует добавить, что F(x) будет строго выпуклой, если каждая из ее
составляющих х,/,(х,) будет вести себя хотя бы несколько "круче",
чем прямая линия, что имеет место, если, например,
fi{xi)>cixfi\xi>Q,
где с, > 0 и а,-> 1 - произвольные постоянные. В случае строгой выпук-
выпуклости F(x) она достигает своего глобального минимума в единственной
точке х, для которой F' (х) = 0.
Определим теперь дополнительные требования к /,(х,), при которых
экстремальная задача I G.3), G.4). будет эквивалентна (т.е. приводить к
совпадающим решениям) алгебраической задаче II:
Ax = Q, Bh = 0, h=f(x). G.5)
Эта система уравнений описывает потокораспределение в многоконтур-
многоконтурной пассивной цепи с постоянными притоками и нагрузками в узлах (ниже
будет рассмотрен и общий случай).
Выделим на схеме цепи некоторое дерево и зафиксируем соответствую-
соответствующую ему "хордовую" систему контуров. Тогда задача I может быть записа-
записана в виде-
F (x) = F (хк, хя) = /(хк)Тхк + f (Хд) тхя G.6)
при
Лк*к +Aaxa=Q, G.7)
где Ак = Дхк) и йд=/(Хд).
Выберем хк в качестве вектора независимых переменных и заменим
G.7) эквивалентным ему выражением (см. разд. 4.5):
xa=BTaxK+RaQ. G.8)
Если теперь подставить G.8) в G.6), то получим задачу на абсолютный
минимум функции F(x) относительно контурных переменных, необходи-
необходимым условием которого является обращение в нуль всех производных по
*г {г = 1,. . ., с):
dF{x)ldxK = ЪР{хIЪхк HdF(x)ldxa)(dxa/bxK) =
x)x
где f'(xK) и /'(хд) — диагональные матрицы порядков cum—] из произ-
производных /, (*.), /= 1 ги/=с+1 и.
93

В G.9) можно перейти отВд к полной матрице контуров В = (?', Ва):
dF(x)ld (xK) = Bf(x) + Bf'(x)x. G.Ю)
В результате экстремальная задача I сведена к решению системы из с
уравнений G.10) и т - 1 уравнений в виде G.8) или G.7). Сравнивая
G.7) и G.10) с G.5), получаем следующее утверждение.
Теорема 1. Для того чтобы экстремальная задача I с критерием миниму-
минимума энергетических потерь была бы эквивалентна алгебраической задаче И
о потокораспределении в пассивной многоконтурной цепи, необходимо и
достаточно, чтобы замыкающие соотношения /г,-= /,¦(*,) для ее ветвей
удовлетворяли условию
Bf'(x)x = 0. G.11)
где В - с х л-матрица контуров, а/'(х) — диагональная матрица из про-
производных f'j(Xj), i = 1, . .., п.
Действительно, условие G.11) является критерием того, чтобы уравне-
уравнения G.10) обратились в уравнения второго закона Кирхгофа.
Векторное уравнение G.10) состоит из следующих покоординатных
(контурных) уравнений:
c!F (x)jJxr = 2 /, (х,-) + 2/'. (jr,-)х,- = 0 G.12)
Следовательно, условие G.11) сводится к тому, чтобы для каждого
установившегося потокораспределения х в любом контуре г одновременно
с равенством
2/¦(*,) = 0 G.13)
г
выполнялось бы
2/',(*|)*| = 0. G.14)
Прежде всего проверим выполнение этого условия для следующих двух
важных случаев:
1) закона Ома, когда /, (х,) =s,Xi. Для него //(*,) =/',(лг,)х,,
и тем самым подтверждается теорема Максвелла;
2) однородной пассивной цепи с одночленной зависимостью
fi(xi) = si(\x,\f-1xi, G.15)
где показатель степени 0~ один и тот же для всех ветвей. Так как здесь
2/',(*/)*,¦ = 02/;•(*,-) = 0,
то теорема справедлива только потому, что 0 не зависит от / и является
общим множителем для суммы.
Исходя из этого, можно прийти к простому следствию: достаточным
признаком эквивалентности задач I и II является выполнение для каждой
94

ветви условия
р/;¦(.*,•)=/;¦(*,¦)*,•¦ . GЛ6>
Нетрудно убедиться, что общим решением этого дифференциального
уравнения является функция G.15), так что признак G.16) полностью ис-
исчерпывает случай однородной цепи с одночленной зависимостью, когда пра-
правомочна экстремальная постановка задачи с "энергетической" целевой
функцией.
Из изложенного формально следует, что рассмотренная задача I оказы-
оказывается несостоятельной для общего случая с произвольными//(л:,-), и по-
потому возникает вопрос о том, какова та общая экстремальная задача, ко-
которая с математической точки зрения будет экивалентна системе уравне-
уравнений Кирхгофа.
7.2. ОБЩИЙ СЛУЧАЙ НЕОДНОРОДНОЙ АКТИВНОЙ ЦЕПИ
Вначале рассмотрим пассивную, но неоднородную цепь с различными
одночленными замыкающими соотношениями G.15), считая, что показа-
показатель степени ft свой для каждой ветви, и вместо целевой функции G.3)
обратимся к несколько более сложной конструкции:
F(x)= ? Sifi (х,) х,- . G.17)
i= 1
Определим, как должны быть связаны между собой постоянные 5,- и ft,
чтобы задачи I и II стали бы эквивалентными. Ход рассуждений, аналогич-
аналогичный приведенному выше, позволяет сформулировать следующее утвер-
утверждение .
Теорема 2. Критерием эквивалентности экстремальной задачи с миними-
минимизируемой функцией G.17) и системы уравнений Кирхгофа является выпол-
выполнение для ее решениях следующих условий:
- «/ (ft (х,-) + /¦', (х,- )х, = 2 fi (х,-) = 0, G.18)
. с.
Следствие. Для эквивалентности этих задач достаточно соблюдения ра-
равенств
5,(.//(х,)+/',(х/)х,) = /,(х,), /= 1,....и. G.19)
Решая дифференциальное уравнение G.19) относительно /,(х,), получим
J 1\ЛП ~ SjXj ,
откуда 6,-= 1/A +ft), /= 1 ,и.
Таким образом, G.17) здесь примет следующий вид:
/¦»= S = /}(*,-)*,-/( 1 +ft). G.20)
/= 1
В частности, если все /3,- = 0, то одинаковый знаменатель 1 + C может
быть исключен из выражения G.20), так как это не повлияет на точку ми-
минимума F(x). и тогда приходим к случаю функции энергетических потерь
(теореме 1)
95

Перейдем теперь к общему случаю неоднородной цепи, содержащей ис-
источники давления Я,- на ветвях и с произвольными замыкающими соотно-
соотношениями v + Н = f(x), для которой выпишем еше раз систему уравнений
второго закона Кирхгофа
By = B(f(x) Я) = 0. G.2i)
Будем искать целевую функцию экстремальной задачи в виде
/•' (х) = х V (х), G.22)
где <р(х) = (^i(Ar,),..., \рп (*„))т - неизвестная вектор-функция.
Необходимые условия экстремума после перехода к контурным нере-
неременным хк выразятся тогда системой уравнений
dF(x)/clxK= В to (х) + / (х)х) = 0, G.23)
где \р' (х) —диагональная матрица порядка п из производных <р ;(*/)•
Сравнивая G.23) с G.21), получим следующее векторное условие их
совпадения:
f{x) -Н = *(х)+ у (х)х = (хтф(х)) = F'(x). G.24)
т.е. градиент минимизируемой функции G.22) должен быть равным/(.т) -
- //. А так как эта функция является суммой однотипных составляющих,
каждая из которых зависит от одной переменной, то она, исходя из G.24),
может быть восстановлена интегрированием по этим переменным:
х <р(х) = Ъ [ 1
(=1 0
где с — произвольная
Таким образом,
F(x)= X J \>iB
i= 1 0
Ufa)- Hi)
постоянная,
и
•.j) dzt = ~L
i- 1
dz
не
xi
f
0
влияющая
fiizddz, ¦
на
Я1
точку экстремума
rx
G.25)
/=10 1-10
или
F(x) = G-Fu, G.26)
где G - величина, называемая в работе [263] объемом цепи, a Fu — суммар-
суммарная мощность источников действующих напоров Я,. В результате получено
утверждение.
Теорема 3. Потокораспределение в произвольной активной многокон-
многоконтурной г.ц. отвечает точке минимума функционала G.25) при условии
соблюдения материального баланса во всех узлах цепи.
Для одночленных /)(х/) функционал G.25), как нетрудно убедиться,
приводит после интегрирования к функции
нЛ G-27)
/
1 +ft-
которая совпадает с G.20) при Я,- = 0 (/ = 1, . . . , п).

7.3. ДВОЙСТВЕННЫЕ ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ
ПОТОКОРАСПРЕДЕЛЕНИЯ
Применим теперь общие положения метода неопределенных множителей
Лагранжа [154, 253] и двойственности для задач на условный экстремум к
нашей общей экстремальной задаче на минимум функционала G.25) при
-iv = <2> 1'№ Уг -fi{x) - Н,, A -¦ полная матрица соединений узлов и
ветвей, Q = {Q\ QmY¦
Построим для нее функцию Лагранжа
ф (х, X ) = I /V,- (z,) dZj + Xх (А х ¦ Q). G.28)
Г- 1 О
Так как ранг А равен т - 1, то для однозначности вектора Xх = (Х[, . . .
• , Х,„ ) достаточно предварительно зафиксировать одно из значений
X/ (см., например, [253]).
Задачей, двойственной к исходной, будет следующая задача на условный
экстремум:
дФ(х, X) - -
max Ф (х, X ) при = у+АТХ=0. G.29)
\ дх
Уравнения связей в G.29), если их сравнить с уравнениями у = Ал 1\ яв-
являющимися аналогами второго закона Кирхгофа, однозначно указывают
на физический смысл множителей Лагранжа в нашей задаче: X - это с точ-
точностью до знака вектор Р узловых давлений. (В случае минимизируемой
функции G.27) и j3,- = j3 X будет совпадать с -Р с точностью до множителя
1 + C). А требование предварительного задания одного из значений X,- соот-
соответствует условию фиксации Р/ в одном из узлов цени.
Таким образом, установившееся потокораспределение в произвольной
г.ц. можно определить также и посредством решения следующей двойствен-
двойственной (по отношению к исходной) экстремальной задачи:
max B X'f yj(zf)dZi - Рл (Ах Q)) G.30)
Р /=1 О
при
у - АТР = 0. у = f{x) • Н. G.31)
Поскольку после умножения G.31) справа скалярно на х можно полу-
получить, что
(у АтР)х = улх - РтАх = 0,
то,следовательно,
РтАх = утх. G.32)
Кроме того,
.V,- У/
I y,dz,- = yiXi - / Xidyh G.33)
о я,-
7. Зак. 384 97

и после подстановки G.33) в G.30) получим двойственную задачу в окон-
окончательной форме
" Г/ _ _
max (- I / Xjdy-i +PTQ) G.34)
р / = i //,
при связях G.31).
Для одночленной зависимости имеем
, ., Я, \ ¦""'•
>-,+//,= s,- л?'; л-,- =
что после подстановки в G.34) дает
ft
max -
р L ' = i i+ft-
_ Если решением исходной экстремальной задачи на минимум G.25) при
Ах = Q является вектор**^ решением двойственной задачи G.30), G.31) -
вектор Р*, то точка (х*, Р*) будет седловой точкой функций Лагранжа
G.28), которая выпукла по х и линейна по Р. Стационарные точки этой функ-
функции находятся из системы уравнений
ЬФ{х, РIЪР = Ах B=0. G.36)
ЪФ(х,РIЬх = у АтР=0, G.37)
у + Я =/(*); G-38)
которые совпадают с законами Кирхгофа.
Известное соотношение двойственности применительно к рассмотрен-
рассмотренной паре экстремальных задач заключается в том, что в точке (х'*,Р*) долж-
должны совпадать значения функционалов G.25) и G.30), что означает обра-
обращение в нуль скалярного произведения
Рт(Ах - Q) = 0. G.39)
Поскольку стационарная точка должна также удовлетворять уравне-
уравнениям связей G.36) —G.38), то, следовательно, справедливо равенство
G.32), поэтому после раскрытия скобок в G.39) имеем
РтАх -PTQ= yTx - PTQ = (f{x) - IJ)Tx -
— — — — A40)
- PTQ =HTx - xTf(x) f PTQ = 0. v
Если вместо одного вектора Q ввести вектор Qu > 0 притоков, т.е. посту-
поступающих в г.ц. расходов жидкости, и Qv < 0 - вектор расходов (нагрузок)
у потребителей, то G.40) запишется в виде равенства
Нтх +PUQU =xTf(x) - PVQV. G.41)
Здесь слева стоит величина общей потенциальной энергии источников дав-
давления и расхода, а справа — кинетическая энергия рассеивания всеми вет-
ветвями цепи на преодоление трения и суммарная потенциальная энергия,
доставляемая потребителям. Очевидно, что G.41) выражает закон сохра-
сохранения энергии для г.ц. в целом.
98

7 4. ПЕРЕХОД К ЗАДАЧЕ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
И ЕДИНСТВЕННОСТЬ ПОТОКОРАСПРЕДЕЛЕНИЯ
Математическое описание потокораспределения в г.ц. в виде задач на услов-
условный экстремум позволяет сделать следующий шаг и перейти к эквивалент-
эквивалентным задачам нелинейного программирования, которые можно отнести или
к классу задач выпуклого программирования с линейными ограничениями,
и;)и к классу нелинейных сетевых транспортных задач. При этом необхо-
химо ввести неотрицательные переменные, как этого требует каноническая
формулировка этих задач, что, кстати, позволяет одновременно решать и
проблему определения истинного направления течения на ветвях цепи.
Рассмотрим такой переход на примере экстремальной задачи с минимизи-
минимизируемой функцией в виде G.27), где /;(„г,) = х, |х,- \&i~ 'xt (ft > 1) при
Ax = Q.
8 связи с этим выделим прежде всего в исходной схеме цепи два под-
подмножества ветвей: пассивных — А = {/://,- =0} и активных —/2 =
- / :Hj > 0 , так что матрица соединений А разобьется соответственно на
две подматрицы А ('' и А B). Направления потоков на активных ветвях
фактически будут известны заранее, так как задание источников напоров
//,• определяет, как правило, их фактическую ориентацию. Что касается
пассивных ветвей, то каждую из них заменим на две — с одинаковыми
сопротивлениями х,- и расходами х\ ^ 0 и х"> 0, но с противоположной
ориентацией, так что искомый расход х,- всегда может быть подсчитан как
разность этих двух неотрицательных величин: х,- -х\ х'/. В результате
получим расширенную схему цепи с "раздвоенными" пассивными ветвя-
ветвями, матрица соединений и вектор расходов которой будут иметь вид
А = (Л<'>. - /(О. Л<2)). х =
где х'" = { Xj > 0, / G /2 } - вектор расходов на активных ветвях.
Таким образом, можно сформулировать следующую задачу нелинейно-
нелинейного программирования:
,(; ) /(O
\X) — Z. +
/e /, 1 + ft
V I
/e /, \ 1 + ft
> min G.42)
при
Ax = A^x' -A(l)x" + A^x'" = Q; x' > 0. x" > 0, x'" > 0. G.43)
Покажем, что целевая функция F (х) является строго выпуклой на
множестве х > 0, для чего достаточно убедиться в положительной опреде-
определенности матрицы F" (х) ее вторых частных производных [74, 154]. Дейст-
Действительно, поскольку F (х) — аддитивная функция, составленная из функ-
функций одной переменной, то все ее смешанные частные произвольные
й~1-1Ъх^ Ъх^ = 0, следовательно, F" (х) имеет в качестве ненулевых лишь
99

диагональные элементы
d2F/dxf = hSixfi-1 =/;(*,-) > 0, G.44)
положительные при любом х,- > 0 для произвольных гладких функций
fi (Xj) в случае их строгого возрастания (что ранее и предполагалось).
Область R допустимых решений х, удовлетворяющих линейным усло-
условиям G.43), представляет собой, как известно, выпуклое многогранное
множество.
Итак, задача G.42), G.43) заключается в минимизации строго выпук-
выпуклой функции, определенной на выпуклой области. Отсюда следует [74],
что любой ее локальный минимум является абсолютным и достигается он
в единственной точке. Таким образом, задача о потокораспределении в
г.ц. с сосредоточенными параметрами имеет единственное решение.
Покажем при этом, что для оптимального решения задачи G.42), G.43)
невозможно одновременное выполнение для каждого i G /t (т.е. для
"раздвоенных" ветвей) неравенств х/> 0 и х"> 0, т.е. одна из каждой
пары этих переменных должна обратиться в нуль и потому обязательно
х'(х"= 0. Предположим противное, например, что х\ > х"> 0. В таком
случае можно вычесть меньший расход из большего, заменив х\ на x'j — x",
а затем положить х\'= 0. Очевидно, что это не нарушит условий материаль-
материального баланса во всех узлах, однако значение целевой функции F (х) явно
уменьшится, так как в ней два слагаемых заменяются на одно
которое по значению всегда меньше их в силу отмеченных выше свойств
функций/} (*,).
Следовательно, любое решение, содержащее циркуляцию в элементар-
элементарном контуре, не может быть оптимальным, и потому для искомого реше-
решения или x'j = 0, или х]' = 0.
Математическое описание потокораспределения в виде задачи нелинейно-
нелинейного программирования дает возможность применять здесь основные положе-
положения теории и методов выпуклого программирования или нелинейных
транспортных задач в сетевой постановке (см. упоминавшиеся уже работы
[35,66,211]).
Конечно, быстродействие методов нелинейного программирования в
случае гидравлических расчетов будет наибольшим, если задачу G.42),
G.43) решать как нелинейную транспортную в сетевой постановке. Однако
и при этом сравнение все равно будет в пользу алгебраического подхода,
т.е. в пользу МКР и МД или, тем более, увязочных методов. И дело не толь-
только в том, что размерность задачи G.42), G.43) увеличивается примерно
вдвое за счет "раздвоения" ветвей. Просто-напросто "неэкономично" ре-
решать замкнутую систему уравнений Кирхгофа методами линейного и не-
нелинейного программирования.
Дальнейший сравнительный анализ и дифференциация методов описания
и расчета потокораспределения в г.ц. с сосредоточенными параметрами
проводится в разд. 7.6.
100

7.5. ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ
И "НОВЫЙ ВАРИАЦИОННЫЙ ПРИНЦИП"
Содержание данного раздела носит постановочный и дискуссионный харак-
характер. Он посвящен "системным" вопросам, связанным с принципами мате-
математического моделирования гидравлических объектов, и степени адекват-
адекватности тех или иных математических описаний реальным процессам течения
жидкости или газа в этих системах. Речь идет не о законах гидравлического
сопротивления как таковых, а о том, насколько правомочно формальное
использование их в виде совокупности замыкающих соотношений при по-
построении математических моделей потокораспределения - без должного
учета, с одной стороны, системного взаимодействия этих течений, а с дру-
другой — приближенности отображения реальной гидравлической системы в
виде довольно абстрактной схемы соединений их ветвей, пересекающихся
в точках-узлах.
Действительно, каждое уравнение А,- = у, + Hj =/} (Xf) достаточно пра-
правильно (в принципе с любой степенью точности) может описать установив-
установившееся течение на основной части соответствующего линейного участка
системы, но ведь оно берется как замыкающее соотношение для всей ветви
в целом, от одного ее концевого узла до другого, т.е. от "точки" до "точ-
"точки", в то время как фактически в местах соединения, например, двух или
нескольких трубопроводов среднего и большого диаметра происходят
"свои", довольно непростые процессы смешения и разделения потоков.
И чем сложнее и крупнее трубопроводная или другая гидравлическая систе-
система, тем ее схемное описание становится, видимо, все более абстрактным.
Возможно, что ключом к изучению этой проблемы является правиль-
правильная постановка и решение вопроса о том, какую же все-таки экстремаль-
экстремальную задачу "решает" реальная система. И должна ли при этом целевая
функция (при моделировании данной системы в виде г.ц.) иметь опреде-
определенный физический смысл, согласующийся, например, с принципом наи-
наименьшего действия, или она может носить формально-математический
характер "нового вариационного принципа " (см. разд. 3.2).
Конечно, в вычислительном отношении подобные моменты представ-
представляются в настоящее время не очень актуальными, поскольку и тот и другой
принцип приводит к совпадающим численным решениям. Однако эта
равносильность критериев имеет место опять же лишь с точностью до замы-
замыкающих соотношений, которые в обоих случаях в настоящее время просто
берутся в виде общего списка для ветвей расчетной схемы.
Как бы то ни было, попытаемся хотя бы наметить эту проблему в науч-
научно-методическом плане, тем более что в литературе по этому поводу не уда-
удалось обнаружить каких-либо специальных разъяснений.
Принцип наименьшего действия — один из наиболее общих физических
экстремальных принципов, которые "выражают объективную тенденцию
определяющих конкретную форму движения количественных характерис-
характеристик принимать минимально или максимально возможное при данных
условиях значение. Таким образом, экстремальные принципы... характе-
характеризуют признак, отличающий объективно происходящее движение системы
от возможных при данных условиях" [13]. Согласно принципу наимень-
наименьшего действия [32], существует такая величина F, называемая действием,
которая в случае действительно происходящего движения имеет минималь-
101

ную величину. Размерность действия равна произведению размерностей
работы и времени. Математически действие (по Гамильтону) выражается
интегралом по времени
F = / Ldt, G.45)
где L — функция Лагранжа изучаемой системы, которая представляет собой
разность между кинетической Т и потенциальной U энергиями этой систе-
системы, т.е. А = Т~ U.
Применительно к данному случаю стационарных режимов течения жид-
жидкости в гидравлической системе функция L не зависит от времени. Потому
минимум действия F должен определяться непосредственно минимумом
энергии L, рассеиваемой системой за каждую единицу времени, в течение
которого имеет место установившийся процесс, вплоть до очередного внеш-
внешнего воздействия, нарушающего равновесие системы. Таким образом,
установившемуся по то ко распределению в произвольной г.ц. должен отве-
отвечать минимум величины
F(x) = I (fi(x,)Xi- HiXi)=f(x)x-HTx=yT(x). G.46)
1 = i
Посмотрим, как соотносится с этим общим положением "новый вариа-
вариационный принцип" (см. разд. 3.2), состоящий в том, что минимизируемая
функция в общем случае должна иметь интегральную форму относительно
расходов х,-у например в виде G.25). И как объяснить формальные мате-
математические выкладки, представленные выше, которые действительно при-
приводят к такой функции?
Обратимся прежде всего к возможному здесь физическому смыслу.
Несмотря на то что выражение G.25), так же как и G.46), имеет размер-
размерность энергии, ее интегральный характер отражает учет "предыстории"
искомого установившегося режима, характеризуемого векторами х, у а Н.
Другими словами, F(x) в G.25) представляет величину энергии, которую
система должна "затратить" на то, чтобы перейти от состояния покоях = О
до конкретного х при заданных условиях Ах = Q. Безусловно, целевая
функция должна иметь аддитивно-интегральный характер, например, для
переходных процессов, но как сумма интегралов по времени от момента
нарушения "предыдущего" стационарного процесса до момента нового
устойчивого равновесия в виде другого установившегося режима работы.
Таким образом, "новый вариационный принцип" представляется проти-
противоречащим принципу наименьшей работы, необходимой для поддержания
любого стационарного процесса, и поэтому единственно правомочным для
формулировки экстремальной задачи о потокораспределении в г.ц. являет-
является, с точки зрения авторов, "энергетический" критерий G.46). Что же
касается формальной стороны дела, которая приводит к G.25), то сущест-
существует только один способ выйти из создавшегося противоречия - это считать
уравнения И,- - yt + Я,- = /,- (*,-) не априори заданными, а искомыми соот-
соотношениями, которые при математическом моделировании гидравлических
систем необходимо определять (уточнять, модифицировать), исходя из
критерия минимума G.46) суммарной энергии, затрачиваемой системой в
момента времени на преодоление трения при каждом установив-
установившемся процессе течения.
102

Проведенное в начале данной главы обобщение теоремы Максвелла о
принципе наименьшего теплового действия для электрической цепи на г.ц.
и является проявлением такого подхода. Сформулированные при этом
утверждения по существу могут служить математическим обоснованием
тезиса, что при любом установившемся потокораспределении всякая гидрав-
гидравлическая система должна моделироваться однородной гидравлической
цепью, а именно: течение жидкости на каждой из ее ветвей должно опи-
описываться одинаковой одночленной зависимостью. Функционалом вида
G.25) также можно пользоваться, но постольку, поскольку для одночлен-
одночленной зависимости он дает те же решения, что и G.46).
Безусловно^, все это требует соответствующих гидравлических экспери-
экспериментов на основе физического моделирования системного взаимодействия
различных течений, а также и теоретических исследований, необходимых
для того, чтобы правильно раскрыть механизм действия принципа наимень-
наименьшего действия на уровне гидравлических систем и вытекающие отсюда
требования к их математическим моделям.
7.6. ДИФФЕРЕНЦИАЦИЯ МЕТОДОВ РАСЧЕТА
ГИДРАВЛИЧЕСКИХ ЦЕПЕЙ
Изложенное выше позволяет более обоснованно классифицировать те или
иные подходы к описанию и расчету потокораспределения и дифференци-
дифференцировать их с физико-математической и вычислительной точек зрения. На
рис. 7.1 представлена общая схема возможных постановок задачи о потоко-
потокораспределении в цепи с сосредоточенными параметрами, эквивалентных
преобразований ее математических формулировок, численных методов
решения.
Что касается исходных постановок задачи, то они, независимо от того,
используются ли при этом алгебраический или экстремальных подходы,
должны отвечать физической сущности установившегося потокораспре-
потокораспределения в гидравлической системе. Во всяком случае, содержание данной
главы указывает на то, что такие, казалось бы, формальные моменты,
как привлекаемые вариационные принципы, основные положения двойст-
двойственности экстремальных задач потокораспределения, вид замыкающих
соотношений, неразрывно связаны с физической природой изучаемых
процессов, т.е. носят физико-математический характер.
Математически это приводит или к замкнутой системе уравнений, или
к задачам на условный экстремум. При определенных требованиях к виду
замыкающих соотношений, соответствующих опять-таки физическим
особенностям течения однофазной жидкости, все эти постановки оказы-
оказываются эквивалентными.
Эквивалентные преобразования задачи и переходы от одной математичес-
математической формулировки к другой, как правило, сочетают в себе обоснован-
обоснованный формализм известных математических приемов с их сетевой интерпре-
интерпретацией, что, в свою очередь, опирается на алгебру г.ц. и соотношения между
ее векторами и матрицами. Практически каждое из таких преобразований
связано с исключением векторов h, P или х (с целью сокращения размер-
размерности задачи и перехода только к контурным или узловым уравнениям)
и фактически всегда имеет своей целью подготовить задачу для ее решения
тем или иным методом. ,.,

<У
я
s
X
«
о
X
s.
—
*х
1
с
е
Of
И
X
1
*х
я
а
с
о
Л
X
о'
"х
НИН
к
s
8.
и
8.
ейного п
ни
X
X*
2 §
X Ф
ii
шейной
ЗОЙ
спортной
чи
S * Я 3
X О Н (Л
X
ё
>s
§
ювых
О1
<1
|
N
Z
'Он
<1
У.
~х
S
i
¦><
и
Z
S
вяз
?,
К
cd
0
о
с
8
расхо
1
о.
с
и
RJ
С
о
X
3
%
о
S
ю
О
II
а
8.
i s

Возможные методы расчета потокораспределения можно разбить на три
основные группы: методы линеаризации уравнений на базе метода Ньюто-
Ньютона и его модификаций, градиентные и методы нелинейного программиро-
программирования.
Метод Ньютона — универсальная основа для разработки алгоритмов
гидравлического расчета. Присущая ему линеаризация системы уравнений
на каждом шаге вычислительного процесса позволяет эффективно исполь-
использовать особенности топологической структуры расчетной схемы цепи и
многократно обращаться к линейным преобразованиям к контурным
или узловым величинам. Это резко снижает размерность системы уравне-
уравнений, которую фактически надо решать, и дает возможность для компакт-
компактного представления и обработки исходной и промежуточной информации
путем сетевой интерпретации вычислительных и логических операций.
Кроме того, линеаризация позволяет использовать богатейший опыт алгорит-
алгоритмизации расчетов линейных электрических цепей.
Методы по контурной и по узловой увязки гидравлических параметров
цепи представляют собой оригинальные, приемлемые даже для ручного
счета реализации метода Ньютона с помощью упрощенных итераций, осу-
осуществляющих приближенное решение систем линеаризованных уравнений
на каждом шаге процесса. Однако эти методы, как уже отмечалось, не обла-
обладают гарантированной сходимостью.
В общем же случае, например при расчете цепей с неплоской схемой
соединений, с переменными параметрами, особенно когда требуется прове-
проведение двойных и тройных циклов итераций (см. гл. 8 и 9), системы линей-
линейных уравнений необходимо решать более точным методом (по схеме Гаус-
Гаусса, методом окаймления или итерационным методом Зейделя и др.).
Методы контурных расходов и узловых давлений (МКР и МД) как раз
и являются совокупностями эффективных приемов сетевой реализации
метода Ньютона и вычислительных методов линейной алгебры, обобщая на
нелинейнысг.ц. известные электротехнические методы контурных токов и
узловых напряжений.
Области предпочтительного применения МКР и МД зависят от типа гид-
гидравлической системы, размеров и структуры расчетных схем, целей ис-
исследования. Проведенные вычислительные эксперименты на примере одних
и тех же цепей при взаимном соответствии начальных приближений по рас-
расходам (для МКР) и узловым давлениям (для МД) выявили большее
быстродействие и лучшую сходимость МКР по сравнению с МД. Некоторые
преимущества МД перед МКР, заключающиеся в том, что: не требуется
выбор системы контуров; начальное приближение в значениях узловых
Давлений может быть достаточно произвольным; проще производить де-
декомпозицию схемы цепи на отдельные фрагменты; легче учитываются
Двухсторонние ограничения на значения давлений в узлах, становятся в
основном 'несущественными при использовании автоматизированных
систем программ для гидравлических расчетов (см. гл. 8).
Экстремальное описание потокораспределения в виде прямой или двой-
двойственной задач на условный экстремум в случае его реализации через
необходимые условия экстремума автоматически приводит к системам
Уравнений законов Кирхгофа и поэтому с вычислительной точки зрения
не дает ничего принципиально нового по сравнению с алгебраическим под-
подходом (см. рис. 7.1). 105

К группе градиентных методов относятся методы нахождения точки
минимума (или максимума) специальной нелинейной функции, заключаю-
заключающиеся в движении по антиградиенту этой функции (метод наискорейшего
спуска) или по направлению, составляющему "острый угол" с ним (на-
(например, методы возможных направлений [74]). Эти методы основаны на
вычислении полного или частичного градиента (в частности, на покоорди-
покоординатном "спуске") или на тех или иных модификациях, учитывающих "ов-
"овражный" характер минимизируемой функции.
Выделение данных методов в отдельную группу весьма условно, по-
поскольку методы, рассмотренные выше, можно также трактовать как
градиентные. Однако речь идет в основном о методах, которые применяют-
применяются в случаях сведения гидравлического расчета к определению точек мини-
минимума функций без связей, например, посредством перехода к задаче на
абсолютный экстремум относительно векторов хк или Р, а также в резуль-
результате замены исходной системы уравнений Кирхгофа специальной функ-
функцией, являющейся суммой квадратов этих уравнений.
Известно, однако, что градиентные методы слишком универсальны,
чтобы быть полезными во всех конкретных задачах, и "скорейшими" они
могут быть названы лишь теоретически. Это подтвердили и проведенные
эксперименты по сравнению различных методов расчета потокораспреде-
ления [209 и др.]: градиентные методы оказались малоэффективными
из-за большого числа итераций и "пилообразной" сходимости (даже при
сравнительно близких к решению начальных приближениях).
Таким образом, анализ и сравнение' различных подходов и методов
расчета потокораспределения, а также вычислительная практика приводят
к выводу о явной предпочтительности здесь методов, реализующих итера-
итерационный процесс Ньютона или его модификаций, которые наиболее эффек-
эффективно используют сетевой характер и вытекающие из этого специальные
свойства системы уравнений Кирхгофа. Вместе с тем экстремальные под-
подходы сохраняют, несомненно, свое не только теоретическое, но и приклад-
прикладное значение, например при постановке и решении задач схемно-структур-
ной и схемно-параметрической оптимизации многоконтурных систем
(см. ч. 2 данной монографии).
Глава 8
ГИДРАВЛИЧЕСКИЕ ЦЕПИ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
8.1. ИСХОДНЫЕ ПОЛОЖЕНИЯ
Поднятие г.ц. с сосредоточенными параметрами означает, что соответствую-
соответствующая физическая или математическая модель реальной системьг базируется
на элементах, основные характеристики которых, т.е. величины гидравли-
гидравлических сопротивлений s,- , действующих напоров Я,- , узловых расходов
Qi , считаются "соредоточенными (усредненными) постоянными. Такие
модели дают, однако, весьма упрощенное описание реальных задач во мно-
многих практически важных случаях, когда требуется учесть: наличие регули-
регулирующих устройств (регуляторов расхода и давления, насосных и компрес-
106

8.1. Обобщенные характеристики регуляторов расхода и давления (РР и РД)
сорных станций), сжимаемость транспортируемой среды и изменение ее
характеристик в процессе течения и прочие факторы.
Обобщая эти случаи, можно прийти к пониманию того, что величины
sit Hi, Qj, вообще говоря, должны считаться функциями неизвестных:
расходов х( , потерь давлений yt , узловых давлений Pj и температур
Т/, определяющих искомое потокораспределение в г.ц., т.е., к примеру,
si = si(xi,PiiCp,TiiCp),Hi=Hi(xi),Q= Qj (Pj ),raePiiCp и 7}>ср - некоторые
средние для ветви i значения. Это означает, что данные характеристики
меняются от одного установившегося режима к другому и как бы опреде-
определяются (регулируются) "самим" потокораспределением. Соответствую-
Соответствующую г.ц. назовем цепью с переменными (регулируемыми) параметрами.
Конечно, фактически все гидравлические системы являются системами
с распределенными параметрами и строгие (эталонные) математические
модели должны в принципе исходить из этого. Вместе с тем это требует
рассмотрения соотношений в дифференциальной или интегральной формах
и приводит к смешанным системам уравнений (см. гл. 10), которые слиш-
слишком сложны, чтобы их можно было широко применять в большинстве
практических случаев.
Таким образом, привнесение в математическое описание всякого рода
упрощений и усредненных характеристик является неизбежным методи-
методическим приемом. С этой точки зрения если два типа гд. - с сосредоточен-
сосредоточенными и распределенными параметрами — считать граничными случаями
моделирования, то гд. с переменными параметрами представляют собой
промежуточный, оптимальный во многих отношениях (с методической
точки зрения, по вычислительной эффективности и практической значи-
значимости) класс моделей. К ним можно прийти "снизу", перестав считать
характеристики ветвей и узлов константами (как это и делается в данной
главе), или получить "сверху", упрощая модели с распределенными пара-
параметрами заменой в них интегральных соотношений некоторыми средними
значениями как искомых величин, так и функций от них.
Начальное представление о регулируемых элементах ТПС можно полу-
получить на примере регуляторов расхода и давления (РР и РД) в ТСС. Назна-
Назначение этих регуляторов, которые могут быть поставлены в источниках,
на вводах у потребителей или непосредственно на участках тепловой сети, -
Поддерживать заданные расходы или давления. Однако возможности вы-
107

полнения ими функций всегда ограничены некоторой "пороговой" величи-
величиной входного параметра.
Обратимся к обобщенным характеристикам РР и РД (рис. 8.1). Из
рисунка видно, что только при Pj > Pj* РР обеспечивает режим регулирова-
регулирования: увеличивает свое внутреннее сопротивление таким образом, чтобы
уменьшить давление на выходе до Pj*, что и обеспечит пропуск заданного
расхода Q*. При Pj < Pj* РР работает в режиме дросселирования, т.е. ведет
себя как элемент с постоянным (минимально возможным для себя) гидра-
гидравлическим сопротивлением Sj*, соответствующим полному открытию
клапана и определяющим в этом режиме пропускаемый расход Q в зави-
зависимости от Pj , так что для РР
Qf, если Pj >Pj*\
(8.1)
y/Pl/sfnpnO<Pj < Pj*.
Аналогично для РД
Р/ ,если Q/ > Qj*;
(8.2)
sfQJ при 0< Qj < Qj*.
Регуляторы, устанавливаемые на участках трубопроводной сети, рабо-
работают по более сложному закону. Фактически их роль сводится к тому, что-
чтобы изменять гидравлические сопротивления s,- в зависимости от расхода
% и перепада давления у-, или какой-либо другой переменной.
Отталкиваясь от этих достаточно простых случаев регулирования и
понимания взаимосвязи между потокораспределением и фактическими
характеристиками такого рода устройств, можно пойти дальше и распро-
распространить понятие элемента с переменными параметрами на более сложные
элементы и даже целые объекты в ТПС, как трубопроводные участки газо-
и нефтепроводов, насосные и компрессорные станции (КС), источники
расхода и давления, абонентские подсистемы. В связи с этим можно исполь-
использовать следующий прием: считать, что реальной ТПС отвечает некоторая
моделирующая ее г.ц. с переменными параметрами, значения которых
перенастраиваются (регулируются, пересчитываются) от одного устано-
установившегося режима к другому как сосредоточенные характеристики узлов
и ветвей цепи. При этом с каждой ветвью можно связывать не один, а
несколько переменных параметров, характеризующих, например, "обоб-
"обобщенное сопротивление" трубопроводного участка, входные и выходные
параметры КС и т.д. (конкретные примеры см. ниже).
Нередко цели расчетов при анализе режимов работы и наладке ТПС
заключаются именно в поиске положений ее регулирующих органов, что,
в свою очередь, зависит от распределения неизвестных еще (до расчета)
гидравлических параметров элементов системы. При этом, как правило,
возможно огромное число сочетаний в значениях переменных параметров
и соответственно множество допустимых (относительно давлений) реше-
решений, удовлетворяющих практическим требованиям. Поэтому в принципе
здесь необходим переход к постановке и решению соответствующих опти-
оптимизационных задач, поскольку по существу речь идет об управлении режи-
108"

мами работы ТПС (см. гл. 17). Эта особенность характерна прежде всего
д!Я задач расчета газотранспортных систем, имеющих множество КС [226.
227].
[гели же гидравлический анализ ТПС проводится посредством много-
многовариантного решения задачи о потокораспределении в отвечающей ей г.ц.
с переменными параметрами, то необходимо принимать во внимание два
обстоятельства: что подлежащая решению система уравнений не должна
быть недоопределенной и что, с другой стороны, задание вместо постоян-
постоянных коэффициентов и правых частей уравнений некоторых функций от
искомых переменных не увеличивает числа неизвестных, а сохраняет зам-
замкнутость (полноту) системы уравнений, если это уже имело место "на
уровне" г.ц. с сосредоточенными параметрами. Усложняются лишь соот-
соотношения, используемые для математического описания, и система уравне-
уравнений становится "еще более" нелинейной. Особая нагрузка здесь падает на
этап задания исходных данных, когда для получения однозначных решений
приходится фиксировать параметры источников напора, положения от-
отдельных регуляторов и т.п.
Другое дело, что функциональные зависимости, характеризующие эле-
элементы с переменными параметрами, зачастую составляются из различных
кривых, выбор которых связан с теми или иными режимами течения,
необходимостью соблюдения технических требований и других логичес-
логических условий, и потому имеют кусочно-линейный и нелинейный характер.
К тому же они бывают взаимно неоднозначными относительно своих пе-
переменных (например, некоторым значениям расхода может соответство-
соответствовать множество значений давления) и недифференцируемыми в отдельных
точках, так что допустимых решений может оказаться много и их нельзя
получить обычными (формальными) методами. Все это требует примене-
применения специальных и более сложных в математическом отношении (по срав-
сравнению с рассмотренными выше) методов расчета, обязательно учитываю-
учитывающих специфические особенности и физическую сущность потокораспределе-
ния в цепях с переменными параметрами.
Известно, что инженерный опыт и даже вычислительная практика здесь
явно опережали этап более или менее строгого осмысливания и формализа-
формализации с обоснованием соответствующих методов и алгоритмов расчета.
Данная глава посвящена вопросам математического описания и расчета
г.ц. с переменными параметрами [133, 135, 137, 140, 147], рассмотрение ко-
которых позволяет в известной степени преодолеть этот разрыв.
8.2. СИСТЕМА УРАВНЕНИЙ ГИДРАВЛИЧЕСКОЙ ЦЕПИ
С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
В отличие от предыдущих глав будем рассматривать теперь неизотерми-
неизотермическое потокораспределение, установившееся в произвольной г.ц., так
что, помимо векторов х, у, h, H и Р, к числу основных добавим также
вектор узловых температур Т= {Тх,..., Тт)т и векторы их граничных
значений для всех ветвей: /@) = (t, @),..., Г„@))т, t (/,) = (f, (L ,) ,...
Кроме того, потребуется также вектор 0 = @j,..., 6m )T узловых расхо-
расходов тепла, состоящий из величин с/ tJQj для узлов, в которых имеет место
109

приток среды с заданными температурой tj и теплоемкостью г; , и из
CjTjQj — в случае стоков (т.е. потребителей с нагрузками Q-; , а также
температурами Tj и теплоемкостями су , подлежащими определению в
результате расчета). i
Тогда равенство начальных температур f,-@) для потоков, .исходя-
.исходящих из общего узла/, может быть описано одним векторным уравнением
t@) = A]T, (8.3)
где A i — (тХ и)-матрица, фиксирующая отдельно начальные узлы всех
ветвей ( заменой нулями всех элементов полной матрицы соединений А,
равных — 1).
Температуры tj (/-,-) в концевых точках ветвей должны определяться
с помощью задаваемой вектор-функции аналитических зависимостей для
ветвей:
r(L)=G(x, P, t@),tTp, /B> w), (8.4)
где trp и tB - векторы температур грунта и наружного воздуха, a w -
вектор остальных параметров, привлекаемых для описания изменения
температуры потоков среды в зависимости от типа системы, целей и тре-
требуемой точности расчета.
Общая система уравнений г.ц. с переменными параметрами включает,
как обычно, уравнения материального баланса во всех узлах:
т - 1
Ах = Q(P), J. QjiPj) + Qm (P^) = 0, (8.5)
в которых вектор-функция Q(P) учитывает возможность взаимного ре-
регулирования значения расходов и давлений в узлах, а последнее равенство
обеспечивает суммарный баланс по цепи в целом за счет переменного
расхода Qm в линейно-зависимом узле.
Следующая группа уравнений отражает уравнения второго закона
Кирхгофа:
Ву = 0, /»=_(^)-10'д+ Ят.д/'т), (8-6)
где ат д - т-я строка матрицы Ар., записанная как столбец. Вместо (8.6)
можно использовать подсистему уравнений
АТР -у = 0.
Баланс расходов тепла во всех узлах можно описать одним векторным
уравнением
J,C@)r@) + A2C(L)t(L}=&, (8.7)
где дополнительно к введенным уже обозначениям С@) и C(L ) — диаго-
диагональные матрицы из значений С/ @)*/_ и С/ (tt)xt; Аг-тп Хи-матрица
конечных узлов ветвей .получаемая из А заменой на нули всех ее элемен-
элементов, равных +1, так что A i + А2 = А .
Кроме того, помимо (8.4), необходимы и замыкающие соотношения,
отвечающие принятым законам гидравлического сопротивления трению:
А = у + Н(х, Р, Т) = f{x, s(x,P,T,d)), (8.8)
tto

rJp // и s — векторы переменных параметров: действующих давлений и
• сообщенных" гидравлических сопротивлений ветвей. Здесь Р и Т могут
использоваться неявно, через их средние (в том или ином смысле) значе-
значения для ветвей цепи. Кроме того, на вид этих соотношений существенно
вгияет характер транспортируемой среды(сжимаемость, вязкость и пр.).
Уравнения (8.3)-(8.8), взятые вместе, образуют систему порядка
4» + Zm относительно х, у, t @), / (L ), Т, m - \ значений Pj и неизвестного
"балансирующего" расхода Qm.
Частным случаем рассматриваемой задачи является расчет изотерми-
изотермического потокораспределения в г.ц. с переменными параметрами. Тогда
обшая система уравнений сокращается до следующей:
Ax=Q(P), "i Qj(Pj)=O; (8.9)
By = 0; '"' (8.10)
Р=*{Рт,У)\_ _ (8.11)
y=f(x,s(x,P))-H(x,P), (8.12)
где Ф - вектор-функция, с помощью которой определяются все узловые
давления, исходя из фиксированного Р'^, и перепадов у{ давления на вет-
ветвях (см., например, (8.6)). Порядок этой системы — m + 2л, неизвестные —
х, у и m значений Q/ или Pj .
Для иллюстрации данных математических моделей конкретизируем их
применительно к газо- и нефтепроводным системам. Например, в случае
установившегося неизотермического течения газа по горизонтальному
газопроводу среднего давления используются зависимости:
/>/(!,) = Pj @) - Si(Л/сР, Т1шср )xf, (8.13)
ti(Li)=ttirp+ (ti @) - f/fI.p)exp(- НЛ.ср. '/.ср)/*,), (8.14)
гдеР,- ср, /,¦ ср — средние значения давления и температуры, широко при-
применяемые в расчетной практике с использованием различных формул
[226] :
2/ Pj (Li) \
pi ср =—\Pi@) + I.
'•ср з\л> л-@) + Л(^)/
или
Pj.cp= (PJ{0) +
i() ,,rp
li. ср = h, rp + A - exp (-7)),
1
или
- t,(L,)\
~~ ';
, rp
где 7 - критерий Шухова.
Здесь
si = eX,Aiz, tticp LJAI % = к(tifcpOTdiLi/Aiс(/>,-_cp)
где а — числовой коэффициент, зависящий от единиц измерения; X,-

коэффициент гидравлического сопротивления, зависящий от диаметра и
шероховатости трубы; Д,- — отношение плотности газа к плотности [воз-
[воздуха; с(Р, ср) - удельная теплоемкость газа; k(t,- cp) - коэффициент
полной теплопередачи от газа в окружающую среду (при средней темпе-
температуре tj_ ср) на ветви /; z,- - коэффициент сжимаемости газа.
Величины Sj и % можно считать обобщенными гидравлическими и тер-
термическим сопротивлением ветви i и соответственно, ее переменными пара-
параметрами, значения которых "определяются" самим неизотермическим
потокораспределением.
При изучении неизотермического течения разносортных нефтей можно
использовать следующее общее уравнение [137, 155] :
1,75
(8.15)
„"'1.877
i/ X j
pV877
где х/, s'j'ns'[' - гидравлические сопротивления трубопровода соответ-
соответственно при ламинарном, турбулентном и переходном режимах течения
(они зависят от потери напора на трение, вязкости и температуры нефти в
начале ветви); х ^рд' и s ^Р1>' — сопротивления фактических или условно
вводимых регуляторов давления и расхода соответственно; р,- и р/н) -
плотности нефти при средней температуре и поступающей в насос соответ-
соответственно; Hj , s ("' их*-"^ — соответственно максимально возможное
давление и гидравлические сопротивления насоса. Таким образом, здесь
фигурирует несколько переменных параметров ветви / по числу перемен-
переменных коэффициентов при xt в различной степени.
В еще большей степени усложняются замыкающие соотношения при
учете таких сложных элементов, как КС, а также при укрупнении расчет-
расчетных схем за счет агрегирования отдельных частей и подсистем ТПС. С
математической точки зрения получаемые при этом системы уравнений
являются сложными системами из линейных и нелинейных уравнений,
включающих неявные и трансцендентные уравления.
8.3. МЕТОДЫ ПОСЛЕДОВАТЕЛЬНОЙ ЛИНЕАРИЗАЦИИ
Для решения данных систем уравнений большой размерности, содержащих
нелинейные зависимости самого общего и произвольного характера, прак-
практически не существует каких-либо достаточно строгих и вместе с тем
эффективных вычислительных процедур, кроме общих положений об
организации итерационных процессов на базе линеаризации (метод Ньюто-
Ньютона и его модификации) или градиентных методов. Речь может идти лишь
о "гибких" методах, обязательно учитывающих физическую сущность
и сетевой характер задач.
В настоящее время основными методами расчета г.ц. с переменными
параметрами являются методы последовательной линеаризации. Они суше-
112

ствсино опираются на специальные свойства и структуру решаемых сис-
систем уравнений и заключаются в последовательном пересчете этих цепей
как цепей со все более точными значениями сосредоточенных параметров,
отвечающих искомому потокораспределению. Данные методы реализуются
б виде так называемых двойных и тройных циклов итераций, которые
математически можно интерпретировать как процессы расщепления общей
системы уравнений на подсистемы и их многократного решения при фик-
фиксируемых значениях наиболее сложных нелинейных коэффициентов и пра-
правых частей.
Общая схема такого рода методов характеризуется следующим. Внеш-
Внешний цикл итераций заключается в определении очередного приближения
для векторов Р к Т и подсчете новых значений всех переменных парамет-
параметров (s, H, Q), включая выполнение имеющихся логических условий и опре-
определение режима работы регулирующих устройств. Внутренний цикл реа-
реализует МКР или МД для очередной увязки расходов и давлений (при зафи-
зафиксированных температурах) по всей схеме цепи. Общий шаг такого про-
процесса последовательных приближрний содержит также анализ сходимости,
например, проверкой на совпадение с задаваемой точностью двух очеред-
очередных значений всех искомых векторов или только некоторых из них.
Рассмотрим данный подход более подробно, но прежде всего применительно
к системе уравнений (8.9) —(8.11), описывающей изотермическое потоко-
распределение. Будем считать, что расчетная схема цепи уже расширена до
циклической схемы, полностью отображающей "кругооборот" в движении
траенпортируемой среды, а узел j = m является опорным линейно-зави-
линейно-зависимым узлом (с заданным давлением Р'т ), который соединен фактически-
фактическими или условными ветвями со всеми другими узлами (см. разд. 4.4).
Тогда группа уравнений (8.9) сведется к однородной системе Ах = 0.
Вычислительный процесс, ориентированный на применение МКР (гл. 5),
будет состоять из выполнения следующих операций:
1. Фиксирование значений всех переменных параметров схемы цепи,
т.е. s = s@),# = Н @), исходя из физических соображений и целей расчета.
2. Построение и решение с помощью МКР системы уравнений относи-
относительно вектора х
Ах =0, Bf(x, х@)) = ВН@), (8.16)
в результате чего определяется х(°).
3. Подсчет узловых давлений
(8.17)
4. Определение новых приближений в значениях переменных параметров
s°) = s(x@),P@),P'm), ЯA) = Я(х<°\ .Р(о); Р'т). (8.18)
5. Анализ сходимости процесса.
6. Повторение в случае необходимости п. 2—5 с переходом от и = 0 к
Л/=1,2,....
В случае использования МД (вместо МКР) п. 2, 3 заменяются одним:
построением и решением с помощью МД системы уравнений относительно
*иР для определениях@) иР@):
(8.19)
8-Зак. 384 113

При расчете неизотермкческого потокораспределения в г.ц. с переменны-
переменными параметрами, когда требуется решение полной системы уравнений
(8.3) —(8.8) относительно векторов xs,P и Г, описанный выше вычислитель-
вычислительный процесс двойных циклов итераций (где "внутренний" цикл связан с
решением системы (8.16) или (8.19), а остальные операции составляют
"внешний" цикл) "погружается" в еще один цикл для пересчета "темпе-
"температурного поля" цепи в соответствии с уравнениями (8.3), (8.4) и (8.7).
При этом во всех последующих операцияхпеременные параметры пере-
считываются уже как функции не только х и Р, но и Т.
Таким образом, предлагаемые здесь методы двойных и тройных циклов
итераций (в различных вариантах) относятся к методам последовательных
приближений, осуществляемых как для векторов искомого решения,
так и для переменных коэффициентов и правых частей ("регулируемых
параметров") исходной системы уравнений посредством группового ослаб-
ослабления невязок тех или иных ее подсистем. С физической же точки зрения
речь идет об итерационном процессе поиска некоторой г.ц. с сосредото-
сосредоточенными параметрами, которая в принципе существует, но своя для каждо-
каждого установившегося потокораспределения. Выполняется это с помощью
двухступенчатой линеаризации, проводимой при каждом прохождении
цикла итерации: сначала путем фиксирования очередного приближения в
значениях переменных параметров, затем - в ходе применения МКР или
МД и сведения задачи к контурным или узловым переменным.
Как и для любых методов последовательных приближений, большую,
часто решающую роль в их сходимости играет выбор начального прибли-
приближения, что требует задания приближенных значений всех искомых векто-
векторов х, Р и Т. Данную задачу можно упростить предварительным заданием
лишь одного из векторов х или Р с тем, чтобы остальные гидравлические
параметры определять (с помощью ЭВМ), исходя из замыкающих соотно-
соотношений и части сетевых уравнений. В результате будет обеспечено более
строгое (физическое) соответствие этих векторов друг другу.
Поскольку перед каждым внутренним циклом итераций фиксируются
все значения температур и переменных параметров, то вопрос о его сходи-
сходимости заключается в выполнении условий сходимости МКР и МД для цепей
с сосредоточенными параметрами. А так как эти требования практически
соблюдаются, то вычислительный процесс во внутренних циклах будет
всегда сходящимся при условии применения точных методов для решения
систем линейных уравнений относительно контурных расходов или узло-
узловых давлений.
Что касается сходимости всего процесса в целом, то она будет опреде-
определяться при условии корректной постановки задачи выбором достаточно
хорошего начального приближения и способами организации внешних
циклов. При этом существенную роль играют различные соображения и
математически обоснованные приемы, направленные на повышение эф-
эффективности методов расчета изотермического и неизотермического пото-
кораспределений. Эти вопросы обсуждаются в следующей главе.
114

Глава 9
ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИИ МЕТОДОВ РАСЧЕТА
ПОТОКОРАСПРЕДЕЛЕНИЯ НА ЭВМ
9.1.0 СПОСОБАХ ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ
МЕТОДОВ РАСЧЕТА ПОТОКОРАСПРЕДЕЛЕНИЯ
Представленные выше математические модели, описывающие потокорас-
пределние в г.ц. с сосредоточенными и переменными параметрами, теоре-
теоретически позволяют ставить задачи по анализу установившихся (нормаль-
(нормальных и послеаварийных) режимов работы сложных трубопроводных и дру-
других гидравлических систем практически с любой степенью детализации
расчетной схемы, с учетом активных и регулирующих устройств, а также
с требуемой точностью в отражении изменения параметров состояния
транспортируемой среды. Вместе с тем, как показал опыт применения
ЭВМ в данной области, накопленный в 60-70-х годах, методы и особенно
алгоритмы, реализующие данные модели, оказались недостаточно совер-
совершенными с точки зрения их надежности, гибкости и быстродействия.
В начале этого периода казалось очевидным, что используемый матема-
математический аппарат численных методов линейной и нелинейной алгебры
является вполне досаточным, а новые сверхмощные ЭВМ вообще снимут
все проблемы, связанные с автоматизацией и эффективностью многова-
многовариантных расчетов потокораспределения в сложных системах. Однако
масштабность и сложность рассчитываемых объектов и соответственно
требования к основным параметрам (быстродействию и емкости памяти)
ЭВМ стали довольно быстро обгонять возможности используемых ЭВМ
и программ расчета. Так, например, однократный расчет ТСС средних
размеров, схема которой имеет порядка 250 ветвей и 50 контуров, но с
широким диапазоном значений гидравлических сопротивлений и наличием
множества регуляторов расходов и давлений, может занять на довольно
распространенной в настоящее время ЭВМ типа ЕС-1030 около часа.
Подобные затраты машинного времени становятся совершенно неприем-
неприемлемыми при проведении многовариантного анализа потокораспределения
в сложных ТПС и тем более в условиях автоматизированного диспетчер^
ского управления режимами их работы. Актуальность проблемы совершен-
совершенствования методов и программ для гидравлических расчетов подчерки-
подчеркивается также очевидным прогрессом в этом направлении в области электро-
электроэнергетики, где постоянно велись и продолжают вестись работы по исполь-
использованию последних достижений вычислительной математики и максималь-
максимальному учету специфики своих задач — в стремлении к трудно достижимой
Цели управления режимами работы электроэнергетических систем в реаль-
реальном масштабе времени.
Рассмотрим некоторые из возможностей для повышения быстродей-
быстродействия методов и алгоритмов расчета потокораспределения и их гибкой
адаптации к особенностям рассчитываемых-ТПС, составу исходных данных
и конкретной постановке задач [142].
1. Учет слабой заполненности матриц гидравлической цепи. Практиче-
Практическая эффективность многих машинных программ для расчета потокорас-
потокораспределения базируется на использовании методов поконтурной или поузло-
115

вой увязки (см. гл. 3), с помощью которых предельно упрощается вычи-
вычислительный процесс решения систем линеаризованных уравнений отбрасы-
отбрасыванием всех внедиагональных элементов в матрицах Кирхгофа и Максвел-
Максвелла. Однако при этом, во-первых, может значительно увеличиться число
необходимых итераций (из-за широкого диапазона коэффициентов гидрав-
гидравлического сопротивления, неудачного выбора системы контуров и, как
следствие, плохого начального приближения) и, во-вторых, процесс вообще
может оказаться расходящимся.
Таким образом, в общем случае данные системы линеаризованных
(контурных или узловых) уравнений, получаемые на каждом шаге про-
процесса, необходимо решать в полном виде, но с обязательным учетом раз-
разреженной (слабозаполненной ненулевыми элементами) структуры матриц
коэффициентов этих систем. Дело в том, что формальное использование
методов линейной алгебры (методов исключения Гаусса, окаймления и др.
[57, 235, 239]) применительно к полным матрицам Кирхгофа и Максвелла
требует выделения порядка с2 или (т- IJ ячеек оперативной памяти
ЭВМ (или половины этого объема), что вряд ли допустимо при сит,
равных нескольким сотням. К тому же это приводит к чересчур длитель-
длительному счету из-за необходимости обработки и нулевых элементов, которые
составляют в этих задачах более 90%.
В настоящее время считается общепризнанным, что одним из средств
преодоления этих трудностей является использование модифицированных
методов исключения (типа метода Гаусса), специально ориентированных
на учет разреженности матриц [28, 45, 232]). Это дает существенный эф-
эффект в экономии памяти ЭВМ и времени ее работы за счет: 1) применения
специальных способов хранения элементов матриц в форме "списков",
позволяющих фиксировать только их ненулевые элементы и без особых
трудностей вносить изменения при появлении дополнительных ненулевых
элементов; 2) использования алгоритмов определения оптимального
порядка исключения неизвестных, обеспечивающих минимизацию числа
появляющихся новых ненулевых элементов и 3) проведения арифмети-
арифметических операций только с ненулевыми элементами. Вместе с тем имеются
некоторые особенности реализаций данных приемов в нашем случае.
В отличие от электрических цепей при расчете потокораспределения
в г.ц. наиболее распространенным и более эффективным в вычислитель-
вычислительном плане является переход к контурным уравнениям. В то же время для
учета разреженности матрицы более выгодной оказывается узловая форма
записи системы уравнений, поскольку для сложных систем заполненность
нулями у матрицы Максвелла меньше, чем у матрицы Кирхгофа. Кроме
того, структура матрицы Максвелла совпадает со структурой схемы цепи
и не зависит от выбора контуров, что упрощает логику алгоритмов упорядо-
упорядочения исключения переменных.
В работе [28] в связи с этим высказано справедливое предложение
о целесообразности комбинации обеих форм записи с тем, чтобы одновре-
одновременно использовать как преимущества вычислительного процесса относи-
относительно контурных переменных (с точки зрения более высокой скорости
его сходимости), так и минимальные требования к памяти в случае перехо-
перехода к узловым уравнениям. Иначе говоря, речь идет о том, чтобы сходи-
сходимость процесса контролировать по невязкам в контурах, а поправки к
решению находить из системы узловых уравнений.
116

Для осуществления такой комбинации необходим эквивалентный пере-
переход от контурной формы к узловой, основанный на теореме Нортона для
электрических цепей. Поскольку сам способ перехода в работе [28] опи-
описан не совсем точно, рассмотрим его подробно на примере цепи, схема
которой изображена на рис. 9.1. Для этого приведем подробное математи-
9.1. Пример схемы г.ц.
С,, ??з ~ узловые (известные) расходы
ческое описание цепи, причем будем параллельно рассматривать обе формы
записи уравнений второго закона Кирхгофа:
+ *i +*3.-Gi ^0, wl(x,P) = P1-P2-slxi = 0,
и, (*)= + *i +*3.-Gi ^0,
и2(х)= -х, + х2 -х4 = 0,
и3(х)= -х2 - х5 + 0з =0;
() ] l -S3X3,
(9.1)
(9.2)
ws (x,
= P2-P3-s2x22 = 0,
= P1-Pi -s3xl=0, (9.3)
= 0.
Здесь (9.1) — уравнения первого закона, а (9.2) и (9.3) — уравнения
второго закона Кирхгофа соответственно в контурной и узловой формах;
Р\ — известное давление в линейно-зависимом узле.
Полагая, что начальное приближение х^ выбрано удовлетворяющим
уравнениям (9.1), т.е. щ {xS^ ) =0, (j- 1,2,3), проведем линеаризацию
всех уравнений в этой точке:
и2
= +&х, + Ах3 =0,
Ах)= -AXi + Ах2 - Д
(х{0) + Ах) = ~Ах2 - Axs = 0,
=0,
(9.4)
и,
i =0,
= 0,
(9 5)
v2(x{0) + Ax)^v2(x{0))-
\A?, (y^ ' + Л V Р+Л РЛ ZZZ Ш fv' ^/ РЛ 4- Л P ЛР Op v( О/ Л v — П
+ Ax, P+AP)^ w2(x<0), F) + AP2 - AP3 - 2х2х^0)Длг2 = О,
+ Ax,P+ AP) ~ tv4(i(°), F) - ДР2 - 2s440) Дл:4 = О,
Длг, P+ AP)^ ws(x@\ P) - AP3 - 2s5xi0)Axs = 0, (9.6)
где AP4 = 0.
Считая хордами ветви / = 1 и 2 и разрешая (9.4) относительно
А*з» Ах4, Ах5, перейдем в (9.5) к системе уравнений относительно контур-

ных поправок:
Далее, следуя [28], отнесем контурные невязки vh(x^) и и2(х^) к со
ответствующим хордам так, что (9.6) примет вид
ДЛ - АР2 - 2slx[0)Axl = -Ui(*@)),
АР2 ~ АР3 -2s2xi0)Ax2 = -v2(xw),
APl~2s3x{o)Ax3=0, (9.8)
-Д/>2 -2х440)Д*4 =0,
-АР3 - 2s5x|0>Ax5 = 0.
Заметим, что (9.8) эквивалентно (9.5), поскольку подстановка величин
2s,-x,- Дх,- (/= 1,..., 5), полученных из (9.8), в (9.5) даст тождества.
Выпишем теперь, исходя из (9.8) .компоненты вектора Ах:
Ах, = (ДР, - АР2 + Vl(x^))l2Slxl0), Ах2 =(АР2 - AP3+v2(x^))l2s2x[
Ах3 = ДЛ/2$з40), Ах4 = -AP2/2s4xi0\ Ах5 = -AP3/2ssxi0). (9.9)
Подставив (9.9) в (9.4), получим после несложных преобразований
искомую систему уравнений относительно АР1,'АР2, АР3:
1 1 \ . 1 _ »i(x@>)
) ' s3xr' ) SixY" 2slx\V)
('ло)
Таким образом, имеем систему уравнений в узловой форме с сим-
симметрической матрицей Максвелла. Однако правые части этих уравнений
представлены здесь не в виде небалансов расходов в узлах, что требуется
в случае стандартной схемы метода узловых давлений (см. гл. S), а как
преобразованные контурные невязки.
Решив (9.10) относительно АР{, получим затем из (9.9) Axlt Ax2,
которые будут совпадать со значениями, если их определить из системы
уравнений (9.7). Далее находится следующее приближение лс*1* = х*0) + Д*
вектора расходов, вычисляются невязки потерь давления в контурах, фор-
формируется и решается система уравнений (9.10) и т.д.
Сделаем некоторые замечания, касающиеся дальнейшего изложения.
Для иллюстрации эффекта от рассматриваемых в данном разделе рекомен-
рекомендаций будем по возможности приводить результаты численных экспери-
экспериментов по их реализации. Понимая» что получающиеся при этом выводы

Таблица 9.1
Параметры гидравлических цепей, используемых для сравнения эффективности
методов расчета потокораспределения
Название
гидравличес-
гидравлической цепи
Количество
ветвей л
узлов т
конту-
контуров с
Диапазон коэффициентов гидравли-
гидравлического сопротивления ветвей
ГЦ-1
ГЦ-2
ГЦ-3
ГЦ4
ГЦ-5
ГЦ-6
160
270
314
243
353
285
111
190
224
130
204
206
50
81
91
114
150
80
3,7 X 10-'
2,4 X 10"8
2,0 X 10~9
3,3 X 10~8
2,49 X 10"'
2,0 X 10"9
-2,07x10°
- 1,93 X 10°
-4,9 X 10+ '
-2,15 X 10
' - 1,14 X 10м
-4,9Х 10+1
существенно зависят от конкретных особенностей рассчитываемых цепей,
приведем в табл. 9.1 характеризующие их параметры.
Далее, в качестве критерия для оценки эффекта выбрано время, затра-
затрачиваемое ЭВМ на увязку цепи, т.е. время, отсчитываемое от момента полу-
получения начального приближения, до момента, когда абсолютная величина
невязки в каждом контуре станет меньше некоторой достаточно малой
величины е, одинаковой для всех цепей. Поскольку все расчеты проводи-
проводились на одной и той же ЭВМ БЭСМ-6 и объем используемой оперативной
памяти был примерно одинаковым, то выбор данного критерия представ-
представляется достаточно обоснованным. К тому же в настоящее время именно
по времени счета принято выносить суждения об эффективности программ
или их отдельных блоков.
В качестве методов, с которыми производится сравнение, используются
получившие наибольшее распространение при расчете гидравлических
цепей методы МКРТ и МКРУ [147] (см. также гл. 5): МКРТ - метод кон-
контурных расходов, на каждом шаге которого решается линеаризованная
система точным методом окаймления; МКРУ - метод контурных расходов
увязочного типа с использованием модификации [20, 259].
Для получения начального приближения используется методика ли-
линеаризации гидравлических цепей, описанная в разд. 6.3 и реализованная
в работе [147]. Если особо не оговорено, начальное приближение для
одноименных цепей одно и то же.
Для удобства сравнения введен коэффициент эффективности кэ, значе-
значение которого есть отношение времени счета по МКРТ к времени счета
сравниваемого метода, т.е. коэффициент, показывающий, во сколько раз
быстрее или медленнее, чем МКРТ, работает конкурирующий метод.
Итак, приведем в табл. 9.2 результаты численных расчетов по методу,
изложенному в данном пункте и условно названному МКРДГК (метод
контурных расходов, на каждом шаге которого проводится разнесение кон-
контурных невязок в узлы, ограничивающие одноименные (контурам) хорды,
и формируется система уравнений в узловой форме, решаемая методом
Гаусса с компактной формой записи, хранения и обработки коэффициентов
матрицы Кирхгофа).
119

Таблица 9.2
Время счета t, мин, количество итераций kN и коэффициент эффективности
кэ при расчете гидравлических цепей методами МКРТ, МКРУ и МКРДГК
Название гид-
гидравлической
цепи
МКРТ
kN
МКРУ
kN
МКРДГК
kN
ГЦ-1
ГЦ-2
ГЦ-3
ГЦ4
ГЦ-5
ГЦ-6
1,89
2,31
6,20
9,20
10,25
27,23
5
8
7
6
5
8
1
1
1
1
1
1
7,04
9,92
64,39
0,23
17,02
155,33
2983
6800
12713
57
5320
21868
0,27
0,23
0,10
40,0
0,6
0,18
0,38
1/13
2,92
1,49
2,80
2,85
5
8
7
6
5
8
4,98
2,04
2,12
6,17
3,65
9,56
Данные табл. 9.2 наглядно свидетельствуют об очевидной в боль-
большинстве случаев эффективности МКРДГК. Лишь для одной цепи (ГЦ-4)
МКРУ оказался в 40 и в 6,5 раз эффективнее соответственно МКРТ
и МКРДГК, что подтверждает хорошее быстродействие увязочных методов
в благоприятных условиях: относительно небольшой диапазон коэффи-
коэффициентов гидравлического сопротивления ветвей, удачливый выбор системы
контуров и т.п.
2. О выборе шага для проверки контурных расходов. В современной
вычислительной практике при решении как оптимизационных задач, так и
задач нелинейной алгебры поправки к очередному приближению, как пра-
правило, вводятся с некоторым коэффициентом, который может быть как
меньше, так и больше единицы, а конкретное его значение выбирается,
исходя из некоторого критерия [253, 256] и др. Критерием обычно служит
минимум той или иной нормы невязок уравнений, например, суммы их
модулей или квадратов. Эффект от введения такого коэффициента состоит
в том, что приближения получаются более точными и, следовательно, умень-
уменьшается число итераций. При этом, однако, использование переменного шага
для приращений аргументов оправдано лишь в тех случаях, когда поиск
его осуществляется намного быстрее, чем решение линеаризованной систе-
системы уравнений. Для задач большой размерности это требование обычно
выполняется.
В случае МКРТ с переменным шагом очередное приближение представ-
представляется в виде
(9.11)
где Ах^^ определяется, как обычно, в результате решения системы ли-
линеаризованных контурных уравнений, а коэффициент Л, называемый ша-
шагом поправки, находится с помощью решения одномерной (относитель-
(относительно Л) задачи на минимум суммарной (по абсолютной величине) невязки
во всех с контурах.
Результаты экспериментальных расчетов по апробации такого подхода,
условно названного MKPTJ1, на примере ГЦ-1 (табл. 9.3) подтверждают
приведенные выше рассуждения: при хорошем начальном приближении
эффекта практически нет, а при грубом сокращается число итераций и соот-
соответственно время счета.
120

Таблица 9.3
Время счета /, мин, количество итераций kN, коэффициент эффективности к3 при
расчете ГЦ-1 методами МКРТ и МКРТЛ с различными начальными приближениями
Название метода
МКРТ
МКРТЛ
1
1
г
,89
,86
Начальное
Хорошее
kN
5
4
Л
1
1,
э
02
приближение
г
4,16
2,7 9
Грубое
kN
11
6
кэ
1
1,49
Исходным здесь был также МКРТ с точным решением систем линеаризо-
линеаризованных уравнений методом окаймления. К качестве конкурирующих мето-
методов одномерной минимизации фигурировали: метод ДСК, предложенный
Девисом, Свенном и Кэмпи, и метод Фибоначчи [256]. Относительно этих
методов можно сказать следующее: при грубом начальном приближении
v'0' метод Фибоначчи эффективнее ДСК, поскольку в принципе позволяет
получить более точное значение Л вдоль Ах\ при хорошем же л:^ точ-
точность в определении Л не столь существенна и ДСК становится предпочти-
предпочтительнее метода Фибоначчи, так как требует для нахождения Л меньшего
числа операций. Анализ результатов расчета как этой, так и других цепей
подтверждает целесообразность введения процедуры определения опти-
оптимального коэффициента для поправок контурных расходов при решении
задач расчета потокораспределения в цепях средней и большой размерности.
3. О методе Брауна. Среди большого числа методов, созданных на базе
метода Ньютона, особого внимания в данном случае заслуживает метод
Брауна, опубликованный в 1969 г. [279] под названием "Метод с квадра-
квадратичной сходимостью, подобный методу Ньютона и основанный на гауссов-
ском исключении". В литературе приведены данные, показывающие эф-
эффективность его применения для расчета ЭЭС, а также результаты сравне-
сравнения с другими методами, из которых следует, что данный метод сходится
даже в тех случаях, когда расходится метод Ньютона.
Математическая сущность метода Брауна достаточно полно и ясно изло-
изложена в работе [279], поэтому опишем кратко лишь его основную идею.
Метод заключается в последовательной линеаризации каждого из уравнений
исходной нелинейной системы, получении из этого линеаризованного урав-
уравнения явного выражения очередной переменной и подстановки ее во все
нелинеаризованные уравнения. И так до тех пор, пока не будет получено
выражение для последней переменной, в котором она уже не зависит от
Других переменных. Далее осуществляется обратный ход (как и в методе
Гаусса) для получения искомых значений всех переменных.
Основная трудность при реализации метода Брауна связана с необходи-
необходимостью формализации процесса подстановок переменных в нелинейные
Уравнения достаточно произвольного вида. Ее преодоление, очевидно,
Должно идти по пути выявления закономерностей преобразования коэффи-
коэффициентов при неизвестных для функций конкретного вида, свойственного
рассматриваемому типу задач. Кроме того, при решении систем уравнений
большого порядка возникает также проблема упорядочения этих подста-
121

новок с цепью уменьшения числа новых ненулевых элементов при соот-
соответствующих преобразованиях матриц гидравлической цепи.
Авторами проведена предварительная оценка степени применимости и
трудоемкости метода Брауна для расчета потокораспределения в гидравли-
гидравлических цепях с использованием систем контурных уравнений и упорядоче-
упорядочена последовательность формул для преобразования коэффициентов в урав-
уравнениях (они не приводятся здесь из-за их громоздкости). Разумеется,
целесообразность практического использования данного метода еще должна
быть подтверждена расчетами реальных объектов, но уже можно сделать
вывод о необходимости его включения в число перспективных методов.
4. О комбинации методов. В предыдущих материалах обсуждались в
основном единичные возможности увеличения эффективности методов
расчета потокораспределения. Здесь рассмотрим совместное использование
некоторых из них для тех же целей.
В п. 1 данного раздела (см. табл. 9.2, ГЦ-4) была приведена информация,
отражающая факт высокого быстродействия в благоприятных условиях
метода увязочного типа, которая в очередной раз объясняет причину широ-
широкого их использования. Вместе с тем там же имеются данные (см. ГЦ-3,
ГЦ-6), указывающие на крайнюю неэффективность МКРУ по сравнению с
методами, в которых используются все элементы матриц Максвелла. Одна-
Однако заранее, до расчета, чаще всего неясно, какой же метод следует приме-
применять, поскольку не существует пока "формальных правил или критериев,
априори обеспечивающих рациональный выбор того или иного метода.
Конечно, опираясь на информацию о параметрах цепи, о процедурах подго-
подготовки ее к расчету, можно сделать некоторые качественные выводы (ти-
(типа: "плохо" - "хорошо") о будущем поведении метода. Но подтвердить
правильность выбора метода, осуществленного на основе этих выводов,
может лишь ход реального вычислительного процесса.
В связи с этим представляется, что достаточно информативным и объек-
объективным критерием, отражающим влияние .всех факторов на вычислитель-
вычислительный процесс, может служить величина некоторой нормы (например, суммы
модулей невязок системы), характеризующая степень "увязанности"
системы уравнений на каждом шаге процесса. Разность же этих величин,
вычисленная по результатам текущего и предыдущего шагов, позволяет
оценить текущую "скорость" процесса. При этом управление вычислитель-
вычислительным процессом будет заключаться в смене метода, как только он переста-
перестанет удовлетворять некоторым требованиям к скорости увязки системы.
Ниже на эмпирическом материале иллюстрируются примеры такого управ-
управления.
Рассмотрим (см. рис. 9.2) поведение суммы модулей невязок системы
с
2 \vr(x^N^)\ (в дальнейшем для простоты написания индекс и предел
г= 1
суммирования будем опускать) в процессе расчета потокораспределения
для ГЦ-1-ГЦ-6, организованного на базе МКРУ. На рисунке в целях мас-
масштабирования приведены значения не 2| vr(x(N))\, а их отношения к
2| vr(x*-°')\ — сумме модулей невязок при начальном приближении * ¦
обозначенные o*-N\ N — номер итерации.
Анализируя приведенные графики, наглядно убеждаемся, что использова-
использование МКРУ для ГЦ-1-ТЦ-6 становится совершенно неэффективным после

9.2. Изменение критерия ст4"' = Z\vr(x( ')\/ % \vr(xx ~') | в процессе расчета по-
токораспределения методом МКРУ (а) и продолжение графиков (б)
I - ГЦ-1, 2 - ГЦ-2, 3 - ГЦ-3, 4 - ГЦ-4, 5 - ГЦ-5, 6 - ГЦ-6
соответственно 7-, 31-, 7-, 75- и 10-й итераций, т.е. после указанных номе-
номеров итераций значение а^ либо возрастает, либо уменьшается очень незна-
незначительно. Очевидно, на следующих итерациях необходимо применять мето-
Ды типа МКРТ, например лучшую на данный момент его модификацию -
МКРДГК. Далее, учитывая, что время выполнения одной итерации МКРУ
123

Таблица 9.4
Время счета t, мин, коэффициент эффективности кэ и количество итераций при
расчете гидравлических цепей комбинированным методом
Название гидрав-
гидравлической цепи
ГЦ-1
ГЦ-2
ГЦ-3
ГЦ4
ГЦ-5
ГЦ-6
0,41
1,0
1,8
0,23
2,03
1,64
ц
4,61
2,31
3,44
40,0
5,05
16,54
Количестве
МКРУ
27
30
20
57
136
16
итераций
МКРДГК
3
5
4
0
2
4
обычно существенно меньше аналогичного времени МКРДГК, логично
повторное применение МКРУ до тех пор, пока не выполнится условие для
перехода к МКРДГК.
В обоснование целесообразности выбора МКРУ как исходного метода,
с которого следует начинать расчет потокораспределения, приведем следую-
следующие рассуждения: во-первых, для некоторых цепей применение МКРУ мо-
может оказаться эффективным до конца процесса и переход к МКРДГК
вовсе не понадобится (так для ГЦ-4 (см. табл. 9.2) решение было достигну-
достигнуто за 57 итераций, на что было затрачено 13,8 с), во-вторых,МКРУ на на-
начальном этапе обеспечивает достаточно быстрое убывание суммы модулей
невязок (см. рис. 9.2), затрачивая при этом меньше времени, чем требует-
требуется на одну итерацию МКРДГК. В табл. 9.4 приведены результаты численных
экспериментов по реализации рассмотренного подхода. А на рис. 9.3
проиллюстрирован ход соответствующих вычислительных процессов.
Реализовывалась комбинация МКРУ и МКРДГК, причем в рамках МКРДГК
использовалась процедура ДСК для поиска величины шага X вдоль направ-
направления Ax(N). Условие для перехода от МКРУ к МКРДГК получено на осно-
основании анализа поведения суммы модулей невязок (см. рис. 9.2) и имеет
вид
Анализируя данные, приведенные в табл. 9.2 и 9.4, можно сделать вывод
о достаточной эффективности рассмотренной комбинации методов - для
большинства цепей решение достигается за меньшее время (или проигрыш
во времени незначителен), чем при использовании одного конкретного ме-
метода. Однако еще более важным является заключение, вытекающее из изло-
изложенного, о принципиальной возможности создания комбинаций методов,
которые освобождают пользователя от предварительного "угадывания"
их предпочтительности и обеспечивают наиболее рациональное использова-
использование достоинств каждого из них в процессе расчета потокораспределения.
В заключение заметим, что приведенная здесь комбинация не является
единственно возможной и авторами опробованы разнообразные варианты
комбинаций, которые отличались друг от друга как составом методов и
формой их взаимосвязи, так и критериями слежения за ходом вычислитель-
вычислительного процесса. Так, например, в некоторых вариантах: в качестве критерия
124

/K
9.3. Изменение критерия а -1|г,.(л- )|/Г|гг(л ) i в процессе расчета потоко-
распределения комбинированным методом и продолжение графика для ГЦ-5
1 - МКРУ, 2 - МКРДГК
выступала евклидова норма вектора невязок системы; в составе МКРДГК
отсутствовала процедура ДСК; МКРУ использовался только в начале
процесса; варьировались на разных этапах расчета значение правой части,
Условия перехода с метода на метод и т.п. Данная же комбинация — резуль-
125

тат выбора среди апробированных и представляется наиболее приемлемой,
поскольку обеспечивает убывание критерия и обладает хорошей вычис-'
лительной эффективностью.
5. Использование специфики ТПС. Рассмотренные выше общие методы
расчета потокораспределения (МКР и МД) эффективно используют сетевой
характер исходных систем уравнений и связанные с этим соотношения меж-
между матрицами и векторами цепи. Однако они исходят из расчетных схем це-
цепей и, естественно, не могут использовать топологические и функциональ-
функциональные особенности ТПС, которые должны учитываться еще на уровне задания
этих схем.
Все средние и крупные ТПС, как правило, построены по иерархическо-
иерархическому принципу, в них всегда можно выделить те или иные относительно са-
самостоятельные подсистемы или фрагменты исследуемой ТПС, которые
можно рассчитывать отдельно. С другой стороны, для каждой такой под-
подсистемы, в свою очередь, всегда имеются возможности для разумного
упрощения (укрупнения) ее схемы без внесения сколько-нибудь заметной
погрешности в результате расчетов. Данные вопросы весьма специфичны
для ТПС конкретного типа и назначения, они подробно рассматриваются в
специальной литературе (см., например, [2, 73, 147, 156, 204, 226 и др.]),
но все они так или иначе сводятся к декомпозиции ТПС и эквивалентиро-
ванию их расчетных схем.
В качестве примера обратимся к двухтрубным ТСС. Естественное деле-
деление тепловых сетей в таких ТСС на подающую и обратную магистрали
позволяет (при их рассмотрении в двухлинейном изображении) рассчиты-
рассчитывать отдельно две подсистемы, состоящие соответственно из участков толь-
только подающей или обратной линий, а затем "состыковать" их через участки,
отображающие потребителей. Эффект здесь достигается, во-первых, за счет
существенного уменьшения размерности решаемых систем уравнений и,
во-вторых, в результате более быстрой и гарантированной сходимости
вычислительного процесса из-за меньшего разброса в значениях гидравли-
гидравлических сопротивлений.
В работах В.Л. Леонаса предлагается на базе использования идей
диакомптики Крона и блочных методов линейной алгебры строить общие и
достаточно универсальные алгоритмы декомпозиции для решения боль-
больших транспортно-энергетических задач. При этом приводятся примеры
быстрого решения задач большой размерности из области ЭЭС. Однако
данные алгоритмы весьма непросты в реализации, особенно применительно
к нелинейным ТПС, и требуют проведения специальных исследований и
алгоритмических разработок.
В данном разделе были рассмотрены лишь некоторые способы повыше-
повышения эффективности методов расчета потокораспределения при их реализа-
реализации на ЭВМ. При этом не отмечались такие важные вопросы, как выбор
начального приближения, системы главных контуров, эквивалентирования
расчетных схем, в силу того что они носят неформальный характер и яв-
являются специфическими для ТПС каждого конкретного типа.
Вместе с тем главные выводы очевидны. Математическое и алгоритми-
алгоритмическое обеспечение проблемы анализа и управления режимами работы ТПС
должно идти не по пути разработки автономных программ для ЭВМ, а в
направлении создания единых программно-вычислительных комплексов,
126

ориентированных на ТПС того или иного типа на основе следующих поло-
положений: а) использования современных достижений соответствующих
разделов вычислительной математики; б) учета сетевой структуры ре-
решаемых,систем уравнений и специфических особенностей ТПС; в) анализа
и активного использования межотраслевого опыта, особенно в области
управления режимами ЭЭС; г) максимальной автоматизации процесса
использования ЭВМ; д) создания автоматизированных банков и архивов
данных.
9.2. МЕТОДИКА РАСЧЕТА ГИДРАВЛИЧЕСКИХ ЦЕПЕЙ
С РЕГУЛЯТОРАМИ РАСХОДА И ДАВЛЕНИЯ
Для расчета г.ц., содержащей регуляторы расходы и давления (РР и РД),
может быть применена специальная методика, в которой используется
предложенный С. Цоем и Г.К. Рязанцевым [259] оригинальный способ
определения параметров вентиляторов и дросселирующих устройств,
обеспечивающих требуемые расходы воздуха на участках вентиляционной
сети. Она во многих случаях оказывается гораздо более быстродействую-
быстродействующей, чем описанный в разд. 8.3 общий подход, заключающийся в последо-
последовательной корректировке всех переменных параметров цепи с помощью
двойных циклов итераций.
Данная методика опирается на предположение о том, что требования о
поддержании необходимых значений расходов и давлений на определенных
элементах (ветвях и узлах) цепи всегда могут быть удовлетворены о по-
помощью некоторого потокораспределения. Правда, положения отдельных
регулирующих органов (т.е. их сопротивления s> ' и х> ^') могут ока-
оказаться при этом вне своих рабочих диапазонов. Тогда все такие сопротивле-
сопротивления фиксируются своими предельно возможными (т.е. минимальными)
значениями s*, после чего повторяется весь расчет. В итоге будет найдено
именно то потокораспределение и те параметры РР и РД, которые факти-
фактически возможны в исследуемой цепи с учетом заданного множества РР
иРД.
0
9.4. Схема цепи с двумя регуляторами (расхода и давления)
Рассмотрим основные особенности этой методики на примере г.ц. с дву-
двумя регуляторами, схема которой приведена на рис. 9.4. Пусть РД, располо-
расположенный на ветви 3, должен поддерживать давление в узле 2, равное F2, а
РР на ветви 7 должен поддерживать расход <77- Тогда соответствующая
Данной схеме система уравнений из узловых и контурных уравнений запи-
127

шется следующим образом:
хх - х2 - хп = 0, х2 - хъ х8 = О,
х3-х6=0, -х5 +х6 +х8 =0, (9.12)
-х4 +xs + х7 = 0;
SiX2 +4РР)л:? +s4xl =#,
s2x\ +х3(РД)л +s6Jf6 + *5*1 + sAx\+Six\ =Д (9.13)
(РД)
2 . 2 , 2 , (РД) 2
4 + S5XS + ^б^б + Si Х3 >
+s* +х^ (9.14)
^ 4 — -*6 """^4^4
'S = " 6 "*" ^4 ^
S7 >s7, если хп =q-i,
(РР) , . (915)
s\ ' = s1, при х-, <q1;
4РД) >хз, если Р2 =Р'2,
при ^>f (9Л6)
где s$)PP) и х|рд^ - коэффициенты гидравлических сопротивлений, каж-
каждый из которых представляет собой сумму сопротивления самой ветви,
содержащей РР или РД, и собственного сопротивления регулятора; х* и
5з - минимальные значения этих коэффициентов (при полностью открытых
регуляторах); Р'6 -заданное (фиксированное) давление в узле б.
В этой системе коэффициенты 4РР^ и х|РД^ являются неизвестными и
их значения зависят от того, каким в конечном итоге будет распределение
расходов и давлений по всем элементам схемы. Условия (9.15) и (9.16)
позволяют лишь оценить состояния регуляторов при каждом потоко-
распределении, для нахождения которого, в свою очередь, требуется инфор-
информация о сопротивлениях регуляторов. Таким образом, система (9.12),
(9.13) сама по себе без учета (9.15), (9.16) является неопределенной.
Для преодоления этой трудности выше (в гл. 8) был предложен метод
двойных циклов итераций, когда каждый внутренний цикл производится
при очередном приближении в значениях syp' и s^^, что делает систе-
систему (9.12), (9.13) замкнутой. Затем во внешнем цикле проверяется выпол-
выполнение условий (9.15), (9.16) и в случае необходимости значения пере-
переменных сопротивлений корректируются по определенному правилу. По-
Подобные операции повторяются до тех пор, пока не будут удовлетворены
требованиям регулирования (9.15), (9.16) или регуляторы не окажутся в
своих предельных положениях.
Другая методика, охарактеризованная в начале раздела, в некоторых
случаях фактически не требует проведения внешних циклов итераций.
Достигается это прежде всего фиксированием расходов на всех ветвях, со-
содержащих РР, и приписыванием их (в качестве нагрузок и притоков) соот-
соответствующим узлам, что переводит эти переменные в разряд известных
величин и позволяет вообще исключить (временно) из рассмотрения дан-
128

T a G Р
ица 9.5
Количество
|
ветвей 1 Р1>
i
353
353
270
270
1 16
85
85
79
79
35
Конечное
в рабочем
диапазоне,
шт.
68
85
79
0
35
Новая методика
состояние РР
предель-
предельное, шт.
17
0
0
79
0
Время
счета,
мин
16,1
2,6
1,2
41,3
1,1
Время счета
по старой
методике,
мин
52,2
26,9
14,7
45,7
3,2
ные ветви. Это существенно упрощает систему уравнений и уменьшает ее
размерность.
Затем фиксированием всех тех узловых давлений, которые должны
поддерживаться с помощью заданных РД, можно удалить из схемы также
ветви, содержащие и эти регуляторы. Предварительно, однако, необходимо
выразить потери напора sf д^х,-2 на этих ветвях (где неизвестными яв-
являются и я/рд) и X,-) из соотношений (9.14), описывающих пути, связы-
связывающие эти узлы с узлом, в котором задано давление (в данном случае
это узел 6), и подставить в контурные уравнения (9.13). Данная процеду-
процедура, конечно, вносит нестандартность в формирование матрицы Кирхгофа и
к тому же делает ее несимметрической, что предъявляет повышенные тре-
требования к выбору метода решения системы линеаризованных уравнений
и к составлению программы для ЭВМ.
Система уравнений, соответствующая указанным преобразованиям,
примет вид
-х1+х2=~Ят, -х2 +х3 +д:8 =0,
-л-3 + х6 = 0, +х5 - дг6 - л-8 =0, *4 - *s = Чп;
(9.18)
ssx28 =
Из рассмотрения полученной системы видно, что неизвестное хп, при-
приняв значение, равное ц1ь перешло в правые части для уравнений первого
закона Кирхгофа в узлах 1 и 5. Первый контур обратился в тождество,
а второй и третий выродились в два различных пути от узла 2 с зафиксиро-
зафиксированным давлением Р2 до узла 6. Вдоль первого пути алгебраическая сумма
потерь напора на участках /, 2 равна величине Н+ Р2 - Р'6, а вдоль второго
аналогичная сумма на участках 4, 5, 8 равна Р2 - Р'ь. Линейная комбинация
этих путей образует контур s^x\ + s2x\ + s8xl + ssx\ + s4xl =H, который
можно использовать в (9.18) вместо одного из них.
После решения системы (9.17), (9.18) для полученного потокораспре-
деления проверяется удовлетворение условий ^рд^ >ij- S7??^ > sy ^ если
они (или одно из них) не могут быть выполнены, то полагается s) ' = s*,
S3 ' =$з> затем восстанавливается исходная система (9.12), (9.13) и с ее
помощью производится расчет искомого потокораспределения.
«• Зак. 384 129

Для иллюстрации вычислительной эффективности данного подхода при-
приведем табл. 9.5, в которой отражены результаты расчетов нескольких
цепей, содержащих только РР, по старой и новой методикам. При этом
варьировались величины расходов, которые должны были поддерживать
регуляторы, чем и объясняется различное число регуляторов (см. табл. 9.5),
находящихся в рабочем и предельном состояниях, для цепей, имеющих
одинаковое число ветвей.
Анализ результатов, приведенных в табл. 9.5, показывает, что новая ме-
методика может сократить время счета во много раз по сравнению со време-
временем на двойные циклы итераций. Она тем эффективнее, чем больше регуля-
регуляторов оказывается в своих рабочих диапазонах. Очевидно, что эта методика
может с успехом применяться и для расчета г.ц. с более сложными геремен-
ными параметрами, например, в случае наличия КС, однако это требует
специального рассмотрения.
9.3. АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ ПРОГРАММ
ДЛЯ ГИДРАВЛИЧЕСКИХ РАСЧЕТОВ
В настоящее время расчет, анализ и управление режимами работы ТИС не-
невозможны без применения ЭВМ. Среди решаемых задач можно выделить
три основные группы:
1. Многовариантные расчеты установившихся нормальных и аварийных
режимов работы ТПС с варьированием расчетной схемы и других исходных
данных.
2. Задачи наладки ТПС, связанные с выбором их переменных парамет-
параметров и планируемых режимов работы. Они возникают не только в про-
процессе эксплуатации, но и при проектировании, когда проверяется работо-
работоспособность и надежность функционирования вновь создаваемой или
развиваемой ТПС.
3. Определение рациональных (оптимальных) с точки зрения эксплуа-
эксплуатации режимов работы ТПС в условиях диспетчерского и автоматизирован-
автоматизированного управления.
В любом случае успешное решение данных задач может быть обеспечено
лишь при условии, что в каждом случае: 1) выбирается подходящий (по
размерам и типу ТПС, параметрам используемой ЭВМ и времени счета)
вариант метода расчета; 2) рационально задаются расчетная схема и исход-
исходная информация — они укрупняются или, наоборот, детализируются таким
образом, чтобы наилучшим образом отвечать постановке вопросов, обеспе-
обеспечивать сходимость выбранного метода расчета и удовлетворительную
точность результатов.
При этом следует отдавать отчет в том, что нет и не может быть "абсо-
"абсолютных" методов и программ, которые гарантировали бы получение реше-
решения на ЭВМ при произвольном (формально допустимом) сочетании исход-
исходных данных. Таким образом, ЭВМ не только не снимает проблемы качест-
качественной подготовки информации, но, напротив, требует четкого представле-
представления о смысле решаемой задачи и реальном содержании, корректности и
взаимном соответствии ее исходных данных.
Специалист, овладевший элементами алгоритмического мышления
и методами активного использования ЭВМ, быстро освобождается от плена
130

ручных и стандартных способов работы. Он понимает, что благодаря уме-
умелой подготовке исходной информации можно не только добиться эконо-
экономии в затратах своего и машинного времени, но и "заставить" ЭВМ решать
все более широкий круг задач эксплуатационной и проектной практики,
совершенно неподъемных для рутинных методов расчета и анализа. Наи-
Наилучшие результаты достигаются в тех случаях, когда пользователь оказы-
оказывается способным самостоятельно вносить изменения в программы для
ЭВМ или осмысленно и четко формулировать требования к дальнейшему
совершенствованию математического обеспечения решаемого класса задач.
В развитии работ по применению ЭВМ и автоматизации процессов их
использования в данной области за прошедшие 20 лет можно довольно
четко проследить следующие три этапа:
1. Разработка отдельных программ, реализующих те или иные методы
расчета потокораспределения. Основной целью многочисленных программ,
разработанных в 60-х годах в различных организациях для ЭВМ первого
и второго поколений (типа "Урал" БЭСМ-2 и БЭСМ-4), было численное
решение собственно системы уравнений или экстремальной задачи, описы-
описывающих потокораспределение (см. обзор, данный в гл. 3). Все остальные
операции, сопровождающие проведение расчетов, а именно: построение
и упрощение расчетной схемы, контроль исходных данных, последователь-
последовательная перенумерация ее элементов, выбор дерева и системы контуров на
схеме, определение начального приближения, обработка результатов рас-
расчета и переход к новым вариантам и другие — делались в основном вруч-
вручную.
Любой новый расчет одной и той же цепи, связанный с простейшими
изменениями в схеме (например, удалением и добавлением ветвей и узлов)
и исходных данных, требовал повторения большого числа операций. С рос-
ростом же размеров и усложнением расчетных схем объем подготавливаемой
информации и всей ручной работы возрастали примерно в квадратичной
(и более) зависимости от числа ветвей и узлов. Расчет одного варианта для
схемы, состоящей из 110-150 узлов и 200 ветвей, мог занять (с учетом
подготовки массивов перфокарт, их проверки и анализа результатов счета)
несколько дней работы квалифицированного сотрудника. А многовариант-
многовариантные исследовательские и проектные расчеты одной и той же крупной Tilt
длились неделями и месяцами. Таким образом, все более актуальной ста-
становилась проблема автоматизации процесса использования ЭВМ.
2. Создание автоматизированных систем программ для гидравлических
расчетов (АСИГР) стало следующим крупным шагом, который обеспечил
здесь переход к качественно новому уровню применения ЭВМ. Эти системы
взяли на себя все основные операции, связанные с преобразованием, упоря-
упорядочением и контролем исходных данных, формированием соответствую-
соответствующих математических моделей, организацией вычислительного процесса,
многовариантностью расчетов и выдачей результатов в удобной форме.
Одни из первых вариантов АСИГР были созданы в СЭИ [130, 135, 147].
3. Новым этапом, который осуществляется в настоящее время, являет-
является переход от автоматизации использования ЭВМ к автоматизации управле-
управления режимами работы ТПС. Речь идет о "погружении" пакетов программ
типа АСИГР в реальные процессы диспетчерского управления этого рода
объектов, что предъявляет новые (дополнительные) требования к формам
131

¦4 Контроль исходных данных
Упорядочение нумерации элементов расчетной схемы
Переход к циклической
схеме
Выбор дерева
Декомпозиция сета |
(в случае групповой релаксации j I
Построение хордовой системы контуров и ее матрицы В
Начальное приближение
Суммирование
расходов по дереву
Назначение расходов
на хордах
Линеаризация уравнении
±
J Метод контурных расходов (MKP)U
Поконтурная увязка
перепадов давлений
Метод
окаймления
¦J Метад узловых давлений I МЛ i
г
Метол Зейделя
Поузловая увязка
расходов
Анализ сходимости по х и Р
_L
Учет регуляторов
расходов (РР)
и давления |РД)
Пересчет
„сосредоточенных"
параметров ветвей
Пересчет
действующих
напоров
..темпера ivpiioi о
поля" сети
•Л Взаимный пересчет отдельных решений, анализ сходимоеги
Возврат к исходной нумерации
t
Контроль и выдача результатов
1
t t
Табличная I 1 Графики
Варьирование схемой и исходными данными
J
9.5. Блок-схема автоматизированных систем для гидравлических расчетов (АСИГР)
и способам алгоритмического и информационного обеспечения: ориенти-
ориентировку на реальные первичные документы и данные, с которыми непосред-
непосредственно оперирует пользователь; создание централизованного и автомати-
автоматизированного информационного обслуживания (например, в виде банка
данных); использование быстродействующих, гибких и достаточно надеж-
надежных (с точки зрения сходимости) численных методов; модульный принцип
построения и привязку всей системы к имеющейся технической базе
(включая устройства для связи с управляемым объектом) и т.д. Первые
очереди такого рода систем созданы или создаются практически во всех
отраслях трубопроводного транспорта. Хорошей иллюстрацией данного
уровня работ может служить, например, пакет программ для управления
режимами работы систем тепло- и водоснабжения, описанный в работе
[81].
132

Развернутая характеристика и описание автоматизированных систем
для диспетчерского управления ТПС выходит за рамки данной книги.
Ограничимся лишь рассмотрением программ АСИГР, которые по-прежне-
по-прежнему остаются одним из основных инструменов для научно-исследователь-
научно-исследовательских и практических расчетов по анализу функционирования ТПС при
их проектировании и эксплуатации.
В СЭИ были разработаны различные варианты АСИГР для ЭВМ БЭСМ4,
БЭСМ-6 и ЕС-1033 [130, 135, 147]. Таким образом, в последней версии
АСИГР учтены в основном те способы повышения эффективности ме-
методов расчета потокораспределения, которые были обсуждены в разд. 9.1.
Для АСИГР принят модульный принцип построения в виде совокупности
отдельных автономных программ (блоков, модулей), которые можно раз-
разрабатывать (и улучшать) отдельно или иметь их в различных модифика-
модификациях. Их общая блок-схема представлена на рис. 9.5.
Глав а 10
ГИДРАВЛИЧЕСКИЕ ЦЕПИ
С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
10.1. ИСХОДНЫЕ ПОЛОЖЕНИЯ
Во многих задачах расчета сложных гидравлических систем принципиаль-
принципиально важным является совместный учет неизотермического характера течения
транспортируемой среды, существенной разнотипности элементов и подсис-
подсистем, а также и других физико-технических особенностей их структуры, ре-
режимов и условий работы. Это относится к таким объектам, как: многони-
многониточные системы магистральных нефте-и газопроводов, функционирующих
в экстремальных природных условиях; системы отопления и вентиляции
многоэтажных зданий и промышленных объектов, при изучении которых
обязателен учет гравитационных напоров и температурных градиентов;
газопромысловые системы типа "пласт — скважины — газосборная сеть"
(пример которой представлен на рис. 10.1) и другим. Необходимая пол-
полнота математического описания, равно как и точность получаемых числен-
численных решений, в данных случаях уже не может быть обеспечена моделиро-
моделированием этих систем как г. ц. с переменными параметрами. Здесь требуется
переход к более строгим математическим моделям — г. ц. с распределен-
распределенными параметрами.
Построение и исследование таких моделей необходимы и с точки зрения
развития самой ТГЦ как следующий шаг в совершенствовании научно-ме-
научно-методической и алгоритмической базы в данной области, не говоря уже о пос-
постоянном стремлении ко все более точным ("эталонным") математичес-
математическим описаниям. Без этого невозможны объективная оценка, классифика-
классификация и дифференциация различных методов, а также анализ и обобщение
богатого межотраслевого опыта.
Если обратиться к литературе, то можно увидеть, что попытка систем-
системного подхода к постановке и численному решению задач расчета слож-
сложных гидравлических объектов делались уже сравнительно давно. Так,
133

10.1. Схема газопромысловой системы
1 — участки газосборной сети; 2 — скважины; 3 — участки пласт—забой; 4
условные ветви; МТ — магистральный газопровод; ГСП — газосборный пункт; ПЛ
в 1969 г. Е.М. Минским и Ю.И. Максимовым [148] подобный вопрос
был поставлен применительно к газопромысловым системам: "... опти-
оптимальной следует считать такую организацию разработки, при которой
на скважинах не будут установлены штуцера и скважины будут давать
максимально возможный дебит. В этом случае величина дебитов скважин
будет автоматически регулироваться сопротивлением газосборной сети".
В этой же работе ими дается содержательная постановка задачи гидравли-
гидравлического (но изотермического) расчета такой системы, а в работах [114,
149] предлагаются соответствующие метод и программа для ЭВМ, бази-
базирующиеся на переходе к сосредоточенным характеристикам элементов
и увязке узловых расходов с помощью решения системы уравнений пер-
первого закона Кирхгофа, выраженных через разности квадратов узловых
давлений.
М.Г. Сухаревым и Е.Р. Ставровским в 1971 г. [226] описан дополни-
дополнительный блок к программе расчета потокораспределения [212], который
производит итеративный пересчет средних температур для ветвей рас-
расчетной схемы. При этом приводится пример приближенного неизотерми-
неизотермического расчета Шебелинского газосборного коллектора в сравнении с
обычным гидравлическим расчетом, который показывает важность учета
неизометричности течения газа для определения фактического распреде-
распределения и давлений по всей схеме. Вместе с тем в их работах [226, 227]
не рассматривается проблема построения более общих описаний и методов
расчета неизометрического потокораспределения.
Современный уровень постановки и решения задач газотермодинами-
газотермодинамического расчета сложных систем определяется главным образом весьма
полным описанием собственно течений различных сред [33, 34, 186],
а с другой стороны, рассмотрением разностных схем на графах [38]. Так,
например, О.Ф. Васильев и А.Ф. Воеводин [33] описывают неустановив-
134

шееся движение весомого сжимаемого газа по трубе (с переменным диа-
диаметром) с учетом тепло- и массообмена с внешней средой, а также реаль-
реальных термодинамических свойств газа. При более общих, чем обычно,
предположениях они получают замкнутую систему из пяти уравнений:
потоков массы (неразрывности), импульса и энергии, а также двух за-
замыкающих термодинамических соотношений. Она описывает как медлен-
медленно, так и быстро протекающие процессы, связанные с появлением разры-
разрывов при образовании ударных волн.
Данные работы являются характерными в том отношении, что основ-
основное внимание в них сосредоточено на тех или иных численных методах
решения подсистем уравнений в частных производных, описывающих
отдельные течения на множестве ветвей расчетной схемы. При этом ста-
стационарное неизотермическое течение, а также и установившееся в системе
потокораспределение рассматриваются, как правило, лишь в качестве
частного случая общего термодинамического расчета. Такой подход не-
нередко оказывается довольно абстрактным и недостаточно работоспособ-
работоспособным в методическом и вычислительном отношениях.
Таким образом, с различных точек зрения представляется очевидной
необходимость в построении и изучении г. ц. с распределенными парамет-
параметрами как специального класса математических моделей, которые должны
заполнить пробел, существующий между относительно простыми моделя-
моделями с переменными параметрами (рассмотренными в предыдущих главах)
и весьма общими и универсальными "разностными" подходами. Эти мо-
модели должны содержать: подсистемы уравнений для ветвей, которые с
заданным приближением будут отражать фактическое изменение парамет-
параметров состояния транспортируемой среды, а также и сетевые уравнения,
отвечающие за совпадение граничных значений этих параметров на кон-
концах ветвей для цепи в целом в соответствии с ее схемой и законами сох-
сохранения. С математической точки зрения это приводит в общем случае
к специальному классу смешанных систем уравнений, включающих замы-
замыкающие уравнения в дифференциальной или интегральной формах, а также
и в частных производных, если это необходимо.
Данные модели сетевого типа можно строить и обосновывать с помощью
различных подходов: с позиций термодинамики и экстремальных прин-
принципов механики, укрупнением разностных схем на графах или путем
развития теории цепей с сосредоточенными и переменными параметрами.
Все они при сопоставимых требованиях должны привести к совпадающим
результатам. Во всяком случае, каждый из этих подходов представляется
интересным предметом для исследований, а их совместное рассмотрение
могло бы, видимо, обогатить все привлекаемые здесь дисциплины.
Данная глава посвящена г. ц. с распределенными параметрами приме-
применительно к неизотермическим, но стационарным процессам потокорас-
пределения. При этом используется материал предыдущих публикаций
СЭИпо данным вопросам [128,131,135,246].
135

10.2. СИСТЕМЫ УРАВНЕНИЙ ГИДРАВЛИЧЕСКОЙ ЦЕПИ
С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Рассматривается произвольная гидравлическая система с установившим-
установившимся неизотермическим течением транспортируемой среды как единая г.ц.,
состоящая из т узлов и п ветвей. Нашей целью является построение такой
замкнутой системы уравнений, решение которой (численными методами
на ЭВМ) даст совокупность кривых, описывающих распределение величин
расхода среды, давлений и температур по всем ветвям и узлам этой г.ц.
В качестве основных переменных возьмем вектор х установившихся
на ветвях расходов среды и две вектор-функции:
p(x,t,t) = (Pi(xutuh) Р„(х„, tn, ln)f ,
t(x,p, 0 = (ti(Xi,Pi, h) tn(xn, р„, ln)f,
составленные из кривых изменения давления и температуры по каждой
из ветвей, где 0 </,- <L,- (/ = 1,. . ., п).
По существу здесь нет проблемы выбора других переменных, так как
на практике замеряются именно расходы, давления и температуры. При
этом давления и методически, и в вычислительном плане будут (для рас-
рассматриваемых гидравлических систем) иметь относительный приоритет
перед температурами, поскольку именно они, как правило, в большей сте-
степени определяют режим работы системы. И переход от одного потоко-
распределения к другому проявляется через изменение Pi(Xj, f,-, /j) за
меньшие промежутки времени, чем через г, (я,, р,-, /,•) из-за высоких тепло-
инерционных свойств тепловой изоляции, массива грунта, в котором
проложен трубопровод и т.п.
Обе вектор-функции A0.1) кратко обозначим через р{1), f (/), 0 </ <
<L, тогда р@), г@) и p(L), t (L) - векторы граничных значений давле-
давлений и температур соответственно в начальных и конечных узлах ветвей.
Кроме того, как и в случае г.ц. с переменными параметрами (гл. 8), по-
потребуются вектор-функции сA) из кривых с,-(/,) распределения изобар-
изобарной удельной теплоемкости по ветвям и их граничные значения с@), c(L).
Изменение параметров состояния транспортируемой среды (при уста-
установившемся ее течении) вдоль одной ветви i независимо от физико-техни-
физико-технических особенностей соответствующего элемента системы может быть —
на некотором уровне абстракции - описано следующей парой интеграль-
интегральных уравнений:
Pi(Lj) = Pj(O) J fi(Xj, Pi(lj), tj(lj), lj)dlj, (Ю.2)
о
где в случае активной ветви в подынтегральной функции A0.2) может
быть учтена характеристика действующего на ветви источника напора
(насосной или компрессорной станции), а в A0.3) — внешний (сосредо-
(сосредоточенный или распределенный) отвод или подвод тепла (чиже будут при-
приведены примеры этих уравнений для ветвей различного типа).
Будем по-прежнему исходить также из того, что все заданные притоки
136

имеют известные температуры t) и теплоемкости с,' (эти величины в
отличие от ?/(/;•) и су(/,) будем обозначать с использованием индекса
соответствующего узла и без указания аргумента в скобках).
Если использовать, как обычно, вектор Р = (Л, • • ¦, Рт - \, РтУ узло-
узловых давлений, то граничные значения р@) и p(L) для ветвей будут связа-
связаны с ними (а через них и друг с другом) следующими уравнениями:
р@) = AJP, p(L) = -А1Р, A0.4)
где А 1 и Аг — матрицы, фиксирующие отдельно начальные и конечные
узлы ветвей. Эти уравнения с помощью промежуточного вектора Р описы-
сывают совпадение граничных значений давления в общих узлах и в целом
эквивалентны уравнениям второго закона Кирхгофа.
Для описания температурного поля цепи в принятой математической
модели, как и ранее (в гл. 8), требуется совпадение друг с другом только
начальных температур ?,@) потоков, выходящих из одного и того же
узла:
/@) =А\т, A0.5)
где Т = (Гь . . . , Tm)r - вектор узловых температур для смешанных в
узлах потоков среды. Величины же расходов дг,-, а также значения /,•(?,)
должны удовлетворять балансовым уравнениям расходов среды и тепла
в узлах цепи:
Ах = Q A0.6)
/f,C@)r@)+J2C(Z.)r(Z,) =0. . A0.7)
Теоретически логично включить в систему уравнений также и условия
t (L) = -AlT. Тогда была бы полная симметрия математической модели
относительно векторов Р и Г, что соответствовало бы положениям термо-
термодинамики. Однако вряд ли это целесообразно, учитывая два момента:
1) весьма абстрактный характер узловых точек в расчетной схеме, ко-
которые не отражают ни физически, не геометрически реальную картину
смешения и разделения потоков жидкости или газа, имеющую место,
например, в местах соединений нескольких труб большого диаметра;
2) необходимость "итерационной гибкости" модели при ее реализации
методами последовательных приближений на ЭВМ, для чего достаточно
обеспечивать сходимость вычислительного процесса, помимо расходов
и давлений, лишь относительно температур уже смешанных в узлах по-
потоков.
Таким образом, задача об установившемся неизометрическом потоко-
распределении в произвольной цепи с распределенными параметрами
может быть сформулирована как задача решения замкнутой системы
уравнений A0.2) — A0.7) порядка 5л + 2т - 1 относительно*, p@),p(L),
t @), t (L), Тит — 1 значений Pj. Данная система уравнений может быть
охарактеризована с двух точек зрения: 1) как система из пар интеграль-
интегральных уравнений A0.2), A0.3), для которых параметры jr,- и граничные
условия связаны подсистемами линейных и нелинейных уравнений A0.4) —
A0.7); 2) как совокупность подсистем A0.6), A0.7) относительно век-
векторов х, t@), t(L), покоординатные связи между которыми описывают-
описываются парами уравнений A0.2), A0.3) с граничными условиями A0.4),

Возможна эквивалентная модификация этой системы посредством
замены в ней вектора Р на вектор у перепадов давлений (или их квадра-
квадратов) с вводом в рассмотрение той или иной системы из с главных кон-
контуров. Для этого следует включить в систему уравнений связь между
векторами у = р@) - p(L), что увеличит число неизвестных на п; под-
подставить в A0.4) выражение D.38) Р черезуя, что, в свою очередь, умень-
уменьшит это число на m - 1, и добавить подсистему контурных уравнений
By = 0 (см. также (8.6)). Таким образом, порядок системы уравнений
увеличивается на с, поскольку размерность вектора у именно на с больше,
чем у Р. Выбор математической формулировки задачи может определять-
определяться, например, методом ее решения.
Пример составления системы уравнений. В качестве иллюстрации рас-
рассмотрим пример составления описанной выше системы уравнений для
условной цепи, схема которой приведена на рис. 10.2. Эта цепь имеет пять
узлов, семь ветвей и три контура. Стрелки на ветвях показывают направле-
направления потоков для начального приближения, а стрелки над номерами кон-
контуров - выбранные направления их обхода.
Предположим, что имеет* место установивший режим течения среды,
обусловленный постоянным ее притоком в узлах 2—4 в количествах
Qi - Q<\ (I 2s I = иг + Ог + Q*) с температурами Г2 - t'4, удельными
теплоемкостями с2 - с\ и фиксированным давлением Р$ в узле 5.
Структура цепи и выбранная ориентация ее ветвей опишется матри-
матрицей соединений
А =
Начальные узлы ветвей фиксируются матрицей
//;• 12 3 4 5 6 7
1
/А
1
2
3
4
5
1
1
-1
2
1
-1
3
1
_
4
-1
1
1
5
-1
1
6
-1
1
7
Г
А, =
1
1
1 1
1
а конечные — матрицей
/А
1
2
А2= 3
4
5
1
1
2
-1
3
-1
4
-1
5
-1
6
-1
7
-1 .
138

10.2. Пример расчетной схемы для описания неизотермического потокораспределения
1—5 — узлы; 1 - хорды; 2 - ветви дерева; 3 - источники расхода; т - 5, п = 7,
с = 3
Если за линейно зависимый узел взять узел 5, то матрицы А, А\ кА2
получаются из данных вычеркиванием в каждой из них последней строки.
Граничные условия A0.4) и A0.5) примут вид
1
II
-1
-1
t@) =
pt
Рг
Ръ
=
Ръ
Р*
Рг
Ръ
Рг
Л
_1
Pi
Рг
Ръ
Р4
Р-
=
' Р4~
P's
Ps
Рг
Pi
Pi
1
1
.1
1
1
1
1
-
1
>i"
7-2
т3
тл
7*5
т3
7-4
т2
т3
7-2
139

Материальные балансы в узлах
Ах ' =
11
1
-1
1
-l -1 Г
1
1
х
'о
Ql
<2з
<?4
Тепловые балансы в узлах, после соответствующих выкладок
-c5(L5)x5t5(L5) ¦ c6(L6)x6t6(L6) +c7@)x7f7@) =0.
+Cs(O)jcsfs(O) = c2Q2t'2,
-c1(Ll)xltl(Ll)+c2@)x2t2@)+c6@)x6t6@) =
-c2(L2)x2t2(L2) - c3(L3)x3t3(L3) -
+ Q3+ Qa)Ts.
Здесь третье уравнение фактически сведется к равенствам:
ci@) = с4@) = с'з, r,@) = r4@) = t'3.
Кроме того, необходимы еще 14 замыкающих уравнений A0.2) и
A0.3) того или иного вида в зависимости от типа ветвей. Так, для ветвей
"газоносный пласт-забой скважины" можно воспользоваться зависимостя-
зависимостями (в наших обозначениях)
где
=t,(O)-<*i(Pi(O)~Pi(L,y),
и s" — коэффициенты, зависящие от проницаемости пласта и кон-
конструкции забоя скважины. Для скважин:
() + 1/
= р,@) -
= tt@) - f
0
Pi
~ ti))dlh
где а\, a", b\, b" - величины, включающие в себя удельную теплоемкость,
коэффициенты теплоотдачи от газа в породу и сжимаемости газа; гпл -
температура пласта; Г,- - геометрический градиент.
Что касается ветвей, соответствующих трубопроводным участкам, то
здесь можно воспользоваться формулами, приведенными в гл. 8, или
более сложными уравнениями (в дифференциальной или интегральной
формах), если это целесообразно по постанове задачи.
Таким образом, будем иметь 44 уравнения с 44 неизвестными: х; р@) v
p(L); t(fl),t(L);P1,Pl,P3,PA; Ти Т2, ТЪ,Т^, Т5.
В случае оперирования с контурами выбранной на схеме главной системе
контуров отвечает матрица
10 0-1-1 1 0
В = | 0 1 0. 0 0-1-1
0 0 10-1 0-1
140

Тогда у = р@) - p(L), By = 0. Кроме того, для выражения Р черезуа
= (у*, Vs. Уь. УпУ потребуются матрица D.33)
/// 4 5 6 7
1
2
Д
4
и вектор
i.
0
0
1
0
0
1
1
0
5
0
0
0
1
1
1
1
1
"т. д
о
о
о
-1
В результате подсистема уравнений
Р(О) = А\
для данного примера примет вид
Pi@) = у4 +ys +Уп +P's,
Рг@) = У 6 +Уу +P's,
РзФ) = У$ +У7 +P's,
р4@) = y*+ys +У7
Ps@) = ysyi +P's,
Рб@) =Уб+У
р7@) = у-, +P's.
10.3. О СМЕШАННЫХ СИСТЕМАХ УРАВНЕНИЙ СЕТЕВОГО ТИПА
И ОБЩЕЙ СХЕМЕ ИХ ДЕКОМПОЗИЦИИ
Построенные выше системы уравнений, описывающие установившееся
неизотермическое потокораспределение в произвольной г.ц. с распределен-
распределенными параметрами, могут быть обобщены в виде специального класса
смешанных систем уравнений, содержащих линейные A0.4)-A0.6),
билинейные A0.7) и интегральные (или дифференциальные) уравнения
A0.2), A0.3). Такое несколько более абстрактное представление позволит
лучше подчеркнуть их основные физико-математические особенности и
обоснованнее применять те или иные численные методы.
Для описания распределения давлений возьмем за основу контурную
систему уравнений. Тогда сетевые законы Кирхгофа могут быть записа-
записаны следующим образом:
"(*) = B, A0.8)
u(p@), p(L)) = 0, A0.9)
где матричные операторы им v представлены как вектор-функции размер-
размерностей т — 1 и с. Для того чтобы зафиксировать в соответствии сориента-
141

цией ветвей цепи взаимосвязь последовательностей значений р,-@) ир,-(?,-)
с заданным узловым давлением Pln, необходимо вместо Р взять его вы-
выражение (8.6) через уа и Р'т, где, в свою очередь, использовать равенства
У'1 ~ Р/@) - Pi(Lj), i = 1, . . . , п. После подстановки данных зависимо-
зависимостей в A0.4) для р@) можно в конце концов получить векторное урав-
уравнение, связывающее граничные значения р @) и р (L):
A'p@)+A"p{L) = b, A0.10)
где А к А — некоторые квадратные матрицы порядка п, а Ь — вектор
правых частей, компоненты которого определяются значением Р'т.
Векторное уравнение A0.7) балансов узловых расходов тепла пред-
представим в виде
w(x, f@), t(L)) = в. A0.11)
Что касается совпадения начальных температур t,-@) потоков среды,
выходящих из общих узлов цепи, то эти условия A0.5) могут быть сведе-
сведены приравниванием и заменой каждой из компонент 7} вектора Т (у =
= 1, ...,«?) начальной температурой f,-@) для ветви /, выходящей из
узла /, к с - 1 равенствам соответствующих значений ?,@) друг другу:
B't(O) = 0, A0.12)
где В' - некоторая (с - 1) X и-матрица из коэффициентов 0,1 или -1.
Таким образом, общая система относительно х, р@), p(L), t @), t (I)
будет состоять из 5и уравнений: m - 1 уравнений в A0.8), с - в A0.9),
и - в A0.10), m - в A0.11), (с - 1) - в A0.10) и 2и замыкающих соот-
соотношений A0.2) и A0.3). Будем предполагать, что все функции в этих
уравнениях вместе со своими частными производными первого и второго
порядков являются непрерывными на некоторых выпуклых областях
допустимых значений своих аргументов и что, кроме того, выполнены
и другие условия, необходимые для сходимости метода Ньютона [57].
Предлагаемый ниже подход можно классифицировать как метод по-
последовательных приближений, сочетающий декомпозицию (расщепление)
общей системы на две подсистемы и итерационный процесс Ньютона для
каждой из этих подсистем со взаимной увязкой их решений.
С физической точки зрения речь идет о разбиении общей задачи о неизо-
неизотермическом потокораспределении на последовательность из трех под-
подзадач: 1) попарного численного решения замыкающих интегральных урав-
уравнений A0.2) и A0.3) для каждой из ветвей цепи; 2) изотермического
расчета для увязки расходов и давлений (при фиксированных температу-
температурах) по всем элементам цепи; 3) пересчета "температурного поля" цепи.
Путем решения данных подзадач в ходе итерационного процесса осу-
осуществляется последовательный пересчет текущих значений векторов
х, р@), p(L), t@), t(L), соответствующих все более точно опреде-
определяемым вектор-функциям рA) и t(l). общая схема такого процесса
сводится к выполнению следующих операций:
1. Решается проблема начального приближения для х, р @), t @) с по-
помощью решения специальных задач или частичного задания и доопределе-
доопределения этих значений.
2. Численным образом производится попарное интегрирование уравне-
уравнений A0.2) и A0.3) при известных начальных условиях р/@) и ?,@) и
142

значениях xt, играющих роль параметров. В результате определяются
(уточняются при последующих итерациях) кривые рA) и t (/) и их гранич-
граничные значения р^Ь/) и tj(L;), i = I,...,n.
3. ПутеН фиксирования t (/) вместе с г@) и t (?) из общей системы
выделяется подсистема A0.8)-A0.10) и A0.2), т.е. ее "изотермическая"
часть, котбрая решается методом Ньютона (см. об этом в следующем
разд. 10-.4).Ее решение обозначим через х, р @), р (L).
4. Далее фиксируется это частичное решение и тем самым вьщеляется
подсистема' A0.11)-A0.12), которая сводится к линейной системе урав-
уравнений с помощью линеаризации (см. разд. 10.4) замыкающих соотноше-
соотношений A0.3): это позволяет заменить t (L) соответствующим линейным
выражением через t @).
В результате получается _и затем решается замкнутая система линей-
линейных уравнений относительно Г,@).
5. Анализируется сходимость всего процесса, например, покоординат-
покоординатной проверкой на совпадение (с задаваемой точностью) искомых векторов
или части из них. В случае необходимости осуществляется переход к п. 2
и т.д.
Сходимость данного вычислительного процесса определяется прежде
всего условиями сходимости метода Ньютона, которые должны выполнять-
выполняться для соответствующих подсистем уравнений. В большой степени она
будет зависеть также от свойств подынтегральных функций в A0.2) и
A0.3) и, конечно, от начального приближения.
Применительно к задачам неизотермического расчета реальных гидравли-
гидравлических систем можно считать, что в случаях корректной их постановки
обязательно существуют решения, отвечающие физической сущности
установившихся процессов потокораспределения. Знание этой стороны
дела помогает успешно решать проблему хорошего начального приближе-
приближения. А специальными приемами, максимально учитывающими топологи-
топологическую структуру расчетной г.ц. и "блочность" решаемой системы урав-
уравнений, может быть обеспечена ускоренная сходимость и практическая
эффективность описанного процесса последовательных приближений.
10.4. ЧАСТНЫЕ СЛУЧАИ ОБЩЕЙ СИСТЕМЫ УРАВНЕНИЙ
И ЛИНЕАРИЗАЦИЯ ЗАМЫКАЮЩИХ СООТНОШЕНИЙ
Выделим в рассмотренной выше системе часть уравнений, а именно
A0.8)-A0.10) и A0.2), относящиеся только к х, р@) и p{L), пред-
предполагая, что потокораспределение в цепи не зависит от температур. По-
Получим замкнутую систему уравнений порядка Зи, имеющую и самостоя-
самостоятельное значение, которую для удобства изложения выпишем отдельно:
«(*) = 2; v(p@), p(L)) = 0; A'p@)+A"p(L) = b, A0.13)
Ч
Pi{Lt) = p,.@) + / nixbpMt), li)dlt A0.14)
0 (/ = 1 .....и).
Общий шаг итерационного процесса Ньютона для решения такой систе-
системы будет состоять из: 1) решения каким-либо из численных методов
Уравнений A0.14) при некоторых начальных условиях р,-@) и параметрах
xi\ 2) построения и решения системы линейных алгебраических уравне-
143

ний относительно приращений (Дх,, . . . , Дх„)т = Д* линеаризацией как
A0.13), так и A0.14) для получения приближенного линейного соотно-
соотношения, связывающего Ap(L) схи Ар@) при переходе от х к х + Дл\
Рассмотрим подробнее операции дифференцирования и линеаризации,
с которыми связана реализация второго этапа. Предположим, что для
выбранных х, р@) получены решения (pi(/i), . . . , р„(,1„)У = рA).
0 </ <L, удовлетворяющие интегральным уравнениям A0.14)!. Последую-
Последующая подстановка этих л:, р@) и результирующего вектора р(/,|) в A0.13)
даст следующие невязки:
и(х) = Q+AQ,
v(p@), p(L)) = АН, A0.15)
А'р@) + A"p(L) = Ъ + АЬ.
Разлагая левые части этих уравнений в ряд и ограничиваясь только
линейными членами, придем к следующей системе:
и'(х)Ах = -AQ,
v'(p@))Ap@) + v\p(L))Ap(L) = АН, A0.16)
А'Ар@) + A"Ap{L) = -Ab,
где
(Эи,(хI
и(л:) = ¦ , / = 1, . .. ,т - 1; / = 1, . . . ,п;
{ b J
V тъ |3w,(p@),p(L))| .
w(p@)) = —— , г = I с; i = 1 л;
1 bpi(O) J
V »^ I 3»r(p@),p(L) | .
u (p(L)) = i -— , г = 1, . . ., с; i = 1,. .., п.
I Ь^Ц) )
Запишем далее общее решение каждого из интегральных уравнений
A0.14) в следующем неявном виде:
где 0 < /,- < /,,-, х,- — параметр.
Тогда линеаризация A0.17) даст
* Др,<0) +
р,( ) +
= Др,@) +
Если ввести
D(x) = diag
144
L'( dipt
о \ dXj
I ' ' Э^/
\ о dXj
Axi(otj + fi).
диагональную
(a,- + 7/), /' =
Эр,-
1 А- С -
0
матрицу
= 1,...,
Эр,-
Эр,- о
п.
bxt
A0.18)

то связь между приращениями граничных значений кривых /?/(/,•) и пара-
параметров Xj примет вид
Ap(L) «= Ар@) + D(x)Ax. A0.19)
Посте подстановки A0.19) в A0.16) получим систему линейных ал-
алгебраических уравнений относительно Ах и Ар@):
и'(х)Лх = -AQ.
(А' + A")Ap@)+A"D{x)Ax = - Ab.
Решив эту систему порядка 2и, определим Ах и Др@) и с их помощью
перейдем к следующему приближению в значениях: параметров х = х + Ах,
начальных условий р @) = р@) + Ар@) - для очередного численного
решения уравнений A0.14) и т.д., пока процесс не сойдется.
Рассмотрим один частный случай системы A0.13), A0.14), когда все
подсистемы в A0.13) линейные, а в A0.14) участвуют не сами граничные
значения р@), p(L), а их покоординатные разности >> = р@) - p(L), т.е.
речь идет о системе
Ах = Q, By = 0, у = р@)- p(L), A0.21)
у,- = / <л(лг,-, рМ), lj)dli, i= I,..., n. A0.22)
о
В этом случае A0.19) сводится к приближенному равенству
Ay =» D(x)Ax, A0.23)
а вместо A0.20) имеем
А Ах = -Д2, BD(x)Ax = АН. A0.24)
Таким образом, процесс Ньютона сведется здесь к тому, что на каждом
шаге: 1) решаются уравнения A0.22) при некоторых*, р@), являющихся
начальным приближением или полученных в результате предыдущего
шага; 2) вычисляются элементы а,- + у,- диагональной матрицы D(x)
в соответствии с A0.18); 3) формируется и решается система линейных
уравнений A0.24) относительно Д*; 4) определяются Ay = -D(x)Ax;
р @) = р@) + Ау; х = х + Ах; 5) производится анализ сходимости про-
процесса проверкой условий | Ajc | < 5? | Ау | < е?, где 8, е - заданные век-
векторы допустимых погрешностей в значениях Axj и Д^,- (;' = 1, . . . , п).
В случае необходимости все пункты повторяются и т.д.
В качестве примера рассмотрим систему с изотермическим течением
газа, для которой с учетом некоторых допущений A0.14) могут быть
представлены следующим образом:
PiiLi) = Р,@) + ! si{.Pl{l,))xfdli, A0.25)
о '
где s,-(/?,-) - заданная функция, /3 - показатель степени. Тогда (см. A0.18))
а,- = S ~ dlt = pxf-1 f s,(j>,(l,№; A0.26)
о dXj ' о
'0. Зак. 384 145

7/ = / s-(Pi)xf( f &xf-\{p,{l,))dlt =
0 ° A0.27)
Формулы A0.26) и A0.27) с учетом непосредственного интегрирова-
интегрирования заданных функций s,(p,-(/,)) на отрезках [0, Lt] дают возможность
подсчитывать элементы матрицы D(x) на каждой итерации.
В частности, при s,(p,-) = const (что имеет место для г.ц. с сосредото-
сосредоточенными параметрами) все yt = 0 (г = 1, ...,«) и система A0.24) по
существу совпадает с той, которая отвечает методу контурных расходов,
описанному в гл. 5.
Глава 11
ОБРАТНЫЕ ЗАДАЧИ ПОТОКОРАСПРЕДЕЛЕНИЯ
И ИДЕНТИФИКАЦИЯ ТРУБОПРОВОДНЫХ СИСТЕМ
11.1. О ПРОБЛЕМЕ ИДЕНТИФИКАЦИИ ТПС
Известно, что задачи, связанные с анализом реальных физико-технических
систем, а тем более с управлением их эксплуатацией и развитием, реша-
решаются в условиях той или иной неопределенности. Факторы неопределен-
неопределенности существенно влияют на процесс принятия решений, а также на сами
решения и их фактическое последействие.
Незнание истинных параметров и топологии трубопроводных систем
(ТПС), явно недостаточная оснащенность их измерительными приборами
и датчиками, большая погрешность и неоднородность тех данных, которые
удается получить, приближенность математического моделирования, усу-
усугубляемая вычислительной погрешностью, и другие моменты — вот те
факторы, из которых складывается неопределенность при управлении
их эксплуатацией. Многие из перечисленных вопросов входят в общую
проблему идентификации реальных объектов.
Даже простой переход от изучения какого-либо класса объектов на
уровне его общего математического описания и формальных методов
решения, когда мы абстрагируемся от проблемы исходных данных и не-
неопределенности в их составе и численных значениях, к анализу конкрет-
конкретного объекта уже требует решения специальных вопросов, связанных с
адекватностью его математической модели, ее оптимальной точностью
и др.
С математической точки зрения рассмотрение вопросов такого рода
приводит к необходимости решения тех или иных обратных задач, когда
искомые и задаваемые величины в исходных математических моделях
полностью или частично меняются ролями и изучается возможность их
численного определения и взаимного влияния при варьировании. Извест-
Известно, что обратные задачи часто оказываются плохо обусловленными и не-
неустойчивыми с точки зрения получаемых решений, т.е. некорректными.
146

Математические методы могут здесь иногда улучшить решение и сделать
его практически приемлемым, но в общем случае этого нельзя гарантиро-
гарантировать. Данные вопросы усложняются еще в большей степени, когда комп-
комплекс "прямых" и "обратных" математических моделей должен фигури-
фигурировать в контуре автоматизированного управления. Здесь уже не обой-
обойтись без разработки специальных алгоритмов, обеспечивающих машинное
слежение за поведением объекта.
Несколько обобщая, идентификацию можно определить как процесс
приближенного отображения (отождествления) функционирующей си-
системы в виде соответствующих математических (или физических) моделей,
способных замещать реальный объект в процессе его анализа и принятия
решений. Идентификация, таким образом, представляет обязательный
этап управления и неизбежно проходит в условиях неопределенности,
охарактеризованной выше. Из этого вытекают и принципиальные требо-
требования к методам идентификации, заключающиеся в том, чтобы напол-
наполнять реальным содержанием математические модели, обеспечивая их адап-
адаптацию как к обратным связям с объектом, так и применительно к целям
и задачам управления.
ТПС — это сложные динамические системы, характеристики которых во
время их работы постоянно меняются по заранее неизвестному закону.
В отличие от электроэнергетических систем (ЭЭС), чьи эксплуатационные
(фактические) параметры гораздо в меньшей степени отличаются от про-
проектных, а нагрузки, напряжения и другие характеристики измеряются
довольно точно, для трубопроводных сетей коэффициенты s,- гидравли-
гидравлического сопротивления, а также и расходы xt на ветвях и у потребителей
известны в основном очень приближенно.
Значения s(, например, в процессе строительства и эксплуатации ТПС
претерпевают значительные изменения (из-за коррозии труб, накипеобра-
зования, появления новых местных сопротивлений, завалов, засоров и пр.),
существенно отклоняются от проектных данных и фактически являются
неизвестными величинами. - Следствие этого - неправильное их задание
в замыкающих соотношениях для ветвей, что вместе с неточным знанием
нагрузок Qj приводит к большим, часто недопустимым погрешностям
в рассчитываемом потокораспределении.
Конечно, трубопроводные и другие гидравлические системы в той или
иной мере оснащены аппаратурой и приборами для измерения давлений,
температур и расходов. Естественно поэтому желание использовать ре-
результаты измерения этих величин для подстановки их в замыкающие
уравнения с целью определения неизвестных коэффициентов гидравли-
гидравлического сопротивления и теплоотдачи отдельных элементов системы.
Собственно, подобные замеры и являются основой существующих "участ-
"участковых" способов гидравлических испытаний, которые требуют специаль-
специальных условий (см. об этом ниже). Однако основная трудность при этом
заключается в необходимости замерять расходы, поскольку массовое
использование тарированных расходомеров является делом весьма отда-
отдаленного будущего. Для большинства же существующих ТПС это уже прак-
практически исключено, к тому же расходомеры ненадежны в постоянной
эксплуатации, требуют периодической тарировки и большинство из них-
увеличивает гидравлические сопротивления участков.
147

Итак, одно из ограничительных исходных положений сводится к тому,
что в общем случае невозможны натурные испытания для замеров всех
величин, составляющих полное решение задачи потокораспределения в
гидравлической системе. Практически осуществимыми являются только:
манометрическая съемка во всех узлах цепи при изотермическом потоко-
распределении (или манометрическая и температурная съемки в неизо-
неизотермическом случае), дополненная одновременными замерами отдель-
отдельных расходов в источниках и у крупных потребителей.
Один из подходов к данной проблеме может заключаться в восста-
восстановлении полного решения математической модели и прежде всего расхо-
расходов на всех ветвях через множество ее частичных решений, замеренных
на реальном объекте. При этом идентификация ТПС должна осуществлять-
осуществляться в полном виде — на уровне ее г.ц. Отсюда и возникает исходная идея
"математического расходомера" [126, 127, 129]1: использовать искусст-
искусственное (или естественное) варьирование режимов работы системы, сов-
совмещенное с многократной манометрической съемкой, для получения
переопределенной системы алгебраических уравнений относительно рас-
расходов в любом из режимов, взятом за базисный. Построив и решив с
помощью ЭВМ эту систему, определим*, а затем и s.
В результате приходим к целому ряду задач. Круг вопросов оказывается
здесь и в математическом, и в прикладном отношениях гораздо шире
этой первоначальной постановки и дает принципиальную возможность
для решения ряда важных задач в области трубопроводного транспорта.
Насколько известно, в литературе до последнего времени не ставилась
задача системного подхода к идентификации гидравлических систем раз-
различного типа на базе их общего математического описания.
Существенно более высокий уровень системных исследований и разра-
разработок по вопросам оценивания состояния и идентификации имеет место
в области ЭЭС. При этом следует выделить выполненные в СЭИ работы
А.З. Гамма и его сотрудников [46], которые и в теоретическом, и в ал-
алгоритмическом планах опережают аналогичные зарубежные публикации.
Эти работы непосредственно неприменимы в ТПС, но с методической
точки зрения представляют несомненный интерес.
11.2. "МАТЕМАТИЧЕСКИЙ РАСХОДОМЕР" ДЛЯ ЦЕПЕЙ
С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
Существует ряд способов определения расходов х,- на отдельных участках
тепловых, водопроводных и других сетей с помощью расходомеров, а
также путем измерения потери ht давления на участке, если известно
значение коэффициента его гидравлического сопротивления st. Приме-
Применение первого способа требует установки расходомеров не только у по-
потребителей, но и на участках сети и их периодической тарировки. Вы-
Вычисление же расходов по данным о потерях давления на участках неред-
нередко приводит к недопустимо большим погрешностям из-за незнания фак-
фактических значений х,-.
1 См. также А.с. № 283746 (СССР). Способ определения расходов и гидравли-
гидравлических сопротивлений/А.П. Мсренков, К.С. Светлов, В.Я. Хасилев. - Опубл. в БИ.
1970, №31, с. 154-155.
148

В этом разделе речь пойдет о методе "математического расходомера"
цля определения установившихся расходов жидкости, газа или гидро-
гидросмеси, а также коэффициентов гидравлического сопротивления на мно-
множестве участков и у потребителей многоконтурной ТПС или другой слож-
сложной гидравлической системы без массового применения расходомеров.
Кроме того, на основе этого метода можно в рамках автоматизированной
обработки данных измерений на ЭВМ расчетным путем устанавливать
факты аварийных ситуаций и локализовывать места аварий.
Целью данного метода является одновременное определение неизвест-
неизвестных расходов Xj и коэффициентов х,- по данным многократной мано-
манометрической съемки в узлах сети и по показателям расходомеров, фик-
фиксирующих только отдельные расходы в системе. Выбор узловых давле-
давлений Р/ (или, что аналогично, перепадов yt давлений) в качестве основ-
основного источника информации обусловливается, во-первых, тем, что это
именно те параметры, которые в большинстве случаев контролируются
при эксплуатации ТПС, и, во-вторых, они относительно легко (по срав-
сравнению с расходами) могут быть измерены. Что касается числа незамеряе-
мых узловых расходов, то оно определяется условием: каждый участок
ТПС должен быть инцидентным хотя бы одному узлу с измеряемым рас-
расходом2 (участок, инцидентный узлу с нулевым расходом, удовлетворяет
этому условию).
Суть данного подхода заключается в использовании не только замы-
замыкающих соотношений, но и сетевых законов Кирхгофа, так что для каж-
каждой расчетной схемы ТПС существует некоторое "пороговое" число ре-
режимов, которому соответствует переход от недоопределенной к пере-
переопределенной системе узловых уравнений. В самом исходном виде эта
идея на уровне моделирования ТПС цепью с сосредоточенными парамет-
параметрами реализуется следующим образом.
В отличие от обычных (прямых) задач потокораспределения, когда
величины х,-, составляющие вектор х, наряду с А, Н и Q (ниже будет пока-
показано, что замер всех узловых расходов не обязателен) считаются задан-
заданными, а х и у -искомыми,здесь требуется по серии из и частичных реше-
решений у, у(и^ (и=1,...,о-1) задачи потокораспределения определить
вектор х, относящийся к одному из режимов, взятому за базисный (его
параметры будут обозначаться J5e3 верхнего индекса), а следовательно, их.
Каждый вектор у = Ат. Р, соответствующий замеренным значениям
узловых давлений (Р1?..., Рт)г = Р, обращает уравнения второго закона
Кирхгофа в тождества, поэтому исходная система уравнений сокраща-
сокращается до
Ах = Q, у+Н = f(x) = SXx =h A1.1)
и становится недоопределенной относительно х и х.
С каждой новой замеренной на участке величиной у^ связан неиз-
неизвестный расход х {"^, и система A1.1), таким образом, все время остается
недоопределенной для любого из режимов. Однако замыкающие соот-
соотношения позволяют по известнымyjt у^ (/ = 1,... ,п; и= 1,..., v— 1)
Доказательство необходимости указанного условия приведено в статье Б.И. Си-
порштейна "Об одном методе расчета сложных газопроводных систем".- Вестн. МГУ.
Сер. 1. Математика, механика. 1976. № 3, с. 76-83.
149

получить коэффициенты г**"*, связывающие величины любых двух неиз-
неизвестных расходов х *" * и xt '.
Действительно, наряду с A1.1) имеем для других режимов
Здесь величины st, как и х", являются неизвестными. Однако в отли-
отличие от ху', которые меняются от режима к режиму, s,- естественно счи-
считать постоянными характеристиками ветвей (по крайней мере во время
натурных испытаний), поэтому их можно исключить и получить для каждой
ветви v — 1 соотношений
Ли)
О, A1.3)
R(u)
ТО
х(и)
_
г 1и> 0
0 '•г'")
и
= R{u)x(u=l,.
где Я,-, #(") также должны быть замерены на всех активных ветвях от-
отдельно оту{ >0, yl"\
Отметим, что вектор х можно считать неотрицательным при условии,
что в матрице А зафиксирована такая ориентация ветвей, которая соот-
соответствует положительным перепадам yt (i = 1,... , п) давления, под-
подсчитанным по замеренным узловым давлениям Pj(j = 1,..., т ). Величи-
Величины у у' также берутся по абсолютной величине. Возможное же при других
режимах изменение направления расходов х\и' учитывается присвоением
знака "минус" коэффициентам г (") при вычислении их по формуле A1.3).
Если ввести диагональные матрицы
A1.4)
и-1) A1.5)
и получим следующую переопределенную (при достаточно большом и)
систему линейных алгебраических уравнений относительно х:
Ах = Q, AR(u)x = Qiu) (и = 1,..., и-1). A1.6)
Система A1.6) содержит и подсистем материальных балансов в узлах,
записанных относительно одного и того же базисного вектора х. Матрицы
R(u^ при этом являются "матрицами приведения" неизвестных х^ к
искомому вектору х.
Все рассуждения полностью сохраняются, если для каждой ветви будут
более сложные законы гидравлического сопротивления. В этом случае
коэффициенты г ^ будут определяться по другим формулам.
Таким образом, задача определения параметров г.ц. с сосредоточенными
параметрами, отвечающей реальной ТПС, может быть сведена в своей
начальной постановке к построению и решению переопределенной системы
уравнений. Решив ее, определим х, а значит, вектор s: Sj = hj/x*[ (i -
= 1,... , и) и векторы х^"), относящиеся к другим режимам (см. A1.5)).
Переопределенность системы уравнений "математического расходо-
расходомера" имеет вполне определенный физический смысл, связанный с неиз-
неизбежной на практике погрешностью замеренных значений, следствием
чего является погрешность коэффициентов г ^ .
150

0
©'
ф
©,
4- ,'@
а
0
©
/ /
//
11.1а,б. Пример схемы для иллюстрации метода "математического расходомера"
а — обычная схема; б — циклическая схема; 1 — задвижка; 2 — фиктивные ветви
Исходные методы решения. Переопределенные системы A1.6) можно
решать методом наименьших квадратов или посредством сведения их к
эквивалентной задаче линейного программирования (что равносильно
применению метода наименьших модулей) :
v т—1
S
и=1
min
1=1
A1.7)
при условиях
-zA) = Q, AR(u)x +
x>0,
где w =
w(u)-z(u) =
> 0,
), A1.8)
wA) >0, zA) > 0, w(u) > 0, A1.9)
0 (м=2,..., v), A1.10)
wi,..., wm_j)r hz = (zi,...,zm_1)f- векторы неотрица-
неотрицательных дополнительных переменных, введенных в качестве неизвестных
невязок (с разными знаками) в уравнения с неточными коэффициентами.
Оба эти подхода были реализованы авторами на различных ЭВМ и апро-
апробированы на ТПС с большим числом участков и различными схемами сое-
соединений. За результаты манометрической съемки были приняты давления
в узлах, полученные предварительно (при заданных величинах гидравли-
гидравлических сопротивлений s,-) одним из следующих методов: 1) в результате
решения для этих сетей на ЭВМ обычной задачи потокораспределения
при различных задаваемых режимах; 2) с помощью пьезометров на гидрав-
гидравлической модели, которая использовалась для моделирования этих же
объектов; 3) путем замеров давлений манометрами на испытательном
стенде и при гидравлических испытаниях реальных объектов [198].
Пример. Поясним применение данного метода на примере цепи, пред-
представленной на рис. 11.1,я. Пусть установившиеся режимы определяются
различным положением исполнительного органа задвижки на ветви 2
151

и разными величинами подачи и отборов в узлах цепи. Причем потреби-
потребитель в узле 4 не меняет своего внутреннего сопротивления во всех ре-
режимах, что дает основание вычислять для него коэффициенты пропор-
пропорциональности по формуле A1.3). Давления измеряются во всех узлах,
а расходы в узлах / и 5. Требуется определить расходы на ветвях цепи
и расходы в узлах 2 и 4. Найдя указанные расходы, можно затем вычис-
вычислить сопротивления ветвей.
Для удобства изложения приведем схему цепи к циклическому виду
(рис. 11.1,6), где замеряются: давления в узлах 1,. .. , 6; расходы в уз-
узлах 1 к 5 (—Qx и 2s) ¦ Определяются расходы на ветвях и в узлах 2 к 4.
Все множество расходов X разобьем на три непересекающихся подмно-
подмножества: Х\ — подмножество неизвестных расходов на ветвях с постоян-
постоянными сопротивлениями (в это подмножество не входят расходы для не-
небазовых режимов, поскольку они могут быть выражены через соответ-
соответствующие расходы на ветвях в базовом режиме); Х2 — подмножество не-
неизвестных расходов на ветвях с переменными сопротивлениями; Х3 - под-
подмножество известных (замеренных) расходов. Для данного примера они
состоят из следующих элементов:
Х\ = \-*1, Х$, Х/\, Х$, Х(,,
<">
Х$, Х(,, X-j, Хд},
и= 1,2,..., V},
Соответственно замеренным давлениям определим перепады давления
(и) _ р(и) р(и) (и) = р(и) _ р(и) (и) = p(uf _p(u) (и) =
У\ - м ~ "г >Уз ri Г4 ' ¦ ¦ ¦ > Уп r s Г4 > У9
= Р\и> - /*6(") (давление в фиктивном узле 6 равно нулю, т.е. Р6 = 0).
Вычислим коэффициенты пропорциональности:
г 1 = (^1 1у\ ) »• • • > ''э = (^9 /У9 ) > и— 2,3,... , v.
Выберем узел 5 в качестве линейно зависимого и составим систему
уравнений типа A1.6) :
1) Xi + x$l) + х2 = Qi ^ - узел 1
2) -*! - х4 + х6 + Jci') = ° - Узел 2
3) —х^ + х4 + xs = 0 — узел 5 • режим 1
4) -х3 - х5 - хп + х9 = 0 - узел 4
5) -х8A) - х9 =-GiO) + Gs0) -узел 6
6)/-,B)^i + х2B) + r3B)x3 = Q[2) -узел!
7) -г,B)дг1 - г4B)х4+ г^2)х6 + х^2) = 0-узел 2
8) -х2B) + /-4B)л:4 + rsB)x5 = 0-узел 5
9) -г3B)х3 - r<2)xs - /-7B)х7+ r9B)x9= 0- узел 4
10) -х8B> - г9B);с9 = -2,B) + Ql2) -узел 6
режим 2
Аналогично записываются 5 уравнений для режима 3. В данном случае
достаточно трех режимов для достижения переопределенности системы.
В данной переопределенной системе из 15 уравнений содержится 13
неизвестных: хи х3,
152
4. *s, х6, х7, х9,

что является необходимым (наряду с указанным ранее условием на из-
мерения узловых расходов), но недостаточным условием для получения
единственного решения, поскольку вследствие ошибок измерений система
несовместна. Обычно находят решение, обладающее определенным свойст-
свойством, например минимизирующее сумму квадратов невязок системы.
В таком случае единственность решения (при условии, что система приве-
приведена к нормальной форме) обеспечивается равенством рангов исходной
и расширенной матриц числу неизвестных. Соблюдение последнего условия
зависит, в свою очередь, от качества режимов (от их контрастности).
Так, для данного примера переопределенность системы не гарантирует
получение единственного решения, если группы уравнений, соответствую-
соответствующие режимам 2 и 3, окажутся линейно зависимыми по отношению к урав-
уравнениям первого.
Сделаем несколько замечаний относительно линейно зависимого узла.
Во-первых, при выборе такого узла следует исходить из того, чтобы он не
препятствовал исключению из системы расходов л;^"^ ? Хг на ветвях с
переменными сопротивлениями. Это означает, что данный узел не должен
быть инцидентным указанным ветвям. Внашем примере узел 5 удовлетво-
удовлетворяет этому требованию, что позволяет, выразив х\!* их]1' из 1-го и 2-го
уравнений для режима 1
1)х2A> = -х,-хз + 2,A), 2)*8A) = хх + х4 - х6,
и подставив их в 3-е и 5-е уравнения, получить
3)*! + х3 + х4 + xs = е,A>,
4) -х3 - х5 - х7 + хд = О,
5) -*, - х,+х6- х9= -2A) + 05A)-
Аналогичные преобразования можно сделать и для подсистем, соответ-
соответствующих другим режимам. В итоге для трех режимов получим пере-
переопределенную систему меньшей размерности (9 уравнений и 7 неизвест-
неизвестных) , содержащую неизвестные расходы только на ветвях с постоянными
сопротивлениями.
Во-вторых, уравнение, соответствующее линейно-зависимому узлу,
несет дополнительную информацию, которая в условиях несовместности
системы может повысить точность находимых затем оценок расходов.
Однако при дальнейшем изложении из методических соображений будут
использоваться только линейно-независимые узлы.
Все изложенное выше позволяет применять основные положения "мате-
"математического расходомера" для разработки ряда важных методик, имеющих
большое значение при эксплуатации и проектировании ТПС; 1) гидравли-
гидравлических испытаний трубопроводных сетей для нахождения их фактических
параметров; 2) определения текущих расходов и гидравлических сопро-
сопротивлений у абонентов сети; 3) оперативного фиксирования аварийной
ситуации с последующим определением расчетным путем места и величины
аварийного расхода (утечки); 4) эквивалентирования (упрощения) рас-
расчетной схемы ТПС; 5) уточнения математического описания течения жид-
жидкости или газа на ветвях цепи в зависимости от режима и др.
В принципе данный метод дает точные решения, и при условии относи-
относительно точных исходных данных для решения поставленной задачи опре-
153

деления фактических параметров г.ц. наиболее простым является описан-
описанный выше переход к переопределенной системе линейных алгебраических
уравнений и ее решение методом наименьших квадратов. Однако на практи-
практике замеры производятся обычно с невысокой точностью и правильность
ответов зависит от: класса точности приборов, применяемых для изме-
измерения давлений в сети; степени разрегулировки при варьировании ги-
гидравлических режимов (поскольку чем более отличаются друг от друга
коэффициенты пропорциональности г^, тем выше точность результа-
результатов) ; числа дополнительных режимов, для которых производятся замеры
и др. При этом матрица нормальной системы уравнений, получаемая в
случае метода наименьших квадратов, бывает плохо обусловленной, так
что решение может значительно отличаться от истинного. В связи с этим
ниже рассматриваются вопросы дальнейшего развития основных положе-
положений "математического расходомера" и разработки более совершенных
математических моделей и методов [134, 204—207].
11.3. НЕЛИНЕЙНЫЕ МОДЕЛИ
ДЛЯ ОЦЕНКИ ГИДРАВЛИЧЕСКИХ ПАРАМЕТРОВ ТПС
Описанный выше способ "математический расходомер" практически позво-
позволяет находить в силу неизбежной погрешности замеряемых величин лишь
оценки Jc,- и s,- искомых параметров ТПС. Отмеченное же совпадение этих
оценок с эталонными значениями Xf и S/ имеет место только в модельных
ситуациях, когда исходные данные фактически не содержат ошибок, по-
поскольку они задаются или вычисляются на ЭВМ путем решения прямых
задач потокораспределения.
На практике компоненты векторов р("\ Q^"\ H^ определяются
по приборам, имеющим зачастую весьма невысокий класс точности. Для
выявления степени влияния ошибок измерений, соответствующих различ-
различным классам точности приборов, на погрешность получаемых оценок
х^"' и ? авторами были проведены вычислительные эксперименты с при-
применением представленных в предыдущем разделе линейных моделей иден-
идентификации ТПС. При этом использовались предположения: об отсутствии
систематических ошибок в показаниях приборов, о нормальном законе
распределения погрешностей измерений.
В результате было установлено, что относительно узкому диапазону
ошибок (от 0,01 до 0,8%) исходных данных может соответствовать до-
достаточно широкий диапазон (от 1,3 до 11% для xt и от 2,4 до 26,3% длях,-)
ошибок в оцениваемых параметрах. (Отметим, однако, что большие отно-
относительные погрешности были характерны лишь для некоторой части оце-
оценок, которая для большинства исследованных объектов составляла обычно
около 10% от их общего количества.)
В связи с этим следующим шагом в развитии математических моделей
и методов для оценивания параметров ТПС с целью повышения их точ-
точности и практической эффективности стали формулировка и численная
реализация нелинейных обратных задач потокораспределения [204-206].
К нелинейным моделям здесь можно прийти по крайней мере тремя путями.
Во-первых, нетрудно получить ту или иную переопределенную систему
нелинейных алгебраических уравнений. Если, например,величины у*- >
Q и Н , измеренные для различных режимов (ы = 1, . . . , и), подста-
154

вить непосредственно в математическую модель потокораспределения
(без какого-либо ее преобразования), то придем к следующей переопре-
переопределенной системе относительно х^ их,- (/ = 1,..., п) :
Ах<-и) = 2(и), (П.П)
s,(l*/w)l)fl =^(И) -Я/"> = я/и). A1.12)
Поскольку число неизвестных здесь равно vn + n, то число режимов,
необходимое для переопределенности A1.11), A1.12), определяется
из условия (от — 1 + n)v > (и + 1)и, т.е. (т - l)v > п. Учитывая, что п =
= т — 1 + с, а также тот факт, что для цепей, не содержащих петель и ду-
дублирующих ветвей, как правило, т — 1 > с > л/2, получим нижнюю гра-
границу для и: v > 2.
В этой же переопределенной системе уравнения A1.12) позволяют
исключить не только s,-, как это делается в методе "математического рас-
расходомера", но hjcEm) :
/> /^IA/^l1/^-1/". A1.13)
Введя диагональную матрицу
D(u) = diag(sign;c/")|fl/")r/'3).
и новые переменные z,- = s ~ '^ (г = 1,... , п), после подстановки A1.13)
в A1.11) получим следующую переопределенную систему, нелинейным
образом связанную с искомыми s,-:
ADwz ~ Q(u) (u= \,...,v). A1.14)
Данные переопределенные системы решаются на ЭВМ с помощью различных
методов ортогонализации для решения систем с прямоугольными матри-
матрицами [235], регуляризации (с целью уменьшения степени плохой обус-
обусловленности системы) и др.
Второй путь связан с применением метода наименьших квадратов,
смысл которого для системы A1.11), A1.12) может заключаться в на-
нахождении минимума сложной нелинейной функции:
= Б {[(Ах^ - Q^y(Ax(u) - <2(u))l + A1.15)
и = \
x^u) - /i("))TEZ(")x(") - /г <">)]},
где S и Х^и> — диагональные матрицы порядка п с элементами, равными
s,- и |.ty(">|'J' соответственно. "
Необходимые условия экстремума для A1.15) сводятся к сложной сис-
системе нелинейных уравнений, решение которой требует преодоления мно-
многих вычислительных трудностей, увеличивающихся по мере роста ошибок
измерений и степени несовместности системы. Поиск работоспособного
метода решения данной задачи привел к следующей модификации метода
Ньютона.
В окрестности некоторого начального приближения Х@) и х\"^ линеа-
линеаризуется система A1.11), A1.12). Полученная в результате этого пере-
переопределенная система линейных уравнений относительно поправок к Х@)
и х^ решается методом наименьших квадратов. В направлении получае-
155

мого вектора этих поправок делается шаг, величина которого определяет-
определяется из условия минимума функции A1.15), например, с помощью метода
Фибоначчи. Отметим, что при нахождений минимума A1.15), исходя из
различных начальных приближений, была установлена унимодальность
этой функции в исследуемой области изменения переменных.
Из других возможных нелинейных формализации задач оценивания
параметров ТПС следует отметить постановку, основанную на физическом
смысле задачи, а именно: требуется, не нарушая условий потокораспреде-
ления, т. е. первого и второго закона Кирхгофа,так подобрать сопротив-
сопротивления ветвей г. ц., которая моделирует данную ТПС, чтобы расхождения
между измеренными потерями давления h^M и значениями h *¦"', полу-
полученными из решения задачи о потокораспределении, были бы (в том или
ином смысле) минимальными. Такой постановке вопроса отвечает, на-
например, следующая задача на условный экстремум:
2 [(SX(U)X(U> -/Озм) <5* * АизмI "* mi" A1.16)
u= 1 M i? x (")
при
^л(и) =Q(»)!Bhiu) =BHJifM,SX^u)x<-u)x^ = /z(u) (u=l,...,u).
A1.17)
Численное решение такой задачи также сопрояжено со значительными
трудностями, обусловленными ее большой размерностью и существен-
существенной нелинейностью функции A1.16). Для их преодоления был разработан
алгоритм, опирающийся на идею групповой релаксации, основные этапы
которого состоят в следующем: задается начальное приближение вектора
s (о), которое используется для расчета потокраспределения, в результате
х @) и xi^l будут удовлетворять условиям A1.17). Далее по зафиксирован-
зафиксированным х^} ищется Х(!) =S(o) + Х(о) Д^(о) > исходя из минимизации A1.16).
При этом, естественно, изменится и xi'A , поскольку должны выполняться
условия A1.17), они определят xS"\ и т. д.
Большинство из названных подходов было реализовано на ЭВМ БЭСМ-6.
И в условиях вычислительных экспериментов векторы оценок s и х^"'
всегда совпадали с эталонными значениями s и х^, что подтверждало
принципиальную правильность данных методов. Одновременно было
установлено, что значения оценок, получаемых в результате решения не-
нелинейных задач, практически оказывались ненамного точнее по сравнению
с теми, которые определялись ранее с помощью линейных моделей.
Таким образом, проблема повышения точности решения задач инден-
тификации ТПС при существующем техническом уровне информационной
базы в этой области не может быть до конца решена лишь на путях услож-
усложнения формально-математической стороны дела. Помимо ориентации на
использование более современных и точных измерительных приборов и
датчиков, необходимо одновременно проводить анализ конкретных целей
и условий идентификации ТПС, учитывать специфические особенности
исследуемых объектов, конкретизировать чересчур общие постановки за-
156

дач, применять комбинированные подходы, формулировать те или иные
требования к расстановке измерительной аппаратуры различного клас-
класса точности и т. п.
Так, к примеру, отмеченный ранее факт наличия больших величин
относительных ошибок у некоторых компонент векторов оценок s и
?(") еще не дает оснований для вывода о полной практической неприем-
неприемлемости результатов оценивания. Дело в том, что идентификация пара-
параметров производится не только с целью определения коэффициентов гид-
гидравлического сопротивления каждого участка ТПС и последующего вы-
вычисления коэффициентов шероховатости труб, но и для определения па-
параметров моделирующей данную ТПС г. ц., способной замещать ее в за-
задачах управления, связанных с многовариантными расчетами потокорас-
пределения. В этом случае судить о пригодности оценок s вместо истин-'
ных значений s нужно именно с такой точки зрения.
11.4. МЕТОДЫ СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ
НА БАЗЕ ЛИНЕЙНЫХ МОДЕЛЕЙ
Выше рассматривались главным образом вопросы математического моде-
моделирования и сравнения различных моделей и методов для идентификации
параметров ТПС с методической и алгоритмической точек зрения. Было
выявлено, что практически они равноценны в смысле значений конечных
результатов как в условиях вычислительных экспериментов, так и при
идентификации ряда реальных объектов. Однако выбор модели, которую
следует рекомендовать для решения тех или иных задач идентификации,
связанных с обработкой результатов реальных испытаний, должен де-
делаться не только и не столько исходя из приемлемости и удобств в вы-
вычислительном отношении, а с учетом одного из главных практических тре-
требований - быть подходящей не только для получения оценок параметров,
но и оценок их дисперсий или стандартных отклонений.
При формальном подходе к использованию схем оценивания, приме-
применяемых в математической статистике, нетрудно прийти к выводу, что они
не соответствуют линейным моделям в основном из-за того, что ошибки
измерений здесь содержатся не только в правых частях, но и в элементах
матриц коэффициентов. В нелинейных же моделях ошибки измерений
сосредоточены в правых частях, тем самым выполняются условия для
оценивания по методу наименьших квадратов. Определение оценок па-
параметров st и х,-(м) и их дисперсий as. и а (и) (/= 1,..., п) можно осу-
осуществить, например, с помощью описанного выше алгоритма минимиза-
минимизации нелинейной функции A1.15), только она в данном случае модифи-
модифицируется следующим образом:
F(s, x(u)) = 2 {(Ах^ -Q(u))T(C(u))-1(/lx(") -Q{u)) +
и= 1
+ (SX{u)x^u) -hWyiGWy^SXMxM-hW)} A1.18)
где С "' и G'"' — ковариационные матрицы ошибок измерений компо-
157

нент векторов Q^ и h ^ (порядков т - 1, п соответственно), позволяю-
позволяющих учесть неравноточность измерений и коррелированность ошибок
измерений.
Заметим, что G^ в отличие от С*-"* - недиагональные матрицы, по-
поскольку ошибки в измерениях компонент векторов h (") нельзя считать
независимыми. Вычислительные трудности, связанные с нелинейностью и
большой размерностью задачи, здесь имеют место в еще большей степени.
В связи со сложностью нахождения оценок параметров и их дисперсий
в нелинейном случае ниже предлагается к использованию способ, который
применяется для оценки качества изделий. Смысл его в данном случае
заключается в том, что в известные после проведения испытаний значе-
значения И *¦"' и Q^u' случайным образом вносятся ошибки, соответствующие
эмпирическим стандартным отклонениям или классам точности исполь-
использованных приборов, после чего оценки сопротивлений и расходов находят-
находятся с помощью самой простой из линейных моделей. Повторив подобные
операции достаточно большое число раз (например, 100), получим соот-
соответствующее количество векторов оценок s и х^и', а это уже позволяет
оценить и их среднеквадратические отклонения [205-206].
Анализом этих значений оценок дисперсий можно выделить участки ТПС,
параметры которых определены с недопустимой погрешностью, и преду-
предусмотреть, к примеру, различного рода технические мероприятия, способ-
способствующие увеличению точности оценок: установку дополнительных рас-
расходомеров, использование приборов повышенного класса точности и т. п.
Практическую и вычислительную эффективность предложенных выше
моделей и методов можно существенно повысить за счет понижения раз-
размерности решаемых задач. Первая возможность здесь связана с переходом
от общего вектора расходов к контурным неизвестным. Другой путь
заключается в разбиении исходной общей системы уравнений на после-
последовательность подсистем меньшей размерности. Применительно к иссле-
исследуемой ТПС это означает поэтапную обработку данных о ее измерениях,
опирающуюся на последовательное рассмотрение отдельных узлов и фраг-
фрагментов ТПС и поочередное оценивание параметров их элементов. При этом
на каждом этапе используются результаты оценивания, полученные на
предыдущем, а параметры участков, инцидентных выбранным узлам,
определяются из соотношений материального баланса. Поэтапная обра-
обработка резко снижает требования и к быстродействию, и к объему памяти
используемых ЭВМ.
11.5. ИДЕНТИФИКАЦИЯ ТПС КАК ГИДРАВЛИЧЕСКИХ ЦЕПЕЙ
С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
Математическое описание неизотермического потокораспределения для
ТПС, моделируемых г. ц. с переменными, зависящими от режима функцио-
функционирования параметрами, имеет вид (см. формулы (8.3) —(8.8), учитывая,
что некоторые из них берутся здесь в упрощенном виде);
Ax=Q, A1.19)
Ву^Р = ф_(Р'т,у), (П-20)
AiXt@)-A3Xt(L)=e, A1.21)
158

г(О)=А\Т, A1.22)
t{L)=G{x,P,t(O),t(L\w), A1.23)
y=F(x,s(x,P,T,d)). A1.24)
Здесь для простоты изложения в A1.21) отсутствует теплоемкость, по-
поскольку, например, в нефте- и газотранспортных системах ее величина
примерно одинакова для потоков среды, инцидентных одному узлу, и по-
потому соответствующее уравнение в (8.7) может быть поделено на эту ве-
величину, и так для всех уравнений. Отсюда и вектор Q в A1.17) состав-
составлен лишь из компонент вида 7N/ и tjQj, а не С/7N/ и CjtjQj, как это
было в (8.7).
Как и в случае сосредоточенных параметров, основной информацией
для идентификации г. ц. с переменными параметрами [207] является
манометрическая съемка, но дополненная одновременными замерами тем-
температур. Использование температуры в качестве информативного факто-
фактора здесь весьма существенно, так как, несмотря на возросшую сложность
математической модели, позволяет в ряде случаев значительно упростить
и вместе с тем сделать более эффективной процедуру идентификации.
Итак, jjycTb для определенного установившегося режима известны
векторы Р, Q, T@), 7{L), представляющие собой измеренные значения
векторов Р, Q, r@), t{L). Кроме того, пусть модели измерений имеют
вид
Р=Р+ЬХ, Q = Q + 62, r@) =Г@) +53, 7(L) =t{L) +54, A1.25)
где 5 а (а = 1, 2, 3, 4) - векторы ошибок независимых измерений, рас-
распределенные по нормальному закону с нулевыми математическими ожи-
ожиданиями и ковариационными матрицами Da соответственно.
Рассмотрим подходы, которые могут быть применены здесь для иден-
идентификации параметров. Но прежде заметим, что идентифицировать сами
переменные параметры Sj или ?/ (см. формулы (8.13), (8.14)) уже не
имеет смысла, поскольку их значения меняются при изменении режима
функционирования системы. В связи с этим идентификации подлежат
не зависящие от режима коэффициенты с?,- и k((i = 1, ..., и), зная кото-
которые можно определить и другие искомые значения переменных парамет-
параметров для любого из режимов.
I. Поскольку измерения A1.25) должны удовлетворять условиям
A1.19) —A1.24), их подстановка дает следующую систему уравнений:
Ax=Q, A1.26)
A,X7{G) -A2Xt(L) = в (t@)J(L),Q), A1.27)
[_{L) =GG@),7(L),x,P,K,d,w), A1.28)
ArP*=F(x, Г(О),Г(?),Л d, м), A1.29)
где.Р*_ вектор, состоящий из величин /*/(/ = 1, 2, ..., ш)для нефтепро-
нефтепроводов или из.Р/ - для газопроводов.
При условии, что в ТПС для данного режима имеется по меньшей мере
с узлов, в которых сходятся не менее чем по два потока (это дает с ли-
линейно независимых уравнений в A1.27) дополнительно к т - 1 уравне-
уравнениям (И .26), так что в итоге их будет с + т - 1 = п), процесс нахождения
решения системы A1.26) —A1.29) может быть разделен на два этапа.
159

На первом, например, методом наименьших квадратов, исходя из A1.26) —
A1.27), находятся оценки х - вектора расходов; на втором, используя
х, из соотношений A1.28) и A1.29) определяются оценки d,-и kt (i =
= 1,...,л).
Таким образом, при нахождении оценок d{ и kt в отличие от случая
с сосредоточенными параметрами мы обошлись информацией, замерен-
замеренной лишь для одного установившегося режима, что подтверждает важную
роль температур при идентификации г. ц. с переменными параметрами.
Вместе с тем очевидно, что одноразовые замеры Р, Q, ?@) и 7(L) могут
содержать грубые ошибки измерений, что соответственно может привести
к грубым ошибкам в оценках параметров. Однако данный подход может
быть использован для оперативной (прикидочной) идентификации, ре-
результаты которой впоследствии можно уточнить, а также в качестве приема
для нахождения начального приближения в более сложных алгоритмах
идентификации.
II. В связи с тем что на практике не всегда могут быть осуществлены
замеры всех компонент векторов A1.25) и, кроме того., указанное выше
ограничение на количество сходящихся потоков в узлах выполняется не
для любого режима, система A1.26)-A1.29) может оказаться недоопре-
деленной. Это приводит к необходимости использования многократных
замеров, соответствующих различным режимам работы ТПС, что в итоге
порождает переопределенность системы типа A1.26) —A1.29) относи-
относительно искомых величин. К переопределенности системы приводит также
и стремление к более достоверным результатам идентификации.
Итак, пусть тепер
величин выступает Р
щая переопределенная система примет вид
ь в качестве измеренных (полностью или частично)
("), qM ftu) @),f(")(L) (« = !,..„„). Соответствую-
?<"> (L) =G(?(U) @),Г(и)
-AT(P*)(U) =
(Г(и) @),7("> (L)
Р(и), к, d, w.),.
@),?(u) (L),P(U
i,e(u)),
>, d, w).
A1.30)
A1.31)
A1.32)
A1.33)
В разд. 11.2—11.4 достаточно подробно рассмотрены способы решения
переопределенных систем нелинейных алгебраических уравнений данно-
данного типа. Все соображения относительно предпочтительности того или ино-
иного способа решения, а также относительно способов оценки достоверности
результатов идентификации остаются в силе и для системы A1.30)-
A1.33). Здесь лишь подтвердим, что наиболее работоспособным способом
решения A1.30) —A1.33) является преход к линейной переопределенной
системе относительно лишь одного вектора х расходов в базовом режиме
с последующим использованием результатов решения этой линейной си-
системы дли получения искомых оценок коэффициентов с?,- и kj. Ниже
рассмотрим только некоторые особенности формирования переопределен-
переопределенных систем и особенности алгоритма идентификации, присущие системам
с переменными параметрами.
В случае неизотермического течения система (см. формулу A1.6))
Ах =Q, AR(u)x =C(u) (u=l,...,v -1) A1.34)
160

может быть дополнена уравнениями, составленными на основании A1.31):
AtXrW+AiXtiDjd G(О),Г(Ь),в), A1.35)
ji (
A1.36)
При этом коэффициенты г/"* могут быть получены, исходя не только
из соотношений A1.33) для давлений, но и с помощью A1.32), описы-
описывающих изменение температуры. Так, для газопроводов из (8.13) имеем
i_ = sign(Ar.(u)) —Г2, A1.37)
i ' \jr,r(.»)(r.(«) ,<"> ) /
^ • г v i, cp i, cp '
cp
а из (8.14)
rP / \fM) @) _
грХХ
rp//
A1.38)
Здесь нижние индексы "р" и "г" у г означают, что использовано соотноше-
соотношение для давлений или для температур. Аналогичные формулы можно по-
получить и для нефтепроводов [207]. Очевидно, что, поскольку г^ фор-
формально должны совпадать с г j"^, они могут быть использованы для вза-
взаимного уточнения и замещения в системе A1.34) — A1.36).
Таким образом, в общем случае имеем переопределенную систему
уравнений с переменными коэффициентами и правыми частями. Основ-
Основными методами решения подобных систем являются методы, заключаю-
заключающиеся в последовательном их пересчете как систем со все более точными
значениями сосредоточенных параметров (см. гл. 8).
Основанная на указанном принципе итерационная процедура идентифи-
идентификации в общих чертах заключается в следующем. Для каждого из и режи-
режимов задается начальное потокораспределение (х^ ) *¦") . Исходя из из-
известных параметров среды (плотности, вязкости, температуры), посту-
поступающей в систему, с помощью алгоритма, реализующего соотношения
типа (8.3), находится распределение этих параметров по ветвям г.ц. Счи-
Считая полученные параметры для данного этапа расчета заданными, состав-
составляется и решается система уравнений A1.34)-A1.36). После этого уточ-
уточняются параметры, неявно входящие в соотношения типа A1.37), A1.38),
и процесс повторяется до тех пор, пока с заданной степенью приближен-
приближенности не совпадут оценки расходов на двух соседних итерациях.
В заключение обсудим вопрос о практической целесообразности иденти-
идентификации на базе цепей с переменными параметрами. Иными словами, не
компенсируют ли ошибки в оценках параметров эффекта от использования
сложных моделей, учитывающих неизотермичность и неоднородность среды?
И не следует ли в таком случае пользоваться при идентификации более про-
простыми в вычислительном отношении моделями с сосредоточенными пара-
параметрами?
Численные эксперименты по идентификации параметров различных
нефте- и газопроводных систем показывают, что при ошибках измерений,.
П.Зак. 384 161

соответствующих классам точности манометров 0,5; 1,0; 1,5, относитель-
относительные погрешности идентифицированных сопротивлений не превышают
соответственно 1,3, 6%. В то же время факторы неизотермичности и не-
неоднородности среды приводят к изменению обобщенных гидравлических
сопротивлений в различных режимах на 20—30%. Следовательно, модели-
моделирование этих систем как г. ц. с сосредоточенными параметрами (когда со-
сопротивления считаются постоянными) сопровождается ошибками, соот-
соответствующими указанному диапазону изменения сопротивлений. Отсюда
следует вывод о практической целесообразности идентификации ТПС
как г. ц. с переменными параметрами, поскольку погрешности иденти-
идентификации оказываются значительно меньше погрешностей моделирования.

Часть вторая
ОПТИМИЗАЦИЯ СТРУКТУРЫ И ПАРАМЕТРОВ
РАЗВЕТВЛЕННЫХ МНОГОКОНТУРНЫХ СИСТЕМ
Глава 12
О ПРОБЛЕМЕ МАТЕМАТИЗАЦИИ И АВТОМАТИЗАЦИИ
ПРОЕКТИРОВАНИЯ ТРУБОПРОВОДНЫХ СИСТЕМ
12.1. ИСХОДНЫЕ ПОЛОЖЕНИЯ
Проблема оптимального проектирования сложных пространственно рас-
распределенных систем трубопроводного транспорта, энергетики и других
отраслей является одной из самых актуальных в народном хозяйстве.
На сооружение, развитие и реконструкцию этих систем ежегодно расхо-
расходуются значительные денежные средства, они стали крупнейшими по-
потребителями металла и энергосилового оборудования. Отсюда очевид-
очевидно первостепенное значение количественного обоснования принимаемых
решений и автоматизации самих процессов, связанных с их оптимальным
проектированием, что требует соответствующего математического, прог-
программного, информационного и организационного обеспечения.
В связи с этим принципиальным моментом (и основным стимулом
для дальнейшего изложения) является общность всего комплекса опти-
оптимизационных технико-экономических задач, составляющих проблему
оптимального проектирования физико-технических систем, с которы-
которыми можно связать (на уровне их проектных схем) соответствующие гид-
гидравлические или электрические цепи. Действительно, основные и весьма
типичные задачи проектной практики в данной области заключаются в
выборе: 1) мест размещения и параметров источников, что фактически
предопределяет в рамках проектируемой системы возможные уровни
централизации снабжения; 2) конфигурации сети (трубопроводной,
электрической или в виде совокупности каналов для транспортировки
воды), которая связывает множество рассредоточенных потребителей с
источниками; 3) физико-технических (дискретных и непрерывных) пара-
параметров всех элементов системы; 4) способов их развития и реконструк-
реконструкции (при наличии уже существующей части объекта проектирования);
->) мероприятий по обеспечению и повышению структурной и техноло-
технологической надежности системы и т. д.
Первые два типа задач обычно решаются (во многом на основе инже-
инженерного опыта и интуиции) отделами перспективного планирования, кото-
которые обосновывают: необходимость создания конкретной системы, разме-
размещение и количество источников, предельные радиусы снабжения от каждо-
каждого из них и в итоге - структуру системы в целом, включая конфигурацию
сети, которая будет осуществлять транспортировку среды или энергии.
удем называть их задачами схемно-структурной оптимизации.
163

Следующий тип задач, который рассматривается для уже определенной
структуры системы (т. е. при заданной схеме ее основных связей), -
это задачи схемно-параметрической оптимизации. Речь идет о выборе
диаметров трубопроводов (или сечений проводников и каналов), сетевых
сооружений (насосных, компрессорных или трансформаторных станций)
и расчетного потокораспределения для того или иного уровня нагрузок
у потребителей. Выполняется это уже в других подразделениях проектных
организаций и, как правило, без проведения многовариантных оптими-
оптимизационных расчетов на ЭВМ (особенно это характерно для тепло- и водо-
снабжающих систем), на основе стандартных нормативов и правил и с
минимальным учетом конкретных особенностей сооружаемого объекта.
Особое значение имеет проблема развития и реконструкции систем,
которая возникает в связи с появлением новых потребителей и ростом
нагрузок. Подобные вопросы становятся все более актуальными и рас-
распространенными, поскольку в настоящее время большинство систем
энерго-, тепло-, водо- и газоснабжения крупных городов и промышлен-
промышленных центров - это постоянно развиваемые и реконструируемые объекты.
Однако эти задачи гораздо более трудные не только в методическом и
математическом плане, но и в организационном отношении, поскольку
появляются уже в ходе эксплуатации систем и решаются разрозненно
и эпизодически.
Весьма злободневной в последние годы стала разработка мероприятий
по обеспечению и повышению надежности вновь проектируемых и сущест-
существующих систем в связи с заметным разрывом между растущими масшта-
масштабами централизованного электро-, тепло-, водо-, газо- и нефтеснабжения
в народном хозяйстве страны, огромной протяженностью соответствую-
соответствующих магистралей и сетей, с одной стороны, и недостаточным уровнем
проектирования, а также организационных и технических средств управ-
управления эксплуатацией и развитием этих систем — с другой. Очевидно, что
требования надежности должны учитываться уже на стадии проектирования
системы при решении вопросов о выборе источников, конфигурации и
"кольцевании' сетей, а также и параметров элементов.
Общность проектных задач проявляется здесь уже на этапе их содержа-,
тельной постановки, но в еще большей степени она становится очевидной
при построении соответствующих матматических моделей и разработке
алгоритмов оптимизации. Исходной базой для такого межотраслевого
рассмотрения могут служить основные положения и методы ТГЦ, изло-
изложенные в первом разделе книги. Определяется это тем, что математические
описания областей допустимых решений в перечисленных выше оптими-
оптимизационных задачах фактически получаются из математических моделей по-
потокораспределения внесением в них тех или иных "степеней свободы"
в зависимости от того, какие схемные и физико-технические параметры
проектируемой системы являются искомыми и подлежат оптимизации.
Конечно, процессы оптимального проектирования сложных физико-
технических систем не могут быть полностью формализованы и автома-
автоматизированы, они будут осуществляться лишь на основе диалога специа-
специалиста-проектировщика и ЭВМ. Но реализация такого диалога не сводится
к простому объединению имеющихся математических моделей и алгорит-
алгоритмов и их "погружению" в реальную проектную практику на уровень первич-
первичных исходных данных и документов. Необходимо более глубокое осмысли-
164

вание процессов проектирования и принятия решений с переходом от рас-
рассмотрения совокупности отдельных математических моделей к поста-
постановке более общих проектных задач и разработке отвечающих им сложных
итерационных процессов комплексной оптимизации с созданием соответ-
соответствующих программно-вычислительных комплексов (ПВК). Подобная
постановка вопросов не является умозрительной. Анализ как отраслевой,
так и математической литературы, который дается ниже, позволяет вы-
выявить ряд узловых проблем, требующих более четкой постановки, комп-
комплексного рассмотрения и решения.
12.2. МЕТОДЫ СХЕМНО-СТРУКТУРНОЙ ОПТИМИЗАЦИИ
Вопросам построения наилучших в том или ином смысле сетей посвя-
посвящено достаточно много работ. Как математические задачи о нахождении
минимальных (по суммарной длине участков) сетей, связывающих "звезд-
"звездное поле" точек (с возможностью генерирования дополнительных узлов),
они начали рассматриваться еще в 30-е годы прошлого столетия Я. Штей-
нером [102], затем усложнены A909 г.) А. Вебером и потому в настоя-
настоящее время получили название проблемы Штейнера—Вебера [23, 169]. Ана-
Аналитических решений, а также работоспособных алгоритмов для решения
данных задач даже относительно небольшого размера нет до сих пор [97].
Математические модели схемно-структурной оптимизации стали пред-
предметом активного изучения в связи со становлением и развитием матема-
математического программирования и применением ЭВМ. Основное внимание
во многих работах [23, 158, 169, 183 и др.] вначале было направлено на
введение той или иной системы координат для описания исходного мно-
множества точек и связей между ними, определение оптимального расположе-
расположения точек ветвления в искомой сети, более содержательную интерпрета-
интерпретацию (на данной формальной основе) задач "пространственной экономи-
экономики" и т. п.
Для нахождения оптимальных точек ветвления сети (точек Штейнера)
ряд авторов [42, 43, 164] использовали градиентные методы, однако это
приводило лишь к локально-оптимальному решению, зависимому от пер-
первоначально выбранной сети. В других работах предлагалось исходить из
нескольких (задаваемых опытным проектировщиком либо с помощью
случайного выбора) начальных вариантов конфигураций сети, для кото-
которых искалось затем наилучшее размещение точек ветвления.
Довольно скоро стало ясным, что решение практических задач в та-
такой постановке дает хорошие результаты лишь в отдельных случаях, ко-
когда требуется оптимизировать конфигурацию сетей без строгой привязки
их к условиям местности или городской застройки, число узловых то-
точек относительно невелико, а ущерб при отклонении фактической трас-
трассировки сети от формально-оптимального варианта с целью обхода пре-
препятствий оказьюается (или считается) несущественным.
Некоторые авторы (например, [164]) пытались преодолеть подобную
ограниченность данного подхода путем введения "зон непроходимости"
и Других ограничений, описывающих запреты на расположение точек вет-
ветвления сети, либо с помощью специальных алгоритмов улучшения реше-
решения. Так, М.Г. Сухарев и Е.Р. Ставровский [226] предлагают при проекти-
165

ровании газосборных сетей для учета местных условий прохождения трасс
вводить соответствующие коэффициенты удорожания к базисной стои-
стоимости прокладки трубопроводов и учитывать их при определении областей
поиска координат точек разветвления.
В целом же задачи схемно-структурной оптимизации при относитель-
относительной простоте их постановки являются весьма трудным объектом для
приложений математических методов оптимизации из-за их многоэкстре-
многоэкстремального характера, большой размерности и важности учета конкретных
ограничений. Здесь могут оказаться полезными в зависимости от объекта
опитимизации и целей расчета различные подходы, в том числе и упро-
упрощенные. Наиболее развитыми и весьма эффективными инструментами
для постановки и решения задач перспективного планирования и разви-
развития сетевых объектов являются математические модели и методы ли-
линейного, кусочно-линейного программирования, а также нелинейные тран-
транспортные задачи, особенно в их сетевой интерпретации.
Еще Дж. Данциг показал [56], что симплекс-мет од для сетевой задачи
линейного программирования (ЛП) сводится к целенаправленному пе-
перебору деревьев этой сети. А теоретические основы построения и алго-
алгоритмизации сетевых потоковых моделей изложены в известной книге
Л. Форда и Д. Фалкерсона [237], которые, в частности, раскрыли двойст-
двойственность задач о максимальном потоке и минимальном разрезе сети. Име-
Имеется ряд монографий отечественных и зарубежных авторов, в которых
рассматриваются различные вопросы теории и методов решения нели-
нелинейных сетевых транспортных и других экстремальных задач на графах
[35, 66, 257]. Применительно к трубопроводным системам (ТПС) наибо-
наиболее полное истолкование сетевых потоковых моделей (на примере задач
оптимизации развития, текущего и перспективного планирования работы
газотранспортных систем и Единой системы газоснабжения страны) дано
в монографии [228].
В работе В.А. Трубина и Г.Н. Юна [41] рассматривается многоэкстре-
многоэкстремальная задача выбора сети авиалиний при следующих допущениях:
1) на полном графе задается множество значений спросов на маршрутах
между различными вершинами; 2) для каждой вершины известна макси-
максимальная пропускная способность расположенного в ней аэропорта; 3) каж-
каждое ребро характеризуется функцией затрат в зависимости от пассажиро-
пассажиропотока, которая предполагается возрастающей, но вогнутой. Требуется
синтезировать сеть авиалиний, отвечающую минимуму суммарных затрат.
Решение ищется с помощью модификации метода ветвей и границ. По-
Подобным задачам оптимального синтеза сетей с вогнутой целевой функцией
посвящены и другие работы Института кибернетики АН УССР [41].
Публикации по применению метода ветвей и границ [289, 24] отно-
относятся и к задачам трассировки электрических сетей. Однако, как сви-
свидетельствуют работы А.И. Лазебника и О.Н. Цаллаговой [105], его реа-
реализация приводит к весьма продолжительному времени счета даже для
сетей среднего размера. Кроме того, для получения нижней оценки здесь
необходимо решать транспортную задачу не менее сложную, чем исходная.
Другой подход, предложенный в работах В.Я. Хасилева и О.А. Некрасо-
Некрасовой [270, .240, 167, 168], а также в работах В.Л. Леонаса и И.Б. Моцку-
са [107, 159], опирается на первоначальное задание исходной избыточ-
166

ной схемы сети. Она должна учитывать все фактические ограничения на
плане города и местности, включать конфигурацию существующей части
системы и содержать все целесообразные для рассмотрения и сколь угод-
угодно многочисленные (но реально допустимые) связи между источниками,
потребителями и точками разветвления сети. Задача как раз и заключа-
заключается в том, чтобы суметь отбросить (отбраковать) ненужные связи и
оставить (выделить) лишь оптимальную подсеть, отвечающую наивыгод-
наивыгоднейшему потокораспределению (электрического тока, жидкости или га-
газа) от источников к потребителям.
Интересно отметить, что в первой своей работе по трассировке элект-
электрических сетей авторы статьи [158] еще базируются на задаче Штейнера.
В дальнейшем же [107, 159] они переходят к постановке, исходящей
из задания не координат узлов, а именно исходной избыточной сети,
и преобразуют ее затем в задачу на безусловный экстремум относитель-
относительно контурных переменных. Для решения последней предлагаются обыч-
обычный и усиленный методы покоординатной минимизации (см. гл. 13),
которые обеспечивают в ряде случаев нахождение и глобального минимума.
Методика "избыточных проектных схем" как специальный подход к
постановке и решению задач схемно-структурной оптимизации сетевых
систем является во многих отношениях более эффективной, чем другие,
благодаря следующим отличительным особенностям:
1) задание избыточной схемы проектируемой или развиваемой системы
относится в ней к "эвристическому" этапу, который выполняется проек-
проектировщиком (пользователем математической модели). Это максимально
приближает постановку задач к реальным условиям размещения объекта
на плане города или местности, упрощает их математическую формулиров-
формулировку и тем самым позволяет решать задачи большей размерности с помощью
относительно простых процедур оптимизации;
2) система условий включает не только уравнения материального ба-
баланса в узлах схемы (что является естественным для любых сетевых ма-
математических моделей), но. и уравнение общего баланса энергии в проек-
проектируемой системе, которое позволяет приближенно учесть второй закон
Кирхгофа. В результате появляется основа для постановки и решения
более сложных задач, когда требуется выбрать не просто схему транспор-
транспортировки среды от источников к потребителям, а именно структуру гидрав-
гидравлической системы, для которой искомое потокораспределение будет фи-
физически осуществимо;
3) в случае пополнения системы условий соотношениями и неравенст-
неравенствами, позволяющими подсчитывать надежность "путей снабжения" и учи-
учитывать "узловые нормативы" к надежности снабжения потребителей, на
базе избыточной проектной схемы можно в принципе ставить и решать
задачи об оптимальных уровнях централизации снабжения с учетом требо-
требований надежности.
Дальнейшее изложение проблемы схемно-структурной оптимизации
(в гл. 13 и 15) сводится к раскрытию основных положений и возмож-
возможностей методики избыточных лроектных схем.
167

12.3. МЕТОДЫ СХЕМНО-ПАРАМЕТРИЧЕСКОЙ ОПТИМИЗАЦИИ
Применение математических методов оптимизации для выбора параметров
трубопроводных, электроэнергетических и других физико-технических
систем имеет большую историю, отраженную в весьма обширной лите-
литературе по методам технико-экономических расчетов. В этой связи прежде
всего обратимся к классической работе В.Г. Шухова A884 и 1895 гг.)
по оптимизации нефтепроводов [272].
Данная публикация начинается с утверждения, что "для жидких тел
(воды, нефти и ее продуктов, свекловичного сока и т.п.) специальными
перевозочными средствами являются трубные проводы". В ней дается
следующая содержательная постановка задачи: "По данному расстоянию
и по количеству перекачиваемой жидкости определить размеры всех частей
сооружения под тем условием, чтобы ежегодные проценты с затраченного
на устройство капитала, сложенные со стоимостью эксплуатации, составля-
составляли возможно меньшую величину". Нетрудно убедиться, что здесь факти-
фактически сформулирован широко используемый в настоящее время критерий
общих расчетных (приведенных к одному году) затрат.
Исходя из этого, В.Г. Шуховым рассматриваются две конкретные задачи:
1) по заданному диаметру трубопровода найти наивыгоднейшую для него
производительность и число насосных станций и 2) по заданной произво-
производительности определить наивыгоднейшие диаметр трубопровода и число
станций для него. Обе задачи сводятся им к задачам на абсолютный экстре-
экстремум относительно двух переменных и решению соответствующих систем
из двух нелинейных уравнений путем "последовательных подстановок".
На основе аналитических выкладок в работе обосновывается вывод о
том, что наивыгоднейший расход по трубопроводу пропорционален квад-
квадрату диаметра трубы. Показывается, что решения для указанных выше
двух задач будут различными: "Если для известной трубы d\ найден наи-
наивыгоднейший для нее расход Qx, то тот же расход можно еще дешевле
перекачать по некоторой другой трубе d2 и тд.". Аналогичную задачу
для паровой сети (для случая одной линии с сосредоточенными нагруз-
нагрузками) рассмотрел Г. Гребер в 1927 г. [285].
В ЗО-е годы аналитические методы технико-экономического расчета
получили большое развитие в нашей стране в связи с периодом индустриа-
индустриализации и созданием систем централизованного электро-, тепло- и водо-
водоснабжения городов и промышленных центров. Именно в эти годы появи-
появились известные работы Л.К. Якимова, A.M. Занфирова, Б.Л. Шифринсова,
В.Г. Лобачева, М.В. Кирсанова, Л.Ф. Мошнина и других авторов.
Л.К. Якимов в работе [274] дал формулу для определения диаметра
магистрали тепловой сети, исходя из минимума суммарных затрат по
сети и допустимого давления в ней. Расчет "отводов сети" проводится
затем последовательно, друг за другом с использованием номограммы
и с последующим округлением диаметров до стандартных значений.
A.M. Занфиров [70] обобщил метод, предложенный Л.К. Якимовым,
на случай "ветвистой сети", когда диаметры ее участков не могут счи-
считаться независимыми переменными. Для отыскивания "относительного
минимума годовой стоимости сети" им используется метод множителей
Лагранжа, и в результате задача сводится к решению системы уравнений,
порядок которой равен сумме числа участков и колец сети. Автор считает
168

данную систему "математически неразрешимой" и предлагает ее решать
графически "совместно с методом приближений".
В области теплоснабжения фундаментальные исследования этого пе-
периода принадлежат Б Л. Шифринсону [269], который в общем виде рас-
рассмотрел задачи технико-экономического расчета разветвленных тепло-
тепловых сетей произвольной конфигурации (но с одним источником) и дал
их формулировку как задач на условный экстремум. В отличие от А.М.Зан-
фирова он, используя аналогию с расчетом электрических сетей, берет в
качестве основных переменных не диаметры, а потери напора на участках
сети, что позволяет существенно упростить вид необходимых условий
минимума общих расчетных затрат по сети в целом. В результате им впер-
впервые с методической и аналитической точек зрения был обоснован для
практического применения метод равномерной потери напора вдоль глав-
главной (наиболее протяженной) магистрали тепловой сети. Данный метод
и до сего времени остается одним из основных проектных методов, при-
причем оптимизация удельной потери напора для каждого объекта заменена
нормированием этой величины, что в условиях ручного счета было вполне
оправданным из-за большого объема проектных работ.
Обширная литература была посвящена методам технико-экономичес-
технико-экономического расчета водоснабжающих систем, и во многих отношениях ее научно-
методический уровень являлся наиболее передовым для ТПС вообще.
Это объяснялось главным образом тем, что данные системы с самого на-
начала своего возникновения строились и развивались как многоконтур-
многоконтурные системы (МКС), что требовало более глубокого осмысливания воз-
возникающих задач и разработки соответствующих расчетных методов.
В.Г. Лобачев в книге [109], помимо систематического и полного изло-
изложения предложенного им "способа расчета многоколечных сетей методом
итераций" (о котором уже говорилось выше, в гл. 2 и 3), рассматривает
также и метод расчета "сложных водоводов и разветвленных сетей по
экономическому принципу". Расчет разветвленной сети сводится к много-
многократному решению так называемой задачи Грасгофа: при заданном рас-
располагаемом напоре отыскивается минимум стоимости водовода, состоя-
состоящего из последовательности труб разных диаметров и с различными рас-
расходами на отдельных участках.
Наибольшее развитие вопросы оптимизации водопроводных сетей на
уровне непрерывных математических моделей и методов условной ми-
минимизации получили в работах М.В. Кирсанова, Д.М. Минца и Л.Ф. Мошни-
на [89, 160]. Ими были раскрыты особые свойства функции затрат для
кольцевых сетей, заключающиеся в том, что она является выпуклой по
напорам и вогнутой по расходам воды на участках. Этот результат свиде-
свидетельствовал о многоэкстремальном характере задачи, однако в то время
отсюда был сделан вывод о невозможности определения наилучшего по-
токораспределения в сети и о необходимости его предварительного назна-
назначения.
В случае задания распределения расходов задача оптимизации парамет-
параметров МКС перестает быть многоэкстремальной и становится задачей вы-
выпуклого программирования. Для ее решения при учете ограничений толь-
только в виде равенств (законов Кирхгофа) можно воспользоваться класси-
классическими методами условной и безусловной минимизации. Именно подоб-
169

ные методы активно применялись во многих работах для техникооконо-
мических расчетов. С их помощью строились "универсальные" зависи-
зависимости (как, например, в статье В.Я. Хасилева [241]), номограммы и гра-
графики, которые служили и служат до сих пор руководством при проек-
проектировании ТПС и других сетевых объектов.
При оптимизации параметров водоснабжающих систем (ВСС) широ-
широкое распространение получил метод, разработанный Л.Ф. Мошниным
[160], который является интересной интерпретацией методов условной
минимизации. Он предназначен для определения оптимальных диаметров
ВСС при заданном ("желательном") распределении расходов. При некото-
некоторых допущениях Л.Ф. Мошнин дал аналитическое выражение стоимости
водопроводной сети как функции от диаметров, расходов и коэффициен-
коэффициентов, получивших, как и сам метод, название "фиктивных расходов". Он
исследовал свойства этих коэффициентов, предложил способ их опреде-
определения, а приравниванием нулю производных от функции стоимости по
диаметрам получил аналитические выражения для определения самих
диаметров. Следует подчеркнуть, что главная заслуга Л.Ф. Мошнина состо-
состоит в том, что он впервые поставил и решил системную-задачу оптимизации
параметров для всего множества участков ВСС (подробнее об этом методе
см. в разд. 15.3).
При проектировании и развитии современных физико-технических
систем аналитические, методы оказались явно недостаточными, так как
по существу они были ориентированы на оптимизацию вновь создаваемых
объектов и не могли учитывать в полной мере: дискретность диаметров
и типоразмеров насосов, конкретные особенности прокладки трубопрово-
трубопроводов , наличие существующей части системы и необходимость в реконструк-
реконструкции отдельных ее элементов, ограничения в виде неравенств (на допусти-
допустимые значения давлений и расходов), разнообразные логические условия.
Появление ЭВМ и развитие математического программирования (линей-
(линейного, динамического, дискретного и др.) стимулировали разработку но-
новых подходов и методов, так что аналитические методы уступили место
алгоритмическим, хотя и сохранили известное значение.
Наибольшее число публикаций по применению ЭВМ для оптимизации
разветвленных систем (PC) различного типа и назначения связано с при-
применением методов последовательного анализа вариантов, особенно дина-
динамического программирования (ДП). В числе первых как в отечественной,
так и в мировой литературе были работы B.C. Михалевича, Н.З. Шора и
других сотрудников Института кибернетики АН УССР [41, 43, 66, 151].
Можно отметить также работы СЭИ [123, 173, 179, 214, 244], М.Г. Суха-
Сухарева и Е.Р. Ставровского [226,227] и др.
Метод ДП является одним из основных для оптимизации PC и в зару-
зарубежной вычислительной практике. Так, в статье- [287] говорится о при-
применении ДП для оптимизации городских коммунальных сетей. Ее авто-
авторы считают, что среди методов ветвей и границ, симплекс-метода, полного
перебора метод ДП является наиболее эффективным. В этой работе при-
приводится пакет программ для оптимального проектирования распреде-
распределительных разветвленных сетей, где основным также является метод ДП.
Сведение к моделям ЛП является другим распространенным подходом
в области схемно-параметрической оптимизации. Его первыми авторами
170

в отечественной литературе применительно к ТПС являются Г.Е. Кикачейш-
вили [87, 88] и А.Е. Мурадян [163]. Идея применения ЛП опирается на
хот факт, что задачи оптимизации PC принимают линейный вид, если в ка-
качестве основных переменных взять длины трубопроводов определенного
стандартного сечения, допускаемых к прокладке на каждом участке. При
этом оптимизация PC, имеющей т узлов и п ветвей, потребует перехода к
задаче ЛП с числом уравнений п + т и числом неизвестных порядка zn, где
z — число стандартных диаметров. Например, при w = 100hz = 15 полу-
получим задачу ЛП с 199 уравнениями и 1500 неизвестными, решение которой
на ЭВМ занимает довольно заметное время.
Одно из основных преимуществ методов ЛП для оптимизации PC заклю-
заключается в том, что их реализации в виде достаточно мощных стандартных
программ имеются, как правило, в составе математического обеспечения
любой ЭВМ. Существенным же недостатком в данном случае является
большая размерность получаемых задач ЛП, а отсюда и большое время
счета. Кроме того, при расчете конкретных объектов необходимо каждый
раз вручную выполнять трудоемкую (и не автоматизированную до сих
пор) работу по формированию соответствующих моделей ЛП, отвечаю-
отвечающих особенностям проектируемой сети и конкретным условиям.
Имеется ряд работ, в которых описывается сведение задач оптимизации
трубопроводных, электроэнергетических и транспортных систем к зада-
задачам кусочно-линейного и выпуклого программирования, к сетевым транс-
транспортным задачам и другим известным математическим моделям и мето-
методам оптимизации. В этом ряду вполне конкурентоспособным остался
и метод "фиктивных расходов" Л.Ф. Мошнина, который упоминался
выше: в статье [162] описаны его эффективные реализации на ЭВМ. Не-
Некоторым развитием данного метода является "дифференциальный алго-
алгоритм" А.Г. Евдокимова [60], который предназначен для оптимизации
МКС, но позволяет находить лишь локальный минимум, соответствую-
соответствующий теоретическим (а не стандартным) значениям диаметров.
Заканчивая обзор литературы по оптимизации параметров разветвлен-
разветвленных и многоконтурных систем, можно прийти к выводу о том, что в на-
научно-методической литературе в основном рассматриваются PC, а. опти-
оптимизация МКС связывается с заданием потокораспределения или сводится
в конце концов к оптимизации PC. Вместе с тем наивыгоднейшее потоко-
распределение должно быть составной частью искомых величин в общей
задаче оптимизации МКС и находиться одновременно с другими парамет-
параметрами системы.
124. ПОСТАНОВКА ВОПРОСОВ
Приведенный выше обзор математической и отраслевой литературы по
моделированию и методам схемно-структурной и схемно-параметричес-
кой оптимизации позволяет дать общую оценку положения в данной об-
области.
Во-первых, несмотря на большое число публикаций, существует из-
известный разрыв между потенциальными возможностями современных
математических методов оптимизации и уровнем их применения в реаль-
реальной проектной практике. Основная часть работ идет по пути формального
171

привлечения математических методов для решения отдельных оптими-
оптимизационных задач по принципу "владею методом — его и применяю", в то
время как первичным должно стать изучение реальной проектной прак-
практики и максимальный учет специфики выделяемых при этом классов
задач с целью создания более адекватного и работоспособного матема-
математического и программного обеспечения.
Следующий важный момент заключается в том, что до последнего вре-
времени основным объектом оптимизации были, как правило, PC, что объяс-
объяснялось объективными причинами: их экономической целесообразностью
(поскольку они являются наивыгоднейшими с экономической точки
зрения, если не учитывать факторы надежности и развития уже сущест-
существующих систем) и возможностью применения для их оптимизации извест-
известных методов, в основном линейного и динамического программирования.
Однако даже применительно к PC исходные математические модели и кон-
конкретные алгоритмы данных методов за прошедшие 10-15 лет подверглись
существенной трансформации в связи с необходимостью оптимизации PC
с большим числом участков, наличием множества источников, насосных
или компрессорных станций, учетом существующего состояния PC, различ-
различными условиями прокладки на отдельных участках и т.п.
Это потребовало, с одной стороны, совершенствования самих алгорит-
алгоритмов, поскольку параметры и мощных ЭВМ оказывались недостаточными
(при формальной реализации методов ДП и ЛП), а с другой - внесения
в них различного рода модификаций для учета специфических особен-
особенностей решаемых задач. Все это нуждается в анализе и обобщении, что яв-
является актуальным при рассмотрении более сложных объектов оптими-
оптимизации.
Далее, подавляющее большинство опубликованных работ ограничива-
ограничивается рассмотрением отдельных задач схемно-структурной и схемно-пара-
метрической оптимизации и, как правило, лишь для вновь проектируемых
систем. В то же время известно, что необходимость учета существующего
состояния систем при решении вопросов об их реконструкции и развитии
существенно осложняет математическую формулировку задач и разработ-
разработку методов и алгоритмов решения, поскольку переводит их в класс мно-4
гоэкстремальных задач с разрывными целевыми функциями.
Среди имеющихся публикаций довольно мало таких, которые посвя-
посвящены комплексной оптимизации именно многоконтурных систем. Од-
Однако в последние годы в связи с бурным развитием систем энергоснаб-
энергоснабжения, трубопроводного транспорта различного типа и назначения и дру-
других систем все более актуальными становятся проектирование и эксплуа-
эксплуатация их как МКС. Это определяется требованиями надежности, что при-
приводит к необходимости обеспечения многостороннего снабжения всех или
части потребителей системы, и, кроме того, их развитием и реконструкци-
реконструкцией, когда вводятся дополнительные источники, подключаются все новые
потребители и относительно простые (вначале) системы превращаются в
сложные PC и МКС.
При этом уровень работ и опыт, накопленный, например, в области во-
водоснабжения, где исторически эти системы с самого начала проектирова-
проектировались и строились как МКС, оказались недостаточными, поскольку они но-
носили отраслевой характер и опирались на слишком жесткие допущения
172

и специальные методы расчета, ограниченные рамками задач условной ми-
минимизации. Таким образом, необходим переход к систематическому рас-
рассмотрению вопросов математического моделирования, дискретной оптими-
оптимизации и синтеза МКС. Он особенно важен еще и потому, что перечисленные
выше типовые задачи оптимизации структуры и параметров PC и МКС не
согласованы по своим постановкам и методам решения, "входам" и
"выходам", информационному обеспечению, что нельзя сделать без по-
построения общих математических моделей многоконтурной оптимизации.
При переходе к рассмотрению более сложных комплексных проблем,
требующих человеко-машинных подходов для своего решения, в извест-
известной степени меняется представление об относительной ценности и эффек-
эффективности привлекаемых или разрабатываемых математических моделей
и методов. В противовес стремлению к максимальной формализации,
которая была довольно характерна для первого этапа широкого приме-
применения математических методов и ЭВМ, в настоящее время все более пред-
предпочтительными и практически работоспособными оказываются гибкие
подходы, основанные, например, на неформальной декомпозиции (расщеп-
(расщеплении) общих задач в те или иные последовательности относительно са-
самостоятельных подзадач меньшей сложности и размерности.
Методы декомпозиции при этом могут иметь двоякое проявление. В од-
одних случаях они отвечают реальной иерархии подзадач, которые можно
выделить еще на этапе общей постановки в соответствии со структурой
исследуемой системы или применительно к отдельным этапам ее планиро-
планирования, проектирования и развития. Другая основа для их применения —
это более формальная декомпозиция общей задачи по каким-либо груп-
группам основных переменных или уравнений, которые последовательно вы-
выделяются, преобразуются и агрегируются, исходя из внутренней логики
исследования и с целью получения более простых (известных) матема-
математических моделей.
В данном случае, например, среди множества переменных, используе-
используемых для математического описания МКС, всегда можно выделить те из
них, которые: а) отражают структурные особенности системы (состав
элементов, распределение источников и потребителей, иерархию связей);
б) совпадают с техническими характеристиками отдельных элементов
(диаметры труб или сечения проводников тока, длины ветвей, единич-
единичные мощности агрегатов НС и другие); в) являются "режимными" па-
параметрами, поскольку описывают потокораспределение в системе (име-
(имеются в виду расходы транспортируемой среды на ветвях и узловые потен-
потенциалы: давления или напряжения); г) характеризуют "внешние связи"
Данной системы (возможные производительности источников, нагрузки
У потребителей и их изменение во времени, экономические показатели
и т.д.). И совершенно естественным для моделирования и алгоритмизации
процессов оптимального синтеза МКС становится подход, состоящий в
поочередном фиксировании той или иной группы переменных с тем, чтобы
можно было формировать и решать более простые подзадачи относительно
переменных, которые остаются свободными. При этом производится:
фиксирование всего или части полученного промежуточного решения,
пересчет "смежных" переменных, получение дополнительной информации
от пользователя и переход к новой подзадаче и т.д.
173

Одной из основных проблем здесь становится обоснованная форма-
формализация совокупности этих процедур и промежуточных этапов в виде
целенаправленных итерационных процессов, а также их реализация и ав-
автоматизация с помощью ПВК. При этом не должна забываться первона-
первоначальная цель, заключающаяся в получении общего оптимального решения,
и потому каждый из этапов и весь процесс декомпозиции необходимо
интерпретировать и анализировать с точки зрения удовлетворения всей
системы ограничений и достижения глобального (или по крайней мере
локального) минимума целевой функции исходной задачи, а также и воз-
возможности изучения поведения решения вблизи своего экстремума. Выде-
Выделение иерархий подзадач на содержательном уровне и формальная деком-
декомпозиция общей задачи часто осуществляются совместно и настолько пе-
переплетаются, что их трудно четко разделить. Тем не менее только актив-
активная алгоритмическая разработка, изучение и практическое применение
идей декомпозиции обеспечат новый уровень применения ЭВМ и продви-
продвижение исследований в данной области. Об этом же свидетельствует и ли-
литература последних лет.
Так, В.В. Кафаров, В.Л. Перов, В.П. Мешалкин и В.В. Асташкин [84]
ставят вопрос о необходимости обобщающей постановки "задачи опти-
оптимизации гидравлических цепей химико-технологических систем" и раз-
разработки соответствующего комплекса программ. И.Д. Зайцев и В.Г. Вай-
нер [69] формулируют общую двухэтапную задачу оптимизации трубо-
трубопроводных сетей на стадии их проектирования: на первом этапе оптими-
оптимизируется "геометрия сети", на втором производится расчет гидравличес-
гидравлических характеристик сети "с выбранной геометрией". Ими предлагается
"универсальный комплекс алгоритмов, полученный благодаря приме-
применению модульного принципа". Однако общая задача ставится как обоб-
обобщение задачи Штейнера с поиском оптимальной геометрии сети "при от-
отсутствии запрещенных областей". Кроме того, они рассматривают сети
лишь с одним источником. Подобный комплексный подход к проекти-
проектированию PC описывается и в зарубежных публикациях [277].
Сказанное подводит к постановке следующих вопросов:
1) о необходимости обобщения многолетнего опыта применения ме-
метода ДП для оптимизации развиваемых и реконструируемых PC со мно-
многими источниками при наличии большой совокупности физико-техни-
физико-технических ограничений и логических условий (см. гл ,14);
2) о математической формулировке общей задачи оптимизации МКС
и разработке гибких алгоритмов многоконтурной оптимизации (гл. 15);
3) об исследовании общей задачи оптимального синтеза МКС с учетом
требований к надежности снабжения потребителей, распределенных по
узлам проектной схемы МКС (гл. 16);
4) о дальнейшей формализации процессов количественного обоснова-
обоснования проектных решений при создании и развитии трубопроводных и дру-
других гидравлических систем - с разработкой соответствующей унифици-
унифицированной вычислительной базы на уровне ПВК (гл. 18);
5) о необходимости более глубокой алгоритмизации и автоматизации
оптимального проектирования МКС на базе современного информационно-
информационного и организационного обеспечения с переходом к созданию человеко-
машинных (диалоговых) систем (гл. 19).
174

Глава 13
СХЕМНО-СТРУКТУРНАЯ ОПТИМИЗАЦИЯ
13 1. ИСХОДНЫЕ ПОЛОЖЕНИЯ МЕТОДИКИ
ИЗБЫТОЧНЫХ ПРОЕКТНЫХ СХЕМ
В данном разделе рассматриваются задача об оптимальной трассировке
(конфигурации) трубопроводной сети на избыточной схеме и приближен-
приближенный метод ее решения в том исходном виде, в каком они были даны в
первых публикациях СЭИ по этим вопросам [167, 168]. Как уже'отме-
уже'отмечалось, принципиальным положением данного подхода является задание
не цифровой модели местности, т.е. координат узлов (источников снаб-
снабжения и потребителей транспортируемой среды) , а непосредственно схемы
их возможных соединений трубопроводной сетью. В предельном случае
такой схемой может служить полный граф (когда каждый узел связан
со всеми другими) , но, как правило, уже на этапе задания схемы проекти-
проектировщик может учесть конкретные условия и особенности объекта и отбро-
отбросить подавляющее большинство заведомо нерациональных и просто нере-
нереальных связей.
Задача выбора наивыгоднейшей конфигурации трубопроводной сети
может быть сформулирована тогда как задача о поиске наивыгоднейшего
нотокораспределения на заданной избыточной схеме, имеющей т узлов и
п ветвей, с тем, чтобы выделить на ней оптимальную подсхему в виде де-
дерева, соединяющую источник снабжения со всеми потребителями.
За критерий оптимальности принимается минимум суммарных приве-
приведенных затрат на сооружение и эксплуатацию всех элементов сети, вклю-
включая затраты электроэнергии на перекачку транспортируемой среды, ко-
которые могут быть выражены как функция от искомых расходов X/, диа-
диаметров di труб. В первой математической модели было сделано допуще-
допущение о предварительном задании величины общей энергии Э источника,
что соответствует при известной производительности источника заданию
его действующего напора. Практически это означает, что эксплуатацион-
эксплуатационные издержки принимаются постоянными и, следовательно, можно решать
задачу на минимум только капиталовложений
л
F(d)= 2 f,(d,)Lh A3.1)
i=i
где /,- - удельная стоимость трубопровода с диаметром dt, включающая
стоимость: одной единицы длины самой трубы, ее прокладки, монтажа и
изоляции. Эти функции в случае непрерывной модели (когда диаметр
трубы может принять любое неотрицательное значение) обычно выража-
выражаются как
- 032)
0, если dt = О,
гДеа,,й,- - коэффициенты, которые получаются в результате аппроксима-
аппроксимации реальных (табличных) значений стоимостных функций fi{dt).
175

Если учесть зависимость диаметра от потери давления ht и расхода xh
полученную из формулы
h^srf = l-L,drllaxf. Xi>0,
Ф
характеризующей течение жидкости, например, в доквадратичной области
гидравлического сопротивления
aL^ A3.3)
то минимизируемая функция A3.1) примет вид
= F(x,h) = 2 itlx?fluhTc"t+-Z e,Z.,sign|jc,|. A3.4)
Здесь я,- = i//"&,-Z-/+a" - экономическая характеристика ветви, не связан-
связанная с показателем степени /3; а — показатель, отвечающий принятой фор-
формуле для S/; ф — коэффициент, зависящий от степени шероховатости
внутренней поверхности трубы; sign |лгж-1 = 0 при х,- = 0 и 1, если xt Ф 0.
Взяв частные производные второго порядка от функции A3.4)
b2F/bh) =au(au + \)
нетрудно увидеть, что существует критическое значение показателя сте-
степени ив A3.2) : гГ= 1/а0, от которого зависит знак вторых производных
по X;. (К примеру, для а = 0,2 и 0 =2, п = 2,5). При и < п", что характерно
для большинства практических задач, функция A3.4) выпукла по h{,
но вогнута по Xj. Именно этот случай и берется ниже в качестве основного.
Система условий составляется из уравнений материального баланса
во всех узлах схемы и энергетического баланса для искомой сети в целом:
Ax = Q, A3.5)
2 hixi = hTx = 3, A3.6)
где всегда hjXf > 0. Уравнение A3.6) является следствием подсистемы
уравнений второго закона Кирхгофа (см. об этом в [167], а также в гл. 7
данной книги), поэтому здесь можно говорить об их приближенном учете.
Предполагается также, что энергия источника полностью тратится на
преодоление трения в сети, т.е. не учитывается энергия, доставляемая
потребителям. Такое допущение приемлемо для многих схемно-структур-
ных задач.
Задача минимизации A3.4) при условиях A3.5), A3.6) и составляет
исходную математическую модель для выбора оптимального дерева тру-
трубопроводной сети на ее избыточной схеме. Целью дальнейших преобразо-
преобразований данной модели является стремление исключить из нее вектор h и
перейти к эквивалентной оптимизационной задаче относительно лишь
вектора расходов х. Такой переход опирается на построение частичной
функции Лагранжа и использование ее для проведения "аналитической"
оптимизации по группе переменных. (Данный прием описан в книге [21]
на примере конкретной задачи.)
176

Исходя из этого и учитывая выпуклость функции затрат F(x, И) по й,
яменим исходную задачу минимизацией частичной функции Лагранжа
ф = Я*>А) + М ^ М/-Э) A3.7)
/=i
при /4х = Q.
Необходимым условием минимума Ф по й и X будет соблюдение сле-
следующих равенств:
ЭФ/Эй,- = 9F/9A,- + Хх,- = -auirrf^hf""-1 + \xt = 0, A3.8)
ЭФ/ЭХ = I й,х,-Э=0, A3.9)
так что из A3.8) получим:
й/ = (ви7г,I/A+0!и)*<в</A+в")^/A+ви)- A3.10)
Подставив эти выражения для й/ в A3.9), определим оптимальное зна-
значение множителя X:
/=l ' '
которое, в свою очередь, позволяет свести A3.10) к выражению й,- как
функции только Xj. А учет последних в A3.4) приводит к следующей
окончательной математической формулировке рассматриваемой задачи:
минимизировать
" 1
2 т^/О+а") I*.! <*u@+l)/(l+au) 1+au +
' I
+ 2 assign |x, I A3.11)
1=1
при линейных условиях A3.5).
Функция A3.11) является вогнутой, а область допустимых решений —
выпуклым многогранным множеством, определяемым системой урав-
уравнений первого закона Кирхгофа, так что задача относится к классу мно-
многоэкстремальных сетевых задач вогнутого программирования.
Известно, что локальные минимумы целевой функции в такой задаче
достигаются в вершинах (угловых точках) многогранного множества.
А так как этим вершинам здесь взаимно однозначно соответствуют де-
деревья исходной схемы, описываемой ее матрицей соединений А (см. об
этом в книге Данцига [56])., то, следовательно, искомое решение содер-
содержится среди деревьев избыточной схемы.
Исходя из сказанного и был выбран метод решения, заключающийся
в Целенаправленном переборе "соседних" деревьев исходной схемы (по
типу симплекс-метода ЛП, но и в его сетевой интерпретации), организуе-
организуемом путем последовательного "поконтурного" преобразования дерева
начального приближения. При этом генерируется множество таких де-
деревьев, так что в процессе их улучшения определяется и соответствую-
12. Зак. 384 177

щее множество локальных минимумов. Дерево, отвечающее меньшему
из них, принимается за оптимальное решение задачи.
Данный алгоритм был реализован в СЭИ О.А. Некрасовой и СВ. Су-
Сумароковым в ряде программ для БЭСМ-2м и БЭСМ-4, но время счета
по ним оказалось довольно продолжительным даже для сравнительно
небольших схем. Проведенный в связи с этим анализ результатов пока-
показал, что эффективность метода "поконтурного" перебора деревьев су-
существенно зависит от: 1) начального приближения, которое, в свою оче-
очередь, связано с порядком перечисления участков исходной избыточной
схемы; 2) числа перебираемых деревьев для одного начального прибли-
приближения; 3) количества начальных приближений.
Таким образом, требовалось повысить вычислительную и практичес-
практическую эффективность имеющегося метода и дать его оценку в сравнении
с другими возможными подходами к решению многоэкстремальных за-
задач данного класса. Весьма интересным и актуальным также было даль-
дальнейшее развитие самой методики избыточных схем для постановки и
решения более сложных схемно-структурных оптимизационных задач.
Этим вопросам посвящен последующий материал данной главы.
13.2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ СОВМЕСТНОЙ ОПТИМИЗАЦИИ
ПРОИЗВОДИТЕЛЬНОСТЕЙ ИСТОЧНИКОВ И КОНФИГУРАЦИИ PC
Рассматриваются две математические модели [144-146], необходимые
для постановки, исследования и решения различных задач схемно-струк-
турной оптимизации PC, а также переход от них к задачам безусловной
минимизации.
Первая модель представляет собой модификацию описанной выше
модели Хасилева-Некрасовой (или модели А), которая потребовалась в
связи с включением в число искомых оптимизируемых величин не только
расходов Х{ (отличные от нуля значения которых отвечают выбранной
конфигурации PC), но и полной энергии Э источников (будем обозна-
обозначать ее как модель В). Она позволяет дать более полное математическое
описание целевой функции (общих расчетных затрат) и учесть во всех
выкладках наличие постоянных составляющих я,- в удельных стоимостных
показателях A3.2).
Вторая модель, являющаяся основной, предназначена для оптималь-
оптимального выбора на избыточной схеме мест размещения и производительностей
источников совместно с поиском наилучшей конфигурации PC. Для крат-
краткости будем называть такую задачу задачей оптимизации структуры PC,
а соответствующую ей модель — моделью С.
Обе эти модели также сводятся в конце концов к минимизации вогну-
вогнутой функции, определенной на выпуклом многогранном множестве зна-
значений вектора х. При этом пока не учитываются возможные дополнитель-
дополнительные ограничения на искомые переменные (в виде неравенств), условия
дискретности диаметров, требования к напорам у потребителей и надеж-
надежности их "путей" снабжения по ветвям получаемой PC, существующая
часть системы (если она имеется) и другие, поскольку это переводит
данные модели из класса относительно простых задач на условный экстре-
экстремум в многоэкстремальные сетевые задачи нелинейного дискретного про-
178

ммирования. Детальный учет указанных ограничений производится
последующем этапе - схемно-параметрической оптимизации PC (гл. 14)
• и путем решения более общих задач многоконтурной оптимизации
/гл 15) и оптимального синтеза МКС (гл. 16).
Начнем с построения модели В. Выше была описана задача на минимум
капиталовложений в сеть с допущениями о предварительном вычисле-
вычислении Э. Модель В позволяет избавиться от этого ограничения и находить
оптимальную конфигурацию PC при наивыгоднейших напорах #, источ-
источников (/е Л)- За критерий оптимальности берется общепринятый в
энергетике минимум приведенных (к одному году) затрат на строитель-
строительство и эксплуатацию объекта:
3 = (?+Гс)К+сэЭт, A3.12)
где К — капиталовложения в сеть; Е — нормативный коэффициент эффек-
эффективности; fc — доля отчислений на амортизацию, ремонт и обслужива-
обслуживание сети; сэ - удельная стоимость электроэнергии; Эг - годовая потреб-
потребность в электроэнергии. При этом, как и прежде, должны соблюдаться
условия A3.5) и A3.6), где Э - расход энергии за единицу времени (обыч-
(обычно в качестве нее берется один час).
Если использовать одно из возможных выражений для годового рас-
расхода энергии Эг на привод сетевых насосов, то A3.12) с учетом A3.4)
конкретизируется следующим образом (для простоты изложения при-
примем C = 2):
3 = F(x, Л, Э) = (f + /с) 2 (*,xfauhf аи + a,Lt) + -^ 2 Q,Hf.
367,2^ ,е,,
где дополнительно к предыдущему пг — число часов использования расчет-
расчетной производительности насосов (в год); тгнас — к л д. насосно-моторной
установки; 2 Q,H; = 3.
/еу,
Необходимые условия экстремума частичной функции Лагранжа
Ф(х, h, Э) - см. A3.7) — в данном случае приводят к уравнениям
ЭФ/Эй, = -(?• +/с><* unixf^hf01"-1 + Ах,- = О,
ЭФ/ЭЭ=с-А = 0,
п
ЭФ/ЭА = 2 h,x, - Э = 0.
Таким образом, множитель Лагранжа А здесь равен константе с =
= сэЛг/367,2т?нас, что в итоге дает следующие выражения для ft, и Э в за-
зависимости от *,-:
1/A+Jвц-1/A+аи)> A3Л4)
()
1=1 '
Если подставить A3.14) и A3.15) в целевую функцию A3.13), то по-
"Учим искомое выражение для минимизируемой функции, в которой
в аналитической форме уже учтен экономически наивыгоднейший расход
179

энергии в источниках:
п
1=1
(?¦+/,)• ? a,L,-affi\xl\+cui я1/О+««0|*,|3ви/A+ви\ A3Л6)
где U = c~^1
Минимизация данной функции при соблюдении условий Ax = Qyi состав-
составляет модель В. Таким образом, задача сведена, как и в модели А, к сете-
сетевой задаче вогнутого программирования относительно лишь вектора х,
но с более сложной целевой функцией, включающей как капитальные
затраты в PC, так и затраты на перекачку транспортируемой среды.
Модель В дает возможность перейти к более общей модели С, с по-
помощью которой можно обосновывать выбор оптимального решения не
только по конфигурации PC, но одновременно и по ее источникам. По-
прежнему задается избыточная схема (У, /), содержащая т узлов и п вет-
ветвей. При этом выделяются два подмножества: Л — узлов-потребителей
с заданными нагрузками и J2 - узлов возможного размещения источ-
источников, но без фиксирования их производительностей и напоров. Известна
лишь необходимая суммарная производительность Q^. этих источников,
равная сумме нагрузок Q/ потребителей (/ ? /i). Требуется наряду с
выбором конфигурации PC определить оптимальное число источников
и их производительности, а также соответственно "зоны" влияния этих
источников, исходя из наивыгоднейшего потокораспределения на исход-
исходной избыточной схеме.
Основная идея построения модели С состоит в некотором дополни-
дополнительном расширении исходной схемы за счет условных связей с целью
сведения данной задачи к предыдущей, когда оказывается возможным
использование модели В. Для этого схема (J, /) пополняется фиктивным
узлом / = т + 1 и подмножеством lm +1 фиктивных связей, соединяющих
этот узел со всеми узлами из /2» так что Im +1 = {/ = Qn + 1,/) , / € У2}..
В узле / = т + 1 назначается фиктивный источник с производительностью
Qm +1 = Се . а Для узлов / ? /2 с возможным размещением фактических
источников вводятся неизвестные производительности х-, равные расхо-
расходам xt на соответствующих фиктивных ветвях i ? Im +1. При этом должно
выполняться условие
2 *,= ? x, = Qm + 1. A3.17)
Система материальных балансов для преобразованной избыточной схемы
запишется следующим образом:
2 fly/JCj = Qj, j ? /j (для узлов-потребителей),
2e«xI- = 0, /?/з (для точек разветвления), A3.18)
2 а/(ос(=0, /?^2 (для узлов с возможным размещением
ie/u/m+,
источников),
180

Qj = Qz (дчя фиктивного источника в ухпе
1),
где #// - элементы пополненной (за счет (т + 1)-й строки и \J2\ столб-
столбцов) матрицы соединений.
Наличие в оптимальном решении величин х, > 0 (/ € /т + 1) будет
означать выбор источников в соответствующих узлах / 6 У2 с произво-
дительностями g; = xt. Нулевые же расходы на фиктивных ветвях будут
свидетельствовать о том, что соответствующие им источники не потребо-
потребовались и они (при выделении искомой структуры PC) должны быть уда-
удалены из избыточной схемы вместе со всеми другими ветвями, для кото-
которых также xt = 0.
Уравнение энергетического баланса в случае нескольких источников
с неизвестными их параметрами может быть записано в виде
I htx, = 2 HjQcfix, = Э,
id i^J2
где Hj(xj) - заданные функции, описывающие связи между их произво-
дительностями и действующими напорами (в аналитической или таблич-
табличной формах).
Целевая функция также усложняется за счет включения в нее слагаемых,
относящихся к фиктивным ветвям и представляющих приведенные расчет-
расчетные затраты на источники в зависимости от их типа, технических характе-
характеристик и стоимостных показателей. При этом капиталовложения и эксплуа-
эксплуатационные издержки по сети (Кс и Зс) в расчете на год выражаются, как и
ранее, через исходные технико-экономические показатели:
Кс = 2 (а,- + bid1)L,; Зс = fcКс + сэЭг,
Капиталовложения Ки в источники трудно математически описать сразу
для всех их типов, да это и не принципиально для данной модели. Сущест-
Существен тот факт, что будем считать их функцией лишь производительностей
источников:
Производственные затраты Зи>/ по источнику складываются, как известно,
из затрат на топливо, амортизацию основных фондов, текущий ремонт,
заработную плату обслуживающего персонала и прочие расходы. Часть из
них представляется соответствующими долями от капиталовложений, а
Другая так или иначе зависит от мощности источника, так что
Таким образом, целевая функция может быть записана в следующем
Достаточно общем виде:
3 = (?4/c) 2 (e/ + M?)I/sign|*,| + c,3r+ ^ Щх{), A3.19)
гДе Wj(xj) = (Е + fK)KK,j{Xj) + W/(Xj) - расчетные затраты на строитель-
ство и эксплуатацию источника в узле/.
181

Нетрудно убедиться, что после всех преобразований, связанных с исполь-
использованием частичной функции Лагранжа и аналогичных тем, которые произ-
производились выше, придем к модели С, состоящей в минимизации функции
F(x)+ 2^ Щх,), A3.20)
где F(х) совпадает с A3.16), при выполнении условий материального ба-
баланса в узлах.
Значение моделей А, В, и С с методической и вычислительной точек зре-
зрения состоит и в том, что в них можно освободиться от связывающих урав-
уравнений и перейти к задаче на абсолютный экстремум. Для- этого достаточно
разрешить систему уравнений первого закона Кирхгофа относительно
выбранной группы зависимых переменных и, подставив их выражения в
целевую функцию, получить в результате задачу на поиск точки абсолютно-
абсолютного минимума этой преобразованной функции.
Рассмотрим подробнее такой переход, но для упрощения изложения
возьмем целевую функцию в виде одной суммы:
п
р/чл — у_1/A + 0(И)||За:м/A+<*ы) /1 ч -> 1 \
i = 1
Соответствующее разделение переменных произведем выбором полного
дерева на исходной схеме, тогда (см. гл. 4)
т.е. в качестве независимых переменных берутся контурные расходы
Хк = (Xj , . . . , Хс) .
Из A3.22) имеем
С
х,= 2 brixr+xf0), i = c+ I,... ,п, A3.23)
где х) — значения расходов на ветвях выбранного дерева и х\ = 0 для
i = {,..., с; brj — элементы матрицы контуров В. После подстановки
A3.23) в A3.21) получим функцию
с
F(xK) =
i = 1
п
+ 2
I = С + 1
с
2
г = 1
До)
Зан/A +аи)
A3.24)
которую необходимо минимизировать по независимым переменным
*,•(/= 1,. . . ,с).
Функция F(xK) в отличие от F(x), которая является вогнутой, имеет
более сложный многоэкстремальный характер. С целью изучения поведения
этой функции были проведены численные эксперименты на ЭВМ для услов-
условной схемы, приведенной на рис. 13.1. Она исследовалась покоординатно
при изменении значений каждой из контурных переменных х,- на отрезке
[~ Qz. > Qx\ > Для чег0 им присваивались некоторые дискретные значения,
начиная с нуля, с различными шагами.
В соответствии с задаваемыми значениями каждой из независимых пе-
182

[ з. 1. Пример схемы г.ц.
Цифры в кружке — номер узла-по-
узла-потребителя с нагрузкой в м3/ч; в узле
j расположен источник; цифры между
узлами-длины участков в м
/40,
ременных пересчитывались расходы на ветвях дерева, входящих в соот-
соответствующий контур. Получаемые значения целевой функции выдавались
на печать, и так для каждого контура. Подобные расчеты проводились,
исходя из различных деревьев. На рис. 13.2 показаны графики, иллюстри-
иллюстрирующие полученные результаты и доказывающие многоэкстремальный
характер минимизируемой функции относительно контурных переменных.
13.3. СРАВНИТЕЛЬНЫЙ АНАЛИЗ МАТЕМАТИЧЕСКИХ МЕТОДОВ
И ВЫБОР АЛГОРИТМОВ СХЕМНО-СТРУКТУРНОЙ ОПТИМИЗАЦИИ
Если обратиться к математическим методам оптимизации, которые могут
быть применены для решения сформулированных выше сетевых задач
на условный и безусловный экстремум с вогнутой или более сложной мно-
многоэкстремальной минимизируемой функцией, то их можно разбить на
следующие три группы:
1) приближенные методы целенаправленного перебора деревьев исход-
исходной избыточной схемы PC, которые характеризуются генерированием мно-
множества деревьев начального приближения и их последующей локальной
оптимизацией (подобный метод описан в разд. 13.1);
2) "усиленные" локальные методы оптимизации с поиском абсолют-
абсолютного экстремума по перебираемым направлениям поиска [107, 159], а
также метод многоконтурной оптимизации (гл. 15);
3) "строгие" методы, среди которых в настоящее время можно выде-
выделить методы: вогнутого программирования [31], ветвей и границ [289, 24]
и построения последовательности планов "в порядке ухудшения оценочной
функции (миноранты или мажоранты) " [63].
Дадим этим методам краткую сравнительную характеристику, опираю-
опирающуюся на результаты некоторых численных экспериментов на ЭВМ, с целью
выбора работоспособных и быстродействующих алгоритмов схемно-струк-
тУрной оптимизации.
Что касается наиболее рациональных алгоритмов перебора деревьев,
™ они будут описаны в конце раздела. А обзор начнем с работ И.Б. Моцку-
са и В.Л. Леонаса [107, 159], в которых сформулирована и практически
апробирована (на задачах оптимизации конфигурации электрических
сетей) идея об усилении локальных методов минимизации посредством
183

тхождения по каждому из выбираемых направлении поиска не локально-
го. а абсолютного минимума.
Данный подход является наиболее подходящим здесь в случае перехода
к задаче безусловной минимизации функции вида A3.24) по контурным
переменным. Вычислительная эффективность подобного процесса весьма
зависит от быстродействия алгоритма одномерной минимизации. Л по-
поскольку функция A3.24) в общем случае принадлежит к классу недиффе-
реНцируемых функций (из-за наличия постоянных составляющих а,- в удель-
удельных затратах и других особенностей), то речь должна идти о методах поис-
поиска экстремума без вычисления производных.
Д.И. Батищев [19] рассматривает подобные методы поиска глобального
экстремума функции от одной переменной с предварительным выявлением
подынтервалов, содержащих по единственной точке локального минимума.
Из этих минимумов выбирается наименьший, который и считается абсо-
абсолютным для исследуемой функции. Для определения подынтервалов ис-
используется процедура построения кусочно-линейной функции, которая
имеет такое же число локальных минимумов, что и исходная; затем для
поиска точек локальных минимумов применяются, например, методы "зо-
"золотого сечения" и ДСК-Пауэлла [253] .
В соответствии с этим авторами была разработана специальная програм-
программа, по которой проводились исследовательские расчеты. Расчеты показали,
что метод глобальной поконтурной минимизации представляет интерес
возможностью получать оптимальные конфигурации сетей не только среди
деревьев, но и в виде кольцевых сетей, что существенно при решении задач
развития структуры систем с учетом их существующей части. Однако
он гораздо более трудоемкий, чем метод перебора деревьев, и время счета
для него оказывается в десятки раз большим при практически совпадаю-
совпадающих результатах.
Другой подход к реализации математических моделей А я В может за-
заключаться в применении общих математических методов вогнутого и дис-
дискретного программирования, например, разработанный в СЭИ В.П. Булато-
Булатовым [31] метод последовательного отсечения подобластей допустимых
решений, содержащих точки локальных минимумов вогнутой функции.
Среди найденных локальных минимумов выбирается наименьший, который
и дает глобальное решение задачи. При оптимизации этим методом конфи-
конфигурации PC на схеме с параметрами т = 35 и п = 51 возникли трудности
из-за медленной сходимости вычислительного процесса отсечений. Для их
преодоления автором метода было предложено осуществлять сдвиг отсе-
отсекающей гиперплоскости на некоторую величину h. Однако это привело к
трудно решаемой проблеме рационального выбора данной величины: при
увеличенном значении h можно пропустить глобальный минимум целевой
функции, а при малых h процесс оптимизации требует чрезмерного машин-
машинного времени даже для сравнительно небольших сетей.
Можно обратиться также к методу ветвей и границ, широко используе-
используемому для численного решения задач дискретного программирования.
Известно его эффективное применение для решения задач оптимизации
электрических сетей, описанное в работах А.И. Лазебника и О.Н. Цаллаго-
в°й [105]. Реализованный ими алгоритм ограниченного перебора вариан-
вариантов сети основан на последовательном делении множества допустимых
185

решений с отбрасыванием подмножеств, которые имеют чрезмерную ниж-
нижнюю оценку минимизируемой функции. Теоретически это обеспечивает по-
получение глобального минимума, но с заданной допустимой погрешностью.
Если эта величина мала, то процесс сходится медленно. Кроме того, рас-
распространение данных разработок на ТПС требует специальных исследований
и соответствующей алгоритмизации.
Подходящим методом для решения задач схемно-структурной оптими-
оптимизации представляется предложенный В.А. Емеличевым и В.И. Комликом
[63] метод построения двойной последовательности планов. Сущность его
состоит в "конструировании" (дополнительно к исходной) более простой
задачи, удовлетворяющей двум условиям: 1) для нее относительно легко
может строиться последовательность планов в порядке ухудшения ее
целевой функции, однако 2) последовательность значений этой вспомо-
вспомогательной целевой функции должна представлять неубывающую нижнюю
границу (миноранту) для допустимых значений минимизируемой функции
исходной задачи.
Проведенные в СЭИ СВ. Сумароковым исследования, связанные с при-
применением такого подхода для решения задач, обсуждаемых в данной главе,
показали возможность построения подобных вспомогательных сетевых
задач и перспективность этого метода.
Задачи схемно-структурной оптимизации являются частными случаями
более общей проблемы оптимального синтеза многоконтурных систем и
потому в принципе могут решаться методом многоконтурной оптимиза-
оптимизации (эти вопросы рассматриваются в гл. 15 и 16).
Таким образом, если говорить о методе, который необходимо выбрать
в качестве рабочего с целью использования его в реальной проектной прак-
практике для схемно-структурной оптимизации систем, имеющих сотни узлов
и ветвей, то на сегодня наиболее эффективным следует признать метод
целенаправленного "поконтурного" перебора деревьев исходной избыточ-
избыточной схемы. Данный вывод согласуется и с возможным применением здесь
описанного выше метода В.А. Емеличева и В.И. Комлика, поскольку отве-
отвечающие ему последовательности планов исходной и вспомогательной
задач должны строиться, опираясь на эффективные процедуры перебора
деревьев.
Предлагаемый ниже алгоритм поиска оптимального дерева (или леса
в случае нескольких источников) на избыточной схеме системы учитывает
многолетний опыт разработки и реализации такого рода алгоритмов в соот-
соответствующих стандартных программах. В него внесен ряд существенных
изменений по сравнению с процедурой перебора, описанной в разд. 13.1.
Во-первых, просмотр каждого контура с целью последовательной замены
его ветвей, принадлежащих дереву, на хорду теперь производится до конца,
так что лучший вариант выбирается с точки зрения всех ветвей, входящих
в обрабатываемый контур. Во-вторых, введен повторный цикл итераций, а
именно: вариант дерева, соответствующий наименьшему значению крите-
критерия (среди всех просмотренных деревьев), вновь берется в качестве дерева
начального приближения и для него повторяется вся процедура "поконтур-
"поконтурного" перебора. Это может дополнительно (иногда довольно значительно)
улучшить решение. В-третьих, процесс минимизации заканчивается лишь в
том случае, когда очередной полный просмотр списка хорд уже не приводит
186

к уменьшению целевой функции. Кроме того, применен способ компакт-
компактного хранения множества обрабатываемых деревьев, что обеспечивает эко-
экономное использование памяти ЭВМ, более быстрый просмотр и обработку
рабочих массивов и т.д.
Все это с учетом перехода к использованию более мощных ЭВМ позволи-
позволило производить рационально организованный перебор значительно больше-
большего числа деревьев и существенно повысить размерность решаемых задач.
Соответствующий алгоритм поиска оптимального дерева на исходной схе-
схеме состоит из следующих основных операций.
1. Строится некоторое дерево начального приближения (ДНП) с расхо-
расходами на ветвях, удовлетворяющими балансам в узлах, для чего:
1.1. Одному узлу/о, выбранному в качестве корня дерева, присваивает-
присваивается метка в/ = 1, а для всех других узлов задается 6j = 0.
1.2. Отыскивается ветвь [/'j, /2], у которой один из ее узлов имеет не-
ненулевую метку; она ориентируется так, чтобы узел с нулевой меткой стал
для нее конечным; затем к меткам начала и конца этой ветви прибавляется
по 1 и она запоминается; такой процесс продолжается до тех пор, пока мет-
метки всех узлов не станут отличными от нуля.
1.3. Проводится "обратный ход" для суммирования расходов вдоль по-
полученного дерева: отыскивается ветвь / = \Ji,'n], метка конца которой
бу = 1; от меток ее концевых узлов вычитается по 1 и на данной ветви
назначается расход Xj, равный сосредоточенному расходу Q/ (с учетом его
знака) в узле/2; далее к величине расхода в его начальном узле/i добав-
добавляется Xj и т.д. — это повторяется для всех ветвей, пока не окажется равной
единице метка выбранного корня /0.
Итогом проделанных операций будет ДНП с известными расходами на
всех его ветвях. Ветви, не вошедшие в ДНП, составят список хорд ir (r =
= 1, . . . , с). Каждая из них замыкает в виде контура некоторую последо-
последовательность ветвей дерева, которую будем обозначать через Dr .
1.4. Для ДНП подсчитывается значение целевой функции Fo, при этом
используются формулы A3.16) или A3.20).
Данные пункты составляют этап получения и расчета очередного ДНП.
На втором этапе осуществляются операции по возможному улучшению
полученного дерева поконтурной заменой его ветвей хордами:
2.1. Для каждой хорды ir отыскиваются ветви / ? Dr, входящие в оп-
определяемый ею контур, и в нем поочередно "проводятся" (см. гл. 2)
контурные расходы, берущиеся равными по модулю (но с обратным зна-
знаком) расходам на этих ветвя"х. Любой подобный пересчет обратит в нуль
расход на одной из них, что переводит данную ветвь в разряд хорд и соот-
соответственно дает новый вариант дерева.
2.2. Определяется значение целевой функции, отвечающее каждому но-
новому дереву, для чего достаточно изменить сумму только тех слагаемых
в F(x), которые относятся к Dr.
2-3. Среди полученных (для всех / S Dr) величин F {х) определяется
наименьшая, и если она оказывается меньше, чем Fo, то запоминается вмес-
вместо Fo, соответствующая ветвь с нулевым расходом заменяет хорду ir,
а вновь полученное дерево принимается как исходное для последующей
оптимизации.
187

Когда операции 2.1-2.3 выполнены для всех хорд одного ДНП, то в па-
памяти ЭВМ остается преобразованное дерево, дающее наименьшее значение
F(x) на множестве просмотренных вариантов. На этом заканчивается одна
"большая" итерация. Следующая такая итерация начинается с построения
ДНП от нового узла / (п. 1.1-1.3), затем проводится его улучшение и т.д.
Всего строится т ДНП - по числу узлов исходной избыточной схемы.
Из всех полученных локально-оптимальных значений F выбирается наи-
наименьшее, а соответствующее ему дерево принимается за новое начальное
приближение, для возможного улучшения которого вновь применяются
п.- 2.1-2.3. Тем самым осуществляется повторный цикл итераций, но с не-
некоторым изменением: в случае перехода к дереву, улучшающему значение
целевой функции, обновляемый список хорд просматривается каждый
раз заново с целью более полного перебора вариантов. Выполнение алгорит-
алгоритма заканчивается, если при очередном просмотре всех хорд не удается
уменьшить значения F.
Алгоритмы "поконтурного" перебора деревьев типа описанного выше
послужили основой для создания ряда стандартных программ, реализую-
реализующих математические модели схемно-структурной оптимизации PC, исходя
из их избыточных проектных схем. Они зарекомендовали себя как эф-
эффективный инструмент для решения проектных задач в области ТПС .
13.4. ПРИМЕРЫ РАСЧЕТОВ РЕАЛЬНЫХ ОБЪЕКТОВ
В настоящее время практически используются следующие три програм-
программы, разработанные на языке Фортран для ЭВМ БЭСМ-6 и ЕС-1033:
1) ТРАССА-1 реализует модель В, т.е. на заданной избыточной схеме
системы и при известных производительностях ее источников обеспечивает
выбор наивыгоднейшей конфигурации PC;
2) ТРАССА-2 решает аналогичную задачу, но с дополнительным учетом
затрат на сооружение ветвей-хорд, не вошедших в оптимальное дерево
(т.е. в минимизируемую функцию все время добавляется стоимость про-
прокладки "кольцующих" ветвей, исходя из минимального диаметра труб,
допускаемых к прокладке).
С помощью этой программы определяется так называемое "оптималь:
но подготовленное дерево" (ОПД), которое может использоваться при ана-
анализе возможных оптимальных решений и, кроме того, служить начальным
приближением при решении более общей задачи оптимального синтеза
многоконтурных систем (см. гл. 15 и 16);
3) СТРУКТУРА позволяет решать задачи, описываемые моделью С, т.е.
оптимизировать структуру PC путем минимизации общих затрат в строи-
строительство и эксплуатацию как источников снабжения, так и сети, связываю-
связывающей их с потребителями.
Предельные параметры исходных схем для всех программ следующие:
п < 500, т < 400, число источников специально не ограничивается. Время
счета зависит от размеров и особенностей конфигурации исходных избы-
избыточных схем. Оно колеблется от секунд до нескольких минут (например,
10 мин для схемы с п = 106). Вместе с тем имеется пример задачи (т = 292,
п = 327), решение которой потребовало более 2 ч машинного времени
БЭСМ-6.
188

Данные программы используются различными организациями для
схемно-структурной оптимизации тепло- и водоснабжающих систем. Приве-
Приведем примеры их применения при проектировании двух реальных объектов:
ТСС города и Пресновского группового водопровода (расчеты выполня-
выполнялись совместно с проектными организациями).
Первый пример относится к одновременному выбору оптимальной кон-
конфигурации тепловой сети и необходимого числа источников с оптимизацией
их производительностей для ТСС одного из крупных городов. По имеюще-
имеющемуся плану города была намечена совместно с проектировщиками избыточ-
избыточная схема, учитывающая расположение улиц и автодорог, переходы через
железнодорожные пути и другие ограничения. Были заданы узлы с намечае-
намечаемыми площадками для размещения новых источников тепла (районных
котельных) и отмечены уже существующие котельные. В результате была
получена схема с т = 80 и п = 106 (из них в 31 узле - потребители, в 12 -
возможные источники тепла, новые и существующие), которая и представ-
представлена на рис. 13.3.
Для подсчета капиталовложений в тепловую сеть использовалась таблица
удельных стоимостей прокладки трубопроводов для непроходных сборных
железобетонных каналов (в сухих грунтах), которая была аппроксимиро-
аппроксимирована зависимостью
#уя = 65 + 586,7 с?1'18.
Остальные показатели здесь были следующими: ф =0,01271 (при коэф-
коэффициенте шероховатости 0,5 мм); а = 0,1905; сэ - 0,021 руб/кВт • ч; /с =
= 0,08; ? = 0,12; пс = 5400; т?нас=0,7.
Расчетные тепловые нагрузки показаны на схеме. Там же указаны и дли-
длины всех ветвей в метрах.Ветви 64-67, 92-93, 23-24 и 41-42 выделены в
особую группу, поскольку они представляют переходы через железную
дорогу, которые удорожают стоимость прокладки трубопроводов.
Исходные технико-экономические показатели по районным котельным:
пТ - 2600 ч/год — расчетное число часов использования отопительной на-
нагрузки; ст = 42 руб/т. у.т. — строимость топлива; Ьуа = 0,17 т/Гкал —
удельный расход топлива на 1 Гкал (с учетом к.п.д. котлов). Были заданы
также возможные диапазоны изменения производительностей источников
и соответствующие им капитальные затраты, которые вычислялись при ус-
установленной стоимости, равной 20 тыс. рубл. на 1 Гкал/ч.
Наличие в системе уже существующих котельных потребовало провести
многовариантные расчеты с целью наилучшего использования новых
перспективных котельных. (Описанные выше программы позволяют за-
заданием соответствующих коэффициентов для подсчета затрат в источники
Добиться обращения в нуль этих затрат для уже существующих источников
и учитывать лишь эксплуатационные расходы.) Были рассмотрены следую-
следующие ситуации:
1 • Первый вариант — три возможных новых источника в узлах 8, 10 и 13,
остальные - существующие котельные с ограниченными производитель-
ностями, причем для котельных в узлах 3 и 6 разрешалось увеличить их
производительность до 300 Гкал/ч.
В результате работы программы был получен оптимальный вариант
стРУктуры ТСС, которая показана на рис. 13.3 (выделена жирными линия-
189

13.3. Избыточная схема и оптимальная структура ТСС
ми). Видно, что вся схема распалась на ряд подсистем. При этом две су-
существующие котельные (в узлах б к 11) используются на полную мощ-
мощность, а остальная нагрузка распределилась между двумя новыми источни-
источниками 8 и 13.
190

2. Второй вариант — учет существующих котельных, но без ограничений
на их производительность, причем с помощью подбора необходимых коэф-
коэффициентов у слагаемых целевой функции учитывались затраты лишь на
расширение этих источников. В этом случае в оптимальном распределении
нагрузок между источниками участвуют 4 котельные в узлах 4, 6, 11 и 12.
расчетные затраты по ТСС здесь снизились на 19% по сравнению с оптималь-
оптимальным решением первого варианта.
Время счета на БЭСМ-6 для каждого из вариантов составило 10 мин.
результаты оптимизации были использованы при принятии окончательно-
окончательного решения о развитии этой ТСС.
Другой объект — Пресновский групповой водопровод (схема показана
на рис. 1.4), являющийся сложной ТПС огромной протяженности (в сотни
км). Местность, по которой он должен пройти, пересечена сетью шоссейных
дорог и линиями электропередач, изобилует озерами и заболоченными
участками. В результате анализа этих особенностей была составлена ис-
исходная избыточная схема с количеством узлов т= 299 (из них 260 узлов -
с водоиотреблением, а остальные - возможные точки разветвления), вклю-
включая три предполагаемые источника.и количеством связей и = 334.
Приведенные затраты, связанные со строительной стоимостью системы,
подсчитывались по формуле, полученной аппроксимацией сметных данных
по удельным капиталовложениям в прокладку труб соответствующего
диаметра на единицу длины:
Kya = 62,5d1'22.
Значения капитальных затрат на насосные станции были заданы таблицей
в зависимости от дискретного ряда их возможных производительностей.
Остальные технико-экономические показатели были следующими (см.
A3.12) и A3.13)): ?=0,12;/с = 0,06; сэ = 0,017 руб./кВт • ч,иг =-8760;
г? = 0,75; а = 0,1876; ф= 0,01372 (при коэффициенте шероховатости
труб 1 мм).
Расчеты проводились по программе СТРУКТУРА. Вся система водопро-
водопроводов распалась на три самостоятельные PC, которые затем были детально
рассчитаны по программе динамического программирования (см. следую-
следующую главу) для определения их оптимальных параметров: диаметров от-
отдельных трубопроводов, оптимальных действующих напоров в источниках
и необходимого минимума дополнительных подкачивающих НС. В резуль-
результате такой оптимизации оказалось, что достаточно установки лишь четырех
НС вместо восьми в варианте, предложенном проектировщиками. В целом
же суммарные расчетные затраты по объекту получились на 5,6% меньше,
чем в проектном варианте.
Кроме данных объектов, проводилась схемно-структурная оптимизация
и других систем различного типа и масштаба. Эти расчеты показали: 1) хо-
хорошее соответствие методики избыточных проектных схем и отвечающих
ей математических моделей реальной проектной практике в области ТСС
и ВСС; 2) относительно небольшую трудоемкость, связанную с освоением
и практическим использованием разработанных программ для ЭВМ, по-
поскольку исходная информация максимально приближена к реальным дан-
данным; 3) экономическую эффективность применения данных разработок
в проектной практике.
191

Глава 14
ОПТИМИЗАЦИЯ ПАРАМЕТРОВ РАЗВЕТВЛЕННЫХ СИСТЕМ
В настоящей главе приводятся математическая формулировка задачи и ал-
алгоритм оптимизации PC, реализованный в стандартных программах для
ЭВМ БЭСМ-6 ЕС ЭВМ, а также излагаются способы, позволившие повысить
эффективность пошаговой оптимизации для данного класса задач.
14.1. УСОВЕРШЕНСТВОВАННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
ДЛЯ ОПТИМИЗАЦИИ ПАРАМЕТРОВ PC
Рассматривается математическая модель для оптимизации параметров
PC, которая предназначена не только для вновь проектируемых, но и
развиваемых систем с несколькими источниками и при сложном релье-
рельефе местности. Она обобщает модели, разработанные в СЭИ (первая публи-
публикация [123] относится к 1963 г.), и учитывает основные требования реаль-
реальной проектной практики в области ТСС и ВСС. Модель, в частности, обеспе-
обеспечивает оптимальный выбор: способов реконструкции существующей часта
систем, мест установки и параметров НС и дроссельных станций (ДС), ко-
которые могут потребоваться для понижения (гашения) избыточного напора
на отдельных ответвлениях, и других характеристик PC.
Для начала обратимся к простой последовательности ветвей, но с отбора-
отборами (нагрузками) в промежуточных узлах и с одним источником в узле
/ = 1 (рис. 14.1). С каждой ветвью связывается следующее соотношение
между ее техническими и гидравлическими параметрами:
L,(l+5 (<?,)) „
¦„ *,? = */*?. A4.1)
где y{kj) — коэффициент, зависящий от шероховатости к, трубы; 5(J,) —
коэффициент местных потерь (задается таблично); а - показатель степе-
степени, характеризующий тип системы, например, для ТСС а = 5,25, для ВСС
а = 5,33; хг- — коэффициент гидравлического сопротивления ветви.
Будем считать, что НС или ДС, если они имеются на ветви, расположены
в ее начальном узле. Тогда конкретное состояние системы можно изоб-
изобразить в виде графика изменения давления по всем узлам/ = 1,, .., т
и участкам i = 1,... , и (для PC т - п + 1). Такой график представим в
виде ломаной, состоящей из наклонных и вертикальных звеньев. Так,
на рис. 14.1 показаны ДС в узле 3 и НС в узле / — 1, а отрезки ломаных,
соединяющие значения давлений в двух соседних узлах, отражают пере-
перепады давления на участках.
Таким образом, состояние каждой ветви i = [/' - 1, / ] может быть
описано с помощью трех величин: исходного узлового давления Р/-г
с которым среда доставляется в начальный ее узел; скачка (подъема
или понижения) давления #у, где Я,- > 0 для НС и Н{ < О в случае ДС;
конечного узлового давления Pj. В качестве вспомогательной величины
введем
192

14.1. Изменение давления вдоль последовательности ветвей
I 1,2,...,/ ¦¦ I,/, ...,/и, —узлы; 1 —ветви; 2 — источник, 3 — отборы
14.2. Различные случаи измене-
изменения давления на ветви /
14.3. Изменение давления в
общем узле /
которую назовем стартовым давлением для ветви /. Этим параметрам
бУДУт соответствовать векторы: Р = {Рх Рт)\Н= (Нх Нп)\
13- Зак. 384
193

На рис. 14.2 представлены возможные случаи изменения давления для:
а) пассивной ветви, когда на ней нет ни НС, ни ДС; б) активной ветви
с НС в узле / — 1, обеспечивающей увеличение давления на величину #.,
и в) активной ветви с дросселированием (понижением) давления в узле
/ - 1 (здесь Н, < 0).
В каждом общем узле /, от которого имеется по меньшей мере два
ответвления, будет более сложная картина дискретного изменения дав-
давления, показанная на рис. 14.3, где н\ , Я/ - стартовые давления для
снабжаемых от узла / ветвей / г, z 2 и т.д. В частном случае эти давле-
давления могут совпадать с Pj, когда в узле / нет станций, изменяющих стар-
стартовые давления для последующих ветвей.
Управление вектором состояний Р осуществляется с помощью диаметров
dj и скачков давления Я,-, которые определены на дискретных множествах:
D - стандартных диаметров труб (сечений проводов) и Т - типоразме-
типоразмеров насосов, уже имеющихся на существующих НС либо разрешенных
к установке на новых станциях. Что касается возможных понижений дав-
давления с помощью дросселирующих устройств (станций), то для них обыч-
обычно не вводится никаких ограничений на возможные значения Н{ < 0.
Итак, в целом управление состоянием PC производится вектором и =
= (dy Я). Каждое управление «.определяет некоторую ломаную кривую,
описывающую соответствующее изменение давления в системе, причем
крутизна ее наклонных звеньев зависит от вектора d, а длина вертикаль-
вертикальных - от Я.
Перейдем к математической формулировке задачи оптимизации пара-
параметров произвольной PC. Заданными являются:
схема PC, т.е. граф (/, /) в виде дерева с указанием существующих
(/ S /,) и вновь проектируемых (/ S /2) ветвей и их длин Lt;
нагрузки Qj у потребителей (Qj > 0, / G /1) ив узлах-источниках
(б.- < 0, / € Jг), такие, чтобы соблюдался их баланс по системе в це-
целом;
подмножество ветвей (г G /3), на которых разрешается сооружение
новых НС (для таких участков задается признак у = 1) или НС и ДС на них
уже имеются G = 2);
стандартный набор D ={di,. .., dz) диаметров труб, допускаемых
к прокладке;
множество Т характеристик насосов, которые могут устанавливаться
на НС;
все необходимые для целевой функции и замыкающих соотношений тех-
технико-экономические показатели и коэффициенты;
ограничения на способы реконструкции для ветвей г € /,, на допус-
допустимые давления Pj в узлах и удельные потери давления Л/уд (см. ниже).
Необходимо найти такое управление и G (Д Г), которое обеспечит
минимум общих расчетных затрат по всей системе, т.е. требуется мини-
минимизировать
F(u) = 2 F.(d.,H., P.) = _ |^ (g.(d.) + z.(x.,h.) + ф.(х., Я.)) +
+ 2 z(P Q), A4-3)
i &J J ' '
194

де g., Zj, ф(, Zj - затраты соответственно на: прокладку участков;
еКТроэнергию, требующуюся на перекачку среды; строительство НС и
энергию, доставляемую потребителям, — они вычисляются, например,
по следующим формулам:
gtW-(E+fe)KvnWLt; A4.4)
A4.6)
где со = сэ«г/367,2т? — константа, а остальные обозначения совпадают с
введенными ранее, в гл. 13.
При этом должна выполняться прежде всего система уравнений, свя-
связывающая вектор Р фазовых переменных с допустимыми значениями
управлений:
ATP=h(d)-H = y. A4.8)
Параметры каждой ветви должны удовлетворять замыкающему соотно-
соотношению A4.1), где dt G D. На переменные Pj налагаются ограничения в
виде неравенств, которые могут иметь различную природу: от необходи-
необходимости учета рельефа местности до технических ограничений на прочность
используемых труб:
P.<P.<P.,jGJ. A4,9)
Выбор допустимых управлений может производиться также с учетом
ограничений на удельные потери давления по ветвям, что будет соответст-
соответствовать заданию диапазонов разрешаемых скоростей течения жидкости
или газа:
h. <A. < h. , i<EI. A4.10)
-', уд I, уд I, уд' v '
Следующие соотношения:
V.(d.)eV(D), /=/,, d.eD.CD; A4.11)
Я.?7^7), /е/з, 7=1,2 A4.12)
отражают условия дискретности диаметров и оборудования для НС, а
также конкретные требования к возможным способам реконструкции
существующих ветвей и использования в перебираемых решениях НС
и ДС (как уже имеющихся, так и вновь сооружаемых).
Матричная запись A4.8) системы уравнений эквивалентна описаниям
изменения давления вдоль каждого из ответвлений в PC:
Рп+ 2 (Я.-А.)-^ + 1=0, A4.13)
где / 1, /у +1 - начальный и конечный узлы ответвления, а /ь
ветви, которые его составляют.
195

Кроме того, вектор Н1 стартовых давлений может быть выделен из
A4.8) расщеплением матрицы А на подматрицы A i и А 2 начальных и
конечных узлов ветвей в схеме PC:
Н'=А\Р+Н или H'=-All>+h.
В результате решения задачи минимизации функции A4.3) при условиях
A4,1), A4.8) — A4.12) должны быть определены оптимальные параметры
PC, а именно: диаметры di для i € /2; ветви / из множества / ь подле-
подлежащие реконструкции, и способы v t ? Vt {dt) этой реконструкции; места
(узлы расположения и параметры НС и ДС для i € /3; давления во всех
узлах, включая и действующие напоры в источниках / S / 2.
Основными особенностями данной модели являются: нелинейная за-
зависимость A4.1) между hj.x^di; дискретность условий A4.11),
A4.12); табличное задание удельных стоимостных показателей К и К
для целевой функции A4.3), а также коэффициентов местных потерь
5 (d{) в A4.1); возможность оптимального учета уже существующих эле-
элементов PC при решении задачи о ее развитии и реконструкции. Если вновь
проектируемые PC характеризуются, как правило, относительно пологой
целевой функцией [241], то при росте числа ограничений и логических
условий допустимая область может сдвинуться в зону большей крутиз-
крутизны минимизируемой функции, а учет существующей части PC вообще
приводит к появлению у этой функции "зон провалов", определяющих
дополнительные локальные минимумы. Все это не только усложняет эту
задачу, но и повышает практическое значение использования современных
методов дискретной оптимизации, особенно динамического программиро-
программирования.
По сравнению с исходной моделью, описанной в работе [123], здесь
учитываются также: наличие в системе нескольких источников снабжения,
рельеф местности, множество индивидуальных характеристик ветвей
и узлов PC. Множественность источников снабжения отражается с помощью
знака у величин расходов: полагается х(> 0, когда соответствующая
ветвь хотя бы частично снабжается от источника, выбранного в качестве
"главного" (т.е. корня дерева, характеризующего оптимизируемую PC);
задается х,- < 0, если снабжение ветви i полностью осуществляется от
любых других источников.
При оптимизации PC, имеющих сложный рельеф местности, а также
в случае сложной совокупности ограничений, описывающих область до-
допустимых решений (корректность которой практически невозможно
проанализировать до расчета), система условий A4.1), A4.8) — A4.12)
может оказаться несовместной. В подобных случаях, когда не сущест-
существует ни одной допустимой "траектории" изменения давлений по всем
элементам PC, математическая модель позволяет выявить "узкие места"
допустимой области, а также определить решение, в наименьшей мере
нарушающее заданные ограничения,
196

14.2. ОБЩАЯ СХЕМА МЕТОДА ДП
ДЛЯ ОПТИМИЗАЦИИ ПАРАМЕТРОВ PC
И СПОСОБЫ ПОВЫШЕНИЯ ЕГО ЭФФЕКТИВНОСТИ
В основу метода решения сформулированной задачи положена пошаговая
оптимизация (динамическое программирование) как наиболее эффектив-
эффективная в данном случае процедура, которая позволяет в должной мере учесть
и математические особенности задачи, и индивидуальные характеристики
каждого из объектов оптимизации.
Предметом ДП в его традиционном описании [21] являются много-
многошаговые процессы оптимального управления во времени для различных
систем. Основная идея алгоритмизации таких процессов заключается в
построении и "наращивании" посредством пошагового перебора множест-
множества условно-оптимальных "траекторий", отражающих в дискретной форме
всю область допустимых решений, с обязательной оптимизацией всех воз-
возможных исходов относительно перебираемых на каждом шаге значений
фазовых переменных. Заключительным этапом является так называе-
называемый "обратный ход", который позволяет выделить из этого множества
наилучшую траекторию, отвечающую заданным краевым условиям ре-
решаемой задачи.
В данном случае эти положения интерпретируются следующим обра-
образом: управляемая система — оптимизируемая PC; роль времени играет
протяженность ее сети от главного источника до потребителей, причем
с каждой ветвью и каждым узлом связывается один шаг процесса при-
принятия решений; управление сводится к выбору диаметров труб на вет-
ветвях, а также узлов для размещения активных элементов (НС и ДС);
фазовые переменные — это давления Р^ в узлах и стартовые давления
Н- — для участков, определяющие конкретное состояние PC.
Одной из предпосылок для применения метода ДП является аддитив-
аддитивность (сепарабельность) целевой функции, что здесь также имеет место:
общие расчетные затраты A4.3) по PC естественным образом складывают-
складываются из отдельных составляющих по ее узлам и ветвям.
Математической формализацией ДП являются функциональные урав-
уравнения рекуррентного типа, описывающие перебор вариантов на каждом
jV-m шаге и сдвиг индексов (на единицу) от шага к шагу. Рассмотрим
вывод этих уравнений для одной магистрали (/ = 1,,.., п; j = 1,...,
и + 1 - см. рис. 14.1), разворачивая процесс ДП от ее конца к началу.
Последнее, вообще говоря, не принципиально, но в случае ТСС и ВСС
представляется более удобным, поскольку давления в концевых узлах,
как правило, фиксируются в то время, как действующие напоры в ис-
источниках входят в число искомых оптимизируемых параметров. Кроме
того, организация многошагового процесса, начиная именно с концевой
ветви (т.е. N = п + 1 — /, / = п, ... ,1), оказывается целесообразной при
оптимизации PC с произвольной схемой соединений, когда необходимо
стыковать" в общих узлах частичные траектории, построенные для
отдельных ответвлений.
Методика ДП, обеспечивающая перебор решений с отсеиванием заведомо
неоптимальных вариантов, должна применяться здесь на каждом шаге
Дважды (см. рис. 14.3): один раз — для оптимального выбора на /-й вет-
и " ~ 1' /1 диаметра с?(-, отвечающего конкретному значению Н/ , и вто-

рой раз - для выбора скачка Я,- давления (включая и случай Ht = 0)
в начальном узле / - 1 этой же ветви применительно к каждому пере-
перебираемому значению давленияР/ _,. Аналитически это может быть описа-
описано следующей парой функциональных уравнений:
F*(Я') = min (g.(d) + zXx ,Н\,P.) + F*{P,)) =
i1 I
r j A4.14)
F*(P ) = min (ф(х H,-P ) + F*(H') =
=^(xrH*) + F*(H'.\ A4.15)
где верхний индекс в виде "звездочки" обозначает минимум целевой
функции и оптимальную величину искомых параметров, соответствую-
соответствующих значению фазовой переменной, указанной в качестве аргумента функ-
функции F. При этом должны выполняться все заданные ограничения A4.9) —
A4.13).
Формальная численная реализация данных уравнений приводит к чрез-
чрезмерным затратам машинного времени и памяти ЭВМ при оптимизации
параметров реальных PC, имеющих сотни участков, десятки стандартных
диаметров и типоразмеров оборудования для НС, а также большое число
узлов с ответвлениями (примеры такого рода систем см. ниже). Это
связано с тем, что прямой порядок вычислений, определяемый уравне-
уравнениями A4.14) и A4.15) для шкал значений, описывающих допустимые
интервалы изменения Н/ и Pj _ l, влечет за собой многократное обра-
обращение к трудоемким формулам типа A4.1) и оперирование с "теорети-
"теоретическими" значениями й{ и Нг При этом требуется дополнительная про-
процедура для пересчета и обработки получаемых решений в связи с необ-
необходимостью округления d*w H. до стандартных значений и т.д.
В связи с этим ниже описывается модифицированная схема метода ДП
для оптимизации параметров PC, которая реализована в СЭИ в послед-
последних вариантах программ для БЭСМ-6 и ЕС ЭВМ [147, 179]. Она макси-
максимально учитывает специфику этих задач и опыт предыдущих алгоритми-
алгоритмических разработок, что позволило увеличить относительное быстродейст-
быстродействие вычислительного процесса в десятки раз по сравнению с первой про-
программой для БЭСМ-2.
Для организации перебора вариантов на ветви i = [f — 1, j ] магист-
магистрали (j = п + 1,.. ., 1; i = п, и — 1,..., 1) произведем разбиение (рав-
(равномерное или неравномерное) диапазона [ Р . .Р • _ {] на М ячеек
("луз"), с каждой из которых свяжем два значения: Pj_i ,, Hi,t
(t = 1,.. ., М). Обратимся теперь к общему TV-му шагу процесса оптими-
оптимизации диаметров на ветви i - п + 1 — N. Будем исходить из того, что в ре-
результате предыдущих N - 1 шагов (для ветвей п, и — 1,. . . , л+1-ЛО
уже определено множество из М частичных условно-оптимальных траек-
траекторий, начинающихся заданным давлением Рп +1 в концевом узле и окан-
оканчивающихся последовательностью значений Р- f, дискретно отражающих
допустимый диапазон давлений в узле /. Для них должны быть известны
19Я

^нимальные значения целевой функции A4.3) :
it' A» t' •" r t> * V> V • * ~S
'• r = 1-1 Г r' ' Г'Т
где в соответствии с A4.7) F(o) = c0Qn+lPn+l, а сумма имеет смысл и
подсчитывается при N > 2.
Вычислительная процедура, обеспечивающая решение уравнения A4.14)
соответствующим перебором вариантов, модифицируется следующим
образом:
1. Вместо того чтобы определять наилучшую для каждого фиксиро-
фиксированного Я/ "теоретическую" величину dt на ветви с помощью прямого
перебора допустимых падений давления А,- = Я,- — Pj t (t - 1,. .., М),
гораздо целесообразнее выполнять все операции, включая и проверку
ограничений, непосредственно на заданном дискретном множестве Dt
возможных значений d] .
Это, в свою очередь, делает предпочтительными естественным осуществ-
осуществление перебора данных стандартных диаметров относительно значений
не Я.', a Pj t, поскольку они являются реальными граничными значения-
значениями для частичных траекторий, построенных в результате выполнения пре-
предыдущих шагов. В итоге -получим Mz (где z — число перечисленных в
?>• значений dt) практически возможных (от узла/ к узлу/ - 1) "про-
"продолжений" для М условно-оптимальных траекторий, уже построенных
от конца магистрали и до узла/ .
2. В соответствии с этим операцию минимизации, указанную в A4.14),
можно организовать теперь для произвольно задаваемой шкалы значе-
значений Pj _, t "просеиванием" всех полученных Mz граничных значений
Pj; _, в узле / - 1 через ячейки этой шкалы. Смысл такой операции сос-
состоит в том, чтобы оставить в каждой ячейке лишь одно значение
P"j _ , <t, отвечающее траектории с наименьшей (с точки зрения всех вари-
вариантов, попавших в данную ячейку) величиной целевой функции.
Ячейка, для которой не оказалось ни одной траектории, остается пустой.
Это будет равносильно выбору не более чем М оптимальных траекторий,
проходящих через обрабатываемый диапазон значений Р- _ t.
Таким образом, если при формальной схеме ДП необходимо перебрать
М вариантов с полным выполнением всех вычислений по формулам A4.1),
A4.3) и другим (и к тому же потребуются дополнительные операции,
связанные с округлением получаемых диаметров до стандартных зна-
значений) , то для описанной модификации нужно подсчитать лишь Mz зна-
значений hf для перебираемых dt иР,- f. Это обстоятельство позволяет: не
производить аппроксимации табличных значений Kya(dt) в A4.4); зара-
заранее вычислить ряд величин (например, d", 6(<i;) в A4.1)), являющихся
общими для всех ветвей PC, и тем самым существенно сэкономить время
на численную реализацию самого процесса пошаговой оптимизации.
Кроме того, для PC, тепло- и водоснабжения А,- является функцией
лько х(. и параметров самой ветви, но не зависит от давлений в ее кон-
199

14.4. "Наращивание" условно-оптимальных траекторий изменения давления
1 — возможные варианты падения давления для ветви; 2 — варианты, выходящие
за пределы ограничений по давлениям; 3 - условно-оптимальные варианты; 4 -
график, соответствующий оптимальному решению для всей схемы
цевых узлах (как, скажем, в газопроводных системах). Это обстоятельст-
обстоятельство дает возможность дополнительно уменьшить время счета, поскольку
набор величин ht и соответствующих слагаемых в A4.3) как функций
лишь известных хг , h,- и стандартных d( может быть посчитан до пере-
перебора вариантов решений для ветви i . А получение Mz возможных зна-
значений Pj _ j осуществляется далее простым "откладыванием"пучка наклон-
наклонных звеньев ломаных, соответствующих этому набору h,-, от каждой
из точек Pj t. Общая картина "наращивания" условно-оптимальных тра-
траекторий изменения давления для трех последовательно соединенных вет-
ветвей дана на рис. 14.4.
Аналогичные приемы уменьшения трудоемкости вычислений можно
использовать и при решении уравнения A4.15) для получения оптималь-
оптимальных скачков давления Hi в начальном узле/ — 1 ветви г. Взятые вместе,
они обеспечивают многократное сокращение времени работы ЭВМ.
3. Следующая модификация процедуры счета позволяет, наоборот,
за счет некоторого удлинения вычислительного процесса существенно
снизить потребность в памяти ЭВМ. Она связана со способом организации
"обратного хода", который необходим для выдачи на печать искомой
оптимальной (с точки зрения всех PC) траектории изменения фазовых
переменных и отвечающих ей параметров ветвей и узлов.
Таким образом, алгоритм оптимизации параметров PC на основе мо-
модифицированной схемы ДП состоит из следующих основных операций:
200

1 Выбора в качестве корня дерева главного источника (как правило,
10 источник с наибольшей производительностью) и главной магистрали
oq - последовательности ветвей, соединяющей корень дерева с наиболее
удаленным потребителем. В соответствии с этим производится упорядо-
упорядочение всех исходных данных.
2. Начального шага процесса оптимизации каждого из ответвлений —
обработки его концевого участка. Для каждого перебираемого диаметра
подсчитываются и запоминаются: потеря давления — по формуле A4.1);
суммарные затраты на прокладку соответствующего трубопровода и на
электроэнергию, которая потребуется для перекачки как по данной ветви,
так и для снабжения зависимых от нее потребителей.
3. Общего шага — перебора вариантов и оптимизации управлений dj,
Hi, т. е. решения уравнений A4.14) и A4.15) модифицированным мето-
методом, описанным выше, для "наращивания" условно-оптимальных тра-
траекторий. Если узел / - 1 оказывается общим для нескольких ответвлений,
то результаты расчета данной ветви запоминаются и далее производится
выбор и расчет концевой ветви (см. п. 2) каждого из этих ответвлений,
но лишь до очередного общего узла и т. д.
4. "Стыковки" условно-оптимальных траекторий (по значениям фазо-
фазовой переменной Pj_ \ >г), полученных для различных ответвлений, в об-
общем для них узле / — 1. Каждый из вариантов траекторий для "главного"
ответвления пробуется на стыковку со всеми меньшими по давлению
Pj_ i <t траекториями другого (или других, если их несколько) ответвлений,
а именно: расчетные затраты для таких траекторий складываются и к ним
добавляются затраты, связанные с возможным дросселированием (из-за
неточности стыковки) давления на ответвлениях. Затем они сравнивают-
сравниваются между собой и для дальнейшего расчета (см. п. 3) оставляется не бо-
более М наиболее экономичных вариантов.
5. Заключительной процедуры "прямого хода" — выбора оптимальной
траектории по минимуму суммарных затрат для всей PC - в том случае,
если узел / - 1 оказывается корнем дерева.
6. Управления процессом оптимизации с целью обеспечения его сходи-
сходимости. Требуемая точность достигается повторением всего счета начиная
с п. 2 с увеличенным числом М точек разбиения допустимых интервалов
изменения фазовых переменных, например, до тех пор, пока не совпадут
(с заданной погрешностью) минимальные значения целевой функции для
двух соседних "больших" итераций.
7. Осуществления "обратного хода" для определения и выдачи на печать
¦оптимальной траектории изменения фазовых переменных и соответствую-
соответствующих параметров всех элементов PC.
Делается это многократным переносом корня дерева и повторением
оптимизации для леса частичных деревьев и ответвлений, на коренные
Распадается при этом PC.
При выполнении п. 2 и 3 в конкретных алгоритмах предусматривается
возможность перебора также и задаваемых способов реконструкции су-
существующих участков PC, т. е., например: прокладки параллельного трубо-
трубопровода, замены его на трубопровод большего диаметра или сохранения
без изменения. Конкретные условия реконструкции описываются с по-
помощью множеств A4.11).
201

Метод ДП и его применение для оптимизации параметров ВСС описаны
также в монографии [223]. Что касается оптимизации произвольных МКС
то данным задачам посвящена следующая глава. В ней же более детально
изложены и приемы трансформации многоконтурной схемы в развет-
разветвленную.
14.3. ПРИМЕРЫ ОПТИМИЗАЦИИ РАЗВИТИЯ
И РЕКОНСТРУКЦИИ РЕАЛЬНЫХ PC
Метод многошаговой оптимизации параметров PC неоднократно реализо-
вывался в СЭИ в виде стандартных программ для различных ЭВМ. Первые
варианты таких программ были разработаны в 60-х годах: сначала для
БЭСМ-2м [123, 124], а затем для БЭСМ-4 [179, 214, 215, 217, 244]. Они
использовались как в исследовательских целях, так и для практических
расчетов при проектировании ТСС и ВСС, что дало возможность осмыслить
и учесть требования реальной проектной практики и вместе с тем разрабо-
разработать способы повышения быстродействия данного метода (часть из них
описана выше).
Накопленный опыт позволил составить более совершенную программу
ДИПР на языке Фортран для БЭСМ-6 и ЕС ЭВМ [139, 142, 147,179], кото-
которая оптимизирует параметры PC, имеющих до 300 ветвей, с учетом: су-
существующей части системы, рельефа местности, различных способов про-
прокладки участков, произвольного числа источников и других требований.
Эта программа прошла проверку в ходе многочисленных расчетов реаль-
реальных объектов и передана многим организациям. Время счета зависит от
числа ветвей и сложности схемы PC, от количества насосных станций,
задаваемых способов реконструкции и точности оптимизации (табл. 14.1).
Охарактеризуем кратко результаты оптимизации некоторых из этих
объектов с целью иллюстрации области применения и практической эф-
эффективности данной программы. Расчет ТСС г. Южно-Сахалинска был
проведен двумя способами: традиционным инженерным методом, бази-
базирующимся на стандартных нормативах и правилах, и методом ДП по про-
программе ДИПР. Полученные с ее помощью оптимальные диаметры и дав-
давления для этой ТСС удовлетворяли всем заданным ограничениям, и ре-
решение в целом оказалось экономичнее проектного по общим расчетным
затратам на 12,6%.
Таблица 14.1
Параметры PC и время счета (на БЭСМ-6)
Наименование объекта
Условная схема
ТСС
г. Даугавпилса
г. Южно-Сахалинска
г. Риги
г. Хабаровска
Пресновский групповой водопровод
Число ветвей
15
48
74
105
183
298
Время счета
1 мин 57 с
4 мин 34 с
18 мин 58 с
20 мин 17 с
44 мин 13 с
1 ч 17 мин
202

Следующий пример относится уже к развиваемой и реконструируемой
ТСС г. Хабаровска. Эта система в связи с большой протяженностью тепло-
тепловых сетей, сложным рельефом местности, наличием колец и отсутствием
групповых распределительных пунктов является одной из наиболее слож-
сложных в стране. Система снабжается от трех источников: двух ТЭЦ и котель-
котельной и, кроме того, имеет четыре НС. В Сибтехэнерго (г. Новосибирск)
была выполнена работа по определению варианта реконструкции данной
ТСС на основе анализа возможных гидравлических режимов ее работы.
Выработанное в итоге решение предполагало перекладку трубопроводов
на 21 участке общей протяженностью 2732 м, установку одной дополни-
дополнительной НС и отключение двух существующих станций.
Эта же задача была решена с использованием программы ДИПР. В ка-
качестве исходного варианта параметров ТСС было взято решение Сибтех-
Сибтехэнерго, что позволило рассчитать потокораспределение в системе и затем
превратить ее в разветвленную "разрезанием" ряда узлов. Далее в каждом
из узлов были заданы допустимые диапазоны давлений с учетом геоде-
геодезических отметок, прочности труб и обеспечения необходимых давлений
у потребителей тепла. Полученный в результате дискретной оптимизации
на ЭВМ вариант предполагает перекладку трубопроводов лишь на семи
участках общей длиной 743 м, что почти в четыре раза меньше, чем в про-
проектном решении. При этом, однако, перекладка трубопроводов на неко-
некоторых из этих участков должна быть произведена с увеличением не на
один, а на два и три типоразмера диаметров. Несмотря на это, общие расчет-
расчетные затраты на реконструкцию во 2-м случае оказались на 6,5% меньше.
Программа ДИПР применялась также для оптимизации Пресновского
группового водопровода, представленного в виде трех PC, на которые он
распадается при оптимизации его структуры (см. гл. 13). Стоимостные ха-
характеристики и технико-экономические показатели для трубопроводных
участков и НС, а также данные о проектном варианте этого объекта были
предоставлены Союзгипроводхозом. Результаты оптимизации также су-
существенно отличаются от проектного решения по значениям диаметров,
местам расположения и числу НС.
Поскольку в оптимальном варианте данного группового водопровода
три его PC имеют по сравнению с проектным меньшую суммарную длину
и несколько больший средний диаметр, то общие затраты энергии на пре-
преодоление трения здесь оказались гораздо меньше. Это, в свою очередь,
определило и совершенно другую картину размещения НС и их производи-
тельностей. Расчет на ЭВМ показал, в частности, нецелесообразность строи-
строительства трех НС, которые фигурировали в проектном варианте. Оптималь-
Оптимальный вариант оказался лучше по общим расчетным затратам на 5,6%.
Таким образом, приведенные модель и алгоритм являются эффектив-
эффективным инструментом для количественного обоснования оптимальных ре-
решений в задачах проектирования, развития и реконструкции PC различного
-типа и назначения. Они могут применяться также и для оптимизации режи-
режимов работы PC при заданных диаметрах трубопроводов (см. об этом в
гл. 17). Помимо самостоятельного значения, эти разработки играют су-
существенную роль при математическом моделировании более общих задач
многоконтурной оптимизации и оптимального синтеза МКС с учетом тре-
требований надежности, которым посвящаются последующие главы.
203

Г л ав а 15
МНОГОКОНТУРНАЯ ОПТИМИЗАЦИЯ
15.1. ОБЩАЯ ЗАДАЧА МНОГОКОНТУРНОЙ ОПТИМИЗАЦИИ
Под общей задачей многоконтурной оптимизации (МКО) понимается
совместная оптимизация параметров активных и пассивных элементов
МКС, включая и потокораспределение в ней. Главное, что отличает данную
постановку от более простой задачи оптимизации параметров PC, — это
произвольный характер конфигурации системы, предполагающий наличие
в ней контуров, обеспечивающих двух- и многостороннее снабжение всех
или части потребителей. Если в случае PC расходы транспортируемой среды
на ветвях устанавливаются однозначно, то для МКС их также необходимо
определять наряду с диаметрами на ветвях и давлениями в узлах.
Это не только увеличивает число искомых оптимизируемых величин,
но и приводит к существенно более сложной многоэкстремальной сетевой
задаче дискретного программирования с десятками и сотнями контуров
в расчетной схеме МКС. Для получения ее численного решения за при-
приемлемое время недостаточно формального привлечения общих идей и
основных положений: декомпозиции, последовательного улучшения реше-
решения, градиентного спуска, пошаговой оптимизации и т. д. Лишь макси-
максимальный учет сетевых и физико-технических особенностей рассматривае-
рассматриваемых МКС может привести здесь к успеху. Содержание данной и последую-
последующих глав отражает попытку такого подхода к проблеме МКО и опирается
на выполненные в СЭИ работы [171, 179, 180, 216, 218-220, 223, 250,
255].
Содержательная постановка и математическая формулировка задачи
МКО включают прежде всего все основные положения задачи оптимиза-
оптимизации параметров PC, поэтому не будем повторять их здесь. Отметим лишь
дополнения и усложнения, которые появляются в связи с многоконтур-
ностью системы и включением вектора х в состав искомых величин. В ос-
основном они сводятся к двум моментам:
1) все составляющие целевой функции A4.3), которые содержат xh
становятся более сложными функциями, поскольку значения расходов уже
не могут быть зафиксированы заранее, как в случае PC;
2) система условий A4.1), A4.8)— A4.12) пополняется подсистемой
уравнений Ах = Q материального баланса в узлах. Уравнения A4.8) целе-
целесообразно оставить лишь для описания изменения давлений в ответвлениях
от "контурной" части системы, для которой вводится матрица контуров В
и соответствующая подсистема уравнений By = 0.
Задача оптимизации параметров и распределения расходов в МКС ха-.
рактеризуется, таким образом, следующими особенностями:
1. Функция цели A4.3) является выпуклой по потерям давления А,-, но
вогнутой по расходам х,- (к данному выводу нетрудно прийти, проанали-
проанализировав знак вторых призводных аналогично тому, как это было проде-
проделано в разд. 13.1).
2. Многоэкстремальность задачи обусловливается вогнутостью целевой
функции, а также наличием постоянных составляющих в стоимостных
показателях и существующей части системы (если решается задача ее раз-
204

*-*
f, -to
15.1. Приемы "разрезания" схемы в узлах слияния потоков
вития и реконструкции). Последнее обстоятельство приводит к тому, что
поверхность функции A4.3) имеет зоны разрывов, содержащие точки ее
локальных минимумов, которые соответствуют решениям с сохранением
существующих ветвей без изменений их параметров.
205

3. Принципиальной особенностью задачи является дискретность основ-
основных переменных dj и //,-, что связано со стандартностью диаметров и типо-
типоразмеров оборудования НС. Зачастую неоднородна и сама структура МКС,
когда различные ее элементы неодинаковы по условиям их сооружения
и техническим решениям (природным и городским условиям, способам
прокладки трубопроводов и т. п.).
В данной задаче нетрудно выделить следующие две подзадачи:
1) определения потокораспределения в МКС '(т. е. векторов х, Ри h) по
ее заданной схеме и с фиксированными диаметрами и действующими дав-
давлениями (векторами d, H), но без учета ограничений в форме неравенств;
2) оптимизации параметров PC, которой можно заменить исходную
МКС для каждого установившегося в ней потокораспределения путем
специально организуемой процедуры "разрезания" схемы МКС в узлах
слияния потоков. Эта процедура занимает важное место в декомпозиции
МКО и фактически является самостоятельной логической подзадачей,
решение которой дает возможность эквивалентным (с точки зрения рас-
распределения расходов транспортируемой среды) образом перейти от МКС
к PC. Основные приемы и возможные случаи "разрезания" схемы МКС
показаны на рис. 15.1. Полученная в итоге разомкнутая схема будет иметь
вид дерева, число ветвей которого совпадает с числом ветвей исходной
схемы, а число узлов равно сумме числа узлов и контуров МКС.
То, что вторая из выделенных выше подзадач является оптимизацион-
оптимизационной, очевидно. Но весьма существенным является тот факт, что и решению
первой подзадачи всегда будет отвечать минимум эксплуатационных затрат
(стоимости электроэнергии на перекачку среды). Это следует из эквива-
эквивалентности алгебраического и экстремального подходов к расчету потоко-
потокораспределения (см. гл. 7) и вытекающего отсюда вывода о том, что каждо-
каждому установившемуся в системе потокораспределению соответствует мини-
минимум необходимой для этого энергии источников.
Таким образом, последовательное решение обеих этих подзадач обеспе-
обеспечит двухэтапную минимизацию целевой функции (общих расчетных затрат)
на множество решений, удовлетворяющих системе ограничений исходной
общей задачи. На этапе расчета потокораспределения при этом фактически
будет решаться следующая задача на условный экстремум той части фун-
функции A4.3), которая зависит от х:
min [S (z,- (хь h, (*,)) + to (pch Н, (*,))) + 2 Zf (Qf, Pj (x))] A5.1)
при A x = 0 и с фиксированными Q, H и d.
Последующая трансформация МКС в PC в соответствии с полученным
потокораспределением дает возможность решить для нее задачу ДП:
min [2 (p,(rf,)+z,(jci,A/) + to(**.^/)) + S Zj(Qi,Pi)\ A5.2)
d.H.P.h /e/ J
с выполнением всей заданной совокупности ограничений и логических
условий A4.8)-A4.12).
Именно данные две подзадачи, для которых имеются весьма эффектив-
эффективные методы решения и их реализации в виде стандартных программ для
ЭВМ, а также отмеченная "экстремальная природа" потокораспределения
206

МКС и составляют основу метода МКО, который описывается ниже в
компактной форме. (Более детальное его изложение дается в монографии
[223].)
15.2. МЕТОД ДЕКОМПОЗИЦИИ МКО И ОБЛАСТИ ЕГО ПРИМЕНЕНИЯ
Основная идея метода МКО заключается в систематическом и последо-
последовательном выделении в исходной задаче оптимизации МКС двух указанных
выше подзадач и многократной увязке их решений в едином итерацион-
итерационном процессе. Делается это разделением всех искомых переменных задачи
на три группы векторов: 1) с? и Я, 2) х, 3) Р и h и поочередного фикси-
фиксирования векторов первой и второй группы. Вектор Р является перемен-
переменным для обеих подзадач и постоянно входит в число искомых величин.
Каждая итерация МКО включает: 1) расчет потокораспределения для
всей МКС и 2) оптимизацию параметров PC, выделяемых в МКС при оче-
очередном перераспределении расходов. Рассмотрим подробно общую схему
возможных алгоритмов, реализующих эту идею декомпозиции МКО, но
сначала - для более простой задачи оптимизации параметров вновь про-
проектируемой МКС, у которой нет еще существующей части системы. Число
источников при этом несущественно, их увеличение требует лишь относи-
относительно простой дополнительной вычислительной обработки.
Пусть заданы: конфигурация МКС, которая отображает все ее связи
между источником питания и узлами потребления, а также необходимые
исходные данные. Основные этапы метода МКО будут состоять тогда в
выполнении следующих вычислительных и логических операций:
1. Задания начального приближения d^0' иЯ*0' (в случае Л^-йитерации
это-<*<"-»> иЯ<"-»>.
2. Формирования и решения задачи расчета потокораспределения в МКС
для определения х^ ' и p(N~1> ( соответствующих зафиксированным
^ (N- 1) ^ (N - 1) и удОВлетвОряющих законам Кирхгофа.
3. "Разрезания" схемы МКС в узлах слияния потоков для превращения
ее в PC. При этом множество / исходных узлов пополнится подмножеством
/' дополнительных узлов, для которых установим нагрузки, равные расхо-
расходам на соответствующих ветвях: Qj = хг1" '\/€/, где / - номер ветви
I/'./].
Если в МКС имеется несколько источников, то после "разрезания"
она распадается на ряд деревьев. Объединение этого леса в одну PC произ-
производится замыканием всех источников на фиктивный узел с помощью
ветвей с нулевыми расходами.
4. Оптимизации параметров полученной PC методом ДП для определе-
определения d(^ иЯ'^, обращающих в минимум (при фиксированном х^N~l*)
Целевую функцию A4.3). При этом учитываются все имеющиеся ограни-
ограничения в виде неравенств,и логических условий, а также конкретные осо-
особенности прокладки трубопровода на каждой ветви.
5. Возвращения к исходной МКС "склеиванием" разрезанных узлов.
6. Перераспределения расходов в МКС в соответствии с новыми зна-
значениями d^ > и Н^ . В связи с этим опять решается задача потокораспре-
потокораспределения и в результате находятся уточненные х(ЛГ) и Р^ .
^^ целевой ^yHKumF(x{N),PiN),h(-N),d(N),HiN) =
~F ¦ 207

8. Управления вычислительным процессом посредством сравнения
W /^-О.атакже*™ и Я™ с </<"-» и/>-<> и повторения
в случае необходимости п. 3-7 с заменой NnaN+ 1.
Компоненты вектора х^ в общем случае по величине и знаку будут
отличаться от компонент х ^N~ ' ^, поэтому в результате "разрезания" коль-
кольцевой схемы МКС на /V-й итерации каждый раз будем получать (пока про-
процесс не сойдется к решению) новое дерево. В окончательном решении не-
необходимо удалить участки с пренебрежимо малыми д:,- и h/. И в результате
получим значения всех искомых переменных, которые определят: уточнен-
уточненную конфигурацию МКС, расчетное потокораспределение в системе, диа-
диаметры на всех ветвях, места размещения и параметры НС и ДС, действую-
действующие напоры в источниках.
Описанный алгоритм применим и для оптимизации развивающихся МКС.
В этом случае в исходных данных указываются параметры всех ее сущест-
существующих элементов и допускаемые способы их реконструкции. На этапе
оптимизации параметров PC будут определяться наряду с параметрами
всех новых участков изменившиеся характеристики тех элементов сущест-
существующей части системы, которые целесообразно реконструировать. Все же
остальные этапы метода МКО не потребуют особых изменений.
Строгого доказательства сходимости данного метода МКО к точке гло-
глобального минимума целевой функции A4.3) не получено. Однако нетруд-
нетрудно показать, что получаемая в ходе итераций последовательность ее значе-
значений должна иметь некоторый предел. Действительно, на этапе оптимизации
параметров PC, которая выделяется в МКС, каждый раз будет находиться
(но при фиксированном х) глобальный минимум функции A4.3) F(d, H),
что следует из математической сущности динамического программирова-
программирования. Далее, на этапе расчета потокораспределения, который выполняется
для корректировки х при известных с? и Я, целевая функция F(x, P) опять
может только уменьшаться в силу отмеченного выше принципа "энерге-
"энергетического" минимума для любого установившегося потокораспределения
за счет уменьшения составляющих общих затрат, связанных с расходами
электроэнергии на перекачку.
Таким образом, теоретически будем иметь неотрицательную монотонно
убывающую и ограниченную снизу (поскольку затраты для реальной МКС
не могут обратиться в нуль) последовательность значений этой функции.
Известно, что для такой последовательности должен существовать конеч-
конечный предел, из чего следует сходимость метода по целевой функции по
крайней мере к ее локальному минимуму.
В то же время вычислительные эксперименты, которые были проведены
в ходе многовариантных расчетов условных и реальных примеров (под-
(подробнее о них см. ниже), показали, что монотонность в уменьшении целевой
функции иногда нарушается из-за дискретности переменных и других осо-
особенностей, усиливающих многоэкстремальный характер задачи, а также
из-за возможного нарушения некоторых ограничений - неравенств на эта-
этапах расчета потокораспределения.
Быстродействие и сходимость этого метода существенно зависят от
начального приближения. В первое время при реализации метода МКО
авторами в качестве исходного допустимого решения брался вариант
со средним по величине (для задаваемого списка) значением диаметра на
208

15 1 а, б, в. Оптимизация структуры
и параметров PC
<; - избыточная схема; решения,
поЛученные методами схемно-стру-
1Турной оптимизации и ДП (б) и
МКС (в) ; числа над ветвями обо-
обозначают: а - длины; б, в - диа-
диаметры
/000 2000
_ -J
всех ветвях, а при решении задачи развития и реконструкции МКС — пара-
параметры элементов ее существующей части. Однако последующие экспери-
эксперименты показали, что существенно более эффективным является предвари-
предварительное определение для исследуемой МКС ее "оптимально подготовлен-
подготовленного дерева" (ОПД), которое учитывает затраты и в кольцующие ветви.
Это можно сделать методом поконтурного перебора деревьев с помощью
программы ТРАССА, описанной в гл. 13.
При оптимизации МКС, показанной на рис. 15.2, итоговое решение,
исходя из средних диаметров, было получено на 14-й итерации, а для ОПД —
на 8-й. К тому же последнее оказалось экономичнее на 4,2%. На рис. 15.3
представлены соответствующие графики изменения целевой функции
(от итерации к итерации), которые иллюстрируют возможный "пилообраз-
"пилообразный" характер поведения данной функции и его зависимость от началь-
начального приближения.
В этих условиях важным является выбор правила остановки процесса
оптимизации. Наиболее строгим, конечно, будет условие совпадения иско-
искомых параметров (и прежде всего диаметров) для двух соседних итераций,
что вполне оправданно для развивающихся МКС. В случае же вновь про-
проектируемых МКС или систем с весьма сложной конфигурацией и множест-
множеством активных элементов такое совпадение искомых параметров может
оказаться труднодостижимым, причем значительная часть заключитель-
заключительных итераций уже не будет, как правило, давать заметного уменьшения
Целевой функции. Поэтому здесь лучше добиваться сходимости по общим
затратам, следя за их совпадением (с заданной точностью) после выполне-
выполнения каждой очередной итерации.
Метод МКО может использоваться и для решения частных или смеж-
смежных задач, имеющих самостоятельное значение. Охарактеризуем наиболее
важные из них.
¦ Выбор наивыгоднейшей конфигурации и параметров новой PC, исходя
3 ее избыточной проектной схемы (которая может содержать множество
14- Зак. 384 209

/j
15.3a, б Изменение функции затрат по итерациям метода МКО
1 - расчет от средних диаметров; 2 - расчет по ОПД; а - оптимизация параметров
МКС на рис. 15.5; б— оптимизация системы на рис. 15- 2
контуров). Список диаметров при этом должен обязательно включать
достаточно малые по величине значения для того, чтобы можно было моде-
моделировать участки с практически нулевыми расходами транспортируемой
среды.
Данная задача является задачей схемно-структурной оптимизации и по-
потому может быть решена одним их алгоритмов поконтурного перебора
деревьев, описанных в гл. 13. Однако для проверки степени приближен-
приближенности этих алгоритмов, а также и с целью возможного улучшения и дета-
детализации структуры получаемой PC и параметров ее элементов здесь воз-
возможно применение и метода МКО, но в модифицированном виде.
После проведения первого цикла итераций и обеспечения сходимости
по диаметрам производится удаление из исходной схемы одной из ветвей
с наименьшими диаметром и потерей давления. Затем новый цикл итера-
итераций — выбрасывание очередной ветви — и т. д. до тех пор, пока схема не
примет вид дерева.
Процесс определения PC существенно ускоряется, если удаление очеред-
очередной ветви производить также и в момент первого возрастания целевой
функции, т. е. в начале итераций, дающих ее "пилообразное" поведение.
Но самое большое сокращение времени счета достигается следующим
приемом. При выбрасывании очередной ветви можно временно исключать
из схемы также и те ветви, которые не входят ни в один из контуров, с
тем, чтобы дальнейшую оптимизацию вести только для остающейся коль-
кольцевой части системы. А после того как она окончательно превратится в
дерево, следует восстановить все временно удаленные участки и произ-
произвести оптимизацию параметров PC в ее полном виде.
2. Выбор конфигурации PC совместно с местами расположения и произ-
водительностями источников. Эта более общая схемно-структурная задача
сводится к только что рассмотренной с помощью расширения исходной
схемы фиктивными ветвями, замыкаемыми на дополнительный узел с
условным общим источником, имеющим суммарную производительность.
При этом: 1) в выражение для целевой функции добавляется еще одна
составляющая Б </у (х,-, Pj) для учета затрат в источники, где х, — неизвест-
ная производительность источника в узле / и .2) в подсистему уравнений
первого закона Кирхгофа добавляются условия материального баланса во
всех узлах / из J2 ив дополнительном узле.
210

\
Так же как и в предыдущем случае, с помощью метода МКО можно
будет постепенно уменьшать до минимально возможного значения диа-
диаметры отдельных участков расширенной схемы, превращая ее в PC с оп-
оптимально выбранными притоками в узлы-источники. Это и обеспечит
совместный оптимальный выбор структуры и параметров искомой PC.
3. Выбор оптимальной конфигурации и параметров развивающейся
системы. Решением данной задачи в общем случае является МКС, даже
если существующая часть системы была разветвленной, и потому здесь
непригодны методы, основанные на переборе деревьев. Применение ме-
метода МКО позволяет решать эту задачу за конечное число итераций при
произвольном характере связей в исходной схеме и различном сочетании
параметров ее существующей части.
Для системы, изображенной на рис. 15.4, а, с помощью МКО был полу-
получен оптимальный вариант ее развития (рис. 15.4, в), который оказался
на 10% экономичнее решения, полученного с использованием алгоритма,
взятого из работы [60] (рис. 15.4, б). (Существующая часть системы на
всех схемах выделена жирными линиями, а значения диаметров (в мм)
для существующих ветвей подчеркнуты. На рис. 15.4, а, б цифры над вет-
ветвями схемы указывают их длину в м, диаметры под ними на существующих
ветвях в мм; пунктиром обозначены" ветви, не вошедшие в решение.)
Оптимальный вариант, показанный на рис. 15.4, в, имеет на один контур
больше, чем их было в существующей части системы, так как в решение
вошла ветвь 13—16. Если же удалить из исходной схемы эту ветвь и снова
применить метод МКО, то получим решение, показанное на рис. 15.4, г.
Для него общие затраты будут на 7,9% больше, чем у оптимального. Это
подтверждает важность и необходимость рассмотрения многоконтурных
решений для развивающихся систем.
15.3. СРАВНЕНИЕ С МЕТОДОМ ФИКТИВНЫХ РАСХОДОВ
И ПРИМЕРЫ РАСЧЕТОВ
Программная реализация метода МКО выполнена в рамках общего ПВК
СОСНА (см. гл. 18), предназначенного для решения комплекса технико-
экономических задач, которые составляют проблему оптимального синте-
синтеза МКС с учетом требований надежности и для которых этот метод являет-
является одним из основных вычислительных инструментов. Приведем примеры
расчетов реальных МКС, связанных с решением отдельных задач проектной
и эксплуатационной практики в области ВСС. При этом проведем срав-
сравнение результатов расчетов по методам фиктивных расходов (МФР) и
МКО.
Суть МФР [160-162] заключается в следующем. Суммарную потерю
Давления Яо на трение в МКС можно представить в виде некоторой функ-
функции от потерь давления А,- на отдельных ветвях, например в виде
п
#о =2 Xihi,
/=i
считая xi здесь некоторыми неизвестными коэффициентами. Л.Ф. Мошнин
исследовал свойства этих коэффициентов и установил, что они подчиняются
первому закону Кирхгофа и, следовательно, могут трактоваться как неко-
211

о.
s
« 2
s 2

ffffff/r/c
15.5. Расчетная схема МКС
Цифры под ветвями — длины; цифры над ветвями — диаметры, полученные
расчете по методам "фиктивных расходов" и МКО
при
торые расходы, доставляемые транзитом от источника до точек слияния
потоков. При этом распределение самих потоков транспортируемой среды
считается известным. Коэффициенты Xj, как и сам метод, получили назва-
название "фиктивных расходов" (или "ситуационных факторов").
Увязав расчетную схему МКС по фиктивным расходам, можно устано-
установить долю участия каждого участка в суммарной потере Но. А продиф-
продифференцировав функцию стоимости объекта по диаметрам и приравняв
производные нулю, получить выражения для наивыгоднейших диаметров
на участках при заданном потокораспределении и в зависимости от х,-. За-
Затем производится округление полученных теоретических диаметров до
их стандартных значений с помощью таблицы "предельных расходов".
Нетрудно показать (впервые это сделано В.Г. Лобачевым [109]), что
фиктивные расходы представляют удобную для расчетов комбинацию
неопределенных множителей Лагранжа для учета уравнений второго закона
Кирхгофа. Можно также установить соответствие между ними и вели-
величинами 0,-, введенными Б.Л. Шифринсоном [269] для получения оптималь-
оптимальных напоров при расчете разветвленных тепловых сетей.
Подбором и корректировкой величин*,-, притоков и нагрузок у потре-
потребителей (с помощью специальных операций) можно учесть рельеф мест-
местности и наличие нескольких источников в системе. Однако за пределами
возможностей метода остается учет двухсторонних ограничений на узло-
узловые давления, типов прокладки трубопроводов и характеристик грунта на
отдельных участках, дискретности диаметров и т. п. Явное преимущество
214

пискретной оптимизации, реализуемой в методе МКО, перед аналитическим
подходом в МФР показывают следующие сравнительные расчеты одних
и тех же ВСС.
Первый объект - ВСС с одним источником, описанная в статье [160],
откуда были взяты все необходимые данные для расчета, а также и реше-
решение, полученное по МФР. На схеме этой системы (рис. 15.5), которая имеет
IS узлов и 26 ветвей, указаны нагрузки потребителей и производитель-
производительность источника в узле 1. Цифры под ветвями схемы обозначают их длины,
а над ними - диаметры, полученные при расчете по двум методам (пер-
(первая - по МФР, а вторая - по методу МКО). Список стандартных диамет-
диаметров содержит 13 значений от 100 до 900 мм. Удельная стоимость проклад-
прокладки трубопроводов взята, как и в работе [160], по формуле
Kc(di) = 2\ +350d!-777.
Решение, полученное по МФР, затем дополнительно обрабатывалось
по программе метода МКО для однотипного получения сравниваемых
экономических показателей. Как видно из представленной таблицы.
Таблица 15.1
Экономические характеристики двух решений для ВСС (рис. 15.5)
Решение
Зэ, руб//год
Зс,руб./год
3s, руб./год
По МФР
По методу МКО
108 561
94 908
379 911
360 535
488 472
455 444
6,7
решение, полученное с помощью метода МКО, гораздо экономичнее ре-
решения по МФР.
Далее проводились сравнительные расчеты для ВСС одного из городов,
расчетная схема которой насчитывает 46 узлов и 62 участка. Этот объект
рассматривался как вновь проектируемая система. Итоговые экономи-
экономические показатели приведены в табл. 15.2.
Таблица 15.2
Результаты расчетов ВСС
Решение
Зэ, руб./год
Зс, руб./год
32, руб./год
По МФР
По методу МКО
194 823
187 124
217 561
182 770
412 384
369 895
10,3
Экономическая эффективность второго решения по сравнению с "анали-
"аналитической" оптимизацией здесь еще выше, чем в предыдущем случае. Понят-
Понятно, что величины и направления потоков для этих двух вариантов не долж-
должны совпадать, так как МФР определяет параметры ВСС для заданного их
распределения, а метод МКО получает оптимальное потокораспределение.
Имеются и другие примеры успешного применения метода МКО для оп-
оптимизации проектируемых и развиваемых сложных ТСС и ВСС (см. гл. 18).
215

Глава 16
ОПТИМАЛЬНЫЙ СИНТЕЗ МНОГОКОНТУРНЫХ СИСТЕМ
С НАГРУЖЕННЫМ РЕЗЕРВИРОВАНИЕМ
16.1. КОНФЛИКТЫ РЕЗЕРВИРОВАНИЯ
Оптимальный синтез МКС - наиболее общая задача, относящаяся к
оптимальному проектированию ТПС и других пространственно распреде-
распределенных физико-технических систем, которая рассматривается в этой книге.
Ее содержательная постановка включает все основные системные технико-
экономические задачи, представленные в предыдущих главах, и сводится
к оптимальному совместному выбору: структуры системы, параметров
всех ее активных и пассивных элементов, расчетного (проектного) потоко-
распределения, а также "структурно-параметрических" мероприятий с це-
целью удовлетворения требований к надежности снабжения потребителей.
Для сложных систем, имеющих большое народнохозяйственное значение
и требующих огромных затрат, какими являются ТПС и ЭЭС, задачи их
оптимального синтеза должны в принципе ставиться и решаться уже на
стадии планирования как комплексные оптимизационные задачи, в кото-
которых совместно присутствуют физико-технические ограничения и вероят-
вероятностные требования к надежности снабжения потребителей.
Тем не менее до последнего времени проблема оптимального синтеза
МКС заменялась рассмотрением последовательности известных задач
оптимизации систем и анализа их надежности, что исключало из поля зре-
зрения актуальные на сегодняшний день вопросы математического модели-
моделирования сложных систем с учетом принципов их резервирования. Но только
на этом пути и на базе взаимополезных межотраслевых методических
обобщений можно построить работоспособные математические модели
и отвечающие им итерационные процессы оптимального синтеза.
Попытаемся предварительно охарактеризовать надежностные и экономи-
экономические факторы, играющие здесь решающую роль. Одним из наиболее важ-
важных вопросов является выбор принципов резервирования проектируемой
системы. Известно, что в теории надежности различают много видов резер-
резервирования, среди которых выделим два: нагруженное (постоянное) резер-
резервирование, при котором "резервные элементы участвуют в функциониро-
функционировании объекта наравне с основными", и ненагруженное (резервирование
замещением или дублирование), когда "функции основного элемента
передаются резервному только после отказа основного элемента" [165].
В любом случае возникают "конфликты резервирования", которые необ-
необходимо учитывать и правильно (оптимально) разрешать.
Реализация принципов ненагруженного и ненагруженное резервирования
в ТПС проявляется, в частности, в так называемых "секционированных"
(разомкнутых) и "обезличенных" (замкнутых) схемах их эксплуатации.
В первом случае задвижки на перемычках между магистралями в нормаль-
нормальных режимах закрыты, во втором открыты, и оба эти способа имеют как
положительные, так и отрицательные стороны.
Эксплуатация систем в "секционированном" виде позволяет относитель-
относительно быстро обнаруживать аварийные магистрали, сокращать аварийные
утечки, а также упрощает наладку их гидравлических режимов работы.
216

Обезличенная схема, в свою очередь, дает целый ряд очевидных эконо-
экономических и "гидравлических" преимуществ: а) уменьшается общее гид-
гидравлическое сопротивление системы и соответственно сокращается расход
электроэнергии на перекачку; б) оказывается возможным при проектиро-
проектировании новых и развитии существующих систем на основе принципа нагру-
нагруженного резервирования существенно снизить затраты на их резервирова-
резервирование уменьшением диаметров труб на отдельных магистралях; в) повышает-
повышается гидравлическая устойчивость и маневренность системы благодаря более
низким действующим напорам, которые потребуются от источников и др.
Вместе с тем в случае многоконтурной схемы эксплуатации отдельные
группы потребителей будут снабжаться по нескольким путям, что серьез-
серьезно затрудняет обнаружение и идентификацию аварийных ситуаций и т.п.
Если обратиться к реальным ТПС, то можно увидеть, что большинство
ТСС в соответствии с официальными рекомендациями работают, за неко-
некоторыми исключениями, по секционированной схеме. Аналогичная ситуация
имеет место в основном и для систем нефте- и газоснабжения. А вот для
ВСС работа по многоконтурной схеме давно уже является традиционной,
она предусматривается на стадии проектирования и осуществляется в усло-
условиях эксплуатации.
Эксплуатационные преимущества секционированной схемы быстро
уменьшаются по мере усовершенствования средств и методов управления
и оптимального проектирования ТПС. Например, трудности наладки режи-
режимов работы МКС уже теперь успешно преодолеваются с помощью приме-
применения современных методов расчета потокораспределения и ЭВМ. С внед-
внедрением же автоматизированного управления, которое возьмет на себя
слежение за фактическими параметрами ТПС, телеконтроль и управление
задвижками, будет решена и проблема дистанционного оперативного
обнаружения и локализации аварийных участков.
Для дальнейшего изложения важно подчеркнуть неразрывную связь,
которая существует между выбранными принципами резервирования, ха-
характером получаемой при этом структуры системы и математической слож-
сложностью возникающих здесь задач. В случае дублирования элементов проек-
проектируемая система почти всегда может быть сведена к PC, в которой допус-
допускаются, однако, "многониточные" участки и лупинги (параллельные тру-
трубопроводы, полностью или частично дублирующие отдельные участки).
Поэтому для оптимизации в этих случаях, как правило, может быть приме-
применен метод ДП.
Понятно, что по чисто экономическим соображениям нереально ставить
вопрос о полном дублировании всех путей снабжения в PC. Включение
же в рассмотрение способов нагруженного резервирования заставляет
рассматривать и оптимизировать системы с более сложными структурами,
что во многих отношениях усложняет проектные задачи и приводит к но-
новым методическим и вычислительным проблемам.
Одним из самых существенных моментов при построении оптимизацион-
оптимизационных математических моделей для обеспечения надежности ТПС и других
МКС является формулировка целей расчетов. Известно, что достижение
оптимума при решении экстремальных задач всегда связано с нахожде-
нахождением некоторого компромисса между какими-то противоположными
¦тенденциями (например, в технико-экономических задачах по существу
217

речь всегда идет об оптимальном соотношении между увеличением капи-
капиталовложений в объект и последующим снижением эксплуатационных
расходов) или между стремлением максимально улучшить какой-либо
обобщенный показатель проектируемой системы и необходимостью
удовлетворить заданным ограничениям.
Аналогичная ситуация имеет место и в рассматриваемых задачах. С од-
одной стороны, любое резервирование требует дополнительных расходов по
сравнению с затратами, определяемыми экономическим оптимумом без
учета требований надежности. Но, с другой, необходимо обеспечить выпол-
выполнение этих требований. При этом возникают два конфликта резервирова-
резервирования, которые могут быть использованы для математической формулировки
задачи с целью получения искомых оптимальных решений.
Первый из них имеет довольно очевидное проявление и заключается в
том, что увеличение капиталовложений в систему в связи с обеспечением ее
надежности должно снижать ущерб от недоотпуска энергоносителя (или
другой транспортируемой среды) потребителям во время аварий. Опти-
Оптимальное решение теоретически должно отвечать здесь общему минимуму
денежных затрат, в сумму которых наряду с общепринятыми приведенны-
приведенными затратами по системе включается и математическое ожидание случай-
случайных величин: ущерба от недоотпуска и затрат на восстановление после
аварий.
Не исключено, что экономические, статистические и социологические
исследования смогут в будущем сделать такой подход реальным и дать
конкретные рекомендации по оценке ущербов. Однако в настоящее время
соответствующие математические модели, несмотря на свою внешнюю
строгость, оказываются в большинстве случаев информационно не обеспе-
обеспеченными. Действительно, соизмерение затрат на повышение надежности
со случайной величиной ущерба может быть получено только как резуль-
результат обработки статистических данных большого объема за ряд лет для од-
однотипных потребителей, т.е. информации, которой сейчас практически
нет. Трудно также соотносить ущербы, которые оцениваются по отпуск-
отпускным ценам производимой продукции, с расчетными затратами по ТПС.
К тому же ущерб от недоотпуска воды, тепла или газа, являющихся основ-
основными видами нагрузки в жилищно-коммунальном секторе, не может быть
до конца оценен в денежном выражении. ¦
Таким образом, возможность использования взаимозависимости между
допольнительными затратами на повышение надежности и снижением
ущербов при аварийных ситуациях для количественной оценки и сравне-
сравнения различных мероприятий по обеспечению надежности ТПС носит пока
довольно абстрактный характер. Выходом из положения может служить от-
казоткатегорииущербови переход к заданию уровней надежности, т.е. к ее
нормированию. Нормирование надежности снабжения потребителей поз-
позволяет использовать в оптимизационных моделях- обычные (традицион-
(традиционные) технико-экономические критерии, но при условии пополнения сис-
системы ограничений соответствующими формулами и неравенствами, опи-
описывающими сопоставление вероятностных показателей надежности с тре-
требованиями потребителей.
С математической точки зрения подобное расширение системы ограни-
ограничений может быть в принципе заменено добавлением в целевую функцию
218

чинейной комбинации всех этих дополнительных условий, взятых с неко-
некоторыми неопределенными множителями (весами, оценками). Тем самым
6yieT построена частичная функция Лагранжа, которая формально экви-
эквивалентна критерию, учитывающему возможный ущерб. Но методически
и практически модели с нормированной надежностью оказываются в нас-
настоящее время более эффективными. Они позволяют легче справиться и
с информационной проблемой с помощью двух приемов: назначением этих
норм (на основании прошлого опыта, имеющихся данных об отказах эле-
элементов, путем экспертных оценок) или через варьирование этими
нормами и последующие многовариантные расчеты для количественного
анализа зоны возможных оптимальных решений.
Общий в „надежностных" задачах конфликт между необходимостью
в дополнительных затратах на обеспечение надежности системы и снижени-
снижением ущерба у потребителей в случае аварийных ситуаций дополняется „про-
„противоборством" факторов, связанных со специальными способами резер-
резервирования. Так, нагруженное резервирование и переход от PC к синтезу
МКС характеризуется следующей конфликтной ситуацией.
С одной стороны, каждый дополнительный элемент, который постоян-
постоянно участвует в функционировании МКС, как и любое работающее оборудо-
оборудование, создаст новый источник потенциальных отказов, что, конечно, по-
понизит надежность расчетного снабжения Kajaix-то узлов системы при нор-
нормальных режимах. С другой стороны, возможность многостороннего пи-
питания потребителей в МКС повышает надежность в аварийных ситуациях,
(но лишь с пониженным уровнем снабжения). В этом противоречии меж-
между повышением надежности аварийного снабжения и ее снижением для
проектных режимов работы системы и состоит, по мнению авторов, конф-
конфликт нагруженного резервирования.
Конечно, предварительно необходимо решать вопрос о характере снаб-
снабжения потребителей в аварийных условиях: осуществлять ли дискретное
их отключение (в соответствии с категорийностью) или производить одно-
одновременный общий переход на пониженное, но заранее регламентированное
снабжение. Кстати, для большинства ТПС в отличие от ЭЭС можно допус-
допустить (на тот или иной период, соизмеримый в большинстве случаев со вре-
временем ликвидации аварий) уменьшенную подачу транспортируемой среды
потребителям. В общем, исходя из конкретных особенностей систем и
требований потребителей, для каждого узла проектной схемы МКС можно
указать его суммарную пониженную нагрузку для случая аварийных ситуа-
ситуаций (которая в отдельных случаях может совпадать и с полной, если такое
понижение для какого-либо узла вообще не допускается).
В связи с изложенным необходимо вначале хотя бы кратко рассмотреть
методику расчета надежности и резервирования МКС (на примере ТПС),
разработанную в СЭИ [170, 199-200, 230, 250-252]. Этому посвящается
следующий раздел. Далее в этой главе излагаются: математическая форму-
формулировка задачи оптимального синтеза МКС с нагруженным резервирова-
резервированием, вопросы ее декомпозиции и алгоритмизации для получения числен-
численных решений [171,218,219,254,255].
219

16.2. МЕТОДИКА РАСЧЕТА НАДЕЖНОСТИ ТПС
Проблема надежности ТПС, которая заключается в обеспечении их способ-
способности централизованно снабжать множество своих потребителей теплом, во-
водой , газом или нефтью в заданных количествах и с требуемыми парамет-
параметрами в течение всего срока эксплуатации (с учетом возникновения аварий-
аварийных ситуаций), становится все более актуальной. Первоочередные меры
здесь прежде всего связывают с повышением качества труб, монтажных
и сварочных работ, усилением ремонтных служб и т.п. Очевидно, однако,
что стопроцентной надежности достигнуть в принципе невозможно. Поэ-
Поэтому чем сложнее и масштабнее становятся системы трубопроводного
транспорта, тем все заметнее усложняются цели и содержание проектной
работы: вместо традиционного последовательного выбора структуры и
параметров элементов систем, исходя из минимизации суммарных расчет-
расчетных затрат, на первый план выходит более общая задача оптимального
построения надежных (в задаваемом смысле) систем из ненадежных
элементов.
ТПС, как и вообще системы энергетики, обладают рядом свойств (часть
из которых отмечалась выше), коренным образом отличающих их от бо-
более компактных („стендовых") объектов, являющихся традиционными и
типичными для прикладной теории надежности, таких, как радиотехни-
радиотехнические устройства, аппараты, машины и т.п. В периоды строительно-мон-
строительно-монтажных работ и длительной экспулатации ТПС подвергаются воздействию
множества случайных и неслучайных факторов, которые невоспроизводи-
мы на испытательных стендах и которые трудно должным образом иден-
идентифицировать при регистрации аварий и других нарушений в условиях экс-
эксплуатации. Имеющаяся информация об аварийности в системах при всей
ее неполноте дает, конечно, возможность оценить общий технический уро-
уровень ТПС и указать на наиболее уязвимые места. Однако эти данные мало-
малочисленны и по природе своей чаще всего не совпадают с той статистической
информацией, которая необходима для получения вероятностных характе-
характеристик.
Надежность, как известно, комплексное свойство и вместе с тем соби-
собирательное понятие, отражающее качество работы отдельных элементов
и системы в целом, и оно может характеризоваться многими показателями,
зависящими как от объекта, так и целей исследования. Однако имеется один
принципиальный момент, связанный с количественной оценкой системной
надежности ТПС, - это малая информативность и „неработоспособность"
во многих случаях обобщенных показателей надежности. Такие показатели,
как „коэффициент готовности системы", „средняя суммарная продолжи-
продолжительность безотказной работы за расчетный период", „пропускная способ-
способность" и т.п., необходимы и полезны, когда речь идет об "одноцелевых"
системах, транспортирующих среду в заданный район (типа магистраль-
магистральных нефте- и газопроводов). Но они становятся бесполезными для ТПС,
имеющих множество относительно равнозначных потребителей, рассредо-
рассредоточенных по всем ее узлам, поскольку не могут охарактеризовать надеж-
надежность снабжения каждого из них. Такие ТПС необходимо рассматривать уже
как объекты не с единичными (скалярными) показателями, а как системы
с „векторной надежностью", отражающей требования именно множества
потребителей.
220

Описываемая ниже методика расчета надежности и резервирования ТПС
ориентирована в основном на ТСС и ВСС, т.е. на системы, не имеющие дос-
достаточного информационного обеспечения, для которых не имеет особого
смысла использование обобщенных показателей надежности . (Что касается
ТПС магистрального типа, то методы расчета их надежности изложены
в монографии Е.Р. Ставровского, М.Г. Сухарева и А.М.Карасевича [213J.)
С учетом сказанного существенными особенностями описываемой
ниже методики являются: 1) параметрическое задание уровней надежнос-
надежности в виде вектора узловых величин (норм), устанавливаемых для предста-
представительных узлов проектной схемы ТПС с учетом категорийности присое-
присоединяемых потребителей; 2) исключение из экономического критерия
величины математического ожидания ущерба от недоотпуска энергоноси-
энергоносителя или воды потребителям; 3) сочетание вероятностных методов расчета
надежности путей снабжения каждого из узлов и детерминированных
методов гидравлического анализа режимов работы ТПС в нормальных и
аварийных ситуациях; 4) рассмотрение двух уровней обеспечения надеж-
надежности потребителей - расчетного (проектного) и пониженного (аварий-
(аварийного) . Основная идея разработки подобной методики состоит в том, чтобы,
используя высокое быстродействие ЭВМ и варьируя априорными значе-
значениями различных параметров и критериев надежности, можно было вы-
выполнять многовариантные расчеты, которые дали бы сравнительную оценку
различных способов резервирования и построения системы.
Предварительно уточним некоторые исходные понятия и определения.
Под элементом линейной части ТПС понимается ее участок между двумя
секционирующими задвижками, выключающими этот элемент при отказе.
Другие элементы ТПС, относящиеся к источникам, сетевым сооружениям
и дополнительному оборудованию (НС, регуляторы, аккумулирующие
емкости и т.д.), будем считать для простоты изложения не влияющими на
надежность снабжения (хотя вероятности их отказов также могут быть
учтены). Отказ — случайное событие, состоящее в нарушении способности
элемента выполнять заданные функции и вызвавшее полный или частичный
перерыв в снабжении одного или группы потребителей. Путь снабжения
какого-либо узла - это последовательность элементов, доставляющих
транспортируемую среду в данную точку.
Будем считать, что для элементов ТПС характерен простейший поток
отказов, который удовлетворяет трем условиям: 1) взаимной независи-
независимости, т.е. отсутствию последействия; 2) ординарности, т.е. невозможности
появления в один и тот же момент времени более одного отказа, и 3) ста-
стационарности, когда предполагается, что процессы старения и износа элемен-
элементов компенсируются планово-предупредительными ремонтами, очередными
реконструкциями и т.п., так что интенсивность потока отказов поддержи-
поддерживается на одном уровне.
Количественно надежность элемента i можно оценить вероятностью
его безотказной работы в течении рассматриваемого периода времени
г> т.е. некоторой функцией Л,(т), так что вероятность отказа этого эле-
элемента равна 1 — R/ (г). Для аналитического представления данной функции
необходимо ввести также интенсивность отказов щ (Lh dh т) - вероят-
вероятность того, что элемент, проработавший безотказно до момента г, откажет
в следующий бесконечно малый промежуток времени. Так же, как это
221

принято для многих технических устройств, работу каждого элемента
(и системы в целом) можно разбить натри периода: приработочный (пус-
коналадочный), нормальной эксплуатации, старения и полного износа.
Здесь имеется в виду период нормальной эксплуатации, причем в соот-
соответствии с предположением о простейшем потоке отказов будем считать
величины wt не зависящими от г и возьмем за основу экспоненциальный
закон, связывающий показатель надежности элемента и интенсивность
его отказов:
Ri(t) = exp(~wi(Li,di)T). A6.1)
В сложных случаях могут использоваться и более общие законы, скажем
распределение Вейбулла.
Уровни (нормы) надежности снабжения потребителей в узле / могут
задаваться различными параметрами, например следующими тремя вели-
величинами: ip. - нормой допустимого снижения отпуска траспортируемой
среды в периоды аварий, определяемой как отношение (в долях от едини-
единицы или в процентах) минимально допустимой подачи к максимальной
расчетной нагрузке; Л^00 - нормой надежности расчетного A00%-ного)
снабжения, которая совпадает с требуемой вероятностью безотказной по-
подачи энергоносителя или воды при нормальных условиях в течение периода
эксплуатации; N? - нормой пониженного снабжения, т.е. требуемой
вероятностью подачи транспортируемой среды во время аварий в коли-
количестве^. • 100% от расчетной величины.
Вероятность R/ безотказного снабжения узла/ вычисляется через надеж-
надежности путей его снабжения от источников или от резервированной (заколь-
(закольцованной) части системы. Для пути лу, состоящего из к элементов,
к
R(n:)= П Ru. A6.2)
и =1
Строго говоря, для подсчета показателя надежности снабжения какого-
либо узла / в МКС необходимо пользоваться более сложными формулами,
зависящими к тому же и от типа системы. Например, для ТСС вместо
A6.2) следовало бы взять следующие выражения:
R)oo= П [\~RdP{tH<tH>i}](l-P{tH<^}) ПД„, A6.3)
I U
Л*=П[1-A-Л,-)A-Л,,/)] ПЯ„, A6.4)
где i — номера элементов, аварийна которых нарушают расчетное снаб-
снабжение узла / ; и — номера элементов нерезервированной части сети, входя-
входящей в путь снабжения узла/ ; R3j — вероятность отключения (задвижками)
аварийного элемента; tH -температура наружного воздуха; t'H - ее расчет-
расчетное значение; tHj _ минимальная tn, при которой отключение элемента
i не нарушает расчетного теплоснабжения узла / (с учетом повышения
температуры воды в подающей магистрали); Р{ tH < fH,i) ~ вероятность
того, что авария на элементе / произойдет при tH < tHt ,¦ ; Р {tH < t^ } -
вероятность понижения Гн против расчетного значения. Однако при дальней-
дальнейшем изложении будем обращаться к упрощенным выражениям типа A6.2) -
222

Для того чтобы использовать эти формулы, требуется знать фактичес-
фактическую картину путей снабжения, т.е. потокораспределение в системе. Именно
в данном пункте методика расчета надежности включает методы гидрав-
гидравлического расчета и анализа режимов работы ТПС. Расчет надежности
снабжения всех узлов системы с помощью выражений A6.2) "вдоль извест-
известного потокораспределения" и сравнение получаемых показателей с узловы-
узловыми нормами позволяют выявить подмножество узлов, требующих тех или
иных мероприятий по резервированию: дублирования каких-то элементов;
кольцевания трубопроводной сети; понижения уровня централизации снаб-
снабжения введением в рассмотрение дополнительного источника и т.п. Любые
мероприятия по резервированию имеют целью выполнение требований:
R^NjJGJi. A6.5)
Такой многопараметрический подход к проблеме надежности ТПС
отвечает многообразию целей "надежностных" расчетов и выработанным
практикой приемам резервирования, а также (специфическим особенностям
систем снабжения, допускающим, как правило, временное снижение подачи
энергоносителя или воды потребителям.
Таким образом, основной целью оптимального синтеза надежных МКС
является обеспечение заданных уровней надежности снабжения ее потре-
потребителей при минимально необходимых для этого затратах. Возможна
также постановка обратной (двойственной) задачи по определению макси-
максимальных уровней надежности, при которых дополнительные затраты и ре-
ресурсы в систему не превысят заданных величин.
16.3. ОБЩАЯ ЗАДАЧА ОПТИМАЛЬНОГО СИНТЕЗА МКС
И ЕЕ ДЕКОМПОЗИЦИЯ
Как уже говорилось, проблема оптимального синтеза надежных МКС
объединяет не только задачи схемно-структурной и схемно-параметри-
ческой оптимизации системы, но и задачу введения в нее некоторой избы-
избыточности, минимально необходимой для удовлетворения заданных требо-
требований потребителей к надежности их снабжения. При этом оптимальное
состояние МКС ищется на конец выбранного преиода времени (например,
года или пятилетки), т.е. оптимизируется лишь один шаг в ее развитии.
Таким образом, данная задача не ставится как динамическая, поскольку
в ней не учитывается многоэтапный характер процесса создания и разви-
развития любой сложной системы трубопроводного транспорта.
Вместе с тем ее нельзя считать и чисто статической, так как во всех
математических формулировках и алгоритмах предусматривается опти-
оптимальный учет существующей части МКС, так что по существу это двух-
этапная задача. При расширенной трактовке "исходного состояния системы"
в качестве такового можно, например, поочередно брать результаты пред-
предварительной оптимизации МКС для некоторых промежуточных моментов
времени. Такой подход при условии его творческого применения в ходе
проектирования одной и той же системы позволяет в принципе решать
и задачи ее поэтапного развития. (Иллюстрацией подобного рассмотрения
может служить работа [173], где описана' попытка математического моде-
моделирования и оптимизации данимики развития газопроводных систем.)
223

Поскольку излагаемая ниже комплексная задача обобщает отдельные
задачи, представленные ранее, то в интересах ее полного описания содер-
содержательная постановка и математическая формулировка будут даны (на
примере ТПС) с повторением отдельных положений и формул. Итак, пред-
предполагаются заданными: избыточная проектная схема системы в виде произ-
произвольного графа (/,/) с длинами Z.,- всех участков и указанием ее сущест-
существующей части L- /; размещение потребителей по узлам схемы (/ ? 7j) и
их расчетные нагрузки Q/ (на конец рассматриваемого периода); воз-
возможные места (/ 6 J-i) расположения источников снабжения и их характе-
характеристики (фактические — для уже существующих источников и проектные
данные — для новых); сортамент D стандартных диаметров труб, разре-
разрешаемых для прокладки; технико-экономические показатели и таблицы,
необходимые для подсчета значений целевой функции; узловые нормы
надежности, характеризующие требования к снабжению потребителей
в нормальных и аварийных условиях; вероятностные характеристики
Rj и Rj надежности элементов линейной части (ветвей) и активных эле-
элементов, размещаемых в отдельных узлах; двухсторонние ограничения
на допустимые значения Р/ узловых давлений и удельных потерь A,-.va
давления или скоростей v{ на ветвях; допускаемые способы реконструк-
реконструкции : V,- - для ветвей и Г,- - для НС (г G /,).
Исходная схема (/, /) должна быть расширена введением фиктивного
общего источника в дополнительном узле т + 1 и соединением его услов-
условными связями i . € Iт + ] со всеми узлами / S J2, в которых возможно
размещение источников.
Требуется определить следующие оптимальные характеристики и пара-
параметры элементов искомой проектируемой МКС: места размещения и произ-
производительности источников (а следовательно, и уровни централизации
снабжения); конфигурацию сети (или сетей), связывающей источники
с потребителями, удовлетворяющей (с учетом ее "структурного" резерви-
резервирования) требованиям надежной транспортировки энергоносителя или
воды ко всем своим узлам; диаметры трубопроводов на ветвях, размеще-
размещение НС и их действующие напоры; расчетное потокораспределение в систе-
системе; существующие элементы, включая источники и НС , подлежащие ре-
реконструкции, и способы этой реконструкции (из числа заданных).
Область допустимых решений описывается большой совокупностью
уравнений, аналитических соотношений между искомыми параметрами
элементов, неравенств и логических условий. Во-первых, это подсистема
уравнений, характеризующая любое потокораспределение на заданной
избыточной схеме:
S «/,•*«= б/> /е/,; A6.6)
IS/
O, jGJ2 U/3?. A6.7)
xt = 2 12/1 =Qz; A6-8)
/ey,
у =Arf; A6.9)
A, = yt + H{ = ft (xlf dj, Lt), i€ /. A6.10)

При этом каждому допустимому распределению расходов и давлений
будет отвечать (с точностью до коэффициента) своя величина, пропорцио-
пропорциональная общей энергии задействованных источникоз и НС:
Э = 2 Н/Х; + 2 Нрс, = 2 hiXi + Z Pj\ Q,\ , A6.11)
где Xj (j ^J 2) - неизвестная производительность источника, равная расхо-
расходу Xj на фиктивной ветви [т + 1,/].
Как и в задачах оптимизации параметров PC и МКС, в общую систему
условий включаются двухсторонние ограничения на допустимые значения
давлений в узлах и удельных потерь давления на ветвях:
Pj^Pj^PjJ^J; /?,-,уд </гЛ уд, hu уд, /е /, A6.12)
а также условия дискретности диаметров труб, оборудования для НС,
возможных производительностей источников и способов реконструкции
существующих элементов системы:
d(еА сд /е/; и,-(</,) ег(д),;е/,; A6.13)
Hi G Г,- С Г, г ? // х/ е Gj CG, j ej2, A6.14)
Специальная группа соотношений должна фиксировать условия резерви-
резервирования проектируемой МКС и требования к надежности снабжения потре-
потребителей. В связи с этим в рассматриваемой ниже постановке основной
целью оптимального синтеза МКС с точки зрения обеспечения надежности
будем считать выполнение для каждого узла одного из условий, соответ-
соответствующих следующих двум случаям:
1. Данный узел включается в резервированную часть проектируемой
системы. Тогда он будет иметь двух- или даже многостороннее снабжение
и при выходе из строя какого-либо элемента, входящего в любой из путей
его снабжения, ему гарантируется по меньшей мере односторонняя подача
транспортируемой среды, но в уменьшенном объеме
Qj><(>jQf, Rj>N*, jGJlt A6.15)
где величины ip/ @ < ^ < 1) отражают заданные нормы пониженного
снабжения потребителей в аварийных условиях.
2. Узел у относится к одному из ответвлений, идущему от кольцевой
части или непосредственно от источника. В этом случае путь лу его снабже-
снабжения, составленный из участков i = ily .. ., /;, считая от начального узла
ответвления, должен обладать надежностью R (яу), которая не может
быть меньше заданной нормы N ?° °, т.е.
'"/
Я (тг,) = П /?,- (Lh dd > NJ 00 . A6.16)
Заметим, что в A6.16) с целью упрощения изложения не фигурируют
показатели надежности активных элементов, которые могут находиться
в числе элементов пути t;- и соответственно влиять на R (тг,). Другими сло-
словами, условно предполагается, что все они равны единице.
Данные положения позволяют в принципе производить (ориентировочно
на предварительном этапе или в ходе итерационного вычислительного про-
ls-3aK. 384 225

цесса) анализ и распределение всех узлов исходной проектной схемы на
два подмножества: J (R^) — содержащее узлы, которые необходимо "за-
"закольцевать", т.е. обеспечить для них многостороннее снабжение от источ-
источников, и J (R100), составленного из узлов, не нуждающихся в резервиро-
резервировании. При этом узлы из J (Л100) образуют "периферию" будущей систе-
системы, a J (R* ) — ее центральную часть, т.е. зону источников, крупных ма-
магистралей и связей между ними, которые в совокупности должны взаимно
резервировать друг друга. Таким образом, выбор этих подмножеств во
многом предрешает структуру синтезируемой системы и соответственно
параметры ее элементов. В частности, тем самым может обосновываться
иерархическое построение МКС (например, деление на магистральные и
распределительные сети), без чего не могут быть достигнуты надежность
и управляемость современных ТПС.
Определение J (R 10° ) естественно считать первичным моментом. Выя-
Выявлять "периферию" на исходной схеме можно с помощью многократного
использования формулы A6.16) и некоторых дополнительных логических
операций применительно к любому начальному приближению или проме-
промежуточному решению относительно конфигурации и параметров элементов
МКС. Однако выбор и оценку надежности путей снабжения следует произ-
производить не от источников к потребителям, а, наоборот, от концевых потре-
потребителей к источникам. В результате для каждого из узлов / S У, будет
выявлен максимальный "радиус" его надежного снабжения путем после-
последовательного перемножения величин Rt для "цепочки" яу ветвей, веду-
ведущих от него к ближайшему источнику, и сравнения получаемых значений
с нормой /V100, так что
J(R100) = {j:R(irj) >N100, /e/,}. A6.17)
Все узлы, не вошедшие в это подмножество, образуют
J(Rlf)=J -J(R100). A6.18)
Что касается / (R^), то с целью обеспечения кольцевания этой части
системы для каждого узла данного подмножества формулируется следую-
следующее упрощенное требование: в искомой структуре МКС должен обязатель-
обязательно существовать контур г, проходящий как через этот узел, так и один из
источников, что требует одновременного выполнения следующих условий:
Б ¦\br,a,i-sign*,! =2,/ <=J(R*);
'е/ ,е/ A6.19)
Е | b,flji signal = 2, / еУ2.
где bri - элементы матрицы контуров В формируемой "кольцевой" части
системы.
Целевая функция представляет собой выражение для общих расчетных
затрат по системе в целом:
F (х, d, Н, Р,Н)=Ъ (gt (dlf Lt) + z, (*,, ht) + ф{ (х,. Я,)) +
A6.20)
+ 2 z, (Qf, P/) + 2 %, (*,-, P,),
226

где gi >zi > ^i ~ приведенные (к одному году) затраты на прокладку трубо-
трубопровода, перекачку транспортируемой среды и сооружение НС на ветви
j • zi — стоимость энергии, доставляемой потребителю в узле j ? Л ; §/ —
общие приведенные затраты на сооружение и эксплуатацию источника в
узле /? J-i-
Задача заключается в минимизации функции A6.20) при соблюдении
всей совокупности условий A6.6) - A6.19). Она в еще большей степени,
чем задача МКО (см. гл. 15),характеризуется многоэкстремальным харак-
характером целевой функции, наличием уравнений самого различного типа
(линейных, билинейных, степенных, трансцендентных) и логических усло-
условий, дискретностью отдельных групп искомых переменных. К тому же
в ней присутствуют не полностью формализованные положения, которые
заранее ориентируют на участие инженера-проектировщика в процессе
построения и обоснования оптимального варианта синтезируемой системы,
т.е. на разработку диалоговых итерационных процедур оптимального
синтеза МКС.
Еще раз отметим, что в данной общей задаче содержатся многие подза-
подзадачи, имеющие самостоятельное значение. Так, если на избыточной проект-
проектной схеме МКС решать задачи, связанные с нахождением лишь наивыгод-
наивыгоднейшего потокораспределения (т.е. ограничить систему условий уравнения-
уравнениями A6.6) - A6.8) первого закона Кирхгофа, замыкающими соотношения-
соотношениями A6.10), описывающими законы течения среды, а также условием
A6.11) энергетического баланса), то придем к задачам схемно-структур-
ной оптимизации PC и МКС (см. гл 13).
Усложнив последние введением узловых норм и оценок надежности
путей снабжения, можно сформулировать задачу оптимизации уровней
централизации снабжения с учетом требования надежности.
Задачу схемно-параметрической оптимизации PC (гл. 14) получим,
если определять минимум A6.20) при выполнении условий A6.9),
A6.10), A6.12)-A6.14), но для заданного распределения расходов и с
применением приемов трансформации кольцевой схемы в разомкнутую
(и наоборот).
Зафиксировав диаметры трубопроводов на всех участках и действующие
напоры в источниках и НС, а также исключив условия, связанные с учетом
требований надежности, и все ограничения в виде неравенств, придем к
известной задаче о потокораспределении в МКС.
И наконец, здесь можно выделить математическую формулировку
задачи МКО (гл. 15), если выбрать (зафиксировать) схему МКС и исклю-
исключить из рассмотрения все величины и условия, связанные с требованиями
к надежности снабжения потребителей.
Данные математические модели справедливы в принципе и для оптимиза-
оптимизации конфигурации и параметров гидромелиоративных систем и систем
каналов по переброске вод, которые могут рассматриваться как единый
класс объектов - "системы многопрофильных каналов" [143, 221, 223].
При этом вместо A6.10) должны быть взяты соотношения, описывающие,
связи между техническими параметрами и стационарным течением воды
по каналам различного профиля, а также добавлены переменные и форму-
формулы для описания объемов земляных работ и их экономической оценки в
Целевой функции.
227

Все рассмотренные подзадачи в той или иной степени выделяются и чис-
численно решаются при разработке и реализации общих алгоритмов оптималь-
оптимального синтеза МКС с нагруженным резервированием, и им отвечают спе-
специальные вычислительные модули в ПВК СОСНА (см. гл. 18).
16.4. АЛГОРИТМИЗАЦИЯ ОПТИМАЛЬНОГО СИНТЕЗА МКС
Методическое значение обобщающих математических моделей заключает-
заключается в том, что они позволяют сделать некоторый новый шаг в формализации
рассматриваемой проблемы. Это неизбежно требует более четкой, по срав-
сравнению с достигнутым уровнем ее изучения формулировки и упорядочения
исходных посылок, а также расширения числа факторов и переменных,
считающихся существенными. Такие модели дают возможность более
обоснованно соотносить содержательную постановку задач с их математи-
математической сложностью и проводить дифференциацию имеющихся подходов
и вычислительных методов для их решения. Вместе с тем эти модели,
чтобы не оказаться чересчур абстрактными, должны быть потенциально
реализуемы (с учетом параметров используемых ЭВМ), а также обеспече-
обеспечены реальной информацией.
Построенная математическая модель для оптимального синтеза МКС,
несмотря на свою упрощенность в отношении учета требований надежности,
позволяет преодолеть известную ограниченность имеющихся в литературе
подходов, которые можно классифицировать следующим образом:
1. Замена задачи обеспечения надежности проектируемой системы много-
многократным рассмотрением задачи анализа ее надежности (о чем говорилось
в начале этой главы).
2. Эквивалентирование (упрощение) математических моделей, которое
достигается двумя способами: а) укрупнением схемы проектируемой си-
системы с соответствующим агрегированием исходных данных; б) перехо-
переходом к эквивалентной (в смысле надежности) конфигурации системы,
в которой фигурируют лишь элементы и подсистемы, непосредственно
влияющие на ее надежность. К этой группе относятся, в частности, методы,
требующие предварительного получения (через решение специальных под-
подзадач) обобщенных агрегированных характеристик и показателей надеж-
надежности для отдельных укрупненных элементов и подсистем.
3. Оптимальный синтез надежных PC, когда конфигурация синтезируемой
системы ищется в виде графа-дерева; при этом, однако, разрешается ис-
использование двух или более ниток (трубопроводов, линий передач) на
некоторых ветвях или их частичное дублирование (т.е. введение лупингов).
Общая схема такого подхода на базе метода ДП была описана в статье
Кеттеля [85].
Подчеркнем еще раз, что оптимальный синтез PC имеет принципиальное
значение при рассмотрении произвольных МКС. Прежде всего это объяс-
объясняется тем, что с чисто экономической точки зрения именно PC является
наиболее выгодным решением, но при условиях, что 1) система синтези-
синтезируется как бы из абсолютно надежных элементов, что делает ненужным
выполнение каких-либо дополнительных требований, связанных с надеж-
надежностью; 2) речь идет об оптимизации вновь проектируемой системы,
когда нет необходимости в учете ее существующей части. Именно поэтому
228

определение экономически наивыгоднейшего варианта проектируемой
системы в виде PC позволяет выявить наименьшую возможную величину
общих затрат как точку отсчета для оценки экономической целесообраз-
целесообразности тех или иных мероприятий по резервированию системы, т.е. для
определения "цены надежности". С другой стороны, последующее удовлет-
удовлетворение требований надежности применительно к полученной оптималь-
оптимальной PC путем необходимого дублирования ее элементов даст в большин-
большинстве случаев другую границу "вилки" (диапазона) возможных затрат
в систему с учетом обеспечения уже и требований надежности. Оптималь-
Оптимальному построению МКС на базе принципа нагруженного резервирования
будет отвечать, как правило, некоторое промежуточное значение целевой
функции, находящееся внутри этой "вилки".
4. Сведение задачи к типовым и хорошо отработанным математическим
моделям (например, линейного, кусочно-линейного, динамического или
стохастического программирования). Этому подчиняется тогда весь про-
процесс математического моделирования рассматриваемой задачи: вводимые
допущения, замена ее дискретной постановки непрерывной, линеаризация
нелинейных зависимостей и т.п.
На этом фоне переход к более общей задаче и ее содержательная деком-
декомпозиция, которая, в частности, может опираться и на перечисленные прие-
приемы, создают новые возможности для комплексной и гибкой алгоритмиза-
алгоритмизации оптимального синтеза МКС с нагруженным резервированием. Предла-
Предлагаемая ниже общая схема алгоритмов декомпозиции представляет один
из возможных способов реализации идеи построения итерационных вычис-
вычислительных процессов с помощью последовательного "расщепления" общей
задачи. Она ориентирована на множественность начальных приближений
с целью обработки более широкой области возможных решений и макси-
максимального приближения к глобальному оптимуму в решаемой задаче. Кроме
того, данная схема рассчитана в принципе на работу в режиме диалога со
специалистом-проектировщиком. Однако для практической реализации
такого режима до последнего времени не имелось соответствующего алго-
алгоритмического и технического обеспечения. Поэтому решение этой пробле-
проблемы остается предметом дальнейших разработок с целью создания человеко-
машинных систем для оптимального проектирования ТПС конкретного
типа и назначения.
Принципиальная блок-схема алгоритмов декомпозиции приведена
на рис. 16.1. Вычислительный процесс, как видно из рисунка, состоит из
девяти основных этапов (шагов). На первом этапе осуществляется выбор
на исходной избыточной схеме МКС "деревьев начального приближения"
(ДНП), обладающих характерными свойствами. Например, дерево кратчай-
кратчайших расстояний (ДКР) от главного источника до узлов потребления содер-
содержит все максимально надежные (с точки зрения схемы) пути яу (./€ J)
одностороннего снабжения, имеющие наибольшие (для каждого /) значения
Д(тг/). В качестве других вариантов ДНП берутся: 1) оптимальное дерево
(ОД) (или несколько деревьев), получаемое в результате решения схемно-
структурной задачи с помощью программы СТРУКТУРА (см. гл. 13);
2) оптимально-подготовленное дерево (ОПД) с учетом затрат в кольцую-
кольцующие ветви, определяемое по той же программе; 3) дерево наименьшей
суммарной длины (ДНД) ; 4) любое другое выбранное дерево на исходной
схеме. 229

] снгриронанмс ДИН -^- '1
2
¦¦'
1
час in M К(
К-зернир.
Опгимича
t
НИНИГГХ
пи: пара
ни|
ем
ме
ров МКС
Назначение анарийных ситуаций
16.1 .Принципиальная блок-схема алгоритмов декомпозиции для оптимального синтеза
МКС
11 — 14 — диалог пользователя и ЭВМ
Второй этап отводится для расчета надежности путей снабжения в ДНП
и выделения в нем двух подмножеств узлов: J (R100), включающего узлы,
которые не будут резервироваться и определят "периферийную" развет-
разветвленную часть системы, и J (R^) "головной" части, узлы которой должны
быть закольцованы (подробнее об этом говорилось выше).
На третьем этапе производится построение "надежной" схемы для
J (R*) посредством резервирования узлов этого подмножества дополни-
дополнительными связями, содержащимися в исходной избыточной схеме. Для
каждого / из / (R*) осуществляестя перебор всех имеющихся в схеме
ветвей, связывающих его со смежными узлами. Включение любой такой
дополнительной ветви в искомую конфигурацию системы приводит к обра-
образованию контура. Поэтому выбирается та из них, которая замыкает контур
с наибольшим количеством входящих в него узлов и проходит через один
из источников. Если в данном контуре окажутся еще не обработанные
узлы из / (R*), то они также считаются зарезервированными, так как их
двухстороннее снабжение уже обеспечено.
В ходе выполнения такой процедуры / (Я100) может оказаться совпав-
совпавшим с У. Это будет означать, что обрабатываемое ДНП не нуждается в резер-
резервировании, и проектируемая система будет далее оптимизироваться как
PC. В общем же случае получим частично закольцованную конфигурацию,
для оптимизации которой используется метод МКО (описанный в преды-
предыдущей главе), это составляет содержание четвертого этапа.
В итоге, исходя из выбранного ДНП, получим такой вариант МКС,
который будет обладать структурной надежностью (с точки зрения ее
схемы и протяженности путей снабжения узлов), а также оптимальным
в отношении: расчетного потокораспределения, диаметров трубопроводов,
действующих давлений и производительностей источников.
230

\\а пятом этапе производится перебор и обработка других ДНП (путем
повторного обращения к предыдущим процедурам) и выбор наиболее
экономичного варианта среди полученных локально-оптимальных решений
-.щя проектируемой системы.
Затем осуществляется перебор наиболее опасных аварийных ситуаций
(моделируется выход из строя головных участков магистралей, идущих
or источников, и для каждой из них обеспечивается повторение всех опе-
операций, необходимых для определения соответствующих оптимальных
параметров элементов, но применительно к пониженному уровню нагрузок
у потребителей, т.е. для Q' = <pjQj). Тут же производится сравнение диамет-
диаметров груб на ветвях, числа НС и действующих напоров для них, полученных
применительно к рассматриваемой аварийной ситуации, с теми, которые
были определены ранее для нормальных условий эксплуатации. Для даль-
дальнейшего расчета оставляются повышенные параметры элементов, если это
увеличение имело место (этапы 6—8).
Девятый этап — формирование итогового оптимального решения (с
проведением необходимых вспомогательных расчетов), а десятый —
определение "цены надежности", т.е. увеличения общих затрат в синтези-
синтезированную МКС по сравнению с ее незарезервированным вариантом.
В общей схеме алгоритмов оптимального синтеза МКС предусмотрены
также "точки диалога" с проектировщиком (см. рис. 16.1) для слежения
за ходом вычислительного процесса, корректировки данных, повторения
отдельных блоков или, наоборот, сокращения и прекращения счета и т.п.
Практической реализации описанного вычислительного процесса в виде
ПВК СОСНА, а также примеру использования этого ПВК в конкретной
задаче посвящена гл. 18.
Глава 17
ОПТИМИЗАЦИЯ УСТАНОВИВШИХСЯ РЕЖИМОВ
РАБОТЫ ТРУБОПРОВОДНЫХ СИСТЕМ
17.1. СРАВНИТЕЛЬНАЯ ХАРАКТЕРИСТИКА РАБОТ
ПО ОПТИМИЗАЦИИ РЕЖИМОВ ЭЭС И ТПС
Методы оптимизации режимов ЭЭС имеют уже большую историю [99],
начало которой относится к концу прошлого столетия, когда появились
первые сравнительно непротяженные электрические системы. В СССР
одними из первых здесь были работы Н.А. Сахарова [194] и Б.Л. Шифрин-
гана, опубликованные в 1927 и 1930 гг. и посвященные наивыгоднейшему
распределению нагрузки между параллельно работающими генераторами
и электрическими станциями. Позднее, особенно в послевоенные годы,
в связи с созданием и развитием объединенных ЭЭС стали активно разра-
разрабатываться теория и методы управления сложными ЭЭС, базирующиеся на
использовании современных методов линейной и нелинейной алгебры,
теории графов, нелинейного программирования и ЭВМ [5, 28, 45, 58, 98,
С)9. 101, 119, 187,191, 202, 203 и др.].
231

Более того, эти дисциплины испытывали известное взаимное влияние
обусловленное физическими аналогиями и математической общностью
своих задач. Можно указать, к примеру, на монографии: Дж. Б. Денниса
[58], рассмотревшего принцип электрической аналогии для постановки
и решения задач линейного и квадратичного программирования;
Л.А. Крумма [98, 99], предложившего еще в 1957 г. для оптимизации
режимов ЭЭС метод приведенного градиента, который фактически стал
одним из первых общих методов выпуклого программирования; Г.Е. Пу-
Пухова и М.Н. Кулика [187], разработавших методы построения и исполь-
использования гибридных (аналогово-цифровых) вычислительных систем, соче-
сочетающих высокое быстродействие и наглядность работы аналоговых уст-
устройств с универсализмом и точностью ЭВМ, для решения задач расчета и
управления режимами как ЭЭС, так и гидравлических систем.
Литература по оптимизации и управлению режимами ЭЭС и Единой
ЭЭС страны насчитывает тысячи наименований. Ее развернутый анализ дан
в -упомянутых книгах Л.А. Крумма, а также в коллективной монографии
[5]. С точки зрения темы данной главы важна сравнительная оценка состоя-
состояния и уровня работ по оптимизации режимов ЭЭС и ТПС.
Несомненно, что методы математического моделирования и расчета
потокораспределения и соответственно анализа режимов тепло-, водо-,
нефте-, газоснабжающих и других гидравлических систем достигли доста-
достаточно высокого уровня, сопоставимого в основном с аналогичными разра-
разработками для ЭЭС. Вместе с тем переход к более быстрым и гибким алго-
алгоритмам гидравлического расчета (см. гл. 9), а также замена многовариант-
многовариантного анализа режимов ТПС их комплексной оптимизацией на строгой мате-
математической основе, что относительно давно уже осуществлено в области
ЭЭС, здесь слишком затянулись. Подобная ситуация объясняется рядом
объективных причин.
Можно начать с того, что проблема оптимизации режимов ТПС не была
такой острой, как для ЭЭС, потому что бурное развитие трубопроводного
транспорта и создание сложных систем началось здесь значительно позднее,
чем в электроэнергетике. При этом даже в случае объединения отдельных
магистралей, распределительных сетей и источников в общие системы схе-
схемы их нормальной эксплуатации оставались в большинстве случаев "сек-
"секционированными", т.е. разомкнутыми, что максимально облегчало управ-
управление их режимами как в расчетном, так и в практическом отношении.
Другой общий для ТПС факт был отмечен В.Я. Хасилевым в 1957 г.
[241]. При некоторых упрощающих предположениях им была выведена
универсальная зависимость относительного изменения общих расчетных
затрат по трубопроводной или электрической сетям при отклонении иско-
искомых параметров от их оптимальных значений, а также ее экономических
и технических показателей. Это позволило количественно оценить значи-
значительно более пологий характер (по сравнению с ЭЭС) влияния нелинейно-
нелинейности основных гидравлических соотношений (между расходом, диаметром
трубы и перепадом давления) на общие экономические характеристики
ТПС.
Вместе с тем меньшая практическая актуальность оптимизации режимов
для ТПС - это лишь частичное объяснение сложившегося положения, тем
более что научно-методическая сторона может и должна в принципе опе-
232

режать практический уровень. Более важная причина заключалась здесь
в математической сложности соответствующих задач нелинейного програм-
программирования, их большой размерности и неразработанности для них эффек-
эффективных и работоспособных численных методов решения.
В последние годы актуальность проблемы оптимизации режимов ТПС
резко возросла по ряду причин. Во-первых, не только нефте- и газотранс-
газотранспортные системы, но и ТПС тепло-, водо- и газоснабжения крупных городов
и промышленных центров превратились в весьма сложные системы, объе-
объединяющие несколько источников и имеющие самые произвольные схемы
соединений, со множеством подстанций и регулирующих устройств. При
этом настоятельные требования эксплуатационной и проектной практики
все в большей степени заставляли переходить от секционированных к
многокольцевым схемам их работы (см. гл. 8, 9). В этих условиях стало
невозможным назначать гидравлические режимы и тем более обеспечивать
автоматизированное диспетчерское управление ТПС лишь с помощью мно-
многовариантных расчетов потокораспределения. Практически нереально учесть
таким путем все множество технических ограничений - сделать это в прин-
принципе можно лишь через решение соответствующих оптимизационных задач.
Современные ТПС - это также и постоянно развивающиеся системы.
Но для того чтобы заниматься разработкой мероприятий по их расшире-
расширению и реконструкции, необходимо уметь определять "узкие места" сущест-
существующих систем, что опять-таки требует предварительной постановки и
решения различных задач по оптимизации режимов их работы.
Еще одной причиной обращения к проблеме оптимизации режимов
ТПС стал опережающий уровень работ по созданию методической и алго-
алгоритмической баз для решения комплекса задач, составляющих пробле-
проблему оптимального проектирования МКС. Появилась возможность исполь-
использования данных разработок применительно к "режимным" задачам, пос-
поскольку в математическом плане их можно считать частными случаями задач
схемно-параметрической оптимизации МКС, но при условии, что структу-
структура системы и все ее технические характеристики являются заданными,
а оптимизации подлежат лишь гидравлические параметры всех элементов.
А поскольку описанные выше математические модели и алгоритмы рас-
рассчитаны на оптимизацию не только вновь проектируемых, но и разви-
развиваемых и реконструируемых систем, то именно это обстоятельство позво-
позволяет применять их (ценой относительно небольших модификаций) и для
оптимизации режимов PC и МКС.
Данные моменты уже нашли свое отражение в литературе, и можно ука-
указать в связи с этим на следующие группы публикаций. Прежде всего, это
работы по применению метода ДП для оптимизации режимов магистраль-
магистральных нефте- и газопроводов [226] и других разветвленных ТПС. Другая
часть публикаций касается использования сетевых потоковых моделей
линейного и кусочно-линейного программирования (являющихся прибли-
приближенными в том плане, что они не учитывают в полной мере уравнений
второго закона Кирхгофа) для управления потокораспределением в Еди-
Единой системе газоснабждения [228] и других много контурных ТПС. Имеют-
Имеются также отдельные работы по относительно частным задачам, связанным
с оптимизацией выходных параметров источников и распределением между
ними суммарной нагрузки.
233

Проблемам оперативного управления потокораспределением в инженер-
инженерных сетях посвящены монографии А.Е. Евдокимова, В.В. Дубровского и
А.Д. Тевяшева [60-62]. В них рассматриваются: математические форму-
формулировки и методы решения этих задач в детерминированной и вероятност-
вероятностной постановках, прогнозирование и моделирование "процессов потребле-
потребления целевого продукта", управление в условиях неполной информации.
В частности, в [60] описывается задача "синтеза оптимальной по энерго-
энергозатратам системы регулирующих органов в сложной инженерной сети",
а в [62] - идентификация моделей объекта управления и окружающей
среды. В то же время в этих книгах не нашли достаточно полного и объек-
объективного отражения исторический аспект и сравнительный анализ литера-
литературы и уровня работ в данной области, а вычислительная база для расчета
и оптимизации потокораспределения сводится в основном к методам
"диктующих точек" и "дифференциальному алгоритму", имеющим огра-
ограниченные области применения.
Таким образом, очевидно, что обсуждаемая проблема продолжает оста-
оставаться актуальной и заслуживает специального рассмотрения с различных
точек зрения. Ниже излагаются следующие вопросы, не выходящие за
рамки традиционных постановок задач математического программирова-
программирования: 1) математическое описание области допустимых гидравлических
режимов ТПС; 2) выбор критериев и математическая формулировка задач
оптимизации потокораспределения и 3) применение методов ДП и МКО
для оптимизации режимов разветвленных и многоконтурных ТПС.
17.2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ОБЛАСТИ
ДОПУСТИМЫХ ГИДРАВЛИЧЕСКИХ РЕЖИМОВ ТПС
По аналогии с ЭЭС [5] назовем установившимся режимом работы ТПС
некоторое ее состояние, определяемое (в случае изотермического течения,
т.е. без учета температур) значениями: действующих напоров и произ-
водительностей источников; перепадов давления и расходов на участках;
напоров и нагрузок у потребителей, характеризующих на протяжении
какого-то периода времени процесс отбора, транспортировки и распреде-
распределения энергоносителя или другой среды и называемых гидравлическими
параметрами режима.
Среди этих режимов ТПС, как и для ЭЭС, будем различать: нормальные,
утяжеленные (ухудшенные), аварийные и послеаварийные. Нормальный —
это такой установившийся режим работы ТПС, при котором обеспечивается
выполнение по крайней мере минимальных требований потребителей к
надежности и уровню их снабжения. Режим, в который система вынужден-
вынужденно перешла из нормального и существование которого (по времени) долж-
должно быть ограничено, поскольку нарушена часть требований к снабжению
(пониженный уровень узловых расходов, выход отдельных давлений за
допустимые пределы, перегрузка оборудования и др.), определим как
утяжеленный. Аварийный режим, подлежащий быстрейшей ликвидации,
возникает при выходе из строя каких-либо элементов ТПС и недопусти-
недопустимых отклонениях в значениях параметров. Послеаварийный — это режим,
в который ТПС переходит из аварийного состояния (например, в резуль-
результате действия автоматики и срабатывания задвижек, локализующих вышед-
234

щую из строя часть системы); чаще всего он является утяжеленным и
необходимы дополнительные мероприятия для восстановления длительно
допустимого (т.е. нормального) режима.
Математическое описание области допустимых режимов ТПС, даваемое
ниже, рассматривается на некотором абстрактном уровне, необходимом
для обсуждения основных методических положений и справедливом в
принципе для установившихся режимов любого из этих типов. Конкрети-
Конкретизация математической формулировки задачи производится на этапе уточ-
уточнения временнбго уровня управления режимами ТПС (см. об этом ниже)
с учетом внешних условий и фактического состояния системы, наличия
необходимых исходных данных и других факторов.
Исходной базой для описания области допустимых режимов являются
математические модели потокораспределения, представленные в первом
разделе книги. Однако эти модели сами по себе не могут дать описания
какой-либо области режимов по следующим двум причинам: 1) они строят-.
ся в виде замкнутых систем уравнений, так что (в случае корректной
постановки задачи) при каждом сочетании исходных данных (коэффи-
(коэффициентов и правых частей) будем получать единственное решение этой
системы, отвечающее физической сущности решаемой задачи; 2) в них не
входят ограничения, описывающие диапазоны возможных значений гид-
гидравлических параметров режимов.
В качестве отправной точки для дальнейших рассуждений обратимся к
модели потокораспределения в виде г.ц. с переменными параметрами
(см. гл. 8). Соответствующая ей система уравнений
Ах = Q(P), A7.1)
Qf(Pj) .+ Qm = 0, A7.2)
/ = i
ЛТР = у, A7,3)
h = у + Н(х) = f(x,s(x,P)) (ПА)
имеет m + 2п уравнений относительно 2и переменных х,- и /г,-, m — 1 пере-
переменных Pj и "балансирующего" расхода Qm в линейно-зависимом узле
т. Для простоты будем считать, что речь идет об изотермическом потоко-
распределении, иначе потребовалось бы вводить переменные, описывающие
изменение температур по всем элементам схемы цепи.
В настоящее время анализ и назначение режимов ТПС (по крайней мере
тепло-, водо- и газоснабжающих систем городов и промышленных центров,
а также и других гидравлических систем) осуществляется в основном с
помощью многократного решения подобных замкнутых систем уравнений
путем варьирования расчетной схемой и другими исходными данными.
Однако оптимизационный подход требует, чтобы еще до расчетов была бы
математически описана та область допустимых режимов, которая должна
быть подвергнута анализу.
Известно, что каждая ТПС обладает той или иной структурной и техни-
технической избыточностью (по производительности источников, пропускной
способности сетей, мощности компрессорных и насосных станций),
а также элементами автоматики, что обеспечивает ей гидравлическую
235

маневренность и способность реализовывать, вообще говоря, бесчислен-
бесчисленное множество потокораспределений. Основная цель математического
описания — это правильно отразить эти "степени свободы" ТПС в системе
уравнений A7.1)-A7.4), что должно превратить ее в недоопределенную
систему условий, имеющую целую область возможных решений. Одно-
Одновременно необходимо перечислить ограничения в виде неравенств и других
условий, отражающие предельные требования к допустимым гидравли-
гидравлическим режимам ТПС: с одной стороны, это известные технические огра-
ограничения (по условиям прочности труб, допустимой работы насосных
станций и т.п.), определяющие максимально возможные для каждого из
элементов ТПС давления и объемы подачи транспортируемой среды, а с
другой - минимальные требования, обусловливающие их нормальную
эксплуатацию.
Исходная неопределенность, отвечающая физическому смыслу и
конкретной содержательной постановке задачи, вводится в систему
уравнений очевидным образом: часть переменных переводится из
категории заданных в искомые величины, причем это может относиться
и к узловым расходам О/, и к действующим напорам Ht , и к гидравли-
гидравлическим сопротивлениям st. В связи с этим потребуется некоторая конкре-
конкретизация ранее введенных обозначений.
Введем дополнительные символы: J\ — подмножество узлов-потре-
узлов-потребителей, нагрузки которых заданы в аналитической форме, например в
виде зависимостей Qj{Pf), в частности, это могут быть фиксированные
значения; //— узлы с неизвестными нагрузками qj1^ >0, так что
/, =/1и//; аналогично J\ и/"- подмножества узлов-источников
с заданными аналитически QfiPj) ^0 и неизвестными q\2' <0 прито-
притоками среды; /з — простые точки разветвления на схеме с <2/ = 0. В итоге
совокупность неизвестных расходов на ветвях и в узлах расширяется до
вектора (х,«7A),^B))={д:/%О)ге/;^1)>О,/е/1'; <?J)<0, /?/?} а век-
вектор правых частей в A8.1) преобразуется (сохраним для него прежнее обо*
начение) в вектор Q(P) = ( Q,{Pj) > 0, /е/,; Q^P/) < 0, /е/2; Q/ = 0.
/?/3M так что вместо A7.1) можно записать
A7.5)
а условие A7.2) суммарного материального баланса примет вид
- 2 QiiPj)- S <?/2) = 2 Of(Pf) + 2 qy\ A7.6)
/еГ, /е/'/ /е/', /е/'/
Аналогичным образом расщепляется вектор действующих напоров:
Н{х) = { Hi (xt) i G/,; 0, / e/2} = (Я т(х), 0т), где i = [/',/+ 1 ] -' ветвь
i с концевыми узлами /, / + 1; / = I\ U/2 — подмножества ветвей соот-
соответственно с заданными аналитически (в частности, фиксированными)
величинами действующего напора (г'6/i), а также пассивных ветвей
(г?/2), для которых Н\ =0. В результате замыкающие соотношения
A7.4) разобьются на следующие две группы:
у, + н,{х) = ftto,sito. Pf. Pf+i)l «ел. A7-7)
yt =f,(x,. % Ph PI+i), ?8)
236

или в векторной форме
yd) + ?=/О>, /2>=/2>. A7.9)
Для гидравлических сопротивлений s,- могут иметь место два рода
ситуаций: 1) возможность непрерывного их изменения в некоторых
пределах (например, путем плавного открывания или закрывания задви-
задвижек на трубопроводах):
s, <*(*,, Pj, P,+ l) <!,, A7.10)
причем будем допускать случай s,- = + °°, что соответствует полному
прекращению течения на этой ветви, и тогда фактически остается лишь
ограничение снизу:
si >n; (iv.li)
2) дискретный характер изменения, когда st может принимать значения
из некоторого списка {$,-д, sii2 , ¦ ¦ ¦ , s^m).
Объединяя эти два случая, будем считать, что для каждого s,- задано
множество St возможных значений, которое может, в-частности: сводиться
к единственной величине, задаваться диапазоном A7.10), полупрямой или
другим образом, так что
S(I /G/ A7.12)
или в обобщенной форме
s(x,P)ES. A7.13)
Нижние и верхние границы (или диапазоны) допустимых значений иско-
искомых величин, отвечающие конкретным физико-техническим ограничениям
для рассматриваемой ТПС и решаемой задаче, могут быть, как правило,
сведены к неравенствам:
? <?B); #<#; _Р<Р<Р' . A7.14)
Таким образом, математическое описание области допустимых режимов
представляет собой совокупность условий, включающую линейные и нели-
нелинейные уравнения и неравенства A7.3)— A7.6), A7.9), A7.13) и A7.14).
В связи с тем что некоторые характеристики активных элементов могут
быть составлены из двух и более аналитических зависимостей (соответст-
(соответствующих различным диапазонам изменения основных переменных) или
даже принимать лишь дискретные значения, ясно, что данная система усло-
условий может иметь и такие нелинейные соотношения, которые недифферен-
Цируемы в отдельных точках или связаны логическими условиями и требо-
требованиями дискретности. Все это резко ограничивает, а в общем случае и
исключает применение традиционных математических методов, опирающих-
опирающихся на непрерывность и дифференцируемость функций, составляющих мате-
математическую формулировку задачи. Поэтому речь должна идти о специаль-
специальных методах (типа метода динамического программирования и других
методов поиска экстремума), оперирующих по возможности лишь со зна-
значениями функций, а также максимально учитывающих специфику этих
237

задач. Для полной формулировки оптимизационных задач и перехода к
возможным методам их решения необходимо предварительно рассмотреть
критерии для оценки и сравнительного анализа режимов ТИС.
17.3. ВОЗМОЖНЫЕ КРИТЕРИИ И МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА
ЗАДАЧ ОПТИМИЗАЦИИ РЕЖИМОВ ТПС
Любая оптимизационная задача строится из двух основных элементов:
области R допустимых решений и целевой функции F, задающей критерий
для сравнения возможных решений. И заключается она в отыскании таких
точек из R, в которых F принимает минимальные (или максимальные)
значения. При этом речь идет, как правило, о точках *(") локального
минимума F, для каждой из которых можно указать такую окрестность
Rv, принадлежащую целиком области R, что неравенство F(x)^ F(x^v^)
имеет место для всех xGRv. Каждая такая точка х^ называется локаль-
локально-оптимальным решением. В случае множественности подобных точек
задача относится к классу многоэкстремальных и ее глобальным реше-
решением считается наилучшее среди локально-оптимальных, т.е. то из х ^ ,
в котором достигается самое меньшее (большее) среди локальных мини-
минимумов (максимумов) F(x^).
Многоэкстремальность в задачах оптимизации определяется свойствами
целевой функции F (ее невыпуклостью, недифференцируемостью в отдель-
отдельных точках и др.), а также и особенностями допустимой области R, кото-
которая может оказаться невыпуклой или несвязной (т.е. состоящей из
нескольких непересекающихся подмножеств). При оптимизации режимов
работы ТПС, как правило, уже на этапе постановки задачи и задания
исходных данных должна формироваться система условий, содержащая
единственную точку минимума F. Однако в сложных случаях необходимо
считаться с возможностью многоэкстремальной задачи.
Содержание и назначение конкретной задачи оптимизации режима ТПС
решающим образом зависит от выбора целевой функции, что, в свою
очередь, определяется рядом факторов: характером рассматриваемых
режимов (нормальные, утяжеленные, послеаварийные и другие), времен-
временным уровнем управления режимами, текущим состоянием системы.
Что касается временных уровней оперативно-диспетчерского управле-
управления ТПС, то, как и в электроэнергетике, здесь можно выделить четыре
аспекта: долгосрочное и краткосрочное планирование; оперативное и
автоматическое управление. К долгосрочному планированию относятся
задачи назначания режимов с большой заблаговременностью (месяц—квар-
(месяц—квартал—сезон—год), а также задачи анализа режимов в связи с развитием и
реконструкцией ТПС. На уровне краткосрочного планирования решаются
задачи подготовки режима работы ТПС на ближайшие сутки или несколько
суток (включая выходные и праздничные дни). Оперативное управление
обеспечивает в течение суток реализацию запланированных режимов
и их коррекцию в случае необходимости, а также предотвращение и ликви-
ликвидацию аварийных ситуаций. Автоматическое управление предполагает
наличие локальных и централизованных средств регулирования (включая
и ЭВМ) и обратную связь с объектом для управления текущими и пере-

Поскольку основной задачей ТИС независимо от их imi<i n mwi.-w
является обеспечение бесперебойного снабжения множества потребителей
.шергоносителем, водой и другой транспортируемой средой при мини-
минимальных народнохозяйственных затратах, то основным критерием для
уровней планирования режимов служит минимизация энергозатрат на
транспортировку и распределение среды:
f\ =2 С/Я/IQ/I + X c,Hj\qj\ + A7.15)
+ v Cj(yi+Hi)Xi + 2
где Cj - удельная стоимость энергии, вырабатываемой источником в узле
/, а с,- — удельная стоимость энергии, затрачиваемой на насосной станции,
расположенной на ветви i .
Кроме A7.15), при планировании режимов, а также при оперативном
управлении могут использоваться и другие целевые функции. Например,
с точки зрения предельного использования ТПС наиболее важной может
оказаться задача о максимально возможной подаче энергоносителя заданно-
заданному подмножеству ее потребителей (при соблюдении минимально допусти-
допустимых ограничений снизу для остальных потребителей). Тогда в качестве
критерия можно взять
F2 = 2 qf -> max, A7.16)
где в J*DJ /'перечисляются номера всех этих узлов-потребителей.
Во многом эквивалентной ей (что зависит от конкретных условий)
будет задача на максимальную пропускную способность отдельных
трубопроводных участков:.
F3 = 2 Xi ~* max, A7.17)
где /*С/ - подмножество- выделенных ветвей расчетной схемы ТПС.
Именно с помощью соответствующего подбора Г* можно в принципе
выявлять зоны снабжения потребителей от одного или минимального
числа источников. Допустимы и другие критерии, что зависит от содер-
содержания и целей оптимизации режимов работы ТПС. Так, например, на
этапе коррекции (стабилизации) ранее намеченных режимов возможен
критерий
F4 = 2 (Pfnn) ~P,f -+ min, A7.18)
где />.(пл) — запланированные значения давлений в узлах, перечисленных
вУ4- В качестве этих узлов рыступают так называемые диктующие точки
ТПС.
Итак, математическая формулировка рассматриваемых задач может
быть сведена к минимизации F\ или F4, максимизации F2 или F3 (или
к нахождению экстремального значения какой-либо другой функции)
при связях и ограничениях, описанных выше, часть из которых может
быть опущена. Примером такого подхода может служить работа [3],
239

посвященная предельным режимам ГСС при планировании топливоснаб-
топливоснабжения экономического района.
Сформулированные выше задачи являются сложными задачами нели-
нелинейного программирования, которые в случае многоконтурных ТПС,
рассматриваемых как г.ц. с переменными параметрами, не имеют еще
эффективных численных методов для своего решения. В связи с этим
и возникает идея об использовании здесь математических моделей
и алгоритмов, разработанных для решения комплекса задач оптималь-
оптимального проектирования разветвленных и многоконтурных систем, описанных
в предыдущих главах данного раздела книги.
17.4. О ПРИМЕНЕНИИ МЕТОДОВ ДП И МКО
ДЛЯ ОПТИМИЗАЦИИ РЕЖИМОВ РАЗВЕТВЛЕННЫХ
И МНОГОКОНТУРНЫХ ТПС
Очевидно, что для оптимизации режимов разветвленных ТПС с успехом
может быть применен метод ДП. Представление расчетной схемы ТПС в
виде графа-дерева существенно упрощает задачи ее расчета и оптимизации
(об этом уже говорилось неоднократно), поскольку вектор расходов
фактически исключается из числа неизвестных величин. Такому выводу
не противоречат и те случаи, когда имеет место попутный расход
транспортируемой среды, например, на собственные энергетические
потребности ТПС (как это делается в газотранспортных системах, где газ
используется для обеспечения работы газоперекачивающих агрегатов на
КС), так как соответствующее уменьшение потока легко учитывается
в процессе вычислений. Таким образом, в качестве основных искомых
параметров здесь выступают лишь действующие напоры в источниках и
насосных подстанциях, а также узловые давления (или их перепады) по
всем элементам расчетной схемы. Дискретность некоторых из этих пере-
переменных, связанная со стандартностью типоразмеров оборудования
активных элементов, также не представляет особых трудностей для
метода ДП.
Из сказанного ясно, что определение наилучшего гидравлического
режима работы разветвленной ТПС можно произвести с помощью програм-
программы метода ДП (гл. 14), предназначенной для оптимизации развития PC.
Действительно, если система является существующей, то, следовательно,
полностью известны ее конфигурация и значения технических параметров
(или их взаимозависимости) всех активных и пассивных элементов.
В результате расчет по данной программе фактически можно свести к
выбору лишь наивыгоднейших давлений и действующих напоров. А это
при известных расходах на ветвях будет означать оптимизацию режима
ее работы по одному из двух возможных (с точки зрения используемого
критерия минимума общих расчетных затрат) показателей качества иско-
искомого решения: 1) минимума общей стоимости электроэнергии, затрачи-
затрачиваемой для перекачки среды, или 2) максимума суммарной энергии,
которая будет доставлена потребителям. Расчеты по оптимизации режимов,
проведенные для ТСС, работающих от нескольких районных котельных,
показали эффективность использования программы метода ДП, предназ-
предназначенной, вообще говоря, для решения общей оптимизационной задачи.
240

Что касается многоконтурных ТПС, то для оптимизации гидравличес-
гидравлических режимов их работы аналогичным образом может быть применен метод
МКО с сохранением всех своих основных положений (гл. 15). Изме-
Изменится лишь вид целевой функции в соответствии с назначением расчета,
а также скорректируется содержание этапа, связанного с оптимизацией
методом ДП разветвленной ТПС, получаемой после разрезания исходной
многоконтурной схемы в точках слияния потоков.
Так как диаметры трубопроводов в рассматриваемой задаче должны
быть заданы, то объектом оптимизации для метода ДП на этом этапе будут
именно узловые давления, действующие напоры, а также рабочие состояния
всех регулируемых органов (регуляторов расхода и давления, дроссельных
станций и др.). В результате будут найдены оптимальные значения s,- и
#,-, отвечающие их заданным (в аналитической или табличной формах)
характеристикам и логическим условиям работы всех элементов с пере-
переменными параметрами, по критерию минимума эксплуатационных затрат
и с учетом всей совокупности заданных ограничений. В соответствии с
этими поправками коэффициентов гидравлического сопротивления и дру-
других характеристик на последующем этапе будет определяться новое пото-
кораспределение уже для многоконтурной схемы ТПС и т.д. от итерации
к итерации, пока не сработает условие сходимости вычислительного про-
процесса.
В следующей главе описано применение метода МКО для выявления
"узких мест" в ТСС г. Новосибирска с целью оптимизации мероприятий по
ее развитию и реконструкции, что по содержанию своих расчетов близко
к рассматриваемой задаче. Вместе с тем описанная (весьма кратко) схема
использования метода МКО носит, конечно, предварительный характер и
потребует дополнительной работы по ее реализации, исследованию и
практической апробации. При этом должны быть уточнены содержательная
постановка и математическая формулировка задач применительно к специ-
специфическим особенностям и условиям функционирования ТПС. различного
типа и назначения с обязательным учетом временных уровней планиро-
планирования и оперативно-диспетчерского управления режимами их работы.
Глава 18
ПРОГРАММНО-ВЫЧИСЛИТЕЛЬНЫЙ КОМПЛЕКС СОСНА
ДЛЯ ОПТИМАЛЬНОГО СИНТЕЗА МКС
18.1. ОБЩАЯ ХАРАКТЕРИСТИКА ПВК СОСНА.
ЕГО ОСНОВНЫХ МОДУЛЕЙ И БЛОКОВ
ПВК СОСНА ("система оптимального синтеза с учетом надежности")
предназначен для использования в трех направлениях: 1) для реализации,
исследования и совершенствования общих алгоритмов оптимального синте-
синтеза МКС; 2) в качестве алгоритмического обеспечения при решении отдель-
отдельных задач оптимального проектирования ТПС; 3) как вычислительная
база и составная часть систем автоматизированного проектирования
(САПР), ориентированных на ТПС конкретного типа.
1/2 16. Зак. 384 241

<
Q
D
f-
c;
S
3
i
Зал
h
а о
UO
5^
E-i
реше
9
С
<N
J
a
табли
E
1
s ?
<
о
ей
OQ
РЭ
1=
s
к
рол
онт
s
go
m >
D
<y
A
cxe
в:
Q
S
a.
s
X
ни я
*
К
8.
e
о
" Z
1 i
CO 3
§¦"
о >,
m z
Q
X
мят
CO
П
s
CTK
3"
X
ей
е
о
о,
С
сл.
ей
PC D
73
3 H
С
3 м
Г , р ,
с Я
С =
w X
S 9
I §
МКС
х f-
155
II

Данный ПВК разработан на языке Фортран и представляет комплекс
программ, реализующих методы схемно-структурной, схемно-параметри-
ческой и многоконтурной оптимизации, гидравлического расчета, а также
алгоритмы логической обработки данных, управления вычислительным
процессом и другие. Пакет построен по модульному принципу, унифици-
унифицирован по всем исходным, рабочим и результирующим массивам данных
и является открытым, т.е. после унификации и согласования "входа"
и "выхода" к нему может быть подключен любой новый модуль, расши-
расширяющий возможности ПВК.
Здесь и далее под модулем будем понимать отдельную программу или
совокупность подпрограмм, которая имеет относительно самостоятельное
значение и может использоваться автономно для решения частных задач.
Блоком же будем считать специальную подпрограмму для выполнения
какой-либо вспомогательной процедуры по обработке информационных
массивов, анализу сходимости процесса, интерпретации результатов
счета и т.п. Функционально ПВК разбит на пять групп блоков и модулей
(рис. 18.1): информационные блоки, вычислительные модули, интерпре-
интерпретирующие, сервисные и управляющие блоки.
Информационные блоки производят ввод данных, их контроль, пере-
переработку, изменение, упорядочение, а перед печатью результатов - возврат
к исходной нумерации, принятой для элементов избыточной проектной
схемы МКС.
Вычислительные модули составляют библиотеку оеновных "инструмен-
"инструментов" для счета и оптимизации и включают (но в унифицированном виде)
все описанные выше стандартные программы: оптимизации конфигурации
и параметров элементов PC, анализа гидравлических режимов, построения
надежной схемы МКС, а также получения различных начальных прибли-
приближений и др.
Интерпретирующие блоки предназначены для анализа и переработки
"выходов" проработавших блоков и модулей во "входы" последующих
процедур при выполнении заданного итерационного процесса, для
управления работой ПВК. К ним, в частности, относятся блоки: RE
("разрезания" многоконтурной гсхемы на деревья) и KLE (обратного
их "склеивания"), а также объединения отдельных модулей и блоков
в новые модули более высокого уровня.
Сервисные блоки осуществляют хранение и обновление основных
массивов исходных данных и промежуточных результатов: запись их во
внешнюю память ЭВМ и списывание оттуда (в случае прерывания счета),
выдачу на печать сигнальной информации, а также промежуточных и
окончательных результатов в виде таблиц. Каждый из управляющих
блоков обеспечивает реализацию того или иного общего алгоритма опти-
оптимального синтеза с помощью соответствующего режима работы ПВК.
В настоящее время ПВК содержит 47 подпрограмм (порядка
5000 операторов). Оттранслированная версия пакета находится в архиве
персональных библиотек БЭСМ-6 (в СЭИ), занимая там 23 зоны, а его
работа производится в режиме полуавтоматической системы сегмен-
сегментации с динамической перегрузкой разделов в соответствии с тем или
иным реализуемым поддеревом из общего дерева разделов (рис. 18.2).
Для записи промежуточных результатов счета используются магнитные
243

барабаны и диски. С помощью ПВК можно синтезировать МКС, имеющие
до 250 ветвей (при необходимости это число можно увеличить расши-
расширением используемой памяти ЭВМ).
Отладка и тестирование ПВК проводились "нисходящим" способом
аналогично тому, как это описано в работе [75]. Такой подход "сверху
вниз", когда к совокупности работающих программ последовательно
подключаются один модуль или блок за другим, приводит, с одной
стороны, к меньшим потерям времени при отладке, а с другой - обеспе-
обеспечивает более естественные условия для численных экспериментов.
Более подробно описание ПВК, включая порядок задания исходных
данных, выбор режима использования, способы повышения надежности
его работы и т.д., дано в работах [254, 255].
18.2. ИСПОЛЬЗОВАНИЕ ПВК СОСНА ДЛЯ ОПТИМАЛЬНОГО СИНТЕЗА
И РЕКОНСТРУКЦИИ РАЗВИВАЕМЫХ ТПС
Отдельные примеры использования ПВК СОСНА для решения типовых
оптимизационных подзадач, возникающих при проектировании и разви-
развитии ТПС, уже фигурировали в предыдущих главах этого раздела.
В данном разделе рассказывается о решении с помощью этого ПВК двух
новых задач. Первая иллюстрирует на примере условной ТПС решение
общей задачи оптимального синтеза с учетом требований надежности.
Вторая задача связана с оптимальной реконструкцией развиваемой
ТСС г. Новосибирска (рис. 1.1 и 1.2). Она весьма интересна в том отно-
отношении, что показывает большие возможности ПВК СОСНА как комплекс-
комплексного инструмента для выявления "узких мест" в структуре и парамет-
параметрах элементов крупных существующих ТПС с выдачей оптимальных реко-
рекомендаций о способах их реконструкции. Это любопытно еще и потому,
что другими способами, в том числе и посредством многовариантного
инженерного анализа возможь^лх мероприятий (с применением программ
гидравлического расчета на ЭВМ), данная задача в должной мере так и
не была решена.
Избыточная схема условной ТПС (рис. 18.3) имеет параметры: т -Т1,
п = 40, с = 19. Последовательность расчетов и характер получаемых резуль-
результатов опишем, исходя из начального приближения в виде "оптимально
подготовленного дерева" (ОПД), поскольку именно это ДНП обеспечило
получение наиболее экономичного решения. Для простоты предположим,
что в рассматриваемой ТПС все потребители относятся к одной категории
и соответственно для каждого из них задана одна и та же требуемая норма
надежности его снабжения N1.00 =0,94.Будем считать также, что для всех
ветвей схемы имеют место одинаковые показатели, необходимые для
подсчета по формуле A6.1) вероятностей Л,- их безотказной работы.
Вычислительный процесс состоит из следующих операций:
1. Анализ путей снабжения (для выбранного ОПД) и построения надеж-
надежной схемы ТПС. Для этого определяются все величины /?,-(/= 1,..., 40),
которые использовались для подсчета надежностей R{iij) путей снабжения
и сравнения их с jV.1 оо .
Начнем с узла/ =22, тогда/?B1-22) =0,9701; ЛB0-21-22) =0,9554;
R(9-20-21-22) = 0,9304. Таким образом, в узле/ = 9 происходит нару-
245

18.3. Избыточная схема условной ТПС для задачи оптимального синтеза
Полужирными линиями — ОПД; цифры между узлами — длины участков
шение проверяемого условия:/?/ > 0,94. И,следовательно, все узлы в пути
снабжения, связывающем его с источником, т.е. узлы 9, 7,4, 11, 1, необхо-
необходимо резервировать. Далее анализируются ответвления от узла 2:
ЛB-12) = 0,9627; /?B-13) = 0,9701 и для последующих расчетов путей
снабжения берется наименьшее из этих двух значений. Тогда R A0—2—12) =
= 0,9374, т.е. узлы 10,8,5 также подлежат резервированию.
Затем подсчитываются R(tTj) для двух оставшихся ответвлений:
#A5-16) = 0,9887; ЛA4--15-16) = 0,9737; ЛF-14 15 -16) = 0,9374;
ЛA8 19) = 0,9812; Я(П-18 19) = 0,9591; ЛC-17 18- 19) = 0,9304.
В результате выявляется вся "головная" часть ОПД, т.е. подмножество
узлов JiR^), которое необходимо закольцевать (на рис. она отделена
пунктирной линией).
Далее производится перебор вариантов "схемного" резервирования
узлов из У(Л?>): для узла 9 возможны две дополнительные связи:
246

Таблица 18.1
Оптимальные параметры элементов для ТПС на рис. 18.3
№ п.п.
Ветвь [/,, /2
Начальное приближение
ОПД
*/> т/ч
d(, мм
МКС
/, т/ч
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
1-3
6-10
10-9
1-11
11-4
4-5
5-3
5-8
8-10
5-6
4-7
7-9
3-17
17-18
18-19
6-14
14-15
15-16
10-2
2-13
2-12
9-20
21-22
20-21
Действующий напор в
источнике
Капитальные вложения, руб.
Общие расчетные затраты,
руб./год
Эксплуатационные расходы на
перекачку руб./год
12,82
5,32
7,64
774,18
746,18
575,82
130,18
241,96
193,96
93,68
158,36
110,36
88,00
48,00
18,00
74,00
34,00
14,00
103,00
21,00
18,00
86,00
12,00
42,00
36,89
819190,00
163269,67
15815,47
100
100
100
500
500
450
250
300
250
200
250
200
200
150
100
200
125
100
200
100
100
200
100
150
129,98
4,97
7,32
657,02
629,02
458,33
13,02
231,35
183,35
103,97
158,68
110,68
88,00
48,00
18,00
74,00
34,00
14,00
103,00
21,00
18,00
86,00
12,00
42,00
39,14
796890,00
160328,81
16888,61
200
100
100
400
400
350
100
250
250
200
200
200
200
150
125
200
125
100
200
125
125
200
100
150
8—9 и 10-9; выбирается вторая, так как она образует контур
10—9—7-4—5—8-10 с большим количеством вошедших в него узлов;
для узла 3 берется связь 1—3, которой соответствует контур 1—3-5—4-
-11—1, и для узла 6 связь 6—10 с контуром 6—10—8—5—6. Все дополнитель-
дополнительные связи показаны на рисунке параллельными пунктирными линиями.
2. Оптимизация параметров выбранной МКС методом МКО (это заняло
2,5 мин на БЭСМ-6). Полученные значения диаметров, расходов, действую-
действующих напоров \и технико-экономических показателей приводятся в табл.
18.1.
247

18.4. Решения для закольцованной части ТПС
при различных у
a- ip = 0,5;6- 1^=0,7; е- </>=1,0
Из таблицы видно, что экономические показатели многоконтурного
варианта ТПС ненамного лучше ее начального приближения — ОПД:
общие расчетные затраты у МКС меньше, чем у ОПД на 1,8%; капиталь-
капитальные вложения в объект на 2,7%, а эксплуатационные расходы, наоборот,
больше на 6,8% за счет увеличения действующего напора в источнике.
Однако решения, представленные выше, не учитывают условий
обеспечения потребителей з аварийных ситуациях, исходя из задаваемых
норм tf их пониженного снабжения. В связи с этим выполняется
следующий этап.
3. Анализ аварийных ситуаций и корректировки оптимального варианта
ТПС для <ff= 1; 0,7 и 0,5. На рис. 18.4 выделена кольцевая часть ТПС.
В качестве наиболее опасных аварий рассматривались случаи выхода из
строя и полного отключения ветвей: 1—11, 11—4, 1—3, 5—3 и 5—4, т.е.
близких к источнику.
Для каждой из них производилась корректировка исходной схемы
ТПС (т.е. удаление из нее соответствующей ветви) и изменение всех
нагрузок у потребителей (посредством умножения их на ^/), а далее —
повторение всего процесса оптимального синтеза с целью определения
оптимальных значений я,-, df и Щ, соответствующих данной аварии.
После подобной обработки всех намеченных аварий искомые d,, В/
окончательно выбирались по принципу "суперпозиции" всех полученных
значений, а именно: для каждой ветви выбирались максимальные из них,
что приводит, конечно, к некоторому избыточному резервированию
ТПС в целом.
Решения для различных значений норм <$ f оказаны на рис. 18.4.
248

Цифры вдоль линий указывают на значения диаметров трудопроводов.
Если этих значений два, то первый диаметр соответствует случаю нормаль-
нормального режима, а второй увеличен в ходе оптимизации ТПС при аварийных
отключениях участков. Если диаметр указан один, то это означает, что его
изменения не потребовалось.
В табл. 18.2 включены результаты соответствующих расчетов. Здесь
цифрами обозначены различные решения: 1 — для нерезервированной
схемы, т.е. решение в виде ОПД; 2 — оптимальное решение ТПС как
многоконтурной системы, но без учета гарантированного уровня снабжения
потребителей во время наиболее опасных аварий; 5-5 - решения для
рассмотренных аварийных ситуаций при заданных i/>/-
В табл. 18.3 сведены общие технико-экономические показатели полу-
полученных решений, а также результаты их сравнения и величины "цен надеж-
надежности". Данный пример показывает работоспособность разработанной
методики и ПВК СОСНА для реализации алгоритмов оптимального синтеза
МКС с нагруженным резервированием.
С помощью ПВК СОСНА были проведены расчеты по оптимальной
реконструкции ТСС г. Новосибирска (см. рис. 1.1 и 1.2). Эта система исто-
исторически развивается как многоконтурная, причем кольцующие перемычки
используются не только в аварийных ситуациях, но и в условиях нормаль-
нормальной эксплуатации. Теплоснабжение города осуществляется от четырех
ТЭЦ, в сети работает пять НС. Ввиду недостаточной увязки планов
строительства тепловых сетей с развитием города направления прокладки
отдельных трубопроводов и их диаметры оказались выбранными
неудачно, что обусловило неравномерную загрузку магистралей. Подоб-
Подобная ситуация крайне осложнила решение вопросов о рациональном с точки
зрения всей системы развитии и реконструкции ТСС.
Новосибирским отделением института Теплоэлектропроект совместно
с СЭИ еще в 1972 г. была выполнена работа, в которой исследовались
вопросы аварийного резервирования и развития ТСС г. Новосибирска
для уровней нагрузок 1975-1980 гг. С помощью многовариантных расче-
расчетов на БЭСМ4 по программам расчета потокораспределения в МКС и
оптимизации параметров PC были выбраны варианты зон обслуживания
ТЭЦ, диаметры новых и реконструируемых трубопроводов, места
установки и параметры НС.
Все сравниваемые варианты количественно и экспертно оценивались
как по их экономичности, так и с точки зрения эксплуатационной надеж-
надежности. Были показаны преимущества работы системы по многоконтурной
схеме перед разветвленной (с закрытыми задвижками на перемычках),
так как это давало очевидную экономию электроэнергии на перекачку
теплоносителя и капиталовложений на аварийное резервирование сетей,
а также повышало гидравлическую устойчивость ТСС в целом. Основные
принципы построения и развития этой ТСС, предложенные в той работе
в основном и реализовывались в последующие годы.
С тех пор прошло много лет и накопились новые проблемы, связанные
с дальнейшим развитием ТСС г. Новосибирска. Поэтому появилась острая
необходимость в новом анализе "узких мест" системы с целью опреде-
определения оптимальных вариантов реконструкции и развития ее структуры
и параметров элементов на выросшие уровни нагрузок. Кроме того, теперь
17. Зак. 384 249

Таблица 18.2
Выбор диаметров на ветвях схемы (рис. 18.4) для нормальных и аварийных
ситуаций
№ п.п.
Ветвь
<Р= 1,0
Авария на ветви
1-11
1-3
11-4
5-3
4-5
1
2
3
4
5
6
7
8
9
10
11
12
1-11
6-10
11-4
4-7
7-9
4-5
5-8
8-10
5-3
5-6
1-3
9-10
700
700
300
200
500
350
350
250
200
350
100
300
150
125
250
200
200
125
100
200
100
100
200
150
100
250
200
150
350
100
350
100
350
100
350
150
125
300
200
200
150
100
100
200
100
150
125
200
200
200
350
125
350
100
350
100
350
150
125
250
200
200
100
150
100
350
125
300
300
250
150
200
150
100
200
250
350
125
350
300
250
300
200
200
350
125
350
250
Та
№ п.п.
блица
Ветвь
18.2 (продолжение)
1
2
Ч> - 0,7
1-U
Авария на
1-3
11-4
ветви
5-3
4-5
4
1
2
3
4
5
6
7
8
9
10
11
12
1-11
6-10
11-4
4-7
7-9
4-5
5-8
8-10
5-3
5-6
1-3
9-10
700
700
300
200
500
350
350
250
200
350
100
300
150
125
250
200
200
125
100
200
100
100
200
150
100
200
200
150
300
100
350
100
350
100
300
150
100
250
200
150
125
100
100
150
100
150
100
150
200
150
250
100
300
100
300
100
250
150
100
250
200
150
100
125
100
250
125
250
250
200
125
150
125
100
150
200
350
125
300
250
200
25 О"
200
200
300
100
350
200
это можно было сделать не посредством многовариантных расчетов по
отдельным программам, а с помощью ПВК СОСНА и на более мощной ЭВМ.
Расчетные нагрузки, производительности источников и все другие необ-
необходимые исходные данные были предоставлены Управлением тепловых
сетей "Новосибирскэнерго". Проведенные на первом этапе многовариант-
многовариантные гидравлические расчеты системы при варьировании числа, параметров
и мест установки НС результатов не дали: удовлетворяющий всем техни-
техническим требованиям вариант так и не был найден. Ввод искомого решения
250

Таблица 18.2 (окончание)
№ п.п.
Ветвь
1
2
1-11
Ч> =
Авария на
1-3
11-4
Э,5
ветви
5-3
4-5
1
2
3
4
5
6
7
8
9
10
11
12
1-11
6-10
11-4
4-7
7-9
4-5
5-8
8-10
5-3
5-6
1-3
9-10
700
700
300
200
500
350
350
250
200
350
100
300
150
125
250
200
200
125
100
200
100
100
150
125
100
200
150
125
250
100
250
100
250
100
250
125
100
200
150
125
125
100
100
125
100
125
100
125
150
125
200
100
250
100
250
100
200
125
100
200
150
125
100
100
100
200
100
200
200
200
100
125
125
100
125
200
350
100
300
200
200
250
200
200
250
100
250
200
Таблица 18.3
Сравнение результатов расчета и
цена, надежности
Решение
Технико-экономические
показатели, руб./год
Общие рас-
расчетные за-
затраты
Стоимость
электроэнер-
электроэнергии на пере-
перекачку
Действующий
напор в источ-
источнике, м вод.ст.
"Цена надежности",
По расчет-
расчетным за-
затратам
По электро-
электроэнергии
1
3; v
4; v
= 1,0
= 0,7
= 0,5
74064,55
83798,08
79562,21
75665,59
11303,95
3481,18
4221,4
5311,69
47,6
14,4
17,6
22,2
13,14
7,42
2,16
-69,20
-62,66
-53,01
в допустимую область был произведен только с помощью ПВК СОСНА,
причем было рассчитано порядка 15 вариантов, отличающихся температур-
температурными графиками (т.е. расчетными расходами теплоносителя), уровнями
нагрузок, конфигурацией ТСС и разрешаемыми способами реконструкции.
Оптимальный вариант реконструкции и развития ТСС г. Новосибирска,
полученный в итоге с помощью ПВК СОСНА, имеет значительно лучшие
показатели по сравнению с соответствующим проектным вариантом: по
расчетным затратам — на 11,7%, по капвложениям—на26,6%. Более того,
оказалось, что в проектном варианте давления в 77 узлах выходят за
допустимые для расчетного потокораспределения пределы. И дополни-
дополнительные расчеты, связанные с корректировкой проектного варианта с
целью введения его в область допустимых решений, показали, что при
намеченных проектировщиками местах установки НС потребуется
реконструкция 25 участков сети вместо намеченных 16, что делает этот
вариант дороже оптимального уже на 23%.

Глава 19
ОБ АВТОМАТИЗАЦИИ
ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ ТПС
19.1. ДИАЛОГОВЫЕ СИСТЕМЫ - НЕОБХОДИМОЕ УСЛОВИЕ
ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ ПРОЕКТИРОВАНИЯ ТПС
Современный этап развития ТПС характеризуется непрерывным ростом их
масштабов, усложнением структуры, усилением внутренних и внешних свя-
связей, повышением роли системных факторов. В этих условиях системный
подход к решению задач их оптимального проектирования и развития, пред-
предполагающий комплексную оценку рассматриваемых решений с точки зре-
зрения экономичности, надежности, управляемости планируемого варианта
системы и других влияющих критериев становится все более необходимым.
Вместе с тем постоянное возрастание объемов проектных работ привело к
разделению труда и решаемых проектных задач по различным организаци-
организациям, инженерным специальностям и отдельным составляющим ТПС.
Например, в области ТСС проектирование магистральных и распредели-
распределительных тепловых сетей ведется в отделениях института ВНИПИ Энергоп-
ром, разводящие (квартальные) сети проектируются отделами Граждан-
проектов и Промстройпроектов, а решения по системам отопления, венти-
вентиляции и горячего водоснабжения закладываются в типовые проекты зда-
зданий. Что касается источников теплоснабжения, то выбор мест их размеще-
размещения, производительностей и способов реконструкции также осуществляет-
осуществляется, как правило, отдельно от остальных подсистем ТСС и без учета требова-
требований надежности и управляемости ТСС в целом. В то же время в ближайшие
10-15 лет, по данным ВНИПИЭнергопрома, предполагается вводить по
1,5—2,0 тыс. км магистральных и распределительных сетей в год, т.е. во
много раз больше, чем в предыдущие пятилетки. Аналогичным образом
растет объем работ, связанных с проектированием систем водо-, газо- и
нефтеснабженйя.
Таким образом, несмотря на то что общая научно-методическая и алго-
алгоритмическая база для постановки и решения задач комплексной оптимиза-
оптимизации и развития ТПС во многом уже создана, единая "сквозная" методоло-
методология проектирования этих систем отсутствует. Положение дел осложняется
еще и тем, что противоречие между высоким уровнем требований к совре-
современный системам, необходимостью системного подхода к их проектиро-
проектированию, с одной стороны, и традиционными малоэффективными и несогла-
несогласованными методами — с другой, не может быть полностью преодолено раз-
разрозненным применением ЭВМ для решения отдельных задач. Дополнитель-
Дополнительное время на подготовку, перфорацию и проверку исходных данных, часто
дублирующих друг друга в разных задачах, на интерпретацию результатов
и передачу их из одной программы в другую может привести даже к боль-
большим затратам времени, чем при обычных инженерных методах расчета.
Большеразмерные модели математического программирования также
оказываются недостаточно эффективными на практике при многовариант-
многовариантных расчетах без должной автоматизации процесса использования ЭВМ.
Сказанное с очевидностью показывает, что. со всех точек зрения потреб-
потребность в систематическом применении современных методов имитационно-
имитационного моделирования и количественного обоснования оптимальных решений

посредством создания практически эффективных человеко-машинных сис-
систем автоматизированного проектирования (САПР) ТПС стала предельно
острой. Решение этой проблемы — обязательное условие дальнейшего со-
совершенствования всего процесса проектирования, а также повышения эко-
экономических показателей и оперативности проектных решений.
Автоматизация оптимального проектирования ТПС различного типа и
назначения должна обеспечить: а) повышение качества и технико-экономи-
технико-экономического уровня проектируемых объектов; б) увеличение производитель-
производительности труда проектировщиков и, следовательно, сокращение сроков,
уменьшение стоимости и трудоемкости проектирования; в) продление
срока безаварийной службы ТПС благодаря более обоснованному выбору
их структуры и параметров элементов с учетом требований надежности;
г) сокращение затрат на восстановление и ремонтные работы и т.п.
Вычислительной и организационной базой для САПР должны стать чело-
человеко-машинные системы. Они будут включать различные ПВК, базу дан-
данных (БД) и систему управления ею (СУБД). Развивающаяся система
ПВК обеспечит целенаправленное накопление унифицированных модулей
и блоков для проведения оптимизационных расчетов и других вычислений,
а также для переработки данных при решении различных проектных задач.
База данных явится общим хранилищем информации, и с помощью СУБД
будет осуществляться ее пополнение, корректировка и выдача для исполь-
использования.
ПВК - это сложные и трудоемкие разработки, требующие длительного
срока (десятков человеко-лет) для их выполнения и предназначенные для
широкого круга пользователей в течение многих лет. Поэтому они должны
удовлетворять целому ряду требований, в частности следующим: 1) фор-
формирование заданий, управление процессом вычислений при решении про-
проектных задач должны быть доступны инженеру-проектировщику, не имею-
имеющему специальной подготовки по программированию пДя ЭВМ; 2) должны
быть обеспечены возможности постоянного расширения и модернизации
ПВК; 3) пользователь должен имет возможность для формирования ис-
исходных данных, их редактирования, а также оперативного вмешательства
в процесс расчетов.
Наибольшая эффективность взаимодействия человека и машины может
быть обеспечена лишь развитым диалогом на языке, близком к естествен-
естественному. При этом активное участие человека и сохранение за ним приоритета
в принятии решений обеспечивает творческий характер процесса проектиро-
проектирования. Формы диалогового взаимодействия могут быть весьма разнообраз-
разнообразными: анкетными, когда заполняются стандартные бланки; в виде перечня
возможных заданий и вплоть до языка директив и языка, все более близ-
близкого к естественному. Важно, чтобы реакция ЭВМ в процессе диалога вы-
вырабатывалась за психологически приемлемое время. Понятно, что чем бо-
более совершенна форма диалога, тем более сложны программные средства
ее реализации. Частной формой диалога является взаимодействие не с
ПВК в целом, а только с базой данных, при этом сам процесс расчета пол-
полностью регламентирован и автоматизирован.
Таким образом, при создании ПВК возникает необходимость в разра-
разработке не только функционально-структурной блок-схемы, отображающей
последовательность и взаимосвязь операций процесса проектирования, но

также и информационной модели, содержащей все необходимые для про-
проектирования данные и последовательность их преобразования. При этом
детальность и обоснованность проработки информационного аспекта оп-
определяет в конечном итоге эффективность процесса проектирования, а
ее трудоемкость соизмерима с разработкой прикладных программ. В
связи с этим для экономии трудозатрат и времени на создание ПВК, по-
видимому, в настоящее время необходимо ориентироваться на специаль-
специально разрабатываемые универсальные СУБД, представляющие собой специ-
специализированные программные комплексы, позволяющие создавать и эксплу-
эксплуатировать информационные массивы сложных баз данных произвольного
типа в режиме коллективного пользования с наименьшими затратами труда
на организацию хранения, поиска и обработки информации. Кроме того,
эти СУБД обеспечивают полную независимость данных от прикладных про-
программ, средства защиты данных в случае аппаратных сбоев или програм-
программных ошибок, а также средства защиты от несанкционированного доступа
к информации в базе данных. К сожалению, такие СУБД разрабатывались
до сих пор в основном применительно к информационно-поисковым зада-
задачам и, видимо, не учитывали в полной мере специфику задач проектиро-
проектирования.
В заключение отметим, что проблема автоматизации проектирования
крупных объектов вообще и ТПС в частности оказалась гораздо сложнее,
чем представлялась многим в 60—70-е гг., когда был развернут широкий
фронт работ по применению математических методов и ЭВМ в различных
областях науки и техники. Быстро возраставшее количество разработанных
математических моделей, численных методов и стандартных программ для
ЭВМ само по себе не смогло автоматически обернуться качественно новым
уровнем планирования, проектирования, диспетчерского управления и т.д.
Потребовалось (и этот этап исследований продолжается в настоящее вре-
время) более'глубокое проникновение в реальные процессы подготовки и при-
принятия решений на базе создания соответствующих проблемно-ориентиро-
проблемно-ориентированных ПВК. Именно в этом направлении ориентированы описанные в дан-
данном разделе книги более общие по сравнению с традиционными математи-
математические модели и алгоритмы многоконтурной оптимизации и оптимального
синтеза МКС с нагруженным резервированием, а также и отвечающий им
ПВК СОСНА.
19.2 АЛГОРИТМИЧЕСКОЕ ОБЕСПЕЧЕНИЕ СИСТЕМ
АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ ТПС
В настоящее время в институтах ВНИПИЭнергопром и Союзгипроводхоз ве-
ведутся работы по созданию САПР-теплосеть (САПР-ТС) как подсистемы об-
общей САПР централизованного теплоснабжения и автоматизированных тех-
технологических линий проектирования (АТЛП) групповых водопроводов и
систем водоснабжения населенных пунктов, которые составят основу
САПР водохозяйственных объектов.
В состав первой очереди разрабатываемых систем включены основные
системные задачи проектирования и развития ТПС, которые, с одной сто-
стороны, являются наиболее трудоемкими и сложными в математическом
плане, а с другой - во многом определяют качество и стоимость проектов.
7ЧЛ

Это задачи: выбора оптимальной структуры системы (мест расположения
и производительностей источников и оптимальной конфигурации сети);
оптимизации ее параметров (диаметров трубопроводов, мест установки и
параметров насосных станций, действующих напоров для источников); вы-
выбора оптимальных способов и параметров реконструкции существующих
элементов, которые и составляют проблему оптимального синтеза
МКС.
Многолетний опыт создания и практического применения математичес-
математических моделей для решения отдельных системных задач, а также ПВК СОСНА
в целом оказался весьма полезным при разработке упомянутых выше авто-
автоматизированных систем. Практически все математическое, алгоритмичес-
алгоритмическое и программное обеспечение ПВК СОСНА вошло в состав технического
и рабочего проектов САПР-ТС, которые выполнены ВНИПИЭнергопромом
совместно с СЭИ. Этот же ПВК взят за основу для АТЛП групповых водо-
водопроводов, разрабатываемой в Союзгипроводхозе.
Наибольшая эффективность методов декомпозиции, реализованных в
пакете для решения задачи оптимального синтеза ТПС (см. гл. 15 и 16), мо-
может быть достигнута при организации активного диалога исследователя и
ЭВМ, позволяющего прерывать, анализировать и корректировать информа-
информационные потоки и тем самым управлять процессом расчета. Режим диалога
позволит "проигрывать" большое число вариантов проектируемой системы,
отличающихся экономическими, надежностными и техническими характе-
характеристиками и ограничениями, способами построения резервных связей, на-
начальным приближением и пр., а также имитировать различные условия раз-
развития системы.
Имеющийся уже опыт эксплуатации ПВК СОСНА показывает, что ис-
использование подобных комплексов вне рамок автоматизированной сис:
темы и без интерактивного режима работы затруднено потому, что требует
слишком больших затрат времени на подготовку исходных данных. Так,
при расчетах реальных ТСС изменение массивов исходных данных для
варьирования способами реконструкции существующих участков, местами
установки НС, диапазонами ограничений на давления в узлах и т.п. оказа-
оказалось настолько трудоемким и чреватым новыми ошибками, что пришлось
прибегать к программному способу изменения соответствующих массивов.
На рис. 19.1 показана принципиальная блок-схема решения задачи опти-
оптимального синтеза ТСС с указанием мест диалога исследователя и ЭВМ. Рас-
Рассмотрим кратко функциональное назначение блоков диалога.
Блок 4. Поскольку точный метод решения рассматриваемой задачи от-
отсутствует, для увеличения числа просматриваемых локальных минимумов
необходимо исходить из различных деревьев начального приближения
(ДНП) (см. гл. 16). Их тип и число должны назначаться (или рассчитываться
решением специальных оптимизационных подзадач) пользователем ПВК в
зависимости от характера решаемой задачи и целей расчета.
Блок 9. В итерационном процессе определения оптимальных параметров
системы может оказаться целесообразным зафиксировать диаметры на от-
отдельных ветвях расчетной схемы, расширить или, наоборот, сократить спи-
список узлов, в которых разрешается установка НС, изменить технические ог-
ограничения и т.д.
Блок 11. Для обеспечения требований надежности параметры системы,
255

Адаптация
решения
к аварийной
ситуации
19.1. Принципиальная блок-схема оптимального синтеза ТСС с учетом требований
надежности
полученные для нормального режима, должны быть скорректированы с уче-
учетом аварийных ситуаций, набор которых может меняться пользователем в
процессе расчета.
Блок 13. В ходе расчетов может оказаться целесообразным переход к
следующему этапу, прежде чем все первоначально намеченные аварийные
ситуации будут рассмотрены.
Блок 14. На данном этапе, наоборот, может выясниться необходимость
рассмотрения дополнительных аварийных ситуаций.
Блок 16. Задачей данного блока является реализация возможностей
возврата: а) к этапу построения дополнительных связей в схеме для рас-
рассмотрения новых вариантов резервирования; б) к этапу выделения резер-
резервируемой части системы, что может быть связано с недостаточностью ин-
информации о характеристиках надежности элементов ТСС и необходимостью
повторения решения задачи для различных значений этих характеристик и
их сочетаний.
256

19.2. Принципиальная схема взаимодействия ПВК СОСНА с базой данных
Блок 18. В процессе расчета может оказаться целесообразным в одних
случаях переход к следующему этапу, прежде чем все первоначально наме-
намеченные варианты ДНП будут рассмотрены, в других - необходимость
рассмотрения дополнительных ДНП.
Блок 20. Первое назначение данной "точки диалога" состоит в том,
чтобы обеспечить возможность варьирования экономическими и техничес-
техническими характеристиками системы, вариантами рассматриваемых техничес-
технических решений и условиями развития системы. Вторым важным ее назначе-
назначением является анализ результатов всех вариантов расчета, записанных в
БД, и выбор окончательного решения.
Один из вариантов ПВК СОСНА создается применительно к ТСС на базе
универсальной СУБД СПЕКТР, которую можно отнести к системам реляци-
реляционного типа. Основными достоинствами этой СУБД являются:
возможность представлять данные (объекты и связи между ними) в ви-
виде совокупности изменяемых во времени отношений различных степеней,
т.е. таблиц, которые привычны, просты для понимания и для работы с
ними;
способность выбирать данные на уровне "полей", что обеспечивает неза-
независимость использования информации от способа ее физической организа-
организации и хранения;
способность устанавливать новые поля внутри существующих файлов,
динамически создавать или аннулировать логические связи между файлами
и расширять общий объем БД без ее реорганизации;
экономичное использование вычислительных ресурсов;
относительная простота использования.
На рис. 19.2 показана принципиальная информационная схема взаимо-
взаимодействия ПВК СОСНА с базой данных. В БД будет содержаться информация
трех типов:
а) нормативно-справочная информация (НСИ), включающая типоразме-
типоразмеры и технические характеристики насосных станций (НС) и труб, применяе-
применяемых в тепловых сетях; таблицы капвложений в строительство НС и тепло-
тепловых сетей для различных диаметров труб, разных конструкций теплопрово-
теплопроводов и условий прокладки; замыкающие затраты на электроэнергию в зави-
257

симости от числа часов использования установленной мощности для разных
районов страны и другие технические, экономические, надежностные и кли-
климатические характеристики;
б) операционные данные (ОД) по системе, включающие информацию о
схемах сетей, диаметрах, гидравлических сопротивлениях и длинах ветвей,
нагрузках потребителей, местах установки и параметрах НС и источников и
т.д.;
в) промежуточные результаты и конечные результаты многовариантных
расчетов, помещаемые в рабочую область (РО) БД.
Выделение РО позволяет средствами языка БД частично реализовать диа-
диалоговый режим работы системы: запоминать, вызывать в оперативную па-
память и анализировать промежуточные и конечные результаты расчетов, кор-
корректировать информационные потоки, производить выбор окончательного
решения и вносить его в состав операционных данных. Полная же реализа-
реализация диалогового режима требует специального алгоритмического и про-
программного обеспечения.

ЗАКЛЮЧЕНИЕ
Данная монография в систематизированном виде отражает следующие
этапы становления и развития ТГЦ:
1. Формирование проблематики, разработка алгебры и общих методов
расчета г.ц. с сосредоточенными параметрами - методов контурных расхо-
расходов и узловых давлений, алгоритмов дискретной оптимизации PC, а также
экстремального подхода.к описанию и расчету потокораспределения в г.ц.
Приложения к системам тепло- и водоснабжения, отопления и вентиляции
A961-1966 гг.).
2. Исследование вопросов регулирования расходов и давлений, а также
учета температур транспортируемой среды в задачах расчета гидравличес-
гидравлических режимов ТПС с переходом к разработке исходных положений ТГЦ с
переменными и распределенными параметрами. Формулировка проблемы
идентификации ТПС и разработка метода "математического расходомера".
Создание автоматизированных систем программ для многовариантных
гидравлических расчетов ТПС. Разработка методик "избыточных проект-
проектных схем" и расчета надежности и резервирования ТПС. Приложения к
системам тепло-, водо- и газоснабжения A967-1973 гг.).
3. Разработка метода много контурной оптимизации для решения много-
многоэкстремальных сетевых задач. Комплексное рассмотрение задач схемно-
структурной и схемно-параметрической оптимизации ТПС, составляющих
проблему их оптимального проектирования, а также общей задачи опти-
оптимального синтеза МКС с нагруженным резервированием. Совершенствова-
Совершенствование и унификация основных математических моделей и алгоритмических
разработок и создание первой очереди ПВК СОСНА. Выход на новые об-
области приложений — системы нефтеснабжения, групповых водопроводов
и каналов для переброски вод A974-1983 гг.).
Все эти исследования и разработки велись в постоянных и взаимополез-
взаимополезных контактах со многими научно-исследовательскими, проектными,
наладочными и эксплуатационными организациями Минэнерго, Минводхо-
за, Миннефтепрома, Мингазпрома и других министерств.
Вместе с тем неслучайно в монографии довольно много места уделено
обоснованию ТГЦ как научно-технической дисциплины и предмета ее ис-
исследований, терминологии и другим вводным разделам. Во-первых, накоп-
накопленный за прошедшие годы опыт и обращение к неизвестным ранее перво-
первоисточникам позволили лучше и глубже оценить значение ТГЦ, имеющей
такое же право на существование, как и теория электрических цепей. В
то же время история ТГЦ сравнительно коротка, так что эта дисциплина
все еще нуждается в самоутверждении.
В настоящее время ТГЦ находится на новом, качественно более слож-
сложном этапе своего развития, который характеризуется переходом к рас-
259

смотрению более масштабных и сложных объектов - больших трубопро-
трубопроводных и гидравлических систем (БТП и ГС), таких, как Единая система
газоснабжения страны, ТСС крупнейших городов, на уровне их более пол-
полных схем и иерархического построения, ВСС для больших территорий,
системы магистральных нефтепроводов Западной Сибири и других. В связи
с этим основная логика развития ТГЦ диктуется необходимостью рассмот-
рассмотрения проблем, привносимых именно сложностью и особыми свойствами
БТП и ГС, что требует существенного повышения всего уровня математи-
математического моделирования, расчетов, управления состоянием, оптимального
проектирования и развития этих систем.
Исходя из этого, представляется, что основные усилия в области ТГЦ
должны теперь направляться на решение следующих вопросов:
создание более полных математических моделей БТП и ГС как неодно-
неоднородных г.ц. со сложной иерархической структурой, отражающих технологи-
технологическое взаимодействие подсистем различных иерархических уровней с уче-
учетом разнообразия физических процессов, происходящих при этом в тран-
транспортируемой среде;
исследование и выбор показателей для количественной оценки свойств
БТП и ГС как целостных объектов с целью последующего учета данных
свойств в моделях анализа и оптимального синтеза;
разработка методов согласования критериев в многокритериальных
задачах планирования состояния и оптимального синтеза БТП и ГС;
разработка способов обоснованного упрощения сложных моделей;
создание диалоговых вычислительных систем, обеспечивающих наиболее
эффективную реализацию и автоматизацию процессов решения задач ана-
анализа, управления состоянием и синтеза БТП и ГС и др.

ЛИТЕРАТУРА
1. Абрамов Н.Н. Графические ме-
методы расчета водопроводных систем.
М.: Наркомхоз РСФСР, 1946. 136 с.
2. Абрамов Н.Н. Теория и методика
расчета систем подачи и распределения
воды. М.: Стройиздат, 1972. 288 с.
3.Абрамова Х.Я., Меренков А.П.,
Хасилев В.Я. Об анализе предельных
режимов газоснабжающих «истем при
планировании топливоснабжения эконо-
экономического района. - Изв. АН Латв.ССР
Сер. физ. и техн. наук, 1979, №2, с. 86-
93.
4.Абрамова Х.Я. Разработка и при-
применение методов оценки предельных
режимов газоснабжающих систем при
планировании и управлении топливос-
топливоснабжением района: Автореф. дис. ...
канд. техн. наук. - Иркутск: СЭИ СО
АН СССР, 1979. 20 с.
5.Автоматизация управления энерго-
энергообъединениями / В Л. Гончуков,
Л.А. Крумм, Ю.Н. Руденко и др.; По ред.
С.А. Совалова, М.: Энергия, 1979. 432 с.
б.АлихашкинЯ.И., Юшкин А.Р. При-
Применение ЭВМ для гидравлических рас-
расчетов водопроводных сетей. - Городс-
Городское хозяйство Москвы, I960, № 11,
с. 17-18.
7. Алтунин B.C. Мелиоративные ка-
каналы в земляных руслах. М.: Колос,
1979. 265 с.
8. Алътшулъ А .Д. Гидравлические соп-
сопротивления. М.: Недра, 1970. 216 с.
9. Андрияшев М.М. Техника расчета
водопроводной сети. М.: Сов. законо-
законодательство, 1932. 62 с.
10. Андрияшев ММ. Гидравлические
расчеты водоводов и водопроводных
сетей. М.: Стройиздат, 1964. 107 с.
11. Антонов Е.П., Хачатурян РА. Воп-
Вопросы оптимизации систем энергоснаб-
энергоснабжения городов. - В сб. научных статей
ГрузНИИЭГС. М.: Энергоиздат, 1981,
с. 19-24.
YI.Aoku M. Введение в методы
оптимизации. М.: Наука, 1977. 344 с.
13. Асеев В.А. Экстремальные прин-
принципы и проблема целесообразности. -
Вопросы философии, 1971, № 8, с. 85-
94.
14. Асташкин В.В., Кафаров В.В.,
Мешалкин В.П., Перов В.Л. Сравнитель-
Сравнительная оценка некоторых алгоритмов ав-
автоматизированного составления мате-
математических моделей гидравлических це-
цепей химико-технологических систем. -
АиТ, 1976, №4, с. 166-174.
15. Атабеков Г.И. Основы теории
цепей: Учебник для вузов. М.: Энергия,
1969. 424 с.
16. Багриновский А.Д., Клебанов Ф.С.
Теоретические вопросы автоматизации
проветривания угольных шахт. М.: Нау-
Наука, 1965. 64 с.
П.Бакаев А-А., Кайдан Л.И. Дина-
Динамическая модель проектирования неф-
тепродуктопроводных систем. - В кн.:
Пробл. построения автоматизированных
систем управления на транспорте. Киев:
Ин-т кибернетики АН УССР, 1980, с. 3-
12.
18. Большее О.А. Исследование теп-
тепловых режимов скважин и промыс-
промысловых газопроводов в северных усло-
условиях методами математического моде-
моделирования: Автореф. дис. ... канд. техн.
наук. М.: МИНХ и ГП им. И.М. Губки-
Губкина, 1974. 22 с.
19. Батищев Д.И. Поисковые методы
оптимального проектирования. М.: Сов.
радио, 1975. 216 с.
20. Белан А.Е. Универсальный метод
гидравлического увязочного расчета
кольцевых водопроводных сетей. - Изв.
вузов. Строительство и архитектура,
1964, №4, с. 69-73.
21. Беллман Р., Дрейфус С. Прик-
Прикладные задачи динамического програм-
программирования. М.: Наука, 1965. 458 с.
22. Беляев Л.С. Решение сложных
оптимизационных задач в условиях не-
неопределенности. Новосибирск: Наука,
1978. 128 с.
23. Бер AM., Белов Е.Н., Поляк Б.Т.
О некоторых задачах оптимизации
- В кн.: Вычислительные методы и прог-
261

раммирование. М.: МГУ, 1966, т 5
с. 115-123.
24. Береснев В.Л,, Гимади Э.Х.,
Дементьев В.Т. Экстремальные задачи
стандартизации. Новосибирск: Наука,
1978.335 с.
25. Берж К. Теория графов и ее при-
применения. М.: Изд-во иностр. лит., 1962.
320 с.
26. Берман Р.Я., Бобровский С.А.,
ГалиуллинЗ.Т. Расчет режимов работы
закольцованной системы газопроводов
на ЭВМ. - Газовая промышленность,
1966, №12, с. 14-16.
27. Бородавкин П.П. Подземные
трубопроводы. М.: Недра, 1973. 304 с.
28. Брамеллер А., Аллан Р., Хэ-
мэм Я. Слабозаполненные матрицы. Ана-
Анализ электроэнергетических систем. М.:
Энергия, 1979. 192 с.
29. БСЭ, 2-е издание, 1955, т. 31,
с. 11-12.
30. БСЭ, 3-е издание, 1978, т. 30,
с. 100.
31. Булате В.П. Методы погружения
в задачах оптимизации. Новосибирск:
Наука, 1977. 161 с.
32. Бухгольц Н.Н. Основной курс
теоретической механики. М.: Наука,
1972. Ч. 2. 332 с.
33. Васильев О.Ф., Воеводин А.Ф.
О газотермодинамическом расчете по-
потоков в простых и сложных трубопро-
трубопроводах (постановка задачи). - Изв.
СО/АН СССР. Сер. техн. наук, 1968,
№13, вып. 3, с. 53-62.
34. Васильев О.Ф., Бондарев Э.А.,
Воеводин А.Ф., Каниболотскип М.А.
Неизотермическое течение газа в тру-
трубах. Новосибирск: Наука, 1978. 128 с.
35. Васильева ЕМ., Левит Б.Ю.,
Лившиц В.Н. Нелинейные транспортные
задачи на сетях. М.: Финансы и статис-
статистика, 1981. 104 с.
36. Васильченко М.П. Расчет коль-
кольцевых водопроводных сетей путем на-
нахождения полных поправочных расхо-
расходов. - Изв. вузов. Строительство и
архитектура, 1964, № 6, с. 80-90.
37. Вишневский К.П. Механизация
расчета кольцевых водопроводных се-
сетей. - Водоснабжение и санитарная
техника, 1961, №4, с. 20-24.
38. Воеводин А.Ф., Шугрин СМ.
Численные методы расчета одномерных
систем. Новосибирск: Наука, 1981. 208с.
39. Волков А.А. Синтез оптималь-
оптимального управления конечным состоянием
потокораспределения в сети. - В кн.:
Поиск экстремума: Труды Ш Всесоюз.
262
симпозиума по экстремальным задачам.
Томск: Томский ун-т, 1969, с. 363-369.
40. Волков А.А., Евдокимов А.Г.
Математическое описание установивших-
установившихся процессов воздухораспределения в
вентиляционных сетях шахт. - Изв.
вузов. Горный журн., 1965, № 2, с.
136-143.
41. Вычислительные методы выбора
оптимальных проектных решений. /
B.C. Михалевич, Н.Э. Шор, Л.А. Галус-
това и др. Киев: Наук, думка, 1977.
178 с.
42. Галиуллин З.Т., Кривошеий Б.Л.,
Ходанович И.Е. Аналитическое обосно-
обоснование выбора оптимального варианта
трасс сети газопроводов. - Газовая
промышленность, 1965, № 2, с. 42-45.
43. ГалустоваЛА., Струтинская СП.,
МомотА.Й. Методика оптимизации элек-
электрических сетей. - В кн.: I Всесоюз.
конф. по оптимизации и моделированию
транспортных сетей: Сб. докл. Киев:
Ин-т кибернетики АН УССР, 1969,
с. 91-98.
44. Гальперин ЕМ. Гидравлический
расчет совместной работы водопрово-
водопроводной сети, насосной станции и напорно-
регулирующих сооружений. -Изв. ву-
вузов. Строительство и архитектура,
1969, №7, с. 131-134.
45. Гамм А.3. Методы расчета нор-
нормальных режимов электроэнергетиче-
электроэнергетических систем на ЭВМ: Учебное пособие.
Иркутск: ИПИ и СЭИ СО АН СССР,
1972. 188 с.
46. ГаммА.З., Герасимов Л.Н., Го-
Голуб И.Н. Оценивание состояния в элек-
электроэнергетике. М.: Наука, 1983. 302 с.
47. Гацулаев С.С., Игнатенко Ю.К.,
Озерова В.Ф., Цайгер М.А. К методи-
методике расчета сложных газопроводных се-
сетей. - Газовое дело, 1970, № 12, с. 14-
17.
48. Гениев Н.Н. Измерители в оцен-
оценке городской водопроводной сети труб.
- Сан. техника, 1928, № 1, с. 40-41.
49. Гениев Н.Н. Примеры расчета
водопроводов. М.; Л.: Гос-издат, 1930.
127 с.
50. Гермейер Ю.Б., Моисеев Н.Н. О
некоторых задачах теории иерархичес-
иерархических систем управления. - В кн.: Проб-
Проблемы прикладной математики и меха-
механики. М.: Наука, 1974, с. 30-43.
51. Горская Н.И. О задаче автома-
автоматического выявления поврежденного
участка в тепловых сетях. - Изв. АН
СССР. Энергетика и транспорт, 1973.
№4. г. 140-147.

52. Горская Н.И. Разработка метода
выявления аварийных ситуаций в тру-
трубопроводных системах и его примене-
применения (н$ примере систем теплоснабже-
теплоснабжения) : Автореф. дис. ... канд. техн. наук.
Иркутск: СЭИ СО АН СССР, 1977. 22 с.
ЪЪ.Григоровский Е.П., Койда Н.У.
Автоматизация расчета многоконтурных
сетевых,1 систем. Киев: Вища школа,
1977. 192 с.
54. Громов Н.К. Городские тепло-
теплофикационные системы. М.: Энергия,
1974. 253 с.
55. Громов Б.Н., Сидлер В.Г. Рас-
Расчет нестационарных гидравлических ре-
режимов тепловых водяных сетей на
ЭЦВМ. - Теплоэнергетика, 1973, № 3,
с. 65-69.
56. Данциг Дж. Линейное програ-
мирование, его применения и обоб-
обобщения. М.: Прогресс, 1966,
600 с.
57 Демидович Б.П., Марон И.А. Осно-
Основы вычислительной математики. М.:
Наука, 1970. 644 с.
58. Деннис Дж. Б. Математическое
програмирование и электрические цепи.
М.: Изд-во иностр. лит., 1961. 216 с.
59Дюскин В.К. Тепловой и гидрав-
гидравлический режим систем водяного отоп-
отопления. М.: Минкомхоз РСФСР, 1950.
148 с.
60. Евдокимов А.Г. Оптимальные
задачи на инженерных сетях. Харьков:
Вища школа, 1976. 153 с.
61. Евдокимов А.Г., Дубровский В.В.
Тевяшев АД. Потокораспределение в
инженерных сетях. М.: Стройиздат, 1979.
199 с.
62. Евдокимов А.Г., Тевяшев АД.
Оперативное управление потокораспре-
делением в инженерных сетях. Харьков:
Вища школа, 1980. 144 с.
63. Емеличев В.А., Комлик В.И.
Метод построения последовательности
планов для решения задач дискретной
оптимизации. М.: Наука, 1981. 208 с.
64. Емеличев ВА., Овчинников В.Г.
Применение метода построения последо-
последовательности планов к решению задачи
обустройства нефтяных месторождений.
ДАН БССР, 1982, т. 26, № 4, с. 344-347.
65. Емеличев В.А., Супруненко Д.А.,
Танаев B.C. О работах белорусских
математиков в области дискретной оп-
оптимизации. - Изв. АН СССР. Техн. ки-
кибернетика, 1982, № 6, с. 25-45.
66. Ермольев ЮМ., Мельник И.М.
Экстремальные задачи на графах. Киев.:
Наук, думка, 1968. 176 с.
67. Ефимов Н.В. Квадратичные фор-
формы и матрицы М.: Наука, 1967. 160 с.
68. Зайченко ЕМ., Меренков А.П.,
Петренко ВЛ., Сидлер В.Г. Исследование
распределения потоков в системах ох-
охлаждения двигателей и агрегатов авто-
автомобилей. — Автомобильная промышлен-
промышленность, 1978, №10, с. 11-14.
69. Зайцев ИД., Вайнер В.Г. К вопро-
вопросу оптимизации трубопроводных сетей
на стадии проектирования. - Экономика
и математ. методы, 1979, т. 15, №1,
с. 171-177.
70. Занфиров А.М. Технико-экономи-
Технико-экономический расчет водяных тепловых сетей. -
Тепло и сила, 1933, №11, с. 4-10.
71. Зингер Н.М., Андреева К.С.,
Вульман Ф.А. Расчет многокольцевых
гидравлических сетей на ЭВМ "Урал". -
Теплоэнергетика, 1960, №12, с. 44-52.
72. Зингер М.Н. Гидравлический рас-
расчет тепловых сетей с переменными
расходами воды у абонентов на ЭВМ
"Урал-1". - Теплоэнергетика, 1962, №7,
'с. 27-32.
73. Зингер НМ. Гидравлические и
тепловые режимы теплофикационных
систем. М.: Энергия, 1976. 336 с.
74. Зойтендейк Г. Методы возмож-
возможных направлений. М.: Изд-во иностр. лит.,
1963.176 с.
75. Йодан Э. Структурное проекти-
проектирование и конструирозание программ.
М.:Мир, 1979.415 с.
76. Каганович БМ. Методы оптими-
оптимизации тепловых сетей при совместной
работе ТЭЦ и котельных: Автореф.
дис. . . . канд. техн. наук. М.: МЭИ,
1971.25 с.
77. Каганович БМ. Дискретная опти-
оптимизация тепловых сетей. Новосибирск:
Наука, 1978. 88 с.
78. Калнин O.K., Карнаушенко В.В.,
Клищенко В.Я. Метод определения гид-
гидравлических параметров действующих
газосборных промышленных коллекто-
коллекторов. - Газовое дело, 1966, №12, с. 6-8.
79. Каменев П.Н. Смешивание пото-
потоков. М.; Л.: ОНТИ, 1936. 188 с.
80. Каменев П.Н. Расчет однотруб-
однотрубных систем водяного отопления. М.:
Минкомхоз РСФСР, 1948. 212 с.
81. Карасев Н.И., Фольгарт В.И.,
Алехин А.Ф. и др. Пакет прикладных
программ для решения задач расчета
параметров стационарного гидравличес-
гидравлического режима систем централизованного
теплоснабжения и водоснабжения про-
промышленных центров. - Управляющие
системы и машины, 1982, №1, с. 113-116.
263

82. Карнаушенко В.В., Калнин О.К.
Определение гидравлических параметров
лупингов и речных переходов на магист-
магистральных газопроводах. - Газовая про-
промышленность, 1969, №10, с.12-14.
83. Кафаров В.В., Перов В.Л., Мешал-
кин В.П. Принципы математического
моделирования химико-технологических
систем. М.: Химия, 1974. 344 с.
84. Кафаров В.В., Перов В.Л., Мешал-
кин В.П., Асташкин В.В. Алгоритм
оптимизации гидравлических цепей хими-
химико-технологических систем. - ДАН СССР,
1976, т. 229, №4, с. 928-931.
85. Кеттелъ Дж. Увеличение надеж-
надежности при минимальных затратах. —
В кн.: Оптимизационные задачи надеж-
надежности. М.: Стандартаздат, 1968, с. 29-43.
86. Кё'ниг Г., Блекуэлл В. Теория
электромеханических систем. М.; Л.:
Энергия, 1965. 424 с.
87. Кикачейшвили Г.Е. Технико-
экономический расчет разветвленных
водопроводных сетей методом линейного
программирования. — Водоснабжение и
сан. техника, 1969, №6, с. 7-8.
88. Кикачейшвили Г.Е. Расчет оптима-
оптимальных параметров систем подачи и
распределения воды. Тбилиси: Сабчота
Сакартвело, 1980. 200 с.
89. Кирсанов М.В. Экономический
расчет водопроводных сетей. М.; Л.:
Минкомхоз РСФСР, 1949. 148 с.
90. Койда НУ. Вариационные прин-
принципы в теории движения жидкости
по сложным трубопроводам. — Изв.
вузов. Энергетика, 1962, №6, с. 111-112.
91. Койда Н.У. Гидравлический расчет
кольцевых трубопроводов методом сече-
сечений. — Теплоэнергетика, 1962, №9,
с. 66-68.
92. Койда Н.У., Ильина Т.П., Казими-
Казимиров Е.Ф., Щербо AM. Вариационные
методы гидравлического расчета трубо-
трубопроводов. Минск: Высш. шк., 1968.
36 с.
93. Константинова В.Е., Светлов К.С.
Исследование систем естественной вы-
вытяжной вентиляции в многоэтажных
зданиях. — Водоснабжение и сан. тех-
техника, 1965, №6, с. 10-13.
94. Корбут АЛ., Финкельштейн Ю.Ю.
Дискретное программирование. М.:
Наука, 1969. 368 с.
95. Кошелев АЛ. Исследование нес-
нестационарных режимов в системах тепло-
теплоснабжения с использованием гидроинтег-
гидроинтегратора и ЭВМ: Автореф. дис. ... канд.
техн. наук. М.: МИСИ им. В.В. Куйбы-
Куйбышева, 1966. 14 с.
264
96. Коишанов В.В. Георг Ом. М.:
Просвещение, 1980. 112 с. ;
97. Кристофидес Н. Теория графов.
Алгоритмический подход. М.: Мир, 1978.
432 с. i
98. Крумм JI.A. Методы приведен-
приведенного градиента при управлении элект-
электроэнергетическими системами. Новоси-
Новосибирск: Наука, 1977. 368 с.
99. Крумм JI.A. Методы оптимиза-
оптимизации при управлении электроэнергети-
электроэнергетическими системами. Новосибирск: Нау-
Наука, 1981. 320 с.
100. Кублановский Л.Б. Определение
мест повреждений напорных трубопро-
трубопроводов. М: Недра, 1971. 136 с.
101. Кудрявцев Л.Д. О некоторых
математических вопросах теории элек-
электрических цепей. - Усп. мат. наук,
1948, т. 3,вып.4, с. 80-118.
102. Курант Р., Робине Г. Что такое
математика? М.; Л.: Госиздат, 1947.
664 с.
103. Курман А.В., Каганер В.М.
Принцип экстремальности и метод расче-
расчета на ЭЦВМ сложных вентиляционных
и гидравлических сетей. - В кн.: Тез.
докл. V Всесоюз. совещ. пользователей
ЭВМ типа "Урал". Секция III. Матема-
Математическое программирование. Тарту: Тарт.
ун-г, 1966, с. 47-53.
104. Лаврентьев В.Л. Исследование
переходных гидравлических процессов
в сетях теплоснабжения: Автореф. дис.
. . . канд. техн наук. Новосибирск:
НИСИ им. В.В. Куйбышева, 1982. 18 с.
105. Лазебник А.И., Цаллагова ОМ.
Оптимизация развития электрической
сети на основе метода ветвей и границ. -
Изв. АН СССР. Энергетика и транспорт,
1979, №3, с. 6-12.
106. Левин AM., Смирнов В.А.,
Черкасова А.Я. Расчет многокольцевых
городских газовых сетей на ЭВМ. -
Газовая промышленность, 1961, №11,
с. 33-34.
107. Леонас ВЛ., Моцкус И.Б. Метод
последовательного поиска для оптими-
оптимизации производственных системи сетей. -
Изв. АН СССР. Энергетика и транспорт,
1965, №1, с. 18-25.
108. Лобачев В.Г. Новый метод
увязки колец при расчете водопровод-
водопроводных сетей. - Сан. техника, 1934, №2,
с. 8-12.
109. Лобачев В.Г. Вопросы рациона-
рационализации расчетов водопроводных сетей.
М.:ОНТИ, 1936. 148 с.
110. Лямаев Б.Ф., Небольсин ГЛ.,
Нелюбов ВЛ. Стационарные и переход-

ные процессы в сложных гидросисте-
гидросистемах. Методы расчета на ЭВМ. Л.: Маши-
Машиностроение, 1978. 192 с.
111. Макаров АЛ., Мелентъев Л.А.
Методы исследования и оптимизации
энергетического хозяйств а. Новосибирск:
Наука, 1! 73. 274 с.
112. Макаров И.П., Щербаков В.Н. Об
одном подходе к идентификации пара-
параметров трубопроводных систем. - В кн.:
Прикладная математика. Иркутск: СЭИ
СО АН СССР, 1978, с. 201 -205.
113. Максименко Ф.Е. Различные
расчеты по курсу водопроводов. М.:
Типо-лит. Рихтер, 1910.102 с.
114. Максимов Ю.И. Метод решения
нелинейной системы уравнений, описы-
описывающей работу систем пласт - сква-
скважины - газосборная сеть на ЭВМ. -
В кн.: Научно-технический сборник по
геологии, разработке, транспорту и ис-
использованию природного газа: Труды
ВНИИГАЗа; Вып. V. М.: Недра, 1965,
с. 67-82.
115. Максимович H.I. Знойные эле-
электрические цепи и их преобразования.
М.; Л.: Госэнергоиздат, 1961. 264 с.
116. Максимович Н.Г. Методы топо-
топологического анализа электрических це-
цепей. Львов: Львов, ун-т, 1970. 260 с.
117. Марков С.А., Пшеничный Б.Н.
Расчет городских газопроводов высо-
высокого и среднего давления. - Газовая
промышленность, 1962, №3, с. 26-30.
118. Маркович ИМ. Режимы энер-
энергетических систем. М.: Энергия, 1969.
352 с.
119. Меерович ЭЛ. Геометрическая
теория электрических цепей. - Элек-
Электричество, 1947, №2, с. 30-39.
120. Мелентъев Л.А. Теплофикация,
М.; Л.: АН СССР. ч. 1, 1944, с. 248;
4.2,1948. с. 276.
121. Мелентьев Л.А. Оптимизация
развития и управления больших систем
энергетики. М.: Высш. шк., 1982. 319 с.
122. Мелентьев Л А. Системные иссле-
исследования в энергетике. Элементы тео-
теории, направления развития. М.: Наука,
1983.456 с.
123. Меренков А.П. Применение ЭВМ
для оптимизации разветвленных тепло-
тепловых сетей. - Изв. АН СССР. Энерге-
Энергетика и транспорт, 1963, №4, с. 531-538.
124. Меренков А.П., Хасилев В.Я.
Расчет разветвленных тепловых сетей
на основе их оптимизации с использо-
использованием ЭВМ. - Изв. СО АН СССР. Сер.
техн. наук, 1963, №10, вып. 3, с. 42-48.
125. Меренков А.П. Решение общей
18. Зак. 384
задачи линейного программирования
модифицированным симплексным мето-
методом. М.: ГИПРОТИС Госстроя СССР,
1965.75 с.
126. Меренков А.П., Светлов К.С.,
Хасилев В.Я. Методы и средства для
управления эксплуатацией и развитием
трубопроводных систем. - В кн.:
Оптимизация и управление в больших
системах энергетики / Под ред. Л .А. Меле-
нтьева, Л.С. Беляева. Иркутск: СЭИ
СО АН СССР, 1970, т. 1, с. 60-80.
127. Меренков А.П, Светлов К.С.,
Сидлер В.Г., Хасилев В.Я. "Матема-
"Математический расходомер" и его приме-
применение в тепловых сетях. - Теплоэнер-
Теплоэнергетика, 1971, №1, с. 70-72.
128. Меренков А.П, Кривошеий Б.Л.,
Рогожина Х.Я., Сидлер Л.Е. Примене-
Применение теории и методов расчета гидрав-
гидравлических цепей к системам с неизо-
неизотермическим течением газа. — Изв.
АН СССР. Энергетика и транспорт,
1971, №6, с. 129-138.
129. Меренков А.П, Сидлер В.Г.
Обратные задачи потокораспределения
в гидравлических цепях. - В кн.: Труды
IV Всесоюз. зимней школы по мат.
программированию и смежным вопро-
вопросам. М.: МИСИ им. В.В. Куйбышева,
1972, с. 8-14.
130. Меренков АЛ., Светлов К.С.,
Такайшвили М.К., Хасилев В.Я. Об
автоматизированных системах программ
для расчета гидравлических режимов
трубопроводных сетей. - Изв. Ан СССР.
Энергетика и транспорт, 1973, №3,
с. 126-131.
131. Меренков А.П., Сидлер Л.Е.
Об одном классе смешанных систем
уравнений и методике их решения. -
В кн.: Дифференциальные и интеграль-
интегральные уравнения. Иркутск: Иркутский
ун-т, 1973, вып. 2, с. 98-105.
132. Меренков А.П. Дифференциа-
Дифференциация методов расчета гидравлических
цепей. - Журн. вычисл. математики и
мат. физики, 1973, т. 13, №5, с. 1237-
1248.
133. Меренков А.П. Математические
модели и методы для анализа и оптима-
оптимального проектирования трубопроводных
систем: Автореф. дис. ... д-ра физ.-мат.
наук. Новосибирск: Секция киберне-
кибернетики Объединенного ученого совета СО
АН СССР, 1974. 34 с.
134. Меренков А.П., Сидлер В.Г.
Идентификация трубопроводных сис-
систем. - В кн.: Фактор неопределеннос-
неопределенности при принятии оптимальных решений
265

в больших системах энергетики. Ир-
Иркутск: СЭИ СО АН СССР, 1974, т. 3,
с. 149-162.
135. Меренков АЛ., Хасилев В.Я.,
Абрамова Х.Я., Сидлер Л.Е. Методы
и программы расчета гидравлических
цепей с сосредоточенными, регулируемы-
регулируемыми и распределенными параметрами. -
В кн.: Труды IV Всесоюз. семинара
по комплексам программ мат. физики
/ Под ред. Н.Н. Яненко. Новосибирск:
ВЦ СО АН СССР, 1976, с. 40-52.
136. Меренков А.П., Хасилев В.Я.,
Храмов А.В. О вычислительной сис-
системе для оптимального проектирования
трубопроводных систем. - В кн.: Проб-
Проблемы повышения эффективности
БЭСМ-6. Иркутск: ВЦ АН СССР -
СЭИ СО АН СССР, 1975, 'с 185-
191.
137. Меренков А.П., Морев А.А.,
Хасилев В.Я. Гидравлические цепи с
регулируемыми параметрами и их при-
применение для описания и расчета много-
многониточных нефтепроводов. - В кн.:
Системы энергетики - тенденции раз-
развития и методы управления. Иркутск:
СЭИ СО АН СССР, 1980, т. 1,с. 193-204.
138. Меренков А.П., Морев А.А.,
Хасилев В.Я. Об эффективности нагру-
нагруженного резервирования в многониточ-
многониточных системах нефтепроводов. - Неф-
Нефтяное хозяйство, 1980, №6, с. 48-52.
139. Меренков А.П., Меренкова Н.Н.,
Ощепкова Т.Б., Храмов А.В. Методы
схемно-структурной и схемно-парамет-
рической оптимизации разветвленных
и многоконтурных систем. - В кн.:
Проблемы нелинейной электротехники:
Тез. докл. Всесоюз. конф. Киев: Наук,
думка, 1981, ч. 2, с. 63-66.
140. Меренков А.П.. Сидлер ВТ.,
Такайшвили М.К. Обобщение электро-
электротехнических методов на гидравлические
цепи. — Электронное моделирование,
1982, №2, с. 3-12.
141. Меренков А.П., Морев А.А.,
Новицкий Н.Н. Расчет и оптимизация
режимов работы многониточных нефте-
нефтепроводов при многокольцевых схемах
эксплуатации. - В кн.: Трубопровод-
Трубопроводный транспорт газа: Тез. докл. Всесоюз.
научно-техн. конф. Уфа: Уфимский неф-
нефтяной ин-т, 1982, с. 64-66.
142. Меренков А.П., Сеннова Е.В.,
Сидлер ВТ. и др. Повышение эффек-
эффективности методов расчета и комплек-
комплексной оптимизации теплоснабжающих сис-
систем. - В кн.: Пятая Междунар. конф.
по централизованному теплоснабжению.
266
Москва; Киев: Информэнерго, 1982,
секция 5, вып. 2, с. 80-95. /
143. Меренков А.П., Сумароков СВ.,
Мурашкин ГЛ., Чупин В.Р. Математи-
Математическое описание систем многопрофиль-
многопрофильных каналов и методы их оптимизации.-
Гидротехническое строительстро, 1983,
№4, с. 33-35. I
144. Меренкова Н.Н. Математические
модели для оптимизации трассировки
и структуры трубопроводных систем. -
В кн.: Вопросы прикладной математики.
Иркутск: СЭИ СО АН СССР, 1977,'
с. 145-158.
145. Меренкова Н.Н. Разработка и
применение математических моделей
для оптимизации производительностей
источников и конфигурации гидравли-
гидравлических сетей на основе их избыточных
схем: Автореф. дис. ... канд. техн. наук.
Новосибирск: Ин-т математики СО АН
СССР, 1980. 22 с.
146. Меренкова Н.Н., Сеннова Е.В.,
Стенников В.А. Схемно-структурная оп-
оптимизация систем централизованного те-
теплоснабжения. - Электронное моделиро-
моделирование, 1982, №6, с. 76-82.
147. Методы и алгоритмы расчета
тепловых сетей / В.Я. Хасилев, А.П. Ме-
Меренков, Б.М. Каганович, К.С. Светлов,
М.К. Такайшвили. М.: Энергия, 1978.
176 с.
148. Минский ЕМ., Максимов Ю.И.
Основы расчета сложных газосборных
сетей на ЭВМ. - Газовая промышлен-
промышленность, 1962, №10, с. 9-12.
149. Минский Е.М., Максимов Ю.И.
Универсальная программа для расчета
работы систем "пласт-скважины - га-
газосборная сеть". - Газовая промыш-
промышленность, 1964, № 10, с. 5-7.
150. Мирзаджанзаде А.Х., Гусейн-
заде М.А., Александров А.В. и др. Не-
Некоторые обратные задачи трубопровод-
трубопроводного транспорта. - Изв. вузов. Нефть
и газ, 1970, №9, с. 95-97.
151. Михалевич B.C. Последователь-
Последовательные алгоритмы оптимизации и их при-
применение. - Кибернетика, 1965, № 1,
с. 45-46; №2, с. 85-89.
152. Моисеев Н.Н. Математика ста-
ставит эксперимент. М.: Наука, 1979.
224 с.
153. Моисеев Н.Н. Математические
задачи системного анализа. М.: Наука,
1981.488 с.
154. Моисеев Н.Н., Иванилов Ю.П.,
Столярова Е.М. Методы оптимизации.
М.: Наука, 1978.352 с.

155. Морев АЛ. Расчет систем мно-
многониточных нефтепроводов при сме-
смешении рфносортных нефтей. - Неф-
Нефтяное хозяйство, 1978, № 2, с. 43-46.
156. Морев А.А.% Методы расчета
режимов систем многониточных нефте-
нефтепроводов , как гидравлических цепей
с регулируемыми параметрами: Авто-
реф. дис. L. канд. техн. наук. М.: МИНХ
и ГП им. И.М. Губкина, 1982. 22 с.
157. Морозов К.Е. Математическое
моделирование в научном познании.
М.: Мысль, 1969. 212 с.
158. Моцкус И.Б., Леонас В.Л.,
Шальтянис В.Л. О нахождении опти-
оптимальной конфигурации распределитель-
распределительных сетей. - Изв. АН СССР. Энерге-
Энергетика и транспорт, 1963, № 2, с. 176-
182.
159. Моцкус И.Б. Многоэкстремаль-
Многоэкстремальные задачи в проектировании. М.: Наука,
1967.215 с.
160. Мошнин Л.Ф. Выбор диаметров
водопроводных линий. - Водоснабжение
и сан. техника, 1940, № 2/3, с. 48-55.
161. Мошнин .Л.Ф. Методы технико-
экономического расчета водопровод-
водопроводных сетей. М.; Стройиздат, 1950.
144 с.
162. Мошнин Л.Ф. Применение ЭВМ
для технико-экономического расчета во-
водораспределительных сетей по методу
фиктивных расходов. - Водоснабжение
и сан. техника, 1975, №5, с. 8-13.
163. Мурадян А.Е. Оптимизация раз-
развития сетей, комплектуемых из стан-
стандартных элементов. - Изв. АН СССР.
Энергетика и транспорт, 1970, № 2,
с. 94-100.
164. Мурадян А.Е., Смотрицкип Я.Ш.
Оптимизация конфигураций распреде-
распределительных электрических сетей при на-
наличии препятствий в месте ветвления. -
Изв. АН СССР. Энергетика и транспорт,
1973, №5, с. 74- 80.
165. Надежность систем энергетики.
Терминология / Отв. ред. Ю.Н. Руденко.
М.: Наука, 1980.44 с.
166. Нгуен Май, Щербачев О.В. Ал-
Алгоритм и программы для определения
оптимальных конфигураций электричес-
электрических сетей с учетом бесперебойности
электроснабжения потребителей. — Изв.
АН СССР. Энергетика и транспорт,
1970, №4, с. 85-90.
167. Некрасова О.А., Хасияев В.Я.
Оптимальное дерево трубопроводной
системы. - Экономика .; :-.'ат. методы,
1970, т. 4, №3, с. 427-432.
168. Некрасова О.А. Оптимальная
трассировка трубопроводных сетей: Ав-
тореф. дис. ... канд. экон. наук. М.:
ЦЭМИ АН СССР, 1970, 16 с.
169. Нутенко Л.Я. Использование
проблемы Штейнера и ее обобщений
для постановки и решения некоторых
задач пространственной экономики: Об-
Обзор литературы. М.: ЦЭМИ АН СССР,
1968.82 с.
170. Об исходных научно-методи-
научно-методических положениях оценки надежности
в энергетике. - Изв. АН СССР. Энер-
Энергетика и транспорт, 1969, № 4, с. 158—
160.
171. Оптимальный синтез многокон-
многоконтурных систем с нагруженным резер-
резервированием / А.П. Меренков, Т.Б. Ощеп-
кова, СВ. Сумароков, В.Я. Хасилев,
А.В. Храмов. - В кн.: Системы энер-
энергетики - тенденции развития и методы
управления. Иркутск: СЭИ СО АН СССР,
1980, т. 1, с. 180-192.
172. Оптимизация и управление боль-
большими системами энергетики (основные
результаты исследований) / Л.С. Бе-
Беляев, Ю.М. Горский, Л.А. Крумм,
А.А. Макаров, А.П. Меренков, Л.С. По-
пырин, Ю.Н. Руденко, И.А. Шер. - Изв.
АН СССР. Энергетика и транспорт,
1980, №3, с. 31-46.
173. Оптимизация развития во вре-
времени сложных газопроводных систем /
А.Н. Арянин, А.К. Арский, Ю.А. Куз-
Кузнецов, А.П. Меренков, Х.Я. Рогожина. -
Экономика и математика, 1970, т. 6,
№1, с. 105-111.
174. Оптимизация развития топливно-
энергетического комплекса / А.С. Некра-
Некрасов, И.Н. Борисова, Ю.С. Кретинина,
Т.М. Полянская, Р.А. Хачатурян. М.:
Энергоиздат, 1981. 240 с.
175. Оре О. Теория графов. М.: Наука,
1968. 352 с.
176. Орлов Р.В., Багриновский А.Д.
Расчет шахтных вентиляционных сетей
на быстродействующих машинах. -
Уголь, 1962, №4, с. 54-56.
177. Ортега Д., Рейнболдт В. Ите-
Итерационные методы решения нелинейных
систем со многими неизвестными. М.:
Мир, 1975.557 с.
178. Основы теорий цепей: Учебник
для вузов / Г.В. Зевеке, П.А. Ионкин,
А.В. Нетушил, СВ. Стахов. М.: Энер-
Энергия, 1975. 752 с.
179. Ощепкова Т.Б. Оптимизация
разветвленных и многоконтур.чых тру-
трубопроводных систем: Авгореф. дис.
... канд. техн. наук. Новосибирск: Ин-т
математики СО АН СССР, 1983. 11 с.
?67

180. Ощепкова Т.Е., Сумарков СВ.
Метод многоконтурной оптимизации и
его приложения. - В кн.: Методы и
программы решения оптимизационных
задач на графах и сетях: Тез. докл.
Всееоюз. совещ. Новосибирск: ВЦ СО
АН СССР, 1980, с. 68-70.
181. Пайус Л.А. Матрицы в техни-
технике. - В кн.: Современная математика
для инженеров / Под ред. Э.Д. Бекен-
баха. М.: Изд-во иностр. лит., 1958,
с. 305-345.
182. Полисар Г.Л., Хасилев В.Я.
Задачи потокораспределения в сложных
тепловых сетях и их решение на элект-
электрических моделях. - ДАН СССР, 1950,
т. 74, № 2, с. 243-246.
183. Попов Ю.И. Определение рас-
расположения точек разветвления в сети
трубопроводов. - Строительство тру-
трубопроводов, 1974, № 12, с. 21-24.
184. Прим Р.К. Кратчайшие связы-
связывающие сети и некоторые обобщения. -
Кибернет. сб., 1961, № 2, с. 95-107.
185. Протодьяконов ММ. Курс про-
проветривания рудников. Екатеринослав:
Тип. "Прогресс" А. Бершицкого, 1911.
143 с.
186. Пустовойт Б.В. Механика дви-
движения жидкостей в трубах. Л.: Недра,
1971.144 с.
187. Пухов Г.Е., Кулик М.Н. Гиб-
Гибридное моделирование в энергетике.
Киев: Наукова думка, 1977. 150 с.
188. Пшеничный Б.Н. Расчет энер-
энергетических сетей на ЭВМ. - Жури, вы-
числ. матем. и мат. физики 1962, № 5,
с. 942-947.
189. Пшеничный Б.Н. О численных
методах гидравлического расчета се-
сетей. - В кн.: Первая Всееоюз. конф.
по оптимизации и моделированию транс-
транспортных сетей: Сб. докл. Киев: Ин^г
кибернетики АН УССР, 1967, с. 77-90.
190. Райбман И.С Что такое иден-
идентификация? М.: Наука, 1970. 117 с.
191. Реза Ф., Силы С. Современный
анализ электрических цепей. М.; Л.:
Энергия, 1964.480 с.
192. Руденко Ю.Н., Чельцов М.Б.
Надежность и резервирование в элект-
электроэнергетических системах. Методы ис-
исследований. Новосибирск: Наука, 1977.
264 с.
193. Савельева Н.П. Трассировка
сети групповых водопроводов. - Водо-
Водоснабжение и сан. техника, 1964, № 7,
с. 9-12.
194. Сахаров НА. Метод наивыгод-
наивыгоднейшего распределения нагрузки между
268
1МИ. J-
ричество, 1927, № S, с. 167-169-
195. Светлов К.С. Расчет воздухо-
воздухообмена в многоэтажных уданиях с
использованием ЭВМ. - Водоснабжение
и сан. техника, 1966, № 11J с. 28-31.
196. Светлов К.С. О применении
ЭЦВМ для расчета воздухдобмена и
аэрации зданий. - В кн.: Методы мате-
математического моделирования' в энерге-
энергетике. Иркутск: Вост.-Сиб. кн. изд-во,
1966, с. 362-369.
197. Светлов К.С. Исследование воз-
воздухообмена в зданиях с использова-
использованием ЭВМ: Автореф. дис. ... канд. техн.
наук. М.: МИСИ им. В.В. Куйбышева,
1967.14 с.
198. Светлов К.С, Сидлер ВТ.,
Юдкин Э.Л., Романов А.Л. О методах
гидравлических испытаний водяных теп-
тепловых сетей. - Электрические станции,
1971, № 11, с. 39-41.
199. Сеннова Е.В. О нормативах
надежности в теплофикационных систе-
системах. - Изв. вузов. Энергетика, 1975,
№4, с. 110-116.
200. Сеннова Е.В. Методика анализа
надежности развивающихся систем теп-
теплоснабжения: Автореф. дис. ... канд.
техн. наук. Новосибирск: НИСИ им.
В.В. Куйбышева, 1975. 28 с.
201. Сеннова Е.В., Стенников В.А.
Об оптимальном проектировании раз-
развиваемых и реконструируемых тепло-
теплоснабжающих систем. - Теплоэнергетика,
1964, №9, с. 26-30.
202. Сешу С, Балабанян Н. Анализ
линейных цепей. М.; Л.: Госэнергоиз-
дат, 1983. 552 с.
203. Сигорский В.П. Методы анализа
электрических схем с многополюсными
элементами. Киев: АН УССР, 1958.
402 с.
204. Сидлер ВТ. О статистическом
подходе к эквивалентированию трубо-
трубопроводных сетей. - В кн.: Вопросы
оценивания и идентификации в энер-
энергетических системах. Иркутск: СЭИ
СО АН СССР, 1974, с. 173-178.
205. Сидлер ВТ. Линейная и нели-
нелинейная модели для оценивания парамет-
параметров гидравлических сетей. - В кн.:
Вопросы прикладной математики. Ир-
Иркутск: СЭИ СО АН СССР, 1977, с. 159-
167.
206. Сидлер ВТ. Разработка и при-
применение методов идентификации пара-
параметров гидравлических сетей: Автореф.
дис. ... канд. техн. наук. Томск: ТПИ
им. СМ. Кирова, 1977. 20 с.

207. Сидлер В.Г., Новицкий Н.Н.
Идентификация трубопроводных систем
как гидравлических цепей с перемен-
переменными параметрами. - Изв. АН СССР.
Энергетика и транспорт, 1984, № 4,
с. 155-1Й2.
208. Системный подход при управ-
управлении развитием электроэнергетики /
Л.С. Беляев, Г.В. Войцеховская,В.А. Са-
Савельев и др. Новосибирск: Наука, 1980.
240 с.
209. Скрипник В.Ф., Такайшвили
М. К., Толмачев а Н.И. Типовые програм-
программы для расчетов сложных гидравли-
гидравлических цепей. - В кн.: Методы мат.
моделирования и использования ЭВМ
в энергетике: Тез. докл. науч. сессии.
Иркутск: Иркут. кн. изд-во, 1963,
с. 101-104.
210. Советский энциклопедический
словарь. М.: Сов. энциклопедия, 1979,
с. 1554.
211. Срогович Е.Б., Рахманин ГД.
К вопросу о математическом модели-
моделировании работы трудопроводных се-
сетей. - В кн.: Первая Всесоюз. конф.
по оптимизации и моделированию транс-
транспортных сетей: Сб. докладов. Киев:
Ин-т кибернетики АН УССР, 1967,
с. 139-151.
212. Ставровский Е.Р., Сухарев М.Г.
Универсальная программа расчета газо-
газосборных сетей. - Газовая промышлен-
промышленность, 1965, №7, с. 10-11.
213. Ставровский Е.Р., Сухарев М.Г.,
Карасевич A.M. Методы расчета надеж-
надежности магистральных газопроводов. Но-
Новосибирск: Наука, 1982. 126 с.
214. Сумароков СВ. Вопросы опти-
оптимального размещения аккумулирующих
емкостей в развивающихся системах
коммунального водоснабжения: Авто-
реф. дис. ... канд. техн. наук. М.: АКХ
им. К.Д. Памфилова, 1972. 26 с.
215. Сумароков СВ. Применение
динамического программирования
для оптимального проектирования рас-
расширяемых и реконструируемых раз-
разветвленных водопроводов. - Изв. вузов.
Строительство и архитектура, 1975,
№11, с. 125-129.
216. Сумароков СВ. Метод решения
многоэкстремальной сетевой задачи. -
Экономика и мат. методы, 1976, т. 12,
№5, с. 1016-1018.
217. Сумароков СВ., Меренкова Н.Н.
Методика оптимизации реконструкции
водопроводной сети. - Изв. вузов.
Строительство и архитектура, 1976, № 3,
с. 128-132.
218. Сумароков СВ., Храмов А.В.
Об одном методе решения многоэкст-
многоэкстремальной задачи оптимизации много-
многоконтурных гидравлических сетей. -
В кн.: Методы оптимизации и исследо-
исследования операций (прикладная матема-
математика). Иркутск: СЭИ СО АН СССР,
1976, с. 157-167.
219. Сумароков СВ., Храмов А.В.
Построение надежной схемы в общей
задаче оптимального проектирования
трубопроводных сетей с нагруженным
резервированием. - В кн.: Методи-
Методические вопросы исследования надеж-
надежности больших систем энергетики. Ир-
Иркутск: СЭИ СО АН СССР, 1976, вып. 12,
с. 163-171.
220. Сумароков СВ., Храмов А.В.
Вопросы оптимального синтеза систем
водоснабжения с учетом надежности. -
В кн.: Вопросы надежности систем
водоснабжения. М.: МИСИ им. В.В. Куй-
Куйбышева, 1978, с. 36-44.
221. Сумароков СВ., Чупин В.Р. О
применении методов теории гидравли-
гидравлических цепей для оптимального проек-
проектирования каналов переброски вод. -
В кн.: Системы энергетики - тенден-
тенденции развития и методы управления,
Иркутск: СЭИ СО АН СССР, 1980,
т. 1с. 216-223.
222. Сумароков С.В., Меренко-
Меренкова Н.Н., Храмов А.В. и др. Проектиро-
Проектирование систем групповых водопроводов
с применением методов дискретной
оптимизации. - Науч. труды Всесоюз.
объединения Союзводпроект, 1981,
№56, с. 62-68.
223. Сумароков СВ. Математическое
моделирование систем водоснабжения.
Новосибирск: Наука, 1983.
224. Сурин А.А. Выбор схемы водо-
водоснабжения. Л.: Гос. науч.-мелиорацион-
ный ин-т, гос. тип. им. Ив. Федорова,
1927. 126 с. '
225. Сухарев М.Г. Об одном мето-
методе расчета газосборных сетей на вычис-
вычислительных машинах. - Изв. вузов.
Нефть и газ, 1965, № 6, с. 48-52.
226. Сухарев М.Г., Спвровский Е.Р.
Расчеты систем транспорта газа с по-
помощью вычислительных машин. М.:
Недра, 1971. 206 с.
227. Сухарев М.Г., Ставровский Е.Р.
Оптимизация систем транспорта газа.
М.: Недра, 1975. 278 с.
228. Сухарев М.Г., Ставровский Е.Р.,
Брянских В.Е. Оптимальное развитие
систем газоснабжения. М.: Недра, 1981.
294 с.
269

229. Такайшвили М.К. Методы рас-
расчета аварийных режимов, надежности
и резервирования тепловых сетей: Авто-
реф. дис. ... канд. техн. наук. Новоси-
Новосибирск: Секция техн. наук Объединен-
Объединенного ученого совета СО АН СССР, 1971.
32 с.
230. Такайшвили М.К., Хасилев В.Я.
Об основных положениях методики
расчета надежности и резервирования
тепловых сетей. - Теплоэнергетика,
1972, №4, с. 14-19.
231. Толмачева Н.И., Хасилев В.Я.
Программа расчета многокольцевых гид-
гидравлических сетей увязочным методом.
М.: ГИПРОТИС Госстроя СССР, 1965,
вып. 1-4. 21с.
232. Тъюарсон Р. Разреженные мат-
матрицы. М.: Мир, 1977. 189 с.
233. Уайлд Д.Д. Методы поиска
экстремума. М.: Наука, 1967. 267 с.
234. Уилсон Р. Введение в теорию
графов. М.: Мир, 1977. 208 с.
235. Фаддеев Д.К., Кубланов-
ская В.П., Фаддеева В.Н. О решении
линейных систем с прямоугольными
матрицами. - В кн.: Труды Мат. ин-та
им. В.А. Стеклова. Л,: Наука, 1968,
т. 96, с. 76-92.
236. Фокс Д.А. Гидравлический ана-
анализ неустановившегося течения в трубо-
трубопроводах. М.: Энергоиздат, 1981. 248 с.
237. Форд Л., Фалкерсон Д. Потоки
в сетях. М.: Мир, 1966. 276 с.
238. Форсайт Дж. Что представляют
собой релаксационные методы? - В кн.:
Современная математика для инжене-
инженеров/ Под ред. Э.Ф. Бекенбаха. М.: Изд-во
иностр. лит., 1959. 500 с.
239. Форсайт Дж., Молер К. Числен-
Численное решение систем линейных алгебраи-
алгебраических уравнений. М.: Мир, 1969. 168 с.
240. Хасилев В.Я. Анализ конфигу-
конфигурации несимметричных тепловых сетей
и его применение к выбору мощности
систем централизованного теплоснабже-
теплоснабжения. - Изв. АН СССР. Отделение техн.
наук, 1945, № 10/11, с. 1105-1114.
241. Хасилев В.Я. Обобщенные за-
зависимости для технико-экономических
расчетов тепловых и других сетей. -
Теплоэнергетика. 1957, № 1, с. 28-32.
242. Хасилев В.Я. Элементы теории
гидравлических цепей. - Изв. АН СССР.
Энергетика и транспорт, 1964, № 1,
с. 69-88.
243. Хасилев В.Я. Линейные и лине-
линеаризованные преобразования схем гид-
гидравлических цепей. - Изв. АН СССР.
270
Энергетика и транспорт, 1964, № 2
с. 231-243.
244. Хасилев В.Я., Меренное А.П.,
Сумароков СВ. Выбор диаметров труб
разветвленных тепловых сетей 'с приме-
применением ЭВМ. - Теплоэнергетика, 1966,
№ 6, с. 60-65.
245. Хасилев В.Я. Вопросы матема-
математического моделирования и оптимизации
гидравлических систем с применением
ЭЦВМ. - В кн.: Методы математическо-
математического моделирования в энергетике. Ир-
Иркутск: Вост.-Сиб. кн. изд-во, 1966,
с. 343-348.
246. Хасилев В.Я. Гравитационные
гидравлические цепи с распределенными
параметрами и методика их расчета. -
Там же, с. 349-362.
247. Хасилев В.Я. Элементы теории
гидравлических цепей: Автореф. дис...
д-ра техн. наук. Новосибирск: Секция
техн. наук Объединенного ученого сове-
совета СО АН СССР, 1966. 98 с.
248. Хасилев В.Я., Светлов КС,
Такайшвили М.К. Метод контурных
расходов для расчета гидравлических
цепей. Иркутск, Москва: СЭИ СО -
ВИНИТИ АН СССР, 1968, № 339-68
деп. 110 с.
249. Хасилев В.Я. О применении
математических методов при проекти-
проектировании и эксплуатации трубопрово-
трубопроводных систем. - Изв. АН СССР. Энер-
Энергетика и транспорт, 1971, №2, с. 18-27.
250. Хасилев В.Я. О методике опти-
оптимизации резервируемых систем водо-
водоснабжения с учетом критериев и пара-
параметров надежности. - В кн.: Проблемы
надежности систем водоснабжения. М.:
МИСИ им. В.В. Куйбышева, 1973,
с. 16-29.
251. Хасилев В.Я., Каганович Б.М.,
Виноградов Н.А., Сеннова Е.В. Об'эф-
фективности нагруженного резервиро-
резервирования в тепловых сетях. - Теплоэнер-
Теплоэнергетика, 1974, №7, с. 66-71.
252. Хасилев В.Я., Меренков А.П.,
Каганович Б.М., Виноградов Н.А. О
проблеме надежности систем теплоснаб-
теплоснабжения с нагруженным резервировани-
резервированием. - Изв. АН СССР. Энергетика и
транспорт, 1976, № 1,с. 146-153.
253. Хедли Дж. Нелинейное и дина-
динамическое программирование. М.: Мир,
1967.506 с.
254. Храмов А.В. Программно-вы-
Программно-вычислительный комплекс СОСНА как
инструмент для pea.-ii.:.u:;<th и иссле-
исследования алгоритмов оптимального син-
синтеза мкогоконгурных гидр'.---.-'.'.' --?скич

систем. - В кн.: Пакеты прикладных
программ. Методы, разработки. Ново-
Новосибирск: Наука, 1981, с. 174-182.
255. Храмов А.В. Оптимальный син-
синтез многоконтурных систем с нагружен-
нагруженным резервированием: Автореф. дис....
канд. техн. наук. Новосибирск: Ин-т ма-
математики СО АН СССР, 1983. 24 с.
256. Химмелъблау Д. Прикладное
нелинейное програмирование. М.: Мир,
1975.534 с.
257. Ху Т. Целочисленное програм-
программирование и потоки в сетях. М.: Мир,
1974. 520 с.
258. Цой С, Рогов Е.И. Основы тео-
теории вентиляционных сетей. Алма-Ата:
Наука, 1965. 283 с.
259. Цой С, Рязанцев Г.К. Принцип
минимума и оптимальная политика уп-
управления вентиляционными и гидравли-
гидравлическими сетями. Алма-Ата: Наука, 1968.
258 с.
260. Цой С. Автоматическое управле-
управление вентиляционными системами шахт.
Алма-Ата: Наука, 1975. 336 с.
261. Цыпкин Я.З. Оптимальность в
естествознании, технике и обществе. -
В кн.: Проблемы управления: Сб. статей
Ин-та проблем управления АН СССР.
М.: Наука, 1975, с. 20-28.
262. Чарныи И.А. Основы газовой
динамики. М.: Гостоптехиздат, 1961.
200 с.
263. Черри Е., Миллар У. Некоторые
новые понятия и теоремы в области
нелинейных систем. - В кн.: Автомати-
Автоматическое регулирование: Сб. материалов
конф. в Кренфилде, 1951 / Под ред.
М.З. Литвина-Седого. М.: Изд-во иностр.
лит., 1954, с. 261-273.
264. Чупин ВЛ Методысхемно-струк-
турной оптимизации систем многопро-
многопрофильных каналов. - В кн.: Численные
методы оптимизации и их приложения.
Иркутск: СЭИ СО АН СССР, 1981,
с. 160-174.
265. Шашков O.K. Расчет потокорас-
пределения в сложных тепловых сетях
при помощи ЭЦВМ. - Изв. вузов. Энер-
Энергетика, 1973, № 9, с. 67-70.
266. Шевелев Ф.Ф. Таблицы для гид-
гидравлического расчета стальных, чугун-
чугунных, асбестоцементных, пластмассовых
и стеклянных водопроводных труб. М.:
Стройиздат, 1973.114 с.
267. Шевяков ЛЯ. Вывод формул
естественного распределения воздуха в
горных выработках из начала наимень-
наименьшей работы. - Горн, журн., 1929, № 1,
с. 3-6.
268. Шеннон Р. Имитационное моде-
моделирование систем — искусство и наука.
М.: Мир, 1978,420 с.
269. Шифринсон Б.Л. Основной рас-
расчет тепловых сетей. М.; Л.: Госэнерго-
издат, 1940.188 с.
270. Шифринсон Б.Л., Хасилев В.Я.
Рациональная трассировка теплопрово-
теплопроводов. - Строительная промышленность,
1944, №2/3, с. 21-24.
27'1. Шухов В.Г., Кнорре Е.Г., Лемб-
ке К.З. Проект Московского водоснаб-
водоснабжения. М.: Контора инж. А.В. Бари,
1891.104 с.
212.Шухов В.Г. Трубопроводы и
их применение к нефтяной промыш-
промышленности. М.: Типо-лит. "Рус. т-ва печ.
и изд. дела", 1895. 38 с.
273. Щербо A.M. Второй итерацион-
итерационный метод гидравлического расчета тру-
трубопроводных сетей с помощью ЭЦВМ. -
Изв. вузов. Энергетика, 1969, № 3,
с.*92-95.
27'4. Якимов Л.К. Предельный радиус
действия теплофикации. - Тепло и си-
сила, 1931, №9, с. 8-10.
275. Яресько Э.И. Расчет водопровод-
водопроводных кольцевых сетей способом распре-
распределения неуравновешенных напоров. -
Водоснабжение и сан. техника, 1959,
№9, с. 23-24.
276. Яськова Э.Н. Исследование и
создание способов организации инфор-
информационного и программного обеспече-
обеспечения для автоматизированной системы
плановых расчетов: Автореф. дис. ...
канд. техн. наук. Киев: Ин-т кибернети-
кибернетики АН УССР, 1979. 28 с.
m.Appleyard J.R. Optimal design of
distribution networks. - Build. Serv.
Eng., 1978, vol. 45, N 11, p. 191-204.
ni.Birkhoff G., Diaz J.B. Nonlinear
network problems. - Quarterly of Applied
Math., 1956, vol. 13, N 4, p. 431-443.
279. Brown K. A quadratically conver-
convergent Newton-like method based upon Gaus-
Gaussian elimination. - Siam Journ. of Nume-
Numerical Analysis, 1969, vol. 6, N 4, p. 560-
570.
280. Carteron J. Calcul des veseaux ma-
illes de conduite a l'aide d'une calculat-
rice electronique. Grenoble: La Houille
Blanche, 11, N special A/1956, p. 173-177.
281. Cross H. Analysis of flow in net-
networks of conduits or conductors. Urbana,
Illinois: Eng. Exp. Station of Univ. of
Illinois, 1936, November, Bull. N 286.
29 p.
2S2.Dubin Ch. Analysis of mesh net-
networks by digital computer. - Interna-
271

tional Watei Supply Congress. Special
Subject N 7. Stockholm, 1964, June.
44 p.
2S3.Duffin RJ. Nonlinear networks,
lla. - Bull. Amer. Math. Soc, 1947,
vol. 53, p. 963-971.
284. Duffy F.L. Gas network analy-
analysis programm for hign-speed computer. -
GAS (USA), 1958, vol. 34, N6,p.47-54.
285. Grober H. Warmetransport und
Warmeschutz. Bericht XII Kongress fur
Heizung und Luftung. Berlin, 1927,
p. 106-118.
286. Hoag L.N., Weinberg G. Pipeline
networks analysis by electronic digital
computer. - Journ. of Am. Water Works
Ass., 1957, vol. 49, N 5, p. 517-534.
287'. Kally E. Computerised planning of
the least cost water distribution network. -
Water and Sewage Works. Reference Num-
Number, 1972, Aug. 31, p. 121-127.
288. Kirchhoff G. Ueber die AuflS-
sung der Gleichungen, auf welche man
bei Untersuchung der linearen Verthei-
lung, galvanische Strome gefuhrt wird.
Leipzig; Annalen der Physik und Chemie
(Poggendorf), 1847, Bd. 72, N 12, S. 497-
508.
289. Lawler EX., Wood D.E. Branch-
and-bound methods: a survey. - Operat.
Res., 1966, vol. 14, N 4, p. 699-717.
290. Maxwell J.C. A treatise of elec-
electricity and magnetism. Oxford, 1873,
vol. l.chapt. 6.
291. Murge D. Essai sur les machines
d'aerage. - Bull, de la Sos. de L'Ind.
Minerale, 1873, part 1, p. 464-472.
292. Ohm G.S. Die galvanische Kette,
mathematisch bearbeitet. В., 1827.
293. Wilson G.G., Kniebs D.V. Distri-
Distribution system analysis with the elektronic
digital computer. - GAS (USA), 1956,
vol. 32, N8, p. 37-44.
294. Fatt I. The network model of
porous media C parts). - Petroleum Trans-
Transactions. АШЕ, 1956, vol. 207, p. 144-180.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоматизация проектирования 163, 253
Активные элементы г.ц. 30
Асимметрия решений для г.ц. 81
Дерево графа 8, 55
— начального приближения 187, 229
Единств енность
100
потокораспределения
Задача о потокораспределении 42
- алгебраическая 42, 49, 93, 104, 109,
111,136
- в контурной форме 63, 104
- в узловой форме 63,104
- для циклической схемы 59
- экстремальная 42, 92, 96, 99, 104
- двойственная 97
- обратная 146
Задачи идентификации ТПС 14 6
в виде переопределенных систем
уравнений 150, 160
линейного программирования 151
в виде нелинейных моделей 154
Задачи оптимизации 163
схемно-структурной 163, 175, 227
схемно-параметрической 164,227
- - режимов ТПС 231, 238
- Штейнера-Вебера 165
- Шухова 168
Закон Кирхгофа 7, 98
- - первый48, 61, ПО, 137
- - второй 48, ПО, 137
- гидравлических сопротивлений 28
- сохранения энергии 98
Замыкающие соотношения 28, 30, 45,
110, 111,136,140
Конфликт нагруженного резервирования
219
Математическая модель для выбора оп-
оптимального дерева г.ц. 176
оптимизации структуры PC 178, 180
оптимизации параметров PC 192
многоконтурной оптимизации 204,
227
оптимального синтеза МКС 223
Матрица соединений 8,17, 49
- контуров 17, 52
- Кирхгофа 67,116
- Максвелла 71, 116
Метод идентификации ТПС 147
- "математического расходомера" 149
- наименьших модулей 151
- статистических испытаний на базе ли-
линейных моделей 157
как г.ц. с переменными парамет-
параметрами 158
Метод оптимизации PC или МКС 165,
168
- динамического программирования
170, 192
- линейного программирования 170
- фиктивных расходов 170, 171, 211
- многоконтурной оптимизации 207
Метод расчета потокораспределения 42
- контурных расходов 67, 105
- узловых давлений 70, 105
- поконтурной увязки перепадов дав-
давлений 35, 38, 68
- поузловой увязки расходов 37, 39, 72
- увязочный модифицированный' 41,
119
- линеаризации г.ц. 82
- комбинированный 122
- последовательных приближений 142
- линеаризации замыкающих соотноше-
соотношений 143
Методика избыточных проектных схем
167, 175
- расчета г.ц. с регуляторами расхода и
давления 113,127
- расчета надежности и резервирования
ТПС 221
Надежность ТПС 220
Неизотермичность течения 109, 111,136,
158
Отказ элемента 221
Параметры узлов и ветвей 14, 16
Преобразования матриц элементарные
53
273

- к контурным переменным 57, 61, 67
- к узловым переменным 71
- для циклической схемы ЬО
Переменные контурные 8, 62
- "поперечные" (последовательные) 10
- "продольные" (параллельные) 10
Преобразования г.ц. линейные 86
- проективные 87
- линеаризованные 89
Принцип наименьшего действия 42, 44,
101
теплового действия 9,92
Программа (пакет программ) АСИГР
131
- ТРАССА 188
- СТРУКТУРА 188
- ДИПР202
- СОСНА 241
Путь снабжения в г.ц. 221
Регуляторы расхода и давления 107, 127
Режим работы ТПС установившийся 234
аварийный 234
послеаварийный 234
Решение системы уравнений первого за-
закона Кирхгофа общее 43, 61
- частное 61
Седловая точка функции Лагранжа 98
Схема цепи 15
циклическая 15, 57
Система гидравлическая 13, 19
теплоснабжающая 19
водоснабжающая 20
газоснабжающая 26
- - магистральных нефте- и газопрово-
газопроводов 23, 111, 161
многопрофильных каналов 23
воздухообмена и вентиляции 25
охлаждения автодвигателей 26
газопромысловая 134, 140
разветвленная 18, 172, 228
многоконтурная 18, 172, 204, 216
Система главных контуров 56
Соотношения между матрицами 60, 62
Способ повышения эффективности мето-
метода расчета г.ц. выбором шага 120
учетом заполненности матриц
115
комбинацией методов 122
использованием специфики
ТПС 126
Теорема Максвелла 9, 42, 92
обобщение на г.ц. 94, 96
Теория цепей гидравлических 4, 11, 259
электрических 7
Узловые нормы надежности снабжения
222
Хорда 8, 15,56
Цепь 11
- гидравлическая 4, 13
с сосредоточенными параметрами
14,62
с переменными параметрами 14, 107
с распределенными параметрами 14,
133, 136
неоднородная 95, 260
- электрическая 13

ОГЛАВЛЕНИЕ
Предисловие 3
Введение ?
О теории гидравлических цепей как научно-технической дисциплине '
Терминология, исходные определения и обозначения ^
Часть первая
ОСНОВЫ ТЕОРИИ И МЕТОДЫ РАСЧЕТА
Глава 1
Гидравлические системы и их гидравлические цепи 19
1.1. Примеры гидравлических цепей 19
1.2. О законах гидравлических сопротивлений 28
Глава 2
Методы ручного расчета гидравлических систем 32
2.1. Графические и аналитические методы 33
2.2. Методы поконтурной и поузловой увязки 35
Глава 3
О применении математических методов и ЭВМ для расчета гидравлических
систем 38
3.1. Вычислительные возможности увязочных методов 38
3.2. Работы общего характера 42
Глава 4
Алгебра и топология гидравлических цепей 45
4.1. Уравнения гидравлический цепи и формы их представления 45
4.2. Матрицы цепи и их линейные преобразования 49
4.3. Декомпозиция векторов и матриц цепи 55
4.4. Циклическая схема цепи 57
4.5. Связи между матрицами и векторами цепи 60
Глава 5
Гидравлические цепи с сосредоточенными параметрами 62
5.1. Исходные системы уравнений 62
5.2. Методы контурных расходов и узловых давлений 66
Глава 6
Геометрические интерпретации и линеаризация гидравлических цепей 73
6.1. Исходные положения и классификация задач 73
6.2. Квадратичные формы гидравлической цепи и асимметрия решений ... 75
275

6.3. Линеаризация гидравлических цепей 82
6.4. Линейные и линеаризованные преобразования схем гидравлических
цепей 86
Глава 7
Экстремальный подход к описанию и расчету потокораспределения 92
7.1. Обобщение теоремы Максвелла о принципе наименьшего теплового
действия на гидравлической цепи 92
7.2. Общий случай неоднородной активной цепи 95
7.3. Двойственные экстремальные задачи потокораспределения 97
7.4. Переход к задаче нелинейного программирования и единственность
потокораспределения /99
7.5. Принцип наименьшего действия и "новый вариационный принцип" . . . 101
7.6. Дифференциация методов расчета гидравлических цепей 103
Глава 8
Гидравлические цепи с переменными параметрами 106
8.1. Исходные положения 106
8.2. Система уравнений гидравлической цепи с переменными параметрами . 109
8.3. Методы последовательной линеаризации 112
Глава 9
Практическая реализация методов расчета потокораспределения на ЭВМ .... 115
9.1. О способах повышения эффективности методов расчета потокораспре-
потокораспределения 115
9.2. Методика расчета гидравлических цепей с регуляторами расхода и дав-
давления 127
9.3. Автоматизированные системы программ для гидравлических расчетов . 130
Глава 10
Гидравлические цепи с распределенными параметрами 133
10.1. Исходные положения 133
10.2. Системы уравнений гидравлической цепи с распределенными парамет-
параметрами 136
10.3. О смешанных системах уравнений сетевого типа и общей схеме их
декомпозиции 141
10.4. Частные случаи общей системы уравнений и линеаризация замыкающих
соотношений '43
Глава 11
Обратные задачи потокораспределения и идентификация трубопроводных си-
систем 146
11.1. О проблеме идентификации ТПС 146
11.2. "Математический, расходомер" для цепей с сосредоточенными парамет-
параметрами 148
11.3. Нелинейные модели для оценки гидравлических параметров ТПС .... 154
11.4. Метод статистических испытаний на базе линейных моделей 157
11.5. Идентификация ТПС как гидравлических цепей с переменными пара-
параметрами 158

Часть вторая
ОПТИМИЗАЦИЯ СТРУКТУРЫ И ПАРАМЕТРОВ РАЗВЕТВЛЕННЫХ
И МНОГОКОНТУРНЫХ СИСТЕМ
Глава 12
О проблеме математизации и автоматизации проектирования трубопроводных
систем
12.1 Исходные положения
12.2. Методы схемно-структурной оптимизации 165
12.3. Методы схемно-параметрическрй оптимизации 168
12.4. Постановка.вопросов 171
Г лав а 13
Схемно-структурная оптимизация 175
13.1. Исходные положения методики избыточных проектных схем
13.2. Математические модели для совместной оптимизации производитель-
ностей источников и конфигурации PC 178
13.3. Сравнительный анализ математических методов и выбор алгоритмов
схемно-структурной оптимизации 183
13.4. Приметы расчетов реальных объектов 188
Глав а 14
Оптимизация параметров разветвленных систем 192
14.1. Усовершенствованная математическая модель для оптимизации парамет-
параметров PC 192
14.2. Общая схема метода ДП для оптимизации параметров PC и способы
повышения его эффективности 197
14.3. Примеры оптимизации развития и реконструкции реальных PC 202
Глава 15
Многоконтурная оптимизация 204
15.1. Общая задача многоконтурной оптимизации 204
15.2. Метод декомпозиции МКО и области его применения 207
15.3. Сравнение с методом фиктивных расходов и примеры расчетов 211
Глава 16
Оптимальный синтез многоконтурных систем с нагруженным резервирова-
резервированием 216
16.1. Конфликту резервирования 216
16.2. Методика расчета надежности ТПС 220
16.3. Общая задача оптимального синтеза МКС и ее декомпозиция 223
16.4. Алгоритмизация оптимального синтеза МКС 228
Глава Р
Оптимизация установившихся режимов трубопроводных систем 231
17.1. Сравнительная характеристика работ по оптимизации режимов ЭЭС
и ТПС 231
17.2. Математическое описание области допустимых гидравлических режи-
режимов ТПС 234
17.3. Возможные критерии и математическая формулировка задач оптимиза-
оптимизации режимов ТПС 238
17.4. О применении методов ДП и МКО для оптимизации режимов развет-
разветвленных и многоконтурных ТПС 240
277

Глава 18
Программно-вычислительный комплекс СОСНА для оптимального синтеза
МКС 241
18.1. Общая характеристика ПВК СОСНА и его основных модулей и блоков 241
18.2. Использование ПВК СОСНА для оптимального синтеза и реконструкции
развиваемых ТПС 245
Глава 19
Об автоматизации оптимального проектирования ТПС 252
19.1. Диалоговые системы - необходимое условие повышения эффективнос-
эффективности проектирования ТПС 252
19.2. Алгоритмическое обеспечение систем автоматизированного проектиро-
проектирования ТПС 254
Заключение . 259
Литература 261
Предметный указатель 273

Лютолий Петрович Меренков
Виктор Яковлевич X а с и л е в
ТЕОРИЯ ГИДРАВЛИЧЕСКИХ ЦЕПЕЙ
Утверждено к печати
Сибирским энергетическим институтом
ордена Ленина Сибирского отделения
АН СССР
Редактор
Е.Я. Коршунова
Редактор издательства
Н.А. Ермолаева
Художник
Л.А. Григорян
Художественный редактор
Н.А. Фильчагина
Технический редактор
Н.А. Торгашова
Корректор
Р.Г. Ухина
Набор выполнен в издательстве
на наборно-печатающих автоматах
ИБ N«29103
Подписано к печати 27.06.85.Т - 01176
Формат 60 Х90 1/16
Бумага для глубокой печати
Гарнитура Пресс—Роман. Печать офсетная
Усл.печ.л. 17,5. Усл.кр.-отт. 17,8.
Уч.-издл. 19,9. Тираж 1550 экз.
Тип. зак. 384. Цена Зр. 10 к.
Ордена Трудового Красного Знамени
издательство "Наука"
117864 ГСП-7, Москва В-485,
Профсоюзная ул., д. 90
Ордена Трудового Красного Знамени
1-я типография издательства "Наука"
199034, Ленинград В-34, 9-я линия, 12