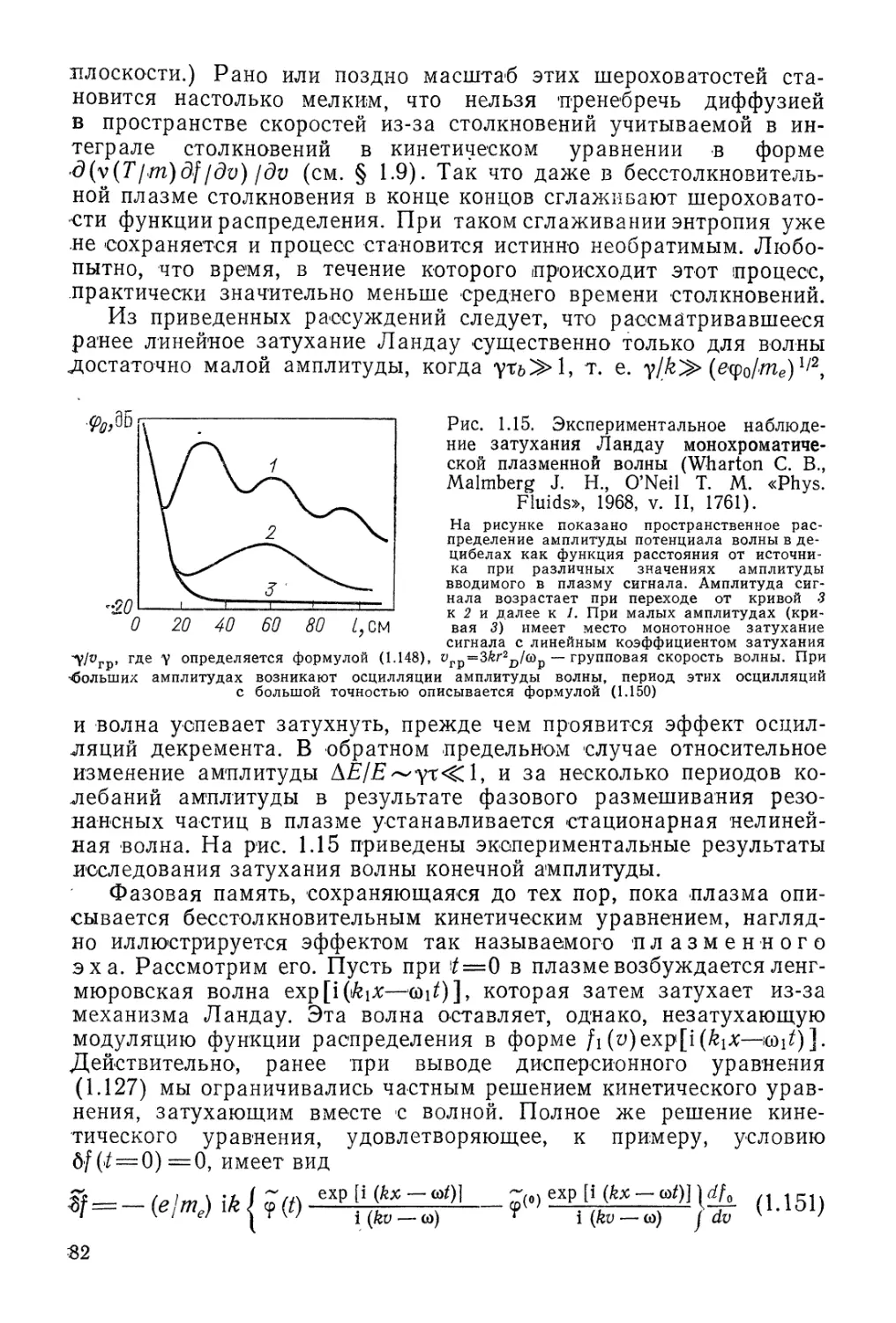
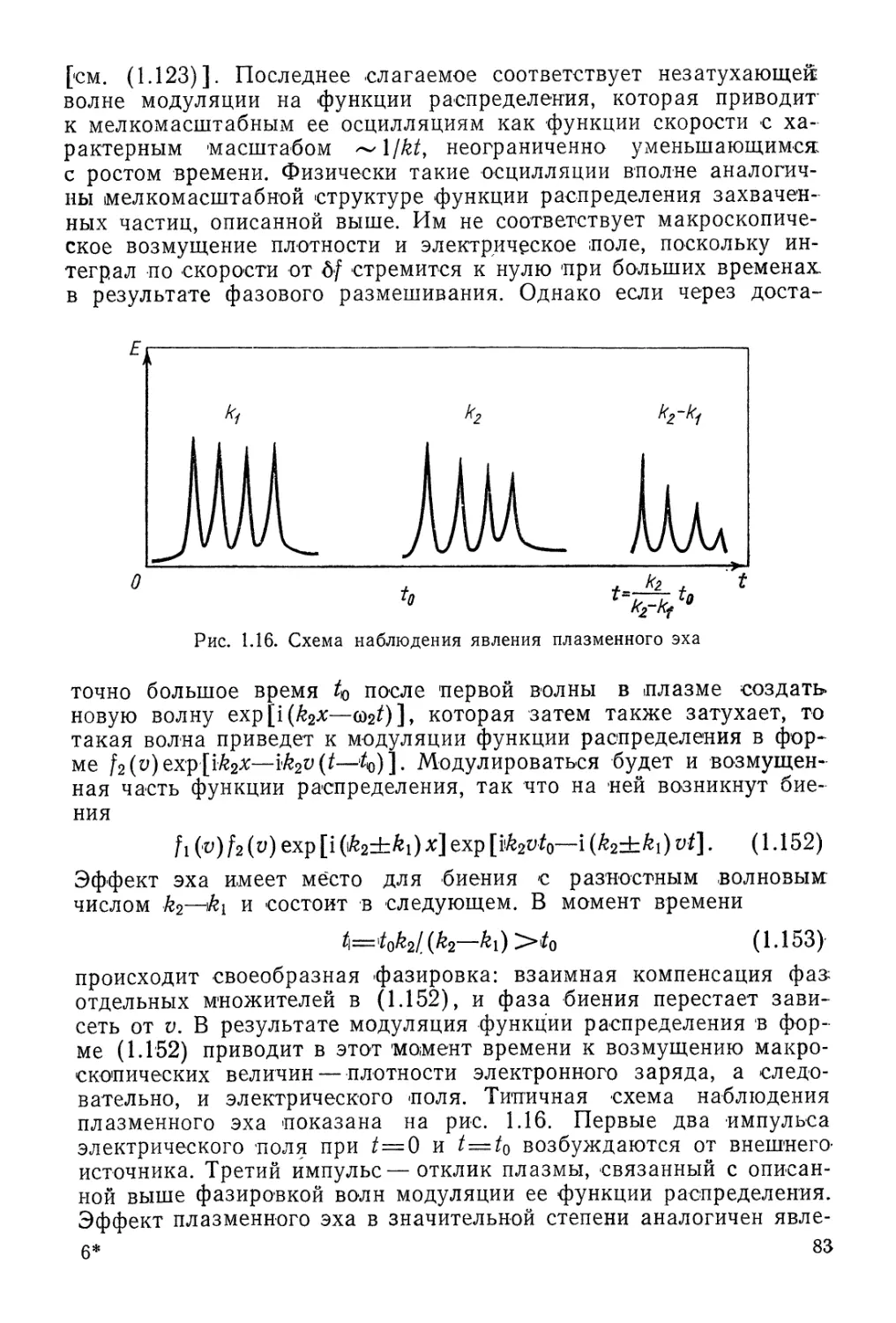
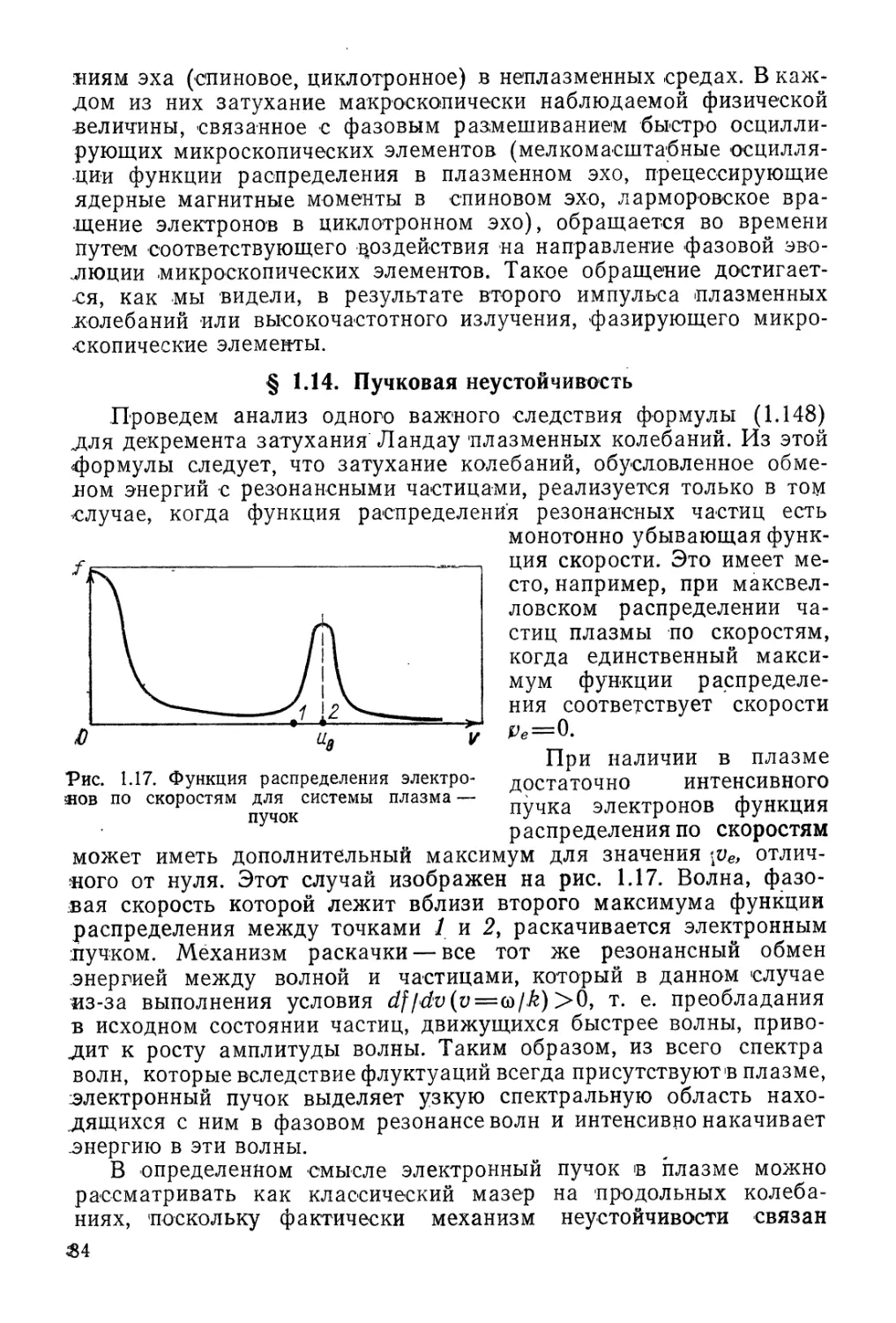
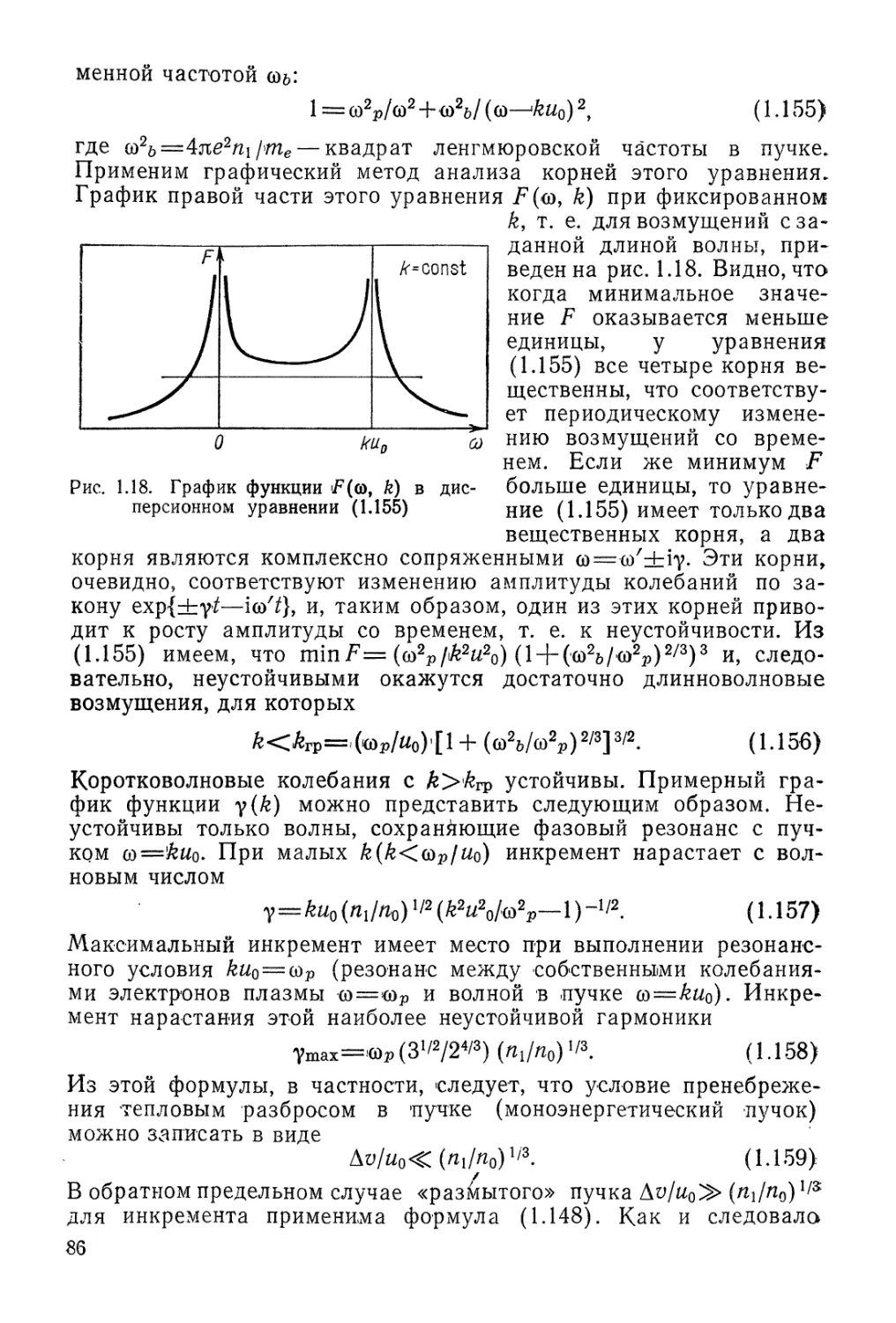
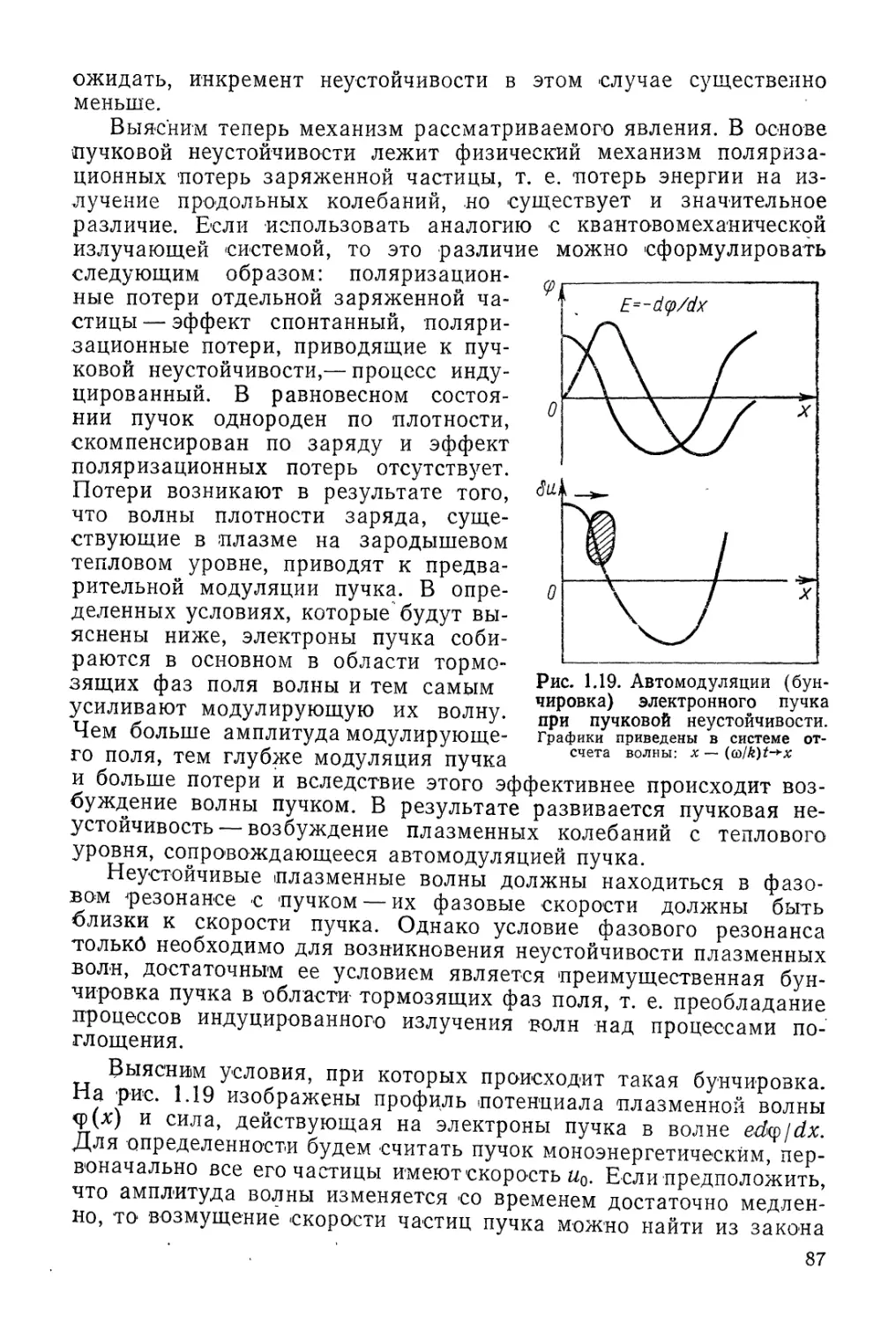
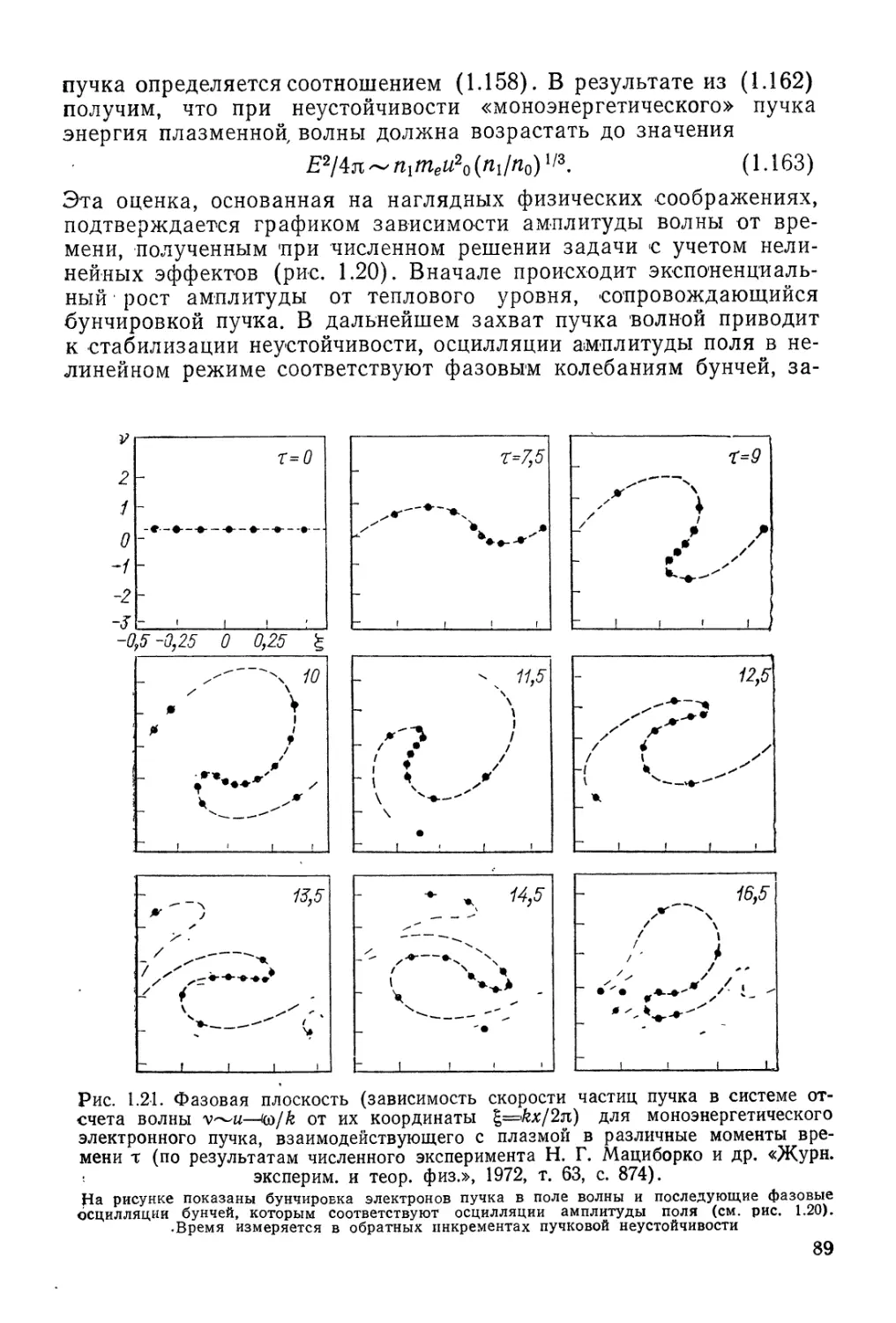
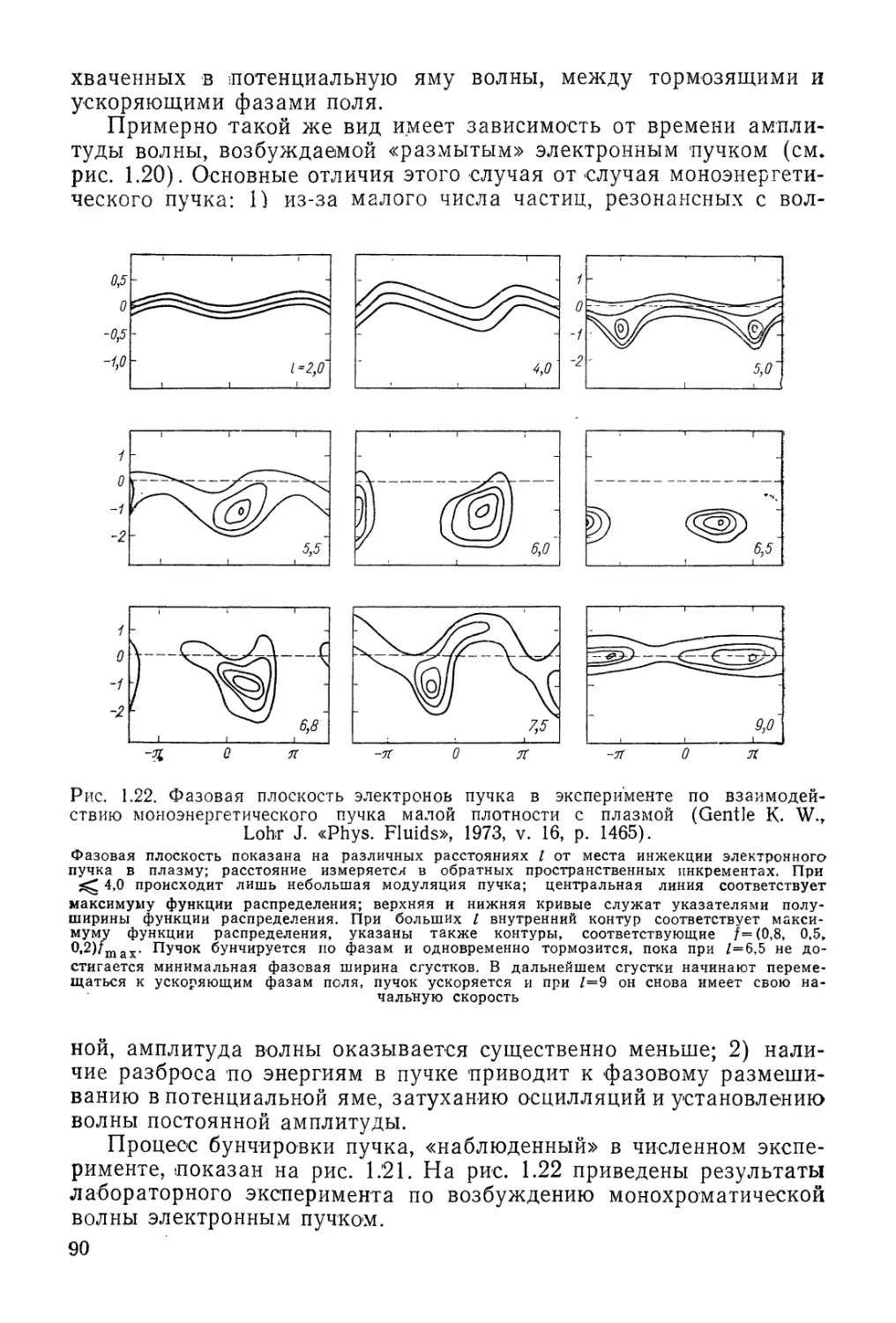
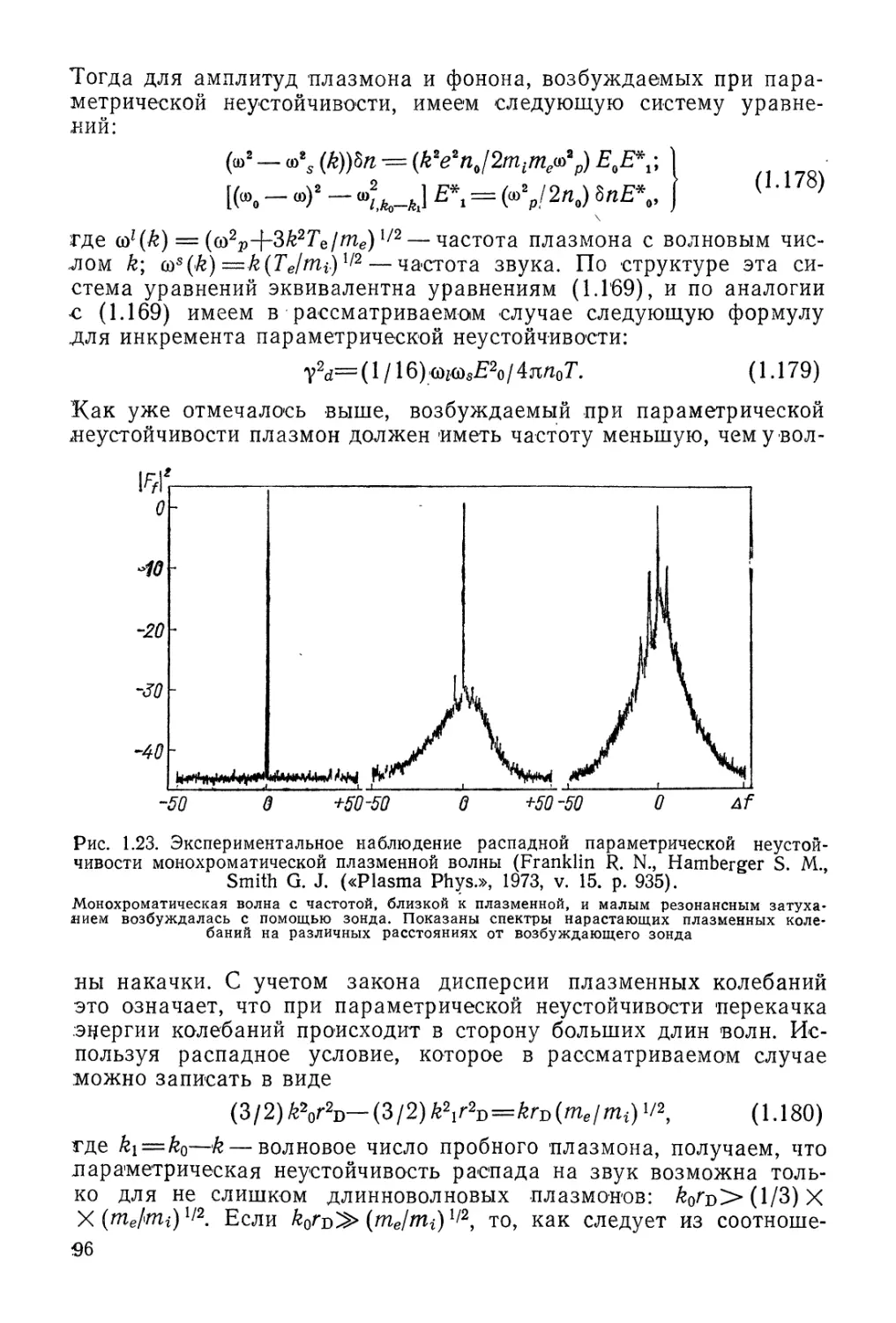
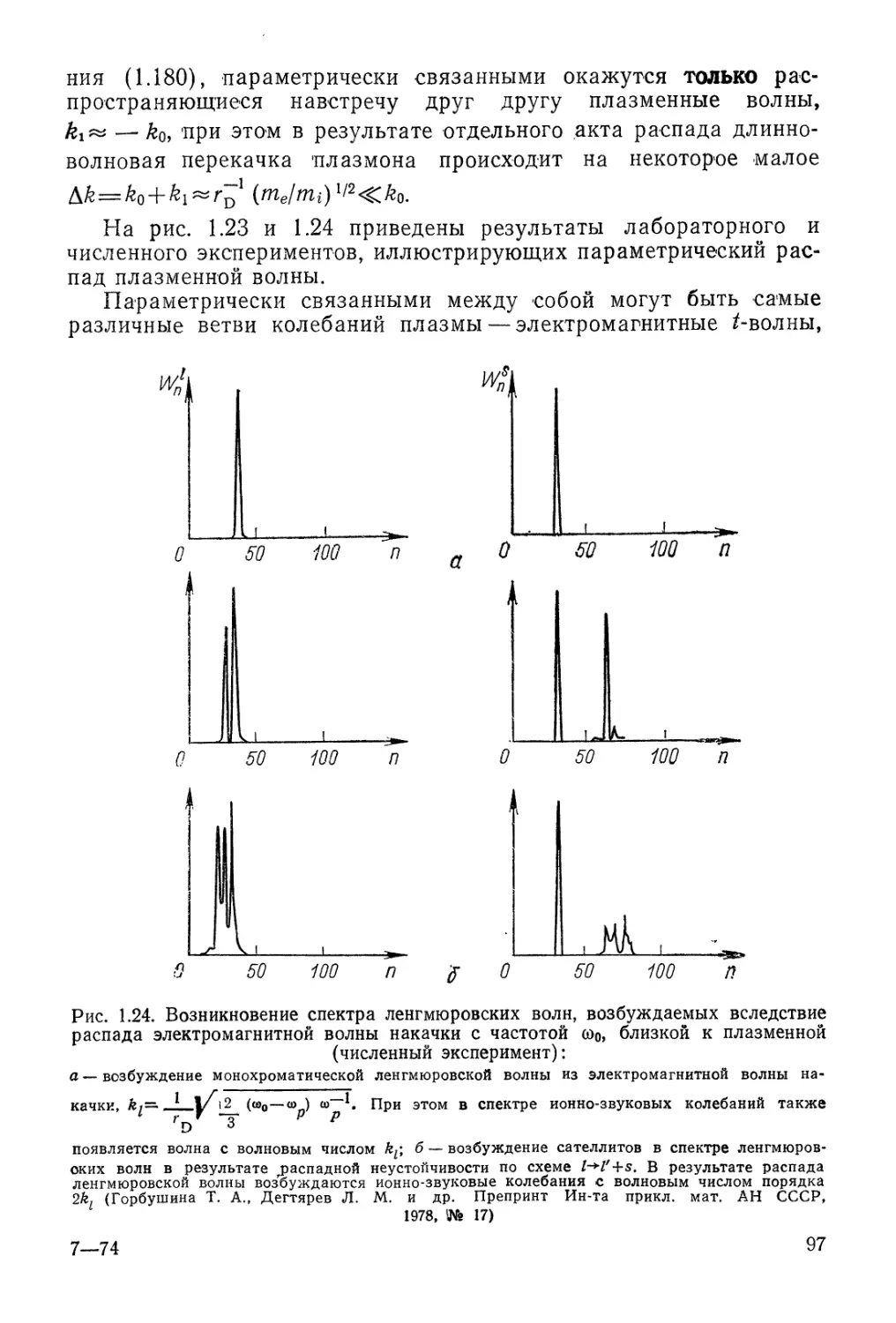
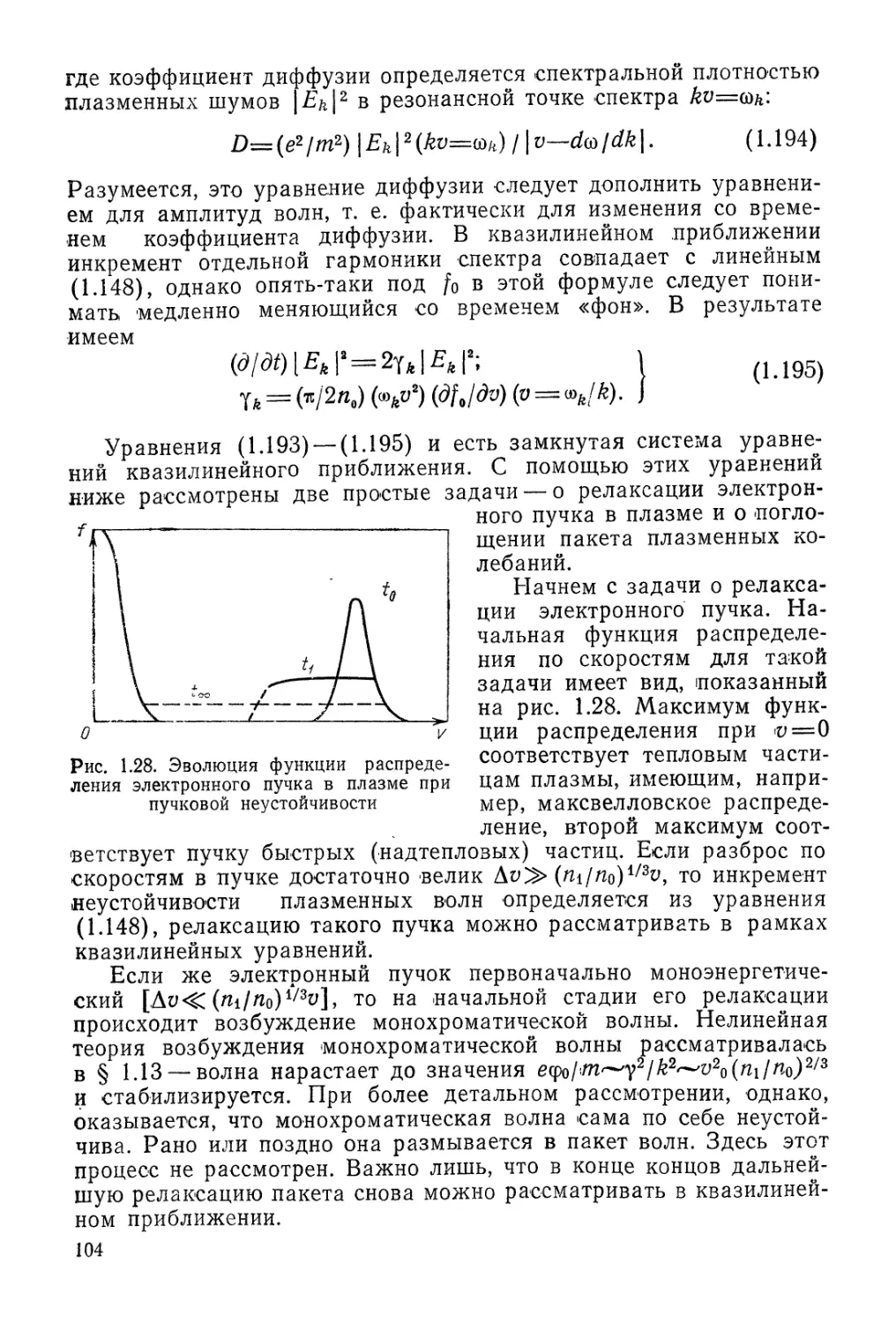
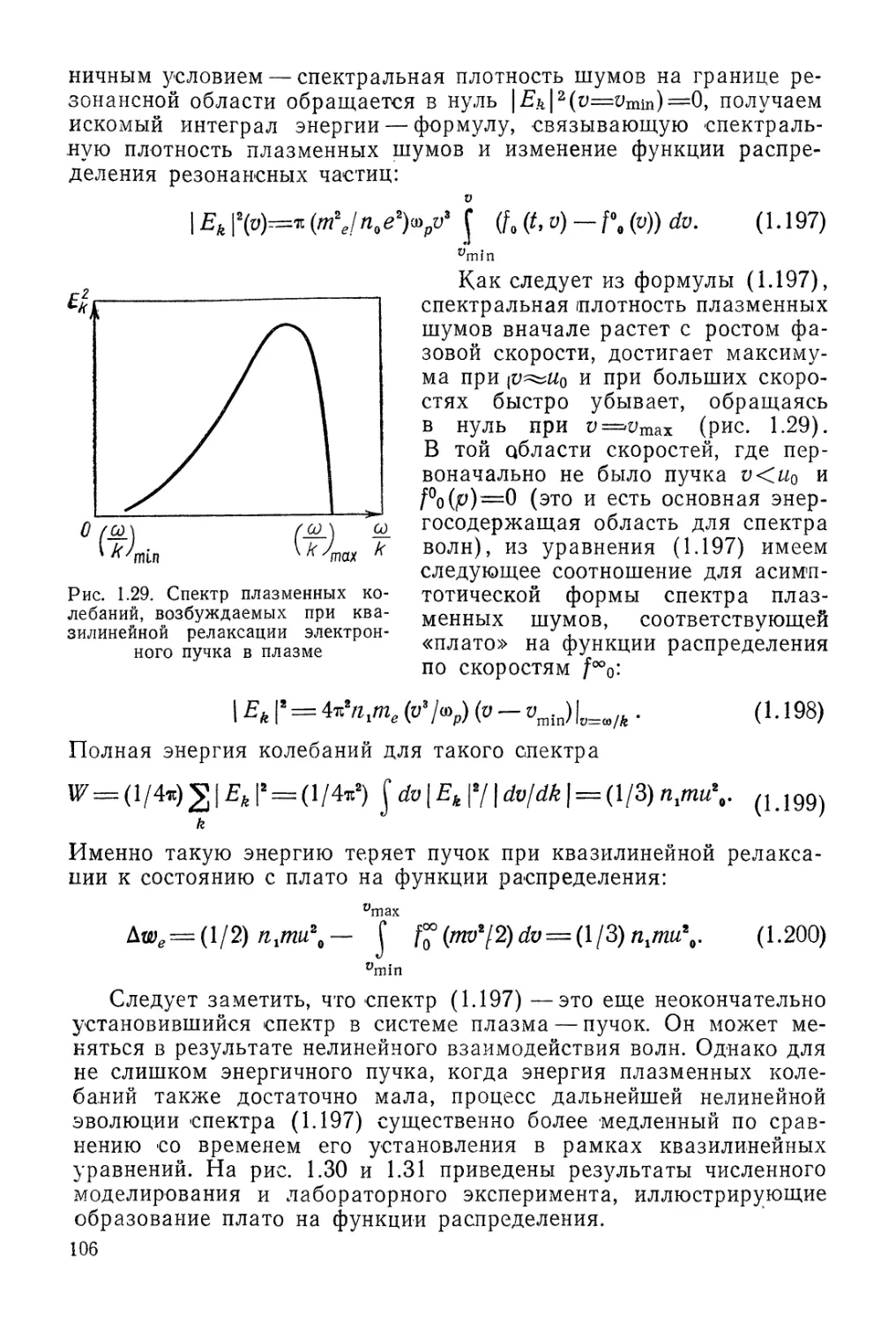
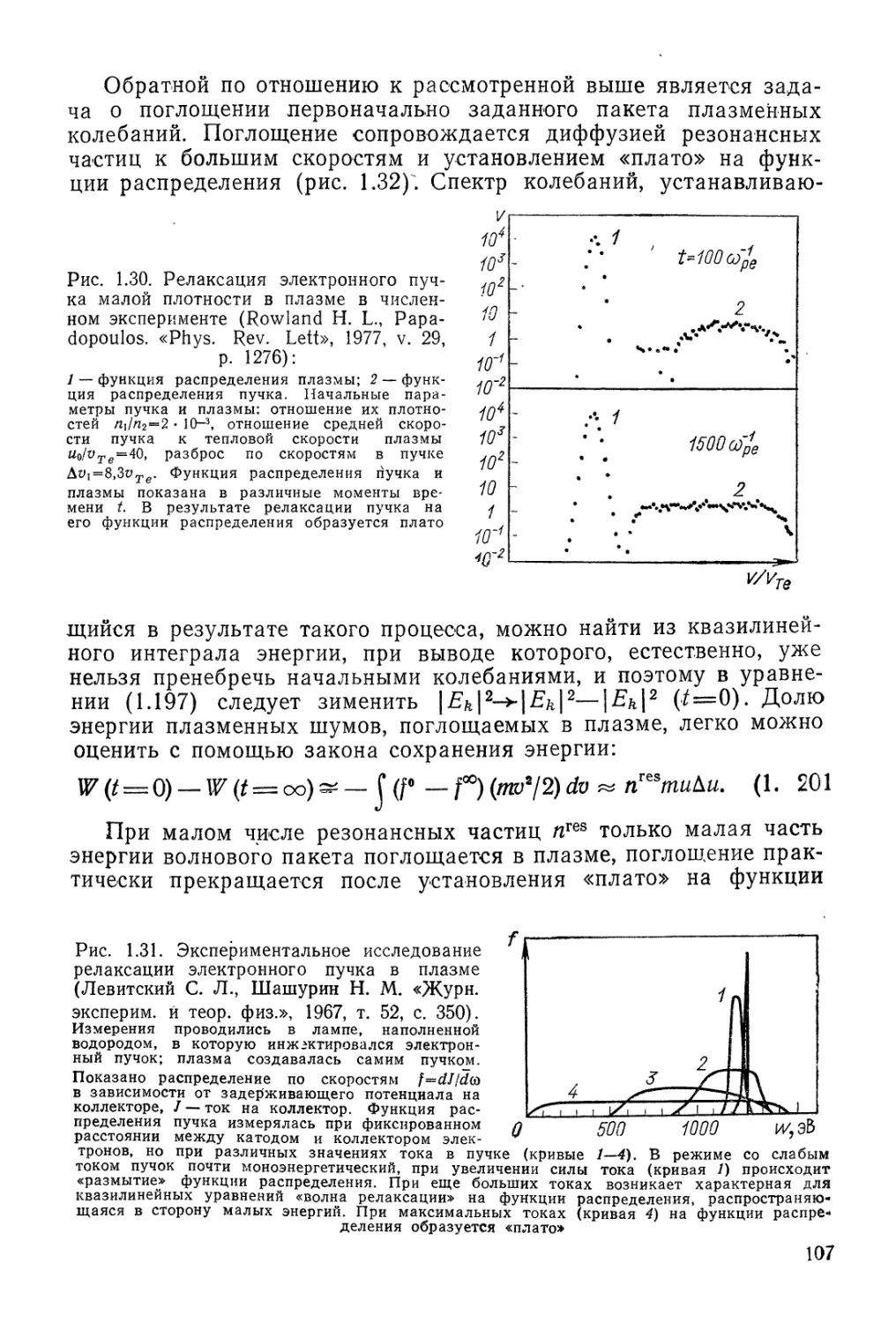
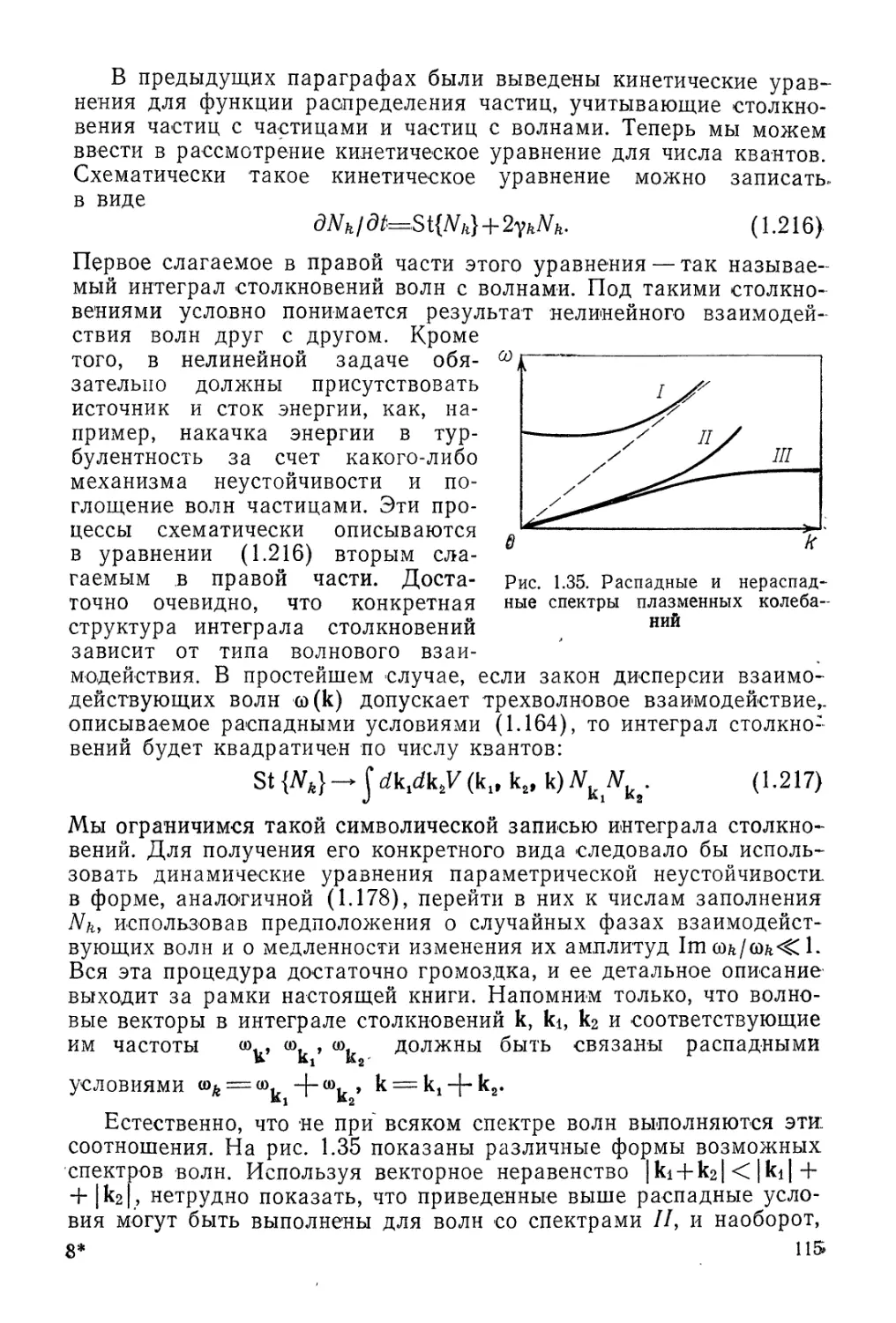
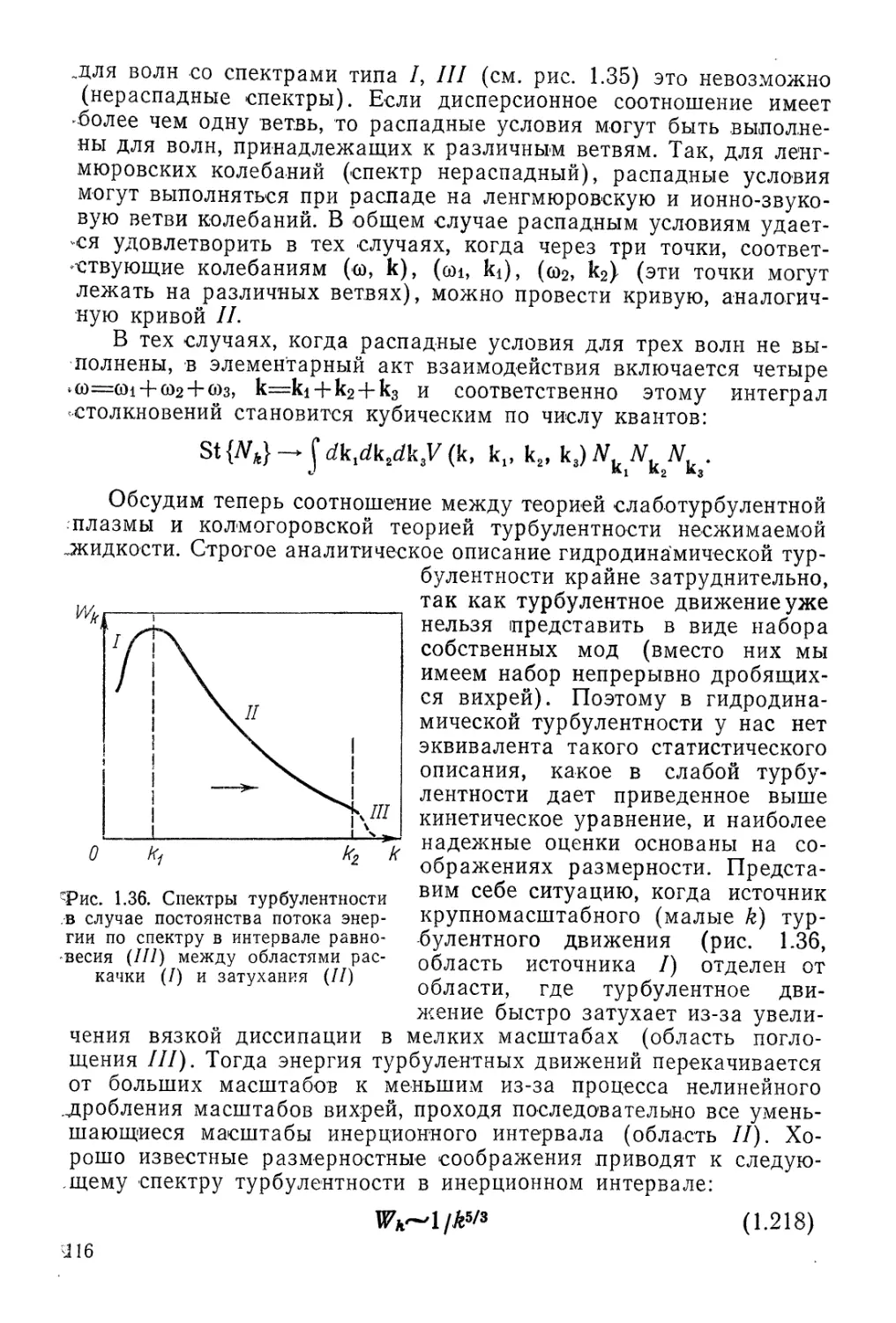
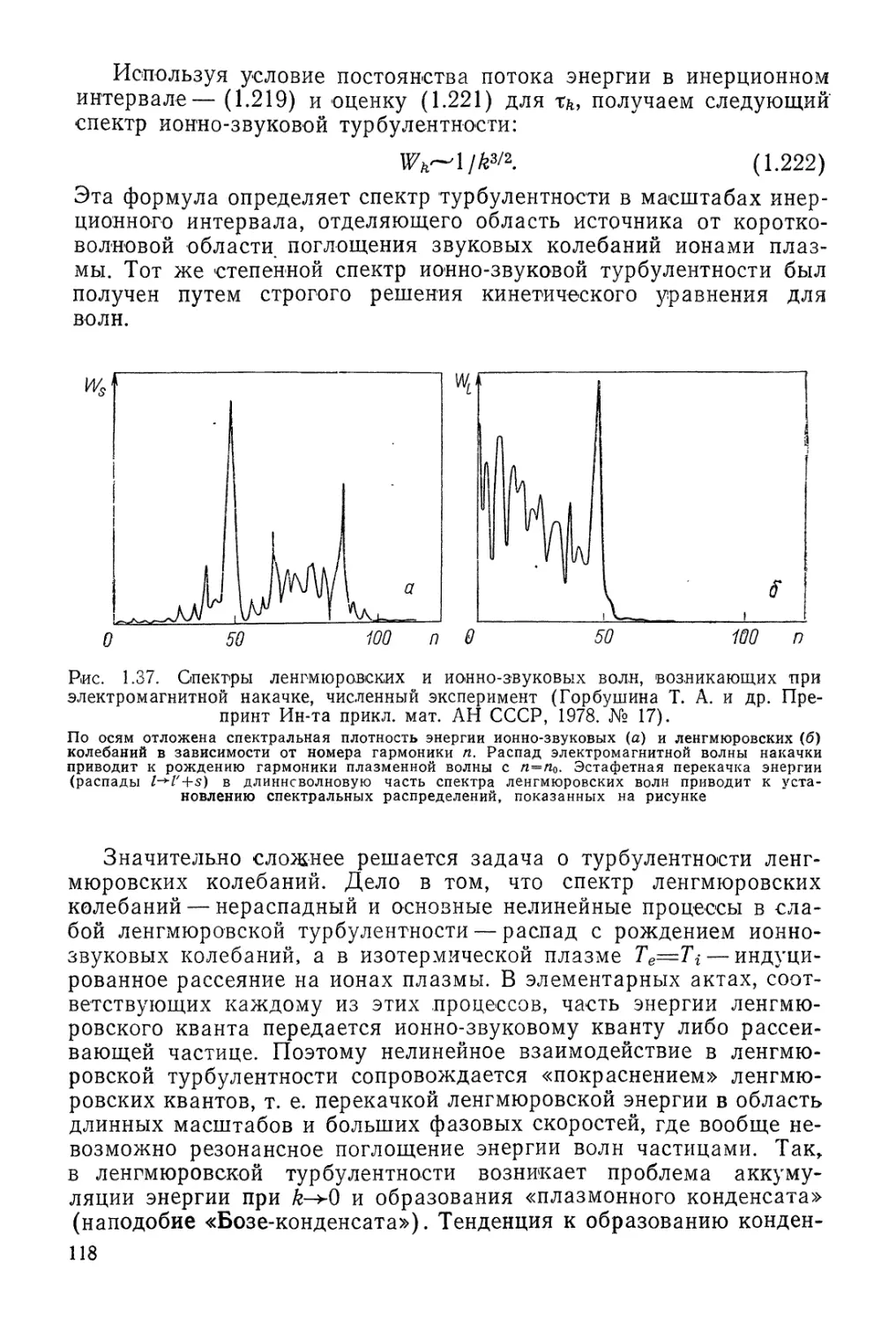
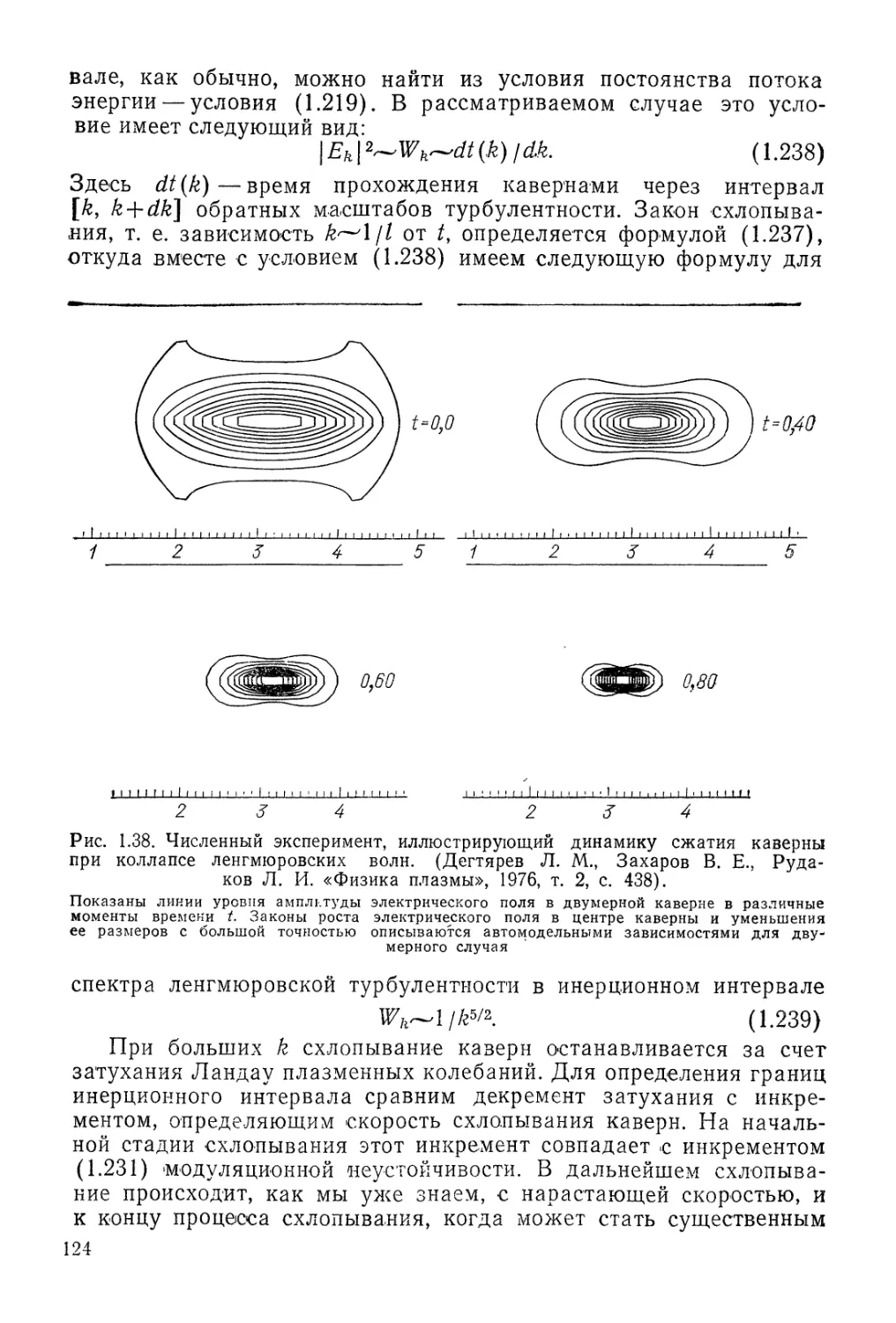
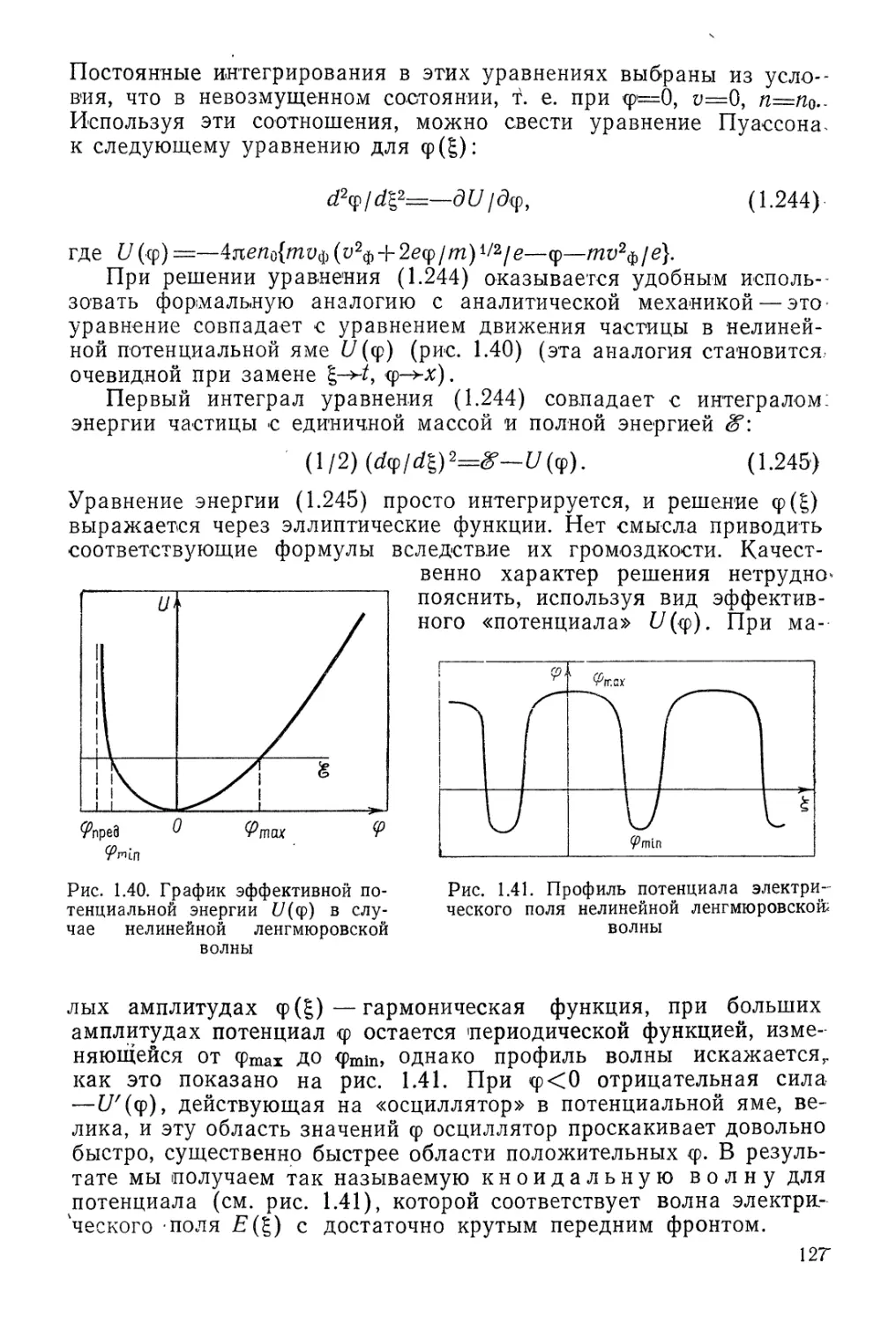
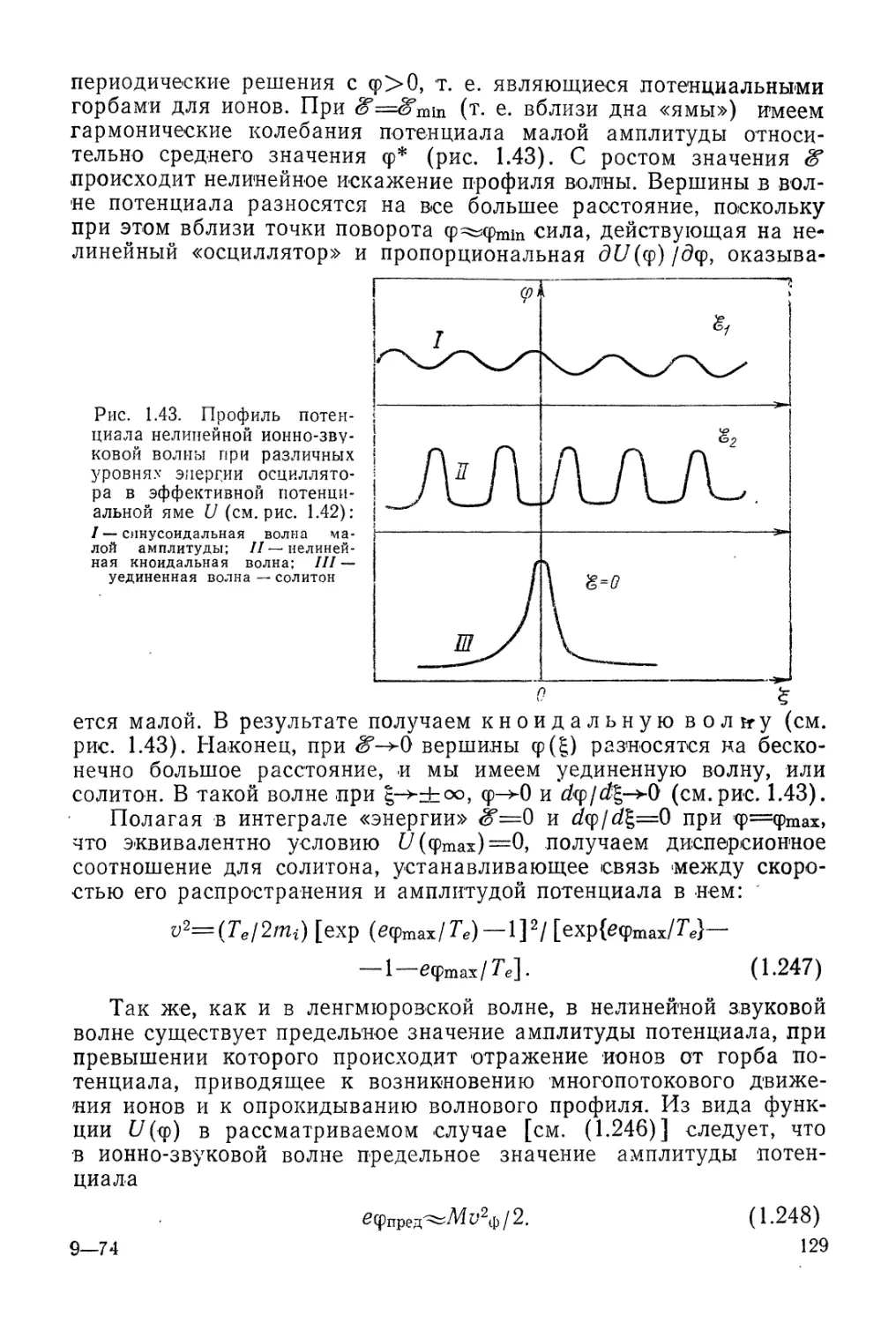
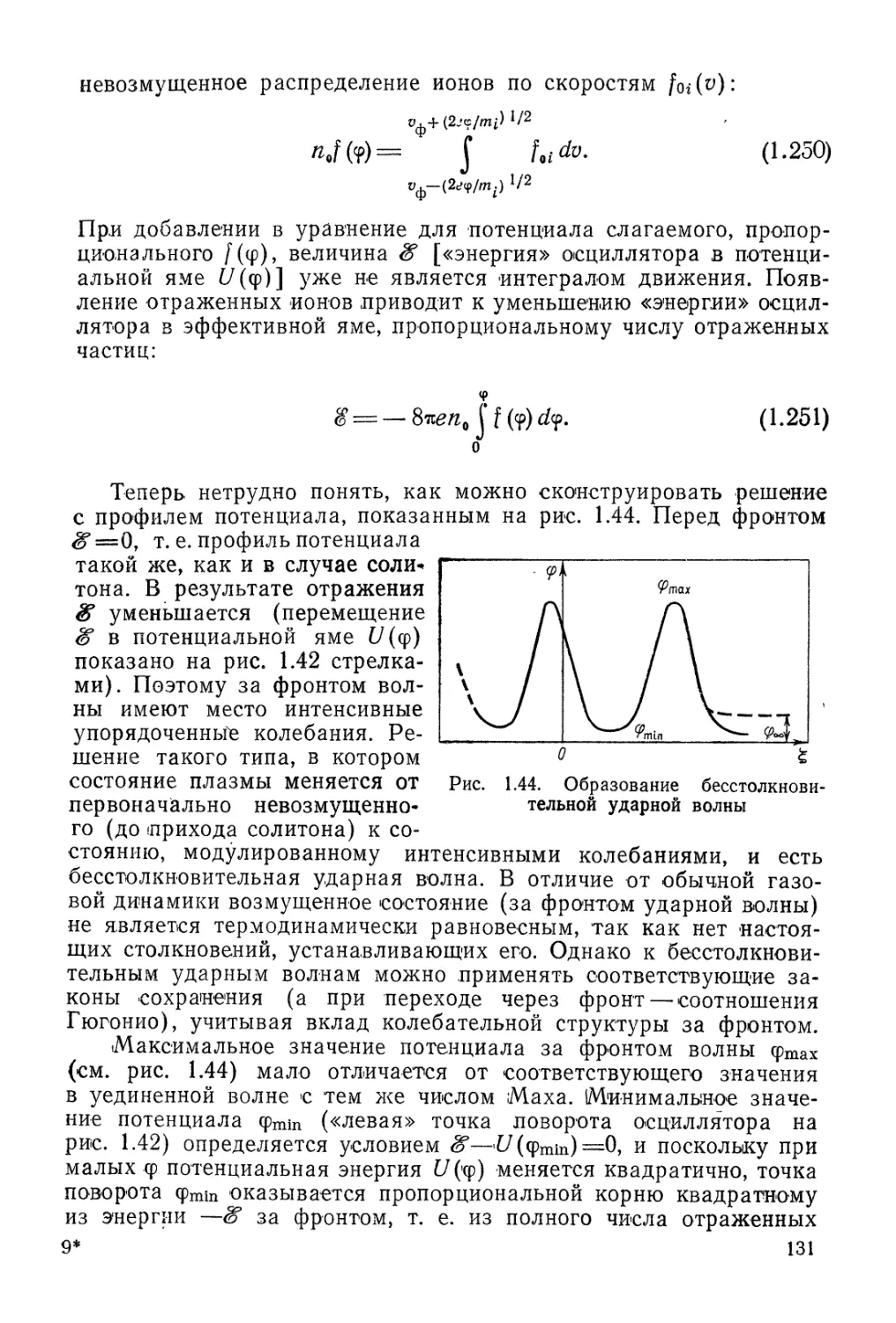
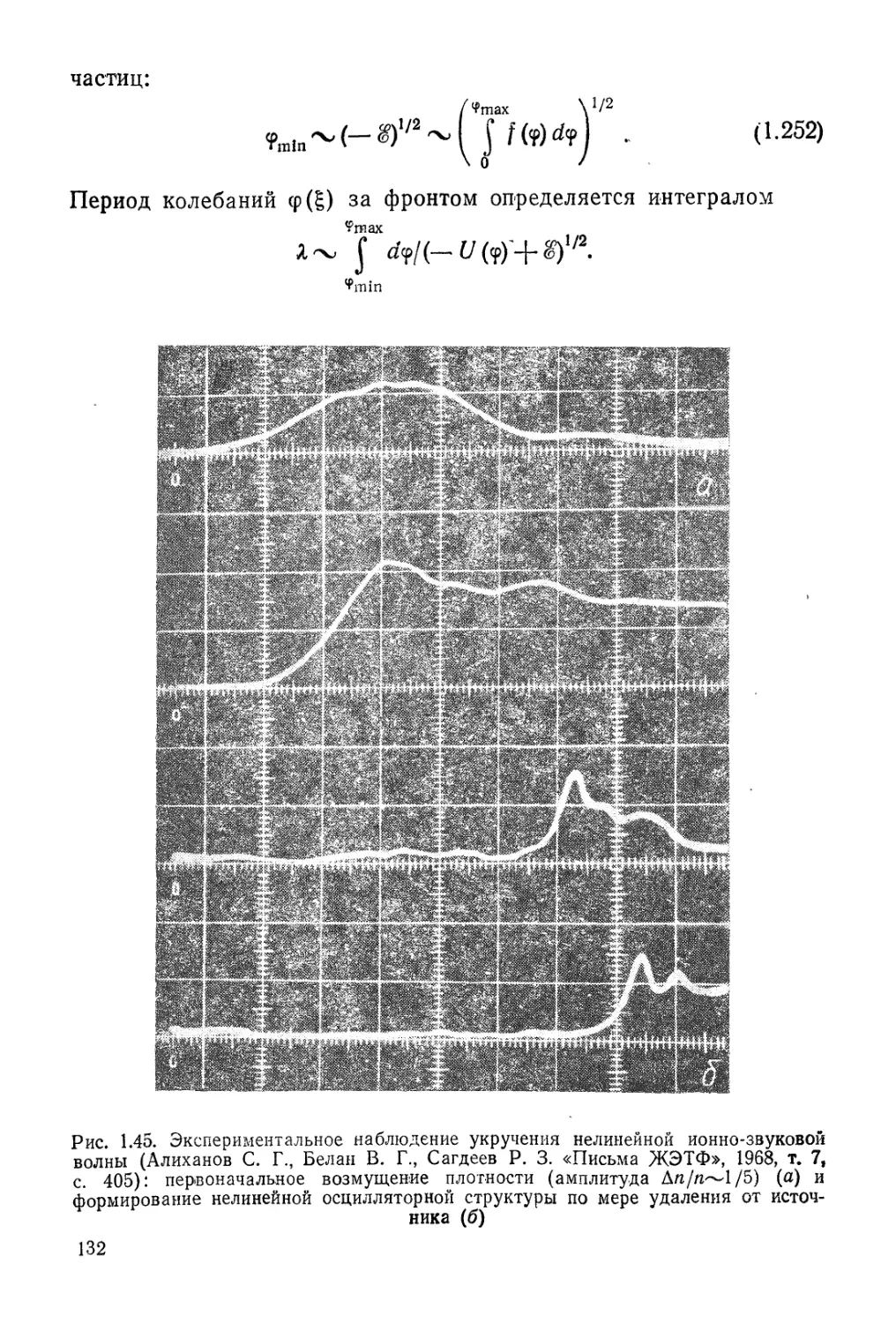
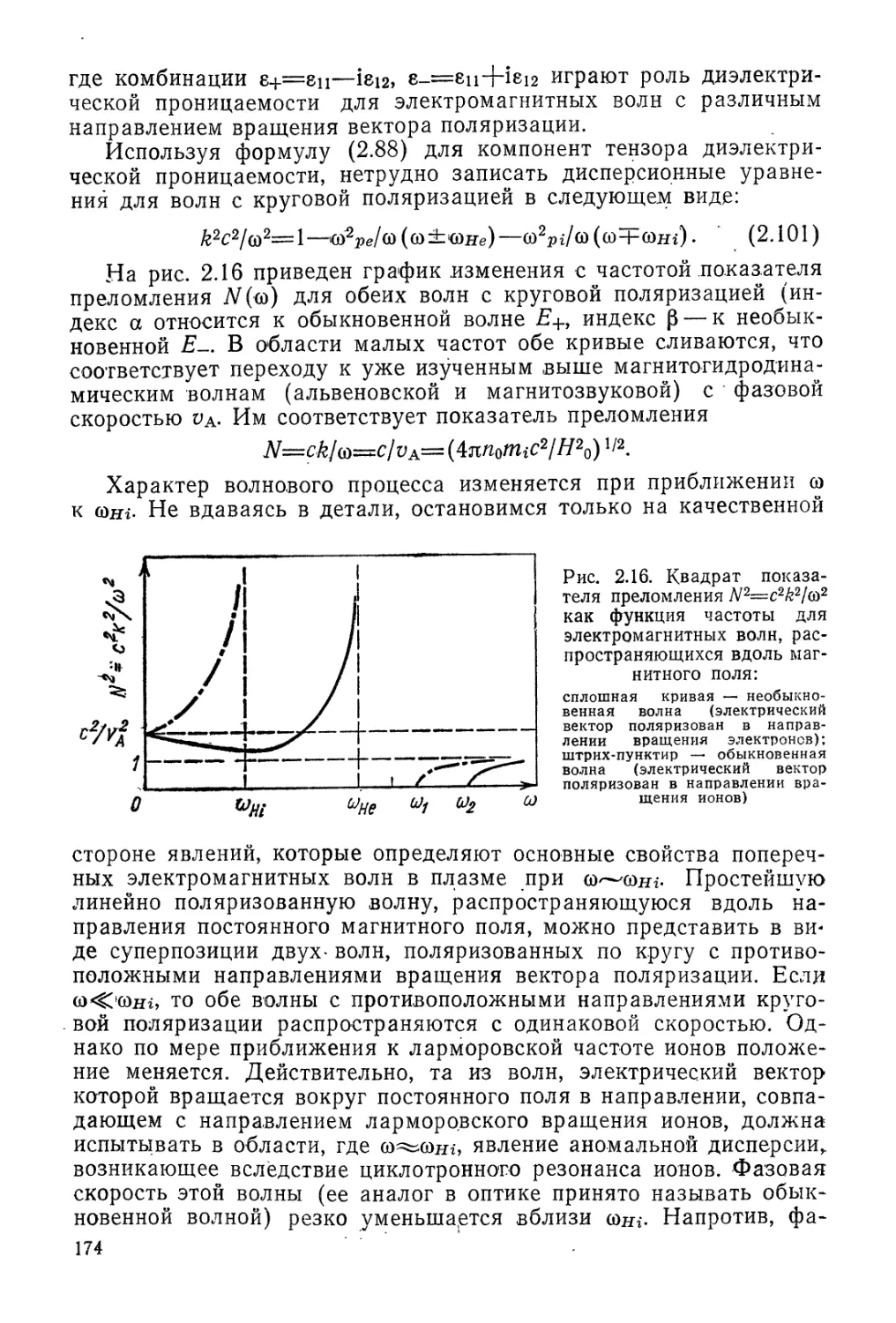
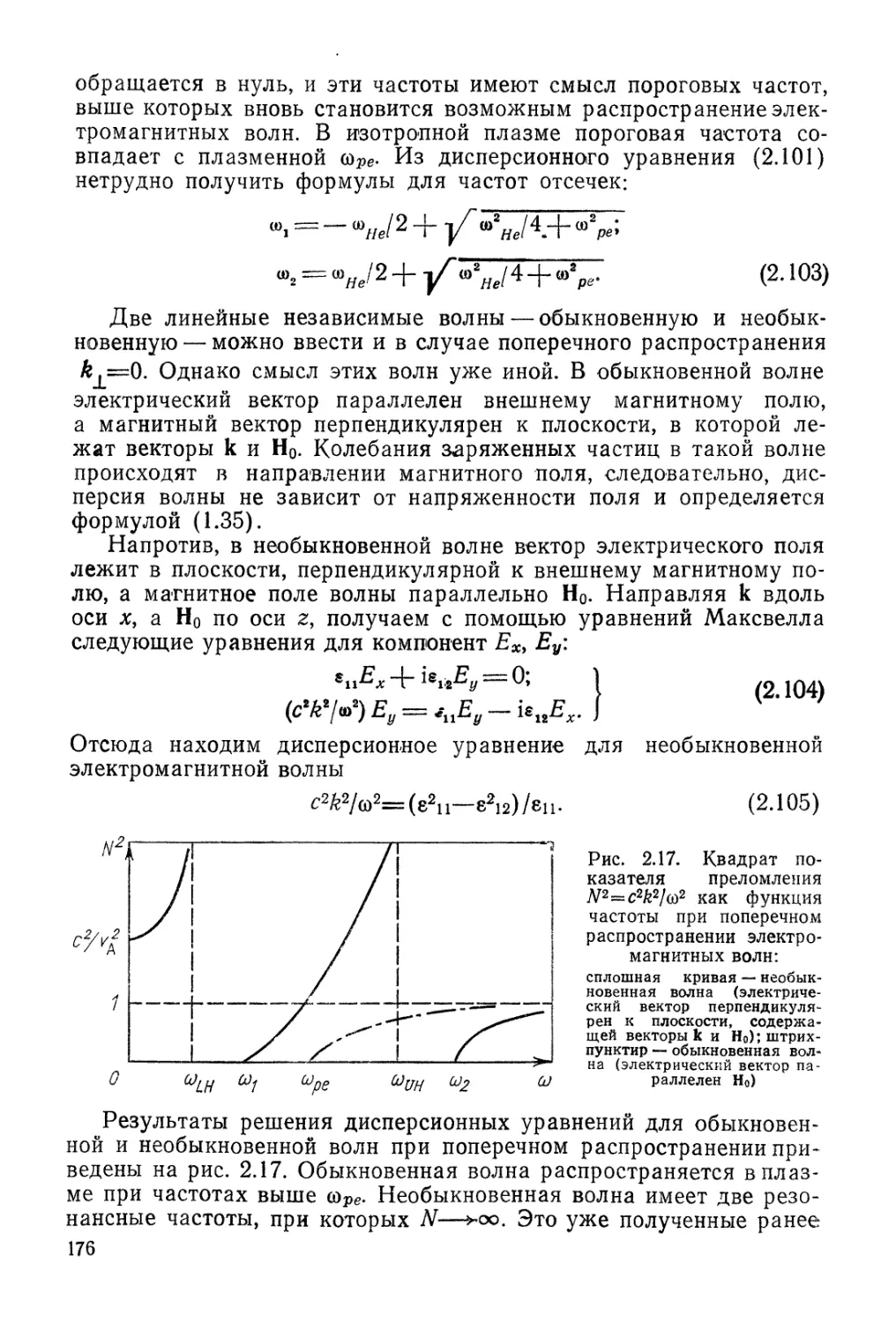
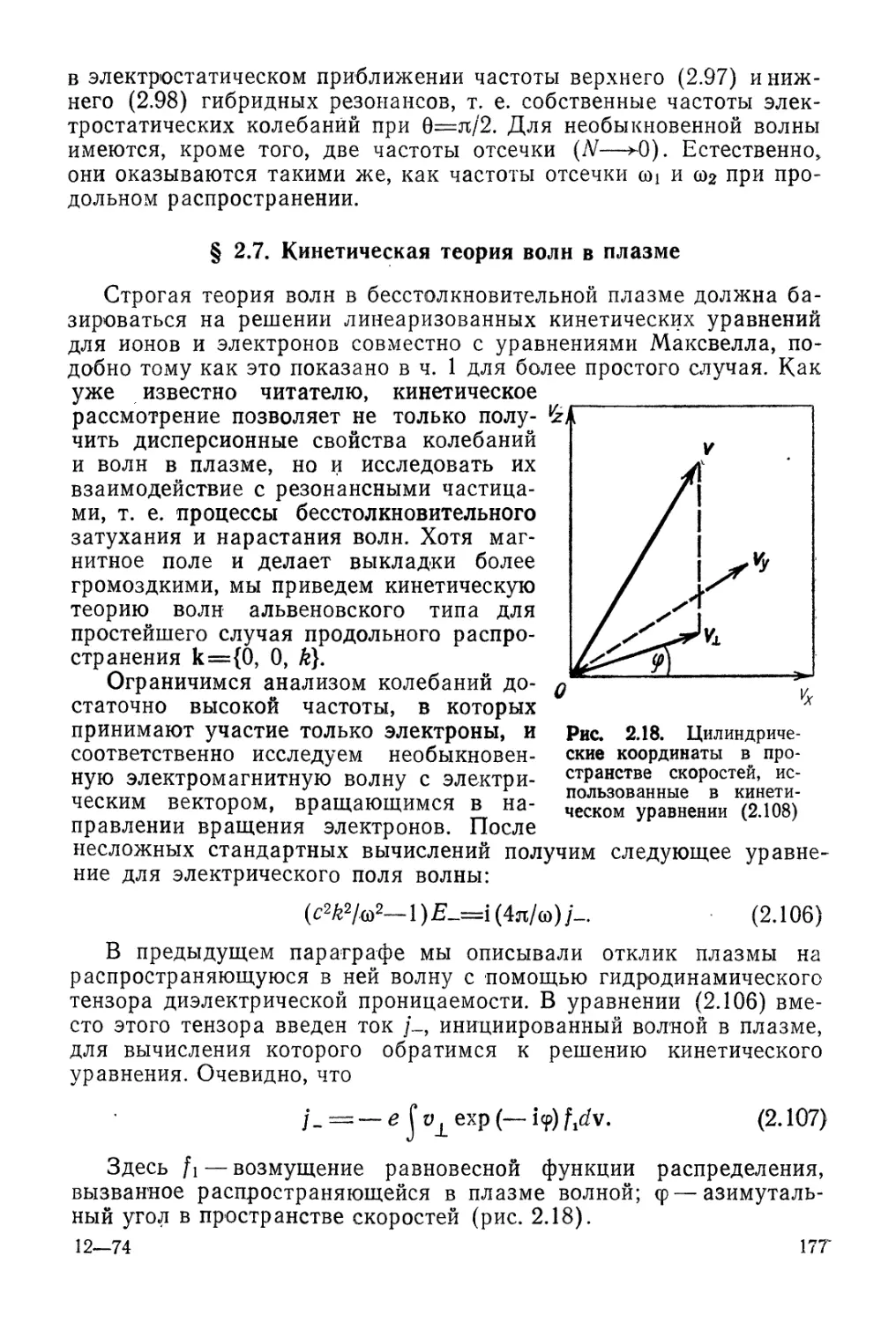
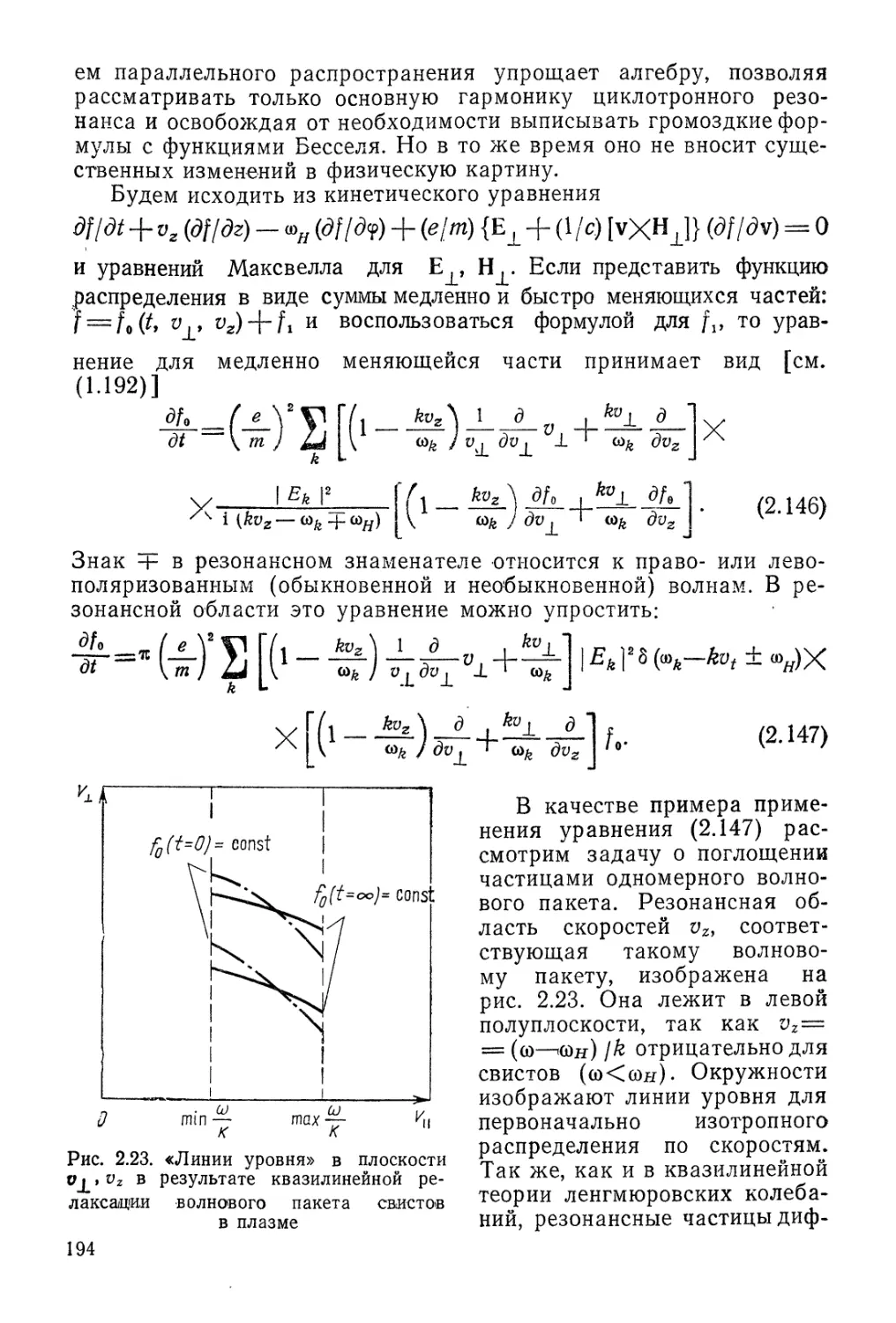
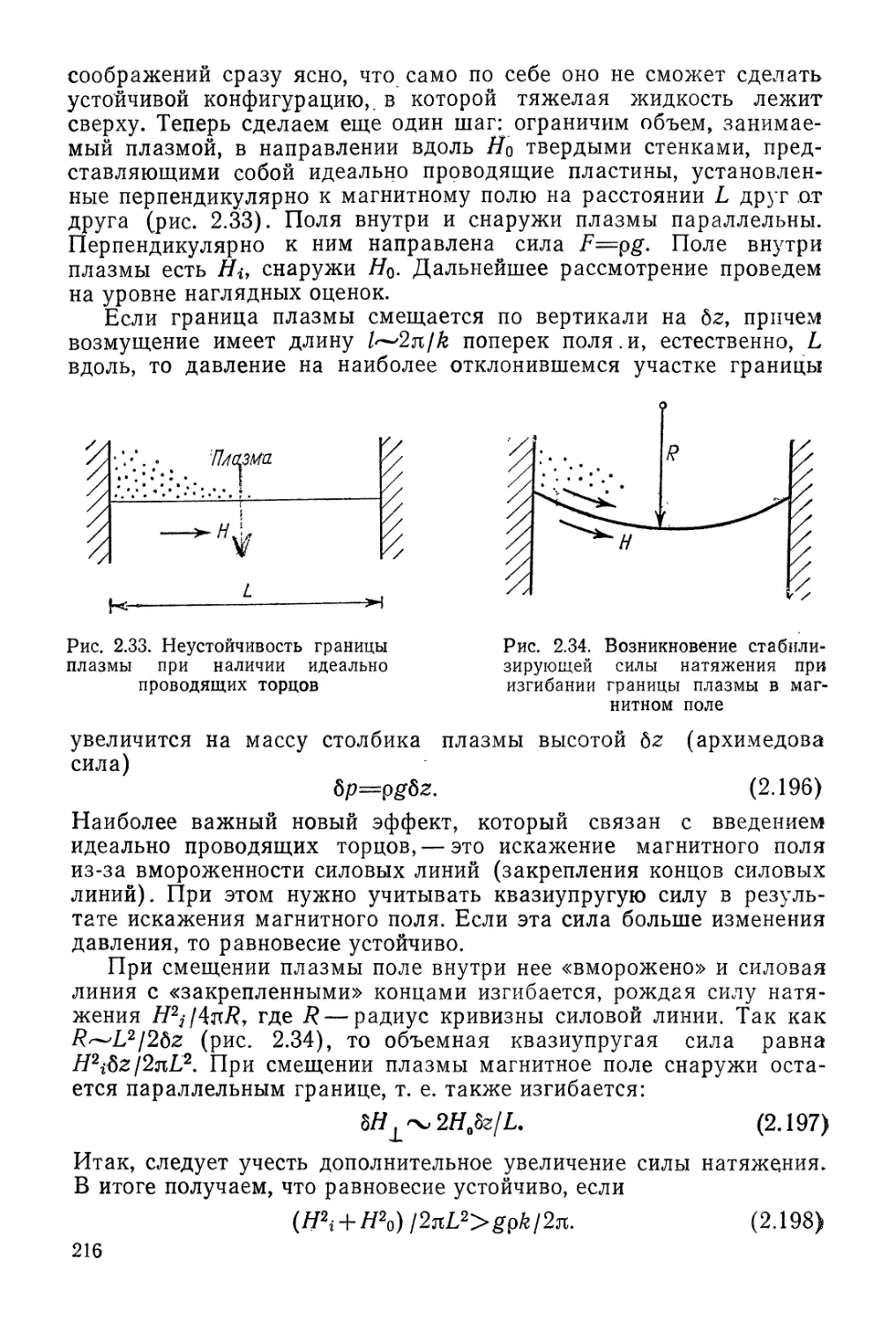
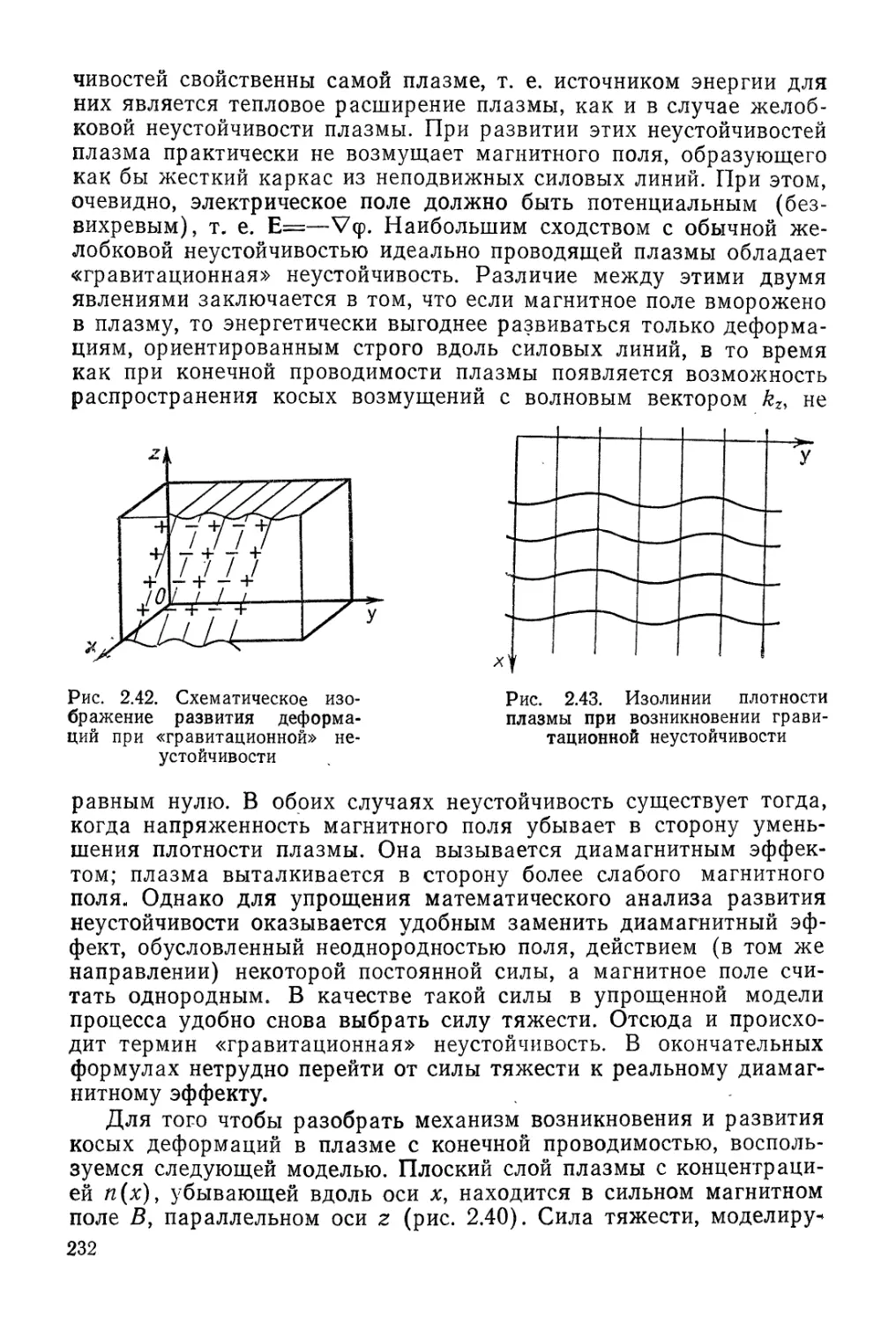
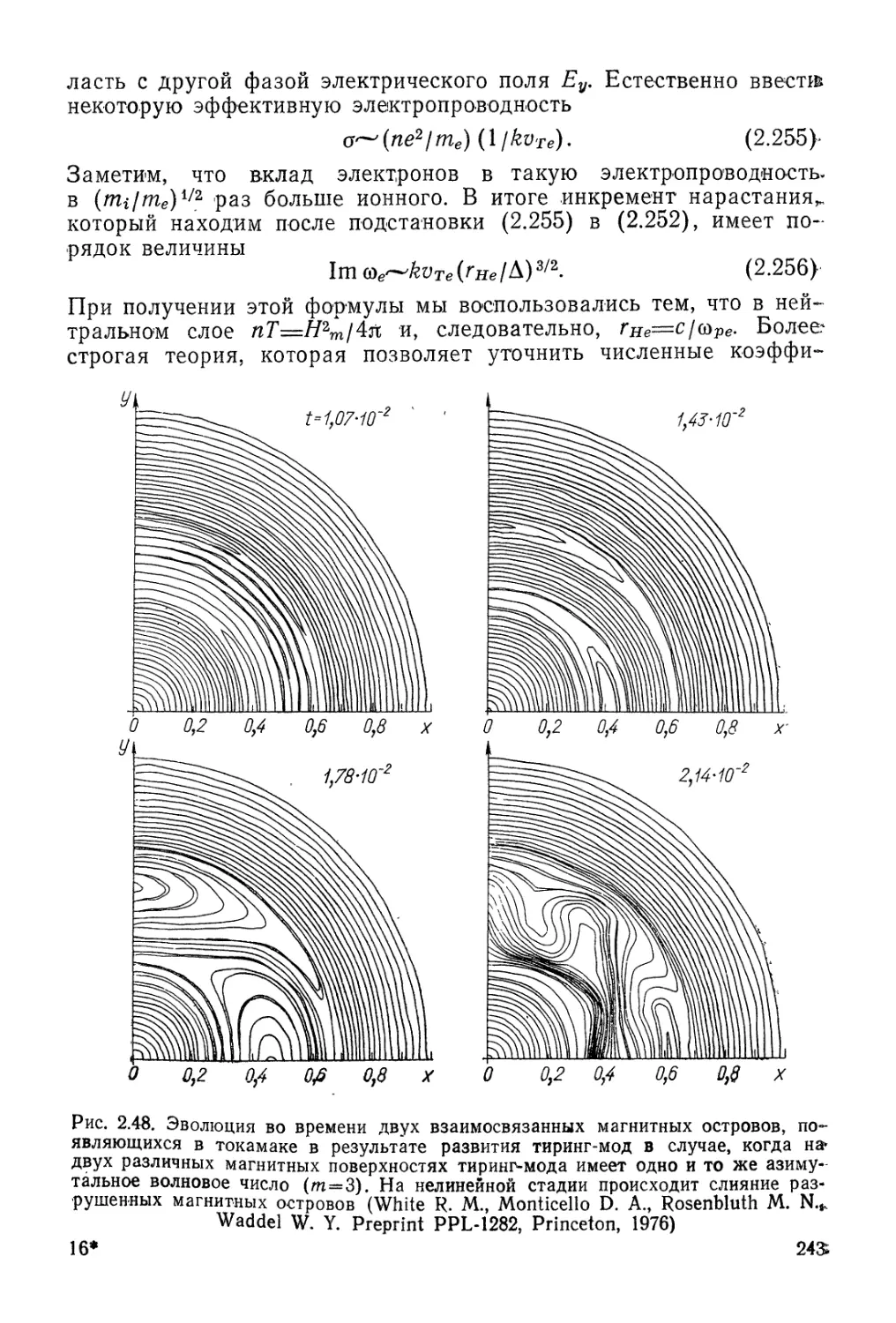
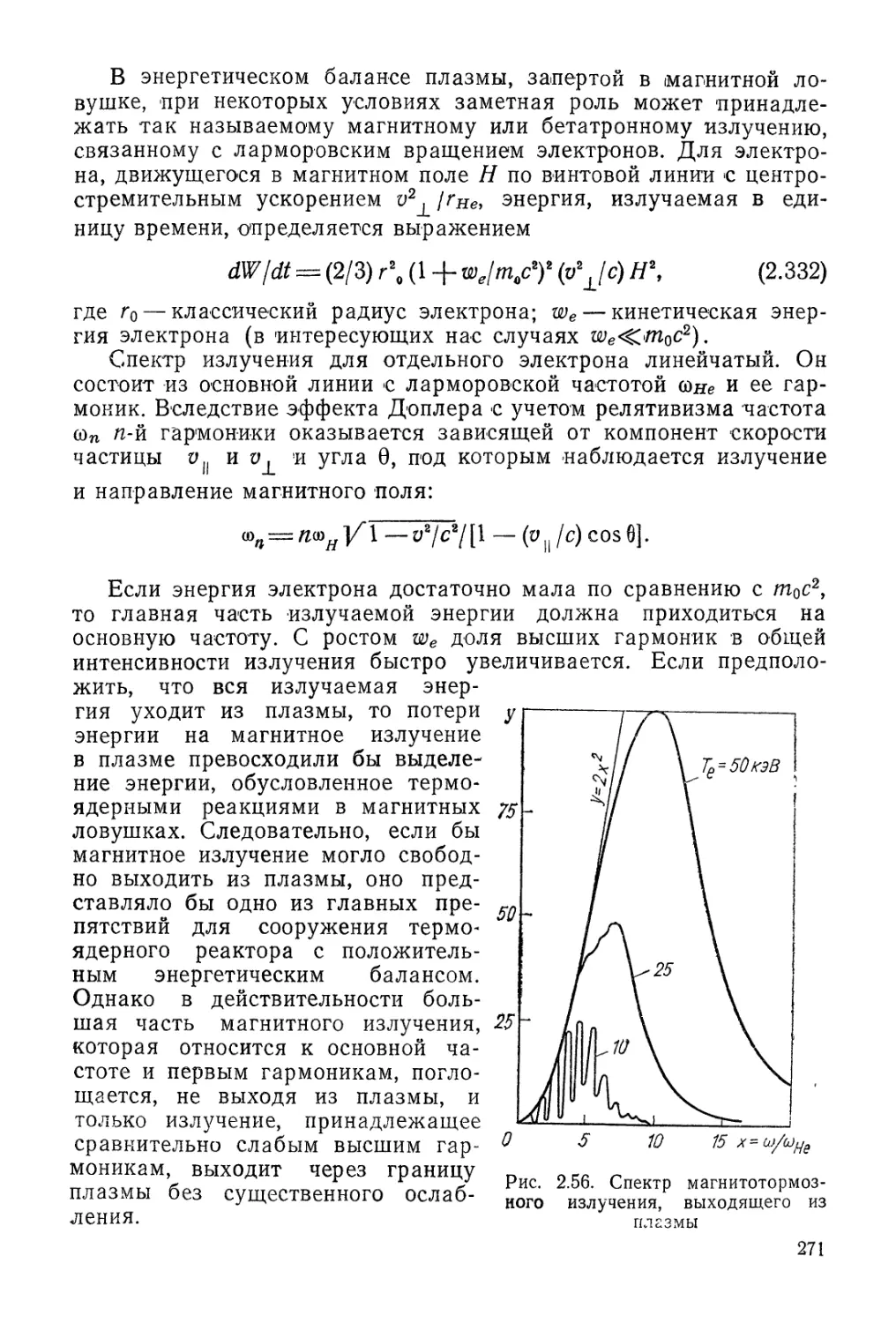
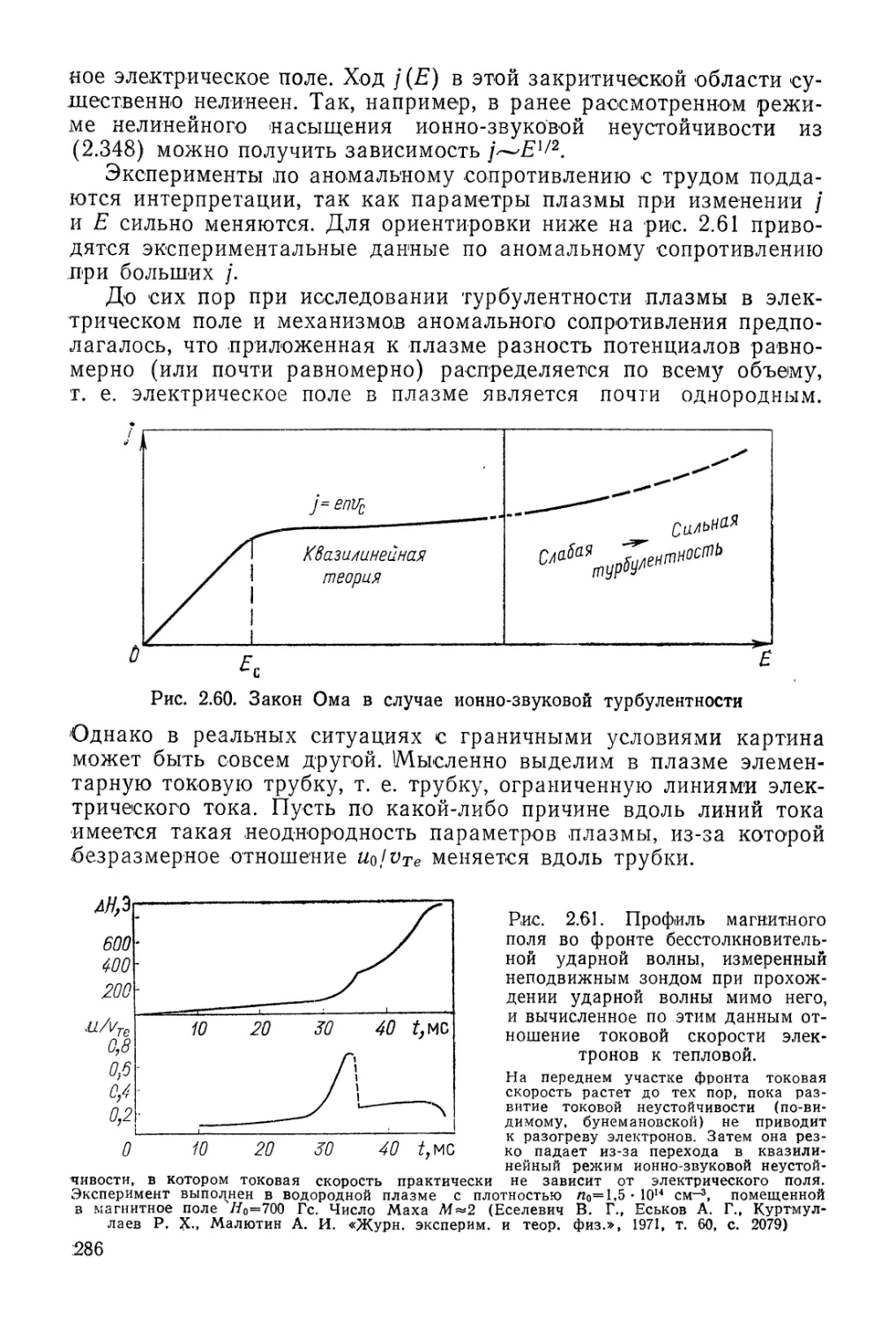
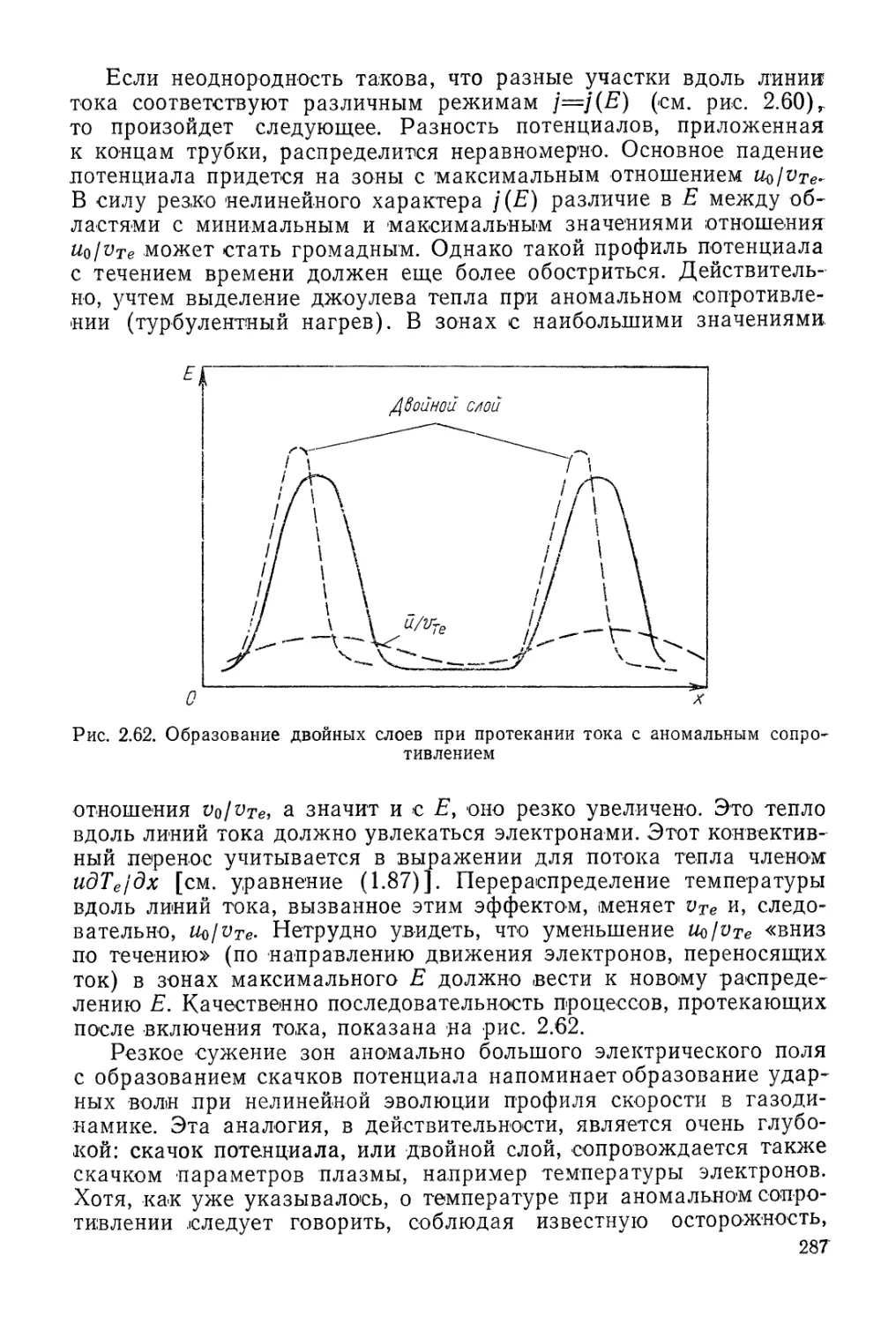
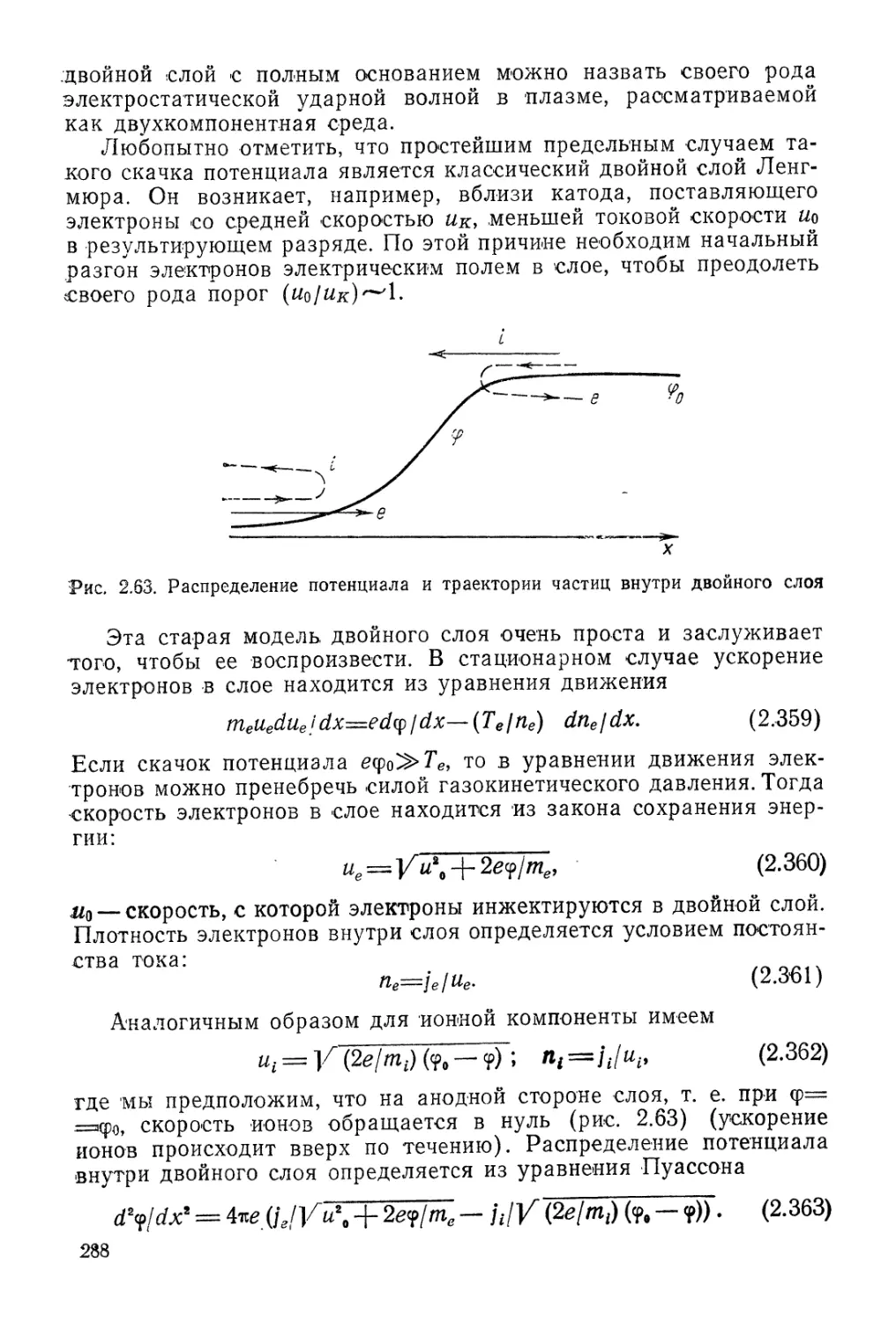
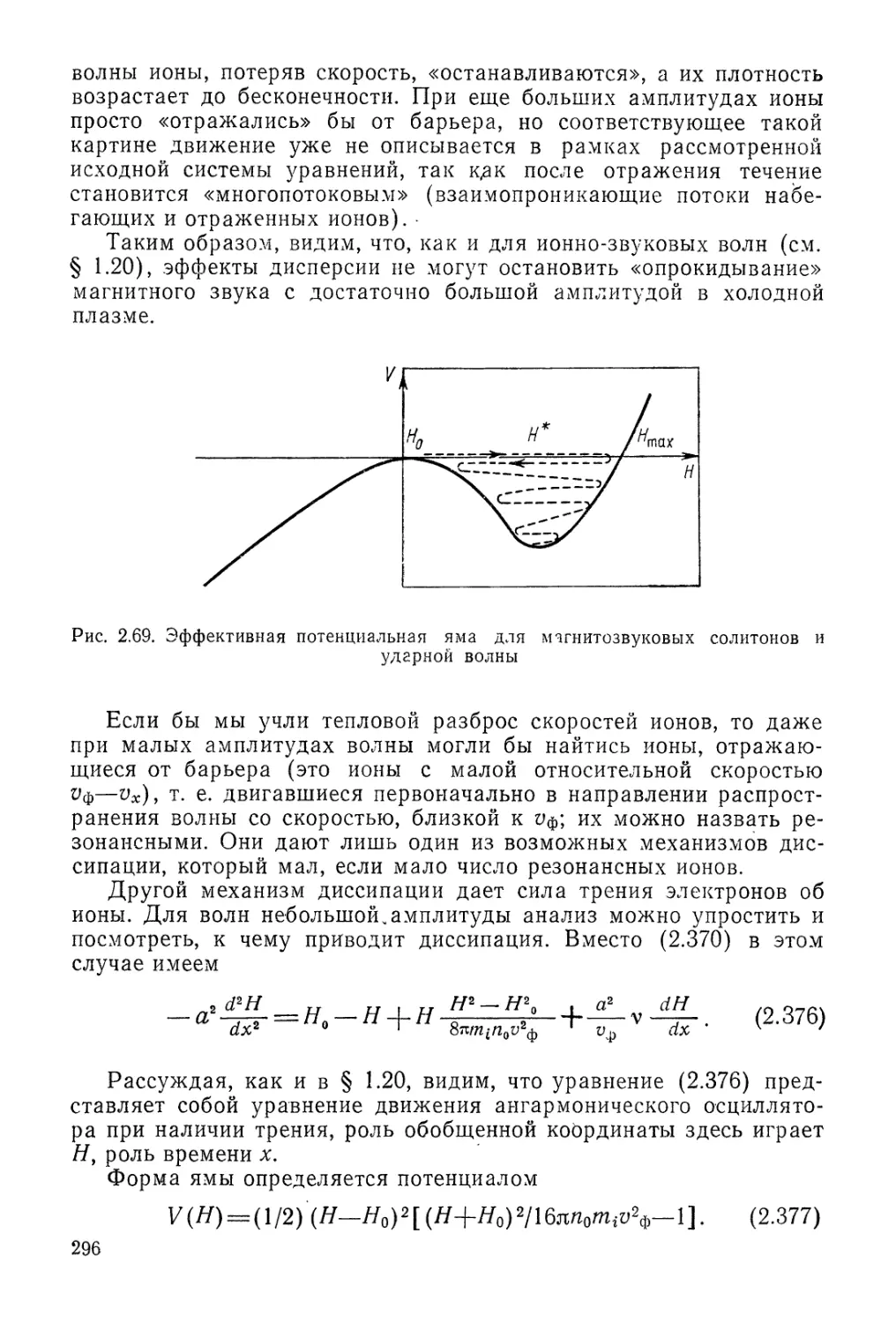
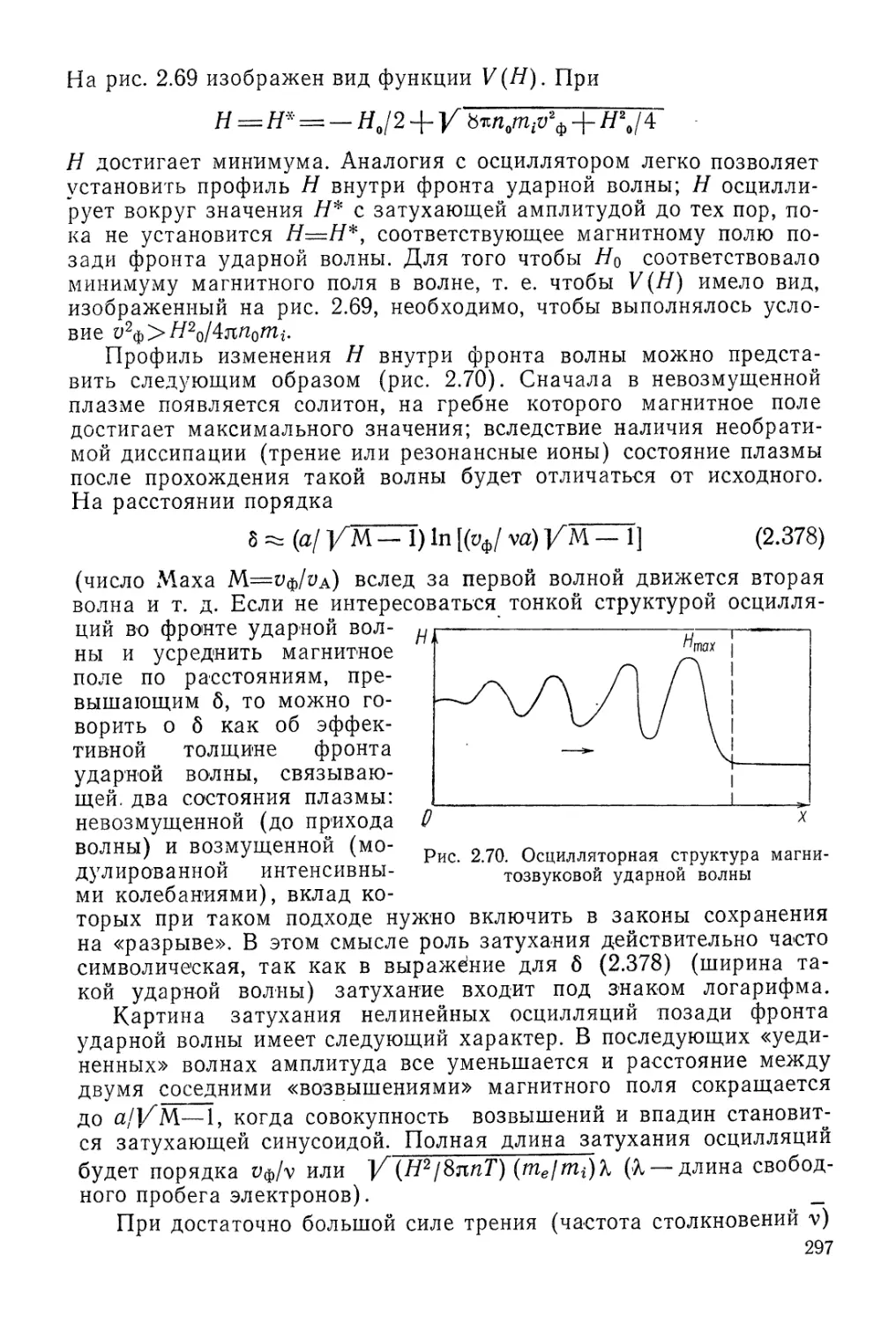
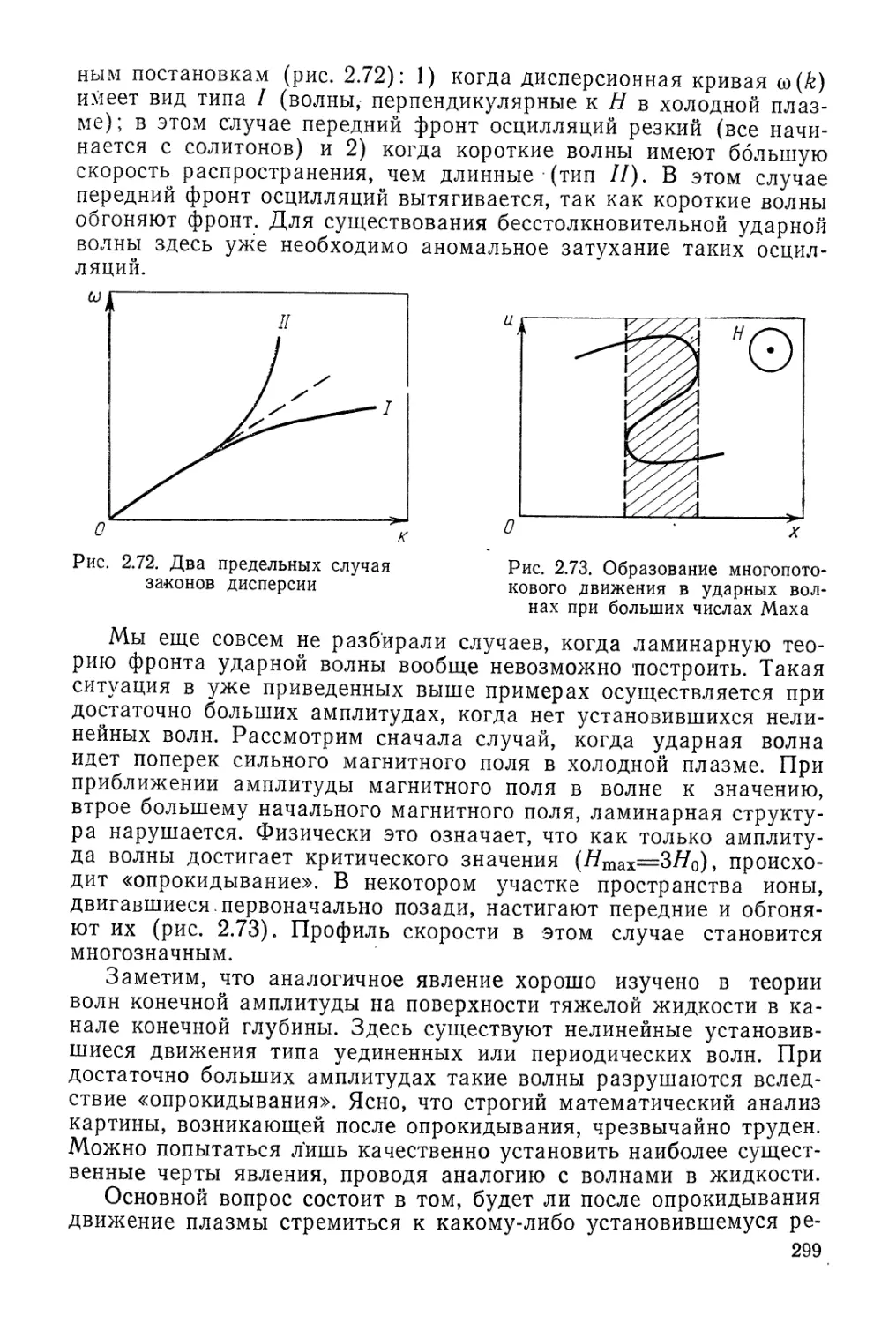
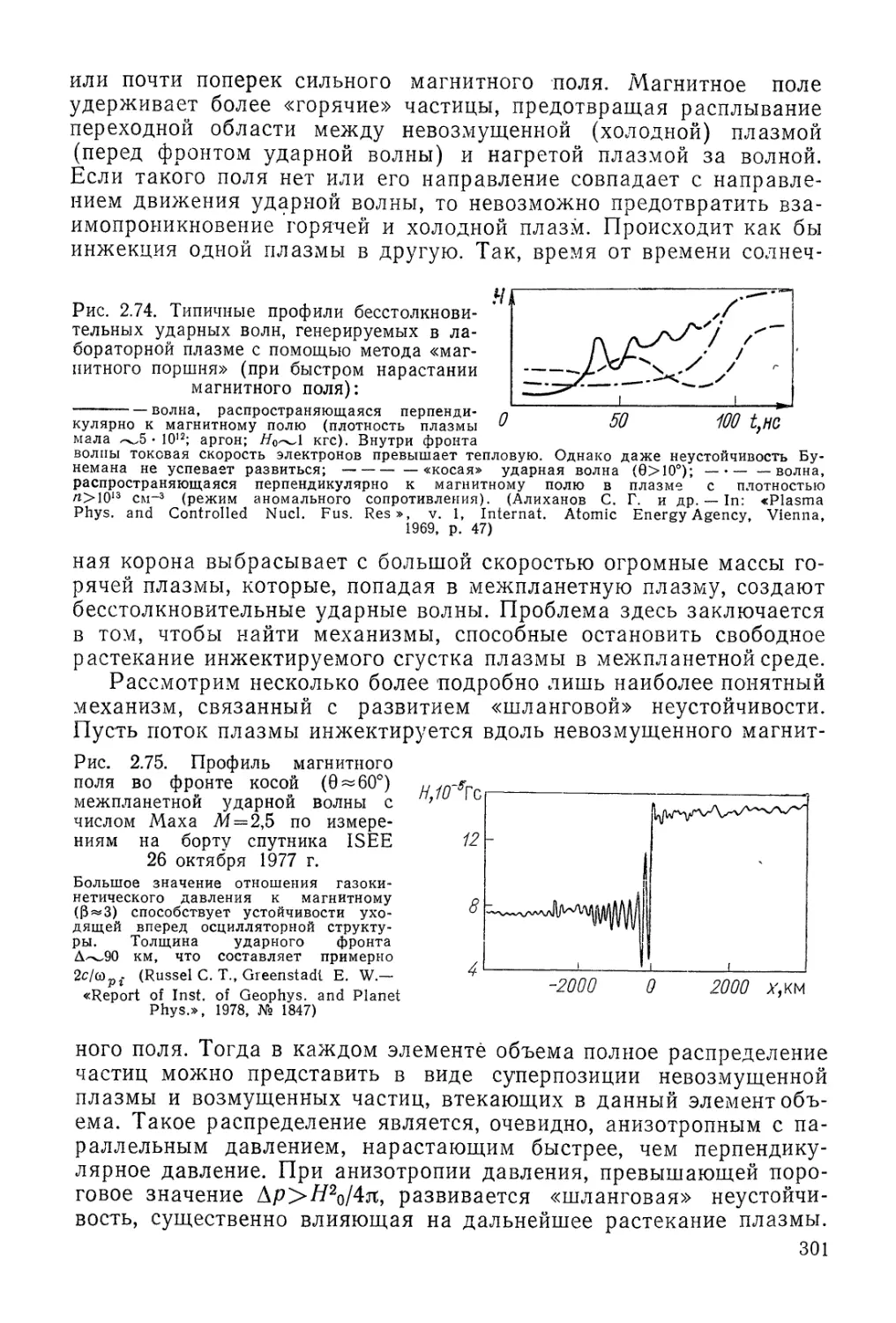
Автор: Арцимович Л.А. Сагдеев Р.З.
Теги: физика плазмы физика астрофизика геофизика физика твердого тела атомиздат физика полупроводников
Год: 1979
Текст
Л. А. АРЦИМОВИЧ, Р. 3. САГДЕЕВ
ФИЗИКА
ПЛАЗМЫ
для
ФИЗИКОВ
МОСКВА • АТОМИЗДАТ • 1979
УДК 533.9
А р ц и м о в и ч Л. А., С а г д е е в Р. 3. Физика плазмы для фи-
физиков.— М.: Атомиздат, 1979.— 320 с.
В книге дано изложение физики плазмы как раздела современ-
современной физики в расчете на широкую физическую аудиторию, имею-
имеющую дело с плазменными явлениями вне собственно физики плазмы.
В этой связи систематически прослеживаются плазменные аналогии
в физике сплошной среды, физике твердого тела и полупроводников,,
геофизике, астрофизике и т. д.
Специалисты по физике плазмы могут почерпнуть из книги ин-
информацию о распространении идей и представлений о различных
процессах, протекающих в плазме, на смежные области физики.
Данная книга представляет собой задуманное академиком
Л. А. Арцимовичем систематическое развитие краткого курса лек-
лекций «Что каждый физик должен знать о плазме» (М., Атомиздат,
1976).
Чтение книги предполагает подготовку на уровне университет-
университетского курса общей физики. Книга предназначена для физиков й
инженеров-физиков широкого профиля.
Табл. 3. Рис. 125. Список литературы 20 наименований.
А г t s i m о v i с h L. A., S a g d e e v R. Z. Plasma Physics for
Physicists. — M: Atomizdat Publishers, 1979.
Acad. Lev Artsimovich, soon after he completed a shorter ver-
version «What should every physicist know about Plasma» (now pub-
published by Atomizdat, Moscow, 1976), invited Acad. Roald Sagdeev
as coauthor. He decided to fill it with appropriate theoretical guideline-
and convert it into Basic course on Physics of Hot Plasmas,
which could be used by much broader audience then fusion commu-
community only.
But unfortunately Acad. Lev Artsimovich left unfinished this book.
Joint work was revised and finished by coauthor in 1978 in order to
give up-to-date picture of principal ideas in the field of Hot Plasma
Physics, originated mainly by fusion research. Later they diffused to
space plasma, to astrophysics as well as to solid-state plasma.
To read this book it requires the knowledge of basic physics of
university level.
Tables 3. Figures 125. Reference 20 items.
20409—132
БЗ—31—26—1979. 1704040000 © Атомиздат, 1979
034@1)—79
ПРЕДИСЛОВИЕ
История появления этой книги такова. Однажды в 1971 г.
Лев Андреевич Арцимович пригласил меня для «очень серьезного»,
как он выразился, разговора. Он показал мне рукопись объемом
страниц в 80 с условным названием «Что каждый физик должен
знать о плазме» *. Несмотря на то что она была написана в при-
присущем Л. А. Арцимовичу ярком стиле, густо насыщена плазменной
физикой, автор не был ею вполне удовлетворен. Дело в том, что
к этому времени он уже опубликовал две книги, в которых неко-
некоторые вопросы физики плазмы и управляемых термоядерных ре-
реакций излагались с точки зрения и языком физика-эксперимента-
физика-экспериментатора с привлечением лишь «минимума теоретических сведений,
который нужен для общей ориентировки в физике высокотемпера-
высокотемпературной плазмы». Надо сказать, что у Льва Андреевича были со-
совершенно четкие требования к теоретикам. Он считал, что теория
плазмы должна иметь прикладной характер, и с изрядной долей
иронии относился к абстрактно-теоретическим «наукообразным»
работам. Лев Андреевич часто любил повторять, что плазму, как
физический объект, можно полностью описать, исходя из простых
«первых принципов» (законов механики и электромагнетизма), и
что теоретики должны заниматься конкретными явлениями и эф-
эффектами, а не уточнением вывода исходных уравнений плазмы.
Во время той первой беседы о книге я получил предложение
стать соавтором и ввести в книгу математический аппарат теории
плазмы в доступной сравнительно широкой физической аудитории
форме. Неизбежную при этом степень упрощения Л. А. Арцимо-
Арцимович сравнил с обычно используемой теоретиками в выступлениях
на семинарах перед экспериментаторами.
Для меня было большой честью получить приглашение участ-
участвовать в работе над подобной книгой как представителю теорети-
теоретиков. Многие вопросы, которые должны были войти в эту книгу,
в разное время докладывались мною на семинарах, которыми ру-
руководил сам Лев Андреевич. Я хорошо помню свое первое выступ-
выступление на семинаре Л. А. Арцимовича в Институте атомной энергии
им. И. В. Курчатова осенью 1956 г., посвященное теоретическому
* Впоследствии она была издана как самостоятельная книга (М., Атомиздат,
1976).
3
предсказанию так называемой «диамагнитной» («зеркальной»)
неустойчивости и связанной с ней в то время потенциальной опас-
опасности для термоядерных ловушек с магнитными пробками.
Примерно десять лет спустя на таком же семинаре докладыва-
докладывалась «неоклассическая теория переноса» в применении к тока ма-
макам. Безошибочное критическое чутье, глубокая физическая интуи-
интуиция и острота реакции, помноженные на редкую доброжелатель-
доброжелательность, превращали семинары Л. А. Арцимовича в настоящую шко-
школу для молодых физиков.
Задача, которую авторы поставили перед собой при написании
книги, заключалась в том, чтобы дать возможность физикам, ра-
работающим в областях, пусть даже далеких от физики горячей
(высокотемпературной) плазмы, составить представление о по-
последней, ее идеях и логике развития. Нам хотелось, насколько это
возможно, использовать аналогии с методами, явлениями и про-
процессами, относящимися к самым разным разделам физики. Мы
много спорили, во многом сходились, но были и разногласия.
Так, например, были существенные расхождения в наших пред-
представлениях «табели о рангах»: «что есть что» в физике плазмы.
Делая скидку на некоторую долю несерьезности, с которой физики
относятся к подобным оценкам, я все же замечу, что одним я;* не-
немногих, к счастью, расхождений в порядке расположения iio зна-
значимости было, например, следующее. Я никак не мог согласиться
(и не соглашаюсь сейчас) поставить эффект «плазменного фоку-
фокуса» выше «бесстолкновительных ударных волн». Конфигурация
с плазменным фокусом, на мой взгляд, хотя и интересна, но пред-
представляет собой одну из модификаций течения плазмы при линч-
эффекте. Однако в основных концептуальных вопросах наши оцен-
оценки сходились.
Основная мысль, которая, можно сказать, красной нитью ;лро-
ходит через книгу, что плазма — эго не только газ частиц — элек-
электронов и ионов, но и газ квазичастиц — волн. Та легкость, с кото-
которой в плазме самопроизвольно могут возбуждаться колебания и
волны, приводит к тому, что приходится предоставить «граждан-
«гражданские права» волнам как квазичастицам. Конечно, высокотемпера-
высокотемпературная плазма практически всегда является классическим объек-
объектом, и наши плазменные квазичастицы не совсем похожи на ква-
квазичастицы— коллективные возбуждения в конденсированных сре-
средах при низких температурах.
В начале 1973 г., когда Льва Андреевича не стало, рукопись
этой книги была еще далека от завершения. В первые месяцы пос-
после смерти Льва Андреевича мне было трудно взяться одному за
рукопись. Вскоре я был назначен директором института, появи-
появились административные заботы, отнюдь не способствующие ни
научному, ни литературному труду. Изредка мне удавалось воз-
возвращаться к прерванной работе, но дело продвигалось вперед очень
медленно. Однако несколько месяцев назад, когда все мы, друзья
и ученики Льва Андреевича, начали готовиться к 70-летию со дня
4
его рождения, решили провести мемориальный международный
семинар, издать книгу воспоминаний о Льве Андреевиче, я обещал
своим товарищам и самому себе закончить работу над старой
рукописью к этой дате. Мне казалось, что живое слово Л. А. Арци-
мовича, факсимиле последних страниц, написанных им за не-
несколько недель до смерти, будут интересны читателям.
За шесть лет, прошедших после кончины Л. А. Арцимовича,
в физике высокотемпературной плазмы, несмотря на заметные
успехи, основные концепции 60—70-х годов не только сохранились,
но и укрепились, получив дополнительные подтверждения и разви-
развитие благодаря новым теоретическим и экспериментальным рабо-
работам. Большой шаг вперед был сделан в физике космической плаз-
плазмы и в плазменной астрофизике, где в значительной степени ис-
используются идеи и представления, развитые в физике высокотем-
высокотемпературной плазмы. Это обстоятельство позволило ограничиться
лишь минимальными изменениями в той части рукописи, которая
была готова к 1973 г. Чтобы сохранить стиль Л. А. Арцимовича,
в целом ряде новых разделов использованы фрагменты из его ра-
ранее опубликованных книг.
Поскольку этот труд не представляет собой исчерпывающую
монографию, приводимый в нем список литературы является, ко-
конечно, неполным. Предлагается лишь перечень наиболее полез-
полезных, по моему мнению, кнцт и обзоров.
Для того чтобы устранить перекос в сторону теории, по понят-
понятным причинам появившийся в книге после смерти Л. А. Арцимо-
Арцимовича, соавтор «разбросал» по книге серию экспериментальных
графиков и результатов, иллюстрирующих развитие основных
представлений физики плазмы. Возможно, читателю подбор этих
экспериментальных иллюстраций покажется пристрастным, пусть
тогда он сделает скидку на вкус физика-теоретика.
Чтобы завершить, работу над рукописью, мне пришлось в зна-
значительной степени отвлечься от привычных повседневных дел, по-
посвятить книге отпуск и воспользоваться большой помощью со сто-
стороны коллег. Я хотел бы особо поблагодарить В. Д. Шапиро и
В. И. Шевченко, самоотверженно разделивших со мной напряже-
напряжение заключительного этапа работы над книгой. Думаю, что без их
помощи этот труд так и не был бы окончен. Неоценимо было уча-
участие А. А. Галеева, с которым меня связывают тесные узы много-
многолетней совместной работы. Я хотел бы также выразить призна-
признательность А. Б. Михайловскому за ряд полезных советов. Наконец,
я хотел бы поблагодарить Атомиздат за настойчивость и большую
помощь.
Декабрь, 1978 г.
Р. 3. САГ ЛЕЕВ
1
ПЛАЗМА БЕЗ МАГНИТНОГО ПОЛЯ
§ 1.1. Общие сведения о плазме
Плазмой называется ионизованный газ, в котором атомы
(все или значительная их часть) потеряли по одному или по не-
несколько принадлежавших им электронов и превратились в поло-
положительные ионы. Это только предварительное определение плазмы
как особого состояния вещества. В дальнейшем будет дано более
точное определение. В общем случае плазма представляет собой
смесь трех компонент. Она содержит свободные электроны, поло-
положительные ионы и нейтральные атомы (или молекулы). Плазма —
это наиболее распространенное состояние вещества в природе.
Солнце и звезды можно рассматривать как гигантские сгустки
горячей плазмы. Внешняя часть земной атмосферы представляет
собой плазменную оболочку — ионосферу. За пределами ионосфе-
ионосферы, в магнитосферу Земли, простираются плазмосфера и так на-
называемые радиационные пояса, которые представляют собой свое-
своеобразные плазменные образования. В земных условиях в лабора-
лаборатории 'И в технике мы встречаемся с плазмой при различных
газовых разрядах, так как любой разряд (молния, искра, дуга
и т. д.) всегда связан с возникновением плазмы.
В развитии исследований по физике плазмы важными стиму-
стимулами всегда были перспективы практического применения. Снача-
Сначала плазма интересовала физиков как своеобразный проводник
электрического тока и как источник света. В настоящее время надо
рассматривать физические свойства плазмы под другими углами
зрения, и тогда плазма предстанет перед нами в новом облике.
Во-первых, плазма — это естественное состояние вещества, нагре-
нагретого до очень высокой температуры, и, во-вторых, это динамиче-
динамическая система — объект приложения электромагнитных сил. Новые
методы подхода к изучению поведения плазмы органически свя-
связаны с большими техническими проблемами, для которых физика
¦плазмы служит научным фундаментом. Важнейшими из них явля-
являются управляемый термоядерный синтез и магнитогидродинамиче-
ское преобразование тепловой энергии в электрическую. Возмож-
Возможно, что в недалеком будущем физика плазмы глубоко проникнет
также в ускорительную технику.
6
Однако исследование явлений, происходящих в плазме, пред-
представляет интерес не только в связи с различными практическими
применениями. Плазма — это материальная среда, образованная
коллективом частиц, которые взаимодействуют друг с другом по
наиболее простым законам — с помощью электростатических ку-
лоновских сил. Физик обязан, исходя из известной микроструктуры
плазмы, объяснить механизм различных процессов, которые про-
происходят в этой среде. Исходные теоретические положения в дан-
данном случае обладают исключительной .прозрачностью. Как прави-
правило, мы находимся здесь в рамках классической физики, так как
квантовые эффекты для обычной плазмы не играют сколько-ни-
сколько-нибудь заметной роли.
Главные усилия экспериментальных исследований в настоящее
время направлены на разработку методов получения плазмы со
все более высокими параметрами: высокой температурой и боль-
большой плотностью. Мы сами создаем объект исследований — высо-
высокотемпературную плазму, стараясь обеспечить для нее
оптимальные условия существования, при которых плазма нахо-
находится в. квазистационариом, устойчивом состоянии.
Прежде чем изучать этот вопрос дальше, уточним определение
понятия плазмы. Электрические силы, связывая разноименные за-
заряды в плазме, обеспечивают, ее к в а з иней тр а л ьн ость, т. е.
приблизительное равенство концентрации электронов и ионов. Вся-
Всякое разделение зарядов, обусловленное смещением группы элек-
электронов относительно ионов, должно приводить к возникновению
электрических полей, которые стремятся скомпенсировать создан-
созданное возмущение; эти поля растут с увеличением концентрации ча-
частиц и в случае плотной плазмы могут достигать очень больших
значений.
Для оценки напряженности поля, возникающего при нарушении
нейтральности плазмы, предположим, что в некотором объеме
произошло полное разделение зарядов и внутри этого объема
остались только заряды одного знака. Электрическое поле в рас-
рассматриваемой области удовлетворяет уравнению Пуассона div E=
=4яр, где р — плотность электрического заряда. Если линейные
размеры области масштаба х, а концентрация заряженных частиц
в плазме равна п, то div Е<-^Е!х^4кпе и, следовательно, Е<^
—Annex. Потенциал плазмы в области разделения зарядов изме-
изменится на ф—Ех^Аппех2.
Рассмотрим пример. Пусть полностью ионизованная плазма по-
получена из водорода, находящегося первоначально при нормальной
температуре и давлении 1 мм рт. ст. В каждом кубическом сан-
сантиметре такой плазмы будет по 7»1016 ионов и электронов. Поэто-
Поэтому если резкое нарушение квазинейтральности произойдет в объ-
объеме с характерным размером порядка 1 мм, то электрическое поле
превзойдет 1010 В/см, и в пределах этого объема возникнет раз-
разность потенциалов порядка 109 В. Ясно, что подобное разделение
зарядов совершенно нереально. Даже в гораздо более разрежен-
7
ной плазме резкое нарушение квазинейтральности в указанных
объемах будет немедленно ликвидироваться возникающими элек-
электрическими полями. Поле будет выталкивать из объема, где
произошла декомпенсация зарядов, частицы одного знака и втя-
втягивать в эту область частицы противоположного знака. Однако
если выделить в плазме достаточно малый объем, то в нем квази-
квазинейтральность может и не сохраниться, гак как поле, созданное
избытком частиц одного знака, окажется слишком слабым для
того, чтобы существенно повлиять'на движение частиц. При за-
заданных концентрации и температуре плазмы имеется характерный
линейный масштаб rD, удовлетворяющий следующему условию:
если #<СПэ> то в пределах объема с линейным размером х разде-
разделение зарядов происходит без существенного влияния на движе-
движение частиц, если же x»rD, то концентрации частиц противополож-
противоположных знаков в указанном объеме почти одинаковы.
Характерную длину rD можно оценить следующим образом.
В области с линейным размером rD потенциальная энергия заря-
заряженной частицы при полном разделении зарядов по порядку ве-
величины равна энергии теплового движения частиц Г*.
Итак, можно привести оценку потенциальной энергии:
^—Т.
Следовательно,
Ту же величину /'d получаем рассматривая экранирование электри-
электрического поля в плазме. Допустим, что в плазму введен «пробный»
точечный заряд q. На достаточно малом расстоянии г от этого
заряда потенциал будет равен q/r. Однако на больших расстоя-
расстояниях ход потенциальной функции изменится вследствие поляри-
поляризации плазмы, вызываемой полем заряда q.
При установившемся статистическом равновесии пространствен-
пространственное распределение электронов и ионов в окрестности пробного
заряда определяется законом Больцмана п—ехр(—U/T). Здесь U
имеет противоположный знак для электронов и ионов. Как нетруд-
нетрудно видеть, возникающая поляризация должна привести к экрани-
экранировке электрического поля в рассматриваемой области. Вблизи
пробного заряда, т. е. при относительно большом абсолютном зна-
значении отношения U/Т9 концентрация частиц с противоположным
знакохм заряда более высокая. Это должно привести к резкому
ослаблению электрического поля. Расчет, основанный на совмест-
совместном использовании уравнения Пуассона и закона Больцмана,
показывает, что на больших расстояниях от заряда q потенциал
Тепловую энергию частиц плазмы естественно измерять в электронволь-
тах. В таком случае и температуру плазмы удобно выражать в электронвольтах:
Г(эВ)=71(град)/11 600. При таком обозначении температура совпадает с ве-
величиной, характеризующей тепловую энергию частиц. В дальнейшем под Т убу-
убудем понимать температуру плазмы, выраженную в электронвольтах, а иод Г° —
температуру плазмы в Кельвинах.
убывает экспоненциально, а область существования сильного элек-
электрического поля вокруг q ограничена сферой с радиусом порядка
rD. Характерная длина экранирования впервые введена Дебаем
при рассмотрении сильных электролитов. В дальнейшем это поня-
понятие было перенесено в физику плазмы. Величину
гв=(Т/4лпе2)^ A.1)
принято называть дебаевским радиусом или д е б а е в-
с к о й длиной. Если дебаевский радиус характеризует прост-
пространственный масштаб областей декомпенсации заряда, то время,
в течение которого эти области существуют, можно найти, разде-
разделив гв на скорость более быстрых частиц (электронов):
Чем выше плотность плазмы, тем меньше масштабы декомпенса-
декомпенсации зарядов в пространстве и во времени. Внутри области, заня-
занятой плотной и холодной плазмой, нарушения квазинейтральности
могут происходить только в пределах достаточно малых объемов.
В редкой и горячей плазме дебаевская длина может оказаться
значительно больше размеров области, занятой плазмой. В этом
случае реализуется независимое движение электронов и ионов и
отсутствует механизм для автоматического выравнивания концен-
концентраций зарядов противоположных знаков.
Используя понятие о дебаевской длине, уточним определение
плазмы как особого состояния вещества. Собрание свободно дви-
движущихся разноименно заряженных частиц, т. е. ионизован-
ионизованный газ, называется плазмой, если дебаевская длина мала
по сравнению с объемом, занимаемым газом. Это определение
принадлежит Ленгмюру, основоположнику учения о плазме.
Следует сделать два замечания о введенных здесь парамет-
параметрах плазмы — концентрации и температуре.
1. Электронная и ионная концентрации в общем случае не
должны быть равны друг другу, так как в плазме могут присутст-
присутствовать не только однозарядные, но также и многозарядные ионы.
Пусть /2i — концентрация однозарядных ионов, Пг — концентрация
ионов с двойным зарядом и т. д., тогда электронная концентрация
пе равна Я1 + 2я2+ ... Однако в дальнейшем мы будем интересо-
интересоваться главным образом случаем, когда концентрации электронов
и ионов равны. (Это, в частности, справедливо для чистой водо-
водородной плазмы.) Учет влияния многозарядных ионов на основ-
основные процессы в плазме обычно не представляет большой труд-
трудности.
2. Введение величины Т как температуры плазмы оправдано
только тогда, когда средняя кинетическая энергия электронов и
ионов одинакова. В общем случае в плазме следует различать по
меньшей мгре две температуры — электронную Те и ионную 7\\
В плазме, которая создается в лабораторных условиях или в при-
приборах, Те обычно значительно превосходит Тг. Различие между Те
9
и Ti обусловлено громадной разницей в массах электрона и иона.
Внешние источники электрического питания, с помощью которых
создается плазма (при различных формах разряда в газах), пере-
передают энергию электронной компоненте плазмы, так как именно
электроны являются носителями тока. Ионы приобретают тепло-
тепловую энергию в результате столкновений с быстро движущимися
электронами. При таких столкновениях относительная доля кине-
кинетической энергии электрона, которая может быть передана иону,
не должна превышать Ameimi. Средняя доля энергии, передавае-
передаваемой при столкновении, еще меньше. Поскольку те<^пц, то элек-
электрон должен испытать большое количество (тысячи) столкновений
для того, чтобы полностью отдать имеющийся у него излишек
энергии. Поскольку параллельно процессам обмена тепловой энер-
энергией между электронами и ионами идет процесс приобретения
энергии электронами от источников электрического питания, и од-
одновременно с этим энергия уходит из плазмы вследствие различ-
различных механизмов теплопередачи,. то при электрическом разряде
обычно поддерживается большая разность температур электронов
и ионов. Этот перепад, как правило, снижается при увеличении
концентрации плазмы, потому что число столкновений между элек-
электронами и ионами в заданном объеме плазмы растет пропорцио-
пропорционально квадрату концентрации.
При некоторых специальных условиях в сильноионизрванной
плазме Т{ может значительно превзойти Те. Такие условия имеют
место, в частности, при кратковременных импульсных разрядах
большой мощности, которые приводят к возникновению и после-
последующей кумуляции ударных волн в плазме.
§ 1.2. Плазменные колебания
Плазма представляет собой среду, в которой легко возбужда-
возбуждаются различные виды колебаний и волн. Рассмотрим наиболее про-
простой вид колебаний, возникающих при микроскопических отклоне-
отклонениях от квазинейтральности. Пусть в некотором месте в плазме
тем или иным способом создается избыток зарядов. Рассмотрим,
что при этом произойдет. Проще всего это сделать на примере
плоского слоя плазмы. Под действием «возвращающей» силы
движение электронов подчиняется уравнению теАх=—еЕх=
——4тше2Дх, где Ах — смещение электронов. Отсюда следует, что
рассасывание избыточного заряда сопровождается колебаниями
~с частотой
соР-=Dдав2/т,I/2. A.2)
Это так называемые ленгмюровские колебания. В этих
колебаниях ионы плазмы практически не участвуют из-за большой
массы. В отличие от звуковых колебаний незаряженного газа, где
упругая сила — градиент давления, здесь главную роль играют
электрические поля, обусловленные декомпенсацией зарядов.
Ленгмюровские колебания могут распространяться в плазме в ви-
10
де волн с частотой со=о)р, которая при использованном нами упро-
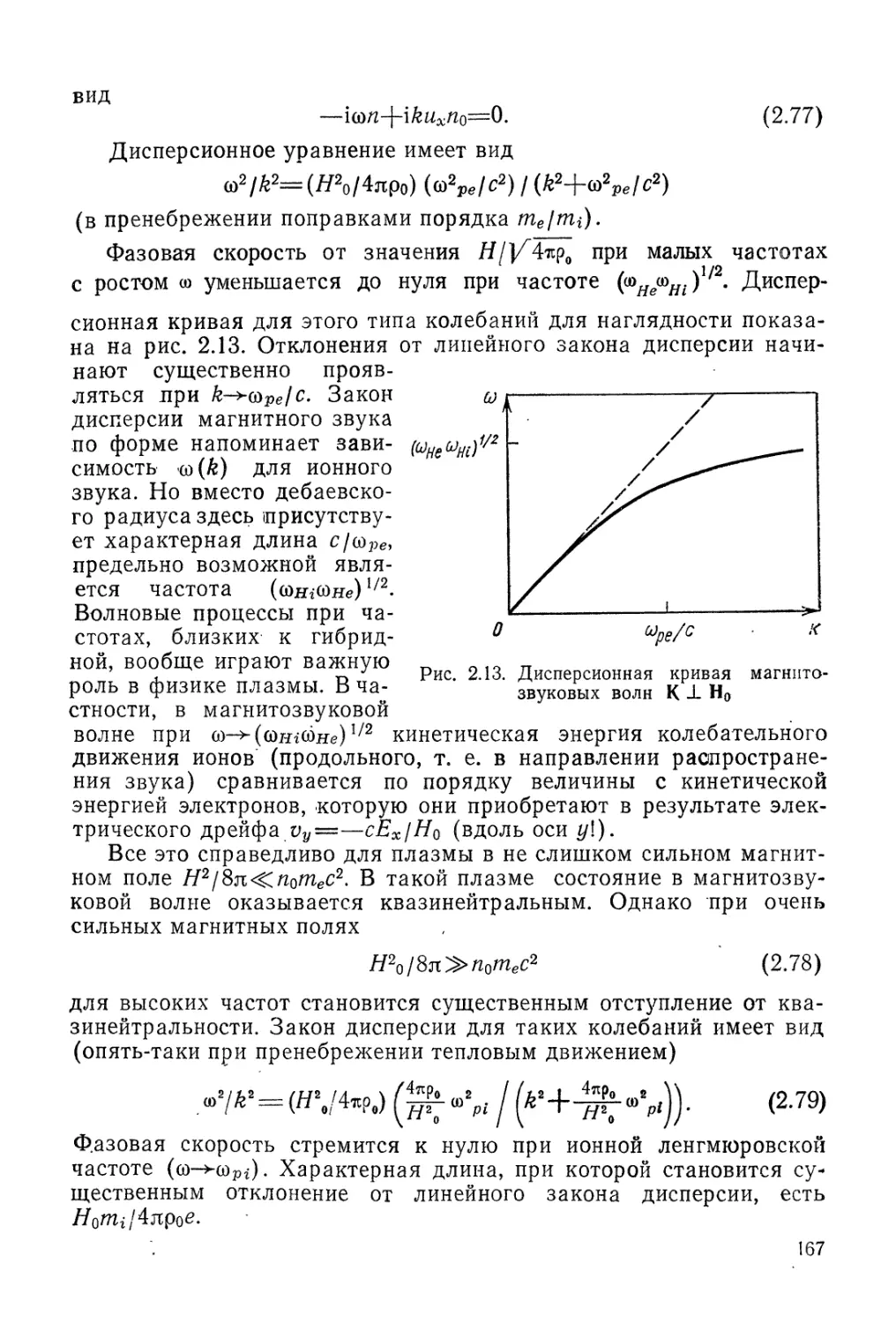
упрощенном подходе оказалась не зависящей от длины .волны. Фазовая
скорость таких продольных волн равна сор/&, где к=2л/Х — вол-
волновое число, X — длина волны. При малых длинах волн (больших
значениях k) нужно учесть также влияние обычного звукового
эффекта, связанного с перепадОхМ давлений в плазме. Для этого
обе упругие- силы нужно сложить. Нетрудно установить, что квад-
квадрат скорости в этом более общем случае равен
A.3)
и соответственно
(д2=4ппе21 me+k2dpe I др3, A.3а)
. Здесь ре—плотность электронного газа (ре—шпе), ре — его
давление. В такой форме свойства электронных колебаний плаз-
плазмы были получены еще Ленгмюром. Он исходил из аналогии элек-
электронных колебаний плазмы со звуковыми волнами и пользовался
уравнениями газодинамики. При вычислении др/др для адиабати-
адиабатического сжатия Ленгмюр положил в уравнении состояния у—
=Cplcv=&l3, считая электронный газ одноатомным. Однако это
справедливо лишь при условии, что в процессе колебаний все вре-
время успевает установиться равнораспределение тепловой энергии
между тремя степенями свободы поступательного движения элек-
электронов. Практически в любой плазме за один период колебаний
2я/сор электроны не испытывают столкновений, и поэтому равно-
равнораспределение не устанавливается. А. А. Власов, пользуясь мето-
методом кинетического уравнения, установил, что в действительности
Y=3.
Этот результат можно получить на основании очень простых
рассуждений, даже не обращаясь к кинетическому уравнению.
Пусть слой газа ограничен двумя параллельными плоскими
стенками, расстояние между которыми медленно изменяется. Если
столкновения между частицами происходят очень редко, то для
компоненты скорости частицы, которая направлена перпендику-
перпендикулярно к стенкам, должно иметь место сохранение адиабатического
инварианта v /=const, где/—расстояние между стенками. Это
нетрудно доказать, рассматривая отражение частиц от подвижной
стенки. Поэтому давление на стенку птиг. будет изменяться про-
пропорционально /г//2, а поскольку л^1//, то р^п3, т. е. y=3. Факти-
Фактически это уравнение состояния для адиабатического сжатия одно-
одномерного газа. Его можно получить также термодинамическим пу-
путем. При указанном значении у соотношение A.3) перепишем
в виде
A.36)
Второе слагаемое в уравнении A.36) меньше первого во всех слу-
случаях, когда речь идет о длинах волн, достаточно больших по срав-
сравнению с дебаевской длиной.
П
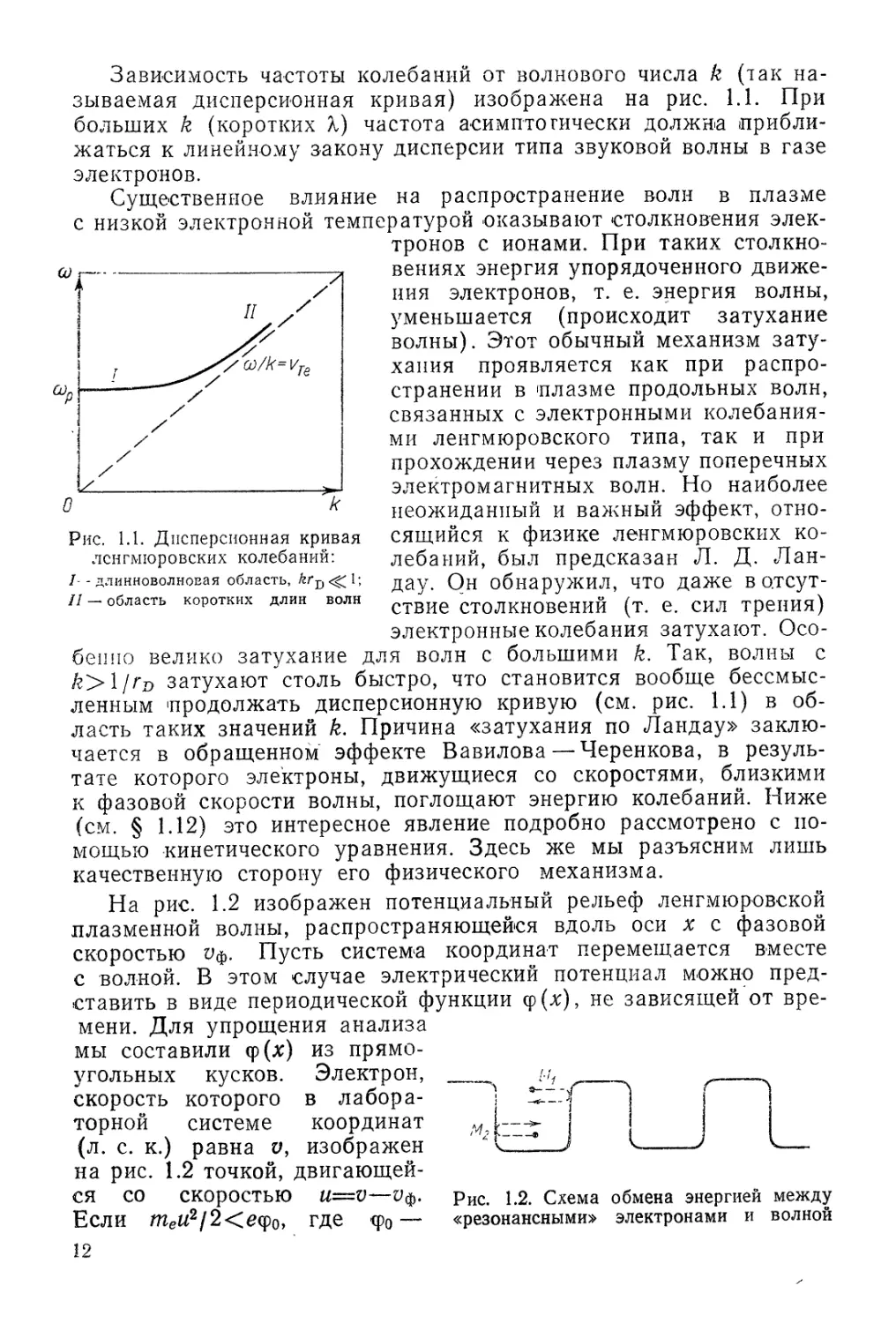
Рис. 1.1. Дисперсионная кривая
ленгмюровских колебаний:
/- - длинноволновая область, ?rD <^ I;
// — область коротких длин волн
Зависимость частоты колебаний от волнового числа k (так на-
называемая дисперсионная кривая) изображена на рис. 1.1. При
больших k (коротких X) частота асимптотически должна прибли-
приближаться к линейному закону дисперсии типа звуковой волны в газе
электронов.
Существенное влияние на распространение волн в плазме
с низкой электронной температурой оказывают столкновения элек-
электронов с ионами. При таких столкно-
столкновениях энергия упорядоченного движе-
движения электронов, т. е. энергия волны,
уменьшается (происходит затухание
волны). Этот обычный механизм зату-
затухания проявляется как при распро-
распространении в 'плазме продольных волн,
связанных с электронными колебания-
колебаниями ленгмюровского типа, так и при
прохождении через плазму поперечных
электромагнитных волн. Но наиболее
неожиданный и важный эффект, отно-
относящийся к физике ленгмюровских ко-
колебаний, был предсказан Л. Д. Лан-
Ландау. Он обнаружил, что даже в отсут-
отсутствие столкновений (т. е. сил трения)
электронные колебания затухают. Осо-
Особенно велико затухание для волн с большими k. Так, волны с
k>l/rD затухают столь быстро, что становится вообще бессмыс-
бессмысленным 'продолжать дисперсионную кривую (см. рис. 1.1) в об-
область таких значений k. Причина «затухания по Ландау» заклю-
заключается в обращенном эффекте Вавилова — Черенкова, в резуль-
результате которого электроны, движущиеся со скоростями, близкими
к фазовой скорости волны, поглощают энергию колебаний. Ниже
(см. § 1.12) это интересное явление подробно рассмотрено с по-
помощью кинетического уравнения. Здесь же мы разъясним лишь
качественную сторону его физического механизма.
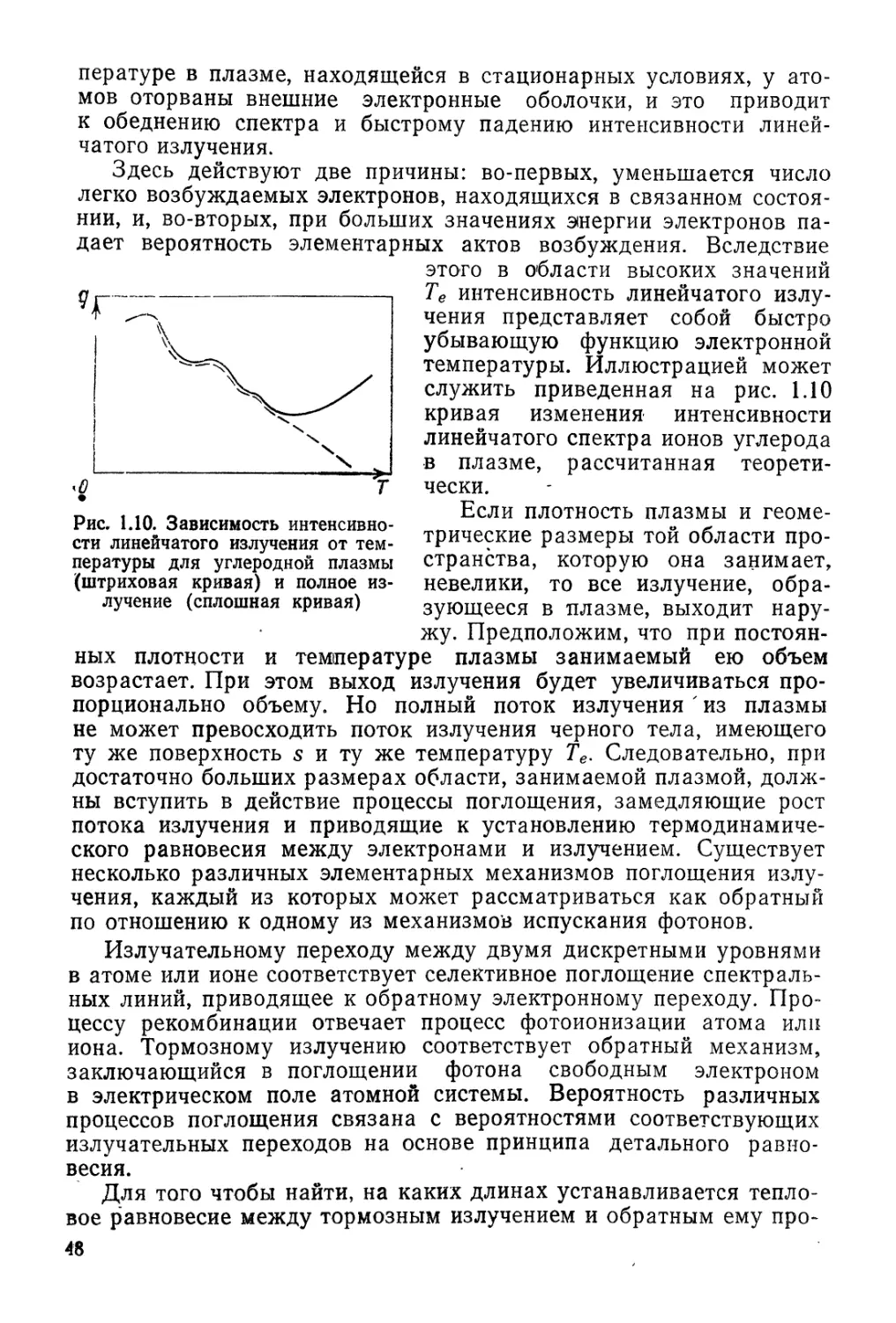
На рис. 1.2 изображен потенциальный рельеф ленгмюровской
плазменной волны, распространяющейся вдоль оси х с фазовой
скоростью Vф. Пусть система координат перемещается вместе
с волной. В этом случае электрический потенциал можно пред-
представить в виде периодической функции ф(лс), не зависящей от вре-
времени. Для упрощения анализа
мы составили <р(х) из прямо-
прямоугольных кусков. Электрон,
скорость которого в лабора-
лабораторной системе координат
(л. с. к.) равна в, изображен
на рис. 1.2 точкой, двигающей-
двигающейся СО СКОрОСТЬЮ U=V—Уф.
Если raew2/2<e<po, где <р0—
12
Рис. 1.2. Схема обмена энергией между
«резонансными» электронами и волной
амплитуда электрического потенциала волны, то электрон будет
заперт в потенциальной яме между двумя потенциальными гор-
горбами, Отражаясь от этих горбов, электрон будет обмениваться
энергией с волной. Такие «резонансные» электроны принадлежат
к узкому участку спектра скоростей, так как обычно* амплитуда
потенциала волны, умноженная на заряд электрона, мала по срав-
сравнению со средней кинетической энергией теплового движения элек-
электрона, Электроны, не принадлежащие к этому участку спектра,
испытывают только относительно слабое воздействие поля волны.
Резонансные частицы можно разделить на две группы: 1) дого-
догоняющие волну (v>v<b) и 2) отстающие от волны (и<Уф). На
рис. 1.2 точка Mi изображает электрон, принадлежащий к первой
группе, а точка Мг — электрон второй группы. В этой системе ко-
координат, движущейся вместе с волной, обе частицы после столкно-
столкновения с потенциальными горбами изменяют направление скорости
(без изменения ее значения). Поэтому в лабораторной системе
координат догоняющий электрон после столкновения будет иметь
скорость У1=Уф—1> + Уф<и, т. е. часть кинетической энергии от
электронов будет передана волне. В противоположном случае от-
отстающий электрон после столкновения с гребнем волны приобре-
приобретает дополнительную энергию. При максвелловском распределении
электронов в плазме по скоростям догоняющих частиц меньше, чем
отстающих, и поэтому суммарный эффект взаимодействия резо-
резонансных частиц с волной должен заключаться в перекачке энергии
волны в энергию теплового движения, что должно привести к зату-
затуханию колебаний. Очевидно, что чем больше концентрация резо-
резонансных частиц, тем более сильным должно быть затухание. При
максвелловском распределении по скоростям оно должно быстро
возрастать с уменьшением Vф. Фазовая скорость, волны падает
с уменьшением длины волны, и для длин волн, меньших дебаев-
ского радиуса гъ, она оказывается порядка тепловой скорости
электронов vTe. В этом случае (область Л на рис. 1.1) затухание
становится настолько сильным, что волны не могут распростра-
распространяться в плазме. В противоположном случае, при v$*>vTe, число
резонансных частиц экспоненциально уменьшается, и затухание
должно быть очень'слабьш.
Приведем грубую оценку скорости изменения амплитуды вол-
волны. Эта величина характеризуется так называемым декремен-
декрементом затухания — логарифмической производной по времени от
энергии .волны y=(l/2W)dWldt, где IF —энергия волны в едини-
единице объема.
При одном столкновении электрон первой группы (опережаю-
(опережающий волну) теряет энергию:
Число столкновений с потенциальными горбами волны, которое
один электрон испытывает за 1 с, равно скорости движения элек-
13
тро'на относительно волны, деленной на расстояние между гор-
горбами Я.
Электрон, опережающий волну, передает ей в единицу времени
энергию 2т (р—со/^Jсо/^Я. Энергия, которую получает электрон,
отстающий от волны, определяется таким же выражением.
Суммируя по всем электронам, захваченным волной ?osin&x,
находим, что изменение энергии волны определяется выражением
dWfdt = Bmev/k!) J (v — Mlkf f\ (v) dv —
-BтвфХ) J (v-tDlk)*r,(v)dv. A.4)
(<ofk)-BeE0/mJi)ll2
Здесь feo(v)—равновесная функция распределения электронов по
компоненте скорости в направлении распространения волны, так
что feo(v)dv — число электронов со скоростями в интервале v, v-\-
+ dv. Считая, что Ео мала и, следовательно, v незначительно от-
отличается от о)/k, можно представить feo(v) в виде
Го (v) = Го (<¦>/*) + df\ldv \v=iDJk (v - ф).
Подставляя это выражение в A.4) и интегрируя, получаем
Be*l*nQ Hk2)E\drjdv\v=2^ , A.5)
Для определения инкремента надо вычислить энергию, запасен-
запасенную в волне. Энергия волны, приходящаяся на единицу объема,
где Е2 — среднее значение квадрата напряженности электрическо-
электрического поля; v% — средний квадрат скорости электронов в волне. Сред-
Средние значения потенциальной и кинетической энергии при продоль-
продольных колебаниях электроноз приблизительно равны. Следователь-
Следовательно, W=E2/4n. Из A.5) получим выражение для инкремента
Для продольных плазменных волн ю^(ор, и окончательно имеем
Продольные ленгмюровские колебания следует учитывать при
рассмотрении спектра теплового (черного) излучения плазмы.
Вклад этих колебаний в равновесную энергию плазменного со-
состояния можно учесть по порядку величины, если положить на
каждую степень свободы Т/ 2 и принять (как это делается в тео-
теории излучения) число степеней свободы равным объему в фа-
фазовом пространстве волновых чисел. Поскольку из-за затухания
14
Ландау существует граница значений волновых чисел km—1/гв,
такая, что колебания с волновыми числами выше нее не могут
раскачиваться, то фазовый объем Кфаз^1 /r3D- Поэтому энергия
колебаний на единицу объема WQ^(llr3v)T/2. Такая оценка спра-
справедлива, так как TL(op<^Tey и поэтому для электронных колебаний
соблюдается статистика Рэлея — Джинса.
Все сказанное выше относится к случаю, когда распределение
электронов термодинамически равновесно, т. е. спектр скоростей
подчиняется закону Максвелла. Если же распределение электро-
электронов по скоростям хотя бы на небольшом участке спектра сильно
отклоняется от равновесного, то становится возможной раскачка
колебаний до очень большой амплитуды, т. е. в этом случае может
иметь место один из видов неустойчивости плазмы.
Из элементарного анализа механизма затухания волн, который
был сделан выше, следует, в частности, что раскачка колебаний
может возникнуть, если функция распределения электронов по
скоростям имеет в 'некоторой области значений максимум. В этом
случае для волн с фазовыми скоростями, несколько меньшими
скорости, соответствующей максимуму функции распределения,
среди резонансных частиц будет преобладать группа «догоняю-
«догоняющих волну»: dfejdo\ >0.
Ф
При сильной раскачке колебания могут играть большую роль
в динамике плазменных процессов. Иногда такую плазму полезно
рассматривать даже как смесь двух газов: собственных частиц
плазмы (электронов и ионов) и квазичастиц — колебаний. Такой
подход положен в основу современной трактовки многих турбу-
турбулентных явлений (см. § 1.15—1.18). В газе «квазичастиц» кроме
ленгмюровских колебаний иногда нужно учитывать также и дру-
другие виды колебаний, в частности низкочастотные. В плазме без
магнитного поля — это продольные колебания ионов. По существу,
колебания, в которых принимает участие вся масса вещества
в плазме, представляют собой не что иное, как распространение
звука со скоростью cs=(dp/dp)i/2. Как известно, в обычном газе
звуковые колебания имеют смысл лишь в том случае, если длина
звуковой волны значительно больше средней длины свободного
пробега атомов или молекул. Оказывается, что в плазме из-за
наличия далыюдействующих кулоновских сил (которые образу-
образуют так называемое самосогласованное поле) могут существовать
звуковые колебания также и в противоположном предельном слу-
случае, т. е. тогда, когда длина звуковой волны значительно меньше
длины свободного пробега. Звуковые колебания в плазме без маг-
магнитного поля рассмотрены в § 1.11.
§ 1.3. Классификация видов плазмы
С помощью введенных понятий о дебаевской длине и плазмен-
плазменной частоте можно классифицировать встречающиеся в природе
плазмы на разреженные и плотные, классические и квантовые.
15
Внутренняя энергия плазмы складывается из кинетических энер-
энергий иО'Нов и электронов и из энергии их электростатического куло-
новского взаимодействия (в плазме, нагретой до релятивистских
температур, нужно учитывать и магнитное взаимодействие). Срав-
Сравним среднюю кинетическую энергию C/2) Г, приходящуюся на
одну частицу, со средней энергией взаимодействия. Из-за дебаев-
ского экранирования взаимодействие заряженной частицы с да-
далекими частицами несущественно, и надо учитывать в основном
лишь ближайших соседей. Среднее расстояние до соседней части-
частицы /-^(l/nI/3, следовательно, энергия взаимодействия приблизи-
приблизительно равна е2п1/3. Поэтому, как правило, плазму можно считать
идеальным газом, если е?/3<Г. Если обе части неравенства воз-
возвести в степень 3/2, то, как легко заметить, неравенство примет
следующий вид: /гг3в^>1. Таким образом, условие идеальности
плазмы можно записать через число частиц в объеме с размерами
порядка дебаевской длины. Это число должно быть много больше
единицы*. При пг3в^>1 тепловая энергия частиц превышает как
энергию электростатического взаимодействия, так и равновесную
энергию электронных колебаний плазмы. Если указанное условие
не выполнено, плазма уже не является газом, а скорее напоминает
жидкость с, вообще говоря, очень сложным и до сих пор неизвест-
неизвестным уравнением состояния. При дальнейшем повышении плотно-
плотности плазмы можно ожидать ее металлизации. При больших плот-
плотностях в плазме должны проявляться также и квантовые эффек-
эффекты. Сначала их следует учитывать в ленгмюровских колебаниях.
Очевидно, это должно произойти тогда, когда квант энергии плаз-
плазменных колебаний станет сравнимым со средней тепловой энер-
энергией, приходящейся на один электрон. При этом условии длина
волны де-Бройля для электронов со скоростями порядка средней
тепловой оказывается сравнимой с дебаевским радиусом. Еще
раньше, когда будет выполнено условие Ъ/т^те—1/я1/3, т. е. дли-
длина воЛ'Ны де-Бройля будет сравнима со средним расстоянием
между электронами, квантовой становится статистика электронов
(распределение Ферми — Дирака вместо больцмановского). Это
так называемая квантовая вырожденная плазма.
В квантовой плазме начинают играть роль обменные взаимо-
взаимодействия, и вид дисперсионного уравнения для плазменных воли
A.36) несколько меняется:
©^=(o*p+ C/5) (l—ars)k2v2F.
Здесь vp — скорость Ферми; а — численный коэффициент
(—0,06); rs — безразмерный параметр, характеризующий отноше-
отношение энергии взаимодействия к энергии Ферми.
* При более строгом анализе следовало бы учесть, что вклады в энергию
кулоновского взаимодействия порядка е2/*1/3 за счет притяжения и отталкива-
отталкивания взаимно погашаются. Однако окончательный критерий идеальности пг3в > 1
остается справедливым.
16
Согласно принципу Паули два электрона с одинаковыми спи-
спинами не могут находиться в одной и той же точке пространства*
поэтому потенциальная энергия взаимного электростатического от-
отталкивания электронов, а значит, и возвращающая сила в плаз-
плазменных колебаниях несколько уменьшаются. Однако, поскольку
обменные силы короткодействующие, они не могут изменить ча-
частоту ленгмюровских волн с бесконечной длиной волны и влияют
лишь на частоту волн с конечной величиной волнового вектора.
Подавляющее большинство плазм в природе можно считать
идеальным газом (космическая, газоразрядная и т. п.). Примером
неидеальной плазмы могут служить сильные электролиты. Наибо-
Наиболее интересными из них являются растворы щелочных металлов
в аммиаке, где хорошо прослеживается переход к жидкому плаз-
плазменному состоянию и металлизации. Представителем квантовой
плазмы молено считать электронный газ в металлах: при плотно-
плотности конденсированного вещества (пе—1023 см~3) квант энергии
плазменных колебаний по порядку величины оказывается равным
единицам электронвольт. Квантовыми свойствами может обладать
и плазма, состоящая из электронов и положительно заряженных
квазичастиц — дырок в полупроводниках. Виды плазмы такого
рода принято объединять под названием плазма твердого
тела. Явление квантового вырождения должно иметь место и для
электронного газа в очень плотном веществе звезд — белых кар-
карликов.
Свойства плазмы усложняются, если одновременно с заря-
заряженными частицами (ионами и электронами) в ней существуют
также нейтральные атомы и молекулы, т. е. плазма не является
полностью -ионизованной.
Степень ионизации п л а з м ы — отношение числа заря-
заряженных частиц к первоначальному числу атомов—определяется
конкуренцией между процессами ионизации (развала атомов)
и обратным процессом рекомбинации, т. е. воссоединения
электронов и ионов в нейтральные частицы. В термодинамически
равновесной плазме степень ионизации не зависит от деталей этих
процессов, и, в принципе, ее можно установить чисто термодина-
термодинамическим путем. Наиболее просто законы термодинамики выгля-
выглядят для идеальной плазмы, т. е. такой, в которой кинетическая
энергия заряженных частиц значительно превышает энергию их
взаимодействия. Допустим, что мы имеем дело лишь с однократ-
однократной ионизацией. Согласно общим принципам статистической фи-
физики отношение вероятностей нахождения электрона в состояниях
с энергией Wi и до2 при заданной температуре,Г равно
tei/g2)exp[(—Wi+w2)/T]. A.6)
Здесь gi и g2 — квантовые веса состояний с энергиями W\ и w2 со-
соответственно. Степень ионизации газа» т. е. отношение числа сво-
свободных электронов к числу нейтральных атомов,, определяется вы-
2—74 1 7
сражением A.6), в котором следует положить W\—w2=I, где / —
энергия ионизации.
В этом случае gi — число квантовых ячеек в фазовом прост-
пространстве для свободного электрона; g2 — квантовый вес стационар-
стационарного энергетического уровня в атоме. Если для простоты не учи-
учитывать возможность перехода электрона на возбужденные уровни
ато'ма и предположить, что основное состояние является невы-
невырожденным, то / — энергия ионизации для основного состояния и
,g2=l. Свободные электроны имеют сплошной спектр по энергиям.
Квантовый вес свободных состояний приблизительно равен объему
^фазового пространства для электрона со средним тепловым им-
,пульсом BтеТI/2>, деленному на элементарный фазовый объем:
В этом выражении Vo — геометрический объем, приходящийся на
• один электрон, т. е. Vu=l/ne. Следовательно,
BmeTf2 .
Мспользуя этот результат, мы получаем так называемую формулу
Саха, которая определяет зависимость степени ионизации газа от
температуры:
njna = (gl[g2) ехр (-//Г) ^ [BmeTf2 \пе B^K] ехр (-ЦТ). A.7)
;В другой записи (более удобной для вычисления отношения
Mejtia при слабой степени ионизации) формула A.7) приобретает
вид
пе[па ^ [(Zrnjf4 /</2 B^K/2 ] ехр (-7/2Т). A.7а)
Из формулы Саха следует, что чем меньше плотность (т. е. кон-
концентрация атомов) газа, тем легче его ионизовать. При плотно-
плотностях, значительно меньших плотности конденсированного вещест-
вещества, высокая степень ионизации достигается еще при температурах
Г<С/. Но при слишком малых плотностях труднее достигнуть
термодинамического равновесия, потому что реже происходят
столкновения между частицами, устанавливающие равнораспреде-
равнораспределение по степеням свободы. В термодинамически неравновесных
плазмах для определения степени ионизации приходится рассмат-
рассматривать специфику процессов столкновений, приводящих к иониза-
ионизации и рекомбинации. Рассмотрение подобных вопросов в настоя-
настоящей книге увело бы нас слишком далеко от поставленной цели.
Общепринято также делить плазму на высоко- и низкотемпе-
низкотемпературную. Это разделение в значительной степени связано с вида-
видами конкретных исследований и их приложений. Так, с высокотем-
высокотемпературной плазмой связаны исследования по проблеме
управляемого термоядерного синтеза. Именно эти исследования
стимулировали бурный расцвет физики высокотемпературной плаз-
мы в 50—60-х годах, позволивший объяснить многие явления т
в физике радиационных поясов, и в некоторых новых областях:
астрофизики. Низкотемпературная плазма является рабочим те-
телом— газообразным проводником для магнитогидродинамических
генераторов.
Холодную плазму в ионосфере можно рассматривать как одну
из природных форм реализации низкотемпературной плазмы. Из-
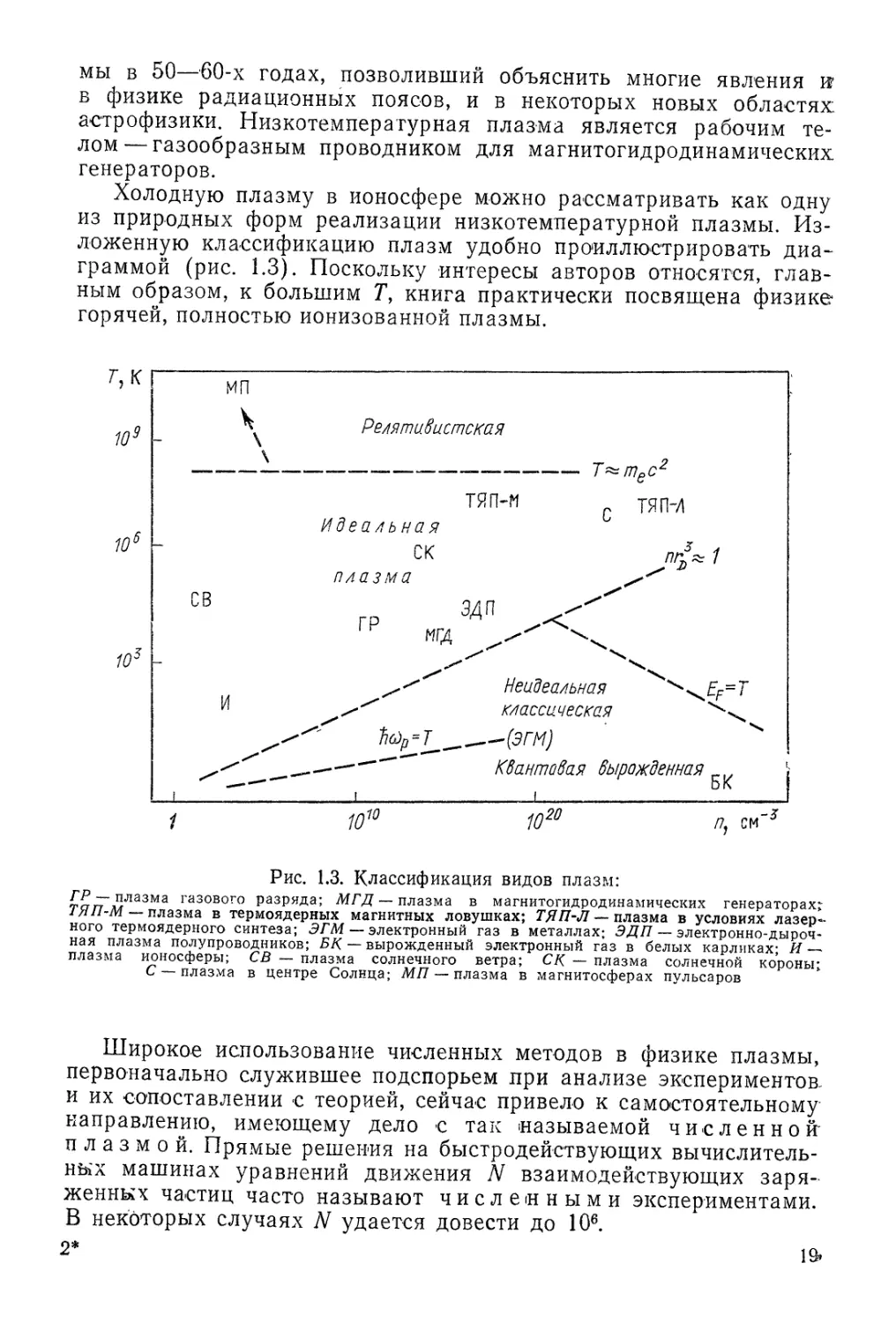
Изложенную классификацию плазм удобно проиллюстрировать диа-
диаграммой (рис. 1.3). Поскольку интересы авторов относятся, глав-
главным образом, к большим Г, книга практически посвящена физике
горячей, полностью ионизованной плазмы.
Г, К
10°
106
МП
Релятивистская
ТЯГИ!
Идеальная
СК
плазма
ТЯГЫ
ГР
мгд
Неидеальная
классическая
Квантовая вырожденная
ьк
I . :
101
10
20
Рис. 1.3. Классификация видов плазм:
ГР — плазма газового разряда; МГД — плазма в магнитогидродинамических генераторах:
ТЯП-М — плазма в термоядерных магнитных ловушках; ТЯП-Л — плазма в условиях лазер-
лазерного термоядерного синтеза; ЭГМ — электронный газ в металлах; ЭЦП — электронно-дыроч-
электронно-дырочная плазма полупроводников; БК — вырожденный электронный газ в белых карликах; И —
плазма ионосферы; СВ — плазма солнечного ветра; СК — плазма солнечной короны;
С — плазма в центре Солнца; МП — плазма в магнитосферах пульсаров
Широкое использование численных методов в физике плазмы,
первоначально служившее подспорьем при анализе экспериментов,
и их сопоставлении с теорией, сейчас привело к самостоятельному
направлению, имеющему дело с так называемой численной"
плазмой. Прямые решения на быстродействующих вычислитель-
вычислительных машинах уравнений движения N взаимодействующих заря-
заряженных частиц часто называют численными экспериментами.
В некоторых случаях yV удается довести до 106.
2* 19»
§ 1.4. Столкновения частиц в плазме
Проанализируем общую картину движения электронов и ионов
в плазме при отсутствии внешних полей. Характер этого движения
определяется законами взаимодействия частиц. В плазме с высо-
высокой степенью ионизации основная форма взаимодействия частиц —
рассеяние в кулоновском поле. Нужно различать три основных
типа элементарных актов рассеяния: рассеяние электронов на
ионах, электронов на электронах и ионов на ионах. Другие эле-
элементарные процессы происходят либо с излучением фотонов (они
будут рассмотрены в § 1.8), л>и^о в них участвуют также и ней-
нейтральные частицы (и тогда они отступают на задний план по мере
повышения степени ионизации). Примером процессов первого рода
;может служить испускание тормозного излучения при электрон-
лонных столкновениях, примером второго — процессы ионизации и'
возбуждения атомов электронным ударом и явления перезарядки
ионов на атомах. Если рассматривается неводородная плазма, то
в общем случае следует учитывать взаимодействие электронов
с ионами, находящимися в различных энергетических состояниях.
В этом случае интенсивность излучения возбужденных ионов мо-
может оказаться очень большой, она будет играть заметную роль
в энергетическом балансе плазменных пр'оцессов.
Мы ограничимся, в основном, анализом взаимодействия частиц
в полностью ионизованной плазме.
Пусть через плазму проходит некоторая «пробная» частица
{в качестве таковой Амы можехМ выбрать любой электрон или ион
плазмы, зафиксировав внимание на его траектории). Эта заря-
заряженная частица испытывает акты рассеяния на своем пути. Если
речь идет о движении легкой частицы среди совокупности тяжелых
частиц (электрона среди ионов), то центры рассеяния можно счи-
считать неподвижными. В указанном случае вероятность рассеяния
на тот или иной угол определяется классической формулой Резер-
форда.
Каждый акт рассеяния, обусловленный пролетом пробной ча-
частицы мимо рассеивающего центра, приводит к повороту траек-
траектории частицы на некоторый угол 8, т. е. к уменьшению скорости
по первоначальному направлению движения от v до v cos 8. В по-
подавляющем большинстве случаев акты рассеяеия происходят на
дальних дистанциях, т. е. при больших расстояниях, и, следова-
следовательно, как правило, сопровождаются очень малым изменением
направления траектории (характерная особенность резерфордов-
ского рассеяния в электрическом поле точечных зарядов!). По-
Поэтому привычная для кинетической теории газов изломанная
траектория частицы, состоящая из отдельных прямолинейных
участков — пробегов, которые соединяют места «столкновений»,
в данном случае не имеет смысла. Вместо этого появляется кар-
картина плавно извивающейся линии, направление ее изменяется под
действием многочисленных, но вместе с тем очень слабых импуль-
:20
сов, обусловленных «столкновениями» с другими частицами. Фак-
Фактически эти импульсы сливаются в непрерывный ряд воздействий,
оказываемых на движущуюся частицу «микрополем» плазмы, об-
образуемым суперпозицией электрических полей отдельных частиц.
В рассматриваемом случае естественно ввести понятие о длине
свободного пробега / как о расстоянии, на протяжении которого
частица сохраняет первоначальное направление своей скорости.
Это определение соответствует следующему равенству:
dv==—vdx/L A.8)
Здесь dv— среднее изменение компоненты скорости по первона-
первоначальному направлению движения при прохождении отрезка пути
dx. С учетом dx=vdt A.8) можно переписать в виде уравнения
движения с .некоторой эффективной силой трения:
mdv/dt——mv (v/l) =—mvv9 A.8а)
где введенную таким образом величину v—v/l называют часто-
частотой столкновений.
Пользуясь определением A.8а), можно представить I с по-
помощью интеграла по угловому распределению рассеянных частиц.
Если вектор скорости поворачивается при столкновении на угол
0, то проекция скорости по первоначальному направлению движе-
движения уменьшается на величину Av=v(l—cosG). Поскольку основ-
основную роль играют акты рассеяния на малые углы (9<С1), то изме-
изменение скорости при элементарном столкновении можно предста-
представить как Av^vQ2/2. Суммарное изменение скорости из-за
рассеяния на нескольких центрах AvN—(v/2J92г*, где суммиро-
суммирование проводится по всем N рассеивающим центрам. При прохож-
прохождении элементарного отрезка пути dx заряженная частица встре-
встретится с ndx j* ds рассеивающими центрами, находящимися на все-
всевозможных прицельных расстояниях. Поэтому элемент площади
ds можно выразить с помощью прицельного расстояния Ъ как
ds=2nbdb, тем более что элементарный угол рассеяния б зависит
именно от Ь. Для малых углов рассеяния 9 справедливо соотно-
соотношение б ^ v. [v, где у .можно найти с помощью компоненты урав-
уравнения движения, перпендикулярной к направлению начальной ско-
скорости:
mv±^ Ze2ll(b2-{-v2t2f2.
Здесь мы предположили, что траектория пробной частицы пред-
представляет собой почти прямую линию, а расстояние наибольшего
сближения практически совпадает с прицельным параметром.
Отсюда
v± ^ BZe2/m) If [b/(b2 + v42f2 ] dt = 2Ze2f mbv>
6
21
т. е. б ^ 2Ze2/mbv2. Следовательно, средняя величина
dv= — dxnv2n Г 62М?= — dxraDtuZV/mV)InF Ib.). A.9)
j \ / \ max' mm' ^ '
bmin
Сравнивая A.9) с формулой A.8), получаем
min)]. A.10)
Величины бтах, &тт оценим исходя из следующих соображений.
Электрическое поле рассеивающего центра можно считать куло-
новским только на расстояниях, меньших дебаевского радиуса г^.
На больших расстояниях оно убывает экспоненциально, и, следо-
следовательно, столкновения, при которых частица проходит мимо рас-
рассеивающего центра на расстояниях, превышающих гс, нужно из
рассмотрения исключить. В действительности, конечно, дебаевское
облако вокруг движущегося заряда лишь в грубом приближении
можно считать сферическим. Время релаксации — установления
такого облака — имеет тот же порядок величины, что и время
пролета зарядом со средней тепловой скоростью расстояния, срав-
сравнимого с радиусом облака. Но строгая теория приводит лишь
к небольшому количественному уточнению окончательного выра-
выражения для длины свободного пробега. Поэтому при вычислении
/ используем указанный метод обрезания предельного параметра
&тах на величине По.
В качестве 6mm можно взять прицельное расстояние, отвечаю-
отвечающее рассеянию на углы 9~1, при которых нарушилось бы при-
приближение малых углов. Полагая 6—-1, находим
bmin~Ze*lmv2. A.11)
Поскольку стоящая под знаком логарифма в A.10) величина,
которая получена таким образом для актов взаимодействия ча-
частиц в плазме, оказывается очень большой (во всех представляю-
представляющих интерес случаях от 104 до 108), то приблизительность оценки
&тах и Ьт\п практически не отражается на точности вычисления / *'.
Предположения, при которых найдено выражение для длины сво-
свободного пробега /, выполняются в случае, когда пробной частицей
является электрон и рассматривается его взаимодействие с иона-
ионами плазмы. Среднюю длину свободного пробега, соответствующую
электрон-ионным столкновениям в плазме, обозначим 1е%. Ее полу-
получают при усреднении выражения A.10) по энергетическому спек-
спектру электронов. Если все ионы в плазме имеют единичный заряд,
то, предполагая максвелловское распределение электронов по энер-
энергиям, получаем следующее выражение для средней длины свобод-
свободного пробега:
* Более строгое рассмотрение, учитывающее квантовые эффекты в кулонов-
ском рассеяний, при условия Zezlhv<A (квазиклассическое приближение 'нару-
'нарушено) приводит к видоизмененному выражению под знаком логарифма. Вместо
Ьтт появляется длина волны де-Бройля ft/mv. Однако численно изменение зна-
значения логарифма незначительно.
22
A.12)
где Те — температура электронов, К; Lk —так называемый куло-
новский логарифм. Он получается при подстановке в выражение
lnFmax/&mm) значейий Ьтах=гв, bmin=qeqi/mev2 и mev2=3Te, qe=
==—qi-=z—e. В очень широких пределах изменения п и Те лога-
логарифм Lk изменяется от 10 до 20. Поскольку в физике плаЗхМЫ
часто достаточно даже довольно грубой оценки величин, характе-
характеризующих процессы столкновений между частицами, то в дальней-
дальнейшем будем считать Lk=15.
Кроме lei можно ввести также некоторые другие усредненные
характеристики процессов столкновения между электронами и
ионами. Эффективное сечение для таких столкновений опреде-
определяется соотношением lei—l/noei, среднее время между двумя со-
соударениями %ei=leilVTe> где Vxe — средняя тепловая скорость элек-
тронов. Частота столкновений vei=l/xei. Указанные величины мож-
можно вычислить по следующим формулам:
е/ ' } A.13)
20(п!(ТУ'2). J
Выражения для всех указанных параметров нетрудно обобщить
на случай, когда столкновения происходят с многозарядными
ионами. Эффективное сечение оге* возрастет в этом случае пропор-
пропорционально квадрату заряда иона, соответственно изменятся и
остальные величины.
Среди различных видов взаимодействия частиц в плазме
столкновения между электронами и ионами играют наиболее важ-
важную роль, определяя, в частности, механизм таких процессов, как
протекание электрического тока и диффузию.
Для полной характеристики кулоновского взаимодействия ча-
частиц в плазме нужно ввести такие же параметры, характеризую-
характеризующие статистический эффект столкновений между идентичными
частицами (электрон-электронные и 'ион-ионные столкновения).
В этом случае расчет осложняется тем, что при анализе элемен-
элементарных актов столкновения нужно учитывать движение рассеи-
рассеивающих центров. Однако очевидно, что учет эффекта может отра-
отразиться только на значении численного коэффициента в формулах
для средней длины свободного пробега, а температурная зави-
зависимость должна иметь одинаковый характер. В частности, выра-
выражение для lee (средняя длина свободного пробега при электрон-
электронных столкновениях) должно совпадать с выражением для
lei с точностью до численного коэффициента, не очень сильно отли-
отличающегося от единицы. Формула для 1ц (средняя длина свободно-
свободного пробега при ион-ионных столкновениях) получается из формулы
для lei при замене Те на 7V Значения хее и rei близки друг к другу.
23
Отношение хц\хее равно (miT3ilmeT3e)i/2. При равных электронной
и ионной температурах ион-иоиные соударения происходят го-
гораздо реже, чем электрон-электро'нные или электрон-ионные.
Рассеивающими свойствами обладают не только хаотические
ми-крополя отдельных заряженных частиц, но и электрическое поле
плазменных колебаний. Попытаемся хотя бы грубо оценить длину
свободного пробега электрона из-за взаимодействия с равновес-
равновесными (Рэлея—Джинса) колебаниями плазмы. Воспользуемся для
этого формулой Av=—v(Ax/l). Пусть Ах порядка нескольких де-
баевских длин, т. е. порядка самых коротких длин плазменных
колебаний. Изменение продольной скорости на этом расстоянии
составит Av = —v(\—cos 9)^—v(Q2/2), где О — угол отклонения
электрона под действием поперечной компоненты электрического
поля колебаний Е±. Значение этого угла можно считать равным
отношению средней поперечной скорости, приобретаемой электро-
электроном в поле Е., к продольной скорости v. Следовательно, угол
б*—'(еЕ112те(др) A/и). Отсюда
Av ъ A18о) (еЕ±/тршрУ; I <x, 8rDv2 (темр/еЕ±)\
Принимая во внимание, что Е2± = B/3)Е2 ^ 8% 1,38- 10~16rV3r3D?
получаем /^ 10* (Г 2/п). Таким образом, при грубой оценке вклад
поля колебаний с Я > rD в процессы рассеяния электронов оказы-
оказывается примерно на порядок (в кулоновский логарифм раз) мень-
меньше вклада, который дают элементарные акты кулоновского
столкновения частиц. Строгий расчет показывает, что и элемен-
элементарные акты кулоновского рассеяния и рассеяние на колебаниях
плазмы могут быть выведены как частные случаи взаимодействия
частиц с флуктуация-ми микрополя. При этом «парные» столкнове-
столкновения— это результат рассеяния на флуктуациях микрополя, прост-
пространственные размеры которого меньше гт>. Флуктуации же с 1>гв
надо рассматривать как суперпозицию плазменных колебаний.
Таким образом, длина пробега электрона из-за рассеяния на
термодинамически равновесном фоне плазменных колебаний на
порядок величины больше пробега по отношению к парным со-
соударениям. Но плазма часто оказывается неустойчивой: амплиту-
амплитуды плазменных колебаний самопроизвольно -нарастают до значе-
значений, которые во много раз презышают равновесные. В таких слу-
случаях длина свободного пробега определяется рассеянием на коле-
колебаниях. Такие плазмы обладают аномальными свойствами.
С введением понятия «длина свободного пробега» удобно еще
раз вернуться к разделению плазм на идеальные и неидеальные.
Условия идеальности w3d>1 можно переписать так: (ор//УтеЗ>1О.
Это условие означает, что за время одного периода колебания
столкновений практически не происходит. В случае неидеаль-
ной плазмы столкновения становятся столь частыми, что колеба-
колебания затухают слишком быстро и само понятие колебаний теряет
смысл.
24
Подведем некоторые итоги.
С помощью проведенного вы-
выше анализа мы попытались
включить взаимодействие за-
заряженных частиц в плазме
в рамки элементарной кинети- \+ze
ческой теории газов, заменяя J.
плавно изгибающиеся траекто-
рии электронов и ионов услов-
условными ломаными линиями и ис'
сводя статистический эффект
многих слабых столкновений к одному условному сильному
удару. Польза от применения таких не очень корректных методов
заключается в том, что имея формулы для средней длины свобод-
свободного пробега, среднего времени между ударами и т. д., можно опе-
оперировать наглядными картинами при анализе основных физиче-
физических процессов в плазме. Существует, однако, вполне корректный
метод анализа кулонозского взаимодействия частиц в плазме, осно-
основанный и а использовании математического аппарата теории кине-
кинетических уравнений.
Остановимся теперь на вопросе об обмене тепловой энергией
между электронами и ионами в плазме. Рассмотрим сначала са-
самый простой случай. Пусть быстрый электрон с импульсом rneve
пролетает мимо неподвижного иона и 'испытывает рассеяние на
угол в. при этом иоиу передается импульс 2/net;,?sin(8/2) (рис. 1.4).
Под действием этого импульса нон приходит в движение, приобре-
приобретая кинетическую энергию
AWi=(l /2mj) Bmevesin(Ql2)J.
Чтобы найти энергию, которую быстрый электрон передает не-
лодв'ижным ионам за единицу времени, нужно умножить Aw на
vj(Q)dQ и проинтегрировать по углам:
—dw ej dt—{Anneal т&в) LK A-14)
(предполагается, что ионы имеют единичный заряд). Выражение
для передаваемой энергии преобразуем следующим образом:
Здесь vet — число столкновений между электроном с кинетической
энергией we и неподвижными ионами в единицу времени. Отно-
Относительная доля энергии, теряемая в среднем при одном столкнове-
столкновении, составляет 2тс\т\ (как и следовало ожидать для наглядной
модели упругого удара двух шаров). Среднее значение энергии
Qeu которую электрон плазмы передает ионам за 1 с, получается
из A.14) интегрированием по максвелловскому распределению
по скоростям:
A.16)
25
Здесь А — атомная масса ионизованного газа. Указанная форму-
формула справедлива только при Te*>Ti\ если Те и 7^ одного порядка, то
выражение A.16) должно быть заменено на следующее:
Qei^(l,2.10-"!А)п(Т°е-Г{) / (T°e)W. A.17)
Для того чтобы получить представление о степени эффектив-
эффективности теплообмена между электронами и ионами плазмы, обра-
обратимся к конкретному примеру. Пусть температура электронов
в водородной плазме поддерживается на уровне 106 К при концен-
концентрации п=Ю13 СхМ~3. Чтобы нагреть ионы от нулевой температуры
до Ti=Tel2, при этих условиях потребуется 1,2 мс. Заметим, что
результат такого вычисления имеет смысл только в том случае,
если в течение рассматриваемого промежутка времени ионы со-
сохраняют всю приобретаемую ими энергию. Ион с энергией, соот-
соответствующей температуре в несколько сот тысяч градусов, за
1 мс проходит примерно 100 м. Для того чтобы в этих условиях
ионная компонента могла нагреваться, необходима эффективная
термоизоляция плазхмы.
Если тепловая скорость электронов значительно превышает
тепловую скорость ионов, то формула A.17) остается справедли-
справедливой и при Гг>Ге, т. е. в том случае, когда*происходит нагрев элек-
электронов более горячей ионной компонентой. Перепишем для этого
случая указанную формулу в виде
A.17а)
где Qie=—Qei — энергия, передаваемая от ионов к электронам
в единице объема за 1 с. Однако если в плазме "с холодными элек-
электронами присутствуют настолько горячие ионы, что vOve, то ско-
скорость теплообмена может значительно возрасти. Рассуждая так
же, как и при выводе формулы A.14), при указанном условии
приходим к следующей формуле для теплопередачи:
A.18)
или после интегрирования по максвелловскому распределению
ионов
Q<e=2,2.1(h"rt/(r,I/2. AЛ8а)
Одной из основных характеристик вещества служит уравнение
состояния, т. е. соотношение между давлением, плотностью и тем-
температурой. Для классической плазмы с изотропным распределе-
распределением по скоростям заряженных частиц уравнение состояния имеет
тот же вид, что и для идеального газа с двумя компонентами:
p=n(Te + Ti). Здесь р — давление плазмы, равное сумме электрон-
электронного и ионного давлений. Как уже указывалось выше, эта форму-
формула справедлива для случаев, когда яг3о>1.
Обычно предполагается, что распределение частиц газа по
энергиям подчиняется закону Максвелла. По отношению к плазме
это предположение нельзя считать бесспорным. Максвелловский
26
энергетический спектр устанавливается в результате столкновений
между частицами газа. Для того чтобы в данном коллективе ча-
частиц при произвольном начальном энергетическом распределении
установилось распределение по Максвеллу для широкой области
энергий, т. е., чтобы успел «отрасти» максв-елловский «хвост», со-
содержащий частицы с энергией w>T, должно пройти время, за ко-
которое частицы должны испытать в среднем ло несколько столкно-
столкновений друг с другом. Причем речь идет о столкновениях идентич-
идентичных частиц. В частности, максвелловское распределение по энер-
энергиям у электронов практически установится за промежуток вре-
времени, примерно в десять раз превышающий среднее время хее
между двумя электрон-электронными столкновениями. В ионной
компоненте максвелловское распределение устанавливается после
десятка ион-ионных соударений. Следовательно, при Тг^Те «мак-
свеллизация» у ионов происходит гораздо медленнее, чем у элек-
тронов (в отношении (me/mi)i/2). Необходимо отметить, что
,в каждой из компонент плазмы процесс максвеллизации, который
едет из-за столкновений между идентичными частицами, протекает
быстрее, чем установление теплового равновесия между обеими
компонентами. Поэтому в плазме электроны и ионы могут быть
распределены по Максвеллу, «о при двух .различных значениях
температуры. Кроме того, если время жизни заряженных частиц
плазмы мало, то у ионной компоненты в области энергий, во мно-
много раз превышающих температуру ионов, энергетическое распре-
распределение может резко отличаться от максвелловского (число та-
таких быстрых ионов во много раз меньше, чем это следует по за-
закону Максвелла, если нет каких-либо механизмов ускорения).
§ 1.5. Явления переноса в плазме
С помощью понятий длины свободного пробега, времени про-
пролета или частоты столкновений можно уже сейчас .построить ка-
качественную теорию процессов переноса в плазме, таких как диф-
диффузия, теплопроводность, электропроводность и т. п.
Движение каждой заряженной частицы в плаз-ме носит случай-
случайный диффузионный характер, которому можно сопоставить коэф-
коэффициент диффузии: D<^v2tT. Макроскопический смысл могла' бы
иметь диффузия электронов слабоионизованнои плазмы, в которой
роль рассеивающих центров играют нейтральные частицы.
Если температура плазмы неоднородна, то в процессе такого
диффузионного движения происходит перенос тепла, описываемый
обычным уравнением теплопроводности с коэффициентом темпе-
температуропроводности %, который по физическому смыслу получается
умножением коэффициента диффузии на теплоемкость: %^Dc.
Отсюда видно, что коэффициент теплопроводности для пол-
полностью ионизованной плазмы прямо пропорционален Г5/2.-Правиль-
-ное значение численного коэффициента определяется строгой ки-
кинетической теорией. В связи с тем, что в плазме существуют раз-
27
личные сорта частиц с различными скоростями и длинами свобод-
свободного пробега, перенос тепла частицами разного сорта происходит
не одинаково. Поэтому не случайно в плазме вводят раздельное
понятие об электронной и ионной теплопроводности (так же, как
и диффузии).
Важнейшим свойством плазмы является способность перено-
переносить ток под действием электрического поля. Основные черты это-
этого явления с точностью до тонких деталей можно разобрать, даже
не прибегая к кинетической теории. Под действием электрического
ноля в плазме возникают направленные потоки заряженных ча-
частиц; иначе говоря, через плазму течет электрический ток. Если
геометрические масштабы движения плазмы гораздо больше сред-
средней длины свободного пробега частиц, а характерное время дви-
движения значительно превышает среднее время свободного пробега,
то столкновения должны играть здесь значительную роль.
При прохождении тока через плазму ионы, как правило, мож-
можно считать неподвижными. Ток создается потоком электронов.
В простейшем случае, когда сила тока постоянна, должно устанав-
устанавливаться равновесие между силой, с .которой действует на элек-
электроны электрическое поле, и силой торможения, обусловленной
столкновениями между электронами и ионами. Последняя равна
среднехму значению направленного импульса, теряемого электро-
электроном при столкновении с ионами. Электрон испытывает за 1 с v^
столкновений, при каждом из которых он теряет импульс гпеи,
где и — направленная скорость электрона. Следовательно, сила
торможения равна mvuv(,i и условие равновесия имеет вид
—eE=meuvei. (LI 9)
Плотность тока в плазме определяется выражением
}=—пеи. (L20)
Следовательно,
}=(пе21 mcvei)E=(ne2Xeil те)Е. A.21)
Это закон Ома для плазмы.
Величина a=(ne2jme)xei — электропроводность плазмы. Под-
Подставляя в эту формулу выражение для xei и численные значения
констант, получаем (при LK=15)
V2c-K A.22)
Эта формула применима для полностью ионизованной плазмы
с однозарядными ионами (водородная плазма). Заметим, что про-
проводимость не зависит от плотности плазмы и с увеличением Те
быстро возрастает. При температуре около 100 млн. градусов элек-
электропроводность водородной плазмы должна более чем на порядок
превосходить электропроводность меди при комнатной темпера-
температуре. Присутствие многозарядных ионов значительно снижает
электропроводность плазмы. В общем случае, если относительные
28
концентрации ионной компоненты плазмы с зарядами Zu Z2. .....
равны сп, а2, .. ., приведенную выше формулу A.22) для а надо
заменить следующей:
ПK/2. A.23)
Для плазмы с очень высокой электронной температурой форму-
формулу A.23) следует видоизменить. Для быстрого электрона эффек-
эффективное сечение рассеяния oei при слишком большом заряде иона
становится значительно меньше геометрического сечения иона.
В этом случае существенную роль в процессе рассеяния начинает
играть взаимодействие электрона с внутренним атомным полем,
в результате чего сечение рассеяния значительно увеличивается по
сравнению с тем значением, которое получим, рассматривая ионг
как точечный заряд. При достаточно больших we эффективное се-
сечение рассеяния электрона определяется уже не зарядом иона Ziy
а порядковым номером атома Za, возрастая пропорционально Z2a.
В промежуточной области энергий, где происходит переход от
зависимости aei—Zzi к a<>r^Z2a, эффективное сечение рассеяния
падает медленнее, чем 1/Т2е. Поэтому электропроводность высо-
высокотемпературной плазмы при наличии в ней тяжелых компонент
возрастает медленнее, чем по закону 73/2, и оказывается очень чув-
чувствительной даже по отношению к малой доле примесей. В водо-
водородной плазме при Те—1О80 вклад одного атома или иона ртути
в процесс торможения электронов в несколько тысяч раз превы-
превышает вклад иона водорода. В слабоионизованной плазме формула
A.23) уже несправедлива, если электроны сталкиваются с ней-
нейтральными частицами чаще, чем с ионами. По физическому смыс-
смыслу ясно, что в этом случае следует вернуться к выражению для
проводимости A.21), но вместо х€\ подставить туда хеп — среднее-
время столкновений электронов с нейтральными атомами и моле-
молекулами:
a=nehenlme. A.24)
Температурный ход коэффициентов электропроводности такой"
плазмы будет зависеть, в частности, от поведения эффективного
сечения рассеяния электронов на нейтральных частицах. Однако
в слабоионизованной плазме определяющим температурную за-
зависимость фактором является степень ионизации. Действительно,
W^l/tto, следовательно, а пропорционально отношению п/щ; зна-
значит, при небольших температурах (Т<^1) а пропорционально силь-
сильно меняющемуся экспоненциальному множителю ехр (—//2Г).
Рассмотрим вкратце применимость закона Ома для плазмы.
Этот закон справедлив, если в плазме устанавливается равновесие
между силами, действующими на электроны со стороны электри-
электрического поля, и силами торможения. Однако должно ли такое рав-
равновесие устанавливаться при любых условиях?
Сила торможения, испытываемая электроном в полностью иони-
ионизованной плазме, находящимся под действием ускоряющего поля,
имеет тем меньшее значение, чем больше скорость электрона. Рас-
29-
смотрим поведение электрона, принадлежащего к далекому хвосту
максвелловского распределения we^>Te. Приращение скорости,
приобретаемое электроном в промежутке между двумя «столкно-
«столкновениями» с ионами, пропорционально xie и, следовательно, растет
как v3. Поэтому если скорость теплового движения v у выбранно-
выбранного нами электрона достаточно велика, то приращение скорости и
может оказаться того же порядка, что и v, или даже превысить
€е. При такой ситуации неприменима упрощенная модель процес-
процесса, в которой считается, что электрон набирает на длине пробега
относительно небольшую упорядоченную скорость и полиостью
теряет ее при мгновенном сильном ударе. В действительности
ускорение и торможение электрона происходят одновременно. В то
время как электрон приобретает упорядоченную скорость, резер-
фордовское рассеяние на ионах постепенно изменяет направление
^го движения. Электрическое поле стремится распрямить траекто-
траекторию, в то время как взаимодействие с ионами изгибает ее. Если
прирост упорядоченной составляющей скорости не компенсируется
рассеянием, то равновесие сил не может установиться и электрон
должен перейти в состояние непрерывнрго ускорения, при котором
его энергия будет все время возрастать. С увеличением энергии
сила торможения падает, и поэтому электрон, вовлеченный в про-
процесс непрерывного разгона полем, будет продолжать ускоряться,
пока он находится в области действия поля. В состояние разгона
нолем переходят те электроны плазмы, которые успевают набрать
на длине свободного пробега дополнительную скорость и, превы-
превышающую их начальную скорость. Указанное условие разгона мож-
-но записать в виде
eExei/me>v. A.25)
Поскольку %ег пропорционально v3/п, то из A.25) следует, что
непрерывное ускорение происходит в том случае, когда Ewe/n пре-
превышает .некоторое граничное услозие. Как нетрудно убедиться,
для водородной плазмы это граничное значение порядка 3-10~12,
-если Е измеряется в вольтах на сантиметр, a we — в электронволь-
тах. В экспериментах с плазмой условие A.25) обычно удовлетво-
удовлетворяется только для электронов с энергией, во много раз превышаю-
превышающей Те. Эти электроны составляют очень небольшую долю всей
электронной компоненты. Поскольку в указанном случае основной
вклад в электрический ток дают составляющие большинство теп-
тепловые электроны плазмы, закон Ома верен с .^высокой точностью.
Однако наряду с обычным током проводимости в плазме будет
существовать дополнительный ток ускоренных электронов, для ко-
которого закон Ома не применим. При большом значении отношения
Ejn условие A.25) будет выполняться также и для электронов со
средней тепловой скоростью. В этом случае в процесс непрерыв-
непрерывного ускорения может перейти основная часть электронной ком-
компоненты плазмы, и тогда закон Ома должен резко нарушиться,
та,к как, вообще говоря, мы имеем дело с нестационарным процес-
процессом ускорения электронов. Расчет показывает, что процесс элек-
30
тронного разгона заметно развивается тогда, когда отношение*
среднего значения и для плаз'мы в целом к средней тепловой ско-
скорости электронов становится больше одной десятой. Отношение
u/ve растет пропорционально v%, и поэтому если для электронов-
со средней тепловой энергией we=Te и/?/е=0,1, то для электронов-
с энергией ЮТе и сравнивается по значению с ve, и такие электро-
электроны оказываются близкими к порогу непрерывного ускорения. Пе-
Переход электронов в состояние непрерывного ускорения можно на-
наблюдать в кольцевых электрических разрядах, когда плазма обра-
образуется внутри тороидальной камеры и ускоряется вихревым
электрическим полем. В экспериментах такого рода при некоторых
условиях действительно наблюдается разгон определенной (отно-
(относительно небольшой) группы электронов плазмы до очень высо-
высокой энергии при сравнительно небольших напряжениях на плаз-
плазменном витке.
Более глубокий анализ поведения потоков разогнанных элек-
электронов показывает, что такие потоки способны возбуждать и рас-
раскачивать в плазме различные колебания и волны, передавая им-
всю энергию или заметную часть ее. В результате этого появляет-
появляется новый механизм торможения ускоренных частиц, прекращаю-
прекращающий разгон после того, как электроны плазмы наберут определен-
определенную порцию избыточной энергии направленного движения. Этот
автоматический механизм не позволяет всем электронам плазмы
перейти в состояние непрерывного ускорения. Ясно, что электро-
электропроводность плазмы в указанном случае нельзя вычислять по фор-
формуле A.22) и что торможение электронов при взаимодействии
с волнами должно приводить к увеличению сопротивления. К на-
настоящему времени накоплен большой экспериментальный материал
по аномалии электропроводности плазмы в сильном электрическом'
поле. Однако для его анализа требуется привлекать более глубокие
и детальные представления нелинейной теории плазменных не-
устойчивостей (см. § 2.19). При высокой плотности плазмы и от-
относительно небольшой напряженности электрического поля найден-
найденные экспериментально значения в пределах погрешностей измере-
измерений совпадают со значениями, определенными по формуле A.23).
§ 1.6. Плазма в высокочастотном поле
Своеобразные свойства плазмы выступают очень отчетлива
в том случае, когда рассматривается ее поведение под действием
электрического поля высокой частоты. В этих условиях сущест-
существенную роль начинает играть механическая инерция электронов.
Рассмотрим простейший случай. Пусть в плазме действует элек-
электрическое поле Е, напряженность которого равна ?оехр(—ico/).
Если частота настолько велика, что за время одного периода из-
изменения поля у отдельного электрона вероятность столкновения
с ионами достаточно мала, то, рассматривая движение электронов»
можно в первом приближении пренебречь силой торможения.
Уравнение движения в этом случае имеет вид
тех=—еЕо ехр (—ico/), A.26)
где х — координата в направлении электрического поля. Интегри-
Интегрируя A.26), получаем
ие=х= (еЕ0/шссо) ехр (-Ш). A.27)
Следовательно,
1=—епис=—пе2Е1\тсЫ. A.28)
Полученное соотношение можно записать в следующей форме:
E=z(—imeto!ne*)]\ A.29)
Таким образам, высокочастотное напряжение сдвинуто по фазе
на 90° назад по сравнению с током. Это означает, что в высоко-
высокочастотном поле плазма обладает собственной «немагнитной» ин-
индуктивностью, которая обусловлена инерцией электронов. При
низких концентрациях немагнитная индуктивность плазменного
проводника может превосходить его обычную («магнитную») ин-
индуктивность. Выясним условия, при которых это может иметь ме-
место. Для однородного цилиндрического плазменного проводника
с радиусом а магнитная индуктивность на единицу длины в еди-
единицах СГСЭ равна
A.30)
Обычная индуктивность (коэффициент самоиндукции) в единицах
СГСМ для проводника длиной 1 см порядка единицы; в СГСЭ она
^составляет величину порядка 1/с2. Следовательно, для плазмы
отношение обычной индуктивности к немагнитной индуктивности
будет порядка Пе2/тес2^3 * 1О~13, где П — число электронов на
1 см плазменного проводника. Эта величина имеет очень простой
смысл. Она рав'на полному числу электронов, которые находятся
внутри отрезка плазменного проводника длиной, равной класси-
классическому радиусу Го=е2/тес2. Формулу A.29), связывающую плот-
плотность тока с напряженностью высокочастотного поля, можно обоб-
обобщить, если учесть торможение электронов, вызванное столкнове-
столкновениями. В этом случае получаем
?=/(A/<х)-ш1в). A.31)
Здесь Ье=те1пе* — немагнитная индуктивность. Такой характер
движения электронов и переносимого ими тока под действием вы-
высокочастотного электрического поля играет решающую роль
в формировании диэлектрических свойств плазмы. В рассмотрен-
рассмотренном выше простейшем случае, когда в плазме существует электри-
электрическое поле ?оехр(—Ш), ускорение электрона i: и его скорость
определяются выражениями A.26) и A.27). Интегрируя по вре-
времени еще раз, находим смещение
х=ф/тоJ)?оехр(—Ш). A.32)
32
Из A.32) следует, что смещение электрона сдвинуто по фазе отно-
относительно действующей силы (F=—еЕ) «а 180°. Это случай, про-
противоположный тому, с которым мы встречаемся, изучая поведение
обычных твердых диэлектриков. При сдвиге по фазе на 180° меж-
между силой, действующей на заряд, и его смещением поляризация
вещества направлена против поля и, следовательно, диэлектриче-
диэлектрическая проницаемость е<1. Диэлектрическую проницаемость можно
выразить через величину электрического момента единицы объ-
объема Р с помощью известной формулы
е=1+4яР/?, A.33)
в плазме
р=:—пеху A.34)
где х — смещение электронов (смещением ионов можно пренеб-
пренебречь, так «как оно очень мало). Из A.32) и A.34) находим извест-
известное выражение
е=1 —<о2р / со2, A.35)
из которого следует, что в плаз^ме не могут распространяться элек-
электромагнитные волны с частотой, меньшей сор. Следовательно, по-
показатель преломления М= ]/e=(l—g>2p/uJI/2, а волновое число
к=2п/1 равно k=±Na>/c=:((olc) (I—co2P/co2I/2.
Дисперсионная кривая для электромагнит-
электромагнитных волн приведена на рис. 1.5. Для электро-
электромагнитных волн, распространяющихся в про-
пространственно-однородной плазме без магнит-
магнитного поля, отсутствует явление «затухания
Ландау». Это связано с тем, что фазовая ско-
скорость волн CD/&—с/A—*й2р/<*JI/2 превышает
скорость света в вакууме и, следовательно,
нет частиц, которые могли бы находиться в ре-
резонансе с такими волнами. Поэтому единст-
единственный очевидный механизм затухания элек-
электромагнитных волн в такой плазме — это тор-
торможение электронов, вызванное столкновения-
столкновениями. В формуле для диэлектрической прони-
проницаемости учет этого эффекта дает мнимую
часть. Действительно, если в уравнении дви-
движения для электронов в поле волны учесть
силу трения электронов и ионов
тех=—е?оехр (~~Ш) —тсх1хеи
то для смещения х получаем
x=(elme(i){<o+ivei) )EQ ехр (—ico/).
Используя A.33) и A.34), находим
е=1—(o2p/(o(<o + ivet)« A.36)
Для электромагнитных волн в плазме, как правило, выполняет-
выполняется неравенство to^Vei. Действительно, для нижней границы частот
3—74 ' 33
Рис. 1.5. Дисперсион-
Дисперсионная кривая электро-
электромагнитных волн в
плазме
с» =^ юр оно эквивалентно условию о)ртРг>1 (условию идеальности
плазмы /2/*3d>1, см § 1.3). По этой причине формулу A.36) с до-
достаточной степенью точности можно представить двумя первыми
членами разложения в ряд по величине yeil<o:
8=1— co2P/co2+icoV^/(o3. A.36a)
До сих пор мы рассматривали движение электронов в электри-
электрическом поле волны в линейном по амллитуде приближении. В этом
приближении электроны совершают быстрые колебания в направ-
направлении электрического поля со скоростью и, определяемой соотно-
соотношением A.27). В следующем порядке по амплитуде усредненный
эффект квадрата быстрых осцилляции приводит для электромаг-
электромагнитной волны с пространственно неоднородной амплитудой к вы-
вытеснению электронов плазмы из областей, занятых электромагнит-
электромагнитным полем. Физику такого вытеснения можно объяснить следую-
следующим образом. Электромагнитное поле, вызывая высокочастотные
колебания электронов со скоростью u(t), создает как бы дополни-
дополнительное высокочастотное давление рЪлг^птеи^, в результате - чего
электроны плазмы стремятся перемещаться к минимуму поля.
Рассмотрим для определенности стоячую электромагнитную
волну. В такой волне электрическое и магнитное поля лежат
в плоскости, перпендикулярной к направлению неоднородности
(ось г)\
Ex=(l/2)Ex(z)exp(—ieo'O+K. с.
Ну=A12)Ну(г)ехр(—Ш)±к. с.
Здесь к. с. означает слагаемое, комплексно сопряженное первому.
Амплитуды полей связаны соотношением
вытекающим из уравнения Максвелла:
rotE=—A/с)<ЭН/а/.
В соответствии со сделанными выше замечаниями электроны
плазмы в волне конечной амплитуды участвуют в двух движе-
движениях— быстрых колебаниях в направлении электрического поля и
медленном смещении вдоль неоднородности:
г=A/2)хехр(—Ы)+г(/)+к. с.
Уравнение движения электронов вдоль оси z имеет вид
mez=—(ejc)uHy=—(\l4) (е/с) (иехр(-Ш) +к. с.) X
Х(Я2/ехр(—Ы)+к. с). A.37)
В последней формуле мы учли, что скорость электронов — вещест-
вещественная величина, и представили ее в виде
tt=(l/2)M(z)-exp(—ico^+iK. с,
где величина u(z) определяется формулой A.27). Проведя в пра-
правой части A.37) усреднение по быстрым колебаниям, получим сле-
34
дующее уравнение для медленного движения электронов по оси z\
пгег=—(е214теы2) (ЕдЕ*/дг+к. с.) =
=— (е2/4те<й2)д\Е\21дг. A.38)
Это уравнение означает, что в поле*электромагнитной волны с про-
пространственно неоднородной амплитудой на электроны плазмы дей-
действует сила высокочастотного давления, направленная против гра-
градиента электрического поля:
Fz=—dpB.4/dz. A.39)
Высокочастотное давление, создаваемое электромагнитной волной,
равно
рв>ч= (<Ai/4me©2) Е2 (г). A.40)
Эта формула получена для стоячей монохроматической электро-
электромагнитной волны, однако в действительности она имеет достаточно
универсальный характер. В частности, такая же формула для вы-
высокочастотного давления получается при рассмотрении движения
электронов в неоднородном продольном электрическом поле ко-
конечной амплитуды: Ez=(\/2)Ez(z)exp(—ico/)+K. с. Пусть частицы
колеблются около точки z0 в поле с амплитудой, возрастающей
в сторону увеличения z. При колебательном движении сила на-
направлена против смещения. Поэтому когда электрон смещается
направо, на него действует возвращающая сила большей величины,
чем при смещении налево. В итоге возникает результирующая си-
сила, действующая в сторону уменьшения 2, т. е. в направлении, об-
обратном градиенту электрического поля.
Ограничиваясь членами, квадратичными по амплитуде поля,
действующую на электроны силу можно представить в виде
F=—(el2) [Е ехр (—Ш) +
+*>г(дЕ1дг)ехр(—Ш)]+к. с.
Соответственно этому движение электронов по z представляется
в виде суммы быстрых колебаний
6z=~(eE/2me(xJ)exp(—mt)+K. с. A.41)
и медленного смещения под действием силы, усредненной по быст-
быстрым осцилляция'м:
. с.]).
Подставляя в правую часть этого соотношения z и проводя усред-
усреднение по быстрым колебаниям, вновь придем к формуле A.40) для
силы высокочастотного давления. Эта сила обращается в нуль для
бегущей плоской волны, во всех других случаях она отлична от
нуля и приводит к вытеснению плазмы из областей, занятых вы-
высокочастотным полем. По этой причине для удержания плотной
3* 35
плазмы могут быть использо-
использованы мощные пучки электро-
электромагнитных волн, получаемые
в современной когерентной
электродинамике.
Механизм удержания разъ-
разъясняется следующим образом.
В достаточно «плотную плазму
электромагнитная волна не
проникает, и вблизи границы
Рис. 1.6. Действие давления электромаг- ПЛаЗМЫ возникает градиент
нитной волны на плазму электрического поля. Тогда
под действием силы высокоча-
высокочастотного давления профиль плотности плазмы искажается—¦
электроны плазмы смещаются в область, свободную от электро-
электромагнитного поля (рис. 1.6). При этом возникает поляризацион-
поляризационное электрическое поле, в результате чего ионы смещаются вслед
за электронами. Уравнения, описывающие равновесие плазмы
с электромагнитным полем, можно записать в виде
—eE0—(e2l4me(>>2)dE2/dz—(lln)dnTejdz=0; A.42)
eEo—(l/n)dnTi/dz=0. (IAS)
(Здесь мы пользовались условием квазинейтральности пе=Пг.) Из
этих уравнений имеем
/г=лоехр{
Те+ Тг) ,
где п0— невозмущенная плотность при Е-+0. Таким образом, до-
достаточно мощную электромагнитную волну
е2\Е\2/те(хJ>Те+Тг
действительно можно использовать для удержания плазмы,
§ 1.7. Проникновение электромагнитной волны в плазму.
Трансформация в плазменные колебания
Поскольку при оз<(Ор диэлектрическая проницаемость плазмы
отрицательна, электромагнитные волны в такую плазму не могут
проникать больше, чем на глубину скин-слоя. Оказывается, в не-
некоторых случаях внутри этого тонкого слоя толщиной порядка
с/юр с электромагнитной волной могут происходить поистине дра-
драматические события. Их проще всего понять, если рассматривать
распространение электромагнитной волны в неоднородной плазме,
плотность и диэлектрическая проницаемость которой зависят от
пространственной координаты. Будем считать, что плотность мо-
монотонно нарастает в глубь плазмы (вдоль г). Пусть в такой плаз-
плазме под углом к оси г распространяется электромагнитная волна,
36
Если (плотность плазмы меня-
меняется достаточно медленно в
масштабах длины волны, т. е.
выполнено условие o>L/c3>l,
где L — характерный прост-
пространственный масштаб измене-
изменения плотности, то задачу о рас-
распространении электромагнит-
электромагнитной волны всюду, за исключе-
исключением особых точек, можно ре-
решать в приближении геометри-
геометрической оптики. В этом прибли-
приближении волновое поле, как и
e-sin 0
Рис.. 1.7. Пространственное распределе-
распределение электрического поля электромагнит-
электромагнитной волны в неоднородной плазме вбли-
вблизи «точки отражения»
в однородной среде, можно искать в виде плоской волны, учиты-
учитывая, однако, что г-составляющая волнового вектора и амплитуда
волны медленно меняются с расстоянием:
Е, Я = (const/A^2) exp /i f kzdz-{- ikyy — iwt}. A.44)
Для простоты предположим, что волновой вектор лежит в плоско-
плоскости yz (плоскость падения). Дисперсионное уравнение этой волны
имеет такой же вид, как и в однородном случае:
к22+к2у=((*2/с2)г.
A.45)
Слева от области, занятой плазмой, т. е. в вакууме, это уравнение,
очевидно, переходит в следующее: &2=со2/с2. Поскольку k2y=
=&2sin29, то дисперсионное уравнение в общем случае можно за-
записать так:
e—sin2e).
Точка e=sin2e называется точкой поворота волны. Структура поля
вблизи точки поворота показана на рис. 1.7. Слева от точки пово-
поворота осцилляторная структура стоячей электромагнитной волны —
результат наложения падающей и отраженной электромагнитных
волн. Справа от точки отражения поле экспоненциально затухает
в глубь плазмы. Более детально структуру поля можно найти, ре-
решив уравнения Максвелла:
rot E = i (со/с) Н;
rotH = — is((«/c)
A.46)
Здесь е-функция координат. Подставляя Н из первого уравне-
уравнения во второе, получаем следующее уравнение для Е:
ДЕ+е(со2/с2)Ё—graddivE=O. A.47)
Аналогичным образом исключая Е, находим уравнение для Н:
AH+8(o2/c2)H-f(l/e)[V>e, rotH]=0. A.48)
37
При исследовании структуры поля будем различать два неза-
независимых случая поляризации волн: 5-поляризацию, когда электри-
электрический вектор перпендикулярен к плоскости падения, т. е. в рас-
рассматриваемом случае направлен вдоль оси х, и Р-поляризацию,
когда электрический вектор лежит в плоскости падения yz, а по
оси х направлено магнитное .поле волны.
Наиболее просто рассматривается случай S-поляризации, когда
уравнение A.47) для электрического поля можно представить
в виде
d2E/dz2 + (со2/с2) (г—sin26)?=0. A.49)
Достаточно далеко от точки поворота е—sin20 решение этого урав-
уравнения можно получить в приближении геометрической оптики; оно
совпадает с формулой A.44), структура поля в этом случае соот-
соответствует структуре, изображенной на рис. 1.7.
Для того чтобы получить решение вблизи точки поворота, надо
задаться конкретной зависимостью 8 от координаты. Будем счи-
считать, что в этой области плотность плазмы меняется по линейному
закону n=no(l+z/L) (здесь Яо — плотность электронов в точке,
\це плазменная частота совпадает с частотой волны). В этом слу-
iae уравнение A.49) приводится к знаменитому уравнению Эйри:
d2E/dz'2—(со2/с2) (z'l'L)E=0> A.50)
где z'=z—Lsin20. Решение этого уравнения, не имеющее особен-
особенности в точке z'—О, выражается через хорошо известную функцию
Эйри. Достаточно далеко от точки z'—О асимптотика этой функции
совпадает с решением, полученным в приближении геометриче-
геометрической оптики [см. формулу A.44) с k2z=—(co2/c2) (z'/L), осцилля-
осцилляции имеют место слева от точки z'=0, экспоненциальное спада-
спадание— справа от точки z'=0].
Рассмотрим теперь волну Р-поляризации, у которой есть со-
составляющая электрического поля в направлении неоднородности
и с которой связаны обещанные в начале § 1.7 драматические со-
события. Дело в том, что в окрестности точки z=0, где осуществля-
осуществляется резонанс со==<Ор, упомянутая выше компонента Ez электриче-
электрического поля падающей электромагнитной волны, казалось бы, могла
раскачивать продольные (ленгмюровские) плазменные колеба-
колебания. Для того чтобы убедиться, что эта «степень свободы» дейст-
действительно реализуется, обратим внимание на неизбежность разделе-
разделения зарядов, так как под действием нормальной компоненты элек-
электрического поля Ez возникает движение электронов в направлении
неоднородности плотности. Рассмотрим детально поведение ампли-
амплитуд поля в окрестности точки 2=0. Воспользовавшись z-компонен-
той второго из уравнений Максвелла A.46), нетрудно найти, что
амплитуда продольного поля определяется соотношением
e?z^#x@)sine. A.51)
38
Анализ поведения магнитного поля можно провести, основываясь
на уравнении A.48), которое в данном случае (Н параллельно
оси х> 8 зависит только от г) запишем в следующем виде:
(Э2Я/<Эг2—A/е) {дг/дг) {дН/dz) +
+ (со2/с2) (g-sin26)#=0. A.52)
Из этого уравнения следует, что точка отражения волны Р-поля-
ризации также определяется условием e=sin26. После прохожде-
прохождения точки отражения z=—iLsin2e магнитное поле волны экспонен-
экспоненциально спадает с характерным размером, имеющим порядок
с}со sin Э.
\
Рис. 1.8. Пространственное распределение электрического поля электромагнитной
волны в неоднородной плазме вблизи точки «плазменного резонанса» и явление
трансформации электромагнитной волны в плазменную
Точное решение уравнения A.52), которое оказывается несколь-
несколько более сложным, чем уравнения Эйри, показывает, что магнит-
магнитное поле не испытывает никакой аномалии в точке плазменного
резонанса г==0 и в формуле A.51) магнитное поле можно считать
постоянным. Тогда электрическое поле в точке 2=0 будет иметь
особенность порядка 1/е. Структура электрического поля в случае
Р-поляризации показана на рис. 1.8. Тонкий слой вблизи особен-
особенности можно рассматривать как своеобразный конденсатор, в ко-
котором происходит накопление энергии до бесконечно большой ве-
величины при пренебрежении диссипацией (столкновениями) и про-
пространственной дисперсией, которая, как известно, соответствует
выносу энергии плазменной волны.
Для того чтобы описанный здесь эффект был заметен, необ-
необходимо, чтобы точка отражения и точка плазменного резонанса не
были разнесены в пространстве слишком далеко. Условие проник-
проникновения электромагнитной волны в область плазменного резонанса
запишем в виде |&гг|~1, где z=Lsin2i9 — расстояние между точ-
точкой отражения и точкой плазменного резонанса. Подставляя сюда
{) sin0, получаем, что электромагнитная волна проникает
39
в область резонанса при углах падения, близких к нормальному:
Однако 9 не может обратиться в нуль (нормальное падение), так
как в этом случае вообще отсутствует продольное электрическое
поле.
Расходимость поля Ег в точке г=0 отсутствует, если учесть
реальные эффекты — столкновения или раскачку продольных плаз*
менных колебаний. Для того чтобы учесть раскачку продольных
колебаний, необходимо ввести поправку к частоте, возникающую
из-за теплового движения [см. уравнение A.36),].
Рассмотрим сначала более простую задачу, когда особенность
в точке резонанса снимается столкновениями. Используя выраже-
выражение A.36а) для диэлектрической проницаемости плазмы при на-
наличии соударений, найдем, что амплитуда продольного электриче-
электрического поля определяется соотношением
EZ=HX(O) sin0/(— (z/L)— iv/co). A.53)
Отсюда следует, что диссипация ограничивает продольное элек-
электрическое поле на уровне
?макс^#*@) Sin 9@/V. A.54)
Такое поле достигается в области шириной
A?~<Lv/g). A.55)
Во всех приведенных выше формулах #^@) —это магнитное поле
в окрестности особенности. Для того чтобы связать его с амплиту-
амплитудой падающей волны Я, необходи-
необходимо решить уравнение A.52). Мы не
будем проводить здесь строгое ре-
решение этого уравнения и приведем
лишь окончательный результат:
sin e#*@)=#(x/©L) 1'*Ф(%) I Bл) ^
A.56)
где T=(<o-L/cI/2sin6. График Ф(т)
приведен на рис. 1.9, при больших т
в соответствии с проведенным вы-
ше Рассмотрением функция Ф(т)
экспоненциально спадает.
Рис. 1.9. График функции Ф(т)
Теперь можно вычислить коэффициент поглощения электромаг-
электромагнитной волны в окрестности плазменного резонанса. Очевидно, что
такой коэффициент поглощения определяется отношением мощно-
мощности диссипации в окрестности резонанса к потоку энергии в падаю-
падающей волне, который, в свою очередь, определяется вектором Пойн-
тинга и равен сН2/8п. Основной вклад в диссипацию, очевидно,
обусловлен продольным электрическим полем. Тогда поглощаемая
мощность равна
P=v $(\E2z\2/8n)dz.
40
Подставляя в этот интеграл формулу A.53) для пространствен-
пространственной структуры продольного электрического поля в окрестности
плазменного резонанса, получаем следующее уравнение для сксь
рости поглощения:
-<*>p(z)r + v>\. A.57)
В пределе малых v подынтегральное выражение является
одним из известных представлений б-функций, а именно
lim , чч2 ,—о- = тс8 (со — шп (г)).
Наличие этой б-функции подчеркивает резонансный характер по-
поглощения —¦ диссипация электромагнитной энергии происходит
только в узком слое плазмы, где плазменная частота совпадает
с частотой падающей волны. В этом случае частота столкновений
определяет только ширину резонансного слоя Аг [см. A.55)],
а скорость поглощения от v не зависит. Это обстоятельство можно
пояснить иначе: Р—vE2MaKcA2, ?макс—1/v [см. A.54)], Az~v, сле-
следовательно, Р не зависит от v. Иначе говоря, роль v является,
в известном смысле, символической.
Следует заметить, что при дальнейшем рассмотрении свойств
плазмы нам довольно часто придется сталкиваться с резонансными
явлениями [черенковский резонанс волн и частиц a)=kv (сы.
§ 1.12), резонанс на плазменной частоте в спектре поляризацион-
поляризационных потерь заряженной частицы (см. § 1.8)]. Все эти резонансы
в значительной степени аналогичны резонансу A.57). Для полу-
получения конечной ширины резонанса мы и в дальнейшем будем до-
довольно часто вводить соударения.
Вернемся к формуле A.57). Выполняя интегрирование по г,
получаем
P=(l/8)#2*@) sin29iLco. A.58)
Коэффициент поглощения электромагнитной волны определяется
отношением мощности, поглощаемой в окрестности резонанса,
к потоку энергии в падающей электромагнитной волне:
При К-+0 почти весь поток отражается от границы плазмы и обра-
образуется стоячая электромагнитная волна. При /С->1 энергия падаю-
падающей электромагнитной волны практически полностью поглощается
в окрестности плазменного резонанса.
Используя приведенное выше выражение для Р и формулу
A.56), связывающую амплитуду магнитного поля в окрестности
резонанса с амплитудой поля в падающей волне, находим следую-
41
щую формулу для коэффициента поглощения электромагнитной
волны:
К=0,25ФЦт). A.59)
Из графика функции Ф'(т) видно, что максимальное значение ко-
коэффициента поглощения достигается при очень малых углах между
направлением распространения волны и градиентом плотности
плазмы:
@о порядка нескольких градусов). Максимальное значение коэф-
коэффициента поглощения
/СШах«0,4. A.60)
Другой механизм ограничения электрического поля в окрестно-
окрестности резонанса связан с выносом энергии из этой области плазмен-
плазменными волнами. Уравнение, описывающее трансформацию электро-
электромагнитной волны в 'плазменные волны, совпадает с уравнением
A.51), в котором теперь нужно учесть пространственную диспер-
дисперсию диэлектрической проницаемости. Тогда в соответствии с A.36)
е(<о, k) = \ — (©Ую2)A + ЗЛ2г2в).
Эта формула получена для плоской волны ?^ехр (\kz). В более
общем случае волновое число следует заменить оператором диф-
дифференцирования ?=\д/дг9 и тогда диэлектрическую проницаемость
следует понимать в операторном смысле
В этом 'случае вместо соотношения A.51) имеем следующее диф-
дифференциальное уравнение для .поля:
3r2Dd2Ez/dz2—(z/L)Ez=Hx@) sin 9. • A.61)
Решение этого уравнения также можно выразить с помощью функ-
функции Эйри, в данном случае она будет определять структуру плаз-
плазменных волн, выходящих из области резонанса. Однако для каче-
качественных оценок нет необходимости получать точное решение урав-
уравнения A.61). Заменяя в этом уравнении д2/дг2 на l/(AzJ, находим
характерный пространственный масштаб, на котором изменяется
амплитуда плазменных колебаний:
iAz~(L/'2DI/3, A.62)
а максимальная напряженность электрического поля
Em*j~>Hx@) Sine(l/*bJ/8. A.63)
Теперь сопоставим оба конкурирующих механизма. Трансфор-
Трансформация в плазменные волны доминирует над столкновительным по-
поглощением, если характерный пространственный масштаб плазмен-
плазменных колебаний A.62) превышает ширину области резонанса, обу-
обусловленную соударениями v<G)(irD/LJ/3. В противном случае
ограничение на величину продольного электрического поля в окре-
окрестности ,2=0 связано с диссипацией на столкновениях.
42
Поток энергии в плазменной волне определяется формулой
vgE2zjAn, где vg=d®ldk — групповая скорость плазменных колеба-
колебаний, в соответствии с формулой A.36) равная vg=3kzr2T)(up. По
порядку величины kz—l/iAiz, поэтому поток энергии, уносимый
плазменной волной, приближенно равен
^?2,/4я^A/4я) (#х@) sin9Jo)PL.
Подставив в это соотношение значение магнитного поля в точке
резонанса из A.56), получим окончательное выражение для пото-
потока энергии в плазменной волне:
vgE2z/4n=c(H2l4n) (Ф2(т) /2я).
Если ввести коэффициент трансформации электромагнитной вол-
волны в плазменную волну, равный отношению потоков энергии
в плазменной и падающей электромагнитной волнах, то нетрудно
видеть, что при углах 0о—(g))L/c)~1/3 он оказывается порядка еди-
единицы. Более точное рассмотрение, основанное на решении урав-
уравнения Эйри для продольного поля, показывает, что этот коэффи-
коэффициент в точности совпадает с коэффициентом поглощения электро-
электромагнитной волны в результате соударений [см. формулу A.59)].
Иначе говоря, в обоих случаях должна теряться одна и та же доля
падающего на плазму потока электромагнитной энергии.
§ 1.8. Излучение плазмы
В плазме без магнитного поля электромагнитное излучение
обычно возникает в результате элементарных процессов неупругото
взаимодействия частиц. Одним из таких процессов является не-
неупругое рассеяние электронов в электрическом поле иона -с поте-
потерей энергии, которая превращается в электромагнитное излучение.
Это так называемое тормозное излучение электро-
электронов — главный источник излучения плазмы при очень высокой
электронной температуре. Оно имеет сплошной спектр: энергия фо-
фотонов Ню, излучаемых в элементарном акте, лежит в пределах от
% (Dp (что соответствует нижней возможной частоте электромаг-
электромагнитных волн в плазме) до we, где we — кинетическая энергия элек-
электрона до столкновения. Как правило, основная доля излучаемой
энергии приходится на частоты соЗ>сор. Действительно, это условие
для квантов с энергией порядка средней тепловой энергии элек-
электронов й.со'-^Те можно преобразовать к виду
е*(теI12[П(Ге)]'2> l/nr3D. A.64)
В правой части неравенства A.64) стоит величина, характери-
характеризующая степень неидеальности плазмы как газа, т. е. обычно чрез-
чрезвычайно малая. Выражение, стоящее в левой части, удобно пред-
ртавить как отношение G0/ГеI/2, где 1о=еАте1%2 с точностью до
численного коэффициента порядка единицы совпадает с боровской
энергией электрона в атоме водорода. Для условий обычного га-
43
зового разряда эта величина порядка единицы. Она становится
меньше единицы для высокотемпературных плазм, но обычно это
с лихвой компенсируется еще более значительным уменьшением
правой части неравенства A.64).
Частотный спектр излучения для элементарных актов тормо-
торможения нерелятивистских электронов с заданной энергией те при-
приближенно можно получить, по существу, в рамках классической
электродинамики. Воспользуемся известной формулой для интен-
интенсивности классического дипольного излучения заряда, движущего-
движущегося с ускорением:
dW/dt=Bl3)e2v2lc*. A.65)
Полную энергию, излучаемую электроном при пролете около рас-
рассеивающего центра (иона), можно представить и как интеграл по
всем возможным частотам:
B/3) (е2/с3) J b2dt = B/3) (е*!съ) 4% J16п [* <?», A.66)
О
где vm — A /2-я) ^v (t) exp (—io>^) dt — разложение ускорения в инте-
—оо
грал Фурье.
Рассмотрим тормозное излучение при столкновениях с больши-
большими прицельными расстояниями, т. е. с малыми углами рассеяния
(8<С1). В этом случае ускорение, испытываемое электроном, почти
перпендикулярно к его первоначальной скорости и приблизительно
равно
v± ^ (Ze2!me) [bj(b2 + v2t2f2]. A.67)
Напомним, что в § 1.4 упругие столкновения были рассмотрены
в этом же приближении. Теперь вычислим компоненту Фурье от
величины ускорения, определяемой формулой A.67):
= A /2«) BZe2b/me) J cos Ы [l/(b2 + v2t2f2 ] dt
6
Возникший здесь интеграл можно выразить через некоторую бес-
селеву функцию от мнимого аругумента. Чтобы не вдаваться в де-
детали теории специальных функций, ограничимся простой интерпо-
интерполяцией интеграла
6
основанной на следующих рассуждениях. При достаточно малых
частотах to^vfb в существенной области интегрирования t^bfv
44
(т. е. при таких t9 когда знаменатель подынтегрального выраже-
ния еще не успевает слишком сильно вырасти) можно положить
l. Тогда интеграл берется и равен
В противоположном предельном случае больших частот
b в той же существенной области интегрирования t^b/v
множитель coso)^ успевает совершить большое число осцилляции,
в результате чего подынтегральное выражение оказывается знако-
знакопеременным и интеграл становится очень малым (экспоненциаль-
(экспоненциально, как следует из теории бесселевых функций). В этом можно
было бы убедиться и с помощью прямых вычислений, например по
методу перевала.
В итоге для приближенной оценки интенсивности тормозного
излучения напрашивается простая интерполяционная формула,
объединяющая оба предельных случая:
llb*v при m<vlb>
О при о)>у/6.
Соответственно энергию, излученную при столкновении с прицель-
прицельным параметром b в интервале частот от оз до co+rfco, приближен-
приближенно можно представить в виде
1Г(со)ЛоМ8/3) (Z2e2clnb2v2)r2od<>)f
где ro=^e2jmc2 — классический радиус электрона. Безразмерная
величина W(<u)d®!% о определяет вероятность излучения кванта
с частотой в интервале от <о до со+йсо. Теперь нетрудно получить
эффективное сечение излучения такого кванта, если проинтегри-
проинтегрировать по всем возможным прицельным расстояниям:
<fo
&тах
(<o)= Г
&min
A6/3) (FeV/ncv*) r\ (*>/«) In (bmjbmj.
mjbmj
В этом выражении в отличие от формулы кулоновского логарифма
&тах, вообще говоря, уже не имеет смысла дебаевского радиуса гр.
Действительно, поскольку W((o) равно нулю при <о>о/6, то
всегда 6тах во всяком случае меньше v /со.
Таким образом, при а/со</ъ следует обрезать логарифм при
&mar==0/<D. Именно так обстоит дело во всех практически интерес-
интересных случаях (о^>(Ор. Если в этом, по существу чисто классическом,
выводе учесть возможные квантовые эффекты хотя бы самым при-
примитивным образом, положив bmin равным длине волны де-Бройля
электрона 6шш=Й/^у, то окончательное выражение для сечения
тормозного излучения
do (ш) ^ Ж> A6/3) (ZV/cft) (c*[v%) (r\(m) In (mjff*n) A.68)
45
оказывается почти совпадающим с результатом квантовомеханиче-
ских вычислений в борновском приближении. Если же интересо-
интересоваться более тонкими деталями, то следовало бы обратиться к до-
довольно громоздкому выражению, полученному в свое время Зом-
мерфельдом путем строгих вычислений. Во всяком случае формула
A.68) правильно описывает зависимости от Z, е2 и скорости элек-
электронов. Из нее следует, что электрон при движении в веществе за
1 с теряет на излучение энергию
dwe(dt = f n^ntvdz (со) =BntZ2 (weI12 , A.69)
где численный множитель В, получающийся с учетом теории Зом-
мерфельда, равен 1,5-Ю-25, если кинетическую энергию электрона
we выражать в электронвольтах. Интенсивность тормозного излу-
излучения плазмы находят, интегрируя выражение A.69) по энергети-
энергетическому распределению электронов. При максвелловском законе
распределения полная энергия, которую излучает 1 см3 плазмы
в 1 с, должна составлять
<7изл=1,5- \0-27neniZ*(Toe)V2. A.70)
В плазме, содержащей ионы нескольких веществ, <7изл будет пред-
представляться суммой выражений вида A.70) со значениями щ и Z,
соответствующими разным компонентам. Из формулы A.70) сле-
следует, в частности, что. присутствие даже очень незначительной
примеси тяжелых ионов в плазме, которая в основном содержит
ионы легкого вещества, должно приводить к резкому возрастанию
интенсивности тормозного излучения.
Выражение A.70) для интенсивности тормозного излучения
справедливо с достаточной точностью при не слишком высоких
значениях Теу когда электроны можно считать нерелятивистскими.
Однако оно нуждается в корректировке при переходе к реляти-
релятивистским электронным температурам (т. е. для значений Т°е—10'9°
и выше). В этой области температур интенсивность излучения,
обусловленного взаимодействием электронов с кулоновским полем
ядер, растет с Те быстрее, чем это следует из формулы A.70). Кро-
Кроме того, при релятивистских скоростях столкновения электронов
с электронами также приводят к увеличению тормозного излуче-
излучения. Выше такие столкновения не учитывались при вычислении
тормозного излучения из-за тождественного обращения в «нуль
второй производной по времени от джюльного момента системы,
состоящей из электронов.
Излучение с непрерывным спектром возникает в плазме также"
в результате процессов рекомбинации электронов с ионами. В эле-
элементарном акте рекомбинации свободный электрон в результате
взаимодействия с электрическим полем иона захватывается на
46
один из дискретных энергетических уровней. При этом излучается
фотон с энергией, равной w€+w8, где ws — энергия связи электро-
электрона на занятом им квантовом уровне. Заряд иона в акте рекомби-
рекомбинации уменьшается на единицу (в частности, рекомбинация одно-
однозарядного иона приводит к образованию нейтрального атома). За-
Захват электрона может происходить не только на наинизший
возможный энергетический уровень, но также и на уровни, соответ-
соответствующие различным возбужденным состояниям атомной системы
с зарядом (Z*—\)е. Поэтому после актов рекомбинации может
присходить высвечивание возбужденных ионов (или атомов) с ис-
испусканием фотонов, принадлежащих к линейному спектру излуче-
излучения вещества плазмы.
Интенсивность рекомбинационного излучения уменьшается с уве-
увеличением кинетической энергии электрона и очень сильно зависит
от заряда ионов.
Для грубой оценки энергии, излучаемой в сплошном спектре
в результате процессов рекомбинации в 1 см3 плазмы за 1 с, мож-
можно пользоваться формулой
<7рек^5 • 1 Ъ-™пещ1\ (Te)-W. A.71)
В общем случае в правой части выражения A.71) надо заменить
rtiZAi на 2n2-Z4i, распространяя суммирование на все разновидности
ионов, присутствующих в плазме. Заметим, что при достаточно
большом времени жизни ионов в плазме благодаря конкурирующим
процессам ионизации — рекомбинации среднее значение заряда
иона данного вещества должно приближаться к некоторому ста-
стационарному значению, которое тем ближе к Za, чем выше элек-
электронная температура. Как следует из сравнения формул A.70.) и
A.71), в плазме с относительно невысокой электронной темпера-
температурой рекомбинационное излучение должно преобладать над тор-
тормозным, в то время как при большом значении Те имеет место
обратное явление.
В низкотемпературной плазме с небольшой степенью иониза-
ионизации главным источником квантового электромагнитного излучения
становятся возбужденные атомы и молекулы. Поэтому излучение
холодной плазмы имеет преимущественно линейчатый характер.
При малых значениях Те интенсивность линейчатого спектра излу-
излучения может на несколько порядков превосходить интенсивность
сплошного спектра рекомбинационного и тормозного излучений.
Поскольку состав линейчатого спектра и интенсивность входящих
в него спектральных линий чрезвычайно сильно зависят от индиви-
индивидуальных свойств атомов и ионов плазмы, то трудно установить
общие количественные закономерности, характеризующие зависи-
зависимость выхода линейчатого излучения от электронной температуры
(в особенности для плазмы, содержащей атомы различных эле-
элементов). Однако можно отметить одну общую закономерность ка-
качественного характера — при достаточно высокой электронной тем-
47
Рис. 1.10. Зависимость интенсивно-
интенсивности линейчатого излучения от тем-
температуры для углеродной плазмы
(штриховая кривая) и полное из-
излучение (сплошная кривая)
пературе в плазме, находящейся в стационарных условиях, у ато-
атомов оторваны внешние электронные оболочки, и это приводит
к обеднению спектра и быстрому падению интенсивности линей-
линейчатого излучения.
Здесь действуют две причины: во-первых, уменьшается число
легко возбуждаемых электронов, находящихся в связанном состоя-
состоянии, и, во-вторых, при больших значениях энергии электронов па-
падает вероятность элементарных актов возбуждения. Вследствие
этого в области высоких значений
Те интенсивность линейчатого излу-
излучения представляет собой быстро
убывающую функцию электронной
температуры. Иллюстрацией может
служить приведенная на рис. 1.10
кривая изменения интенсивности
линейчатого спектра ионов углерода
в плазме, рассчитанная теорети-
теоретически.
Если плотность плазмы и геоме-
геометрические размеры той области про-
пространства, которую она занимает,
невелики, то все излучение, обра-
образующееся в плазме, выходит нару-
наружу. Предположим, что при постоян-
постоянных плотцости и температуре плазмы занимаемый ею объем
возрастает. При этом выход излучения будет увеличиваться про-
пропорционально объему. Но полный поток излучения ' из плазмы
не может превосходить поток излучения черного тела, имеющего
ту же поверхность 5 и ту же температуру Те. Следовательно, при
достаточно больших размерах области, занимаемой плазмой, долж-
должны вступить в действие процессы поглощения, замедляющие рост
потока излучения и приводящие к установлению термодинамиче-
термодинамического равновесия между электронами и излучением. Существует
несколько различных элементарных механизмов поглощения излу-
излучения, каждый из которых может рассматриваться как обратный
по отношению к одному из механизмов испускания фотонов.
Излучательному переходу между двумя дискретными уровнями
в атоме или ионе соответствует селективное поглощение спектраль-
спектральных линий, приводящее к обратному электронному переходу. Про-
Процессу рекомбинации отвечает процесс фотоионизации атома или
иона. Тормозному излучению соответствует обратный механизм,
заключающийся в поглощении фотона свободным электроном
в электрическом поле атомной системы. Вероятность различных
процессов поглощения связана с вероятностями соответствующих
излучательных переходов на основе принципа детального равно-
равновесия.
Для того чтобы найти, на каких длинах устанавливается тепло-
тепловое равновесие между тормозным излучением и обратным ему про-
48
цессом поглощения, воспользуемся следующими рассуждениями*
В уравнение, учитывающее изменение энергии излучения, надо до-
бавить слагаемое, учитывающее поглощение —Щсо)/тф. Здесь по*
смыслу Тф — время свободного пробега фотона с частотой со. Оно,,
очевидно, связано с длиной свободного пробега фотона /ф=стф. Из
уравнения A.69) имеем для одного электрона
(ш).
Учитывая теперь наряду с излучением A.68), A.69) и погло-
поглощение, получаем
(Z2e2/c) X
X (c2lv2)r2Qv In (mev2l«>h)) — Щсо)/тф.
(Угловые скобки означают усреднение по максвелловскому рас-
распределению электронов.)
В экспериментальной физике лабораторной плазмы обычно?
имеют дело с такими условиями эксперимента, при которых про-
пробеги фотонов во много раз превышают линейные размеры плаз-
плазменных образований (в некоторых специальных случаях, когда
исследуется очень плотная плазма, узкая спектральная область
вблизи линии поглощения может представлять исключение). В та-
таких оптически прозрачных плазмах фотоны не удерживаются и
плотность энергии излучения значительно меньше равновесной^
т. е. плотности черного излучения. По мере увеличения размеров
плазменного образования сначала должно устанавливаться равно-
равновесие для малых частот, как это следует из формулы (Г.68).
Черное излучение может установиться лишь внутри простран-
пространственно протяженных или достаточно плотных плазм, например
в звездах. В таких плазмах при очень высоких температурах чер-
черное излучение может давать основной вклад в плотность энергии
(а значит и в давление). Так, при плотности частиц в звездах по-
порядка 1024 см~3 плотность энергии излучения аТ4 превышает пТ,.
если температура становится больше десятка килоэлектронвольт..
Это условие не выполняется для Солнца, температура в центре
которого порядка 1,5 кэВ. Но и в солнечной плазме черное излуче-
излучение играет важную роль. В частности, механизм переноса тепла во
внутренних слоях Солнца в значительной степени определяется
черным излучением: Такой перенос тепла квантами из спектра
черного излучения называют лучистой те п л oinp овод-
нос т ь ю. Коэффициент лучистой теплопроводности нетрудно оце-
оценить, если известны средний пробег фотонов вблизи максимума
распределения Планка ftco—'5 kT. Коэффициент диффузии таких фо-
фотонов D—A /3)/ф^7. Поток фотонов равен —Dgrad%. Поток энер-
энергии, переносимый фотонами,
4—74 4 9
где йлоЯф — плотность энергии черного излучения аТ*. Таким об-
образом, qc^—4DaT3 grad Т. Это означает, что коэффициент лучи-
лучистой теплопроводности х—D/3IфСаТг.
Пробег фотонов в такой плазме, как солнечная, определяется
в основном механизмом поглощения, обратным тормозному излу-
излучению. Его можно связать со средним временем свободного проле-
пролета Тф фОТОНОВ 1ф=СГф.
Интересующую нас величину Тф найдем из условия, что в рав-
равновесии между электронами и излучением IF (со) должно представ-
представлять собой распределение Планка. Следовательно,
Vs* №«« A6/3) (Z'e'lc) (c2/v2) r\v in (тг1Щ). A.72)
Для мягких фотонов (/too < Те)9 которые могут излучаться электро-
электронами, принадлежащими максвелловскому распределению, формулу
A.72) можно привести к совсем простому виду. Распределение
Планка превращается в спектр Рэлея — Джинса Щсо)==Г3со2/я2с3,
а угловые скобки, символизирующие усреднение по максвелловско-
максвелловскому распределению электронов, можно убрать, приписав ve смысл
средней тепловой скорости C/2)?Г=то2е/2. Таким образом, на-
находим, что
'С(©2/«>2р)г*^. A.72а)
Величина т*ег отличается от среднего времени столкновения элек-
электрона с ионом лишь тем, ,что вместо кулоновского логарифма Ьк
здесь стоит, вообще говоря, несколько меньшая величина.
Этот результат можно получить достаточно простым способом,
используя мнимую часть диэлектрической проницаемости:
8=1—,(о2р /о (@ + ive) .
До сих пор мы исследовали электромагнитное излучение
в плазме. Но мы уже знаем, что в плазме кроме электромагнитных
колебаний возможны также колебания плотности заряда — плаз-
плазменные волны, и естественно ожидать, что часть потерь энергии
заряженной частицы в плазме будет связана с возбуждением про-
продольных колебаний — поляризационными потерями. Важная осо-
особенность поляризационных потерь состоит в том, что основная доля
энергии, теряемой в этом случае заряженной частицей, остается
в плазме в виде колебаний плотности заряда и в конечном счете
усваивается плазмой в результате поглощения при соударениях
либо затухании Ландау плазменных колебаний. Однако не сле-
следует забывать, что в неоднородной плазме существует и другой
механизм — трансформация в электромагнитные колебания "(см.
§1.7).
Поляризационные потери можно также интерпретировать как
потери энергии при кулоновских столкновениях с большими при-
прицельными параметрами, когда из-за дальнодействующего харак-
характера кулоновских сил во взаимодействие с налетающей частицей
50
может одновременно вовлекаться большое число частиц плазмы.
С макроскопической точки зрения это обстоятельство проявляется
в поляризации плазмы как сплошной среды при пролете заряжен-
заряженной частицы, т. е. в возбуждении уже знакомых нам плазменных
колебаний.
Для иллюстрации механизма поляризационных потерь ограни-
ограничимся для простоты случаем нерелятивистских скоростей частицы.
Перейдем к фурье-представлению электрического потенциала ко-
колебаний, вызываемых такой заряженной частицей:
? (U г) = A/2*L J dkda, exp {ikr - Ы) ^ A.73)
Плотность заряда, создаваемая точечным зарядом, движущим-
движущимся со скоростью v, определяется как ре=—#6(г—vt). Разложим
б-функцию по плоским волнам:
8 (г — v/) = A /2тс)а Г Г 6 (со — kv) exp {ikr — Ы} dk <fa.
Тогда фурье-компонента плотности заряда —еЬ (г—vt) есть
Восдользуемся уравнением Пуассона, записанным для каждой
фурье-компоненты:
причем в(<о)=1—со2р/со2— обычная диэлектрическая проницае-
проницаемость холодной плазмы для волны с фиксированной частотой [см.
A.35)]. Тогда для отдельной фурье-гармоники потенциала имеем
следующее уравнение:
9ke = - (8Л/е (со) к2) § (со - kv). A.76)
Отсюда сразу следует, что заряженная частица возбуждает только
те гармоники потенциала, которые находятся в фазовом резонансе
с этой частицей, т. е. скорость движения частицы в направлении
распространения волны должна совпадать с фазовой скоростью
волны kv cos 9=co. Мощность излучения определяется формулой
dW/dt= — jE, A.77)
где j=—ev6(r—\t)—плотность тока, создаваемая движущимся
электроном; Е=—Vtp — электрическое поле плазменных колеба-
колебаний; черта в правой части A.77) соответствует усреднению по рас-
расстояниям, большим по сравнению с длиной волны. С помощью A.76)
получим
dWldt=8n2e4v/ Bn)* $ dkd<o(klk4((u))8((d—kv). A.78)
4* 51
Подынтегральное выражение имеет особенность при частотах
»&)=±й)р. Эта особенность аналогична рассматривавшейся в § 1.7
:и имеет резонансный характер. Однако если при распространении
электромагнитной волны в неоднородной плазме резонанс имеет
пространственный характер [возникает в слое сор!(г) =зсо], то
в эффекте поляризационных потерь резонанс возникает в спектре
по частотам (при интегрировании по частоте). Для устранения
-особенности подынтегрального выражения по аналогии с § 1.7 вве-
введем малое затухание. Тогда с учетом мнимой части е(ю) получим
Кроме действительной части это выражение имеет мнимую часть,
которую в пределе v-Я) можно представить как
limlm [l/(»f — <»2n + iv:o)] =
Согласно формуле A.78) в интеграле, определяющем мощность
-потерь, существен только вклад от 6-функции. Выполнив интегри-
интегрирование, придем к следующей формуле для мощности потерь:
dW/dt = 16*Va>y BiuL j dU (® — kv)/?2. A.79)
Для получения окончательной формулы следует проинтегри-
проинтегрировать в A.79) по k{{ и по k±. Последний интеграл логарифми-
логарифмически расходится при больших &±, и его необходимо обрезать при
kmax—l/b. Здесь Ъ — минимальный прицельный параметр «коллек-
«коллективных» столкновений, т. е. расстояние, на котором становится не-
лрименимым описание плазмы как сплошной среды. Очевидно, что
Ь порядка радиуса дебаевского экранирования заряда гв=
= (Г/4я^2/2оI/2. Окончательный результат для скорости потерь
имеет вид
dW/dt=(e2G>2Plv) In (о/©р*). A.80)
Величина, стоящая над знаком логарифма в этой формуле, — отно-
отношение скорости частицы к тепловой скорости, т. е. порядка
10—100. Поэтому In (v/iopb) по порядку величины не сильно отли-
отличается от единицы. В этой связи напомним, что потери энергии на
парные соударения с учетом многократного рассеяния по сравне-
сравнению с формулой A.80) содержат большой множитель — так назы-
называемый кулоновский логарифм, т. е. величину порядка 20. Подобно
тому как рассеяние на тепловых флуктуациях в кулоновский лога-
логарифм раз меньше рассеяния при парных столкновениях, потери
энергии на излучение плазменных волн (поляризационные потери)
в кулоновский логарифм раз меньше потерь энергии при парных
столкновениях. Следует иметь в виду, что поляризационные потери
существенно увеличиваются при переходе от отдельных зарядов
к пучкам заряженных частиц. В этом случае в актах излучения
участвуют не отдельные электроны, а «бунчи» (сгустки) когерент-
но излучающих частиц, на которые разбивается пучок из-за не-
неустойчивости. При этом в формуле A.80) для мощности потерь
следует заменить е на Ыдфеу где NЭф — число частиц в бунче, и со-
соответственно этому потери, рассчитанные на одну частицу, возра-
возрастают пропорционально М>ф(МЭф»1). Самой сложной задачей
является определение эффективного заряда бунча. Эту задачу
можно решить только в рамках самосогласованной теории неустой-
неустойчивости, основывающейся на кинетическом подходе.
§ 1.9. Кинетическое уравнение для плазмы
Идеальную плазму можно, как и обычный газ незаряженных
частиц, описывать с помощью кинетического уравнения для функ-
функции распределения частиц в фазовом пространстве. В этом случае,
разумеется, нужно вводить свою функцию распределения для каж-
каждого сорта зарядов. В координатной записи функция распределе-
распределения f(x, у у z, vx, vy, vz, t) определяет плотность частиц на единицу
объема в фазовом пространстве вблизи точки с геометрическими
координатами х, у, z и компонентами скоростей vx, vv\ vz для мо-
момента времени t. Используем более компактную форму записи,
в которой функция распределения имеет вид f (r, v, t) и относится
к точке с векторными координатами г, v. Интеграл от функции
распределения по всему объему в пространстве скоростей дает
ллотность в данном элементе геометрического объема
„(г, .*)=f/(r, v, t)dv.
к)
Как показано выше, на заряженные частицы плазмы могут
воздействовать силовые поля двух типов: а) регулярные поля, со-
создаваемые внешними источниками или избыточными зарядами
в объемах с размерами, превышающими дебаевскую длину (как,
например, для колебаний плазмы), и б) случайные микрополя от-
отдельных частиц, вызывающие процессы рассеяния (столкновения).
Кинетическое уравнение описывает изменение функции распреде-
распределения f (r, v, г\) во времени под действием указанных полей. Допу-
Допустим сначалау что микрополя относительно слабо влияют на про-
процессы в плазме (это справедливо для плазмы с низкой концентра-
концентрацией и очень высокой электронной и ионной температурами).
В этом случае изменение f в некотором заданном элементе фазо-
фазового объема происходит вследствие того, что каждая фазовая
точка, изображающая отдельную частицу, непрерывно перемеща-
перемещается в геометрическом пространстве и пространстве скоростей.
Причиной движения в пространстве скоростей может быть наличие
в плазме макроскопического электрического поля Е (в общем слу-
случае Е — функция геометрических координат). Вычислив потоки
частиц, входящих в элементарный объем фазового пространства
й выходящих из него, нетрудно получить уравнение баланса ча-
частиц
dfldt=-(dr/dt) (dfldr)-(dvldt) (df/dy). A.81)
53
Поскольку dvldt=iqElmt где q и т — соответственно заряд и мас-
масса частицы, то A.81) равносильно уравнению
dfl&t=—vdfldr—(qElm)idfldv). A.82)
Это и есть кинетическое уравнение для заряженных частиц плаз-
плазмы (для электронов или ионов). В формуле A.82) dffdr обознача-
обозначает вектор с компонентами df/дх, df/dy, dfjdz и соответственно
df/dv есть вектор с компонентами dfldvXy df/dvy, df/dvz. Перене-
Перенесем все члены уравнения A.82) в левую часть и перепишем его
в следующем виде:
dfldt=dfldt+vdfldr+ (qE/m)dfldv=O. A.83)
В такой форме кинетическое уравнение имеет наиболее наглядный
смысл, так как A.83) означает сохранение плотности частиц в эле-
элементе фазового объема, движущемся вместе с выделенной группой
частиц. Формула A.83) —прямое следствие постоянства числа ча-
частиц и величины движущегося фазового объема (фазовый объем
сохраняется по теореме Лиувилля, поскольку движение происхо-
происходит в макроскопическом потенциальном поле).
Электрическое поле в плазме создается не только внешними
источниками, но также объемными зарядами электронов и ионов.
Вклад объемных зарядов плазмы в напряженность электрического
поля учитывается в дополнительном уравнении для Е:
div Е=4яр=4яе (J fidv— J f,dv). A.84)
Поле Е в этом уравнении называется самосогласованным
(поскольку существует обратная связь между Ей/). Пренебреже-
Пренебрежение микрополями отдельных частиц, Т; е. кулоновскими столкнове-
столкновениями, справедливо, если ограничиться изучением процессов, ра-
разыгрывающихся за времена, меньшие среднего времени свободного
пробега. Многие быстропротекающие явления в разреженной плаз-
плазме, где столкновения редки, можно рассматривать в рамках такого
приближения: колебания, развитие некоторых видов неустойчиво-
стей и т. п. Система уравнений A.83) и A.84), описывающая пове-
поведение бесстолкновительной плазмы, широко известна под названи-
названием «уравнения Власова».
В случае когда значительную роль в поведении плазмы играют
не только макроскопические поля Я>Го, но имикрополя отдельных
частиц, ответственные за процессы кулоновского рассеяния, равен-
равенство A.83) перестает быть справедливым. В отдельном акте куло-
кулоновского столкновения вектор скорости электрона (или иона) ис-
испытывает конечное изменение, и частица перебрасывается из одной
области пространства скоростей в другую. Поэтому в малом эле-
элементе фазового объема, который движется вместе с принадлежа-
принадлежащими к нему частицами вдоль фазовой траектории, определяемой
действием макроскопического поля, полное число частиц в общем
случае не должно оставаться постоянным. Учитывая роль куло-
новских столкновений, заменим A.83) следующим соотношением:
dfldt=St{f]. A.85)
54
Выражение, стоящее в правой части, называется интегралом
столкновений. Для того чтобы найти этот интеграл, нужно
вычислить результирующий эффект миграции частиц в пространст-
пространстве скоростей, происходящий вследствие процессов кулоновского
рассеяния. Не будем приводить здесь явное выражение для строго-
строгого интеграла столкновений не только потому, что такие вычисле-
вычисления выходят за рамки данной книги, но и потому, что многие свой-
свойства плазмы можно выяснить с помощью более простых приближе-
приближений. К наибольшим упрощениям ведет интерполяция интеграла
столкновений формулой
St{f}=(fo-/)/T. A.86)
Это так называемое т-приближение в кинетической теории. В при-
приведенной формуле т обозначает среднее время свободного пробега
частиц.
В правой части 'A.86) f0 — равновесная максвелловская функ-
функция распределения. Физический смысл правой части уравнения
A.86) заключается в том, что в результате столкновений восста-
восстанавливается максвелловское распределение по скоростям, / экспо-
экспоненциально приближается к */о с характерным временем устано-
установления т. Как видно из рассмотрения столкновений между
частицами плазмы, понятие т как среднего времени между столк-
столкновениями неоднозначно. Различные процессы в плазме характе-
характеризуются разными т, причем это различие может быть чрезвычай-
чрезвычайно большим. Так, время обмена энергиями между электронами
и ионами приблизительно в mi\me раз больше времени потери
импульса электронами при соударении с ионами. Даже для оди-
одинаковых частиц время столкновения зависит еще и от скорости.
Это означает, что пользоваться кинетическим уравнением в т-при-
ближении следует весьма осторожно. Выбирать т в интерполяцион-
интерполяционной формуле, заменяющей интеграл столкновений, нужно в зави-
зависимости от конкретной постановки задачи. Так, например, в задаче
о законе Ома следует выбрать х равным среднему времени потери
импульса электронами при столкновениях с ионами.
Покажем, как с помощью кинетического уравнения для элек-
электронов в т-приближении можно получить формулу для электро-
электропроводности. В этом случае кинетическое уравнение имеет вид
(eElme)df/dv=(fo—f) fr<*. A.87)
Пусть f=;fo+fl. При достаточно малом электрическом поле второй
член представляет собой лишь относительно небольшую добавку
к /о, и поэтому можно пренебречь произведением двух малых со-
сомножителей (еЕlme)dfi/dv. Тогда
(еЕ1те)д1о1ду=-и1хеи A.88)
Отсюда / = - е j vfx (v) dv = (ezEfme) zei j fodv = (ne*/me) zelE,
т. е. -приходим к выведенной в § 1.5 формуле электропроводности.
55
Теперь раскроем смысл приближения слабого электрического
поля. Условие fi^jfo можно объяснить с помощью формулы A.88),
пользуясь также тем, что по порядку величины dfo/dv^folvT-
В итоге получаем (eEjme) (tei/VrJ'Cl или (еЕ 1Те)!кег<^1. Это зна-
значит, что энергия, приобретаемая электроном в электрическом поле
на длине свободного пробега, должна быть намного меньше теп-
тепловой.
При нахождении коэффициента электронной теплопроводности
нужно учитывать столкновения электронов друг с другом и
с ионами. Напротив, в задаче об ионной теплопроводности пол-
полностью .ионизованной плазмы т — среднее время столкновения
иона с ионами; столкновения же ионов с электронами здесь можно
не учитывать, так как ионы' практически не рассеиваются на элек-
электронах. В тех случаях, когда существенны столкновения заряжен-
заряженных частиц с нейтральными атомами и молекулами, вводятся
другие характерные времена т. Следует еще раз подчеркнуть, что
кажущийся произвол, связанный с выбором т, в действительности
можно устранить при корректном подходе к отдельным конкрет-
конкретным задачам о поведении плазмы в различных физических про-
процессах.
Для определения коэффициента теплопроводности восполь-
воспользуемся методом кинетического уравнения. Если плазма находится
в стационарном состоянии, а внешнее электрическое поле отсут-
отсутствует, то
vdfldx=(fo-f)!x. A.89)
Здесь х — направление градиента температуры. Для достаточно
плотной плазмы, в которой длина свободного пробега I—vx мала
по сравнению с характерными линейными размерами, функцию
можно разложить в ряд по степеням малого параметра т: /=»/о +
+ /i+ ..., где /о — максвелловская функция распределения*:
(—mv2/2T(x)).
В следующем приближении имеем
f1 = -,vdf0/dx=[-n,v(ml2^/2] X
X (mv2l2T*/2— 1/2T312) exp (—mv2/T) дТ/дх.
Каждая компонента плазмы переносит поток тепла
<7 = J (v[2) mv2f (v) dv = f (v/2) mv2fQdv — f (v[2)*mv2Udv.
Первый из этих интегралов равен нулю. Вычисляя второй инте-
интеграл, находим, что
q=3nnx{Tlm)dTldx. A.90)
Суммарный поток тепла для плазмы получится, если сложить по-
потоки тепла, которые переносятся электронами и ионами. Однако
* Этот упрощенный расчет выполняется для одномерной модели плазмы.
56
из A.90) следует, что ионный поток тепла исчезающе мал по срав-
сравнению с электронным (так как те/т*<С1). Поэтому коэффициент
теплопроводности плазмы
x=3nm(Tel<me). A.91)
где т — время между двумя столкновениями для электронов. Здесь
нужно учитывать любые столкновения электронов (как друг с дру-
другом, так и с ионами). Но поскольку хее—teu то порядок величины
не изменится, если положить
и^C/2)ялтв*(Гв/тв). О-92)
Правильный численный множитель в этом выражении для коэф-
коэффициента теплопроводности дает строгая кинетическая теория
с точным, а не приближенным интегралом столкновений. Не прово-
проводя здесь слишком громоздких вычислений, приведем результат
такой строгой теории:
х=3,203(лГла//п)> A.93)
где ,,,= C,5.1071*) (Tfln).
Таким образом, в плазме носителями тепла и электрического
тока являются электроны (по крайней мере в отсутствие магнит-
магнитного поля).
В этом смысле плазма близка по своим свойствам к металлам.
Естественно, что и для плазмы справедлив аналог закона Видема-
на—Франца, утверждающий, что отношение коэффициента тепло-
теплопроводности к коэффициенту электропроводности пропорционально
температуре. Это следует из A.22) и A.93).
Однако упрощенная форма интеграла столкновений в т-при-
ближенни хотя и описывает установление максвелловского рас-
пределения, но не отражает основную особенность кулоновского
рассеяния, которая приводит к медленному («диффузионному»)
изменению вектора скорости частиц, имеющему место в результате
многократного рассеяния на малые углы. Л. Д. Ландау привел
интеграл столкновений между заряженными частицами к специаль-
специальной диффузионной форме (напоминающей диффузию по Фокке-
ру—Планку)^ учитывая рассеяние частиц только на очень малые
углы. Но даже этот вывод довольно громоздок. Воспользуемся
некоторыми дополнительными упрощениями, чтобы проиллюстри-
проиллюстрировать идею диффузионного подхода к интегралу столкновений.
При этом ограничимся рассмотрением функции распределения, за-
зависящей лишь от одной компоненты скорости f(v) (это значит,
что по двум другим составляющим скорости проведено интегри-
интегрирование), и будем считать, что рассеивающие заряженные части-
частицы находятся в состоянии теплового рашовесия с некоторой тем-
температурой Г.
В диффузионном приближении влияние многократных столкно-
столкновений приводит, вогпервых, к появлению силы динамического тре-
трения iFTp=—mw и, во-вторых, к диффузионному блужданию ско-
57
рости рассеиваемой частицы под действием толчков, создаваемых
тепловым движением рассеивающих зарядов. Соответственно в ин-
интеграле столкновений появятся два члена. Один из них, который
описывает регулярное изменение скорости из-за силы трения
dv/dt=—w, дает в левой части кинетического уравнения слагае-
слагаемое d(dv/dt)f/dv, т. е. —d(vvf)/dv. Оно совершенно аналогично
члену divr {(dvjdt)n)y т. е. div (v/i), в обычном уравнении непре-
непрерывности. Поэтому нет нужды в более строгом доказательстве.
Другой член описывает диффузию д(D\(v) df /dv) jdv с некоторым
коэффициентом ?>(<?>), который можно выразить через ту же часто-
частоту столкновений v, вводя эффективный шаг блужданий скорости
D(v)—Av2v. Строгое рассмотрение многократного рассеяния долж-
должно дать величину Av2. Однако при сделанном выше упрощающем
предположении о том, что рассеивающие частицы имеют опреде-
определенную температуру Г, ответ получить еще легче. Под действием
столкновений с рассеивающими зарядами, по сути дела играющи-
играющими роль термостата, функция распределения f(v) рассеиваемых
частиц должна стремиться к максвелловской с температурой тер-
термостата Г, так что интеграл столкновений
St{f}=(d/dv) [—vvf+D(v)df/dv] A.94)
должен обращаться в нуль в тех случаях, когда функция распре-
распределения f совпадает с максвелловской:
fo=const -exp (—mv2j2T).
Отсюда находим, что
D(v)=—(Tlm)v A.95)
и диффузионный интеграл столкновений
St{f}=-(dldv)[v(vf+(T/m)dfldv)].
Полученный результат весьма просто обобщается на трехмерный
случай, когда тензор коэффициентов диффузии
вид которого также можно определить из условия обращения
в нуль интеграла столкновений для равновесной максвелловской
функции распределения с температурой, равной температуре тер-
термостата:
D^ = -(T/me)v(v^!v>). .(L96)
Учитывая также возможность столкновения электронов с несколь-
несколькими рассеивающими центрами, интеграл столкновений запишем
в виде
st {f>=- 53 'к{Vj [vJ+р*1щ) (v^lzJ) wdv^ (I -97)
/p
53
58
В некоторых случаях, когда под действием каких-либо внешних
факторов (например, плазменной волны) в некоторой области про-
пространства скоростей у функции распределения рассеиваемых ча-
частиц появляются большие градиенты, в интеграле столкновений
для этой области скоростей достаточно удержать только вторую
производную. В этом случае эффективной оказывается следую-
следующая форма интеграла столкновений:
St{/}=-u2v((?2(/-f0) /^2), A.98)
которая также описывает установление максвелловского распреде-
распределения /о-
Детальный анализ свойств плазмы, связанных с влиянием
столкновений и строгим методом кинетических уравнений, слишком
громоздок и не входит в задачу авторов книги. Следует иметь
в виду, что (как уже отмечалось) для большого круга проблем
в физике плазмы (например, связанных с колебаниями и волна-
волнами) правая часть кинетического уравнения не существенна, если
речь идет о поведении плазмы за времена, значительно меньшие
времени свободного пробега.
§ 1.10. Гидродинамическое описание плазмы
Для понимания многих плазменных процессов очень полезной
оказывается гидродинамическая модель плазмы, в которой плазма
изображается как смесь электронной и ионной жидкостей. Эта мо-
модель применима для плазмы, у которой характерный линейный раз-
й~ер Ь во много раз превосходит длину свободного пробега /,
а характерная длительность процессов tp велика по сравнению со
временем между двумя столкновениями т. Величины L и iv обрат-
обратно пропорциональны скорости изменения функции распределения
частиц в пространстве и во времени: 1/L—A//) (bf/дх), \\tv^
—•(l/f) (df/dt). В этом случае, как было показано ранее,-функцию
распределения / для каждой компоненты плазмы можно разло-
разложить по малому параметру / или т. В нулевом приближении
f=f0=(ml2nT)l'2nexv (—m(v—uJl2T),
где п=п(ху t)\ T—T(x, t); u=u(x, t) (для простоты ограничиваем-
ограничиваемся одномерной задачей). В гидродинамической модели вся инфор-
информация о локальных свойствах любой компоненты содержится
в трех величинах: плотности п, температуре Т и средней скоро-
скорости и, которые пока остаются произвольными функциями х и /.
Подставляя в кинетическое уравнение разложение для f(f=fQ+
+fi+ .. .)> получаем в нулевом приближении
dhldt+vdfoldx+(qE im)dfoldv = St{f}. A.99)
Здесь в правой части оставлен интеграл столкновений для полной
функции распределения /, поскольку St{/0}=0, a St{f} имеет нуле-
вой порядок относительно параметра малости т//р *. В данном слу-
* St {f} не является аддитивной функцией аргумента, и поэтому нельзя на-
написать St {/}=St {/0}+St {fi} + ...
59
чае в уравнении A.99) мы имеем в виду строгое выражение инте-
интеграла столкновений, а не упрощенный вид в т-приближении. При
этом нас не должно смущать, что в строгом виде интеграл столк-
столкновений весьма громоздок. Как будет видно из дальнейшего, со-
совсем не обязательно знать явный вид интеграла столкновений,
можно использовать лишь некоторые его общие свойства — законы
сохранения. Ограничимся вначале анализом поведения электрон-
электронной и ионной компонент плазмы. Процессы ионизации и рекомби-
рекомбинации, вызывающие появление или исчезновение новых заряжен-
ньЬ^астиц, при этом учитывать не будем.
Что^м—построить гидродинамическую модель, проинтегрируем
уравнение A.99) для выбранной компоненты по всему пространст-
пространству скоростей. Интегралы от двух первых членов уравнения A.99)
представим в следующем виде:
(df./дх) dv = d ^vf.dvydx = d (nu)/dx
Здесь изменен порядок дифференцирования по t и х соответствен-
соответственно и интегрирования по dv, так как в кинетической теории t> x, v —
независимые переменные. При интегрировании третьего члена
уравнения A.99) по частям получается тождественный нуль:
Даже без конкретизации вида интеграла столкновений ясно, что
при отсутствии ионизации и рекомбинации полное число частиц
сохраняется.
Итак, имеем уравнение непрерывности
dn/dt+d(nu) jdx=O. (L100)
Умножим теперь уравнение A.99) на v и опять проинтегрируем.
Поступая так же, как и при выводе A.100), получаем
f}dv. A.101)
Если для обеих компонент плазмы (электронной и.ионной) сред-
средняя скорость и одинакова, то интеграл j v St{f)dV должен обра-
обращаться в нуль, так как не происходит оередачи импульса от одной
компоненты к другой. При этом условии равенство A.101) можно
с помощью A.100) привести к виду
nm(duldt + uduldx)=—d{nT)ldx+qEn. A.102)
Это уравнение Эйлера для заряженной жидкости. Заметим, что
в общем случае при наличии электрического поля щфие, и поэто-
поэтому между компонентами плазмы возникает сила трения. Эту силу,
которая для электронной компоненты на единицу объема равна
60
а для ионной компоненты
нужно прибавлять к правой части равенства A.102). Наконец,,
умножая уравнение A.99) на v2 и еще раз интегрируя, после не-
несложных выкладок с использованием A.100) и A.102) получаем
dTldt+udTldx+2Tduldx=0. A.103)
Это соотношение найдено в предположении о том, что интегралы
fjvSt{f}dv и J v2St {f}dv равны нулю. Первое условие справедли-
справедливо при щ=ие, а второе — ери Ti=Te. Если Т{фТе, то происходит
обмен тепловой энергией между компонентами плазмы и интеграл
J v2Si{f}dv не обратится в нуль ни для одной из них.
Уравнение A.103), очевидно, есть не что иное, как уравнение
одномерной адиабаты (v=3). Действительно,
так как р—пТ, а из A.100) dn/dt=—пди/дх. Для трехмерного
случая в результате аналогичных, но более громоздких вычислений,
можно получить в векторной форме следующую полную систему
уравнений «двухжидкостной» плазменной гидродинамики с уче-
учетом сил трения:
nemed\xefdt = — grad neTe — neeE -f- F€i.
В уравнениях AЛ05) du/dt—duldt-\-(ugrad)u. Векторное обозна
чение (ugrad)u расшифровывается как вектор с компонентами:
Сила трения F равна импульсу, передаваемому в единице объема
за секунду от частиц одной компоненты плазмы к частицам дру-
другой, в т-приближении ее можно записать в следующем виде:
Fei=—nme (Ue—Ui)Vei,
где Vei — частота столкновений между частицами разного сорта.
Аналог уравнения A.103) в трехмерном случае имеет вид
дГ/df+u grad Г+B/3)Г<Ну u=0 A.106>
(Ему соответствует показатель адиабаты 7=5/3.) Заметим, что*
при выводе уравнений основного гидродинамического приближе-
приближения из кинетического уравнения не обязательно знать явный вид
интеграла столкновений. Нет необходимости также вычислять по-
прав-ку /i в явном виде. Знание этой поправки позволило бы нам,
6*
найти диосипативные добавки (вязкость, теплопроводность и т. д.)
к уравнениям A.102), A.103) и к трехмерным обобщениям A.105),
A,106), но тогда нужно было бы задаться определенным видом
интеграла столкновений. При строгом рассмотрении эта задача
является довольно громоздкой. Она упрощается, если интеграл
столкновений на этом этапе представить в упрощенной форме т-
приближекия. Именно так был ранее найден коэффициент тепло-
теплопроводности.
Следует обратить внимание на то, что уравнения A.104) и
A.105), образующие основу гидродинамического приближения
в теории плазмы, были выведены из более общего .кинетического
уравнения, однако их можно получить гораздо более простым пу-
путем при анализе макроскопических свойств плазмы. Уравнения
A.104) имеют смысл закона сохранения числа частиц каждого
сорта, а уравнения A.105) суть второй закон Ньютона примени-
применительно к движению единичного объема — электронной и ионной
компонент плазмы — под действием градиентов давления, электри-
электрического поля и сил взаимного трения.
В описанной картине плазма является смесью двух взаимопро-
взаимопроникающих жидкостей, взаимодействующих друг с другом через
самосогласованное электрическое поле и силу трения из-за парных
•соударений. Во многих задачах, когда плазма сохраняет свою ква-
квазинейтральность пе—П{=п, удобно пользоваться и более простой
моделью одножидкостной гидродинамики. Складывая уравнения
A.105) для ионов и электронов и принимая во внимание, что чле-
члены, обусловленные трением между электронной и ионной компо-
компонентами, сокращаются, получаем
(и grad)u]=—grad(/?i+pe), A.107)
где
Это основное уравнение одножидкостной гидродинамики плазмы
уже не содержит электрического поля.
Следует подчеркнуть, что в плазме электрическое поле, как
правило, возникает и в том случае, если нет внешнего источника.
Вообще говоря, согласно условию сохранения квазинейтральности
потоки электронов и ионов через любую замкнутую поверхность
должны быть равны. Поскольку электроны подвижнее ионов, то
при возникновении градиента давления электронный поток из об-
области высокого давления в область более "низкого сначала превы-
превысит поток ионов. Вследствие этого произойдет поляризация плазмы
и появится электрическое поле, которое будет тормозить электро-
электроны и ускорять ионы.
До сих пор рассматривался случай полностью ионизованной
плазмы. В слабоионизованной среде заряженные частицы, пред-
представляющие слабый раствор плазмы, не могут разогнаться под
действием собственных градиентов давления вследствие торможе-
62
ния из-за частых столкновений с нейтральными частицами. Основ-
Основной вклад в силу трения должны давать столкновения ионов с ней-
нейтральными атомами и молекулами:
FTP=—niiWivio. A.108)
Когда градиент полного давления плазмы grad(p* + Pe) уравно-
уравновешивается трением о нейтральный газ, движение плазмы носит
характер диффузии. Действительно, из условия баланса силы тре-
трения и градиента давления имеем
—grad р—miUnvio—0;
и——(nmmo^gradp. A.109)
В случае однородности температуры 7(r)=const, следовательно,
и=— (T/nrriiVio) grad n.
Подставляя это выражение для скорости в уравнение непрерывно-
непрерывности
dn/dt + div nu=0,
получаем
dnfdt=(T/miVio) div grad n. A.110)
Это уравнение описывает диффузионный процесс с «коэффициентом
диффузии
0=Т/тто. A.111)
Заключая разбор гидродинамического описания плазмы, следу-
следует подчеркнуть, что деление плазм на гидродинамические и кине-
кинетические было бы в корне ошибочным. Один и тот же плазменный
объект б одно и то же время может обнаруживать и гидродина-
гидродинамические, и кинетические (беестол'кнов'ительные) свойства. Так,
например, плазма газового разряда в макроскопических масшта-
масштабах, как правило, достаточно хорошо описывается в рамках ги-
гидродинамической модели (включая явления переноса: диффузия,
закон Ома и т. д.). Вместе с тем в микроскопических масштабах
(с характерными размерами, много меньшими длины свободного
пробега) поведение той же плазмы газового разряда всегда носит
бесстолкновительный характер. В такой плазме вообще можно
пренебрегать обычными столкновениями. К процессам, которые
нужно рассматривать в микроскопической шкале, относятся коле-
колебания плазмы, распространение электромагнитных волн, затухание
волн по Ландау. Таким образом, граница раздела между разными
методами описания является границей раздела не видов плазм,
а явлений, происходящих в них. Подобно тому как явления с ха-
характерными длинами, значительно превышающими длины свобод-
свободного пробега, составляют особый предмет — гидродинамическое
описание плазмы, микроскопические процессы с характерными
масштабами, много меньшими длины свободного пробега, состав-
составляют самостоятельный раздел физики плазмы — бесстолкновитель-
ную плазму, описываемую системой бесстолкновительных кинети-
63
ческих уравнений. Следует иметь в виду, что кинетическое описа-
описание плазмы намного более громоздко, чем описание в рамках ги-
гидродинамических уравнений, и было бы крайне тяжело для описа-
описания всех бесстолкяовительных процессов применять кинетический
метод. Однако в некоторых случаях этот метод описания бесстолк-
новительной плазмы можно существенно упростить путем перехода
.к уравнениям своеобразной бесстолиновительной гидродинамики.
Физическая причина возможности такого перехода совершенно
иная, чем в обычной гидродинамике.
Дело в том, что бесстолкновительная гидродинамика обычно
применяется для описания волновых и колебательных процессов,
когда кроме частоты столкновений возникает еще один характер-
лый временной масштаб — частота колебаний. Если в столкнови-
тельном случае переход к гидродинамике, т. е. пренебрежение теп-
тепловым движением частиц, означает малость длины свободного про-
пробега vt/v по сравнению с характерным пространственным масшта-
масштабом задачи L, то в беюстолкновительном случае переход к гидро-
гидродинамике и пренебрежение тепловым движением возможны при
условии малости параметра vT/(o по сравнению с длиной волны Я.
Последнее условие фактически означает, что бесстолкновительная
гидродинамика применима, если тепловая скорость частиц много
меньше характерной скорости возникающих в плазме волновых
движений. Система уравнений бесстолкновительной гидродинами-
гидродинамики состоит из уравнений A.104) и A.105), в которых не учиты-
учитывается сила трения.
§ 1.11. Звук в плазме
В начале книги говорилось о ленгмюровских колебаниях. Было
отмечено, что кроме электронных колебаний существуют также и
звуковые (иногда их называют ионно-звуковыми), обу-
обусловленные движением ионов. Свойства всех видов колебаний мож-
можно исследовать единым методом на основе кинетических уравнений
(см. § 1.12). Здесь же мы проведем более простой и наглядный
анализ звуковых колебаний плазмы в рамках гидродинамической
модели.
Как и в любой сплошной среде, при звуковых колебаниях плаз-
плазмы роль квазиупругой возвращающей силы играют силы газового
давления. В одножидкостной гидродинамике плазмы [см. уравне-
уравнение A.107)] давление складывается из суммы электронного <и
ионного p=pi+pGy и соответственно этому хорошо известное вы-
выражение для скорости звука в обычной сплошной среде cs=
= (dp;dpI/2 трансформируется в [д(р;+ре)/ф]1/2. Как обычно,
здесь под частной производной подразумевается так называемая
адиабатическая производная, вычисляемая при постоянной энтро-
энтропии. Тогда c2s=y(Te-\~Ti) jrrii при *v = 5/3.
Процессы последовательного сжатия и расширения плазмы
¦в звуковых волнах можно считать адиабатическими, если возни-
<64
кающие при этом перепады температур не успевают выравниваться
из-за теплопроводности. Сравним член дТ[dti, описывающий коле-
колебания температуры в уравнении баланса тепла, с членом %АТ, опи-
описывающим теплообмен. В звуковой волне при Т—exp [i(kx—wt)]
производная по времени dT/dt=—icoT, а второй член превращается
в %А7=—yk2T. Тогда условие адиабатичности dTjdt*>y\k2T примет
вид <о^>&2х- Но электронная и ионная компоненты плазмы имеют
сильно различающиеся коэффициенты теплопроводности (см.
§ 1.9). Труднее выполнить условие адиабатичности для электрон-
электронной компоненты. Неравенство ay^>Jz2x можно представить в виде
A.112)
где X — длина волны. Подставляя сюда вместо % электронную тем-
температуропроводность %е—leVTe/З, получаем неравенство
А,>Bя/в/3) (пц\теу1\ A.113)
Это значит, что полностью адиабатическими являются только зву-
звуковые колебания с длиной волны, по крайней мере на два порядка
большей длины свободного пробега электронов. При обратном
условии
4(I/2Я A.114)
но при \^>U звук изотермичен для электронной компоненты, «о
адиабатичен для ионной. Выражение для скорости звука в этом
случае можно записать так:
c5=(re/mi+E/3)ri/miI/2. A.115)
Таким образом, аналогия со звуком в обычном сжимаемом газе
не является полной из-за двухкомпсшентности плазмы. Однако по-
настоящему аномальные свойства плазмы проявляются при еще
более коротких длинах волн. Обычный звук с приближением длины
волны к длине свободного пробега начинает все сильнее затухать
(из-за вязкости и теплопроводности) и при условии %<Cl вообще
не может существовать. Ясно, что любое возмущение плотности
в свободномолекулярном потоке рассеивается из-за теплового дви-
движения отдельных частиц. В плазме же при отсутствии парных
столкновений частицы взаимодействуют через самосогласованное
электрическое поле. Подобно тому как электрическое поле такого
типа приводит к ленгмюровским колебаниям электронов, возникает
возможность существования и колебаний звукового типа, в кото-
которых участвуют и ионы, если частоты колебаний настолько малы,
что ионы успевают реагировать на изменения поля.
Таким образом, упругая связь между электронной и ионной
компонентами в коротковолновом звуке осуществляется благодаря
возникновению электрического поля, а температуры электронов и
ионов в такой звуковой волне остаются постоянными.
Сделаем небольшое отступление и отметим одно общее обстоя-
обстоятельство, весьма важное для волновых процессов в плазме. Вооб-
Вообще говоря, как и в любой физической системе, колебания в плаз-
5—74 65
ме являются -нелинейными. Однако исследование волновых и коле-
колебательных процессов в плазме целесообразно начать с линейной
теории. В линейной теории рассматриваются колебания плазмы
достаточно малой амплитуды, соответствующие малым возмуще-
возмущениям исходного равновесного состояния плазмы, на фоне которого
они развиваются. В кинетической теории малость амплитуды коле-
колебаний означает, что возмущение функции распределения, связан-
связанное с колебаниями и волнами, ъо всей физически важной области
скоростей мало по сравнению с исходной равновесной функцией
распределения: f=fo + 6f; 6f<Cfo. Соответственно этому в гидроди-
гидродинамической теории следует считать, что все физические величины,
связанные с колебаниями и волнами, также достаточно малы:
б/г<ло, ар<тах(Г, тсо2/?2), 6и<<о/?, |<1/?,
где Ьп — возмущение плотности в колебаниях; ср— их характерный
потенциал; 6м и g — характерное значение скорости и смещения
частиц в колебаниях соответственно. Поэтому основная математи-
математическая процедура, которая превращает общие уравнения колеба-
колебаний, будь то кинетические уравнения или уравнения гидродинами-
гидродинамики, в уравнения линейной теории, — это процедура линеаризации.
Линеаризация означает, что все физические величины, характери-
характеризующие состояние плазмы, представляются в виде суммы их рав-
равновесного значения и возмущения, связанного с колебаниями и
волнами, и' в исходных уравнениях пренебрегается слагаемыми
второго и более высокого порядка по амплитуде возмущений.
Вернемся теперь к рассмотрению бесстолкновительного звука,
ограничившись в этом параграфе линейной теорией. Можно ожи-
ожидать, что, как и в стол'кновительном случае, рассматриваемая зву-
звуковая волна достаточно медленная — ее фазовая скорость много
меньше тепловой скорости электронов. Фактически это означает,
что возмущение, создаваемое волной, является квазистатическим
для электронов и в изменяющемся со временем электрическом по-
поле волны они всякий раз успевают «подстроиться» под стационар-
стационарное распределение Больцмана:
пе=по ехр{е<р/ Те}. A.116)
Для колебаний малой амплитуды следует, как мы уже знаем, ли-
линеаризовать эту формулу. В результате линеаризации находим, что
возмущение электронной плотности связано с потенциалом волны
следующим соотношением:
A.116а)
Для ионов, наоборот считаем выполненным условие
Как отмечалось выше, это и есть условие применимости бесстолк-
новительной гидродинамики. Поэтому движение ионов в бес-
бесстол кновительной звуковой волне будем рассматривать с помощью
линеаризованной по амплитуде возмущений гидродинамической
66
системы уравнений без силы трения:
Сравнивая различные слагаемые в этих уравнениях, нетрудно по-
показать, что силой давления [последнее слагаемое в травой части
A.117)] при выполнении условия со>>tori можно пренебречь.
Сделаем еще одно дополнительное предположение, а именно
будем считать, что длина волны рассматриваемых здесь ионно-
звуковых колебаний все же достаточно велика по сравнению с де-
дебаевской. Тогда, поскольку ионно-звуковая волна для электронов
является квазйстатической, к ней применимы соображения § 1.2
о квазинейтральности плазмы. Оторвать электроны от ионов с по-
помощью их энергии взаимодействия в волне можно только на рас-
расстояниях масштаба дебаевской длины. Ионно-звуковые колебания
с длинами волн много больше дебаевской длины являются квази-
квазинейтральными: б/ге=^6пг=б^. В этом случае с учетом A.116а)
систему уравнений A.117) можно записать в виде
, )
который совпадает с видом линеаризованных уравнений обычной
газовой динамики изотермического газа (y=1). Фазовая ско-
скорость звуковой волны в таком газе равна
а>/к=(Те1т{I'2. A.119)
Но в рассматриваемом здесь случае плазмы звук с таким законом
дисперсии является бесстолкновительным. Подобно ленгмюров-
ским колебаниям звук также испытывает бесстолкновительное за-
затухание из-за резонансного взаимодействия с тепловыми части-
частицами плазмы. Физический механизм затухания был разъяснен
в § 1.2 на примере ленгмюровских колебаний. Звуковая волна
может затухать в результате взаимодействия как с ионами, так
и с электронами. Однако поскольку параметр (x}/kvTi={Te/TiI^,
то при выполнении условия Те^>Тг (горячие электроны, холодные
ионы) в резонанс со звуковой волной попадает лишь небольшое
количество ионов на «хвосте» распределения Максвелла, и затуха-
затухание на ионах оказывается экспоненциально малым. С ростом
ионной температуры все больше и больше ионов может попадать
в резонанс. При этом если Гг~Ге, то уже основная масса ионов
даст вклад в затухание Ландау ионно-звуковых колебаний,
а декремент затухания станет сравним с частотой колебаний, т. е.
распространение ионного звука окажется невозможным. Поэтому
существование слабозатухающих бесстолкновительных ионно-зву-
ионно-звуковых колебаний требует неизотермичности плазмы, т. е. Те^>Тг.
Что же касается бесстолкновительного затухания звука на
электронах, то его декремент является малым по отношению
5* 67
к частоте ~ (те/т^1/2. Качественно это можно разъяснить следу-
следующим образом. Фазовая скорость волны существенно меньше теп-
тепловой скорости электронов !со/?уте~ {те/тг)У2 и резонансное
затухание на электронах возникает в той области электронной
функции распределения, где ее градиенты df/rfv малы и, как
следует из формулы A.5), см. § 1.2, соответственно -мало и бес-
столкновительное затухание. Подробно вопрос о бесстолкновитель-
ном затухании ионно-звуковой волны рассмотрен в § 1.12.
Отклонение от квазинейтральности в ионном звуке, как уже
отмечалось выше, становится существенным на очень малых дли-
длинах волн, сравнимых с дебаевской длиной. Распределение электро-
электронов в такой коротковолновой ионно-звуковой вол-не-» по-прежнему
остается больцмановским и Ьпе определяется формулой A.117).
Систему уравнений A.118) для ионов следует дополнить урав-
уравнением Пуассона -для потенциала ионно-звуковой волны. Полу-
Получающаяся при этом система уравнений, которая описывает корот-
коротковолновый ионный звук, имеет -вид
dt^ — iTJn,) дЬпе(дх\ L A.120)
дЧпе\дх*=.(Ьъе*п,{Т^ (8я, — Ъпв) ]
Подставляя в эти уравнения все волновые величины в виде
exp{i(kx—о/)}, приходим к следующему дисперсионному урав-
уравнению:
eo2=co2piAV2D/(^2r2D+l), A.121)
где со2рг=4яе2/г/ш* — квадрат ионной плазменной частоты. В пре-
пределе длинных волн Х^гв из уравнения A.120) следует получен-
полученный ранее закон дисперсии A.119). С уменьшением длины волны
становится существенной дисперсия фазовой скорости — фазовая
скорость уменьшается при продвижении в область коротких длин
волн и, наконец, при й->оо (А<СПэ) стремится к нулю, а частота
ионного звука стремится к ионной плазменной коР{.
Полученный результат имеет .весьма простое объяснение. Из-за
теплового движения частота электрического поля, действующего
на электроны, сдвинута по Доплеру: co-^jco—kvTe\. Для очень
коротких длин волн (Х<^гт>) kvTe^tope, т. е. эффективная частота
поля, действующего на «средний» электрон, существенно больше
электронной плазменной частоты, и электроны не успевают участ-
участвовать в колебаниях. В результате для столь коротких длин волн
плотность электронов остается практически невозмущенной и мы
вновь получаем ленгмюровские колебания зарядов одного знака
относительно зарядов другого знака, так же как и в высокочас-
высокочастотных ленгмюровских колебаниях (см. § 1.2). Единственное раз-
различие состоит в том, что если в. высокочастотных колебаниях
происходят колебания электронного заряда относительно непо-
неподвижных ионов, то в коротковолновом ионном звуке ионный заряд
со
со/к=с
Рис. 1.11.
Ветви колебаний в однородной
изотропной плазме
решетки.
колеблется на электронном фоне и соответственно этому частота
этих колебаний 'совпадает с ионной плазменной.
Результаты -проведенного в книге исследования колебаний
изотропной плазмы суммированы на рис. 1.11. Кроме электромаг-
электромагнитной волны со*= ((o2Pe+k2c2I12 в такой плазме существуют две
ветви чисто 'продольных колебаний. Это высокочастотные ленгмю-
ровские колебания оУ= ((o2pe-\-3k2v2TeI/2 и низкочастотные ионно-
звуковые колебания с законом дисперсии cos(&), определяемым
формулой A.121). В этих
формулах индекс t относит-
относится к электромагнитной вол-
волне (от слова transversal —
поперечный), индекс I —
к продольной плазменной
волне (от слова longitudi-
longitudinal — продольный), индекс
5 — к ионно-звуковой волне
(от слова sound — звук).
Обратим здесь внимание на
существование достаточно
глубокой аналогии между
продольными колебаниями
в. плазме и упругими коле-
колебаниями атомов и ионов в узлах кристаллической решетки
Роль электрических сил, возникающих яри колебаниях заряда
в плазме, в решетке выполняют упругие силы, возвращающие ато-
атомы (ио'ны) к -положениям равновесия. При этом, например,
в двухатомной решетке 'существуют две ветви колебаний — опти-
оптическая ветвь, в которой атомы (либо ионы) разных сортов при
колебаниях движутся навстречу друг другу <и которая аналогична
колебания^ плотности заряда — ленгмюровским колебаниям
в плазме, и акустическая ветвь, в которой атомы (ионы) сме-
смещаются в одном направлении и которая аналогична ионно-звуко-
вым колебаниям плазмы.
До сих пор при рассмотрении колебаний, плазмы мы исполь-
использовали гидродинамическую систему уравнений. В следующем
параграфе излагается кинетическая теория колебательных и вол-
волновых процессов в ллазме. Такой подход позволяет не только
получить ^ с едино? точки зрения все уже известные нам ветви
колебании, но и количественно строго рассмотреть эффект резо-
резонансного взаимодействия колебаний с частицами. По этой причине
кинетическая теория имеет крайне важное значение в теории
коллективных взаимодействий в плазме.
§ 1.1-2. Кинетическая теория волн в плазме
Наиболее важной демонстрацией метода самосогласованного
поля в кинетической теории плазмы является вывод дисперсион-
дисперсионного соотношения для различных типов колебаний плазмы с по-
69
мощью бесстолкновительного кинетического уравнения. Предполо-
Предположим, что распространение плоской монохроматической волны
с частотой со и волновым числом к сопровождается появлением
(из-за поляризации плазмы) самосогласованного электрического
поля с потенциалом
<р = ср exp {ikx — iwt}.
Также как -и в гидродинамической модели малых колебаний,
р. кинетической теории используется метод линеаризации. Функцию
распределения ионов (электронов) ищем в виде
fi = f0i(v)+6fi{X,V, t).
Здесь fa — функция распределения в равновесном состоянии
(невозмущенная). Поправку 6fif связанную с предполагаемой зву-
звуковой волной, считаем малой. Тогда кинетическое уравнение для
нее примет вид
dufifdt+vdufildx— {е/гпг) (дфх) dfoi/dv = О A.122)
(в последнем слагаемом слева мы пренебрегли нелинейным чле-
членом (e/nii) (dq>/dx)ddfildv, поскольку он имеет второй порядок
малости). Из уравнения A.122) видно, что б/* пропорционально ср
и, следовательно, также ведет себя как 'exp[i(kx—Ы)]. Подстав-
Подставляя в A.122) 6fi = 8fiexp{i(kx—со/)}, получаем
— i (со — ко) bfi — (efmt) ik ?dfoi/dv = 0. A.123)
Таким образом, воамущение плотности ионов
^dv, A.124)
Рассуждая точно так же, для возмущения плотности электронов
можно написать
По сравнению с формулой A.124) здесь заменены, все индексы
ионов (заряд и масса). Теперь воспользуемся тем, что электриче-
электрический потенциал и пространственный заряд еF/г*—Ьпе) связаны
уравнением Пуассона
к*у = 4>*е (Ьп1 — Ьпе). A.126)
Выразив плотность заряда с помощью A.124) и A.125) и под-
подставив в A.126), получим следующее уравнение:
mi \ J to — kv ' те J со — kv
\ A.127)
эквивалентное обращению в нуль диэлектрической проницаемости
плазмы:
+ пн_ с kdUdv d%) \ AЛ28)
где «е, 8i — вклад электронов и ионов в диэлектрическую прони-
проницаемость. Конкретный вид ге и е* очевиден из соотношения A.128).
Уравнение A.127), которое в неявном виде содержит зависи-
зависимость со = со(&)—закон дисперсии, называется общим диспер-
дисперсионным уравнением колебаний плазмы без
магнитного поля. Из уравнения A.127) можно вывести
ранее исследованные свойства всех видов продольных колебаний
плазмы.
Рассмотрим сначала звуковые колебания. Прежде всего при-
приведем оба слагаемых в фигурных скобках правой части уравнения
A.127) к более простому виду. Начнем со второго слагаемого,
представляющего собой вклад электронов. В предыдущем пара-
параграфе показано, что- средняя тепловая скорость электронов на-
намного больше фазовой скорости звуковых волн (x)fk<^vTe (или
co<c?t>re). По этой причине в основной области интегрирования
в знаменателе подынтегрального выражения 1/(со—kv) для элек-
электронов можно пренебречь со по сравнению с kv. Упрощенный
интеграл §(dfoe/dv)dvlv для максвелловского распределения
электронов по скоростям /гое=Яо(^е/2яГеI/2ехр(—mev2/2Te) равен
—ПоШе/Те, Т. е. 8е== 1 /&2Г2О.
При вычислении «ионного» 'интеграла (первое слагаемое в фи-
фигурных скобках) следует предположить, что фазовая скорость
волб существенно превышает среднюю тепловую скорость ионов
(u^kvTi- Согласно § 1.11 это условие выполняется лишь в плазме
с холодными ионами Ti<^Te. Если в знаменателе выражения для
ионов в формуле A.126) пренебречь kv по сравнению с <о, то
интеграл тождественно обратится в нуль. Следовательно, нужно
удержать второй член в разложении
В результате получаем
\Ш*>) (kvh2) dv=- (*M J hidv=
что приводит к следующей формуле для .е*: Si = — (о2Рг/со2.
Подставив в A.127) полученные выражения для интегралов,
представим дисперсионное уравнение в виде
&= Dле2п/гт) {&№^пц1Те}. A.129)
Нетрудно убедиться, что результат полностью совпадает с диспер-
дисперсионным" уравнением бесстолкновительных звуковых колебаний,
71
¦которое получено ранее при гидродинамическом рассмотрении
A.121).
Физический смысл бесстолкновительного затухания волн
в плазме детально исследовался в § 1.2 на примере ленгмюров-
ских колебаний. Бесстолкновительное затухание своим возникно-
возникновением обязано поглощению энергии волны частицами, движущи-
движущимися со скоростью равной фазовой и поэтому длительное время
сохраняющими фазовый резонанс -с 'волной. Поэтому (при рас-
рассмотрении количественной стороны эффекта естественно исполь-
использовать закон сохранения энергии в системе волна — резонансные
частицы. Для его вывода обратимся к дисперсионному уравнению
A.127). Учтем, что диэлектрическая проницаемость плазмы, ко-
которая определяется интегралами по скоростям частиц, входящими
в правую часть A.127), в действительности имеет небольшую
мнимую часть, математическая 'причина ее возникновения — на-
наличие особенности (полюса) подынтегрального выражения в точ-
точке v=xu/\k. Появление мнимой части диэлектрической проницае-
проницаемости как раз и приводит к возникновению 'бесстолкнов'ительного
затухания волны. Разобьем диэлектрическую проницаемость на
действительную я мнимую части:
е(<о, *)=е'(ю, k)+ie"(a>, k).
Тогда действительная часть частоты 'ю/(а>=«о/+гу) будет реше-
решением действительной части дисперсионного уравнения:
•8'(о/, k)=0.
Уравнение для у— это мнимая часть дисперсионного уравнения.
При у<;>©', т. е. при е"<^е', уравнение
1те'(о)+е"(<о)=0
можно привести к виду
удг'1дп'=—г"(а>'), A.130)
разложив ¦г/(<д-\-[у) в ряд с точностью до первого члена по ty/co.
Домножим обе части уравнения A.130) на ы\Е\2/Ал. Тогда, учи-
учитывая, что
d\E\ydt=2y\E\>,
а диэлектрическая проницаемость е связана с проводимостью а
соотношением e=i4jwj/(o, представим уравнение для у ъ следую-
следующем виде:
dfdtv дг/дхо(Е2/8п) =— Re-a(?2). A.131)
Здесь угловые скобки означают усреднение по длине волны коле-
колебаний. Это уравнение выражает закон сохранения энергии в си-
системе волна — резонансные частицы. Величина
ш = со<?е/(Эсо(Я2/8я} A.132)
имеет смысл энергии монохроматической продольной волны, кото-
которая -складывается из потенциальной энергии (энергии электриче-
72
ского поля) волны w1J0T= (?2/8я) и энергии колебаний частиц
яУкол. Используя 'приведенные выше выражения для ге и е*, для
энергии ионно-звуковой волны получаем
). A.133)
Вклад в эту энергию дают кинетическая энергия колебаний ионов
колебательная энергия электронов
(считалось, что только квадратичные по амплитуде волны вели-
величины имеют отличное от нуля среднее значение, и в соответствии
с этим оставлено под знаком среднего только слагаемое, пропор-
пропорциональное б/z), и, наконец, потенциальная энергия волны
( ?2/8я). Для длинноволновых ионно-звуковых колебаний основ-
основной вклад в энергию обусловлен колебательной энергией частиц —
естественный результат, поскольку для длинноволновой звуковой
волны с малым разделением зарядов электрическое поле также
мало, иначе говоря, плазма почти квазинейтральна.
Изменение во -времени энергии волны определяется диссипа-
диссипацией, связанной с взаимодействием волна — резонансные частицы.
Диссипируемая мощность пропорциональна Re а, и ее можно
представить в виде работы поля волны Е над резонансными час-
частицами: Rea?2=(!/Pe3?).
Возвращаясь к амплитуде потенциала электростатической вол-
волны фь, закон сохранения энергии в системе волна — резонансные
частицы запишем в следующей форме:
k-^E). A.134)
Диссипация энергии волны, связанная с резонансными частицами,
как ясно из приведенного выше вывода, выражается через мнимуй
часть е (со, k), ее легко можно найти из конкретной формулы для
е (со, к) [см. A.128)]. Мы, однако, проведем здесь независимый
выдод формулы для диссипируемой мощности ( /Рез? ), посколь-
поскольку такой вывод,проясняет физический смысл бесстолкновительного
затухания Ландау.
Ток Я>ез просто выражается через возмущение равновесной
функции распределения резонансных частиц
где суммирование проводится по двум сортам частиц— электро-
электронам и ионам. Подставляя сюда функцию распределения б/ из
73
уравнения A.123), можно легко вычислить «среднее в правой части
"уравнения A.134). Рассмотрим, для примера, ионный вклад:
(ГЕ) = ({(*72*1<) j n^d!l/dJ ехР 0 (Ь* - <¦*» + к. с. | X
X { - ^ % exp {i (?x - arf)} + к. с. J) = A /4) (е2/^-) 9*kk^vdfJdoX
(kv — <D) — K.c.)dv. A.135)
Здесь проведено усреднение по времени и учтено, что величины
6f,f <р — вещественны. Использованное ранее комплексное представ-
представление этих величин справедливо только в линейной теории, при
вычислении же квадратичных комбинаций, таких. как (/?)>
в приведенных выше формулах для 6/ и ф надо прибавить комп-
комплексно сопряженные слагаемые и множитель 1/2.
Из A.135) следует, что из-
• v=co/k + i/kr менение амплитуды волны свя-
___ | \ занос резонансной областьюско-
\^у ~~v ростей р^ы/к, в которой имеется
особенность подынтегрального
Рис. 1.12. Обход особенности, возни- выражения. Здесь мы вновь стал-
кающей в кинетической теории коле- киваемся С ОДНИМ ИЗ ТИПОВ резо-
баний плазмы из-за резонанса Лан- нансных плазменных явлений,
дау о которых уже упоминалось
в § 1.7. В данном случае речь
идет о резонансе между частицей и волной, фазовая скорость кото-
которой совпадает со скоростью частицы ь = щ\к (резонанс Ландау).
Как и раньше, для того чтобы устранить особенность в резонансе,
введем в рассмотрение бесконечно 'малое затухание волны, свя-
связанное со столкновениями. Тогда из кинетического уравнения со
stoss-члеяом в форме A.86), следует, что учет столкновений при-
приводит к замене co-^co + i/t. Положение полюса v=<x)/:k + i/kx сме-
смещается с действительной оси в верхнюю 'полуплоскость. Отсюда
следует, что при интегрировании по v в формуле A.135) особен-
особенность подынтегрального выражения в точке v=wjk надо обходить
снизу (рис. 1.12), в результате имеем
lim \Hko-ш—i/x) = #{1/(&> —m)}-J-k8(fo — со). A.136)
1/0
Здесь символ 0* — главное значение, ё(х)—дельта-функция. Та-
Такое направление обхода особенности принято называть правилом
обхода Ландау.
Подставляя в A.135) l/{kv—со) из A.136), выполняя интегри-
интегрирование по v с учетом б-функции и суммируя вклад от ионов и
электронов, приходим к следующему уравнению для амплитуды
волны:
^j[l(/)]p
X{dfoi/ dv-\- (mi/ trie) dfoe/ dv}.
v=to/k A.137)
74
Для звуковой волны с законом дисперсии со = &GУтгI/2, предпо-
предполагая равновесные функции распределения электронов и ионов
максвелловскими, получаем
Т ^ - (*/8I/2 « {(mjmtf2 + (TJTf2 exp (- Ге/2Г,)}, A.138)
что подтверждает возможность существования слабозатухающей
G<С<о) звуковой волны в неизотермической (Te^>Ti) плааме.
Ионно-звуковые колебания плазмы напоминают фононы в ме-
металлах. Вместо неравенства Т{<^Те в металлах T<^EF (EF—
энергия Ферми электронов). Таким образом, роль Те играет EF.
Скорость звука в металлах порядка (EF/niiI12, а закон дисперсии
напоминает зависимость, показанную на рис. 1.11.
В термодинамически равновесной плазме для ионно-звуковых
колебаний устанавливается спектр Рэлея—< Джинса. Взаимодейст-
Взаимодействие электронов с такими тепловыми шумами звуковых волн дает
вклад в длину свободного пробега по сравнению с парными куло-
новскими столкновениями (как это было в случае ленгмюровских
колебаний). Нетрудно представить, что 'при неустойчивых ионно-
звуковых колебаниях, когда уровень шумов становится достаточно
большим, длина свободного пробега может в основном опреде-
определяться коллективным взаимодействием электронов с ионно-зву-
ковыми колебаниями.
Основная неустойчивость, специфическая для ионного звука,—
это неустойчивость, возникающая в плазме с достаточно большим
электрическим током. Действительно, в 'плазме с током электроны
должны иметь относительно ионов среднюю скорость иОеу связан-
связанную с плотностью тока соотношением j=enuOe. Тогда функция
распределения электронов имеет вид
.foe= С exp[—me(v—uoe) 2/<2Г].
Используя эту функцию распределения для электронов и пред-
предполагая, что ионы сохраняют ма'ксвелловское распределение (их
токовая скорость в гп{/ше раз меньше скорости электронов), полу-
получаем из A.137) следующую формулу для декремента:
у=—(я/8) ^М (со—ки<>еIк(Те1пцУ'2+
Видно, что при иОе>ы/]к~ (Те/гП{I12 вклад электронов в декремент
меняет знак, т. е. электроны вместо поглощения могут раскачивать
ионно-звуковые колебания. Если ионная температура достаточно
мала, то этот эффект перевешивает ионное затухание, и возникает
своеобразная когерентная накачка ионного звука электронами.
Развитие такой неустойчивости может привести к резкому воз-
возрастанию электрического сопротивления. Но плазма с сильно
возбужденными хаотическими ионно-звуковыми колебаниями на-
находится в своеобразном турбулентном состоянии, трудно поддаю-
поддающемся теоретической интерпретации. Основной метод, используе-
75
мый теоретиками, .заключается в представлении 'подобной турбу-
турбулентности как некоего газа квазичастиц — волн (в данном случае
ионно-звуковых). В такой теории, которая здесь рассмотрена ни-
ниже, нелинейные эффекты при больших амплитудах волн интерпре-
интерпретируются как столкновения квазичастиц — волн.
Ионно-звуковая неустойчивость реализуется только при не
слишком больших скоростях электронного потока, когда направ-
направленная скорость электронов меньше их тепловой скорости. При
больших скоростях электронов, (больших электрических токах)
возникает так называемая неустойчивость Бунемана —
раскачка связанных друг с другом колебаний «плотности заряда
электронной и ионной компонент плазмы.
Известно, что в плазме возможны два типа колебаний плот-
плотности заряда: быстрые электронные со ^ соре и медленные ионные
о<сорг. Если направленная скорость электронов достаточно вели-
ка> то в результате доплеровского сдвига частоты возможно свое-
своеобразное пересечение этих двух ветвей колебаний. При этом мед-
медленные ионные колебания со—wPi в системе отсчета, движущейся
вместе с электронным потоком, попадают в резонанс с быстрыми
колебаниями электронной плотности |со—kuoe\~(x>pe. В этих усло-
условиях •« возникает неустойчивость Бунемана. Дисперсионное урав-
уравнение для этой неустойчивости, как обычно в случае продольных
колебаний, соответствует обращению в ' нуль диэлектрической
проницаемости. Чтобы проиллюстрировать основные черты не-
неустойчивости в терминах диэлектрической проницаемости, доста-
достаточно учесть лишь основной вклад ионов и электронов, соответ-
соответствующий первым членам разложения интеграла jA.127). Резуль-
Результат имеет вид
8= 1— C02pi/c02—|G)V/(CD— kltrQeJ. A.140)
Для (о<С!&г/ое последнее слагаемое можно разложить: оJре/(со—
—\kuoeJ^^аJре/^2^2ое+2(о2ре0)/^3^3ое. Подставим это разложение
в уравнение A.140) и рассмотрим его решение для частного выбо-
выбора волнового числа k=<dpeluoe- Тогда из A.140) получим
ОK = —С02ргС0ре/2. A.141)
Это кубическое уравнение имеет комплексный корень co^co'+iy
с положительной мнимой частью, соответствующий экспоненциаль-
экспоненциальному росту амплитуды со временем Е*-*exp(yt). Инкремент на-
нарастания амплитуды волны, определяемый из A.141), равен
T = C^24/3)^f4?. AЛ42)
Более строгий анализ исходного уравнения . A.140) показал бы,
что это и есть максимум инкремента и достигается он как раз
при k = d)pe/uOe. С развитием этой неустойчивости связывают рез-
резкое торможение электронного потока и, следовательно, механизм
так называемого аномального сопротивления (см.
§ 2.19) плазмы, наблюдающегося при достаточно больших силах
тока l—enuoe>envT<i.
76
С использованием такой неустойчивости можно сконструиро-
сконструировать своеобразный линейный ускоритель для ионов в электрон-
электронном потоке. В этом случае (взаимопроникающие электронный и
ионный потоки) неустойчива волна плотности заряда в электрон-
электронном пучке со—\kuOe^z—хоре, одновременно находящаяся в черенков-
ском резонансе с ионным пучком iu^ktioi. Инкремент неустойчи-
неустойчивости определяется формулой A.142), а частота колебаний нахо-
находится из уравнения A.141) с учетом доплеровского сдвига
частоты в результате направленного движения ионов:
« = К/ + A/24/3)»У»^. A-143)
Как следует из A.143), неустойчивая волна движется быстрее
ионного пучка. Поле такой волны и реализует высокочастотное
поле линейного ускорителя. В такой волне резонансные частицы
(в данном случае ионный пучок) должны ускоряться. При этом,
как обычно в линейных ускорителях, 'процесс 'непрерывного ускоре-
ускорения должен обеспечиваться поддержанием непрерывного 'синхро-
'синхронизма между волной и ускоряемыми частицами: Ui(z)=<®/k(z).
Воспользовавшись также приведенным выше условием резо-
резонанса (неустойчивой волны с электронным пучком и тем, что
о><Ссоре, условие синхронизма можно переписать в виде
U(z)=UOe(u/(dpe(z). A.144)
Если мощность, поглощаемая от электронного пучка, достаточно
мала, то ток в пучке должен 'сохраняться: neu0e=oonst Поскольку,
кроме того, частота ускоряющей волны постоянна co==const, а яри
нерелятивистских энергиях скорость ускоряемых ионов и растет,
как обычно в линейных ускорителях, пропорционально ?1/2, то
видно, что синхронизм между ионами и ускоряющей их волной
может быть легко обеспечен за счет профилированного из^шнения
плотности в электронном пучке:
пе~1/я1&. A.144а)
Вообще, рассмотренная выше схема в значительной степени
аналогична линейному ускорению. Основное отличие состоит в том,
что мощность, необходимая для ускорения, не вводится в ускори-
ускоритель извне, а из-за неустойчивости черпается от электронного пуч-
пучка в самом процессе ускорения (так называемый коллектив-
коллективный м ето дускор е ни я),
Механизму неустойчивости Бунемана можно дать еще одну
важную трактовку. Для волны плотности заряда в электронном
пучке со—kuoe~—Ыре производная de/dco«—2ДоРе, т. е. отрица-
тельца. Из формулы A.132) следует, что в этом случае энергия
волны отрицательна. Так называемая отрицательность
э^е е р г и и , волны означает, что при распространении такой
волны в среде энергия среды (в данном случае электронного по-
потока) уменьшается. Тогда любой механизм диссипации (в рас-
рассмотренном -здесь примере это ускорение ионов) должен \чриво-
Т7
дить к дальнейшему уменьшению энергии среды, а следовательно,
и к росту амплитуды волны отрицательной энергии, т. е. к неустой-
неустойчивости. Этот результат следует также из уравнения A.134) для
амплитуды волны: диссипация (Re dr>0) в случае волны «отрица-
«отрицательной энергии» (?8/<5со<0 приводит к неустойчивости (d/dt)E2'>0.
В этом смысле рассмотренная неустойчивость является при-
примером достаточно широкого класса неустойчивостей волн с отри-
отрицательной энергией. Волны отрицательной энергии возможны
в неравновесных средах с запасом свободной энергии, таких, на-
например, как электронные пучки. Диссипация энергии этих волн
(в плазаме такая диссипация может быть связана не только со
столкновениями, но и с затуханием Ландау) является причиной
неустойчивости. Неустойчивости волн отрицательной энергии так-
также хорошо известны в радиофизике (резистивные генераторы и
усилители на поглощении). В последнем случае механизм дисси-
диссипации связан с 'поглощением электромагнитной энергии в стенках
резонатора или волновода.
§ 1.13. Кинетическая теория волн в плазме
(ленгмюровские колебания)
Рассмотрим свойства высокочастотных электронных (ленгмю-
ровских) колебаний на основе дисперсионного уравнения A.127).
В этом случае речь идет о быстрых волнах с фазовой скоростью,
существенно большей тепловой скорости электронов; что же
касается ионов, то они не успевают участвовать в таких колеба-
колебаниях из-за их большой массы. Поэтому для ленгмюровских коле-
колебаний в уравнении A.127) достаточно ограничиться электрон-
электронным вкладом. В знаменателе соответствующего интеграла
в A.127) (u^kv — по крайней мере для скорости электронов по-
порядка средней тепловой, т. е. в существенной области интегриро-
интегрирования по скоростям. Тогда для вычисления интеграла можно
воспользоваться разложением
1/(ю—kv) = l/co + to/ico2+ (ЬJ/со3 + (fo>K/o>4. A.145)
Подстановка A.145) в электронный интеграл в дисперсионном
уравнении A.127) и последующее интегрирование по частям при-
приводят к следующим результатам:
{lfa)fdfoe/dvdv=O
(«/о обращается в нуль на пределах интегрирования и->-±оо);
(W) J vdfoeldvdv=~(k/<o2)n;
(й2/©3) J v2dfOe)dvdv = O
{dfoe/dv — начальная функция как производная от максвелловской
функции распределения);
(?3/<о4) J v*dfoeldvdv=—3(?3со4) {Tejme)n.
78
Разложение, аналогичное A.145) с последующим интегрированием,
можно было бы осуществить и с первь!м интегралом оправа
в дисперсионном уравнении A.127). Однако этот член, являю-
являющийся результатом учета движения ионов, оказывается втг/тераз
меньше. Поэтому им можно пренебречь.
В итоге вместо A.127) получаем
^2^й2(со2Р/оJ + ЗоJрй2(Ге/те)/(о4) A.146)
и яри <u*>kvTe приходим к уже известному закону дисперсии для
электронных колебаний 'плазмы: со2=1со2р + 3^2Ге/те. Очевидно, что
такое дисперсионное уравнение соответствует диэлектрической
проницаемости
е = 1 -но У со2 A + 3k2 (Те1те) /со2).
Нетрудно 'получить формулу для энергии ленгмюровской волны
с помощью общей формулы A.132). В случае ленлмюровской вол-
волны с &гб<С1, когда тепловые поправки малы, эта формула при-
принимает совсем простой вид:
W=(E2/4n). A.147)
Интересно отметить, что для такой ленгмюровской волны, так же
как и для гармонических колебаний в аналитической механике,
имеет место так называемая теорема вириала — среднее
значение кинетической энергии колебаний частиц
№кол = ( пот8и2е/2)=(Е2/8п)
равно среднему значению потенциальной энергии волны
Этот результат также вполне естествен — уже из качественного
рассмотрения, проведенного в § 1.2, известно, что высокочастот-
высокочастотные ленгмюровские колебания можно рассматривать как гармони-
гармонические колебания электронов относительно неподвижных ионов.
Декремент затухания ленгмюровских колебаний определяется
формулой A.137), где в данном случае существен только элек-
электронный вклад. В результате для декремента затухания получаем
выражение, отличающееся от приближенной формулы § 1.2 лишь
численным 'множителем я/2:
у = B*e4mJ?) *dfeofdv \v^/k A.148)
(мы учли, что для ленгмюровских колебаний <Эе/Ао = 2со2Р/ю3^2/со).
Для плазмы с максвелловским распределением ло скоростям из
A.148) имеем формулу для декремента затухания, впервые полу-
полученную Л. Д. Ландау:
Y= — (я/8)х'2 (cDp/?3r3D) exp {-3/2-l/2?2r2D}. A.149)
Подчеркнем интересную особенность затухания Ландау —как
всякое явление, описываемое кинетическим уравнением A.122) без
79
столкновений и поэтому сохраняющим энтропию (в соответствии
с Я-теоремой Больцмана), такое затухание должно быть обрати-
обратимым. Для того чтобы разъяснить это, обратимся еще раз к ка-
качественной картине, рассмотренной в § 1.2. Там мы для простоты
считали, что 'потенциал волны имеет прямоугольный 'профиль (см.
рис. 1.2). Для такого идеализированного профиля частицы, за-
захваченные в потенциальную яму волны, т. е. движущиеся доста-
достаточно медленно относительно волны
меняют свою скорость только при столкновении со стенкой потен-
потенциального барьера. Для этого случая мы разделили частицы на
две группы: частицы, догоняющие волну и, следовательно, теря-
теряющие свою энергию при таком столкновении, и частицы, отстаю-
отстающие от волны, а значит, получающие энергию. В максвелловской
а 5 в
Рис. 1.13. Динамика поведения резонансных электронов на фазовой плоскости
плазме частиц второй группы (т. е. более медленных) больше,
поэтому волна затухает. Следует, однако, иметь в виду, что после
столкновения эти две группы частиц меняются местами; частицы,
которые отставали от волны и которых было больше, теперь опе-
опережают волну и при следующем столкновении со стенкой потен-
потенциального барьера отдают волне энергию. Поэтому «затухание»
меняет знак и является осциллирующей функцией времени с пе-
периодом, равным периоду колебаний частицы в потенциальной яме:
%ъ~\Щеу1т)хР. A.150)
Строго говоря, такая картина имеет место только в том случае,
когда все захваченные частицы синхронно колеблются в потенци-
потенциальной яме. В действительности период колебаний частиц в яме
зависит от их энергии: т~ \Ik\v—<о/&|.
Для того чтобы понять, как это обстоятельство влияет на за-
затухание Ландау, рассмотрим поведение траекторий частиц на
фазовой плоскости (я, v). Фазовая плоскость для случая частиц,
захваченных волной прямоугольной формы, показана на рис. 1.13.
Частицы движутся с постоянной скоростью между стенками по-
потенциальной ямы, а затем скачком меняют скорость, переходя
80
Рис. 1.14. Зависимость от времени?
амплитуды монохроматической волны:
/ — волна малой амплитуды, когда существен-
существенно затухание Ландау; Я —волна большой
амплитуды, для которой происходит быстрое-
выключение затухания в результате фазовых
осцилляции резонансных частиц
из верхней части фазовой пло-
плоскости в нижнюю, и наоборот.
Будем считать, что вначале
было больше частиц, движу-
движущихся медленнее волны, т. е.
находившихся в нижней части
фазовой плоскости (см. рис.
1.13,а, заштрихованная часть
фазовой плоскости). Из бес-
столкновительного кинетиче-
кинетического уравнения следует, что
функция распределения сохра-
сохраняется при движении частиц
(теорема Лиувилля) и поэтому
при отражении от границ по-
потенциальной ямы заштрихованные участки переходят в верхнюю^
часть фазовой плоскости. Быстрее всего колеблются частицы
с большей энергией, и они раньше других перейдут наверх, части-
цы с меньшей энергией останутся в нижней части плоскости*
(см. рис. 1.13,6), через несколько периодов колебаний частиц карти-
картина фазовой плоскости чрезвычайно усложнится (см. рис. 1.13,в),
на котором перемежаются заштрихованные и незаштрихованные
участки фазовой плоскости). Вообще, если представить себе две
частицы с несколько различающимися энергиями ei и е2, то им
будут соответствовать разные периоды колебаний в потенциаль-
потенциальной яме iAT=(dr/de)Ae. Даже если эти частицы начинают дви-
двигаться по своим траекториям с одинаковыми начальными фазами
Q—kx, то через время ^--т2/Ат их фазы разойдутся на величину
А9~1 и они могут оказаться в разных частях фазовой плоскости.
В итоге «происходит своеобразное размешивание частиц по всей
фазовой плоскости.
Число частиц, движущихся быстрее и медленнее волны, при-
примерно выравнивается, и затухание волны прекращается. Ампли-
Амплитуда волны как функция времени, полученная при точном решении*
задачи с волной синусоидальной формы, показана на рис. 1.14.
Она качественно соответствует рассмотренной здесь упрощенной
картине.
В принципе можно представить ситуацию, когда все частицы,,
двигаясь по своим фазовым траекториям, вновь окажутся, на-
например, в нижней части фазовой плоскости и восстановится за-
затухание. Однако для системы с большим числом частиц вероят-
вероятность такого события крайне ;мала (иначе говоря, время «возврата»
чрезвычайно велико), и с большой степенью точности -можно счи-
считать, что в результате фазового размешивания в плазме устанав-
устанавливается волна постоянной амплитуды. Фазовое размешивание
(см. рис. 1.13) приводит к мелкомасштабным осцилляциям на
функции распределения. (На этом рисунке все время переме-
перемежаются заштрихованные и незаштрихованные участки на фазовой
6-74 81
плоскости.) Рано или поздно масштаб этих шероховатостей ста-
становится настолько мелким, что нельзя 'пренебречь диффузией
в пространстве скоростей из-за столкновений учитываемой в ин-
интеграле столкновений в кинетическом уравнении в форме
•d(v(T/m)df/dv) jdv (см. § 1.9). Так что даже в бесстолкнозитель-
ной плазме столкновения в конце концов сглаживают шерохозато-
сти функции распределения. При таком сглаживании энтропия уже
не сохраняется и процесс становится истинно необратимым. Любо-
Любопытно, что время, в течение которого происходит этот процесс,
практически значительно меньше среднего времени столкновений.
Из приведенных рассуждений следует, что рассматривавшееся
ранее линейное затухание Ландау существенно' только для волны
достаточно малой амплитуды, когда уть>1, т. е. y/k^> (еуо/теI/29
О 20 40 60 80 /,см
Рис. 1.15. Экспериментальное наблюде-
наблюдение затухания Ландау монохроматиче-
монохроматической плазменной волны (Wharton С. В.,
Malmberg J. H, O'Neil Т. М. «Phys.
Fluids», 1968, v. II, 1761).
На рисунке показано пространственное рас-
распределение амплитуды потенциала волны в де-
децибелах как функция расстояния от источни-
источника при различных значениях амплитуды
вводимого в плазму сигнала. Амплитуда сиг-
сигнала возрастает при переходе от кривой 3
к 2 и далее к /. При малых амплитудах (кри-
(кривая 3) имеет место монотонное затухание
сигнала с линейным коэффициентом затухания
~y]vvv, где Y определяется формулой A.148), arp=3&r2D/cop — групповая скорость волны. При
^больших амплитудах возникают осцилляции амплитуды волны, период этих осцилляции
с большой точностью описывается формулой A.150)
и волна успевает затухнуть, прежде чем проявится эффект осцил-
осцилляции декремента. В обратном предельном случае относительное
изменение амплитуды АЕ/Е~ух<С\, и за несколько периодов ко-
колебаний амплитуды в результате фазового размешивания резо-
резонансных частиц в плазме устанавливается стационарная нелиней-
нелинейная волна. На рис. 1.15 приведены экспериментальные результаты
исследования затухания волны конечной амплитуды.
Фазовая память, сохраняющаяся до тех пор, пока плазма опи-
описывается бесстолкновительным кинетическим уравнением, нагляд-
наглядно иллюстрируется эффектом так называемого плазменного
эха. Рассмотрим его. Пусть при !/=0 в плазме возбуждается ленг-
мюровская волна exp[i(Ai*—<o\t)]9 которая затем затухает из-за
механизма Ландау. Эта волна оставляет, однако, незатухающую
модуляцию функции распределения в форме fi{v)exp[i(kiX—KO\t)].
Действительно, ранее при выводе дисперсионного уравнения
A.127) мы ограничивались частным решением кинетического урав-
уравнения, затухающим вместе с волной. Полное же решение кине-
кинетического уравнения, удовлетворяющее, к примеру, условию
( = 0) =0, имеет вид
~ А exp [i (kx — со/)] ~@) exp [i (kx — со^)]) df0 ,
i (kv — со)
i (kv — со) f dv
[см. A.123)]. Последнее .слагаемое соответствует незатухающей
волне модуляции на функции распределения, которая приводит
к мелкомасштабным ее осцилляциям как функции скорости с ха-
характерным 'масштабом ~ l/kt, неограниченно уменьшающимся
с ростом времени. Физически такие осцилляции вполне аналогич-
аналогичны мелкомасштабной структуре функции распределения захвачен-
захваченных частиц, описанной выше. Им не соответствует макроскопиче-
макроскопическое возмущение плотности и электрическое поле, поскольку ин-
интеграл по скорости от df стремится к нулю (при больших временах
в результате фазового размешивания. Однако если через доста-
Рис. 1.16. Схема наблюдения явления плазменного эха
точно большое время t® после 'первой волны в плазме создать
новую волну exp[i(&2*—©я*)], которая затем также затухает, то
такая волна приведет к модуляции функции распределения в фор-
форме f2(v)exp[ik2x—\k2v{t—t^)\. Модулироваться будет и возмущен-
возмущенная часть функции распределения, так что на ней возникнут бие-
биения
^o—i(k2±ki)vt]. A.152)
Эффект эха имеет место для биения с разностным волновым:
числом k2—>&i и состоит в следующем. В момент времени
t\=4Qk2/(k2—ki)
A.153)
происходит своеобразная фазировка: взаимная компенсация фаз;
отдельных множителей в A.152), и фаза биения перестает зави-
зависеть от v. В результате модуляция функции распределения в фор-
форме A.152) приводит в этот ъшмент времени к возмущению макро-
макроскопических величин —плотности электронного заряда, а следо-
следовательно, и электрического «поля. Типичная схема наблюдения
плазменного эха показана на рис. 1.16. Первые два импульса
электрического поля при ^=0 и t=tQ возбуждаются от внешнего^
источника. Третий импульс—отклик плазмы, связанный с описан-
описанной выше фазировкой волн модуляции ее функции распределения.
Эффект плазменного эха в значительной степени аналогичен явле-
6* 83
.ниям эха (спиновое, циклотронное) в неплазменных средах. В каж-
каждом из них затухание макроскопически наблюдаемой физической
•величины, связанное с фазовым размешиванием быстро осцилли-
осциллирующих микроскопических элементов (мелкомасштабные осцилля-
осцилляции функции распределения в плазменном эхо, прецессирующие
ядерные магнитные моменты в спиновом эхо, ларморовское вра-
вращение электронов в циклотронном эхо), обращается во времени
путем соответствующего воздействия на направление фазовой эво-
эволюции микроскопических элементов. Такое обращение достигает-
достигается, как мы видели, в результате второго импульса 'плазменных
колебаний или высокочастотного излучения, фазирующего микро-
микроскопические элементы.
§ 1.14. Пучковая неустойчивость
Проведем анализ одного важного следствия формулы A.148)
для декремента затухания Ландау 'плазменных колебаний. Из этой
формулы следует, что затухание колебаний, обусловленное обме-
обменом энергий с резонансными частицами, реализуется только в том
случае, когда функция распределения резонансных частиц есть
монотонно убывающая функ-
функция скорости. Это имеет ме-
место, например, при максвел-
ловском распределении ча-
частиц плазмы по скоростям,
когда единственный макси-
максимум функции распределе-
распределения соответствует скорости
При наличии в плазме
достаточно интенсивного
пучка электронов функция
распределения по скоростям
может иметь дополнительный максимум для значения \ve, отлич-
отличного от нуля. Этот случай изображен на рис. 1.17. Волна, фазо-
фазовая скорость которой лежит вблизи второго максимума функции
распределения между точками 1 и 2, раскачивается электронным
лучком. Механизм раскачки — все тот же резонансный обмен
энергией между волной и частицами, который в данном случае
мз-за выполнения условия dfldv(v=&lk)>6, т. е. преобладания
в исходном состоянии частиц, движущихся быстрее волны, приво-
приводит к росту амплитуды волны. Таким образом, из всего спектра
волн, которые вследствие флуктуации всегда присутствуют в плазме,
электронный пучок выделяет узкую спектральную область нахо-
находящихся с ним в фазовом резонансе волн и интенсивно накачивает
энергию в эти волны.
В определенном смысле электронный пучок в плазме можно
рассматривать как классический мазер на продольных колеба-
колебаниях, 'поскольку фактически механизм неустойчивости связан
Рис. 1.17. Функция распределения электро-
аюв по скоростям для системы плазма —
пучок
с инверсностью заселенности уровней для частиц со скоростями,
близкими к фазовой скорости волны (условие (dfo/dv) |о=='<о/Л>0).
Скорость нарастания амплитуды плазменных волн, возбуждае-
возбуждаемых электронным пучком, определяется формулой A.148). Из
этой формулы, в частности, следует, что для возникновения не-
неустойчивости необходимо, чтобы интенсивность пучка в плазме
превышала некоторую минимальную величину или чтобы пучок
был сильно надтепловым, т. е. приходился на далекую область
«хвоста» максвелловского распределения тепловых частиц плаз-
плазмы. Очень слабый пучок, очевидно, не сможет повлиять на функ-
функцию распределения электронов по скоростям таким образом,
чтобы ее производная могла изменить знак. Если же в области
скоростей (резонансных с неустойчивыми волнами) можно прене-
пренебречь вкладом плазменных частиц, то очевидно, что функцию
распределения в резонансной области скоростей можно предста-
представить в виде fe~fii/Av, где щ—плотность пучка; Av— тепловой
разброс в пучке (ширина его функции распределения по скоро-
скоростям). Производная от функции распределения dfe/dv~tii/(AvJ,
и в этом случае для инкремента нарастания находим из A.148)
формулу
2), A.154)
которая часто используется для оценок.
Формулы A.148) и A.154) описывают неустойчивости пучков
с большем тепловым разбросом. Дело в том, что из-за нестацио-
нестационарности волно'вого процесса, в данном случае роста амплитуды
волны при неустойчивости, резонанс волна — частица имеет конеч-
конечную ширину по скорости \v—4x>/&|~y/&. Именно на такую мини-
минимальную ширину по фазовым скоростям размыт пакет волн из-за
мнимой части частоты. Формула A.154), чпри выводе которой пре-
пренебрегал ось конечной шириной резонанса волна — частица, отно-
относится к случаю сильно размытых пучков, когда тепловой разброс
в пучке существенно больше ширины резонанса и для каждой
неустойчивой волны на функции распределения пучка выделяется
своя небольшая группа резонансных частиц.
В обратном предельном случае Av<^yjk весь пучок как целое
находится в резонансе с неустойчивой волной. Именно в этом
случае следует ожидать развития наиболее сильной пучковой не-
неустойчивости. Дисперсионное уравнение для такой неустойчивости
можно получить из общего уравнения A.127). При вычислении
интеграла по скоростям в этом уравнении следует выделить об-
область тепловых скоростей, в которой интеграл по v вычисляется
обычным путем (разложением по параметру kv[(o), и область ско-
скоростей пучка, при рассмотрении которой можно считать пучок
имеющим б-образное распределение по скоростям: /Oe=^i6 (t;—щ).
Однако нагляднее вывести искомое уравнение по аналогии с дис-
дисперсионным уравнением неустойчивости Бунемана, считая элек-
электроны пучка своего рода отдельным сортом частиц со своей плаз-
85
F-
г
ки0
со
менной частотой соь:
1 = (о2р/(о2+-со2ь/ (a--ku0J, A.155)
где (д2ь=4ле2П1/те — квадрат ленгмюровской частоты в пучке.
Применим графический метод анализа корней этого уравнения.
График правой части этого уравнения F({u, k) при фиксированном
k, т. е. для возмущений с за-
заданной длиной волны, при-
приведен на рис. 1.18. Видно, что
когда минимальное значе-
значение F оказывается меньше
единицы, у уравнения
A.155) все четыре корня ве-
вещественны, что соответству-
соответствует периодическому измене-
изменению возмущений со време-
временем. Если же минимум F
больше единицы, то уравне-
уравнение A.155) имеет только два
вещественных корня, а два
корня являются комплексно сопряженными ю=<о/±гу. Эти корни,
очевидно, соответствуют изменению амплитуды колебаний по за-
закону ехр{±у*—ico'O, и, таким образом, один из этих корней приво-
приводит к росту амплитуды со временем, т. е. к неустойчивости. Из
A.155) имеем, что minF= (co2pl\k2u20) A + (оJь/о>2рJ/3K и, следо-
следовательно, неустойчивыми окажутся достаточно длинноволновые
возмущения, для которых
*<А!Р=,(«Юр/Ио)'[1 + (со2ь/со2рJ/3]3/2. A.156)
Коротковолновые колебания с #>&гр устойчивы. Примерный гра-
график функции y{k) можно представить следующим образом. Не-
Неустойчивы только волны, сохраняющие фазовый резонанс с пуч-
пучком со=й«о. При малых k(k<(ovju0) инкремент нарастает с вол-
волновым числом
Рис. 1.18. График функции F(®, k) в дис-
дисперсионном уравнении A.155)
20fco2P—l)-ll2. A.157)
Максимальный инкремент имеет место при выполнении резонанс-
резонансного условия kuQ=(x)p (резонанс между собственными колебания-
колебаниями электронов плазмы <о=<ор и волной в пучке a)=ku0). Инкре-
Инкремент нарастания этой наиболее неустойчивой гармоники
Vmax='C0pC1/2/24/3) (njnoyi*. A.158)
Из этой формулы, в частности, следует, что условие пренебреже-
пренебрежения тепловым разбросом в 'пучке (моноэнергетический пучок)
можно записать в виде
Av/uo<(nl/no)V3, A.159)
В обратном предельном случае «размытого» пучка Av/uq^ (щ/п0I^
для инкремента применима формула A.148). Как и следовала
86
ожидать, инкремент неустойчивости в этом случае существенно
меньше.
Выясним теперь механизм рассматриваемого явления. В основе
пучковой неустойчивости лежит физический механизм поляриза-
поляризационных «потерь заряженной частицы, т. е. 'потерь энергии на из-
излучение продольных колебаний, но существует и значительное
различие. Бели использовать аналогию с квантовомеханической
излучающей системой, то это различие можно сформулировать
следующим образом: поляризацион-
поляризационные потери отдельной заряженной ча-
частицы— эффект спонтанный, поляри-
поляризационные потери, приводящие к пуч-
пучковой неустойчивости,— процесс инду-
индуцированный. В равновесном состоя-
состоянии пучок однороден по плотности,
скомпенсирован по заряду и эффект
поляризационных потерь отсутствует.
Потери возникают в результате того,
что волны плотности заряда, суще-
существующие в плазме на зародышевом
тепловом уровне, приводят к предва-
предварительной модуляции пучка. В опре-
определенных условиях, которые будут вы-
выяснены ниже, электроны пучка соби-
собираются в основном в области тормо-
тормозящих фаз поля волны и тем самым
усиливают модулирующую их волну.
Чем больше амплитуда модулирующе-
модулирующего поля, тем глубже модуляция пучка
Рис. 1.19. Автомодуляции (бун-
чировка) электронного пучка
при пучковой неустойчивости.
Графики приведены в системе от-
отсчета волны: х — (<dlk)t-+x
и больше потери и вследствие этого эффективнее происходит воз-
возбуждение волны пучком. В результате развивается пучковая не-
неустойчивость—возбуждение плазменных колебаний с теплового
уровня, сопровождающееся автомодуляцией пучка.
Неустойчивые плазменные волны должны находиться в фазо-
фазовом резонансе с 'пучком — их фазовые скорости должны быть
близки к скорости пучка. Однако условие фазового резонанса
толькб необходимо для возникновения неустойчивости плазменных
волн, достаточным ее условием является преимущественная бун-
чировка пучка в области тормозящих фаз поля, т. е. преобладание
процессов индуцированного излучения волн над процессами по-
поглощения.
Выясним условия, при которых происходит такая бунчировка.
На -рис. 1.19 изображены профиль потенциала плазменной волны
<р(х) и сила, действующая на электроны пучка в волне edep/dx.
Для определенности будем считать пучок моноэнергетическйм, пер-
первоначально все его частицы имеют скорость щ. Если предположить,
что амплитуда волны изменяется со временем достаточно медлен-
медленно, то возмущение скорости частиц пучка можно найти из закона
87
сохранения энергии
(те/2) (u—(dlkJ—ey=const,
A.160)
т. е. 6и= (е<рlme) I (tio—<о/Л). С течением времени первоначально
синусоидальный профиль волны скорости в пучке искажается, час-
частицы с и>и0 забегают вперед, частицы с и<и0 отстают. При этом
частицы -пучка собираются в областях с повышенной крутизной
профиля скорости и(х) (в системе отсчета волны движение на-
направо). При выполнении условия Мо>©/6 (см. рис. 1.19) частицы
собираются в области тормозящих фаз 0<||=(й^/2я)<1/г. Ана-
Аналогичным образом если ыо<ю/й, то частицы будут бунчироваться
в области фаз 1/2<5<1> где они ускоряются электрическим полем
волны, и неустойчивости не может быть.
Из приведенного анализа вытекает, что при взаимодействии
электронного пучка с плазмой неустойчивыми оказываются только
те волны, для которых выполнено условие
'Со^&г/о- A.161)
В этом случае электронный пучок разбивается на сгустки, стяги-
стягивающиеся к тормозящим фазам электрического поля, и амплитуда
волны растет со временем. Такой рост 'продолжается до тех пор,
пока сгустки, на которые разобьется электронный пучок, не ока-
окажутся захваченными возбуждаемой им плазменной волной. Как
следует из анализа, приведен-
приведенного в § 1.13, захваченные ча-
частицы попеременно смещаются
от тормозящей фазы поля
к ускоряющей и наоборот и
в среднем за [период таких ко-
колебаний не обмениваются
энергией с волной. В резуль-
результате захват частиц пучка вол-
волной должен приводить к ста-
стабилизации пучковой неустой-
неустойчивости. Поскольку ширина
резонанса плазменная волна —
пучок \v—'<u/)k\'*~ylk, то усло-
условие захвата частиц пучка
имеет вид
Рис. 1.20. Нелинейная эволюция ампли-
амплитуды монохроматической волны, возбуж-
возбуждаемой при пучковой неустойчивости:
/ — неустойчивость «моноэнергетического»
пучка, в нелинейном режиме амплитуда вол-
волны испытывает глубокие осцилляции
АЕ1Еп
12/3, соответствующие синхронным
колебаниям частиц пучка в потенциальной
ЯМе; // — неустойчивость «размытого» пучка
в плазме. В результате фазового размешива-
размешивания резонансных частиц амплитуда волны до-
достаточно быстро выходит на стационарный
уровень
88
A.162)
Воспользуемся тем, что элек-
электрическое поле плазменной
волны Е—&<р, волновое число
в области неустойчивости k**&
^(йр/Uo, инкремент неустойчи-
неустойчивости «моноэнергетического»
пучка определяется соотношением A.158). В результате из A.162)
получим, что при неустойчивости «моноэнергетического» пучка
энергия плазменной, волны должна возрастать до значения
Е2/4п ~ пхтви\ (щ/поI/3. A.163)
Эта оценка, основанная на наглядных физических соображениях,
подтверждается графиком зависимости амплитуды волны от вре-
времени, полученным (при численном решении задачи с учетом нели-
нелинейных эффектов (рис. 1.20). Вначале происходит экспоненциаль-
экспоненциальный рост амплитуды от теплового уровня, -сопровождающийся
бунчировкой пучка. В дальнейшем захват пучка волной приводит
к стабилизации неустойчивости, осцилляции амплитуды поля в не-
нелинейном режиме соответствуют фазовым колебаниям бунчей, за-
V
2
1
0
ч
-Z
-J
r=0
-
-
-
~ ' i ! :
47,fr -0,25 0 0,25
_ 0
\
I
9
i
10
/
t
Ц5
f
i i
У
!
-—-
\
/
>»
(
f ,
_
Ж'
- /
/
1
" \
V
\
!
>
*
11,5
\
i
-
-
i
\
\ Г
12,5
-
- чч
Рис. 1.21. Фазовая плоскость (зависимость скорости частиц пучка в системе от-
отсчета волны v^u—4d)/k от их координаты 1=&х/2п) для моноэнергетического
электронного пучка, взаимодействующего с плазмой в различные моменты вре-
времени т (по результатам численного эксперимента Н. Г. Мациборко и др. «Журн.
•; эксперим. и теор. физ.», 1972, т. 63, с. 874).
На рисунке показаны бунчировка электронов пучка в поле волны и последующие фазовые
осцилляции бунчей, которым соответствуют осцилляции амплитуды поля (см. рис. 1.20).
• Время измеряется в обратных инкрементах пучковой неустойчивости
89
хваченных в потенциальную яму волны, между тормозящими и
ускоряющими фазами поля.
Примерно такой же вид имеет зависимость от времени ампли-
амплитуды волны, возбуждаемой «размытым» электронным 'пучком (см.
рис. 1.20). Основные отличия этого случая от случая моноэнергети-
моноэнергетического пучка: П из-за малого числа частиц, резонансных с вол-
0,5
0
-0,5
-1,0
I =2,0
4,0
6,0
6,5
о
Рис. 1.22. Фазовая плоскость электроноь пучка в эксперименте по взаимодей-
взаимодействию моноэнергетического пучка малой плотности с плазмой (Gentle К. W.r
Lobr J. «Phys. Fluids», 1973, v. 16, p. 1465).
Фазовая плоскость показана на различных расстояниях / от места инжекции электронного
пучка в плазму; расстояние измеряется в обратных пространственных инкрементах. При
^ 4,0 происходит лишь небольшая модуляция пучка; центральная линия соответствует
максимуму функции распределения; верхняя и нижняя кривые служат указателями полу-
полуширины функции распределения. При больших / внутренний контур соответствует макси-
максимуму функции распределения, указаны также контуры, соответствующие /=@,8, 0,5,
0,2)/юах. Пучок бунчируется но фазам и одновременно тормозится, пока при /=6,5 не до-
достигается минимальная фазовая ширина сгустков. В дальнейшем сгустки начинают переме-
перемещаться к ускоряющим фазам поля, пучок ускоряется и при /=9 он снова имеет свою на-
начальную скорость
ной, амплитуда волны оказывается существенно меньше; 2) нали-
наличие разброса по энергиям в пучке 'приводит к фазовому размеши-
размешиванию в потенциальной яме, затуханию осцилляции и установлению
волны постоянной амплитуды.
Процесс бунчировки пучка, «наблюденный» в численном экспе-
эксперименте, показан на рис. 1.21. На рис. 1.22 приведены результаты
лабораторного эксперимента по возбуждению монохроматической
волны электронным пучком.
90
§ 1.15. Параметрическая неустойчивость
Авторы надеются, что читатель уже привык к мысли, что
плазма — это не только большое число заряженных частиц, но -и
ансамбль большого числа осцилляторов — элементарных мод ко-
колебаний, каждое из которых характеризуется определенным зна-
значением волнового числа и частоты. В равновесной плазме все эти
колебания находятся в зародышевом -состоянии на уровне тепло-
тепловых флуктуации. При отклонении от равновесности (электрический
ток в плазме, пучок быстрых частиц и др.) некоторые ветви коле-
колебаний (ионно-звуковая, плазменная) могут возбуждаться до весь-
весьма значительного уровня в результате какого-либо из описанных
в предыдущих параграфах механизмов линейной неустойчивости.
Пока амплитуда колебаний мала, все электромагнитные моды —
осцилляторы можно считать гармоническими и независимыми друг
от друга. Однако поскольку плазма — среда нелинейная, то при
достаточно больших амплитудах возникает связь между модами —-
осцилляторами. Одна из форм этой связи, которая рассмотрена
в настоящем параграфе, напоминает хорошо известное явление
параметрического резонанса, описываемого в механике в простей-
простейшем случае уравнением Матье.
Ситуация такого рода получается, если в плазме возбуждено
колебание с некоторой конечной амплитудой. Нелинейность плаз-
плазмы приводит к тому, что малые волновые возмущения (пробные
волны) на фоне заданного колебания (будем называть его «вол-
«волной накачки») оказываются параметрически связанными, подобно
тому как это имеет место в системе параметрически связанных
осцилляторов. По аналогии с задачей о параметрическом осцилля-
осцилляторе Матье можно поставить вопрос об устойчивости такой систе-
системы, иначе говоря, о том, не может ли присутствие «волны накач-
накачки» приводить к нарастанию пробных волн. Первое, что сразу
бросается в глаза, условие резонанса Матье /гю>о=2ш, должно
быть дополнено ограничением на волновые числа nko=2k, так как
в -плазме каждый элементарный осциллятор характеризуется не
только частотой, но и волновым числом. Одновременное выпол-
выполнение этих условий явилось бы слишком жестким ограничением,
поскольку кроме условий параметрического резонанса со и k для
каждой ветви колебаний связаны друг с другом еще законом
(&) {Ь)
р ) {)
Более реальной оказывается возможность параметрического
возбуждения одновременно по крайней мере пары волн. Разви-
Развивающаяся при этом параметрическая, т. е. нелинейная, неустой-
неустойчивость в плазме часто именуется «распадной». Она состоит в том,
что в присутствии 'волны накачки с частотой соо и волновым век-
вектором к0 нарастает одновременно пара волн <oi, ki и со2, к2, удовле-
удовлетворяющих условиям
ггхг}
91
Соотношения A.164) допускают весьма наглядную квантовую ин-
интерпретацию. При такой интерпретации набор элементарных
мод—осцилляторов, присутствующих в плазме, можно рассмат-
рассматривать как некий газ «квазичастиц» с энергией г—Ню и 'импульсом
р=Йк (фотоны для электромагнитных колебаний, фононы —для
ионно-звуковых и т. д.)- Тогда соотношение A.164) есть не что
иное, как законы сохранения энергии и импульса при распаде ис-
исходного «кванта» (©о, ко) на два других— (соь к^, (со2, к2)..
Первым теоретически предсказанным и детально исследован-
исследованным еще в 1962 г. типом параметрической рас-падной неустойчиво-
неустойчивости явилась неустойчивость электронной ленгмюровской волны
накачки.
Волнами с индексами 1 и 2 в условиях A.164) в этом случае
являются другая плазменная волна и ионно-звуковая волна, по-
поэтому предполагается неизотермичность плазмы (Те^$>Тг). Эта
неустойчивость часто называется распадом «плазмон—К1лаэмон +
+ фонон», хотя задача совершенно не квантовая. В дальнейшем
параметрическая неустойчивость исследовалась для самых раз-
различных ветвей колебаний и волн. Несмотря на разнообразие ти-
типов волн в плазме «и вытекающий отсюда большой выбор пара-
параметрических связей, все параметрические неустойчивости имеют
одинаковую природу. Поэтому удобно начать их рассмотрение
с какой-нибудь простой модели. Очевидным обобщением уравне-
уравнения Матье на случай волновой среды могло бы служить, напри-
например, следующее уравнение:
d2u[dt2 — s2[l+acos(v0t-k0?c)]d2ujdx2 + Lu = 0. A.165)
Подобно тому как в уравнении Матье модулируется собственная
частота осциллятора, здесь модулируется скорость распростране-
распространения волны. Слагаемое Ей, где L — линейный оператор, добавлено,
чтобы учесть возможное отклонение от линейного закона диспер-
дисперсии co=&s, коэффициенты в этом члене в принципе также можно
модулировать.
Будем искать условия параметрического возбуждения в урав-
уравнении A.165) одновременно пары элементарных волн. Для этого
приведем уравнение A.165) к виду, напоминающему уравнение
гармонического осциллятора с правой частью (вынуждающая
сила). Удобно перейти к фурье-компонентам Uk= ^juexp(ikx)dx
и перенести слагаемое, учитывающее влияние волны накачки,
в правую часть:
d2uk/dt2-]-<s>2 (k) uk = —(\j2) s2 (k0 — kf a exp (— imj)
- A/2) s2 (k. + kf a exp (Ц/) i^+ft , A.166)
где <u2(k)=s2>k2 + L(k)—закон дисперсии волн (для простоты
считаем, что модулируется только скорость распространения волн).
92
Вынуждающая сила будет в резонансе с собственной частотой
осциллятора соь, если выполнено условие
% ±<°ко-к=тк- A.167>
Выберем в этом условии знак минус, тогда приведенное соотно-
соотношение совпадает, как нетрудно -видеть, с распадным условием
A.164) для частоты. В этом случае в правой части уравнения
A.166) существенно только первое слагаемое. Волна uk_k, в свок*
очередь, описывается аналогичным уравнением:
d2u\_k /dt + <»\o__k u*ko_k = - A /2) s*k> exp D0 uk -
- A/2) a {2k0 - kf s* exp (- Ц/) u\Q_k. A.168>
При выполнении резонансного условия на частоту а>0— <»ко_к—<*>&
в правой части уравнения A.168) также существенно только пер-
первое слагаемое.
Итак, рассмотренное здесь параметрическое взаимодействие
волн в нелинейной среде ничем не отличается от параметрическо-
параметрического резонанса в системе двух связанных осцилляторов uk, tiko_k .
Однако эта аналогия стала полной лишь в силу использованного*
предположения — мы опустили слагаемое ~u>k+k в лравой
части уравнения A.166) и аналогичный член в уравнении A.168)..
Дело в том, что для одновременного возбуждения осцилляторов
uko-k> uk0+k Д°лжны выполняться два распадных условия для
частоты:
Их совместное выполнение практически маловероятно. Поэтому
хотя в литературе и были попытки исследования этого случая, онв
не 'представляют существенного 'интереса в общем случае и здесь
не рассматриваются.
Параметрическая связь между осцилляторами приводит к сме-
смещению частоты. Будем интересоваться случаем, когда поправка
к частоте становится мнимой и, следовательно, соответствует не-
неустойчивости. Решение системы уравнений A.166), A.168) ищем
в в-иде
uk = uk exp (- Ы)\ u\_k =Ъ\_к exp {- i (ш- ш0) t).
Подстановка в A.166) и A.168) дает следующую систему урав-
уравнений
] AЛб9>
[(со - %J - ш^_к } ~u*ko_k = (as2/2) k*Zk. J
При малой параметрической связи частота осцилляторов близка,
к линейной: ©=<оА + 1у, |y/<»*I<1- Тогда, используя распадное
условие :@fe='@o— \_Й , получим из условия разрешимости си-
системы A.169) -следующее уравнение для у:
f = a W (k. - kfl 16ш,ш^ . A.170)
Неустойчивость развивается при у2>0, т. е. при а>*<»Л Л>0,
это вместе с распадным условием для частоты означает, что для
возникновения параметрической неустойчивости необходимо, чтобы
«.>-*; •4Ht. A.171)
Смысл полученного результата достаточно очевиден на «кванто-
«квантовом» языке: квант волны накачки (»соо, й0) имеет большую часто-
частоту, а, следовательно, и большую энергию, чем квант любой из
образующихся отри распаде пробных боли, поскольку при распаде
часть энергии уносится вторым квантом.
После обсуждения такой символической модели рассмотрим
уже упоминавшийся выше распад плазменной волны на плазмен-
плазменную волну и звук.
Основной нелинейный эффект, приводящий к связи плазменных
и звуковых колебаний, — это модуляция плотности -плазмы низко-
низкочастотной звуковой волной. Рассмотрим, как с учетом этого
эффекта меняются уравнения для плазменных и звуковых колеба-
колебаний. Естественная физическая величина, характеризующая высоко-
высокочастотные ленгмюровские колебания с большим разделением за-
зарядов,— это электрическое аюле колебаний ?(Й, х). В линейной
теории уравнение для электрического ноля монохроматической
ленгмюровской волны сводится к хорошо -известному дисперсион-
дисперсионному уравнению A.146):
[со2—со2р—3k2Te/m]E(to, k)=0. A.172)
В присутствии звуковой волны происходит модуляция плотности
плазмы, в результате чего в слагаемом (хJрЕ 'появляется нелиней-
нелинейный член, пропорциональный дпЕ. С учетом этого слагаемого
ллазменная волна уже не является более монохроматической,
в ней рождаются новые гармоники на биениях ленгмюровской и
звуковой волн. Нетрудно обобщить уравнение A.172) на случай
немонохроматичности ленлмюровской волны. Очевидно, что при
этом следует заменить частоту со на оператор дифференцирования
ло времени со-ид/d/ 'и аналогичным образом волновое число k —
на оператор дифференцирования по координате k->(\/i) (д/дх).
Б итоге вместо A.172) получаем следующее дифференциальное
уравнение для электрического поля ленгмюровской волны:
(д2/д12—З/Wp {д2/дх2) — ,оJр) Е=<ь*рЕЪп/п0, A.173)
где ®2р — квадрат ленгмюровской частоты, рассчитанной тто невоз-
невозмущенной плотности п0 (нелинейный член, возникающий в резуль-
результате модуляции плотности /плазмы звуковой волной, перенесен
в правую часть уравнения).
94
Для низкочастотных квазинейтральных колебаний, напротив,,
электрическое 'поле весьма мало и звуковые колебания наиболее
естественно описываются такими величинами, как скорость 'ионов
в волне либо возмущение плотности. Уравнение для -возмущения
плотности в монохроматической звуковой волне опять-таки может
быть получено простым обобщением линейного дисперсионного-
уравнения. Считая волну достаточно медленной <D/&<C?>re и квази-
квазинейтральной, с учетом результатов § 1.11 запишем следующее
уравнение для бя:
[A/*VD ) + e. («, Щ Ьп («, Л) = 0. A.174>
Это уравнение, в принципе, учитывает и кинетические эффекты,,
связанные с ионами, что может быть существенно при выполнение
условия (d/k~vTi. Если же частота и волновое число низкочастот-
низкочастотной моды таковы, что выполнено условие w/\k*^>vTiy то ионы можно*
описывать гидродинамически. В этом случае, как мы знаем, Si =
= —оJРг/(о2 и уравнение A.174) «переходит в следующее:
[со2—ЩТе1пц)]Ы(в>9 ?)=0. A.175)
Связь 'ионно-звуковых колебаний с высокочастотными ленгмюров-
скими осуществляется из-за существования сил высокочастотного»
давления (см. § 1.7). В этом параграфе было показано, что при
наличии высокочастотных колебаний кроме обычного газокинети-
газокинетического давления электронов возникает еще и высокочастотное
рв>ч=A/16я)(?2),
где угловые скобки, как обычно, означают усреднение по высокойг
частоте. Звуковая волна приводит, с одной стороны, к модуляции:
плотности плазмы, а следовательно, и кинетического давления
~ЪпТе, а с другой стороны, из-за возникновения биений
ленгмюровских волн — к модуляции высокочастотного давления
^( ?2)/16jt. Поэтому в уравнении A.175) для Ьп следует сде-
сделать замену:
Кроме того, так же как и в уравнении для высокочастотной ленг-
мюровской волны, 'подставим в A.175) вместо со и к операторы
дифференцирования id/dt и (l/i)d/dx. В результате получим сле-
следующее уравнение для модуляции плотности плазмы медленных
квазинейтральных движений:
(d2ldt2—(Telmi)d2ldx2)8n=(\ll6nmi)d2ldx2{E2e). A.176)
Будем искать решение уравнений A.173 и A.176) в виде коле-
колебаний, удовлетворяющих распадным условиям A.164):
(k0 k)x f <U77>
— i((D0 — a>)f}-|-K. с. J
95
Тогда для амплитуд -плазмона и фонона, возбуждаемых при пара-
параметрической неустойчивости, имеем следующую систему уравне-
уравнений:
(ю« _ со2, (k))bn =
[К - -J -
p)
\ = («
A.178)
где tol{k) = (со2р-)-Зй2Ге//ПеI/2 — частота плазмона с волновым чис-
числом Л; (ds(k)=k(Te/mi)l/2 — частота звука. По структуре эта си-
система уравнений эквивалентна уравнениям A.169), и по аналогии
с A.169) имеем в рассматриваемом случае следующую формулу
для инкремента параметрической неустойчивости:
A.179)
Как уже отмечалось выше, возбуждаемый при параметрической
неустойчивости плазмон должен 'иметь частоту меньшую, чем у вол-
-50
Рис. 1.23. Экспериментальное наблюдение распадной параметрической неустой-
неустойчивости монохроматической плазменной волны (Franklin R. N., Hamberger S. M.,
Smith G. J. («Plasma Phys.», 1973, v. 15. p. 935).
Монохроматическая волна с частотой, близкой к плазменной, и малым резонансным затуха-
затуханием возбуждалась с помощью зонда. Показаны спектры нарастающих плазменных коле-
колебаний на различных расстояниях от возбуждающего зонда
ны накачки. С учетом закона дисперсии плазменных колебаний
это означает, что при параметрической неустойчивости перекачка
энергии колебаний происходит в сторону больших длин 'волн. Ис-
Используя распадное условие, которое в рассматриваемом случае
можно записать в виде
C/2)?V2d— C/2)^2i/'2D=^D(me/mi)V2> AЛ80)
где ki = k0—k — волновое число пробного плазмона, получаем, что
параметрическая неустойчивость распада на звук возможна толь-
только для не слишком длинноволновых плазмонов: &(/d>A/3)X
Х(те//ПгI/2. Если korj)^> (me/miI12, то, как следует из соотноше-
96
ния A.180), параметрически связанными окажутся только рас-
распространяющиеся навстречу друг другу плазменные волны,
ki?& — fco, 'при этом в результате отдельного акта распада длинно-
длинноволновая перекачка 'плазмона происходит на некоторое малое
На рис. 1.23 и 1.24 приведены результаты лабораторного и
численного экспериментов, иллюстрирующих параметрический рас-
распад плазменной волны.
Параметрически связанными между -собой могут быть самые
различные ветви колебаний плазмы — электромагнитные /-волны,
50
100
50
100
50
100
50
100
о
50
100
п
ff о
50
100
П
Рис. 1.24. Возникновение спектра ленгмюровских волн, возбуждаемых вследствие
распада электромагнитной волны накачки с частотой со0, близкой к плазменной
(численный эксперимент):
а — возбуждение монохроматической ленгмюровской волны из электромагнитной волны на-
качкк, k
f=- ^1 l/ i2_^ (w0—<
rD 3
w"~.
При этом в спектре ионно-звуковых колебаний также
rD 3
появляется волна с волновым числом kt\ б — возбуждение сателлитов в спектре ленгмюров-
оких волн в результате граспадной неустойчивости по схеме 1-+U+S. В результате распада
ленгмюровской волны возбуждаются ионно-звуковые колебания с волновым числом порядка
2k (Гб Т А Д Л М. и др. Препринт Ин-та прикл. мат. АН СССР,
1978, 1№ 17)
7—74
97
плазменные /-волны, ионно-звуковые s-волны. Но непременное
условие параметрической неустойчивости — частота волны накачки
должна быть больше.частоты всех возбуждаемых в результате
неустойчивости волн. Не вдаваясь в детали соответствующих вы-
вычислений, которые легко провести в рамках намеченной выше
общей схемы, приведем условия возникновения всех возможных
типов параметрических неустойчивостей изотропной плазмы и ин-
инкременты нарастания амплитуды (табл. 1.1).
Таблица 1.1
Условия распадных параметрических неустойчивостей волн в плазме
Волны, участ-
участвующие в рас-
распаде
/->/'+ S
t->l + S
t-*l + lr
t->tr + l
t-+tf + S
Условие распада
*о>Ъ^1/3)(/п*//и*I/2
со' =^ 2сор
сор^ъ* (vTe /с)
сор^(о* (vTe /с)
Инкремент нарастания
(eE0'me<*LvTe )(со/(о5I/2
(eE0/me^vTe )(оЛ>5I/2
(еЕ0/ю*тьс) <ар
(еЕ0/те<й*с)(<й*(*рI12
\{оЕ,)/ (ть<*^Тв')](<*'иРL2 Н'«>)
Некоторые из приведенных в таблице параметрических неустой-
неустойчивостей соответствуют явлениям вынужденного комбинационно-
комбинационного рассеяния, известным из других разделов физики. Так, напри-
например, распад по схеме t-^-t' + s соответствует хорошо известному
в физике твердого тела явлению Мандельштама — Бриллюэна —
рассеянию света интенсивными звуковыми колебаниями решетки.
Раопад по схеме t-*~V' + / — это явление рассеяния Рамана —
рассеяние света на оптических колебаниях решетки.
Порог параметрической неустойчивости в однородной плазме
определяется диссипацией энергии пробных волн. Затухание одно-
одного из двух раскачиваемых возмущений не может полностью ста-
стабилизировать неустойчивость, а только уменьшает ее инкремент.
Действительно, обратимся вновь к задаче о распаде плазменной
волны и учтем сначала затухание низкочастотной моды колебаний.
При этом соответствующий ей осциллятор становится затухающим
с декрементом затухания vs, соответственно этому левую часть
первого из уравнений A.178) следует видоизменить, введя в нее
слагаемое 2ivs(o6n. Дисперсионное уравнение получается по общей
схеме. Решая его в предположении, что *у == Im co<Cvs, получаем,
что в этом случае развивается диссипативная1 параметрическая
неустойчивость с инкрементом
7=vVvs. A.181)
98
И только при учете затухания плазменной волны (его легко учесть
введением в левую часть второго из уравнений A.178) слагаемого
2ive(coo—оз), где ve — затухание плазмона), когда уравнение
A.181) трансформируется .в следующее:
возможна стабилизация параметрической неустойчивости. Порого-
Пороговое значение амплитуды накачки, -при которой происходит такая
стабилизация, определяется из условия
Предшествующее рассмотрение относилось к начальной стадии
параметрической неустойчивости, когда амплитуду волны накачки
можно считать постоянной,
а амплитуды пробных волн
нарастают со временем по
экспоненте. При достаточно
больших амплитудах проб-
пробных волн становятся суще-
существенными нелинейные эф-
эффекты, связанные с измене-
изменением амплитуды волны на- п , ос о
/otrt7II П^ЛЛ „„Л „„„ л Рис. 1.25. Зависимость от времени амплитуд
качки. Обратимся ДЛЯ КОН- при взаимодействии трех волн при распад-
кретности к задаче о пара- ной неустойчивости
метрической неустойчиво-
неустойчивости плазменной волны. Уравнение для изменения ?0 легко можно
получить из A.173), причем очевидно, что dE0/dt~$nEu Распад
при больших амплитудах пробных волн описывается, таким обра-
образом, системой из трех связанных нелинейных уравнений для Ео>
Ei, Ьп. Эта система уравнений допускает точное аналитическое ре-
решение. Оно, однако, слишком громоздко для этой книги. Опуская
вывод, приведем графики зависимостей E0(t\) и Ex(i)y полученные
при точном интегрировании уравнений взаимодействия трех волн
(рис. 1.25). Как видно, амплитуда пробной волны Е\ достигает
максимального значения, равного начальному значению амплиту-
амплитуды накачки ?о(О) (накачка при этом минимальна), в дальнейшем
энергия перекачивается от пробной волны к волне накачки и т. д.
Характерный период осцилляции порядка величины обратного
инкремента неустойчивости. Энергия, переходящая в 'ионно-звуко-
вые колебания, мала по сравнению с энергией плазменной волны
в (os/cop раз — именно такая доля энергии уносится фононом при
элементарном акте распада — «плазмон-*плазмон+фонон».
§ 1.16. Резонансное взаимодействие волн
и частиц (квазилинейная теория)
Плазму, в которой в конце концов возбуждается большое ко-
количество волн — мод колебаний (например, из-за неустойчивостей,
рассмотренных ранее), можно назвать турбулентной, если
7* 99
Ы\
i
А У'
УЛ У'
Ш
УХ
Л
амплитуды волн существенно превышают уровень тепловых флук-
флуктуации, а их фазы случайны. Вообще говоря, если уровень колеба-
колебаний становится очень большим, то могут стираться описанные
выше характерные черты отдельных мод. Поэтому специально вы-
выделяют более простой случай не очень больших амплитуд — так
называемое приближение слабой турбулентности.
Нелинейность плазмы приводит к взаимодействию между модами
типа рассмотренной в предыдущем параграфе распадной неустой-
неустойчивости, так что коэффициенты в раз-
разложении по собственным колебаниям
становятся медленно меняющимися (в
масштабе периода колебаний) функ-
функциями времени.
Важная особенность плазменной
турбулентности, отличающая ее от
турбулентности жидкости, связана
w w. w, _ с тем, что в плазме значительную,
1< ~к~ 1<з ~к а иногда и Доминирующую роль игра-
1 z ет известный из предыдущих парагра-
Рис. 1.26. Перекрытие зон ре- |фов эффект резонансного взаимодей-
зонансов Ландау для волн ! ствия ВОЛн с частицами. В старшем
с близкими фазовыми скоро- * « ¦,
стями и «коллективизация» порядке по амплитуде поля такой эф-
резонансных частиц фект соответствует индуцированному
излучению и поглощению волн части-
частицами, скорости которых связаны с частотами и волновыми векто-
векторами волн черенковским условием (резонанс Ландау):
со=Ь. A.182)
Здесь уместно доставить вопрос о том, как будет меняться
функция распределения резонансных частиц по скоростям при
излучении и поглощении волн. Этот вопрос уже рассматривался
в § 1.13 для изолированной монохроматической волны. В этом
случае основной эффект обратного воздействия волны на частицы
заключается в захвате резонансных частиц волной и их фазовых
осцилляциях в (Потенциальной яме. Зависимость периода фазовых
колебаний от энергии частиц приводила к фазовому размешива-
размешиванию, так что функция распределения в узком интервале скоростей
\v—(olk\r^(e(po/m)^2 испытывала мелкомасштабные осцилляции,
сглаженная по этим осцилляциям функция распределения была
постоянна вдоль траекторий.
Траектории резонансных частиц существенно отличались от
невозмущенных, и решение задачи удалось 'получить только бла-
благодаря тому, что уравнения движения частиц при достаточно мед-
медленном изменении амплитуды волны имеют точные интегралы.
Уже при наличии двух-трех волн строгий анализ движения резо-
резонансных частиц становится безнадежно сложным, и аналитическое
решение задачи для этого случая до сих пор не получено. Ситуа-
Ситуация, однако, существенно упрощается в предельном случае очень
100
большого числа волн, когда можно использовать статистический
подход, считая случайными их фазы.
Действительно, предположим, что в плазме возбужден широкий
пакет волн, фазовые скорости которых достаточно плотно запол-
заполняют некоторый интервал (<(о/&)тах>^> (co/?)min, так что области
захвата соседних волн перекрываются. Очевидно, что для этого
должно быть выполнено условие
Рис. 1.27. Броуновское дви-
движение резонансных частиц
в пространстве скоростей
б (<со/?) < {(e/mk) (E\8kI/2} ^ A.183)
где 6(со/&), 6k — расстояние между соседними гармониками по
фазовой скорости и волновому числу соответственно; ^ — спект-
спектральная плотность энергии электрического поля плазменных шу-
шумов. Тогда энергия плазменных шумов
на интервале 8k равна E2k6k, среднеквад-
среднеквадратичный потенциал на этом интервале
(E2k8k)l/2lk и условие A.183) действи-
действительно соответствует перекрытию потен-
потенциальных ям для соседних волн
(рис. 1.26). При выполнении этого усло-
условия происходит своеобразная «коллекти-
«коллективизация» резонансных частиц между,
двумя любыми соседними волнами. Если
фазы волн случайны, то в результате
толчков со стороны многих волн ско-
скорость частицы как бы участвует в броу-
броуновском движении. В фазовом про-
пространстве это броуновское движение
складывается со свободным движением
частиц, так что результирующие тра-
траектории имеют вид, изображенный на рис. 1.27. С тече-
течением времени броуновские траектории частиц хаотически, но
достаточно плотно заполняют nav фазовой плоскости весь учас-
участок резонансных скоростей частиц: ('со/&)тах>0> (W^)min. Отно-
Относительно полной ширины пакета волн в этом случае «предпола-
«предполагается, что она существенно больше ширины потенциальной ямы,
созданной 'пакетом:
Д (©/Л) = (W&) max-(CD/6) min> (eifo/mI^ A.184)
где q>o=[Jd??V&2]1/2 — среднеквадратичный потенциал в пакете
волн. Устанавливающаяся в этих условиях функция распределе-
распределения, разумеется, содержит мелкомасштабные шероховатости и
сохраняет (в отсутствие столкновений) энтропию, но физический
смысл имеет только сглаженная функция распределения, которая
соответствует росту энтропии и описывает диффузию резонансных
частиц в лоле волны, В результате диффузии функция распреде-
распределения будет выравниваться, т. е. стремиться к постоянному значе-
значению, на участке (co/&)max>f > (co/&)mm, заполненном траекто-
траекториями частиц (постоянство сглаженной функции распределения
101
на траекториях имело место и в случае монохроматической
волны).
Процесс диффузии резонансных частиц можно описать в рам-
рамках так называемого квазилинейного приближения. При получении
уравнений этого приближения предполагается, что амплитуды
возбужденных в плазме волн не слишком велики, так что нели-
нелинейными взаимодействиями между колебаниями можно прене-
пренебречь, а единственный нелинейный эффект, который принимается
во внимание, связан с обратным воздействием колебаний на рас-
распределение резонансных частиц по скоростям, в результате чего
возбуждение и поглощение колебаний происходят на медленно
меняющемся под действием самих же колебаний «фоне».
Мы не будем вдаваться в детали обоснования уравнений квази-
квазилинейного приближения (хотя такое обоснование уже давно прове-
проведено), а ограничимся наиболее простым выводом этих уравнений
для случая взаимодействия с плазмой ленгмюровских колебаний.
Будем считать плазму однородной, а колебания одномерными.
В соответствии со сделанным выше замечанием функцию рас-
распределения резонансных частиц по скоростям представим в виде
/=/o(f, v)+bf(t, v, x). A.185)
Здесь fo(t, v)—медленно меняющаяся функция распределения,
характеризующая фон, на котором развиваются колебания;
б/(/, v9 х) —осциллирующая в пространстве и во времени добавка
к функции распределения, характеризующая эти колебания. Оче-
Очевидно, что
(б/)=0, т. е. tf>=f0. A.186)
Скобки здесь означают усреднение по временному интервалу,
большому по сравнению с периодом колебаний, и по простран-
пространственному интервалу, большому по сравнению с длиной волны.
Тогда уравнение для fo получается простым усреднением исход-
исходного кинетического уравнения и имеет вид
dfoldi=(eim)(E&6f/dv). A.187)
Здесь кроме соотношений A.185) и A.186) учтено отсутствие сред-
среднего электрического поля в плазме (Е)=0. Слагаемое, перене-
перенесенное в правую часть уравнения A.187), определяет изменение
/о из-за наличия среднеквадратичного эффекта быстрых осцилля-
осцилляции (так называемый квазилинейный интеграл столкновений).
При получении его явного вида учтем, что в плазме возбужден
достаточно широкий пакет волн, т. е.
(кх-шкЩ. A.188)
k
В этих формулах оэ& — частоты линейных плазменных мод, опреде-
определяемые соотношением A.36); Ek{t)—амплитуды этих мод, мед-
102
ленно меняющиеся со временем в результате взаимодействия с ре-
резонансными частицами. Поскольку величины б/ и Е по физическо-
физическому смыслу должны быть вещественны, то очевидно, что в разло-
разложениях A.188) Ek- и Я-ь-гармоники комплексно сопряжены, т. е.
выполняются условия:
Е-к=Е%; f-k=f*k; G>_ft=—©л. A.189)
Используя эти условия, уравнение A.187) перепишем в виде
A.190)
(гармоники с к'ф—k из этой суммы исчезают при усреднении).
Выше отмечалось, что эффектом нелинейного взаимодействия
гармоник в квазилинейном приближении пренебрегается. Соответ-
Соответственно этому для связи fk и Ek=—ikyk используем формулу ли-
линейной теории A.123). Единственное отличие от линейной теории
состоит в том, что в этой формуле под fo понимается меняющаяся
со временем фоновая функция распределения; формула A.123)
применима, если «фон» изменяется со временем достаточно мед-
медленно в масштабе периода колебаний | (l//o)d/o/cW| <Ссо/г.
Учитывая также, что в согласии с замечаниями, сделанными
.в § 1.12, резонансный знаменатель kv—со& в этой формуле следует
понимать в смысле A.136), получаем окончательно следующую
формулу для fk:
fh=(eim)Ek(dfo/dv) (&l(kv—m) +in6(kv—a>h)). A.191)
Подставляя fk в A.190) и учитывая, что 3>(\\х)—нечетная,
а 8(х)—четная функция аргумента, получаем следующее уравне-
уравнение для /0:
dfjdt = («V*) (djdv) 121 Eh I2 8 {kv - со) dfjdvl A.192)
В правой части уравнения A.192) хможно перейти от суммиро-
суммирования к интегрированию по волновым числам с помощью соотно-
соотношения
2 = (l/2ic)Jdft = (l/ic) J dk.
k k>0
В этой формуле учтено, что элементарный «интервал» k, прихо-
приходящийся на одно колебание, bk=Lj2n (L —линейный размер плаз-
плазмы, всюду для простоты полагается L=l). Формулы для случая
ЬФ\ получаются с помощью очевидной замены |Ek\2-+L\Eh\2.
Выполняя в A.192) интегрирование по k с помощью б-функции,
можно записать это уравнение в виде квазилинейного уравнения
диффузии по скорости
dfoldt={didv) (Ddfo/dv), A.193)
103
где коэффициент диффузии определяется спектральной плотностью
плазменных шумов \Ek\z в резонансной точке спектра kv=®k'.
D=(e2lm*)\Ek\2(kv=(x)h) l\v—d®ldk\. A.194)
Разумеется, это уравнение диффузии следует дополнить уравнени-
уравнением для амплитуд волн, т. е. фактически для изменения со време-
временем коэффициента диффузии. В квазилинейном приближении
инкремент отдельной гармоники спектра совпадает с линейным
A.148), однако опять-таки под /0 в этой формуле следует пони-
понимать медленно меняющийся со временем «фон». В результате
имеем
1^ ,ч}
A.195)
Уравнения A.193) —A.195) и есть замкнутая система уравне-
уравнений квазилинейного приближения. С помощью этих уравнений
ниже рассмотрены две простые задачи — о релаксации электрон-
электронного пучка в плазме и о погло-
поглощении пакета плазменных ко-
колебаний.
Начнем с задачи о релакса-
релаксации электронного пучка. На-
Начальная функция распределе-
распределения по скоростям для та;кой
задачи имеет вид, показанный
на рис. 1.28. Максимум функ-
функции распределения при <у = 0
Рис. 1.28. Эволюция функции распреде- соответствует тепловым части-
ления электронного пучка в плазме при Цам плазмы, имеющим, напри-
пучковой неустойчивости мер, максвелловское распреде-
распределение, второй максимум соот-
соответствует пучку быстрых (надтеплозых) частиц. Если разброс по
скоростям в пучке достаточно велик Av^> (ni/no)i/3v, то инкремент
неустойчивости плазменных волн определяется из уравнения
A.148), релаксацию такого пучка можно рассматривать в рамках
квазилинейных уравнений.
Если же электронный пучок первоначально моноэнергетиче-
моноэнергетический [Да<< (/2i/ftoI/3u], то на начальной стадии его релаксации
происходит возбуждение монохроматической волны. Нелинейная
теория возбуждения монохроматической волны рассматривалась
в § 1.13 — волна нарастает до значения eyolm<~y2lk2-—u2o(ni/ftoJ/3
и стабилизируется. При более детальном рассмотрении, однако,
оказывается, что монохроматическая волна сама по себе неустой-
неустойчива. Рано или поздно она размывается в пакет волн. Здесь этот
процесс не рассмотрен. Важно лишь, что в конце концов дальней-
дальнейшую релаксацию пакета снова можно рассматривать в квазилиней-
квазилинейном приближении.
104
Таким образом, будем считать разброс по скоростям в пучке
достаточно большим, так что применимы квазилинейные уравнения.
Тогда волны с фазовыми скоростями в некотором интервале, где
dfo/dv>O, оказываются неустойчивыми. Возбуждение волн сопро-
сопровождается диффузией частиц пучка по скоростям, и в первоначаль-
первоначальной области неустойчивости устанавливается «плато» на функции
распределения (см. рис. 1.28). Однако такая функция распределе-
распределения неустойчива, «а ее переднем фронте производная dfo/dv поло-
положительна и происходит возбуждение волн. Область неустойчиво-
неустойчивости и соответственно область диффузии в пучке все время смеща-
смещаются к меньшим скоростям. В результате на функции распределе-
распределения возникает как бы волна релаксации, имеющая вид ступеньки
с крутым фронтом и распространяющаяся в область малых ско-
скоростей. Перед фронтом шумы остаются на тепловом уровне, за
фронтом возбуждены интенсивные плазменные шумы, и функция
распределения близка к «плато». Процесс релаксации заканчива-
заканчивается, лишь когда частицы пучка продиффундируют до скоростей,
сравнимых с тепловой скоростью плазмы. Окончательные границы
«плато» определяются из следующих соотношений:
ff=M°»in)./Г=Р.(О- AЛ9б>
Здесь /jj°—окончательная функция распределения в резонансной об-
области, имеющая вид «плато» df™ldv = O; fM(v) — максвелловская
функция распределения тепловых частиц плазмы; f%{v)—началь-
f%{v)—начальная функция распределения в пучке. Очевидно, что
Vmin^vr, vmdiX^Uo. A.196a)
Высоту «плато» можно найти, воспользовавшись законом сохра-
сохранения числа частиц в резонансной области:
откуда имеем приближенно
f™ ^ njuo.
Спектральную плотность энергии плазменных шумов в резонанс-
резонансной области ?>min<&)/?<утах найдем с помощью так называемого
интеграла энергии квазилинейных уравнений. Для его получения
подставим в правую часть квазилинейного уравнения диффузии
\Ek\2(df/dv) (kv=co) из уравнения A.195) для \Ek{t)\2. В резуль-
результате приходим к следующему соотношению:
) (d/dv)
Проинтегрируем это уравнение по времени и пренебрежем
вкладом тепловых шумов ?Г2л(/=О). Интегрируя получившееся со-
соотношение по скорости в пределах от Ущш ДО v с очевидным гра-
105
ничным условием — спектральная плотность шумов на границе ре-
резонансной области обращается в нуль |?ft|2(a=i>min)==0, получаем
искомый интеграл энергии — формулу, связывающую спектраль-
спектральную плотность плазменных шумов и изменение функции распре-
распределения резонансных частиц:
| Ек \2(v)^
Рис. 1.29. Спектр плазменных ко-
колебаний, возбуждаемых при ква-
квазилинейной релаксации электрон-
электронного пучка в плазме
/ j (f. (t, v) - f\ (v)) do. A.197)
°min
Как следует из формулы A.197),
спектральная «плотность плазменных
шумов вначале растет с ростом фа-
фазовой скорости, достигает максиму-
максимума при [V^Uq и при больших скоро-
скоростях быстро убывает, обращаясь
в нуль при v=>vmaX (рис. 1.29).
В той области скоростей, где пер-
первоначально не было пучка v<u0 и
f°Q(p)=O (это и есть основная энер-
госодержащая область для спектра
волн), из уравнения A.197) имеем
следующее соотношение для асим'п-
тотической формы спектра плаз-
плазменных шумов, соответствующей
«плато» на функции распределения
по скоростям f°°0'
Полная энергия колебаний для такого спектра
A198)
хти\. AЛ99)
Именно такую энергию теряет пучок при квазилинейной релакса-
релаксации к состоянию с плато на функции распределения:
u20— Г
A.200)
Следует заметить, что спектр A.197) —это еще неокончательно
установившийся спектр в системе плазма — пучок. Он может ме-
меняться в результате нелинейного взаимодействия волн. Однако для
не слишком энергичного пучка, когда энергия плазменных коле-
колебаний также достаточно мала, процесс дальнейшей нелинейной
эволюции спектра A.197) существенно более медленный по срав-
сравнению со временем его установления в рамках квазилинейных
уравнений. На рис. 1.30 и 1.31 приведены результаты численного
моделирования и лабораторного эксперимента, иллюстрирующие
образование плато на функции распределения.
106
Обратной по отношению к рассмотренной выше является зада-
задача о поглощении первоначально заданного пакета плазменных
колебаний. Поглощение сопровождается диффузией резонансных
частиц к большим скоростям и установлением «плато» на функ-
функции распределения (рис. 1.32). Спектр колебаний, устанавливаю-
Рис. 1.30. Релаксация электронного пуч-
пучка малой плотности в плазме в числен-
численном эксперименте (Rowland H. L., Рара-
dopoulos. «Phys. Rev. Lett», 1977, v. 29,
p. 1276):
1 — функция распределения плазмы; 2 — функ-
функция распределения пучка. Начальные пара-
параметры пучка и плазмы: отношение их плотно-
плотностей П\1п2=2 • 10-3, отношение средней скоро-
скорости пучка к тепловой скорости плазмы
Uo/vTe = 40, разброс по скоростям в пучке
At>i=8,3t>T<?. Функция распределения пучка и
плазмы показана в различные моменты вре-
времени t. В результате релаксации пучка на
его функции распределения образуется плато
ю4
10'
iOz
10
1
iff1
юг2
104
10s
1OZ
10
1
к
*
-•
-
ч.
/• 1
• •
UIQQcDpQ
Z
•*
•
1500 00 L
4
V/V-,
те
щийся в результате такого процесса, можно найти из квазилиней-
квазилинейного интеграла энергии, при выводе которого, естественно, уже
нельзя пренебречь начальными колебаниями, и поэтому в уравне-
уравнении A.197) следует зименить \Ek\2-*\Ek\2— \Ek\2 (t=0). Долю
энергии плазменных шумов, поглощаемых в плазме, легко можно
оценить с помощью закона сохранения энергии:
W(t = 0) — W{t = oo)^— UP —f°°)(mv2l2)dv^nresmuLu. A. 201
При малом числе резонансных частиц nTes только малая часть
энергии волнового пакета поглощается в плазме, поглощение прак-
практически прекращается после установления «плато» на функции
Рис. 1.31. Экспериментальное исследование
релаксации электронного пучка в плазме
(Левитский С. Л., Шашурин Н. М. «Журн.
эксперим. и теор. физ.», 1967, т. 52, с. 350).
Измерения проводились в лампе, наполненной
водородом, в которую инжектировался электрон-
электронный пучок; плазма создавалась самим пучком.
Показано распределение по скоростям f=dJ/d(u
в зависимости от задерживающего потенциала на
коллекторе, / — ток на коллектор. Функция рас-
распределения пучка измерялась при фиксированном п
расстоянии между катодом и коллектором элек- v
тронов, но при различных значениях тока в пучке (кривые 1—4). В режиме со слабым
током пучок почти моноэнергетический, при увеличении силы тока (кривая /) происходит
«размытие» функции распределения. При еще больших токах возникает характерная для
квазилинейных уравнений «волна релаксации» на функции распределения, распространяю-
распространяющаяся в сторону малых энергий. При максимальных токах (кривая 4) на функции распре-
распределения образуется «плато»
107
2
Too
.
V
Рис. 1.32. Поглощение пакета
ленгмюровских колебаний
^г 1 распределения резонансных частиц.
В этих условиях дальнейшее погло-
поглощение 'плазменных колебаний воз-
возможно только при учете обычной
столкновительной диффузии, рас-
рассмотренной в § 1.9. Дело в том, что
если квазилинейная диффузия при-
приводит к установлению «плато» на
функции распределения, dfo/dv^O,
то столкновения стремятся вернуть
наклон функции распределения
к равновесному значению. В резуль-
результате возникает конкуренция между
влиянием волн и влиянием столкно-
столкновений, при достаточно частых столк-
столкновениях функция распределения
сильно отличается от вида «плато»
и затухание Ландау сохраняется.
Чтобы продемонстрировать это,
введем в квазилинейное уравнение
диффузии также и диффузионный
член, соответствующий парным
столкновениям. Для рассматривае-
рассматриваемой задачи, в которой функция распределения существенно ме-
меняется лишь в узкой резонансной области, достаточно удержать
только член со старшей . производной {djdv)v{Tfm) (df/dv), не
учитывая динамического прения.
В результате конкуренции между квазилинейным воздействием
волн на частицы и столкновениями в резонансной области должно
установиться некоторое квазистационарное распределение
(dfojdt=O), подчиняющееся уравнению
Интегрируя уравнение A.202) один раз, находим*
dfo/dv^idfu/dv) li[l-\-D(v) /via/ItJ]. A.203)
D(v)^(e2lm2) (\Ek\2lv) (kv=(d) -^-коэффициентдиффузии в ре-
резонансной области. Полученный наклон функции распределения
подставим в формулу для декремента затухания y=(tt/2)X
\X(@3/k2) (df/dv). В результате
Y^Yb/ [ 1 ~\~е2(Е2) lm2v (¦©/?) 3Д^] • A -204)
В этой формуле уь — декремент затухания Ландау, рассчитанный
по максвелловской функции распределения. Для достаточно узко-
* При этом интегрировании учитываем, что вне резонансной зоны скоростей
наклон функции распределения — максвелловский dfu/dv.
108
го пакета можно записать E2kAk^(E2), что и было сделано при
выводе формулы A.204).
Формулу A.204) можно интерпретировать следующим образом.
Запишем ее в виде
7^Yb/(l+Ti/T2), A.205)
где Ti — характерное время установления локального максвеллов-
ского распределения в резонансной области Av, ti~(l/v) (v/AvJ;
%2 — характерное время квазилинейной диффузии под действием
волнового пакета. Если Ti<Ct2, то столкновения успевают восста-
восстановить максвелловскую функцию распределения, и мы получим
обычное затухание Ландау. В случае T2>Ti функция распределе-
распределения близка к «плато», и затухание стремится к нулю. На рис. 1.33
показаны результаты исследования аналогичного эффекта зависи-
зависимости коэффициента усиления звука в решетке от амплитуды.
Рис. 1.33. Зависимость коэффициента элек-
электронного усиления звука от мощности вво-
вводимого в кристалл звукового потока.
В достаточно сильном электрическом поле, когда
скорость дрейфа электронов оказывается «сверх-
«сверхзвуковой», резонансное взаимодействие звуковой
волны с электронами проводимости приводит к ее
усилению. Сплошная кривая — результат расчета,
основанного на идеях, аналогичных изложенным
в этом параграфе (см. формулу A.204I (Гальпе-
(Гальперин Ю. М., Каган В. Д. «Журн. эксперим. и теор.
физ.», 1970, т. 59, с. 1057); ^.—эксперимент
(Иванов С. Н., Котелянский И. М., Мане- j{f* jff3 ЯВТП/СМ2
фельд Г. Д., Хазанов Е. И. «Письма ЖЭТФ», '
1971, т. 13, с. 283)
Отметим, что формула A.205) применима и в случае погло-
поглощения монохроматической волны. В этом случае (см. § 1.2) при
выполнении условия 7ьТ&<С1 фазовое размешивание резонансных
частиц, захваченных в потенциальную яму, быстро «выключает»
поглощение. Столкновения, также .как и в случае пакета волн, вос-
восстанавливают максвелловское распределение резонансных частиц
»~ затухание плазменной волны. Одновременный учет обоих фак-
факторов вновь приводит к формуле A.205), где в данном случае
T2=l/&(eq>0/'/nI/2 — период фазовых колебаний захваченных ча-
частиц, определяющий время фазового размешивания, ti=(l/v)X
X (со/&J[1/ (<?фо/т)]—характерное время установления максвел-
ловского распределения в области захвата Av—(?фО/тI/2.
§ 1.17. Резонансное взаимодействие волм
и частиц (индуцированное рассеяние)
В квазилинейных уравнениях учитывается только обычное ре-
резонансное взаимодействие волн с частицами (резонанс Ландау
<о—kv=0). Среди большого количества, вообще говоря, более сла-
слабых нелинейных эффектов высокого порядка (возникающих в бо-
более высоких порядках разложения по амплитуде волн) важную
109
роль может играть появление биений на разностных частотах
между двумя любыми парами волн в спектре слабой турбулентно-
турбулентности. Если рассматривать такие биения как новые волны, то усло-
условие их резонанса Ландау с частицами имело бы вид
V-°»*, = (k.-k.)v. A.206)
Очень часто из-за условия o^klk^$>vT обычный резонанс Ландау
со—kv=0 выполняется только для надтепловых частиц, и из-за ма-
малого числа резонансных частиц обычные квазилинейные эффекты
излучения и поглощения волн слишком малы. В этих условиях
важную роль может играть резонанс на биениях, поскольку усло-
условие A.206) может выполняться для основной массы тепловых
частиц. Например, для ленгмюровских колебаний соответствующая
скорость биений ((oko — <t>k)[(ko—ki)=3(ko + ki)rBVTel2 всегда су-
существенно меньше тепловой скорости электронов. Поэтому хотя'
резонанс A.206) и возникает в старших порядках по амплитуде
поля, в него вовлекается большое число частиц, и он может ока-
оказаться весьма существенным в динамике слектра волн.
Резонансные условия A.182) и A.206), также как и -распад-
ные условия A.164), допускают наглядную квантовую интерпре-
интерпретацию. Мы знаем, что колебания, возбужденные в плазме, можно
рассматривать как газ «квазичастиц» — элементарных «квантов»
колебаний с энергией Йсоь и импульсом Нк. В § 1.15 было показа-
показано, что распадные условия A.164) соответствуют законам сохра-
сохранения энергии и импульса в процессах распада (слияния) квантов.
Законы сохранения энергии и импульса при излучении (погло-
(поглощении) кванта резонансной частицей запишутся в виде
где Awe, Ар соответствуют изменению энергии и импульса при
излучении (поглощении) кванта. Определяя Ар из второго условия
и подставляя в первое, сокращая на постоянную Планка (ведь
фактически рассматривается чисто классический случай!), прихо-
приходим к резонансному условию A.182). Аналогичным образом резо-
резонансное условие A.206) вытекает из законов сохранения энергии
и импульса при неупругом рассеянии частицей кванта («). > k0) c
превращением в квант (a>k , kj.
В задачах турбулентной плазмы «числа заполнения» для кван-
квантов плазменных колебаний велики, поэтому процессы рассеяния
также становятся индуцированными, как и излучение и поглоще-
поглощение волн при обычном резонансе Ландау A.182).
Рассмотрим более детально этот процесс индуцированного,рас-
индуцированного,рассеяния для случая плазменных колебаний. Оказывается, такой про-
процесс можно интерпретировать как параметрическую неустойчи-
неустойчивость плазменных и ионно-звуковых колебаний в изотермической
плазме Te=Ti. В этом случае затухание низкочастотной моды
(биения), обусловленное резонансным взаимодействием с ионами»
по
настолько велико, что декремент затухания может иметь порядок
частоты, и в этом случае вообще не имеет смысла говорить об
ионном звуке. Таким образом, если в обычной параметрической не-
неустойчивости рост пробных .плазменной и ионно-звуковой волн
возникает в результате их параметрической связи на «фоне» плаз-
плазменной накачки, то в механизме индуцированного рассеяния рост
пробной плазменной волны из волны накачки обусловлен излу-
излучением и поглощением резонансными частицами (в данном случае
ионами) «квантов» биений на разностной частоте. Чтобы описать
этот эффект, движение ионов в низкочастотной моде биений следу-
следует рассматривать в кинетическом приближении. В этом приближе-
приближении линейное уравнение для возмущения плотности плазмы сов-
совпадает с уравнением A.174). Для учета связи низкочастотных
движений с высокочастотными ленгмюровскими в это уравнение
нужно добавить слагаемое, возникающее при учете высокочастот-
высокочастотного «давления». Как было показано в § 1.15, это означает замену
k2r2B8n-^k2r2j)8nJr (k2/ 16ятвсо2р) (?2>.
Выделяя в высокочастотном давлении биение двух ленгмюровских
волн — основной волны Ео (накачки) и пробной Е\, получаем сле-
следующее уравнение для возмущения плотности плазмы в биениях:
Ьп [e~l (ш, k) + k2r2D] = — {к2(Ыте<*>%) Е.Е*г. A.207)
Здесь -мы использовали обозначения со=соо—<oi, k=ko—&i; co0 и
coi, kQ и ki — частоты и волновые векторы двух ленгмюровских волн
(основной и пробной) соответственно.
Уравнение A.207) следует дополнить уравнением для ампли-
туды пробной ленгмюровской волны Е\, Это уравнение было полу-
получено в § 1.15 [см. A.178)]:
[К - «О1 - < ] Е\ = (шу 2/г9) ЬпЕ\. A.208)
Связь пробной ленгмюровской волны ?\ с волной накачки Ео,
осуществляемая через биения, естественно приводит к нелинейно-
нелинейному сдвигу частоты o)i по сравнению с ленгмюровской: coi=
=co*(Ai)+&a>, 6со<сог, мнимая часть бсо определяет инкремент на-
нарастания пробной амплитуды Ei при неустойчивости индуцирован-
индуцированного рассеяния. Уравнение для бсо, как обычно, получается из
условия разрешимости уравнений A.207) и A.208). Определим
Ех из A.208): ?*1^о)р6/2^*о/4я0б(о* и подставим результате A.207).
Преобразуем последнее уравнение. Разобьем диэлектрическую
проницаемость ионов на действительную и мнимую части (см.
§ 1.12): ei=e'i'+ie,"i. Будем для простоты считать, что 8"г<Се'г и
s'i определим из условия квазинейтральности: e/i=e/e=l/&V2D.
Тогда из. уравнения A.207) получим следующую формулу для
инкремента нарастания пробной волны при индуцированном рас-
рассеянии:
t7. A.209)
ill
Как мы уже знаем, мнимая часть диэлектрической проницаемо-
проницаемости связана с особенностью .подынтегрального выражения в фор-
формуле A.128) при d=(d/&, т. е. для скоростей, соответствующих
резонансу Ландау между частицами и биением. Будем считать,
что скорость резонансных ионов существенно меньше их тепловой
скорости, а функция распределения ионов по скоростям совпадает
с максвелловской. Вычисляя при этих предположениях е"г- и под-
подставляя результат в A.209), приходим к окончательной формуле
для инкремента индуцированного рассеяния:
Im бсо= (я/8) 1/2©Р?2оЗ(й2о—*2i)rD(/ni/me) 1/2/128яя0Г| k0—kx |.
A.210)
Неустойчивость на индуцированном рассеянии возникает в том
случае, когда пробная волна имеет большую длину волны, чем
накачка: Ао>&1.
Очевидно, что когда пробная плазменная волна возникает не
из монохроматической накачки, а из пакета плазменных волн, то
инкремент неустойчивости также можно получить из A.210') с по-
помощью очевидной замены |?10|2/4-^ 2[?\ Г [множитель 1/4
возникает из-за используемой здесь нормировки, см. A.135)]. Тог-
Тогда вместо A.210) имеем
й)=3«)/оGг^/8^I/2 X
(k\-k\) l\k.-kx |32
A.211)
Остановимся на некоторых интересных следствиях этой форму-
формулы. Прежде всего видно, что при индуцированном рассеянии пе-
перекачка энергии происходит в длинноволновую часть ^спектра
[инкремент в A.211) положителен при k&>k\\. Это достаточно
очевидный результат — при рассеянии на плазме с равновесной
максвелловской функцией распределения преобладают процессы
поглощения виртуальных квантов, поэтому часть энергии рассеи-
рассеивающегося плазмона поглощается частицей и рассеянный плазмон
должен иметь меньшую частоту и, следовательно, меньшее волно-
волновое число. Число плазмонов Nh при рассеянии, естественно, сохра-
сохраняется. Кроме того, поскольку энергию плазменных волн можно
представить в виде Nkh®k=NhU(uv(\+3k2r2T>l2), а при рассеянии
изменяется только небольшая тепловая поправка к частоте, то
энергия плазменных волн в процессе рассеяния также остается
примерно постоянной. Действительно, с помощью A.211) нетрудна
показать, что
112
Максимальную величину инкремента, характеризующего индуци-
индуцированное рассеяние, легко можно получить из A.210), а именно
при (соо—coi)/!'&o—к\\я&отг имеем
7таХ^сор(?2о/64яя0Г). A.212)
Изменение волнового числа плазмона в отдельном акте Ak рассея-
рассеяния определяется соотношением со0—со^З&Д&гЪ'СОр^&Угг. Отсюда
Ak^^(melmi)l/2l3rj). Таким образом, в области не очень малых вол-
волновых чисел кгъ>{Ще\тхУ12 перекачка по спектру носит диффе-
дифференциальный характер. Так же, как и при параметрической не-
неустойчивости с рождением ионно-звуковых волн в этом случае
в процессе индуцированного рассеяния оказываются связанным»
друг с другом две распространяющиеся навстречу плазменные вол-
волны &0^—k\. Изменение волнового числа при рассеянии ko-\-k\^Ak
мало по сравнению с шириной спектра. Из уравнения A.211) в этом
случае нетрудно показать, что характерный инкремент, определяю-
определяющий скорость нелинейного изменения всего спектра, уменьшается:
по сравнению с A.212) в (k/AkJ раз:
Экспериментальный результат, иллюстрирующий явление индуци-
индуцированного рассеяния плазменных колебаний, приведен на рис. 1.34..
Рис. 1.34. Экспериментальное исследование
неустойчивости монохроматической волны,
обусловленной индуцированным рассеянием
на частицах плазмы (Измайлов А. Н. и др.
«Письма ЖЭТФ», 1970, т. 12, с. 73).
Эксперимент проводился в цезиевой плазме с тем-
температурой /-х_2000 К. Возбуждались две ленгмю-
ровские волны — основная и пробная, частоты
КОТОРЫХ УДОВЛеТВОрЯЛИ УСЛОВИЮ | COi—:COo | >—-^
<^kvTe. Показано распределение амплитуды
пробной волны по длине плазменного шнура в от- 0 5 10 15 20 ,V,CM
сутствие основной волны (кривая /) и при нали-
наличии основной волны B), частота которой больше,
чем у пробной. Рост амплитуды связан с неустойчивостью индуцированного рассеяниям
уменьшение амплитуды при больших х связано с затуханием основной волны до значений,,
при которых инкремент индуцированного рассеяния становится меньше декремента затуха-
затухания Ландау
Инкремент определяет, в частности, скорость длинноволновой:
перекачки энергии в спектре колебаний A.197), возбуждаемых
при релаксации электронного пучка в плазме. Поэтому квазили-
квазилинейная теория процесса релаксации, изложенная в первой
части данного параграфа, применима, если при максимальном уров-
уровне энергии колебаний W, определяемом формулой A.199), инкре-
инкремент нелинейной перекачки энергии по спектру остается меньше
инкремента лучковой неустойчивости. В этом случае вначале про-
происходит квазилинейная релаксация пучка, а затем возбужденный-
пучком .спектр колебаний постепенно трансформируется в резуль-
8-74 ИЗ»
тате индуцированного рассеяния. Для сильно размытого пучка
Ли^>v согласно A.154) инкремент лучковой неустойчивости
Тлин—(йрЩ/По. Волновое число неустойчивых колебаний /г^ор/ио,
шоэтому параметр кЧ^^Т/ти20 и сформулированное выше условие
применимости квазилинейной теории можно записать в виде
уу/ \\\ПъТ\ X
X (теи20/Т) (те1пц)~пц(Т1тви20Jте^>1. A.214)
..Для энергичных пучков, когда параметр е<С1, имеет место так
называемый эффект нелинейной стабилизации пучковой неустой-
неустойчивости. Энергия плазменных колебаний, возбуждаемых пучком,
растет до значения sW. В дальнейшем откачка колебаний из ре-
.зонансной для пучка области спектра, связанная с индуцирован-
индуцированным рассеянием, стабилизирует пучковую неустойчивость, и ко-
.лебания все время поддерживаются на уровне eW. Поскольку ко-
коэффициент диффузии частиц пучка по скоростям пропорционален
плотности энергии колебаний в резонансной области, то время
.диффузии, т. е. время релаксации пучка, возрастает вМ/е раз по
сравнению с квазилинейным. Происходит как бы просветление
-.плазмы для электронного пучка — явление, часто наблюдающееся
в космической плазме (плазма солнечного ветра, магнитосферная
плазма), где пучок проходит огромные расстояния без существен-
существенной потери энергии.
§ 1.18. Нелинейное взаимодействие волн
в слабой турбулентности
До сих пор мы исследовали взаимодействие в слаботурбулент-
слаботурбулентной плазме между газом частиц — электронов либо ионов и газом
.квазичастиц — элементарных волновых движений. В данном пара-
параграфе рассмотрена слабая турбулентность и проанализировано
взаимодействие между волнами, т. е. внутри газа квазичастиц.
Физический механизм, лежащий в основе такого взаимодействия,
-связан с исследованной в § 1.14 параметрической неустойчивостью
и проявляется в процессах распада и слияния элементарных вол-
волновых квантов. Газ элементарных волновых движений можно за-
задавать функцией распределения квантов определенного типа (ленг-
мюровских, звуковых) по волновым числам Na (t, k), подобно то-
тому как электроны и ионы плазмы характеризуются функцией рас-
распределения по скоростям fa(t, v). Выше мы вводили спектральное
распределение энергии колебаний по волновым числам Wk=
= |?fe|2/8rt (либо Ek= (\Ek\2-\-\Hk\2/8n для электромагнитных ко-
. лебаний). Поскольку энергия отдельного кванта равна ftco/г, то
имеем очевидное соотношение
Nh=Whlm A.215)
(рассмотрение удобно проводить в системе единиц с Н— 1—так
: как-рассматриваются чисто классические эффекты, то постоянная
Планка из окончательных формул должна выпасть).
,114
. д рд
ные спектры плазменных колеба-
колебаний
В предыдущих параграфах были выведены кинетические урав-
уравнения для функции распределения частиц, учитывающие столкно-
столкновения частиц с частицами и частиц с волнами. Теперь мы можем
ввести в рассмотрение кинетическое уравнение для числа квантов.
Схематически такое кинетическое уравнение можно записать,
в виде
dNk I dt=St{Nk} + 2ykNk. A.216)
Первое слагаемое в правой части этого уравнения — так называе-
называемый интеграл столкновений волн с волнами. Под такими столкно-
столкновениями условно понимается результат нелинейного взаимодей-
взаимодействия волн друг с другом. Кроме
того, в нелинейной задаче обя-
обязательно должны присутствовать
источник и сток энергии, как, на-
например, накачка энергии в тур-
турбулентность за счет какого-либо
механизма неустойчивости и по-
поглощение волн частицами. Эти про-
процессы схематически описываются
в уравнении A.216) вторым сла-
слагаемым в правой части. Доста- Рис. 1.35. Распадные и нераспад-
точно очевидно, что конкретная
структура интеграла столкновений
зависит от типа волнового взаи-
взаимодействия. В простейшем случае, если закон дисперсии взаимо-
взаимодействующих волн со (к) допускает трехволновое взаимодействие,,
описываемое распадными условиями A.164), то интеграл столкно-
столкновений будет квадратичен по числу квантов:
<2>k) W • A.217)
Мы ограничимся такой символической записью интеграла столкно-
столкновений. Для получения его конкретного вида следовало бы исполь-
использовать динамические уравнения параметрической неустойчивости.
в форме, аналогичной A.178), перейти в них к числам заполнения
Nk, использовав предположения о случайных фазах взаимодейст-
взаимодействующих волн и о медленности изменения их амллитуд Im со&/со/1<С1.
Вся эта процедура достаточно громоздка, и ее детальное описание
выходит за рамки настоящей книги. Напомним только, что волно-
волновые векторы в интеграле столкновений k, ki, кг и соответствующие
им частоты (о , со , «). должны быть связаны распадными
условиями <*>Л = ш +а)к> k = k1-f-k2.
Естественно, что не при всяком спектре волн выполняются эти
соотношения. На рис. 1.35 показаны различные формы возможных
спектров волн. Используя векторное неравенство |ki + k2| < |ki| +
+ |k2|, нетрудно показать, что приведенные выше распадные усло-
условия могут быть выполнены для волн со спектрами //, и наоборот,
8* 115
..для волн со спектрами типа /, /// (см. рис. 1.35) это невозможно
(нераспадные спектры). Если дисперсионное соотношение имеет
-более чем одну ветвь, то распадные условия могут быть выполне-
выполнены для волн, принадлежащих к различным ветвям. Так, для ленг-
мюровских колебаний (спектр нераспадный), распадные условия
могут выполняться при распаде на ленгмюровскую и ионно-звуко-
вую ветви колебаний. В общем случае распадным условиям удает-
удается удовлетворить в тех случаях, когда через три точки, соответ-
соответствующие колебаниям (со, к), (ом, ki), (co2, к2) (эти точки могут
лежать на различных ветвях), можно провести кривую, аналогич-
аналогичную кривой //.
В тех случаях, когда распадные условия для трех волн не вы-
выполнены, в элементарный акт взаимодействия включается четыре
,о)=оI + со2 + о)з, k=ki + k2 + k3 и соответственно этому интеграл
-столкновений становится кубическим по числу квантов:
St ШЛ > Г Нк Нк Нк V (к к к к \ N N N
J *М **2 **3
Обсудим теперь соотношение между теорией слаботурбулентной
плазмы и колмогоровской теорией турбулентности несжимаемой
.жидкости. Строгое аналитическое описание гидродинамической тур-
турбулентности крайне затруднительно,
так как турбулентное движение уже
нельзя щредставить в виде набора
собственных мод (вместо них мы
имеем набор непрерывно дробящих-
дробящихся вихрей). Поэтому в гидродина-
гидродинамической турбулентности у нас нет
эквивалента такого статистического
описания, какое в слабой турбу-
турбулентности дает приведенное выше
кинетическое уравнение, и наиболее
надежные оценки основаны на со-
соображениях размерности. Предста-
Представим себе ситуацию, когда источник
крупномасштабного (малые k) тур-
турбулентного движения (рис. 1.36,
область источника /) отделен от
области, где турбулентное дви-
движение быстро затухает из-за увели-
увеличения вязкой диссипации в мелких масштабах (область погло-
поглощения ///). Тогда энергия турбулентных движений перекачивается
от больших масштабов к меньшим из-за процесса нелинейного
.дробления масштабов вихрей, проходя последовательно все умень-
уменьшающиеся масштабы инерционного интервала (область //). Хо-
Хорошо известные размерностные соображения приводят к следую-
.щему спектру турбулентности в инерционном интервале:
Wk^\jk^ A.218)
^116
"Рис. 1.36. Спектры турбулентности
;в случае постоянства потока энер-
энергии по спектру в интервале равно-
равновесия (///) между областями рас-
раскачки (/) и затухания (//)
{закон Колмогорова — Обухова). Эти соображения основаны на
предположении о постоянстве потока энергии по спектру в инер-
инерционном интервале. Количественно это условие записывается
в виде
A.219)
Здесь Wk — спектральная плотность турбулентных движений; т&—
характерное время перекачки энергии, зависящее от k\ kjx имеет
смысл скорости переноса в /^-пространстве. Поскольку этот процесс
вызван нелинейным слагаемым (vy)V'—'kv2 в уравнении Эйлера
A.102), то из соображений размерности имеем
llXh^kv. A.220)
Здесь v—скорость в турбулентных пульсациях масштаба krl.
Очевидно, что энергию этих пульсаций kWk можно записать в виде
n0Mv2, и из A.220) имеем размерностную оценку
l/Xk~k[kWk]№, A.220а)
которая вместе с условием A.219) дает закон турбулентности Кол-
Колмогорова — Обухова. Интересно найти аналог колмогоровского
спектра в слабой турбулентности плазмы, когда такой спектр мо-
может быть получен не только из размерностных оценок, но и из
точного решения кинетического уравнения. Однако сложность плаз-
плазменной задачи состоит в том, что даже в изотропной плазме су-
существуют различные взаимодействующие между собой ветви коле-
колебаний: плазменные, звуковые, электромагнитные, так что некоего
универсального - спектра с простой степенной зависимостью не
существует. Поэтому искать такой спектр имеет смысл лишь в не-
некоторых случаях, когда возбужден определенный тип волн. При
этом наиболее просто решается вопрос о спектре ионно-звуковой
турбулентности.
Пусть, источник такой турбулентности находится в области до-
достаточно длинных масштабов. Спектр ионно.-звуковых колебаний
в области больших длин воли, когда несущественна дисперсия фа-
фазовой скорости, — распадкый, причем во взаимодействие вовлека-
вовлекаются колебания с коллинеарными (или, точнее, почти коллинеар-
ными) волновыми векторами. Процесс коротковолновой перекач-
перекачки энергии связан тогда со слиянием ионно-звуковых квантов,
которое описывается уравнением A.217). Из этого уравнения име-
имеем следующую оценку т* (с учетом соображений размерности)
llXh~e*kWklnoTe. A.221)
Вследствие распадности спектра ионно-звуковых колебаний энер-
энергия турбулентных пульсаций kWh входит в формулу для тГ~
в первой степени. Эта энергия нормируется на тепловую энергию
в плазме поткхJ1к2=поТе. Величина {йк=Ь{Те\кыУ1г — единственная
•в рассматриваемой задаче имеющая размерность частоты.
117
Используя условие постоянства потока энергии в инерционном
интервале— A.219) и оценку A.221) для та, получаем следующий
спектр ионно-звуковой турбулентности:
A.222)
Эта формула определяет спектр турбулентности в масштабах инер-
инерционного интервала, отделяющего область источника от коротко-
коротковолновой области, поглощения звуковых колебаний ионами плаз-
плазмы. Тот же степенной спектр ионно-звуковой турбулентности был
получен путем строгого решения кинетического уравнения для
волн.
50
100
Рис. 1.37. Спектры ленгмюровских и иоино-звуковых волн, возникающих при
электромагнитной накачке, численный эксперимент (Горбушина Т. А. и др. Пре-
Препринт Ин-та прикл. мат. АН СССР, 1978. № 17).
По осям отложена спектральная плотность энергии ионно-звуковых (а) и ленгмюровских (б)
колебаний в зависимости от номера гармоники п. Распад электромагнитной волны накачки
приводит к рождению гармоники плазменной волны с л=я0. Эстафетная перекачка энергии
(распады t-+l'+s) в длинноволновую часть спектра ленгмюровских волн приводит к уста-
установлению спектральных распределений, показанных на рисунке
Значительно сложнее решается задача о турбулентности ленг-
ленгмюровских колебаний. Дело в том, что спектр ленгмюровских
колебаний — нераспадный и оснозные нелинейные процессы в сла-
слабой ленгмюровской турбулентности — распад с рождением ионно-
звуковых колебаний, а в изотермической плазме Те=Тг — индуци-
индуцированное рассеяние на ионах плазмы. В элементарных актах, соот-
соответствующих каждому из этих процессов, часть энергии ленгмю-
ровского кванта передается ионно-звуковому кванту либо рассеи-
рассеивающей частице. Поэтому нелинейное взаимодействие в ленгмю-
ленгмюровской турбулентности сопровождается «покраснением» ленгмю-
ленгмюровских квантов, т. е. перекачкой ленгмюровской энергии в область
длинных масштабов и больших фазовых скоростей, где вообще не-
невозможно резонансное поглощение энергии волн частицами. Так,
в ленгмюровской турбулентности возникает проблема аккуму-
аккумуляции энергии при А-^0 и образования «плазмонного конденсата»
(наподобие «Бозе-конденсата»). Тенденция к образованию конден-
118
сата в процессе нелинейного взаимодействия плазмонов хорошо
видна в численном эксперименте (рис. 1.37). Разгадка парадокса
«конденсации» плазменных колебаний имеет важное значение в фи-
физике нелинейных колебаний и турбулентности плазмы. Эта про-
проблема подробно обсуждается в следующем параграфе.
§ 1.19. Модуляционная неустойчивость и коллапс
ленгмюровских волн
Оказывается, что «конденсат» — достаточно интенсивный газ
длинноволновых плазмонов — неустойчив относительно процесса
модуляции его плотности и образования каверн — областей лока-
локализации более высокой концентрации волновой энергии, из кото-
которых под действием силы высокочастотного давления вытеснена
плазма. Физический смысл неустойчивости можно разъяснить до-
достаточно наглядно. Представим себе, что «на первоначально одно-
однородном фоне ленгмюровских волн хотя бы в результате флуктуа-
флуктуации возникла область, где амплитуда колебаний электрического
поля несколько превышает средний уровень. В результате в этой
области возрастает и высокочастотное давление, так что электроны
из нее вытесняются. Возникающее при поляризации плазмы ква-
квазистатическое электрическое поле вытягивает ионы вслед за элек-
электронами, образуется квазинейтральный профиль пониженной плот-
плотности. Как движутся плазмоны на таком профиле плотности?
Мы знаем, что каждый плазмон — это квазичастица с энергией
сок(г)^соРоA+6/г(г) /2/2o) + C/2)?2r2DG)po и импульсом к (здесь п =
= яо+б/г — плотность плазмы; соро— плазменная частота, соответ-
соответствующая невозмущенной плотности). Поэтому уравнения движе-
движения плазмона, записанные в гамильтоновой форме, имеют вид
dk/dt = - дш/дг ;= - тр.№1дг,
dvjdt = д®}дк = 3kr2D «v
Из этих уравнений очевидно, что профиль с пониженной плотно-
плотностью играет роль потенциальной ямы для плазмона. Действитель-
Действительно, в этом случае сила F—-dk/dt ускоряет те плазмо'ны, которые
движутся на дно ямы, и тормозит движущиеся в обратном направ-
направлении. В результате достаточно медленные плазмоны захватыва-
захватываются в потенциальную яму, возрастают высокочастотное давление
и, следовательно, деформация профиля плотности, потенциальная
яма становится глубже, что приводит к дальнейшему росту локаль-
локальной интенсивности ленгмюровских волн и высокочастотного дав-
давления. Таким образом, развивается неустойчивость автомодуляции
пространственного распределения плазмонов — стягивание их
в сгустки-каверны.
Из проведенного анализа ясно, что при неустойчивости изме-
изменяется характер траекторий плазмонов. Если в отсутствие взаимо-
взаимодействия плазмоны двигались по пролетным траекториям с по-
119
стоянной скоростью dco/dk, то при развитой модуляционной не-
неустойчивости они оказываются запертыми в кавернах, аналогично
тому как достаточно сильная волна захватывала резонансные ча-
частицы плазмы в потенциальную яму. Так же как эффект захвата
резонансных частиц волной не описывается квазилинейными урав-
уравнениями, захват плазмонов в каверны и развитие модуляционной
неустойчивости нельзя описать в рамках слабой турбулентности.
Возникающая в результате модуляционной неустойчивости турбу-
турбулентность ле'нгмюровских волн является сильной — волновые дви-
движения, из которых она слагается, существенно отличаются от ли-
линейных мод колебаний. Ниже проведен качественный анализ этой
проблемы.
Начнем с простого эвристического рассмотрения модуляционной
неустойчивости, использующего аналогию между распределением
плазмонов в неоднородной плазме б/г (г) и больцмановским рас-
распределением заряженных частиц в потенциальном поле <р(г). Хо-
Хорошо известно, что функция распределения электронов в таком
поле имеет вид
/(v) = по (т/2яГK/2 ехр{—/ш>2/2Г+вф/ T}. A.224)
Интегрирование по скоростям в этой формуле приводит к распре-
распределению Больцмана для плотности распределения электронов в по-
потенциальном поле.
По аналогии с максвелловским распределением равновесную
функцию распределения плазмонов в отсутствие деформаций плот-
плотности условно представим в виде
Nk = N9 ехр {— k2lk2}jn3/2k\ A.225)
Из закона дисперсии ленгмюровских волн имеем
=2 (со—»соРо) /3(DPoftV2D, поэтому равновесное распределение мож-
можно представить следующим образом:
Мк = No ехр{ - 2(« - <оро)/3%Д V 2D}/<№.
При наличии деформаций плотности плазмы б/г (г) величина со—
—соро=(Р./'2в/2-|-б/г/2/2о)(Оро (первое слагаемое— кинетическая энер-
энергия плазмона, второе — его потенциальная энергия). В этом слу-
случае равновесное распределение плазмонов A.225) трансформиру-
трансформируется в следующее:
Nt =JVoexp {— k2jk* — bnjd>k*r*u.}ln3/2k*. A.226)
Если равновесное распределение A.225) —аналог максвелловского
распределения для частиц, то распределение A.226)—аналог
больцмановского распределения в потенциальном поле ф(г). Инте-
Интегрируя по к, находим полную плотность плазмонов
j dkNk^Noexp {- Sn/3?VD/20}. A.227)
120
Из этой формулы действительно следует, что плазмоны имеют тен-
тенденцию скапливаться в местах провала плотности плазмы. Воз-
Возмущение плотности плазмонов определяется формулой
в полной аналогии с возмущением электронной плотности 8п=
—щеу/Те. Соответствующее возмущение высокочастотного давле-
давления
*Pm = -PMlWr^n. A.228)
(ро=(Е2) /8п — равновесное давление плазмонов) по знаку об-
обратно возмущению плотности, что, собственно говоря, и приводит
к неустойчивости.
Для получения количественной формулы напомним, что линеа-
линеаризованные уравнения медленных квазинейтральных движений
плазмы имеют вид [ср. с A.118)]
— nQmiioyv = —ikbp; — i<D$n-\-iknjD = O, A.229)
где 6р — суммарная вариация давления в плазме, слагающаяся
из вариаций высокочастотного и газокинетического давлений:
Подставляя в A.229) 8/?вч из формулы A.228), получаем следую-
следующее дисперсионное уравнение:
ш2=1т [1 — (E2)/k2r2D l6m.T\lmi. A.230)
Условие неустойчивости со2<0, т. е.
(?2) /16я/го7>/г2г2Б, A.230а)
и в процессе накопления длинноволновых (к->-0) плазмонов по
каналам слабой турбулентности обязательно должна возникнуть
модуляционная неустойчивость. При (Е2) /l6nnoT^>kzr2j) имеем
из A.230) следующую оценку для инкремента модуляционной не-
неустойчивости:
Im со^ ((Е2) 11 блистая) i/2^
-^сор (me(E2) j гщ 1 бппоТ) W. A.231)
Весьма важным является вопрос о дальнейшей динамике образую-
образующихся в результате модуляционной неустойчивости каверн. Для
запертых в каверне плазмонов кинетическая энергия порядка по-
потенциальной, т. е.
к*г\ъ\Ъп\1п.. . A.232)
Длина волны запертого плазмона определяет одновременно ха-
характерный размер каверны l^ljk. Под действием силы высокоча-
121
стотного давления плазма вытесняется из каверны. Рост \6п\ со-
сопровождается охлопыванием каверны, так как /^1/FяI/2. При
этом плотность энергии колебаний возрастает и происходит уско-
ускорение процесса выталкивания плазмы и схлопывания каверны, ко-
который, таким образом, носит взрывной характер. Естественно воз-
возникает вопрос о том, что останавливает схлопывание. Ограничим-
Ограничимся качественным анализом этого вопроса, основывающимся на со-
соотношении A.232) между длиной волны запертых ллазмо'нов и
глубиной модуляции плотности, а также на условии постоянства
числа запертых в каверне плазмонов. Так как глубина модуляции
плотности в каверне обычно невелика \8п\/по<1 и соответственно
мало изменение частоты плазмона б(о<Со), то последнее условие
означает, что j <fr | ?р=соп* A.233)
и, таким образом, высокочастотное давление в каверне возрастает
при схлопывании обратно пропорционально ее объему |?|2'^Л/Is
(s принимает значения 1, 2, 3 в зависимости от размерности ка-
каверны). В то же время для схлопывания необходимо преодолеть
давление вытесняемой плазмы 8пТ, которое согласно A.232) воз-
возрастает как 1~2: Отсюда следует, что динамика каверны существен-
существенно зависит от ее размерности. В одномерной каверне (локализация
ленгмюровской энергии только по одному измерению) газокинети-
газокинетическое давление при схлопывании возрастает быстрее высокоча-
высокочастотного. В результате лри некотором / установится баланс дав-
давлений и образуется солитон — ленгмюровский сгусток конечного
размера, который, однако, неустойчив относительно модуляции
в двух других измерениях.
В двумерном случае E=2) если только в начальный момент
времени высокочастотное давление в камере превышало газоки-
кетическое, то в дальнейшем схлопывания каверны не остановить.
Наконец, в трехмерном случае высокочастотное давление при
схлопывании возрастает быстрее >газоки:нетического и процесс схло-
схлопывания идет с нарастающей скоростью. В каждом из двух слу-
случаев схлбпывание каверны с запертыми в ней плазмонами проис-
происходит до столь малых размеров, что длина волны плазмона
становится сравнимой с дебаевской длиной (а фазовая скорость срав-
сравнимой с тепловой скоростью) и «включается» резонансное погло-
поглощение плазмонов частицами плазмы — затухание Ландау. Явле-
Явление схлопывания образующихся при модуляции неустойчивости
каверн с плазмонами, которое имеет характер взрыва и ограничено
только затуханием Ландау, получило название коллапса ленг-
мюровских волн. Коллапс ленгмюровских волн описывается
полученными в параграфе о параметрической неустойчивости урав-
уравнениями A.173) и. A.176) для электрического поля и вариаций
плотности. Особенность рассматриваемого случая по сравнению
с решениями, полученными в § 1.14, связана с тем, что из-за нали-
наличия сильного взаимодействия моды колебаний, описываемые урав-
уравнениями A.230), A.231), существенно отличаются от линейных.
122
Связь между вариацией плотности в каверне и высокочастот-
высокочастотным давлением определяется уравнением A.176), в котором в мно-
многомерном случае следует заменить оператор дифференцирования
д2/дх2 на оператор Лапласа А.
Из этого уравнения следует, что схлопывание каверны с плаз-
монами носит характер «взрыва», когда сколь угодно малые раз-
размеры каверны и сколь угодно большие значения плотности энертии
в ней достигаются за конечное время. Действительно, полагая, что
скорость схлопывания каверны превышает скорость звука, сохра-
сохраним в левой части уравнения A.176) только первое слагаемое.
Кроме того, из условия захвата плазмонов каверной A.232) нахо-
находим, что
г2вА. A.234)
Таким образом, получим вместо уравнения A.176) следующую
оценочную формулу:
A.235)
Из этой формулы следует, что рост б/г и \Е\2 происходит быстрее,
чем по экспоненте, т. е. по закону «взрыва» 1/(/о—t)a9 a>0, U —
время «взрыва», т. е. время достижения особенности. Из уравнения
A.235) следует, что
\E\^\;{U-i)\ A.236)
а законы изменения Ьп и I со временем находим из условия A.233)
постоянства числа запертых в каверне плазмонов. В случае трех-
трехмерных каверн имеем
~1*Г»~<»/Г:1 „.237,
Более точно динамику ленгмюровского коллапса рассчитывали чис-
численными методами (рис. 1.38) и подтвердили взрывной характер
схлопывания, описываемый формулами A.236) и A.237).
Выясним теперь, как выглядит картина ленгмюровской турбу-
турбулентности при наличии коллапса каверн. Вначале энергия ленгмю-
ровских волн по каналам слабой турбулентности перекачивается
в длинноволновую область модуляционной ^неустойчивости. Из-за
этой неустойчивости энергия ленгмюровских волн локализуется
в большом числе случайно расположенных каверн, коротковолно-
коротковолновая перекачка запертых в кавернах ленгмюровских колебаний осу-
осуществляется в процессе коллапса.
Между длинноволновыми масштабами модуляционной неустой-
неустойчивости /о—2мгт>(\6лп0Т1(Е2)I/2 (см. рис. 1.36, область /) и ко-
коротковолновыми масштабами области поглощения /*—2ягв (об-
(область ///) лежит инерционный интервал. Через масштабы инерци-
инерционного интервала ленгмюровская энергия проносится схлопываю-
щимися кавернами. Спектр турбулентности в инерционном интер-
123
вале, как обычно, можно найти из условия постоянства потока
энергии — условия A.219). В рассматриваемом случае это усло-
условие имеет следующий вид:
\Ek\*~Wk~dt(k)ldA. A.238)
Здесь dt(k)—время прохождения кавернами через интервал
[k, k + dk] обратных масштабов турбулентности. Закон схлопыва-
схлопывания, т. е. зависимость k^l/l от t, определяется формулой A.237),
откуда вместе с условием A.238) имеем следующую формулу для
t=0,0
t=0,40
0,60
ом
} I 1 I I Г I I I I
¦L.U.l.J L.U.1
Рис. 1.38. Численный эксперимент, иллюстрирующий динамику сжатия каверны
при коллапсе ленгмюровских волн. (Дегтярев Л. М., Захаров В. Е., Руда-
Рудаков Л. И. «Физика плазмы», 1976, т. 2, с. 438).
Показаны линии уровня ампльтуды электрического поля в двумерной каверне в различные
моменты времени t. Законы роста электрического поля в центре каверны и уменьшения
ее размеров с большой точностью описываются автомодельными зависимостями для дву^
мерного случая
спектра ленгмюровской турбулентности в инерционном интервале
Wh~\lW\ A.239)
При больших k схлопывание каверн останавливается за счет
затухания Ландау плазменных колебаний. Для определения границ
инерционного интервала сравним декремент затухания с инкре-
инкрементом, определяющим скорость схлопывания каверн. На началь-
начальной стадии схлопывания этот инкремент совпадает с инкрементом
A.231) -модуляционной неустойчивости. В дальнейшем схлопыва-
схлопывание происходит, как мы уже знаем, с нарастающей скоростью, и
к концу процесса схлопывания, когда может стать существенным
124
поглощение, соответствующий инкремент возрастает в to/to—t—-
— (k*/koK/2 раз, &* и ko — волновые числа соответственно в облаете
поглощения и в области источника, где образуются каверны. Та-
Таким путем из условия
находим, что затухание Ландау становится существенным при вол-
волновых числах
A/3 -*-1/4) r~!.
A.240>
Это и есть обратные масштабы длин волн в области поглощения-
ленгмюровской турбулентности.
§ 1.20. Стационарные нелинейные волны
Не следует думать, что волны в плазме можно «довести» до*
нелинейного уровня только из-за наличия неустойчивостей. Боль-
Большой раздел в физике плазмы составляет изучение регулярных
нелинейных волн, возникающих в результате каких-либо упорядо-
упорядоченных механизмов, аналогич-
аналогичных, например, механизму ге-
генерации ударных волн в обыч-
обычной газодинамике движущим-
движущимся поршнем. Ведь так же, как
и в газовой динамике, для
волн с линейным законом дис-
дисперсии должны происходить о' х
хорошо известное укручение и
опрокидывание фронта. Эта
нелинейная деформация про-
профиля волны (рис. 1.39) за-
заключается в том, что участки профиля, которым соответ-
соответствуют большие скорости, стремятся опередить участки с мень-
меньшей скоростью, и в конце концов образуется разрыв. Если
в газовой динамике рост крутизны фронта ограничивался дис-
сипативными эффектами, то в плазме главную роль могут
играть эффекты дисперсии, т. е. зависимости фазовой скорости от
длины волны. Роль дисперсии в ограничении нелинейного укру-
чения профиля можно пояснить следующим образом. Увеличе-
Увеличение крутизны переднего фронта означает рождение высших гар-
гармоник в 'волне под влиянием нелинейности. В первом (линейном)
приближении по амплитуде всякая волна остается гармонической
в форме exp{ikx—Ш}. Во втором приближении тот же механизм,,
который был описан в § 1.14 и приводил к параметрической связи
различных типов волн, ,в случае монохроматической волны приво-
приводит просто к рождению второй гармоники. Разлагая по амплитуде
\волны, получаем следующее уравнение для поправки второго при-
125*
Рис. 1.39. Нелинейное укручение фронта
волны
•ближения:
(d2/dl2 — v\d2[dx2) E2 + LE2= AE\ exp {2i (kx — ш/)}. A.241)
Здесь Е — электрическое поле волны, индексы 1 и 2 соответствуют
амплитудам первой и второй гармоник, оператор L описывает от-
отклонение от линейного закона дисперсии волны oo=t%&. В извест-
жои смысле уравнение A.241) имеет вид уравнения движения
«осциллятора» под действием вынуждающей силы, пропорциональ-
пропорциональной Ei. Ясно, что вторая гармоника может эффективно возбуждать-
возбуждаться только тогда, когда эта сила находится в резонансе с собствен-
собственной частотой осциллятора, т. е. если удвоенной исходной частоте
2со соответствует (в законе дисперсии) волновое число 2k. Такой
резонанс может осуществляться лишь для линейного закона дис-
дисперсии со—v$k, дисперсия фазовой скорости означает, что вынуж-
вынуждающая сила смещается из резонанса и перекачка во вторую гар-
гармонику становится менее эффективной.
Для того чтобы увидеть, как дисперсия остановит процесс не-
нелинейного укручения профиля, рассмотрим случай, когда фазовая
^скорость уменьшается с ростом волнового числа. Тогда нелинейная
добавка к фазовой скорости и дисперсионная добавка, появляю-
появляющаяся при укручении профиля, имеют разный знак и поэтому мо-
могут компенсировать друг друга. Такой закон дисперсии имеют
.ленгмюровские и коротковолновые ионно-звуковые колебания, и
в этих случаях следует ожидать появления нелинейных стационар-
стационарных волн. В таких волнах все величины зависят от комбинации
х—v$t (уф — скорость распространения волны). Эти волны
можно рассматривать как асимптотическое состояние исходного
волнового пакета при достаточно больших временах, когда эффекты
нелинейного укручения и дисперсии успевают стабилизировать
друг друга.
Рассмотрим сначала нелинейную ленгмюровскую волну. Напом-
Напомним, что для волны достаточно большой амплитуды, когда выпол-
выполнено условие уь^ь<1 (уь — линейный инкремент, %ъ — период ко-
.лебаний захваченных частиц), фазовое размешивание полностью
«выключает» кинетический эффект взаимодействия резонансных
частиц с волной. Поэтому нелинейную волну можно исследовать
'С помощью более простых гидродинамических уравнений A.100)
;и A.102), дополненных уравнением Пуассона:
(Щдх);)
A.242)
d2fjdx2 = 4я? (п — п0).
"Полагая, что п=п{Ъ), v — v(l), <p=<p(g), 1-х—t^t, можно про-
проинтегрировать первые два уравнения из приведенной системы:
dnjdt-{-d(nv)ldx =
(L243)
126
Постоянные интегрирования в этих уравнениях выбраны из усло-
условия, что в невозмущенном состоянии, т. е. при ф—О, v=0y n=n0.-
Используя эти соотношения, можно свести уравнение Пуассона,
к следующему уравнению для ф(?):
A.244)
При решении уравнения A.244) оказывается удобным исполь-
использовать формальную аналогию с аналитической меха-никой — это<
уравнение совпадает с уравнением движения частицы в нелиней-
нелинейной потенциальной яме U(q) (рис. 1.40) (эта аналогия становится,
очевидной при замене ?-W, <p->-x).
Первый интеграл уравнения A.244) совладает с интегралом:
энергии частицы с единичной массой и полной энергией S\
A/2) (d<pldlJ=S>— U(q>). A.245)
Уравнение энергии A.245) просто интегрируется, и решение ф(|)
выражается через эллиптические функции. Нет смысла приводить
соответствующие формулы вследствие их громоздкости. Качест-
Качественно характер решения нетрудно*
пояснить, используя вид эффектив-
эффективного «потенциала» U(<p). При ма-
и
{
к
/
/1 ё
^S 1
-л
г
и
\J
Рис. 1.40. График эффективной по-
потенциальной энергии U(q>) в слу-
случае нелинейной ленгмюровской
волны
Рис. 1.41. Профиль потенциала электри-
электрического поля нелинейной ленгмюровскош
волны
лых амплитудах ф(|)—гармоническая функция, при больших
амплитудах потенциал <р остается 'периодической функцией, изме-
изменяющейся от фтах до фт1п, однако профиль волны искажаетсяг
как это показано на рис. 1.41. При <р<0 отрицательная сила
—^/7(ф), действующая на «осциллятор» в потенциальной яме, ве-
велика, и эту область значений <р осциллятор проскакивает довольно
быстро, существенно быстрее области положительных <р. В резуль-
результате мы получаем так называемую кноидальную волну для
потенциала (см. рис. 1.41), которой соответствует волна электри-
электрического поля ?(?) с достаточно крутым передним фронтом.
127
Нелинейное укручение профиля волн
в рассматриваемом случае остановлено
в результате дисперсии, а обмен энергии
с резонансными частицами полностью
«выключен» из-за фазового размешива-
размешивания этих частиц. Предельное значение
амплитуды потенциала в этой волне
Фпред^—ти2ф/2е, как это следует из вида
потенциальной ямы ^(ф). Возникновение
такого ограничения потенциала можно
объяснить так. В области отрицательных
Ф (см. рис. 1.40) профиль потенциала
Рис. 1.42. График ?/(ф) для представляет собой потенциальный горб
«нелинейной ионно-звуковой для электронов. При достаточно боль-
волны шой высоте rOpga фт1п=фпред тепловые
частицы плазмы не могут переваливать через него и останавли-
останавливаются в системе отсчета волны. При еще больших амплитудах
появляются отраженные электроны, возникает многопотоковое
движение частиц, приводящее к опрокидыванию профиля волны.
Таким образом, в плазменной волне дисперсионные эффекты оста-
останавливают процесс .нелинейного укручения и опрокидывания волно-
волнового профиля только для волны не слишком большой амплитуды:
Рассмотрим теперь другой предельный случай — нелинейную
жшно-звуковую волну. Фазовая скорость ионно-звуковой волны
•существенно больше тепловой скорости ионов, поэтому движение
ионов в волне можно рассматривать с помощью гидродинамиче-
гидродинамических уравнений. Ско^рость и плотность ионов определяются тогда
•формулами A.243) с соответствующими заменами заряда и массы
заряженной частицы г-*—е, те-+гпг. Что же касается электронов,
то, как уже отмечалось ранее (см. § 1.10), тепловая скорость элек-
электронов существенно больше фазовой скорости волны, и поэтому
для них поле волны практически квазистащшнарно. В этом случае
лля электронов простейшей моделью является распределение
Больцмана A.116). Тогда уравнение Пуассона для потенциала
шонно-звуковой волны вновь сводится к уравнению движения не-
нелинейного осциллятора [см. уравнение A.244)]. Эффективная
««потенциальная яма» iU(<p) в этом случае имеет вид
A.246)
+Геехр
График функции ?/(ф) показан на рис. 1.42. Так же, как и
в случае ленгмюровской волны, ограничимся качественным анали-
анализом решения, основывающимся на интеграле «энергии» A.245). Из
вида графика ?/(ф) следует, что в случае сверхзвуковой волны
Юф>{Те1гПгУ12 значениям 8 в интервале <Утш<^<0 соответствуют
J28
периодические решения с ф>0, т. е. являющиеся потенциальными
горбами для ионов. При &=^т[п (т. е. вблизи дна «ямы») имеем
гармонические колебания потенциала малой амплитуды относи-
относительно среднего значения <р* (рис. 1.43). С ростом значения &
происходит нелинейное искажение профиля вол'ны. Вершины в вол-
волне потенциала разносятся на в-се большее расстояние, поскольку
при этом вблизи точки поворота ф^фщщ сила, действующая на не-
нелинейный «осциллятор» и пропорциональная <3?/(op)/dop, оказыва-
Рис. 1.43. Профиль потен-
потенциала нелинейной ионно-зву-
ковой волны при различных
уровнях энергии осциллято-
осциллятора в эффективной потенци-
потенциальной яме U (см. рис. 1.42):
/—синусоидальная волна ма-
малой амплитуды; // — нелиней-
нелинейная кноидальная волна; /// —
уединенная волна — солитон
ЛА
AJUt.
ется малой. В результате получаем кноидальную вольту (см.
рис. 1.43). Наконец, при <§Т->0 вершины ф(?) разносятся на беско-
бесконечно большое расстояние, и мы имеем уединенную волну, или
солитон. В такой волне при |->-±оо, ф^О и dtp/dt-r+O (см. рис. 1.43).
Полагая в интеграле «энергии» <?Г=0 и dkp/dg=O при ф=фтах,
что эквивалентно условию ?/(фтах)=0, получаем дисперсионное
соотношение для солитона, устанавливающее связь -между скоро-
скоростью его распространения и амплитудой потенциала в нем:
V2=(Tel2ini) [ехр (ефшах/Ге)— I]2/ [ехр^фшах/^}—
— 1— ефтах/7У|. A.247)
Так же, как и в ленгмюрозской волне, в нелинейной звуковой
волне существует предельное значение амплитуды потенциала, при
превышении которого происходит отражение ионов от горба по-
потенциала, приводящее к возникновению многопотокового движе-
движения ионов и к опрокидыванию волнового профиля. Из вида функ-
функции ?/(ф) в рассматриваемом случае [см. A.246)] следует, что
в ионно-звуковой волне предельное значение амплитуды потен-
потенциала
9—74 129
Воспользовавшись дисперсионным соотношением A.247), не-
нетрудно показать, что для солитона такая амплитуда соответствует /
критическому числу Маха Мпред=^ф/ (Ге//ЛгI/2^1,6. Стационар-
Стационарный ионно-звуковой солитон возможен только при числах Маха
М<МпРед, при больших числах Маха.дисперсия не останавливает
нелинейное укручение и опрокидывание волнового профиля.
Рассмотренная здесь уединенная волна — солитон представляет
собой симметричный горб потенциала. Такая волна возможна
только в отсутствие какой-либо диссипации, когда условия за фрон-
фронтом волны повторяют условия перед ее фронтом, т. е. решение
строго обратимо. Наличие диссипации приводит к нарушению сим-
симметрии и возникновению своеобразной ударной волны, связываю-
связывающей два различных состояния плазмы: невозмущенное (перед
фронтом) и модулированное интенсивными колебаниями (за фрон-
фронтом). Структура ударной волны существенно зависит от конкрет-
конкретного механизма диссипации. Кроме чисто столкновительного за-
затухания .колебаний возхможны также коллективные механизмы дис-
диссипации, связанная с ними ударная волна называется б е с-
с то л кн о в и те л ьн о й. г:, v ъ^)
Рассмотрим, как происходит формирование бесстолкновитель-
ной ударной волны. Ограничимся случаем достаточно малых ам-
амплитуд волн, когда удается построить ламинарную теорию. Будем
считать, что обычная диссипация из-за парных столкновений частиц
отсутствует, но примем во внимание эффект отражения ионов от
переднего фронта, играющий роль бесстолкновительной диссипа-
диссипации. В построенной выше гидродинамической теории такое отра-
отражение вообще отсутствовало, если только амплитуды были не
слишком велики: ф<фПред (М<1,6), Однако в действительности
ионы имеют распределение по скоростям, и для небольшой группы
резонансных с волной ионов эффект отражения возможен и при
малых амплитудах волны. Если число отраженных ионов невели-»
ко, то можно найти форму профиля устанавливающейся в этих
условиях ударной волны.
При учете отраженных ионов уравнение для потенциала A.246)
модифицируется таким образом, что
Л,—Ло/(фтах) Уф/ (У Vвф//П<) l'2+2n0f (ф) . A.249)
В этой формуле Пг — плотность ионов, проходящих над потенци-
потенциальным горбом, которая определяется ранее полученной гидроди-
гидродинамической формулой. Из добавленных слагаемых первое соответ-
соответствует вычитанию отраженных ионов из полного числа ионов щ,
второе представляет собой вклад в плотность отраженных ионов.
Величина nof (ф) есть полная плотность отраженных ионов в точке
с потенциалом ф. Коэффициент 2 перед последним членом
в A.249) возникает из-за наличия двух групп движущихся на-
навстречу друг другу частиц. Конкретный вид /(<р) легко найти, зная
130
невозмущенное распределение ионов по скоростям foi(v):
nj(?)= J Uidv. A.250)
!/2
Пр.и добавлении в уравнение для потенциала слагаемого, пропор-
пропорционального /(ф), величина & [«энергия» осциллятора в потенци-
потенциальной яме 0(у)] уже не является интегралом движения. Появ-
Появление отраженных ионов .приводит к уменьшению «энергии» осцил-
осциллятора в эффективной яме, пропорциональному числу отраженных
частиц:
о
A.251)
Теперь нетрудно понять, как можно сконструировать решение
с профилем потенциала, показанным на рис. 1.44. Перед фронтом
?>=0, т. е. профиль потенциала
такой же, как и в случае соли-*
тона. В результате отражения
5 уменьшается (перемещение
6 в потенциальной яме ?/(ор)
показано на рис. 1.42 стрелка-
стрелками). Поэтому за фронтом вол-
волны имеют место интенсивные
упорядоченный колебания. Ре-
Решение такого типа, в котором °
состояние плазмы меняется ОТ Рис. 1.44. Образование бесстолкнови-
первоначально невозмущенно* тельной ударной волны
го (до (Прихода солитона) к со-
состоянию, модулированному интенсивными колебаниями, и есть
бесстолкновительная ударная волна. В отличие от обычной газо-
газовой динамики возмущенное состояние (за фронтом ударной волны)
не является термодинамически равновесным, так как нет -настоя-
-настоящих столкновений, устанавливающих его. Однако к бесстолкнови-
тельным ударным волнам можно применять соответствующие за-
законы сохранения (а при переходе через фронт — соотношения
Гюгонио), учитывая вклад колебательной структуры за фронтом.
Максимальное значение потенциала за фронтом волны фщах
(см. рис. 1.44) мало отличается от соответствующего значения
в уединенной волне с тем же числом Маха. Минимальное значе-
значение потенциала фшт («левая» точка поворота осциллятора на
рис. 1.42) определяется условием <%—i?/((pmin)—0, и поскольку при
малых ф потенциальная энергия ?/(ф) меняется квадратично, точка
поворота фщт оказывается пропорциональной корню квадратному
из энергии —8 за фронтом, т. е. из полного числа отраженных
9* 131
частиц:
A.252)
Период колебаний cp(g) за фронтом определяется интегралом
Рис. 1.45. Экспериментальное наблюдение укручения нелинейной ионно-звуковой
волны (Алиханов С. Г., Белан В. Г., Сагдеев Р. 3. «Письма ЖЭТФ», 1968, т. 7,
с. 405): первоначальное возмущение плотности (амплитуда Д/г/д^Л/5) (а) и
формирование нелинейной осцилляторной структуры по мере удаления от источ-
источника (б)
132
Очевидно, что этот период конечен и логарифмически зависит от
энергии
1— &)~ 1пA/ф,шп). . . A.253)
Наконец, появление уходящих на бесконечность ионов приводит
к скачку потенциала фоо. Такой скачок пропорционален /, и при ма-
малом числе отраженных ионов сроо^Сфтш.
При больших числах Маха, когда возникают многопотоковое
движение ионов и опрокидывание волнового фронта, изложенная
выше так называемая ламинарная теория бе с столки о-
в и тельной ударной волны неприменима. В принципе может
Рис. 1.46. Опрокидывание нели-
нелинейной ионно-звуковой волны
при больших числах Маха в
численном эксперименте (Али-
ханов С. Г., Сагдеев Р. 3., Че-
ботаев П. 3. «Журн. эксперим.
и теор. физ.», 1969, т. 57,
с. 1565).
Показана фазовая плоскость ионов
(у, х) после опрокидывания фронта
волны. Видно появление впереди
фронта ионно-звуковой волны ионов,
убегающих вперед со скоростями
~ 2и. Наличие этих ионов приво-
приводит к образованию подножия на
профиле потенциала (и плотности)
в волне
возникнуть неустойчивость многопотокового движения ионов типа
рассмотренной в § 1.14 пучковой неустойчивости электронов. Не-
Неустойчивость подобного типа, как известно, переводит анергию уло-
рядоченного движения в энергию хаотических турбулентных пуль*
саций. Связанная с неустойчивостью аномальная диссипация
может в определенных условиях привести к формированию некото-»
рого турбулентного слоя конечной толщины, играющего роль фрон-
фронта турбулентной бесстолкновительной ударной
волны.
Иллюстративные примеры генерации нелинейных ионно-звуко-
вых волн приведены на рис. 1.45 (лабораторный эксперимент
с плазмой низкой плотности) и на рис. 1.46 (одномерный числен-
численный эксперимент).
2
ПЛАЗМА В МАГНИТНОМ ПОЛЕ
§ 2.1. Движение заряженных частиц в магнитном поле
Наиболее интересные и важные для различных приложений
свойства плазмы обнаруживаются при анализе ее поведения в маг-
магнитном поле. Под действием магнитного поля плазма теряет изо-
изотропию и млогие ее свойства радикально меняются. При наличии
магнитного поля появляется возможность создать плазменные кон-
конфигурации, занимающие ограниченную часть пространства и, так
сказать, подвешенные в вакууме. Это уже нечто совершенно не
свойственное обычному газу. В этих условиях плазма приобретает
некоторые новые свойства, отличающие ее от всех других состоя-
состояний вещества.
Поскольку в конечном счете все характерные черты плазменных
процессов обусловлены законами движения частиц, то прежде чем
заняться магнитными свойствами плазмы как макроскопической
субстанции, нужно проанализировать вопрос о влиянии магнитного
поля на движение электронов и ионов.
Как известно, в однородном магнитном поле заряженная ча-
частица движется в общем случае по винтовой линии. Проекция тра-
траектории на плоскость, перпендикулярную к вектору магнитного по-
поля Н, представляет собой окружность радиусом Гн—mv^cjeH,
где v,—поперечная составляющая скорости частицы. Это так
называемая ларморовская окружность. Вращение по этой
окружности происходит с ларморовской частотой ын=еНjmc.
Вдоль силовых линий частица движется с постоянной скоро-
скоростью v{r
Рассмотрим теперь движение частицы в неоднородном магнит-
магнитном поле. В физике плазмы мы обычно встречаемся только с таким
уровнем неоднородности, при котором «а расстоянии порядка лар-
моровского радиуса частиц вектор Н остается почти постоянным
по величине и направлению: другими словами, в «микромасшта-
«микромасштабах» магнитное поле изменяется очень медленно. Выясним, какие
изменения вносит слабая неоднородность поля в характер движе-
движения частиц. Допустим сначала, что напряженность магнитного по-
поля изменяется вдоль силовой линии.
134
Наблюдая за траекторией частицы, которая навивается на эту
силовую линию, можно установить, что форма траектории заметно
меняется на протяжении отрезков, в пределах которых происходит
существенное увеличение или уменьшение напряженности магнит-
магнитного поля Н. При движении в сторону возрастания поля траекто-
траектория становится более крутой и она похожа на сжимающуюся пру-
пружину. Если же частица движется в сторону ослабевающего поля,
то ее траектория становится более пологой.
Причину этого эффекта нетрудно обнаружить. Заряженная ча-
частица, вращающаяся по ларморовской окружности, создает коль-
кольцевой ток и, следовательно, эквивалентна элементарному диамаг-
нетику с магнитным моментом ix=w±jH9 где w±—кинетическая
энергия поперечного движения. Действительно, согласно теореме
Ампера магнитный момент кольцевого тока |л=(//с)яг2я; величи-
величина электрического тока, соответствующая ларморовскому враще-
вращению, /=ео)я/2я. Теперь, подставляя записанные выше выражения
для сон и Гн, получаем
^ = mv2J2H = w±[H. B.1)
На диамагнетик, находящийся в неоднородном магнитном поле,
действует сила F=—jigrad#. В частности, если gra*d# направ-
направлен вдоль силовой линии, то
F=-ixdH/dt, B.2)
где дифференцирование проводится вдоль направления поля. Под
действием указанной силы скорость продольного движения изме-
изменяется по закону
mdv „ Jdt = — (wJH) '(dHJdl). B.3)
Умножая обе части последнего равенства на у(|, получаем
dw H Jdt = — (wJH) (dH[dl) (dtjdt) = — (wJH) (dH/dt). B.4)
При движении в постоянном магнитном поле w±-\-w{l = const. По-
Поэтому B.4) можно преобразовать к виду
dw±/dt = (wJH) (dH/dt). B.5)
Отсюда следует, что
dw±/w± = dH(H; wJH = const. B.6)
Таким образом, при движении заряженной частицы в магнит-
магнитном поле, напряженность которого достаточно плавно изменяется
вдоль силовых линий, отношение wJHm меняется, а следова-
следовательно, остается постоянным и магнитный момент, связанный
с ларморовским вращением. Сохранение величины w±JH имеет
более общий и глубокий смысл — оно представляет собой прояв-
проявление принципа адиабатической инвариантности при квазипериоди-
квазипериодическом движении. Связь с этим принципом разобрана в § 2.3.
135
grad H
Рис. 2.1. Дрейф частиц в не-
неоднородном магнитном поле
Рассмотрим теперь движение ча-
частиц в неоднородном поле, .напряжен-
.напряженность которого изменяется в направ-
направлении, перпендикулярном к силовым
линиям. Остановимся сначала на про-
простейшем случае, когда скорость пер-
перпендикулярна к магнитному полю.
х Траектория частицы изображена на
рис. 2.1. Магнитное поле направлено
перпендикулярно к плоскости черте-
чертежа. Напряженность поля увеличива-
увеличивается в сторону возрастания координа-
координаты х. В этом случае траектория части-
частицы в плоскости ху уже не будет пред-
представлять собой окружность, так как
величина ларморовского радиуса спра-
справа будет меньше, чем слева. Очевидно, что траектория- не замы-
замыкается после одного полного оборота. При каждом обороте части-
частица описывает петлю и передвигается на некоторое расстояние Ау
вдоль оси у, т. е. перпендикулярно к градиенту магнитного поля.
После нескольких оборотов траектория обрисуется достаточно ясно.
Она будет представлять собой дорожку, сплетенную из петель, по
которой частица движется .вдоль направления, .параллельного оси у.
Такое движение называется магнитным д р е й ф о м. Скорость
дрейфового движения частицы вдоль дорожки мала по сравнению
со скоростью ее ларморовского вращения (по условию предпола-
предполагается, что напряженность поля' слабо -.изменяется на расстоянии
масштаба ларморовского радиуса).
Обратим внимание на одну особенность дрейфового движения
в неоднородном магнитном поле. Совершая его, частица не уходит
в область более сильного или более слабого поля. Напротив, ча-
частица движется по узкой дорожке таким образом, что в пределах
ее траектории напряженность поля сохраняет одно-и то же значе-
значение. Это означает, что адиабатическая инвариантность Н име-
имеет место также <и .при магнитном дрейфе. В неоднородном магнит-
магнитном поле дрейфовое движение может быть связано также с нали-
наличием у частицы продольной скорости i>(|. Механизм возникнове-
возникновения такого дрейфа можно понять, рассмотрев рис. 2.2. На этом
рисунке жирными линиями показаны'силовые линии неоднород-
неоднородного магнитного поля. В общем случае о,ни являются криволиней-
криволинейными. В точке Mi, где скорость частицы параллельна вектору Н,
сила Лоренца равна нулю. Однако при дальнейшем движении ча-
частица по инерции соскользнет с силовой линии, и это приведет
к тому, что в точке Мг у частицы появится небольшая слагающая
скорости, перпендикулярная <к магнитному полю. С появлением по-
поперечной скорости будет автоматически связано появление силы
Лоренца. Под действием этой силы частица приобретает дрейфо-
136
Рис. 2.2 Происхождение центробежно-
Г0 дреифа
вую скорость, которая направлена перпендикулярно к плоскости
рисунка.
Рассматривая частные случаи (например, движение частиц
в магнитном поле, создаваемом прямолинейным проводником с то-
током), нетрудно убедиться, что дрейф частицы, связанный с про-
продольной скоростью и||Э происходит в том же направлении, в кото-
котором совершается дрейфовое движение, обусловленное наличием
у частицы поперечной скорости v..
Дрейфовое движение возникает не только при неоднородности
магнитного поля, но также и тогда, когда на заряженную частицу
в однородном магнитном поле действует дополнительная сила
немагнитного происхождения
(например, со стороны элек-
электрического или гравитационно-
гравитационного поля), направленная пер-
перпендикулярно к вектору Н.
Для выяснения основных
закономерностей дрейфового
движения рассмотрим следую-
щую задачу. Частица с заря-
дом е и массой т движется
в однородном магнитном поле,
направленном по ОСИ Z, при
наличии дополнительной силы
F, направленной вдоль оси у.
Величину Е будем считать медленно изменяющейся функцией вре-
времени (ее можно рассматривать так же, как функцию 2, поскольку
слагающая скорости частицы вдоль линий магнитного поля оста-
остается постоянной и поэтому z=0и*). Условие медленности измене-
изменения юзначает, что F остается почти постоянной за время одного
ларморовского оборота частицы, т. е. Bя/оодг) \F/F\ <Cl.
Запишем уравнения движения частицы:
х = юну; B.7)
y = -vHx + F(t)lm. B.8)
Выберем следующие начальные условия: jc(O) = O; у @) = 0;
х@) = 0; y@) = v0. При указанных условиях
х = «>ну, B.9)
У = -»шнУ+*®1т. B.10)
Общее решение уравнения B.10) имеет вид
t
у = A sin mHt -f- В cos »Ht + ^- f (F (u)/m) sin [»H (t — u)] du, B.11)
137
где А и В — константы интегрирования. Поскольку ^@)=0, нужно
положить 5=0. Преобразуя интеграл, получаем
у = Asm V ^
F (и) cos соя (t — u)du. B.12)
б
Дифференцируя B.12), находим
у = Лшя cos соя^ -[- (Т7 @)//ио)я) sin о>я? -}-
4- A/да>я) f Z1 (и) sino^ (t — а) Л*. B.13)
о
При принятом предположении о медленном изменении F послед-
последний член выражения B.12) пренебрежимо мал по сравнению со
вторым. Действительно,
f F (и) cos соя (t — и) du
и, следовательно-, отношение третьего члена ко второму порядка
A /соцг) | i^1//71. Точно так же можно пренебречь .последним членом
в выражении для у. Принимая во внимание начальные условия, из
B.9) и B.12) получаем следующие соотношения:
t
$ B.14)
0
У = (о.Ы sin «>Ht - (F @)/mco2H) cos mj + F ((Цтон. B.15)
Выражения для компонент скорости частицы имеют вид
x = v0 sin (oHt — (F @Iтън) cos <*>Ht + F (t)lm<*H\ B.16)
у = ^ cos Юд* + (F @)[rnmH) sin (оя?. B.17)
Малые члены в B.14) — B.17) отброшены.
Полученные формулы нетрудно интерпретировать. 'Мъг видим,
Что движение частицы в однородном магнитном поле при наличии
медленно (меняющейся дополнительной силы F_LH представляет со-
собой суперпозицию равномерного вращательного движения с угло-
угловой скоростью соя и перемещения в направлении, параллельном
[FXH], с дрейфовой скоростью
ud = F(f)lrm>ff = cF(t)[eH. B.18)
138
Линейная скорость вращательного движения остается в этом слу-
случае неизменной. При заданных начальных условиях
WH. B.19)
v± =
Постоянство v± связано с адиабатической инвариантностью отно-
отношения v2. /Я. Центр ларморовской окружности перемещается с дрей-
дрейфовой скоростью вдоль оси х. При этом его координата медленно
изменяется:
yc=F(t) /ты2н. B.20)
Перейдем к анализу конкретных случаев дрейфового движения.
Если частица движется перпендикулярно к силовым линиям не-
неоднородного магнитного поля, то влияние неоднородности можно,
заменить действием дополнительной силы:
F = — }xgrad# = (— w, /Я) grad Я. B.21)
Дрейфовое движение будет связано с компонентой F в направле-
направлении, перпендикулярном к Н. Из B.18) и B.21) находим дрейфо-
дрейфовую скорость для рассматриваемого случая:
ud = (mv2±cl2eH2) grad± Я, B.22).
где grad. Я обозначает компоненту grad Я по направлению, перпен-
перпендикулярному к Н. Дрейфовая скорость направлена параллельно
[НХё^Я]. Если движение
происходит в области, где
rotH=0, то формулу B.22)
можно привести к более про-
простому виду. При наличии ком-
компоненты gradЯ в направлении,
перпендикулярном к Н, сило-
силовые линии безвихревого маг-
магнитного поля должны быть
криволинейными. Для того что-
чтобы связать величину grad^H
с геометрией силовых линий,
рассмотрим рис. 2.3, на котором изображены .два небольших
участка силовых линий в плоскости кривизны (для простоты пред-
предполагаем, что мы имеем дело с семейством плоских кривых).
Точка 0 — центр кривизны для силовой линии 1. Интеграл по кон-
контуру abed равен H2dl2—H\dlu где dl\ и dl2 — длина отрезков сило-
силовых линий. В безвихревом случае этот интеграл обращается в нуль.
Следовательно,
H2dl2=Hidtu B.23)
но
Рис. 2.3. Связь между кривизной си-
силовых линий и неоднородностью маг-
магнитного поля
dL = i
B.24)
139
и
H2=HlJt-(dH/dnNn. B.25)
Подставляя выражения для dl2 и Я2 в B.22), получаем следующее
соотношение, связывающее проекцию grad# на направление нор-
мал-ик силовой линии с величиной R:
— (l/H)(dH/dn)=llR. B.26)
В рассматриваемом частном случае (плоские силовые линии) оче-
очевидно, что grad±H=dHfdn. Поэтому формулу B.26) можно запи-
записать в виде
(l/tf)grad±#=l/R. B.27)
Для вычисления па можно теперь использовать следующую фор-
формулу:
ud = v\[2mHR. B!28)
Строгий расчет показывает, что она остается справедливой в са-
самом общем случае, если только неоднородность поля достаточно
мала (в смысле, указанном ранее). Как уже говорилось выше, при
движении вдоль кривой силовой линии возникает дрейф, причиной
которого служит инерционный эффект. Если от криволинейного
движения перейти к движению в системе координат, в которой
продольная скорость равна нулю, то необходимо учесть действие
центробежной силы
F = m*]]IR, B.29)
направленной перпендикулярно к силовой линии. Согласно B.18)
эта сила вызывает дрейфовое движение со скоростью
направленной параллельно вектору [HXgrad#]. В общем случае
дрейфовая скорость частицы в неоднородном магнитном поле рав-
равна сумме выражений B.28) и B.30):
Заметим, что положительно и отрицательно заряженные частицы
дрейфуют в противоположных направлениях.
В общем случае движение заряженной частицы в неоднородном
поле можно представить как суперпозицию следующих движений.
1. Вращения по ларморовской окружности со скоростью v . ,
которая изменяется пропорционально VH.
2. Движения центра ларморовской окружности вдоль силовой
линии со скоростью о A (при этом я^ + о*!, = const).
3. Дрейфового движения центра ларморовской окружности со
скоростью tid, определяемой уравнением B.31).
НО
Соединяя мгновенные поло-
положения центров ларморовского
вращения, находим осевую ли-
линию траекторий, которую мож-
можно рассматривать как усред-
усредненный путь частицы.
Выясним теперь, как проис-
происходит дрейф при наличии элек-
электрического поля. Если на ча-
частицу, находящуюся в одно-
однородном магнитном поле, дей*
ствует также электрическое
поле Е, направленное перпен-
перпендикулярно к Н (скрещенные
поля), то F=eE и, следова-
следовательно, iid=cE/H. В этом слу-
случае дрейфовая скорость не за-
зависит ни от заряда, ни от мас-
массы частицы. Она направлена
параллельно [ЕхН]. Центр
ларморовской окружности, по
которой вращается частица,
смещается в сторону электри-
электрического поля. В интервале
©н
0н
Рис. 2.4. Траектория частицы в скрещен-
скрещенных электрическом и магнитном полях
при быстром (а) и медленном (б) вклю-
включении электрического поля
времени от t=t\ до /=/2 это смещение согласно B.20) составляет
Воспользуемся этой формулой в дальнейшем при анализе диэлек*
трических свойств плазмы в.магнитных полях.
На примере движения частицы в скрещенных полях наглядно
иллюстрируются различия в характере движения при быстрых и
медленных изменениях силы, вызывающей дрейф. Пусть в момент
времени /=0 частица покоится в начале координат (оси хну вы-
выбираются, как и ранее, рис. 2.4). Допустим, что ?*@) =0 и напря*
женность электрического поля очень медленно нарастает до неко-
некоторого предельного значения Е. При vo=O и F@)—eE@)=0 тра-
траектория частицы изображается плавной кривой (рис. 2.4,6) *. Зна-
Значение Ау монотонно нарастает от 0 до еЕ/<пш2н- Если же при /=0
напряженность электрического поля скачком (сон^<С1) нарастает
до предельного значения Е, то с помощью общих, формул B.14)
и B.15) нетрудно установить, что траектория частицы будет пред-
представлять собой циклоиду (рис. 2.4,а). Дрейфовые скорости в обоих
случаях при больших t оказываются одинаковыми, однако во
За исключением очень небольших шероховатостей в начальной части кри-
кривой, вызванных присутствием малых членов, которые не учтены в формулах
B.12) и B.13). r J v v J
141
втором случае частица будет испытывать также ларморовское вра-
вращение с линейной скоростью, равной скорости дрейфа.
Если напряженность поперечного электрического поля изме-
изменяется с частотой (о=@я, то мы имеем дело с так называемым
циклотронным резонансом. При прежних начальных усло-
условиях (равенство нулю начальных координат и скорости) и F =
=е?0 sin ©я* из B.11) и B.14) следует:
t
у = с{EJH) fsinwjsinш (t — и)du-
и)dull
= (cEJ2<t>ffH)(sm<*>Htcos«>Ht); } B.32)
t
x = соя fydt — (cEJ2<*>HH) {2A — cos <*>Ht) — <*>Ht sin <*>Ht).
6
При (DHt > 1
x ^ — (cEJ2H) t sin <aj; }
v e/ ' H B.33)
у ^ — (cEJ2H) t cos t»Ht, J
т. е. траектория образует спираль, радиус которой растет пропор-
пропорционально времени. При этом энергия частицы увеличивается про-
пропорционально t2.
§ 2.2. Примеры движения частиц в магнитном поле
Общие законы кинематики заряженных частиц в сильных маг-
магнитных полях можно проиллюстрировать на конкретных примерах.
Укажем сначала на один важный результат, вытекающий из зако-
закона сохранения отношения w±/H. Энергия поперечного ларморов-
ского вращения ш^ =t<yosin2<х, где w0 — полная кинетическая энер-
энергия частицы, а а — угол между векторами v и Н. При движении
в постоянном во времени магнитном поле w0 не изменяется. Поэто-
Поэтому постоянство w.JH означает, что сохраняется отношение
sin2 а/Я.
Пусть в некоторой точке траектории a=ai и #=#ь При таких
начальных условиях угол а в любой точке траектории можно най-
найти с помощью равенства sin2 a jH=sin2 ai/ Ни откуда
sin a = sin a, У7ЦЩ. B.34)
Если частица движется вдоль силовой линии в сторону возра-
возрастающего поля и достигает точки, в которой W.—W9, то угол a
становится равным я/2 и, следовательно, продольная скорость
142
Рис. 2.5. Осевая линия траекто-
траектории частицы в поле с магнит-
магнитными пробками
обращается в нуль. Это означает, что в указанной точке направлен
ние продольного движения изменяется. Отразившись от области
сильного магнитного поля, частица уходит обратно в сторону бо-
более слабого поля. Таким образом, области сильного поля при не-
некоторых условиях могут играть для заряженных частиц роль свое-
своеобразных магнитных зеркал. Через такие зеркала могут прохо-
проходить только частицы с малым начальным углом наклона ось Физи-
Физический механизм, вызывающий отражение частиц от областей
с сильным магнитным полем, достаточно ясен. Здесь проявляется
действие диамагнитной силы \igvadH, которая направлена в сто-
сторону слабого поля.
Движение заряженных частиц в магнитных полях при опреде-
определенных условиях может оказаться финитным, т. е. будет происхо-
происходить в ограниченной области про-
странства. Это, в частности, может
иметь место из-за отражения части-
частицы от магнитных зеркал.
Пусть напряженность поля на-
нарастает вдоль силовых линий в обе
стороны от некоторой средней
области, где Н^Н\ (рис. 2.5). Час-
Частица, находящаяся в этой обла-
области, будет заперта в пространстве
между магнитными зеркалами (зонами сгущения силовых линий),
если угол наклона ее траектории оц превосходит некоторое мини-
минимальное значение, и будет колебаться вдоль ограниченных участ-
участков силовых линий. Магнитное поле, в котором можно организо-
организовать «длительное хранение» заряженных частиц, используя
эффект отражения от магнитных зеркал (или пробок), можно соз-
создать, например, с помощью длинного прямого соленоида, плот-
плотность намотки в котором увеличивается при приближении к тор-
торцам. Роль гигантской магнитной ловушки в природе выполняет
магнитное поле Земли, удерживающее заряженные частицы в рай-
районе так называемых радиационных поясов.
Частицы, оказавшиеся в ловушке с магнитными зеркалами,
совершают не только колебательные движения вдоль силовых ли-
линий. В поле с искривленными силовыми линиями они будут также
дрейфовать перпендикулярно к Н <(см. рис. 2.5). Однако такой
дрейф не приведет к уходу частиц из ловушки, так как инвариант-
инвариантность sin2 а при наличии дрейфа не нарушается. В отсутствие элек-
электрического поля и при постоянном во врехмени магнитом поле час-
частица может ускользнуть из ловушки только в результате удачного
для нее столкновения с какой-либо другой частицей.
. В качестве другого примера рассмотрим траекторий заряжен-
заряженных частиц в винтовом тороидальном поле. Такое поле создается
в системах для получения высокотемпературной плазмы, исполь-
используемых в исследованиях по управляемому термоядерному синтезу.
В этом случае магнитное поле есть суперпозиция двух полей:
143
магнитного поля Н , создаваемого током, текущим вдоль кольце-
кольцевого плазменного витка, и продольного магнитного поля HQ внеш-
внешнего происхождения, замкнутые силовые линии которого парал-
параллельны току (рис. 2.6). При этом НЬ^>Н^ и радиус поперечного
сечения плазменного витка, в котором происходит движение час-
частиц, мал по сравнению с радиусом кольца R. Предполагается, что
имеет место симметрия по отношению к главной оси тороидаль-
тороидальной системы.
Рис. 2.6. Тороидальное винтовое магнитное Рис. 2.7. Проекция траектории
поле частицы в тороидальном поле
иа плоскость х, у
Для описания траектории частицы в винтовом тороидальном
поле введем координаты х, у и в (рис. 2.7). Осевая линия кольце-
кольцевого тока пересекает плоскость чертежа в точке О, где х—у=0.
Координата 8 определяет угол поворота вокруг главной оси торо-
ида. Предположим далее, что Н зависит только от г=У%2-\-у2.
Продольное магнитное поле Нв\ обратно пропорционально расстоя-
расстоянию до главной оси тороидальной системы и при r/i?<Cl опреде-
определяется равенством
- (xlR0)\,
B.35)
где Но — напряженность продольного поля в точке О.
В рассматриваемой магнитной системе движение, центра лармо-
ровской окружности частицы будет складываться кз перемещения
вдоль силовой линии со скоростью v{] и магнитного дрейфа со
скоростью tid. Нетрудно показать, что если соблюдается условие
H(?/HB<^rjR, то влиянием Н^ на дрейфовую слагающую ско-
скорости можно пренебречь. В этом случае дрейфовая скорость на-
направлена по оси у и равна
ud ^ [у2 _]_ (i/2) v2 ][(oHRQ =5r [v20 — A/2) v2 ]I«>HRO, B.36)
144
где v0 — неизменная величина вектора скорости частицы. Поскольку
Н =5= #б, а Я9 согласно B.35) мало изменяется вдоль силовой линии,.
то v2± также испытывает лишь небольшое изменение при движе-
движении частицы и, следовательно, иа можно считать в первом прибли-
приближении постоянной величиной. Слагающие результирующей ско-
скорости движения по осям х и у определяются выражениями
=vn (HJH)(x[r)+ud, B.37>
Уравнение траектории в плоскости ху имеет вид
% = -(ua[va)dx B.38>
ИЛИ
drfdx = -(udfva) (HJHJ. B.39>
Следует различать два разных класса траекторий. К первому
из них принадлежат траектории так называемых пролетных час-
частиц, у которых вектор скорости составляет не слишком большой
угол с вектором Н, вследствие чего они свободно перемещаются
вдоль силовых линий. Ко второму классу относятся траектории
так называемых запертых частиц. У таких частиц угол наклона
скорости к направлению магнитного поля относительно велик, и,
поэтому они колеблются вдоль ограниченных участков силовой ли-
линии между областями с более сильным полем. Поскольку напря-
напряженность магнитного поля вдоль силовой линии изменяется отно-
относительно мало, то в силу адиабатического постоянства отношения
v2±IH ларморовская скорость v^ любой частицы испытывает от-
относительно малые колебания вдоль траектории» В частности, для*
запертых частиц V. должна в любой точке траектории иметь зна-
значение, близкое к результирующей скорости t/о. Определим с по-
помощью уравнения B.39) форму траектории для пролетных и за-
запертых частиц. .
Для того чтобы не усложнять вычислений, рассмотрим траек-
траектории таких пролетных частиц, у которых продольная скорость v^
в любой точке траектории не слишком мала по сравнению с vq,
т, е. движение частицы не очень сильно замедляется в областях
с максимальным значением HQ '(при х, близких к г). При указан-
указанном условии ввиду практической неизменности v± значение v{]
относительно слабо изменяется при движении частицы. Следова-
Следовательно,, правую часть уравнения B.39) можно в первом приближе-
10—74 145.
мш считать величиной постоянной. Обозначим ее С. Нетрудно
убедиться, что | С\ < 1. Действительно,
mvc
где г —ларморовскии радиус частицы в поле тока — величина, по
общему условию достаточно малая. Заметим, что Съ 1/#ф и практи-
практически не зависит от #0. Из B.39) следует, что г = го — Сх. Если
пренебречь членами второго порядка малости относительно С, то
B.39) можно привести к виду (х— СгоJ+У2=^2о. Это уравнение
окружности, центр которой смещен на расстояние Сг0 относитель-
Рис. 2.8. Траектории пролетных
частиц
Рис. 2.9. Траектории запретных ча-
частиц
но осевой линии винтового магнитного поля (рис. 2.8). При своем
движении частица отклоняется от силовой линии на расстояние
где г9 — ларморовскии радиус в результирующем магнитном поле. При
соблюдении условия Яф/Яе < r[R это отклонение может в несколь-
несколько раз превысить ларморовскии радиус, но оно остается малым по
сравнению с Го. Следовательно, пролетные частицы с не слишком
малой v{{ хорошо удерживаются в винтовом поле. Более деталь-
детальный анализ показывает, что это имеет место для любых пролетных
частиц.
Выясним теперь поведение запертых частиц. В этом случае ин<
<С^ и продольная скорость v[{ сильно изменяется вдоль траекто-
траектории, обращаясь в нуль в точках отражения от области с более
сильным полем (рис. 2.9), между которыми происходит колебание
частиц. (В плоскости ху частица колеблется между точками Mi и
„М2). В данном случае в уравнении Д2.39) правая часть уже не
146
является постоянной величиной. Из адиабатической инвариант-
инвариантности v2^/H следует, что
где хт — абсцисса точки отражения*. Дрейфовую скорость ud
в этом случае также можно считать практически постоянной. Ин-
Интегрируя B.39) с учетом указанной зависимости для v]{ , получаем*
Здесь фш — значение угла ср в точке отражения. На рис. 2.9 изо-
изображена форма траектории в проекции, напоминающая банан. Как
нетрудно убедиться, смещение Агт для запертых частиц значитель-
значительно превосходит смещение для пролетных частиц (в отношении,,
пропорциональном ]/r2R/r для двух противоположных предель-
предельных случаев). Следует отметить, что компенсация дрейфа при дви-
движении запертых частиц происходит в результате того, что точки
поворота траектории М\ и М2 расположены симметрично относи-
относительно экваториальной плоскости плазменного витка. Такое рас-
расположение точек поворота будет иметь место только при наличии,
аксиальной симметрии по углу 8. В противном случае траектории
могут стать незамкнутыми, что должно ухудшать удержание час-
частиц в магнитной системе рассматриваемого типа, которая может
служить простейшим примером «замкнутой магнитной ловушки».
В идеальном случае частицы могут уходить из такой ловушки толь-
только в результате кулоновских столкновений друг с другом.
Вопрос о влиянии кулоновских столкновений на время удержа-
удержания частиц и сохранение тепловой энергии в замкнутых ловушках
будет обсуждаться ниже (см. § 2.17). Здесь мы ограничимся толь-
только одним замечанием по указанному поводу. Поскольку при своем,
движении в магнитном поле запертые частицы сильнее отклоняют-
отклоняются от линии поля, то кулоновские столкновения быстрее выбрасы-
выбрасывают их из магнитной ловушки. Для иллюстрации сравним
рис. 2.10,а и б. На рис. 2.10,а показана проекция траектории ча-
частицы в однородном магнитном поле до и после столкновения;
с другой частицей, сопровождающегося относительно небольшим
изменением вектора v. Смещение происходит на расстояние поряд-
порядка доли ларморовского радиуса.
На рис., 2.10,6 показано, как изменяется форма траектории
запертой частицы при столкновении в точке MQ, которое приво-
приводит к небольшому повороту вектора скорости с изменением знака
* Строго говоря, это справедливо только в области, где | v,, | <C^i • По-
Поэтому дальнейшие вычисления сохраняют силу лишь при не слишком малых зна-
значениях угла ф.
10* 147
¦^н (P\\ <^v±)- В этом случае траектория смещается по радиусу г
та расстояние
~ 2Arm ^ 2rH (HJHJ (r/R) VRfF.
Поскольку (HB[HJ(r[R)> 1 и #/г»1, то смещение запертой части-
частицы при столкновении в винтовом поле во много раз превосходит
-смещение- частицы при столкновении в неискривленном магнитном
поле и одинаковых значениях импульса и напряженности магнит-
магнитного поля.
§ 2.3. Адиабатические инварианты движения частиц
в магнитном поле
Вернемся к выводу о сохранении магнитного момента jx заря-
заряженной частицы при движении в слабо меняющемся в пространст-
пространстве магнитном поле. К этому вопросу можно подойти с более об-
_щей точки зрения. В классической механике при описании почти
периодического (квазипериодического) движения консервативной
системы говорят о некоторых приближенно сохраняющихся вели-
величинах— адиабатических инвариантах. Так, например, если у маят-
гника с медленно (адиабатически) меняющейся во времени длиной
подвеса L (простейший случай квазипериодического движения)
это изменение за период колебаний невелико, то справедлив закон
-сохранения адиабатического инварианта:
B.40)
где v — скорость осциллятора; х — координата, характеризующая
^его смещение от положения равновесия. Интеграл берется между
двумя крайними точками траектории.
В общем случае произвольной консервативной системы, опи-
описываемой i обобщенными координатами дг и соответствующими
grad И
Рис. 2.10. Изменение траектории частицы при столкновении в однородном (а) и
тороидальном (б) полях
148
обобщенными импульсами piy выражение для адиабатического ин-
инварианта имеет следующий вид:
§ B.41)
аде предполагается, что по координате qi имеет место квазипери-
квазипериодическое движение. Таким образом, если система обладает N
степенями свободы и по каждой степени свободы совершается ква-
квазипериодическое движение (с медленно по сравнению с периодом
меняющимися параметрами), то существуют N адиабатических ин-
инвариантов.
Ларморовское вращение заряженной частицы вокруг силовых
.линий магнитного поля можно трактовать с этих позиций. В опре-
определение адиабатического инварианта B.41) в случае ларморовско-
го вращения частицы нужно подставить p=mv^ и dq=rHdq, где
гн — ларморовский радиус частицы, а ф — фаза вращения. Тогда
2тс
It = m f v±rHdc?=2r.m2v21cleH = D%fe) тер, B.42)
о
т. е. ji=:const. Таким образом, видим, что сохранение магнитного
момента \х заряженной частицы есть следствие общего принципа
адиабатической инвариантности.
Первый адиабатический инвариант \х можно записать и по-дру-
по-другому:
lL=:T>r2HH(lf2%) (е21тс2) = const, B.43)
что означает сохранение магнитного потока через площадку, огра-
ограниченную ларморовской окружностью при вращении частицы в маг-
магнитном поле.
Применительно к общему случаю движения заряженной части-
частицы- в магнитном поле, изменяющемся во времени и пространстве,
условия сохранения адиабатической инвариантности магнитного
момента \х имеют следующий вид:
| ЩН| <«V 1/Я| grad Я | < \\гн. B.44)
Если заряженная частица заперта между двумя магнитными
зеркалами (колеблется вдоль силовых линий, не выходя за преде-
пределы ограниченной области пространства), то такому движению так-
также можно сопоставить соответствующий адиабатический инвари-
инвариант /=f/да dl. Здесь интеграл берется вдоль силовой линии меж-
между двумя точками отражения частицы (где v^ обращается в нуль),
причем v.. можно выразить с помощью следующих соотношений:
9 {J\± ±
Отсюда находим v,. и, подставляя в формулу для адиабатического
инварианта /2 (назовем его вторым, в отличие от |л — первого ади-
адиабатического инварианта), получаем
B.45)
149
Для выполнения условий сохранения второго адиабатического
инварианта движения частицы нужно, чтобы за период одного ко-
колебания частицы между магнитными зеркалами магнитное поле
вдаль силовой линии изменилось мало. Изменение поля вдоль си-
силовой линии, по которой движется частица, может быть вызвано
двумя причинами: 1) пространственной неоднородностью магнит-
магнитного поля, приводящей к дрейфу частицы поперек (при таком
дрейфе частица все время переходит с одной силовой линии на
другую — с отличающимся, вообще говоря, магнитным полем); 2)
изменением общей картины силовых
линий из-за нестационарности магнит-
ного тюля. В этом последнем случае
энергия частицы уже не является ин-
интегралом движения, но адиабатиче-
адиабатический инвариант /2 сохраняется в обыч-
обычном смысле.
Иногда можно говорить и о треть-
третьем адиабатическом инварианте движе-
движения "заряженной частицы в магнит-
магнитном поле. Такой инвариант соответ-
соответствует дрейфовому движению частицы
поперек силовой линии магнитного по-
поля, если оно носит циклический харак-
Рис. 2.11. Движение частицы теР- Так, движение заряженной части-
в магнитном поле Земли цы в изображенном на уже знакомом
нам рис. 2.5 магнитном поле может
быть периодическим и для дрейфа. Вращаясь вокруг силовой линии
и совершая продольные колебания вдоль силовой линии между об-
областями с большим магнитным полем, частица медленно [с дрей-
дрейфовой скоростью, описываемой выражением B.22] обходит сило-
силовую трубку по некоторой поверхности, изображенной на рис. 2.5.
Третий инвариант движения частицы используется в физике
плазмы значительно реже первого и второго, поэтому мы не будем
здесь вдаваться в детали. Укажем лишь, что роль /з играет маг-
магнитный поток внутри силовой трубки, охватываемой дрейфовой
траекторией частицы (см. рис. 2.5). Магнитный поток в такой си-
силовой трубке сохраняется, если за период обращения частицы со
скоростью дрейфа вокруг силовой трубки магнитное поле изме-
изменяется мало. Всеми описанными свойствами может обладать дви-
движение электронов и протонов в радиационных поясах Земли
(рис. 2.11).
Первый адиабатический инвариант — это, естественно, магнит-
магнитный момент. Второй адиабатический инвариант соответствует дви-
движению запертых частиц между магнитными зеркалами, располо-
расположенными у полюсов. Третий инвариант соответствует дрейфовому
движению, частиц в неоднородном магнитном поле Земли. Электро-
Электроны согласно формуле B.36), примененной к случаю магнитного
поля Земли, дрейфуют с запада на восток, а ионы — в обратном
150
направлении. Время полного обхода вокруг земного шара при та-
таком дрейфе для частиц, движущихся по силовым линиям с макси-
максимальным удалением от центра Земли R> имеет порядок 2neR2/iic.
Это значит, что третий адиабатический инвариант (магнитный по-
поток через поверхность, охватываемую дрейфовой траекторией точки
отражения частицы от магнитного зеркала) сохраняется, если маг-
магнитное поле мало меняется за время порядка 2neR2/\xc.
Большое принципиальное значение в динамике движения заря-
заряженных частиц имеет вопрос о точности сохранения адиабатиче-
адиабатических инвариантов. Разберем этот вопрос на примере \х. В этом
случае точность сохранения адиабатического инварианта |д, опре-
определяла бы длительность запертого движения частицы между маг-
магнитными зеркалами. Как уже говорилось, понятие об адиабатиче-
адиабатической инвариантности \х имеет смысл при условиях B.44). Естест-
Естественно было бы ожидать, что сохранение инварианта является
результатом разложения по малому параметру е^—'|/?| /соя|#| или
(гн/\Н\) |grad#|. Тогда следовало бы ожидать нарушения адиа-
адиабатической инвариантности в следующем порядке по этому малому
параметру. Однако более тонкие соображения показывают, что,
вообще говоря, точность адиабатического инварианта гораздо вы-
выше. Оказывается, он сохраняется с так называемой экспоненциаль-
экспоненциальной точностью |Д|л/[л|-—ехр{—1/s}. Математический аппарат,
используемый для доказательства этого утверждения, требует
лишь, чтобы функции, описывающие поведение полей, в которых
движется частица, были достаточно гладкими по отношению к из-
изменению аргументов г и t.
Для иллюстрации обратимся к рассмотренному в § 2.2 движе-
движению частицы в однородном магнитном поле и поперечном электри-
электрическом поле, включенном при ?=0. Скорость ларморовского вра-
вращения частицы в этом случае согласно выражениям B.9), B.12),
B.13) равна
t
1 с •
я = (а Л sin wj \ F (u) cos (Ь„ (t — и) du\
Л О
B.46)
Если электрическое поле возрастает по закону E(t)=Eo(l—
—ехр{—Ы})> то изменение магнитного момента после включения
поля (при />1/а) равно A\i^(eAE0/H) (а/кдя). Низкая (порядка
а/(дн) точность сохранения адиабатического инварианта объяс-
объясняется тем, что изменение электрического поля не является доста-
достаточно гладким. Так, производная F(t)—eE(t) по / испытывает раз-
разрыв при i=0. Если включить электрическое поле достаточно плав-
плавно, ситуация изменится. Пусть, например, напряженность поля
151
зависит от времени по закону
E(t) = (aEjV*j J exp(— a*%*)d*.
—00
Такая форма зависимости означает, что «включение» происходит
при /=—оо, а при /->оо E-*-Eq. Вычисляя входящие в B.46) ин-
интегралы, находим, что при t->oo
* ° H H \ B.47)
vy = vQ cos (DHt -f- 5 sin mHtt j
где ?^(l/2)(^0/mco//)exp(-«J//a2).
Отсюда v2=v2q~\~12 и, следовательно, Ajut/jji=g2/^2o=
= A/4) (в2?2о/1>20т2<о2я)ехр(—2co2Ha2).
Таким образом, изменение адиабатического инварианта в рас-
рассмотренном примере с идеально плавным включением действитель-
действительно оказывается экспоненциально малым.
§ 2.4. Кинетическая теория плазмы
в магнитном поле
Поведение ансамбля большого числа заряженных частиц в маг-
магнитном поле можно описывать с помощью функции распределения
/(г, v, /) (для каждого сорта зарядов), которая определяется так
же, как и для плазмы в отсутствие магнитного поля. Но в кинети-
кинетическое уравнение, которому подчиняется такая функция распреде-
распределения, нужно добавить еще одно слагаемое, учитывающее действие
силы Лорецца (e/c)[vXH]. Такое кинетическое уравнение имеет
вид
5f/«+vgrad/+(e/m){E+(l/c)[vXH]}Cf/(?v)=St{f}. B.48)
Это уравнение отличается от кинетического уравнения A.83)
слагаемым (е[т) IЕ +~ [vX Н]| (df/dv) [вместо (е[т) Е (df/dv)].
Однако может возникнуть вопрос, не изменится ли также ха-
характер столкновений между заряженными частицами при наличии
магнитного поля. Траектории частиц, пролетающих друг от друга
на расстояниях, сравнимых со средним ларморовским радиусом
или больших его, в процессе рассеяния будут испытывать также
искривление из-за магнитного поля. В результате дебаевской экра-
экранировки поля каждого отдельного заряда практически нужно учи-
учитывать лишь парные взаимодействия между частицами на расстоя-
расстояниях, меньших дебаевскотч) радиуса.
Отсюда сразу же следует первый вывод: влияние магнитного
поля ка процесс рассеяния несущественно, если дебаевский радиус
rD плазмы меньше среднего ларморовского радиуса частиц гн—
152
—mvTc\eH, где vT — средняя тепловая скорость. В применении
к электронам, ларморовский радиус которых в "[/т^/я^ раз мень-
меньше, чем у ионов при той же энергии, неравенство гв<гн можно
Привести к виду
сон<сор, B.49)
или
Н214л<птес2. B.50)
В конкретных условиях экспериментов с плазмой оно соблюдается
только при не очень сильных магнитных полях. Однако несколько
более углубленный анализ показывает, что нарушение условия
юн<сор еще не равнозначно сильному влиянию магнитного поля на
элементарные акты столкновений. Это связано с тем, что сечение
кулоновского рассеяния [см. формулу A.10)] содержит так назы-
называемый кулоновский логарифм Lk, возникающий, грубо говоря,
вследствие обрезания (отбрасывания) столкновений, происходящих
на расстояниях, больших г^. В силу логарифмической зависимости
сечения рассеяния от расстояния, на котором происходит обреза-
обрезание, величина сечения не слишком чувствительна к параметру об-
обрезания. Следовательно, влиянием магнитного поля на процесс
столкновений можно пренебречь вплоть до таких параметров плаз-
плазмы, при которых выполняется более мягкое условие
ln©H/<op<LK. B.51)
Оно неприменимо лишь для очень экзотических плазм (в чудовищ-
чудовищно сильных магнитных полях).
Для теории плазмы выполнение неравенства B.51) означает,
что интеграл столкновений в правой части кинетического уравне-
уравнения Больцмана сохраняет ту же форму, что и при отсутствии маг-
магнитного поля. Естественно, остаются прежними и формулы для
длины свободного пробега заряженных частиц, времени между
двумя столкновениями и все другие следствия в § 1.3.
Понятие самосогласованного поля в общем случае нужно рас-
распространять и на магнитное поле. Это значит, что в уравнении
Максвелла для магнитного поля
следует учесть самосогласованный ток j, переносимый зарядами
плазмы. Поскольку по определению для любого сорта частиц /zv—
= f vfdv, то вклад каждого сорта частиц в плотность тока есть
env=e §vfdv и в итоге \=Ъвк \vfkdv, где суммирование проводят
по всем сортам частиц.
Для плазмы, состоящей из электронов и однозарядных ионов
одного сорта, полная система уравнений кинетической теории
с самосогласованным полем имеет вид:
153
B.52)
Эти уравнения, так же как и соответствующие уравнения A.84),
A.85) для плазмы без магнитного поля, являются основой для
исследования динамики и установления уравнений гидродинамиче-
гидродинамического приближения для плазмы в магнитном поле. Гидродинами-
Гидродинамическое приближение пригодно для описания плазмы, которая про-
простирается на расстояния, значительно превышающие длину сво-
свободного пробега /. Существование магнитного поля в такой плазме
по-разному сказывается на ее свойствах в зависимости от соотно-
соотношения между длиной свободного пробега / и средним ларморов-
ским радиусом частиц гя. Если /<С/*н (плотная плазма с относи-
относительно невысокой температурой, сравнительно небольшая напря-
напряженность магнитного поля Я), то влияние магнитного поля
проявляется слабее. В противоположном случае, когда /^>гя, тра-
траектория частицы на длине свободного пробега успевает свернуться
в винтовую линию. В этом случае можно пользоваться приближен-
приближенной кинетической теорией плазмы в так называемом дрейфо-
дрейфовом приближении. В дрейфовом кинетическом уравнении
функция распределения частиц описывает плотность распределе-
распределения центров ларморовских кружков в фазовом пространстве. В дан-
данном случае фазовое пространство представляет собой обычное ко-
координатное пространство г (г — радиус-вектор центра ларморов-
ского кружка), t>,, —скорость движения заряда вдоль силовой
линии магнитного поля; \х— магнитный момент частицы.
Такое фазовое пространство описывается лишь пятью независи-
независимыми переменными вместо шести (г, v). Левая часть дрейфового
кинетического уравнения представляет собой уравнение непрерыв-
непрерывности для функции /(г, O|j,|i) в этом упрощенном фазовом про-
пространстве:
—#- = St{/}. B.53)
Здесь скорость ud имеет компоненту v.. вдоль силовой линии маг»
нитного поля, а скорость движения поперек магнитного поля опре-
определяется уравнениями дрейфового движения с учетом всех воз-
возможных типов дрейфа. Составляющая силы F||t действующая
вдоль магнитной силовой линии, задается уравнением B.21).
Интеграл столкновений при описании плазмы в дрейфовом при-
приближении необходимо преобразовать к новым переменным v{l, ц
вместо v.
154
При вычислении плотности тока в такой плазме нужно соблю-
соблюдать некоторую осторожность. Дело в том, что ток }d=enudy созда-
создаваемый перемещением центров ларморовских кружков, не описы-
описывает полного переноса заряда. Существует еще дополнительный ток
даже при покоящихся центрах ларморовских кружков, обусловлен-
обусловленный их диамагнитным моментом |и. При равномерном распределе-
распределении диамагнетиков со средним моментом ju, и плотностью п в про-
пространстве обтекающий ток возникает лишь на границе. Он приво-
приводит к ослаблению магнитного поля на величину A#=4jmjLt. При
неоднородном распределении в пространстве возникает и объем-
объемный ток. Его плотность jd определяется из уравнения
rot ДН = rot 4%п\1 = 4яjD/c; |
}
Это есть искомый дополнительный ток. С помощью функции рас-
распределения представим его в следующем виде:
B.54а)
Единичный вектор —Н/# означает, что магнитные моменты час-
частиц ориентированы против поля.
Вернемся к условию 1^>гн, выделяющему область сильного
влияния магнитного ноля на траектории частиц в плазме и, следо-
следовательно, на всю кинетику плазмы в целом. Учитывая, что l—vTx
и rH=VTt<uH, где т — время свободного пробега, условие /»гы
можно представить в виде
<онт>1. B.55)
Неравенство B.55) называют критерием замагничен-
ности плазмы, а плазму, удовлетворяющую этому критерию,
за магничен ной. Оно требует дополнительной конкретизации
для электронов и ионов. При одинаковых температурах и длинах
свободного пробега имеем
Поэтому для одной и той же плазмы электроны могут быть «за-
магничены», а ионы нет. Как раз такая ситуация часто осуще-
осуществляется в низкотемпературной плазме МГД-генераторов. В вы-
высокотемпературных или достаточно разреженных плазмах замаг-
ниченными оказываются и электроны, и ионы. К таким плазмам
относятся: плазма в магнитных термоядерных ловушках, в верх-
верхних слоях ионосферы, в магнитосфере Земли, солнечной короне,
в газовых разрядах при низком давлении.
Во многих представляющих интерес случаях процессы, проте-
протекающие в плазме, охватывают промежутки времени, меньшие вре-
времени соударения, но значительно превышающие период ларморов-
ского оборота частиц в магнитном поле. При этом можно прене-
155
бречь парными соударениями частиц, т. е. опустить интеграл*
столкновений в правой части дрейфового кинетического уравнения:
B.53). Тогда оно описывает поведение своеобразной бесстолкнови-
тельной плазмы в магнитном поле. Подобная модель часто исполь^
зуется для исследования колебаний и волн в плазме и для анализа
некоторых важных неустойчивостей плазмы в магнитном поле.
§ 2.5. Гидродинамика плазмы в магнитном поле
Гидродинамическое приближение для плазмы в магнитном по-
поле можно получить так же, как это было сделано в § 1.5 для
плазмы без магнитного поля.
При рассмотрении плазмы, свойства которой меняются на рас-
расстояниях Lp, значительно больших длин свободного пробега I за
промежутки времени тр, большие времени свободного пробега,,
функции распределения ионов и электронов следует считать близ-
близкими к максвелловским. В такой плазме состояние каждой заря-
заряженной компоненты задается плотностью п(г, t), температурой
Г (г, ¦/) и средней макроскопической скоростью u (r, t). Уравнения
для этих величин, т. е. уравнения гидродинамики, выводятся, как
и в § 1.5, нахождением моментов от кинетического уравнения
B.52). Эти вычисления аналогичны вычислениям, проведенным
в § 1.10, поэтому их не стоит повторять. Нужно лишь учесть, что
кинетическое уравнение B.52) содержит дополнительное слагае-
слагаемое в правой части с силой Лоренца
(e/mc)[vXH](dfldv). B.56)
Простое интегрирование по dv (нулевой момент) этого слагаемо-
слагаемого дает нуль. Это и не удивительно, так как сила Лоренца не мо-
может изменить баланс числа частиц, учитываемый уравнением не-
непрерывности: dn/dt-\-divnu—0.
В уравнении Эйлера_, получающемся при вычислении момента
первого порядка — умножении на v и последующем интегрирова-
интегрировании по dv (по частям) член с силой Лоренца дает
Это есть не что иное, как средняя сила Лоренца, действующая на
все частицы одного сорта в единице объема. Итак, в старом урав-
нении Эйлера для плазмы без магнитного поля A.102) добав-
добавляется слагаемое (е/с)л[иХН] в правой части:
тп (du/dt)=—gTad р+епЕ+{е/с)п[иХЩ. B.57)
Уравнение для температуры остается неизменным, если не учи-
учитывать возможного изменения теплопроводности. Таким образом,
каждая заряженная компонента плазмы в гидродинамическом при-
приближении описывается системой уравнений A.100), A.106) и
B.57). Учтем теперь столкновения между частицами разного сорта.
156
Так же как и в § 1.10, это дает силу взаимного трения между ком-
компонентами плазмы в уравнениях Эйлера. Тогда уравнения движе*
ния двухжидкостной гидродинамики для квазинейтральной плазмы,,
состоящей из электронов и такого же числа ионов одного сорта
(т=Пе=п)> принимают вид
^ п[щХЩте(Щ-ие)че1п\ B.58У
^r ге(щ — *е)че1п. B.59)
По отношению к этим уравнениям справедливо замечание, сде-
сделанное в § 1.10 в связи с анализом гидродинамического приближе-
приближения в теории плазмы. По существу для упрощенного вывода урав-
уравнений динамики плазмы в гидродинамическом приближении как
в отсутствие, так и при наличии магнитного поля нет нужды
в использовании аппарата кинетических уравнений, поскольку име-
имеем здесь дело с простым применением самых общих законов дина-
динамики к движению микроскопических элементов обеих компонент
плазменной субстанции.
Переход к описанию плазмы как единой жидкости можно про-
провести, складывая уравнения B.58) и B.59). При этом обычно пре-
пренебрегают инерцией электронов, а суммарная электрическая сила,.
действующая на элемент объема плазмы, обращается в нуль из-за
квазинейтральности. Также исчезает сумма противоположно на-
направленных и равных по величине сил трения между ионами и-
электронами* Сумма сил Лоренца (еп/с) [(щ—пе) ХН] приводится
к виду (l/c)[jXH] (сила Ампера), так как еп{щ—ue)—j.
В результате уравнение Эйлера одножидкостной гидродинами-
гидродинамики плазмы в магнитном поле (ее чаще называют магнитной гидро-
гидродинамикой) имеет вид
и = (ад + mSeVimi + nQ; B.60>
j
Плотность тока j можно выразить через Н из уравнения Максвел-
Максвелла rot Н=Dя/с)]. Исключив j, силу Ампера можно представить
в виде
(l/c)[jXH] = (l/4n)[rotHXH].
Векторное произведение в правой части удобно раскрыть с по-
помощью известного векторного тождества
A/2) gracU2= (a grad) a+ [aXrot a].
В применении к рассматриваемому случаю это дает
(l/4jt)[rotHxH]=—grad#2/8n+(l/4rt)(Hgrad)H. B.61>
Первый член в правой части уравнения B.61) можно интерпре-
интерпретировать как градиент магнитного давления Я2/8я. Второй член-
15Г
называют силой натяжения силовых линий магнитного поля. Он
отличен от нуля только для магнитного поля с кривыми силовыми
линиями. Соответствующая ему сила всегда оказывается направ-
направленной в сторону, противоположную искривлению силовой линии.
В магнитной гидродинамике неизвестными величинами являют-
являются плотность /г, скорость и, давление р и магнитное поле Н. Число
уравнений для определения этих величин должно соответствовать
числу самих неизвестных функций. Три уравнения (для определе-
определения пу и, р) у нас есть. Это уравнение непрерывности для пу урав-
уравнение Эйлера для и B.60) и уравнение состояния для давления.
Недостающее уравнение для магнитного -поля выводится по сле-
следующей схеме. Нужно воспользоваться уравнением Максвелла
rot Е= — A /с) (dH/dt) и подставить в него электрическое поле Е,
выраженное через плотность тока с помощью закона Ома. Но
при наличии магнитного поля связь между / и Еу т. е. закон Ома,
отличается от результата, полученного в ч. 1.
Для того чтобы выяснить характер связи в общем случае, об-
обратимся снова к уравнениям, характеризующим поведение обеих
компонент плазмы. Умножая уравнения B.58) на те и B.59) на
Л1{ и вычитая одно из другого, получаем
B.62)
В правой части этого выражения отброшены члены порядка
те\тхУ а в левой — инерционные члены, поскольку предполагается,
ято заметное изменение плотности тока может происходить лишь
за времена тР^>тег и на расстояниях Lp>/. Теперь удобно пред-
представить B.62) в следующем виде:
, B.63)
Это соотношение является обобщением закона Ома для плазмы,
находящейся в магнитном поле. В частности, когда ток течет па-
параллельно магнитному полю и плазма является однородной (т. е.
градиент давления отсутствует), соотношение B.63) совпадает
с выведенным в предыдущей главе соотношением A.21) с той лишь
разницей, что Е надо заменить на Е'=Е+A/с) [иХН]. Однако
в общем случае уравнение для j отличается от простого закона
Ома дополнительными членами в правой части, из которых первый
пропорционален градиенту электронного давления, а второй со-
содержит векторное произведение [JXH]. Эти дополнительные чле-
члены имеют простое физическое истолкование. В выражении для j
появляется величина (e/meVei)Vpe, так как ток в ионизованном
газе может быть вызван не только электрическим полем, но также
и разностью электронных давлений в различных точках простран-
пространства. Член, содержащий [JXH], свидетельствует о влиянии маг-
магнитного поля на движение электронов в плазме.
158
Из-за указанных дополнительных членов между плотностью то-
тока и напряженностью электрического поля нет простой связи. При
заданных значениях Е' плотность тока может иметь самые раз-
различные значения. Эта неопределенность существенно ослабляется:
в том случае, когда плазма находится в квазистационарном состоя-
состоянии, т. е. при du/di=0.
В квазистационарном состоянии основные уравнения B.60.) ш
B.63) принимают вид
4 B.64>
B.65)
Сделав естественное допущение о том, что gradpe и gradp* на-
направлены параллельно друг другу, находим из B.64), что*
grad/?iJLj. Обращаясь к B.65), видим, что вектор Е' должен иметь
две взаимно перпендикулярные компоненты Е' п и Е', из которых.
Е'„ И j, a E'J|gradA-
Из B.65) находим, что j1( =cE'r Следовательно, для компонен-
компоненты j1( справедлив закон Ома. Компонента Е' не создает тока.
Она уравновешивает градиент ионного давления
B.66>
Неколлинеарность векторов Е' и j приводит к эффекту Холла —
появлению составляющей тока, перпендикулярной к электрическо-
электрическому полю.
Физический смысл этих результатов можно разъяснить на осно-
основе простых соображений. Ввиду того, что ток создается электрона-
электронами, сила [JXH], действующая на плазму со стороны магнитного
поля, приложена к электронному газу. Эта сила, в частности, соз-
создает перепад электронного давления ре. Из-за условия квазиней-
квазинейтральности pi следует за изменением ре. Однако градиент pi может
поддерживаться только в том случае, если существует сила, ме-
мешающая выравниванию ионных давлений. Она должна быть на-
направлена так же, как grad/?*, т. е. перпендикулярно к j и Н. Такой
силой как раз и является компонента электрического поля Е'^ _L j~
Она обеспечивает сохранение квазинейтральности плазмы, не да-
давая ионам оторваться от электронов. Для этой компоненты закон
Ома, очевидно, не имеет силы. Если плазма неподвижна (статиче-
(статический случай), то по отношению к компоненте электрического поля,
параллельной току, справедлив закон Ома в обычной форме: j=,
=оЕ||.
Для того чтобы исключить электрическое поле из уравнений
магнитной гидродинамики, возьмем rot от обеих частей уравне-
шия B.63):
Далее, используя rotE=—A /с) (ОНjdt) и rot H = 4jtj/c, полу-
получаем недостающее уравнение для магнитного поля
^XgradTe]+?AH. B.68)
Это уравнение можно привести к более симметричному виду, если
<. помощью уравнения Эйлера исключить второе слагаемое справа
ж учесть, что rot du jdt=d rot u/dt—rot[uXrotu].
Итак,
ir ^AH. . B.69)
Член, содержащий [grad /?Xgrad T.i], обычно не играет важной
роли, за исключением тех случаев, когда плотность и температура
зависят от координат совершенно по-разному. Для простоты не
будем его учитывать. Последнее слагаемое в правой части этого
уравнения описывает процесс своеобразной диффузии магнитного
лоля. Отложим на время обсуждение этого явления и рассмотрим
случай, когда проводимость плазмы достаточно высока и этим
членом можно пренебречь. Тогда уравнение B.69) является обоб-
обобщением известного уравнения переноса rot u из обычной гидроди-
гидродинамики— так называемого уравнения «приклеенности» линий вих-
вихря скорости к веществу. В достаточно большом магнитном поле
еН/Mc^u/Lp уравнение упрощается:
ДН
Именно это уравнение часто используется вместо четвертого, не-
недостающего уравнения магнитной гидродинамики. В частном слу-
случае плоского движения, когда магнитное поле имеет лишь одну
^компоненту, например Я2, зависящую от двух координат х и у,
я скорость и имеет только компоненты их и щ, уравнение B.70)
-Приобретает вид
^-+~ (UxHz) + _|_ (Uy нг) = il f^+JjL\ Нг, B.71)
напоминающий уравнение непрерывности для плотности при плос-
плоском движении (если отвлечься от правой части).
it 60
Уравнение B.70) называют уравнением «вморожеиности» для
магнитного поля. Рассмотрим это явление подробнее. Плазма —
хороший проводник. Поэтому если она быстро движется, пересекая
силовые линии магнитного ноля, то появляются индуцированные
токи, которые изменяют распределение напряженности магнитного
поля. Общий характер этого изменения таков, как будто при своем
движении плазма увлекает вместе с собой линии поля. Линии поля
ведут себя так, как будто они были «вморожены» в плазму (или
склеены с ней).
Для того чтобы лучше понять, в чем состоит это явление, рас-
рассмотрим частный случай движения плазмы. Пусть плазма запол-
заполняет объем, в котором создано магнитное поле, направленное па-
параллельно оси г. При этом напряженность поля изменяется по
некоторому закону в плоскости, перпендикулярной к направлению
z, т. е. в плоскости ху. Концентрация плазмы постоянна вдоль си-
силовых линий, но также может быть функцией координат х и у.
Предположим, что плазма движется перпендикулярно к сило-
силовым линиям. Выделим мысленно в пространстве тонкий столбик
плазмы, параллельный Н. Пусть площадь его сечения плоскостью
ху равна dS. При движении плазмы выделенный столбик испыты-
испытывает сжатие или расширение, в результате чего его поперечное
сечение изменяется. Поскольку полное число частиц внутри стол-
столбика должно сохраняться, справедливо соотношение ndS—const.
Кроме того, должно оставаться постоянным также значение магнит-
магнитного потока, проходящего через сечение dS. В плазме с достаточно
хорошей электропроводностью даже незначительное изменение
хмагнитиого потока, если оно происходит быстро, приведет к возник-
возникновению большого индукционного тока. Магнитное поле этого тока
скомпенсирует изменение потока. Сохранение потока означает, что
HdS=const.
Из сказанного выше следует, что в рассматриваемом случае
при движении плазмы отношение Hjn остается постоянным. Если
плазма сжимается, то напряженность поля в ней возрастает, рас-
расширение плазмы влечет за собой ослабление магнитного поля. Пе-
Перераспределение плотности в результате быстрых деформаций при-
приводит к соответствующему изменению распределения напряжен^
ности поля в пространстве. В этой связи между деформациями
плазмы и поля, вытекающей из сохранения магнитного потока
в движущемся материальном элементе, объема, и заключается вмо-
роженность силовых линий.
Нужно, однако, отметить, что постоянство отношения Я/п не
является законом: оно имеет место только в том конкретном слу-
случае, о котором говорилось выше. При других геометрических усло-
условиях соотношение между напряженностью поля и концентрацией
в быстро движущейся плазме может иметь иную форму. Так, на-
например, в аксиально-симметричной плазменной струе, движущейся
под действием электродинамических сил, обусловленных током, ко-
который проходит через плазму (рис. 2.12) в каждом элементе объ-
11—74 ' 161
Рис, 2.12. Вмороженность магнитного поля
В плазме аксиально-симметричной струи
ема во время его движения остается постоянным отношение Н/пг,
где г — расстояние от данного элемента объема до оси системы.
Еще одно замечание может оказаться полезным. Вмор.ожен-
ность силовых линий не следует считать явлением, специфически
связанным со свойствами плазмы. Аналогичный эффект будет на-
наблюдаться в любом хорошем проводнике, движущемся в магнит-
магнитном поле с достаточно высокой скоростью. Вообще уравнениям
магнитной гидродинамики подчиняется не только движение плазмы
в магнитном поле, но и движение любой другой газообразной или
жидкой среды, обладающей способностью проводить электрический
ток. Примером таких сред
могут служить расплавлен-
расплавленные металлы. Классические
опыты Альвена по магнит-
магнитной гидродинамике были
проведены с жидкой ртутью.
Теперь вернемся к исход-
исходному уравнению B.70) и
разберемся в механизме
«диффузии» магнитного по-
поля, описываемой правой
частью этого уравнения. Как мы уже отмечали, явление вморожеи-
ности магнитного поля связано с возникновением индукционных
токов, сопровождающих движение плазмы. Сколь бы велика ни
была проводимость плазмы, за достаточно большой промежуток
времени должна проявиться диссипация (затухание) этих токов
из-за конечного сопротивления. Это, разумеется, должно привести
к изменению магнитного поля. Так, например, если из-за деформа-
деформации сжатия в какой-либо силовой трубке внутри плазмы было соз-
создано сгущение силовых линий магнитного поля, то в конце концов
в результате затухания индукционных токов магнитное поле ослаб-
ослабнет. Можно сказать, часть силовых линий уйдет наружу. Этот про-
процесс, как следует из уравнения B.70), носит диффузионный харак-
характер. Соответствующий коэффициент диффузии магнитного поля
пропорционален удельному электрическому сопротивлению плазмы
DM=c2/4nG*. Часто этот коэффициент диффузии магнитного поля
называют коэффициентом магнитной вязкости и обоз-
обозначают символом vm. Происхождение этогб термина связано с ана-
аналогией между диффузией магнитного поля и вязким просачиванием
rotu в гидродинамике из-за обычной вязкости.
Подведем некоторые итоги анализа роли магнитного поля в гид-
гидродинамике плазмы. В уравнении движения появляются дополни-
дополнительные силы, связанные с магнитным полем [см. уравнение
* Очевидна связь между коэффициентом диффузии магнитного поля и из-
известной формулой для глубины скин-слоя. Предположим, что на границе прово-
проводящей среды приложено переменное магнитное поле частоты со. Тогда за период
колебаний поле успевает продиффундировать на глубину 5~ (Dm/cd)!/2===
= (c2/4ttGco)V2, т. е. на глубину скин-слоя.
162
B.57)]. Видоизменяется закон Ома для плазмы в магнитном поле:
электропроводность плазмы остается неизменной лишь для элек-
электрического тока, текущего вдоль силовых линий магнитного поля;
поперечные же магнитному полю токи могут сильно изменяться
(в частности, возникает эффект Холла), если выполнено условие
(Oiiete^h иначе говоря, если плазма «замагничена».
Зависимость электропроводности плазмы от магнитного поля —
это лишь частный случай влияния магнитного поля на коэффици-
коэффициенты переноса. Если средний ларморовский радиус частиц плазмы
меньше длины свободного пробега, то все явления переноса в плаз-
плазме поперек магнитного поля заторможены. Это относится, напри-
например, к теплопроводности плазмы поперек силовых линий магнитно-
магнитного поля. Области с различными температурами могут сосущество-
сосуществовать в такой плазме рядом друг с другом, поскольку частицы со-
совершают ларморовское вращение вокруг силовых линий магнитно-
магнитного поля, перемещаясь в направлении градиента температуры на
величину порядка гн при редких соударениях (это свойство плаз-
плазмы, помещенной в магнитное поле, используется в так называе-
называемой магнитной термоизоляции).
При некоторых условиях влияние магнитного поля оказывается
еще более кардинальным. До сих пор мы считали, что гидродина-
гидродинамическое приближение (так же, как и в случаях без магнитного
поля) справедливо лишь для плазмы с характерным масштабом
пространственного изменения Lp, значительно превышающим дли-*
ну свободного пробега: Lp>/. Представим себе теперь плазму
с очень большой длиной свободного пробега 1^>LP. Гидродинами-
Гидродинамическое описание такой плазмы в обычном смысле может показаться
недопустимым. Действительно, в этом случае будет происходить
свободный обмен частицами между областями с различными на-
начальными значениями концентрации и температуры. В результате
возникает состояние с функцией распределения, представляющей
собой как бы случайную смесь различных максвелловских функ-
функций, и ни о какой температуре каждой локальной области гово-
говорить нельзя. Только в результате достаточно частых столкновений,
которые мы учитывали при выводе гидродинамических уравнений,
перемещение частиц затормаживается и восстанавливается ло-
локальное максвелловское распределение. Оказывается, с первой из
этих задач с успехом может справиться также и сильное магнит-
магнитное поле (даже когда нет столкновений). Конечно, это свойство
магнитного поля относится только к движению частиц поперек
магнитных силовых линий.
Таким образом, магнитное поле при полном отсутствии соуда-
соударений приводит к возможности реализации своеобразного гидро-
гидродинамического приближения для плазмы при ее движении поперек
магнитных силовых линий.. Условием применимости такой гидро-
гидродинамики должно быть, как можно ожидать по аналогии с обыч-
обычным случаем, следующее соотношение:
LP>rH B.72)
11* ' 163
(здесь роль длины свободного пробега играет средний ларморов-
ский радиус). В этой физической картине гидродинамические
свойства плазмы не распространяются на ее движение вдоль си-
силовых линий магнитного поля, так как частицы могут свободно
перемещаться вдоль Н. Поэтому магнитная гидродинамика плазмы
при условии Ьр^>Тн (иногда ее называют бесстолкнови-
тельной гидродинамикой) имеет смысл лищь когда речь
идет о движении плазмы поперек Н. Так же, как и в обычной маг-
магнитной гидродинамике, силовые линии магнитного поля при дви-
движении бесстолкновительной плазмы переносятся вместе с ней, ина-
иначе говоря, Н подчиняется уравнению вмороженности. Претерпевает
изменение уравнение адиабаты, связывающее давление плазмы
с плотностью р=р(р).
Эту связь можно найти из следующих простых соображений.
Рассмотрим плазму внутри элементарной силовой трубки. Пусть
первоначально давление плазмы было равно р, температура 7\
плотность п, а магнитное поле внутри силовой трубки Н. Если
в процессе эволюции состояния плазмы происходит сжатие (рас-
(расширение) за время, значительно превышающее период обращения
ионов в магнитном поле, то сохраняется магнитный момент \i=
— w./H каждой частицы (вследствие адиабатической инвариант-
инвариантности). Это автоматически означает, что остается неизменным так-
также и средний магнитный момент р,—7\/# (приходящийся на
одну частицу плазмы). Иначе говоря, температура плазмы меняет-
меняется пропорционально Н. Из-за вмороженности магнитного поля
Н-—л, поэтому для давления плазмы получаем я7\—тг2, т. е. по-
показатель адиабаты для плазмы в магнитном поле у. ==2, если
в процессе изменения состояния плазмы совсем не происходит
столкновений. При очень медленных процессах столкновения успе-
успевают погасить разность температур вдоль и поперек Н, вследствие
чего показатель адиабаты даже для очень разреженной высоко-
высокотемпературной плазмы становится равным 5/3.
С такой гидродинамикой (при условии /»LP) часто приходит-
приходится иметь дело в физике высокотемпературной плазмы, в магнито-
магнитосфере Земли и т. п.
§ 2.6. Колебания и волны в плазме
с магнитным полем
Упругие свойства плазмы, помещенной в магнитном поле, во-
вообще говоря, существенно меняются. Это должно следовать из то-
того, что изменяется характер движения частиц плазмы в поле вол-
волны, иначе говоря, отклик частиц плазмы на поле волны. С этой
точки зрения удобно разделить все типы колебаний и волн плазмы
на два класса: 1) волны, в которых частицы совершают колебания
практически вдоль направления магнитного постоянного поля, т. е.
волны с j|| Но, и 2) волны, в которых главную роль играют токи,
164
текущие поперек направления внешнего магнитного поля jJ.H0.
Это условное деление само по себе означает, что волновые свойст-
свойства плазмы в магнитном поле неизотропны.
Таким образом, в плазме, помещенной в магнитном поле, долж-
должны существовать электромагнитная волна с электрическим векто-
вектором вдоль Но, т. е. с к±Н0, имеющая тот же закон дисперсии
A.45), что и электромагнитные волны в изотропной плазме (обык-
(обыкновенная волна), а также электростатическая волна с Е и к!|Но
и законом дисперсии A.36).
Для волн, распространяющихся под углом к магнитному полю,
деление на электростатические и электромагнитные, проведенное
в первой части книги, уже не является строгим. Ниже показано,
что волны являются электростатическими только в пределе боль-
больших показателей преломления Л/=&с/со>1. Дисперсионные харак-
характеристики электростатических волн, вообще говоря, менее всего
чувствительны к постоянному магнитному полю.
Если частота таких колебаний значительно превышает лармо-
ровскую частоту электронов а>не=еНо1гпес1 то магнитное поле не
успевает оказывать заметное воздействие на быстрое колебатель-
колебательное движение электронов. Условие пренебрежимой малости влия-
влияния магнитного поля в этом случае имеет, очевидно, вид о)Ре>«Нб>.
Для большинства практических приложений это действительно так.
Для ионно-звуковых колебаний из условия пренебрежимости влия-
влиянием магнитного поля, казалось бы, должно следовать, что
о)^>сояе, о)ш. Это было бы очень жестким ограничением на вели-
величину магнитного поля. Однако в условии о^сож? под частотой о>
следует понимать истинную частоту ионно-звуковой волны в систе-
системе отсчета, движущейся вместе со «средним» электроном io-j-kv.
Второе слагаемое значительно больше первого, так.как тепло-
тепловая скорость электронов существенно превышает фазовую скорость
ионно-звуковых колебаний. Отсюда можно заключить, что магнит-
магнитное поле не влияет заметно на иоино-звуковые колебания даже
при поперечном распространении, если kvre^^He- В противопо-
противоположном предельном случае звуковые колебания могут существен-
существенно изменить свой характер в присутствии магнитного поля. Так,
например, если звук малой частоты распространяется поперек маг-
магнитного поля, то каждое сжатие шпг разрежение плазмы должно
приводить к сжатию или разрежению силовых трубок. Магнитное
поле сообщает плазме дополнительную упругость, что приводит
к увеличению скорости звука. Для частот, значительно меньших
ионной ларморовской частоты, скорости распространения этих волн
(их принято называть магнитозвуковыми) можно найти, используя
соотношение cs— V др/дру в котором, однако, для р нужно взять
сумму давления плазмы и давления магнитного поля рт=#2/8я.
При дифференцировании надо учесть, что вследствие вморожен-
ности магнитное поле Н пропорционально р. Следовательно,
и
дрт1др=Н*14пр. B.73)
365
Определяя давление плазмы, следуетчучесть, что при медленных
звуковых колебаниях (со<Ссояг) в бесстолкновительной плазме
у каждой частицы отношение WJH сохраняется постоянным. Сле-
Следовательно, «температура» Т±, определяющая среднее значение
кинетической энергии для движения перпендикулярно к силовым
линиям, должна при звуковых колебаниях изменяться' пропорцио-
пропорционально Я.. Пусть р обозначает давление плазмы. Оно равно
п(Тг-\-Те). Эта величина пропорциональна р#, а так как #<—'р, то
давление должно быть пропорционально р2. Следовательно,
др1др=2р/р=2(Тг+Те) /mi. B.73а)
Пользуясь B.73) и B.73а), можно написать следующее выраже-
выражение для скорости магнитозвуковых волн:
B.74)
В тех случаях, когда газокинетическое давление плазмы зна-
значительно меньше магнитного давления (такую плазму иногда на-
называют «холодной»), в выражении B.74) можно пренебречь пер-
первым членом, и скорость звуковых волн оказывается совпадающей
с так называемой альвеновской скоростью Va=HIV'4itp.
Разумеется, полученные из наглядных соображений свойства
низкочастотных магнитозвуковых колебаний можно было бы дока-
доказать прямыми вычислениями, линеаризуя уравнения магнитной
гидродинамики, подобно тому как это делалось при рассмотрении •
колебаний плазмы в гидродинамическом приближении. Такие вы-
выкладки оказываются необходимыми, если интересоваться свойст-
свойствами магнитного звука при частотах, сравнимых или превышаю-
превышающих соя*- В приближении «холодной» плазмы, т. е. когда тепловое
движение ионов и электронов в волне, распространяющейся попе-
поперек магнитного поля, не учитывается, выкладки оказываются не-
несложными. Прежде всего запишем, линеаризованные уравнения
движения ионов и электронов в поле волны сжатия:.
Нг = Н0-\- Нг ехр (— Ы -J- ikx);
Е «= (Ех; Еу; 0) ехр (— Ы + ikx);
— ra{\^uxi — еЕх -f- (вIс) uyiHQ\
иуе = - сЕх/Нв + i (фн) (сЕу(Н0);
ntifauyi = еЕу — (е[с) их{На;
ихе = сЕу/Н, + (ЧшНе) (сЕх!н°)-
Далее учтем уравнения Максвелла для компонент поля волны
i*?, = +1(«>/с)Я8;
B.75)
Drc/c) noe (uyi — иуе).\
Считая плазму квазинейтральной (ni=tie=n), нетрудно прийти
к выводу, что Uxi=Uxe=Ux, а уравнение непрерывности принимает
166
вид
B.77)
Дисперсионное уравнение имеет вид
со2/Р=(Я20/4яро)((о2ре/с2)
(в пренебрежении поправками порядка /
Фазовая скорость от значения Я/]/терв при малых частотах
с ростом ш уменьшается до нуля при частоте {^Не^шL2' Диспер-
Дисперсионная кривая для этого типа колебаний для наглядности показа-
показана на рис. 2.13. Отклонения от линейного закона дисперсии начи-
начинают существенно прояв-
проявляться лри k->(uvelc. Закон
дисперсии магнитного звука
по форме напоминает зави-
зависимость со(&) для ионного
звука. Но вместо дебаевско-
го радиуса здесь присутству-
присутствует характерная длина с/соре,
предельно возможной явля-
является ЧаСТОТа ((ОЯгСОНе) 1/2«
Волновые процессы при ча-
частотах, близких к гибрид-
гибридной, вообще играют важную
роль в физике плазмы. В ча-
частности, в магнитозвуковой
волне при ы-*((дн{(днеI/2 кинетическая энергия колебательного
движения ионов (продольного, т. е. в направлении распростране-
распространения звука) сравнивается по порядку величины с кинетической
энергией электронов, которую они приобретают в результате элек-
электрического дрейфа vy=—cExlH0 (вдоль оси у\).
Все это справедливо для плазмы в не слишком сильном магнит-
магнитном поле Я2/8я<Сп0тес2. В такой плазме состояние в магнитозву-
магнитозвуковой волне оказывается квазинейтральным. Однако при очень
сильных магнитных полях
Я20/8я»п0тес2 B,78)
для высоких частот становится существенным отступление от ква-
квазинейтральности. Закон дисперсии для таких колебаний имеет вид
(опять-таки при пренебрежении тепловым движением)
B.79)
Ф.азовая скорость стремится к нулю при ионной ленгмюровской
частоте (co->(opi). Характерная длина, при которой становится су-
существенным отклонение от линейного закона дисперсии, есть
167
и)ре/с
Рис. 2.13. Дисперсионная кривая магнито-
звуковых волн К J- Но
Тепловое движение частиц, не учтенное в проведенном рассмот-
рассмотрении, сделало бы все вычисления весьма громоздкими, так как
пришлось бы заниматься кинетической теорией. Иногда учет теп-
теплового движения не только приводит к количественным поправкам,
но и дает качественно новые физические результаты. Только так,
например, можно получить характерные типы колебаний плазмы,
распространяющиеся почти поперек магнитного поля с частотами,
близкими к целым кратным циклотронных частот ионов и элек-
электронов. Эти типы колебаний называют модами Берн штейна.
Новые типы колебаний могут возникать в плазме и при рас-
распространении вдоль магнитного поля. Наиболее важными среди
них являются магнитогидродинамические альвенов-
ские волны. Вывод свойств этих волн с помощью уравнений
магнитной гидродинамики не представляет трудности.
Пусть направление оси z совпадает с направлением вектора по-
постоянного магнитного поля Яо. Альвеновские волны распространя-
распространяются вдоль Яо и являются поперечными, т. е. соответствующие им
компоненты скорости плазмы и. колебаний магнитного поля пер-
перпендикулярны к Яо, а следовательно, и к направлению распростра-
распространения волны. При таких поперечных смещениях плазмы, первона-
первоначально однородной, не возникает ни сжатий, ни разрежений, т. е.
плотность плазмы, а также давление в процессе распространения
альвеновских волн остаются постоянными. В этом случае уравне-
уравнение Эйлера магнитной гидродинамики B.60) с учетом B.61) при-
принимает вид
ро<Эи/д/=—§гаёЯ2/8я+A/4я)(Ндгас1)Н. B.80)
Линеаризация означает, что нужно отбросить член с магнитным
давлением (как квадратично малый). Второе слагаемое в правой
части дает A/4я) (Hod/dz) H. Итак, линеаризованное уравнение
движения имеет вид
ро<Эи/<«=A/4я) (Нод/дг)Н. B.81)
В качестве урагвнения для магнитного поля волны возьмем урав-
уравнение B.70), в котором член rotfuXH] для случая альвеновских
волн упрощается:
rot [uX Но] = Ноди/дг,
а само уравнение принимает вид
dH/dt=H0duldz+(c2l4no) (d2H/dz2). B.82)
В пренебрежении магнитной вязкостью уравнения B.81) и
B.82) легко объединить, исключив любую из переменных и или Я.
В итоге получается обычное волновое уравнение
llv2A{d2u!dt2)=d2uldz2 B.83)
с линейным законом дисперсии b)=kvA. Учет магнитной вязкости
приводит, как нетрудно увидеть, к затуханию волны. Роль упругой
возвращающей силы в магнитогидродинамических волнах играет
168
сила натяжения силовых линий. Поэтому удобно представить аль-
веновские волны как колебания упругих нитей (силовых линий
магнитного поля), нагруженных плазмой (из-за эффекта вморо-
женности).
Квадрат показателя преломления iV2=&2c2/co2, соответствующий
альвеновской волне, равен Annmic2/Н2. Ему можно дать наглядное
толкование на языке дрейфового движения заряженных частиц
в скрещенных электрическом и магнитном полях (см. § 2.1). Дви-
Движение со скоростью с[ЕХН]/#2 не приводит к электрическому
току, так как и ионы, и электроны движутся вместе. Дрейфовое
движение в следующем порядке приводит к смещению зарядов
в направлении электрического поля [см. формулу B.31)]: х=
B)?
(/
Теперь диэлектрическую проницаемость можно выразить через
электрический момент Р единицы объема е=1+4яР/?г, где Р—
=—пех. Пренебрегая смещением электронов (оно меньше ионного
в Шх\те раз), получаем диэлектрическую проницаемость в области
низких_частот 4лпгп{С2/Н2. Соответствующий показатель преломле-
преломления У г для подавляющего большинства плазм чрезвычайно велик.
Таким образом, магнитогидродинамические волны представляют
собой просто замедленные поперечные электромагнитные колеба-
колебания. В очень разреженной плазме они плавно переходят в обычные
электромагнитные волны в вакууме. Однако в нашей магнитогидро-
динамической модели не учтен ток смещения, и поэтому такой пре-
предельный переход невозможен.
Величина альвеновской скорости не содержит характеристик
теплового движения плазмы. С этим обстоятельством связана за-
замечательная особенность магиитогидродинамических волн: их
свойства универсальны, где бы они ни распространялись, в прово-
проводящей ли жидкости, помещенной в магнитное поле (С. Лундквист
в своих классических опытах генерировал волны в жидкой ртути),
или в бесстолкновительной плазме. В последнем случае, разумеет-
разумеется, теряет смысл понятие магнитной вязкости и затухание может
быть вызвано эффектами бесстолкновителы-юго взаимодействия
волна — частица, примером которого в отсутствие магнитного поля
является резонанс Ландау.
В бесстолкновительной плазме появляется эффект аномальной
дисперсии и двойного лучепреломления, когда частота волны по
мере увеличения становится сравнимой с ларморовской частотой
ионов.
Самое общее описание волн в такой неизотропной среде, как
плазма в магнитном поле, основано на введении тензора диэлек-
диэлектрической проницаемости. Из уравнения Максвелла легко можно
получить связь между тензорами диэлектрической проницаемости
и проводимости:
e<fe=6iH-i Dя/ш) а*- B.84)
Это соотношение — тензорное обобщение рассмотренного в ч. 1 со-*
отношения между диэлектрической проницаемостью и проводи-
169
мостыо плазмы. Компоненты тензора проводимости от — коэффи-
коэффициенты в тензорном обобщении закона Ома:
ji=.OikEk. B.85)
Формула B.84) получена для плоской волны, пропорциональной
ехр (—icoH-ikr).
В приближении «холодной плазмы» компоненты тензора ди-
диэлектрической проницаемости зависят только от частоты (времен-
(временная дисперсия). Для получения их конкретного вида необходимо
с помощью уравнений двухжидкостной гидродинамики B.58) и
B.59) определить токи, которые инициируются в плазме полем ко-
колебаний.
Пусть плазма помещена в однородное внешнее магнитное поле
НоII Oz, другие внешние поля отсутствуют. Плазму будем считать
однородной и пренебрежем столкновениями и тепловым движением.
Последнее означает, что в уравнениях B.58) и B.59) можно опус-
опустить слагаемые с компонентами тензора давления. Наконец, пред-
предположим, что в равновесии в плазме отсутствуют какие-либо пото-
потоки Uo=O. В этом приближении уравнения двухжидкостной гидро-
гидродинамики для электронов и ионов (а=е, г) имеют вид
- Ь*. = (ejmj Е + (ejmac) [и. X HJ. B.86)
Решение этих уравнений имеет вид
«„=(«.« (•'-•1ЯвГ<ья,+•*.**); B 87)
(JiJEz;
Определяя с помощью этих соотношений ток в плазме
получаем с учетом B.84) и B.85) следующий тензор диэлектри-
диэлектрической проницаемости:
е11 е12 0 \
•и «.. 0 , B.88)
О 0 е33/
где ^^l-
а
со (со2 —
со2 '
а
170
Таким образом, магнитное поле существенным образом влияет
на диэлектрические свойства плазмы, приводя, во-первых, к ани-
анизотропии направлений вдоль и поперек поля (si 1=^833), а во-вторых,
к появлению недиагональных компонент тензора диэлектрической
проницаемости, соответствующих вращению вектора электрическо-
электрического поля волны в перпендикулярной магнитному полю плоскости
(эффект Фарадея).
Читатель уже знает, что в плазме без магнитного поля су-
существуют три ветви колебаний: высокочастотные колебания плот-
плотности заряда (ленгмюровские волны), электромагнитные волны и
ионный звук. Очень важное свойство плазмы в магнитном поле
состоит в том, что в ней, вообще говоря, уже не существуют не-
независимые продольные и поперечные волны: колебания плотности
заряда инициируют в плазме магнитное и вихревое электрическое
поля.
Действительно, пусть в плазме под углом к магнитному полю
распространяется продольная волна. В отличие от изотропного слу-
случая анизотропия тензора диэлектрической проницаемости приво-
приводит к тому, что вектор тока не будет коллинеарен вектору электри-
электрического поля. Наличие перпендикулярной к направлению распро-
распространения компоненты тока j* приводит, как следует из уравнения
Максвелла
rot Н=A/с) (дЕ*/д^ + Dл1с)?, B.89)
к возбуждению магнитного и вихревого электрического полей,
а следовательно, к связи продольных колебаний плазмы с электро-
электромагнитными. Именно из-за этого обстоятельства исследование вы-
высокочастотных колебательных и волновых -свойств плазмы в маг-
магнитном поле существенно усложняется. Однако в пределе очень
больших показателей преломления плазмы Л/>1 можно прибли-
приближенно рассматривать чисто продольные колебания в магнитном
поле, поскольку связанные с ними вихревые электрические поля
будут пренебрежимо малы.
Действительно, из уравнения Максвелла
rotE=— (llc)(dH/dt) B.90)
имеем следующую оценку для вихревого электрического поля:
#, B.91)
или с учетом уравнения rot H=4ftjf/c
E*~D7W>/k*c*)j*. B.92)
Кроме того, используя уравнение Пуассона
div Е'=4яр, B.93)
имеем с учетом уравнения непрерывности
(№с*№)Е*. B.94)
171
Таким образом, даже при сильно выраженной анизотропии ]ч—jl
для плазмы с большим показателем преломления (N^kc/w^l)
Предполагая .V»l, рассмотрим чисто продольные (электро-
(электростатические) колебания плазмы в магнитном поле. Введя, как
обычно, электростатический потенциал колебаний Е=—V<p, запи-
запишем уравнение Пуассона в следующем виде:
(д*<р/дхгдх,)ы?=О. B.95)
Для плоской волны с учетом конкретного вида тензора
B.95) имеем следующее дисперсионное уравнение:
из
-^COS26-
1 ре
<*>- — СО'
//с?
<* pi
ОJ
' pi
in
B.96)
со
Здесь 0 — угол между направлением волнового вектора и магнит-
магнитным полем. В изотропной плазме дисперсия частоты электроста-
электростатических (ленгмюровских)
j колебаний была связана
I только с тепловым движени-
| ем. Уже весьма слабое маг-
магнитное ПОЛе С02дге/0Jре ^
^ 3k2r2D' меняет дисперсию
электростатических колеба-
колебаний и тем самым приводит
к зависимости частоты этих
колебаний от угла 0. Чтобы
не тратить лишних слов на
описание дисперсионных ха-
характеристик, приведем ре-
результаты решения алгебраи-
алгебраического уравнения B.96)
в виде графиков со=ю@)
(рис, 2.14).
В плазме, помещенной в,магнитное поле, существуют три вет-
ветви электростатических колебаний. Наиболее высокочастотная из
них (при о)ре>о)не) соответствует ленгмюровским колебаниям, при
6—>0 частота этой волны совпадает с плазменной о)ре, с ростом 0
частота этой ветви растет вплоть до так называемой частоты верх-
верхнего гибридного резонанса:
<*>ин~\Ш pe + (D Не) ' BШ)
Частота второй ветви с ростом 0 убывает от сояе при 0=0 до ча-
частоты нижнего гибридного резонанса
Рис. 2.14. Ветви электростатических колеба-
колебаний плазмы в магнитном поле
Л/2
B.98)
172
при е=л/2. Наконец, частота • третьей, самой низкочастотной вет-
ветви, для которой существенно движение ионов, совпадает с ионной
циклотронной сонг вплоть до углов, весьма близких к я/2, а именно
я/2—e«me/mft)i/*.
Исследование дисперсионных свойств волн в плазме, помещен-
помещенной в магнитное поле, при произвольных значениях показателя
преломления — довольно громоздкая задача, выходящая за рам-
рамки настоящей книги. Ограничимся рассмотрением дисперсионных
характеристик волн, распространяющихся вдоль или поперек маг-
магнитного поля.
При продольном распространении (k.=0) в качестве элемен-
элементарных мод колебаний естественно взять волны с круговой поля-
поляризацией. Это вызвано тем,
что в волне, распространяю-
распространяющейся в такой плазме, -прак-
-практически на всех частотах
существует ток Холла, при-
приводящий к повороту вектора
электрического поля. В ка-
качестве двух линейно незави-
независимых мод колебаний с кру-
круговой поляризацией следует
рассматривать волны, у ко-
которых электрический вектор
вращается соответственно
в сторону вращения элек-
электронов и ионов в магнитном
поле. Для каждой из этих
волк удобно ввести комби-
комбинацию компонент -доля ?±==
—ЕХ±[ЕУ (такие же комби-
комбинации вводятся для других
физических величин Н±, j±
и т. п.). Поскольку Е±—
(\kz—Ш), то очевид-
\
v
i
Рис. 2.15. Вращение вектора электрического
поля в обыкновенной и необыкновенной
циркулярно-поляризованных волнах
но, что в волне ?+ Ех—cos (kz—со^), Еу-*ът (kz—(ot) и электри-
электрический вектор вращается по часовой стрелке, т. е. в сторону вра-
вращения ионов (рис. 2.15). Аналогичным образом для волны ?L:
Ex^cos (kz—ю?), Ey——sin (kz—Ы) и электрический вектор вра-
вращается в сторону вращения электронов.
Для волн круговой поляризации уравнение Максвелла rotE==
= — A/с) (dHjdt) записывается в следующем виде:
H±=4zi(kc/®))E±. B.99)
Аналогично другие уравнения Максвелла rot Н= A /с) X
X(dD/d/) с помощью тензора диэлектрической проницаемости
<2.88) можно представить в виде
H±=±i(<d/kc)e±E±9 B.100)
173
где комбинации е+=8ц—iei2> e-=en+iei2 играют роль диэлектри-
диэлектрической проницаемости для электромагнитных волн с различным
направлением вращения вектора поляризации.
Используя формулу B.88) для компонент тензора диэлектри-
диэлектрической проницаемости, нетрудно записать дисперсионные уравне-
уравнения для волн с круговой поляризацией в следующем виде:
' B.101)
На рис. 2.16 приведен график изменения с частотой показателя
преломления iV(co) для обеих волн с круговой поляризацией (ин-
(индекс а относится к обыкновенной волне Е+, индекс р — к необык-
необыкновенной Е-. В области малых частот обе кривые сливаются, что
соответствует переходу к уже изученным .выше магнитогидродина-
мическим волнам (альвеновской и магнитозвуковой) с фазовой
скоростью va- Им соответствует показатель преломления
Характер волнового процесса изменяется при приближении о)
к сонг. Не вдаваясь в детали, остановимся только на качественной
со
Рис. 2.16. Квадрат показа-
показателя преломления N2—c2k2/(d2
как функция частоты для
электромагнитных волн, рас-
распространяющихся вдоль маг-
магнитного поля:
сплошная кривая — необыкно-
необыкновенная волна (электрический
вектор поляризован в направ-
направлении вращения электронов);
штрих-пунктир — обыкновенная
волна (электрический вектор
поляризован в направлении вра-
вращения ионов)
стороне явлений, которые определяют основные свойства попереч-
поперечных электромагнитных волн в плазме при о—(от- Простейшую
линейно поляризованную волну, распространяющуюся вдоль на-
направления постоянного магнитного поля, можно представить в ви-
виде суперпозиции двух* волн, поляризованных по кругу с противо-
противоположными направлениями вращения вектора поляризации. Если
о)*С'сояг, то обе волны с противоположными направлениями круго-
круговой поляризации распространяются с одинаковой скоростью. Од-
Однако по мере приближения к ларморовской частоте ионов положе-
положение меняется. Действительно, та из волн, электрический вектор
которой вращается вокруг постоянного поля в направлении, совпа-
совпадающем с направлением ларморовского вращения ионов, должна
испытывать в области, где со^сош, явление аномальной дисперсии,,
возникающее^ вследствие циклотронного резонанса ионов. Фазовая
скорость этой волны (ее аналог в оптике принято называть обык-
обыкновенной волной) резко уменьшается вблизи соя;- Напротив, фа-
174
зовая скорость так называемой необыкновенной волны, которой
соответствует противоположное направление вращения электриче-
электрического вектора, в области частот, близких к соя*, растет при увели-
увеличении со. Поэтому в области значений со, близких к сонг, в плазме
должно наблюдаться «двойное лучепреломление». Волны такого
типа играют важную роль в физике околоземной плазмы. Они
легко генерируются в естественных условиях и распространяются
в магнитосфере Земли на очень большие расстояния вдоль силовых
линий геомагнитного поля. Их часто называют ионными (или
электронными) свистами — «свистящими атмосфериками».
При очень больших значениях частот," в области, где со стано-
становится сравнимой с ларморовской частотой электронов о)яе, должна
наблюдаться аномальная дисперсия для необыкновенной волны,
электрический вектор которой вращается вокруг магнитного поля
в ту же сторону, что и электроны плазмы. При частотах соЗ>сонг
ионы практически не участвуют в волновом движении, т. е. волна
становится чисто электронной. В металлах и полупроводниках,
помещенных в магнитное поле, такие волны называют гелико-
геликонами.
Если частота этих волн мала по сравнению с сояе, то закон их
дисперсии имеет вид
0)= (с2&2/С02ре)с0яе. B.102)
В такой волне основное движение электронов — дрейф в скре-
скрещенных Е- и Но-полях, который приводит к возникновению холлов-
ского тока, перпендикулярного к электрическому полю. Затухание
геликона в металлах и полупроводниках связано со столкновения-
столкновениями. Столкновения приводят к возникновению компоненты тока
вдоль электрического поля, которая мала по сравнению с холлов-
ской в отношении v/сояе- Соответственно этому столь же мало за-
затухание геликона: Y/'W^v/coHe. Именно благодаря этому обстоя-
обстоятельству возможно распространение геликонов в плотной
металлической плазме с большими частотами столкновений
с-1 при использовании сильных магнитных полей
(L Э.
Аномальная дисперсия на резонансных частотах всегда сопро-
сопровождается аномальным' поглощением (т. е. резким увеличением
затухания волны). Это поглощение обусловлено тем, что при при-
приближении частоты обыкновенной волны к соЯг ионы все время на-
находятся в резонансе с электрическим полем волны и, ускоряясь
под действием этого поля, непрерывно отбирают у него энергию.
Это явление используется в так называемом циклотронном методе
нагрева плазмы. С необыкновенной волной то же самое происходит
при .фасоне.
При частотах, больших резонансных, вплоть до так называе-
называемых частот отсечки, coi — для обыкновенной, сог — для необыкновен-
необыкновенной, находятся области непрозрачности, в которых распростране-
распространение электромагнитной волны невозможно. При частотах отсечки k
175
обращается в нуль, и эти частоты имеют смысл пороговых частот,
выше которых вновь становится возможным распространение элек-
электромагнитных волн. В изотропной плазме пороговая частота со-
совпадает с плазменной соре. Из дисперсионного уравнения B.101)
нетрудно получить формулы для частот отсечек:
ре>
Не>
ре-
B.103)
Две линейные независимые волны — обыкновенную и необык-
необыкновенную— можно ввести и в случае поперечного распространения
k,=0. Однако смысл этих волн уже иной. В обыкновенной волне
электрический вектор параллелен внешнему магнитному полю,
а магнитный вектор перпендикулярен к плоскости, в которой ле-
лежат векторы к и Но. Колебания заряженных частиц в такой волне
происходят в направлении магнитного поля, следовательно, дис-
дисперсия волны не зависит от напряженности поля и определяется
формулой A.35).
Напротив, в необыкновенной волне вектор электрического поля
лежит в плоскости, перпендикулярной к внешнему магнитному по-
полю, а магнитное поле волны параллельно Но. Направляя к вдоль
оси х, а Но по оси г, получаем с помощью уравнений Максвелла
следующие уравнения для компонент Ех, Еу:
B.104)
Отсюда находим дисперсионное уравнение для необыкновенной
электромагнитной волны
2=(е2п-е212)/еи. B.105)
Н2\
с?у*
А
I
1
1
! /
аш а1
"ре
ш2
0J
Рис. 2.17. Квадрат по-
показателя преломления
М2=с2&2/со2 как функция
частоты при поперечном
распространении электро-
электромагнитных волн:
сплошная кривая — необык-
необыкновенная волна (электриче-
(электрический вектор перпендикуля-
перпендикулярен к плоскости, содержа-
содержащей векторы к и Но); штрих-
пунктир — обыкновенная вол-
волна (электрический вектор па-
параллелен Но)
Результаты решения дисперсионных уравнений для обыкновен-
обыкновенной и необыкновенной волн при поперечном распространении при-
приведены на рис. 2.17. Обыкновенная волна распространяется в плаз-
плазме при частотах выше соре. Необыкновенная волна имеет две резо-
резонансные частоты, при которых N—мх>. Это уже полученные ранее
176
в электростатическом приближении частоты верхнего B.97) и ниж-
нижнего B.98) гибридных резонансов, т. е. собственные частоты элек-
электростатических колебаний при Э—я/2. Для необыкновенной волны
имеются, кроме того, две частоты отсечки (N—Я)). Естественно»
они оказываются такими же, как частоты отсечки coi и 02 при про-
продольном распространении.
§ 2.7. Кинетическая теория волн в плазме
Строгая теория волн в бесстолкновительной плазме должна ба-
базироваться на решении линеаризованных кинетических уравнений
для ионов и электронов совместно с уравнениями Максвелла, по-
подобно тому как это показано в ч. 1 для более простого случая. Как
уже известно читателю, кинетическое
рассмотрение позволяет не только полу-
чить дисперсионные свойства колебаний
и волн в плазме, но и исследовать их
взаимодействие с резонансными частица-
частицами, т. е. процессы бесстолкновительного
затухания и нарастания волн. Хотя маг-
магнитное поле и делает выкладки более
громоздкими, мы приведем кинетическую
теорию волн альвеновского типа для
простейшего случая продольного распро-
распространения к={0, 0, k).
Ограничимся анализом колебаний до-
статочно высокой частоты, в которых
принимают участие только электроны, и
соответственно исследуем необыкновен-
необыкновенную электромагнитную волну с электри-
электрическим вектором, вращающимся в на-
направлении вращения электронов. После
й
Рис 2.18. Цилиндриче-
Цилиндрические координаты в про-
пространстве скоростей, ис-
использованные в кинети-
кинетическом уравнении B.108)
несложных стандартных вычислений получим следующее уравне-
уравнение для электрического поля волны:
— I) ?_=i DяДо) /_. B Л 06)
В предыдущем параграфе мы описывали отклик плазмы на
распространяющуюся в ней волну с помощью гидродинамического
тензора диэлектрической проницаемости. В уравнении B.106) вме-
вместо этого тензора введен ток /_, инициированный волной в плазме,
для вычисления которого обратимся к решению кинетического
уравнения. Очевидно, что
/. = — е j v± exp (— i<p) f,dv.
B.107)
Здесь fi — возмущение равновесной функции распределения,
вызванное распространяющейся в плазме волной; <р — азимуталь-
азимутальный угол в пространстве скоростей (рис. 2.18).
12-74 YIT
Решим теперь кинетическое уравнение B.48). Для этого пред-
представим функцию распределения в виде f=fQ-j-f{. Величина f\ про-
пропорциональна exp [ikz—ico1/}, для нее линеаризованное кинетическое
сравнение записывается в следующем виде:
- i (со - kvz) U - (е/тес) [v X HJ ^--
- (е[те) (е + -i- [v X Н]) dfJdv = O. B.108)
Используя полярные координаты в пространстве скоростей с осью
шдоль постоянного магнитного поля vx — v . cos <j>; vy = v. sin 9, не-
нетрудно доказать, что слагаемое
— (е/ШесУ [vX Но] dfif&v= (eH0/mec) (v^dfx/dvy—v^fi/dvx)
переходит в он^/г/^ф. Что касается двух последних слагаемых, то,
используя вытекающее из уравнений Максвелла соотношение меж-
между амплитудой электрического и магнитного полей волны Н=
= (Ф)[кХЕ], можно представить их в следующем виде:
- (е/те) (Ех cos 9 + Ey sin 9) [A - Ь» dfjdv±+
Здесь учтено, что в стационарном состоянии равновесная функция
.распределения может зависеть только от v, , vz. Подставляя Ех, Еу
в виде Ех= (Е+-\-Е-) /2, ЕУ=(Е+—E-)/2i, получаем кинетическое
уравнение
- i (ш - kvz) U+»Hdft/df=(еBте) Е_ exp (i?) [A -
— Ао,/ш) df,(do± + (kojm) дЦдог\. B.109)
Отметим, что в вынуждающей силе сохранено только слагае-
слагаемое, пропорциональное ?_ехр (i(jp), с которым связан ненулевой
аклад в ток B.107).
Решение кинетического уравнения B.109) записывается в виде
/, = - i (e[2me) E_ exp (i?) [A - to» df,[dv± +
+ (Ьо±[*) df./d0a][(k0M - т + mHg). B.110)
Вычисляя с помощью ,fi ток B.107), приходим к следующему дис-
дисперсионному уравнению:
= — Bпе*[те<в) J d\v± [A — kvz[<») df9!dv± +
m) dfu[dv2][(kv2 -<» + <»He). B.111)
Для получения дисперсионных характеристик электромагнитной
волны в холодной плазме и ее декремента затухания разобьем
равновесную функцию распределения на две части — функцию
Д78
распределения основной массы частиц (тепловых)., определяющих:
дисперсию волны, и функцию распределения небольшой группы
резонансных частиц, взаимодействие которых с волной приводиг
к ее затуханию.
Для электрической волны круговой поляризации, электрический-
вектор которой вращается в ту же сторону, что и электроны, усло-
условие резонансного взаимодействия с электронами имеет вид
(d—>kzVz=(i)He, B.112)
т. е. частота волны с учетом доплеровского сдвига совпадает с цик-
циклотронной частотой. При этом частицы долгое время находятся при:
одной и той же фазе поля и могут эффективно обмениваться;
энергией с волной. Условие резонанса B.112) записано для не-
необыкновенной волны. Для обыкновенной волны аналогичный резо-
резонанс имеет место с ионами
(О—^2=0)Нг. ' B.113)
При распространении электромагнитной волны под углом к маг-
магнитному полю возможны и другие резонансы. Подробно этот во-
вопрос рассматривается в следующем параграфе.
Пренебрегая вкладом теплового движения в дисперсию волн*,
интеграл в правой части уравнения B.111) можно вычислить пре-
предельным переходом v±—И), v±—Я). Тогда получим
J к-1х+^ ГО - ^)|r+<fo»«w*.]*-
Учтем теперь вклад резонансных частиц, используя символическую»
запись
1 l(kvz — ш -f- соя) = 3>\{kvz — ш -|- соя) -|- k§ (kvz — со -f- <оя),
смысл которой был разъяснен ранее. Слагаемое с главным значе-
значением вещественно и поэтому приводит только к малой (пропор-
(пропорциональной плотности резонансных частиц) поправке к частоте.
Пренебрегая этой поправкой, сохраним в интеграле лишь вклад от
5-функции. Вычислив для резонансных частиц интеграл по vz, при-
приведем дисперсионное уравнение к виду
ГI\ fkVz \ df0
± 1Д (о
\ • 2ГС?2 СО f
Не' те | k | J
со dvz
Если пренебречь правой частью, то это уравнение, естественно, со-
совпадет с дисперсионным уравнением для ?1_-волны, полученным
в § 2.6 из гидродинамических уравнений (напомним, что мы рас-
рассматриваем высокочастотную ветвь и не учитываем движение ио-
12* it»
нов). Но кроме частоты при кинетическом рассмотрении может
быть получен также и декремент затухания волны.
Из уравнения B.114) имеем следующую формулу для декре-
декремента затухания:
._
4ll
Для плазмы с максвелловским распределением резонансных час-
частиц по скоростям интеграл по v± в B.115) легко вычисляется; де-
декремент циклотронного затухания необыкновенной волны в резуль-
результате взаимодействия с резонансными электронами имеет вид:
d)) W \
B.116)
Как уже отмечалось выше, область аномального поглощения на-
.ходится при частотах, близких к циклотронной:
В этой области основная масса частиц плазмы попадает в ре-
резонанс с волной. С ростом расстройки |оз—соне| число резонанс-
резонансных частиц экспоненциально уменьшается.
Уже известно, что когда функция распределения резонансных
частиц отличается от максвелловской (например, если резонанс-
резонансные частицы образуют пучок), их взаимодействие с волной может
приводить к нарастанию ее амплитуды, т. е. к неустойчивости. Так
же, как в случае ленгмюровской волны, пучковая неустойчивость
циклотронной волны может быть двух типов — гидродинамической
и кинетической.
Рассмотрим гидродинамическую неустойчивость циклотронной
волны, возникающую при взаимодействии с плазмой моноэнерге-
моноэнергетического электронного пучка, все частицы которого имеют один и
тот же продольный и поперечный импульс:
Такая функция распределения соответствует как бы пучку осцил-
осцилляторов (назовем их ларморовскими), имеющих одну и ту же ско-
скорость движения вдоль магнитного поля, но равномерно разме-
размешанных в равновесном состоянии по фазам вращения в магнит-
магнитном поле.
Для рассмотрения пучковой неустойчивости окажется важным
учет релятивистской зависимости циклотронной частоты от энергии
180
электронов. В релятивистском случае формула для циклотронной
частоты шяе=^0/тес переходит в следующую:
, B.118)
где w^m^Y^l-^-p^/mV — энергия частицы. Переход к реляти_
висте кому случаю очень прост. Для этого следует заменить
l/rne(djdv) на д/др. В результате вместо B.111) получим следую-
следующее дисперсионное уравнение:
11 kvz —• со + <*>#* V о) / др^ > <о cfy?z
B.119)
Разделим функцию распределения /о на две — функцию для тепло-
тепловых нерелятивистских частиц плазмы и функцию релятивистского
пучка B.117). Для частиц пучка интеграл по продольным и попе-
поперечным импульсам легко вычисляется интегрированием по частям.
В результате приходим к следующему дисперсионному уравнению:
С»А« _ ш2 + со2рсо/((о — шНе)=
= ^ A/2) [со2, (ЛV - ш2)/(со - Ьо - соя/] (*в±о/с«). B.120)
Здесь учтено, что для неустойчивой волны приближенно должно
выполняться условие циклотронного резонанса B.112), и поэтому
в правой части дисперсионного уравнения сохранены только сла-
слагаемые со старшей степенью (квадрат) резонансного знаменателя.
Подчеркнем, что при нерелятивистском рассмотрении частиц пуч-
пучка вклад пучка содержит только первое слагаемое, пропорциональ-
пропорциональное k2c2.
Таким образом, нерелятивистское рассмотрение применимо
лишь для медленных волн с большим показателем преломления
iV»l? в общем же случае нужно учитывать релятивистскую зави-
зависимость массы и циклотронной частоты частиц пучка от их
энергии.
Решение дисперсионного уравнения можно получить аналогич-
аналогично тому, как это было сделано для пучковой неустойчивости в от-
отсутствие магнитного поля. Частота наиболее неустойчивой волны
определяется из условия
(^/0»J=8-, B.121)
т. е. дисперсионные свойства такой волны те же, что для иссле-
исследовавшейся выше необыкновенной волны. Наличие пучка малой
ллотности приводит к возмущению ее частоты.
Полагая, что эта волна находится в циклотронном резонансе
с электронным пучком
B.122)
181
для мнимой части добавки к частоте, т. е. для инкремента нара*
стания, получаем из дисперсионного уравнения .следующее соот-
соотношение:
Приведенная формула для инкремента нарастания содержит вкла-
вклады от двух возможных механизмов неустойчивости электронного
пучка в магнитном поле — циклотронного и мазерного. Остановим-
Остановимся на этом вопросе более подробно.
Так же, как и в отсутствие магнитного поля, в рассматривае-
рассматриваемом случае для возникновения неустойчивости кроме резонансного
условия B.122) должно выполняться условие бунчировки частиц
пучка в тормозящих фазах поля волны.
Для 'электронного пучка в магнитном поле возможны два ме-
механизма бунчировки. Один из них существенно связан с продоль-
продольной неоднородностью поля волны — это бунчировка электронного
пучка по продольным фазам kz, при которой частицы пучка стяги-
стягиваются в сгустки, локализованные в области тормозящих фаз. Та-
Такой механизм аналогичен бунчировке электронного пучка в отсут-
отсутствие магнитного поля, с той разницей, что в рассматриваемом
случае электромагнитной волны бунчировка осуществляется из-за
наличия продольной компоненты силы Лоренца, (обусловленной
магнитным полем волны) (е/с) [v, Н]2.
Можно воспользоваться условием A.161), если под а> пони-
понимать частоту волны в системе отсчета, вращающейся вместе с элек-
электронами. Таким образом, условие бунчировки по продольной фазе
имеет вид
со—юн<Й02. B.124)
И опять, как без магнитного поля, стабилизация неустойчиво-
неустойчивости происходит в результате захвата электронов пучка в эффек-
эффективные потенциальные ямы. При колебаниях электронов в этих
потенциальных ямах меняется продольная фаза. -Период этих ос-
осцилляции определяется формулой A.150) с заменой Е на (v^jc)H.
Таким образом,
ec). B.125)
Амплитуда поля, при которой происходит стабилизация неустой-
неустойчивости, так же как и в изотропной плазме, определяется из усло-
условия у%ъ~\. Связанная с такой бунчировкой неустойчивость назы-
называется циклотронной. Однако в магнитном поле возможен еще
один механизм бунчировки — группировка частиц пучка по фазам
вращения в магнитном поле. В отличие от первого механизма этот
механизм бунчировки является чисто релятивистским. Поясним,,
как происходит группировка электронов по фазам вращения в маг-
магнитном поле (рис. 2.19).
182
(С
U)< CJu
В системе отсчета, вращаю-
вращающейся вместе с электроном, ча-
частота изменения действующего
на электрон электрического поля
ю'—(оя (о/ — частота поля
с учетом доплеровского сдвига,
со'=со—kzvz). Если циклотронная
частота не зависит от энергии, то
ускорение электрона на первом
полупериоде изменения поля ком-
компенсируется торможением его на
втором полупериоде и суммарное
изменение энергии равняется ну-
нулю. Однако, поскольку с учетом
релятивизма dwH/dwKO, то в об-
области тормозящих фаз поля ци-
циклотронная частота возрастает.
В этом случае, при о)г>10я такое
возрастание циклотронной часто-
частоты означает, что область тормо-
тормозящих фаз 'поля проходится мед-
медленнее [т—1/(о/—соя)], электро-
электроны здесь группируются и энергия
передается от электронов пучка к волне.
Таким образом, при d<dH/dw<0 условие бунчировки электронов
в той области* фаз, где они тормозятся волной, т. е. условие воз-
возникновения неустойчивости имеет вид
на
(О
Рис. 2.19. Группировка частиц по
фазам ларморовского вращения
B.126)
Нерелятивистская группировка по продольной фазе существен-
существентолько для' достаточно медленных электромагнитных волн
& т. е. Л/"(со)^>1. В этом случае в формуле для инкремента
доминирует первое слагаемое и имеет место нерелятивистская ци-
циклотронная неустойчивость.
При раскачке быстрой электромагнитной волны ы>Лс сущест-
существенным оказывается релятивистский эффект зависимости цикло-
циклотронной частоты от энергии. Неустойчивость этого типа называют
мазерной.
Как и следовало ожидать, вклады от обоих механизмов груп-
группировки [слагаемые в квадратных скобках в выражении B.123)
для инкремента] противоположны по знаку. Это объясняется тем,
что условия группировки B.124) и B.126) противоположны. Ин-
Интересно отметить, что <при .со=&с, т. е. для среды с показателем
преломления iV(co)-—'1, соответствующие вклады компенсируют
друг друга и неустойчивость отсутствует.
Происхождение самого термина «мазерная неустойчивость»
связана с использованием квантовомеханической интерпретации.
При такой интерпретации электронный пучок рассматривается как
183
газ осцилляторов с уровнями энергии wn—nd)He (п=0, 1, 2, ...)..
Как и в обычном мазере, для неустойчивости необходима неэкви-
неэквидистантность энергетических уровней, т. е. в данном случае зави-
зависимость соне от энергии. Тогда квант поля, излученный при пере-
переходе осциллятора на более низкий энергетический уровень
п—>-п—1, не может поглотиться при переходе п—>~п-\-1, и проис-
происходит усиление поля излучения.
Уровень амплитуды поля, возбуждаемого при хМазерной не-
неустойчивости, определяется из условия
До)Н==: (d(uH/dw) Aw^y B.127)
(расстройка частоты о/—<он порядка инкремента у). При таких:
амплитудах происходят эффективная бунчировка и захват частиц,
при движении по фазе ср. Изменение энергии частицы за характер-
характерное время развития неустойчивости t^l/y
bw = eEv±ft. B.127a>
Из B.127) и B.127а) получаем следующую оценку для макси-
максимальной амплитуды электрического поля волны:
^>)°Л(Т'К)Л B.128)
Мазерная неустойчивость позволяет получать большие амплитуды
электромагнитных волн в генераторах мощного электромагнитно-
электромагнитного излучения, основанных на использовании интенсивных пучков
электронов (циклотронные мазеры А. В. Гапонова-Грехова).
Кроме резонансного взаимодействия частиц с волнами сущест-
существует еще важный класс взаимодействий, при которых нельзя чет-
четко выделить группу частиц, ответственную за затухание или не-
неустойчивость. Это так называемое нерезонансное или адиа-
адиабатическое взаимодействие. Одним из самых наглядных
примеров могут служить неустойчивости плазмы, требующие для
своего возникновения, как правило, еще более сильной анизотро-
анизотропии функции распределения fo iv\> v\\)-
Неустойчивость в рассматриваемом случае может возникать
для волн, распространяющихся под произвольным углом к магнит-
магнитному .полю. Для простоты рассмотрим ставший уже традицион-
традиционным предельный случай волны, распространяющейся вдоль маг-
магнитного поля, т. е. альвеновскую волну.
В действительности при выполнении приведенного ниже крите-
критерия неустойчивости возмущение не носит волнового характера
(формально это проявляется в том, что со2 становится отрицатель-
отрицательным). Тем не менее будем говорить для краткости о «неустойчиво-
«неустойчивости на альвеиозской волне», имея в виду, что при уменьшении ани-
анизотропии рассматриваемый тип возмущений переходит в альвенов-
ские волны, у
Так же как и рассмотренную выше гидродинамическую неустой-
неустойчивость резонансного типа нерезонансную неустойчивость" можно
184
получить из общего дисперсионного уравнения кинетического при-
приближения. Для возмущений альвеновского типа в дисперсионном
уравнении следует учесть также вклад ионов.
Уравнение B.111) нетрудно обобщить:
v±
dv2
^f4 B.129)
Рассмотрим возмущение с длиной волны X, много большей сред-
среднего ларморовского радиуса электронов и ионов (и характерным
временем изменения амплитуды, значительно превышающим пери-
периоды обращения частиц в маг-
магнитном поле). Тогда интеграл
для ионов легко вычисляется
путем разложения по пара-
параметрам:
B.130)
Для электронов вообще доста-
достаточно ограничиться членом
старшего порядка по 1/оояе.
В результате получим следую-
следующее уравнение:
^нп
Р\\ > Pl
"Не
dv,
Рис. 2.20. «Шланговая» неустойчивость
, др. b2vjvz\
dv:
Для плазмы с изотропным распределением частиц по скоростям
отсюда следует дисперсионное уравнение альвеновской волны о=
=kv&. При достаточно большой анизотропии
B.131)
рассматриваемая мода колебаний становится апериодически неус-
неустойчивой:
mi. B.132)
Эта неустойчивость допускает наглядную физическую интерпрета-
дию. Воспользуемся тем, что альвеновские волны можно наглядно
представить как колебания «упругих нитей» — силовых линий маг-
магнитного поля. Рассмотрим силы, возникающие при малом искрив-
искривлении силовой линии в анизотропной плазме (рис. 2.20).
Так как .частицы «привязаны» к силовым линиям, то при дви-
движении по искривленному участку силовой линии возникает цен-
185
тробежная сила
стремящаяся увеличить искривление. Здесь учтено, что при выпол-
выполнении условий B.130) можно пользоваться дрейфовым приближе-
приближением, в рамках которого плазма рассматривается как совокупность
квазичастиц — ларморовских кружков с сохраняющимся магнит-
магнитным моментом \х= wJH. Распределение частиц тогда удобно-
описывать функцией f(\i, ?/{|), где v{] — скорость вдоль постоянно-
постоянного магнитного поля; w^—энергия вращения. Поскольку, кроме
того, каждая квазичастица обладает магнитным моментом
—jiH/Я, ориентированным против магнитного поля Н, то на них
в неоднородном магнитном поле будет действовать сила, связанная
с наличием тока намагничивания:
JV = rot J tifdv„ dp; F^ = [p<H] = [rot j |i/ fav „) dv „ d^XHJ.
Эта сила вместе с силой «натяжения» линий магнитного поля
стремится вернуть силовую линию в положение равновесия.
Если ^#>^и, + ^#> то система уходит от положения равнове-
равновесия, т. е. возникает неустойчивость. В рассматриваемом возмуще-
возмущении отлична от нуля лишь компонента k^ волнового вектора. После
несложных выкладок получихМ следующее условие неустойчивости:
Р\\—Р±>н*о14'к>
Поскольку при выполнении условия B.131) результирующая
сила все время уводит систему от положения равновесия, неустой-
неустойчивость носит апериодический характер. Инкремент у легко найти^
приравняв сумму сил FR—F^— FH к произведению массы элемента
плазмы на ускорение: v=(d/dt)c(EJH0). Но так как из уравнений
Максвелла E=Hy/kc, то v=y2H/kH0. Подставляя значение F, по-
получаем [см. формулу B.132)]
f^^(Pl]-p±-H\!^)/P. B.133)
В проведенном анализе действительно трудно было бы выде-
выделить какую-то группу резонансных частиц, ответственных за неус-
неустойчивость. Этот конкретный вид адиабатической неустойчивости
называют «шланговой» или центробежной (за очевидную анало-
аналогию с капризным поведением садового шланга, по которому пода-
подается мощная струя воды). Квазилинейный подход, применяющий-
применяющийся для описания поведения плазмы при развитии адиабатических
неустойчивостей, учитывает отсутствие резонансных частиц, а со-
186
20
40
60 t
Рис. 2.21. Роет флуктуации магнит-
магнитного* поля <Я2 I /8я> при шланговой
неустойчивости (численный расчет
Березина Ю. А., Сагдеева Р. 3.
«Докл. АН СССР», 1969, т. 184, с. 570).
Флуктуирующее магнитное поле Нj_ изме-
измеряется в единицах Яо; - время выражено
в обратных инкрементах шланговой не-
неустойчивости; усреднение проводится по
длине волны. В начальном состоянии Р ц —
=30#V8Jt, ^=6,6Я2о/8Л возмущение маг-
магнитного поля выбиралось в виде монохро-
монохроматической волны с круговой поляризацией.
Экспоненциальный рост амплитуды поля
сменяется регулярными осцилляциями, со-
соответствующими одномодовому режиму (монохроматическая волна). Перехбд в турбулент-
турбулентный многомодовый режим со стохастическим пространственным распределением поля при-
приводит к затуханию осцилляции и установлению квазистационарного состояния
отзетствующая квазилинейная диффузия затрагивает практически
все частицы плазмы. На рис. 2.21 показаны результаты численно-
численного анализа шланговой неустойчивости для двухтемпературной
Т и, Tj) бесстолкновительной гидродинамической модели.
§ 2.8. Взаимодействие волн с частицами плазмы
в магнитном поле и квазилинейная диффузия
В этом параграфе будет продолжено исследование резонансно-
резонансного взаимодействия волн и частиц в магнитном поле.
Кроме резонансов B.112), B.113), возникающих при продоль-
продольном распространении электромагнитной волны, в магнитном поле
возможны и другие резонансы между частицами и волной. Прежде
всего это резонанс Ландау между продольным движением частиц
и волной:
®=kzvz. B.134)
Такой резонанс обычно существен, когда волна имеет составля-
составляющую электрического поля в направлении магнитного поля и ча-
частицы, продольные скорости которых vz близки к соответствующей
проекции фазовой скорости волны a>/kz, эффективно обмениваются
энергией с электрическим полем волны. Резонанс B.134) вполне
аналогичен резонансу Ландау в изотропной плазме, детально ис-
исследованному в ч. 1.
Новой особенностью волн в магнитном поле является возмож-
возможность появления магнитных потенциальных ям, движущихся вме-
вместе с волнами. Для примера рассмотрим случай магнитозвуковой
волны, распространяющейся под углом к магнитному полю. Про-
Продольная составляющая электрического поля в такой волне прене-
пренебрежимо мала, и резонанс Ландау связан с существованием для
частиц магнитной потенциальной ямы. •
При (о<Ссош сохраняются магнитные моменты электронов и ио-
ионов. В неоднородном магнитном поле волны на эти моменты дей-
стзуетсила — ^V#. Волна с заданными со и k создает периодиче-
периодическую картину сгущений и разрежений силовых линий магнитного
187
поля, движущуюся с фазовой скоростью волны со/А. Под влиянием
силы —[iVH резонансные частицы, скорости которых удовлетво-
удовлетворяют условию B.134), будут отражаться от областей сгущения си-
силовых линий и захватываться в магнитную потенциальную яму.
Рассуждения, аналогичные изложенным в ч. 1, приводят к вы-
выводу о том, что декремент затухания волны, обусловленного рас-
рассматриваемым механизмом, как обычно, должен зависеть от про-
производной функции распределения в резонансной точке:
^\v^lkdv. BЛ35)
Фазовая ^скорость магнитозвуковых волн по порядку величины
равна #e/|/*p; в достаточно сильном магнитном поле эта скорость
значительно превышает тепловую скорость частиц, так что, вообще
говоря, и здесь затухание оказывается экспоненциально малым.
Период фазовых колебаний в магнитном поле получается из фор-
формулы A.150) с помощью очевидной замены eE=ekzq>—*~\xk2H. Та-
Таким образом,
B.135а)
Очевидно, что линейное затухание магнитозвуковой волны име-
имеет место при достаточно малых амплитудах поля волны, когда ча-
частота 1/ть существенно меньше декремента затухания. Как мы уже
знаем, при больших амплитудах захват резонансных частиц в по-
потенциальную яму, созданную волной, и их фазовые осцилляции
в этой яме выключают затухание Ландау и приводят к колебаниям
амплитуды поля волны со временем.
Для магнитозвуковых волн также возможна пучковая неустой-
неустойчивость при обращении знака производной функции распределе-
распределения в формуле B.135).
Для того чтобы получить общие условия резонанса волн и ча-
частиц в магнитном поле, рассмотрим, как будет происходить движе-
движение частиц в электрическом поле волны в произвольном случае на-
наклонного распространения к—{0, k^, kz). Будем считать для про-
простоты, что существенны только компоненты электрического поля,
перпендикулярные к внешнему магнитному полю Но. Тогда урав-
уравнения движения заряженной частицы (электрона или иона) будут
иметь вид (рассматривается нерелятивистское движение)
т (dvxjdf) = еЕх ехр (—Ы -f- \k±x -f- \kzz) -f- (el
1 J \ B.136)
lc)vxH..j
m (dvy idt) = eEy ехр (— Ш + ik±x -f- \kzz) — (el
Отсюда для v=vxJrivy получим
m (dvjdt) + i (eHJc) v = eE+ ехр (-Ы + ik±x + \kzz)% B.136a)
188
где E+=Ex-\-iEy. Замена v = v exp (—шн() в уравнении B.136а)*
дает
dv/d(=(eE+lm) exp {—mt+mnt + ikk ±x-]-ikzz), B.137)
Теперь воспользуемся тем, что рассматривается, как обычно,,
волна малой амплитуды. В данном случае это значит, что волна,
не слишком сильно возмущает траекторию частицы. Иначе говоря,.
в экспоненте, стоящей в правой части уравнения B.136а), под х и
z будем понимать их невозмущенные значения, соответствующие
свободному движению частицы в магнитном поле:
dx/dt=vx cos сон^—vy sin соя ?;
dy/dt—vx sin (uHt-r-Vy cos юн*;
dz/dt=vz.
Тогда экспоненциальный множитель принимает вид
4f (t) =5 exp [i (шя — со — ?2y2) f + i (k±vy/iDH) A — cos «>Ht) —
В итоге возмущенное движение частицы определяется зависимо-
зависимостью от времени экспоненциального множителя iF(t). Функция
f я @ = ехР[(—**±0*/»я) sin V +} (кх°у1тн) A — cosmHt)\ B.138>
является периодической по t с периодом 2jiyW, и ее можно пред-
представить в виде ряда по exp (iruant). Коэффициенты разложения
для функции вида B.138) после несложных преобразований мож-
можно выразить через бесселевы функции (именно так появляются
цилиндрические функции в теории колебаний замагниченнои плаз-
плазмы). Мы не будем вдаваться в дальнейшие детали вычисления..
Остановим внимание лишь на следующем существенном обстоя-
обстоятельстве. С учетом сказанного выше результирующая вынуждаю-
вынуждающая сила [правая часть уравнения B.137)], представляющая со-
собой действие поля волны на частицу, оказывается суммой элемен-
элементарных гармонических сил вида
&~п exp (—mt+itUdnt+ikzVzt).
Соответственно реакция частицы на такое воздействие есть проста
сумма влияний отдельных сил: vn^&~nl'(жоя-Mkflz—с°)- Наиболь-
Наибольшего эффекта взаимодействие достигает при условии резонанса
<u—kzvz=n®H. B.I39)
Здесь, очевидно, п принимает все целые значения: /г=±1, ±2, ...
Резонанс при п=1 для электронов уже был рассмотрен ранее
для случая взаимодействия с частицами необыкновенной электро-
электромагнитной волны, распространяющейся вдоль внешнего магнитно-
магнитного поля. Это циклотронный резонанс между электронами и злек-
189*
трическим полем волны, вектор которого вращается в ту же сто-
сторону, что и электроны. В условии резонанса учитывается допле-
ровский сдвиг частоты о/—со—kzvz (в. радиофизике условие резо-
резонанса с п=\ часто называют резонансом при нормаль-
нормальном эффекте Доплер а). Если бы в предыдущем параграфе
было учтено движение ионов в необыкновенной волне, то условие
их резонанса с волной имело бы вид
B.140)
{Поскольку ионы вращаются в сторону, обратную направлению
вращения электрического вектора, то резонанс возможен только
при достаточно большом доплеровском сдвиге частоты, когда из-
за этого сдвига частота меняет знак.)
Аналогичным образом условия резонансного взаимодействия
обыкновенной электромагнитной волны с ионами и электронами
имеют вид
B.140а)
Ш—kzVz±=—(Оке-
Таким образом, наряду с циклотронным резонансом с'я=1 воз-
возможен также циклотронный резонанс с п=—1. Это так называе-
называемый циклотронный резонанс при аномальном
эффекте Доплера. Заметим, что он возможен только при доста-
достаточно большой продольной скорости частиц vZi превышающей фа-
фазовую скорость волны (o/^z-
Резонансы в условиях нормального и аномального эффектов
Доплера были изучены довольно давно при рассмотрении излуче-
излучения заряженных частиц в магнитном поле. Оказалось, что физиче-
физическая картина, соответствующая этим двум резонансам, совершен-
совершенно различная.
При нормальном эффекте Доплера излучение происходит из-за
наличия поперечной составляющей энергии частиц, в данном слу-
случае ларморовского осциллятора, и сопровождается переходом это-
этого осциллятора на более низкий энергетический уровень. Резонанс
.возможен и в отсутствие продольного движения частиц vz—Я). Ре-
Резонанс же при аномальном эффекте Доплера соответствует излу-
излучению волн в результате существования продольной энергии заря-
заряженной частицы. Излучение сопровождается увеличением попереч-
поперечной энергии частицы, т. е. возбуждением ларморовского осцилля-
осциллятора.
Так же, как излучение отдельной заряженной частицы, пучко-
;вая неустойчивость при аномальном эффекте Доплера развивается
из-за присутствия продольной -составляющей энергии пучка, т. е.
^обыкновенная электромагнитная волна может возбуждаться' элек-
электронным пучком, движущимся вдоль магнитного поля. При нор-
нормальном эффекте Доплера пучковая неустойчивость развивается
из-за существования поперечной составляющей энергии пучка лар-
Й90
моровских осцилляторов. Действительно, инкремент пучковой не-
неустойчивости необыкновенной волны, полученный в предыдущем?
параграфе, обращается в нуль при v.—>~0.
Рассмотрим циклотронную неустойчивость электромагнитных:
волн. Для многих физических приложений, в первую очередь для.
физики магнитосферы, чрезвычайно важной оказывается цикло-
циклотронная неустойчивость ионных и электронных свистов, т. е. обык-
обыкновенной волны при ю<<ош и необыкновенной волны при ю<;
~ сон<?. Показатель преломления таких волн достаточно велик
(ck/to^l), и поэтому при рассмотрении их неустойчивости можно
не учитывать релятивистские эффекты в движении резонансных ча-
частиц.
Кроме гидродинамической циклотронной неустойчивости, кото-
которая исследовалась в предыдущем параграфе, возможна также ки-
кинетическая неустойчивость. В этом случае так как резонансные ча-
частицы имеют неравновесную функцию распределения (пучок, ани-
анизотропия распределения по скоростям), то может происходить об-
обращение знака декремента циклотронного затухания в формуле-
B.115). Эта формула описывает взаимодействие резонансных элек-
электронов с необыкновенной волной, но ее можно легко обобщить на;
случай взаимодействия с такой волной резонансных ионов:
-Отметим, что как и в ч. 1, формулы для декремента (инкремен-
(инкремента) амплитуды волны можно получить не только формальным ре-
решением дисперсионного уравнения, но и с помощью простого энер-
энергетического подхода, основанного на балансе энергии в .системе:
волна — резонансные частицы.
Из формулы для циклотронного декремента (инкремента) не-
необыкновенной волны следует, что условие возникновения цикло-
циклотронной неустойчивости имеет вид
J
± ± |Д СО Jdv± ~ О) dv2 J |0г=(а,--соя)/*
B.142>
Покажем, как это условие реализуется в плазме с неизотропным
максвелловским распределением по скоростям (с разными про-
продольной и поперечной температурами):
U ~ exp {-mv\[2T± - mv\/2T |(}.
Выполняя интегрирование по у±, находим, что критерий неустойчи-
неустойчивости в этом случае имеет вид
TJTa +K»(\-Т±1Тп)]<0 (для электронов); B.143),
TJTn — (юя,/ю) A - Туг,,) <0 (для ионов). B.143а>
19k
При этом для необыкновенной волны циклотронная неустойчи-
неустойчивость на электронах возникает при ^>^ц (нормальный эффект
Доплера), а на ионах —при 7^ > Т± (аномальный эффект Доплера).
Для обыкновенной волны неустойчивость на ионах и электронах
имеет место при обратных соотношениях между температурами.
Циклотронная неустойчивость свистов (или геликонов) играет
фундаментальную роль в динамике радиационных поясов Земли.
В существовании такой неустойчивости можно убедиться, если
конкретные функции распределения частиц радиационных поясов—
энергичных протонов и электронов — подставить в критерий
B.142). На рис. 2.22 показаны примеры функций распределения
энергичных частиц в магнитосфере Земли по данным измерений
на спутниках.
Рис. 2.22. Контуры линий уровня функции распределения протонов в радиацион-
радиационном поясе Земли.
Скорость дана в масштабе 10г см/с на деление. Три показанных распределения соответ-
соответствуют трем последовательным областям пространства вдоль траектории спутника, на ко-
котором проводилось измерение функции распределения протонов. Условия для ионно-цикло-
тронной неустойчивости выполняются за счет распределения с опустошенным «конусом потерь»
(Williams D. J. Physics of Hot Plasma in Magnetosphere. Ed. by B. Hultgvist, L. Stenflo.
London, Plenum Press, 1975)
Для конкретности проведем дальнейшие выкладки для х\шдель-
ного максвелловского распределения с неизотропными температу-
температурами. Это, конечно, является идеализацией, так как «резонансные»
частицы, вызывающие неустойчивость в .магнитосферной плазме,
разумеется, не описываются максвелловским распределением.
Из B.143) следует, что неустойчивость имеет место даже при
очень малой анизотропии температур |7\—7^ |/7\ <^1, при этом,
однако, инкремент у оказывается экспоненциально малым. Дейст-
Действительно, у пропорционально
f. [vz = (со - шн)/кж] ~ ехр {-(т/2) [(со - шя)»/ГпЩ).
При о>«^а>я. k* = m*/v*Af и так как согласно B.143) неустойчивость
имеет место для <о<о>я. \Т{{ — Т±\!Т^ то для наиболее „опасных"
192
волн инкремент у будет пропорционален
ехр {- (m,/2) {v*JT) [Т/(Т „ - Т±)}*}.
Следует заметить, что в реальной ситуации при малой анизотро-
пии рассмотренная неустойчивость может и не возникнуть, если,
например, в «обрезанном» максвелловском распределении отсутст-
отсутствуют частицы с большими продольными скоростями:
ответственные за раскачку колебаний. Это приводит к тому, что на
практике нарастание волн вследствие подобной неустойчивости мо-
может быть заметным лишь при достаточно высокой степени анизо-
анизотропии, тем большей, чем больше отношение магнитного давления
к плазменному.
Пусть, например, ^>^ц- Не будем заранее считать анизотро-
анизотропию температур малой, т. е. не будем предполагать выполненным
условие со<Ссонг. Оценим, при какой степени анизотропии экспонен-
экспонента ехр{—(гаг/2)[(со—сошJ/?^, &2]}, входящая в выражение для ин-*
кремента, станет порядка единицы:
mi(°-»/HO7'ii*i~1- B-144)
Квадрат волнового вектора k2 можно выразить через со с помощью
дисперсионного соотношения для «холодной» плазмы, вывод кото-
которого приведен выше (см. § 2.6):
&2С2/(й2=С02огУ [(Ояг (о)Нг—0)) ]
(если речь идет о волне, вектор поляризации которой вращается
в направлении вращения ионов в магнитном поле). Подставляя
й2=со2ог0J/[с2о)нг(сонг—со)] в B.144) и учитывая, что согласно
B.143) для неустойчивости необходимо ш<ОсошA — ^\\il^±i) ПОЛУ"
чаем
. B.145)
При этом условии инкремент неустойчивости становится заметным.
Аналогичное условие имеет место и для волны, поляризованной
в направлении вращения электронов. Ясно, что при прочих равных
условиях электронная ветвь должна иметь больший инкремент.
Развивая последовательно аналогию с продольными колебани-
колебаниями, для рассматриваемого взаимодействия между частицами и
волнами при циклотронном резонансе можно рассмотреть квази-
квазилинейную стадию, которая должна учитывать обратное влияние
волн на распределение частиц по скоростям (в данном случае по
vz и Vj). Для простоты и здесь ограничимся простейшими случая-
случаями, а именно ионными и электронными циклотронными волнами
(свистами), распространяющимися вдоль Яо. Ограничение случа-
13—74 193
ем параллельного распространения упрощает алгебру, позволяя
рассматривать только основную гармонику циклотронного резо-
резонанса и освобождая от необходимости выписывать громоздкие фор-
формулы с функциями Бесселя. Но в то же время оно не вносит суще-
существенных изменений в физическую картину.
Будем исходить из кинетического уравнения
dfjdt + vz (df(dz) - шя (df[d<e) + (elm) {E± + A /с) [vXHJ} (dffdv) = 0
и уравнений Максвелла для Е±, Н±. Если представить функцию
распределения в виде суммы медленно и быстро меняющихся частей:
"f = f9(f, v±9 »g) + fi и воспользоваться формулой для f19 то урав-
уравнение для медленно меняющейся части принимает вид [см.
A.192)]
'дГ) L
ИГ
х-
(kvz —
dv
±
B.146)
Знак -ь в резонансном знаменателе относится к право- или лево-
поляризованным (обыкновенной и необыкновенной) волнам. В ре-
резонансной области это уравнение можно упростить:
т
v±dv±
Ль
/\ V ?Л* t Art
k-kvt±
B.147)
II
Рис. 2.23. «Линии уровня» в плоскости
v±>vz в результате квазилинейной ре-
релаксации волнового пакета свистов
в плазме
194
В качестве примера приме-
применения уравнения B.147) рас-
рассмотрим задачу о поглощении
частицами одномерного волно-
волнового пакета. Резонансная об-
область скоростей vZj соответ-
соответствующая такому волново-
волновому пакету, изображена на
рис. 2.23. Она лежит в левой
полуплоскости, так как vz=
= (со—<сон) Jk отрицательно для
свистов (со<соя). Окружности
изображают линии уровня для
первоначально изотропного
распределения по скоростям.
Так же, как и в квазилинейной
теории ленгмюровских колеба-
колебаний, резонансные частицы диф-
фундируют до тех пор, пока не достигается установившееся состоя-
состояние «плато». Для достаточно узкого волнового пакета [А(со/?)<
С/&] установившееся состояние таково, что
{[1 - (Ь2/со)] (dUdvj + (kvj*) (dfo[dvz)} = 0. B.148)
При достижении такого состояния диффузия прекращается, как это
видно из сравнения B.148) с уравнением B.147). Это условие
определяет плато для рассматриваемого случая по аналогии с ус-
условием dfo/dv=Q (плато в квазилинейной теории ленгмюровских
колебаний). Линии уровня установившегося распределения по ско-
скоростям (линии равных значений функции распределения), удовлет-
удовлетворяющего уравнению B.148), определяются уравнением
V±tVz—:^=const B.149)
В этом можно убедиться, если функцию распределения вида
f[(v2.-\-v2z)/2 — ®vz(k] подставить в уравнение B.147). Линии уров-
уровня представляют собой окружности, но их центры смещены вправо
на, расстояние (о/& (см. рис. J2.21). Сравнивая условия «плато»
с уравнением B.115) для декремента
затухания, видим, что декремент зату- '^ к
хания свистов в состоянии плато обра- и у^У^1
щается в нуль (аналогично случаю х /
ленгмюровских колебаний). * ^ у _^
Квазилинейная диффузия такого ти- *^ у 7 "*~ ^ {
па, если она возникает в результате * е ' °
неизотропной неустойчивости плазмы ^ ^
в ловушке с магнитными пробками,
например в магнитосфере, приводит ?ис- 2-24- «^енгмюровские коле-
к диффу^и вектора скорости частиц из бания ^SSSSS п^™""
юбласти удержания в конус потерь.
Оказывается, что в условиях магнитосферы Земли это важнейший
механизм, определяющий время жизни частиц в радиационных по-
поясах.
Эта диффузия связана с возбуждением электромагнитных волн
типа свистов. Однако к диффузии в конус потерь может приводить
и другой механизм, связанный с возбуждением электростатических
колебаний. В лабораторных магнитных ловушках плазма помеще-
помещена в сильное магнитное поле и, как правило, электронная цикло-
циклотронная частота превышает плазменную. Электроны в этих усло-
условиях оказываются замагниченными.
Рассмотрим колебания, электрический вектор в которых почти
перпендикулярен к магнитному полю. Из-за замагниченности элек-
электронов их движение при колебаниях происходит не вдоль электри-
электрического вектора, как в изотропной плазме, а только вдоль магнит-
магнитного поля (рис. 2.24). В результате частота колебаний существен-
13* 195
но уменьшается по сравнению с электронной плазменной соре, и
такие низкочастотные колебания могут оказаться в резонансе с за-
захваченными в ловушку ионами.
Действительно, из дисперсионного уравнения продольных коле-
колебаний плазмы B.96) следует, что при о)ре<С(Он<? частота электрон-
электронных ленгмюровских колебаний в замагниченной плазме
o)=copecos0 B.150)
(см. рис. 2.14, вторая ветвь колебаний).
Покажем, что взаимодействие этих колебаний с захваченными
в ловушку ионами действительно приводит к неустойчивости. При
не слишком малых значениях отноше-
отношения kzjk частота со остается все же су-
существенно больше ионной циклотрон-
циклотронной частоты. В этом случае магнитное
поле не влияет на взаимодействие
ионов с волной (незамагниченные
ионы) и эффективное взаимодействие
имеет место при условии выполнения!
' резонанса Ландау. Тогда влияние
Рис. 2.25. Функция распределе- магнитного поля на ионы проявляется
ния с «конусом потерь» только в том, что магнитное поле
«размешивает» их функцию распреде-
распределения по углам ларморовского вращения. Поэтому функция рас-
распределения ионов в ловушке имеет вид
Ионы с достаточно малой поперечной скоростью v.<vzVHm/H0—1
(Нт/Н0 — «пробочное» отношение) попадают в конус потерь и ухо-
уходят из ловушки. В результате этого функция распределения ионов
в ловушке имеет вид, представленный на рис. 2.25. Покажем, что
при такой функции распределения ионов всегда существуют рас-
распространяющиеся почти перпендикулярно к магнитному полю не-
неустойчивые электростатические колебания, и определим фазовые
скорости этих колебаний.
Пусть для определенности волна распространяется по оси у.
Инкремент неустойчивости y^dgfdvy, где g — функция распреде-
распределения, проинтегрированная по поперечным, (по отношению к вол-
волне) компонентам скорости vx, vz. Для возникновения неустойчиво-
неустойчивости необходимо, чтобы
{v*rv3)dvxdvz\ar4k>Q. B.152)
Левую часть этого неравенства распишем следующим образом, пе-
переходя к интегрированию по полярным координатам v., vg,f:
J dvxdvydvz (d[dvy) f (v\, vz) 6 (vy — a>(k) =
= B»[k) J v±dv±d<fdo9 (dldv'j) f {v\, vz) S (v± sin у — wjk).
Интеграл по <р легко вычисляется, и в итоге условие неустойчиво-
неустойчивости записывается следующим образом:
J (df!dv2±)Jv2±dv2! j/V^—ш2/?2 > 0. B.153)
Если бы в подынтегральном выражении отсутствовал множитель
[v*± — а>7^2]~1/2> то Для Функции распределения (см. рис. 2.23) инте-
интеграл в левой части неравенства B.153) обратился бы в нуль. Ин-
Интеграл положителен при выполнении условия
B.154)
поскольку в этом случае при интегрировании по v. наиболее суще-
существенна область, где dfJdv2±^>0. Таким образом, неустойчивыми
оказываются все колебания с фазовыми скоростями, удовлетво-
удовлетворяющими неравенству B.154).
Условие возникновения неустойчивости, так же как и инкремен-
инкременты нарастания, конечно, можно получить и из дисперсионного урав-
уравнения ленгмюровских колебаний, приведенного в ч. 1. В этом
уравнении необходимо учесть, что электроны замагничены, а в ре-
резонанс с колебаниями могут попадать.только ионы, и, следователь-
следовательно, только их нужно рассматривать в кинетическом приближении.
Функция распределения ионов определяется формулой B.151).
С учетом этих замечаний дисперсионное уравнение преобразуется
следующим образом:
[ 1 — (о>%>2) cos2 б — (Аъе'/т^2) J k (df*Jdv) (kv — <d) -' dv = 0.
B.155)
Будем считать, что ионы определяют только мнимую часть ча-
частоты, и соответственно этому в последнем слагаемом учтем только
мнимую часть резонансного знаменателя:
Im [l/(kv—G))]=ji6(kv—со).
Преобразуем интеграл по скоростям, переходя к полярным коор-
координатам г>^,ф, vx и интегрируя по <р:
Г k (dfJdVj) sin 98 (kv± sin <p — ш) v±dv±d<pdvz =
= . Г-L^.-^ V.dO.dvJ
J «±dv± /^i-»' ± Х \
Окончательно получим следующее дисперсионное уравнение:
197
Из этого уравнения следует, что частота колебаний определяется
формулой B.150), а инкремент нарастания амплитуды
2А>2 ю2 Г df dv2*dvz
[см. условие возникновения неустойчивости B.153)]. Возникающая
при выполнении условия B.153) неустойчивость хорошо известна
в физике плазмы. Это так называемая конусная неустойчи-
неустойчивость, которая должна весьма существенно влиять на динамику
частиц в ловушках с сильным магнитным полем. Из-за неустойчи-
неустойчивости функция распределения, показанная на рис. 2.23, должна пе-
переходить в состояние с плато в той области скоростей, где перво-
первоначально dfQ/dv2.^>0. В этом случае происходит диффузия частиц
в пространстве скоростей в сторону убывания v±, т. е. уход ча-
частиц в конус потерь. Таким образом, развитие конусной неустойчи-
неустойчивости должно стать причиной быстрого ухода плазмы из ловушки.
§ 2.9. Равновесие плазмы в магнитном поле
Подобно тому как в механике обычной жидкости простейшим
случаем является гидростатика, т. е. раздел гидродинамики, изу-
изучающий равновесие жидкой или газообразной среды, в магнитной
гидродинамике плазмы можно выделить раздел о равновесии плаз-
плазмы в магнитном поле. В таких состояниях левая часть магнитоги-
дродинамического уравнения Эйлера B.57), описывающая инер-
инерцию плазмы, полагается равной нулю, и в результате получается
уравнение
(l/*)[iXH]=gradp, B.158)
означающее, что сумма объемных сил, действующих на плазму,
равна нулю в любой точке внутри плазмы.
Первым следствием условия равновесия плазмы B.158) являет-
является постоянство ее давления вдоль силовых линий магнитного поля,
так как [jXH]±H. В произвольном случае магнитное поле может
иметь довольно сложный характер и свойства равновесного состоя-
состояния плазмы оказываются непростыми. Задачи такого рода имеют
важное значение в проблеме управляемого термоядерного синтеза.
Здесь же мы рассмотрим простейший случай равновесия плазмы
в магнитном поле с прямолинейными и параллельными друг другу
силовыми линиями магнитного поля, иначе говоря, равновесие
плазмы в продольном магнитном поле. Магнитное поле имеет толь-
только одну компоненту #z, которая является функцией координат х
и у (в плоскости, перпендикулярной к полю). В этОхМ случае усло-
условие равновесия принимает вид
др/дх=—A/8л)дНМдх;
др/ду=— A/8я) дНМду. B.159)
198
Следовательно,
. p+#2z/8jt=const. B.160)
Это соотношение показывает, что магнитное давление #2/8я за
пределами области, занятой плазмой, больше, чем внутри нее, на
величину Ртах- Максимальное давление, при котором плазма мо-
может удерживаться полем заданной напряженности Яо, определяет-
определяется из условия
Апах=#2о/8Я. BЛ61)
Видно, что магнитное поле внутри плазмы оказывается меньше
внешнего поля; это следствие того, что плазма представляет собой
диамагнетик. В этом случае плазма должна полностью вытеснять
поле из занимаемой ею области пространства.
До сих пор, говоря о равновесии плазмы в магнитном поле, мы
использовали лишь одно из уравнений магнитной гидродинамики —
уравнение Эйлера, в котором считали du/dt=O. Выясним, совмести-
совместимо ли это допущение с остальными уравнениями магнитной гидро-
гидродинамики. Исходя из уравнения
приходим к выводу о неизбежности диффузии магнитного поля
внутрь объема, занимаемого плазмой, т. е. в область более слабого
поля. Таким образом, магнитное поле, вообще говоря, будет изме-
изменяться во времени. Но тогда давление плазмы, жестко связанное
с магнитным давлением условием равновесия B.160), тоже долж-»
но меняться, т. е. будет происходить изменение распределения
плазмы в пространстве. Этот встречный процесс также имеет диф-
диффузионный характер. Коэффициент диффузии плазмы, очевидно,
имеет такой же порядок величины, как и ?)м=?2/4л0, если давле-
давление плазмы сравнимо с давлением магнитного поля р—#2/8я.
Уравнение, описывающее процесс диффузии плазмы в магнит-
магнитном поле при /?<C#2/8jt, можно вывести следующим образом. Рав-
Равновесие плазмы достигается в результате протекания тока плотно-
плотностью
1=(с/Н)Чр. ~ B.163)
Электрический ток связан с относительным движением электронов
и ионов плазмы со скоростью Цеп. Электрическое сопротивление
такому току есть следствие силы трения между электронами и ио-
ионами плазмы:
B.164);
где Tei=l/vei — время свободного пробега электронов по «отношению
к соударениям с ионами. Точно так же, как рассматривался дрейф
заряженных частиц под действием произвольной силы F, можно
говорить о дрейфе электронов и ионов под действием силы трения.
Скорость такого дрейфа
ud=c(me/e#2/i)ve<[jXH]. B.165)
199
Она одинакова для ионов и электронов, поскольку разные знаки
зарядов ионов и электронов компенсируются взаимно противопо-
противоположными направлениями сил трения. Поэтому в процессе такого
дрейфа электрическая нейтральность плазмы не нарушается. Под-
Подставим теперь найденную скорость па движения плазмы под дей-
действием сил трения в уравнение, непрерывности. Получим уравнение
диффузии
- B.166)
В результате проведенного анализа можно сделать вывод, что
в реальном случае плазмы с конечной электропроводностью стро-
строгого равновесия не существует, так как скорость плазмы отлична
от нуля. Это значит, что инерционный член в уравнении Эйлера,
вообще говоря, не обращается в нуль и можно говорить лишь
о приближенном выполнении условия равновесия. Это условие вы-
выполняется с тем большей точностью, чем меньше относительная
величина инерционного члена.
Допустим, что Тр — характерное время, за которое происходит
изменение плотности плазмы. Тогда сделанное приближение спра-
справедливо при условии
\ппци/хР\<(Цс)\}ХЩ.
Подставляя и из B.165), получаем
1/сОнгТр <С|С0яеТег- B.167)
Отсюда видно, что чем выше степень замагниченности плазмы, тем
с большим правом можно говорить о ее равновесии.
Из рассмотренной картины диффузии плазмы в магнитном по-
поле вытекает еще одно следствие: диффузия связана со столкнове-
столкновениями между частицами разного сорта — между электронами и ио-
ионами (столкновения между одинаковыми частицами в рассмотрен-
рассмотренном приближении не приводят к диффузии, так как не дают силы
трения). Используя уравнение диффузии плазмы B.166), нетрудно
оценить время диффузии (т. е. время, за которое распределение
плотности плазмы существенно изменится). Это время
zp^L%/DL^L%Ho[c*p. B.168)
Таким образом, данное равновесие плазмы имеет конечное время
жизни порядка тр.
Полезно привести еще один вывод коэффициента диффузии
плазмы поперек магнитного поля, рассматривая случайные блуж-
блуждания частиц вследствие столкновений. За время одного свободно-
свободного пробега %ег электрон в среднем испытывает одно кулоновское
столкновение, в результате которого он смещается в плоскости,
перпендикулярной к Я, на расстояние порядка ларморовского ра-
радиуса г не- При многократных столкновениях согласно статистиче-
статистическим законам складываются квадраты отдельных смещений. По-
Поэтому за время t частица сместится перпендикулярно к Я на рас-
200
стояние
*хъгну{ры- BЛ69)
Кроме того, среднее смещение при таком диффузионном процессе
должно быть порядка ty^D^t. Следовательно,
D±^r2Hehel- B.170)
Вследствие квазинейтральности плазмы скорость ее диффузии в на-
направлении, перпендикулярном к Я, должна практически совпадать
со скоростью диффузии электронов, так как при сравнимых значе-
значениях температуры электроны из-за меньшей величины ларморов-
ского радиуса блуждают поперек поля гораздо медленнее, чем
ионы. Поэтому формула B.170) дает оценку коэффициента диф-
диффузии для плазмы в целом. Среднее время между двумя столкно-*
вениями т=/па/я?2. Поэтому
D± ^ г2я/х ^ v^^ne'/eWm.o ^ с2р[оН\ B.171)
По порядку величины этот результат совпадает с найденным ра«
нее коэффициентом диффузии B.166).
В диффузию рассмотренного типа дают вклад только столкно-
столкновения электронов с ионами, но не электронов между собой. Это
обстоятельство может ускользнуть от внимания, если ограничить-
ограничиться лишь грубой моделью случайных блуждений. Вот почему ма-
макроскопический подход, основанный на силе трения, особенно по-
полезен. Он автоматически учитывает, что столкновения между элек-
электронами не создают средней силы* трения, а следовательно, и
диффузионного дрейфа.
Очевидно, что теплопроводность плазмы в направлении, перпен-
перпендикулярном к Я, также должна резко снижаться при увеличении
напряженности поля. В противоположность диффузии, которая
обусловлена столкновениями между ионами и электронами, тепло-
теплопередача в плазме поперек силовых линий происходит в основном
в результате ион-ионных столкновений (если Тг не слишком мало
по сравнению с Те). Это объясняется тем, что интенсивность тепло-
теплопередачи зависит от ширины той области, в пределах которой при
наличии градиента температуры перемешиваются траектории ча-
частиц с различной тепловой энергией. Коэффициент теплопроводно-
теплопроводности-в направлении, перпендикулярном к Я, пропорционален квад-
квадрату ширины области перемешивания, а эта ширина по порядку
величины сравнима с ларморовским радиусом. Поэтому теплопере-
теплопередача в основном идет через ионную компоненту Х^ ^= г2н.!*ц.
Отсюда видно, что коэффициент ионной теплопроводности в на-
направлении, перпендикулярном к силовым линиям, уменьшается
примерно в .(<°шТиJ раз по сравнению с тем значением, которое
он имеет в отсутствие магнитного поля. Коэффициент поперечной
теплопроводности для водородной плазмы можно вычислить, поль-
201
зуясь следующей формулой:
н±^ 2-10-1С/г2/#2/7\. B.172)
В различных приложениях физики плазмы рассматриваются
достаточно сложные типы равновесия плазмы в магнитном поле
(так называемые магнитогидродинамические равновесные конфи-
конфигурации). Однако и в таких произвольных случаях сохраняется
основной вывод, сделанный здесь на примере магнитного поля,
имеющего только одну компоненту: равновесие имеет условный
характер, так как оно с течением времени разрушается из-за диф-
диффузии и теплоотвода. В сложных равновесных конфигурациях вы-
выражения для коэффициентов диффузии и теплопроводности плаз-
плазмы поперек магнитного поля могут заметно отличаться от B.171)
и B.172). Это можно понять, если вспомнить, насколько сложны-
сложными могут быть дрейфовые траектории электронов и ионов в произ-
произвольных магнитных полях. В таких полях в качестве элементар-
элементарного шага в схеме случайных блужданий частицы может входить
величина, намного превышающая ларморовский радиус частицы.
Некоторые эффекты такого типа, важные для исследований по уп-
управляемым термоядерным реакциям, рассмотрены в параграфе, по-
посвященном токамаку.
§ 2.10. Примеры равновесия плазмы в магнитном поле.
Токамак
Простейшим конкретным примером применения основных урав-
уравнений магнитогидродинамики B.60), B.63) может служить изоли-
изолированный плазменный столб цилиндрической формы, удерживае-
удерживаемый магнитным полем протекающего в плазме продольного тока
(рис. 2.26). При равновесии радиальный градиент давления в плаз-
плазменном столбе должен быть равен электродинамической силе
(l/c)jzHo, где jz — плотность продольного тока, а #ф— напряжен-
напряженность магнитного поля тока. Силовые линии этого поля имеют
кольцевую форму. Величины \ъ и #ф в случае цилиндрической
симметрии связаны соотношением
следовательно,
-dpldr = (\M (HJr) (d[dr) (г#ф). B.173)
Отсюда
— J (dpfdr) r'dr = (l/8ic) a2H\ (a). B.174)
о
Здесь верхний предел интегрирования по г принят равным радиу-
радиусу сечения плазменного цилиндра а. На границе плазмы /7=0. По-
202
этому
— f (dpfdr) r2dr = 2 j /^ = /7a2 B.174a)
6 0
где ^ — среднее значение давления плазмы в столбе. Из B.174) и
B.174а) следует, что р пропорционально квадрату напряженности
магнитного поля на границе плазмы:
Вакуум
к"?
Плазма
Вакуум
Образование плазменного столба, удерживаемого давлением
магнитного поля протекающего по нему тока, носит название л и-
нейного п'инч-эффекта. При пропускании тока через пря-
прямую разрядную трубку, заполнен-
заполненную газом, сначала должна воз-
возникнуть плазма (в результате иони-
ионизации газа), затем под действием
электродинамических сил она начи-
начинает сжиматься и в результате мо-
может образоваться стянутый к оси
плазменный столб. Ток в этом слу-
случае выполняет сразу три функции:
он создает плазму, нагревает ее за
счет джоулева тепла и уравновеши-
уравновешивает давление плазмы в сжатом
плазменном столбе с помощью дав-
давления собственного магнитного
поля. В начальный период исследо-
исследований по физике высокотемпера-
высокотемпературной плазмы этот метод достиже-
достижения высоких температур благодаря
своей кажущейся простоте пред-
представлялся очень перспективным.
Казалось, что если пропустить через газ при низком давлении им-
импульсный ток достаточно большой силы, то за ничтожный проме-
промежуток времени в разрядной трубке возникнет раскаленный плаз*
менный шнур с огромной температурой.
Однако практически в экспериментах с такой геометрией не
удалось поднять температуру плазмы выше ^1-106 К, и то всего
лишь на несколько микросекунд. Как показали эксперименты, раз-
развитие кратковременного импульсного разряда с большой силой то-
тока не приводит к образованию квазистационарного состояния, опи-
описываемого условием равновесия B.173). Постфактум сейчас мож-
можно сказать, что при некоторой проницательности это можно было
бы предвидеть заранее. Не учтенным оказался важнейший физиче-
физический фактор — неустойчивость «гибкого» проводника, каковым яв-
является плазменный столб с током. За очень короткий промежуток
времени (в обычных условиях эксперимента — за несколько микро-
203
Рис. 2.26. Равновесие плазменного
столба, удерживаемого магнитным
полем собственного осевого тока
(пинч)
секунд) в плазменном шнуре развиваются деформации, напомина-
напоминающие «перетяжки» и «изгибы» (рис. 2.27). Они разрушают пра-
правильную геометрическую структуру плазменного образования, в ре-
результате чего плазма начинает сильно взаимодействовать со
стенками и быстро охлаждается.
На этом конкретном примере мы впервые встретились с одной
из центральных проблем физики плазмы — проблемой устойчиво-
устойчивости плазменных конфигураций. Общий ана-
анализ относящегося сюда широкого комплек-
комплекса явлений составит содержание ряда сле-
следующих параграфов.
Хотя первая попытка получить высоко-
высокотемпературную плазму в равновесном со-
состоянии путем использования линейного
пин-эффекта оказалась неудачной, однако
дальнейшее развитие этой основной идеи
в конце концов увенчалось успехом. Два
основных элемента, добавленных в процес-
процессе развития к первоначальной идее, со-
состояли: 1) в стабилизации неустойчивости
«мягкого» плазменного проводника с током
при помощи сильного продольного поля
f
Рис. 2.27. Деформации типа «перетяжка» (а) и «изгиб» (б)
внешнего происхождения. Силовые линии продольного поля обра-
образуют как бы жесткий каркас, препятствующий нарастанию любых
макроскопических деформаций в плазменном шнуре, и 2) в замы-
замыкании плазменного цилиндра в кольцо для устранения потерь
энергии на концах (при наличии концов, опирающихся на элек-
электроды, невозможно получить плазму в квазистационарном состоя-
состоянии с достаточно высокой температурой).
Итак, мы пришли к системе, получившей название «токамак».
Она изображена на рис. 2.28. Кольцевой плазменный виток удер-
удерживается в равновесии магнитным полем тока Н^ и стабилизиру-
стабилизируется продольным полем #0. Ток в плазме можно создать индук-
индукционным путем (например, надев камеру, в которой должен об-
образоваться плазменный виток, на сердечник трансформатора).
Однако, как нетрудно видеть, для того чтобы добиться равновесия
плазмы, кроме полей #ф и #в нужно ввести также поле Н±, на-
204
правленное вдоль главной оси тороидальной системы (перпендику-
(перпендикулярно к плазменному кольцу). Это поле необходимо для того, что-
чтобы скомпенсировать электродинамическую силу радиального рас-
расталкивания кольцевого плазменного тока. При взаимодействии по-
поля Яjl с током / возникает сила A/с)/Я^(на единицу плазменно-
плазменного кольца). При указанном на рис. 2.28 направлении Я^ эта сила
в каждом элементе кольца направлена по радиусу к оси торои-
тороидальной системы.
В обычных условиях | Н, | < | Я (а)|, поэтому присутствие Я^
не нарушает общей картины поля. Линии результирующего маг-
магнитного поля имеют винтовую структуру. Они навиваются вокруг
Рис. 2.28. Магнитное поле и ток
в токамаке
Рис. 2.29. Тороидальные магнит-
магнитные поверхности
кольцевой осевой линии плазменного витка. Как было указано
в § 2.2, в таком поле траектории заряженных частиц принадлежат
к двум различным классам: существуют «пролетные» и «запертые»
частицы. Рассматриваемая как единое целое, плазма свободно рас-
растекается вдоль винтовых силовых линий.
Прежде чем заниматься анализом условий равновесия в такой
тороидальной системе, следует обратить внимание на одну харак-
характерную для нее черту топологии магнитного поля. Пусть плоскость
5 представляет собой поперечное сечение системы. Силовая линия,
проходящая через точку Мх на этой плоскости, обходя один раз
вокруг тороида, пересечет плоскость 5 в точке М2, в следующий
раз — в точке Af3 и т. д. (рис. 2.29). Множество точек Ми 7И2,
Мз, ... в общем случае будет бесконечным. Однако для некоторых
линий поля оно может быть конечным, и это означает, что такая
линия поля замыкается сама на себя. Это так называемые выро-
вырожденные линии. К их числу, в частности, принадлежит осевая линия
витка, на которой поле тока обращается в нуль. Ее след (см.
рис. 2.28) обозначен буквой О.
Поведение силовой линии, многократно обходящей вдоль торо-
тороида, определяется положением изображающих точек Ми М2, ...
Пусть после нескольких обходов точка М приблизилась к началь-
205
ной точке Мх. При следующем обходе угол поворота вокруг О бу-
будет уже больше 2я. Где в таком случае расположится следующая
точка? Естественно предположить, что Мп+\ лежит между М\ и
М2, следующая Мп+2 — между М2 и Мъ и т. д., и после многих об-
обходов изображающие точки образуют гладкую замкнутую кривую.
В таком случае можно говорить о существовании семейства маг-
магнитных поверхностей. Каждая из них, образно выражаясь,
изготовлена из одной бесконечной силовой линии. Линия поля, по-
порождающая магнитную поверх-
поверхность, плотно устилает ее.
Магнитные поверхности в то-
камаке образуют множество вло-
вложенных друг в%друга торойдов.
В континууме этих тороидов каж-
каждый, взятый наудачу, образуется
одной силовой линией. Однако
среди магнитных поверхностей
„ пол г есть счетное множество «выро-
Рис. 2.30. Стелларатор — «восьмерка». г
Стрелками обозначена силовая ли- Жденных», которые создаются
ния замкнутыми силовыми линиями.
В этом случае на поверхности
укладывается непрерывное множество линий поля, смещен-
смещенных друг относительно друга. Л. Спитцер высказал гипотезу
о том, что магнитные поверхности существуют также и для
таких тороидальных полей, в которых винтовые силовые ли-
линии, поворачивающиеся вокруг кольцевой оси, создаются толь-
только с помощью внешних источников специальных винтовых обмо-
обмоток) или же деформацией всей магнитной системы — например,,
превращением кольцевого соленоида в восьмерку (рис. 2.30).
Однако теоретический анализ показывает, что в случае таких
несимметричных полей можно говорить о системе вложенных друг
в друга магнитных поверхностей лишь в некотором приближении.
В общем случае структура магнитного поля является довольно
сложной. Отдельные магнитные поверхности оказываются разде-
разделенными системой тороидальных трубок («волокон»), между кото-
которыми силовые линии ведут себя совершенно хаотически. Очевидно,,
что вопрос о существовании магнитных поверхностей имеет боль-
большое значение для перспективы использования различных магнит-
магнитных систем для удержания горячей плазмы. Поскольку плазма
свободно растекается вдоль силовых линий, ее давление р в усло-
условиях равновесия должно быть одинаковым в разных точках одной
и той же магнитной поверхности.
Таким образом, магнитные поверхности представляют собой
семейство плазменных изобар. Если (вместо того чтобы обрисовы-
обрисовывать плавную кривую) «изображающие» точки М\, М2... запол-
заполнят некоторую широкую зону в поперечном сечении плазменного
витка, то в пределах этой зоны плазма может находиться в равно-
равновесии только при условии gradp—0. Очевидно, что обращение
206
в нуль градиента давления в сечении плазменного витка равно-
равносильно появлению аномально большой утечки плазмы в направле-
направлении, перпендикулярном к Я.
Представляет немалый интерес хотя бы вкратце разобрать во-
вопрос о топологии магнитных поверхностей. Если заданы источники
магнитного поля, т. е. система электрических токов, то вектор маг-
магнитного поля Н(г) можно в принципе считать заданным (вычис-
(вычисленным по формуле Био—Савара). Это позволяет написать систе-
систему уравнений для силовых линий магнитного поля, используя их
определение как линий, касательная к которым параллельна Н
в каждой точке. Оказывается, что найти решение этой, казалось
бы, простой системы уравнений в общем случае не так-то просто.
Основная идея подхода к этой проблеме заключается в исполь-
использовании, на первый взгляд, неожиданной аналогии с гамильтоно-
выми уравнениями динамики материальной точки. В данном слу-
случае это означает, что координата вдоль силовой линии играет роль
времени, а некий «гамильтониан», описывающий силовые поля,
в которых «движется» рассматриваемая материальная точка, тогда
должен быть периодической функцией времени. Теперь становится
понятной сложность задачи. Ведь в классической механике вопрос
об устойчивости движения с такими гамильтонианами сводится
к знаменитой проблеме о так называемых малых резонансных зна-
знаменателях. Формально разложение в ряд Фурье нелинейной перио-
периодической функции содержит бесконечное число членов с потен-
потенциальной возможностью соответственно бесконечного числа резо-
нансов.
Весьма сходная проблема небесной механики — о движении
планет при учете возмущающего резонансного влияния друг на
друга — как известно, приводит к неустойчивости множества воз-
возможных орбит и выделению некоторых устойчивых состояний.
«Резонансные» возмущения, нарушающие тороидальную сим-
симметрию магнитного поля в токамаке, могут создаваться не только
из-за неидеальной геометрии наружных проводников с током, но
и в результате внутренних неоднородностей собственного тока, те-
текущего по плазме. Такие неоднородности могут быть и следствием
мелкомасштабных неустойчивостей плазмы. В предельном случае
достаточно сильных микронеоднородностей поведение силовых ли-
линий магнитного поля может напоминать стохастическое движение
броуновской частицы. Такое стохастическое разрушение структуры
магнитных поверхностей может стать препятствием для длитель-
длительного удержания плазмы в термоядерных ловушках.
Эти качественные рассуждения можно проиллюстрировать на
примере разрушения плоских магнитных поверхностей при наложе-
наложении мелкомасштабного возмущающего поля. Пусть магнитные си-
силовые линии являются прямыми, лежащими в плоскостях yz. На-
Напряженность этого поля примем постоянной и равной Яо. Примем
угол между Но и осью z зависящим от координаты х. Если при
х=0 Hq\\0z, to вблизи х=д простейшей формой такой зависимости
207
может служить Ну—(х/Ь8)Но. Физически для реализации описы-
описываемого поворота силовых линий нужно иметь электрический ток,
текущий вдоль силовых линий по плазме.
Наложим возмущающее магнитное поле Hx = H1cos(k2z-\-kyy).
Тогда «уравнения движения» для силовых линий с учетом возму-
возмущений можно записать в виде dx\dl-= (H± /Яо) cos {kzz-\-kyy)y
dyldl=xlLs, где / — координата вдоль силовой линии Но. Интегри-
Интегрируя второе из этих уравнений, получаем у==хо1 / Ls+{I I Ls) I xdl.
x0
Выберем хо, удовлетворяющее условию kz=—ky(xolL8). Оно
означает, что возмущение находится «в резонансе» с невозмущен-
невозмущенной силовой линией в плоскости х=хОу иначе говоря, фаза возму-
возмущения постоянная вдоль /. При этом условии
B.175)
Теперь немедленно воспользуемся аналогией с уравнением дви-
движения электрона в поле монохроматической электростатической
волны при условии резонанса со/й=у0 (vo— невозмущенная ско-
скорость) :
= ^Ecos(k tvdtY
Правила соответствия очевидны:
j
Тогда ширина зоны захвата ?а — (е(р/тI/2— (eE/km)l/2 электрона
полем волны соответствует ширине Ax = (HJH0) (Lsfky)/2 зоны ре-
резонансного возмущения магнитного поля. Картина возникающего
расщепления магнитных поверхностей на плоскости ху у в точности
совпадает с картиной поведения фазовых траекторий частицы на
О
а
У О
Рис. 2.31. «Резонансное» разрушение магнитных поверхностей: регулярное (а) и
стохастическое (б), приводящее к броуновскому движению силовых линии
208
плоскости v, x (рис. 2.31,а). Аналогом осцилляции захваченных;
электронов на этом рисунке являются так называемые магнит-
магнитные островки.
Для возмущения, представляющего собой суперпозицию отдель-
отдельных гармоник #я= 2 Hlkcos(kzz-\-kyy)t нетрудно провести рас-
суждения, приводящие к установлению аналога квазилинейного
приближения для электронов (см. § 1.16). Условием применимости
такого приближения должно являться перекрытие зон резонансов..
соседних гармоник возмущения. Это квазилинейное уравнение, ко-
которое описывает стохастическое поведение силовых линий магнит-
магнитного поля (см. рис. 2.31,6), легко написать по аналогии с A.192)^
пользуясь введенными выше правилами соответствия:
s
01 ~ дх ( U Н\ "" х дх
В рассматриваемом приближении «диффузия» силовых линий
описывается с помощью соответ'ствующей плотности вероятности?
/я(/,г).
После этого небольшого отступления проанализируем равнове-
равновесие кольцевого плазменного витка, используя уравнения магнитной
гидродинамики. В первом приближении можно считать, что плаз-
плазменный виток имеет в поперечном сечении форму окружности ра-
радиуса а. Вне этого круга р и / обращаются в нуль. Тороидальная?;
поверхность радиуса а представляет собой граничную поверхность,
плазменного витка, «оторванного» от стенок вакуумной камеры,,
внутри которой этот виток находится. Вместе с тем это одна из;
магнитных поверхностей тороидального поля. Другим независимым
параметром, определяющим геометрию системы, является большой
радиус плазменного витка R. В дальнейшем будем предполагать^,
что a<g.R (это практически всегда выполняется в эксперименте).
Заметим, что при малом отношении aj\R плазменный виток по*
свойствам должен приближаться к прямому цилиндру.
Поскольку в задачу входят два главных параметра а и R, от-
отвечающих двум степеням свободы, то нужно найти два условия
равновесия витка — по малому и большому радиусам. Для первого
можно пренебречь влиянием тороидальности и использовать урав-
уравнение равновесия, справедливое для прямого плазменного цилинд-
цилиндра. При этом плазма находится под действием полей Яф и #8,
(в первом приближении поле Я. роли не играет), и поэтому урав-
уравнение равновесия должно представлять собой обобщение соотно-
соотношений B.173) и B.174). Такое обобщение можно получить, считая,
что напряженность обоих полей и давление плазмы зависят только'
от г (т. е. от расстояния между данной точкой и точкой О в попе-
14—74 _
речном сечении). Простые вычисления показывают, что для равно-
равновесия необходимо, чтобы соблюдалось следующее равенство:
*'•' " р+ТГ\18к = Н\(а)[8п + Н\(аI*ъ B.176)
где #*0— усредненное значение H2Q в плазме. Это равенство мож-
ео записать также в следующем виде:
= 1ш1с + (Н\ (а) -7
B.177)
Более детальный анализ приводит к выводу, что соотношение
B.177) справедливо также и для тороидальной системы после вне-
внесения небольшого уточнения, которое относится к величине Нв(а).
При строгом расчете HQ(a) в B.177) должно соответствовать
Л0 на поверхности плазмы при ф=я/2 (рис. 2.32).
Выясним теперь происхождение и величину сил, которые могут
вызвать изменение R. Существуют следующие причины их появ-
появления:
1. Согласно законам электродинамики в кольцевом проводнике
с током должна возникать радиальная сила растяжения, пропор-
пропорциональная /2. При
а/#<С1 она равна
{Pl2c2){dgjd\R)y где
& — коэффициент са-
самоиндукции провод-
проводника.
2. Плазменный ви-
виток должен растяги-
растягиваться также под дей-
действием внутреннего
давления. Растягиваю-
Растягивающее усилие можно
определить, вычислив
работу, совершаемую давлением плазмы при бесконечно малом
изменении R, и разделив эту работу на Ш. Таким путем нетруд-
нетрудно найти, что полное растягивающее усилие равно 2л2а2р.
3. Существует также радиальная пондеромоторная сила, обу-
обусловленная различием в напряженности продольного магнитного
поля вне и внутри плазмы. Механизм возникновения этой силы
можно разъяснить, обратившись к рис. 2.32, на котором изображен
-небольшой отрезок плазменного витка. Кольцевые силовые линии
внутри плазмы стремятся сократиться, вследствие чего возникают
силы F\ и F2, приложенные к торцам отрезка. Их равнодействую-
равнодействующая направлена внутрь. Как нетрудно установить, она равна
Я2а2Д8/3, где Л0 — угловая длина отрезка. Если бы напряженность
поля внутри и снаружи витка была одинакова, то эта сила должна
была бы уравновешиваться боковым давлением силовых линий, по-
поэтому результирующая сил бокового давления должна быть равна
H2(a)a2AQ/8. В общем случае при Н2{а)ФН2 остается разностный
1210
<Рис. 2.32. Происхождение пондеромоторной
силы, растягивающей виток по радиусу
эффект. В расчете на всю длину витка он дает силу радиального?
растяжения, равную
|f ^ 4 . B.178>
Для равновесия плазменного витка необходимо, чтобы сумма трех
радиальных растягивающих усилий компенсировалась силой F.
взаимодействия тока / с поперечным полем Я ,. Следовательно,
условие равновесия по большому радиусу имеет вид
%+[H'()H*\ 2R±- B.179>
Если плазменный виток создается внутри тороидальной камеры,
изготовленной из материала с высокой электропроводностью, то
коэффициент самоиндукции можно принять равным
2>=2яД[1пF/а)+/<], B.180)
где Ь — радиус поперечного сечения камеры; U — внутренняя
индуктивность плазмы на единицу длины витка (при равномерном^
распределении тока по сечению /^1/4, а при сильном скин-эффек-
скин-эффекте /г^О). Используя B.177) и B.180), можно исключить из уравне-
уравнения B.179) член, содержащий Я2 (а)—Я2. В результате условие
равновесия по R принимает вид
В установках, предназначенных для получения плазменных
витков в режимах эксперимента с не очень большой длитель-
длительностью, компенсация растягивающих усилий может происходить
автоматически, так как при радиальном расширении шнура в про-
проводящей оболочке камеры возникают токи Фуко. Они создают по-
поперечную слагающую магнитного поля Я., необходимую для ком-
компенсации растяжения. Как показывает несложный расчет, состав-
составляющая н± пропорциональна / и смещению Н±^B1/с) (в/Л2).
Итак, равновесие должно устанавливаться при определенном
смещении
8 = (b*j2R) [In Ца + 8^/Я2ф (а) + (/, - 1)/2]. B.182>
В экспериментальных установках b<^R9 и поэтому равновесие
устанавливается при относительно небольших смещениях плазмы
относительно центра поперечного сечения камеры.
В режимах с большой длительностью компенсация растяжения
с помощью токов Фуко оказывается недостаточной, и приходится
создавать дополнительные источники поперечных полей, размещая
кольцевые проводники с током вблизи камеры. С помощью таких:
проводников можно управлять положением витка в камере, изме-
изменяя величину б.
14 * 211
§ 2.11. Устойчивость границы плазмы
в магнитном поле
Кроме диффузии существует еще одна причина распада равно-
равновесия плазмы в магнитном поле. Подобно тому как в механике
равновесие тела или материальной точки в поле сил не всегда бы-
бывает устойчивым, плазма, обладающая, выражаясь формально,
бесконечным числом степеней свободы, также может оказаться
неустойчивой относительно малого отклонения от положения рав-
равновесия. Имеет смысл говорить лишь о таких неустойчивостях, ко-
которые разрушают равновесие плазмы за время меньшее, чем время
диффузии.
Допустим, что плазменная конфигурация находится в состоянии
равновесия. Это означает, что все параметры, характеризующие
свойства плазмы (плотность, температура, распределение частиц
по скоростям), должны оставаться постоянными во времени. Будет
ли такое состояние сохраняться длительное время или же под
влиянием случайных флуктуации параметров возникнут быстро на-
нарастающие возмущения, которые вызовут резкое нарушение исход-
исходного равновесия плазмы? Такова в общей постановке задача об
устойчивости.
Поскольку плазма представляет собой механическую систему
с бесконечным числом степеней свободы, то в строгом смысле сло-
слова полный теоретический анализ ее устойчивости по отношению
к разным видам возмущений может оказаться практически неосу-
неосуществимым. Общепринятый подход, сложившийся к настоящему
времени в физике устойчивости плазмы, состоит в последователь-
последовательном рассмотрении различных неустойчивостей, начиная с самых
простых моделей — магнитогидродинамических и постепенно ус-
усложняя их, чтобы ввести в рассмотрение эффекты конечной дисси-
диссипации, многокомпонентность плазмы, кинетические эффекты.
Существенно, что различные механизмы нарушения равновесия
.допускают классификацию по скорости развития связанных с ними
возмущений. Это позволяет ориентировать теорию на последова-
последовательное рассмотрение неустойчивостей и условий их стабилизации,
начиная с тех, которые вызывают наиболее быстрые перемещения
шлазмы и поэтому являются самыми опасными. Наиболее же
-опасными нарушениями равновесия являются те, которые можно
считать магнитогидродинамическими. При возмущениях магнито-
гидродинамического типа макроскопические участки плазмы могут
приобрести скорости порядка тепловой скорости ионов. При таких
возмущениях плазма ведет себя в магнитном поле аналогично
идеально проводящей жидкости (или, точнее говоря, как идеаль-
идеальный проводник, лишенный собственной жесткости).
В связи с большими математическими трудностями обычно вы-
выделяют более простую задачу исследования устойчивости относи-
относительно возмущений малой величины или амплитуды. Метод исполь-
используемого в этом случае теоретического анализа заключается в том,
212
что плазма с заданными равновесными параметрами, такими как
плотность, температура, магнитное поле, подвергается малой вир*
туальной деформации, при которой возникают добавки к равно-
равновесным значениям тех же параметров. Судьба такого состояния
плазмы затем прослеживается с помощью уравнений магнитной
гидродинамики плазмы (если такая модель описания плазмы
оправдана). Предположение о малости амплитуды облегчает ма-
математическое исследование этих уравнений, так как пренебрежение
квадратами и более высокими степенями малых величии дает
уравнения, линейные относительно неизвестных величин р, и, Н.
Но даже такая упрощенная (линейная) теория устойчивости для
произвольных равновесных конфигураций оказывается довольно
сложной.
Часто теории устойчивости плазмы приходится опираться на
методы, разработанные в обычной гидродинамике.
Самый простой, но чрезвычайно важный вид неустойчивости
равновесия плазмы удобнее всего проиллюстрировать на примере
уже рассмотренного выше равновесия с резкой границей в про-
продольном магнитном поле. Как будет видно из дальнейшего рассмо-
рассмотрения, почти все основные типы магнитогидродинамических не-
устойчивостей различных равновесных конфигураций «генетически»
связаны с этим простейшим случаем. Поэтому неустойчивости
плазмы с резкой границей посвящается отдельный параграф.
Итак, пусть плазма занимает полупространство #>0. Магнит-
Магнитное поле внутри плазмы для начала положим равным нулю. При
х<0 имеется магнитное поле, рдаправленное вдоль оси z с давле-
давлением #2о/8я, уравновешивающим давление плазмы. Дополним
рассмотренную здесь модель равновесия введением некоторой
силы тяжести pg", направленной вниз по оси х (естественно, что
речь идет о силе тяжести, компенсированной действием магнитного
поля на плазму). Мы предположили, что магнитное поле при х =
=0 скачком меняется от нуля до Яо, т. е. границу плазмы считаем
бесконечно тонкой. Мы уже знаем, что из-за диффузии магнитно-
магнитного поля внутрь плазмы (и встречной диффузии плазмы) толщина
этой границы должна быть конечной. Поэтому сделанное выше
предположение означает, что мы будем интересоваться только
явлениями с пространственными масштабами (длинами волн не-
неустойчивости, в данном случае), значительно превышающими
толщину переходного слоя б. В частности, будем исследовать де-
деформацию равновесия плазмы (см. рис. 2.31), представляющую
собой волнообразное искривление поверхности раздела вдоль ко-
координаты у с длиной волны Я, значительно превышающей толщи-
толщину переходного слоя.
Само наличие неустойчивости рассматриваемого равновесия
плазмы очевидно из аналогии с известной в обычной гидродинами-
гидродинамике неустойчивостью тяжелой жидкости над легкой в поле тяжести.
Малая деформация поверхности раздела дает возможность «язы-
«языкам» легкой- жидкости всплывать в поле тяжести, «языки» же тя-
213
желой жидкости опускаются. В данном случае плазма играет
роль тяжелой жидкости, магнитное же поле — легкой (в рассма-
рассматриваемом случае можно говорить даже о невесомой жидкости).
Количественное описание неустойчивости такого рода можно
дать с помощью подстановки малых величин <6р, и, 8р в уравнения
магнитной гидродинамики. Так, изменение плотности должно опи-
описываться уравнением
dSp/dt+u grad po+po div u=0, B.183)
в котором пренебрегается членом, содержащим произведение двух
малых величин и и 8р. Задача еще более упростится, если прибли-
приближенно считать плазму несжимаемой жидкостью (такое приближе-
приближение обычно справедливо при рассмотрении движений со скоростя-
скоростями, много меньшими скорости звука). Тогда из уравнения непре-
непрерывности получается условие несжимаемости divu=0, т. е.
дих/дх-]-диу1ду=0. Скорость плазмы можно найти из уравнения
Эйлера podu/d't=—grad 8p, в котором также отброшены члены,
содержащие произведение малых величин. Вместо скорости и
удобно ввести другую переменную — смещение плазмы из положе-
положения равновесия g, определяемую с помощью формулы и=дЦд1.
Условие несжимаемости теперь принимает вид
дЫдх+дЪУ1ду=0, B.184)
а уравнение Эйлера
р0д2ЦдР=—grad 8p. B.185)
Эти уравнения, вообще говоря, нужно дополнить граничными
условиями на границе, разделяющей плазму и магнитное поле, и
уравнениями Максвелла для магнитного поля в области вне
плазмы.
Но в рассматриваемой здесь частной задаче путь к ответу ока-
оказывается более простым. Смещение при волнообразной деформа-
деформации с длиной волны X зависит от у по гармоническому закону
$ (х, у, t) =?(*) exp (iky — iarf), B.186)
где &=2я/А,, а ы — собственное значение частоты, соответствую-
соответствующее волновому числу k. Подставляя искомый вид \ B.186) в урав-
уравнения B.184) и B.185), получаем
?xJdx + Щ = 0; B.187)
— 9о<*>% = — dbp/dx; B.188
B.189)
Здесь учтено, что 8р=8р(х) exp (iky—mt). Из уравнений B.188)
и B.189) можно исключить 8р, если первое из них умножить на
iky второе продифференцировать по ху а затем сложить оба урав-
уравнения:
'тгх + dljdx = 0. B.190>
214
Из B.190) определяем |у и, подставляя его в уравнение BЛ87),
находим
d%/dx2- k4x = 0. B.191)
Общее решение этого уравнения имеет вид суммы двух экспонент
exp (±kyx) с произвольными коэффициентами. Из физических со-
соображений ясно, что по мере удаления от границы х=0 создавае-
создаваемое волнообразное искривление первоначально плоской границы
должно сказываться все слабее. По этой причине из двух возмож-
возможных экспонент следует удерживать лишь затухающую при л:->оо,
т. е.
\=%exp(-kx). B.192)
где §я — постоянный коэффициент.
Изменение давления при смещении плазмы бр можно найти
из следующих соображений. В равновесии действие силы тяжести
внутри плазменного слоя уравновешивается градиентом давления
Pog—dpo(x)/dx=0, B.193)
в результате чего давление плазмы должно зависеть определен-
определенным образом от координаты • я: р=р(х). При смещении на рас*
стояние §х р=ро(#+Ы» и, раскладывая это выражение в ряд, по-
получаем с учетом B.193)
8p^(dp/dx) g*=pogg*. B.194)
Далее подставляя B.194) в уравнение B.189), приходим к ю2?у=
=i&?^Pog". Заменив gx на ?у, с помощью B.190) легко получить
<о2|2/=—kgly. Иначе говоря, дисперсионное уравнение для частоты
<о имеет вид
tf=-kg B.195)
и дает мнимые собственные значения, соответствующие экспонен-
экспоненциально растущим во времени решениям.
Дисперсионное уравнение B.195), если в нем изменить на про-
противоположный знак в правой части, совпадает со знаменитым
уравнением волн тяжести в океане — так называемых «гравита-
«гравитационных» волн. Это совпадение не случайно, ведь в задаче об
устойчивости удержания плазмы магнитным полем мы, образно
выражаясь, поставили жидкость (плазму) «с ног на голову», т. е.
против силы тяжести. Этот пример неустойчивости равновесия
плазмы исторически был исследован раньше всех прочих (не-
(неустойчивость Крускала—Шварцшильда). Теперь, двигаясь шаг за
шагом от простых ко все более сложным видам равновесия, изу-
изучим, как изменяется их устойчивость.
Первым очевидным шагом на пути обобщения модели Круска-
Крускала—Шварцшильда является допущение, что и в объеме (полупро-
(полупространстве), занимаемом плазмой, имеется магнитное поле (более
слабое по условиям равновесия, чем снаружи). Из интуитивных
212
соображений сразу ясно, что само по себе оно не сможет сделать
устойчивой конфигурацию,. в которой тяжелая жидкость лежит
сверху. Теперь сделаем еще один шаг: ограничим объем, занимае-
занимаемый плазмой, в направлении вдоль #0 твердыми стенками, пред-
представляющими собой идеально проводящие пластины, установлен-
установленные перпендикулярно к магнитному полю на расстоянии L друг от
друга (рис. 2.33). Поля внутри и снаружи плазмы параллельны.
Перпендикулярно к ним направлена сила F=pg. Поле внутри
плазмы есть Ни снаружи Яо. Дальнейшее рассмотрение проведем
на уровне наглядных оценок.
Если граница плазмы смещается по вертикали на бг, причем
возмущение имеет длину l^2njk поперек поля.и, естественно, L
вдоль, то давление на наиболее отклонившемся участке границы
1 Плазма
у,
нн
у
у
Рис. 2.3о. Неустойчивость границы
плазмы при наличии идеально
проводящих торцов
Рис. 2.34. Возникновение стабили-
зирующей силы натяжения при
изгибании границы плазмы в маг-
магнитном поле
увеличится на массу столбика плазмы высотой Ьг (архимедова
сила)
6p=pg8z. B.196)
Наиболее важный новый эффект, который связан с введением
идеально проводящих торцов, —это искажение магнитного поля
из-за^вмороженности силовых линий (закрепления концов силовых
линий). При этом нужно учитывать квазиупругую силу в резуль-
результате искажения магнитного поля. Если эта сила больше изменения
давления, то равновесие устойчиво.
При смещении плазмы поле внутри нее «вморожено» и силовая
линия с «закрепленными» концами изгибается, рождая силу натя-
натяжения #2,-/4л#У где R — радиус кривизны силовой линии. Так как
т* (?fi2i> ^РИС* 2'34^' Т0 объемная квазиупругая сила равна
И iSzlznL2. При смещении плазмы магнитное поле снаружи оста-
остается параллельным границе, т. е. также изгибается:
B.197)
Итак, следует учесть дополнительное увеличение силы натяжения.
В итоге получаем, что равновесие устойчиво, если
{Н\ + Н\) /2nL2>gpkl2n. B.198)
216
Поскольку существуют возмущения со сколь угодно малыми Х =
==2я/&, то резкая граница плазмы всегда неустойчива даже при
учете стабилизирующего влияния силы натяжения. Это наводит
на мысль о том, что если граница плазмы (как в любом реальном
случае) слегка размыта, то в формуле B.198) нельзя рассматри-
рассматривать возмущения с длиной волны, меньшей толщины границы (ска-
(скажем, б), т. е. возмущения, удовлетворяющие условию ?6>1. Дей-
Действительно, возникающая при смещении элемента неоднородной
плазмы квазиупругая сила остается такой же, как и в предыду-
предыдущей задаче: H28zj2nL2, то архимедова сила g8p (бр— разность
плотностей смещенного элемента и окружающей плазмы) изме-
изменится. Действительно,
8p=8zdpoldz, B.199)
так что условие устойчивости есть
H2l2nL2>gdpoldz^g9l6, B.200)
т. е. размытая граница плазмы ширины б на самом деле может
быть устойчива.
Постановка задачи с введением гипотетической силы тяжести
g может показаться слишком искусственной. Однако в любом ре-
реальном равновесии плазмы в магнитном поле роль такой эффек-
эффективной силы тяжести играет любая перпендикулярная к магнит-
магнитному полю сила, действие которой не зависит от знака заряда.
Такой силой может быть, во-первых, центробежная сила, связан-
связанная с движением частиц вдоль искривленной силовой линии.
Очевидно, при этом следует заменить g-яа v*l{/R, где R— ради-
радиус кривизны силовой линии, а я2 — средний; квадрат скорости про-
продольного движения ионов (электронов). Во-вторых, эта сила мо-
может быть связана с дрейфом в неоднородном магнитном поле (см.
§ 2.1). Если эта неоднородность вызвана кривизной силовых ли-
линий, то замена производится следующим образом: g-+v2J2R.
Складывая оба эффекта, получаем
n ±|| +Р±)/Р. B.201)
Отсюда видно, что выпуклая граница плазмы должна быть не-
неустойчива. Для стабилизации силой натяжения силовых линий не-
необходимо, как это видно из B.200) и B.201), чтобы ^
Я2, > DL2P/6) (?„ +?L/2)/& B.202)
где L — эффективная длина силовой линии; R — радиус ее кривиз-
кривизны; б — толщина размытой границы.
В заключение этого параграфа следует заметить, что если плаз-
плазма движется ускоренно, то аналогом g является ускорение гра-
границы а. Инкремент нарастания возмущений в этом случае есть
ImcD'—' У a/I. Такого типа неустойчивости наблюдаются в экспери-
217
ментах по «инерциальному» методу удержания в термоядерном
синтезе. Сюда относятся методы быстрого сжатия плазмы нара-
нарастающим аксиальным магнитным полем (так называемый «0-
пинч»), быстро сжимающаяся под действием мощного лазерного
излучения капля плотной плазмы.
§ 2.12. Желобковая неустойчивость плазмы
и энергетический принцип устойчивости
в магнитной гидродинамике
Тенденцию плазмы обнаруживать неустойчивость вблизи вы-
выпуклых участков границы можно интерпретировать как следствие
диамагнетизма плазмы. Будучи диамагнетиком, плазма стремится
распространяться в сторону более слабого магнитного поля. Имен-
Именно поэтому если поверхность плазмы лежит в области, где напря-
напряженность магнитного поля убывает от границы плазмы наружу, то
положение границы может оказаться неустойчивым.*
Для замкнутых магнитных ловушек справедлива следующая
теорема. Нельзя создать такое магнитное поле, напряженность ко-
которого возрастает наружу от гра-
границы плазмы вблизи каждой точ-
точки поверхности тороидальной
плазменной конфигурации. Нор-
Нормальная к поверхности плазмы
компонента grad|//| меняет знак
вдоль границы.
Простой иллюстрацией может
служить система токамак. В этом
случае Я убывает от границы
плазмы наружу на внешней сторо-
стороне тороидального плазменного
витка и возрастает на внутренней
стороне витка. Указанное свойство замкнутых ловушек, естественно,
вызывает сомнение в возможности устойчивого удержания плазмы
в таких системах. Появляется следующий вопрос: не может ли
плазма отдельными «языками» вытекать в область более слабого
поля? Ответ на этот вопрос зависит от того, имеем ли мы дело с
плазмой высокого давления, для которой параметр $ = 8пр/Н2—1,
или же с плазмой низкого давления, для которой {$<Cl. В этих
двух крайних случаях условия устойчивости совершенно различны.
При р^1 на поверхности плазмы могут образовываться и раз-
развиваться локальные возмущения типа «языков» (рис. 2.35). Вслед-
Вследствие вмороженности поля в плазму образование отдельного языка
приводит к искривлению силовых линий с увеличением магнитной
энергии. Соответствующая работа производится расширяющейся
плазмой благодаря ее тепловой энергии. Если «язык» встречает
более слабое поле, то он будет распространяться все дальше, ц это
означает неустойчивость границы плазмы. В данном случае не-
.218
Рис. 2.35. Образование «языка» на
поверхности плазмы
устойчивость имеет локальный характер, т. е. она зависит от мест»
ной геометрии поля.
Как уже говорилось, в замкнутых ловушках на отдельных уча-
участках поверхности плазменного витка геометрия поля благоприят-
благоприятствует развитию «языков» (это имеет место там, где\ поверхность
плазмы двояковыпуклая). Поэтому плазма с р—1 в тдких систе-
системах должна быть более неустойчивой. Об этом не следует забы-
забывать при обсуждении перспектив использования высокотемпера-
высокотемпературной плазмы.
Созершенно иная ситуация складывается в том случае, если
давление плазмы исчезающе мало по сравнению с магнитным дав-
давлением. Заметим, что это условие
фактически соблюдалось во всех ис-
исследованиях, выполненных до сих пор
на установках типа токамак. При
C<Cl возмущения плазмы не могут
вызвать заметных искажений формы
силовых линий. Следовательно, ло-
локальные деформации типа «языков» Рис< 2Ж Желобковая дефор-
автоматически стабилизируются, и все мация
возмущения внутри плазмы или на ее
границе могут носить только характер перестановки целых систем
трубок.
Плазма, заполняющая магнитную трубку, образованную очень
тонким пучком силовых линий, стремится расшириться и поэтому
будет перемещаться в ту сторону, где объем трубки увеличивает-
увеличивается. Этот объем &V= § \6Sdl> где 65 — площадь поперечного сечения
трубки и dl — элемент длины силовой линии. Вследствие неизмен-
неизменности магнитного потока 6Ф по длине трубки можно написать
6V= I bSHdljH=\ №dl/H=№J dljH. B.203)
Вмороженность силовых линий означает, что при всех переме-
перемещениях данной трубки, заполненной плазмой низкого давления, 6Ф
остается постоянным. Следовательно, объем трубки изменяется
пропорционально \dl\H. Поскольку плазма, как и всякий другой
газ, имеет естественную тенденцию к увеличению объема, то в про-
процессе перемещения трубки \dl\H играет роль, аналогичную по-
потенциальной энергии.
Описанные здесь перемещения отдельных элементов плазмы,
при которых силовые трубки меняются местами, замещая друг
друга, называются перестановочными, или конвектив-
конвективными, деформациями. Появление таких деформаций на границе
плазмы с внешним полем приводит к тому, что поверхность плаз-
плазмы приобретает «желобковую» структуру (рис. 2.36), ориентиро-
ориентированную вдоль силовых линий. Поэтому иногда говорят также о де-
деформациях желобкового типа — самых опасных врагах равновес-
равновесных конфигураций.
Критерий устойчивости по отношению к таким деформациям до*
219
пускает простую формулировку, если воспользоваться введенным
выше понятием о «потенциальной энергии» U.
Граница плазмы устойчива в том случае, если при выходе маг-
магнитной трубки с плазмой изнутри на поверхность с образованием
выступа происходит возрастание U, т. е. имеет место условие
б^ий/ЖО. B.204)
Вариация интеграла берется между двумя бесконечно близкими
силовыми линиями по нормали к границе плазмы. При другом зна-
знаке неравенство B.204) означало бы неустойчивость границы плаз-
плазменной конфигурации.
Полученный критерий устойчивости имеет достаточно ясный
физический смысл. Для устойчивости необходимо и достаточно,
чтобы напряженность поля, усредненная вдоль силовой линии, воз-
возрастала от границы плазмы на-
наружу. Это частная форма извест*
; ного принципа «минимума Я».
Заметим, что согласно B.203)
j dl/H=-6V/6O. Поэтому \dl\H
можно назвать «удельным объе-
объемом» магнитной трубки.
Для того чтобы установить
область применимости критерия
устойчивости B.204), надоснача-
Рис. 2.37. Иллюстрация связи потен- ла устранить неопределенность
циальной энергии и поперечного тока в выражении для U, которая за-
заключается в том, что не указаны
пределы интегрирования по длине силовой линии. Неопределен-
Неопределенность исчезает в том случае, когда силовые линии на поверхности
плазмы замкнуты, так как очевидно, что при этом интеграл §,dl/H
должен распространяться на всю длину силовой линии. Для уточ-
уточнения можно ввести следующее определение потенциальной энер-
энергии U магнитной поверхности с замкнутыми силовыми линиями:
U=—{llN)§dllH. B.205)
Здесь N — число обходов вдоль магнитной системы, после которых
силовая линия замыкается на себя.
Потенциальная энергия JJ является однозначной характеристи-
характеристикой поверхности. Для того чтобы убедиться в этом, рассмотрим
две близкие магнитные поверхности и определим ток, протекаю-
протекающий между ними через перегородку, проведенную вдоль одной из
магнитных силовых линий (рис. 2-37). Суммарный ток dl> прохо-
проходящий через перегородку, очевидно, не должен зависеть от выбора
силовой линии:
dl=§ j±dndl = const. B.206)
Здесь dn — элемент нормали к магнитной поверхности и ]± —'ком-
—'компонента плотности тока, перпендикулярная к Я. Интеграл берется
220
вдоль силовой линии. Согласно основному уравнению баланса сшв
в равновесии
!± = (c!H)(dp[dn). B.207>
Из B.206) и B.207) следует, что
cdp <j> dljH = const. B.208)*
Таким образом, поверхность p=const должна совпадать с по-
поверхностями, на которых эффективная «потенциальная энергия» U
имеет одинаковое значение.
То обстоятельство, что разобранные неустойчивости равновес-
равновесных конфигураций плазмы в магнитном поле оказалось возмож-
возможным трактовать с помощью энергетических соображений, отражает'
важную особенность магнитогидродинамической теории устойчиво-
устойчивости. На более рафинированном математическом языке магнитогид-
магнитогидродинамической теории устойчивости можно сформулировать даже*
общий, так называемый энергетический принцип, заключающийся*
в следующем. Введем бесконечно малое смещение |(г, t) элемента-
объема плазмы из положения равновесия, при этом u=d\jdt. Ока-
Оказывается, что линеаризованные уравнения общей теории устойчиво-
устойчивости идеально проводящей плазмы можно привести к одному век-
векторному уравнению
д%Цд? = — КЪ, B.209>
в котором К — некоторый дифференциальный оператор, действую-
действующий на g как на функцию координат. Говоря формально, уравне-
уравнение в виде B.209) аналогично уравнению, описывающему колеба-
колебания произвольной неоднородной упругой среды, где К играет ролы
соответствующего обобщенного коэффициента упругости. Несмотря
на кажущуюся громоздкость, вывод энергетического принципа не-
невызывает затруднений. Прежде всего в линеаризованных уравне-
уравнениях магнитной гидродинамики следует перейти к переменной g;
(смещение) вместо u (=dg/d/). Затем следует исключить возмуще-
возмущения всех остальных величин, выразив их через g.
Выберем .в качестве основного уравнения B.60). Левая часть
этого уравнения после линеаризации примет вид pog. Линеаризо-
Линеаризованную правую часть
выразим через g. Так, первое слагаемое претерпевает следующие
преобразования; 8p=(dpldp)8p, и с учетом уравнения непрерыв-
непрерывности
=div pol=po div g+g grad p0.
Окончательно получим бр==—YPdivg+ggrad/?. Таким же образом
с помощью уравнения можно выразить 6Н через смещение g. В ре-
221
зультате уравнение, линеаризованное и выраженное через |, при-
принимает вид
Pi =?{!}, B.210)
где
-L UXrot [IXH]] ^г [Н X rot rot [1XH]]). B.210a)
Здесь р — давление; р — плотность; Н — напряженность магнитно-
магнитного поля; j — плотность тока (все величины в равновесии). Уравне-
Уравнение B.210) математически полностью эквивалентно уравнениям,
описывающим малые колебания упругой среды. Роль обобщенного
коэффициента упругости принадлежит оператору %=Р/р. По ана-
аналогии с механикой упругих сред естественно ввести в рассмотрение
потенциальную энергию малых колебаний bW=-^- I %K%dV-
Явное выражение для 8W нетрудно получить с помощью
B.210а). Если 6W>0 для всех g?=0, то отклонения от положения
равновесия не могут нарастать во времени и, следовательно, плаз-
плазма магнитогидродинамически устойчива. В противном случае, когда
•bW может принимать отрицательные значения, коэффициент упру-
упругости К отрицателен по отношению к некоторым деформациям, и,
следовательно, рассматриваемая система неустойчива. Границу
между устойчивыми и неустойчивыми конфигурациями образуют
такие состояния, в которых исчезает упругость по отношению к од-
одному определенному типу смещений. В этом случае наряду с исход-
исходным равновесным состоянием существуют близкие к нему равно-
равновесные состояния, соответствующие смещению | в направлении
упругости, равной нулю. Таким образом, для нахождения границы
устойчивости достаточно определить, при каких условиях появля-
появляются близкие равновесные состояния, т. е. достаточно исследовать
уравнение Р1=0.
Равновесные состояния, для которых можно найти возмущения,
соответствующие нулевым собственным частотам, по сути дела,
представляют собой безразличные равновесия. Такова в кратких
•чертах общая программа магнитогидродинамической тебрии устой-
устойчивости. В выражении для потенциальной энергии 6W два слагае-
слагаемых [см. две фигурные скобки в формуле B.210а)]. Первое опи-
описывает изменение внутренней тепловой энергии плазмы, второе —
¦изменение магнитной энергии при перестройке конфигурации.
Неустойчивости желобкового типа связаны с высвобождением
внутренней энергии плазмы (при расширении). Они соответствуют
деформациям равновесной конфигурации, имеющим вид желобков,
вытянутых вдоль силовых линий магнитного поля. При таких сме-
смещениях силовые линии магнитного поля не «растягиваются» и не
-«изгибаются», на что пришлось бы затрачивать энергию [это вто-
второе слагаемое в B.210а)].
222
Так как смещения в желобковых возмущениях поперечны си-
силовым линиям магнитного поля (§JLH), то можно сделать еще
одно важное обобщение: энергетический принцип, формально выве-
выведенный из уравнений магнитной гидродинамики, имеет разумный
смысл и для разреженной плазмы в дрейфовом приближении, так
как для наиболее опасных возмущений (|JLH) движение происхо-
происходит поперек силовых линий, когда снова применима своеобразная
гидродинамика, бесстолкновительная и с неизотропным давлением..
Не следует думать, что магнитная часть потенциальной энергии
всегда играет стабилизирующую роль. Если при выборе равновес-
равновесной конфигурации проявить беспечность, то именно высвобождение
избытка энергии магнитного поля при перестройке конфигурации:
явится источником наиболее бурных проявлений магнитогидроди-
намической неустойчивости. Тенденция к сокращению длины сило-
силовых линий и приводит к неустойчивости. Примером может служить
неустойчивость пинча. Иногда высвобождаемую при этом энергию»
называют энергией пинчевания.
§ 2.13. Стабилизация магнитогидродинамических
неустойчивостей в термоядерных ловушках
Устойчивость плазмы при пинч-эффекте являлась предметом
многочисленных исследований. Самые первые фотографии плаз-
плазменного шнура, сжатого протекающим по нему собственным токому
показали, что он неустойчив относительно деформаций типа пере-
перетяжек («шеек») и изгибов («змеек»).
Из общих соображений неустойчивость пинча с продольным то-
током, текущим по поверхности, очевидна по той причине, что всюду
от границы плазмы наружу магнитное поле падает.
Для стабилизации такого пинча еще в середине 50-х годов бы-
было предложено использовать сильное магнитное поле, направленное
вдоль оси пинча. Действительно, в этом случае при деформациях
пинча затрачивается работа на увеличение энергии этого магнит-
магнитного поля, что и вызывает стабилизирующий эффект. Этот эффект
резче всего проявляется для возмущений с большим волновым век-
вектором, т. е. с малой длиной волны вдоль оси пинча. Напротив,,
в длинноволновых возмущениях изменения продольного магнитного-
поля малы, и относительно возмущений с длиной волны, значи-
значительно большей радиуса пинча, неустойчивость остается.
Условие устойчивости пинча относительно «змеек» и «шеек»
можно получить наглядно следующим образом. Рассмотрим сна-
сначала змейкообразные возмущения пинча (рис. 2.38). Предположим,
что внутри пинча радиуса а имеется вмороженное продольное по-
поле Hit а снаружи — азимутальное поле тока, текущего по его по-
поверхности, Н. Если пинч изгибается (длина изгиба А,), то силовые
линии азимутального поля сгущаются с внутренней стороны и раз-
разрежаются снаружи. Поэтому на внутреннюю часть пинча (обра-
(обращенную в сторону центра кривизны) действует большее магнитное
22а
'Рис. 2.38. Неустойчивость пинча
относительно деформаций типа
«змеек»
давление. Кроме того, из-за искрив-
ления^ силовых линий вмороженно-
вмороженного продольного поля возникает си-
сила натяжения, действующая в об-
обратном направлении.
Силу, действующую со стороны
азимутального поля на плазму,
можно подсчитать следующим об-
образом. Выделим вокруг пинча ци-
цилиндрический объем радиуса А,,
как бы срезанный плоскостями,
проходящими через центр кривиз-
кривизны. Так как силовые линии азиму-
азимутального поля лежат в этих пло-
плоскостях, то полная сила, действую-
действующая на единицу длины пинча в направлении смещения, склады-
складывается из соответствующей составляющей магнитного давления на
чгорцах:
2а f (tf 2/8rc) 2%rdr
а
'{где угол наклона a=k/2R, a R— радиус кривизны) и давления
та боковые поверхности, которым можно пренебречь. Вблизи от
искривленного пинча поле Н можно описывать так же, как и для
^бесконечно длинного проводника с током H=Hoa/r. Ho=H(a) —
поле на поверхности пинча. Однако на расстояниях г^Х эффект
возмущения исчезает и интеграл следует «обрезать» при г-—•%. По-
Поэтому действующая на единицу длины шнура сила, вызванная
шозмущением поля, при искривлении есть
(l/R) J (#78*) 2%rdr = {Н\!Щ In (Я/а) а\
о
а2,
Сила натяжения, как обычно, равна
— (H2il4nR) ш2=— (H
так что полная сила
6F=(a2/4#) [#20ln(Va)— #V|-
Отсюда возникает известное условие устойчивости
H2ilH%>\nXla. B.211)
Так как из условия равновесия p-\-H2i/8n=H2ol8n следует, что
Л2г<Н2о, то ясно, что пинч нельзя полностью стабилизировать
сильным внутренним продольным полем относительно длинновол-
длинноволновых возмущений.
Если продольное магнитное поле имеется и внутри, и вне шну-
шнура с аксиальным током, то полное поле оказывается винтовым.
В таком поле шнур, искривившись по винтовой силовой линии,
сможет пролезть между силовыми линиями поля, не искривляя их.,
224
Такая неустойчивость имеет место, если возмущение поверхности
шнура винтовое и если шаг этого винта А, совпадает с шагом си-
силовой линии на поверхности пинча 2na(Hz/H9) или оказывается
больше него. Следовательно, пинч устойчив относительно винтовых
возмущений с длиной волны
Я<2шЯ2/Яф (критерий Крускала—Шафранова). B.212)
Таким образом, в обоих случаях существует максимальная дли-
длина волны возмущения, еще стабилизируемого магнитным полем.
Для системы типа токамак при возмущениях с длиной волны, рав-
равной периметру тора, K=2nR критерий устойчивости Крускала —
Шафранова имеет вид R<aHzfH^ т. е. плазма тем более устой-
устойчива, чем больше безразмерный параметр q=(a/R) (Hz\H ) (так
называемый запас устойчивости).
Условие устойчивости относительно деформаций типа «шеек»
(см. рис. 2.27) можно найти следующим образом. Пусть радиус
шнура изменился на да. Тогда из-за сохранения магнитного пото-
потока поле внутри шнура меняется на 6#=—Нг26а/а. Кроме того,
азимутальное поле вне шнура Н=21/са> где / — полный ток, поэто-
поэтому 6#=—Нуба/а. Полное изменение разности магнитных, давле-
давлений изнутри и снаружи пинча
8pm=—(H2il4n) Bба/а) + (Я2/4я) (ба/а),
так что условие устойчивости имеет вид
#2;>#2/2. B.213)
Итак, достаточно сильное продольное поле подавляет «шейки»,
но не может стабилизировать пинч относительно длинноволновых
«змеек». Дополнительные меры по стабилизации — окружение
плазменного шнура проводящей коаксиальной оболочкой. При сме-
смещениях шнура в оболочке должны наводиться индукционные токи,
взаимодействие с которыми стремится вернуть шнур в исходное
положение.
Сочетание этих способов стабилизации в свое время широко
применялось для создания высокотемпературной плазмы.
Стабилизация по Крускалу — Шафранову представляет собой
использование квазиупругой силы натяжения достаточно сильного
магнитного поля. Критерии, которые были получены выше для
идеализированной геометрии пинча с поверхностным током, конеч-
конечно, нельзя применять для реальных равновесий в буквальном
смысле. Ток всегда распределен каким-либо образом по сечению
плазменного шнура. Поэтому внутри плазмы сосуществуют обе
компоненты поля: и аксиальная, и азимутальная, т. е. суммарное
магнитное поле является винтовым. В винтовом поле невозможна
обычная перестановочная желобковая неустойчивость, так как из-
за того, что шаг силовой линии на каждой магнитной поверхности
различен, трубки «перепутываются» при радиальном смещении и
15-74 225
возникает та же самая квазиупругая сила натяжения. Чем сильнее
меняется шаг винта силовой линии в равновесии при переходе от
одной магнитной поверхности к другой, иначе говоря, чем сильнее
перекрещенность силовых линий (так называемый шир), тем более
устойчивым должно быть равновесие.
Наличие шира в магнитной системе с вращательным преобра-
преобразованием поля означает, что уюл поворота силовых линий Q яв-
является функцией от координаты г, т. е. изменяется при переходе
от магнитной оси к периферии плазменного витка. В литературе
по теории устойчивости в качестве меры шира чаще всего прини-
принимается величина
6s=(r2/L)<ffi/dr), B.214)
где L — длина плазменного витка (для круговых систем L—2nR).
В настоящее время очень распространена точка зрения, согласно
которой шир можно рассматривать как некоторое универсальное
средство борьбы с широким классом плазменных неустойчивостей.
Поэтому прежде чем специально останавливаться на выяснении
роли шира в подавлении неустойчивостей магнитогидродинамиче-
ского типа, сделаем отступление в сторону, чтобы разъяснить
происхождение формулы B.214).
Элементарное возмущение, возникшее в плазменном шнуре,
можно представить в виде следующей функции координат:
Ч^ехр [i (пф—kzz) ],
где z — координата, отсчитываемая вдоль плазменного шнура;
kz — компонента волнового вектора в этом направлении; п — целое
число. Для простоты здесь используется модель «выпрямленного»
витка, что допустимо при слабой тороидальности системы (а<^Я).
Рассмотрим, как это возмущение распространяется вдоль сило-
силовой линии. Обозначим элементарный отрезок длины силовой ли-
линии dl:
Дифференцирование функции *F по / дает
r)H^-k2Hz] V.
Здесь Aj—волновой вектор вдоль силовой линии. Возмущение по-
постоянно вдоль силовой линии, т. е. k{] =0, если
Hg) = kf(HjH.). B.215)
В этом выражении ?ф = я/г— компонента волнового вектора
по азимуту ф.
Вводя длину плазменного шнура L, можно записать условие
B.215) в следующей форме: kzL=nQ. Поскольку kz=2nmlL, где
т — целое число, то указанное условие удовлетворяется только для
замкнутых силовых линий, у которых Q=2nmln.
226
Выясним, как будет изменяться фаза функции W при переходе
от силовой линии, лежащей на поверхности с радиусом г0, для
которой условие B.215) выполнено, к бесконечно близкой силовой
линии, лежащей на поверхности с радиусом г (как и ранее, будем
рассматривать область лишь вблизи магнитной оси). Разлагая
dVdl по малому параметру Ьг=г—г0, находим
—й1^** B'216>
где 0S определяется формулой B.214). Для магнитных систем ти-
типа токамак в этОхМ выражении можно положить Hz/H—l.
Из B.216) следует, что при заданных значениях волнового век-
вектора k и относительного радиального смещения бг/г0 фаза воз-*
мущения на силовой линии, равная k{{ /, будет тем ближе к посто*
янной величине, чем меньше величина шира 6S. Смысл этого
результата нетрудно уяснить. Если речь идет о маг-
нитогидродинамических возмущениях в плазме
низкого давления, то сохранение постоянства фа-
фазы при переходе от одной силовой линии к другой
означает наименьшее возмущение магнитного по-
поля. Следовательно, при значениях '9S, очень близ-
близких к нулю в системе без магнитной ямы, возму-
возмущения перестановочного типа могут свободно рас-
распространяться по радиусу, вызывая неустойчивость
плазмы.
При увеличении д8 такие деформации будут
стабилизироваться, так как с перемещением плаз-
плазмы в направлении г в этом случае будет связано
сильное искажение поля. Если 6s^0, то возмуще-
возмущение, которое на некоторой магнитной поверхности
имело форму выступа, совпадающего с силовой
линией, должно при переходе к близкой магнитной
поверхности изогнуться так, чтобы образовался
плазменный «язык» сложной формы. Его боковые
края как бы закреплены вдоль внутренней силовой лобковая де-
линии, а наиболее далеко продвинувшийся по г формация при
гребень расположен параллельно внешней силовой наличии шира
линии (рис. 2.39). Дополнительную магнитную
энергию, которая соответствует такому искажению формы поля
(напомним, что силовые линии вморожены в плазму), можно по-
получить только в результате работы сил давления плазмы. Условие
стабилизации заключается в том, что накладывается ограничение
на максимальную величину р или на величину градиента давле-
давления плазмы.
Проведем упрощенную оценку конкуренции двух сил, действу-
действующих на смещенный элемент плазмы. Дестабилизирующая сила
p/Rs связана с кривизной силовой линии магнитного поля, где
J?s — радиус кривизны для прямолинейного плазменного столба,
15*
Rs=rH2lH\. Возмущение давления при смещении ? равно
^ \
1 \
Hz
z
Итак, сила, стремящаяся вывести плазму из равновесия, F{ =
=-(llRa)(dpldr)t
Стабилизирующую силу натяжения (Ну)Н/4ъ можно оценить сле-
следующим образом: Fg ~ #0& t| 6#,/Фя, где А|( определяется выраже-
выражением B.216); ЬН' можно найти, рассматривая искривление силовой
линии при выпячивании «языка» на расстояние ?: 8#^ ~ #0S&,,.
Минимальный характерный размер 6г, занимаемый областью,
в которой происходит возмущение, естественно считать имеющим
тот же порядок величины, что и длина волны возмущения по ази-
азимуту (по ф), т. е. k^8r^l. В итоге из условия /r2>i7i получаем
известный критерий Сайдэма стабилизации локальных возмущений
широм:
- (8*/Н\) dpjdr< К (Н*/Н\) A /г) 8V B.217)
Специально введенный здесь численный множитель К<^\ подчер-
подчеркивает, что использованная оценка не
может претендовать на большую точ-
точность. Правильное значение должна
дать строгая теория.
Количественный вывод критерия
Сайдема представляется весьма по-
поучительным. Мы ограничимся мини-
минимальными математическими выклад-
выкладками, предельно упростив задачу, но
стараясь сохранить основные черты
Рис. 2.40. Стабшшза- стабилизации желобковой неустойчи-
^ойчГостГГпомо: вос™ с помощью шира. Выберем пло-
щью шира скую геометрию, напоминающую уже
рассмотренную ранее в задаче Крус-
кала — Шварцшильда об устойчи-
устойчивости размытого (без резкой границы) равновесия плазмы под
действием силы тяжести, уравновешиваемой давлением магнитного
поля. В эту задачу необходимо ввести шир, т. е. поворот силовых
линий равновесного магнитного поля. На рис. 2.40 изображена
именно такое равновесие. С ростом х, по мере продвижения в глубь
плазмы, магнитное поле, при х—0 для определенности направлен-
направленное строго по оси z (перпендикулярно к плоскости рисунка), при-
приобретает компоненту по оси у. Будем считать, что вблизи плоскос-
плоскости х=0 эта компонента магнитного поля ведет себя как Hy—HxjLs.
Для установления соответствия между плоской задачей и цилинд-
цилиндрической геометрией, для которой дано определение шира 0s, за-
заметим, что Ну соответствует Н .
Приращение Яф за счет изменения угла поворота dQ/dr имеет
вид dHy=z(rfL)(dh/dr)Hdr. Сравнивая его с приращением Ну при
изменении х, получаем б5/г-
228
Нетрудно видеть, что возмущение такого равновесия, выбран*
ное, как и в старой задаче Крускала — Шварцшильда, в виде
ехр{—Ш-{-Игу}, имеет при хфЬ компоненту волнового вектора
вдоль силовой линии k{{ —kQx. По этой причине и возникает ста*»
билизирующая сила натяжения силовых линий, учтенная ранее
в упрощенном рассмотрении. Однако строгое рассмотрение должно
учитывать также и возмущение магнитного давления
б(H2z+H2y) /8n^(Hz6Hz+Hy8Hy) /4я. B.218)
При дальнейшем анализе воспользуемся методом отыскания
границы устойчивости, основанным на поиске решения, соответст-
соответствующего условию со2=0, т. е. случаюлулевой упругости (см. § 2.12).
Компонента уравнения Эйлера по оси у превращается в простое
условие баланса сил ikdHzHz—H'ydHx (газокинетическое давление
плазмы считаем пренебрежимо малым, как и в большинстве задач
о желобковой неустойчивости плазмы). С помощью этого уравне-
уравнения возмущение магнитного давления можно переписать в следую-
следующем виде:
Основная компонента уравнения Эйлера — по оси х (в направлен
нии действия силы тяжести) — теперь принимает вид
^ l = 0. B.2.9)
Воспользуемся еще уравнениями
B.220)
B.221)
B.222)
полученными из условия вмороженности магнитного поля dH/dt =
=rot[uXH], уравнения непрерывности и условия div Н=0 соот-
соответственно. Исключая все переменные, кроме 6НХ, нетрудно полу-*
чить одно уравнение для возмущения магнитного поля:
8H"x—k26Hx— Dnp'g/H2y) 8Нх=0. B.223)
Теперь видно, в чем заключался дефект простого вывода, осно*
ванного на балансе сил: не был учтен член со второй производной
(обязанный своим происхождением возмущенному давлению маг*
нитного поля).
Обращает на себя внимание изящная аналогия между исследуе*
мым уравнением и уравнением Шредингера с потенциальной ямой
\\х2 для известной задачи нерелятивистской квантовой механики
о «падении» частицы на притягивающий центр. Не удивительно,
что ход рассуждений, который будет сейчас проведен, очень напо-
напоминает рассуждения, содержащиеся практически в любом курсе
квантовой механики.
229
В окрестности сингулярности х=0 (именно в этой точке ?ц=0)
будем искать решение уравнения B.223) в виде хп, пренебрегая
членом &28#х. Подставляя искомое решение в усеченное уравне-
уравнение
surf 4тср'? *lj п /О 00А\
ОП х -г™—Oflx^=\J, \L*LLlt)
Рис. 2.41. Баллонная мода неустойчивости
получаем выражение для показателя л= 1/2 ± ]/l/4-j-a , где
а=4яр'gL2slH2. Нетрудно увидеть, что характер решения меняется
при условии а< —1/4. В этом случае решение можно представить
в виде •—х =ехр (ivln*), где v= V \а\—1/4. Это значит, что
вблизи х=0 решение имеет бесконечно много нулей. Поэтому ре-
решения, затухающие на
бесконечности, можно
сшить с любым решением
вблизи х=0.
При v^<0 этого сде-
сделать нельзя. Поэтому
критическое значение
|<х| есть 1/4. Это означа-
означает, что в формуле B.217)
численный коэффициент нужно принять равным 1/4. Отметим,
кстати, что в упомянутой квантовомеханической задаче о «паде-
«падении» на центр условием захвата частицы потенциальной ямой
также является а^—1/4.
У неустойчивости сайдэмовского типа есть аналог и для равно-
равновесных систем совсем другого вида, в частности не имеющих «ши-
ра», но обладающих свойствами магнитной потенциальной ямы
«в среднем», как говорят, имеющих «средний минимум Я». Приме-
Примером может служить магнитная ловушка, магнитное поле которой
обладает минимумом J dl/H.
Однако, как уже говорилось, трудно добиться, чтобы магнитное
поле возрастало наружу во всех направлениях. Поэтому на ло-
локальных участках поверхности, где магнитное поле убывает в сто-
сторону от плазмы, возможно возникновение локальных деформаций —
так называемых «баллонных» мод (рис. 2.41). Эта неустойчивость,
как и мода Сайдэма, вызывается конечной величиной р и стабили-
стабилизируется, если сила натяжения силовых линий достаточно велика.
Как уже говорилось, кроме неустойчивостей, причиной которых
является стремление плазмы к расширению в направлении, пер-
перпендикулярном к магнитному полю, может существовать особый
тип неустойчивости, свойственный самой магнитной конфигурации.
Эта неустойчивость обусловлена тем, что вдоль силовых линий
винтового магнитного поля действуют максвелловские-натяжения
(неустойчивость пинчевания). Силовые линии стремятся сократить-
сократиться путем деформации, при которой они выпрямляются, а плазмен-
плазменный шнур винтообразно извивается. Если малые винтовые дефор*
230
мации описываются обычным выражением я|>—exp[i(#cp—kz)], то
п называется номером моды. При я=1 возмущения соответствуют
простому однозаходному винту, при п=2 — двухзаходному и т. д.
Стабильность плазменного витка по отношению к винтовым дефор-
деформациям зависит от коэффициента запаса q.
Согласно критерию Крускала — Шафранова при q>\ стабили-
стабилизируется наиболее опасная первая мода винтовой деформации.
Если q>n, то обеспечена устойчивость по отношению ко всем вин-
винтовым модам вплоть до /г-й. Детальный анализ показывает, что
при очень больших q (четыре и более) должны быть стабилизиро-
стабилизированы все винтовые возмущения. Именно поэтому величина q и бы-
была названа коэффициентом запаса но винтовой неустойчивости.
Подведем итог описанию магнитогидродинамической неустой-
неустойчивости идеальной плазмы с вмороженными силовыми линиями.
Все три рассмотренных выше типа возмущений: желобковые или
перестановочные деформации, баллонная мода и винтовое извива-
ние плазменного шнура с продольным током — при невыполнении
условий устойчивости развиваются очень быстро и практически
полностью уничтожают эффект магнитной термоизоляции. Инкре-
Инкремент нарастания для перестановочных возмущений порядка Vija
(где Vi — тепловая скорость ионов), а для винтовых возмущений
порядка vAjaf т. е. неустойчивость развивается, как говорят, за
«инерционные» времена.
Всякая попытка нагревать магнитогидродинамически неустой-
неустойчивую плазму представляется совершенно бесполезным делом. Од-
Однако, как мы видели, все указанные виды неустойчивости в плазме
низкого давления сравнительно легко подавляются при использо-
использовании магнитных систем с большим отношением H^jH^ удов-
удовлетворяющих условию минимума В или же обладающих широм.
§ 2.14. Магнитогидродинамическая неустойчивость равновесия
при конечной электропроводности
До сих пор, говоря о магнитогидродинамической картине устой-
устойчивости плазмы, мы исходили из представления об идеальной вмо-
роженности магнитного поля в плазму. Реальная плазма из-за на-
наличия сил трения между электронами и ионами обладает конечной
электропроводностью. Во многих случаях, когда идеальная беско-
бесконечно проводящая плазма оказывается устойчивой, добавление да-
даже небольшого электрического сопротивления «размораживает»
силовые линии, и они перестают увлекаться плазмой. В результате
может появиться новый класс так называемых диссипативных не-
устойчивостей, как правило, имеющих характер более медленного
тихого просачивания плазмы в магнитном поле. Это просачивание
тем медленнее, чем меньше электрическое сопротивление. Среди
неустойчивостей, связанных с конечной проводимостью плазмы,
условно выделим следующие виды: «гравитационную» и токово-
конвективную, или «штопорную», неустойчивость. Эти типы неустой-
231
чивостей свойственны самой плазме, т. е. источником энергии для
них является тепловое расширение плазмы, как и в случае желоб-
ковой неустойчивости плазмы. При развитии этих неустойчивостей
плазма практически не возмущает магнитного поля, образующего
как бы жесткий каркас из неподвижных силовых линий. При этом,
очевидно, электрическое поле должно быть потенциальным (без-
(безвихревым), т. е. Е=—Vcp. Наибольшим сходством с обычной же-
лобковой неустойчивостью идеально проводящей плазмы обладает
«гравитационная» неустойчивость. Различие между этими двумя
явлениями заключается в том, что если магнитное поле вморожено
в плазму, то энергетически выгоднее развиваться только деформа-
деформациям, ориентированным строго вдоль силовых линий, в то время
как при конечной проводимости плазмы появляется возможность
распространения косых возмущений с волновым вектором kZi не
+ U
Рис. 2.42. Схематическое изо-
изображение развития деформа-
деформаций при «гравитационной» не-
неустойчивости
Рис. 2.43. Изолинии плотности
плазмы при возникновении грави-
гравитационной неустойчивости
равным нулю. В обоих случаях неустойчивость существует тогда,
когда напряженность магнитного поля убывает в сторону умень-
уменьшения плотности плазмы. Она вызывается диамагнитным эффек-
эффектом; плазма выталкивается в сторону более слабого магнитного
поля. Однако для упрощения математического анализа развития
неустойчивости оказывается удобным заменить диамагнитный эф-
эффект, обусловленный неоднородностью поля, действием (в том же
направлении) некоторой постоянной силы, а магнитное поле счи-
считать однородным. В качестве такой силы в упрощенной модели
процесса удобно снова выбрать силу тяжести. Отсюда и происхо-
происходит термин «гравитационная» неустойчивость. В окончательных
формулах нетрудно перейти от силы тяжести к реальному диамаг-
диамагнитному эффекту.
Для того чтобы разобрать механизм возникновения и развития
косых деформаций в плазме с конечной проводимостью, восполь-
воспользуемся следующей моделью. Плоский слой плазмы с концентраци-
концентрацией п(х), убывающей вдоль оси х, находится в сильном магнитном
поле В, параллельном оси z (рис. 2.40). Сила тяжести, моделиру-
232
ющая влияние неоднородности магнитного поля, направлена по
оси х. Допустим, что в плазме возникает флуктуация плотности
вида п\>—ехр (—mt-\-ikyy-{-ikzz). В результате такого возмущения
изолинии плотности плазмы в каждом горизонтальном сечении
приобретают волнистую форму (рис. 2.43). Это означает, что флук-
флуктуации плотности указанного вида представляют собой малый сдвиг
косых слоев плазмы вдоль оси х.
Вследствие существования силы тяжести, перпендикулярной
к Н, должно происходить дрейфовое движение частиц, скорость ко-
которого направлена по оси у и имеет разный знак для ионов и
электронов. В однородной плазме такое движение не может соз-
создать разделение зарядов. Однако, если возникают возмущения
плотности, зависящие от координаты у, потоки заряженных частиц
из соседних объемов плазмы не компенсируют друг друга, и поэто-
поэтому происходит электрическая поляризация косых слоев с образо*
ванием объемных зарядов (см. рис. 2.42). В идеально проводящей
плазме 1ггф0 заряды должны были бы компенсироваться в резуль-*
тате перетекания вдоль силовых линий, поэтому косые деформации
не могли бы развиваться. Однако при конечной проводимости
плазмы полная компенсация не происходит, и из-за возникновения
электрического поля начальное возмущение должно возрастать.
В этом легко убедиться из рис. 2.42. В результате дрейфового дви-
движения на левой стороне каждого выступа (т. е. косого слоя, сме-
смещенного вперед) появляется положительный заряд, а на правой
стороне — отрицательный. Величина этих зарядов зависит от ско-
скорости, с которой они отводятся током вдоль силовых линий. Элек-
Электрическое поле, создаваемое зарядами в плазме, вызывает дрейф
в направлении [ЕХН]. Этот дрейф направлен таким образом, что
выступы в распределении плотности смещаются в направлении по-
положительной оси ху т. е. вперед, а впадины — в противоположном
направлении. Это означает раскачку колебаний плотности, т. е.
развитие неустойчивости.
Рассмотрим количественную сторону указанного механизма. Ли-
Линеаризованное уравнение движения имеет, вид
—iconomiU+Vpi=(l/c)[jiXH]+mi/zig. B.225)
В плазме с достаточно хорошей проводимостью косые возмущения
должны нарастать медленно, поэтому инерционный член в уравне-
уравнении B.225) при kz=?0 относительно мал. Проектируя это вектор*
ное уравнение на оси х и у, находим следующие соотношения меж-^
ду компонентами тока и градиента давления:
LH + mgn = dpjdx, B.226)
— (llc)jlxH=dPlldy. B.226a)
Из условия квазинейтральности в рассматриваемом процессе по-
получаем
di v j, = di v j/+ ikzj12 == 0. B.227)
233
Из B.226) и B.226а) следует, что
div }± = — ik^cgnJH. B.228)
Подставляя это выражение в B.227), находим
jiz=(miCglH) (nikylkz). B.229)
Уравнение непрерывности имеет вид
— i шл1 + п0 div п± + i n9kzu2 + u V л. = 0. B.230)
Поперечная скорость движения плазмы удовлетворяет условию
div u . =0. Действительно,
и± = - (с[Н>) [V ?г X Н] + (т.фН*) [g X Н].
где ф1—электрический потенциал, связанный с возмущением
в плазме. Следовательно,
Таким образом, второй член в выражении B.230) исключается.
Продольным движением ионов также можно пренебречь, по-
поскольку оно представлено в B.230) членом, содержащим множи-
множитель nokZi который мал по сравнению с V/i *. С учетом этих заме-
замечаний уравнение непрерывности B.230) можно записать в следую-
следующей форме:
—i(oni—(c/H)ifcyipi(dnQldx) =0. B.232)
Далее из закона Ома находим
/l2=i?z<T<pb B.233)
где о — электропроводность плазмы. Последнее соотношение спра-
справедливо в том случае, если продольный ток в невозмущенной плаз-
плазме отсутствует.
Решая систему уравнений B.229), B.232) и B.233), получаем
следующее выражение для инкремента нарастания малых возму-
возмущений:
Y=— ico = 02^/o)s, B.234)
где
ю2?=—gA /по) {dtio/dx); cos= (k\\k\)®ядояЛ«. B.234а)
Согласно B.234) инкремент растет с уменьшением kz. При очень
малых kZy когда (os становится порядка cog, в уравнении B.230)
следует сохранить поперечный инерционный член. Это означает,
что исследуемая неустойчивость переходит в желобковую с инкре-
инкрементом y=(dg. Таким образом, «гравитационная» диссипативная
неустойчивость является продолжением желобковой для случая
с конечной проводимостью.
* В плазме могут развиваться только косые возмущения, очень сильно вы-
гянутые вдоль силовых линий, для которых kz относительно невелико.
234
Для того чтобы перейти к реальному случаю плазмы, находя-
находящейся в неоднородном магнитном поле, нужно заменить фиктивную
силу pg истинной силой диамагнитного выталкивания.
Если R — радиус кривизны силовой линии неоднородного маг-
магнитного поля, то замену нужно провести по уже известному ре*
цепту:
g=(llR){2plp). B.235)
Очевидно, что в системах, удовлетворяющих условию «минимум
Я», «гравитационная» неустойчивость подавляется так же, как и
желобковая. Однако косые деформации с не слишком малым от-
отношением kzjky нельзя стабилизировать при помощи шира. Поэто-
Поэтому в ловушках без магнитной ямы «гравитационная» неустойчи-
неустойчивость может приводить к аномальной утечке частиц из плазмы-
Вследствие диссипативного характера «гравитационной» неустой-
неустойчивости она тем менее опасна, чем выше температура плазмы.
Если в равновесном состоянии по плазме вдоль магнитного поля
течет ток и при этом существует градиент температуры в направ-
направлении, перпендикулярном к Н, то может возникать так называемая
токово-конвективная неустойчивость. С ней также связана раскач-
раскачка косых деформаций в плазме, но при этом, в противоположность
«гравитационной» неустойчивости, главную роль играют не воз-
возмущения плотности, а возмущения температуры и электропровод-
электропроводности.
Пусть в плазме с начальной температурой То(х)> которая из-
изменяется вдоль оси х, происходит флуктуация температуры, при-
причем Т\=Т—Го зависит от координат и времени по закону
ехр(—iarf+iftj^-HifezZ). Поскольку проводимость есть функция тем-
температуры плазмы, то возникают также возмущения проводимости
Oi—(d<fldT)T\. Из-за наличия продольного тока возмущения долж-
должны приводить к электрической поляризации косых слоев, которая
будет носить такой же характер, как и в случае, когда на плазму
действует сила тяжести.
Выясним условия раскачки малых возмущений. Из закона Ома
для продольной составляющей тока следует, что
ju=OiEo+<toEu B.236)
где Eq — начальная напряженность электрического поля в плазме;
Е\— возмущение поля. Из уравнений непрерывности для ионов и
электронов получаем
% iv «|V<= ^+^ ?+ nt\k,v12l = 0; B.237)
vr.=?+^?+«.i*AM = a B.238)
Время нарастания возмущений очень велико по сравнению со вре-
временем релаксации зарядов в плазме. Поэтому можно считать, что
в рассматриваемом процессе квазинейтральность плазмы практик
235
чески не нарушается. Вычитая выражение B.237) из B.238), по-
получаем
Vizi—viZe=0, B.239)
что эквивалентно условию /iz=0. Добавим теперь уравнение теп-
теплового баланса. Учитывая, что в неравновесной плазме энергия
переносится вместе с веществом в результате дрейфового движе-
движения, можно записать это уравнение в виде
- |»7\ + (cEJH) dTJdx = -X[{k\Tl. B.240)
Здесь х|, —продольная температуропроводность плазмы. Посколь-
Поскольку электрическое поле потенциально, то E\v\E\z-=ky\kz. Из B.236),
B.240) и условия /iz=0 легко получить дисперсионное уравнение
токово-конвективной неустойчивости:
- i со = т = - X и k\ if (cEJH) {ky\kz) (l/ae) dojdx. B.241)
В плазме с невысокой электронной температурой теплопровод-
теплопроводность мала, и первым членом в B.241) можно пренебречь. В таком
случае косые деформации, для которых знак kyjkz совпадает со
знаком dao/dx, будут нарастать, т. е. должна иметь место токово-
" конвективна я неустойчивость.
Однако в высокотемпературной плазме продольная теплопро-
теплопроводность при не слишком малых значениях kz быстро выравнивает
возмущения температуры. Инкремент нарастания возмущений у
может достигать больших положительных значений только при
&2-Я). В тороидальной геометрии роль kz выполняет компонента
волнового вектора &1(. Как было выяснено в предыдущем парагра-
параграфе, при наличии шира величина k.. может быть очень мала только
вблизи магнитной поверхности с замкнутыми силовыми линиями.
Она быстро увеличивается при смещении от такой поверхности
в радиальном направлении. Это означает, что шир подавляет то-
ково-конвективную неустойчивость. Расчеты показывают, что роль
токово-конвективной неустойчивости в энергетическом балансе вы-
высокотемпературной плазмы относительно невелика и уменьшается
с ростом Т.
Следует отметить, что модификация неустойчивости такого типа
часто наблюдается в низкотемпературных газовых разрядах во
внешнем магнитном поле. Она также имеет свой аналог в элек-
электронно-дырочной плазме твердого тела.
§ 2.15. Неустойчивость тиринг-моды
Значительно более сложной является неустойчивость плазмы
с конечной электропроводностью, при которой происходит «разрыв»
силовых линий магнитного поля. Эта разновидность неустойчивости
получила название «разрывной», или тиринг-моды (от английско-
английского слова tearing — «разрыв»).
236
В известном смысле ее можно 'представить себе как некоторое
расширение области винтовой неустойчивости для магнитных сис-
систем с продольным токбм. В области устойчивости идеально прово-
проводящей плазмы, определяемой условием Крускала — Шафранова,
в плазме с конечной проводимостью появляются области возмож-
возможного развития медленной неустойчивости, изменяющей структуру
винтового магнитного поля из-за локального пинчевания. При этом
в шнуре вблизи замкнутых силовых линий происходит расщепление
магнитных поверхностей и выделяются винтовые волны — локаль-
локальные пинчи.
Эта мода неустойчивости играет важную роль в токамаке. Счи-
Считают, что релаксационные колебания, наблюдаемые в токамаке
в некоторых режимах, связаны с тем, что внутри плазменного шну-
шнура из-за тиринг-неустойчиво-
сти время от времени происхо-
дит перестройка магнитной
конфигурации, при которой
избыток энергии магнитного
поля передается плазме. Нё^
устойчивость такого типа мо-
может оказаться важной также "^
в астрофизике и геофизике.
Математические методы ис- Рис- 2М- Тиринг-неустойчивость ней-
трального слоя
следования тиринг-моды весь-
ма нетривиальны. Это свя-
связано с тем, что малое электрическое сопротивление в линеаризо-
линеаризованных уравнениях для возмущений входит в малый коэф-
коэффициент перед старшей производной. Это как раз та самая
ситуация, в которой математика призывает к особой бдительно-
бдительности. В некотором смысле теория гидродинамической устой-
устойчивости успела «набить себе шишки» в классической задаче об
устойчивости течения Пуазейля по трубе, прежде чем В. Гейзен-
берг и С. Лин сумели «укротить» известное уравнение Зоммер-
фельда —Орра, в котором вязкость примерно таким же образом
входила в малый коэффициент при старшей производной.
Физический смысл возникших для тиринг-моды математических
осложнений можно разъяснить следующим образом. В некотором
очень узком слое из-за конечной проводимости плазмы происхо-
происходит в буквальном смысле «разрыв» магнитных силовых линий. Не
случайно эта неустойчивость иногда называется «разрывной». При
этом разорванные «концы» силовых линий соединяются заново
(как говорят, происходит «пересоединение»), но, образно выра-
выражаясь, с другими партнерами. Не удивительно, что такая карди-
кардинальная перестройка топологии магнитного поля требует адекват-
адекватно сложного математического описания.
Рассмотрим плоскую модель тиринг-неустойчивости, появляю-
появляющейся в задаче о возмущении равновесия плазмы в.так называем
мом нейтральном слое. Пусть давление плазмы достигает макси-
237
мума в плоскости х=0, магнитное поле, направленное по оси z,
равно нулю при х=0 и нарастает при удалении в обе стороны ог
нейтральной плоскости с характерным масштабом изменения х^
«»Д. При этом направление магнитного поля в нижней полуплос-
полуплоскости обратно направлению его в верхней (рис. 2.44). Такой скачок
магнитного поля поддерживается током /0, текущим вдоль оси у.
Даже из простых интуитивных соображений ясно, что такое рав-
равновесие обладает большим избытком свободной энергии, заклю-
заключенной в магнитном поле. Потенциально этот избыток энергии мог
бы освободиться, если бы, условно говоря, произошла «анни-
«аннигиляция» встречных магнитных полей. Физическим механизмом
такой аннигиляции могло бы быть линчевание, разбиение первона-
первоначально плоского токового слоя на отдельные жгуты (см. рис. 2.44).
При таком пинчевании возмущение выбирается в виде
ехр t—iwt-\-ik2). Нужно учитывать возмущения скорости и магнит-
магнитного поля «х, uz, Нх, Hz. Электрическое поле возмущения направ-
направлено по оси у. Уравнение Эйлера дает
B.242)
B.243)
Воспользовавшись условием несжимаемости \kUz-\-duxjdx—Q (как
будет видно, при этом возникнут очень медленные движения),
уравнения B.242) и B.243) после несложных алгебраических пре-
преобразований можно привести к уравнению для их.
B.244)
—iupuz=—\kp— A /4лс) jHx.
В этом уравнении потенциальным источником неустойчивости
является член (i/4nck)j'oHx. С помощью условия вмороженности
его можно привести к виду — A/4ш?)/'оЯ<&с. Он дает отрицатель-
отрицательный вклад в упругость: f#0>0 (рис. 2.45). С точки зрения энерге-
энергетического принципа он соответствует третьему слагаемому (энер-
(энергии пинчевания) в выражении B.210а).
Однако столь легкая доступность этого энергетического резер-
резервуара является иллюзорной. Возмущения, изображенные на
рис. 2.44 и соответствующие
неустойчивости типа локаль-
локального пинчевания в окрестности
плоскости *=0, молчаливо
предполагают разрыв и пере-
пересоединение силовых линий
магнитного поля. Но это не-
невозможно, если плазму счи-
тать идеальным электрическим
прОВОдНИКОМ, Основная идея
теории тиринг-неустойчивости
Рис 245 Профиль магнитного поля и заключается в том^что в неко-
производной от плотности тока торой, очень малой окрестно-
233
сти нейтральной плоскости учитывается конечное, хотя и весьма
малое, электрическое сопротивление. Его учет размораживает си-
силовые линии магнитного поля, тем самым снимая топологический
запрет на разрыв и пересоединение силовых линий.
.Таким образОхМ, можно «осуществить доступ» к источнику сво-
свободной энергии и вызвать неустойчивость, которая может рассмат-
рассматриваться как один из случаев неустойчивостей волн с отрицатель-
отрицательной энергией. Общие принципы такого рода неустойчивостей, разо-
разобранные в ч. 1, как раз и показывают, что неустойчивость появ-
появляется, если можно обеспечить конечную величину диссипации
энергии волны.
Электрический ток в возмущении рассматриваемого, здесь типа
направлен по оси у и равен
jy=<y[Ey-(uxHolc)]. B.245)
Всюду, за исключением некоторой окрестности нейтральной
плоскости, электропроводность плазмы можно считать бесконечной,
т. е. пренебрегать левой частью уравнения B.245). В то же время
найдется такая окрестность х=0, в которой магнитное поле столь
мало, что в уравнении B.245) придется пренебречь вторым чле-
членом правой части. Назовем такой слой сингулярным. Очевидно,
его толщина б будет зависеть также от того, насколько быстро
спадает их при приближении к нейтральной плоскости. Закон спа-
спадания их в окрестности х—0 существенным образом зависит от
конкуренции членов правой части уравнения B.244). Член в левой
части пренебрежимо мал, так как неустойчивость тиринг-моды раз-
развивается очень медленно (со мало). В то же время старшую про-
производную в правой части этого уравнения следует сохранить, хотя
коэффициент, стоящий перед ней, мал по тем же причинам. Оценку
6 нетрудно провести, если приближенно третий член в правой части
уравнения B,244) представить в виде
и сопоставить его по порядку величины с первым членом правой
части того же уравнения. (Второй член при х->0 становится очень
малым, так как /V^O при Х-+-0). Итак, получаем
(сор/А2) (wx/62)—Я0/у/4яс. B.246)
Для оценки величины ]у достаточно сопоставить его с любым
из двух членов правой части уравнения B.245). Например, со сла-
слагаемым а(их/с)Но. Такой произвол связан с тем, что на границе
между внешней областью, где в уравнении B.245) пренебрегают
членом в левой части, и сингулярной областью, в которой прене-
пренебрегают вторым членом справа, все члены имеют один и тот же
порядок величины. С учетом этого приближенное равенство
B.246) дает после подстановки jy и Я0^//т6/А следующую оценку:
a^V/V/W^^X'2- <2-247>
239
Теперь рассмотрим внешнюю область, в которой электропровод-
электропроводность условно считается бесконечной. Уравнение для возмущения
магнитного поля rot Н—4л)/с с учетом div Н=0 можно представить
как
ik[Hx—(l/k2) (d2Hxldx2)] = Dn/c)jy , B.248)
(пока еще оно является совершенно точным и применимо всюду).
Для внешней области в уравнении B.244) пренебрегают членами
с инерцией, так как со мало. Тогда jy=—\(jf^jkH^)Hx.
Подставляя в B.248), получаем
\k[Hx— A /?2) {d2Hx/dx2) + (WoIс)Hx/k2H0] =0. B.249)
Перед последним шагом к решению задачи удобно рядом с этим
уравнением для магнитного поля во внешней области написать
уравнение для магнитного поля во внутренней области
ik[Hx-(\jk2) (d*Hxldx*)] = Dnlc)oEy B.250)
в соответствии с уже обоснованным пренебрежением вторым сла-
слагаемым в законе Ома B.245).
Правый член в B.250) как раз и учитывает конечную диссипа-
диссипацию (омическую) энергии возмущения, которая является ключом
к задаче о неустойчивости типа отрицательной энергии.
Оценим полный баланс диссипируемой энергии. Для этого
умножим обе части уравнений B.245) и B.250) на Еу, проинтегри-
проинтегрируем по всему плазменному слою и сложим оба уравнения. Физи-
Физический смысл правой части получившегося выражения ясен: это
джоулево тепло J jEdx, Левая часть представляет собой измене-
изменение энергии магнитного поля .возмущения. Дестабилизирующую
роль, как уже говорилось, играет член с j'o/Ho. Мы не будем вни-
вникать в характер решения для возмущения магнитного поля во
внешней области. Строгое рассмотрение подтверждает, что сущест-
существуют возмущения, для которых слагаемое с j'o/Ho доминирует.
Тогда нетрудно оценить изменение энергии магнитного поля воз-
возмущения по порядку величины (\kjk2) J (j/olHo)HxEydx^^(ilk)X
Х(с/4пА)НхЕу. В итоге получаем }*словие баланса между ростом
энергии магнитного поля возмущения и джоулевой диссипацией:
(llAk)HxEy~{4nfc)GE2y6. B.251)
Так как электрическое поле легко выразить через магнитное с .по-
.помощью уравнения Максвелла rotE=—(l/c) (dH/dt), то уравне-
уравнение B.251) с учетом Еу=(<й/кс)Нх дает заготовку для получения
дисперсионного уравнения
1/А—Dя/с)а(со/с)б. B.252)
Для магнитогидродинамической тиринг-моды величину 5 мы
уже оценили [см. B.247)]; таким образом, дисперсионное урав-
уравнение принимает вид
1 /А <^ D«/с) о (»/<?) (ш1/4/Л1/2о1/4) (с1/2Д1/2р1/4/</2). B.253)
240
Очевидно, оно всегда дает неустойчивый корень с инкрементош
неустойчивости
Im ш л, Л2/5Д^/о8/5Дв/У/5. B-254)
Эта оценка по порядку величины согласуется с точным отве-
ответом. Можно показать, что имеется полная аналогия рассмотрен-
рассмотренной плоской задачи о неустойчивости нейтрального слоя с зада-
задачей о неустойчивости равновесия плазмы в винтовом магнитном
поле. Роль нейтральной плоскости играет магнитная поверхность,,
на которой &„=(), т. е. шаг винта силовой линии магнитного поля;
совпадает с шагом винта возмущения. Пересоединяющимися явля-
являются проекции силовых линий азимутального магнитного поля*?
s,
Рис. 2.46. Движение частиц в узком слое вблизи ней-
нейтральной плоскости
в винтовой системе координат с шагом винта, соответствующим?
нейтральной магнитной поверхности. Инкремент неустойчивости
имеет такой же порядок величины, что и B.254). Именно этот тиш
тиринг-моды привлекают для объяснения некоторых неустойчиво-
стей в токамаке.
'Выражение B.252), использованное здесь как заготовка для
получения дисперсионного уравнения, в действительности имеет
значение, выходящее за рамки простого машитогидродинамиче-
ского приближения. Так, например, при известной осторожности:
его можно применить даже для случая бесстолкновительной плаз-
плазмы. Равновесие с нейтральным слоем бесстолкновительной плазмы. |
может иметь физический смысл для так называемого геомагнитно-
геомагнитного, хвоста Земли и в некоторых астрофизических ситуациях. В та-
такой задаче следует представлять себе характер движения частиц,
в магнитном поле, меняющем знак при переходе через нейтраль-
нейтральную плоскость х=0. Вообще говоря, всюду, за исключением не-
небольшой окрестности х=0, «магнитное поле как бы привязывает
частицы к своим силовым линиям, восстанавливая тем самым гид-
гидродинамический характер движения плазмы. Однако всегда най-
найдется хотя бы узкий слой некоторой толщины 6i, внутри которого*
движение частиц не замагничено: они как бы движутся по узкому
коридору, отражаясь от его стен. Примерный вид траекторий заря-
заряженных частиц изображен на рис. 2.46. Толщину этого коридора
6i можно оценить следующим образом. Очевидно, частицы могуг
16-74 241
.«проникать за его пределы (с возвратом назад) на расстояние по-
;рядка ларморовского радиуса. Хотя в столь неоднородном маг-
магнитном поле представление о ларморовском радиусе имеет смысл
только по порядку величины, оценим его vrmcjeH^b\. Да-
.лее учтем, то Но/Нт8\/А. Отсюда 6i—(ДгяI/2.
Естественно считать, что эта величина в бесстолкновительной
.задаче и будет аналогом толщины сингулярного слоя для тиринг-
моды. В отсутствие столкновений формальное вьиражение для элек-
электропроводности о=пе2х/те дает бесконечность. Тем не менее мож-
можно воспользоваться этим выражением, если под т подразумевать
^величину, близкую к той, которая используется в теории твердого
тела и плазмы при рассмотрении явления аномального скин-эффек-
скин-эффекта. В выражении для а время свободного пролета (ускорения) т
¦не обращается в бесконечность даже при отсутствии столкновений,
так как в среднем за время порядка x^\\kv частица сместится
вдоль слоя на расстояние порядка длины волны и попадет в об-
Рис. 2.47. Магнитные силовые линии в верхней части плоского нейтрального слоя
плазмы на начальной стадии развития тиринг-неустойчивости (а) и в сильно не*
линейном режиме (б) по результатам численного моделирования:
• изолинии равной плотности плазмы. На начальной стадии неустойчивость приво-
приводит к формированию магнитных островов вблизи центра нейтрального слоя. В дальнейшем
происходит объединение групп островов (Зеленый Л. М., Липатов А. С. «Физика плазмы»,
1979, т. 5)
242
ласть с другой фазой электрического поля Еу. Естественно ввести*
некоторую эффективную электропроводность
o<->(ne2lme)(llkvTe). B.255}>
Заметим, что вклад электронов в такую электропроводность,
в (rrii/me)i/2 раз больше ионного. В итоге инкремент нарастания^
который находим после подстановки B.255) в B.252), имеет по-
порядок величины
Im uv- ЬтДгне/ДK/2. B.256)
При получении этой формулы мы воспользовались тем, что в ней-
нейтральном слое пГ=Я2ш/4л; и, следовательно, Гне=с/ауре. Более."
строгая теория, которая позволяет уточнить численные коэффи-
t= 1,07-10
-2
1,4J-10"
Рис. 2.48. Эволюция во времени двух взаимосвязанных магнитных островов, по-
появляющихся в токамаке в результате развития тиринг-мод в случае, когда на*
двух различных магнитных поверхностях тиринг-мода имеет одно и то же азиму-
азимутальное волновое число (т=3). На нелинейной стадии происходит слияние раз-
разрушенных магнитных островов (White R. M., Monticello D. A., Rosenbluth M. N.*
Waddel W. Y. Preprint PPL-1282, Princeton, 1976)
16* 24$
щиенты, потребовала бы использования методов кинетической
теории.
Считается, что инкремент неустойчивости B.256) слишком мал
,для того, чтобы вызвать заметные эффекты в нейтральном слое
геомагнитного хвоста. Если в силу каких-нибудь обстоятельств,
.например из-за наличия в равновесии небольшой вертикальной
компоненты магнитного поля, движение электронов в сингулярном
слое замагничено, то нужно учесть ионы. Действуя по уже исполь-
.зованному рецепту 6—(гшАI/2; a~(/ze2/mO (l/kvTi), легко найти
инкремент неустойчивости, который в этом случае оказывается го-
гораздо большим, чем определяемый формулой B.256):
Iffl о>г— (пц \те) i/*Im о>е. B.257)
Этот режим неустойчивости, по-видимому, может играть важную
роль в геофизике. Энергия, высвобождаемая из-за тиринг-неустой-
чивости геомагнитного хвоста, считается ответственной за явление
так называемых магнитосферных суббурь — процессов
гвзрывообразного вторжения плазмы геомагнитного хвоста в маг-
магнитосферу и ионосферу Земли.
Развитие бесстолкновительной тиринг-моды в плоском ней-
нейтральном слое иллюстрируется на рис. 2.47, который получен
в численном эксперименте. Для сравнения на рис. 2.48 показаны
конфигурации магнитных поверхностей в токамаке, полученные
шри исследовании гидродинамической тиринг-моды численными
методами.
§ 2.16. «Дрейфовая> неустойчивость плазмы
Магнитная гидродинамика даже при учете конечного электри-
электрического сопротивления остается всего лишь некоторой приближен-
приближенной моделью описания плазмы. Она неполностью учитывает неко-
некоторые важные степени свободы, как, например, относительное дви-
движение ионной и электронной .компонент. Неустойчивости, связанные
с такими дополнительными степенями свободы, могут играть в фи-
физике плазмы большую роль. Разумеется, плазма должна быть до-
достаточно разреженной, чтобы реализовать их. Среди этих неустой-
неустойчивостеи основную роль играет так называемая дрейфовая
неустойчивость. Соответствующий ей тип движения плазмы —
«дрейфовые» волны — складывается из практически свободного
перетекания электронов вдоль силовых линий магнитного поля и
.движения ионов в основном поперек магнитных силовых линий.
В самой простой форме для описания этих эффектов в об-
обобщенном законе Ома нужно учесть градиент давления электро'Н-
ной компоненты. Исследование этого эффекта привело к обнару-
обнаружению так называемых дрейфовых неустойчивостеи, теория кото-
которых к 'настоящему времени разработана достаточно детально.
Попытаемся в общих чертах изложить основные представления
о физическом механизме явлений, относящихся к этому классу.
1244
С чисто математической точки зрения мы будем при этом все вре-
время только скользить по поверхности теории, оставаясь «а грани
качественного и количественного анализа. Нетрудно найти оправ-
оправдание для такого нестрогого подхода. Дело в том, что, переходя от
¦изучения относительно простых видов магнитогидродинамической
неустойчивости идеально проводящей плазмы к эффектам, связан-
связанным с диссипативным'и силами, и далее — к дрейфовым -неустой-
чивостям, мы вступаем в район все более сложных теоретических
построений, которые к тому же имеют гораздо меньшую опору со
стороны эксперимента.
Одним из исходных пунктов в исследовании нобого класса не-
неустойчивостей служит уравнение движения электронной компо-
компоненты. В наиболее общем случае его можно записать в виде
[см. B.58)]
теп ^ + 7Л = _*лЕ-^[и.ХН]-^. B.258)
Последний член в правой части есть сила трения между электро-
электронами и ионами.
Изучая механизм развития диссипативных неустойчивостей, мы
использовали проекцию этого уравнения -на направление, парал-
параллельное Н, и при этом пренебрегали инерционным членом и вели-
величиной Vpie, считая их малыми по сравнению с силой трения. Имен-
Именно на указанных допущениях основано применение закона Ома
в его простейшей форме j=crEi.
Теперь поступим иначе: пренебрежем силой трения, но будем
учитывать Vpie. При этом из B.258) следует, что
B.259)
Инерционный член по-прежнему считается малым. Соотношение
B.259) в теории дрейфовых неустойчивостей часто используется
в качестве эквивалента закона Ома.
Рассмотрим снова плоский слой плазмы, в котором при отсут-
отсутствии возмущений концентрация п(х) плавно меняется вдоль осих.
Магнитное поле Н, как и ранее, будем считать однородным и на-
направленным вдоль оси г. Допустим далее, для простоты, что тем-
температура электронов Те постоянна по всему слою. Для «стандарт-
«стандартных» .возмущений плотности типа плоской волны (exp(ikyy +
-\-\kzz—icoO) из B.259) в линейном приближении следует уравне-
уравнение для .возмущения плотности электронов П\е\
B.260)
где <ф1 — возмущение электрического потенциала. Это так назы-
называемое больцмановское распределение, уже использовавшееся
ранее.
^Если так же, как это было сделано при анализе гравитацион-
гравитационной 'неустойчивости, пренебречь продольным движением ионов и,
кроме того, учесть, что поперечное движение обусловлено элек-
245
трическим дрейфом, то уравнение непрерывности можно записать
в виде
—mnu—iky(c(pi/HQ)dnoldx=O. B.261)
С помощью B.260) и B.261) из условия квазинейтральности tiie—
—Пц можно найти дисперсионное соотношение
a^—kyicTe/eHo) A/ло) (dtio/dx). B.262)
Здесь [A1По)dtioIdx]-1 — характер-ный размер неоднородной
плазмы, который имеет тот же порядок величины, что и радиус
поперечного сечения плазменного шнура а.
Эта волна называется дрейфовой, так как скорость ее распрост-
распространения в направлении, перпендикулярном к Н, по порядку вели-
величины совпадает со скоростью дрейфового движения 'Неоднородной
плазмы (при Ti^Te величина этой скорости пропорциональна
ГнеУте/а—гтУтг/а)- Пределы применимости полученного выраже-
выражения для частоты дрейфовой волны вытекают из условия, чтобы
фазовая скорость в продольном направлении (o/kz лежала в интер-
интервале, определяемом неравенствами
vTe Vmjmi < Ч^г < vTe. B.263)
Если CD/&2 приближается к vTe, то необходимо учитывать инер-
инерционный член в уравнении для электронов; при этом выражение
для со изменяется. В другом крайнем случае, когда co/&z стремится
к vTe V trie/nti, дрейфовая волна в плазме с голодными ионами
(Те*$>Тг) переходит в ионно-звуковую, при этом существенное зна-
значение приобретает продольное движение ионов. Если же ионы име-
имеют температуру, близкую к электронной, то vTe Vте\^г^/'^ти и
поэтому вступает в действие сильный механизм затухания волны
на ионах (затухание Ландау), вследствие чего волна не может
распространяться. Заметим, что из условия со/^>^гг следует, что
kz\kv<rm\a. B.264)
В сильном магнитном поле /*яг/#<С1, и, таким образом, дрейфовая
волна должна быть сильно вытянутой ©доль (Магнитного поля.
Рассмотрим теперь свойства дрейфовых волн для привычной
геометрии плазменного шнура в магнитном поле, ограничиваясь,
как обычно, случаем, когда Яф <С#2. При слабой тороидальности,
т. е. в случае, когда радиус сечения плазменного шнура а очень
мал по сравнению с длиной витка L, элементарное волновое воз-
возмущение зависит от координат по закону expi(mp—2wnz\L).
Волновой вектор k^ в направлении магнитного поля для такого
возмущения обращается в нуль на замкнутой силовой линии
с углом полного поворота Q, равным 2ят//г. Согласно B.215)
вблизи такой замкнутой линии, лежащей на магнитной поверхно-
поверхности радиуса г,
ku = k,(Arlr)b* B.265)
246
где Ь§— величина шира, k^ — азимутальная составляющая волнового
вектора. Выражение, определяющее частоту волны для тороидаль-
тороидальной системы, должно быть аналогично B.262) при замене ky на k .
Из условия (x)/k^>vTi и выражения B.262) для со следует
&r<rHi/Qs. B.266)
Таким образом, при наличии шира дрейфовая волна с индекса-
индексами п и т локализована в узкой области вблизи магнитной поверх-
поверхности с радиусом Го, «а которой шаг возмущения совпадает с ша-
шагом силовой линии. Если температура ионов не очень сильно отли-
отличается от температуры электронов, то за пределами области
B.266) возмущения типа дрейфовых волн быстро затухают. Сле-
Следует отметить, что, ка:к показывает детальный анализ различных
механизмов возбуждения дрейфовых колебаний, в большинстве
случаев ширина области локализации возмущений плазмы оказы-
оказывается во много раз меньшей, чем rHi/Qs-
Пренебрегая влиянием сил трения и сил инерции в уравнениях
движения, получаем для частоты дрейфовых волн чисто веществен-
вещественную величину. Это означает, что такие волны представляют собой
гармонические колебания, распространяющиеся в пределах своей
области локализации без заметного затухания или нарастания.
Они не !могут приводить к переносу частиц поперек магнитного
поля, т. е. вызывать аномальную диффузию плазмы. В этОхМ можно
убедиться на основе следующих достаточно общих соображений.
При медленных колебаниях типа дрейфовых волн в плазме
с достаточно высокой температурой справедливо соотношение
B.260), связывающее продольные компоненты градиентов давле-
давления и электрического потенциала. Вследствие очень большой про-
продольной теплопроводности плазмы электронная температура долж-
должна сохранять постоянное значение во всех точках одной и той же
силовой линии. Поэтому, интегрируя обе части B.259) вдоль Н,
получаем
T B.267)
В замкнутой магнитной системе с вращательным преобразова-
преобразованием каждая бесконечная силовая линия порождает и повсюду
плотно заполняет тороидальную магнитную поверхность. Очевид-
Очевидно, что уравнение B.267) связывает значения пе и ср во всех точ-
точках такой поверхности, а фо изменяется только при переходе от
одной магнитной поверхности к другой. Таким образом, на каждой
магнитной поверхности устанавливается больцмановское распре-
распределение электронов.
Из B.267) следует, что для всех компонент градиента элек-
электронного давления, лежащих на заданной поверхности, справедли-
справедливо соотношение
dpelds=-eneEs. B.268)
247
При возбуждении дрейфовых волн поведение электронной ком-
компоненты описывается уравнением
UeXtt]. B.269)
В силу B.268) проекция [иеХН] на любое -направление, касатель-
касательное к выбранной магнитной поверхности, равна нулю. Отсюда сле-
следует, что компонента скорости иеп, перпендикулярная к магнитной
поверхности, также равна <нулю, т. е. переход электронов от одной
магнитной поверхности к другой запрещен.
Если учесть силу трения между электронами и ионами, то
у частоты может появиться мнимая добавка (a>=(oo + iv)> что озна-
означает раскачку дрейфовых волн. Единственным условием для их
раскачки является неоднородность плазмы по отношению к рас-
распределению плотности или температуры. Поэтому в литературе по
теории плазмы неустойчивости такого типа иногда называются
также универсальными неустойчив остям и.
Рассмотрим сначала случай, когда температуру в невозмущен-
невозмущенной плазме (т. е. в исходном состоя-нии) можно считать постоян-
постоянной по всему объему, а 'плотность плазмы неоднородна. Пусть
в слое плазмы возникает возмущение типа плоской волны
(ехр (—i<ut-\-ikyy-\-ikzz)). Из уравнения движения B.258) при уч-е-
те малого инерционного члена следует, что
jI± = (c/H>) [UX (- i пют,щ + VA)b B.270)
Движение ионов в первом приближении определяется электриче-
электрическим дрейфом. Поэтому в уравнении B.270) вместо и^ можно под-
подставить [(c/#2)HxV(p]. Принимая во внимание условие divji=O,
находим следующее соотношение между компонентами плотности
тока:
k B.271)
Применяя известную формулу векторного анализа*, получаем из
B.270) и B.271)
div ju = (wmiC/H*) H -rot n и*. B.271а)
Используя выражение для иг, можем привести B.271) к виду
B.272)
Линеаризованное уравнение непрерывности имеет вид [см.
уравнение B.261)]
—i®nt—(c/H)iky<pdno!dx=0, B.273)
а уравнение движения для электронов в направлении, параллель-
параллельном магнитному полю (с учетом силы трения), можно записать
следующим образом:
\kztix Te=enoikzxp+ (me /v) /u. B.274)
* div[AXB]«B.rotA—A-rot B.
248
Решение системы B.272) —B.274) дает следующее дисперсионное
уравнение:
<о2—icosco + icos0d=O, B.275)
где (x)s=(k2zlk2v)(x)He(uHi%ei; (tei=l/v), a <ud=—(kycTeteHno)X
X{dno/dx) —дрейфовая частота B.262). При очень частых соуда-
соударениях, а следовательно, малых хеи cds<C(Dcz из дисперсионного
уравнения имеем w^±i(coscDdI/2- Скорость нарастания этой так
называемой дрейфово-диссипативной неустойчиво-
сти становится максимальной и сравнимой с самой дрейфовой ча-
частотой Im @^@B ПрИ УСЛОВИИ C0s—Wd-
Эти соотношения реализуются лишь в достаточно холодной
плазме газового разряда или в условиях ионосферы (когда время
свободного пробега электронов может еще уменьшиться в резуль-
результате столкновений с нейтральными частицами). Поэтому дрейфо-
во-диесипативная неустойчивость такого типа не представляет
опасности для высокотемпературной плазмы в магнитных ловуш-
ловушках. Но в свое время, на заре термоядерных исследований, счита-
считалось, что -моделирование магнитного удержания плазмы можно
проводить в сравнительно холодной плазме газового разряда. Тог-
Тогда ,в течение длительного времени оставалось неразгаданным явле-
явление так называемой бомовской аномальной диффузии. На основе
некоторых данных ранних исследований диффузии плазмы поперек
магнитного поля Д. Бом постулировал, что коэффициент аномаль-
аномальной диффузии
D± = cT[lGeH. B.276)
Он предположил, что причиной такой аномалии является неустой-
неустойчивость неизвестной природы, переводящая плазму в турбулентное
состояние.
Многие первые попытки разгадать механизм этой гипотетиче-
гипотетической неустойчивости оказались безрезультатными. Но сразу, как
только была открыта дрейфово-диосипативная неустойчивость, од-
одного взгляда на ее максимальный инкремент г-^ыа—кс(Т/еН) (п!\п)
было достаточно, чтобы сделать вывод: если существует диффузия
Бома, причиной должна быть именно эта неустойчивость.
В высокотемпературной плазме, как правило, cos>o)d, и для ча-
частоты колебаний получаем
co=cod + i(co2d/cos). B.277)
Чем больше %еи тем больше cos и меньше инкремент неустойчиво-
неустойчивости. Точно такую же роль играет шир, увеличивающий эффек-
эффективную величину k п, а значит, и cos. Поэтому дрейфово-диссипа-
тивная неустойчивость такого типа оказывается неопасной.
Следует также отметить, что в высокотемпературной плазме,
где обычные силы трения между электронами и ионами малы, на
первый план выступает бесстолкновительный аналог дрейфово-
диссипативной неустойчивости, в которой роль диссипативных сил
играет затухание Ландау. Сама неустойчивость принимает в ука-
249
занном. случае вид резонансной раскачки дрейфовых волн элек-
электронами, продольная скорость которых совпадает с фазовой ско-
скоростью волны co/kz.
Оценку инкремента неустойчивости нетрудно провести традици-
традиционным методом, вычисляя работу поля волны над резонансными
частицами (to^kzvz). Кинетическое уравнение для электронов
в дрейфовом приближении будет иметь вид [см. B.53)]
•*i-i. t i ЕУ df* eEzdh Л
Это уравнение отличается от обычного линеаризованного уравне-
уравнения A.83) наличием слагаемого (с(Еу/Н0) (dfo/dx)), учитывающе-
учитывающего перенос электронов со скоростью электрического дрейфа
сЕу/Но. Тогда поправка ft к функции распределения
'.-та D &-??}¦
Вычислим работу электрического поля волны над резонансными
электронами:
т f Ezvzdvz f By df0 eEz df0
, — — elm i г— \c-rj- az— -^—> =^=
J<o — kzvz У Ho ox> me dvz)
( Ey_ o|/e_
Z\C H д*
B.279)
Знак этой работы, определяющий устойчивость или неустойчивость
системы, зависит от конкуренции двух слагаемых. Второе из них
описывает обычное затухание Ландау и при отсутствии эффекта
типа пучковой неустойчивости (df/dv>0) играет стабилизирую-
стабилизирующую роль. Первое же слагаемое описывает высвобождение энер-
энергии при расширении плазмы и является источником дрейфовой не-
неустойчивости.
Вычисление суммы в B.279) проводится автоматически для
случая, например, максвелловского распределения плазмы f®—•
r^cnQ(x)exp (—mev2zj2T) с однородной температурой и дает
—d). B-280)
Здесь учтено, что Ey—(skvlkz)Ez (из Е=—grad(p); ©d определяется
соотношением B.262). Таким образом, для простой дрейфовой вол-
волны, описываемой формулой B.262), имеет место точная взаимная
компенсация обоих конкурирующих процессов. Однако при учете
неоднородности температуры первое слагаемое может перевесить,
и тогда возникает неустойчивость. Кроме того, более тонкие рас-
рассуждения показывают, что с уменьшением длины волны дрейфо-
дрейфовых колебаний в направлении, перпендикулярном к силовым ли-
линиям магнитного поля, частота со всегда оказывается меньше, чем
дает простая модель B.262). Это также ведет к неустойчивости.
250
Такая неустойчивость уже не зависит от деталей конфигурации
плазмы. Поэтому ее также иногда называют универсальной.
Наиболее эффективным средством борьбы с ней является шир —
перекрещенность силовых линий магнитного поля.
По этой причине рассматриваемая форма неустойчивости не
представляет катастрофической опасности для удержания энергии
и частиц в плазме. В конечном счете малая эффективность этой
разновидности дрейфовой неустойчивости связана с тем, что при
медленных дрейфовых колебаниях электроны успевают распреде-
распределяться по Больцману.
Большую опасность представляет неустойчивость, обусловлен-
обусловленная не градиентом плотности, а градиентом температуры. Эта
неустойчивость называется те мпер атурно-др ейфовой. До-
Допустим для простоты, что спад те*мпературы от осевой линии плаз-
плазменного витка к его поверхности происходит по гораздо более кру-
крутой кривой, чем спад концентрации, т. е. (din T/dlnn) ^>1. В ука-
указанном случае в линеаризованном уравнении непрерывности для
ионов можно пренебречь членом, содержащим dtio/dx, но при этом
уже нельзя исключить член, пропорциональный продольной скоро-
скорости пи. Следовательно, уравнение непрерывности принимает вид
—шгц+ikzuiztio=O. B.281)
Физический смысл этого соотношения заключается в том, что при
движении, для которого div/ZoUj. =0, единственной причиной изме-
изменения плотности может быть только продольное сжатие или раз*
режение плазмы.
Компоненту скорости щг можно найти из уравнения, описы-
описывающего продольное движение ионов плазмы:
—шпотгЩх-{-ъкг(поТ1-\-П1То) =—i&zcpi?. B.282)
Если пренебречь теплопроводностью, то уравнение теплового ба-
баланса можно записать в виде
—icoTi—i (c/H) tfyyidTo/dx=O. B.283)
Электроны можно считать распределенными по Больцману. Это
означает, что имеет место соотношение eq>i=(tiiln)To. Подставляя
это выражение для cpi в уравнение B.282) и решая систему
B.282) — B.283), получаем следующее уравнение для определе-
определения со:
, B.284)
где (uT—(cleH)ky(dT/dx); Cs=V2Tlmt. При (OT^>kzcs уравнение
B.284) сводится к более простому:
со3=A/2)сог&2А B.285)
Последнее уравнение имеет три корня, среди которых один дейст-
действительный и два комплексных. Один из комплексных корней соот-
соответствует раскачке малых возмущений. При этом инкремент ока-
оказывается порядка частоты.
251
Более строгий теоретический анализ показывает, что в плотной
плазме неустойчивость имеет «место, если \)—(d\n T/dlnn) >2/3.
В разреженной плазме, где роль сил трения играет затухание Лан-
Ландау, неустойчивость должна проявляться при ц>2 для длинновол-
длинноволновых колебаний (/гугт<^1) и при ц>\ для коротковолновых
{куГт—'1). Раскачка имеет место при a)T>2kzcs). Для подавления?
этой разновидности дрейфовой неустойчивости потребовался бы
более сильный шир. Поэтому ее нельзя исключить как возможный
источник дополнительной потери тепла из плазмы в токамаке.
Интересные модификации дрейфовых неустойчивостей возмож-
возможны в многокомпонентной плазме. Примером такой плазмы может
служить плазма с примесями. Вообще проблема примесей является
одной из основных проблем управляемого синтеза. В 'магнитных
ловушках вблизи стенок камеры неизбежно наличие некоторого
количества тяжелых ионов примесей (ионов, выбитых из стенок)
с большим зарядовым числом Z>1. Хорошо известно, что нали-
наличие примесей нежелательно для проблемы управляемого термо-
термоядерного синтеза, поскольку даже небольшое число примесей
с большим зарядовым числом существенно увеличит потери на из-
излучение (см. § 1.8).
Менее известным является тот факт, что наличие примесей при-
приводит к появлению новой ветви дрейфовой 'неустойчивости плазмы.
Механизм этой неустойчивости становится довольно простым, если
использовать изложенный выше подход к дрейфовым волнам.
В рассматриваемом теперь случае неустойчивыми оказываются
достаточно медленные возмущения, фазовая скорость которых
вдоль магнитного поля мала по сравнению с тепловой скоростью
водородных ионов, но существенно больше тепловой скорости тя-
тяжелых примесных ионов:
B.286)
В этом случае не только электроны, но и водородные ионы успева-
успевают приобрести больцмаиовское распределение B.260). Что же ка-
касается примесных ионов, то их плотность находится из гидродина-
гидродинамического уравнения непрерывности B.261). В этом случае из-
условия квазинейтральности имеем вместо B.262) следующую
формулу для частоты медленных дрейфовых движений в трехком-
понентной плазме:
(elTe)ne=—(elTi)n**o—(ckvlHo) {dnhldx) (Z/оз),
]
B.287)
Так же, как и в случае универсальной дрейфовой неустойчиво-
неустойчивости, раскачка рассматриваемой здесь дрейфовой волны связана
с тем, что в формуле для работы электрического поля волны над
резонансными частицами B.279) наряду с обычными для однород-
однородной плазмы слагаемыми, пропорциональными Ez(dfo/dvz), имеется
также слагаемое, пропорциональное Ey(dfoldx). При этом в силу
252
условия B.286) основной вклад в работу поля над частицами даег
взаимодействие с резонансными ионами водорода (в отличие or
универсальной дрейфовой неустойчивости, при которой vTi<
<^lkz<(oTe и существенно только резонансное взаимодействие вол-
волны с электронами). В этом случае инкремент нарастания дрейфо-
дрейфовой волны
Y ~ [dfjdvz + (kyjkz) (cmHleH0) {dfjdx)] \ v_4k. B.288>
Считая температуру плазмы однородной, получаем из B.288) сле-
следующее условие возникновения неустойчивости:
l + G^/co) (сТн/еНо) (l/n^o) (dn^jdx)<Q. B.289)-
Используя формулу B.287) для частоты, это условие можно за-
записать в виде
Те!(Те+Тн) + (dnHoldx){Z(dnioldx)]-i«). B.290)
Очевидно, для возникновения рассматриваемой неустойчивости
знаки градиентов плотности для основных и примесных ионов-
должны быть противоположными, что действительно имеет место*
у стенок камеры. Эта неустойчивость может быть опасна тем, что-
приводит к усиленной диффузии примесных ионов в глубь плазмы.
Любопытным аналогом дополнительной примесной компоненты
могут служить частицы, запертые в тороидальных ловушках. Раз-
Различие между пролетными и захваченными частицами наиболее
существенно проявляется для медленных возмущений с '(o/kz<^vTu
В электрическом поле, обусловленном таким возмущением, про-
пролетные ионы и электроны успевают приобрести больцмановское-
распределение B.260), в то время как возмущение плотности за-
захваченных частиц можно определить из уравнения непрерывносга
B.261). В этом уравнении, однако, надо учесть, что из-за столкно-
столкновения частицы покидают конус захвата с некоторой частотой v^
С учетом этого следует модифицировать уравнение непрерывности^
B.261) следующим образом:
i шп\г + i ky9 ^8-g* - va< = 0, B.291>
где 6— ]/e —доля захваченных частиц в равновесном состоя-
состоянии *. При вычислении vi следует учесть, что из-за существования
конуса захвата функция распределения в равновесном состояний'
имеет большие градиенты по скорости (меняется на интервале ско-
* Поскольку глубина магнитной ямы, в которую захватываются частицы,,
порядка |хД#, где A#=//oa/#, a/R — отношение малого радиуса тора к большо-
большому, то из максвелловского распределения по скоростям будут захватываться*
только частицы с достаточно малыми продольными скоростями:
,, T vTVa/Rl
Таким, образом, доля захваченных частиц b = Ve , e = a/R.
253
рости w^ У evT). В этом случае в интеграле столкновений Ландау
достаточно учесть только слагаемое со старшей (второй) произ-
производной [см. уравнение A.98)]. Таким образом, vi=v/e. Тогда из
уравнения непрерывности B.291) имеем следующую формулу для
^возмущения плотности захваченных частиц (электронов и ионов):
nf=- 1/(со + i v/s) (c/H0) ky<?b (dn.Jdx). B.292)
Ъ этом случае из условия квазинейтральности
вместо формулы B.262) имеем для частоты дрейфовых колебаний
•следующее дисперсионное уравнение:
2 = — <»d УТЦш + i vjs) -f <»d ]/7/(ш + iv, /в). B.293)
Здесь ш — частота дрейфовых колебаний, определяемая уравне-
уравнением B.262). Слагаемое в левой части дисперсионного уравнения
описывает вклад пролетных электронов и ионов, имеющих больц-
мановское распределение (для простоты считаем, что ионы и элек-
электроны имеют одинаковую температуру: Те=Т{). В правой части
дисперсионного уравнения представлены вклады от затертых элек-
электронов и запертых ионов. Исследуем случай, когда V2/e<co<Ve/s,
наиболее важный для термоядерных ловушек. Тогда из B.293)
зшеем следующее решение дисперсионного уравнения:
2«) = *d yT[l— i(v,/e©)] + i°> Ы3/21*е)>
т. е.
(о = (У7[2) md -f i {^dj2ve) ss — 2iv,/e. B.294)
Таким образом, при
VeVz<co2d83/4. B.295)
имеет место так называемая дрейфово-диссипативная неустойчи-
неустойчивость на запертых частицах. Эту моду неустойчивости, тго-видимо-
¦му, невозможно полностью подавить. Поэтому следует ожидать,
^что она служит дополнительным (но не катастрофическим) кана-
каналом утечки из тороидальных плазменных ловушек.
§ 2.17. Микронеустойчивость плазмы и аномальная диффузия
В отличие от крупномасштабных магнитогидродинамических не-
устойчивостей, способных вызвать катастрофическое изменение
исходного равновесия плазмы, мелкомасштабные неустойчивости
(микр о неустойчив о сти) типа дрейфовых не приводят к не-
немедленному изменению равновесия. Следует ожидать, что они вы-
вызывают появление мелкомасштабных пульсаций с характерными
•пространственными размерами порядка наиболее неустойчивых
длин волн исходных линейных возмущений. А характерные часто-
частоты пульсаций, вообще говоря, должны вести свое происхождение
Таблица 2.Г
Систематизация микроиеустойчивостей неоднородной плазмы
Тип неустойчивости
Дрейфово-Дйссипативная
Дрейфовая („универсальная")
Дрейфово-температурная
Дрейфовые неустойчивости
на запертых электронах и ио-
ионах
Токово-конвектйвная
Характерная
длина волны
rHi ^^l <^-a
Х±<гя.
^j_ ^ тт
^1 > rHi
Частота
tod
tod
tod
tod (a/R)l/2<
Апериодическая
Инкремент
нарастания
"*^C tod
CO
'^k\\VTe ^
<(a/R)lI2tod
от частот наиболее неустойчивых мод неустойчивости. Установле-
Установление же амплитуд пульсаций в возникающем нелинейном режиме
является наиболее трудной задачей. Из об-
общих соображений можно лишь заключить,
что неустойчивости с большим инкремен-
инкрементом нарастания, вообще говоря, должны
приводить к большим амплитудам. В ука-
указанном смысле полезно провести система-
систематизацию микронеустойчивостей равновесия
плазмы в магнитном поле на основе прове-
проведенного в § 2.14—2.16 анализа (табл. 2.1).
Спектры низкочастотных флюктуации
плазмы, возникающих из-за микронеустой-
микронеустойчивостей, которые наблюдались на токама-
ке в Принстоне, приведены на рис. 2.49.
Наиболее важным следствием турбулент-
турбулентных пульсаций, возникающих в результате
микронеустойчивостей плазмы, является
увеличение потоков частиц и тепла поперек
удерживающего плазму магнитного поля.
В среднем такое турбулентное просачива-
просачивание плазмы поперек Н носит диффузион-
диффузионный характер, поэтому часто говорят об
аномальных диффузии и тепло-
теплопроводности.
В случае, если возникающая турбу-
турбулентность может быть представлена в виде
суперпозиции большого числа слабо взаи-
взаимодействующих между собой элементар-
элементарных колебаний, явление аномальной диф-
16'
Рис. 2.49. Спектр флук-
флуктуации плотности плаз-
плазмы в токамаке, измерен-
измеренный методом рассеяния
пучка микроволнового
излучения. (Okabaya-
shi M., Arunasalam V.
«Nucl. Fusion». 1977, v. 7,
p. 497)
Верхняя граница спектра
(он резко обрывается при*
частотах 103 кГц) согласует-
согласуется с оценкой максимальной
частоты дрейфовых волн по-
формуле B.262) при
255
'фузии можно описывать на языке метода слабой турбулент-
турбулентности. Первым шагом в этой схеме является использование
.квазилинейного приближения. Функция распределения электро-
электронов (ионов), как обычно, разбивается на быстро осциллирую-
осциллирующую и медленно меняющуюся части. Ограничимся кинетическим
уравнением в дрейфовом приближении:
dfli [EXH0] f , H
Аномальная диффузия появляется при усреднении второго и
третьего членов этого уравнения, т. е. за счет пульсаций вследст-
вследствие электрического дрейфа и блужданий силовой л'инии магнит-
магнитного поля. Для 'простоты не будем рассматривать последний эф-
эффект (его физический смысл практически уже разобран в § 2.10
при обсуждении разрушения магнитных поверхностей). Поле ко-
колебаний Еу представим в виде
0
к
Выражение для быстро осциллирующей части уже /получено
в § 2.16 [см. формулу B.278)]. После обычной процедуры усред-
усреднения (для сравнения ом. § 1.16) получаем уравнение для мед-
медленно меняющейся части
A4 bLJL\F* Tm ! ( с д * е kz д
dt~~ 2J\h дх т ky ^zjyk <*-kzvz [ И дх ^ т ky dvz )
B.297)
Здесь в явном виде содержится диффузионный член с коэффициен-
коэффициентом диффузии резонансных частиц
D±=2 (cEydHfIm (V° - *A>- B.298)
k
Таким образом, задание спектра флуктуации электрического
ноля автоматически определяет скорость диффузии.
Любопытное вырождение возникает для мод с k (| =0:
где -у — мнимая часть частоты соответствующей моды. Модами
с k{l=0, в частности, являются двумерные (в плоскости перпенди-
перпендикулярной к Н) конвективные ячейки. Как и в обычной несжимае-
несжимаемой жидкости, они представляют собой движение апериодического
типа (Reco = O). Следовательно, остается лишь мнимая часть, свя-
связанная с затуханием. При наличии диффузионного размешивания
такое затухание равно yk = k2yD.,. Тогда B.298) переходит в
D±=2 (cEkyIH*J (l!k*yDJ- С2-2")
к
256
И в итоге для коэффициента аномальной диффузии получается,
иная, чем в B.298), зависимость от амплитуды флуктуации элек-
электрического поля:
D, = ( V — с2Е\ /#2\1/2 /о 300)
V к )
Самый трудный этап решения задачи об аномальном переносе
частиц и тепла заключается в нахождении спектра турбулентно-
турбулентности |?к|г- Квазистационарный спектр пульсаций, который уста-
устанавливается после развития неустойчивости, — результат действия
двух факторов: 1) вследствие неустойчивости энергия непрерывно
накачивается в неустойчивые моды пульсаций; 2) из-за нелиней-
нелинейного взаимодействия между модами энергия передается по спектру
в область затухания. Последний процесс для большинства микро-
неустойчивостей плазмы не укладывается в рамки приближения
слабой турбулентности. Приходится привлекать - размерностные
оценки, также как это делается обычно в теории гидродинамиче-
гидродинамической турбулентности.
Коэффициент диффузии можно записать в виде
D~v2vx. B.301)
Здесь Vp—'пульсационная скорость плазмы; т — характерное вре-
время исчезновения корреляции. В данном случае т~ 1/|т|> поскольку
здесь нет другого масштаба времени, характеризующего необра-
необратимость турбулентного режима. Амплитуду пульсаций определим
из следующих соображений. С одной стороны, -неустойчивость при-
приводит к нарастанию амплитуды пульсаций dvp/dt\~yvPj с дру-
другой— нелинейные члены типа (vV)v вызывают перекачку энергии
в те части спектра, где флуктуации затухают. Из условия баланса
между этими двумя процессами и определяется стационарное
значение амплитуды -пульсаций
IТ! VP ^ (vp!x I) vp> B.302)
где Х± — характерный размер турбулентных пульсаций поперек Н.
Определяя из B.302) vp ^ | у | Я±, получим
?>^[у|Я8г B.303)
Естественно в качестве Я взять длину волны неустойчивости.
Для максимального Я <v/ [A//г) (dn/dx)]^1 и инкремента
достигаемого при условии u>s^wd (см. §2.16), окончательно полу-
получим
D± ^ сТое/2ъеНь. B.304)
Коэффициент диффузии, принятый в гипотезе Бома, имеет такой
же -порядок величины. Нетрудно видеть, что при достаточно боль-
17—74 257
ших Но получился бы меньший коэффициент диффузии. В самом
деле, при неизменном ky и ограниченном снизу ?2^2ot/L с ростом
Но значение cos станет больше со^.
Значение магнитного доля #*, выше которого происходит ука-
указанное изменение режима турбулентной диффузии, можно оценить
из условия «>s^cod при ky~\la, fez~2jt/L. В результате получаем
e) 1/3^-4/3^-1^ B.305)
В высокотемпературной плазме с малой частотой соударений ve
практически всегда приходится иметь дело с гораздо большими
полями, следовательно, диффузия из-за дрейфово-диссипативной
неустойчивости не опасна.
§ 2.18. Энергетический баланс плазмы в токамаке
Бели неустойчивости в плазме подавлены, длительность удер-
удержания частиц и энергии в магнитных ловушках определяется про-
процессами диффузии и теплоотдачи. Изложим некоторые результаты
теоретического анализа закономерностей, которым 'подчиняются
эти процессы.
Для конкретности ограничимся случаем токамака, но в дейст-
действительности выводы будут иметь более общий характер. Диффу-
Диффузионная скорость потока 'плазмы иг направлена по 'малому ра-
радиусу, и, на первый взгляд, для ее определения можно восполь-
воспользоваться формулой для прямолинейного плазменного шнура:
иг=—(с*/о FP) dp/dr [ср. с формулой B.171)].
Однако диффузия плазмы в токамаке содержит дополнитель-
дополнительные слагаемые, играющие гораздо более важную роль. Отбросим,
не столь принципиальные дополнительные эффекты: сжатие плаз-
плазменного шнура, обусловленное взаимодействиехМ продольного тока
с создаваемым им азимутальным полем, дрейфовое движение
в вихревом электрическом поле, возникающем лишь при изменении
продольного поля Яе.
Ключевая роль принадлежит в рассматриваемом случае то-
тороидальной поправке «tor. В замкнутых системах дрейфовое дви-
движение частиц, вызванное тороидальной неоднородностью основно-
основного магнитного поля, должно было бы приводить к быстрому накоп-
накоплению объемных зарядов (рис. 2.50).
Из-за наличия тороидальной компоненты магнитного поля (#ф),
создаваемой в случае токамака током по плазме, эти заряды
должны компенсироваться вследствие перетекания вдоль силовых
линий. В результате возникает своеобразная перманентная цирку-
циркуляция зарядов: тороидальный дрейф все время стремится их раз-
разделить, движение же по ф со скоростью v^HJH возвращает из-
258
быток заряда обратно (см.
рис. 2.50). Рассуждая так же
как при выводе выражения для
скорости диффузии плазмы
поперек прямолинейного маг-
магнитного поля (см. § 2.9), не-
нетрудно заключить, что появле-
появление новых токов приведет
к дополнительной силе трения
между электронами и ионами,
а следовательно, и к дополни-
дополнительному дрейфу под действи-
действием этой силы. Проделаем нуж-
нужные выкладки, пользуясь ма-
математическим языком магнит- о ПСЛ ™
,; Рис. 2.50. Разделение зарядов из-за то-
нои гидродинамики. УСЛОВИЯ рОидального дрейфа и перетекание за-
равновесия по г и ф имеют вид ряда в тороидальной ловушке
,г = 0;] B.306)
B.307)
В качестве простейшего заменителя тороидальной силы снова
введем искусственную тяжесть FtOr=—pg, ориентированную, как
показано на рис. 2.50, вдоль направления от внутреннего к внеш-
внешнему обводу тора. Тогда
Считая, что в целом тороидальная поправка к равновесным пара-
параметрам плазмы р(г) и р(г) мала (т. е. выполнено условие г/7?<§С1),
из уравнения B.307) находим
p = po(r) +rp0(r)gcos<p. B.308)
Теперь это выражение нужно подставить в B.306). Нетрудно ви-
видеть, что получится уравнение, в котором некоторые члены вовсе
не зависят от угла «р, а другие члены пропорциональны cos ф. При-
Приравняв эти части нулю по отдельности,'получим
(обычное условие равновесия плазмы с прямыми силовыми линия-
линиями, в данном случае играющее роль нулевого приближения);
Это уравнение как раз и дает выражение для тока вдоль силовых
линий, компенсирующего разделение зарядов из-за тороидального
дрейфа, вызываемого силой Ftor.
17* 259
Скорость результирующего дрейфового движения и*г плазмы
под действием обусловленной током /9 силы трения (FB = jJenzei)
получаем из закона Ома
B.310)
B.311)
Итак, из B.309) и B.310) получаем
и\ - - сшг (dpjdr) g cos ф., Н\9
т. е. тороидальная поправка к диф-
диффузионному растеканию плазмы
оказывается знакопеременной по
углу ф. Картина такого растекания
скорее напоминает своеобразную
диффузионную конвекцию (рис.
2.51). Но если определить средний
поток плазмы по углу ф, то он ока-
оказывается отличным от нуля, и на-
направлен наружу. Действительно,
интеграл от потока частиц по углуф
дает
Рис. 2.51. Диффузионная
конвекция плазмы в тока-
маке вследствие конечной
проводимости
> = J л.(г)к^
Первый член в правой части обращается в нуль. Чтобы найти
8п(г, ф) —тороидальную поправку к плотности плазмы, будем счи-
считать, что температура плазмы однородна вдоль магнитной поверх-
поверхности, т. е. дп^бр. С учетом этого из B.308) находим
Ьп = (по[ро) Ьр = -g- rp0 (r) g cos <p.
Тогда
J bnu*rd<f = - (тггУ (dpjdr) g*PJo „Н\) (п.[р.) B.312)
Если ввести иг — усредненное значение диффузионной скорости,
разделив B.312) на 2япо(г), то для пг получим
иг*= -(г2/2) (с2 (dpjdr)
„H\pQ).
B.312а)
Возвращаясь к настоящей тороидальности, в частности к силе
2p/R вместо искусственной тяжести pg, для усредненной скорости
г/тор получаем
r).
B.313)
260
Сумму иг и t/тор можно рассматривать как эффективную диф*
фузионную скорость радиального потока плазмы в тороидальной
ловушке. В этом случае имеем
ф^ + 2-^^р. B.314)
Параметр q=^(r/R)(HB/H ) часто называют «коэффициентом запаса
устойчивости» (по отношению к винтовым возмущениям). В усло-
условиях экспериментов на установках токамак при г —а он обычно
лежит в пределах от 3 до 5. Величина q связана с углом вращения
силовых линий соотношением <q = 2n/Q. Формула B.314) эквива*
лентна следующему соотношению между эффективным значением
суммарного коэффициента диффузии и обычным коэффициентом
диффузии ?)°, соответствующим магнитному полю с прямыми
силовыми линиями (см. B.171)):
e,,)^t). B-315)
Если в нем выразить q через Q, то получается формула, справед-
справедливая также и для систем типа стеллараторов:
?rs = d°i О +8*1°1/QV- B.315а)
Эту формулу часто называют формулой Пфирша — Шлютера.
Второй член, характеризующий здесь тороидальную поправку
к коэффициенту диффузии для устойчивой плазмы, относительно
велик (на установках токамак отношение Dp.s/^)°j_ должно было
бы составлять 10—20). Но даже с учетом этой поправки скорость
диффузии оказывается небольшой. Однако практически в сущест-
существующих экспериментальных установках не удается получать плаз-
плазму, в которой все виды неустойчивости подавлены. Поэтому коэф-
коэффициент поперечной диффузии во много раз (на несколько поряд-
порядков) превышает значение коэффициента, вычисляемого согласно
Пфиршу и Шлютеру.
Однако нужно иметь в виду, что указанное выражение B.315)
для D. справедливо лишь в том случае, если плазма имеет
достаточно высокую концентрацию, и поэтому при вычислении
скорости потока частиц можно пользоваться магнитогидродина-
мическим приближением. Для этого необходимо, чтобы в каждом
элементе объема распределение частиц по скоростям было пол-
полностью изотропным.
В плазме с низкой концентрацией и высокой температурой
влияние тороидальное™ «а процессы переноса может быть более
сильным, чем указывалось выше. Это объясняется той ролью,
которую в таких процессах играют частицы, запертые в ограни-
ограниченных участках силовых линий между областями сильного поля.
261
При низкой концентрации такие частицы образуют в системе как
бы отдельный статистический ансамбль. Очевидно, что о сущест-
существовании отдельной группы запертых частиц можно говорить в том
случае, если за время колебания одной такой частицы между
точками отражения вероятность ее перехода из «запертого» со-
состояния в «пролетное» мала.
Очень грубую оценку коэффициента поперечной диффузии D'^
для запертых частиц можно получить при помощи соотношения
D'±^(krJ/^ B.316)
где Дг —смещение частицы в направлении, перпендикулярном к Я,
за 'промежуток времени ть- Примем Дг по порядку величины рав-
равным полуширине «банана»—серповидного сечения траектории за-
яертой частицы. Для того чтобы частица сместилась на расстояние
Дг, ее скорость должна повернуться на угол порядка Va/R (так
как для запертых частиц угол 0цМ составляемый направлением
скорости с плоскостью, перпендикулярной к Я, имеет порядок
величины У^ a/R, и .при изменении этого угла соответственно из-
изменяется ширина серповидного сечения).
Поскольку кулоновские столкновения носят характер много-
многократного рассеяния, 'при котором суммарный угол поворота ско-
скорости Да статистически складывается из «малых отклонений, то
время -л можно определить при помощи соотношения
Х[—т(ДаJ—xajJR, где <т— время между двумя соударениями
электрона с ионами.
Подставляя в B.316) выражения для Дг и п, находим
D\^{r\eh){H\lH\), B.317)
где г не — ларморовский радиус электронов.
Отношение концентрации запертых частиц к концентрации всех
частиц в плазме порядка Уа/R. Поэтому эффективный коэффици-
коэффициент диффузии плазмы должен быть порядка D'^Y^a/R. Окончатель-
Окончательно, с учетом численного множителя, для получения которого по-
потребовалось бы воспроизвести громоздкие вычисления так назы-
называемой неоклассической теории переноса, коэффициент диффузии
равен
Эта величина превышает тороидальную поправку в формуле
B.315) в отношении (R/rK12, т. е. для существующих установок
по ^меньшей мере в несколько десятков раз. Таким образом, ока-
оказывается, что при чисто классическом (ламинарном) рассмотрении
эффект тороидальное™ может увеличить диффузионный поток
в 'плазме низкой плотности в 1000 и более раз.
262
Проведем наглядное сопо-
сопоставление скоростей диффузии
в двух рассмотренных пре-
предельных случаях: магнитогид-
родинамическом и так назы-
называемом банановом — построим
условный график зависимости
коэффициента диффузии от ча-
частоты столкновений ve= 1 /те
(рис. 2.52). Условность такого
представления очевидна хотя
бы из того, что в действитель-
действительности выражения B.315) и
B.318) для коэффициентов
диффузии содержат прямую
зависимость коэффициента от
' IV
/// 1 / //
I /
1/
I
Ч Нд f
11
Рис. 2.52. Зависимость коэффициента
диффузии плазмы от частоты соударе-
соударений:
/ — магнитогидродинамический режим; // —*
область плато; /// — банановый режим
ффца от
температуры помимо зависимости ve от температуры. В обоих
предельных случаях ход D(ve) изображается прямыми. Наклон
?>G.s(ve) (в банановом режиме) в 3,6(JR/аK/2 раза больше. Этот
режим реализуется при
ve<(r/Rf2(HJHb)(vTJr).
Если это условие не выполнено, то запертые электроны не успе-
успевают описать бананообразную траекторию. Да и само разделение
электронов на запертые и пролетные теряет смысл.
Магнитогидродинамический предел, в свою очередь, наклады-
накладывает ограничение на частоту столкновений ve снизу. Для приме-
применимости гидродинамического приближения необходимо, чтобы
длина свободного пробега была существенно меньше характерного
пространственного размера. Для продольного (вдоль Я) движения
электронов в качестве такого размера следует выбрать гНь/Н —
среднее расстояние вдоль силовой линии -между областями с мак-
максимумом и минимумом поля в тороидальном витке. Следовательно,
в режиме частых столкновений
9
Видим, что рассмотренные пределы банановой и магнитогидроди-
намической диффузий разделены на рис. 2.47 областью, где час-
частота столкновений лежит в интервале
Kir) (HJHJ (r[Rf2<ve<(vTe[r) (HJHB). B.319)
Практически это довольно широкий интервал, так как ,(#/гK'2»1.
^Как же ведет себя коэффициент диффузии в этой промежуточ-
промежуточной области? Ответ на этот вопрос следует из «неоклассической»
теории диффузии: в интервале B.319) практически исчезает за-
зависимость от частоты столкновений. Можно сказать, что этот ответ
является наиболее неожиданным результатом «неоклассической»
теории. Физический смысл этого результата становится более
263
понятным, если воспользоваться аналогией с затуханием Ландау.
Неоднородная часть тороидального магнитного поля магнитной
ловушки как бы играет роль поля волны (в данном случае -следо-
-следовало бы назвать ее магнитостатической). Запертые частицы вполне
аналогичны резонансным частицам в механизме затухания по
Ландау. А вместо силы трения F9 = jB/ne*ei выступает сила тре-
трения электронов о магнитостатическую волну, как бы играющую
роль посредника между электронами и ионами. Эта аналогия су-
существенно упрощает выкладки.
Итак, тороидальное магнитное поле #Q = #O[1 — (r/R) cos 9]. Не-
Неоднородная добавка 6#=—#0(r//?)-cos<p, как уже говорилось,
имитирует лоле волны. Вызываемая ею поправка f{ к искомой
функции распределения «резонансных» (запертых) электронов
удовлетворяет линеаризованному кинетическому уравнению
+ (с/еН0) р (grfcd S#)9 (df./dr) = - vj,. B.320)
Здесь индексы || и ср означают выбор компонент grad6# вдоль
силовой линии и оо ф соответственно. Второе слагаемое в B.320)
конкретизирует член —(\x/m)gvadH(df/dvI а третье слагаемое
описывает влияние дрейфа резонансных частиц в неоднородном
магнитном поле. Отсутствие традиционного члена —iofi означает,
что резонансными являются частицы с 1>„«0, как и следовало
ожидать. Учитывая, что
(grad 8Я) „ = - (HJR) sin <? (HJHJ;
(gradStf)9 = (#„/#) sin 9,
после несложных выкладок, напоминающих вычисления в § 2.7
[см. вывод формулы B.108)],, находим решение уравнения B.320):
ехр(±
Далее по аналогии с тем, как в теории затухания Ландау вычис-
вычислялась работа поля волны над резонансными частицами (j*E),
найдем радиальный поток резонансных частиц из-за тороидального
дрейфа (ntir):
^^ B.322)
В этом выражении интегрирование по ф, и d\{] заменяет инте-
интегрирование по пространству скоростей. Так как знак дрейфа яв-
264
ляется знакопеременным по углу ф, то «мы усреднили это выраже-
выражение также по всем углам ф. При вычислении интеграла по ?>ц
следует учесть, что
1га . и .,,. . -,• . = ± ^т-1 5 (v„)
(Hy/tfjv^/r+iv tf9 v IK
(при v-й), рассуждая так же, как и при вычислении резонансного
полувычета, соответствующего затуханию Ландау). В конце кон-
концов, несложные выкладки с учетом B.321) и B.322) для равно-
равновесной функции распределения вида fo=n(r)fM (/м — максвеллов-
ское распределение) дают
(cTJeHJidnfdr).
Таким образом, для коэффициента диффузии в 'промежуточной
области частот столкновений (ее принято называть областью нео-
неоклассического плато — см. рис. 2.52) имеем
D\ = уЩ(ттНе[^) (cTJefty. B.323)
Зависимостью аналогичной той, которая изображена на рис. 2.52
для D. (ve), обладает и коэффициент температуропроводности, по-
поскольку перенос тепла поперек магнитного поля в тороидальном
витке определяется такими же дрейфовыми движениями частиц,
прерываемыми время от времени столкновениями. Особенно важ-
важную роль должна играть ионная температуропроводность из-за
большого элементарного шага перескоков ионов. Ведь толщина
ионных «бананов» в rm/гне раз больше. Опуская выкладки, ана-
аналогичные только что 'проделанным, приведем коэффициент темпе-
температуропроводности ионов в режиме плато:
Хр±1 = C/2) У^(ггш1ЯГ) (cTtfeHJ. B.324)
Отсюда видно, что скорость теплоотвода в режиме плато растет
с температурой ионов как 73/2г-. Чем сильнее нагреваются ионы,
тем больше они отдают тепло в результате теплопроводности.
Поэтому в течение длительного времени рост температуры ионов
существенно отставал от роста мощности нагрева в современных
лабораторных установках.
В банановом режиме согласно неоклассической теории пере*
носа ионная температуропроводность
!Н\). B.325)
Скорость теплоотвода с ростом температуры в этом режиме долж-
долж1/2
на падать как Т71/2.
Однако выйти в банановый режим оказалось не так-то просто.
Входящая в условие
B.326)
265
частота столкновений ионов водородной плазмы в реальных усло-
условиях эксперимента, по-видимому, увеличена из-за столкновений
с многозарядными ионами примесей. Во всяко-м случае, в настоя-
настоящее время режим плато в токамаках преобладает,
it f Процесс изменения режима «неоклассического» переноса с рос-
ростом температуры удобно проследить с помощью семейства зависи-
зависимостей Хи (п)> соответствующих различным температурам (рис. 2.53)-
Каждая из изображенных кривых ведет себя аналогично x±i (v/)
при фиксированной температуре. В области плато Xjj тем боль-
больше, чем больше Г. Однако границы этой области для разных
кривых не совпадают. С ростом температуры v* должна падать,
и в конце концов нагрев плазмы при /г=const должен привести
к «банановому» режиму.
Рис. 2.53. Семейство зависимостей
X i / (п) (аналогично ведет себя и ко-
коэффициент диффузии) при трех фик-
фиксированных значениях температуры
согласно «неоклассической» теории.
Изменение режима переноса тепла при
нагреве показано стрелкой A-+2-+3). При
достаточно большой температуре режим
1лато сменяется банановым режимом.
Наличие примесей с большим зарядом мо-
может затянуть режим плато. Смещение гра-
границ плато при увеличении концентрации
примеси показано стрелками D)
На рисунке стрелка-ми показана последовательность смены ре-
режимов теплоотвода; рост X±t(T) в области плато сменяется па-
падением в банановом режиме. Пунктиром показано изменение
зависимости х^(я)как результат увеличения v* (при наличии при-
примесей).
В условиях джоулева нагрева плазмы при протекании по ней
тока CfB9 создающего полоидальное поле Н , температура электро-
электронов, как правило, оказывается значительно выше ионной. Баланс
тепла в ионной компоненте является следствием конкуренции
между передачей энергии ионам при их столкновениях с электро-
электронами и «неоклассическим» тепло отводом. Так называемый
скейлинг (зависимость от основных параметров) для ионной
температуры в этом случае несложно установить, рассуждая сле-
следующим образом. Передача тепла от электронов ионам пропорцио-
пропорциональна n(Te — Ti)\T*J2 [см. формулу A.17а)]. Потерю тепла
ионами оценим, считая, что тю порядку величины в уравнении теп-
теплопроводности ATi~Ti/r2. Тогда nTi/x^nx±i(Ti/r2). Из условия
баланса тепла имеем соотношение пропорциональности
/гг% rjy \ /rjio/2 /rT* /,#/.2\ /О QO7\
ft \1 е i i)l I *V/ /.. yl ilГ ). (Z.oZl)
266
Для отношения (Те — T^jJ^J2 удобна интерполяция (Те —
^ 0,33 УТ19 освобождающая от Те. В интервале изменения пара-
параметра Те/Тг от 1,6 до 10 погрешность такой интерполяции не боль-
больше 15%. Это вполне допустимо для экспериментов на токамаках.
Теперь, подставляя х 11 в соответствии с формулой B.324), из
B.327) нетрудно найти, что температура ионов подчиняется скей-
лингу*
Ti^{IBHbR2tifl2>. B.328)
При выводе B.328) полоидальное поле Н выражено через ток IQ
с помощью очевидного соотношения Яф^= с1в [г. Удивительно, на-
насколько хорошо результаты измерения ионной температуры в то-
Рис. 2.54. Экспериментальные ре-
результаты исследования зависимо-
зависимости ионной температуры в тока-
маке от силы тока и амплитуды
магнитного поля.
Прямые / и // соответствуют измене-
изменению ионной температуры, вычисленно-
вычисленному на основе «неоклассической» тео-
теории при двух различных предположе-
предположениях о радиальном распределении то-
тока и плотности. Прямая / соответст-
соответствует однородному распределению плот-
плотности и тока, прямая // — случаю
п^(\—r2ja2), /g ^.A— г2/а2). Точки—
результаты эксперимента Q 1 2 5 4 5 5 7 8 (I$H9R2n)i/J
камаках с омическим нагревом укладываются в рамки такого
скейлинга (рис. 2.54).
Процессы установления баланса тепла по электронной компо-
компоненте оказалось невозможным объяснить на основе «неоклассиче-
«неоклассической» теории: слишком уж мала вытекающая из нее теплопровод-
теплопроводность плазмы (в Гт/гне раз меньше ионной). Поэтому даже сла-
слабые остаточные неустойчивости (скорее всего из семейства дрей-
дрейфовых) вызывают дополнительную утечку тепловых электронов.
Для 'прямого одноступенчатого нагрева ионов можно использо-
использовать энергию пучков быстрых ионов, инжектируемых извне в плаз->
му (первоначально в виде пучков нейтральных, быстро теряющих
связанный электрон, атомов тяжелого водорода). Надо только
убедиться, что энергия этого пучка не будет перехватываться
электронами.
Если тепловая скорость электронов значительно превышает
тепловую скорость ионов, то формула A.17а) остается справед-
справедливой также и при Т{^>Теу т. е. в том случае, когда происходит
нагрев электронов более горячей ионной компонентой. Перепишем
* Это соотношение сейчас широко известно под названием «формула Арци-
мовича». — Прим. Р. 3. Сагдеева
267
для этого случая указанную формулу в виде
Qie = A,2-10- 17/А) п G\ - Te)IT3J\ B.329)
где Qie — энергия, передаваемая от ионов к электронам в единице
объема за 1 сек. Однако если в .плазме с холодными электронами
постоянно присутствуют горячие ионы, так что Утг^^ге, то ско-
скорость теплообмена может значительно возрасти. Рассуждая так
же, как и при выводе формулы B.329), мы при указанном условии
приходим к следующей формуле теплопередачи:
Qt.e = 2.2-10-14/z/j/77, B.330)
Из 'сравнения формул B.329) и B.330) вытекает интересное
следствие, демонстрирующее одно из специфических свойств вы-
высокотемпературной 'плазмы. Предположим, что через 'плазму про-
проходит быстрая тяжелая заряженная частица с энергией в интер-
интервале от 105 до 10б эВ. Основные потери энергии у такой частицы
будут обусловлены столкновениями с электронами плазмы, и имен-
именно этот физический механизм должен определять длину пробега
быстрой частицы в плазме. Если движение происходит в водород-
водородной плазме и при этом скорость частицы vTi^>VTe, то для грубой
оценки торможения частицы можно пользоваться формулой
B.330), полагая 7\=B/3)oy, где w — энергия частицы. При этом,
как 'показывают аналогичные подсчеты, потери энергии частицы
на единицу массы пройденного вещества в плазме будут того же
порядка, что и в нейтральной среде. Однако положение сущест-
существенно изменится, если заставить частицу проходить через плазму
с достаточно высокой электронной температурой. Если даже
7^<С B/3) до, но VTe^Vru то потери энергии значительно умень-
уменьшаются и будут определяться формулой
Qie ^ (l,210-17/^) n FilTf). B.33П
Здесь Qie — энергия, теряемая частицей за 1 сек; А — масса части-
частицы (для протона Л=1). Уменьшение Q означает соответствующее
увеличение пробега частицы. Если на своем пути в плазме частица
может генерировать ядерные реакции, то общий выход реакций
во много раз возрастет при увеличении электронной температуры
(если, конечно, нам удастся заставить быструю частицу пробыть
в плазме достаточно долгое время).
Рассмотрим интересный пример, принадлежащий одному из ав-
авторов (Л. А. Арцимовичу). Пусть пучок быстрых дейтонов про-
проходит через тритиевую плаз'му. Если температура плаз'мы невели-
невелика, то выход реакций будет очень мал. При w^lOO кэВ вероят-
вероятность того, что частица испытает в плазме с близкой к нулю
температурой на полной длине своего пробега одно ядерное столк-
столкновение, составляет 2-10~б. Энергетический КПД, т. е. отношение
Освобождаемой ядерной энергии к начальной энергии дейтонов,
близок к 0,04%. Вероятность и энергетический КПД реакций
268
Последние (факсимиле) страницы рукописи академика Л. А. Арцимовича,
быстро возрастают с увеличением Те и при Ге^6-103 эВ КПД
приближается к единице, а при Ге^104 эВ значительно ее превос-
превосходит. Таким образом, в принципе появляется возможность энер-
энергетического использования "реакций D + T-^-He + я в режиме про-
прохождения потока быстрых заряженных частиц через 'плазму с до-
достаточно высокой электронной температурой. В 1961 г., когда были
проведены эти оценки, такая перспектива казалась практически
маловероятной. Однако в настоящее время появилась возможность
инжектирования быстрых ионов в «магнитные ловушки» с боль-
большим временем жизни заряженных частиц (например в токамаки).
По отношению к такому пучку горячая плазма может служить
эффективной «ядерной мишенью». В результате ионы плазмы ока-
оказываются двух сортов: тепловые и быстрые. Этот вариант токама-
ка называют «двухкомпонентным». Все же, по-видимому, более
важное значение будет иметь использование такого метода инжек-
ции для простого повышения ионной температуры плазмы. Осо-
Особенно успешным оказалось применение такого метода нагрева на
токамаке PLT в Принстоне (рис. 2.55).
Инжектор
Рис. 2.55. Принципиальная схема, показывающая расположение инжекторов ней-
нейтральных частиц вдоль большого периметра токамака PLT в Принстонской
плазменной лаборатории.
При суммарной мощности инжекции Р^Л,Ъ МВт в плазме с плотностью п^Ъ • 1013 см~э
(в центре) была получена температура ионов Гс^,5,5 кзВ. При этом ионы оказались
в банановом режиме с коэффициентом теплопроводности в несколько раз меньше, чем
по скейлингу для «плато». (Препринт PPL-783851, Принстонская плазменная лаборато-
лаборатория, 1978.)
270
В энергетическом балансе плазмы, запертой в магнитной ло-
ловушке, лри некоторых условиях заметная роль может 'принадле-
'принадлежать так называемому магнитному или бетатронному излучению,
связанному с ларморовским вращением электронов. Для электро-
электрона, движущегося в магнитном поле Н по винтовой линии с центро-
центростремительным ускорением v2. /rHey энергия, излучаемая в еди-
единицу времени, определяется выражением
dW/dt = B/3) г\ A +
(v\(c) H\
\
B.332)
где г0 — классический радиус электрона; хюе — кинетическая энер-
энергия электрона (в 'интересующих нас случаях we<.m0c2).
Спектр излучения для отдельного электрона линейчатый. Он
состоит из основной линии с ларморовской частотой сояе и ее гар-
гармоник. Вследствие эффекта Доплера -с учетом релятивизма частота
(оп п-й гармоники оказывается зависящей от компонент скорости
частицы v. и v, !и угла 9, под которым наблюдается излучение
и направление магнитного поля:
»n = n*HV\-v4c4[\-(vJc) cost].
Если энергия электрона достаточно мала по сравнению с т0с2,
то главная часть излучаемой энергии должна приходиться на
основную частоту. С ростом we доля высших гармоник в общей
интенсивности излучения быстро увеличивается. Если предполо-
предположить, что вся излучаемая энер-
энергия уходит из плазмы, то потери
энергии на магнитное излучение
в плазме превосходили бы выделе-
выделение энергии, обусловленное термо-
термоядерными реакциями в магнитных
ловушках. Следовательно, если бы
магнитное излучение могло свобод-
свободно выходить из плазмы, оно пред-
представляло бы одно из главных пре-
препятствий для сооружения термо-
термоядерного реактора с положитель-
положительным энергетическим балансом.
Однако в действительности боль-
большая часть магнитного излучения,
которая относится к основной ча-
частоте и первым гармоникам, погло-
поглощается, не выходя из плазмы, и
только излучение, принадлежащее
сравнительно слабым высшим гар-
моникам выходит через границу магнитотормоз-
плазмы без существенного ослаб- ного ИЗЛучения, выходящего из
ления. плазмы
271
Упрощенно излучение, в конце концов выходящее из плазмы,
можно представить 'себе как суперпозицию равновесного излуче-
излучения (по Рэлею — Джинсу) при малых частотах я</г* (здесь п —
номер гармоники), где важен эффект перепоглощения, и высоко-
высокочастотной доли излучения электронов плазмы я>д*, практически
свободно покидающей плазму. Оценку /г* можно сделать, считая,
что при п=п* обе ветви спектральной интенсивности излучения
(Рэлея — Джинса и прямого излучения электронами) сравнивают-
сравниваются по порядку величины.
Рис. 2.57. Магнитотормозное излучение релятиви-
релятивистских электронов в межзвездном магнитном поле
является главным источником наблюдаемого ра-
радиоизлучения нашей Галактики и других галак-
галактик, радиогалактик, а также остатков вспышек
сверхновых и квазаров.
Здесь приведен спектр радиоизлучения радиогалактики
Лебедь А. Радиосветимость около 1045 эрг/с (б). Спек-
Спектральная деталь вблизи ^,@=56 кэВ в спектре рентге-
рентгеновского излучения пульсара НегХ-1, обнаруженная при
рентгеновских наблюдениях с баллона (Trumper J. е а
«Astrophys. J. Lett», 1978, v. 219, p. 105. Максимум при
56 кэВ интерпретируется как излучение горячей плазмы
на циклотронной частоте и соответствует напряженности
магнитного поля 5 • 1012 Гс (б)
10
Представление о результатах, полученных в строгой теории
переноса излучения, может дать рис. 2,56, на котором изображено
спектральное распределение интенсивности магнитного 'излучения,
выходящего из -плоского слоя плазмы, для случая 8ппТ/Н2=1. По
оси абсцисс отложена частота в единицах со#е, а по оси ординат —
распределение интенсивностей- по спектру. Масштаб по оси орди-
ординат выбирается таким образом, чтобы спектр черного тела в об-
области низких частот (т. е. там, где он соответствует закону
Рэлея—Джинса) изображался параболой у=2х2.
Так как вследствие поглощения спектр излучения плазмы дол-
должен зависеть от толщины излучающего слоя, ее удобно выражать
в безразмерных единицах. Безразмерная толщина слоя а0 опре-
определяется соотношением ао= Dпп0е/Н)а, где а —толщина слоя
в сантиметрах. Графики, приведенные на рис. 2.56, построены для
случая, когда ао=1О4. Различные кривые изображают спектр маг-
магнитного излучения, соответствующий разным значениям темпера-
температуры -плазмы. Если при не слишком высоких Те на спектральной
272
кривой ясно видны отдельные гармоники, то при более высоких'
температурах кривые имеют форму, характерную для сплошного*
спектра.
Из-за эффекта Доплера при высоких температурах отдельные-
линии, принадлежащие к высоким гармоникам, сливаются друг
с другом.
В предельном случае сверхсильных магнитных полей (имею-
(имеющих смысл для астрофизических приложений), магнитотормозное-
излучение смещается в рентгеновскую часть спектра. На рис. 2.57,б
изображен спектр такого излучения от нейтронной звезды Нег-Х»
§ 2.19. Аномальное сопротивление в плазме
и образование двойных слоев
Среди большого разнообразия неустойчивостей плазмы имеет'
смысл отдельно выделить те, которые не зависят или почти не
зависят от специфики краевой задачи, будь то конкретная геомет-
геометрия лабораторной плазменной установки, тип равновесной кон-
конфигурации плазмы или формы ее течения. Одним из важнейших,
классов таких неустойчивостей, безусловно, следует считать не-
неустойчивости плазмы с током, плотность которого превышает опре-
определенное критическое значение.
Самым распространенным примером является ионно-звуковая
неустойчивость (см. § 1.12). Если причиной, вызывающей неустой-
неустойчивость, является превышение некоторого критического значения
тока, то из общих соображений ясно, что рост такой неустойчиво-
неустойчивости должен автоматически привести к механизму, ограничиваю-
ограничивающему рост тока. Иначе говоря, должно появиться дополнительное
электрическое сопротивление — так называемое аномальное..
Итак, пусть электронная функция распределения имеет неко-
некоторую скорость и0 относительно ионной функции распределения,
Таблица 2.2'
Неустойчивости плазмы с электрическим током, относящиеся
к проблеме аномального сопротивления
Тип неустойчивости
Неустойчивость Буне-
мана
Ионно-звуковая
Электростатически е
моды k2± > k2z
Неустойчивости наv
гармониках циклотрон-
циклотронной частоты
Порог неустойчивости
и0 > vTe
*o>(Te/mi)l/2
Очень низкий, иногда
<vTl
Частота
Инкремент возрастания
<ьни / vTe
18—74
273
превышающую критическое значение для возникновения неустой-
неустойчивости. Вследствие такой неустойчивости электроны в дополнение
к обычной потере импульса из-за парных столкновений теряют
-еще часть его с 'излучением колебаний и волн различного типа.
Рассмотрим таблицу неустойчивостей такого типа, возникающих
лри превышении критического значения скорости. В табл. 2.2 пере-
перечислены основные неустойчивости, имеющие отношение к проблеме
аномального сопротивления в плазме. Простейшая неустойчи-
неустойчивость— это неустойчивость Бунемана (см. § 1.12). Исходные
функции распределения электронов и ионов в этом случае имеют
вид двух 6-функций, сдвинутых друг относительно друга на вели-
величину средней скорости щ. Неустойчивость представляет собой
раскачку продольных электростатических колебаний плазмы со
скоростью нарастания порядка плазменной ионной частоты.
Другой пример неустойчивости, которую практически можно
¦считать модой того же типа, — это уже упоминавшаяся неустойчи-
неустойчивость йонно-звукового типа. Эти колебания возникают при дрей-
дрейфовых скоростях электронов щ9 меньших тепловых скоростей. По
порядку величины инкремент нарастания ионно-звуковых колеба-
колебаний— это плазменно-ионная частота, уменьшенная в отношении
дрейфовой скорости электронов к тепловой. В предельном случае
U(r+-VTe ионно-звуковая неустойчивость почти ллавно переходит
,в бунемановскую неустойчивость.
При наличии магнитного поля появляются и другие типы не-
неустойчивостей. Одна из них, также обязанная своим появлением
электронной (Мнимой части (электронного полувычета) в ионно-
циклотронных волнах, называется неустойчивостью Драммонда—
Ррзенблюта. Она возникает тогда, когда ток протекает вдоль
магнитного поля, в то время как первые две неустойчивости в из-
вестно'м смысле инвариантны л о отношению к существованию
магнитного поля, если оно не очень велико (соне<С(Оре). Неустой-
Неустойчивость Драммонда — Розенблюта, по-видимому, не создает за-
заметного аномального сопротивления, потому что она приводит
к небольшим скоростям нарастания флуктуации и, по-видимому,
легко подавляется простыми квазилинейными эффектами, типа
эффекта образования плато.
Более важную роль может играть класс неустойчивостей отно-
относительно электростатических возмущений k2±^>k2z. Иначе говоря,
это волны, у которых составляющая волнового вектора вдоль маг-
магнитного поля значительно меньше поперечной составляющей вол-
волнового вектора, а частоты значительно меньше электронной л ар-
моравской частоты, но больше ионной. Эта мода напоминает моду,
.возникающую при наличии конуса потерь (см. § 2.8):
со — kv { k2 \ со — ku0 — kzv2
B.333)
274
В приближении со>А^Гг, kno^kz\Te уравнение B.333) переходит
в дисперсионное уравнение для так называемой модифицирован-
модифицированной неустойчивости Бунемана:
B.334)
Инкремент нарастания по порядку величины равен
при
krHe ъ1,кг = kuJvTe. B.334a>
Приближение B.334) справедливо, если дрейфовая скорость замет-
заметно превышает vTi. Если это условие не выполнено, имеют места
неустойчивости кинетического типа:
Re (ш- ku.) ^ кг (Ttltne)l/2[(\
Im да=: «1/2 rnrfcr((й ~kUo):
B.335}
Неустойчивости такого типа имеют место, когда ток течет перпен-
перпендикулярно к магнитному полю.
Самой сложной проблемой является связь между линейной тео-
теорией неустойчивости и величиной аномального электрического со-
сопротивления в состоянии, когда наступает нелинейное насыщение
роста неустойчивости. Для решения этой проблемы прибегают
к мобилизации арсенала методов нелинейной теории поля в плаз-
плазме, теории слабой турбулентности (см. § 1.16—1.18), размерност-
ных оценок (в тех случаях, когда возникающая при аномальном,
сопротивлении турбулентность оказывается сильной) и т. д.
Приведем некоторые общие рассуждения, практически не зави-
зависящие от конкретной модели нелинейной стадии. Строгая постанов-
постановка задачи о проводимости а должна проводиться с учетом обмена
импульсом между электронами и колебаниями. Обычная формула
для проводимости плазмы G=ne2/mv содержит частоту столкнове-
столкновений электронов v с рассеивающими центрами (ионами, нейтраль-
нейтральными атомами) по отношению к потере импульса. Если электроны
плазмы раскачивают некоторые типы .колебаний или волн ©след-
©следствие неустойчивости, то имеет место аномальная потеря импульса
(передача колебаниям, т. е. коллективным движениям ионов). Для
нахождения veff можно воспользоваться законом сохранения коли-
количества движения в системе электроны — волны. Средняя потеря
импульса электронами за единицу времени равна
VefftfVZoUo^s—F. B.336)
18* 275
Если этот .импульс передается волнам с плотностью энергии
то изменение количества движения волн равно
B.337)
где Y*k — вклад электронов в мнимую часть частоты. Приравнивая
<2.336) и B.337), получаем
veHmnono ^ j fkWk (к/шк) [dk/W], B.338)
т. е.
veff = a/mnQu0) J fkWk ± [ik/B*K]. B.339)
Таким образом, задача сводится к нахождению W' у* следует
понимать в квазилинейном смысле.
В справедливости соотношения B.338) можно было бы убе-
убедиться и с помощью квазилинейного уравнения диффузии для элек-
электронов на примере ионно-звуковых колебаний.
Наличие аномального сопротивления приводит к аномальному
выделению джоулева тепла в плазме /2/aeff. Такой нагрев плазмы
часто 'называют турбулентным, поскольку механизмом, определяю-
определяющим природу аномального сопротивления плазмы, является тур-
турбулентность, вызванная неустойчивостью. При отсутствии парных
соударений турбулентный нагрев неодинаков для электронной и
.ионной компонент плазмы. Более того, нельзя даже говорить о воз-
возрастании температур электро-нов и ионов, подразумевая темпера-
температуры в традиционном смысле (максвелловского распределения ча-
частиц). Под температурой таких плазм обычно условно понимают
средние хаотические энергии компонент.
Как правило, в процессе турбулентного нагрева ллазмы быстрее
увеличивается температура электронов. Можно установить простой
критерий, связывающий скорость нагрева электронов со скоростью
нагрева ионов. Вывод такого критерия основан на использовании
законов сохранения .количества движения и энергии пр«и взаимо-
взаимодействии электронов и ионов с колебаниями. На электроны плазмы
действует сила трения
F=—vefftfomuo. B.340)
Работа этой силы, очевидно, затрачивается «на нагрев электронов
плазмы:
dwjdt ^ veumeu\ = A//О j Цг fkWk (k uo)/«>k. B.341)
В стационарном состоянии насыщения, достигаемого, когда рост
неустойчивости ограничивается нелинейными эффектами, количест-
количество движения колебаний (а вместе с тем и их энергия) передается
ио'нам. Таким образом, в состоянии насыщения ионы должны по-
276
глощать энергию колебаний со скоростью порядка f T\^V^k'
В результате нагрев ионов должен происходить со скоростью
dwjdt^ilfn,) J fkWkdklB*y. B.342)
Теперь разделим уравнение B.341) на B.342):
dwjdwt 'v, j fkWk (k.u,/»k) dk I j.fkirkdk. B.343)
Если в формуле B.343) приближенно положить
J 4\Wk <*«./»k)dk ~ (* • uohk) J YWk«
то для отношения скорости нагрева электронов к скорости нагрева
ионов получим оценку
dweldwi~uo((ol\k). B.344)
Это соотношение в том виде, в котором оно получено, не зависит
от типа неустойчивости -и поэтому носит универсальный характер.
Для большинства неустойчивостей оно действительно приводит
к более быстрому нагреву электронов. Так, при ионно-звуковой не-
неустойчивости, как правило, &0>со/& и, следовательно, dwe\dw{^>\.
Для этого примера полезно привести выражение B.339) к бо-
более наглядному виду. Подставим в него максимум инкремента
нарастания колебаний ионно-звукового типа у*к^оШо/?>ге, достигав-
мый при k^f^. Тогда получим следующее соотношение:
veff—cop№>07V B.345)
Таким образом, зная плотность энергии колебаний W в режиме
насыщения неустойчивости, можно было бы найти veff. Для нахож-
нахождения W в нелинейной теории плазмы имеется регулярный метод—
теория слабой турбулентности. Но этот метод не всегда применим.
Даже простейший случай неустойчивости Бунемана следует рас-
рассматривать с позиций сильной турбулентности. Существующие тео-
теории сильной турбулентности могут претендовать лишь на оценки
по порядку величины.
Ионно-звуковая неустойчивость представляет собой удобный
пример исследования с помощью метода слабой турбулентности.
Мнимая часть частоты в данном случае значительно меньше, чем
ее действительная часть, поскольку дрейфовая скорость может
быть много меньше средней тепловой скорости электронов. Нели-
Нелинейной теории ионно-звуковой неустойчивости и вычислению ано-
аномального сопротивления посвящено много работ. Остановимся на
этом вопросе несколько подробнее. Плотность энергии Wk моды
колебания ^ волновым вектором к нарастает дри малых амплиту-
амплитудах экспоненциально. Затем при больших амплитудах должны
включаться эффекты нелинейного насыщения и, возможно, возник-
277
нет установившееся или квазиустановившееся состояние. Тогда
можно найти спектр W , компенсируя линейное нарастание одним
из эффектов, связанных с нелинейным насыщением. Нелинейный
член, исходя из соображений размерности, символически предста-
представим в следующем виде:
О = {2Тк - Аок (W/nJe)} Wk. B.346)
Для ионно-звуковых колебаний запрещены резонансы трехвол-
новых взаимодействий (см. § 1.18), поэтому единственным эффек-
эффектом, который дает член порядка W2, может быть эффект нелиней-
нелинейного рассеяния волны на ионах (см. § 1.17). Это эффект, который
обусловлен наличием знаменателей типа со—со'—(к—к') -v, т. е.
резона-нсов Ландау на нелинейных биениях, возникающих от каж-
каждой произвольно выбранной пары волн. Эти биения попадают
в резонанс с ионами, и часть энергии поглощается, а другая часть
переходит в волну с меньшей частотой. На самом деле квадратич-
квадратичный член представляет собой некое довольно сложное интеграль-
интегральное выражение, слишком громоздкое для целей данной книги.
Величину этого члена оценим следующим образом: так как данный
эффект связан с тепловым движением .ионов, то оператор А лро-
порционален малому множителю Т{/Те (поскольку речь идет об
ионном звуке, то по определению необходимо, чтобы Тг<.Те). По-
Поскольку он безразмерен, предположим, что он просто равен
A<^Ti/Te. Эту оценку подтверждает строгая теория слабой турбу-
турбулентности. Итак,
W^lO-HTe/Ti) (uolvTe)nTe. B.347)
Численный множитель дает строгая теория. Это приводит к следую-
следующей формуле для эффективной частоты соударений:
(Te/Ti). B.348)
Таким образом, если бы по плазме удавалось пропускать ток,
существенно превышающий критическое значение, так что элек-
электроны теряли бы импульс из-за когерентного излучения фононов,
т. е. ионно-звуковых колебаний, то в ко-нце концов установился
бы некий стационарный спектр, и veff определялась бы формулой
B.348).
Укажем, что если по плазме с первоначально изотермическими
ионами и электронами (ионно-звуковые колебания невозможны)
протекает ток в режиме аномального сопротивления вследствие
неустойчивости Бунемана, то рано или поздно этот режим должен
смениться на .ионно-звуковой. Это связано с тем, что электроны,
как было отмечено, нагреваются в kuo/ы раз быстрее, чем ионы, и
плазм'а в конце концов становится неизотермической. Ионно-зву-
ковая же неустойчивость в этом смысле является самоподдержи-
самоподдерживающейся, так как при ио^с8 электроны всегда получают больше
тепла, чем ионы.
278
В рассмотренной модели аномального сопротивления имеется
трудное место. Ни одна из четырех величин щ, cSy Te « Tif которые
входят в формулу B.348), в «настоящей плазме при отсутствии ре-
реальных парных соударений (при наличии лишь рассеяния «а
флуктуациях) уже не может иметь своего обычного смысла. Нач-
Начнем с электронной температуры. Если нет парных соударений, то
очень трудно ожидать, что функция распределения будет максвел-
лсвской. Даже если не требовать, чтобы функция распределения
электронов была максвелловской, и характеризовать ее 'неким
средним тепловым разбросом, то необходимо, чтобы f% имела до-
довольно быстро сходящиеся «хвосты». В этом случае можно было
Hem
дисрфузии
'Не
Конус диффузии
Рис. 2.58. Квазилинейная диффузия электронов при ионно-звуковой неустойчи-
неустойчивости
бы, по .крайней мере условно, говорить о температуре электронов.
Но с ионами ситуация еще более сложна, если они взаимодейству-
взаимодействуют только с волнами (нет парных соударений).
Перейдем к обсуждению возможного вида функций распределе-
распределений ионов и электронов. Воспользуемся двумерной картиной про-
пространства скоростей, показанной на рис. 2.58. Здесь по оси абсцисс
отложена компонента скорости частиц вдоль направления проте-
протекания тока, а по оси ординат — поперечная компонента.
Пусть, первоначально имеется обычное максвелловское распре-
распределение электронов и ионов. Для максвелловского распределения
линии равного значения функции распределения в этой плоскости
являются окружностями. Центр таких окружностей для ионов (по-
(положение максимума функции распределения) находится в начале
координат. Для электронов он смещен «а величину щ: они пере-
переносят ток. Взаимодействие волн с частицами особенно сильно тог-
279
да, когда осуществляется резонанс Ландау. Взятая наугад волна
с фазовой скоростью со/& взаимодействует с частицами, находя-
находящимися вблизи прямой (см. рис. 2.58). Именно для таких частиц
осуществляется резонанс. Наконец, есл.и рассмотреть волны все-*
возможных направлений и разных значений фазовых скоростей, то
можно убедиться, что все частицы, находящиеся в окрестности ли=-
нии, соответствующей условию резонанса Ландау, испытывают дей-
действие поля волн. Но в ионно-звуковом спектре отсутствуют волны
со скоростями меньше некоторой (ю/6<и*) (см. § 1.11, 1.12).
Частицы с Ку* в квазилинейном приближении не взаимодей-
взаимодействуют с волнами. Здесь взаимодействие оказывается гораздо бо-
более слабым, оно связано с нелинейными эффектами следующего
приближения. Ионов в области взаимодействия с волнами доволь-
довольно мало; таким образо1М, лишь малая доля ионов подвергается
мощному воздействию со стороны волн. В нулевом приближении
функция распределения ионов в основной области практически не
деформируется. В резонансной же области возникает сильная де-
деформация из-за квазилинейной диффузии в пространстве скоро-
скоростей. Когда парные столкновения не играют роли, такое изменение
функции распределения ионов очень существенно. Оно сильно
меняет -ионную мнимую часть в дисперсионном уравнении (ион-
(ионный полувычет, пропорциональный числу ионов, которые могут
находиться в резонансе). Это, как правило, весьма малая величина,
очень чувствительная к тому, что происходит на «хвосте» ионного
распределения.
С электронами же происходит следующее: область запрещен-
запрещенных скоростей, внутри которой отсутствует резонанс между части-
частицами и волнами, сравнительно невелика, потому что скорость зву-
звука в Y™>i!m>e раз меньше средней тепловой скорости электронов.
В принципе можно пренебречь тем, что происходит внутри этого
небольшого кружка. Но возникает другая сложность. Очень труд-
трудно представить себе, чтобы ток раскачивал волны, почти попереч-
поперечные своему направлению. Действительно, из теории ионно-звуковой
неустойчивости следует, что волны с волновым вектором, практи-
практически поперечным направлению тока, имеют малую мнимую часть
и практически их можно считать устойчивыми.
Таким образом, приходим к выводу, что здесь образуется не-
небольшой конус в пространстве скоростей, в котором нет волн для
резонанса с электронами. Эти электроны свободно ускоряются
электрическим полем, вызывающим ток в плазме. Вклад таких
электронов может сильно уменьшить сопротивление плазмы. Ка-
Какая же доля электронов попадает в этот конус потерь и дальше
свободно ускоряется? Задачу можно разбить на два предельных
случая. Сначала целесообразно выделить более простой случай,
когда имеется хотя бы слабое магнитное поле #о, перпендикуляр-
перпендикулярное к плоскости (см. рис. 2.58). Такое магнитное поле медленно
вращает электроны (в сравнении с частотой плазменных ,колеба-
280
ний). Но оно может быть достаточно быстрым в масштабе времени,
в котором появилось бы убегание электронов в «конус потерь». И,
таким образом, в среднем все электроны за один ларморовский
оборот оказываются взаимодействующими с волнами. В этой зада-
задаче для электронов не возникает дополнительной трудности. Хотя
feo и «е сводится к максвелловскому распределению, тем не менее
можно говорить о средней электронной температуре.
Итак, будем считать, что если Ихмеется слабое поперечное маг-
магнитное поле, то все результаты для эффективного числа соударе-
соударений можно переносить даже и на далекие моменты времени, когда
могло бы существенно сказаться искажение электронного распре-
распределения, его отклонение от максвелловского распределения. Имен-
Именно такая ситуация имеет место с бесстолкновительными ударными
волнами поперек магнитного поля (см. § 2.20).
Однако проблемы, связанные с ионным распределением, оста-
остаются и 'в этом случае. Дело в том, что ионы не успевают переме-
перемешиваться под действием магнитного поля, и поэтому ионное рас-
распределение может приобрести довольно экзотическую форму и
в конце концов станет сильно отл.ичаться от максвелловского.
(Можно ожидать, что основная часть -ионов будет холодной, а ка-
какая-то часть ионов, движущихся со скоростями, 'начиная от скоро-
скоростей порядка скорости звука, будет нагреваться. По-видимому,
в ближайшее время нельзя без использования численных методов
-найти вид такого сложного ионного распределения.
Более простыми должны быть закономерности при малой не-
нелинейности, когда достаточно ограничиться только квазилинейным
приближением. В таком приближении насыщение неустойчивости
достигается- вследствие квазилинейной деформации функции рас-
распределения ионов, в результате которой даже в неизотермической
плазме появляется группа ионов с большими скоростями v^>cs.
Такие ионы, резонансно поглощая ионно-звуковые волны, должны
уравновешивать раскачку колебаний электронами.
Рассмотрим процесс нелинейного, в данном случае квазилиней-
квазилинейного, насыщения колебаний. Пусть уравнение для спектра неустой-
неустойчивых волн имеет символический вид [см. уравнение B.346)]
dWJdt = 2fkWk - 2y<kIFk - A (W/n0Te) Wk. B.349)
Нарастание колебаний при u>cs приводит к увеличению сопро-
сопротивления, т. е. возникает сила трения, действующая на электро-ны.
Если приложенное электрическое поле, создающее ток, не слиш-
слишком велико, то, как следствие реакции электронов на увеличившееся
сопротивление, щ должно уменьшаться до тех пор, пока плазма
не окажется на пороге' неустойчивости. Это означает, что нелиней-
нелинейные члены в уравнении B.349) играют малую роль, а насыщение
колебаний определяется условием у*к ^ у'к для всех первона-
первоначально неустойчивых волн. Иначе говоря, для всех первоначально
281
неустойчивых волн должно выполняться условие при всех резо-
резонансных скоростях (®=kv)
Yk = fk- т'к ^ WJdv + imJmt) (dflofdv)] = O. B.350)
Условие B.349) при пренебрежении лоследним членом не со дер- *
жит амплитуды установившихся колебаний W^ и, следовательно,
с его помощью сразу нельзя -вычислить veff. Эффективную частоту
столкновений для такого режима насыщения 'Неустойчивости (его
иногда называют «пороговым» или квазилинейным) можно найти
из закона Ома, подставив в него найденное выражение для
j=enoUo^enovc. Считая j=enovc=®E, находим
veff=eE/meVc. B.351)
Теперь с помощью соотношения B.339), связывающего veff с энер-
энергией колебаний, можно найти W:
W/n0Te =* {eErD(nJe) (vTe[vc). B.352)
С ростом Е увеличивается W, и при достаточно больших полях
уже -нельзя пренебречь нелинейным членом в уравнении B.349).
Кажущиеся простыми формулы для порогового (квазилинейного)
режима на самом деле сложны. Казалось бы, для нахождения
Uo^vc достаточно линейного выражения для мнимой части часто-
частоты. Однако Y?:k очень чувствительно к виду ионного распределения
при больших скоростях ионов, т. е. на хвосте функции распределе-
распределения. Такие ионы, поглощая колебания, увеличивают свою энергию
и быстро меняют вид своей функции распределения (из-за квази-
квазилинейных эффектов). В результате быстро меняется -у'к и, следова-
следовательно, vc.
Если тепловая энергия, поглощаемая частицами плазмы, не
отводится наружу, то можно ожидать, что в конце концов выде-
выделится некоторая группа ионов, поглощающая всю энергию волн.
Поступим следующим образом. Ионное распределение разобьем
на группу холодных и горячих ионов. В таком упрощенном (двух-
групповом) приближении можно найти величины, характеризую-
характеризующие протекание тока. Группа ионов, которые попадают в резонанс
с ионно-звуковыми колебаниями и затем ускоряются, сравнительно
невелика. Обозначим их концентрацию X. Введем эффективную
температуру таких резонансных ионов 7V^m2-u22\ Тогда из B.344)
имеем
B.353)
Оценивая ионный декремент как yi^^(^2
(в предположении, что Т{^Те) и сравнивая его с электронным
(см. табл. 2.2 в начале параграфа), получаем
Хъ(те1пцУ'1(Т{1Тв)М. B.354)
282
Теперь мы имеем два уравнения B.353) и B.354) для трех неиз-
неизвестных X, щ/с8 и Т{/Те. Для нахождения третьего уравнения рас-
рассмотрим импульс резонансных ионов. Импульс, теряемый электро-
электронами при рассеянии, переходит к ионам. Поэтому распределение
ионов по скоростям должно быть анизотропным. Функцию
распределения ионов представим в виде /;(v, Q)==>fiOi(v)-\-
+/aii(v, 9), где анизотропная часть fau может быть оценена из
следующих соображений. При поглощении колебаний резонансный
ион 'в среднем поворачивается на угол AQ^^W/miCsVi. Относитель-
Относительное приращение энергии ионов -в том же процессе имеет порядок
величины ATi/Ti—W\Т{. Таким образом, размешивание по углу,
стремящееся сделать распределение изотропным, в Vi/cs раз силь-
сильнее. Тогда
Недостающее уравнение получим из условия, что работа силы тре-
трения dPi/dt затрачивается на нагрев электронов (dPi/dt)iio^
^^nodTe/dty т. е.
XmiCsUo^Te. B.355)
Окончательный результат решения полученной системы уравнений
имеет вид
Uo^cs(mi!me)V\ Т^Те, Хъ(те1пцу/К B.356)
Итак, средняя хаотическая энергия этих горячих жшов по порядку
величины близка к средней хаотической энергии основной массы
электронов. Это своего рода скейлинг для квазилинейного режима
аномального сопротивления.
Этот скейлинг относится к случаю тока, поперечного или почти
поперечного к магнитному полю. Представим себе теперь, что маг-
магнитное поле у нас либо савс.ем отсутствует, либо действует в на-
направлении протекания тока. Тогда сразу исчезает тот механизм,
который перемешивает все электроны, и задача об электронной
функции распределения усложняется. Как поступить в этом слу-
случае? По-видимому, невозможно ввести двухгрупповое распределение
электронов, потому что нет явно выраженных двух групп электро-
электронов, как это было в случае с ионами. Наоборот, возникает плавный
переход от медленных электронов ко все более быстрым, и ;В конце
концов с течением времени, как показывает качественный анализ,
значительная доля электронов попадает в область скоростей, где
практически нет волн. Это явление напоминает убегание электро-
электронов в газе с лоренцевекими столкновениями, когда частота соуда-
соударений падает со скоростью v~3. Взаимодействие электронов с ион-
но-звуковыми волнами обладает именно такими свойствами.
Вопрос о том, какой вид в конце концов примет закон Ома
в такой плазме, на сегодняшний день остается открытым. Одна из
распространенных точек зрения такова: значительная доля элек-
электронов попадает в режим убегания, функция распределения элек-
электронов в проекции на параллельную полю скорость оказывается
283
сильно вытянутой в направлении тока, отношение средней дрейфо-
дрейфовой скорости электронов к средней тепловой скорости электронов
может стать равным единице.
Рассмотрим теперь аномальное сопротивление из-за какой-ни-
какой-нибудь другой неустойчивости (см. табл. 2.2 в начале § 2.19). Наибо-
Наиболее низким порогом возбуждения (малым значением по) обладают
электростатические неустойчивости с kz <С&, в плазме с током,
текущим поперек магнитного поля. Нелинейное насыщение этих
видов неустойчивости не поддается рассмотрению с помощью ме-
методов теории слабой турбулентности. Обратимся, например, к слу*
чаю модифицированной неустойчивости Бунемана [см. формулу
B.334)].
Дисперсионное уравнение B.334) отличается от обычного ура-
уравнения Бунемана лишь заменой шр1 на u>pi/Vl +аJре/@*яе и °V Ha
шрАг/^]/1 +a)Wc°2He- Можно оценить амплитуду колебаний в ре-
режиме насыщения так, как это часто делается в теории сильной
турбулентности. Сравним линейный dnjdt и нелинейный (uV)u
члены в уравнении для электронов
В нелинейной стадии эти члены должны конкурировать друг с дру-
другом, приводя к квазистационарному режиму насыщения неустой-
неустойчивости. Приравнивая их по порядку величины, получаем
q
Отсюда можно сделать следующую оценку плотности энергии ко-
колебаний:
2"о*21 ?к 1727; *= теп,и\, krHe ^ 1. B.357)
к
Теперь с помощью формулы B.339) получим
Vef f я&йнЩ} Vre. B.358)
Эта неустойчивость, как правило, раскачивается медленнее, чем
ионно-звуковая (при Ге>7\), но она может иметь место и в плаз-
плазмах с большой ионной темлературой. В отличие от ионного звука
для этой неустойчивости не требуется выполнения условия Те^>Т{.
Явление аномального сопротивления, как это следует из прове-
проведенного обсуждения, по-прежнему остается одним из самых труд-
трудных разделов физики коллективных процессов в плазме. По сути
дела, на сегодняшний день в арсенале теории кроме некоторых
полуколичественных соображений и оценок имеется несколько мо-
моделей для частных предельных случаев. Общий же сценарий pea-
284
лизовать не так-то просто. Анализ даже квазилинейного режима
аномального сопротивления, освобожденный от учета нелинейного
взаимодействия волн, в общем виде не проведен. Здесь полезным
оказывается численный эксперимент (рис. 2.59).
Подводя итоги, отметим, что качественный ход аномального
закона Ома /=/(?), т. е. вольт-амперная характеристика, должен
иметь вид, изображенный <на рис. 2.60. При докритической плот-
плотности тока (uolvTe)<(uolvTe)cr все устойчиво, линейная часть
графика /=/(?) соответствует классической электропроводности:
из-за столкновений. Вблизи порога токовой неустойчивости мо/0те^
(щ/) сг резко возрастают флуктуации, а следовательно, и эф~
-1000
1000 v
2000
Рис. 2.59. Численное модели-
моделирование асимптотического по-
поведения ионно-звуковой не-
неустойчивости (Morse R. L.r
Nielson С. W. «Phys. Rev.
Lett.», 1971, v. 26, p. 3). По-
Показана зависимость от времени
дрейфовой скорости и и тепло-
тепловой скорости vте электронов,
а также фазовая плоскость и
функция распределения элек-
электронов при ^=400.
Эксперимент проводился с реальным отношением масс электронов и ионов, при напряжен*
ности электрического поля E0=0,Q2me(npev0Tele и начальном отношении температур TJT^l..
Время измерялось в обратных плазменных частотах 1/@ре, скорости — в единицах vuTJ2zt.
Графики иллюстрируют появление на функции распределения наряду с сильно размытым
электронным «керном» (/) группы убегающих электронов B) в асимптотическом режиме
u**svTer^j. Срыв ускорения на начальной стадии связан с возникновением ионно-звуковой'
неустойчивости в результате преимущественного нагрева электронов
фективная частота соударений (в результате рассеяния электронов*
на флуктуациях). Конкретное значение порога (uolvTe)Cr зависит от
того, какой из типов токовой неустойчивости оказывается сущест-
существенным. Резкое увеличение verf при достижении порога неустойчи-
неустойчивости приводит к появлению излома на кривой j(E). В масштабах,
принятых для .измерения классической электропроводности, кривая
зависимости j(E) в области 'неустойчивости практически парал-
параллельна оси абсцисс. Для того чтобы создать ток, существенно
превышающий критический, потребовалось бы приложить громад-
285*
ное электрическое поле. Ход j(E) в этой закритической области су-
существенно нелинеен. Так, например, в ранее рассмотренном режи-
режиме нелинейного насыщения ионно-звуковой неустойчивости из
B.348) можно получить зависимость /—Е1/2.
Эксперименты ,по аномальному сопротивлению с трудом подда-
поддаются интерпретации, так как параметры плазмы при изменении /
и Е сильно меняются. Для ориентировки ниже на рис. 2.61 приво-
приводятся экспериментальные данные по аномальному сопротивлению
при больших /.
До сих пор при исследовании турбулентности плазмы в элек-
электрическом поле и механизмов аномального сопротивления предпо-
предполагалось, что приложенная к плазме разность потенциалов равно-
равномерно (или почти равномерно) распределяется по всему объему,
т. е. электрическое поле в плазме является почти однородным.
j= епщ
/\ Квазилинейная
/ 1 теория
Сальная
Рис. 2.60. Закон Ома в случае ионно-звуковой турбулентности
Однако в реальных ситуациях с граничными условиями картина
может быть совсем другой. Мысленно выделим в плазме элемен-
элементарную токовую трубку, т. е. трубку, ограниченную линиями элек-
электрического тока. Пусть по какой-либо причине вдоль линий тока
имеется такая неоднородность параметров плазмы, из-за которой
безразмерное отношение Uo!vTe меняется вдоль трубки.
Рис. 2.61. Профиль магнитного
поля во фронте бесстолкновитель-
ной ударной волны, измеренный
неподвижным зондом при прохож-
прохождении ударной волны мимо него,
и вычисленное по этим данным от-
отношение токовой скорости элек-
электронов к тепловой.
На переднем участке фронта токовая
скорость растет до тех пор, пока раз-
развитие токовой неустойчивости (по-ви-
(по-видимому, бунемановской) не приводит
к разогреву электронов. Затем она рез-
резко падает из-за перехода в квазили-
квазилинейный режим ионно-звуковой неустой-
неустойчивости, в котором токовая скорость практически не зависит от электрического поля.
Эксперимент выполнен в водородной плазме с плотностью /го=1,5-1О14 см-3, помещенной
в магнитное поле #0=700 Гс. Число Маха М«2 (Еселевич В. Г., Еськов А. Г., Куртмул-
лаев Р. X., Малютин А. И. «Журн. эксперим. и теор. физ.», 1971, т. 60, с. 2079)
286
Если неоднородность такова, что разные участки вдоль линия
тока соответствуют различным режимам j=j(E) (см. рис. 2.60) г
то произойдет следующее. Разность потенциалов, приложенная
к концам трубки, распределится неравномерно. Основное падение
потенциала придется на зоны с максимальным отношением щ\ъТе-
В силу резко 'нелинейного характера j(E) различие в Е между об-
областями с минимальным и максимальным значениями отношения
uo/vTe может стать громадным. Однако такой профиль потенциала
с течением времени должен еще более обостриться. Действитель-
Действительно, учтем выделение джоулева тепла при аномальном сопротивле-
сопротивлении (турбулентный нагрев). В зонах с наибольшими значениями:
ооинои. слои
Рис. 2.62. Образование двойных слоев при протекании тока с аномальным сопро-
сопротивлением
отношения Vo/vTe, а значит и с Е> оно резко увеличено. Это тепло
вдоль линий тока должно увлекаться электронами. Этот конвектив-
конвективный перенос учитывается в выражении для потока тепла членом
идТе/дх [см. уравнение A.87)]. Перераспределение температуры
вдоль линий тока, вызванное этим эффектом, меняет vTe и, следо-
следовательно, щ/VTe- Нетрудно увидеть, что уменьшение UojvTe «вниз
по течению» (по направлению движения электронов, переносящих
ток) в зонах максимального Е должно .вести к новому распреде-
распределению Е. Качественно последовательность процессов, протекающих
после включения тока, показана да рис. 2.62.
Резкое сужение зон аномально большого электрического поля
с образованием скачков потенциала напоминает образование удар-
ударных воли при нелинейной эволюции профиля скорости в газоди-
газодинамике. Эта аналогия, в действительности, является очень глубо-
глубокой: скачок потенциала, или двойной слой, сопровождается также
скачком параметров плазмы, например температуры электронов.
Хотя, как уже указывалось, о температуре при аномальном сопро-
сопротивлении следует говорить, соблюдая известную осторожность,
287
двойной слой с полным основанием можно назвать своего рода
электростатической ударной волной в плазме, рассматриваемой
как двухкомпонентная среда.
Любопытно отметить, что простейшим предельным случаем та-
такого скачка потенциала является классический двойной слой Ленг-
мюра. Он возникает, например, вблизи катода, поставляющего
электроны со средней скоростью ик, меньшей токовой скорости щ
в результирующем разряде. По этой причине необходим начальный
разгон электронов электрическим полем в слое, чтобы преодолеть
своего рода порог ()!
X
Рис. 2.63. Распределение потенциала и траектории частиц внутри двойного слоя
Эта старая модель, двойного слоя очень проста и заслуживает
того, чтобы ее воспроизвести. В стационарном случае ускорение
электронов в слое находится из уравнения движения
meuedueIdx=edy/dx— (Telne) dnejdx. B,359)
Если скачок потенциала e^*>Tei то в уравнении движения элек-
электронов можно пренебречь силой газокинетического давления. Тогда
-скорость электронов в слое находится из закона сохранения энер-
энергии:
;, B.360)
щ — скорость, с которой электроны инжектируются в двойной слой.
Плотность электронов внутри слоя определяется условием постоян-
постоянства тока:
ne=jeIUe. B.361)
Аналогичным образом для ионной компоненты имеем
?)(90-ср); /*<=;>;, B-362)
где 'мы предположим, что на анодной стороне слоя, т. е. при ср=
=афо, скорость ионов обращается в нуль (рис. 2.63) (ускорение
ионов происходит вверх по течению). Распределение потенциала
«внутри двойного слоя определяется из уравнения Пуассона
d\!dx* = ^е(ЦУи\ + 2e<flme - UlV Be/m,) (?• - ?)) • B.363)
288
Первый интеграл этого уравнения дает электрическое поле в слое:
~ Е2 = 4* (jeme уи\ + 2е<?!те — jemeu0
ri). B.364)
Отсюда с помощью очевидного условия Е=—dq)/dx-+-0 при ф->
-мро получили некий аналог вольт-амперной характеристики
двойного слоя — соотношение, связывающее скачок потенциала
с плотностью электронного и ионного токов:
U = U V2e<fjntl(me ]/V0 + 2е9о/те - тм0). B.365)
В наиболее важном случае ец)о^>теи2о из B.365) приходим
к так называемому условию Ленгмюра
U=nVm№e- B.366)
Распределение потенциала, определяемое- интегрированием
уравнения B.364)% см. на рис. 2.63, распределение плотности заря-
зарядов в слое находим по формуле р =—1/4я#ф/^х2. Слева, в катод-
катодной части двойного слоя, имеется избыток электронов (р<0). Вну-
Внутри слоя происходит ускорение электронов, их плотность падает, и
в анодной части двойного слоя возникает избыток ионов (р>0).
Как уже упоминалось выше, двойной слой Ленгмюра—структура,
в значительной степени аналогичная нелинейным электростатиче-
электростатическим волнам (см. § 1.20). Однако имеются и некоторые важные
различия. Прежде всего двойной слой — стационарная структура.
Кроме того, в двойном слое электрический заряд локализован
в узкой области пространства, вне слоя имеет место квазинейтраль-
квазинейтральность. Поскольку плотность электронов в слое падает вниз по те-
течению, а плотность ионов — в обратном направлении, то очевидно,
что с помощью только двух компонент — ускоренных электронов
и ионов — нельзя обеспечить квазинейтральность по обе стороны
от двойного слоя. Для этого необходимы еще две группы частиц —
холодные ионы в катодной части двойного слоя и холодные элек-
электроны в его входной части (см. рис. 2.63). Обе эти группы частиц
отражаются от потенциальных горбов, каким является для них
распределение потенциала в слое. При #фо!Э>7\> эти частицы не
проникают глубоко внутрь слоя и не влияют существенно на рас-
распределение потенциала в нем, они нужны только для обеспечения
квазинейтральности по обе стороны от слоя.
Еще одну важную особенность двойного слоя легко усмотреть
из уравнения B.359). Воспользовавшись условием B.361), это
уравнение можно записать в виде
(meii—Te;u)duldx=edq>ldx. B.367)
Отсюда следует, что ускорение электронов в направлении возрас-
возрастания ф, необходимое для возникновения двойного слоя, можно
19-74 289
6х
обеспечить только при выполнении условия
теи\>Те. B.368)
Уже известно, что это неравенство одновременно определяется
условием возникновения бунемановской неустойчивости. Таким об-
образом, в окрестности слоя Ленгмюра можно ожидать возбуждения
интенсивных электростатических колебаний с частотой порядка
ионной плазменной. Строгая теория двойного слоя, учитывающая
турбулентность, которая возникает вследствие бунемановской не-
неустойчивости, еще не построена. По всей видимости, развитие не-
Рис. 2.64. Профили потенциала элек-
электрического поля на фронте тепловой
ударной волны, измеренные через
время А^=10-8 с.
Тепловая волна возбуждалась в аргоновой
плазме (ло=2 • !013 см~3, Ге=10 эВ) локаль-
локальным нагревом до температур порядка
300 эВ. Разлетающиеся горячие электроны
тормозились двойным электрическим слоем на фронте тепловой волны (Иванов А А и др
«Письма ЖЭТФ», 1971, т. 13, с. 591)
устойчивости не останавливает процесс инерционного ускорения
электронов электрическим полем, однако в результате взаимодей-
взаимодействия с турбулентными пульсациями у электронов появляется так-
также хаотическая скорость V{v2). Если считать, что внутри двой-
двойного слоя направленная скорость электронов растет пропорцио-
пропорционально хаотической V{v2)> то остаются качественно справед-
справедливыми все старые формулы Ленгмюра с заменой me-+mefi—2me.
Вне двойного слоя в области, примыкающей к нему «снизу
по течению», следует ожидать -раскачки чисто электронной плаз-
плазменной .ветви колебаний быстрыми электронами, ускоренными по-
полем внутри слоя. Эти электроны играют роль пучка на фоне более
холодных электронов плазмы. Правдоподобная качественная кар-
картина двойного слоя с учетом неустойчивостей -изображена на
рис. 2.63.
Любопытное явление, по сути дела представляющее собой дви-
движущийся двойной электрический слой, было получено в лабора-
лабораторных экспериментах (рис. 2.64) по так называемым электронным
бесстолкновительным тепловым волнам.
§ 2.20. Бесстолкновительные ударные волны
Другой интересный пример важной роли коллективных процес-
процессов в плазме — бесстолкновительные ударные волны. В обычной
газодинамике толщина фронта ударной волны ограничена снизу
величиной порядка длины свободного пробега молекул в газе,
в плазме же благодаря «коллективным» свойствам возможно су-
существование специфических ударных волн, толщина которых зна-
290
чительно меньше длины свободного пробега. Простейшим приме-
примером являются уже рассмотренные в § 1.20 решения для ионно-зву-
ковых солитоноб.
Рассмотрим теперь ситуацию при наличии, магнитного поля.
Представим себе (рис. 2.65) ударную волну с толщиной А, значи-
значительно меньшей длины свободного пробега /. Более быстрые части-
частицы (v>u) из области слева (нагретая
ударной волной плазма), казалось бы,
могли, свободно двигаясь в сторону
невозмущенной плазмы, размыть пере-
переходную область до толщины /, равной
длине свободного пробега. Какие
эффекты могут предотвратить такое
расплываиие переходной области?
1. Самый простой случай имеет
место при наличии магнитного поля,
параллельного плоскости фронта. Та-
Такое магнитное поле заворачивает
ИОНЫ И электроны плазмы на расстоя- Рис- 2-65- Схематическое изо-
г сражение фронта оесстолкно-
ниях порядка их ларморовского ра- вительной ударной волны
диуса гн. Следовательно, можно ожи-
ожидать, что А-—\гн- Достаточно сильное магнитное поле (#2/8я^>/?Г)
препятствует размыванию даже в том случае, если оно не обязатель-
обязательно лежит в плоскости фронта. Это связано с тем, что скорость удар-
ударной волны при Н2/8л^>пТ намного превышает тепловую скорость
частиц, и, следовательно, доля ионов (электронов), обгоняющих
волну, экспоненциально мала. В задачах этого типа возникает
следующий кажущийся парадокс. Состояния с обеих сторон фрон-
фронта ударной волны связаны соответствующими законами сохра-
сохранения (адиабатой Гюгонио), согласно которым энергия поступа-
поступательного движения невозмущенной плазмы трансформируется во
внутреннюю энергию плазмы после прохождения ударной волны.
Что же приводит к диссипации, если А<С/? В возмущенном со-
состоянии за фронтом волныv основная доля внутренней энергии
плазмы приходится на интенсивные плазменные колебания. Про-
Происхождение таких нелинейных колебаний не обязательно связано
с неустойчивостью плазмы. Оно тесно связано со специфическими
дисперсионными свойствами плазмы (см. § 1.20). Иначе говоря,
как и в нелинейной динамике ионно-звуковых волн, главную роль
здесь играют конкуренция нелинейного укручения и отклонения
от линейного закона дисперсии.
2. Когда магнитное поле мало, вообще отсутствует или перпен-
перпендикулярно к фронту волны, механизм, мешающий расплыванию
фронта ударной волны, имеет иную природу. Предположим, что
вследствие расплывания некоторая доля быстрых частиц про'ник-
нет в невозмущенную плазму перед фронтом ударной волны.
Тогда состояние плазмы в этой области представит собой смесь
равновесного невозмущенного распределения частиц и некоторой
29!
группы быстрых частиц, т. е. станет неравновесным (в итоге рас-
распределение частиц по скоростям будет отличаться от максвеллов-
ского). Неравновесная плазма неустойчива по отношению к рас-
раскачке различного фода колебаний. Флуктуирующие электрическое
и магнитное поля колебаний, возникающих вследствие неустойчи-
неустойчивости, приводят к рассеянию ионов и электронов. Иначе говоря,
при наличии такого сорта флуктуирующих полей нужно переопре-
переопределить понятие длины свободного пробега, подобно тому как это
было сделано в задаче об аномальном сопротивлении.
Путь построения теории ударной волны без столкновений та-
таков. Сначала строится ламинарная теория, основанная на пред-
представлении о регулярных нелинейных колебаниях (солитонные ре-
решения), затем исследуется устойчивость таких решений. Наконец,
в неустойчивых случаях (а также тогда, когда ламинарных реше-
решений вообще не существует) строится «турбулентная» теория.
В ламинарной теории следует учесть влияние затухания на ха-
характер нелинейных установившихся волн, так как в отсутствие
затухания эти волны описывают обратимые движения. Так, состоя-
состояние плазмы до и после прохождения уединенной волны (оолито-
но;в) одно и то же. Ясно, что учет диссипации должен нарушить
обратимость, и состояния плазмы до и .после уединенной волны
будут различны. Если воспользоваться для -нелинейных движений
плазмы уравнениями сохранения потоков массы, импульса и энер-
энергии, то для установившихся движений эти уравнения, по опреде-
определению, должны связывать состояния, подчиняющиеся уравнениям
адиабаты Гюгонио. Состояния до и после уединенной волны без
учета затухания тривиально удовлетворяют адиабате Гюгогою. Как
изменится форма уединенной волны, если учесть диссипацию? Со-
Состояние после прохождения уединенной волны должно отличаться
от исходного, причем различие это, конечно, определяется конкрет-
конкретным механизмом и величиной диссипации.
Кроме того, адиабата Гюгонио не зависит от конкретного меха-
механизма диссипации. В теории толщины ударной волны в обычной
газодинамике этот кажущийся парадокс разрешается следующим
образом. В зависимости от коэффициентов вязкости, теплопровод-
теплопроводности и других величин, характеризующих диссипацию, меняется
и сама форма переходной зоны (ее толщина). В разреженной же
плазме «толщина» уединенной волны (при малой диссипации) за-
задается "независимо от адиабаты Гюгонио дисперсионными свойст-
свойствами. Решение кажущегося парадокса в случае разреженной плаз-
плазмы заключается в том, что состояние плазмы остается «возмущен-
«возмущенным»: в плазме остаются интенсивные колебания, вклад которых
в потоки импульса и энергии нужно учитывать. Это означает, что
внутри фронта ударной волиы самопроизвольно нарастают регу-
регулярные колебания конечной амплитуды.
В случае разреженной плазмы, находящейся в магнитном поле,
когда длина свободного пробега значительно больше среднего лар-
моровского радиуса л оно в, формальное газодинамическое описание
292
применимо (для движений поперек силовых линий) и внутри про-
пространственных областей, меньших свободного пробега. Необходи-
Необходимо только, чтобы все величины мало менялись на расстоянии по-
порядка ларморовского радиуса.
Рассматривая структуру фронта ударной волны, распростра-
распространяющейся перпендикулярно к магнитному полю в разреженной
плазме, будем считать, что всюду
внутри фронта выполнено условие ма- - П Уп
лости ларморовского радиуса по срав- Т
нению с любым характерным разме-
размером. Рассмотрим более простой случай
«холодной» плазмы (р<С#2/8я). Пусть # у-
механизмом затухания будет некото- У /и
рое условно введенное трение между :.:У
ионами и электронами. Его конкрет-
ный механизм (при определенных Рис< 266 СистеМа координат
УСЛОВИЯХ ОН МОЖеТ быть СВЯЗаН С аНО- для рассмотрения процессов
мальным сопротивлением) обсудим внутри фронта ударной волны
позже. Задача заключается в том,
чтобы составить систему дифференциальных уравнений для вели-
величин, характеризующих плазму и самосогласованные электромаг-
электромагнитные поля внутри фронта ударной волны, и исследовать ее.
Введем систему координат, в которой фронт волны покоится;
магнитное поле направим по оси z\ пусть zy — плоскость
фронта. Электрический ток переносится электронами в направле-
направлении у (рис. 2.66). Инерция электронов в этом направлении будет
существенно влиять на структуру фронта, так как она определяет
отклонение закона дисперсии магнитного звука от линейного (см.
§ 2.6). Наконец, для простоты примем, что внутри фронта выпол-
выполняется условие квазинейтральности щ=пе, где яг-, пе — плотность
числа ионов и электронов в соответствии с аналогичной задачей
о линейных магнитозвуковых колебаниях поперек магнитного поля
(см. §2.6).
В набор величин, определяющих плазму и поля, входят: я, Я,
их (скорость плазмы в направлении распространения волны, т. е.
по оси х), иу (скорость электронов, переносящих ток), Еу (напря-
(напряженность электрического поля вдоль оси у). Поле Ех можно ис-
исключить, пользуясь условием квазинейтральности. В системе от-
отсчета, где фронт волны покоится, для этих пяти неизвестных име-
имеется пять уравнений: 1) уравнение сохранения потока частиц;
2) уравнение сохранения потока импульса; 3) уравнение движения
электронов в направлении переноса электрического тока — по оси
у; 4) и 5) уравнения Максвелла для соответствующих компонент
rot E и rot H. Исходную систему после несложных преобразований
можно свести к дифференциальному уравнению второго порядка
для одной из переменных, например Н. Выпишем эти уравнения
с учетом сделанных приближений:
293
(d/dx) пи = 0; (d/dx) (Mnu2/2 -f Я2/8тг) = 0;
mnu (duyldx) = — enEy -f- (efc) nuH — vmnuy\
dEy(dx = 0; dH/dx = (Avne/с) иу.
B.369)
Последний член в правой части уравнения движения для электро-
электронов соответствует силе трения электронного газа об ионный.
Исключая из этих уравнений все переменные, кроме Я, можно
получить одно уравнение второго порядка для Я. Если на время
не учитывать вклад силы трения, это уравнение примет вид (с точ-
точностью до членов с melnii)
—Г
dx [
dH ///2-
dx
[Stzi
B.370)
Это уравнение определяет профиль изменения Я в исследуемой
установившейся волне. Интегрируя один раз, приведем его к виду
B.371)
(здесь а,2=тес21Апще2=с21(й2ре). В зависимости от выбора констан-
константы интегрирования С мы получаем различные решения. Удобно
проследить за характером решений
в зависимости от С, построив (рис. 2.67)
интегральные кривые на фазовой пло-
плоскости (Я, Я7).
Решения уравнения B.371) долж-
должны описывать периодические волны
конечной амплитуды (кноидальные
волны). Исключение составляет реше-
решение, соответствующее частному слу-
случаю С=0. Этот случай относится к ре-
решению типа магнитозвукового солито-
на. Действительно, такой выбор соот-
соответствует условию dH/dx=0 при Я=
Н
Рис. 2.67. Фазовые кривые для
нелинейных магнитозвуковых
волн
у у
=Я0. При этом уравнение принимает вид
± а -^-=/„а
dx (Н2
X
B.372)
Если выбрать определенный знак перед корнем в равенстве
B.372), то получим, что нельзя построить физически, разумное ре-
решение для Я на всей оси х. Однако существуют решения всюду
294
непрерывные (до второй производной включительно), в которых
при некоторых х=Х\ производная Я' меняет знак. В этой точке Я
достигает своего максимального значения Ятах. Уравнение
(dH/dx) (х\)=0 связывает амплитуду магнитного поля Ятах со ско-
скоростью распространения волны и играет роль, аналогичную дис-
дисперсионному уравнению
B.373)
B.374)
2=
=0.
Отсюда находим для скорости солитона
1>2ф= (Ятах+Я0) 2/
В предельном случае малых амплитуд (Ятах
находим ско-
скорость магнитного звука.
Характерный пространственный масштаб солитона 6—с/соре,
что соответствует длинам волн, при которых появляется дисперсия
фазовой скорости. Простое аналитическое выражение для профиля
магнитного поля в уединенной волне легко получить для малых
амплитуд (Ятах—Н0<Н0). Оно имеет вид
у
II 2' i7^=
— 1 sh
Г
.—1
B.375)
На рис. 2.68 показаны профили солитона для различных значе-
значений числа Маха М=аф[Яо/]/Л4гслот/]-\
Решение солитонного типа исчезает при достаточно больших
Уф и Я. Критической является амплитуда Ятах=ЗЯ0 (т. е. Vф =
z=2H0iyr4nn0nii). При приближении амплитуды волны к критиче-
критической плотность ионов на гребне волны стремится к беско-
бесконечности. Физически это
означает следующее. Уеди-
Уединенная волна представля-
представляет собой «горб» электри-
электрического потенциала ф. В си-
системе координат, связанной
с волной, поток ионов из
д:=:сх) набегает на этот по-
потенциальный барьер со ско- о х
ростью Vф. При не слишком рис 268 • магнитозвуковых соли.
больших амплитудах на- тонов для различных чисел Маха
чальная кинетическая энер-
энергия иона Ш{Ю2ф/2 превышает высоту потенциального барьера ефтах,
и ионы, несколько задержавшись, переваливают через него. Однако,
как следует из решения, с ростом амплитуды волны потенциаль-
потенциальный барьер становится настолько высоким, что ец)тах>пци2ф/2. Мо-
Момент ^фтах^^т^2ф/2 соответствует амплитуде Ятах=ЗЯ0 (иначе
говоря, критическое число Маха равно двум). На гребне такой
295
волны ионы, потеряв скорость, «останавливаются», а их плотность
возрастает до бесконечности. При еще больших амплитудах ионы
просто «отражались» бы от барьера, но соответствующее такой
картине движение уже не описывается в рамках рассмотренной
исходной системы уравнений, так кдк после отражения течение
становится «многопотоковым» (взаимопроникающие потоки набе-
набегающих и отраженных ионов). •
Таким образом, видим, что, как и для ионно-звуковых волн (см.
§ 1.20), эффекты дисперсии не могут остановить «опрокидывание»
магнитного звука с достаточно большой амплитудой в холодной
плазме.
Рис. 2.69. Эффективная потенциальная яма для магнитозвуковых солитонов и
ударной волны
Если бы мы учли тепловой разброс скоростей ионов, то даже
при малых амплитудах волны могли бы найтись ионы, отражаю-
отражающиеся от барьера (это ионы с малой относительной скоростью
^Ф—vx)9 т. е. двигавшиеся первоначально в направлении распрост-
распространения волны со скоростью, близкой к Юф\ их можно назвать ре-
резонансными. Они дают лишь один из возможных механизмов дис-
диссипации, который мал, если мало число резонансных ионов.
Другой механизм диссипации дает сила трения электронов об
ионы. Для волн небольшой,амплитуды анализ можно упростить и
посмотреть, к чему приводит диссипация. Вместо B.370) в этом
случае имеем
, а2
i v
v
dH
dx
B.376)
Рассуждая, как и в § 1.20, видим, что уравнение B.376) пред-
представляет собой уравнение движения ангармонического осциллято-
осциллятора при наличии трения, роль обобщенной коЬрдинаты здесь играет
Я, роль времени х.
Форма ямы определяется потенциалом
B.377)
296
На рис. 2.69 изображен вид функции V(H). При
Я = Я* = -Я0/2 + /
\ + Я 20/4
Я достигает минимума. Аналогия с осциллятором легко позволяет
установить профиль Я внутри фронта ударной волны; Н осцилли-
осциллирует вокруг значения Я* с затухающей амплитудой до тех пор, по-
пока не установится Н=Н*, соответствующее магнитному полю по-
позади фронта ударной волны. Для того чтобы Яо соответствовало
минимуму магнитного поля в волне, т. е. чтобы V(Я) имело вид,
изображенный на рис. 2.69, необходимо, чтобы выполнялось усло-
условие и2ф>Н20/4лП0ГПг.
Профиль изменения Я внутри фронта волны можно предста-
представить следующим образом (рис. 2.70). Сначала в невозмущенной
плазме появляется солитон, на гребне которого магнитное поле
достигает максимального значения; вследствие наличия необрати-
необратимой диссипации (трение или резонансные ионы) состояние плазмы
после прохождения такой волны будет отличаться от исходного.
На расстоянии порядка
8 ^ (а/ УМ—1)In[@ф/ va)УМ—1] B.378)
(число Маха М=уф/уа) вслед за первой волной движется вторая
волна и т. д. Если не интересоваться тонкой структурой осцилля-
осцилляции во фронте ударной вол-
волны и усреднить магнитное
поле по расстояниям, пре-
превышающим б, то можно го-
говорить о б как об эффек-
эффективной толщине фронта
ударной волны, связываю-
связывающей, два состояния плазмы:
невозмущенной (до прихода
Рис. 2.70. Осцилляторная структура магни-
тозвуковой ударной волны
0 X
волны) и возмущенной (мо-
(модулированной интенсивны-
интенсивными колебаниями), вклад ко-
которых при таком подходе нужно включить в законы сохранения
на «разрыве». В этом смысле роль затухания действительно часто
символическая, так как в выражение для б B.378) (ширина та-
такой ударной волны) затухание входит под знаком логарифма.
Картина затухания нелинейных осцилляции позади фронта
ударной волны имеет следующий характер. В последующих «уеди-
«уединенных» волнах амплитуда все уменьшается и расстояние между
двумя соседними «возвышениями» магнитного поля сокращается
до а/УМ.— 1, когда совокупность возвышений и впадин становит-
становится затухающей синусоидой. Полная длина затухания осцилляции
будет порядка v$/v или V(Н2/8ппТ) (те/т{)\ (Л, —длина свобод-
свободного пробега электронов). __
При достаточно большой силе трения (частота столкновений v)
297
характер решения уравнения B.376) полностью меняется. Этот
случай в бесстолкновительной плазме очень важен при аномальном
сопротивлении. До сих пор мы считали затухание [последний член
в уравнении B.376)] малым. В противоположность этому случаю
при с/(Оре<.с2теу/4ппе2иф можно пренебречь дисперсией, т. е. чле-
членом со второй производной в B.376). Толщина фронта ударной
волны тогда дается выражением
А^^2/4яаУф(М—1). B.379)
Конкретную величину А получим, если для а воспользуемся выра-
выражением из теории аномального сопротивления при ионно-звуковой
неустойчивости.
До сих пор речь шла о структуре волны, распространяющейся
строго поперек магнитного поля. Нетрудно обобщить предыдущее
рассмотрение на случай волн, не перпендикулярных к Н. Диспер-
Дисперсионные эффекты резко чувствительны к направлению распростра-
распространения волны. Если волна распространяется не строго поперечно, то
характерной длиной дисперсии является (?/(ОргH (при У~me/mi<^
<С0<^1). Инерция электронов для таких волн несущественна, но
зато учитывается гиротропия плазмы. Уравнение для Я в этом
случае можно угадать из простых соображений о роли дисперсии.
Действительно, для этого достаточно в уравнении B.376) под дли-
длиной дисперсии а понимать (?/ю^N. В результате получим для Н
следующее уравнение:
co2pi v dx2
Но здесь меняется не только длина, но и характер дисперсии (ю/ft
с ростом k увеличивается). В уравнении B.380) изменился знак
«эффективной массы». В пре-
пренебрежении затуханием
adH/dx мы снова имеем
нелинейные периодические
установившиеся волны. Осо-
Особым решением и здесь явля-
являются уединенные волны, но
в этом случае это уединен-
уединенные волны «разрежения»
(рис. 2.71). Профиль же
ударной волны будет иметь
вид, показанный на рис. 2.71.
Любопытно, что внутри
фронта ударной волны магнитное поле достигает минимального
значения, меньшего, чем в невозмущенной плазме. Отличие от пре-
предыдущего случая заключается и в том, что передний фронт осцил-
осцилляции не является резким.
Таким образом, задача о ламинарной структуре нелинейных
осцилляции внутри фронта ударных волн сводится к двум различ-
298
Рис. 2.71. Осцилляторная структура
сой» ударной волны
ско-<
ным постановкам (рис. 2.72): 1) когда дисперсионная кривая со(&)
имеет вид типа / (волны, перпендикулярные к Я в холодной плаз-
ме); в этом случае передний фронт осцилляции резкий (все начи-
начинается с солитонов) и 2) когда короткие волны имеют большую
скорость распространения, чем длинные (тип //). В этом случае
передний фронт осцилляции вытягивается, так как короткие волны
обгоняют фронт. Для существования бесстолкновительной ударной
волны здесь уже необходимо аномальное затухание таких осцил-
осцилляции.
Рис. 2.72. Два предельных случая Рис. 2.73. Образование многопото-
законов дисперсии кового движения в ударных вол-
волнах при больших числах Маха
Мы еще совсем не разбирали случаев, когда ламинарную тео-
теорию фронта ударной волны вообще невозможно построить. Такая
ситуация в уже приведенных выше примерах осуществляется при
достаточно больших амплитудах, когда нет установившихся нели-
нелинейных волн. Рассмотрим сначала случай, когда ударная волна
идет поперек сильного магнитного поля в холодной плазме. При
приближении амплитуды магнитного поля в волне к значению,
втрое большему начального магнитного поля, ламинарная структу-
структура нарушается. Физически это означает, что как только амплиту-
амплитуда волны достигает критического значения (#тах=3#0), происхо-
происходит «опрокидывание». В некотором участке пространства ионы,
двигавшиеся.первоначально позади, настигают передние и обгоня-
обгоняют их (рис. 2.73). Профиль скорости в этом случае становится
многозначным.
Заметим, что аналогичное явление хорошо изучено в теории
волн конечной амплитуды на поверхности тяжелой жидкости в ка-
канале конечной глубины. Здесь существуют нелинейные установив-
установившиеся движения типа уединенных или периодических волн. При
достаточно больших амплитудах такие волны разрушаются вслед-
вследствие «опрокидывания». Ясно, что строгий математический анализ
картины, возникающей после опрокидывания, чрезвычайно труден.
Можно попытаться лишь качественно установить наиболее сущест-
существенные черты явления, проводя аналогию с волнами в жидкости.
Основной вопрос состоит в том, будет ли после опрокидывания
движение плазмы стремиться к какому-либо установившемуся ре-
299
жиму или же переходная область (заштрихованная, см. рис. 2.73)
будет неограниченно размываться, как это имело бы место в обыч-
обычном газе без столкновений. В теории поверхностных волн через не-
некоторое время после опрокидывания возникает установившееся
течение, называемое прыжок воды или бор, представляющее
собой некоторую переходную область конечной толщины, которая
обычно заменяется идеализированной математической поверхно-
поверхностью, разделяющей два плоскопараллельных потока. При переходе
через эту поверхность удовлетворяются соответствующие законы
сохранения. В известном смысле «бор» представляет собой аналог
ударной волны. Стационарность ширины переходного слоя физи-
физически обеспечивается тем, что участки профиля, выдвигающиеся
вперед при опрокидывании, в конце концов, описав дугу, под дей-
действием силы тяжести падают и «смешиваются» с покоившимися.
В плазме роль силы тяжести выполняет магнитное поле, заворачи-
заворачивающее ионы. Хотя распределение их по скоростям еще далеко от
максвелловского, состояния плазмы с обеих сторон переходной об-
области можно связывать законами сохранения потоков массы, им-
импульса и энергии. Ширину переходной области можно оценить как
радиус кривизны ионов после опрокидывания в Амагнитном поле.
Так как в волне с числом Маха большем двух амплитуда скорости
v^vA, то ширина переходного слоя (или ширина бесстолкнови-
тельной ударной волны) 6—vmiC/eH^c/(dPi.
Однако многоскоростное течение со скоростями, перпендикуляр-
перпендикулярными к магнитному полю, возникающее после опрокидывания, дол-
должно быть неустойчиво. Действительно, если для простоты рассмот-
рассмотреть двухпучковое распределение ионов при разности скоростей
пучков, превышающей тепловую скорость, то возникает неустойчи-
неустойчивость относительно раскачки колебаний с волновым вектором, по-
почти параллельным скорости пучка. В «боре» также имеет место
неустойчивость сходной природы (встречные потоки); это просто
неустойчивость тангенциального разрыва, возникающая при сопри-
соприкосновении падающей струи с поверхностью покоившейся жидко-
жидкости. В случае же двух встречных ионных потоков, движущихся
поперек магнитного поля, двухпотоковая неустойчивость сильнее
всего развивается при частотах порядка нижней гибридной. Макси-
Максимальный инкремент неустойчивости по порядку величины также
равен ((он&йнеI/2. Таким образом, плазма турбулизуется. В отли-
отличие от аномального сопротивления такая турбулентность приводит
к аномальной вязкости.
Большое разнообразие типов структур фронта бесстолкнови-
тельных ударных волн, соответствующее описанным выше моде-
моделям, наглядно иллюстрируется лабораторными экспериментами
(рис. 2.74) и измерениями ударных волн в солнечном ветре
(рис. 2.75).
Выше мы рассмотрели вопрос о бесстолкновительных турбу-
турбулентных ударных волнах в плазме, распространяющихся поперек
300
или почти поперек сильного магнитного поля. Магнитное поле
удерживает более «горячие» частицы, предотвращая расплывание
переходной области между невозмущенной (холодной) плазмой
(перед фронтом ударной волны) и нагретой плазмой за волной.
Если такого поля нет или его направление совпадает с направле-
направлением движения ударной волны, то невозможно предотвратить вза-
взаимопроникновение горячей и холодной плазм. Происходит как бы
инжекция одной плазмы в другую. Так, время от времени солнеч-
Рис. 2.74. Типичные профили бесстолкнови-
тельных ударных волн, генерируемых в ла-
лабораторной плазме с помощью метода «маг-
«магнитного поршня» (при быстром нарастании
магнитного поля):
- волна, распространяющаяся перпенди-
кулярно к магнитному полю (плотность плазмы
мала ^ч^5 • 1012; аргон; #о^Л кгс). Внутри фронта
волны токовая скорость электронов превышает тепловую. Однако даже неустойчивость Бу-
немана не успевает развиться; «косая» ударная волна @>1О°); — •— —волна,
распространяющаяся перпендикулярно к магнитному полю в плазме с плотностью
/г>1013 см-3 (режим аномального сопротивления). (Алиханов С. Г. и др. — In: «Plasma
Phys. and Controlled Nucl. Fus. Res», v. 1, Internal. Atomic Energy Agency, Vienna,
1969, p. 47)
ная корона выбрасывает с большой скоростью огромные массы го-
горячей плазмы, которые, попадая в межпланетную плазму, создают
бесстолкновительные ударные волны. Проблема здесь заключается
в том, чтобы найти механизмы, способные остановить свободное
растекание инжектируемого сгустка плазмы в межпланетной среде.
Рассмотрим несколько более 'подробно лишь наиболее понятный
механизм, связанный с развитием «шланговой» неустойчивости.
Пусть поток плазмы инжектируется вдоль невозмущенного магнит-
Рис. 2.75. Профиль магнитного
поля во фронте косой (9 — 60°)
межпланетной ударной волны с
числом Маха УМ = 2,5 по измере-
измерениям на борту спутника ISEE
26 октября 1977 г.
Большое значение отношения газоки-
газокинетического давления к магнитному
C«3) способствует устойчивости ухо-
уходящей вперед осцилляториой структу-
структуры. Толщина ударного фронта
А/^,90 км, что составляет примерно
2c/api (Russel С. Т., Greenstadt E. W.—
«Report of Inst. of Geophys. and Planet
Phys.», 1978, № 1847)
ного поля. Тогда в каждом элементе объема полное распределение
частиц можно представить в виде суперпозиции невозмущенной
плазмы и возмущенных частиц, втекающих в данный элемент объ-
объема. Такое распределение является, очевидно, анизотропным с па-
параллельным давлением, нарастающим быстрее, чем перпендику-
перпендикулярное давление. При анизотропии давления, превышающей поро-
пороговое значение Ар>Я20/4л;, развивается «шланговая» неустойчи-
неустойчивость, существенно влияющая на дальнейшее растекание плазмы.
301
100
500
1000 х
Рис. 2.76. Структура бесстолкновительной ударной волны, распространяющейся
параллельно магнитному -полю в плазме с большим р (Н. Volk, D. Auer, 1971).
Показаны профили плотности в волне в различные времена t: расстояние измеряется
в ионных ларморовских радиусах, время — в обратных частотах ларморовского вращения
ионов. Вследствие сжатия на фронте волны продольное давление ионов превышает попе-
поперечное. Развивающаяся при этом шланговая неустойчивость создает эффективную диссипа-
диссипацию в ударной волне, препятствующую укручению ее профиля. Создается квазистационар-
квазистационарная структура фронта шириной порядка нескольких ионных ларморовских радиусов
Вследствие развития «шланговой» неустойчивости магнитные си-
силовые линии будут извиваться беспорядочным образом, так что
магнитное поле становится турбулентным. Обратное влияние этой
турбулентности на растекание частиц учитывается квазилинейными
уравнениями для функций распределения частиц. С точки зрения
сохранения адиабатических инвариантов
и ] =
(dl — длина элемента силовой линии магнитного поля) по мере
нарастания турбулентного магнитного поля уменьшается продоль-
продольное и увеличивается поперечное давление плазмы. Иными словами,
рассеяние частиц на нерегулярностях магнитного поля играет роль
эффективных соударений, приводящих к изотропизации давления
плазмы.
Аналитическая теория этого явления построена для слабых
ударных волн. В общем же случае используют численное модели-
моделирование (рис. 2.76). Толщина' ударной волны без столкновений
оказывается, как и следовало ожидать из размерностных сообра-
соображений, порядка нескольких ларморовских радиусов иона.
302
§ 2.21. Генерация и усиление магнитного поля
До сих пор, рассматривая поведение плазмы в магнитном поле,
мы молчаливо считали, что само существование последнего задает-
задается извне внешними источниками, хотя, разумеется, принималось во
внимание влияние электрических токов, текущих по плазме.
В астрофизических приложениях невозможно обойти вопрос
о происхождении исходного магнитного поля. Оказывается, маг-
магнитная гидродинамика сама по себе способна объяснить, каким
образом движение проводящей среды (будь то плазм# или рас-
расплавленный металл) генерирует магнитное поле. В основе меха-
механизма генерации магнитного поля, так называемого динамо-про-
динамо-процесса, лежит явление растягивания магнитных силовых линий при
L t>0
Рис. 2.77. Схема усиления магнитного подя в процессе дифференциального
вращения плазмы вместе с вмороженными силовыми линиями
движении проводящего вещества вместе с вмороженными в него
силовыми линиями магнитного поля. В частности, при турбулент-
турбулентном движении плазмы различные точки, пронизываемые силовой
линией, со временем удаляются друг от друга, приводя к растяги-
растягиванию и запутыванию силовых линий. При этом, однако, возника-
возникают сильные градиенты магнитного поля, а в некоторых областях
даже образуются конфигурации со встречным направлением маг-
магнитного поля. Поэтому ясно, что в таких конфигурациях становит-
становится важной диссипация поля из-за взаимной диффузии («аннигиля-
(«аннигиляции», по терминологии § 2.15 о тиринг-моде) магнитных силовых
линий. Эти же процессы мешают усилению поля в случае растяги-
растягивания силовых линий в процессе регулярного движения в одной
плоскости. Классическим примером ламинарного движения такого
рода является дифференциальное вращение, когда силовые линии,
соединяющие две точки, лежащие на различном расстоянии по ра-
радиусу от оси вращения, со временем растягиваются в спирали
(рис. 2.77). Из-за условия div H=0 число силовых линий, направ-
направленных по спирали к оси вращения, должно быть равным числу
силовых линий, уходящих по спирали от оси вращения. Поэтому
при сильном закручивании спиралей пучки силовых линий, имею-
303
щие противоположные направления (к оси и от оси), находятся на
близком расстоянии друг от друга и быстро аннигилируют вслед-
вследствие взаимной диффузии полей. Кроме того, обратное воздействие
сил натяжения магнитных силовых линий на вращающуюся плазму
рано или поздно приводит к ее торможению, т. е. к прекращению
дальнейшего усиления поля.
Невозможность длительного усиления поля в двумерном слу-
случае нетрудно доказать и на математическом языке. Для этого вос-
воспользуемся уравнением B.70) для магнитного поля с учетом дви-
движения проводящей плазмы. Это уравнение является основным
в теории так называемого кинематического динамо, в которой дви-
движение (поле скорости v(r, /)) задано. В двумерном случае удобно
вместо напряженности магнитного поля ввести векторный потен-
потенциал
H=rotA. B.381)
В случае двумерного движения в плоскости (х, у) векторный по-
потенциал имеет только одну компоненту вдоль оси z, так что урав-
уравнение B.70) сводится к виду
dA2/di+ (и V) Az= (c2/4jta) AAZ. B.382)
Второй член в левой части B.382) описывает усиление магнит-
магнитного поля при движении его силовых линий с плазмой, а правая
часть учитывает диффузию магнитных силовых линий. Эффект уси-
усиления доминирует при условии AnoV\L^>\, где V9 L — характерные
скорость и масштаб движения соответственно. Однако само усиле-
усиление не может длиться бесконечно долго, так как в таком процессе
не создается новых силовых линий, а старые в конечном счете дол-
должны исчезнуть в результате взаимной диффузии. Последнее не-
нетрудно понять из аналогии (замеченной Я. Б. Зельдовичем) урав-
уравнения B.382) с уравнением теплопроводности, которое, как изве-
известно, имеет только одно стационарное решение, соответствующее
,42=const.
Учитывая огромные пространственные масштабы, характерные
для космической плазмы, и ее достаточно высокую 'проводимость,
можно показать, что для нее условия усиления поля часто выпол-
выполняются с хорошим запасом. В качестве классического примера
обычно ссылаются на Крабовидную туманность, магнитное поле
которой, по-видимому, претерпело эволюцию указанного типа. Сце-
Сценарий должен выглядеть примерно так. Около тысячи лет назад
в результате взрыва сверхновой в центре Крабовидной туманности
образовалась нейтронная звезда, вращающаяся с угловой частотой
порядка 30 об/с, а внешняя проводящая оболочка старой звезды
была сброшена и разлетается теперь примерно со скоростью
1500 км/с. В результате магнитные силовые линии, вмороженные,
с одной стороны, в разлетающуюся оболочку, а с другой, в быстро
вращающуюся нейтронную звезду, за время, прошедшее с момента
взрыва, должны были совершить Л^ЗО об/сХЗ-1010 с^Ю12 об.
Магнитный поток, пронизывающий старую звезду, по-видимому, по
304
порядку величины составлял величину, равную потоку через такук>
типичную звезду, как наше Солнце, т. е.
= 2*/?2n?n^ 1023 Гс-см2,
где Bq^= 1 Гс — среднее по поверхности магнитное поле Солнца,,
a i?Q = 7-105 км — радиус Солнца. Если теперь предположить, что
примерно один процент этого потока остался вмороженным в раз-
разлетающуюся оболочку, то к настоящему моменту магнитный по-
поток, пронизывающий Крабовидную туманность, с учетом много-
многократного закручивания силовых линий составит около 1033 Гс-см2.
Учитывая, что размер Кра-
бовидной туманности при-
примерно равен расстоянию,
которое пролетела оболоч-
оболочка за тысячу лет, т. е. при-
примерно 3-1018 см, находим
магнитное поле в Крабовид-
ной туманности Я=10~4 Гс.
Оценка синхротронного из-
излучения энергичных электро-
электронов в таком магнитном поле
дает поток энергии излуче-
излучения, по порядку величины
совпадающий с наблюдае-
наблюдаемым. Сторонники такой мо-
модели считают это аргумен-
аргументом в пользу изложенной
простой модели усиления
поля.
Точно так же, как и для
плоского движения, было
доказано, что и некоторые
другие регулярные движе-
движения, обладающие высокой
симметрией, не могут усили- идальным магнитным полем
вать и поддерживать поля
в течение длительного времени. К такого рода движениям относит-
относится дифференциальное вращение проводящего ядра вместе с вморо-
вмороженным в него полоидальным магнитным полем. Дифференциаль-
Дифференциальное вращение ядра (обычно более быстрое в центре) приводит к за-
закручиванию в тор полоидальных магнитных силовых линий
(рис. 2.78). Напряженность тороидального поля при этом растет
линейно со временем, так как каждый новый оборот силовых ли-
линий увеличивает магнитный поток через меридиональную плоскость.
Однако полоидальное поле при этом экспоненциально затухает
20-74 3Q 5
Рис- 2.78. Генерация тороидального поля
из-за магнитной вязкости (диффузии силовых линий). В конце
концов начнет затухать и тороидальное поле. Следовательно, что-
¦'бы генерировать стационарное магнитное поле, нужно найти под-
подходящий механизм поддержания именно полоидального магнитно-
магнитного поля. Более того, это поле важно для объяснения дипольного
магнитного поля некоторых планет и звезд. Что же касается
внутреннего тороидального поля, то его наличие не сказывается
на характере внешнего поля.
Буллард и Эльзассер предложили в качестве такого механизма
использовать преобразование тороидального магнитного полявпо-
.лоидальное в процессе конвекции проводящей среды. Такое дви-
движение дополняет уже рассмотренное неоднородное вращение и
снимает цилиндрическую симметрию задачи. Возникновение же
конвекции, например в ядре Земли и в атмосферах звезд, является
результатом обычной гидродинамической неустойчивости среды,
подогреваемой снизу в поле тяжести. Рассматривая процесс подъ-
подъема петли тороидального поля в восходящих конвекционных пото-
потоках, можно показать, что силы Кориолиса поворачивают такую
яетлю в меридиональную плоскость и таким образом поддержива-
поддерживают полоидальное магнитное поле. Итак, в системе полоидаль-
ное п о л е+тор о и д а л ьно е возникает обратная связь.
Ю. Паркер предложил феноменологические уравнения, реализую-
реализующие обратную связь между полоидальным НР и тороидальным Нт
полями. Эти уравнения имеют следующий наглядный вид:
где Tr — коэффициент генерации тороидального магнитного поля
из полоидального вследствие дифференциального вращения, а Г с—
коэффициент генерации полоидального поля из тороидального
вследствие конвекции. Нетрудно убедиться, что в пределе слабой
диффузии эти уравнения описывают экспоненциальное нарастание
полей во времени при условии, что знаки коэффициентов связи по-
полоидального и тороидального полей одинаковы:
# г,Р~ехр (yt); y2=TRTc. B.384)
Задачу о генерации магнитного поля планет и звезд в строгой
•аналитической постановке решить не так-то просто. Поэтому часто
пользуются численными методами, предложенными еще Буллар-
дом и Эльзассером. Однако задача о генерации магнитного поля
значительно упрощается в случае, когда турбулентное движение
с мелкими масштабами возбуждает существенно более гладкое
магнитное поле. Тогда в разложениях Фурье поля скоростей и маг-
магнитного поля главные вклады определяются совершенно разными
306
масштабами. Это означает, что в формулах фурье-разложения
u (r, t) = J uk (t) exp (ikr)d3k; . B.385)
H (r, *) = J Hq (t) exp (iqr)rf3q, B.386>
следует иметь в виду, что q2<^k2. По этой причине имеет смысл
усреднение магнитного лоля по мелкомасштабному движению сре-
среды (черта сверху над Н(г, /)).
Итак, существенное различие масштабов позволяет предста-
представить магнитное поле в виде суммы медленно меняющегося («круп-
(«крупномасштабного») поля Н и мелкомасштабных флуктуации h (яв-
(являющихся мгновенным откликом на движение среды). Здесь по-
полезно отметить некоторую аналогию с квазилинейным приближени-
приближением (§ 1.17). Представим магнитное поле в виде
Н (г, t) = Н (г, t) + h (r, t). B.387>
Из уравнения B.70) нетрудно получить уравнение для быстро
меняющейся части
dh/dt = rot [uXH] + ДЬ^уЧтса. B.388).
Воспользуемся медленностью изменения Н по сравнению с v. Счи-
Считая для простоты, что магнитная вязкость достаточно велика, пе-
перепишем это уравнение в виде
(РГ. v) u = (сш/4т) F% B.389>
где k2 — некоторый средний по спектру турбулентных пульсаций,
скорости квадрат волнового вектора.
Уравнение для медленно меняющейся части магнитного поля:
получаем, усредняя уравнения B.70) по мелкомасштабным флук-
туациям, подобно тому как это делалось при выводе квазилиней-
квазилинейного уравнения для функции распределения:
= rot ]u X h] + (с2/4тго) Д Н.
Подставив сюда найденное выше выражение для h, получим
dH/dt = Dтсо/с2&2) rot [ u X (Н • V) и] + (с2/4по) ДН. B.390>
Черта сверху в этом уравнении означает усреднение по турбулент-
турбулентным пульсациям скорости. В теории кинематического динамо поле
скоростей считается заданным. Для турбулентного движения за-
задание усредненных характеристик движения осуществляется обыч-
20* 3 07 "
.но с помощью корреляционной функции для скоростей
Так как а, [3=1,2,3 соответственно числу измерений в про-
пространстве, то Као является тензором. Естественно считать, что он
зависит только от (г—г"). Проще всего такой тензор можно пред-
представить в следующем виде:
К^(т9г') = А(т-т')Ь^ + В(г-т')хах^ + С(т-т')8^х^ B. 91)
где ДВи С — некоторые функции (г — г'); е—полностью анти-
антисимметричный единичный аензор; ха, х^ — компонейты радиус-векто-
радиус-вектора (г—г7). Если положить г—г7—0, то в правой части B.391)
останется только первый член. Тогда свертывание тензора по ин-
индексам а и C дает v2=3A@). Средний квадрат скорости является
самой общей характеристикой турбулентного движения. Часто при
описании изотропной турбулентности этим и ограничиваются, т. е.
в правой части B.391) сохраняют лишь член с А. Если провести
усреднение в интересующем нас уравнении B.390), сохраняя лишь
вклад, содержащий Л, то получится тождественный нуль. Удержа-
Удержание третьего члена в B.391) придает турбулентному движению
своеобразную особенность. Проведем сначала вычисления, а затем
вернемся к обсуждению физического смысла. Умножая обе сторо-
стороны выражения B.390) на *ь^д!дх ъ и свертывая по индексам а
и р, получаем С@)=—A/3) (v-rotv). Именно этот член дает не-
исчезающий вклад при усреднении в рассматриваемой модели ди-
камо. Проводя несложные выкладки, получаем
dH/dt = — (Aizo/c2k2) (v -rot v) rot H + (с74тоз) Д Н. B.392)
Турбулентное движение с (v-rotv)^O удобно представлять на-
наглядно как статистический ансамбль вихрей, каждый из которых
в среднем имеет преимущественное направление вращения (знак
rotv) в зависимости от направления своего поступательного дви-
движения (знак v). Любопытна аналогия с поляризацией нейтрино и
антинейтрино, которая, конечно, является чисто внешней.
Расписывая уравнение B.392) по компонентам, находим, что
между различными компонентами появляется обратная связь.
'Правда, она несколько отличается от предложенной Паркером.
Итак, как это было показано Стенбеком и Краузе, гиротропная
турбулентность, в которой (vrotv)^O, способна обеспечить усиле-
усиление и поддержание магнитного поля. Характерное время нараста-
нарастания можно получить, оценивая коэффициент связи из уравнения
B.392) и используя выражение для тем-па нарастания в упрощен-
308
ной модели Паркера:
у ъ 4mv2q/c2k.
B.393)
Поскольку при выводе уравнения для мелксшасштабных флуктуа-
флуктуации магнитного поля главным считается член, описывающий диф-
диффузию поля, то на темп роста поля накладывается следующее
ограничение: у < c2k2/4w, т. е. с2/4тса > Yv2qlk* •
Наконец, выше поле скоростей считалось заданным. На самом
же деле с ростом напряженности магнитного поля возрастает воз-
воздействие его на движение среды. Тем самым мы выходим за рам-
рамки кинематического приближения. Верхний предел магнитного
поля, который еще можно достичь, определяется из условий при-
приближенного равенства энергии магнитного поля и кинетической
энергии плазмы.
Кроме динамо существуют механизмы генерации магнитного
поля, связанные с так называемыми сторонними силами (сторон-
(сторонними ЭДС). Такую роль могут играть термоэлектрические эффек-
эффекты в плазме. Так, в уравнениии B.69) для магнитного поля при-
присутствует слагаемое, которое в плазме с неколлинеарными гради-
градиентами давления и температуры приводит к появлению вихревой
компоненты электрического поля. Этот эффект связан с учетом сил
давления в обобщенном законе Ома. В отсутствие движения среды
и магнитной вязкости уравнение B.69) принимает простой вид:
]. B.394)
Отсюда следует, что при неколлинеарных градиентах VTe и Vn
в плазме самопроизвольно нарастает магнитное поле. Из общих
соображений следовало бы ожидать,
что магнитное поле может нарастать
до тех пор, пока плотность энергии
магнитного поля станет сравнимой
с плотностью тепловой энергии плаз-
плазмы (H2l%n^nT). Однако гораздо
раньше магнитное поле замагничивает
электроны, и поэтому в законе Ома
появляются дополнительные члены,
связанные с так называемой термоси-
термосилой в направлении поперек градиента
температуры и направления магнитно-
магнитного поля. Физический смысл такой тер-
термосилы и порядок ее величины можно
Рис. 2.79. Возникновение тер-
термосилы из-за существования
разности длин пробега элек-
электродов в областях с разными
температурами
уяснить из рис. 2.79. Здесь электроны, движущиеся из области
с большей температурой в область с меньшей температурой, име-
имеют соответственно большую длину пробега относительно кулонов-
ских соударений. Вращаясь в магнитном поле, они передают в про-
процессе столкновений импульс плазме в направлении поперек гради-
309
ента температуры и магнитного поля, создавая термосилу порядка
где о)не=?Н/тес, а численный коэффициент можно получить из бо-
более строгой теории явлений переноса, выходящей за рамки книги.
Включая эту термосилу в закон Ома B.65), преобразуем уравне-
уравнение для магнитного поля к виду
dHldt=Ofil[Xelme] rot [HXVrj + (c/e/i)[VrexV/z]. B.395)
Дополнительный член слева можно интерпретировать как увлече-
увлечение магнитного поля тепловыми потоками со скоростью
u=—0,8UeVTe/me. B.396)
Именно этот процесс оказывает стабилизирующее воздействие на
рост поля и приводит к насыщению поля на уровне, определяемом
ПО ПОрЯДКу веЛИЧИНЫ уСЛОВИеМ (дн^е'—'1.
Здесь же следует отметить, что в плазме с первоначально кол-
линеарными градиентами я и Г к неколлинеарности последних мо-
могут привести малые возмущения градиента температуры при нали-
наличии возмущений магнитного поля. Для того чтобы убедиться в этом,
в уравнение теплопроводности следует включить так называемые
косые потоки тепла (за счет явления, аналогичного эффекту Хол-
Холла). В итоге получим уравнение
qJL=-5,7 {пТехМте) [©HeXVrj,
где численный коэффициент находит обоснование в строгой теории
переноса. В результате уравнение теплопроводности принимает вид
—5,7 div (neTex2e[idHeXVrj/me). B.397)
Выбирая ось х вдоль невозмущенных градиентов п0 и ГОе, а возму-
возмущение магнитного поля вдоль оси z в виде Нг=Н\ ехр (—kotf-f-
-\-iky), линеаризуем уравнения B.395) и B.397) относительно ма-
малых возмущений:
—i®Hi=—(ikcTiefen0} (dnojdx);
— C/2) iam0Tie=—3,16noToeTek2Tle/me—
Пренебрегая членом в левой части последнего уравнения по срав-
сравнению с членом, описывающим незамагниченную теплопровод-
теплопроводность, и разрешая систему уравнений относительно Ни находим,
что магнитное поле нарастает экспоненциально с инкрементом
7^1,8(te/men)(grad/2.gradre). B.398)
Описанная выше самопроизвольная генерация магнитного поля
предсказана А. Дыхне и В. Болыыовым в задаче о плазменной ко-
короне капельной мишени, облучаемой лазерным светом. Подавление
теплопроводности плазмы в результате роста магнитного поля су-
310
щественно сказывается на гидродинамике сжатия мишени и может
оказаться препятствием на пути к осуществлению лазерного термо-
термоядерного синтеза. Кроме того, если мишень облучается сфериче-
сферически-несимметричным потокОхМ лазерного света, то импульс световой
волны, поглощаемой электронами скин-слоя, может иметь компо-
компоненту вдоль скин-слоя. Это приводит к генерации тока электронов
и соответственно магнитного поля, охватывающего область погло-
поглощения излучения. Поскольку напряженность магнитного поля при
этом оказывается пропорциональной интенсивности излучения, то
эффект становится существенным лишь при очень больших потоках
лазерного излучения.
СПИСОК ЛИТЕРАТУРЫ *
1. Арцимович Л. А. Управляемые термоядерные реакции. М., Физматгиз, I960.
2. Арцимович Л. А. Замкнутые плазменные конфигурации. М., «Наука», 1969.
3. Веденов А. А., Велихов Е. П., Сагдеев Р. 3. Устойчивость плазмы.— «Успехи
физ. наук», т. 73, с. 701, 1961.
4.- Sagdeev R. Z., Galeev A. A. Nonlinear plasma theory. Benjamin, NY—L,
1969.
5. Альвен X. Космическая электродинамика. Пер. с англ. М., Изд-во иностр.
лит., 1952.
6. Ахиезер А. И. и др. Электродинамика плазмы. М., «Наука», 1974.
7. Гинзбург В. Л. Распространение электромагнитных волн в плазме. М., «Нау-
«Наука», 1960.
8. Гинзбург В. Л., Рухадзе А. А. Волны в магнитоактивной плазме. М., «Нау-
«Наука», 1967.
9. Толант В. Е. Основы физики плазмы. М., Атомиздат, 1975.
10. Иванов А. А. Физика сильнонеравновесной плазмы. М., Атомиздат, 1977.
11. Кадомцев Б. Б. Коллективные явления в плазме. М., «Наука», 1976.
12. Ломинадзе Д. Г. Циклотронные волны в плазме. Тбилиси, «Мецниереба»,
1975.
13. Михайловский А. Б. Теория плазменных неустойчивостей. Т. 1. Неустойчи-
Неустойчивости однородной плазмы. Изд. 2-е, перераб. и доп. М., Атомиздат, 1975;
Т. 2. Неустойчивости неоднородной плазмы. Изд. 2-е, перераб. и доп. М.,
Атомиздат, 1977.
14. Пикельнер С. Б. Основы космической электродинамики. М., Физматгиз, 1961.
15. Piddington. Cosmical Electrodynamics. Wiley Inters. NY-L, 1966.
16. Силин В. П. Параметрическое воздействие излучения большой мощности на
плазму. М., «Наука», 1973.
17. Силин В. П., Рухадзе А. А. Электромагнитные свойства плазмы и плазмо-
подобных сред. М., Атомиздаг, 1964.
18. Спитцер Л. Физика полностью ионизованного газа. Пер. с англ. М., Изд-во
иностр. лит., 1957.
19. Стикс Т. X. Теория плазменных волн. Пер. с англ. М., Атомиздат, 1965.
20. Цытович В. Н. Нелинейные эффекты в плазме. М., «Наука», 1967.
* Изложение в этой книге следует в значительной степени содержанию и
стилю [1—4].
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Адиабатические инварианты 135, 150
Альвеновские волны 168
Аномальная вязкость 300
Аномальное сопротивление 76, 273,
277, 284, 285
Арцимовича формула 267
Бома коэффициент диффузии 249,
257
Булларда — Эльзассера механизм
генерации магнитного поля 306
Власова уравнение 54
Вмороженность магнитного поля 161
Волны бесстолкновительные ударные
• без магнитного поля 130
в магнитном поле 292, 299
¦— дрейфовые 244
— кноидальные 127
— магнитогид родин амические (аль-
(альвеновские) 168
— магнитозвуковые 165
— отрицательной энергии 77
— электромагнитные необыкновен-
необыкновенные 174
обыкновенные 174
Время свободного пробега электро-
электрона 21
иона 23
фотона 49
Вязкость магнитная 162
Гидродинамика магнитная 157
—¦ плазмы без магнитного поля 59
— бесстолкновительная 64
— двухжидкостная 61
— одножидкостная 62
— в магнитном поле 157
бесстолкновительная 164
двухжидкостная 157
Давление высокочастотное 34
— магнитного поля 157
Дебаевский радиус экранирования 9
Декремент затухания колебаний
(волн) электронный, плазменных
79
ионно-звуковых 75
Динамо-механизм генерации магнит-
магнитного поля в движущейся плазме
304
Дисперсионная кривая 12
Дисперсионное соотношение (урав-
(уравнение) колебаний плазмы 37
Диффузии коэффициент Бома 249,
257
в магнитном поле 199
—¦ — в тороидальных ловушках 261
Диффузия аномальная 249, 255, 257
— «банановая» 262
— в пространстве скоростей (квази-
(квазилинейная) 104
— магнитного поля 162
— неоклассическая 262
— плазмы в магнитном поле 199
Диэлектрической проницаемости тен-
тензор 170
Длина свободного пробега ионов 21
электронов 21
Дрейф заряженной частицы в скре-
скрещенных полях 14
магнитный 136
За'магниченности плазмы критерий
155
Запас устойчивости 227, 231
Запертые частицы в тороидальных
магнитных ловушках 205, 262
Захват частиц волной 14
Индуцированное рассеяние колеба-
колебаний (волн) 109, ПО
313
Инкремент нарастания неустойчиво-
неустойчивости (см. Неустойчивости)
Ионизация 17
Ионизационное равновесие по Саха
18
Интеграл столкновений 55
в форме Ландау 58
Квазилинейная теория 102
циклотронной неустойчивости
193
ионно-звуковой неустойчивости
279
дрейфовых неустойчивостей
254
Квазинейтральность 7
Квантовая плазма 16
Кинетическое уравнение для заря-
заряженных частиц 54
для волн 115
Когерентное излучение 53
Коллапс плазменных волн 122
Коллективный метод ускорения 77
Колмогорова — Обухова спектр тур-
турбулентности 117
Критерий замагниченности плазмы
155
— Сайдэма 228
— устойчивости плазмы Крускала —
Шафранова 225
Кулоновский логарифм 21
Ландау затухание колебаний 12
Ларморовская орбита 134
— частота 134
Ленгмюра двойной слой 287
Ленгмюровская плазменная частота
электронов 10
ионов 68
Магнитный момент заряженной ча-
частицы 135
Магнитное зеркало 143
Магнитная ловушка 143
Магнитная термоизоляция 163
Магнитные островки 209
— поверхности 205
Магнитная яма 221
Магнитное (бетатронное) излучение
271
Магнитного поля генерация (см. Ди-
Динамо-механизм) 309
за счет термосилы 309
Маха критическое число 130
для ионно-звукового соли-
тона 130
•— для магнитозвукового со-
литона 295
«Минимума Н» принцип 221
Натяжения силовых линий магнитно-
магнитного поля сила 157
314
Неизотермическая плазма 9
Неоклассическая диффузия 262
Низкотемпературная плазма 19
Неустойчивость Будкера — Бунемана
76
— Драммонда — Розенблюта 274
— ионно-звуковая 75
— конусная 195
— модуляционная 119
— пучковая 15, 84
— распадная параметрическая 91, 98
— шланговая 184
— циклотронная 180
— мазерная 182
— равновесия плазмы в магнитном
поле 213
баллонная 230
гравитационная 231
дрейфовая 248
диссилативная 249
запертых частиц 253
¦ —• примесная 252
температурная 251
токово-конвективная 235
желобковая 218 '
Крускала — Шварцшильда 215
тиринг-моды 236
«Осцилляции» затухания 80
Перестановочные (конвективные)
возмущения 220
Пинч-эффект 203
Плазменное эхо 82
Плазменный конденсат 118
«Плато» на функции распределения
(квазилинейное) 105
«Плато-режим» неоклассической диф-
диффузии 263
Правило обхода Ландау 74
Пролетные частицы в тороидальных
ловушках 145
Разрушение магнитных поверхностей
(резонансное) 207
Распад плазменной волны 92
Рассеяние частиц на колебаниях 24
Резонанса плазменного точка 39
Резонанс волна — частица 12
—- гибридный верхний 172
нижний 167
— циклотронный 142
Рекомбинация 17
Рекомбинащшнное излучение 47
Релаксация электронного пучка в
плазме 104
Сайдэма критерий 228
Самосогласованное поле 54
Саха формула 18
Сечение тормозного излучения 45
Солитон ионно-звуковой 129
— магнитозвуковой 294
Стабилизация неустойчивости пучко-
пучковой 88
продольным полем 225
широм 228
Степень ионизации 17
Температура электронов 9
— ионов 9
Теплообмен между электронами и
ионами 26
Тормозное излучение электронов 43
Трансформация электромагнитной
волны в плазменную 43
Теплопроводность (температуролро-
водность плазмы без магнитного
поля) 57
— замагничен'ная 201
—• неоклассическая 265
Трансформации волн коэффициент 43
Турбулентность 99
— ионно-звуковая 118
— слабая 100
Токамак 204
Убегания электронов эффект 30
Устойчивости плазмы запас 227, 231
критерий Крускала — Шафра-
нбва 225
энергетический принцип 211
ОГЛАВЛЕНИЕ
Предисловие 3
1. ПЛАЗМА БЕЗ МАГНИТНОГО ПОЛЯ 6
§ 1.1. Общие сведения о плазме 6
§ 1.2. Плазменные колебания Ю
§ 1.3. Классификация видов плазмы 15
§ 1.4. Столкновения частиц в плазме 20
§ 1.5. Явления переноса в плазме 27
§ 1.6. Плазма в высокочастотном поле 31
§ 1.7. Проникновение электромагнитной волны в плазму. Трансформация
в плазменные колебания 36
§ 1.8. Излучение плазмы . 43
§ 1.9. Кинетическое уравнение для плазмы 53
§ 1.10. Гидродинамическое описание плазмы 59
§ 1.11. Звук в плазме 64
§ 1.12. Кинетическая теория волн в плазме , 69
§ 1.13. Кинетическая теория волн в плазме (ленгмюрозские колебания) . 78
§ 1.14. Пучковая неустойчивость 84
§ 1.15. Параметрическая неустойчивость 91
§ 1.16. Резонансное взаимодействие волн и частиц (квазилинейная теория) 99
§ 1.17. Резонансное взаимодействие волн и частиц (индуцированное рас-
рассеяние) 109
§ 1.18. Нелинейное взаимодействие волн в слабой турбулентности . . . 114
§ 1.19. Модуляционная неустойчивость и коллапс ленгмюровских волн . 119
§ '1.20. Стационарные нелинейные волны 125
2. ПЛАЗМА В МАГНИТНОМ ПОЛЕ . . , 134
§ 2.1. Движение заряженных частиц в магнитном поле 134
§ 2.2. Примеры движения частиц в магнитном поле 142
§ 2.3. Адиабатические инварианты движения частиц в магнитном поле . 148
§ 2.4. Кинетическая теория плазмы в магнитном поле * 152
§ 2.5. Гидродинамика плазмы в магнитном тюле 156
316
§ 2.6. Колебания и волны в плазме с магнитным полем . . ¦ . . . 164-
§ 2.7. Кинетическая теория волн в плазме 177
§ 2.8. Взаимодействие волн с частицами плазмы в магнитном поле и
квазилинейная диффузия 187'
§ 2.9. Равновесие ллазмы в магнитном поле .198
§ 2.10. Примеры равновесия плазмы в магнитном поле. Токамак . . . 202
§ 2.11. Устойчивость границы плазмы в магнитном поле 212
§ 2.12. Желобковая неустойчивость плазмы и энергетический принцип
устойчивости в магнитной гидродинамике 218
§ 2.13. Стабилизация магнитогидродинамических неустойчивостей в термо-
термоядерных ловушках 223-
§ 2.14. Магнитогидродинам'ическая неустойчивость равновесия при конеч-
конечной электр отгроводности 231
§ 2.15. Неустойчивость тиринг-моды 236
§ 2.16. «Дрейфовая» неустойчивость плазмы 244
§ 2.17. Микронеустойчивость плазмы и аномальная диффузия .... 254
§ 2.18. Энергетический баланс плазхмы в токамаке 258
§ 2.19. Аномальное сопротивление в плазме и образование двойных слое!з 273
§ 2.20. Бесстолкновительные ударные волны 290
§ 2.21. Генерация и усиление магнитного поля 303
Список литературы 312
Алфавитно-предметный указатель 313
ИБ № 1108
Лев Андреевич Арцимович,
Роальд Зиннурович Сагдеев
ФИЗИКА ПЛАЗМЫ ДЛЯ ФИЗИКОВ
Редактор Л. В. Белова
Художественный редактор А. Т. Кирьянов
Переплет художника О. В. Камаева
Технический редактор Н. А. Власова
Корректор Н. А. Смирнова
Сдано в набор 02.03.79. Подписано к печати
20.07.79. Т-11959. Формат 60x90/i6. Бумага тип. №2
Iарнитура литературная. Печать высокая Усл.
печ. л. 20. Уч.-изд. л. 21,54. Тираж 7100 экз.
Зак изд. 75364. Зак. тип. 74. Цена 2 р.
Атомиздат, 103031 Москва К-31, ул. Жданова, 5
Московская типография № 10 Союзполиграфпрома
при Государственном комитете СССР по делам
издательств, полиграфии и книжной торговли.
113114 Москва М-114, Шлюзовая наб., 10.
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Атомиздат совместно с издательством «-North Holland» (Ни-
(Нидерланды) наметил издание коллективной монографии «Физика
плазмы» в 6 томах под общей редакцией академика Р. 3. Сагдеева
(СССР) и академика М. Н. Розенблюта (США). Авторы обзоров —
известные специалисты по физике плазмы из СССР, США, Франции,
Японии, Италии и других стран. Монография будет издана на рус-
русском и английском языках в 1981—1983 гг. Объем каждого тома —
30 л.
Тома 1 и 2. Общая физика плазмы.
Под ред. А. А. Галеева (СССР) и проф. Р. Н. Судана (США).
В томах детально излагаются основы классической физики
плазмы, нелинейной теории плазмы и физика плазмоподобных сред.
Включены обзоры по следующим вопросам: движение заряженных
частиц в электрическом и магнитном полях, кинетическая теория
плазмы и интеграл столкновений, элементарные процессы в плазме,
магнитная гидродинамика, классическая теория процессов, процес-
процессы излучения в плазме, колебания и волны в плазме, микроне-
микронеустойчивости однородной плазмы, микронеустойчивости неоднород-
неоднородной плазмы, диагностика плазмы, численная плазма, нелинейные и
ударные волны в плазме, взаимодействие волн и частиц, теория
слабой турбулентности, аномальный перенос в плазме, взаимодей-
взаимодействие пучков заряженных частиц с плазмой, параметрические не-
неустойчивости, коллапс ленгмюровских волн, сильная турбулентность
и механизмы диссипации ВЧ-энергии, релятивистская плазма, не-
неидеальная плазма, плазма твердых тел.
Тома 3 и 4. Управляемый термоядерный синтез.
Под ред. акад. Е. П. Велихова (СССР) и проф. Б. Коппи
(США).
Излагаются основные идеи и современный уровень исследова-
исследований по проблеме управляемого термоядерного синтеза. Отражены
результаты исследований по замкнутым открытым магнитным ло-
ловушкам, а также по важнейшим импульсным методам осуществле-
осуществления управляемых термоядерных реакций.
В тома включены обзоры по следующим вопросам: основные
концепции термоядерного синтеза, импульсные разряды малой дли-
длительности, плазменные инжекторы, открытые магнитные ловушки,
гибридные ловушки, нагрев плазмы в открытых ловушках, замкну-
замкнутые магнитные ловушки (общие принципы), неоклассическая теория
процессов переносов, неустойчивости в замкнутых ловушках и ано-
аномальный перенос, различные методы нагрева плазмы в замкнутых
ловушках, токамаки и стеллараторы (основные экспериментальные
результаты), лазерный термоядерный синтез, пучковый термоядер-
термоядерный синтез.
Том 5. Космическая плазма.
Том 6. Астрофизическая плазма.
Под ред. проф. Р. А. Сюняева (СССР), проф. Ч. Ф. Кеннела
(США).
В материалах томов отражен современный уровень исследова-
исследований по космической и астрофизической плазме. Включены обзоры
но элементарным и коллективным процессам излучения в космиче-
космической плазме, ускорению заряженных частиц в космосе, происхожде-
происхождению космического магнитного поля, пересоединению магнитных си-
силовых линий, Солнцу, солнечным вспышкам и солнечному ветру,
магнитосфере планет, плазме астрофизических объектов и теории
гравитирующих систем.