Московский государственный технический университет им. Н. Э. Баумана
Зайцева А. В.
ИНФОРМАТИКА
Пособие для студентов (под редакцией Жукова А. Е.)
Москва, 2010 г.
Аннотация
В настоящем пособии изложены основы теоретической информатики.
В первой главе даны элементы теории множеств. Приведены основные термины, определения и свойства; продемонстрирована работа с диаграммами Эйлера — Венна и характеристическими функциями; введены понятия отношения и отображения множеств.
Вторая глава посвящена комбинаторике. Даны базовые комбинаторные понятия и схемы; разобраны как элементарные, так и некоторые нетривиальные задачи; рассмотрены математические аспекты биномиальных коэффициентов.
В третьей главе рассматриваются основы теории чисел (делимость, свойства остатков, наибольший общий делитель, алгоритм Евклида) и, в частности, элементы модульной арифметики (обратимость чисел по умножению, сравнения и системы сравнений первой степени).
В четвёртой главе пособия описана работа с различными системами счисления; затронут вопрос представления чисел в двоичном коде.
Материал изложен доступным языком и сопровождается наглядными примерами. В конце каждой главы приведены задачи для самостоятельного решения.
Пособие предназначено для студентов первого курса, обучающихся по специальностям «Комплексное обеспечение информационной безопасности автоматизированных систем» и «Компьютерная безопасность».
2
Оглавление
Предисловие....................................................6
1.	Элементы теории множеств....................................7
1.1.	Основные термины и определения..........................7
1.2.	Числовые множества......................................9
1.3.	Способы задания множеств................................9
1.4.	Операции над множествами. Диаграммы Эйлера — Венна.....10
1.4.1.	Задача 1.1. Вычисление мощности множества по диаграмме Эйлера — Венна...................................14
1.5.	Характеристическая функция множества...................17
1.5.1.	Задача 1.2. Вычисление мощности множества с помощью характеристических функций.................................18
1.5.2.	Характеристическая функция подмножества..............19
1.6.	Отношения на множествах.................................20
1.6.1.	Свойства бинарных отношений.........................22
1.7.	Отображения............................................23
1.7.1.	Типы отображений....................................25
1.7.2.	Композиция отображений. Обратное отображение........27
1.7.3.	Подстановки на множестве............................28
1.7.4.	Задача 1.3. Уравнение с подстановками...............30
1.8.	Принцип включения-исключения...........................30
1.8.1.	Задача 1.4. Элементарная задача на формулу включения-исключения.................................................32
1.9.	Задачи для самостоятельного решения....................33
2.	Основные комбинаторные понятия и схемы.....................36
2.1.	Два основных правила комбинаторики.....................36
2.1.1.	Задача 2.1. Правило произведения....................37
2.1.2.	Задача 2.2. Правило суммы...........................37
22.	Основные схемы выборок.................................38
2.2.1.	Размещения с повторениями...........................38
3
2.2.2.	Размещения без повторений, перестановки.............39
2.2.3.	Сочетания без повторений............................39
2.2.4.	Сочетания с повторениями............................41
2.3.	Примеры комбинаторных задач.............................42
2.3.1.	Задача 2.3. Пассажиры в купе........................42
2.3.2.	Задача 2.4. Игральные карты.........................43
2.3.3.	Задача 2.5. Количество чисел определённого вида.....44
2.4.	Свойства биномиальных коэффициентов.....................45
2.4.1.	Симметрия...........................................46
2.4.2.	Рекуррентность......................................46
2.4.3.	Максимальное значение...............................47
2.4.4.	Треугольник Паскаля.................................47
2.4.5.	Свёртка Вандермонда.................................48
2.4.6.	Бином Ньютона.......................................49
2.4.7.	Задача 2.6. Выражение, имеющее	в основе бином
Ньютона....................................................50
2.4.8.	Задача 2.7. Преобразование биномиальных коэффициентов..............................................51
2.4.9.	Задача 2.8. Дифференцирование бинома Ньютона........51
2.4.10.	Задача 2.9. Интегрирование бинома Ньютона..........52
2.4.11.	Алгебраическое доказательство свёртки Вандермонда...53
2.5.	Полиномиальные коэффициенты............................54
2.5.1.	Задача 2.10. Шашки на доске.........................55
2.5.2.	Разложение степени полинома на слагаемые............56
2.5.3.	Задача 2.11. Коэффициенты разложения................56
2.6.	Задачи для самостоятельного решения....................57
3.	Основы теории чисел........................................59
3.1.	Основные термины и определения.........................59
3.2.	Базовые теоремы........................................60
3.3.	Свойства остатков......................................62
3.4.	Наибольший общий делитель и наименьшее общее кратное...63
4
3.4.1.	Функция Эйлера......................................64
3.4.2.	Задача 3.1. Делимость чисел.........................66
3.4.3.	Основное свойство НОД...............................68
3.4.4.	Алгоритм Евклида....................................69
3.4.5.	Расширенный алгоритм Евклида........................69
3.5.	Модульная арифметика...................................71
3.5.1.	Множество вычетов...................................71
3.5.2.	Сравнение по модулю.................................73
3.5.3.	Сравнения первой степени............................75
3.5.4.	Китайская теорема об остатках.......................77
3.5.5.	Системы сравнений первой степени....................79
3.6.	Задачи для самостоятельного решения....................80
4.	Системы счисления..........................................82
4.1.	Непозиционные системы счисления........................82
4.1.1.	Римские цифры.......................................82
4.1.2.	Система остаточных классов..........................82
4.2.	Позиционные системы счисления..........................83
4.2.1.	Представление натуральных чисел.....................83
4.2.2.	Представление дробных чисел.........................85
4.2.3.	Арифметические действия в b-ричной системе счисления.88
4.2.4.	Двоичный код........................................91
4.3.	Задачи для самостоятельного решения....................92
Ответы и указания к задачам...................................94
Список рекомендуемой литературы...............................98
5
Предисловие
В настоящем пособии изложены основы теоретической информатики — дисциплины, использующей математические методы для изучения информации и информационных процессов.
В первой главе пособия даны элементы теории множеств, лежащей в основе большинства математических дисциплин. Множество является ключевым объектом математики и логики.
Вторая глава посвящена комбинаторике — разделу математики, изучающему дискретные объекты. В данном пособии рассматривается перечислительная комбинаторика, которая занимается подсчётом количества различных комбинаций, образуемых заданными объектами (элементами конечных множеств) и удовлетворяющих тем или иным условиям. Комбинаторика тесно связана с теорией вероятностей.
В третьей главе рассматриваются основы теории чисел (дисциплины, изучающей целые числа) и, в частности, модульной арифметики. Они имеют непосредственное отношение к криптографии — науке, занимающейся шифрованием информации.
В четвёртой главе описана работа с различными системами счисления', затронут вопрос представления чисел в двоичном коде, т. е. в том формате, в котором данные хранятся и обрабатываются в подавляющем большинстве современных компьютеров.
Материал изложен доступным языком и сопровождается наглядными примерами (они выделены пунктирной рамкой). Примеры зачастую приводятся раньше теории, что способствует лучшему пониманию материала благодаря плавному переходу от простого к сложному, от частного к общему.
В конце каждой главы даны задачи для самостоятельного решения, позволяющие закрепить пройденный материал.
Пособие предназначено для студентов первого курса, обучающихся по специальностям «Комплексное обеспечение информационной безопасности автоматизированных систем» и «Компьютерная безопасность».
6
1.	Элементы теории множеств
Теория множеств — это раздел математики, в котором изучаются общие свойства множеств. Данная теория лежит в основе большинства математических дисциплин, в том числе математического анализа, геометрии и теории вероятностей.
1.1.	Основные термины и определения
Под множеством понимают совокупность (набор) объектов, обладающих определённым свойством. Эти объекты называются элементами множества.
Утверждение «Множество М состоит из элементов а, Ь, с» записывается следующим образом: М = {а,Ь,с]. Вводится понятие принадлежности: а&М {а принадлежит множеству Л/), d^M (d не принадлежит множеству М).
Количество элементов множества называется мощностью множества. Мощность множества М обозначается \м\.
Если множество содержит конечное число элементов, оно называется конечным, в противном случае — бесконечным.
Так, например, множество натуральных чисел {1,2,3,...} является бесконечным.
Множество букв русского алфавита {а, б, в,..., э, ю, я} конечно, его мощность равна 33.
Элементами множеств могут быть любые объекты, в том числе и сами множества.
Например, {ИУ8-11, ИУ8-12,...} — множество групп первого курса потока ИУ8, а каждая группа есть множество студентов.
Говорят, что множество А является подмножеством множества В (или «лежит в множестве В», или «включено в В»), если любой элемент, принадлежащий Л, также принадлежит В. Обозначают это отношение как А о В.
7
Множество студентов группы ИУ8-11 лежит в множестве студентов кафедры ИУ8.
Множество групп первого курса потока ИУ8 лежит в множестве всех групп потока ИУ8.
Если Лс й и йс Л, то множества А и В равны. Очевидно, что из равенства множеств следует равенство их мощностей, но обратное неверно.
Множество корней уравнения х2 + 5х - 6 = 0: А = {-6,1}.
Множество корней уравнения 2х2 + 10х -12 = 0: В = {-6,1}.
А = В.
Множество, не содержащее ни одного элемента, обозначается символом 0 и носит название «пустое множество».
Множество людей, пробегающих стометровую дистанцию за 5 секунд, — пустое.
Справедливо утверждение: УЛ, 0сЛ — пустое множество является подмножеством любого множества.
Справедливо утверждение: УЛ, ,4с,4 — любое множество лежит в самом себе.
Если А^В и АфВ , то говорят, что А «строго лежит в В», А является собственным, или нетривиальным, подмножеством множества В. Обозначение: А^В.
В рамках каждой задачи определяют т. и. универсальное множество. Это множество, которое включает в себя все множества, рассматриваемые в рамках определенной ситуации или рассуждения. Оно обозначается буквой U. К примеру, если в задаче рассматриваются множества студентов, изучающих те или иные дисциплины в МГТУ им. Баумана, и никакие другие люди в за-
В некоторых источниках символом CZ обозначают любое подмножество, а для указания на собственное подмножество используют значок С .
8
даче не участвуют, то в качестве универсального множества можно взять множество всех студентов вуза.
1.2.	Числовые множества
N — множество натуральных чисел: {1,2,3,4,...}.
Z — множество целых чисел:	3, — 2, — 1,0,1,2,3,.
Q — множество рациональных чисел. Оно состоит из всех обыкновенных дробей вида тп/п, где т g Z, п g N.
В — множество вещественных (действительных) чисел.
С — множество комплексных чисел. Его элементы имеют вид x+iy, где хе В, уеВ, i— «мнимая единица», т. е. число, удовлетворяющее уравнению Z2 = -1.
I — множество иррациональных чисел. Оно состоит из вещественных чисел, не являющихся рациональными. Пример: л/2 е I, л е I.
No — множество «натуральных чисел с нулём»: {0,1,2,3,4,...}.
В+ — множество положительных вещественных чисел.
Очевидно: NcN0 cZcQcBcC ; IcB; В+ с В.
1.3.	Способы задания множеств
Перечислением элементов.
М = {1, 2, 3};	К = {2, 4, 6, 8,...};	L = ’{1,2, 4, 8,...} .
Описанием.
М = {х g N | х < 4} ;	К = {х | х = 2п, п g N);	L = |х | х = 2к, к е No} ;
Q = {х | х = т/п, т е Z, п е N) .
Словесно.
М — множество натуральных чисел от 1 до 3 включительно;
К — множество положительных чётных чисел;
L — множество целых неотрицательных степеней двойки;
9
Q — множество рациональных чисел;
Р — множество простых чисел.
Рекурсивно.
Для множества К:
1.	2<=К.
2.	Vx G К, Х + 2 G К .
3.	Других элементов нет.
Для множества L:
1.	IgZ.
2.	Vx g Л, 2x g L .
3.	Других элементов нет.
1.4.	Операции над множествами. Диаграммы Эйлера — Венна
Объединение множеств Лий — это множество, состоящее из элементов, которые принадлежат хотя бы одному из этих множеств: А или В.
A иВ = {х | (х g A) v (х g В)} .	(1-1)
Пересечение множеств А и В — это множество, состоящее из элементов, которые принадлежат и Л, и В.
А гВ = {х | (х g А)л(х g В)} .	(1-2)
Разность множеств А и В — это множество, состоящее из тех элементов Л, которые не принадлежат В.
А\В = {х | (х g А) л (х £ В)} .	(1-3)
Симметрическая разность множеств А и В — это множество, состоящее из элементов, которые принадлежат ровно одному из множеств (т. е. либо Л, либо В, но не обоим множествам одновременно).
АЛВ = (Аг>В)\(АглВ),
(1-4) АЛВ = (А\В)и(В\А).
Дополнение множества Л (до универсального множества) — это множество, состоящее из всех элементов U, которые не принадлежат Л.
10
A = {x | (x g U)/\ (x £ Л)} .
(1-5)
Пусть A = {1,2,3,7}, В = {2,4,5}. Тогда:
4иВ = {1,2, 3, 4, 5,7};
+Ы = {2{;
Л\В = {1,3,7};
ВЫ = {4,5};
ЛАВ = {1,3,4, 5, 7}.
Результат операции дополнения зависит от того, что считается универсальным множеством. Если в рамках данной задачи мы оперируем числами от 1 до 10, то имеет смысл выбрать U = {1,2,..., 10}, и тогда
Л = {4, 5, 6, 8, 9,10};
В = {1, 3, 6, 7, 8, 9,10}.
Результатом операции над множествами может быть пустое множество. Пусть А = {1,2,3, 7}, С = {4, 5} . Тогда А о С = 0 .
Для наглядной иллюстрации результатов операций над множествами используют диаграммы Эйлера — Венна, в которых множества условно изображаются кругами (или другими фигурами) на плоскости.
Пример 1. Пусть U— множество студентов группы ИУ8-11. Пусть С — множество тех из них, которые в школе изучали язык C++. Пусть D — множество студентов, знающих Delphi. Ниже представлены диаграммы Эйлера — Венна для различных множеств, которые могут образоваться в результате операций над исходными множествами. В некоторых случаях множества, не участвующие в операции, изображены пунктиром для большей наглядности.
11
С — студенты, не изучавшие C++.
D — студенты, не изучавшие Delphi.
CAD — студенты, изучавшие либо C++, либо Delphi, но не оба языка сразу.
C\D — студенты, изучавшие C++ и не изучавшие Delphi.
С <jD — студенты, изучавшие хотя бы один из двух рассматриваемых языков программирования.
С <jD — студенты, не изучавшие ни один из рассматриваемых языков.
I) — студенты, изучавшие Delphi.
D\C — студенты, изучавшие Delphi и не изучавшие
С г!) — студенты, изучавшие оба этих языка.
С г!) — студенты, изучавшие не более одного языка.
12
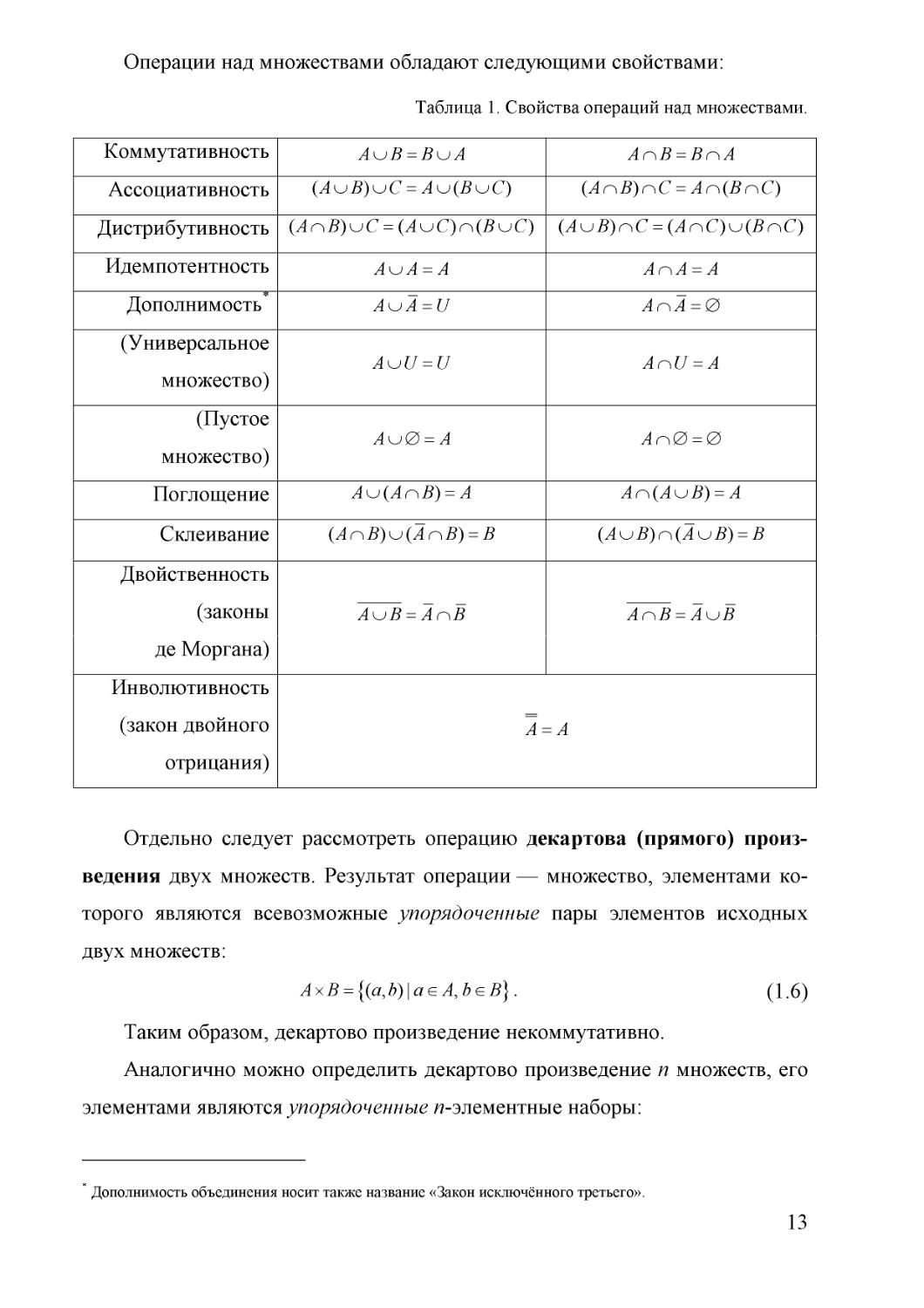
Операции над множествами обладают следующими свойствами:
Таблица 1. Свойства операций над множествами.
Коммутативность	A <jB = B<jA	ArB=BoA
Ассоциативность	(А^В)^С = А^(В^С)	(АглВ)глС = Агл(ВглС)
Дистрибутивность	(Ar>B)uC = (A<jC)g3(B<jC)	(AuB)nC = (AnC)u(BnQ
Идемпотентность	A^jA = A	A-A = A
Дополнимость	A<jA = U	Ar, A = 0
(Универсальное множество)	AoU = U	AoU =A
(Пустое множество)	Ao0 = A	Ло0 = 0
Поглощение	Axx(ArxB) = A	А rx (А о В) = A
Склеивание	(АпВ)и(АгУ) = В	(AuB)n(AuB) = B
Двойственность (законы де Моргана)	AxxB = A rB	AoB = A uB
Инволютивность (закон двойного отрицания)	A = A	
Отдельно следует рассмотреть операцию декартова (прямого) произведения двух множеств. Результат операции — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств:
А хВ = {(а,0 | а е Л, b е В] .	(1.6)
Таким образом, декартово произведение некоммутативно.
Аналогично можно определить декартово произведение п множеств, его элементами являются упорядоченные н-элементные наборы:
Дополнимость объединения носит также название «Закон исключённого третьего».
13
A1xA2x...xAn={(a1,a2,...,an)la1eAi,...,aneAn}.	(1.7)
Декартов квадрат множества определяется как А2 = Ах А. Декартова степень Л" — это прямое произведение множества А самого на себя и раз.
Для иллюстрации декартова произведения можно, например, отметить соответствующие «координаты» точек на плоскости (рис. 1.1).
Пример 2. Если S = {Иванов, Петров, Сидоров} —	5	•••
множество студентов группы, а К = {2,3,4,5} — 4— ф ф множество оценок, которые они могут получить, то прямое произведение SxK фактически описывает все возможные комбинации: каждый из сту-	♦
дентов может получить любую из оценок.	j______|______|
Иванов Петров Сидоров SxK = {(Иванов, 2), (Иванов, 3), (Иванов, 4), (Иванов, 5), (Петров, 2), (Петров, 3), (Петров, 4), (Петров, 5),	Рисунок 1.1.
(Сидоров, 2), (Сидоров, 3), (Сидоров, 4), (Сидоров, 5)}	декартово произведение.
1.4.1.	Задача 1.1. Вычисление мощности множества по диаграмме Эйлера — Венна
Построить диаграмму Эйлера — Венна для множества D = AS(BS(C\A)) и выразить его мощность через мощности множеств А, В, С и их пересечений. Диаграмму будем строить последовательно.
Поскольку в задании ничего не сказано о том, что собой представляют множества А, В, С и как они пересекаются между собой, рассмотрим самый общий случай (рис. 1.2):
Рисунок 1.2. Исходные множества.
14
На первом шаге изобразим множество Е, являющееся результатом операции С\А (рис. 1.3). Множество В в данной операции не участвует. На втором шаге построим F = BEE (рис. 1.4); множество А здесь не задействовано. Наконец, определим область диаграммы, соответствующую I) = AAI- (рис. 1.5).
Е = С\А.	F = BAE = Bk(C\A).	D = A kF = АЛ(ВЛ(С\А)).
Выразим мощность полученного множества D.
Из диаграммы видно, что в состав множества D входят в том числе и те элементы, которые принадлежат только множеству А и никакому другому. Значит, в формуле для |£>| будет фигурировать |А|.
|С| = |Л| + ...
Отметим палочками те области диаграммы, элементы которых окажутся учтёнными в формуле за счёт этого слагаемого:
Рисунок 1.6. Элементы множества Л.
Рассуждая аналогичным образом, приходим к выводу, что без мощностей \В\ и |С| также не обойтись:
|Д| = |Л| + |£| + |С| + ...
Данная формула затронет следующие участки диаграммы:
15
Рисунок 1.7. Элементы множеств Л, ВиС.
Из чертежа видно, что элементы, лежащие в пересечении двух множеств,
оказываются учтены дважды, а элементы, входящие в АглВглС,— трижды. Однако для корректного подсчёта мощности множества D необходимо получить такую формулу, чтобы внутри каждого закрашенного контура было ровно по одной палочке, а в белых областях диаграммы — ни одной.
Для этого вычтем попарные пересечения множеств. Слагаемые, входящие в формулу для |£>| со знаком «—», будем для наглядности отмечать горизон
тальными чёрточками. Горизонтальные и вертикальные палочки, сливаясь, образуют «+», что символизирует взаимное уничтожение.
Сначала избавимся от лишней палочки между Л и С (рис. 1.8):
1с1=И+1в1+Н-И^с|-...
Поскольку между Л и В, а также между В и С, по две лишних палочки, необходимо вычесть их по два раза (рис. 1.9):
|Г>| = |Л| + |В| + |С|-|ЛпС|-2|ЛпВ|-2|ВпС|-...
Рисунок 1.8.
Промежуточный этап. |£>| = |Л|+|2?| + |С|-|ЛпС|-...
Рисунок 1.9. Промежуточный этап.
|Г>| = |Л| + |В| + |С|-|ЛпС|-2|ЛпВ|-2|ВпС|-...
16
Мы добились желаемого результата во всех областях, кроме центральной: в ней остались два «нескомпенсированных» минуса. Поэтому необходимо прибавить к формуле удвоенную мощность пересечения всех трёх множеств. Итоговый результат: |Z>| = |Л| + |в| + |С|-|Л оС|-2|ЛоВ|-2|ВоС| + 2|Л оВоС|.
1.5.	Характеристическая функция множества
Характеристическая функция множества, или индикатор множества, указывает на принадлежность элемента этому множеству.
Если М = {1,2,3}, то Zm(2) = 1, Zm(5) = 0.
Очевидно, что два множества равны тогда и только тогда, когда равны их характеристические функции, что позволяет перейти от операций над множествами к арифметическим операциям над характеристическими функциями и использовать их свойства для упрощения выражений и доказательства тождеств.
Характеристические функции множеств, являющихся результатами основных операций над множествами А и В, выражаются через /Дх) и /Дх) следующим образом:
Пересечение: xAii = ха-Хв-
Объединение: Хл .в = ХА + Хв~ХА-Хв-
Разность: хА\В = хА~хА-хв-
Симметрическая разность: хл,в = ХА + Хв - 2• хА • Хв •
Дополнение: Xa=^~Xa-
В справедливости данных формул нетрудно убедиться, изучив таблицу значений функций при всех возможных расположениях элемента х: первая строка соответствует случаю, когда он не принадлежит ни одному из двух множеств, вторая — ситуации, когда х принадлежит В, но не принадлежит Л, ит. д.
17
Таблица 2. Операции над множествами и их характеристические функции.
Ха	Хв	%Аг\В	XauB	Ха\в	Хв\А	Ха	Хв	Ха&в
0	0	0	0	0	0	1	1	0
0	1	0	1	0	1	1	0	1
1	0	0	1	1	0	0	1	1
1	1	1	1	0	0	0	0	0
Нетрудно заметить, что %А -%А = %А.
◄ В самом деле, характеристическая функция может принимать только два значения — 0 и 1, — а для обоих этих чисел данное свойство справедливо. ►
Таким образом, подтверждается свойство идемпотентности Аг>А = А. Остальные свойства операций над множествами доказываются через характеристические функции столь же легко.
В случае конечных множеств, из определения характеристической функции следует её взаимосвязь с мощностью множества:
И = Е^(х)-	(1.9)
x&U	V 7
Пусть М = {1, 2, 5}, U = ’{1,2, 3, 4, 5} .
H| = Zm(1) + Zm(2) + Zm(3) + Zm(4) + Zm(5) = 1 + 1 + 0 + 0 + 1 = 3.
Это даёт возможность выражать мощность рассматриваемого множества через мощности других множеств и их пересечений путём преобразования выражения для характеристической функции.
1.5.1. Задача 1.2. Вычисление мощности множества с помощью характеристических функций
Возьмём множество D = ЛЛ(ВЛ(С \ А)) из задачи 1.1 и выразим его характеристическую функцию через хА, хв, %с .
'У — 'У — у _ у . у
Ле Лс\а Лс Ла Лс ?
Xf =Хвле=Хв +Хе-2-Хв-Хе= Хв+(.Хс ~Ха-Хс)-2-Хв-(.Хс-Ха-Хс) =
= Хв + Хс - Ха  Хс ~2' Хв  Хс +2' Ха- Хв  Хс',
18
XD=XA^ = %A+ %F	ХА' %F = %a+(%b+ %C- ХА' %C~2-Хв' %c+2-ХА' Хв' %c)-
-2-Xa-(.Xb +Xc-Xa-Xc-2-Xb-Xc +2'Xa-Xb-Xc) = Xa + XB + Xc ~XA-XC ~ -2-Xb-Xc+2-Xa-Xb-Xc-2-Xa-Xb-2-Xa-Xc+2-Xa-Xa-Xc+4-Xa-Xb-Xc--4-Xa-Xa-Xb-Xc =Xa +Xb +Xc-Xa-Xc~2'Хв'Xc +2’ XA ’ Xb' Xc ~2'XA ' Xb,
а значит, \D\ = |Л| + |В| + |С|-|Л оС|-2|ВоС| + 2|Л оВоС|-2|Л оВ|.
Именно такой результат был получен в задаче 1.1, что подтверждает правильность решения.
1.5.2. Характеристическая функция подмножества
Заметим, что В о А о Vx g U, %в (х) < %А (х).
◄ В самом деле, если для некоторого элемента аА1 окажется, что
Хв (а) > хА (а) > это будет означать, что (а) = 1, (а) = 0, т. е. а е В и а <£. А, а это противоречит определению подмножества. Остальные три возможных комбинации значений описаны ниже.
Z/x)	zB(x)	Комментарий
0	0	Элемент не принадлежит множеству А (отсюда автоматически следует, что и множеству В он не принадлежит).
1	0	Элемент принадлежит Л, но не принадлежит В.
1	1	Элемент принадлежит множеству В (отсюда автоматически следует, что он принадлежит и множеству Л).
Распространённой ошибкой является попытка вычислить мощность разности множеств |Л \В| как разность их мощностей. На самом же деле, как видно из формулы для характеристической функции разности, вычитать из |Л| нужно не общее количество элементов множества В, а количество элементов, лежащих в их пересечении: |Л\В| = |Л|-|ЛпВ|. Следовательно, формула |Л\В| = |Л|-|в| справедлива тогда и только тогда, когда второе множество целиком лежит в первом: В о А .
19
1.6. Отношения на множествах
Отношение — это математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи.
«-местным (н-арным) отношением R на множествах А1,...,Ап называется подмножество прямого произведения А1х...хАп.
Пусть S = {Иванов, Петров, Сидоров} — множество студентов группы, а К = {2,3,4,5} — множество оценок, которые они могут получить. Прямое произведение SxK описывает все возможные комбинации (см. пример 2).
Если по окончании первой сессии в зачётке Петрова стоят только пятёрки, а Сидоров получал за экзамены только двойки и тройки, то пары (Петров, 2), (Петров, 3), (Петров, 4), (Сидоров, 4) и (Сидоров, 5) не будут лежать в данном отношении студентов и оценок. Отношение R, «студенты и их оценки за первый семестр» будет иметь вид:
R, = {(Иванов, 2), (Иванов, 3), (Иванов, 4), (Иванов, 5), (Петров, 5), (Сидоров, 2), (Сидоров, 3)}.
Аналогично можно задать отношение R2, описывающее успеваемость во втором семестре; оно может выглядеть иначе.
Таким образом, отношение, в отличие от прямого произведения, описывает конкретную ситуацию, некое свойство, связывающее элементы множеств.
Математическое понятие отношения имеет широкое практическое применение. В частности, на нём основаны реляционные базы данных (англ, relation — отношение), в которых связи между данными задаются таблицами: каждая строка таблицы соответствует одному элементу отношения. К примеру, сведения о курсовых проектах студентов могут храниться в таком виде (таблица 3):
20
Таблица 3. Отношение «Курсовые проекты».
Студент	Научный руководитель	Оценка за курсовой проект
Иванов	Волков	5
Петров	Медведев	5
Сидоров	Волков	4
В математике, как правило, отношения задаются не на разных множествах, а на декартовой степени одного.
Бинарным отношением на множестве М называется подмножество R декартова квадрата МхМ (т. е. подмножество множества всех упорядоченных пар элементов из М). Будем говорить, что элементы х и у множества М находятся в отношении R, если упорядоченная пара (x,y)eRcMxM . Обозначение: xRy .
Пример 3. Рассмотрим различные отношения на множестве студентов S = {Иванов, Петров, Сидоров} .
В качестве отношения R1 возьмём свойство «Первый студент учится лучше второго студента». Допустим, Петров — круглый отличник, средний балл Иванова за сессию равен 4, а средний балл Сидорова — 2.5. Тогда отношение будет выглядеть так:
Д = {(Петров, Иванов), (Петров, Сидоров), (Иванов, Сидоров)} .
Теперь рассмотрим отношение R2, сформулированное как «Первый студент учится не хуже второго студента». По сравнению с Д добавятся три пары, потому что любой студент сам с собой состоит в отношении R-. — он не может учиться хуже самого себя:
R2 = {(Петров, Иванов), (Петров, Петров), (Петров, Сидоров), (Иванов, Иванов), (Иванов, Сидоров), (Сидоров, Сидоров)}.
Отношение R-. «Первый студент сидит за одной партой со вторым» может иметь, например, такой вид:
21
Д, = {(Иванов, Петров), (Петров, Иванов)} .
Допустим, что Иванов и Сидоров имеют свои сайты в Интернете. Тогда отношение R4 «Первый студент посещал сайт второго» может выглядеть так: R4 = {(Иванов, Иванов), (Петров, Иванов), (Сидоров, Иванов), (Иванов, Сидоров), (Петров, Сидоров), (Сидоров, Сидоров)}.
1.6.1. Свойства бинарных отношений
Бинарное отношение R на множестве М может обладать следующими свойствами:
Рефлексивность о VxgM, xRx, т. е. любой элемент множества М состоит в отношении R сам с собой.
Иррефлексивность (антирефлексивность) о Vx g М, ->(х7?х) . Ни один элемент множества М не состоит в отношении R сам с собой.
Если взять вышерассмотренные отношения (пример 3), то Д и R3 иррефлек-сивны, т. к. в них нет ни одной пары вида (х, х), a R-. рефлексивно, т. к. все три пары вида (х,х) принадлежат этому отношению. R4 не обладает ни тем, ни другим свойством, т. к. Иванов и Сидоров посещали собственные сайты, а Петров своего сайта не имеет и посещать его не мог.
Симметричность <=> Vx, у g М, xRy => yRx.
Антисимметричность о Vx,y eM,(xRy /\yRx)=>(x = у). Как следует из данного определения, в антисимметричном отношении могут присутствовать пары вида (х, х).
Асимметричность о \/x,y<=M,xRy=>^(yRx). Асимметричность подразумевает иррефлексивность.
Отношение R3 из примера 3 симметрично: если Иванов сидит за одной партой с Петровым, то Петров, соответственно, сидит с Ивановым. Отношения R, и R-., сравнивающие успеваемость студентов, антисимметричны. Более того, отношение R, является асимметричным. R4 не обладает ни одним из данных свойств.
22
Транзитивность о Vx,y,zeM, (xRy лyRz) => (xRz).
Отношение R-. из примера 3 не является транзитивным: согласно определению, наличие пар (Иванов, Петров) и (Петров, Иванов) влечёт за собой необходимость присутствия пар (Иванов, Иванов) и (Петров, Петров) .
Отношения R-. и R4 транзитивны, в чём нетрудно убедиться, поочерёдно подставляя все фамилии в определение транзитивности в качестве х, у и z.
Полнота о \/x,y&M,(xRyvyRx). Как следует из определения, необходимым условием полноты отношения является его рефлексивность.
Отношения R, и R, из примера 3 не являются полными, т. к. в них отсутствуют пары вида (х, х). R4 не содержит пары (Петров, Петров), поэтому также не является полным.
Отношение R2 обладает свойством полноты.
Рефлексивное симметричное транзитивное отношение называется отношением эквивалентности.
Рефлексивное антисимметричное транзитивное отношение называется отношением частичного порядка.
Антирефлексивное антисимметричное транзитивное отношение называется отношением строгого порядка.
R, из примера 3 — отношение строгого порядка. R2 — отношение частичного порядка.
Классическими примерами отношений эквивалентности, частичного порядка и строгого порядка являются арифметическое равенство, нестрогое неравенство и строгое неравенство, соответственно.
1.7. Отображения
Пусть X и Y — два множества. Закон /, согласно которому каждому элементу х g X поставлен в соответствие единственный элемент у g Y , называется отображением множества X в множество К, или функцией, заданной на X со значениями в У:
23
f'.X^Y о Vxel,3!jer :/(*) = у.
Формат представления цифровых изображений Bitmap, в котором каждая точка (пиксель) прямоугольного рисунка описывается значением цвета, по сути является отображением множества пикселей Р = X х Y (каждая точка задаётся своими координатами (х,у)) в множество цветов:
RGB = {#000000, #000001, ..., #FFFFFF} .
Слово «шар» переводится с английского не только как «карта», но и как «отображение» (также — «mapping»).
Пример 4. Пусть S = {Иванов, Петров, Сидоров) — множество студентов группы, а К = {2,3,4,5} — множество оценок, которые они теоретически могут получить за контрольную работу. Тогда соответствие
Иванов	5
Петров	5
Сидоров	3
является отображением множества S в множество К', каждому элементу первого множества сопоставлен ровно один элемент второго, каждый студент получил за контрольную работу ровно одну оценку.
Элемент у = /(х) называется образом элемента х. Сам х в этом случае является прообразом у. Для каждого х g X существует ровно один образ, а элемент у g Y может иметь один или несколько прообразов, а может не иметь ни одного прообраза.
Полный прообраз элемента у g Y — это множество всех таких х g X, что /(х) = у:
'0') = {хеУ |/(х) = у).
Вернёмся к примеру 4.
Образ Иванова — 5.
Полный прообраз 5 — {Иванов, Петров) .
Прообраз 3 — Сидоров.
24
2 и 4 не имеют прообраза.
При небольших мощностях множеств, отображения можно задавать таб-
Отображения на бесконечных множествах, как правило, задаются формулой.
f: В В, /(х) = х2 — отображение (функция) на множестве вещественных чисел (хе(-оо;+оо)), графиком которого является парабола.
g: В+	В, g(x) = х2 — отображение, графиком которого является правая ветвь
параболы. хе(0;+оо).
А:В^В+,А(х) = х2 — не отображение, поскольку для элемента х = 0 не существует образа в множестве В+ (А(0) = 0 £ В+).
1.7.1. Типы отображений
Существуют следующие типы отображений:
Инъекция. Отображение f: X Y инъективно о
Vx15х2 G X, у Ф х2 => /(у) Ф f(x2) .
Альтернативная формулировка: Vy,x2 G X, (/(у) = /(х2) о у = х2).
Неформально говоря, разным элементам X соответствуют разные образы в У.
25
Отображение из примера 4 не инъективно, поскольку и Иванов, и Петров получили оценку 5.
Соответствие посетителей кинотеатра и их мест в зале является инъективным отображением, поскольку двое зрителей не могут сесть на одно место. (Подразумевается, что каждому посетителю досталось по одному билету, в противном случае соответствие не будет отображением.)
Отображение f: В В, fix) = х2 не инъективно, поскольку, например, /(-2) =/(2) = 4 .
Отображение g: В+ В, g(x) = х2 инъективно, поскольку функция g(x) на интервале хе(0;+оо) строго возрастает.
Сюръекция. Отображение f: X Y сюръективно о
Vy g Y, Ex g X : f(x) = у .
Иными словами, для любого элемента из Y найдётся хотя бы один прообраз в X.
Отображение из примера 4 не сюръективно, поскольку ни один студент не получил оценку 2.
Соответствие всех родившихся в двадцатом веке людей и годов рождения {1901,1902,2000} является сюръективным отображением, поскольку не было ни одного года, когда на Земле не родился ни один человек. (Примечание: данное соответствие действительно является отображением, поскольку каждому человеку сопоставлен ровно один год рождения.)
Отображение f: В В, fix) = х2 не сюръективно, поскольку, например, ни при каком xg(-qo;+oo) функция fix) не принимает значения -1.
Отображение / :В^[0;+оо),/(х) = х2 сюръективно.
Биекция, или взаимнооднозначное отображение.
Отображение f -.X^Y биективно о оно инъективно и сюръективно.
Соответствие студентов группы и их порядковых номеров в журнале — взаимнооднозначное отображение.
26
Отображение к: В+ В+, Л(х) = х2 биективно.
В вышерассмотренных примерах можно заметить некоторую закономерность для конечных множеств:
Необходимым условием инъективности отображения f: X Y является соотношение |х| < |У|.
◄ В самом деле, каждый элемент множества X должен иметь образ в У, а значит, если в множестве X окажется хотя бы на один элемент больше, чем в К, то по крайней мере два элемента X будут иметь общий образ, и инъективность выполняться не будет. ►
Необходимым условием сюръективности отображения f: X Y является соотношение |х| > |У|.
◄ Согласно определению отображения, один элемент множества X не может иметь несколько образов в У, а значит, если в множестве Y окажется больше элементов, чем вХ, то некоторым элементам Y «не хватит» прообразов. ►
Необходимым условием биективности отображения f: X Y является равенство |х| = |У|.
1.7.2. Композиция отображений. Обратное отображение
Если / :Х , g:Y Z, то их композицией (произведением) называют отображение h: X Z, h(x) = (J ° g)(x) = g(/(x)), х g X.
Композиция отображений некоммутативна, т. е. g(/(x)) /(g(x)) , или f°g*g°f*
Пусть / : В -> В, /(х) = х2 ,g: В -> В, g(y) = sin у .
f ° g = g<J(*)) = sin (x2) , g ° f = /(g(y)) = (sin y)2.
Композиция отображений ассоциативна', (J °g)°h = f .
В некоторых источниках произведение g( f (х)) обозначают g ° f . Поскольку композиция отображений некоммутативна, порядок записи множителей следует обговаривать заранее. В данном пособии множители записываются слева направо, в порядке применения: g(f (х)) = f ° g .
27
Пусть f : В В, /(х) = х2, g: В В, g(y) = sin у, h: В В, A(z) = z +1.
f ° g = g(f(x)) = sin (x2), (/ ° g) о h = sin (x2) +1.
g°/z = /z(g(y)) = siny + l, /o(go/z) = sin(x2) + l.
Тождественным отображением на множестве X называется отображение Ix : X X : Vx g X, 1Х (х) = х .
Отображение g: Y X называется обратным к отображению f: X Y <=> f °g = Ix > g° J = I? - этом случае отображение g обозначается как f 1.
Отображение f имеет обратное тогда и только тогда, когда оно биективно.
Отображение f: В В, f(x) = sin х не является биективным, для него не существует обратного.
Отображение f: [-л/2\ л/2] -> [-1; 1], f (х) = sin х биективно. Обратным к нему является отображение f 1 : [—1; 1] [-л-/2;л-/2], f 1 (у) = arcsiny.
1.7.3. Подстановки на множестве
Если X — конечное множество, то биективное отображение сг: X X называется подстановкой. Подстановки задаются таблицей из двух строк: в первой строке перечисляются элементы множества X в лексикографическом либо ином удобном порядке , во второй — их образы.
Пусть Х = {1,2,3,4}.
Подстановки на множестве X.
<1 2 3 4^	<123 4^ fl 2 3 4^
Ci	? С9	5 Со	• . .
3 1 4 2	2 3 4 1	1 2 3 4
Лексикографический порядок последовательностей предполагает, что последовательность а предшествует последовательности Ъ, если для некоторого \ их начальные отрезки длины \ равны, а (3+1 )-й член последовательности а меньше. По такому принципу, например, расположены слова в словаре: «ТЕОРЕТИК» предшествует слову «ТЕОРИЯ» (т. к. «Е» < «И»), а число «100» идёт раньше, чем «90» (ведь 1 < 9).
Если множество состоит из чисел, то логичнее сортировать его элементы естественным образом, от меньших к большим (т. е., например, 90 < 100).
28
Композиция (произведение) подстановок определяется так же, как и произведение отображений. Если подстановка сг переводит элемент хеХ в элемент у того же множества, а подстановка т переводит у в z g X, то композиция от переведёт х в z.
Первая подстановка переводит 1 в 3, вторая — 3 в 4. Поэтому произведение cTjO-2 переведёт 1 в 4. Аналогичным способом находятся образы остальных элементов. В результате:
<1 2 3 4)
Нетрудно убедиться, что произведение подстановок в общем случае некоммутативно'.
<1 2 3 4)
Тождественной подстановкой на множестве X называется подстановка / : Ver, /сг = сг/ = сг .
Для множества	X = {1,2,3,4}	тождественной является подстановка
<1 2 3 4)
12 3 4
Подстановка т: X X называется обратной к подстановке сг: X X <=> от = тег = /. В этом случае подстановка т обозначается как сг 1.
Чтобы найти обратную подстановку, достаточно поменять местами строчки таблицы. Ради удобства следует переупорядочить столбцы так, чтобы элементы верхней строки оказались в том же порядке, что и в исходной подстановке (например, в лексикографическом).
<1	2 3 4)	.J <3	1 4	2)	<1 2	3 4)
Ol	5 ^1
3	1 42	1	23	4	24	1 3
29
1.7.4. Задача 1.3. Уравнение с подстановками
„	fl 2 3 41 2 3 4)
Решить уравнение о-° \	=	относительно а.
3142	2341
Решение. Можно подобрать подстановку сг поэлементно: композиция подстановок переводит 1 в 2, второй сомножитель переводит 4 в 2, значит, первый сомножитель должен переводить 1 в 4, и т. д. Однако грамотнее будет
воспользоваться свойствами подстановок.
Домножим обе части
справа на подстановку, обратную ко второму множите-
лю:
1 2 3 4И1 2
3 1 4 2 ° 3 1
3 4| J 1 2 3 4 [1 2 3
4 2 ~ 2 3 4 1 ° 3 1 4
В силу ассоциативности умножения:
1 2 3 4И 1 2 3 4)	fl
°	, или просто СГ =
23413142	2
2	3	4Н1	2	3	4
3	4	1 ° 3	1	4	2
Осталось только найти обратную подстановку и выполнить умножение:
1	2	3	4	3	1
сг =	°
2	3	4	1	1	2
4 2) Г1 2 3
3 4 Г 4 1 3
Нетрудно убедиться
в правильности
ответа, подставив найденную подста-
4
2
4
2
новку в исходное уравнение.
1.8.	Принцип включения-исключения
Как правило, посчитать мощность пересечения множеств гораздо проще, чем найти мощность результата других операций. Формула включения-исключения (формула перекрытий) позволяет выразить мощность объединения произвольного числа множеств через мощности этих множеств и их пересечений.
|4^-^4| = Е|4|- Е |4°4|+ Е |4^4^4|--+(-1Г1|4^-^4|- (1.10)
\<i<n	\<i<j<n	\<i<j<k<n
Так, например, для п = 4 формула примет вид:
|4ол2одол4| = |4| + |л2| + |д| + |л4|-|4ол2|-|4од|-|4ол4|-|л2од|-|л2ол4|--14 о л41+14 о 4 о 41+14 о 4 о а41+14 4 ° 41+|4 ° 4 ° 41 -|4 ° 4 ° 4 ° 41 •
30
Убедиться в её справедливости для небольших значений п можно самостоятельно с помощью диаграмм Эйлера — Венна или характеристических функций.
|ЛоВ| = |Л| + |В|-|ЛоВ|;
|ЛоВоС| = |Л| + |В| + |С|-|ЛоВ|-|ЛоС|-|ВоС| + |ЛоВоС|.
Докажем формулу перекрытий более строго.
Лемма. Для V/veN справедливо равенство:
П(1-ц) = 1-^ц + 2 a/z.- 2 ца^+... + (-1Г1- Е ah-a^ + (-1)4-4 -(1.11) /=1	/=1	\<i<j<n	\<i<j<k<n	l<z1<. ..<in_]<n
◄ Докажем лемму методом математической индукции.
Для п = 1 равенство (1.11) выполняется: (1 - ах) = 1 - ц.
Можно даже проверить менее тривиальный случай, п = 2:
(1 -а})(1 -а2) = I -(Д +а2) + ца2.
Предположим теперь, что равенство верно для некоторого N, и проверим его
для N +1.
у+1	Л м	\
П(1-й0= По-я,) •(1-«w+i)=
/=1	V /=1	)
= !-E^ + 2 а>аг Е чд4+-+(-141 • 2 ач
.	г=1	\<i<i<N	\<i<i<k<N	1<г, <N
Л N
+ Е а>аГ Е	+	2 ач--а^ +(-^Nav..aN
ч г=1	\<i<j<N	\<i<j<k<N	ISijC..	у
E +... + (-1/4- E ач--а^ +(~^Nav..aN
\<i<j<k<N	!<!!<..	у
Л N
= i-E^^ E a^aj- E + •+(-i/-1- E ач-а^ +(-1)w«i--«w -
4 i=l \<i<j<N	\<i<j<k<N	!<!!<.. .<iN_r<N	j
-«w+i+Eay^i“ E ч«а+1+ E + •+(-1Г- E +
i=l	\<i<j<N	\<i<j<k<N
+(— 1) a,.. ,aNaN+x —
31
aiaiaN+\
a +а
l<i<j<k<N+l
1<1<J<N+1
a...aNaN+, =
W+1 Cl Cl
U1 • • •UW+1 •
Доказательство формулы включения-исключения:
◄ Выразим характеристическую функцию множества А = Д и...иД через ха
рактеристические функции множеств Д,...,Д , обозначив последние как
соответственно. По закону де Моргана, А = Д о...о Ап = Д о...о Ап.
Тогда =1-Z_n n_ =i-fj(i-z). i=l	i=l
Применив формулу (1.11), получим:
/л=Ёх_ Е 2 zjGZ, + ... + (-i)”+1Zi---z„ =
/=1	\<i<j<n	\<i<j<k<n
= ЕА“ Е Xa^Aj + Е Xa^Aj^a, +-- + (—1)”+1 Ха^..^А„-
/=1	\<i<j<n	\<i<j<k<n
Мощность множества связана с характеристической функцией соотношением (1.9), откуда следует формула (1.10). ►
Формула включения-исключения позволяет ответить на вопрос, сколько элементов обладает хотя бы одним из заданных свойств Д,...,Рп, если известно, сколько элементов обладает свойством Д , сколько — свойством Д , сколько — свойствами Д и Д одновременно и т. д.
1.8.1.	Задача 1.4. Элементарная задача на формулу включения-исключения
Пусть U— множество студентов группы ИУ8-11, \и\ =25. Пусть С — множество тех из них, которые в школе изучали язык C++, |С| =17. Пусть D — множество студентов, знающих Delphi, \D\ = 12. При этом 7 человек знают оба языка программирования. Сколько студентов группы не знают ни одного языка?
32
Для ответа на этот вопрос необходимо посчитать мощность множества CrJM'uB
Из диаграммы Эйлера — Венна (рис. 1.11) видно, что |со£>| = |t/|- |Со£>|.
В свою очередь, |Со£>| = |С| + |£>|-|Сп£>| = 17 + 12-7 = 22 .
Тогда |Со£>| = 25 -22 = 3 .
Формула включения-исключения находит широкое применение в комбинаторике.
1.9.	Задачи для самостоятельного решения
1.	Есть ли разница между записями А = 0 и В = {0} ?
2.	Пояснить разницу между записями А = {1} и А = 1.
3.	Проиллюстрировать законы де Моргана с помощью диаграмм Эйлера — Венна.
4.	Доказать законы де Моргана с помощью характеристических функций.
5.	Вывести характеристическую функцию симметрической разности из формул (1.4) (предполагается, что характеристические функции остальных операций известны) и убедиться, что оба выражения дают один результат.
6.	Верны ли тождества? Проверить с помощью диаграмм Эйлера — Венна, доказать с помощью характеристических функций.
а)	(Л\В)\С = (Л\С)\(В\С);
б)	Лп(В\С) = (ЛпВ)\С;
в)	(АиВ)\С = (Л\С)о(В\С) .
7.	Упростить выражение: (А п В п С n X) о (A n С) о (В n С) о (С n X).
8.	Выразить операции: а) о,\ через п,А. б) п,\ через о, А. в) через А,\. Универсальное множество и операция дополнения недоступны.
33
9.	В базе данных хранится информация о фильмах и персонах, имеющих отношение к кинематографу.
а)	Какие отношения можно установить на множестве фильмов? Какими свойствами обладают эти отношения?
б)	Какие двухместные отношения можно задать на множествах персон и фильмов?
в)	Будет ли соответствие между актёрами и фильмами отображением? А наоборот?
10.	Пусть S— множество студентов группы, К = {2,3,4,5} — множество возможных оценок за контрольную работу. Всегда ли соответствие S К будет отображением?
11.	Пусть ведомость для зачётов и экзаменов имеет вид таблицы, в строки которой вписаны фамилии студентов, а в столбцах указаны возможные результаты: «Недопуск», «Неявка», «Незачёт», «Зачёт», «Неуд.», «Удовл.», «Хор.», «Отл.». Напротив каждой фамилии ставится отметка (галочка) в соответствующей ячейке.
а)	Будет ли соответствие Студенты Результаты отображением?
б)	Может ли результат экзамена по физике быть сюръекцией?
в)	Может ли результат зачёта по информатике быть инъекцией?
12.	Указать такие множествах и У, что отображение f \Х будет: Инъективным, но не сюръективным. / Сюръективным, но не инъективным. / Не сюръективным и не инъективным.
a)	/(х) =/g(x);
б)	/(x) = log2x;
в)	/(х) = е--5;
г)	/(x) = secx = —!—; COSX
Д) /(х) = arrtg(x);
е)	/(х)=|х-1|+1;
ж)	f (х) = sin(2x) +1.
34
13.	Для функций из задачи 12 указать такие множества Хи У, что 3/ 1: У X. Выразить обратную функцию.
14.	Является ли соответствие f :N0 f(n) = п\ отображением? Если да, яв-
ляется ли оно инъективным, сюръективным?
15.	Решить уравнение относительно сг:
.fl 2 3 Е	<12 3
а)	° сг =
^3 1 4 2 J	^2 3 4
<1	2	3	4	5?	<1 2
б)	сг°
1^4	3	1	5	2)	\2 1
.<1 2	3	4	5	6?	<12345	6?	<1	2345	6
В)	ОСГО	=
^6 3	1	2	5	4J	^1	64325^^2	36541
4 •
1J
3 4 5?
5 4 3 Г
16.	В потоке 95 студентов. Из них 25 получили тройки за экзамен по информатике, 47 — по физике, 39 — по алгебре, 22 — по геометрии. Известно, что 42 студента имеют как минимум по две тройки, причём 23 из них — ровно по три. Пять человек сдали на тройки все четыре экзамена. Сколько человек закрыло сессию без троек?
35
2.	Основные комбинаторные понятия и схемы
Комбинаторика — это раздел математики, изучающий дискретные объекты. В данном пособии рассматривается перечислительная комбинаторика, которая занимается подсчётом количества различных комбинаций, образуемых заданными объектами (элементами конечных множеств) и удовлетворяющих тем или иным условиям.
2.1.	Два основных правила комбинаторики
Правило суммы: Пусть есть события А и В, которые никогда не наступают одновременно. Пусть событие А имеет п исходов, В — т исходов. Тогда событие, заключающееся в том, что реализовано одно из событий, А или В, может осуществиться п + т способами.
Пример: в зоомагазине продаётся 5 различных щенков и 3 различных котёнка. Мы хотим купить ровно одного зверя. Щенка мы можем выбрать пятью способами, котёнка — тремя, итого событие «мы купили домашнее животное» имеет 8 различных исходов.
Правило произведения: Пусть есть события А и В, событие А имеет п исходов, а В, независимо от исхода А, — т исходов. Тогда одновременное выполнение этих событий имеет п-т исходов.
Пример: в зоомагазине 5 различных щенков и 3 различных котёнка. Мы хотим купить одного щенка и одного котёнка. Выбираем их независимо, не обращая внимания на то, уживутся ли два конкретных зверя друг с другом. Тогда различных вариантов выбора — 15.
Обратите внимание на формулировку правила произведения: события А и В не обязаны быть полностью независимыми, важно лишь то, что число исходов во всех случаях одинаково.
36
2.1.1.	Задача 2.1. Правило произведения
От дома до зоомагазина можно пройти пятью различными маршрутами. Мы хотим дойти до магазина одной дорогой, а вернуться — другой. Сколькими способами можно прогуляться?
Решение. Примем за событие А поход в магазин (в таком случае оно имеет 5 исходов), а за событие В — возвращение. Если в результате события А был выбран маршрут №1, то событие В может реализоваться такими способами: {№2, №3, №4, №5}. Если поход в магазин осуществился по маршруту №2, то событие В имеет исходы: {№1, №3, №4, №5}. И т. д. Таким образом, сами исходы события В зависят от реализации события А, однако их количество во всех случаях постоянно и равно 4. Поэтому к данной задаче применимо правило произведения. Различных способов прогулки будет 5•4 = 20.
Данные правила можно обобщить на произвольное количество событий.
2.1.2.	Задача 2.2. Правило суммы
Имеется три генератора случайных чисел, каждый из которых отвечает за соответствующий разряд дисплея. Первый генерирует цифры {1,2,3,4,5,6}, второй— {1,2,...,8}, третий— {0,1,...,9}. Сколько чисел, у которых цифра «1» встречается не менее чем в двух разрядах, можно вывести на дисплей с их помощью?
Решение 1. Разобьём задачу на 4 непересекающихся события, каждое из которых удовлетворяет заданному требованию:
Ап — цифра «1» в первом и втором разрядах, в третьем разряде — не «1»;
Ап — цифра «1» в первом и третьем разрядах, во втором разряде — не «1»;
А23 — цифра «1» во втором и третьем разрядах, в первом разряде — не «1»; Айз — цифра «1» во всех трёх разрядах.
Поскольку третий генератор может выдать 10 различных цифр, событие А^ имеет 9 исходов (ПО, 112, ..., 119).
По тем же соображениям:
А13 = 7 (121, 131, ..., 181);
37
А23 = 5 (211, 311, ...,611).
Событие А12з имеет 1 исход (111).
Согласно правилу суммы, всего можно вывести на дисплей 9 + 7 + 5 + 1 = 22 числа.
Можно было подойти к решению с другой стороны.
Решение 2.
Bn — цифра «1» в первом и втором разрядах: 11*. Это событие имеет 10 исходов.
Bn — цифра «1» в первом и третьем разрядах: 1*1.8 исходов.
В23 — цифра «1» во втором и третьем разрядах: *11.6 исходов.
Однако правило суммы напрямую здесь неприменимо, поскольку события не являются взаимоисключающими: во всех трёх случаях возможен исход 111, и, таким образом, при сложении он будет учтён 3 раза вместо одного.
Поэтому окончательный ответ: 10 + 8 + 6- 2 = 22.
2.2.	Основные схемы выборок
2.2.1.	Размещения с повторениями
Сколько 5-буквенных слов можно составить из букв русского алфавита, если под словом понимать не осмысленную последовательность букв, а любую? (Т. е. «слово» может начинаться даже с мягкого знака.)
В данной задаче можно выделить 5 событий: «Выбрана 1-я буква», «Выбрана 2-я буква» и т. п. События эти независимые, каждую букву можно выбрать 33-мя способами независимо от того, какие символы стоят на других позициях. Итого, по правилу произведения, образуется ЗЗ5 «слов».
В общем случае число способов упорядоченной выборки к элементов из п с возвращением, или число размещений с повторениями из п элементов по к, равно
%=пк.	(2.1)
Буква «А» взята от английского слова «arrangement» («размещение»); черта над буквой символизирует возможность повторения элементов.
38
2.2.2.	Размещения без повторений, перестановки
Сколько 5-буквенных «слов» можно составить из 33 магнитов с различными буквами?
В данной задаче можно выделить те же 5 событий: «Выбрана 1-я буква», «Выбрана 2-я буква» и т. п. Однако, поскольку каждая буква присутствует только в одном экземпляре, события будут зависимы друг от друга: например, если первая буква — «А», то вторая буква не может быть «А». Тем не менее, независимо от того, какая буква оказалась на первом месте, вторая буква может быть выбрана 32-мя способами. Аналогично, на третье место можно поставить одну из оставшейся 31 буквы и т. д. По правилу произведения получаем 33-32-31-30-29 «слов».
В общем случае число способов упорядоченной выборки к элементов из п без возвращения, или число размещений без повторений из п элементов по к, равно
,	Ц I
Акп=н-(П-\у...-(п-к + б) = ^—^].
Если к>п, то Лк=0 (нельзя составить слово длины 34, используя 33 магнита).
Если к = п, то размещение без повторений называется перестановкой п элементов:
Рп=С.	(2.3)
Буква «Р» — от англ, «permutation». Отметим, что 0! = 1.
2.2.3.	Сочетания без повторений
Пусть в зоомагазине продаются пять различных щенков: {болонка, колли, овчарка, терьер, чау-чау}. Сколькими способами можно купить трёх щенков?
Задача отличается от предыдущей тем, что не имеет значения, в каком порядке мы возьмём щенков из клетки — важно лишь то, какие три щенка окажутся у нас на руках. Если мы взяли сначала колли, потом болонку, потом чау-чау, — это то же самое, как если бы мы выбрали первой болонку, а затем 39
чау-чау, а затем колли. Трёх собак можно переставить 3! способами; значит, для каждого размещения без повторений 3! = 6 комбинаций будут считаться за одну.
Если бы мы размещали щенков по порядку, то число способов было бы равно
5!	Л; 5!
Л; = —. Тогда способов выбора без учёта порядка будет	= 1° •
Можно даже указать эти комбинации в явном виде:
{болонка, колли, овчарка};
{болонка, колли, терьер};
{болонка, колли, чау-чау};
{болонка, овчарка, терьер};
{болонка, овчарка, чау-чау};
{болонка, терьер, чау-чау};
{колли, овчарка, терьер};
{колли, овчарка, чау-чау};
{колли, терьер, чау-чау};
{овчарка, терьер, чау-чау}.
В общем случае число способов неупорядоченной выборки к элементов из п без возвращения, или число сочетаний без повторений из п элементов по к, равно
Ск _ п\ п к\-(п-к)\'
Буква «С» — от англ, «combination». Ограничения на верхний индекс те же, что и для размещений без повторений: если к > п, то Скп = 0.
Заметим, что, в силу симметричности формулы, Скп = С” *.
◄ В самом деле, сочетание без повторений разбивает множество из п элементов на два подмножества: из к элементов и из п-к элементов. Число способов выбрать подходящие к элементов (взять трёх щенков из пяти) равно числу способов выбрать элементы, которые не подходят (оставить в клетке двух щенков из пяти). ►
40
2.2.4.	Сочетания с повторениями
Пусть в зоомагазине продаются щенки пяти пород: {болонка, колли, овчарка, терьер, чау-чау}. Представителей каждой породы — неограниченное количество. Сколькими способами можно купить трёх щенков, если считать щенков одной породы неразличимыми?
Отличие данной задачи от предыдущей в том, что возможны, например, такие комбинации:
«чау-чау, чау-чау, чау-чау»;
«болонка, колли, колли»;
«колли, овчарка, терьер».
Задача сочетания без повторений сводилась к подсчёту количества размещений без повторений и последующему делению их на число перестановок, дающих один результат. Здесь подобный метод не сработает, поскольку это число зависит от выбранных пород.
Если были выбраны 3 разных щенка, то 3! размещений дадут одно и то же множество.
Если состав — 2 + 1, то нужно делить число размещений на 3 (пример: «болонка, колли, колли» = «колли, болонка, колли» = «колли, колли, болонка»). Если все три собаки — одной породы, то ни на что делить не надо.
Следовательно, перейти от неупорядоченной выборки с возвращением к упорядоченной выборке не удастся, здесь нужен иной подход.
Расставим в ряд пять клеток — по числу пород. Первая — для болонок, вторая — для колли, третья — для овчарок и т. д.:
болонки | колли | овчарки | терьеры | чау-чау
Рассадим по этим клеткам выбранных нами щенков. Получается, что в каждой клетке может сидеть от нуля до трёх собак. Например, выбор трёх чау-чау будет выглядеть так:
|	|	|	| 00®
Выбор болонки и двух колли — так:
0	| 00	|	|	|
41
Выбор колли, овчарки и терьера — так:
Очевидно, что наш выбор можно однозначно закодировать при помощи битовой последовательности, в которой нули будут обозначать собак, единицы — перегородки между клетками. Три вышерассмотренных случая будут записаны как 1111000, 0100111 и 1010101, соответственно.
По условию, собак (т. е. нулей) три. Перегородок (т. е. единиц) окажется на единицу меньше, чем клеток, а именно — 4. Задача сводится к формированию последовательностей длины 7 бит, состоящих из трёх «0» и четырёх «1». Это не что иное, как сочетание без повторений Cf: из 7 разрядов выбираются 3 места для нулей, причём в одном разряде не могут стоять два нуля; тогда 4 разряда для единиц определяются автоматически.
Итак, выбрать трёх собак из 5 пород можно С33+5ч = С73 = 35 способами.
В общем случае число способов неупорядоченной выборки к элементов из п с возвращением, или число сочетаний с повторениями из п элементов по к, равно
(к + п -1)!
к! • (и -1)!
(2-5)
2.3.	Примеры комбинаторных задач
2.3.1.	Задача 2.3. Пассажиры в купе
В купе поезда имеется 10 занумерованных сидений, по 5 с каждой стороны. Из 10 пассажиров четверо желают сидеть лицом по направлению движения, трое — спиной; ещё троим безразлично, как сидеть. Сколькими способами могут разместиться пассажиры?
К этой задаче можно подходить с различных сторон.
Решение 1. Разместить четверых пассажиров по пяти сиденьям, расположенным «лицом», можно Л54 = = 5! = 120 способами. Аналогично, рассадить тро-
их пассажиров напротив них можно Л53 = — = 60 способами. Таким образом,
42
автоматически определятся три места для трёх оставшихся пассажиров. Рассадить их можно 3! = 6 способами. Поскольку все выборки выполняются независимо друг от друга, общее число комбинаций равно 120 • 60 • 6 = 43200.
Решение 2. Выберем среди трёх пассажиров, которым безразлично, где сидеть, одного человека, который сядет лицом. Сделать это можно тремя способами. В каждом из трёх случаев будут сформированы две группы по 5 человек: множество тех, кто сидит лицом, и тех, кто сидит спиной. Теперь нужно рассадить каждую группу на своей скамье. В соответствии с формулой перестановок и правилом произведения получаем 515! = 14400 способов размещения для каждого из трёх случаев (независимо от того, какой из «безразличных» пассажиров сел лицом). Поэтому окончательный ответ — 3-51-5! = 43200.
Ответ: 43200.
2.3.2.	Задача 2.4. Игральные карты
Колода состоит из 52 игральных карт. Сколькими способами можно выбрать из неё 10 карт так, чтобы среди них оказалось хотя бы 2 туза?
Сразу заметим, что подход «Выбрать двух тузов, а затем ещё 8 любых карт» неверен, т. к. в этом случае одна и та же комбинация окажется учтена несколько раз! Например,
{червовый туз, крестовый туз} о {пиковая дама, бубновый туз, десятка треф, (...)} и {бубновый туз, крестовый туз} о {пиковая дама, червовый туз, десятка треф, (...)} — это одна комбинация, которую мы при таком подходе будем считать за несколько различных. Поэтому необходимо разбить задачу на взаимоисключающие случаи.
Решение 1. Задача разбивается на следующие события: «Выбрано 2 туза», «Выбрано 3 туза», «Выбрано 4 туза» (ведь в колоде 4 масти).
В первом случае необходимо выбрать двух тузов из четырёх и 8 карт, не являющихся тузами (их всего 48). Обе выборки являются сочетаниями (ведь порядок размещения карт в руке не имеет значения) без повторений (мы
43
не можем, например, дважды выбрать червового туза) и производятся независимо друг от друга, поэтому число исходов равно С4 • С48 .
Рассуждая аналогичным образом, приходим к выводу, что трёх тузов и семь других карт можно выбрать С4 • Cj8 способами, а четырёх тузов и ещё шесть карт — С4 • С48 = С48 способами.
А	4 4о	4о
Тогда, по правилу суммы, не менее двух тузов окажется выбрано в следующих случаях: С4 • С48 + С4 • С478 + С4 • С48.
Решение 2. Можно подойти к задаче с другой стороны: найти число неподходящих способов и вычесть из общего числа комбинаций.
Число способов выбрать 10 карт из 52: С™.
Первый случай: «Не выбрано ни одного туза». Это С4° С48 = С48 вариантов.
Второй случай: «Выбран 1 туз». Это С4 С48 вариантов.
Тогда число комбинаций, удовлетворяющих условию, составляет с52 с4 • с48 с4 • с48.
Ответ: 2570881764.
2.3.3.	Задача 2.5. Количество чисел определённого вида
Сколько существует чисел от 0 до 999 999 включительно, в записи которых присутствует хотя бы по одной из следующих цифр: {1,2,3,4} ?
Решение. Будем рассматривать числа как последовательности длины 6, где на каждой позиции может стоять любая из 10 цифр (например, последовательность 004280 соответствует числу 4280, а последовательность 000000 — числу 0). Очевидно, что всего таких последовательностей |t/| = 106.
Выделим среди них последовательности, обладающие свойством «в записи числа присутствует хотя бы одна цифра 1», и обозначим это множество как Р}. Аналогично введём множества Р2, Р3, Р4 — индексы указывают на наличие хотя бы одной соответствующей цифры.
Требуется вычислить мощность множества Р = Plr>P2r>P3r>P4. Воспользовав-
шись законом де Моргана, перейдём к виду: Р1иР2иР3иР4 . Тогда
44
а вычитаемое можно найти по формуле включений-
исключений (1.10), для наглядности обозначив множества 2) как Aj (свойство «в записи числа цифра j не встречается ни разу»):
|4 о...ол4|= ^|4|- Е|4ПЛ|+ Е|4	пА|-|4
1<г<4	1<г<;<4	l<i<j<k<4
Все Д имеют одинаковую мощность, равную 96 (в формировании разрядов числа участвуют 9 цифр вместо 10). Таких слагаемых— 4 штуки, по числу множеств.
Все 4 ° 4 также имеют одинаковую мощность 86 (в формировании числа могут участвовать все цифры, кроме i и у). Этих слагаемых столько, сколько существует способов выбрать индексы i и j из четырёх возможных, т. е. С4 =6.
Тройные пересечения 4 ° 4 п 4 имеют мощность 76 (таких пересечений С4 = 4 штуки), и, наконец, пересечение всех четырёх множеств содержит б6
элементов.
Следовательно, искомая величина равна \Р\ = 106 - 4 • 96 + 6 • 86 - 4 • 76 + б6 = 23160.
Ответ: 23160.
2.4.	Свойства биномиальных коэффициентов
Число сочетаний Скп определено только для неотрицательных целых чисел п и к. Биномиальный коэффициент, часто встречающийся в комбинаторных задачах и теории вероятностей, является обобщением данной форму-
(и А
(обратите
Л ) внимание, что верхний и нижний индексы в данной записи поменялись местами), однако мы во избежание путаницы будем продолжать использовать обозначение Ск.
Если 0 < к < п, то Ск =-:--. Отсюда следует: С° = 1 и С” = 1 для \/п > 0 .
к! • (п - Л)!
45
Если 0<n<k или k<0, то Ск=0. Таким образом, для всех п<0 выполнено С” = 0.
Если п<0<к , то Скп = (~\)к  Ск_п+к_х . Значит, для всех п<0 справедливо С„°=1.
Исследование биномиальных коэффициентов с отрицательными значениями п выходит за рамки данного пособия. Далее полагается, что п > 0 .
2.4.1.	Симметрия
Как уже было показано в разделе 2.2, биномиальные коэффициенты обладают следующим свойством:
(2-6)
2.4.2.	Рекуррентность
Биномиальные коэффициенты можно выразить через коэффициенты с меньшими значениями индексов:
(2-7)
◄ Действительно:
(л-1)!
(л -1)!	_ (л -1)! • к + (л -1)! • (л - к)
(к -1)! • (л - к)! к! • (л - к -1)! к! • (л - к)! к! • (л - к)!
Можно подойти к доказательству логически. Неупорядоченная выборка к элементов из п разбивается на два взаимоисключающих случая: «Элемент х (в качестве которого можно взять произвольный элемент рассматриваемого множества) входит в выборку» и «Элемент х не входит в выборку». В первом случае остаётся выбрать к-1 элементов из оставшихся л-1, это СД) способов. Во втором случае необходимо по-прежнему выбрать к элементов, но из тех же л-1 (т. к. один элемент гарантированно не входит в выборку). Это можно сделать Скч способами. Применяя правило суммы, получаем искомое тождество. ►
46
2.4.3.	Максимальное значение
Если п чётно, то своего максимального значения биномиальный коэффициент Скп достигает при к = п/2. Если п нечётно, то максимум достигается
при двух значениях индекса: к = (и -1)/2 и к = (и +1)/2.
◄ Рассмотрим, при каких значениях к справедливо неравенство Скп4 < Ск > Ск+1, т. е. достигается нестрогий максимум.
Левая половина неравенства преобразуется к виду:
и!	и!
(к -1)! • (и - к +1)! к! • (и - к)!
Сократив обе части на-------:----
к! • (п - к +1)!
получаем к < п - к +1, или к < (и +1)/2.
Правая половина неравенства:
п\	п\
к\-(п-к)\ (к +1)! • (и - к -1)!
Сократив на--------:----
(£ + !)!• (п-к)\
получаем к +1 > п - к, или к > (и -1)/2.
Итак, нестрогий максимум коэффициента Ск при фиксированном п достига
ется при (n-V)/2<k <(и + 1)/2. Если п чётно, то единственное целое значение индекса к на данном отрезке— к = п/2 . При нечётном п, k = (n-V)/2 и к = (п + 1)/2. В силу симметричности биномиальных коэффициентов, оба значения к дадут одно и то же значение коэффициента. ►
2.4.4.	Треугольник Паскаля
Треугольник Паскаля является наглядной иллюстрацией вышеприведённых свойств биномиальных коэффициентов. Коэффициенты в нём располагаются в шахматном порядке; индекс п увеличивается на 1 с каждым переходом на новую строку; в пределах одной строки индекс к возрастает слева направо от 0 до п. Строится треугольник начиная с вершины (Со° =1), «боковые стороны» состоят из единиц (С„° = С” = 1), а остальные коэффициенты получаются путём сложения двух вышестоящих (Ск =Ск^ +Ск_г). На рисунке 2.1 изображены первые 11 строк треугольника Паскаля (0 < п < 10).
47
п
О	1
1 1	1
2	12	1
3	13	3	1
4	1	4	6	4	1
5	1	5	10	10	5	1
6	1	6	15	20	15	6	1
7	1	7	21	35	35	21	7	1
8	1	8	28	56	70	56	28	8	1
9	1	9	36	84	126	126	84	36	9	1
10	1	10	45	120	210	252	210	120	45	10	1
Рисунок 2.1. Треугольник Паскаля.
2.4.5.	Свёртка Вандермонда
Задача 2.4 является иллюстрацией к важному соотношению — свёртке
Вандермонда. Если переписать полученные ответы
z^2 z^8	. z^3 z^7	. z^4 z^6	__
^4 ’^48 “Г^4 ’^48 “Г^4 ’^48 ~
rlO _(^0 z^lO _ Z^l z^9 52	^4 ’ ^48	^4 ’ ^48
в виде
z^lO _ z^C) zrlO . xrl z^9	. z^2 z^8	. z^3 z^7	. z^4 z^6
'-'52	'—'4	* ^48	'^'4 * ^48	'^'4	* ^48	'^'4	*	^48	'^'4 * ^48 >
то становится очевидно, что выбор 10 карт из 52 можно интерпретировать как сумму всех возможных взаимоисключающих вариантов: «выбрано 0 тузов и 10 не-тузов», «выбран 1 туз и 9 не-тузов», ..., «выбрано 4 туза и 6 не-тузов».
В общем случае свёртка Вандермонда имеет вид:
CL = Z«<-'.	(2.8)
z=0
Если подставить в неё значения п = 4 (количество тузов в колоде), т = 48 (количество других карт в колоде), Л = 10 (количество выбираемых карт), то получим справа от знака равенства 5 слагаемых, совпадающих с вышеприведённой формулой, т. к. биномиальные коэффициенты, у которых верхний
48
индекс отрицательный либо превышает нижний, обнулятся. Таким образом, формула свёртки Вандермонда справедлива при любых соотношениях индексов к, т и п.
2.4.6.	Бином Ньютона
Биномом Ньютона называется следующее соотношение:
(х+Я^ХС»"-'.	(2.9)
к=0 3 /	.	\3	s~ik к 3—к	/"’О 0 3 .	1 2 . /^2 2 1 . z^3 30	3 . о 2 . о 2	.	3
(х + у) — / j С3 х j' — (L3 х у + (L3X у + С3 х у + (L3 х у — у + Зху + Зх у + X . к=0 2
<х-у)г = ХС‘Х‘(-У^‘ = С?х°(-у)г +С\х'(-у)' +Cix\-yf = уг-2ху + хг. к=0
Из бинома Ньютона следует несколько важных свойств биномиальных коэффициентов.
Если задаться значениями х = у = 1, то выражение (2.9) сведётся к виду
£с‘ = 2".	(2.10)
к=0
◄ С точки зрения комбинаторики данное свойство объясняется следующим образом.
Пусть требуется найти количество битовых последовательностей длины п.
С одной стороны, в каждом из п разрядов может стоять один из двух символов (либо 0, либо 1), и, согласно схеме размещений с повторениями, число таких последовательностей равно 2”.
С другой стороны, задачу можно разбить на взаимоисключающие случаи, в каждом из которых последовательность содержит ровно к нулей и п-к единиц, 0 < к < п . Для каждого случая количество таких последовательностей равно числу способов расставить к нулей по п позициям, т. е. Скп. По правилу суммы, С°+С’+... + С” = 2”. ►
Если подставить в бином Ньютона х = -1 и у = 1, то получится
Х(-1)Х=0,	(2.11)
£=0
49
или, в развёрнутом виде: С„° -С\ + С3п -С3п +... + (-1)”С” = 0. Перенеся коэффициенты, перед которыми стоит знак «минус», в правую часть, обнаружим следующее свойство: сумма всех коэффициентов с чётным индексом к равна сумме всех коэффициентов с нечётным к. С учётом формулы (2.10), каждая из этих сумм равна 2”1.
2.4.7.	Задача 2.6. Выражение, имеющее в основе бином Ньютона
Найти значение выражения:	 22^3 • (-3)7 4 .
к=1
Решение. Данное выражение по своей структуре напоминает бином Ньютона (2.9), однако не совпадают пределы суммирования, индексы биномиальных коэффициентов и показатели степени.
Наименее «гибкой» составляющей бинома является биномиальный коэффициент, поэтому начинать «подгонку» выражения под бином Ньютона нужно с него. Чтобы привести коэффициент вида Ск 1 к виду Ск, необходимо принять п равным 8 и сделать замену переменных: k-l = t. Тогда исходное выражение примет вид: ^С4 • 2241 • (-3)"' . t=0
Теперь необходимо привести множитель 22' 1 к виду х‘: 22' 1 = 22' - 2 1 = 44/2 .
Аналогично выделяем из (-3)"' составляющую у8 ': (-3)" ' = (-3)8 ' • (-3) 2 = (-3)8 4 /9 .
6	4‘ f—зУ^ 1	6
Выражение свелось к	С4 — -—-— = — С4 • 44 • (-3)8 4.
t=o	9	18 t=0
Для полного соответствия суммы биному Ньютона с параметрами п = 8, х = 4, у = -3 недостаёт двух слагаемых:
С4 • 44 • (-3/ ' = С4 • 44 • (-3/ ' - С8 • 48 • (-3)° - С87 • 47 • (-3)1 = г=о	г=о
= (4-3)8 -48 -8-47 • (-3) = 1-48 +24-47 = 5• 48 +1 = 3 2 7 681.
Тогда ^Се'- — -^—^— = ——=182045. t=o 2	9	18
Ответ:	1 • 274' 3 • (-3)7 4 = 18204.5 .
к=\
50
2.4.8.	Задача 2.7. Преобразование биномиальных коэффициентов
Упростить выражение: ^Скм-Ск -2к.
k=N
Решение. Чтобы интерпретировать данное выражение как бином Ньютона, необходимо избавиться от двойного коэффициента: ск	М\________к\ _ М\
м к к\-(М-к)\ N\-(k-N)\ N\-(M-k)\-(k-N)\
= М\___________= cN ck_N
N\-(M-N)\ (M-k)\-(k-N)\ M M~N' MM	м
Тлгпя Ск 7к —	r<k-N ~к _	pk-N ,ук
i ui да / мм -мк - ±	мм • mm_n • z, — мм • / j mm_n • z, .
k=N	k=N	k=N
Замена переменной: k-N = t. M	M-N	M-N
s~ik-N syk _ s~iN M r^t+N _ s~iN syN
^M * / j ^M-N *	— ^M * / j ^M-N *	— ^M *	* / j ^M-N *	*
k=N	t=0	t=0
В таком виде сумма представляет собой бином Ньютона (2.9) с параметрами п = М -N, х = 2, у = 1,а значит, выражение сведётся к следующему: C^-2w-(2 + 1)m~w =C^-2n-3M-N.
м
Ответ: £ Скм •	-2к =C*-2N • 3M~N.
k=N
2.4.9.	Задача 2.8. Дифференцирование бинома Ньютона
Упроститъ выражение: ^к-Ск-2к.
к=1
Решение 1. Слагаемые данной суммы имеют вид к-Ск-хк, к = 1...п, в то время как слагаемые бинома Ньютона не содержат множителя к'. Ск-хк- уп~к. Однако множитель появится при дифференцировании этих слагаемых по переменной X'.
(Ск  хк  уп-к)' = Ск  у"-к • (хк У = Ск  у"-к  к  хк-г.
Воспользуемся этим и продифференцируем обе части бинома Ньютона (2.9) по х, приняв у = 1:
Z	X f
((х+1)-)’=|£су I » „.(x+ir^^fcy-)' о „.(x+ir^zc.'.w-1. \£=0	/	к=0	к=0
51
В качестве нижнего предела суммирования можно сразу взять к = 1, ведь слагаемое, соответствующее к = 0, равно нулю.
Итак,	х*1 =и (х + 1)”1. Подставив х = 2, получим -2*1 =и-3”1, а
к=1	к=1
значит, искомое выражение к • Скп • 2к = 2 • п • 3”1 к=\
Решение 2. к -Ск =
к-п\ _ п\ _	n-(n-V)\
к\-(п-к)\~ (к-1)\-(и-к)\~ (к-1)\-(п-к)\
Тогда к • Ск • 2к = п • Ск2  2к. Замена: к -1 = t. Выражение примет вид:
п-^С'п_х-2м =2-п-^С‘„_1 -2‘ = 2-и-(2 + 1)”"1 = 2-//-3" 1 . t=0	t=0
Ответ: У к • Ск • 2к = 2 • п • З”-1. и
к=\
2.4.10. Задача 2.9. Интегрирование бинома Ньютона
п (—2)
Упростить выражение:
X
Решение 1. Слагаемые данной суммы имеют вид Ск----, к = 0...и, в то время
Л + 1
как слагаемые бинома Ньютона не содержат знаменателя: Ск-хк -у"к. Однако
знаменатель появится при интегрировании этих слагаемых:
f Скп • хк • у" kdx = Ск  уп~к  f xkdx = Ск-уп~к + С, где С — константа.
J	J	к + \
Воспользуемся этим и проинтегрируем обе части бинома Ньютона (2.9), при-
няв у = 1:
(x + l)n+1 п + \
(x + l)n+1 п + \
хк+\ к + \
Определим, при каком значении С данное равенство справедливо. Поскольку С не зависит от х, мы имеем право подставить в равенство любое значение переменной. Задавшись значением х = 0, получим:
1И+1	п
1___ Qk и_____
n + \~h п'к + \
1
п + \
52
Итак,
к=0
хк+1
к + 1
(x + l)n+1 1
п + 1 п + 1
п (-2/+1 (-1)”+1 -1
Подставив х = -2, получим УСк--—-— = -— --------------, а значит, искомое выраже-
t=o к +1	п +1
,к (-2/ = (-1)и+1-1 ( П = (-!)"+! ” к + 1 п + 1 L 2) 2(и + 1)
Решение 2. —— =--------------
к +1 к! • (п - к)! • (к +1)
п\ =	(л+i)!	= с;.
(к +1)! • (п - к)! (к +1)! • (п - к)! • (п +1) п +1
Тогда fck-^-
1 ”
---Е С^+1 • (-2/ • Замена: к +1 = t. Выражение примет вид: п + 1 к=0
1	П+\	1	П+\	1	Л п+\	\
—7 • Е С, • (-2Г = ——— • 2 c«+i • (-2У = . ( п • 2 С, • (-2У -1 • и + 1	-2-(и + 1)	-2-(п + 1) VS	)
Избавимся от суммы, воспользовавшись биномом Ньютона (2.9):
-2-(и + 1) v	7 -2-(и + 1) 2-(и + 1)
Ответ: У Ск
/ j п к=0
(-2/ к + 1
(-!)”+! 2(и + 1)
О, если п нечётно;
1 ----, если п чётно. п + 1
2.4.11.	Алгебраическое доказательство свёртки Вандермонда
Формулу (2.8) можно получить не только комбинаторными рассуждениями, но и алгебраически, с использованием бинома Ньютона.
◄ Рассмотрим выражение (х+1)”+Я! = (х +1)” • (х +1)".
Левая часть равенства в соответствии с биномом Ньютона (2.9) представляется в виде:
(x + nn+m=f° Х°+С1 х1 +С2 х2 + + Ск хк + +сп+тхп+т yx-rkj	^п+тЛ '^-'п+111	'^-'п+111	' •••'{^’п+тЛ'	' '"'^п+тЛ
Каждый из сомножителей в правой части представляется аналогично в виде многочлена:
(х +1)” • (х +1)" = (С°х° + С'X1 + С2х2 +... + С”х”) • (С° х° + С'X1 + С2 X2 +... + С"хт).
\	7	\	7	\ и	п	п	п 7 \ т	т	т	т 7
Рассмотрим коэффициенты при различных степенях х после перемножения скобок.
При х°: С°п-С°т (берётся х° из первой скобки и х° из второй).
53
При х1: С„° • Ст + Сп • С° (первая степень получается как х° • х1 и х1 • х°).
При х2: С„° С2т+С'п-С'т + С2  С°т (вторая степень образуется при перемножении слагаемых со степенями: 0и2, 1 и 1,2и0).
При хк: с°п-Скт+С1п-Скт1+... + Скп-С°т=ХС1п-Скт1.
/=0
С другой стороны, как было показано выше, коэффициент при хк равен Ск+т, ч. т. д. ►
2.5.	Полиномиальные коэффициенты
Сколькими способами можно переставить буквы в слове «МАТЕМАТИКА»?
Если бы все буквы данного слова были различны (условно обозначим их как {М15 Ар Тр Е, М2, А2, Т2, И, К, А3}), то количество перестановок в соответствии с формулой (2.3) определялось бы как До = 10!. Однако, если мы поменяем местами « Mj» и « М2», или « Tj» и « Т2», или три буквы «А», то последовательность символов не изменится. Следовательно, количество перестановок необходимо разделить на 2! = 2 (это число способов поменять местами две буквы «М»), затем ещё раз на 2! (перестановки «Т») и, наконец, на 3! = 6 (перестановки «А»), ——— = 151200 способов.
2!-2!-3!
Альтернативный подход к задаче заключается в следующем. Необходимо расставить три буквы «А», две буквы «М», две буквы «Т», одну «Е», одну «И» и одну «К» по десяти позициям. Выбор трёх позиций для «А» осуществляется С30 способами. Вне зависимости от этого выбора, остаётся 7 позиций для двух «М»: это С2 вариантов расстановки. Из оставшихся пяти свободных мест два займут «Т»: С2 комбинаций. Для «Е» и «И» будет С2 и С2 способов, соответственно, а позиция для «К» определится автоматически (Q'M). То-
54
гда, согласно правилу произведения, число комбинаций будет равно
’3 Г2Г2Г1Г1_Ю!	7!	5!	3!	2!
10 7 5 3 2 3!-7! 2!-5! 2!-3! 1!-2! 1!-1!
10!
3! - 2! - 2!
= 151200.
Эта комбинаторная схема называется перестановкой с повторениями. С точки зрения теории множеств, задача формулируется так: «Сколькими способами можно разбить н-элементное множество на к различимых (например, пронумерованных) подмножеств мощности , ..., пк, соответственно, причём подмножества могут быть пустыми (д > 0)?» Альтернативная формулировка: «Сколькими способами можно присвоить п различным предметам к меток так, чтобы ровно р из них получили метку I, //2 — 2, ..., пк — к, причём р + ... + пк =пЪ> Ответом на оба вопроса служит формула
или, с помощью выборок, Р(п,р,п2,...,пк) = С^ С2П1 • С„И!П1 „2 •... • Q .
2.5.1.	Задача 2.10. Шашки на доске
Сколькими способами можно разместить 5 белых и 7 чёрных шашек на доске 8x8 ? Правилами игры пренебречь.
Решение 1. Имеется п = 64 клетки, р = 5 белых шашек и /?2 = 7 чёрных. Введём объекты третьего типа, «фиктивные шашки», которые будут стоять на пустых клетках. Их количество: р = п-р -п2 =52 . Тогда, согласно формуле (2.12),Р(64,5,7,52) = ^.
Решение 2. Выбрать клетки для пяти белых шашек можно С654 способами. Останется 59 мест для семи чёрных шашек: С579. Согласно правилу произве-_	64!	59!	64!	~
дения, существует С654-С579 = —= 5!7!52! комбинации.
Заметим, что порядок помещения шашек на доску не имеет значения: если бы первыми ставились шашки чёрного цвета (С674), а затем белого (С557), окончательный результат не изменился бы.
55
2.5.2.	Разложение степени полинома на слагаемые
Полиномиальные коэффициенты используются при разложении выражения вида (у + х2 + ... + хк)п в сумму одночленов:
(y+x.+^ + xJ^ 2 Р(«;«1Л2,...,^)-^-x2”2-...-x/i .
0<г^ <п
nl+...+nk=n
(x + y + z)2= X р(2; «1 л2 Лз) • х”1 • У”2 •	= Р(2; 0,0,2) • х° • у0 • z2 + Р(2; 0,1,1) • х° • у1 • ? +
0<^ <2 nl+n2+ni=2
+Р(2- 0,2,0) • х° • у2 • z° + Р(2; 1,0,1) • х1 • у° • ? + Р(2; 1,1,0) • х1 • у1 • z° + Р(2; 2,0,0) • х2 • у° • z° = = z1 + 2yz + у2 + 2xz + 2ху + х2.
Заметим, что при к = 2 формула (2.13) сводится к биному Ньютона (2.9). уу |	п
◄ (x,+v= Y	_	-х,=	►
0<И;<И	б<пх<п	^\) '	7^=0
п1+п2=п
2.5.3.	Задача 2.11. Коэффициенты разложения
2 Найти свободный член в разложении (5 + х2 +—)9.
х
Решение. Применив формулу (2.13), получим:
2	( 2 А”3
(5 + х2+— )9 =	Р(9;и1,и2,и3)-5^-(х2)”2- - =	Р(9,пх,п2,п3)-5”'-2”3-х2”^”3 .
Х	0<ni<9	\Х)	0<И;<9
и1+и2+и3=9	и1+и2+и3=9
Свободный член — это слагаемое, не содержащее х. Он образуется, когда показатель х равен нулю. Следовательно, необходимо найти решения системы:
о VI £f VI о ч		VI £f VI о <	
< р + п2 + п3 = 9 о 	п3 = 2п2
2п2 -п3 =0	р = 9- Зп2
р 9 6 3 0
Перебрав все возможные значения и2, получим: и2 0 1 2 3.
и3 0 2 4 6
Тогда свободный член равен
Р(9; 9,0,0) • 59 • 2° + Р(9; 6,1,2) • 56 • 22 + Р(9; 3,2,4) • 53 • 24 + Р(9; 0,3,6) • 5° • 26 = 20228501.
Ответ: 20228501.
56
2.6.	Задачи для самостоятельного решения
17.	Сколькими способами можно выбрать пару букв «гласная + согласная» из слова «функция»?
18.	Сколькими способами можно выбрать на шахматной доске одну белую клетку и одну чёрную?
19.	Сколькими способами можно выбрать на шахматной доске белую и чёрную клетки так, чтобы они не лежали на одной горизонтали или вертикали?
20.	Сколькими способами можно выбрать четыре баллончика с краской из имеющихся шести?
21.	Найти число способов раскрасить четыре стены дома, если имеется шесть различных красок и:
а)	Ограничений нет;
б)	Все стены должны быть разного цвета;
в)	Все стены должны быть разного цвета и одна из стен должна быть красной (красный входит в число шести предоставленных цветов).
22.	В колоде 52 карты (по 13 каждой масти). Найти число способов выбрать четыре карты, по одной каждой масти, если:
а)	Ограничений нет;
б)	Выбранные карты должны быть разного достоинства.
23.	Сколькими способами можно распределить шесть посылок между тремя курьерами? Каждый курьер может взять от нуля до шести посылок.
24.	Сколькими способами можно посадить за круглый стол 5 мужчин и 5 женщин так, чтобы лица мужского и женского пола чередовались?
25.	В киоске продаются шоколадные батончики восьми видов. Найти число способов купить:
а)	Пять батончиков;
б)	Пять различных батончиков;
в)	20 батончиков.
57
26.	На первом этаже пятиэтажного здания в лифт вошло семь человек. Найти, сколькими способами они могут распределиться между четырьмя этажами, если:
а)	Учитывать только количество людей, вышедших на том или ином этаже;
б)	Имеет значение, какой человек на каком этаже покинул лифт.
27.	Найти число способов раздать 15 одинаковых воздушных шариков четверым детям, если:
а)	Ограничений нет;
б)	Каждый ребёнок должен получить хотя бы по два шарика.
28.	В коллективе 7 мужчин и 5 женщин. Сколькими способами можно набрать группу из шести человек так, чтобы среди них было как минимум две женщины?
29.	Сколькими способами можно покрасить 10 вагонов в три цвета, если каждый цвет должен присутствовать хотя бы на одном вагоне?
30.	Найти сумму всех пятизначных чисел, которые образуются перестановкой цифр 1, 2, 3, 4, 5.
31.	Найти сумму всех четырёхзначных чисел, которые образуются при помощи цифр 1, 2, 3, 4, 5, 6, 7.
а)	Цифры в числе могут повторяться;
б)	Каждая цифра встречается в числе не более одного раза.
32.	Найти значение выражения: ^Ск2к.
к=1
33.	Упростить выражение: ^к-Ск-2т~к -,т,п = const. к=\
34.	Найти значение выражения:	(к -З)2 • Ск2 • (—8)*+1 • (—З)21 2/с .
к=0
35.	Упростить выражение:	.
к=о к + 2
36.	Найти значение выражения: ^(С';)2 .
к=0
58
3. Основы теории чисел
Теория чисел, или высшая арифметика, — это раздел математики, изучающий целые числа и сходные объекты. В данном пособии рассматривается элементарная теория чисел, изучающая целые числа без использования методов других разделов математики.
3.1. Основные термины и определения
Если для некоторого целого числа а и целого числа d ф 0 существует такое целое число q, что d-q = a, то говорят, что число а делится нацело на d. При этом число d называется делителем числа а, число а называется кратным числа d, а число q называется частным от деления а на d. Отношение делимости обозначают как d | a («d делит «»); реже — a:d («а делится на J»).
Ноль делится на любое целое число, отличное от нуля. \/а g Z\{0},a 10.
Любое целое число, отличное от нуля, делится само на себя. Va g	| а .
Единица является делителем любого целого числа. \/а g Z, 11 а.
Числа ±1 и +а являются тривиальными делителями числа а.
Вне зависимости от делимости целого числа а на целое число Ь ф 0, число а всегда можно разделить на b с остатком, т. е. представить в виде: a = b-q+r, где 0 < г < |Z>|. В этом случае q — неполное частное, г — остаток от деления а на Ь. Число а делится нацело на b тогда и только тогда, когда остаток от деления а на b равен нулю.
а = 16, Ь = 3. 16 = 3- 5 + 1. 5 — частное, 1 — остаток. О< 1 <|з|.
а = -16, Ь = 3 . -16 = 3-(-6) + 2. -6 — частное, 2 — остаток. О<2<|з|.
а = 16, b =-3 . 16 = (—3)- (—5)+1. -5 — частное, 1 — остаток. О < 1 < |-3|.
а = -16, Ь =—3 . -16 = (-3)-6 + 2.6 — частное, 2 — остаток. О < 2 < |-3|.
а = -15, Ь = 3 . —15 = 3-(—5) + 0. -15 делится нацело на 3, или 31 —15, или -15:3.
Для конкретных двух чисел ап b (Ь*о), частное и остаток определяются однозначно.
59
◄ Предположим, что помимо чисел q и г, удовлетворяющих соотношению a = b-q+r , 0<r<|Z>| , существуют числа q' и /' , 0<r'<|Z>| , для которых a = b-q'+r'.
Тогда a = b-q+r = b-q'+r'. Полагая для определённости, что г'>г, приведём выражение к виду Ь • (q - q') = гг .
Очевидно, что левая часть равенства делится нацело на Ь, а значит, и правая часть должна обладать этим свойством. Однако из определения остатка следует, что 0 < г '-г < |Z>|. Значит, равенство возможно только в том случае, когда г'-г = 0, а следовательно, q-q' = Q, т. е. г' = г и q' = q. Итак, числа q и г определяются единственным образом. ►
Остаток от деления а на b обычно обозначают как Rb (а).
Как правило, при рассмотрении вопросов делимости целых чисел ограничиваются положительными, т. е. натуральными числами. Далее в данном разделе под «числом» будет пониматься натуральное число, а под «делителями» — натуральные делители, если не указано иное.
Простое число — это натуральное число, имеющее ровно два делителя: единицу и само себя. Сама единица не является простым числом по определению. Все остальные натуральные числа (т. е. натуральные числа, имеющие нетривиальные делители) называются составными.
Собственным делителем числа называется всякий его делитель, отличный от самого числа. У простых чисел существует ровно один собственный делитель — единица.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29... — простые числа.
4, 6, 8, 9, 10, 12, 14, 15, 16, 18... — составные числа. Нетривиальные делители числа 12: 2, 3, 4, 6.
3.2.	Базовые теоремы
Теорема 1. Простых чисел бесконечно много.
Самое старое из известных доказательств этого утверждения принадлежит Евклиду:
60
◄ Предположим, что множество простых чисел конечно: {/?15 р2,рк]. Возьмём число N = рх р2 рк +1. Оно не делится ни на одно из к простых чисел (в остатке всегда будет 1), а значит, оно либо само является простым, либо делится на простое число, которого нет в выбранном наборе. Следовательно, наша гипотеза неверна, и множество простых чисел бесконечно. ►
Теорема 2. Для любого п, на числовой оси найдутся п подряд стоящих составных чисел.
◄ Возьмём последовательность чисел (и+1)! + 2, (и+1)! + 3, ...,(и+1)! + и+1. Поскольку (и+1)! делится и на 2, и на 3, ..., и на и + 1, то первое число последовательности будет также делиться на 2, второе — на 3 и т. д., а значит, все эти п чисел являются составными. ►
Чтобы найти пять подряд идущих чисел, ни одно из которых не является простым, нужно вычислить (5 +1)! = 6! = 720 и прибавить к результату числа от 2 до 6: 722, 723, 724, 725, 726.
Разумеется, это не единственный вариант. Последовательности {24,25,26,27,28}, {32,33,34,35,36} и т.п. тоже удовлетворяют условию. Вышеприведённый алгоритм лишь гарантирует существование хотя бы одной такой последовательности для произвольного п.
Теорема 3. Любое натуральное число п>2 может быть разложено в произведение простых чисел, причём единственным образом (с точностью до порядка сомножителей).
◄ Если число п не имеет нетривиальных делителей, то оно простое. Если имеет, то его можно представить в виде п = • //2, причём 1<п} <п и 1<п2<п. К числам И; и //2 можно применить аналогичные рассуждения. Сомножители каждый раз уменьшаются, а значит, процесс конечен. Он прервётся, когда все сомножители будут простыми.
Предположим, что у числа п существует два разложения:
и =	• /?2“2 рт№т = q/1 -q/2 qsPs, где а, >1, /3} >1, т. е. фиктивных сомножи-
телей нет.
61
Поскольку первое разложение содержит простой сомножитель д, то и второе должно делиться на т. е. содержать в себе этот сомножитель: рх = qf для некоторого I. Перенумеруем индексы таким образом, чтобы выполнялось Px = qx. Тогда:
Р?-Р^ Ртат =Р^cLPs 
Предположим, что а, ф Д, например, ах> /Зх. Разделим обе части равенства на Р^:
р^Р'-р2аг---рпат =\-q^-...-qsPs •
Левая часть равенства делится на р}, а правая — нет. Это невозможно, а значит, и i-a“2 ртат = ^q2h---qsPs •
Применяя те же рассуждения к остальным сомножителям нового равенства, приходим к выводу, что оба разложения содержат одни и те же простые числа в одинаковых степенях; количество сомножителей также совпадает (т = 5). ► 16 = 24; 24 = 23-3'; 7 = 7\
3.3.	Свойства остатков
Rd (п + cd) = Rd (п) для Vw, с g 1, d ^0.
◄ Пусть Rd(n) = r, a q — неполное частное от деления п на d. Тогда n = q-d+r . n + cd = (q-d + r) + cd = (q+c)-d+r , т. e. г является остатком от деления (n+cd) на d. ►
7?10(74) = 7?10(-16) = 4 , т. к. -16 = 74 +(-9)-10.
Остаток от деления суммы чисел равен остатку от деления суммы остатков: Rd(d + nd = Rd (,Rd(nd + Rd(nd) Для	g + 0.
◄ Пусть Rd(n} +/+) = г. Тогда r\+n2=qd+r для некоторого целого q.
Пусть Rd(n1) = r1. Тогда nA=q1-d+r1. Аналогично, T?d(«2) = r2, a n2=q2-d + r2. В этом случае сумму остатков можно представить как
Rd(d) + Rd(nd = rl+r2= (d -q.-d) + (п2-q2-d) = (n1+n2)-(qi+q2)-d = = (q-d + r)-(qi+q2)-d = (q-qi-q2)-d + r.
62
Из данной записи видно, что г является остатком от деления суммы остатков на d. ►
7?10(35 + 57) = 7?10(92) = 2;
Rw (7?10 (35) + 7?10 (57)) = До(5 + 7) = Rw (12) = 2 .
Остаток от деления произведения чисел равен остатку от деления произведения остатков:
Rd(b-nd = Rd (A/Oi) АО2)) для , d + о.
◄ Пусть Rd(i\ -п2) = г. Тогда -и2 = q-d + r для некоторого целого q.
Пусть Rd(nx) = rx. Тогда nx=qx-d+rx. Аналогично, А(/72) = /2, a n2=q2-d + r2. В
этом случае произведение остатков можно представить как
Rd (d )-Rd(n2) = ri-r2= -Qi-d)- (п2-q2-d) = n,-n2-(qxn2 + q2n,)-d + q,q2d2 = = (q-d + r)-(qxn2 + q2nx)-d + qxq2d2 = (q-qxn2 -q2nx + qxq2d)-d + r.
Таким образом, г является остатком от деления произведения остатков на d. ►
7?10(36-53) = 7?10(1908) = 8 ;
До (7?10 (36)  7?10 (53)) = До (6 • 3) = Rw (18) = 8 .
3.4.	Наибольший общий делитель и наименьшее общее кратное
Наибольший общий делитель чисел а и b — это наибольшее число, которое делит и <т, и Ь. Обозначается НОД (а,Ь) или просто (a,Z>).
Если (а,Ъ) = 1, то числа а и b называются взаимно простыми.
Наименьшее общее кратное чисел а и b — это наименьшее число, которое делится и на а, и на Ь. Обозначается НОК(а,Ъ) или просто [а,Ь\.
Если числа а и b взаимно просты, то [а,Ь] = а-Ь.
(12,16) = 4, [12,16] = 48.
(75,16) = 1 —числа 75 и 16 взаимно просты. [75,16] = 1200.
Заметим, что НОД нуля и любого числа равен этому числу, а НОК нуля и любого числа равно нулю.
63
Если числа а и b представлены в виде произведения степеней простых к	к
чисел (а = П ptа‘ , аг.> 0 , Ъ = pfl , Д>Ъ), то их НОД равен произведению /=1	/=1
этих простых чисел с минимальным из двух показателей
к
(ЯОД(а,/>) = Плтт(“"А) ), а Для нахождения НОК нужно взять максимальные
к
показатели степени: НОК(а,f] дтахИ А)
/=1
<	а = 23-5-112 Ъ = 23-32-53	1-Н	1-Н Гг> Тг> 7^ 7ч 7ч и и < J	НОД(а,Ь) = 23-З0^1 -11° = 23-51 =40 НОК (a, b) = 23 • З2 • 53 • 112 = 1089000
Из данного примера видно, что НОК(a,Z>)• НОД(а,Ь) = а-Ь .
◄ В самом деле, для НОД выбирается минимальный из двух показателей, для НОК — максимальный, а значит, в произведении в любом случае будут присутствовать множители вида ptai  pf‘, 1 = 1...к . ►
Для трёх и более чисел данное равенство в общем случае неверно.
а = 12	а = 22 • 3	НОД(а,Ь,с) = 2' =2
< Z> = 16 => 	Ъ = 24	=> 	НОК(а,Ъ,с) = 2?	=144
с = 18	с = 21-32	НОД (а, Ь,сУ НОК (а, Ь, с3
= 288; но а- b-с = 3456.
НОД трёх (и более) чисел можно вычислять последовательно:
НОД (а,Ъ,с} = НОД (НОД (а,Ь),с).
НОД (12,16,18) = НОД (НОД (12,16), 18 j = НОД (4,18) = 2 .
3.4.1.	Функция Эйлера
Функция Эйлера ср(п) определена для всех натуральных чисел и равна количеству натуральных чисел, не превосходящих п и взаимно простых с ним.
(р(п) = |{х g N | (х < п) /\ НОД (х, п) = 1}|.
Из определения следует, что <Д1) = 1 : ровно одно натуральное число, не превосходящее 1, взаимно просто с единицей, и это число — сама единица.
64
Если п представлено в виде произведения степеней простых чисел
к
п = П&а‘ ’Т0
i=l
(Р(п) = П • П 0 -	) = П ^а‘ ~	) •
7=1	7=1
(3.1)
◄ Обозначим множество чисел из диапазона [1;лг], делящихся на /?, как Д,
7 = 1...к. Количество таких чисел равно |Д| = |_и/д) = и/д•• Количество чисел,
взаимно простых с н, т. е. не делящихся ни на одно из /? , равно
Применяя формулу включения-исключения
(1.10)	и учитывая, что все /? попарно взаимно просты (а значит,
. л I 11 \
Д г', А. =-), получаем:
Р^
(р(п) = п-^п/рг +	—-----—-— + ... + (-1)” =
\<i<k	\<i<j<k PiPj	\<i<j<l<k PIPjpl
Как было показано в разделе 1.8:
l-5>,+ 2 хгх}- Z W/+ • + (-1)”х1"^ = П(1-х>) (формула (1.11)). В дан-1<7<£	\<i<j<k	\<i<j<l<k	7=1
к
ном случае у = 1/д , тогда (p(n) = n-J~[(l-l/pI). Представив п как произведение
7=1
степеней простых чисел и внеся эти числа в соответствующие скобки, полу-
к
чим альтернативный вариант формулы: ср(п) = ]~~[Ср4 -р,а‘ ') • ►
7=1
Очевидно, что для простых чисел р <р(р) = р-1, а <з(/?“ ) = /?“ '•(/?-!) для
произвольного а .
Функция Эйлера мультипликативна : если т и п взаимно просты, то (р(т  п) = (р(т)  (р(п) . В *
В теории чисел мультипликативной называют такую арифметическую функцию (т. е. функцию
f : N —> С ), что Д(1) = 1 и f(lTTll) = f (pri)  f (pi) для любых двух взаимно простых чисел т и п.
65
(р(2) = 2-1 = 1 (это число 1);
(з(5) = 5-1 = 4 (числа 1, 2, 3, 4);
(3(500) = (з(22 • 53) = (22 - 21) • (53 - 52) = 2 • 100 = 200,
или, применяя вышерассмотренные свойства: (3(500) = (з(22 • 53) = (з(22) • (з(53) = (21 • 1) • (52 • 4) = 200.
3.4.2.	Задача 3.1. Делимость чисел
Сколько чисел из диапазона [1000; 7000] не делится ни на одно из следующих чисел: {4,6,9}?
Решение. Обозначим множество чисел из диапазона [1000; 7000], делящихся на 4, как А4. Аналогично введём множества Д, и 4 для чисел, делящихся на 6 и 9, соответственно. Тогда искомую величину можно записать в виде |Л о А6 о Л,|, или, в соответствии с законом де Моргана (табл. 1), |л4 о А6 о Д,|. Далее воспользуемся свойством дополнения и формулой перекрытий (1.10): |л4оЛ6оД| = |А|-|Л4оЛ6оД| =
= |А|-|Л4|-|Лб|-|Д| + |Л4оЛб| + |Л4оД| + |ЛбОД|-|Л4 пД пД>|.
Мощность универсального множества равна 6001.
В самом деле, число №1 равно 1000, №2— 1001, №3 — 1002, ..., №х — 7000, тогда х = 7000 -1000 +1 = 6001.
Вычислим теперь мощность множества А4.
Представим диапазон [1000; 7000] как разность двух непересекающихся множеств : [1000; 7000] = [1; 7000] \ [1; 999].
Среди чисел [1; 7000] на 4 делятся: {4,8,12, ...,7000}. Иными словами, это те числа, которые при делении на 4 дают частные: {1,2,3, ...,1750}. Очевидно, что их 1750 штук.
Если рассмотреть теперь диапазон [1;999], то последним числом, делящимся
на 4 без остатка, будет
999
4
•4 = 249-4 = 996, где символ |_xj означает округле-
66
ние х до ближайшего целого числа в меньшую сторону , а количество этих
чисел —
999
4
= 249. Тогда |Д| = 1750-249 = 1501.
Для проверки правильности результата можно выписать множество А4 в яв
ном виде: {1000,1004,1008,..., 7000}. Каждый элемент разделим на 4 — их коли
чество от этого не изменится: {250,251,252,...,1750}. В новом множестве эле-
мент №1 равен 250, №2 — 251, ..., №<т — 1750, откуда а = 1750-250 + 1 = 1501.
Аналогично находим мощность |Д| =
7000
6
999
6
= 1166-166 = 1000 .
В самом деле: А6 ={1002,1008,1014,...,6996};
мощность множества частных
{167,168,169,...,1166} равна 1166-167 + 1 = 1000.
1+1=
7000
9
999
9
= 777-111 = 666.
А4оА6 — это множество чисел, делящихся
и на 4, и на 6, т. е. делящихся на
Я(ЭК(4,б) = 12. |Л4
7000
12
НОК(4,9) = 36, а значит, |Д о Д |
ЯОК(б,9) = 18, |ДоД| =
7000
18
999
12
= 583-83 = 500.
7000
36
999
18
-- =194-27 = 167. 36
= 388-55 = 333.
Наконец, ЯОК(4,6,9) = 36 — пересечение трёх множеств совпало с множеством А4 О Ад .
Осталось подставить полученные числа в формулу:
Существует много способов округления чисел. Вот два метода, часто встречающиеся в математике:
|_хJ = max {z G Z | z < х}, до ближайшего целого в меньшую сторону. Пример: |_2.4J = 2 , |_ —2.4J = —3 . Рх~| = min {z G Z | z > x} , до ближайшего целого в большую сторону. Пример: |~2.4~| = 3 , |~— 2.4~| = —2 . Встречается также функция [х] (целая часть числа), но её определение неоднозначно. Некоторые источники полагают [х] = |_XJ , другие интерпретируют её как отбрасывание части числа, стоящей после запятой. В первом случае [—2.4] = —3 , во втором — [—2.4] = —2 . Поэтому данное обозначение не рекомендуется к использованию.
67
|п|-|л4|-|4|-|Д>|+|4 ^4|+|4 ° 4|+|4 4|-|4 ° 4 4>| =
= 6001-1501-1000-666 + 500 + 167 + 333-167 = 3667.
Ответ: 3667.
В общем случае количество чисел из диапазона [1;«], делящихся на d.
равно
п ~d
Если диапазон имеет вид [а; />], а, Ъ g N, необходимо представить
его как [1; Л] \ [1; а -1] — тогда искомое число будет равно
Заметим, что
Ь_ ~d
а-\
Ь-а+1 d
Пусть а = 4, Z> = 13, <7 = 4.
= 3-0 = 3 (три числа из диапазона [4; 13] делятся на 4, это {4,8,12}),
но
Ь-а + 1 d
= 2 — на самом деле данная формула отвечает на вопрос,
сколько чисел из диапазона [1; 10] делятся на 4, это числа {4,8}.
Отношение делимости определено и для отрицательных целых чисел. Если диапазон чисел, рассматриваемых в задаче, имеет вид [-«;/>], а,йеК,
его можно представить как [-а;-!] '+{0} о[1;Л]. Очевидно, что числа из множества [—<зг;—1] имеют те же делители, что и противоположные им числа из отрезка [1;<Д.
3.4.3.	Основное свойство НОД
Va, Ъ g N, НОД (а, />) = НОД (а + с/>, />) для Vc g Z .
◄ Пусть HOД(ab') = d. Тогда a = a'-d, b = b'-d, где а' и Ь' — некоторые целые числа. Число (а + с/>) можно выразить как а'-<7 + с-(/>'-<7) = (а'+<?•/>')• <7, т. е. d является его делителем.
Докажем, что d является именно наибольшим общим делителем для (а + cb) и b. Предположим, что НОД(a+cb,b) = d', d'>d. Это означает, что (а + cb) = к• d',
68
b = m-d'. Но тогда а = (a+cty-cb = k-d'-c-m-d' = (k-cm)-d', т. е. а делится на d' и НОД (a,b) = d'> d —противоречие. Следовательно, HOД(a + cb,b) = d. ►
Следствие. Если 0 < b < а, то НОД (a, Z>) = НОД (b, Rb (а)).
НОД (96,72) = НОД (72, /?72(96)) = НОД (72, 24) = 24 .
3.4.4.	Алгоритм Евклида
Алгоритм Евклида позволяет находить наибольший общий делитель чисел без разложения их на простые сомножители. Он основан на следствии из основного свойства НОД (см. раздел 3.4.3).
Пусть нужно найти НОД (а,Ь).
Е Большее число обозначить за а, меньшее— за b. а <—max (а, Л) , b <— min(a,Z>) .
2.	Вычислить остаток от деления большего числа на меньшее, г = Rb(a).
3.	Если остаток равен нулю, перейти к пункту 6.
4.	Заменить большее число остатком, а <— /.
5.	Перейти к пункту 1.
6.	Наибольший общий делитель равен меньшему числу (Ь).
Пример 5. Найти НОД (504,624).
Итерация 1. а = 624, b = 504, г = 624 -1 • 504 = 120.
Итерация2. а = 504, b = 120, г = 504-4-120 = 24 .
Итерация 3. « = 120, Ь = 24, г = 120 - 5 • 24 = 0.
НОД (504,624) = 24.
3.4.5.	Расширенный алгоритм Евклида
Соотношение Безу. Для любых двух целых чисел а и Ь, не равных нулю одновременно, найдутся такие целые числа х и у, что НОД(a,b) = x-a+y-b. ◄ Заметим, что при нахождении наибольшего общего делителя с помощью алгоритма Евклида, НОД исходных чисел равен остатку, полученному на предпоследней итерации, который, в свою очередь, выражается через остатки, найденные на предыдущих шагах. Последовательно проходя все итерации 69
снизу вверх, можно представить НОД (a, Z>) в виде линейной комбинации а и Ь. ►
В примере 5 был получен результат: НОД (504,624) = 24.
Из итерации 2: 24 = 504-4-120.
Заменим число 120 выражением, полученным на итерации 1:
24 = 504 - 4 • (624 -1 • 504) = 504 - 4 • 624 + 4 • 504 = 5 • 504 - 4 • 624 .
Итак, 24 = 5-504-4-624.
Вышеописанный процесс называется расширенным алгоритмом Евклида.
Числа хи у, называемые коэффициентами Безу, определены не однозначно. Например, можно переписать соотношение Безу в виде
НОД(a,b} = x-a+y-b = x-a+y-b + (b-a-a-b') = (x+b')-a+(y-d)-b, откуда следует, что если х и у удовлетворяют соотношению, то числа х + Ь и у-а также будут ему удовлетворять.
24 = 5-504-4-624; 24 = 629-504-508-624; 24 =-619-504 + 500-624 и т. д.
Пример 6. Найти НОД(1000,129) и выразить его через линейную комбинацию этих чисел.
Итерация 1. (1000,129). 97 = 1000-7-129.
Итерация 2. (129,97). 32 = 129-1-97.
Итерация 3. (97,32). 1 = 97-3-32.
Итерация 4. (32,1). 0 = 32-32-1.
Следовательно, ЯСД(1000,129) = 1.
Из итерации 3: 1 = 97 - 3 • 32.
Подставляем сюда выражение для числа 32 из итерации 2:
1 = 97-3-(129-1-97) = 97-3-129 + 3-97 = -3-129 + 4-97.
Подставляем 97, найденное на итерации 1:
1 =-3-129 + 4-(1000-7-129) = -3-129 + 4-1000-28-129 = 4-1000-31-129.
70
Итак, ЯОД (1000,129) = 1 = 4-1000-31-129 — одна из возможных линейных комбинаций.
3.5.	Модульная арифметика
3.5.1.	Множество вычетов
Множеством вычетов по модулю п называют множество всех возможных остатков от деления на и: Zn = {0,1,2,..., и-1}.
Z4 ={0,1,2,3} .
На множестве Z,, можно определить операции сложения и умножения.
Результатом операции сложения чисел по модулю п является остаток от деления суммы чисел на п. а + Ъ (mod и) = Rn(а + V).
Результатом операции умножения чисел по модулю п является остаток от деления произведения чисел на п. а-Ъ (modи) = Rn(a-b).
5 + 7 (modlO) = 7?10(5 + 7) = 2 .
6-3 (modlO) = 7?10(6-3) = 8 .
Все элементы Zn обратимы по сложению: для VaeZn, ЭЪ g Zn .а + Ъ (modи) = 0. Обозначение: Ъ = -а.
7	+ 3(modl0) = 0, т. е. число 3 является обратным числу 7 по сложению по модулю 10 и наоборот. -7 (mod 10) = 3 .
5	+ 5 (modlO) = 0, т. е. число 5 обратно самому себе по сложению по модулю 10. -5 (modlO) = 5 .
Когда говорят об обратимости элементов Zn, обычно подразумевают операцию умножения: элемент aeZB обратим по модулю п о .а-Ъ (mod и) = 1. Обозначение: Ъ = ах.
7-3(mod 10) = 1, т. е. число 3 является обратным числу 7 по модулю 10 и наоборот: 71 (modlO) = 3.
71
Число 5 не обратимо по модулю 10, т. к. 5-Ь не даст в остатке 1 при делении на 10 ни при каких значениях Ь.
Теорема. Элемент aeZB обратим по модулю п <=>НОД(а,п) = 1, т. е. а и п взаимно просты.
◄ (=>) Если aeZB обратим по умножению, то	:a-Z>(mod«) = l. Это оз-
начает, что а• Ъ = q• п +1 для некоторого целого q. Тогда a b-q n = \.
Предположим, что НОД(а,п) = d> 1. Тогда a = a'-d, n = n'-d . Подставляя эти числа в полученное выражение, получим (a'-dyb -q-(n'-d') = \ , или (сГ-b-q-n') -d = 1. Левая часть равенства делится на Э, правая не делится — это невозможно, а значит, d = 1.
(<=) Если НОД(а,п) = \, то, согласно соотношению Безу (см. раздел 3.4.5), найдутся такие числа х и у, что а• х + п• у = 1, или а-х = п-(-у) +1. Это означает, что 7?п(а-х) = 1, т. е. ax(mod«) = l. Если коэффициенты Безу подобраны так, чтобы х лежал в множестве вычетов Zn, то число х является обратным к а: х = а \ Если x£Zn, то a '=7?n(x), ведь a-Rn(x) (modw) также будет равно 1 в силу свойств остатков (см. раздел 3.3). ►
В множестве вычетов Z10 количество обратимых элементов равно числу элементов, взаимно простых с 10. Применив функцию Эйлера, находим это число: <Д10) = <Д2 • 5) = (2 -1) • (5 -1) = 4. Это элементы {1,3,7,9}:
Г1 (modlO) = 1; 3 1 (modlO) = 7; 7 1 (modlO) = 3; 9 1 (modlO) = 9 .
Для нахождения обратного элемента используется расширенный алгоритм Евклида.
Найти 129 1 (modlOOO).
В примере 6 с помощью алгоритма Евклида было получено, что НОД(1000,129) = 1. Следовательно, число 129 обратимо по модулю 1000. Расширенный алгоритм Евклида даёт соотношение 1 = 4 1000-31 129 . Значит, 129 1 (modlOOO) = -31 (modi000) = 969 .
72
Действительно, 129 • 969 (mod 1000) = 125001 (modlOOO) = 1.
3.5.2.	Сравнение по модулю
Говорят, что целые числа а и b сравнимы по модулю п (a = Z>(mod«)), если:
a)	Rn(a) = Rn(by,
б)	п | (а - Ь) \
в)	а = Ь + сп для некоторого с е Z .
Нетрудно убедиться, что все три формулировки эквивалентны. а = 32 , Ъ = -8 , п = 10 .
а)	Д0(32) = Д0(-8) = 2;
б)	a-Z> = 32-(-8) = 40, 101 40;
в)	32 = -8 + 4-10.
Выполнение любого из этих условий говорит о том, что 32 = -8 (mod 10).
Не следует путать сравнение с равенством. Так, например, 32(modl0) = 2 (слева от знака равенства записана операция приведения по модулю 10, справа— результат), поэтому можно записать 2 = 32 (mod 10), подразумевая, что 2 является остатком от деления 32 на 10. Формулировка 2 = 32 (mod 10) также справедлива, поскольку числа 32 и 2 сравнимы по модулю 10. Верна и запись -8 = 32(modl0) , в чём мы убедились выше. Однако формулировка -8 = 32(modl0) некорректна: слева от знака равенства должен стоять элемент множества Z10.
Сравнение по модулю является отношением эквивалентности (см. раздел 1.6.1).
Если ц = (modw) и a2=b2 (modw), то
ц + а2 = Z>j + b2 (modw) и ц • а2 = Ь, • b2 (modw) .
Иными словами, сравнения по одному и тому же модулю можно складывать и перемножать друг с другом и с другими числами.
73
27 = 17 (modlO), -11 = 9 (modlO) .
Сложение соответствующих чисел даст верное сравнение 16 = 26 (mod 10).
Умножение также справедливо: -297 = 153 (mod 10).
Прибавив к обеим частям сравнений одно и то же число, например, -12, мы снова получим верные сравнения: 15 = 5 (mod 10), -23 = -3 (mod 10).
Умножив обе части сравнений на одно и то же число, например, 3, опять придём к корректным сравнениям: 81 = 51(modl0), -33 = 27 (mod 10).
Однако сравнения в общем случае нельзя делить друг на друга или другие числа, тем более что, строго говоря, операция деления на множестве вычетов Zn не определена. Но числа можно умножать на обратные, при условии,
что таковые существуют. Достаточное условие делимости сравнений можно сформулировать так: если a = Z>(mod«) , d\a , d\b и Я<Л'/(<7,//) = 1 (т. е.
а b
3d 1 (mod и)), то справедливо — = — (mod и). d d
-6 = 9 (mod 5). Поскольку число 3 взаимно просто с модулем (ЯОД(3,5) = 1), можно разделить на 3 обе части сравнения (на самом деле домножить на 3 ' ) и получить верное сравнение -2 = 3 (mod 5).
При этом сравнение -6 = 9 (mod 15) нельзя делить на 3, поскольку числа 3 и 15 не взаимно просты, и сравнение -2 = 3 (mod 15) окажется неверным.
Иногда, однако, деление даёт корректный результат даже при невыполнении условия взаимной простоты, поэтому данное условие является достаточным, но не необходимым:
25 = 125 (modlO) . Деление обеих частей на 5 даст верное сравнение 5 = 25 (mod 10), несмотря на то, что НОД (5,10) Ф1.
Если а = b (modи), d\a, d\b, d\n, то можно разделить на dвсё сравнение, а Ъ (	,пУ
включая модуль: — = — mod— .
d d \	d J
74
-6 = 9 (mod 15). Можно перейти к новому модулю, поделив все числа на 3: -2 = 3 (mod5).
3.5.3.	Сравнения первой степени
Решить сравнение: 862x = (585-54)-110(mod725).
Решение. Для начала следует упростить выражение, произведя все возможные операции по модулю 725: 862 (mod 725) = 137 ,
(585 - 54)-110 (mod 725) = 58410 (mod 725) = 410 .
Сравнение приняло вид 137х = 410 (mod725).
Числа 137 и 725 взаимно просты (в этом можно убедиться, например, при помощи алгоритма Евклида), а значит, 3137 1 (mod 725). Применив расширенный алгоритм Евклида, находим, что 24-725-127-137 = 1, или -113-725 + 598-137 = 1.
Итак, 137 1 (mod725) = 598. Если домножить обе части сравнения на это число, то коэффициент при х в левой части сравнения окажется равен единице (по определению обратного числа), а значит:
х = 598-410 (mod725) = 245180 (mod725) = 130.*
В множестве вычетов Z725 лежит ровно одно решение сравнения. Остальные решения — это все целые числа, сравнимые с ним по модулю 725.
Ответ: х = 130 (mod725).^
В общем случае, решение сравнения + x = Z>(modm), где НОД(а,т) = 1, имеет вид х = а' • Ъ (mod m).
Не обязательно при нахождении 137 1 брать число, лежащее в множестве вычетов. Подойдёт любое число, сравнимое с ним по модулю 725, например, -127:
х = -127 -410 (mod 725) = -52070 (mod 725) = 130 .
Можно также записать ответ в виде X = 130 + 725z, z G 1.
75
Решить сравнение: 30х = 20 (modlOOO).
Решение. 30 и 1000 не взаимно просты, ЖЛ'/(30,1000) = 10 . Следовательно, не существует 30 1 (modlOOO). Однако это не означает, что решений нет.
Если переписать сравнение в виде
ЗОх = 20 + 1000Л, Л g Z,
и сократить обе части на 10, то получим
Зх = 2 + 100Л, к g Z, что равносильно сравнению Зх = 2 (mod 100).
Решениями этого сравнения будут целые числа
x = 3"1-2(modl00) = 67-2(modl00) = 134(modl00) = 34(modl00), т. е. числа, сравнимые С 34 по модулю 100. х = {...,-166,-66,34,134,234,...,934,1034,...} . Из них ровно 10 чисел (от 34 до 934) будут лежать в множестве вычетов Z1000. Таким образом, данное сравнение имеет 10 решений по модулю 1000.
Ответ: х = 34 + 100Л (modlOOO), к = 0...9 .
Решить сравнение: ЗОх = 15 (modlOOO).
Решение. НОД (30,1000) = 10.
Перепишем сравнение в виде
ЗОх = 15+ 1000Л, Л g Z.
Мы не можем сократить равенство на 10, поскольку 15 на 10 не делится. Данное равенство можно сократить только на 5.
6х = 3 + 200Л, к g Z .
6х-200Л = 3, к g Z .
Поскольку х и к — целые числа, то левая часть равенства чётна при любых значениях переменных, в то время как правая часть нечётна. Это невозможно, а значит, решений нет.
Конечно, можно написать проще: X = 34 + 100z, z G 1. Однако, поскольку исходное сравнение рассматривалось по модулю 1000, желательно, чтобы в ответе фигурировало это число.
76
В общем случае, сравнение a-x = /?(mod/??) имеет решения тогда и только тогда, когда d | Ъ, где d = НОД (а,т). Количество решений по модулю т равно
d. Частное решение имеет вид х0 =| — | -| — j| mod— |, а общее решение запи-\d ) \d j\ d j
772
сывается как х = х0 + £• — (mod/??), к = 0 ...d-1.
3.5.4.	Китайская теорема об остатках
(к	А
Лемма 1. Если НОД= 1 для всех i = \...к, то НОД\ ]~[ д,/?? = 1.
\ /=1	)
◄ Каждое из чисел а также число т, можно представить в виде произведения степеней простых сомножителей. Если ц и т взаимно просты, это означает, что среди сомножителей ц нет ни одного делителя т. А значит, и в произведении всех таких ц делителям т неоткуда взяться, и оно по-прежнему будет взаимно просто cm.k
т = Д -17 , ц= 23-57 , а2 =5-И2,	= 22 -З2 . Ни одно из ц не содержит в своём
разложении простых чисел 7 и 17, поэтому и их произведение этих чисел содержать не будет: ца2а3 = 25 • З2 • 58 • 112.
Лемма 2. Если аДт для всех i = \...k и НОД{а^а^ = 1 для всех / j, то
(к А
Пч \ \т.
\ /=1 J
◄ Из делимости т на ц следует, что каждое из чисел а},...,ак содержит в своём разложении только те простые числа, которые присутствуют в т, причём в степенях, не превосходящих соответствующие показатели в числе т. Из попарной взаимной простоты ц следует, что простые сомножители у всех ц различны. Значит, при перемножении этих чисел показатели не увеличатся, и т будет делиться на произведение ц . ►
т = 25 -З2 -58 -7-И2 -17 , ц= 23-57 , а2=112, а3=32 -7. Все ц попарно взаимно просты, поскольку не содержат совпадающих простых сомножителей. Поэтому,
77
чтобы получить их произведение, достаточно выписать три разложения последовательно: ца2а3 = 23 • 57 • 112 • З2 • 7 . Это число делит т.
Китайская теорема об остатках. Если натуральные числа тх,т2,...,mt попарно взаимно просты, то для любых целых чисел bx,b2,...,bt система сравнений
х = Z>j (modОт;) (3-2) x = bt (mod от,)
имеет решения, и любые два решения отличаются на величину, кратную т, 	.
◄ Покажем, что система (3.2) имеет решения.
Пусть т = т}-	. Вычислим вспомогательные параметры ni=mlmi, i =	.
По Лемме 1, ЯОД (от,, у) = 1 для всех /, ведь у является произведением всех модулей, кроме тг.
Согласно соотношению Безу, для всех i = найдутся такие целые числа kt и qf, что k^+q^ =1. Это означает, что к^ = l(modOT;). Для всех остальных модулей	выполнено к^ = 0(modот.), поскольку mj являются делителями
Число х0 = '^bikini является решением системы (3.2). В самом деле: /=1
х0 (modOTj) = bxkxnx +b2k2n2 + ... + btktnt (пкИотД = bx -1 + Z>2 • Q + ... + bt • 0 (modOTj) = bx (пкИотД ; для остальных модулей проверка выполняется аналогично.
Докажем вторую часть теоремы.
Пусть у — другое решение системы (3.2). Тогда у-х0 = 0(mod/у) для всех /, т. е. mi\(xl-x0'). По Лемме 2, от|(у-х0) (ведь все модули попарно взаимно просты), а значит, два решения отличаются на величину, кратную т. ►
Следствие. В диапазоне [0; от — 1] всегда лежит ровно одно решение.
78
3.5.5.	Системы сравнений первой степени
Из доказательства китайской теоремы об остатках следует, что решения системы сравнений (3.2) вычисляются следующим методом:
1.	т = тх- .
2.	д = m/mi, i =	.
3.	Для каждого i = найти такие целые числа kt и qt, что Ад + <?гтг = 1.
t
4.	Частное решение системы: х0 =	(mod/??).
/=1
5.	Общее решение: х = х0 (mod/??), т. е. х = х0 + zm, z g Z.
Найти решения системы:
х = 6 (mod8) < х = 5 (modl3).
х = 3 (mod 15)
Решение. Все модули попарно взаимно просты:
НОД (8,13) = НОД (8,15) = НОД (13,15) = 1.
Следовательно, выполняется условие китайской теоремы об остатках и мож
но переходить к вычислениям.
1.	m = 8-13-15 = 1560.
2.	р = т/8 = 13• 15 = 195 , //2 =/??/13 = 8- 15 = 120, п3 = т/15 = 8-13 = 104 .
3.	При помощи расширенного алгоритма Евклида находим: 3-195-73-8 = 1, -4-120 + 37-13 = 1, -1-104 + 7-15 = 1.*
4.	х0 =6-(3-195) + 5-(-4-120) + 3-(-l-104)(modl560) = 798.
Ответ: x = 798 + 1560z, zgZ.
Для проверки нужно подставить полученное частное решение во все три сравнения. Разность левой и правой частей сравнения должна делиться нацело на соответствующий модуль.
Числа Ад вычисляются неоднозначно. Например, выразить 1 через 195 и 8 можно было не только как 3 • 195 — 73 • 8, но и как —5 • 195 +122 • 8 . Поскольку полученные значения отличаются на величину, кратную 1560, подойдёт любое из них.
79
Например, 798 = 6 (mod 8) о 81 (798 -6). 792 делится на 8, следовательно, найденное решение удовлетворяет первому сравнению.
Если числа тх,т2,..., mt не являются взаимно простыми, это не означает, что решений не существует. Система (3.2) имеет решения тогда и только тогда, когда = Ъ} (mod НОД (т^т^. В этом случае решения отличаются на величину, кратную т = НОК(т}, и находятся методом последовательной
подстановки.
Найти решения системы:
х = 2 (mod6) х = 5 (mod 9)
Поскольку НОД (6,9) = 3, а 2 = 5 (mod3), решения существуют.
Перепишем первое сравнение в виде х = 2 + 6q и подставим х во второе срав
нение:
2 + 6q = 5 (mod 9) <=> 6q = 3 (mod 9); 2q = 1 (mod3) ;
<7 = 2(mod3) <=> q = 2 + 3k', x = 2 + 6-(2 + ЗЛ) = 14 + 18Л .
Ответ: x = 14 (mod 18).
3.6. Задачи для самостоятельного решения
37.	Указать все такие п, для которых значение функции Эйлера (Дп) нечётно.
38.	Указать все такие п, для которых сДп) = 2.
39.	Известно, что n = p-q, р и q— простые числа. « = 348913, (Дп) = 347620 . Найти pvtq.
40.	Сколько чисел из диапазона [-3500;6000] делится хотя бы на одно из следующих чисел: {12,14,20} ?
41.	Найти НОД чисел:
а)	789612 и 456618;
80
б)	485236 и 231844;
в)	487836 и 535884.
42.	Найти:
а)	6191 (modlOOO);
б)	27’1 (modlOOO);
в)	880 1 (modl021);
г) 659 1 (mod 1016).
43.	Решить сравнение:
а)	455x^(666+ 536)-406 (mod 982);
б)	235х = (132 + 448)-268 (mod458) .
44.	Решить систему сравнений наиболее оптимальным способом: x = 10(modl3) x = 4(mod9)
х = 4 (mod 7)
а) < х = 1 (modl2) б) < х = 0(mod8) . х = 1 (mod 7)
7х = 4 (modl7)
45.	Решить систему сравнений: -px = 0(modll) .
9х = 6 (modl3)
81
4.	Системы счисления
Система счисления — это способ представления чисел с помощью письменных знаков (цифр).
Системы счисления подразделяются на позиционные, непозиционные и смешанные.
4.1.	Непозиционные системы счисления
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе.
4.1.1.	Римские цифры
Канонический пример непозиционной системы — римская система счисления, использующая в качестве цифр латинские буквы: 1=1, V = 5, X = 10, L = 50, С = 100, D = 500, М = 1000. Цифры записываются в порядке убывания:
1678 = MDCLXX VIII (1000 + 500 + 100 + 50 + 10 + 10 + 5 + 1 + 1 + 1 ).*
Римские цифры используются для записи номера века (XVIII век), монарха (Екатерина II), важного события (XX съезд КПСС) и т. и.
4.1.2.	Система остаточных классов
Система остаточных классов (СОК) определяется набором попарно взаимно простых чисел m2,mt. Каждому целому числу х из отрезка [0; т-1], m =	, ставится в соответствие набор вычетов (bx,b2,...,bt} , где
х = Z>j (modОт;)
<...	, ()<b<mi для всех i =	. Существование и однозначность та-
x = bt (modmz)
Современная римская система не является полностью непозиционной, поскольку в ней допускается запись меньшей цифры перед большей, и в этом случае вместо сложения осуществляется вычитание. Например, VI = 6 (5 + 1), а IV = 4 (5-1), т. е. в первом случае цифра I означает число 1, а во втором — -1. Однако сами древние римляне записывали число 4 как ПП, и их система счисления была чисто непозиционной.
82
кого представления гарантирует китайская теорема об остатках (см. раздел 3.5.4).
Сложение и умножение чисел в этой системе производится поразрядно, по соответствующему модулю.
4.2.	Позиционные системы счисления
В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от местоположения (разряда). Привычная для нас десятичная система счисления является позиционной.
В записи числа 222 (двести двадцать два) используются три одинаковые цифры, однако самая правая цифра означает число 2, следующая — 20, а крайняя левая — 200.
Позиционная система счисления определяется натуральным числом b > 1, т. и. основанием системы счисления. Систему счисления с основанием b называют Zj-ричной (в частности: двоичной, троичной, восьмеричной, шестнадцатеричной нт. и.).
4.2.1.	Представление натуральных чисел
Натуральное число х в ^-ричной системе счисления представляется в ви-
де х = ^акЬк, где ак — это целые числа, называемые цифрами. 0<ак<Ь. Ко-к=0
гда />>10, для обозначения дополнительных цифр используются буквы латинского алфавита: 10 = А, 11 = В и т. д. Число х в />-ричной системе счисления записывается как х = (ап_1ап_2...а1а0) ; в большинстве случаев скобки не ставятся.
68310 = 6-102+8-101+3-10°.
68А16 = 6-162+8-161+10-16° = 167410.
В />-ричной системе счисления само число b записывается как 10ь.
◄ 106 = 1-Ь1 +о-ь° = ь. ►
83
Перевод из произвольной 6-р и мной системы в десятичную был продемонстрирован выше. Для осуществления обратного перевода нужно делить исходное число, а затем частные, на Ь, пока очередное частное не обнулится. Остатки будут цифрами 6-ричного представления, от младших разрядов к старшим.
Перевод десятичного числа 1674 в шестнадцатеричную систему:
1674 = 104-16 + 10;
104 = 6-16 + 8;
6 = 0-16 + 6.
Остатки читаются снизу вверх, десятичное число 10 заменяется шестнадцатеричной цифрой А. Получаем 68А16.
Если числа небольшие, можно воспользоваться методом исчерпывания, т. е. начать с больших степеней.
Перевод десятичного числа 1674 в шестнадцатеричную систему.
162 = 256 , 163 = 4096. 162 <1674<163, значит, максимальная степень основания равна 2.
256 укладывается в числе 1674 шесть раз: 1674 = 6-256 + 138.
16 укладывается в числе 138восемьраз: 138 = 8-16+10.
1 укладывается в числе 10 десять раз.
Частные читаются сверху вниз, образуется число 68А16.
Перевод чисел из а-ричной системы в ^-ричную может быть осуществлён через десятичную. Однако, если а = Ъс для некоторого натурального с, перевод между системами можно произвести напрямую, поскольку в этом случае ровно с разрядов ^-ричной системы соответствует одной а-ричной цифре, и переводить число можно поразрядно.
Поскольку 8 = 23, три двоичных разряда задают одну восьмеричную цифру. Допустим, требуется перевести в двоичную систему число 7438.
7„ = 111,, 4„ = 1009, 3„ = 011,. Тогда 743„ = 111100 011,.
о	2 > о	2 > о	2	’ ’	о	2
84
Чтобы перевести число из ^-ричной системы в а-ричную, где а = Ьс, нужно разбить его на группы по с разрядов, начиная с младших. Слева к числу можно приписать нули так, чтобы количество разрядов стало кратно с. Каждая группа разрядов заменяется одной <т-ричной цифрой.
11010110, =011'010'110, =326„. 2	2	о
4.2.2. Представление дробных чисел
Десятичная дробь— это дробь со знаменателем 10”, иеК. Она записывается следующим образом: целая часть в десятичной системе счисления, затем разделитель (запятая или точка), затем дробная часть в десятичной системе счисления.
Аналогично, /ьричная дробь — это дробь со знаменателем bn, п g N.
При переводе дробных чисел между различными позиционными системами счисления, рассматривают отдельно целую часть, отдельно — дробную,
а результат складывают.
513 _5 8125
16 ~ 10000
5.812510.
с13 С 13 1Ш 11012
5— = 5 + — = 101, +------- 16
16	24	100002
= 101.11012.
5—= 516+^ = 5.D 16	ю16
16 •
Работа с целыми числами описана в разделе 4.2.1. Для перевода дробной части Л-ричной дроби в десятичную систему нужно вычислить линейную
комбинацию х = ^акЪ к. к=\
0.1101, =1-2"1 + 1 - 2 2 + 0 - 23 +1 - 2 4 = — + — + — = —.
2 4 16 16
Перевод дроби (как обыкновенной, так и десятичной) из десятичной системы в Л-ричную осуществляется следующим образом: число умножается на Ь, целая часть произведения отбрасывается, превращаясь в очередной разряд ^-ричной дроби.
85
тт •• г 13
Переведем дробь — в двоичную систему счисления.
16
13 „ 13 л5 тт	.	-Г
—• 2 = — = 1-. Целая часть равна 1, запоминаем ее и отбрасываем.
2 = -| = Д. Целая часть равна 1, запоминаем её и отбрасываем.
^2 = ^. Целая часть равна 0, запоминаем её.
—•2 = 1 • Целая часть равна 1, дробная часть равна 0 — алгоритм завершён.
Цифры читаются сверху вниз: 0.11012.
Процесс мог оказаться бесконечным.
Переведём дробь 0.2 в двоичную систему счисления.
0.2 • 2 = 0.4. Целая часть равна 0, запоминаем её.
0.4 • 2 = 0.8. Целая часть равна 0, запоминаем её.
0.8-2 = 1.6. Целая часть равна 1, запоминаем её и отбрасываем.
0.6-2 = 1.2. Целая часть равна 1, запоминаем её и отбрасываем.
Следующим числом будет 0.2, которое уже встречалось на первом шаге алгоритма. Таким образом, процесс зациклится, и двоичная дробь примет вид: 0.001100110011...2 = 0.(0011)2.
Возможна и обратная ситуация: дробь, бесконечная в десятичной системе счисления, будет конечной в системе с другим основанием.
- = 0.333. =0.Т. 3
Несократимая дробь — будет конечной в ^-ричной системе счисления п
тогда и только тогда, когда п | Ь* для некоторого натурального t.
10 = 2-5, поэтому в десятичной системе счисления конечными будут только те дроби, знаменатель которых не содержит никаких простых делителей, кроме
з
2 и 5. Например, обыкновенная дробь — конечна, т. к. 50 = 2-5* 21102 ;
86
3	6	7
—	= — = О.О6,„. Дробь — бесконечна, т. к. 24 имеет 3 в качестве простого де-50 100	10	24
лителя, а 3 не делит 10 в какой бы то ни было степени.
12 = 22-3, следовательно, в двенадцатеричной системе счисления конечными
будут только те дроби, знаменатель которых не содержит никаких простых
7
делителей, кроме 2 и 3. Дробь — конечна, т. к. 24 = 23-3|122 ;
7	42	36,,	3
—	= — = —— = 0.36,,. Дробь — бесконечна, т. к. ее знаменатель содержит
24 144 10012	12	50
делитель 5.
Любое рациональное число (дробь —) можно представить в виде перио-п
дической дроби (возможно, с нулевым периодом). Верно и обратное: любая периодическая дробь является рациональным числом.
= 0.111... = 0.(1)10 — чистая периодическая дробь (период начинается сразу
после разделителя), длина периода равна 1;
= 0.050505... = 0.(05)10 — чистая периодическая дробь, длина периода равна 2;
7
— = 0.291666... = 0.291(6)10 — смешанная периодическая дробь (имеется предпе-
риод), длина периода равна 1.
—	= 0.25000... = 0.2510 — конечная десятичная дробь (период равен нулю).
Чистую периодическую дробь можно интерпретировать как дробь со
знаменателем 10”-1, иеК, т. е. состоящим из п девяток. Аналогично, в
Zj-ричной системе счисления знаменатель периодической дроби равен bn -1 и записывается в своей системе как п цифр (Ъ -1).
0-(74)10 =	74 ” 99 ’
О.(74)16 =	_ 7416 _ 116 _ 116 ” FF16 162 -1 ~ 255
87
Заметим, что О.(9)1о = 1. Одно из наиболее простых обоснований выглядит
так:
◄ - = 0.333. .. Умножим обе части на 3: 1 = 3 0.333.... Умножение в правой час-
3
ти можно выполнить «столбиком», поразрядно, т. к. переносов не будет. Получим 1 = 0.999.... ►
Ещё один способ доказательства:
◄ Обозначим 0.999... = х. Умножим обе части на 10: 9.999... = 10х. Вычтя из
второго уравнения первое, получим 9.000... = 9х, т. е. х = 1. ►
Аналогичный парадокс наблюдается во всех системах счисления.
О.(2)3 =У = 1; 0.(6),=^ = 1; o.(F)16 =5^ = 1 ит. д. 2,	6,	Ей
Перевод смешанной периодической дроби в десятичную систему счисления удобнее всего проиллюстрировать на примере:
0(211	21	2	7	23
0.2(211 = 0.2, + 0.0(211 = 0.2, + Л Л = 0.2, +---— = - + — = —
10,	10.-22.	3 8-3 24
Перевод дробей между системами с основаниями b и Ьс можно осуществлять напрямую, как и для целых чисел, но дробная часть числа разбивается слева направо, и недостающие нули приписываются справа.
0.01001, =0.010'010, =0.22 ’
0.10(01)2 = 0.100'101'010'101'010..,2 =0.45252..,8 = 0.4(52)8 ;
0.6(2)8 = 0.6222..,8 =0.110010010010..,2 =0.1(100)2.
4.2.3. Арифметические действия в /ьричной системе счисления
Арифметические действия в ^-ричной системе счисления осуществляются теми же способами, что и в десятичной: сложение, вычитание, умножение — «столбиком», деление — «уголком». Принцип таков: b единиц одного разряда превращаются в одну единицу следующего по старшинству.
88
Сложение. A8C4i6 + 78Ei6 = ? *1	*1	*1
A 8 С 4 7 8 E В 0 5 2
Пояснение:
(4 + E)i6 = 4 + 14 = 16 + 2 = 1216. Пишем 2, переносим 1 в следующий разряд.
(С + 8 + 1)16 = 12 + 8 + 1 = 16 + 5 = 15 16. Пишем 5, переносим 1 в следующий разряд.
(8 + 7 + 1)16 = 16 = 1016. Пишем 0, переносим 1 в следующий разряд.
(А + 1)16 = В16.
Проверка: A8C4i6 + 78Ei6 = 43204 + 1934 = 45138 = B052i6.
Вычитание. 5218 - 2358 = ?
_5 2 1 2 3 5 2 6 4
Пояснение:
1 < 5, занимаем единицу из следующего разряда. (11 - 5)8 = 8 + 1 - 5 = 4. (2 - 1) < 3, занимаем из следующего разряда. (11 - 3)8 = 8 + 1 - 3 = 6.
(5- 1) - 2 = 2.
Проверка: 5218 - 2358 = 337 - 157 = 180 = 2648.
Умножение. 12023 • 2113 = ?
Для начала рассмотрим умножение на одноразрядное число на примере 12023 • 23:
12 0 2 X
2
10 111
Пояснение:
(2 • 2)3 = 4 = 113. Пишем 1 и переносим 1 в следующий разряд.
(0 • 2 + 1)3 = 1.
89
(2 • 2)з = 4 = 113. Пишем 1, переносим 1.
(1 - 2 + 1)3 = 3 = 103.
Проверка: 12023 • 23 = 47 • 2 = 94 = 101113.
Теперь можно решить пример целиком:
12 0 2 2 1 1 12 0 2 +	12 0 2
10 111 1 1 0 2 0 2 2
Пояснение:
Верхнее число умножается на цифры нижнего числа, начиная с младшего разряда. Каждое следующее произведение записывается со смещением на один разряд влево. Затем произведения складываются так, как если бы в пустых разрядах справа стояли нули (т. е. необходимо сложить «столбиком» числа 12023, 120203 и 10111003).
Проверка: 12023 • 2113 = 47 • 22 = 1034 = 11020223.
Деление. 100101002 : 10112 = ?
Пояснение:
100102 делим на 10112, частное равно 1, остаток равен 1112. Сносим следующий разряд делимого (1).
11112 делим на 10112, частное равно 1, остаток равен 1002. Сносим следующий разряд (0).
10002 < 10112, поэтому пишем в частное 0 и сносим следующий разряд (0).
90
100 002 делим на 10112, частное равно 1, остаток равен 1012. Деление завершено.
Проверка: 100 1 0 1 002 : 10112 = 148 : 11 = 13 (неполное частное) и 5 в остатке, т. е. 11012 и 1012, соответственно.
4.2.4. Двоичный код
В подавляющем большинстве современных компьютеров данные представляются в двоичном коде, т. е. при помощи двух знаков, обычно обозначаемых цифрами 0 и 1. Используя п двоичных разрядов (бит), можно, согласно схеме размещений с повторениями (2.1), закодировать 2” различных комбинаций.
Программист вправе самостоятельно выбрать способ кодирования данных в своей программе (например, создать код, в котором двоичная комбинация 11 будет означать число 1, а 10 — число 3), однако для упрощения работы с числами разумнее всего воспользоваться одним из существующих способов их двоичного представления, основанных на двоичной системе счисления.
Самой наглядной формой представления целых чисел со знаком является прямой код, где старший бит отведён под знак числа, а остальные — под его модуль. Числа, хранящиеся в таком виде, удобно перемножать: модули умножаются отдельно, знак определяется исходя из старшего бита. Однако вычитание чисел в прямом коде потребует выполнения сложных алгоритмов.
Также используется обратный код, в котором положительные числа записываются так же, как и в прямом коде, а отрицательные инвертируются. Обратный код также называется «дополнением до единицы», поскольку н-битное отрицательное число, будучи сложенным со своим модулем, даст 2”-1 — число, состоящее из п единиц. Обратный код упрощает вычитание чисел, заменяя его операцией сложения.
Широко распространён дополнительный код. Дополнительный код положительного числа совпадает с его прямым (и обратным) кодом, дополнительный код отрицательного равен обратному коду, сложенному с единицей.
91
Это представление также называется «дополнением до двух», так как код отрицательного «-битного числа представляет собой число, которое, будучи сложенным со своим модулем, даст 2”. Дополнительный код, как и обратный, заменяет операцию вычитания операцией сложения, а кроме того, позволяет не задумываться о знаке операндов при сложении и вычитании: старший бит участвует в арифметических операциях наравне с остальными.
Пусть на хранение целого числа отведено 3 бита.
Если в поставленной задаче мы оперируем только положительными числами, то можно интерпретировать эти три бита как цифровые разряды двоичного числа, от О (ООО) до 7 (111) — т. и. беззнаковое целое число.
Если требуется хранить и отрицательные числа, то старший бит будет знаковым, следующие два — цифровыми. Варианты представления чисел приведены в таблице 4.
Таблица 4. Двоичные коды длиной 3 бита.
Код	3	2	1	0	-0	-1	-2	-3	-4
Прямой	011	010	001	000	100	101	ПО	111	—
Обратный	011	010	001	000	111	по	101	100	—
Дополнительный	011	010	001	000	—	111	по	101	100
Как видно из таблицы 4, диапазоны чисел, представляемых в том или ином коде, различны. Прямой и обратный коды длиной п бит позволяют записать числа от -2”1 -1 до +2" 1 -1, при этом ноль представляется двумя способами («положительный ноль» и «отрицательный ноль»), В дополнительном коде можно получить числа от -2”1 до +2" 1 -1, при этом ноль только положительный.
4.3. Задачи для самостоятельного решения
46.	Перевести число во все системы счисления с основаниями от 2 до 10: а) 122125;
б)	26127;
92
в)	1210203;
г)	131034.
47.	Перевести двоичную дробь в десятичную, восьмеричную и троичную системы счисления.
а)	0.1110(01)2;
б)	10.0(1 юоо 1)2.
48.	Выполнить сложение и проверить результат с помощью вычитания:
а)	10101012 + 11010012.
б)	18А16 + ЗСВ16.
49.	Перевести числа 21 и 25 в указанную систему счисления, выполнить умножение в этой системе и проверить результат с помощью деления.
а) Двоичная; б) восьмеричная; в) троичная.
93
Ответы и указания к задачам
1. А — пустое множество. В — множество, единственным элементом которого является пустое множество.
2. В первом случае А — множество, во втором — число.
6.	Все три тождества верны.
7.	С. Указание: воспользоваться законами дистрибутивности и де Мор
гана.
8.	а) ЛоВ = (ЛоВ)Л(ЛЛ5) , Л\В = ЛЛ(ЛоВ) . б) Аг>В = (А^В)Л(АЛВ) , А \ В = (А >и В)ЛВ . в) A jB = U\B)\B , Ar,B = (A\B)AA.
9.	а) «Является сиквелом»; «вышел раньше»; «получил больше “Оскаров”» и т. и. б) «Является режиссёром»; «написал сценарий»; «сыграл в фильме» и т. и. в) Нет, т. к. один актёр мог сыграть в нескольких фильмах. / Нет, т. к. в одном фильме появляется несколько актёров.
10.	Нет, т. к. кто-то из студентов мог прогулять контрольную работу и
не получить оценку.
11.	а) Да, т. к. множество результатов покрывает все возможные ситуации, и напротив каждого студента будет стоять ровно одна галочка, б) Нет, т. к. экзамен подразумевает оценку, и никто из студентов не получит «Зачёт» или «Незачёт», в) Может, если количество студентов в группе не превышает четырёх: один получит «Недопуск», второй — «Неявку», третий — «Зачёт»,
четвёртый — «Незачёт».
14.	Да. / Нет, т. к. 0! = 1! = 1. / Нет, т. к. не каждое натуральное число является факториалом некоторого числа (например, у 3 нет прообраза).
15. а) ['
2 3	4)	(1	2 3 4 5)	ч <1	2	3 4	5
. б)	.в)
1 2	4)	(5	3412)	(2	6	4 1	3
6
5
16.	37. Указание: из условия следует, что: М = 95, |д| = 25, |4| = 47 , |4| = 39, |Л4| = 22 ,
1</<У<4
= 42
144441+|44441+144441+144441 23
|4444| = 5 (сим-
волы пересечения множеств опущены). Требуется вычислить 4 ^4 и4 °4
94
Наиболее объёмные вычисления связаны с раскрытием выражения
1</<У<4
по формуле включения-исключения: в объединении задействованы шесть множеств (В1 = ДД, В2 = ДД, В6 = ДД), что даёт 15 слагаемых вида |дд|, 20 слагаемых вида |ддд| и т. д. (в общей сложности 63 слагаемых). Однако все пересечения множеств Д будут сводиться к А1А2А3, Д Д Д, А,А3А,, ДДД или ДДДД , поэтому после упрощения формула примет вид
U 44 = S |44|-2-	|ДДД| + 3-|ДДДД| • Окончательное выражение
1</<у<4	1</<у<4	l<i<j<k<4
для подсчёта ответа:
4 и и Л3 и Л4
M-SI4I+
1</<У<4
+ 2• |ДДДД |,
где М— множество студентов, сдавших на «3» ровно три экзамена.
17.	3-4 = 12.
18.	32-32 = 1024.
19.	32-24 = 768.
20.	С4 =15.
21.	а) Д4 = 64 = 1296 . б) Д4 = 360 . в) 4- Д3 = 240 .
22.	а) Д43 = 134 = 28561. б) Д4 = 17160 .
23.	Д6 = З6 = 729. Указание: распределяются фактически не письма между
курьерами, а курьеры между письмами.
24.	2-5!-5! = 28800 . Указание: все пять женщин одновременно сядут на стулья либо с чётными номерами, либо с нечётными. Мужчины, соответственно, займут оставшиеся пять мест.
25.	а) С85 = 792 . б) С85 = 56 . в) С820 = 888030.
26.	а) С47 = 120. б) Д7 = 47 = 16384 .
27.	а) С4 —816. б) С4 —120. Указание, сразу раздать по два шарика каждому ребёнку, а потом распределять оставшиеся.
28.	=812.
95
29.	310-3-210+3. Указание: ввести три множества событий Д «z-й цвет не используется», z = 1,2,3, и применить формулу включения-исключения.
30.	3999960. Указание: в каждом разряде каждая цифра встречается — к раз, где к— количество имеющихся цифр, N— количество чисел, составленных из данных цифр.
31.	а) 10670044. б) 3732960.
32.	39 -29 -1 = 19170.
33.	п-Зп-х-2т-\
34.	2648.
zz-2”+1+l	1	1	1	п
35.		. Указание: ---------------=--------------------. Для получения по-
(п + l)(zz + 2)	к + 2 к + \ (к + 1)(Л + 2)
еле дней дроби необходимо проинтегрировать бином Ньютона дважды.
36.	С'о5 -1 = 155117519. Указание: воспользоваться свойством симметрии и
свёрткой Вандермонда.
37.	1 и 2.
38.	3, 4, 6.
39.	383 и 911.
40.	1630.
41.	а) 6. б) 4. в) 12.
42.	а) 979.6) 963. в) 811. г) 979.
43.	а) 574. б) 106.
44.	а) 673(modl092). б) 256(mod504). Указание: сравнения с одинаковыми правыми частями можно объединить в одно сравнение по модулю, равному НОК их модулей.
45.	2332(mod2431).
46.	а) 122125 = 932 = 11101001002 = 322104 = 16448 = 10211123 = 12459 = 41526 = 25017.
б)	26127 = 989 = 11110111012 = 331314 = 17358 = 11001223 = 13189 = 43256 = 124245.
96
в)	1210203 = 5369 = 438 = 1101101102 = 123124 = 6668 = 32235 = 20106 =
11647.
г)	131034 = 1110100112 = 7238 = 467 = 1220223 = 5689 = 33325 = 20556 = 12357.
43	7
47.	а) — = 0.8958(3) = 0.71(25)s = 0.2(2001)3. б) 2—= 2.3(8) = 2.3(07)8 =2.10(1)3.
48	18
48.	а) 101111102 (в десятичной системе: 85 + 105 = 190). б) 555i6 (394 + 971 = 1365).
49.	а) 101012 • П0012 = 10000011012. б) 258 • 318 = 10158. в) 2103 • 2213 =
2011103. (В десятичной системе: 21 • 25 = 525.)
97
Список рекомендуемой литературы
1.	Белоусов А. И., Ткачёв С. Б. Дискретная математика.— М.: Изд-во МГТУ им. Н. Э. Баумана, 2004. — 744 с.
2.	Виленкин Н. Я., Виленкин А. Н., Виленкин П. А. Комбинаторика. — М.: ФИМА, МЦНМО, 2006. — 400 с.
3.	Грэхем Р., КнутД., Паташник О. Конкретная математика. Основание информатики. — М.: Мир, 1998. — 703 с.
4.	Девенпорт Г. Высшая арифметика. Введение в теорию чисел.— М.: Наука, 1965. — 176 с.
5.	Жуков А. Е. Элементы комбинаторики (с дополнениями Д. А. Жукова). — М.: МИФИ, 2008. — 128 с.
6.	Кнут Д. Искусство программирования, том 1. Основные алгоритмы. — М.: Вильямс, 2000. — 720 с.
7.	КнутД. Искусство программирования, том 2. Получисленные алгоритмы. — М.: Вильямс, 2001. — 832 с.
8.	Яблонский С. В. Введение в дискретную математику.— М.: Высшая школа, 2006. — 384 с.
98