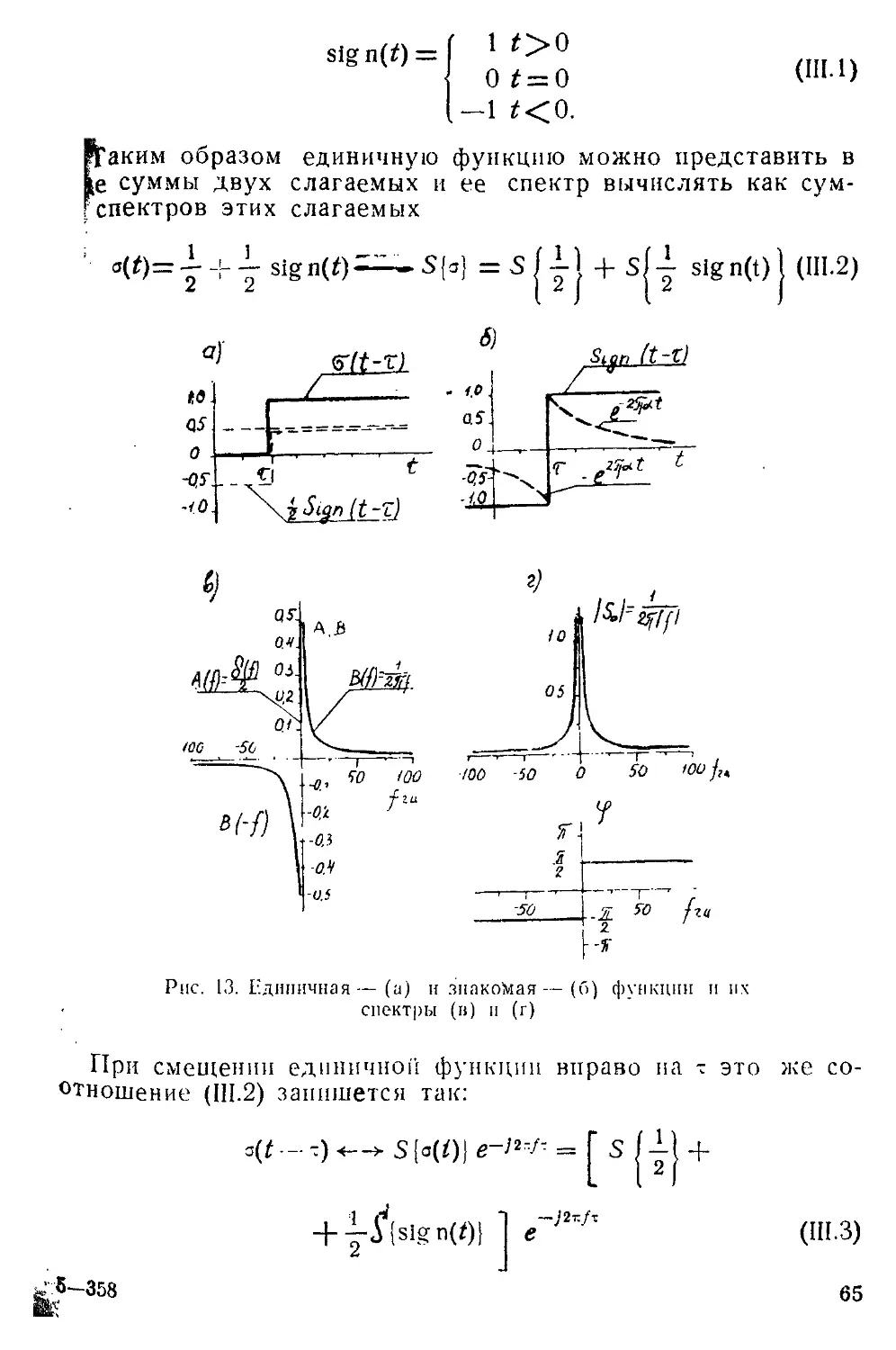
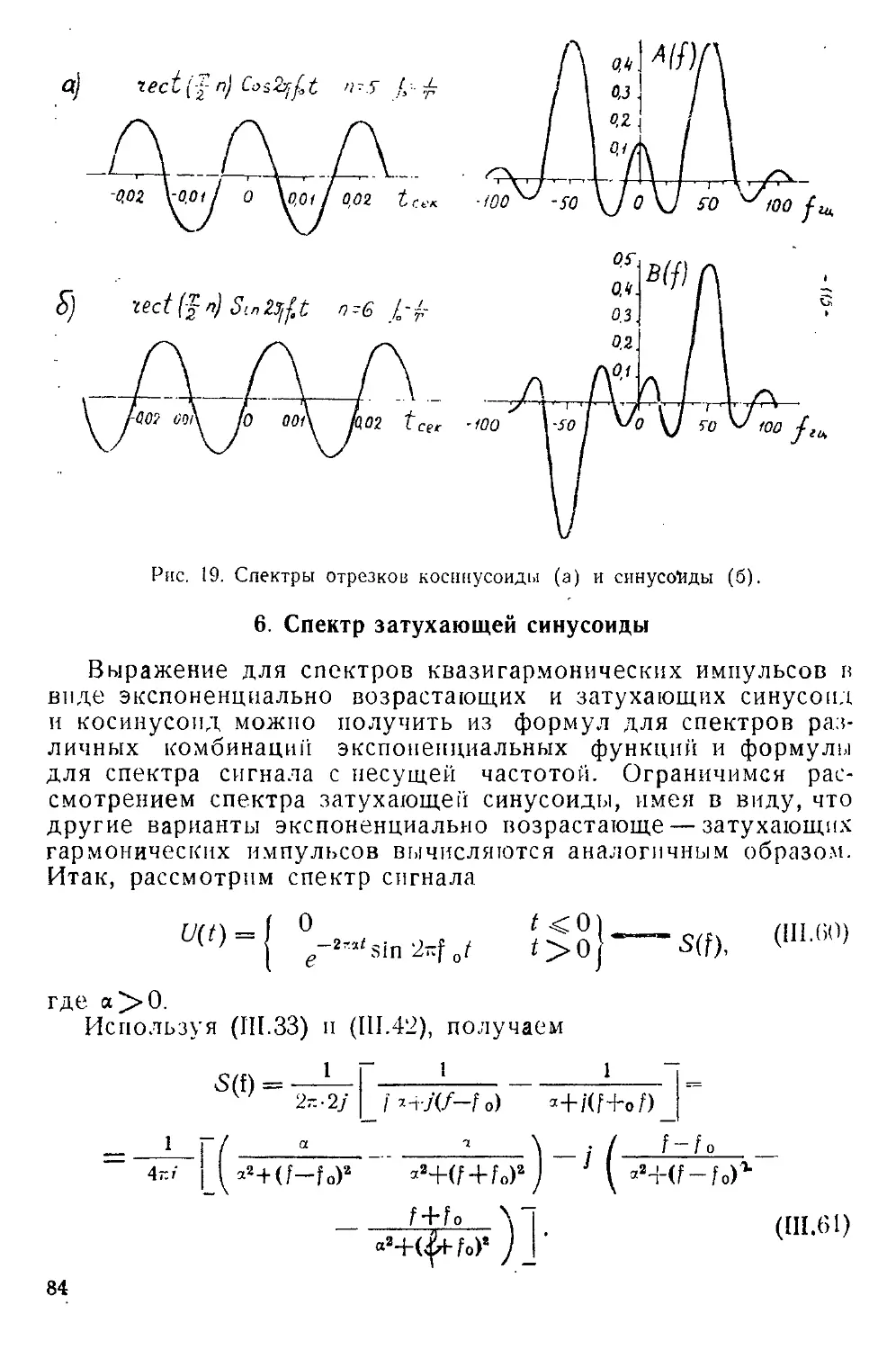
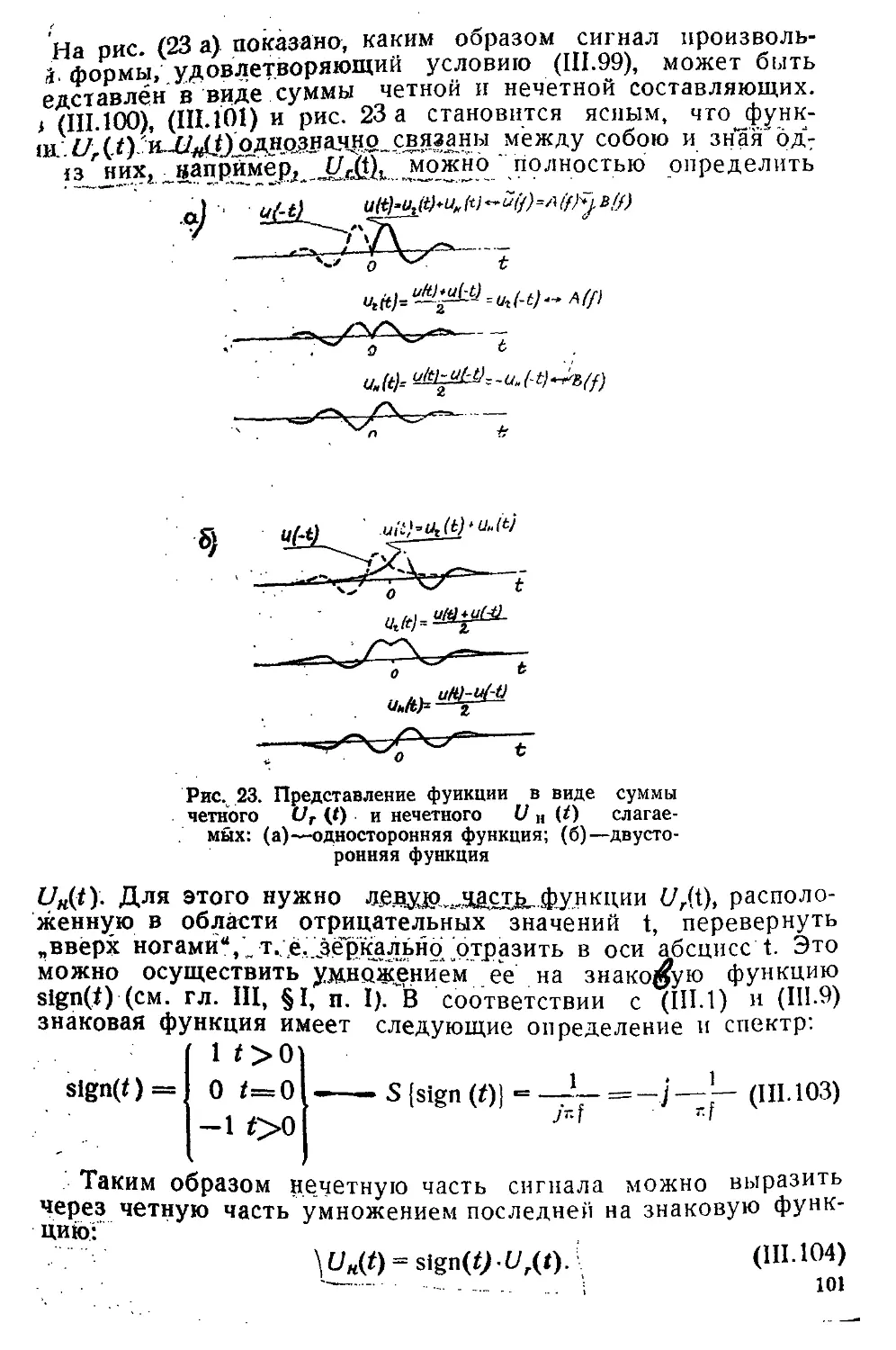
Текст
ИНИСТЕРСТ80 ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО
ОБРАЗОВАНИЯ СССР
Московский Ордена Трудового Красного Знамени
.ститут нефтехимической и газовой промышленности
им. И. М. Губкина
КАФЕДРА ПОЛЕВОЙ ГЕОФИЗИКИ
Ю. В. НАПАЛКОВ
УТВЕРЖДЕНО
Ученым Советом института
в качестве учебного пособия
СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ
В СЕЙСМОРАЗВЕДКЕ
ЧАСТЬ I
ОСНОВЫ ТЕОРИИ СПЕКТРОВ
УЧЕБНОЕ ПОСОБИЕ ДЛЯ СТУДЕНТОВ
ПЕЦИАЛЬНОСТИ 0105 — ПОЛЕВАЯ ГЕОФИЗИКА
Москва — 1974
Предисловие
Спектральные представления, основанные на преобразова.
;и Фурье, получили и настоян1,ее время ншрокое примене-
е во всех областях науки и техники, занимающихся пере-
чеь и преобразованием информации. Особенно плодотвор-
м оказалось применение спектральных представлений в
I росах, связанных с преобразованием сигналов линейными
огемами обработки и передачи. Понятие о спектре сигнала
частотной характеристике линейной системы позволило
сьма просто и наглядно описать процесс прохождения сир
ла через линейную систему.
Развитие и и1ирокое применение спектральных представле-
1'г позволяет сейчас говорить о спектральном нечислении
к об определенном разделе прикладной математ1!ки, приме-
емом при описа.чии преобразования сигнала линейной си-^-
мой на ос1.ове ^штегральпого п1)ео6разования Фурье. Ана-
|Гичио этому в прикладной математике существуют и дру-
е ви1.ь1 исчислении, например, операционное исчисление,
ень олизкос по содержанию к спектральному, но оспован-
'е ]1а применении преобразования Лапласа. Естественно,
о в сейсморазведке, занимающейся переработкой информа-
1И с^ геологическом строении среды, представляемой упру-
г%.п сейсмическими волнами в земной коре, идеи и метод]>1
:ектрального исчисления находят самое ншрокое примеие-
0. Они являются базой при рассмотрении многих теорети-
о::их вопросов, связанных с возбуждением, распростране-
1ем, регистрацией, обработкоГ] и интерпретацией искусствен-
) возбуждаем1>1х сейсмических волн, вплоть до построения
.":смо-геологического разреза,
К сожалению, н учебном плане специальности „полевая
^чфизика" института не предусмотрено специального курса
5 теории линеГтых систем и спект])альпому или операп,и-
,,'Ому исчислению, а объем сведений, получаемых студен-
II по этим вопросам в курсах математики, явно недо-
С л ^^ Время отсутствуют какие-лиоо учеб:1ые
-Х'окп и разделы в учебниках, глс студе1ггы могли 6-^^. •
'Хр?рчуть необходимые сведения в достаточно ко\/
пактной форме. На дневном факультете геологии и геос]
зики минимум необходимых сведений по спектральным пр€
ставлеииям приходится сообщать в геофизических курс
(гравиразведка, сейсморазведка). Студенты-заочники лише:
возможности получить даже и эти сведения. Настоящее уче
ное пособие имеет целью в какой-то мере исправить э
положение.
Первая часть настоящего учебного пособия посвяще
основным вопросам математического аппарата преобразов
-чин Фурье, на котором базируются спектральные представл
ньЯ. Первая глава является вводной. В ней рассматривают!
понятия о линейной системе и принципе суперпозиций (нал
женин) и приводятся основные сведения об элементарн!
функциях, наиболее употребляемых при разложении сигнал*
на элементарные составляющие.
Вторая глава является основной, В ней излож'.'ны оснои
теории преобразования Фурье и основные свойства частотнь
спектров. При изучении спектрального исчисления на э"
главу надо обратить особое внимание.
В третьей главе приведены примеры вычисления спектре
некоторых характерных функций. Подразделение рассмотре
ных функций на разрывные и непрерывные носит условнь
зсарактер, так как отрезки непрерывных функций имеют ра
рывные концы. В этой же главе рассматривается спект
,,сейсмической волны", под которой понимается сигнал, осно
ными особенностями которого являются зависимость как с
времени, так и от координат пространства, и убывание^ а!
"плитуды с расстоянием. '
Вопрос о связи между амплитудно-частотным и фазйво-ч
стотным спектрами сигнала, которым заканчивается /трет)
глава, более естественно было бы осветить во второе гла1
при описании основных свойств спектра. Однако при из^тюж
НИИ этого вопроса необходимо оперировать с понятиям\1 и
^е^фала свертки, теоремы о произведении спектров, спект].
единичной функции, в результате чего этот параграф оказа.
ся последним.
Изложение материала не претендует на математическу.
строгость и полноту. Более подробное и строгое изложени
многих вопросов мол{но найти в монографиях, приведенных ,
списке литературы.
Автор будет благодарен всем, кто сообщит ему свои з)
мечания по поводу содержания части I данного учебного п<)
собия. 1
ГЛАВА I
ЛИНЕЙНЫЕ СИСТЕМЫ И ПРИНЦИП НАЛОЖЕНИЯ
§ г. ЛИНЕЙНЫЕ СИСТЕМЫ
I. Системы передачи сигналов в сейсморазведке
Совокупность методов и способов исследования геологи-
кого строения верхней части земной коры путем изучения,
|1ения распространения упругих волн в геологической сре-|
'называется сейсмической разведкой, или сокращенно сейс-
разведкой. В большинстве методов сейсморазведки нсполь-
йтся упругие волны, вызванные искусственными источни-
ми: взрывами, ударами, вибраторами и пр. При этом оказы-
■ются известными точки возбуждения волн (источники) и
чки приема волн (приемники). Упругие волны, вызванные
:инсчным или групповым источником, распространяются з
элоЬ5ческой среде и регистрируются приемниками. Вслед-
йие неоднородности геологической среды возникают раз-
1чные|, типы волн, распространяющиеся по разным путям и с
13ным'и скоростями (отраженные, преломленные, рефрагиро-
1нные, дифрагированные, однократные, многократные, про-
>ЛБиые, поперечные, обменные, поверхностные и пр.). В
^■1-сморазведке обычно полезной оказывается волна какого-
1бо одного типа, а остальные волны оказываются помехами,
сложняющими регистрируемую волновую картину. Кроме
ого, волновая картина обычно осложняется так называемы-
й нерегулярными волновыми помехами, которые возникают
результате дробления фронта регулярной волны на малых
о размерам неоднородностях среды. Вследствие малой про-
яжениости регулярных обрывков волнового фронта эти вол-
ы проявляются в соседних точках приема как независимые,
ерегулярные колебания почвы. Для выделения нужных волн
'й фоне многочисленны}^ регулярных и нерегулярных помех в
сейсморазведке применяются различные способы частотной и
гространственной селекции, т. е. фильтрации по частотам и
юлновым числам, осуществляемые специальными аппаратур-
шми устройствами. В результате такой предварительной об-
5
работки полезный сигнал, очищенный от помех и ис
ный фильтрами, используется в дальнейшем для интер
ци» сейсморазведочных данных, т. е. для вычисления ,
стей, построения временных и глубинных сейсмически,
резов, построения структурных карт и пр. Путь сейсмич;
волны от источника через геологическую среду, прием!
фильтрующую аппаратуру и аппаратуру, переводящую ь
в соответствующий элемент разреза, можно рассматрив4^^-
систему приема, передачи и обработки сейсмическогон:
ла. Вся система передачи сейсмического сигнала от ист
ка до сейсмического разреза может рассматриваться ка|{
следовательность отдельных звеньев: источник, геологич^
среда (с ее отдельными элементами), приемная и фил; "
щая аппаратура (с ее отдельными звеньями), ностроител:
резов (с его отдельными элементами-этапами). Изучение.
ЭТ011 обобщенной систем1I передачи может быть разби-
этапы изучения отдельных звеньев систем!,!, причем для'
ных задач разбиение системы па звенья и более мелкие
менты может осуществляться по разному. ТакиМ' образе
сеГ1сморазведке, как и во многих других областях тех'
имеющих дело с передачей и преобразованием сигн.
большинство задач теории передачи сигналов могут .
сведены к схеме: входно!'! сигнал — передающая система
образователь) —^выходно!! сигнал.
Обычно задача исследования сводитс5. к нахожденик
НОИ из упомянутых функций по двум другим известным (|
циям. к указанной схеме исследования можно свестигС
разнообразные вопросы теории сейсморазведки: возбуж;!
сейсмических волн, их распространение в среде, фильтр;
и т. п. Например, в качестве входного сигнала мокно
сматривать импульс давления или смещения в области
буждення упругих волн, передающей системой мож-ую
тать геологическую среду, а выходным сигналом—унр
волну (давление, смещение) в точке приема. Любое 'з
сейсморегистрирующего канала, а также весь канал в и
"могут рассматриваться как передающая система со с
входным и выходным сигналами. Аналогичным образов
терференционн!,!е систем!>!, применяемые в сейсморазвед:
целью осуществления селекции по направлению распро
нения се1Смического излучения, также могут рассматри
ся как системы, преобразующие входной сигнал в выход
2. Понятие о линейной систе1У1е
Линейно!! системо!"! передачи (преобразования) сигн
наз!51вается система, у которое! амплитуда выходного сиг
иро1юр!и10пальна амплитуде входного сигнала. Зависи^
амплитуды выходного сигнала от амплитуды входного с
1СЛЛ ПОЛОЖИТЬ в A.17) х= Х1-\-х^, то получим
Полученное соотношение A.18) доказывает аддитивность
гобрязрвания, осуществляемого дифференциальным урав-
тёшЖ\7), вследствие чего дифференциальное уравнение
(Л|0 типа называется линейным, ^метим, .-цю-есдл-в-дра-
^рдасти при4ав-итБ—н«€4иаянное слагаемое-, то уравнение вс-
:';ется формально цч"Р""'-"^^ ("''р прррмрннмр н перд^-'^ ^тр-
■^ду и птгутгтпу1ат—щ{—нронзосдепий),—НО иербстанет удав-
■4»прдтк гнпйетву аддитинностм. в силу причин, аналогич-
IX указанным выше, по отношению к линейны.м алгебран-
ским уравнениям, для линейных систем, передаюш,их сиг-
.^^ в соответствии с преобразованием A.17), постоянная сос-
.«*ляющая всегда равна нулю. Отметим, что коэффициенты
, уравнения A.17) для систем с переменными параметрами
|)гут быть функциями времени, что не наруишт аддитивно-
и этого уравнения.
, Далее рассмотрим о^шрацию интегрирования, причем в ви-
) примера воспользуемся интегралом специального вида,
^■торый в дальнейшем будет играть больи1ую роль — инте-
(^.алом_ свертки. Этот интеграл осуществляет так называемую
,ерацш6 «свертывания" двух функций хИ) и у(^), в резуль-
|1те чего образуется функция 2{^). Этот интеграл имеет важ-
,)е физическое содержание, но мы пока рассмотрим его фор-
^лльно. Интеграл свертки функций x{^) и у{() записывается
,1к;
гЦ)= { .V(т)•у(^-x)с/x = л|.V. у]. A.19)
Положп.м х=Х1-\-Х2- Тогда интеграл свертки примет
д:
ос
= I д:,(-)-у(^-г)йх+ I л:,(х).у(^-х)й'г =
-=А\хи У]-\-А{х^, У\- A-20)
Страницы 8-13
в данном экземпляре кннгн
отсутствуют
Г1олучси}1ое выражение доказывает линейность операц
свертывания относительно функций х((). Очевидно, что ^,\
логичнь1е рассуждения можно привести и относительно фу;
ции у{^). Линейность операции сверт1,1вания одновременно (
начает линейность эквивалентной операции, осуществляем
частотной фильтрацией сигналов. Поэтому частотные 15С|
жения сигнала, осуществленные линейной системой, наз;:;
ются также линейными искажениями.
Наконец, преобразование сдвига сигнала во времени, к
изменение начала отсчета времени, также удовлетвори
условиям аддитивности и однородности и поэтому тг!:;
является линейным преобразованием.
§ 3. ЭЛЕМЕНТАРНЫЕ СИГНАЛЫ
1. Выбор элементарных сигналов
В предыдущих разделах было показано, что к линейн!,
системам применим принцип наложения (суперпозиции). I!
этому изучение свойств этих систем может быть осущес
нлено путем исследования реакции систем!^! на какой-лиг'
специально выбранный сигнал достаточно простой форм1
который легко создать экспериментальным путем и описа,
аналитически. Такой сигнал простой формы буде.м называ:
элементарным сигналом. Вопрос о передаче системой сигг
ла произвольной формы может решаться на основе прпнци!
суперпозиции, для чего иходно11 сигнал разлагается на су.>
му элемептарн1.1х сигналов, каждое из слагаемых пропуск
ется через систему, а выходной сигнал получается в резу::
тате суммирования реакций системы на эти элементар!;;-
сигнал[>1. Естественно, что в выборе элементарн1>1х сигнал^
имеется некоторый произвол, и их выбор определяется тс
что элементарный сигнал должен б1)!ть достаточно "удо;
ным" для теоретических и экспериментальных исследован;-:
Это „удобство" определяется условием, что должен име1
достаточно простоГ! и удобный математический аппарат .т ^
а) разложения сигнала сложно!! формы па консч]!у[о :■.";
бсско1и:)чну1о сумму выбранных элементарных сигналов;
б) вычисления реакции основных типов лиис1П1Ых систем
элементарный входной сигнал;
в) синтеза выходного сигнала в результате суммирования р'
акцш"! систем1I на элементарные сигналы. '
С экспериментальной точки зрения необходимо име'
возможность достаточно простыми средствами физичес;-.:
осуществлять выбранные элементарные сигналы. Указанны
условиям обычно в наибольше!! степени удовлетворяют и*
прерывные сигналы в виде гармонических функций (спи;
соиды пли косинусоиды) и разрывные сигналы: единична
функция, прямоугольная функция и единичный импульс.
14
:>
л настоящее время еще нет общепринято!! терминологии
I поводу названий указанных элементарных разрывных
нкций. Например, единичный импульс иногда называют
ной импульсивной функцией, дельта-функцией, функцией;
оака. или импульсом Дирака. Аналогично этому, разные
(мины применяются и к другим разрывным функциям. В
-ьнейшем будут применяться первоначально указанные
зания разрывных функций в соответствии с терминологией,
мененной в монографии |19]. Ниже приводятся основные
(дения по поводу указанных элементарных сигналов.
2. Гармонические элементарные сигналы
К гармоническим элементарным сигналам относятся снну-
1дальные и косинусоидальиые функции, которые записыва-
ся в обычном виде:
и (^)-А 81П (ш ^ + ?1) - Л соя (о) ^ -|- ?2) =
= Л 81П B- [I: + фО = ^ СОЙ B- /^ + фг). A.21 >
В этих выражениях у\—амплитуда гармонического колеба-
О—
я, ш = 21т/== круговая частота колебания (число радиа-
в в секунду), /— частота колсбангп! (число |V0лебани^^ в
кунду, герцы). Г"-период колебания, ср — фазовый сдвиг
лебания. Последний определяет полпчипу колебания в па-
льный момент времени, при
аф) = А К1П ?1 = А сов ср2. A.22)
Таким образом элелгеитариый гармонический сигнал оире-
'ляется тремя параметрами: ^амплитудой, частотоГ! и фазой,
при разложении сигнала на сумму элементарных гармоник,
рмоники могут отличаться лруг от друга по этим трем па-
метрам. Гармонические сигналы могут б)>1ть описаны как
нусоидальными, так и косинусоидальи1>1ми функциями, и
аимный переход между ними осуи[,ествляется путем изме-
;ния фазы колебания на — . Частота колебаиги! (герцы)н-«.е;
'Яду)- и круговая частота (радианы и секунду) имеют раз
-рность, обратную времени, так что произведение
Л/^ 0J? = 2тг//? ([.23)
Г}
':■' 15
является безразмерной величиной (измеряется в рад1
йлн градусах). На рис. I а гармонический сигнал показ
виде функции времени ^. Поэтому начальная фаза колеС
выражается также в единицах времени и равна
Що)=йЗ,
о) иП1=<^((-^)={1]^
У и(Ь}=^[е(Ь-'(:-'^'^)-^(±-'с- ^}]г7вси^%1)
лТ
^-гГ-2-
Рис. 1. Элементарные функции: гармоническая (а),
единичная (б), прямоугольный импульс (в)
ш 2к/ 2г.
(I.
' Круговая частота о) является производной от безразмери
го аргумента '^ тригонометрической функции ио време
|19], так что можно записать
та(.
A.2
В большинстве случаев рассматриваются тригонометричс
кие функции постоянной частоты. Тогда
4г . л^
У=^ 0I а -— = (О = С0П51.
а1
(и
16
''Зц некоторых специальных случаях приходится иметь дело
;^'азигармрническими функциями, у которых частота меня-
'^я^о~временем. В этих случаях колебание можно записать
иде л
и{1) = А$\пЩ1) + <^\, A.27)
о
До сих пор рассматривались колебания, происходящие во
змени, и поэтому аргументом элементарных гармоник яв-
лось время. В сейсморазведке при рассмотрении вопросов
:пространения волн приходится иметь дело с процессами,
горые носят колебательный характер не только во време-
, но и в пространстве. Собственно, именно такие процессы
явления, которые распространяются во времени, в простран-
}е, и называются волнами. Аргументом таких волновых про-
ссов является линейная комбинация функций времени и ко-
динат пространства. При рассмотрении одномерного случая,
гда плоская волна распространяется вдоль координаты х,
от аргумент имеет вид:
Ф<=ш^ — ^x = ^^>^~-x = 2-{^^-~у.x)^ A.28)
V
В этом выражении V — скорость распространения волны,
— волновое число, V—круговое волновое число. Термин
руговое" волновое число не является общепринятым и
шей здесь по аналогии с термином „круговая частота" с
;лью отличия этой величины от волнового числа у.. В каж-
>1Й заданный момент гфемеии г'—^] сигнал становится функ-
1ей только расстояния х и описывает отклонения величины
),.вт нуля в различных точках х:
^(л:)=--Л81п(^х)==--Л51пB7:хА-). A.29)
, болновые числа часто иаз1лвают пространственными часто-
Ши, т. к. для колебания в пространстве волновое число х и
дуговое волновое число V являются аналогами частот!.! / и
и .. , 1 21С
^уговои частот!>1 I", а дл1!иа волп1>1 X == — ■—- является ана-
\ I- ')
1^гом периода Т колебания, происходящего во времени.
оченная аналогия позволяет рассматривать основные вопро-
1.теори11 спектральных представлений на каком-либо одном
№1ке (например, частотно-временном), а затем переносить
рученные результат1>1 на аналогичные явления в простран-
^ённо-волновую область. Одновременное использование ча-
■Отно-временных и пространственно-волновых представлений
^358 17
оказывается необходимым при рассмотрении вопросов ра
странеиия волн одновременно и во времени и в прост!
ве. Схема разложения сигнала на сумму элементарных г
нических (косинусоидальных) составляющих приведен
рис. 2 а.
1
о)
. 5)-
О ~0,01 0.09 0,03 0,О^ 0,01 с се*
о 0.01 0.09 0,03 0,01/ 0,05 Ссе*
Рис. 2. Разложение сигнала па сумму
тарных функций:
а—гар.чоннческих функций; б—единичных
ций, в—единичных импульсов
3. Разрывные элементарные сигналы
ГЕдиничная функция. Единично)! функцией называется |
рывная функция, которая при определенном значении а^
мента { = - скачком меняет свое значение от О до некотор1
значения а, и дальн!е остается постоянно!! при произволь^:
увеличении аргумента. Значен!1е _.я может быть принято
единицу, вследствие чего эта функция и названа единична
Эту функцию называют также функцией Хевисапда. Чтс*
подчеркнуть, что амплитуда единичной функци!! равна е)
нице, ее иногда обозначают 1(< —-). Аналит!1ческое опре)
ление еД1!Нично1) функцн!! вы1лядит так: |
1 1 ^>^
A
Вид единичной функц1!и, возникающей в момент време
т, показан !1а рис. 1 б. Произвольнь1й сигнал можно приб
»«енно представить в виде сумм1>! последовательно возник'
18
сх в моменты т^ единичных функций с амплитудами а^(^—■«;)^
)■( показано на рис. 2 б, т. е. в таком виде:
с ^^@-^11»;(^-^;)- A-31)
Амплитуда каждого такого импульса равна разности зна-
[ИЙ функци11 в точках Т; и т/_1, т. е.
Ф - 'ч) = <^ - ^1)т'и) - ^(^^-01, A-32)
3 0|(^—х) — единичная функция с единичной амплитудой.
;ы'гно интервалы между значениями -,. берутся одинаковыми,
^ что т; =/Лт. Тогда разложение по единичным функциям
жно записать так:
Щ^) ^^<'{^-' /Ат)[(/г - ^/-11. A.33)
При уменьп1ении интервала Дт апроксимация сигнала сум-
й'единичных функций уточняется, и в пределе сумма пере-
дит в точное интегральное выражение. При Д-—»0, /Дт -»■ т
Лт->-с?г, т. е. получаем
= 7 <^ - -) ^^^ (^'=1 <* - -) ^'(^) ^-- A-34)
йГх
I Единичную функцию называют иначе огра}1Ичиваюш,ей или
^зающей функцией. /1,ля того чтобы ограничить, обрезать
гакцию в момент ^ —т „слева", ее нужно помножить на
М-т), а для того, чтобы ограничить в момент {= •: „спра-
, нужно ее помножить на [1—а(^ — -:)].
Прямоугольный импульс
"Прямоуголыплм импульсом длительностью Д^ называется
эрывная функция, которая мгновенно принимает единичное
ачение в какой-то момент времени ^ — т^, остается равной
рнице в течение времени Д- и мгновенI0 принимает
ние О при ^ — -2=-:^ + А-. Прямоугольный импульс длитель-
стью А-, можно представить как разность двух единичных
|нкций, взаимно смещенп1>1х на Дт. Вид прямоугольного им-
Пьса показан на рис. 1 в. Иногда прямоугольную функцию
|ывают вырезающей функцией, так как если из какой-либ^'
Нкции требуется вырезать кусок длительностью Дт, то эг
функтЬо в нужном месте надо помножить на прямоугольную
функцию заданной длительности.
Вследствие широкого применения прямоугольной функции
при описании различных физических и технических вопросов,
в литературе в последнее время для обозначения этой
ции применяется специальный термин „гее!"* [6|.
Часто бывает удобно, чтобы при изменении длительности
прямоугольной функции, ее площадь оставалась постоянной,
равной единице. Тогда ее амплитуда принимается равной 1/Дх,
и она получает следующее аналитическое выражение:
гес1(Ду) = ^ Иг^ - - тО - а(Г - х^)!
^^Г'('-'+т1--'('---|
A.35)
где -^1, Х2,т:. —времена соответственно начала, конца и
ны прямоугольного импульса. Поскольку в дальнейшем мы
будем применять прямоугольный импульс главным образом с
нормированной площадью, то символом гее! будем
ваться для обозначения прямоугольного импульса в форме
A.35). При этом прямоугольный импульс единичной площади
длительностью Ах с центром на времени х будем обозначать
гес1 (Дх, х). Произвольный сигнал ^{^) приближенно может
быть представлен как последовательность прямоугольных
пульсов, возникающих в моменты х. с амплитудой 6'(х/)-Дх^,
где Лх^- — интервал между соседними импульсами. Обычно
принимают Дх^ = Дх = сопз! постоянной величиной, так что
X; —/Дх. Тогда разложение сигнала по прямоугольным
пульсам можно представить в таком виде (рис. 2 в):
^(^)=^^^{^^^)■^ес^(^-, х)Дх, A.36)
где х = гЧх,
Очевидно, что при произвольном виде сигнала 0A:) умень- -^
шенис длительности апроксимнрующих прямоугольников Д-
будет приводить к более точному воспроизведению сигнала
последовательностью прямоугольных импульсов по A.36).
Единичный импульс
Единичным импульсом называется разрывная функция, ко
торая при значении аргумента, равном нулю, скачком прини
мает бесконечно больиюе значение, имеющее бесконечно ма
лую протяженность, в то время как площадь этой функци|
* ,гесГ — гес(ап2к: — прямоугольник (англ.).
20
|павна условной единице. Иначе говоря, это бесконечно
ротки до длительности пмнульс с конечной площадью.
ничный импульс обычно обозначают буквой 8, и если он
никает в момент Ь~-, то его записывают 8(^ —-:). Единичный
импульс можно определить следующим образом:
о(^).-.^0 1Ф0 ]
'(Щ)а1^ (' ^<0</Л A-37)
Единичный импульс может быть получен из
ного импульса путем сокращения длительности последнего
до "нуля. Пдисокращеции. длительности прямоугольного
пульса, как следует из A.35), его ^мпл^IТ^да беспредельно
возрастает, а площадь остается постоянной, равной единице..
Таким о"^разом
•Н^т)-'('-'-т)
гц- -) = Ит гес1(Ат,-:) = \\т ~ -^ ^ — <!.38)
Из A.38) также следует, что еди.н'Лчный тшпульс является
производной от единичной функции, т. е. можно записать
г{Ь--)^±о{1-'.). A.39)
При разложении произвольного сигнала на су.мму
угольных импульсов и уменьшении длительности этих
пульсов, имея в виду A.36) и A.38), получим:
бУ@ = Ит21^('Д^)-гес1(Дт, т)Дх= I {;(т)8(^-т)Л, A.40)
.0
Полученное 1?ыражение позволяет представить функцию
ий1егр.алом свертки самой себя с единичным импульсом, что
иногда бывает полезно при математических выкладках.. Это
соотношение можно интерпретировать следующим «бразом;
умножение функции 1]{-) Iа единичный импульс о(^ —т)
резает из этой функции одно ее значение 0A), которое яв-
•^яется постоянной относительно переменной интегрирования
^личиной и может быть вынесено за знак интеграла. Интег-
{ирование оставшегося иод знаком интеграла единичного им-
%льса по определению A.37) дает единицу. В результате
лучается тождество, утверждающее, что функция, представ-
л^е.нная в разных формах записи, равна само11 себе.
О^ойство единичного импульса при умножении на какую-
■'Шбо функцию вырезать ее значение в момент действия еди;
,%чного импульса называется фильтрующим свойством §-функ-.
Щ*и-([6] и др.).
ГЛАВА II
1. Переход 01 днснрстцого спектра к сплошному
1. Ряд Фурье. Понятие о дискретном спектре
В дайной главе рассматриваются основные йопросы
рии разложения сигналов на элементарные гармонически!;
(синусоидальные и косинусоидальные) функции, то есть раз
ложение в ряд или интеграл Фурье. Как будет следовать и^
дальнейи1его, основной задачей этого разложения является
нахождение комплексных амплитуд гармоник, совокупность
которых (дискретная для периодических сигналов и сплошная
для непериодических сигналов) называется частотным
тром сигнала. В более общем случае безотносительно к
ложению функции времени, применяются термины „изобра
жение по Фурье", „Фурье-образ", „трансформанта ио Фурье*
и др. Операция нахождения спектра по сигналу называется
прямым пЛ^о^Р^-^оианием Фурье, или анализом (частотным
или волновым). Операция нахождения сигнала по его спектру
носит название обратного преобразования Фурье, или синтеза
(во времени или пространстве). Как будет показано в
нейшем, прямое и обратное преобразования Фурье являются
симметричными, т. е. определяются одинаковыми
ческими операциями. Вследствие этого, часто нецелесообразно
приписывать преобразуемым функциям термины „сигнал" п
„спектр", а более удобным оказывается говорить об операции
преобразования Фурье и называть преобразуемые функции
„трансформантами по Фурье", или „Фурье-трансфор.мантами".
Рассмотрим ограниченный по времени сигнал и{()
ностью 7"с и представим его в виде суммы элементарных
монических функций с частотами, увеличивающимися на
одну и ту же величину Ди)=:2тсД/. Для определенности пусть
это будут косинусоиды с разными амплитуда.ми, частотами и
фазами. Тогда можно исходный сигнал {/(О записать в виде
следующей суммы;
[У@=Со+^ (/л|со8BилД;^_(р„), ("-^^
Т1—\
где л =1,2,3, . .—порядковый номер гармоники. В общем
случае сумма A1.1) может иметь бесконечное число слагаемых,
причем каждое слагаемое представляет собой косинусоидаль-
ное колебание с амплитудой Ся, частотой ^^ = пА^ и
вым сдвигом ф„. Постоянная Со является постоянной
тавляющей сигнала. При «=1 слагаемое представляет собоГ)
косинусоиду с частотой
А/ = Й^/Г, A1.2)
22
^.де X — период колебания. Эта первая гармоника в
нии @.1) обладает наибольптм периодом Т н наименьшей
частотой Д/пз всех гармоник разложения. Она называется
новной гармоникой разложения, а Т и Д = Л/ называются
ответственно основным периодом и основной частотой этого
разложения. Заметим, что постоянную составляющую сигнала
(при я = 0) можно рассматривать как „нулевую гармонику"
разложения, период которой равен бесконечности, а частота
равна нулю. Однако по причинам, которые станут ясными в
дальнейп1ем, се нельзя внести в общую сумму и
нить суммирование и нг^начение га = 0. Все последующие
слагаемые представляюг^обой синусоиды с кратными
тами и периодами соответственно
'\ "
Таким образом все последующие периоды укладываются
целое число раз в основной период. Разложение функции в
ряд вида (П.1), состоящий из суммы гармонических функций
с кратными периодами и частотами, называется разложением
в ряд Фурье. Сумма в правой части A1.1) представляет ряд
^урье.
Из A1.1) следует важный вывод, что записанная сумма есть
периодическая функция с периодом Т. Поэтому суммой
гонометрических функций вида A1.1) можно
вать только периодические функции, причем основной
од разложения Т (период первой гармоники) равен периоду
этой исходной периодической функции. Если не
кая, ограниченная по времени длительностью Т^, функция
представляется в виде ряда Фурье A1.1), то полученное
ложение совпадает с исходно!! функцией на интервале ее
ществования, а вне этого интервала, где иа) = 0, лает
одическое повторение этой функции с периодом Т.
Напомним, что периодической функцией! с периодом Т
зывается функция, значения которой не изменяются, если к
ее аргументу прибавить или отнять целое число периодов
пГ{п = 0±1, ±2,-..), т. е.
и{{) = и(^ ± п7). A1.4)
. Основным свойством периодической функции является не-
з^ависимость значения интеграла этой функции на интервале,
{ратном периоду, от положения этого интервала на оси
цисс, т. е.
")""'и{Ь)М^'""{'иЦ) с11, A1.5)
а Ь
где а и 6 —произвольные точки на оси /, а /я = 1, 2, 3
целые числа, Г — период периодической функции ^7@-
23
На рис. 3 приведены примеры периодических функций ц
указаны их периоды повторения Т. При выборе основного
периода при разложении в ряд Фурье A1.1) сигнала
ностью Гс необходимо, чтобы период разложения Т был не
меньше длительности сигнала Тс-
_к
л п
п п п п ,
и
га
Рис. 3. Прлмеры периодическлх
функций
ДМДйД-
-)
6) ^^иииихл^
ел
^\7-Г
и гг,^:
■'V-
-ь-
Рис. 4. Изменение интервала поиторе-
мня иернодической последоватсльУюстл
сигналов.
В противном случае "^повторяющиеся сигналы будут
дываться друг на друга, суммироваться в местах наложения,
и получитс-я периодический сигнал, каждьи! период которого
не совпадаН^г с исходным сигналом, т. е. разложение A1.1)
дет соответствовать сигналу иной формзл (рис. 4а). Если
выбрать Г = Г(.. то разложение A1.1) буде'У апроксимировать
периодическую функцию с периодом, совпадающим по форме
и длительности с исходным сигналом (рис. 4 6). Если выбрать
период повторения Т, большим длительности сигнала Тс, то
риоды полученной периодической функции, даваемой рядом
Фурье (П.1) будут включать сигнал и ,,пуст1Iе" места, как
казано на рис. 4 в, г. Из сказанного следует, что ирии-разложе-
,ди^11 в_рн,^..Фу^^ье^аер^1адичй^^I<сш Фу.н1<шч1^вопрос„о^ыборе. ос-
^^йеьйЛёДЦДда^^ые возникает, ллк^ как ^^м .равед _периоду 'ис-
■^дв<»й периолинвской-.-фуакции. В результате этого п интер-
^^гармоник (частот) в разложении ^оказывается однозначно
опрМеленным, равным Д/=-?-.
о)
с»
го
@.
I г\1
Мм., ч
100 <!0
/^'
I
г
ЧГ\19
УС 1бО 40
100
/"
■«О -50
(х1з * I
^0 ^00 А<4
-150 - «О
,7п;
*-)|-г-.
' г'» *>
с ?1 »1
50 /в<? Угч
Рис. 5. Дискретные спектры:
а)—односторопн ий; б)—двусторопн и и
В сейсморазведке обычно приходится иметь дело с
лами импульсного типа, так что разложение периодическоГ!
функции в ряд Фурье само по себе представляет
ный интерес. При апрокспмпции импульсного сигнала одним
^шриодом периодической функции, даваемой рядом Фурье,
возможен некоторый произвол в выборе Т, котор1лй
чивается лишь условием Г> Т^. Выбранное значение Т
деляет вид апроксимируюиХёй периодическо11 функции и шаг
■в/ между гармониками, т. е. в.ид-..саот.ветсхвующего спектра.
Остановимся на понятии „спектр", которым мы до сих пор
пользовались, имея в виду, что смысл его интуитивно ясен.
Совокупность амплитуд (^^ гармоник в разложении A1.1)
носит название амплитудного частотного спекхрд, а
ность фазовых сдвигов ф„ — фазового частотного спектра
сигнала. Для краткости их часто называют „амплитудный
"Спектр" и „фазовый спектр". Амплитудный и фазовый спектры
"Можно изобразить в виде точек в системе координат (С«, /)
^ (фш ^), однако более принято изображать их в виде
кальных линий соответствующей величины, как показано на
рис. 5 а. В связи с таким их изображением дискретные сиект-
.ры называют линейчатыми спектрами. Из сказанного следует,
25-
что ^1е2ио^^.ч^^сш^м_^X^^!^Iи1ям_с_ош:в.ет^^ линейчатые (дис-
кретные)-Х1Шкх41ы^-Чтобы представить 11ериодиче"с"кую
цию в виде ряда Фурье A1.1), необходимо вычислить
туды Сп, фазы фд и основную частоту Д/^ или, иначе говоря,
определить амплитудный и фазовый спектр1>1 разлагаемой
функции.
Как уже отмечалось, основная частота (частота первой
гармоники) определяется по периоду функции в соответствии
с A1.2). Для определения остальных параметров {Сп и ср„)
обычно сумму A1.1) представляют в ином виде:
иц)^со+1 спсо5^2т:п^!^^(^I„) =
л = 1
^Со-{- 2 Спсо$<(^со5 2-п^1{ г Е С« зШ ф„ 31П 2-яД//=
Со
= ^1 (а„С08'27:п^}^ -\-Ь„51п27:пА!1). A1.6)
В (П.6) обозначено:
«о = 2Со I
а„ — Спсо8(рп \ (И.7)
Из A1.7) следует, что
С . Сп = У а1 + Ь1,
Ч^п^-- A1-8)
Таким образом каждая гармоника разложения A1.1) или
"A1.6) определяется двумя параметрами Сп и ф^, либо двумя
параметрами а„ и &„, причем зная одну из этих пар можно
но A1.7) или по (И.8) найти вторую пару.
Из теории рядов Фурье известно, что параметры а^ и Ь,^
могут быть определены по заданной периодической функции
и{1) с периодом Т по формулам
а„ = - ^]'' и{Ь) С05 2:т пЬ\1М
Т _7-/2
'^ -т/г
A.1.9)
26
Постоянная составляющая сигнала — находится но
муле для а„ при л = 0.
Доказательство формул A1.9) можно наГ1ти в любом учеб-
•иике по математическому анализу или по теории рядов Фурье
(см. например [7], [12], 118]). Здесь мы не будем приводить
доказательства этих соотношений, так как ниже будет
веден вывод аналогичных формул для коэффициентов ряда
Фурье в комплексной форме.
2. Комплексная форма ряда Фурье. Понятие о комплексном
дискретном спектре
Обычно бывает удобнее применять ряд Фурье не в виде
■суммы де11ствительных гармоник, даваемо!! выражением A1.1)
или A1.6), а в более компактно!! комплексно!'! форме, которая
может быть получена !!3 действительно!! форм!)! A1.6)
ющим образом.
Выразим в A1.6) синус1л и коси!!ус!I через показательн1,1е
функции по формулам Эйлера:
С08 2- я ^Н = ^- ■,
12г.п1^Г1 _^-12^и(
$\п2^ п^П = ~ ~ . (П. 10)
где е — основание !!атуралы11,1х логарифмов,
/ — мнимая единица.
Тогда вместо (II.6) получим разложение и{Ь) в следующем
виде:
^^^) - 7 + „^ ("" ^ + ^« ^^ ] =
'■^ ■ « = 1 2 ' „_1 2 • \ ■ /
Из^ A1.9) следует, что коэффициенты а„ являются четно!!
функцией, а коэффициенты 6„ —нечетно!! функцие!"!
тельно номера гармои1!Ки п, т. е.
27
Поэтому, если во 2-ой сумме выражения A1.11) изменить
зн;1К у й на отрицательный, то всю сумму можно
вить в виле:
где
,7@= 2 ^п^^е^^'^"*''- I зУ'""" A1.13)
«5(«)=-^=^^- (4)
Подставляя в A1.14) выражения для а„ и Ь„ по (П.9),
чим:
о 2 Т'г С05 2я пД//- ; 51п 21СЯД// ,,
^{п) = - ] и{() г (И=
' -Т12 *
Совокупность выраженнГ! A1.13) и A1.15) представляет
бой пару взаимно однозначных комплексных дискретных
образований Фурье. По сравнению с ранее записанной
вительной формой (П.1) и A1.6) эта комплексная форма ряда
Фурье A1.13) обладает следующими особенностями:
1) ряд представляет сумму комплексных гармоник
^;2х«4// _ ^рд 2;: /гД//' + /зШ 2- лД/ I (Л. 16)
с комплексными амплитудами 5(я);
2) ряд представляет сумму членов как по положительным,
так и по отрицательным значениям п, так что каждой гармо-
Iике с положительной частотой /„ =г /гД/ соответствует такая
же по амплитуде гармоника с отрицательной частотой /„ =
= — п^\\
3) комплексная амплитуда 5(„) может быть выражена
рез модуль \3(п)\ п фазовую функцию <р(,г), и таким образом,
содержит в себе как амплитудный, так и фазовый спектр
сигнала, т, е. является ко.мплексным спектром сигнала:
5,„, = |5,„)Н"^''' = ^.~/'-^. A1.17)
Модуль |5'(„)| представляет собо11 амплитудно-частотный
спектр сигнала, а ф(„)—его фазовый частотный спектр. Из
A1.14) следует, что
!-5(«I=7А„^-&^^^ A1.18)
а,
(п)
1Ы
23
Оба спектра, амплитудньи! и фазовый, существуют как в
области положительных (л>0), так н отрицательных частот
(п <С0)- Вслелхтвие__не_четности Ьм относительно,., п •4за„а_о_вый
спектр, при атркаахельных-насхохах меняет знак.
^Сравнивая A1.18) и A1.8), можно получить, что
|5(„)|=-|«. A1.19)
Таким образом в комплексной форме ряда Фурье
туды гармоник вдвое меньше, но число их вдвое больше, так
как каждая гармоника действительной формы ряда
ется на две одинаковые гармоники с разными по знаку
стотами.
— В результате амплитудный спектр сигнала оказывается
стоящим как бы из двух половинок по положительным и
рицательным частотам, симметричных относительно нулевой
стоты. Только одна гармоника не распадается на две
ричные половинки — это постоянная составляющая сигнала,
соответствующая нулевой частоте. Именно поэтому в
жениях A1.6) и A1.11), чтобы получить постоянную
щую из общей формулы для а„ A1.9) при п~0, пришлось ее
представить в виде ~ и не включать в общее выражение
суммы. В дальнейшем следует иметь в виду, что
но-частотный спектр симметричен относительно нулевой ча-
^тоты. Если он изображается для простот1>1 только в области
положительных частот, как это показано на рис. 5 а, то
зательно имеется симметричная часть в области отрицательных
частот (рис. 5 б). Каждая гармоника спектра сдвинута на
зу, определяемую ' В1)гражением A1.18). Для положительных
частот (/г>0) фазовый сдвиг отрицателен, что определяется
отрицательным знаком мнимой части показателя степени спект-
ра^A1,17). Отрицательный фазовьп! сдвиг соответствует
щению гармоники в сторону положительных времен, т. е. за-
"'^Зйыванию соответствующих гармоник. В области
тельных частот (/г<0) фазов))И1 спектр меняет знак и
вится положительным, что соответствует опережению
ник во вре.мени.
Ряд Фурье может состоять из бесконечного числа
мых (гармоник), однако в теории рядов Фурье доказывается,
что при возрастании частоты (номера гармоник п) члены ря-
Да должны стремиться к нулю [18]. Поэтому можно всегда
с некоторого значения граничной частоты (^ считать, что
вклад остальных гармоник в структуру сигнала и спектра
•пренебрежимо'мал. Для некоторых функ'циГ! просто!! формы
•ряд Фурье может содержать лшнь конечное число слагаемых,
'так что последнее слагаемое определяет граничную частоту
1я в точном смысле. В любом случае приближенного или
29
точного определения граничной частоты, эта частота
ляет ширину спектра, причем вследствие симметричности
спектра относительно нулевоГ[ частоты, пшрина спектра
зывается равной удвоенной граничной частоте 2 1^.
В теории рядов Фурье доказывается, что для
сти функции тригонометрическим рядом Фурье она должна
подчиняться определенным условиям, которые именуются
ловиями Дирихле, или условиями ограниченного изменения
(ограниченной вариации). Эти условия сводятся к тому, что
периодическая функция в пределах одного периода должна
быть кусочно-непрерывной, иметь конечное число максимумов
и минимумов и конечное число разрывов первого порядка
(т. е. конечной амплитуды). При этом в точках
сти ряд сходится к значению функции, а в точках конечного
разрыва — к полусумме значений функции в точке разрыва.
Сейсмические сигналы заведомо удовлетворяют указанным
условиям, так что мы не будем в дальнейшем беспокоиться
о существовании спектров сигналов и останавливаться на
этом подробно. Отметим только, что указанные условия
раниченной вариации являются достаточными условиями, но
не необходимыми. В ряде случаев и при несоблюдении
торых из этих условий ряд будет существовать и сходиться
к заданной функцЛи.
3. Определение коэффициентов ряда Фурье.
В предыдущем разделе были получены соотнопгения
имно однозначного дискретного преобразования Фурье в
де A1.13) и A1.15). Для осуществления разложения функции в
ряд Фурье по A1.13) необходимо вычислить коэффициенты
ряда 5(„) по формуле A1.15), полученной из соотношений A1.14)
и A1.9), последнее из которых было приведено без
тельства. Вычислим коэффициенты ряда Фурье A1.13) из
ловия минимального среднеквадратичного уклонения. Это
значит, что если тгодобранные каким-либо способом
циенты ряда A1.13) дают некоторую опшбку в представлении
функции ^(^) этим рядом, то выбирается способ определения
коэффициентов, дающиС' минимально возможное значение
суммы квадратов этих ошибок. Математически это можно
записать так:
и{Ь) - 2 '5(«) е + <^. 5(„)),
где е(г', 5{п)) — ои1ибка аироксимации, даваемая суммой всех
членов ряда, которая поэтому является функцией значений
всех коэффициентов ряда 5(л), а также времен ^.
енты ряда ищутся из условия минимального
ного уклонения:
30
1т 1ч I
]2Т!.11&/(
"сИ--- ^'' 82 (Л 5(„))й?^ = т1п.
-7J
A1.20)
Каждый искомый коэффицие}!! 3{п} определяется из
ношения A1.20) независимо от остальных коэффициентов по
правилу нахождения экстремума функции. Так например для
нахождения коэффициента ряда с номером |л нужно
ференцировать A1.20) по 5(ц.), приравнять результат нулю и
вычислить из полученного уравнения выражение для 5(|1.).
Проделаем эти операции:
"^^М { -г/г ' !«'. ^ и
г/2
I
-т/2
2[^@-2'5(.)-'""'']^'"''"^^ = 0. A1.21)
Разбивая интеграл A1.21) на два и приравнивая их друг
другу, получаем
^\ и{Ь)е (И= 1^ 2 5(„)е сИ =
-г/2 —Г, 2 «=-<»
00 7-/2 ;2хД//(л + |1)
== 2 ^(л) ] « й^г^- ■ A1-22)
л=-«, -г/г
Полученный в правой части интеграл отличен от нуля
только при « = — [>., т. е. когда подынтегральная функция
равна единице. В других случаях из-за ортогональности
монических (синусоидальных и косинусоидальных) функций,
интеграл от их произведения, взятый по основному периоду
(интервалу ортогональности), равен нулю. Таким образом
имеем:
г/2 ^-'^^^/'(«■ь^^^^^.т при \пу^\^, A123)
-т/2 \ Т при п--= —\>.,
и в правой части A1.22) остается только один коэффициент
5{п) с номером п = — (а, умноженный на Т. В результате
лучаем:
"■(' V(^)е'''"''^'' а1=^ Т-8{~1>). A1.24)
-7/2
Имея в виду, что номер коэффициента [л — пронзвольныСг
из п, получаем искомую формулу A1.15) для определения
эффициентов 8{п) ряда (П.ТЗ):
3{п)=— \ 11{1)е йЬ. A1.25)
^ -'Г|2
31
§ 2. ИМПУЛЬСНЫЕ СИГНАЛЫ. СПЛОШНЫЕ СПЕКТРЫ
I. Переход от дискретного спектра к сплошному
Сейсмическая запись представляет собой наложение п(
следовательности сеГ1СМ11ческих импульсов, время прихода, т
тенсивность и форма которых определяются положением г(
ологических границ и физическими свойствами среды. В св5
зн с этим в сейсморазведке основной интерес представляв
'^^ и/{)=и{0.1;)
^002 О.ОЧ'^ 0,0* 01^011 (се/с
и.а
«01
т
15м1
»-7 е 1-'/-)\2
А.
2ЦГ* 3-6 ' ! п
<' Ч),ог 1^06 дал о,10"о,п Т.сег ""?.'"'
15(к]1
Н- Т^О, Юг^,к -^
■1бО -50
л» ♦
I 50 1до Ы
Рис. 6. Связь дискретности спектра с
стью сигнала
изучение сиектрон отдельных сейсмических импульсов,
знанных определенными геологическими объектами, и интер-
фереционных картин, возникающих в результате наложения
нескольких отдельных импульсов. Поэтому перейдем к
смотрению своAСтв спектров отдельных импульсн1Iх
одических) сигналов, которые определяются интегральны.м нре-
образовапием Фурье.
Используя уже рассмотренный вып1е аппарат дискретного
преобразования Фурье (ряда Фурье), получим спектр
ного сигнала из спектра периодического сигнала путем бес-
иред(;льного увеличения периода повторения этого сигнала.
Прежде всего посмотрим, что будет происходить с
ным (линейчатым) спектром периодической
сти импульсов, следующих через период Г, если не меняя
форму самого импульса увеличить период его повторения и
т раз, т. е. сделать его :рапн1.1м Т„г==/га Г (рис. .6). Как
следует из основных соотноп1ений для ряда Фурье A1.2), A1.13)
и A1.15), при увеличении основного периода периодической
.32
функции интервал Д^ между гармониками спектра
ется. Если этот интервал при периоде Т был Д^ = —,топри
увеличении периода в т раз он станет в т раз меньше:
В то же время, судя по A1.15), где основной период Т
находится в знаменателе, амплитуды гармоник одной и той
же частоты при возрастании основного периода в т раз
улЩаыидются во столько же раз. В результате можно
лать вывод, что растяжение основного периода приводит к
'гоМХг^ПН-^^'^*^""'^^' более плотно заполняют ось частот, а
и^^^мплитуды уменьшаются (рис. 6 б). Увеличивая период до
бесконечности, можно от периодической функции, состоящей
из последовательности импульсов, перейти к отдельному
пульсу. При этом частотный интервал между гармониками
спектра будет беспредельно уменьшаться, амплитуды
ник станут бесконечно малой величиной, а сумма A1.13)
рейдет в интеграл, выражающ,ий спектр одиночного сигнала
в виде сплошной функции частоты 5([). В результате из A1.15)
при Г -* оо будем иметь:
«ДГ-Г; ]:-^\-*A1 A1.26)
Иш 5(«) = Ит — ^1'' и{1) е ''^""^'^ (Ц -
/■-=0 Т -г/2
где обозначено
а\ 1 Щ)е ^■'"^'йг'=5(Г)•«?/, A1.27)
5(/)= 1 и{1)е~'>'^^' а{ =
= Л ^{^) С05 2- гмь^1 |° М(Ь^^п 2^ ис1Ь (п.21)
Аналогично, переходя п A1.13) к пределу при Г -*■ со и
учитывая A1.27), получаем:
со —оо
-^/ г 5(П81п2г \(с1\ A1.29)
~ 00
33
Выражения A1.28) и A1.29) представляют собой пару взаим
но однозначных интегральных преобразований Фурье. Форму
ла A1.28) позволяет вычислить спектр 5([) импульсного сиг
нала ^{^) (операция анализа), а формула A1.29) осуществляр;
обратную операцию определения сигнала по его сплошном\
спектру (оиеращгя синтеза).
В соответствии с данной выше терминологие!!, касающе1|
ся дискретного преобразования Фурье, эти операции аналлзг
и синтеза обычно называют прямым и обратным
ным преобразованием Фурье, а сами функции V{() и 5(|^) на
зывают трансформантами по Фурье или Фурье-трансформаи-
тами.
2. Понятие о комплексном сплошном спектре
импульсного сигнала
Полученная формула обратного иреобразопанпя Фурье
A1.29) представляет собой разложение и.мпульсного сигнала
на интегральную сумму бесконечно болыиого числа
ных гармоник вида
с бесконечно малыми амплитудами, плотность распределения
котор1Iх по частоте )' описывается функцией 5(/). Последняя
определяется но сигналу иптег1)ал1>11ым преобразованием
A1.28). Функция частот1>1 5(П "о A1.28) в общем случае
ется комплексно!"! !! иредстапляет сплошной комплексп1>[11
спектр !1мнульс1!Ого сигнала и{(). Как в комплексно!'!
ции, в не1'| можно 151>|дел!!ть де1Ствительну!о (вещественную,
реальную) част!^ и М1т.ч!ую часть, или модуль и фазов>;-'
функц!1ю, т. е. можно записать комилскси!)!!! С!!ектр в так!1^
вариантах:
5(П - \5(!)с-е-^'^-'' = Ке|5(/)| ^■ /1тE(П1 =
= |5(/)|со5ф(/)-/;;5(/):8шф(П = Д/)-/5(/), A1.311
Ке{5(П|=^(/); \т{3{!)]=-'ВЦ). A1.32)
В 1!оследне\! в!>1ражении С11мвол1>1 Ке и 1т, 1!111роко пр;:ме-
няем1Iе в теории функции комплексного переменного, о6о:1-
начают действительную и мнимую части комплексного
жения *. Абсолютные значения действительной и мнимой ча-
стс!! обозначены в правой части A1.31) Л([) и ВЦ).
вие больше!! компактности последних обозначений мы и
дальнейп1ем будем им!1 пользоваться чаще. В выражении
* Кс(геёО -действительный, 1п1 Aгаа21па1ге) — мнимый (французск.).
34
/1131) |5(П| б'^ть модуль комплексного выражения 5(П> Эф([)—^
6'фазовая функция (называемая в теории? функции комп-'
лексного переменного „аргументом" [13]). Эти. величины свя-
зоты между собой соотношениями:
^(Г) = |5{/I-со8д@; Л(П=15(П1-81п(р(П,
Ке{5(/)} _ Ж/)
С05ф(П =
|5(/)| |5(Л1
^^^(^)==__М^I=^). A1.33)
^^^1' Пе{81Л} А(/) ^ '
Модуль [5(/)] комплексного спектра характеризует
туды гармоник спектра в зависимости от частот!)!, т. е.
тотный состав сигнала. 0!1 называется амплитудно-частотным
с'пектром импульсного сигнала. /1,ля краткости его иногда
зывают просто „частотн!)!М спектром" или „амплнтудшлм
спектром". Фазовая функция ф(/) характеризует взаимн1)!й
сдвиг гармоник спектра по времени и называется фазово-ча-
стртным спектром или сокраще!!но — фазовым спектром
нала. Аналогично дискретному фазовому спектру
ческого снг!!ала, !1епрер!>1вный фазовый спектр отдельного
импульса в области 1!Олож!!тель!!Ь!х частот отрицателен, что
сцответствует запаздыванию гармо!1нк относительно нулевой
гармоники (иостоя1!ной составляющей сигнала). При одном и
том же частотном составе (амплитудном спектре) разное
имное расположение 1'прмо1!!1К (разн]Iе фазов!ле спектр!,!)
водит к разно!'! форме сиг!1ала, т. е. фазов1>1й спектр
рует конкретную форму сигнала. Кроме того, фазов1,1й спектр
ЗЙр.еделяет положение сигнала !1а оси времени. Фазов!>1й
спектр может б1,!ть в!,1раже1! как в угловой мере ф(/')
сы, радианы), так !! во временно!'! (секунд1>!) [20]
Щ!)=^- (П.34)
, Запаздывание сигнала ^{^) на Дт записывается в виде
Ц^—Дт) и отражается на фазовом спектре следующим
зом. Все спектральные составляющие сигнала запаздывают
на Дт, т. е. фазы гармо1!ик во временной форме приобретают
вид
АМ/) = ~^ = Д^(/)-Ат = ^-Д^. ("-35)
35
При этом в угловой мере фазовый спектр получает слага
емое, линейно зависящее от частоты:
(р,(/) = ф(П - 27:/Ат = ф(/) - Дф(П. A1.36)
При запаздывании сигнала во времени это линейное
гаемое фазового спектра отрицательно. Более подробно этот
вопрос рассматривается ниже, при изложении теоремы
щения.
Взаимно однозначное соответствие между функцией и ее
спектром обычно обозначается каким-либо специальным сим.
волом. До настоящего времени такого общепринятого
ла нет, и разные авторы применяют различные обозначения.
Мы будем применять двустороннюю стрелку и записывать
взаимно однозначное соответствие между функцией и ее
спектром в таком виде:
и(Ь) 5(/). A1.37)
Остановимся на размерности полученного сплошного
ра. При предельном переходе A1.27) и A1.28) амплитуды
моник дискретного спектра имели конечную величину и
уменьшались по величине, а число этих амплитуд возрастало
пропорционально увеличению периода Т. В пределе, при
7->оо амплитуды спектральных составляющих делаются
конечно малыми величинами, а совокупность их непрерывно
заполняет ось частот. В результате этого амплитудный спектр
непериодического сигнала представляет собой сплошную (н
отличие от дискретной) функцию, имеющую с.мысл и
ность плотности спектральных амплитуд. К понятию
сти" приходится обычно прибегать при совместном
рении и сопоставлении как дискретных, так и сплошных
личин и функций.
3. Изображение сплошных спектров
Спектры сейсмических, сигналов в общем случае являются
непрерывными комплексными функциями частоты, так что
прос об их г^эафическом изображении сводится к выбору
иболее удобного способа изображения комплексной функции.
,Как следует из предыдущего, и в частности, из A1.31), A1.33),
!ушО'=о^ШгШ^цакхр. -хигнала.. есть совокупность двух функций:
либо амплитуАН-0---Ч.астотного спектра |5(|')| и фазового спектра
*ф|(|)^либо действительной Ке[5(П} = А{\)\\ мнимой 1т~{5(П) = —
В{^) частей комплексной функции.
С точки зрения теории комплексных функций наиболее
тественно спектры сигналов изображать на комплексной
кости в векторной форме, как это принято в математике для
комплексных величин. Для этого в прямоугольной системе
зв
тсоординзт по горизонтальной оси откладываются значения
^йствительной части спектра А{[), а по вертикальной оси—
мяймой Щ!) как функции частоты. Рассматривая А{}) и ВЦ) как
компоненты вектора |5(/)| в прямоугольных координатах,
лучаем в соответствии с формуло!! A1.31) для каждого
ния частоты ^ значение модуля вектора |5(/}| и его
ния (фазового угла) ф(/'). Для изображения совокупности
чений модуля и фазы от частоты достаточно изобразить па
комплексной плоскости геометрическое место концов
тора 5(|^) для различных частот с обозначением значений ча-
стот" для__последовательности точек на этой кривой,
'"■^ШТрис. 7 а приведен пример сигнала в виде экспоненциально
затухающей синусоиды, а на рис. 7 6 —спектр этого сиг}1ала
на комплексной плоскости. Для практических целей
ние на.дсомплексной плоскости оказывается неудобным, т. к.
иэ^а отсутствия равномерной шкалы частот
ства и.„особедности . спектров. и.роявляю.тся ледостаточно на-
ГДЯД1Ю. В связи с этим в практике сейсморазведки более
пдинятр раздельное изображение величии |5(/)} и ({;(П> либо
яд| и ;5(/) в прямоугольной системе координат, когда по
оси абсцисс отложены частоты. Первый, вариант изображения
п о каз ы&аети №6 с рё д с тв е н'н 6"Тм и л и туд ^>^ |5(/)| и фазовые
ги ф(/) р,а.зличных частотных гармоник спектра и поэтому
наиболее наглядно характеризует спектральный состав сигнала.
Пример такого изображения спектров приведен на рис. 7 в.
Пвй„...изображении снектров^безЬтноситедьно абсолютных зна-
4^ин спектральных плотностей их амплитуд модули спектров
д^мируют, т. е. делают максимальные значения амплитуды,
#5.'1Н!!?Л^™^А!^Й.^1^^?• ^сли' важно подчеркнуть амплитудные
.тоот^юшёния нескольких спектров, то спектры изображают не
нормированными или их нормируют по отношению к одному,
о|ШШ1Рму спектру.
Выше отмечалось, что вид фазового спектра сигнала за-
^^ит от выбора начала отсчёта времени. Чтобы исключить
влйяНТйе-ттоложения сигнала на оси времени и выделить часть
ф_азового спектра, определяющую форму сигнала, фазовый
^ектр изображают во временной форме. При таком
жении смещение сигнала во времени приводит к смещению
^^^Я"^?!"*^ спектра по вертикали, но не аввлияет на его фор-
*?У (рис. 7 г). Главным зIачением фазового спектра
ется такое его положение во временном представлении, при
котором он стремится к нулю при беспредельном увеличении
а/Г?^*^^'' л^^^" ^^ ''"''■ ^^ приведен пример фазового спектра
^«Шь^'зр.РР.ажшишго. в угловом представлении (пунктирная
.линия), и несколько фазов1.1х спектЬов^'ТГШ.'изображенных
:^ ' ''^ Временном иредставлении (сплоп1ные линии).
'«вное значение фазового спектра А/(/') показано жирной
Яией.
37
VЧс• и
^
—1
—!
х'
11
^
-г
/ 1
1 1
Й
/
«=^'~^
-•-
ш
«-в
%
38
"Изображение комплексного частотного спектра в виде
оаздельных кривых А{}) и В{}) применяется редко, главным
"ббразом при вычислениях спектров по заданному сигналу
/ |^из) пли сигнала по заданному спектру (синтез).
тельные схемы спектрального анализа и синтеза обычно
вают построены на основе раздельного вычисления
тельной части А{/) и мнимой части В{^}. Пример
ния Аф н -^СП для сигнала на рис. 7 а приведен на рис. 7 в.
Наконец, в практике исследования вопросов прохождения
сигналов через линейные системы передачи пшроко нспользу-
{0Т2Я-Л0гарпфмические координаты для,изображения спектров
сигналов и частотных характеристик систем. В логарифмичес-
■ктгйгсистеме координат по вертикали отклад1>1ва[отся
мы нормированного значения амплитудно-частотной характе-
{Тистики, а по горизонтали—логарифмы частот. Системы
динат отличаются между собою принятыми основаниями
гарифмов, из которых наиболее употребительными являются
двоичные логарифмы (единица измерения—бит), натуральные
логарифмы (единица измерения—непер) и десятичные
мы (единица измерения—белл). Наиболее употребительная
тическая единица — децибелл (одна десятая часть белла). Если
в^ логарифмических координатах строится нормированный
амплитудно-частотный спектр, то его максимальное значение
равно единице, а остальные значения—меньше единицы. В
зультате ЭТ010 все логарифмы оказываются отрицательными,
а в. максимуме спектра логарифм единицы равен нулю. По
горизонтали обычно логарифмические шкалы частот
вываются непосредственно в значениях частот (в герцах). Для
-изображения, фазоврхо спектра логарифмический масштаб
обычно применяется только для оси частот, а для углов сме-
щения^1спользуется линейная шкала. Пример изображения
плитудного ~"ТГ" фазового спектров описываемым способом в
логарифмических координатах (для того же сигнала рис. 7 а)
приведен на рис 7 д.
§ 3. ОСНОВНЫЕ СВОЙСТВА СПЕКТРОВ
1. Симметричность спектрального преобразорания
Как отмечалось выше и следует из('Н.Э4), нахонгдение
тра по сигналу и сигнала по спектру сводится в принципе
к совершению аналогичных операций умножения на
ную гармонику и интегрирования по соответствующему
гументу. Поэтому можно говорить о „симметрии" прямого и
обратного преобразования Фурье. Знак в показателе комплекс-
".~.1зрмоннк следует учитывать лишь когда оба преобра-
здващя, "прямое и обратное, рассматриваются одновременно,
^.^совокупности. При рассмотрении каждого из преобразований
39
в отдельности знак может быть взят произвольным, так как
юн будет оцЁеделять только знак фазового спектра.^
Оба преобразования Фурье могут быть записаны в общем
виде
C(х) = "р(*)е'''''ТйГС. A1.38)
—00
Полагая здесь х = / и С= I, можно считать, что ^(^) есть
спектр сигнала Р{1), так что из A1.38) получим выражение
мого" преобразования Фурье. Полагая x — ^ и 1'=/, получим
выражение „обратного" преобразования Фурье, когда ^(/)
дет является сигналом, а Р(?) его спектром.
Чтобы подчеркнуть симметрию спектрального
вания, в прикладной математике, и в частности в
ведке, некоторые авторы предлагают ввести специальные
мины, подчеркивающие аналогию некоторых основных
тий и параметров для сигналов и их спектров и условность
в общем случае разделения трансформант Фурье на сигналы
и спектры. Например, аналог понятия периода (сигнала во
времени) предлагается для Фурье-трансформанты называть ре-
диод (период периодического по частоте спектра) |21].
рия прямого и обратного преобразования Фурье приводит к
тому, что все основные свойства сигналов имеют своих
логов для спектров и наоборот.
2 Симметричность амплитудно-частотного спектра и
кососимметричность фазово-частотного спектра
Преобразование Фурье (как прямое так и обратное)
полагает интегрирование по аргументу в бесконечных
пределах (т:<»). Для прямого преобразования A1.28) это
всегда необходимо, т. к. импульсы физических процессов
обычно имеют начало-момент своего возникновения,
рый можно принять за начало отсчета времени, так что
весь импульс будет расположен в области положительных
времен. сЗбратное преобразование Фурье предполагает
рирование в бесконечных пределах как по положительным,
так и по отрпцательи1>1м частотам. Са^Ш1_ш^себЁ-нал_ичие__отри-
идтрльцых ча^:тот и- их-,.физш1&ааш .хмыа1-на_шлж1ш..-вызы-
вать недоумения. Если ппибегнуть _к^]тз.ппгии .ча.ашты__коле-
бани_я..г частотой вращения^.то положительные и
ные частоть! будут соответствовать врашению_какого2Либо те-
ла в~"разнь1е_с11Щ1Ш1ы,--а.р^?,",рляю1п.т1я их "у.^еряя_.дд.ст.!?Тт1—не-
подвижному ^I0Л0ЖРНИ1п ятргп т^>лп,
~В соответствии с выражением A1.33) амплитудно-частотный
спектр представляет собой модуль комплексного спектра,
торый оказывается симметричным относительно нулевой
стоты, т.е.
|'^(/)! = |5(-/)| A1.39)
40
?|
,оЖомним, что отрицательные частоты возникли, когда для
^ее компактной записи выражения ряда Фурье A1.1) мы че-
I формулы Эйлера A1.10) ввели отрицательные номера ди-
ретных гармоник —п и получили запись ряда Фурье в комп-
|:СНОй формеA1.13) и A1.14). При этом все амплитуды гар-
шк стали вдвое меньше, а число гармоник удвоилось за
|т появления „отрицательных дублеров". Таким образом
шетричность амплитудно-частотного спектра есть следст-
"лГомплексности спектра, т. е. представления спектра в
шактной форме в "виде вектора па комплексной плоскости.
%о, что вторая симметричная, иолов1!на спектра никакой до-
|нительно11 информации не несет. Поэтому обычно для
^оты изображают лишь одну правую половину амплитуд-
|;Ь спектра, однако Iельзя забывать о существовании его
юй симмет1)пч11оГ1 половины. Из формул (II..33) следует,
'^йствительиая часть спектра является четной функцией
ШгьГ, а ^1П^^I.мая часть — нечетно]'! функцией частоты. Кро-
го, д.ая__1|^у.Тёёой частоты всегда мнимая часть спектра
.нулю, а "действительная равна среднему значению (по-
^ои сосгавляющей) сигна.'!а. Поэтому можно записать
Л(/) = Л(--Г); ВЦ) ~В{-}),
Л@) _7 и{{)с1^; 5@) = 0. A1.40)
й|.Пр11нимая это во внимане, из выражений A1.33) можно ио-
'|нть, что ф|азово-частотная характеристика сигнала всегда
|яется нечетно11. (кососимметричноГ!) функциеГ! частоты и
1^3 и у л ю., н_а.. I !у л е.в о 1). частоте
Ф(^=^--Ф(~П. Ф@) 0. A1.41)
^||Таким образом введение и непременное использование от-
РЩательных частот в комплексных спектрах вызвано не мо-
Д3|»ем спектра, а фазовым спектром, которыГ! для частот раз-
'•'^'^о. знака также меняет свой знак.'
^^1^Щйа^^а,значение фазового спектра на нулевой частоте
^^^чает, что гармоника с нулевой частотой не сдвинута в
^ШШЛё_Р.тн.ослт-«льно начала в^?€мени. Поскольку мнимая со-
с*^ляющая спектра на нулевой частоте равна нулю, то эта
Е^^10ника представляет собой косинусоиду, которая симмет-
'^^^0 расположёна относительно начала времени и бесконеч-
Шянута вдоль оси времени. При.'. увеЛйчени!! 'частоты
^симметрии гщшо-ник (максимум у косинусоиды и нуль.
Лид) сдвшаются относительно .начала отсчета времен.
р"йДля каждого абсолютного значения частоты имеются две
^^Моники, соответствующие положительной и отрицательной
Ш''*"Оте, причем вследствие кососимметричности фазового-
41
спектра, они сдвинуты в разные стороны от нуля времен и
одинаковую величину по времени (фазе). Запаздывание сигца
ла во времени, т. е. сдвиг его по оси времен вправо, приво
дит к увеличению отрицательных фазовых сдвигов.
Отметим также, что вследствие A1.39), A1.40) и A1.41), ос
ратной (сопряженной) по знаку аргумента функции соотвог
■ствует сопряженный спектр. Это значит, что
:)- 3{!) = Аи)-уВ{1)~-^\8(!)\-е-^-''^' \
где 5(/') обозначен комплексны!! спектр, сопряженны!! спект
РУ 5(/).
3. Спектры симметричной и кососимметричной функции
Симметричной относительно точки 1 = - функцией
ется функция, у которой равноотстоящие от этой точки
чения попарно равны между собой, т. е.
и{^-^')^и{' — 1). (ИМ)
Если си.мметрия наблюдается относительно точки ■г = 0, то
функция называется четной, так как ее значения не
ся при перемене знака у аргумента, т. е. б'(^) ^ 6'(—2?).
Рассмотрим спектр такоС! функции, причем для простоты
положим - = 0. /1ля этого подставим в общее выражение для-
спектра A1.28) четную функцию и{Ь)'^и{— Ь). Так как в пер
вом интеграле содержится произведение двух четных
ций, то его подынтегральная функция четная и каждому
чению Ь будет соответствовать такое же и с тем же знако.\!
значение подынтегрально!! функции с аргументом {—^). Во
втором интеграле произведение четной функции иA) на
четную ^\п2т.)(: дает нечетную функцию, интегрирование
торой в бесконечных пределах (+ оо) дает нуль, т. е. мнимая
часть спектра исчезнет. В результате спектр четной функцш:
окажется состоящим только из действительной части, и
плитудно-частотный спектр будет равен ее абсолютному
чению, а фазовый спектр станет равным 0'^/(^Л^и^и,'Р((/^<^^
5{!) = А{п = У ^{^)со82^!^(И = 2 Т ^(^)со52т4^с^^. (и.44)
При этом для определения спектра достаточно интегрнр"'
вание проводить только по одной из полуосей абсцисс.Г1р"
^отсутствии фазово-частотной характеристики отпадает
ходимость рассматривать амплитудно-частотный спектр сиМ'
метричным относительно нулевой частоты и оказывается во-т
можным рассматривать его только для положительных мас-
42
от с удвоенными амплитудами (рис. 8 а). Здесь сказывается
^шаетрия прямого и обратного преобразования Фурье: при
^'есимметричном расположении сигнала относительно
го' времени модуль спектра оказывается симметричн1^1м
сительно нуля частот, а при несимметричном расположении
модуля спектра (расположении только в области
но.] /^/^/
а] '^т-'оН)
0,02
сог Г с
8) иа-1:}=и1т-1}
100 -50 О 10 (Ои /га
, 50 100 [гц
Рис. 8. Спектры симметричного импульса,
а) — четного, б) — сметенного па время т.
ПЫХ частот) сигнал оказывается симметричным относительно
иуля времен. Функция, симметричная относительно точки
^^.'^» может быть получена из четной функции путем смеще-
"'И начала координат из точки симметрии в какую-либо сто-
ролу на -с. Как будет показано в следующем параграфе (см.
теорему о смещении функции во времени), этот сдвиг не от-
РДйится на амплитудно-частотном спектре, и приведет лишь
•^, возникновению линейного фазового спектра. При этом
ст1ектр усложнится, станет комилексн1,1м, т. е. будет
жать как действительную, так и мнимую части (рис. 8 б).
Преобразование A1.44) называется косинусным преобразо-
ва^ем Фурье.
[зй'^'^^^'^-^'^^^"^'^^"^^*^^ относительно точки ^ = х функцией на-
йв^ется такая функция, у которой зн.ачения равноотстоящих
^~а.Той точки ординат равны по абсолютной величине и про-
,№Оположны по знаку, т. е.
иЦ — и) - (/Гт —О-
43
При этом, если ^з..=:0, (то получается обычная нечеп
функция, для которой и{1) ■= — и{(:).
При вычислении спектра для такой функции можно п
помощи рассуждений, аналогичных предыдущим, придти
выводу, что в A1.28) из-за нечетности подынтегральной фу»
ции первьи"! интеграл ранен нулю. Во втором интеграле н(
а/ иA)'.-и(-1)
)^ иA-ф-а(Ы)
^'О.С/Тсе^г
/^А^?
-/00 -30 о 50 100 Аи,
-/ОС -50 О Л то Л;,
Я
-100 -30
Рис. 9. Спектр кососпмметричпого импульса,
а) — нечетного, б) — смещенного на время т
изведение двух нечетных функций образует четную функцию
и интеграл сохранится. В результате, для спектра нечетнои
функции получим
A1.45)
т. е. спектр является чисто мнимоГ! величиио!!.
Из A1.45) следует, что
— нечетная функция частоты^ та<г-тп!гзтга1^?--й(-/')~-ее&»адает со
здд4<ом час'юты /. 4]оэтому0разовый сдвиг можно определить
как (рис. 9 а) '
^ '^ |5(/)| |б(/I ^ ^ Р*' ^ '
♦4
'''д^-51дл — специальный символ, обозначающий так называе-
^1,ую знаковую функцию, равную + 1 при положительных зна-
''чеяйях аргумента н — 1 — при отрицательном аргументе. В
,.результате
О ^~- О A(Л7)
Аналогично предыдущему смещение нечетной функции
(центра кососимметрии) приведет к усложнению выражения
спектра, т. к. вызовет появление действительной его части и
фазового спектра (рис. 9 б). При этом надо помнить, что
зовый сдвиг ф(П. как и всюду прежде, имеет в комплексном
вы]^жении спектра отрицательный знак A1.18; 11.31; 11.42 и др.),
чтр^срртветствует запаздыванию гармоник с положительны-
мй^астотами и опережению гармоник с отрицательными ча-
с|до'ами.
Преобразование A1.45) называется синусным
нием Фурье.
4. Косинусное и синусное преобразование Фурье
■ Пдоизвааьн^ю функцию (сигнал) С/(^) мсжио лредставить в
^виде суммы симметричной (чётной) функции G.^(^) = Ц.(-^ ^) и
"йососймметричиой (нечетной) функции ОнЦ)-^—^н(^)- Функ-
цш~'^^(^] н {У^^^) йогут быть выражены через исходную
цию ^{^) следующим образом:
и^(() = тШ=:^- [/,(-0, A1.48)
Склад!,!вая б'Д/) и и„(^), легко проверить, что
^^^)-= ^ДО-г ^„@- A1-49)
^1Ш!м^^яя прямое п1)еобразова11ие Фурье к A1.49) в
ветствии со сказанным в пред1)!лущем пункте, получаем, что
ЙШй^Я .часть сигнала (У(^^ дает кос11нусную срставляющую
спектра, а нечётная часть сигнала цр^рбразуется в синусную
часть спектра. Ппртп т мпу пчоп-г иуприпй ^я^г^иии\' гие^ктр^
^ Вторая-^рдзривиий фазовьж спектр 3 --р Ы^д([)(П:47). Рас-
45
смотрим поведение амплитудно-частотного спектра и его сч;
нусной и косинусной составляющих. Соотношение между эп^
ми величинами можно по A1.33) представить в таком виде:
Из A1.50) следует, что всегда
15(П1>и(ти |5(П|>^(Г)|
и когда
5@ = 0
Л([) = 0
!5(ГI=И(ПН
|5@1=\^(П\|-
(П-оО
(П.51
(П.52)
Поэтому, если изобразить |5(/)|, А{1) и В(}) в единой си1'.
теме координат, то |5(|)| будет идти всегда вне (снаружи)
А{}) и В{1), и нигде не будет с ними пересекаться. Далее,
продифференцируем A1.50) по частоте. Тогда получим
|5(Г>
На частотах, где
а! а/
5(П = 0, -^^^
A/
а где
а^■
^5(Г)-
ал
чГ
а/ '
A1.53)
A1.54)
Отсюда следует, что |5(/) касается Л([) в точках .б(П=" О
и касается ВЦ) в точках А{1)-=0. В результате можно
зать, что амплитудно-частотный спектр является огибающе;:
для синусной и косинусной (действительной и мн1гмой)
тей этого спектра. Пример этому приведен на рис. 7 в, где
изображен!^! в единой системе координат модуль !5(П| "
тавляющие А{1) и В{1) спектра сигнала, приведенного на
рис. 7 а.
§ 4. ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕОБРАЗОВАНИИ
СИГНАЛОВ И СПЕКТРОВ
I. Теорема о линейности спектрального преобразования
(теорема суперпозиции).
Пусть имеется несколько сигналов ИхИ), ^2@'''^л@ '■ '^""
ответствующие им спектры:
^1@ 5 А
^,@—5 ,(^
Ь„@--5^6^'
46
Тогда спектр суммы этих функций, умноженных на посто-
^няые числа С,-, равен сумме спектров этих функций, умно-
^нных на эти же числа, так что можно записать:
и4П= 2 С,и/{1)*—.-5,(!)= 2 С,5,(/). A1.55>
/г 1 Ь I
Доказательство этого соотношения непосредственно
ет из прямого преобразования Фурье. Применяя к сумме
функций интегральное преобразование A1.28), можно в
вой части заменить интеграл от суммы суммой интегралов и
вынести постоянные коэффициенты С,, за знак интегралов.
Тогда и получим соотношение A1.55). Его можно проинтер-
цретировать и в обратном порядке — от спектров к сигналам.
Можно считать, что даны спектры 5ДП, а результат
нения обратного преобразования Фурье к сумме спектров
ет сумму сигналов [/^(П. Поэтому можно }(е фиксировать
мание на „спектрах" и „сигналах", а сформулировать
риваемое СВ011СТВ0 п более общем виде: преобразование Фурье
от линейной комбинации функций приводит.к той же
ной комбинации Фурье—трансформапт этих функци!). Таким■
бТ5"разом трансформация Фурье обладает свойством
ности и является липопплм преобразованием.
2. Теоремы о дифференцировании сигнала и спектра
(теорема о спектре производной).
Сигнал II его производная являются разтлми но виду
циями, но их свойства зависят друг от друга. Очевидно, что
спектры сигнала и его производной также должны б1,1ть
заны между собой опред(!лени1лм образом. То же самое
но сказать и о связи сигналов, соответствующих спектру, и
его производно!!. Рассматриваемая здесь теорема В1>1ясняет
эту связь.
Начнем рассмотрение со спектра ироизводно11 сигнала-
Пусть""~дано такое соответствие между сигналами и их спект
рами
Для нахождения 51([) по 5*(П применим к и'@ прямое
преобразование Фурье и проинтегрируем полученное вг.фа-
*ение по частям. Тогда
47
ЗгИ)-1е-^''''иу)си-1е-^''''ащ
^иц)е-^'''
о» 00 ~12г.Ц - -(Ь
- 1 щоае ' = '
—00 ^
— эо
— 00
I—>з
В полученном выражении нервьи! член представляет спектр
исходной функции, умноженный на /ш=у2я/'. Второй члев
определяется поведением исходной функции в бесконечности.
Все физические процессы, сигналы не могут бесконечно нро-
должаться,. Е.о_..в.р.емени. Они когда-то начинаются'и когда-то
пре.крашакися. Поэтому . можно считать, что из физнн.^ск11х
соображений исходный сигнал удовлетворяет условию
Ит ^^^)-0.,
' - ± ОЭ
Тогда из A1.56) получаем
51(П = ./2«Г^"?(П. A1.57)
Применив это правило последовательно п раз и считая,
что С1{1) — дифференцируема нужное число раз, а ее
водные при 1 = 0 также равны нулю, получаем
В некоторых задачах приходится рассматривать сигнал!.!
(воздействие на линейную систему), которые в момент (=-.
скачком меняют свое значение от О до какой-то конечной
личины У{-). Обычно этот момент принимается за начало
счета времени, т. е. ': = 0, так что это значение равно (/(+0)
'(значение функции справа от ^=0, предел, к которому
мится функция при -[-г?>0, в то время как при (—{) — 0
[]{—0) = 0). Тогда значение ^7(—схз)-0 приходится заменит!,
значением {7D-0) и вместо A1.57) записать
^'@^-51(П"-/2«/5(/)- Ц+0). A1.59)
■48
е вдаваясь в дальнейшие подробности, укажем лить, что
Ь1_. .последующих ироизводных исходной функции будут
делиться значениями как самой функции, так и ее про-
ых в точке ^=4-0-- В общем случае при ненулевых на-
X условиях вместо A1.58) будем иметь
^'0 - -> 5„(Г) = (У2:г/)« 5(П - (У»)'""' V(+0, -
■и2г.^Г'и[
(л-1)
A1.60)
1Под _(У<Дц^" имеется в виду и])ел_ельное значение (« — 1) про-
и^одной функции (/(/) при (->0 сирава^ т. е.. и области
ложительных „значений времен.
;||В больитнстве технических задач приходится иметь дело
срулевыми начальными условиями, при которых справедли-
вМ^выражеиия A1.57), A1.58). В результате можно сказать, что
ф|>фрр('нтгрпвпиию функции. ВО времснной области соответ-
С^ует умножение ее спектра на его аргумент у'ю == у'2-/. Но
1^1 этом нельзя забывать о требовании соблюдения нулевых
й|.ча.иьн1>1х условий.
' Аналогичн1,1е соотно1иепия можно получить и при
рении обратного варианта это1'1 теоремы, т. е. вида сигнала,
ответствующего ироизводио!! о г спектра.
■> Этот сиснал равен
^.(П
5'и2.1)е''^"с1!
Т е"^-' с18 (У2«П. (И.61)
; Интегрируя это выражение но частям аналогично
лению интеграла A1.56) и имея в виду, что спектры сигналов
стремятся и бесконечности к нулю, получаем
С/,(О
У2г
' 'е^''"8и2.!)\
ос
.)■
— 00
8{12г.Пс1е
угк//
у1- -30
A1.62)
Полученное соотношение между сигналами, соответствую-
*гй^ми спектру и его производной, аналогично выражению
Щф7), что является следствием симметричности прямого и
^Рртного преобразования Фурье. Ясно, что A1.62) может
. --^ {обобщено и на случай л-ой производной спектра, анало-
''И'^ю (П.58), соответствующей л-ой производной сигнала (с
иу^вымм начальными условиями).
3. Теоремы об интегрировании сигнала и спектра
(теорема о спектре интеграла)
Условия теорем1I относительно интеграла от сигнала <;
ключаются в следующем
Если
[/{0--5(Г)
и
Ф@= / и{()сИ^-> ЗА!),
— 00
то требуется выразить 5_1(/) через 5(/).
Из условия теоремы следует, что
ас
Поэтому, применив результат!)! предыду1це1Ч теоремы,
но записать
Ь'@—- 5{!) = }2-П 5_1(/ )- Ф(о). (II' '■^)
или
При нулев1Iх начальных условиях, т. е. когда Ф@) ■■--=
== I 6/(^)^^ = 0 и весь стиал расположен в области про-
— 00
должительн!.1х ^, получаем
При л-!<ратиом интегрировании сигнала, !ьм«т спектр
5-пЦ) будет выражаться через спектр исходного сигнала и
виде
п
Таким образом инте1рирование сигнала приводит к
нию его спектра на аргумент уш = ;2-/'. Аналогично этой
реме можно пр1!вести „парную" теорему об изменении фор-
м!)! сигнала при 11птегрирован1!и его спектра. Ее можно
мулировать так:
пусть
^(^) —5(П,
требуется В1,1разить сигнал 11-1{(), которы!! соответств;,от
спектру
через си1нал ^{^)
50
По аналогии с предыдущими теоремами можно предполо-
йть, что интегрирование спектра приведет к делению сигпа-
, ?а на аргумент I.
Это можно получить как следствие из предыдущей
мы и соотношения A1.62). Применяя A1.62) к 5_1(/) и 5(П
сто 5(/) и 5(П = 5,(П). получаем 5(П=5_1(П, так что
и-1{^) = -^^^'^ . A1.67)
Вопрос о начальных условиях необходимо иметь в виду и
в данном случае. При этом }1адо учесть, что спектры
ных физических процессов и бесконечности всегда стремятся
1? Нулю, а постоянная составляющая спектра сейсмических
сигналов в принципе должна иметь также нулевое значение.
4. Теоремы о смещении сигнала во времени и спектра
по частоте (теорема смещения)
Рассмотрим, как изменяется спектр сигнала, если
тить этот сигнал во времени без изменения форм1)[, или
че говоря, если изменить начало координат на оси времени.
Условие теоремы запин1ется так:
если ^у(^)^->5(П,
то требуется выразить спектр смещенного на - сигнала .5^@
через спектр ^О") сигнала и{().
Для определения 5т;(/) применим к смещенной функции
прямое преобразование Фурье и произведем замену
ных, обозначив ^1 = ^—-. Тогда, заменив ^гг!";-}-- и сИ^сИи
получаем
5.(/)= Г иЦ-.)е-"^'' А1= Т ^(^,)^-^""'+^'-^й/,=
— ОС — эо
^е ' ' ] Щ,)е '^ A1^=^6 ' ^ 5(/). A1.68)
— 00
Интеграл в правой части A1.68) равен спектру исходного
несмещенного сигнала. То обстоятельство, что
ние происходит по переменной 1^, а не I, не имеет значения,
т. к. интегрирование нроиз1юдится в бесконечных пределах,
т. е. по всем значениям времен.
В результате получаем, что смещение сигнала вдол!. оси
§р.емен на время ± - соответствует умножению спектра па
"^н.ожитель е'^''^^^'', который можно назвать функ]и1е1
ния:
5±.( /) = |5.( /)! еН" = е^>'^^-8{\) ^ $Г^
_ ^±У2:"/х |^( ^ у^ ^ухл ^ 1^^ ^^1 еЫ/)±г-М1 A1.69)
4* О
^ 51
Ил равенства A1.69) следует, что
?±.({) = ?({) ± 2«Ь, {И.70
т. е. смещение сигнала во времени не изменяет его амплц
тудно-частотный спектр, а отражается только на его фазовом
спектре. Последний получает слагаемое в виде линейной
функции частоты (± 2х{т) —прямой линии, наклон которой
определяется интервалом смещения сигнала - (рис. 8 6; 9 б)
При неизменном амплитудно-частотном спектре смещение
сигнала по времени приводит к изменению действительно!!
А{1) и мнимой 5({) частей спектра.
Как уже указывалось раньп]е, смещение сигнала вправо,
т. е. запаздывание сигнала во времени приводит к смещению
фазового спектра в области положительных частот в
тельную сторону.
Рассмотренная теорема о смещении сигнала во времени
имеет очень важное значение в сейсморазведке, где
дится иметь дело с сигналами, приходящими к сейсмоприем-
никам в разное время. В частности, на применении этой
ремы базируется теория направленного приема сейсмических
волн. Из результата A1.70) следует, что для создания искус-
ственноГ! задержки сигнала, задерживающее устройство долж--
но пропускать сигнал без изменения его амплитудно-частотно- .
го спектра и изменять его фазовый спектр, вычитая из не- "
ходного фазового спектра сигнала линейную функцию частоты. ■
Далее рассмотрим парную теорему о смещении спектра по '
оси частот и о влиянии этого смещения на форму сигнала. В
этой теореме устанавливается связь между двумя сигна.л[ам!1
^(^) и и^{{), имеющими спектр1>|, одинаковые по форме, но *
смещенп1>1е по частоте на А^. Условие теоремы записывается "
так: если 3{()<- -^и({), то требуется выразить через С/@ сигнал
Применив к 5A' ± Д[) обратное преобразование Фурье A1.29)
и проведя рассуждения п выкладки, аналогичные
ным в предыдуп1,ей теореме, можно получить
^^{^)=^{^)■е^'^^^". (п.71)
Из полученного результата следует, что при умножении
сигнала па е^'^"'^^^ его спектр смещается по частоте на фА?.
Заметим, что в данном случае знак ^\ в аргументе спектра
5(}'|^А|) и а.показателе степени функции смещения в A1.71)
меняется на обратный, в то время как в предыдущей
ной) теореме знак у смещения т сохранялся. Это есть
вие разных знаков у показателей комплексных гармоник в
прямом и обратном преобразованиях Фурье.
52
Шри умножении сигнала ^{^) на гармонику соз2::А^/ (несу-
частота при так называемой „балансной" модуляции 119])
)Ответствми с рассмотренной теоремой получаем
ищ соз21:М^ = ^\ ии)е'''■'^' + ^{^)е~^'^'''\^ ■
[Ьи~ Д/)-) .^(?-|-Д^)I•
(II.72)
а ОоЬ^Уо.С! СОЬ Тсек гСО НОЮС -50 С 50 <0С '50 2С0 (щ
-м/ ^1I
кс1Л1-'0.02 ООзЬе/г -250 200 но -(ОО-^О о 50 100 150 200 250 I г и.
Рис. 10. Теорема о смещении спектра по частоте
В результате спектр исходною сигнала 5@ распадается на
|е одинаковые части с половинной амплитудой, которые
|сполза1отся по частоте в разные сторон1.1 на Д{ (рг.с. 10).
5. Теорема изменения масштабов сигнала и спектра
I (теорема масштабов)
«: Если у сигнала С/(/) аргумент заменить на а1{а Ч= 1), то из-
^нится его горизонтальны!! маспггаб. При а>1 сигнал
дет сжиматься, а при а< 1 - растягиваться по оси времени,
жабы при изменении горизонтального маси1таба не менялась
1цадь сигнала, рассмотрим функцию СУд(^) = а6'(а/)*П1осмот-
I, как будет меняться ее спектр при изменении горизон-
(Лййого масштаба вследствие изменения коэффициента а.
^^^ким образом условие теоре.м!.! можно записать так:
^яа Ыр, <- -> 5([) и 6'а@ = аЬ(,а1) ^ -. 5^@, то требуется ны-
Разить 5а({) через 5({).
Для определения 5а( П представляем сигнал Gй@ в вырз-
^йнне прямого преобразования Фурье A1.28):
I- 53
00
,1'
■ 00
~]г-^/1
-/г^г^С'»
5„(П-а Г и{т)е ' сЦ= ]■ ^{а^)е
с1{ак) =*
ц-г. ■■ '■■
иЦ^)е " й?г,=5|'^) .
(П.?::
Интегралы в прамо!! части представляют собой спектр И[
Х0ДН011 функции ЬA), иолученньп! мри частотах //а.
\щ\-Ш
О 50 100 1^0 1-1и
■НО -100 50 О 50 ЮС 150 ^1 и,
а^^^ {'0.5)
18./
А
' о 'о^^О.О'* 0,06 ^се«: -^0 О 50 ^г.
Рис, и. Теорема масштабов
Таким образом при изменении горизонтального масштаба
сигнала горизонтальный масп1таб соответствующего ему
ра меняется в обратном наиравлении: при растяжении
ла спектр сжимается, при сжатии — растягивается.
В результате можно сделать общий качественный вывод,
что 1шдее длительным во времени сигналам соответствуют
б о л се_ узкие сн «у^Ж''- ,11— ДАО барот, более , коротким сцгн ал а ^^
Л2^1^Щ1 Я^^^^^е^сxво^шл:ьЗ^ Р^^с. И
приведен пример взаимного соответствия растяжения сигнал;'
и спектра по осям абсцисс.
54
6. Теоремы об дифференцировании и интегрировании сигнала
и спектра по параметру (теорема о параметре)
Свойства сигнала могут зависеть от какой-нибудь физичес-
,^ой1величины а, независимой от времени распространения
нала (• В этом случае форма сигнала зависит от параметра а,
^ что его спектр также будет содержать этот параметр.
Независимость параметра а, от времени I определяет его
зависимость и от частоты ^ в спектре. Из математического
Анализа известно |17|, что при дифференцировании или ик-
тегрировании интеграла от функции по параметру в случае
||ёпрерывности функции и ее производной по аргументу и
параметру можно дифференцировать и интегрировать по
раметру саму подынтегральную функцию. Очевидно, это
вило интегрально-дифференциальных операций по параметру
в равной степени может б1>1ть применено как к прямому, так
и к обратному преобразованию Фурье. Поэтому рассмотрим
только прямое преобразование.
Считая, что трансформанты но Фурье содержат параметр
«, можно записать
3A0.)= Т и{{, у.)е~'''''-^' М. A1.74)
Тогда рассматриваемые теоремы отдифференцировании и
интегрировании по параметру преобразования Фурье могут
быть записаны так:
A1 — ОС (}1
[\, ^)с1х = 1 {]' и{1, а)йо. \ е "''"'''' сИ
A1.75)
A1.76)
7. Теоремы о произведении спектров и сигналов
(теорема свертывания)
В_т_еорпп линейных систем часто приходится и.меть дело
"СО спектром, который может быть представлен в виде
изведения двух комплексп1.1Х функциГг частоты. Наиболее
пичным примером этого может служить ше.ктр сигнала на
выходе линейной систем1>1, которьп! получается в результате
ум_ножения спектра входного сигнала на комплексную
ную характеристику системы. Форма сигнала и временная
трансформанта частотной характеристики обычно бывают
вестны. В результате спектр выходного сигнала оказывается
^едставленным в виде произведения двух функций частотгл
, 1(/) ч >5»(П, для каждой из 1<'ото])ых известна прсменная трапе-
форманта по Фурье б'Дг') и G,@- Произведение этих сз;^.^
ров 5@ = 5х(^)-8г(П также представляет собой спектр неког
рой функции времени 11{(), которая определяется функция^
^хСО и и^{1). В упомянутом вьпие примере это будет слгн^
на выходе линейно)! системы, который часто является иек,
мой функцией, определяемой по входному сигналу и изб^'с-
ным свойствам (характеристикам) линейной системы.
Рассматриваемая теорема о произведении спектров по;я!г.,
ляет выразить сигнал й{() через функции ОгЦ) и ^'■;^(^) в ц\[.
де интегрального соотиоп1епия специального вида:
00
— ОС
^{^)■---^ I и^(-)-и,{1--.)Aх, {п.ц
которое носит название „интеграла свертки". Операция, кч,.
торую нужно произвести над функциями G,@ и и^{() по сц.
отношению A1.77), чтобы получить ^{^), называется „операт;-
ей свертывания", или „конволюцией" функции С1{(:) и с/з!/)
Иногда эта интегральная операция A1.77) называется „склад
кой", или „композицией" двух функций [5].
Заметим, что ^7,@ и 0,@ мы уже не называем
ми", а используем более общее понятие — функции времени,
или временные трансформанты по Фурье. Точно также 51(^I!
8г(П. строго говоря, нужно называть не спектрами, а фупк
циями частоты, или частотными трансформантами по Фуры'.
Дело в том, что одна из функций частоты представляет с"-
бой частотную характеристику системы, а ее временная трап-
сформанта — временную характеристику системы. Впрочем о1-
меченная терминологическая особенность не так уж сущее !-
венна, так как вдемйнная характеристика представляет собой
реакцию системы"" на входной сигнал в виде единичного им
пульса, и таким образом имеет право называться выходны.м
сигналом системы. В то же время частотная характерно гика
системы представляет собой частотную трансфор.мант} по
Фурье этой временной характеристики, т. е. ее спектр.
Итак, содержание теоремы о произведении спектров
тоит в том, что если имеется Фурье — соответствие между
парой сигналов и спектров
^2(Г)'
5,(П^->^Л@.
и^И), (Ь'.78)
то произведению спектров 5( П = 5x1 /)• 52( [) соответствуе I
нал
•^(П = -51(П-52(П--^@. {И.79)
который определяется через исходные сигналы 1';(<) у С'з@
операции их свертывания A1.77).
56
ля доказательства этого утверждения запишем выражение
ого преобразования Фурье для 51(П^-^ ^1(^). помножим
выражение на ^гС П> внесем его справа под знак ннтегра-
сделаем несложные преобразования. Тогда получим
- 00
= Т и,{.)\8,A)е-'^'^'''\а.'^
- 00
= .1' иг{-)
г 00
I
00
Т и^а -)е '^^^йг^й-. AГ-80)
Имея в виду теорему смещения сигнала во времени, мож-
Н.0 считать, что выражение в квадратных скобках последнего
Жнства представляет собой спектр смещенной на - функции
— -с). Меняя порядок интегрирования, последнее
ние можно записать в виде
Г
- 00
" " ' ~''''^Ч1=8,(\)-8,{1) = Щ). (И.81)
^ и1{-)-и^и — -)а~
00
. в полученном соотноиении A1.81) слева записано в!Iраже-
ад;е.,.прямого преобразования Фурье (определение спектра) для
функции, стоящей в квадратных скобках. Имея в виду пра-
вую'часть A1.81) и условие теоремы A1.79), убеждаемся в
справедливости искомого соотнои1ения A1.77), то есть
мы свертывания.
, ^перацпю свертывания двух функций A1.77) в виду ее ши-
р^ого использования обычно для краткости обозначают ка-
кр1-либо специальным символом, часто звездочкой между
свертываемыми функциями. Применив это обозначение,
зультат рассмотренной теоремы свертывания можно записать
так:
5(П= ■5,(п-5г([)^-. иц)='их(()., и,(П- (пт
Рассмотрим парную теорему.г- теорещ; о „.др,^I13в^^дсиип
ФушщигГ"(сигналов). Она может оказаться полезной при
смотрении формы сигнала в виде произведения двух функ-
Чин, например, выделении в виде множителя члена,
ризующего затухание или расхождение волны, или при
ляции сигналом высокой несущеГ! частоты.
Содержание теоремы о произведении функций может быть
-формулировано аналогично предыдущему. 1^сли между па-
Рвми функций времени 6/д@, ^^«(О " "х спектрами 5,(|^) и
*вA) имеются соотношения A1.78), то спектр 5@ сигнала,
ного произведению исходных сигналов
Определяется операцией свертывания спектров 5^(/) л 52@-
Запишем произведение сигналов в виде произведения ц^
юбратных Фурье-преобразований
^@= ^1@-^2@= Я 5,Ц^,).3,{/и)е'"^^-''^'\и-^1г, A1.84
— 00
II обозначим
Подставляя эти обозначения в A1.84), получаем
Очевидно, справа в A1.85) стоит обратное преобразовани(:
Фурье от функции в квадратн[Iх скобках, так что можно за
писать результат рассматриваемой теоремы в тако.м виде:
00
^@ • - * 5 ,(уЪ)■ 5,(Л ~ У!,)с1/, = 5^(/7),52(//). A1.86;
в правой части полученного выражения A1.86) стоит
ка спектров 51(/) и ЗзСГ), так что результат теоремы о произ
ведении сигналов можно кратко выразить так:
С;,@-^2@ —5х/*5,(/). (П.87:
Это вполне аналогично результату предыдущей теоремь
{11.82). При записи спектров как функций кру10вых частот а
правую часть соответствия A1.86) нужно разделить на 21с11].
§ 5. ОПЕРАЦИЯ СВЕРТЫВАНИЯ !
1. Механизм операции свертывания
Интеграл снерт1:и двух функций имеет многочисленные
менения в различных областях физики и техники, где он
лучает различные специфичные названия: теорема Бореля,
интеграл Дюамеля [9), интеграл суперпозиции [6] и др.
Физический смысл операции свертывания двух функци11
наиболее наглядно проявляется при ее нспользованпи в
кой-либо конкретное физической задаче, когда свертываемым
функциям придан определенны!! физический смысл.
дены общие соображения о структуре интеграла свертки A1.77)
и механизме операции свертывания двух функций как
деленной математическое! операции.
Прежде всего обрат!!м внимание на аргу.мент у второС!
функции в A1.77). Если С/у^х) и ^'^(■с) изобразить в одинаковои
системе координат, как показано на рис. 12 а, б, то и^{х—/)
58
I
^)
ф
и, (г)
игЫ)
' 1
0
аоЛ>
' 0,011
\
0,06
1 '
<^08 Та
и,{Ы}
»начает, что функция 114:}) смещена вправо по оси времен г,
ре. запаздывает на время ^ (рис. 12 в). Тогда функция,
писанная в виде И^{1—X), представляет собой смещенную по
Ь} времен на / и перевернутую задом наперед функцию
Шт). Переворот фу,нкции происходит таким образом, что на
^^те остается и совпадает сама с собой единственная орди-
^га функции ^(О), т. е. по-
^рот осуществляется вокруг
^чки на оси времен 1-—1
рГис. 12 г). Далее, в соответ-
Ьвии со структурой интегра-
|а свертки, функции 1)-^) и
Ш< — ">=) перем}1ожаются и
ве:1ультат перемножения ин-
гегрируется. Такая
ра осуществляется при раз-
Цшчных взаимных сдвигах
ремножаемых сигналов I, так
рто результат операции
тывания оказывается функ-
[Б^ей взаимного сдвига свер-
гываемых сигналов (рис. 12д).
В результате операции
тывания двух функций
мени С/1(-с) и 114:}) получается
новая функция вре.^ени,
ределяемая свойствами свер-"
гываемых функций и
ным сдвигом между ними.
Если свертываемые функции
занимают конечный интервал
на оси времен, то их
ведение со взаимным
гом отлично от нуля на ин-
гервало нремен1г, не превы-
иающем сумму длительностеГг этих функций, так как их
ведение становится равн1,1м нулю, когда области их сущест-
:ювання по т не перекрываются. Но результат операции
тывания может оказаться нулевым и при перекрывающихся
;игналах, так что длительность функции свертки может быть
короче, чем суммарная длительность свертываемых функций.
Если вспомнить, что с^вертке двух функциГ! соответствует
:1еремножение сротвстствующих им спектров, то становится
^сным, чго со. спектральной точки зрения результат сверты-
:^ания определяется соотношением частотных диапазонов
:пектров. Если частотные диапазоны спектров не
ется, то результат перемножения спектров так же, как и
ввертывание сигналов, окажется нулевым.
0,0» 'Ссчк
Рмс.
12. Операция свертывания
функций 1!\A) и ИгЦ)
Отметим одну из наиболее важных физических интерп
таций интеграла свертывания.
В главе I (§2) было показано, что интеграл свертки 0(
ществляет линейное преобразование сигналов. Имея в ви,
описанное действие операции свертывания, нетрудно из сам1
общих соображении дать физическую интерпретацию эт(
операции применительно к линейным системам. Представи
себе, что л_и1[1е]1ная система возбуждается последовательн!
стью единичных импульсов с амплитудой, меняющейся и
времени пропорционально огибающей (УхС':)- Обозначим ре;}1,
ци1р линейной системы на единичный импульс через
и,{'^) =-- /ч--).
Возможность представления сигнала последовательностьц.
единичных импульсов по принципу суперпозиции
валась в гл. I (§3). Произведение/У^(т,•)•^'^^(^---С;) = ^^{'^)•к{^—-;)
будет представлять собо11 реакцию системы на импульс
плитуды Ь'1{"/) в момент -■, а реакция системы па иоследовл-
тельность всех импульсов, т. е! на весь входной сигнал, ска-,
жется по принципу суперпозиции равной сумме этих
ных реакци!! (в случае дискретноA последовательности
ных импульсов), !у1и интегралу свертки 6'1(-) и //(т) (в случа('!
СПЛ0П1Н0Й -последовательности импульсов, составляющих:
СИЛ0П1Н0}'! сигнал).
Рассмотри.м далее некоторой? частные, но важн;1!е случ;и1
интеграла свертки двух функций.
2. Свертка одинаковых функций
Предположим, что ^/гСО^^аСО» ■• <^'- свертываются
ковые функции. Тогда в соответствии с теоремой о
дении спектров в обозначениях (§4 п. 7), получаем
— 00
в результате свертки одинаковых функций получается
функция, которая по сравнению с исходной имеет
ный в квадрат амплитудно-частотный спек1р и удвоенный фа-
зово-частотныи спектр.
3. Свертка «сопряженных» функций
Расс.мот])им операцию свертки двух функций 01A) и из(—{),
имеющих противоположные знаки аргументов. Так как в со-
ответств1П1 с рассмотренными свойствами спектров перемена
знака аргумента сигнала преобразует его спектр в сопряжен-
60
рУЖ функции с разными знаками аргумента здесь дли крат-
^^й также названы „сопряженными". Если использовать
.■мврцные обозначения
чп
•Интеграл свертки ^1@ и Щ - ^) заиии1ется с иеремеиой
зяша. у аргумента ^^{^), т. с.
= ^1{!)-5,{!)^\5т-т)\-е''"~''' A1.89)
•" Амплитудный и фазовый спектры результирующего
ла оказываются равными
A[.90)
■г. е. амплитудные спектры перемножаются, а фазовые спект-
:Йк~9Ь1чйтаются.
"^ ЧертоГ; сверху обозначен комилексно-сопряженныГ! спектр.
■Полученное соотиопюнпе A1.89) между функпиями ^'1@ "
ЩГ) называется функпиеп взаимной корреляции, а
вующий еГ; спектр 5( [) = 51(П-52(/) — взаимным спектром рас-
<Жатриваемых функций.
Предположим далее, что^свертываемые сопряженные
кции одинаковы по фор.ме, т. е.
В соответствии с предыдущим эти сигналы имеют одииа-
'^<^§Ме_.амплитудные спектры и
ные по зк"
ровфазо!;
амплитуда V.. :,^^ Vл.-. о
адетртного спектра
Ц0= Т ^1(х).;(.-0о!^—>15(П|-151(ГГ
■•■ ОС
\ «р@-0. (П.91)
ФуIкция а{() В A1.91)называется автокорреляционной фуя^
цией сигнала Ь'хСО. '^ полученный в правой части A1.91)спект.
называется энергетическим спектром этого сигнала. '
Автокорреляционная функция не имеет фазового снек;р^
и является представителем некоторого класса сигналов, о,-,.
ладающпх одинаковым спектральным составом (т. е. оди^а.
ковыми амплитудными спектрами) и различной фор.мой, он,
редсляемой фазов1Iм спектром. Равенство нулю фазового
спектра автокорреляционной функции означает, что все гзр.
МОНИКИ ее спектра оказываются в фазе в момент ^==0. В р^.
зультате в этот момент сигнал обладает максимально во;).
можпой амплитудой при данном амплитудном спектре. Налк.
чие фазовых характеристик у других сигналов с таким же
частотп1,1м составом может только расфазировать гармоняю!
в этот момент времени и уменьшить амплитуду сигнала,
„размазать" сигнал по времени.
Таким образом можно сказать, что автокорреляцион;;;1я
функция обладает .макси.мальной амплитудной
ностью по сравнению с другими функциями того же спехг-
рального состава.
Рассмотренн1>1е выше понятия „автокорреляционной" 1'
„взаимноГг' корреляционно!! функций операций
ции" и „взаимной корреляции", а также „энергетического" \:
„взаимного спектра" имеют важное значение в теории слу-_
чайных функций, и в частности, в теории фильтрации слу-'
чайных сигналов лине11Н1IМи системами. В теории случайн!Iх
функций автокорреляционная функция и энергетический'
спектр применяются для характеристики и описании
рого класса случайн1>1х функци]!, разнообразной „случайноп"
формы, но обладающих одинаковым частотн1>1м составом.
Иногда вместо терминов „автокорреляция" и „взаимная
реляция" употребляются тер.мин1>1 „автовариация" и ..кроссв;:-
риация" или „аптовариация" и „ковариация". Эти термин!.;
вводят, чтоб111 отличать эти понятия от математических
нятий „функций" авто- и взаи.мо-корреляции", которые
логичны авто-и кроссвариации, но являются нормированными
функциями с .максиму.мом, равпы.м единице. Корреляционном
функции обычно присваивают какое-либо определенное обо;!-
начение, причем часто ее обозначают буквой В. Функция
взаимной корреляции сигналв^с индексами т\\ п обозначается
Вт.п{^)> '1 автокорреляционная функция снабжается одинаковым;!
индекса.ми, например ВпЛЦ-
4. Свертка сигнала с единичным импульсом и гармоникой
Предположим, что одна из свертываемых функций,
мер ^^^{^), представляет собой единичный импульс, т. е. {^гСО^
=1Ъ{^), а вторая функция {.']@ является сигналом. Тогдг)
свертка сигнала с единичной функцисГ! будет иметь вид
62
I
00
{^1@*5«1)= ^• ^^{^)■Ч^г--^)а'^. A1.92)
— со
Единичная функция о(/, — т) отлична от нуля только в мо-
мент ^1--=^ "• Поэтому умножением С'хС") на о{'A-) из сигнала
урезается его значение в момент - = ^^, которое
ся независимым от неременной интегрировании т и поэтому
)лржет быть в1>1несено за знак интеграла. Интеграл от
ничного импульса равен единице. Поэтому
Полученн1)П1 результат указывает, что _свсртка сигнала с
единичным импульсом позволяет выделить одно значение
сигнала в^ момент действия этого импульса.
'' Рассмотрим далее, что получится, если сигнал „свернуть"
с комплексной гармонической функцией. Предположим, что
У^(() ^ е^^'^^о'. Тогда преобразование свертки дает
11{1)-= I 11х{~):е' д.- = е' ] ^1(')е й- =
— оо - —оо
= 5г{и)е1'^-^^* =\5А\ Л■е^'''-^"^^''. A1.94)
Так как 51(|'„) представляет собой амплитуду гармоники
сдектра ^x{^) с частотой /ц, то полученный результат
ставляет комплексную гармоническую составляющую спектра
сигнала 1/1@. Таким образом операция свертывания сигнала
с^зрмоникой выделяет гармонику из спектра сигнала, т. с.
.осуществляет операцию гармонического (спектрального) ана-
^за.
5. Энергия сигнала и спектра (теорема энергий)
Запин1ем выражение для автокорреляционно!! фу1!кции:
= I 5(/)- 5{Пе' с?г- .1- |5(ПГб ^/. A1-90)
—оо — 00
г^ассмотрим это равенство д.чя начального момента
ни /=0.
Получим
ба
в лево!! части выражения A1.96) стоит интеграл от квад],
та амплитуд исходного сигнала, который выражает энергн
сигнала. В правоГ! части аналогичный интеграл от квадоа-,
амплитудно-частотного спектра. Отсюда можно заключт.
что каадрЗ-Х Амплитудного спектра представляет собой ило-,
ность распределения энергии по частоте в спектре сигнал,-
Поэтому квадрат амплитудно-частотного спектра называете
обычно энергетическим спектром. Соотнои1еиие A1.96) выра
жает энергию сигнала через ее амплитуды и спектральны
■составляющие. Его часто называют теоремой Рейли (Релея!
ГЛАВА т
СПЕКТРЫ НЕКОТОРЫХ ФУНКЦИЙ
§ 1. СПЕКТРЫ РАЗРЫВНЫХ ФУНКЦИЙ
1. Спектры знаковой функции и единичной функции
В главе I в качестве элементарной функции б1Iла описаи;
единичная функция, которая представляет собой мгновеипьп:
скачок а.мплитуды от нуля до постоянной величины, приия
той за единицу. Если этот скачок произошел в момент вре
меии -, то единичная функция определяется по A.30) с за
паздывающим аргументом (рис. 13 а)
а(^--) = р^<^ A.30;
Вычисление спектров одиничиоГ! функции встречает дне
формальные трудности:
а) нижний предел интегрирования не имеет оиределенногг
значения, т. к. при ( = 0 а{1) меняется скачком от О до 1;
б) интеграл Фурье от функции з(^) оказулвается расходящим
ся, т. к. единичная функция не стремится к нулю при безгр.'
иичиом увеличении времени.
Однако спектр едиIичио11 функции существует, так чп
обе эти трудности преодолимы.
/1,ля преодоления первой трудности представим
ную функцию в виде суммы четного и }1ечетного слагаемых
Четная часть будет представлять собой постоянную велич:
ну 1/2, а нече,тная часть — кососимметричиую разрывную фут
цию, при ^—0 скачком меняющую значение от --1/2 ;|-
-1- 1/2. Подобная разрывная функция с единично!! амплит»
дой называется знаково!! функциеГ! и обозначается об(.1Ч111
81йп F и ДР-1*- Функц!1я 81дп ужс исиользопалась ранее (П.41>)
и равна (рис. 13 б)
* 31дп — по-анг;1И1'1ски—знак, отметка, признак.
64
81?П@:
1 ^>0
О ^ = 0
—1 ^<0.
(Ш.1)
й'аким образом единичную функцию можно представить в
|[е суммы двух слагаемых и ее спектр вычислять как сум-
спектров этих слагаемых
о}-
«е.
О
6)
МЫ!
а5]
-10.
^ -?.+
ИшпИ!-^} -^
А
81^П (К)
-<^'
Г 171^г ^
100 -50
^, П ЮО 100 -ю о 60 1(Ю1;
/-
1
2
У
1
-50
- "■■"""! ' г
2 '
Рис. 13. Ь-димпчпая — (а) и 311ако;иая — (б) функции них
спектры (и) и (г)
При смешении единично!! функции вправо на т это же
отношение A11.2) запишется так:
а(^-.-)^_> 5@@) е-/2^А
[1
+
+1-^^C1-п(^)}
5-358
-)гт.)-.
(Ш.З)
65
Подобная ситуация изображена на рис. 13 а, где един;щ
ная функция, изображенная жирной линией, смещена относи
тельно нуля вправо на т. На такое же время смещены и ел
гающие ее симметричная и кососимметричная части, изобра,
женные пунктиром, хотя на внешнем виде постоянного сщ;
метричного слагаемого это смещение не отразилось.
Найдем спектры обоих слагаемых A11.2). Постоянной велц.
чине 1/2, как наиболее растянутой вдоль оси ^ функции, в со-
ответствии с теоремоГ! масштабов будет соответствовать нац.]
более узкий спектр —одна спектральная линия на частотс|
|'=;0, которую можно выразить через символ единичного им
пульса:
I—5^1 = 1^/). (Ш.4,
Более подробно это соотношение A11.4) будет обосновано
ниже при рассмотрении спектра единичного импульса. Спектр
получается чисто дс1ств11тельный, так как постоянная
чина при т=О является симметричной функцией.
Функция 5,1й.пB') кососимметрична, так что
разование сводится к синусному преобразованию и спектр яи-
ляется чисто мнимо11 величино!!. При непосредственном
числении синусного преобразования Фурье от 51§ п {^) мы
встретимся со второ)! из указанных выше трудностей —
грал окажется расходящимся, т. е. не будет стремиться к
ределенному пределу. Для вычисления этого интеграла
меним косвенный прием и проинтегрируем экспоненциально
затухающую кососимметричную функции вида
в-^'181^П@ = [^~"''^>^0
где а>0.
Эта функция изображена на рис. 13 б пунктирной линией.
Применив к ней прямое преобразование Фурье A1.28),
чаем
Г е '"''' 5^§п{^) е ~'*"^' й1^-2]Х е ''"' 51ёп {I) зШ 2тг Г ^ Л =
■ 00
1
о
= -721 е '"'51п2и/^^^. A11.6)
66
|Интеграл в правой части A11.6) является табличным и его
^^чение приведено в справочниках по высшей математике
ц.. например [2|, стр. 379, ф. 459). В результате имеем
00 —2п;а<
-2жп(
[а81п2тсД4- /соз2и/и =
27:(ао+/2) о
/
2М^^+Р)
/
пт
а,0 2г:(а2+р)
1
2^-1
A11.7)
^1 Имея в виду, что
5 E1^п(^)) - Пт 5 {е--^"*'*5щпи )] Ит е"^~'" з1^п(/) A11.8)
ос-» а->0
используя A11.6) и A11.7), получаем выражение для спектра
1аковой функции:
2
З1'ёп@ ■
1 5{81§п@1 = ~ = —^
2 I & ^'^' 2к/ 12п/
A11.9)
В результате но A11.3), A11.4) ' и A11.9) спектр единичной
рункции равен
,(/)__5{а@!=|з(/) + -^=|5([)-у^. (Ш.Ю)
Отметим,|что единичная функция а(—1), направленная от
)уля в сторону отрицательных [^времен, будет иметь сопря-
сенный спектр, т. е.
2 2г./
Из полученного выражения A11.10) следует, ,'что действи-
гельная и мнимая части спектра единичной функции
ственно равны
АA) = -^Ч1).
^'> = Т.7
5*
(III. П)
($74
Действительная часть А{{) и мнимая ВЦ) рассматриваемого
спектра изображены на рис. 13 в. Следует обратить внимание
на то, что действительная часть Л(/) отлична от нуля только на
нулевой частоте ([=0). В то же время, мнимая часть, а стало
быть и модуль |5|з)|, на нулевой частоте принимает
нечные значения. В результате оказывается, что наличие дей-
ствительной части спектра — (^) никак не сказывается на
ведении амплитудного спектра ]уЗ(/)| и фазового спектра ?(/)
которые равны соответственно
|5(/)| = —-,
С05 ?(П = ^^^ = 21г1 Л • ~ 8(П = О,
1^п = ^а^«п(|)■ AИ.12)
в связи с этим обстоятельством часто оказывается
точным выводить спектр упрощенным способом и получать
его в виде одной мнимой части A11.10) [19 и др.]. Однако в
некоторых специфических задачах действительную часть
ра единичной функции приходится учитывать. Вид
ного и фазового спектров единичной функции при т = 0
казан па рис. 13 г. Как следует из рис. 13 г, а также A11.10),
A11.11), A11.12), спектр единичной функции содержит все
тоты, но низко-частотные составляющие обладают большей
амплитудо!!, так как амплитуда гармоник с повьппеиием
стоты убывает по гиперболическому закону. Часто входной
сигнал в виде единичной функции применяется при
ниях аппаратуры. В сейсморазведочных станциях об1Iчно
ется спепГйальная кнопка „собственный процесс", при помощи
которой можно на вход усилителей подавать включение
стоянного напряжения. При производстве подобных
ний следует иметь в виду, что подача на вход аппаратуры
сигнала в виде единичной функции равносильна подаче
ра с преобладанием низкочастотных составляющих, так что
проверка аппаратуры при таком испытании производится
главным образом в низкочастотном диапазоне частот.
2. Спектр прямоугольного импульса.
'В главе I (§3) было приведено выражение A.35)
гольного импульса с постоянной единичной площадью в
де разности двух единичных функций, возникающих с интер-
68
|лом Дт, равным длительности импульса (рис. 14 а). Там уже
называлось на специальное обозначение этого импульса, в
^ответствии с которым п^рямоугольный импульс единичной
^ощади длительностью Д- с центром в точке т, обозначает-
A11.13)
а)
иA}^гес1(лг,1)
>
4
^)
5ф = ^спс{/)
о г, г ^ ^«* .±
1—дС ^ "^ *Г
"' Рис. 14. Прямоугольный импульс (а) и его спектр
(б)
■ { Подчеркнем, что этим символом обозначен прямоуголь-
'ный импульс с единичной площадью, так как иногда это же
/^обозначенпе применяется для прямоугольного импульса с еди-
|Ничной амплитудой.
{ Используя теорему суперпозиции (гл. И, §4), можно спектр
■^прямоугольного импульса получить как сумму спектров сла-
|,гаемых в левой части A11.13). Для этого используем выраже-
^лие для спектра единичной функции A11.10) н теорему смеще-
:=ния (гл. II, §4),- в результате чего получим
^
4
1
гес1(Д-:,
_\
еЧФ
81 п г./Ах
- ^ 2:с/Дт
е *
—У2;1/-
- -е
. 2,=/Дт -1
У
A11.14)
;• Единичные импульсы на нулевой частоте в спектре A11.10)
Цри вычитании взаимно уничтожались, так как их функции
.•смещения на нулевой частоте равны единице. В полученном
■ Выражении A11.14) первый множитель представляет собой
ствительную часть спектра прямоугольного импульса. Второй
^множитель является функцие/! смещения и указывает
жение центра прямоугольника на оси времен. Если выбрать
Начало времен так, чтобы тг:10, то
69
гесКДх) _-^^?^^^^ =-!^ (ШЛО)
71/Дт; шДх '
Вследствие четности прямоугольного импульса при т=;0
его спектр A11.15) получился в виде чисто действительной
ции, представляющей собой синусоиду с амплитудой, убьша-'
ющей по гиперболическому закону. Эту функцию A11.15) иног.
да называют „синус-кардинал" [6, 26] и обозначают
лом 81п с:
81п гЛ-Г . ,, V /щ ,,,
——-^5шс(П. (П1-1Ь)
яДт/
Применяются и другие термины (функция отсчетов,
вая функция, интерполяционная функция [211). ^ид этой
ции показан на рис. 14 6 сплошной линией.
Таким образом полученное соответствие по Фурье A11-15)
можно записать в виде
гес1@™ 31пс(П- A11.17)
Амплитудный спектр прямоугольного импульса равен
солютному значению (модулю) синус-кардинала (П1.15)
51п гДт/
|з1пс(П|
гЛ-с/
A11.18)
Он показан на рис. 14 б пунктиром. Амплитудно-частотный
спектр прямоугольного импульса A11.18) имеет нули,
ющие с нулями зШтсДх/ и расположенные на значениях
мента
! =^ —
" д. '
где й=1, 2,---—целые числа. Первый нуль расположен на
частоте {^ — —•, период которой равен длительности импульса.
Дх
Остальные нули следуют на оси частот через постоянный
тервал ^1. При удлинении импульса увеличение Дт приводит
к пропорциональному уменьшению ^1, т. е. к сжатию всего
спектра к началу координат, что находится в соответствии с
теоремой маспгтабов (гл. II, § 4). Поэтому для расширения
спектра прямоугольного импульса и обогащения его
частотными составляющими необходимо уменьпшть его
тельность.
Из A11.16) следует, что
11т81пс(/)=1, A11.19)
т. е. на нулевой частоте спект]) имеет максимум, равный
нице.
70.
^зоаый спектр прямоугольного импульса с центром в на-
Ё[е,коордннат из-за симметрии этого импульса равен нулю.
рямоугольный импульс A11.13) и его спектр A11.15) находят
фокое применение в разнообразных технических вопросах.
^пример прямоугольным импульсом удобно моделировать
Етёму конечной длительности, считывающую сигнал с вос-
Шоизводящего носителя. При оптической записи и воспроиз-
р,ении прямоугольным импульсом молено описывать считы-
|к)щую щель шириною (длительностью) Дт, а при воспроиз-
гдении с магнитного носителя — ширину зазора из немагнит-
|ого материала в сердечнике считывающей головки. Спектр
ррямоугольиого импу;1ьса может рассматриваться как частот-
|ая характеристика воспроизводящей (считывающей) щели, в
' гзультате чего могут быть оценены частотные искажения,
|озникающие при воспроизведении записанных сигналов, и
|ыбраиа ширина щели, обеспечивающая допустимые искаже-
шя.
3. Спектр единичного импульса
Единичный импульс определен в гл. I §3 в виде соотно-
деиий A.37) (рис. 15 а) и может быть получен из прямоуголь-
10Г0 импульса гест(Дт) при Д-:-»-0.
а). 8)
иаЯа)
1$Коп^1^(
/'
Рис. 15. Единичный импульс (а) и его спектр (б)
Используя A11.15) и сокращая до нуля длительность пря-
'моугольного импульса Дт, получаем
ИтгесиД-) = о@-—~Иш81пс(П = 1- A11.20)
• К аналогичному результату можно придти и други.ми
тями, например рассматривая единичный импульс как
водную от единичной функции. Тогда, имея в виду спектр
единичной функции A11.10) и теорему о спектре производной
(гл. II, §4), можно легко получить для спектра единичного
импульса результат A11.20). Этот результат означает, что
сцектр единичного импульса представляет собой постоянную
величину (единицу), то есть содержит все частоты с
ковыми амплитудами. Как спектр импульса, симметричного
относительно начала координат, он обладает только
тельной частью и нулевым фазово-частотным спектром
71
(рис. 15 6). Таким образом спектр единичного импульса яв.
ляется наиболее широким из всех возможных спектров, чт^
находится в соответствии с теоремой масштабов, так щ
единичный импульс является самым коротким из всех во-),
можных импульсов.
Если центр прямоугольного импульса, используемого длй
получения единичного импульса, расположен не в начале
ординат, а находится на времени ± -:, то в соответствии с
теоремой смещения спектр единичного импульса получает
множитель смещения е*-'*"-''^ и становится равным
Ь{{ ± т)-
• е ь;2«/%
§ 2 СПЕКТРЫ НЕПРЕРЫВНЫХ СИГНАЛОВ И ФУНКЦИЙ
1. Спектр экспоненциально затухающей функции
В дальнейшем могут представлять интерес
но затухающие функции следующих видов.
Двусторонняя одпополярная затухающая
ная функция (рис. 16 а)
,+ гг.л,1
и,{П={ 1
о—2гл„<
1<0
( =0
/>0.
A11.21
Двусторонняя разнополярная затухающая
ная функция (рис. 16 б)
,-(-2от,/
^.(/)- О
о—2па^
I <0
^>0.
A11.22)
Односторонняя затухающая экспоненциальная функция
(рис. 16 в)
^а@
A11.23)
Везде а>0.
Как видно, эти функции отличаются друг от друга
дением их левых частей.
72
Вычислим спектр двусторонней экспоненциальной фуик-
^и A11-21):
■-; 00 _ 12п/{
— 00
-00
Хе сИ-= г е сИ-\- ] е сИ ■
■' О
— 00
1
2ф,-1П
1
—27;@(а4-//) о
-(=с.-//)~ _^"' 2п{^,+]/,) (о
1 . 1
8 -2^(<,,4 )/)/■
Выделяем действительную и мнимую части
A11.24)
51(Г)-\51(/)|е
+
+7/ . "а—у7
2г.( а\+/-) 2Ц «Н/'
Л(/) =
ч-
+ /Г ^: I т
2г.( .^+/2) 2я( а\ ^Р) 2^( ,2+/')( »^ ^/.)
_ @1,4-аа)(а,-агЧ-/')
2;:(=.?4-Я)(а^+Я
5,(/) = -^ -^ 1_ =х1±ьЛ:1-_
«^ +/'1
A11.26)
Н «?+/')( =-2+/^)
Амплитудный и фазовьп! спектры соответственно равны
*§: "р,(/)
5,(/)|= ■
/(°1-°2) ^ ЯЬ-Ч)
С05 91(/) = °'''''+^' —
A11.27)
73
Примеры |5,(/)| и ср1(]^) приведены на рис. 16 а. Если ра^
сматриваемая двусторонняя функция симметрична, т. е. а,,
= «2 = *» то спектр становится действительной функцией ч
стоты
151(/)|==|Л(/)| =
2а
(П1.28|
^>Ч1' 11 е'*'"''''
-30 -10 о 10 го 30 Глее*.
Рнс. 16. Экспоненциальные функции и их спектры
Рассмотрим спектр разнополярной экспоненциально
хающей функции, который вычисляется вполне аналогично
предыдущим. Разница только в том, что 1-ып интеграл в
A11.24) отрицателен
•5»(/)= ) {--е )е с1^ 'г \ е е Ш =
^Ф,+^■/) 2ф,-у/) 2г(.|+я) 2г.{а\+р)
^\2гии
г.{4+/^) Н4+Р)
-)■
A11.29)
74
т.
ла) =
^ _^2{'^\+Р)Ьч{4+Р)
В{Г)==
^ (Д|-»8)(а|Д,-Я)
A11.30)
Эбычным образом получаем амплитудньп! и фазовый
ектры
1
1
^е (/)_? -! + °2+2У^ _ /{А+4^2Р)
С08 92(П^
(я,-л,)(а,я,-^^
I/"
V ('?+У^)(=^+;2)[(о<,-.2)Ч4/^]
A11.31)
Для кососи-мметричной функции при «1=92 спектр оказы-
|^етсй чисто .мнимым:
Л(П=0, В,{1) = —!—-,
~(а--\-р)
^=<"--^-^4-л-|^'<«|=;;,;^;яу
4^
A11.32)
2(Й = 7«!8П(/).
{Наконец спектр односторонней экспоненциально-затухаю-
1,ей функции может быть получен из любой из рассмотрен-
Ь1Х выше двусторонних функций, если убрать ненужную
асть, снабдив ее бесконечно большим затуханием а = сх:.
Для функции 6^3@ (И1.23), изображенной на рнс. 16 в, ус
рая у ^/^(О A11-22) левую часть, из A11.30) при а1 = сх), пол
чаем
^^' 2г.(»+УУ) 27:(а2+/') 2;:(«'+'П 2г.(а2+/») '
A11.33
Амплитудный И фазовый спектры соответственно равн)
>'+у' _ ^
• 4-/2J — 2г.|/"аг+/2
а
2. Спектр колокольной функции
В предыдущих примерах полученный спектр по своей фор
ме оказывался совершенно непохожим на форму исходнок
импульса. Можно считать, что, как правило, форма сигнала
н его спектр оказываются различными по внешнему виду
функциями. Однако из этого правила есть и исключение. Для
рассматриваемого ниже так называемого колокольного мм
пульса форма исходного импульса и его спектр подобны.
Колокольным импульсом называется функция вида
У@ = ае'"™'^'-^—-^С/)- A11.37)
Импульс симметричен относительно начала координат, так
что его спектр содержит только действительную часть.
числяем этот спектр:
5(П=а"? е е (И-а 3 е И =
.-00 — <»
4а'' Ор [ 2т. Dг»)М
= 2ае ^ ^ И =
■ Л- -B.)'('<./+; ~^—\
4»'' оэ \ <я(« /
а '''' »
= 2ае \ е сИ = — е 1е их-
и гя о
-/'
е
2. К'
AП..З!^)
7й
Последний интеграл является табличным [2]. Если удоб-
К^'иметь здесь_ множитель, равный единице, то можно поло-
Ъ^ь й; = 2аУ к. В результате получилось соответствие
где
Ь =
2а
2а]/«,
-B™/)'
„-("/)'
A11.39)
5)
-(^
-0,02
Рис. 17. Колокольная функция (а) и ее спектр (б)
Как видно из A11.39), структура колокольного импульса и
р спектра одинаковы и их форма отличается только масш-
ными множителями а и Ь. Вид колокольного импульса и
[о спектра приведен на рис._^ 17. Название „колокольный"
'звано соотцотетвон1Ю форм^этого импульса.
При увеличении параметра а колокольный импульс
йся, а амплитуда его увеличивается. Одновременно его
ктр расптряется. При бесконечном увеличении а форма
'локольного импульса стремится к единичному импульсу на
емени ^ = 0, а его спектр — к постоянной величине — еди-
Це. Можно рассмотреть и обратны!! процесс—стремление
нулю. В этом случае удобнее положить а=1, чтоб|д
ектр стремился к единичному импульсу (одио11 гармонике
частоте ^ = 0), а колокольный импульс бесконечно
лся до постоянной величины — единицы.
3. Спектр сигнала с несущей частотой
Рассмотрим, как изменится спектр сигнала, если сам сиг-
1л умножить на гармонику постоянной частотыд/'Й^. т. е. про-
^дулировать амплитуду несущеГ! частоты А^ формо!'! сигнала
77
без постоянной составляющей. Такая модуляция называв'
„балансной модуляцией" [19]. Она упоминалась выше в вид
примера использования теоремы смещения спектра по част,
те (гл. II, §4, п. 4). Итак, рассмотрим спектр 51@ функцни
если
^г{^)-= ^;(Осо8 27:Д[/ 51(П.
С/@~5(П.
Используя известную формулу Эйлера, можно сигнал :M1
писать в такой форме
Далее, используя теорему смещения спектра по частого,]
можно получить выражение для искомого спектра в виде по-
лусумм1л спектров
(/,(()—5,(П = ||5(?-ДП45(Н-4/)]. A11.41I
I
Из выражения A11.41) следует, что при умножении
ной функции на гармоническую функцию частоты Ь.\, спектр
исходного сигнала расщепляется на два спектра, подобных
исходному и смещенных в разные стороны на частоту Д/^.
плитуды двух смещенн1>1х спектров одинаковы и равны
вине амплитуд исходного спектра.
Меняя „несущую" частоту Д/^, -можно смещать спектр
ходного сигнала по частоте. На таком принципе работают
которые конструкции частотных анализаторов. В этих
заторах одна половина раздвоенного спектра гасится филы-
рами, а вторая пропускается мимо остро-резонансного
ра ПОСТОЯННО!! частоты, вырезающего из спектра при его
ремещении отдельные частотные составляющие.
Рассмотрим далее спектр того же сигнала,
го синусоиду, т. е.
^гСП ^2@ - ^(<) 81П 2т:Д/^.
Рассуждая аналогично предыдущему, получаем
—5а(П = ^Г5(?-А/)-5(Г+Д01, (Ш.42)
где
ЦО—'5(Г).
78
|ёсли полученное выражение A11.42) помножить на у и сло-
ть с A11.41), то
5л(/) = 51(/) + /5,(/) = 5(^-Д/). (Ш.43)
)то соответствует обычиоС! записи теоремы смещения
нектра по частоте в комплексном виде.
* "Если несущая гармоника смещена внутри огибающей 1/{\}
время ± X, то вместо A11.43) будем иметь
Гак как А/ и т — постоянные величин1>1, то перв1IЙ миожи-
|ль е^^*"^-'^' представляет собою постоянное комплексное чис-
с единичным модулем, которое не оказывает влияния на
зоцесс вычисления спектра и создает лишь постоянное до-
элнительное слагаемое в его фазовом спектре. Поэтому
)жно записать искомый спектр в виде
[/^(/)__^±^2'^V^5(^--ДП=.|5(/• _Д^)|.е^'^<^'±*^^^^> A11.44)
Таким образом смещение несущей частоты относительно
)дулирующей огибаюп1,ей не влияет нфастотный состав
ала, т. е. его амплитудно-частотный~сТ1ектр при этом не
|еняется. Происходит лишь взаимное перемещение гармо-
\к, определяемое возникновением постоянного слагаемого в
|азово-частотном спектре ± 2тЛ^'..
4. Спектры односторонних косинусоиды и синусоиды
а) Односторонняя косинусоида-
При заполнении единичной функции о{^) гармоникой
|)8 2тг/^о^ получается функция
^/1@ = 0@соз2л[о^ = 1^^0527:/о* 001^ ^^51(П- AП-45)
1о ^-<0|
Спектр единичной функции в соответствии с (ШЛО) равен
'О - - — 8@ — / — • Умножение единичной функции на ко-
2 2я/
инусоиду приводит по A11.40) и A11.41) к раздвоению спект-
а, в результате чего он примет вид
A11.46)
Для односторонней косинусоиды, расположенной в об п.
сти^отрицательных времен, будем по аналогии иметь
=(.-1) 1з(/) + /_^,
^^^(п=^^^~[щ+!о)-^ч!^!о)^ + ^
+
а)
Со5 20Л ■ ^=^о»«
AП.4?
А-/31
ЦО'АУ-ЦП^Х/ о\/0,О2К/0,О^ Ьсек
-л?
о $0 /г«
' I
31
^
/ \/о.о1\/ш\/о \Дог \/ооч Х/Ьсе
.^0
ь-ЩфШ
Рис. 18. Спектры косинусоиды (а) и синусоиды (б)
Спектр полной ДВуСТОрО1ГН0Н К0СИНуС0ИД1,Г ПОП'ЧаСТСЯ 11
результате сложения спектров ее обоих половинок и равен
соз21г^„/ -6-(/) = 5х(/) + 5,(Г)=^^Ш«)--!-^^ЬМ_. A11.48)
Он'представляет собоГ! два единичных импульса
ной площади и одинаковой полярности, расположенных па
частотах косинусоиды ■;/„ симметрично относительно нули
(рис.* 18 а). ^
б) Односторонняя синусоида-
Рассматривая аналогичные операции для синусои-и.1 в соох-
ветствии^с (ШЛО) и A11.42) получаем
и.
,(_О-+=(-0з)п2::/„^=Г о />0 ] „ - .4
Ь1п2;:/„^ ^<0| '^'
, A11.49)
5^,^^-1_|е1Ж,ЬЧЬк)_у 1
чп^
{Ш
{[+/о)-Ч(-Го)
+ }
2" \ /+/„
Спектр полной двусто|)онней синусоиды
тектров баСП и ^аСП двух половинок, т. е.
A11.50)
равен сумме
18Ш21:1,1 5@=5,@+ 5,(/):^^у[г(/+^)-о([-/„)] =
^ =н-/!
ЧГг/о)
(/"-/о) 1 _ ГЧГ±1о)
ЩЧо)
-\-(А\''(^-т е \^=-^D^о^ е ^ч-
-(^ '-^Л/Л^
ъ^
AП.51)
.Таким образом сиоктр полной синусоиды представляет
рбой два единичных импульса иоловинноГ! илониади, распре-
реленпых симметрично относительно нуля на частоте
иды ± }о " имеющих иротивоио;южнук) полярность. Так как
пектр существует то.чько в двух этих точках ± /о. ''"о фазо-
ый сиект]) представляет собой также два значения углов
•Ь — па ЭП1Х частотах. Модуль спектра синусоиды совпадает
мо,хулем спектра косинусоиды, так что ЭТ1[ две
ческие функции различаются только фазовыми спектрами,
'пектр синусоиды мол<ет б1,1ть изображен условно .с-^а&том
"'Зои^!'^ ''век-таа в виде л,вух разнополярпых единичных им-
.ульсов на частотах ±[о> '^эк показано на рис. 18 6. Заметим,
1Т0 при вычислении спектров синусоиды и косинусоиды еди-
4ичп!>1й импульс В спвктре единичной функции оказался
обходимым и сыграл главную роль.
5. Спектры отрезков косинусоиды и синусоиды
В технических приложениях сигналы и в частности гармо-
1ические сигналы всегда имеют начало и конец. В связи с
*тим рассмотрим, как изменится спектр гармонической
ции, если из нее вырезать кусок определенной длительности,
".—358 81
причем для простоты примем, что этот кусок выбран с ис!1г.
ром в начале координат. Заполним симметричный относитель.
но точки 1 = О прямоугольный импульс единичной илощалм и
длительности Д- гармонической несущей частотой [о. При :!„.
полиеиии этого прямоугольника косинусоидой соз 25г'|'(, 1
сматриваемый сигнал имеет такой вид:
^1{^) = тес\{^-)■со$2^4^ —
'51(/).
Спектр этого сигнала может быть получен разными
ми: сверткой сомножителей в частотноС! области, из теоремы
смещения спектра по частоте и пр. Воспользовавшись
жением A11.15) для спектра вьфезающей функции гес1(Ат) ц
применив теорему о смен1,ении спектра по частоте (гл. II, §4),
или спектр сигнала с косинусоидальной несущей гармон! "
A11.41), получаем
^коа
5а(/)-
1 г з1пгДт(/-Ь/„)
2 г.Дт(/^+/о)
+
31ппЛ-(/-/о)
7сДт(/-/о)
A11.5::)
Это выражение легко и1)еобра;<уе1ся к такому виду
1
5,(/) =
-д-
■■(Р-11)
\151п-Л- / сойгА-
„—/„СОЙ 7;Д-/.ям1 тсА- ;^\.
(Ш.о.З)
косинусоид1^1, симметр!^!'
представляет собой де1Г
зависит от длителькост];
оба слагаемых в A11.52)
Таким образом спектр отрезка
ного относительно начала координаТ;
ствительную функцию, вид которой
вырезающей функции. При Дт-^'со
стремятся к нулю и только на частотах [ п --/у сох,раняет1;я
постоянное единичное значение. В результате при безграни':-
ном удлинении отрезка косинусоиды ее спектр стремится'к
двум единичным импульсам половинной амплитуды, располр-
женным на частотах I == ^- 1о AП.48), т. е. к спектру чисту!'
косинусоиды.
Рассмотрим частн1I11 случа;!, когда длительность отре,'
косинусоиды равна целому числу ее полуиериодов, т. е.
^т{М
Ат =
■п —
1-де п
1, 2,
целые числа.
AИ.
Подставляя это значение
преобразований, получаем
\т в
A11.53), после неслож!•:1^1^
5,(/)
2?о
2 Г
г 51П ' СОЗ —П —/о С05 «ЗШ —П
2 /о 2 ■'° 2 /о 2
Е 51П '■— I ■ СОЗ — П — СОЗ
2 2
•5Ш
■п
A11.55)
52
или
51E) =
( 1.
2е(-1)* . - ,
—8ш — п1 для «-четных,
т.п^^"—!) 2 '
2(-1) 2 г. .
——^ соя ПК для Л'нечетных,
-•«§2-1) 2
A11.56)
Для вычисления спектра отрезка синусоиды с симметрич-
вой вырезающее огибающс!! функцией используем соотноше-
1ия A11.15) и A11.42). Тогда, ^аналогично предыдущему, полу-
|аем выражение для искомого спектра:
2У
—5 (п = 1Г _«^-Д-(/+/о) _ «!п ^^-ч-Го)
—у
•-д^/^-^?) I
соз тЛ-\ .51п тсА- [„ - /"о 51п^-Дт[-С08 гА-:^^
A11.57)
^ Спектр получается чисто миим|,1й, так как исходный
ал кососимметричсн. Далее рассмотрим спектр с целым чис-
ом нолупериодов.^Подставив A11.54) ^^ A11.57), получаем
52(/)
2У
г.-гф—\)
зш — соз ^'05 ?-81П—- A11.58)
.2 2 2 2 '
В зависимости от четности числа вырезаннI1х полуперио-
|1,ов синусоиды п получаем
у . ^^ '> - 51п 9 Л;
5,(/) =
у-^<-'> 1 [соз"^.;
для я-четных,
д,;!Я /г-нсчетных,
A11.59)
[Где по-прежнему
Примеры спектров отрезков синусоиды и косинусоиды
приведены на^рис. 19 а, б.
83
а) гесЬЦ-п) Со5Ь:(л '!г^ г.ф
О.Ог 1сек -100^^ -50
02 I сег ■ 100
Рис. 19. Спектры отрезков коснпусоид!.! (а) и синусо'иды (б).
6. Спектр затухающей синусоиды
Выражение для спектров квазигармоническпх импульсов в
виде экспоненциально возрастающих и затухающих синусоид
и косинусоид можно получить из формул для спектров
личных комбинацт'1 экспоненциальных функций и формулы
для спектра сигнала с несущей частотой. Ограничимся
смотрением спектра затухающей синусоиды, имея в виду, что
другие варианты экспоненциально возрастающе — затухающих
гармонических импульсов вычисляются аналогичным образом.
Итак, рассмотрим спектр сигнала
^@
_[ о ^<0)
5@,
A11.E0)
где а>0.
Используя A11.33) и A11.42), получаем
5({) = т
2--2У
1
1
1^-^Л/Чо) '+К1+оП
Ат.г-
^Ч(/-?о)^
^+{/ +
^0~'('
?-/о
'''+(^-/о)'-
(Ш.61)
84
После простых преобразовании имеем
1 Гок + /1-[']-У2«^
5(П-
2" (а2+/2-;2J^4.р
|5(П1 = :^-
!о
^'^ У[12^,^-{1Уг4.гр
С08<?( ) =
2а/
К (»='+/? .-/^)Н4.^'
A11.62)
A11.63)
Пример экспоненциально затухаюпшго колебательного им-
1ульса и соответствуюи1,его ему спектра приведен на рис. 7.
■ж
7. Спектр импульса Берлаге
Импульсом Берлаге в сейсморазведке называется возраста-
ще-затухающий гармонический импульс, описываемый выра-
ением [3, 4]
иц)
1е '"'81п2-/о^ ?>0.
О ^<0
A11.64)
В результате исследования формы сейсмического сигнала,
•I в частности области его начала (область первого
ния волны), было установлено, что начало записи волны име-
гт плавный непрерывный характер. В те же время анрокси-
нация этой волны внезапно начинающейся затухающей
соидой, односторонней синусоидой и пр. неминуемо нриво-
а,ит к разрыву скорости. Предложенная Берлаге формула для
апроксимации волнового сейсмического импульса дает
рерывное гладкое возрастание амплитуды сигнала в
ный момент времени и поэтому более подходит для его
мации аналитическим выражением.
Вычисление спектра импульса Берлаге произведем в два
этапа. Сначала вычислим спектр огибающей (без гармоники
заполнения), котор)>1й может представлять самостоятельны!"!
интерес. Дальше по теореме смещения спектра найдем спектр
с гармоническим заполнением этой огибающей.
Используя выражение спектра односторонне затухающе,;
экспоненциальной функции A11.33) н теорему о производно|1
спектра (II.62), можно сразу записать
<71@ = *е'
^5х(П
_ й8(^)
- ^ / 1 \ ^ (-1) (-1)
ат^П I 2г(а+,7) ) BгJ (^-ь/-
-1)
-Ь/7)^
1^
(«+/[)*
(Ш.().5)'
Таким образо.м для 01'ибающе11 импульса Берлаге
ем спектр в виде
1
т
51(П =
1
B-J а2-{2+у2а/
27{
(-=-№+4''Р
(а2_^ 2J..|.4,2^ 2
A11.66)
2^/'
С08?х([)
/" (а^_р)-' + 4«'/-^
A11.67)
Используя полученное выражение A11.65) н теорему смг-
п;ония спектра по частоте A11.42), .можно получить компле1СС-
ное выражение спектра импульса Берлаге
5Ш ---^[51(/ + М--5,(/--Ь)] =
B^)-2у [\а+,\1^Щг. [.+/(^_|„)].
A11.68)
Далее обычи1,1ми алгеб|)аическими преобразованиями
деляется действительная и мнимая части комплексного сиек1-
ра A11.68):
1 2/'о(а4-//') _ 1 2/о(о.+Л) _
5(П-
B..)- [(..нЛ)'+/^о]^ Bг.Г [„,+|2_^.^.,,^|.
Bг)'
[(-+/,!-Г)'+4-?']
A11.61')
86
Выражения для модуля и фа:I,1 комплексного спектра
111.69) привод';ть не будем из-за их громоздкости. Они могут
ыть рассчитаны по известным дейстпительной и мнимой
стям. Пример импульса Берлаге и его спектра приведен
,|)ИС
20.
на
<=^)
иЦУ-ЬГ^'^ЗспЯЩ
^
ч(='г,5-
Рис. 20. Импульсы Берлгпс (а) и их спектры (б).
§ 3 СПЕКТР СЕЙСМИЧЕСКОГО СИГНАЛА
1. Понятие О многомерном спектре.
До слх пор рассматрива,;1ся сигнал одной переменной —
времени Л Фурье-трансформанта которого оказывалась функ-
щие]г1 также одно'йеременной частоты. Для описания физичес-
|ких процессов часто оказывается необходимым рассматривать
[■сигналы нескольких независимых переменн1>1х, например вре-
'мекн Ь и координат пространства х, у, г. По каждое! из этих
переменных функция может быть подвергнута
нию Фурье, причем при преобразовании по пространственным
координатам х, у, г Фурье-трансформанта становится
цией волновых чисел, соответственно:
/_ . _ _[_ .. — 1_
У-х '^ ,"/ > /.V —■ 1/ ' У.г
V,
V
A11.70)
х> ' у. \/г~ ^^°'^"*'"^^^'^^^'^ скорости по координатам.
где У^, V ■_
Произведя преобразование Фурье по всем независимым
переменным многомерной функции, мы приходим к понятию
многомерного спектра этой функции. Для формального
сания многомерных спектров физическая сущность
ных несущественна. Поэтому будем исходить из обобщенного
вида преобразования Фурье, где переменным сигнала и
ра не придается конкретного физического содержания.
Если функции ^{x) и Р(х) связаны преобразованием Фурье,
то
д(х) Р(/.), ^—^х,
87
т. е.
—00
Р(-,)^ I ^(к)е ' их
- 00
(П1.71)
Фурье-трансформация многомерной функции ^{x, у, г)
жет быть произведена по каждой иа переменных {х, у, г), в
результате чего может быть получен многомерней спектр
Р{^х> ''■г "^г)- Ограничимся двумерным преобразованием Фурье
в координатах (х, у)—- —(л,, -/у), имея в виду, что его
пространение на большее число координат можно
ти аналогичным образом чисто формально.
Рассмотрим функцию двух переменных ^{x, у), где х и у
могут быть переменными любой физической породы, но для
определенности будем считать их расстояниями. /]Цвумернос
прямое и обратное преобразокание Фурье записывается
дующим образом:
00 00 \гх{г. к4-' у)
Я{х, у)= .1 1 Р{у;.,у;)е' ''■ ^У^аг^ёу.^.
— 00 —ж ^
■' —<х> — 00
{111Т2)
Двумерная Фурье-трансформанта Р{у-^(, '■у) является
цией двух новых переменных, по размерности обратных
менным X я у и имеющим смысл волновых чисел
ственных частот). Функция /'(/д-, Уу) представляет собой
мерный спектр двумерного сигнала C(л;, у). Обозначим дво!'!-
ное Фурье-преобразонание двумя двусторонними стрелками:
^^x, у):=Р(-/,, Уу). @1.73)
Основные свойства двумерного преобразования
ны свойствам одномерного преобразования и могут быть
лучены точно таким же способом, рассматривая двумерныГ)
сигнал последовательно как одномерный сигнал по одной, н
затем по второй переменной. Так, например, если
^^x, у)г=г-Р(х,,, /.у)
дх
дЯ(х, у)
ду
дЧ1(х,у)_
дх ду
^х,у{У-ху У-у)
(П1.74)
88
о при нулевых начальных условиях
Рхр-х> '■у) = (/2'^)= ■*-х• ■'у ■ Р(-^л, ''у)
(III 7Г)>
■' Наибольший практический интерес имеет операция свер-
"-.шания для двумерных функций, т. е. теорема произведения
.вумерных спектров. Если имеется соответствие
Л(х, у):=-гРг(-'^л-, ■^у)= И(?,(.г, у)е"'"^'''"^"'''^сгх^у, A11.76>
' —00
C(х, у) :гг=т Р(>с,^, ■'■у) = Рхк'-х, ■^у)-Р2(\' '"у)'
(?(.V, у) = и Р,{ X - с, у - ■п).р,{^, т)) сгИг, A11.77)
о
Смысл этого соотношения вполне аналогичен смыслу со-
этветствующего одномерного интеграла сверт1Iвання. В свя-
и с двумерностью рассматриваемых сигнала и спектра мож-
о говорить о плоскости сигнала и плоскости спектра и изо-
^ажении сигнала и спектра в виде рельефа на
ющих плоскостях. Преобразование Фурье осущсствлаёт
ражение одной плоскости сигнала в другую плоскость. Ёс-
й~число переменных у сигнала и спектра больше двух, то
ожно говорить о многомерных плоскостях или объемах.
Функции нескольких переменных, которые можно пред-
тавить в виде произведения функций, зависящих только от
дной переменной, называются фун.вдид^д.С^1а34^М1ШШ^111.-,
я леременн1,1ми или сепарабельными функциями*. Например,
ели ^{x, у) — функция с разделяющимися переменными, то
3 можно представить в виде
^^x, у)=^^г^x)■^,{у). {ш.щ
Если двумерный сигнал представлен сепарасельной функ-
ией A11.78), то его двойной спектр также разбивается на
ва со>!пожителя, т. е. также является сепарабельным. При.
гом сомножители сигнала и спектра попарно связаны одно-
ерным преобразованием Фурье:
^1(X) Р,{-^х); 0,{у)—-Р,{-^у)
* Ле ЗерагаИоп — нем., ьсрагаНоп — англ. — отделение, разделение.
Й9
00 со ; о-ггу V *— Иху. V
— 00 —00
-Р^'х)-Р,{\)- (.79)
Различные многомерные функции могут оказаться сеиара-
•бельными в различных системах координат. В приведенном
.выше соотноше1Л1И A11.79) имелось в виду, ч?о х и у, а так-
же Хд. и -^у образуют прямоугольные системы координат, так
что функция A11.78) и ее спектр A11.79) сепарабельны в прн.
моугольной системе координат.
2. Представление сейсмического сигнала на пространственно-
временной и частотно-волновой плоскостях
Сейсмические волны, как и иолигл любой природы,
пространяются с течением времени в пространстве. Поэтому
для описания явления распространения сейсмической волн1,1
в пространстве в общем случае приходится рассматривать
четырехмерные функции с четырьмя переменными: временем
I и координатами пространства х, у, г. В результате
ческую волну можно рассматривать как четырехмерный
нал, которому соответствует четырехмерный спектр: по ча-
■стоте / и по трем пространственным частотам (волновым
слам) х^, у.^,, -/.^, соответствующим трем пространственным ко-
• ординатам х, у, г. Для простоты рассмотрим
ние следа фронта плоско!! волны вдоль оси х со скоростью
1/^. Аргумент этого волнового процесса является функциен
двух независимых переменных: времени I и расстояния х, "
волновой процесс может быть представлен в таком виде:
^//'^_-М = С/A/^-х). AИ.80)
Заданная точка среды (х=сопз1) колеблется около своего
среднего положения во времени, и функция G@.
щая это движение, называется формоГ! волны. В заданнь!!'
произвольный момент времени (^ = сопя!) волновой процесс
С(—х) описывает отклонение точек среды в данный мом(М1Т
В1)емени. Эта функция называется профилем волны.
При рассмотрении пр(Л1,есса распространения волн1л вдоль
.чинии наблюдения х суи1,ественными является поведение скО'
рости вдоль х- В простей1пем случае волна движется вдо.'И'
оси X с постоянной скоростью, так что в A11.80) V — это чо-
^стоянная истинная скорость. Если ось х, вдоль которой иа-
■ЙО
дюдается волна, не совпадает с направлением ее распрост-
анения, то плоский фронт волны распространяется вдоль
'"ей X с постоянной 1<:ажуи1ейся скоростью, всегда большей ис-
йнной скорости. Кажущуюся скорость принято в сейсмораз-
зедке обозначать звездочкой.
Из понятия кажущейся скорости следуют связанные с ним
оняти,р кажущейся длины волнь! ).*, кажущегося волнового
'исла X* и кругового волнового числа V*. В результате, и.меем
ледующне соотношения
еличинами:
V
между истинными и кажущимися
V* г=
V
51П;
V*
созе
Х*= У*-Т,
= 2-/*
A11.81)
|р — угол между лучом волны и линией наблюдения — назы-
I вается углом выхода волны,
§■—угол падения волны на линию наблюдения, является до-
пол^[ительным к углу е. При постоянной истинной
сти V, плоской волне и прямолинейной линии
ния все величины в A11.81) являются постоянными.
В случае необходимости приведенные выражения для вол-
чы вдоль оси X могут быть распространены и на волну в
трехмерном пространстве. Для плоской волны вместо х
дует написать длину пути волны в пространстве в виде
мали, опущенной из начала координат на плоскость фронта
^олны:
г = X С05 я-|-у С05 Р -Ь г С05 7, AИ.82)
»-;№ а, р, 7 — углы вектора г с осями координат;
X, у, г—координаты конца вектора г.
Тогда плоская волна в трехмерном пространстве запиншт-
ся в виде
где г определяется по A11.82).
Если 4'ронт этой плоской волны параллелен какой-либо
13 осей, например у, то ,3 :-1 ~ , соз р = О и
г — лгсоз а-|-гсозтс- A11.84)
Если фронт параллелен двум осям, например у и г, то
аналогично получаем, что С08р = со8 7 = 0, а С05а=1, так что
приходим к линейному случаю г = х. В дальнейшем для
стоты будем рассматривать главным образом линейшлй
чай.
Страницы 92-93
в данном экземпляре кннгн
отсутствуют
Подставим этот результат в A11.86) и заметим, что часюг
Iый спектр 5,A^, х) A11.87) остался функцией расстояния х,
которое входит только в -.
Применяя Фурье-преобразование (х-—->-/.), находим вод,
НОВО!'! спектр исходного сигнала:
5(/, /)= .1 5^(})-е -е их =
—00
= 51(П } е Aх==
—00
Здесь о(-/) — единичны!'! импульс, а -/-х — волновое число,
ответствующее конкретным значениям скорости V сигнала и
его спектральным составляющим. При V = сопз! ^^
нально частоте спектральн1Iх составляющих сигнала.
В результате получаем двойное преобразование Фурьг
для идеально регулярной плоско;! волны:
где
8Ц,-^)^Ч1)-Ч-'--ч), A11.89)
5,(П и -.1=1
Идеально регулярная плоская полна на плоскости (х, О
об^зазует цилиндрическую поверхность с осью, определяемо;!
уравнением
I —- = I,-- С0П51,
V ^
или
Наклон этих прямых к осям координат х и (
ся значением кажущейся скорости V* волны вдоль линии
блюдения
— =1/^ A11.91)
Параметр ^, определяет начало отсчета времени и
сматриваемую фазу волны. Для первого вступления прямо11
волны /1 = ~ О, если д; и 1: отсчитываются от источника. Д.'*'
последующих фаз прямоГ! или глубинной волны при д;=0,
^=^^ — значение времени прихода волны в точку наблюд''-
ния.
94
Независимо от наклона оси сиифазности волны растяжение
10ЛНЫ по оси времени будет постояннным, определяемым
тественной формой волны. "
юй формы, прип1едшие к
[сущимися скоростями I/*
1енно-временной плоскости
г
Иными словами, волны одинако-
линии наблюдения с разными ка-
1/*, будут иметь на простра!!ст-
разные наклоны оси спнфазности
-)
<0
005 01 0M 1с<^:<
I ' ■ ■ ' 1
50 ЮО 150 200 /гч
^,- -уК = 0,2 Юс^.к « '; 0 = .'Л:,?0О5юЪек /,..-
Рис. 21. Идса,1Ы1о-рсгулярные волны (а) п и.х лкумерные спектры (б).
оси цилиндрической поверхности рельефа), но одинаков1>1е
-представления, т. е. одинаковую форму волны. В связи с
-ТИМ, разные наклоны оси синфазности, соотвстствуюн1,ие раз-
1ЫМ кажущимся скоростям, будут давать разное растяжение
1рофиля волны (х-представленIя) (рис. 21 а). При увеличе-
1ИИ кажущейся скорости направление оси синфазности
ближается к оси X и профиль волны растягивается. При приб-
1ижении кан<уп1ейся скорости к бесконечности профиль вол-
дЫ растягивается до бесконечности. Это обозначает, что х-
":ечения (параллельные оси х) проходят вдоль оси сннфазно-
.=ти по ее постоянным значениям. При уменьпгении
ся скорости и ее стремлении к истинной скорости профиль
^олны, даваемый х-сечепием, сокран1ается и стремится к
ютинному профилю волны вдоль луча. При этом наклон оси
синфазности стремится к направлению, соответствующему
тинной скорости распространения волны.
Отметим, что вертикальная полоса на плоскости {х, I),
раниченная значением времени ( ~^I, соответствует записи
-ейсмограммы в интервале времен 0<^<г?1. Горизонталь-
1ая полоса, ограниченная значением х = Хх, соответствует
/частку профиля (линии наблюдения) в пределах 0<д:<а:1.
95
Рассмотрим теперь, как этот же самый идеально регуляр,
ный плоский сигнал будет выглядеть в виде двумерного
-спектра на частотно-волновой плоскости (^Э0-
Из A11.89) следует, что частотный спектр сигнала опреде,
ляется первым множителем, который не зависит от кажущец.
оя скорости и волнового числа. Эта спектральная функция
(частотный спектр сигнала) представляет собой инлиндричес.
кую поверхность с осью, параллельной оси волновых чисел
/. Все сечения этого рельефа плоскостями, перпендикулярны-
ми оси у., будут давать одни и те же частотные спектры
нала. Сечения, перпендикулярные оси частот / и
ные оси цилиндрической поверхности, будут давать
ные величины (рис. 21 б).
.фактор распространения волны с кажущейс$^ скоростью
V* определяется вторым множителем A11.89), который
ляется единичным импульсом и отличен от нуля только при
равенстве нулю его аргумента. Таким образом этот
тель описывает плоскость Aт~5с), нормальную к плоскости (?,/.)
и образующую след пересечения по линии
V. -^- = о
у*
или
1
ф;!-ё!- (Ш.92)
Наклон э'юй линии к осям координат I и /. определяется
обратным значением величины кажущейся скорости волны,
т. е. градиенто.м времени
ё. A11.93)
а! "~ V'- ~
Пересечение плоскости 5|х ^^-) с цилиндрическое! ип-
■ О \ V*]
верхностью ЗхЩ) образует сечение, проекция которого и;^
вертикальную и^Iоскость /-= О образует неизменный частог-
Н1,1й спектр воли1,1. Проекция этого же сечения на
кальную плоскость / = О образует волновой спектр сигнале,
положение и растяжение которого определяется
ем секуще!! илосскости 5. Чем больше скорость, тем меньпю
наклон секущей плоскости о, тем более сжат спектр по
новым числам. При V* =: оо (§• =0) плоскость 8 проходит по
оси / и волновой спектр стягивается в вертикальную линию,
выходящую из начала координат. При уменьшении скорости
волновой спектр растягивается и смещается в область боль-
]иих значений волновых чисел. Это понятно, так как при
изменной частоту / увеличение скорости приводит к
циональному у^е^ъИ1[ению длины волны и, стало быть, 1^'
96
■!<'-]у положение котороA определяется кажущейся ско-
V*/
■еньишнию соответствующего волнового числа. Проекция
^ения на плоскость /—О будет соответствовать двойному
.ёктру сигнала в форме A11.89). Таким образом двумерный
*ектр идеально регулярной плоской волны представляет со-
эй сечение цилиндрической поверхности 51(|') плоскостью
^тью волны.
Такие сечения изображены на рис. 21 б.
V Дри одно.м и том же частотном диапазоне, но при разных
ажущихсн скоростях, например при рассмотрении разных
ре выхода одной и той же отраженно11 волны, волны с
ольшими значениями кажущихся скоростей группируются па
^стотно-волновой плоскости в области меньших значений
рлнового числа /. и обладают более узким волновым сиект-
5'м (вследствие большего растяжения профиля волны). Если
ксматривать волны различных типов, то низкоскоростные
Ъмехи, обладающие обычно более низкочастотными
рами, по сравнению с полезными отраженными волнами,
руппируются блинке к оси волновых чисел и в области низ-
их частот. При нанесении ,областей существования" полез-
ых волн и помех на плоскости ([, у.) наглядно видно, каки-
ш параметр|ми должна обладать аппаратура, осуществляю-
дая селекцию волн.
■ Полоса Д/, параллельная оси ■/., соответствует частотному
Шапазону, а полоса Д-/., параллельная оси (, диапазону вол-
ов1Iх чисел (пространственных частот) для сигналов на всех
ременах ^ и во всех точках наблюдения х. Сектор, образо-
анн1.п[ двумя прямыми, выходящими из начала координат,
)граничивает соответствующий диапазон градиентов и кажу-
дихся скоростей для всех волн сейсмолснты (или
го разреза).
Как отмечалось выше, дискретность сейсмических записей
"по X с шагом между каналами Ах, приводит к
сти спектра по волновым числам с периодом Дх = — .:
Следует также иметь в виду, что амплитудно-частотньи!
спектр располагается симметрично как для частот, так и для
|волновых чисел обоего знака, и поэтому будет симметрично
эасположен во всех четырех квадрантах системы координат
1/, ■/). На рис. 21 б показан только один 1свадрант.
Посмотрим, как изменение амплитуды волн[>1 вдоль линии
наблюдения х отразится па ее двумерном спектре ]26, 27].
Представим регулярн[.1й сейсмически!'! сигнал в виде A11.85)
и запии1е.м общую форму его двойного преобразования
Фурье:
§(/•, у.) = 1 Г а{х)-и,(( - —") е~''^'^' е'''^'"аШх. A11.94)
7—358 97
Найдем сначала частотный спектр, т. е. выполним преоо-
разование { — - /:
= а(х)Т ^Л^ — ■^)е~'^^'^' с1(^а{х)-8,{})е~'^''^\ {111.%)
где - = ~, а 51(/)—частотный спектр сигнала (У,A).
ченное выражение подвергнем преобразованию (х - - х), имея
в виду, что в A11.95) множитель ^^(х) не зависит от х:
^)
В полученном выражении Ь{у.)-^—^ а{х)■
функции а{х), а лу———отноитение заданных значений с;:о-
ростн и частоты сигнала. Полученное выражение A11.96) а; г)-
логично спектру идеально регулярной волны A11.89), рассм.^г-
ренному ^з<^^№|йд^ядуш,с^к^ротдоле. Разница заключается в тс.\;,
что вместо ед^шйчного импульса, определяющего секущую
плоскость, в данном случае спектр 51(/) сигнала Й'хСЛ
ется на волновой спектр Ь с тем же волновым аргументом
|х —— У Частотный спектр5](/) по-прежнему образует
дрическую поверхность с осью, параллельной оси х. Волно-
ш
тоянном значении аргумента.
вой спектр Ь (х -] имеет постоянные значения прр
образующего линии
С0П81 = С,
V
у + С, A11.97)
аналогичные следу секущей плоскости в случае идеально ?''"
гулярпой волны. В результате этого волновой спектР
ь(у.—^]образуст цилиндрическую поверхности, направлеииб?
98
ки которой определяется скоростью V по соотношению
В1.93). Двумерный спектр образуется пересечением этих ци-
дандрических поверхностей н поэтому является объемной
кигурой, а не плоской, как в случае идеально регулярной
,олны. Пример изображения регулярной волны на плоскости
^, Щ и нх спектров на плоскости ([,«) приведен на рис. 22,
а)
а(х] - ^Ш
3(и)-2,({L(зг-^)
^■■
/
о 005 0,1
\/*=5.000» сек-
а=1/'/^-0,2Ю'сек м->
Рис. 22. Регулярная волна (а) и ее двумерный спектр (б),
11ирина спектра функции регулярности может быть исполь-
рвапа для оценки степени регулярности волны. Чем уже
рот спектр, т. е. чем уже поперечное сечение соответствую-
Ьей ему цИ'Линдрической поверхности, тем регулярнее вол-
К, т. е. тем более постоянна ее амплитуда. Наклон оси по-
йхности волнового спектра Ь определяется обратным значе-
№м кажущейся скорости и уменьшается при возрастании
Ш При V* - 00 эта ось совпадает с осью / обе цилиндричес-
ре поверхности пересекаются под прямым углом, и фигура,
)бразованная их пересечением представляет собой спектр
8{1г.)==8т-Ь{-^). A11.98)
Как следует из A11.85) и A11.9^, при 1/* = оо регулярный
ргнал и его двумерный спектр являются сепарабельными
фикциями, т. е. функциями с разделяющимися переменными.
Р^тальные свойства двумерных спектров регулярной волны
Йалогичны спектрам идеально регулярной волны.
I, В частности, при дискретно!! волновой картине по коорди-
^те X, спектры оказываются периодическими по переменной
В области 1^ также располагаются более высокоскоростные
99
(например отраженные) волны, а в области оси / — более ннз-
коскоростн1>[е волны, которые обычно оказываются помехами
(поверхностные, кратные отраженно-преломленные волны и
др.). При изображении на плоскости (^, /) областей
вания полезных волн и помех можно наглядно представить,
как должна переходить граница между областями
ния и подавления, т. е. какими параметрами должна
дать аппаратура, осуществляющая селекцию полезных волн.;
/
§ 4. СВЯЗЬ МЕЖДУ АМПЛИТУДНО-ЧАСТОТНЫМ
И ФАЗОВО ЧАСТОТНЫМ СПЕКТРАМИ СЕЙСМИЧЕСКОГО СИГуАЛА
I
I. Связь между действительной и мнимой частями
комплексногоухигнала. Понятие о преобразовании Гильберта
В сейсморазведке сейсмические волны,
ственными источниками, всегда имеют „начало". Поэтому
всегда можно так выбрать начало координат (времени или
пр"бстранства), чтобы весь сигнал располагался в области
положительных значений аргумента, и выполнялось бы
ловие
^{^)=-0 ^<0. A11.99)
«
Именно такую функцию, удовлетворяющую условию A11.99),
мы будем в дальиейп]ем называть сигналом.
Ранее (гл. II, §3) указывалось, что любую функцию-в
ответствии с соотношениями A1.48) и A1.49) можно
вить в виде суммы ее четной (симметричной) и нечетной
симметричной) частей.
При этом четная часть сигнала
^^(^)=.^т±Ч(IЛ^=.и^(^_^) ац), (Ш.юо)
имеет своей Фурье-трансформантой действительную часть
комплексного спектра, а нечетная часть сигнала
у^(^)= ^(^>^^(-0 ^ _ ^^(__^) ^вф A11.101)
соответствует мнимой части комплексного спектра сигнала,
так что
^(^) = ^x^) + ^«(^) ^—> $(/) = Л(/) - /5(/). (Ш. 102)
Отсутствие сигнала при отрицательных значениях
та, выраженное условием A11.99), обусловливает связь
четной и нечетной составляющими сигнала.
100
На оис B3 а) показано, каким образом сигнал ироизволь-
й формы, удовлетворяющий условию A11.99), может быть
едетавлён в виде суммы четной п нечетной составляющих.
1 (Ш 100), (Ш.101) и рис. 23 а становится ясным, что функ-
1К а (О'^^-^лШолР^^'З^а^ш^^ между собою и зная'од:
{з'них^ напрймер^_^[/^^^^_можно■ полное определить
щ
Ц}'и^(Ь)*иМ
и.1ь>^а^
Рис. 23. Представление функции в виде суммы
четного От (О и нечетного 1) н (^^
мых: (а)—односторонняя функция;
ронняя функция
{/„(О- Для этого нужно ад.вуао._аа.стк-.ФХнк1Щи (/^.A),
женную в области отрицательных значений I, перевернуть
„вверх ногами",", т.;е,^^ерк^льно отразить в оси абсцисс 1. Это
можно осуществить умножением ее на знаковую функцию
81дп(<) (см. гл. III, §1, п. I). В соответствии с A11.1) и A11.9)
знаковая функция имеет следующие определение и спектр:
1 1>^\
5 {81^п (^)! = -}.-^-\—У A11.103)
818П@ =
О /=0
-1 ^>0
г-\
Таким образом нечетную часть сигнала можно выразить
через четную часть умножением последней на знаковую
цию:
\и^{1)-%\^Щ).и,{1У\
A11.104)
101
Аналогично четная часть сигнала может быть получена а
результате умножения нечетной его части на знаковую функ
цию, т. е.
аД1) = 51ёпA)Л*[;„0). {111.105}
Характерна полная симметрия преобразовании A11.104) и
A11.105). Однозначная связь между четной и нечетной
ляющими сигнала естественно влечет за собой однозначную
с'йЯВ^ЁПйёжду действительной и мнимой частями его спектра.
При этом временные соотношения A11.104) и A11.105)
разуются в частотной области в соотношения свертки межл\
соответствующ,ими спектрами. В результате можно записать
уравнение связи между действительной и мнимой частям1!
спектра сигнала, т. е. функции, удовлетворяюш,ей условии»
A11.99):
-/б(П-5{81§п(ОиЖ0. ' AИ-106
Симметрия преобразований A11.106) является следствием
с^иметрии преобразований A11.104) и A11.105). Далее остаетс!
|^^|(щ:,ат)ь., свертки A11.106) более подробно в виде интеграль
:»й!^;,;1г#Щб|>4з<:^ва.иий. В соответствии с теоремой о произведе
1ги'"т^т\"-^]?<<^^|-'^^^^ интеграла сверх
киД11.77).соотарш||114р^ (ЩЛОб) получаем:
. ^п -00 /-.^'^М'
СШ.ю?;
Ш,~~1 Т М)
^ -^;»^■^^'=--г^:.-^■^А.(ПI.108
/т ^лй"^^"*^""^^ пард:интегральных преобразований A11.107) ы
AПЛШ) ставит в^ однозначное соответствие
ции А(^) и. ВЩ-Эу.а,Я№^щ^лльте преобразование называется
преооразо,ван4е^I'^^^щ трансформацией Гильберта [8, 11].
'Рункцищ, связанные между собой преобразованием Гиль-
оерта,.часто называются сопряженными по Гильберту функ-'
диями>
.,. Хак-им образом тщдсформации Гильберта в частотной об-
■■'?Л?!?^соответствует операция умножения сигнала на знако-
§№„М.н{сцию во временной области.
т
Из сказанного следует важный вывод, что функциям,
удовлетворяющим условию A11.99), т. е. равным нуЛю"'при
рицательных значениях аргумента, соответствуют комплекс- :
^•ые Фурье-трансформанты, действительная и мн»мая часть.|
которых связаны между собой преобразованием Гильберха,. I
Если условие A11.99) не выполняется, то между 0,^) и(У„(/)'
однозначной связи нет. Следовательно и в спектре Л({) и Щ)
оказываются независимыми (рис. 23 б).
2. Понятие об аналитическом сигнале
Аналитическим сигналом называется комплексный сигнал,!'
действительная й'Тйним'ая"части которого связаны преобразо-| \
ванием Гильберта. Пусть имеется действительный сигнал в
виде функции времени и{(). Тогда можно определить
женную по Гильберту функцию У@, так что
у^^^^1. 7 -Ш±а.; иц)^-1. Т -^с1^. (Ш.шэ)
*^ т: —оо ^—x п — 00 (—X
Из сопряженных по Гильберту функций и{{) и 1^@ можно
составить комплексную функцию времени
Щ^)='^{^)+/V^п, (Ш.ио)
которая и будет представлять собой аналитический сигнал.
Как всякую комплексную функцию аналитический сигнал
можно представить в виде
Г(^)-а(Ое^''^-о@со5'Ф) + /а@81п'Ф). (ИМИ)
где ^^
A11.112)
я
уи)-аЦ)81ттп I
1^1/A) = ^.
A11.114)
В этих выражениях д(/) —модуль, а'1^/) — фазовая
ция аналитического сигнала. Исходный сигнал ^{^) в
ствии с A11.112) может быть представлен в виде двух
телей—амплитудного а{^) и фазового со8Щ{). Цо свойству
модуля комплексной функции амлллхудиьШ . множитель а({)
является огибающей для составляющих, аналитического
нала С/({) я УЩ. Кроме Т|рро, вследствие однозначной связи
между и{{) и V{^), д{^) иТ/ГО также однозначно связаны
ду,собой, в результате чего исходный сигнал С/@ может быть
представлен любым другим сигналом V(^), а{{) и 'Щ{).
103
Наибольший интерес представляет использование сигнале
ац) и 1Н:п-
Сигнал а(() представляет собой положительную функцик,
огибающую исходный знакопеременный сигнал (-/@> такт,
он- является более плавной и простой по форме функцией
которую можно использовать для сопоставления волн (во.!
новой корреляции), автоматическо!'! амплитудой регулировк
сигналов, оптической обработки и других операциС! по обр^
ботке се11смических иаблюдепи!'!. Представляет интерес п ф-'
зовая функция 'VС^), также содержащая в себе всю информ;]
цию исходного сигнала ^{^). В главе I отмечалось, что в со
ответствии с A.25) и A.26) обычную частоту ( гармоиическоп
сигнала можно рассматривать как производную по времен!
от лине^шо надрастающего со временем фазового угла. Есл1
фаздвый"угол ЩО является более сложноГ! функцией време
ни, как это имеют место в фазе аналитического сигнала, тс
производная фазы по времени уже не будет постоянной ве
личиной, а окажется функцией времени. В связи с этим мож
но ввести о^бщенное понятие частоты каЛ производной ф.
-З^в^ГР—З^^ГУ"* 1^^ 5?^"^^*^**' которая окажется переменной во
ВД®И.ели..8еличино11. Для каждого заданного момента времен!
эта "частота называется мгновенной частотой. Таким образов;
.аналитический, сигнал Щ^) и исходный действительньш сиг-
щл Щ() могут |0ыть охарактеризованы мгновенцой частотой
(III.! 15)
Эта мгновенная частота является функцией времени, и
этому обладает собственным частотным спектром. Она
жет быть использована в качестве функции, однозначно
сывающей сигнал ^^^^) и представляюще!! этот сигнал в
цессе его передачи 1г обработки B5]. Аналитически!'! сигнал
можно рассматривать как обобщение комплексного
ческого сигнала. Так, в частном случае при
С{0 - соз2-;/
получаем .
1Д0 = 2-//', Г=сопя1; 1/@ " %\x\2т.^^,
й@ I, Щ1)-- <:о%Щ^^^ ]ъ\х\1-\\ - с'''^^^. AП.П6;
Действительны!! гармонический сигнал ссу&Ч-пЦ в этом 1,мые-
ле является частным случаем действительного снгна.гта ^{^).
Проведем аналогию между комплексным (аналитическим)
сигналом и комплексным спектром. У спектра сопряженность
по Гильберту де!1Ствительной и мнимой частей Л(/) и В(})
лялось следствием условия A11.99), по которому сигнал для
104
Страницы 105-106
в данном экземпляре кннгн
отсутствуют
Вид функции 1п=(^( показан на рис. 24. Это острый
,.^г на частоте !,^!, который приближенно может быть
"?апоксйМирован единичным импульсом. Поэтому выражение
(Ш 126) может быть заменено приближенным соотношением
,(П==1Т'^>5(Г,-Пс^/. (-127)
т. -оо /I
■пф
Рис. 24. Функция
1п
I 1-5!
"ИЛИ
^@
Г«^0
A11.127)
Таким образом фазово-частотиый спектр сигнала
женно.пропорционален логарифмической крутизне
но-частотного спектра и обратно пропорционален частоте.
ЛИТЕРАТУРА
А-
-Л-тбеков Г. И. Теория л1И1еп}1ых электрически.х цепеГг. «Советское
радио». 19Ж^
II 2\^Р°^тейн И. Н., Се ме и дя ев К. А. Справочник по математике.
113Д 4-е «Гостехтеорнздат», 1954.
•5. Гамбурцев Г. А. Основы сейсморазведки. «Гостоптехиздат», 1959.
4. Г
5. Г
УРВнч И. И. Сейсмическая разведка. Изд. 2-е. «Недра», 1970.
..„, г/'г'''„"^Р М. Ф., Берне Дж. Л. Переходные процессы в линейных си-
.те.мах Изд. 2-е. «Физматгиз», 1961.
О- 1 уд мен Дж. Введение в Фурье-оптнку. «Мир», 1970.
1П7
7. Джексон Д. Ряды Фурье н ортогональные полиномы «И. Л.», 1948
8. Д II т к и н В. А.. Прудников А. П. Интегральные преобразования I
операционное исчисление. Серия: Справочная математическая библиотека
«Физматгиз», 1961.
9. К о н т о р о 1^1 ч М. и. Операционное исчисление и процессы в
ческих цепях. Изд(!»«Наука», 1964.
10. Лебедев Н. Н. Специаль}1ые функции и их приложение «Гостехтеор
и^ат», 1953.
11. Т и т ч м а р Н1 Е. Введение в теорию Чштсгралов Фурье. «Гостехиздат»
1948. -^Н-
12. Тол стон Г. П. Ряды Фурье. «Гс^стеориздат»., 1951.
13. Свешников А. Г., Тихонов А. Н. Теория функций комплексного
переменного. И.зд. 2-е. «Наука», 1970.
14. С не д дон И. Преобразования Фурье. «И. Л.», 1955.
15. Фаддеева В. И. Вычислительные методы линейной алгебры. «Тех-
теориздат», 1950.
16. Фихтенгольц Г. М. Курс диффсрециального и интегрального
исчисления. Том I. Изд. 7. «Наука», 1969.
17. Фифтенгольц Г. М. Курс дифференциального и интегрального
числения. Том И. Изд. 7. «Наука», 1969.
18. Фихтенгольц Г. ДА. Курс дифференциального и интегрального
числения. Том 111. Изд. 5. «Наука», 1969.
19. Харкевич А. А. Спектры и анализ. Изд. 4-е. «Физ.матгнз», 1962.
20. Худзи некий Л. Л. О частотно-фазопо'м анализе сейсмических волн.
Сб. статей. Динамика земной коры. ИФЗ им. О. Ю. Шмидта АН СССР
«Наука», 1965.
21. Новое в сейсморазведке. Обзор зарубежной литературы. Раздел III
Автор обзора А. А. Богданов. ВНИИОЭНГ, 1970.
22. Современные достижения в методике и^технике разведочной и
вой геофизлки. Обзор зарубежной литературы. Авторы/обзора А. С. Петухов.
А. Л. Богданов, В. Г. Горохов, М. М. К р е*? б е г. ВНИИОЭНГ, 1970'
23. Аналоговая и цифровая обработка сейсмических данных. Обзор
бежной литературы. Авторы обзора А. А. Богданов и др. ВНИИОЭНГ, 1969.
24. Справочник геофизика, том IV, Сейсморазведка. «Недра», 1966.
25. Теория передачи сообщений. Труды международной конференции.
П. ЛА а р к у. Ж. Лаге. Новые методы передачи речи. «И. Л.», 1957.
26. О. Сгаи. В. ОотоНе, А. Роп1апс1, 1Ь Нетоп, ^\1. 1аусг§пе. Ье ЯИга-
8е еп ,ч|5тЦие. Тоте I. РиЬИсаНопз йе Лшзти! {гапда18Aи ре1гои. Раг15, 1966
(Г. Гро и др. Фультрация в сейсморазведке. Том I).
27. Магк К. ЗтИН, Мо15^па1у5|8 апA ти1ир1е 5е1згаоте1ег 1Ьеогу. ОеорИу-
«168, уо1 XXI, Х» 2, АрШ 1956.
(.Марк К. С.МИТ. Анализ помех и теория грунпировання сейсмографе?).
о г л А в л Е II И !•
3
1рсдисловие .
лава I. Линейные системы и принцип наложения
§ 1. Лине)'шые системы
1. Системы передачи сигналов в сейсморазведке 5
2. Понятие о линейной системе' (>
§ 2. Линейные преобразования. Пр!И1цип наложения (супсрнозн-
ции).
1. Основные свойства линейи1.1х преобразований
2. Принцип наложения (суперпозиции)
3. Основные виды линейных нреобразоваиий
§ 3. Элементарные сигналы-
1. Выбор элементарных сигналов 14
2. Гармонические элементарные сигналы 15
3. Разрывные илементарныс сигналы 18
Глава II. Сигналы и спектры
§ 1. Периодические сигналы. Дискретные спектр).!.
1. Ряд Фурье. Понятие о дискретмо.м спектре 22
2. Комплексная форма ряда Фурье. Понятие о комплексном
дискретном спектре 27
3. Определение коэффициентов ряда Фурье 30
^ 2. Импульсные.сигналы. Сплошные спектры.
1. " рехол от дискретного спектра к сплошному 32
2. Понятие о ко.мплексном сплошном спектре импульсного
■сигнала 34
3. Изображение сплоишых спектров 36
^ 3. Основные свойства спектров
1. Симметричность спектрального преобразования -^
2. Симметричность амплитудно-частотного спектра и кососиммет- "^
ричность фпзово-частотпого спектра 40
3. Спектры симметричной и кососн.мметричной функций .... 42
4. Коснпусиое и синусное преобразс/ваннс Фурье 45
§ 4. Основные теоремы о преобразовании сигналов и спекгроп
1. Теорема о линейности спсктрал1Л10го преобразования (теорема
суперпозиции) 46
2. Теоремы о днфференцироваиип сигнала и спектра (теоре.ма
о спектре производной) 47
3. Теоремы об интегри1)опап1П1 сш-иала и спектра (теорема о
спектре интеграла) 50
4. Теоремы о смещении сигнала во времени и спектра по
те (теорема смещения) 'Л
^>• Теореммал)б изменении масигтабов сигнала п спектра (гсоре-
ма масштабов) 53
• 1еоремы о дифференцировании и нптсгриропанпи сшнала и
спектра по параметру (теорема о параметре) 55
10а
7. Теоремы о произведенпп спектров и сигналов (теорема
тывания) 5?
§ 5. Операция свертывания.'
1. Механизм операции свертывания 56
2. Свертка одинаковых функций 6С
3. Свертка «сопряженных» функции . , . , , 6С
4. Свертка сигнала с единичным импульсом и гармоникой ... 62
5. Энергия сигнала и спектра (теорема энергий) 6':
Глава III. Спектры некоторых функций
§ 1. Спектры разрывных функций.
1. Спектры знаковой функции и единичной функции ... 64
2. Спектр прямоугольного импульса Ск
3. Спектр единичного импульса . IV ■
§ 2. Спектры непрерывных сигналов и функций.
1. Спектры экспоненциальной затухающей функции 72
2. Спектр колокольной функции 7*.'
3. Спектр сигнала с песущей частотой 7/
4. Спектры односторонних косинусоиды и синусоиды Т->
Ъ. Спектры отрезков косинусоиды и синусоиды 81
6. Спектр затухающей синусоиды 84
7. Спектр импульса Берлаге 8-''
§ 3. Спектр сейсмического сигнала
1. Понятие о многомерном спектре 87
2. Представление сейсмического сигнала на
менной и частотно-волновой плоскостях 90
3. Двумерные спектры идеально-регулярной и регулярной волны 93
§ 4. Связь между амплитудно-частотным и фазово-частотным
спектрами сейсмического сигнала
1. Связь между действительной и .мнимой частями комплекснс^^о
сигнала. Понятие о преобразовании Гильберта . . . '; 100'
2. Понятие об аналитическом сигнале ....,.,., 103
3. Связь между модуле;.! и фазой частотного спектра и
ческого сигнала - . 105
Литература ' ■ •. .. 10"
Редактор С. И. Щеглова
^%Но в набор 30./Х1 1973 г. Подписано к печати 21/У1-74 г.
. ^^.7 Формат 60X90716 Печ. л. 7
!1|^_500 экз. Цена 20 коп. Заказ Ла 358
Серпуховская типография