Теоретические основы обработки геофизической информации - Никитин А.А.

Автор: Никитин А.А.
Теги: прикладная геология и геофизика геологические методы поисков и разведки интерпретация результатов геология геофизика
Год: 1986
Похожие
Теория нейтронных методов исследования скважин
Разведочная геофизика
Промысловая геофизика
Курс гравиразведки.
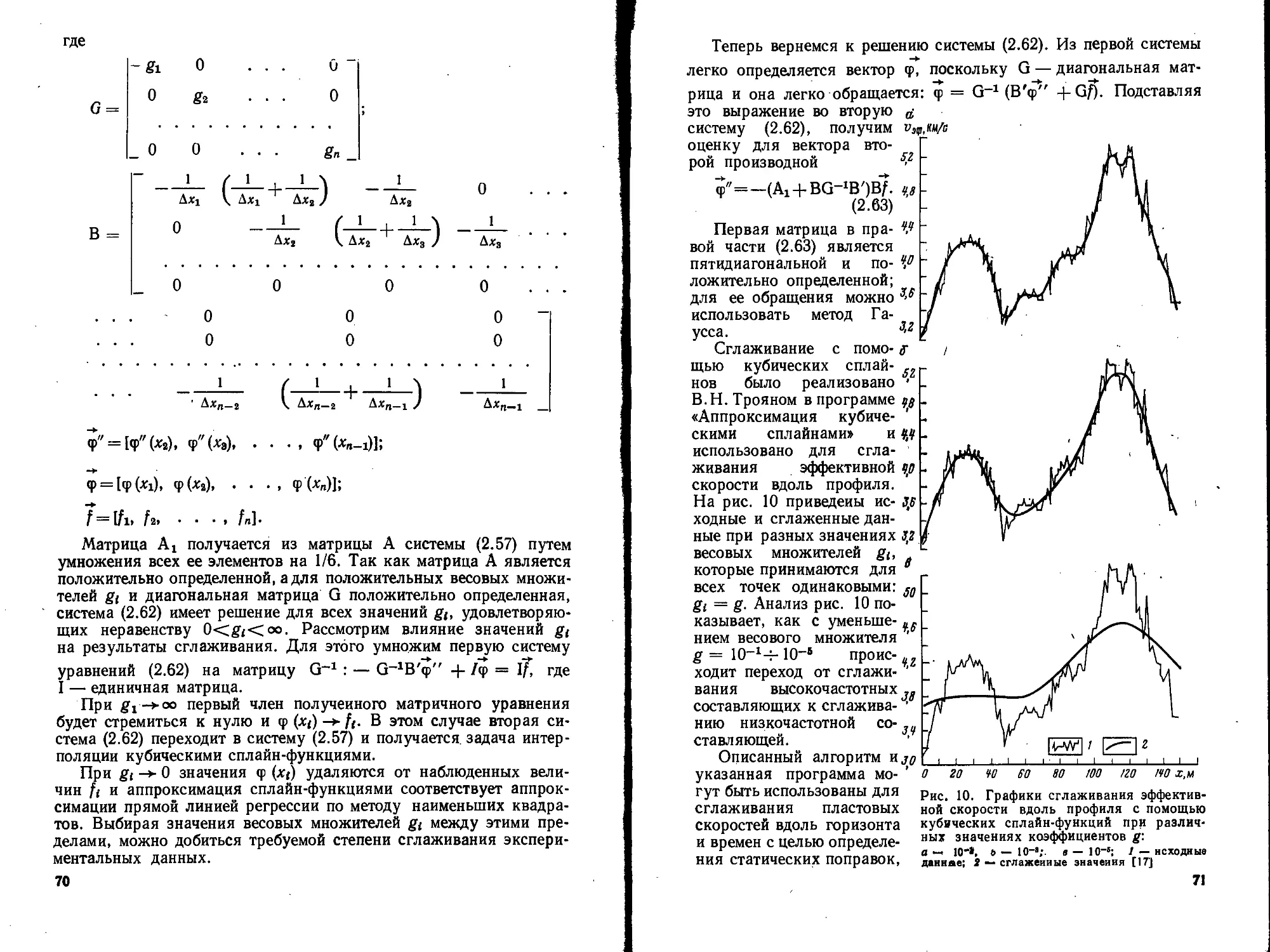
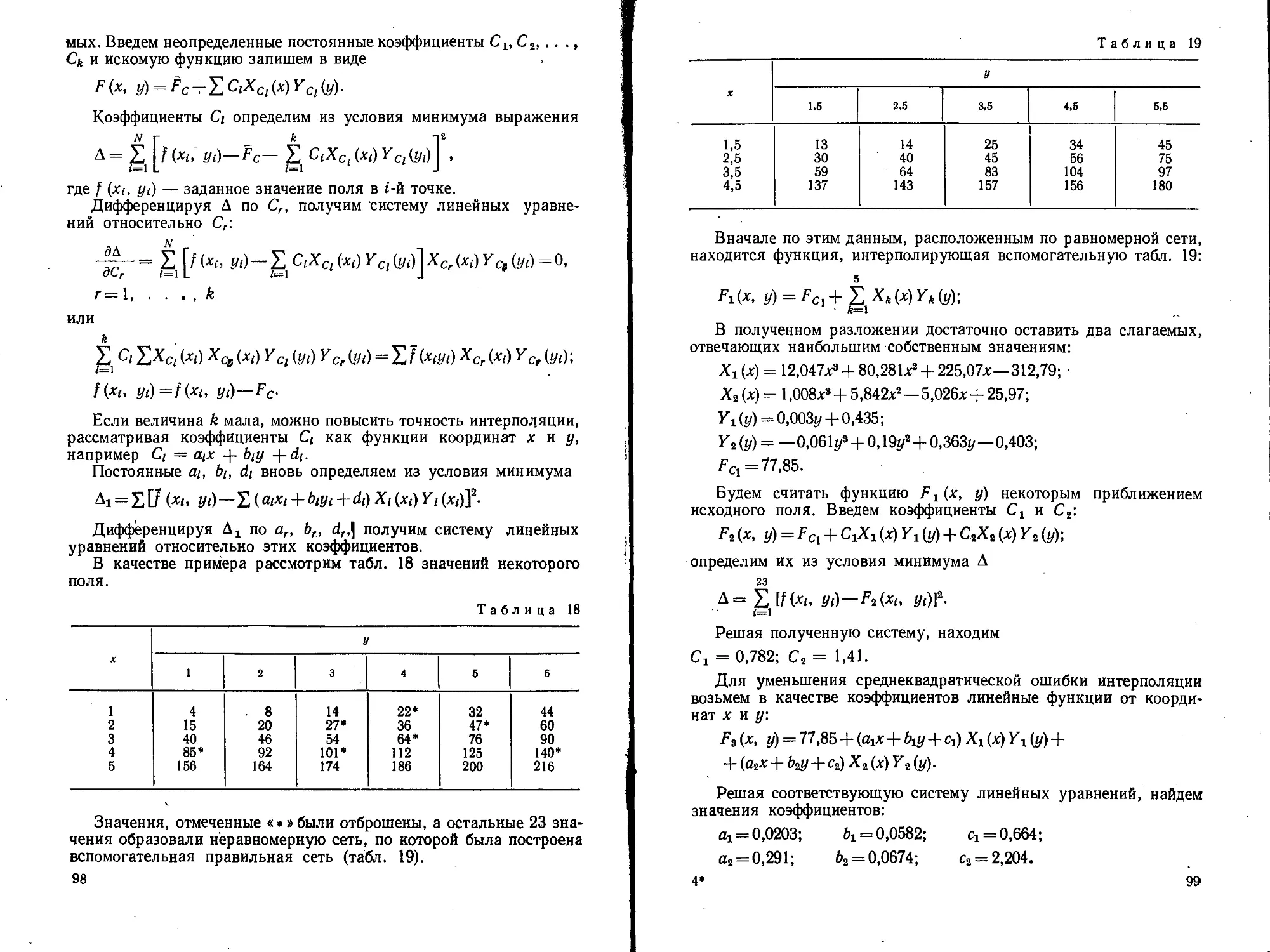
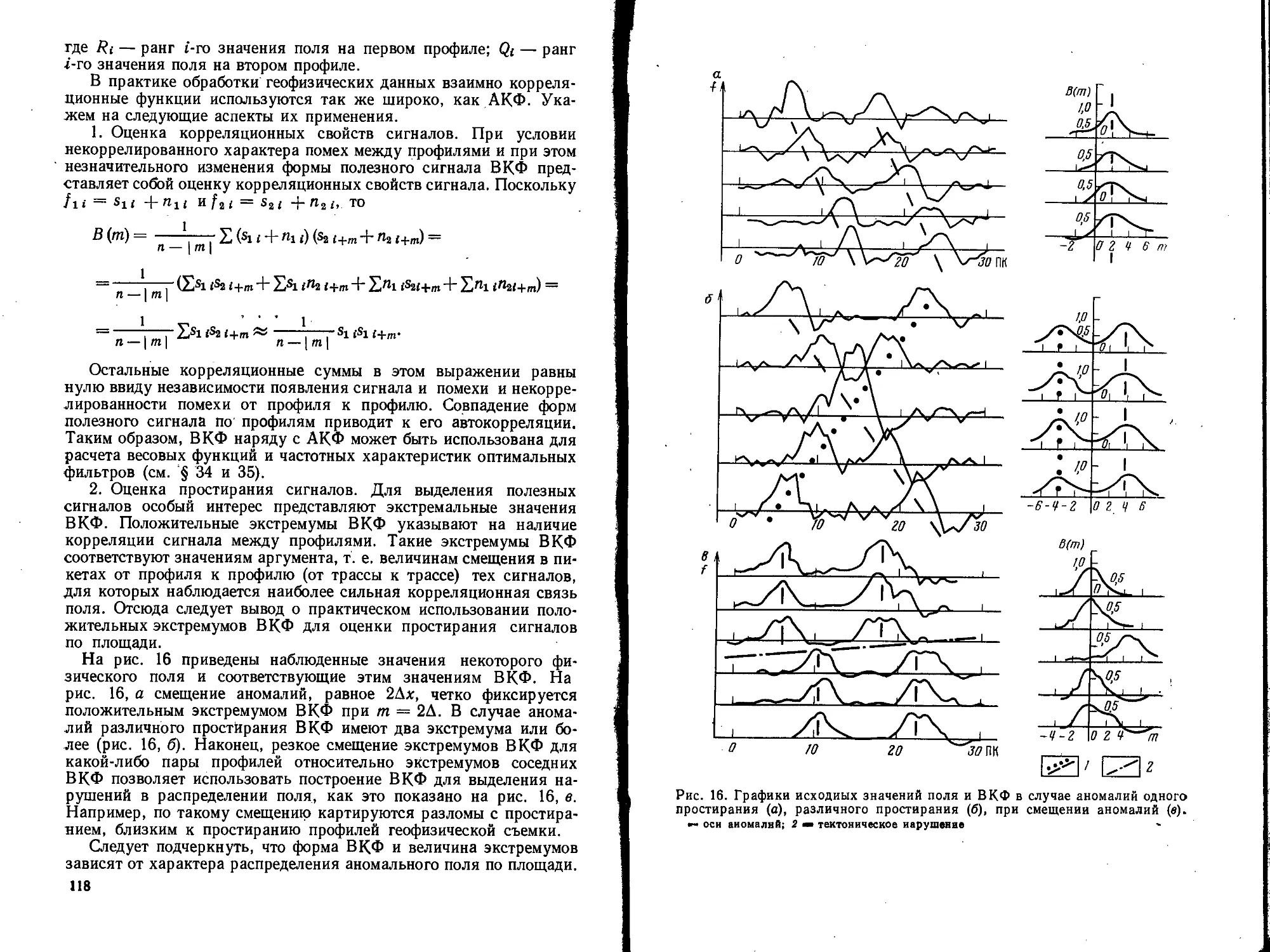
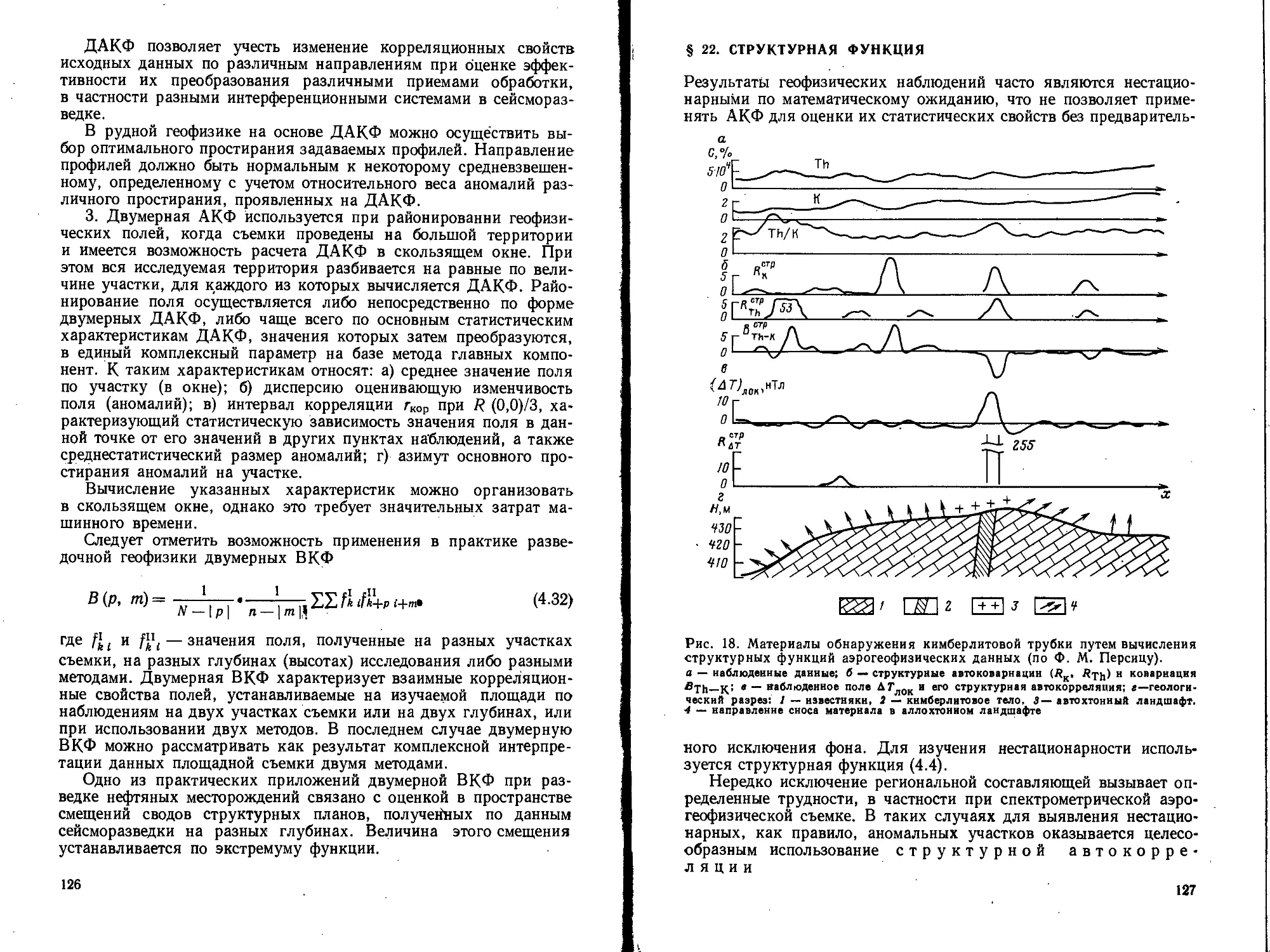
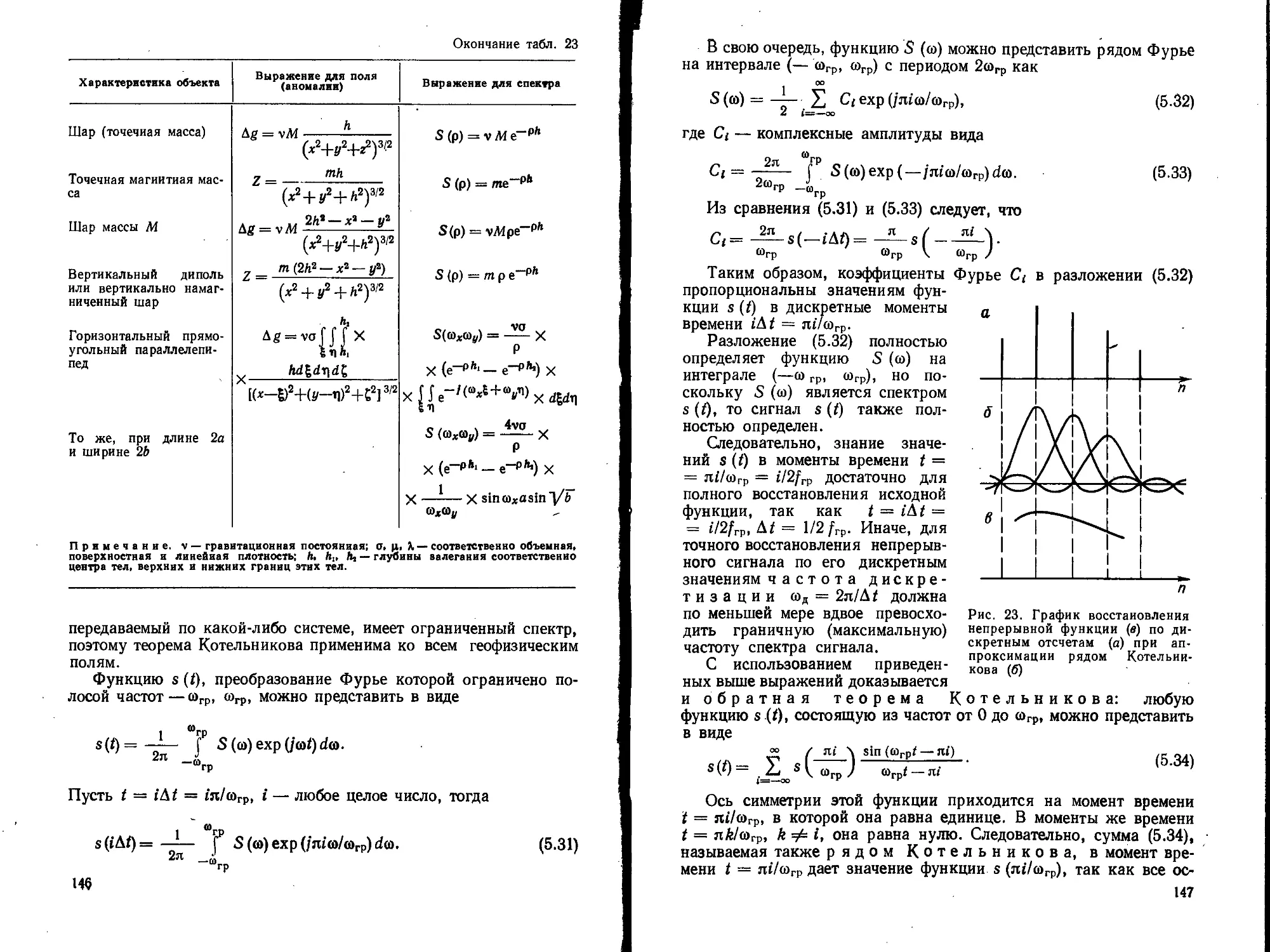
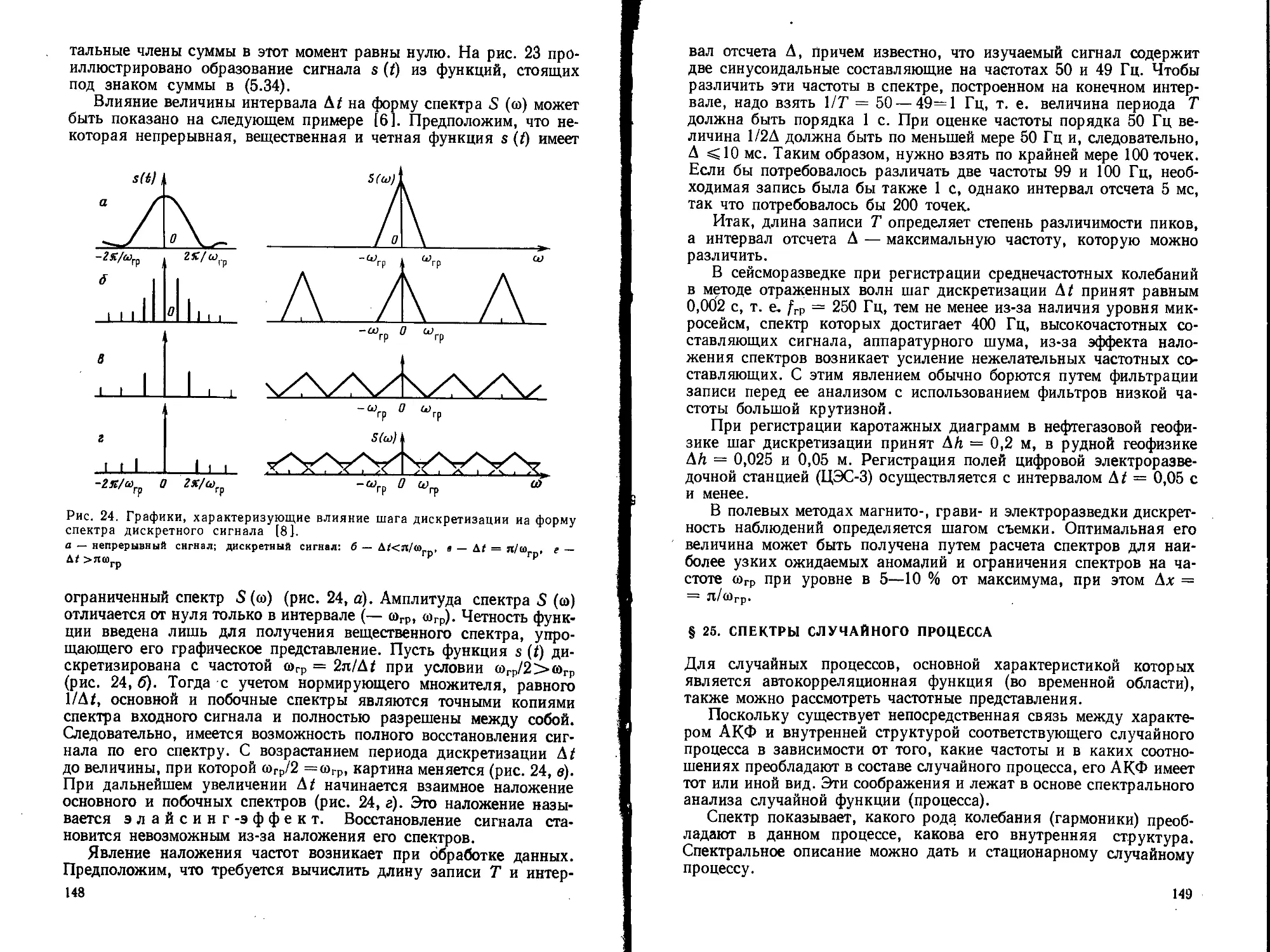
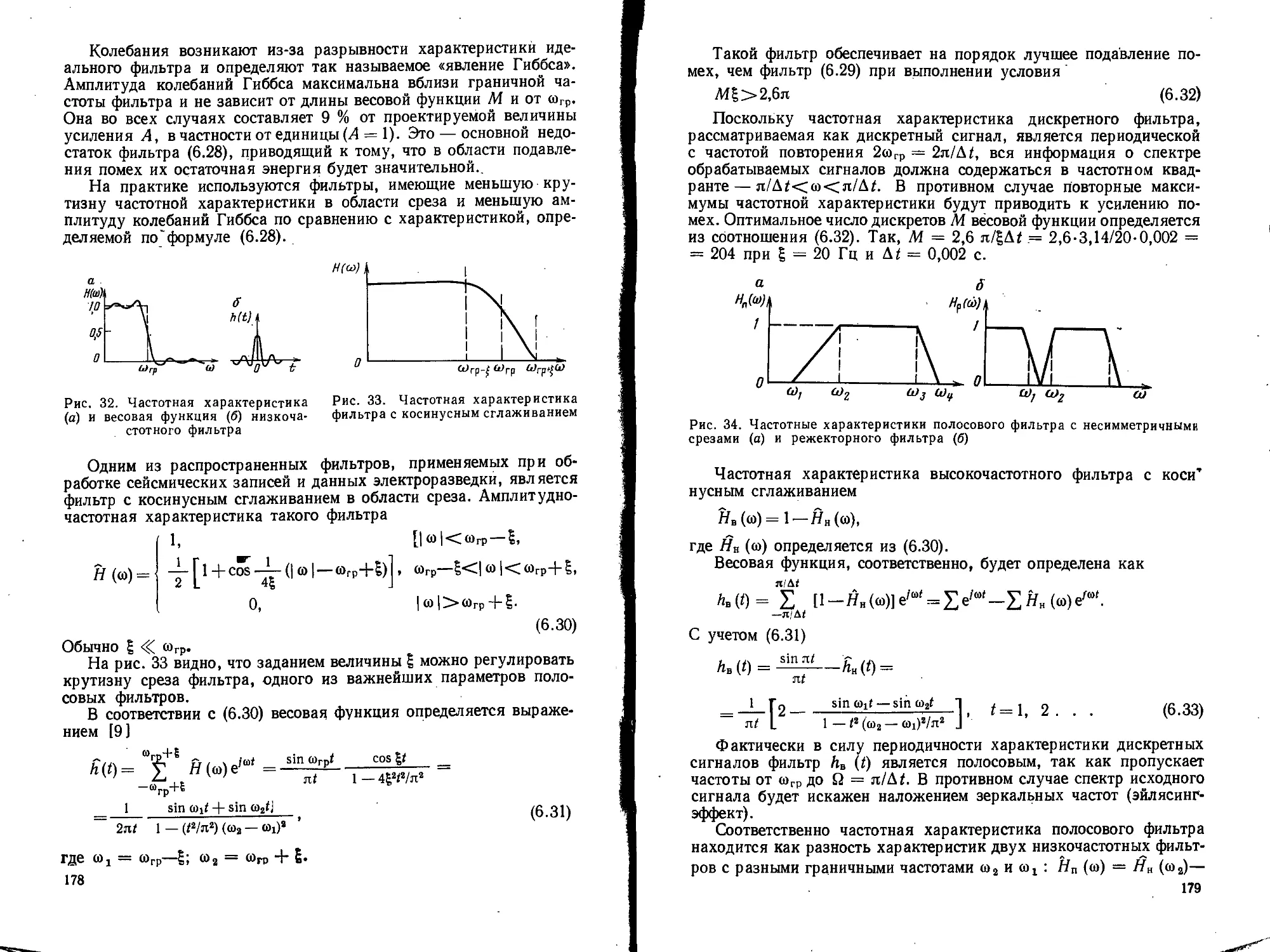
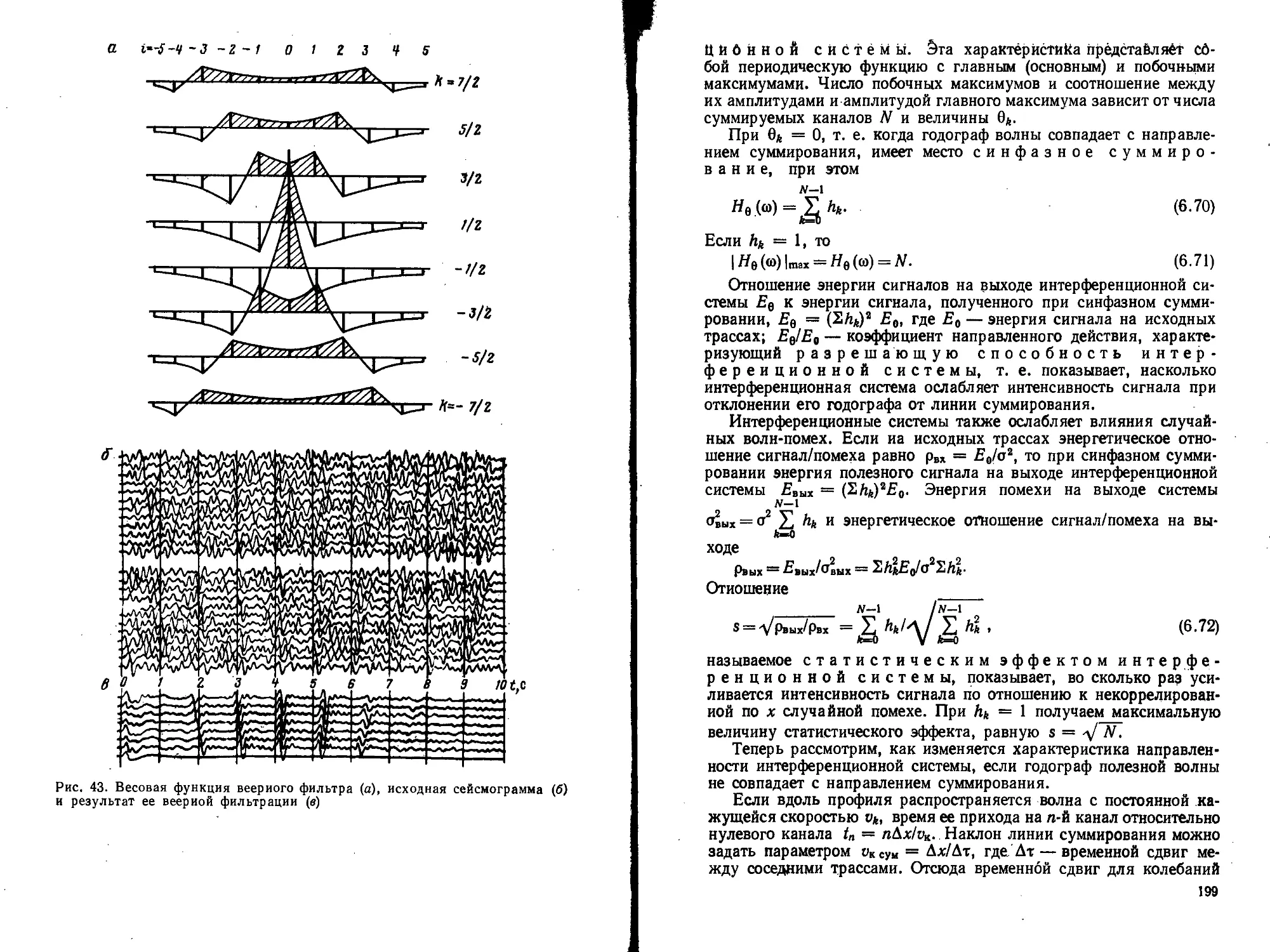
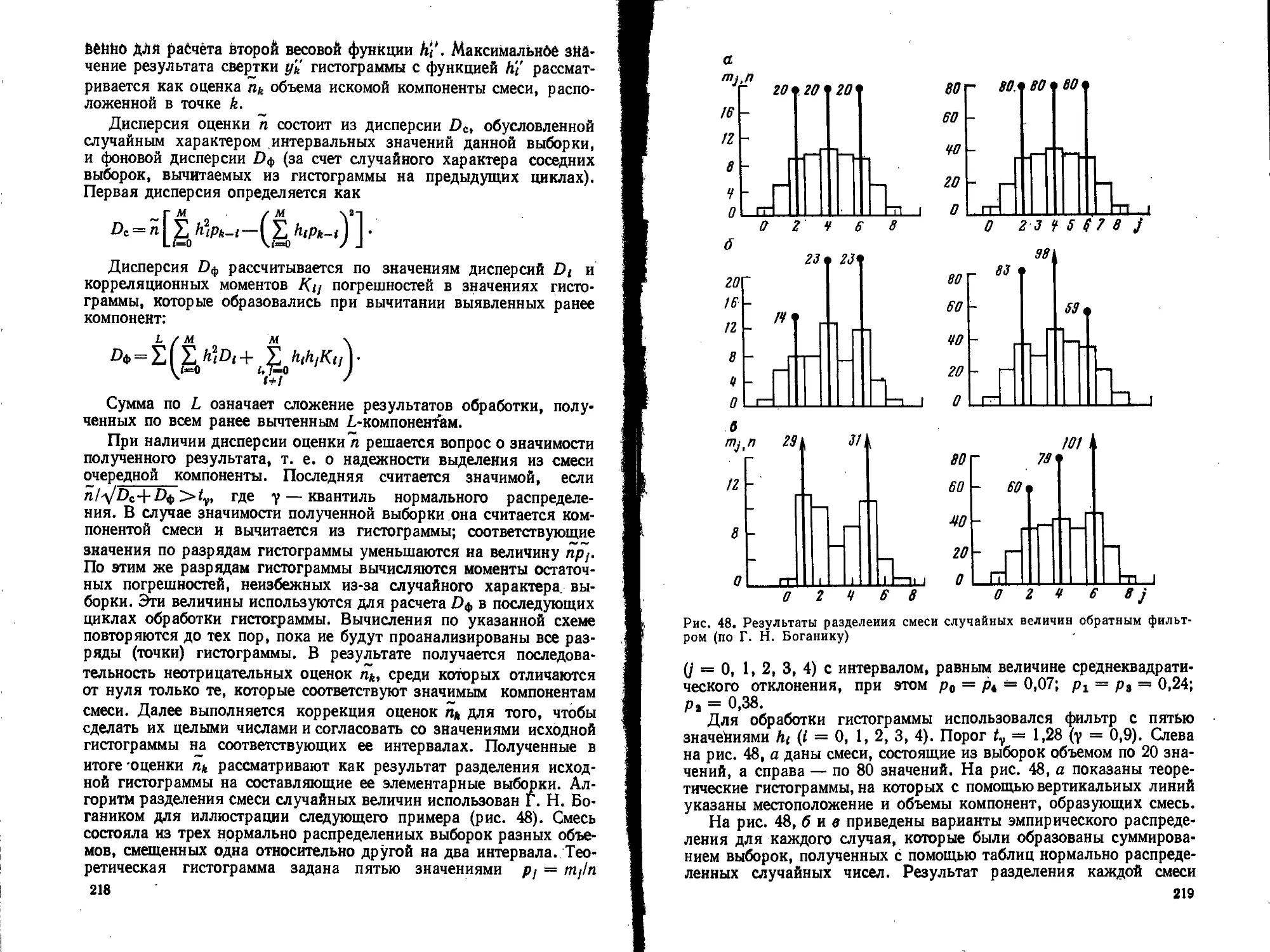
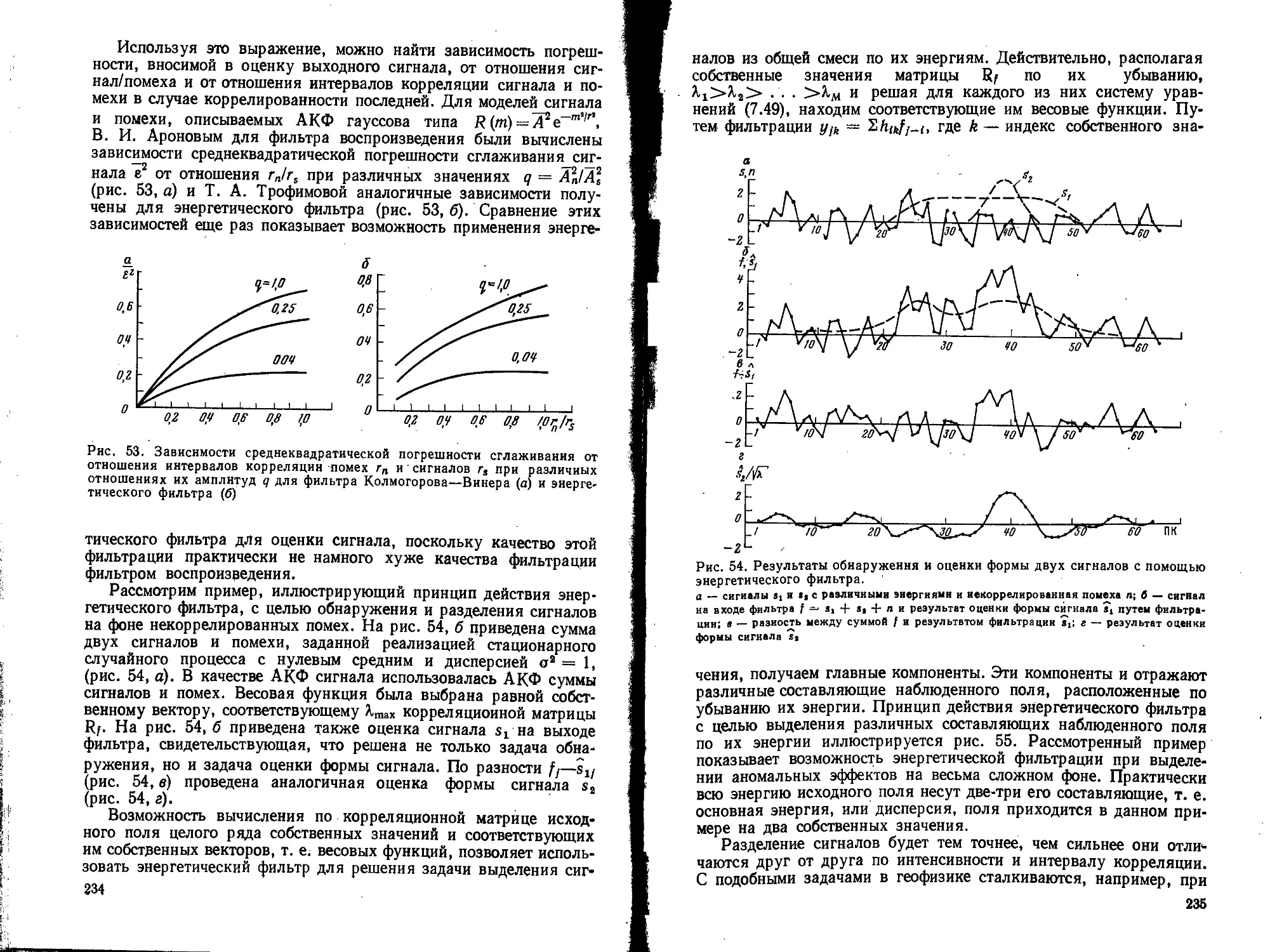
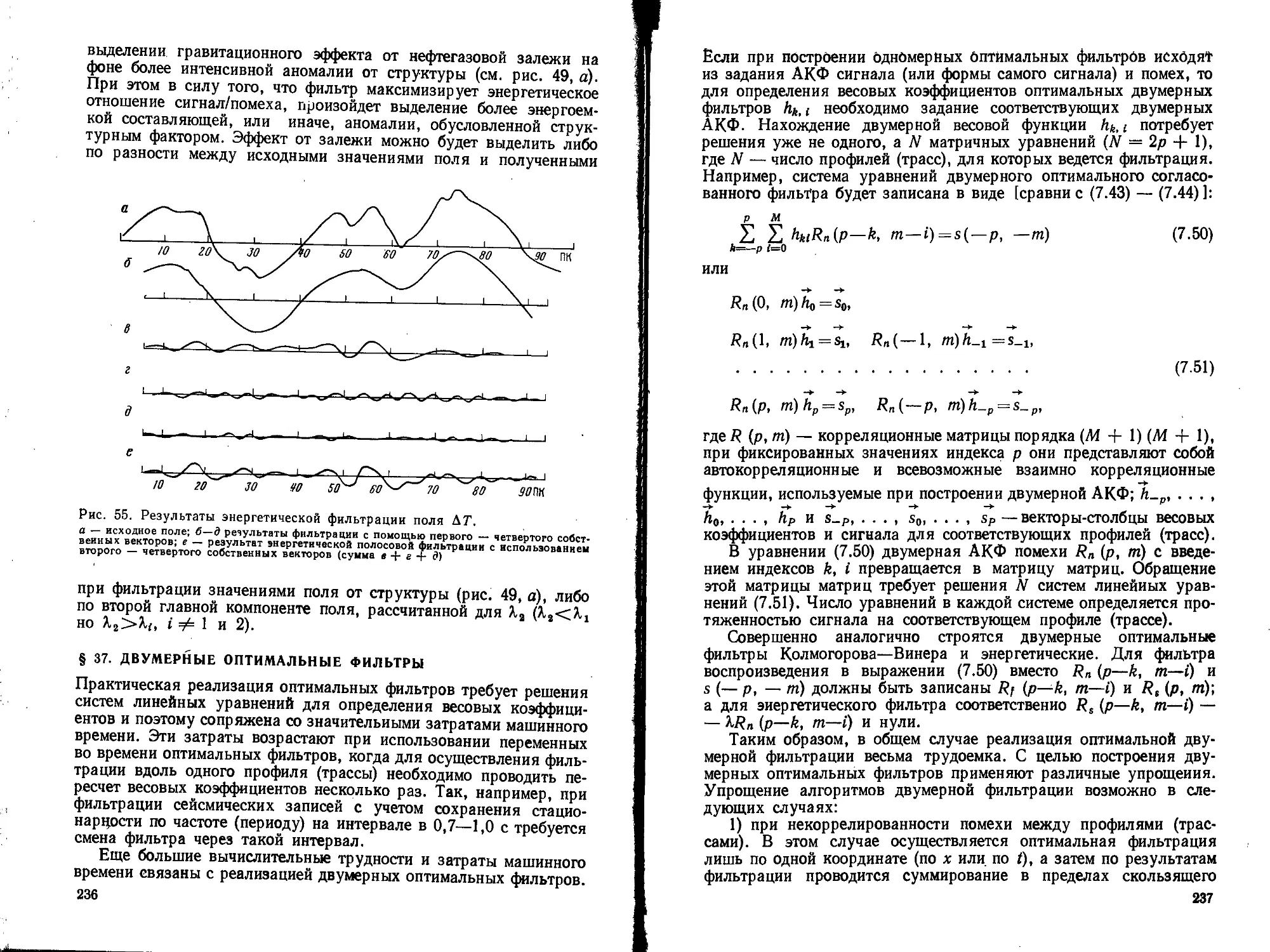
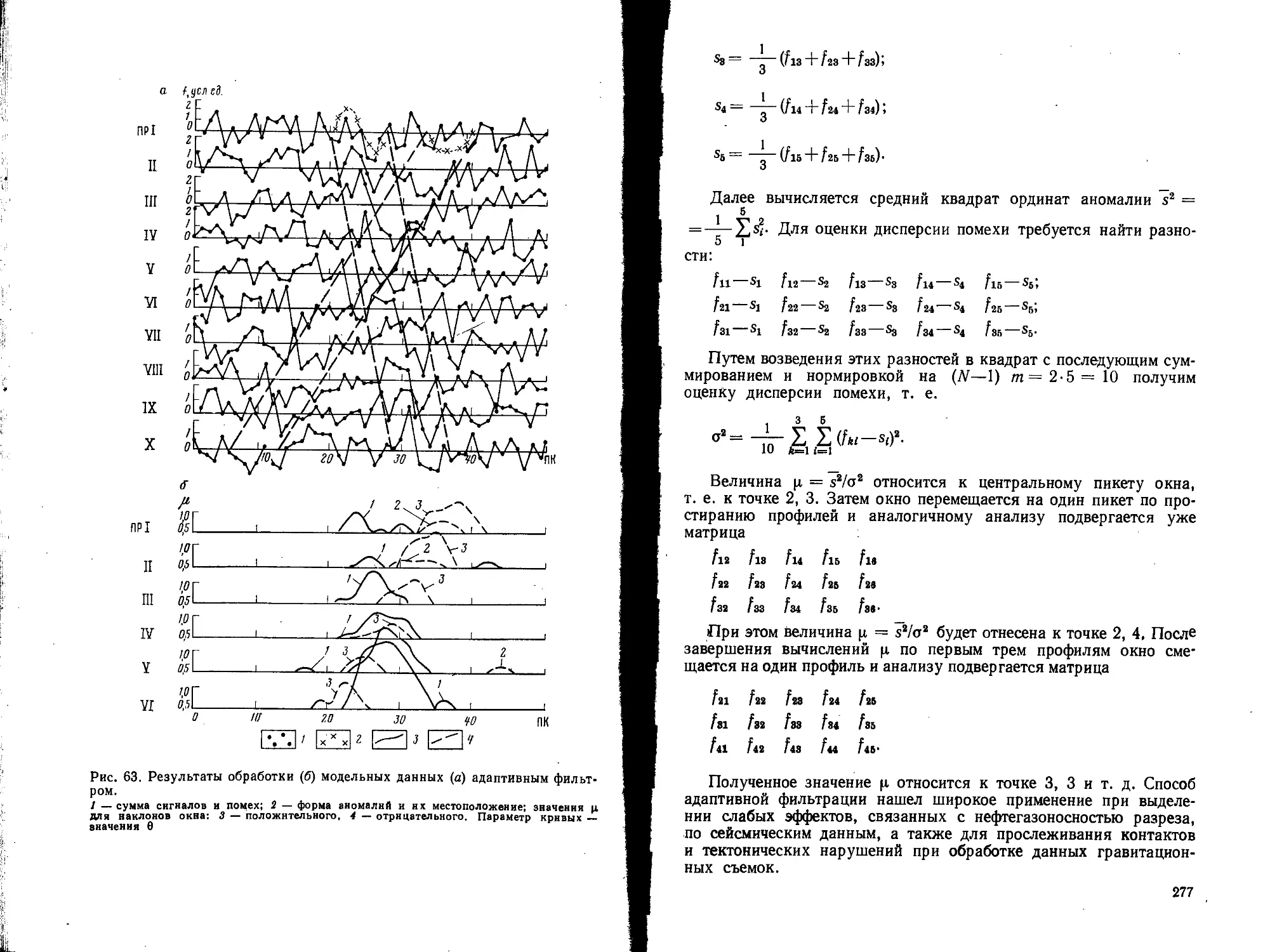
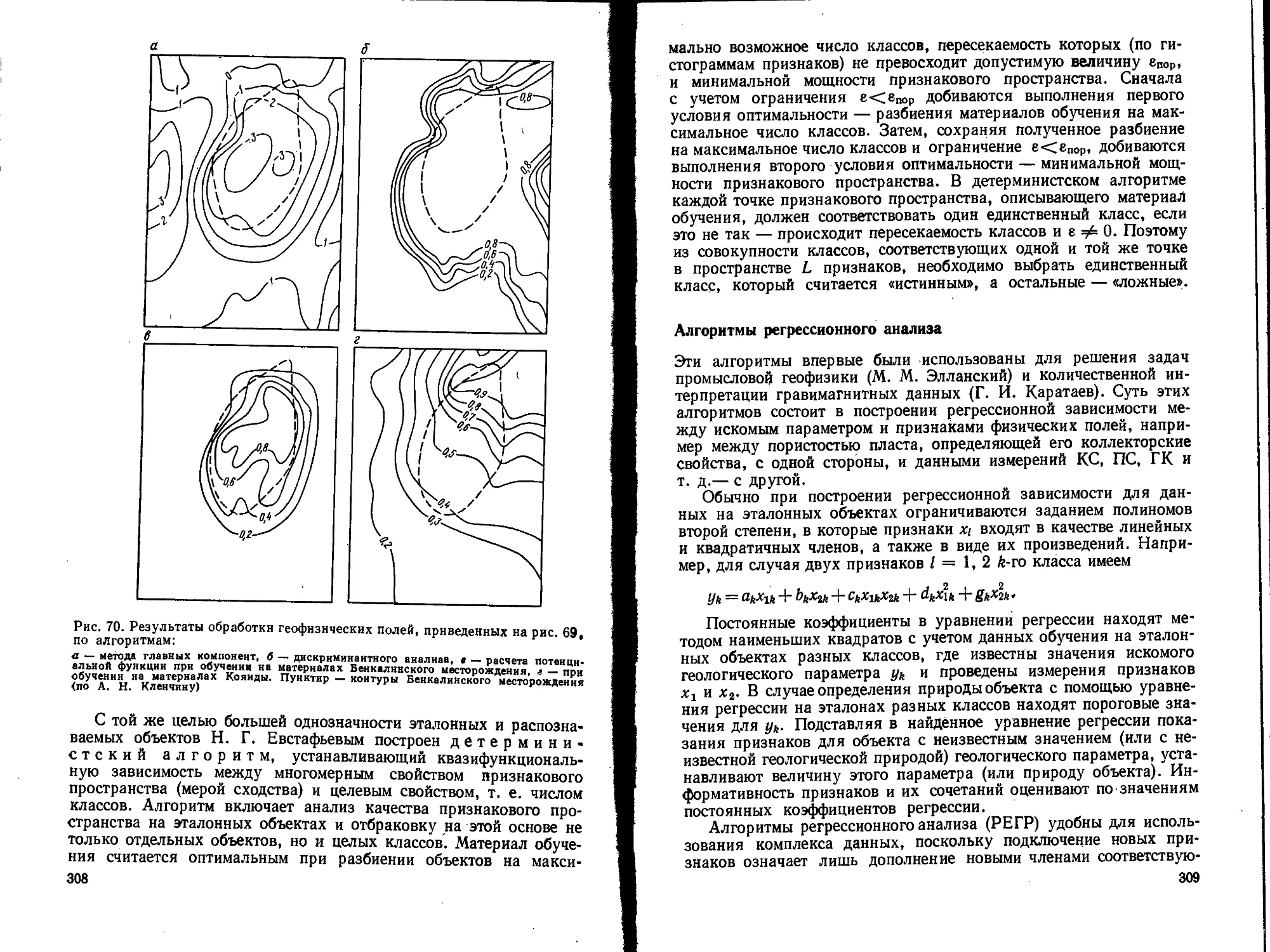
Текст
                    
А.А.НИКИТИН
ТЕОРЕТИЧЕСКИЕ
ОСНОВЫ
ОБРАБОТКИ
ГЕОФИЗИЧЕСКОЙ
ИНФОРМАЦИИ
Допущено Министерством высшего и среднего специального
образования СССР в качестве учебника для студентов вузов,
обучающихся по специальности «Геофизические методы
поисков и разведки месторождений полезных ископаемых».
МОСКВА „НЕДРА" 1986
УДК 550.83 : 519.2

Никитин А. А. Теоретические основы обработки геофизической информации:
Учебник для вузов.— М.: Недра, 1986.— 342 с.
Даны понятия об информации и ее обработке, сведения о квантовании
сигналов по времени.
На базе современного математического аппарата (статистический, спек-
тральный, корреляционный, факторный анализы) рассмотрено решение наи-
более типичных Задач обработки геофизической информации (сглаживание
и интерполяция данных, выделение сигналов на фоне помех, изучение свойств
физических полей, классификация геологических объектов и др.).
Для студентов вузов по специальности «Геофизические методы поисков
и разведки месторождений полезных ископаемых».
Табл. 25, ил.— 72 список лит.— 19 назв.
Рецензенты: Кафедра геофизических методов разведки (Иркутского
политехнического ии-та); В. И. Аронов, д-р физ.-мат. наук (Всесоюзный
научно-исследовательский геологоразведочный нефтяной ии-т)
и», ГОРЬКОГО
БИБЛИОТЕКА
м. г. У.
1903010000—287
”	043(01)—86
34—86
© Издательство «Недра», 1986
ВВЕДЕНИЕ
Обработка геофизической информации — важнейший этап ана‘
лиза экспериментальных данных всех методов разведочной геофи-
зики. Основой получения геофизической информации (геофизиче-
ских данных) являются измерения. Измерение — это нахождение
значения физической величины опытным путем с помощью специ-
альных технических средств. В разведочной геофизике предметом
измерения являются физические свойства горных пород и физиче*
ские поля, создаваемые горными породами. Техническими средст-
вами их измерения служат аналоговые и цифровые приборы. Ре-
зультат измерения представляет собой число, выраженное в соот-
ветствующих физических единицах измерения. Это число — эле-
мент измерительной информации. Иначе говоря, геофизическая ин-
формация — это измерительная информация, доставляющая ко-
личественные сведения о каком-либо физическом свойстве, физиче-
ском поле или явлении геологической среды, геологического
объекта.
Объем геофизической информации непрерывно растет, что опре-
деляется как увеличением объемов геофизических работ, так и
повсеместным переходом на цифровую регистрацию физических
полей. Этот переход обусловлен преимуществами цифровой аппа-
ратуры по сравнению с аналоговой, основные из которых: 1) высо-
кая точность и быстродействие; 2) возможность выдачи результа-
тов измерений непосредственно в ЭВМ; 3) безошибочный перенос
дискретных сигналов из одних запоминающих устройств в другие
и передача информации на большие расстояния; 4) многократное
усиление и воспроизведение дискретных сигналов без потери ин-
формации; 5) способность работать в системах автоматического
контроля и управления.
Цель обработки геофизических данных — извлечение полезной
информации из результатов измерений (наблюдений) отдельных
геофизических методов и их комплексов. В отличие от первичной
обработки исходных данных, включающей определение координат
точек наблюдений, введение различных поправок (в частности,
уравнивание опорной сети в гравиразведке), увязку наблюдений
по площади съемки, обработка исправленных данных (перед про-
ведением количественной интерпретации) решает задачи преобра-
зования, фильтрации и анализа с целью подавления помех, выде-
ления и разделения полезных сигналов (аномалий). Количествен-
ная интерпретация выделенных путем обработки сигналов сводится
к количественной оценке геометрических и физических параметров
источников аномалий. Если методика и методы количественной
интерпретации геофизических аномалий существенно зависят от
регистрируемого физического поля, то теоретические основы мё-
3
•годов обработки, направленных на извлечение полезной инфорг
мации, являются едиными для всех геофизических методов, мето-
дика их применения также не зависит от типа анализируемого фи-
зического поля. Это обстоятельство и позволяет рассматривать
обработку информации для всех геофизических методов в едином
курсе. Создание подобного курса по интерпретации пока прежде-
временно, хотя вопросы интерпретации гравитационных и магнит-
ных аномалий читаются совместно. Следует также отметить, что
с развитием методов обработки грани между обработкой данных
и количественной интерпретацией постепенно стираются.
Существуют два подхода к обработке и интерпретации резуль-
татов геофизических наблюдений: детерминированный и вероят-
ностно -статистический.
Основой детерминированного подхода, исполь-
зуемого главным образом при интерпретации, является примене-
ние аналитических методов теории потенциала (в грави-, магнито-,
терморазведке, электроразведке постоянным током и естественного
поля), уравнений Максвелла (в электроразведке переменным то-
ком) и теории упругости (в сейсморазведке). Решение обратных
задач при этом находится в форме единственно возможного реше-
ния, т. е. либо в виде определенной функциональной зависимости,
либо в виде числа как частного значения функции для искомого
значения ее аргумента.
Применение детерминированного подхода (аналитических ме-
тодов) при обработке и интерпретации можно считать оправдан-
ным, если производятся преобразования и анализ интенсивных
аномалий от геологических объектов с заметной дифференциацией
физических свойств, благоприятными для решения поставленных
задач размерами, формой и глубиной залегания.
В настоящее время при обработке и интерпретации геофизиче-
ских данных все большее значение приобретает в е р о я т -
„ ностно-статистический подход. Это связано с ха-
рактерной особенностью геофизических наблюдений, заключаю-
щейся в том, что полученные в отдельных точках данные следует
рассматривать как случайные события. Случайно также располо-
жение разнообразных геологических объектов, точек и даже пло-
щадей исследования, поскольку при съемке другими исполните-
лями и в другое время могут изменяться контуры площади и по-
ложение точек сети наблюдений. Наконец, и пожалуй самое глав-
ное, из-за наложения помех, вызванных погрешностями измерений,
геологическими неоднородностями, неучтенными вариациями по-
лей и другими причинами, само физическое поле реализуется слу-
чайным образом.
Следовательно, в практике обработки и интерпретации иссле-
дователь имеет дело с данными, которые с большим основанием
описываются случайными величинами и процессами, чем анали-
тическими функциями. Изучение этих величин и процессов требует
привлечения аппарата теории вероятностей и ее различных прило-
жений. При вероятностно-статистическом подходе результатом
4
решения является уже не число и не функция, а распределение
вероятностей, заданное для возможных значений искомого пара-
метра.
Подавляющее большинство методов обработки базируется на
использовании вероятностно-статистического подхода. В соответст-
вии с указанными подходами в развитии методов обработки геофи-
зической информации можно выделить два этапа.
Первый этап — 1930—1960 гг.— характеризуется исключи-
тельно детерминированным подходом к обработке данных, начиная
с простых приемов интерпретации (усреднение, методы характер-
ных точек, касательных и т. д.) и кончая развитием методов ана-
литического продолжения гравимагнитных полей (Б. А. Андреев,
А. Н. Тихонов, В. Н. Страхов и др.). Интенсивно развиваются ме-
тоды частотного анализа (Л. А. Рябинкин, Ф. М. Гольцман,
И. И. Гурвич, А. К. Урупов, К. В. Гладкий, С. А. Серкеров,
В. Н. Страхов и др.).
На рубеже 50- и 60-х годов работы А. Г. Тархова,
Л. А. Халфина, Ф. М. Гольцмана, И. Г. Клушина явились нача-
лом принципиально нового вероятностно-статистического подхода
к обработке геофизических данных. Этот подход получил широкое
развитие прежде всего в сейсморазведке (Ф. М. Гольцман, С. А. На-
хамкин, Е. А. Козлов, С. В. Гольдин, А. К. Яновский, Е. А. Ро-
бинсон и др.), затем в других методах структурной и рудной гео-
физики (А. Г. Тархов, А. А. Никитин, Г. Й. Каратаев, И. Г. Клу-
шин, С. А. Серкеров, Н. Н. Боровко, В. И. Аронов, Т. Б. Кали-
нина, В. И. Шрайбман, К. В. Хортон и др.) и каротаже (Ш. А. Гу-
берман, М. М. Элланский, Г. Н. Зверев и др.).
Второй этап — 1960—1980 гг.— наряду с вероятностно-ста-
тистическим подходом характеризуется дальнейшим углублением
и расширением функционально-аналитических методов интерпре-
тации, а также широким развитием цифровой обработки данных
на ЭВМ. С 1970 г. происходят отмирание аналоговой техники и од-
новременно интенсивное внедрение ЭВМ в производственных и на-
учных организациях страны. Для этого этапа характерно также
взаимное обогащение методов и методик обработки информации,
разработанных в разных методах разведочной геофизики. Так, на-
пример, приемы оптимальной фильтрации сигналов, созданные
в сейсморазведке, используются при обработке данных рудной
геофизики, приемы распознавания образов, развитые сначала для
обработки данных комплекса методов в промысловой геофизике,
получили распространение в рудной геофизике и сейсморазведке,
методы аналитического продолжения гравимагнитных полей при-
обретают значение при анализе волновых полей в сейсморазведке
и т. п.
В последнее время все большее число исследователей понимают
необходимость слияния детерминированного и вероятностно-ста-
тистического подходов. Этому в значительной мере способствует
развитая А. Н. Тихоновым теория регуляризации. Параметр ре-
гуляризации, используемый при решении системы линейных урав-
5
нений, к которым сводится большинство задач обработки и интер-
претации, выполняет ту же роль, что и дисперсия помех при ве-
роятностно-статистическом подходе.
Применение современных методов обработки геофизической ин-
формации невозможно без использования ЭВМ, парк которых не-
прерывно растет.
Наряду с созданием региональных вычислительных центров,
начиная с 1980 г., геофизические экспедиции оснащаются специа-
лизированными вычислительными комплексами ГВК на базе ЭВМ
СМ-2 или СМ-4 и спецпроцессоров ПС-2000 и ПС-3000.
Необходимость использования ЭВМ при обработке геофизиче-
ских данных вызывается следующими причинами:
1)	все возрастающим объемом цифровой информации, получае-
мым при измерениях на земле и под землей, на море, в воздухе
и космосе.
Так, например, в одной 24-канальной сейсмограмме с длитель-
ностью записи до 6 с при дискретности измерений 0,002 с (это со-
ответствует 500 числам в 1 с) содержится 500-24-6 = 72-103 чисел
(или машинных слов), что при 15-разрядном машинном слове дает
72-103-15 = 10е бит информации. В Казахстане еще в конце 60-х гг.
ежегодно по результатам геохимических съемок получали 107 чи-
сел, а по результатам электро- и гравимагниторазведочных работ —
10е чисел.
Увеличение информации в настоящее время происходит за счет
появления новых систем наблюдений, например в электро разведке—
это переход на пространственные и временные измерения поля;
2)	более полным использованием исходной информации при ее
цифровой регистрации. Так, при ручной корреляции волн на сей-
смограмме информация о разрезе обеспечивается десятками, в луч-
шем случае первыми сотнями чисел. Например, для корреляции
отражений от трех горизонтов на 24-канальной сейсмограмме ис-
пользуют 72 числа, т. е. 72 отсчета времени, для корреляции от-
ражений от пяти горизонтов — 120 чисел. Возможность получения
динамических характеристик записи при этом практически исклю-
чается. Применение ЭВМ и современных методов обработки сущест-
венно повышает информативность геофизических измерений и,
в частности, каждой сейсмограммы. Изучение динамических и ки-
нематических особенностей сейсмической записи и совместная их
обработка приводят к решению принципиально новых геологиче-
ских задач, направленных на оценку вещественного состава пород,
прогноз нефтегазоносности;
3)	увеличением глубинности и повышением разрешающей спо-
собности геофизических методов.
Достигнутая глубинность сейсморазведки к началу 70-х годов
составляла в среднем по СССР 2,5 км. Внедрение методики общей
глубинной точки и современных методов фильтрации сейсмических
полей позволили за 10 лет увеличить глубинность сейсмических
методов в основных нефтегазоносных провинциях страны до 5—6 км.
Глубинность методов рудной геофизики к началу 80-х годов
6
составляла в среднем по стране 230 м при колебании от первых де-
сятков метров до 500 м. В ближайшее десятилетие необходимо ее
увеличение до 1000—2000 м, что невозможно достичь без самого
широкого использования приемов выделения слабых сигналов и об-
работки данных комплекса геофизических полей.
Требование повышения разрешающей способности геофизиче-
ских методов обусловлено прежде всего усложнением решаемых
с их помощью геологических задач. На XII пятилетку перед оте-
чественной геологической службой поставлена задача освоения
районов Восточной Сибири. В то же время большая часть террито-
рии Восточной Сибири перекрыта трапповыми покровами и много-
летней мерзлотой. Как траппы, так и мерзлые породы представ-
ляют собой помехи, по существу, для всех методов разведочной
геофизики. В области нефтегазовой геофизики следует подчеркнуть,
что фонд антиклинальных структур с мощностью залежей более
100 м практически исчерпан и необходим поиск малоамплитудных
поднятий, а также залежей, связанных с литолого-фациальными
замещениями пород. Кроме того, уменьшился и средний размер
структур, перспективных на нефтегазоносность. Если до 70-х го-
дов средний размер ловушек углеводородов оценивался в 100 км2,
то к началу 80-х годов он снижается до 50—60 км2. Таков далеко
не полный перечень проблем, стоящих перед обработкой геофизи-
ческих данных.
Подчеркнем, что при решении все усложняющихся геологиче-
ских задач с помощью современных методов обработки существен-
ным является правильное задание физико-геологической модели
объекта исследования [3, 15], поскольку эти модели принципиально
влияют, а нередко определяют последовательность и выбор спосо-
бов обработки.
Для обработки геофизической информации в настоящее время
применяются практически все разделы современной математики,
которые, естественно, нельзя охватить в одном курсе. Поэтому ос-
новная цель новой дисциплины «Теоретические основы обработки
геофизической информации», введенной в учебные планы подго-
товки специалистов-геофизиков, выделить главные направления
в развитии современных методов обработки геофизической инфор-
мации и дать основы математического аппарата тех разделов ана?
лиза физических полей, которые получают наибольшее применение
в практике производственных и научных организаций.
При написании учебника автор опирался на десятилетний опыт
преподавания курса «Теоретические основы регистрации и обра-
ботки геофизических данных» в Московском геологоразведочном
институте им. С. Орджоникидзе.
ГЛАВА 1
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ В ЗАДАЧАХ
ОБРАБОТКИ ГЕОФИЗИЧЕСКИХ ДАННЫХ
§ 1. СОБЫТИЕ И ВЕРОЯТНОСТЬ
Теория вероятностей изучает закономерности случайных событий
во времени и пространстве и приемы их количественного описания.
Наблюдаемые при проведении экспериментов события делятся
на достоверные, невозможные и случайные. Каждый эксперимент,
состоящий из серии любых геофизических измерений, сопровож-
дается соблюдением определенного комплекса условий. Этот комп-
лекс условий, включающий регистрирующую аппаратуру и мето-
дику измерений, должен оставаться неизменным иа протяжении
всего эксперимента. Если при этом событие может как произойти,
так и не произойти, оно называется случайным. В качестве
события при геофизических измерениях выступают: появление кон-
кретного значения физического параметра (при измерениях физи-
ческих свойств) или физического поля (например, при регистрации
силы тяжести), появление аномалии какого-либо поля, факт соот-
ветствия определенных значений поля конкретному типу горных
пород и т. д.
Характерная особенность геофизических наблюдений состоит
в том, что полученные в отдельных точках данные целесообразно
рассматривать именно как случайные события ввиду случайности
расположения геологических объектов, обусловливающих появ-
ление конкретных значений поля, случайности расположения са-
мих точек наблюдений по площади исследований и наложения по-
мех, вызванных разнообразными причинами.
В отличие от случайного события, достоверным назы-
вается событие, которое при том же комплексе условий экспери-
мента обязательно происходит, а невозможным — то, ко-
торое заведомо не может произойти при этом комплексе условий.
Например, факт измерения значения полного вектора магнит-
ного поля в диапазоне от 0,33 до 0,66 Э является достоверным со-
бытием, а, наоборот, измерение значения поля свыше 0,66 Э (или
ниже 0,33 Э) будет невозможным событием, поскольку такой ве-
личины полного вектора магнитного поля на Земле не существует.
Два события называются несовместными, если
появление одного из них исключает появление другого при одном
и том же эксперименте; например, наличие и отсутствие аномалии
какого-либо физического поля в одной и той же точке наблюдения—
несовместные события.
Суммой событий называется событие, состоящее в по-
явлении хотя бы одного из этих событий.
8
Допустим, диапазон измеренных значений поля разбит на п
градаций. Событие, состоящее в появлении значения поля из пер-
вых двух градаций будет суммой двух событий, первое из которых—
появление значений из первой градации, второе — появление зна-
чений из второй градации. Соответствующее утверждение можно
высказать о сумме трех, четырех, . . . , п событий.
Произведением событий называется событие, со-
стоящее в совместном появлении всех этих событий.
Пусть событие А состоит в том, что значения магнитного поля
Z от 0 до 100 иТл соответствуют гранитам, а событие В — значения
поля Z от 50 до 200 нТл соответствуют измененным породам, тогда
произведением событий АВ является событие, включающее значе-
ния магнитного поля, соответствующие измененным разновидно-
стям гранитов, т. е. от 50 до 100 нТл. При этом сумме событий,
А + В (Д U В) будут соответствовать или значения поля Z грани-
тов, или значения поля Z измененных пород, или значения поля Z
измененных разновидностей гранитов. События А и В, в отличие
от приведенного выше примера с градациями значений поля, в дан-
ном случае являются совместными.
События Др Д2.....Ап образуют полную группу
событий, если они попарно несовместны, а в сумме образуют
достоверное событие, т. е. какое-либо из них обязательно происхо-
дит, причем только одно.
Примером полной группы событий являются п градаций, на ко»
торые разбит весь диапазон измеренных значений поля.
Противоположными событиями называются
два несовместных события, образующих полную группу, напри-
мер наличие и отсутствие аномалии какого-либо поля являются
противоположными событиями. Противоположными событиями бу-
дут значения поля из первой градации и значения поля из всех
остальных градаций, на которые разбит диапазон значений поля.
Количественной мерой степени объективной возможности того
или иного события А служит вероятность события
Р (Д), которая измеряется отношением числа т благоприятствую-
щих событию А исходов к общему числу п всех равновозможных
исходов экспериментов, т. е. Р (Д) = т/п. Это — классическое
определение вероятности. Оно сводит понятие вероятности к по-
нятию равновозможных событий и исходит из соображений сим-
метрии, как, например, в тривиальных примерах с бросанием мо-
неты или игральной кости. Однако задачи, связанные с симметрией
эксперимента, на практике встречаются весьма редко. Так, вероят-
ность распада атома радиоактивного вещества за конечный отрезок
времени на основании симметрии определить нельзя.
Поэтому на практике чаще всего используют статистиче-
ское определение вероятности, при котором ве-
роятностью события называют относительную частоту его появле-
ния при многократном воспроизведении комплекса условий экспе-
римента. При большом числе опытов частота события А стремится
к вероятности Р (Д) в ее классическом определении. Следовательно,
9
при статистическом определении вероятность события находится
лишь при достаточно многочисленных опытах, что является недо-
статком этой статистической вероятности.
Вероятность события А, вычисленная при условии, что прои-
зошло событие В, называется условной вероятностью
Р (А/В) события А.
Допустим, событие А состоит в наличии гранитов на некоторой
площади исследований и вероятность их встречи равна Р (Л). По-
сле проведения геофизических измерений (эксперимента), фикси-
рующих аномальными значениями поля распространение гранитов,
в чем состоит событие В, вероятность встречи гранитов Р (Л) пе-
реоценивается и становится равной Р (А/В).
Два события называются независимыми, если по-
явление одного из них не изменяет вероятности появления другого,
т. е. для независимых событий Р (А/В) = Р (Л), а для зависимых
Р (А/В) ^=Р (Л).
Виды различных событий, соответствующие им вероятности
и свойства этих вероятностей сведены в табл. 1. Следствием этих
свойств вероятностей является формула полной вероятности, на
основе которой определяется вероятность события Л, происходя-
щего вместе с одним из событий Н2, .... Нп, образующих
полную группу. События Hit Н2, . . . , Нп часто называют гипоте-
зами. Согласно формуле полной вероятности
П
P(A)=^P(Hl)P(A/Hi).	(1.1)
Следствием свойств умножения вероятностей (см. табл. 1, п. 5)
и формулы (1.1) является формула Бейеса, или теорема
гипотез, или формула обратных вероятностей.
На основе формулы Бейеса решается задача о нахождении ве-
роятности Р (Ht/Л) гипотезы Ht при условиях, что в результате
проведенного эксперимента произошло событие Л, а гипотезы Нх,
Н2, . . . , Нп образуют полную группу, причем их вероятности до
опыта известны и равны соответственно Р (HJ, Р (Н2), . . . ,
Р (Нп). Согласно формуле Бейеса
п
P(Hi/A)— Р(Н()Р(А/Н{)/ &P(Ht)P(A/Ht).	(1.2)
С помощью этой формулы переоцениваются вероятности гипотез
Р (Hi), называемые априорными, т. е. известными (или за-
данными) до опыта. После проведенного эксперимента, в результате
которого появилось событие Л, вероятностей Р (Н{) изменяются.
Новые вероятности Р (Нс/А) называют апостериорными,
т. е. полученными после эксперимента.
Пример. На площади исследований фундамент кристаллических пород
представлен гипербазитами, гранитами и гнейсами. По данным сейсмиче-
ских измерений известен нижний предел а для Значений скорости продоль-
ных волн ор, используемый для выделения по этим скоростям гипербазитов.
Из опыта предшествующих работ иа аналогичных по геологическому строе-
10
Таблица 1
п/п	Событие	Вероятность события	Свойства вероятности
1	Достоверное U	P(U)	Р (U) = 1
2	Невозможное V	P(V) .	р (V) = о
3	Случайное А	Р(Л)	О Р (Л) 5= 1
4	Противоположное А	Р(А)	Р (Л) = 1-Р (Л)
5	Произведение двух событий (пересече- ние) АВ (А Л В)	Р (АВ)	Независимые события Р (АВ) = Р (А)Р (В) Зависимые события Р (АВ) = Р(А/В)Р (В) = Р (В/А) (Л)
	Произведение п со- п бытий JJ Ai	чн	Независимые события р(п ^=]W) \Z=I / i=l
6	Сумма двух событий (объединение) А +	Р (А + В)	Несовместные события Р (А + В) = (Р (Л) + Р (В) Совместные события Р (Л + В) = Р (Л) + Р (В)-Р (АВ)
	Сумма п-событнй	'(?, 4')	Полная группа
	п		
	HI		р( Е лч = Е ри«)= 1 \1=1 / (=1 Любая группа / n \ п р А J = Ер - - ^P(AtAl)+^J(AiAlAk) + + . . . + (-1) р"-1 (Л,Л, . . .Л„)
иию участках значения vp^a наблюдались: на гипербазитах в 80, на гра.
нитах в 10, а на гнейсах в 5 % случаев. На одной из "точек площади прове.
денные измерения показали, что vp выше порогового значения а. Требуется
найти вероятность того, что фундамент участка в этой точке сложен гипер-
базитами [7].
Решение. Введем полную группу событий: Ht— фундамент, представ-
лен гипербазитами; Я2 — гранитами; Hs — гнейсами; событие А — изме-
ренное значение vp превышает порог а. Очевидно, что Р (А/Hi) — 0,8;,
Р (A/Ht) = 0,10; Р (A/Ht) = 0,05. Поскольку до проведения сейсмических
работ никакому типу пород не отдается предпочтения, то Р (Hi) = Р (Ht) =
= Р (Яз) = 0,33. По формуле Бейеса (1.2) переоцениваем априорную веро-
ятность Р (Hi) — 0,33, вычисляя апостериорную вероятность Р (А/Hi):
Р (AlHi) = 0,33 0,8: (0,33-0,8 + 0,33-0,10 + 0,33-0,05) = 0,84.
И
Формула Бейеса играет чрезвычайно важную роль. На ее ос-
нове решаются задачи выделения сигналов на фоне помех (см.
§ 40), обработки данных комплекса геофизических полей (см. § 46),
определения параметров источников аномалий при количествен-
ной интерпретации и др. [5].
Понятие вероятности события допускает также простую геомет-
рическую трактовку. Геометрическая вероятность
обобщает классическое определение на бесконечное множество
экспериментов. К понятию геометрической вероятности приводит
задача о бросании точки в некоторую ограниченную область G,
содержащую меньшую по размерам область g, причем все положе-
ния падения точки в область G считаются равновозможными.
Если событие А состоит в попадании точки в область g,
то Р (Л) = мера g/мера G, где под мерами областей g и G можно
понимать длины отрезков, размеры площадей или объемов.
Понятие геометрической вероятности используется при решении
задачи Бюффона, заключающейся в определении вероятности пе-
ресечения наугад брошенной иглы длиной 21 одной из параллель-
ных прямых, отстоящих друг от друга на плоскости на расстоянии
2а, причем /<а. Эта вероятность равна Р = 21/па. Важность этой
задачи по определению вероятности пересечения рудной жилы
длиной 21 одним из профилей площадной геофизической или гео-
логической съемки совершенно очевидна. На основе задачи Бюф-
фона И. Д. Савинским (1964 г.) были рассчитаны «Таблицы вероят-
ностей пересечения эллиптических объектов прямоугольной сетью
наблюдений», а также решены и другие задачи выбора оптималь-
ных сетей геофизических наблюдений.
Расчет сетей при таком подходе ориентируется лишь на геомет-
рию объектов и основывается на предположении, что объекты четко
фиксируются аномалиями в физических полях. В то .же время при
слабой дифференциации по физическим свойствам вмещающих по-
род и искомых объектов последние даже при значительных разме-
рах могут не выделяться аномальными значениями поля. Для
уверенного выделения аномалий от таких объектов обычно тре-
буется накопление аномального эффекта по большому числу точек
наблюдений. Таким образом, в общем случае расчет сетей геофи-
зических наблюдений следует проводить с учетом необходимости
накопления аномального эффекта.
} 2. СЛУЧАЙНАЯ ВЕЛИЧИНА
Расширением понятия случайных событий, состоящих в появле-
нии числовых значений, является случайная величина X.
Случайной называют величину, принимающую в резуль-
тате эксперимента одно, и только одно возможное значение, заранее
неизвестно какое именно и зависящее от случайных причин, ко-
торые не могут быть учтены. Случайная величина является обосно-
ванной моделью для описания данных геофизических измерений
в силу целого ряда случайных факторов, влияющих на показания
12
геофизического поля. Как и для результата отдельного экспери-
мента, для случайной величины можно установить статистические
закономерности, т. е. определить вероятности ее значений.
Случайные величины бывают непрерывные и дискретные. Пер-
вые из них принимают значения на числовой оси в рабочем диапа-
зоне прибора. Примером непрерывных случайных величин является
запись полного вектора магнитного поля в аэромагнитной станции
или сейсмическая запись в аналоговых станциях. Дискретная
случайная величина принимает вполне определенные значения хи
х2, . . . , хп с вероятностями plt р2...рп. Все возможные п
значений случайной величины при этом образуют полную группу
п
событий, т. е. pt = 1. где п конечно (или бесконечно).
Примером дискретных случайных величин являются данные
Измерений физических свойств горных пород, значения физических
полей, разбитых на п градаций.
В связи с обработкой на ЭВМ непрерывные случайные величины
обычно преобразуются в дискретные.
Универсальной характеристикой случайной величины является
функция распределения F (х), определяющая для
каждого значения х на числовой оси вероятность того, что случай-
ная величина X примет значение меньше х, т. е. F (х) = Р (Х<х).
Эта функция существует как для непрерывных, так и для дискрет-
ных величин. Она обладает следующими свойствами: F (х) непре-
рывна справа;
limF(x) = l;	limF(x) = 0;
Х-+-00	Х-+ОО
F (х2) > F (xj при x2>xf,
F(*2<X<x2) = F(x2)-F(x1). •	(1.3)
Значение случайной величины, для которого функция распреде-
ления принимает конкретно заданное значение, называется кван-
тилью распределения. Иначе, квантиль — есть аргу-
мент функции распределения.
Другая важная характеристика случайной величины — плот-
ность распределения f (х).
В силу (1.3)
Р (х<Х<х+ Дх) = Г(х+ Дх)—F(x).
Отсюда lim [F(x + Дх)—F(x)]/bx = F'(х),	Функция f (х) =
д*—о
= F' (х) характеризует плотность, с которой распределены зна-
чения случайной величины в данной точке. Плотность распределе-
ния обладает следующими свойствами: f (х) определена при тех же
значениях, что и F (х), за исключением тех точек, где F' (х) не су-
ществует; f (х) > 0;
lim f(x) = O;
J f(x)dx = 1;
—СО
13
Р (*1<Х<х2) =f f (x)dx.	(1.4)
*1
Функцию распределения можно выразить через плотность по-
редством интеграла с переменным верхним пределом, т. е.
Л*1) = f f(x)dx.	(1.5)
—00
В табл. 2 приведены основные числовые характеристики слу-
	Таблица 2
Характеристика (параметр) случайной величины	Формула для нахождения характеристики случайной величины
7-квантнль (квантиль поряд- ка у)	£	= F (М = т; tv = F~r Су)> г«е г-1 (?)—функция, обратная функции рас- пределения F (х)
Математическое ожидание MX (или среднее значение х) Мода Мо	МХ = 'х= £ XiPt l=i Мо — такое значение X, при котором плот- ность распределения f (х) максимальна
Медиана Me (или квантиль по- рядка 0,5)	Р (X < Me) = Р (X > Me) = F (Me) = 0,5
Дисперсия DX	DX = М (X—MX)2 = (xt - MX)*pi (=1
Среднее квадратическое откло- нение (стандарт) а	a=±V5x
Коэффициент вариации V	V = а/MX = '\I~DXIMX
Центрированное и иормирован- на отклонение	xi = (Xi — MX)/^DX
Начальный момент k-ro по- рядка а&	n i-=l
Центральный момент k-ro по- рядка Цк Асимметрия распределения А Эксцесс распределения Е	ИЛ = M (X-MX)k = (Xi-MX)kPl /=1 A = p.,/03 F. = u4/or« — 3
чайной; величины, широко используемые при обработке экспери-
ментальных данных.
Если результат эксперимента описывается двумя случайными
величинами и больше, то говорят о системе случайных
величин, включающей, например, измерения различных фи-
14
зических свойств горных пород, данные измерений разных полей,
различные параметры аномалиеобразующих объектов и т. д.
Случайные величины X и Y называются независимыми,
если плотность их совместного распределения f (х, у) = f (х) f (у),
в противном случае X и Y зависимы.
Характеристикой связи (зависимости) двух случайных величин
X и Y служит корреляционный момент (или момент
связи): КХу = М (ЛЬ, где Л = X—MX, t = Y—MY — цен-
трированные случайные величины.
Для дискретных величин X и Y
КХу = Ц (xt-MX) (У!-MY) p(j,	(1.6)
где Ру = Р (X — Xt\ Y ~ yj] — вероятность того, что система
(X, Y) примет значения xty}.
Для характеристики связи между X и Y часто используют
безразмерную величину — коэффициент корреляции
ГхУ = ХХу/ахОу	(1-7)
Коэффициент корреляции характеризует степень линейной связи
(зависимости) между X и Y. Его величина гХУ изменяется от — 1
до + 1. При гху">0 имеет место положительная корреляция (при
гХу = 1 — положительная функциональная зависимость), при
Гху<0 — отрицательная.
Случайные величины, для которых гХУ (или Хху) равен нулю,
называют некоррелированными.
Система п случайных величин Xj.Хп (в случае двух слу-
чайных величин Хх = X, Х2 = Y) имеет п2 корреляционных мо-
ментов, или ковариаций Кц — М (XtXj), которые принято
располагать в	виде Кп	матрицы К12	. . .	Кт	
К = КЧ =	К 21	Хм	...	Кт	(1-8)
	Кп1	кпг ...	Кпп	
Матрица (1.8) называется ковариационной, причем из
(1.6) легко видеть, что Kq — Кр и Кр— D(. Матрица, составлен-
ная из коэффициентов корреляции rtj = р называется кор-
реляционной
1 Tig ... Гщ
Гп1 Гпг ...	1
Две основные характеристики случайной величины — среднее
и дисперсия — обладают следующими важными для применения
1В
свойствами: 1) если а — постоянное число, то Ma = a, Da — 0;
2) если случайная величина Y — аХ, то MY = аМХ, DY = a2DX;
п	п
3) если Y = Х то МУ = У, MXi; для зависимых случайных
i=i	i=i
величий
DY=t DXi+2% Kif,	(1.10)
1=1	i<i
для независимых случайных величин
ОУ = £о(;	(1.10')
1
4)еслиУ = Пх<) то MY = Ц MXlt
п	п
ДУ = ПОХ< + 2 (MXt)*DXt,	(1.11)
1=1	1=1
где Х{ — попарно-независимы;
5) если
У = У а(Х {+ ад—
i=i
линейная функция, то
MY^pa/MXi + ao,
DY = У dtDXi 4- 2 Y WiKii = X Д <Wi/0i<i/.	(1.12)
Для различных случайных величин существуют разные соот-
ношения или законы, устанавливающие связь между возможными
значениями случайной величины и соответствующими им вероят-
ностями.
Для описания распределения геофизических показателей (фи-
зических свойств горных пород, физических полей и т. д.) наи-
большее применение получили:
1)	нормальный закон распределения с плот-
ностью распределения
f (х) = — -ехр [—(х—х)’/2о2]
л/ 2 л <з
и функцией распределения
F (х) = - L- J exp [ — (/—х)2^2] dt,
V 2Л О —оо
16
где х и ст — параметры распределения.
При х = 0 и ст = 1
W = 7=^ ехр (—х*/2),	(1-13)
д/2л
Г(х) = Ф(х) = —Jexp(—W2)dt	(1.14)
'у 2 л —оо
Причем Ф (— х) = 1—Ф (х). Так, Ф (0) = 0,5, Ф (— 1) = 0,1587;
Ф (1) = 0,8413.
Нормальный закон имеет широкое распространение в природе;
в частности, плотность и скорость упругих волн для образцов
пород обычно распределены нормально.
Для нормально распределенной величины практически все рас-
сеяние, т. е. отклонение от среднего х, укладывается в интервале
х ± Зст. Это следует из формулы, определяющей вероятность по-
падания случайной величины на заданный интервал (хт, х2),
Р (xi<X<x2) = Ф[(х2—х)/ст]—Ф[(хх—х)/ст].	(Ы5)
Согласно формуле (1.15), вероятности попадания случайной
нормально распределенной величины в интервалы х ± ст, х ± 2ст
и х ± Зст будут равны соответственно:
Рх — Ф [(х + ст—х)/ст]—Ф[(х—ст—х)/ст] = Ф (1) — Ф ( — 1) —
= 0,682;
Р2 = Ф(2)—Ф(—2)= 0,955 (95,5 %);
Р8 = Ф(3)—Ф( — 3) = 0,997 (99,7 %).
Поскольку все значения случайной величины, а именно 99,7 %,
укладываются в интервал Зст, способ оценки диапазона возможных
значений случайной величины носит название «правило трех
сигма». Из этого правила следует приближенный способ опре-
деления: ст = (хтах—х)/3.
Асимметрия и эксцесс нормального закона равны нулю.
Случайная величина, логарифмы значений которой распреде-
лены нормально, имеет логнормальный закон рас-
пределения. По этому закону обычно распределены значе-
ния кажущегося сопротивления пород, магнитной восприимчи-
вости сильно магнитных разностей пород, концентраций химиче-
ских элементов в горных породах;
2)	равномерный закон распределения с плот-
ностью
I 0, х<а, x>ft,
ж—"	17
Им. ГОРЬКОГО
БИБЛИОТЕКА
м. г. у.
и функцией распределения
F(x) =
(х—а)/(Ь—а),
О,
1,
a<Zx<Zb,
х<.а,
х~>Ь,
(1-17)
используется при априорном задании распределений параметров
аномалиеобразующих объектов (глубины залегания, мощности
и т. д.) или параметров аномалии (амплитуды, протяженности).
Среднее значение и дисперсия случайной величины, распреде-
ленной по равномерному закону, равны соответственно MX —
= (а + Ь)/2 и DX = (Ь—а)г/\2. Вероятность попадания случай-
ной величины в интервал (xlt х2)
Р (xt < X < х2) = (х2—*i)/(b—а).
Асимметрия, ввиду симметрии плотности, равна нулю, а эксцесс
равен — 1,2;
3)	закон Пуассона для дискретной случайной величины,
принимающей последовательно значения X — 0, 1, 2, . . . , т . . .
с вероятностью Рт = атехр (— а)/т! и дискретной функцией рас-
пределения
Лп= Z [amexp(—a)}lm\	(1.18)
m=0
Для закона Пуассона х — D = а, а — параметр распределе-
ния, т. е. этот закон является однопараметрическим, в отличие от
нормального закона, определяемого двумя параметрами х и D = о3.
Закон Пуассона используется при анализе результатов изме-
рений, в процессе которых проводится расчет суммы импульсов,
фиксирующих радиоактивный распад какого-либо элемента за
время t. При этом параметром распределения является величина
а — kt, где к — постоянная распада для данного элемента. ____
Закон Пуассона асимметричен и его асимметрия А = 1/V а,
а эксцесс Е — 1/а, т, е. распределение правоасимметрично и имеет
положительный эксцесс.
Распределение суммы двух независимых случайных величин Хг
и Х2, распределенных по закону Пуассона с параметрами аг и а2,
также подчиняется закону Пуассона с параметром 0 = 0!+ а2.
При решении задач математической статистики важную роль
играют три распределения %4 (или Пирсона). Стьюдента и Фишера,
используемые при изучении систем случайных величин, каждая
из которых имеет нормальное распределение. Распределе-
нию х2 подчиняется сумма конечного числа квадратов независи-
мых нормально распределенных величин с МХ{ = 0 и DXi = 1,
т. е.
х?=£х< или х?=Е [(У;-МУг)/7ОУ]2,	(1.19)
1=1	1=1
где Yi — произвольные независимые и нормально распределенные
18
величины с М%? = г и Dx? = 2г, число г называется числом сте-
пеней свободы.
Распределение Стьюдента (или /-распределе-
ние) с г степенями свободы имеет случайная величина вида
i = Х/^(£ Х^!г = Х/д/%^
(1-20)
Независимые случайные величины Х( распределены нормально
с MXt = 0 и DXt = 1, Mt = 0 (при г>1) и Dt = r/(r—2) (при
/>2).
Если Xi — произвольные независимые нормально распределен-
ные случайные величины, то величина
Х-МХ /	/_1_ у» (Xi — AlXf)8
д/ЬГ / V r U Dx‘
(1.21)
также является распределением Стьюдента. При увеличении г
распределение Стьюдента приближается к нормальному.
Распределение Фишера (или ^-распределение)
имеют случайные величины вида
т	п
(1.22)
т i=i п Д
где Xt и Y{ — независимые нормально распределенные величины
с МХ{ = MYt = 0; т и п — число степеней свободы Е-распреде-
ления. Математическое ожидание и дисперсия этого распределения
MFmn=n/(n~2) при п>2;
rip ____ (W -|- и — 2)
тп~ m(n — 2)s(n—4)
при п>4.
Обоснованием возможности использования на практике число-
вых характеристик случайных величин и их распределений при
проведении массовых экспериментов являются закон больших чи-
сел и центральные предельные теоремы.
Закон больших чисел устанавливает сходимость по
вероятности среднего арифметического, вычисленного по независи-
мым наблюдениям одной и той же величины, к математическому
ожиданию, т. е. среднее арифметическое случайной величины с уве-
личением числа наблюдений становится все более близким к ее
математическому ожиданию. Для среднего арифметического, рав-
ного Y ——У Xi, согласно свойствам математического ожидания,
П i=l
получаем МУ=МХ и DY = — X DXi = -^— • Таким образом,
n2 1=1	п
среднее арифметическое есть случайная величина со сколь угодно
малой дисперсией и при большом числе экспериментов ведет себя
почти как неслучайная. Закон больших чисел устанавливает в точ-
2*
19
ной количественной форме это свойство устойчивости среднего ариф-
метического. Другие формы закона больших чисел устанавливают
сходимость частоты события к его вероятности.
Так называемые центральные предельные тео-
ремы теории вероятностей устанавливают сходимость суммы
случайных величин к нормальному закону распределения. По-
скольку на геофизические измерения влияет большое число неза-
висимо действующих факторов, свойство нормальности сумм слу-
чайных величин приобретает большое значение. Это свойство имеет
место для неодинаково распределенных слагаемых при условии
конечности их дисперсий. Опыт показывает, что центральными
предельными теоремами можно пользоваться для суммы сравни-
тельно малого числа случайных величин, порядка десяти, и даже
меньше.
Для анализа ошибок измерения и фильтрации геофизических
полей особое значение имеют два положения: 1) если Хх, . . . , Хп
взаимно независимые нормально распределенные величины, то их
п	п
сумма Y =YtXl имеет нормальное распределение с MY 1=УМХ{,
f=l	1
п
DY =Y,DXt 2) если случайные величины XL...Хп не всегда
1
независимые нормально распределенные величины, то линейная их
комбинация Y = axXi +агХг + . . . апХп имеет нормальное рас-
пределение со средним и дисперсией, определяемой по (1.12).
§ 3.	СТАТИСТИЧЕСКИЕ ОЦЕНКИ
При количественном анализе результатов измерений используют
выборки случайных велияин. При этом важно организовать экспе-
римент таким образом, чтобы вероятность быть выбранным была
бы одинакова для любого элемента выборки — так называемая
репрезентативная выборка.
Множество всех возможных значений случайной величины,
в котором распределение изучаемого параметра совпадает с ее рас-
пределением, называют генеральнойсовокупностью.
Выборка, извлекаемая из генеральной совокупности,— лишь один
из возможных вариантов наблюденных значений изучаемой слу-
чайной величины.
Если представить, что весь массив горной породы разбит на
элементарные образцы, подобные тем, которые отбирают для опре-
деления физических свойств, то совокупность таких образцов
можно считать генеральной совокупностью, а извлекаемые из гор-
ного массива несколько десятков образцов с целью определения по
ним физических свойств всей горной породы, представляют выборку
из этой совокупности.
Важно обеспечить отбор образцов таким образом, чтобы вы-
борка была бы репрезентативной (представительной), т. е. надо
поставить эксперимент так, чтобы образцы отбирались равномерно
20
Генеральная совокупность является математической моделью
соответствующего действительного множества, и цель экспери-
мента — сделать заключения- ло имеющейся выборке о всей сово-
купности, из которой она взята.
Выборками являются результаты наблюдений физических по-
лей по точкам площади, типам пород, методам измерений и т. д.
При таком подходе точная информация о распределении изучаемых
величин отсутствует, поэтому одной из основных задач математи-
ческой статистики является оценка числовых характеристик (па-
раметров), плотности и функции распределения по отдельным вы-
боркам наблюдений.
Оценкой неизвестного параметра 9 назы-
вают случайную величину 0rt = f (хь . . . , хп), являющуюся
функцией наблюденных значений xlt . . . , хп. Часто используется
также термин «статистика».
Под статистикой понимают любую функцию от наблю-
денных данных. Оценка — это построенная по определенному пра-
вилу статистика.
Закон распределения оценки зависит от закона распределе-
ния и от числа элементов в выборке п. Представление о точности
и надежности оценки связано с понятиями доверительного ин-
тервала и доверительной вероятности.
Доверительным интервалом (0П—е, Ъп + е) для
параметра 9 называется такой интервал, в пределах которого не-
известное значение параметра 9 находится с вероятностью у, не
меиыпей заданной. Величина у называется доверительной
вероятностью (уровнем доверия) и обычно полагается рав-
ной 0,9; 0,95; 0,99. Равенство Р (9n—e?<0<0n + ev) = у озна-
чает, что с вероятностью у неизвестное истйнное значение параметра
попадает в интервал (0„—е7, 0„ + ev).
Практическое применение нашли опенки, которые характери.
зуются следующими свойствами:
1)	несмещенностью, состоящей в том, что математиче-
ское ожидание оценки 9„ равно истинному значению, т. е. М 0П = 9.
Несмещенность важна лишь для малых выборок п = 10-j-20;
2)	состоятельностью, имеющей место при условии,
что с увеличением числа наблюдений п оценка приближается (по
вероятности) к истинному значению параметра, т. е.
Р {I 9„—91 <е} —► 0 при п —► оо;
3)	эффективностью, заключающейся в том, что наи-
лучшей из всех возможных оценок является оценка с минимальной
дисперсией, т. е. D ($п) = min. Такими свойствами обладают
обычно несмещенные оценки. Если несмещенная оценка 0° имеет
дисперсию М (0°—9)2 = D§°n = <р„, величина <p„/Af (бп—9)2 ко-
личественно характеризует эффективность оценки Фп;
21
4)	асимптотической нормальностью, т. е. с
увеличением числа независимых наблюдений в выборке распреде-
ление оценки должно приближаться к нормальному, иначе
F — ______—<х } ->Ф(х) при п->оо,
где Ф (х) — функция (0, 1)-нормального распределения; (0, 1) —
означает нулевое среднее и единичную дисперсию.
Среди различных методов нахождения оценок параметров рас-
пределений, построенных по выборочным данным и обладающих
перечисленными выше свойствами, наибольшее применение имеют
методы моментов и максимального правдоподобия.
Суть метода моментов состоит в том, что в силу за-
кона больших чисел все выборочные моменты при п -> сю сходятся
по вероятности к соответствующим моментам исходного распреде-
ления. Это позволяет для вычисления оценок параметров исполь-
зовать формулы, приведенные в табл. 2.
Оценками наибольшего правдоподобия параметров 0Х, . . . , 9т
являются такие их значения, при которых достигает максимума
функция
Р(хъ . . . , xn/0i......0т) =
п
= £ Inf (Х1......хп/91,	, 0J-
t=i
где f (*1, . . . , хп/9) — условная плотность распределения, на-
зываемая функцией правдоподобия.
Согласно методу максимального правдопо-
добия оценки находятся из системы уравнений
дР/д9/ = 0, /=1, . . . , т.	(1.23)
По сравнению с методом моментов эти оценки определяются
по более сложным выражениям, к которым приводит решение си-
стемы (1.23), но зато они являются более эффективными.
Например, используем метод максимального правдоподобия для нахож-
дения параметров нормального распределения (среднего х и дисперсии а2)
по п наблюдениям . . . , хп. Функция правдоподобия примет вид
п
Р (xi, . . . , хп/х, а2) = у* In |—ехр[—(хг—х)2/2о21 =
2_j	( д/2л а	I
?=i
п
=—— 1п(2л)—-In а2—-V
2	2	2 / ,	2а2
1=1	_
Соответствующая система уравнений (1.23) для нахождения х и а2 будет
п
дР _ Xj—~x _q.	дР _   п	.
дх ~ , а2 “ ’	да2 “	2а2
1=1
22

п
+т£^=°.
1=1
из которой имеем
х~ — £ X/;	а2 = — 2} (х{— х)2.
П i=l	П i=l
При статистическом анализе геофизических данных широко
используются числовые характеристики (параметры распределе-
ний), приведенные в табл. 3. Эти
характеристики, определяемые по
выборкам, являются случайными
величинами. Следовательно, не-
обходимо указать их оценки и
соответствующие этим оценкам до-
верительные интервалы (см.
табл. 3).
Имея выражения для диспер-
сий оценок и их доверительных
интервалов, можно рассчитать
количество п независимых наблю-
дений для оценки числовой харак-
теристики с заданной точностью
ev (см. табл. 3).
Статистическими оценками фун-
кции F (х) и плотности f (х) рас-
пределения являются соответствен-
но статистическая функция рас-
пределения (называемая также
выборочной функцией распределе-
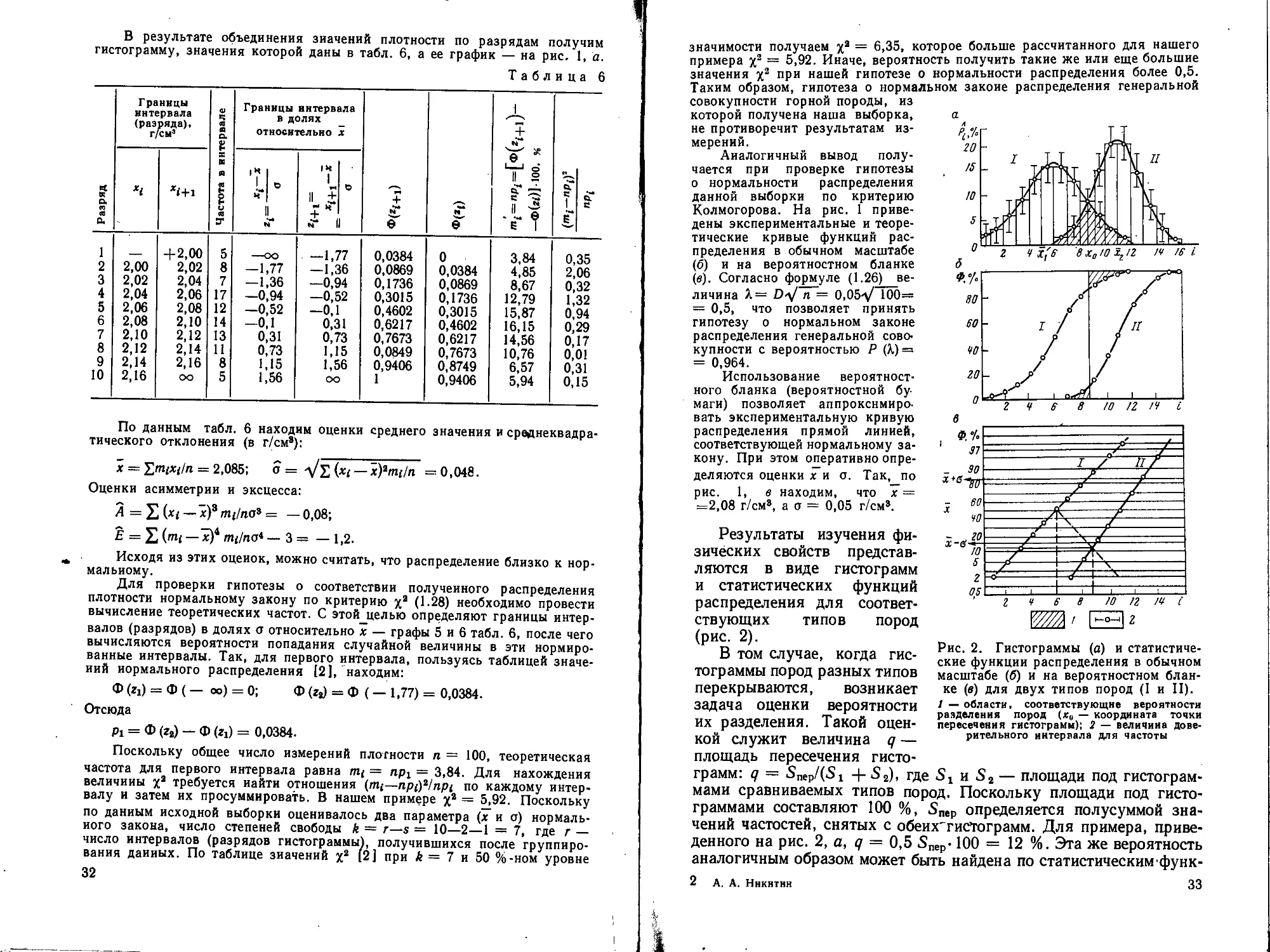
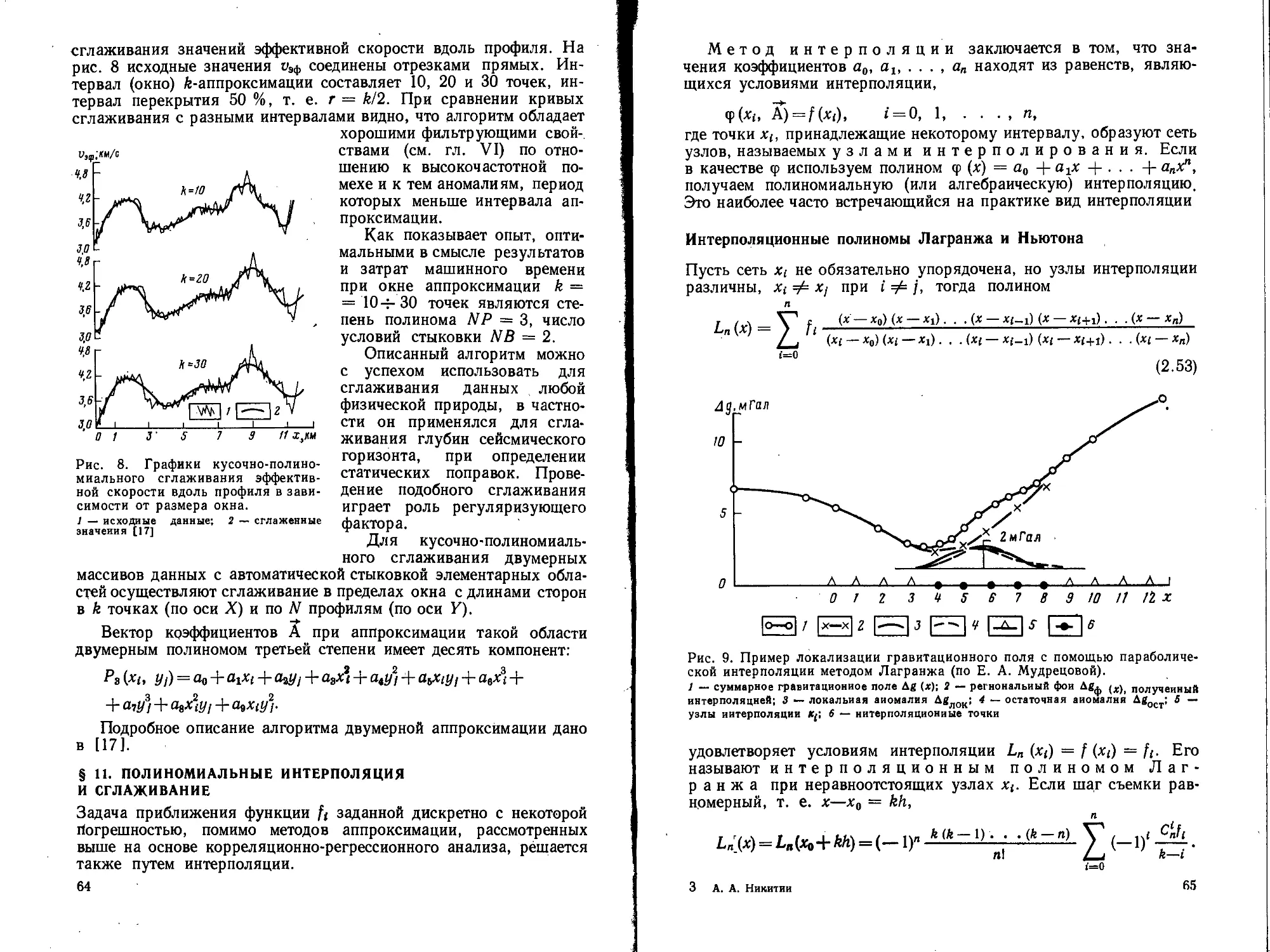
Рис. 1. Графики плотности нормаль-
ного распределения и гистограммы (а),
функции нормального распределения и
статистические функции распределения
в обычном масштабе (б) и на вероятно-
стном бланке (в).
Распределение: 1 — экспериментальное. 2—
теоретичеокое, 3 — области, соответствую-
щие доверительной вероятности 95 %. х —
среднее значение случайной величины; о —ее
среднеквадратическое отклонение; D — макси-
мальное отклонение теоретического распреде-
ления от экспериментального
ния, функцией накопленных частот, кумулятивной кривой) и гис*
тограмма.
Цод статистической функцией распреде-
ления случайной величины понимается частота события, что
Х<х, т. е.
Р (X < х) = Fn (х) = п (х)/п.
24
Для нахождения этой функции при фиксированном х следует
найти число значений X, меньших фиксированного х, а затем по-
лученный результат разделить на общее число значений случайной
величины п. Функция Fn (х) представляет дискретную ступенча-
тую функцию, скачки которой соответствуют значениям X и равны
частотам этих значений.
Г истограмма описывает распределение частот pi =
определяемых для каждого значения Xi случайной величины X.
Для построения гистограммы весь диапазон значений X разби-
вается на некоторое число градаций (разрядов) и подсчитывается
число значений случайной величины mit приходящееся на каждую
i-ю градацию, которое затем нормируется по общему числу значе-
ний п. По оси абсцисс откладываются градации (разряды), а по
оси ординат — соответствующие этим разрядам частоты pi (рис. 1, а)
называемые иногда частостями. На основе гистограммы обычно
строят статистическую функцию распределения (рис. 1,6). Если
границы (или середины) разрядов на гистограмме обозначить че-
рез х1( . . . , хг, то
Л.(*1) = 0; К{хг) = рй Fn(xs) = p1 + p2;	. .
K(Xr) = £pi-	(1-24>
z=i
При построении гистограмм не существует строго обоснованных
методов определения числа разрядов г. Обычно пользуются одним
из трех эмпирических правил: 1) определяют г « aJ п; 2) г нахо-
дят по интервалу группирования исходных данных Дх, равного
погрешности (двойной или тройной ее величине) измерения пара-
метра); 3) г определяют по величине Дх, вычисляемой по формуле
Стерджеса
Дх = (Хтах—Xmin)/(1 4" 3,321g п)-	(1-25)
При этом в каждом разряде гистограммы не должно быть менее
пяти значений, в противном случае проводится объединение не-
скольких разрядов. Общее число разрядов также должно быть не
менее пяти.
Для изображения статистической функции распределения часто
используют вероятностный бланк (рис. 1, а), на котором функ-
ция нормального распределения всегда представлена прямой ли-
нией.
Построение гистограмм и статистических функций распределе-
ния является основой обработки данных физических свойств гор-
ных пород и различных количественных признаков геофизических
полей при оценке их информативности (см. § 5).
25
§ 4. СТАТИСТИЧЕСКАЯ ПРОВЕРКА
ПРОСТЫХ ГИПОТЕЗ
Для проверки предположения о характере закона распределения
изучаемого признака, а также для сравнения отдельных числовых
характеристик различных выборок между собой используют по-
нятие гипотезы и критерия значимости.
Любое предположение относительно распределения случайной
величины X называют статистической гипотезой, а
правило, по которому на основании имеющихся данных принимают
или отвергают гипотезу, называют критерием ее проверки.
Для выработки критерия надо указать интервал, в пределах ко-
торого возможные значения параметра встречаются наиболее часто.
Если теоретическое значение параметра 0 укладывается в этот ин-
тервал, то гипотеза не противоречит исходным данным. Область,
в которой вероятность наблюдения статистической величины —0
достаточно велика, называется областью принятия™-
п о т е з ы. Область с малой вероятностью определения —9
называется областью непринятия гипотезы или критической
областью. Для проверки гипотезы задают уровень значимо-
сти, т. е. некоторое малое число 8. Если гипотеза верна, т. е. 0П =9,
критерий приводит к неверному решению в 100 8 % случаев и к вер-
ному решению в 100 (1—г) % случаев. Выделяют односторонние
и двусторонние критерии. Односторонний критерий
устанавливает область гипотезы как 0n< 0i-e, а двусторон-
ний критерий определяет эту область как 9ei2<:9n<9i-ei2-
В последнем случае область принятия гипотезы определяется
доверительным интервалом. При малом числе данных симметрич-
ная оценка приводит к неоправданно большим доверительным ин-
тервалам ввиду резкой асимметрии распределения выборочной
дисперсии. Поэтому при малом числе данных применяют асиммет-
ричные доверительные оценки, рассчитываемые таким образом,
чтобы вероятности на концах кривой распределения были бы равны
между собой.
Гипотеза называется простой, если требуется прове-
рить одну единственную гипотезу, например о виде распределения
или о равенстве числовых характеристик, и сложной, если
проверяется не одна, а две гипотезы и больше, например, когда
требуется установить наличие нескольких типов пород по данным
одного или комплекса геофизических методов. Для проверки ги-
потезы соответствия статистической функции распределения ?п (х)
теоретической функции F (х) (например, функции распределения
нормального закона) в практике обработки геофизических данных
получили распространение критерии Колмогорова и Пирсона.
Согласно критерию Колмогорова вычисляется ве-
личина
l = DVn, ~	(1.26)
где D = max) F (х) — F (х) | — максимум модуля отклонения ста-
26
тистической и теоретической функций распределения. По величине
Л в соответствии с ее распределением
Р(Х)=1 — £ (—1)*ехр(—2W)	(1.27)
k=*—00
находится вероятность Р (1).
Если Р (1) мала (обычно меньше 0,5), гипотеза о соответствии
статистической Fn (х) и теоретической F (х) отвергается.
Например, для X, равной 0,3, 0,7, 1,1, значения Р (К) равны
соответственно 1,00, 0,71, 0,18.
Согласно критерию Пирсона
X2 = Z (mi — npiYInpi,	(1.28)
1==1
где mi — число значений случайной величины в i-м разряде гисто-
граммы; pt — вероятности сравниваемого с экспериментальным
теоретического распределения.
По значению х2 и числу степеней свободы k = г—s (s — число
наложенных связей) с помощью таблиц вероятностей Р (%2) опре-
деляется вероятность того, что величина, имеющая распределение
X2 с k степенями свободы, превысит данное значение %2. Если эта
вероятность мала, гипотеза о соответствии экспериментального
распределения теоретическому отвергается. Например, для k = 5
и х2 = 1>5, 4,35, 15,1 значения Р (х2) соответственно 0,9, 0,5, 0,01.
Число степеней свободы определяется разностью между числом
разрядов г и числом наложенных связей s.
При сопоставлении статистической функции с нормальным за-
коном распределения s = 3, поскольку для вычисления теорети-
ческих значений pi используются оценки среднего и дисперсии,
полученные по выборке (это дает две связи), а задание конкрет-
ного вида распределения—нормального, добавляет еще одну связь.
Теоретические частоты определяют следующим образом. На-
ходят оценки среднего и дисперсии х и а2. Полученные эксперимен-
тальные данные, т. е. значения случайной величины, центрируют
и нормируют, переходя к значениям X — (X—х)/ст, вычисляют
концы разрядов гистограммы:
Xi=(xi — х)/а;	Xf+i = (xt+1—х)/а.
Далее определяют теоретические вероятности pt попадания зна-
чений X в интервале (xj; xi+1), например для нормального закона
по формуле pt = Ф (х,+ 1)—Ф (х/), и, наконец, находят теорети-
ческие частоты mi = npi.
Следует отметить, что при использовании критерия х2> в от-
личие от использования критерия Колмогорова, необходимость
вычисления оценок среднего и дисперсии по выборочным данным
учитывается путем уменьшения числа степеней свободы. На изме-
нение числа степеней свободы влияет и изменение числа разрядов
27 '
гистограммы, т. е. способ группировки данных. Критерий Колмо-
горова такого согласования не предусматривает, поэтому он может
приводить к завышенным значениям вероятности Р (1).
Н. В. Смирновым предложены критерии для проверки гипотезы
о принадлежности двух выборок к одной и той же генеральной со-
вокупности (иначе, о том, что распределения какого-либо признака
в двух генеральных совокупностях, из которых мы взяли выборки,
одинаковы).
Мерой расхождения двух статистических функций распределе-
ния Fni (х) и Fni (у) для первого критерия является
Dnin2 = max\Fni(x)—Fn2(y)\.	(1.29)
Определяется параметр 1	+ «а и по таб’
лице для распределения критерия Колмогорова находится вероят-
ность Р (1<17) = у. При гипотеза об одинаковом распре-
делении двух выборок X и Y отвергается с вероятностью у.
Для проверки однородности двух выборочных распределений
используется также критерий %2 в виде
(1.30)
где rn't и т \ — соответственно частоты сравниваемых выборок
X и Y.
Этот критерий при больших их и п2 распределен по закону %2
с г—1 степенями свободы.
Особое значение имеют непараметрические кри-
терии, применение которых не требует заранее устанавливать
законы распределения сравниваемых совокупностей, т. е. когда
неизвестны семейства функций распределений, к которым принад-
лежат плотности распределения. Согласно критерию Вил-
кок с о н а независимые наблюдения двух выборок xt (i = 1.
ni) И «//(/= 1....п2)	располагаются в общую последователь-
ность в порядке их возрастания, и для этой последовательности
рассчитывают число инверсий U, равное сумме количества всех у/,
стоящих впереди каждого xt. Например, в последовательности
У1, хъ х2, у 2, ys, yit ха, уъ, ув, xlt ... Xt и х2 дают по одной ин-
версии с у-с, ха дает четыре инверсии с у1У у2, у2, у2 и х2 — шесть
инверсий.
Гипотеза о принадлежности выборок одной и той же совокуп-
ности отвергается, если общее число инверсий превосходит выб-
ранную с учетом уровня значимости границу. Эта граница опреде-
ляется из условия нормального распределения для общего числа
инверсий U со средним U = пуг212 и дисперсией DU = пхп2 (пх 4-
+ лг + 1)/12, т. е. критическая область определяется с помощью
значений функций (0, 1)-нормального распределения.
28
Для двустороннего критерия нижняя и верхняя границы со-
ответственно:
Uy = и—;
Ut^U + ta+W2^DU,	(1-31)
где у — 1—е; 8 — уровень значимости; t^+^/2 — квантиль (0, 1)-
нормального распределения порядка (1 +?)/2. При условии,
U>U^, либо U < ЦТ гипотеза о принадлежности выборок одной
и той же совокупности отвергается.
Указанные критические границы Uy и Uy являются прибли-
женными, так как основаны на асимпотически нормальном рас-
пределении U. Однако это приближение вполне удовлетворительно
при п1>10, п2>1 0. При nx<10 и п2<10 критические значения
для U определяются по специальным таблицам [2].
Пример. По образцам гранодиоритов двух массивов измерена плот-
ность, результаты Х( и у; (в г/см8) приведены в табл. 4. Проверить по крите-
Таблица 4
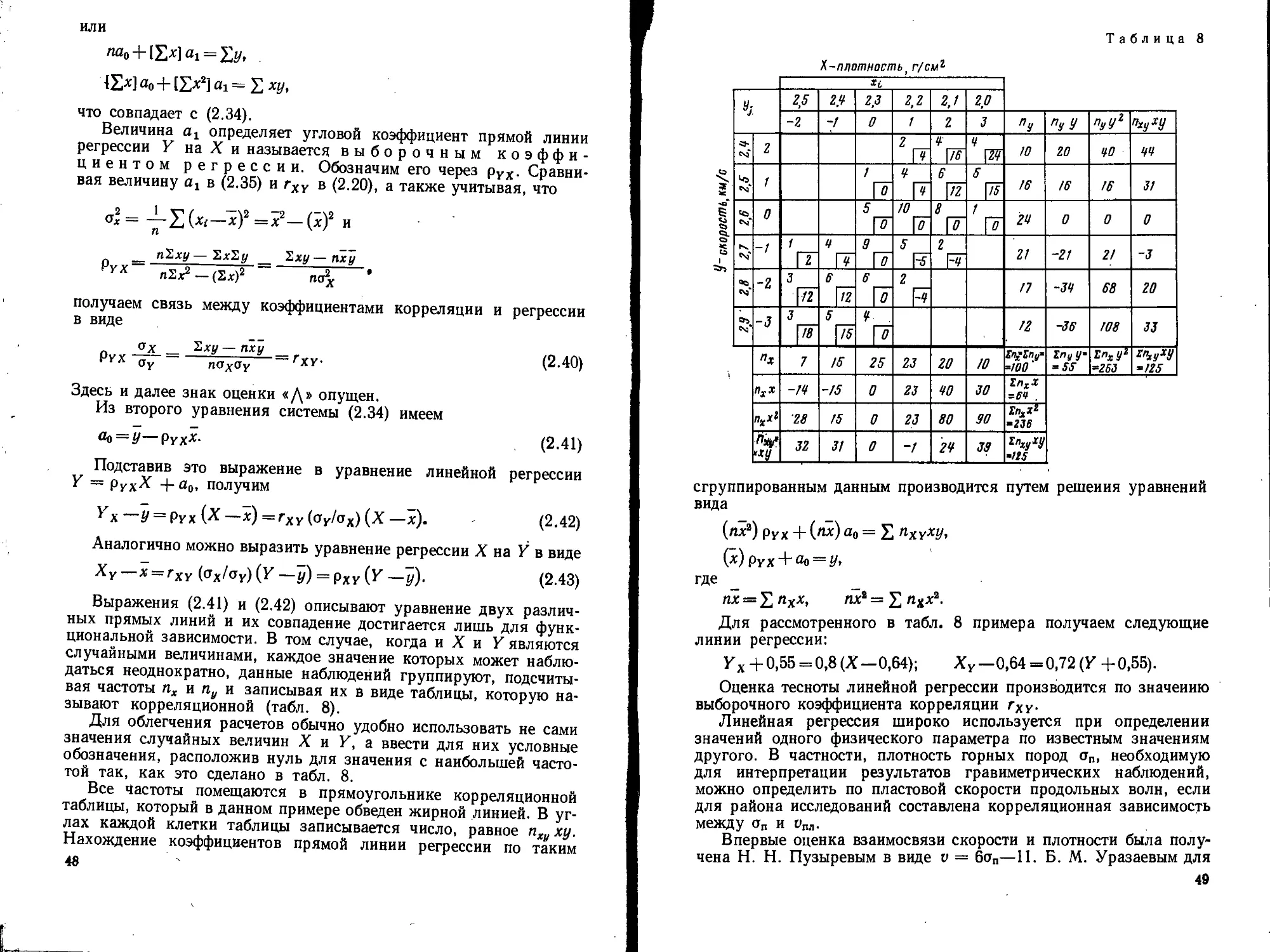
Образцы I массива	Плотность, г/см’	Образцы II массива	Плотность, г/см’	Образцы I массива	Плотность, г/см’	Образцы 11 массива	Плотность, г/см3
*1	2,96	У1	2,98	х7	3,05	Уа	3,14
*3	2,96	Уа	2,98	Xg	3,05	У»	3,15
Xg	3,00	Уч	3,02	X,	3,08	У»	3,16
*4	3,03	«4	3,07	*10	3,11	Ут	3,16
*S	3,03	Уа	3,10	*11	3,14	Ун	3,16
х»	3,04	Уч	3,12	*и	3,14	Ун	3,16
рию Вилкоксона гипотезу о равенстве средних значений плотности по двум
массивам при уровне значимости е = 0,05.
Решение. Составим общую последовательность наблюдений по возраста-
нию: хь х2, уъ у2, х3, уз, х4, х5, хв, х„ х8, у4, хв, Уз, Хю, у», Хп, у,, х12,
Уа, Уа< Уи>, Ун. У12-
Число инверсий у на х равно сумме произведений riki, где Г( — номера
тех у], которые сменяются в последовательности наблюдениями х*.; kt —
число наблюдений в серии наблюдений х*. следующих за yrf.
U = 2 + 3-5 + 4 + 5 + 6 + 7 + 12 = 51;
U = П1-ла/2= 12-12/2 = 72.
Среднее квадратическое отклонение для числа инверсий
ou = ^JdU = V12-12/12(12+ 12+ 1) = 12^/2* = 16,92;
5 = 72— 1..96-17 « 38,7;	(7+95 = 72 + 1,96-17 = 105,3.
Так как 38,7<U — 51 < 105,3, результат применения критерия Вилкоксона
не противоречит гипотезе о равенстве средних.
29
Часто вместо сравнения самих распределений, когда выбороч-
ное распределение построить трудно, ограничиваются проверкой
гипотезы о равенстве числовых характеристик: среднего, дисперсии
и других моментов распределения.
Для сравнения средних двух выборок X и У можно использо-
вать расчет доверительных интервалов (см. табл. 3):
X ±	; у ± th-
Если эти интервалы пересекаются, то с вероятностью у можно ут-
верждать равенство средних х и у.
Учитывая асимптотическую нормальность распределений х и у
(согласно центральной предельной теореме), можно говорить об
их равенстве с вероятностью у при выполнении условия
I х—у |	tv (fyn-i + Су/пъ,	(1.32)
где tv—у-квантиль (0, 1)-нормального распределения.
Критерий (1.32) удовлетворительно работает при пх>»30 и
п2>30. По пересечению доверительных интервалов можно прове-
рить гипотезу о равенстве любых других числовых характеристик
двух выборок.
Более точный метод сравнения двух выборок базируется на
критерии Стьюдента. Если распределения выборок
предполагаются нормальными, то равенство х = у с вероятностью у
удовлетворяется при выполнении условия | где
X — У
пхпа (П1 + па — 2)
/11 + па
(1.33)
а —у-квантиль распределения Стьюдента с k = (пх + п2—2) —
степенями свободы. Например, при у = 95 % и k = 10, 20, 40
критическое значение равно соответственно 2,23, 2,09, 2,02. Для
приведенного выше примера по проверке гипотезы о равенстве
средних значений плотности двух массивов х = 3,05; ох — 0,06;
у = 3,10; ау = 0,07.
Согласно критерию (1.33)
t =	0.05	/ 12-12-22	0,05-11,6 ~ . g
V0,043 + 0,059	V 24	“	0,32	’
Таким образом, t = 1,8 меньше табличного значения, равного
tv = 2,07 (для k = 22), и гипотеза о равенстве средних этих вы-
борок выполняется.
Метод сравнения дисперсий в предположении о нормальности
распределения обеих выборок основан на критерии Фи-
шера
Е= аМ	1	(1.34)
где о? и о| — выборочные дисперсии, причем О1>Ог.
30
Величина F подчиняется распределению Фишера с («1—1) и
(п2—1) степенями свободы.
Гипотеза о равенстве дисперсий принимается с вероятностью
7 при F<zFv, где А —у-квантиль распределения Фишера. На-
пример, для у = 95 то и rtj—1 = n2—1 — 10, 20, 30 критические
значения Fv равны соответственно 2,98, 2,12, 1,84.
Нетрудно видеть, что гипотеза о равенстве дисперсий плотности
двух гранитных массивов согласно критерию Фишера F = а2/а2 =
= 0,072/0,062 — 1,37 выполняется с вероятностью не менее 95 %.
§ 5. ОБРАБОТКА ДАННЫХ ИЗМЕРЕНИЙ
ФИЗИЧЕСКИХ СВОЙСТВ ГОРНЫХ ПОРОД
Применение основных понятий теории вероятностей и математиче-
ской статистики, статистической проверки гипотез проиллюстри-
руем на примере обработки данных измерений физических свойств
горных пород. Эта обработка включает: построение статистических
оценок плотности и функции распределения с целью компактного
представления данных о физических свойствах; вычисление оценок
числовых характеристик (см. табл. 2); определение точности оце-
нок (доверительных интервалов) согласно табл. 3; проверку гипо-
тезы о законе распределения изучаемых данных в соответствии
с § 4; оценку формы и силы корреляционных связей между различ-
ными физическими свойствами, анализ множественных связей,
рассматриваемых в гл. II.
Допустим, что в результате п = 100 измерений плотности горной по-
роды на денситометре с погрешностью 6 = ± 0,01 г/см8 получены данные,
приведенные в табл. 5.
Таблица 5
Плотность, г/см3	Частость, mi	Плотность, г/см’	Частость, mi	Плотность, г/см'	Ч астость, mi
2,00	5	2,06	7	2,12	3
2,01	3	2,07	6	2,13	5
2,02	5	2,08	6	2,14	6
2,03	4	2,09	8	2,15	4
2,04	3	2,10	6	2,16	4
2,05	10	2,11	10	2,17	3
				2,18	2
Для построения оценки плотности распределения — гистограммы не-
обходимо провести группирование данных согласно эмпирическим правилам.
По формуле Стерджеса (1.25) имеем
Дх = J^max^ymin. = 2'18-2,00 = Q г/см8
14-3,321gn	1 + 3,32-2
Такой же интервал группирования получаем, исходя из равенства ин-
тервала двойной погрешности измерений: Дх = 26 = 0,02 г/см8. Проведем
группирование данных, начиная с больших значений плотности, учитывая,
что в каждом разряде гистограммы не должно быть менее пяти значений.
31
В результате объединения значений плотности по разрядам получим
гистограмму, значения которой даны в табл. 6, а ее график — на рис. 1, а.
Таблица 6
| Разряд	|	Границы интервала (разряда), г/см®		Частота в интервале	Границы интервала в долях относительно х				+ ё"	It*	% ‘001 [(»)ф— —(— -du = -ш	сГ с 1 г 'w-	сГ е
	xi	xi+i		|Н L н“	О	IX 1 II ± г	о					
1			4-2,00	5			—1,77		0,0384	0	3,84	0,35	
2	2,00	2,02	8	-1,77		—1,36		0,0869	0,0384	4,85	2,06	
3	2,02	2,04	7	—1,36		—0,94		0,1736	0,0869	8,67	0,32	
4	2,04	2,06	17	—0,94		—0,52		0,3015	0,1736	12,79	1,32	
5	2,06	2,08	12	—0,52		—0,1		0,4602	0,3015	15,87	0,94	
6	2,08	2,10	14	—0,1		0,31		0,6217	0,4602	16,15	0,29	
7	2,10	2,12	13	0,31		0,73		0,7673	0,6217	14,56	0,17	
8	2,12	2,14	11	0,73		1,15		0,0849	0,7673	10,76	0,01	
9	2,14	2,16	8	1,15		1,56		0,9406	0,8749	6,57	0,31	
10	2,16	оо	5	1,56		ОО		1	0,9406	5,94	0,15	
По данным табл. 6 находим оценки среднего значения и сраднеквадра-
тического отклонения (в г/см8):
х = TjiWlln = 2,085; о = л/Е (*£ — x)2miln = 0,048.
Оценки асимметрии и эксцесса:
А = 2 (xi — *)3 пц/па2 = — 0,08;
Е = У, (mt — х)1 mj/na* — 3 = — 1,2.
Исходя из этих оценок, можно считать, что распределение близко к нор-
мальному.
Для проверки гипотезы о соответствии полученного распределения
плотности нормальному закону по критерию х2 (1.28) необходимо провести
вычисление теоретических частот. С этой целью определяют границы интер-
валов (разрядов) в долях а относительно х — графы 5 и 6 табл. 6, после чего
вычисляются вероятности попадания случайной величины в эти нормиро-
ванные интервалы. Так, для первого интервала, пользуясь таблицей значе-
ний нормального распределения [2], находим:
Ф(31) = Ф(— °о) = 0; Ф(г,) = Ф (— 1,77)= 0,0384.
Отсюда
Pi = Ф (г2) — Ф (3j) = 0,0384.
Поскольку общее число измерений плотности п = 100, теоретическая
частота для первого интервала равна гп( = npi — 3,84. Для нахождения
величины х2 требуется найти отношения (mi—npi)2/npi по каждому интер-
валу и затем их просуммировать. В нашем примере х2 = 5,92. Поскольку
по данным исходной выборки оценивалось два параметра (х и о) нормаль-
ного закона, число степеней свободы k — г—s = 10—2—1 = 7, где г —
число интервалов (разрядов гистограммы), получившихся после группиро-
вания данных. По таблице значений х2 [2J при k = 7 и 50 %-ном уровне
32
значимости получаем у? = 6,35, которое больше рассчитанного для нашего
примера х2 = 5,92. Иначе, вероятность получить такие же или еще большие
значения х2 при нашей гипотезе о нормальности распределения более 0,5.
Таким образом, гипотеза о нормальном законе распределения генеральной
совокупности горной породы, из
которой получена наша выборка,
не противоречит результатам из-
мерений.
Аналогичный вывод полу-
чается при проверке гипотезы
о нормальности распределения
данной выборки по критерию
Колмогорова. На рис. 1 приве-
дены экспериментальные и теоре-
тические кривые функций рас-
пределения в обычном масштабе
(6) и на вероятностном бланке
(в). Согласно формуле (1.26)_ве-
личина Х= D-у/ и ~ 0,05^ 100=
= 0,5, что позволяет принять
гипотезу о нормальном законе
распределения генеральной сово-
купности с вероятностью Р (Х) =
= 0,964.
Использование вероятност-
ного бланка (вероятностной бу-
маги) позволяет аппроксимиро-
вать экспериментальную кривую
распределения прямой линией,
соответствующей нормальному за-
кону. При этом оперативно опре-
деляются оценки х и а. Так, по
рис. 1, в находим, что х =
=2,08 г/см8, а о = 0,05 г/см8.
Результаты изучения фи-
зических свойств представ-
ляются в виде гистограмм
и статистических функций
распределения для соответ-
ствующих типов пород
(рис. 2).
В том случае, когда гис-
тограммы пород разных типов
перекрываются, возникает
Рис. 2. Гистограммы (а) и статистиче-
ские функции распределения в обычном
масштабе (б) и на вероятностном блан-
ке (в) для двух типов пород (I и II).
задача оценки вероятности
их разделения. Такой оцен-
кой служит величина q —
1 — области, соответствующие вероятности
разделения пород (х(| — координата точки
пересечения гистограмм); 2 — величина дове-
рительного интервала для частоты
площадь пересечения гисто-
грамм: q = Snep/GSr + S2), где и S2 — площади под гистограм-
мами сравниваемых типов пород. Поскольку площади под гисто-
граммами составляют 100 %, Snep определяется полусуммой зна-
чений частостей, снятых с обеих'гистограмм. Для примера, приве-
денного на рис. 2, a, q = 0,5 Snep-100 = 12 %. Эта же вероятность
аналогичным образом может быть найдена по статистическим функ-
2 А. А. Ннкнтнн
33
циям распределения (графикам накопленных частот) (рис. 2, б)
и особенно просто на вероятностном бланке (рис. 2, в).
Для значений частот, соответствующих разрядам гистограммы,
следует оценивать их точность а(р) = д/р(1—рУп (см. табл. 3)
и построение гистограмм дополнять доверительными интервалами
(см. рис. 2, а). Перекрытие доверительных интервалов гистограмм
двух типов пород свидетельствует о невозможности разделения
этих пород по физическому параметру.
Вероятность разделения пород двух типов у = 1—q. При ве-
роятности у = 50 % гистограммы полностью перекрываются и,
следовательно, породы по физическому параметру не различаются.
Обычно при у, меньшей 75 % (q > 25 %), разделение пород по
физическому параметру практически невозможно.
В том случае, когда исходные выборки имеют нормальное рас-
пределение, вероятность разделения
у = ф(*°	ф( *о у	(1.35)
где х0 — точка пересечения гистограмм; xlt хг и olt а2 — соответст-
венно оценки средних и среднеквадратических отклонений двух
выборок.
Эту вероятность удобно определять графически по расстоянию
между кривыми накопленных частостей по линии, проходящей
через точку х0. Например, для случая, приведенного на рис. 2,
имеем х0 = 9, xt — 6, xt = 11, ах = 3, а2 = 2 и соответственно
у = 87 %.
Важным моментом при обработке данных измерений физиче-
ских свойств пород является разделение гистограмм сложной формы,
в частности с двумя и большим числом экстремумов, отражающих
смесь некоторого числа разнотипных пород. Эта задача решается
путем фильтрации гистограммы оптимальным фильтром сжатия
(обратный фильтр), рассмотренной в § 34.
С использованием табл. 3 возможно оценить необходимое число
измерений при заданной точности n = tyD/e%.
Например, пусть при измерении плотности By = 0,01 г/см8; а оценка
дисперсии D = [0,03 г/см0]а. При доверительной вероятности у= 0,95 ве-
личина ty = 1,65. Следовательно, для нашего примера п = 1,65*Х
Х0,038/0,012 « 25.
Все приведенные приемы обработки данных измерений физиче-
ских свойств горных пород аналогичным образом используются
при обработке наблюдений геофизических полей, в частности при
решении задач распознавания образов (см. § 44). При этом гисто-
граммы наблюденных значений физических полей строятся над
объектами с известной геологической природой, служащими эта-
лонами при распознавании неизвестных объектов. Вероятность
разделения гистограмм является мерой информативности измеряе-
мых признаков.
ГЛАВА II
КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ,
ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ
ГЕОФИЗИЧЕСКИХ ДАННЫХ
Решение задач сглаживания, интерполяции и аппроксимации гео-
физических данных проводится на основе вероятностно-статистиче-
ского и детерминированного подходов. В рамках первого подхода
наибольшее применение получили методы корреляционно-регрес-
сионного анализа (см. § 6—10), а в рамках второго — методы ин-
терполяции с помощью полиномов Ньютона, Лагранжа, сплайн-
функций (см. § 11) и системы гармонических функций (см. § 12).
§ в. КОРРЕЛЯЦИЯ И РЕГРЕССИЯ
Важной задачей обработки геофизических данных является изу-
чение зависимостей между изучаемыми признаками (например,
между различными физическими свойствами горных пород), между
показаниями различных методов (например, между глубиной за-
легания сейсмического горизонта и аномальными значениями силы
тяжести в гравиразведке) и т. д. Другой распространенной задачей
обработки геофизических данных является их аппроксимация не-
которой зависимостью, в частности полиномом заданной степени.
Изучение и построение указанных зависимостей предусматривают
оценку тесноты связи и формы проявления этой связи. Тогда за-
дачи обработки решаются на основе корреляционно-регрессионного
анализа.
Зависимость, при которой изменение одной величины вызывает
изменение распределения другой, называется статистиче-
ской (стохастической). При статистической зависимости разли-
чают корреляцию, когда устанавливают существование
взаимосвязи между двумя (или более) случайными величинами
и оценивают силу (тесноту) этой связи, и регрессию, когда
выясняют характер (форму) зависимости между величинами X
и У и возможность оценки У по X (или X по У), причем либо X,
либо У, либо X и У являются случайными величинами.
Оценка тесноты связи производится путем расчета коэффици-
ента корреляции, определяющего и степень взаимосвязи между
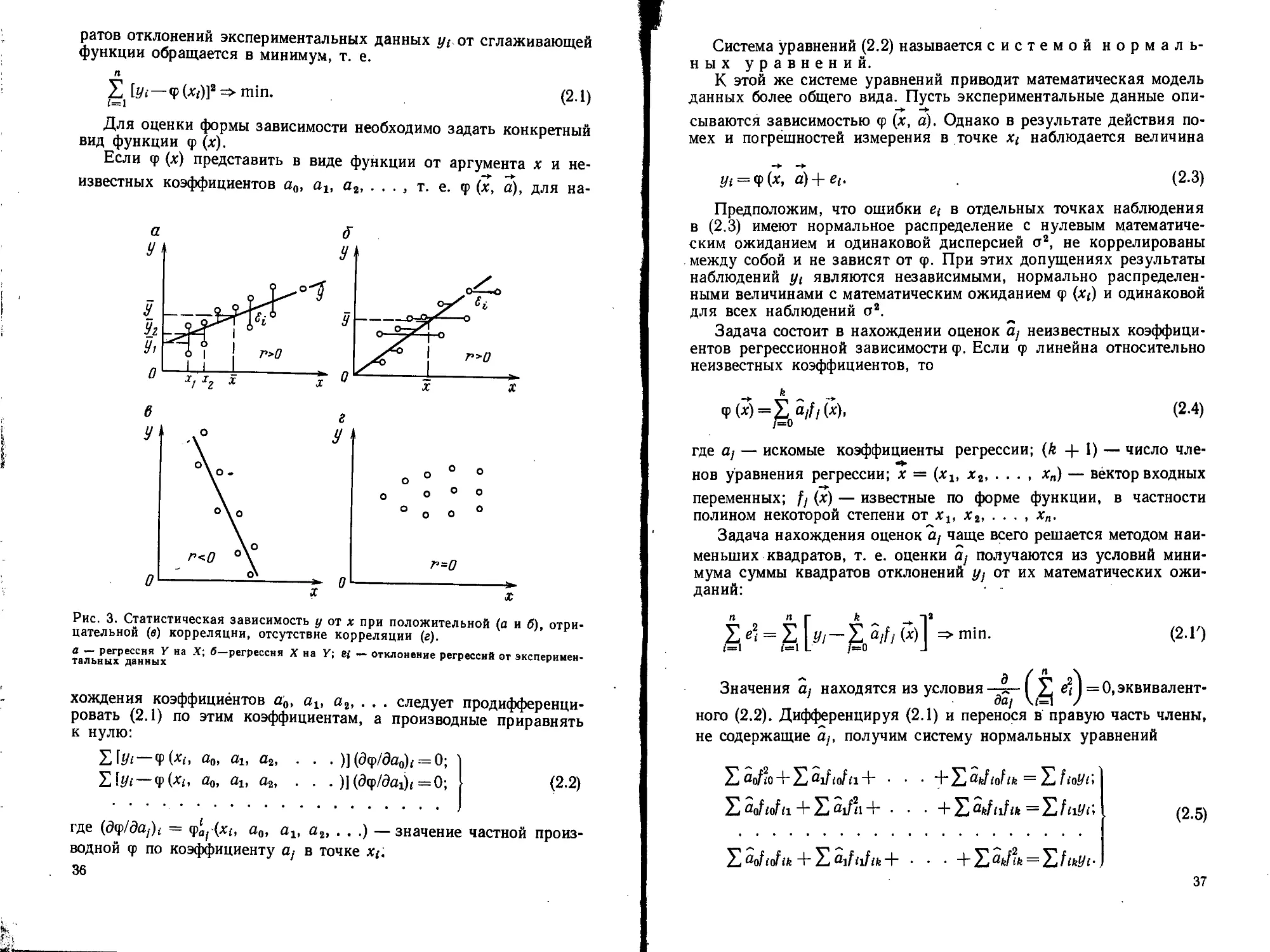
случайными величинами.
На основании регрессионного анализа наблюдаемое «облако»
точек (рис. 3) аппроксимируется уравнением регрессии. Под рег-
рессией понимают сглаживание экспериментальной зависимости по
методу наименьших квадратов. Согласно этому методу сумма квад-
2*	35
ратов отклонений экспериментальных данных yt от сглаживающей
функции обращается в минимум, т. е.
п
S [*/» —ф (я?)]2 => min.	(2.1)
i=l
Для оценки формы зависимости необходимо задать конкретный
вид функции ф (х).
Если ф (х) представить в виде функции от аргумента х и не-
известных коэффициентов а0, аг, о2, . , . , т. е. ф (х, а), для на-
Рис. 3. Статистическая зависимость у от х при положительной (а и б), отри-
цательной (в) корреляции, отсутствие корреляции (е).
а — регрессия У на X; б—регрессия X на У; а/ — отклонение регрессий от эксперимен-
тальных данных
хождения коэффициентов а0, alt а2, . . . следует продифференци-
ровать (2.1) по этим коэффициентам, а производные приравнять
к нулю:
ф(Х{, о0, аь а2, • • . )](дф/до0)( = 0;
—ф(х<, «о, «1> «2, • • . Ждф/дах^О;
(2-2)
где (d^/da^t = фа( (xj, а0, аъ а2, . . .) —значение частной произ-
водной ф по коэффициенту а,- в точке хь
36
Система уравнений (2.2) называется системой нормаль-
ных уравнений.
К этой же системе уравнений приводит математическая модель
данных более общего вида. Пусть экспериментальные данные опи-
сываются зависимостью ф (х, а). Однако в результате действия по-
мех и погрешностей измерения в точке Xi наблюдается величина
уг = ф(х, а)+е{.	(2.3)
Предположим, что ошибки ei в отдельных точках наблюдения
в (2.3) имеют нормальное распределение с нулевым математиче-
ским ожиданием и одинаковой дисперсией а2, не коррелированы
между собой и не зависят от ф. При этих допущениях результаты
наблюдений yt являются независимыми, нормально распределен-
ными величинами с математическим ожиданием ф (xi) и одинаковой
для всех наблюдений а2.
Задача состоит в нахождении оценок at неизвестных коэффици-
ентов регрессионной зависимости ф. Если ф линейна относительно
неизвестных коэффициентов, то
-> k ~
Ф (x)=^a/fj(x),	(2.4)
где а/ — искомые коэффициенты регрессии; (k + 1) — число чле-
нов уравнения регрессии; х = (х1( х2, ... , хп) — вектор входных
переменных; f] (х) — известные по форме функции, в частности
полином некоторой степени от xlt х2,   . , хп.
Задача нахождения оценок а/ чаще всего решается методом наи-
меньших квадратов, т. е. оценки О/ получаются из условий мини-
мума суммы квадратов отклонений yt от их математических ожи-
даний:
п	п Г k	-1»
2^1 = 2 [.У/ —	wj =>min-	(2.1')
О	"	5 ( V 2^ л
Значения а, находятся из условия-х-I >. ei I = 0, эквивалент-
на/ /
ного (2.2). Дифференцируя (2.1) и перенося в правую часть члены,
не содержащие «/, получим систему нормальных уравнений
S аоА) + £01ЛоЛ1+ • • • + S akfloflk = X fioUi>
S	+ • • • +^Okfnfik = Xfi^
(2-5)
X aoftofik 4- S alf ilf ik +
+S aJ2ktky i-.
37
Приняв обозначения для коэффициентов системы (2.5)
cji = S f ijf ч
и для свободных членов
=*= Д f чУь
(2.6)
(2.7)
систему нормальных уравнений можно записать в виде
СыАо 4" coiQi +
Cioao + cuai +
(2.8)
СмАо + CkAi + • • • +	= bk.
В настоящее время наиболее распространенным является пред-
ставление системы нормальных уравнений в матричной форме
F'FA = F'Y,
(2.9)
где ’ F — прямоугольная матрица размерности h х (k +1), за-
дающая значения функции при проведении п наблюдений,
f ю	fn
	fao	fai
F =		
_ fno fnl
fik
fzk
~r~
r;
(2.10)
+ CfaAk = Ьо\
+
ft — вектор, определяющий значения функций fj в i-й точке на-
блюдений,

(2.П)
fik
38
A — вектор искомых оценок неизвестных коэффициентов уравне-
ния регрессии,
(2.12)
«л .
Y—n-мерный вектор наблюдений,
У1
У2
(2.13)
/А.
Знак «штрих» означает транспонирование.
Матрица
F'F = M	(2.14)
называется информационной матрицей Фишера.
Эта матрица — квадратная, положительно определенная и невы-
рожденная при n > fe + 1 и если хотя бы (k + 1)-наблюдение про-
ведено в разных точках пространства входных переменных. Сле-
довательно, для нее существует обратная матрица
C = (F'F)-1 = M-1.	(2.15)
Тогда решением системы нормальных уравнений (2.9) является
вектор неизвестных коэффициентов
A = (F'F)-1F'Y = M-1F/Y = CF'Y.	(2.16)
Учитывая (2.16) и то, что истинные значения коэффициентов
регрессии А = CF'Y, можно получить выражение для ковариацион-
ной матрицы оценок неизвестных коэффициентов:
К = М[(А—А) (А—А)']=а®С,	(2.17)
где М — знак математического ожидания.
Отсюда следует, что ковариация двух любых оценок aj и at
klt = a*c]b	(2.18)
где Сц — соответствующий элемент обратной матрицы С.
39
Мерой отклонения оценки регрессии от истинной зависимости
является дисперсия предсказания по уравнению
регрессии значений (дисперсия аппроксимации). Эту диспер-
сию предсказания как функцию входных переменных можно за-
писать в виде
Г Й	k	“12	f k	“j 2
d(x) = M £	— Z fj (x)at = M Z fj	=
L/=o	/=o	J	L/=o	J
= Z £ fl (x)fj (x)M[(al—ai)(aj—aj)] = a2f' (x) (F'F)-1/(x) =
J=o /=0
= a*T'(x)Cf(x).	(2.19)
Фундаментальную роль в анализе уравнения регрессии играет
матрица С = в структуре которой содержится вся информа-
ция о статистических свойствах исследуемой модели (2.3).
Примеры нахождения оценок неизвестных коэффициентов и изу-
чения информационной матрицы М и матрицы С даны в следующих
разделах.
§ 7.	ОЦЕНКА ТЕСНОТЫ КОРРЕЛЯЦИОННОЙ СВЯЗИ
Характеристикой связи между двумя случайными величинами X
и Y, представленными физическими параметрами или геофизиче-
скими полями, служит коэффициент корреляции (1.7). Поскольку
средние значения и дисперсии X и У в (1.7) неизвестны, исполь-
зуется оценка (состоятельная и несмещенная) коэффициента кор-
реляции, называемая выборочным коэффициентом
корреляции:
л ! п
rXY = " ^Xi “Х) —У"> =
ПОхаУ 1=1
. п
-	=—^	(xtyt—пху),	(2.20)
ЛОХ°У i=l
где х, у, ах, ау — оценки средних значений и среднеквадратиче-
ских отклонений X и Y.
Свойства выборочного коэффициента корреляции гху состоят
в следующем: 1) абсолютная величина гху не превосходит еди-
ницы, — 1 < rxy < 1; 2) если гху — 0, величины X и У не свя-
заны линейной корреляционной связью, такие величины называют
некоррелированными, в случае нормального распре-
деления X и У из равенства гху = 0 следует назависимость X
и Y, т. е. некоррелированность и нормальное распределение слу-
чайных величин приводит к их независимости; 3) с возрастанием
40
'Г
1.
абсолютной величины гху линейная корреляционная зависимость
становится все более тесной и при | гХУ | = 1 переходит в функцио-
нальную.
При оценке корреляционной связи различают: коэффициент
корреляции, коэффициент ранговой корреляции, частный коэффи-
циент корреляции, множественный коэффициент корреляции, кор-
реляционное отношение.
Коэффициент корреляции гху оценивает тесноту лишь линей-
ной связи между X и Y. Доверительный интервал для гху в пред-
положении нормальности распределения X и Y (при доверитель-
ной вероятности у) будет
гХу zfc ^<v-t-i)/2 (1—гху)/д/й,	(2-21)
где А?-Н)/2—у-квантиль (0,1)-нормального распределения;
(1—?xy)/Vn—среднеквадратическое отклонение для гху.
Поскольку величина гХУ оценивает тесноту линейной связи, то
при значениях гху, выходящих за пределы доверительного интер-
вала (2.21), гипотеза об отсутствии линейной связи отвергается
с вероятностью у.
При отсутствии линейной связи коэффициент корреляции ра-
вен нулю, однако при этом выборочный коэффициент не обяза-
тельно будет равен нулю. Его колебания вокруг нуля можно учесть,
указав пределы, в которых при справедливости гипотезы об отсутст-
вии связи должен находиться с близкой к единице вероятностью у
выборочный коэффициент корреляции. Эти пределы с учетом (2.21)
равны ± f(i+V)/2 Vl/n.
Пример [71. Проверить гипотезу о наличии связи между величинами
кажущихся сопротивлений (КС) рв,55 и pli05, р0>55 и pi(7B, измеренных в неф-
тенасыщенных пластах терригенных отложений зондами различной длины —
0,55, 1,05 и 2,75 м, если выборочные коэффициенты корреляции по 20 пластам
составили: г13 = 0,91 (для зондов 0,55 и 1,05 м), ri3 = 0,15 (для зондов
0,55 и 2,75 м).
Решение. Пределы, в которых с вероятностью у = 0,95 должен нахо-
диться коэффициент корреляции при гипотезе об отсутствии связи, состав-
ляют: 0,91 ± /o.»7sW2O = 0,91±1,96-0,22 = 0,91 ±0,44. Так как гХУ >0,44,
гипотеза о наличии связи между ро)33 и р i,05 принимается с доверительной
вероятностью 0,95.
Для р0,55 и р2175 эта гипотеза отвергается, так как каждый односторон-
ний доверительный интервал по величине больше ri3. Полученные резуль-
таты можно объяснить особенностями залегания изучаемых пластов. Так,
малая мощность и невыдержанность пластов по площади приводит к усред-
нению величии КС при увеличении длины зонда и к ослаблению связи с КС
при малой длине зонда.
Более точный критерий некоррелированности величин X и Y
основан на том, что при отсутствии связи величина
t = г х у it—2 /	1—7Ху	(2.22)
распределена по закону Стьюдента с (п—2) степенями ’свободы.
41
Гипотеза об отсутствии связи отвергается, если |Л>Лт+1)/2>
где — (1 +?)/2 — квантиль распределения Стьюдента с
(п—2) степенями свободы.
Если коэффициент корреляции имеет значимое отличие от нуля,
то его распределение тем сильнее отличается от нормального, чем
меньше число наблюдений п и чем больше его абсолютное значение.
Распределение гху может быть приближенно приведено к нор-
мальному с помощью так называемого z-преобразования Фишера:
z = 0,51n[(l+гху)/(1 —гху)]; az = |l/V^Z3.	(2.23)
Это преобразование можно применять уже при п > 10.
В том случае, когда определяется взаимосвязь между случай-
ными величинами X, Y (физическими параметрами), распределен-
ными не по нормальному закону, а произвольно, зависимость ме-
жду X и Y следует оценивать с помощью коэффициента
ранговой корреляции Спирмена р. Для вычис-
ления р каждая наблюденная величина преобразуется с помощью
рангов (табл. 7), образуются разности D для п пар рангов, которые
Таблица 7
п	Плотность ап, г/см’	Магнитная восприимчивость х-1(А ед. СИ	Ранги		Разность рангов D	О!
			°п	X		
1	2,58	6	5,5	1	4,5	22,25
2	2,65	10	10	5,5	4,5	22,25
3	2,52	8	3	3	0	0
4	2,68	42	12	16	4	16
5	2,70	12	14	7	7	49
6	2,73	НО	17	18,5	1,5	2,25
7	2,71	ПО	15	18,5	3,5	12,25
8	2,58	8	5,5	3	2,5 •	6,25
9	2,49	20	1	10	9	81
10	2,50	25	2	12	10	100
И	2,73	206	17	20	3	9
12	2,68	61	12	17	5	25
13	2,64	20	9	10	1	1
14	2,68	20	12	10	2	4
15	2,73	33	17	14,5	2,5	6,25
16	2,78	10	19,5	5,5	14	196
17	2,78	33	19,5	14,5	5	25
18	2,59	30	7,5	13	5,5	30,25
19	2,53	8	4	3	1	1
20	2,59	13	7,5	8	0,5	0,25
2D2 = 605
возводятся в квадрат и суммируются, т. е.
р = 1—6SD*/(n8—п).	(2.24>
Если два ряда рангов равны, разности D равны нулю и р = 1.
Если ряды рангов обратны, то р = — 1.
42
Этот критерий позволяет ответить на вопрос о знаке имеющейся
корреляции.
Для проверки гипотезы об отсутствии связи между X и Y следует
сравнить коэффициент р с его доверительным интервалом, равным
в предположении о нормальности распределения р± /(1+у)/2д/1/(п— О»
Указанным интервалом можно пользоваться при п > 10.
В случае одинаковых значений X и Y вместо (2.24) вычисляется
р=1 —6SD*/[n(n8—1)—6(T+(/)L	(2.25)
где Т = 1/12 S (t2—1) t, t— количество одинаковых значений X’,
U = 1/12 S (и2—1) и, и — количество одинаковых значений Y.
Для примера, приведенного в табл. 7, в соответствии с (2.25)
р = 1—6-605; (20-399 — 6.11) = 0>54.
Доверительный интервал ^(y+i)/2	—0 ПРИ V — 0>95 равен
+ 0,45. Поскольку 0,54 >0,45, гипотеза о наличии корреляцион-
ной связи между оп и х выполняется.
Расчет коэффициента ранговой корреляции был использован
для изучения связи между х и стп, определяемыми по керну корен-
ных пород в картировочных скважинах. При этом р находится
в пределах скользящей палетки, включающей 15—20 скважин.
Значение р‘ относится к центру каждой палетки.
После вычисления р в пределах всей площади исследования
строится карта изолиний р (рис. 4). Анализ карт изолиний р, по-
лученных по различным рудным районам, позволил установить,
что неизмененные эндогенными процессами горные породы незави-
симо от их состава и генезиса характеризуются положительной
корреляционной связью между х и оп. В зонах проявления гидро-
термально-метасоматических процессов происходит нарушение этой
связи между плотностью и магнитной восприимчивостью вплоть
до появления обратной связи между ними.
Таким образом, построение карт изолиний коэффициентов ран-
говой корреляции позволяет использовать результаты петрофизи-
ческих измерений (х и оп) Для выделения площадей гидротермально-
измененных пород, к которым обычно приурочены месторождения
полезных ископаемых. Промышленные месторождения, как уста-
новил В. И. Пахомов, располагаются в пределах областей наруше-
ния положительной корреляции между х и стп, тяготея к наиболее
градиентным изменениям величины р.
Если случайная величина Y линейно зависит от системы слу-
чайных величин . . . , Xk, то теснота линейной связи характе-
ризуется множественным коэффициентом кор-
реляции
Vk
Е bir(Y ,	(2.26)
f=i
43
0 5001000 tSOO»
|^|z !'• |j E3P E±3J I 4- P
X/ X/ 7
/ X /* f
10
Рис. 4. Карта изолиний коэффициента ранговой корреляции (по В. И. Па-
хомову).
1 и 2 — метасоматиты разных формаций; 3 — месторождения; 4 — изолинии коэффици-
ента ранговой корреляции; 5 — граниты среднезериистые; 6 — граниты рапакиви;
7—9 — гиейсы разного состава; 10 — тектонические нарушения
где Пу— выборочный коэффициент корреляции величины с У;
bi — решение системы линейных уравнений вида
Rb = r;	(2.27)
г = (г1У.....г*у); R — корреляционная матрица, составленная
из выборочных коэффициентов парной корреляции rtj.
Допустим, что Y линейно зависит от двух переменных и Х2,
тогда система (2.27) примет вид
1
г12
г12
1
Ip!
J L ь2
Г r1Y 1
L I'iY J
44
или by 4- 6ar12 = г1У, отсюда by = (г1У—r12rzY)/(l— rf2); ЬуГ12 +
+ b2 = г2У; b2 = (г2У—г 12г 1У)/(1—Г|2).
Множественный (выборочный) коэффициент корреляции с уче-
том (2.26) будет
=	/ Ь1у — Г12Г2у) Г1У (г2у — Г12Гуу) Г2у _
V 1 — Л12	1 ~~ Л12
Vr12 ~ 2г12г1Уг2У "Ь г2У
1-^2
Степень влияния одной из величин, например Xj на Y (при по-
стоянном значении Х2) оценивается частным (парциальным)
коэффициентом, корреляции величин Ху и Y по
отношению к Х2
ЛУ/2 = (^1У — fnfгу)/ д/(1 —Лг) (1 —Лу) •
Аналогично определяются частные коэффициенты корреляции
Г12/У И Г2У/1-
Частный коэффициент корреляции определяется на значимость
так же, как и обычный коэффициент корреляции. Однако при этом
число степеней свободы при исключении каждой величины умень-
шается на единицу. Если исключается одна величина, как в рас-
смотренном примере для г1У/2, то число степеней свободы равно
п—2—1 = п—3.
Вычисление частных коэффициентов корреляции обычно дает
возможность оценивать искажающее влияние тех факторов, ко-
торые при эксперименте плохо контролируются или вообще не
контролируются.
Гипотеза, согласно которой множественный коэффициент кор-
реляции равен нулю (против 7?*+1>»0), проверяется на основании
Лкритерия:
F = (n-k-l)Rl+i/k(l-R2k+i).	(2.28)
Если FcFy (п—k—1, k), где —у-квантиль распределения Фи-
шера с (п—k—1) и k степенями свободы, гипотеза о наличии ли-
нейной связи между Y и Ху, . . . , Xk отвергается с вероятностью у.
В качестве меры связи нескольких ^-параметров (признаков),
допускающих ранжирование, используется коэффициент
согласованности Кендалла и Смита 1F:
r=12Sw/^(n8—п),	(2.29)
где!|
w п г k	I2
= Е [2/0-*(»+ 1)/2] .
где rtj — элементы матрицы результатов ранжирования R — {г<у),
i = 1, . . . , /г; j — 1, . . . , п; i-я строка матрицы содержит резуль-
таты ранжирования по i-значениям (объектам), следующим в од-
46
ном и том же порядке. В случае отсутствия связи M.W — \lk, при-
чем 0 < W С 1.
С помощью корреляционного отношения производится оценка
тесноты нелинейной корреляционной связи. Корреляцион-
ное отношение т) представляет собой отношение межгруп-
повой дисперсии DM к общей дисперсии данных D:
t] = VDm7D,	(2.30)
где DM — дисперсия групповых средних относительно общей сред-
ней, (N{ — объем /-й группы),
. р _
£>м=— S	(2.31)
1 П(
у =—£ niyi—общее среднее величины У (п{ — частота значе-
п £=2
ния yt); у,- — среднее значение У в /-й группе (групповое среднее,
р
соответствующее /-му значению аргумента X);n=£ Nj—объем
/”1
всей совокупности значений;
D = — £ nt(yi_yf.	(2.32)
п i=l
Если величина У связана с X функциональной зависимостью,
отношение D^JD = 1, если У связана с X корреляционной зави-
симостью, DM/D<1.
Корреляционное отношение я обладает свойствами: 1) 0^т]< 1
(с ростом т] корреляционная связь становится более тесной); 2) если
т] = 0, корреляция между X и У отсутствует; 3) если г) = 1, ве-
личины X и У связаны функциональной зависимостью; 4) т) > | rXy I
5) если т] = | гху |, имеет место линейная корреляционная зави-
симость.
В отличие от коэффициента корреляции отношение я оценивает
тесноту связи любой формы, однако не позволяет суд ть о раз-
бросе вокруг кривой определенного вида.
§ 8. ВИДЫ РЕГРЕССИЙ И ИХ ПРИМЕНЕНИЕ
ЛИНЕЙНАЯ РЕГРЕССИЯ
Линейной регрессией между величинами X и У называется корре-
ляционная зависимость вида
У=а0 + а1Х.	-	(2.33)
Согласно (2.2) для линейной регрессии получаем (dy/da^i = х«;
(дц>/да0){ = 1 и
Е [yi—(а0 + OiXi)]Х( =0;
Elz/i — (ао + ад)]1 = О.
46
Система нормальных уравнений запишется в виде
IS *21 ai + IE х] ао = Е ху;
[Е х] tti + па0 = Е У,	(2-34)
где Sx = Sx/; Sy = Sy/; Sx2 — Sxf; Sxy — 2xiyi, если Y —
случайная величина, а значения X заданы точно.
Коэффициенты регрессии из этой системы соответственно
„	—„	п%ху — £х£у
Используя представление системы нормальных уравнений в мат-
ричной форме (2.9) для модели (2.33), т. е. yt = а0 + aixi, имеем
X'XA^X'Y,	(2.36)
где матрица
~ 1	хг ~
1	х2
1 х„
Соответственно матрица
Xi
Хг
1 хп _
(2.37)
а матрица
1
1
х8
ёу ] (2-38>
-Уп _
Выражение (2.36) для нахождения коэффициентов а0 и at с уче-
том (2.37) и (2.38) примет вид
п
Ех
Е* 1Г ао ] = Г Т.У ]
Е*2 JI ai J L Zxy 1
(2.39)
47
или
л«0 + IE*] Д1 = £у, .
<Е*] «о+IE*2] «1 = Е ху .
что совпадает с (2.34).
Величина ах определяет угловой коэффициент прямой линии
регрессии Y на X и называется выборочным коэффи-
циентом регрессии. Обозначим его через рух. Сравни-
вая величину а! в (2.35) и rXY в (2.20), а также учитывая, что
^=-£(*<-*)2=*2-(;)2 и
п
_ пЯху — SxSy _ Sxy — пху
Рух“ nSx2 — (Sx)2 ~ па2х *
получаем связь между коэффициентами корреляции и регрессии
в виде
ах _ Sxy—nxy
Pvx-^----------------гху-	(^-40)
Здесь и далее знак оценки «Д» опущен.
Из второго уравнения системы (2.34) имеем
Оо = У— Рухх-	(2-41)
Подставив это выражение в уравнение линейной регрессии
У = Рух% +ао> получим
Ух—У = РуХ(Х—x)=rXy(aY/ax)(X—х).	(2.42)
Аналогично можно выразить уравнение регрессии X на У в виде
Ху —x = rXY (gx/gy) (Y —у} = Рху	—у)-	(2.43)
Выражения (2.41) и (2.42) описывают уравнение двух различ-
ных прямых линий и их совпадение достигается лишь для функ-
циональной зависимости. В том случае, когда и X и У являются
случайными величинами, каждое значение которых может наблю-
даться неоднократно, данные наблюдений группируют, подсчиты-
вая частоты пх и пи и записывая их в виде таблицы, которую на-
зывают корреляционной (табл. 8).
Для облегчения расчетов обычно удобно использовать не сами
значения случайных величин X и У, а ввести для них условные
обозначения, расположив нуль для значения с наибольшей часто-
той так, как это сделано в табл. 8.
Все частоты помещаются в прямоугольнике корреляционной
таблицы, который в данном примере обведен жирной линией. В уг-
лах каждой клетки таблицы записывается число, равное пху ху.
Нахождение коэффициентов прямой линии регрессии по таким
48
Таблица 8
Х-плотность, г/см1
			Xi									
У~ скорость, кы/с			2,5	2,4<	2.3	2,2	2.1	2,0				
			-2	-/	0	/	2	3	пЧ	ПцУ	"цУг	ОхуХу
		2				2 И	4 |7У	Ч Р?	Ю	20	40	44
		/			1 [о	4 [7	5 р2	5 р5	/в	/в	/6	31
		0			5 [У	10	8 рг	/ Г*	24	0	0	0
		-/	1 [Т	4 И	9 [7	5 [7	2 нп		21	-21	2/	-з
		-2	3 рУ	6 [7F	6 |7	2 F			/7	-34	68	20
		-3	3 /8	5	4				12	-36	Ю8	33
		"х	7	75	25	23	20	/0	*100'	= 55	6nxyi =253	ХПхУХУ =125
		пхх	-14	-/5	0	23	40	30	=БЧ .			
			28	/5	0	23	80	90	^xxZ •236			
		<ху	32	31	0	-/	24	59	•125			
сгруппированным данным производится путем решения уравнений
вида
(л?) рук + (лх) о0 = £ пхуху,
(х)рух + «о = !/,
где
пх = £ «хх, «х2 = £ «х^2-
Для рассмотренного в табл. 8 примера получаем следующие
линии регрессии:
Y х + 0,55 = 0,8 (X—0,64);	Ху—0,64 = 0,72 (У + 0,55).
Оценка тесноты линейной регрессии производится по значению
выборочного коэффициента корреляции гХУ.
Линейная регрессия широко используется при определении
значений одного физического параметра по известным значениям
другого. В частности, плотность горных пород ап, необходимую
для интерпретации результатов гравиметрических наблюдений,
можно определить по пластовой скорости продольных волн, если
для района исследований составлена корреляционная зависимость
между оп и цпл.
Впервые оценка взаимосвязи скорости и плотности была полу-
чена Н. Н. Пузыревым в виде v = 6оп—Н. Б. М. Уразаевым для
49
эффузивных и метаморфических пород были найдены зависимости
v = 3,64 стп — 4,73 и v = 2,47 ац — 1,55. Эти связи обычно ме-
няются в зависимости от возраста горных пород и района иссле-
дований. Так, для восточного борта Прикаспийской впадины уста-
новлено стп = 0,2 цпл 1,6 (при ипл<2,8 км/с), стп = 0,13 опл 4-
+ 1,98 (при 1>пл > 2,8 км/с).
Оценка глубины залегания фундамента Н (или другой геологи-
ческой границы) по данным гравиразведки (или магниторазведки)
Н = fliAg 4- а0 может служить еще одним примером использова-
ния линейной регрессии.
Для определения коэффициентов а0 и необходимо иметь ряд
скважин с известными значениями Н или значения глубин, опреде-
ленные другим методом.
Пример [7]. На участке проведены измерения приращения силы тяжести
Agi в пунктах бурения скважин. По скважинам определены глубины Hi за-
легания фундамента. По этим данным найдены: выборочный коэффициент
корреляции Ag и Н, равный г = — 0,9, средние значения Н = 175 м и Ag =
= 50 мГал, среднеквадратические отклонения Оц = 15 м; од4 = 9 мГал.
1. Построить уравнение регрессии для расчета Н по Ag и оценить ошибку
такого прогноза при доверительной вероятности у = 0,9.
2. Можно ли использовать полученное уравнение на участке, на кото-
ром контрольная скважина показала Н = 250 м при Ag = 2,5 мГал.
Решение. 1. По формулам (2.40) и (2.41) находим коэффициенты регрес-
сии Н — а0 4- OiAg : ах = — 0,9 (15/9) = — 1,5; а0 = Н—а^в = 175 4-
4- 1,5-50 = 250.
Уравнение регрессии Н — — 1,5 Ag 4- 250. Ошибка прогноза Н по Ag:
± /(i-|-y)/2	—г* <Ун~ ± 1,645 л/1 —0,9s -15 = 4- 10,8
2. При Ag = 25 мГал Н должно находиться с вероятностью у = 0,9 в пре-
делах (Н—10,8; Н + 10,8), где прогнозное значение Н= — 1,5-25 4-
4- 250 = 212,5 м.
Так как это условие не выполняется, использовать уравнение регрессии
для расчета Н на другом участке нельзя.
Нелинейная регрессия
Нелинейной (криволинейной) регрессией называется любая за-
висимость, отличающаяся от линейной. Примером является пара-
болическая регрессия второго порядка
^x=ao + aiX + aaXs.	(2.44)
Система нормальных уравнений в матричной форме (2.36) при
этом запишется в виде
1	1
х?	4
*1 4 а0
2
%2	^1
50
1	1
Х1	хг
2	2
Xt	X2
Хп
У1
Уъ
-Уп _
После перемножения матриц получаем
' п Ех
Ех Ех2
. Ех2 Е*8
Ех2 
Ех3
Ех1
 а0 ~
ai
. а2 .
Г Zy 1
Е*0 .
LE^J
или
лао4-(Е*) 01+(Е*2) fl2=Е//;
(Ех) По + (Ex2) Oi + (Ех3) а2 = £ху;
(Ех2) Оо++ (Ех4) аг=Ех21/.
(2.45)
Параболическая регрессия используется при определении сред*
ней плотности пластов с помощью акустического каротажа (по ско-
рости), по результатам которого найдена скорость продольных
волн ор:
I	I	2
Оп = во + OlVp 4* в20р.
Для терригенных пород платформенного типа, например, а0 =
= 1,75, вх = 0,266, в2 = — 0,015 (оп в г/см8, а ир в км/с).
Среднеквадратическая ошибка одного определения оп по этому
способу составляет 3—5 %.
Широкое применение находят и другие виды нелинейной рег-
рессии. Так, экспоненциальная зависимость плотности от пласто-
вой скорости установлена для пород Южного Сахалина в виде
ип = 2,6—0,95 ехр (—0,4 опл)> Для палеозойских отклонений По-
волжья связь между опл и рпл надежно аппроксимируется регрес-
сией вида опл = а 4- 5 In рпл.
Экспоненциальные виды регрессии нашли применение в гео-
химии. Так, в первичном ореоле рассеяния зависимость содержа-
ния элемента от расстояния х до границы рудного тела описываются
кривой
<р (х) = а exp [ —-X (х—т)а] 4- Ь$,
где йф — уровень фоновых содержаний химического элемента;
X — обратная величина показателя миграционной способности
элемента; т — координата центра ореола.
А. П. Соловов использовал эту зависимость для описания рас-
пределения содержаний элементов во вторичных элювиальных орео-
лах рассеяния от маломощных рудных тел жильной формы.
Нормальные уравнения для нахождения коэффициентов а, X,
т — нелинейны. Поэтому для их решения применяют итерацион-
ные методы, причем первое приближение при оценке коэффициентов
51
задают, исходя из физических предпосылок. Например, для при-
веденного выше уравнения первое приближение получают по наи-
большему участку опробования, где In bt (i = 1, п) соответствует
параболической зависимости otxj. Такое приближение определяется
условием минимизации суммы
S = у1. (in Ь( — In и Х/п	,
1
которая дает линейную относительно величин (In а—1ктг), — X
и 2Х/п систему уравнений.
Следует отметить также тесную корреляционную связь времен
регистрации в сейсморазведке t0 и электроразведке /ЗСБ, установ-
ленную по данным сейсмокаротажа и кривым электромагнитных
зондирований становлением поля в ближней зоне (ЗСБ). Эта связь
при совпадении глубин отражающего сейсмического и опорного
геоэлектрического горизонтов описывается уравнением t0 =
= 2а^^зсв> на ее основе можно прогнозировать среднюю скорость
по данным ЗСБ:
оСр = Н/а
Коэффициент а определяется опытным путем по данным сейсмо-
каротажа и кривым ЗСБ. Совместное использование скорости,
определяемой по ЗСБ, с данными ОГТ обеспечивает более надеж-
ные и точные оценки скоростного разреза.
В электроразведке получение регрессии между глубиной зале-
гания опорного горизонта и кажущимся сопротивлением Н =
= а0 + П1 In рк позволяет заменить наблюдения дорогостоящим
методом ВЭЗ измерениями более производительным методом сим-
метричного профилирования с целью картирования горизонта.
Множественная регрессия
Эта регрессия получается при исследовании связи между несколь-
кими (три или более) величинами. Так, линейная множественная
регрессия Y на Хх и Х2 имеет вид
Y = а0 -|- Я1Х1	(2.46)
Система нормальных уравнений для нахождения коэффициентов
а0, ai, аг в матричной форме (2.36) при этом записывается следую-
щим образом:										
	" 1 *11	1 *12	•	• • •	• •	1 - *lrt		- 1 1	*11 *12	*21 *22		а0 ai
	_ *21	*22	•	*2л _		1	*1л	*2п _		_ Ch _
52
(2.47)
па0 + Yixiai Н- — Sz/i
(S*i) ao + (S*l) Qi + (Лх1хг) аг — Yixiy<
(Hxi) ao “H ai + (S-^) a2 ~ ^хгУ-
Для (2.46) удобно искать уравнение связи в виде
У —у — ах (Xi—Xi) + <*2 (Х2 —*2),
(2.48)
где
ГХ1У — ГХ2У'’Х1Х2 0у
ai =---------й------- • --;
1—гх,х2	ах,
ГХ2У — ГХ1УХ1Х2 Оу
а2 —---------5-------*----->
I — Гу V	Оу
Л 1 Л 2	Л 2
гхху> гх2у и гххх2— выборочные коэффициенты корреляции ме-
жду Хх и У, Х2 и У, Хх и Х2.
Теснота связи оценивается множественным коэффициентом кор-
реляции (2.26).
Множественная линейная регрессия успешно применялась
Г. И. Каратаевым для определения глубины залегания складча-
того фундамента на территории Западно-Сибирской плиты по дан-
ным гравиразведки (Ag) и аэромагниторазведки (АТ) в виде Н—Н =
= а0 + axAg + а2АТ, где Я —среднее значение глубины в за-
данном окне.
Множественный нелинейный регрессионный анализ используется
для построения петрофизических моделей (М. М. Элланский) про-
дуктивных нефтегазовых пластов по данным геофизических иссле-
дований скважин (ГИС), в частности зависимости величины пори-
стости пласта от показаний стандартного комплекса ГИС, вклю-
чающего для разведочных скважин КС, ПС, ИК, ДС, ГК, НК,
АК. При этом уравнения регрессии ограничиваются квадратич-
ными членами показаний соответствующих зондов.
53
Аналогичные регрессионные модели строятся для других фи-
зических параметров. Так, для глин месторождений Узень, Жеты-
<5ай (Южный Мангышлак) использование данных о кажущемся
сопротивлении рк, интенсивности нейтронного гамма-каротажа
/Нгк и скорости продольных волн иР по акустическому каротажу
лриводит к уравнению регрессии
<Тп = 2,28 0,28 In Рк -j- 0,36/ нгк—0,017ир
при коэффициенте множественной корреляции = 0,75.
Важными вопросами при построении множественных регрессий
являются задание степени используемых полиномов и возможность
исключения членов регрессии с малыми значениями коэффициен-
тов. Эти вопросы решаются на основе дисперсионного анализа
в § 14.
§ 9. КОРРЕЛЯЦИОННЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ
ГРАВИТАЦИОННЫХ И МАГНИТНЫХ АНОМАЛИЙ
Корреляционные методы преобразования гравитационных и маг-
нитных аномалий, развитые в работах Г. И. Каратаева, В. И. Шрай-
<5мана, М. С. Жданова и других, основываются на реализации
двух процедур:
1) установления статистической зависимости между изучаемой
теологической характеристикой, чаще всего глубиной залегания
некоторого горизонта, заданной по геологическим данным (апри-
орная информация по данным бурения или сейсморазведки), и гео-
физическим полем или совокупностью полей на этом эталонном
геологическом пространстве Н3 = АХ3, где Н3 — геологическая
характеристика; А — оператор статистической связи, которым
обычно является полином заданной степени; Xs = (Xf, . . . ,
Хп ) — вектор геофизических полей (или параметров);
2) последующего применения этого оператора с целью прогно-
зирования искомой геологической характеристики по геофизиче-
ским полям Япр = Хпр, где Япр — прогнозируемое значение гео-
логической характеристики; Хпр = (Х"р, . . . , Х"₽) — вектор гео-
физических полей, измеренных на прогнозируемой области.
Для получения более эффективного решения задачи прогноза
геологической характеристики Предлагается на основе использо-
вания эталонных данных выделять из суммарного наблюденного
поля такую компоненту, которая наилучшим образом связана с
изучаемым геологическим объектом (характеристикой).
Идея создания метода выделения компоненты геофизического
поля, наилучшим образом связанной с изучаемым геологическим
объектом, т. е. такого метода, который мало зависит от ненадежно
определяемых физических свойств горных пород и в то же время
использует априорную, информацию об изучаемом объекте, реали-
зуется в так называемых корреляционных методах преобразования
геофизических аномалий [18].
54
Таким образом, корреляционные методы пре-
образования аномалий заключаются в выделении иа
наблюденного геофизического поля F остаточной аномалии F0CT,
наилучшим образом (в смысле корреляционной зависимости) свя-
занной с изучаемой геологической характеристикой Н. Остаточ-
ную аномалию ищут в виде разности наблюденного поля и неко-
торого полинома Lk по системе функций ft, ... , fk, т. е.
Fост — F — Lk (х, у),
где
k
Lk(x, y)='^iajfl(x, у).
При этом полином Lk (х, у) называют трансформационным мно-
гочленом (иначе, Lk — регрессионная зависимость); Яу (/ = 1..
k) — коэффициент трансформационного многочлена; fi, ... , fk~
базисные функции; k — размерность трансформационного много-
члена; (х, у) — координаты точек плоскости наблюдений.
Трансформационный многочлен должен наилучшим образом
описывать составляющую геофизического поля, обусловленную
влиянием геологических факторов, являющихся помехами при
выделении искомой остаточной аномалии. В роли такой составляю-
щей, в частности, выступает региональный фон.
Система базисных функций выбирается с учетом структуры ком-
поненты поля, обусловленной влиянием помех. Этот выбор основан
на априорных сведениях о помехах. Задание той или иной системы
базисных функций приводит к различным методам преобразования
геофизических аномалий.
После выбора системы базисных функций преобразование гео-
физических аномалий сводится к определению коэффициентов
трансформационного многочлена яу, которое осуществляется в рам-
ках двух подходов.
При первом подходе (подход А) оператором связи изучаемой
геологической характеристики с геофизическими параметрами (по-
лями) является уравнение линейной регрессии, т. е.
k
Fост k — ga/Zy + flo,	(2.49>
где F^k — полезная остаточная составляющая геофизического-
поля F\ k — общее число геофизических параметров fk-i = H„
fk = F.
При втором подходе к определению полезной остаточной состав-
ляющей (подход Б) оператор связи позволяет непосредственно осу-
ществлять прогноз значений изучаемой геологической характери-
стики Н:
£—2
= ak-iFост k 4-	Gyfy+Оо»	(2 • 50>
где Яу — коэффициенты уравнения прямой регрессии; — рас-
55
четные значения геологической характеристики Н; F"cTk — про-
гнозная остаточная составляющая геофизического поля F; k — об-
щее число параметров fk^1 = F, fk = Н.
При решении прогнозных геологических задач, когда искомой
величиной является геологическая характеристика, преобразова-
ние геофизического поля целесообразно проводить на основе под-
хода Б. Когда же цель обработки — выделение из суммарного на-
блюденного поля составляющей, связанной с геологической харак-
теристикой, более эффективен подход А.
Коэффициенты af, определяемые на базе подхода А, формируют
простой трансформационный многочлен, а в рамках подхода Б —
прогнозный трансформационный многочлен.
Корреляционный метод трансформации
геофизических аномалий
Этот метод основан на задании базисных функций:
fps = F(x + pAx, y+s&y), р, s = 0, ±1........±п;
|pl + |s|>0.
Трансформационный многочлен при этом
£(2л+1>»- 1 = S apsF(x-f-pAx, y+s&y)	(2.51)
р. s=—п
IР 1+1 S|>0
Аналогичным образом записываются все аналитические транс-
формации геофизических полей, поэтому множественная регрессия
указанного вида названа трансформационным многочленом. Число п
является максимальным смещением по х (пДх) и по у (пЛу) исход-
ного поля и называется порядком трансформаци-
онного многочлена. Размерность трансформационного
многочлена, определяемая по числу его коэффициентов, равна
k = (2п + I)2 — 1.
Остаточная составляющая геофизического поля
FoctH*. y) = F(x> У)~ X ар/(х + рДх, у + зДг/),
р. s=—п
|Pl+ls|>0
или
F0CTk(x, у) = % cpsF(x + pAx, y+sby),
р, s=—n
где Cqo = 1; cps = — aps; p, s = 0, ± 1, . . . , ± n, | p | +1 s|>0-
Обычно на коэффициенты cps накладывается дополнительное
ограничение, связанное с их нормировкой на заданное число Q.
Тогда функцию Fn, получаемую в результате всех указанных пре-
образований, называют корреляционной трансфор-
56
мантой геофизического поля F, п — порядком этой транс-
форманты:
Fn(x, y) = '^cspF(x-\-p\x, y + sby),
где
Coo ~ QJ (1 iZj ftps); Cps= QflpJ (1 iZj ftps I 
\	p,S=—n z	\	p, s=—n z
I p Ж s\>0
Корреляционная трансформанта аналогична по виду выра-
жениям для аналитических трансформаций поля, однако ее отличие
состоит в том, что она вычисляется из условий, обеспечивающих
наилучшую ее корреляцию с изучаемой геологической характери-
стикой (по эталонным профилям).
В качестве примера описанного метода трансформации рассмотрим вы-
деление прогнозной корреляционной трансформанты гравитационного поля
[18]. На рис. 5, а представлены графики изменения аномалии Буге Ag и
глубины залегания границы Н вдоль профиля наблюдений. Из графика за-
висимости Ag от Н (рис. 5, б) видно, что между Ag и Н корреляция весьма
слабая. Кроме того, локальные максимумы на кривой Ag смещены относи-
тельно соответствующих поднятий структуры Н. Задача решалась на основе
подбора коэффициентов трансформации вида
1
AgJ'P (х) = £ CppAg (х 4-рАх), Дх=50 м,
р=—1
при этом минимизировалась ошибка приближения Н по Ag"₽.
Были получены следующие коэффициенты: с_х = 0,5; с0 = 1, сх = — 1
(при расчетах Q = 0,5). Результат выполненной трансформации с этими
коэффициентами приведен на рис. 5, а. Коэффициент корреляции гдв я бли-
зок к единице. Для сравнения на том же рисунке дан график трансформации
по методу Андреева—Гриффина: 6Ag (х) = &g (х) — [Ag (х + Ах) +
+ Ag(x—Ах)]/2.
Полученная йчомалия практически не коррелируется с глубиной за-
легания геологической границы Н (рис. 5, г), и в этом существенное отличие
корреляционной трансформанты от аналитического продолжения полей.
Корреляционный метод разделения
геофизических аномалий (КОМР)
Если влияние геофизических факторов-помех описывается полино-
мом некоторой степени от координат точек площади исследований,
то система базисных функций задается в виде
fps — xpys, р, 8 = 0, 1, . . . , п, 0<рЧ-8<п,
где х, у — координаты точек площади исследования.
Тогда трансформационный многочлен, называемый геофизи-
ческим фоном
п
L — F^n(x, у) = £ apixpys,	(2.52}
р» s==0
0<р-Н<п
где п — порядок фона.
57
Этот вид преобразования называется также тренд-анали-
зо м геофизического поля.
В качестве примера применения тренд-анализа приведем аппрок-
симацию наблюденного поля (рис. 6, а) полиномом второй степени
L2 (х, у) = 17,76 + 1,436x4- 0,703г/—0,098х2—0,024/— 0,072хг/.
Рис. 5. Выделение прогнозной корреляционной трансформанты поля Ag
[18].
а — графики изменения аномалий Ag и глубины залегания границы Н; 1 — аномалий
Буге; 2 — глубины, залегания границы Н, 3 — прогнозная корреляционная трансфор-
манта AgyP, 4 — трансформированная аномалия Д£тр по методу Андреева—Гриффина;
корреляционные графики зависимости; б — Ag от Н; в — Ag JP от Н, i — Agrp от Н
Остаточную составляющую n-го порядка вычисляют по фор-
муле
^ост (X, у) = F (х, y)—Z apsxpys-
р» 8=0
0<p4-s<n
Корреляционный метод разделения геофизических аномалий
•отличается от тренд-анализа тем, что коэффициенты полинома,
описывающие влияние помех, находят на основе априорной инфор-
58
мации об изучаемой геологической структуре таким образом,,
чтобы выделяемая остаточная составляющая поля коррелировалась
с этой структурой наилучшим образом. В том случае, когда нужно
учесть изменение геолого-геофизических характеристик в преде-
лах площади исследований, используют уравнение регрессии с пе-
ременными по площади коэффициентами (см. кусочно-полиноми-
альную аппроксимацию, § 10):
k-i
Foct (х, у) = ^а{(х, y)fj+a0,
Рис. 6. Наблюденное поле Ag одного из районов Польши (а) и его региональ-
ная составляющая в виде полинома второй степени (б) (по 3. Файклевичу)
где а/ (х, у) — переменные коэффициенты регрессии, которые ап-
проксимируются многочленами от координат:
а{(х,
у) = а$+ i <$х?у\
р, s=>0
0<p4-s<n/
k— 1.
/=1, 2, . .
Как и при постоянных коэффициентах регрессии, полезную оста-
точную составляющую (называемую структурной составляющей}
представляют в виде разности исходного поля и помехи:
^‘сДх, y) = F(x, у)—С(х, у),
где
По
L*(x, у} — £ с$х?у*.
р, s=0
0<p+s<»4
5»
Полином L* называют структурным трансформационным мно-
гочленом; п0 — его порядком.
Коэффициенты а/ и aps ищут методом наименьших квадратов,
т. е. из условия
Г	k~1	I2
2 F (х, у)— L* (х, у)— £ а}(х, у) fj—a0 => min.
L	/=1	J
Рис. 7. Результаты использования корреляционного метода разделения
аномалий &g.
л — карта изогипс в м; б — изоаиомалы модельного поля Ag в мГал; я — карта прогноз-
ной остаточной составляющей поля Ag второго порядка в мГал. На картах Приведены
эталонные профили (по В. И. Шрайбмаиу и М. С. Жданову)
Выбор порядка и размерности трансформационного многочлена
проводится на основе критериев: 1) минимума дисперсии остаточ-
ной составляющей разделяемого геофизического поля; 2) минимума
модуля коэффициента корреляции между трансформационным мно-
гочленом и изучаемой геологической характеристикой; 3) мини-
мума погрешности эталонного оператора на независимой контроль-
ной выборке.
Эффективность корреляционного метода разделения аномалий
показана на рис. 7. В гравитационном поле геологическая струк-
тура, изображенная в виде изогипс глубины залегания (рис. 7, а),
отображается локальными аномалиями, осложненными помехами
в виде других локальных аномалий (рис. 7, б). В связи с этим ко-
эффициент корреляции между глубинами, по которым построена
геологическая структура, и аномалией Ag, вычисленной по дан-
ным трех эталонных профилей, равен лишь 0,018.
На основе корреляционного метода разделения аномалий ре-
шение базировалось на априорных данных о глубине залегания
геологической границы по эталонным профилям. Эффективность
решения задачи по описанной методике В. И. Шрайбмана и
М. С. Жданова иллюстрируется табл. 9.
Выделение корреляционным методом фоновой составляющей пер-
вого порядка приводит к увеличению по модулю коэффициента
корреляции остаточной составляющей с глубиной залегания гео-
логической границы до —0,88.
60
Таблица 9
Порядок прогнозных остаточных составляющих	Коэффициент	корреляции	Погрешность приближения глубины е, м	Среднеквадрати- ческое отклонение составляющих Ag, мГал
	Дйпр и Н *ост п и 11	Ag"p и Н		
0	0,018			143	2,2
1	—0,88	0,46	68	1,3
2	—0,90	0,36	63	0,9
3	—0,97	0,50	33	1,3
4	—0,99	—0,63	22	1,9
Прогнозная остаточная составляющая второго порядка выде-
ляется на базе двух критериев: минимума дисперсии остаточной
составляющей и минимума модуля коэффициента корреляции фона
и геологической границы. Эта составляющая характеризуется ко-
эффициентом корреляции с границей г = 0,9 при погрешности
« = 0,63 м. На карте прогнозной остаточной составляющей Ag
(рис. 7, в) хорошо отображаются особенности изучаемой геологи-
ческой структуры. Рассмотренный пример указывает на возмож-
ность замены дорогостоящих сейсморазведочных работ на грави-
разведку и проведения сейсмических исследований лишь с целью
получения эталонных данных. Корреляционные методы приобре-
тают особое значение в районах Восточной Сибири, где значитель-
ные территории покрыты трапповыми покровами и выполнение
•сейсморазведочных работ затруднено. В этих условиях сейсмораз-
ведкой отрабатывают участки с отсутствием траппов, которые яв-
ляются эталонными для построения трансформационных много-
членов. Затем, используя полученные корреляционные зависимо-
сти, по данным гравиразведки определяют геологические характе-
ристики (в частности, глубины залегания исследуемых горизон-
тов) на площадях с развитием траппов.
При другой методике корреляционных преобразований в гра-
вимагниторазведке, реализованной в автоматизированной системе
комплексной интерпретации АСКИНТ (В. С. Славкин, П. А. Бес-
прозванный и др.), по эталонным участкам с известной глубиной
залегания исследуемого горизонта (например, фундамента) опре-
деляется информативность остаточной составляющей (или струк-
турной составляющей) гравитационного поля: AgCTp = Ag—Agj, =
= ah, где h = H—H; Н — глубина до поверхности фундамента;
Н — ее среднее значение в скользящем окне, размеры которого
зависят от масштаба исследований; Agj,— региональная состав-
ляющая (от фундамента); а — статистический показатель грави-
активности, измеряемый в мГал/км,
На эталонных участках определяются значения a, AgcTV, Agj>.
Затем поле Ag$ интерполируется в межэталонную область путем
61
его аппроксимации полиномом. Прогнозная глубина исследуемого
горизонта (поверхности фундамента) находится из выражения
ЯПР = (Ag-Ag3P)/a + Н.
§ 10. КУСОЧНО-ПОЛИНОМИАЛЬНАЯ АППРОКСИМАЦИЯ
СЕЙСМИЧЕСКОЙ ИНФОРМАЦИИ
В тех случаях, когда исходная информация характеризуется об-
ластями существенно различной степени гладкости, при сглажи-
вании экспериментальных данных полиномами не получают удов-
летворительных результатов. С целью повышения эффективности
сглаживания такого материала разработаны алгоритмы поинтер-
вальной аппроксимации с автоматической стыковкой (В. Н. Троян,
Б. А. Окунев), используемые при сглаживании значений эффек-
тивных скоростей, времени t0 вдоль профилей, глубин сейсмиче-
ских горизонтов.
Рассмотрим алгоритм аппроксимации одномерной кривой, пред-
ложенный В. Н. Трояном [17].
На основании априорных представлений (или на эталонных
участках) о степени гладкости исходных данных выбирают эле-
ментарный интервал обработки (окно сглаживания), содержащий
k точек. Величина такого интервала (размер окна) обычно равна
половине минимального периода геофизической аномалии, обус-
ловленной искомым объектом. В пределах этого интервала проводят
сглаживание полиномом до четвертой степени, т. е. модель экспе-
риментальных данных в окне имеет вид
Y = XA + n,
где А = (а0, alt а2, а3> а«) — вектор коэффициентов полинома;
X — структурная матрица,
п — случайная компонента (помехи, погрешности измерений) с ну-
левым средним и дисперсией ст®.
Дисперсия оценок коэффициентов полинома
D(A) = a®(X'X)-1,
дисперсия аппроксимации
а®=(1/(*—5))(Y—ХА)' (Y—ХА).
Начиная со второго интервала, содержащего k точек, коэффи-
циенты ai определяются по исходным данным уже этого интервала,
но с учетом коэффициентов, найденных на первом интервале. Так
как точность аппроксимации будет максимальной в центре интер-
вала, переход со старого интервала на новый следует осуществлять
с перекрытием, обычно составляющим половину интервала, т. е.
62
k/2 точек. При этом линейные связи между найденными оценками
Ал_ т предыдущего интервала и искомыми коэффициентами Ал но-
вого интервала можно представить в виде системы уравнений
CA = W, где матрица С определяет характер связей:
1	xi	х]	х? xi
с_ 0	1	2х/	Зх?	4х?
0	0	2	6х/	12х?
_ 0	0	0	6	24xz	_
Тогда
Сто, л-1 + Ях, n-iXi + а?, л-хЛ/ + о®. n-iX3[ + а4, n-iX/
W	®i, п~1 “I-	л—1Х/ 4- 3dg_ n—iXi 4* 4а$, л—хх;
2<Хг, л-x + баз, л-i-^i 4* 12а4, Л_1Х?
_	баз, л—14- 24а4, л_iXz	_
Число линейных связей должно быть всегда меньше числа ко-
эффициентов. Индекс I определяется формулой I = (и—1) (k—г),
где г — число точек перекрытия.
Число строк в матрице С равно числу линейных связей. Если
матрица С состоит лишь из первой строки, стыковку интервалов
аппроксимации проводят только по значению функции (число ус-
ловий стыковки NB — 1). Если матрица включает первые две
строки, стыковку выполняют по функции и первой производной
(NB — 2), когда три строки — по функции первой и второй произ-
водных (NB — 3) и т. д. Компоненты вектора W представляют со-
бой значения функции аппроксимации, ее первой, второй и третьей
производных, вычисленные по коэффициентам Ал_х интервала п—1
в точке с координатами X/. Далее вычисляются оценки А коэффи-
циентов аппроксимации n-го участка, ковариационная матрица
оценок D (А) и дисперсия аппроксимации ст2.
. Для равноточных наблюдений с учетом формулы (2.16) при по-
лучении оценок параметров любого участка с номером п, начиная
со второго, осуществляют расчеты:
An = (X'X)-1X/Y„;
a;=a'+w;q-a’s-,
D(A) = ct2R,
где
Q = [C(X'X)-1C']-1C;	S = C'Q;
R = (X'X)-1—(X'X)-1 С' [С (X'X)-1 С']-1 C (X'X)-1.
В качестве примера описанного алгоритма кусочно-линейной
аппроксимации рассмотрим использование этого алгоритма для
63

Рис. 8. Графики кусочно-полино-
миального сглаживания эффектив-
ной скорости вдоль профиля в зави-
симости от размера окна.
1 — исходные данные; 2 — сглаженные
значения [17]
сглаживания значений эффективной скорости вдоль профиля. На
рис. 8 исходные значения аЭф соединены отрезками прямых. Ин-
тервал (окно) ^-аппроксимации составляет 10, 20 и 30 точек, ин-
тервал перекрытия 50 %, т. е. г = fe/2. При сравнении кривых
сглаживания с разными интервалами видно, что алгоритм обладает
хорошими фильтрующими свой-
ствами (см. гл. VI) по отно-
шению к высокочастотной по-
мехе и к тем аномалиям, период
которых меньше интервала ап-
проксимации.
Как показывает опыт, опти-
мальными в смысле результатов
и затрат машинного времени
при окне аппроксимации k —
= 10-5-30 точек являются сте-
пень полинома NP = 3, число
условий стыковки NB = 2.
Описанный алгоритм можно
с успехом использовать для
сглаживания данных любой
физической природы, в частно-
сти он применялся для сгла-
живания глубин сейсмического
горизонта, при определении
статических поправок. Прове-
дение подобного сглаживания
играет роль регуляризующего
фактора.
Для кусочно-полиномиаль-
ного сглаживания двумерных
массивов данных с автоматической стыковкой элементарных обла-
стей осуществляют сглаживание в пределах окна с длинами сторон
в k точках (по оси X) и по V профилям (по оси Y).
—►
Вектор коэффициентов А при аппроксимации такой области
двумерным полиномом третьей степени имеет десять компонент:
Подробное описание алгоритма двумерной аппроксимации дано
в [17].
§ 11. ПОЛИНОМИАЛЬНЫЕ ИНТЕРПОЛЯЦИЯ
И СГЛАЖИВАНИЕ
Задача приближения функции ft заданной дискретно с некоторой
Погрешностью, помимо методов аппроксимации, рассмотренных
выше на основе корреляционно-регрессионного анализа, решается
также путем интерполяции.
64
Метод интерполяции заключается в том, что зна-
чения коэффициентов а0,	.ап находят из равенств, являю-
щихся условиями интерполяции,
ф(%ь A) = f(x/), i = 0, 1, . . . , п,
где точки xlt принадлежащие некоторому интервалу, образуют сеть
узлов, называемых узлами интерполирования. Если
в качестве <р используем полином <р (х) = а0 + агх + . . . + алх",
получаем полиномиальную (или алгебраическую) интерполяцию.
Это наиболее часто встречающийся на практике вид интерполяции
Интерполяционные полиномы Лагранжа и Ньютона
Пусть сеть Х[ не обязательно упорядочена, но узлы интерполяции
различны, Х{ Ф Xj при i Ф j, тогда полином
л
Рис. 9. Пример локализации гравитационного поля с помощью параболиче-
ской интерполяции методом Лагранжа (по Е. А. Мудрецовой).
1 — суммарное гравитационное поле Ag (х); 2 — региональный фон АЯф полученный
интерполяцией; 3 — локальная аномалия Д2ЛОК; 4 — остаточная аномалия Авост: 5 —
узлы интерполяции К[, 6 — интерполяционные точки
удовлетворяет условиям интерполяции Ln (xt) = f (х() = ft. Его
называют интерполяционным полиномом Лаг-
ранжа при неравноотстоящих узлах х{. Если шаг съемки рав-
номерный, т. е. х—xQ = kh,
п
Lnr(x) = L„(xo+^) = (-l)n	• -(fe~n) У (-1/-^-.
n!	4_j	к—I
1=0
3 А. А. Никитин
65
Пример интерполяции полиномом Лагранжа гравитационного
поля рассмотрен на рис. 9..
Полином Лагранжа приближает не случайную величину, а
гладкую функцию f (х) с погрешностью
| f (x)—Ln (х) | <	I (х—х0) (х—xi) . . . (х—хп) I,
(П + 1)1
где Мп+1 = шах | /(”+1) (х) |.
Интерполяционный полином Лагранжа можно представить в
форме
Ln(x) = f(x0) + (x—x0)f(x0, xi) + (x—х0)(х—xi)f(xo, *i> х2) +
+ . . . + (х—х0)(х—х1). . . (х—хл_1)/(х0, хъ .... хп),
(2.54)
которая более удобна для вычислений при последовательном до-
бавлении одного или нескольких узлов. Выражение (2.54) назы-
вают интерполяционным полиномом Ньютона.
В формуле (2.54) выражения вида
/(Хь Х;)=[/ (X/)— f (хг)]/(Х/ — Х{)
определяют разделенные разности первого порядка,
выражения вида
f(xt, х/, xk) = [f(xt, Xk)—f(Xh Xj^Xit—Xi)
определяют разделенные разности второго порядка, и т. д. Соот-
ветственно разности k-ro порядка f (xlt х2, . . . , xk+1) находят
через разности (k—1)-го порядка:
/(*1, х2......хк+1) = [f (х2......**+1)	—
—/4*1. *2......**)]/(**+!	—*1)-
Интерполяционные полиномы (2.53) и (2.54) используют при
решении задачи прогноза значений некоторого параметра (или
поля) в области, где либо измерение параметра невозможно из-за
наличия мешающих природных факторов, либо эти факторы носят
иной характер, чем тот, который наблюдался бы при отсутствии
в этой области аномального эффекта, например, от нефтегазовой
залежи.
В практике обработки в последнее время широкое развитие
с целью интерполяции получили сплайн-функции.
Сплайн-интерполирование
Этот способ приближения сочетает хорошие аппроксимационные
качества на всем интервале обработки (х0, хл) с локальным харак-
тером сплайна.
Простейший линейный сплайн — кусочно-линейная
функция фх (х), «натянутая» на точки (х(, ft), как на «частокол».
Здесь и далее полагают сеть узлов х< строго возрастающей, т. е.
*o<*i< • •  хп, что обычно имеет место на практике.
€6
полагая фз' (х£) = Mt, по-
Оценка погрешности при неравномерной сети xt
IФ1 (*)—f(х)|< М#,
для равномерной
IФ1W—f (х) К MJPIS,
где М2 = шахЦ" (|)|; |<(х0, хп)-, h — шаг по профилю, при
неравномерной сети h — величина максимального расстояния ме-
жду точками наблюдения.
Можно построить и параболические (квадратичные) сплайны
ф2 (х), однако их мало используют, а выражения для них громоздки.
Кубические сплайны <р 8 (х) представляют собой на
каждом шаге (х£, х£+1) кубический полином. Они удовлетворяют
условиям интерполяции ф3 (хг) = ft, а также дополнительному
условию гладкости: требуется, чтобы производные <рз (х) и фз' (х)
были непрерывны на всем интервале обработки (х0, хл). Поскольку
Фз (х) — кусочно-линейная функция,
лучим
Фз (х) =	— (X—Xl) + Mt,
Xi+l — Xi
Интегрируя это выражение 2 раза
стоянные интегрирования из условий интерполирования, получим
представление сплайна ф3 (х) на интервале х£, х£+1 в виде
Фз (х) = Мt (xi+1~x)-- + М(+1. 	Х{)3--)-
7	6(х1+1-х{)	t+1 6(Xi+1 —Х£)
। Г___ М i (Xj-l-1 Xj)* *1 / Xj-j-i X \
L	6 J\ Xi+l—Xi /
, n	Mi+Hxe+1 — Xi)2 1/ x —Xi
+l/<«-----------5-------J -
Значения Mt определяются из условий непрерывности, которые
приводят к системе уравнений
Xi-Xi-1 М , Xi+j- Xj-1
6
от Xi до х и определяя по-
(2.55)

3
=_l£±l—fl-----fi—fbl_,	i=l, 2..........n— 1.
Xi+l — Xi Xt — Xt-!
Эту систему представим в виде
Дх(_1ф" (xi—i) + 2 (Axi-i + Дхг) ф" (xt) + Дх£ф" (Xi+1) =
= 6(ДА/Дх(—Afi-i/Axi.O, 1 = 2, .... п— 1,	(2.56)
где Дх( = х{+1—х(; ДА = ft+i—ft; ф" (х() = М£.
Система (2.56) состоит из (п—2) линейных уравнений и служит
для определения неизвестных значений вторых производных
ф" (хг), по которым совместно с заданными значениями ft находят
коэффициенты кубического полинома (2.55). Перед расчетом сле-
дует задать значения ф” (х) в точках хх и хп, которые для куби-
3*	67
ческих сплайн-функций обычно полагают равными нулю: <р" (х2) =
= <р" (хл) = 0.
Формулу (2.56) можно представить в матричной форме:
A<p" = Y,	(2.57)
где
2 (Д х,-|-Д х2)	Дх2	0	0 • . .
Дх2 2 ( Ах2-|-Ах3) Дх3 0	. . .
О	Длгз 2 (Дхз+Дх,) Дх, . . .
О
О
О
0	0	0	0 . . . Дх„_2 2 (Д«„_2+Дхя_1) J
ф"=[ф"(^), ф"(*з). • • • - ф"(*п-1)];
Y = [6f-^-----£M-W'(xi), 6f^-------
L \ Дх2 Д*1 /	\ Д*з Д*2 /
— Дх2ф" (х2),
\ Д*п-1
^-2-)_Дхп_1Ф"(х„)].
Матрица А является трехдиагональной, симметричной и имеет
положительные диагональные элементы. Следовательно, ее можно
считать положительно определенной. Ввиду этого обеспечивается
существование и единственность решения системы (2.57), которое
можно получить обычным методом исключения Гаусса.
До сих пор рассматривалось применение кубических сплайн-
функций для интерполяции. Однако они используются и для сгла-
живания экспериментальных данных.
Пусть вновь на оси абсцисс в точках Xi<x2< . . . <хл заданы
значения функции наблюдений fu f2, . . . , fn. Краевые условия
задаются в точках хг и хп значениями первой либо второй произ-
водной искомой функции ф (х) : ф' (хх) и ф' (хл) или ф" (хх) и
ф" (хл). Для расчета сглаживающей функции ф (х) примем условие
пропорциональности разности ft—ф (хг) скачку третьей производ-
ной в точках 1 = 2,..., п—1:
gilfi — ф(хг)] = аг,' gi>0; i = l, . . . , п,
где	— —
ах = Li (хх); а{ = L,' (х,)—Ц-\ (xt); an = —Ln-i (x„);
Lc (*z) — полиномы, определяемые формулой кубического сплайна,
Lt (х) = ai (x—Xi)3 + bt (x—xif + (x—x{) + d{,
t = l, 2.......n— 1;	(2.58)
a.i — коэффициенты пропорциональности, которые должны быть
положительными; gi — весовые множители.
68
Искомыми параметрами являются коэффициенты alt bt, Ct, dt,
число которых равно 4 (п—1). Сплайн-функции на границах ин-
тервала xt, х<+1 удовлетворяют условиям:
qj(xi) = Li(xi)=dt;
Ф (xl+1) = Lt (х,+1) = аДх^ + b{kx2 + cihxi +df;
Ф (xi)= i(xi) = ci\	(% 59)
ф (Xi+i) = Li (xi+1) = 3ai^x2i + 2bi^Xi + c{-t
ф" (xi) = L"i(xi)=2bi-,
Ф (xf+]) — L\ (*t+i) =	+ %bi-
Значения искомых коэффициентов находят, используя условия
(2.59) для функции и второй производной, а также учитывая, что
Ф М = fi- После несложных преобразований, имеем:
а‘= to" <**+»)— f" Ml;
6Дх/
bt— — ф"(х/);
2 т ih	(2.60)
* =	—V-1*”" (*+i) + Ф" Ml;
Дх/ 6
di = fi', &fi = fi+i—ft-
Используя условия (2.59) и уравнения (2.60), получим систему
из (п—2) уравнений с (п—2) неизвестными ф" (xt) (для i = 2,
3, . . . , п—1) и с п неизвестными ф (xi) (i = 1, . . . , п) в виде
- -у— 1ф" (*i)—ф" (*2)1 = gi [fi—Ф (*i)L
—— 1ф" (xi-i)~ф" (х,)]-----г- 1ф" (х<)-ф" (^+1)1 =
Axi-i	Axj	(2.61)
= gilfi—Ф (x,)L » = 2, .... n— 1,
—! [ф" (xn_i)—ф" (x„)] = gn [fn — ф (xn)] •
Axn_i
Помимо этого имеем еще (n—2) уравнения относительно тех же
неизвестных, которые получаются из условий (2.56) путем замены
fi на ф (xi).
Полагая краевые условия для второй производной в виде
ф'7 (*i) = ф" (хп) = 0, запишем системы уравнений (2.56) и (2.61)
в матричной форме:
— В'ф"+ 6ф= Gf;
AxJ"4-bJ = 0	(2.62)
69
где
~gi	0	...	О
О	g2	...	О
_ О О ... gn _
 —— Г-^+-Ч	—Ь	о
Д«1	\ ДХ1 Дх2 /	Дх2
о ----1—	(-!-+-!-')-—
Дх2 \ Дх2 Дх3 J Дх3
О	О	О	О
ООО
ООО
ф" = [ф"(х8). ф"(*э).......Ф" (*»-!)];
Ф = [ф(Х1), ф(х2)........ф (хл)];
f = fz< • • • » /nJ-
Матрица Ах получается из матрицы А системы (2.57) путем
умножения всех ее элементов на 1/6. Так как матрица А является
положительно определенной, а для положительных весовых множи-
телей gi и диагональная матрица G положительно определенная,
система (2.62) имеет решение для всех значений gi, удовлетворяю-
щих неравенству 0<gt<co. Рассмотрим влияние значений gt
на результаты сглаживания. Для этого умножим первую систему
уравнений (2.62) на матрицу G-1 : — С-1В'ф'' + /ф = If, где
I — единичная матрица.
При gi—>оо первый член полученного матричного уравнения
будет стремиться к нулю и ф (х<) -» ft. В этом случае вторая си-
стема (2.62) переходит в систему (2.57) и получается, задача интер-
поляции кубическими сплайн-функциями.
При gt -> 0 значения ф (х<) удаляются от наблюденных вели-
чин fi и аппроксимация сплайн-функциями соответствует аппрок-
симации прямой линией регрессии по методу наименьших квадра-
тов. Выбирая значения весовых множителей gi между этими пре-
делами, можно добиться требуемой степени сглаживания экспери-
ментальных данных.
70
Теперь вернемся к решению системы (2.62). Из первой системы
легко определяется вектор <р, поскольку G — диагональная мат-
рица и она легко обращается: <р = G-1 (В'ф" + Gf). Подставляя
это выражение во вторую о-
систему (2.62), получим v^iw/c
оценку для вектора вто-
рой производной	S’2
(2.63)
Первая матрица в пра-
вой части (2.63) является
пятидиагональной и по- W
ложительно определенной;
для ее обращения можно 3>в
использовать метод Га-
усса.	3>г
Сглаживание с помо- g
щью кубических сплай-	h_h
нов было реализовано ’	ьитен
В.Н. Трояном в программе щ
«Аппроксимация кубиче-
скими сплайнами» и 9,9
использовано для сгла-
живания эффективной 9,0
скорости вдоль профиля.
На рис. 10 приведены ис- SJ5
ходные и сглаженные дан-
ные при разных значениях
весовых множителей gi,
которые принимаются для в
всех точек одинаковыми:
gi = g. Анализ рис. 10 по-
казывает, как с уменыпе-
нием весового множителя '
g = 10-14-10~5 проис-
ходит переход от сглажи- *’
вания высокочастотных Jg
составляющих к сглажива- 
нию низкочастотной со-
ставляющей.
Описанный алгоритм hj#
указанная программа мо- ’
Рис. 10. Графики сглаживания эффектив-
ной скорости вдоль профиля с помощью
кубических сплайн-функций при различ-
ных значениях коэффициентов g:
а 10”*, ь — 10-’;. в — Ю-5; 1 — исходные
даннае; 1 — сглаженные значения [17]
гут быть использованы для
сглаживания пластовых
скоростей вдоль горизонта
и времен с целью определе-
ния статических поправок,
71
а также и для сглаживания полей в различных геофизических мето-
дах. Степень сглаживания регулируется весовыми множителями,
которые выбираются либо путем визуального анализа результатов
на экране дисплея (при интерактивной системе обработки), либо
по характеристике сглаживания, рассчитанной В. Н. Трояном
[17].
Следует подчеркнуть, что в отличие от рассмотренного в § 10
алгоритма кусочно-полиномиальной аппроксимации, в котором
априорная информация задается размером окна и степенью поли-
нома, весовые множители gt при сплайн- интерполяции не имеют
конкретного физического смысла. В то же время они выполняют
роль регуляризующего фактора и можно считать, что обратная
величина g{ пропорциональна погрешности (дисперсии) отклоне-
ния наблюденных значений от сглаживающей кривой.
В целом сплайн-интерполяция не всегда дает удовлетворитель-
ные результаты, особенно при обработке двумерных массивов дан-
ных. Тригонометрическое или кусочно-полиномиальное интерполи-
рование обеспечивают более устойчивые результаты.
§|12. ИНТЕРПОЛЯЦИЯ СИСТЕМОЙ
ГАРМОНИЧЕСКИХ ФУНКЦИЙ
Практическое применение при интерполяции потенциальных гео-
физических полей и полей различных геологических параметров
в условиях неоднородности сети наблюдений, особенно при нали-
чии пересеченного рельефа местности, наличия существенных оши-
бок наблюдений, получила система гармонических функций, пред-
ложенная В. И. Ароновым [1]. Интерполяция значений f (xtyt)
исходного поля по площади съемки основана на аппроксимации
системой гармонических функций
ф(х, «/) = LaA(x—хь у—Hi, Zj),	(2.64)
где
G( = —!------------г-1----------;	(2.65)
2л [(x-x^ + ^-^W2
at — коэффициенты, определяемые таким образом, чтобы выпол-
нялось неравенство
max | f (xh (x{, yi) | < e0; {x,, yt}£P\	(2.66)
P — множество пунктов наблюдений в исследуемой области; е0 —
величина, выбираемая равной среднеквадратическому значению
помехи; z± — параметр, принимаемый большим шага наблюдений
Ax (z^Ax). При z^ —> со ф —ф, где ф — целая функция, т. е.
этот метод интерполяции является асимптотически оптимальным.
Значения at определяются из решения системы уравнений
AX=F,	(2.67)
72
где X — вектор-столбец значений а{; F— матрица исходного поля
/ (xi, yi)', А = [atil — матрица, элементы которой
ao=Zi/[(x;—Х/)2 + (у{—г//)2 + z2]3/2. i, j = l, . . . , п;
п — число исходных значений f (xi, у с).
Система линейных уравнений (2.67) решается методом итера-
ций. При значительной неравномерности сети наблюдений (шаг
наблюдений меняется в несколько раз) скорость итерационного
процесса падает при гг > Дхтах. Последнее условие необходимо
для получения высокой точности приближения. В связи с этим
более целесообразным становится использование аппроксимации
ф(*, y) = miairGir(.x—xl, y—yi, zr), r=l, 2, . . .	(2.68)
r i
При каждом фиксированном значении г ведется сортировка
исходных значений поля f (х<, yi) таким образом, чтобы минималь-
ное расстояние между ними было не менее zr/2. Максимальное зна-
чение zr выбирается равным размеру максимального «белого» пятна
(пропуска в наблюдениях) в исходных данных.
При аппроксимации системой (2.68) последовательно выде-
ляются компоненты интерполируемого признака <р, соответствую-
щие различным значениям шага наблюдений Ах, в результате
чего интерполяция становится возможной практически при любой
неоднородности исходной сети и восстанавливает одновременно
локальные и региональные составляющие поля.
Как указывалось, величина е0 в (2.66) выбирается равной
среднеквадратическому значению помехи и является, по существу,
всей той априорной информацией, которая необходима при исполь-
зовании этого алгоритма интерполяции.
Описанный метод интерполяции может быть использован и для
нахождения тренда. С этой целью нужно соответствующим обра-
зом изменить параметр z функции Gir при вычислении <р (х, у)
по уже полученным значениям а(г. Например, если требуется
понизить уровень влияния локальной составляющей с интерва-
лом корреляции гл. значения ztr должны быть увеличены на число
г0 = гл. Значения тренда <р (х, у, г0) вычисляются по выражению,
аналогичному (2.68):
ф(х, У, го)~ ZZa<rGo-(x—xlt у—УС, zr + zn).
г I
Подобный прием интерполяции рассмотрен И. Д. Савинским.
ГЛАВА III
ДИСПЕРСИОННЫЙ И ФАКТОРНЫЙ АНАЛИЗЫ
ГЕОФИЗИЧЕСКИХ ДАННЫХ
Основой дисперсионного и факторного анализов являются изуче-
ние и сравнение дисперсий наблюденных данных и их линейных
комбинаций, при этом измеренные значения геофизических полей
полагаются случайными величинами.
§ 13.	ОСНОВЫ ДИСПЕРСИОННОГО АНАЛИЗА
Задача дисперсионного анализа — оценка влияния того или иного
фактора Y или комбинации таких факторов на распределение из-
меряемых величин Хъ . . . , Хр, проявляющееся в изменении ма-
тематического ожидания при неизменной дисперсии.
Одно из основных требований, которому должны удовлетворять
результаты геофизических измерений, состоит в том, чтобы они не
содержали систематических ошибок. Факторами, вызывающими
систематические ошибки, являются погрешности аппаратуры, ме-
тодики измерений, оператора, а также неучтенные изменения фи-
зических условий наблюдения.
Рассмотренные в § 4 критерии относились к проверке гипотезы
о равенстве средних двух случайных величин (выборок). В то же
время, когда решается задача, например, о систематической ошибке
гравиметра как фактора, влияющего на показания силы тяжести,
измерение на двух приборах (гравиметрах) может оказаться не-
достаточным.
Для получения обоснованного вывода следует провести изме-
рения при нескольких состояниях фактора, т. е. на нескольких
приборах, и убедиться в отсутствии или наличии систематической
ошибки в полученных результатах. Совершенно аналогично мы мо-
жем рассматривать аномалию того или иного геофизического поля
как фактор, для надежного установления которого необходимо вы-
полнить измерения поля на нескольких профилях, т. е. при раз-
личных состояниях фактора. При комплексной интерпретации гео-
физических полей различными состояниями фактора (комплексного
параметра) будут данные измерений различных геофизических по-
лей.
В общем случае дисперсионный анализ применяют для того,
чтобы установить, оказывает ли существенное влияние некоторый
фактор Y, имеющий ряд состояний Ylt . . . , Yp, на изучаемую
величину. Попарное сравнение средних значений при этом исклю-
чается, поскольку с возрастанием числа средних увеличивается
и наибольшее различие между ними: среднее новой выборки может
74
оказаться больше наибольшего или меньше наименьшего из сред-
них, полученных до нового эксперимента.
Идея дисперсионного анализа состоит в сравнении фактор-
ной -дисперсии, обусловленной воздействием фактора, и
остаточной дисперсии, вызванной случайными при-
чинами. Если различие между этими дисперсиями значимо, фактор
Y оказывает существенное влияние на систему величин Xlt ... ,
Хп. В этом случае средние при каждом состоянии фактора (груп-
повые средние) также будут иметь значимое различие.
Однофакторный дисперсионный анализ
Пусть на нормально распределенную случайную величину X (гео-
физическое поле) воздействует фактор Y (систематическая ошибка
прибора, аномалия и т. д.), имеющий р состояний (р — число при-
боров, профилей и т. д.), т. е. имеем:
*и. *12. • • • . *ш при состоянии Vi (xi);
*Р1, *Р2. . . . , *рЛ при состоянии Ур(*р).
Измеренные значения поля можнб представить в виде табл. 10.
Таблица 10
Номер измерения	Состояние фактора			
	У1	У2		ур
1	*11	*12		Х1Р
2	*21	*22		*ар
п	*л1	*Л2		*лр
				
Групповая средняя	*1	*2	. . .	ХР
Групповая дисперсия	с?	‘1	• • •	°р
Еще раз подчеркнем, что в качестве состояний фактора Yit ... ,
Yp можно рассматривать измерения поля разными приборами,
на разных профилях или измерения р полей на одном и том же
профиле.
Пользуясь этими- статистическими данными, необходимо про-
верить нулевую гипотезу, согласно которой групповые средние рас-
пределений равны между собой. Если проверяемая гипотеза верна,
при сопоставлении средних значений по каждому состоянию фак-
тора не должно быть значимого расхождения между ними, если
75
такое расхождение обнаружено, нулевую гипотезу следует отбро-
сить.
Обозначим: хг — среднее значение из п измерений, выполненных
по первому состоянию фактора (т. е. первым гравиметром или по
первому профилю и т. д.); х2 — среднее из измерений по второму
состоянию фактора и т. д,, так что
- 1 " 1 п
х1 =-----2 х{1; . . хр =-----2 х(р;
п 1 = 1	П i=l
о?, ... , Пр —дисперсия по состояниям фактора.
Обозначим через х общее среднее всех измерений, т. е.
х=----£ Ё хч< или х= — Ё xi-
ptl j=l 1 = 1	р 1=1
Тогда величина
Р л
s=E£(x(/-%)2	(3.1)
/=1 i=i
является общей суммой квадратов отклонений измеряемых
сначений от общей средней х, а
р _	_
S4) = nSi(x/—х)2	(3.2)
называется факторной суммой квадратов отклонений
групповых средних (средних по состояниям фактора) от общей
средней. Величина Зф характеризует разброс между различными
состояниями фактора Y. Наконец, величина
Зост = S (хп—xi)2 + • • • + S (xip—xpf	(3.3)
i=i	i=i
называется остаточной суммой квадратов отклонений
наблюденных значений внутри групп (или состояний фактора),
она характеризует остаточное рассеяние случайных погрешностей
результатов измерений. Очевидно, что
Зост = 3 — Зф.	(3-4)
Для расчетов S и Зф часто бывают более удобными формулы
р п	/ р п \2
-----IZEd;
/=1 1=1	рп \j=i 1=1
. Р / л	\2	, / р л	\2
Зф=—-Г(Ё—(ЁЁ*о)«
п j=i \;=1 J	рп \/=i i=i	/
Для сумм (3.1) — (3.3) получаем соответствующие выражения
общей, факторной и остаточной дисперсий:
D — S/(pn— 1); Рф = 5ф/(р —1); Don = S0CT/p (п— 1).	(3.5)
76
Чтобы проверить нулевую гипотезу о равенстве средних для
различных состояний фактора, достаточно применить критерий
Фишера, сравнивая факторную и остаточную дисперсию, т. е.
Г = Рф/Р0СТ =	S*/(p ~ —	(3.6)
Sqct/P (П — О
Если F<zFv, где Fy —у-квантиль распределения Фишера с
(р—1) и р (п—1) степенями свободы (числителя и знаменателя),
гипотеза о равенстве средних выполняется, т. е. х± = . . . = хр.
При этом отсутствует систематическая ошибка, вызванная влия-
нием гравиметра как фактора, если Yи . , Yp— различные
приборы, или можно говорить об отсутствии аномалии при на-
блюдениях по р профилям съемки и т. д.
Если имеет место влияние фактора на измеряемую ве-
личину. С помощью корреляционного отношения ц = Пф/ст можно
количественно оценить это влияние. Чем ближе отношение л к еди-
нице, тем сильнее влияние фактора.
В том случае, когда число измерений при различных состоя-
ниях фактора разное и равно nt, для определения дисперсий а2
(по состояниям фактора), факторной и остаточной дисперсий вы-
числения проводят по формулам:
где
D* = —!— £ п, (х/—х)2,	(3.8)
!р -1 /=»
где
. р п1	. р _
;=—S2/"=—
Ро<Я = у ] S 1^ (*</-------(3.9)
р
где N = П]— общее число измерений.
Пример. На исследуемом объекте предполагается функциональное из-
менение намагниченности насыщения, проявляющееся на фоне случайных
ошибок измерений. Для проверки этой гипотезы отобрано по 12 образцов
с 10 различных участков, равномерно расположенных по площади. Для
каждого образца измерена намагничеииость насыщения Js и результаты
прологарифмированы, т. е. хц = 1g J${/ с учетом близости распределения
данных измерений к логарифмическому закону распределения. По каждому
77
из участков, являющихся состояниями фактора, вычислены средние xj и
дисперсии а2 (табл. 11).	.у
Требуется проверить гипотезу об отсутствии функционального измене-
ния J$ на уровне значимости 0,05.
Решение. По формулам (3.8) и (3.9) имеем:
1 10 - 110_
Дф =——Е 12 (х/— х)2 « 6,06; х = —У Xi« 2,37;
9 1=1	10 М
10	а2
Рост = У 11 —= —— • 3,05 = 0,305.
>1	110	10
Таблица 11
Номер участка	Х1		Номер участка	Х1	
1	2,51	0,25	6	3,55	0,60
2	3,09	0,37	7	3,01	0,49
3	2,68	0,40	8	2,19	0,20
4	1,16	0,23	9	2,08	0,12
5	2,00	0,21	10	1.41	0,18
По таблице значений распределения Фишера [2] находим критическую
границу критерия Фишера F0,»5 (9, ПО) = 1,96.
Поскольку Юф/Эост = 19,9 >1,96, гипотеза о наличии функциональ-
ного изменения намагниченности насыщения принимается с вероятностью
0,95.
Решающее правило дисперсионного анализа применяется при
условии равенства дисперсий при всех состояниях фактора. Когда
число измерений по всем состояниям одинаково, т. е. п} — п, ис-
пользуется критерий Кочрена:
р
G = Отах/Е О^гпах = ГПЭХ О/»	.'	(3.10)
/=1
Гипотеза о равенстве дисперсий принимается с вероятностью у,
если G меньше критической границы Gv (р, п—1), определяемой
из таблицы значений распределения Фишера [2].
При неравных числах измерений при каждом состоянии фак-
тора применяют критерий Бартлетта.
Двухфакторный дисперсионный анализ
В случае одновременного действия двух факторов, наприйер, когда
измерения проводятся различными приборами несколькими на-
блюдателями, требуется оценить, обусловлен ли разброс получен-
ных значений и средних его значений в группах различием между
приборами или различием между наблюдателями.' Аналогичная
задача возникает при оценке влияния двух разных геологических
факторов на показания того или иного геофизического поля.
78
Основная идея дисперсионного анализа в данном случае заклю-
чается в разложении суммы квадратов отклонений от общего сред-
него на компоненты, отвечающие предполагаемым факторам из-
менчивости.
Допустим, имеются два фактора (признака) А и В, по которым
можно расклассифицировать данные наблюдения. Пусть по фак-
тору А все наблюдения делятся на г групп (состояний) А г, Аг,
а по фактору В — на о групп (состояний). Таким образом, все на-
блюдения разбиваются на rv групп.
Для простоты положим, что в каждой группе имеется лишь одно
наблюдение, т. е. общее число наблюдений Af = rv. Обозначим хц
наблюдение, попавшее в группу Ai по фактору Лив группу В}
по фактору В. Соответствующие средние значения будут:
X/ — у Xi/', Xj —	- 2^ Xjj,
1	° г
Результаты наблюдений для факторов А и В можно представить
в виде табл. 12.
Таблица 12
Состояние фактора А1	Состояния фактора В]				
	В1	вг		BV	
						.
Аг	*11	*12		*10	*1
Аг	*21	*22		*20	*2-
*					
					мнж
Аг	*Г1	Кг 2		*Г0	Хг-
					
xi	*1	х.г		х.о	
где Х(.—средние по строкам; x.j— средние по столбцам.
Для вычисления сумм квадратов 5фЛ, ЗфВ и 50Ст при двух-
факторном анализе используются формулы:
79
Величины 5ф А и ЗфВ являются суммами квадратов разностей
между строками и между столбцами.
Для проверки степени значимости расхождений, обнаруженных
в средних по строкам и столбцам, вычисляются критерии
$Ф а/(г — О
$ост/(г — 1) (о — 1)
5фВ/(о-1)
$ост/(г-1) (и — 1)
— Д^ост,
(3.11)
(3.12)

При ГдС^утабл принимается гипотеза об отсутствии расхож-
дений в средних значениях по строкам, при FB<Z/\>табл — гипо-
теза об отсутствии расхождений в средних значениях по столбцам.
Если гипотеза о равенстве средних по строкам и столбцам не-
верна, величина eft = (г—1) (£>фЛ — DOcr)/rv и eft = (и— 1) (£>ф в—
—D0CT)/rv являются мерами систематического изменения (тренда)
средних значений соответственно по строкам и столбцам.
Двухфакторный дисперсионный анализ рангов
Рассмотренные выше задачи дисперсионного анализа решались
в предположении о нормальном характере случайных отклонений.
Если закон распределения случайных отклонений неизвестен,
для сравнения нескольких, в общем случае зависимых выборок
измеренных значений (например, для сравнения данных по
нескольким профилям съемки) относительно их средних значений
можно использовать ранговый метод, известный как двухфакто-
рный дисперсионный анализ рангов, или критерий Фрид-
мана.
Предполагается, что имеется п выборочных групп (п измерений
по каждому профилю) при р вариантах условий (р — число про-
филей или методов). При этом критерий Фридмана фактически
применяется в рамках модели однофакторного дисперсионного ана-
лиза,. в котором второй фактор В представляет собой однородные
группы или повторные измерения, связанные с одним и тем же со-
бытием, например наличием аномального эффекта (первый фак-
тор А).
С помощью критерия Фридмана проверяется нулевая гипотеза
о том, что различные условия, т. е. наблюдения по разным профи-
лям или разными методами не оказывают влияния на распределе-
ние измеренных значений, иными словами, ранги п измерений
распределены случайным образом по р условиям.
80
Если в предположении справедливости нулевой гипотезы сфор-
мировать суммы рангов для каждого из р условий, они либо не бу-
дут отличаться друг от друга, либо их отличия будут носить слу-
чайный характер. Если отдельные условия вызывают систематиче-
ское изменение (в частности, аномальный эффект), р столбцов бу-
дут иметь различные ранговые суммы. Проверка нулевой гипотезы
состоит из упорядочения (ранжирования) измеренных значений
в каждой строке, суммирования полученных рангов по каждому
из столбцов и вычисления статистики Фридмана
р / «	\2
Хя =----73-JT- Щ ~3«(p+1),	(3.13)
где п — число строк (число наблюдений по каждому профилю);
р — число столбцов (число профилей); ЯКц — сумма рангов для
Р j __	Ч.
i-го условия; S(W— указывает на необходимость суммирова-
ния рангов по каждому условию, возведения в квадрат полученных
сумм и последующего суммирования этих квадратов по всем р
условиям.
Статистика (3.13) при не слишком малых выборках (р = 4,
п>4, р = 3, п>9) распределена как %2 с (р—1) степенями сво-
боды, и решение принимается на основании %2-критерия.
Критерий Фридмана, по существу, аналогичен F-критерию
Фишера на однородность выборок.
Пример. Допустим, что иа участке из трех профилей съемки по трем
пикетам каждого профиля имеются измерения поля Za (в нТл) (табл. 13).
Таблица 13
ПР	пк		
	1	2	3
I	78	92	84
11	63	71	69
III	52	57	65
Таблица 14
	пк		
ПР	1	2	3
I	1	3	2
II	1	3	2
III	1	2	3
			=
	= 3	= 8	= 7
Требуется установить наличие или отсутствие аномального эффекта
в этих наблюдениях (предполагается, что предварительно проведено исклю-
чение региональной составляющей).
Решение. В соответствии с формулой (3.13) прораижируем по порядку
значения AZ на каждом профиле в направлении от наименьших к наиболь-
шим, т. е. наименьшее значение получает ранг 1, следующее по величине —
ранг 2 и т. д. Проранжированные данные приведены в табл. 14.
Далее суммируем ранги в каждом столбце и полученные суммы возво-
дим в квадрат, т. е. 2/?^ = 3, (ХТ?^)2 = 9; 2/?;а = 8, (2/?;а)2 = 64;
2/?Zs = 7, (2/?,3)2 = 49.
81
Подставим полученные значения в (3.13): %2 = 12 (9 + 64 + 49)/(3-3-
• 4) _ 3.3.4 = и.
Поскольку найденная величина превышает критическое, равное 9,24,
принимается решение о наличии аномального эффекта в данной выборке.
Использование статистики Фридмана при обработке геофизи-
ческих данных началось в самые последние годы, однако на ее ос-
нове уже построены эффективные алгоритмы выделения слабых
аномалий на фоне произвольно распределенных помех (см. § 43).
§ 14. ДИСПЕРСИОННЫЙ АНАЛИЗ
ПРИ ИЗУЧЕНИИ ТРЕНДА
Дисперсионный анализ — основа решения многих важных задач
обработки геофизических данных: анализа распределения характе-
ристик физических свойств пород в различных направлениях на
поверхности земли и по глубине; сопоставления различных физи-
ческих параметров по «контрастности» их как признаков тех или ,
иных особенностей, например по степени изменчивости, обуслов-
ленной некоторой аномалией, с помощью корреляционного отно-
шения и т. д. Широкое применение дисперсионный анализ нашел
при изучении регрессионной зависимости и тренда (регрессионной
поверхности). При этом с помощью дисперсионного анализа ре-
шаются задачи: 1) согласования регрессионной зависимости (или
тренда) и исходных данных; 2) эффективности увеличения степени
полинома в уравнении регрессии; 3) оценки значимости постоянных
коэффициентов в уравнении регрессии.
Согласованность регрессионной зависимости (или поверхности
тренда) с исходными данными оценивается путем разделения об-
щей изменчивости величины на регрессию (или тренд), принимае-
мую за искомый'фактор, и остаток (отклонение от регрессии, тренда).
При этом регрессию для модели однофакторного дисперсного ана-
лиза можно представить в виде табл. 10, в которой состояниям фак-
тора соответствуют значения Y при фиксированных X, т. е. со-
стояниями фактора будут xlt . . . , хр, а исходными данными
Ун.......Утр • • • > Ур1....УрПр, В частных случаях П1 = . . . =
= Пр = П, = п2 = . . . = пр — 1.
Число степеней свободы, соответствующее общей изменчивости
в регрессионной зависимости (в тренде), равно v = N—1, где N —
р
= 2 п,-—число наблюдений. Число степеней свободы, соответст-
/=>
вующее уравнению регрессии vper, равно числу членов полинома т,
используемого для построения регрессии (тренда). Число степеней
свободы для отклонений от регрессии vOtk = N—щ—1. Тогда об-
щую схему дисперсионного анализа для проверки согласованности
уравнения регрессии (тренда) с исходными данными по критерию
Фишера можно представить в виде табл. 15.
Если регрессия (тренд) играет существенную роль, дисперсия
отклонения от регрессионной зависимости будет мала по сравнению
82
Таблица 15
Фактор
(источник дисперсии)
Тип дисперсии
Число
степеней
свободы
Регрессия
Отклонение от регрес-
сии
Общая изменчивость
(общая дисперсия)
Oper = — Ehl-У/)2
т /=1
1 р "
о0гк=—---------Е Е (уи-ш)2
N — т — 1 /=1 (=1
D ™ „ 1 . Е Е (уц — у)2
N — 1 /=1 i=l
Р/—значения поверхности ре-
грессии. Критерий Фишера - D^/D^ < F? табл.
с дисперсией самого уравнения регрессии. При проверке гипотезы
о наличии или отсутствии тренда рассматривается частное от де-
ления оценки дисперсии уравнения регрессии на оценку дисперсии
отклонений Пррг/Потк исходных данных от регрессии. Сравнение
этих дисперсий по критерию Фишера позволяет ответить на вопрос,
можно ли рассматривать эти дисперсии как несущественно отли-
чающиеся одна от другой, т. е. существенна ли роль регрессии по
сравнению с влиянием случайных ошибок измерений. Если разли-
чия нет, математическая модель для описания регрессионной за-
висимости (тренда) выбрана неверно (или тренд отсутствует).
Часто согласованность уравнения регрессии с эксперименталь-
ной зависимостью проверяют путем сравнения гипотезы Нг о зна-
чимости коэффициентов, т. е. аг, ... , ат^ 0, с гипотезой Но,
когда ах = . . . = ат — 0 (регрессии нет). Если значение F-кри-
терия превысит допустимое, соответствующее заданному уровню
значимости и числу степеней свободы, гипотеза HQ отвергается.
Эффективность увеличения степени в уравнении регрессии оце-
нивается в том случае, когда при использовании полиномов в тренд-
анализе последовательно увеличивают их степень. Это приводит
к постепенному увеличению числа слагаемых. Тогда дисперсион-
ный анализ применяют для изучения вклада добавляемых компо-
нентов регрессии в общую изменчивость.
Критерий эффективности увеличения порядка регрессии строится
как разность между дисперсиями регрессий последующего и пред-
шествующего порядков. Частное от деления полученной дисперсии
на дисперсию регрессионной зависимости (тренда) последующего
порядка имеет F-распределение, если дальнейшее увеличение сте-
83
Таблица 16
Фактор (источник дисперсии)	Тип дисперсии	Число степеней свободы	Критерий Фишера
Уравнение регрес- сии степени k + 1	т /=1	m	£>(*—!> per
Отклонение от урав- нения регрессии сте- пени k + 1	n(*+D	1	v °™ - N-m-\ Х ₽ П)	N—m—\	
			^OTK < Fy табл
Уравнение регрессии степени k	S /=1	s	p(A) per ^OTK < Fy Табл
Отклонение от урав- нения регрессии сте- пени k	х £ хм* 7 Xml? Г । 1	1 <е> X	N—s—\	
Увеличение степени уравнения регрессии от k до k + 1	р(М-1)_р№) = р per	per ^раэм	m—s	Рразн < D <F у табЛ
Общая изменчивость (общая дисперсия)	II 1 - Хм* Хм~= «с" "i «= । №9	N—l	
пени полинома не дает эффект. Схема оценки эффективности уве-
личения степени полинома приведена в табл. 16.
Когда требуется оценить эффект, обусловленный лишь одним
коэффициентом регрессии в уравнении поверхности тренда, такая
оценка проводится путем исключения данного члена полинома с по-
следующим повторным вычислением сумм квадратов для регрессии
и отклонения. Вклад исключенного члена является разностью двух
дисперсий. Значимость этого члена проверяется с помощью отно-
шения дисперсии для уравнения с исключенным членом Орег.н к дис-
персии для полного уравнения регрессии Dper.n. Для критерия Фи-
шера число степеней свободы равно соответственно 1 (для числи-
теля) и N—m—1 (для знаменателя).
Схема оценки значимости исключенного коэффициента приве-
дена в табл. 17.
Решение рассмотренных в этом параграфе задач также может
быть проведено на основе дисперсионного анализа рангов.
84
Таблица 17
Фактор	Тип дисперсии	Число степеней свободы	Критерий Фишера
Регрессия всех чле- нов	1 Р Орег. п —	 ({// — 1//)2 т /=1	tn	Орег п < Dotk табл
Отклонение от регрес- сии	Dotk — ,,	, X Af — m— 1	N—m—\	
Регрессия после ис- ключения k-ro члена	1 p Орег.н —	, Zfe 1//) m — 17=1	m—1		V ч И	S	g С	й	₽- 8. S О Q V
Отклонение с учетом исключения k-ro чле- на	^отк. H	X N — m — 2 P П/	N—m—2	
Регрессия	только k-ro члена	Dper k — t)per. n — ^рег. и	1	Ррег. k < D < Fy табл
Общая изменчивость (общая дисперсия)	W — 1 /=1 (=1	M— 1	
§ 15. ФАКТОРНЫЙ АНАЛИЗ
Задачей факторного анализа является изучение внутренней струк-
туры ковариационной (или корреляционной) матрицы, полученной
в результате измерений нескольких случайных величин Х1.....
XN. В качестве таких величин, как и при дисперсионном анализе,
могут быть использованы данные измерений того или иного геофи-
зического поля по различным профилям, данные измерений раз-
ными методами по одному и тому же профилю, значения различных
параметров (глубина залегания, геометрические размеры и т. д.)
искомого геологического объекта, полученные в разных точках
наблюдений.
Результаты измерений запишем в виде матрицы
Хц Хц . . . Хщ
Y _	*21	*22	• • •	*2л	/о
*N1	*W2	• • • xNn
85
для которой различные строки могут означать: измерения по N
профилям съемки, в каждом из которых содержится п пикетов;
измерения по N — разными методами по одному и тому же про-
филю с п пикетами и т. д.
Различные случайные величины или признаки Х3, ... , XN
обычно связаны между собой статистической зависимостью, причем
влияние одних признаков может оказаться превалирующим, т. е.
остальные признаки не несут какой-либо существенной информа-
ции, в частности о геологическом объекте исследования.
Например, если значения одного из признаков могут быть вос-
становлены по значениям остальных при наличии его сильной кор-
реляционной зависимости от последних, прямые измерения такого
признака не несут дополнительной информации по сравнению с той,
которую дают все остальные признаки. Это обстоятельство можно
объяснить поведением некоторой небольшой группы т (т N)
независимых, но непосредственно не измеряемых факторов, которые
определяют поведение всех исходных N признаков. Поэтому же-
лательно полученную при измерениях информацию выразить через
эти непосредственно не наблюдаемые факторы. Для перехода к та-
ким новым факторам используется внутренняя структура информа-
ционной матрицы Х'Х-М, которая при условии нормального рас-
пределения и центрирования Х1У . . . , XN выражается как
2X1 2ХхХ2 ... ZXiXN
В = Х'Х=	‘	’ SX*X"
. . . 2Хдг
Диагональные члены этой матрицы являются дисперсиями слу-
чайных величин (признаков) Хх, . . . , XN, а внедиагональные
члены — их ковариациями.
После нормировки ковариаций на соответствующие произве-
дения среднеквадратических отклонений матрица (3.17) преобра-
зуется в корреляционную матрицу R:
1	Г12	...	r1N
г> _	r21	1	...	r2N
(3.18)
rNl rN2 • • •	1
В факторном анализе стараются выбрать небольшое число фак-
торов, способных объяснить ковариационную (или корреляцион-
ную) матрицы. При этом важно найти минимальное число таких
новых случайных величин (или факторов) flt . . . , fm, которые
превращали бы матрицы (3.17) и (3.18) в диагональные. Другими
словами, после учета действия т факторов все связи (корреляции)
между величинами Xt должны стать незначимыми, а сами факторы
fi, . . . , fm — независимыми.
S6
Основная математическая модель факторного анализа записы-
вается в виде системы равенств
+ i = l, . . . , N-, tn<N,	(3.19)
где fj — j-й простой фактор; величины fj независимы друг от друга
и от погрешностей измерений ег, N — заданное число простых
(начальных) факторов; ei — случайные величины, описывающие
ошибки измерений, статистически независимые друг от друга с ну-
левым средним, их дисперсии принимаются одинаковыми и рав-
ными о5, если это не так, т. е. Det = of, преобразование Х{ =
= aXilat приводит к случаю Det = о2; at/ — коэффициенты пе-
рехода от системы случайных величин ft к системе случайных ве-
личин Хг, они называются нагрузками i-й случайной величины
на /-й фактор (факторные нагрузки).
Матричная запись равенств (3.19)
X = Af + e.	(3.20)
При записи модели факторного анализа (3.19) и (3.20) предпо-
лагается, что величины Х{ центрированы. Максимально возможное
число факторов т при заданном числе случайных величин опреде-
ляется неравенством (N	—т)г, которое учитывает тре-
бование о том, чтобы задача не вырождалась в тривиальную.
Факторный анализ базируется на основной теореме, сводящейся
к следующему. Пусть исходные величины Xj и Х2 обусловлены
одним фактором ft, тогда их ковариацию, а при соответствующей
нормировке коэффициент корреляции, можно записать в виде
ri2 = ^ijChi’
В общем случае, когда N случайных величин выражаются че-
рез т факторов, коэффициент корреляции
т
г12 = ЙЦЙ21 + #12^22 + • • • +fllma2m = aVa2/-
Следовательно, коэффициент корреляции любых двух незави-
симых величин Xi и Xj можно выразить суммой произведений ко-
эффициентов (нагрузок) некоррелированных между собой факто-
ров.
Построив матрицу F размерностью N х т из строк, элемен-
тами которых являются коэффициенты ац, например t-я строка
имеет вид ац, а12, .... а1т, получим основную теорему фактор-
ного анализа в виде
R = FFZ	(3.21)
Таким образом, задача факторного анализа сводится к линей-
ному преобразованию W-мерного пространства в /n-мерное путем
представления корреляционной матрицы факторами. Эта задача
не решается однозначно. Представление корреляционной матрицы
R факторами, или факторизацию матрицы R, можно
87
произвести разными способами. Например, если удалось осущест-
вить факторизацию с помощью некоторой матрицы F, любое ее
линейное ортогональное преобразование (или ортогональ-
но,е вращение) приведет к такой же факторизации. Цель
процедуры вращения факторов — представление каждой исходной
случайной величины Xi одним или небольшим числом факторов.
Нагрузки остальных факторов при этом близки к нулю. Может
оказаться, что первая факторизация будет неблагоприятной, т. е.
трудно поддающейся физической или геологической интерпрета-
ции. Тогда следует начать вращать факторы, т. е. подбирать но-
вые матрицы F, причем это следует делать до тех пор, пока не по-
лучим результаты, легко поддающиеся либо физическому, либо
геологическому истолкованию.
Следовательно, в факторном анализе переход к новым случай-
ным величинам выполняют, ориентируясь на поведение взаимных
корреляций (или ковариаций) Х{.
В аналитических методах обработки и интерпретации к анало-
гичным задачам приводит анализ положительно определенных сим-
метричных матриц, которой, в частности, является и корреляцион-
ная (ковариационная) матрица. При этом для изучения простых
структур факторных нагрузок (структура факторных нагрузок
считается простой, когда большинство из не намного отличаются
от нуля и лишь некоторые из них имеют относительные большие
значения) минимизируется так называемая целевая функ-
ция, зависящая от ац, и для ортогонального вращения исполь-
зуется выражение
т т г N	/ W \ / N \ "1
°-’.?, £<£“»)]
где параметр у меняется от 0 до 1.
При у = 1 метод вращения носит название варимакс и яв-
ляется наиболее распространенным. В этом случае минимизация G
эквивалентна максимизации
, т N
4 Е Е (4-4)2,
N /=1 i=i
где
1 N
а/ = — Е 4/1 / = 1, • • • , т,
N f=i
т. е. варимакс максимизирует разброс квадратов нагрузок для каж-
дого фактора, что приводит к увеличению больших и уменьшению
малых значений факторных нагрузок.
При у = 0 вращение, получаемое в результате минимизации
функции G, называется квартимакс. Минимизация G в этом
случае эквивалентна максимизации
, т N
у “i (-=1
88
где
, т N
?-J-EE4,.
Wm /=1 i=i
т. е. квартимакс максимизирует дисперсию квадратов факторных
нагрузок, иначе, выбираются факторные нагрузки с достаточно
большим диапазоном их значений.
Использование факторного анализа при обработке геофизиче-
ских данных связывается с разложением наблюденного поля на
аномальные составляющие, обусловленные основными источни-
ками, создающими суммарное поле. Эти аномальные составляющие
и являются искомыми факторами. Обработка данных комплекса
геофизических (геохимических) признаков с помощью факторного
анализа позволяет осуществлять классификацию полей признаков
по комплексным параметрам, каждый из которых выступает в ка-
честве фактора.
Существенную роль в факторном анализе играет физическое
или геологическое истолкование выделяемых факторов. К сожа-
лению, далеко не всегда удается дать интерпретацию факторам.
Поэтому факторный анализ чаще всего применяется в модификации
метода главных компонент (или компонентного анализа), в кото-
ром первые главные компоненты имеют более прозрачный физи-
ческий смысл.
§ 16.	МЕТОД ГЛАВНЫХ КОМПОНЕНТ
К новым случайным величинам для той же модели (3.19) можно
перейти, ориентируясь преимущественно на поведение дисперсий.
Главная компонента определяется как линейная комбинация ис-
ходных случайных величин
Y/ = ^a(iXl- / = 1..........N,	(3.22}
при этом первая главная компонента
Ух= £ааХ, = а1Х	(3.23}
i=i
обладает максимальной дисперсией среди всех возможных линей-
ных комбинаций вида (3.23).
Дисперсии линейных комбинаций Yt располагаются в убы-
вающем порядке, т. е. стг(У1) > ст2 (Yг) > . . ; > ст2 (УN), при.
следующей нормировке коэффициентов
N
причем
л -*,-»
У а2ц = а 1а,	(3.24}
где I — единичная матрица.
89-
Пусть В — ковариационная матрица X (3.17), Л1Х — матема-
тическое ожидание X, тогда дисперсия Yt‘.
DY! = М (Уу—MY,)« = Л4 (У у—МУ у)' (У у—МУ,) =
. =m(Jx— а'/Мх) (aiX—ajMx) = 0^.	(3.25)
С учетом нормировки коэффициентов atj (3.24) для (3.25) полу-
чаем отношение двух квадратичных форм в виде
Ху = ауВ ау/ау lay.	(3.26)
Для получения—максимума (3.26), т. е. максимума дисперсии У у,
необходимо продифференцировать (3.26) по а) и производную при-
равнять к нулю, т. е.
—(a/Bay—Xyajlay) =0.
да
После дифференцирования получаем Вау—Ху lay = 0, или
(В—Ху1)ау = 0.	(3.27)
Из (3.27) следует, что Ху является собственным значением ко-
вариационной матрицы исходных данных В, а вектор а{ (а{1, . .г. ,
°In) — собственным вектором этой же матрицы для Ху.
При соответствующей нормировке исходных величин X на их
среднеквадратические значения вместо ковариационной матрицы
В в (3.27) можно записать корреляционную матрицу R, т. е.
(R—XyI)ay = O.	(3.28)
Дисперсия главной компоненты
DY у = ayRay = ayXyay = XyayOy = Х^.	(3.29)
Практически нахождение собственных значений и собственных
векторов корреляционной (или ковариационной) матрицы сводится
к следующему:
1)	вычислению коэффициентов корреляции для случайных
величин Х{ и Ху и составлению из них корреляционной матрицы
1	...	I"1N	~
R __	Г21	1	• • •	r2N
-	rNl	r№	• • •	1	-
2)	составлению матрицы R—XI и приравниванию ее определи-
теля |R—XI | к нулю, т. е.
1—X	г12	... rlN
id__it I— Г2)	1	• • • Ггы
rN1	rN2
90
1 - X
3)	раскрытию определителя | R—II | и нахождению его корней,
или, иначе, собственных значений Хх, . . . , kN матрицы R. Напри-
мер, для %i и Х2 имеем:
1 — X Г12
1 — X
= 0;
(1—Х)^—Г?2 = 0;	1—X = zb Г12^	Х1=1-]-Г12» Хг=1—Г12-
Очевидно, что для матрицы R размерности N получим N собст-
венных ее значений;
4) нахождению собственных векторов af матрицы R путем ре-
шения системы линейных уравнений вида
- 1—Ху Г21	г12 1 —Ху .	rlN r2N		 01/ ' Й2/	=	- 0 - 0	; (3.30)
rNl	Cv2	.	1 —Ху _		- aNj -		. 6 J	
(1—\)а1/-|-г:12а2/+ • • -	=
Г21Я1/ + (1—Ху)а2/ + • • •	=
rN	lall + r + • • • +(1—X/)aJvy = 0,
N
при этом
 В результате решения системы (3.30) для каждого Ху получаем
набор (систему) собственных векторов: аг = (а1Х, а1В, .... a1N);
—>
а2 = («21> «22> • • • , a2jv)> Un ~ (flWl> aN2< ' • • > 0Nn)-
Система собственных векторов является ортогональной, а из
ортогональности следует некоррелированность векторов, отсюда
справедливость выражения (3.29). Таким образом, корреляцион-
ная матрица оказывается расщепленной на N ортогональных ком-
понент.
Некоррелированные, нормированные с учетом (3.24) линейные
комбинации (3.22) Yf =	и называются главными
компонентами. Линейная комбинация (3.23) для собст-
венного вектора, соответствующего максимальному собственному
значению Х^, называется первой главной компо-
нентой. Соответственно для следующего по величине собствен-
ного значения X линейная комбинация (3.22) дает вторую главную
компоненту и т. д. Метод построения и изучения комбинаций вида
(3.22) получил название компонентного анализа или
метода главных компонент. Собственные значения
X, являются дисперсиями соответствующих им главных компонент
(3.22).
Геометрически нахождение главных компонент приводит к пе-
реходу к новой ортогональной системе координат; первая коорди-
91
натная ось находится таким образом, чтобы соответствующая ей
линейная комбинация случайных величин (3.22) обладала бы наи-
большей дисперсией, т. е. эта комбинация извлекала бы возможно
большую дисперсию из наблюденных данных. Далее находится
ортогональная этой линейной комбинации ось, которая делает то
же самое с оставшейся дисперсией и т. д. Иначе, в JV-мерном про-
странстве величин . . . , XN ось наибольшей протяженности
W-мерного эллипсоида рассеяния X определяется направляющими
косинусами, равными компонентам вектора аг (при
Проекция вектора наблюдений X на это направление ах имеет наи-
большую дисперсию по сравнению с проекциями на другие направ-
ления. Каждый собственный вектор а, определяет ось эллипсоида
рассеяния.
От новых координат, учитывая ортогональность преобразова-
ния, можно вернуться к старым:
N
х, = Z ацУ1,	(3.31)
/=1
где Yj — j-я главная компонента, а ац — вес /-й компоненты в t-й
случайной величине.
Соотношение (3.31) является основным в методе главных ком-
понент и отличается от (3.19) тем, что число факторов здесь т = N.
Оно не содержит остаточных составляющих, так как все N глав-
ных компонент исчерпывают всю дисперсию исходных данных.
В методе главных компонент нет необходимости делать какие-
либо предположения о величинах X, даже не обязательно считать
их случайными (это могут быть и аналитические функции), хотя
чаще всего их рассматривают как выборку из генеральной нормаль-
ной совокупности (о нормальном характере распределений Xt здесь
следует говорить лишь потому, что элементами корреляционной
матрицы служат вторые центральные моменты, которыми задается
многомерное распределение). Однако главные компоненты не инва-
риантны относительно изменения масштаба тех шкал, по которым
отсчитываются разные величины Xt.
Анализ методом главных компонент целесообразно использо-
вать тогда, когда все величины Xt измерены в одних и тех же еди-
ницах и для нахождения главных компонент берется ковариацион-
ная матрица. Заметим, что используемый обычно прием представ-
ления данных в нормализованной форме (X;—xi)l<3t не имеет стро-
гого обоснования при произвольном уравнивании величин, несу-
щих разную информацию, как это обычно допускается в методе
главных компонент.
Физическая интерпретация собственных значений и главных
компонент не всегда оказывается возможной и существенным об-
разом зависит от специфики решаемой задачи. Хотя факторный
анализ чаще всего использует главные компоненты, вычисление
собственных значений и собственных векторов при этом разли-
92
чается тем, что собственный вектор приводится к такому виду, при
котором его длина равняется величине" собственного значения.
Полученный вектор и называется фактором, а его вес пропорцио-
нален вкладу в общую дисперсию.
Как в факторном, так и в компонентном анализе важное зна-
чение имеет оценка числа основных факторов. Собственные значе-
ния характеризуют относительный вклад каждого собственного
вектора в суммарную дисперсию. Длины векторов, представляющих
факторы, равны квадратным корням из собственных значений,
поэтому факторы оценивают также соответствующие дисперсии,
точнее, среднеквадратические отклонения. Для оценки основных
факторов располагают собственные значения X/ матрицы R в по-
рядке их убывания, а затем отбрасывают те из них, которые мало
отличаются от нуля. Чаще всего оставляют несколько первых зна-
чений %/, которые в сумме составляют 70—90 % от общей диспер-
N
сии К/.
Количество оставшихся собственных значений и дает оценку
числа основных независимых между собой факторов. На практике
оказывается полезным сохранять столько факторов, сколько имеется
собственных чисел, больших или равных единице, т. е. вновь со-
храняются все те факторы, которые дают наибольший вклад в дис-
персию. Однако, если исходные величины Xi слабо коррелированы
или не коррелированы,. половина или более факторов может иметь
собственные значения, большие единицы. В результате получается
не только очень большое число факторов, но и вероятность того,
что ни один из них не допускает никакой физической интерпрета-
ции.
§ 17. ОБЛАСТИ ПРИМЕНЕНИЯ ФАКТОРНОГО
И КОМПОНЕНТНОГО АНАЛИЗОВ
Как факторный, так и компонентный анализы базируются на изу-
чении внутренней структуры ковариационной матрицы исходных
данных. Это изучение включает: 1) нахождение собственных зна-
чений и собственных векторов матрицы; 2) вычисление линейных
комбинаций исходных величин с собственными векторами вида
(3.22); 3) оценку числа основных, независимых векторов т\ 4) фи-
зическое или геологическое истолкование факторов и главных
компонент.
В настоящее время факторный и компонентный анализы наи-
большее применение получили при решении следующих задач.
Разделение поля на ортогональные составляющие
Пусть система случайных величин Xt, ... , Хы представляет дву-
мерный массив измеренных значений того или иного наблюденного
поля по N профилям в виде (3.16). По этим данным вычисляются
93
ковариации для различных пар профилей, т. е. btj = —— Ё хмх{1,
Я /г=1
i, / = 1, . . . , N, где п — число пикетов по профилю; N — число
профилей; Xki = xki—Xi; Xi =---xftl- — измеренное значе-
Л Л=1
ние поля на /г-м пикете i-ro профиля.
По полученным ковариациям составляется ковариационная
матрица
Ьц ^12
&21	^22
- bNi bNi
blN
biN
•
bxN -
для которой находятся максимальное собственное значение Amax
из уравнения |В—%maxI| = 0 и соответствующий этому значению
собственный вектор матрицы В из системы линейных уравнений
(В—%maxI) аг = 0, т. е,-
(Ьц—Атах) йц + Ьцйц + . • . -\-bxfjaifj =0;
^21^11 + (&22— Ащах) 012• • • +^2^1№=0
^Ма11 + ^№#12 + • • •	— Атах) = О-
Вектор определяется с учетом нормировки = 1. Физи-
ческий смысл этой нормировки состоит в том, чтобы преобразован-
ные данные не отличались по масштабу от исходных (т. е. чтобы
не происходило усиления исходных данных). Затем вычисляется
значение первой главной компоненты Yx = aJX, или
Хц *12
Yife = (0u, Он, • • • » а™)
х23.
Хц
- XN1 XNi
Xln
Хгп
Хцп-
Физический смысл величин: Уц (k — 1, . . . , п) — определяют
весовые коэффициенты для значений поля по каждому пикету
исходной съемки: ах< (i = 1, . . . , N) — определяют весовые ко-
эффициенты для значений поля каждого профиля. При этом оценка
составляющей наблюденного поля, характеризующаяся наиболь-
шей дисперсией (такой составляющей обычно является фоновая,
или региональная, составляющая), равна произведению вектора-
столбца Уц на вектор-строку ац с добавлением к каждому эле-
94
менту образующейся матрицы среднего значения поля по про-
филю xi, т. е.
• • » alN) 4“ xi —
Кцйц + Xi	Yпаи + х2 . . .
Y12ЙЦ + xi	Y12012 + х2	. . .
YllalN ~^xn
Y lifllN + XN
- У1п0ц + Х1	УщОи + Хг . . . Ущ01М-|-хм
Рис. 11. Результаты оценки региональной составляющей поля A# путем
выделения первой главной компоненты (по А. Н. Кленчину).
а — исходное поле Ag; бив — соответственно региональная (первая главная компо-
нента) и локальная составляющие; пунктир—контур месторождения
Поскольку х?й чаще всего является оценкой региональной со-
ставляющей, разность х°" = xlk—x^k оценивает поле локальных
аномалий. Эффективность описанной процедуры обработки с по-
мощью метода главных компонент иллюстрируется рис. 11.
Как было отмечено, к недостаткам компонентного анализа от-
носится неинвариантность его решения к изменению масштаба
исходных данных, именно поэтому при оценке региональной со-
ставляющей целесообразно использовать ковариационную мат-
рицу, а не корреляционную матрицу исходных данных. При рас-
чете корреляционной матрицы R можно получить искаженный
масштаб искомого поля.
Применение метода главных компонент для выделения регио-
нальной составляющей при обработке наблюденных геофизических
полей свидетельствует о ее надежной оценке этой составляющей
в случае существенного преобладания ее энергии (дисперсии) над
95
энергией (дисперсией) локальных аномалий. Как показали спе-
циальные исследования, форма локальных аномалий практически
не искажается. Существенное преобладание энергии региональ-
ной (фоновой) составляющей прежде всего сказывается на Лтах,
величина которого должна составлять не менее 70—90 % суммы
собственных значений £Х,-.
Таким образом, первая главная компонента при обработке гео-
физического поля получает четкое физическое истолкование как
региональная (или фоновая) его составляющая.
Аналогичную обработку можно было бы провести для второго
по величине собственного значения Х2 ковариационной матрицы
наблюденного поля, и новая полученная составляющая, являясь
ортогональной к региональной, давала бы поле локальных анома-
лий, обладающих наибольшей дисперсией по сравнению с остав-
шимися невыявленными локальными аномалиями. Однако физиче-
ское истолкование второй, третьей и т. д. главных компонент при
этом было бы затруднено тем обстоятельством, что при выделении
локальных аномалий существенное значение имеет не только их
дисперсия, но и форма.
В целом метод главных компонент — эффективный способ
оценки региональной составляющей при минимуме априорной ин-
формации. Для ее выделения достаточно лишь выполнения пред-
положения о существенном преобладании дисперсии этой состав-
ляющей над дисперсией локальных аномалий.
Интерполяция наблюденных полей
Одна из основных задач интерполяции, решаемых на базе компо-
нентного анализа,— сведение информации всех методов исследо-
ваний в данном районе в узлы регулярной (прямоугольной или
квадратной) сети.
Двумерная интерполяция по регулярной сети может быть про-
ведена путем разложения исходного поля f (xt, у,) на составляющие,
зависящие лишь от одной координаты Xk (xi) и (у<). Для ди-
скретных наблюдений по прямоугольной сети (n х JV, где п —
число точек по профилю, AZ—число профилей) задача формулируется
следующим образом: требуется найти такие функции Xk (х) и Yk (у),
k = 1......п, которые удовлетворяли бы минимуму выражения
N п	П2
Е Е р(*. Уд~Y>^k(Xi)yk(ni)\ =>min.
/=1 £=1 L	k	J
Эта задача сводится к решению системы уравнений
N
XtaisXi = ^xs, s=l,2, . . .,N,
по определению собственных значений и собственных векторов
симметричной матрицы А = (а^}.
96
Пусть f =	— среднее значение поля. Элементы мат-
рицы А вычисляют по формуле
ач=а,ч = — £ fjs/; fls = fts—f; fsi = fSl—f.
nN S=1
/= 1, 2, . . . , N, i = l, . . . , n.
Если в качестве ортонормированной системы выбрать векторы,
то коэффициентами искомого разложения будут векторы Хк (х<),
которые связаны с векторами Yk (у}) соотношением
к	К
Таким образом, заданная функция f (xi, y.j) в каждой точке ока-
жется представленной суммой
k
Если требуется получить аналитическое выражение функции,
интерполирующий заданную таблицу значений ,поля, тогда в полу-
ченном разложении f (xi, yj) каждый вектор следует рассматривать
как значения функции одного аргумента (X и У) в заданных точ-
ках. При наличии подходящих методов одномерной интерполяции
можно в аналитическом виде получить функции Xk (х), Yk (у) и
искомую функцию F (х, у) = Т +%Xk(x)Yk(y).
Следовательно, описанный прием позволяет свести задачу ин-
терполяции функции двух переменных к интерполяции функций,
зависящих от одного аргумента.
Решение задачи двумерной интерполяции по нерегулярной сети
М. Н. Смирновой сведено к решению задачи, описанной выше.
При этом для сети с произвольным расположением точек наблюде-
ний строится вспомогательная прямоугольная сеть, шаг по осям
которой выбирается так, чтобы в каждый Z-й прямоугольник по-
пало хотя бы одно наблюденное значение поля. К центру каждого
прямоугольника относят среднее значение заданной функции, вы-
численное по значениям, попаЬшим в i-й прямоугольник. На ос-
новании решения для интерполяции в случае регулярной сети
строится поверхность, наилучшим образом интерполирующая ука-
занные средние значения заданного поля. Обозначим ее Fc (х, у),
т. е.
Fc{x, y) = FcY£XCk(x)YCk(y).
В разложении обычно ограничиваются одним, двумя слагае-
мыми, соответствующими наибольшим собственным числам. Допу-
стим, в соответствии с требуемой точностью надо оставить k слагае-
4 А. А. Никитин	97
мых. Введем неопределенные постоянные коэффициенты Ск, С2..
Ck и искомую функцию запишем в виде
F(x, y) = Fc + LClXCl(x)YCl(y).
Коэффициенты Ci определим из условия минимума выражения
N г	_ ft	I2
Л = Z f (xt, yi)—Fc— £ CiXC[ (xt) YCl (yi) ,
i=l L	/=1
где f (xi, yi) — заданное значение поля в i-й точке.
Дифференцируя А по Сг, получим систему линейных уравне-
ний относительно Сг:
Z [f(xt, yi)-EC/XCz(xi)yCz(yI)]xCr(x()VzCe(^)=O,
r= 1, . . . , k
или
k
g Ci %XCl (Xi) xce (Xi) YCl (yi) YC[(yi) = Zf (xtyi) XCr (xt) YCr (y{);
f(xt, yi)=f(x{, yi)—Fc.
Если величина k мала, можно повысить точность интерполяции,
рассматривая коэффициенты Ct как функции координат х и у,
например Ci — сцх + tyy +d[.
Постоянные а/, bi, di вновь определяем из условия минимума
Ах = Е U (хь yi)—Z( ЯМ + btyt +di)Xi (xz) Yz (xz)]2.
Дифференцируя Дх no ar, br, dr,\ получим систему линейных
уравнений относительно этих коэффициентов.
В качестве примера рассмотрим табл. 18 значений некоторого
поля.
Таблица 18
X	У					
	1	2	3	4	Б	6
1	4	8	14	22*	32	44
2	15	20	27*	36	47*	60
3	40	46	54	64*	76	90
4	85*	92	101*	112	125	140*
5	156	164	174	186	200	216
Значения, отмеченные «»»были отброшены, а остальные 23 зна-
чения образовали неравномерную сеть, по которой была построена
вспомогательная правильная сеть (табл. 19).
98
Таблица 19
X	У				
	1.5	2.5	3.5	4,5	5,5
1,5	13	14	25	34	45
2,5	30	40	45	56	75
3,5	59	64	83	104	97
4,5	137	143	157	156	180
Вначале по этим данным, расположенным по равномерной сети,
находится функция, интерполирующая вспомогательную табл. 19:
5
Fi (х, у) = FC{+^ Xk (х) Yk (у);
— 1
В полученном разложении достаточно оставить два слагаемых,
отвечающих наибольшим собственным значениям:
Х2(х) = 12,047х® +80,281х2 +225,07х—-312,79; 
Х2 (х) = 1,008х3+ 5,842х2—5,026х+ 25,97;
Л (у) = 0,003у + 0,435;
У2 (у) = —0,061z/3 + 0,19z/2 + 0,363z/—0,403;
FCi = 77,85.
Будем считать функцию (х, у) некоторым приближением
исходного поля. Введем коэффициенты Сх и С2:
F. (х, у) = FCl + СхХх (х) Ух (у) + СвХ8 (х) У2 (у);
определим их из условия минимума А
23
А= Z yi)—F2(Xi, у{)]2.
1=1
Решая полученную систему, находим
Cj = 0,782; С2 = 1,41.
Для уменьшения среднеквадратической ошибки интерполяции
возьмем в качестве коэффициентов линейные функции от коорди-
нат хну:
Fs(x, y) = 77,85 + (aix+biy + c1) X1(x)Y1(y) +
+ {flzX + tty)+c2) X2 (x) Y 2 (y).
Решая соответствующую систему линейных уравнений, найдем
значения коэффициентов:
ах = 0,0203; Ьх = 0,0582;	сх = 0,664;
а2 = 0,291; Ь2 — 0,0674; с2 = 2,204.
4*
99
Среднеквадратическая ошибка интерполяции в первом случае
oj = 37,6/23, во втором — Ог = 25/23.
Ошибку интерполяции можно уменьшить, если воспользоваться
методом итераций. При этом за начальное приближение неизвест-
ных значений функции в узлах таблицы принимается среднее, вы-
численное по всем известным значениям функции в остальных
узлах. На каждом шаге итерации описанным методом разложения
определяется интерполирующая функция. Значения этой функции
вычисляются только в тех узлах таблицы, в которых они были
заданы. В остальных точках используются исходные значения поля.
На каждом шаге итерации в дискретном представлении функции
оставлялись только два основных слагаемых. В результате послед-
него, шестого приближения о! = 0,63. Полученная интерполя-
ционная функция приведена в табл. 20.
Таблица 20
	У					
X	1	2	3	4	5	6
1	3,72	7,95	14,6	23	32,8	43,4
2	15	20,1	27,7	37,4	46,8	60,7
3	40,1	45,8	54,1	64,5	76,4	89,3
4'	85	91,6	100,6	111,6	124,2	138
5	155,8	163,9	174,1	186,3	200,2	215,6
Фильтрация наблюденных полей
Эта фильтрация с использованием метода главных компонентов бу
дет рассмотрена в § 35. Забегая вперед, отметим, что в задачах
линейной фильтрации можно использовать не ковариационную,
а корреляционную матрицу, поскольку при линейной фильтрации
весовые коэффициенты фильтра последовательно перемещаются
со смещением на один пикет по исходным значениям поля и для
принятой их нормировки масштаб профильтрованного, т. е. полу-
ченного в результате обработки, сигнала не изменяется по срав-
нению с масштабом исходных данных (входным сигналом).
Классификация геологических объектов
по комплексу геофизических признаков
Эта классификация на базе метода главных компонент будет рас-
смотрена в § 47. При решении задачи классификации производится
обработка данных комплекса признаков. Поскольку размерности
признаков обычно совершенно разные, необходима предваритель-
ная их нормировка на среднеквадратические значения и перевод
признаков в безразмерные величины. Следовательно, в дальнейшем
используется корреляционная матрица признаков, порядок ко-
торой определяется числом признаков.
100
Первая главная компонента при обработке данных комплекса
является комплексным параметром, которому можно дать физиче-
ское истолкование как составляющей в пространстве N признаков,
обладающей в нем наибольшей энергией (или дисперсией).
Планирование физического эксперимента
В настоящее время внимание исследователей обращено главным
образом на совершенствование методов обработки при заданном
способе проведения эксперимента. Выбор же условий самого экс-
перимента, т. е. как, где, когда проводить измерения, определяется
в значительной степени интуицией и опытом исследователей. Про-
блема извлечения максимума полезной информации об изучае-
мых геологических объектах и явлениях при минимальных затра-
тах времени и средств остается одной из важнейших задач разве-
дочной геофизики.
Следовательно, необходимо использовать не только способы
рациональной обработки данных, но и способы оптимального пла-
нирования физического эксперимента для получения максимума
информации при минимуме затрат времени и средств.
Эксперимент, который проводится при соблюдении требования
оптимизации, называется экстремальным (или оптимальным). Пла-
нировать можно экстремальные и регрессионные эксперименты.
Экстремальные эксперименты встречаются в тех
случаях, когда исследователя интересуют условия, при которых
изучаемый процесс (явление) удовлетворяет тому или иному кри-
терию оптимальности наблюдений. Такие эксперименты характерны
для задач по выбору числа и условий проведения опытов, необхо-
димых для достижения заданной точности или надежности, как,
например, это было сделано при оценку числа измерений плотно-
сти горных пород в § 5. Расчет необходимого числа независимых
наблюдений по методу максимума правдоподобия с целью обнару-
жения сигнала с заданной надежностью (см. § 38) является еще
одним примером указанного типа эксперимента.
Регрессионные эксперименты проводятся в тех
случаях, когда модель искомого объекта или явления можно вы-
разить с помощью регрессионной зависимости. Построение мате-
матической модели геологического объекта, в частности одного
его физического параметра, например пористости нефтегазонос-
ного пласта, по данным комплекса геофизических признаков яв-
ляется типичным примером регрессионного эксперимента. В этом
случае важность применения факторного анализа для оптимизации
проведения эксперимента несомненна, хотя планирование экспе-
римента сочетает в себе методы регрессионного анализа и решения
экстремальных задач на базе линейного,. нелинейного и динамиче-
сого программирования.
Планирование регрессионных экспериментов начинается с вы-
яснения факторов Хх, . . . , XN, определяющих особенности иско-
мого объекта или явления. Совокупность этих факторов X =
101
= (Xr......XN) образует пространство размерности N, называе-
мое факторным пространством или пространством
контролируемых (управляемых) величин. Факторы могут быть ко-
личественными и качественными. Так, мы можем контролировать
число и виды используемых геолого-геофизических методов иссле-
дований.
Каждый фактор в эксперименте может принимать одно или
несколько значений, называемых уровнями. Перед планированием
эксперимента оцениваются границы областей определения факто-
ров и выбираются интервалы их изменения.
Эксперимент, в котором реализуются все возможные сочетания
уровней факторов, называется полным факторным
экспериментом. Если число уровней каждого фактора
равно двум (например, наличие и отсутствие фактора), а число
факторов — N, имеем полный факторный эксперимент типа 2N = п,
где п — число опытов. Сам план эксперимента представляет собой
матрицу планирования, в которой строки соответствуют различным
опытам, а столбцы — различным факторам.
Задачей факторного (регрессионного) эксперимента является
установление связей между факторами и реакцией (откликом) мо-
дели искомого объекта, записываемой в общем виде как yi —
—► —►
= yi (X, a), j — 1, ..., L, в предположении, что при этой записи
У/ зависят также от совокупности ряда неизвестных параметров
а (а0, .... aL). Оптимальный эксперимент надо будет ставить
таким образом, чтобы при минимальном числе опытов (результа-
тов измерений), варьируя значениями Хг, ... , XN по специ-
ально сформулированному критерию, построить оптимальную ма-
тематическую модель объекта. В зависимости от степени информа-
тивности относительно вида функции У] (X, а) эксперименты ста-
вятся либо для определения и (или) для уточнения значений пара-
метров О(, либо для оценки вида функции у/. Обычно оптимизи-
руется лишь одна функция yjt наиболее важная для исследования,
поскольку одновременная оптимизация нескольких функций прак-
тически невозможна.
>
Располагая минимальными сведениями относительно Y (X, а),
можно принять регрессионную модель
ы
Y = a0 + aiXi + . . . +ад/Х# = ^а<Х(=а,Х,
j=o
где а = (а0, . . . , aN).
При проведении и наблюдений образуется прямоугольная мат-
рица размерности п (N + 1):
*10 *ц ... Хщ
Y *го Х21	. . . х^н
ХпО ХП1 ... %nN
102
Матрица Х'Х = М является информационной матрицей с об-
ратной матрицей С = (Х'Х)-1 = М-1, или матрицей ковариаций.
В зависимости от того, какие требования предъявляются к мо-
дели, приходят к той или иной формулировке требований к мат-
рице плана X, т. е. к выбору числа и последовательности заполне-
ния строк матрицы X.
Формализация этих требований связана с критериями оптималь-
ности, которые обычно формулируются в терминах свойств мат-
рицы М или матрицы М-1. Именно эти матрицы непосредственно
связаны с оценками модели и функционально зависят от матрицы X.
Смысл наиболее распространенного критерия D-оптимальности
состоит в минимизации дисперсии всех коэффициентов регрессии,
рассматриваемых как вектор а0, . . . , aN.
Этот критерий гарантирует, что в области планирования не
—* —►
окажется точек/в которых точность оценки поверхности Y (X, а)
будет слишком низкая. Дисперсия вектора коэффициентов, назы-
ваемая обобщенной, задается определителем ковариационной мат-
рицы С = М-1, и ее минимизация соответствует максимизации
определителя информационной матрицы М. Геометрически этот
критерий обеспечивает минимум объема эллипсоида рассеяния оце-
нок коэффициентов at. При другом важном критерии .Е-оптималь-
ности минимизируется максимальное собственное значение мат-
рицы М-1. Если эллипсоид рассеяния очень вытянут в одном на-
правлении, часть коэффициентов at попадает в неблагоприятные
условия и этот критерий позволяет уменьшить такую опасность.
После построения модели выясняется, в какой мере каждый фак-
тор влияет на критерий оптимальности. Количественной мерой
этого влияния является величина коэффициента регрессии, т. е.,
чем больше коэффициент at, тем сильнее влияние фактора Xt.
Вопросам планирования физического эксперимента в разведоч-
ной геофизике в настоящее время уделяется сравнительно мало
внимания, решена лишь задача оптимизации параметров линейного
фильтра в случае задания двух уровней как по нижней, так и по
верхней частотам среза частотной характеристики.
ГЛАВА IV
КОРРЕЛЯЦИОННЫЕ ХАРАКТЕРИСТИКИ
ГЕОФИЗИЧЕСКИХ ПОЛЕЙ
В рассмотренных выше методах обработки и анализа геофизических
данных в качестве модели измеренных значений использовались
понятия случайного события, случайной величины и системы слу-
чайных величин. В то же время в практике обработки широкое
распространение получили методы, связанные с представлением
результатов геофизических измерений в качестве случайных про-
цессов.
Применение модели случайного процесса для описания геофи-
зических данных, полученных по профилям, по трассам сейсмо-
граммы в вертикальной плоскости, скважинам и т. д., существенно
расширяет круг решаемых при обработке задач. Особую роль при
этом играют корреляционные функции случайных процессов,
имеющие и большое самостоятельное значение.
§ 18. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ
СЛУЧАЙНЫХ ПРОЦЕССОВ
Случайным процессом, или случайной функ-
цией F (/) называется непрерывная или дискретно заданная
функция, которая в результате эксперимента может принимать
тот или иной конкретный, но априори неизвестный вид. Эта функ-
ция может изменяться либо по времени t (например, при записи
упругих колебаний на сейсмограмме), либо по глубине h (каротаж-
ная диаграмма), либо по горизонтали х, т. е. вдоль профиля наблю-
дений при наземных, морских и воздушных съемках. Для большей
определенности в этом параграфе будем считать, что случайный
процесс изменяется по времени.
Конкретный вид случайного процесса, устанавливаемый в ре-
зультате эксперимента, называется его реализацией. Та-
ким образом, случайный процесс описывается семейством реализа-
ций, которое в каждый фиксированный момент времени ti превра-
щается в обычную случайную величину, называемую сечением
случайного процесса. Понятие случайного процесса
при этом является обобщением понятия системы случайных вели-
чин X (G), X (<2).....X(ti), . . . , X(tn).
На рис. 12 показаны случайные процессы двух типов. Если рас-
смотреть случайную величину X (ti) как сечение случайного про-
цесса в момент ti, то эта случайная величина имеет закон распре-
деления, который зависит от ti, и плотность распределения можно
обозначить f (хк, ti). Такая плотность распределения не является
104
исчерпывающей характеристикой случайного процесса X (t), по-
скольку описывает только закон распределения X (/) для данного,
хотя и произвольного значения времени tr, она не может служить
оценкой зависимости случайных величин X (t{) при разных t. Бо-
лее полной характеристикой является многомерный закон распре-
деления с плотностью f (xlt х2, . • • , хт, tlt t2, ... , tn). Однако
даже для двух случайных величин не всегда удается найти сов-
местную плотность и функцию распределения, поэтому для прак-
тических задач обработки ограничиваются рассмотрением и изу-
чением простых числовых характеристик случайного процесса:
математического ожидания, дисперсии и корреляционной функции.
Рис. 12. Случайные процессы:
а — некоррелированный, б — коррелированный
Под математическим ожиданием (средним зна-
чением) случайного процесса понимают неслучайную
функцию М [X (t) ], которая при .каждом фиксированном значе-
нии времени tt равна математическому ожиданию соответствую-
щего сечения случайного процесса тх (t) ~ М [X (01-
Под дисперсией случайного процесса по-
нимают неслучайную функцию Dx (0> значение которой для фик-
сированного 0 равно дисперсии соответствующего сечения про-
цесса Dx (0 = D [X (0 ].
Из рис. 12 видно, что для различных пр своей внутренней струк-
туре случайных процессов их математические ожидания и диспер-
сии (разброс вокруг математического ожидания) практически оди-
наковы и, следовательно, для описания основных особенностей
случайного процесса этих двух характеристик явно недостаточно.
Для случайного процесса, представленного на рис. 12, а, харак-
терно незакономерное, скачкообразное для различных значений tt
изменение, быстро затухающее по мере увеличения расстояния
между ti. Наоборот, для случайного процесса Х2 (f) (рис. 12, б)
имеет место плавное закономерное изменение исходных данных
между значениями ti. Хотя внутренняя структура обоих процессов
различна, это различие не отмечается ни по математическому ожи-
Д 105
данию, ни по дисперсии, для его описания требуется введение но-
вой характеристики, называемой корреляционной или автокорре-
ляционной функцией. Эта функция оценивает степень зависимости
между различными сечениями случайного процесса по величине
корреляционного момента, являющегося функцией двух аргумен-
тов и i2 и уменьшающегося с увеличением расстояния между
ними.
Таким образом, автокорреляционной (корреля-
ционной) функцией называют неслучайную функцию Rx (tit})
двух аргументов ti и tj, которая для каждых двух значений tt и tf
равна корреляционному моменту соответствующих сечений слу-
чайного процесса: Rx (t{, tt) = М [X (tt) X (tj) ], где X(t{) и
X (tj) — центрированные случайные величины, т. е. X (t{) =
= X (ti) — MX (ti)-, X(tj) = X (tj) — MX (tj).
Для случайных процессов Xr (t) и X2 (t) (см. рис. 12) при близ-
ких их математических ожиданиях и дисперсиях получаются со-
вершенно различные автокорреляционные функции: для Хх (t)
эта функция быстро убывает с увеличением расстояния между tt
и tj, а для Х2 (t) — медленно убывает.
Основные свойства автокорреляционной функции (АКФ) сле-
дующие: 1) (ti, tj) = Rx (tj, t^, т. e. АКФ симметрична отно-
сительно своих аргументов, поскольку корреляционный момент
двух случайных величин X (tt) и X (tj) не зависит от последова-
тельности, в которой эти величины рассматриваются; 2) при = tj
Rx (й, fy) =	(О, т- е- АКФ при tt = tj обращается в диспер-
сию случайного процесса и необходимость в дисперсии как само-
стоятельной характеристики процесса отпадает, для его описания
достаточно ограничиться математическим ожиданием и АКФ;
3) при сложении неслучайной функции ср (t) и случайного процесса
АКФ процесса не меняется; 4) при умножении случайного процесса
на неслучайную функцию ср (t) АКФ процесса умножается на про-
изведение <p (t{) <p (tj), В частности, когда <р (t) = С — постоянная
величина, АКФ умножается на С2.
Практические приложения теории случайных процессов с целью
обработки экспериментальных данных связаны с понятиями ста-
ционарности и эргодичности случайного процесса.
Стационарным случайным процессом на-
зывается такой случайный процесс, для которого все числовые ха-
рактеристики не изменяются при сдвиге аргумента t. Это означает,
что MX (t) = const, DX (t) = const,
Rx(ti,1tj) = Rx(ti, ti + ty, tj = ti+x.	(4.1)
Иначе говоря, для стационарного случайного процесса матема-
тическое ожидание и дисперсия не зависят от расположения интер-
вала (t{, tj) по оси t, для которого они определяются, а автокорре-
ляционная функция зависит только от расстояния между t{ и tj
и является, таким образом, функцией лишь одного аргумента т.
Поскольку АКФ, с одной стороны, определяется через матема-
106
тическое ожидание, а с другой — при /t- = tj — t совпадает с дис-
персией процесса, условие (4.1) является основным для выполне-
ния стационарности. Примером стационарного процесса может
служить сейсмическая запись с автоматической регулировкой ее
амплитуд на любом интервале длительностью 0,7 с (иногда до 1 с).
За счет увеличения низкочастотных составляющих от начала
записи к ее концу сейсмическая запись для больших интервалов
времени (> 1,5 с) уже не удовлетворяет условию стационарности
главным образом из-за увеличения видимого периода АКФ (рис. 13).
7}	7z
Рис. 13. Реализации нестационарных случайных процессов.
Нестационарный: а — по математическому ожиданию, б — по дисперсии, в — по АКФ
Случайный процесс обладает свойством эргодичности,
если средние значения его числовых характеристик, определенные
на достаточно большом временном интервале, равны средним зна-
чениям тех же характеристик по множеству реализаций, т. е. когда
усреднение по множеству реализаций эквивалентно усреднению
по времени для любой достаточно «длительной» реализации. В этом
случае одна единственная реализация дает представление о свойст-
вах случайного процесса в целом, являясь как бы его «полномоч-
ным представителем».
Свойство эргодичности для стационарного случайного процесса
обычно выполняется при стремлении к нулю его автокорреляцион-
ной функции при т -> со.
На практике свойство эргодичности служит основанием доста-
точности использования лишь одной реализации для определения
числовых характеристик случайного процесса.
107
На рис. 13 приведены примеры эргодических процессов, для
которых стационарность соблюдается отдельно по интервалам Тг
и Т2, а на общем интервале Т измерения являются нестационар-
ными соответственно по математическому ожиданию, дисперсии
и АКФ-
Для стационарного эргодического процесса, описываемого реа-
лизацией наблюденного геофизического поля F по профилю (по
трассе) с текущими значениями /2, . . . , fn, соответствующие
оценки математического ожидания, дисперсии и автокорреляцион-
ной функции следующие:
f = —ЕА, —Е(Л-Г)2;	(4.2>
п i=l	п 1=1
п—
Жт)=—S (Л-7)(Л+г-7)-	(4.3)
П —|TJ i=l
где т — разность аргументов, т = ti—tf, принимающая последо-
вательно значения 0; ± А; ± 2А; . . . , выраженные в дискретных
величинах расстояний А между значениями поля f{ и fi+x.
Для описания нестационарного эргодического процесса может
быть использована структурная ф у н к ц и я:
С(т)=тЛтг Д	(4-4>
Взаимно корреляционная функция (ВКФ) является оценкой
корреляционной связи двух случайных стационарных эргодиче-
ских процессов Fi и F2:
1	п~'х'
в(т)=Т^7Г £	<4-5>
Ввиду ограниченности по времени реализаций эксперименталь-
ных данных все приведенные выше выражения являются оценками
соответствующих характеристик случайных процессов. При этом
существенную роль играет свойство эргодичности, благодаря ко-
торому все характеристики случайного процесса вычисляются лишь
по одной реализации. Для получения оценок математического ожи-
дания и автокорреляционной функции случайного процесса необ-
ходимо было бы наблюдать один и тот же профиль не менее несколь-
ких десятков раз, что, конечно, практически невозможно. В то же
время рассмотрение одной лишь реализации случайного процесса
возвращает нас к математической модели экспериментальных дан-
ных в качестве случайной величины; Однако для случайной вели-
чины не имеется числовых характеристик вида (4.3) — (4.5), т. е.
характеристик, зависящих от интервала т между наблюденными
значениями ft и ft+x и в этом состоит принципиальное отличие
модели случайного процесса от модели случайной величины.
108
§ 19. АВТОКОРРЕЛЯЦИОННАЯ ФУНКЦИЯ И ЕЕ ПРИМЕНЕНИЕ
Автокорреляционная функция, или функция автокорреляции, оп-
ределяется выражением (4.3). Без ограничения общности можно
положить среднее значение f — 0 (поскольку среднее значение по
профилю или по трассе всегда можно вычесть из наблюденных дан-
ных), тогда, обозначив т через т, имеем
п-\т\
R(rri) =--!— У	(4.6)
n —|m| 1ST
Рис. 14. Реализация стационарных случайных процессов и их АКФ:
а — некоррелированного, б —• коррелированного
*
где А — значение.поля р i-й точке профиля (трассы, скважины),
i = 1, . . . , и; п — число точек (пикетов) профиля; т — интервал,
принимающий последовательно значения 0; ± А; ± 2А; . . . ,
± Л4А (Л4	п), которые выражают расстояние (в пикетах) между
ft и fl+m. Ввиду свойства симметрии АКФ — четная функция, т. е.
Я (m) = R (— т), поэтому для её вычисления достаточно огра-
ничиться нахождением R (т) лишь при т > 0. Нетрудно видеть,
что при т = 0 АКФ равна дисперсии
. п
R(0) = —=
n 1
109
при т — 1 АКФ выражает корреляционную связь значений поля
для соседних пикетов
Я(1)=—“г(/1/2fafз“Ь • • • + fn-ifn);
п — 1
при т = 2 АКФ выражает корреляционную связь значений поля,
полученных через пикет,
К (2) —	- (Л/з+^Ч- • • • -\-fn-Jn)-
и т. д.
Наряду с выражением (4.6) используется нормированная АКФ,
определяемая как
Ян (т) = К (т)/Я (0) = R (m)ID.	(4.7)
Нормированная АКФ при различных значениях т совпадает
с коэффициентом корреляции для двух случайных величин, одна
из которых представляет значения наблюденного поля по профилю
(трассе), а другая — те же значения поля, но смещенные относи-
тельно предыдущих на т пикетов. Отсюда же следует, что ненор-
мированная АКФ оценивает ковариацию этих случайных величин.
Для приведенного на рис. 14, а случайного процесса корреля-
ционная связь между значениями поля отсутстует и АКФ близка
к нулю для всех т >0 (при т — 0; R	Это будет некорре-
лированный процесс. Для процесса, представленного на рис. 14, б,
корреляционная зависимость значений поля от расстояния т
уменьшается медленно — это коррелированный случайный про-
цесс.
Поскольку АКФ при каждом значении смещения т оценивает
ковариацию двух случайных величин, а нормированная АКФ —
коэффициент корреляции, по АКФ легко построить ковариацион-
ную матрицу, а по нормированной АКФ — корреляционную мат-
рицу в виде
-	1	Яи(1)	• . . RB(M) -
Ru(m-k}~	'	1	. ; ; ;	.
_ RK(M)	RK(M — 1)	...	1
(4.8)
Здесь k = 0, . . . , M.
В практике обработки геофизических данных нашли применение
следующие типы АКФ (рис. 15).
1.	Единичный импульс Кронекера (рис. 15, а):
f 1, tn — 1,
^н(/п) = | 0( т_£0>
110
a.
г
a
.	5(Ы)
Рис. 15. Основные типы АКФ и их спектры:
а — единичного импульса Кроиекера, б — треугольного типа, »—
марковского типа, « — гауссового типа, [д — затухающей по экс-
поненте косинусоиды
его ненормированная АКФ описывается единичным^импульсом,
называемым дельта-функцие и,]
(со,	/71 = 0,	°?
6(m) = <	J 6 (m)dm = 1.'
v ’ I 0,	m^=0;
(4.9)
Дельта-функция 6 (m) — математическая модель предельно ко-
роткого однополярного импульса единичной площади, которая
используется для характеристики белого (некоррелированного)
аппаратурного шума. Ее также часто применяют для описания
АКФ погрешностей измерений.
2.	АКФ треугольного типа (рис. 15, б)
Ян(/П =
1 —т/г0,
0,
m < г0;
т>г0
;Г(4.10)
описывает корреляционные свойства погрешностей, возникающих
при определении эффективных скоростей способом встречных го-
дографов в сейсморазведке, а также аппроксимационные свойства
контактной поверхности в гравиразведке.
3.	АКФ марковского типа (рис. 15, в)
Ян (т) = ехр (—а | т |)	(4.11)
с экспоненциальным затуханием корреляционных свойств измере-
ний по профилю. Корреляционная матрица для АКФ вида (4.11)
при ехр (— а) = г имеет вид
(4-12)
а соответствующая ей обратная матрица
	- 1	—г
	— Г	1+г
R-1= 	Ц_ 1 — г2	0	—г
0	0	. . .	0 ~
—г	0	. . .	0
1+г	—г	. . .	0
0	0	0	0	. . .	1 _
(4-13)
Поскольку только для АКФ марковского типа при наличии
корреляции можно выразить обратную корреляционную матрицу
аналитически, выражение (4.11) часто используется в теоретиче-
ских исследованиях для оценки влияния корреляции при анализе
тех или иных алгоритмов обработки геофизических данных.
4.	АКФ гауссового типа (рис. 15, г)
RH (ттг) = ехр (—тЧг*).	(4.14)
113
Применение АКФ этого типа оказывается эффективным при
описании корреляционных свойств аномалий гравитационного
поля, представленных моделью случайного процесса, причем при
г < Д это будет некоррелированный процесс, при г>Д — корре-
лированный процесс.
5.	АКФ затухающей по экспоненте косинусоиды (рис. 15, д)
R„(/n) = exp(—а | т |) cos fyn,	(4.15)
где а — коэффициент затухания; 0 — видимый период колебаний.
Выражение (4.15) используется для описания формы корреля-
ционной функции сейсмических колебаний, представленных мо-
делью случайного процесса, а также для описания АКФ погреш-
ностей в гравиразведке.
По АКФ определяется интервал, или радиус, кор-
реляции исходных данных — гД, т. е. такое расстояние, на-
чиная с которого значения поля f( и fi+r можно считать некорре-
лированными, а при нормальном законе распределения ft и неза-
висимыми друг от друга. Для некоррелированного случайного
процесса ковариационная матрица В и корреляционная матрица R
становятся диагональными, впервой из них по диагонали располо-
жены значения дисперсии, во второй — единицы, т. е. для некор-
релированного процесса корреляционная матрица является еди-
ничной.
Для определения интервала корреляции гД используют раз-
личные оценки. Наиболее распространено оценивание гД по за-
данному значению в = 0,14-0,3 R (0). При этом будет таким
значением аргумента АКФ, начиная с которого выполняется со-
отношение | RB (m)|«<e для всех т>г.
Часто г определяется как
00	00
г2 = [ | Rh (т) | dm или rs=? f Rl(m)dm.	(4-16)
о	о •	.
Все эти оценки г дают разные по величине интервалы корреля-
ции, поэтому при обработке данных надо использовать лишь одно
из определений. В частности, для оценки ширины гравитационных
и магнитных аномалий более подходящей является величина г2,
для сейсмических сигналов — г3.
При нормальном распределении ft для быстрой приближенной
оценки можно воспользоваться соотношением r4 == l/2v, где v —
число пересечений среднего значения поля по профилю, приходя-
щееся на один пикет (на один дискрет Д).
Величиной интервала корреляции обычно ограничивают дли-
тельность АКФ при расчете весовых коэффициентов фильтра (см.
гл. VI и VII) и ширину аномалии по профилю (или длительность
сигнала по трассе).
Форма АКФ и интервал корреляции нашли применение при
решении следующих задач обработки геофизических данных:
1)	оценка корреляционных свойств сигналов (аномалий) и по-
мех. Поскольку наблюденные значения геофизического поля в об-
113
щем случае равны сумме сигнала и помех, ft = s{ + п{, при отсутст-
вии корреляции между сигналом и помехами (чаще всего при об-
работке данных исходят из предположения о том, что появление
сигнала не зависит от появления помех и наоборот) АКФ поля
можно представить в виде четырех АКФ:
R (т)=------------------------j-(ZsA+m + En>ni+m +
+ Zs/ni+m + Snisi+m)-	(4.17)
Последние две суммы этого выражения ввиду указанного пред-
положения равны нулю. Отсюда следует, что при слабом влиянии
помех на сигнал (малой их интенсивности по сравнению с интен-
сивностью сигнала) АКФ является оценкой корреляционных
свойств сигнала и, наоборот, на интервале отсутствия сигнала
АКФ наблюденного поля представляет собой оценку свойств по-
мех.
Опыт показывает, что сигналы, соизмеримые по интенсивности
с уровнем некоррелированных помех, не влияют на оценку свойств
помех при интервале оценивания п, в 4—5 раз превышающем дли-
тельность сигнала (ширину аномалии);
2)	расчеты весовой функции и частотной характеристики оп-
тимальных фильтров (см. § 34—36) базируются на знании АКФ
сигнала и помех. Отметим также, что совпадение формы неслу-
чайного сигнала с формой АКФ помех, как показано А. К. Янов-
ским, свидетельствует о невозможности разделения сигнала и по-
мех, поскольку при этом спектры сигнала и помех совпадают. На-
оборот, различие формы сигнала и АКФ помех говорит о необхо-
димости дополнительной обработки с целью отфильтровывания
частотных составляющих помех;
3)	трансформация наблюденного поля. Расчет АКФ равносилен
применению способа трансформации с частотной характеристикой
Н (— со), обладающего тем преимуществом, что характер преобра-
зования определяется особенностями самого исходного поля и ре-
зультаты такого преобразования можно непосредственно интерпре-
тировать. Кроме того, в ряде случаев пересчет поля в нижнее по-
лупространство в магнито- и гравиразведке целесообразно прово-
дить не по наблюденному полю, а непосредственно по его АКФ,
поскольку АКФ мало чувствительна к ошибкам измерения. Бли-
жайшая особая точка при этом, как показано В. Н. Страховым,
залегает в 2 раза глубже, чем в случае исходной аномалии. Малая
чувствительность АКФ к ошибкам измерения определяется интег-
ральным эффектом нахождения каждого значения АКФ (при вы-
числении каждого значения АКФ участвуют наблюденные значе-
ния по всему профилю);
4)	разделение наблюденного поля на однородные по статисти-
ческим характеристикам участки. Такое разделение проводится
с целью геологического картирования по геофизическим полям.
В качестве статистических характеристик чаще всего используются
114
среднее значение, дисперсия и интервал корреляции, вычисляемые
в окне заданного размера. Так, например, И. Г. Берлянд, исполь-
зуя расчет указанных характеристик по данным региональной гра-
витационной съемки в Предуралье, провела картирование основных
типов пород по изменению интервала корреляции, дисперсии и
среднего значения, которые рассчитывались по отрезкам профиля
длиной 10 км со смещением этих отрезков на 1 км;
5)	оценка глубины залегания источников аномалий в магнито-
и гравиразведке по интервалам корреляции. Как показано С. А. Сер-
керовым, для положительных аномалий силы тяжести глубина
залегания
й<г/л, г=----------f | RAtri) | dm.	(4-18)
л о
Для знакопеременных аномалий выполняется соотношение
1,3 h < г < 2 л/г.
Шаг съемки по профилю с интервалом корреляции связан со-
отношением Дх 1,36 h = 0,43 г.
6)	проверка стационарности наблюденного поля (по С. А. Кап-
лану и А. К. Яновскому) может быть осуществлена по отношению
двух оценок дисперсии АКФ:
mmax
2	У #н (т)
U _ q‘ = (n + 2"h + 1) т,__________.	(4.19)
(mmax — ttli) "И
2
0
Если Я<1, исходная реализация наблюденного поля стацио-
нарна, если Н>1—нестационарна;
7)	оценка разрешающей способности сейсмической записи. От-
ношение
wii	mmax
P = £R£(m)/ £ Ян(т),	(4.20)
где тг = 14-2 Т; /Птах=—5-j- 10 Т (Т — видимый период сигнала),
предложенное А. А. Зеновым, позволяет количественно оценить
разрешающую способность. Очевидно, что если Р « 1, то запись
имеет хорошее разрешение (вся энергия сигналов сосредоточена
на малом интервале времени), если Р<0,5, то запись плохо раз-
решена, т. е. можно считать, что многофазное исходное колебание
связано с положением нескольких волн.
Часто для оценки АКФ приходится использовать короткие от-
резки профилей, поэтому вопросы точности определения АКФ при-
обретают большое практическое значение.
Если закон распределения измеренных значений fi нормаль-
ный и для каждого смещения /пД величина R„ (m) представляет
собой эмпирический коэффициент корреляции, погрешность оценки
АКФ можно найти как
оЛн= ±[1 —7?$(m)]/Vn—/п.	(4.21)
115
Надежным значением 7?н (w) для 95 %-ной доверительной ве-
роятности является такая величина, для которой 17?н (/п) |> 1,96стЛн.
В общем случае дисперсия оценки АКФ определяется выраже-
нием
м
f^K = 2YlR2B(m)/n.	(4.22)
Оценка (4.21), в частности, показывает, что надежным значе-
нием АКФ при интервале оценивания п > 50 являются величины
Rn (т) > 0,25.
Соотношение (4.22) может быть положено в основу расчета не-
обходимой длительности реализации (длины профиля) для надеж-
ного оценивания АКФ. Из (4.22) следует, что Одн = 4гКоР/п, от-
сюда п>4гкор/стлн.
Допустим, что АКФ выражается функцией 7?н (т) =
= ехр (— а| т |) х cos 0т. Для п = 2л/г/0, k = 1, 2, . . . , имеем
(2 + р,)2 [1 — exp (— 4nfe/|i)]
' кор —-----------------------------------------
р. = 0/а.
4а (1 + Ц2)
Следовательно,
2	а2 (2 + р,2) [ 1 — ехр (— 4nfe/ц)]
4^(ц+1/р)	(4,23)
По (4.23) с учетом того, что п = 4гКорА*2. можно рассчитать
необходимую длительность реализации сейсмической записи с ап-
риорным значением р.
В заключение заметим, что, хотя АКФ была введена как харак-
теристика случайного процесса, формально построение АКФ ис-
пользуется и для детерминированных, аналитически заданных сиг-
налов (аномалий), однако при этом в формуле (4.6) уже не следует
проводить усреднение по числу участвующих в определении АКФ
точек.
- Таким образом, АКФ детерминированного сигнала st
R (т) = Hsfsi+/n
Для непрерывных сигналов и реализаций случайных процес-
сов суммирование во всех приведенных выше выражениях заме-
няется интегрированием.
§ 20. ВЗАИМНО КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
И ЕЕ ПРИМЕНЕНИЕ
Взаимно корреляционная функция (ВКФ) представляет собой
оценку корреляционных свойств двух случайных процессов. Для
эргодических случайных процессов ВКФ вычисляется по данным
отдельных реализаций fu и В качестве таких реализаций мо-
116
гут быть взяты данные по двум профилям, скважинам, трассам
и т. д. При этом вычисление ВКФ производится по формуле
п—\т 1
В(т)=-----(4.24)
п — | т | i=i
где т = 0, ± А; ± 2Д; . . . ; ± МА; п — число точек для каждой
реализации.
Допустим, что по реализации найдены их. средние значения:
fi = %/« и f2 = Sf2t/n. Тогда без ограничения общности можно
считать, что /х = /2 — О и выражение (4.24) запишется в виде
п—\т\
В(т)=-----!— £ fiihi+m-	(4.25)
п — | т | ;=1
При пг = О
В (0)= —£fl i/г Z = fllf21+ /12/22 + • • • + /ln/2n,
п
т. е. при вычислении В (0) перемножаются значения поля для одно-
именных пикетов профилей (дискретов времени по трассе и т. д.).
При т = ± А:
В(1) =----~~ Z/i cfz i+i = /11/22 + /12/28+ • • • +/ln-1/2,1!
п — 1
B(—1) = ----^—E/lz/2Z-l =/12/21 +/13/22+ • • • +/ln/2n-l,
т. е. при вычислении В (± А) перемножатюся значения поля, сме-
щенные на один пикет (дискрет времени). При этом будем считать,
что смещение А соответствует смещению последующего профиля
(например, второго) на один пикет влево относительно предыду-
щего (например, первого). Наоборот, смещение — А соответствует
смещению предыдущего профиля на один пикет вправо относительно
последующего при расположении профилей.
Положительное смещение последующего профиля относительно
предыдущего для коррелированного от профиля к профилю полез-
ного сигнала дает положительной экстремум ВКФ при А, отрица-
тельное же смещение профилей для аналогичного сигнала дает по-
ложительный экстремум ВКФ при — А.
В том случае, когда обработке подвергаются не исходные дан-
ные, а их ранги (ранг определяется как порядковый номер элемента
в возрастающем ряду значений), по аналогии с введением коэффи-
циента ранговой корреляции вводится ранговая взаимно
корреляционная функция
n£”{[J?z-(n-m+l)/2][<>z-(n-m+l)/2]}
BRQ (m) =	-------—-------------:-------------.	(4.26)
£ [Z_(n_m+l)/2p
i=l
1'7
где Ri — ранг i-ro значения поля на первом профиле; Qi — ранг
г-го значения поля на втором профиле.
В практике обработки геофизических данных взаимно корреля-
ционные функции используются так же широко, как АКФ. Ука-
жем на следующие аспекты их применения.
1.	Оценка корреляционных свойств сигналов. При условии
некоррелированного характера помех между профилями и при этом
незначительного изменения формы полезного сигнала ВКФ пред-
ставляет собой оценку корреляционных свойств сигнала. Поскольку
/l<==Sl<+^l<K/:2i = S2<4_,I2i>TO
В (т) = -------- 2 (S1 i + «1 i) (Sa i+m + n2 i+m) ~
n — I m I
=----"--Г (Ssl <S2 i-f-m + S5! i°2 i+m + is2f+m + i^al+m) =
n — | m |
=  7ТГ £S1 iSa i+m «   7—- 81 iSl i+m-
n — I tn I	n — I m I
Остальные корреляционные суммы в этом выражении равны
нулю ввиду независимости появления сигнала и помехи и некорре-
лированности помехи от профиля к профилю. Совпадение форм
полезного сигнала По профилям приводит к его автокорреляции.
Таким образом, ВКФ наряду с АКФ может быть использована для
расчета весовых функций и частотных характеристик оптимальных
фильтров (см. § 34 и 35).
2.	Оценка простирания сигналов. Для выделения полезных
сигналов особый интерес представляют экстремальные значения
ВКФ. Положительные экстремумы ВКФ указывают на наличие
корреляции сигнала между профилями. Такие экстремумы ВКФ
соответствуют значениям аргумента, т. е. величинам смещения в пи-
кетах от профиля к профилю (от трассы к трассе) тех сигналов,
для которых наблюдается наиболее сильная корреляционная связь
поля. Отсюда следует вывод о практическом использовании поло-
жительных экстремумов ВКФ Для оценки простирания сигналов
по площади.
На рис. 16 приведены наблюденные значения некоторого фи-
зического поля и соответствующие этим значениям ВКФ. На
рис. 16, а смещение аномалий, равное 2Ах, четко фиксируется
положительным экстремумом ВКФ при т = 2Д. В случае анома-
лий различного простйрания ВКФ имеют два экстремума или бо-
лее (рис. 16, б). Наконец, резкое смещение экстремумов ВКФ для
какой-либо пары профилей относительно экстремумов соседних
ВКФ позволяет использовать построение ВКФ для выделения на-
рушений в распределении поля, как это показано на рис. 16, в.
Например, по такому смещению картируются разломы с простира-
нием, близким к простиранию профилей геофизической съемки.
Следует подчеркнуть, что форма ВКФ и величина экстремумов
зависят от характера распределения аномального поля по площади.
118
Рис. 16. Графики исходных значений поля и ВКФ в случае аномалий одного
простирания (а), различного простирания (б), при смещении аномалий (в).
>- оси аномалий; 2 в тектоническое нарушение
При наличии аномалии одного и того же простирания ВКФ имеют
один экстремум (см. рис. 16, а), причем его величина тем больше,
чем больше аномальных значений поля участвует при вычислении
ВКФ. В случае аномалии различного простирания ВКФ имеют,
как правило, несколько экстремумов, абсциссы которых указывают
на смещение аномалий от профиля к профилю. Чем больше ано-
малий одного и того же простирания наблюдается на площади, тем
больше величина соответствующего экстремума ВКФ. В то же
время для интенсивных аномалий (практически не искаженных
помехами) различного простирания при небольших смещениях их
относительно друг друга ВКФ могут иметь лишь один экстремум
вместо двух.
При обработке сейсмических записей построение ВКФ между
трассами обеспечивает оценку суммарной (кинематической и ста-
тической) поправки, определяемую абсциссой максимального зна-
чения ВКФ. Зная закон распределения скоростей, а следовательно,
и величину кинематической поправки от трассы к трассе, опреде-
ляют статическую поправку для пункта взрыва как разницу между
абсциссой максимума ВКФ и величиной кинематической поправки.
Определение кинематической и статической поправок в сейсмо-
разведке позволяет перейти на автоматическую корреляцию отра-
женных волн, в основе которой лежит использование ВКФ. Однако
при этом существенное значение приобретают вопросы надежности
вычисления экстремумов ВКФ и точности определяемых по ним
величин смещений.
Надежность значений ВКФ может быть оценена исходя из того,
что для каждого смещения mA величина В (т) представляет собой
коэффициент корреляции. Поэтому погрешность оценки определе-
ния значений нормированной ВКФ Вн (tri) в предположении о
нормальном характере распределения значений поля находится
как
°вн (т) = [1—Вн (т)]/д/п—т, Ви (т) = 'В (m)/afiaf2,	(4.27)
Надежными значениями Вн (т) для 95 % -го уровня доверия яв-
ляются значения Вн (т)>1,96 оВн(т).
Дисперсия величины смещения тэ для экстремума ВКФ мо-
жет быть оценена по формуле Яновского
Отэ = 2 [1—Вн (^а)] гкор А/пАсо Вн (тэ),	(4.28)
где Гкор — интервал корреляции полезного сигнала, определяемый
00
как гкор— £ R.H(tri)dm-, т9 — абсцисса экстремума ВКФ;
Вн (тэ) — значение ВКФ в точке экстремума; со — соо Асо, соо —
видимая частота спектра сигнала, Асо — среднеквадратический
разброс частот по спектру; nA — интервал оценки ВКФ, т. е. об-
щее число дискретов при определении ВКФ.
120
По величине (4.28) определяется доверительный интервал Для
смещения тэА, в пределах которого выделяются оси синфазности
или аномалий.
При оценке о„э для потенциальных полей в формуле (4.28)
можно принять со0 = 2jiv0, причем для знакопеременной аномалии
v0 = 1/mA, а для знакопостоянной аномалии v0 — 1/2 mA, где
т — ширина аномалии.
3.	Оценка отношения сигнал/помеха. Указанная оценка может
быть получена по экспериментальным данным без привлечения
особых априорных сведений о сигнале и помехе. Если сигнал, за-
данный в виде случайного процесса вдоль профиля (трассы), пред-
' т
ставить в виде А (х) — 51a<s(x—xi) (s (х) — форма сигнала; а/ —
1
его амплитудные значения), то математическое ожидание величины
А (х) (согласно теореме Кэмбелла) равно МА (х) = nas (х) (п —
среднее число аномальных значений на единице длины профиля;
а — среднеквадратическая амплитуда сигнала). Отсюда в предпо-
ложении об'отсутствии корреляции помехи вдоль профиля, получим
значение автокорреляционной функции
R (0) = па2 + т — 0,
R(m) = na2R:(m), т=/=0.
Аналогичное выражение для взаимно корреляционной функции
данных двух профилей и /2 при отсутствии корреляции помехи
между профилями и неизменности формы сигнала от профиля к
профилю будет В (т) ~ na2Bs (m).
Приведенные выражения АКФ и ВКФ показывают, какие основ-
ные величины влияют на их оценку. Если учесть, что в результате
вычисления АКФ по профилю получаем оценку суммы АКФ сиг-
нала и АКФ помехи, то разность между значениями АКФ при
т = 0 и ВКФ для положительного экстремума (в частности, для
максимума) даст оценку дисперсии помехи RH (т) — В„ (ms) =
= 1—Вн (/«э) — о2. При расчете ВКФ принимается a1fi = af2 — а2,
В то же время, учитывая выражение (4.26) и некоррелированный
характер помех, можно считать, что Вн (тэ) — а2. Следовательно,
выражение
____В (nts) _ Дн (тэ) _ °*	29)
/?(0)-В(тэ) 1-ВнИэ)	’
обеспечивает оценку величины отношения сигнал/помеха.
Нетрудно показать, что оценка (4.29) справедлива не только
для модели сигнала в виде случайного процесса, но и для модели
детерминированных сигналов (аномалий).
121
§ 21. ДВУМЕРНЫЕ КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
Для описания корреляционных свойств двумерных геофизических
полей используют двумерную автокорреляционную функцию
(ДАКФ), которая при центрированных значениях, поля на каждом
профиле, т. е. при	. = fN — 0, определяется выражением
N — | р I га — \т\
R(p, т)=—•—!— Е Е fkifk+pk+m, (4.30)
N — | р | п — | т | fe=i f=i
где fkt — значение поля на /г-м профиле в t-й точке; р — опреде-
ляет смещение между профилями съемки (р = 0; ± Ар; ± 2Ар, ...);
т — смещение между точками по профилю (т — 0; ± Ах;
± 2Ах, . . . ); п — общее число точек по профилю (трассе); JV—
общее число профилей (трасс).
С целью изучения структуры ДАКФ выпишем выражение (4.30)
для различных фиксированных значений р. При р = 0
К(0, m) = 4"T~M ZZWfei+m==
“ЧгСп	+ „ Ll
/V \ Л —| tn |	П ““ | tn |	/
т. е. при р = 0 ДАКФ равна сумме всех одномерных функций ав-
токорреляций, вычисленных для каждого профиля и усредненных
по их общему числу N.
При р = 1
R (!, щ) = —££ fk (fk+1 l+m =
ZZ1^2<+m+ • • •
т. e. при p = 1 ДАКФ равна усредненной сумме одномерных функ-
ций взаимной корреляции, вычисленных для значений поля по
каждой паре соседних профилей (трасс). Аналогично при р — 2
получаем сумму функций взаимной корреляции, вычисленных для
значений поля, расположенных через один профиль, при р = 3 —
через два профиля и т. д.
Для выражения ДАКФ (4.30) справедливо соотношение R (р,
т) — R (— р, — т), поэтому при расчетах ДАКФ можно огра-
ничиться вычислением значений либо R (р, ± т), либо R (± р, т).
Двумерную автокорреляционную функцию следует строить на
плоскости смещений /иАх и рАр, где для различных значений рДр
откладываются сумма автокорреляционных (при р = 0) и взаимно
корреляционных (при р > 1) функций. Такое представление дву-
мерной АКФ в изолиниях ее рельефа на плоскости (т, р) позволяет
наглядно отобразить корреляционные свойства геофизических по-
лей по площади, а для сейсмической информации — по времени
и в пространстве (рис. 17).
122
Точность оценки ДАКФ обычно значительно выше точности
оценки одномерных АКФ из-за большого числа значений поля,,
используемых для ее определения.
Нормированная ДАКФ рассчитывается как
RH(p, ni) = R(p, m)/R(Q, 0).
Описанное построение ДАКФ по формуле (4.30) справедлива
для регулярной сети.
Значения ДАКФ как для регулярной, так и для произвольной
сети наблюдений на площади съемки находятся по выражению
Л(р)=ЕАА+р.	(4-31>
а
Рис. 17. Графики исходного поля Za (а) и их нормированнаи двумерная ав-
токорреляционная функция (б)
в котором производится усреднение значений поля по заданным
интервалам группирования с радиусом-вектором р. В частности,.
р = V /и2 Ах + р*Ьу<
Из (4.31) следует, что алгоритм вычисления R (р) сводится
к определению, группированию и усреднению произведений зна-
чений поля для всех пар точек, попадающих в пределы круга ра-
диуса р. Количество таких пар произведений равно п (п—1)/2
(где п — число точек в круге) и обычно вполне достаточно для
надежного определения величины R (р). При графическом по-
строении ДАКФ по формуле (4.31) она аналогична одномерной
АКФ, а в случае изотропности поля — совпадает с последней. По-
этому выражение (4.31) целесообразно использовать для изотроп-
123
ных полей и при расчете основных статистических характеристик
(среднего, дисперсии, интервала нулевой корреляции, на котором
значения корреляционных функций равны нулю) в пределах окна,
выбранного с целью районирования поля.
Оценку интервала корреляции по ДАКФ можно провести по
любому направлению с использованием выражений, приведенных
в § 19.
Для оценки точности определения ДАКФ погрешности вычис-
ляются по различным направлениям раздельно, что позволяет по-
строить их рельеф на плоскости.
Использование ДАКФ в практике обработки геофизических дан-
ных во многом аналогично применению одномерных АКФ.
1.	При отсутствии корреляции помех как вдоль профиля, так
и между профилями ДАКФ представляет собой оценку корреля-
ционных свойств аномального поля. Подобно тому, как вычисление
одномерной АКФ является основой для расчета весовых функций
и частотных характеристик оптимальных фильтров, так и вычисле-
ние ДАКФ следует рассматривать как начальную процедуру при
построении двумерных фильтров, в частности алгоритмов прост-
ранственно-временной фильтрации в сейсморазведке (см. гл. VII).
Построение ДАКФ на аномальном участке при проведении маг-
нитных и гравиметрических съемок позволяет существенно сни-
зить влияние помех в случае оценки формы аномалии. ДАКФ мо-
жет быть с большим успехом, чем само наблюденное поле, исполь-
зована для пересчетов потенциальных полей.
В задачах фильтрации геофизических полей возникает необхо-
димость построения корреляционной матрицы по ДАКФ. Эта мат-
рица будет определяться по аналогии с (4.8) как R (р—k, т—I).
При р = т — 0; ± 1; ± 2 получаем значения матрицы, при-
веденные в табл. 21.
В силу симметрии ДАКФ R (р, т) = R (— р, — т), корреля-
ционная матрица симметрична относительно главной диагонали.
2.	Двумерная автокорреляционная функция дает возможность
определять основные простирания аномалий. На рис. 17, б приве-
ден пример определения простирания аномалий по ДАКФ, вычис-
ленной для магнитного поля Za в одном из районов Северного
Криворожья. Графическое изображение ДАКФ в изолиниях позво-
ляет установить два направления простираний: меридиональное,
которое выделяется визуально по графикам исходного поля, и се-
веро-западное, не проявляемое достаточно четко на графиках Za.
ДАКФ в общем случае аналогична розе-диаграмме изолиний поля,
применяемой, в частности, для выявления микроструктур полей
при микромагнитных съемках. Если изолинию интервала корреля-
ции, определенного абсциссой R (0,0)/3, аппроксимировать эл-
липсом, азимут направления большой оси эллипса будет оценивать
основное простирание аномалий по площади, а коэффициент сжа-
тия эллипса, численно равный отношению малой полуоси эллипса
к большой,— количественно характеризовать степень анизотро-
пии поля.
и ц а 21		сч 1	(-2, 2)	£	(-2, 0)	(г ‘I—)	C4	(0 ‘I—)	см	о	О о.	
Ч 50			ас	ас	ас	ас	ac	ac	ас	ас	ас	
сз												
	7	g	(i ‘г—)	(о ‘г—)	! сч	7	О 7	1 7	О	o' _о.	7 о	
			ас	ас	ас	ас	ac	ac	ас	ас	ас	
		о II g	(о ‘г—) if	(I— ‘г—) а	1 см’ 1 й;	(0 ‘I—) if	(I- ‘I—) if	fe— ‘I—) if	R (0, 0)	R (0, -1)	R (0, -2)	
		?	(г ‘i-	(I ‘I-	(0 ‘I-			О	СМ		О	
		g	1 *	ft?	1 о?	0) if	0) if	0) if	1) и	1)а	I) и	
	1	т	(I ‘I-	(0 ‘I-	(I- ‘1-		о	г—		о	7	
			ас	ас	г. ас	0) if	0) if	О ft?	I) и	1)И	I) и	
		о ц	(0 ‘Г	1	1	о	7	оГ 1	о	7	сТ 1	
			1 Of	ас	ас	R (0,	o’ ft?	о ft?	ас	‘I) и	ас	
		сч	сТ	^^4	S'	oT		S'	СЧ		О	
				о	<О.				CJ	см	сч.	
			ас	ас	ас	ac	ac	ас	ас	ас	ас	
												
	о II			О’	1		S'	1		S'		
	л	g	R (0,	0) if	0) if	ac	‘I) if	ас	R (2,	R (2,	R (2, 1	
		о II g	S'	1	о?	o'	7	О? 1	S'	1	сТ 1	
			о О?	R (0,	о ft?	R (1,	R (1,	ас	R (2,	R (2,	R (2, 1	
			о		см	О		см	О		ei	
	о.		о						сч			
124
ДАКФ позволяет учесть изменение корреляционных свойств
исходных данных по различным направлениям при оценке эффек-
тивности их преобразования различными приемами обработки,
в частности разными интерференционными системами в сейсмораз-
ведке.
В рудной геофизике на основе ДАКФ можно осуществить вы-
бор оптимального простирания задаваемых профилей. Направление
профилей должно быть нормальным к некоторому средневзвешен-
ному, определенному с учетом относительного веса аномалий раз-
личного простирания, проявленных на ДАКФ.
3.	Двумерная АКФ используется при районировании геофизи-
ческих полей, когда съемки проведены на большой территории
и имеется возможность расчета ДАКФ в скользящем окне. При
этом вся исследуемая территория разбивается на равные по вели-
чине участки, для каждого из которых вычисляется ДАКФ. Райо-
нирование поля осуществляется либо непосредственно по форме
двумерных ДАКФ, либо чаще всего по основным статистическим
характеристикам ДАКФ, значения которых затем преобразуются,
в единый комплексный параметр на базе метода главных компо-
нент. К таким характеристикам относят: а) среднее значение поля
по участку (в окне); б) дисперсию оценивающую изменчивость
поля (аномалий); в) интервал корреляции гкор при /? (0,0)/3, ха-
рактеризующий статистическую зависимость значения поля в дан-
ной точке от его значений в других пунктах наблюдений, а также
среднестатистический размер аномалий; г) азимут основного про-
стирания аномалий на участке.
Вычисление указанных характеристик можно организовать
в скользящем окне, однако это требует значительных затрат ма-
шинного времени.
Следует отметить возможность применения в практике разве-
дочной геофизики двумерных ВКФ
В (р, т) = —±—---------1— ZZ fl {$+р {+т.	(4.32)
ЛГ — I р | п — I т |Д
где fh и — значения поля, полученные на разных участках
съемки, на разных глубинах (высотах) исследования либо разными
методами. Двумерная ВКФ характеризует взаимные корреляцион-
ные свойства полей, устанавливаемые на изучаемой площади по
наблюдениям на двух участках съемки или на двух глубинах, или
при использовании двух методов. В последнем случае двумерную
ВКФ можно рассматривать как результат комплексной интерпре-
тации данных площадной съемки двумя методами.
Одно из практических приложений двумерной ВКФ при раз-
ведке нефтяных месторождений связано с оценкой в пространстве
смещений сводов структурных планов, получейных по данным
сейсморазведки на разных глубинах. Величина этого смещения
устанавливается по экстремуму функции.
126
§ 22.	СТРУКТУРНАЯ ФУНКЦИЯ
Результаты геофизических наблюдений часто являются нестацио-
нарными по математическому ожиданию, что не позволяет приме-
нять АКФ для оценки их статистических свойств без предваритель-
Рис. 18. Материалы обнаружения кимберлитовой трубки путем вычисления
структурных функций аэрогеофизических данных (по Ф. М. Персицу).
а — наблюденные данные; б — структурные автоковарнацин (J?K, -ftTh) н ковариация
ЯТЬ—К’ * ~ наблюденное поле ДГЛОК и его структурная автокорреляция; а—геологи-
ческий разрез: I — известняки, 2 — кимберлитовое тело, 3 — автохтонный ландшафт.
4 — направление сноса материала в аллохтонном ландшафте
ного исключения фона. Для изучения нестационарности исполь-
зуется структурная функция (4.4).
Нередко исключение региональной составляющей вызывает оп-
ределенные трудности, в частности при спектрометрической аэро-
геофизической съемке. В таких случаях для выявления нестацио-
нарных, как правило, аномальных участков оказывается целесо-
образным использование структурной автокорре-
ляции
127
.	mmax	_
/?стр(т)= ----1---- 1 КН-АС/Ятах)]2.	(4.33)
п — ттах	т=1
I т
fi (т) =--£ fi~mt
ТП —т
где т и ттг1Х — переменный и максимальный интервалы усредне -
ния исходного поля fa т = 1, 2, . . . ,	[f{ (т) — ft (rnmax) ] —
ордината структурной функции i-й точки профиля.
Для стационарного процесса при т„,ах -> со структурная функ-
ция совпадает с дисперсией процесса. Преимущество структурной
функции (4.33) по сравнению с АКФ состоит в ее относительно
большей устойчивости к нестационарное™ процесса по математи-
ческому ожиданию.
При изучении зависимости двух различных полей ft и f2 исполь-
зуют построение структурной ковариации
В^р (т) =-----1---- X 171 i i (^max)] X
П — fnmax — m
X [fa <(/«)— МИтах)]-	(4.34)
На рис. 18, а приведены данные аэрогеофизической съемки по
регистрации содержания Th, К, отношения Th/K, а на рис. 18, в—
магнитного поля (АТ')лок над кимберлитовой трубкой, на рис. 18, б,
в их структурные автокорреляции и структурная ковариация Th
и К. Дальнейшее преобразование значений этих функций в единый
комплексный параметр приводит к однозначной локализации ким-
берлитовой трубки.
ГЛАВА V
СПЕКТРАЛЬНЫЙ АНАЛИЗ
ГЕОФИЗИЧЕСКИХ СИГНАЛОВ
Спектральный анализ занимает центральное место при обработке
геофизических данных. Разложение наблюденного поля на различ-
ные частотные составляющие, что и представляет сущность спек-
трального анализа, уже само по себе дает много информации о
структуре поля. При этом важно подчеркнуть применимость спек-
трального анализа для описания свойств геофизических полей,
заданных как детерминированными, так и случайными функциями.
Необычайно широки и разнообразны возможности спектрального
анализа при фильтрации исходных данных, оценке погрешностей
и сравнении эффективности обработки данных различными прие-
мами.
В настоящее время спектральный анализ объединяет методы
анализа Фурье и статистического анализа временных, в том числе
любых дискретных последовательностей наблюденных значений
геофизических полей. Отметим, что при обработке данных конеч-
ной длительности, к которым относятся все геофизические наблю-
дения, спектральный анализ оказывается более предпочтительным,
чем автокорреляционный анализ.
§ 23.	СПЕКТРЫ ДИСКРЕТНО ЗАДАННОГО СИГНАЛА
В связи с использованием ЭВМ практические приложения ана-
лиза Фурье при обработке геофизических полей обусловлены пред-
ставлением исходных данных как сигналов, заданных в дискрет-
ные моменты наблюдения, т. е. Si = s (х = iAx = iA) данных по
профилю (трассе). Кроме того, в большинстве методов, регистри-
рующих потенциальные поля, наблюдения проводятся дискретно.
Вначале рассмотрим основные понятия спектрального анализа для
детерминированных сигналов. При расчете таких сигналов сущест-
венным является их модельное представление. Различают перио-
дические и непериодические сигналы. Сигнал s(х), для которого
справедливо соотношение s (х + Т) = s(x), где Т — некоторая
постоянная, называется периодическим. Величину Т на-
зывают периодом сигнала. Для непериодического
сигнала такого Т не существует, например для s (х) = е~х,
а для так называемого апериодического сигнала
полагают величину Т стремящейся к бесконечности.
Рассмотрим разложение дискретно заданного сигнала по перио-
дическим функциям синусов и косинусов. Такой сигнал можно
рассматривать как полученный из непрерывного сигнала s (х) дли-
тельностью Т при отсчете значений сигнала через интервалы А,
5 А. А. Никитин	129
что дает п = 77 Д дискретных значений s<. Для удобства вычисле-
ний полагаем, что п четцое и равно 2г, а начало отсчета значений
сигнала помещено в его центр, так что текущий индекс i для абс-
циссы сигнала s{ изменяется по целым числам от — г до г—1: — г,
— г + 1, . . . , — 1,0, 1......г — 2, г — 1.
Известно, что практически любую периодическую функцию 1
можно представить в виде конечного ряда Фурье
Г—1
8~(Х) = ЛО + 2 X (Amcos2nrnf1x+Bmsin2nffif1x)-|-.4ncos2nn/:1x,
m=l
(5.1)
содержащего г констант Ат и Вт, которые можно определить так,
чтобы дискретные и непрерывные значения сигнала совпали в
точках х = /Д, т. е. s (х) = st. Функция s (х) является приближе-
нием к исходной непрерывной функции s (х) в интервале
— T/2<zx<zT/2. Заменяя х на 1'Д в (5.1) и полагая s (/Д) = s<,
получаем систему п уравнений для п неизвестных констант:
Г “1
s( = Ло 2 У, Amcos 2nmfiiД + Вт sin 2nmf1iA) +
+ Ап cos 2nnfiiA,	(5.2)
i — — r, —r+1, .... —1, 0, 1, ... , r—1.
Для величины = 1/пД решение системы (5.2) упрощается,
поскольку синусы и косинусы образуют ортогональную систему,
удовлетворяющую соотношениям:
г-1 У sin i=s— г	2nki		2л mi	=с		k, m—целые;
	п		п			
					о,	k=£ tn,
Г—1 У sin- /——Г	2n£i п	sin-	2nmi п	__ ,	n/2,	k = m = 0,
					0,	k — m = 0-,
					0,	k=£tn,
г—1 У cos <=— г	2яМ	-cos	2nmi		n/2,	k = my=0,
	п					
					n,	k = m = 0-
Приведенные соотношения ортогональности используются для
нахождения коэффициентов Ат и Вт в (5.2). При этом обе части
(5.2) умножаются на cos (2nmi/n) или sin (2лт11п) и ведется сумми-
1 Согласно условиям Дирихле функция в пределах периода Т ограни-
чена и может иметь лишь конечное число разрывов.
130
рование по i. С учетом их ортогональности получаем выражение
для коэффициентов Ат и Вт:
Ат = (]./п) У si cos(2nmi/n);
Г_Г"Г	(5.3)
Вт(\/п) У s{ sin(2nmi/n).
i г
где т = 0, 1, . . . , п/2.
Коэффициенты Ат и Вт называются коэффициентами
Фурье, а их вычисление — анализом Фурье (гармоническим
анализом).
Величина ft = 1/пА называется основной частотой
сигнала, она соответствует периоду, равному длине интервала об-
работки, в частности длине профиля. Величина измеряется либо
в периодах на метр (километр), если А измерено в метрах (кило-
метрах), либо в периодах в секунду или герцах, если А измерено
в секундах.
Исходный сигнал s< в результате разложения (5.1) представляется
суммой синусоидальных и косинусоидальных функций вида sin
2nmf1i и cos 2nmf1t, частоты которых кратны основной частоте
fm = mfi, иначе они называются гармониками основ-
ной частоты, их периоды Тт = Т/т, а амплитуды Ат
и Вт. Наивысшей из частот является частота fr = г/nA = 1/2Д.
Эта частота соответствует периоду, равному двум интервалам
отсчета, и называется частотой Найквиста.
Коэффициент Ао в разложении (5.2), как нетрудно видеть из
(5.3), является средним значением сигнала на интервале его периода.
Выражения, аналогичные (5.3), можно получить, если начало
отсчета помещено в первую точку сигнала, а отсчет ведется слева
направо, тогда
п	п
Ат = (1/п) У st cos (2nmi/n), Вт = (1/n) J] st sin (2nmt7n). (5-3')
z=i	j=i
Широко используется тригонометрическая форма ряда Фурье,
для которой вводятся амплитуда Rm ифаза <рт т-й гар-
моники, связанные с коэффициентами Фурье соотношениями
Rm = л/ Ат + Вт,	<рж = arctg (— Вт/Ат).	(5.4)
Тригонометрическая форма ряда Фурье
г—1
s~(x) = /?o Н- 2 }* ж cos (2л/п/1Х | фж) I Rn cos 2sitifiX,
m=l
Распределение амплитуд гармонических составляющих сигнала
Rm в зависимости от частоты (номера гармоники) называется ам-
плитудным спектром (или амплитудно-частотным), рас-
пределение фаз этих составлякйцих фт от частоты — фазовым
спектром (или частотно-фазовым).
5*	,	131
Амплитудный и фазовый спектры периодического сигнала яв-
ляются линейчатыми, дискретными, они состоят из отдельных «ли-
ний», соответствующих дискретным частотам: 0; fi, 2/\ — и т. д.
(рис. 19).
Значения амплитудного /?т и фазового <pm спектров рассчиты-
ваются относительно принятого начала отсчета. Если изменить
начало отсчета, которое для (5.3) было взято в центральной точке
сигнала, амплитуда гармоник останется прежней, а фаза соответст-
венно изменится. Фаза хар актер изует'"смещение т-й гармоники
с амплитудой Rm относительно выбранного начала отсчета.
Рис. 19. Наблюденное поле &g (а} и его спектры (б).
1 — спектр Фурье; 2 — спектр, построенный по методу-максимума энтропии
Если просуммировать все значения гармонических составляю-
щих, полученных в точках задания сигнала, с учетом величины
их амплитуды и фазового сдвига относительно начала отсчета, ре-
зультат суммирования приведет к амплитудным значениям сигнала.
Пример. Проиллюстрируем технику вычисления амплитудного и фазо-
вого спектров для сигнала, заданного следующими значениями: V-1, — 3, 1,
3, 2, 1.
Решение. Начало отсчета примем в центральной точке сигнала, т. е.
абсцисса сигнала i изменяется от — г до г—1, где г = 3: si = — 1, — 3, 1
3, 2, 1; i= — 3, — 2, — 1,0, 1,2. Общее число дискретов п = 2г=6.
Коэффициент Alt например, получается следующим образом, если его
рассчитывать по формуле (5.3):
Ai = — Г(- 1) cos 2л+(—3)cos	+
6 L	6	6
, ,	2л-1-(—I) . _	2л-0 , о 2л-1-1 ,
4- 1 • cos------- 4- 3 cos------Р 2 cos-------Р
6	6	6
+ bcos 1 =—(1 + 1,54-0,5 + 3 + 1-0,5)=-
6 J 6
= — -6,5= 1,083.
6
В табл. 22 приведены значения амплитудного и фазового спектров этого
сигнала.
132
Таблица 22
Номер гармоники	Ат т	вт		ч>т
0	0,5	0	0,5	0
1	1,083	0,722	1,3	—33°40'
2	0,25	—0,433	0,5	60°
3	—0,167	0	0,167	0
При изучении спектров сигнал удобно выражать через комплекс-
ные амплитуды, образующие комплексный спектр:
^m = Rm^P( 1'фт)^Ат ]Вт~
1	Г-1
=----- У, stexp(—j2nmf1i),	(5.5)
П i=—r
где / = V —1 •
С учетом (5.5) дискретный ряд Фурье (5.2) запишется в виде
г—1
s<= У Smexp(j2nmfii),	(5.6)
me—г
где S-m — S*m образуют комплексно сопряженный
спектр сигнала.
Величины
I Sm |2 = SX = Rm	(5-7)
определяют энергетический спектр сигнала. При этом
сумма амплитуд энергетического спектра позволяет получить
среднюю мощность сигнала
, Г—1	Л—1	г—1
— T.s^Ro+2 XRm + R2n^ у |Sm|2.	(5.8)
п i=—r	m=l	m=—г
Вклад в среднюю мощность, вносимый членом 27?™ в выражение
/?о + 2 27?™ + 7?2, разделяется в сумме 2|S™|2 на две ча-
сти, каждая из которых равна | Sm j2 = 7?™: одна соответствует
частоте mf lt другая частоте — mf1.
Таким образом, практически любой Дискретно заданный геофи-
зический сигнал можно представить в виде амплитудного и фазо-
вого спектров, образованных гармониками основной частоты 1/лД,
полагая интервал задания сигнала его периодом. Максимальной
из этих частот является частота 1/2А, поэтому сигнал st имеет ог-
раниченную полосу частот.
Выражения (5.3), (5.5), (5.7) представляют собой различные
виды обратного дискретного преобразования Фурье, а (5.2), (5.6) —
прямого преобразования Фурье.
133
Для восстановления сигнала по заданным его спектрам (ампли-
тудному и фазовому) удобно использовать тригонометрическую
формулу
Si = Ko + 2 £ tfmcosp^+9J+tf„cos-^.	(5.9)
m=l	\ П	/	П
Пример. Необходимо рассчитать значение сигнала в точке i = — 2
при его заданных амплитудном Rm (Ro — 0,5, Rt = 1,13, R2 = 0,25, Rs =
= 0,167) и фазовым <pm (0, —30°, 60°, 0°) спектрах (табл. 22).
Решение. Для того чтобы воспользоваться формулой (5.9), требуется
знание помимо Rm и <рт величины п. Отношение последней гармоники сиг-
нала к его первой гармонике’^ = 1/пД):
frp/fi = пД/2Д = п/2.
Следовательно, величина п равна удвоенному значению номера послед-
ней гармоники, т. е. п = 2г. Для нашего примера п = 2'3 = 6. Отсюда
sZ=-2 = 0,5 + 2 cos (+
+ Ri cos ( 2jl2(6 2) +	+ 0,167 cos 2Tt3(6 2) = — 2,96.
В тех случаях, когда спектральный анализ проводится для
дискретно полученных наблюдений, интервал, выбранный для об-
работки, определяет нижнюю частотную границу спектра =
= l/TA, а шаг наблюдений Л — верхнюю частотную границу
fTp — 1/2А. Величиной 1/ТА характеризуется также спектральная
разрешающая способность, т. е. разность между последовательно
разделившимися частотами А/ = 1/ТА.
При анализе спектров сигналов, полученных путем дискрети-
зации непрерывных наблюдений (аналоговых сейсмических запи-
сей, аэрогеофизических наблюдений, данных каротажа КС, ПС
и т. д.) возникает явление наложения частот, рассмотренное при
анализе спектров непрерывных периодических сигналов (см. § 24).
С дискретизацией непрерывных сигналов тесно связан вопрос вы-
бора оптимального шага геофизической съемки. Однако прежде,
чем переходить к этим вопросам, приведем выражение для спект-
ров’ двумерных дискретных сигналов.
Разложение дискретно заданного сигнала в двумерный ряд
Фурье имеет вид
п ы .
„ V* V*	2лт/Дх 2лрЛДр .
sik = ) ) атв cos----------cos —z—— +
Li Lt P nbx N&y
i=l fe=l
n N
, V* V1 о	2лп»'Дх . 2лрЛДи
Г > > Ртр COS---------SIH  у +
La l—i	п&х N&y
1-1 fe=l
n N
, V* V1 • 2лт/Дх 2лрЛДи ,
+ > > Утр «И-----------COS ; У +
Z_j Ди н пДх	N&y
M fe=l
134
n N
+ ^^8тР 8’П
i=l fe=l
2л mi Ax
пДх
s}n 2npfeAy
ЛГДр ’.
(5.10)
где тир — номера гармоник в направлениях х и у.
Рис. 20. Двумерный амплитудный спектр в пространстве (а) и на плоскости
в изолиниях (б)
Коэффициенты гармоник вычисляются по формулам:
n N
к ХП V''	2nmi&x	2npkAy
атв =----- > > st* cos--------cos —-——;
тр nN LL nAx NAy ’
1=1 Л=1
n N
a x V4 V4 2лпг/Дх . 2лр/гДу
pmp = —гг > > s«cos ——sin  -zr—;
nN La L-i	nkx	NAy
ы
n N	(5.11)
x V* V* •_ 2лт/Дх	2 л р/г Ду
Ymp = —T7-) ) s^sin-----------COS ; *;
nN La La	nAx NAy
i=l fe=l
n N
я x W1	• 2лпг/Дх	2лрйДу
Smp=—) S<feSin----------------Sin \	,
F nN La La	n^x	N&y
где x = 1, если m = 0 и p = 0; x = 2, если m = 0 или p = 0;
x = 4, если m>0 и p>0.
Начало гармонического ряда при вычислениях по (5.10) и (5.11)
помещено в начало координат системы X и У. Гармоники могут
быть рассчитаны вплоть до значений т = п/2 и р = N/2. По ко-
эффициентам Фурье (5.11) соответствующим образом находят ам-
плитудный спектр:
Rmp —	&тр 4" Ртр ~Ь Утр + 5тр>
О характере двумерного спектра можно судить по рис. 20.
135
При изучении геофизических полей Земли широко используется
разложение по сферическим функциям, поскольку
с их помощью выражаются распределения сигналов (наблюденных
данных) по сферической поверхности.
Сферические функции являются комбинациями синусо-косинус-
ных функций и функций Лежандра, причем зависимость сфериче-
ской функции от долготы определяется рядом Фурье, а от широты—
функциями Лежандра:
N п
s(X, ф)= У, У (Л<„m) cos пгк + В^ sin тк)Р{п} (cos <р),	(5.12)
п=0 /п=0
где А, — долгота; <р — дополнение широты до 90°, а функция
Рп"1’ (cos ф) — соответствующий полином Лежандра первого рода
степени п и порядка т.
Замечание о быстром преобразовании Фурье
Рассматривая процесс вычисления амплитудного и фазового спект-
ров, нетрудно видеть, что синусы и косинусы встречаются с одними
и теми же аргументами. Алгоритм (Маркус Бат, 1974 г.), позволяю-
щий объединить их и тем самым ускорить процесс вычисления спект-
ра, получил название алгоритма (способа) быстрого пре-
образования Фурье, сокращенно БПФ. Принцип этого
алгоритма заключается в следующем. Обозначим дискретно задан-
ный сигнал через s{, где i = 1, 2...п, причем п — четное число.
Этот ряд значений сигнала разделяется на две части: первая со-
стоит из дискретов с нечетными индексами, а вторая — с четными,
причем i = 1, 2, . . . , п/2, т. е.
Xi = Sa/-i = Si, s8, ...» sn_j,
yt= Sm = $2, 84, . . . , sn.
Используя эти выражения, можно записать дискретные преоб-
разования (ДПФ) трех рядов (суммарного и двух частичных
и t/О как
=-----У s< ехр (—j2nmiln)’,
п ,=1
„ "/2	;
Х%,2) = —	xi ехр (—/4л/ш7п);
о "/2
у(Л/2) = - £ у{ ехр ^j4ntni/n),
п i=\
Число Членов в равно и, а в Х^/2) и У^/2) равно п12. Дан-
ные три ряда связаны между собой, и их преобразования также
связаны, что следует из разложения
п/2
—£ {х,ехр[—/(2шп/п)(2/—1)]+
п i—1
136
। n/2
+ ut exp [—j (2nmi/n) 2i]} = exp (j2nm/n)-£ xt x
n (=1
Л/2
X exp [ — j (4ntn/N) i] 4-У yt exp [—j (4лт/п) i] =
n i=l
=-^- exp (j2nm/n) Xm2) + -у- Ут2><
Заменяя m на m 4- n/2, находим
v(n/2)   y(n,2).	y(n/2)  y(»/2)
Am-|-n/2 — Am >	I m+n/2 — ‘m •
поскольку
4nmi/n -> (4n/n) (m 4- n/2) i — (4nmi/n) + 2ni,
что в случае целого i составляет показательную функцию без из-
менений. Отсюда получаем
5(Дп;2 = (1/2) ехр [/ (2л/п) (т + п/2)] Х^„/2 + (1/2) У^/2 =
= -(1/2) ехр (]2пт/п) х£/2) + (1/2) У £/2).
Формулы для т = 0, 1,2,..., (п/2) — 1
5<тл) = ехр(/2лт/п) Х(”/2> + -±- У("'2>;
для т + п/2 = п/2; п/2 4- 1,	, п—1
S^n 2 = - -у-ехр /(2лт/п) ХЙ/2) +	У<£/2).
Эти формулы позволяют вычислять преобразование заданного
ряда по преобразованиям двух частных рядов xt и yt. Если же
п/2 — четное число, процесс можно продолжить, т. е. каждый ряд
Х( и у( можно снова разделить на два частных ряда и найти преобра-
зование каждого из них и так далее, пока число членов в частных
рядах четное. Последнее условие выполняется при n = 2к, k —
целое число. При этом описанный процесс продолжается до тех
пор, пока в каждом из частных рядов не останется по одному члену.
Преобразования Фурье этого члена совпадают, что видно из выра.
жения для
Основное преимущество БПФ по сравнению с обычным преоб-
разованием Фурье — увеличение скорости вычислений благодаря
меньшему числу операций. Число арифметических операций в ал-
горитме БПФ 2kn = 2n logs п, а при обычном преобразовании
Фурье п2. При п = 4096 и k = 12 выигрыш во времени состав-
ляет 171 раз.
137
§ 24. СПЕКТРЫ НЕПРЕРЫВНЫХ СИГНАЛОВ
И ИХ ДИСКРЕТНЫХ АНАЛОГОВ
Спектры непрерывных сигналов
Любой непрерывный периодический сигнал (более точно, сигнал,
удовлетворяющий условиям Дирихле) может быть представлен
в виде ряда Фурье
оо
s(0=Ao + 2 У, (Amcos2nrnfit + Bmsin2nmfit),	(5.13)
т=\
где = 1/7 — основная частота; Т — период сигнала.
Коэффициенты Фурье Ап и Вт находятся путем умножения
(5.13) на cos 2nmf1t и sin 2nmfit и интегрирования по t на отрезке
[— 7/2, 7/2] с использованием свойств ортогональности функций
синуса и косинуса:
!	7/2
Ат—------- f s(t)cos2nmfitdt-,
Т — Т/2
1 г'2
Вт=------- J s(0sin2nmfitdt.
Т —Т/2
(5.14)
Амплитудный, фазовый, комплексный, комплексно-сопряженный
и энергетический спектры непрерывных периодических сигналов
определяются по тем же формулам (5.4), (5.5), (5.7), что и спектры
дискретно заданных сигналов:
Rm— Am-\-Bm> фщ — arctg ( Bm/Am);
7/2
Sn= — I s(0exp(—/2nmfi0d0	(5.15)
T —7/2
I $т I = SmSm — Rm>
Все эти спектры, как и спектры дискретно заданного сигнала,
являются линейчатыми, однако не имеют ограничения по частоте,
так как /гр = 1/2А -> оо при А -> 0.
Формула для восстановления (синтеза) непрерывного периоди-
ческого сигнала по его спектру в комплексной форме (обратное
преобразование Фурье) принимает вид
s(0 = У Smexp(/2nmf10.	(5.16)
т=—оо
Далеко не всегда геофизические сигналы можно считать перио-
дическими, поэтому практическое значение имеет рассмотрение
спектров апериодических непрерывных сигналов. Апериодический
сигнал можно считать периодическим с неограниченно увеличи-
вающимся периодом. По мере того как 7 стремится к бесконечно-
сти, частотный интервал между соседними гармониками в спектре
становится бесконечно малым, что приводит к непрерывному рас-
пределению амплитуд по частоте,
138
Запишем уравнение (5.16) в виде
s(/) = X (TSm)exp(j2nmt/T)/T.	(5.17)
В пределе, когда Т -> оо; m/T -+ f-, 1/Т -+ df, (TSm) ->S (f),
выражение (5.17) стремится к интегралу
s(/) = У S (f) ехр (/2л//) df.	(5.18)
—00
Аналогично выражение (5.15) можно переписать в виде
T/2
TSm= f s(/)exp(—j2nmtlT)dt.
—T/2
В пределе, когда Т -> оо, получаем
00
S(/) = У s(/)exp( —j2nft)dt.
—00
(5.19)
Уравнения (5.18) и (5.19) являются уравнениями прямого и об-
ратного преобразования Фурье для апериодического непрерывного
сигнала, их называют Инте-	£(t)
тралами Фурье. Ампли- а	_
тудный и фазовый спектры апе-	\.
риодического сигнала	---:-------------------*-
/?(/)= д/Аа(/) +В2 (/);	(5.20)
<p(/) = arctg[ —В(/)/А (/)],
где коэффициенты Фурье
А (/) = У s (/) cos 2nftdt,
—00
В (f) — f s(t) sin 2nftdt.
s(t)
Рис. 21. Непрерывный сигнал
(5-21) в Ф°Рме убывающей экспоненты
'	7 с периодом Tt (а) и его ампли-
представляют собой непрерывные спектры (б)^ И *аз0ВЬ1и ф
функции частоты и являются
сплошными. Амплитудный и фазовый спектры для сигнала вида
( ехр(—at),	/>0,
S(*)=l	0,	/<0
приведены на рис. 21.
Произведение комплексного S (/) и комплексно-сопряженного
S* (/) спектров образует спектр мощности апериодиче-
ского сигнала
F(/) = S(/)S*(/)
(5.22)
139
Другая форма преобразования Фурье апериодических сигна-
лов связана с введением круговой частоты со = 2nf, при этом урав-
нения (5.18), (5.19), (5.22) принимают вид:
s (0 = —L. f S (со) exp {jcnt) dco;
—оо
S(®) = f s(Oexp(—jat)dt;	(5.24)
W (co) = S(®) S* (co).	(5.25)
Соответствующие выражения для двухмерного преобразования
Фурье:
(5.23)
Рис. 22. Система коорди-
нат для случая двумерной
круговой симметрии.
у = г sin 0;
= Р ®1пф
Ханкеля. Прямое
с учетом системы координат, приведенной на рис. 22, имеют вид:

s (х, у) = ——
(2л)’
(йу) ехр [/ (<ох • X + а>у • у)] daxd<ay-,
(5-26)

у) ехр [—/ (шж • X+,соу • у)] dxdy,
(5.27)
а — х = г cos 0,
б — е>х = р cos ф.
где сох, (£>у — пространственные часто-
ты (волновые числа) по направлениям
осей х и у.
Особый интерес представляет дву-
мерное пространство с круговой сим-
метрией. В этом случае преобразова-
ния Фурье эквивалентны преобразо-
ваниям Ханкеля, или спектрам
и обратное преобразования Ханкеля
S (р) = 2л j г S (г) Jo (pr) dr;
{5.28)
s(r)= j pS {р) J0 {pr) dp,
где г = V*2 + “2 :
(5.29)
p = д/®2 + tt»2 ; Jo{/pr) — функции
Бесселя нулевого порядка.
Свойства преобразований Фурье
При спектральном анализе геофизических данных широко исполь-
зуются основные свойства преобразований Фурье, которые приве-
дем для апериодических сигналов, но которые справедливы как для
дискретных, так и для непрерывных сигналов:
140
1)	свойство линейности, состоящее в Том, ЧТо если Sj (0
имеет спектр Sj (со), т. е. Sj (t) ♦+ Sx (со), a s2 (t) — спектр S2 (со),
т. е. s2 (0 ** S2 (со), то (0 ± a2s2 (0 «-» (со) ± a2S2 (со),
где ах и а2 — постоянные числа. Это свойство распространяется
на любое конечное число сигналов и соответствующих им спектров;
2)	свойство симметрии прямого и обратного преобразо-
ваний Фурье заключается в отличии только в знаке экспоненты.
Для четных сигналов исчезает и это различие, т. е.
S (®) = 2 J s (0 cos (0 &td i** s (0 = 2 f S (®) cos cofdco.
о	0
Отсюда следует вывод о том, что фазовый спектр для четных
сигналов тождественно равен нулю;
3)	свойство подобия, состоящее в том, что сжатие (растя-
жение) сигнала приводит соответственно к растяжению (сжатию)
спектра. Вследствие обратной размерности времени и частоты спектр
во столько раз растягивается (сжимается), во сколько раз сжи-
мается (растягивается) сигнал при сохранении их формы. Если
s (0 ♦+ S (со) и а — постоянное число, то s (a0-w(l/a)S (co/a). От-
сюда следует важный практический вывод о том, что, чем сигнал
короче, тем спектр шире;
4)	свойство запаздывания сигнала на время т, при-
водящее к изменению фазового сдвига каждой гармоники на сот
без изменения амплитудного спектра, т. е. если s (0 ++ S (со),
то s (t ±т) «->• ехр (± /сот) S (со);
5)_свойство смещения спектра на величину со0, ко-
торое приводит к умножению сигнала на комплексную величину,
т. е. если S (со) ++ s (0, то S ( со ±<о0) <-<• ехр (± /соо0 s (0.
Таким образом, временная функция оказывается комплексной.
Вещественный характер сигнала сохраняется при смещении спектра,
если выполняется условие S (— со) = S* (со). Разлагая выражение
еХр (zp /соо0 с помощью формулы Эйлера и используя свойство
линейности, получаем два важных соотношения:
s (0 cos coq/ ++ (1/2) (S (со + со0) -Ь S' (со — о>о)]>
s (0 sin соо/ ** (1/2) [S (со + соо)—S (со—соо)].
Это означает, что спектр раздваивается на одинаковые части,
которые смещаются относительно друг друга по частоте на ± соо.
Приведенные соотношения используются для объяснения рас-
щепления частоты как явления, вызываемого амплитудной моду-
ляцией;
6)	свойство дифференцирования сигнала, со-
стоящее в том, что если s (0 ++ S (со), то s' (0 ++ /coS (со) и
S' (со) ~ - jtf (0.
Таким образом, дифференцирование сигнала приводит к обога-
щению спектра высокочастотными составляющими и уничтожает
составляющие с нулевой частотой. Дополнительно появляется сдвиг
фаз на л/2 для всех гармоник. Приведенные результаты распро-
141
ограняются на любую производную высшего порядка п, т. е.
s<"> (/) ** (j®)nS (со); S<<*> (со) +* (— jt)ns (0;
7)	свойство интегрирования сигнала, заключаю-
оо
щееся в том, что если s (/)<->• S (со), то f s(t)dt «-> (l//co)S(co).
—ОО
Последние два свойства применяют в тех случаях, когда запись
одного сигнала является производной или интегралом другой.
Например, скорость v (t) = s'(t) ** i(oS (co) = coS (co) exp I/ (n/2) ]
и ускорение a (t) = s" (/) «+ — <o2S (co) = a>2S (co) exp (/л);
8)	свойство свертки двух сигналов. Сверткой сиг-
налов (функций) называется выражение
00
J Si^Sa^—T)dT = s1(0*sa(/).
—оо
Спектр свертки сигналов равен произведению спектров этих
сигналов, т. е.
ОО
f Si(0sa(/—Si (со) S2 (со);
—00
В частном случае свертки с функцией обратного времени, т. е.
когда s2 (i) = Sj (— t),
s (/)* s (—0 ~ S (®) S* (co) = I S (co) Is;
9)	свойство свертки двух спектров аналогично
предыдущему, т. е. свертка двух спектров равна произведению
функций:
j Si (со) S8 (со—v) dv = Si (со)* S8 (со) ++ Si (f) s8 (t).
—oo
Используя это свойство, легко получить выражение для энергии
апериодического сигнала, выраженной через спектральную плот-
ность:
J &(t)dt = J s(/)[-^— J S(co)exp(/cof)dcold/==
= J S(co)dco f s(/)exp(j<i>t)dt= —J— f S(co)S*(®)dco =
—OO	—00	2л —oo
=	“ |S(co)|adco.	(5.30)
2Л — 90
Спектры некоторых непрерывных сигналов
На основе приведенных выше свойств преобразований Фурье
рассчитываются спектры сигналов, использование которых имеет
важное значение для изложения дальнейшего материала.
142
1. Дельта-функция Дирака, определяющая импульс единичной
площади в виде
6(0 = 0, /=/=0;
f &(t)dt=\,	/ = 0,
—00
имеет спектр, равный единице, т. е. 6 (0 «->• 1. Это следует из свой-
ства свертки сигналов, поскольку свертка с единичным импульсом
не меняет сигнала.
2. Функция единичного скачка (Хевисайда), или- ступенчатая
функция,
( 1, t >0,	Г е ,
“«“{о. ко, »(0=
т. е.
-^-«(0=6(0; jcoSB(®) = l.
at
Это справедливо и для суммы единичной функции с постоянным
числом. Мнимый спектр имеет только нечетная функция, равная
и (0 — 1/2; и (0 — 1/2 ~ 1//<о.
Учитывая спектр постоянного числа, получаем
и (0 ** яб (со) — //со.
3.	Прямоугольная функция (прямоугольный импульс) единич-
ной высоты и длительностью т
(1, |*|<т/2,
S(°“l0, |*|>т/2
имеет спектр, равный
5(со) = J ехр (—/®0 dt = т [sin (сот/2)/ (сот/2)].
Отсюда следует, что прямоугольный спектр в полосе частот
— со0/2 < со < со02 имеет функция s (0 = sin лсоо//ясоо0 называе-
мая функцией отсчета.
4.	Треугольная функция (треугольный импульс)
s(0 = {
111 С т/2,
|0>т/2,
рассматриваемая как свертка двух прямоугольных функций, имеет
спектр
S (со) = sin® (<вт/4)/(<вт/4)® = [ 1 — cos® (сот/4)/(<вт/4)®].
5.	Знаковая функция
, I -1, />0
«““I-1, КО,
имеет спектр S (со) = — 2//со,
143
6.	Косинусоида cos <ooZ имеет спектр л [6 (cd + ®0)+ 6 (©—соо)].
Для отрезка косинусоиды
( cos at,	т/2 < t < т/2,
0,	|<|>т/2,
который можно рассматривать как произведение косинусоиды и
прямоугольного импульса (что приводит к раздвоению спектра
прямоугольника) имеем спектр
з (со) = т Г Sin [(<Р — <о0) т/2]
2 I (со — Оо) т/2
sin [(о 4- о0) т/2]
(о + Ор) т/2
Форма спектра определяется числом периодов косинусоиды
п = соот. Для полупериода косинусоиды, когда п = 1/2 с дли-
тельностью х = 1/2со0,
т Г sin (от/2 — л/2) , sin (<от/2 + я/2)
2 L ©т/2 — л/2	ют/2 + л/2
__ 2т cos (ют/2)
л 1 — (оЧ’/п1
7.	Затухающая экспонента (функция Лапласа) ехр (—а|/|),
.используемая для оценки АКФ некоторых типов помех, имеет
спектр S (со) = 2а/(а2 + со2).
8.	Колоколообразная функция (функция Гаусса) ехр (—а/2),
применяемая для аппроксимации АКФ аномалий Ag над анти-
клинальными структурами, имеет спектр
S (со) = л/п!а ехр (—со2/4а).
9.	Функция Бергале, применяемая для описания сейсмических
импульсов t ехр (— a/) sin соо/ имеет спектр
S (со) = 2сОо(а + /<в)/[(а + /со)2 + со2]2.
10.	Для гравитационных и магнитных аномалий от тел простей-
ших форм С. А. Серкеровым рассчитаны спектры, приведенные
в табл. 23.
Дискретизация непрерывных сигналов.
Теорема Котельникова
Как уже отмечалось, в практике обработки геофизических данных
используются в основном дискретно заданные сигналы. Поэтому
зарегистрированные аналоговые записи необходимо подвергнуть
дискретизации таким образом, чтобы информация о физическом
поле была бы минимально искажена.
Интервал дискретизации непрерывного сигнала определяется
на основе теоремы (прямой) Котельникова. Любой
сигнал s (/), описываемый функцией с ограниченным спектром,
определяется однозначно своими значениями, расположенными че-
рез интервал А/ = л/согр = 1/2 /гр. Заметим, что любой сигнал,
144
Таблица 23
Характеристика объекта	Выражение для поля (аномалии)	Выражение для спектра
Бесконечная линия по- люсов	(т-магнитная масса)	Z = 2m			 х2 + Л2	S(®) = "|/2л m | w | e—। 'h
Бесконечный горизон- тальный круговой ци- линдр, бесконечная ли- ния полюсов или одно- полюсная линия	Ag = 2vA,	-	 хг + Л2	S(<n) = V2nvA,e-l‘olh
Бесконечная дипольная линия или намагничен- ный бесконечный гори- зонтальный круговой цилиндр	й2 —X2 Z = 2т —	-— (х2 + Л2)2	S(co) ~ l/2n m |co | e— 1 “1 A
Бесконечная горизон- тальная полоса шириной 21		S(to) = 2Д/2зт vp S'n—- x (0 X e— 1W1 tl
	\	Л sretg л )	
Бесконечная горизон- тально заряженная по- лоса шириной 2/ или пря- моугольная призма бес- конечной длины шириной 2Z, расположенная так, что верхняя грань парал- лельна поверхности зем- ли при вертикальном на- магничении	Z = 2m ^arctg х	_ »dg н )	5((о) = 2У2я m^5-^ X CO Xe-lal*
Бесконечная вертикаль- ная материальная пло- скость Бесконечная вертикаль- но заряженная полоса	х2 +	S (и) = У2 л vp —— x l“l x (e-lе-|ш|Лг) S (co) = У2л m —— X |co| x (e-l«>|h._ e~
	x2 + hl х2-|- Z = m In	 x2 + hf	
Бесконечная горизон- тальная материальная полуплоскость	Ag = 2vp(-y + + arctg — h /	S(<B) = vp —e-l(0'h_ /co — У2л vp e~'“' h
Бесконечная горизон- тальная дипольная пла- стинка шириной 21	,	4m/(ft2-H2-x2)	S(ш) = 2У2л m sin co I X X е-1®1Л1®1 G)
	“ (х»+л*—	
145
Окончание табл. 23
Характеристика объекта	Выражение для поля (аномалии)	Выражение для спектра
Шар (точечная масса)	Ag = vM				S (p) = V M e“pft
Точечная магнитная мае-	,	tnh	S (p) = me~₽fc
са		
Шар массы М	ЛЛ 2Л» —x’-y2 ад == v M	—	S(p) = vMpe" ph
Вертикальный диполь или вертикально намаг- ниченный шар	„	m(2ft2-x2-y2)	S (p) = m p e~pft
	(х2 + у2 + Л2)3/2	
Горизонтальный прямо- угольный параллелепи- пед	Ла AS=VOIUX x	hd^di\dZ	S(ox<b#) = X P X (e“ph‘ — e_phl) X
	[(*-E)2+(i/-n)2+E2]3/2	X e~/(“*E+V’) x dgdr]
То же, при длине 2а и ширине 2Ь		S (<в*Шу) =	X P X (e_p*‘ — e_ph’) X
		X —-— X sin<B*asin УГ
Примечание, v — гравитационная постоянная; а, ц. X — соответственно объемная,
поверхностная н линейная плотность; h, Л„ Л, — глубины залегания соответственно
центра тел, верхних и нижних границ этих тел.
передаваемый по какой-либо системе, имеет ограниченный спектр,
поэтому теорема Котельникова применима ко всем геофизическим
полям.
Функцию s (t), преобразование Фурье которой ограничено по-
лосой частот—а>гр, (огр, можно представить в виде
1 ®Гр
s(t)=—— j S(a>)exp(/®i)d®.
—“гр
Пусть t = iSt = in/©гр, i — любое целое число, тогда
1 ®гр
s(iAi)=------- £ S (ш) ехр (/ni«>/(»rp) d®.
—ш
ГР
(5.31)
U6
В свою очередь, функцию S (со) можно представить рядом Фурье
на интервале (— ©гр, согр) с периодом 2©гр как
S (со) = — £ Ct ехр (/ш©/®гр),	(5.32)
где Ci — комплексные амплитуды вида
2л гр
Ci — —-- J S(®)exp(—/nt©/©rp)d®.	(5.33)
2шгр _Шгр
Из сравнения (5.31) и (5.33) следует, что
Ct =	-?-s(-i).
мгр	шгр \ мгр /
Рис. 23. График восстановления
непрерывной функции (в) по ди-
скретным отсчетам (а) при ап-
проксимации рядом Котельни-
кова (б)
Таким образом, коэффициенты Фурье С{ в разложении (5.32)
пропорциональны значениям фун-
кции s (0 в дискретные моменты
времени iAt = ni/©rp.
Разложение (5.32) полностью
определяет функцию S (со) на
интеграле (—со гр, согр), но по-
скольку S (со) является спектром
s (/), то сигнал s (/) также пол-
ностью определен.
Следовательно, знание значе-
ний s (?) в моменты времени t =
= п1/шгр = i/2frp достаточно для
полного восстановления исходной
функции, так как t = iAt =
= i/2frp, Д/= 1/2/Гр. Иначе, для
точного восстановления непрерыв-
ного сигнала по его дискретным
значениям частота дискре-
тизации сод = 2л/Д/ должна
по меньшей мере вдвое превосхо-
дить граничную (максимальную)
частоту спектра сигнала.
С использованием приведен-
ных выше выражений доказывается
и обратная теорема Котельникова: любую
функцию s (0. состоящую из частот от 0 до ®гр, можно представить
в виде
”	/ ni \ sin (согр/ — nt)
s (0 — 2j s \ шгр ) шгр/ — nt
£~~ -oo	r	r
(5.34)
Ось симметрии этой функции приходится на момент времени
t = nil&rp, в которой она равна единице. В моменты же времени
t = nk/a>rp, k Ф i, она равна нулю. Следовательно, сумма (5.34),
называемая также рядом Котельникова, в момент вре-
мени t — nt/corp дает значение функции s (ш7©гр), так как все ос-
147
тальные члены суммы в этот момент равны нулю. На рис. 23 про-
иллюстрировано образование сигнала s (t) из функций, стоящих
под знаком суммы в (5.34).
Влияние величины интервала А/ на форму спектра S (<о) может
быть показано на следующем примере [6]. Предположим, что не-
которая непрерывная, вещественная и четная функция s (t) имеет
Рис. 24. Графики, характеризующие влияние шага дискретизации иа форму
спектра дискретного сигнала [8].
-2л/«гр о гх/шгр
а — непрерывный сигнал; дискретный сигнал: б — Д/<л/<ог , в — Af = л/со ,
Д* >Л(1)гр	Р	Р
ограниченный спектр S (<о) (рис. 24, а). Амплитуда спектра S (со)
отличается от нуля только в интервале (— согр, <огр). Четность функ-
ции введена лишь для получения вещественного спектра, упро-
щающего его графическое представление. Пусть функция s (t) ди-
скретизирована с частотой ®гр = 2л/А/ при условии согр/2>®гр
(рис. 24, б). Тогда с учетом нормирующего множителя, равного
1/Af, основной и побочные спектры являются точными копиями
спектра входного сигнала и полностью разрешены между собой.
Следовательно, имеется возможность полного восстановления сиг-
нала по его спектру. С возрастанием периода дискретизации Ai
до величины, при которой <огр/2 =согр, картина меняется (рис. 24, в).
При дальнейшем увеличении А/ начинается взаимное наложение
основного и побочных спектров (рис. 24, г). Это наложение назы-
вается элайсинг-эффект. Восстановление сигнала ста-
новится невозможным из-за наложения его спектров.
Явление наложения частот возникает при обработке данных.
Предположим, что требуется вычислить длину записи Т и интер-
148
вал отсчета Д, причем известно, что изучаемый сигнал содержит
две синусоидальные составляющие на частотах 50 и 49 Гц. Чтобы
различить эти частоты в спектре, построенном на конечном интер-
вале, надо взять МТ = 50 — 49=1 Гц, т. е. величина периода Т
должна быть порядка 1 с. При оценке частоты порядка 50 Гц ве-
личина 1/2Д должна быть по меньшей мере 50 Гц и, следовательно,
Л <10 мс. Таким образом, нужно взять по крайней мере 100 точек.
Если бы потребовалось различать две частоты 99 и 100 Гц, необ-
ходимая запись была бы также 1 с, однако интервал отсчета 5 мс,
так что потребовалось бы 200 точек.
Итак, длина записи Т определяет степень различимости пиков,
а интервал отсчета Д — максимальную частоту, которую можно
различить.
В сейсморазведке при регистрации среднечастотных колебаний
в методе отраженных волн шаг дискретизации Д/ принят равным
0,002 с, т. е. frP = 250 Гц, тем не менее из-за наличия уровня мик-
росейсм, спектр которых достигает 400 Гц, высокочастотных со-
ставляющих сигнала, аппаратурного шума, из-за эффекта нало-
жения спектров возникает усиление нежелательных частотных со-
ставляющих. С этим явлением обычно борются путем фильтрации
записи перед ее анализом с использованием фильтров низкой ча-
стоты большой крутизной.
При регистрации каротажных диаграмм в нефтегазовой геофи-
зике шаг дискретизации принят Д/i = 0,2 м, в рудной геофизике
Д/г = 0,025 и 0,05 м. Регистрация полей цифровой электроразве-
дочной станцией (ЦЭС-3) осуществляется с интервалом Д / = 0,05 с
и менее.
В полевых методах магнито-, грави- и электроразведки дискрет-
ность наблюдений определяется шагом съемки. Оптимальная его
величина может быть получена путем расчета спектров для наи-
более узких ожидаемых аномалий и ограничения спектров на ча-
стоте (оГр при уровне в 5—10 % от максимума, при этом Дх =
л/(Орр •
§ 25. СПЕКТРЫ СЛУЧАЙНОГО ПРОЦЕССА
Для случайных процессов, основной характеристикой которых
является автокорреляционная функция (во временной области),
также можно рассмотреть частотные представления.
Поскольку существует непосредственная связь между характе-
ром АКФ и внутренней структурой соответствующего случайного
процесса в зависимости от того, какие частоты и в каких соотно-
шениях преобладают в составе случайного процесса, его АКФ имеет
тот или иной вид. Эти соображения и лежат в основе спектрального
анализа случайной функции (процесса).
Спектр показывает, какого рода колебания (гармоники) преоб-
ладают в данном процессе, какова его внутренняя структура.
Спектральное описание можно дать и стационарному случайному
процессу.
149
Отличие спектров стационарного случайного процесса от спект-
ров детерминированных сигналов состоит в том, что для случай-
ного процесса амплитуды гармоник будут случайными величинами.
Спектр стационарной случайной функции описывает распределе-
ние дисперсий по различным частотам.
Если для стационарного случайного процесса построена АКФ,
его спектр вычисляется по автокорреляционной функции. При этом
получаем различные выражения для спектров случайного процесса
в зависимости от того, как задана его автокорреляционная функ-
ция: в виде дискретно заданного сигнала с периодом Т, в виде
непрерывного периодического или апериодического сигнала. По-
скольку АКФ — четная функция, при разложении в ряд Фурье
учитываются только четные (косинусные) гармоники. Тогда для
АКФ (i) как дискретного сигнала имеем
Sm = У. К(/)ехр(— j2amr/n) = -^— £ R(i) cos 2nmi.. • (5.35)
П i=—r	П i=—r	П
для АКФ в виде непрерывного периодического сигнала R (т) с пе-
риодом Т
Т/2	Т/2
sm = у- R (т) cos — с/т = ~ R (т) cos соттс/т; (5.36)
о	и
для АКФ, заданной в виде апериодической функции,
S (со) = J К(т)ехр(—/сот)с/т = 2[ К (т) cos сотс/т.	(5.37)
—оо	О
Поскольку нечетные гармоники для спектра АКФ отсутствуют,
выражение (5.37) совпадает с энергетическим спектром. Чаще всего
функция S (со) в (5.37) называется спектральной плот-
ностью случайного процесса.
По аналогии с разложением в ряд Фурье, случайная функция
(процесс) может быть представлена в виде так называемого кано-
нического разложения
0 “
Х(/)= 2 (Amcoscom/ + Bmsina>mO,	(5.38)
m=0
где Am и Bm — некоррелированные случайные величины с нуле-
вым математическим ожиданием и дисперсиями, одинаковыми для
каждой пары случайных величин D (Am) = D (Bm) = Dm, опреде-
ляемых по (5.36) при разных т.
Спектральное разложение (5.38) представляет стационарную
случайную функцию, разложенную на гармонические колебания
с частотами ©х, . . . , ©m, . . причем амплитуды этих колебаний
являются случайными величинами.
150
По свойству о дисперсии линейной функции некоррелированных
случайных величин (см. табл. 2) находим дисперсию случайного
процесса
Dx=D[X (01 = S (cos2 &mt + sin2 &mt) Dm =
fll=0
oo
= 2Ж
0
Таким образом, дисперсия стационарной случайной функции
равна сумме дисперсий всех гармоник ее спектрального разложе-
ния.
Спектр стационарного случайного процесса изображается в виде
спектра дисперсий для (5.35) и (5.36), а сумма всех ординат этого
спектра равна дисперсии случайного процесса. Спектр стационар-
ного случайного процесса в виде спектральной плотности представ-
ляет собой сплошную линию, однако площадь, ограниченная этой
линией (кривой) S (®) по-прежнему должна быть равна дисперсии
оо
случайного процесса: Dx = f S(co)<i®.
о
Очевидно, что через спектральную плотность случайного про-
цесса можно выразить его АКФ:
Я(т) =
1
2л
ОО	00
f S (со) ехр (/сот) da =----------J S (со) cos ardr.
—оо	Л О
(5.39)
Выражение (5.37) использовано для расчета энергетических
спектров распространенных в геофизике моделей АКФ (см. рис. 15).
На рис. 15 приведены спектры наиболее распространенных АКФ.
Спектр АКФ единичного импульса (спектр белого шума) является
сплошным (см. рис. 15, а). Спектр АКФ треугольного типа (см.
рис. 15, б) выражается зависимостью IT (со) = 2 (1—cos сог)/лг®2
(г — интервал корреляции) и представлен затухающими по ве-
личине экстремумами, расположенными через интервал 2л/г0.
Спектр АКФ марковского типа [затухающей экспоненты
ехр (— ат) ] приведен на рис. 15, в и описывается выражением
IT (со) — al [л (а2 + со2)]. Спектр АКФ гауссова типа IT (©) =
= гд/я"ехр(—®8г2/2) имеет такую же, как АКФ, колоколооб-
разную форму (см. рис. 15, г). Спектр АКФ затухающей по экспо-
ненте косинусоиды выражается формулой
а
W (со) = —— (------------------------------1--------------------
' ’ 2л V а’ + (о + Р)2 а2 + (<о — Р)2
и представлен на рис. 15, г.
Приведем энергетические спектры и АКФ некоторых распро-
страненных моделей случайных процессов, используемых в
гравиразведке и других геофизических методах:
151
1)	для случайного процесса с равномерным энергетическим
спектром
I А, 0 =£ ®<®гр>
Г(®)= Л
( 0,	®>®гР,
описывающего белый шум с ограниченной полосой,
9 7	2Л V
R (т) =---f W (®) cos aid® =---- f cos ©id® =
2л о	2л о
__ Л coгр sin согрт
л согрт ’
2)	для случайного процесса, описывающего ошибки наблюдений
при работе с гравиметрами (по С. А. Серкерову), АКФ имеет вид
R (т) = R (0) ехр (—ат) cos 0т,
а энергетический спектр
U7 (®) = -АВ. Г----5------1-----2------1.
2л L а’ + (о + Р)2 а2 4- (со — р)2 J
3)	для случайного процесса, описывающего аномалии от беско-
нечного горизонтального слоя со случайным расположением беско-
нечных горизонтальных контактов (по В. Н. Глазневу),
R(t) = 21nf
V н.
, 4Я| + т2
In--------,
4/^ + т2
где Hi и Н2 — глубины залегания верхней и нижней границ го-
ризонтального слоя. Соответствующий энергетический спектр
W (®) = R (0) f 2 In	— [ехр (-гоН^-ехр (—2®Н2)];
\ Л1 / со
4) для контактной поверхности, заданной в виде случайного
процесса величинами z, характеризующими отклонение границы
раздела от Н, где Н — глубина залегания контактной поверхности,
причем | z \/Н < 1, получаем следующие типы АКФ и их спектров.
При избыточной плотности Аоп = const гравитационный эффект
двухслойной среды на уровне Н, как известно, равен Ag (?) =
= 2nGA<rnz (?), где G—гравитационная постоянная, и R (т)х =
= (2nGAcrn)2R (т)2, где R (т)х и R (т)г — АКФ аномалий границы
раздела и самой границы, т. е. контактной поверхности. Энергети-
ческий спектр при этом будет
^(®)1 = (2лОАоп)а^(®)г.
Тогда энергетический спектр аномалии на оси х, с которой сов-
падает начало координат, на высоте Н от средней линии контактной
поверхности
W (®) = (2л0АОп)4 * * * 8 ехр (—2®//) W (®)г.
152
Если распределение z полагать белым шумом, то
( (2лОДоп)2 А ехр (—2аН), О С со С ©гр,
U7(®) — I	qj	©>югр.
Тогда при (огр —> оо (достаточно считать согр > (3-4-4)///) АКФ
имеет вид
R (т) = —— J W (®) ехр (/ют) d© =
= —— (2лОДоп)2 A J ехр (—2©Н) cos ©rd© =
2л	о
= —(2лСДоп)2А-----—------
2л '	’	4Я« + т®
Если
U7(©)= ехр (—©720),
д/2л
при R (т) = R (0) ехр (— 0т2) имеем
W (®) = (2лОДоп)2-ехр (—2©Н — ©а/40).
V20
Если контактную поверхность аппроксимировать последова-
тельностью взаимно независимых функций вида f (х) = ЬгЦх* + г2),
где z — глубина залегания эквивалентного цилиндра, радиус кор-
реляции элемента контактной поверхности гг = лг, то
U7 (©) = д/я /2 л ft2 ехр (—2©Гг/л);
W (®) = у/л/2 пЬг (2nfAan)z ехр [—2© (Н + гг/л)].
При определении энергетических спектров (спектральной плот-
ности) по АКФ, полученных по экспериментальным данным, сле-
дует иметь в виду, что длина АКФ сказывается на разрешающей
способности спектра. На рис. 25 приведена АКФ сейсмической за-
писи длительностью 180 мс и ее спектры, которые рассчитаны для
различных интервалов АКФ. Из рассмотрения этих спектров сле-
дует, что они становятся все менее разрешенными при уменьшении
интервала АКФ.
Для спектрального анализа нестационарных случайных про-
цессов используется понятие текущего спектра. При этом
применяются преобразования Фурье с той лишь разницей, что
пределы интегрирования изменены таким образом, чтобы учесть
нестационарность изменения процесса по времени. Учет неста-
ционарности производится либо интегрированием от — оо до не-
которого момента времени t0 и дальнейшего дифференцирования
результата, либо интегрированием от т0 до т0 + бт0 на небольшом
интервале.
163
В случае первого приема обработки определяется текущий
спектр Фурье
У»
5(т0, (!))== I s(/)exp (—jatjdt.	(5.40)
—00
в предположении, что s (f) = 0 для />т0.
Рис. 25. Автокорреляцион-
ная функция (а) и оценки
ее спектров (б) при различ-
ной длительности АКФ
(1-3) [Н]
О 20 40 60	80 100 f,Гц

Текущий спектр является функцией двух переменных <в и т0.
Он характеризует процесс формирования спектра, причем
S (®) = lim S (со, т)
Т->оо
Подставив (5.40) в (5.30), находим
-J- ” |S(T, ®)|«d®= I1 |5(П|‘Л,
ZJl —00	—ОО
а продифференцировав это выражение по верхнему пределу интег-
рала, получаем
*00
®)lad® = ls(To)l8-
хЛ —оо uCq
Правая часть последнего выражения — мгновенная мощность
сигнала, т. е. мощность (энергия) в момент времени т0, а
d'/difJS (то,со)а — мгновенная спектральная плотность мощности
(энергии).
154
Согласно второму приему оценки спектров нестационарных со-
бытий определяется текущий спектр в виде
/0+Дт„/2
s(t0, га, Ат0) = f s(f)exp(—(5.41)
to— Дт0/2
где t0 — центральная точка в окне длительностью Ат0.
Этот спектр принято изображать с помощью изолиний на гра-
фике с осями т0 и ®, его построение использовалось при анализе
дисперсии сейсмических поверхностных волн и при обработке ко-
роткопериодных геомагнитных вариаций.
Следует отметить, что аналогичный подход используется при
построении автокорреляционных функций, когда вычисляется те-
кущая АКФ, например при изучении распределения силы тяжести
или вектора АТ с целью районирования гравитационного и маг-
нитного полей.
§ 26. г-ПРЕОБРАЗОВАНИЕ И РАЗЛОЖЕНИЕ СИГНАЛОВ
ПО ДРУГИМ СИСТЕМАМ ОРТОГОНАЛЬНЫХ ФУНКЦИЙ
При построении линейных фильтров и их анализе широко исполь-
зуется z-п реобразование последовательности дискретных
значений, которым является полином
п—1
^(г)—fo + fiz 2 + • • • +fn-iz ' ,)== 2 ft2 1-	(5.42)
Если сигнал описывается последовательностью —1, —3, О,
1, 3, 2, его z-преобразование в соответствии с (5.42) будет
F (?) = (— 1) г° + (3) г-1 + 0 • z~2 + г~8 + Зг-1 + 2z"8 =
= — 1 —Зг-1 + г-8+Зг-1 + 2г"5.
По заданному z-преобразованию однозначно восстанавливается
исходная последовательность значений. Например, если / (г) =
= 1—г-2, исходная последовательность /7 = 1,0, — 1.
Если сравнить z-преобразование с преобразованием Фурье ди-
скретно заданного сигнала
. п-1	___
Sm = — У. ft ехр (—jai/n),	j = V— 1,
п (=0
это выражение, отбросив нормирующий множитель 1/п, можно
представить следующим образом:
Sm = fo + fiexp(—/a>) + f2exp(—2/a>) + f8exp(—3/®)+ ...
(5.43)
При сравнении (5.43) с (5.42) видно, что под символом единич-
ного сдвига z понимается комплексная величина ехр (/®А). Таким
образом, z-преобразование — особая запись. комплексного спектра
дискретной последовательности значений. С помощью z-преобра-
155
зования очень удобно представить операцию свертки двух сигна-
лов:
Pl (z) = f 10 + /llz 1 + /12z 2+ • • • +/1Л-1Z ''i
Fz (z) = /20 + f21Z 1 + fzz^ 2 + . . . + m_iZ (m ’’ 
Перемножив оба z-преобразования, получим
/^(z) f'l(z) =/20/10+ /WllZ-1 + f2o/12Z-2+ • . . +/Wln-lZ—(n—1,+
+ f21floZ_1 + f21fllZ-2+ • • . +f21fln-lz—<n—1) +
+ /22floZ~2+ • • • +/22/1 n-lz—!) +  • . +
+ fz m-lfl n-iZ_(n+m—2) = /20/10 + (/20/11 +/21/ 10) Z-1 +
+ (f20А2+ fllf21 +/22/10) Z~2 + . . . +/2 m-1/1 n-lZ~(n+"’~I). (5.44)
При сопоставлении выражения (5.44) с (5.42) видно, что пер-
вый член правой части (5.44) представляет собой начальный (нуле-
вой) элемент полученной свертки. Коэффициент при г1 — первый
ее элемент, коэффициент при г-2 — второй элемент и т. д., а вся
правая часть (5.44) есть z-преобразование полученного нового
сигнала, т. е.
r(z) = F2(z)/?i(z),
что совпадает со свойством ппеобразований. Фурье свертки двух
сигналов.
Выражения (5.42) и (5.43) описывают одностороннее z-преобра-
зование, когда последовательность дискретных значений задается
только для положительных значений I. В более общем случае z-пре-
образование определяется через спектр вида
S(co) = £ /гехр(—j®«)
i=—00
и называется двусторонним z-п реобразованием
F(z)= f /fz-‘.	(5.45)
/=—ОО
Уравнение (5.45) определяет z-преобразование при условии,
что независимая переменная z лежит на единичной окружности.
В случае изменения со от — оо до оо комплексная переменная z
вращается по единичной окружности в плоскости г, так как г =
= ехр (ico) = cos соА/ + / sin coAf, делая при этом один оборот
в направлении против часовой стрелки. При любом изменении со
на величину ± 2л/Д в плоскости г происходит циклическое повто-
рение, ‘которое является следствием процесса дискретизации сиг-
нала, а абсолютная величина | z | = 1.
Допустим, что а возрастает скачками, равными л/2Д, в интер-
вале от 0 до 2л/Д. Тогда соответствующие значения г с учетом, что
г = ехр (/ соА), равны 1; /; — 1; — /; 1 соответственно при со = 0;
л/2Д; л/Д; Зл/2Д и 2л/Д.
156
При дальнейшем увеличении со от ®гр до 2согр значения z повто-
ряются.
Для некоторых функций z-преобразование можно выразить ана-
литически.
1. Дельта-функция. Пусть дискретный эквивалент единичного
импульса представляет собой последовательность fi = (..., О, О,
1, 0, 0, . . .), где точка над цифрой указывает на начало координат
по оси времени, т. е. t = 0. Тогда
1=—оо
т. е. спектр 6-функции — постоянная величина.
Между последовательностью значений Д — (1, 0, 0, . . .) и еди-
ничным импульсом 6 (/) существует четкая аналогия. Если еди-
ничный импульс задержан на два интервала дискретизации, т. е.
/,= (..., 0, 0, 0, 0, 1, 0, .. .) z-преобразование будет F (z) — z~2.
2. Единичная (ступенчатая) функция. Она описывается после-
довательностью fi = (. . . , 0, 0, 1, 1, 1, . . .) и ее z-преобразование
будет
F1(z)=l + z-1 + z-2+ . . . =(l-z-1)-1= —L-Г-
I^Kl.
Если эта последовательность сдвинута на два интервала дискре-
тизации, т. е. fi = (. . . , 0, 0, 1, 1, 1, 1, . . .), ее z-преобразование
Fa(z) = z2 + z+l + z-1 + z-2+ . . . -г2Ег(г), |г-х |<1.
Fi (z) и F2 (г) сходятся при | z |>1 или | г"11< 1, так как имеют
единственную особую точку z = 1.
3. Затухающая экспонента. Зададим ее дискретами fi =
= А ехр (—aiA), i > 0. Тогда ее z-преобразование
F{z) = A (1+ехр(—aA/)z-1 + exp( — 2aAi)z~2 + • • •) =
= Л/( 1—ехр (—aA/) г-1); | ехр (—aA£)z-11 < 1.
Наряду с преобразованием (5.45) иногда используется преобра-
зование Лапласа, выражаемое соотношением
F(z) = Е	(5-46)
(«в—-00
Переход от z-преобразования к преобразованию Лапласа осу-
ществляется заменой г на г-1, при этом амплитудный спектр не из-
меняется, а фазовый — меняет знак на противоположный.
Отметим, что одностороннее z-преобразование (5.42) по форме
совпадает с двусторонним (5.45), за исключением нижнего предела.
Двустороннее z-преобразование можно записать в виде
t=o	1=0
157
Первая сумма здесь представляет собой одностороннее z-преобразо-
вание, которое сходится для | z !>/?!, где — верхний предел
последовательности (ft)*'1- Вторая сумма сходится для |z|<R2«
где R g — верхний предел последовательности (fi)~*ft.
Обратное z-преобразование может быть записано через контур-
ный интеграл
Л= V-f F(z)zl~'dz, /=0, 1, 2, . . .
2л/ с
Контур интегрирования С включает все точки F (z), а интегри-
рование ведется против часовой стрелки. Контур С выбирается
так, чтобы он лежал внутри области сходимости ряда (5.42) и вклю-
чал в себя начало координат: z = 0. Величина контурного интег-
рала определяется особыми точками подынтегрального выражения.
Применяя теорему Коши, имеем
Л = Zres[F(z)z‘-1], i = 0, 1, 2, . . . ,
причем суммируются все особые точки, заключенные в контуре С.
Поскольку особые точки F (z) могут быть как внутри, так и вне
контура интегрирования, теорема Коши обеспечивает две возмож-
ности при нахождении ft, а именно ft — Sres [F (z) г1-1], т. e.
все полюсы находятся внутри единичной окружности, и fi =
= — Sres [F (z) z1-1], т. e. все полюсы расположены вне единич-
ной окружности.
На основе (5.42) z-преобразование позволяет вычислить ком-
плексный спектр как функцию вещественной переменной. Запишем
(5.42) в виде
^(z) = fo + fiexp(—/©Д) + /гехр(—/а>2Д)4- ....	(5.47)
В соответствии с (5.47) для данной частоты © = ©0 комплексный
спектр находится как сумма векторного ряда.
В качестве примера найдем комплексный спектр F (г) последовательно-
сти чисел ft'= (. . . , 0, 0, 0, 1,2, 3, 4, 0, 0, . . . л) для частот, равных 0,
л/2Д, 2л/2Д, Зл/2Д [8].
Из выражения (5.47) следует, что значение спектра для со = 0 можно
найти простым суммированием F (1) = 1 + 2 + 3 + 4 = 10, так как все
экспоненциальные множители ехр (— /цнД) в (5.47) становятся веществен-
ными и равными единице. Для более высоких частот получаем:
<о = л/2Д;	Д(г)= 1+2е_/я/2—3 + 4е_,3я/2 = — 2 + 2/;
со = л/Д; F (г) = 1 + 2е“/я + 3 + 4е_/я = — 2;
со = Зл/Д; F (г) = 1 + 2е_/3я/2 — 3 + 4е“/я/2 = -2 — 2/.
Отсюда значения амплитудного и фазового спектров для заданных частот со:
Rm	фт
0	10	0
л/2Д	2^2	Зл/4
л/Д	д/2	— л
Зл/2Д 2 VF — Зл/4.
158
Значения амплитудного и фазового спектров для частоты о = 2л/Д
будут такими же, как и для частоты со = 0, в силу свойства периодичности
спектра, так как 2л/Д = согр.
Помимо преобразования Фурье, z-преобразования и преобра-
зования Лапласа в обработке геофизических данных находит при-
менение разложение полей по другим системам ортогональных
функций. Часто рассматривают эти системы на отрезке Т [— 1, 1 ],
т. е. с периодом, равным 2.
На отрезке Т [— 1, 1] получают систему полиномов
Лежандра:
Фо (t) = —L_;	ф1 (t) = д/3/F t- <р2 (0 = д/5/2 (3/а/2 — 1/2);
уг
фз(0 = л/7/2 (5£а/2—3t/2); . . . ; ф„ (£) = д/(2п+ 1)/2 Рп (t),
где
Рп (/) = —----------1)»
' ’	2"л1 dtn к '
— общий вид полинома Лежандра.
На этом же отрезке Т [— 1,1] рассматривается система поли-
номовЧебышева
фл(/) = 2п(2л)—1/2Тл (/),
где Тп (0 — полиномы Чебышева:
T0(t), . . ., Tn(f) = -^~ cos (п arccost).
Из полиномов Чебышева путем замены % = 1—2 ехр (— 2pf)
получаем функции Чебышева
р„(0 =2п(р/я),/2Тл(1-2ехр(-2рО).
В последнее время все большее внимание уделяется функ-
циям Уолша, представляющим собой ортонормированную
систему функций типа прямоугольных волн (рис. 26). Эти функции
принимают значение только 1 или — 1 и обозначаются символами
IT (k, i), где k — частота следования, i — текущий дискрет сиг-
нала.
Для дискретного сигнала Д, заданного на интервале (0, п)’,
т. е. О < i п—1, п — 2Г, где г — целое положительное число,
рассматривают систему функций Уолша как заданную либо на
интервале (0, 1), либо на интервале (0, л), состоящую из п дискрет-
ных базисных функций W (k, i), по которым и проводится разло-
жение дискретного сигнала. Такая система образует квадратную
матрицу размерности п, номера строк которой k, а каждая строка
обозначает функцию Уолша с номером i, причем 0 < k < п—1.
Спектр Уолша определяется соотношением
S{k)=^-YftW{k, I),	(5.48)
п
159
а обратное преобразование Уолша
Я— 1
ft= 2 S(k)W(k, 0.
i=0
С увеличением k растет частота следования, что аналогично
росту частоты в преобразовании Фурье.
На рис. 26 приведено восемь функций Уолша на интервале
(0, 1), при этом функции задаются системой уравнений:
W(k, 0 = 0;	/<0,	/>1; а
№(0,0=1;	0 <=/<!;
W (2k, t) = W(k, 2t) +
+ (— 1)*№[Л, 2 (/—1/2)];
Рис. 27. Спектральные характери-
стики белого шума (а) и импульса,
возбужденного электроискровым ис-
точником (б), полученные иа основе
дискретного преобразования Фурье
(/) и преобразования Уолша (2) (по
Б. Л. Пивоварову)
Рис. 26. Графики восьми функций
Уолша
Г(2Л+1, t) = W(k, 204-
+ (— l)*+1№[fc, 2а—1/2)],
k = 0, 1, 2, . . .
Каждая последующая функ- -------------------------------
ция Уолша, как видно из рис. 26,
образуется из предыдущей путем ее сжатия на первой половине
интервала и повторения этого сигнала на второй половине интер-
вала с тем же или обратным знаком.
Приведенные на рис. 27 спектры Фурье и Уолша получены по
реализации белого шума, заданного 64 дискретами. Их сравнение
позволяет говорить о возможности применения функций Уолша
для частотного анализа сигналов. Спектральные кривые близки
по форме, совпадают их положения экстремумов, хотя соотношение
интенсивностей несколько различается.
Функции Уолша образуют ортонормированную систему функ-
ций, что делает их удобными для использования в преобразованиях
и при вычислении спектров, но основное их достоинство состоит
в быстроте вычислений. Преобразование Уолша можно выполнить
160
быстрее, чем БПФ, поскольку используются только операции сло-
жения и вычитания. При преобразовании Уолша отсутствует так
называемое явление Гиббса (см. § 30), однако при вычислении
корреляционных функций и сверток, например в сейсморазведке,
возникают трудности, обусловленные коррекцией записей за влия-
ние функций отклика регистрирующей аппаратуры.
§ 27.	ОСНОВНЫЕ ПРИЛОЖЕНИЯ СПЕКТРАЛЬНОГО АНАЛИЗА
ПРИ ОБРАБОТКЕ ГЕОФИЗИЧЕСКИХ ДАННЫХ
Использование спектрального анализа в геофизике чрезвычайно
широко и разнообразно.
1.	Оценка спектрального состава изучаемых полезных сигна-
лов и помех. Это центральная проблема, возникающая при разра-
ботке регистрирующей аппаратуры и алгоритмов обработки во всех
без исключения геофизических
методах.
Так, например, по спектраль-
ному составу волн, возбуждаемых
поверхностными источниками, мак-
симум спектров полезных отра-
женных сигналов приходится на
диапазон от 20 до 40 Гц (рис. 28),
для низкочастотных поверхност-
ных волн (они же и низкоскорост-
ные v = 0,2 ч- I км/с) —на диапа-
зон 5—10 Гц и, наконец, частот-
ный спектр микросейсм, весьма
широк и достаточно постоянен.
Поэтому при разработке сей-
сморегистрирующей аппаратуры
с целью выделения полезных си-
гналов необходимо учесть подавле-
ние как низкочастотных, так и
высокочастотных составляющих
общего спектра регистрируемых сигналов. Если при регистрации
не удалось осуществить оптимальное их подавление, это дости-
гается при дальнейшей обработке записей на ЭВМ.
При регистрации потенциальных полей в магнито-, грави-,
терморазведке и ряде методов электроразведки нельзя отделить
низкочастотные составляющие, к которым относятся региональный
фон, аномалии от крупных объектов, а также полезные сигналы
от высокочастотных составляющих, обусловленных погрешностями
измерений (рис. 29).
2.	Исследование возможностей тех или иных преобразований
(методов обработки) геофизических полей. В качестве примера при-
ведем спектры основных преобразований, используемых в магнито-
и гравиразведке (по К. В. Гладкому). Анализ спектров этих преоб-
разований (рис. 30), называемых частотными характеристиками
6 А. А. Никитин	161
Рис. 28. Спектры возбуждаемых
поверхностными источниками
волн:
1 — поверхностных, 2 — отраженно-
преломленных, 3 н 4 — отраженных,
5 — микросейсм, 6 — аппаратурного
шума (по М. Б. Шнеерсону)
трансформаций гравитационных и магнитных аномалий, показы-
вает, что операции усреднения поля и перерасчета поля в верхнее
полупространство подчеркивают низкочастотные составляющие и
подавляют высокочастотные. Пересчет поля в нижнее полупрост-
ранство и вычисление высших производных, наоборот, подчерки-
вают высокочастотные составляющие и не подавляют низкочастот-
ные, т. е. аномалии, протяженные по профилю. Вычисление высших
производных после предварительного пересчета поля в верхнее
полупространство обеспечивает выделение частотных составляющих
в пределах некоторого интервала, ограниченного как со стороны
низких, так и со сторон'ы высоких частот, и представляет собой
полосовой фильтр (см. § 30).
Приведенные на рис. 30 частотные характеристики являются
идеальными. На практике преобразование поля ведется дискретно
Рис. 29. Спектры региональной (/),
локальной (2) аномалий и погреш-
ностей наблюдений (3) в гравираз-
ведке
Рис. 30. Спектры основных преобра-
зований в грави- и магниторазведке.
/ — усреднение; 2 — аналитическое про-
должение в верхнее полупространство; 3—
аналитическое продолжение в нижнее по-
лупространство; 4 и 5 — вычисление выс-
ших производных; 6 — вычисление про-
изводных на высоте
в пределах некоторого заданного окна, т. е. сигнал, для которого
рассчитывается спектр, считается периодическим. С учетом этого
С. А. Серкеровым были построены частотные характеристики ряда
наиболее распространенных приемов вычисления высших (вторых)
вертикальных производных силы тяжести и пересчета поля в ниж-
нее полупространство, из которых следует, что все используемые
схемы вычисления высших производных идентичны между собой
и подвержены влиянию высокочастотных составляющих. Из срав-
нения спектров идеальных и применяемых на практике характе-
ристик следует, что до некоторой частоты они совпадают, а далее
либо стремятся к нулю, либо осциллируют около некоторой по-
стоянной величины (сравни рис. 30 и рис. 38). Таким образом,
после некоторой частоты происходит искажение результатов пре-
образования поля. Однако по отношению к погрешностям наблю-
дений спад частотной характеристики благоприятен, поскольку
при этом гасятся высокочастотные составляющие, преобладающие
162
г
в спектре погрешностей наблюдений. Следовательно, чем резче
происходит спад частотной характеристики, тем вычислительная
схема менее чувствительна к погрешностям в исходных данных.
3.	Синтез (восстановление) сигналов по спектрам. С этой целью
используется построение спектров исходного геофизического поля
и вычисление по формулам обратного преобразования Фурье зна-
чений сигнала в заданном из определенных априорных соображе-
ний интервале частот. В частности, для оценки региональной со-
ставляющей f обычно достаточно взять лишь несколько первых гар-
моник
3
fi = Ro + 2 Е Rm cos (Ф„ + 2nmiln)
т=1
и тем самым осуществить один из приемов низкочастотного сглажи-
вания.
4.	Построение линейных, в том числе оптимальных, фильтров
и оценка погрешностей линейной фильтрации. Это весьма важная
и разнообразная область применения спектрального анализа (см.
гл. VI и VII).
5.	Совместный анализ наблюдений напряженности магнитного
поля Земли и силы тяжести. Значения магнитного ДТ и гравита-
ционного Ag тюлей заданы в дискретных точках по площади i — О,
1, . . . , п—1; р = 0, 1, . . . , N—1. Объединение полей в каждой
точке производится на основе выражения
f Pi = ^Tpl + jbgpi.
Дискретное преобразование Фурье примет вид
п-1 N-1	.
5 (сох, (ои) = — У Е fpi ехр [—2л/	+ -^-)1 >
nN i=o р— о	L \ я Д' /J
где kx = 0, 1, . . . , п/2, и ky = 0, 1, . . . , N/2 — волновые
числа; сох = 2лkx, <оу = 2nky — пространственные частоты (см.
§32).
Подобный анализ выполняется с целью нахождения намагни-
ченности и плотности пород для случая, когда оба вида аномалий
(ДТ и Ag) вызываются одним и тем же телом.
По характеру изменения формы двумерных спектров, построен-
ных в ячейках заданного размера, производится районирование
наблюденного поля так же, как это делается по изменению формы
двумерных АКФ.
6*
ГЛАВА VI
ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ
ГЕОФИЗИЧЕСКИХ ПОЛЕЙ
Одной из основных задач обработки геофизических полей является
выделение сигналов (аномалий) на фоне помех. С этой целью ис-
пользуются разнообразные приемы преобразования исходного поля,
которые в конечном итоге описываются с позиции линейной или не-
линейной фильтрации.
В настоящее время в разведочной геофизике наиболее широко
применяются линейные фильтры. Преобразование записей упругих
волн по времени (временные фильтры), по времени и по скорости
в пространственно-временной области (интерференционные системы)
в сейсморазведке, различные способы усреднения и пересчетов
полей в верхнее, нижнее, боковое полупространства в магнито-
и гравиразведке — это приемы линейной фильтрации.
Предварительная оценка спектральных или корреляционных
свойств полезных сигналов и помех позволяет обоснованно реали-
зовать нужное преобразование, т. е. провести фильтрацию исход-
ных данных с целью выделения полезного сигнала и подавления
помех. Прежде чем перейти непосредственно к понятию о линейной
фильтрации, рассмотрению различных типов линейных фильтров,
необходимо выяснить, в рамках каких моделей сигналов и помех
ведется построения этих фильтров.
Подчеркнем, что построение любого преобразования поля, т. е.
любого фильтра, проводится в рамках вполне определенной мате-
матической модели наблюденного поля.
§ 28.	МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПОЛЯ.
ПОНЯТИЯ СИГНАЛА (АНОМАЛИИ) И ПОМЕХИ I
Обоснованный [выбор (или задание) математической модели поля
и соответствующая ей постановка задачи преобразования поля яв-
ляются исходным положением (принципом) в обработке геофизи-
ческих данных.
Общепринятой моделью геофизического поля является адди-
тивная модель, т. е. такая модель, в которой результаты
измерения поля fj представляют собой сумму полезной составляю-
щей сигнала (аномалии) S/ и осложняющей ее помехи (или помех) /i;-:
f/=S/ + «/.	(6.1)
Для некоторых типов сейсмических вол'н рассматривают муль-
типликативную модель, когда
fj=Sjnj,
164
однако эта модель несложным преобразованием всегда может быть
приведена к виду (6.1), поскольку In fj = In st + In n,.
Понятия сигнала (аномалии) и помехи в разведочной геофизике
носят не абсолютный, а относительный характер. Поэтому в каж-
дом конкретном случае следует выяснить, что принимать за сигнал
(аномалии) и что считать помехой.
Под сигналом понимается форма проявления поля, в ко-
торую облечена полезная информация. Такое определение чаще
всего используется при описании сейсмических и электромагнит-
ных волн. При регистрации естественных потенциальных полей
обычно применяют термин «геофизическая аномалия»,
под которой понимается отклонение физического поля от его нор-
мальных значений. Нормальное поле — геофизическое
поле, обусловленное однородными по конкретному физическому
параметру горными породами. Однородность зависит от масштаба
исследований. Понятие нормального поля различно для искусст-
венно возбуждаемых (электрические и магнитные поля постоян-
ных токов, переменные электромагнитные поля) и естественных
(магнитного, гравитационного, электромагнитного и теплового) по-
лей.
В первом случае нормальное поле определяется полем заданного
источника в однородной среде, которая обычно отождествляется
с полупространством. Во втором либо нормальное поле рассчиты-
вается аналитически, либо данные наблюдений пересчитывают
в величины, которые для однородного полупространства равны
нулю или константе, как, например, в методе кажущихся сопро-
тивлений электроразведки. При рассмотрении естественных полей
нормальные поля Земли также описываются некоторыми аналити-
ческими выражениями, коэффициенты разложений которых опре-
деляются по данным наземных или спутниковых наблюдений на
всей поверхности Земли или в околоземном пространстве. Напри-
мер, нормальное магнитное поле Земли определяется как сумма
первых десяти гармоник разложения этого поля в ряд по сфери-
ческим функциям (международное аналитическое поле — МАП).
Оно изменяется во времени в связи с западным дрейфером магнит-
ного полюса, поэтому периодически рассчитывается для опреде-
ленного года (эпох), в промежуточные годы для него вводятся со-
ответствующие поправки.
Для естественных полей различают материковые, региональные
аномалии и локальные аномалии различных порядков. Региональ-
ные аномалии охватывают площади в тысячи и десятки тысяч квад-
ратных километров, локальные — от тысяч квадратных километ-
ров до десятых и сотых долей квадратного километра. Такое пред-
ставление позволяет выделить несколько условных нормальных
уровней поля в зависимости от класса аномалий.
За локальную аномалию можно принять такую
составляющую наблюденного поля, которая по линейным разме-
рам (площади) значительно (в 5 раз и более) меньше изучаемых
профилей (площадей) наблюдений, т. е. число характеризующих
165
локальную аномалию’ точек в несколько раз меньше общего числа
наблюдений. При решении разведочной геофизики используют
главным образом региональные и локальные аномалии.
При изучении локальных аномалий за нормальное поле прини-
мается сумма нормального поля Земли, материковых и региональ-
ных аномалий, причем действие первых двух составляющих можно
считать постоянным в пределах изучаемых профилей и площадей
наблюдений.
Выделение региональных и локальных аномалий из суммарного
поля носит условный характер. Так, при выполнении детальных
съемок крупного масштаба для небольших площадей региональную
аномалию, являющуюся отражением, как правило, крупных струк-
турных единиц подземного рельефа, можно принять за постоянную.
Однако при этом крупные локальные аномалии начинают высту-
пать в роли региональных для более мелких аномалий. Например,
при проведении гравиразведки с целью прямых поисков нефти
и газа аномалия, обусловленная структурой, будет региональной
для аномалии, созданной залежью углеводородов. Такие «регио-
нальные» аномалии называют фоновыми. За фоновую ано-
малию принимаются составляющие поля, которые по линей-
ным размерам (площади) значительно (в 5 раз и более) превышают
локальные аномалии.
Под помехой следует понимать всякие возмущающие поля,
препятствующие выделению сигнала, аномалии. Различают помехи
геологического происхождения, вызванные влиянием перекрываю-
щих и подстилающих пород, неоднородностью верхней части раз-
реза, рельефом местности и т. д., и помехи негеологического проис-
хождения — временные вариации полей, блуждающие токи и т. д.
Кроме того, помехи делят на случайные, обусловленные большим
числом неконтролируемых факторов, действие каждого из которых
незначительно (например, случайные погрешности измерений),
и неслучайные (например, фоновая составляющая при выделении
локальной аномалии).
Поскольку любое наблюденное геофизическое поле представ-
ляет собой суперпозицию различных аномалий (сигналов) и помех,
основная задача при его изучении состоит в выделении аномалий
(сигналов), обусловленных изучаемыми геологическими объектами
на фоне помех, а также в разделении поля на составляющие различ-
ной природы. После разделения полей и выделения аномалий (сиг-
налов) проводится физико-геологическая интерпретация послед-
них, включающая установление геологической природы аномалий
и количественное описание их источников. Геологическая природа
аномалий (сигналов) наиболее надежно определяется путем ком-
плексной интерпретации геофизических данных (см. гл. IX); фи-
зические и геометрические параметры источников аномалий —
путем количественной интерпретации.
В математической модели геофизического поля (6.1) сигнал
(аномалия) может быть представлен либо детерминированной, т. е.
аналитически заданной по форме и своим параметрам, функцией,
166
либо случайным процессом с известными (заданными) или неиз-
вестными корреляционными (спектральными) свойствами. Для
модели (6.1) помеха чаще всего описывается случайной функцией,
для которой могут быть известны (заданы) или не известны корре-
ляционные (спектральные) свойства.
Относительный характер понятий сигнала и помехи нетрудно
проиллюстрировать математической моделью вида
fl = $рег / + $лок / +	(6-2)
для которой наблюденное поле представлено суммой региональной
и локальной аномалий и некоррелированной помехой, обуслов-
ленной, например, методическими и аппаратурными погрешно-
стями.
Очевидно, для задачи выделения региональной составляющей
локальная аномалия является помехой и, наоборот, при выделе-
нии локальной аномалии региональная составляющая выступает
в качестве помехи.
Наложение некоррелированной случайной помехи на полезный
сигнал позволяет рассматривать наблюденное поле fa как случай-
ный процесс. Причем, учитывая неизбежное изменение физических
свойств горных пород и геометрических характеристик исследуе-
мых объектов по площади наблюдений, наиболее обоснованным
следует считать задание статистической модели наблюдённого
поля. В то же время целый ряд задач эффективно решается в рам-
ках детерминированной модели поля, при которой fa полагается
аналитически заданной функцией, например при аналитическом
продолжении гравитационных и магнитных полей в верхнее и ниж-
нее полупространство. При этом влияние погрешностей сводится
к нулю путем предварительного сглаживания исходных данных.
Отметим, что при решении задач выделения сигналов в рамках
регрессионного и факторного (компонентного) анализов модель
наблюденного поля описывалась системой случайных величин.
В конечном счете выбор той или иной модели исходного поля
определяется полнотой априорной информации, а точнее, совер-
шенством физико-геологической модели исследуемого объекта. При
малой изученности объектов исследований физико-геологическая
модель груба и, соответственно, априорная информация о форме,
параметрах сигналов и свойствах помех практически отсутствует.
В ходе дальнейших исследований с увеличением объема информа-
ции об объектах изучения, используя механизм обратных связей,
уточняют физико-геологическую модель. Это, в свою очередь, по-
зволяет осуществить выбор более совершенной модели исходного
поля.
Важно подчеркнуть возможность уточнения модели поля в про-
цессе самой обработки. Так, изучение спектрального состава (см.
гл. V) и корреляционных характеристик поля (см. гл. IV) позво-
ляет получить достаточно определенную априорную информацию
о свойствах сигналов и помех. Наличие априорной информации
о сигналах и помехах дает возможность применять оптимальные
167
процедуры обработки данных (см. гл. VII и VIII) для их [разделе-
ния.
Большое значение для выделения сигналов имеет их коррели-
рованность (прослеживаемость) от профиля к профилю (от трассы
к трассе в сейсморазведке). Поэтому площадные наблюдения спо-
собствуют более успешному решению задачи выделения сигналов
на фоне помех.
Рассмотрим на нескольких примерах конкретизацию статисти-
ческой модели (6.1) — (6.2).
1. Построение модели сейсмограммы начнем с введения пред-
ставления об элементарной [волне как основном элементе сейсмиче-
ской записи:
f(t) = as(t—r) + n(t), s(t—x) = Q при t—т<0,	(6.3)
где а — амплитуда, характеризующая интенсивность волны; s (0 —
форма волны по времени; т — время регистрации вступления волны;
п (t) — нерегулярная помеха, связанная с микросейсмами и с на-
ложением тех волн, которые при существующей методике наблюде-
ний и обработке не выделяются раздельно.
Для совокупности К сигналов, например однократных отраже-
ний, модель запишется в виде
к
f (0 = Z akSk (i—tk) + П (О-	(6.4)
fe=i
Волновые параметры ak, Sk, tj, полностью предопределены глу-
бинными факторами, воздействие которых в явном виде в модели
(6.4) не рассматривается.
Модель, описывающую совокупность регулярных и квазирегу-
лярных помех, можно представить аналогично (6.4)
L М
f(O=E Z ад»>(Мл)+л(0.	(6.5)
/=1 т—1
где I = 1, . . . , L — число классов, включающих tn = 1, . . . , М
различных типов волн.
Наконец, для модели многоканальной сейсмограммы, в кото-
рой отображена система наблюдений, путем введения индексации
по пунктам взрыва i = 1, . . . , 1 и пикетам приема /=!,...,/
с учетом (6.4) и (6.5) имеем
к	L м
f (0 = EiakijSkil (^ Tfti/)"b Zj almiishnij	4" ПЦ (O'
k=l	I =1 m=l
Эта модель носит общий характер, поскольку она не привязана
к особенностям того или иного сейсмического метода. В каждом
же методе по-своему определяются классы полезных волн и волн-
помех.
В качестве аналитического представления формы сигнала пред-
ложен ряд формул. Так, нередко сигнал описывают с помощью
функции s (0 = а ехр (— 02£2) sin (соо/ + <р), t > 0, для которой
168
параметры 0 и <р позволяют получать колебания с разным характе-
ром изменения огибающей.
Часто в качестве формы сигнала используют непосредственно
форму АКФ или ВКФ, построенных по наблюденным данным.
При статистической модели времена прихода волн xk принимают
распределенными по закону Пуассона, а амплитуду сигналов —
либо по закону Гаусса (для тонкослоистых толщ), либо по закону
Джефриса (для толстослоистых толщ). Для закона Джефриса среди
коэффициентов отражения, среднее значение которых близко к
нулю, встречаются и довольно большие, причем они фиксируются
чаще, чем этого следовало бы ожидать при нормальном законе.
Первоочередная задача обработки состоит в обнаружении по-
лезных волн на фоне некоррелированных помех, а затем их отде-
ление от коррелированных волн-помех. При этом обычно опреде-
ляются параметры как полезных волн, так и волн-помех. Для ре-
шения задач по обнаружению и разделению сигналов используются
линейные и нелинейные фильтры различных типов.
2. Модели экспериментального материала в гравиразведке для
площадных наблюдений можно свести к виду
fki = ®рег hi W + V 5лок kl (Ю +	(6-6)
1=1
где 0О и 0/ — векторы неизвестных значений параметров аномалий.
При количественной интерпретации эти векторы включают в себя
и значения параметров искомого геологического объекта. Для ре-
гиональной составляющей, заданной в виде регрессии (тренда)
первого порядка
sper kf (а0, аъ а2) = a0 + a1xi + a2yk,
вектор 0 включает три неизвестных параметра а0, аъ а2.
Форма локальных аномалий может быть задана аналитически,
т. е. рассчитана для определенной модели объекта, либо автокор-
реляционной функцией.
. В практике обработки данных гравиразведки для описания кор-
реляционных свойств аномалий и помех при поисках антиклиналь-
ных ловушек нефти и газа получила распространение автокорре-
ляционная функция гауссового типа
R (т) = А2 ехр (—m2/r2),
где А2 — средний квадрат амплитуды аномалии (или помех); г—
интервал корреляции. Обычно полагают, что интервал корреля-
ции аномалии в 5 раз и более больше интервала корреляции помех.
Пример выделения аномалии с'такой формой АКФ рассмотрен
в § 34. Процесс обработки начинается с выделения региональной
составляющей. С этой целью можно использовать уже рассмотрен-
ные выше приемы регрессионного, компонентного и спектрального
анализов. В то же время выделение региональной аномалии —
это процесс низкочастотной фильтрации, выделение локальной
169
аномалии на фоне региональной и некоррелированных помех —
процесс полосовой фильтрации.
Таким образом, при обработке геофизических полей с целью
выделения различных составляющих особое место занимает филь-
трация наблюденных данных, в частности линейная фильтрация.
§ 29. ПОНЯТИЕ О ЛИНЕЙНОЙ ФИЛЬТРАЦИИ.
СВЕРТКА
Под фильтрацией понимается преобразование эксперимен-
тальных данных для выделения полезной информации, создавае-
мой сигналом (аномалией), на фоне различного типа помех, накла-
дывающихся на сигнал и тем самым затрудняющих его выделение.
Такое выделение можно осуществить по частоте (частотная филь-
трация), по времени (временная фильтрация), по направлению
коррелируемости сигнала, в частности по скорости в сейсмораз-
ведке (скоростная фильтрация), одновременно и по времени и по
направлению (пространственно-временная фильтрация в сейсмо-
разведке) и т. д.
Преобразование экспериментальных данных, иначе — входных
данных f (t) или f (х), в некоторую выходную функцию у (/) или
у (х) проводится путем применения оператора фильтра L:
y(tj) — L[f(tj)]r j = l, . . . , п.	(6.7)
Последовательность у (tj) получается как результат воздейст-
вия оператора L на входную функцию f (f). Операторы L могут быть
линейными и нелинейными.
Линейным оператором L (или линейным фильтром)
называется оператор, который удовлетворяет двум свойствам: если
С — некоторая постоянная, а A (t) и /2 (/) — различные входные
функции, то
L[C/(0J=cL[4(01;	(6-8)
L[M0W0]=W0] + MM0b
Фильтры, которые не удовлетворяют этим условиям, называют
нелинейными. В частности, расчет автокорреляционной
или взаимно корреляционной функции является примером нели-
нейной фильтрации. Класс линейных фильтров (операторов) опи-
сывается выражением
т
y(t)= J h(t—x)f (x)dx.	(6.9)
To
Это выражение, называемое интегралом Дюамеля или интег-
ралом свертки, характеризует широкий класс преобразо-
ваний наблюденного поля: фильтрацию, сглаживание, интерпо-
ляцию.
Сигнал на выходе любой физический системы (например, элек-
трических фильтров) не может предшествовать по времени соот-
170
ветствующему сигналу на входе, т. е. если f (/) = 0, t<zT0, то
у (О = L [/(/)]= О, t<T0.	(6.10)
Фильтр, удовлетворяющий условию (6.10), называется физи-
чески осуществимым или каузальным.
Если для физических фильтров, например электрических, ус-
ловие каузальности обязательно, то для фильтров, реализуемых
на ЭВМ, оно теряет свою важность. Более строго, физически осуще-
ствимым называется фильтр, удовлетворяющий двум условиям:
1) линейный оператор h (t) = 0 при /<0; 2) Л (I) -> 0 при t оо,
причем
f \h(t)\dt< оо.
о
Дискретным аналогом интеграла Дюамеля, т. е. дискрет-
ным аналогом свертки, является выражение
!/(//) = £л(//-т)/(^),	/=0,1..........п. (6.11)
«=о
Учитывая, что фильтрация может быть осуществлена как по
времени, так и по любой пространственной координате, запишем
(6.11) в виде
///=£Л/-Л>	/ = о, 1.......п.	(6.11')
т=о
Другая форма свертки получается путем замены i = /—т:
м
yi-lLhds-i, 7 = 0, 1, . . . , п.	(6.12)
<=о
Переход от (6.11) к (6.12) определяет свойство перестановочно-
сти (коммутативности) операции свертки, состоящее в том, что
результат свертки у, остается одним и тем же независимо от того,
какая функция fj или hj сдвигается по оси времени, если эта же
функция одновременно обращается во времени.
Функция hi в (6.12) называется весовой функцией,
которая представляет собой последовательность чисел Ло,
h^, . . . ,
Операция, или уравнение свертки (6.12), является важнейшим,
наиболее часто применяемым преобразованием в цифровой обра-
ботке геофизических данных. Суть этой операции легко уяснить
из следующего примера. Пусть входная функция, т. е. исходные
данные, задана тремя дискретами: fj = f0, flt f2, а весовая
функция — двумя дискретами: hi = h0, ht.
В соответствии с формулой (6.12) имеем:
при / = 0 t/o = Wo;
при j = 1	yi = hofi + hifo,
при / = 2	y2 = h0f2 + h1fi-,
при / = 3 yz = hif2.
171
Процесс получения выходной функции у, может быть изобра-
жен путем перемещения перевернутой по времени весовой функции
вдоль значений входной функции согласно схеме
fo>	fl,	f 2
К h0
К,	h0
[hi, h0
hi, ho-
i Таким образом, процесс свертки состоит из четырех операций:
обращения во времени весовой функции, ее смещения вдоль исход-
ных значений поля, умножения и суммирования (интегрирования).
Общее число значений выходной функции г/;- больше значений
входной функции и равно п 4- М—1. Крайние члены выходной
последовательности (для рассматриваемого примера — у0 и г/8) по-
лучаются при неполной весовой функции, и их значения искажены
(так называемые краевые эффекты). Поэтому в практике обработки
их не учитывают.
Уравнение свертки (6.12) устанавливает связь между входным
и выходным сигналами через весовую функцию и при построении
любых линейных фильтров является основополагающим. Проблема
фильтрации по существу и состоит jb нахождении весовой функции,
исходя из заданных критериев цели обработки, выбранной мате-
матической модели экспериментального материала, полноты апри-
орной информации о сигнале и помехах.
Свертка некоторой функции /у с-единичной функцией 6,, опреде-
ляемой как
=J b /==°’
'' 10, /V0,
(6.13)
дает в результате саму исходную функцию fjt в чем нетрудно убе-
диться, положив hi = 1, 0, 0.
ото свойство в сочетании со свойством коммутативности позво-
ляет определять неизвестную весовую функцию некоторой си-
стемы. С этой целью в качестве входной функции следует взять
fj = б/, тогда по формуле свертки получим
м	м
У1= Z htfj-i = £ /г,6/_( = /г/.
1=0	4=0
Операцию [свертки часто обозначают звездочкой, т. е. вместо
(6.12) записывают
y = h*f.	(6.14)
Представление свертки в виде (6.12) и (6.14) называют синте-
зом во временной области, если все три величины
у, h и f являются функциями времени.
172
Используя преобразование Фурье, в частности свойство о
свертке двух сигналов (см. § 24), свертку во временной области (6.12)
можно записать в частотной области в виде произведения двух ком-
плексных спектров Н (со) и F (со), т. е.
Y (со) = Н (со) F (со),	(6.15)
где
Н(со)= ]’ h(t)e~iaidt	(6.16)
«•30
называется частотной характеристикой фильтра
и весовой функции; F (со), Y (со) — спектры соответственно вход-
ной и выходной функций.
При дискретном задании весовой функции Н (со) определяется
через дискретное преобразование Фурье.
Обратное преобразование Фурье позволяет получить весовую
функцию h (f), если заданарсастотная характеристика фильтра
Я (со)Я
/i(0 = — J’ Я (co)Je/w/dco.	(6.17)
2л —оо
Амплитудный спектр функции у (t) равен произведению ампли-
тудных спектров функций h (t) и f (t), а фазовый — сумме фазовых
спектров этих функций,^, е.:
/?!/((0) = ^((0ВД(0);	(6.18)
сру(со) = ср/ (со)н-(со).	(6.19)
Частотная характеристика Н (со) является [комплексным спект-
ром; через амплитудный и фазовый спектры она выражается как
Я(®) = 7?4((о)е/<р<<ш),	(6.20)
где (со) = | Я (со) | = д/Л2 (со)-FB2 (со) — амплитудно-
частотная характеристика фильтра, или к о -
эффициент передачи линейной системы;
срЛ (со) = arctg [— В (®)1А (со)] — фазово-частотная ха-
рактеристика фильтра.
Амплитудно-частотная характеристика определяет усиление
спектральной составляющей сигнала на определенной частоте при
прохождении его через линейной фильтр. По фазово-частотной
характеристике для любой частоты определяется временная за-
держка, создаваемая фильтром на заданной частоте. Rh (со) и <рл (со)
полностью характеризуют фильтр.
Для вещественных сигналов на входе и выходе фильтра вы-
полняется следующее свойство симметрии:
| Я (со)| = | Я (—со) |;	<р(— со) = — <р(со).
173
Если применить обратное преобразование Фурье к выражению
(6.15), получим
1/(0 = 4“ Гя(со)/=’((о)е'^(0 =
= 4- f /?/,(©)£(©) o'(6.21)
2л _oo
Таким образом, для получения результата фильтрации во вре-
менной области необходимо сначала выполнить прямое преобразо-
вание Фурье входного сигнала и весовой функции, затем перемно-
жить их спектры и, наконец, найти обратное преобразование Фурье
от произведения спектров.
Частотная характеристика фильтра Н (со) определяется через
ее действительную А (со) и мнимую В (со) части или амплитудно-
частотную R (со) и фазово-частотную ср (со) характеристики:
Н (со) = А (со) + jB (со) = R (со) ехр [/<р (со)].	(6.22)
Построение, или синтез, фильтров в частотной области через
характеристики R (со) и ср (со) — весьма распространенный прием,
что определяется простотой описания с их помощью желаемых ха-
рактеристик фильтра. Расчет фильтров во временной области часто
используется при построении оптимальных фильтров (см. гл. VII).
Для широкого класса фильтров R (со) и ср (со), так же как А (со)
и В (со), не являются независимыми друг от друга: каждая из них
может быть однозначно определена из другой функции путем пре-
образований Гильберта. В частности, вещественная
А (со) и мнимая В (со) части частотной характеристики физически
реализуемого фильтра связаны следующей парой преобразований
Гильберта:
4 (а) = — { 4 * * * В (v) dv; в (и) = -L- Г -4	dv.
Л J V — со	л J V — со
—оо	—оо
Таким образом, учитывая изложенное, можно сделать вывод
о том, что фильтрация — это линейное преобразование исходных
данных. Целью этого преобразования является изменение спек-
трального состава входного сигнала, а именно: пропускание одних
спектральных компонент и ослабление (подавление) других.
В аналоговых устройствах обработки данных частотная филь-
трация осуществляется физически реализуемыми фильтрами, пред-
ставляющими собой определенную совокупность элементов элек-
трических схем. Для выбора необходимого режима фильтрации
требуется расчет схемы физического фильтра с определением па-
раметров ее деталей (резисторов, конденсаторов и т. д.). При циф-
ровой обработке частотная фильтрация может быть реализована
либо во временной, либо в частотной области.
Для цифрового фильтра весовая функция является временной
последовательностью определенных дискретных значений. Соот-
174
ветственно цифровым фильтром называют фильтр, сиг-
налы на входе и выходе которого представлены последователь-
ностями дискретных значений.
Спектр выходной функции, получаемой в результате фильтра-
ции, может содержать только те частоты, которые присутствуют
и в спектре входного сигнала, и в спектре весовой функции. При
фильтрации обычно происходит увеличение длительности сигна-
лов по сравнению с входными сигналами. Для установления нор-
мального режима фильтрации требуется совмещение всех значений
весовой функции со значениями входного сигнала.
Цифровые фильтры в отличие от физически реализуемых всегда
заданы дискретной весовой функцией и, следовательно, имеют
ограниченный частотный диапазон с <огр = ± л/Д/, At — шаг ди-
скретности по времени.
Принципиальное отличие цифрового фильтра от физически
осуществимого заключается в том, что с помощью цифровых фильт-
ров возможно реализовать весовую функцию на времени /<0.
Начало отсчета, т. е. точка t — 0, может быть расположено в лю-
бом месте весовой функции цифрового фильтра: у ее первой орди-
наты, у последней, в центре и т. д. Эта особенность цифровых фильт-
ров является важным их преимуществом по сравнению с физиче-
скими фильтрами, работающими в режиме реального времени, бла-
годаря чему при обработке данных на ЭВМ предоставляется воз-
можность проведения фильтрации в обратном направлении, т. е.
с конца исходной последовательности значений к ее началу. Про-
ведение фильтрации сначала в прямом, а затем в обратном направ-
лении позволяет исключать влияние фазовых искажений весовой
функции, что особенно существенно в тех случаях, когда фазово-
частотная характеристика фильтра не определена.
Если в уравнении свертки (6.12) весовая функция не изменяет
своих значений в процессе фильтрации (обработки) всей исходной
совокупности данных, говорят об инвариантном во вре-
мени фильтре. Если свойства входного сигнала во времени
(или по х) изменяются, следует использовать переменные
во времени фильтры, т. е. фильтры с изменяющейся во вре-
мени весовой функцией.
Фильтры, определяемые уравнением свертки (6.12), называются
нерекурсивными в отличие от рекурсивных, для
которых выходной сигнал выражается не только через выходную
функцию, но и через профильтрованные ранее значения:
М	L
У1=Е hifi-i — £ bflj-l.	(6.23)
i=0	fZi
В уравнении рекурсивного фильтра (6.23) величины входного
сигнала определяются через прошлые и текущие значения вход-
ного сигнала и прошлые значения выходного сигнала.
Рекурсивный фильтр — это фильтр с обратной связью. Именно
благодаря обратной связи общее число весовых коэффициентов
ht и bt для рекурсивного фильтра оказывается существенно меньше,
175
чем для нерекурсивного. Это основное преимущество рекурсивных
фильтров, заключающееся в их экономичности, т. е. в значительно
меньших затратах времени на обработку по сравнению с затратами
времени для обычных фильтров-сверток.
§ 30. ПОСТРОЕНИЕ ФИЛЬТРОВ
ДЛЯ ЗАДАННОГО ДИАПАЗОНА ЧАСТОТ
Фильтры, построение которых проводится в частотной области,
делятся ‘на три основных типа:
1)	низкочастотные фильтры — фильтры, ампли-
тудно-частотная характеристика
ние в полосе пропускания | со |<
а
Н(ш) в	в
Рис. 31. Частотные характеристики
идеальных низкочастотного (а), вы-
сокочастотного (б) и полосового (в)
фильтров
которых имеет постоянное усиле-
и нулевое вне ее (рис. 31, а);
2)	высокочастотные
фильтры — фильтры, ампли-
тудно-частотная характеристика
которых постоянна в полосе
пропускания | со | > со2 и равна
нулю вне ее (рис. 31, б);
3)	полосовые филь-
тры — фильтры, обеспечиваю-
щие равномерное усиление
в полосе пропускания | сох | <
< | со | со2 и нулевое усиление, т. е. бесконечное подавление
за пределами указанного диапазона (рис. 31, в).
Частоты сох и со2 являются граничными частотами,
или частотами среза фильтра.
На рис. 31 приведены амплитудно-частотные характеристики
идеальных фильтров. Реальные фильтры имеют характеристики,
которые представляют ту или иную аппроксимацию характеристик
идеальных фильтров. Основой при построении (синтезе) фильтров
любых типов служит низкочастотный фильтр, поскольку частот-
ная характеристика идеального высокочастотного фильтра
Нв(со)=1 —Ян(со),	(6.24^
где Нн (со) — характеристика низкочастотного фильтра; в качестве
1 — рассматривается характеристика фильтра, пропускающего
без искажений все частоты, а частотные характеристики полосовых
фильтров могут рассматриваться как комбинации характеристик
низкочастотных и высокочастотных фильтров:
/7п(со) = Ян(со2)—Ян(сО1);	(6.25)
Нп (со) = Нв (coi)—Нв (со2).
Следует выделить также режекторный фильтр (за-
граждающий полосовой), предназначенный для подавления очень
узкого диапазона частот, например 50 ±2 Гц. Его характеристика
определяется через характеристики полосовых фильтров и (или)
комбинации низкочастотных и высокочастотных фильтров.
176
Наибольший интерес, как правило, представляют .фильтры, не
вносящие фазовых сдвигов, поэтому стараются использовать ве-
совые функции, мнимая часть частотных характеристик которых
В (со) равна нулю. Рассмотрим построение идеального низкочастот-
ного фильтра вида
(А, I со I <
Я(®) =	(6.26)
( 0, | со |> соь	'	'
где | со | < сох — область пропускания сигнала; | со |>сох — область
подавления сигнала; А — действительное число, определяющее
усиление, фильтра в полосе пропускания. Обычно весовая функция
нормализуется таким образом, чтобы усиление в полосе пропуска-
ния фильтра было равным единице, т. е. А = 1. Поскольку Н (со)—
действительная величина, равная А или нулю, то амплитудная
характеристика определяется только ее вещественной частью, а
фазовая характеристика ср (со) = 0. Следовательно, весовую функ-
цию h (t) находим из обратного преобразования Фурье:
h (t) = -U Jr₽ H (co) e/w/dco = — JrP cos coWco =
2л	л 0J
у4 » j Лсого sin CDpp^	zz*
=-----sin (orD/ =------------.	(6.27)
Tit	JT	CDpptf
Эта функция имеет форму интегрального синуса sin х/х и беско-
нечна по времени. Величина А согр/л — постоянна и без ограниче-
ния общности ее можно полагать равной единице, ®гр = ®1-
Для реализации цифровой фильтрации во временной области,
естественно, используются только фильтры с операторами ограни-
ченной длины М, т. е. вместо h (t) применяется некоторая функция
h (t), равная нулю при 11 ]>Л1 /2. При этом очевидно, что частотная
характеристика ограниченного фильтра h (/) будет уже не Н (со),
а другая характеристика
ЛС/2	М/2
Я(со) = J h(t)e~ia>tdt = £	(6.28)
— MI2
Весовая функция
л ( SIH СОгп^/сОгр/,
'Н , о,
Функция h (/) и соответствующая ей частотная характеристика
приведены на рис. 32. Весовая функция представляет собой сим-
метричную кривую с максимумом в центре при t = 0. Видимый
период колебаний (осцилляций) близок к 2л/согр. Частотная харак-
теристика Н (со) весьма существенно отличается от характеристики
идеального фильтра, показанного пунктиром, особенно вблизи
граничной частоты. Это отличие проявляется в виде плавного пе-
рехода в области ступенчатого изменения и колебаний самой ча-
стотной характеристики.
/=—ЛС/2
|/|<М/2,
(6.29)
177
Колебания возникают из-за разрывности характеристики иде-
ального фильтра и определяют так называемое «явление Гиббса».
Амплитуда колебаний Гиббса максимальна вблизи граничной ча-
стоты фильтра и не зависит от длины весовой функции М и от югр.
Она во всех случаях составляет 9 % от проектируемой величины
усиления А, в частности от единицы (А = 1). Это — основной недо-
статок фильтра (6.28), приводящий к тому, что в области подавле-
ния помех их остаточная энергия будет значительной,.
На практике используются фильтры, имеющие меньшую кру-
тизну частотной характеристики в области среза и меньшую ам-
плитуду колебаний Гиббса по сравнению с характеристикой, опре-
деляемой по'формуле (6.28).
Рис. 32. Частотная характеристика
(а) и весовая функция (б) низкоча-
стотного фильтра
ff
hit)
Рис. 33. Частотная характеристика
фильтра с косинусным сглаживанием
Одним из распространенных фильтров, применяемых при об-
работке сейсмических записей и данных электроразведки, является
фильтр с косинусным сглаживанием в области среза. Амплитудно-
частотная характеристика такого фильтра
Я(©) =
1,
Г1 Ч-COS (I © I — ®гр+£)
2 L 4£
О,
[| ©|<®гр — £,
©гр-® I < ®гр4""
| © |>©гр + I-
(6.30)
Обычно I < ©гр.
На рис. 33 видно, что заданием величины | можно регулировать
крутизну среза фильтра, одного из важнейших параметров поло-
совых фильтров.
В соответствии с (6.30) весовая функция определяется выраже-
нием [9]
h(t) = £ Я(ю)е/т/ = —n Мгр<
-о>Гр+&	nt
1______sin (од/ + sin a>2t;
~ 2nt 1 — (/2/л2) (<o2 — ©i)8
COS 5<
1 — 452/2/rt2
(6.31)
где ©j — ©гр I; ©2 — ©rp 4~ £•
178
Такой фильтр обеспечивает на порядок лучшее подавление по-
мех, чем фильтр (6.29) при выполнении условия
М|>2,6л	(6.32)
Поскольку частотная характеристика дискретного фильтра,
рассматриваемая как дискретный сигнал, является периодической
с частотой повторения 2согр = 2л/Д/, вся информация о спектре
обрабатываемых сигналов должна содержаться в частотном квад-
ранте— л/Д/<(о<л/Д/. В противном случае повторные макси-
мумы частотной характеристики будут приводить к усилению по-
мех. Оптимальное число дискретов М. весовой функции определяется
из соотношения (6.32). Так, М = 2,6 л/|Д£ = 2,6-3,14/20-0,002 =
= 204 при | = 20 Гц и Д / = 0,002 с.
Рис. 34. Частотные характеристики полосового фильтра с несимметричными
срезами (а) и режекторного фильтра (б)
Частотная характеристика высокочастотного фильтра с коси’
нусным сглаживанием
/7В (<о) = 1 —	(со),
где Нн (®) определяется из (6.30).
Весовая функция, соответственно, будет определена как
я/Д<
йв(0= Е
—л;Д<
С учетом (6.31)
Лв (0 = .“—hu(t) =
nt
= J_[2_______sinwit-sitW—1	f==1 2	(6 ,зз)
nt L 1 — <* (co2 — <01)г/л2 J
Фактически в силу периодичности характеристики дискретных
сигналов фильтр hB (/) является полосовым, так как пропускает
частоты от (огр до Q = л/Д t. В противном случае спектр исходного
сигнала будет искажен наложением зеркальных частот (эйлясинг-
эффект).
Соответственно частотная характеристика полосового фильтра
находится как разность характеристик двух низкочастотных фильт-
ров с разными граничными частотами <о2 и : Нп (®) = Н„ (<о2)—
179
—Ня ((Oj). Отсюда h„ (/) = й2 (/) — Л^(0, где h2 (t) и h± (t) — ве-
совые функции, определяемые через Ня (и2) и Ня (©J.
Для симметричного полосового фильтра с косинусным сглажи-
ванием [19]
hn (0 = —7-	2 (sin (d2t— sin ©J0.	(6.34)
nt 1 — 4|2/2/л2
Задавая различную крутизну срезов низкочастотных фильтров,
получим весовую функцию полосового фильтра с несимметричными
срезами (рис. 34, а) [19]:
_	1 Г sin co3f + sin со4/__sin со4/ + sin co2< 1	„r.
" 2nt L 1 — /2 (<o4 — со3)2/л2	1 — t2 (co2 — Ш1)2/я2 J
Смысл частот <o2, <o3 и <o4 ясен на рис. 34, а.
По формуле (6.35) рассчитываются весовые функции широкого
класса фильтров: прямоугольных при ©4 да ©2 и <о3 да ©4, трапе-
цеидальных и треугольных при <о2 = <о3.
Весовую функцию режекторного фильтра можно получить как
разность весовых функций низкочастотного и полосового фильтров
или же как разность весовых функций двух полосовых фильтров.
Отметим, что задание граничных частот накладывает существен-
ные ограничения на длину применяемых весовых функций: чем
уже полоса пропускания и круче срезы характеристики, тем длин-
нее должна быть весовая функция. С учетом соотношения (6.32)
ширина [пропускания должна удовлетворять условию
Д© > 10л/ЛШ.	(6.36)
Особенно критичным к выбору величины | является режектор-
ный фильтр (рис. 34, б). При	(<о2—©J/2 он не обеспечит не-
обходимого глубокого подавления частотных составляющих в по-
лосе режекции, при	(<о2—©J/2 теоретически достигается су-
щественное подавление, однако в силу соотношения (6.32) это
требует применения очень протяженных по времени (до 0,2—0,4 с)
весовых функций. Ввиду этого для построения режекторного
фильтра следует использовать рекурсивную фильтрацию (см. § 31).
Помимо фильтров с косинусоидальным сглаживанием для
аппроксимации частотной характеристики идеального низкочастот-
ного фильтра используются еще два подхода, связанных с синте-
зом фильтров Баттерворта и Чебышева.
Фильтры Баттерворта наиболее точно аппроксими-
руют характеристику идеального фильтра, причем усиление убы-
вает монотонно с возрастанием частоты и амплитудно-частотная ха-
рактеристика не имеет колебаний ни в полосе пропускания, ни за
ее пределами (рис. 35). Преимуществом этих фильтров является
простота аналитического выражения и возможность управления
степенью-подавления в переходной зоне.
Фильтры Баттерворта обычно задаются квадратом частотной
характеристики в виде
|Яб(®)|2 = 1/[1 + (®М2п],	(6.37)
180
где <ос — частота среза фильтра; п — целое число, определяющее
порядок фильтра.
При и -> О усиление фильтра согласно (6.37) стремится к еди-
нице.
Из рис. 35 следует, что чем выше порядок фильтра, тем быстрее
характеристика приближается к прямоугольной характеристике
идеального фильтра. При со/<ос = 1 характеристика Нъ (©) при-
нимает значение 1/V 2 = 0,707 независимо от п.
Отметим, что наклон частотной характеристики при переходе
от области пропускания к области подавления определяется ее
крутизной К (©). Обычно крутизна К (со) измеряется в де-
цибеллах на октаву. Децибелл (дБ) — логарифмическая мера от-
ношения двух сопоставляемых
величин, например \Н (©Л и
|/7(ft>i)|. Крутизна
К(©) = 201g | Я[(ю2)\/\ Н^)\,
(6.38)
где ©, и — частоты с интерва-
лом-в Гоктаву, т. е. ©а = 2®i-
В частности, область пропус-
кания характеристики Нъ (©) на
уровне \/^ 2 = 0,707 при ©/©гр =
= 1 соответствует ослаблению
в 3[дБ. ^Действительно, согласно
(6.38) имеем 20 1g Мл/2 =
= 20 1g 0,707 - — 3 дБ.
Рис. 35. Частотные характера-
стики фильтров Баттерворта пер-
вого, третьего и пятого поряд-
ков
Величину п для фильтра Баттерворта выбирают, ориентируясь
на желаемую степень ослабления в полосе подавления фильтра.
Например, какое значение п необходимо использовать в уравнении
(6.37), чтобы на частоте 2©с получить ослабление 48 дБ на октаву.
Из определения децибелла (6.38) с учетом (6.37) получаем
201g [| Н (©а) |/| Н (ах) | ] = 101g [| Н (ю2) |а/| Н (©х) |3] =
= 1Q 1g-1	=
1/[1 + (а>1/сос)2л]<о1/о>с=2
= 101gj[ , 11  1 = 48; 1g 2я = 4,8; n = 8.
JL 1/(1 + 22Л) J
Следовательно, для ослабления в 48 дБ п = 8. Обычно ослаб-
ление изменяется на 6 дБ при изменении п на единицу.
Далее по частотной характеристике Нъ (©) необходимо найти
весовую функцию ЛБ (/) цифрового фильтра. Проще всего это сде-
лать в комплексной плоскости с помощью преобразования Лапласа.
Высокочастотный фильтр Баттерворта определяется через ча-
стотную характеристику низкочастотного фильтра как | Нв (со) ]3 =
181
= 1—| Ня (<o) |2. При этом (оя, (ов — частоты срезов соответствую-
щих фильтров. Очевидно, с учетом (6.37)
| нв (©) |2 = 1--------------J'(й)/ -с-)2га 4
1 + (<о/а>с)2"	1 + ((0/(0с)2"
(6.39)
Другим типом фильтров, удачно аппроксимирующих частот-
ную характеристику идеального низкочастотного фильтра, являются
низкочастотные фильтры Чебышева, определяемые квад-
Рис. 36. Частотные характери-
стики фильтров Чебышева
с е — 0,6 и N = 3 (/) и Бат-
терворта третьего порядка (2)
ратом амплитудно-частотной характе-
ристики в виде
|Z74((o)|2=l/[l + e2Cw((o/(oH)b
(6.40)
Уравнение (6.40) — фильтр Чебы-
шева с характеристикой | Нч (©) |2,
имеющей одиночный выброс в полосе
пропускания сигнала и монотонно
убывающей в области подавления по-
мех (рис. 36). Размах этого выброса
6 = 1— (1 +е2)-х/2.
В уравнении (6.40) CN ((о/(он)
представляет собой полиномы Че-
бышева N-ro порядка, получаемые
с помощью рекуррентного соотноше-
ния Со ((о) = 1; С!((о) = (о; Cw+1 (о>) + CN ,((о) = 2(0 CN ((о).
Например, пусть е — 0,6, т. е. о = 0,14, a N = 3. В пределах
полосы пропускания частотная характеристика колеблется от 0,86
до 1, что соответствует приблизительно 1,3 дБ. Характеристика
для фильтра Чебышева на рис. 36 сравнивается с характеристикой
фильтра Баттерворта третьего порядка. Из этого сравнения следует,
что фильтр Чебышева имеет большую крутизну среза, чем фильтр
Баттерворта того же порядка. «Платой» за увеличение крутизны
среза является появление выброса на характеристике в полосе
пропускания.
Полосовые фильтры Баттерворта и Чебышева вначале исполь-
зовались при обработке данных сейсмологии. В настоящее время
они применяются в сейсморазведке благодаря их экономичности
по сравнению с традиционными полосовыми (с косинусным сгла-
живанием) фильтрами. Экономия машинного времени достигается
путем реализации этих фильтров в рекурсивной форме.
Типичным примером линейной фильтрации вдоль пространствен-
ной координаты х, т. е. по профилю, являются трансформации поля
силы тяжести и магнитных полей. К трансформациям относятся
операции усреднения, сглаживания, пересчет поля в верхнее й
нижнее полупространства, вычисление высших производных.
(Спектральные характеристики идеальных фильтров этих преоб-
разований были приведены на рис. 30.) В основу трансформации
заложен принцип линейной фильтрации с целью подавления по-
182
мех и наиболее четкого выделения полезной информации (аномалии).
Так, при усреднении поля в скользящем окне, включающем п
точек, весовая функция в (6.12) постоянна и ее коэффициенты
hi = 1/п. Если ограничить частотную характеристику усреднения
Н (<о) = [sin (©п)/2 ]/ [<оп)/2 ] основным (первым) экстремумом, по-
давление частотных составляющих наблюденного поля будет про-
исходить до частоты © = 2л/п.
Поэтому оптимальный размер палетки усреднения (окна) свя-
зан с заданием граничной частоты спектра аномалий, подлежащих
выделению.
Аналогом низкочастотного фильтра с косинусным сглажива-
нием в гравиразведке является фильтр Страхова с частотной ха-
рактеристикой
Н (®) = 1 — {1 — [cos (<о Дх/2)]2N [р.
Варьируя величинами N и р, подбирают нужную форму частот-
ной характеристики. Обычно = 154-30, р = 3.
На базе операции усреднения, используя разницу результатов
суммирования данных в окнах разной длины, можно построить
полосовой фильтр
1	М,	,
fi = 2/И1+ 1 fl+‘ ~ 2Л12+1 t=£Mi fl+ {‘
Фильтрующие свойства этой операции ^сследованы К. Сейа
при выделении аномалий силы тяжести с помощью преобразований
Фурье. Им рекомендовано ее применение при = 1, М2 = 3
и Afj = 3, ТИ2 = 7.
Аналитическое продолжение поля f в верхнее полупространство
осуществляется на основе интеграла Пуассона
f'(x,
1
Л
оо
HI. 0)
—00
[(£-х)2 + Я?]
lh) =
(Hi — высота пересчета), который можно представить как свертку
исходного поля f (|, 0) с весовой функцией
h(x, =	+
Поскольку весовая функция четная, ее частотная характери-
стика
H(0))=_2^(_£^_dx =
nJ
О
2Я1 я „-!<>», | __ - [<> ( н,
л 2Я1
Частотная характеристика е 1 н‘ экспоненциально убывает с
ростом пространственной частоты что свидетельствует о низко-
183
частотном характере операции аналитического продолжения поля
вверх. Аналитическое продолжение в нижнее полупространство
имеет частотную характеристику Н (©) = е“Н1 и приводит к вы-
сокочастотной фильтрации поля (см. рис. 30).
Для практической реализации вычислений интеграла Пуассона
в гравиразведке существуют разные вычислительные схемы.
В качестве примера, иллюстрирующего характер весовых функ-
ций и частотных характеристик аналитического продолжения поля
как операции линейной фильтра-
а h(x)	ции, приведем две схемы вычис-
I/ г	лений:
j _	1) по способу сеток, основан-
ному на теореме о среднем значе-
2"	нии функции:
Рис. 38. Частотные характеристи-
ки аналитического продолжения
поля в иижнее полупространство.
,	*	«Я „
1 — точное преобразование е ; 2 —спо-
соб сеток; 3 ~ способ Страхова
Рис. 37. Весовые функции аналити-
ческого продолжения поля в иижиее
полупространство для способа сеток
(а) и Страхова (б)
Д§(х, -Н1) = 4Д^(х, 0)-Д^(х + Яь 0)-Дйг(х-Я1, 0)-
— Д^(х, 7/i);
Н (©) = 3,750—2,352 cos ©—0,148 cos 2©—0,07 cos 3© —
—0,04 cos 4©—0,025 cos 5©—0,0115 cos 6©, H1=\\
2) по способу Страхова, основанному на замене функции
Ag (х, Нх) интерполяционными многочленами Лагранжа:
—H^1,3M9bg(x, 0)-2,3258[Д£(х+/Л/2, 0) +
+ Д^(х-Я1/2,0)]-0,5683[Д^(х + Я1, 0) + &g(x-Hlt 0)]-
—0,1931 [Ag(x + 2tflt 0) +Ag(x—2ЯЬ 0)]—0,0178 [Ag (хД-
4-ЗЯь 0) + Д£(х—ЗЯЬ 0)]—0,0041 l.[Ag(x+6Wi, 0) +
+ Д£(х—6ДЬ 0)]—0,0030[Д£(х+9/Л, 0) + Ag(x—9Яь 0)];
Н (ш) = 7,3029—4,6516 cos 0,5©— 1,1366cos © —
—0,3862 cos 2©—0,0356 cos 3©—0,00822 cos 6©—0,006 cos 9©,
Hi=l.
Соответствующие этим (вычислительным схемам весовые функ-
ции приведены на рис. 37, а частотные характеристики — на
рис. 38.
§ 31. ПОСТРОЕНИЕ ФИЛЬТРОВ
в комплексной плоскости
z-преобразование с целью синтеза линейных фильтров приоб-
ретает в последнее время все большее значение в связи с возмож-
ностью реализации режекторных фильтров, фильтров Баттерворта
и Чебышева в рекурсивной форме, обеспечивающих существенную
экономию машинного времени, что особенно важно при обработке
огромного потока сейсмической информации.
Рассмотрим некоторые свойства z-преобразования, связанные
с фильтрацией данных. Начнем с операции свертки у = h*f. За-
меняя входную и весовую функции f и h их z-преобразованиями
Z7 (2) = fo + М 1 ^rfiz 2+ • • • +/м2 ",
77 (z) = Ао hxz h2z 2+ . . . -\-hMz м,
получим, как это следует из (5.44), последовательность
7/(z)F(z) = Wo + WiZ-1 + W2z-2+ . . . +
-\-hofnZ " + W#z 1+ WiZ * + . . . 4~
+ hifnZ п + Wог 2 + • • • + Wnz " + . . . +
+ ^м/п2	= hofo + (Aofx + hif0) z 1 +
+ (Wa + Wi + Wo)2 2 + . . . +hMfnz	(6.41)
Сопоставив полученный результат с результатом свертки (6.12),
нетрудно, заметить что первый член (6.41) — это нулевой элемент
выходного сигнала, коэффициент при z-1 — первый элемент вы-
ходного сигнала, коэффициент при z~a — второй элемент и т. д.,
т. е. правая часть (6.41) представляет собой z-преобразование вы-
ходной функции у:
. Y(z) = H(z)F(z)=y0 + y1z-'+ . . . +ynz~iM+n). (6.42)
z-преобразование удобно для количественного описания фазовых
соотношений, важных при реализации фильтрации сейсмических
данных.
Многочлен вида (6.42) может быть представлен в виде произве-
дения биномов:
У (z) = a0(ai + 2-1)(a2 + z-1)(a84-z-1) . . . (aM+z-1),	(6.43)
где alt а2, . . . — корни многочлена.
Во временной области разложение (6.43) эквивалентно покас-
кадной свертке множества сигналов, охарактеризованных двумя
ординатами
—аъ 1; — а2, 1; —а3, 1;	. . . ; —ам, 1,
185-
т. е. можно записать
t/ = a0(—аъ 1) * (—аа, 1)»(—а8, 1)* . . . *(— ам, 1).
Рассмотренные свойства г-преобразований позволяют опреде-
лить понятие минимально-фазового сигнала.
Если сигнал у (t) представлен всего двумя ординатами, т. е. у (г) =
— у0 + z/iZ-1, то при у0<.У1 он называется минимально-фазовым
или сигналом с минимальной задержкой. При	сигнал на-
зывается максимально-фазовым или сигналом с мак-
симальной задержкой. При у0 = уг оба определения равноправны.
Рис. 39. Геометрическая интерпретация системной функции при двух нулях
и двух полюсах (а) и Н (г) = 2 + г-1 = 2 (z+ 0,5)/г в плоскости г-1 (б).
J — положение нулей, 2 — положение полюсов
Сигнал с множеством ординат, т. е. сигнал вида (6.42) или (6.43),
будет минимально-фазовым, если каждый из биномов аг + z-1,
а2 + г-1, . . . является минимально-фазовым, и, наоборот, сигнал
будет максимально-фазовым, если каждый из биномов максимально-
фазовый. Другими словами, на основании (6.43) сигнал можно счи-
тать минимально-фазовым, если все корни а2, . . . его полинома
у (г) больше г. Поскольку г = е/<0 выражает задержку по времени
и в комплексной плоскости представляет собой окружность еди-
ничного радиуса (рис. 39), сигнал является минимально-фазовым,
если все корни alt а2, . . . его полинома лежат внутри единичного
круга е/и или на этом круге. При z = е_/“ корни полинома будут
расположены, наоборот, вне единичного круга.
Допустим, что весовая функция в общем виде может быть за-
писана как частное от деления, двух многочленов, представленных
их z-преобразованиями:
(6.44)
186
Для такого отношения значения весовых коэффициентов а{ и bt
определяют тип фильтрации — рекурсивной или нерекурсивной.
Если хотя бы один коэффициент а; 0, а все коэффициенты bt,
кроме первого, равны нулю, фильтрация является нерекурсивной.
Если же, кроме того, имеется хотя бы один из коэффициентов bt 0,
кроме первого Ьй =# 0, то последовательность выходной функции
зависит от текущих и прошлых значений входного сигнала, а также
от прошлых (профильтрованных) значений выходного сигнала.
В этом случае фильтрация будет рекурсивной, т. е. фильтрация
с обратной связью.
Действительно, с учетом (6.44) выходная функция пвинимает
вид
У(г) = В(г)Л(г)/В(г)
или
У(г)В(г) = В(г)Л(г).	(6.45)
Перейдем к представлению выражений (6.45) во временной об-
ласти, заменив произведение г-преобразований сверткой времен-
ных рядов: у *b = f *а. Например, пусть
Л (г) = а0 + а^1 + а2г~г\
В (г) = 1 + fejZ-1 + b2z~2.
Перемножая соответствующие z-преобразования согласно (6.45),
получим:
Уо= / оао>
УоЬ1 + У1 = f oai+fia0,
2/0^2 + У1К + Уч —	+	(6.46)
У1Ьч + уФг + Уз = Ла2 + /А + /А»
Выходная функция у0, ylt у2 находится из уравнений (6.46)
следующим образом:
Уо —
У1= Mi + f iao—Уо^ъ
Уч — fo&i 4“ f iai +	—(уо^ч ~Ь У1Ь1),
Уз = f А + fidi+f A—(yibi +1/261),	(6-47)
....................4.........
У! = fi-i^i + f 1-1O.1A—(yi-ibi + Z//-1&1),
или в общем виде
М	L ,
У1= Z aifi-i— У biyj^i,
i=0
что совпадает с определением рекурсивной фильтрации (6.23).
187
d Рекурсивная фильтрация может представлять интерес лишь
в тех случаях, когда М + L<P, где Р — число весовых коэффи-
циентов нерекурсивного фильтра, и расчет по (6.47) оказывается
экономичнее, т. е. быстрее, чем по обычной формуле свертки (6.12).
} Такая экономичность обеспечивается при синтезе узкополосных
и особенно режекторных фильтров. Затраты машинного времени
 могут быть снижены в 5—10 раз и более.
Проблема расчета весовой функции рекурсивных фильтров сво-
дится к определению корней z-полиномов числителя и знаменателя
выражения
Н (z) = А (г)/В (г).	(6.48)
В силу (6.43) числитель и знаменатель могут быть представлены
произведениями биномов, поэтому для частотной характеристики
имеем
м
«0 П (* -
Я(г) = ^--------------,	(6.49)
П—рг2-1)
i=Fl
где ri и pi — корни соответствующих полиномов.
Множитель а0 является масштабным и на форму частотной ха-
рактеристики не влияет.
Числитель в (6.49) равен произведению членов, описывающих
нули H(z), а знаменатель — произведению членов, представляю-
щих полюсы z-преобразования, т. е. корни числителя являются
«нулями», а корни знаменателя — «полюсами» Н (z). С точностью
до постоянного множителя эти корни полностью характеризуют
свойства фильтра. Если мы установим положение нулей и полюсов
на комплексной плоскости, тем самым определим и амплитудно-
частотную и фазово-частотную характеристики фильтра. Пусть,
например, Н (г) определяется двумя нулями rj и г2 и двумя полю-
сами plt рг, положение которых дано на рис. 39, а. Тогда ам-
плитудно-частотная характеристика
IН (z) | = t\r<JpiPi,	(6.50)
а фазово-частотная характеристика
агсЯ(2) = ф1 + фа—(0i + 0a).	(6.50')
Весьма существенно, чтобы все корни знаменателя, т. е. «по-
люсы», были по модулю больше единицы. В противном случае
фильтр оказывается неустойчивым, поскольку не может быть опи-
сан ограниченным числом весовых коэффициентов. [Покажем это
на примере.
Пусть а0 =1; аг = а2 = 0; 60 — 1; Ь± = — 2; Ь2 = 0. Тогда полюс
этого фильтра, определяемый равенством 1 + Ьг~1 = 0, будет р = — 1/2 =
= - 0,5.
Найдем выходную последовательность ’при входном импульсе f = (1,
0, 0, . . .). Отклик фильтра иа этот сигнал определяет импульсную
188
реакцию фильтра, а ее z-преобразоваиие представляет системную
функцию Н (г), или частотную характеристику. Из системы уравнений (6.47)
для указанного фильтра находим выходные значения: уд = а0 = 1; у1 =
= ааЬх = 2; уг = айЬ] = 4; у3 = — а06^ = 8; t/4 = agb\ = 16 и т. д.
Таким образом, весовая функция расходится.
Подставляя в полученные значения у = (а0; aabx, aab\‘, aobl; а0Ь* . . .)
числовые значения, равные ад = 1 и Ьх = 0,9, имеем (полюс р = 1/0,9 =
= 1,1) импульсную реакцию в виде (1, — 0,9, 0,81,—0,729, 0,656, . . .), т. е.
фильтр является устойчивым, так как весовая функция фильтра сходится.
Приведенный пример показывает эффективность применения
рекурсивного фильтра по сравнению с применением обычного
фильтра-свертки. Действительно, при а0 = 1, Ьг = 0,9 для нахож-
дения каждого отсчета выходного сигнала при использовании ре-
курсивного фильтра вида yj = а0Х/—b^j-r (рекурсивный фильтр
первого порядка) требуется выполнить одно умножение и одно сло-
жение. При а0 = 1 и !>i = 0,9 ряд h.{ сходится медленно и надо
вычислить по крайней мере 20 членов ряда, прежде чем. их вели-
чина станет меньше 0,1. Это означает, что при выполнении нере-
курсивной фильтрации на ЭВМ для получения каждого отсчета
выходной последовательности требуется выполнить около 20 пар-
ных операций сложения — умножения, чтобы обеспечить удов-
летворительную точность. В приведенном примере рекурсивной
фильтрации на вычисления нужно затратить времени практически
в 20 раз меньше.
Убывание (по абсолютной величине) отсчетов весовой функции
рекурсивного фильтра первого порядка определяется величиной
коэффициентов Ьг. При приближении b к единице это убывание
замедляется.
Заметим, что фильтр с весовой функцией, г-преобразование
которой имеет все корни, по модулю большие единицы, называется
минимально-фазовым в соответствии с определением минимально-
фазового сигнала. Заметим также, что при нахождении системной
функции Н (г) можно использовать переменную г, а не г-1 = е_/“.
При этом Н (г) не изменяется, так как отсчеты выходной функции
описываются той же системой (6.47) и критерий устойчивости
| Ь|<1 сохраняется. Однако существенное различие между ука-
занными случаями состоит в том, что при использовании переменной
г~1 полюсы находятся вне единичной, окружности, а при исполь-
зовании переменной z— внутри нее. В обоих случаях единичная
окружность делит z-плоскость и z-’ -плоскость на устойчивые и
неустойчивые области. Критерии, обеспечивающие положение
полюсов вне z-1-плоскости и внутри z-плоскости, выполняются
для всех устойчивых фильтров. Положение нулей на устойчи-
вость фильтров не влияет.
Преимущество построения частотной характеристики (сис-
темной функции) Н (z) в виде (6.49), т. е. при одновременном
использовании нулей и полюсов, можно проиллюстрировать
на следующих примерах:
1.	Исследуем функцию Н(z) =2-t-z~I. Она имеет нуль
гх = —2 и полюс первого порядка (в нулеz-плоскости). Положе-
189
ния нуля и полюса относительно единичной окружности в г-1-плос-
кости показаны на рис. 39, б. Точка С на единичной окружности,
отвечающая угловой частоте' й, при интервале дискретизации
А/= 1 с является изображением величины г-1 = e~iQ. При этом,
как следует из рис. 39, б, значение амплитудно-частотной характе-
ристики | Н(г) | для © = й определяется расстоянием между точ-
кой С и нулем гх. Значение | Н (г) | для других частот можно по-
лучить перемещением переменной z-1 по единичной окружности и из-
мерением для каждого z-1 расстояний Сгг. При этом фазовый сдвиг
измеряется углом <р (©) = 0 (©).
Поскольку сама системная функция Н (г) не меняется от того,
в какой плоскости она определяется г- или г-1-плоскости, рассмот-
рение нулей и полюсов должно приводить к одинаковым резуль-
татам независимо от формы представления Н (г). В z-плоскости
для точек С на единичной окружности для данного примера ам-
плитудно-частотная и фазовая характеристики при © = й соот-
ветственно будут: | Н (й) | = 2СгГ/Ср7; <р (©) = 0—ф.
2.	Построим фильтр, направленный на подавление постоянной
составляющей входного сигнала. Такой фильтр позволяет пода-
вить самые низкочастотные составляющие. При этом идеальный
фильтр для подавления постоянной составляющей должен иметь
нулевое усиление при а = 0 и равномерное пропускание для всех
остальных частот. Приемлемая аппроксимация такого идеального
фильтра может быть реализована с помощью функции
Яа(г) = (1-г-1)/(1-61г-1).
Эта системная функция имеет нуль г1 — 1 и полюс pr = l/b^
Для любой частоты © амплитудно-частотная характеристика пред-
ставляет собой отношение Cr-JCp±, где С — точка на единичной
окружности. Очевидно, что усиление | Я2 (®) I равно нулю при
Сгг = 0 и приблизительно постоянно и близко к единице для ча-
стот, на которых Сг± = Срг. Иначе, полюсрг должен располагаться
ближе к для того, чтобы приблизить значение характеристики
к единице для любой частоты, кроме © -> 0. Еще одно требование
вытекает из критерия устойчивости | b± |< 1, т. е. полюс должен
находиться вне единичной окружности.
Например, для b = 0,95 ,
Яа(г) = (1—2-1)/(1—0,95г-1).	[(6.51)
Из амплитудно-частотной характеристики, нормализованной
относительно максимального усиления (для © = л) (рис. 40), видно,
что фильтр полностью подавляет постоянную составляющую и про-
пускает все более высокие частоты с постоянным усилением. Так, _
для частот 0,03©™ и 0,15 ©гр усиление соответственно будет
0,95 | Ятах | и 0,99 | Яшах |. Следовательно, фильтр-Я2 (г) является
весьма универсальным средством для подавления постоянной со-
ставляющей.
190
Н(ы)г
0,25Ыц qfG)r? 075ь)г, u>rf
Рис. 40. Нормализованные ампли-
тудно-частотные характеристики для
режекторных фильтров, настроен-
ных на подавление постоянной со-
ставляющей (а) и частоты 0,25 шн (б).
Слева показано расположение нулей
(/) и полюсов (2) фильтров в г-1-пло-
скости
Основным параметром, влияющим на форму характеристики
| Н2 (z) |, является расстояние между полюсом и нулем: чем оно
короче, тем уже диапазон подавляемых частот.
Для представления фильтрации во времени умножим обе части
формулы (6.51) на (1 — 0,95 г-1) F (г), т. е. имеем
(1— 0,95г-1)У(г) = (1— z~l)F(z).	__
Отсюда вытекает рекурсивная формула для получения /-го зна-
чения выходной функции с целью подавления постоянной состав-
ляющей:
=	x/-i~|-0,95r/z_1.	(6.52)
3.	Проведем синтез режекторного рекурсивного фильтра для
подавления промышленной частоты 50 Гц. Отметим, что для фильтра,
устраняющего частоту <ofe, сле-
дует расположить н ули, т. е.
корни числителя, в точках
z [ = 1, для которых
2 = e-'“A,(Ai=l) = 2Re +
+ J2/m = COS <0 A £ — / sin ©Af,
ZRe = COS (О* Д/, ZIm = sin <dk&t.
(6.53)
Эти точки в z-плоскости на-
ходятся на единичном круге
под углами ср* = ± ®аД^, из-
меренными в радианах, или
Фа = ± (180/л) со*. Д/ в граду-
сах (см. рис. 40). Из рис. 41, а
видно, что фильтр с одним ну-
лем устраняет нежелательную
частоту ©а> но вместе с тем ис-
кажает все остальные частоты.
Для ослабления указанных
искажений в характеристику
Н (z) (6.49) следует ввести пару комплексно-сопряженных корней
знаменателя, т. е. полюсов, расположенных в непосредственной бли-
зости к нулям. Эти полюсы в силу обеспечения устойчивости | &t|< 1
должны быть вне единичной окружности. Наиболее удобно для даль-
нейших расчетов расположить полюсы на продолжении лучей, соеди-
няющих начало координат с нулями фильтра. Амплитудно-частот-
ная характеристика, как уже отмечалось, будет выражаться от-
ношением длин векторов Ci\ICpt. При этом амплитудно-частотная
характеристика становится более остронаправленной (рис. 41, б).
Путем приближения полюса к нулю регулируется направленность
фильтра, и таким образом можно сузить полосу подавления (ре-
жекции) до искомого предела.
Пример. Построим фильтр при шаге дискретизации Д< = 0,002 с с целью
подавления частоты 50 Гц.
191
Решение. Найдем действительную и мнимую части ZRe и z/mB (6.53).
Очевидно, что <р60 — ± 2л X 50-0,002 (180°/л) = 36° и, согласно (6.53),
ZRe == cos 36° = 0,809; zjm = sin 36° = 0,588. Следовательно, корни чис-
лителя располагаются в точках с координатами г01 = 0,809 + j 0,588,
г02 = 0,809—j 0,588. Расположим полюсы на лучах под тем же углом <р
вблизи, но вне единичной окружности. Пусть |z|= 1,02. Тогда z'Re =
= 1,02 zRe = 0,825 и полюсы (корни знаменателя) получим в виде
Pi = 0,825 + /0,600; р2 = 0,825 — /0,600.
a
-Ц-р -CJ/c Q Ct)K <Vrp “&>гр	О	^гр
Рис. 41. Амплитудно-частотные характеристики \Н (со) Црежекторных фильт-
ров с одним нулем (а) и с нулем и полюсом (б) в z-плоскости
Таким образом, выражение для системной функции режекторного
фильтра будет
Н (z) =	(1 —	_
U	(1,02 — piz-* 1) (1,02 — р2г-!)
0,962 (1 — l,618z-i + г~8)	(б зд
1 — 1,587г-1 + 0,981г-2 * * * * *	’	V • 1
Отсюда реализация рекурсивного фильтра во временной области выра-
жается в виде
уп = 0,962 (/ „ -1,6-f„_2) - 0,981 г/„_2 +1,587г/,,
При дискретизации Д/ = 0,001 с <рво = 18° и нули Н (г) расположены
в точках г12 = 0,951±/0,309. Если при этом полюсы разместить возле
нулей при |г|= 1,01, их координаты будут р12 = 0,960 ±/0,312. Тогда
z-преобразование весовой функции (системная функция)
Н = 0.980(1 — 1,902г-1 + г-2)
U 1 — 1,882г-1 4-0,980г-2
I Подчеркнем еще раз то обстоятельство, что применение рекур-
I сивных фильтров эффективно, если необходимо иметь большую кру-
i тизну частотной характеристики. При этом реализация обычной
1 свертки сводится к очень длинным весовым функциям, например
для подавления частоты 50 Гц при обработке сейсмических записей
их длина достигает 100 коэффициентов (0,2 с) и более. Реализация
рекурсивного фильтра (6.54) требует всего пяти весовых коэффици-
ентов, т. е. этот фильтр по крайней мере в 40 раз экономичнее обыч-
ного нерекурсивного фильтра-свертки.
Сложность построения рекурсивных фильтров с использованием
нулей и полюсов системной функции резко возрастает при увели-
192
чении числа ее особых точек, поэтому на практике получили при-
менение лишь фильтры низкого порядка.
§ 32. ДВУМЕРНЫЕ ЛИНЕЙНЫЕ ФИЛЬТРЫ
Площадной характер наблюдений потенциальных геофизических
полей, многоканальность сейсмических записей, регистрация ка-
ротажных кривых по профилю скважин вызывают необходимость
построения двумерных линейных фильтров. В общем случае такие
фильтры приводят к двумерной пространственной фильтрации.
В сейсморазведке преобразование волновой картины, регистри-
руемой по времени t и в пространстве (по х), называют пространст-
венно-временной фильтрацией.
Аналогичный характер (пространственно-временной) фильтра-
ции имеет место при обработке данных частотных зондирований
в электроразведке, когда результаты измерений представляют в
вертикальной плоскости (И, х).
Двумерный аналог свертки (6.12), определяющий двумерную
фильтрацию входных данных fp/ (/ = 0, 1, . . . , п, п — число пи-
кетов, р = 0, 1, .... N, N — число профилей), имеет вид
t/pl = 'EZhkifP-k,i-i,	(6.55)
к i
где hki — матрица весовых коэффициентов; индекс k = 0,1, . . . ,
..., К изменяется по профилям; индекс i = 0, 1, . . . , I изменяется
по пикетам.
Часто отсчет значений весовых коэффициентов производят от
центральной точки весовой функции, при этом k изменяется от
— А72 до J</2, a i — от — Z/2 до Z/2.
В частотной области двумерная фильтрация определяется про-
изведением двумерных спектров весовой функции Н (&х, coj и
входной функции F (<аи, их):
Y (сох, ау) = И (®х, <лу) F (сох, аи),	(6.56)
где (пх = 2л/тАх и <ли =	— пространственные частоты
(тАх и М&у — протяженности сигналов вдоль профиля и по пло-
щади).
Формулы (5.26) и (5.27) выражают прямое и обратное преобра-
зование Фурье для сигналов (аномалий), описывающих геофизи-
ческое поле по площади съемки.
Для сейсмических записей прямое и обратное преобразования
Фурье, связывающие упругую волну / (/, х) с ее спектром, выра-
жаются следующим образом:
ОО 00
S (и, kx)= J J f(t, х)ехр[ — j (atkxx)] dtdx,
—00 —00
(6.57)
f	Г f S (“- k*) exP I/ M + Ml d&dkx.
(2л)2
7 А. А. Никитин
193
Здесь <о = 2л/Г определяет йрёмеййук) я а С16 t у, ййё-
личина k.x — пространственную частоту.
По аналогии с и = 2л/Т (Т — период сигнала по времени)
для сейсмических сигналов kx = 2л/Хк, где %к — кажущаяся длина
волны. Очевидно, что %к = TvK (ук — кщкущаяся скорость волны)
и, следовательно, пространственная частота kx = 2л/Хк = 2л/Ток=
= и/ок- Пространственные частоты часто называют волно-
выми числами, ив связи с этим употребляется термин «вол-
ночисловая фильтрация». Двумерная пространственная фильтра-
ция по координатным осям х и у используется для различных ви-
дов потенциальных полей (гравитационных, магнитных) и в сей-
смологии при обработке площадных наблюдений.
При входном сигнале fpt и весовой функции hki для пространст-
венных координат х и у выходная функция ypj определяется сверт-
кой (6.55). Соответствующее уравнение в волновой области выра-
жено (6.56).
По аналогии с частотной характеристикой идеального фильтра
низких частот (6.26) частотную характеристику двумерного низко-
частотного фильтра можно задать в виде:
(1, |их|<л/Дх, |иД < я/Ьу,
(®х, ®») —I |иж|>л/Ах, |(0(,|>л/Аг/,	'
где л/Ах и л/Д# — граничные значения волновых чисел, или, иначе,
волновые числа Найквиста. Эти числа обычно не одинаковы по
разным осям.
В общем случае обратное преобразование Н (их, <ои) дает
*
Л(х, у) =	- f Н(ах, ©^ехрЩи^Ч-ш^йсо/Ц,.
4Я —я/ Дх —я/ Д{/
(6.59)
Если положить Ах = A# = 1, для дискретных данных получим
I к
Н (®х, юи) = 4 hki cos i wx cos ka>p	(6.60)
и
i 1/2Дшх 1/2Д®„
= — У У Я(mA(ox, pAojJcos^Ao^Jcos^A®^). (6.61)
n n^O p^O
Эту процедуру применяют по следующей схеме: 1) вначале вы-
бирают функцию Я (сох, а>и), удовлетворяющую требованиям для
разделения сигналов по волновым числам; 2) вычисляют hik по
(6.61); 3) проводят свертку hik с исходным полем fp,j, в результате
чего получают выходную функцию yp,j как результат фильтрации.
Для.сглаживания полей, т. е. выделения низкочастотных со-
ставляющих, применение частотной характеристики (6.58) ввиду
194
ее периодичности приводит к нежелательному усилению высоко-
частотных составляющих наблюденного поля на зеркальных ча-
стотах. Поэтому вместо (6.58), как и в одномерном случае, целесо-
образно использовать сглаживание Н (сох, сой). Так, В. Н. Стра-
ховым выбор частотных характеристик с целью сглаживания гра-
витационных полей предлагается проводить по форме
Я (сох, ®й) = Н (<ох) Н (<ой) = {1 — [1 - (cos ихДх/2)2ЛГ‘]р‘) X
X {1—[1-(cos®,Ai//2)2JV’]p’}.
(6.62)
Варьируя параметрами /Vj, 7v2 и plt рг, можно подобрать нуж-
ную для данных условий форму частотной характеристики. Наи-
более часто употребляемыми яв-
ляются значения 2Я1>г = 30-? 60;
Pi, 2 = Зч-4. Большие значения
Nlt а рекомендуются для сглажи-
вания аномалий силы тяжести,
меньшие — при сглаживании вто-
рых производных гравитацион-
ного потенциала.
Использование сглаживания
обеспечивает резкое уменьшение
влияния случайных ошибок на
результаты пересчета полей.
В области волновых чисел час-
тотные характеристики, с помощью
Рис. 42. Различные виды филь-
трации в частотио-волиочисловой
области:
которых реализуется соответствен-
но усреднение в квадрате со сто-
роной L, вычисление вторых про-
а — частотная, б — волночнсловая,
а — скоростная, а — частотно-волно
числовая, д — частотно-скоростная,
е — по скорости н волновому числу
изводных и продолжение поля
в нижнее полупространство на глубину Н, имеют простой вид:
Н1 ((Ох, ®й)
sin s>xL sin s>yL .
wxL a>yL ’
Hz(<i>x, (Uy) — (0* + (0y‘,
Ha(ax,
(Dy) = exp (ff V®x + ®y )•
Последние две характеристики безгранично возрастают при
увеличении х и у, поэтому на практике вместо точных выражений
используются приближенные формулы.
Особое место двумерная фильтрация занимает при обработке
сейсмических записей. Ее различные модификации (рис. 42, а—ё)
имеют самостоятельное значение.
Известно много модификаций пространственно-временнбй филь-
трации сейсмических записей, которые различаются моделью вол-
нового поля, видом частотных характеристик, целью применения.
В отличие от одноканальных временных фильтров, базирующихся
на частотном различии сигналов и помех, двумерные, фильтры осу-
7»	195
ществляют выделение сигналов по признаку кажущейся скорости
и степени коррелированное™ по заданному направлению. Огра-
ничимся рассмотрением двух групп двумерных фильтров: ско-
ростных фильтров, осуществляющих выделение сиг-
налов с прямолинейными осями синфазности, иинтерферен-
ционных систем, в которых отсутствует поканальная
фильтрация и процедура фильтрации сводится к суммированию
некоторого числа трасс вдоль заданной линии с весами, постоян-
ными для каждой трассы.
Скоростная (или частотно-волночисловая) фильтрация основана
на различии кажущихся скоростей полезных сигналов и волн-по-
мех. Идеальная частотная характеристика такого фильтра в об-
ласти двумерного спектра при | пк |> окгр Н (со, kx) = Н (vK) — 1
и равна нулю за пределами этой области, т. е. на плоскости (со, kx)
область пропускания фильтра образует сектор (см. рис. 42, в).
По внешнему виду области пропускания фильтр называется веер-
ным и при этом является пропускающим. В том случае, когда
области пропускания и подавления меняются местами, веерный
фильтр будет режекторным.
Амплитудная частотная характеристика веерного фильтра, про-
пускающего без искажения сигналы внутри веера кажущихся ско-
ростей — i>K1< ок< %2, выражается уравнением
Я (со, ^={0,
— I со |/vK гр «£ kx < I (0 |/ок гр,
I СО |/^к гр, ky^> | СО |/Uk гр'
(6.63)
Для того чтобы веерный фильтр не вносил фазовых искажений,
его фазовая характеристика должна быть равна нулю. С помощью
обратного преобразования Фурье получим
ЯДсо) = -L- ?Я(со, kx)^dkx =
м —->г>
1	' “ У"к гр e/^dkx = sin [(| <01/рк гр) X]
2п -|ю 1/и	*	пх
I W|/VK Гр
(6.64)
Формула (6.64) определяет частотную характеристику одно-
мерного фильтра по направлению х для обработки записей, заре-
гистрированных на расстоянии х от центра базы фильтруемых
трасс.
Пространственно-временная весовая функция получается из
(6.64) путем вторичного обратного преобразования Фурье с учетом
его четности по аргументу <о:
h(t, х)=— F Ях (со) е/0/Ясо =	\
2л
ОО
—f sinf—i-^-LxAcoscoidco.
ft % J \ Vk rp /
0
(6.65)
196
Если теперь учесть дискретный характер записи как по t (i =
= t/&t = 0, ± 1, . . . , ± Т), так и по х, при этом число каналов
N берется четным и k = х/Ах = ± 1/2; ± 3/2; . . . , ± (N—1) 2,
то весовая функция веерного фильтра, пропускающего волны с ка-
жущимися скоростями | vK |>Ркгр= Ах/А/ принимает вид
htk=l/na(k2—i2).	(6.66)
Графическое изображение весовой функции веерного фильтра
для Г=±5и^=8 приведено на рис. 43, а. Результат приме-
нения веерного фильтра (6.66) при Т=±50иЛ/=18к сейсмо-
грамме рис. 43, б с целью выделения волн с разными направлениями
их распределения показан на рис. 43, в.
Большое распространение при обработке геофизических данных
получили преобразования, связанные с направленным суммирова-
нием, т. е. суммированием исходных данных по направлению кор-
реляции полезного сигнала (аномалии). В сейсморазведке сумми-
рование сейсмических трасс вдоль заданной линии с весами hK,
постоянными или меняющимися от трассы к трассе, реализуется
в интерференционных системах. При этом линии суммирования
соответствуют форме годографов полезных сигналов [6].
Общая формула результирующей трассы при обработке интер-
ференционными системами может быть представлена в виде
• N-1
=	(6.67)
где т* — временной сдвиг на k-й трассе (относительно произволь-
ного начала отсчета), определяемый годографом волны.
Если на сейсмотрассах наблюдается регулярная волна f (t, х)
с годографом вступления t (х) = у* (/) = f (t—tk), то из (6.67)
следует выражение, описывающее выходную функцию интерфе-
ренционной системы:
ЛГ-1	N—1
y(t)=L Ы(t-tk + т*) = Z W	(6.68)
k=0	k=0
где величины 0* = —т* определяют отклонение годографа от
Даданной линии суммирования.
Применяя свойство преобразований Фурье о запаздывании функ-
ции (см. § 24), найдем спектр профильтрованных данных
У(о>) = Нв(®)Г(®),
где
N-1
Нв(а>) == ^	(6.69)
F (и) — спектр волны f (I) на трасее k = 0.
Форма годографа волны зависит от направления ее подхода
к линии наблюдения, поэтому функцию Нв (<в) называют харак-
теристикой направленности интерферен-
197
Рис. 43. Весовая функция веерного фильтра (а), исходная сейсмограмма (б)
и результат ее веерной фильтрации (в)
Ц И б н н о й системы. &та характеристика прёдстайляёт сб-
бой периодическую функцию с главным (основным) и побочными
максимумами. Число побочных максимумов и соотношение между
их амплитудами и амплитудой главного максимума зависит от числа
суммируемых каналов /V и величины 0*.
При 0* = 0, т. е. когда годограф волны совпадает с направле-
нием суммирования, имеет место синфазное суммиро-
вание, при этом
N—1
(6.70)
Если hk — 1, то
|Яе(®)1тах = Яе(®) = ^.	(6.71)
Отношение энергии сигналов на выходе интерференционной си-
стемы Ее к энергии сигнала, полученного при синфазном сумми-
ровании, Ее = (2Л*)2 ^о. гДе — энергия сигнала на исходных
трассах; Ее/Ев — коэффициент направленного действия, характе-
ризующий разрешающую способность интер-
ференционной системы, т. е. показывает, насколько
интерференционная система ослабляет интенсивность сигнала при
отклонении его годографа от линии суммирования.
Интерференционные системы также ослабляет влияния случай-
ных волн-помех. Если иа исходных трассах энергетическое отно-
шение сигнал/помеха равно рвх = Е0/с*, то при синфазном сумми-
ровании энергия полезного сигнала на выходе интерференционной
системы Евых = (W2£<r Энергия помехи на выходе системы
N—1
Ствых = о2^ hk и энергетическое отношение сигнал/помеха на вы-
ходе
Рвых = ^ВЫХ^^ВЫХ = S/IjEq/O' S/lft-
Отношение	______
_______ N-\	J N—l
s = д/рвых/рвх =	Л*/Д/ 2 Л* ’	(6.72)
называемое статистическим эффектом интерфе-
ренционной системы, показывает, во сколько раз уси-
ливается интенсивность сигнала по отношению к некоррелирован-
ной по х случайной помехе. При hk = 1 получаем максимальную
величину статистического эффекта, равную з = л] N.
Теперь рассмотрим, как изменяется характеристика направлен-
ности интерференционной системы, если годограф полезной волны
не совпадает с направлением суммирования.
Если вдоль профиля распространяется волна с постоянной ка-
жущейся скоростью Vk, время ее прихода на n-й канал относительно
нулевого канала tn — nAxlvK. Наклон линии суммирования можно
задать параметром оКсум = Дх/Дт, где Дт— временной сдвиг ме-
жду соседними трассами. Отсюда временной сдвиг для колебаний
199
п-и трассы относительно нулевой т„ = пАх/оксум- Отклонение го-
дографа волны от линии суммирования
Хп ~ пДх — 1/Ц& сум)-	(6.73)
Подставив (6.73) в (6.69), получим
N-1
Нв (<о) = £ /гпе-/пД^ = Н (kx),	(6.74)
п=0
где kx — разностное волновое число, характеризующее различие
пространственных частот волны kxB и линии суммирования kxcy№,
kx — kx B — kx cyM = (й/Vk в w/Uj сум = ©/Од-
Параметр 1/ик имеет смысл разностной кажущейся скорости
И 1 / V к = 1/Окв—1/Оксум-
Характеристика направленности интенференционной системы
представляет собой функцию разностной пространственной частоты
и вычисляется как спектр дискретной весовой функции. Характе-
ристика Н (kx) является периодической функцией пространствен-
ной частоты с периодом kx = 2л/Ах, и ее называют обобщен-
ной характеристикой интерференционной
системы ввиду того, что ее аргумент — пространственно-вре-
менной параметр [6]. При hn = 1 из (6.74) следует, что
N-1
H(kx}=- £ е-/пД*\	(6.75)
п=0
Выбрав начало отсчета х в центре базы системы, получим по-
следовательность равных весовых коэффициентов в виде четной
функции. При этом Н (kx) будет функцией с нулевой фазовой харак-
теристикой. Для вычисления (6.75) надо найти сумму N членов
геометрической прогрессии со знаменателем, равным е-/Лх*х, поме-
стив начало отсчета каналов в центр базы суммирования. Тогда
характеристика направленности (6.75) примет вид
H(k\— sin (N^xkx!^)
х . sin (ДхЛ*/2)
(6.76)
Функция (6.76) зависит от величин N и Ах, имеет период 2л/Ах
и максимум, равный Н (kx)max = Н (0) = N.
Обычно для построения обобщенной характеристики направ-
ленности (рис. 44) используют относительные значения Н.
Эти характеристики зависят от изменения числа суммируемых
каналов (рис. 44, а и б), от увеличения базы суммирования /УАх
(рис. 44, б) и изменения vK (рис. 44, в).
Увеличение числа N при постоянном шаге Ах ведет к сужению
области пропускания, определяемой главным максимумом характе-
ристики, и к расширению области подавления, к которой относят
интервал между главным и побочным максимумами, его граничные
значения 2л//УАх и 2л (N—1)//УДх.
При увеличении шага между каналами в 2 раза (см. рис. 44, б)
при тех же значениях N вдвое увеличивается база суммирования.
200
При этом период функции Н (kx) уменьшается вдвое и соответст-
венно сокращаются размеры областей пропускания и подавления.
Для волны с vK = const от Н (kx) легко перейти к Н (со), для
чего значения kx следует пересчитать в соответствующие значения
= kxVx, где % — разностная кажущаяся скорость волны от-
носительно линии суммирования. Характеристика Н (со) с перио-
Рис. 44. Характеристики
направленнЬсти интерфе-
ренционных систем для
сейсмических плоских волн
[6].
а — при Дх = const; б — Дх' =
= 2Дх = const; в — для ок
(при N = 4) равной: 1 — оК1
2 — 2v'K, 3 — 4 t»R. 4 —оо
дом Q = kxvK = 2nvK/Ax растянута по оси со пропорционально
величине vK (см. рис. 44, в).
Для синфазно суммированной волны = °°. Н (<л) = const
форма колебаний при суммировании не искажается. Спектры ос-
тальных волн, годографы которых отклоняются от линии суммиро-
вания, подвергаются искажениям тем значительнее, чем больше
это отклонение, т, е. чем меньше разностная скорость vK (см.
рис. 44, в).
Характеристики направленности, приведенные на рис. 44, оп-
ределяют процесс обработки по методу регулируемого направлен-
ного приема (РНП).
Совершенно аналогичные характеристики будут оценивать ка-
чество приемов обработки потенциальных полей, направленных на
выделение аномалий путем скользящего суммирования исходных
данных в пределах N профилей, например способ межпрофильной
корреляции (см. § 41).
Характеристики направленности могут быть использованы при
анализе преобразований двумерных потенциальных геофизических
полей,- если аномалию описать выражением f (х, у) = f (у—фх),
где ф — азимут простирания аномалии (сравни с описанием сейсми-
ческой волны s (t, х) = s (t—x/v)). Выражение для азимута про-
стирания при линейном смещении аномалии от профиля к профилю
Ф = arctg (0Ax/At/), где Ах, At/ — расстояния между пикетами
и профилями; 0 — число пикетов, на которое смещена аномалия
между соседними профилями.
201
ГЛАВА VII
ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ ФИЛЬТРЫ
Рассмотренные в гл. VI линейные фильтры были построены на ос-
нове задания тех или иных частотных характеристик. При этом
предполагалось, что области повышенных амплитуд частотных ха-
рактеристик соответствуют частотным составляющим полезных
сигналов, а области отсутствия частотных характеристик — ча-
стотным составляющим помех, т. е. построение фильтров осущест-
влялось в рамках детерминированного подхода к обработке данных.
Такие фильтры не учитывают того обстоятельства, что на практике
спектры сигнала и помех часто занимают перекрывающиеся между
собой диапазоны частот.
При наличии перекрывающихся спектров фильтры с прямоуголь-
ной частотной характеристикой, используемые в гл. VI, не могут
полностью выделить сигнал на фоне помех, поскольку при этом
они пропускают некоторую часть помех и подавляют определенную
часть полезной информации.
Таким образом, все приведенные в гл. VI фильтры можно рас-
сматривать как неоптимальные. При этом возникает
вопрос о построении оптимальных фильтров, позволяющих
иаилучшим образом выделять сигналы на фоне помех. На постав-
ленный вопрос ответ дает теория оптимальной фильтрации, осно-
ванная на критериальном подходе к построению линейных фильт-
ров.
§ 33. КРИТЕРИАЛЬНЫЙ ПОДХОД
К ПОСТРОЕНИЮ ЛИНЕЙНЫХ ФИЛЬТРОВ
При критериальном подходе к построению фильтров задача состоит
в том, что на основе известных корреляционных (или спектральных)
свойств сигнала и помех требуется реализовать такой фильтр, ко-
торый будет либо воспроизводить, либо обнаруживать искомый
сигнал наилучшим образом с точки зрения некоторого критерия.
В настоящее время в практике обработки геофизических полей
нашли применение три основных критерия построения линейных
фильтров: минимум среднеквадратического отклонения профильт-
рованного сигнала от желаемого (заданного априори); максимум
пикового отношения сигнал/помеха и максимум энергетического
отношения сигнал/помеха на выходе фильтра. В соответствии с ука-
занными критериями решаются задачи сглаживания, воспроизве-
дения, обнаружения и разделения сигналов. Построение оптималь-
ных фильтров в отличие от неоптимальных требует задания апри-
орной информации о корреляционных или спектральных характери-
стиках как сигнала, так и помех, В то же время для оптимальных
202
фильтров возможна Оценка погрешностей фильтраций, которые
являются предельно достижимыми для неоптимальных фильтров.
При построении оптимальных фильтров используется аддитив-
ная модель поля (6.1): ft = Sy + п/. Из-за наличия помехи Пу пол-
ное восстановление сигнала з/ по наблюденному полю ft путем ли-
нейной фильтрации обычно невозможно. Профильтрованный вы-
ходной сигнал yi в той или иной степени всегда будет отличаться
от S/. Поэтому вполне разумно для выделения сигнала выбрать
такой критерий, при котором среднеквадратическое отклонение
требуемого, т. е. желаемого, сигнала от профильтрованного было бы
минимально. Этот критерий, как видим, исходит из задания желае-
мого выходного сигнала. Обозначим его через зу. В частности,
можно считать, что желаемым выходным сигналом является точ-
ная копия входного сигнала зу, т. е. Sj = Sj. В общем случае желае-
мым сигналом может быть любая заданная от координат х или t
функция.
Фактический выходной сигнал будет отличаться от желаемого
на величину 8у = у/—S/, которую можно рассматривать как по-
грешность воспроизведения желаемого сигнала. Качество линей-
ного фильтра можно оценить либо средним значением модуля 8у,
т. е. |е|, либо средним значением квадрата в/, т. е. е4. Крите-
рий минимума среднеквадратического от-
клонения еа, предложенный А. Н. Колмогоровым (1941г.).
и Н. Винером (1949 г.), придает большой вес значительным погреш-
ностям 8/ и игнорирует малые. Очевидно, что, полагая у1 =
= Z htfj-t, где hi — весовые коэффициенты фильтра, получим вы-
ражение критерия минимума среднеквадратического отклонения
eJ=^ZW/-t-S/y=>min.	(7.1)
Минимизация ъл (см. § 34) позволяет определить значения hi
через корреляционные характеристики сигнала Зу и помехи Пу.
По своему принципу критерий (7.1) близок к критерию наимень-
ших квадратов, применяемому с целью вычисления коэффициентов
регрессионных зависимостей (см. гл. II). Проводя аналогию ме-
жду этими критериями, можно считать, что для метода наимень-
ших квадратов желаемым сигналом является заданная модель рег-
рессионной зависимости. Как критерий минимума среднеквадрати-
ческого отклонения, так и критерий наименьших квадратов исхо-
дят из статистической модели экспериментального материала (на-
блюденного поля), т. ё. работают в рамках вероятностно-статистиче-
ского подхода. При детерминистской модели поля в рамках детер-
минированного подхода аномалия обычно задается в виде аналити-
ческой, ограниченной функции, а относительно помех не делается
каких-либо предположений. Обратные задачи разведочной геофи-
зики при детерминированном подходе являются некорректно по-
ставленными как из-за наличия помех во входном сигнале, так и
203
ввиду принципа эквивалентности. Основой построения решений
некорректных задач служит сформулированный А. Н. Тихоновым
(1963 г.) принцип регуляризации. В конечном итоге этот принцип
сводится к учету априорной информации о свойствах искомого
решения и о помехе во входных данных на базе так называемого
регул яр изующего функционала (или стабилизатора). Суть регу-
ляризации, по А. Н. Тихонову, состоит в том, что при решении
системы линейных уравнений, к которым сводится реализация всех
оптимальных фильтров, производится минимизация отклонений
точного решения рт от приближенного ра с учетом стабилизатора—
регулирующего функционала й (р):
II Рт—ра lit + ай (р) => min,	(7.2)
где а — параметр регуляризации; й (р) — стабилизатор, учиты-
вающий априорные свойства искомого решения; £2 — евклидово
пространство с квадратичной метрикой.
Выбор стабилизатора неоднозначен и определяется характером
решаемой задачи. Фактически его введение является «штрафом»,
накладываемым интерпретатором на решение за его нежелательные
свойства, в частности за негладкость, т. е. искажение помехами.
При решении задачи построения фильтров с целью выделения
сигналов на фоне помех регуляризации сводится к регуляризации
по помехам. Для некоррелированной помехи стабилизатор является
не чем иным, как ее дисперсией, которая неизбежно учитывается
при построении фильтров на основе статистической модели на-
блюденного поля.
Таким образом, в рамках вероятностно-статистического подхода
не требуется использование принципа регуляризации, точнее, он
реализуется несколько иными критериями, чем (7.2). Однако если
при решении задач обработки геофизических данных достижения
вероятностно-статистического подхода велики, то при количествен-
ной интерпретации аномалий возможности такого подхода пока
весьма ограниченны. Именно поэтому критерий (7.2) получил ши-
рокое применение прежде всего в задачах количественной интер-
претации аномалий в гравиразведке.
На основе критерия минимизации отклонений профильтрован-
ного сигнала от желаемого (7.1) и близкого к нему критерия
наименьших квадратов решаются задачи преимущественно по
оценке формы сигнала (выделение сигнала) и оценке формы корре-
ляционной связи.
Совершенно иной критерий оптимизации используется в тех
случаях, когда требуется решить вопрос лишь о наличии сигнала
известной формы, т. е. только установить факт его наличия в на-
блюденном поле. При этом говорят о задаче обнаружения
сигнала, в отличие от задачи выделения его.
; Поскольку форма сигнала считается известной, нетнеобходи-
мрсти ограничивать искажение его фильтром. С целью уверенного
обнаружения (установления факта наличия) сигнала фильтр дол-
204
жен обеспечить максимально возможное превышение его ампли-
туды над помехой, использовав при этом различия в корреляцион-
ных или спектральных свойствах сигнала и помех.
При визуальном обнаружении сигнала применяются отношения
сигнал/помеха нескольких типов. При корреляции волны на сей-
смограмме, а также узких аномалий потенциальных полей исполь-
зуют пиковое отношение сигнал/помеха
Pi = Лэкс/<т,	(7.3)
где ЛЭкс — экстремальное значение сигнала (максимальное или
минимальное); о — среднеквадратический уровень помех.
При расплывчатой форме сигнала (аномалии), т. е. при отсутст-
вии ясно выраженного экстремума, более приемлемым оказывается
отношение средних квадратов
|12 = ?/о2,	(7.4)
т
где s2— средний квадрат амплитуды сигнала, s2=£s2/m; т—
число аномальных значений; о2 — дисперсия помех.
Обе оценки для отношения сигнал/помеха (7.3) и (7.4) содержат
параметры интенсивности сигнала и помехи. В то же время оче-
видно, что ни амплитуда сигнала, ни среднеквадратический уро-
вень помех не являются достаточными для полного и объективного
описания отношения сигнал/помеха.
При описании сигнала (аномалии) помимо интенсивности су-
щественное значение имеет его протяженность, при описании по-
мехи величина ст2 является достаточной лишь в случае ее некорре!-
лированности.
Наиболее полной характеристикой для отношения сигнал/по-
меха следует считать энергетическое отношение,
которое для заданного по форме сигнала и некоррелированной по-
мехи будет
p = ^s2/o2 = s2/n/a2,	(7.5)
а в случае коррелированной помехи
p = sR7’s,	(7.6)
где s', s — соответственно вектор-строка и вектор-столбец ординат
сигнала; R71 — обратная корреляционная матрица помехи.
Критерии оптимизации при построении фильтров обнаружения
основаны на максимизации отношения сигнал/помеха на выходе
фильтра (это так называемый согласованный фильтр, см. § 35) и
энергетического отношения сигнал/помеха на выходе фильтра
(энергетический фильтр, см. § 36).
205
Приведенные выражения (7.3) — (7.6) представляют собой раз*
личные типы отношений сигнал/помеха на входе фильтра.
Для того чтобы получить выражения для пикового и энергети-
ческого отношений сигнал/помеха на выходе фильтра, обозначим
профильтрованные значения полезного сигнала и помехи соот-
ветственно через S/ и nf.
sj = 2h(Sj-i; nt = 2hirij^i,
где Sj и nt — значения сигнала и помехи на входе фильтра.
Профильтрованное значение сигнала в точке х0 равно хВЫх (х0) =
= s'h.
Энергия сигнала на выходе фильтра определяется суммой квад-
ратов ординат профильтрованных значений:
Es вых =	s/ = £	hiSj_lJ.
Возведя элементы внутренней суммы этого выражения в квадрат
и учитывая, что	= Rs (т—0 корреляционная мат-
рица сигнала, получим энергию профильтрованного сигнала в виде
Esвых = Е ЕhmRs (т — i)ftt =h'RJi.
т i
Совершенно аналогично получим выражение для мощности
помехи на выходе фильтра
Еп вых — h'Rnh,
где Rn = Rn (m—i) — корреляционная матрица помехи.
Пиковое отношение сигнал/помеха на выходе фильтра в неко-
торой точке х0
Цвых	(x0)/na (х) = (sVT) /A'R„A,	(7.7)
П*=Еп, вых, .
где "s — вектор координат заданного по форме сигнала (s0,
Si, . . . s„,); h — вектор искомых весовых коэффициентов фильтра;
Rn — корреляционная матрица помехи.
Критерий максимума пикового отноше-
ния сигнал/помеха сводится к максимизации выражения
(7.7). Впервые этот критерий предложен Д. Норсом (1943 г.). Оче-
видно, что числитель (7.7) равен квадрату произведения строки из
координат сигнала на столбец из координат искомой весовой функ-
ции Л. Знаменатель, оценивающий энергию помех на выходе фильтра,
206
равен произведению следующих матриц:
(йо, йх,
₽„(М) Rn(M—i) . . . R„(0)
й0
Й1
Йм
В частности, если s = (s0, sx), а помеха задана двумя значениями
ее автокорреляции Rn (0) и Rn (1), мы имеем
=__________(Mi + Siftp)2__________________(Mi + Мо)2________,
.. . Г/?П(О)Я„(1) 1/M	(Л§+ h?)/?Л(0)+2й0Л1Я„(1) ’
(Mi) I	III
L/?„(i)/?n(o) J W
так как перемножение матриц знаменателя дает
/Йо\
[йоЯп (0) + Й!₽„ (1); йо₽„ (1) + йх7?я (0)]	=»
= (й2+й?)₽я(0) + 2йой1/?я(1).
Полагая й? + й? = Rh (0) и й0Й! = Rh (1), получим
______(Ml + Sl^o)8______
я„(о) яЛ(о)+2/г„(1) /гЛ (I)
(78)
Критерий максимума энергетического
отношения сигна л/п о м е х а соответственно состоит в
максимизации энергетического отношения^ си гнал/помеха на вы-
ходе фильтра, т. е. max pBMx=max Е,,лых/п*.
Если сигнал и помеха заданы своими автокорреляционными
функциями Rs и Rn, то
Рвых —
Л Rsft Т t___________
h'R^i ^,ZhihlRn4
(7-9)
где Rstf и Rni/ — элементы корреляционных матриц сигнала и по-
мехи.
Выражение (7.9) представляет собой отношение двух квадратич-
ных форм. Раскрывая это выражение для случая, когда сигнал
207
и помеха заданы двумя значениями их автокорреляционных функ-
ций, с учетом (7.8) получим
rRs(0) /?s(i)-| /V
(h0, /ii)
L/?s(l) RS(O)J \h^
РВЫХ	ГЯл(О) Я„(1)Т /ho
(ho, Л1)	(
Ltfn(l) /?n(0)J Ux
__ Rs(0)Rh(0) + 2Rs(V)Rh(l)
Rn(0)Rh(0) + 2Rn(l)Rh(l)
(7.10)
Сигнал Sj в модели исходного поля f = s;- + nt можно рассмат-
ривать и как детерминированный, т. е. заданный своей формой.
При этом требуется расчет его автокорреляционной функции.
§ 34. ФИЛЬТР КОЛМОГОРОВА—ВИНЕРА
Фильтр Колмогорова—Винера строится на основе критерия мини-
мума среднеквадратического отклонения е/ профильтрованного
сигнала У/ — Y.hcfi-i от желаемого st:
? = (ЕМ/-«—S/^.	(7.11)
Черта сверху означает усреднение ошибки отклонения в2 по всем
j-m значениям. В общем случае этот фильтр решает задачу сглажи-
вания, т. е. (7.11) полностью совпадает с (7.1).
Перепишем (7.11) с учетом возведения в квадрат и усреднения
входящих в него членов:
e‘=(EW/-l) —2s)EW/-i + S/ =
=	+	1, И1 = 0, 1...M.
mi	m
Очевидно, что
= Rf(m— i),	(m),
где Rj (m—i) — корреляционная матрица исходного поля f\
— взаимно корреляционная функция желаемого сигнала s
и исходного поля f. Отсюда
* = Е Е hthmRf (т- i)-Е hmB~f(rn) -Й,2.	(7.12)
т i	т
Для нахождения минимума еа необходимо взять производную 82
по hm и приравнять ее к нулю, т. е. из (7.12) следует, что
-^- = EA/Rf(/n-i)-B7f(/n) = 0.	(7.13)
dhm t
208
Анализ (7.13) показывает, что необходимым и достаточным ус-
ловием обращения (7.11) в минимум для нахождения весовой функ-
ции фильтра ht является решение матричного уравнения вида
£/i{R,(m-0 = B7,(m).	'	(7-14)
Уравнение (7.14) представляет собой дискретный аналог урав-
нения Колмогорова—Винера, которое для непрерывных случайных
процессов выражается как ^h(;t)Rf(t—x)dx = B'-sf (t) и из-
вестно под названием уравнения Винера—Хопфа. Впервые оно
получено А. Н. Колмогоровым, однако для решения задачи филь-
трации было предложено Н. Винером.
Если сигнал s и помеху п считать независимыми друг от друга,
то их взаимно корреляционная функция будет равна нулю и пра-
вую часть (7.14) можно записать как
(/и) = B7s (т) + В?п (т) = В~ (т).
Учитывая также, что для fj = Sj + п/ корреляционная матрица
Rf = Rs + Rn, уравнение (7.14) перепишем в виде
^hi [7?s (т—i) + Rn(m—i)] = Въ (m).	(7.15)
i
Уравнение (7.15) по известным автокорреляционным функциям
сигнала и помехи и по взаимно корреляционной функции желае-
мого сигнала Sj с исходным s/ позволяет найти весовую функцию
фильтра сглаживания.
Если принять, что желаемый сигнал s совпадает с исходным s,
т. е. s = s, то B~s (т) = Rs (т) и уравнение (7.15) преобразуется
следующим образом:
Е ht [7?s (m—i) + Rn (m—i)] = 7?s (m).	(7.16)
Уравнение (7.16) по известным АКФ сигнала и помехи позво-
ляет рассчитывать весовую функцию фильтра, называемого фильт-
ром воспроизведения исходного сигнала.
Уравнение (7.16), так же как и уравнение (7.15), можно записать
в виде системы линейных уравнений:
при т = 0 h0[Rs(Q) + Rn(Q)] + h1[Rs(l) + Rn(l)]+ . . . +
+ hM [Rs(M\+Rn(M)] = Rs(Q)-
при m=l /iolRs(l) + Rn(l)] + /ii[R,(O) + Rn(O)]+ . . . +
+ hM [Rs (M-1) + Rn (M-1)] ±= Rs (1);	(7.17)
при m=M ha[Rs(M)+Rn(M)]+h1[Rs(M-l)]+Rn(M-l)] +
+ . . . +hM [Rs(V + Rn (0)] = R,(M).
В этой системе учтена четность автокорреляции R (— т) = R (т).
209
Проиллюстрируем нахождение весовых коэффициентов из урав-
нений (7.15) и (7.16) на простой числовой модели.
Пример. Пусть полезный сигнал на входе фильтра представлен двумя
значениями s0 = 3 и sx = 1. Этот сигнал осложнен некоррелированной по-
мехой с единичной дисперсией и нулевым средним: п0 = 1; ni = 0; i 0.
Зададим желаемый сигнал s/ на выходе фильтра в виде единичного: 0, 1, 0.
Тогда функция взаимной корреляции В- (т) в правой части (7.15) будет
B?s(0)= 1 и B?f (l)= 3.
Функция автокорреляции входного сигнала без учета его усреднения
состоит из двух значений: Rs (0) = Sq + sj = 10 и Rt (1) = SqS, = 3, со-
ответственно для помехи Rn (0) = Пд + nJ = 1 и Rn (1) = n<fil = 0.
Решение. Уравнение Колмогорова—Винера (7.15) в матричной форме
с учетом полученных выше
ГЯ,(0) + /?„(0)
(Л»> МI
LRs(l) + Rn(l)
Последние выражения
значений
Л.(1) + Я„(1)
R»(0) + R„(0)J
системе линейных уравнений (7.17) примут вид:
в
hg[Rs (0) + Rn (0)] + hl [Rs (1) + Rn (1)] = B?f (0);
ft0[Rt (1) + Rn (1)] + [/?,(0) + Rn (0)] = B?s (1).
Подставив полученные числовые значения, имеем
Г Ло-11 4-ЛгЗ= 1,
(1, 3) или <
( fto-3-l-fti-ll =3.
(Ao. hi)
Отсюда Ло = 0,018,	= 0,268.
Для того чтобы не было усиления сигнала на выходе фильтра за счет
свертки, т. е. чтобы масштаб выходного сигнала соответствовал масштабу
входного сигнала, весовые коэффициенты обычно нормируют к единичной
энергии: Лц + ftj = 1. С учетом этой нормировки получаем Ло =
= 0,018 <0,018» + 0,268» = 0,067,	= 0,998.
Профильтрованный сигнал, согласно свертке, будет представлен значе-
ниями: у0 = soho = 0,201; yi = htSi + AjSq = 3,061; yt =s1h1 — 0,998.
Для рассмотренного фильтра с учетом (7.8) и (7.10) найдем пиковое
и энергетическое отношения сигнал/помеха на входе фильтра:
R,(0) R,<0) + 2R,(l)R,(l)
R.(0)R.<0)"9'”’	---------R.(0)R,(0)	'°’’*
Здесь Rh (0) = hg + hl = 1, /?h(l) = hghi = 0,067 — значения АКФ ве-
совой функции.
ОчеЬиДно,
и (m) = R
SS	S
/11
(Л«. hl) I
\3
Применяя свойства преобразований Фурье линейности и свертки
функций (см. § 24) к (7.16) Н (со) [ Ws (со) + Wn (<*>)! =	(со),
получим выражение для частотной характеристики фильтра вос-
произведения
Н (<о) = W, (©)/[№, (со) + Wn (®)1,
что для фильтра воспроизведения (7.16), когда s=s
(m), получим систему уравнений
3\
) = (10, 3).
11/
(7-19)
210
где Ws (со) и Wn (со) — соответственно энергетические спектры сиг-
нала и помехи, которые, в частности, могут быть рассчитаны по
их автокорреляционным функциям. Если сигнал s, во входной
последовательности не является случайным процессом, а представ-
лен аналитически заданной функцией, вместо Ws (со) следует пи-
сать | S (со) |2. Из выражения (7.19) видно, что фильтр Колмого-
рова—Винера эффективен именно в задачах сглаживания и вос-
произведения, для которых необходимо большое отношение сиг-
нал/помеха. Действительно, при большом отношении сигнал/по-
меха Wn (со) < W, (со) частотная характеристика Н (со) 1. Сле-
довательно, весовая функция есть дельта-функция и фильтр точно
воспроизводит сигнал.
Таким образом, из (7.16) и (7.19) следует, что для построения
оптимального фильтра воспроизведения сигнала необходимо зна-
ние автокорреляционных функций сигнала и помехи или их спектров
на входе фильтра.
Преимущество оптимальных фильтров по сравнению с неопти-
мальными состоит в возможности получения оценок качества филь-
трации. Так, для фильтра воспроизведения качество оценивается
среднеквадратической погрешностью
ё2=—С WsWWnM da
Л J U7,(®) + «М®)
о
(7.20)
Если спектральная плотность помех мала по сравнению со
спектральной интенсивностью сигнала, т. е. Wn (со) W, (со), то
г2 = J- f Wn (©) dio = Rn (0) = о2,
Л 0
что означает равенство среднеквадратической погрешности сгла-
живания (воспроизведения) сигнала дисперсии помех о2.
Применение фильтра Колмогорова—Винера не ограничивается
решением задач сглаживания и воспроизведения сигнала, оно зна-
чительно шире. Поэтому приведем примеры использования фильтра
для решения наиболее часто встречающихся в практике обработки
геофизической информации задач.
Выделение аномалий в гравиразведке
При обработке данных гравиразведки фильтр Колмогорова—Ви-
нера был использован И. Г. Клушиным с целью сглаживания вы-
сокочастотных составляющих поля, его исследованием также за-
нимались В. И. Аронов, С. А. Серкеров, П. Ганн и другие.
Весовую функцию фильтра воспроизведения И. Г. Клушин
определял на основе обратного преобразования Фурье частотной
характеристики (7.19):
ОО
hi — — \-----------------cos coiAxdco	(7.21)
' л] «7,(<о) + W'n(o)	v '
о
211
В этом выражений учтена четность Н (со) [см. (7.19)1, которая
следует из симметрии энергетических спектров.
Спектры Wt (со) и ,Wn (®) в гравиразведке предложено опреде-
лять через АКФ гауссова типа, т. е.
72
Rs (пг)= —ехр (—/и2//-?);
у2л
Rn (т) —  7— ехр (—т2//^) >
___	_ у2п
где А2 и п2 — средняя интенсивность аномалии и помех.
Соответствующие этим спектрам энергетические спектры:
оо
Fs(<o) =f А2 ехр (—m2/rs2) cos comd/n =
о
= 7Prs (д/лУ2) ехр ( — a>2rs2/4);
ОО
Wn (®) = f n2 ехр (—tn/rfy cos asmdm =
0
= n2rn (д/л /2) exp ( — co2/-2/4).
Отсюда частотная характеристика фильтра воспроизведения
аномалии будет представлена в виде
и (ю) =-------------------=---------!--------=
«М®) + Wn(a) 1 + Wn(a>)/Ws(a)
.____________________1_________________
1 + (п2г„/Л%) ехр [ - а2 (г2 - г2)/4]
Полагая, что аномалия по интенсивности соизмерима с уровнем
помех, т. е. п2 = А2, а ее интервал корреляции rs в 5 раз больше
интервала корреляции помехи rn = 1, получим
Н (со) ----------!--------
' ’	1 + (1/5) ехр (6<йа)
С учетом (7.21) имеем
ОО
. _ 1 f cos m/Axdto
1 + (1/5) exp (6ш2)
0
Этот интеграл можно вычислить, воспользовавшись формулой
трапеций. Переходя к дискретной свертке, получим профильтро-
ванные значения поля fc.
у. — — 2 f t (0,293 5i~e,8‘A* + 0,172	=
У1 п 1 \	0,8/Дх	0,4/Дх )
— 0,148/ j + 0,136 (//+1 + f /-1) + 0,107 (f/+i + f y_j) +
+ 0,069 (fj+з + f /-з) + 0,033 (fi+t + f /-«)•
Пример, иллюстрирующий сглаживание высокочастотной по-
мехи, соизмеримой по интенсивности с аномалией силы тяжести,
приведен на рис. 45.
212
Если модель наблюденного поля включает помимо локальной
составляющей региональный фон: f = sper + smK + п, то при ус-
ловии независимости их появления между собой и от помехи спектр
наблюденного поля Wf (ш) = U7per (<о)+№Лок (®) + Wn («), где
№Рег (<о), Н7ЛОК (®) И Wn (со) — энергетические спектры соответст-
венно регионального фона, локальной аномалии и помех.
Следовательно, частотная характеристика фильтра Колмого-
рова—Вииера для выделения (воспроизведения) локальной ано-
Рис. 45. Результаты выделения аномалии на фоне помех по критерию Кол-
могорова—Винера:
1 — заданная аномалия; 2 — аномалия, осложненная помехой; 3 — результат фильтра-
ции (по И. Г. Клушнну)
малии, осложненной региональным фоном и погрешностями на-
блюдений (помехами), примет вид
Я(ю)=------------^лок (т)---------- (7.22)
№per (®) 4" ^лок (<о) + Wn (со)	' 7
При этом фильтр Колмогорова—Винера соответствует полосовому
фильтру. При аппроксимации энергетических спектров U7per (со),
И^лок (<*>), Wn (со) выражением W (со) = Ааг (д/л /2) ехр (— <о2г/4)
получим частотную характеристику такого полосового фильтра
с учетом (7.22)
ц	= _____________________1 + сехр ( — <оааа/8)__________________
1 + са ехр ( — <оааа/4) -j- d2 ехр ( — <оа6а/4) + 2с ехр ( — <оааа/8) ’
(7.23)
где
2	2	2	,2 2 2
О —Грег — Глок!	О —Гп — Глок!
J2	-П
(Л — Рег Рег . J2 	.
т	Г
плок лок	лок лок
Результат применения частотной характеристики (7.23) к сум-
марному полю Ag (рис. 46, а) позволяет провести выделение ло-
кальных аномалий с высокой достоверностью (рис. 46, б) и тем
самым подчеркнуть основные структуры кристаллического фунда-
мента (рис. 46, в). По эталонным профилям I и II на схеме поверх-
ности фундамента (см. рис. 46, в) проводилась оценка параметров
А рег И Грег и Л^лок и Глок, помеха принималась некоррелированной
и оценивалась по погрешностям наблюдений. Для регионального
213
Рис. 46. Результаты выделения
локальных аномалий &g на фоне
регионального поля и помех
с целью картирования поверх-
ности кристаллического фунда-
мента на одном из участков Цен-
тральной части Московской сине-
клизы (по С. А. Серкерову).
л — наблюденное поле Ag в уел. ед.;
б — поле локальных аномалий Д£ в —
структурная схема поверхности кри-
сталлического фундамента
фона были получены Лрег — 0,64 км’, Грег= 50,9 км, для локаль-
ных ПОДНЯТИЙ 11ок = 0,16 км’, Глок = 24 км.
Обратная фильтрация
Обратная фильтрация широко используется в сейсморазведке для
повышения разрешающей способности сейсмических записей, в ча-
стности для подавления реверберационных волн-помех в морской
сейсморазведке. Цель обратной фильтрации — максимально при-
близить сейсмический импульс к дельта-функции, т. е. в конечном
итоге получить импульсную сейсмограмму. Поэтому обратный
фильтр часто называют фильтром сжатия. Идеальный
обратный фильтр имеет частотную характеристику
Н (©) = l/S(to) = S*(©)/|S (©)(’.	(7.24)
где S (®) — спектр желаемого сигнала; S* (ш) — комплексно-
сопряженный спектр сигнала.
214
Очевидно, что на выходе фильтра получим сплошной спектр
Y (со) = Н (со) F (со)-> 1, если F (со) » S (со), который и соот-
ветствует дельта-функции или единичному импульсу.
Первые попытки реализации обратной фильтрации были свя-
заны с использованием характеристики (7.24). Однако нетрудно
видеть, что, если спектр сигнала на некоторых частотах принимает
близкие к нулю значения, например из-за его искажения помехами,
на тех же частотах \Н (со)| -> оо и фильтр становится неустойчи-
вым. Дальнейшие исследования обратной фильтрации были на-
правлены на ее стабилизацию путем введения в знаменатель (7.24)
дополнительного члена для исключе-
ния возможностей деления на нуль,
т. е.
//(©) = S*(©)/(|S (u>)f + a).	(7.25)
Рис. 47. Сигналы:
1 — исходный, 2 — зеркально отраженный относи-
тельно оси ординат
Величину а предлагалось задавать равной 5 или 10 % от мак-
симальной частоты сигнала S (со). Это, естественно, приводило
к существенному повышению устойчивости обратного фильтра, но
в то же время возникала новая проблема уже по определению оп-
тимальной величины а. Использование общего уравнения фильтра
Колмогорова—Винера (7.15), в котором в качестве желаемого сиг-
нала следует принять дельта-функцию, позволяет однозначно ре-
шить вопрос о величине а и тем самым построить оптималь-
ный обратный фильтр.
Положим s (/) = б (0, тогда функция взаимной корреляции
B~s(r) = б (/) s (/—т) = s (—т). Следовательно, уравнение Кол-
могорова—Винера для реализации обратного фильтра примет вид
ZhiRf(m—i)=s(—т)
или
£ hi [Rs (m—0 + Rn (m—i)] = s(—m).	(7.26)
Используя свойства преобразований Фурье, из (7.26) получаем
частотную характеристику оптимального обратного фильтра
Яовр (®) = S* (со)/(| 5 (©) |« + Wn (©)).	(7.27)
Сравнивая (7.27) с (7.25), видим, что оптимальной величиной
стабилизатора а является не что иное, как спектральная плот-
ность помех. Во временной области вычисление весовой функции
оптимального обратного фильтра сводится к решению системы
линейных уравнений вида (7.17), где в правой части вместо авто-
корреляционной функции сигнала следует подставить значения
самого сигнала, симметрично отраженного относительно оси ор-
динат (рис. 47).
В случае некоррелированной помехи с дисперсией о® система
уравнений (7.26) для нахождения обратного фильтра минимально-
го
фазового сигнала (если сигнал минимально-фазовый, обратный
фильтр относится к физически осуществимым фильтрам, для ко-
торых s (т) = 0 при т<0) принимает вид:
ho[Rs(0) + ai] + h1Rs(l) + . . . + hMR,(M) = s(0)-,
/*otfs(l) + MKs(O) + a2]+ • • • + hMRs(M—V) = 0;	„ o
/i0Rs(M) + /i17?s(M-l)+ . . . +/iM[7?s(0) + o2]=0.
Во-первых, из этой системы следует, что устойчивость обрат-
ного фильтра достигается путем введения дисперсии помехи. Иначе
говоря, регуляризация решения обеспечивается стабилизатором,
тождественно совпадающим с дисперсией помех. Во-вторых, до-
пущение о минимальной фазовости сигнала освобождает от необ-
ходимости рассчитывать форму импульса. Пользуясь свободой
выбора постоянных коэффициентов при весовой функции фильтра,
положим s (0) = 1, тогда для нахождения значений h{ достаточно
знания корреляционной матрицы наблюденного поля Rf (т—t) =
= Rs (m—i) + Rn (m—i).
Применение обратной фильтрации не ограничивается задачами
повышения разрешающей способности сейсмической записи. Не-
сомненно, она может использоваться и в других методах разведоч-
ной геофизики. На базе обратного фильтра, например, основана
поточечная интерпретация геофизических параметров в каротаже,
реализованная Г. Н. Зверевым [13].
Если после обратной фильтрации реализуется полосовой фильтр
с заданной частотной характеристикой Н„ (<л), такая фильтрация
называется корректирующей. Частотная' характери-
стика корректирующего фильтра Нкор (со) = НовР (со) Нп (со).
Оригинальное применение обратного фильтра предложено
Г. Н. Богаником для преобразования наблюденной гистограммы
mJ / = 0, 1, . . . , L, £ mz = 1 I некоторого случайного параметра
\	/=о	/
с дискретной плотностью распределения р/ (j = 0, 1, . . . , L,
jT, Pf = 1) и объемом выборки п в функцию, наименее отличающуюся
от единичной дельта-функции 6/. При этом весовая функция об-
ратного фильтра находится из системы линейных уравнений
м
2 hf [bf-i + 6z_i/(n-1)] = npk4l(n-1),	(7.29)
/ = 0, 1, . . . , M- k = Q, 1, . . . , L + M,
где
fl при i = /,
— 10 при i =/= /;
216
bj_i — элементы корреляционной матрицы (bj-t = bi-j),
L-l+i
bi-i= 2 PkPk+J-t-
fe=0
Вариационный ряд случайной выборки объемом п (гистограмма)
преобразуется в функцию, которая в среднем по множеству реали-
заций наименее отличается от 6-функции с амплитудой п, распо-
ложенной в заданной точке k. От объема выборки п зависят только
диагональные элементы матрицы системы (7.29).
В (7.29) к величине 60> являющейся максимальным значением
автокорреляционной функции дискретной плотности (гистограммы),
добавляется слагаемое 1/(п—1). Например, в случае L—M = k = 2
система (7.29) принимает вид:
(b0 Н---——'j h0 + bihi + bi/it =--—
bih^ (Ьо -----—hi + b^ =----------— pi;
\ n — 1 /	п — 1
+ bihi + (b0 -|	— 'j hi =---— p0.
\ л — 1 / n — 1
Обратный фильтр служит для разделения смеси однотипных
случайных величин, известных с точностью до их математических
ожиданий и объемов выборок. Сначала по совокупности из N зна-
чений изучаемого параметра строят исходную гистограмму т/ (j=0,
1, . . . , L). Интервал Д между соседними разрядами принимают
равным величине среднеквадратической погрешности определения
параметра. Анализ гистограммы выполняют путем циклического
повторения последовательных операций выявления, оценивания и вы-
читания из смеси составляющих компонент в порядке убывания
их объемов. В качестве исходных параметров задают теоретиче-
скую гистограмму распределения случайных величин р/ (/ = 1,
1, . . . , L) и порог а, соответствующий принятому значению до-
верительной вероятности у выявления компонент смеси.
При каждом цикле анализируется гистограмма — исходная
либо остаточная, полученная из исходной после вычитания ком-
понент смеси, установленных в предыдущих циклах. В этой гисто-
грамме выделяется наибольшая по объему выборка путем ее свертки
с весовой функцией. Для расчета весовой функции необходимо
знать объем п искомой выборки, неизвестный заранее. Поэтому
задача решается способом последовательных приближений. Первая
оценка п' объема максимальной компоненты смеси находится по
гистограмме п' — пгтах/ртах, где mmax и ртах — максимальные зна-
чения соответственно наблюденной и теоретической гистограмм.
Величина п' используется для вычисления первой весовой функции
h'i, с которой свертывается гистограмма. Максимальное значение
результата свертки yk (k = 0, 1, . . . , L + М) дает вторую оценку
п" объема' искомой компоненты смеси, используемую соответст-
217
йеййо для расчета второй весовой функции hi*. Максимальное зна-
чение результата свертки y'k гистограммы с функцией h'i рассмат-
ривается как оценка nft объема искомой компоненты смеси, распо-
ложенной в точке k.
Дисперсия оценки п состоит из дисперсии £)с, обусловленной
случайным характером интервальных значений данной выборки,
и фоновой дисперсии Дф (за счет случайного характера соседних
выборок, вычитаемых из гистограммы на предыдущих циклах).
Первая дисперсия определяется как
De = п I Д	htPk—i \ I •
Дисперсия Оф рассчитывается по значениям дисперсий Dt и
корреляционных моментов Ktj погрешностей в значениях гисто-
граммы, которые образовались при вычитании выявленных ранее
компонент:
L / М	М	\
4	t+I	/
Сумма по L означает сложение результатов обработки, полу-
ченных по всем ранее вычтенным L-компонентам.
При наличии дисперсии оценки п решается вопрос о значимости
полученного результата, т. е. о надежности выделения из смеси
очередной компоненты. Последняя считается значимой, если
пЛуТЭсЧ-Дф >*v, где V — квантиль нормального распределе-
ния. В случае значимости полученной выборки она считается ком-
понентой смеси и вычитается из гистограммы; соответствующие
значения по разрядам гистограммы уменьшаются на величину пр].
По этим же разрядам гистограммы вычисляются моменты остаточ-
ных погрешностей, неизбежных из-за случайного характера, вы-
борки. Эти величины используются для расчета Дф в последующих
циклах обработки гистограммы. Вычисления по указанной схеме
повторяются до тех пор, пока ие будут проанализированы все раз-
ряды (точки) гистограммы. В результате получается последова-
тельность неотрицательных оценок п*, среди которых отличаются
от нуля только те, которые соответствуют значимым компонентам
смеси. Далее выполняется коррекция оценок п* для того, чтобы
сделать их целыми числами и согласовать со значениями исходной
гистограммы на соответствующих ее интервалах. Полученные в
итоге-оценки п* рассматривают как результат разделения исход-
ной гистограммы на составляющие ее элементарные выборки. Ал-
горитм разделения смеси случайных величин использован Г. Н. Бо-
таником для иллюстрации следующего примера (рис. 48). Смесь
состояла из трех нормально распределенных выборок разных объе-
мов, смещенных одна относительно другой на два интервала. Тео-
ретическая гистограмма задана пятью значениями pt = mj/n
218
a
Рис. 48. Результаты разделения смеси случайных величин обратным фильт-
ром (по Г. Н. Ботанику)
(/ = О, 1, 2, 3, 4) с интервалом, равным величине среднеквадрати-
ческого отклонения, при этом р0 = pt = 0,07; рх = ра = 0,24;
р3 = 0,38.
Для обработки гистограммы использовался фильтр с пятью
значениями hi (i = 0, 1, 2, 3, 4). Порог tv = 1,28 (у = 0,9). Слева
на рис. 48, а даны смеси, состоящие из выборок объемом по 20 зна-
чений, а справа — по 80 значений. На рис. 48, а показаны теоре-
тические гистограммы, на которых с помощью вертикальных линий
указаны местоположение и объемы компонент, образующих смесь.
На рис. 48, б и в приведены варианты эмпирического распреде-
ления для каждого случая, которые были образованы суммирова-
нием выборок, полученных с помощью таблиц нормально распреде-
ленных случайных чисел. Результат разделения каждой смеси
219
изображен с помощью вертикальных линий, расположение и вы-
сота которых соответствуют параметрам выявленных компонент,
оценки объемов этих компонент указаны числами. Пример иллю-
стрирует общую закономерность: с уменьшением объемов выборок
задача выделения отдельных компонент из наблюденной смеси слу-
чайных величин решается менее точно.
Фильтр прогнозирования
Оптимальный фильтр Колмогорова—Винера используется для ре-
шения задачи прогноза (предсказания) значений поля в некоторых
«будущих», например еще не измеренных, точках Xk = k&x (&>1).
При этом в правой части уравнения (7.14) желаемым сигналом s/
является входной сигнал f{, т. е. s7- = fjt в последующие (будущие)
моменты времени. Тогда = Rf (т + k) и уравнение Кол-
могорова—Винера принимает вид
У, i) = Rf(m + k).	(7.30)
1=0
Практическая реализация фильтра прогноза (7.30) сводится
к многократному решению систем линейных уравнений для каж-
дого заданного значения k = 1, 2....Правая часть выражения
(7.30) при k — 1 представляет собой автокорреляционную функцию
исходного поля без ее значения в нуле, при k = 2 — ту же функ-
цию без первых двух значений АКФ исходного поля и т. д. При
k<0 уравнение (7.30) соответствует фильтру запаздывания.
Фильтр прогнозирования предсказывает будущие значения
сигнала по предшествующим значениям («истории») сигнала и по-
мехи. Следовательно, его можно с успехом использовать для ре-
шения задач интерполяции поля в любые наперед заданные точки.
Широкое применение получил алгоритм обратной фильтрации
с прогнозированием, включенный в стандартную процедуру циф-
ровой обработки сейсмических записей.
На основе фильтра прогноза строится новый метод оценки энер-
гетических спектров, отличающийся существенным увеличением
разрешающей способности по сравнению с методами расчетов спект-
ров Фурье. Этот метод, предложенный И. Бургом, исходит из мак-
симизации энтропии стационарного нормального случайного про-
цесса и поэтому получил название метода максимума
энтропии. И. Бургом показано, что спектральная плотность,
отвечающая максимуму энтропии случайного процесса,
W (со) =------------
2<Х>гр
_______£z+i_____________
I	2
1 + У hu ехР (— /штЛ)
/=1
где соГр = 1/2Д, Di+i и Ц, { находятся из системы уравнений про-
220
гнозирующего фильтра
"R(0) R(l) . . . R(l) ~
R(l) R(0)	. . .	R(/-l)
R (Z) R(Z—1)
Di+i
0
(7-31)
Эта система уравнений преобразует входной сигнал, заданный
его АКФ R (т), в белый шум с дисперсией Di+1. Она, по существу,
описывает обратный фильтр с прогнозом на один интервал и сов-
падает с системой (7.28). В то же время дисперсию прогноза можно
найти через средний квадрат разности между входным сигналом
в момент I 4- j и предсказанным его значением yi, т. е. Di+j =
= (h+}
Используя специальный метод вычисления hi,i, можно полу-
чить рекуррентное соотношение hu— ht-ц — htihi+ci—i и значения
автокорреляционной функции для т = I + 1, выраженные через
весовые коэффициенты фильтра (7.31):
«4-1
R (/ + 1) = - £ hl+1(R (i + 1 -/).	(7.32)
Первый индекс при коэффициенте й/+ц обозначает номер ите-
рации, иначе — длину фильтра прогнозирования (число его ко-
эффициентов), вычисляемого на данном этапе.
Алгоритм метода максимума энтропии начинается с того, что
полагают I = 0, тогда уравнение (7.31) запишется как
[R (0)]• 1 = £>х. При определении АКФ при нулевом сдвиге сред-
няя мощность одночленного фильтра прогноза Dr — R (0). При
расчете двучленного фильтра прогноза вида (1, йХ1) сначала свер-
тывается входной сигнал /х, f2, . . . , fn, и ошибка прогнозирова-
ния — fl+t—huff, j — 1, . . . , п. Если фильтр прогноза обра-
тить и провести фильтрацию в обратную сторону, то 8/ = fj—huff+i
j = 1, ... , п—1.
Средняя энергия при прямом и обратном направлении свертки
1	"-1
221
или
£а= ,Лп XW/+i-W/)2 + (f/-W/+i)2l-
X {Fl LJ /^1
На основании максимума энтропии htt определяется так, чтобы
Е2 была бы минимальной, т. е. dEJdhu — 0:
п—1
dEJdhu=[\l{n-1)] g [-Ш1+М/) + Лн (f/+i + f2/)] = 0.
Отсюда
Ли = 2Ш+1£ (f/ + f/+i) = 2R (1)7(R (0)+О
В то же время можно вычислить htt, не используя АКФ и не
делая предположений относительно поведения исходных данных
за конечными интервалами их определения. Уравнение (7.31) при
I = 1 имеет вид
Г R (0)	R (1) ] Г 1 1 = Г Dt
L R (1)	R (0) J L Ли J “ L 0 . ’
Эти уравнения решают относительно R (1) с использованием
оценки и R (0). Тогда получают R (1) = R (0) ЛХ1.
По формуле (7.32) вычисляют значение АКФ при I = 1, т. е.
R (2), благодаря которому из системы (7.31), уже состоящей из
трех уравнений, находят й21, й22 и Ds. Этот итерационный процесс
продолжается др тех пор, пока не будет достигнута заданная погреш-
ность D/+1, либо пока не будут использованы все значения ис-
ходного поля для коротких реализаций. Наконец, по формуле для
W (<о) с известными hu и Di+1 находят спектральную плотность
(энергетический спектр), для вычисления которой следует исполь-
зовать алгоритм быстрого преобразования Фурье.
Метод максимума энтропии обеспечивает высокую разрешаю-
щую способность спектра за счет надежной оценки более длинной
АКФ наблюденного поля. Достигаемый при этом эффект аналоги-
чен расчету спектра по длинной АКФ (см. рис. 25). Одновременно
со спектром получаем более надежную оценку АКФ, что сущест-
венно при обработке данных по малому числу наблюдений вдоль
профиля. Однако важно, чтобы число членов фильтра ошибки
прогноза не превышало бы величины [(л + / + 1)/(л—4—1) 1 D/+i,
так как при чрезмерном увеличении разрешенное™ спектра на нем
появляются ложные максимумы и наблюдается расщепление ча-
стоты.
Пример, иллюстрирующий высокую разрешенность энергети-
ческого спектра по методу максимума энтропии, приведен на
рис. 49. Из рисунка видно, что помимо пика для постоянной состав-
ляющей четко выделяются еще- два экстремума, соответствующие
составляющим поля Ag с различной протяженностью. По этим
экстремумам спектра представляется возможность оценить отно-
сительную интенсивность составляющих поля и их протяженность.
222
&	i	i
Рис. 49. Результаты обработки исходной кривой Ag с помощью энергетиче-
ского фильтра (а) и оценки энергетического спектра кривой Ag (б).
1 — исходная кривая Ag; 2 — результат энергетической фильтрации; 3 — разность ме-
жду / и 2; 4 — спектр Фурье; о — спектр, рассчитанный по методу максимума энтропии
и =
Наибольшему значению спектра отвечает составляющая поля про-
тяженностью в 3/4 профиля, а второму по величине максимуму —
составляющая с протяженностью около 1/4 длины профиля. Ос-
новная составляющая поля определяется структурным фактором,
а вторая по протяженности — эффектом от нефтегазовой залежи.
По «хвосту» энергетического спектра находится интенсивность
некоррелированных помех — погрешностей измерений поля Д#.
§ 36. СОГЛАСОВАННЫЙ ФИЛЬТР
Согласованный фильтр строится на основе критерия максимума
пикового отношения сигнал/помеха и предназначен для решения
задачи обнаружения сигнала, т. е. установления факта его нали-
чия, а в общем случае за счет существенного искажения формы сиг-
нала. При этом полагают, что полезный сигнал задан по форме
и ее искажение при фильтрации не имеет существенного значения.
Выбор формы сигнала (аномалии) может быть осуществлен либо
путем решения прямой задачи, либо посредством анализа наблю-
денных значений над аномальными объектами на соседних, ана-
логичных по геологическому строению участках. При обработке
сейсмических записей оценка формы сигнала производится по АКФ
или ВКФ исходных трасс. Кроме того, в сейсморазведке, напри-
мер, существуют такие типы источников, как вибрационные, для
которых форма возбуждаемых в упругой среде волн известна. Поэ-
тому задача фильтрации сигналов известной формы, т. е. детерми-
нированных сигналов, в разведочной геофизике представляет прак-
тический интерес. Ее значение непрерывно, возрастает в связи
223
с поисками глубокозалегакицих месторождений, аномальные эф-
фекты от которых искажены помехами различной природы, а ин-
тенсивность помех превосходит амплитуду полезных сигналов.
Для нахождения частотной характеристики согласованного
фильтра исходим из аддитивной модели поля fj = s/+ П/, в которой
Sj — известный по форме сигнал, а помеха — стационарный слу-
чайный процесс. Вывод частотной характеристики проведем для
апериодического сигнала. Если известна форма сигнала s (х), оче-
видно, известен и его спектр 3(со), т. е.
s(x) = (l/2n) f 3(со)e/“Mco, где S(co) = У s(x)e~iaxdx.
—00	—00
Сигнал на выходе фильтра с частотной характеристикой Н (со)
можно представить в виде
8вых(х) = (1/2л) f е/ш*Я(со) S(co)dco.	(7.33)
—00
Энергия помех на входе фильтра выражается через спектраль-
ную плотность (энергетический спектр) Wn (со):
n2(x)=J_ f rn(co)dco.
2л —оо
Выражение для энергии помех на выходе фильтра получим,
если учтем, что при преобразовании стационарного случайного
процесса (т. е. помех) линейным фильтром его спектральная плот-
ность умножается на квадрат модуля частотной характеристики
фильтра | Н (со) |2, т. е.
Пвых(х) = 4- У | Н (со) |2 W„ (со) da>.	(7.34)
2л — оо
Пиковое отношение сигнал/помеха в точке х0 на выходе фильтра
определяется как
Рвых — ®вых (Хо)/Мвых (х).	(7.35)
Используя выражения (7.33) и (7.34), получаем
Рвых- 2Я
00
J ехр (/сохо) Н (со) S (со) dco
—00
У | Н (со) |а Wn (со) da>
—00
(7.36)
К ;На выходе фильтра у (х0) = «вых (х0) + «вых (х0), при этом
требуется максимизация рвых. Иными словами, необходимо, чтобы
8вых (х) Пвых (х).
224
Частотную характеристику искомого фильтра получим, если
воспользуемся известным неравенством Буняковского—Шварца,
согласно которому
I f el^H (со) S (©) do < f | H (®) |2 Wn (©) da x
I -00	—00
C |S ((0)1*
) Wn (И)
da.
Отсюда с учетом (7.36)
1
2л
JAWJLdtt>,
wn (о)
Очевидно, выражение (7.37)
Рвых- Если принять частотную
характеристику
Я((о) = е-/“*о S* (a)/Wn (®),
(7.38)
то максимально достижимое
значение пикового отношения
сигнал/помеха рВых согласно
(7.36) будет
(7.37)
является верхним пределом для
1 Г | S (<в) |2 .
Цвых Ш8Х —	\	Ct (О •
2я 1
(7.39)
Рис. 50. Графики спектров сигнала
(/), помехи (2) и частотной харак-
теристики согласованного филь-
тра (3)
Таким образом, выражение (7.38) является частотной характе-
ристикой искомого согласованного фильтра.
Физический смысл неравенства (7.37) состоит в том, что согла-
сованный фильтр пропускает интервал частот (®, ® 4- Д<о) в тем
большей степени, чем больше спектральная амплитуда полезного
сигнала и чем меньше спектральная мощность помех в том же ин-
тервале (рис. 50). При этом, как следует из (7.39), отношение сиг-
нал/помеха иа выходе фильтра будет тем больше, чем больше от-
личие спектра сигнала от спектра помехи.
Без ограничения общности можно принять х9 = 0, тогда из
(7.38) имеем
H(<o) = S*(<o)/IFn((o).	(7.40)
Если помеха представляет белый, некоррелированный шум, то
Wn (a) = const и
Н (со) = cS* (a).	(7.41)
Из (7.41) следует, что частотная характеристика фильтра пол-
ностью определяется спектром сигнала, иначе говоря, согласована
8 А. А. Никитин	225
со спектром сигнала. Отсюда и название фильтра — согласованный.
Если от спектральных представлений (7.41) перейти в область
пространственной координаты х, получим
h(x) = cs(—х), ht = cs(—г).	(7.42)
Из (7.42) следует, что при некоррелированной помехе весовая
функция фильтра полностью определяется формой сигнала, т. е.
ее форма согласована с формой сигнала. Нетрудно видеть, что
роль константы в (7.42) играет величина, обратная дисперсии по-
мех, т. е. с = 1/о2. Это следует из выражения (7.40), если, исполь-
зуя свойство преобразований Фурье о свертке двух функций, от
частотной области перейти в пространственную (или временную):
м
Wn (®) Н (со) = S* (<о)	2 htRn	(7.43)
i=0
Формула (7.43) представляет собой систему линейных уравнений
согласованного фильтра при заданных АКФ помех и форме сиг-
нала, ее можно записать в матричной форме:
“ Rn (0) Rn (1)	... Rn (М) “
R»(l) R„(0)	. . . R„(M-1)
(йо, hi, . . . , hM)
Rn(M) Rn(M — V) ...	R«(0) _
= (s-m> s-m+i. • • • » So)	(7-44)
или в виде
М„(0) + Мл(1)+ • • • +hMRn(M) = s(-M),
ад„(1) + ад„(0) + . . . +Ладп(М-1) = а(-М+1),
ад„(Л4)+адп(Л1-1)+ . . . +hMRn(0) = s(0).
При не коррелированной помехе Rn (0) = о2, Rn (т) = 0 и из
приведенных выше уравнений следует, что h{ = s (— i)/o2.
Уравнение оптимального согласованного фильтра (оптималь-
ность фильтра следует из того, что любой другой фильтр создает
меньшее отношение сигиал/помеха) можно получить приравнива-
нием производной дрвых/дй( к нулю. Согласно выражению (7.7)
дрвьж  2 (ft's) s (ft'Rn ft) — 2Rn ft (ft's)8  о
dhi
(h' Rn ft)2
Равенство числителя нулю выполняется, если положить
Rnh = s; h'Rn=s‘
h = Rnll
(7.46)
226
Таким образом, мы вновь получили уравнение (7.43), однако
при таком подходе к построению согласованного фильтра следует
учесть, что в правой части (7.45) сигнал должен быть переверну-
тым, т. е. отсчет его значений производится с конца. Проиллюстри-
руем нахождение весовой характеристики согласованного фильтра
на простой числовой модели.
Пример. Пусть, как и для фильтра Колмогорова—Винера, сигнал и по-
меха заданы значениями (s0, sx) = (3,1), (n0, nt) = (1, 0), т. e. (Rn (0) = 1,
Rn (1) = 0.
Решение. В соответствии с (7.44) получим
( °’ 1 L Rn (1) Rn (0) J
(ho. fci) [ о j ] = <sb so)-
иля
Отсюда ft0 = Ь Й1 = 3. С учетом нормировки весовой функции
ho+ hl = 1; h0 = 0,316, hi = 0,948.
Найдем пиковое и энергетическое отношение сигнал/помеха на выходе
фильтра с учетом (7.8) и (7.10):
__ (hpSi -f- hi$o)a__________(hpSi 4- hjSo)2________
ЦВЫХ~ A'R h ~ Kn(0)Rft(0) + 2/?n(l)/?ft(l) ~
= 10
1
(h<A>)2 + (hoSj + hjSo)2 + (hiSi)2 .. „
Ряых =	11 1"1	* —	—	1 1 1 =: ll»O.
/?„ (0) (0) + 2Л„ (1)	(1)
Из сравнения полученных значений рВых и рвых с аналогичными
значениями для фильтра Колмогорова—Винера видим, что согла-
сованный фильтр обеспечивает большие как пиковое, так и энерге-
тическое отношения сигнал/помеха.
Другой пример, иллюстрирующий применение согласованного
фильтра, приведен на рис. 51. Из рисунка видно, что весовая функ-
ция в случае коррелированной помехи уже не согласована с фор-
- мой сигнала. Таким образом, согласованность форм сигнала и ве-
совой функции имеет место лишь для некоррелированной помехи.
Максимальное значение профильтрованного сигнала, приходящееся
на ПК 50, соответствует центральной точке полезного сигнала.
В этом случае решена задача обнаружения сигнала за счет иска-
жения его формы.
Согласованная фильтрация нашла применение при обработке
сейсмических записей. Пример ее применения для обнаружения
вступления рэлеевской волны приведен на рис. 52. Здесь макси-
мальная амплитуда профильтрованного сигнала указывает иа
вступление волны, имеющей период 30 с. Форма весовой функции
при этом определялась формой сигнала с частотой, линейно меняю-
щейся от 0,02 до 0,06 Гц, и длительностью 630 с.
8*	227
Рис. 51. Пример обнаружения сигнала на фоне коррелированной помехи.
а — помеха и ее автокорреляционная функция R (т); б — полезный сигнал зр в — сиг-
нал 4* помеха; г — весовая функция согласованного фильтра Лр д — результат согла-
сованной фильтрации; е — апостериорная вероятность наличия сигнала заштрихована
область значений Рр больших 0 5
Все более широкое использование согласованной фильтрации
мы находим в варианте построения корректирующих фильтров,
частотная характеристика которых равна произведению частот-
ных характеристик обратного и согласованного фильтров.
Сравнивая выражения для частотных характеристик обратного
(7.27) и согласованного (7.40) фильтров, при | S (со) |2 < (со)
получаем, что оптимальный обратный фильтр является фильтром,
максимизирующим пиковое отношение сигнал/помеха.
Рис. 52. Исходная сейсмическая
трасса с записью рэлеевской волны г
(/) и выходной сигнал согласован-	ЛдЛа,-.____
ного фильтра (2) [8]	! Змин j
В заключение подчеркнем, что согласованный фильтр наиболее
эффективен при решении задач обнаружения весьма слабых сигна-
лов.
§ 36. ЭНЕРГЕТИЧЕСКИЙ ФИЛЬТР
Энергетический фильтр строится на основе критерия максимума
энергетического отношения сигнал/.помеха на выходе фильтра
и предназначен для выделения сигналов (аномалий), различаю-
щихся по энергии. Этот фильтр занимает промежуточное положе-
ние между фильтром воспроизведения Колмогорова—Винера и со-
гласованным фильтром, поскольку он строится как фильтр обна-
ружения (максимизируется отношение сигнал/помеха), а решает
задачу выделения, т. е. оценки формы сигнала. В отличие от со-
гласованного фильтра для этого фильтра требуется задание авто-
корреляционных функций сигнала и помех, т. е. знание формы
сигнала несущественно, и априорная информация о сигнале и по-
мехах совпадает с той информацией, которая необходима при по-
строении фильтра воспроизведения. Оценка формы сигнала при
максимизации отношения сигнал/помеха оказывается возможной
потому, что максимизируется не пиковое отношение, т. е. отноше-
ние лишь в одной точке, а энергетическое — по всей длине фильтра.
Энергетическое отношение сигнал/помеха на выходе фильтра
(7.9)
рвых —h Rsh/h Rnh,
—►	—>
где ft' и h — соответственно вектор-строка и вектор-столбец весо-
вых коэффициентов фильтра; Rt и Rn — корреляционные матрицы
сигнала и помехи.
Энергетический фильтр должен иметь весовые коэффициенты hi,
определяющие максимум выражения (7.9) при условии нормали-
зации весовой функции £ft, = 1.
229
Для Нахождения весовых коэффициентов обозначим рВЫх че-
рез А. Продифференцируем А, по h, а производную dK/dh прирав-
няем к нулю, т. е.
А — h' Rs h'/h' R„ /г,
дк  (h' Rn hj (R, ft) - (h' Rs ft) Rnh =Q
dh	(h' R„ftja
—► —►
Поделив обе части числителя последнего выражения на ft'RnA
и учтя введенное обозначение для А, получим матричное уравнение
Rs/i—A Rn h = 0 или
[Rs—AR„] h — 0, или
м
Y, [Rs(m—i)—kRn(m—i)]hi = Q.	(7.46)
z=o
Уравнение (7.46) может быть записано в развернутой матричной
форме:
~ R,(0)	Rs(l)	. . . RS(M) -
ед	ед	. . .	я,(л<-1)
RS(M) RAM-1) . . .	Rs(0)
“ R„(0)	R„(l)
ед	ед
RAM)
RAM-1)
Ao
Ai
_.Rn(M) RAM-1)
- Am _
(7.47)
0 _
Значения автокорреляционных функций сигнала и помехи счи-
таются известными, заданными. Неизвестными являются параметры
А и значения весовых коэффициентов.
Решение системы линейных уравнений (7.47) составляет так
называемую проблему нахождения собственных значений. Пара-
метр А при этом является собственным значением корреляционной
230
матрицы (Rs—R„), а весовая функция — соответствующим ему
собственным вектором той же матрицы.
Таким образом, построение энергетического фильтра сводится
к задаче компонентного анализа, при которой также находятся
собственные значения корреляционной матрицы и соответствующие
этим значениям собственные векторы.
Для корреляционной матрицы (Rs—R„) в уравнении (7.47)
собственные значения Хо, Лх, . . . , являются действительными
и положительными. Это свойство собственных значений хорошо
согласуется с физическим смыслом параметра X.
Поскольку Хтах представляет собой энергетическое отношение
сигнал/помеха, т. е. отношение двух действительных положитель-
ных чисел (энергий сигнала и помех), оно само должно быть дейст-
вительной и положительной величиной.
Система (7.47) имеет ненулевое решение, если определитель
матрицы, составленный по разности двух матриц Rs и Rn, равен
нулю. В этом случае существует (Л4 + 1) собственных значений
и соответствующих им собственных векторов, удовлетворяющих
уравнению (7.47). Все собственные значения можно расположить
в порядке убывания и выбрать среди них максимальное, которое
будет соответствовать максимальному отношению сигнал/помеха на
выходе фильтра. Собственный вектор, связанный с этим ХтаХ, сле-
дует выбрать в качестве искомой весовой функции. Следовательно,
из всех (М + 1) собственных значений Х<, удовлетворяющих урав-
нению (7.47), решение задачи о максимизации рвых обеспечивается
вектором матрицы (Rs—XmaxRn).
Из сказанного выше раскрывается физический смысл Хтах:
Хтах — не что иное, как максимум энергетического отношения
сигнал/помеха на выходе фильтра. Поэтому профильтрованный
выходной сигнал yt = с весовой функцией, представлен-
ной собственным вектором, соответствующим Хтах, является пер-
вой главной компонентой в терминах метода главных компонент.
Физический смысл Хтах позволяет считать, что выходной сиг-
нал ус, соответствующий первой главной компоненте, обеспечивает
выделение составляющей наблюденного поля, которая обладает
наибольшей энергией. В модели поля// = sper/ + 8лок/+ п/ такой
составляющей, как правило, оказывается региональный фон, в мо-
дели fj — sMk i + П] — локальная аномалия.
Рассмотрим построение энергетического фильтра на той же
простой числовой модели, использованной нами в § 34 и 35.
Пример. Пусть сигнал (s0, Sj) = (3,1) и помеха (л0, nx) = (1, 0), их
автокорреляции R, (0) = 10; Rt (1) = 3; Rn (0) = 1, Rn (1) = 0.
Решение. Составим матричное уравнение (7.47):

Определитель матрицы, заключенный в фигурные скобки,
3
10 —X
10 —X
3
D =
= (10 —	— 9 = 91— 20Х + Х2.
231
Приравниваем определитель D к 0 для нахождения Хг и Ха: 20Х +91 = 0,
откуда получаем Х1а = 10±V100—91 = 10 ± 3, т. е.	= 13; Ха = 7'.
Выбираем собственное значение X, имеющее максимальную величину, т. е.
Хтах = 13, и подставляем его в исходное уравнение:
г ю —13 з	Ipl _Г°Т
L 3	10-13 IL hl J “ [ О ]'
Умножая матрицу на вектор h (h9, hi), получаем систему из двух урав-
нений с двумя неизвестными:
— ЗЛо 4- ЗЛ1 = 0,
31ц — 3hi — 0.
Эта система имеет бесчисленное множество решений, и для нахождения
весовой функции надо воспользоваться условием нормировки весовых ко-
эффициентов /iQ-|-ftj= 1. Тогда получаем Л0 = Л1 = О,7О7.
Рассчитаем пиковое и энергетическое отношение сигнал/помеха на вы-
ходе фильтра в соответствии с (7.8) и (7.10):
ых =	(^t + sifto)2 = 0,707-3 + 0,707-3 = 8.
В“Х /?п(0)/?А(0) + 2/?„(1)/?Л(1)	1
/?,(0)RA(0) + 2R,(l)/?A(}) _ 10-1 + 2-30,5 = 13
В“Х Rn(0)Rh(0) + 2Rn(l) RH(1)	1
при этом RA (0) — 1; /?А (1) = 0,5.
В рассмотренном примере, как и следовало ожидать, Хт.» =
= Рвых = 13, поэтому рвых можно было бы и не вычислять. Срав-
нивая значения р и р, полученные ранее для фильтров Колмого-
рова-Винера (см. § 34) и согласованного (см. § 35), видим, что
наибольшее энергетическое отношение достигается для энергети-
ческого фильтра, а наибольшее пиковое отношение — для согла-
сованного фильтра.
Задача определения весовой функции энергетического фильтра
существенно упрощается, если помеха является некоррелирован-
ной, в частности, представляет собой процесс типа «белого шума».
В этом случае корреляционная матрица помехи — единичная, ее
диагональные элементы равны единице, а все остальные — нули:
г 1	0	... От
L о о ...	1 J
Тогда матричное уравнение (7.46) записывается в виде
(Rs—XI) Л=0	или
2	(т—0—X/ (т— 0] h = 0.	(7.48)
232
В развернутой форме уравнение (7.48) представляется
“К8(0)-Л	R,(l)	...	R,(M) -
ад) /г,(0)—х . . .
Ло
/ii
R,(M)	RS(M-1)
- 0 -
о
RS(O)-X _ _hM
(7-49)
О
Весовая функция здесь, как и в рассмотренном выше примере,
равна собственному вектору, соответствующему максимальному
собственному значению корреляционной матрицы сигнала. Этот
вывод имеет принципиальное значение в связи с тем, что в прак-
тике обработки экспериментальных данных оценку АКФ сигнала
Rs (m) при слабых помехах можно проводить непосредственно по
АКФ наблюденного поля Rf (т), т. е. вместо корреляционной мат-
рицы Rs в уравнении (7.49) использовать матрицу fy.
При обнаружении сигнала известной формы весовая функция
согласованного фильтра максимизирует отношение квадрата ам-
плитуды сигнала в его центральной точке к мощности помех, а при
обнаружении сигнала, заданного его автокорреляционной функ-
цией, весовая функция энергетического фильтра максимизирует
отношение энергий иа интервале, равном длине фильтра. Поскольку
в последнем случае в полосе частот, на которую приходится макси-
мальная энергия сигнала, мощность помех уменьшается, искаже-
ние формы сигнала при использовании энергетического фильтра
будет существенно меньшим, чем в случае согласованной филь-
трации.
Качество энергетического фильтра, как и фильтра Колмого-
рова—Винера, можно охарактеризовать величиной среднеквадра-
тической погрешности отклонения результата фильтрации yh полу-
ченного при точно заданных АКФ сигнала и помехи, от результата
фильтрации полученного при неточно заданных АКФ, т. е.
в2 = Е («//~ У/)2- Если ввести понятия автокорреляционных функ-
ций Rn (т) и Rf (т) соответственно для весовых коэффициентов hi
и /ц и их взаимокорреляционной функции ВА^ (т), то величина
в* будет
м
М
?33
Используя это выражение, можно найти зависимость погреш-
ности, вносимой в оценку выходного сигнала, от отношения сиг-
нал/помеха и от отношения интервалов корреляции сигнала и по-
мехи в случае коррелированности последней. Для моделей сигнала
и помехи, описываемых АКФ гауссова типа R (т) = А2е~т’/гг,
В. И. Ароновым для фильтра воспроизведения были вычислены
зависимости среднеквадратической погрешности сглаживания сиг-
нала 7 от отношения rn/rs при различных значениях q = Л1/А?
(рис. 53, а) и Т. А. Трофимовой аналогичные зависимости полу-
чены для энергетического фильтра (рис. 53, б). Сравнение этих
зависимостей еще раз показывает возможность применения энерге-
Рнс. 53. Зависимости среднеквадратической погрешности сглаживания от
отношения интервалов корреляции помех гп и сигналов г, при различных
отношениях их амплитуд q для фильтра Колмогорова—Винера (а) и энерге-
тического фильтра (6)
тического фильтра для оценки сигнала, поскольку качество этой
фильтрации практически не намного хуже качества фильтрации
фильтром воспроизведения.
Рассмотрим пример, иллюстрирующий принцип действия энер-
гетического фильтра, с целью обнаружения и разделения сигналов
на фоне некоррелированных помех. На рис. 54, б приведена сумма
двух сигналов и помехи, заданной реализацией стационарного
случайного процесса с нулевым средним и дисперсией о2 — 1,
(рис. 54, а). В качестве АКФ сигнала использовалась АКФ суммы
сигналов и помех. Весовая функция была выбрана равной собст-
венному вектору, соответствующему XmaJt корреляционной матрицы
Rf. На рис. 54, б приведена также оценка сигнала sr на выходе
фильтра, свидетельствующая, что решена не только задача обна-
ружения, но и задача оценки формы сигнала. По разности fj—s1(
(рис. 54, в) проведена аналогичная оценка формы сигнала s2
(рис. 54, г).
Возможность вычисления по корреляционной матрице исход-
ного поля целого ряда собственных значений и соответствующих
им собственных векторов, т. в; весовых функций, позволяет исполь-
зовать энергетический фильтр для решения задачи выделения сиг-
234
налов из общей смеси по их энергиям. Действительно, располагая
собственные значения матрицы Rf по их убыванию,
Xi>X2i> • • • и решая для каждого из них систему урав-
нений (7.49), находим соответствующие им весовые функции. Пу-
тем фильтрации y/k —	где k — индекс собственного зна-
а

-21-
Рис. 54. Результаты обнаружения и оценки формы двух сигналов с помощью
энергетического фильтра.
а — сигналы а, и а, с различными энергиями и некоррелированная помеха п; б — сигнал
на входе фильтра f =- а, + з, + л и результат оценки формы сигнала а", путем фильтра-
ции; а — разность между суммой t н результатом фильтрации а,; е — результат оценки
формы сигнала s.
чения, получаем главные компоненты. Эти компоненты и отражают
различные составляющие наблюденного поля, расположенные по
убыванию их энергии. Принцип действия энергетического фильтра
с целью выделения различных составляющих наблюденного поля
по их энергии иллюстрируется рис. 55. Рассмотренный пример
показывает возможность энергетической фильтрации при выделе-
нии аномальных эффектов на весьма сложном фоне. Практически
всю энергию исходного поля несут две-три его составляющие, т. е.
основная энергия, или дисперсия, поля приходится в данном при-
мере на два собственных значения.
Разделение сигналов будет тем точнее, чем сильнее они отли-
чаются друг от друга по интенсивности и интервалу корреляции.
С подобными задачами в геофизике сталкиваются, например, при
235
выделении гравитационного эффекта от нефтегазовой залежи на
фоне более интенсивной аномалии от структуры (см. рис. 49, а).
При этом в силу того, что фильтр максимизирует энергетическое
отношение сигнал/помеха, произойдет выделение более энергоем-
кой составляющей, или иначе, аномалии, обусловленной струк-
турным фактором. Эффект от залежи можно будет выделить либо
по разности между исходными значениями поля и полученными
Рис. 55. Результаты энергетической фильтрации поля ДТ.
а — исходное поле; б—д результаты фильтрации с помощью первого — четвертого собст-
венных векторов; е — результат энергетической полосовой фильтрации с использованием
второго — четвертого собственных векторов (сумма в + е -f- д)
при фильтрации значениями поля от структуры (рис. 49, а), либо
по второй главной компоненте поля, рассчитанной для Х2 (Xa<Xi
но Х2>ХЬ i =/= 1 и 2).
§ 37.	ДВУМЕРНЫЕ ОПТИМАЛЬНЫЕ ФИЛЬТРЫ
Практическая реализация оптимальных фильтров требует решения
систем линейных уравнений для определения весовых коэффици-
ентов и поэтому сопряжена со значительными затратами машинного
времени. Эти затраты возрастают при использовании переменных
во времени оптимальных фильтров, когда для осуществления филь-
трации вдоль одного профиля (трассы) необходимо проводить пе-
ресчет весовых коэффициентов несколько раз. Так, например, при
фильтрации сейсмических записей с учетом сохранения стацио-
нарцости по частоте (периоду) на интервале в 0,7—1,0 с требуется
смена фильтра через такой интервал.
Еще большие вычислительные трудности и затраты машинного
времени связаны с реализацией двумерных оптимальных фильтров.
236
Если при построении Одномерных Оптимальных фильтров исходят
из задания АКФ сигнала (или формы самого сигнала) и помех, то
для определения весовых коэффициентов оптимальных двумерных
фильтров hk.t необходимо задание соответствующих двумерных
АКФ- Нахождение двумерной весовой функции hk,i потребует
решения уже не одного, а Л/ матричных уравнений (N — 2р 4- 1),
где N — число профилей (трасс), для которых ведется фильтрация.
Например, система уравнений двумерного оптимального согласо-
ванного фильтра будет записана в виде [сравни с (7.43) — (7.44) ]:
р м
S S hkiRn(p—k, m—i)=s(—p, —т)	(7.50)
А=—р 1=0
или
/?п(0, m)k0=s0,
Rn(l, m)hi = s1, Rn(— 1, m)h_i=s_i,
................................................ (7.51)
Rn(p, m)hp = sp, Rn(—p, m)h~p = s_p,
где R (p, m) — корреляционные матрицы порядка (M + 1) (Л4 + 1),
при фиксированных значениях индекса р они представляют собой
автокорреляционные и всевозможные взаимно корреляционные
функции, используемые при построении двумерной АКФ; h-p, ....
ft0, . . . , hP и s_p, . . . , s0, ... , sP —векторы-столбцы весовых
коэффициентов и сигнала для соответствующих профилей (трасс).
В уравнении (7.50) двумерная АКФ помехи Rn (р, т) с введе-
нием индексов k, i превращается в матрицу матриц. Обращение
этой матрицы матриц требует решения N систем линейных урав-
нений (7.51). Число уравнений в каждой системе определяется про-
тяженностью сигнала на соответствующем профиле (трассе).
Совершенно аналогично строятся двумерные оптимальные
фильтры Колмогорова—Винера и энергетические. Для фильтра
воспроизведения в выражении (7.50) вместо Rn (р—k, т—i) и
s (— р, — т) должны быть записаны Rf (p—k, m—i) и Rs (р, т);
а для энергетического фильтра соответственно Rs (p—k, m—i) —
— ^Rn (p—k, m—i) и нули.
Таким образом, в общем случае реализация оптимальной дву-
мерной фильтрации весьма трудоемка. С целью построения дву-
мерных оптимальных фильтров применяют различные упрощения.
Упрощение алгоритмов двумерной фильтрации возможно в сле-
дующих случаях:
1)	при некоррелированности помехи между профилями (трас-
сами). В этом случае осуществляется оптимальная фильтрация
лишь по одной координате (по х или по t), а затем по результатам
фильтрации проводится суммирование в пределах скользящего
237
окна, включающего N профилей (трасс) по заданному направлению
сигнала. Если с помощью подбора соответствующих фильтров
в сейсмостанции удалось добиться оптимальной фильтрации по
времени, а нерегулярные волны-помехи при этом являются некор-
релированными между каналами, методы РНП и ОГТ можно счи-
тать реализующими оптимальные двумерные согласованные фильтры;
2)	при учете корреляции помех как по координате х (по про-
филю), так и по координате у (между профилями), но при опреде-
ленной симметрии двумерной АКФ помехи, которая позволяет
представить двумерную АКФ в виде произведения одномерных
автокорреляционных функций, полученных раздельно по х и по у.
Так, при R (p—k, m—i) = Rx (m—i) Ry (p—k) = Rmi Rpk из
равенств ^RmiRy = и ^RpkRki = 6pZ следует
(7.52)
Согласно (7.52) алгебраическое дополнение элемента Rmp,lk
для матрицы матриц R (р—k, т—i) можно представить в виде
Rmp,ck= RmliR^k- Это соотношение позволяет получить уравнение
для весовых коэффициентов hki при известных выражениях для
матриц Rx (m—i) и Ry (p—k), характеризующих корреляционные
связи при сдвигах в направлениях по х и по у.
Уравнение свертки для выходного сигнала тогда получим в виде
ypl = -£hkZh{fp_kj_{,	(7.53)
где весовые коэффициенты hk являются решением системы Rkih — s,
T.e.h = [7?wl] s, а коэффициенты h( — решением системы ROT//i ==s.
Таким образом, двумерная согласованная фильтрация здесь
сводится к раздельно реализуемой фильтрации по координате х
для каждого профиля и по координате у, т. е. между профилями.
Для получения соответствующих весовых коэффициентов hi
и hk необходимо раздельное обращение матриц Rx и Ry, что позво-
ляет значительно упростить построение двумерных фильтров. В ка-
честве примера рассмотрим вычисление весовых коэффициентов
для модели помехи марковского типа;
Kml—rx i Kpk—'y >
где rx = e~Ax; rb = е~ь».
Как известно, матрица, обратная
АКФ марковского типа, имеет вид
матрице, построенной по
	1	— гх	0	0 "
Rm*= —Ц- 1-^	— гх	1+4	— гх	. .	0
	0	0	0	1 _
238
С учетом этого получаем обратную матрицу Rmp.» в виде де-
вяти элементов:
Rmp.'ik —
— ^(1 + ^)
-- гх (1
(1+г2)(1+4)
--гх(1 + г»)
гХГу
— ^(1+d)
ГХГу
Оптимальная согласованная фильтрация
для каждой точки площади (х{уь) величины
состоит в вычислении
Уы
____1____
0-^)0-^)

(ffe+i, < + i +
+ fit. i-f-1 + fk. (-1) + ~-rry-— (fk+1, t+1 + fk+1, i-1 +
+	i+1+ /*-!. l-l)-
На рис. 56 приведен пример раздельной фильтрации по х и по t
для девяти трасс с целью выделения на фоне нерегулярных корре-
лированных помех полезного сигнала на времени 3,2 с. Вначале
была осуществлена фильтрация по х в предположении марковской
корреляции помехи по х (рис. 56, б). Затем к полученному резуль-
тату добавлена оптимальная согласованная фильтрация по t. В ре-
зультате достигнуто существенное увеличение отношения сиг-
нал/помеха (рис. 56, в);
3)	при аппроксимации двумерных спектров сигналов и помех
изотропными спектрами на основании предположения о централь-
ной осевой симметрии поля. Для изотропных двумерных сигналов
с центрально осевой симметрией это можно сделать путем замены
<а на р = у/+ ®у в формуле (7.23). Реализация двумерного
оптимального фильтра и в данном случае становится возможной
за счет сведения его к одномерному в силу изотропности поля.
Если способ построения корреляционной матрицы по одномер-
ной АКФ (см. § 19) распространить на построение корреляцион-
ной матрицы по двумерной АКФ, мы сможем реализовать двумер-
ную оптимальную фильтрацию в самом общем случае, не прибегая
к обращению матрицы матриц.
Покажем такую возможность на следующем примере. Пусть
для двумерной АКФ
R ,N-\p\ n-|m| ? ? Мр~к’ т~1
значения р = т = 0; ±1; ±2. Элементы матрицы матриц
R (p—k, т—') при этом будут представлены таблицей значений
(см. табл. 21).
239
Рис. 56. Результаты двумерной оптимальной фильтрации сейсмической за-
писи по х и t\
а — исходные сейсмические трассы; б — результат фильтрации исходных трасс по х;
в — результат фильтрации данных, приведенных на рис. о. по t
Для получения коэффициентов ковариации через значения
двумерной АКФ R (р, т) можно использовать следующие выра-
жения:
rw = #(P> т)‘, k, i = l, 2, . . ., nxn;
r- г i — IT, г k — И
m = [i—r] — n -------1 + nl------ •
L » J L n J
Квадратные скобки здесь обозначают целую часть от деления
указанных в них индексов.
Найдем rw = R (р, т). При k = 2; i = 9; п = 3 согласно при-
веденным выражениям rae = R (—2,1).
Таким образом, для трех смещений по профилю т и трех сме-
щений между профилями р получаем матрицу размером 9X9.
240
С учетом симметрии двумерной АКФ /? (р, т) = /? (— р, — т)
эта матрица симметрична относительно главной диагонали, на
которой расположена дисперсия поля /? (О, 0) = о2.
Если весовые коэффициенты и значения двумерного сигнала
в (7.50), представленные матрицами вида
Рис. 57. Результаты двумерной энергетической фильтрации при обработке
данных ВСП.
о — исходный временной разрез ВСП; б — данные обработки
расположить по строкам, в которых сначала идут значения весо-
вых коэффициентов h^i (и сигнала) при k = 0 (р = 0), а индекс
i (т) пробегает все значения, затем идут значения hki (и spm) при
k = 1 (р = 1) и т. д., мы сведем случай умножения матрицы ве-
совых коэффициентов на матрицу матриц с учетом приравнивания
этого произведения к матрице сигнала к случаю нахождения ве-
совых коэффициентов одномерного фильтра. При этом вектор-
строка из девяти весовых коэффициентов фильтра умножается на
матрицу, приведенную в табл. 21, а произведение приравнивается
к вектору-строке из девяти значений сигнала.
После нахождения весовой функции путем решения системы
линейных уравнений проводится двумерная свертка ypj —
— Yfikifp-i, i-i, обеспечивающая двумерную оптимальную филь-
трацию поля.
241
Пример, иллюстрирующий применение двумерного энергети-
ческого фильтра, рассчитанного по описанной выше методике, при-
веден на рис. 57. На рис. 57, б показан результат обработки участка
профиля ВСП по одной из скважин в Чу-Сарысуйской депрессии.
На исходном разрезе (рис. 57, а) прослеживаются две интерфери-
рующие системы волн: 1) падающие продольные волны и парал-
лельные им многократные нисходящие волны-помехи; 2) восходя-
щие волны, несущие полезную информацию об отражающих гори-
зонтах.
Обработка проводилась с целью выделения отраженных волн,
подавляемых нисходящими и другими волнами-помехами. В ре-
зультате двумерной энергетической фильтрации полезный сигнал,
характеризующийся меньшей интенсивностью, по сравнению с вол-
нами-помехами, уверенно выделяется. Дополнительное применение
к полученному результату обратной фильтрации позволит достичь
и временной разрешенности поля.
При нахождении весовых функций оптимальных фильтров, осо-
бенно двумерных, требуется решение системы линейных уравнений
большого порядка. Для решения систем уравнений этого типа раз-
работан специальный алгоритм Левинсона, позволяющий в N раз
сократить время вычислений и объем памяти, занятый коэффи-
циентами матрицы. Описание алгоритма можно найти в [11].
ГЛАВА VIII
ВЫДЕЛЕНИЕ СЛАБЫХ ГЕОФИЗИЧЕСКИХ
СИГНАЛОВ НА ОСНОВЕ
ПРОВЕРКИ СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Критерии оптимальной фильтрации и соответствующие им алго-
ритмы обработки исходных данных обеспечивают выделение сиг-
налов на фоне помех, однако принятие решения о наличии или от-
сутствии полезного сигнала после фильтрации осуществляется
интерпретатором визуально. Это обстоятельство делает последний
этап обработки весьма субъективным, особенно для случая обна-
ружения слабых сигналов. Достаточно вернуться к рис. 51, г, на
котором приведены результаты фильтрации согласованным фильт-
ром, чтобы увидеть три примерно равных по своей амплитуде мак-
симума. Хотя наибольший из них и соответствует искомому сиг-
налу, тем не менее при обработке геофизических данных в подоб-
ной ситуации и два других максимума можно было бы принять
за полезный сигнал. Следовательно, при фильтрации слабых сиг-
налов не хватает обоснованной процедуры принятия решения о
наличии сигнала.
В разведочной геофизике слабым сигналом (слабая
аномалия) принято считать сигнал, который соизмерим по интен-
сивности с уровнем помех или ниже этого уровня. Йх визуальное
обнаружение практически исключено. Тем не менее проблема об-
наружения слабых сигналов в разведочной геофизике приобретает
все большее значение в связи с поисками месторождений, залегаю-
щих на больших глубинах, а также с поисками объектов, аномаль-
ные эффекты от которых осложнены интенсивными помехами са-
мой разной природы. Под обнаружением сигнала,
обычно понимают факт установления его наличия. Однако, уста-
навливая факт наличия сигнала, мы тем самым относим сигнал
к определенной точке наблюдения, частично решая одновременно
и задачу выделения сигнала, состоящую в оценке параметров и
формы сигнала. Нередко после обнаружения сигнала удается пе-
рейти и к оценке его формы. Поэтому, рассматривая алгоритмы
обнаружения слабых сигналов и оценку их параметров, можно
считать, что решаем задачу их выделения.
Общей задачей фильтрации является извлечение полезной, ин-
формации из смеси сигнала и помех. Рассмотренные в гл. VI и
VII приемы обработки исходных данных в значительной степени
направлены на достижение возможно большего отношения сиг-
нал/помеха, исходя из того, что именно помехи в конечном итоге
ограничивают чувствительность метода и, следовательно, чем сла-
бее помеха, тем лучше. Ф. Вудворд подчеркивает: «Такой подход
243
справедлив до тех пор, пока он приводит к цели, однако он не со-
держит постановки задачи об извлечении полезной информации.
Кроме того, не существует общей теоремы, утверждающей, что
максимальное отношение сигнал/помеха на выходе фильтра обеспе-
чивает максимальное извлечение информации». Под максимальным
извлечением информации в настоящее время понимается получение
апостериорных вероятностей, в частности для задачи обнаруже-
ния сигнала — апостериорных вероятностей наличия и отсутствия
сигнала.
Результатом развития статистической теории оптимальной филь-
трации в середине 50-х годов, благодаря трудам В. А. Котельни-
кова, Ф. Вудворда, Д. Мидлтона и др., явилась статистическая
теория оптимального приема. При оптимальном приеме, в отличие
от оптимальной фильтрации, результатом обработки данных яв-
ляются условные вероятности интересующих нас событий, напри-
мер вероятность наличия полезного сигнала. Статистическая тео-
рия приема, в свою очередь, возникла на базе теории проверки ста-
тистических гипотез. В теории приема также фигурирует параметр
отношения сигнал/помеха. Однако роль этого параметра здесь бо-
лее скромная, поскольку вопрос о наличии (отсутствии) сигнала
решается без его помощи. Для решения задач обнаружения (и вы-
деления) сигнала используются критерии принятия статистических
гипотез, которые позволяют установить порог принятия решения
о наличии сигнала. При этом оптимальная фильтрация входит как
составная часть общего решения.
§ 38. КРИТЕРИИ ПРИНЯТИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
Статистическое решение связано с понятием статистиче-
пении задачи обнаружения сигнала
е гипотезы: 1) гипотеза о наличии
сигнала, т. е. когда наблюденное
поле ft = Si + щ, эту гипотезу
называют ненулевой, обозначим
ее Ht; 2) гипотеза об отсутствии
сигнала, т. е. когда ft = nt, эту
гипотезу называют нулевой, обо-
значим ее Но. Для каждой гипо-
тезы по значениям ft можно по-
строить оценку плотности их рас-
пределения — гистограмму. Такие
условные плотности распределе-
ния значений Л, обозначаемые со-
ответственно Р (F/Ho) и Р FtHj),
где F = flt . . . , fm, называются
о д о б и я. Функции правдоподо-
бия для задачи обнаружения сигнала приведены на рис. 58, где
Р (FIHO) соответствует оценке плотности распределения помех
и может быть построена на участках, на которых заведомо отсутст-
244
с к о и
имеют
гипотезы,
место две стати
Рис. 58. Графики плотностей
распределения гипотез Но и Нх
для оценки вероятностей ошибок
первого и второго рода

п
О
вуют полезные сигналы, Р (FIHх) соответствует оценке плотности
распределения суммы сигнала и помехи, причем если среднее зна-
чение помех равно нулю, то среднее значение сигнала является
величиной а. Вся область значений вектора F разделяется на две:
область So, которая образует множество значений ft, соответст-
вующих гипотезе Но, и область 51я которая образует множество
значений fit соответствующих гипотезе Ях. Точка h на оси /, раз-
деляющая эти области, называется порогом принятия
решения о наличии той или иной гипотезы.
Принятие решения (статистического решения) о наличии (от-
сутствии) сигнала не может быть безошибочным. Ошибки неиз-
бежны, поскольку заключение о наличии или отсутствии сигнала
дается на основании обработки данных, осложненных помехами.
Все критерии принятия статистических решений о наличии сигнала
и вытекающие из них алгоритмы обработки связаны с вероятно-
стями ошибок, возникающих из-за помех. Принятие решения со-
провождается ошибками двух родов. Ошибка первого
рода заключается в том, что принимается гипотеза Нь в то
время как в действительности выполняется гипотеза Но. Такая
ошибка в случае обнаружения сигнала означает, что принимается
решение о наличии сигнала, в то время как на самом деле он от-
сутствует. Эта ошибка называется ошибкой обнаруже-
ния ложного сигнала. Она появляется тогда, когда
наложение помех создает ситуацию, похожую на полезный сигнал.
Ошибка второго рода заключается в том, что прини-
мается гипотеза Нй, в то время как в действительности справедлива
гипотеза Н^. Такая ошибка означает, что принимается решение
об отсутствии сигнала, в то время как сигнал имеется. Эта ошибка
называется ошибкой пропуска сигнала. Она по-
является тогда, когда помехи настолько искажают сигнал, что соз-
дается ситуация, похожая только на помеху.
С ошибками обнаружения ложного сигнала и пропуска сигнала
связаны соответствующие вероятности. Вероятность ошибки об-
наружения ложного сигнала
а= J Р (FIHO) dF = [P (f/Яо) dF,	(8.1)
а вероятность ошибки пропуска сигнала
h
р = f Р (F/Hi) dF = f Р (F/HJ dF.	(8.2)
So	—op
Вероятности а и p на рис. 58 заштрихованы.
Если ввести априорные вероятности для гипотез Но и Hi —
Ро и рх, то
9 = роа + р!р	(8.3)
определяет полную безусловную вероятность ошибки, связанную
245
как с обнаружением ложного сигнала, так и с пропуском сигнала.
Величина
Т=1-Р	(8.4)
называется вероятностью правильного обнару-
жения сигнала или надежностью обнару-
жения. Соответственно вероятность правильного необнаруже-
ния сигнала <р = 1—а.
Учитывая, что при выборе порога h потери, обусловленные
различными ошибками, могут быть разными с экономической
точки зрения, вводят понятие цены для ошибок первого и вто-
рого рода — Са и Ср. Произведение Саа называют риском
(потерей), соответствующим гипотезе Но. В задаче обнаружения
сигнала это будет потеря, обусловленная неправильным решением
о наличии сигнала. Обнаружение ложного сигнала неизбежно при-
ведет к затратам средств на его проверку другими геофизическими
методами или же горно-буровыми работами. Аналогично произве-
дение Сар есть риск (потеря), соответствующий гипотезе Ях. Про-
пуск действительного сигнала (аномалии) может привести к про-
пуску месторождения полезного ископаемого, при этом потери
могут быть весьма велики.
Средний риск при принятии решения
r(ft) = PoCaa + piCpp.	(8.5)
Величина среднего риска г зависит от Л, поскольку от h зависят
значения а и ($.
Естественный критерий принятия статистических решений свя-
зан с минимизацией среднего риска. Согласно критерию ми-
нимального риска, или критерию Байеса, вы-
бирается такое значение h, которое обеспечивает минимум выра-
жения (8.5). Для нахождения величины г (й) с учетом (8.1) и (8.2)
выпишем выражение (8.5), к которому добавим и от которого выч-
тем одну и ту же величину
JC^PtF/HJdF:
r(h) = J CfipJtF/HJdF+j CaPoP(F/Ho)dF +
+ $ С$Р1Р(FIHJdF — SC^PtFIHJdF.
St	Si
После объединения первого члена с третьим, а второго с чет-
вертым получаем
г(Л)= f C^p1P(F/H1)dF+ С [СаРйР (F(H0)—
S»So4-Si	Si
- С^Р1Р (F/Hi)] dF = C₽P1 + f [CaPoP {F/He)—C^P1P (F/HJ] dF.
St
В последнем выражении первое слагаемое положительное, поэ-
тому для минимизации риска нужно выбрать область 5t, иначе,
246
порог h, таким образом, чтобы подынтегральная функция была
отрицательной, т. е. Сор0Р(Г/Я0)<СрР1Р(Е/Я1).
Из этого следует, что
Л = Р(Р/Я1)/Р(Р/Я0)>Сар0/С₽р1 = Л.	(8.6)
Отношение функций правдоподобия Л = Р	(F/Ho) на-
зывается коэффициентом правдоподобия. Для
критерия минимального риска коэффициент правдоподобия в слу-
чае выполнения гипотезы (гипотезы о наличии сигнала) должен
превосходить величину порога h, равную C^pJC^pi. Таким обра-
зом, применение критерия минимального риска возможно лишь
при известных ценах ошибок первого и второго рода и априорных
вероятностях р0 и pv Достоверная оценка Са и Ср требует тщатель-
ного анализа большого статистического материала, который может
быть получен в районах с хорошей геолого-геофизической изу-
ченностью. В ином случае приходится считать Са = Ср, т. е. при-
писывать пропуску сигнала и обнаружению ложного сигнала оди-
наковый вес. При этом следует минимизировать безусловную ве-
роятность ошибки (8.3), что приводит к правилу принятия решения
[см. также 8.6) при Са = Ср] в виде
A>p0/p1 = /i.	(8.7)
Правило (8.7) соответствует критерию Котельни-
кова (или идеального наблюдателя). Если при обработке геофи-
зических данных априорные вероятности наличия и отсутствия
сигнала (р0 и р^ считать равными, что отвечает максимальной не-
определенности этих событий, то порог h в (8.7) становится равным
единице:
Л>1=Л.	(8.8)
Правило принятия решения (8.8) соответствует критерию
максимального правдоподобия. Согласно этому
критерию решение о справедливости гипотезы Нг принимается
тогда, когда вероятность Р (F/Hi) больше вероятности Р (F/Ho)
в (8.6), т. е. h ~ 1. Критерий Котельникова при заданных вероят-
ностях До и Pi позволяет на основе формулы Байеса (1.2) оценить
апостериорную вероятность наличия сигнала:
p(HJF) — ------Р1Р ---------=—^Ра)— -.	(8.9)
1 7 рхР(Р1Нг) + рлР{Р1Н^ (рМ)Ь+\
Когда задание априорных вероятностей является нецелесооб-
разным, используются следующие три критерия: минимакса, Ней-
мана—Пирсона и Вальда.
Согласно критерию минимакса порог h находится
при минимизации максимально возможного риска. Поскольку г (h)
зависит от р0 и Pt наименьший риск имеет максимум при некотором
значении pj = 1—р*, не равном ни нулю, ни единице, ибо как при
Рл1, так и при р-> 0 риск г->-0. Если выбрать критическое
значение р* и определить порог h =Саро/С^Р\, действительный
247
риск при любом, отличающимся от pi значений р! не превзойдет
риска, рассчитанного для h = h*. Значение р‘ находится из урав-
нения дг!дрг = 0. Из (8.5) легко видеть, что dr (h)ldpx = С$—Саа,
т. е. уравнение для нахождения р\ будет Ср0 = Соа.
Правило принятия решения при отсутствии сведений об апри-
орных вероятностях и о ценах Са, Ср дает критерий Ней-
мана —П и р с о н а. Согласно этому критерию минимизируется
величина 0 вероятности пропуска сигнала при условии, что вероят-
ность обнаружения ложного сигнала а не превосходит заданной
величины а0, т. е. min 0 при а = а0. При известной функции прав-
доподобия P(FIH0) и заданной величины а0 из (8.1) можно найти
порог Л, соответствующий разбиению области наблюдений F на
So и Sx. В этом нетрудно убедиться, если в (8.1) перейти от m-мер-
ной выборки поля F к одномерной переменной коэффициента прав-
доподобия Л, положив
Р (F/HJ dF — P (AJHi) dA; Р (F/Ho) dF = P dk.
Правые и левые части указанных равенств выражают одну и
ту же условную вероятность принятия решения о наличии сигнала
и его отсутствии. Области So и Sx при переходе от переменной F
к переменной Л преобразуется в числовую ось Л, на которой зна-
чение Л = Л 0 является порогом для принятия решений. Таким
образом:
а= f P(A/tf0)dA;	(8.10)
Ло
Ло
0= J P(A/Hx)dA.	(8.11)
—00
Для критерия Неймана—Пирсона вероятность а равна заданной
величине а0, отсюда заданным является и пороговое значение Ло.
Для всех рассмотренных выше критериев и соответствующих
им правил принятия решения характерно было условие фиксиро-
ванного объема выборки поля F, а именно его m-мерная размер-
ность. Существует подход к установлению правила принятия ре-
шения, при котором размер выборки т не фиксируется, а ограничи-
вается в процессе наблюдений в зависимости от уже ранее прове-
денных наблюдений. При таком подходе наряду с принятием ре-
шения о выполнении Но и Нг возможно принятие решения о необ-
ходимости продолжить наблюдения, т. е. отказаться на данном
этапе от принятия одного из решений о справедливости Но и
Если же принимается решение о выполнении Но или Я1( наблю-
дения на этом заканчиваются. Целесообразность такого подхода
очевидна при проведении дорогостоящих экспериментов, напри-
мер при подсчете запасов с помощью бурения скважин. Этот под-
ход был разработан А. Вальдом и получил название последо-
вательного анализа. При последовательном анализе
размер выборки наблюдений т заранее неизвестен и является слу-
248 J
чайной величиной. Область наблюдений делится уже не на две, а
на три области: 50, и Snp (промежуточная область). Если мы
попадаем в промежуточную область, необходимо продолжить на-
блюдения.
Критерий Вальда сводится к следующему правилу:
при т-м наблюдении принимается решение о гипотезе Но, если
f/(l—a)<A(f1........../*)<(!—р)/а,	(8.12)
k = 1, . . . , tn— 1;
A(ft, .... fm) < p/(l—а)<1,
и о гипотезе Hit если справедливо (8.12) и
A(fx.........fm) >(1-Р)/а^>1-
Как видно, критерий Вальда основан на сравнении коэффици-
ента правдоподобия с порогами, зависящими от задания вероятно-
стей ошибок первого и второго рода.	/
Таким образом, правила принятия решения для всех критериев
сводятся к нахождению коэффициента правдоподобия Л и сравне-
нию его с некоторыми пороговыми значениями Ло (или Л).
Для решения задачи обнаружения слабых геофизических сиг-
налов используются критерии максимального правдоподобия и
Неймана—Пирсона. В сейсморазведке применяются фильтры, по-
строенные на минимаксном критерии.
Проиллюстрируем применение рассмотренных выше критериев и со-
ответствующих им правил для решения задачи о наличии аномалии в точке
при условии, что амплитуда поля в ней в 3 раза больше среднеквадратиче-
ского значения фона помех <Тф. Без ограничения общности положим, что
помехи распределены нормально с нулевым средним и Оф= а2 = 1, а также
некоррелироваиы. Соответственно нормальным будет и распределение суммы
аномалии и помех со средним а0 = 3 и дисперсией а* = 1.
Отсюда функции правдоподобия будут
Р (F/Ha) = (д/а Van) ехр (-
И
Р (F/HJ = (1/о V&T) ехр [ - (/ - а0)«/2ст»],
а коэффициент правдоподобия примет вид
Л = Р (FIHi)IP (FIH0) = ехр ( - -Д- +	> Ло = Л.	(8.13
\	2а* а* /
Для критерия максимального правдоподобия априорные вероятности
р0 и pi и цены ошибок Св и Ср равны, т. е. порог Ло = h = 1, что обеспе-
чивает граничную величину для f из (8.13), равную /пор = at/2 = 1,5, так
как Oq/202 = /а0/а2. Таким образом, искомое значение поля можно считать
аномальным.
Применим критерий Котельникова, для которого Ло = h = Po/pi. Про-
логарифмировав (8.13), найдем
а2 /
fnop =-------1 In Ло -(
До \
Др \ Ар	а21пЛо
2а* / . 2 во
249
Пусть Ло = р»)Р1 = Ю, тогда пор = 2,4 и заданное значение поля яв-
ляется аномальным. Только при Ло = Pol Pi = 100 (/пор = 3,03)- его нельзя
считать аномальным.
Для критерия минимального риска пороговое значение Ло = Cap0/Cppj.
Пусть цена пропуска аномалии в 10 раз выше цены обнаружения ложной
аномалии, тогда Са/Ср = 0,1. При p0/pj = 10 и а„/о2 = 9 из (8.13) находим
/пор =1,5, т. е. в этом случае более высокая цена пропуска аномалии ском-
пенсировала более низкую величину априорной вероятности наличия ано-
малии и в результате получен тот же порог, что и для критерия максималь-
ного правдоподобия.
Для применения критериев минимакса и Неймана—Пирсона необхо-
димо вычисление вероятности а и 0. С учетом (8.1) и (8.2) имеем
“-----У ехр (— ха/2) dx ±= 1 — ф(
а 'у2л ^пор~~ао	\ о
<т
= 1-_Фг_д°-+ glnft>Y
\ 2о а0 )
(8.14)
где
Ф (() = —!— У ехр ( — [х*/2) dx.
2л — оо
Аналогично для вероятности 0 получим
(1пор~аа)
=------!= f ехр ( - х»/2) Лг = ф<7пор~
о 'у 2я	V °
= ф( __go_ + .gjn4o Y
\	20 а0 )
Отметим, что для критерия максимального правдоподобия (Ло = 1)
согласно (8.14) и (8.15) в нашем примере а ~ 0 = 7,5 %.
Выражение для среднего риска (8.5) при Са = 6 Ср имеет вид
г (h) = ср (ьРо Г1 - ф (-3L-+ gln^Y| + Р1ф	+ -SJaAAl.
I L \ 2о о® /J \ 2о во /)
В нашем примере
г (Л) = Ср ^ро [1 - Ф (у- In + 1 ,б)] + Р1Ф (у In X
X
РрЬ
1 — Ра

250
Для drldpi — 0 имеем Соа = Ср₽. Подставляя сюда выражение для
аире учетом Ср/Са = Mb, получаем
— ф(— In—------------1,5'1 = 1- ф(— In—----------Н.бУ
b \ 3	1 — pt /	\ 3	1 — рл )
При заданном значении поля наименее благоприятная величина ра
соответствует максимальному г (h). Например, при b = 1 из последнего
уравнения следует, что р0 = 0,5, т. е. при равных ценах ошибок наименее
благоприятным случаем является равенство априорных вероятностей pj =
= ₽! = 0,5. Этот случай соответствует критерию максимального правдо-
подобия.
Наконец, для применения критерия Неймана—Пирсона необходимо из
выражения (8.14) определить Ло или fnop при заданной величине а = 5 %:
01пЛо ^ = 1—а= 0,95; go^ а 1п Ло _165
V 2а at 7	2а ав
С учетом (8.14) получаем Ло = 1,57 (fnop = 1,57), т. е. заданное значе-
ние поля можно вновь считать аномальным. При этом из (8.15) 0 = 16 %,
т. е. вероятность пропуска аномалии достаточно велика.
§ 39. НАДЕЖНОСТЬ ОБНАРУЖЕНИЯ СИГНАЛА
Под надежностью обнаружения сигнала (ано-
малии) понимается вероятность его правильного обнаружения
у = 1—0, где Р — вероятность ошибки пропуска сигнала.
Надежность обнаружения сигнала позволяет оценить качество
проводимой обработки (фильтрации) данных. Вспомним, что для
согласованного фильтра качество фильтрации оценивалось по ве-
личине пикового отношения сигнал/помеха на выходе фильтра.
Надежность же обнаружения, как увидим, определяется по вели-
чине энергетического отношения сигнал/помеха, что подчеркивает
преимущество последнего перед пиковым отношением.
Найдем вероятности ошибок первого и второго рода для задачи
обнаружения сигнала известной формы и амплитуды на фоне не-
коррелированных помех с нулевым средним и дисперсией о2. При
этом гипотеза об отсутствии сигнала Но состоит в том, что ft = nt,
а гипотеза о наличии сигнала — в том, что ft = s< + nt, i =
= 1, . . . , m. Полагая распределение помех нормальным, полу-
чаем следующие выражения для функций правдоподобия:
p.(f/h0)= L wp(-fW). . . —-L.............х
V 2л а	V2л а
X ехр (—/„/За2) =	- т ехр( —£ /1/2а21;	(8.16)
(у2л ) а 41	7
P(F/H1)= —А_—ехр [—(fi—S1)a/2o2] . . . _L X
-у2л а	-у2л °
X ехр [—(fm—sm)2/2o*] =	1 ехр х
(V2^) а
251
[т	1
i	j
(8.17)
Соответственно из (8.16) и (8.17) коэффициент правдоподобия
т
Е»?
1
т
1
л_. Р(^1)
Р (F/Ht) ”’г \	2<т2 1 о2 7
Согласно рассмотренным выше критериям, решение
сигнала принимается при Л>Л0 = й. Тогда с учетом
i.si ]
= ехр
(8.18)
о наличии
(8.18)
Л = ехр
или после логарифмирования
1 т
ф = — EfiSt>lnA0 + p/2,
а2 1
где р = £s2/ct2 = /ns2/o2 — энергетическое отношение сигнал/по-
меха; <р — корреляционная сумма заданного сигнала с наблюден-
ными значениями поля.
Вероятность ошибки обнаружения ложного сигнала а — это
вероятность того, что при отсутствии сигнала si величина <р ока-
жется больше порога Ло и будет принято неправильное решение
в наличии сигнала, т. е. при ft = nt
Ф = Ц- 2n{s, >1п Ло + р/2
(8.19)
и для вычисления а необходимо определить вероятность осущест-
вления такого неравенства. Поскольку помеха — некоррелиро-
ванная случайная величина с нулевым средним, математическое
ожидание и дисперсия величины ф, также имеющей нормальное
распределение, будут соответственно:
Мф = 0; Dtp = У, = р.
Отсюда плотность распределения ф при отсутствии
Р (ф/#0) = —-— ехр (—ф2/2р) = —-— ехр х
Г.	(1П Ло + р/2)2 1
L 2р J
(8.20)
сигнала
(8.21)
Следовательно, вероятность ошибки первого рода с учетом
(8.20)
ОО	00
а= f Р(ф/Я0)б/ф = У Р (ф/Я0)^ф =
’пор	1п Ло+Р'2
= 1 _ф(_1пЛо+р/2 ),	(8.22)
252
где
ф (f) = —i— г ехр (—х®/2) dx.
л/in -io
Аналогично находим вероятность ошибки пропуска сигнала 0
как вероятность того, что величина ф окажется меньше порога Ло,
несмотря иа наличие сигнала, т. е. при f{ .= sj + nt
ф= _l_£(Sf_]_nj)St<lnA0+ р/2,
аа
ИЛИ	;
ф = “V Е П,5(<1п Ло— р/2.
(J*
Плотность распределения ф при наличии сигнала, когда М<р =
= Dq> = р, будет
Р (Ф/# i) = -т=г ехр [—(<р—р/2)а/2р! =
-у2лф
= ~ - ехр [ (1пА»~Р/2)а j.	(8.23)
Следовательно, вероятность ошибки второго рода
’пор	,п Ло—
0= J Р(ф/я1)йф= у Р(Ф/я1)^ф = фГ 1пЛа~р/-2-у
\ Vp )
(8.24)
Надежность обнаружения сигнала, определяемая как вероят-
ность правильного обнаружения сигнала,
у=1 — 0=1 — ф/ 1п А».Т1Р/2 \ .	(8.25)
V Vp )
Рассмотрение полученных [вероятностей а, 0 и у [показывает,
что качество обработки определяется через энергетическое отно-
шение сигнал/помеха и порог принятия решения Ло.
Для критерия максимального правдоподобия Ао = 1 и из
выражений (8.22), (8.24) и (8.25) следует:
а = 0 = 1 — ф(Ур/2);	(8.26)
? = ф(Л/р/2).	(8.27)
Характеристики обнаружения сигнала, представляющие за-
висимости между надежностью обнаружения и энергетическим от-
ношением сигнал/помеха, для критерия максимального правдо-
подобия приведены на рис. 59.
Для критерия Неймана—Пирсона (8.22) порог принятия ре-
шения находится при заданных значениях а0 и Р-
253
Характеристики обнаружения сигнала иллюстрируют тот факт,
что для достижения большей надежности требуется и большее
отношение сигнал/помеха. Это утверждение описывается количест-
венной зависимостью с помощью характеристики обнаружения.
По кривым рис. 59 при заданной надежности для критерия макси-
мального правдоподобия (а для критерия Неймана—Пирсона также
и заданного значения а) определяется требуемая величина энерге-
тического отношения р. Из (8.22) и (8.25) нетрудно получить
Рис. 59. Характеристики обнаружения сигнала:
1 — по критерию максимального правдоподобия, 2 — по критерию Неймаиа—Пирсона
где Ф"1 — функция, обратная интегралу вероятности.
Из (8.27) соответственно имеем
р = 4 [Ф-1 (т))а.	(8.29)
Таким образом, характеристики обнаружения позволяют еще
до начала обработки оценить возможности выявления тех или иных
сигналов (аномалий). Например, надежность обнаружения сигнала,
соизмеримого с уровнем помех, т. е. sa =аа, при 10 аномальных
значениях по критерию максимального правдоподобия равна 95 %
(р = тз2/в2 = 10). Для критерия Неймана—Пирсона при одном
и том же отношении р обнаружение характеризуется различной
надежностью в зависимости от величины а. Так, например, для
р = 10 можно обеспечить высокую степень надежности 99 % (ве-
роятность пропуска сигнала 1 %), однако при этом будет большая
вероятность обнаружения ложного сигнала — 20 %. Наоборот,
небольшая величина надежности — 80 % при р = 10 связана с ма-
лой долей ложных сигналов — 1 %, но с большой вероятностью
пропуска действительного сигнала — 20 %.
254
Все приведенные выше выражения справедливы и для случая
обнаружения сигнала на фоне коррелированных помех, для которого
энергетическое отношение сигнал/помеха р = s' RJT’s, где s'
из — вектор-строка и вектор-столбец значений сигнала; R71 —
обратная корреляционная матрица помехи.
При обнаружении сигнала по нескольким профилям (трассам)
N
Рх = X Ра» W Рк— отношение сигнал/помеха на k-м профиле.
В частности, при рх = . . . = pN = р имеем р2 = Л/р и соответст-
венно надежность обнаружения по критерию максимального прав-
доподобия
у = Ф(УЛ/р/2).	(8.30)
Если форма сигнала заранее неизвестна, оценка энергетического
отношения может быть проведена по исходным данным следующим
образом. По функциям взаимной корреляции в предположении
коррелируемое™ сигнала от профиля к профилю рассчитывается
величина s2/ct2 = Ви (тв)/[1—Вл (ms)]> где Вя (тз) — экстремаль"
ное значение нормированной ВКФ - Протяженность сигнала М оцени"
вается по величине интервала корреляции, определяемого с помощью
АКФ- Отсюда р = з2т/ст2. Эта оценка р является усредненной,
т. е. для некоторого среднестатистического сигнала, тем не менее
она позволяет до начала обработки установить возможности выде-
ления слабых сигналов.
На основе количественной зависимости между р и надежностью
обнаружения у определяется понятие достоверная гео-
физическая аномалия (достоверный сигнал). Наибо-
лее распространенным подходом к оценке достоверности геофизиче-
ских аномалий является такой, при котором под аномалией пони-
мается совокупность не менее трех точек со значениями в них поля,
превышающими тройную среднеквадратическую погрешность на-
блюдений ст. Интуитивно предполагая наличие связи между на-
дежностью обнаружения аномалии и числом аномальных точек,
для увеличения достоверности аномалии на практике сгущают
сеть наблюдений. При этом интерпретаторы считают возможным
' пренебречь условием о наличии трех точек со значениями, боль-
шими Зст, при выделении протяженных по профилю или площади
аномалий. Такой подход действительно оправдан. Пусть, напри-
мер, мы исходим из приведенного выше подхода к определению
достоверности аномалии, т. е. когда имеются три точки (т = 3)
со значениями st/a > 3. При этом р > 27, что по критерию макси-
мального правдоподобия соответствует надежности обнаружения
у > 99,5 % (см. рис. 59). Следовательно, согласно действующим
инструкциям по магнито-, электро- и гравиразведке, аномалию
предлагается считать достоверной, если надежность ее обнаруже-
ния по критерию максимального правдоподобия не менее 99,5 %,
Отсюда вполне очевидно, что аномалию протяженностью в семь
255
точек, но уже при отношении s/o = 2 также можно считать досто-
верной, ибо р = s2m/o2 > 27. Из тех же соображений полагаем,
что аномалия с отношением s/o = 1 будет достоверной при т > 27.
Проведенный анализ позволяет дать более точное определение
понятия «достоверная аномалия»: под достоверной аномалией сле-
дует понимать такую составляющую поля, отношение энергии ко-
торой к мощности (в частности, к дисперсии) помех а2 превосходит
порог, соответствующий заданной вероятности (надежности) обна-
ружения у. Например, при у = 99,5 % порог р = 10 (см. рис. 59).
При проведении радиометрических наблюдений за аномалию
принимается одна точка (т = 1) со значением s/Оф = 2, где Оф —
среднеквадратический уровень фона пород. Из критерия макси-
мального правдоподобия следует, что р = 4иу = 84%.По кри-
терию Неймана—Пирсона при а = 20 % и р = 4 надежность у =
= 88 %, т. е. доля, приходящаяся на пропуск аномалии р = 12 %,
почти в 2 раза меньше вероятности обнаружения ложных аномалий
(а = 20 %).
Другой практический вывод из характеристик обнаружения
сигнала по критерию максимального правдоподобия состоит в по-
лучении объективного критерия для выбора параметров геофизи-
ческой съемки. Действительно из (8.27) следует, что
в7ст=(2/Ут')ф-1(у).	(8.31)
Задавшись надежностью обнаружения аномалии от интересую-
щего нас объекта, по выражению (8.31) можно найти шаг съемки
при некотором отношении s/o, величину которого оценивают пред-
варительно либо путем решения прямой задачи, либо по функциям
взаимной корреляции.
Наконец, по надежности обнаружения оценивается предель-
ная глубина исследований геофизическим методом. Глубина зале-
гания геологических объектов является одним из параметров, от
которого зависят ординаты и энергия аномалии. Поэтому исполь-
зовав решение прямой задачи для заданной модели и оценив дис-
персию помех по наблюденным данным, нетрудно установить за-
висимость энергетического отношения аномалия/помеха от глу-
бины залегания искомого объекта, т. е. р = f (ft). Далее из (8.29)
при заданной допустимой надежности обнаружения у0 получим
пороговое значение рпор = 4 [Ф~1 (у0)Р и по зависимости р =
— f (ft) оценим предельную глубину исследований объекта, для
которого решена прямая задача данным геофизическим методом.
При выводах, которые следуют из анализа надежности обна-
ружения, мы исходили из предположения отсутствия корреляции
помех. Только в этом случае надежность обнаружения аномалии
растет пропорционально увеличению числа аномальных значений
поля /и, таккак р = ($2/ст8) т, и чем больше т при одном и том же
отношении s*/o8, тем больше р*, а следовательно, и вероятность
правильного обнаружения аномалии у. Однако на определенном
256
этапе сгущения сети (на определенной стадии детализации анома-
лии) увеличение т не будет приводить к увеличению р, поскольку
уменьшение шага наблюдений по профилю в конечном итоге при-
ведет к коррелированное™ помех, обусловленных, в частности,
эффектами от поверхностных неоднородностей.
Пусть АКФ помехи треугольного типа (см. рис. 15, б), тогда
дисперсия помехи D = r/т2, где гх — интервалы корреляции по-
мехи по профилю. Отсюда энергетическое отношение р = s2/n/parx,
и чем больше т, тем больше гх, т. е. сгущение сети путем увеличе-
ния т будет скомпенсировано возрастанием величины гх. При этом
выигрыша в увеличении энергетического отношения не будет. Сле-
дующий путь повышения надежности обнаружения аномалии —
увеличение р за счет увеличения числа независимых наблюдений
аномалии по ряду профилей. Тогда р = 8*т№о*гх, где N — число
профилей, по которым прослежена аномалия. Однако на опреде-
ленном этапе сгущения сети профилей появится корреляция помех
между профилями и р =	где ги — интервал корреля-
ции помех между профилями. И вновь увеличение числа незави-
симых наблюдений путем сгущения сети компенсируется ростом гу.
В то же время практические возможности выделения аномалий
при использовании данных площадных съемок существенно рас-
ширяются. При достаточно большом числе N мы достоверно сможем
обнаружить аномалию, по интенсивности меньшую уровня помех
и в то же время небольшой протяженности по профилю.
Увеличение надежности обнаружения аномального эффекта мо-
жет быть достигнуто также путем использования данных комплекса
геофизических методов.
Если для каждого независимого физического параметра анома-
лия связана с одним и тем же геологическим объектом, ее надеж-
ность у = ф(д/2р//2) где pi — отношение аномалия/помеха для
l-го параметра,	— число параметров.
§ 40.	СПОСОБ ОБРАТНЫХ ВЕРОЯТНОСТЕЙ
Способ обратных вероятностей предназначен для обнаружения
заданных по форме сигналов. В отличие от способа обработки со-
гласованным фильтром, он включает порог принятия решения и вы-
числение апостериорных (обратных) вероятностей наличия сигнала
по формуле Байеса. Способ обратных вероятностей в геофизике,
предложенный А. Г. Тарховым (1959 г.), вначале был использован
О. А. Демидовичем (1964 г.) в задачах рудной электроразведки,
а затем получил широкое применение и в других методах разведоч-
ной геофизики.
Рассмотрим обнаружение детерминированного, т. е. заданного
по форме сигнала, на фойе некоррелированных помех с позиции
проверки статистических гипотез.
1.	Модель поля и постановка задачи. Пусть результаты изме-
рений вдоль профиля представляют собой сумму сигнала S; и помехи
9 А. А. Никитин	257
nt  fi — Si + n(. Помеху будем считать стационарным эргодиче-
ским процессом, некоррелированной и нормально распределенной
с нулевым средним и дисперсией о2.
Требуется на основе имеющейся последовательности значений
поля F = (fi....., /т) с определенной вероятностью установить,
является ли эта последовательность суммой сигнала и помехи, т. е.
fi = st + п(, или она представлена лишь одной помехой, т. е.
ft = ni. Такая постановка задачи приводит к сравнению двух ста-
тистических гипотез Нх и Яо; при наличии сигнала выполняется
гипотеза Я1( при его отсутствии — гипотеза Нй.
2.....Оценка формы сигнала и корреляционных свойств помех.
Форма полезного сигнала s0 может быть получена путем решения
прямой задачи для подходящей физико-геологической модели иско-
мого объекта и вмещающей среды, либо просто по наблюденным
визуально сигналам (аномалиям) на соседних, сходных по геоло-
гическому строению объектах, либо, наконец, путем расчета ВКФ
или АКФ. При этом ординаты сигнала целесообразно определять
исходя из заданной величины надежности обнаружения сигнала
у = 95 % (99 % и т. д.), например согласно критерию максималь-
ного правдоподобия. Пусть получен сигнал с ординатами s0 = (sOi,
......	.. som). Для этого сигнала по критерию максимального прав-
доподобия энергетическое отношение сигнал/помеха р0 = 2s0(/o2,
а заданной величине надежности обнаружения у соответствует от-
ношение р. Если р =/= р0, все ординаты сигнала s0 следует умно-
житьна Vp/Po, что и обеспечивает обнаружение сигнала S/ =
= -v/p/PoSo i с заданной надежностью у.
Оценка корреляционных свойств помехи проводится на заве-
домо безаномальных участках съемках путем расчета АКФ и не-
обходима для проверки некоррелированного характера помехи
и определения дисперсии^о2.
3.	Выбор критерия принятия решения. Для обнаружения^из-
вестного по форме сигнала в теории оптимальной фильтрации (см.
гл. VII) следует использовать критерий максимума пикового от-
ношения сигнал/помеха. Этот критерий обеспечивает построение
согласованного фильтра. При проверке статистических гипотез
выбор критерия определяется наличием априорной информации
(см. § 38). Если цены ошибок первого Са и второго рода и апри-
орные вероятности наличия р0 и отсутствия рг сигнала полагать
равными, т. е. Са = Ср, р0 = plt что соответствует максимальной
неопределенности событий наличия и отсутствия сигнала, следует
выбрать критерий максимального правдоподобия. Согласно [этому
критерию задача обнаружения сигнала состоит в нахождении ко-
эффициента правдоподобия А = Р	(F/Ho), где Р (F/Hi)
и Р (F/Ho) — функции (условные плотности распределения) прав-
доподобия соответственно при наличии и отсутствии сигнала, и
в сравнении А с порогом Ао = 1.
По формуле Байеса от вычисления коэффициента правдоподо-
бия можно перейти к вычислению вероятности гипотезы о наличии
258
сигнала, т. е. от вероятности Р (FjH^ к вероятности р (HJF),
иначе, к обратной вероятности. Именно поэтому рассматриваемый
прием обработки данных получил название способа обрат-
ных вероятностей, поскольку результатом обработки
является получение апостериорных (обратных) вероятностей на-
личия сигнала.
При равных априорных вероятностях наличия сигнала (гипо-
теза Hj) и его отсутствия (гипотеза Но), т. е. Po~Pi~ 0,5, со-
гласно формуле Байеса (8.9) получаем:
р (Hi/F) = (Р1/р0) Л/[(Р1/р0) Л + 1] =Л/(Л + 1).	(8.32)
С учетом (8.32) правило принятия решения по критерию
максимального правдоподобия будет следующим: при p(//1/F)>0,5—
есть сигнал; при p(HilF)<0,5—нет сигнала, так как порог приня-
тия решения Ло=1.
4.	*Построение и анализ алгоритма обнаружения. Для случая
некоррелированной помехи нормального типа с нулевым средним
и дисперсией о2 согласно выражениям (8.16) и (8.17) была полу-
чена формула для вычисления коэффициента правдоподобия ((8.19)
в виде
/	. т	1 т \
(833>
Если теперь заданный сигнал sx, . . . , sm перемещать вдоль
профиля наблюдений как весовую функцию линейного фильтра,
получим распределение коэффициента правдоподобия по профилю
(, т	1 т	\
(8-34)
2аа «=1	a2 £=i	/
где индекс / характеризует смещение сигнала вдоль профиля от
пикета к пикету.
Согласно критерию максимального правдоподобия для тех пи-
кетов, где Л/>1, будем принимать решение о наличии сигнала,
а по формуле Байеса (формуле обратных вероятностей) решение о
наличии сигнала принимаем по величине апостериорной вероят-
ности
рДЯ1/£)>0,5,	(8.35)
где
p/(/f1/F) = Ay/(Ay+ I)-
В основном алгоритме обнаружения (8.34) первый член под
знаком экспоненты представляет собой энергетическое отношение
сигнал/помеха р и при вычислениях остается неизменным; второй
член является сверткой, обеспечивающей фильтрацию исходных
данных, т. е. сам процесс обнаружения, по критерию максимума
пикового отношения сигнал/помеха. Весовой функцией при этом
служат ординаты сигнала, нормированные на дисперсию помехи о2,
т. е. hi = st/o2. Следовательно, в алгоритме обнаружения сигнала
(8.34) и (8.35), полученном на основе проверки статистических ги-
9*	259
потез, с одной стороны, обеспечивается оптимальная согласован-
ная фильтрация исходных данных, с другой — возможность вы-
числения апостериорной вероятности наличия сигнала, т. е. из-
влечение максимума информации о полезном сигнале.
Рассмотрим реализацию алгоритма (8.34) — (8.35) на числовом
примере.
Пусть исходные данные представлены 12 значениями: fi = — 2, — 2,
О, 2, — 1, 3, 2, 1, —2, 0, 1, —2. Среднее значение f = 0, а дисперсия
оа = 3. Пусть сигнал задан ординатами s/ = 1, 2, 4, 2, 1. Очевидно, его
энергия £«2 = 26, а энергетическое отношение сигнал/помеха р = Y.s2/o2—
= 8,67, что соответствует достаточно высокой надежности обнаружения
сигнала по критерию максимального правдоподобия (см. рис. 59) 93 %;
р/2 = 4,34.
Нахождение корреляционных сумм в (8.34) <р = (l/o2) прово-
дится согласно схемы:			
		' Mi	Ml
	f&a	Ма	ftsz
s8 =	Ms’	=	Ms’ 2б =	ИТ-Д-
	ftst	Мб	м«
	fbSt>	. Ms	Ms
Фз = 2	3/аа; ф4 = 24/оа; ф6=26/аа и т. д.		
Расчет апостериорной вероятности (8.35) с учетом (8.34) сведем в табл. 24.
Таким образом, решение о наличии сигнала следует принять лишь для
ПК 6, для которого вероятность р/ (Hi/F) > 0,5.
Таблица 24
пк		Ф/=2)/°2	—р/24-фу	лу=ехр(_р/2+ф/)	P/=A;./(A/+l)
3	—4	—1,33	—5,87	0,00	0,00
4	7	2,33	—2,01	0,13	0,12
5	7	2,33	—2,01	0,13	0,12
6	17	5,67	1,33	3,78	0,79
7	13	4,33	—0,01	0,99	0,50
8	7	2,33	—2,01	0,13	0,12
9	—3	—1,00	—5,34	0,00	0,00
10	—3	—1,00	-5,34	0,00	0,00
Обнаружение заданного по форме сигнала на фоне коррелиро-
ванных помех включает те же самые процедуры, что и в случае не-
коррелированных помех. Отличие состоит в том, что для описания
статистических свойств помех требуется оценка корреляционной
матрицы Rn (т—i) по ее АКФ. Алгоритм обнаружения при этом
сводится к вычислению коэффициента правдоподобия:
A^exp^-^-S/ifSi + S/iJ;.^,	(8.36)
где весовые коэффициенты hi являются решением системы линей-
ных уравнений YfaRn (tn—i) = s (— /и), т. е. определяются аца-
260
логично согласованному фильтру. Величина ^h{Si в (8.36) опреде-
ляет энергетическое отношение сигнал/помеха, а второй член пред-
ставляет собой свертку, обеспечивающую фильтрацию данных по
критерию максимума пикового отношения сигнал/помеха.
Решение о наличии сигнала принимается при Л/>1 или при
Pj (Я1//г)>0,5 [см. формулу (8.35)]. Пример обнаружения сигнала
на фоне коррелированной помехи с треугольной функцией автокор-
реляции приведен на рис. 51 (интервал корреляции гКоР = 3),
Энергетическое отношение сигнал/помеха для этого примера р =
= sWakopO2 = 5,5.
5.	Оценка качества обработки. Завершающим этапом любой
обработки является оценка ее качества.
К оценке качества в способе обратных вероятностей отнесем
надежность обнаружения, оценку параметров сигнала и величину
разрешающей способности алгоритма. Надежность обнаружения
оценивается по величине энергетического отношения сигнал/по-
меха р, которая еще до начала обработки может быть получена из
расчета ВКФ данных соседних пар профилей s2/o2 =
= Вя (тэ)/11—Вя (/Пэ)] и нахождения интервала корреляции сиг-
нала по АКФ- Анализ надежности обнаружения, в частности, с ис-
пользованием критерия максимального правдоподобия показы-
вает, что возможности обнаружения слабых сигналов вдоль оди-
ночных профилей ограничены: вдоль профиля можно провести на-
дежное обнаружение (у > 95 %) сигнала, по интенсивности соиз-
меримого с помехой s2 = о2, лишь при достаточной его протяжен-
ности (/и > 10).
Для оценки параметров сигнала используются следующие вы:
ражения. Оценка амплитуды сигнала после фильтрации
=	(8-37)
Дисперсия этой оценки (8.37) при р > 1 есть величина, обрат-
ная энергетическому отношению сигнал/помеха:
Da = оя = ± 1/д/Р-	(8.38)
Из выражения (8.38) следует важный практический вывод о том,
что возможности интерпретации слабых сигналов (аномалий) весьма
ограниченны. Действительно, для проведения количественной ин-
терпретации требуется знание амплитуд аномалии с погрешностью
не более 10 %, т. е. — ± 0,1, следовательно, р должно быть
при этом не менее 100.
Для оценки протяженности сигнала (аномалии) получить явное
выражение трудно, можно лишь воспользоваться формулой (8.38)
соответственно для дисперсии и среднеквадратического отклонения
протяженности /пА, когда сигнал задан в форме прямоугольного
импульса (а~ = ± 1/д/р)-
Оценка положения сигнала на профиле сводится к определе'
н^ю его центральной точки х0 по максимальному значению коэффи*
f	261
циента правдоподобия Лу (при Лу> 1) или по апостериорной ве-
роятности pj (при >0,5).
Дисперсию оценки положения центральной точки сигнала можно
найти по приближенным формулам:
Dz = 2 (mA)2/p2;	= ± д/2тЛ/р,	(8.39)
где т — ширина прямоугольного импульса, совпадающего по энер-
гии с искомым сигналом.
Очевидно, что при р — 10 и т = 10 (s2/o2 = 1; т = 16) средне- .
квадратическая погрешность оценки местоположения сигнала
о~ = ± д/2 = 1,4Д, т. е. местоположение слабых сигналов
устанавливается достаточно точно.
Возможности разрешения двух близко расположенных по про-
филю сигналов оцениваются с позиции решения задачи о разли-
чении сигналов, при которой гипотеза Н± является гипотезой о
наличии сигнала slt т. е. когда ft = s1( + nit а гипотеза Но — ги-
потезой о наличии сигнала s2, т. е. когда = s2i + Тогда ко-
эффициент правдоподобия
Г 1 т
Л = ехр	(52г-й)4
L2aa
i m	1
(8.40)
Основная операция в алгоритме (8.40) — получение величины
<р = У, (sXi—s2() fi, нахождение ее статистических характеристик
При условии равенства энергий сигналов Esl = ES2 (т. е. psl =
= pS2 = р) и априорных вероятностей psi — pS2 = 0,5 приводит
к надежности различения по критерию максимального правдопо-
добия в виде
? = O(V2p(l-/-12)/2),	(8.41)
где г12 = EsxrSa/ZffqOsj — коэффициент корреляции, между sx и s2.
Безусловная вероятность ошибки различения сигналов будет
q = 1—у. Наибольшей ошибкой различения при одинаковом от-,
ношении сигнал/помеха обладают сигналы, для которых коэффи-
циент корреляции г12 максимален. Так, для одинаковых по форме
сигналов r12 = 1 и при р = 10 из (8.41) следует, что у = 50 %
и q = 50 %, т. е. сигналы неразличимы. В то же время для оди-
наковых по форме, но противоположных по знаку сигналов г12 —
= — 1 и при р = 10 из (8.41) у « 100 %.
§ 41.	СПОСОБ МЕЖПРОФИЛЬНОЙ КОРРЕЛЯЦИИ
Площадная съемка ведет к увеличению информации о полезном
сигнале при его корреляции по нескольким профилям и вследствие
этого расширяет возможности выделения слабых сигналов. Рас-
смотренные^в § 40 алгоритмы обнаружения допускают обобщение
и на двумерный случай. Выделение двумерных сигналов, или ано-
малий, приводит к возможности решения принципиально новой
задачи — разделению интерферирующих между собой аномалий,
262
т. е. когда аномальные эффекты от объектов, различающихся своим
простиранием, накладываются друг на друга и наблюдаемые поля
приобретают сложный интерференционный характер. Накопление
аномальных эффектов за счет использования наблюдений по пло-
щади позволяет обнаруживать и выделять сигналы при минимуме
априорной информации о сигнале и помехах.
Как следует из анализа характеристики надежности обнаруже-
ния (см. § 39), повышение надежности сигнала у связано не только
с увеличением числа т, но и с увеличением независимых наблюде-
ний за счет числа профилей N, по которым прослеживается сигнал.
Алгоритм способа межпрофильной корреляции аномалий вы-
текает из решения задачи обнаружения заданного по форме сиг-
нала, прослеживаемого по N профилям, на фоне некоррелирован-
ных (как вдоль профилей, так и между ними) помех с дисперсией о2.
При такой задаче сравнивается гипотеза Нг о том, что многомер-
ный вектор наблюденного поля Fb.. N содержит и сигнал, и по-
меху, с гипотезой Но о том, что тот же вектор наблюденного поля
Fi,,,n содержит только помеху.
Вследствие условия некоррелированности помехи между про-
филями гипотезам Нг и Но соответствуют следующие функции
правдоподобия:
Р (Fi. . . jv/Hi) = Р (Fi/Hj . . . Р (FM-
P(Fi... n/H0) = Р (Ft/H0) . . . Р (Fn/H0),	(8.42)
где Fi...л — матрица из наблюденных значений поля fkt, состоя-
щая из N строк и т столбцов, где т — протяженность сигнала по
каждому из профилей, причем fki = ski + Пн для гипотезы
и fkt — nki — Для гипотезы Но.
Входящие в (8.42) функции правдоподобия по отдельным про-
филям определяются формулами (8.16) и (8.17), на основании ко-
торых для (8.42) получаем:
P(F,. . .N/HJ = т- -—ехр Г--J-SS^-s^)2!;
cmN (2л)тЛ2 L 2аа k i	J
~	(8.43)
P(Fb..»/H.)= >(^..rap(--X-??ft).	(8.44)
Отсюда коэффициент правдоподобия
A = P(F1...N/Hl)/P(F1...N/H0) =
==exp(-ib_??s‘‘+ ±№4		(8,45)
Если ввести индексы / для смещения сигнала вдоль профиля
и р для смещения сигнала между профилями, рабочий алгоритм
263
для вычисления Л примет вид:
Лр/=ехр( —--±-£ Zskifp-k.j-iy (8.46)
где т — четное; I — оценивает смещение центральной точки сиг-
нала от профиля к профилю, I = 0; ±1; ± 2, . . . , (N + 1)/2 <
< р < М — (N—1)/2; М — общее число профилей.
Первый член под знаком экспоненты в (8.46) определяет энер-
гетическое отношение сигнал/помеха в окне из Ntn точек, а второй
член — представляет двумерную свертку, обеспечивающую филь-
трацию исходных данных путем расчета двойной корреляционной
суммы <рр/ наблюдаемых значений поля fkl с заданным по форме
двумерным сигналом sftj.
По формуле Байеса нетрудно от вычисления по (8.46) перейти
к вычислению вероятности наличия сигнала по (8.35). Однако по-
стараемся из (8.46) извлечь алгоритм обработки при отсутствии
сведений о форме сигнала. Если двумерную свертку в (8.46) за-
писать в виде
Фр/=	*	(8-47)
о i k
то при отсутствии сведений о форме сигнала для его выделения
ограничимся лишь результатом суммирования данных по несколь-
ким профилям, т. е. нахождением сумм
(8-48)
Выражение (8.48) отражает межпрофильное суммирование ис-
ходных данных и в принципе обеспечивает оценку формы сигнала,
если помехи остаются некоррелированными. При таком суммиро-
вании интенсивность помехи возрастает в aJN раз, а амплитуда
сигнала возрастает в N раз. Общий выигрыш в отношении
сигнал/помеха получается b^N, раз, причем он достигается лишь
при суммировании в направлении корреляции сигнала (простира-
ния аномалии). Величина смещения /, т. е. смещение центральной
точки аномалии от профиля к профилю, определяется по экстре-
мумам ВКФ данных соседних пар профилей. Поскольку ВКФ для
каждого смещения I = 0; ± Ах; ± 2Ах; . . . представляет собой
выборочный коэффициент корреляции, величина Вя (Z) будет на-
дежной, если превышает двойную — тройную ошибку ее опреде-
ления, т. е.
oBh = [1-Bh(0]/V^>
Надежные оценки Вя (/) получаются в тех случаях, когда
имеется несколько аномалий (сигналов) одного и того же прости-
264
рания, либо одиночные аномалии с большой энергией. Поэтому
способ межпрофильный корреляции в основном эффективен при
выделении и разделении групп аномалий одного и того же прости-
рания. Для решения задачи разделения аномалий должно наблю-
даться несколько надежных экстремумов ВКФ, причем доверитель-
ный интервал для смещения I определяется дисперсией вида,
(А. К. Яновский)
Dt = 2 [1 — В2 (/,)] Гкор Ах/пАх®2Вн (/,),	(8.49)
где Гкор — интервал корреляции, /-Кор =	(т) dm\ (т) —
нормированная АКФ;<о = (оо+ Асо; ®0 — частота максимума спектра
аномалии; А® — среднеквадратическая частота спектра.
Разрешающая способность алгоритма межпрофильной корреля-
ции связана с надежностью оценивания величины Вн (/) и самого
смещения I.
В случае наложения аномалий, различных, но близких по про-
стиранию, получается расплывчатый экстремум ВКФ. Для более
точной оценки смещения I, характеризующего направление каждой
аномалии, требуется расчет ВКФ для данных, расположенных
через профиль, два профиля и т. д.
Обработка данных по способу межпрофильной корреляции вклю-
чает следующие процедуры:
1.	Расчет нормированных ВКФ для данных соседних пар про-
филей Вн (/). Максимальное смещение /тах при вычислении ВКФ
должно соответствовать максимально возможному смещению ано-
малий от профиля к профилю. Величина 1тзх обычно не менее пяти
и, как правило, не более 15 дискретов.
2.	Определение смещения 13 по положительным экстремумам
ВКФ с оценками значимости Вн (/э) и дисперсией величины /9 по
(8.49). Обычно ВКФ имеет не более трех экстремумов. В случае
расплывчатых экстремумов ВКФ, когда достоверная оценка ве-
личины 13 затруднена, следует провести вычисление ВКФ для
данных, расположенных через профиль или через два профиля.
Расплывчатые экстремумы обусловлены интерференцией аномалий
близкого простирания или широкими аномалиями. Расчет допол-
нительн'ых ВКФ позволяет уточнить величину смещения для каж-
дой интерферирующей аномалии. Если экстремум ВКФ не разде-
ляется на два, его расплывчатость объясняется широкой аномалией.
3.	Задание направлений суммирования и выбор базы суммиро-
вания. Направления суммирования задают по результатам оценок
13 по ВКФ с учетом доверительного интервала 13 ±о/э и значимости
Вв (Z9). Обычно величина о/э — не менее шага съемки по профилю,
поэтому разброс значений 13 в пределах одного пикета можно не
учитывать. Вычисление нормированных ВКФ дает возможность
оценить отношение сигнал/помеха $2/ст2 = Вя (Z9)/[l—В„ (13)], что,
в свою очередь, позволяет найти базу суммирования А/, т. е. число
профилей для дальнейшего суммирования, с учетом заданной на-
дежности у по (8.30).
265
При s4/o2 = 1, Вн (/э) = 0,5 обычно достаточно принять N = 3,
поскольку протяженность аномалии по профилю т > 5, что в це-
лом обеспечит надежность обнаружения аномалии по критерию
максимального правдоподобия у > 97 % (р> 15). Лишь для очень
узких аномалий (при т = ЗА) надо выбирать N > 5. При s2/oa<; 1,
когда Вн (/э) = 0,3-j-0,4, N > 5 4-7. Число профилей больше
девяти даже в случае съемок крупного масштаба задавать не имеет
смысла.
4.	Нахождение сумм вида (8.48) по каждому заданному направ-
лению суммирования. Так, при /э = А, что соответствует смеще-
нию аномалии в один пикет и базе суммирования N = 3, схема
вычислений имеет вид
fsi
fai /зг
fu + faa + f 33
f 12 + faa + /з4
fai
fn
fit
fai + /32 + f43
f 22 + f 33 + f 44
и т. д.
fin—3 + /2П-2 + /ЗП-1
fin—2 + /гп-1 + /зп
fln-1 fin
fin
fin-3 + fan-2 + fin-1
_ fan—2 + fan-i + fm
fan-i fan
fan
Полученные суммы на приведенной схеме отмечены квадрат-
ными скобками. Результаты суммирования относятся к среднему
из суммируемых профилей. При этом часть информации теряется
(по одному, двум значениям с каждого конца профилей). Для при-
ведения масштаба данных суммирования к исходному результаты
суммирования следует разделить на N.
5.	Выделение аномалий и аномальных зон по коррелируемым
особенностям суммарного поля. При этом надежными аномалиями
следует считать лишь те, которые коррелируются по числу профи-
лей, превышающему базу суммирования. Аналогичный алгоритм
заложен в сейсморазведочных методах регулируемого направлен-
ного приема и общей глубинной точки. Однако выбор направления
суммирования с учетом экстремумов ВКФ повышает надежность
разделения сигналов.
Для оценки разрешающей способности межпрофильной корре-
ляции следует воспользоваться обобщенной характеристикой на-
правленности (6.75).
Разделение аномалий магнитного поля Za, обусловленных, с
одной стороны, контактами пород, а с другой — тектоническими
нарушениями, по способу межпрофильной корреляции проиллю-
стрировано на рис. 60.
266
Bt.14
Рис. 60. Результаты обработки поля Za способом межпрофильной корреляции.
а — исходные данные Za; б — функции взаимной корреляции; результаты суммирова-
ния по пяти профилям: а — северо-восточного простирания, е — северо-западного про-
стирания; 1 н 2 — смещение осей аномалий; 3 — зона пониженных значений поля
На рис. 61 приведена геологическая карта участка с результа-
тами статистической обработки. Исходные данные магнитного поля
приведены на рис. 60, а. Сеть съемки 250 X 50 м. Точность наблю-
дений ± Ю нТл. Графики поля Za свидетельствуют о его сложном
характере. Какие-либо четкие аномальные зоны, связанные с кон-
тактами различных пород, с тектоническими нарушениями, харак-
терными для местных геологических условий, выделить трудно.
Построение ВКФ (см. рис. 60, б) позволило зафиксировать два
основных направления аномалий: северо-восточное и северо-запад-
ное. Дальнейшее суммирование исходных данных в пределах пяти
Рис. 61. Геологическая карта с результатами статистической обработки.
1 — разломы; 2 — контакты пород; 3 — порфириты; 4 — конгломераты; 5 — песчаники;
6 — алевролиты; 7 — яшмы; 8 — кремнистые сланцы; 9 — осн геофизических аномалия,
выделенные по результатам обработки
профилей вдоль установленных направлений аномалий (см. рис. 60,в
и а) дает возможность обнаружить отдельные аномалии и аномаль-
ные зоны, проследить характер их изменения по площади. На
рис. 60, в четко выделена зона отрицательных значений Za, кото-
рая хорошо увязывается с областью распространения порфири-
тов на геологической карте. Помимо этой зоны уверенно прослежи-
ваются две положительные аномалии северо-восточного простира-
ния, из которых одна приурочена к разлому того же простирания,
а другая — к контакту песчаников и яшм. На рис. 60, г также
четко выделяются две аномалии. Одна совпадает с установленным
тектоническим нарушением северо-западного простирания, другая,
более интенсивная,— фиксирует нарушение, подтвержденное в
дальнейшем при тщательном изучении керна картировочных сква-
жин.
.268
§ 42.	СПОСОБ АДАПТИВНОЙ
(САМОНАСТРАИВАЮЩЕЙСЯ) ФИЛЬТРАЦИИ
Рассмотренный способ межпрофильной корреляции эффективен
в тех случаях, когда можно рассчитывать на наличие нескольких
аномалий одного и того же простирания, либо широких аномаль-
ных зон. При этом слабые одиночные аномалии, отличающиеся
по своему направлению от превалирующих, не будут выявлены.
Одним из наиболее эффективных приемов выделения слабых сиг-
налов при минимуме априорных сведений о форме сигнала в общем
случае является способ адаптивной (самонастраи-
вающейся) фильтрации. Под адаптацией, самонастрой-
кой, понимается «приспособляемость» алгоритма обработки к из-
менению свойств сигнала (его формы и параметров) и помех, в ча-
стности к изменению дисперсии помех о2.
Оценка этих свойств производится непосредственно в процессе
обработки. Получение подобных оценок возможно лишь по данным
площадных наблюдений, когда имеется уверенность в корреляции
сигнала по нескольким профилям. При использовании адаптив-
ных (самонастраивающихся) процедур обработки (см. также § 43)
основное значение приобретают критерии многомерного статисти-
ческого анализа. Рассмотрим применение одного из таких крите-
риев, содержащего алгоритм решения задачи обнаружения сигна-
лов на фоне помех и их разделения по различным направлениям.
Эта задача формулируется следующим образом.
Пусть имеются данные геофизических наблюдений F по пло-
щади в виде двумерного массива fki, где k — номер профиля,
i — номер пикета на профиле. Положим, что поле F представляет
собой аддитивное наложение некоррелированных нормально рас-
пределенных помех на совокупность неизвестных по форме сигна-
лов различного направления. За сигнал принимается любой ре-
гулярный процесс с математическим ожиданием, не равным нулю,
процесс регистрируется по нескольким профилям (трассам) с ли-
нейным смещением (или без смещения) от профиля к профилю,
Рассмотрим в поле F окно, включающее N профилей и т точек по
каждому профилю, т. е. определяющее матрицу размером
fk+l, t+l> fk+l, t+2> • • • , fk+l, l+mi
fk+2, i+1+0, fk+2, /+2+0, • • • » fk+2, i+m+0,
fk+N, /+1+0Л» fk+N, /+2+0ЛП • • • , fk+N, i+m+eN-
Индексы k + 1, i + 1 указывают на положение левого верхнего
угла выбранного окна, 0 — его наклон к простиранию профилей,
определяемый величиной смещения на один (0 = 1), два (0 = 2)
пикета и т. д. последующего профиля относительно предыдущего;
0Г<; 0< 02; 0 = 0, ± A, ± 2А, . . . Величины 0Х и 02 задаются
интерпретатором в зависимости от возможных направлений сигна-
269
лов. Наибольшая величина 0, т. е. 02, отвечает максимально воз-
можному углу, образуемому направлением осей сигналов с направ-
лением профилей. С изменением индексов I и k связывается пере-
мещение окна соответственно по простиранию и вкрест простира-
ния профилей.
Задача состоит в том, чтобы получить оптимальный для неко-
торого критерия алгоритм обработки в указанном окне и решить,
является ли соответствующий ему участок съемки аномальным или
безаномальным.
Не уменьшая общности, рассмотрим окно в левом верхнем углу
матрицы F при 0 = 0, относительно которого и проведем необхо-
димые рассуждения. Таким образом, имеет место матрица вида
	/н»	flit • • • ,	flm
F (2V, т, 0 = 0) =	fiit	fiit	• • • t	fim
	-f Nit	fxz • • v t	f Nm -
(8.50)
Допустим, что в пределах окна дисперсия помехи изменяется
незначительно, т. е. оы = о2. Тогда векторы-строки матрицы (8.50)
имеют /n-мерное нормальное распределение с векторами средних
значений flt . . . , fN и одинаковыми корреляционными матрицами
D = о21, где I — единичная матрица. Иначе говоря, = /11, . . . ,
fim) — вектор-строка распределена нормально с параметрами (/lt
D); In = Owi> • • • » fwm) — вектор-строка распределена нор-
мально с параметрами (fN, D).
В пределах окна (8.50) возможны три случая.
1.	Участок поля внутри окна является безаномальным, т. е.
f! = . . . = fN и векторы-строки Д распределены соответственно
с параметрами (0, D). Это гипотеза Но.
2.	В окне присутствует аномалия, но ее направление не совпа-
дает с наклоном окна . В этом случае векторы-строки распреде-
лены с параметрами (fk, D), причем	Это гипо-
теза Н}.
3.	В окне имеется аномалия и ее направление совпадает с на-
клоном окна, т. е. /\ == /2 =_. . . = fN = f и векторы-строки fk
распределены с параметрами (/, D). Это почти нулевая гипотеза Н*о,
Последний случай соответствует сохранению формы и парамет-
ров аномалии (сигнала) от профиля к профилю. В первом и третьем
случаях все строки матрицы (8.50) являются выборками одного
и того же вектора. Решение о наличии первого и третьего случаев
заключается в проверке нулевой гипотезы Но о том, что векторы
средних значений векторов-строк равны: h = fa = . . . = fN —f.
Гипотеза Но легко сводится к чисто нулевой гипотезе Но путем
—>	—*
образования (N—1) новых векторов гъ ... , где векторы
270
z = fk-i — fk распределены с параметрами (0, D*). Следовательно,
гипотеза Но состоит в том, что все векторы zft имеют нормальное
распределение с параметрами (О, D*) и при ее проверке мы отде-
ляем первый и третий случаи от второго. Задача отделения первого
случая от третьего решается как проверка гипотезы Но о том, что
векторы-строки Д распределены с параметрами (0, D), в то время
•*>
как для гипотезы Hi векторы-строки Д распределены с парамет-
рами (f, D). Остановимся на задаче проверки гипотезы Но. Для
этой проверки в теории статистических решений существует кри-
терий, основанный на ^-статистике Хоттелинга: Т2 = A7'R-1/,
f = (Д, . . . , fm) — оценка вектора математических ожиданий,
причем
1 N
h=-^-Zfki,	(8.51)
I?-1 — обратная корреляционная матрица помехи.
В нашем случае R = D — о21 и
к = = (8's2>
Отсюда
tn
Т* =--------------^4------------- (8.53)
----!-----2 Е
ki
Гипотеза Но принимается, если 7’2<Та(7'а — порог принятия
решения при заданной вероятности ошибки первого рода), и от-
вергается если T22>7t-
С учетом (8.51) перепишем формулу (8.53) в виде
m / N
m z=i \ N J
1
и> =
(8.54)
N m /	N у
n ES(f«—— Е(«)
m(N— 1) л=1 t=i \ Л/ й /
Величина w в случае выполнения гипотезы Но (отсутствие
аномалии в окне) имеет так называемое центральное F (0, qlt ga)-
распределение с qt = m и q2 = m (N—1) степенями свободы, а
в случае выполнения гипотезы (наличие, аномалии в окне) —
нецентральное F (b, qlf «/^-распределение с теми же степенями
свободы qr и q2 и параметром нецентральное™
b = N^gla2,
(8.55)
271
где si — компоненты вектора аномалии (сигнала)
_ N
Sl = (UN) Y Ski.
k=i
Если провести анализ выражения (8.54), нетрудно увидеть,
что при наличии аномалии числитель с точностью до множителя,
равного N, представляет собой оценку среднего квадрата ампли-
туды сигнала в окне размером mN. Для нахождения этой оценки
сначала следует усреднить наблюденные значения fk{ по N профи-
лям согласно (8.51), а затем вычислить их средний квадрат ампли-
туды вдоль профиля по т точкам, т. е.
- т f N \2
S2=—	(8.56)
т i=\ \ N fe=i / .
Знаменатель (8.54) выражает оценку дисперсии помехи в том
же сжне. Для ее получения из наблюденных значений fki следует
—мячбсть усредненные по N профилям значения поля, а результат
возвести „в квадрат и усреднить, т. е.
N т f	N
& = -Tv % Е	Е fkJ •	(8.57)
m(N — 1) i=i \ N k=\	/
Таким образом, выражение (8.54) в случае наличия аномалии
(сигнала) в окне с точностью до множителя N представляет собой
оценку отношения среднего квадрата амплитуды аномалии к дис-
персии помех, т. е. если р, = sVo2, то
w — N\k	(8.58)
Основной алгоритм адаптивной фильтрации сводится к вычис-
лению оценки отношения сигнал/помеха ц в окне, состоящем из
mN точек:
N т /	N	v '
-———т— Ё Ё (/« —— Ё fki)
m(N — V) k-ii=i\ N Л=1	/
С величиной ц. непосредственно связан параметр нецентраль-
ное™ (8.55) для нецентрального F (b, qlt q2)-распределен и я
b = Nmp.	(8.60)
Для принятия решения о наличии аномалии, т. е. гипотезы Hlt
необходимо выбрать порог d: при W>d (р>рпор) следует прини-
мать решение о наличии аномалии, а при W<Zd — решение об от-
сутствии аномалии в окне (гипотеза Но). Для нахождения порога
используем критерий Неймана—Пирсона, т. е. порог d будем уста-
272
навливать путем задания вероятности ошибки первого рода а, где
ОО
а = J PF(0.q„q2)(X)dx’
PF (01 ff2) (х) обозначает плотность центрального /•'-распределения.
Для а = 1 и 5 % значения порога d приведены в табл. 25.
Таблица 25
(N—1)т	т				
	5	7	9	15	20
		а =	1 %		
10	5,64	5,20	4,94	4,56	4,40
15	4,56	4,14	3,89	3,67	3,37
20	4,10	3,70	3,46	3,23	2,94
30	3,70	3,30	3,07	2,84	2,55
60	3,34	2,95	2,72	2,50	2,20
		а = 5 %			
10	3,33	3,14	3,02	2,84	2,77
15	2,90	2,71	2,59	2,40	2,33
20	2,71	2,50	2,39	2,20	2,12
30	2,53	2,33	2,21	2,01	1,93
60	2,37	' 2,17	2,04	1,84	1,75
Соответственно для (8.59) пороговое значение цПоР = d/N.
Надежность обнаружения аномалии (при W^>d) по критерию
Неймана—Пирсона определяется как у = 1—Р, где р — вероят-
ность ошибки второго рода;
d
Р — f PF (6, qt. q2) (*) dx, Pp ((,, (?11
—00
—плотность нецентрального F-распределения. Примеры характе-
ристик обнаружения сигнала для заданных значений т и N при-
ведены на рис. 62.
Из графиков рис. 62 следует, что при фиксированных ц. и т
надежность обнаружения резко возрастает с накоплением ано-
мального эффекта по N профилям. Надежное обнаружение (с ве-
роятностью у >95 %) для аномалий, соизмеримых по интенсив-
ности с уровнем помех, s2 = о2 возможно для нешироких аномалий
(т = 5-5-7 А) при накоплении аномального эффекта не менее чем
по пяти профилям; для аномалий с т = 9 и 11 такая надежность
достигается при N = 3 (а = 5 %). Естественно, что возможности
накопления сигналов в сейсморазведке гораздо шире, чем в дру-
гих'методах. Известны примеры выделения слабых сигналов, когда
в накоплении участвовало 600 каналов.
273
Существенное значение имеет выбор размеров окна. В сейсмо-
разведке размер окна по времени определяется периодом сигнала.
Так, при частоте fs = 40 Гц период составляет 0,025 с. Число N
обычно выбирают не менее 12. При обработке данных потенциаль-
ных полей размер окна оценивается путем построения двумерной
АКФ исходных данных. В ряде случаев целесообразно проводить
обработку при разных размерах окна.
Рис. 62. Характеристики обнаружения сигнала адаптивным фильтром,
а в %; а — 5, 6 — 1; значения т: 1 — 5. 2 — 7
Адаптация алгоритма обработки (8.59) связана с перемещением
окна сначала вдоль профилей с шагом, равным расстоянию между
пакетами, а затем вкрест простирания профилей с шагом, равным
расстоянию между профилями. Для каждого такого смещения вы-
числяется отношение сигнал/помеха ц или статистика W. При этом
получается непрерывная оценка ц (или W) по всей площади съемки.
При р.>рПор (W>d) принимается решение о наличии аномалии.
Совершенно аналогичные вычисления осуществляются в пределах
окон с различными значениями 0. Подобный анализ позволяет,
с одной стороны, выделить аномалии на фоне помех, с другой —
провести их классификацию по разным направлениям. Как следует
из выражения (8.59), величина ц. находится лишь по наблюденным
значениям поля, априорные сведения о форме аномалии при этом
не привлекаются. Форма и параметры аномалии могут изменяться
в пределах съемки существенно. Для принятия решения о наличии
аномалии важно лишь, чтобы ее энергия превосходила дисперсию
помех. Изменения формы аномалии и дисперсии помех раздельно
не сказываются на конечном результате обработки, поскольку в
алгоритме существенна лишь достаточно большая величина отно-
шения сигнал/помеха, т. е. р.2>ц.ПоР-
На рис. 63 приведены результаты обработки модельных данных
адаптивным фильтром. На случайную реализацию, состоящую из
274
50 значений, в пределах каждого профиля наложены две аномалии,
местоположение которых указано на рис. 63, а. Одна аномалия
знакопеременная и задана с положительным смещением от профиля
к профилю на один пикет (0 = 1), другая — отрицательная со
смещением 0 = — 3. Обе аномалии соизмеримы по интенсивности
с уровнем помех и визуально не прослеживаются. Обработка по
алгоритму (8.59) с учетом выбора порога по (8.58) включала вычис-
ления р. для окон N = 5 и т ~ 7 с наклонами 0 = 0; ± Г, ±2
и ± 3. Результаты обработки приведены на рис. 63, б в виде гра-
фиков р>|лПор = 0,66 (Цпор = d/N = 3,30/5 = 0,66, см. табл. 25).
Надежность обнаружения обеих аномалий, если положить для них
р. = 1, составляет приблизительно 95 % (см. рис. 62, б). Таким
образом, обработка данных по алгоритму адаптивной фильтрации
позволяет уверенно проследить обе аномалии даже в местах их
перекрытия.
На рис. 63, б выделена также ложная аномалия: 0 = — 2,
совпадающая по местоположению с аномалией при 0 = — 3. Эта
ложная аномалия по простиранию меньше числа профилей М
заданного окна и ее отбраковка не представляет труда.
Из рассмотрения вопросов по разрешающей способности адап-
тивной фильтрации следует, что определяющим при ее оценке яв-
ляется исследование параметра нецентральности Ь. Это рассмотре-
ние показывает, что выделение знакопеременных аномалий прово-
дится более «чисто», чем знакопостоянных. Для знакопостоянных
аномалий со значениями р > 1 происходит выделение ложных
осей, простирание которых близко к истинному в пределах 0 =
= ± Д, с достаточно большой вероятностью. Примером могут слу-
жить результаты обработки модельного материала на рис. 63, б,
где зафиксирована ложная аномалия с направлением оси, близким
к истинному. Поэтому в практике обработки следует задавать зна-
чения 0 = 0; ± 2Д; ± 5Д. Максимальная величина 0 опреде-
ляется углом 45° относительно простирания профилей. Если этот
угол больше 45°, сеть профилей должна быть повернута на 90°.
В качестве примера реализации алгоритма (8.59) приведем
схему вычислений ц при параметрах окна т = 5; N = 3; 0 = 0.
Исходная матрица значений поля в окне имеет вид
/11	/12.	/13	/14	/15	.
/21	/22,	/23	/24	/25
/з1	/з?	/зз	/ 34	/зь
Оценка формы аномалии проводится путем суммирования зна-
чений поля без смещения между профилями, так как 0 = 0.
Ординаты аномалии в окне, если она имеется, будут:
si= ~7~ (/11 + /21+/31);
О	/
Sa = —(/12 + /22 + /за);
О
275
Рис. 63. Результаты обработки (б) модельных данных (а) адаптивным фильт-
ром.
/ — сумма сигналов и помех; 2 — форма аномалий и нх местоположение; значения ц
для наклонов окна*. 3 — положительного, 4 —• отрицательного. Параметр кривых —
значения 0
S3 — ""T-(f 13 Т f 23 Н-f зз) >
О
s4 — —5- (/14+/24+/34);
Sb = (fib + f25 + /зб) •
О
Далее вычисляется средний квадрат ординат аномалии s2 =
.	5
=------Для оценки дисперсии помехи требуется найти разно-
5 1
сти:
/11--S1	fli--Si	/13 S3	fl4-S4	/16 Sb‘,
hi — Sj	hi — ®2	/28—S3	hi—S4	h5 — sB;
hi—si	hi—s2	/зз—S3	/34 — s4	fsB—s5.
Путем возведения этих разностей в квадрат с последующим сум-
мированием и нормировкой на (N—1) /п=2-5= 10 получим
оценку дисперсии помехи, т. е.
1	3	6
Величина ц = s2/o2 относится к центральному пикету окна,
т. е. к точке 2, 3. Затем окно перемещается на один пикет по про-
стиранию профилей и аналогичному анализу подвергается уже
матрица
/12	/13	fit	fib	fi»
fit	hi	f 24	fib	f 2»
hi	/зз	/34	ha	fat-
При этом величина ц = s2/o2 будет отнесена к точке 2, 4, После
завершения вычислений ц по первым трем профилям окно сме-
щается на один профиль и анализу подвергается матрица
hi	fn	faa	fu	f 25
hi	ha	ha	fat	fse
/41	/42	/43	fu	fib-
Полученное значение ц относится к точке 3, 3 и т. д. Способ
адаптивной фильтрации нашел широкое применение при выделе-
нии слабых эффектов, связанных с нефтегазоносностью разреза,
по сейсмическим данным, а также для прослеживания контактов
и тектонических нарушений при обработке данных гравитацион-
ных съемок.
277
FvV FT7]? Fvh FF7U |д|*
Ш7 PvTk Ш} 1^1/g
Рис. 64. Геологическая схема с осями аномалий р..
1 — альбититы; 2 — плагиограниты; 3 и 4 — мигматиты соответственно бнотнт-плагно-
клаэовые н плагноклазовые; 5 — диабазы; 6 — пегматиты; 7 — гнейсы; S — геологи-
ческие границы; 9 — тектонические нарушения по геологическим данным; а — установ-
ленные, б — предполагаемы; 10 — оси аномалий ц, определенные путем адаптивной
фильтрации
На рис. 64 приведена геологическая схема одного из участков
Северного Криворожья с выделенными осями аномалий ц., полу-
ченными в результате обработки данных магнитной ^ъемки (рис. 65)
адаптивным фильтром. Для выбора параметров обработки — раз-
меров и наклонов окна — была использована двумерная АКФ
исходного поля (см. рис. 17). Рельеф ДАКФ показывай» что кор-
реляция практически пропадает (коэффициент коррел^ии <0,3)
на расстояниях 5—7 пикетов (т) и 4—5 профилей (N) бт ее центра.
Таким образом, при обработке наиболее подходящими размерами
окна mN следует считать 5 X 5 и 7 X 5. Рельеф ДАКФ отмечает
278	'
Рис. 65. Наблюденные графики Za и результаты их обработки адаптивным
фильтром.
1 — графики Za; 2—4 — графики аномалий |Л соответственно для субмериднонального
северо-западного и северо-восточного простираний
два основных простирания аномалий: субмеридиональное (0 = 0)
и северо-западное (0 == 3). Если первое из них картируется по гра-
фикам Za визуально, то второе — на них вообще не выделяется
По графикам значений р четко прослежен целый ряд аномальных
зон, визуальное выделение которых по исходной карте Za было
исключено. Через всю площадь участка прослеживается зона се-
веро-западного простирания, параллельно которой в юго-западной
части участка отмечается несколько аномалий меньшей протяжен-
ности. Эта зона связана с тектоническим нарушением, не выделен-
ным по геологическим данным. Остальные выявленные аномалии р
обусловлены дайками диабазов, контактами пород различного со-
става, разломом северо-восточного простирания, установленного
ранее по геологическим данным.
279
§ 43. НЕПАРАМЕТРИЧЕСКИЕ ПРИЕМЫ
ОБНАРУЖЕНИЯ СИГНАЛОВ
В основе рассмотренных выше способов выделения геофизических
сигналов на фоне помех лежит предположение о нормальном рас-
пределении помех. Такие способы можно назвать параметрическими,
поскольку нормальный закон характеризуется двумя парамет-
рами — средним и дисперсией (для коррелированных помех —
корреляционной матрицей). В то же время предположение о нор-
мальном законе распределения помех не всегда имеет место на прак-
тике. В связи с этим необходимо применение так называемых н е -
параметрических способов (алгоритмов) обра-
ботки, которые оказываются эффективными в тех случаях, когда
использование статистических приемов, базирующихся на нормаль-
ном законе распределения, является сомнительным или вообще
невозможным.
Основное достоинство непараметрических способов состоит в
том, что их построение не требует предположения относительно
вида распределения. При решении задачи обнаружения сигнала
на фоне помех распределение последних может носить любой ха-
рактер. Весьма вероятно, что большинство типов помех, осложняю-
щих обнаружение геофизических аномалий, не имеет нормального
распределения. В частности, помехи, создаваемые геологическими
неоднородностями верхней части разреза, с большей достоверностью
можно считать имеющими равномерное распределение, чем нор-
мальное.
Изучение помех, возникающих при измерении геофизических
полей в скважине, проведенное С. М. Махмутовым, указывает на
наличие двух дополнительных экстремумов в их распределении
соответственно при очень низких и очень высоких значениях из-
меряемого параметра по сравнению с нормальным законом. На-
личие подобных экстремумов связывается с помехами технического
характера, такими, как сбои при движении скважинного снаряда.
Таким образом, отказ при построении алгоритмов выделения сиг-
налов от конкретного вида распределения помех, кстати, как и са-
мих сигналов, если они представлены случайным процессом, по-
зволит обнаруживать сигналы в тех случаях, когда параметриче-
ские способы не являются эффективными.
Использование непараметрических способов обработки геофи-
зических данных связано с применением знаковых, ранговых и
знаково-ранговых статистик.
Знаковая статистика — произвольная функция век-
тора /, т. е. последовательности наблюденных значений поля,
/1( ...,/„ с компонентами sgn / = (sgn flt ... , sgn /„), где
sgnf,= —(8.61)
IM 1-1, A<0.	;
Например, пусть
280
/ = (—1, 2, 3, —5, 0, 5).	(8.62)
Его знаковая статистика будет — 1, 1, 1, — 1, 1, 1.
Алгоритм, использующий только знаки элементов вы-
борки наблюдений, называется знаковым.
Порядковая статистика — упорядоченная вы-
борка, в которой все элементы вектора / (Л, • • . , /п) расставлены
в возрастающем порядке. Для того же примера (8.62) порядковая
статистика будет — 5, — 1, 0, 2, 3, 5.
Рангом Rt элемента выборки fa называется порядковый но-
мер этого элемента в порядковой статистике. Так, для примера
(8.62) с учетом его порядковой статистики получаем
/<=—5, —1, 0, 2, 3, 5	fa= — 1, 2, 3, —5, 0, 5
=	2, 3, 4, 5, 6, ИЛИ R{ = 2, 4, 5, 1, 3, 6.
Ранговая статистика — это произвольная функция
от рангового вектора R (f) = R . . . , R (fn), представляющего
перестановку чисел 1, 2, . . . , п, которая получается при замене
элементов выборки их рангами.
Ранговый алгоритм — есть сравнение ранговой ста-
тистики с некоторым заданным порогом.
Знаково-ранговый алгоритм использует зна-
ково-ранговую статистику R*, зависящую как
от вектора рангов R (f), так и от вектора знаков sgn f выборки fa
Например, значение знаково-ранговой статистики для первого
элемента выборки (8.62)
. п
^=^-Zsgn(|/1|-|fA|)+-J- =
Z k=\
= _1_(1 —1 —1 _ 1.+1 _ 1) + 3 = 2.
Рассмотрим алгоритмы обнаружения сигналов, построенные на
указанных статистиках, на их основе получим непараметрические
аналоги способов обратных вероятностей, межпрофйльной корре-
ляции и адаптивной фильтрации.
Знаковый алгоритм обнаружения детерминированного (задан-
ного своими значениями) сигнала Si на фоне некоррелированной
помехи с нулевым средним и симметричным распределением имеет
вид
1 п
У1 = — Е sgn st sgn fj^t +	> ho,	(8.63)
где ho — порог принятия решения, равный (1/2) (ФйЧ/л+л):
а — заданная вероятность ошибки первого рода; Ф«’ — величина
обратная интегралу вероятности при фиксированном значении а.
Так, при а = 5 % ta = 0,52.
В качестве иллюстрации работы алгоритма (8.63) рассмотрим
следующий пример.
281
Пусть требуется обнаружить сигнал s (+ 1, + 5, — 5, — 1) в выборке
f =.— 1, 2, 3, — 5, 0, 5. Очевидно, что максимальная величина (8.63) будет
наблюдаться при значениях s, и равных — 5. Найдем при этом величину
выходного сигнала yj.
Сначала определим знаковые статистики: sgn f = (— 1, 1, 1, — 1, 1, 1)
и sgn s = (1, 1, — 1, —1). Отсюда у3 = (1 + 1 + 1—1) +2 = 3. Порог при-
нятия решения: Ло = (1/2) (0,52 -у^4 + 4) = 2,52. Поскольку профильтро-
ванное значение сигнала 3>А0, принимается решение о наличии сигнала.
Другой, более эффективный вариант знакового обнаружения
детерминированного сигнала имеет вид
У/ = £ si sgn fi-i > h0.	(8.64)
Для рассмотренного примера на основе (8.64) получаем yt —
= 1 + 5 + 5-1 = 10.
Значение yt существенно выше порога 2,52, рассчитанного при
заданной 5 %-ной вероятности ошибки первого рода.
Алгоритмы обнаружения сигналов, построенные на ранговых
статистиках, наиболее эффективны при обнаружении сигналов, не
содержащих постоянной составляющей. Хотя эти алгоритмы можно
использовать с целью обнаружения сигналов и с постоянной со-
ставляющей, их эффективность будет ниже эффективности знаково-
ранговых алгоритмов.
Приведем один из основных ранговых алгоритмов, получивший
название алгоритма Вилкоксона,
п
У1 = Е SiRf-i > h<!-	(8.65)
1=1
Порог й0 определяется из соотношения
ho = ta. (я&$пфп) 1 +	(8.66)
где ta. — квантиль нормального распределения при заданной ве-
роятности ошибки первого рода (при а — 5 %, ta = 0,52);
. л
<	2	1 V* 2
^sn — Щп--Osn> Wsrt—-------
n i=i
1 n
atn=—E st»
n i=i
фп и фп — соответственно среднее и дисперсия функции R] в (8.65).
Найдем, например, значение порога для алгоритма (8.65), когда сиг-
нал задан в виде s; = (+ 1, + 5, — 5, — 1). Тогда
Wsn = 52/4 = 13; ci3fi = 0; Ь3ц ~ 13;
ф« = (1 + 2 + 3 + 4)/4 = 2,5,
282
так как сигнал представлен четырьмя значениями и его ранговая статистика
включает ранги 1, 2, 3, 4:
ф2 = 2-1,52 + 2'0,52 == 5.
Таким образом, по (8.66) получаем й0 = 0,52 (4-13-5),/2= 8,3. Макси-
мальное значение выражения (8.65) при использовании исходного вектора
наблюдений (8.62) с учетом того, что
s/= 1, 5, — 5, — 1,	f/= — 1, 2, 3, —5, 0, 5,	/?< = 3, 4, 1, 2
будет
4
У1 = У	1-3 + 5-4 —5-1 —1-2= 16.
/г—1
Поскольку yi>h0, принимается решение о наличии сигнала.
3на к о в о-ранг о вый алгоритм обнаруже-
ния детерминированного сигнала имеет вид
(8.67)
Z {osl	Z i=l
Порог принятия решения
Ло = (fa +n2as„/V^).	(8.68)
Z
В качестве примера, иллюстрирующего выполнение операций в (8.67),
вновь рассмотрим обнаружение сигнала st = (1, 5, — 5, — 1) в исходной
выборке (8.62).	__
Согласно (8.68) порог для обнаружения такого сигнала ft0 = 2V13-
0,52д/4/3 = 5,0, а значение у/ в (8.67) будет
у/=_Ьц.3.1 + 5-41+(-5)Н-D+ (- 1)-2-1] +
Z
-4- —[1-3 + 5-4-5-1 -1-2] = 13 + 8 = 21.
2
Очевидно, что yt = 21>Л0 = 5,0.
Из рассмотренных примеров видно, что знаково-ранговый ал-
горитм наиболее эффективен по сравнению со знаковым и ранго-
вым алгоритмами. Следует отметить, что устойчивость ранговых
алгоритмов, настроенных на нормально распределенную помеху,
всегда больше устойчивости неранговых алгоритмов, настроенных
на ту же нормально распределенную помеху. Это свойство ранго-
вых алгоритмов имеет место при любом законе распределения
помех.
Алгоритмы (8.63) — (8.65) и (8.67) являются соответствующими
аналогами алгоритмов способа обратных вероятностей. Обработка
по наиболее эффективному из них — знаково-ранговому алгоритму
включает три основные процедуры: 1) задание окна, размер кото-
рого определяется длительностью детерминированного сигнала т
(в пределах этого окна находится ранг и знак каждого значения
исходного поля, а также рассчитывается величина (1/2)
283
постоянная для данного сигнала); 2) нахождение свертки вида у, =
= (1/2) X sgn/j_i; 3) сравнение статистики (8.67) с поро-
говым значением h0, определяемым по (8.66), и принятие решения
о наличии сигнала, если	и об отсутствии сигнала, если
yi<Zh0.
Для выделения неизвестных по форме сигналов в § 41 и 42 со-
ответственно были рассмотрены способы межпрофильной корреля-
ции и адаптивной фильтрации. На основе ранговых статистик не-
трудно получить их непараметрические аналоги.
Пусть= (fn, . . . , /1п) и/2 = (f21, . . . , fin) — наблюденные
значения по двум профилям съемки (это могут быть и наблюденные
значения на одном и том же профиле по двум методам) и пусть
/?=(/?!,..., Rn) и Q = (Qx, . . . , Qn) — ранговые векторы этих
наблюдений. Решение о наличии сигнала на обоих профилях сле-
дует принять, если
y=iRiQi>h0.	(8.69)
i=i
Статистика (8.69) — не что иное, как коэффициент ранговой
корреляции Спирмена (см. гл. II). Порог принятия решения для
(8.69)
/lo = (fa + 3Vn)nS2/12.
Если в выражении (8.69) учесть среднее значение рангов по
каждому профилю и его нормировку на дисперсию, получим ран-
говую взаимо корреляционную функцию BR0
[см. формулу (4.26)].	RQ
По экстремальным значениям (4.26) можно найти смещение
сигнала (от профиля к профилю), как это делается в способе меж-
профильной корреляции. Аналог процедуры суммирования для
межпрофильной корреляции найдем, если проранжируем значения
исходного поля по направлению суммирования. Ранжировке под-
вергаются значения поля с разных профилей, после чего для рангов
этих значений находится медиана /?* = (/V + 1)/2 и проводится
выбор значения поля, соответствующего
Следовательно, ранговый аналог межпрофильной корреляции
включает: 1) оценку простирания аномалий по экстремумам ран-
говой ВКФ; 2) ранжирование исходных данных по направлению
простирания аномалий (направлению суммирования); 3) выбор
центрального элемента ранжированного ряда значений. Значение,
соответствующее центральному элементу ранжированного ряда,
есть медиана, т. е. вместо среднего значения по N профилям съемки
здесь в качестве оцейки аномалии используется значение поля,
соответствующее медиане рангов.
Допустим, по семи профилям вдоль направления суммирования
значения поля расположились с 1 по 7 профиль следующим обра-
284
зом: 2, — 82, 3, 1,4, 123, 5. Располагаем этот ряд значений в воз-
растающем порядке с присвоением ранга:
fk= — 82, 1, 2, 3, 4, 5, 123,
Pft=l, 2, 3, 4, 5, 6, 7.
где k — индекс для профиля; Rk — (N + 1)/2 = (7 + 1)/2 = 4.
Результатом обработки будет значение поля, равное 3, соответст-
вующее Rk = 4.
Рис. 66. Выделение слабого сигнала путем нелинейного накопления.
1 — сигнал; 2 — сигнал + помеха; 3 — результат линейного накопления; 4 — резуль-
тат нелинейного накопления
Описанный прием целесообразно использовать, когда на фоне
сравнительно небольших по абсолютной величине значений поля
появляются резкие выбросы, явно искажающие результаты наблю-
дений. К таким искажениям относятся помехи импульсного типа
при каротаже. Ранговый вариант межпрофильной корреляции по-
зволяет провести подавление помех подобного типа. При обычном
же суммировании, в основе которого лежит предположение о нор-
мальном характере распределения помех, резкие выбросы оказы-
вали бы существенное влияние и были бы приняты за аномалии.
Пример, иллюстрирующий эффективность ранговой межпрофиль-
ной корреляции, иначе, нелинейного накопления, по сравнению
с линейным накоплением при искажении результатов наблюдений
помехой, распределение которой наряду с центральным имеет два
боковых экстремума, приведен на рис. 66.
Непа'раметрический аналог адаптивной фильтрации основан на
использовании статистики (критерия) Фридмана, в то время
как параметрическая адаптивная фильтрация строится на базе
статистики Хоттелинга.
При применении статистики Фридмана процедура обработки
сводится к ранжировке значений поля в каждой строке того же
285
окна, включающего N профилей и т пикетов по каждому профилю^
суммированию полученных рангов по каждому из столбцов и вы-
числению величины %’ в виде [см. формулу (3.13) ]
т z N
12 Ё *«)
%? = У , 1» -ЗЛГ(т + 1),
Nm (т +1)
N	т
где R( = У Rm — сумма рангов для t-ro пикета окна; У, Rj — ука-
k=i	i=i
зывает на необходимость суммирования квадратов полученных
сумм рангов по всем пикетам.
Рнс. 67. Выделение слабого сигнала с помощью непараметрической адаптив-
ной фильтрации (по С. М. Махмутову).
а — сигнал; б — сигнал 4- помеха по 11 профилям; в и г — значения, полученные соот-
ветственно с помощью параметрической и иепараметрнческой адаптивной фильтрации
Величина называемая статистикой Фридмана, имеет рас-
пределение Пирсона (хи-квадрат) при (т—1) степенях свободы,
когда сигнал в выбранном для анализа окне отсутствует. Это поз-
воляет найти величину порога при решении задач обнаружения
неизвестного по форме сигнала на фоне некоррелированных помех.
Пример применения статистики Фридмана рассмотрен в § 13.
Как и в параметрическом варианте адаптивной фильтрации,
окно, включающее mN точек, перемещается сначала вдоль профилей

со смещением, равным одному пикету, а затем вкрест их простира-
ния со смещением на один профиль. Это позволяет определить ме-
стоположение сигналов по площади съемки.
Пример, приведенный на рис. 67, свидетельствует о преиму-
ществе непараметрической адаптивной фильтрации по сравнению
с параметрической при обнаружении сигнала на фоне ненормально
распределенных помех.
В заключение подчеркнем, что при обработке геофизических
данных с целью выделения сигналов на фоне помех нельзя, как
правило, ограничиваться использованием лишь одного приема,
одного алгоритма обработки, особенно в сложно построенных в гео-
286
логическом отношении районах. Неизбежные изменения формы
наблюдаемых аномалий и свойств помех, в том числе характера
их распределений, приводят к