Введение в механику сплошных сред (в приложении к теории воли) - Бреховских Л.М., Гончаров В.В.

Автор: Бреховских Л.М. Гончаров В.В.
Теги: океанология рельеф морского дна дно океана физика атмосфера
Год: 1982
Похожие
Механика сплошных сред
Общий курс физики Т.1. Механика
Курс теоретической физики. Часть 1. Механика и электродинамика
Общий курс физики. Том I. Механика.
Текст
                    АКАДЕМИЯ НАУК СССР
Отделение океанологии,
физики атмосферы и географии
Л. М. Бреховских, В. В. Гончаров
ВВЕДЕНИЕ
В МЕХАНИКУ
сплошных
СРЕД
В ПРИЛОЖЕНИИ
К ТЕОРИИ ВОЛН
ИЗДАТЕЛЬСТВО «НАУКА»
Москва 1982

УДК 551.463: 551.51
Бреховских Л. М., Гончаров В. В. Введение в механику
сплошных сред (в приложении к теории волн). М.: Наука, 1982.
В книге излагаются основы механики сплошных сред, а также
некоторые прикладные вопросы, среди которых большое внимание
уделено изложению теории волн в жидкостях. При этом широко
используются навыки физического мышления, приобретенного
читателем в процессе изучения других физических предметов. В
результате авторам при небольшом объеме книги удается дать
основные представления о теории упругости, гидродинамике и
магнитогидродинамике. Без излишне сложной математики, но на
высоком научном уровне излагаются необходимые сведения об
основных уравнениях движения в упругих., жидких средах и в
проводящей жидкости. Изложены также теория упругих волн в
твердых телах, теория гидродинамических и звуковых волн в
жидкостях, простейшие понятия о турбулентности и т. д. Изложение
материала сопровождается многочисленными примерами и
задачами, для большинства из которых приведены решения.
Книга рассчитана на студентов, аспирантов и научных
работников физических и геофизических специальностей: физики океана»
атмосферы, твердой оболочки Земли, плазмы и др.
Ил. 99. Библиогр. 39 назв.
Ответственный редактор
доктор физико-математических наук
профессор Г. И. БАРЕНБЛАТТ
Б 1.[^"0,410 26-82, кн. 2 © Издательство «Наука», 1982 г.
055(02) -82

ПРЕДИСЛОВИЕ
В основу этой книги положен курс лекций, который
авторы в течение ряда лет читали студентам
Московского физико-технического института. Преподавание
механики сплошных сред физикам имеет славные
традиции как в нашей стране, так и за рубежом:
достаточно назвать курсы Фока, Зоммерфельда, Ландау и
Лифшица, на которых воспитывались поколения
физиков. Однако в настоящее время бурного развития
многих отраслей физики студенты обычно слушают
лишь небольшой курс механики сплошных сред. За это
время им нужно без сложной математики дать
представление об основных идеях и методах этого важного
раздела теоретической физики. Эту задачу можно
выполнить, только если наиболее полно использовать
знания и интуицию, уже полученные
студентами-физиками в других курсах. Все эти обстоятельства мы
постарались учесть в предлагаемой читателю книге, в
которой изложены наиболее важные, по нашему
представлению, аспекты механики сплошных сред, как
классические, так и активно развивающиеся в
настоящее время, такие, как теория турбулентности.
Обращаясь к механике сплошных )сред, физики и геофизики
обычно интересуются волновыми движениями.
Именно поэтому в нашей книге уделяется большое
внимание (как в изложении теории, так и в задачах)
вопросам распространения волн в сплошных средах:
сейсмических, гидродинамических, акустических, магни-
тогидродинамических.
Авторы не ставили своей целью строгое изложение
принципов механики сплошных сред и готовы принять
от механиков определеннее упреки в этом отношении.
Но эта книга и не рассчитана на механиков. При
изложении какого-либо раздела авторы стремились к
3

постепенному усложнению рассматриваемого круга
проблем. Именно с этой целью вначале излагается
теория упругости, которая в рамках нашей книги
представляется более простой по сравнению с задачами
гидродинамики. Более глубокому усвоению материала
должны способствовать и многочисленные примеры и
задачи с решениями, помещенные в конце каждой ела-
вы, которые следует рассматривать как неотрывную
часть курса. Для тех читателей, которые хотели бы
глубже изучить какой-либо конкретный вопрос, в
конце книги помещена основная литература по всем
затронутым здесь проблемам.
Авторы приносят глубокую благодарность Г И. Ба-
ренблатту, А. Г. Вороновичу, Г. С. Голицыну и
Л. А. Островскому за прочтение рукописи и ряд
ценных замечаний, а также И. Ф. Трещетенковой за
большую помощь при оформлении рукописи.
Л. М. БРЕХОВСКИХ, В. В. ГОНЧАРОВ

Часть первая
ТЕОРИЯ УПРУГОСТИ
Все'реальные тела под действием приложенных сил
деформируются, т. е. меняют свою форму и объем. Теория упругости
изучает поведение упругих твердых тел, деформации в которых
исчезают при снятии нагрузки. При этом нагрузка должна
сниматься постепенно, малыми порциями, как говорят, квазистатически,
В случае же резкого прекращения действия приложенных сил в
упругом теле могут возникать колебания.
Мы видим, что в теории упругости исключаются такие
явления, как пластические или остаточные деформации,
релаксационные процессы и т. п. Кроме того, мы будем рассматривать
только малые деформации, при которых изменение расстояния
между двумя близкими точками тела оказывается малым по
сравнению с расстоянием между ними в недеформированном
состоянии. При этом можно ограничиться лишь малыми членами
низшего порядка, что соответствует линейной теории упругости.
Деформации упругого тела могут вызываться и
сопровождаться изменениями температуры тела. Мы ограничимся
изучением лишь таких деформаций, которые происходят при
постоянной температуре или постоянной энтропии, т. е.
изотермических или адиабатических деформаций. Квазистатическое
деформирование упругих тел обычно является изотермическим — тело
успевает принимать температуру окружающей среды. Напротив,
при динамических процессах, например волновых движениях, в
упругих телах передачи тепла от одного участка тела к другому
практически не происходит. Следовательно, эти процессы
являются адиабатическими. Для изотермических и адиабатических
процессов основные механические законы деформирования тел
имеют одинаковый вид и отличаются лишь эмпирически
получаемыми значениями численных коэффициентов, называемых
упругими постоянными. В силу этого мы, как правило, не будем
оговаривать, какой процесс рассматривается в данном
конкретном случае.
о

Глава 1
ОСНОВНЫЕ ВИДЫ ДЕФОРМАЦИИ
УПРУГИХ ТЕЛ
В этой вводной главе на основе закона Гука и соотношения
Пуассона рассмотрены простейшие деформации упругих тел, такие,
как растяжение, сдвиг, кручение, изгиб.
§ 1. Законы линейной теории упругости
1.1. Закон Гука. Упругое поведение тел в конечном счете
определяется их атомно-молекулярной структурой, которая не
рассматривается механикой сплошных сред. Поэтому для
установления законов теории упругости следует, обратиться к
эксперименту. При этом утверждения, которые основываются на опыте
и не выводятся каким-либо логическим путем, следует отличать
от следствий, которые вытекают из них чисто логически.
Основные законы упругого поведения изотропных тел, т. е.
тел, свойства которых одинаковы по всем направлениям, могут
быть получены из следующих двух опытных фактов:
1) при достаточно малых силах F удлинение б/
цилиндрического бруска из упругого материала длиной / пропорционально
растягивающей силе F, приложенной к торцам бруска (рис. 1.1):
F~6/;
2) при растяжении брусок сжимается в поперечном напраз
лении, причем относительное сжатие оказывается
пропорциональным относительному продольному растяжению: 6А/Л~6///,
где h — характерный поперечный размер бруска.
Опытный факт 1 является законом Гука, выражающим
линейность соотношения между силой и деформацией. Установим,
как сила F связана с длиной бруска /. Скрепим два бруска,
каждый длиной /, торцами (рис. 1.2) и снова приложим к концам
сложного бруска силу F. Очевидно, что на каждый брусок в
отдельности будет действовать растягивающая сила F, которая
приведет к удлинению б/. Удлинение составного бруска будет
26/. Следовательно, при одной и той же силе удлинение в 2 раза
более длинного бруска больше в 2 раза, т. е. удлинение
пропорционально длине бруска: bl~Fl.
Определим теперь, как зависит сила F от площади
поперечного сечения бруска S. Для этого сложим два одинаковых бруска
вместе боковыми гранями и приложим к торцу каждого из них
силу F. Мы получим по-прежнему удлинение б/, как будто брусок
был один, но в целом мы видим, что к двум брускам была
приложена сила 2F. Следовательно, при удвоении площади
поперечного сечения то же самое удлинение, что и раньше, получается
при удвоенной силе, т. е. при том же удлинении сила
пропорциональна площади поперечного сечения.
6

поэтому закон I ука можно записать в виде
FIS-E61/1, (1.1)
где Е — коэффициент пропорциональности, называемый модулем
Юнга (постоянная материала). Силу, приходящуюся на
единицу площади, g=F/S называют напряжением, а относительное
удлинение е = 6///— деформацией. Таким образом, согласно
закону Гука напряжение равно произведению модуля Юнга на
деформацию.
В соответствии с опытным фактом 2 можно ввести еще одну
постоянную материала v, называемую коэффициентом Пуассона
и связывающую деформации в продольном и поперечном
направлениях:
6h/h = —vW, (1.2)
или если 61/1 выразить через F с помощью (1.1), то
** = —!£.. (1.3)
h Е S v '
Знак минус в (1.2) введен потому, что согласно опыту для
подавляющего большинства тел при положительном 6/ имеем
отрицательное 6Л.
Закон Гука (1.1) и соотношение (1.2), являющиеся
опытными фактами, составляют основу линейной механики изотропных
Упругих деформируемых сред. Ее законы вытекают из этих
фактов так же, как из законов Ньютона вытекает классическая ме-

ханика, из уравнений Максвелла — электродинамика, и так же,
как из нескольких начал вытекает термодинамика.
1.2. Дифференциальная форма закона Гука. Принцип
суперпозиции. Для решения практических задач часто бывает
полезным записывать закон Гука (1.1) в дифференциальной форме.
Для этого введем величину смещения и{х) точек бруска вдоль
продольной оси (ось х на рис. 1.3) и вычислим изменение длины
бесконечно малого элемента бруска, длина которого до
деформации Ах=хг—хи после деформации она будет х2+и(х2)—
— [xi + u(xi)]=kx-\—- Ах. Таким образом, для произвольного
dxLx
х изменение длины 6(Дх) = —-А*. Деформация элемента Ах рав-
дх
на г = 6(Ах)/кхжди/дх. Подставляя это выражение в (1.1),
вместо 61/1 получаем закон Гука в дифференциальной форме
c=F/S=Edu/dx. (1.4)
Говорят, что тело однородно деформировано, когда
деформация г=ди/дх постоянна по всему телу. Дифференциальная
форма закона Гука важна при расчете неоднородных деформаций,
в частности, соотношение (1.4) позволяет простым
интегрированием определить смещения точек бруска.
Важным следствием линейности соотношений (1.1) и (1.2)
является принцип суперпозиции, который состоит в следующем.
Если при некоторой силе F имеется некая деформация е и если
представить F как сумму F=F1 + F2+ +Fn, т. е. суперпозицию
п сил, то и деформацию е можно представить как сумму п
деформаций: e = et + e2+ ... +еп, причем каждая г{ может быть
получена из F< с помощью соотношений (1.1) и (1.2) так, как будто
бы остальных сил не существует. Мы используем принцип
суперпозиции для рассмотрения конкретных, сначала простых,
примеров однородной деформации тел.
§2. Однородные деформации
2.1. Тело под действием гидростатического давления. Возьмем
снова тело в виде бруска и поместим его в резервуар с
жидкостью, находящейся под давлением р (рис. 1.4). Сила,
действующая на поверхность тела, всюду нормальна к поверхности, и
напряжение, равное давлению (силе, отнесенной к единице
площади), также одинаково во всех точках. Пользуясь принципом
суперпозиции, задачу разобьем на три отдельные задачи:
1. Продольное сжатие б/А под действием сил, приложенных
к торцам. Согласно (1.1) имеем для него 6/t//=—р/Е.
2. Удлинение б/2 в продольном направлении от сил,
приложенных к горизонтальным боковым граням. Согласно (1.3)
имеем 6lJl=vp/E.
3. Аналогичное удлинение в результате действия сил,
приложенных к вертикальным боковым граням (параллельным
плоскости рисунка): 6Ul=vp/E.
8

Суммарная продольная деформация будет
' Ы/1 = ЫХЦ + 612/1 + Ы3/1 = -4(1- 2v).
Е
В силу симметрии задачи, очевидно, мы можем аналогичные
выражения получить для поперечной деформации в плоскости
рисунка: 6й/й = — р(1— 2v)/£, и то же самое для поперечной
деформации в направлении, перпендикулярном чертежу 6w/w.
Рассчитаем относительное изменение объема тела. До
деформации брусок имел объем V = lhw. В результате деформации он
изменился на величину 6V, которая может быть найдена с точ~
ностью до линейных по деформациям членов как
Отсюда 6V/V- — Зр(1—2v)/£, что можно записать и так:
p=-KbV/Vt /t=£/[3(l-2v)]. (1.6)
Величину К называют модулем объемного (всестороннего)
сжатия. Из выражения (1.5) следует, что всегда у<с7г» так как в
противном случае модуль /С<0, т. е. при повышении внешнего
давления тело расширялось бы.
2.2. Продольная деформация при запрещенных боковых
смещениях. Рассмотрим следующий пример однородной
деформации (рис. 1.5). Пусть брусок растягивается или сжимается в
направлении х силой Fx. Предположим, что смещения в
направлении у запрещены. При сжатии это легко можно осуществить,
поместив брусок вплотную между двумя неподвижными
стенками, перпендикулярными плоскости рисунка. Предполагается, что
грани бруска могут свободно скользить по стенкам. Боковые
стенки бруска, перпендикулярные оси г, предполагаются
свободными.
В данном случае на грани бруска, нормальные к оси у, со
стороны неподвижных стенок будет действовать сила FV9
которая вносит дополнительный вклад в смещение 6/х. Последний
может быть найден с помощью формулы, аналогичной (1.3)-
В результате для продольного смещения получаем
lx Е $х Е S/
где 5Х и Sy— площади граней бруска, нормальных
соответствующим осям х и у; Fy— неизвестная пока сила реакции стенки.
Последнюю легко найти, если написать аналогичное выражение для
Деформации в направлении оси у:
1У Е Sy Е Sx '
9

которая по условию задачи равна нулю. Следовательно, Fv/Sv=
=vFJSx. Подставляя это напряжение в выражение для 6ljlxy
находим
Последняя формула может быть записана также в виде:
Fx/Sx=E9^lx/lxy £эф = Е/ (1 -v2), (1.6)
что вполне аналогично закону Гука (1.1) для свободного
стержня, но только вместо Е фигурирует эффективный модуль Юнга
£эф. В дальнейшем будет видно, что через Е выражается
скорость продольных волн в тонких стержнях, а через
Е9ф—скорость продольных волн в тонких пластинах.
2.3. Деформация чистого сдвига. Рассмотрим новый важный
вид однородной деформации. Предположим, что на рис. 1.6, а
изображено сечение квадратного бруска, к боковым граням
которого, как это показано на рисунке, приложены касательные
силы G. Предположим, что силы распределены по граням
равномерно по всей их площади. Для этого можно применять,
например, жесткие накладки типа изображенной на рис. 1.6, б для
грани ВС. Очевидно, мы будем иметь двумерную задачу.
Рассмотрим единицу длины бруска, ограниченную с одной стороны
сечением ABCD. Результирующие силы и моменты сил,
действующие на брусок, равны нулю, следовательно, последний
находится в равновесии.
Деформации и касательные напряжения, возникающие при
такого рода силах, называются сдвиговыми. Покажем, что сдвиг
осуществляется при известных нам растяжениях и сжатиях
прямоугольных брусков. В самом деле, рассмотрим брусок
квадратного сечения PQRT, содержащий как составную часть брусок
ABCD и находящийся под действием сил растяжения и сжатия,
приложенных к его граням, как это показано на рис. 1.7, а. Если
теперь обратиться к условиям равновесия, например, отдельно
части AQB, то нетрудно видеть, что на грань АВ со стороны
квадрата ABCD должна действовать касательная сила — G
('рис. 1.7, б). Следовательно, на грань А В квадрата ABCD по
третьему закону Ньютона действует касательная сила G.
Аналогично и для остальных граней бруска ABCD.
Пользуясь соотношениями (1.1) и (1.3), не составляет труда
рассчитать растяжение и сжатие граней бруска PQRT, т. е.
деформации диагоналей АС и BD бруска ABCD. Если D —
невозмущенная длина диагонали, то для ее растяжения (или сжатия)
6D имеем
6D/D = G/ES+vG/ES=(l+v)G/ESy (1.7)
где учтено, что площадь грани PQ равна y2S (S — площадь
грани АВ)..
10

Деформацию сдвига обычно характеризуют изменением углов
между гранями бруска, которое непосредственно связано с
деформацией диагоналей. Проще рассмотреть этот вопрос на
несколько другой модели. На практике простейшую деформацию
чистого сдвига обычно осуществляют так, как это изображено
на рис. 1.8. Грань DC предполагается жестко закрепленной.
Сила G, осуществляющая сдвиг, касательна к грани АВ и
равномерно распределена на ней. В результате деформации точки А
и В переходят соответственно в А' и В' Диагональ АС сокраща-
11

ется, диагональ BD растягивается. Нетрудно видеть, что
деформации на рис. 1.8 те же, что получаются при приложении сил,
как на рис. 1.6. Следовательно, система сил здесь та же самая.
Силы на гранях AD, DC и СВ, показанные на рис. 1.8
стрелками, возникают вследствие реакции опоры.
Свяжем угол Э с силой G. Очевидно, что Q&AA'/AD =
=J2AEJAD9 но AEttbD, AD=D/y2, следовательно,
9«26Z)/D»2(l+v)G/£S. (1.8)
Если ввести новые обозначения: g = G/S — напряжение сдвига,
H=£/[2(l+v)] (1.9)
— модуль сдвига, то легко получаем соотношение
g=ne. (l.io)
Очевидно, должно быть jx>0, иначе сдвиг происходил бы в
направлении, обратном приложенным силам. Следовательно,
согласно (1.9) v>—1. Учитывая также ограничение на v (см.
п. 2.1), получаем окончательно интервал, в котором должны
быть заключены значения v: —l<v<72.
Случай v<0 (растяжение бруска в поперечном направлении
при растяжении его в продольном) для реальных материалов,
как правило, не встречается, так что фактически имеют место
неравенства
0<v<V2. (1.11)
§ 3. Неоднородные деформации
3.1. Кручение стержня. Рассмотрим теперь важный случай
неоднородной деформации. Предположим, что левый торец
стержня кругового сечения и конечной длины L закреплен (например,
приклеен к стенке), а к правому приложен крутящий момент М
(рис. 1.9). В результате произойдет закручивание стержня.
Точки на его поверхности, первоначально лежащие на линии АВ,
окажутся теперь на АВ', а радиус О В на правом торце перейдет
в радиус ОВ', повернувшись и а угол ф. Если радиус стержня а,
то длина дуги ВВ' раяна acp, а угол между линиями АВ и АВ'
будет От=аф/1. Деформации предполагаются настолько
малыми, что все конечные приращения можно заменить
дифференциалами.
Определим величину крутящего момента, необходимого для
закручивания стержня на угол ф. Для этого выделим из стержня
малые элементы, внутри которых деформацию можно считать
однородной, и воспользуемся выведенными выше формулами.
Вначале выделим мысленно из стержня цилиндрический слой
(трубку) длиной AL, заключенный между цилиндрическими
поверхностями радиусов г и г+Д|Г (естественно, г<а). Этот
цилиндрический слой в увеличенном масштабе изображен на
рис. 1.10, а. Выделим далее из него малый элемент CDEF
объемом ALA/Дг. При закручивании стержня этот элемент сместится
12

в направлении от Я к С и, кроме того, перекосится, поскольку
смещение точки Е будет несколько меньше смещения точки F.
Смещение элемента как целого, не влияющее на напряженное
достояние тела, нас интересовать не будет, а перекос
представлен на рис. 1.10, б, где изображен вид выделенного элемента
сбоку (с направления, нормального к площадке CDEF). Как
нетрудно видеть, угол перекоса d = r<p/L (ср. с выражением для Фш).
В выделенном малом элементе мы имеем уже известную
деформацию чистого сдвига. Согласно выражению (1.10) этой
деформации соответствует сдвиговое напряжение £=|хФ=|лгф/1,,
вызванное силами AG (рис. 1.10, б). Так как площадь приложения
силы AG равна Д/Дг, то, следовательно, AG=gA/Ar. Сила AG
создает относительно оси стержня момент AM = AGr=grA/Ar.
Теперь, если учесть все элементы, составляющие отрезок трубы
(рис. 1.10, а), то в последней формуле нужно заменить А/ на
2яг. Поэтому момент, действующий на отрезок трубы, будет
Л1Лг = 2яг2^Дг, или, подставив значение g, получаем:
Млг=/лгФ, hr = 2n\ir*br/L. (1.12)
Последняя формула дает связь между крутящим моментом Л4Дг
и углом закручивания ф для тонкостенной цилиндрической
трубы радиусом г, толщиной Дг«;/* и длиной L. Величина / дг
называется крутильной жесткостью стержня.
Если стенка трубки имеет конечную толщину, то выражение
для крутящего момента найдется интегрированием формулы
(1.12) nor:
Mw = /^Ф, fr%~rx '= ^{r}-r[\ (1.13)
где г4 и г2— соответственно внутренний и наружный радиусы
трубы. В случае сплошного цилиндрического стержня в выражении
(1.13) следует положить г2=ау Ti = 0, в результате получим:
Af=fcp, f=niiak/2L. (1.14)
Мы видим, что при заданных ф и L крутящий момент
пропорционален четвертой степени радиуса.
3.2. Изгиб балки. Балкой называется тело, длина которого
много больше его поперечных размеров. Для простоты возьмем
случай, когда сечение балки не изменяется вдоль ее длины.
Прежде всего рассмотрим деформацию балки под действием
поперечных сил. Свяжем кривизну балки в данном ее
поперечном сечении с моментом внешних сил, который действует на это
сечение. Выделим небольшой элемент балки (длиной 1)у
имеющий в результате изгиба радиус кривизны /?, который
предполагается большим по сравнению с поперечными размерами балки.
Продольный разрез этого элемента, проходящий через ось
балки,'изображен на рис. 1.11. Не вдаваясь в подробности, будем
предполагать, как это в свое время сделал Д. Бернулли, что
плоские сечения балки после изгиба также остаются плоскими. Эле-
13

мент балки ABCD в результате изгиба деформируется так, что
первоначально прямая линия АВ растягивается, прямая CD
сжимается, а «нейтральная» линия EF сохраняет свою длину.
Проходящее через нейтральную линию сечение балки,
перпендикулярное плоскости рисунка, называется нейтральным сечением.
Элемент балки ABCD в результате изгиба превращается в
A'B'C'D\ а нейтральная плоскость — в нейтральную поверхность.
Чем дальше некоторый слой материала балки удален от
нейтрального сечения, тем больше его деформация.
Рассмотрим слой, удаленный от него на расстояние у. Его
длина после изгиба равна %(R+y). Учитывая, что
первоначальная его длина, совпадающая с длиной нейтральной линии на
рис. 1.11, была /=х#> имеем для удлинения Ы=ху. Но так как
X=l/R, то 6l=yl/R. Согласно закону Гука (1.1) напряжение,
действующее в этом слое, будет AF/AS = E6l/l = Ey/R, где AF— сила,
действующая на элемент AS площади поперечного сечения.
Чтобы получить момент сил, действующий на все поперечное
сечение, необходимо произведение AFy = Ey2AS/R проинтегрировать
по всему поперечному сечению: М = J ydF. В результате по-
лучаем:
M = EI/R, / = j^d5, (1.15)
s
где /— момент инерции поперечного сечения балки относительно
поперечной оси, лежащей в нейтральном сечении. Последняя,
как легко видеть, при чистом изгибе (исключаются растяжения
и сжатия, одинаковые для всех волокон балки) проходит также
через центр тяжести поперечного сечения. В самом деле, при
чистом изгибе суммарная сила растяжения, действующая на все
сечение, равна нулю. Следовательно, \ dF = (E/R) J ydS = О,
5 s
что выполняется, если прямая у = 0 проходит через центр
тяжести поперечного сечения.
Уравнение (1.15), связывающее радиус кривизны изгиба с
моментом сил, является основным в теории изгиба балки. В
частности, из него следует, что балка тем жестче, чем больше момент
инерции /, т. е. чем больше материала балки удалено от
нейтральной поверхности, как, например, в случае двутавровой
балки.
3.3. Форма нагруженной балки. Перерезывающая сила. Для
решения практических задач необходимо выразить радиус
кривизны R, входящий в (1.15), через уравнение нейтральной линии
изогнутой балки. Если направить ось х вдоль нейтральной линии
недеформированной балки, а ось z— перпендикулярно к ней в
плоскости изгиба, то уравнение нейтральной линии можно
записать так: z=z(x). Для кривизны балки по известной формуле
14

имеем
R d*a[ \dx) J dx* y '
(мы предполагаем деформации достаточно малыми, чтобы
можно было пренебречь (£)г по сравнению с единицей).
Применим формулы (1.15) и (1.16) для определения формы,
которую принимает консольная (жестко закрепленная в стенке)
балка в случае нагрузки на конце (рис. 1.12). Если рассмотреть
некоторое сечение балки на расстоянии х от ее начала, то
согласно (1.15) и (1.16) действующий в этом сечении момент сил,
обусловленный напряжениями, равен M=EIz". Он
уравновешивается моментом, который создается силой F: F(L—х).
Результирующий момент, действующий на часть балки АВ, равен нулю,
поскольку эта часть балки находится в равновесии:
EIz"+F(L—x)=0. (1.17)
Интегрируя это уравнение 2 раза, получаем
s^—^/l — JL^ + dx + C,.
2Е1 \ 3 ] Х 2
Постоянные интегрирования С{ и С2 определяются из граничных
условий z|x=0 = 0, г/|я=0 = 0 и оказываются равными нулю. Таким
образом,
z = — — (L— -) (1.18)
Прогиб на конце балки (стрела прогиба) Zmax пропорционален
кубу длины балки:
Zn^FDftEL (1.19)
Если изгибающий момент меняется вдоль балки, как,
например, в рассмотренной выше задаче, то в каждом сечении балки
возникает так называемая перерезывающая сила Fny
направленная перпендикулярно нейтральной поверхности балки. Легко
получить выражение для этой силы через момент М(х), если
рассмотреть равновесие малого элемента балки Д*. Из уравнения
равновесия моментов для этого элемента М(х+Ах)—М(х) +
+FnAx& —Ax+FnAx = 0 следует, что
дх
Fn(x)=—dM/dx. (1.20)
Физическая причина возникновения перерезывающей силы
связана с появлением при изгибе в каждом сечении балки
касательных напряжений, суммой которых и является эта сила.
Наличие касательных напряжений говорит также о возникновении
сдвиговых деформаций при изгибе, что влечет за собой
искривление первоначально плоского сечения балки.
15

Таким образом, использованная нами при выводе основного
уравнения (1.15) гипотеза Бернулли о том, что сечения
остаются плоскими, строго говоря, не выполняется. С другой стороны,
как показывает опыт, все результаты, полученные на основе
уравнения (1.15), хорошо подтверждаются на практике,
например приведенный нами расчет формы консольной балки (1.18).
Объяснение кажущегося противоречия заключается в том, что
при выводе основной формулы нет необходимости предполагать,
что плоские сечения остаются плоскими. Достаточно лишь
принять гипотезу о пропорциональности продольных напряжений
расстоянию от деформированного слоя до нейтральной
поверхности балки. Уточненный расчет на основе общих уравнений
теории упругости подтверждает эту гипотезу и вместе с ней
формулу (1.15).
Задачи
1.1. Стержень длиной /, находящийся в поле силы тяжести, подвешен за
один конец (рис. 1.13). Поперечное сечение стержня 5, модуль Юнга и
плотность материала Е и р соответственно. Найти распределение напряжений в
стержне и его полное удлинение.
Решение. Рассмотрим сечение стержня на расстоянии х от точки
подвеса (рис. 1.13). В этом сечении на участок Ох действует сила, равная весу
нижней части стержня: F=gpS(l—х). Следовательно, напряжение в точке х
будет F/S=gp(l—х). Воспользовавшись дифференциальной формой закона
Гука (1.4), запишем
*f = -LZ_ = *p(/_.v).
dx Е S £v '
Интегрируя это уравнение с учетом граничного условия и|Жв0=0, получаем
u(x)=gpx(l—х/2)/Е. Полное удлинение стержня u(l)=gpl2l2E.
1.2. На верхний торец стоящей вертикально на жесткой опоре колонны
действует сила F0 (рис. 1.14). Как должна меняться площадь поперечного
сечения колонны S(x), чтобы напряжения во всех точках были одинаковыми?
Найти при этом общее уменьшение длины колонны.
Решение. Пусть Sm — площадь верхнего торца колонны, Е и р —
соответственно модуль Юнга и плотность материала. В некотором сечении х
площади S(x) возникает напряжение
S(x)^S(x)J у> Sm'
X
постоянное по условию задачи. Отсюда после умножения на S(x) и
дифференцирования получаем уравнение S'(x)= — (pgSm/F0)S(x), которое легко
интегрируется:
S(*:=Smexp[-^-(/-*)]
Поскольку при таком изменении площади деформация будет однородной, то
изменение длины колонны будет 6l=Fol/ESm.
16

1.3. Показать, что эффективный модуль Юнга при продольной деформации
бруска прямоугольного сечения при запрещенных смещениях в обоих
поперечных направлениях равен £8ф=£(1— v)/[(l+v) (1—2v)].
Указание. По аналогии с выводом формулы (1.6) записать для
деформаций по каждой из осей выражения:
I..
__ J_
"~~ Е
= 0 =
v
V
т
Е
v
Т
Fr
3_ = Q==_L]j_____
1г Е S, Е Sx
г
V
Е
v
~~Ё
откуда н следует искомая формуле.
Рис. 1.13
N
£-
&
Рис. 1.15
1.4. Для передачи момента М0 используется полый вал с отношением
внутреннего радиуса к внешнему, равным а. Предполагая, что максимально
допустимое напряжение для материала вала есть gmax, определить минимально
возможный внешний радиус вала R и соответствующую ему массу единицы
длины вала.
Решение. При кручении вала возникают сдвиговые деформации,
причем gmax = |A0max = H^fcp/£, гАе ^ "" модуль сдвига; L — длин а вала; <р — угол
закручивания. Последний можно найти на основе формулы (1.13):
2LM0 2MqL 1
Ф
nfi (Я* — г4) nycR* 1 - а4
Требуемый внешний радиус вала определится из условия £max = M-#<p/L=
= 2М0/[я#3(1— а4)], что дает Л3=2М0/[я^тах(1--а4)]. Масса единицы длины
цилиндрического вала будет
т = ря#а (1 — а*) = ря *- -~т, ТТГ =
Utf™/ (1-а»)*'ч1 + а*}1/в
:ря
„ ^_2Л^_у/.(1_а»)У.
d+a2)'7'
f ZMo\
\ 8тах I
17

Отсюда также следует, что изготовление полого вала оказыается
предпочтительным по сравнению со сплошным (а~0) с точки зрения экономии
материала.
1.5. Концы балки с погонным весом р покоятся на двух опорах,
расстояние между которыми L. Найти форму балки.
Решение. Сила реакции на каждой опоре N=Lp/2 (рис. 1.15).
Изгибающий момент в сечении х слагается из момента собственного веса части
балки рх2/2 и момента силы реакции опоры — pLx/2. В результате с учетом
(1.15) и (1.16) получаем уравнение
*=—шх(х-1)'
решение которого, удовлетворяющее граничным условиям z|x=o,l = 0, будет
z=-£kiiL'-2Lxi+x3)-
При этом стрела прогиба z(L/2)=—(5/384) pL4/EI.
1.6. В условиях задачи 1.5 считать балку невесомой, но к ее середине
приложить силу F.
Решение. Силы реакции — F/2. Уравнение для моментов при 0^*^[L/2
45удет £/z" = F*/2. Решением этого уравнения, удовлетворяющим граничным
условиям 2(0)= 0 и z/(L/2)=0 (последнее в силу симметрии задачи
относительно точки x=L/2), является
z (х) = Fx (4*2—3L2) / (48£/).
Стрела прогиба в этом случае равна z(L/2) =—FL3/(48£Y).
1.7. Тонкий стержень длиной L подвергается сжатию с торцов силой F
(рис. 1.16). Показать, что при достаточно малых F<.Fi стержень не будет
иметь деформаций изгиба (устойчивость). Рассчитать критическую силу Fu
называемую силой Эйлера.
Решение. При изгибе стержня в его произвольном сечении х возникает
момент М(х) =Fz(x) (рис. 1.16). В соответствии с (1.15) и (1.16) имеем
уравнение равновесия z"+a2z=0, a2=F/EIt общим решением которогв является
функция z=Asinax+Bcosax. Но при х=0 и x = L должно быть z=0,
откуда для возможных видов равновесия стержня получаем £=0, А —
произвольно и аЛ£=ля (л=1, 2,...). Для каждого п имеем силу Fn =
= п2п2ЕЦЬ2. Наименьшая из них, соответствующая л=1, будет Fi=n2EI/L2.
Если внешняя сила F<FU то стержень будет оставаться прямолинейным. При
F=FX равновесие оказывается возможным при любом большом прогибе.
Однако при немалых прогибах линейная теория, получающаяся при
пренебрежении (z')2 по сравнению с единицей в (1.16), становится неверной. Расчет на
основе точного выражения для кривизны (1.16) приводит к однозначной связи
между силой F>FX и формой, которую принимает стержень.
1.8. Определить энергию, запасенную в стержне длиной / при его сжатии
силой fo-
Решение. Искомая энергия равна работе, совершаемой силой при
переходе от свободного состояния к напряженному. Чтобы исключить из
рассмотрения кинетическую энергию частиц стержня, расчет работы следует
проводить при квазнстатической деформации. Для этого нужно предположить,
18

что все время выполняется закон Гука (1.1): /7/5=£м//, где через и здесь мы
обозначаем смещение торца стержня, к которому приложена сила. В этом
случае приращение работы dA = Fdu=(ES/l)udu, откуда после
интегрирования в пределах от 0 до и получаем
A=ESu*/2l=F0ul2.
Плотность энергии (на единицу объема) при этом равна половине
произведения напряжения на деформацию: &=A/SI=FquI2SL
1.9. Найти кинетическую энергию частиц стержня при резком его
сжатии продольной силой F0.
Решение. Предполагая, что сила остается постоянной в процессе
деформации, имеем для работы A — F0u. Последняя переходит как в упругую
Рис. 1.16 Рис. 1.17
энергию, полученную в предыдущей задаче: &=Fou/2f так и в кинетическую Г:
А = &+Т. Отсюда T=& = F0u/2.
1.10. Определить, изменение радиуса R вращающегося вокруг своей оси
тонкостенного кругового цилиндра.
Решение. Для элемента цилиндра Д/=/?Д<р имеем
центростремительную силу ^цс=р5/?Аф(о2/?, где р —плотность материала; S —площадь
сечения цилиндра плоскостью, содержащей его образующую н ось вращения
(рис. 1.17). Эта сила является равнодействующей сил, растягивающих данный
элемент: Fnc=2Fsin(A(p/2) «FAtp, откуда имеем для напряжений F/S—
= р/?2о)2. Теперь по закону Гука
6(2я#) 6# 1 F рсо2/?2 сл р#3соа
1.11. Определить относительное смещение точек стержня, движущегося
в направлении своей длины с постоянным ускорением а.
Решение. Пусть р — плотность стержня, Е — модуль Юнга, / — длина
стержня и S — площадь его поперечного сечения. В произвольном сечении х
действует сила F(x)=pSxa, вызывающая движение стержня с ускорением а.
Эта сила обусловлена действием внутренних напряжений F(jc)/S=pjta=£dw/d*.
Интегрируя последнее уравнение при условии м(0)=0, находим и=рах2/2Е,
1.12. Найти смещение точек стержня, вращающегося вокруг одного из
торцов с частотой о.
19

Решение. Центростремительная сила участка стержня х>*<ь равная
F^ = Г Sptfxdx = Spa* (Р - ха)/2,
обеспечена действием внутренних напряжений в сечении х: F4C=^SEduldx.
Интегрируя получившееся уравнение, находим
и(х)=р(д*х{Р—хЩ)/2Е.
Глава 2
ВОЛНЫ В СТЕРЖНЯХ,
ВИБРАЦИИ СТЕРЖНЕЙ
В предыдущей главе мы рассмотрели простейшие виды
деформаций, не зависящих от времени. Если же (как это часто и
бывает) внешние воздействия на упругое тело изменяются во
времени, то возникает волновое движение, в результате которого
возмущение (деформация) передается от одних участков тела к
другим с конечной скоростью.
Мы рассмотрим простейшие типы волн в стержнях, получим
уравнения, описывающие распространение этих волн вдоль
•стержня, а также введем ряд важных понятий, свойственных
волновым движениям любой природы.
-§ 4. Продольные волны в стержне
4.1. Волновое уравнение. Ударим в продольном направлении по
торцу длинного стержня. Вдоль стержня побежит возмущение —
продольная волна. Выведем уравнение, описывающее
распространение этой волны. Направим координату х вдоль стержня.
Смещение сечения стержня, которое в состоянии покоя
характеризовалось координатой х, обозначим через и(х, /), так что при
продольной деформации указанное сечение займет положение
х+и(х, t), где / — время. Если рассмотреть малый участок
стержня Ах между сечениями х и х+Ах, то, воспользовавшись
дифференциальной формой закона Гука (1.4), легко определить
силу F(x), действующую в сечении х:
F/S=Edu/dx, (2.1)
где, как и выше, S — площадь поперечного сечения стержня; Е —
модуль Юнга. Аналогичное выражение можно написать и для
силы, действующей в сечении х+Ах. Разность этих сил
F(x+Ax)—F(x) « (dF/dx)Ax создает ускорение элемента
стержня, заключенного между сечениями х и х + Ах. Так как масса
этого элемента равна pSAx (р — плотность материала стержня),
20

а ускорение d2ufdt2t то по второму закону Ньютона имеем
Сократив здесь на Да: и подставив значение F из (2.1), получаем
искомое волновое уравнение для продольных волн в стержне:
d2u/dt2 = c2d2u/dx2t с=1Щ (2.2)
Подстановкой нетрудно убедиться, что его решением будет
и{х, t) =f(x-ct) +g(x + ct)y (2.3)
где / и g — произвольные функции. Первый член в (2.3)
представляет собой волну, распространяющуюся в направлении
положительных х со скоростью с без изменения формы, второй —
волну, распространяющуюся с той же скоростью в обратном
направлении.
4.2. Гармонические волны. В случае гармонических волн»
когда f и g — синусоидальные функции с круговой частотой со,
имеем
и(х, t)=acos(kx—(ut+tyj+bcosikx+at+fy). (2.4)
Здесь а и Ъ — постоянные, называемые амплитудами волн; \pi
и \J)2—также постоянные начальные фазы волн; >k = со/с —
волновое число. Последнее можно также записать в виде 6=2лД, где
Ь=2яс/(й = Тс — длина волны; Т — ее период. Как и в (2.3),
первый член (2.4) описывает волну, распространяющуюся в сторону
положительных #, второй — в обратном направлении.
Для удобства промежуточных выкладок оказывается
полезным записывать волны вместо (2.4) в комплексной форме
и(х, t) =Л exp[i(kx—со*) ] +В ехр[—i{kx+tot) ], (2.5)
где Л = аехр(п|э1); В = Ьехр(^2) —постоянные, называемые
комплексными амплитудами волн. Физический смысл имеет только
вещественная часть выражения (2.5), совпадающая с (2.4). Если
мы совершаем линейные операции над комплексными волнами:
сложение волн, дифференцирование по времени или
координатам и т. п., то ясно, что вещественная часть окончательного
результата будет равна результату тех же операций только над
вещественной частью исходных волн. Если же операции
нелинейны, например определение энергии волн — квадратичной по и
величины, то с самого начала нужно перейти к вещественной
форме.
§ 5. Отражение продольных волн
5.1. Граничные условия. В стержне бесконечной ддины волна
будет распространяться в одном и том же направлении сколь
угодно долго. Однако в действительности стержень всегда имеет
конечную длину, и волна отражается от его конца. Если стержень
21

граничит с другими, то в последнем появляется уходящая от
границы прошедшая волна. Процессы отражения и прохождения
волн зависят от свойств границы — граничных условий.
Рассмотрим некоторые граничные условия, предполагая, что граница
расположена при х=х0.
1. Абсолютно жесткая граница, смещение частиц которой за^
прещено. Математически это условие записывается в виде
и|«*=0. (2.6)
Практически этот случай реализуется, если торец стержня
приклеен к массивной стенке из материала с очень большим
модулем Юнга.
2. Абсолютно мягкая (свободная) граница, например
стержень в достаточно разреженной среде или вакууме. На границе
такого типа исчезают силы (напряжения)
S дх
= 0 или &
|*=ж. дх
= 0. (2.7)
|**=дгв
Хорошим приближением абсолютно мягкой границы служит
граница с воздухом.
3. Неразъемный контакт двух стержней одинакового сечения
с различными материальными постоянными: р1э Ei и р2, Е2.
Очевидно, что в этом случае слева и справа от границы одинаковы
смещения и силы (напряжения):
(их — ы2)д^ = 0, {EJuJdx — Е2ди2/дх)х=х% = 0. (2.8)
5.2. Законы отражения волн. Мы ограничимся наиболее
простым случаем гармонических волн, поскольку на его основе не
составляет труда получить законы отражения для импульса
произвольной формы. Предположим, что волна f(x—at) может быть
представлена в виде интеграла Фурье по гармоническим волнам:
оо
f(x — ct)= Г Л (со) exp [i (kx — со/)] dco, k = со/с.
Используя далее законы отражения для гармонических волн и
принцип суперпозиции, справедливый в силу линейности уравне-*
ния и граничных условий, легко найти закон отражения для
волны f(x—ct).
Таким образом, пусть по стержню, занимающему область
оо<*<;0, распространяется продольная гармоническая волна
и+=А exp[i(kx—со*)] в направлении его конца х — 0 (падающая
волна). Рассмотрим случай абсолютно жесткой границы.
Нетрудно видеть, что одна падающая волна и+ не может
удовлетворить граничному условию (2.6). Следовательно, должна
возникнуть распространяющаяся в обратном направлении волна
частоты ©': и_=ЛУехр[—i(k'x+to't)], k'=<d'/c. Постоянная V
называется коэффициентом отражения. Смещение частиц
стержня будет складываться из смещений, обусловленных каждой из
22

волн:
u(x,t)=A{exp[i(kx—(ot)] + Vexp[—i(k'x+(*'t)]}.
Подставляя суммарное смещение в граничное условие (2.6) при
х0 = 0, получаем
ехр(—i(ot) + Vexp(—tco7)=0 или exp[i(<o'—to)t]=—V. (2.9)
Поскольку в последнем соотношении правая часть постоянна, то
должна быть постоянной и левая. Отсюда следует, что со'=(о,
т. е. частоты падающей и отраженной волн равны. При этом
также k'=k и коэффициент отражения V= — 1. Таким образом,
полное волновое поле в стержне имеет вид
и(х, t) =A[exp(ikx)—exp(—ikx)]exp(—i(ot) =
=2iAsmkxexp(—i(i>t). (2.10)
Аналогичным способом получается закон отражения от
свободной границы. В этом случае коэффициент отражения V=l.
Заметим, что равенство частот падающей и отраженной волн
мы получили автоматически, требуя выполнения граничного
условия во все моменты времени. Нетрудно видеть, что это
обстоятельство будет иметь место во всех случаях, когда время не
входит явно в граничное условие.
Свойство сохранения частоты в значительной степени
облегчает решение задач об отражении волн. Рассмотрим, например,
случай контакта двух полубесконечных стержней из разного
материала, но одинакового сечения. Как и выше, предположим,
что слева падает гармоническая волна i4exp[i(&iJt—©01» *i =
= co/clf ct=y£i/pt. Поскольку частота волны сохраняется,
решение соответствующих волновых уравнений слева от границы
(*<0) и{ и справа (х>0) и2 можно искать в виде:
щ (х, t) =<pi (х) ехр (—Ш), и2 (х, t) =<р2 (х) ехр (—Ш).
При этом для функций ф! и ф2 получаем обыкновенные
дифференциальные уравнения:
ф; + far = 0, k, = о/с/, с,- = УЯ//Р/, /=1,2. (2.11)
Общее решение этих уравнений запишем в виде:
Фх = А ехр (ikxx) + VA ехр (— 1кгх)%
Ф2 = WA ехр (ik2x) + А2 ехр (— ik2x). (2.12)
При этом члены exp(ikjX) соответствуют волнам,
распространяющимся направо, а ехр(—ik^x)—налево. Поскольку при *>0
никаких источников волн нет, то во втором стержне могут быть
только волны, уходящие от границы {условие излучения),
следовательно, Л2==0. Подставляя (2.12) в условия (2.8) при *0 = 0,
получаем систему двух уравнений для определения коэффици-
23

ентов отражения V и прохождения W: \ + V=Wy ikiEi(\—V) =
= ik2E2W. Отсюда получаем формулы Френеля:
где n = cjc2— коэффициент преломления; m = p2/pi—отношение
плотностей.
§ 6. Продольные колебания стержней
При прекращении действия вынуждающей силы стержень конеч-
ной длины продолжает колебаться на некоторых «собственных»
частотах. Эти частоты, а также форму колебания (вид функции
и(х, t)) можно найти, решая волновое уравнение (2.2) при
соответствующих граничных условиях. Пусть, например, имеется:
стержень, концы которого х=0 и *=/ неподвижны, т. е. и|х=о =
= u|x=z = 0. Будем искать решение в виде и(х91) = ф(х)ехр(—Ш)~
Подставив его в (2.2), для функции ф(л:) получаем
обыкновенное дифференциальное уравнение ф"+£2ф = 0, & = оа/с. Условие
при *=0 выполнится автоматически, если положить у(х) =
=Asinkx. Удовлетворяя теперь условию при х=/, находим
sin£/=0. Отсюда следует, что имеется набор волновых чисел
kn = nn/lf п=1,2, (2.14)
при которых выполняются оба граничных условия.
Последнее равенство с учетом формулы £п = о)п/с определяет
для рассматриваемого случая счетный набор собственных частот
(дп = ппс/1. (2.15)
При этом для соответствующих собственных колебаний
получаем
ип(ху t)=Ansmknxexip(—i(unt)f (2.16)
или, представив комплексную амплитуду в виде Лп=апехр(гфп)
и выделяя вещественную часть,
utl(xt t) = ап sin №- х\ cos К< - г|)л); (2.17)
Ял и t|?n при этом остаются произвольными.
На рис. 2.1 изображено распределение амплитуд колебаний
ansin(nnx/l) по длине стержня для разных п. Мы видим, что
величина п—1 дает число узлов (точек, где ип = 0), имеющихся на
стержне, не считая его концов. Обратим внимание также на то,
что в стержне могут существовать только такие колебания, у
которых на длине стержня укладывается целое число полуволн.
Это видно также из уравнения (2.14), если с учетом kn=2n/Xn
записать его в виде l = n\J2.
В случае свободного стержня конечной длины (граничные
условия и'(0) =и'(1) = 0) единственным отличием от
рассмотренного .случая будет выбор решения в виде у(х) =А cos&x, произ-
24

водная от которого обращается в нуль при д:=0. Уравнение для
собственных частот то же (sin /?/=0), так что формулы (2.14) и
(2.15) остаются в силе. Таким образом, частоты собственных
колебаний закрепленного и свободного стержней одинаковы.
Форма собственной функции отличается сдвигом на четверть
периода:
(2.18)
ип U,t) = ап cos (-у- х\ cos (юя* —1|>„).
На рис. 2.2 изображена форма нескольких первых колебаний
стержня. Вновь на длине стержня укладывается целое число
полуволн. Отсюда понятно, почему частоты колебаний
оказываются одинаковыми для закрепленного и свободного стержней.
Однако здесь уже величина п (а не п—1) дает число узловых точек
на длине стержня.
§ 7. Волны кручения в стержне.
Крутильные колебания
Предположим, что к одному концу стержня кругового сечения,
рассмотренного в § 3, внезапно приложен крутящий момент.
Тогда вдоль стержня побежит волна кручения. Деформацию в
каждом сечении х мы будем характеризовать углом
закручивания ф=ф(лс, t), равным углу поворота данного сечения вокруг
оси х. Напряженное состояние в каждом сечении будет
характеризоваться моментом кручения М(х, t). Пользуясь формулой
(1.14), нетрудно связать между собой обе эти величины. В самом
Деле, применив (1.14) к участку стержня, ограниченному двумя
сечениями на весьма малом расстоянии Але друг от друга, и
обозначив угол закручивания этого участка через Дф=<р(я+Д*)—
~~~Ф (*) = (ду/дх) Д*, получим, положив в (1.14) L = Ax и ср = Д(р,
25

М (х) =fAcp = |iJta4A(p/(2A;e) или в пределе Ах-^О
т*)=»т%- (2Л9)
Аналогично рассчитывается результирующий крутящий момент,
действующий на тот же элемент А* и равный разности моментов
на каждом из сечений:
М(х+Ьх)-М(х) = ?£&х = ^&&х.
По второму закону Ньютона этот момент приводит к угловому
ускорению рассматриваемого элемента стержня вокруг оси х.
Поскольку момент инерции нашего элемента равен лра4Д*/2, a
угловое ускорение d2cp/dtf2, то окончательно получаем:
*I = J_*8, ,= l/Z. (2.20)
Это вновь волновое уравнение, совпадающее с (2.2) для
продольных волн, но с другой скоростью распространения. Заметим,
что эта скорость не зависит от радиуса стержня.
Граничными условиями для уравнения (2.20), очевидно,
будут: закрепленный конец ф|ж»хо=0; свободный конец Л1|х=ЗСо=0
или, воспользовавшись (2.19), (dy/dx)x=XQ=0't жесткий контакт
двух стержней одинакового радиуса, но из разных материалов с
|*ь Pi и М<2, р2 соответственно — равенство углов закручивания
q>i|*=*b=<Pa|*-* и моментов М: M,1(^q)i/^1)x«JCo=[i2(5<p2/^)x=Xo, что
аналогично (2.8),
Таким образом, как уравнения, так и граничные условия для
продольных и крутильных волн совпадают между собой с
точностью до обозначений. Поэтому все результаты § 5 и 6
непосредственно переносятся на этот случай, с той только разницей,
что роль продольного смещения играет угол закручивания ф, а
вместо модуля Юнга Е нужно ввести модуль сдвига \i.
Например, формула (2.15) для собственных частот колебаний остается
в силе, но с новым значением с.
§ 8. Волны изгиба в стержнях
8.1. Уравнение для изгибных волн. В стержне могут
распространяться волны еще одного типа, называемые изгибными. Они
возникают при ударе по стержню в поперечном направлении,
сопровождающемся местным изгибом, который и побежит от места
удара в виде волны. Предположим, что стержень имеет плоскость
симметрии, совпадающую с плоскостью чертежа на рис. 2.3, и
что колебания происходят в этой плоскости. Смещения стержня
£ предполагаем достаточно малыми, чтобы считать длину
нейтральной линии неизменной и, следовательно, пренебрегать
растяжениями стержня.
На рис. 2.3 изображен участок стержня, по которому бежит
волна изгиба. Если выделить малый элемент стержня Д*, то,
26

как мы знаем, в сечении возникает перерезывающая сила F(x),
с которой участок стержня по одну сторону сечения действует на
другую. Второй закон Ньютона для элемента Д* можно записать
в виде
pSQbx^Fix+W-FW^-Zf-to, (2.21)
dt* дх
где р — плотность; 5 — площадь поперечного сечения стержня.
Кроме того, при изгибе в каждом сечении стержня возникает
момент сил М(х), который согласно (1.15) и (1.16) при |д£/дл:|<
<1 равен
М(х) = Е1д^. (2.22)
Полный момент сил, действующий на элемент Д#, будет
складываться из разности моментов М в двух сечениях М(х+Ах) —
—М(х) « (дМ/дх)Ах и дополнительного крутящего момента
F(x)hx, обусловленного перерезывающей силой. В результате
общий крутящий момент (F+dM/dx)hx должен
уравновешиваться моментом р/Дх(д2а/д<2), возникающим из-за инерции
вращения элемента Дх вокруг оси, нормальной к плоскости чертежа.
Здесь р/Дх—момент инерции выделенного элемента; а — угол
наклона нейтральной линии в данной точке к оси х. При
\dl)ldx\^i\ a^iga=d%ldx, поэтому уравнение баланса
моментов будет
7 J!L=J?M +Fm (2.23)
дРдх дх v '
Отметим отличие этой формулы на динамический член
pl(dz%/dt2dx) от выражения для перерезывающей силы через
момент в статическом случае (1.20).
Продифференцировав выражение (2.23) один раз по х и
подставив в него М из (2.22) и dF/дх из (2.21), получим уравнение
для смещения £ (ху t):
PI-*L=EI^+pS^. (2.24
дРдх* дх* ^ dt2 v
Обычно на практике для описания изгибных волн
используют упрощенное уравнение, пренебрегая членом в левой части
(2.24), возникшим из-за учета вращения элемента Дх Для
обоснования этого приближения введем радиус инерции г0
поперечного сечения, определяемый соотношением I=r02S и
совпадающий по порядку величины с поперечными размерами стержня.
Кроме того, пусть Т и К будут характерными масштабами
времени и длины изменения £(х, t). Тогда по порядку величины имеем
Для члена в левой части (2.24) pl(d%/dt2dx2) ~ г025р^А2Р, а для
второго в правой части pS(d%/dt2) ~pS%/T2. Отношение этих
величин имеет порядок г02Д2. Последняя величина обычно
пренебрежимо мала по сравнению с единицей, ибо поперечные разме-
27

ры стержня г0 малы по сравнению с длиной волны X. В
результате получаем уравнение для волн изгиба в виде
*L + f>±*L = Om (2.25)
Заметим, что это уравнение получается, если сразу
воспользоваться выражением (1.20), т. е. статическим выражением для
перерезывающей силы через момент.
8.2. Граничные условия. Гармонические волны.
Распространение волн изгиба описывается уравнением четвертого порядка,
что влечет за собой ряд интересных особенностей. В частности,
граничных условий должно быть больше. Выпишем их для
некоторых случаев:
а) зажатый конец (рис. 2.4, а) — обращается в нуль как
смещение £, так и его производная (угол наклона):
*=0; (2.26)
б) свободный конец (рис. 2.4, б) — момент М и
перерезывающая сила F равны нулю или с учетом (2.22) и (1.20)
дх*
= 0;
(2.27)
в) опертый конец (рис. 2.4, в) — равны нулю смещение и
момент:
си-£Ц-°- (2'28)
Общее решение уравнения (2.25) уже нельзя представить в
виде волн произвольной формы, распространяющихся с
постоянной скоростью, как это было для продольных и крутильных
волн в стержне. Поэтому рассмотрим гармонические изгибные
волны в стержне, положив
Е(х, 0=ЛФ(*)ехр(—Ш). (2.29)
Подстановка этого выражения в (2.25) приведет к
обыкновенному дифференциальному уравнению для функции Ф(*):
|£-**Ф = 0, * = (JL.)VV4, (2.30)
общее решение которого можно записать в виде
Ф (х) =Л+ехр (ikx) +А _ехр (—ikx) +
+ В+ехр (kx) + £-ехр (—kx), (2.31)
и соответственно для £; (х, t)
l(x, t) =A+exp[i(kx—(*t)] +Л_ехр[—i(kx+(ot)] +
+ B+exp[kx—mt) +B-exp[—kx—i®t]. (2.32)
28

Здесь первые два слагаемых соответствуют незатухающим
волнам, распространяющимся в положительном (А+) и
отрицательном' (А-) направлениях с фазовой скоростью
сф = ± ©/* = ± f—^-1 со1/. (2.33)
Поскольку Сф зависит от частоты, т. е. имеет место дисперсия
(см. § 9), волновое возмущение конечной длительности при
распространении будет изменять свою форму.
Два других слагаемых в (2.32) с коэффициентами В+ и В-
соответствуют гармоническим (колебаниям с экспоненциально
убывающей или возрастающей амплитудой. Очевидно, что
решения такого типа могут существовать только при наличии концов
стержня или каких-либо его неоднородностей, ибо в противном
случае мы получили бы бесконечно большие амплитуды
колебаний при х->-±оо.
8.3. Отражение волн. Изгибные колебания. Рассмотрим
отражение гармонической волны Aexp[i(kx—cot)] (—оо<х^0),.
например, от зажатого при *=0 конца стержня. Как и в случае
отражения продольных волн, частота о сохраняется. В общем
решении (2.32) следует положить В- = 0 (ограниченность
решения при х-+— оо). Кроме того, положим Л+=Л, Л_=УЛ, В+ = Ю„
Подстановка (2.32) в граничное условие (2.26) при х0=0 дает
1 + V+W=0, 1(1—V) + W=0. Отсюда для коэффициентов V и W
находим:
V=—(l—I)l(l + i), W=-2i/(l + i), (2.34)
т. е. на отраженную волну ЛУехр[—i(kx + ®t)] накладывается
экспоненциально затухающее с удалением от конца стержня
колебание AW ехр (kx—Ш).
Аналогично случаю продольных волн находятся собственные
изгибные колебания стержня конечной длиной /. Для этого
целесообразно общее решение уравнения (2.30) записать в виде
Ф (х) =Accos kx+A8sin kx + Bech kx+B.sh kxt (2.31'}
который следует из (2.31), если экспоненциальные функции
выразить через тригонометрические и гиперболические. При этом
новые комплексные постоянные Лс, Л„ Вс, В, просто выражаются
через амплитуды волн Л+, Л_, В+, В_.
Для примера рассмотрим случай стержня, лежащего на двух
опорах, растояние между которыми /. Из граничных условий
(2.28) при jc0=0 имеем Ае+Ве = В—Ас=0,т.е.Лс=£с=0.Теперь
также из (2.28), но при х0 = 1 получим систему однородных
уравнений относительно величин А, и В,:
Aab\nkl+B.shkl=Ot _ Aasinkl+Bashkl=0.
Последняя имеет ненулевое решение только в случае, если
sinfc/=*0, £„/=/ш, л=1,2,... При этом Вв = 0, а А$=А произволь-
29

но, так что £п(*, О =А sin£nxexp(—tot). На длине стержня, как
и в случае продольных колебаний, укладывается целое число
полуволн. Однако собственные частоты колебаний уже не
совпадают с (2.15), а с учетом (2.30) равны
сол= V Ег*МпЩ1у.
(2.35)
В общем случае произвольных граничных условий на концах
стержня получается однородная алгебраическая система
четырех уравнений относительно величин АСу Вс, А31 В3 вида
в.
= 0, C={cfm}t /,m=l,2,3,4.
При этом элементы с^т матрицы С будут зависеть от волнового
числа k. Собственные значения kn найдутся из требования
существования нетривиального (ненулевого) решения системы, т. е.
g(k) =det С=0. Например, в рассмотренном выше случае
С =
11 0 0
-11 0 0
cos kl ch kl sin kl sh kl
—coskl chkl —slnkl shkl
g k) =-- 4 sin kl shkl.
§ 9. Дисперсия волн и групповая скорость
9.1. Распространение негармонических волн. Как уже
отмечалось в предыдущем параграфе, изгибное возмущение
произвольного вида изменяет свою форму при распространении. Этот факт
является общим для всех волновых процессов, у которых
фазовая скорость гармонических волн зависит от частоты. В этом
случае говорят, что имеется дисперсия. Зависимость частоты
волны от волнового числа (о = со(&) называют при этом
дисперсионным соотношением. Ввиду важности этого вопроса в теории
волн приведем некоторые общие закономерности
распространения волн в средах с дисперсией.
Вначале рассмотрим распространение негармонической
волны в среде с дисперсионным соотношением со = со(&). Пусть в
момент времени /=0 какое-то возмущение (например, £(*, 0) в
случае волн изгиба) задано функцией f(xf 0). Представим ее в
виде интеграла Фурье
/(х,0)= \~f(k)exp{ikx)dk,
где f{k) —пространственный спектр Фурье начального
возмущения. Нетрудно видеть, что при произвольном t возмущение f (х, t)
30

может быть записано в виде
оо
/ (х, f) = j f(k) exp {i [kx — ю (k) t\) dk =
•-00
оо
= j / {k) exp [tfc (x — сф<)] dk, (2.36)
•-co
где c^(k)=(o(k)/k — фазовая скорость. Выражение (2.36) при
tf=0 переходит в функцию f(x, 0) и, кроме того, удовлетворяет
уравнению для волн, так как каждая гармоническая волна
ехр{*[&*—со(k)t]} ему удовлетворяет (например, уравнению
(2.25) в случае изгибных волн при сф из (2.33)).
Рассмотрим теперь (2.36) внимательнее. Если бы скорость
распространения каждой гармоники сф=о)/& не зависела от
волнового числа k ((u(k) —линейная функция k), как это было для
продольных волн в стержне, то возмущение перемещалось бы в
направлении х со скоростью сф, не меняя своей формы. В самом
деле, при сф=const из (2.36) следует
/(*,*) = j 7(£)e*p[t£(jt — c^t)]dk = f{x — сф<,0). (2.37)
•-0О
Волны такого типа называют бездисперсионными.
Для изгибных волн фазовая скорость отдельных гармоник
зависит от волнового числа, или, что то же, от частоты. Поэтому
отдельные гармонические составляющие в возмущении (2.36),
распространяясь каждая со своей скоростью, складываются в
различные моменты времени с разными фазами, что и приводит
к изменению формы начального возмущения. Как правило,
начальный профиль волны расплывается, амплитуда возмущения
падает и оно переходит в нечто похожее на синусоидальный цуг.
9.2. Распространение узкополосных возмущений. В теории
волн важную роль играют так называемые узкополосные
возмущения f(x, t), пространственный спектр которых f(k) отличен or
нуля лишь в малой окрестности некоторого k0. Такие возмущения
можно записать в виде:
f(x, t)=F(x, t)exp[i(k0x—toQt)], (Оо = (о(Ло), (2.38)
т. ё. в виде волны, огибающая которой F(x, t) медленно по
сравнению с exp[i(k0x—сооО] меняется в пространстве и во времени.
Такая волна называется модулированной гармонической волной^
В начальный момент £ = 0 имеем (F0(x) =F(xy 0))
се
/ (х, 0) = j / (k) exp (ikx) dk = F0 (x) exp(ik0x),
*-00
где функция f(k)&0 при \k—k0\>\bk\ и \Hk\4Zk,,. Если
31

положить £=£0+х, то
оо
F0(x) = §l(k0+K)txp(ixx)d*. (2.S9)
—00
Для того чтобы получить возмущение f(xt t) в произвольный
момент времени /, воспользуемся выражением (2.39), положив в
нем k=k0+n и разложив функцию ©(&) в ряд Тейлора в
окрестности kQ:
/(*,*)- j7(*)exp[i(v + »«-^--^-| *t-...\Ux.
—00 *о
Поскольку интегрирование практически распространяется
только на область малых х, мы можем при не слишком больших /
ограничиться линейным членом в разложении для со (Л):
оо
/ (х, t) ж exp [t (V - <V)1 J f(*о + x) x
-оо
*«p[<(*-£|j)«]a».
Величина d(u/dk=crv называется групповой скоростью волны.
С учетом этого обозначения и выражения (2.39) узкополосное
возмущение в произвольный момент времени имеет вид
модулированной гармонической волны
f(x9 t) =F0(x—cr]>t)exp[i(k0x—(d0t)), (2.40)
т. е. огибающая F0(x—сгр0> не меняя своей формы,
перемещается в пространстве с групповой скоростью.
Очевидно также, что энергия возмущения сосредоточена в
области пространства, где огибающая F0(x—crpt) отлична от нуля.
Следовательно, при распространении узкополосных возмущений
энергия переносится также с групповой скоростью.
Отметим, что так будет происходить только на ограниченном
интервале времени, пока отброшенный в разложении частоты
член дает лишь малый набег фазы:
2
Понятие дисперсии и групповой скорости справедливо для
волн любой природы. В частности, для известных нам
продольных волн в стержне сгр = сф=с (дисперсии нет), а для изгибных
распространяющихся волн со= (£>02/р) hk2 и
Сгр *= £ = 2 (Щ\ = 2^ = 2Сф. (2.41)
ak \ Р / Л
Групповая скорость в 2 раза больше фазовой.
32

Задачи
2.1. Определить непосредственно (без обращения к интегралу Фурье)
коэффициент отражения продольной плоской волны произвольного вида от
закрепленного конца стержня.
Решение. Пусть стержень, расположенный при дс<0, закреплен в сече-
ниИ х=0. Общее решение волнового уравнения запишем в виде
u(xtt)=f(x—ct)+g(x+ct)t
где f(x—ct) — падающая волна. Отраженную волну g{x+ct) можно найти,
приравняв к нулю смещение при х=0, что дает f(—ct)+g(ct)=0.
Следовательно, функции g(Q и /(£) одного переменного g должны быть связаны
соотношением g(g)=— f(—£)• Таким образом, u(xt t)=f(x—ct)—f(—x—ct)t т. е.
коэффициент отражения, как и для гармонических волн, равен —1.
2.2. Найти коэффициенты отражения и прохождения продольной
гармонической волны на границе двух стержней с параметрами рь Eit Si и р*, £*, S»
соответственно, предполагая, что стержни жестко соединены невесомой
накладкой из абсолютно жесткого материала (рис. 2.5).
Решение. Для гармонических волн ищем решение в виде:
Ui=A[txp(ikix) + Vexp(—iftix)]exp(—Ш), th—AW exp[l(kaX+®t)]t
где kj=ialCj\ Cj2=Ejlpit /=1, 2. При жестком сцеплении стержней На
границе смещение торцов одинаково: Ui\x—о=«2|*—с Второе граничное условие
вытекает из требования равенства сил, действующих на накладку со стороны
каждого стержня:
Подстановка выражений для щ и и2 в граничные условия дает
откуда имеем
Si VpiEt + S2 Vp*E* ' = Si VpiEi + s* Vp%e% '
В частности, если стержни изготовлены из одного материала, то
V - (Si - 5a)/(Sx + Sa), W = 2S1I(Sl + S2).
2.3. Определить коэффициент отражения продольной гармонической
волны от конца стержня, на котором задан импеданс Z*=—F/(Si;)|x—о> т. е.
отношение напряжения (с обратным знаком) к скорости.
Решение. Согласно закону Гука F/S=Edu/dx, учитывая также, что
v = duldt=—i(ou, получаем в соответствии с условием задачи Z=(Elmu)dul
fdx. Подставляя сюда
" =» A [exp (Ikx) + V ехр (— ikx)] ехр (— к»*), k = ю/г, с = УЩр,
имеем
z^Eik(l-V) х-у
io(l+V) rapi + V
2 Л. М. Бреховсхиос, В. В. Гончаров 33

К^=/7
№>2i
^
л-^
"' 7
Л*7
л^
^
V,0<tf<l/fi
\t=i/c
6/c<t2<2l/c
Vt~2l/c
Vs.
Рис. 2.6
Рас. 2.7
<Г
лткуда
V Ер — Z pc — Z
YEp+Z pc + Z'
2.4. Пользуясь определением импеданса в задаче 2.3, найти импеданс Z&
при х=0 для стержня с параметрами Et р, если при х=1 импеданс равен Zi.
Решение. Гармоническое решение волнового уравнения в стержне
будет tt=(asin£;t+6cos£*)exp(—tot). Найдем соотношение между
амплитудами волн а и Ь, используя заданный импеданс Zi\
Ek (a coskl — b sin kl)
• = — ipc -
a/b—tgkl
'l Sv \x=l to (a sin kl + b cos kl) 'r~ alb tg kl + 1
Определив отсюда отношение a/b, получим импеданс при х=0:
Eka ipctgkl — Zt Zl — ipcigkl
Za = = — ipc ————— = qc ■ .
tob K ipc + Ztigkl r pc — iZttgkl
2.5. Определить входной импеданс полу бесконечного стержня с
параметрами рис.
Решение. В стержне может существовать только уходящая от его
конца волна u=aexp[i(kx—со/)]. Следовательно,
Е ди\ Eik ^гтг-
хх^° щи дх \x==z0 ко
2.6. Подобрать параметры стержня конечной длины (р, с, /) таким образом,
чтобы коэффициент отражения гармонической продольной волны для
изображенной на рис. 2.6 системы был равен нулю.
Решение. Положив по результатам предыдущей задачи Zz=p2c2,
найдем по формуле задачи 2.4 входной импеданс
Рас» — ipc tg kl
рс — Zp,^ tg kl
Теперь обратимся к выражению для коэффициента отражения через Z/, полу-
2о = ^1х=о=:Рс"
34

ценному в задаче 2.3, откуда следует, что У=0 при Zi=piC{. Нетрудно
видеть, что так будет, если Л/= (я/2) (2я+1) (л=0, 1, 2, ...) и рс=Ур1С1р2с2.
Действительно, тогда tgfc/-M», a Zi(pc)2/P2C2aPi£i. Таким образом, для
согласования двух стержней нужно взять третий размером в нечетное число
четвертей длины волны из такого материала, чтобы pc=ypiCip2c2.
2.7. Рассмотреть процесс распространения возмущений в стержне
конечной длиной /, налетевшем со скоростью v0 в момент времени *=0 на
абсолютно жесткую стенку.
Решение. При t>0 со стороны стенки на стержень действует сила f(t),
которая в соответствии с волновым уравнением для F(x, t)=SEdu/dx будет
распространяться со скоростью с=уЯ/р. Следовательно, что 0<t<l/c будем
иметь F(x, t)=f(t+x/c) (f(£)=0 при £<0). В момент времени t=l/c это
возмущение дойдет до свободного конца стержня х=—/. В результате
возникает отраженное возмущение, так что при l/c<t<2l/c F(x, t)=f(t+x/c) +
+g(t—x/c). Поскольку на свободной границе F(—I, 0В0» т0 f(*—Цс) +
+g(t+llc)=0 или g(g)=— f(t—211с). Поэтому при 0<t<2l/c
F(x, t)=--f(t+x/c)-f(t-x!c-2l/c).
Найдем теперь выражение для скорости частиц стержня:
О о
Постоянная интегрирования а(0=0 для 0<t<2l/ct так как v(О, /)=0.
Подставив в v(x, t) выражение для F(xt t)t получим
• х
V(X,t):
t-X/C-2llC -1 r
+ j '©« --ii-K'+f)-
_,„+,(,_f_i)]
так как f(t—2l!c)—0 при t<2l/c. Теперь легко найти явный вид функции
f(l), воспользовавшись условием, что v(—l, t)=v0 при 0<t<l/c
(возмущение еще не добежало до левого конца стержня):
°° * ~ES lf {t"l,C) ~ f (t) + f{t ~ Ш = ~~ES f(/)'
ибо f(t—llc)=0 при t<l/c. Отсюда находим f(t)——ESvolc или (с учетом
/U)=0 при КО) /(&)=-£S(i>o/c)Oa), где 9(£)=1 при 1>0 и 6(1) =0
35
2*

при &<0. Для моментов времени 0<<<2//с окончательно запишем:
F (х, t) = - ES -^ [9 (< + х/с) - 9 (t - х/с- 2Цс)},
С
v(x,t) = -v0lQ(t + x/c)-Q(t) + Q(t-x/c-2l/c)].
Отсюда видно, что при f>l/c напряжение снимается (F(x, t)=0) с участка
стержня —/<х<с/—2/, скорость всех точек которого равна —vq. В
частности, при t=2l/c напряжение снимается со всего стержня, который будет
двигаться как целое со скоростью —v0 (отскок стержня). Диаграмма возмущений
в стержне в различные моменты времени показана на рис. 2.7.
2.8.. Проверить выполнение закона сохранения количества движения
(импульса) при отскоке стержня.
Решение. В течение времени контакта 211 с со стороны стенки на
стержень действует постоянная сила F0=F(Ot t) ••■=— ESvq/c (см.
предыдущую задачу). Выражая полный импульс этой силы F02llc через скорость v0 и
массу стержня m=p/S, получаем
21FJC = - 2ESv0l/c* = - 2p/St>0 =
e _ mv0 — mv0 = nw \t>2l/e - mv \t<0
— закон сохранения количества движения.
2.9. Рассмотреть движение стержня длиной / при коротком (х<£.1/с)
действии силы Fo на левый его торец.
Решение. После удара по стержню побежит импульс сжатия F(x, t) =
=— F0U(t—х/с) при Q<t<l/ct где Н(£) = 1 на интервале 0<£<т и
1Щ)=0 вне его. В момент времени t=ljc импульс достигнет правого конца
стержня и отразится. При условии, что F(lt t)=Q, для 0<t<2l/c получим
F(x, t) =-F0[n(t-x/c)-Tl(t+xIcrr-Wc)].
Найдем выражение для скорости частиц стержня (см. задачу 2.7):
х
ES dt
о
{rt-X/C t+X/C~2l/C -J
i I'm* I nH
+ U(t + x/c- 2L/c) - П (/ - 2l/c) + ax (*)].
Далее при t<2l/c имеем П(/—2//c)^=0, при t<l/c v(lt t)=Q=
=F0c[ax(t)—U(t)]/ESt т. e. ai(t) = U(t) при i<l/c. Но тогда c>(0, 0 =
= FQcU(t)/ES = 0 при T<t<l/ct следовательно, v(ti, t)=0 и при i<t<2l/ct
так как отраженный импульс еще не добежал до левого конца стержня.
Поэтому «i(/)=0 для Цс<.К2Цс и окончательно при 0<t<2l/c
v (х, t) = -^ [П (* -ж/с) + П (/ + х/с-21/с)].
36

Отсюда следует, что каждый элемент стержня за отрезок времени 0<*<2//с
будет дважды иметь скорость Vo—F0clES в течение времени т (элементы
стержня, близкие к его правому концу, часть времени х будут двигаться с
удвоенной скоростью, а оставшуюся часть — покоиться). В результате любой
произвольный участок стержня за время 211с сместится на расстояние Оо=
^2voX=2(FoclES)x. В дальнейшем после отражения импульса от левого, уже
свободного конца стержня этот процесс повторится и т. д. Таким образом,
движение каждой точки стержня будет состоять из быстрого перемещения в
течение времени т, затем покоя и т. д.
2.10. Показать, что рассмотренное в предыдущей задаче движение
упругого стержня после кратковременного удара удовлетворяет законам сохранения
импульса и энергии.
Решение. Импульс внешней силы F0x должен быть равен импульсу,
уносимому волной сжатия: &=[iv0t где \L=*pScx— масса возмущенного
участка стержня. Непосредственной подстановкой в &=\Wq выражения Vo через
Fo убеждаемся в сохранении импульса:
'^ = pSrTlf=FoT-
Если ввести среднюю скорость перемещения стержня как целого
- JfL v<>x F»c*x F*x F*x
V=a 21 °~~ I °~~ ESI e pSl e m f
где m — масса стержня, то получим классический закон сохранения
количества движения в механике твердого тела: Ftfttssmv.
Вычислим теперь энергию, уносимую импульсом сжатия. Для кинетической
энергии имеем £Гк = Ц0о2/2, потенциальная энергия в соответствии с задачей 1.8
будет
n 2 E\S ) 2 £c*° 2 K ° *
Таким образом, полная энергия импульса равна
Fac
»=3»n + ^K=K = p5^=pScT-^-t;o = Fo^-
С другой стороны, при действии силы Fo в течение времени т левый конец
стержня смещается на расстояние Ио/2«а0т, т- е- работа силы A=*FoVtft=&. Закон
сохранения энергии также выполняется. Заметим, что кинетическая энергия
среднего движения
т- т ~F0x 1 v 1 тс
^cp=T^=T,- = -F0,0t- = tt^
значительно меньше полной энергии 8.
2.11. Определить коэффициенты отражения и прохождения изгибной
волны от сосредоточенной в сечении х=0 массы т.
Решение. Имеем при *<D и х>0 соответственно:
Ь (*, i) = exp [i (kx — at) J + V exp [— i (kx + со/)] + Vx exp (kx — Ш),
Ca (xt t) = W exp [i (kx — (at)] + Wx exp (—kx — Ш).
37

В сечении х=0 должны быть непрерывны смещения, угол наклона и момент:
ЯП *Ы ас I
b«U)-b«U), ■§-
^ u; **■ Uo w \х=о
Разность перерезывающих сил при х=0 вызывает движение массы с
ускорением d^ild^:EI(d%2ldx^—d%ldx^)xmm0=rn(d%ldt2)xmm0.. Подставляя в эти
условия выражения для Ci и С2> получаем:
l+V + V1 = W + Wlt i(l-V) + V1 = iW-Wl,
-(\ + V) + V1 = — W + Wlt *(1 —V) + Ki-iV —1Pi =
= — (m/EI)<sHl + V+Vd,
откуда r(
e 4*E/ —ma*(l+i) ' ~~ + ~* 4iEI - mafi (i + i) '
2.12. Определить коэффициенты отражения и прохождения изгибной волны
от закрепления, запрещающего смещения, но не препятствующего поворотам.
Решение. Эта задача отличается от предыдущей только граничными
условиями: £,(0, <)вЬ(0. 0=0, (дЫдх)х=0= (дУдх)х=0, (a2Ci/dx2).-0=
= (d2C2/d*2)x=o. На перерезывающую силу условия не накладываются. Этим
условиям соответствует система уравнений
\ + V+ Vi=W+Wi=0t i(l—V) + Vx=iW—Wu
-(1 + V) + Vi—V+Vi
с решением V=-(l-i)/2, №=(1+0/2, Vi = ^i =—^= —(1+0/2.
2.13. Определить собственные частоты изгибных колебаний зажатого с
обоих концов стержня длиной /.
Решение. Аналогично рассмотренному в п. 8.3 случаю стержня на
опорах получим уравнение для определения собственных частот: cos kl=* l/chkl.
При kl>\ имеем £п/»я/2+пя и <On»V£r02/p(n2/4/2) (2n+1)2.
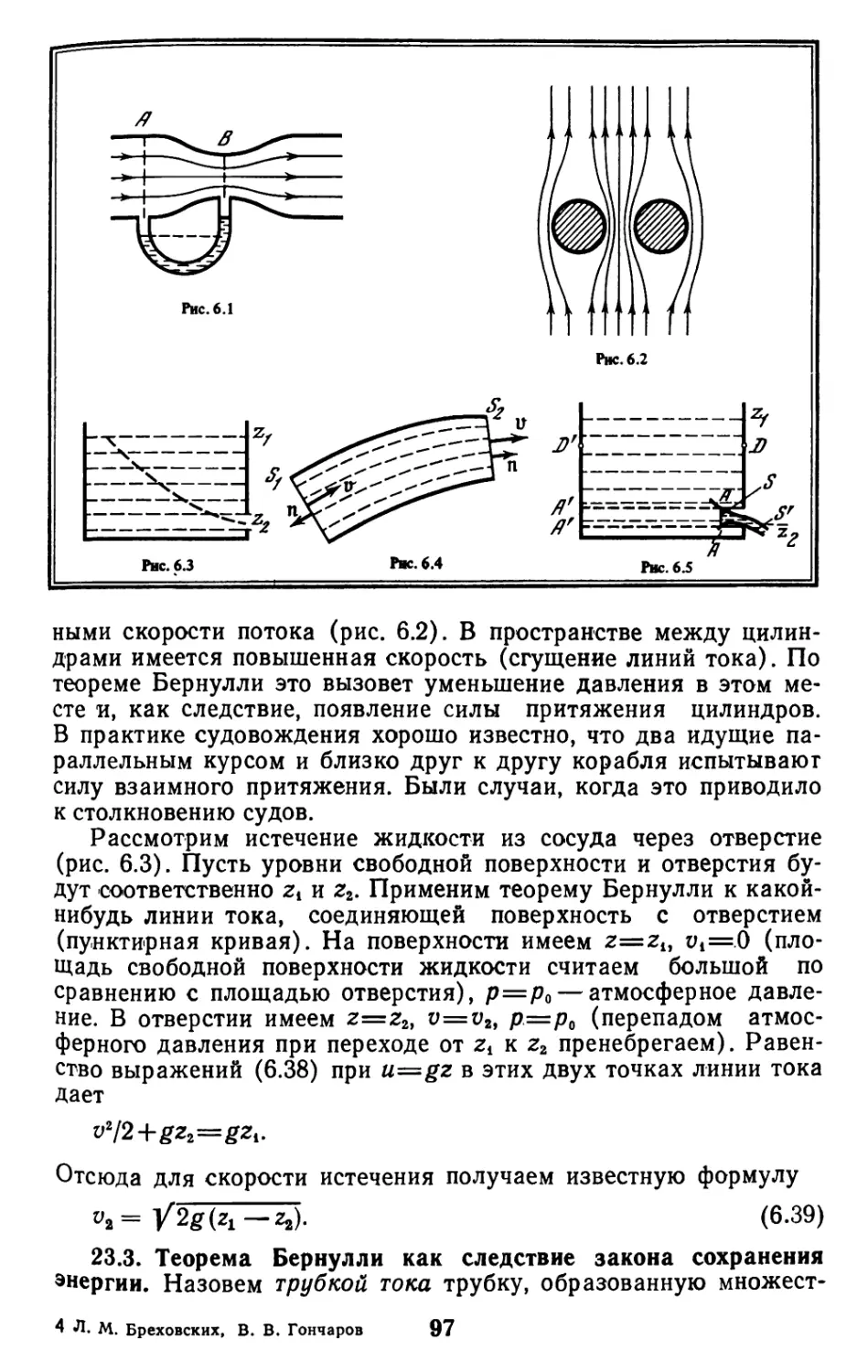
Глава 3 ^
ОБЩАЯ ТЕОРИЯ НАПРЯЖЕНИЙ
И ДЕФОРМАЦИЙ
Перейдем теперь к общей теории поведения упругого тела под
действием внешних сил. Наше рассмотрение в этой главе не
будет ограничено изотропными телами, свойства которых одинако-i
вы по всем направлениям, но приложимо и к анизотропным.
§ 10. Описание состояния деформированного тела
10.1. Тензор напряжений. При воздействии внешних сил на упру
гое тело произвольной формы происходит относительное пере-|
мещение его частей, сопровождающееся появлением внутренние]
38

сил между ними. Для выявления этих сил рассечем
деформированное (говорят также — напряженное) тело произвольной
поверхностью на две части. При этом для сохранения равновесия
любой из частей необходимо приложить к поверхности раздела S
силы, равные действующим до разреза со стороны отброшенной
части. Эти силы и характеризуют напряженное состояние
материала. Для их описания выберем некоторую точку поверхности S
и введем декартову систему координат хи х2, х3 с осью xiy
направленной по нормали к S в данной точке. Возьмем малый
участок поверхности 5 площадью AS1 = Ax2Axs, включающий
выбранную точку. На него будет действовать сила AFb величина
которой пропорциональна площади ASb а направление
произвольно1. Обозначим проекцию этой силы на ось хк (Л=1, 2, 3)
через AFia и введем не зависящую от ASt величину
о^ДЛа/AS*. (3.1)
Аналогично, если брать поверхности раздела, проходящие
через данную точку, но перпендикулярные осям х2 и лг3, получим
еще шесть величин, определяемых напряженным состоянием тела
в точке:
o2h=AF^/AS2, Оз*=AF3fc/AS8, (3.2)
где площади Д52 и AS8 соответственно равны Дд^Д^з и &х±Ах2.
Соотношения (3.1) — (3.2) вводят девять величин oih (i, k= 1,2,3),
которые, как мы сейчас покажем, полностью определяют
напряженное состояние тела в данной точке. Для этого достаточно
показать, что, зная oiht мы можем вычислить силу, действующую
на произвольно ориентированную площадку (вектор нормали п
произволен).
Рассмотрим бесконечно малый элемент объема,
изображенный на рис. 3.1. Он ограничен: а) гранью ABC площадью AS и
нормалью п, на которую действует пока еще неизвестная сила
AF, пропорциональная AS, так что AF=fAS с компонентами по
осям fAS\ б) гранями ОВС, О АС и ОАВ, внешние нормали
которых противоположны единичным векторам координатных осей
х< (*=1, 2, 3) соответственно, а площади равны AS*=
= AScps(n, x<)=AStti, где п{— проекции вектора нормали п на
оси хи Согласно определению величин о{к компоненты силы,
действующей на каждую из этих граней, запишем так:
—OifcASt = —Oihtii AS, —a2fcA S2=—(Wb AS,
—аЗЛД S3=—оЬКпг AS.
Знак минус здесь введен с учетом, что силы противоположны
направлению осей координат (см. рис. 3.1).
На самом деле распределение сил на AS\ эквивалентно силе AFi и моменту
ДМЬ Мы предполагаем, что тг = lim АЩ/ASi = 0.
39

Поскольку выделенный объем находится в равновесии, сумма
всех поверхностных сил должна быть равна нулю. Объемные
силы здесь можно не учитывать, так как они пропорциональны
AXtAXzAXs и при Д*г>0 становятся бесконечно малыми по
сравнению с поверхностными, которые пропорциональны АхАх2
и т. п. Равенство нулю суммы проекций этих сил на ось х{ дает
fAS—diMiAS—a«M2AS—as</i3AS = 0. Отсюда, сокращая на AS и
принимая правило о суммировании по дважды встречающемуся
индексу, получаем
ft=o*nA. (3.3)
Таким образом, величины о* полностью определяют
напряженное состояние тела. Кроме того, соотношение (3.3) позволяет
заключить (см. теорему Г приложения), что величины о*
задают тензор второго ранга, поскольку п и f — векторы.
Тензор о* называют тензором напряжений. Докажем, что в
наших предположениях (т^О) он симметричен (0^=0^). Для
этого рассмотрим параллелепипед бесконечно малого объема
AV=A^1Ax2Axs, ребра которого совпадают с отрезками
координатных осей. На рис. 3.2 изображено сечение этого
параллелепипеда плоскостью х3 = 0. Стрелками показаны компоненты сил,
действующих на его грани. Напомним, что А/7* означает силу,

направленную по оси хку приложенную к площадке,
ориентированной нормально оси *<. Для равновесия параллелепипеда
необходимо, чтобы суммы действующих на него сил и моментов
были равны нулю. Равенство нулю суммы сил обеспечивается
тем, что силы, действующие на противоположных гранях, равны
по величине и противоположны по направлению. Для равенства
нулю моментов, например, относительно оси хя должно быть
AFi2A^i = A^2iA^2, поскольку моменты сил АЛ* и AF2i
противоположны. Выражая здесь AFi2 и AF2i через о1а и o2i по
формулам (3.1), (3.2) и сокращая на объем AxiAx2AxSt получаем o2i =
=ai2. Аналогично доказываются равенства c3i = als и o2S = oi2.
Следовательно, симметрия величин cih доказана.
С учетом симметрии тензора oik равенство (3.3) можно
переписать в виде
и = 0гьпк. (3.4)
Компоненты тензора напряжений о*, вообще говоря,
являются функциями точки, и лишь в случае однородных деформаций
это постоянные величины.
10.2. Тензор деформаций. Опишем теперь деформации в
упругом теле, возникающие при действии внешних сил. Для этого
нужно знать, как сместились все точки тела при
деформировании. Положение каждой из них до деформации определялось в
некоторой системе координат радиус-вектором rs={*i, x2t х3},
после деформации — радиус-вектором r'sfjc/, х2\ х/}.
Величина u = r'—г (Ui=Xi'—Xi) называется вектором смещения.
Деформация тела будет полностью определена, если известна вектор-
функция и(г). Последняя, безусловно, зависит от г, так как
только в этом случае в упругом теле возникают напряжения (силы).
Если и не зависит от г, то происходит перенос тела как целого,
не сопровождающийся внутренними напряжениями.
При известном векторе смещений и (г) не составляет труда
рассчитать изменение расстояния между произвольными, в
частности близкими, точками. В самом деле, пусть х{ и х{ + с1х{—две
бесконечно близкие точки, квадрат расстояния между которыми
а
до деформации был d/2=5] dx? = dXidxi=dx?. После деформа-
Ции координаты этих точек соответственно будут1 x/=x{+Ui(xh)
и Xi+dXi+UiiXb+dXb) ttx{+dXi+Ui(xh) +a(dtii/dxk)dxk.
Следовательно, квадрат расстояния между ними после деформации будет
/ ди. \*
(dlj = Idxt + ~-dxk\ = dx) +
Л ди. ди{ ди,
+ 2 —- dXidxk + —-1 —i- dxkdxm.
dxk dxk dxm
1 Здесь и ниже под щ(хк) подразумевается и,(*ь х2, хг).
41

*ik
Используя далее очевидные соотношения
. ди, ди, duu t ч
2 —- dXidxk = —- dXidxk ^ dxtdxk9
dxk dxk dxt
dut dut 4 , дит dum
—±- —L dxt dxm = -SL —SL dXidXki
dxk dxm dxi dxk
запишем (dl)2 в виде:
(diy=KdP + 2etbdxkdXb
-ifi + ^L + ^^\ (3.5)
2 \9Xk dxi d*i *xk)
Поскольку (dl')z—dl2—скаляр, a dx{ и dxk— векторы, то в
силу теоремы 2f приложения величина е^ является тензором
второго ранга, называемым тензором деформаций. Его
компоненты в общем случае являются функциями координат и
постоянны лишь в частном случае однородной деформации.
Симметричность тензора е* (e*=ew) очевидна. В случае малых
деформаций в (3.5) можно ограничиться линейными по отношению к
и{ членами, тогда
Ш.З. Физический смысл компонент тензора деформаций.
Вначале рассмотрим диагональные элементы, например e^^dujdxi.
Пусть Xi и Х1+Ах{— две близкие точки, лежащие на оси х±.
После деформации эти точки могут сойти с оси хи но их
координаты по этой оси соответственно будут Xi + ut(xif дс2, #8) к xt +
+ Axi + ui(xi+Axi9 x2t хл). До деформации расстояние между
точками было A*i, после деформации расстояние вдоль оси Xi
будет AXi + UiiXi + AXi)— u^{xi)^Axi+(duildxi)Axi. Для
приращения расстояния имеем (dujdxi) &х1и Если последнее отнести
к первоначальному расстоянию A#i, то мы получим
относительное удлинение вдоль оси xt. Аналогично и по другим осям, так
что диагональные элементы тензора деформаций вц^ди^дхи
е22=диг1дхг, e3s=dujdxs дают относительные удлинения
(сжатия) вдоль координатных осей.
Найдем изменение объема V = Ах±АхгАхя элементарного
параллелепипеда с длинами ребер, равными до деформации Axt,
Д*2, А*3. После деформации, как мы видели, длины ребер
соответственно будут (1+вц)Ахи (1+е22)Д#2, (1+е3з)Д*з. Если не
учитывать квадратичные и кубичные по щ члены, то объем
параллелепипеда после деформации определится как У' =
= (1 + £ц + ^22 •+ £м) AXi Дл:2Дх3. Для относительного изменения
вбъема имеем
(V'—V)/V=eii + e22+e>s = ehki (3.7)
42

т# е. след теЬзора eih. Последняя величина согласно теореме 3
приложения является инвариантом, следовательно,
относительное изменение объема, как это и должно быть, не зависит от
выбора системы координат.
Перейдем теперь к выяснению физического смысла
недиагональных элементов тензора деформаций и рассмотрим,
например, компоненту ei2. Возьмем снова элементарный
параллелепипед с ребрами длиной Дхь Д#2> Ах8, параллельными осям
координат. На рис. 3.3 изображена грань параллелепипеда, лежащая
до деформации в плоскости xtx2. В результате деформации
вершины О, А, В, С смещаются, выходя в общем случае из
плоскости #1*2. Обозначим через О', А\ В', С проекции новых
положений соответствующих точек на плоскость XiX2. Учитывая
малость деформаций и, следовательно, углов ть f2 (рис. 3.3),
имеем:
Yi ~ *б Yi ~ : ~ 1— » Y2 ~ 1 ~ "7— »
так что
2eu = |!L + -f2L = Yi + Yi = eu + «bi. (3.8)
ОХх ОХъ
Таким образом, сумма симметричных недиагональных
компонент тензора деформаций eit+e2l определяет изменение угла
между соответствующими гранями параллелепипеда. Как мы
знаем (см. п. 2.3), перекос углов означает сдвиг.
Следовательно, недиагональные элементы тензора деформаций е*
описывают сдвиговые деформации.
Соответствующим поворотом системы координат всегда
можно привести тензор деформаций к диагональному виду в любой
фиксированной точке. Поэтому в такой системе сдвиговых
деформаций не будет, а будут только удлинения и сокращения
вдоль осей. В частности, мы видели (см. рис. 1.7), что
однородную сдвиговую деформацию куба можно рассматривать как
совокупность сжатия вдоль одной из диагоналей и растяжения
вдоль другой.
§ 11. Уравнения равновесия |
и движения сплошной среды
11-1. Вывод уравнения движения. Выделим в упругой среде
некоторый объем V, частицы которого, вообще говоря, могут
находиться в движении. По второму закону Ньютона сила инерции
в этом объеме j pudV (р — плотность вещества, точки сверху
означают дифференцирование по времени) должна
уравновешиваться: а) силами F, приложенными к его поверхности и
возникающими вследствие влияния соседних частей тела; б)
объемными силами J foedV. К последним относится, например, сила
43

тяжести с объемной плотностью pg. В результате равновесия
этих сил имеем уравнение движения
fpudV= U<*dV + F. (3.9)
Воспользовавшись выражением (3.3), выразим
поверхностные силы через тензор напряжений о*:
Ft = J //dS = loiktikdS, (3.10)
где S — поверхность объема V; n={n*} — внешняя нормаль к
ней. В приложении (теорема 4) доказана теорема Гаусса —
Остроградского для произвольного тензора, так что (3.10) можно
записать в виде F{= \ (doJdx^dV. В результате для t-й
компоненты уравнения (3.9) получаем
1[р«<-(Ы,-^р = о.
Отсюда в силу произвольности объема V следует равенство
нулю подынтегрального выражения, что и является искомым
уравнением движения:
pui^iMt+P*. (3.11)
dxk
Если деформированный объем находится в равновесии (и{ не
зависят от времени), то следующее из (3.11) уравнение
^ + (/об)< = 0 (3.12)
дхк
является уравнением равновесия деформированного тела.
Отметим, что в равновесии деформированное состояние
упругого тела может поддерживаться только внешними силами, в
частности приложенными к его поверхности. При этом
последние войдут в граничное условие к уравнению (3.12), а именно:
если р{ есть поверхностная плотность внешних сил, то в
соответствии с (3.3)
Pi=Giknh\8. (3.13)
11.2. Тензор модулей упругости. Теперь, для того чтобы
иметь возможность решать уравнение (3.11), необходимо
выразить тензор напряжений через тензор деформаций, к чему мы
сейчас и перейдем.
В общем случае при упругих деформациях между тензорами
напряжения и деформаций должна существовать
взаимно-однозначная связь типа Ofc=G<A(eiz). При достаточно малых
деформациях разложением функций Gih в ряд Тейлора получаем ли-
44

нейные соотношения между а* и ejt—обобщенный закон Гука:
aik=Cwe»* (3.14)
где Cihji=(dGih/deji)0—тензор четвертого ранга, являющийся
характеристикой вещества. Он называется тензором модулей
упругости. Поскольку каждый индекс в Cikji принимает три значения,
тензор модулей упругости не может иметь более 81
независимой компоненты. В самом же деле их существенно меньше.
Действительно, воспользовавшись симметрией тензоров oih и
ejh установим свойства симметрии тензора Ст. Для этого
запишем цепочку тождеств
Oik = Cikjiefi = Cikijeij = Cjkijefi = вы = Cktt&th
Если теперь попарно приравнять подчеркнутые члены
(Cih]i— Cikij) eit= О, (Cikji—Caw) ец=0,
то из произвольности тензора eit следует равенство нулю
выражений в скобках, т. е.
См=Сад, С*ш=Cjwi. (3.15)
Следовательно, тензор модулей упругости симметричен
относительно перестановки индексов в первой и второй парах.
Теперь не составляет труда подсчитать, что число
независимых компонент тензора упругости не превышает 36.
Действительно, при фиксированных i и k имеется лишь шесть
независимых величин Сш. В свою очередь, к независимым Cikn приводят
лишь шесть из возможных девяти комбинаций индексов i и k.
Более того, можно показать, что число независимых компонент
тензора Cikjl должно быть фактически еще меньшим. Для этого
следует воспользоваться энергетическими соображениями.
§ 12. Энергия деформированного тела
12.1. Плотность энергии. Для того чтобы деформировать
упругое тело, нужно совершить определенную работу. Рассчитаем
эту работу в предположении, что деформация тела совершается
квазистатически, т. е. настолько медленно, что в каждый момент
времени тело находится как в механическом, так и в
термодинамическом равновесии. Выделим некоторый объем тела V,
ограниченный поверхностью S с внешней нормалью п. На этой
поверхности в соответствии с (3.4) распределены силы o^nhy
действующие на наш объем. Пусть вектор смещений и{(т) получает
приращение бы, (г). Работа поверхностных сил, совершенная над
телом при этом переходе, будет 6Л= ) офхЬщйЭ. По теореме
Гаусса — Остроградского для вектора о*6и{ получаем
45

При квазистатическом процессе первый интеграл справа
обращается в нуль согласно (3.12) и предположению об отсутствии
объемных сил (/Об = 0). Второй же интеграл выражается через
тензор деформаций, так как в силу симметрии тензора о^
oih6(du{/dxh) = (о*/2)6[ (dujdxk) + {dujdx<) ] =с*6еЛ.
С другой стороны, работа 8А изменяет внутреннюю энергию
выделенного объема. Если также учесть возможное изменение
энтропии, то по известному термодинамическому тождеству
имеем
\tedV = j ТШУ+ \oik6eikdV,
V V V
где е и s — внутренняя энергия и энтропия единицы объема
соответственно; Т — температура. В силу произвольности объема V
последнее соотношение может быть записано в
дифференциальной форме
de^Tds+Oikdetb. (3.16)
Если вместо внутренней энергии е ввести свободную энергию
/=е—Ts (df=ds—sdT—Tds), то выражение (3.16) примет вид
df=—sdT+oikde^ (3.160
Последняя запись более удобна для изотермических процессов.
Таким образом, если известны е или f как функции s, eih или
7, eikf то компоненты тензора напряжений о* могут быть
найдены из соотношений
oik= (де/де<ь)а= (df/deih)T. (3.17)
Если в процессе деформирования тела мы все время остаемся в
рамках адиабатического или изотермического процесса, то
дифференциал dW=oihdeih имеет смысл дифференциала запасаемой
в теле энергии. Функцию W(eih) называют, может быть
несколько условно, потенциальной или упругой энергией. Соотношение
(3.17) в этих обозначениях записывается в виде
oik=dW/deih. (3.17')
В соответствии с обобщенным законом Гука (3.14) oik—
линейная функция е^. Следовательно, И?(е*) должна быть
однородной квадратичной функцией компонент тензора деформаций:
W=42Cmeihe5l. (3.18)
Нетрудно видеть, что из (3.170 и (3.18) с учетом соотношений
симметрии (3.15) следует (3.14).
Компоненты тензора модулей упругости CikJi будут разными
в зависимости от конкретного термодинамического процесса,
поскольку W—e для адиабатического процесса и W=f для
изотермического. В соответствии с этим вводят адиабатические и
изотермические упругие постоянные.
46

12.2. Число независимых компонент тензора Модулей
упругости. Воспользуемся выражением (3.18) для подсчета
независимых компонент тензора Сти Прежде всего заметим, что этот
тензор всегда можно определить так, чтобы он был
симметричен по перестановкам'пар индексов ik и jl:
Cihil,=zC}lih- (3.19)
Действительно, учитывая, что немые индексы можно
переставлять как угодно, имеем
W = —Cikiieikefi = —(Cibfieikefi + CfukefAidfi =-^С'т&и&п*
где тензор С/т={С<ш+Ст)/2 уже удовлетворяет требуемым
свойствам симметрии.
Подсчитаем число связей, даваемых соотношением (3.19).
Число независимых пар ik9 как и пар //, равно шести, а не
девяти в силу симметрии ло отношению к индексам внутри каждой
пары. Очевидно, что число уравнений (3.19) равно числу
сочетаний из шести пар по две, т. е. (6Х5)/2=15. В результате
заключаем, что максимальное количество упругих постоянных
кристалла самой сложной симметрии не может превышать
36—15 = 21. Чем выше симметрия кристалла, тем меньшим
количеством различных упругих постоянных он описывается.
Рассмотрим, например, кристалл с кубической решеткой.
В нем направления хи х2 и xs равноправны. Поэтому
^1111==^2222=ЬззЗЗ- (3.20)
Далее, имеется зеркальная симметрия, т. е. если замеиить дг< на
—Xi (ur+—Ui)y то ничего не должно измениться. Но при этом
согласно (3.6), например, е12->-—ei2. В этом случае величина W
не изменится, если члены типа Ciii2enei2 будут отсутствовать.
Обобщая это утверждение, можно сказать, что Cifti,= 0, если
какой-либо индекс в четверке встречается нечетное число раз
(один или три раза). В результате наряду с (3.20) остаются
отличными от нуля компоненты Сц22 = С22п = С1Ш = СЗЛ11 =
г=С2239 = Сзз22, С1212==С2121==С1221==С2Ц2= . . .1=Сз223- С уЧеТОМ ЭТИХ
соотношений плотность энергии (3.18) для кубического
кристалла запишем в виде
+
+ 4C1212(^ + ^13 + ^3)]. (3.21)
§ 13. Упругое поведение изотропных тел
13.1. Обобщенный закон Гука для изотропного тела. Выражение
Для энергии в изотропном упругом теле не должно меняться при
любом вращении системы координат. Это означает, что в него
Должны входить лишь инварианты тензора eih (см.
приложение). Так как, с другой стороны, W является однородной квад-
47

ратичной функцией eik, то ее вид определяется однозначно:
W = ±(exl + e22 + e33f+ |i (e"u + ^ + ^ + 2^ + 2^ + 2^),
где Л- и [I — два скаляра, так называемые упругие постоянны^
Ламе. Теперь по формуле (3.17') находим
Gih=dW/deik=Kejfiik+2iie{ki (3.22)
что и является обобщенным законом Гука для изотропной среды.
Сравнивая (3.22) с общей формулой (3.14), получаем:
Сип== А+ 2^1, C»iai2 = 2|A, С1122==Л. (о.2о)
Остальные, отличные от нуля компоненты тензора модулей упру4
гости получаются циклической перестановкой индексов с уче^
том свойств симметрии. Отметим, что имеется равенство С11И =
= ^1122 "Г^ 1212»
13.2. Связь постоянных Ламе с Е и v. Очевидно, что посто-j
янные Яиц должны выражаться через введенные в § 1 модуль]
Юнга Е и коэффициент Пуассона v. Для того чтобы найти со-!
ответствующие выражения, рассмотрим два простейших вида;
деформации.
1. Растяжение стержня при запрещенных боковых
смещениях^ Эффективный модуль Юнга £,эф= (1—v)£"/[(l+v) (1—2v)]:
для этого случая получен в задаче 1.3. Выразим его через
постоянные Ламе. Здесь деформация будет однородной, причем
a2 = u3 = 0. Согласно определению тензоров напряжения и
деформации имеем o11=Feci/SXl, M/l=[ui(xi + kxi)—u(xi)]/&xi =
= ди1/дл:1 = е11. При вычислении Д/// учтено, что вследствие
однородности деформации относительное удлинение всего стержня
такое же, как и бесконечно малого его отрезка. В результате с
учетом (3.22) и выражения для £эф получаем
Fxx /1 . о ч с Ь1 (1 —v) £
—- =<Jii = (^ + 2ц)еи = £Эф— = —- - еп.
Sx. и \ ' г/ и ф l (1+v)(1_2v)
Отсюда следует соотношение
Х+2^= (l-v)£/[ (1 +v) (1—2v) ]. (3.24)
2. Всестороннее сжатие. Объемный модуль сжатия К дается
выражением (1.5). В этом случае а11 = о22=0зз = —Р, AV/V=
= ец + е2г+ел$ = 3еп. Из (3.22) имеем Оц = (2\i+3X)eiiy
следовательно, р= — [(2[А + ЗЯ)/3] (ДК/К). Сравнивая последнее
выражение с (1.5), находим
2jx+3>j=£/(1— 2v). (3.25)
В результате из (3.24), (3.25) получаем искомые выражения:
(l+y)(l_2v)' р 2(l+v)' х+и'Г '
v = - . (3.26)
2 <* + !*>
48

Отсюда видно, что постоянная Ламе \х совпадает с модулем
сдвига, определяемым выражением (1.9).
13.3. Уравнения движения для изотропной среды. После того
как найдена связь между тензорами напряжений и деформаций
в виде формулы (3.22), не составляет труда конкретизировать
уравнения движения (3.11). Из (3.22) находим
л*. г дхи ^ '* дх. г дх. дх. дх. дх.
dxk °xk dxk dxk \ dxk dxt J дх.
но deJdXi^deJdx^diduJdx^/dXi, где dujdxh=ekh=8 —
относительное изменение объема. Теперь
dxk * дх* ^V ^Ч
Учитывая также, что d2ujdxh2 = Ди<, где Д — оператор Лапласа,
уравнение (3.11) запишем в виде
р -^1 = ц Ли, + (X + ц) -£- + (/*)„ (3.27)
или в векторной форме, поокольку G = divu, a dQ/dx{—i'-я
компонента градиента:
P-S" = Iх Аи + (1 + и) Srad div u + *<*• (3-28>
01л
Уравнения равновесия получаются автоматически, если
положить в (3.27) или в (3.28) левую часть равной нулю:
^Au+(X + ^)graddivu+fo6 = 0. (3.29)
При решении конкретных задач часто бывает полезным
использовать иную форму уравнений, которая получается из
(3.27) — (3.29) с учетом известного векторного тождества Ди =
= graddivu—rot rot и. Тогда, например, (3.29) запишем в виде
{X + 2\х) grad div u—\i rot rot u + fo6 = 0. (3.30)
Задачи
3.1. Какому виду деформации соответствуют следующие тензоры
напряжений:
1. а<* = а при i=k, (лл=0 при Ьфк.
Решение. Напряжения по всем осям одинаковы, следовательно,
всестороннее сжатие
2. Gik = o при /, Л=1, 2, 3.
Решение. Найдем вид тензора в главных осях. Характеристическое
Уравнение (см. приложение) (а—Х)3+2а3—За2(а—Я)=0 имеет корни ^ = 30,
2==^з==0. Следовательно, в главных осях отлична от нуля только
компонента сгц'^За, что соответствует растяжению (сжатлю) вдоль оси х\.
49

3. ai2=o*2i = a, остальные a,* = 0.
Решение. Поскольку отличны от нуля и равны друг другу лишь два
недиагональных элемента тензора напряжений, то он соответствует чистому
«сдвигу. В главных осях ац'=— 022'=а и а33'=0 (см. также п. 2.3).
3.2. Определить максимальные нормальное и тангенциальное напряжения в
некоторой точке, напряженное состояние которой описывается тензором о\л.
Решение. Целесообразно рассмотреть задачу в главных осях, где
тензор напряжений имеет диагональный вид с сги = Хь о22=^2, Озз=Яз. Выражение
для силы, действующей на площадку с нормалью n={/ii, П2, пз}> запишется в
виде F«={A,ircb X2n2l Х^гн). Нормальная компонента силы равна /7п=Лл< =
^^/г^+Хг^+^зЛз2, тангенциальная — соответственно Ft2=sF2—Fn2=
= Xl2nl2+X22n22+Xu2n<i2— (Mi2-f-M22+A,3n32)2. Для того чтобы найти
максимальные напряжения, нужно определить условные экстремумы функций
Fn(nu п2, Из) и Ft2(nu п2, п3) при уравнении связи n<2=Mi2+n22+^32=l.
Составляя, например, для Fn функцию Лагранжа On=Fn+y(tn2—1), находим
экстремальные точки как решение системы уравнений:
дФл/ди1 = 2(Х1 + у)л1=»0, (Х2 + У)п2 = 01 (Х9 + у)п3 = 0 л!=1.
* Предполагая все Я» различными, получаем решения системы:
a)nl=»±lf Ла = пз="0, F-A*, dO = 2 (Яа - Xt) dn\ +
+ 2(XZ-X1)dn\y
1) tL - ii ~ 0, «a=-J=l, F^X., <*!>„ ;= 2 (Xi - X2) dn\ +
+ 2(XZ-X2)dn\,
B)n1=-na=-0, rt3=±l, F„ = X8, dQ>n=n2(X1 — Xz)dn\ +
+ 2(X%-Xz)dn\.
£сли для определенности Я1>Я2>Яз и |^i|>|X3|, то max|Fn| = |Xi|.
Аналогичная система уравнений для тангенциальных напряжений имеет
-вид:
пг [Х\ - 2^ (Mi + Х2п22 + Xin2) + V] = 0,
л. [Х\ - 2Я* (MJ + Х2п\ + Хзп28) + V] = 0,
n3lXl-2b8(k1nl + X2nl + \9nl) + y]==Oi п2=1,
решением которой, соответствующим минимуму тангенциального напряжения
(Ft2 = 0)t будет направление главных осей. Максимум Ft2 достигается в
точках:
п8 = 0, л1 = л1= ±|^2/2, Fi = (X1-X2)/2t
щ = 0, пх = л3 = ± /2/2, F, = (Xt- ХО/2,
П1 = 0, П2=Лз=±К2/2, ^ = (Я,-Яз)/2.
Следовательно, максимальное тангенциальное напряжение достигается на
площадке, делящей пополам угол между направлениями максимального и
минимального главных напряжений.
50

3.3. Выразить тензор etk через о*<а в обобщенном законе Гука для
изотропного тела.
Решение. Воспользовавшись (3.22), найдем свертку
Okk = ЗХет.п + *№тт = № + 2& етт .
откуда следует, что emm=(5mml(Z\+2\k). Теперь (3.22) можно записать и так:
а<-*= ЗЯ + 2(Х °тт ** + *»*»•
В результате получаем
*ik = 1JT V'* ~ ~ЗК+2^°тт *'*) в
3.4. Рассчитать на основе обобщенного закона Гука растяжение стержня
длиной / и поперечной площадью S под действием силы F. При этом найти
связь между постоянными £, v и X, ц.
Решение. В данном случае отличной от нуля будет только компонента
тензора напряжений оц. Следовательно, атт = Оц и по формуле предыдущей
задачи:
611 = 2ц V " ЗЯ. + 2И/ GU ~~ I* ЗХ + 2ц °ш
Но G\\=F/S, вц=А///, e22=AA//i, где Л —размеры стержня в одном из
поперечных направлений. Тогда в соответствии с (1.1) и (1.3) ец — Gn/E, е22=
=— vo~n/£. В результате получим выражения (3.26) для £ и v через X и ji.
3.5. Определить деформацию сплошного шара радиусом R, помещенного в
жидкость с давлением р. Найтн относительное изменение объема шара.
Решение. Запишем уравнение равновесия шара (3.30) с fo6=0:
(Л + 2fi) grad div u — u rot rot u = 0.
В силу сферической симметрии u=£/(r)r/r, при этом очевидно, что rotu = 0 и
divu=3C=consl. Но
«-[^f]-v(i)+,f-.i +
/i/'-l/ г
г—*—:
U
= U'+2 — = — (r*U)'t
поэтому U(r) = Cr+d/r2. Вследствие условия ограниченности U при г=0 имеем
^=0, т. е. U=Cr. Определим компоненты тензора напряжений (рис. 3.4):
V = X («„ + ",„,+ «„<,) + 2раг/. = (ЗХ + 2ц) и„ = (За + 2ц) С.
Из-граничного условия аГг|г=я = —р окончательно имеем:
с=—Р/(Зл+2ц), (/•=— рг/(3л+2ц).
51

Относительное изменение объема
АУ _ [R + U(R)]*-R* _
V ~~ R9
Зр ^ _ Л
К
[+Т1
— 1
U(R)
ЗК + 2[1
;лак-и должно быть, определяется формулой (1.5).
3.6. Определить деформацию упругого пространства
с шаровой полостью радиусом Rt давление внутри
которой р.
Решение. Как и в задаче 3.5, и=£У(г)г/г, где
U=bf+a/r2. Из условия ограниченности смещения на
бесконечности 6=0, т. е. и(г)=а/гг. Далее, аГг=
=М (—2а/г3) + (а/г3) + (а/г*) ]—2ц2 а/г3=-4|ia/r3. Но
агг|л=— 4[ш/#3=—*р, откуда a=pR5/4\i и,
следовательно,
r+VM
Рис. 3.4
— 7
1 р Я» г
Г» Г
3.7. Определить деформацию бесконечного полого цилиндра, наружный и
внутренний радиусы которого равны Rx и R2 соответственно, предполагая, что
давление внутри рь а снаружи р2.
Решение. Положив, как и в задаче 3.5, divu = C, u = U(r)r/r
^■{|Ь х2})> найдем dlvи—TV(Ulr)+2Ulr=*r-ld(rU)ldr=C. Отсюда
U^Cr/2+bfr, urr=>dU/dr=C/2-b/r*y u^^Ufr^ С/2+ b/r*t
arr-(* + |i)C-2|i*/r«.
Из граничных условий находим:
(Х+ ц) С—2fib//?!2=—Pi, (Х+ц) С—2|Li6//?22«— р2,
<что дает
/tfpjL —/ffifr Pi—ра ^i^> 1
U = - : г"г+
2 (*+rt (*;-*;)
2Ц
■«;
3.8. Определить деформацию Цилиндра радиусом /?, вращающегося вокруг
,своей оси с частотой со.
Решение. В системе координат, связанной с цилиндром, имеем
объемную (центробежную) силу с плотностью !об = рсо2г, так что уравнение
равновесия примет вид (A,+2|i,)graddivu—jirot rotu=pco2r. Как и выше, и =
= U(r)r/rt rotu=0, divu=r-l(r£7)', grad divu= [r-{(rU)']'r/r=— pco2r/
/(K+2\i)y так что
1 d Г 1 d I
pco*
X + 2ц
Отсюда
c7 =
pco3 г3
Я + 2^г 8
6r
52

Далее,
1 К 3 и
а =* — рсо2г2 — — рсоМ + (X + и) &.
Приравняв (7гг|л=0, найдем &=1рю2#Ч(Х+2ц)][(2Х+3|1)/(Х+м.)] и
окончательно
8(X + 2ji) v Я. + И- ;
*Глава 4
ВОЛНЫ В УПРУГИХ СРЕДАХ
В этой главе мы продолжим исследование волновых движений
в твердых упругих средах, начатое в гл. 2. Здесь из общих
уравнений теории упругости будут получены волновые уравнения для
двух типов волн, распространяющихся в упругих средах:
продольных и поперечных. Подробно исследуются также простые
решения этих уравнений в виде плоских волн, процесс их
отражения от плоских границ. Будут рассмотрены также
поверхностные волны Релея и Лява.
§ 14. Свободные волны
в однородной изотропной среде
14.1. Продольные и поперечные волны. Рассмотрим, какие
волновые движения могут существовать в упругой среде. Для
изотропных сред нужно исходить из уравнений движения (3.28).
Ограничимся лишь свободными волнами, положив fo6=0:
д2и
Р—= nAu + (*>+n)graddivu. (4.1)
at*
Это уравнение не похоже на обычное волновое, так как в нем в
неявном виде содержатся уравнения для двух типов волн —
продольной и поперечной. Для того чтобы убедиться в этом,
представим вектор смещения и в виде:
u=u2 + ut, u, = grad<p, u, = roti|>, (4.2)
гДе ф и ij) — функции времени и координат, называемые в
дальнейшем скалярным и векторным потенциалами. Заметим, что в
таком виде можно представить произвольный вектор и. При
этом векторы U/ и и, удовлетворяют уравнениям:
rotu; = 0, divu, = 0. (4.2')
53

Подставляя (4.2) в уравнение (4.1), с учетом grad diviii=s
= Ди* получаем
^_М^Ди/ + ^_^Ди,= о. (4.3)
Считая среду однородной (р, X, ц — постоянные) и применяя к
(4.3) поочередно операции div и rot, с учетом (4.2') имеем:
\дР р V \dfi р 1
dlyfe.-JLA.uUo. rot&-JLAu,U0.
\dt* p ) \дР p V
Но если div и rot некоторого вектора равны нулю, то без
ограничения общности можно положить этот вектор тождественно
равным нулю, считая, что и, и uf определяются с точностью до
произвольного, зависящего только от времени вектора. В
результате мы получили два волновых уравнения:
dt2 р dt* р
Аналогичные уравнения справедливы и для потенциалов <р и
if. Их легко получить из уравнений для и* и и, соответственно.
При этом следует учесть, что скалярный потенциал ф может
быть определен с точностью до произвольной функции времени,
а векторный ф — с точностью до произвольного потенциального
векторного поля A = gradf(*i, х2у xs, t). Волновые уравнения для
Ф и if обычно записывают в таком виде:
дгф? = с? Аф, с? = (К + 2ц) /р,
(4.4)
d2q/dt2 = ct2Mbt ct2 = ix/p.
Нетрудно убедиться, что решением уравнения для ф является
ф=/(пг-с,0, (4.5)
где f—произвольная достаточно гладкая функция; res
= {*i, *2, х*}—радиус-вектор; п — единичный вектор
произвольного направления. В самом деле, вводя £=nr—ctt, имеем
dw d* dm " 2 d2q> „
= -X--^- = — C/-^-, <f> = a-±. Далее, с учетом nr=/i<*i
a% at at, aga
получаем:
ftp __ J<v_ Jt_ = dy а2ф __ 2 &y_
dXi dg дхх г (% дх* x d? '
Аналогично вычисляя производные по х2 и xSy находим
дф = .*£=я.**_*Ф, таккак П2 = у1Л1 = 1.
т а** • <• <*? tix
54

Таким образом, мы видим, что уравнение (4.4) для ф
удовлетворяется.
Покажем, что выражение (4.5) описьшает волну, которая без
изменения формы перемещается в направлении п со скоростью
сг. Действительно, ср остается постоянным в точках, где
nr—с^=const, (4.6)
которые в любой фиксированный момент времени t лежат в
плоскости, перпендикулярной п и называемой фронтом волны,
С изменением времени фронт перемещается в пространстве,
оставаясь перпендикулярным п. Скорость перемещения легко
найти, дифференцируя (4.6) по времени: ndr/dt=Ci. Отсюда
видно, что скорость перемещения фронта (скорость волны) равна
Си Волны с плоскими фронтами, как, например, волна,
описываемая выражением (4.5), называются плоскими волнами.
Наконец, нетрудно видеть, что (4.5) описывает волну,
смещения в которой происходят в направлении распространения
волны п (продольная волна). Это видно из (4.2), поскольку и =
= grad(p, ui=d(p/dxi=nid(f/dli u = nd(p/d|.
Аналогично можно убедиться, что решение второго
уравнения (4.4) имеет вид
*=F(nr—с,/), (4.7)
где F — произвольная вектор-функция скалярного аргумента
£ = nr—ctt. Это также плоская волна с фронтами,
перпендикулярными направлению распространения п. В отличие от
продольной волны смещения в последней перпендикулярны п
(поперечная волна). В самом деле,
u = rot*=VX*=nXdi|>/d£-Ln.
Рассматриваемую волну называют также сдвиговой,
поскольку, как нетрудно убедиться, воспользовавшись системой
координат, одна из осей которой совпадает с п, из всех
компонент тензора деформаций отличны от нуля лишь
недиагональные, описывающие, как мы видели ранее, сдвиговые
деформации. Скорость распространения поперечной волны равна ct и
совпадает со скоростью волн кручения в стержне.
Сравнивая сг и си определяемые выражениями (4.4), видим,
что с,/с,=У(^+2^)/ц._Поскольку всегда \i>0 и для реальных
веществ Я>0, то сг>^2си
Отметим, что величина
1 р (l+v)(l — 2v)p р
определяется эффективным модулем Юнга при растяжении
(сжатии) стержня с запрещенными боковыми смещениями (см.
задачу 1.3). Именно такие растяжения и сжатия происходят в
55

продольной волне: смещения, перпендикулярные направлению
распространения, равны нулю.
Частным, но весьма важным случаем плоских волн (4.5) и
(4.7) являются гармонические плоские волны:
Ф = А expU —Спг — Cit)] = А exp [i(кг — со/)], к = —п,
I ci '] ci
(4.8)
•ф = В exp \i — (пг — ctt)] = В exp [i (иг — со/)], и = — п,
L ct \ ct
где А и В — произвольные комплексные постоянные; к и и —
волновые векторы; £=|к| и х= |х|—волновые числа; со —
частота волны; соответственно период Г=2я/со и длины волн Хг=
= 2я/£ = 2лС//со, А,* = 2я/х=2яс*/со. Для продольной и_поперечной
волн одинаковой частоты &/x = ct/c/ss:y2/2, ЯД^У2. Если
совместить, например, ось xt с направлением волновых векторов,
то
Ф=Л exp[i(kxt—со/) ], tf=B exp[/(x*i—со/) ]. (4.9)
Выражения для потенциалов волн, распространяющихся в
обратном направлении, запишем в виде:
Ф=Л ехр[—iikXi + at) ], i|>=B ехр[—f (хл^ + со/) ]. {4.10)
Заметим, что продольные и поперечные волны
распространяются без дисперсии (скорость распространения не зависит от
частоты). Именно поэтому плоские волны произвольной формы
(4.5) и (4.7) распространяются без искажений.
14.2. Граничные условия для упругих волн. В безграничной
и однородной упругой среде продольные и поперечные волны
распространяются независимо, не взаимодействуя друг с
другом. Если же параметры Л, \i и р меняются в пространстве, то по
мере распространения, например, продольной волны возникают
поперечные и наоборот. Эти процессы проще всего проследить
на примере отражения плоской волны от плоской границы
между двумя различными средами. В этом случае волновые поля в
каждой из сред будут описываться уравнениями (4.4) с
соответствующими значениями параметров с* и сД Взаимодействие
волн будет осуществляться на границе и должно учитываться в
граничных условиях. Рассмотрим граничные условия на
некоторых типах границ раздела.
1. Граница между двумя упругими полупространствами без
проскальзывания («склейка»). При этом на границе раздела S
должны быть равны векторы смещения и одноименные
компоненты тензора напряжений, соответствующего площадке на
Границе:
(«p>-»f>)s = o, K?-o<3?)s = o,
где /=1, 2, 3; п — индекс оси, направленной нормально к 5.
56

2. Граница между двумя упругими полупространствами с
проскальзыванием («смазка»). Равны нормальные смещения и
напряжения, касательные напряжения обращаются в нуль:
к° - «г»)я =0' <«й - os>s =°- <# и- <# is=o. /*«•
Во втором выражении суммирования не происходит, несмотря
на повторяющийся индекс.
3. Граница с абсолютно жестким телом при наличии
«склейки»:
к,|в = 0, /=1,2,3.
4. Граница с абсолютно жестким телом при наличии
«смазки»:
и«|я = 0, оП;|в = 0, \фп.
5. Граница упругого тела с вакуумом (свободная граница):
OniU = 0, /=1,2,3.
Рассмотрим, например, как будет происходить отражение
упругих волн от свободной границы. Пусть уравнение граничной
плоскости есть х$ = 0 и ось х3 направлена из упругой среды в
сторону вакуума. Граничные условия будут
031 | х3=0 = 032 U=o = Ом | «з-о = 0. (4.11)
Выберем направление осей хи х2 так, чтобы нормаль к фронту
плоской волны, падающей из упругого полупространства на
границу, лежала в плоскости xtxs (плоскость падения). Тогда
мы будем иметь плоскую задачу, причем от координаты хг
никакие величины, характеризующие волны, зависеть не будут.
Выразим компоненты тензора напряжений, входящие в
граничные условия (4.11), через вектор смещений и,
воспользовавшись законом Гука (3.22) и формулой (3.6). Тогда граничные
условия запишем так:
\дх9 axj^, дх,\х^0 Г ™ дх% дХ1\х^0
(4.12)
Учитывая, что плоскость падения волны, по предположению,
совпадает с плоскостью xtxit видим, что падающей может быть
одна из трех волн:
а) поперечная волна, смещение в которой перпендикулярно
плоскости падения: и2ф0, и± = и3 = 0; в сейсмологии, имея в виду
отражение волн, приходящих из глубин земли на ее поверхность,
эту волну называют горизонтально поляризованной;
б) поперечная волна со смещением, лежащим в плоскости
падения: щфО, и*ф0, и2=0;
в) продольная волна, смещение в которой лежит в
плоскости падения: и±ф0, и^фО, ы2 = 0.
57

Волны «б» и «в» называют вертикально поляризованными
волнами.
В силу линейности уравнений (4.4) и граничных условий
(4.12) справедлив принцип суперпозиции, так что можно
рассматривать отражение различно поляризованных волн
независимо.
Заметим также, что в (4.12) первым и третьим граничными
условиями взаимно связаны на границе производные от ui и ы3.
Эти условия не содержат и2. Наоборот, второе условие содержит
только и2. Это означает, что при отражении волны типа «а»
волны типа «б» и «в» не возникают. В то же время эти две
последние волны на границе могут взаимодействовать и их нужно
рассматривать совместно. Другими словами, волны
разделяются по принципу поляризации. Волну горизонтальной
поляризации можно рассматривать независимо от волн вертикальной
поляризации. В дальнейшем мы ограничимся только отражением
гармонических волн.
14.3. Отражение горизонтально поляризованной волны.
В этом случае смещение в падающей ( + ) и отраженной (—)
волнах запишем так:
«2+ = К exp [i (x^i + щх3 — cot)],
"2- = *L exp [I {\хх — н'3х3 — w'f)], (4.13)
где b+ и b-— комплексные амплитуды волн. Так как хь х3 и
и/, Из'— компоненты волновых векторов в падающей и
отраженной волнах, то
XJ + xj = ха = ©»/£*, х? + и;' = х'" = ©'"/<?. (4.14)
Подставляя сумму выражений (4.13) в граничное, условие
(duJdXi) Жз-о = 0, получаем
b_=-^b+exp{t[(x1-x;)x1-((o-co')/]}, (4.15)
что может быть выполнено при всех Xi и t только в случае, если
о)/ = (о и x/=Xi. Таким образом, при отражении от неподвижной
границы частота волны не меняется (о)/ = со, х' = х) и проекция
волнового вектора на границу (ось xt) также не меняется (х/=
= Xj). Согласно (4.14) это означает также и х3'=х8, так что
b- = b+, (4.16)
т. е. амплитуда отраженной волны равна амплитуде падающей.
Коэффициент отражения У=Ь_/Ь+ равен единице.
Равенство x/ = Xi имеет простой физический смысл.
Действительно, запишем (4.13) в виде:
и2+ = b+ехр (т3дс3) exp [ i {\xi—(ot) ],
u2- = &-exp (—i'x3x3) exp [ t(%Xi—®t) ],
58

Рис. 4.1
-н
/7
ф
fi,**,/*
Ъ
ft'^nft
i
Рис. 4.3
Рис. 4.5
где 1 = х, = х/. Таким образом, падающая и отраженная волны
имеют общую зависимость от jc± и t в виде фактора
exp[l'(l*i—(dOL т. е. скорость передвижения волн вдоль
границы одна и та же, равная v = со/|. Назовем углом падения ч угол,
составленный нормалью к фронту падающей волны и осью xs
(рис. 4.1), и углом отражения ч' аналогичный угол для
отраженной волны. Тогда, очевидно, g = X! = xsinf = xsin^/ и равенство
^i,=x1 означает также y' = Y— угол падения равен углу
отражения.
Отметим, что равенство частот и проекций волновых
векторов на границу для падающей и отраженной волн получено из
требования выполнения граничных условий для всех точек
границы и любых моментов времени. Это обстоятельство является
59

общим правилом при исследовании явлений отражения, а также
преломления волн (исключение составляют движущиеся
границы). Поэтому в дальнейшем мы всегда будем полагать в
отраженных и преломленных волнах частоты и проекции волновых
векторов на плоскую границу равными соответствующим
величинам в падающей волне. Провести доказательство этого
факта в каждом конкретном случае не составляет труда.
§ 15. Отражение
вертикально поляризованных волн
15.1. Коэффициенты отражения и трансформации. В этом
случае w2=0, а щ и us в граничных условиях (4.12) целесообразно
выразить через потенциалы в соответствии с (4.2):
JUL_$h ^ + |h. (4Л7)
дхх д*з д*з дхг
Из трех компонент вектора t|> здесь фигурирует лишь i^, индекс
у которой в дальнейшем будем опускать. Подстановка этих
выражений в первое и третье граничные условия (4.12) дает:
дххдх3 дх* д£ )
[ \дх\ dxxdxzJ удх^ л*а
= 0. (4.18)
сРф
Учтем теперь, что падающая и отраженные волны зависят от
времени t и координаты xt (вдоль границы) одинаковым
образом, а именно содержат один и тот же множитель
exp[i(gjti—со/)]. Поэтому имеем dldXi = i\, d/dt=—/ш, а
волновые уравнения (4.4) и граничные условия (4.18) запишем так:
-^ + (#-£а)ф = 0, ^i+(xa-^)^=0, k=<o/ch к=<о/ъ,
дх\ дх\
(4.19)
(£+<*L-(£-*•)_-* '-т(«'-7-)-
Если для сокращения записи опустить один и тот же фактор
expi(£*i—cotf), то общее решение уравнений (4.19) примет вид:
<р=а.ехр (—iksXs) +а+ехр (ikzxb), &3=Vfc2—I2,
(4.20)
i|)=6_exp (—ixs*s) +&+ехр (ws*s), х3=Ух2—I2
Здесь а. и Ъ-—постоянные, имеющие смысл амплитуд
соответственно продольной и поперечной волн, распространяющихся в
сторону отрицательных xs, а а+ и Ь+— то же, для волн,
распространяющихся в сторону положительных xs.
60

Подстановка выражений (4.20) в граничные условия (4.19;
дает связь между амплитудами:
k3(a+—а_)+/?(*>+ + &-)= 0,
(4.21>
кл(Ь+-Ь-)-р(а++а-)=0.
Эта система уравнений описывает все случаи отражения от
свободной границы плоских гармонических волн с поляризацией в
плоскости падения. Так, например, если на границу падает
только продольная волна (6+s=0), то, обозначив через Vti=a-/a+
коэффициент отражения продольной волны, Vlt =
b-/a+—коэффициент трансформации продольной волны в поперечную,
получаем:
k&b + P* Мз + Р*
Коэффициенты Vn и Vtt можно выразить также через угол
падения волны. Напомним, что величина | равна проекциям
волновых векторов продольной и поперечной волн на ось хи
равенство которых обусловлено одинаковой скоростью
распространения всех волн вдоль границы. Обозначим через в угол
падения продольной волны, составленный нормалью к фронту волны
и осью х*. Имеем очевидное (рис. 4.2, а) соотношение
%=k sin 0 = х sin Y, (4.23)
позволяющее найти угол отражения поперечной волны f при
заданном 0. Учитывая определение Лихв (4.19), получаем
sin y = (ct/ci)sm 0 = —sin 0. (4.24)
х
Поскольку всегда ct<Zch то всегда и ^<0. Далее, нетрудно
получить &8 = k cos 0, х3=х cos f, р=—xsctg 2у и
у cos 6fg>2Y-(c//c<) cosy ^ 2coseig2y
cosQtg%2y + (ct[ct)cosy ' cos 0 tgf 2y + (ctfct) cos у
(4.25)
^Аналогичные формулы получаются и при падении
поперечной волны (a+s=0). Отсаженными будут поперечная и
продольная волны (рис. 4.2, б). Для коэффициентов отражения
поперечной волны Vtt = b-/b+ и трансформации поперечной волны в
продольную Vtl=a-fb+ получим:
Vtt = Vlh V =-3L^=—C-^VU. (4.26)
Л8 ctCos "
15.2. Особые случаи отражения. Рассмотрим некоторые
свойства коэффициентов отражения и трансформации. Так, при
нормальном падении имеем 0 = ^ = 0, Vn=Vtt=—1, Vlt=Vtl = 0 —
полное отражение с изменением фазы волны на я, трансформа-
61

ция волн отсутствует. Заметим, что случай нормального
падения поперечной волны ничем не отличается от рассмотренного
в п. 14.3 отражения горизонтально поляризованной волны.
Однако там для коэффициента отражения получилось значение +1.
Отличие объясняется тем, что выше речь шла о коэффициенте
отражения для волны смещения и2у в то время как здесь — о
коэффициенте отражения для потенциала волны \f>. Поскольку и2
получается из tf> операцией д/дхл, то это и дает разные знаки для
коэффициента отражения.
Интересная особенность при отражении наблюдается в
случае, если
cos0tg22v = —cosy, (4.27)
ct
при этом Vu=Vtt = 0, Vlt=— ctg2f = — (c,cos8/CjCOS4)tg2f.
Падающая продольная волна при отражении полностью
трансформируется в поперечную и наоборот. Выразив с помощью (4.24)
Ч через 6, можно получить выражение для угла падения 0, при
котором происходит такой переход. Оказывается, что для всех
возможных комбинаций упругих постоянных угол 0 лежит в
пределах 37°<0<9О°. При этом соответствующий угол у находится
в интервале 25°<ч<45°.
Посмотрим, когда, кроме рассмотренного выше случая
нормального падения, отражается только волна того же типа, что
и падающая, т. е. не происходит трансформации волны при
отражении. Для этого потребуем равенства нулю коэффициента
трансформации Vn=0 или согласно (4.22) р = |-1(|2—х2/2)=0.
Поскольку |=xsinf, получаем sin2^ = V2, f=450. Следовательно,
преобразования не происходит, если угол падения сдвиговой
волны равен 45° Это же в принципе могло бы быть, если при
падении продольной волны отраженная сдвиговая волна
распространялась под углом 45° Однако последнее невозможно при
падении обычной * продольной волны, так как согласно (4.24) и
условию Ci/ct>y2 имеем sin0= (ci/ct)sin ч>1.
Отметим также, что выражение (4.25) для коэффициентов
отражения и трансформации в случае вещественных 0 и к
справедливо не только для гармонической, но и для произвольной
плоской волны. Действительно, представим последнюю в виде
суперпозиции плоских гармонических волн, т. е. разложим ее
в интеграл Фурье. Каждая из гармонических составляющих при
отражении умножается на не зависящий от частоты
вещественный коэффициент. В результате после отражения получается
тот же интеграл Фурье, умноженный на этот же коэффициент.
При падении на границу продольной волны всегда 0 и], а
следовательно, и VUi Vu вещественны.
Введение неоднородных продольных волн (см. ниже п. 15.3) также не
помогает, ибо при этом одна из волн (падающая или отраженная) будет
экспоненциально возрастать при удалении от границы.
62

15.3. Неоднородные волны. Несколько иная ситуация может
быть при отражении поперечных волн. Если угол падения т
достаточно велик, так что sin *(>ct/ch согласно (4.24) и (4.20)
имеем:
sin0>l, l>k, ft8 = 'l*a|.
|ft8| = Aff^k* = *V sin* у —(ct/cif. (4.28)
В выражении для |£3| берется арифметическое значение корня.
Потенциал продольной волны (4.20) с учетом множителя
exp[*46*i—®01 и а+ = 0 запишем так:
ф = Vtlb+exp[ |kz\х% + iilXi—Ы) ]. (4.29)
Таким образом, в этом случае возбуждается продольная
волна, распространяющаяся вдоль границы со скоростью и = а>/|„
с амплитудой, экспоненциально убывающей при удалении от
границы {неоднородная волна).
Коэффициент отражения поперечной волны согласно (4.26)
и (4.22) равен
v« = 77Г7Тх£ - <*Р Н tob а = 2arctS Щг-■ (4-3°)
i|M*s + P р2
Следовательно, отраженная волна отстает по фазе от падающей
на величину а. Однако по энергии отражение является полным,
поскольку | V** | = 1. Это и естественно, так как
возбуждающаяся вблизи границы продольная неоднородная волна (4.29) не
несет энергию в направлении оси хЛ. Однако форма
произвольной негармонической плоской волны будет при отражении
изменяться из-за потери фазы а в каждой гармонической
составляющей.
Имеется весьма тесная аналогия рассмотренного эффекта с
явлением полного внутреннего отражения в акустике или в
оптике, когда волна падает из среды с меньшей скоростью
распространения волн на границу со средой, где скорость волн боль
ше. Здесь вместо другой среды мы имеем другой тип волн
(отражение продольной волны при падении на границу
поперечной). Для полного отражения существенно, что ct>ct. Отсюда
ясно, почему аналогичного эффекта не возникает при падении
продольной волны. В этом случае возбуждаемая поперечная
волна всегда уходит от границы и уносит с собой определенную
долю энергии. Действительно, при падении продольной волны
под углом 8 имеем |=6sin8. При этом согласно (4.20) х3 =
-Ух2—k2s\n2Q = k']/(cl/ct)2—sin20 всегда вещественно.
Легко видеть (см., например, (4.28)), что полное внутреннее
отражение поперечной волны наступает при углах падения f >
>Y*p, где sinifKp = ct/c^l/y2, т. е. ^Кр^45°. При этом коэффици-
ент трансформации
V„ = — 2х3р/(£3хз+р2),

вообще говоря, отличен от нуля. Однако при угле падения f=*
=45°, как показано выше, Vu обращается в нуль, и неоднород-
ная волна отсутствует.
§ 16. Поверхностные волны
16.1. Волна Релея. При определенных условиях (см. (4.27))
лишь две волны удовлетворяют двум граничным условиям на
свободной границе. Найдем аналогичные ситуации, учитывая
также и неоднородные волны. Если потребовать равенства нулю
коэффициента отражения для волн того же типа, что и
падающая, из (4.22) имеем
^зХз—р2 = 0. (4.31)
Отсюда, воспользовавшись выражениями для р, k3, xs из (4.19),
(4.20), получаем уравнение
4ГУ^=Г Ух3^1" (2£2-*2)2, (4.32)
корни которого |п определяют искомые волны.
Несложные преобразования приводят к уравнению третьей
степени относительно величины s = x2/£2:
f(s) = ss-8s2 + 16(3/2-<72)s-16(1-<72) =0, (4.33)
где q = ct/ct<l—отношение скоростей поперечных и
продольных волн. Если уравнение (4.32) имеет корень |2<х2 (s>l), то
для этого корня должно быть и £2<£2, чтобы левая часть (4.32)
была вещественной, как и правая. Это будет случай обычных,
распространяющихся под соответствующими углами наклона к
границе волн. Можно показать (см. также задачу 4.6), что при
коэффициенте Пуассона v<0,26 имеется пара таких корней,
соответствующих случаю, рассмотренному в п. 15.2 (см.
формулу (4.27)).
С другой стороны, уравнение (4.33) всегда имеет корень s =
=50<1. Действительно, для функции f(s) имеем f(0) =
=—16(1—q2)<C0, f(l) = l>0, т. е. на отрезке O^s^ 1 функция
f(s) проходит через нуль. При этом соответствующее значение
£о>и>£, поэтому х8 и &з—'чисто мнимые величины,
следовательно, как поперечная, так и продольная волны являются
неоднородными. В результате решение волновых уравнений (4.4),
удовлетворяющее граничным условиям (4.18), запишем в виде
совокупности двух волн, скалярный и векторный потенциалы
которых даются соответственно выражениями:
q> = aexp(\ki\xi)exp[i(l0xi—(dt)]i
(4.34)
^=aVltexp(\7i3\xs)exp[i{loXi—(dt)],
Совокупность последних называется поверхностной волной
Релея, возмущение в которой сосредоточено в узком
приповерхностном слое толщиной ~1/|&,|. Компоненты смещения щ и и%
64

в волне Релея найдутся элементарно из формулы u=Vcp + roti|>,
где ^^{О» Ф» 0}. Скорость распространения волны Релея вдоль
границы, определяемая выражением и = ©/|0 = (со/х) (х/Ы =
^slcu всегда меньше скорости поперечных и, следовательно,
продольных волн (s0<l). Мы видим также, что v не зависит
0т частоты волны, так как коэффициенты уравнения (4.33),
определяющего s0, не зависят от частоты. Следовательно, волна
релея распространяется без дисперсии (произвольный импульс
сохраняет свою форму). Как мы знаем, для всех упругих тел
справедливо неравенство 0<^<1/У2. При учете этого анализ
уравнения (4.33) показывает, что 0,8741 ^v/ct^,0,9554. Таким
образом, скорость волны Релея мало отличается от скорости
сдвиговых волн, но всегда меньше ее.
Волна Релея играет важную роль в сейсмологии, поскольку
она хорошо прослеживается на больших расстояниях от
эпицентра землетрясения. Широкое применение нашли волны
Релея и в ультразвуковой технике для поверхностной
дефектоскопии материалов.
16.2. Поверхностные волны Лява. В однородном
полупространстве со свободной границей не может существовать
поверхностная волна, у которой вектор смещения был бы параллелен
границе и перпендикулярен направлению распространения —
волна горизонтальной поляризации. Однако такие волны могут
распространяться в слоистой среде, например в слое, лежащем
на упругом полупространстве, изображенном на рис. 4.3.
Теорию этих волн дал Ляв в 1911 г., именем которого они и
названы.
Пусть толщина слоя будет //, его упругие постоянные X и ц,
плотность р. В подстилающем полупространстве
соответствующие величины будут Xiy \it и ple Пусть волна распространяется
в направлении оси xt. Смещения в направлении оси х2
обозначим через и без индекса, так как остальные компоненты равны
нулю. Волну будем считать гармонической с частотой со.
Смещение и в каждой из сред должно удовлетворять своему
волновому уравнению, которое получается из уравнения (4.4) для -ф
применением операции rot:
Ди+х2и=0, х2 = р(о7|ы, —Я^^^О,
(4.35)
Ды + Х12и=0, х12=р1со2/М'1» *з^0.
В качестве граничных условий нужно потребовать:
а) на свободной границе х3=—И условия типа (4.12), из
которых для горизонтально поляризованной волны остается
только второе;
б) предполагая контакт сред при х5=0 жестким («склей-
ка»), потребуем непрерывности смещения и и составляющей
тензора напряжений o2s = 2|i,e82 = iidtt/dxs. В результате получим
^ Бреховскюс. В. В. Гончаров 65

следующие граничные условия для смещения и:
-.-«и, ■»£
ди
дх3
dui =о.
1ж,=+о 5*з \Xf=~H
(4.36)
Выражения для а как в слое, так и в упругом полупространстве
будут содержать один и тот же фактор exp[i(|Xi—(ot)\,
который, как правило, для сокращения записи мы опускаем. При
этом систему уравнений (4.35) с учетом d/dt=—i(o, d/dxt = i\
перепишем в виде:
а*2
(4'?7)
Очевидно, что мы получим поверхностную волну лишь в том
случае, если смещение и с ростом хл будет экспоненциально
убывать в однородном полупространстве. Для этого необходимо,
чтобы (J2>0, или, что то же, £2>хД при этом
и=Вехр(—pjcs), *8>0. (4.38)
Для однородного слоя общее решение уравнения (4.37),
удовлетворяющее условию при хл =—Н (4.36), имеет вид
u=Acos[-{(x3 + H)], — #<хз<0. (4.39)
Подставляя (4.38) и (4.39) в граничные условия (4.36) при
х, = 0, получаем:
A cos чН = В, —iiA^sin^H = —ii^B. (4.40)
Выразив отношение А/В из первого соотношения и подставив
его во второе, находим
tgyH =J!lJL. (4.41)
И У
Введя новую переменную ц = ^Ну причем
|2 = х2-(Л/Я)2, ън=1(кНу-(ъНу-г\\
уравнение (4.41) запишем в виде
tg Л= Ы|А) [(хЯ)»-(х1Я)»-Ч»],А/л. (4.42)
Корни цп этого уравнения и соответствующие им значения |«
будут определять параметры поверхностных волн Лява.
16.3. Свойства волн Лява. Проанализируем возможность
существования корней цп графически. В случае, когда ц
действительно, т. е. х2>£2, очевидно существование по крайней мере
одного корня T]t (рис. 4.4, а, где изображены две ветви функции
66

tgri и правая часть уравнения (4.42)). Если же х2<£2, то ^<0
и -п^а'г)'—чисто мнимая величина (неоднородная волна в слое),
так что (4.42) перейдет в уравнение
Ш л'= {-»М I Ыну-ЫМУ+ц'ТЧч', (4.420
не имеющее корней (рис. 4.4, б, верхняя кривая представляет
собой thri', а нижняя — правую часть уравнения (4.42')).
Таким образом, для существования поверхностных волн Лява
необходимо, чтобы
*,<£<*. (4.43)
При этом конечное число N волн Лява определяется соотноше-
нием Af=[//yx2—Xi2/jt] + l. Здесь [а] означает целую часть а.
Величина ап = со/£п, равная фазовой скорости распространения
волны Лява вдоль границы, очевидно, будет зависеть от
частоты, т. е. волна Лява обладает дисперсией. Из неравенства (4.43)
также следует, что фазовая скорость волны Лява больше
скорости сдвиговых волн в слое, но меньше скорости аналогичных
волн в полупространстве: cti>vn>ct.
Рассмотрим структуру волны Лява номера п с Чп=Цп/Н. Из
(4.38) и (4.39) с учетом (4.40), а также множителя
.exp[i'(£n*i—(ot)] имеем:
= ( An cos [уп (*3 + н)] ехр [I (5-л — со/)], — Я < х3 < 0,
I An cos уп Н ехр [— рп*3 + i (lnxt — coif)], х3 > 0,
(4.44)
где Ап—постоянная, характеризующая амплитуду я-й волны.
На рис. 4.5 схематически изображены смещения ип в трех
первых волнах Лява при #Ух2—Xi2/jt = 2,5 в зависимости от
координаты *3. Смещения равны нулю на узловых плоскостях:
7Л*з + #)=я/2, Зя/2,
Задачи
4.1. На плоскости х3=0 задано распределение смещений
"1=Лехр[1(£*1—©01, H2=5exp[t(£*i—со/)], H3=CexpU(gx,—со/)].
Найти волновое поле в упругом полупространстве х3>0.
Решение. Смещение и2 \Ха=о соответствует поперечной волне
горизонтальной поляризации вида ы2=#ехр [iЦх{+ Ух2—£2х3—(ot) ], совпадающего с
заданным распределением и2 при *3=0. Смещения "1^1=0 и «з|^=0 определяют
волны вертикальной поляризации с потенциалами:
ф=Л1ехр[/(^1 + Аг3х3—со/)], ф2=Ф=^2ехр[/(^1+х3дг3—©0],
*3 = У*2-£2, Хз = |Х2__|2.
Учитывая выражения (4.17), потребуем выполнения условий при *3=0:
^4i—/хзД2=Л, ikzA{ + i\A2=C.
67
з*

Отсюда определяются амплитуды волн:
Al~ Р + иА ' Ai~ ' |» + K,A3
4.2. Найти коэффициент отражения V горизонтально поляризованной
волны от абсолютно твердой стенки в условиях «склейки».
Решение. Для горизонтального смещения и=и2{хи хг) имеем волновое
уравнение d2u/dt2==Ct2Au. Его решением будет сумма ti а дающей и отраженной
гармонических волн вида
u=A+exp[i(lxl+xiX3—co/)]+4+Vexp[t(£xi—х3*з—©/)],
где хз=У(о2/е<2—£2. На абсолютно твердой стенке смещение равно нулю:
м1са=о =0> что Дает 1 + ^=0, откуда V=—1.
4.3. Рассмотреть отражение гармонической вертикально поляризованной
поперечной волны от абсолютно твердой стенки в условиях «смазки»
(проскальзывание).
Решение. Потенциалы <р и i|) = {0, ф, 0} удовлетворяют волновым
уравнениям:
Их решением для падающей плоской гармонической поперечной волны будут
функции:
Ф = BVtl ехр [/ (Ixi ~ ЬэХз — ©/)],
-ф = В exp [i (1хх + х3*з — со/)] + ВУн ехр ft (g*x — х3*з — «/)],
где £з=У(<о2/с/2)— |2, Хз=У((о2/с*2)—£2. Поскольку при *з = 0 имеется
проскальзывание, то граничными условиями будут равенства нулю нормального
смещения и касательного напряжения:
*i~-(*+£L-e-
2 а*? 2 ^
»Ии=2К,.и=2^д-5- +
*3
=0
Подставив в эти условия выражения для ф и ф, находим
« (1 + V«) - *aV« = 0, lk3Vtl - (Е» - Vix») (1 + Vu) = 0.
Отсюда легко получить, что Уц =—1 и Vu=0t т. е. имеем полное отражение с
обращением фазы.
4.4. Выяснить качественно, какие» волны и с какими волновыми векторами
возникают при отражении продольной волны от плоской границы раздела
двух упругих сред.
Решение. Будем обозначать величины, характеризующие среду при
лг3>0, индексом 1, а при х3<0 — индексом 2. Для выполнения граничных
условий во все моменты времени и на всех точках границы необходимо, чтобы
частоты волн со и проекции их волновых векторов на границу совпадали.
Теперь не составляет труда по заданному волновому вектору падающей волны ki
построить волновые векторы как отраженной, так и прошедших в другую сре-
68

ду волн* что н представлено на рис. 4.6. Концы волновых векторов всех волн
должны лежать на одной прямой, перпендикулярной оси хх и проходящей
через точку (£, 0). Кроме того, все возникающие при отражении волны должны
уходить от границы. Длины волновых векторов соответственно равны:
*i = *i = fiV«7ii Л2 = о)/с/2, х/ = ©/с//>Л/| /=1,2.
Из условия равенства горизонтальных проекций волновых векторов можно
также найти соотношения между углами падения 0i, отражения 0/, Yi и
преломления 02, Уг:
0'i = 0i, kx sin 0i=xj siL /i = £2 sin 02=x2 sin Y2.
/
I/
/l
/ 1
/ 1
/ /
fW/-^>
^-
s
Рис. 4.6
Рис. 4.7
4.5. Найти коэффициенты отражения и преломления при падении
продольной гармонической волны на границу раздела между двумя одинаковыми
упругими средами с проскальзыванием.
Решение. Совокупность возникающих волн изображена на рис. 4.6.
Решение соответствующих волновых уравнений имеет вид (общий множитель
exp[i(lx{—Ш)] опущен):
ф1 = Аг [ехр (— ik8x3) + У и ехр (^3*зЧ, *i = AxVlt exp [inpj, x3 > 0,
Фг = AXWU exp (— ik&J, i|?2 = AxWlt exp (—injcj, x3 < 0,
где ^з=УЛ2—£2, k^a/ci, х3=Ух2—£2, x=o)/ct. В качестве граничных условий
при *з=0 нужно взять
Выражая последние через потенциалы ф, и \|)j, получаем:
k»V-vn)-ivlt = ktwtl-iwlt,
Р (1 + VH) - x,V„ = рГ„ +x3Wrt,
fts(1 - Va) = pVu, k3Wu = рГи, P = 1/1 <la -x«/2?
Решая эту систему алгебраических уравнений, находим:
*W
W„ =
Vlt Ра + *з*э
= Г„.
4-6. В п. 15.2 было показано, что при определенных условиях (4.27) в
случае падающей на свободную границу упругого полупространства продольной
69

волны существует только отраженная поперечная волна и нет отраженной
продольной. Показать, что это возможно только при коэффициенте Пуассона
V<Vmax, И НЭЙТИ Vmax.
Решение. Условие (4.27) записывается также в виде (4.31) или (4.33).
Следовательно, требуется показать, что при достаточно больших v уравнение
(4.33) не имеет корней, больших единицы, соответствующих однородным вол-
в:ам. На рис. 4.7 представлен график функции f(s). Очевидно, что для
существования корней 5i,2>l полинома f(s)=s*—8524-16(3/2—^2)s—16(1 —^2)
необходимо, чтобы при s>l имелось два экстремума функции f(s). Поскольку
/'(s)=3s2—16s+16(3/2—Я2)* то выражение для точек экстремума будет s± =
= (4/з) (2±УЗ?2—V2)'. Отсюда следует, что для существования корней Si,2>l
необходимо, чтобы q2=ct2/ci2^l/e. Выражая теперь отношение ct2/ct2*=
= |i/(A,+2ji) через Е и v по формулам (3.26), получаем (1— 2v)/(l— v)>!/3,
или v<0,4.
Однако, как видно из рис. 4.7, условие наличия экстремума не является
достаточным для существования корней Sif2>1. Для этого нужно также
потребовать, чтобы /(s+)<0. Вводя параметр а=УЗ</2— 1/г, <72=(1+2а2)/6,
s+ = 4(2-fa)/3 и вычисляя f(s+). последнее условие запишем в виде
19—30а2— 16а3^0. Отсюда находим предельное значение ао«0,68. Корни Sit2
существуют только при а>ао. Это дает ^2>0,32 и окончательно v<vmax«
«0,26.
4.7. Рассмотреть собственные горизонтально поляризованные волны в слое
с одной свободной и другой абсолютно жесткой границей.
Решение. Абсолютно жесткая граница соответствует полупространству
с бесконечно большой скоростью распространения волн. Следовательно,
решение задачи можно получить предельным переходом jlii-^oo в выражениях для
волн Лява (4.42), (4.44). При этом tgrj-^oo и г)п= (2я+1)я/2 (я=1, 2, ...),
|п=Ух2—(2п—1)2я2/4#2. Смещение (4.44) перепишем так:
ип = Апcos [2п - 1) я (*3 + Я)/2ЯJ ехр [I &пхг - о*)].
Узловые плоскости задаются уравнениями *3/#=—1 + 1/(2я—1),
—1+3/(2п—1), ..., 0. Всего п плоскостей, последняя совпадает с нижней
границей слоя *3=р.
4.8. Определить параметры гармонических, горизонтально поляризованных
волн, которые могут распространяться в слое упругого материала толщиной #1
со свободными границами. ]
Решение. Для горизонтального смещения tt2=«(*i, *з, t) имеем волно-j
вое уравнение d2u/dt2=ct2Au с граничными условиями на свободных стенках]
(дн/д*3)Ха==0,//=0. Решение ищем в виде u^O(xz)exp[i(lxl—©/)]. Для функ-|
ции Ф(*з) получаем обыкновенное дифференциальное уравнение Ф"+]
+ (х2—£2)Ф=0, х = со/с* и граничные условия Ф'|Ха=0 = Ф' \х%=н =0- Уд°в*|
летворим как уравнению, так и условию при *3 = 0, выбрав решение в виде]
Ф=Лсозу*з, у=1 н?—£2. Подставив это решение в условие при хг=Н, по-!
лучаем уравнение для определения возможных значений у: sinY#=0. Теперь
находим допустимые значения уп=*пл/Н (п=0, 1, 2, ...), а также]
£п=Уи2—п2я2/Н2. Имеется конечное число птах<хЯ/я волн, распространяю-'
щихся вдоль слоя. При n>nmax величина £п чисто мнимая, что соответствует j
колебаниям с экспоненциально убывающей вдоль Х\ амплитудой. Смещение]
70

ип (*ь *з, 0 запишем так: ип = Ап cos (— *3j exp [j^i — Ш)]. В
частности, при /1=0 получаем волну с постоянной амплитудой поперек слоя и
распространяющейся вдоль *i со скоростью ct. При л=1, 2, амплитуды воли
меняются по толщине слоя, имеется п узловых плоскостей, на которых «Л=0.
4.9. Найти групповые скорости горизонтально поляризованных волн в слое
со свободными границами.
Решение. В задаче 4.8 было найдено горизонтальное, волновое число
я-й волны 1п=Ук2—п2я2/Н2. Будем рассматривать случай п^птйт. Для
фазовой скорости имеем
vn = <«>/&, = cJV\ - (пп/хН)* > ctJ
для групповой —
(сгр)п = Ш^Г1 = '/ (О**)""1 = '* Kl-,n«/x^a< с,.
Для волны любого номера п имеем простое соотношение сТ^ = с%2.
Глава 5
ВОЛНЫ В ПЛАСТИНКАХ
Упругий слой с плоскопараллельными свободными границами
называют пластинкой. Горизонтально поляризованные поперечные
волны в пластинке (смещения параллельны границам) были
рассмотрены в задачах 4.8 и 4.9 предыдущей главы. Однако
основной интерес представляет случай вертикально поляризованных
волн в пластинках (смещения лежат в «вертикальной»
плоскости, образованной направлением распространения волны и
нормалью к границам).
В этой главе мы проведем классификацию основных типов
волн, встречающихся в пластинках. Проанализируем ряд особых
случаев их распространения, а также осуществим предельный
переход к волнам в тонких пластинках.
§ 17. Классификация волн
17.1. Дисперсионные соотношения. Пусть пластинка имеет
Толщину 2А, а ее границы x3=±h. Как уже отмечалось выше (см.
п- 15.1), смещения в вертикально поляризованных волнах при
соответствующем выборе осей координат можно описать двумя
не зависящими от х2 скалярными функциями: скалярным
потенциалом ф(д:1, х5, t) и компонентой ^(хи х3у t) векторного
потенциала я|>={0, г£, 0}. При этом для компонент вектора смещений
u==={"i', «2, и3} имеем (см. (4.17)):
„* *t Ц2 = 0) Ыз = |ф.+^ (51)
охг дх3 дх3 дхх
71

Функции ф и ^ удовлетворяют волновым уравнениям (4.4). ПрJ
отражениях на границах сохраняются частоты волн и проекций
их волновых векторов на границы. Поэтому зависимость ср и \|J
от Xi и t примем в виде фактора ехр[((£*!—со/)]. В результат^
цолучаем уравнения (4.19) для ф и -ф с общим решением (4.20)1
которое, переопределив произвольные постоянные, можно запи^
сать так:
у= (C{cosksXs + dsinksXsjexplidXt—cat) ],
г|?= {Di cos к3*з+As sin x3*s)exp [*'(£*!—cot) ], (5.2)]
к3 = УйГ—?> k = (o/ch Из = )Лса — £* x = <o/ct.
Подставляя теперь эти выражения в граничные условия (4.19)]
при Xi=±h, получаем однородную систему уравнений относи
тельно постоянных Си С2, Du D2:
1С t
Г2
Г1
= 0.
Здесь элементы матрицы A={aih} (t, k=l, 2, 3, 4) имеют вид::
ап = — 02i = Oi sin а/, а22 = — °i2 = Ф^ s*n а*»
а1з = Ягз = <*/ cos а/, аи = 024 = фЛ cos а/,
fl3i = a4i = — 'М cos а'» аз2 = а42 = а* cos а и
-*зз
— а43 = — iph ^п а/> ам = — fl44 = а* s*n а*>
где oi = k$h=1k?—l% о, = х3А=Ух2-ГЛ, р=(Б1-х1/2)/6.
Сложим и вычтем почленно друг из друга первые два
уравнения, затем проведем аналогичную процедуру и со второй па-;
рой уравнений. В результате получим эквивалентную систему3
вида
0 0
0 0
vL cos al iph cos at I
alsinal — iph sin оt
| — iph cos al at cos at
0 0
0 0
iph sin ot ot sin a.
IICl
d
Pi
= 0.
(5.3)
Представляет интерес ненулевое решение этой системы,
условием существования которого будет равенство нулю ее
определителя:
(opt sin оi cos at + p2h? cos a/ sin at) (oiOt cos oi sin a* +
+ pW sin a/cos a,) = 0. (5.4)
При фиксированной частоте со и, следовательно,
фиксированных k = (dfct и х = (о/с* выражение (5.4) можно рассматривать
как уравнение для определения возможных значений проекций
72

волновых цекторов на ось *t: £ = |п(со). Напротив, при фиксиро-
анном значении £ это уравнение определяет возможные
частоты волн о) = (оп(Ю- Волны такого типа называются собственны-
ми или нормальными, волнами (или также модами), а
соответствующие им значения £п или (оп — собственными значениями.
Выражения (о = (опШ можно рассматривать как дисперсионные
соотношения для мод. При этом величина (сф)Л=(о/^ имеет
смысл фазовой скорости волны, a (crp)n=d(o/rfg — ее групповой
скорости.
17.2. Симметричные и антисимметричные нормальные
волны. Полную систему нормальных волн в свободном упругом
слое можно разбить на два класса, отвечающих обращению в
нуль по отдельности каждого из сомножителей дисперсионного
уравнения (5.4).
1. Симметричные нормальные волны с дисперсионным
уравнением
ом tg Gi + p2h2 tg ot ■* 0. (5.5)
При этом из (5.3) следует, что C2=£i = 0 и D2 = i(ph cos оJ
lot cos Gt)Cit Поэтому согласно (5.2)
9 = C1cjsfesxs, tf=Z)2sinxsA:3. (5.6)
Здесь и, как правило, ниже множитель exp[t(g*i—(о/)] опущен.
Теперь с учетом (5.1) легко найти
Ui = ilC{ cos &sxs—k3D2 cos x8*s, u{ (—x3) = Щ (x9),
(5.7)
us = —kbCi sin fas + i%D2 sin x8*8, и8 (— x8) =—и8 (*a),
откуда и следует симметрия нормальной волны относительно
плоскости х3=0.
2. Антисимметричные нормальные волны с дисперсионным
уравнением
OiOt tg о,+p2/i2tgc, = 0, (5.8)
потенциалами (Ct = 0, Z)2 = 0, D i = i(oi cos Oi/ph cos ot)C2)
q> = C2sin&3*3, ty = Dicosnixi (5.9)
и антисимметричным относительно плоскости *s=0 смещением:
"i = i\Cz sin ksxs + XjDi sin xs#s, Hi (— *8) = —wt (x8),
(5.10)
ws = &3C2 cos £3*3 + i^Di cos X3JC3, Ыз (—x8) = и8 (*8).
Воспользовавшись периодичностью тригонометрических
функций в дисперсионных уравнениях (5.5) и (5.8), можно показать,
Чт° при любом фиксированном % имеется счетное число
собственных значений соп(|) (л=1, 2, ...). Если же фиксировать
частоту о, то дисперсионные уравнения будут иметь лишь конечное
число вещественных корней 1п(со). Действительно, при |2>со2/с«1
Личины ot и о, становятся чисто мнимыми, а тригонометриче-
73

ские функции переходят в гиперболические, непериодические н|
вещественных корней gn в (5.5) и (5.8) будет не более чем по]
одному. Однако и в этом случае существует бесконечное число]
корней £Л2<0, которые уже не соответствуют распространяю-!
щимся волнам, а представляют собой колебания с одинаковой
фазой вдоль слоя и экспоненциально меняющейся амплитудой
Ф, ф~ехр(± |£Л|*1—со/) —разновидность неоднородных волн. I
17.3. Критические частоты волн. С уменьшением частоты <J
число распространяющихся волн, для которых £п2>0, становит*]
ся все меньше и меньше. Граничная частота (а)„р)п, на которой]
Н-я мода становится ^распространяющейся, называется ее крщ
тической частотой. На частотах ниже критической собственное
значение £п(со) становится чисто мнимым. Ввиду непрерывное™
перехода от вещественных |п к чисто мнимым £п[(<йкр)п] =0, а|
фазовая скорость волны сф=б)/£я равна бесконечности. Этим об4
стоятельством можно воспользоваться для определения крити!
ческих частот упругого слоя. Действительно, переходя в (5.5) ц
пределу при ^0, перепишем его в виде tgx/i/tg£/i=0, откуда;
для симметричных волн непосредственно следует: I
(л ТСС л
■xh = — h = п,п, (шкрк = «1 —. "i = 0, 1, 2,
ct h
(5.1ll
kh=— ft = -J-(2n2-l), {aKp)nt=^-fL(2n2-l), /4=1,2,...]
При (о=(а)кр)п, из (5.3) и (5.7) имеем CV=0, и3 = 0, и4=|
=f—Z)2xcosx*3exp(— tot), т. е. синфазная вдоль слоя стояча:
поперечная волна. На толщине слоя 2Л укладывается четно»
число полуволн: хЛ = п1л, 2h/(К/2) =2nt. Если же (о=((оКР)п2, т<
D2=0, ut = Q, и3=—Ct£ sin £*8 ехр (—iat) —стоячая продольна:
волна с нечетным числом полуволн по толщине слоя.
Аналогичные результаты получаются и для антисимметрии
ных волн на критических частотах, а именно:
Крк=у(2пз-1)-^' "з = 0,
их = Dxx sin ххо ехр (— Ш)9 п3 = 1, 2,...;
(5.15
С,
(®кр)п4 = пАп —, иг = 0,
h
и3 = С2& cos£*3 ехр (— Ш), я4 = 0, 1,
Здесь уже по толщине слоя укладывается нечетное число сдв#
говых полуволн или четное продольных полуволн.
В общем случае произвольной частоты нормальная вол
содержит как продольную, так и поперечную компоненты. В №
которых случаях нормальную волну в упругом слое удобно пре;
74

Рис. 5.3
ставлять парой продольных и парой поперечных плоских волн,
взаимно переходящих друг в друга при отражении от границ
слоя. Действительно, выражения для потенциалов (5.6) и (5.9)
можно записать в виде:
4>=C{exp[i(%xi+kixi—(dt)]±exp[i(%xi—kix—(i>t)]}9
(5.13)
^=D{exp[i(lxi + Hixi—(ot)]^exp[i(lxi—7i3x3—(ot)]}.
Верхний знак в (5.13) относится к симметричной нормальной
волне, а нижний — к антисимметричной. Волновые векторы всех
четырех волн к={£, £,}, к'={|, — k3], х={£, х,}, х'={£, —х3}
изображены на рис. 5.1, углы 8 и ^ связаны соотношением (4.24):
Ci sin i = ct sin 9.
17.4. Некоторые особые случаи. Представление нормальной
волны в виде совокупности плоских волн (5.13) часто
оказывается полезным для анализа, поскольку мы можем использовать
известные особые случаи отражения плоских волн. Так,
например, при угле падения поперечной волны, равном 45°,
продольная волна не возникает (см. п. 15.2), следовательно, на
определенных частотах (см. задачу 5.2) нормальная волна будет
образована только парой плоских поперечных волн,
распространяющихся под углом f = 45°
Следующая особенность имеет место для нормальных волн,
°бразованных плоскими волнами, распространяющимися под
75

taKHMH углами 60 и fo, при которых от свободной границы не
отражается волна того же типа, что и падающая. Как уже отме*
чалось в п. 16.1 (см.также задачу 4.6),таких углов будет две па*
ры, если коэффициент Пуассона материала v<0,26. Поэтому в
.Этом случае всегда можно найти частоту, на которой комбинация
плоских волн с волновыми векторами, изображенными на
;рис. 5.2, а, соответствует нормальной волне заданного номера п
;(см. задачу 5.3). В силу симметрии на той же частоте
нормальную волну образует и система плоских волн с волновыми
векторами, изображенными на рис. 5.2, б. Амплитуды плоских волн
!С волновыми векторами х и к' связаны между собой
коэффициентом трансформации Vlt. То же относится и к паре ких'
Однако ни одна из этих комбинаций не будет относиться ни к
симметричным, ни к антисимметричным нормальным волнам. Более
'того, поскольку частоты и проекции волновых векторов на
границу у всех волн, изображенных на рис. 5.2, а, б, одинаковы, то
;любая их комбинация с произвольными комплексными
амплитудами, например сдвиговой волны в каждой паре, также
образует нормальную волну. В частности, можно выбрать эти
амплитуды таким образом, чтобы получить симметричную или
антисимметричную нормальную волну.
§ 18. Нормальные волны низшего порядка
18.1. Кваэирелеевские волны на границах пластинки. Среди
нормальных волн пластинки особое место занимают симметричная
и антисимметричная моды низшего порядка, критические
частоты которых равны нулю (nt = 0 в (5.11) и л4 = 0 в (5.12)). Эти
моды отличаются от остальных также тем, что соответствующее
им распределение смещений частиц по толщине пластинки
имеет минимально возможное из всех мод число перемен знака.
Так, для симметричной моды низшего порядка продольное
смещение не меняет знака на отрезке [—А, А], для
антисимметричной моды аналогичен характер вертикального смещения частиц.
На критических частотах этот факт легко установить,
анализируя уравнения (5.11), (5.12) и соответствующие им выражения
для смещений частиц. Отсюда можно заключить, что этим
модам соответствуют максимально возможные по величине корнв
\г дисперсионных уравнений (5.5) и (5.8) и, следовательно (см,
(5.2)), минимальные положительные (или чисто мнимые)
значения вертикальных волновых чисел х3 и ks. Именно в этой
случае смещения частиц (см. 5.7)) будут иметь наименьшее
число осцилляции по толщине пластинки.
На высоких частотах этим модам соответствуют большие пс
модулю отрицательные значения о,2 (|2>(о/с,2>о)2/с/2).
Действительно, положив в дисперсионных уравнениях (5.5) и (5.8)
tga/ = Hh|a,|«W —2ехр(—2|а/|)], tga* = ith|a,|«
«Щ —2ехр(—2|a,|)],
76

для симметричной и антисимметричной мод соответственно
получим:
fp(l) «2[а^ехр(—2|а,|) + р2Л2ехр(—2|а,|)],
(5.14)
/ра)-2[р2Л2ехр(-2|а,|)+а^ехр(-2|а,|)],
где /Р(£) =OiOt+P2h2- Правые части этих уравнений малы,
поэтому собственные значения £с и £а близки к корню £р
уравнения /РШ=0» соответствующего волне Релея (ср. с (4.31)). При
Е^бр Функция fv(l)ttf/(lP)(%—|р), так что для |с и |а имеем:
|с = ^р — е, £a = gp + e,
pW [ехр (- 21 a, J) - ехр (- 2 | а, |)L.
—2 пу "' <5'15)
гдее>0в силу//(^р)<0и |а«|<|а^|.
Таким образом, на высоких частотах фазовая скорость (о/£с
низшей симметричной моды несколько выше фазовой скорости
о)/£р волны Релея, которая, в свою очередь, несколько выше
фазовой скорости ©/ga низшей антисимметричной моды.
Выражение для смещения, например, ut в соответствии с
(5.7) и (5.10) имеет вид:
Wic =
c<[CJ^f+('- *)ЭД -же*-*--».
(5.16)
\sh\k3]x3 /1 _ х2 \ sh|х81 *31
ch\ct\
,. _ г \sh\k3]x3 /. х* \i
exp[i(lPx1 + ex1—(i)t)].
На рис. 5.3 представлены распределения u^(xs) для этих мод,
которые аналогичны смещениям в волнах Релея у каждой из
границ. Вследствие взаимодействия этих «квазирелеевских»
волн могут возникать интересные явления. Пусть на верхней
границе пластинки x5=h возбуждается волна Релея. Последнюю
можно представить как полусумму симметричной и
антисимметричной мод с одинаковыми фазами. При этом суммарное
поле в окрестности источника будет практически отличным от
нуля лишь у верхней границы, так как у нижней возмущения от
обеих мод взаимно сократятся. Однако в силу различных
фазовых скоростей мод на расстоянии Т/2г от места возбуждения
фазы волн будут отличаться на я. Следовательно, суммарное
возмущение будет отличным от нуля уже только у нижней
границы. В дальнейшем волны снова сконцентрируются «у верхней
границы и т. д. Это явление аналогично переходу энергии от
одного осциллятора к другому, если их резонансные частоты
Равны и между ними имеется слабая связь.
18.2. Юнговская и изгибная волны. Низшие моды в
пластинке отличаются тем, что они существуют при любых как угодно
низких частотах (критические частоты для них равны нулю).
77

Обратимся сначала к симметричной моде и рассмотрим
дисперсионное уравнение (5.5) для случая |о*| = |£3|Л<1, |(J*| =
= |хз|Л<С1 (случай тонкой пластинки). Это уравнение
принимает вид
О|7Л2+/?2 = *2-£2+Р2 = 0.
Отсюда следует, что а*2<0, т. е. £2>Л2,— случай неоднородной
по толщине пластинки продольной волны. Учитывая значение р,
получаем
£2 = х* __ рсоМЯ + 211) = ©^ (5 17
4 (к»-Л») 4|1 <* + (!) 4л*
где
g, 4^ + 0 = _£_д£й; (5л8)
р(А + 2ц) p(l-v»j р '
£Эф— эффективный модуль Юнга для стержня при запрещенных
боковых смещениях по одной из осей (см. (1.6)). Для смещения
частиц в этой волне из (5.7), (5.8) с учетом |£sjts|<t;l и |х3*э|<
«1 находим:
(5.19)
Смещения практически только продольные и постоянные по
толщине пластинки, поэтому симметричную волну на низких
частотах часто называют «юнговской» продольной волной в
пластинке. В силу независимости фазовой скорости от частоты (спл—
материальная постоянная) эта волна распространяется без
дисперсии.
Перейдем теперь к анализу антисимметричной волны в
тонкой пластинке. Здесь уже при |а<|<1 и |о<|«;1 в разложении
дисперсионного уравнения (5.8) следует удержать члены более
высокого порядка, так как в противном случае |2 просто
выпадает. Положив tgOittOi + o*/3 и аналогично для tgo,,
перепишем (5.8) в виде
о? + р2Л2[1 + (о?-а2)/3] = 0.
Отсюда для распространяющихся волн |2>0 с необходимостью
следует требование а*2<0 или £2>х2>£2—неоднородная по
толщине пластинки как продольная, так и поперечная волны. Если
разрешить последнее уравнение относительно £2, то с точностью
до малью величин порядка Ух2—k2h получим дисперсионное
соотношение
%2= ± ^*а . (5.20)
Здесь отрицательные значения £2 соответствуют нераспростра-
няющимся волнам. Распространяющаяся нормальная волна с
78

t2>0 называется изгибной волной в тонкой пластинке. В
последней, как следует из (5.10), вследствие малости ksxs и хах3
смещения частиц преимущественно происходят в поперечном
направлении и, так же как в юнговской волне, не зависят от хг.
Изгибная волна обладает дисперсией, ее фазовая и
групповая скорости соответственно равны:
_ (5.21)
сгр = ^ = 2 /4/3V^i^l-c?/c?c,.
§ 19. Уравнение изгиба тонкой пластинки
19.1. Приближение тонкой пластинки. Волны изгиба играют
важную роль во многих случаях, но выделение изгибной волны
из полной совокупности нормальных волн в пластинках часто
вызывает излишние сложности. Однако можно получить
приближенное уравнение для изгиба, с самого начала рассматривая
пластинку как тонкую.
Такое уравнение впервые было получено С. Жермен в
1815 г. Позднее теория изгиба пластинки была рассмотрена
также Кирхгофом при следующих предположениях:
1) смещение любой точки пластинки мало по сравнению с
ее толщиной, углы наклона границ также малы;
2) серединная плоскость пластинки не подвергается ни
растяжению, ни сжатию;
3) линейные элементы, перпендикулярные серединной
плоскости до деформации, остаются прямолинейными и
перпендикулярными ей;
4) силы внутренних напряжений в пластинке,
перпендикулярные серединной плоскости, малы по сравнению с силами,
действующими в этой плоскости.
На основе этих предположений получим приближенное
уравнение для смещений серединной плоскости в перпендикулярном
направлении, которое обозначим через £(*!, х2, t) = иЛ(хи х2у 0, /)•
Учитывая, что согласно предположению 2 ui\X3B=0 = u2\x3=o = Of
разложим Ui(Xi) в ряд и ограничимся только линейным по х3 членом
«1 = а*з, где a» (duJdx3)X3=0. На рис. 5.4 АВ — положение
некоторого малого участка серединной плоскости до деформации, а
А'В'— то же, после деформации; MN и M'N'— аналогично для
отрезка, первоначально перпендикулярного серединной
плоскости. Очевидно, что a=dujdxs—угол отклонения линейного
элемента от его начального вертикального положения. По
предположению 3 этот элемент должен остаться перпендикулярным
серединной плоскости, наклон которой равен —д%)дхи тогда а =
^—-dfydxi и Wi«—х3д%/дх^ Аналогично получим ы2«—х3д%/дх2.
79

Теперь легко найти следующие компоненты тензора деформаций:
сц — — л3 , е22 — х3 , еп — х3
а* ° ах* " • а** " "ах^х,
(5.22)
Обращаясь к обобщенному закону Гука (3.22), запишем
o3Z = (b. + 2\i.)esa + %(ell + en), или
С учетом этого из (3.22) также находим
оп = (Х + 2(х)еп + Це22 + е33) =
- 2^ [2 (X + ц) % + te22] + -А- а33.
Я,
ГГ2^аз3
<к;
33 1
Но в соответствии с предположением 4
<С|ои|, поэтому, опуская член с o3i и учитывая (5.22),
получаем
где также использована связь Лице модулем Юнга Е и
коэффициентом Пуассона v (3.26). Аналогично
(5.24)
Остальные компоненты тензора напряжений найдем из условия
равновесия упругого элемента (3.12-) в отсутствие объемных сил:
— + — + — = 0. Отсюда для i = 1,2 с учетом (5.23) и (5.24)
дхх дх2 дх3
nd. С Л Л2 Л2
получаем—- = —- Д £, где А = —г + —т~операторЛап-
J d*3 i - va дхх -ъ ~ дх\ дх\ v
ласа по горизонтальным переменным. Интегрируя последнее
равенство по х3 с учетом ais|x3=±/i = 0, находим
—- 4£# ■£"•'-■•«• (5-25)
19.2. Уравнение С. Жермен. Найдем теперь поперечные силы,
возникающие при деформации пластинки. Из условия равнове-
80

сиядазл/дя^Оимеем
дОзз^^ dc3i до32 = E(h* — x\)
дх3 дхг дъ 2(l-va)
Проинтегрировав это уравнение по хл в пределах толщины слоя
(—Л, +Л), получим разность нормальных напряжений на
границах пластинки ? = а3з|х3=л—азз|х3—л-
£Z = D£t (5.26)
Q =
2Eh*
3(1-v»)
Величина
D=2Eh>/3(l-v2) (5.27>
называется жесткостью пластинки при изгибе, или
цилиндрической жесткостью, а q есть не что иное, как нормальная к
пластинке внешняя сила, отнесенная к единице площади
{распределенная нагрузка). Уравнение (5.26), являющееся условием
равновесия пластинки под действием распределенных внешних сил
q, называется уравнением С. Жермен.
Определим изгибающие моменты, возникающие при
деформации пластинки. Для момента, отнесенного к единице
площади и параллельного оси х2, с учетом (5.23) получаем
*,=] о**. - - ^ (Ц + v Щ |■ а* _
Аналогичное выражение с заменой индексов 1^2 справедливо
и для момента, параллельного оси xt.
19.3. Волны изгиба в тонкой пластинке. В случае изгибных
колебаний пластинки распределенной силой q будет сила
инерции элемента пластинки, взятая с обратным знаком: q =
= — 2p/id2£/d/2. Подставив эту силу в уравнение (5.26), получим
уравнение, описывающее распространение изгибных волн в
пластинке:
-a+iilt-O. (5.29>
В случае одномерной волны, направив координату xt вдоль
направления ее распространения, имеем
i!i + ^J!L = o. (5.зо>
дР ^ 2рЛ дх\ У f
Последнее уравнение отличается от уравнения (2.25) для изгиб-
нь1х волн в стержне только коэффициентом перед вторым
членом. Поэтому все полученные для стержня результаты пол-
81

ностью переносятся на случай одномерных изгибных волн в
пластинке. В частности, дисперсионным соотношением для изгибных
волн в пластинке будет
12=±У2^Щ(о. (5.31)
Отметим, что последнее совпадает с выражением (5.20) для
антисимметричной нормальной волны в тонкой пластинке (см.
задачу 5.7). Учитывая предположения при получении выражения
(5.20), видим, что одним из условий справедливости теории
изгибных волн, изложенной в этом параграфе, является малость
толщины пластинки по сравнению с длиной волны.
Задачи
5.1. Найти дисперсионные соотношения и вид собственных функций
нормальных волн в пластинке при ш->оо.
Решение. Обратимся, например, к дисперсионному уравнению для
симметричных волн (5.5). Исключая рассмотренные в п. 18.2 низшие
нормальные волны, заметим, что при о>->оо величина at должна оставаться конечной и
вещественной, например ЛУх2-—£п2=Ло)У1/с*2— 1/сф2=ап. Отсюда, Сф~2=
=ct~2—an2/(h2(u2)-+ct-2. Следовательно, фазовая скорость нормальных волн
•близка к ctf но тогда £птех, Р«х/2, Oi**hyk2—n2=i\oi\, |cri|-*-<», tgai =
= ttH | <T| | «/*, a (5.5) переходит в уравнение
an\°l\ *nVcl-c)
8 " xW» cph
с решением Ot = an&nn. Аналогичные результаты имеют место и для
антисимметричной волны, с той лишь только разницей, что а*«я/2+яя. Таким
образом, при G>-*-oo нормальные волны почти по всей толще пластинки являются
суммой двух поперечных плоских волн, распространяющихся под малыми
углами к горизонтали, и только в непосредственной близости от границ к ним
добавляются неоднородные продольные волны.
5.2. Найти частоты, на которых нормальные волны в пластинке
образованы только парой поперечных волн, распространяющихся под углом 45°. Найти
также смещения частиц в этих волнах.
Решение. При угле падения у — 45° имеем £ = х sin у=х/У2, а< =
= хЛ/У2=о)Л/У2с,, P=l~l(l2—х2/2)=0. По условию задачи в (5.2) d = C2=0.
Дисперсионные уравнения (5.5) и (5.8) и выражения для смещений (5.7) и
{5.10) имеют вид:
для симметричной волны
Г(2п— 1) x31 .„„ . /2n— 1 *, \
«i = - А*з cos 1 yj n~\< "з = tDtl sin y-yf n -y J «
для антисимметричной соответственно
82

sino/ = 0, xh= V2nn, e>n = Y2nn—f
«i = Z>i«8 sin \V2nn 2jA , tt3 = (gDi cos (К^лл ^4 .
5.3. В п. 17.4 указано на аномальный характер нормальных волн, образо-
ванных плоскими волнами с такими углами падения 0О и у0, при которых or
свободной границы не отражается волна того же типа, что и падающая.
Найти частоты о)п, соответствующие этим волнам.
Решение. Принимая во внимание соотношение (4.31) GiCt= p*h2t
справедливое для углов падения 90 и Yo, заметим, что в этом случае
дисперсионные уравнения (5.5) и (5.8) совпадают:
sin (0/ + а,)
tgo^+tga^—: =0.
1 l cos at cos at
Отсюда имеем Oi + ot=nn и (с учетом также Oi~((uh/ci)cos%, <х« =
= ((uhlct)cos Yo)(on = (nn/h)cict/(ci cos yo+ct cos 0o).
5.4. Тонкая пластинка лежит на параллельных линейных опорах,
расстояние между которыми /. Определить форму, которую она принимает под
действием собственного веса.
Решение. Если толщина пластинки 2Л, плотность материала р, то на
единицу площади будет действовать поперечная сила q=—2phg. Направив,
ось Х\ перпендикулярно опорам, запишем уравнение С. Жермеи
— = -« = - — ,
интегрируя которое, находим
С=—(а*14/24) + axl*+bxx2+cxi + d.
Постоянные интегрирования можно определить из граничных условий,
которыми будут равенство нулю смещений на опорах *i = 0, / и моментов
относительно опор. С учетом (5.28) получаем:
d=0, 6-0, — (a/V24)+a/3+c/=0, — (a/2/2) +6a/=0,
откуда
a=a//12, c = —a/3/24, £= — (ax,/24) (*,3—2/x12+/3).
5.5. Найти форму тонкой круглой пластинки с заделанными краями,
которую она принимает под действием силы тяжести.
Решение. Как и в предыдущей задаче, q=—2phg. Функция С(*ь х2) R
силу радиальной симметрии зависит только от r=~\'xi2+x22. При этом
уравнение С. Жермен в полярных координатах примет вид
1 d ( d Г 1 d ( dl \Т\ 2phg
Проинтегрировав это уравнение 2 раза по г, получим
а , * d I dl\ ar2 , f г , .
Постоянная а должна быть равна нулю, так как в противном случае в соот-
83

ветствии с (5.25) напряжение ст<з|г=о=°°. Интегрируя еще 2 раза по г, на.
.ходим £=— ar*l64 + br2/4+cln{r/R)+d. Вновь из условия конечности £(0) по-
.лучаем С=0. Кроме того, в случае заделанных краев пластинки имеем
C(/?)=dC/dr|B = 0, что дает
—а#3+86/?=0, —ct#4-M6W2+64d=0,
юткуда находим
b=aR2/8t £*=—аЯ4/64 и £=-(а/64) (г*—2/?2г2+^4)=_(^/64) (^2_г2)2
5.6. В условиях задачи 5.5 считать, что пластинка невесомая, а к ее центру
лриложена сила Fq.
Решение. Из условий равновесия на пластинку при r=R действует
сила реакции с плотностью на единицу длины — F0/2nR. Следовательно, на
Л
краю пластинки действуют касательные напряжения о>з, такие, что I ondx^m
-ft
= —F0I2jiR. С учетом формулы (5.25) имеем
~^ = Е ^1 \<h>-xl)dx3=Dd-M\
2nR 2(1 — va; dr I J 3' 3 dr '
'r^Rlh
r=R
Всюду, кроме точки г=0, для деформации пластинки справедливо уравнение
Д2_£=0 (см. уравнение. (5.26)) или в случае цилиндрической симметрии
•/--i[r(A-£)']'=0. Отсюда (A-Z)' = a/r. В частности, D(A-t))'rs=R=aD/R=
= F0/2nR или a=Fo/2nD. Проводя следующие интегрирования по г, получаем
Из условия конечности £(0) имеем с=0. Условия tt(R)=dt,ldr\R=0 дают
bR2+d=0, 2bR+F0R/8nD=0, откуда
b=-F0/\faDt d=F0R2l\6nD и £=(F0/16nZ))[2r2ln(r//?)+^2-r2].
5.7. Показать, что дисперсионное уравнение (5.31) для изгибных волн
в тонкой пластинке совпадает с уравнением (5.20) для антисимметричной
нормальной волны наименьшего номера на низких частотах.
Решение. Учитывая соотношения х=со/с*, k = a>lciy ct2=\i/p, ci2=(K+
4-2ц)/р, запишем выражение (5.20) в виде
Р = + У± А -=^== ± ¥1а л/ШШ
~ 2А ct Vc?-c' 2Л У |x(X + (i)
Теперь выразим % и ц через £ и v с помощью (3,26). В результате получим
выражение
* 2h * Е У D
совпадающее с (5.31).
5.8. Решить задачу об отражении гармонической изгибной волны
А exp [/(AjiXi+rjA^—0)01, падающей на опертый при *i = 0 край пластинки.
Решение. Найдем вначале общее решение вида £=ехр [£(5х1+т)дг2—со/) ]
для уравнения (5.29). Подставив это выражение в уравнение (5.29), получиы
84

следующую связь между g, г\ и со: (62+п2)=*4, где £4=2рЛсо2/£. Отсюда
имеем четыре возможных значения g:
g1 = *1=K^-Tla, g2 = -^, Ь = /ХЬ Xl = K*2 + T)2, 64 = -^.
В нашем случае, исключая растущую при *i-*~oo волну и опуская множитель
exp [i(i)X2—(ut)]f запишем
£ = A lexp (1кгхх) + V exp (— Нць) +1 exp (хл)].
Удовлетворим теперь граничным условиям на краю пластинки:
CU--0. "-U-—* 4 + v4 =0,
что дает l + V+№=0, —ki2(l + V)+xi2W^0 и окончательно V=—1, №=0.
5.9. В условиях задачи 5.8 край пластинки считать свободным.
Решение. В этом случае изменятся только граничные условия, в
качестве которых следует потребовать при *i = 0 равенства нулю касательного
напряжения и момента:
"aU-.-^-4-t
В результате для коэффициентов V и W получаем систему уравнений:
ikx (1 - V) + XiW = 0, — (k\ + vna) (1 + V) + (xj — vti2> IT = 0.
Отсюда легко находим:
f К tf — Tj« [^» + (1 — v) П*! — K^* + Tf t^> — (1 — v) n«l _t
_ 2t VW~tf[k* - (1 - v) if ]
i /*2 — V [Л2 + (1 г- v) r|aJ + Yk* + V [Л2 — (1 - v) л2] '
5.10. Показать, что вдоль свободного края пластинки может
распространяться волна, возмущения в которой отличны от нуля лишь в окрестности края.
Найти фазовую скорость этой волны.
Решение. Будем считать падающую волну в предыдущей задаче
неоднородной, т. е. r\>kt £i = i'y, Y==Vt12—^2- Тогда отраженная волна Vr=exp(—#1*1)
возрастала бы экспоненциально при *i->-oo. Следовательно, должно быть V=0
или
Yr\2 - k* [k2+ (1 - v) Ti2] = Yk2 + л2 Ik2 - (1 - v) rf ].
Возводя обе части этого равенства в квадрат, легко находим
т|«=#1 (1—v2) = Зрсо2/£Л2,
0ткУДа для фазовой скорости волны имеем
сф = ©/т|=у£/Зрг|Л.
Заметим, что при этом формула для W, выписанная в предыдущей задаче, дает
^=1. Таким образом, общее выражение для смещения £ (см. задачу 5.8) в
рассматриваемом случае, если учесть также фактор ехр [Ццх2—<ot)]t дает
£ = A (exp (KiJF7*5*i) + exp(Y^f+k2xx)] exp [i (r\x2 -0/)].

Часть вторая
ГИДРОДИНАМИКА
Глава 6
ОСНОВНЫЕ ЗАКОНЫ ГИДРОДИНАМИКИ
ИДЕАЛЬНОЙ ЖИДКОСТИ
Движение жидкостей и газов (в дальнейшем мы будем говорить
чаще о жидкостях, хотя все сказанное относится и к газам),
являющееся предметом гидродинамики, отличается от движения
твердых упругих тел следующими особенностями:
1) жидкость (без учета вязкости) не оказывает
сопротивления сдвигу;
2) смещения точек жидкости в результате ее течения могут
быть не малы даже при малых силовых воздействиях;
3) на характер движения жидкости существенным образом
может влиять внутреннее трение (вязкость).
Если первая особенность ведет к упрощению уравнений
движения по сравнению со случаем твердого тела, то две другие —
к их усложнению. Усложнение существенно пересиливает
упрощение, и в результате гидродинамика оказывается весьма
сложной наукой. Некоторые ее аспекты, например теория
турбулентности, не до конца разработаны даже в настоящее время, хотя
основные принципы гидродинамики, с которых мы начнем, были
установлены еще Эйлером, Бернулли и Лагранжем.
Вначале будем рассматривать идеальную жидкость, т. е.
жидкость без внутреннего трения и, следовательно, без перехода
механической энергии в тепловую. Будем пренебрегать также
теплообменом между различными объемами жидкости. Это
означает, что все процессы протекают при постоянной энтропии и
напряженное состояние жидкости характеризуется одной
скалярной величиной — давлением р.
§ 20. Способы описания движения жидкости
20.1. Эйлеров и лагранжев способы задания движения
жидкости. Движение жидкости будет вполне определено, если все
величины, характеризующие жидкость (скорость движения частиц
v, давление р, плотность р, температура Гит. п.), будут заданы
86

как функции координат и времени. Это способ задания движения
усидкости по Эйлеру. При этом, фиксируя некоторую точку
пространства, мы следим за изменением во времени соответствующих
величин в этой точке, а фиксируя момент времени, мы знаем
изменение этой величины от точки к точке. Однако никакой
информации о том, какая именно частица жидкости находится в
данной точке в данный момент времени и как она перемещается в
пространстве, мы непосредственно не имеем.
Другой способ описания течений, в основу которого положено
описание движения отдельных жидких частиц, называется лаг-
ранжевым. При этом все величины, в том числе и координаты
движущейся частицы жидкости, определяются как функции
времени t и некоторых переменных & (/=1, 2, 3),
идентифицирующих определенную частицу: xi=xi(lk9 t), p=p&ht t), p=p(|k, t)
и т. д. В качестве переменных.£fc обычно используют начальные
координаты частиц жидкости, так что &=*ДБЛ| /0). Таким
образом, при лагранжевом описании фиксируется внимание на
определенных частицах Жидкости и прослеживается, как изменяются
со временем их местоположение, скорость, а также давление,
плотность, температура и другие величины в их окружении.
Эти два описания движения вполне равноправны, и выбор
одного из них в каждом конкретном случае диктуется только
соображениями удобства. Так, например, большинство приборов
измеряют характеристики жидкости (в фиксированной точке
прибор стоит на месте), т. е. дают эйлерову информацию. Если же
покрасить (пометить) часть жидкости, то по растеканию краски
получают лагранжеву информацию о движении. Способ Лагран-
жа также проще описывает процессы диффузии, связанные с
непосредственным перемещением частиц.
20.2. Переход от одного описания к другому. Связь между
двумя описаниями в общем случае является весьма сложной.
Например, если известно давление в лагранжевом описании
P»(6*i 0» то для получения давления в точке {xt} 'p9(xh, t)
(эйлерово описание) нужно найти начальное положение {|fc} той
частицы, которая в момент времени t придет в точку {хк}. Другими
словами, нужно разрешить относительно |к систему уравнений
*<=-*<(Ьь, 0 ('=1. 2, 3), что дает p9(xh, /)=p,[6«(*fc> t), t]. Для
существования обратных функций &(хк, t) необходимо и
достаточно, чтобы якобиан преобразования
*(ЕьЬ.Еа) \dh) к '
был отличен от нуля. В некоторых случаях важно знать, как
меняется якобиан / со временем. Нетрудно показать (см. задачу
6.1), что
— _ = —L =divv. (6.2)
J at dxk
87

20.3. Субстанциональная и локальная производные по времени*
В описании Лагранжа частная производная по времени от какой-
либо величины Соответствует скорости ее изменения для данной
жидкой частицы. В частности, 1>»=д**/д/ и dvjdt есть скорость и
ускорение частицы соответственно. В эйлеровом же описании
частные производные по х{ и t являются компонентами градиента
и скоростью изменения соответствующей величины в данной
точке пространства. Поэтому величина dv(xh, t)jdt уже не является
ускорением частицы, находящейся в момент времени / в точке
{xh}, так как в момент времени t+kt в точке {хк} находится уже
другая частица. Так, например, в водопаде скорость в данной
точке {xh} постоянна (d\/dt=0), в то время как под действием;
силы тяжести частицы ускоряются. Найдем выражение для
ускорения частиц жидкости в описании Эйлера. Пусть за время:
А/ частица, находящаяся в момент времени t в точке {**},
переместится в точку {xh+kxk}. Тогда i-я компонента ускорения
найдется как
lim [Vi(xk + Дхь t + At) — v{(xki t)]/M =
= lim [Vi {xky t) + (dvt/dxk) Ax* + {dojdt) M —vt (xky t)]/M.
At-+o
Учитывая теперь, что Um(AxJkt)=vh, получаем
д*-и>
foi <tot / д д \
—-*■+*■£-{£+»■£;)"• (6-3>
или в векторной форме
a = ^ + (vV)v=(-i-+vV)v. .(6.3')
Аналогично находится скорость изменения произвольной
(скалярной или векторной) величины / для данной частицы. Эту
величину называют субстанциональной, или материальной,
производной, а также полной производной, или производной по
траектории, и обозначают dffdt (в литературе также встречается
обозначение Df/Dt). Частную же производную df/dt в эйлеровом
описании называют также локальной. В наших обозначениях
связь между субстанциональной и локальной производными
имеет вид
d/dt=d/dt+(vV). (6.4)
Мы в основном будем пользоваться эйлеровой формой описания
движения.
Для дальнейшего полезно получить выражение для
субстанциональной производной от интеграла по некоторому объему V,
состоящему из одних и тех же частиц, т. е. движущемуся вместе
88

с жидкостью:
Здесь F—произвольная скалярная или векторная функция. Если
перейти под интегралом к переменным Лагранжа х{=х{(%к, /),
то интегрирование при любых / будет проводиться по
фиксированному объему V0, который занимали частицы в начальный
момент времени. Следовательно, мы имеем право менять местами
d/dt и интегрирование по VV Таким образом,
± = ± jF/dExdbdb = J^(F/) dWWb. (6.5)
где / — якобиан преобразования (6.1). Возвращаясь в (6.5) к
переменным Эйлера (обратное преобразование), запишем
л J / я J\dt ^ J dt )
Воспользовавшись теперь (6.2) и (6.4), окончательно получаем
V V
§ 21. Система уравнений гидродинамики
21.1. Уравнение неразрывности. Одним из фундаментальных
уравнений гидродинамики является уравнение неразрывности,
или закон сохранения вещества. Он выражает тот очевидный
факт, что масса жидкости в объеме, охватывающем все время
одни и те же частицы, сохраняется. Математически это можно
записать так:
-£jW = °- (6.7)
V
Применив формулы (6.6) и (6.4), перепишем (6.7) в виде
f/ia+vVp + pVvW = 0, (6.8)
откуда в силу произвольности объема К, приравняв нулю
подынтегральное выражение, получаем искомое уравнение
неразрывности
iL + vVp + pVv=0 или |B.+ V(pv) = 0, или
iP. + pVv.-=0. (6.9)
89

Интегральная форма уравнения неразрывности (6.8) имеет
простой физический смысл, который становится ясным, если,
используя теорему Гаусса — Остроградского, преобразовать
интеграл по объему от vVp+pVv= V(pv) в поверхностный
fv(pv)dV = fpvndS,
где п — вектор внешней нормали к поверхности S,
ограничивающей объем V. В результате из (6.8) получаем
-|-jpdK = —fpvndS (6.10)
v s
— скорость изменения массы жидкости внутри фиксированного
объема V равна массе жидкости (с обратным знаком),
вытекающей в единицу времени из объема через его поверхность S.
Заметим, что этот факт можно было бы взять за исходный и с
помощью обратных преобразований вновь получить формулу (6.8).
21.2. Уравнение Эйлера. Перейдем теперь к выводу
уравнения движения жидкости, называемого также уравнением
Эйлера. Для этого достаточно применить второй закон Ньютона:
производная по времени от количества движения (импульса)
некоторого объема жидкости равна сумме сил, действующих на этот
объем:
-LjpvdK = F + F$, (6.11)
v
где F= J pfdV — внешняя объемная сила (f — сила, отнесенная
v
к единице массы); Fe—хила, действующая на объем V со
стороны окружающей среды через ограничивающую поверхность S.
В идеальной жидкости поверхностные силы определяются
только силами давления р и равны (с обратным знаком) силам,
действующим со стороны объема V на окружающую жидкость. Так
как давление действует по нормали к S, то Fs=^~ J pndS, где
s
п —внешняя нормаль к 5. По теореме векторного анализа,
аналогичной геореме Гаусса, имеем
Fs = - CpndS = - ГVpdV (6.12)
5 V
В результате (6.11) с учетом (6.12) и выражения для внешних
сил запишем в виде
^]^pl + pviVv)]dV=U-Vp + pf)dV. (6.13)
V V
90

Если теперь, приняв во внимание уравнение неразрывности (6.9),
преобразовать подынтегральное выражение в левой части
следующим образом:
jL(pV)+pv(Vv) = p£ + v(£ + pVv) =
= prfT=pir + p(vV)v*
а также воспользоваться произвольностью объема V> то
получаем искомое уравнение Эйлера
^•£ + «»*>»--? + !. (6.М)
21.3. Полнота системы уравнений. Уравнение (6.14) вместе с
уравнением неразрывности (6.9) составляет четыре скалярных
уравнения для пяти скалярных величин (плотности р, давления
р и трех компонент вектора скорости v{). Следовательно, система
уравнений пока незамкнута. Замыкающими для нее являются
термодинамическое уравнение состояния, связывающее три
величины, например давление /?, плотность р и энтропию s:
P=p(p,s), (6.15)
и уравнение для энтропии. Как мы уже условились выше,
энтропия данной жидкой частицы остается постоянной, г. е.
Заметим, что требование изэнтропичности процессов в идеальной
жидкости не противоречит возможности изменения энтропии в
заданной точке пространства. Это изменение может происходить
в связи с приходом в данную точку новых частиц жидкости.
Энтропию 5 можно исключить из уравнений, для этого нужно
взять от (6.15) субстанциональную производную по времени и
обозначить
с2=(др/ф).. (6.17)
В результате получаем
dp/dt=c2dp/dt\ (6.18)
где с2 уже следует считать заданной функцией рир. Как будет
видно ниже (ом. гл. 12), с является скоростью звука в среде.
Если жидкость является баротропной, т. е. давление зависит-
то л ько от плотности
Р=р(р), (б-19)
то последнее уравнение и будет замыкающим для системы (6.9),
(6.14). Вид функции /?(р) зависит от свойств рассматриваемой
Жидкости или газа. В частности, для идеального (термодинами-
91

чеоки) газа имеем уравнение адиабаты pVT = const, где ^( = cp/cv—
отношение теплоемкостей газа при постоянном давлении и
объеме. Но V=l/p—удельный объем, поэтому р=р0(р/ро)т-
Полная замкнутая система уравнений (6.9), (6.14) и (6.18)
или (6.19) называется системой уравнений гидродинамики
идеальной жидкости. Для решения конкретных задач к уравнениям
нужно добавить соответствующие граничные условия. Так, на»
пример, на неподвижной границе с абсолютно твердым телом
должна обращаться в нуль нормальная компонента скорости
vnt на тангенциальную компоненту в случае идеальной жидкости
никаких ограничений не накладывается из-за отсутствия
напряжений сдвига.
Примером силы f, входящей в уравнение Эйлера (6.14),
является сила тяжести. При этом f равна вектору g(g,= |g| =
=9,81 м/с2), направленному к центру Земли. В уравнения могут
войти также силы притяжения Луны и Солнца, которые
учитываются в теории морских приливов. В динамике океана и
атмосферы оказывается существенной неинерциальность системы
отсчета, связанной с вращающейся Землей. При этом в систему
уравнений гидродинамики должны быть введены силы инерции:
центробежная fu6=fi2r= V(fiV/2), где Q — частота вращения
Земли, и сила Кориолиса ffc=—2fiXv. Заметим, что все
рассмотренные нами силы, кроме кориолисовой, являются
потенциальными, т. е. представимыми в виде градиента от потенциальной
функции: f=— Vu.
Рассмотрим здесь также важное в приложениях упрощение
уравнений гидродинамики, связанное с предположением о
несжимаемости жидкости. В этом случае плотность каждой частицы
должна оставаться постоянной: dp/dt=dp/dt+\Vp=0. При этом
из уравнения состояния (6.18) вовсе не следует, что dp/dt=0,
так как в несжимаемой жидкости скорость звука с бесконечно
велика. Таким образом, в несжимаемой жидкости уравнение
(6.18) заменяется на dp/d/=0 и с учетом уравнения
неразрывности будем иметь
dp/df+vVp = 0, Vv=0, (6.20)
так что система гидродинамических уравнений остается
замкнутой.
§ 22. Гидростатика
22.1. Основные уравнения. Рассмотрим теперь случай
покоящейся жидкости. Положив в (6.14) v=0, получаем уравнение
гидростатики
Vp=pf. (6.21)
Важным является случай, когда внешние силы имеют потенциал
и: f=-—Яи, тогда (6.21) запишем так:
Vp=—pVw. (6.22)
92

Последнее уравнение далеко не всегда имеет решение.
Действительно, слева стоит градиент /?, правую же часть можно будет
представить в виде градиента только при определенной
зависимости р от координат. Действительно, применив к правой и
левой частям уравнения (6.22) операцию rot, получим VpxVw=0,
Следовательно, векторы Vp и Vu должны быть параллельными.
Рассмотрим подробнее случай жидкости (газа) в поле силы
тяжести. При этом u=gz (ось z направлена вертикально вверх)
и уравнение (6.22) примет вид
др/дх=др/ду=0, dp/dz=—pg. (6.23)
Отсюда следует, что p=p(z) —функция только z, и если
предположить, что р постоянно, то
p=—pgz+const.
Постоянная интегрирования определяется из условия на
границе; если при z=z0 задано р=р0у то при произвольном z
P=Po—pg(z—z0). (6.24)
Однако, если рассматривать большие перепады высот, плотность
р уже нельзя считать постоянной. Температура также может
зависеть от г.
Рассмотрим для примера случай изотермической атмосферы.
Уравнение состояния (считаем газ атмосферы идеальным) имеет
вид
P=XRIv)pT, (6.25)
где R— универсальная газовая постоянная; \i — молекулярная
масса газа. Подставляя (6.25) в (6.23), находим:
|i dz ^' p0 RT ,
где p0 —значение плотности при z=0. Таким образом, мы
полумили известную барометрическую формулу
P = р0ехр
(-*,). <6.26>
описывающую изменение плотности с высотой в изотермической
атмосфере. В случае, когда в атмосфере T=T(z),
соответствующая формула для p(z) получена в задаче 6.9.
Аналогично можно рассмотреть и случай баротропной
жидкости (или газа), описываемой уравнением р=р(р), что имеет
место, например, для изэнтропической атмосферы (р=р0(р/р0)т).
22.2. Условие гидростатического равновесия. Частота Вяйся-
ля. Выясним теперь, при каких условиях в поле силы тяжести
состояние равновесия будет устойчивым для общего уравнения
состояния р=р(р, s). Подставив его в (6.23), получаем
-ИГ= & = <•£+у* (6.27>
dz аг дг
93

где Y=(dpjds)p. Рассмотрим частицу жидкости объемом V0,
находящуюся в точке z. На эту частицу действует сила тяжести
—gp(z)Vo и (если жидкость находится /в равновесии) равная ей,
но направленная в противоположную сторону сила Архимеда.
Если теперь сместить частицу на расстояние £ по вертикали, то
из-за сжимаемости изменится ее объем «а величину Д V, в то
время как ее масса и энтропия сохраняются. В результате сила,
действующая на смещенную частицу, будет
F=-gp(z)V0+gp(z + t)(V0+AV)
— снова вес и сила Архимеда. Разложив p(z+£) в ряд и
ограничиваясь линейными по £; и Д V членами, получим
[р (г) dz V0\
Изменение объема можно подсчитать, воспользовавшись
уравнением состояния, примененным к нашей частице. С учетом Д5=0
с точностью до малых первого порядка имеем
Ap=c2Ap=c2A(m/V)=c2p(z)V0A(l/V)= — c2p(z)AV/V0y
где m = p(z) Vo — масса частицы жидкости. Отсюда
V0 с2р (z) dz
Следовательно, AV/V0=(gfc2)l, и окончательно для силы,
действующей на смещенную частицу, получаем
F = gp (г) V0(j^ + g/c2) С = - rnN%
где
N2 = ~s{jjt + g/c2) (6*28)
— так называемая частота Вяйсяля, имеющая важное значение,
в теории внутренних волн. Состояние равновесия будет
устойчивым только в том случае, если сила противоположна смещению,
для чего необходимо
Л^>0 или ±*£- + g/(?^0, (6.29)
р dz
т. е. плотность должна достаточно быстро уменьшаться с
высотой. Точнее, если dp/dz>—gpfc2, то состояние равновесия будет
неустойчивым, возникнут конвективные движения.
Заметим также, что в выражении для частоты Вяйсяля
можно исключить член p^dp/dz, воспользовавшись (6.27):
!£ = _,/<*_ JL*
р dz рс* dz
94

при этом
^=lyi, (6.30)
и если энтропия постоянна во всем пространстве (ds/dz=0), то
состояние равновесия становится безразличным.
§ 23. Теорема Бернулли
и закон сохранения энергии
23.1. Теорема Бернулли. Эта теорема имеет место для стационар-
ново (v не зависит от /) течения идеальной баротропной
жидкости, уравнение состояния которой р=р(р). Обратимся сначала
к уравнению Эйлера (6.14), где в этом случае член dv/dt=0t а
член (vV)v запишем, используя известное векторное тождество:
(vV)v = i- V(i;2) — vxrotv. (6.31)
Кроме того, предположим, что внешние силы имеют потенциал
f=—Vu, и введем новую функцию wy называемую энтальпией и
определяемую в термодинамике как
w=E+pV=e+p/py (6.32)
или в дифференциальной форме
<to = de + - — 4-dp. (6.32')
Р Ра
Здесь w и внутренняя энергия е относятся к единице массы
жидкости. Дифференциал внутренней энергии de=Tds—pdV в
нашем случае изэнтропических процессов (ds=0) упрощается и
равен
de = —pdV=p/p2do. (6.33)
В результате для дифференциала энтальпии имеем
dw=dp/p. (6.34)
Уравнение Эйлера теперь запишем в виде,
V(v2/2+w + u)=vXrot\. (6.35)
Назовем линией тока линию, касательная к которой в каждой
точке совпадает по направлению с вектором скорости v в этой
точке. В общем случае линии тока изменяют свое положение со
временем. В случае же стационарного движения линии тока
неподвижны и совпадают с траекториями частиц жидкости.
Выберем какую-либо линию тока и спроектируем уравнение (6.35) на
направление касательной к этой линии в произвольной точке.
Векторное произведение vXrotv всегда нормально куй поэтому
при проектировании даст нуль. Проекция градиента дает
производную d/dl, где dl— элемент длины линии тока. В результате
95

имеем d(v2/2 + w + u)/dl=0, илк
v*/2 + w + u=Cl. (6.36)
Таким образом, величина v2/2 + w + u постоянна вдоль линии
тока. Это и есть содержание теоремы Бернулли *. Выражение
(6.36) называют интегралом Бернулли. Постоянная С, в общем
•случае будет разной для различных линий тока. Однако в
частном случае безвихревого движения (rotv=0) из (6.35) имеем
V(v2/2 + w + u)=^0t
так что
v2/2 + w + и=const, (6.37)
где постоянная уже одинакова для всех точек жидкости.
В случае течения несжимаемой жидкости (p=const) из (6.34)
следует, что с точностью до постоянной w=plp, поэтому (6.36)
записывается в привычном виде
v2/2+p/p+u=Ct. (6.38)
23.2. Некоторые применения теоремы Бернулли. Рассмотрим
течение несжимаемой жидкости в трубке с сужением (рис, 6.1).
Где давление больше, е широком месте А или в узком В? Ответ
на этот вопрос непосредственно следует из теоремы Бернулли.
В самом деле, поскольку в узком месте скорость v больше
(через поперечное сечение трубки в А и В протекает одинаковая
масса жидкости в единицу времени), то согласно (6.38) давление
в В будет меньше (и при этом можно считать постоянным).
Сделав в Л и В небольшие отверстия и соединив их стеклянной
трубкой с ртутью внутри, мы по разным уровням ртути в правой и
левой частях трубки определим разницу давлений в Л и В.
Устройство, изображенное на рис. 6.1, служит для определения
скорости течения жидкости и называется трубкой Вентури. Присвоим
величинам р, v в А индекс 1, а в точке В — индекс 2. Тогда по
теореме Бернулли
Pi/p + y12/2=p2/p + y22/2.
Кроме того, vt и v2 связаны соотношениями viSl=vlS2t где St и
S2 — площади поперечных сечений трубки в Л и В
соответственно. Из двух получающихся равенств находим
u1=[2(p1-p2)/p(S17S22-l)],\
Таким образом, зная разность давлений pt—р2у находим
скорость в широкой части трубки ut.
Пусть теперь плоский поток жидкости обтекает два близко
расположенных друг к другу цилиндра с осями, перпендикуляр-
Вообще говоря, эта величина постоянна и вдоль линии, касательная к
которой совпадает с направлением вектора rot v (линия вихря). Мы ограничи
лись лишь наиболее распространенной формулировкой теоремы Бернулли.
96

Рис. 6.1
Рис. 6.2
v£",
Ал
Рис. 6.3
Рве. 6.4
щ.
S'
Рис. 6.5
ными скорости потока (рис. 6.2). В пространстве между
цилиндрами имеется повышенная скорость (сгущение линий тока). По
теореме Бернулли это вызовет уменьшение давления в этом
месте и, как следствие, появление силы притяжения цилиндров.
В практике судовождения хорошо известно, что два идущие
параллельным курсом и близко друг к другу корабля испытывают
силу взаимного притяжения. Были случаи, когда это приводило
к столкновению судов.
Рассмотрим истечение жидкости из сосуда через отверстие
(рис. 6.3). Пусть уровни свободной поверхности и отверстия
будут соответственно 2t и z2. Применим теорему Бернулли к какой-
нибудь линии тока, соединяющей поверхность с отверстием
(пунктирная кривая). На поверхности имеем z=ziy 01=0
(площадь свободной поверхности жидкости считаем большой по
сравнению с площадью отверстия), р=р0 — атмосферное
давление. В отверстии имеем z=z2t v=v2f р=р0 (перепадом
атмосферного давления при переходе от г4 к z2 пренебрегаем).
Равенство выражений (6.38) при u=gz в этих двух точках линии тока
дает
v2/2+gz2=gzt.
Отсюда для скорости истечения получаем известную формулу
"2 = Y2g(z1-z2). (6.39)
23.3. Теорема Бернулли как следствие закона сохранения
энергии. Назовем трубкой тока трубку, образованную множест-
4 Л. М. Бреховских, В. В. Гончаров 97

вом линий тока, проходящих через произвольный замкнутый
контур. Рассмотрим участок трубки тока, ограниченный двумя
сечениями площадью 5t и S2. Предполагая в этих сечениях
давление, скорость жидкости, ее плотность и потенциал вяешних сил
постоянными, обозначим их через ри vu pt, ui и р2, Vi, рг, иг
соответственно. Пусть поток жидкости направлен от St к S2. За
некоторое время А/ в рассматриваемый участок трубки тока
войдет масса жидкости piS^A/. За это же время через 52 выйдет из
этого участка масса жидкости p2S2v2At. В случае стационарного
течения эти массы равны между собой:
AM=piSiviAt=p1S2v2M. (6.40)
Давление pi на входе нашего участка трубки тока производит
над втекающей через St жидкостью работу, равную PiS^A/.
Наоборот, в S2 вытекающая жидкость производит над внешней
средой работу p2S2v2At. Разница этих работ должна по закону
сохранения энергии равняться увеличению энергии количества
жидкости, протекшего за время А/ через трубку, т. е.
piSiviAt—p2S2v2At=AM {Е2—Е,), (6.41)
где Ei и Ег — энергия единицы массы жидкости в сечениях S4 и
Sa. Эта энергия в любой точке жидкости складывается из
кинетической и2/2, потенциальной и и внутренней е энергий:
E=v2/2 + u+e. (6.42)
Подставляя это выражение в (6.41) с учетом также (6.40),
нетрудно получить
Pl р, 2 2^ 2^ 2 2 х * г
Вводя теперь по (6.32) энтальпию в сечениях трубки а>«=.е«+
+Р»/р<, вновь приходим к теореме Бернулли (6.36), которая, как
мы видим, является следствием законов сохранения энергии и
массы жидкости, протекающей по трубке тока.
23.4. Закон сохранения энергии в нестационарном случае.
Выясним теперь, как может быть записан закон сохранения энергия
в общем случае нестационарного движения идеальной жидкости.,
Энергия единицы объема жидкости (плотность энергии) согласно
(6.42) равна
9 = рЕ = —ри2+Ра + ре.
Предполагая независимость от времени u(du/dt=0), найдем
изменение во времени плотности энергии 8\
Ы 12 ) dt v Ы dtyv '
Воспользовавшись уравнением неразрывности (6.9), преобразуем
98

первое слагаемое:
(i"'+u)w—(t"+")v<w-
Второе слагаемое преобразуется с учетом уравнения Эйлера
(6.14) с потенциальными внешними силами f=— Vu:
pv— = — pv —— pvVu —pv(v V)v.
dt p
Здесь в соответствии с (6.34) Vp/p=Vw. Учитывая также (6.31)
и тождество v(vXrot v) =0, получаем
— pv(vV)v = — pvV (у2/2).
Группируя теперь соответствующие члены, легко находим
dS/dt = — (v2/2 + и) V (р v) — pv V (vV2 + и + w) + д (ps)/dt.
Вычислим теперь производную по времени от плотности
внутренней энергии ре, используя выражения (6.32) и (6.33):
d (ре) «а р de + edp = {pip) dp + edp = (e + p/p) dp = wdp.
Отсюда с учетом уравнения неразрывности (6.9) имеем
д (ps)/dt = w дР/dt = — w V (р v) (6.43)
и окончательно
Проинтегрируем последнее равенство по произвольному, но
фиксированному объему V. Интеграл по объему от правой части
преобразуем в интеграл по охватывающей этот объем
поверхности S, применив теорему Гаусса—< Остроградского к вектору
А=р(и2/2+ы+ад)у. В результате получаем интегральную форму
закона сохранения энергии в движущейся жидкости
i"I(pf+pu+p*)dV=-$p{^+u+w)v»dS- <6-45)
V S
Здесь выражение слева соответствует изменению энергии объема
У- Из закона сохранения энергии следует, что поверхностный
интеграл справа дает поток энергии через S, и, таким образом,
вектору
N==pv(v2/2 + u + w)=pY(v*l2 + u + E + p/p) (6.46)
можно приписать смысл вектора плотности потока энергии.
Выражение l/2v2 + u + w при этом нужно рассматривать как
количество энергии, переносимое единицей массы жидкости.
Существенно, что здесь к механической энергии v2/2 + u добавляется w, а не
внутренняя энергия е. Это происходит потому, что, кроме просто-
го переноса энергии, в процессе движения среда производит над
99 4*

данным объемом жидкости определенную работу, например
сжимая его. Это дает дополнительный поток энергии pv. В самом
деле, рассмотрим адиабатическое движение жидкости внутри
трубки тока (см. выше). Поток энергии в сечениях S4 и S2^b
стационарном случае должен быть один и тот же. Но согласно (6.41)
этим потоком не может быть (величина АМЕ—масса
перенесенной жидкости, умноженная на энергию единицы массы.
Действительно, из-за отличия от нуля левой части (6.41) эта величина
не сохраняется. Как видно из (6.36), сохраняющейся величиной
является v2/2 + w + u или AM(v2/2+u+w), поскольку ДЛ1 тоже
сохраняется.
Заметим, что в случае несжимаемой жидкости имеем de=0,
в то время как согласно (6.34) dw=p-ldp. Учитывая, что г и w
определяются с точностью до произвольных постоянных, в этом
случае можно положить е = 0, w=pfp, т. е. е и w существенно
различаются.
Пользуясь выражением (6.45), легко получить теорему Бер-
нулли. В самом деле, рассмотрим стационарное (d/dt=0)
движение жидкости и в качестве объема V выберем участок трубки
тока между поверхностями Sd и 52. Поскольку на боковой
поверхности трубки тока 0П=О, то из (6.45) получаем
РЛ$1 (OJ/2 + иг+ тг) = p2u2S2 {v\l2 + ц + w%).
Аналогично на основе интегрального закона сохранения массы
(6.10), примененного к тому же участку трубки тока, имеем
p1u1S1=p2^252.
Поделив теперь первое равенство почленно на второе, мы вновь
придем к теореме Бернулли, т. е. равенству (6.36).
§ 24. Закон сохранения импульса
24.1. Тензор плотности потока импульса. Импульс единицы
объема жидкости, по определению, равен pv. Найдем его производную
по времени. Учитывая уравнение неразрывности (6.9) и
уравнение движения (6.14), имеем
Объединив теперь второй и четвертый члены в правой части в
d(pViVh)/dxh и положив dp/dXi=d(6ihp)dxh, где 6ik — символ Кро-
некера, получаем
4" (Р"<) = - -Г" №* + Pv<Vk) + л- <6-47)
dt dxk
Введем следующее обозначение:
Uik = pbik + pvflk, (6.48)
100

так что
^-(P^)=-^f + A. (6.49)
и проинтегрируем последнее равенство по произвольному
фиксированному объему V:
v v *! v
Здесь первый интеграл в правой части преобразуем в интеграл по
поверхности S, охватывающей объем V> воспользовавшись
теоремой Гаусса— Остроградского для тензора (см. теорему 4
приложения) . Тогда
± J т dV = - J UiknkdS + J /, dV, (6.50)
V S V
где nk — компонента единичного вектора внешней нормали к S.
Таким образом, изменение импульса в объеме V связано с
потоком импульса через граничную поверхность и с действием
внешних сил. Если последние отсутствуют (f(=0), то (6.50)
переходит в закон сохранения импульса:
-Jj-Jp*/ dV - - §UiknkdS (6.51)
— изменение импульса объема V равно потоку импульса,
втекающего в V через граничную поверхность. В связи с этим
тензор называют тензором плотности потока импульса.
24.2. Теорема Эйлера. При решении практических задач
гидродинамики часто возникает необходимость расчета силы,
действующей со стороны протекающей жидкости на окружающую
среду. Найдем эту силу в случае стационарного движения
жидкости в отсутствие внешних сил. Для этой цели воспользуемся
законом сохранения импульса (6.51), который для
стационарного движения примет вид
J Tliknk dS = j (рбЛ + pofik) nkdS = 0. (6.52)
s s
Выберем в качестве 5 поверхность некоторого участка трубки
тока. В плоскости чертежа этот участок изображен на рис. 6.4.
На входном торцевом сечении трубки Si скорость v——vn, а на
выходном S2 v=im, где u=.|v|. Интеграл J pv{vhnkdS по боко-
вым стенкам трубки исчезает, так как vhnh=xn=Q (скорость на-
101

правлена вдоль стенки). Поэтому (6.52) можно записать в виде
j/?nt-dS = — j pViVkfikdS. (6.53)
5 St+S,
Здесь слева имеем t-ю компоненту интересующей нас силы Ft
действующей со стороны жидкости в трубке на окружающую
среду. Далее на Si имеем vhnh=\n—— v, а на S2 vhnh=\n = vm
В результате (6.53) примет вид
F{ = — J pv2n{dS — j* pxfiriidS. (6.54)
St s,
Таким образом, результирующая сила, действующая со
стороны протекающей жидкости на границы выделенного участка
трубки тока (включая и его торцы), равна сумме сил —
J pv*ndS (/=1, 2), приложенных к торцевым сечениям. Это
s/
утверждение обычно называют теоремой Эйлера.
Заметим, что векторная величина
Рх = — Jpt/2ndS (6.55)
St
есть не что иное, как импульс, втекающий в единицу времени в
трубку через Sit Знак минус обусловлен тем, что внешняя
нормаль п на Si направлена противоположно v. Аналогично
Р2 = jpi>2ndS (6.56)
— импульс, вытекающий в единицу времени из трубки через S».
Теперь (6.54) перепишем следующим образом:
F^-P,, (6.57)
т. е. сила р равна потере импульса (за единицу времени)
жидкостью, заключенной в момент времени t в выделенном участке
трубки тока. Если теперь умножить обе части равенства (6.57)
на dt и поменять знаки, то получим классическую формулировку
теоремы об изменении количества движения:
—Fdt=(P2-Pi)dt
Здесь —F по третьему закону Ньютона соответствует силе,
действующей со стороны окружающей среды на протекающую в
трубке жидкость; —Fdt — ее импульс, а правая часть —
приращение количества движения за время dt.
24.3. Применение теоремы Эйлера. Теорема Эйлера широко
используется при расчете характеристики стационарного потока
жидкости. Найдем, например, силу, действующую на стенки
трубы со стороны протекающей по ней жидкости. Если труба
цилиндрическая с прямолинейной образующей, то Р1=Р2, и Pi!=Pt
102

на торцах, следовательно, результирующая сила, действующая со
стороны жидкости на стенки трубы,- равна нулю. Нетривиальный
результат получается, если рассмотреть искривленную трубу и,
возможно, с переменным сечением. Участок такой трубы
изображен на рис. 6.4. Выражение для полной силы, действующей на
границы этого участка трубы, имеет вид
F= \pndS = FCT+ f pndS + j* pndS.
S St s»
Здесь первый член представляет собой искомую силу, действую-
щую на боковые стенки трубы, второй и третий члены — силы,
действующие на торцевые сечения St и S2.
Теперь с учетам теоремы Эйлера (6.54) получаем
Fct = — J (р + pf2)ndS — J (p + pv*)ndS. (6.58)
Si s9
Мы видим, что для определения этой силы достаточно знать
характеристики потока на входном и выходном отверстиях. В
случае, когда торцевые сечения St и 52 являются плоскими (их
площади мы также обозначим через S4 и S2) и значения
характеристик потока р\ р, v на каждом из них постоянны, выражение
(6.58) упрощается:
FCT = — Sx (рг + до») пг — S2 (р2 + p2t;a2) п2. (6.58')
Здесь индекс 1 относится к входному сечению, а индекс 2 — к
выходному.
Применим теперь теорему Эйлера для определения так
называемого коэффициента истечения струи. Выше с помощью
теоремы Бернулли мы определили скорость истечения жидкости из
сосуда через отверстие (см. формулу (6.39)). Однако
неправильно было бы думать, что расход жидкости за единицу^ времени
можно вычислить, умножив v2 на площадь отверстия S. Хотя при
подходе к отверстию из сосуда все частицы имеют одинаковую
по величине скорость v2, но направления этих скоростей разные.
Опыт показывает, что на небольшом расстоянии от отверстия
струя сжимается и линии тока становятся параллельными.
Обозначим площадь поперечного сечения струи в этом месте S'.
Расход жидкости будет равен v2S'. Отношение S'/S и называется
коэффициентом истечения струи. Из-за сложности потока в
сосуде вблизи обычного круглого отверстия этот коэффициент не так
легко вычислить. Однако в одном случае, а именно когда к
отверстию изнутри сосуда присоединена цилиндрическая трубка с
контуром, совпадающим с отверстием («насадок Борда», рис.
6.5), этот коэффициент можно найти с помощью теоремы Эйлера.
Со струей вытекает за время Д/ количество движения (им-
пУльс), равное pu22S'Af. Чтобы создать такое количество
движения, к жидкости должна быть приложена сила F% импульс
которой F&t равен вышедшему количеству движения. Единственной
103

силой, возникающей здесь, является сила давления на стенки со*
суда. Поскольку с помощью' насадка Борда мы удалили
выходное отверстие АА от стенок, то скорость жидкости вблизи них
практически отсутствует и, следовательно, давление на стенки
может быть определено из законов гидростатики. При этом
давления на стенки в любых противолежащих точках D и & равны
по величине и уравновешивают друг друга. Исключение
составляет участок А'А\ лежащий против отверстия. Гидростатическая
сила на этом участке, равная pg(zt—z2)S, и обеспечивает поток
количества движения жидкости через отверстие (мы
предполагаем, что линейные размеры отверстия много меньше Zi—z2):
pg(*i—z2)S=pvz2S'.
Если теперь учесть формулу (6.39) для скорости истечения vZt
мы легко получим, что коэффициент истечения в этом случае
равен S'S = 72. Отметим, что неуравновешенная гидростатическая
сила в сечении А'А' вызовет движение сосуда в сторону,
противоположную вытекающей струе (реактивное движение).
Заметим также, что без насадка Борда скорость жидкости на
стенках вблизи отверстия будет отличной от нуля. Но тогда в
соответствии с теоремой Бернулли давление на стенки в
окрестности отверстия будет несколько ниже гидростатического. Это
приведет к увеличению неуравновешенного гидростатического
давления на противоположном участке и в связи с этим к
увеличению коэффициента истечения жидкости до значения S'/S =.0,61
(см. задачу 7.8).
§ 25. Вихревое движение жидкости
Течение жидкости называется потенциальным, если во всей
жидкости rotv=0. Если же rotv=^=0 хотя бы в части объема,
занимаемого жидкостью, движение последней называется
вихревым. Рассмотрим ряд основных свойств вихревого движения.
25.1. Циркуляция скорости. Интеграл
Г-^vdr, (6.59)
взятый вдоль некоторого замкнутого контура /, называется
циркуляцией скорости вдоль этого контура. Преобразуем его в
интеграл по произвольной поверхности S, опирающейся на контур
/. Для этого воспользуемся известной теоремой Стокса, согласно
которой для произвольного вектора А имеем
фХйт = Г nrotAdS,
где п — нормаль к 5. Здесь предполагается, что контур /
ограничивает одноовязную область на S, т. е. он может быть стянут в
104

точку. Теперь для циркуляции получаем
Г= jnrotvdS. (6.60)
Из этой формулы, в частности, следует, что в потенциальном
течении (rotv=0) циркуляция скорости по любому замкнутому
односвязному контуру равна нулю. Отсюда, в свою очередь,
следует, что в потенциальном течении не может быть замкнутых
линий тока. Действительно, если бы имелась замкнутая линия тока,
то, выбрав ее в качестве I в (6.59), мы получили бы Г#0,
поскольку v и dx на контуре всюду совпадали бы по направлению
и vdx была бы всюду положительной величиной. Здесь
требование односвязности контура является существенным, так как
теорема Стокса справедлива только для таких контуров /, которые
могут быть стянуты в точку, все время находясь в области,
занятой жидкостью. В противном случае, например при
потенциальном обтекании идеальной жидкостью цилиндра, циркуляция
скорости по контуру, охватывающему цилиндр, может быть отлична
от нуля.
25.2. Теорема о сохранении циркуляции скорости. Важную
роль в теории вихревых движений играет теорема Томсона
(лорда Кельвина) о сохранении циркуляции, доказанная им в 1869 г.:
циркуляция скорости по любому замкнутому контуру,
перемещающемуся вместе с жидкостью, сохраняется.
Для доказательства этой теоремы выберем замкнутый
контур, состоящий из фиксированных частиц и, следовательно,
перемещающийся вместе с ними («жидкий» контур), и найдем
полную производную по времени от интеграла (6.59) по этому
контуру:
Поскольку полная производная, по определению, учитывает
перемещение частиц, мы должны принять во внимание изменение
контура со временем, т. е.
Во втором члене в квадратных скобках dr/dt=v и, кроме того,
vd\=d(v2/2). Первый член преобразуется на основе уравнения
Эйлера (6.14) с учетом потенциальности внешних сил /=—Vu ir
выражения для дифференциала энтальпии в адиабатических
процессах Vw—Vp/p (см. (6.34)). В результате
d\/dt=—Vu— 4w=— V(u+w).
Теперь (6.61) оказывается равным нулю как интеграл по замк-
105

нутому контуру от полного дифференциала:
djf = j)d(v*/2-u-w)=0.
i
25.3. Теоремы Гельмгольца о вихрях. Для нас будут важны
некоторые следствия из теоремы Томсона, установленные
независимо несколько ранее (1858 г.) Гельмгольцем.
Предварительно введем понятие о вихревых линиях и вихревых трубках.
Векторную величину ©=rotv часто называют вектором
вихря, или просто вихрем. Вихревой линией называют линию,
касательная к которой в каждой точке коллинеарна вектору вихря.
Из вихревых линий можно образовать вихревую трубку. Для
этого надо взять замкнутый контур и через каждую его точку
провести вихревую линию. Теоремы Гельмгольца формулируются
в этих терминах.
Теорема 1. Элементы идеальной жидкости, лишенные
вихрей в начальный момент времени, будут лишены их и в
дальнейшем.
Для доказательства учтем, что согласно теореме Томсона
циркуляция по замкнутому контуру
r=(£vdr
остается неизменной. Пользуясь теоремой Стокса, ее можно
выразить через интеграл по произвольной «жидкой» поверхности
S, опирающейся на /:
F^= fnrotvdS,
который, следовательно, также должен оставаться неизменным.
Если в начальный момент времени всюду на S rotv=0, что
дает Г=0 по любому контуру, лежащему на S, то, следовательно,
и в дальнейшем это свойство должно сохраниться для этой
«жидкой» поверхности. В самом деле, если бы в какой-то части S
вихрь стал бы отличным от нуля, то можно было бы взять в
качестве / контур, охватывающий такую часть 5, где n rot v не
меняет знак,, и получить Г=^=0 по этому контуру, что противоречит
сказанному выше.
Таким образом, при движении идеальной жидкости в поле
потенциальных сил вихри возникнуть не могут. Очевидно и
обратное утверждение: если rotv^O в начальный момент времени, то
в силу сохранения Г вихрь не может исчезнуть.
Теорема 2. Вихревая линия состоит все время из одних и
тех же частиц, т. е. движется вместе с жидкостью.
Для доказательства построим какую-либо вихревую трубку и
рассмотрим циркуляцию Г по произвольному односвязному
контуру /, лежащему на поверхности трубки. Представим ее в виде
интеграла (6.60) по поверхности S, являющейся частью поверх-
106

ности вихревой трубки. В начальный момент мы имеем Г=0,
поскольку n rot v=0 по определению вихревой трубки. Из теоремы
Томсона следует, что для контура /ив дальнейшем Г=0, т. е.
всегда nrotv=0 для S, движущейся вместе с жидкостью.
Другими словами, S всегда будет являться частью поверхности
вихревой трубки. Так как S (вместе с /) может быть выбрана в
любом месте вихревой трубки, то, следовательно, частицы,
составляющие ее поверхность, все время будут находиться на вихревой
трубке. Сделав последнюю бесконечно тонкой, мы получим
вихревую линию. Следовательно, и вихревая линия будет состоять
все'время из одних и тех же частиц.
Теорема 3. Поток вектора вихря <o=rotv через поперечное
сечение вихревой трубки, т. е. величина J nco dS, остается посто-
янным вдоль данной вихревой трубки. Здесь нормаль п
выбирается совпадающей по направлению со. В частности, если
торцевая поверхность S достаточно мала, так что вихрь со в ее
пределах можно считать постоянным, то вдоль вихревой трубки будет
сохраняться величина ©S, называемая интенсивностью вихревой
трубки.
Доказательство этой теоремы непосредственно следует из того
факта, что поток вектора со через любую замкнутую поверхность
S0 равен нулю. Действительно, по теореме Гаусса —
Остроградского
fn<odS= (divcodV^O,
s. V
так как div<o=divrotv=0. Выберем в качестве S0 поверхность,
ограничивающую конечный участок вихревой трубки: S0=Sj +
+S2 + S7, где 5' — боковая поверхность, a St и о2 — поверхности
торцов. Поток вектора со через S' равен нулю по самому опреде^
лению вихревой трубки (nrotv=0). Следовательно, остаются
только потоки по поверхности торцов вихревой трубки:
J* n&dS+ Г rmdS = 0.
St st
Здесь первый член отрицательный, поскольку п направлен
противоположно со на S^ Поэтому и в силу произвольности выбора
поверхностей Sj и S2 мы получаем утверждение теоремы.
Из постоянства интенсивности вдоль вихревой трубки
следует, что такая трубка не может начинаться и кончаться в
жидкости. Вихревые трубки замкнуты или начинаются и кончаются на
бесконечности, а также на стенках или на поверхности жидкости.
Заметим, что на основании первой теоремы Гельмгольца,
казалось бы, можно было бы заключить, что свойство
потенциальности движения жидкости сохраняется с течением времени. В
действительности же, как это хорошо известно из опыта, вихри
постоянно возникают и исчезают, например кольцеобразные вихре-
107

вые нити дыма, смерчи в атмосфере и т. п. Причинами этого
являются неидеальность жидкости (вязкость и отличие уравнения
состояния от р=р(р)), а также непотенциальные внешние силы.
Задачи
6.1. Показать, что J~~l(dJ/dt)=d\v v, где /=[д(*ь х2% хг)]1[д(%и h> 6з)1—
жкобиан преобразования от эйлеровых координат к лагранжевым.
Решение. В соответствии с формулой (6.1), правилом
дифференцирования определителей и соотношением dXi/dt = Vi — i-n компонента скорости —
имеем
dJ _ d(vlt х2, х9) d(xlt vtf х3\ d(xlt *», v3)
dt а (ь, h. 1з) + а(Ь, Ь, £*) + [д (Ь, Ь. Еа)
Здесь в каждом из трех полученных якобианов преобразуем элементы строки,
содержащие v<[x*(gm, 0» *], к сумме трех слагаемых, воспользовавшись
правилом дифференцирования сложной функции:
dit "" d*k dlf *" d*x ag, + ад, ag; + d*3 dlf "
Теперь, разбивая каждый якобиан на сумму трех в соответствии с правилом
вычисления определителей, получаем, например, для первого якобиана
d(vi> *%> *з) _ дуг d(xlt д^, *8) dvx d(x2t x%i х3)
«(БьЬ.Ь) д*г а(Ь,Ь.Ь) а% *<Ь.Ь.Ь)
at^ а(*8, *а, *3v а^х
а*8 з&.ь.Ь) =axx •
так как два других якобиана равны нулю из-за совпадения строк
определителя. Аналогично находим:
d(xltv2tx3) dv2 J
0(ei.b.Ei) а*а '
И окончательно
d±- j ** jdiw
lT=/ax,-yd,vv-
fl(*i, *», t?3) ^ ар8 j
affix,b,b),=i а*8
\
6.2. Получить уравнение неразрывности в переменных Лагранжа.
d р
Решение. В силу уравнения неразрывности — I р(**,t)dV=Q, где
V — объем, движущийся вместе с жидкостью. Переходя под интегралом к
переменным Лагранжа, находим
^-J|pl**<b. «. ^Jdv-jf^ р(Ь. о wv =
и. V.
■I
-^-W,').']<w=o.
108

В силу произвольности объема Vo получаем искомое уравнение неразрывность
в лагранжевой форме:
6.3. Пусть при /^0 и *з^0 задано поле скоростей частиц жидкости в
описании Эйлера: ^, = ^2=0, а3(*з, /) =/(*з). Найти лагранжево описание
этого движения, рассмотреть частный случай /(*з)=У2£*з.
Решение. Поскольку v{ = v2=Q, то в координатах Лагранжа {£*}
имеем зависимость только от \ъ: *з=*з(£з> t)t Xi=£b Jt2=£2. Но тогда
0з(£з, 0 = [д*з(£з, 0]/^=/[*з(?3'0]. что дает после интегрирования
(учитывая, что при *=0 *з=£3)'=1 [<**з//(*з)1. В частности, для /(*з)=У2£*з
-1
имеем У2£*=2(У*з—У£з). Отсюда находим
*з=Ь+Г2£|з'+£'2/2, *&, 0-УЙЬ+Л Мбз, 0е*.
т. е. получилось движение частиц жидкости с постоянным ускорением g
(движение в водопаде).
6.4. Радиус сферы, находящейся в жидкости, изменяется по закону
R=R(t) (R(Q)=R0). Найти этот закон, если известно, что при t>0 и
r>R(t) скорость частиц жидкости описывается формулой vr (г) = v (г) =
= иоЯо2/г2.
Решение. Нам задала скорость в эйлеровой координате г. Найдем
ее выражение в лагранжевой координате х, где х — положение фиксированной
частицы при / = 0. Имеем по условию задачи
Интегрируя это уравнение с учетом г(х, 0) = х, находим:
г(х, 0 = (*3+3tfo3i>oOV\
у (х, /) = /?o2wo(x8+3/?o2^rVi.
Интересующий нас закон изменения радиуса будет
R(t) =r(R0t t) =#о(1+30о///?о)1/§.
6.5. Написать дифференциальное уравнение для определения линий тока
в жидкости, скорость частиц которой в каждой точке пространства известна:
Решение. Пусть линия тока задана параметрическим уравнением
xtB=Xi(s), или в векторной форме r=r(s), где s —длина дуги вдоль линии
тока. Поскольку вектор касательной к линии тока dr/rs параллелен вектору
скорости v, то dr/ds = Cyt C=const. Следовательно, искомым уравнением будет
1 йхг 1 dx2 1 dx9
vx ds v2 ds v3 ds
6.6. Показать, что при стационарном течении жидкости (dVi/dt=0)t
а также для течения, в котором Vi(xk, 0=а'(*О/(0, линии тока и
траектории частиц совпадают.
109

Решение. В общем случае траектории частиц жидкости находятся из
решения уравнений
dXi/dt = vc(xk, /),
которые можно также записать в виде
"Г1 (**. ') dxi/d* = v? (xk% t) dx2/dt = v? (xkt t) dxjdi.
Линии тока находятся из уравнений
v~l (xk% t) dxjds = с*;1 (xk% t) dxjds = i£x (xk, t) dxjds,
в которых время / является параметром. В стационарном случае у< = у,(х/1),
в результате чего обе системы уравнений становятся эквивалентными.
Аналогично и во втором случае: уравнения для линий тока ai~ldx\lds=a2~{dx2/ds =
=az~xdxblds и уравнения для траектории ai~l(xk)dxildt = a2~l(Xk)dx2ldt =
= az-l(Xh)dxz/dt совпадают.
6.7. Показать, что во вращающейся как целое с круговой частотой Q
жидкости вектор вихря (oesrotv=2£2.
Решение. Имеем в компонентах
о)1=6Ч>з/дх2-—6Ч;2/д*з» ^^dvi/dxz—dvsfdxu <oz=dv2/dxi—dvildx2.
Подставляя сюда соответствующие компоненты вектора
v-Qxr = {Qa — QA. ^з*l — О А. О А - Ga*ib
который и описывает вращение жидкости как целое, имеем
(0i=2Qi, со2=2&2, <0з=2йз, w=2Q.
6.8. Получить дифференциальные уравнения для вихревых линий в
жидкости для общего случая и проинтегрировать их для частного случая,
рассмотренного в предыдущей задаче.
Решение. Если r=r(s) (Xi = Xi(s)) — параметрическое уравнение
вихревой линии, то, по ее определению, rfr/ds=Cco, где G)=rotv— вектор вихря
С=const. Расписывая полученное равенство по компонентам, легко получаем
(u\-ydx\jds=<u2~xdX2lds=а>з~14хзЛ&
В случае вращения жидкости с частотой Q имеем в соответствии с задачей 6.7
o)=2Q. Тогда, как легко видеть, уравнение для вихревых линий
(2Qi)'4xl/ds= (2Q2)-ldx2fds= (2Qz)^dxz/ds^
является уравнением прямой линии, параллельной вектору Q:
(*1— *10)/Ql= (*2—*20)/Й2= (*3—*Зо)/&3,
что и должно быть в силу постоянства вектора вихря <o=2Q.
6.9. Определить зависимость давления идеального газа от высоты в поле
силы тяжести, если температура газа изменяется по закону 7=7(2).
Рассмотреть частные случаи: a) 7=70=const; б) 7=70(1— z/H)(z<H)\
в) 7=7о(1-27#2) (*<#).
Решение. Уравнение состояния идеального газа p=(#/n)p7(z), где
\i — молекулярный вес газа. Отсюда p=[iplRT(z), причем при 2=0 имеем
p0=\ipolRTo (ц/Я=ро70/Ро). Подставляя р в уравнение гидростатики (6.23),
НО

долучаем уравнение, которое легко интегрируется:
dp Р0Г0 dz вко лл
Т = -*~7~^' Р = Рвехр --«а- -ГГТ^
Р Ро Г(*)'
gPo Г Г0
Ро J Г(г)'
В частных случаях «а» — «в» имеем:
г
а) 7\(z) = Г0, J T0/T(z)dz=z и для р получаем формулу (6.26);
о
г г
б) Г (г) = Гв (1 -а/Я), J Го/Г (г) =- J (1 - г/ЯГ*Л =
о о
= -Я1п(1-г/Я) шр(ж)~р9(1-ж/Н)*, *i~ghWp%l
в) Г (ж) - Г, (1-*■/№),
в
J (Го/Г (z)) Л = (Я/2) In | (1 + £/Я)/(1 - ад л
в
■ Р W - Ро [(I - */Я)/(1 + */# И*1. «• - <*i/2 - ^РвЯ/2ро.
6.10. Пусть жидкость с уравнением состояния р=ро(р/ро)* находится в
ноле силы тяжести. Определить гидростатическое распределение давления.
Решение. Пользуясь уравнением (6.23) и учитывая заданную связь
р=р(р), находим
5-1 амУ7^
'=Р«(
s Ро /
6.11. Цилиндрический сосуд с несжимаемой жидкостью в поле силы
тяжести вращается с постоянной угловой скоростью Q вокруг вертикальной оси
цилиндра. Определить форму свободной поверхности.
Решение. Напишем уравнение Эйлера во вращающейся системе
координат:
dv Vp
_ = ___^-ацб.
где аЦб=&2г — центробежное ускорение. В цилиндрических коордянатах в
условиях равновесия (v=0) имеем:
р дг рг ду р дг
После интегрирования этой системы уравнений получаем
p(r,z)=p0-gp2+pfi2r2/2,
где Ро=р(0, 0). На свободной поверхности р(г, г) =ра — атмосферное
давление, что дает
Ро—Ра Q2 л
г(г) = + — гК
g9 2g
111

6.12. Определить зависимость давления от расстояния до центра Земли,
считая вещество Земли несжимаемой жидкостью плотности р. Вращением
Земли пренебречь.
Решение. Уравнение гидростатики (6.22) в этом случае имеет вид
dp/dr=—pduldr=—pg (г).
Зависимость ускорения силы тяжести от г можно найти из закона всемирного
тяготения g(r)=yM(r)lr2, где М(г)=4/зяг3р — масса жидкости, заключенная
в сфере радиусом г; у=6,67-Ю-8 см3/(с2-г)—гравитационная постоянная.
В частности, известное значение ускорения силы тяжести на поверхности
Земли будет g0=zg(R)=yM(R)/R2, где # —радиус Земли (#=6400 км,
go=9,81 м/с2). Теперь легко получить
dp/dr^-pgor/R, p(r) =p&+gop(R2-r*)/2Rt
где ра — давление на поверхности Земли. Максимальное давление в центре
Земли равно р(0) =Ра+£оро#/2. Среднюю плотность вещества Земли можно
оценить, воспользовавшись выражением g0 через у и R: p — 3go/(4nyR), что
дает для р(г) и р(0) соответственно:
Р (г) = ра + (SgllSny) (1 - г*//?а), Р (0) = рш + 3^/8*7 » 10« атм.
6.13. Пусть 2о — высота уровня жидкости в сосуде, z— высота отверстия
над основанием сосуда. Определить расстояние, на котором вытекающая из
сосуда жидкость достигнет плоскости основания сосуда. При каком z (при
заданном z0) это расстояние будет максимальным?
Решение. Горизонтальная, скорость истечения жидкости в соответствии
с (6.39) есть t>=V2g(zo—z). При свободном падении в поле силы тяжести
частицы жидкости достигнут основания сосуда за время to=y2z/g.
Пройденный за это время горизонтальный путь равен
x(z)=u/0=2yz(z—z0).
Максимальное удаление струи от сосуда достигается при z=z0/2 и равно
Xm&x = Zo.
6.14. Определить S (z) — зависимость площади сечения сосуда от
вертикальной координаты при условии, что скорость изменения уровня жидкости в
сосуде dz/dt при ее истечении через отверстие была постоянной.
Решение. Скорость истечения жидкости a=V2£(z—Zo). Приняв
коэффициент истечения жидкости через отверстие постоянным и равным к, найдем
для массы жидкости, вытекающей в единицу времени, выражение
dm
— = 9hso = pks V2g (z — zQ)t
где s — площадь отверстия. С другой стороны, эта величина связана с
изменением уровня жидкости в сосуде формулой
dmldt=pS(z) dz/dt.
Приравнивая эти величины, находим
ks V2j
S(2)=lwrYz-z-
112

6.15. Идеальный газ, находящийся в сосуде под давлением ро,
адиабатически вытекает через малое отверстие в стенке сосуда. Определить скорость
истечения газа, если давление в окружающей среде равно р.
Решение. Для сжимаемого газа следует применить уравнение Бернулли
в виде v02l2+w0=v2/2+wt где ш —энтальпия. Выбирая начальную точку
линии тока на достаточном удалении от отверстия, где i>o=0, находим для
скорости истечения у2=2(ш0—w). Воспользовавшись далее выражением для
дифференциала энтальпии при адиабатическом процессе (dw = dp/p) и уравнением
адиабаты р=Ро(р/ро)т> y=cp/cVi получаем
JP Y-lp. \PJ Y-l P
так что
(Y-l)/Y
у - i po L V Po J
___ 2У /p0 __p\
V-Apo P/
Выразим также скорость истечения
скорость звука в газе, а именно:
с2 = dp/dp = с\ (р/Ро){у~1)/у = ТР/р,
Рве. 6.6
газа через
02 = 2(*?-*')/(7-1),
(6.62)
где Со2 — квадрат скорости звука в покоящемся газе; с2 — то же, на выходе
газа из сосуда.
6.16. Найти массу газа, вытекающего в единицу времени через отверстие
площади So (в условиях предыдущей задачи). Вычислить эту величину при
истечении газа в вакуум и объяснить полученный результат (коэффициент
истечения принять равным единице).
Решение. Для требуемой величины имеем
dmttt = Sopv = s0Po (p/p0)1/v Ptfft - 1)]* (Po/po^ U - (P/Po)iy~l)/y}Vt =
= [2/(Y - l)]1/f PoVo f(P/Po)2/V - (P/Po)(V+1)/Yl1'4.
Отсюда, в частности, получаем, что при истечении газа в вакуум
(p=0)dm/dt=0 — заведомо неверный результат. Чтобы получить
правильную фабулу, обратимся к трубке тока (рис. 6.6), вдоль которой v2/2+w =
= const. Продифференцировав это выражение вдоль трубки тока, получаем
vdv/dt+dw/dl=vdv/dl+p-ldpldl=0.
С другой стороны, вдоль трубки тока сохраняется поток массы pvs = const.
Следовательно,
vsdp/dl+psdv/dl+pvds/dl = 0.
Отсюда для относительного изменения площади сечения трубки тока имеем
J_ ds _ J-— _L^£_— 1 dv 1 dp dp
s dl v dl "~ p dl ~~ _ v dl p dp dl ~~
_ J_£? _Li£. 1 dv I v2\
~~ ~~ v dl ~~ pd2 dl ~~~~ v dl\ c* J
113

Теперь ясно видно, что при v<c трубка тока сужается (dsfdKO). Когда
скорость истечения газа равна скорости звука (v=c), ds/dl=Ot т. е. площадь
сечения трубки минимальна (s \vmee=sm)i затем при v> с трубка начинает
расширяться. Рассчитаем параметры газа в сечении трубки sm(vm = cm).
Воспользовавшись формулой (6.62), полученной в задаче 6.15, имеем ст2=2(с02—ст2)/
/(Y— 1), откуда cm2=vm2=2c02/(y+\). Далее, из соотношения ст2=
— co2(Pm/Po)(v~1)/v следует
PjPo = (e>J)T/C^I} = (2/(7 + Ш^Ч Pm/Po = [2/(Y + DF**-1*.
Можно ожидать, что минимальное сечение трубки тока sm будет наблюдаться
вблизи отверстия. Тогда скорость изменения массы газа в сосуде будет
равна
**« - РлАА - PAY + l)J(1+v)/l2(^1)1PoV..
Глава 7
ПОТЕНЦИАЛЬНОЕ ТЕЧЕНИЕ ЖИДКОСТИ
Мы видели, что в случае идеальной баротропной (/?=р(р))
^кидкости, движущейся в поле потенциальных сил, вихри не
исчезают и не возникают. Поэтому если в начальный момент
времени имеется потенциальное течение (т. е. всюду rotv.=0), то
4Эно останется потенциальным всегда, Конечно, в реальной
жидкости постоянно наблюдаются возникновение и исчезновение
вихрей. Однако все же целесообразно рассмотреть некоторые
задачи потенциального течения, так как в ряде случаев оно
является хорошим приближением к течению реальной жидкости, а
уравнения гидродинамики при этом существенно упрощаются.
§ 26. Система уравнений гидродинамики
для потенциального движения
-26.1. Потенциал скорости. Прежде всего отметим, что при
потенциальном движении поле скоростей частиц жидкости полностью
описывается одной скалярной величиной, а именно потенциалом
ф(*ь ,t). При этом V—Vcp и выполняется условие
потенциальности течения rotv=rot Vcp.= 0. Далее, воспользуемся уравнением
Эйлера (6.14), которое с учетом векторного тождества (6.31),
выражения для дифференциала энтальпии (6.34) и условия
потенциальности внешних сил (f=— Vw) легко преобразуется к ви-
ДУ
V (dy/dt+v2/2 + w + u) =0.
Отсюда непосредственно следует так называемый интеграл Ко-
juu — Лагранжа
dy/dt+v2l2+w + u=F(t)t (7.1)
114

где F(t)—произвольная функция времени. Последнюю всегда
можно обратить в нуль, перейдя от ф к новому потенциалу q/=
=Ф+ \ F(t)dty что, очевидно, не сказывается на значении v.
и
В результате, опуская штрих у ф', выражение (7.1) можно
записать и в таком виде:
£ + .£ + ■,+ « -0. (7.1'>
Заметим, что выражение (7.1) вместе с (7.Г) является
интегралом уравнения Эйлера (6.14) в случае потенциального течения
идеальной жидкости.
Наиболее простой вид уравнения потенциального течения
идеальной жидкости имеют при предположении о несжимаемости
последней: dp/dt=0 (мы в этой главе ограничимся более жестким
условием р—const во всей массе жидкости). В этом случае г
точностью до постоянной, которую также можно включить в ф„
w=p/p, а уравнение неразрывности (6.9) также упрощается:
сНуу=0или
Аф—0,/ (7.2)
где, как всегда, A = div grad — оператор Лапласа.
Таким образом, решение задач потенциального течения
идеальной несжимаемой жидкости сводится к интегрированию
одного скалярного уравнения (7.2) с учетом граничных условий. По
найденному потенциалу ф(л\, t) не составляет труда найти v=
= Уф, а также давление /?, равное в соответствии с (7.1')
Отметим, однако, что при использовании последней формулы
следует проявлять определенную осторожность, поскольку
входящий в (7.3) потенциал найден с точностью до произвольной
функции времени F(t), влияющей на истинное значение давления
р. Эту функцию можно найти, например, задав р в одной точке.
26.2. Плоское течение. Функция тока. Полнее всего
разработана теория потенциального движения идеальной несжимаемой
жидкости в случае плоского течения (когда от одной
координаты, например от *3=г, ничего не зависит и vs=vt=0). Тогда
целесообразно ввести так называемую функцию тока ф(х, у, t),
такую, что уравнение неразрывности divv=dvjdx+ovy/dy=0
будет выполнено автоматически. Для этого, очевидно, нужно
положить
vx=dty/dy, Vy^—д^/дх. (7.4)
Термин «функция тока» обусловлен тем, что линиями тока
течения являются линии г|>= const. Действительно, поскольку, по
определению, направление касательной к линии тока совпадает с
115

вектором v, мы имеем для линии тока у=у(х) соотношение
dy/dx=vyfvXy или vxdy—vvdx=0.
Отсюда с учетом (7.4) получаем
&dx + &-dy = d* = 09
дх ду
т. е. i|)=const на линиях тока.
С помощью функции тока ф простым образом определяется
также поток жидкости через участок плоской кривой,
соединяющей какие-либо две точки Л и В. По определению, он равен
в
N= J Hid/, (7.5)
А
где п —единичный вектор лормали к кривой; dl — элемент ее
длины. В выражении (7.5) имеем (рис. 7.1):
^ /^
Vn = vx cos (nx) + Vy cos (ny),
dl cos (nx) = dl cos 8 = dy,
dl cos (ny) ■= dl cos (л/2 + 9) = dl sin 9 = — dx,
где x и у — орты соответствующих осей. Поэтому с учетом (7.4)
можно написать
в в
А А
— поток жидкости через участок кривой равен разности
значений функций токи на его концах.
Заметим, что пока мы еще не пользовались условием
потенциальности течения, так что понятие о функции тока можно
относить также и к вихревому течению. Выразим вихрь <D=rotv=
= coVz через функцию тока двумерного течения
\ дх ду 1 \ дх* ду* I Y v
Отсюда следует, что в случае потенциального течения (ю=0)
мы можем находить •§ из уравнения
Дг|)=0. (7.8)
Таким образом, в случае двумерного потенциального течения
идеальной несжимаемой жидкости как потенциал скорости
<р(л', у, /), так и функция тока я|К*, у, t) удовлетворяют
уравнению Лапласа, т. е. являются гармоническими функциями
пространственных переменных.
116

0 <z
Рис. 7.1
Рис. 7.2
#\
а У\
<г
Рис. 7.3
a #L
6
?\
_,. if,t,V
_/Cnz
<
\
H3ft\ -
9 Г ч
4
1 к
Рис. 7.6"
Рис. 7.4
Полезно, наконец, установить связь между потенциал'ом ф и
функцией тока яр. Воспользовавшись выражениями для скорости
V=Vq> и (7.4), получаем:
дц1дх=д$1ду, дц)/ду=—дур!дх. (7.9)
Отсюда также следует, что
дх дх ду ду т
(7.10)
т- е. условие ортогональности семейств линий ф=const и t|)=
== const.
117

Функции ф и \|) в известном смысле равноправны. Допустим,
что мы имеем течение, определяемое потенциалом ф.
Ортогональное к семейству линий ф = const семейство кривых соответствует
линиям тока i|)=const. Поскольку обе функции удовлетворяют
уравнению Лапласа, можно представить себе другое, так
называемое «сопряженное» течение, для которого \|) будет
потенциалом, а ф — функцией тока.
§ 27. Применение теории аналитических функций
в задачах гидродинамики
27.1. Комплексный потенциал. На функции ф и \|э можно
посмотреть и с другой стороны, которая открывает широкие
возможности применения в гидродинамике аппарата теории
функций комплексного переменного. Напомним, что функция
комплексного переменного каждой хточке z=x+iy множества
комплексных чисел ставит в соответствие комплексное число F(z).
Из всего класса функций комплексного переменного
замечательным является подкласс аналитических функций, в частности
обладающих свойством дифференцируемости, т. е. существования
предела
Г'(»)-Шп f?<' + f>-fW , (7.11)
называемого производной функции F(z). Дифференцируемость
функции комплексного переменного не эквивалентна требованию
дифференцируемости ее вещественной и мнимой частей, а
накладывает более сильные условия на последние. А именно: если
F(z)=a{xty) + l^{x9y)9 (7.12)
где а и (J—вещественные функции, то для дифференцируемости
функции F(z) необходимо и достаточно выполнение условий
Коши — Римана:
да/дх=д$/ду, д$/дх=—да/ду. (7.13)
Эта теорема является одной из основополагающих в теории
функции комплексного переменного и вытекает из требования
существования предела (7.11), а именно из независимости последнего
от направления приращения Дг. Поясним это простым расчетом
предела (7.11) по двум взаимно перпендикулярным
направлениям: если Az==A*, то
F' = lim [а{х+ Их, у) + Щх+Ьх, у)—а\х% у)—ф(х, у)1/Ах—
Ах-н)
= да/дх + id$/dx,
если Az=iAy, то
F' = lim [а(х, у+Ау)+ф(х, у+Ду)— а(х, у) — Щх, у)\ЦАу=
Ду-н>
= dp/d# — ida/dy.
118

Приравнивая вещественные и мнимые части последних
выражений, мы'и получим условия Коши —Римана (7.13). Вспомним
теперь, что именно этим условиям (см. (7.9)) удовлетворяют
потенциал ф и функция тока tf двумерного течения идеальной
несжимаемой жидкости. Следовательно, последние можно
рассматривать как вещественную и мнимую части аналитической
функции F(z), называемой комплексным потенциалом. Из условий
Коши — Римана нетрудно также получить, что вещественная и
мнимая части любой аналитической функции F(z)
удовлетворяют уравнениям Лапласа. Например, дифференцируя первое
уравнение (7.13) по х, второе по у и складывая полученные
выражения, для а имеем:
д2а/дх2 + д*а/ду2=Аа=0.
Аналогично доказывается, что и Д(*=0.
Таким образом, любой аналитической функции F(z)
соответствуют два взаимно сопряженных течения с потенциалами: ф£=
= ReF(z) {^=\mF(z)) и y2=lmF(z) ($2=ReF(z)). Часто
бывает удобнее получать потенциал сопряженного течения
несколько иначе, а именно (pa=Re(±i/7(z)) (ty2 = lm(±iF(z))).
27.2. Примеры двумерных течений. Приведем несколько про-
етейших примеров функций F(z) и соответствующих им течений
1. Пусть F(z)=az, где а —< вещественная постоянная.
Имеем y + fy=ax+iayf следовательно, ц>=ах, $=ау— течение с
постоянной скоростью vK=a, линии тока ($=const) параллельны
оси х. Чтобы получить сопряженное течение, введем новую F(z),
получающуюся из старой умножением на мнимую единицу со
знаком минус (—i). В результате для сопряженного течения
имеем F(z) =—iaz=ay—iaxy <р=ш/, <ф=— ах. Здесь скорость также
постоянна vv=a, а линии тока Oj)=const) параллельны оси у.
2. Пусть теперь
F(z)=m 1п2, (7.14)
где 2=^=0; m — вещественно. Для анализа этого случая
целесообразно ввести в плоскости (*, у) полярные координаты г и Э так,
что
х=г cos 9, y=r sin 8, z=x+iy=r exp (iQ).
Тогда, подставляя г (г, в) в (7.14), получаем:
F(z)=m (In г+i6), cp=mlnr, г|з=т0.
Здесь линиями тока будут лучи 0 = const, а линиями равного
потенциала— окружности r=const (рис. 7.2). Скорость частиц
жидкости направлена по лучам и равна
иг=дф/дг=т/г.
При mi>0 скорости всех частиц направлены от точки г=0. В этой
точке мы имеем источник жидкости. Масса жидкости, протекаю-
119

щей в единицу времени через произвольную окружность (r=s
= const), равна
2nrvr=2nm
и в соответствии с законом сохранения вещества не зависит or
радиуса г. Эта величина называется производительностью
источника. При т<0 мы имеем в точке г=0 сток жидкости.
Комплексный потенциал для сопряженного течения получим,
умножив (7.14) на —i:
F(z)=—im\nz=m(Q—i\nr), ф=т0, t|? = — mlnr. (7.15)
В этом случае линиями тока будут концентрические окружности
г = const (пунктир на рис. 7.2), а линиями равного потенциала —
лучи 0=const (сплошные прямые на рис. 7.2). Для скорости
получаем
*г = 0, * = .!.£ = «.
г дд г
Следовательно, мы имеем вращение частиц жидкости вокруг
точки г=0 со скоростью, обратно пропорциональной расстоянию г
до этой точки. При т>0 вращение происходит против часовой
стрелки, а при т<0 — по часовой стрелке. Здесь мы имеем так
называемый вихревой источник с циркуляцией вдоль любой
линии тока, равной
T=ve2nr=2nm. (7.16)
Отметим, что это обстоятельство не противоречит
предположению о потенциальности течения и утверждению теоремы Том-
хона. В данном случае точка г=0 является особой и поэтому
исключается из рассмотрения, вследствие чего область,
ограниченная линией тока, не является односвязной и теорема Томсоиа
неприменима. Движение жидкости всюду, за исключением точки
г=0, потенциально.
27.3. Конформные преобразования. Наибольшие успехи в
решении задач двумерного течения идеальной несжимаемой
жидкости были достигнуты при использовании известного в теории
аналитических функций аппарата конформных изображений.
Допустим, что у нас решена какая-нибудь определенная задача о
двумерном потенциальном течении в некоторой области с
определенными граничными условиями, т. е. найден комплексный
потенциал F(z). Перейдем с помощью конформного
преобразования к другой комплексной переменной £, связанной с z формулой
z=f (£). При этом комплексный потенциал преобразуется к виду
F(z)=F[f(Z)] = <b&)>
который в плоскости £ будет соответствовать какому-то новому
течению. С помощью этой процедуры иногда удается получить
решение весьма сложных задач. Продемонстрируем метод кон-
120

формных преобразований на сравнительно простой задаче
течения в клинообразной области.
Рассмотрим в качестве .исходного течения протекание
жидкости с постоянной скоростью в полупространстве у>0 при
наличии твердой стенки при у=0 (vx=v0y ^=0; рис. 7,3, а). Такому
течению соответствует введенный выше комплексный потенциал
F(z)=v0z. Преобразуем теперь полуплоскость у>0
конформным преобразованием z=R(l/R)a (а>0, R>0) в клиновидную
область плоскости переменного Е; (рис. 7.3, б). При этом
комплексный потенциал запишем в виде
Ф(5)=*вЛ(6/Я)".
Введем в плоскости Е; полярные координаты г и 0 так, что £=
=ге1в. Тогда
Ф (£) = v0R (r/R)« exp (*а8) = v0R (r/R)a (cos a0 + i sin a0).
Отсюда для потенциала скорости и функции тока получаем
следующие выражения:
ф=VqR (r/R)a cos a0, ф= v0R (r/R)a sin a0.
И окончательно для компонент скорости имеем:
vr = — = v0a I—) cosa0, vB = —SL = — i;0a /—) sin a0.
dr \R J r ae \R ]
(7.17)
Нетрудно видеть, что vQ обращается в нуль на лучах 0=0 и
0=я/ос, где могут быть без нарушения течения поставлены
твердые стенки. Этот факт является непосредственным следствием
конформности преобразования, сохраняющего угол (в данном
случае прямой) между стенкой и линией q)=const. Таким
образом, мы получили решение задачи о течении в клине с раствором
я/a. На рис. 7.3, б изображен случай а=4.
Как следует из (7.17), при а>1 и г->0 скорости рг->0 и ив-Ю,
т. е. в угловой точке скорость частиц жидкости обращается в
нуль. Если же ос<1, мы получаем решение задачи об обтекании
клина. На рис. 7.3, в изображен случай а=2Л. При этом из
формулы (7.17) следует, что i>r-*oo и i>e-^<» при г->0.
Комплексный потенциал /7(z)=<p+ft|) можно рассматривать
как аналитическую функцию, осуществляющую конформное
преобразование некоторой области на плоскости z, называемой
также областью течения, на плоскость комплексного потенциала.
В ряде случаев полезно также рассматривать конформное
преобразование области течения на плоскость комплексной скорости
w{z)=F>{z) = d^+idJL = vx-ivy. (7.18)
ох ох
Можно также осуществить отображение плоскости потенциала
на плоскость комплексной скорости w(F)=w[z(F)], где z(F) —
121

отображение, обратное F(z). Если функция w(F) известна, to
комплексный потенциал F(z) можно найти, интегрируя
очевидное дифференциальное уравнение:
dF/dz=w(F). (7.19)
Использование такой процедуры при решении конкретных задач
гидродинамики проиллюстрировано на примере решения задач
7.7 и 7.8.
§ 28. Стационарное обтекание
кругового цилиндра
28.1. Решение задачи методом конформного преобразования.
Задача обтекания кругового цилиндра важна как сама по себе, так
и потому, что, взяв ее в качестве исходной, можно решить
методом конформного преобразования задачи обтекания
цилиндрических тел более сложной формы.
Пусть на плоскости z=x+iy=rexp(iQ) (рис. 7.4, а) задана
окружность r=R (R — радиус цилиндра). Будем искать решение
уравнения Лапласа Аф=0 при условии, что на поверхности
цилиндра r=R нормальная компонента скорости равна нулю, а при
г-+оо невозмущенный поток имеет компоненты скорости vK=
=—и0, 1>„=0. Выражая последние через потенциал, запишем
граничные условия в виде:
(*P/^Us = 0' (<*p/d*Uo=-<V (д<р/ду)г^=0. (7.20)
Вместе с функцией тока t|) (Atf=0) <р образует комплексный
потенциал F(z)=(p(x9 y)+ity(x, у). Отобразим, далее, область вне
окружности \z\ >R конформным преобразованием на плоскость
£ с разрезом от —1 до +1, изображенную на рис. 7.4, б. Это
преобразование хорошо известно и называется преобразованием
Жуковского:
l=l + ir]=(zIR + Rlz)l2, (7.21)
При этом окружность z=/?exp(i8) стягивается в отрезок,
простирающийся от £=.—1 до £=1 и проходимый дважды.
В результате F(z) примет вид
Ф-(С)=Ф[(2/Л+Л/2)/21=.ф1(6>л)+*+1(6,л)-
Условие (дф/дг)г=д—0 переходит в (дф4/дт])л=о=0, так как при
конформном преобразовании сохраняются углы между линиями
(прямой угол между границей и нормалью к ней в данном
случае). Далее, при г->оо имеем
Ь * ^ { 2 R 2R ^ 2R
122

что дает q>(*, y)-xpi(x/2R, y/2R) при r->oo. Следовательно,
дф I =о = * дфг 1
dq> I _ „ _ 1 ^Pi
дх \r^ w 2/? ag
где х=У|2+т]2, откуда получаем искомые условия:
(*Pi/^)x-~> = - 2/^0» (дфх/дт])^ = 0.
Таким образом, мы получили задачу обтекания бесконечно
узкой полосы набегающим со скоростью —2Rv0 потоком.
Решением этой задачи является поток со скоростью, одинаковой во
всех точках пространства: vl=—2Rv0i vn=0. Комплексный
потенциал последнего равен (см. § 27)
<b(Z)=-2Rv£.
Возвращаясь от Е; к переменной г в соответствии с (7.21),
получим выражение для комплексного потенциала исходной задачи:
F(z) =-2Rv0Z(z) =-RVo(zfR+R/z) =
=—i>o[rexp(*0) + (R2/r)exp(—iQ)l (7.22)
Отсюда для потенциала имеем
<p=ReF(z)=—i>0[r+#7r]cose. (7.23)
Для компонент скорости потока получаем:
0г=дф/дг=—«.(I— #7/*2)cos6,
(7.230
vB=г-1дср/дв=v0(\ +Rz/r2) sin 9.
Естественно, что граничные условия (7.20) для <р выполняются.
В самом деле, (дф/дг)г«=д=0, а при г->оо ф-> —v0rcosQ=—v0xi
следовательно, (дф/д*)г-о»=—v0y (д<р/ду)г-+оо = 0. На
поверхности цилиндра (r=R) находим
vr= 0, vB=2v0 sin 0. (7.24)
Максимальная скорость имеет место в «плоскости миделя» (6=
=я/2), где v=.Ve=2v0.
28.2. Коэффициент давления. Давление в любой точке
жидкости можно найти, используя теорему Бернулли:
p0 + pt,02/2.=p2+pt;2/2, (7.25)
где р0 и v0—(давление и скорость на бесконечности; р и v — те
Же величины в произвольной точке. Поскольку мы знаем
распределение скорости v по поверхности цилиндра (7.24), легко
находится распределение на ней давления:
p=p0 + 9(v02-v2)l2=p0+pv02(l-4smzQ)/2. (7.26)
Мы видим, что давление в лобовой точке (0=0), равное р0 +
+ 72р^02, превышает давление на бесконечности. Такой же
величины оно достигает и <в симметричной точке за цилиндром
123

(0=я). При приближении к плоскости миделя (0=±я/2)
давление монотонно «падает до величины po—3Upv0zy меньшей р0.
Параметр
К= -^=^0=l-4sin2G
V. ?v\
называют коэффициентом давления. Он не зависит ни от радиуса
цилиндра , ни от плотности жидкости, ни от скорости потока. Это
одно из проявлений общего закона гидродинамического подобия,
о котором подробнее речь пойдет ниже. Благодаря закону
подобия изложенную теорию обтекания цилиндра можно проверить,
измеряя зависимость коэффициента давления от G на
каком-либо случае с определенными значениями R, v0 и р. Полученный
результат будет относиться к любому случаю обтекания цилиндра.
Эксперимент с реальной жидкостью не подтверждает
формулы (7.27). Он показывает, что значение К действительно равно
единице в передней критической точке (8=0), где поток
разветвляется, и уменьшается при приближении к плоскости
миделя. Однако в последней К не падает до значения К=—3, как это
должно было бы быть согласно формуле (7.27), а в задней
критической точке (9=я) не возрастает снова до /С—1. Это
обусловлено тем, что в реальной жидкости безотрывное обтекание
цилиндра, изображенное на рис. 7.4, невозможно. Линии тока в
области л;/2<9<я отрываются от поверхности цилиндра, и в
этой области образуются вихри, о чем мы будем говорить
позднее. Однако это не означает, что теория обтекания тел идеальной
жидкостью не имеет смысла. Цилиндр просто относится к числу
плохо обтекаемых тел. Для хорошо обтекаемых профилей
(например, самолетного крыла) эта теория оправдывается опытом
значительно лучше.
28.3. Парадокс Даламбера — Эйлера. Обратимся еще к одной
особенности обтекания тел идеальной жидкостью, а именно к так
называемому парадоксу Даламбера — Эйлера. Частный случай
этого парадокса легко установить, обратив внимание на
симметрию выражения для давления на поверхности относительно
плоскости миделя Э=я/2 (см. формулу (7.26)). Вследствие этого
сила лобового сопротивления, действующая на цилиндр в
направлении потока, равна нулю. Хотя это утверждение и называется
парадоксом, оно непосредственно следует из теоремы Эйлера и
формулируется следующим образом: при обтекании тела с
гладкой поверхностью идеальной несжимаемой жидкостью сила
лобового сопротивления, действующая на него со стороны потока,
равна нулю.
Для доказательства этого утверждения предположим
сначала, что обтекаемое тело (рассматривается общий трехмерный
случай) помещено в жесткую цилиндрическую трубу,
образующая которой параллельна скорости потока на бесконечности
(рис. 7.5). Боковая поверхность трубы S', так же как и поверх-
124
(7.27)

ность обтекаемого тела S", будет составлять поверхность
некоторой трубки тока. Рассмотрим два поперечных сечения трубы
52 и Si справа и слева от тела, удаленные от него на достаточно
большое расстояние, где скорость потока можно считать
невозмущенной и равной —v0. Согласно теореме Эйлера полная сила,
действующая на жидкость, заключенную между поверхностями
S'+Si+S2 и S", равна разности потоков импульса жидкости
через торцевые поверхности St и S2. Площади St и S2, как и
скорости в этих сечениях, равны, следовательно, и полная сила Fn=0.
рассмотрим проекцию этого векторного равенства на
направление потока вдали от тела. Поскольку на S' силы давления
перпендикулярны v0, интересующая нас проекция складывается из
силы F, действующей на жидкость со стороны обтекаемого тела,
и сил давления на торцах: F+^Sj—/?2S2=0. Отсюда с учетом
S^Sz и pi=p2—p0 получаем, что и F=0. Следовательно, по
третьему закону Ньютона равна нулю и сила лобового
сопротивления, действующая со стороны потока на тело. Предполагая
теперь стенки трубы удаленными на бесконечность, получаем, что
сила лобового сопротивления равна нулю и при обтекании тела
в безграничном пространстве.
Если наложить на картину течения однородный поток со
скоростью v0, то жидкость на бесконечности будет в потоке —
случай, когда тело движется с постоянной скоростью в покоящейся
жидкости. Мы видим, что сила сопротивления его движению
также равна нулю.
28.4. Циркуляционное обтекание цилиндра. При обтекании
цилиндра однородным потоком также равна нулю и сила,
действующая в перпендикулярном потоку направлении (симметрия
формулы для давления (7.26) относительно плоскости 0=0).
В случае же циркуляционного обтекания тела эта сила может
быть отличной от нуля. Ее обычно называют «подъемной» силой
по аналогии с подъемной силой крыла самолета.
Наложим на изученное выше течение при обтекании
цилиндра циркуляционное движение вокруг его оси. Описание
совокупного течения можно осуществить, взяв для комплексного
потенциала сумму выражений (7.22) для симметричного потока и
(7.15) (с учетом (7.16)) для циркуляционного течения. В
результате для суммарного течения получим
F(z)=-v0(z+R2/z) +Г1п(г)/2ш\ (7.28)
Отсюда, определив ф и «ф, можно найти все характеристики
течения. Конечно, на поверхности цилиндра (r=R) нормальная
компонента скорости vr равна нулю. Тангенциальная компонента
была найден^ ранее отдельно для каждого из двух
составляющих течений. Полная скорость ve будет их суммой. Поэтому с
Учетом (7.16) и (7.24)
v\r-R=v9\r-R=2vQsinQ + ri2nR. (7.29)
125

Подставляя найденное значение скорости циркуляционного
потока на поверхности цилиндра в формулу Бернулли (7.25),
для распределения давления в этом случае получаем
'-*+гр[-.-(*ь*«+гг)']-
-/>.+ {p^i^sin^-^sine-k-L.)'] (7.30)
Давление р симметрично относительно плоскости миделя (9 =
=я/2). Поэтому, как и в безциркуляционном обтекании, в
соответствии с парадоксом Даламбера — Эйлера нет силы,
действующей на цилиндр в направлении потока. Однако давление р на
поверхности цилиндра несимметрично относительно плоскости
0=0 (член — (2IX/ji#)sin9 в (7.30)). Следовательно, значения
давления на нижней и верхней половинах поверхности цилиндра
будут разными. Это и понятно. Действительно, наложим
мысленно на симметричный поток (см. рис. 7, 4, а) циркуляционное
течение против часовой стрелки (положительное Г). Тогда над
цилиндром скорости обоих течений будут складываться, а под
цилиндром вычитаться. Результирующая скорость сверху будет
больше, чем снизу. Это означает, что по теореме Бернулли
давление снизу будет больше, чем сверху, и на цилиндр будет
действовать результирующая сила («подъемная» сила), направленная
снизу вверх (по оси у). Величина этой силы, отнесенная к
единице длины образующей цилиндра, равна
Я/2
/^ = _2 j pRsinQdQ.
-Я/2
В самом деле, в силу симметрии р относительно плоскости
миделя (6=я/2) интегрирование поля давлений достаточно провести
от —сгс/2 до я/2 и результат удвоить. Элемент площади цилиндра
будет равен RdQ, а проекция на ось у силы, действующей по
нормали на единичную площадку, равна —р sinG. В результате и
получается приведенная формула.
Теперь подстановка явного выражения для давления (7.30)
с учетом только несимметричного члена дает
Я/2
F„ = .НЕЕЙ- Г sin» 6d9 = ро„Г. (7.31)
-Я/2
Подъемная сила оказывается пропорциональной как . скорости
набегающего потока :>0, так и величине циркуляции Г. В
частности, если Г поменяет знак (направление циркуляции по часовой
стрелке), то и «подъемная» сила поменяет направление на
противоположное.
Отметим, что формула F=pv0T для подъемной силы
справедлива при обтекании любого цилиндрического тела (не обяза-
126

тельно круглого сечения). Доказательство этого утверждения
является предметом теоремы Жуковского.
Интересно, что на использовании силы, даваемой
выражением (7.31), была основана идея так .называемых роторных
движителей для судов. Действительно, если на корабль вместо парусов
поставить вращающийся вокруг вертикальной оси цилиндр, то
при наличии ветра возникает сила, перпендикулярная
направлению ветра. Однако такие движители не получили
распространения.
§ 29. Обтекание сферы потенциальным
потоком
29.1. Потенциал и скорости частиц. На примере с цилиндром
мы видели, что решение двумерных задач потенциального
обтекания тел стационарным потоком идеальной жидкости сводится
к поиску конформного преобразования, переводящего область,
занимаемую телом, в более простую, решение задачи обтекания
которой известно. В общем случае трехмерных задач мы уже не
можем использовать аппарат конформных преобразований к
должны непосредственно решать уравнение Лапласа с
соответствующими граничными условиями. Продемонстрируем метод
решения уравнения Лапласа на сравнительно простой задаче
обтекания сферы *.
Предположим, что на бесконечности жидкость покоится, а
сфера движется с постоянной скоростью v0. Потенциал скорости
частиц жидкости ф (v=Vcp) должен удовлетворять уравнению
Лапласа (7.2), условию на бесконечности и условию на
поверхности сферы — равенство нормальных к
поверхности сферы составляющих скорости частиц
жидкости и точек сферы. Первые равны (vr/r)reJl, вторые v0T=
=v0r/r, где предполагается, что качало системы координат
помещено в центр сферы (рис. 7.6). Теперь полная математическая
формулировка задачи будет:
Дф=0, v 1^00=0,
(7.32)
VT
= ?£, r = YX2+y2+z2.
r=R г
Хорошо известным фундаментальным решением уравнения
Лапласа, удовлетворяющим условию на бесконечности, является
Ф=Л/г, где А — постоянная. Это решение описывает, например,
гравитационный потенциал точечной массы или электрический
потенциал точечного заряда. Однако в силу своей сферической
симметрии оно не может служить решением нашей задачи,
которая не обладает такой симметрией, так как выделено
направление скорости v0. Поэтому мы возьмем другое простое решение
В 'силу цилиндрической симметрии задачи и в этом случае можно .было бы
свести задачу к двумерной, если ввести функцию, аналогичную \|э. Однако мы
этого делать не будем.
127

уравнения Лапласа — потенциал диполя (двух близко
расположенных зарядов противоположного знака), равный BV (1/г),
где В — постоянный вектор, называемый моментом диполя.
Действительно, уравнение Лапласа будет удовлетворяться, так как
операции дифференцирования, например д/дх, переставимы с
операцией А. Условие на бесконечности также будет выполнено,
так как | V (1/г) | ~1/г2 при г->оо.
Скорость сферы v0 входит в граничное условие при r=R
(7.32) линейно, поэтому естественно искать решение нашей
задачи в виде
<f=Av0V(\/r)=-Av0r/r'.
Отсюда скорость частиц жидкости v=Уф будет равна
v=— A v0/rs + ЗА (v0r) г/г5.
Подстановка этого выражения в условие на поверхности сферы
(7.32) дает
—Av0r/R' + 3AvJR3=v0r.
Отсюда находим A=R3/2. В результате имеем:
<p=_±*L(V)> V = -1£-V0+A«1(VLL, (7.33)
Y 2 г3 ; 2 г3 2 г3 г*
что и является решением задачи об обтекании сферы.
Если теперь наложить на найденное течение однородный
поток со скоростью —v0, то получается решение задачи, когда
покоящаяся сфера обтекается потоком, скорость которого на
бесконечности равна —v0. Для вектора скорости этой новой задачи
на основании (7.33) имеем
v = -v0-±^v0+^(-^ (7.34)
0 2 г3 ° 2 г3 г*
и соответственно для компонент скорости
vr = v — = —0Оcos9 _i-5LuoCos8 + «f-^r^ocos0 =
r 2 r3 2 r3
==_t,oCOSe(i-^),
i;e = u0sine (l + y^-),
(7.35)
В последнем выражении мы учли, что t;oe = ^osin0.
На поверхности сферы (r=R), как и должно быть, vr=0 и
ue = t;=72t;oSine. (7.36)
Отсюда следует, что v=0 при 8=0 и 8=л —передняя и задняя
критические точки. Пользуясь теоремой Бернулли, легко найти
распределение давления по поверхности сферы. Подставив в
128

(7.25) вместо v выражение (7.36), получаем
р = Л> + V. Р^(1 - % sin2 0). (7.37)
Давление является симметричным по отношению к плоскости
миделя (0=л/2) и минимальным на ней. Коэффициент давления
аналогично (7.27) будет
к = P^9± = j _ 1 sin2 0# (7в38)
V.|«S 4
29.2. Присоединенная масса. В силу симметрии давления
относительно плоскости 0 = я/2, как и в случае с цилиндром,
полная сила, действующая со стороны потока на сферу, равна нулю
(в соответствии с парадоксом Даламбера — Эйлера). Однако
неправильным было бы думать, что сила, необходимая для
разгона покоящегося шара массой m с постоянным ускорением а до
скорости v0, будет равна та. Как оказывается, для этого
необходима большая сила, т. е. при разгоне шара (или другого тела)
возникает сила сопротивления жидкости. Это обстоятельство не
противоречит утверждению парадокса Даламбера — Эйлера,
поскольку последний имеет место лишь при стационарном (v0=
=const) обтекании. В нашем же случае разгона шара задача
становится нестационарной.
Проще всего определить требуемую силу из энергетических
соображений. При конечной скорости шара v0 время действия
силы F равно T=v0/a. Пройденный шаром при этом путь будет s=
=aT2/2 = v02/2a. Следовательно, работа силы F равна Fs=
= Fv02/2a. Эта работа идет на повышение кинетической энергии
шара и жидкости, которая в начальный момент времени также
покоилась. Таким образом,
Fv\l2a = mv\l2 + j (Pv2/2)dV,
v
где интегрирование проводится по объему всей жидкости (г>
>/?). Отсюда легко получаем, что
F=ma+Ma9
где выражение
Af = -£. [v*dV (7.39)
0 r>R
называется присоединенной массой. Из (7.33) имеем:
vr = (v0R3/r3) cos 9, vB = (v0R*/2r3)sin 9, v2 = (t;20#e/re) x
x(l + 3cos29)/4.
В результате после интегрирования
r>R
5 Л. M. Бреховскнх, В. В. Гончаров 129

Следовательно,
М = 7зя/?3р= (V.) 7,я/?3р = 72Ушр, (7.40)
где Vm —лбъем шара. Таким образом, присоединенная масса
ускоренно движущегося в жидкости шара равна половине массы
жидкости, заключенной в его объем.
Задачи
7.1. Пусть жидкость вращается вокруг вертикальной оси так, что частота
вращения цилиндрического слоя радиусом г равна Й(г). При какой
зависимости Q (г) движение будет потенциальным?
Решение. Скорость частиц жидкости найдется как
v = {и, v) = Q х R = {— Qy, Qx],
где R= {*, у, z) = {г, г). Отсюда для го = rot v имеем:
w=o)Vz, <u = dv/dx—du/dy=Q+xQ'xlr+Q+yQ'y/r=2Q+rQ'.
При потенциальном движении (о) = 0) Q(r) определяйся из уравнения
Q'=dQldr=—2Q/r, решением которого будет функция Q (г) = Q0a2/r2, где
fi0 2== Q (а); а — произвольно.
7.2. Найти форму свободной поверхности при потенциальном вращении
жидкости (см. предыдущую задачу) в поле силы тяжести.
Решение Вводя центробежную силу инерции pQ2r=pQ02(a4/''4)r с
потенциалом на единицу массы жидкости 1/2&о2а4/г2 и потенциал силы тяжести
gz (ось z направлена вертикально вверх), запишем уравнение Бернулли (6.38)
в виде
р/р+Q02a4/2r2+gz=gz0=const.
Поскольку движение безвихревое, то постоянная Zq одинакова для всех точек
жидкости (см. п. 23.1). Отсюда получаем уравнение свободной поверхности
жидкости (р=0):
z=z0—Q02a*/2gr2.
Мы видим, что 2->—оо при г->0.
7.3. Предполагая, что слои жидкости вращаются в поле силы тяжести
вокруг вертикальной оси с частотой Q0 при г<а и Qoa2lr2 при r>at найти
форму свободной поверхности.
Решение. Форма свободной поверхности при г<а была нами найдена
в задаче 6.11: z(r)=H+ (Q02/2g)г2, Н=(р0—pe)/gp. При г>а она получена в
предыдущей задаче. Связь между постоянными Н и z0 можно определить из
условия непрерывности функции z{r) при г=а: Zo=H+Q02a2lg. Окончательно
уравнение свободной поверхности может быть записано в виде
&0а2 (г*/*, г<а,
z{r)==H +~^~{2-а*/г\ г>а.
Нетрудно убедиться также, что при переходе через точку г=а остается
непрерывной и dz/dr.
7.4. Получить выражение для комплексного потенциала F(z) в случае
обтекания цилиндра с эллиптическим сечением (рис. 7,7) набегающим вдоль
130

оси х со скоростью v0 потоком несжимаемой жидкости. Считать, что
направление скорости совпадает с направлением одной из главных осей эллипса.
Решение. Найдем конформное преобразование z=f(£) области вне
эллипса в плоскости z=x+iy на внешность окружности |С|># в плоскости
£=5+иг)- Для этого, написав уравнение эллипса в полярных координатах
x=flcos9, y=bsinQt z=acos9+ibsin9, преобразуем его к виду
а + Ь
е"
2 в
■•#*•■
■Ь R*
W Re"
Теперь легко видеть, что искомым конформный преобразованием будет
преобразование Жуковского, записанное в
более общей форме, чем (7.21):
*-/(«-•
а + Ь
2R
Для того чтобы при |z|->oo
преобразование было тождественным, удобно
положить #=(а+Ь)/2. Тогда 2=g+(a2—62)/4£.
Обратное преобразование имеет вид £=
<8
Рис. 7.7
= 1/2(2+У22—а2+Ь2). В плоскости £ мы
Получили задачу обтекания кругового цилиндра радиусом /?=(а+&)/2 потоком,
набегающим со скоростью
дф (6, Л) I дф (*, у) | дф
<£
Mtl-
дх
Щ-
!—»••
*1 1|С|-м
решение которой описывается комплексным потенциалом (7.22): ф(£) =
=— ^о[£+(а+Ь)2/4£]. При подстановке в последнее выражение £(z)
получаем искомый комплексный потенциал обтекания эллиптического цилиндра:
2 L г + V* — а* + Ь* J
= -Т(* + Ь)[ — + — j
7.5. Найти комплексный потенциал в случае обтекания эллиптического
цилиндра набегающим под углом а к оси х потоком (ось х направлена так же,
как и на рис. 7.7).
Решение. Сначала решим эту же задачу для кругового цилиндра.
Поворот системы координат соответствует конформному преобразованию
£=zexp(—ia), подстановка которого в (7.22) дает решение задачи для
кругового цилиндра:
Fk (*) = —v0exp (— fa) г + — exp (ia).
В случае обтекания эллиптического цилиндра, как и в задаче 7.4, совершим
конформное преобразование £=1M2+Vz2—д2+^2)» отображающее область
Вне эллипса на внешность окружности радиусом /?=(а+6)/2. Далее, исполь-
131
5»

зовав вместо (7.22) потенциал FK(z), получаем
w 2 L а+Ь
г- V# — a* + P
exp (ia)
a-b
7.6. Найти комплексный потенциал в случае обтекания бесконечно тонкой
полосы шириной 2а набегающим под углом а к оси х потоком со скоростью
v0 (рис. 7.8). Рассмотреть частные случаи а = 0
и а=л/2.
Решение. Полоса является частным
случаем эллипса с равной нулю вертикальной
полуосью. Положив в Fd(z) (см. задачу 7.5) Ь=0,
получаем
У*
шиииМмшхъ
-/г
ста 1
л
F (г) = — v0 (г cos a — iYz2 — a2 sin a)=
ftic.7.8
Ы-Ь>луУ*-а*
voy
При a=0, как и должно быть, тонкая пластинка не влияет на поток: F(z) =
= —v0z. При a = Jt/2 поток набегает перпендикулярно плоскости пластинки и
F(z)=iv^z2—а'1. Заметим, что комплексная скорость, равная F'(z)t
обращается в бесконечность на краях пластинки (z=dba).
7.7. Пусть несжимаемая жидкость, заполняющая полупространство'*<О,
с давлением р\ на бесконечности вытекает из отверстия размером 2D в плоской
стенке LU (плоская задача, рис. 7.9, a, АВ и А'В* являются границами струи)
в свободное полупространство дс>0, где давление равно рч. Получить
отображение области течения z=x+ty на плоскость комплексного потенциала
F=q)+n|> и плоскость комплексной скорости w = u—iv.
Решение. Отметим, что задача имеет зеркальную симметрию
относительно оси *, причем последняя является линией тока (if|yeo=const). Без
ограничения общности можно положить я|>|у=о=0. Линией тока будет и
линия LAB. При *-*оо поток становится однородным (u=d^/dy=vot i> =
=—д$/дх=0), следовательно, ty=v0y при *->оо и на линии тока LAB
ty=v0d. Аналогично на линии тока UA'B' ^ — —v0d. Теперь ясно, что
отображение области течения на плоскости потенциала F=q>-M4|) является полосой
(рис. 7.9, б).
L Я
uffd
-V
ц
л
[
Г
Г
ч
is
h'
б
-?
L
Рис. 7.9
132

том на
Скорость жидкости vo при *-*оо можно найти по теореме Бернулли:
pllp = p2lp+Vo2/2t i;0=V2(pi—Рг)/р. Отсюда также следует, что на участках
А В и А'В' скорость постоянна по модулю |и0| и меняется от v={0, — Vq]
до v={v0,0} на АВ и от v={0, v0) до v={i>q,0} на А'В'. На участке
LA (L'A') v={0, v}f причем v монотонно убывает (возрастает) от и=0 при
у=±оо до —v0( + v0). Из сказанного следует, что отображение области
течения на плоскость комплексной скорости — полукруг (рис. 7.9, в).
7.8. Воспользовавшись результатами задачи 7.7, получить выражение для
комплексного потенциала в случае истечения жидкости через отверстие и
вычислить коэффициент истечения.
Решение. Предварительно получим преобразование w = w(F) (в
обозначениях задачи 7.7), отобразив каждую из областей на рис. 7.9, б и в на
полуплоскость £>0 комплексной переменной £=£+/т| (рис. 7.10): g=g(/7) =
= l(w). Первое отображение, как легко проверить, определяется функцией
£=ехр(—nF/2v0d)t второе — преобразованием Жуковского (7.21) с поворо-
i / w . lv0\
я/2: £ =— "л|~ ' I , обратным которому будет
преобразование о> = 0о(У£2+1—£)• Следовательно, отображение полосы в плоскости
потенциала на полукруг в плоскости комплексной скорости имеет вид
w(F) = v0 {[1 + ехр (- nF/v0d)]K __ ехр (- nFfiv^)}.
Но так как w=F't то искомое преобразование F(z) можно найти из
уравнения
dF г- / nF \
Vod2= ; =(V\+**+a)dFt а = ехр - —т ,
/l+a'-a V 2v0d)
интегрирование которого дает обратное преобразование z=z(F):
z=C-(2d/n) [rtf^M+a+Vr+^+lntyf+a3— 1) ].
Комплексная постоянная C=C'+iC" может быть определена из известных
соотношений на линиях тока. Рассмотрим, например, линию тока LAB (см.
рис. 7.9, а), на которой -ф=^о^, F=q>+iv0d (—оо<ф<оо). Подставляя это
значение F в выражение для z(F)t получаем <х=ехр(—£я/2—у), 7=яф/21><4 и
: С - (Щп) {у + in/2 - ie~v + */l-<T2V +
'•\$=
M'
+ ln[Kl+exp(-m-2v)- 1]}.
(7.41}
Если q>->oo, то z-*-x+id, у-*00» ln{[l+exp(wi—2уг*—
—1}«— 1п2—Ы—2у. Следовательно, x+id=
= C'+iC"+ (p/v0—2d (1 —1п2) In+id, откуда С"=0.
На участке LA линии тока, соответствующем ф<0,
имеем z=iy, у<0» ехр(—y)>1- Следовательно,
/
С-
ф 2d г
JL _ — 1п | К1 - ехр (— 2у) — 11 = 0
v0 п
0
-/
но VI— ехр(—2Y)=*Yexp(—2Y)—1, |У1—ехр(—2у) —
—11 «ехр(—y), поэтому С'=0. Таким образом,
комплексная постоянная в выражении (7.41) С=0.
/Г
\6
Рис. 7.10
133

Коэффициент истечения, равный, по определению, k=d/Dt найдем из
условия z(ivod)=iD9 что дает D=d(jt+2)/nt 6=я/(я+2) «0,61.
7.9. Найти присоединенную массу на единицу длины кругового цилиндра,
движущегося с ускорением в несжимаемой жидкости в направлении,
перпендикулярном его оси.
Решение. Поступая аналогично расчету присоединенной массы для
шара, найдем кинетическую энергию жидкости в слое единичной (в
направлении оси цилиндра) толщины, возмущенной движущимся со скоростью v0
цилиндром. Для этого, добавив к комплексному потенциалу (7.22),
описывающему обтекание цилиндра, член v0z, получим комплексный потенциал при
движении цилиндра со скоростью tw F(z)=—voR2lz= — (v0R2/r)exp-i0, откуда
Ф=—(v0R2/r)cos 6. Для скорости частиц жидкости находим
Следовательно, кинетическая энергия в слое единичной толщины равна
о R
где M=pnR2— присоединенная масса на единицу длины, равная массе
жидкости, вытесненной цилиндром.
7.10. Рассчитать присоединенную массу движущегося в жидкости с
ускорением а шара на основе решения динамических уравнений.
Решение. В силу справедливости уравнения Лапласа при движении
шара в несжимаемой жидкости в любой момент времени t можно
воспользоваться выражениями (7.33), положив в них v0=a£. Тогда для потенциала и
скорости частиц жидкости имеем:
1 *■ 1 R* 4 , 3 Я8 (аг)г 4
со =з — 1 аг. v=— a 1-4- /.
ф 2/*' 2 г» ^ 2 г» г«
Давление на поверхности шара можно найти с помощью интеграла Коши —
Лагранжа (7.1), где следует положить w=0, ш=р/р, кроме того, учтем, что
<р-*0, v-й), р-*Ро при г-^оо. Тогда
о* I дф I о р
Р U* - Р# - Р -И - Р 77 = Ро~ «2* (1+3 cos* 9)+ faR cos9.
Сила, действующая на шар в направлении его движения, найдется
интегрированием последнего выражения по поверхности шара:
271 Я
Fx=~ Jp^^5 = -/?> J JL-ja>/'(l+3cos»0) +
5 oo
+ о a/* cos 9 cos 0 sin e d® d<V-
134

Первые два слагаемых в этой формуле симметричны относительно плоскостг
перпендикулярной направлению движения, и при интегрировании дадут нул*
Таким образом,
я
oaR С 2 1
Fx = -R22n y« cos29sinede = —я#3ра = уУшра = А1а,
где М = рУш/2 — присоединенная масса, совпадающая с выражением (7.37).
7.11. Пусть тонкостенная сфера (сферический буй) массой т и радиусом
R находится в равновесии в стратифицированной жидкости плотностью ро(*)
на горизонте Zq (т=4/зя/?3р(г0)). Определить период малых колебаний буя.
Решение. Если вывести буй из состояния равновесия, сместив его на
расстояние £ по вертикали, то на него будет действовать возвращающая сила,
пропорциональная частоте Вяйсяля (см. формулу (6.28)) с с=оо;
1 ф
F=mN2(z)%=—mg ™£- С учетом присоединенной массы сферы, равной
р аг
т/2, запишем уравнение движения буя:
|-/п£ + тЛР(г0)£ = 0.
Отсюда для частоты колебаний буя и периода имеем (о2=2/з#2(2о),
Т=уЪл/Ы(г0).
7.12. Определить силу давления, с которым нужно действовать на
бесконечно легкую и растяжимую сферическую оболочку в несжимаемой жидкости,
чтобы ее радиус начал увеличиваться с ускорением а. Найти присоединенную
массу расширяющейся сферы.
Решение. Через промежуток времени А* скорость растяжения оболочки
будет v=aAt. Сферически-симметричным решением уравнения Лапласа для
жидкости с граничным условием v\R=(d<p/dr)R=aAt является функция
(p=—aAtR2/r. При этом скорость частиц жидкости найдется как v(r) =
= dq>/dr=aAtR2/r2. Вычислим энергию всей жидкости:
оо оо
Е =. -| 4я Г Л* dr = 2яр (аЫ)* R* f -j- = 2яЯ8р (аД/Д
R R
Эта энергия должна равняться работе действующей силы F=4nR2p, равной
A=FAR=Fa(At)2/2. Приравняв Я и Л, находим:
Р=4я#3ра=Ма, М=4я#3р,
где М — присоединенная масса, равная утроенной массе вытесненной сферой
жидкости.
135

7.13. Показать, что в несжимаемой жидкости для увеличения радиуса
цилиндрической оболочки требуется бесконечно большая сила на единицу длины
образующей цилиндра.
Указание. Показать, что в цилиндрически-симметричном случае
энергия жидкости в слое единичной толщины по образующей цилиндра для
расширяющейся со скоростью v\R=v0 оболочки равна бесконечности.
Глава 8
ТЕЧЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
На течение любой реальной жидкости существенное влияние
оказывает вязкость. Как мы видели, в идеальной жидкости,
находящейся в поле потенциальных сил, не может возникать
вихрей — потенциальное течение жидкости всегда остается
потенциальным. В действительности же мы постоянно наблюдаем
возникновение и исчезновение вихрей. Неверным является также
положение теории идеальной жидкости о существовании отличной
от нуля тангенциальной составляющей скорости на поверхности
твердого тела. Опыт, однако, показывает, что на поверхности
любого неподвижного тела все компоненты скорости частиц
жидкости равны нулю. В силу этого на жестких поверхностях
собирается тонкий слой пыли, несмотря на то что поверхность обтека1
ется скоростным потоком (например, пылинки на вращающихся
лопастях вентилятора).
§ 30. Уравнения гидродинамики
вязкой жидкости
30.1. Коэффициент вязкости и вязкие напряжения. Вязкость
(сила трения) проявляется только при деформациях в жидкости.
Если же жидкость движется как целое, то силы трения не
возникают. Для того чтобы учесть эти силы, рассмотрим следующий
элементарный опыт. Возьмем две бесконечные плоские и
параллельные друг другу пластины, расстояние между которыми равно
А. Пусть одна из пластин, например верхняя, движется
относительно другой с постоянной скоростью v0 (течение Куэтта, рис.
8.1). Обозначим через F силу, которая должна быть приложена
при этом к верхней пластине. Опыт показывает, что эта сила,
отнесенная к единице площади пластины, прямо пропорциональна
скорости v0 и обратно пропорциональна расстоянию Л:
F/S=r)v0/h. (8.1)
Коэффициент пропорциональности ц называют ньютоновским
коэффициентом вязкости. В теоретических расчетах часто бывает
удобнее вводить величину v=r]/p, называемую кинематической
136

вязкостью. В качестве примера приведем численные значения
коэффициентов т] (в г-см"1-с"1) и v (в см2-с~!) для воды и
воздуха при температуре 20° С:
ц = 0,01 fv=0,01 (вода),
т1 = 1,8-10-4, v = 0,15 (воздух).
Коэффициенты вязкости зависят от температуры, причем для
жидкостей вязкость быстро убывает при возрастании
температуры, а для газов она несколько растет.
Закон (8.1) поддается обобщению на случай произвольного
течения. Для этого направим ось х вдоль вектора скорости
течения в некоторой точке и выделим мысленно из всего объема,
занимаемого жидкостью, малый параллелепипед с длинами ребер
Ал:, Ду, Дг (рис. 8.2), такими, что Д*/<Д* и Ду<Дг. Обозначим
через Д5=Дл:Д2: площади граней, перпендикулярных оси у.
Скорость частиц жидкости на нижней грани выделенного объема
будет vx на верхней vx+Avx. На основании (8.1) получаем, что
137

Для поддержания такого перепада скорости vx между нижней и
Верхней гранями должна существовать «перерезывающая» сила
AF, такая, что
AF/AS=r|AoJAy.
Полагая Ду-Я) и А5->0, получаем одну из компонент, так
называемого тензора вязких напряжений
<зхд = lim — =* ri -* (8.2)
Высказанные соображения можно рассматривать как
наводящие, позволяющие построить формальную теорию движения
вязкой жидкости, к чему мы сейчас и приступим.
30.2. Уравнение Навье— Стокса. В § 24 мы видели, что
уравнения Эйлера для идеальной жидкости и равных нулю внешних
сил могут быть записаны в виде закона сохранения импульса
dfdt(pvi)=-dnjdxhf (8.3)
где nih=p6ik+pViVk — тензор плотности потока импульса.
Обобщим последнее уравнение, вводя в TLih дополнительные члены,
учитывающие действие вязких сил. Для этого положим
TliK=P&iH+pv{vh—oih, (8.4)
где тензор о* назовем тензором вязких напряжений. Его явное
выражение можно .найти из общих соображений. Как мы уже
отмечали, трение может возникнуть только в случае, когда
различные участки жидкости движутся с разными скоростями.. Следо-
вательно^р* должен зависеть от градиентов скорости (см.
формулу (8.2)). Предполагая, что'эти градиенты невелики,
представим тензор Oik в виде разложения по ним, удерживая только
линейные члены. Из требования обращения в нуль oih в случае,
если жидкость вращается как целое, следует, что градиенты
скорости должны входить в Oih только в комбинациях
dvjdxk+dvjdxif dvjdxm, (8.5)
равных нулю при таком движении. Действительно, при вращении
жидкости как целого с угловой скоростью Й=.{Й1, Q2, й3} имеем
y=QXi\ где г — радиус-вектор произвольной частицы жидкости
при условии, что начало координат выбрано на оси вращения.
Отсюда непосредственно следует dvm/dxm=div v—0. Кроме того,
например,
vi=Q2xi—Qsx2t v2=Qixi—Qix3} dvjdx2 + dv2/dxi=0t
Наиболее общим выражением для тензора второго ранга,
удовлетворяющего указанным выше условиям, является
*»-в(?+тЧ + *г^ (8-6)
\dxk дх( ) дхт
138

где а и Ь — постоянные, не зависящие ни от скоростей, ни от их
градиентов. Последний член в этой формуле, пропорциональный
скорости изменения объема жидкой частицы, существен только
в сжимаемой жидкости, например при исследовании звуковых
волн в вязкой жидкости.
Уравнение движения жидкости с учетом вязких сил,
называемое уравнением Навье — Стокса, можно получить при
подстановке выражения для тензора плотности потока импульса в виде
(8.4) с учетом (8.6) з уравнение (8.3). При этом, предполагая
коэффициенты а и Ь не зависящими от координат, имеем
Ъ°г ■ dp dp ty д / * ч , &°i ,
34 , . «ч
+ а
dxt dxh дх( dxk
Учитывая также уравнение неразрывности (6.9), получаем
искомое уравнение
(*+-£)
*> , .«„ , ,. , и *»'
^ +«*., + (.+4^-. (8.7,
или в векторной форме
P^L=p^+(vV)v]=-Vp + aAv + (a + 6)V(Vv). (8.8)
В случае несжимаемой жидкости (Vv=0) последний член в
правых частях (8.7) и (8.8) выпадает и (8.8) принимает вид
р Vdf+(v V)v]=_ Vp+aAifi (8,9)
что является уравнением Навье — Стокса для несжимаемой
жидкости.
30.3. Вязкие силы. Член doihldxh в правой части уравнения,,
(8.3), или, что то же, члены, содержащие коэффициенты а и & в
(8.7), можно рассматривать как i-ю компоненту вязкой силы,,
действующей на единицу объема жидкости:
/, = a^ + (a + 6)T^ = aAt;/ + (a + 6)^-(divv). (8.10)
Покажем, как может быть вычислена сила, действующая на
твердое тело со стороны установившегося (стационарного)
потока вязкой жидкости. Окружим тело некоторой воображаемой
замкнутой поверхностью S' (рис. 8.3). В стационарном случае
уравнение (8.3) переходит в dUihldxh=0. Интегрируй последнее
по объему жидкости, заключенной между поверхностью S' и
поверхностью тела S, и применяя теорему Гаусса для тензора П<*
139

получаем
— j \1*пк dS + j* Ucknk dS = 0, (8.11)
где n={nu n2, ns} — внешняя нормаль как к S', так и к
поверхности тела S.
Частицы вязкой жидкости прилипают к поверхности
обтекаемого тела, поэтому их скорость на 5 равна нулю, и первый
интеграл в (8.11), равный в соответствии с (8.4)
Fi = —\ рщ dS%+ j aiknk dS, (8.12)
s s
определяет силу, действующую на тело со стороны набегающего
потока. Здесь первое слагаемое не относится к вязким силам, а
представляет собой результирующую сил давления жидкости на
тело. Вязкую силу определяет второй член выражения (8.12)
Fl = j oiknkdSy (8.13)
5
плотность которой на единицу поверхности тела, как и для сил
в упругом теле, равна
f/=oihnh. (8.14)
С учетом (8.11) полная сила, действующая на тело со
стороны потока, может быть вычислена по характеристикам
последнего на произвольной поверхности S' вне тела:
Fi = \ (— РЪ — PViVknk + Oiktik) dS. (8.15)
5'
В некоторых случаях такой подход является более простым по
сравнению с вычислением интеграла (8.12) .непосредственно по
поверхности тела. Действительно, последняя может иметь
сложную форму. К тому же в окрестности тела поток жидкости
сильно возмущен, т. е. существенно отличен от однородного потока в
отсутствие тела. На больших же расстояниях от тела, где может
быть выбрана поверхность S', возмущение потока будет малым.
Благодаря этому его характеристики могут быть найдены,
например, линеаризацией уравнений движения относительно
отклонений характеристик потока от их невозмущенных значений.
§31. Примеры течений вязкой жидкости
31.1. Течение Куэтта. Применим уравнение Навье—Стокса
(8.9) к рассмотренному выше случаю (рис. 8.1), .называемому
течением Куэтта. Пусть ось х совпадает с направлением
скорости v0, а ось у направлена нормально пластинкам. Начало
координат возьмем на нижней неподвижной пластинке. В силу
симметрии задачи скорость и давление в произвольной точке
жидкости могут зависеть только от координаты у: vx=v = v(y), /? =
140

= р(#). Кроме того, движение стационарно (d/dt=0), поэтому
для компонент уравнения (8.9) будем иметь
др/ду = 0, d2v/dy* = 0.
Отсюда легко находим р=р0=const и v=Ay+B. Постоянные А
и В сразу определятся из граничных условий: и=0 при у=0,
v = v0 при y=h. В результате получаем В=0 и A = v0fh. Итак, в
нашем случае
v = vQy/h.
Найдем силу f, действующую на единицу площади нижней
пластины со стороны жидкости. Поскольку силы давления не
дают тангенциальной составляющей, для вычисления последней
можно воспользоваться формулой (8.14) с oih из (8.6).
Предполагая, что индексы 1, 2 соответствуют координатам х, у9 с учетом
в (8.6) только первого члена (несжимаемая жидкость) находим
/|v=0 = a dv/dy=av0/h. (8.16)
Эта сила, очевидно, должна быть равна силе (8.1), приложенной
к верхней пластине. В результате получаем а=т].
Итак, в окончательном виде уравнение Навье — Стокса для
несжимаемой жидкости запишем в виде
Р \Ч~+ (V V)V] = ~ Vp + Т1ЛУ> (8Л7)
В гидродинамике важным является понятие о коэффициенте
сопротивления, характеризующем отношение силы / к так
называемому скоростному напору i/2pvm2:
CD = 2f/piPn, (8.18)
где vm—^средняя (или некая характерная) скорость потока.
В случае течения Куэтта vm=v0/2i f=2t]vm/h и
CD = 4v/tU=4/Re, (8.19)
где Re=umft/v — число Рейнольдса: v = r\/p — кинематическая
вязкость жидкости.
31.2. Течение Пуазейля между двумя пластинками.
Рассмотрим две неподвижные параллельные друг другу пластинки,
расстояние между которыми равно h. Пусть между пластинками
имеется стационарное течение жидкости, которое должно
поддерживаться продольным градиентом давления, созданным
внешними силами. Ось х снова выберем в направлении скорости
течения, а ось у перпендикулярно пластинкам. Для такого
течения скорость жидкости может зависеть только от
координаты у (vx=v(y)). Компонента по оси у уравнения (8.17) имеет
вид
др/ду=0,
т. е. давление не зависит от у, а зависит только от координаты х
141

вдоль потока. Компонента уравнения (8.17) по оси х будет
*L = ±°L. * (8.20)
ду* л дх '
Здесь левая часть является функцией только у, а
правая—только х. Следовательно, и правая и левая части могут быть только
постоянными. Интегрируя (8.20), получаем:
|L = _ilL + A v = -J-y* + Ay+B, &=-^ = const.
ду t\ 2у\ дх
(8.21)
Постоянные интегрирования А и В найдем из граничных
условий: v = 0 .при t/=0, А. При этом получаем В = 0, A = bh/2r\ и
окончательно
,_£,(»-,) — ££,(»_„). (8.22)
Профиль скорости в поперечном направлении параболический
(рис. 8.4). Определим силу, действующую со стороны
протекающей жидкости на единицу площади каждой из пластин. Как и в
случае течения Куэтта (см. формулу (8.16)), имеем
Ь = ъЩ = *.«_*.*-. (8.23)
' Лду\9тш 2 dx 2
Здесь /х>0, dp/dx<0t т. е. сила направлена в сторону движения
жидкости (положительные х)9 а давление падает при
увеличении х.
Найдем среднюю скорость потока
h
vm = J- [vdy = — bh2 = L*. # (8.24)
Л J ^ 12л Щ dx '
0
и коэффициент сопротивления no (8.18)
CD=12/Re, Re=vMh/v. (8.25)
Так же как и для течения Куэтта, CD зависит только от числа
Рейнолытоя Re.
31.3. Течение Пуазейля в круглой трубе. Пусть радиус
трубы равен Rt ось х направлена по оси трубы. Отличной от нуля
будет лишь компонента скорости вдоль оси х, зависящая только
от расстояния до оси трубы (vx=v(r)t г=у*/2+г2). Расписывая
уравнение Навье — Стокса (8.17) по компонентам, получаем:
—др/дх+т) Д v = 0, dp/dy^0t dpfdz=0. (8.26)
Из двух последних равенств следует, что р=р(х)у но так как
v = v(r), то из первого уравнения (8.26) находим —др/дх=Ь =
= const. Оператор Лапласа в цилиндрически-симметричном
случае (v = v(r)) имеет вид
142

^ = r-'dldr{rdldr).
Теперь первое уравнение (8.26) принимает вид
d/dr(rdv/dr) =—Ьг/т). (8.27)
Проинтегрируем его по г:
— — br* л- л di? __ br у А
и потребуем, чтобы dvjdr было всюду конечно, в том числе и
при г=0. Для этого нужно положить Л = 0. Повторное
интегрирование по г дает
v = — br2/4г\ +В.
На поверхности трубы r=R имеем и=0, следовательно 5 =
= Ь/?2/4т]. Окончательно
Ъ (Т?2 — Г2) = L^.(£2_r2). (8.28)
4г| 4т] dx
Профиль скорости снова получился параболическим. Для
средней скорости имеем
R 2Я R
я/?а J J 2tf2n J 8л
0 0 о
Теперь легко получить известную формулу Пуазейля для объема
жидкости, протекающей через трубу за единицу времени
(расход жидкости):
8л 8л
Щ&. (8.29)
dx
Для силы, действующей на единицу площади трубы (п
направлено противоположно г), найдем
fx=-4(dv/dr)r=R=bR/2 = -(dp/dx)R/2.
Полная сила, действующая на единицу длины трубы 2nRfx=
= —7iR2(dp/dx)9 как и следовало ожидать, уравновешивается
градиентом давления.
Коэффициент сопротивления CD также определяется только
числом Рейнольдса:
CD = 2fx/pv*m = 8v/vmR = 16/Re, Re = vmD/vt (8.30)
где D = 2R — диаметр трубы.
На практике рассмотренные нами течения жидкости
осуществляются при достаточно малых скоростях (малые числа"
Рейнольдса). При этом формула (8.29) находится в хорошем
согласии с опытом.
143

31.4. Обтекание сферы медленным течением вязкой жидкости.
Пусть неподвижная жесткая сфера диаметром D = 2R
обтекается однородным на бесконечности стационарным потоком вязкой
несжимаемой жидкости. Направим ось х вдоль скорости потока
v0 на бесконечности (рис. 8.5). В уравнении Навье — Стокса
(8,17) пренебрежем квадратичным («инерционным») членом
p(vV)v, предполагая, что скорость потока достаточно мала.
Оценить условия применимости этого приближения можно
сравнением порядков отбрасываемого члена и, например, «вязкого»
члена r]Av в правой части. Характерным пространственным
масштабом нашей задачи будет диаметр сферы D, следовательно,
квадратичный член по порядку величины ~pv*jD. Вязкий же
член имеет порядок ~r\v0/D2. Условием малости первого члена
по сравнению со вторым будет VoD/v = Re4£l. Таким образом,
наше рассмотрение будет пригодно для малых чисел Рейнольд-
са, что, как мы видим, означает одновременно малость
инерционного члена по сравнению с вязким.
Итак, пренебрегая инерционным членом в (8.17), а также
вспоминая условие несжимаемости (Vv=0), получаем
следующую замкнутую систему уравнений:
Vp=T]Av, divv=0. (8.31)
Граничными условиями в нашем случае будут равенства
скорости нулю на поверхности сферы и v0 на бесконечности:
vLr=0, vxl^ = v„ t>, 1^ = 0.1^= 0, (8.32)
где r=i/x?+y2+z2. Представим v в виде потенциальной (Уф)
части и некоторой добавки w:
v=Vcp+w(x, у9 z). (8.33)
Подставляя последнее выражение во второе уравнение (8.31),
получаем
Acp+Vw = 0. (8.34)
Функцию ф ищем в виде, удовлетворяющем условию Уф|г-» =
= v0:
ф-^ + С^ + С,-^!), (8.35)
где Ct и С2 — произвольные постоянные. Найдем Дф, учитывая,
что Д(1/г)=0 и
Ar=r~2d(r2dr/dr)/dr=2/r.
В результате из (8.35) получаем
Дф=2С1д/дх(1/г). (8.36)
Теперь, чтобы удовлетворить уравнению (8.34), функцию w,
обращающуюся в нуль при г-*оо, следует положить равной
w=— 2CtVx/r.
144

Подставляя последнее выражение вместе с (8.35) в (8.33),
для скорости имеем
= (". —7—£) ** + *(—£ + ЗС./Г») t. (8.37)
Условие v=y0V# при г-*оо удовлетворяется, потребуем теперь
выполнения условия на поверхности сферы (у|г=л=0). Положив
ЗС2=С1/?2, мы обратим в нуль при r=R второе слагаемое в
(8.37), пропорциональное г. Оставшееся слагаемое,
направленное по оси х и равное v0—4CJ3R (C2 = CiR2/3) при г=/?,
обратится в нуль на поверхности сферы, если
ft-VM (8.38)
Таким образом, для скорости частиц жидкости при обтекании
сферы получаем
¥=(l_3^_l^jVe-iu5if,_«L\i-f (8.39)
\ 4 г 4 г3 ) ° 4 г* V г* } г V '
или в компонентах
/, 3 R l R3\ 3 Я*2 Л Яа\
"«-"•('-тт-т-)-?"'—('--)•
-— 7^ ('-?■)•
31.5. Формула Стокса. Для того чтобы найти давление /7,
обратимся к первому уравнению (8.31). Подставляя в него v из
(8.33) и учитывая, что wv=wz = 0, Дауж~ДОЛ*) =0, имеем
V/? = r]A(V(p)=VCnA(p),
или с учетам (8.36) и (8.38)
Vp= V l24C1d(l/r)/djcJ = V (-3Ur\v0Rx/rs).
Решением последнего уравнения, равным нулю на
бесконечности, будет
p=->/2r)V0Rx/r*. (8.41)
Найдем силу F, действующую на сферу со стороны потока.
Очевидно, Fy=Fz = 0 в силу симметрии потока относительно оси
х- В направлении х со стороны вязких сил на единицу площади
поверхности сферы согласно (8.29) действует сила
г' / <hi . ^ \ ( dvA , dVk \ Ч
145

Здесь, как всегда, xt=xf x2=yf хг=г. Далее, находим
дхь
r )r=R [ дг dxfc r )r^R [ дг г* Jr=R { дг }r=R
При дифференцировании мы считали, что Vt=vx зависит только
ют г. Хотя последний член в vx (формула (8.40)) и будет
содержать х?=х*9 однако результат его дифференцирования по xi
при r=R обращается в нуль. Второе слагаемое в выражении для
•силы // равно нулю:
дхг г )r=R \дг r% )r=R {dxt
r=R
(dvjdxh=0 в силу несжимаемости жидкости). В результате для
вязкой силы, учитывая также vi = vx из (8.40), получаем
'•'-«-(£Ь,-т-?('-й- <8-<2>
Кроме того, на оферу действует также сила давления,
компонента которой на ось х, отнесенная к единице поверхности, с учетом
(8.41) равна
рх _ 3 т)ид х2
R "" 2 R R* '
Полная сила, действующая на единицу поверхности сферы,
будет суммой последнего выражения и (8.42), что дает
/x=7*W#. (8.43)
Сила, действующая со стороны потока на всю сферу,
найдется умножением этой величины на поверхность сферы 4я/?2:
Fx=6nr\Rv0. (8.44)
В результате мы получили известную формулу Стокса для
силы сопротивления при медленном движении сферы в вязкой
жидкости. Напомним, что в случае обтекания тела идеальной
жидкостью эта сила равна нулю.
Коэффициент сопротивления (8.18) при движении сферы в
вязкой жидкости определяется следующим образом:
Со = -^4- = -^-, Re=-^, D = 2R. (8.45)
nR2pvl Re v
При движении шарообразных тел в поле силы тяжести в
пределе при t-+oo устанавливается постоянная скорость, которую
мы получим, приравняв силу сопротивления Fx весу тела за
вычетом силы Архимеда ^UnR'g (р{—р). (pi — средняя плотность
вещества падающего тела, р — плотность жидкости). Отсюда
146

для установившейся скорости находим
9 v V Р /
Как мы уже отмечали, приведенное выше решение вместе с
формулами (8.44) — (8.46) справедливо только для движений с
малыми числами Рейнольдса (Re<Cl), т. е:.??для малых скоростей
Vco, большой вязкости v или мелких частиц (D мало). Для
выяснения пределов применимости теории нужно уточнить
полученный результат, учтя нелинейные (инерционные) члены. При
этом с точностью до первых степеней Re для CD имеем формулу
Со = — [I -\ Re), показывающую, что линейная теория с
Re \ 16 /
точностью до 10% справедлива при Re<72. Это условие следует
всегда помнить при применении формулы Стокса. Так,
например, предельная скорость (8.46) достаточно мала и достижима
лишь при малых радиусах падающих тел. А именно: из Re=
= 2/?i>oo/v<72 с учетом (8.46) находим
*<l(^^^Yl/- ЙЛИ ,в<1 (2L|fL_,|y* (8.47>
В частности, для дождевых капель в воздухе /?<3-10"3 см
(о.< 12 см/с).
§ 32. Пограничный слой
32.1. Вязкие волны. Рассмотренное в гл. 7 решение уравнения
Лапласа (Дф=0, v=Vq>) для потенциального течения
несжимаемой жидкости удовлетворяет также и уравнению Навье —
Стокса (8.17). Действительно, при этом Av=A(V<p) = V(A<p) =0 и
дополнительный вязкий член в (8.17), равный т)Ду, также
обращается в нуль. Однако потенциальное решение для идеальной
жидкости не удовлетворяет граничным условиям на поверхности
обтекаемого тела в 'вязкой жидкости ввиду равенства там нулю
полной скорости. Для ряда важных случаев это отличие
проявляется лишь в тонком пограничном слое вблизи границы
обтекаемого тела.
В качестве примера приведем так называемые вязкие волны,
возникающие при периодических колебаниях безграничной
пластинки в своей плоскости. Пусть последняя расположена в
плоскости {х, у), ограничивающей полупространство z>0,
заполненное однородной несжимаемой вязкой жидкостью. Зададим
скорость точек пластинки в виде гармонического колебания
0*|.-о = 0о ехр (—Ы), 0у|г-о=0х|*-о=3О. (8.48)
Идеальная жидкость оставалась бы при таких колебаниях
пластинки в покое из-за проскальзывания. В вязкой жидкости в
силу условий прилипания выражения (8.48) определяют скорости
частиц жидкости при z=0, т. е. являются граничными условиями.
147

Найдем решение уравнения Навье — Стокса (8.17),
удовлетворяющее этим условиям. Из соображений симметрии уу=0, а
две другие компоненты скорости vx и vt могут зависеть только
от 2. Из условия несжимаемости divv=0 (dvjdz=0 в нашем
случае) следует, что компонента vt постоянна, но так как при
^=0 она обращается*в нуль, следовательно, vt^0 при всех 2.
В результате нелинейный член в (8.17) p(vV)\=pvx(dvx/dx)Vx
также тождественно равен нулю. Компонента по оси z этого
уравнения дает dp/dz=0 (/?=const), а компонента по оси х
будет (vx=v)
д° d*v .. Л /о лг\\
— = v , v = — . (8.49)
dt dz* р v ;
Мы получили линейное уравнение типа уравнения
теплопроводности. Его решение, удовлетворяющее условию (8.48), будем
искать в .виде
v = v0 ехр [ i (kz—<dt) ]. (8.50)
Подставляя это выражение в (8.49), получаем:
—ш = — vk\ Л=уЖ=±1(1 + 0/У2]У©М (8.51)
Из условия ограниченности решения при z-*-oo следует
требование Im£>0, которому удовлетворяет лишь выражение (8.51) со
знаком плюс. В результате (8.50) запишем
v = v0 ехр (—Vco/2t;z) ехр [I (V©/2vz—ю*) ], (8.52)
что и является выражением для вязкой волны. Ее амплитуда
убывает в е раз лри удалении от пластинки на расстояние
6=V2W^. (8.53)
Чем меньше вязкость, тем меньше величина б — толщина слоя,
в пределах которого в основном сосредоточены колебания
жидкости. На расстояниях z>6, как и в идеальной жидкости, v=0.
32.2. Пограничный слой. Качественные соображения.
Допустим, что мы исследуем обтекание какого-либо тела вязкой
жидкостью. Будем последовательно использовать жидкости с
уменьшающимся коэффициентом вязкости, надеясь получить течение,
приближающееся к случаю обтекания идеальной жидкостью.
Казалось бы, что при достаточно малых т) мы достигнем
желаемого результата, так как вязкий член в уравнении Навье —
Стокса при t)->0 становится все меньше и меньше. Как мы видели,
мерой отношения вязкого члена (rjAv) к инерционному
(p(vV)v) является число Рейнольдса. Если L — характерный
масштаб задачи (размер тела) и v0 — характерная скорость
потока, то по порядку величины
г)А v
р (v V) v
= _!_, Re = -^>L. (8.54)
Lv0 Re
148

При v-^0 Re->oo, и вязкий член мал по сравнению с
инерционным. Однако оказывается, что эта оценка справедлива всюду,
кроме непосредственной близости к поверхности тела — в так
называемом пограничном слое, ввести который имеет смысл,
если число Рейнольдса потока велико.
Формальной причиной введения в рассмотрение
пограничного слоя является понижение порядка дифференциального
уравнения (8.17) при отбрасывании вязких членов, а следовательно,
и уменьшение числа граничных условий, потребных для
единственности решения задачи. Из-за этого мы уже не можем
требовать равенства нулю тангенциальной составляющей скорости
частиц жидкости на поверхности тела, а должны допустить
проскальзывание. Но это противоречит опыту, поскольку в
жидкости со сколь угодно малым коэффициентом вязкости частицы
прилипают к поверхности тела. Противоречие снимается
введением пограничного слоя. Определим толщину последнего h как
расстояние, на котором скорость частиц жидкости изменяется от
v=0 на границе (тело предполагается неподвижным) до
значения v„, соответствующего обтеканию тела идеальной жидкостью
(точнее, отличающееся от v0 на фиксированную малую
величину). Такое изменение v обусловлено только вязким членом в
уравнении Навье — Стокса, порядок которого (|tjAv| ~r)vjh2)
должен быть таким же, как и порядки остальных членов
уравнения. Следовательно, чем меньше вязкость т|, тем тоньше
пограничный слой и тем больше by~vjh2. В результате при любом
малом tj в пограничном слое вязким членом tjAv уравнения
(8.17) пренебрегать нельзя.
Рассмотренная выше зона вязкой волны также является
пограничным слоем для случая бесконечной пластинки. Вне этой
зоны жидкость остается в покое, как если бы она была
идеальной. Толщина зоны б уменьшается при уменьшении вязкости.
Однако случай бесконечной пластинки является особенным, так
как при этом тождественно обращается в нуль нелинейный
(инерционный) членр(уУ)у.
Рассмотрим другой, хотя тоже идеализированный случай,
позволяющий получить результаты гораздо более общего
значения,—случай обтекания потоком полубесконечной (в
направлении потока) тонкой пластинки (рис. 8.6). Пусть последняя
расположена в плоскости z=0, неограниченна в направлении у и
занимает область х^О в направлении х. Уравнения
гидродинамики вместе с граничными условиями для этого случая имеют
вид:
-^L + (vV)v = --^- + vAv, yv = 0,
dt р i
Х>0
(8.55)
149

Характерным масштабом изменения величин вдоль оси х
будет расстояние точки наблюдения от ребра пластинки (х),
поскольку другого пространственного масштаба, кроме х, в нашей
задаче не существует. Вдоль оси z (в пределах пограничного
слоя) характерным масштабом будет толщина последнего h(x)^
Приравняв по порядку величины вязкий (vAv) и инерционный
((vV)v) члены в уравнении (8.55), можно оценить значение
к(х). Как мы уже отмечали, для вязкого члена
v|Av|^v|d2v/^2|-vt;o/A2W.
При этом учитывается, что |d2\/dzz| > |d2v/dx2| ~ vjx2 (h(x)<^
<Ck). Поскольку основная компонента скорости v есть vx~v0y то>
оценивая инерционный член, получаем \(vV)v\~\v0dvx/dx\~
~v02/x. Итак, приравнивая порядки вязкого и инерционного
членов, находим:
где Re = vQx/v^>\ —число Рейнольдса. Требование Re>l
необходимо, чтобы вне пограничного слоя вязким членом можно
было пренебречь. Толщина пограничного слоя растет с увеличением
х9 как Ух. Отметим, что число Рейнольдса для пластинки можно
ввести и так:
ReA=^W. * YRe.
v h(x)
Не составляет труда также оценить вязкую силу,
действующую на единицу площади пластинки со стороны потока (см.
(8.14)):
1/| = П
** , *« I - ^ - I **
дг дх \ дг
-IE!L.=pЗL=pf^.V/,
•А(х) кЛ(ж) к\ х /
(8.57)
Соответственно для коэффициента сопротивления CD имеем
С-а-р-)"- ' . (8.58)
pv20 V v0x J К Re
32.3. Уравнения Прандтля пограничного слоя. Для
количественного описания .пограничного слоя при больших числах
Рейнольдса можно воспользоваться тем обстоятельством, что
слой является весьма тонким. Это позволяет, как было
показано впервые Прандтлем, существенно упростить уравнение
Навье — Стокса в области слоя. Ограничиваясь плоской
задачей (д/ду=0, 0У=О), запишем уравнения (8.55) по компонен-
150

(8.59)
там:
dvx t dv dvx \ fa I d*vx d2vx \
dt ex dz p a* \ a*a az2 /
a* ax ^ az p dz \ d# a*)
90* \ dv* _o
ax az
Проведем оценку порядка величин входящих в эти уравнения
членов на примере обтекания тонкой полубесконечной
пластинки, хотя опыт показывает, что полученные результаты будут
иметь более общую применимость.
В области пограничного слоя 0^.z^.h(x) положим:
Vx~V99 ±~±9 A-!, Л~-^<*
дх х dz h V**
(Re = Sf> l)
Проинтегрируем последнее уравнение (8.59) по z в пределах от
нуля до z4 (O^Zi^A(x), vs|s_0 = 0):
«.U--j£*
Но по порядку величины dvjdx—vjx, а интегрирование от нуля
до zt эквивалентно умножению на h. Следовательно, vt~v0h/x^.
<.vx. Оценивая теперь порядки величин в первом и втором
уравнениях (8.59), например vxdvjdx~v02/xt vxdvjdx~v2hlx?y
мы видим, что
dp/дх ~ vQ2/x, dp/dz ~ v 02h/x2 < др/дх.
Поэтому можно положить dp/dz=0, р=р(х), т. е. давление
считать постоянным по толщине пограничного слоя и равным,
например, его значению на верхней границе слоя, где жидкость
ведет себя как идеальная. Это давление можно вычислить, решая
Уравнения движения идеальной жидкости для области вне
пограничного слоя, т. е. считать р известной функцией.
Пренебрегая теперь в первом уравнении^ (8.59) d2vjdx2~
~vjx2 по сравнению с d2vjdz2~v0/h2, получа'ем систему двух
Уравнений, называемых уравнениями Прандтля пограничного
слоя:
dvx dvr dvr i Ип d2vx
dt ^ * dx * dz pdjc dz*
(8.60)
dvx { to г ^q
dx dz
151

Эти уравнения вместе с граничными условиями (v=0 на
поверхности тела и vx-+v0 на бесконечно большом удалении от него)
вполне определяют течение. Отметим, что в пределах
пограничного слоя течение не является потенциальным:
(тоЩу-
до9
do,
dx
dz
дох
dz
В ряде задач бывает полезной интегральная форма
уравнений Прандтля, полученная Карманом. Для вывода последней:
преобразуем инерционный член в (8.60):
до,
до,
Vx'
док
дх
дг дх dz dz дх * dz
Здесь мы также использовали второе уравнение (8.60). С учетом;
последнего выражения проинтегрируем первое уравнение (8.60)
по z от нуля до h:
h „ h
с до, r dol
h dp , .. dvx
р ах
dz
(8.61>
Преобразуем члены этого выражения, введя обозначения
vx\z=h = v0:
J dt dt J ° dt J дх дх J x 0ax
oo oo
h z.
к (* doz
»Л|о=»л|»-* = »в J -^z~dz =
0
h z. h
Г дох d С j . - 2 dh
= — Щ \-r-dz = — v0—\ Vxdz+Vo—.
J dx dx J dx
о о
В результате, предположив также, что dvjdz\lmsh=0t получаем
искомую интегральную форму уравнений Прандтля:
1Н—f+£l°^-
— vn
п
-f vxdz =
-h dp
dv,
dx J p d* dz
о
(8.62)
32.4. Решение уравнений пограничного хлоя в простейшем
случае. Рассмотрим снова стационарное обтекание тонкой
полубесконечной пластинки. В этом случае (8.60) допускает так
называемое автомодельное решение, когда vv=vj(ti), у,=
= voyv/v0xg(t))i £ = yuoz7v#, и уравнения Прандтля сводятся к
152

обыкновенному дифференциальному. Мы учтем, однако, что
согласно опыту (как, впрочем, и точному расчету) профиль
горизонтальной скорости vx(z) неплохо аппроксимируется функцией:
i>x=t/0sin£, %=nz/2h, O^z^h. (8.63)
В стационарном случае d/dt=0, кроме того, и др/дх=0. В
самом деле, давление р находится из решения задачи об
обтекании идеальной жидкостью, поток которой не возмущается
бесконечно тонкой пластинкой.
Подставляя vx из (8.63) в интегральное уравнение (8.62),
находим:
Л Я/2
О О
h Я/2
\vxdz = vc -%L j smldl=-^v0
В результате получаем для h(x) обыкновенное
дифференциальное уравнение
h%-=^-*-t (8.64)
ах v0 4 — я
решением которого при условии Л(0) =0 будет функция
кЮ-У^тЛ1. (8.65)
Отсюда видно, что полученная из качественных соображений
формула (8.56) дает правильный порядок для толщины
пограничного слоя.
Сила, действующая на единицу площади пластинки со
стороны жидкости, будет
U = Л (dvx/dz)z=0 = Wi/2/i = V2po2o /(4 —я)/2 УчЩр.
В случае пластинки конечной длиной L в направлении потока
для силы, действующей на полосу единичной ширины, имеем:
L
о
■p0'W~I,31pTTs' Re = ~
Отсюда для коэффициента сопротивления CD=2F/pv*L следует
выражение
CD = 1,31//Ri,
153

которое также подтверждает качественную формулу (8.58).
Кроме того, это значение CF мало отличается от рассчитанного на
основе точного численного решения уравнений Прандтля для
автомодельного случая (вместо 1,31 там стоит коэффициент
1,328).
Задачи
8.1. В выражении (8.6) постоянные а и b независимы. Найти связь между
ними в предположении, что среднее давление рт в вязкой жидкости равно
давлению р, входящему в уравнения гидродинамики.
Решение. Среднее давление в жидкости определяется через инвариант
тензора напряжений о/<л=— рб<*+0<* следующим образом:
Рт = - Vs^ik = Р — Vetfjfc,
где а,-* —тензор вязких напряжений. Если рт=р, то сг*а=0, или при
подстановке (8.6)
2а dvtjdxk + 36 dvk/dxk = О, b =—»/«*-
Отметим, что предположение рт=р не следует из общих физических
закономерностей. Чтобы учесть возможное различие рт и р, иногда наряду с
коэффициентом вязкости х\ = а вводится некий новый коэффициент ц (вторая
вязкость), так, что рт = р—liVv. При этом Ь=— 2/3а+|и=ц—2/зт|. Однако, как
было показано экспериментально, вторая вязкость \i отлична от нуля лишь в
малом числе специальных случаев. В обычных классических жидкостях и
газах jli=0.
8.2. Из уравнения Навье — Стокса (8.8) получить уравнение для вихря
со =rotv.
Решение. Уравнение (8.8) с учетом а=т) и векторного тождества (6.31)
запишем в виде
~^+v('?")+wxv=~7'+TlAv+(T1+6)v (Vv)'
Применяя к полученному уравнению операцию rot и воспользовавшись
известными векторными тождествами:
rot (Уф) = 0, div rot а = 0, rot (фа) = ф rot а — а х Vф,
rot(axb) = (bV)a-(aV)b + a(Vb)-b(Va),
получаем искомое уравнение
EHL + (у V) со — (ю V) v + со (V v) = — VpxVp/pa + vA о.
Ы
Последнее с учетом векторного тождества A© =V(V© )— rot rot CD можно
переписать и в таком виде:
d&ldt +(vV)©-(©V)v + ©(Vv) = - Vpx Vp/p* — v rot rot a>.
8.3. Используя уравнения предыдущей задачи, получить выражение для
изменения во времени циркуляции вектора скорости в вязкой жидкости.
Решение. Проинтегрируем уравнение для вихря по произвольной
«жидкой» (движущейся вместе с жидкостью) незамкнутой поверхности S:
154

\ [dnldt— (©V)v + ©(Vv)]ndS =
5
• — f (VpxVp/pa) ndS — v f rot (rot to) ndSt
где d®/dt=^d&/dt+(\V)(0. Интеграл в левой части преобразуется по
формуле, аналогичной (6.6) для интеграла по объему:
j [dtoldt — (ш V) v + © (V v)] n dS = (d/А) Г юп dS.
S 5
Далее, по формуле Стокса
Г con dS = J (rot v)n dS = ф v d г = Г, f rot (rot to) n dS = <£ rot to d r,
где /—замкнутый контур (граница S). В результате для изменения
циркуляции имеем
— ■= — j(VpxVp/p*)ndS — v(T)rotfi>dr.
s /
Если v=0 и уравнение состояния имеет вид р=р(р) (баротропная
жидкость), то VpXVp= (dp/dp)VpXVp=0 и последнее выражение переходит
в теорему Томсона для идеальной жидкости. В общем случае изменение
циркуляции, следовательно возникновение и исчезновение вихрей, увязано
с вязкостью и небаротропностью жидкости.
8.4. Считая поле скоростей в несжимаемой жидкости заданным, найти
выражение для лапласиана давления (Ар).
Указание. Применить к уравнению Навье — Стокса (8.17)
оператор div.
Отв ет:
Др = - pV [(v V) v] = - 9d2v^k/dx.dxk,
8.5. Найти профиль скорости и силу трения для течения Куэтта между
двумя соосными цилиндрическими трубами кругового сечения, одна из
которых движется относительно другой вдоль образующей со скоростью v0.
Решение. Пусть радиус неподвижной трубы Ru движущейся — R2.
Скорость частиц жидкости направлена вдоль образующей и зависит
только от расстояния до оси г: уж = у(г). При этом инерционный член в
уравнении Навье — Стокса (vV)v = 0. Радиальная и продольная составляющие
этого уравнения имеют вид:
др/дг=0, dp/dx=t)Av = r\r-l(rv')'.
Отсюда с учетом симметрии задачи получаем р—const (др/дх=0) и
v(r)=A]n(r/Rx)+B.
Постоянные А и В определяются из граничных условий (v(R\)=Ot
*(««)-*о):
В = 0, A = v0/\na, а = /?2/#ь v(r)=v0\n(r/Ri)f\na.
Сила трения, действующая на единицу площади /-го цилиндра (/=1, 2),
155

равна с учетом направления нормали
, dv
= (-1)/+1л
r=Rf Я/I*1 а
Как и должно быть, сила, действующая на единицу погонной длины,
одинакова по величине для каждого из цилиндров, но противоположно
направлена:
Fx = 2nRffxf = (- 1)/+12п^о/\п а,
8.6. Рассчитать профиль скорости для течения Пуазейля между соос-
ными цилиндрами. Найти расход жидкости.
Решение. Компоненты уравнения Навье —Стокса будут аналогичны
полученным в предыдущей задаче, но здесь уже следует считать
др/дх=const. Интегрируя дважды уравнение для v(г), получаем
1 dp г
и(г) = — -гг* + А In— + В.
4т] dx ^ Ri
С учетом граничных условий (и| л1==с;|д§=0) находим:
4т, dx 1 4я dx v г l7/ Ri
г- *? dp\l г» ,.„1} in (//ft)]
4t] <te L «J Ina J
Отсюда для расхода жидкости имеем
Q = 2^ro(r)dr=JL_^^(aS_1)(1+a,_^.
Я»
8.7. Рассчитать с учетом силы тяжести течение Пуазейля в круглой
трубе, образующая которой наклонена к горизонту под углом 9.
Указание. Исследовать течение аналогично рассмотренному в
п. 31.3, учитывая в уравнении Навье — Стокса силу тяжести, направленную
вертикально вниз. При этом в выражении для v изменится только значение
постоянной Ь, которая теперь будет равна 6= — (др/дх)—pgsinO.
8.8. Найти профили скорости и давления в случае течения Куэтта
между двумя соосными цилиндрами радиусов R\ н /?2, вращающихся
вокруг общей оси с угловыми скоростями (Oi и ©г соответственно.
Решение. Совместим ось z с осью цилиндров и введем в
перпендикулярной плоскости полярные координаты гиф. Очевидно, что р=р(г),
vt = vr = 0 и v<p=v(r). В полярных координатах имеем:
r dr г dtp ' г дг\ дг)^ г* дфа х ^
„ v д др х dp dp dp др .
v =vcosq>t (vV)= — —-, — = — — = — соБф, — =—втф.
у г дф дх г дг дг ду дг
С учетом этих выражений запишем уравнение Навье — Стокса по компо-
156

нентам:
/1 dp v*\ If v 1 d [ dv\] .
T~ — — cos ф = v — — ■—■ \r — sin Ш,
\p dr r J T \[r* r dr\ dr )\ Y>
/1 dp v*\ . fti Id/ dv\\
Отсюда легко следует
Р
Общим решением последнего уравнения будет функция t;(r)=Qor+Qp#i2/r_
dp v2 1 d I dv \ v* d Г 1 d 1
л решением последнего уравнения будет функция t;(r)=Qor+Q
Удовлетворяя граничным условиям (o(/?i)=g>i/?i, 0(/?2)=<02#2), находим:
О —— О .... /i-i
а* — 1 р а1 — 1
г
Rt
-щ),
R*
= «i
+
*Ь*^-4&-)+4("4-)]
Из формулы для и (г) также следует, что слой жидкости на расстоянии г
от оси вращается с угловой скоростью (o(r)=Qo-\-QPRi2lr2t т. е. движение
вязкой жидкости является комбинацией вихревого вращения с постоянной
частотой Q0 и потенциального вращения с частотой QPRi2/r2 (см. задачу 7.1).
8.9. Определить вязкие напряжения в течении Куэтта между двумя
вращающимися цилиндрами, а также момент вязких сил М(г) относительно оси
вращения.
Решение. Вязкие напряжения будут одинаковыми в любой плоскости,
проходящей через ось. Поэтому нам достаточно найти а*у|х-о.
Воспользовавшись выражением (8.6) „ имеем
-(£+£)
Подставляя в эту формулу vx и vv из задачи 8.8, найдем:
Отсюда для момента вязких сил получаем
М = 2лгохуг = - 4ЯГ, ^f^- *•*».
Как и должно быть, М постоянен. Заметим, что этот факт можно было бы
взять за исходный при выводе уравнения для v(r).
8.10. Получить выражение для вязких волн между двумя параллельным»
стенками, отстоящими друг от друга на расстояние dt предполагая, что одна
из стеиок покоится, а другая колеблется в своей плоскости по закону
и = у0ехр(—ко/). Найти амплитуду вязкой силы на неподвижной плоскости.
157

Решение. Пусть уравнение неподвижной плоскости z=dt подвижной —
£=0. Общее гармоническое решение уравнения для вязких волн (8.49) имеет
вид (v=vx)
w=^sh[(l+orW^d-z)]+^ch[(l+OyW^(^-2)]}exp(-tW).
Из условия v(d)=Q следует В = 0. Удовлетворяя условию при z=0, находим:
Ash [(1+0 а] = v0t а = \^^dt
sh [(!+/) а (\-zld)] .
" = <" shfd+Оа] еХр(-|(0/)'
Для вязкой силы на единицу площади неподвижной стенки имеем
- . dv I a (1 +t)exp(— Ш)
* U=<f » snl(l + 0«]
a (1 -f i) exp (— farf)
0 d sh a cos a + i ch a sin a
При этом амплитуда вязкой силы F= \fx\ будет равна
F = т]0о ^— (sh8 a cos» a + ch8 a sin8 af,/e = V2 -^j- a (ch8 a — cos8 a)%.
Глава 9
ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ
Все рассмотренные в предыдущей главе случаи движения
вязкой жидкости относились к так называемым ламинарным
течениям. Термин «ламинарный» возник вследствие того, что при
окрашивании струй жидкости следы краски в таком течении
располагались слоями. Как показывает опыт, при достаточно
малых скоростях потока жидкости течение всегда является
ламинарным, однако при увеличении скорости всегда переходит в
так называемое турбулентное течение, являющееся уже
существенно нестационарным. Скорость частиц жидкости в каждой
точке турбулентного течения, так же как давление и другие
характеристики, изменяется во времени нерегулярно, случайным
образом даже при постоянных внешних условиях. Данная глава и
будет посвящена изложению основных проблем и методов
теории турбулентности.
158

§ 33. Качественные закономерности.
Гидродинамическое подобие
33.1. Переход ламинарного течения в турбулентное. Впервые эта
явление в трубках круглого сечения изучалось еще в 1839 г. Ха-
геном. Однако систематические исследования возникновения
турбулентных течений с установлением критерия перехода были
проведены только в 1883 г. Рейнольдсом. При этом было
установлено, что определяющим фактором при переходе
ламинарного течения в турбулентное является не величина скорости
потока v0t а число Рейнольдса Re=v0D/vt где D — характерный
пространственный масштаб (диаметр трубы); v — кинематическая
вязкость. Напомним, что число Рейнольдса характеризует
отношение сил инерции к вязким силам в уравнении Навье — Сток-
са. Рейнольде установил, что существует критическое число*
ReKp, такое, что при Re<Re„p поток будет ламинарным, а при
Re>Re„p — турбулентным.
Переход ламинарного течения в турбулентное легко
фиксировался при наблюдении окрашенных струй. При ламинарном
движении струя имела вид ровной линии. При переходе к
турбулентному движению струя завихрялась, краска размываласьг
постепенно расплываясь по всему сечению трубки. Изменение
числа Рейнольдса при течении в одной и той же трубке можно
осуществлять как изменением скорости потока, так и
изменением вязкости жидкости, например подогревая ее или заменяя на
другую. Серия подобных опытов, проведенных Рейнольдсом^
подтвердила высказанный им критерий и позволила
экспериментально измерить величину Re„p. В опытах Рейнольдса с плавным
входом в трубку было получено ReKp= 12 830. Дальнейшие
исследования показали, что величина Re^ существенно зависит
от степени турбулизированности (возмущения) ©ходящего
потока, обусловленной в том числе и влиянием входных условий в
трубку. Так, в случае трубки с острыми краями ReKp=2800.
Напротив, особые предосторожности (плавный переход, гладкие
стенки, отсутствие вибраций) позволяют «затянуть»
ламинарный режим до Re = 20 000 и выше. Однако многочисленными
опытами было также установлено, что при Re^2000 течение всегда
ламинарно, точнее, любые возмущения потока, входящего в
трубку, затухают в ней и движение на некотором расстоянии от
начала трубки становится ламинарным.
Аналогичная картина наблюдается и для пограничного слоя.
Здесь, как мы уже отмечали в гл. 8, число Рейнольдса можно
определить двояким образом:
Reh=v0h(x)/v, Rex=v0x/v,
где h(x) —толщина пограничного слоя (в соответствии с (8.65)
Refc«5YRex).
Естественно, что число Рейнольдса растет при
продвижении вдоль пограничного слоя, поскольку толщина послед-
159

него увеличивается. Оказывается, что критическое число
Рейнольдса существует и в этом случае. Его значение Re/,— 103ч-104
зависит от степени возмущенности набегающего потока.
Мы видим, что по порядку величины значение критического
Reh для пограничного слоя получается примерно тем же, что и
для трубки. Поскольку Re* растет при продвижении вдоль
потока (увеличении х)9 существует критическая точка х=л:кр, где
Reh достигает критического значения. На некотором интервале,
включающем точку *кр, характер течения в пограничном слое
изменяется от ламинарного к турбулентному. В начале этого
интервала течение практически ламинарно и лишь изредка
появляются и исчезают «пятна» турбулентных пульсаций, а перед
областью полностью турбулентного движения уже участки
ламинарного течения наблюдаются лишь спорадически.
Величина критического значения Re*, а следовательно, и
удаленность области перехода от начала пограничного слоя
существенно зависят от гладкости поверхности. Шероховатости,
сравнимые с Л, весьма способствуют переходу ламинарного течения
в турбулентное.
Теоретически описать переход от ламинарного течения к
турбулентному не удается. Даже более простая задача
вычисления критического числа Рейнольдса в общем случае также не
решена, хотя принципиально подход к решению этой задачи ясен.
Он основывается на том, что как ламинарное, так и
турбулентное движения жидкости являются решениями уравнения
гидродинамики, причем переход данного ламинарного течения в
турбулентное происходит из-за потери его устойчивости, т. е. из-за
быстрого роста первоначально малых возмущений, всегда
имеющихся в реальном «ламинарном» потоке. Таким образом,
исследовав исходное ламинарное решение уравнений
гидродинамики на устойчивость, можно найти некоторое критическое
значение числа Рейнольдса Reb при котором решение начинает
терять устойчивость. Один из возможных путей развития этого
процесса при Re>Ret описывается гипотезой Ландау, согласно
которой гидродинамическая система переходит в новое
устойчивое состояние, являющееся суммой исходного ламинарного
движения и наложенного на него периодического колебания.
С дальнейшим ростом числа Рейнольдса это движение также
может потерять устойчивость при Re=Re2, что приведет к
дополнительному периодическому колебанию. Ландау предположил,
что этот процесс возникновения все новых колебаний с ростом
Re будет продолжаться и дальше. В результате в
гидродинамической системе с большими числами Рейнольдса должно
возбудиться большое число колебаний (степеней свободы) с
различными, вообще говоря, несоизмеримыми частотами. Такое
состояние гидродинамической системы называется развитой
турбулентностью.
В ряде экспериментов (см., например, приведенное ниже
описание следа за обтекаемым жидкостью цилиндром) на первый
160

взгляд подтвердилась гипотеза Ландау о последовательном
усложнении состояния гидродинамической системы. Однако
практически удавалось заметить лишь несколько начальных стадий
этого процесса, после которых внезапно осуществлялся переход
к турбулентному режиму.
В последнее время возникли новые представления о развитии
турбулентного движения. Чтобы понять их, заметим, что
формально состояние гидродинамической системы можно описать,
разложив реальное поле скорости по заданной ортогональной
системе функций. Тогда коэффициенты ф< этого разложения
можно рассматривать как обобщенные координаты
гидродинамической системы, а их производные по времени р<=д< — как
обобщенные скорости. Для течений в ограниченных областях число
обобщенных крординат (степеней свободы) будет счетным, но
высокие номера i, соответствующие малым масштабам, из-за
вязкости возбуждаются слабо. Поэтому практически
возбуждается конечное число N степеней свободы. Пространство (ди Р<)
размерностью 2N называется фазовым пространством течения,
а линия в этом пространстве, описывающая изменение состояния
системы,— фазовой траекторией.
В гипотезе Ландау каждая возбуждаемая степень свободы
соответствует в фазовом пространстве так называемому
простому аттрактору. Для стационарного течения — это неподвижная
точка (положение равновесия типа фокуса), а для
периодического— замкнутая линия (предельный цикл). До последнего
времени этим и ограничивали возможности гидродинамической
системы, их нерегулярность (турбулентность} связывалась с
большим числом возбуждаемых степеней свободы. Однако
несколько лет назад была выдвинута гипотеза о возможном
существовании в гидродинамической системе так называемых «странных»
аттракторов, существенно отличающихся по своим свойствам от
простых. Характерным примером такого рода является
аттрактор Лоренца, полученный при решении модельной системы трех
уравнений и содержащий две неподвижные точки <в фазовом
пространстве. Точка в этом пространстве, изображающая
состояние системы, находится некоторое время в окрестности одной из
них и описывает вокруг нее несколько раскручивающихся
циклов, а затем переходит в окрестность другой неподвижной
точки, отходя от первой на достаточно большое расстояние. В
дальнейшем процесс многократно повторяется нерегулярным
(псевдослучайным) образом. Странные аттракторы такого рода были
получены и при анализе других модельных задач, но их
существование в задачах, описываемых уравнениями
гидродинамики, пока еще строго не доказано.
Введение в теорию понятия о странных аттракторах
качественно меняет представление о возникновении и развитии
турбулентности. В этом случае псевдослучайное поведение
гидродинамической системы может проявляться и при возбуждении
малого числа степеней свободы. Конечно, и здесь остается в силе за-
6 Л. М. Бреховскнх, В. В. Гончаров |g|

дача об описании движения с обязательным для турбулентности
возбуждением большого числа степеней свободы. Однако эта
теория пока еще далека от завершения, в то время как
потребности практики уже давно требовали сведений о структуре
турбулентных течений. В этом, казалось бы, тяжелом положении
помогают опыт, а также теория подобия и размерности, которые
позволяют как пересчитывать результаты модельных
экспериментов на реальные масштабы, так и получать новые
результаты.
33.2. Понятие о подобных потоках. Рассмотрим задачу
обтекания некоторого тела с поверхностью S однородным на
бесконечности потоком вязкой несжимаемой жидкости. Плотность
жидкости во всем пространстве будем считать постоянной.
Задача заключается в решении уравнений гидродинамики
р — + p(vV)v = — Vp+TjAv, divv = 0, (9.1)
dt
с граничными условиями
v|fl=0, v\„„ = v,Vx9 r2 = x2+t?+z2. (9.2)
Поверхность тела S в общем случае описывается уравнением
f(x/D, y/D, z/D)=0, где D — некоторый характерный размер
тела. В случае кругового цилиндра диаметром D функция /=
= (x2+y2)JD2—4/i- В общем случае эта функция будет содержать
наряду с D и некоторые безразмерные параметры,
характеризующие отношение размеров тела по разным направлениям.
Так, для эллиптического цилиндра, положив D равным одной из
главных осей эллипса, имеем f=(x2+y2/a2)/D2—74, где а
—отношение главных осей.
Помимо координат точек пространства и времени, решение
нашей задачи зависит от четырех размерных параметров: т), р,
v0 и D. Если бы опыт ставить для каждой их комбинации, то
ввиду большого их числа задача была бы практически
невыполнимой. Однако в случае однородной (р = const) жидкости
число параметров можно легко свести к трем, исключив также и
давление р. Для этого достаточно вместо уравнения Навье —
Стокса воспользоваться уравнением для вихря <o = rotv,
получающимся из (9.1) применением операции rot с учетом
векторного тождества (6.31) (см. также задачу (8.2):
—+ rot(oxv) = vA©. (9.3)
dt
Теперь уравнения содержат три размерных параметра: v, D, v0.
Для дальнейшего уменьшения числа параметров введем
безразмерную скорость v'=v/i;0, безразмерные координаты х'=
= x/D, у*'=у/D, z'=z/D и соответствующее им безразмерное
время t'=v0t/D. Другими словами, теперь мы будем измерять
расстояние, скорость и время соответственно в единицах Dt v$
162

и D/Vq. Граничные условия при этом не будут содержать
никаких размерных параметров:
V \пх,,у.,г,)=0 = О, V |г,_ = V V, г' = r/D, V = DV. (9.4
Посмотрим теперь, как запишется уравнение для вихря (9.3).
Имеем прежде всего, поскольку д/дх=0-*д/дх, д/ду=Б-1д/ду'у
д/д2=0-1д/д2'у
<u = rot\=(v0/D) rotV=t;0<D7A
где через rot' обозначена операция ротора в штрихованных
координатах. Далее, в силу dfdt= (vjD)dfdt' перепишем
уравнение (9.3) в виде
К да>'
— + — rot — <oxt;0v' = —А — ю .
Da dt' D [D ° J D* D
Окончательно, разделив на v02/D2 и введя число Рейнольдса
Re=0oZ)/v, получим
— + rot' (*>' XV) = — Д'ю'. (9.5)
dt' ' Re v '
В результате последнее уравнение вместе с сохранившими свой
вид условием несжимаемости W=0 и определением вихря
co'=rotV, а также с граничными условиями (9.4) вполне
определяет задачу обтекания и содержит всего один параметр —
число Рейнольдса Re. Это означает, что при заданных Re и
безразмерных координатах все течения, возникающие при
обтекании геометрически подобных тел, будут выглядеть одинаково,
т. е. описываться одной и той же функцией безразмерных
переменных. Иначе говоря, для геометрически подобных тел скорость
частиц обтекающей жидкости, измеренная в единицах v0l
зависит только от координат и времени, измеренных в единицах D
и D/v0 соответственно, и от числа Рейнольдса
v = t;0G(£,X * J£L,Re\ (9.6)
\D D D D I
где G — некоторая универсальная функция для данной
геометрии течения. Этот важный результат называется законом
подобия Рейнольдса.
Мы уже отмечали проявление этого закона в случае
обтекания цилиндра идеальной жидкостью, где число Рейнольдса
просто не входит. Не составляет труда найти явный вид
универсальных функций G для рассмотренных в предыдущей главе
простейших течений Куэтта и Пуазейля (для последних в качестве
характерной скорости можно взять среднюю скорость потока). Эти
функции оказываются не зависящими от числа Рейнольдса.
Давление в жидкости принято измерять в единицах pv02/2.
При этом, как следует, например, из уравнения задачи 8.4, в
безразмерных переменных давление также определяется универ-
163 6*

сальной функцией. Это относится и к силам, действующим со
стороны потока на обтекаемое тело. Единицей измерения этой
силы будет величина pv02D*/2. Именно поэтому рассчитываемый
в предыдущей главе для ряда течений коэффициент
сопротивления Cf = f/i/2pv02 оказывался зависящим только от числа Рей-
нольдса.
Закон подобия послужил основъй для широкого
распространения модельных опытов «в аэродинамических трубах, позволяя
результаты измерений на небольшой модели применять к
реальным крупным объектам. Этот закон вытекает из весьма общих
соображений теории размерностей, к чему мы и перейдем.
33.3. Применение теории размерностей. Задача обтекания
несжимаемой жидкостью тела любой формы содержит четыре
независимых размерных параметра: [j\]=ML~iT~it [p]=ML~3y
[D\=Lt [v0]=LT-\ где v0 — скорость потока на бесконечности,
а через Af, L и Г, как обычно, обозначены размерности массы,
длины и времени соответственно. Поверхность тела, как уже
отмечалось, вполне определяется одной величиной D и
некоторой безразмерной функцией, описывающей форму тела.
Конкретный вид уравнений, точнее, величина входящих в них
размерных коэффициентов, зависит от числового значения
размерных параметров задачи, в частности от единиц, в которых они
измеряются. Очевидно, что значение, например, плотности р
будет разным, если мааса измеряется в граммах или тоннах, а
длина — в ангстремах или метрах.
С другой стороны, физические закономерности, описываемые
нашими уравнениями, не должны зависеть от произвола в
выборе единиц измерения. Например, течение Пуазейля в трубе нр
должно измениться, если диаметр трубы измерять вместо
метров в километрах. Отсюда следует, что в безразмерных
переменных в уравнения, описывающие физические процессы, могут
входить только безразмерные комбинации исходных
размерных параметров. Этот на первый взгляд тривиальный принцип и
лежит в основе применения теории размерностей в
гидродинамике. В некоторых случаях из него следуют весьма общие и
далеко не тривиальные результаты. Например, он позволяет
свести сложные уравнения в частных производных, описывающие
течение жидкости в пограничном слое, к обыкновенному
дифференциальному уравнению, решение которого получить
значительно проще. Здесь мы воспользуемся принципом теории
размерности для выявления основных безразмерных параметров,
определяющих поведение гидродинамической системы.
Итак, попытаемся найти безразмерную комбинацию
размерных величин ц, р, D и v0 в виде
Re = Dmvn0r\kpl. (9.7)
Не теряя общности, можно положить т=1. Подставляя теперь
размерности всех параметров и приравнивая нулю суммарные
164

степени М9 Т и L, получаем соответственно уравнения:
£ + /=0, /г+/г=0, l + n—k—3/=0.
Отсюда следует явное значение показателей степени lynuk: 1=1,
л=1, £=—1. В результате из (9.7) находим для безразмерной
комбинации Re=Dv0p/r\=Dv0/v, т. е. ранее определенное число
Рейнольдса.
Нетрудно сообразить, что в других, более сложных случаях
характер течения может определяться большим числом
безразмерных параметров. Например, в случае, когда играет роль сила
тяжести, к указанным выше четырем размерным параметрам
добавляется еще ускорение силы тяжести g (размерность [g] =
= LT-2). Теперь, кроме числа Re, можно образовать еще одну
независимую безразмерную величину, например Fr = u„2/gA
называемую числом Фруда. В этом случае, чтобы течения были
подобны, должны быть одинаковыми числа Re и Fr.
Для нестационарного течения с характерным временем Т
(например, период колебаний) в качестве размерного
параметра добавляется, кроме того, и Т. При этом наряду с Re
возникает еще одна безразмерная комбинация, которую обычно
определяют как Sh=D/v0T и 'называют числом Струхаля.
В сжимаемой жидкости уравнения гидродинамики, как мы
видели, содержат размерный параметр с, равный
адиабатической скорости звука. Новой безразмерной комбинацией может
служить fA=v0/c— число Маха.
Процесс передачи тепла в неравномерно нагретой жидкости
описывается уравнением теплопроводности, содержащим
параметр х, размерность которого совпадает с размерностью
параметра v. Поэтому в качестве дополнительного безразмерного
параметра в этом случае можно принять так называемое число
Прандтля Pr=v/x.
33.4. Картина обтекания кругового цилиндра при различных
числах Рейнольдса.- Мы установили, что характер обтекания
тела в несжимаемой жидкости при пренебрежении силой
тяжести вполне определяется одной величиной Re. Однако при
различных значениях Re картина обтекания существенно разная.
Показательной является полученная на опыте картина
обтекания кругового цилиндра—(тела, являющегося типичным для
плохо обтекаемых тел.
1. В случае малых чисел Рейнольдса (Re<l) имеем
ламинарное обтекание цилиндра (рис. 9.1). Характер течения такой
же, как и при стоксовом обтекании сферы, внешне похожий на
картину обтекания цилиндра идеальной жидкостью.
2. При бблыпих числах Рейнольдса (KRe<40) в
окрестности Re= 1 лежит первое критическое значение числа
Рейнольдса, при переходе через которое исходный ламинарный поток
становится неустойчивым. Однако новый тип течения
определяется окончательно при Re>10 и изображен на рис. 9.2. За
цилиндром образуются два вихря, но течение остается стационар-
165

ным и ламинарным (смена устойчивости). Причину образования
вихрей можно понять, рассмотрев изменение скорости и
давления вдоль поверхности цилиндра. Вне пограничного слоя эти
величины определяются из решения задачи об обтекании
цилиндра идеальной жидкостью. Согласно формулам (7.24) и (7.27)
скорость равна нулю в критических точках О и О' (8 = 0, я) и
максимальна в миделе (0=±я/2). В соответствии с теоремой
Бернулли давление будет максимальным в критических точках
и минимальным в миделе. Поэтому жидкие частицы движутся
за миделем против возрастающего давления, что приводит к их
166

замедлению, которое будет наибольшим для частиц вблизи
поверхности из-за малой их скорости. В некоторой точке А за
миделем эти частицы останавливаются. Частицы, находящиеся за
точкой А вблизи поверхности, движутся навстречу тем
частицам, которые находятся дальше от цилиндра и замедляются в
меньшей степени. Существование противопотока вблизи
цилиндра и приводит к возникновению вихря, а также сил,
«отталкивающих» поток от цилиндра. В результате этого происходит отрыв
пограничного слоя от тела. Чем больше число Рейнольдса, тем
ближе точка А к миделю и тем больше сопротивление потоку
(область высокого давления за миделем уменьшается).
3. При дальнейшем увеличении числа Рейнольдса (Re>40)
достигается следующее его критическое значение. Стационарное
движение теряет устойчивость. Один из вихрей удлиняется,
отрывается и уплывает с жидкостью. Затем удлиняется и
отрывается другой. Вихри отрываются попеременно. На их месте
возникают новые вихри, которые в дальнейшем также отрываются.
В результате за цилиндром образуется так называемая
вихревая дорожка Кармана (рис. 9.3). Движение становится
нестационарным, но периодическим.
4. Для больших чисел Рейнольдса (Re>1000) вихри уже не
успевают сформироваться и заменяются быстротурбулизирую-
щимися областями, поочередно отрывающимися от цилиндра и
уплывающими вместе с жидкостью. В области значений Re-*
— 103-ь 104 турбулентность за цилиндром увеличивается,
движение становится нерегулярным. Отдельные части жидкости
закручиваются во всех трех измерениях, задача перестает быть
плоской. При Re—105 турбулентная область продвигается вплоть
до поверхности цилиндра, картина обтекания имеет вид,
изображенный на рис. 9.4. За цилиндром имеется так называемый
турбулентный след.
Характерным является при увеличении числа Рейнольдса
изменение коэффициента сопротивления цилиндра
CD=2F/pv0W,
где Т7 —сила, действующая .на единицу длины цилиндра со
стороны потока. Экспериментально определенная зависимость
Cp(Re) представлена на рис. 9.5. При малых не показанных на
рисунке числах Рейнольдса (Re<l), как и в случае сферы (см,
формулу (8.45)), коэффициент сопротивления падает с
увеличением Re. Это падение, постепенно замедляясь вследствие
продвижения точки отрыва пограничного слоя к передней
критической точке, продолжается до Re—103. При Re порядка
нескольких тысяч наблюдается возрастание CD, связанное с турбулиза-
цией струи за цилиндром. После этого наступает область
примерно постоянного CDt после которой (при Re, несколько
больших 105) коэффициент сопротивления резко падает. Это явление
называется «кризисом сопротивления» и связано с турбулиза-
цией пограничного слоя. Действительно, при не очень больших
167

числах Рейнольдса пограничный слой будет ламинарным вплоть
до точки А на рис. 9.2, являющейся точкой его отрыва от
поверхности цилиндра. При Re—105 число Рейнольдса для
пограничного слоя Reh=t;0A/v достигает критического значения в какой-
то точке левее Л, а в этой точке слой становится турбулентным.
При этом значительно возрастает поток количества движения,
приводящий к притоку жидкости к поверхности цилиндра от
внешней области пограничного слоя с более быстрыми
частицами. В результате жидкие частицы продвигаются в направлении
возрастающего давления существенно дальше, чем в случае
ламинарного потока. Однако мы знаем, что продвижение точки
отрыва пограничного слоя по потоку снижает коэффициент
сопротивления (справа от миделя увеличивается область
повышенных давлений). Это и приводит к кризису сопротивления. При
дальнейшем увеличении числа Рейнольдса точка отрыва
пограничного слоя (уже турбулизированного) снова продвигается
влево, что приводит к возрастанию CD.
Прандтль для демонстрации кризиса сопротивления делал
такой опыт. На сферу, обдуваемую в аэродинамической трубе
при определенных числах Рейнольдса, он насаживал кольцо из
тонкой проволоки так, чтобы плоскость кольца была
перпендикулярна найравлению воздушного потока. Это приводило к тур-
булизации пограничного слоя и соответственно к снижению
коэффициента сопротивления. В более детальных опытах было
установлено, что при начальной турбулентности потока
(^турб),/а/Уо = 5-10-3 кризис сопротивления наступает при Re„p =
= 2,7-105 (здесь под Re„p понимается то значение Re, при
котором CD=0,3). Еоли же начальная турбулентность
увеличивалась до 2,5- 10~а, то ReKP падало до значения 1,25-105.
§ 34. Законы усредненного турбулентного
движения
34.1. Уравнения Рейнольдса для усредненного потока.
Нерегулярность турбулентного течения, казалось бы, делает
невозможным какой-либо его теоретический анализ. Скорость потока
в данной точке изменяется случайным образом, повторение
опыта при тех же начальных условиях дает другой результат. Это
происходит не потому, что здесь неприменимы основные
уравнения гидродинамики, а из-за того, что малейшие
неконтролируемые изменения условий приводят к существенному изменению
течения. Однако, как показал впервые Рейнольде, можно
получить определенные закономерности для средних величин в
турбулентном потоке, применяя к нему аппарат теории
вероятностей как к статистическому процессу.
Предположим, что мы можем иметь достаточно большое
количество «реализаций» данного потока при одних и тех же
граничных и начальных условиях. Характеристики потока (в
частности, компонента v{ скорости в каждой точке) будут случайно
168

изменяться от реализации к реализации из-за влияния, как выше
было сказано, неконтролируемых факторов. Скорость в любой
точке для любой реализации может быть представлена в виде:
t>,=<tO + 6i;t., <6t>,> = 0, (9.8)
где <и<> — средняя по достаточно большой совокупности
реализаций скорость; 6v{ — случайное отклонение от этого среднего в
данной реализации, флуктуация скорости. Таким образом,
совокупность реализаций можно рассматривать как статистический
ансамбль. Усреднением по этому ансамблю, которое мы будем
обозначать угловыми скобками, и получаются уравнения Рей-
нольдса для усредненного потока. Однако предварительно
сделаем два замечания.
1. Мы используем ряд правил усреднения, известных из
теории вероятностей. В основном они почти очевидны, например
среднее от суммы равно сумме средних «v1+va> = <v1> + <v2»,
и будут использоваться по ходу дела. Здесь следует упомянуть
лишь одно, быть может, наиболее нетривиальное правило, а
именно
(dv/ds)=d(v)/ds, (9.9)
где s означает хи х2, хл или /, a v — одна из компонент скорости,
давление или любая другая характеристика потока (плотность,
температура и т. п.). Формула (9.9) выражает тот факт, что
операции дифференцирования и усреднения можно менять местами.
2. Развиваемая ниже теория основана на усреднении по
совокупности реализаций. Нетривиален вопрос о возможности
сравнения ее с экспериментом, поскольку в последнем (прежде
всего при измерении реальных процессов в океане и атмосфере)
обычно получают лишь одну реализацию. Поэтому вместо
усреднения по ансамблю обычно получают пространственные или
временные средние измеряемых величин. Последние будем
обозначать чертой сверху:
t г/*
im/) = -L J v{t + x)dx. (9.10)
-Г/2
Возникает вопрос о соответствии тех и других методов
усреднения. Например, стремятся ли временные средние при
неограниченном увеличении интервала осреднения к величинам,
усредненным по совокупности: limv(t) = (v). Те случайные процессы,
Т-х»
для которых это имеет место, называются эргодическими.
Легко видеть, что необходимым условием эргодичности случайного
процесса является независимость v от времени t, так как в
противном случае Нтг;(/) не существует. Такое же требование
должно выполняться и по отношению к моментам разного
порядка, образованным из случайной функции v(t). Например,
169

твтокорреляционная функция в точках tt = t и t2 = t+x
*<т)=<(»(0-<»»(»(/+т)-<о»> = <во(0вЬ(<+т)> (9.11)
должна зависеть лишь от разности t2—ti = x. Другими словами,
все моменты случайной величины v(t) не меняются при сдвиге
соответствующих моментов времени на одну и ту же величину
U. Случайные процессы, удовлетворяющие этому условию,
называются стационарными. Аналогом стационарности при
усреднении по пространству являются так называемые однородные
случайные процессы, моменты которых зависят только от
разности координат соответствующих точек пространства,
например пространственная функция корреляции
6(г.-г1)=<во(/,г1)во(/,г1)>. (9.12)
Мы будем предполагать стационарность и однородность
турбулентных течений, с которыми будем иметь дело.
Однако условие стационарности случайного процесса не
является достаточным для его эргодичности. Можно показать,
что достаточным будет следующее условие на
автокорреляционную функцию (9.11):
lim6(x)=0, (9.13)
означающее статистическую независимость между v(t) и
v(t+x) при больших т.
Теперь перейдем к усреднению уравнений гидродинамики
несжимаемой жидкости. Усредним по совокупности реализаций
уравнение сохранения импульса (8.3):
a<v=_i<n£^
v dt dxk '
где p предполагается постоянной, а
Uik = pbik + pvtvk — aiki Oik = Л —L + -=— I • (9-l5)
dvt dvk
*k dxt
Усредняя тензор плотности потока импульса П<*, с учетом (9.8)
имеем
&ишУ= «vd+toi (<vh}+6vh) =<viXvh> + <$vi6v%>9
^скольку iivi){v1)) = <kviXvh>t «Viy6vky = {v{){6vky = 0. Таким
образом,
Шй> = <р>вЛ+р<о*><о1к>—<аЛ>+р<ви<6%>>
&*Х=г)(д^{)/дхк+д^к)/дх<). (9.16)
В результате для средних величин <и<> и <р> имеем уравнение
(9.14), как и в отсутствие турбулентности, но только с
добавкой в тензоре потока импульса члена р(6и<6иЛ>.
Уравнение (9.14) можно записать также в виде,
аналогично

ном уравнению Навье — Стокса. Для этого, усреднив уравнение
неразрывности divv=0 (условие несжимаемости), получаем
d(vh>/dxk=0, следовательно, ^«^><^>J/^=<uA>^<^>/^.
После этого из (9.14) и (9.16) находим
d<v.> d<v>> д<р>
р—+р <«*>!£----*-" +
34.2. Турбулентное трение. При отсутствии турбулентности
выражение в скобках в правой части (9.17) содержало бы
только один член r\dv{/dxkf возникающий из-за вязких напряжений.
Теперь к нему добавляется член
Tih=-P<8v$vk>, (9.19
называемый напряжением Рейнольдса. Следовательно,
турбулентные пульсации, так же как и вязкие силы, могут передавать
импульс от одних частей жидкости к другим. Это легко понять
и физически. Пусть средний профиль скорости течения в
плоскости xt у имеет вид, изображенный на рис. 9.6 пунктирной линией
(длина стрелок пропорциональна величине скорости).
Поскольку, кроме среднего потока, имеются еще и случайные добавки к
скорости — турбулентные пульсации, то частицы жидкости
пересекают линии тока осредненного движения и переносят
импульс, например, из точки О, где он больше, в точку А, где
импульс осредненного движения меньше. Этот процесс вполне ана-
лбгичен переносу импульса из одних частей потока к другим
молекулами или атомами, чем обусловлена молекулярная вязкость
жидкости.
Рассмотрим поток вблизи твердой стенки хл = 0 в
направлении оси xlf осредненные характеристики которого горизонтально
однородны (т. е. не зависят от х^ и х2). Тогда в (9.17) следует
учитывать лишь одну компоненту полного тензора напряжении
о'и=р (v0< v.y/dx,—<в»1б»|».
Это выражение формально можно записать в виде:
a,i,=p(v+/C)^<y1>/^„ K=—(6vM (c^iO/d*,)-1. (9.19)
Величина К называется кинематическим коэффициентом
турбулентной вязкости, В разных областях потока она, естественно,
может быть разной (даже принимать отрицательные значения)^
В частности, на самой стенке (6^1 = 6^ = 0) К обращается в нуль-
Однако обычно величина К на несколько порядков превышает
коэффициент молекулярной вязкости v.
Турбулентные пульсации скорости могут переносить из одних
частей потока в другие, кроме импульса, также и частички с
более высокой температурой, создавая турбулентную теплопровод-
171

ность, или посторонние примеси, например дым, создавая
турбулентную диффузию. Аналогично коэффициенту К можно ввести
понятие о коэффициентах турбулентной теплопроводности и
турбулентной диффузии.
34.3. Турбулентный пограничный слой. Рассмотрим течение
вблизи плоской безграничной стенки. Средние характеристики
потока предполагаем не зависящими от х — координаты в
направлении средней скорости течения. В случае ламинарного
течения уравнение Навье — Стокса, так же как в случае течения
Куэтта, дает:
d*v/dy2 = 0, др/ду = 0. (9.20)
Ось у направлена перпендикулярно стенке. Из (9.20) находим
v=Ay+B, p=const. На самой стенке у=0 имеем v=0,
следовательно, В = 0. Обозначим через Т0 величину вязкого
(тангенциального) напряжения т] (dv/dy) на стенке. Тогда
т0 = л(^/^)у=о=Лл, А=Т0/ц.
В результате получаем линейный профиль скорости
t>=(To/T))i/. (9.21)
Перейдем теперь к турбулентному движению, описываемому
уравнением (9.17). Учтем, что в усредненном потоке отлична от
нуля только jc-компонента средней скорости, которую мы
обозначим через (v) = (vx(y)). Тогда из (9.17) получаем
где т'=—p<8i>«6i>v> — напряжение Рейнольдса. При этом
средние величины (&vx6vyy также могут зависеть только от у.
Проинтегрировав один раз последнее уравнение, находим
4±£L + X>=c.
dy
Постоянную интегрирования С можно определить из условия на
стенке (f/=0), где т'=0 (6vx=6vv=0)f следовательно,
d<v>
С = т,-
dy
у=о
В результате имеем
nlp>- + T' = To, (9.23)
dy
т. е. сумма вязких и турбулентных напряжений остается
постоянной величиной т0, не зависящей от удаления от стенки.
При малых у в непосредственной близости от стенки в левой
части (9.23) главным является первый член (вязкие
напряжения), так как.т'**0. Эта область называется вязким подслоем,
172

потому что профиль средней скорости в нем совпадает с
полученным при ламинарном течении (9.21). Однако движение в
вязком подслое не является ламинарным: в нем имеются заметные
турбулентные пульсации скорости. Наоборот, при достаточном
удалении от стенки в левой части (9.23) превалирует второй
член, так что можно приближенно положить
т'=— p(6vx6vy}^r0. (9.24)
В этой области поток импульса в направлении у, а также
величина градиента средней скорости d(v}/dy определяются
исключительно турбулентным трением, а молекулярная вязкость при
этом несущественна. Выясним, от каких величин может здесь
зависеть величина d(vyjdy. Поскольку молекулярная вязкость
не играет роли, то остаются только три размерные величины р,
у и т0 — существенная величина, определяющая поток
импульса от стенки в жидкость. Из этих трех величин можно составить
лишь одну комбинацию той же размерности, что и градиент
скорости, а именно (то/р)''1*/-1. Мы учли при этом, что согласно
(9.24) размерности квадрата скорости и величины т0/р
совпадают. Обычно вводится величина u#s (т0/р)'\ называемая
динамической скоростью или иногда скоростью трения. Таким образом,
вне вязкого подслоя будем иметь
^L=A^Lt (9.25)
iy У
где А — некоторая универсальная безразмерная постоянная.
Удобно ввести безразмерную координату £ = */(i>*/v). При этом
уравнение (9.25) перепишем без изменений
*¥-=**•* (9.25)
а его общее решение запишем в виде
<1>>=(Л1п£+В)1;„ (9.26)
где В — еще одна универсальная безразмерная постоянная.
Область значений £;, в которой выполняется этот закон, называется
логарифмическим пограничным слоем. Постоянные А я В могут
быть определены из опыта.
В терминах £; изменение скорости в вязком подслое,
аналогичное закону (9.21), запишем в виде
<»> = ».;. (9.27)
Опыт показывает, что закон (9.27) справедлив приблизительно
при £<8, в то время как логарифмический закон (9.26)
справедлив при £>30 с Л«2,5 и £«5,5. В промежуточной области
8<£<30 полученный в опыте профиль скорости отклоняется от
того и другого закона и соответствует плавной переходной
кривой. М. Д. Миллионщиков существенно усовершенствовал теорию
173

турбулентного пограничного слоя, получив вместо (9.26) закон,
справедливый вплоть до £ = 8. Приведем схему его рассуждений.
Используя понятие о коэффициенте турбулентной вязкости
(9.19), запишем уравнение (9.23) в виде
(4 + pK)ii2L = Te. (9.28)
dy
Коэффициент молекулярной вязкости определяется в
теоретической физике как r) = CplrvT, где /т — длина свободного пробега
молекул; vT — средняя тепловая скорость; С — некоторая
постоянная порядка единицы. Предположим, что для р/С также
справедлива аналогичная формула рК=р/и*, где /—«длина
свободного пробега» при турбулентном перемешивании. Для получения
логарифмического закона (9.26) при больших £ надо
предположить, что / пропорционально £; это мы фактически раньше и
сделали. М. Д. Миллионщиков предположил, что
t>.//v«x(C-C), (9.29)
где х и £<>— безразмерные универсальные постоянные, причем
£о имеет смысл безразмерной толщины вязкого подслоя.
Формула (9.29) означает естественное предположение, что закон
линейного возрастания / начинается не от стенки, а от внешней
границы вязкого подслоя £ = £0.
При таком усовершенствовании теории вместо закона (9.26)
получается следующий:
i2LeJ-in[i + x(C-Co)] + Co. ОС. (9.30)
Закон (9.27) при £<£<> остается в силе. Формулы (9.27) и (9.30)
при £; = £<> переходят друг в друга с непрерывной первой
производной. При £»1 закон (9.30) должен переходить в (9.26),
откуда можно установить связь между универсальными
постоянными Л, В и х, £0; Л=1/х, В=£в+х~Чпх. Полученный закон
для профиля средней скорости в зависимости от £ хорошо
согласуется с экспериментальными данными при х»0,4, £0«7,8 (Л«
«2,5, £«5,5). Параметр х обычно называют постоянной
Кармана.
§ 35. Локально-изотропная турбулентность
35.1. Качественные соображения о структуре развитой
турбулентности. До сих пор мы анализировали средние
характеристики турбулентного потока. Однако для ряда практических задач
требуется знать и статистические свойства пульсационных
скоростей 6v и прежде всего их корреляционные функции
{корреляционный тензор):
Вц(ги г2, /)=<6i>,(rlt t)6vs{ru OX (9.31)
В случае однородной турбулентности компоненты этого тензора
будут зависеть только от разности r=rj—г2. С точки зрения тео-
174

рии случай однородной турбулентности является наиболее
простым, но практически редко встречающимся в реальных
турбулентных потоках. Однородность турбулентности нарушается,
например, из-за наличия границ в реальном потоке, а также из-
за анизотропии, вносимой зависящей от координат средней
скоростью течения. С другой стороны, есть основания надеяться,
что мелкомасштабные возмущения потока с большими числами
Рейнольдса будут локально-однородными и изотропными в
небольших пространственных областях. Несколько поясняет это
утверждение качественная картина возникновения развитой
турбулентности, предложенная еще в 20-х годах нашего
столетия Ричардсоном и развитая А. Н. Колмогоровым и А. М.
Обуховым, которым в основном и принадлежат изложенные ниже
результаты.
Пусть мы имеем обтекание тела размером L0 жидкостью с
характерной средней скоростью v0. Предположим, что число
Рейнольдса среднего движения достаточно велико: Re=v0L0/v^>
>ReKp, где ReKp соответствует переходу к турбулентному
режиму. При возникновении турбулентности из-за неустойчивости
ламинарного режима в первую очередь появляются возмущения
с масштабом L^L*. Их характерная скорость vs— величина
порядка [<(6t>)2>J\ сравнимая с изменением средней скорости
hv0~v0 на расстояниях порядка L0. Свою энергию эти
возмущения черпают непосредственно из осредненного движения,
следовательно, они будут неоднородными в пространстве, как и
средний поток. Число Рейнольдса пульсаций масштаба Lt (Rei =
= viLJv) будет еще значительно превышать ReKP. Поэтому они
сами оказываются неустойчивыми, создавая возмущения с более
мелким масштабом L2. Последние при Re2 = i>2Wv^>ReKp также
неустойчивы и порождают пульсации масштаба LS<L2 и т. д.
Вязкость при этом никакой роли не играет, так как числа
Рейнольдса для каждого масштаба велики, и процесс обусловлен
только нелинейными эффектами. Поэтому энергия при передаче
от какого-либо масштаба к более мелкому не теряется и
определяется не зависящей от масштаба величиной е — энергией на
единицу массы, передаваемой за единицу времени от более
крупных масштабов к более мелким. В частности, порядок ее вели-"
чины может быть определен из соображений размерности как
убыль энергии исходного течения. Единственной величиной
размерности [е]=//Т"3, которая может быть составлена из L„ и v0,
будет
e~v0'/L0. (9.32)
Процесс дробления крупных возмущений на более мелкие
продолжается вплоть до вступления сил вязкости, т. е. до таких
масштабов LN (iV»l), для которых Rew = fl*Wv~l (или,
точнее, Rejv~ReKp). Движение этих масштабов уже
гидродинамически устойчиво и не распадается на более мелкие.
Поступающая к этим масштабам в единицу времени энергия е переходит
175

в тепло из-за действия вязких сил. Таким образом, параметр е
определяет также диссипацию энергии единицы массы
жидкости за единицу времени (см. задачу 9.9):
2 М dxk **t ) /
При распаде основного потока на возмущения масштаба Lx
возникают пульсации всевозможных направлений, а не только
в направлении скорости v0 усредненного потока. Другими
словами, движение в масштабах Li более изотропно, чем
усредненный поток. Аналогично при образовании масштаба L2 из Lt
изотропия пульсаций будет возрастать, а влияние основного потока
ослабевать и т. д. В результате уже после нескольких стадий
«размножения» турбулентное движение становится изотропным.
Иначе говоря, в развитой турбулентности почти все возмущения,
за исключением лишь наиболее крупных, будут статистически
однородными и изотропными.
Масштаб Lt~L0 называют обычно внешним масштабом
турбулентности, a LN — внутренним, или колмогоровским,
масштабом. Чем больше число Рейнольдса Re исходного потока, тем
больше и число его дроблений с последовательно
уменьшающимися Ln до LN. Поэтому при достаточно больших исходных
числах Рейнольдса будет существовать весьма представительный
интервал масштабов Ln (1<л<с#), таких, что /,!»£„>£*,
называемый инерционным интервалом масштабов, или просто
инерционным интервалом. Эти возмущения уже «забыли» о
структуре основного потока, а силы вязкости для них еще не
существенны. Поэтому основными определяющими параметрами в
этом интервале будут масштаб возмущений Ln и скорость
передачи энергии е. Ряд высказываний о характеристиках течения в
этом интервале масштабов можно получить из соображений
размерности.
Определим прежде всего порядок пульсационной скорости vn
для масштабов Ln. Последняя может зависеть только от Ln и е,
из которых можно составить лишь одну комбинацию размерно-
. сти скорости
vn~{*Ln)u. (9.33)
Используя формулу (9.32), мы можем также записать
vn~v0{Ln/L0jf*. (9.33')
Число Рейнольдса для произвольного масштаба Ln равно
Kert = —- Re, (9.34)
v vL;/. ^ До )
где Re =y0L0/v —число Рейнольдса основного потока. Если
предположить, что наши оценки справедливы вплоть до внутреннего
176

масштаба турбулентности LNi для которого Re*~l, то,
пользуясь (9.34), можно оценить порядок величины LN и
соответствующей пульсационной скорости vN:
Z,*~L0Re~,/4, vN~v0Re~lu. (9.35)
Таким образом, LN и vN уменьшаются при увеличении числа
Рейнольдса исходного потока пропорционально Re-8'4 и Re~'4
соответственно.
35.2. Статистические характеристики локально-изотропной
турбулентности. Мы видели, что в развитом турбулентном потоке
только мелкомасштабные (Ln<c£0) пульсации являются
статистически однородными и изотропными. Поэтому, если
интересоваться только последними, нужно отделить от них
крупномасштабные (Ln~L0) компоненты движения. Этого можно
достичь, например, рассматривая лишь относительное движение
жидких частиц в малых объемах пространства. Действительно»
можно ожидать, что векторное случайное поле би*^)—б^(г2)
будет однородным и изотропным в любой области пространства,
размеры которой много меньше L0 (|rt—г2|<с£0). Такое поле
называют локально-изотропной турбулентностью. Векторный
характер турбулентной скорости приводит к необходимости
рассматривать так называемый структурный тензор векторного поля
' Д/(г) = ([&,(г1)-во/(гя)][?о,(г1)-во/(г1)]>, г = гх-г2. (9.36
Если исходное поле 6v статистически однородно, то между
тензорами Di5(r) и 5<j(r) имеется очевидная связь, следующая из.
(9.36) с учетом (9.31):
Я,,(г)=2[Ву(0)-Я,Дг)]. (9.37)
Для векторных случайных полей понятие изотропности
является более сложным по сравнению со случаем скалярного поля
(в последнем структурная или корреляционная функция зависит
только от /-=1^ = 1^—г2|). Действительно, рассмотрим
компоненту 0ц(г) структурного тензора. Если вектор разности г=
= г4—г2 направлен по оси хи то Dti=Drr — структурная
функция продольных (адшь г) составляющих вектора 6v. Если вектор
г перпендикулярен оси xi9 то Dn=Dtt описывает корреляцию
поперечных компонент вектора 6v. Нет оснований считать
величины DTT и Dtt равными, т. е. в векторном изотропном поле
каждая компонента структурного тензора D{} зависит не только от
модуля вектора г, но и от его ориентации. Однако эта
зависимость должна быть вполне определенной и найти ее можно из
общих соображений симметрии, определив вместе с этим и число
независимых компонент тензора D{j.
Зададим в точках г4 и г2 единичные векторы произвольного
направления аир соответственно. Ориентацию вектора г =
= rt—г2 характеризует единичный вектор т/г (г= |г|).
Спроектируем векторное поле 6v на направления а, р и найдем структур-
177

D(r>™, -^,opj = /?(r)ap+S(r)
ную функцию получившихся скалярных полей:
D = <a* [6uft(Гх) — fit;* (г2)] pm [бит (гх) — fum (r2j]) = афтйк.л (i>
В изотропном поле величина D не должна меняться при
одновременном повороте векторов г/г, a, р на произвольный угол.
Отсюда следует, что функция D может зависеть лишь от
сохраняющихся при таких поворотах величин г, ra/г, гр/r и ар:
D (г' ljf' Т"*ар)= a^D^(1> (9'38)
В силу линейности правой части последнего равенства по ah и fim
не составляет труда выписать общий вид левой части:
(га) (г0) =
г»
= а*РлЯ(г) + <**Рт -^S (г) = а*рт |# {Г)ЬШ + S{r)%^
Сравнивая эту формулу с (9.38), в силу произвольности векторов
« и р заключаем, что
Dtf(f) =R(r)6if + S(r)^3-. (9.39)
г г
Таким образом, если в общем случае симметричный тензор
второго ранга D{j имеет шесть независимых компонент, то в
изотропном случае их всего лишь две. Обычно компоненты структурного
тензора выражают через продольную и поперечную
компоненты, рассмотренные выше в примере с Diim А именно: направив
вектор г вдоль оси xi (г/г={1, 0, 0}), для продольной
компоненты получаем Drr = Dn = R+S. Аналогично для поперечных
компонент имеем Dtt = D22 = Di3=R. Следовательно, R=Dtt, S =
= Drr—Dtt и
Dif = Dtt (r) 6t7 + [Drr (г) - Dtt (/*)] ^-. (9.390
В случае несжимаемой жидкости, который мы и
рассматриваем, число независимых компонент тензора D{j сводится к одной,
так как имеется связь между Dtt и Drr. Для упрощения
выкладок установим эту связь для изотропного векторного поля 6v.
Рассмотрим сначала величину дВ^(т)1дх{ (по повторяющемуся
индексу подразумевается суммирование). В силу г=г4—г2 имеем
д/дх{=д/дхУ\ где т±ша{х1{1\ х2{1\ *3(1)). В результате с учетом
(9.31) и условия несжимаемости (d&vjdxh=0) находим
Дифференцируя справедливое для изотропных полей соотноше-
178

ние (9.37), имеем аналогичное уравнение для структурного
тензора:
dDJdx^O. (9.40)
Последнее оказывается справедливым и в общем случае
локально-изотропной турбулентности, когда корреляционный тензор
Вц не изотропен. Если теперь в уравнение (9.40) подставить
выражение (9.390, учитывая при этом соотношения дг/дх+=х{/гу
д(хк/г)/дх{=6{к/г—хкх{/г\ будем иметь
dDif
дх{
_ dDtt *! . / dDrr
dr г [ dr
2 х/
+ (Drr~Dtt)-—'-
dDtt\
dr j
= 0.
1-^+
Отсюда непосредственно следует искомое выражение поперечной
компоненты через продольную:
Dtt==Drr + ±.^SL = ±± {r2Drry (9.41)
2 dr 2r dr
Важную роль в корреляционной теории случайных полей
играют спектральные разложения корреляционных и структурных
функций в интеграл Фурье. Например, в случае однородного
векторного поля для компонент корреляционного тензора (9.31)
имеем
оо оо
Bi{ (г) = j Fit (k) ekp (ftr) dfc = j Ftt (k) cos kr dk. (9.42)
Мы воспользовались здесь также условиями симметрии
Bij(ri—r2)=B{j(r2—ri), /7<i(k)=/7ti(—к). Аналогичное
представление для структурного тензора D{j в силу (9.37) будет
оо
Da (г) = 2 j (1 — coskr) Fif (k) dk. (9.43)
-OO
Отметим, что условия сходимости интеграла в (9.43) при к-*0
менее жесткие, чем интеграла (9.42), что также говорит о более
широком классе процессов, описываемых изотропными
структурными функциями.
В изотропном случае пространственный спектральный тензор
F{i(k) должен выражаться через две скалярные функции. По
аналогии с (9.39) и (9.390 запишем
Fif(k) = F(k)blf + G(k) ^J-=Ftt(k)bif+(Frr-Ftt) Л|*'-
В несжимаемой жидкости при подстановке (9.43) в условие
179

(9.40) получаем
оо
j sin(kr)^F,/(k)dk = 0,
откуда при произвольном г следует, что k{Fij(k)=0 и,
следовательно,
G(ft) = -F(ft), Frr(k) = 0, Fif{k)^[b(f-^)Ftt. (9.44)
Пространственная спектральная плотность поля скорости
непосредственно связана с кинетической энергией турбулентных
пульсаций. Например, для однородной и изотропной
турбулентности след Вц корреляционного тензора Bijf (взятый при г=0,
определяет среднюю пульсационную энергию единицы массы
жидкости:
Вц (0) = (to, (г) bot (г)> = (во?) + <fo22> + (bv\) = <fiv*>.
С другой стороны, с учетом (9.42) и (9.44) имеем:
Вц (г) = J F„ (k) cos kr dk, F„ (к) = Uu $Лрн (ft) - 2F* (ft).
Здесь интегрирование по к выполним в сферических
координатах: dk=ft2 sin QdQdydk, kr=ftrcos0 (полярная ось направлена
вдоль г). Для изотропного случая легко находим
оо пая
Ви (г) = Г Г f cos (kr cos 6) Fu (ft) ft2 sin QdQdydk =
0 0 0
oo
sinftr
о
Положив r=0 и
= 4n J ~pF« (ft)fta<ift. (9.45)
£ (k) = 4*£a-£i-- = 4jtfcaF« {k), (9.46)
найдем для средней пульсационной энергии единицы массы
жидкости выражение
г= *«{*)
ао
2 =JE(k)dk. (9.47)
0
Функция £(ft) называется спектральной плотностью энергии.
С помощью (9.46) и (9.43) спектральный тензор F<j(k')
выражается через E(k) следующим образом:
ISO

Аналогичное (9.45) выражение для следа структурной
функции D{i(r) имеет вид (см. задачу 9.2)
оо
Du (г) = 2Dt, + Drr = 4 Г (1 + s-^j Е (k) dk. (9.49)
О
Приведем также спектральные разложения функций Drr и Dtt
через E(k) (см. также задачу 9,10):
(9.50)
О
35.3. Гипотезы подобия Колмогорова. Мы уже говорили, что
в развитом турбулентном потоке с большими числами Рейнольд-
са мелкомасштабные компоненты пульсаций (Ln<^L0) будут
локально-изотропными и не зависящими от средних характеристик
потока. Следовательно, структура турбулентности при Ln<L0
может зависеть только от двух размерных параметров: б и v—»
первая гипотеза Колмогорова. Отсюда, в частности, следует, что
структурные функции Drr(r) и Dtt(r) при всех r<£.L0 должны
иметь вид D„(r) =Z)rr(e, v, г) (аналогично и Dtt). Составляя из
е и v величины с размерностями скорости i>v=(ev),/4 и длины
£v=(vs/e),/4, а также вводя безразмерную комбинацию r/Lvt
выпишем структурные функции, имеющие размерность [и2], в виде:
Drr^vlbrir/Lv), Du = vlftt(r/Lv), r<^Loy (9.51)
гДе frr(t) и ftt(|) —некоторые универсальные функции; | =
= r/Lv=re,/4v~3/4. Последние связаны друг с другом соотношением,
следующим из (9.41):
ftt(t) = frr(t)+^f'rr(t)-
Отметим также, что параметры Lv и vVy как и должно быть,
совпадают с определяемыми (9.35) минимальным масштабом
турбулентности LN и соответствующей ему скорости частиц vN.
В этом легко убедиться, учтя также (9.32). Таким образом,
первая гипотеза Колмогорова утверждает, что если измерять
скорость в единицах vN9 а расстояние — в единицах LNt то
статистические характеристики локально-изотропной турбулентности
определяются некоторым универсальным образом. Эквивалентное
(9.51) выражение для спектра E(k) размерности [E] = [Lvz]
181

будет
E(k)=L,vv2<p(Lvk), (9.52)
где ф(|) — новая универсальная функция.
В более узкой области, а именно, в ранее определенном
инерционном интервале масштабов LN^r<^,L^ (1/L0<£<I/L*)
можно сделать некоторые заключения относительно явного вида
функций /rf, ftt и ф. Здесь структура турбулентности целиком
определяется только величиной е и не зависит от вязкости. Это
утверждение является второй гипотезой подобия Колмогорова^
которая позволяет установить асимптотический вид функций
frr(l) и fail) в (9.51) при |»1. Записав, например, Drr в виде
D^eV'M'e'Vv8''),
будем искать асимптотику функции /гг(£) при больших £,
положив /Гг = Сг|Л и выбирая п так, чтобы параметр v выпал.
Однозначно получаем /г=2/3, следовательно,
Drr (г) = СгеV/э, Dtt(r)= Cte2V/a. (9.53)
Связь между универсальными постоянными Сг и Ct найдем из-
(9.41):C« = V,Cr.
Таким образом, в произвольном развитом турбулентном
потоке с большим числом Рейнольдса средний квадрат разности
скоростей в двух точках, расположенных на не слишком
больших или малых расстояниях г друг от друга (LN^r<^L0)9
пропорционален г2/». Это утверждение, впервые сформулированное в
1941 г. А. Н. Колмогоровым, называется законом 2/3
Колмогорова. С ростом г до масштабов среднего течения (порядка 1„)
этот закон должен замедляться, выходя на некоторую
постоянную, но уже не универсальную, а зависящую от исходного
потока.
В терминах спектра E(k) аналогичное закону 2/а
утверждение было впервые сформулировано в том же 1941 г. А. М.
Обуховым. Поскольку размерность спектра [£J=L[i;2], то, составляя
из е ([eJ=L2/F) и k (U]=L_1) величину размерности Е,
однозначно находим закон
Е(k) = Сггя'4г*\ L?<*k <L*\ (9.54)
называемый законом 5/з для спектра турбулентности в
инерционном интервале. Эквивалентность законов 2/3 и 5/з легко
устанавливается непосредственной проверкой справедливости формулы
(9.49) для спектрального разложения свертки D{i(r) (см.
задачу 9.4). При этом также можно найти связь между
универсальными постоянными d и Сг: Сг= (211ьь)Г(Ч*)С{.
Высказанные А. Н. Колмогоровым и А. М. Обуховым
гипотезы о структуре развитого турбулентного потока оказали
большое влияние на ход дальнейшего развития теории
турбулентности. Сами гипотезы, а также вытекающие из них следствия
подвергались неоднократной проверке в многочисленных экспери-
182

ментах. При этом во всех опытах, где соблюдались условия
локальной изотропности, наблюдалось достаточно хорошее
соответствие с теорией.
Задачи
9.1. Проинтегрировать уравнение турбулентного пограничного слоя (9.28),
определяя коэффициент турбулентной вязкости k в соответствии с гипотезой
Миллионщикова (9.30).
Решение. Переходя в (9.28) к безразмерным переменным 1/=<а>Д>.,
£= (tu/v)*/, где с»= (To/p)1//f, с учетом (9.30) получаем
[1+х(С—Ca)]rft/A£C—1.
Интегрируя это уравнение, имеем
и'=х-Чп[Ц-х(£-&>)]+В, £>&>.
Постоянная В находится из условия непрерывного перехода при £=&> в закон
изменения скорости в вязком подслое (9.27): £ = £о; следовательно, с/=
-х-Чп[1+х(С-Со)]+Ь.
9.2. Получить выражение (9.49) для свертки йц(г) через спектр E(k),
Решение. На основе (9.43) с учетом Fa (k) =E(k)/2nk2 имеем
оо
. > Е(к) „
coskr)~^"
—во
Переходя к сферическим координатам (dk=k? sin QdQdydk, kr=fcrcos9),
интегрируем по угловым переменным:
ОО Я2Я
Da = Г Г Г [1 — cos (krcos 9)] —— sinMBdydk
0 0 0
оо
= 2 f Е (k) I Г [1 — cos (£rcos9)J sin 9d9
о
00
\dk-
--«j««(i-^)*
0
9.3. Получить обратное (9.49) выражение спектра E(k) через свертку
Du(r).
Решение-. Применяя операцию V к исходной формуле предыдущей
задачи, находим
VD«(r)- f katakr-^-A.
183

Обращая это выражение по Фурье, получаем
00
J-£(*)==iIsinkrVD»(rMr
-00
или, умножая скалярно на вектор к,
00
EW = -^7 j sin кг V/>,,(/•) dr.
-оо
В случае локально-изотропного поля kVZ>i<(r) = (kr/r)D</, что приводит при
интегрировании по углам в сферических координатах к выражению
1 Г • и и u^W л k d Г sinfer dDu
Е (k) = ^~Т \ (sin kr — kr cos kr) Dndr = — — — \ — — dr.
2nk J K li 2я dk J k dr
о 0
9.4. Предположив, что закон 5/з для спектра E(k) справедлив для всех
масштабов 0<&<оо, найти структурную функцию /)«(г).
Решение. Воспользуемся выражением (9.49) для свертки Dn(r) через
спектр Е (k) = C,8Viri/a:
De<r)-4C1.".J(l-^)*-'/4».
Делая под интегралом замену переменной £=&г, dk=d\lrt получаем закон 2/э
для Du(r):
РО
Dtt (г) = АСхЛвш'тш\ А = J (l —^-) Г^
«■
9.5. На основе решения предыдущей задачи найти связь между
универсальными постоянными для спектра E(k) =C1et/i£~"*/• и структурной функции
Drr=Cre,/ir*/* в инерционном интервале.
Решение. Используя (9.49), (9.53) и соотношение С«=4/зСг, найдем
выражение для свертки Da(r) в инерционном интервале:
_П
3
^м&тсА|/§'
Сравнивая его с выражением, полученным в предыдущей задаче, заключаем
Сг= 12/цАС{. Следовательно, для установления связи между *СГ и С\
достаточно вычислить интеграл
О о
оо
= - -f- Х*и (I - sin |) |» + у j (1 - cos I) Г*/. d|,
о
184

Здесь первый член обращается в нуль, а второй выражается через Г-функциюз
00 оо
о о
—~Г (-%>«£ Г <»/,>.
В результате для Ст получаем
^-Tf-F'(Th-f'(T)c-
9.6. В некоторых случаях в пространстве выделяют некоторую прямую
линию (например, ось Х\) и рассматривают локально-изотропное поле скорости
лишь на этой прямой. В частности, разложив свертку Du(r) в одномерный
I?
интеграл Dn(r)=2\ (1—coskr)V(k)dk, вводят понятие об одномерном
спектре турбулентности V(k). Получить связь между V(k) и спектром E(k)>
а также выражение для V(k) в инерционном интервале.
Решение. Дифференцируя Dn(r) по г, находим /)«'(г) =
ksinkrV(k)dk. Обращение по Фурье дает
i
оо
Сравнивая эту формулу с выражением E(k) через йц'(г), полученным в
задаче 9.3, заключаем
dV(k)
£(£) = — k
dk
В инерционном интервале выражение для V(k) будет аналогичным E(k)t но
с другой универсальной постоянной Vr(&) = Cvei'•^*■*y',. С учетом связи между
V(k) и £(Л)=С1е*/^1/*легко получаем Су=8/бСь
9:7. В экспериментах обычно измеряют турбулентную скорость лишь в
одной точке пространства г0 (6v(r0, /))» но в течение большого промежутка
времени. При этом рассматривают случайное поле f(r0, /, т)=*6у(г0, /+т)— 6v(r0, /)•
Используя гипотезу «замороженной» турбулентности (гипотезу Тейлора) о
простом переносе картины случайного поля 6v(r) со средней скоростью потока
<v>, связать статистические характеристики поля f(r0, /, т) с
пространственными характеристиками поля 6v(r).
Решение. Направим ось Х\ вдоль направления средней скорости в точке
г0 и обозначим последнюю через <v>. На основе гипотезы «замороженности»
запишем 6v(r0, /+т)=6у[г0—<v>t, t]. Но тогда можно ввести продольную
временную структурную функцию
0j/.W - <l*i (ro» t + т)- *, (r0, *)]a> =
» <[toi (U - <"> *. t) - b>i (r0, *)]•> = Drr «v> t)
185

и аналогично поперечную D\t (t)=Du«v>t). Свертка временного структур,
ного тензора Dlu (т) = 2£>^[(т)+/)'г (т)=£««у>т) может быть представлена
в виде одномерного интеграла
оо
&U W = 2 f (1 — cos cot) IF (со) Ло.
-00
oo
Но, с другой стороны, функция Da(r) = 2 f (l—coskr)V(k)dk, следова-
—oo
тельно,
00
D*u (т) = Dti «t» t) = 2 j [1 - cos (ft <»> t)] V (к) dk.
•-00
Заменяя переменную интегрирования ю = <и>£, находим
t °с ? V(o>/<t»)
Dj, (т) = 2 I (1— cos сот) Г(со) &о = 2 (1 —cos ют)—* <fo,
^ -ОО -00
откуда следует соотношение
Г(©)= V| —) или У(*) = <у>1Р (*<»».
В частности, в инерционном интервале масштабов
^ (о) = — Суъж/* (—) '= Ct,ee/» <y>v« со-1/».
9.8. Получить в случае вязкой несжимаемой жидкости уравнение для
изменения во времени кинетической энергии £=pv2/2.
Решение. Дифференцируя кинетическую энергию по времени (р=const),
находим dE/dt=pvdv/dt = pVidv{/dt. Используем теперь закон сохранения
импульса (8.3) J
a dvt dUik
где П<А=р6<*+р»<1>А—о<»; CT,A=ri(di></d**+di>»/d*0 для несжимаемой
жидкости. В результате
дЕ Щк д до,
ir=~ *-%;=~ "^(в|Пл) + "'* "^Г=
где dvk/dxk = 0 в силу несжимаемости; pVi2vk/2=Evkt —d(pVi2vk/2)/dxk =
= —pViVbdvildxk—Edvkldxh=—pViVkdvi/dxk. Следовательно,
дЕ д ty
186

Последний член в этой формуле обычно обозначают через ре, где
dv. Ш fdvk \ dvt ttf v (lpo{ dvk \2
e = — ^л-ГГ=^| — 4 — ' '
1 fy /
' = — aik ~Z— = v ■
dxk dx-) dxk 2 \ dxk ^дх{
имеет смысл удельной (для единицы массы) диссипации энергии в единицу
времени.
9.9. Представив скорость потока в виде суммы средней и турбулентной
составляющих v=<v>+6v, получить уравнение для изменения во времени
энергии среднего потока Яс=р«1>»2/2 и турбулентной энергии £т=р<(би)2>/2.
Решение. Вычисление dEc/dt аналогично расчету dE/dt> нужно только
вместо уравнения Навье — Стокса воспользоваться уравнением Рейнольдса.
Это, как уже отмечалось, вызывает появление дополнительного члена
p(fiVi6vk) в тензоре плотности потока импульса (9.16). При этом для dEc/dt
в правой частч появляется добавочный член
д д д <vi>
- р <vi> -^- <ЧЧ> = ~ ^7" (Р <»i > <Ч6иА»+Р <b>fiok> -^—.
Следовательно,
IT = ~ аГ1{Ес+<р>) <Vk>~~<Vi> <(J{k> + р <6t;M><^>] -
d<vt>
-Рв0 + Р<44>"^— .
d<vb> \а
/:а<и-> d<vk>\ v /d<vt>
где <ай>- i, ^—+ —j ; ес = т(^—+ —
Усредним теперь уравнение для dE/dt предыдущей задачи
д<Е> л / dvf
dt u*k
д / dvi \
^^т 0 / P \
— = - — \Er < V + -J- <(fc,)»bvk) > 4- <вдв*л> - <tofioih>)
и вычислим входящие в него величины, например
<Evk> = — р <«^> 4- 4>а «vk> + 6vk)> =
- (Ес + Ет) <vk> + р <vt> <bvfivk> + -^- <(«*,)• бил>.
В результате для dET/dt=d(Ey/dt—dEc/dt получаем
— рет — р <6vi6vk> —j£— ,
/d6vl d6vk\ v / I d6v{ ddvkyK
где fart-i, ^+-^J • ^ e* = T\(^r+l^J / " СреДНЯЯ
удельная энергия диссипации для турбулентного движения. Слагаемое
p(6Vi6vkyd{Vi}fdxkt входящее в уравнения для Ес и Ет с разными знаками,
описывает переход энергии от среднего течения к турбулентному и обратно.
187

9.10. Получить интегральное представление структурных функций Drr и
Dtt через спектр E(k) (см. (9.50)).
Решение. Из (9.41) и (9.49) легко получить дифференциальное
уравнение, связывающее DTT(r) и след Du(r):
Du М-Т7 ^Dn WJ + Dn M = — — ^SDrr Mb
1 r
Интегрируя последнее при условии Drr(0) =0, получаем Drr = —\ l2DH(l)x
Xd£ или с учетом (9.49)
г оо
о о
Если теперь проинтегрировать по переменной Б, то найдем
оо
1 , cosfcr sinfcr\ _,.ч ..
0
Интегральное представление для Dtt (г) легко следует из соотношения Dttmm
= 72ф«-Дгг):
оо
гч л Г/ 2 sin£r cos£r , sin/tr\ ^/t4 „
Глава 10
ПОВЕРХНОСТНЫЕ
И ВНУТРЕННИЕ ВОЛНЫ В жидкости
Начиная с этой главы, мы перейдем к изучению особого,
важного во многих приложениях случая движения жидкости — к
волнам. Основной отличительной чертой волновых движений
является то, что благодаря им возможен перенос энергии в
жидкости на большие расстояния без переноса массы. Разнообразие
сил, действующих на жидкие частицы при их движении,
приводит к многообразным волновым движениям. Мы рассмотрим
основные типы волн в жидкости в так называемом линейном
приближении, когда волны распространяются независимо друг от
друга.
В этой главе мы получим линейные уравнения для волн в
жидкости и рассмотрим волны, обусловленные действием силы
тяжести. Это прежде всего гравитационные поверхностные
волны, возникающие на свободной поверхности жидкости, напри-
188

мер поверхности океана. К гравитационным также относятся и
внутренние волны, возникающие на резких или размытых
границах раздела в толще жидкости. Кроме того, в этой главе мы
рассмотрим капиллярные поверхностные волны, обусловленные
силами поверхностного натяжения.
§ 36. Линейные уравнения для волн в жидкости
36.1. Линеаризация уравнений гидродинамики. При изучении
волновых процессов в жидкости мы должны исходить из
основных уравнений гидродинамики, полученных в гл. 6 (см. (6.9) %
(6.14) и (6.18)):
4L + (W)v = -^--gVz-2Qxv,
dt р
(Ю.1
Здесь в уравнение Эйлера мы включили силу тяжести,
направленную вертикально вниз, и силу Кориолиса —2QXv,
возникающую во вращающейся с частотой Q жидкости (например, на
вращающейся Земле). Центробежная сила инерции,
являющаяся, как-отмечалось в п. 21.3, потенциальной, может быть
формально включена в потенциал силы тяжести, что изменит
направление местной вертикали. Мы остановимся на теории рас-
пространения волн в идеальной жидкости, не затрагивая к тому
же вопросы их возбуждения.
Важным обстоятельством при исследовании волновых
движений в жидкости является нелинейность уравнений
гидродинамики (10.1), так что точная теория волн в жидкости будет
нелинейной теорией. Это приведет к влиянию одних волновых процессов
на другие {взаимодействие волн) и к значительному
усложнению процесса распространения волн каждого отдельного вида.
Однако если возмущения жидкости, вызываемые волнами, в
некотором смысле малы, то уравнения гидродинамики могут быть
линеаризованы относительно этих возмущений. При этом теория
волн в жидкости становится линейной и вступит в силу принцип
суперпозиции (волны распространяются независимо друг от
друга). Точный смысл условий малости возмущений мы обсудим
ниже (см. гл. 14). Здесь же мы просто будем считать в
уравнениях гидродинамики значение скорости v малой величиной, а
возмущенные значения давления р и плотности р мало
отличающимися от их равновесных значений р0 и р0 соответственно.
После этого, положив Р=р0+р', р = р0+р'> преобразуем
уравнения (10.1), сохраняя лишь линейные по vss{w, vt w}, рг и р'
члены {линеаризация уравнений). Для состояния равновесия
имеем уравнения гидростатики:
v0=0, dp0/dz=—gp0 (г). (10.2)
189

При линеаризации нелинейный член (vV)v в уравнении Эйлера
выпадает, член же Ур/р преобразуется следующим образом:
Ур _ УРо + Ур' ^ Ур0 | Ур' УРо
Р Ро(1+р7Ро) Ро Ро Ре Ро
Аналогично преобразуется нелинейный член в уравнении
неразрывности
У (pv) =У [ (p0+p')v]«(dp0/dz)w + poW
и в уравнении состояния (с учетом (6.4))
dp dp'
dt dt
dz \ dt dz )
Если теперь вспомнить, что VPo=(dp0fdz)Vzt а также учесть
уравнение гидростатики (10.2), то легко выписать линейную
систему уравнений гидродинамики (штрихи у р' и р' опущены):
dt ро р,
JE_ + ^ta, + p0Vv = 0, (10.3)
dt dz
dt с* dt V0 g
где N2(z) =—g(p0-ldp0fdz+g/cl) —введенная выше (см. (6.28))
частота Вяйсяля.
36.2. Линейные граничные условия. Для свободных волн в
качестве «возвращающих» сил могут выступать силы,
возникающие на границах области, занятой жидкостью. Наиболее
важной с этой точки зрения является свободная поверхность. В
самом деле, пусть в состоянии равновесия поверхность жидкости
является плоской. При выведении ее из этого положения
существуют двоякого рода силы, стремящиеся вернуть поверхность в
прежнее состояние: сила тяжести и сила поверхностного
натяжения. В результате на поверхности жидкости возникает
возмущение, распространяющееся во все стороны в виде волны.
Силы, возникающие на поверхности жидкости, должны
входить в граничные условия для уравнений (10.3). Получим их в
предположении, что в состоянии равновесия свободная
поверхность является плоской (z=0). Пусть возвышение
возмущенной поверхности описывается выражением £ = £(*, у, t).
Скорость возвышения поверхности d\\dt должна совпадать с
вертикальной скоростью частиц среды (w(x, у, z, /))» на ней
находящихся (поскольку эти частицы не могут ни опережать
поверхность, ни отставать от нее), что можно записать в виде
190

Это так называемое кинематическое граничное условие на
свободной поверхности жидкости.
Во втором, динамическом условии на свободной поверхности
жидкости учитывается наличие скачка давления по обе стороны
от границы, обусловленного силами поверхностного натяжения.
Если давление в жидкости p0(z)+p, а давление над
поверхностью /?а, то по известной формуле Лапласа
Po(t)+p\*=t-P*=-oR-\ (10.5)
где о — коэффициент поверхностного натяжения; /?-1 — сумма
главных кривизн поверхности £, равная для поверхности 2=
я-1 = v (v vYi + WJp). (Ю.6)
Граничные условия (10.4) и (10.5) также оказались
нелинейными. Линеаризуем их, считая возмущение поверхности £
малым. При этом, применяя формулу (6.4) для полной
производной по времени, из (10.4) получаем
--* -о.
• w\ —
12=0
dt
Аналогично из (10.5) с учетом (10.6) и р0(0) =р& имеем
■SLt+"'u+ "-оД-г+
где А- = д2/дх2+д2/ду2— оператор Лапласа по горизонтальным
переменным. В результате, ограничиваясь только линейными
членами, с учетом уравнения гидростатики (10.2) получаем ли-
нейные граничные условия на невозмущенной свободной
поверхности г=0:
ши = -|-, />L, = «p0(0)C-a/U. (Ю.7)
36.3. Линейные уравнения для гидродинамических волн.
В основных уравнениях (10.3) для волн в жидкости учтено из-
менение ее плотности за счет сжимаемости, которое
описывается первыми двумя членами в уравнении состояния (третье
уравнение (10.3)):
-*- = -L-*-. (Ю.8)
dt с* dt v r
Наиболее важным следствием сжимаемости жидкости являются
акустические волны, которые будут рассмотрены ъ гл. 12. Здесь
же рассматриваются поверхностные и внутренние волны, для
которых сжимаемость проявляется лишь в виде некоторых малых
поправок, которыми мы пренебрегаем.
191

Формально переход к несжимаемой жидкости можно
осуществить, потребовав постоянства плотности в жидкой частице:
d9/dt=0. (10.9)
При этом непосредственно из точного уравнения неразрывности
(6.9) следует, что при движении жидкости
W=0. (10.10)
С другой стороны, из точного уравнения состояния (6.18) при
условии (10.9) имеем c~2dpfdt=0. Но в общем случае dp/dt=£0t
например из-за изменения гидростатического давления, поэтому
в несжимаемой жидкости следует считать скорость звука с = оо.
Этот результат отражает тот факт, что в несжимаемой жидкости
упругие возмущения распространяются мгновенно. Теперь уже
не составляет труда получить из (10.3) линейные уравнения
гидродинамики несжимаемой жидкости:
_*L+ Vp. + g_£.Vz + 2Qxv = 0,
* Ро Ро
(10.11)
Vv=0,^-Po-^ = 0,
ot g
тде частота Вяйсяля N2(z)=—gpo^dpofdz. Граничные условия
(10.7), не содержащие скорости звука с, останутся неизменными.
Условием применимости приближения несжимаемой
жидкости (с=оо) будет требование, чтобы скорость распространения
рассматриваемых возмущений была значительно меньше
скорости звука.
§ 37. Гравитационные поверхностные волны
37.1. Основные уравнения. При возмущении плоской свободной
поверхности жидкости в гравитационных *волнах возвращающей
силой является сила тяжести. В граничном условии (10.7) ее
влияние описывается членом gpo(0)£, равным давлению столба
жидкости высотой £. Исключим в наших уравнениях действие сил
поверхностного натяжения, силы Кориолиса, архимедовых сил,
положив для этого о=0, Q=0, р0=const (#2=0, р=0)
соответственно, и введем обозначения: uss{a, v) — горизонтальная
компонента скорости частиц, V- = txd/dx+eyd/dy. Тогда из (10.11)
получаем уравнения для гравитационных поверхностных волн:
_*L + ^£ = 0,-^L+-L^=0( Vu + -*L = 0. (10.12)
dt ро dt р0 дг " дг
Из этих уравнений можно исключить горизонтальную скорость
*i и давление /?, выразив последние через вертикальную
компоненту скорости частиц w:
= —v--r-r-» A_p = Ро a,a » (10.13)
dt ' dtdz ' u dtdz
192

и для w получить уравнение
-уДо>=0. (10.14)
Граничное условие на свободной поверхности г=0 для w легко
следует из (10.7), где о=0 и р берется из (10.13):
(•^•-Н„-°- (10Л5)
Кроме того, предполагая на уровне z=—Н наличие границы
жидкости с абсолютно твердым дном (рис. 10.1), добавим еще
условие равенства нулю нормальной (вертикальной)
компоненты скорости частиц жидкости при z=—Н:
а>|— я=0. (10.16)
37.2. Гармонические волны. Будем искать решение уравнения
(10.14), удовлетворяющее граничным условиям (10.15) и
(10.16), в виде распространяющейся в горизонтальном
направлении гармонической волны:
w(xt уу z, /)=Ф(г) exp [t(kr—co/)Jf (10.17)
где k={kX9 kv] — волновой вектор; г={х, у). Подставив это
выражение в (10.14) — (10.16), получаем краевую задачу для
функции Ф (г):
^_£2Ф==0, f-^—^O) = Ф(-#) = 0.
_£2ф=0, (^-^ф) = Ф(-#) = <
Граничное условие при z=—Н удовлетворяется, если выбрать
решение уравнения для Ф в виде
<b(z) = bshk(z + H) . (10.18)
sh kH
Подстановка последнего в граничное условие при z=0
показывает, что волна (10.17) существует не при произвольных
значениях k и о, а только при удовлетворяющих дисперсионному
соотношению
tf^gkthkH. (10.19)
Отсюда следует, что фазовая скорость гравитационной
поверхностной волны зависит от частоты (волнового числа):
Сф = co/k - VW УШНЦгН. (10.20)
Следовательно, последняя распространяется с дисперсией, что,
в частности, приводит к изменению формы негармонической
поверхностной волны. Не составляет труда найти и групповую
скорость гравитационной поверхностной волны, т. е. скорость рас-
7 Л. М. Бреховскнх, В. В. Гончаров 193

пространения огибающей спектрально-узкого волнового пакета
(см. §9):
которая, как мы видим, также зависит от волнового числа k.
Смещение поверхности £(*, у, t) Ьпределяется из граничного
условия (10.7)
-~- = — "°£ = Ч=о = Ь ехР К <кг ~ ®')].
откуда
£ = а exp [t (кг — со/)], а = tfe/co. (10.22)
194

Пульсации давления на произвольной глубине z, обусловленные
волновым движением, найдутся из (10.13), откуда с учетом
Д_ = — kz получаем
^^^Ш"^^1^^-^ С»-23)
Если воспользоваться дисперсионным соотношением (10.19), то
последнее выражение можно записать и в таком виде:
p = pogJLchAJ^) kr_
ш ch kH
= Poga Chku{ltH) exp [i (kr - ©<)]• (Ю.23')
en kH
Далее, из уравнений (10.13) легко находится горизонтальная
скорость частиц жидкости в волне
ц = . к ь ch k(z + Н) ехр [t (кг _ Ы)1 (Ю24)
к sn kH
направление которой совпадает с направлением
распространения волны к. Если обозначить через \ горизонтальное смещение
частиц жидкости, также совпадающее с направлением k (d\\dt=-
= —tool=и), и соответственно через х\ — вертикальное смещение
частиц (dr\/dt=—tcorj = o;)t то, положив & = о)Лехр[*'(а—я/2)]
(а=Л ехр (t'a), А— амплитуда смещений свободной
поверхности) и выделяя вещественные части, получаем:
* „ k chk(z4-H) . /f , , ч
I = — А— —u\7" ; sin (кг— at + a),
k shkH
4 = Ashk{2 + H)cos(kr-G>t + a).
1 shkH v '
Исключая теперь зависимость от ty находим траектории
движения частиц жидкости в гравитационной поверхностной волне:
а| а^ 6 shkH shkH
являющиеся эллипсами с отношением полуосей arJal=th k{z+H).
В случае стоячей поверхностной волны, образованной двумя
бегущими волнами типа (10.17) с одинаковыми частотами со и
амплитудами й, но с противоположно направленными
волновыми векторами к
w = 2b sh*(2 + //) cos (кг) ехр (— Ш),
shkH
аналогичный расчет смещений частиц приводит к выражениям:
I = 2 А — chMz + //) sin (kr) cos (a>* — a),
k shkH \ / v '
t] = _ 2A sh/g(z + 7/) cos (kr) cos (®f — a),
sh kH
195 7«

При этом траекториями частиц будут прямые линии
т, = _ th k (z + Н) ctg (кг) Ь (Ю.26)
наклон которых зависит как от вертикальной z, так и от
горизонтальных х, у координат. Отсюда видно, в частности, что при
кг=0, ±я, ±2я,... частицы движутся по вертикальным
прямым, а при кг= ±я/2, ±Зя/2,... — по горизонтальным.
На основании выражений для скоростей частиц жидкости
(10.17) с учетом (10.18) и (10.24) нетрудно убедиться, что
rot v=0, т. е. движение в поверхностной волне является
потенциальным: v=Vcp, где
Ф = |сЬ*^+Я)ехр№-а)/)1. (10.27)
37.3. Приближения мелкой и глубокой воды. Обычно в
теории гравитационных поверхностных волн рассматривают два
крайних случая, различающихся соотношением между Н и
длиной волны Я=2я/&,
1. Мелкая вода —#/Я<1 (£Я<1). При этом в (10.19) и
(10.20) имеем th kH^kH, в результате
© = ygBfe, сф = У^Н. (10.28)
Дисперсия волн отсутствует (^=const). Для компонент
скорости из (10.18) и (10.24) в том же приближении имеем:
»-b(l+i)e«p[l(kr—/)], u = f|6exp^(kr^co/)]
(10.29)
Отсюда, в частности, следует, что |и|^>|ш|, т. е. скорость
практически постоянна по сечению жидкого слоя и направлена
параллельно дну. Этот факт также легко установить, анализируя
траектории (10.25). Отношение полуосей эллипса ап/а6=
= k(z+H)<kH<^l, так что частицы жидкости в поверхностной
волне на мелкой воде движутся по сильно вытянутым вдоль
горизонтальной оси эллиптическим орбитам.
2. Глубокая вода — ЩХ^Х (&//»1). В этом случае в
(10.19) следует положить th£#»l, что приводит к
дисперсионному соотношению для волн на глубокой воде:
(o2=gfc. (10.30)
Для фазовой и групповой скоростей находим:
Из выражений (10.17), (10.18), (10.23) и (10.24),
пренебрегая всюду величинами ехр (—kH) по сравнению с единицей,
196

получаем:
w = b exp (kz) eftp [i (kr — со/)], u = i — b exp (&z) exp [i (kr — ©/)],
(10.32)
p = p0 — b exp (£z) exp [i (kr — <of)].
Таким образом, все возмущения жидкости в поверхностной
волне на глубокой воде экспоненциально убывают при углублении.
Волновое движение практически отсутствует уже на глубине
порядка длины волны Я. Для траекторий движения частиц
жидкости (10.25) имеем а,1=ац=А exp {kz), что дает
|*+л2=Л2ехр (2*2)
— окружности, радиус которых экспоненциально убывает с
глубиной.
Конечно, любой заданный слой жидкости глубиной Н в
зависимости от длины распространяющихся волн может быть как
мелкой, так и глубокой водой. Очень длинные волны всегда
распространяются без дисперсии. Примером таких волн могут
служить приливные волны или волны цунами в океане.
Дисперсионное соотношение (10.19) удобно изображать графически (см.
рис. 10.2), где хорошо заметны линейный бездисперсионный
участок в окрестности начала координат (длийные волны) и далее
дисперсия, соответствующая при kH^l волнам на глубокой
воде.
37.4. Энергия волн. Величину энергии волны любого вида
обычно определяют как превышение энергии некоторого объема
жидкости, возмущенного волной, над ее величиной в состоянии
покоя. В случае поверхностных волн в качестве объема удобно
выбрать столб жидкости, ограниченный в вертикальном
направлении плоскостью z=—Н и свободной поверхностью, в
направлении движения волны, которое мы примем совпадающим с
осью ху—двумя плоскостями х=х0и х=х0+Х (X — длина волны),
в поперечном направлении аналогичные плоскости отстоят друг
от друга на единицу длины. При этом для кинетической энергии
нашего объема имеем
Xf+A о
Ек = £± Г Г v4xdz.
Квадрат скорости частиц жидкости с учетом выражений
(10.17), (10.18) и (10.24) запишем в виде
р2 = ffl *ha* (г + Н) 2 {kx _ f at)
+ ***kiM + mco*lkx-*t + a' + ±) ,
^ sh*kH \ ^2)
197

где ВехрО*а')=&. Напомним, что при вычислении
квадратичной величины v2 нужно учитывать только вещественную часть
комплексных выражений. Возвращаясь к вычислению
кинетической энергии, замечаем, что
где f(t) —произвольная функция. Поэтому
о
£«="Т"^ § [sh*k(z + H) + ch*k(z + H))dz =
-Я
о
f ch [2* (Я+ z)]d2f
= Ро^ В*
4 sh*kH
и окончательно после интегрирования получаем
Ек = £°L g = b£L*L = &£*_ Лав (Ю.ЗЗ)
4 kthkH 4 оЯ 4 '
Здесь учтено дисперсионное соотношение (10.19) и вместо В =
= |&1 использована амплитуда смещений свободной
поверхности А=\а\ (см. (10.22)).
Аналогично для приращения потенциальной энергии имеем
х / с о v хс х
о V-Я -Я / оо о
Подставляя в интеграл вместо £; вещественную часть выражения
(10.22) A cos (kx—(ut+a) и интегрируя, получаем
£п=Ро^Д2=£к> (10.34)
4
Таким образом, кинетическая и потенциальная энергии в
бегущей поверхностной волне равны друг другу и постоянны во
времени.
В случае стоячей поверхностной волны
£=Л cos kx cos ((ot—a)
аналогичные вычисления приводят к системе выражений:
£п = Md!^cos2((of — а) = Ро£^л2[1 + cos(2o)f — 2а)],
£к =Po£d^sin2(co* — а)=^лМ1 — cos (2со* — 2а)], (10.35)
4 8
£„+£п = const.
Кинетическая и потенциальная энергии, оставаясь в сумме по-
198

стоянной величиной (энергия волны), изменяются во времени с
удвоенной частотой в пределах от 0 до р0£АЛ2/4. Средние по
периоду кинетическая и потенциальная энергии стоячей волны
равны между собой.
§ 38. Капиллярные волны на поверхности
жидкости
38.1. Чисто капиллярные волны. Исследуем теперь волны,
обусловленные силами поверхностного натяжения. Действие
этих сил описывается членом —оД-£ в граничном условии
(10.7). Исключая волновые движения других типов (р0=const,
N2=0, Q=0, g=0) в (10.7) и (10.11), вновь получим уравнение
(10.14) для вертикальной компоненты скорости. Однако
граничное условие на невозмущенной свободной поверхности 2=0
будет уже другим. А именно: положив во втором уравнении (10.7)
£=0 и действуя на него оператором <?Д-/<Э/, имеем
д Л
— А р
= -аАА А
Отсюда, выражая d^/dt через w с учетом первого условия (10.7)
и А_/7 из справедливого и в этом случае соотношения (10.13),
находим
(И+^-Ч».-0' (10-36>
где^=а/р0.
Капиллярные волны, как мы увидим ниже, являются
высокочастотными волнами с малой длиной волны. Во всех
практических задачах поэтому можно полагать &#->оо, как в случае
бесконечно глубокой жидкости. Решения уравнения (10.14) при
этом должны обращаться в нуль при z->*—оо. Если искать
решение в виде гармонической волны (10.17), то для Ф(г) и
w{x, У, 2, /) будем иметь:
Ф(г)=Ь exp (kz), w = bexp (kz) exp [f(kr—со/)]-
Подставив w в граничное условие (10.36), получим
дисперсионное соотношение для капиллярных волн
о)2 = ^3. (10.37)
При этом фазовая и групповая скорости волн равны:
сф = УуЬ; сгр=±У^=--±сф. (10.38)
Выражения для давления р и горизонтальной компоненты
скорости и совпадают с соответствующими выражениями для
гравитационных волн на глубокой воде (10.32). Поэтому и
траектории частиц жидкости в капиллярной волне являются
окружностями.
199

38.2. Гравитационно-капиллярные волны. Учтем теперь
совместное действие сил тяжести и поверхностного натяжения. В
однородной (р0=const), несжимаемой (£2=оо) и невращающейся
(й=0) жидкости остаются справедливыми уравнения (10.12) —
(10.14), граничное условие (10.16), а также решения (10.17),
(10.18), (10.22)—.(10.24) в виде гармонических волн. Все
отличие от рассмотренных выше случаев заключается в
использовании полного динамического граничного условия для р на
свободной поверхности (10.7), которое для w будет комбинацией
условий (10.15) и (10.36):
/ d*w _
gh_w + yk_Ajv V =s0.
/z«=o
Соответственно с этим изменится только дисперсионное
соотношение для волн
tf=(gk+4k*)\hkH. (10.39)
Отсюда находим квадрат фазовой скорости
cJ=(g/k+>tk)thkH. (10.40)
В частности, для волн на глубокой воде (kH^l) имеем:
G)2 = g£+^3, cf^gfk + tf. (10.41)
При малых k (длинные волны) основным в правой части
является первый член, и мы имеем уже исследованный выше
случай гравитационных волн (ср. с (10.19)). Фазовая скорость
падает с ростом k. Напротив, при больших k (короткие волны) в
(10.41) следует удерживать лишь второй член — капиллярные
волны. Фазовая скорость растет с увеличением к. При некотором
й = Л0 = 2яАо фазовая скорость волны будет минимальна.
Приравнивая производную от правой части второго уравнения
(10.41) нулю, находим:
К = Veiy> К = 2яVylg> toWi = V2(gyyu. (10.42)
Для границы вода — воздух «у «73 см8/с2 получим &0» 1,714 см,
соответствующая частота /0=(£ф)тиДо=13,5 гц и (fy)mm=
= 23,1 см/с.
Отметим, что длина волны Х0 является граничной,
разделяющей гравитационные и капиллярные волны. При А,>Х„
превалируют гравитационные силы, при А,<А,0 — капиллярные.
Для групповой скорости гравитационно-капиллярных волн на
глубокой воде (&#;»1), дифференцируя (10.41) по к> имеем
2(uCrp = g+3<ik\
следовательно,
с =g + 3y#'= сф g/y+3k* _ % k\ + №
* 2о) 2 gft + k*~ 2 kl+k*
= - . (10.43)
giy+v 2 *;+*•
200

Отсюда получаем, как это и должно быть, для гравитационных
волн (£0>£) выражение (10.21) при &#>1, а для капиллярных
(Л0<*)—выражение (10.38). На рис. 10.3 дано схематическое
изображение дисперсионных зависимостей б>(&) и сф(к) для
гравитационно-капиллярных волн.
§ 39. Внутренние гравитационные волны
39.1. Вводные замечания. Во внутренних волнах
максимальные вертикальные смещения частиц имеют место не на
поверхности жидкости, а внутри нее, например на границе раздела
двух жидкостей с различными плотностями. В океане
последний случай наблюдается при расположении опресненной воды
над более тяжелой водой с большей соленостью. Такие случаи
были названы «мертвой водой». При этом часть мощности
двигателя корабля может расходоваться на возбуждение
внутренних волн, что приводит к снижению его скорости.
В такой простейшей двухслойной модели жидкости
внутренние волны совершенно аналогичны поверхностным. Они также
сосредоточены вблизи границы раздела. Если предположить,
что по обе стороны от границы жидкость заполняет целиком
каждое полупространство, то дисперсионное соотношение для
внутренних волн будет тождественным соотношению (10.30)
для гравитационных волн, но с другим, эффективным значением
ускорения силы тяжести. Действительно, пусть граница раздела
двух жидкостей с плотностями рА и ра (p2>Pi) расположена на
уровне 2=0 и волны распространяются вдоль оси х. В каждой
из жидкостей решением уравнения (10.14) будут гармонические
волны:
wi = bi ехр (—kz) ехр [i(kx—Ы) ], z>0,
(10.44)
ш2=62ехр (kz) ехр [i(kx—(ot)]t z<0.
На границе раздела должны выполняться кинематическое и
динамическое граничные условия. Первое из них (t£>j!«-* — </£/<#,
/=1, 2) дает в линейном приближении равенство вертикальных
скоростей
wi\z-o = dtt/dt=w2\l=0.
Второе (равенство полных давлений по обе стороны от
границы z=£) приводит к соотношению — gpi£+Pi = — gfat+Pi.
С учетом выражения для давления в жидкости (10.13)
получаем два условия, связывающих вертикальные компоненты
скорости частиц при z=0:
<"i U = w2 U> ek* (р2 - Pi) щ L.= <* (л 1г_ P1 Ir)^;
/ = 1.2. (10.44')
Отсюда при подстановке выражений (10.44) имеем связь меж-
201

ду амплитудами волн по обе стороны от границы bt = b2=b и
искомое дисперсионное соотношение
&=-AL-gk, Ap=p2-Pl. (10.45)
Р1 + Р2
Естественно, что последнее выражение переходит в (10.30) при
р! = 0 (граница с вакуумом).
Однако внутренние волны могут возникать не только в
случае резкого скачка плотности, но и тогда, когда равновесная
плотность po(z) является непрерывной функцией вертикальной
координаты, как это и имеет место практически всегда в океане
и атмосфере. Особенно большие вертикальные градиенты
плотности в океане наблюдаются в пределах сезонного и главного
термоклинов, где и внутренние волны оказываются более всего
выраженными. Спокойная гладь моря вовсе не означает такое
же спокойствие на глубине. Там могут распространяться
внутренние волны, амплитуда вертикальных смещений частиц для
которых может достигать многих десятков метров.
39.2. Основное уравнение для внутренних волн.
Приближение Буссинеска. При выводе уравнения будем исходить из
линейных уравнений (10.11) гидродинамики несжимаемой и не-
вращающейся (£2 = 0) жидкости. Напомним, что входящие в
эти уравнения равновесная плотность и частота Вяйсяля
являются функциями только вертикальной координаты: р0(2), ^(г).
Положив v={u, до}, перепишем систему (10.11) в виде:
^ + ^ = 0, Vu = -^,
dt р0 dz
(10.46)
dt ро dz р0 ' dt \ р0 / g
Последняя легко сводится к одному уравнению относительно
вертикальной компоненты скорости частиц w. В самом деле,
исключая из первых двух уравнений и и учитывая, что V-2=
=Д_, выразим давление р через w:
Д-'=*Ц- <10-47>
Далее, применив к третьему уравнению оператор dAJdt и
подставив d(p/po)/dt из четвертого, а Д-р —из (10.47), получаем
искомое уравнение
-*-(&w+ ±**L*!L) + N*(z)A_w^0. (10.48)
dt2 \ р0 dz dz J
Здесь частота Вяйсяля равна N2(z)=—gp0~idp0/dz (см. (6.28),
где в силу несжимаемости жидкости следует положить с2->оо).
Часто, например для волн в океане, используют упрощенное
уравнение, пренебрегая в (10.48) членом, явно содержащим
202

po~ldp0/dz, по сравнению с Awt т. е.
-|^-Дш + ЛР(г)Д_а; = 0. (10.49)
Это приближение соответствует замене р0(г) в системе (10.46)
везде, кроме N2(z), на постоянную, скажем, р00=р0(0) и
называется приближением Буссинеска. Оценки показывают, что для
рассматриваемых нами ниже линейных задач теории волн это
предположение оправдывается (см. в связи с этим также
задачу 10.8). Поэтому мы также воспользуемся приближением
Буссинеска главным образом для упрощения выкладок, хотя отказ
от этого приближения принципиальных трудностей не
вызывает.
39.3. Волны в безграничной среде. Волны, описываемые
уравнением (10.49), могут распространяться и в безграничной
среде. Наиболее простой вид они имеют в случае постоянной
частоты Вяйсяля (Af2 = const). Рассмотрим для этого случая
гармонические плоские внутренние волны вида
иу = 6ехр [f(xR—(o/)] = bexp [t(kr+ft2z—©f)l, (10.50)
где x={k, kt} = {kx, kv, kz} — волновой вектор волны; о — ее
частота; Ь — амплитуда; R={r, z} = {x, у, z). Подстановка
выражения (10.50) в уравнение (10.49) дает связь между х и со —
дисперсионное соотношение для внутренних волн:
<** = №—?—<=№— = tf2sin29, (10.51)
№ + klz ха
где 8 — угол, составляемый волновым вектором х с вертикалью.
Отсюда следует, что:
1) могут существовать только волны с частотой <о<#;
2) при заданном направлении распространения волны 0
частота (о однозначно определяется соотношением (10.51), длина
волны (а значит, и ее фазовая скорость) при этом может быть
произвольной.
Совместим ось х с направлением горизонтального волнового
вектора k={£x, kv). Тогда выражение (10.50) перепишем
следующим образом:
w = Ь ехр [ I (х£—о>0 ],
где l=x sinO + zcosO; <o=N|sin6|. Поскольку w не зависит
от х, очевидно, что решением уравнения (10.49) с JV2=const
будет являться и выражение вида
w = F(l) ехр (—Ш), (10.52)
где F(l) —произвольная функция. В справедливости этого
утверждения легко убедиться прямой подстановкой (10.52) в
уравнение (10.49).
203

Таким образом, гармоническое возмущение в виде плоской
волны произвольного вида (10.52) во все моменты времени
находится в одной и той же области пространства (стоит на
месте). Этот факт может быть объяснен, если обобщить наши
рассуждения относительно групповой скорости в одномерном
случае (см. § 9) на случай зависимости частоты волны от
волнового вектора g)=iG)(x) = (o(kxy kVi kz).
Пусть при /=0 возмущение среды описывается выражением
w - F (R) ехр (Ы0Ц) = е!хр (йе0 R)] j Ь (х) exp [i (х — х0) R] Ас.
(10.53)
Если функция F(R) является медленно меняющейся по
сравнению с ехр (ix0R), то функция 6(х), характеризующая
спектральную плотность возмущения, будет быстро убывать за
пределами некоторой малой окрестности точки х = х0. В произвольный
момент времени t функция w(Rt /), являющаяся решением
некоторого уравнения для волн с дисперсией <о=<о(х) и
удовлетворяющая начальным условиям (10.53), имеет вид
оо
w(R,t) = [b (х) ехр {/ [х R — со (х) t]} dx » ехр [i (x0R — ©0f)] х
•-оо
оо
х j Ь{х) ехр {i (х — к0) [R — VM со (x) |* t]} dx,
*-oo
где cdo = co(x0). Здесь мы воспользовались разложением ю(х) =
= о)о+[Vxco(x)]xo(x—х0). Сравнивая последнее выражение для
w с (10.53), заключаем, что
o>(R, 0 =ЛЯ—Crp(xo)/]exp[/(x0R—<Оо01,
где вектор сгр, называемый групповой скоростью волны, равен
„„.„.^(„-{i.i.A.}. (Ш.54)
Мы видим, что огибающая плоской гармонической волны
^(R—crp/) сохраняет свое значение на плоскостях R—с,.р*=
s= const, перемещающихся в пространстве с групповой
скоростью.
В случае плоских внутренних волн в безграничном
пространстве непосредственный расчет для <о(х) из (10.51) приводит
к выражениям:
dk х* dk, 4s р х» \ А» )
(10.55)
204

Легко убедиться, что хсгр=о)/гг(Лг-/?г)/х2=0, т. е. сРР
перпендикулярна волновому вектору х, причем ее горизонтальная
проекция совпадает с направлением к, а вертикальная
противоположна kz (см. (10.55) и рис. 10.4).
Теперь становится очевидным, что получить
перемещающийся в пространстве волновой пакет внутренних волн можно
только в случае, когда плоская гармоническая волна модулирована
по фронту (перпендикулярно направлению распространения).
Именно в этом направлении будет перемещаться возмущение,
а следовательно, и энергия.
Для давления в плоской гармонической внутренней волне
(10.50) с учетом (10.47) получаем
, ®К
Р = — РФ -тг- ехР I* О"1 + k*z — ®01- (10-56)
Кг
При этом Vp=txp— градиент давления, параллелен
направлению распространения волны х= {k, kz).
Обращаясь теперь к первому уравнению (10.46), найдем
горизонтальную скорость частиц жидкости во внутренней волне:
u=-r—Vj> = — Ь —exp[t(kr + A>zZ— со*)]. (10.57)
кор0 k2
Тогда с учетом также (10.50) для полной скорости частиц
жидкости имеем v={u, w} = (—ktk/k2 + Vz)w. Отсюда находим
vx=uk+£zw=w(—kt+kt) =0.
Таким образом, частицы жидкости движутся в плоскости,
содержащей ось z и вектор х, по прямым линиям,
перпендикулярным х. Следовательно, внутренние волны являются
поперечными волнами.
При отражении от границы внутренняя волна имеет
интересные особенности, если плоская граница не является
горизонтальной (наклонное дно океана, рис. 10.5). При отражении от
неподвижных границ, как мы знаем, сохраняются частота
волны и проекция волнового вектора на границу. Поскольку для
внутренних волн частота однозначно определяет угол
волнового вектора с вертикалью, то здесь уже угол падения в обычном
смысле (угол волнового вектора с нормалью к границе) не
будет равен углу отражения. Волновой вектор отраженной волны
должен составлять тот же угол с вертикалью 0, что и в
падающей волне. Приравнивая проекции волновых векторов
падающей волны х и отраженной х' на границу, легко найти связь
между длинами этих векторов. Совмещая плоскость, в которой
лежат нормаль к границе и волновой вектор падающей волны,
с плоскостью чертежа (рис. 10.5), имеем
х' cos (я/2—в—-ф) =х cos (я/2—в+ф)
205

или
х' sin (в + ф) = х sin (в—-ф).
Таким образом, при отражении изменяется длина волны
(волновое число), что ничему не противоречит, так как при
данной частоте длина волны может быть любой. Интересно
также отметить, что в «падающей» волне (у которой волновой
вектор направлен к границе) энергия бежит от границы
(направление СгР), а в «отраженной», напротив, к границе.
Следовательно, правильнее было бы отраженную волну назвать
падающей и наоборот. Именно так будет происходить отражение
спектрально узких пакетов волн (обязательно модулированных
и по фронту).
§ 40. Внутренние волны в волноводе
Рассмотренные в предыдущем параграфе плоские внутренние
волны при постоянной частоте Вяйсяля представляют весьма
грубое приближение к реальным процессам. В океане, однако,
близкими к ним могут быть короткие внутренние волны, для
которых изменение частоты Вяйсяля на длине волны мало.
Существование таких волн возможно в изотермической атмосфере,
так как при этом частота Вяйсяля будет постоянной
(ро~1ф0/^2=const по уравнению гидростатики при р0/ро=const).
Однако постоянная температура атмосферы также
сравнительно редкое явление, поэтому представляется целесообразным
провести анализ внутренних волн для более реалистичной
зависимости N(z). Для океана эта зависимость схематически
представлена на рис. 10.6, а.
40.1. Качественный анализ уравнения для внутренних волн.
Итак, считая частоту Вяйсяля функцией только вертикальной
координаты z, ищем решение уравнения (10.49) в виде
гармонической волны, распространяющейся в горизонтальном
направлении:
w = 0>(z) exp [t(kr—<о*)]. (10.58)
Подставив это выражение в (10.49), получаем уравнение для
функции Ф(г):
££+#(—-0<D = O. (10.59)
В качестве граничных условий на плоской нижней границе г=
= — Н потребуем Ф(—#)=0 (абсолютно жесткое дно океана
или поверхность Земли для атмосферы). Верхнюю границу для
океана следует считать свободной с граничным условием
(10.15), которое при подстановке (10.58) переходит в условие
/4Ф_**ф\ =0 (1060)
206

В случае атмосферы в качестве второго граничного условия
можно взять условие ограниченности решения при z-*oo.
Таким же, но при z->-—оо должно быть условие для модели
бесконечно глубокого океана.
Ряд важных особенностей внутренних волн можно выявить
из качественного анализа уравнения (10.59). При заданной
частоте о решение уравнения (10.59), удовлетворяющее
граничным условиям, существует лишь при вполне определенных
значениях k=kn(со), называемых собственными значениями.
Соответствующие им решения Фп(г) называются собственными
функциями задачи. Прр подстановке собственной функции и
собственного значения в выражение для вертикальной
компоненты скорости (10.58) мы получаем нормальную волну\ или
кратко, моду. Зависимость £=&п(<о) или обратная ей <о = <йп(&)
является дисперсионным соотношением.
В случае свободной поверхности жидкости (2 = 0) в системе
нормальных волн всегда имеется мода Ф0(г) с максимальным
значением при z=0 — поверхностная мода, причем Ф0(г)
обращается в нуль только на дне океана. В случае глубокой воды
(&//»1) нетрудно убедиться, что уравнению (10.48) и условию
(10.15) удовлетворяет поверхностная волна (10.32) с
дисперсионным соотношением (10.30) при произвольной зависимости
N2(z) (задача 10.10).
Переходя к анализу внутренних волн, заметим, что в
области zz<z<zi (см. рис. 10.6, а), где a><N(z)t ф" и Ф согласно
(10.59) имеют разные знаки. Следовательно, в этой области
решение уравнения (10.59) носит осциллирующий характер, т. е.
на интервале z2<z<zt Q)(z) может один или больше раз
обратиться в нуль. Это моды различного порядка, причем обычно
приписывают моде номер, на единицу больший числа
переходов функции Ф(г) через нуль. В этом случае Фп(г)
аналогична квантовомеханической -ф-функции для частицы в
потенциальной яме. При z<z2 и z>Zi (см. рис. 10.6, а) частота волны со>
>N(z) и функции Ф", Ф согласно (10.59) имеют одинаковый
знак. Поэтому функция Ф(г) уже не является осциллирующей,
а экспоненциально убывает при удалении от z4 и z2.
Следовательно, для экспериментального наблюдения внутренних волн
следует помещать датчик в слои, где частота Вяйсяля велика,
например в термоклин в океане.
На рис. 10.6, б изображена вертикальная структура мод
трех первых номеров для профиля N(z), представленного на
рис. 10.6, а. Обратим внимание на практически равное нулю
значение всех собственных функций при z=0, хотя при расчете
предполагалось, что плоскость z=0 — свободная поверхность с
граничным условием (10.60). Этот факт обусловлен
справедливостью для внутренних волн в океане так называемого
приближения «твердой крышки» (ш|1=0=0), часто используемого в
задачах океанологии, когда исключаются поверхностные волны.
207

Пусть для некоторой моды номера п найдены дисперсионное
соотношение А=Ап(ю) и собственная функция Фп(2), Для
определенности нормированная на единицу (max|<Dn(z) | = 1). Тогда
в соответствии с (10.58) для вертикальной скорости в данной
моде имеем
wn(r, 2, /)=&пФп(г) exp [i(Kr-<ot)]. (10.61)
Далее, из общих уравнений (10.60) и (10.61) легко найти
давление в волне р„, горизонтальную скорость частиц жидкости ипэ
приращение плотности в данной точке рп, а также из
соотношения d1jdt=w — вертикальное смещение частиц жидкости
Ur,2,f):
Рп = Фо тг ь* т1 ехР Р ft*—®01»
К dz
к d<D
ия = ^6я-2-ехрр(1уг-»*Я.
(10.62)
Рп = *Р0—* Ь„ФЛ(2)е2р[1(кпг- со/)],
£, = — ЬпФп (г) exp [i (k^r — at)].
(О
Отметим, что изменение плотности в данной точке рп(г, 2, /)
можно представить в виде pn=—(dpn/dz)%n. Отсюда следует, что
плотность меняется только за счет прихода в данную точку
частиц с другой плотностью, как это и должно быть в
несжимаемой жидкости.
Аналогично тому, как это было сделано для поверхностных
волн (см. § 37), можно вычислить энергию л-й моды в столбе
жидкости от дна до поверхности с поперечными размерами в
длину волны (X=2njk) вдоль направления распространения и
единичной длины в перпендикулярном. Подробный расчет,
проведенный в задаче 10.12, показывает, что кинетическая энергия
равна потенциальной, и для полной энергии волны
справедлива формула
£Й=Д!£!\Jg<«(0)+ §№(г)Ф2п(г)йг\, ^ = Х"-
(10.63)
Естественно, что для поверхностной волны (л=0, Ф0(0) = 1) в
однородном слое (р0=const, ЛР = 0) выражение (10.63)
переходит в сумму выражений (10.33) и (10.34).
Простейшей является волна первого порядка (первая мода),
в которой согласно рис. 10.6, б все точки термоклина
смещаются при данных ги/в одну сторону, так что весь термоклин как
208

целое приобретает волнообразную форму. Если при этом
длина волны значительно превышает эффективную толщину
термоклина (zt—z2) (см. рис. 10.6, а), но все же значительна
меньше расстояния от него до границ жидкости, то для такой
волны справедливо дисперсионное соотношение (10.45).
Напомним, что последнее получено для бесконечно тонкого слоя
скачка (Zi=22=z0, N-+OQ, pa=Po(22)>Po(2i)=Pi). Волновые движе-
ния в этом случае концентрируются вблизи уровня ги z2 и
экспоненциально убывают при удалении от него (см. (10.44)).
Для оценки встречающихся на практике величин возьмем
случай двух граничащих друг с другом однородных
полупространств с типичным для океана относительным перепадом
плотности Ар/р0=(ра—pi)/pe«10"3. Тогда из (10.45) получаем для
волн с периодом 7,=2я/©=1200 с: Л=2лД= (G>7g)2p0/Ap, А,—
= 1,2 км.
40.2. Модель океанского волновода. Для иллюстрации
общих закономерностей рассмотрим следующую модель
волновода в океане (рис. 10.7). В верхнем, прилегающем к свободной
поверхности слое воды (—fti<z<0), частота Вяйсяля в котором
мала из-за перемешивания водных масс, положим Л^=0.
Область термоклина моделируется слоем жидкости (—h2<z<— ht)
с постоянной достаточно большой частотой Вяйсяля N2. В
придонном слое (—Я<2<С—h2) частоту Вяйсяля будем считать
постоянной и равной Ns<N2. Равновесная плотность жидкости
p0(z) предполагается непрерывной на границах раздела слоев:
z=— Л4 и z=— h2.
Выпишем для этого случая решение уравнения (10.59),
удовлетворяющее условию (10.60) на свободной поверхности и
обращающееся в нуль на дне (г=—Я). В приповерхностном слое
(Nt = 0) функция Ф (г) =0t(z) имеет вид
Oi (г) =at sh kz+ bi ch kz, —/i1<z<0.
Связь между постоянными ax и bt можно найти из условия
(10.60): bi^a^lgk, так что
Ol(z)=ai(shkz+bchkz), b=(^lgk. (10.64)
В области термоклина (—h2<z<—hx) общим решением
уравнения (10.59) является функция
Ф2 (г) = a2sin[ka2{z + ht)] + Ьг cos [ka^ (z + ht)]t
a2=VNl/<o*-l. (10.65)
Наконец, записав решение в придонном слое в виде
Ф3 (z) = 03sh[feag (* + #)]> «а = У1 — #>2, (10.66)
мы удовлетворим условию при z=—Н.
Потребуем теперь выполнения граничных условий на
горизонтах раздела слоев z — —ht и z=—h2y а именно равенство
209

z,
fl
■4
•4
■N
\
Ъ
&&
H2 /У
Z
-»-
Рис. 10.7
К
Рис. 10.9
нормальных скоростей w = dt,/dt и полных давлений р0+р по
обе стороны от границы. В случае непрерывной p0(z) (см.
(10.440) эти условия для функций ФДг) Х/=1, 2, 3) примут
вид:
Oi (-Ai) = Ф* (-А4), Ф/ (-/14) = Ф/ (-Л4),
Ф2 (-А2) = Ф3 (-Л2), Ф/ (-h2) = Ф,' (-А2).
Здесь, как обычно, штрихом обозначена производная по z. Под-
210
(10.67)

становка в (10.67) функций ФДг) приводит к однородной
системе уравнений относительно амплитуд ai9 b,:
(—sh pt+6 ch pi) ^ = 62, (ch pi—fi sh p1)a1=aaa1,
— aaSina + 62cosa = fl3shp3, a2 cos a + 62 sin a = 03 — chp8,
(10.68)
где введены следующие обозначения:
Pi=£fti, a=kcx>2d2l d2=hi—h2t Ps=^a3rfe,
(10.69)
d9=H—h%.
Приравнивая нулю детерминант системы уравнений
(10.68) или же просто исключая, например, величины аи Ь2 и
а3, получаем уравнение для определения собственных значений
Ыю):
[l—6thfc+a;(e — thfc)^]sina — с^х
х[б —thPx —(1 —8thp1)t-^3]cosa=0. (10.70)
Ll ae J
Если частота волны со задана (тем самым фиксированы
значения величин <х2 и аз), то, выражая из (10.69) волновое число к
через а (k=ola2d2) и подставляя последнее в рь р, и б,
получаем в результате в левой части (10.70) функцию только
переменной <т. Корни последней an(co) (л=0, 1, 2, ...) и
определяют собственные значения kn(<o) = on((o)Ju2d2.
40.3. Поверхностная мода. Условие «твердой крышки». Если
частота волн (u>Nk>Nit то в (10.70) а2 вместе с с становятся
чисто мнимыми (<t2=i]/l—N22/(u2). При этом sina=tsh|a|>
cosa=ch|a|, а уравнение (10.70) уже не будет содержать
осциллирующих по о членов. В силу этого последнее имеет
только один вещественный корень &0(о)), соответствующий
поверхностной волне. Как мы уже отмечали выше, на глубокой воде
(&0Я>1) поверхностная волна (10.32) является решением
исходной системы уравнений при произвольной зависимости N(z).
Покажем теперь, что в нашем конкретном случае и при
(o<N2 наименьший по модулю корень а0 уравнения (10.70)
соответствует поверхностной волне. Предположив, что при этом
do вместе с pt и р3 малы, разложим левую часть (10.70) в ряд
Тейлора, ограничиваясь только линейными членами:
а0—<х2 (б—pi—рз/аз) = 0.
Отсюда, подставляя выражения (10.69) и б из (10.64),
получаем обычное дисперсионное уравнение co2=gHk2 для поверхност-
211

яых волн на мелкой воде. При этом для величины а» имеем
*.-*А4-,^—-lj«.<—-в—<1.
где параметр
Be^e_J_^«^-<l. (10.71)
g р0 dz 9о ^
Здесь Др (порядка 10~3 г/см3 в реальных случаях) — перепад
равновесной плотности p0(z) в термоклине. Следовательно,
наше предположение о малости <т0 в условиях океана оказалось
справедливым. Отметим, что и условие мелкой воды выполнено:
S g
а параметр &=(u2/gk0=k0H также мал.
Собственные значения высших номеров kn(q>) (п=1, 2, ...—
внутренние моды) соответствуют значениям an>0o
(последовательные ветви tga при записи (10.70) в виде tgo=F(o)). При
этом волновые числа волн &n=an/a2d2>£o, а параметр б
становится еще более малым. Отсюда следуют два важных вывода.
1. При равных частотах внутренние волны существенно
короче (длина волны меньше) поверхностной. Следовательно,
фазовая скорость последней значительно больше фазовой
скорости внутренних волн.
2. Для внутренних волн хорошо выполняется условие
«твердой крышки» (w\z=0=0). В самом деле, если ввести амплитуду
внутренней волны в термоклине А = Уаг2+Ь22 (см. (10.65)), то
из системы (10.68) легко получить оценку для величины at:
a1«a2(ch2p1+a22 sh2 pt)-M.
При этом на свободной поверхности 2=0 из (10.64) следует,
что
O1(0)=a1a«a2(ch2p1+a22sh2p1)-M6<i4.
Справедливость условия «твердой крышки» обусловлена
тем, что пропорциональная Apg сила, приводящая к заметным
вертикальным смещениям (; внутренних слоев жидкости,
вызывает лишь незначительное смещение свободной поверхности
(~£Др/р), где совершается работа против полной силы тяжести
<~Р*).
40.4. Внутренние моды. Анализ внутренних волн в
волноводе проведем в приближении «твердой крышки», что
соответствует параметру 6, равному нулю. В частности, дисперсионное
212

уравнение (10.70), определяющее собственные значения,
примет вид
tga = F(a),F(a) = a2(thp1 + ^)(aUhp1^-l)"
(10.72)
Правая часть последнего, являющаяся функцией только а,
обращается в нуль при а=0.
Рассмотрим сначала случай достаточно высоких частот Л/г1<
<<u<N2t для которых ps = £yi— N32/cD2ds вещественно. В этом
случае при сг<1 правая часть (10.72) отрицательна, а при a-v
-►оо F(o)-+F00=a2(l+<Zs)I(а22—«s). Если a22><xs или с
учетом (10.65), (10.66)
со2 < й)а2 = N1/(2 - Nl/h 5), (10.73)
то функция F(a) имеет асимптоту о=аа, определяемую из
уравнения а\ th Pi th Ps|<T-a1=as.
На рис. 10.8 схематически изображены графики правой и
левой частей уравнения (10.72) для (о<соа (а) и со>соа (б).
Точки пересечения кривых соответствуют корням уравнения
(10.72) an(<o), определяющим собственные значения Лп(со) =
=an(co)/a2d2. К|ак видно из рисунка, значения an(co) заключены
в следующих пределах:
пп—я/2<(Тп(<й) <яя при <о>о)а или <о<о)а, но а<аа,
(л— 1)я<ап(а))<лл;—я/2 при о)<соа и а>аа.
Воспользовавшись выражениями (10.65) и (10.69), выпишем
дисперсионное соотношение (связ^ между <х> и k) для
внутренних волн в неявной форме
&=Nl А \—. (10.74)
Отсюда заключаем, что при &->оо (короткие волны) <u->N29 т. е.
частоты всех внутренних мод становятся близки к
максимальной частоте Вяйсяля. При этом правая часть уравнения (10.72)
всегда мала (F(o) ~ос2<1) и оп-+гт,.
Собственные функции Ф(г) в области частот N9<co<N2
достигают максимального значения в термоклине, а при удалении
от него экспоненциально убывают (см. (10.64) и (10.66) при
6 = 0), причем скорость убывания растет с увеличением
частоты, т. е. на высоких частотах внутренние волны сосредоточены
в термоклине.
В области низких частот (g><Ns) параметр a,=yi—-М37со2
вместе с ра становится чисто мнимым. Следовательно, в
выражении (10.66) sh[ka3(z+H)] переходит в i sin [k\as\ (z+H)]
213

и собственная функция Ф(г) становится осциллирующей и при
z<—h2. В дисперсионном уравнении (10.72) следует также
положить thps=*tg |р3|, так что его правая часть уже будет
осциллирующей функцией а. Мы ограничимся анализом случая
очень низких частот (<о-*0) (гидростатическое приближение).
При этом «г^Л/г/оэ-^оо, <х8»iNJiur+oo, но параметр o=kN2d2l(u
остается конечным, следовательно, k=(?(u/d2N2-+0. Тогда а=
=Л^2/сф, ^z = iN^dJc^=ioNMN2d2i где сф=со/£ — фазовая
скорость волн. Переписав теперь дисперсионное уравнение (10.72)
в виде
tga=(tfA + c*tg |M)/(tfAtg 1М-СфВДГ2), (10.75)
заметим, что последнее зависит только от сф и не зависит от
частоты. Это означает, что на низких частотах фазовые
скорости внутренних мод, являющиеся корнями уравнения (10.75),
не зависят от частоты, т. е. низкочастотные внутренние волны
в волноводе распространяются без дисперсии (<о= (сф)ЛЛ).
Собственные функции Ф(г) на низких частотах в верхнем
слое (—hi<z<0) будут линейно убывать при удалении от
границы термоклина вплоть до нуля при z=0. Однако в слое ниже
термоклина амплитуда внутренней волны может быть
сравнима с ее амплитудой в термоклине. Более того, при Nsds>N2d2
(IM>cj), как это обычно наблюдается в условиях океана,
первая внутренняя мода будет иметь максимальную амплитуду в
слое ниже термоклина.
Проведенный анализ позволяет схематически представить
ход дисперсионных кривых системы поверхностной (я = 0) и
внутренних (1—3) волн в океане (рис. 10.9). Можно показать,
что в общем случае произвольной N(z) (см. задачу 10.17)
каждая дисперсионная кривая является монотонно возрастающей
(d(oldk=cTV>0). В области низких частот дисперсионные
кривые линейны с уменьшающимся при увеличении номера моды
наклоном. Отметим, однако, что в реальных условиях океана на
частотах, сравнимых с частотой вращения Земли, ход
дисперсионных кривых будет иным (см. гл. 11).
Отметим /также, что в случае волн в атмосфере в качестве
модельной задачи лучше было бы взять неограниченный в
положительном направлении слой z>—At с отличной от нуля
частотой Вяйсяля (Ni<N2). При этом волноводные моды
(захваченные волны) возможны только на частотах <о>Л^. На более
низких частотах в верхнем слое атмосферы могут существовать
не захваченные волноводом распространяющиеся волны, в
частности гармонические плоские волны. В этом случае из области
возбуждения (обычно низкие слои атмосферы) энергия будет
уходить вверх.
214

Задачи
10.1. Пусть при *=0 возбуждается спектрально-узкий пакет
гравитационных поверхностных волн на глубокой воде, содержащий N>1 периодов
колебаний частотой о)0, модулированный медленно меняющейся функцией времени:
w\x-o=F(t)exp(—«DoO, ^(0=0 при *<0 и />Г=2яЛ7<о0. Определить: а) число
гребней волн Ni на поверхности, которое увидит неподвижный наблюдатель;
б) сколько колебаний #2 совершит наблюдатель, находящийся в лодке при
прохождении данного волнового пакета.
Решение. Пакет волн распространяется с групповой скоростью, т. е.
w(x, t)=F(t—x/crp)exp[i(k0x—(a0t)]t k0=(oQ2lg. Для стороннего наблюдателя
в момент времени t пакет будет занимать в пространстве интервал длиной
L = Tcrpt на котором уложится число волн Ni = Lkol2n—TkoCTpl2n=
=2я(ЛГ/юо)£оСгр/2я=М:гр/Сф. Но так как для волн на глубокой воде сгр=Сф/2,
то Ni = N/2. Для наблюдателя, находящегося в лодке в точке х, время
прохождения пакета волн равно Г, за которое лодка совершит N2=Ta)ol2n=N
колебаний.
10.2. В каком случае наблюдатель с берега реки со скоростью течения а0
может увидеть неподвижную стоячую волну (со=0) с гребнями поперек русла.
Решение. Форму свободной поверхности, имеющую вид стоячей волны
для неподвижного наблюдателя, можно записать таким образом:
а
£ = a cos kx exp (— Ш) = -т {exp [i (kx — со*)] + exp [— (kx + at)]}.
В системе координат, связанной с движущейся водой jc'=x—»0^» имеем
£«- — {ехр [*(**' — со^)]+ехр[—i(kx'+to%t)])t со^=.со — kv0> ®%=*<o+ko9.
Но в этой системе координат должно выполняться обычное дисперсионное
соотношение для волн (со—kv0)2=gk= (со+£у0)2» что возможно только при
о)=0 и k—g/vo2. При этом £=acos (gxlv02)=acos [k(x,+Vot)].
Таким образом, в неподвижной относительно воды системе координат мы
имеем бегущую со скоростью течения навстречу ему волну, которая для
наблюдателя на берегу соответствует неподвижной (со=0) возмущенной
свободной поверхности с пространственным периодом возмущения 2n/k=2nvo2fg.
10.3. Показать, что в бегущей поверхностной волне центр тяжести «всей»
жидкости остается на одной глубине, а в стоячей совершает колебания с
удвоенной частотой.
Решение. В состоянии покоя (£=0) центр тяжести жидкости
находится на уровне г0=—Н/2 (см1, рис. 10.1). Рассчитаем вертикальное смещение
центра тяжести Az столба жидкости шириной в длину волны А, при £#0. По
определению центра тяжести имеем
\dx Г (z — z0 — Az)dz = 0.
о *-н
Отсюда интегрированием с учетом периодичности u f £dx = 0 ) находим, что
А«=(2//Л)"1Г Qdz. Для бегущей волны £=acos (kx—mt) получаем Az=
о
= аг/4Н, для стоячей t=a cos kx cos cof имеем Az=a2(l+coe 2co/)/8#.
215

10.4. Найти волновое поле при отражении гармонической гравитационно*
капиллярной волны от абсолютно жесткой вертикальной стенки.
Решение. Пусть стенка расположена перпендикулярно оси х при х=0.
Запишем падающую волну в виде (10.17) с Ф(г) из (10.18):
ш+ » М> (г) ехр [/ (V + V - «М-
где а) и £=У&*2+£у2 удовлетворяют дисперсионному соотношению (10.39).
При отражении волны сохраняются ее частота о) (волновое число k) и
проекция волнового вектора kv на границу, так что для отраженной волны получаем
ш. - VW> (г) ехр [I (- V + kyy - со/)],
где V—коэффициент отражения. На жесткой стенке обращается в нуль
нормальная составляющая скорости частиц и», для которой в соответствии с
формулой (10.24), справедливой также и для гравитационно-капиллярных волн,
имеем:
К
(и+)х «= i — W>' (ж) ехр [/ (hjc + k^ - со*)],
kx
(ujx- - / — VW (г) ехр [I (- ^ + ^ - Ш)].
Приравнивая сумму (и+)х+(м-)« нулю при ж=0, находим V=l.
Следовательно, полное волновое поле для х<0 будет
ш ■* ю+ + tfL. в= 26Ф (z) cos Л^хехр [* (fc^ — со*)].
В случае нормального падения волны на стенку (Ау=0) получаем стоячую
поверхностную волну.
10.5. Определить частоты собственных колебаний несжимаемой жидкости
в бассейне глубиной И с прямоугольным горизонтальным сечением длиной L
и шириной D. Стенки бассейна жесткие. Найти наименьшую частоту колебаний.
Решение. Общим гармоническим решением уравнения (10.14) для волн
в бассейне будет функция t»=bO(z)exp(—Ш){(х,у), где f(xty) —
комбинация экспонент вида exp[i(±kxx±kvy)], a>2=g£th£#. Но в предыдущей задаче
показано, что коэффициент отражения поверхностных волн от вертикальных
жестких границ равен единице. Следовательно, w{x, у, z, t) будет иметь вид
стоячих волн как по х, так и по у. При этом, если положить /(*,#)==
=cos£xxcos£yi/, то нормальные к стенкам бассейна х=0 и у=0
составляющие скорости частиц ux = k-2d2w/dxdz и uv=k~2d2wldydz обратятся в нуль.
Потребовав, чтобы эти скорости обращались в нуль на противоположных стенках
их\ХятЬ=0 и uy\VmmD=0, получаем соответственно sinfcxL=0, {kx)n=nn/L
(п=0, 1, 2, ...) и sinkvD=0t (ky)m=mnlD (m=0, 1, 2, ...). Отсюда для
волновых векторов и частот собственных колебаний имеем:
Положив для определенности L>Dt найдем наименьшую частоту co^in = ^Jo e
= (gn/L)th(nHIL) Ofemin=fcio=Ji/L). Например, для #=40 м, L=l км
находим fmln^lO"2 ГЦ.
216

10.6. Получить дисперсионное уравнение для волн в жидком слое
толщиной Я, состоящем из двух жидкостей с плотностями pi и р2, граничащих на
глубине Л. Верхнюю границу слоя (z=0) считать свободной, нижнюю (z=
= —Я) — абсолютно жесткой.
Решение. Ищем решение уравнения (10.14) в виде а>=Ф(;г)ехр[/(кг—
—©01, где функция Ф(г) удовлетворяет уравнению Ф"—£2Ф=0. При —Л<
<z<0 и —Я<2<—h запишем общее решение последнего уравнения в виде:
OiW^bishkz+Cichkz, <b2(z)=b2shk(z+H)
соответственно. При этом Ф2(—Я)=0. На свободной границе (z=0) функция
Ф! удовлетворяет условию (Ф/—gfc^i/w2)z-o=0. Отсюда имеем связь между
постоянными Ь\ и C\i b\=gkc\lto2. Условия для Ф1 и Ф2 на границе раздела
следуют из условий (10.44'):
Ф1(-Л)=Ф2(-А), ^2ApФi(-Л) = (D2[p2Ф2/(-A)-p1Фl,(-/i)], /-1, 2,
Ар«р2—pi.
Отсюда получаем связь между постоянными Ь\у С\ и Ь2:
—blshkh+clchkh=b2shkdi d=H—h,
gk2&pb2shkd=(d2(p2b2chkd—piblchkh+plclshkh)k.
С учетом bi=gkci/<u2 находим
aPshkd shkd w*
Cl1=S(^chkh-gkshkh a = chM tf-gkthkh 2
и дисперсионное уравнение для волн в слое
(a*-gkthkh)(b>2- — gkth kd)=, — (i>*\hkd(gk-Gfith
\ Pa /Pa
10.7. Провести анализ дисперсионного уравнения предыдущей задачи,
рассмотрев частные случаи: а) £Л»1, Ы>1; б) Др/ра<1.
Решение. Исходное дисперсионное уравнение является квадратным
относительно о2. Следовательно, оно содержит две ветви дисперсионных кривых:
соо=*)о(£) и coi = coi(&). В случае «а», положив thkh^thkd=\t легко находим
©о2 =sgk — поверхностная волна на глубокой воде и ©i2=Ap^/(pi+p2)
—волна на границе раздела двух сред. В случае «б» (pi«P2=Po) выпишем явный
вид уравнения для со2
{l+thkhthkd)e>*—gk(thkh+thkd)^2+g2k2(AplpQ)thkhthkd=^0 и его корни
Разложив квадратный корень в ряд Тейлора, получаем: (Oo2=gkthkH —
поверхностная волна в слое и
со? » — gk (cth М + cth kdr1 (10.76)
Ре
— внутренняя волна на разделяющей поверхности с учетом границ z=0 и
2=— Я.
10.8. Получить дисперсионное соотношение для плоских внутренних волн
в жидкости с постоянной частотой Вяйсяля, не обращаясь к приближению
Буссинеска. Установить критерий применимости последнего в этом случае.
217
kh).

Решение. Будем искать решение уравнения (10.48) с N2=—£Ро_1Фо/
/dz=const в виде гармонической волны w = b<D(z)exp{i(kr—©/)}, k={kXt kv}>
г={дс, у). Подставив это выражение в (10.48), получаем
Ф"—2цФ'+ (Л^2/о>2— 1)#Ф=0, [i=N2/2g.
Исключая Ф' подстановкой Ф=ехр(цг)ф, находим
ф"+ [(ЛГ2/ю2-1)*2-ц2]ф=0,
решением которого будет функция ф(г) = bexp(iktz)t где £г2= (ЛР/ю*— l)k2—ц*.
В результате мы получили решение уравнения (10.48) в виде плоской
гармонической волны
ьу(г, z, t) = be»*exp {i(xR—со/)}, и={к, *«}. R=(r. *}
с дисперсионным соотношением G)2=iV2fc2/(x2+|j,2). Последнее будет совпадать
с (10.51) в приближении Буссинеска, если можно пренебречь величиной
V?= (Ny2g)2=[(2p0)-ldp0/dz]2 по сравнению сх2, т. е. прих> | (2p0)-ldpoldz\t
что и будет критерием применимости приближения Буссинеска для линейных
внутренних волн. В океане это условие выполняется для внутренних волн с
длиной до нескольких сотен километров.
10.9. Найти направление групповой скорости для волн с дисперсионным
соотношением, полученным в задаче 10.8.
Решение. Вычислим сгр= {(d(d/dk)k/k, dmjdki}, используя
дисперсионное соотношение (D = J/V&(x2+n2)~"1/*:
д(о/дк=Ы(х2+\12Гч* (kt2+v2), d<o/dkt=—N(7i2+\i2r9/*kkz.
Представим сгр в виде сгр=Ах+Ац, где \±=(NkzlK2)(H2+[i2)~^t (ktk/k—
—kVz) — вектор, перпендикулярный направлению распространения волны х,
а Ац= (^/х)(х2+|л2)"8/* |и2х/х — параллельный. Если теперь обозначить через
а угол между вектором групповой скорости сгр и нормалью к х (равный нулю
в приближении Буссинеска согласно п. 39.3), то для а получаем tga«
= |Лц/Л_|_| = kk~1\i2(x2+\i2)~~l. Угол а может быть велик, если волна
распространяется в направлении, близком к горизонтальному (&х«0). Вектор груп*
повой скорости за счет А\\ оказывается не малым, в то время как вычисленный
по (10.55) в приближении Буссинеска он мал. Отметим также, что слабо
модулированный в направлении распространения волновой пакет будет в отличие
от расчета в приближении Буссинеска медленно двигаться в направлении Хо
со скоростью перемещения огибающей, равной
| Лц| = (Nk/x) (х2+ц2Г8/» ц2=сфц2/(х2+|^2), сф=(о/х.
10.10. Показать, что волновое решение в виде поверхностной волны в
однородной (р0 = const) бесконечно глубокой жидкости удовлетворяет
уравнению для внутренних волн (10.48) и граничному условию (10.15) при
произвольной зависимости N(z).
Решение. Непосредственной подстановкой в (10.48) выражения для
ловерхностной волны t0 = exp(fcz)exp[t(kr—tot)], a)2=g&, получаем тождество
( [ N2 (г) 1 1 N2 (г)
_ о* _ k2 + #» - —— k - N2 (z) k2 \ w = —— k (a* - gk) w = 0.
218

Таким образом, уравнение удовлетворяется. Аналогично проверяется и
граничное условие
(-
_ш] «=» - *»
gb_w) «=» — k* (tf — gfyw^ = 0.
10.11. Найти наименьший корень 0\ (первая внутренняя мода)
дисперсионного уравнения (10.72) при условии, что нижний слой однороден (ЛГ8=0) и
толщина среднего слоя dr+0 (W^2 при этом остается постоянной).
Установить, в каких случаях слой конечной толщины d2 можно заменить резкой
границей раздела жидкостей с разной плотностью.
Решение. При ЛГ3=0 из (10.66) и (10.69) имеем Оз=1, Рз=&*з.
Дисперсионное уравнение (10.72), которое в этом случае удобнее анализировать
при фиксированном волновом числе &, перепишем в виде
f„ ua thpt + thPa
iga=afcd,a,thMhpg_^.
При dr+О наименьший корень этого уравнения будет также стремиться к нулю
(МЛ)-*0). Тогда, разложив функцию tg<x в ряд и ограничиваясь лишь
главным членом, получаем ^«/^(cthPi + cthPa). С учетом выражения (10.69) для
а находим дисперсионное соотношение первой внутренней моды a>i2(fc) =
=^22^2(cthPi+cthp3)""1. Далее, воспользовавшись выражением для N22, в
пределе при dz-+0 получим N22d2=—gp0~l(dp0ldz)d2-+gAplp0t где Др=—(dp0/
ldz)d2=ps—Pi — разность плотностей жидкости на нижней и верхней границах
термоклина. В результате имеем формулу
©i2(A;)=^(Ap/po)A;(cthpl + cthp3)-1,
аналогичную дисперсионному соотношению для волн на границе раздела
(10.76) (см. задачу 10.7). Если d2 будет малой, но конечной величиной, то для
справедливости последней формулы следует потребовать малости корня o*i (k).
Это будет, как легко видеть из разложения для o*i2, в случае, если: а) kd2<^\
(d2X4Z\) —толщина слоя мала по сравнению с длиной волны; б) kd2/$i =
= d2//*i<l и Ыг/Рз=^2/^з<1 —толщина неоднородного слоя мала по
сравнению с толщинами однородных слоев. При выполнении этих условий
неоднородный слой конечной толщины можно заменить резкой границей раздела, если
интересоваться только первой внутренней модой. Для высших мод такой
переход невозможен.
10.12. Вычислить энергию я-й моды в столбе жидкости от дна до
поверхности с поперечными размерами в длину волны вдоль направления
распространения и единичной длины в перпендикулярном.
Решение. Для кинетической энергии, совместив ось х с направлением
к
распространения, имеем ЕК =» -*~ \ v2dxdz, y2=|u|2+w2. Воспользовавшись
о
вещественными частями выражений для ииш (см. (10.61) и (10.62)) и
интегрируя по х, получаем
£« - -г1'К)? IN+~k (0,;),j dZt
219

Это выражение, проинтегрировав второе слагаемое по частям и учтя условие
(10.60), можно записать и в таком виде:
V
^^Г*п «OJ(0)+ |л"(*)Ф;|(1)А . (10.77)
Обращаясь к вычислению потенциальной энергии, заметим, что ее плот*
ность 8П можно определить как работу в поле архимедовых сил, затрачиваемую
на перемещение частицы жидкости с горизонта z—£ на горизонт z. В силу
2
несжимаемости жидкости имеем еп = # I [po(;z—£)-^Ро (£)]<*£» где р0(г—Е) —
масса единицы объема перемещаемой частицы; р0(£) —масса вытесненной ею
жидкости. Разложив подынтегральное выражение в ряд Тейлора по перемен*
ной g—z+£ и интегрируя, получаем
— 2 „ " 2
Здесь р=—fytpoldz — изменение плотности среды в точке г. Потенциальная
энергия л-й моды теперь будет равна
£--11 1е-А|&.
А /Се 0 ч
о \о -Я /
где £>=£(*, #, 0, /) —смещение свободной поверхности жидкости. При
вычислении первого интеграла по z заметим, что изменение плотности в окрестности
свободной поверхности равно р0(0) н £=z. Поэтому, так же как для
поверхностных волн,
J
р№=--~Ро(0)^.
Подставляя теперь в выражение для Еп вещественные части £nt Рп и £по из
(10.62) и интегрируя по х, получаем для потенциальной энергии моды
выражение, полностью совпадающее с выражением для кинетической энергии
(10.77). Полная энергия волны равна сумме выражений для Ек и £_:
Еп
у -^Г Л„ «Ф» (0) + JiV» (г) Ф* (i) „ (10.78)
Естественно, что для поверхностной волны (л=0, ф0(0) = 1) в случае
однородного слоя (p0=const, N2=0) выражения для Ек и Еп совпадают с (10.33).
10.13. Определить коэффициенты отражения и прохождения при падении
плоской гармонической внутренней волны на горизонтальную границу раздела
двух жидкостей с частотами Вяйсяля N\ и Na. Плотность при переходе через
границу считать непрерывной.
220

Решение. При отражении сохраняются частота волны о и проекция
волнового вектора на границу, поэтому волновые поля в средах, откуда падает
волна (z<0) и куда она проходит (z>0), имеют вид
и>х = Ь exp[i{kx+kizz—®t)]+bVexp[i(kx—kuz—<ot)], z<0,
(o2=bWexp[i(kx+k2zZ—<nt)]t z>0. (10.79)
Частота внутренней волны определяется только углом волнового вектора с
вертикалью 9j, следовательно, (d = N\ sin 81=^2 sin О2, ^и^ЛУ^,2/©2—1, fe*=
=^уЛГ22/со2— 1. Коэффициенты отражения V и прохождения W найдем из
граничных условий, которыми будут равенства вертикальных скоростей и
волновых давлений (см. (10.13)):
(Щ - ttbWo - 0, А_рг |2=0 - р0 (0) (Pwjdtdz)^ =
- Л-Л Ufb Ро (0) (PWildtdz)^.
Отсюда с учетом (10.79) получаем систему уравнений для V и W: \ + V=W>.
Лц(1—V)=k2iWt из которой легко находим:
Кг - Кг УЫ\-&- УК-<*% 2kU
" - ■ — w
10.14. Найти аналогичные задаче 10.13 коэффициенты V и W, считая ча~
стоты Вяйсяля в средах одинаковыми (Ni=N2=N)t но плотности pi и р^
(pi>p2) разными.
Решение. В этом случае в выражениях (10.79) следует положить.
kiz=k2z=kz==yN2l(u2—lk (угол преломления равен углу падения). Условие
равенства вертикальных скоростей на границе сохраняется. Второе граничное-
условие изменится. В самом деле, приравнивая полные давления на границе,
получаем Рю(0)—Pig£+Pi|z-o=P2o(0) —p2g£+P2U-o. Отсюда с учетом*
wl\l-(i=dtjdt, Рю(0)=Р2о(0), &-pj = pjd2Wjldtdz имеем
р* (-*д^+-**)_-р> г**-"* ~^L-
Подставляя в граничные условия выражения для wx и w2 находим:
1 + V = W, — pi£*a.(l + V) + рхО)*^ (1 - V) = - ptfPW + №*ibzW.
И окончательно для V и W получаем (Ap=pi—р2):
(to VN2 - со* — gk) Ар w _ 2tp!Q V N2 — (о*
~ (Pi + p2) ^ /tf2 — coa + Apg* (pi + pa) to ^iV*-(o»+ Apgfc "
Естественно, что при непрерывной р0(г) (Ap=0) V=0, W=l.
10.16. Из результатов задачи 10.14 получить волну, сосредоточенную ъ
окрестности скачка плотностью Ар между двумя жидкостями с равными
частотами Вяйсяля.
221

Решение. Интересующая нас волна соответствует чисто мнимым
значениям kg=±l\kz\=±:ty<u2—N2/(ot т. е. ее частота (0>N. Выберем в обеих
средах kt=i\kz\ и воспользуемся выражениями для wx и w2, выписанными в
предыдущей задаче. Тогда
ш, = Ь[ехр(— |k|z) + Vexp(|fcz|z)]exp[t(kr—©f)], z<0,
го2=ЫРехр(— |Лх|г)ехр[|(кг—©/)], z>0.
Таким выбором знака kz мы обеспечили экспоненциальное убывание при
z->±oo членов, пропорциональных bV и &Н7. Однако первый член в ха>\ дает
-бесконечное поле при z->—оо. Мы исключим это, положив 6=0, но bV и MP
конечными, т. е. V и № бесконечными. Приравнивая знаменатель выражения
для V в задаче 10.14 нулю при kt=i\kz\t найдем дисперсионное соотношение
<оУсо2—Л^2=Др^/(р1+р2). Если разрешить это уравнение относительно ©,
получится явная форма дисперсионного соотношения ®2(k) =V[Apgik/(pi+P2)]2+
+#4/4+#2/2, которое при N=0 переходит в (10.45).
10.16. Получить условия ортогональности собственных функций
внутренних мод в волноводе при различных собственных значениях.
Решение. Собственная функция Фп(г) удовлетворяет уравнению
<Dn"+£2(#2/<0n2— 1)ФП = 0 и граничным условиям Фп(—#) = (ФП'—gk2/
/о)Л2)г=о. Умножив уравнение для Фп на собственную функцию Фт,
проинтегрируем полученное выражение по z от —Н до нуля. После интегрирования
о
члена I Ф*Ф dz 2 раза по частям получаем выражение
Ji
о о
фтфл' \°-Н ~ <">„<. 1-Я + J ФЯФ> + *» j (J - 0 ФяФт* = 0-
-я -я "
Поскольку Фт(г) удовлетворяет таким же, как и Фп(г), уравнению и
граничным условиям, но с ют2, то при подстановке в последнее выражение фп/(0) =
= (£*7<Оп2)Фп(0), Фт,(0) = (^2/0)т2)Фш(0), Фт(-Я) =ФЯ (-Я) =0 И
Фт" = -k2{N2/tom2— 1)Фт НЗХОДИМ
**1(^"""4) ф«<°>ф«<°>+|у ф»«^^
Для различных значений о)п2=:0)т2 отсюда следует равенство нулю
выражений в квадратных скобках, что является условием ортогональности
собственных функций ФЛ(г) и d>m(z). Нормируя последние таким образом, что при
п=т выражение в квадратных скобках было равно единице, запишем условие
юртонормированности собственных функций в виде
о
Ф„ (0) Фт (0) + Г1 f № (г) Ф„ (г) Фт (г) dz = 6^, (10.80)
где бпт — символ Кронекера. При такой нормировке выражение (10.78) для
лолной энергии (см. задачу 10.12) записывается в виде £„=peg|&n|aA,n/2<Dn2=
=Pogkn|an|2/2, где an=ibnla>n — амплитуда вертикальных смещений.
222

10.17. Получить выражение для групповой скорости внутренних волн *
жидком слое через интеграл от собственной функции ФЛ(г) и доказать, что
дисперсионные кривые wn(k) монотонно растут с увеличением к.
Решение. Обратимся еще раз к краевой задаче для функции <S>n(z)t
которая зависит также и от Р=£2:
Ф; (I, Р) + Р {№ (*)/afi (P)J - 1} Ф„ (*, Р) = 0,
фп (- Я, Р) = Ф; (0, Р) - teP/co* (Р)] фп (0, Р) « 0.
Наряду с Фп(2, Р) рассмотрим функцию Fn(z, Р)=дФп(г, Р)/др
(производная от собственной функции по спектральному параметру), которая является
решением краевой задачи, получающейся дифференцированием по р уравнения?
и граничных условий для Фп(г, Р):
<.+.(Н'.~(5--5,2К
f„(-//,P) = 0, F>.»=-^- Fn(0,P)+*(-^- ±.^.]фп(0,Р)..
Проведя процедуру, аналогичную использованной в задаче 10.16 (умножение
уравнения для Fn на Фп, интегрирование от —Я до нуля по 2, интегрирование
по частям и подстановка Фп/|г=о, я из граничных условий и Фп"(2) из
уравнения) , и группируя члены с d<on2/d$t находим
|- *Ф* (0) + JiWjif М^ = *Ф£ (0) + J (ЛР - а>*) Ф*<
Производную da>n2/dp легко выразить через групповую скорость я-й моды
(сГр)«. В самом деле, d(j>n2/d$=2(i>n.{dG>n[dk)dkld$=(un (сгр)n/k= (сф) п (£ГР) п,.
где (Сф) п — фазовая скорость волны. В результате выражение для групповой
скорости внутренней волны /i-й моды будет иметь вид
о
(«ip)« ~ (*ф)п — (10-81)
• «oj(0)+Jiw;*
-я
Это выражение можно представить и в несколько ином виде, если,
воспользовавшись уравнением для Фп(г), записать (N2—о)Л2)Фп=— (йп2Фп"1к2 и про-
интегрировать по частям:
о о
2 2 ° 8 °
-я -н
223

U U
Проведя такую процедуру и в интеграле знаменателя Г №<D*dz =» f (N* —
-я -я
о
— ©*) Ojdz + o* Г Ojrfz, получим
V» - (СФ>* — ; (»0.8Г)
-я -я
Отсюда непосредственно следует неравенство 0<(сГр)п<(сф)п, т. е.
групповая скорость всегда положительна и меньше фазовой скорости внутренней
волны. В силу первого условия (cTV)n=d<£>n/dk>0 имеем монотонный рост
дисперсионных кривых <1>п = со„(й). Поскольку
d d (о\ с -u/k 1
dk** dk\k)~ k А^гр-"Ф'
то фазовая скорость моды убывает с ростом &.
Глава 11
ВОЛНЫ ВО ВРАЩАЮЩЕЙСЯ ЖИДКОСТИ
В гл. 10 были рассмотрены гравитационные волны в жидкости,
имеющие большое значение в динамике океана и атмосферы.
Важную роль в атмосферных и океанских процессах играют
волны, связанные с вращением Земли. Этим волнам, а также
влиянию вращения Земли на гравитационные волны и будет по-
-священа настоящая глава.
В системе координат, связанной с вращающейся как целое
с постоянной угловой скоростью 12 жидкостью, на частицы,
движущиеся со скоростью v, действует сила КориоЛиса —2mQXv
(m — масса частицы). Эта сила нормальна к v, и ее
воздействие на жидкую частицу аналогично действию силы Лоренца на
электрон в магнитном поле (e/c)Hxv. При этом возникает
дополнительное движение частицы по окружности. В сплошной
среде частицы жидкости не могут двигаться независимо.
Взаимодействие между ними приводит к возникновению градиента
давления в среде. Совместное действие силы Кориолиса и
градиента давления и приводит к возникновению волновых
движений.
Вначале мы рассмотрим простейшие инерционные волны во
вращающейся жидкости. Затем изучим совместно внутренние и
224

инерционные волны, называемые также
гравитационно-гироскопическими волнами. Завершается глава исследованием волн
Россби, особо важных для глобальных процессов в океане и
атмосфере.
§41. Инерционные (гироскопические) волны
41.1. Уравнение для волн в однородной вращающейся
жидкости. В линейном случае интересующие нас волны в
несжимаемой вращающейся жидкости описываются линейной системой
уравнений гидродинамики (10.11). Для того чтобы исключить
другие возможные волны, запишем эту систему уравнений для
однородной (р0 = const, TV2=0), вращающейся с постоянной
угловой скоростью Я жидкости:
iL + Z£. + 2axv = 0, i£=0, Vv=0. (11.1)
dt po dt
Направим ось z системы координат параллельно вектору Q,
тогда 2QXv={—Fv, Fu, 0}, где v={u, и, w}\ f=2Q — параметр
Кориолиса. Запишем систему (11.1) по компонентам:
(11.2)
Получим из этой системы уравнение для вертикальной
компоненты скорости частиц жидкости w. Для этого, действуя на
первое уравнение системы оператором д/дх, на второе — д/ду,
складывая полученные выражения и учитывая четвертое
уравнение (11.2), находим
dt ре дх
dt p0 dz
= 0, -£ + Fu+-LfL
dt po dy
du , dv __ dw
dx dy dz
= 0
1 a / \ d*w . j?( dv du\
Наоборот, действуя на первое уравнение (11.2) оператором
д/ду, на второе — д/дх и вычитая, получаем
d fdv du\ __рдш
dt [dx dy)~~ dz
Теперь уже не составляет труда найти
I л д , ч / д* , V2\ dw А du I аа , Р d \ dw
(11.3)
" dt \
dtdy дх) dz
и получить искомое уравнение
JLto + pZL^O, AsA_ + -|L. (11.4)
dt2 dz2 dz2
8 Л. M. Бреховских, В. В. Гончаров 225

Волновые решения, удовлетворяющие этому уравнению,
называются инерционными или гироскопическими волнами во
вращающейся жидкости.
41.2. Плоские гармонические инерционные волны. Если
подставить в (11.4) решение в виде гармонической плоской волны
w = b exp[f(xR—<ut)] = bexp[i(kr+ktz—Ы)]> (11.5)
то легко получается дисперсионное соотношение для волн
k2 k2
со2 = F г— =Р-1 = fac0S2 0 (11.6)
*» + *; *2
где Э — угол волнового вектора х с вертикалью
(направлением вектора угловой скорости Q). Таким образом, как и в
случае плоских внутренних волн, для данной частоты фиксирован
угол 0. Длина волны при этом может быть произвольной.
Частота инерционной волны не может превышать величину F=2Q—
удвоенную частоту вращения жидкости. Для групповой
скорости волн crv=V^={{da)/dk)k/kt dw/dk,} находим ды/дЬ —
= — (D&/x2, d(uldkt = Fk2lK* и
С—2-i + ^V, (п.-п
XX X
3
или, учитывая формулу k = x—ktVz и вводя Q = FVz/2,
со х . 20 /11 т/\
сгр= 1 (И.7')
XX X
Групповая скорость нормальна направлению распространения
волны х (сгрх = 0), но в отличие от внутренних волн ее
горизонтальная проекция (а не вертикальная) противоположна
соответствующей проекции вектора х (рис. 11.1). Аналогия с
внутренними волнами сохраняется и при отражении от границ:
волновой вектор х' отраженной волны должен составлять с
вертикалью (направлением Q) тот же угол, что и волновой вектор х
падающей волны. Длина волны в общем случае произвольного
наклона границы меняется при отражении.
Движение частиц жидкости в инерционных волнах будет
отличным от их движения во внутренних. Напомним, что в
последних частицы двигались по прямым линиям,
перпендикулярным волновому вектору и лежащим в плоскости, содержащей х
и ось z. Для волны (11.5), воспользовавшись (11.3), найдем
горизонтальные компоненты скорости:
«-_£(*,+ /£*,)«. v = -±-(ky-iLkx)w. (11.8)
Непосредственной проверкой получаем, что v={u, v, ш}±х.
226

Рис. 11.2
Н
Si
I
1 F
i
i
i
i
i
i
r-i—-
to
1
1
1
1
1 "
V
1 ^*
1 ^—
*m
\ Л
(Ok
Рис. 11.3
(л /70#е/?а;я0стяая
Лаляа
РисЛМ
F
Wni,n
" гпьп
Рис. 11.5
Рис. 11.6
/700е/и7//0£тная
f0 fojwa
2 00S7//&/
00S7ffZ>/
00У7//Ы /fyttfa, W0.
Рис. 11.7
227

Действительно,
xv = kxu + kyU -f kzw =
\ k* © k* k* © & )
Без ограничения общности можно положить kv=0 (kx=k).
Кроме того, в (11.5) положим b=Bexp (to), *|> = fe«x+fefz—о)/+а.
Тогда для вещественных частей (11.5) и (11.8), которые
только и имеют смысл, будем иметь:
k k f k
и = £-w = -5cosi|\ v = -Bsino|), w=Bcosty.
k k 0) k
Теперь легко видеть, что
va = и2 + V2 + W2 =
(k2 F2 k1 \ к2
-J- cos2 ф + — -j- sin2 ф + cos2i|) I Б2 = -£ В2 = const.
Здесь мы также использовали дисперсионное соотношение
(11.6).
Таким образом, частицы жидкости в инерционной волне
движутся с постоянной скоростью. Учитывая также
периодичность процесса с частотой <о, можно заключить, что траектории
частиц — окружности во фронтальной плоскости
(перпендикулярной х радиусом A = yiB/iok (Лсо=|у|). Причем во всей
фронтальной плоскости движение синфазно, т. е. вся плоскость
движется как единое целое (без деформаций) и таким образом,
чтобы траектория каждой ее точки была окружностью.
Различные фронтальные плоскости имеют разные фазы движения,
поэтому в жидкости возникает градиент давления, естественно,
направленный по х (Vp~x).
Рассмотрим баланс сил и ускорение частиц в инерционной
волне. Вектор ускорения каждой жидкой частицы ацс
(центростремительное ускорение) лежит во фронтальной плоскости.
В соответствии с уравнением Эйлера (ацс = dv/dt =
=—Vp/p0—2QXv) центростремительное ускорение может быть
вызвано только составляющей силы Кориолиса !ц, лежащей во
фронтальной плоскости. Ее другая составляющая
уравновешивает возникающий градиент давления. В самом деле, !ц=
= —2Q±Xv, где |fl±| =Q cos6 — составляющая вектора Й,
нормальная фронтальной плоскости. Так как Qj_J-V, то /ц=
= 2Quco90 = (i>|v| =оА4 — известное выражение для
центростремительного ускорения при движении материальной точки по
окружности с угловой скоростью со.
41.3. Волны в однородном жидком слое. Приложение к
геофизике. Простейшее решение для инерционных волн в жидком
228

слое получается в случае, если границы слоя перпендикулярны
вектору угловой скорости Q. Считая, например, границы
абсолютно жесткими и расположенными при 2=0 и z=—Я,
запишем решение уравнения (11.4) в виде суммы двух плоских волн
(11.5) с противоположными по знаку, но равными по
модулю kz:
w = b sin [kz(z+H)] exp [i(kr—©01, (11.9)
где k= |k|; kz и <o удовлетворяют дисперсионному соотношению
(11.6). Как и должно быть, &у|2=_н=0; приравняв нулю вертит
кальную скорость на верхней границе (ш|х=0 = 0), найдем воз^
можные значения kz:
sinkzH=0t kz = nn/H, л=1,2,
Дисперсионное соотношение для инерционных мод в жидком
однородном слое получится при подстановке последнего
выражения в (11.6):
„,,*.*£(* +**)-1 (н.,0)
Примерный ход дисперсионных кривых показан на рис. 11.2,
цифры соответствуют номеру моды. Частота любой из мод
монотонно убывает с ростом волнового числа k, т. е. групповая
скорость d<u/dk отрицательна. Это, в частности, означает, что
спектрально-узкий волновой пакет будет перемещаться в
противоположном вектору к направлении.
В природе инерционные волны наблюдаются в океане и в
атмосфере. Для волн, длина которых очень мала по сравнение
с радиусом Земли, кривизной последней можно пренебречь и
считать приближение жидкого (воздушного) слоя с
плоскопараллельными границами достаточно хорошим. Однако надо
отметить, что на вращающейся Земле направление оси z,
совпадающее с направлением местной вертикали, будет
параллельно Q только на полюсах. Это вносит в нашу задачу
некоторые особенности, чтобы понять их, направим ось у, как это
принято в задачах геофизики, с юга на север, ось х — с запада
на восток (перпендикулярно плоскости рис. 11.3). В этом случае
й={0, Qv, QJ = {0, Qcoscp, Qsincp}, где ф —широта места.
Уравнение для вертикальной компоненты скорости, аналогичное
(11.4), запишем в виде (см. задачу 11.1)
-^ Aw + 4 (Q V f* w = 0, (11.11)
где оператор (QV)2= (Qyd/dy+Qtd/dzy^QyW/dyt+^yQ&l
/dydz+at*d2!dz\
В задачах геофизики часто используют так называемое
«традиционное» приближение. При этом пренебрегают членами,
содержащими Q„. Мы видим, что для гармонических волн вида
229

(11.5), когда d/dy = ikv, d/dz = ikZi это справедливо, если
fflAI<|^x&x| или \kv\ <g£ \k2\ tgcp. Другими словами,
пространственный масштаб изменения волнового поля в
вертикальном направлении должен быть значительно меньшим, чем
в горизонтальном, а широта места не должна быть слишком
малой. В этом приближении уравнение (11.11) переходит в
(11.4) с параметром Кориолиса F = 2 Q sin ф.
§ 42. Гравитационно-гироскопические волны
42.1. Общие уравнения. Простейшая модель среды.
Гравитационно-гироскопическими называются волны, в которых,
кроме силы Кориолиса, важную роль играют также
гравитационные силы. Рассматривая их, мы будем учитывать и плотност-
ную стратификацию среды p0(z). При этом первые два и
последнее уравнения (11.2) останутся в силе, изменится лишь
третье уравнение и добавится уравнение состояния
*L + ±f + gJL = 0, ^-р^^О. (11.12)
Ы р0 дг р0 dt g
Ограничимся приближением Буссинеска, считая явно входящую
в уравнения р0 постоянной. Нижнюю границу слоя (z=—Н)
будем предполагать абсолютно жесткой (до|,=_н=0), а верхнюю
(2=0) —свободной с граничными условиями (10.7) при а=0:
Выражения (11.3) для давления и горизонтальных скоростей
остаются справедливыми, поскольку они получены без
обращения к третьему уравнению (11.2). С их помощью уже не
составляет труда получить из (11.12) и (11.13) уравнение и
граничные условия только для w:
JLb„, + F**°+N*& w = 0,
dt* дг* ^
-- Ш+р)т-^1гй- (1M4)
Представим вертикальную скорость в виде гармонической волны
^=0(z)exp[t(kr—<о/)], ^={К kv). (11.15)
Тогда из (11.14) для функции <D(z) получаем следующую
краевую задачу:
ф» + &2 АР(»Ь-<* ф = 0> ф(_#) = ф'(0)__^!_ф(0)=0.
(11.16)
Собственные значения М<о) этой задачи и соответствующие им
собственные функции Фп(г) определяют волновые моды во
вращающемся жидком стратифицированном слое.
W
230

Рассмотрим вначале наиболее простую модель жидкого слоя
с N2 (z) = const, для которой решение задачи можно довести
до конечных формул. Это позволит нам получить
представление о возможных волновых движениях во вращающемся
жидком слое. В этом случае решением уравнения (11.16),
обращающимся в нуль при z = — Я, будет функция
(D(z)=b sin a(z+#), а = £У(ЛГ2—<d2)/(<d2—Т72), (Ц.17)
где параметр а может быть и чисто мнимой величиной a = iaf
(при этом sina(z+H)=isha'(z+H))\ Подстановка выражения
(11.17) в граничное условие при z=0 приводит к
дисперсионному уравнению для волновых мод:
go G)a — F2 '
Мы будем анализировать (11.18), фиксируя частоту волн <в, и
ограничимся только такими его корнями, которые приводят к
вещественным значениям k (распространяющиеся моды).
42.2. Классификация волновых мод. Прежде всего отметим,
что при всех <o>F уравнение (11.18) имеет по крайней мере
один корень а0 (наименьший по модулю), соответствующий
поверхностной волне. При kH<£l (длинные волны) его можно
найти, положив tga^a. В результате, учитывая также смысл а2 из
(11.18), получаем:
oQ2 = H(N2—a2)/g, <i>2 = F2+gHk2. (11.19)
Отсюда следует, что частота поверхностной волны всегда выше,
чем /7=2Qsin9. При gHk2^F2 имеем обычное соотношение для
поверхностных волн на мелкой воде (<х>/к)2=сф2=дН.
В случае <u2>N2>F2 уравнение (11.18) имеет только этот
единственный корень а0. Далее, замечаем, что это уравнение не
имеет волновых решений типа (11.15) с вещественными со и Л
в случаях, если N2>F2>a>2 или Р>ЛР>(о2. При этом <т2<0 и
знаки правой и левой частей уравнения (11.18)
противоположны. В результате нам остается рассмотреть два случая:
1) N2><u2>F2 — случай внутренних волн, возмущенных
вращением Земли;
2) F2>(d2>N2 — случай инерционных (гироскопических)
волн, возмущенных наличием силы тяжести и стратификацией.
Не будем рассматривать малые а — поверхностные волны,
имеющиеся в первом случае. Тогда, поскольку в условиях
океана параметр E = H(N2—(o2)lg<HN2/g<^l (ср. с (10.71)),
правая часть (11.18) мала. В результате имеем корни а„«ля (п=
= 1, 2, ...). Эти корни соответствуют волнам, для которых
хорошо работает приближение «твердой крышки» (до|1=0~
~ sin аЛ «0). Дисперсионное соотношение для этих волн
получится из (11.18), если учесть, что <уп~пл:
со2 = (п V/72 + N2k2Hz) I (п2п2 + k2H2). (И .20)
231

На высоких частотах о>/7 (но ю<#) дисперсионное
соотношение совпадает с (10.74), где следует положить ап(о))=/гя.
Для длинных волн (£#<1) вращение всей жидкости приводит
к дисперсии:
са2=Р+(ЛГ2-Л) (kH/nn)2. (11.21)
Дифференцируя дисперсионное соотношение (11.20) по ky
найдем для групповой скорости выражение
где сф=<й/к — фазовая скорость волны, стремящаяся к
бесконечности при &->0. Из последней формулы следует, что для
внутренних волн сгр>0, дисперсионные кривые монотонно
возрастают с ростом ку а для инерционных волн сгр<0 —
монотонный спад последних.
42.3. Гравитационно-гироскопические волны в океане. В
реальных условиях океана качественно картина остается
подобной рассмотренной выше, за исключением того факта, что при
заданной N(z) могут существовать как внутренние, так и
инерционные моды. Это обстоятельство обусловлено тем, что в
реальных условиях волновод образуется не только дном и
поверхностью, как это было в случае N=const, но и конкретной
зависимостью N(z). Рассмотрим, например, типичное для океана
изменение N с глубиной, схематически представленное на
рис. 11.4. Вертикальной пунктирной линией отмечено значение
параметра Кориолиса F. В верхнем перемешанном слое океана
частота Вяйсяля мала, так что может оказаться при z>—ht
F>N(z). В слое термоклина частота Вяйсяля может достигать
Л^п~6 ц/ч (Г—10 мин). Здесь мы будем иметь уже обратное
соотношение N(z)>F. Аналогичная картина будет и в слоях
воды ниже термоклина, где Nz(z) сравнительно велика, и
только на больших глубинах параметр Кориолиса вновь может
превысить значение частоты Вяйсяля 4.
В зависимости от величины со картина волновых движений
в стратифицированной жидкости будет разной. Рассмотрим
последовательно характерные области частот волн.
1. Пусть со больше максимальной частоты Вяйсяля Nm.
Тогда для вещественных k (распространяющиеся моды)
коэффициент при Ф(г) в уравнении (11.16), равный
*(«)-» NtfjFf . 01.23)
будет отрицательным при всех возможных z. Следовательно,
функции <D(z) и Ф"(г) имеют одинаковый знак, т. е. мы имеем
иеосциллирующее решение уравнения (11.16) и максимальное
по модулю его значение достигается на границах слоя. В силу
1 В реальных случаях часто по всей толще воды N(z) >F.
232

ф(—Я)=0 имеем тах|Ф(г) | = |Ф(0) |, так что при <x>>Nm в
жидкости существует только поверхностная мода.
2. Пусть теперь F<<o<Nm. При zi<z<z1 (см. рис. 11.4)
коэффициент a2(z)>0, что приводит к осциллирующей функции
ф(г). Вне этого интервала {z<zi и z>z2) a2(z)<0, и функция
ф(г) не имеет осцилляции. Максимальное значение |Ф(г)|
может достигаться как на границе z=0 при малых k
(поверхностная волна), так и в области термоклина — внутренние моды.
Номер последней обычно приписывают на единицу больше
числа переходов функции Ф(г) через нуль при zt<z<z2. Поэтому
более высокие номера мод соответствуют более быстро
осциллирующим функциям Ф(г), т. е. большим значениям параметра
a2 (z) и, следовательно, большим волновым числам k (см.
(11.23)). При удалении от границ волновода z=zi и z=z2
собственная функция убывает тем быстрее, чем больше волновое
число и номер моды. Оценку собственного значения можно
получить, записав решение уравнения (11.16) в приближении ВКЦ,
что дает
ja(z)dz~/ет, kn~nn/со2— F*'A //V2(z) — tfdz. (11.24)
*X ZX
На высоких частотах ((u-+Nm) волновое число &п->оо. В случае
низких частот (ю-*/7) при оценке входящего в (11.24)
интеграла можно положить '0<Af(z). В результате (11.24) переходит в
аналогичное (11.21) выражение
о2 = F2 + ( j N(z)dz/пЛ ». (И.25)
Таким образом, в области частот /7<<o<JVm система
собственных волн в жидком океанском слое содержит поверхностную
волну, сосредоточенную в приповерхностном слое, и счетный
набор внутренних мод, локализованных в термоклине.
3. Рассмотрим теперь волны на частотах <o<F. Прежде $се-
го, отметим, что поверхностная волна в этом случае не
существует. Этот факт следует, например, из условия при г=0 в
(11.16). Действительно, при &<F Ф(0) и Ф'(0) в соответствие
с (11.16) имеют разные знаки, поэтому при удалении от
поверхности (отрицательные z) |Ф(г) |>|Ф(0) |, чего в
поверхностной волне не может быть по определению. Для анализа другие
волн заметим, что при w<F имеем аа(г)<0 в области
термоклина (w<N(z)) и, наоборот, a2(z)>0 вне его (<a>W(z)).
Последнее может быть, например, в приповерхностном и
придонном слоях (см. рис. 11.4). Характер решения уравнения
(11.16) в них аналогичный, поэтому мы ограничимся лишь
анализом приповерхностного перемешанного слоя. Пусть
минимальное значение частота Вяйсяля в последнем равно Nmi».
Тогда при o)<iVmln для всех z коэффициент a2(z)<0, функция
233

Ф(г) не осциллирует и собственных решений уравнения (11.16)
не существует. Если же Nmin<(o<Ff например в слое zs<z<0
йа рис. 11.4, то в последнем функция Ф(г) уже осциллирует,
следовательно, имеется счетный набор собственных значений
задачи (11.16), соответствующих инерционным модам. Оценкой
собственных значений для них, аналогичной (11.24), будет
kn ~ пп У?* — <&!\ V(»2 — N2(z)dz.
г»
Отсюда следует, что kn увеличивается с ростом номера моды и
уменьшением частоты со. Для длинных волн (&z3<Cl, co«F»
^N(z)) получаем
©*«Р(1—z/ifeV/iV).
Инерционные волны сосредоточены в приповерхностном слое
г>гл и при удалении от него экспоненциально затухают тем
быстрее, чем выше номер моды и ниже частота.
Проведенный качественный анализ волновых движений во
вращающейся жидкости с произвольной зависимостью N(z)
позволяет представить ход дисперсионных кривых co(fe) системы
гравитационно-гироскопических волн в океане. Схематически
без соблюдения масштаба эти зависимости приведены на
рис. 11.Д (цифры соответствуют номеру моды). Монотонный
характер дисперсионных кривых следует, например, из
выражения для групповой скорости волн через интеграл от собственной
функции, полученного в задаче 11.6.
Отметим, что инерционные волны в океане (и в атмосфере)
являются сравнительно редким явлением, поскольку условие
F>N(z) выполняется не часто. Однако в океане наблюдают их
в- вырожденном виде — так называемые инерционные
колебания. № этом случае ускорение частиц создается только силой
Кориолиса (Vp = 0). Движение частиц происходит по
горизонтальным круговым орбитам с центростремительным
ускорением, равным кориолисовой силе, и имеет частоту со = /\
Инерционные колебания являются решением исходной линейной
системы уравнений (10.11) вида
р=о, w = 0, р=0, и=b exp (—iFt), v = —ib exp (—iFt)
(см. также задачу 11.7) и существуют по всей толще океана.
§ 43. Волны Россби
43.1. Приближение р-плоскости. Существенным фактором,
обусловливающим наличие еще одного типа волн во
вращающейся жидкости, является зависимость вертикальной составляющей
частоты вращения от горизонтальной координаты. В
простейшем случае для описания этих волн, называемых волнами
Россби, можно обратиться к уравнениям (11.2) для однородной
вращающейся жидкости в прямоугольных координатах. Однако
234

параметр Кориолиса в последних следует уже не считать
постоянным, а предполагать линейно-зависящим от одной из
горизонтальных координат, например от у: F=F0+\$y. Если вновь
обратиться к геофизическим приложениям, то такое
представление есть не что иное, как следующий линейный член
разложения вертикальной составляющей частоты вращения Земли Qr^=
= Qsinqp по степеням у в соприкасающейся плоскости (см.
рис. 11.3). При этом
F=2Q sin<p = 2Q (siiKp0+A<p cos<p0) = F0+$y,
(11.26)
F0=2 Q sin <p0, p = 2 Q cos ф0//?0,
где ф0 — широта места; R0 — радиус Земли, у=/?0Д<р.
Учет члена $у в (11.26) часто называют учетом ^-эффекта,
соприкасающуюся плоскость в этом случае называют $-плоско-
стью, а анализ волны на р-плоскости — приближением
^-плоскости. Мы также ограничимся этим приближением. Следует
помнить, что описанное приближение учитывает только
вертикальную составляющую частоты вращения Земли, т. е. мы
остаемся в рамках «традиционного приближения».
43.2. Баротропные волны Россби. Рассмотрим случай,
когда в однородной жидкости вертикальная скорость частиц равна
нулю (w = 0) и ни одна из величин, характеризующих жидкость,
не зависит от вертикальной координаты г. Баротропное
движение жидкости будет двумерным, что позволяет ввести функцию
тока i|) (и=д$/ду, и = —dty/дх). При этом, как мы уже видели
в §26,
rotv =(i^--^Vz = -A i|)Vz, (11-27J
\дх ду]
и из (11.2) легко следует уравнение для $
±^+А=0. (11.28)
01 ох
Это уравнение с учетом выражения (11.27) можно записать в
таком виде:
d (2QJ
d(rotv) = — pi; dt = V^- dy,
dy
что является линеаризованным законом сохранения момента
количества движения во вращающейся жидкости: изменение
вихря частицы жидкости при ее смещении в направлении у
обусловлено только градиентом частоты вращения окружающих
частиц.
Нас интересуют решения уравнения (11.28) в виде
гармонической плоской волны:
tp = ft exp [i(kxx+kvy—©/)].
235

Непосредственная подстановка последнего выражения в
уравнение приводит к закону дисперсии волн:
<о=—$kjk\ k2=kj- + kv\ (11.29)
являющемуся существенно анизотропным в горизонтальной
плоскости. В частности, поскольку <о и kx имеют разные знаки,
гармонические волны Россби могут распространяться только в
отрицательном направлении оси х (на запад). Перепишем
(11.29) в виде
(*«+p/2<o)2 + V = P2/4co2,
что соответствует в плоскости (kXy ky) уравнению окружности
радиусом р/2(о с центром в точке (—р/2со, 0) (рис. 11.6). При
фиксированной-частоте <о концы возможных волновых векторов,
Проведенных из начала координат, должны лежать на этой
окружности. Дифференцированием дисперсионного
соотношения (11.29) по kx и kv получаем выражение для групповой
скорости волн Россби:
(11.30)
где kx=—£cosa; &v=&-sina. Легко видеть (см. рис. 11.6), что
вектор групповой скорости направлен от конца вектора к к
центру окружности. В частности, если волна бежит точно на
запад (а=0), то групповая скорость направлена на восток.
Поскольку -ф — функция тока, то касательная к линии ty^
= const, перпендикулярная вектору к (фронт волны), совпадает
по направленно с вектором скорости частиц. Следовательно,
последние движутся по прямым линиям, перпендикулярным
волновому вектору к (поперечные волны). Так же как и для дру-
тих волн с анизотропной дисперсией (внутренние и
инерционные), отражение волн Россби от границ (берег) имеет
определенные особенности (см. задачу 11.8).
' Отметим также, что осцилляции давления в рассмотренной
нами баротропной волне Россби, как это следует из системы
(11.2), отличны от нуля:
бледонательно, последние не будут равными нулю и на
свободной поверхности. Это означает, что в реальных условиях
океана баротропные волны Россби несколько (весьма
незначительно, как будет показано ниже) отличаются от описанных выше.
43.3. Совместный учет стратификации и р-эффекта.
Рассмотрим теперь в приближении р-плоскости случай плоскостра-
тифицированного жидкого вращающегося слоя. В системе
уравнений (1.0Л1.) положим 2Q = 2QzVz = FVz, где F = F0 + ру, a F0 и р
236

определяются соотношениями (11.26). Далее, распишем
систему (10.11) по компонентам:
ii-fb+J-JL^O. * + Fu + -i.3Ee0|^ + i-* +
dt рв дх dt р0 ду dt р0дг ^
+ г1яО, (11.31)
Ро
=0, -*-==р0 — до,
дх ду дг dt ° g
и в качестве граничных условий потребуем равенство нулю
вертикальной скорости на дне (z=—#) и давления (выражение
(11.13)) на свободной поверхности (z=0):
»U« = (J-Prfw) =о- (И-32)
Для упрощения выкладок ограничимся приближением Бусси-
неска, положив явно входящую р0 в (11.31) постоянной.
Будем искать гармонические решения системы (11.31),
(11.32) методом разделения переменных в виде:
и = Р (z)U(x, у) ехр (— ко/), v = Р (г) V(х, у) ехр (— i(ot),
w = mW (z) G (x, у) ехр (— Ш)9 р = pJP (z) G (xf у) ехр (— Ш),
(11.33)
Р = Ре — IF Ф G {х, У) ехр (- Ш).
s
Такой выбор зависимостей диктуется системой уравнений
(11.31). В самом деле, подстановка последних в (11.31)
приводит к уравнениям, содержащим либо только функции от дс, t/,
либо только функции переменной z, и лишь в четвертом
уравнении они связываются:
Р © G (х9 у) [ дх ду \
где параметр разделения v — постоянная величина. В
результате получаем отдельно задачу для функций от горизонтальных
координат
-t(o(/-FK+—=0, -i(*V + FU+d4-=0, ^+^=£vg>G
дх ду дх ду
(11.34)
и краевую задачу для P(z) и W(z)
/>' = (#«_ tf)W, W'= — vP, W(—H)=—m(P + gW)^o=0.
(11.35)
Система уравнений (11.34) после несложных
преобразований сводится к одному уравнению, например для V(x, у)
Д.К + Д- + v(©a — Я)К = 0. (11.36)
ш дх
237

Здесь параметр Кориолиса F=F0+$y зависит от у. Мы
положим его постоянным и равным F0i предполагая, что
рассматривается «малая» окрестность прямой у=0, где ,р*/<СЛ>, т. е. y<^L
(L~FJ$— интервал существенного изменения F). Однако в
этой окрестности должно укладываться большое число длин
волн Я=2я/&, следовательно, с учетом (11.26) имеем
£L = £#0tg<p0>l. (11.37)
Поскольку kR0^>l (условие справедливости приближения р-
плоскости), из рассмотрения исключается только узкая
полоса, охватывающая экватор (очень малые ф0). Если теперь
искать решение (11.36) в виде волны V=A exp[i(kxx+kyy)]9 то
легко получить выражение для параметра разделения v через
компоненты горизонтального волнового вектора k={kXi ky}:
v=(/j2 + ^P/co)/(o)2-/7o2). (11.38)
Мы видим, что v зависит от kx, т. е. от направления
распространения волн по горизонтали.
Краевая задача (11.35) для функций P(z) и W(z) также
легко переписывается только для функции W(z):
W"+v[N2(z)— cd2]№=0, W(—H) = [W'(0)— gvW(0)]=0,
(11.39)
где параметр v определяется выражением (11.38). Если
частота волн достаточно высока, то, пренебрегая членом с р в (11.38),
получаем уже рассмотренную в п. 42.1 краевую задачу для
гравитационно-гироскопических волн. Критерием этого
приближения будет £2> | &*'р/а) | или с учетом kx~k и (11.26)
со><ор=2 Q cos <pe/*#o. (11.40)
Частота щ весьма мала (kR0 велико), в частности щ<^.Р0 в силу
условия (11.37). Следовательно, критерию (11.40)
удовлетворяют частоты <^F0t т. е высокочастотные (длинные)
инерционные волны, и тем более поверхностные и внутренние моды,
частоты которых <o>/v Если минимальная частота Вяйсяля в
океане также значительно превышает <Dp(jVmln»cop), что обычно
и бывает, то влияние изменчивости параметра Кориолиса не
сказывается на инерционных волнах всех частот.
43.4. Волны Россби в океане. Рассмотрим настолько низкие
частоты волн о), чтобы второе слагаемое в числителе
выражения (11.38) превзошло первое:
^ I ^х$ I ВI cos a I 2Q cos ф0 , , i л„ i /11 л i \
(О < —— = -!-! L = —™-|Cosa| =a)p[cosa|> (11.41)
I Л2 I k kR0
где kx=—fccosa; a — угол, составляемый вектором k с
отрицательной полуосью х (западное направление). В этом
случае для волн, распространяющихся на запад (&*<0, cosa>0),
параметр разделения v будет положительным, и решение урав-
238

нения (11.39) в области JV2(z)>u)P2><d2 будет осциллирующим.
Набор собственных функций (мод), соответствующих этим
решениям, определяет волны Россби в океане. Для волн,
распространяющихся на восток (&х>0), при <u<F0 параметр v будет
отрицательным и собственные функции задачи (11.39),
соответствующие вещественным <о и к, не существуют. Следовательно,
как и в простейшем случае п. 43.2, волны Россби
распространяются только в западном направлении.
Собственные значения vn задачи (11.39), вообще говоря,
являются функциями частоты со. Однако в интересующей нас
области низких частот <d2<<dp2<N2(z) входящей в (11.39)
частотой со2 можно пренебречь. Тогда собственные значения 0<v0<
<Vi<.. .<vn<-.. уже не будут зависеть от частоты и
определяются только стратификацией N2(z) (гидростатическое
приближение). Подстановка vn в (11.38), где также можно
пренебречь ©СЛ, приводит к дисперсионному соотношению для волн
Россби
(*,+ £)'+*; = -£._vA (П.42)
которое, так же как для волн п. 43.2, в плоскости (kjkv)
является уравнением окружности с центром в точке (—р/2©, 0), но
меньшего радиуса. Последний_с ростом частоты <о падает вплоть
до нуля при (<оп) max = Р^ЛVvn, являющейся максимально
возможной частотой для волн Россби номера п. При этом волна
распространяется строго на запад (ky=0), а ее волновое число
(£n)min = — **=P/2cD = /Y|/vn с увеличением номера моды п
растет (vn>vn_i) и частота (con)max падает.
Дисперсионное соотношение (11.42) можно разрешить
относительно со:
г*х о k cos а /11 л о\
<о„ = -— = Р — (11.43)
Отсюда следует, что при заданной длине волны h=2n/k частоты
максимальны для волн, бегущих точно на запад (£у=0). При
фиксированном а максимально возможная частота и
соответствующее ей волновое число равны:
ЫтахИ= -^, (kn)min = YbFr (И-44)
2^оУЧ
Волна Россби наименьшего номера (л=0) называется баро-
тропной. Ее собственное значение v0 может быть найдено в
предположении, что W0 — линейная функция z:
W0(z)=b(l + z/H), v0=l/g#. (П.45)
При этом в безразмерных координатах (l = z/H) главный член
в коэффициенте при функции W в уравнении (11.39), равный
239

Л^Я/^Др/р, будет мал. Следовательно, решение (11.45)
удовлетворяет как граничным условиям (точно), так и уравнению
(с высокой степенью точности) краевой задачи (11.39).
Заметим, что баротропная волна Россби существует и в
однородном слое. Отличие этой волны от изученной в п. 43.2,
определяемое величиной F02/gHk2 (ср. (11.29) и (11.43)), невелико для не
очень длинных волн.
Волны с номерами п>0 называются бароклинными волнами
Россби, Для них существенна стратификация среды (N2(z)^0)9
и собственная функция имеет по крайней мере один максимум
в толще океана. Горизонтальная скорость частиц жидкости, при
этом меняет свое направление на обратное. Для бароклинных
волн Россби хорошо выполняется приближение «твердой
крышки» (ш|1в0 = 0). По аналогии с (11.45) собственное значение vn
бароклинных волн записывают в виде vn=l/g#n, причем Я—
= Я0>Я1>Я2> ... >#„> ... Величины Нп размерности
длины называют эквивалентной глубиной.
В заключение представим дисперсионные зависимости для
всех волн в несжимаемой вращающейся жидкости графически
(рис. 11.7). При этом в силу анизотропии волн Россби нужно
построить дисперсионную поверхность <о = ш(Лж, ky)t сечение
которой плоскостью (<о, kx) и представлено на рис. 11.7. Полная
поверхность <o(ftx, kv) получится мысленным вращением
картинки вокруг оси (о. При этом частоты волн Россби будут
уменьшаться в соответствии с множителем cos а (см. (11.43)).
Дисперсионные поверхности для остальных волн будут
практически поверхностями вращения. На рисунке приведены также без
соблюдения масштаба типичные для океана периоды волн.
Задачи
11.1. Получить уравнение для волн в однородной вращающейся жидкости
в случае произвольного направления вектора угловой скорости Q по
отношению к осям координат.
Решение. Если применить к первому уравнению (11.1) операцию rot,
то с учетом rotVp=0 и rot(G Xv)=—(Q V)v систему (11.1) запишем по
компонентам в виде:
д (dw dv\ Л /Л„ч Л д I ди dw \ Лт_
— — — — — 2 av ы = о, — — — т~ - 2 (GV) v = о,
dt \ду dz) к dt \дг дх)
(11.46)
д I dv ди\ Л /Л„ч ди t dv dw
*-(аГ-*Г2(ШГ)'-0, ^+1Г = -1Г
Продифференцируем теперь первое уравнение по у, второе —по х и вычтем
одно из другого. В результате будем иметь
д А аа /dv , ди\ t n/„„Jdv ди\ л
Д_ш — —. + — +2 (QV) — ) = 0.
dt dt dz \ду ^ дх} ^ к *\dx ду)
Дифференцируя последнее соотношение по t и воспользовавшись третьим w
240

четвертым уравнениями (11.46), получаем искомый результат:
ot2
11.2. Найти нормальные волны в однородном слое с горизонтальными
абсолютно жесткими границами, отказавшись от «традиционного приближения*
(вектор Я не вертикален).
Решение. Ищем решение уравнения предыдущей задачи в виде
a> = <D(z)exp[t(kr—со/)],
при этом для функции Ф(г) получаем уравнение
FzFu <»2-F2 k
<Г/ + 2^-£-1!—Ф' + £а LO = 0, F=2QZ, F1|=2QT,^
^-(о* F2-co2 г г \\ k
общее решение которого имеет вид
ф (z) = b+exp (ia+z) + b-exp (ia-z),
где a+ и a_ — корни характеристического уравнения
FF 0)2 _ Я
fla + 26 " a-fe2 Le0.
f|__o)a F2-cd2
Эти корни будут a±=k/±kz"t где
f2-^ ' * К (F^-ca2)2
Пусть теперь границы слоя расположены на уровнях 2=0 и 2=—/f, тогда
решение Ф(г), обращающееся в нуль при 2=0, имеет вид
<D(z) = b exp (ikz't) sin a£z.
Очевидно, что удовлетворить условию на нижней границе (Ф(—#)=0) можно-
только в-случае вещественных kx", т. е. если
\2
со»<^ + ^|=4Й»+4(а|),
при этой kz"H=nn (л= 1,2,3,...). Отметим, что полученное решение
отличается от (11.9), соответствующего «традиционному приближению» (Qk=0
в нашем случае). В частности, частота инерционных волн может-быть больше
параметра Кориолиса FZ=2QZ.
11.3. Получить дисперсионные зависимости для нормальных волн задач»
11.2.
Решение. Искомые дисперсионные соотношения получатся, если решить
относительно а) уравнение kz"H=nn предыдущей задачи. Имеем
^(^ + ^1- "а) __ п2я2
(F2-*2)2 ~~ *2Яа
241

откуда следует квадратное уравнение относительно со2:
корнями которого будут
со2± = {2п*пЧ* + {F\ + F\) «/» ± kH [(F\ + F\)2 k*H* +
+ 4n2n2PzP{l ]v'}/[2 (n»n« + #»#2)].
Следовательно, имеются две ветви дисперсионных кривых. Заметим, однако,
что в случае ОкФ 0 (направление Q совпадает с осью z) co+2=Fx2=4Qr2,
со2-=/г22л2я2(л2л2+#г#2)-1, так что только
ветвь со- соответствует инерционным волнам
(см. 11.10)). Рассмотрим подробнее случай
Ок^О. При kH-+Q (длинные волны) имеем
<*\ = Fl±J-LkH =
г пп
ЬН ( |Л
г пп г \ kl
Дисперсионные кривые стремятся к частоте
2QZ, но каждая со своим не равным нулю
наклоном (групповой скоростью) cTV=-±F\\HI2nn>
Для реальных условий Й=2я/24 ч, Ж104 м имеем сгр<0,5 м/с. В случае
коротких волн (kH-+co) находим:
«4- П + F\ = 4Q* + *(ojf «4-0.
•Отметим горизонтальную анизотропию дисперсионных соотношений, а именно
зависимость от направления распространения (вектора к). На рис. 11.8
схематически показан вид дисперсионных зависимостей, заметно отличающихся от
полученных в «традиционном приближении> (см. рис. 11.2).
11.4. В приближении Буссинеска получить уравнение для волн в
стратифицированной вращающейся с произвольно направленной частотой Q жидкости.
Указание. Ход преобразований общей системы уравнений (10.11)
аналогичен проведенному в задаче 11.1. Следует учесть, что
е(р0 =const в приближении Буссинеска).
Ответ:
77 Дш + 4 (ov)a w + N* (*) A-w = °-
11.5. Провести качественный анализ гравитационно-гироскопических мод
я слое с горизонтальными абсолютно жесткими границами на основе анализа
решений уравнения предыдущей задачи.
г/вЯ/Ьк/к)*
Рис. 11.8
242

Решение. Подставив a> = (D(z)exp[i(kr—cof)] в уравнение, получаем
F*F, N*-<* + F2
Ф" - 2ik !*-=— Ф' + k2 Ф = О,
co'-F2 co2-F2
где /7n=2Qk//j; Fz=2Qx. Если теперь представить <b(z) в виде
Ф (г) = exp [i*F„ Fzzl(tf - ^]ф (*),
то уравнение для \|)(z) не будет содержать первой производной:
(Л^а — а>«) (со2 — Р|) -f- co2F2„
Ч>" + *» -^ L4> = 0.
(cdI-F2)'
Собственные решения (моды) должны обращаться в нуль на границах слоя
0И0)=\|)(—Я)=0), что возможно только в случае, если ф(z) —
осциллирующая функция. Для этого достаточно потребовать, чтобы коэффициент при»
ф в последнем уравнении был положителен:
[#а (г) - со2] (со2 - F\) + ©V* > 0.
Отсюда легко находим условия на возможные частоты волн 0)-2<©2<(0+2г
где
со2± (г) = {№ + F\ + F2,j ± [(tf2 + F\ + F2 )■ - 4JWj]K}/2 =
= {#'+ ^ + Я„ ± [(tf2 - F\ - F\ )a + 4^F2, ]*}/2,
причем g)-2^Fi2<g)+2 при любых #2(z)>0. Частота F2 является особой
точкой уравнения для ф, разделяющей различные ветви дисперсионных кривых.
А именно: при
F22<aJ*<mM{<dl(z)} =
= 7 {"шах + 1 + П + Г "тах - ^ - F\ )2 + ^F» ]*}
(NmAi=maxN(z)) нормальные моды, локализованные в слоях с большим»
значениями N(z), соответствуют внутренним волнам. В случае, когда
min {со2. {г)}1=
= \ «in+ П + А - Km- П- n^ + 4Nlinf\}%}<^< п
(Nmin = minAf(z)), собственные моды соответствуют инерционным волнам,,
сосредоточенным в слоях с малыми частотами Вяйсяля. Для длинных вол»
(£-►0) из уравнения для ф имеем (о2—F22)2/^2-hx2=const (в случае Fn =
=2 ftk/fc#0). Поэтому при k-+0 для ф(г) получаем
ф" + (F2F2,|/а2) \|) = 0, il? = Ь sin (F2F„г/а), F2F„ /а = пя/Я
и для дисперсионных зависимостей имеем
со2 = F\ ± {FZF ц /пя) ЛЯ, со = Fz ± F „ /2пя) ЛЯ
— результат, аналогичный случаю однородной жидкости (задача 11.3).
11.6. Получить выражение для групповой скорости нормальных мод
краевой задачи (11.16) через интеграл от собственной функции.
243

Указание. Поступая аналогично решению задачи (10.19), находим
11.7. Показать, что колебательный процесс вида «=6ехр (—iFt),
v=—ibexp(—iFt), ш = 0, F=2QZ (инерционное колебание) удовлетворяет
системе уравнений вращающейся стратифицированной жидкости ,(10.11) без
«традиционного» приближения.
т Решение. Очевидно, что Vv=0. Далее, из уравнения
состояния d(plpo)/dt=(N2/g)w заключаем, что р=0.
Подставляя теперь и, v и w в уравнение Эйлера, для давления
получаем;
dp dp \ др
дх ду р0 дг r у
Отсюда следует, что
Рис. 11.9
р = р (», /) = - 2Ь (iQx + Qy) exp - (Ft) J p0 '£) (%.
Если принять 6=1 м/с, Q=2n/24 ч-1 и #=104 м, то
— весьма малая величина. Поэтому можно положить psO, и инерционные
колебания будут такими же, как при расчете в «традиционном приближении».
11.8. Найти отраженную волну при падении баротропной волны Россби
«а абсолютно жесткую вертикальную стенку.
Решение. Пусть падающая и отраженные волны имеют вид:
ф1 = аехр [i(kixx+kiyy-4ot)]t $2=aVexp [ifaxX+fayy—tot)].
В плоскости (kx, kv) проведем волновой вектор падающей волны (рис. 11.9)
(k! = {^ix, kly})t конец которого (точка А) лежит на окружности радиусом
Р/2о) с центром в точке Е с координатами (—Р/2со, 0). Пусть линия MEN.,
-составляющая угол у с осью х, параллельна стенке. При отражении
сохраняются частота волны со и проекции волнового вектора на границу.
Следовательно, конец волнового вектора отраженной волны (k2={k2Xt k2v}) также
лежит на той же окружности (точка В). В силу равенства проекций
волновых векторов к, и к2 на границу точка В является пересечением окружности
•с прямой АВ, перпендикулярной стеике. Очевидно, что в общем случае для
волновых векторов угол падения не равен углу отражения. Однако последнее
справедливо для групповых скоростей волн. В самом деле, векторы группо-
зой скорости с, (/=1, 2) направлены от концов волновых векторов к центру
окружности и в силу EF±AB составляют равные углы (AAEF и /JFEB) со
стенкой. Если ввести векторы ko=OF и kj.=FA, то для ki и к2 будем иметь:
^1= ^о + kj_» к* — ко — k_i_.
Поэтому полное волновое поле я|>=г|)1+^2 можно записать и так:
тр = a [exp (i к±т) + V ехр (— i k^r)] exp [i (к0г — со/)].
Коэффициент отражения V найдем, потребовав, чтобы стенка бн«а линией
244

тока, т. е. г|)=0 на линии MN. Отсюда, предполагая, что стенка проходит
через начало координат (х=0, #=0), имеем кхг=0 на MN и V= —1,
следовательно,
ур == 2ia sin к±г exp [t (квг — со/)].
11.9. Рассмотреть баротропные волны Россби между двумя
параллельными абсолютно жесткими стенками 1\ и Г2.
Решение. Пусть L — расстояние между стенками, одна из которых,
например Ти проходит через начало координат. Функция тока \|),
обращающаяся в нуль на Гь определяется последним выражением предыдущей задачи.
Другая стенка (Г2), на которой kjj^kjj», также является линией тока.
Следовательно,
tf \Гл = 0 или sin k±L = 0, (k±)n = nn/Ly п =1, 2, 3,
Обозначим AAEF=б (см. рис. 11.9), тогда
ft
k , = -— sin б, 0 < б < я
± 2ю
(случай — я^б<0 соответствует замене ki**k2). Таким образом, при
заданной частоте волн со получаем конечное число собственных углов бп, таких, что
sin ort = 2пп — , п ^ —
п PL 2яш
Распространяющихся мод не будет при w>pL/2n. Частота, на которой
возникает распространяющаяся мода номера п (n-я критическая частота), равна
<1)п='Р£/2ял.
11.10. Определить траектории движения частиц жидкости в волновом поле
*|), образованном двумя баротропными волнами Россби, равных частот и
амплитуд, распространяющихся под углами сЬа к оси х.
Решение. Волновое поле двух волн Россби запишем в виде
ф = a exp [/ {k^ — о/)] [exp (ikyy) + exp (— ikyy)], a = A exp (i6).
Найдем компоненты смещения частиц, жидкости (£, г\) вдоль координатных
осей (в вещественной записи):
и 1 дф 2Л
— ко — ко ду о * *
» 1 д\|) 2Л t
т] = —Г" = ~ — = — kxcoskuy cos ф,
— «a ко дх со * "
где ф=£жх—<оН-0. Выражение для траекторий получится при исключении
из этих формул зависимости от времени. С учетом также выражений
k= (Р/со) cos a, kx——fccosa, &y=£sina будем иметь
— уравнение эллипса с полуосями
Д- = 2 ^—cosa sinasinf—sin 2a I , au = 2 —-- cos2 a cos (--sin2a) .
* со* I \2g) /I y со2 | \2co / I
11.11. Для двух баротропных волн Россби предыдущей задачи найти
уравнения для линий тока if=const.
245

Решение. В вещественной форме уравнение \|) = C=const имеет вид
2Л cos kyy cos (k^c — со/ + 0) = С.
Исключим время /, переходя к движущейся со скоростью а>/£х системе
координат х'=х—(ot/kx + Q/kx. В этой системе уравнения для линий тока будут
coskyycoskxx'=C/2A. Картина линий тока в плоскости (х\ у) схематически
представлена на рис. 11.10. Стрелками показано направление движения
частиц. Таким образом, получилась периодическая (шахматная) структура
чередующихся циклонических (против часовой стрелки в северном полушарии) и
антициклонических (по часовой стрелке) вихрей. В
неподвижной системе координат (х, у) вся картина
смещается на запад со скоростью о)/£ж. При этом скорость
1пл частиц в фиксированной точке будет Меняться такик
^ образом, что частица совершает движение по эллипти-
f \ глл Г/М ческим орбитам (см. задачу 11.10).
о ню о
■^, 11.12. Определить собственные значения vn(<o)
краевой задачи (11.39) в случае постоянной частоты Вяй-
(ГЙ МЙ ГО) сяля для частот ю<#.
L / \wP \ 1 Решение. При N=const решение уравнения
(11.39), обращающееся в нуль в точке z=—Я, имеет вид
ft*-11-10 W=Ъ sin [iv(N2—со2) (z+Я)].
Удовлетворяя условию при 2=0, получаем:
otga= {N*—a>*)H/gt a=yv(W2_G)2)#.
При a<N для типичных значений N2 и Н величина (N2—©2)Я/#<1.
Следовательно, нулевой корень можно найти разложением функции tg а в ряд:
a02=v0 (ЛГ2—со2) Я2 = (W2-co2)H/gt v0 = 1 IgH.
Собственные значения оп более высоких порядков мало отличаются от нулей
функции tga, т. е. оп~пп (я=1, 2, ...). Следовательно, vn&n2n2lfP(N2—<u2)
и при N2Xo2 уп«п2я2/#2Я2.
11.13. Получить дисперсионное соотношение для бароклинных волн Рос-
сби в слое с постоянным значением N и выяснить, при каких условиях
частота волн Россби (o^CFo (условие применимости формулы (11.43)).
Решение. Подставив рассчитанное в предыдущей задаче собственное
значение vn=n2n2/N2H2 в выражение для v (11.38), получаем
nW b2 + kx¥>/a>
Введем величины f=co/N и /о=Л>/#, а также положим fcx=fccosa. Тогда
для определения безразмерной частоты f получаем уравнение третьей степени
где параметр б = р cos a/Nk = 2 (Q/N) cos ф0 cos a/kR0 (в соответствии с
(11.26)). Последний при условии kR0>\ (как это и должно быть в
приближении р-плоскости) будет малой величиной (6<1). Случай <D<fo
соответствует пренебрежению членом с /3 в последнем уравнении, что приводит к
246

следующей формуле для f и со=#/:
б£2#а лл cos ф0 cos а
/= , <о = 2Й —
*2Яа + п*п% ' kRQ[\ + (nW/k*H2) Fl/N*]
Условием применимости этого приближения будет
в//о = [1 + ("Я/ОД'/оГ1 б//0<1,
что заведомо выполняется, если б//0< 1 или kRo tg ф0> 1.
Глава 12
ЗВУКОВЫЕ ВОЛНЫ
В гл. 10 и 11 мы познакомились с волнами, которые
существуют и в несжимаемой жидкости. Для волн этого типа
сжимаемость среды проявляется лишь в виде некоторых поправок
(например, в дисперсионных уравнениях), которыми мы
пренебрегали.
В этой главе мы обратимся к звуковым или акустическим
волнам, для которых эффект сжимаемости среды является
определяющим фактором. По своей природе звуковые волны
родственны продольным упругим волнам в твердых телах (см.
гл. 2 и 4) и обусловлены силами упругости, возникающими при
деформациях элемента объема жидкости.
В океане акустические волны играют огромную роль, такую
же, как, скажем, электромагнитные волны в атмосфере.
Последние быстро затухают в морской воде, в то время как
звуковые волны могут распространяться на тысячи километров.
Поэтому они широко используются для исследования океана, а
также как средство связи и передачи информации. В
атмосфере звуковые врлны очень низких частот (инфразвук) тоже могут
распространяться на тысячи километров.
В этой главе мы получим линейные акустические уравнения,
из которых следует волновое уравнение, описывающее
распространение звука в жидкости. Рассмотрим простейшие решения
этого уравнения в однородных и неоднородных средах. Изучим
распространение звука в волноводе, типичным для которого
является подводный звуковой канал в океане. Будут также
затронуты вопросы излучения и распространения звука от
сосредоточенного в ограниченной области пространства источника.
§ 44. Плоские волны в покоящейся жидкости
44.1. Система линейных акустических уравнений. В линейной
постановке звуковые волны должны описываться линейной
системой уравнений гидродинамики (10.3), где нужно положить
5=0, N2=0f Q=0:
247

^ + 7Г = 0' f + ^ = o, 'f = ^f • 02.1)
ar p0 a/ at c* dt
Здесь последнее уравнение является уравнением состояния, а
величина с2=(др/др)в (5 —энтропия) — квадрат
адиабатической скорости звука или просто скорости звука.
Исключая из (12.1) плотность р, легко получить два
уравнения линейной акустики:
£ + ^ = 0, -Ljg + Vv=0, (12.2>
dt ро рис2 dt 7
которые сводятся к одному уравнению, например относительно
акустического давления р:
-^^—Ap+ir^vp=0- (12-2'>
с2 dt2 р0
Последний член в левой части этого уравнения мал, например,
по сравнению со вторым, если плотность среды р0 постоянна
или если пространственный масштаб ее изменения L велик по
сравнению с длиной звуковой волны X. Действительно, третий
член по порядку величины равен kp/L=2npfXL, в то время как
второй k2p=(2n/'k)2p. При L»A, третьим членом можно
пренебречь по сравнению со вторым. Тогда мы получаем волновое
уравнение, которое и будет основой для дальнейшего:
br-FlF-0- <|2-3>
где скорость звука может быть функцией координат с=с(г).
Если какое-то решение р(г, t) этого уравнения известно, то
скорость v(r, t) в любой момент времени t находится
интегрированием первого уравнения (12.2):
t
v(r, /j=v(r, t0)— — V fp(r, T)dr. (12.4)
Po J
to
44.2. Плоские волны. Волновое уравнение (12.3) для
давления в случае с = const имеет решение в виде плоских волн,
подробно рассмотренных в § 14 при анализе продольных упругих
волн. Если совместить ось х с направлением распространения
волны, то соответствующее решение уравнения (12.3) запишем
в виде
Р(х, t)=f(x-ct)+g(x+ct), (12.5)
где / и g—произвольные функции. При этом f(x—ct)
представляет собой волну, распространяющуюся в положительном, а
g(x+ct) —в отрицательном направлениях.
В плоской волне имеется простое соотношение,
связывающее скорость частиц среды с давлением. В самом деле, взяв,
248

например, первый член в (12.5) и подставив его в (12.4),
находим
/ x-ct
y(r,/)=v(r,g- — V (7(*-<rr)dT = v(r, t0)+±V Г ftl)dt.
Po J p0c J
Действуя на интеграл с переменными пределами оператором V,
для единственной отличной от нуля компоненты скорости vx
получаем
vx(x9t) = — f(x — ct). (12.6;
Аналогично находим для обратной волны
Vx(x,t)± -g(X + d). (12.7;
Величина р0с, равная отношению акустического давления р к
скорости частиц жидкости в плоской волне, называется
волновым сопротивлением среды, обратная величина 1/р0с—
волновой проводимостью среды.
В акустике часто используют монохроматические источники
звука, работающие на некоторой частоте со. Излучаемые таким
источником волны будут гармоническими, так что акустическое
давление представляется в виде /?=t|)(r) ехр(—Ш). При этом
волновое уравнение (12.3) переходит в так называемое
уравнение Гельмгольца:
ЬуЬ+к2у = 0у k2 = «>2lc\ (12.8)
Простейшим решением этого уравнения является плоская
волна г|э=Л ехр (Лг), причем для волнового вектора к=
= {kx, ky, kz) имеем
k2x+k2y+kl = <**/(?. (12.9)
Для звукового давления в результате получаем
p=Aexp[t'(kr—©/)]. (12.10)
В гармонических волнах скорость частиц выражается через
давление согласно первому уравнению (12.2):
v=Vp/wop0. (12.11)
В плоской волне, учитывая (12.10), для колебательной
скорости жидких частиц имеем
v = ^-- ехр[*(кг —©/)]. (12.12)
Рос k
Таким образом, скорость v совпадает по направлению с
вектором к.
249

Две гармонические плоские волны равных частот и
амплитуд, но противоположно направленных (к'=—к), образуют
стоячую волну:
р = 2 A coskrexp(— ко/), v = — — sinkrexp(— Ш). (12.13)
р0с k
В последней узловые плоскости для давления (р = 0)
определяются уравнениями кг= (я/2) +пл и отстоят друг от друга на
половину длины волны. Скорость частиц жидкости на этих
плоскостях максимальна. Напротив, плоскости максимума давления
кг=пл соответствуют узловым плоскостям для скорости.
44.3. Излучение плоских волн. Неоднородные волны.
Плоские звуковые волны можно получить, создавая на некоторой
плоскости распределение давления или нормальной скорости.
В простейшем случае нормальная скорость одинакова по всей
плоскости, как, например, при изучении звука колеблющимся
поршнем. Пусть на плоскости 2=0 задано vz(t)=f(t), нетрудно
проверить, что решением акустических уравнений (12.2) будет:
vx=vv=0, vz = f(t—zlc), p=p0cf(t—z/c).
В случае произвольного распределения* давления или
нормальной скорости на плоскости целесообразно воспользоваться
разложением этого распределения в интеграл Фурье по t, а
также по х и у и получить решение для отдельных компонент
разложения. Пусть, например, на плоскости 2=0 имеем
распределение давления
р\г=0=А exp [i(kxx+kvy—<ut)]A (12.14)
Решением волнового уравнения (12.3), совпадающим с (12.14)
при z = 0, будет гармоническая плоская волна
р {х, у, z, /) = A exp [i (kxx + kyy + kzz — Ы)]9 kz = Yk* — k\,
(12.15)
где k±=^kx2+kv2 — проекция волнового вектора k на плоскость
2=0. Волну (12.14) называют «следом» плоской волны (12.15)
на плоскости 2=0. След является волной той же частоты и
амплитуды, а его волновое число равно проекции волнового
вектора к на данную плоскость. Таким образом, зная след волны в
плоскости, т. е. одну из гармоник Фурье при разложении
давления или нормальной скорости в плоскости, легко получить
его продолжение в пространстве в виде плоской волны.
Выражение (12.15) имеет интересное обобщение на случай,
когда k±>k=<u/c, т. е. когда проекция волнового вектора на
плоскость превышает его длину. В этом случае величина kt =
=-]/k2—k±2 = iyk±z—k2 чисто мнима и акустическое давление в
р(х, у, 2, t) = A exp (— |£*|2)ехр [b(kjc+k^—^t)\. (12Л6)
среде будет
250

Волну такого вида называют неоднородной плоской волной. Ее
фронты совпадают с плоскостями kxx+kvy=const, но
амплитуда волны уже не постоянна в этой плоскости, а
экспоненциально убывает при удалении от поверхности z=0. Плоскости
равных амплитуд z=const ортогональны фронтам волн.
Скорость частиц жидкости в неоднородной волне не
совпадает с направлением ее распространения, а имеет компоненту
и в перпендикулярном направлении. В самом деле, используя
(12.11) и полагая для простоты ky=0, находим:
vx= - ~ = -£-Лехр(— \kz\z)exp[i(kxx — со/)],
кйр0 ох сор0
(12.17)
vz = - = i—— Лехр(— \kz\z)exp[i(kxx — <ot)].
tcup0 дг (op0
Компоненты скорости сдвинуты по фазе друг относительно
друга на я/2, что соответствует эллиптическим траекториям
частиц.
Понятие неоднородной плоской гармонической волны
можно обобщить, записав ее в виде (12.10) и считая волновой
вектор к комплексным k=k'-Wk", но по-прежнему
удовлетворяющим соотношению (12.9) при вещественном положительном
значении k2 = (d2/c2. При этом имеем волну р = ёхр[—к"г+
+ i(k'r—©Oli распространяющуюся в направлении вектора к'
с фазовой скоростью сф=й)/&' и переменной в пространстве
амплитудой. Подставляя k=k/ + k// в (12.9) и приравнивая по"
отдельности вещественную и мнимую части слева и справа в
равенстве, получаем:
k'k" = *Х + k'jk'y + k£ = 0,
(12.18)
к'2— к" = &=<&/*.
Отсюда следует, что плоскости постоянной фазы k'r=const
ортогональны плоскостям постоянной амплитуды к"г=const.
Поэтому, как и в простейшем случае (12.16), неоднородная
плоская волна распространяется в направлении, задаваемом
вектором к', и имеет амплитуду, быстрее всего убывающую в
перпендикулярном направлении. Из (12.18) также следует, что
k2<k'2 или сф2=((й/к')2<((д/к)2 = с2, т. е. фазовая скорость не-
однородной волны всегда меньше скорости распространения
обычной плоской волны. Следовательно, и длина волны Х' =
= (2n/k')<2nlk также меньше длины обычной плоской волны
той же частоты.
Неоднородные волны не могут существовать в
неограниченном однородном пространстве, так как их амплитуда будет
неограниченно возрастать в одном из направлений. В случае же
ограниченных сред с ними часто приходится встречаться. На-
251

пример, именно с учетом последних решается задача об
излучении звука произвольным распределением давлений или
нормальных скоростей на некоторой плоскости. Как мы увидим
ниже, при преломлении плоских волн на границах раздела сред
неоднородные волны могут превращаться в обычные и
наоборот.
44.4. Энергия звуковых волн. В § 23 дано выражение для
энергии единицы объема жидкости
Е=1/^2+ри+ре,
где р=р0 + р/ и р=р0+р^ (см. ниже) —-полные величины, а не
приращения. Энергия жидкости во внешнем потенциальном
поле и в нашем случае равна нулю. Поскольку мы
ограничиваемся линейным приближением, то в выражении для энергии
следует удерживать члены не выше квадратичных. Поэтому для
плотности кинетической энергии имеем £,K=1/2(po+p/)fl«
~72роа2. Проанализируем £,в=|(р0+р/)е— плотность
внутренней энергии. Согласно (6.33) ее приращение при переходе из
равновесного состояния р„, р0 в возмущенное р=р0 + р/, р=р0 +
р ,
+р' будет £„ = P j -^у". Но р(р)=р0+су, следовательно,
р. р
%о4> , ^Ур'Ф' ~- р' . * Р^_РоР' , IpY
J Р1 J Р* Ро Ро 2 р0
Ро О
2 Ро
Здесь первый член соответствует приращению внутренней
энергии за счет работы сил равновесного давления и является
линейным по отношению к акустическому давлению р'. Второй же
член соответствует работе против сил акустического давления,
именно это слагаемое называют внутренней энергией звуковой
волны. Заметим, что для гармонической плоской волны среднее
по времени или пространству значение р' равно нулю, в
результате чего линейное слагаемое выпадает, а второе остается.
Таким образом, опуская штрихи у приращений р' и р',
запишем выражение для плотности акустической энергии в виде:
Е = ЕК + ЕВ, EK = j9ov*,
(12.19).
Е _ с* Р2 1 рр ^_ 1 р2
р0 2 2 ро 2 Рос2
В частности, для бегущей плоской волны, в которой давление и
скорость связаны простым соотношением v=±p/p9c> имеем:
£к==£. = 1 * E=-?-=p0v*. (12.20)
2 р0с2 Ро<?2
Получим теперь закон сохранения энергии. Для этого, про-
252

дифференцировав Е из (12.19) по времени и учтя (12.2),
найдем
Щ:=^^-^1т^7----^р-р^у = ~^(рП (12.21)
01 01 р0с2 01
Проинтегрировав это выражение по некоторому объему V и
применив теорему Гаусса — Остроградского, получим
±{JEdV = -jjpvndS. (12.21').
V s
Отсюда следует, что 1=р\ является вектором плотности потока
акустической энергии. Что это так и должно быть, легко
пояснить простыми физическими соображениями: pndS — сила
звукового давления, действующая на площадку dS с нормалью п,
pvndS — мощность этой силы, a I=pv —вектор плотности
потока мощности (энергии в единицу времени) через единичную
площадку.
В плоской волне р=р(пг—ct), v = п р ~~ ° , распрост-
Рос
раняющейся в направлении п, вектор плотности потока энергии
равен
I =£-n = P(fv*n = Ecn. (12.22)
Рос
Направление вектора I совпадает с направлением
распространения волны, а его величина равна плотности энергии,
умноженной на скорость волны. Другими словами, энергия в
бегущей плоской волне переносится со скоростью звука, что и
должно быть из-за отсутствия дисперсии волн.
В случае гармонических плоских волн, записанных в
комплексном виде (12.10), при вычислении Е и потока I,
являющихся квадратичными величинами, следует оперировать только с
вещественными частями выражений для р и v. Например, для
неоднородной волны (12.16), полагая в ней для простоты ky=
= 0, учитывая также (12.17) и обозначая Л=|Л|ехрО'а), <р=
=&«*—(ot+a, получим:
/x = !4^exp(-2|Mz)(l + cos2<p),
(12.23)
\А I2 1 k I
1г = —' ' ' 2l ехр(— 2\kz\z)sm2q>.
2сйр0
Обратим внимание на тот факт, что в направлении z поток
энергии каждую половину периода меняет свой знак на
противоположный, так что средний за период волны поток энергий
253

/2=0. В направлении х средний поток энергии остается
отличным от нуля:
7х = Цг^ехр(-2|Л,|г). (12.24)
2(оро
Вспомним, что неоднородная волна (12.16) возникает при
заданном на плоскости 2=0 распределении давления (12.14) с
k±>k и соответственно с фазовой скоростью (d/k±<c—
скорость звука в среде. Следовательно, возмущения, бегущие
вдоль плоскости со скоростью, меньшей скорости звука в среде,
не излучают акустической энергии. Для обычной
гармонической плоской волны (12.10) с вещественным к аналогичный
расчет приводит к выражению
Г = ИЛ1, /,-?£, /,= 7^, 1г=1^, (12.25)
2р0с k k k k
т. е. к излучению звука.
§ 45. Распространение звука в неоднородных средах
45.1. Отражение плоских волн на границе раздела сред.
В предыдущем параграфе рассматривались звуковые волны в
однородной безграничной среде. Простейшим примером
неоднородной среды является случай, когда две жидкости,
отличающиеся как плотностью, так и скоростью звука, разделены
плоской границей. Рассмотрим задачу отражения плоской
гармонической волны от такой границы. Плотность и скорость звука
в среде, из которой падает волна (z<0 на рис. 12.1),
обозначим через р! и Ci соответственно. Эти параметры в другой среде
(z>0) равны р2 и с2. Будем предполагать, что нормаль к
фронту падающей волны лежит в плоскости чертежа (рис. 12.1).
В этих предположениях падающую волну можно записать в
виде
р4+=Лехр [l(lx+kiaz—fut)]9 z<0, (12.26)
где А — амплитуда волны; к={£, 0, kit}\ kiz = y(a2/cl2—I2 — ее
волновой вектор.
Поскольку граница неподвижна в отсутствие звуковых волн,
то, как мы уже видели (см., например, § 14), граничные
условия могут выполняться при всех t и х, только если частота
со и проекция волнового вектора на границу будут
одинаковыми для всех волн. Следовательно, выражение для отраженной
волны, уходящей от границы в первой среде, будет иметь вид
pr=VAехр [Щх—к1яг—Ы)]9 z<0, (12.27)
где V — коэффициент отражения] k/={g, —kiz) — волновой
«вектор, изображенный на рис. 12.1.
254

fgte,y,z)-0
Рис. 12.2
0
If
1
1 я
Ч|к'
1
Рис. 12.4
РИс. 125
Пусть вторая среда — вакуум (свободная граница), тогда
акустическое давление, создаваемое суммой падающей и
отраженной волн на границе z=0, должно обращаться в нуль.
Отсюда легко находим значение коэффициента отражения V=
=—1. При этом для суммарной нормальной составляющей
255

скорости на границе в соответствии с (12.11) получаем
значение
»« = — %■ ехР V (Iх —©О!»
в 2 раза большее нормальной скорости в падающей волне.
Аналогично решается задача в случае границы с абсолютно
твердым телом, на которой должна обращаться в нуль
суммарная нормальная скорость viz=0. При этом для коэффициента
отражения получаем V=l9 т. е. на абсолютно твердой границе
давление удваивается. В общем случае границы двух сред мы
должны добавить преломленную (прошедшую) волну,
распространяющуюся во второй среде и уходящую от границы:
p2=WAexp[i(tx+k2lz—<о/)], (12.28)
где W — коэффициент прозрачности границы; к2={£, 0, k2t}
(£2=u)/c2, kiz=l/k22—V)—волновой вектор, имеющий равную
-с kt и к/ проекцию на границу (см. рис. 12.1). На последней, по
обе ее стороны, должны быть равными звуковые давления и
нормальные составляющие скорости частиц. С учетом (12.11)
эти условия примут вид:
(Pt + PTUo = ftLo'
(12 29)
Pi \ дг дг /z=z0 ^ дг
Отсюда с учетом выражений (12.26) — (12.28) и следуют
уравнения для определения двух неизвестных коэффициентов V
и W:
1 + V = W, b*.(i — V) = — W. (12.30)
•Pi Р2
Обычно вводятся угол падения волны 8i и угол преломле*
ния 62 (см. рис. 12.1), тогда условие равенства проекций
волновых векторов на границу запишем в виде известного закона
преломления
jfe1sine1=/52sinGa (12.31)
или, если учесть, что ki = (o/cit £2=со/с2,
sin91/sin92=n, n=kjki=ci/c2. (12.310
Далее, вводя величину m=p2/pit с учетом £iZ=£4COs9b k2t=
= k2 cos62 из (12.30) получаем формулы Френеля:
У __ m cos 9Х — п cos 9а __ m cos Ъг — V п2 — sin2 9г
mcos 9Х + п cos92 mc0s 9Х + /п2 — sin2 9Х
(12.32)
™, _ 2m cos 61 2т cos 9t
mcos91 + ncos9t тcos Эх + Км2 — s'm2^
256

При нормальном падении волны на границу (е1=е2=0) из
последних формул следует:
v==rE^= 9:c:zpiC: •w = 2pf (12.32-)
m + n hf№ + PiCi Pa^a+pxCx v '
Таким образом, при нормальном падении коэффициенты
отражения и прозрачности определяются только волновыми
сопротивлениями (называемыми также импедансами) Zl=plcl и
Z2=p2^2 сред. Формулы (12.32') можно записать и в таком
виде:
Как видно из (12.32), эти формулы остаются справедливыми и
при наклонном падении волны на границу, если под
импедансами Zi и Za понимать величины
Zi = PA/cos 6lf Z2'= p2^2/cos 92. (12.34)
Нетрудно проверить, что так определенные Z, и Z2 равны
отношению давления и нормальной к границе скорости частиц
соответственно в падающей и прошедшей волнах
Zi = Pt/vu> Z2 = p2/v22 (12.35
и называются нормальными импедансами соответственно в
первой и второй средах.
Отметим, что для определения коэффициента отражения
плоской волны от границы оказывается достаточно знать
только так называемый входной импеданс границы Z^, равный
нормальному импедансу Z2 на границе z=0. Так как нормальный
импеданс не должен испытывать скачка при переходе через
границу (поскольку непрерывны vt и р), то, очевидно, нормальный
импеданс полного поля на границе со стороны первой среды
должен быть равен ZBI. Поскольку во второй среде в
рассматриваемом нами случае нормальный импеданс всюду (в том числе
и на границе) равен постоянной величине Z2, то ZBX=Z2,
поэтому
El
vi9
1 + V PiCi = 1 + V z _ Рг I =z
1-V cosO* 1-V X v2Z Le 2'
откуда получаем для V выражение (12.33). В общем случае
pz(z) и c2(z) могут быть произвольными функциями г.
Выражение (12.33) для V остается в силе с заменой Z2 на ZBX.
Последний должен быть получен отдельно.
45.2. Особые случаи. Полное прохождение и полное
отражение.
Рассмотрим некоторые наиболее интересные случаи.
1. Из формул (12.32) при et-Mt/2 имеем V-+— 1, W-+0.
Отсюда следует, что Pi=Pi++pr=0 и /?2=0, т. е. не может быть
9 Л. М. Бреховских, В. В. Гончаров 257

плоской волны, распространяющейся вдоль границы раздела
двух жидких сред.
2. Отраженная волна отсутствует. Как следует из (12.32),
У=0 при угле 0i, удовлетворяющем условию mcos0i=
=Уп2—sin20t. Отсюда легко найдем угол полной прозрачности
границы:
0/ = arcsin V (m2—nz)/(m2— 1). (12.36)
Конечно, не при любых m и п такой угол существует.
Необходимо, чтобы величина под корнем была положительной и
меньшей единицы.
3. Скорость звука во второй среде больше, чем в первой
(л,<'1). При этом если угол падения 0j больше некоторого
критического значения 0„р, где sin0Kp=n, то из (12.31) легко
видеть, что не существует вещественного угла 02 для прошедшей
волны. Однако для гармонических волн формулы (12.32)
остаются справедливыми и в этом случае. При этом их удобнее
представить в виде:
у mcosQt-iVsmtQj-n* 2mcosQ1
"mcosei + iKsin^-n*' mcosQi + iVsWQi-n*'
(12.37)
Отсюда, записав коэффициент отражения в виде V=
= |У|ехр(«р) (<р — фаза), имеем:
|У|=1, ф = — 2arctgi^^=^- . (12.38)
11 m cos 9i
Прошедшая волна экспоненциально затухает при удалении от
границы, т. е. является неоднородной:
p2=AWехр[— ^Ysin^i—п2 z+i(lx—a>t)].
Поскольку последняя не уносит энергию от границы,
коэффициент отражения оказался равным единице (по модулю).
В этом случае говорят о полном внутреннем отражении волн.
Комплексность коэффициента отражения на закритических
(01>0кр) углах падения приводит к искажению формы
отраженной негармонической плоской волны. В самом деле, разложим
падающую на границу плоскую волну с произвольной
зависимостью р от времени в интеграл Фурье по гармоническим
волнам со всевозможными частотами. В случае 0i<0KP, когда V
вещественно и не зависит от частоты (см. (12.32)), для
отраженной волны получим тот же интеграл, умноженный на V.
В случае же комплексных значений V не зависящая от
частоты фаза коэффициента отражения Эквивалентна изменению
длины пробега отраженной гармонической волны в среде на
величину ср/&, уже зависящую от частоты. В результате профиль
отраженной волны, так же как и прошедшей, из-за
комплексности искажается.
258

45.3. Энергетические соображения. Вопросы взаимности.
При отражении и прохождении волн должен выполняться
закон сохранения энергии, который формулируется так: энергия,
поступающая к границе раздела в падающей волне, равна
энергии, уносимой от границы отраженной и прошедшей волнами.
Рассмотрим нормальные к границе составляющие среднего по
периоду вектора плотности потока энергии (12.25) в падающей,
отраженной и прошедшей волнах:
/tz = id]1cosG1, 4 = _LUL|vpCoselt
2рЛ 2р!С!
/2z = ^|WTcos02. (12.39)
2р2с2
Приравняв поток энергии, притекающей к границе, к
уходящему от нее, получим * (1 — IV Р) = 21 W I2, что вполне со-
Pi<?i Ра<?2
гласуется с формулами (12.33), (12.34).
Как следует из (12.30), акустическое давление в прошедшей
волне будет в 1 + V раз больше, чем в падающей. Например,
при нормальном падении плоской волны из воздуха (piCi=
= 42 г/(см2-с)) в воду (р2с2«1,5-105 г/(см2-с)) получаем из
(12.32) 1/«1, т. е. амплитуда давления в воде будет в 2 раза
превышать амплитуду давления в падающей волне. Если же
волна падает из воды в воздух, то У« — 1, W=0, т. е. звуковое
давление в прошедшей волне будет во много раз меньше
звукового давления в падающей. Таким образом, при переходе
звуковой волны из одной среды в другую и обратно отсутствует
симметрия по отношению к значению звукового давления.
Такая же картина будет наблюдаться и по отношению к скорости
частиц жидкости в волне.
Рассмотрим, как будет обстоять дело по отношению к
потокам энергии от границы и к ней. Вычислим отношение
нормальных составляющих потоков энергии в падающей и прошедшей
волнах, определяемых выражениями (12.39):
!2Z _ COS 62 РхСх | дег2, _ COs62Pi£i_, j , у |2 (12.40)
/+ cosOx р2г2 cos0ip2c2
Остановимся сначала на случае нормального падения волны на
границу (6i=62=0). Воспользовавшись также выражением
(12.32'), для отношения нормальных составляющих потоков
энергии (в данном случае и полных потоков) имеем формулу
/+ (Р2С2 + рл)а'
которая уже будет симметричной по отношению к замене pt*-^
-^р2, Cf-*c2 и обратно. Следовательно, при нормальном падении
во вторую среду перейдет вполне определенная часть энергии
259
?•

падающей волны независимо от того, из какой среды падает
волна.
Аналогично и в общем случае наклонного падения волны
для нормальных составляющих потоков энергии получаем с
учетом (12.32) симметричную по отношению к замене pi*=*p2l
Ci+±c2j 01^^02 формулу
1чл __ л Р1С1Р2С2 cos Ьг cos 9а
l\z (РЛ cos &а + Рг^а cos Gi)2
Заметим, что здесь мы исключаем случай полного
внутреннего отражения, когда во второй среде поток энергии параллелен
границе раздела и /2*=0.
Укажем также на взаимность углов, при которых
коэффициент отражения обращается в нуль. При падении волны из
первой среды это угол 0/, определяемый из (12.36). При замене
0/->02', т~>1/т, /1-И//1 из этой же формулы мы получим угол
полного прохождения при падении волны из среды 2: sin02/=
=]/(m2—n2)l(m2—l)/n=(sin0/)/rt. Мы видим, что эти углы
связаны между собой законом преломления c2sin01/=^1sin0/,
т. е. также симметричной по отношению к замене с^съ 8/=*=*
^0/ формулой.
45.4. Плавно неоднородная среда. Приближение
геометрической акустики. Волновое уравнение (12.3) для давления
остается справедливым и в случае непрерывной зависимости
скорости звука от координат. Введя зависящий от координат
показатель преломления \i(r)=cjc(r) (с0 — скорость звука в
некоторой фиксированной точке), для гармонических волн
снова получим уравнение Гельмгольца, которое аналогично (12.8):
Дф+*0У(г)Ф=0, k02=(o2/c02. (12.41)
Мы видели, что в случае постоянной скорости звука
уравнение Гельмгольца имеет решение в виде плоской волны
постоянной амплитуды. В общем случае переменного ц(г) на высоких
частотах (&0->оо) запишем решение уравнения (12.41) в виде
*(r)=i4(r)exp[fft„f(r)], (12.42)
Здесь амплитуда Л (г) —медленно меняющаяся функция
координат, которую можно считать постоянной в малой
окрестности точки г (но большой по сравнению с Я0=2я/&0). Фаза
f(r) —также медленно меняющаяся функция, которую в той же
малой окрестности можно представить в виде линейной
функции координат, разложив f (г+бг) в ряд. Таким образом,
выражение (12.42) можно рассматривать как локально-плоскую
волну. Подставив выражение (12.42) в уравнение (12.41) и
приравнивая по отдельности нулю вещественную и мнимую
260

части, получаем систему уравнений:
ДЛ-*0М[(У/)2-^]=0,
(12.43)
2VAVf+AAf=0.
На высоких частотах (£<>-*<») в первом уравнении (12.43)
можно пренебречь членом АЛ, в результате будем иметь так
называемое уравнение эйконала
(V/)2=n*(r). (12.44)
Кривые, касательные к которым в каждой точке нормальны
к поверхностям постоянной фазы волны / (г) = const,
направлены по вектору V/ и называются лучами. Пусть r=r(s) —
уравнение луча, где s — длина дуги вдоль него. Единичный вектор
нормали к фронту волны n=V//|V/| =V//ji должен быть равен
производной dr/ds или \idr/ds=Vf. Продифференцируем это
уравнение по s и воспользуемся векторным тождеством (6.31)
^L = (nV)V/ = — (V/V)V/ = lV-^- Lv/xrot(V/).
ds jli ji 2 ц
Здесь мы также учли формулу (6.31). В результате с учетом
уравнения эйконала (12.44) и rot(V/)=0 получаем
дифференциальное уравнение луча
Найдя луч и интегрируя вдоль него уравнение эйконала,
найдем акустическую длину пути
/ = jV
ds. (12.46)
Здесь предполагается, что при 5 = 0 /=/0 = 0.
Для определения амплитуды волны Л (г) обратимся ко
второму уравнению (12.43). Его первый член с учетом V/=jm
будет 2VA\in = 2\idA/ds. Чтобы преобразовать второй член
уравнения, рассмотрим трубку лучей, выходящих из какого-либо
малого участка (площади dS0) начального фронта /0=0
(рис. 12.2). Проинтегрируем функцию A/=V(V/) по объему,
заключенному между стенками этой трубки и двумя близкими
фронтами, расстояние между которыми равно ds, и применим
теорему Гаусса—Остроградского:
J A/ dV « Д/ dS± ds= J V/ n dS « мА — VidSv
V dSi+dSt
Отсюда в пределе при ds-+0 и dS<r*-0, введя величину *=
= limdS/dS0 (расширение лучевой трубки), получаем хД/=
Л5в-»о
=d/ds(|nx). В результате амплитуда волны Л(г) удовлетворя-
261

ет обыкновенному дифференциальному уравнению
2к^-^- + Л-^-(рс) = 0 или А(л^х) = 0. (12.47)
as as ds
Следовательно, вдоль луча справедливо равенство
^2|jix=const.
На исходной «поверхности f0=0 имеем Л=Л0, |г=|г0, х=х0=
= 1, поэтому окончательно выражение (12.42) примет вид
Ф=ЛУ|*о/1*и exp (ik0f) =Аоус(г)/с0к exp (ik0f). (12.48)
Таким образом, мы получили локально-плоскую волну,
которую можно считать плоской в достаточно малой области.
Амплитуда этой волны медленно меняется в пространстве. При
расчете скорости частиц жидкости по (12.11) достаточно
дифференцировать только экспоненту, содержащую большой
параметр k0, что приводит к выражению
v = —р— п. (12.49)
Вектор скорости направлен по лучу. Вектор среднего за период
волны потока энергии также направлен по лучу и равен в
соответствии с (12.22) 1=|р|2п/(2р0с). Средний поток энергии
через любое сечение данной лучевой трубки dS, равный
2р0с 2р0с0
сохраняется в силу уравнения для амплитуды (12.47).
Следовательно, последнее является просто законом сохранения
потока энергии.
Развитая теория, называемая приближением геометрической
акустики, значительно упрощается, если скорость звука зависит
только от одной координаты, например z—
слоисто-неоднородная среда. При c=c(z) в (12.45) имеем Vji~Vz и лучи будут
плоскими, например z=z(x) в плоскости у—О. Введем
касательный к лучу вектор n=dr/ds и умножим уравнение луча
(12.45) скалярно на орт е« оси х. Поскольку exVji=0, находим
(шпеж= const на данном луче. Если теперь ввести угол
скольжения луча % так, что ne«=cosx (рис. 12.3), получаем известный
закон Снеллиуса
M,(z)cosx(z)==[x0cosxo, (12.50)
где ^0=^(^0); Хо—х(2о); z0 — произвольная фиксированная
координата.
Теперь очевидно, что
& ^v _l_ ]/*l-COS2X ^ yVa(g)--rfc08»X»
-—=tgX=± = Л! »
dx cos x Mo cos Xo
262

или после интегрирования
г
^ = ±fi0cosx0(' * (12.51)
J |Ац»(г)-^со5»Хо
Аналогично для эйконала /(*, 2) из (12.46) следует
J J .cosx J Hocosfo
0 x9 x0
(* IX2 — Ц? COS2 Ya
+ \Л U ^-d^ = (^ —X0)MoCOSXo±
J Ho cos Xo
z
:fW« — n»cosaXodz.
2o
Необходимым условием применимости приближения
геометрической акустики с учетом отбрасывания члена АЛ в первом
уравнении (12.43) будет требование
ДЛ/Л<£02. (12.52)
Другими словами, изменение амплитуды волны на ее длине
должно быть мало. Этот критерий, конечно, не очень удобен,
так как амплитуда волны заранее неизвестна. Если обратиться
к выражению (12.48), то легко видеть, что необходимым
условием будет малое изменение параметров среды на длине волны.
Однако амплитуда наряду с \i определяется и параметром
расширения лучевой трубки х, поэтому в условие применимости
приближения должны входить также и геометрические
свойства лучей. Приближение геометрической акустики без
каких-либо затруднений переносится и на уравнение (12.20, где учтена
зависимость плотности среды р0(г) от координат. При этом
изменится только выражение для амшлитуды волны в (12.48):
Л=Л0Ур0с/(рооСо>0, гДе роо = Const.
45.5. Уравнения акустики движущихся сред. Рассмотрим
теперь случай, когда среда, в которой распространяется звук,
сама имеет некоторое движение, например течения в океане,
атмосферный ветер. Получим акустические уравнения в случае
горизонтального, зависящего только от вертикальной координаты
ветра: \0={и0(г), 0, 0}. Здесь мы уже не можем использовать
линеаризованную систему уравнений гидродинамики (10.3),
полученную для покоящейся жидкости. Легко видеть, что в
случае v0=7^0 в линеаризованное уравнение Эйлера войдут два
дополнительных члена (y0V)v=u0(z)dv/dx и (vV)v0=
= tt>dv0/dz, а в уравнение неразрывности — один и0др/дх=
= (и0/с2)др/дх (здесь v={a, v, w} — акустическая скорость
частиц).
263

В результате вместо системы акустических уравнений
(12.2) получим следующую:
д\ . dv , dvft Vp
h U0 f- W 2- = ' — ,
dt dx dz p0
(12.53)
* + «.£ + .¥»*.»-«.
являющуюся исходной для построения акустики движущихся
сред. В частности, может быть развито приближение
геометрической акустики, учитывающее искривление (рефракцию)
лучей из-за наличия среднего движения. Мы ограничимся
анализом сравнительно простой задачи отражения плоской волны от
однородного полупространства той же плотности и скорости
звука, как и в среде, откуда падает волна, но движущегося с
постоянной скоростью и0 параллельно границе раздела в
плоскости падения волны (рис. 12.4).
В первой, покоящейся, среде звуковое поле падающей и
отраженной волн запишем в виде
рг = A[exp(tfeu2:)+Kexp(^w2)]exp[/(^—©it)], ku= l/ ^—g2.
В движущейся среде прошедшая звуковая волна удовлетворяет
уравнению, следующему из (12.53) при dv0fdz=0:
(ir+"•£)'"-'г4*-0-
Это уравнение также имеет решение в виде плоской уходящей
от границы волны:
р2 = AW exp [i (k2xx + kvZ — u)af)],
= Г^-Цр^)» gl%
На границе г=0 должны выполняться условие равенства
давлений в каждой из сред (Pi|z—о=Р2| *—о) и кинематическое
условие (10.4), где £(*, t) —вертикальное смещение точек
границы. В нашем случае, линеаризуя это условие, найдем
1 Ь=о dt ,Zs=0 dt ° dx
Отсюда следует, что dQdt = — ml = wx |^0 и w2 |2t=0 = —^- +
+ щ -^- = (l — М -|Ц wx Ц0, где k = со/с0; М = и0/с0—число Маха.
В результате с учетом выражения для w$ через р§ (/=1, 2) из
264

первого уравнения (12.53) при 2=0 получаем:
(1 + V)exp[i(£x—©0] = Wехр Щ^х—ю,0],
(1 - М -f) -^- (1 - V) exp [i (£х - ©0] =
= ,„. *" n rexp[f<*■*-"»')]■
(0)a — k2XU0) p0
Для выполнения этих условий одновременно для всех х и /
необходимо, чтобы Ш2=а) и £2*=£. Следовательно, длина волно-
вого вектора в движущейся среде k2=Vk\x+klz =
=k(\—Nil/k) (k = <d/c0) будет меньше, чем в падающей волне,
если последняя бежит по течению (5>0, как на рис. 12.4), или
же, наоборот, больше при £<0. Угол преломления 62
выражается через 6i из соотношения
£2sin Q2=l=k sin 0lf sin 02= (1—M sin Gj)-1 sinQt.
При больших углах падения в направлении течения (£>0)
возникает явление полного внутреннего отражения, а именна
при sin в4>1— Msin6i, откуда sinGiXl+M)"1.
Если ввести параметр <х=1—MsinGj, то формулы для
коэффициентов отражения и прозрачности запишем в виде:
у __ a2 cos 9Х — У а2 — sin2 вг ^ __ 2а2 cos ег
~~ а2 cos ех + У а2 — sin2 Qt ' ~~ а2 cos 0Х + У а2 — sin2 0х
45.6. Волноводное распространение звука. Классическим!
акустическим волноводом является переговорная труба,,
соединяющая мостик с машинным отделением на старых судах.
Однако мы будем интересоваться только геофизическими
волноводами, когда распространение волн свободно во всех
горизонтальных направлениях и ограничено в вертикальном
направлении.
Простейшим примером такого волновода является
однородный океан с плоским горизонтальным, абсолютно
неподатливым дном. На его поверхности 2=0, как всегда, имеем р=0 и
V=— 1 согласно п. 45.1. Следовательно, при z<0 выражение
для поля записывается в виде:
р = Asmkzzexp[i{lx — (ot)], кг = У©2/*:2 — £2. (12.54>
На дне z=—H должно выполняться условие ср|_-я—О, т. е.
coskzH=0, kzH=—n/2 + nnt /г=1, 2, (12.55)
Отсюда получаем дисперсионное соотношение для нормальных-
волн (мод):
265

«»-'[-Нг(-1ГГ
(12.56)
Здесь k=(o/c; с^п)=ml%n —фазовая скорость моды.
Выражение для давления в моде номера п имеет вид
Рп = Лфп (z) exp [i {\пХ — ©0],
(12.57)
">"=sin[i (»-т)2]
Групповая скорость волны равна
Как видно из (12.56), при фиксированной частоте оэ только
для конечного числа мод горизонтальное волновое число £п
будет вещественным. Эти моды называются
распространяющимися. Для мод высших номеров |п становится чисто мнимой
величиной, а возмущение в волне экспоненциально убывает в
направлении х. Наименьшая частота о)п, при которой мода номера
п является распространяющейся, называется критической
частотой, равной согласно (12.56) а)п=я(м—*/2)с/Н.
Волновод с абсолютно мягкой верхней границей и жесткой
нижней является чрезвычайно идеализированной моделью
океанского волновода. Следующим, уже неплохим приближением
к действительности является модель «жидкого дна», когда оно
представляется в виде однородного жидкого полупространства
плотностью р2 и скорости звука с2. Если с2>с (с — скорость
звука в слое), то существуют незатухающие моды,
соответствующие таким возмущениям (12.54) в жидком слое, фазовая
скорость которых меньше скорости звука в дне, т. е. £>о)/с2.
При этом в полупространстве z<— Н распространяется
неоднородная волна
р2=Вехр [УГ-<о2/с22(г+Н)+1(1х-Ы)Ъ (12.58)
которая не переносит энергии в направлении от границы.
Для определения параметров нормальных волн в этом
случае приравняем отношение plw\t=-H, которое можно найти,
пользуясь (12.54), входному импедансу жидкого
полупространства z2 = pJw2\z=-H, определяемому из (12.58) (напомним,
что i(i>pw = dp/dz):
^igkzH=-J^ .
266

Отсюда, вводя величину o=ktH=Hy<i>2/c2—|2, получаем
дисперсионное уравнение для определения £я (со):
tga = -fi/ ■ \ * = -• *•= —■ (12.59)
Это уравнение при достаточно высоких частотах будет иметь
конечный набор корней an(co), таких, что пп—я/2<оп(ю) ^
^.пп (л=1, 2, ...). Соответствующие им нормальные волны
записываются в виде (12.57) с фп=sin (o«z/tf), |n=
=kyi-on2/k2H> и сф<п\=сЦ1-оп2/к2Н\ Критической частотой
л-й моды, определяемой условием ап=пя—я/2, будет согласно
(12.59)
V 2/ я Ki-^2 г 2
В реальных условиях океана волновод для акустических волн
может создаваться не только в результате отражения от
поверхности и дна, но также в результате рефракции звуковых
волн в слоях с переменной скоростью звука с (z). Типичный
вертикальный профиль скорости звука в глубоком океане
изображен на рис. 12.5, а. Скорость звука минимальна на «оси»
подводного звукового волновода («звукового канала») z0 и
увеличивается кверху за счет роста температуры, а книзу за счет
роста гидростатического давления. При этом энергия волн,
фазовая скорость которых C4,=g)/£=c(z1)=c(z2), будет в
основном локализована в слое жидкости z2<z<Zi. Вне этого слоя
волны будут неоднородными. Лучи, соответствующие этим
волнам, изображены на рис. 12.5, б.
Параметры распространения нормальных волн можно
найти, если искать решение волнового уравнения (12.3) с c=c(z)
в виде
р=Лф(г)ехр [t(S*~©01-
В результате для функции cp(z) имеем обыкновенное
дифференциальное уравнение
аналогичное уравнению (10.59) для внутренних
гравитационных волн. Добавив к нему граничное условие, например q>(0) =
= 0 на свободной поверхности, и условие непрерывности р и
w на жидком дне, получим краевую задачу для определения
собственных значений сф(п) и соответствующих им собственных
функций фп(г).
Качественный анализ решений этой краевой задачи
аналогичен проведенному выше для внутренних гравитационных
волн. При этом оказывается, что для фиксированной, достаточ-
267

но высокой частоты сот имеется конечное число
распространяющихся мод* для которых сф(п)<с2 — скорости звука в дне. Эти
моды экспоненциально затухают при z>zl(n)(co) и 2<22<п)(<о),
где Сф(п)=£(21(п))=с(г2(Л)). Моды, для которых с(—#)<
<Сф(п)<Сг, имеют амплитуду одного порядка величины от дна
до поверхности и подобны рассмотренным выше модам в
однородном жидком слое на жидком полупространстве. На
критических частотах соЛ фазовая скорость соответствующей моды
равна скорости звука в дне.
§ 46. Сферические волны
46.1. Сферически-симметричное решение волнового уравнения.
Сферически-симметричная волна, излучаемая пульсирующей
сферой малого радиуса, называемой в акустике монополем,
является другим (после плоской волны) простейшим решением
волнового уравнения (12.3). Получим это решение, записав
(12.3) в сферических координатах:
iZ-Hi'ZHfr'* (12-6"
где p=p(r, t)\ r=yx2+y2+z2. Легко видеть, что функция гр
удовлетворяет одномерному волновому уравнению, общее
решение которого имеет вид, аналогичный (12.5) с заменой х на г.
Это приводит к следующему общему решению для давления
P(rJ):
г г
являющемуся суммой расходящейся (/) и сходящейся (g) волн.
Как и в случае обычных плоских волн, профиль давления в
сферически-симметричной волне остается неизменным, но его
величина уменьшается по мере увеличения г.
Подставив (12.62) в (12.4) с t0=— оо и выполнив простые
преобразования интеграла, получим, что скорость частиц
направлена по г и равна
t
vr = v = ±-?- + — Г pdt. (12.63)
Рос 9or J
Здесь знак минус соответствует сходящейся волне, плюс
—расходящейся. Второй член в этой формуле, зависящий от
предыстории волны, убывает с ростом г значительно быстрее первого,
так что на больших расстояниях, как и в плоской волне, v&
~р/р0с В несжимаемой жидкости (с-^оо) первый член
выпадает, а второй остается и соответствует
сферически-симметричному решению уравнения Лапласа для потенциала скорости.
Поэтому этот член называют неволновым,, а первый —
волновым членом. Расстояние, на котором неволновой член сущест-
268

вен, называют неволновой зоной, а те расстояния, на которых
им можно пренебречь,— волновой зоной.
Если излученный импульс имеет конечную длительность,
т. е. />->0 и v->0 при f->-±oo, то из (12.63) следует, что суммар-
оо
ный импульс волны Г pdt=0. Следовательно, сферически-сим-
•-О0
метричная волна в отличие от плоской не может состоять
только из областей сжатия (р>0) или разрежения (р<0).
В случае гармонической зависимости от времени функций
f и g в (12.62) придем к гармоническим
сферически-симметричным волнам вида:
А
р = —exp[i(±kr — о/)],
(12.64)
v= -^-(±1 + —)exp[i(±kr — o)t)].
p0cr \ kr)
Здесь выражение для v получено из р с помощью 02.11).
Легко видеть, что границей волновой и неволновой зон служит
расстояние Го порядка длины волны kr0~ 1. При kr<l превалирует
неволновой член, при kr^l имеем волновую зону.
Пусть скорость поверхности пульсирующей сферы,
излучающей сферически-симметричную волну, задана законом vT=
= у0ехр(—Ш). Пренебрегая в линейном приближении (малые
v0) изменением радиуса сферы /?0, приравняем эту скорость ее
значению в волне (12.64) с верхним знаком (уходящая волна)
при r=R0. В результате для амплитуды давления А находим
А= Ро^ехр(_^о) (12>б5)
46.2. Объемная скорость. Импеданс сферической волны.
Если радиус пульсирующей сферы мал (kR0<£l)t то выражение
(12.65) упрощается: А»— i(dp0Ro2vQ. В этом случае вместо
скорости точек сферы обычно вводят величину
V0=4nRo2v0, (12.66)
называемую объемной скоростью излучателя и равную объему
жидкости, который вытесняется сферой в единицу времени. При
этом выражения (12.64) перепишем так:
Р = - -^ V0exp[i(kr-<»t)h
(12.67)
Покажем теперь, что любой малый по сравнению с длиной
волны излучатель, а не только пульсирующая сфера излучает
269

сферическую волну (12.67), если только он имеет отличную от
нуля объемную скорость V0. Рассмотрим для этого излучение
звука при возникновении в некотором объеме V избытка или
недостатка вещества. Изменение массы вещества в объеме dV
будем характеризовать величиной (ро+р)<7(г, t)dV, где q(r, t) —
заданная функция; р0+р —полная плотность. В этом случае
исходное уравнение сохранения вещества (6.7) запишем в виде
jf§(Po + P)dV = ^(Po+p)qdVt
откуда легко следует обобщение уравнения неразрывности (6.9)
-J+vVp + (Po + p)Vv=(p0+p)<7.
01
Линеаризируя это уравнение относительно акустических
величин v и р, предполагая q также малым, получаем
-^- + PoVv = Po<7 или ^- + p0c2Vv = p0cY (12.68)
at ot
Отсюда с учетом линейного уравнения Эйлера (12.4) следует
неоднородное волновое уравнение
Ap-±*£-=~9o*Lf (12.69)
н са а/2 ™ ot '
а также неоднородное уравнение Гельмгольца для
гармонических процессов
&p+k2p=mp0q, k=(o/c. (12.70)
Фундаментальным решением последнего, соответствующим
точечному, т. е. малому по сравнению с длиной волны источнику
00
в точке г=0 с <7=<7об(г) и с объемной скоростью V0 = \\\qdV=
-оо
=q0t и будет выражение (12.67) для р.
Определим энергию, уносимую сферически-симметричной
гармонической волной, для чего найдем вектор плотности
потока энергии р\у направленный по г. Полагая V0= | V0|exp(ta),
q>=kr—(ut+a и беря вещественные части выражений (12.67)»
имеем
©Ро \Vo\ - ю I V01 / • I COS ф \
pv = —^- ' 0| smcp——^- sin qH —1 =
4я г 4псг \ кг ]
16яа га V 2kr ) v '
Отсюда для усредненного по периоду волны суммарного
потока энергии через сферу радиусом г получаем
/ = 4яг> = ^£-k2\ V0|a. (12.72)
270

Член, содержащий sin2cp/£r в выражении (12.71) и
соответствующий неволновому члену в выражении для скорости, при
усреднении дает нуль. Однако этот член в случае малых по
сравнению с длиной волны размеров излучателя играет
основную роль в сопротивлении, которое оказывает среда при
излучении звука.
Введем импеданс расходящейся сферически-симметричной
волны на произвольном расстоянии г, т. е. величину Z=p/v>
равную согласно (12.67)
Z=ipe©r/(f*r—1). (12.73)
На малых расстояниях, в частности на поверхности
пульсирующей сферы малого радиуса R0 (kR0<, 1), импеданс определяется
в основном неволновым членом и является часто мнимым: £|ло=
=—icopoRo. Следовательно, давление на поверхности сферы
будет равно p\Ro=—i(DpoRoV\R<i=p0R0ay где а—ускорение
точек сферы. Полная сила, действующая на всю поверхность
сферы, при этом имеет вид F=4np0R0*a=Ma, где Af=
=4яр0/?о3 — присоединенная масса пульсирующей сферы,
помещенной в несжимаемую жидкость (см. задачу 7.13). Таким
образом, при расчете сопротивления среды для излучателей
малых размеров можно использовать присоединенную массу,
рассчитанную для несжимаемой жидкости.
46.3. Акустический диполь. Рассмотрим систему из двух мо-
нополей, расположенных на расстоянии г0 друг от друга
(рис. 12.6). Пусть объемные скорости излучателей одинаковы
и равны У0, но излучатели работают в противофазе. Выражение
для суммарного звукового поля согласно (12.67) имеет вид
tcopo у Г exp (Ik 1 г + г0/2 \) exp (ik \ г - г0/2 1) 1 по 74\
Р 4я Ч |г+г0/2| I г — r0/21 J"
При г»Го, как следует из рис. 12.6, |г±г0/2|»
«r[l±(ro/2r)cos0]. Сохраняя члены порядка г0/г только в
экспонентах, найдем
p_2e2XLsin(-^cose )exp(ikr). (12.75)
Таким образом, мы снова получили сферическую волну
exp(ikr)/r, но с множителем sin[(£r0/2)cos 0], определяющим
характеристику направленности излучающей системы. Эта
характеристика многолепестковая, если kr0^>l, так как в этом
случае функция sin[ (£ro/2)cos0] несколько раз достигает мак*
симума и проходит через нуль при изменении 0 от нуля до л.
Случай, когда монополи находятся на расстоянии, малом по
сравнению с длиной волны £г0«<1, соответствует
акустическому диполю. Сохраняя при этом в (12.74) члены порядка г/г0 и
271

в знаменателях (что важно для малых расстояний &г«1),
получаем
р= £^LVor /1+ ±)CosQexv(ikr). (12.76)
Характеристика направленности акустического диполя косину-
-соидальная. Линия, соединяющая монополи, от которой
отчитывается угол G, называется осью диполя, а произведение
Уо1*о — его моментом. Максимум излучения приходится на
направление вдоль оси диполя, в перпендикулярном направлении
•излучение отсутствует.
Отметим, что выражение (12.76) может быть записано и
так:
p„i^K0r0v[i^-], (12.77)
т. е. поле диполя получается при дифференцировании поля мо-
нополя в направлении оси диполя.
Если монопольный источник соответствовал излучению
пульсирующей сферы, то, как можно показать, дипольный
источник соответствует осциллирующей в жидкости сфере, т. е.
движению центра жесткой сферы по закону v=v0exp(—tot).
При этом, так же как и для пульсирующей сферы, сила
сопротивления среды для осциллирующей сферы малого радиуса
определяется присоединенной массой шара при ускоренном
прямолинейном движении его в несжимаемой жидкости:
(2л#о73)ро (см. (7.40)).
Задачи
12.1. При / = 0 заданы давление p(xt 0)=р<>(*) и скорость частиц
#(х, 0) = t;0(jc). Найти решение одномерного волнового уравнения p(xt t).
Решение. Общее решение волнового уравнения имеет вид p(xt t) =
=f(x—ct)+g(x-\-ct)t при этом скорость частиц v(x, t) = (poc)~l[f(x—ct) —
—g(x+ct)]. Подставляя в последние выражения значения р и1 v при /=0,
наводим:
/ (*) +£ (*) = Ро (х), / (х) —g (х) = QoCVo (х).
Отсюда непосредственно следует, что f(x)=l/2[po(x)+pocv0(x)], £(*) =
= 72[А>(*)— PoCv0(x)] и р(х, t) = 42[Po(x—ct)+p0cv0(x—ct)+p0(x+ct)—
—pocv0(x+ct)].
12.2. Пусть на плоскости 2 = 0 задано распределение нормальных
скоростей vz\z=o=Voexp [i(kxx—(ut)]. Найти излучаемую при этом звукОцую
волну.
Решение. След на плоскости z=0 излучаемой звуковой волны должен
совпадать с заданным распределением нормальной скорости, а именно
p^A^p[i(kjc + kzz-^t)]t k2 = /со2/*2 - k%.
Нормальная скорость на плоскости 2=0 при этом равна
1 др
/соро дг
= А exp [i (kjc — со/;].
272

Отсюда для амплитуды звуковой волны А получаем
Ро^о Ро<*>о p9cv0
А = '
У «Р/с* -k\ cos 9
где 9 — угол, составляемый волновым вектором k={kXt kz) с осью z.
12.3. Плоская гармоническая волна p+=Aexp[i(kx—ю/)],
распространяясь в трубе, отражается от ее конца, закрытого подвижным поршнем
массой т на единицу площади. Рассчитать импеданс препятствия и коэффициент
отражения.
Решение. Отраженную от поршня
волну запишем в виде р_=ЛУехр [—i(kx+
+ 0)01- Под действием суммарного
давления поршень придет в движение со
скоростью, определяемой вторым законом
Ньютона, mdv/dt=p или для гармонических
процессов v=pl(—mm). Таким образом,
для импеданса поршня получаем Z=p/v=
=— torn. Теперь по (12.33) найдем
коэффициент отражения
V= (кот+р0с)/(torn — рос).
Рис. 12.7
12.4. В условиях предыдущей задачи считать, что безмассовый поршень
толщиной Л{£Л<1) изготовлен из упругого материала с модулем Юнга Е
и оперт на абсолютно жесткую стенку.
Решение. В этом случае смещение и(0) частиц жидкости при ж=0
будет определяться законом Гука p(0)=Eu(0)/h. Следовательно, скорость
будет v(0)=— i(ow(0). Для импеданса при х=0 и коэффициента отражения
находим:
Z-i
iE
(oh
V =
iE — p0coh
iE + PqCcdA
12.5. Найти входной импеданс ZBx жидкого слоя толщиной d, за которым
расположено жидкое полупространство с входным импедансом Z2 для
падающей под углом к границе слоя плоской волны. Акустические параметры
слоя ро, с0. Рассмотреть частный случай однородного жидкого
полупространства с параметрами р2, с2.
Решение. Проекции на границу волновых векторов волн в
полупространстве ж слое (рис. 12.7), как и их частоты, будут одинаковыми, например
\ и со. Решение в слое —d^z<0, опуская общий множитель exp [i&x—(ot)]f
запишем в виде:
р=Л0 sin kQtz+Bo cos kozz,
k
vz = —— (Л0 cos k^z — £0 sin kozz),
tcopo
Положив здесь z0=0, найдем Л0 = —-V (0), £0=p(0). Следовательно, в лю-
RqZ
10 Л. М. Бреховских, В. В. Гончаров 273

бой точке — d^z^O
ta)p0
Р (z) = -— vz (0) sin *ofz + p (0) cos k02*t
'Roz
k
V2 W = Vt (°) C0S k0Z2 ~~ — P (°) Sil1 ^OZ2'
fop0
Для импеданса будем иметь
tf0tg(*ozz)+Za
Z W = у t -у ♦ /fc ч Zo» (12.78)
Zo + tZ2 tg (kozz)
где Z0=(Dpo/^oz=po^o/cos 9o — нормальный импеданс плоской волны в слое.
В частности, входной импеданс ZBX=Z(—d) будет равен
Z2-iZ0tg(k02d)
z"~ ь-ъыы z- (12-79)
В однородном полупространстве (г>0) имеется только уходящая от границы
волна р2«ехр [i(tx+k2tZ—<ot)], k2z=i(o2/c22—t2. Поэтому импеданс
Z2~Z (0) = (рМ^ = <*P2/k2Z= арщ/У<*/$ - £2.
12.6. Определить параметры однрродного слоя р0, с0, d, расположенного
между двумя полупространствами с pi, сх и р2, с2, так, чтобы падающая под
углом из первой (или второй) среды волна не отражалась (полное
прохождение).
Решение. Коэффициент отражения от слоя V можно найти из (12.33),
где следует положить Zi = <Dpi/fciz, Au=y(<D/ci)2—£2, Z2=ZBX —входному
импедансу опирающегося на однородное полупространство слоя. Выражение
для Zbi через Z2=cop2/£2z и Z0=(upQ/k0z было выписано в предыдущей задаче.
По условию V=0, т. е. Zi=ZBX, или в соответствии с выражением (12.79)
Z2~iZ0tg(k0Zd)
l" Z0-iZttg(k02d) °*
Это уравнение справедливо в трех случаях: 1
1) Z0=Zi=Z2 — нормальные импедансы всех трех сред равны;
2) k0zd=nn (п=1, 2, ...) и Zi=Z2\ в случае нормального падения
волны имеем piCi=p2c2 и d=nk/2 — толщина слоя равна целому числу полуволн;
3) k0zd=(n+l/2)n (п=0, 1, ...), Z0=yZiZ2, т. е, нормальный импеданс
слоя должен быть равен среднему геометрическому из импедансов
полупространств. В случае нормального падения рой)=Ур1^Р2С2, </=(2я+1)Х/4 (п=
=0, 1, ...)—по толщине слоя укладывается нечетное число четвертей волн
(ср. с задачей 2.6).
12.7. Определить коэффициент отражения плоской волны, падающей из
жидкого полупространства с с<> и ро под углом 90 на упругое полупространство
плотностью рь Скорости продольных и поперечных волн в упругом
полупространстве равны ci и с% соответственно.
Решение. В упругом полупространстве возбуждаются только
вертикально поляризованные уходящие от границы волны. Проекции волновых век-
274

торов на границу для всех волн одинаковы, т. е. k0z = k0smQo=l=kx = KXt
£0=G)/c0f k=(u/ci, x=(o/ct (рис. 12.8). Поэтому потенциалы <р и $ для
упругого полупространства запишем в виде:
y=Wl exp[i(lx+kzz—(ot)]t
tj)=U7texp[i(£*+xz2—со/)], 2<0,
где fe=V(o2/o2—£2;-х*=У(о2/с*2—£2. Воспользовавшись формулами (4.2),
(3.22) и (3.6), получим выражения для нормальных скоростей частиц и
компонент тензора напряжений на границе:
°хг 1*=о = ~ Pic? №*Щ + № - *а) Wtl
Здесь также опущен общий множитель /°Оусо
exp[i&x — (ot)]. Так как жидкость не
сопротивляется сдвигу, то o~zx|r=o=0, т. е. Wt =
= —2kzl/(2t2—>i2)Wi. По обе стороны от
границы должны быть равны нормальные
компоненты скорости. Давление в жидкости
равно нормальному напряжению, взятому с
обратным знаком, так как последнее в отличие
от давления определяет действие
окружающей среды на данную частицу. В результате для входного импеданса упругого
полупространства имеем
fiffC-l
Рис. 12.8
*в* = -
р1(0 (2g»-xV + 4£aMz
(12.80)
Коэффициент отражения вычисляем по (12.33):
V = (ZBX - Z0)/(Z х + Ze), Z0 = - p0CD/*0f.
k0z=V<»2/<%-l2- (12.8D
12.8. Вдоль границы жидкого и упругого полупространств может
распространяться поверхностная волна Стонели, аналогичная релеевской волне на
границе упругого полупространства с вакуумом. На основе результатов
предыдущей задачи получить уравнение, определяющее скорость
распространения этой волны.
Решение. Искомая волна должна быть неоднородной и убывающей
экспоненциально как в упругом полупространстве, так и в жидкости.
Следовательно, kz=— tyg2—ю2/с,2=— коуЗ^Я xz=—1'У62—o)2/ct2=— toys—Stt
*о*=-1'У12-о>2/с02 fo>yS=3oT где Sz = l/c,2; S,= l/^2; S0=l/c02; 5=1/^2;
c« — скорость волны Стонели1. Мы видим, что с9<с0, c9<ct<Ci. В жидкости
с удалением от поверхности будет убывать амплитуда отраженной волны
ехр [i(lx—k0zz) ] =■ exp (tgx—©yS—Sqz) , в то время как амплитуда падающей
волны будет нарастать в этом случае. Поэтому мы должны потребовать для
поверхностной волны У=оо или в соответствии с (12.81) ZBx=—Z0.
Выражая ZBX и Zo через введенные нами величины S, S0, Si и Sti получаем урав-
275
10*

нение для определения S, т. е. скорости волны Стонели:
fs(S) = fR(S)-lJLSl VS ~Sl =0,
Pi у s— s0
fR (S) = 4S Y'S^Si yiT^St- (2S- St)*.
Уравнение /b(S)=0 уже встречалось нам в теории релеевских воли и
определяет скорость волны Релея. Уравнение /«(5)=0 всегда имеет корень
S>max{S0, S,}. Действительно, при S-*oo функция /e(S)-*2S(S*—Sj)>0.
С другой стороны, Ы$0)->—°°» если ^о>5«, и fa(St)=— S^— (po/pi)S<2(S<—
—5,)1/f(Si—5оГу§<0, если S0<St. Следовательно, на концах интервала
(max{S0, S<}, «>) функция f»(S) имеет разные знаки, поэтому в некоторой
точке S>max{S0, St) /»(S)=0. В частности, при St<S0<S (сл<с0<с{)
нетрудно получить:
В этом случае скорость волны Стонели немного ниже скорости звука в
жидкости, что соответствует слабому ее затуханию в жидкости при удалении от
границы. Отметим также, что в уравнение f«(S)=0 не входит частота волны,
т. е. волны Стонели? так же как и волна Релея, распространяются без
дисперсии.
12.9. Рассмотреть звуковые волны с учетом силы тяжести, предполагая,
что скорость звука и энтропия постоянны во всей жидкости.
Решение. Уравнение состояния р=р(р) в силу постоянства
равновесной энтропии справедливо и для равновесных значений: р0=р0(р).
Интегрируя уравнение гидростатики —gpo=dpoldz=(dp0/dpo)adp0ldz=c2dpoldz с
учетом, что с2=const, получаем po(z) = Po(0) ехр (—gz/c?). Отсюда также
следует, что частота Вяйсяля N2(z)=—g(p0-ldpoldz+glc2)=0. При этом
система линеаризованных уравнений гидродинамики (10.3) переходит в
следующую систему акустических уравнений:
TT + v(£)-°' ^t-f + ^*-o.
Отсюда, например, для величины ^=р/ро следует
1 && g д& л
с2 dt2 с2 дг
Если искать решение последнего уравнения в виде fr=A ехр [i(xr— со/)],
х={хл, xv, х*}, то легко получить связь между х и со: co2=x2c2+i'gxz. С
другой стороны, если ввести еще вектор k={fcx, kVt kt}, так что х*=&х, Kv = ky,
-Xz=ki+iar то, разделив в соотношении между х и © вещественную и мнимую
части, находим a=—gl2d2 и со2= {k2+a2)c2. Таким образом, имеем звуковую
волну
р = Ар0 (0) ехр (— gz/2c*) ехр [i (кг — со/)],
276

распространяющуюся в направлении вектора к. Дисперсионное соотношенве
для этой волны имеет вид G)=cy#4-g2/4c\ сф = (o/k=<?У 1 +g2/4k2c*t т. е.
появляется дисперсия длинных звуковых волн, если &<&min—g/2A Частот!
(0min=^/2c является минимальной частотой звуковых волн в поле силы
тяжести. Для воды o)min«3-10-"3c~l, длина волн, для которых дисперсия
существенна, Х>Ятах = 2я/Лт1п = 4яС2/£«3000 КМ. * "
12.10. Получить дисперсионное соотношение для
гравитационно-акустических волн в изотермической атмосфере.
Решение. Считая газ атмосферы идеальным, запишем равновесное
уравнение состояния в виде Po(*)=Po(0)po(z)/po(0). Волновые процессы в
атмосфере протекают при постоянной энтропии pp~v=const, где y=cplcv—\t4-
Следовательно, скорость звука с2= (dp/dp)»=yp0lp0=const и p0(z) =
— c2p0(z)/y. Проинтегрировав теперь уравнение гидростатики dp0/dz=
= (c2ly)dpo/dz=—gp0(z), получим р0 (z) =р0(0) exp (—ygz/c2) и ЛР.=
= —g(po~ldpoldz+glc2) = (y—\)g2lc2. В результате линейная система
уравнений гидродинамики (10.3) примет вид:
at ро Ро ot аг
dp 1 dp N2
Вводя величину &,=plp0y для гармонических процессов частоты © имеем!
(N2 N2 \
\g © /
— — $>— -^- о; + V v = 0.
с2 с2
Поскольку коэффициенты этой системы постоянны, ищем решение & и v в
виде, пропорциональном ехр (Ьт) — {£, х*}, что приводит к следующей
связи между х и си:
I* _ ^/с2 - l2N2№ + xj + i (N2 + g2/<*) xz/g = 0.
Отсюда следует, что xr = /k+ia и
a=-(N2+g2lc2)12g=(\l2)p0-*dpoldz=-yg/2c2,
I2 + k\ — cd2/c2 — £Wa/coa + a2 = 0.
Разрешая последнее уравнение относительно ю2, получаем две ветви
дисперсионных соотношений:
о>±2= [ (£2+а2)с2/2] {1 ± [ 1—4A;W2c-2(A;24-a2)-2sin2 О]1/»},
где &2=£2+&z2; в — угол волнового вектора к= {£, kt} с вертикалью.
Максимум второго слагаемого под корнем, который достигается при £2=а2,
равен #2sin26/c2a2<4(Y—1)/y2«0,8. Поэтому путем разложения в ряд получим
2 k2 + a2 Г _ 2#Wasin29
, Г. , - 2#Wasin29]
1 1 + 1 -+-
Первая ветвь а>±2» (й2+а2)с2{1— #W2sin28/[c2(#4-a2)2]}, рассчитанная с
ошибкой не более 8%, соответствует акустическим волнам, распространяю-
277

щимся при £2>а2 без дисперсии. Дисперсия, а также слабая (порядка 10%)
зависимость от N2 и анизотропия звуковых волн имеют место при £2<а2.
Минимальная частота распространяющихся звуковых волн (umin = ^CLC=yg/2c.
Вторая ветвь G)2,= AWsin2 9/(£2+а2) соответствует внутренним волнам.
12.11. Найти звуковое поле от точечного гармонического источника
объемной скорости Vo в полупространстве, ограниченном плоской абсолютно
жесткой или свободной границей.
Решение. Пусть уравнение границы 2=0, а источник находится в
точке с координатами {0, 0, z0/2}. Нужно найти решение уравнения Гельмгольца
(12.8), имеющее вид (12.67) в окрестности источника (r2=x2+y2+(z—Zo/2)2),
с равной нулю компонентой скорости vz при 2=0 в случае абсолютно
жесткой границы или р|2—0=0 — в случае свободной границы. Нетрудно видеть,
что этим условиям удовлетворяет суммарное поле от данного источника и
дополнительного, помещенного в симметричную относительно границы точку
{0, 0, —20/2} с объемной скоростью dfc-Vo, где знак плюс — для абсолютно
жесткой границы, знак минус — для свободной. Этот метод решения носит
название метода мнимых источников. В результате звуковое поле в
полупространстве z>0 имеет вид (12.74) (свободная граница), где г0=— z0Vz.
Отсюда, в частности, следует, что монополь вблизи свободной границы (fczo<Cl)
излучает как диполь, ориентированный в вертикальном направлении.
12.12. Сравнить звуковые энергии, излучаемые монопольным источником
в свободном пространстве и на расстоянии zo/2<Cfc-1 от свободной границы.
Решение. Энергия, излучаемая монополем объемной скорости Vo в
свободном пространстве, определяется формулой (12.72) /т=р0с£2| У0|2/8я.
В случае же работы этого монополя вблизи свободной границы следует
рассчитать поток энергии от дипольного источника, давление для которого
определяется выражением (12.76), где г0=г0 в соответствии с результатами
задачи 12.11. При расчете потока звуковой энергии I=pv можно положить
Лг>1. В этом случае при вычислении скорости v=VpA'(opo достаточно
дифференцировать только экспоненту: vT=(z0k2/4nr)VoCOsQexp(ikr). В
результате получаем
Усредняя это выражение по времени и интегрируя по поверхности полусферы
радиусом г, для суммарного потока энергии находим
Я/2
1„ = 2я -^ | V, |« z\k* j cos* в sin 9 d& = -g£- | V01« (*,*)' A*.
0
Таким образом, наличие свободной поверхности вблизи от излучателя резко
снижает величину излучаемой энергии:
/d//m=(Zo*)76<l.
278

Глава 13
МАГНИТНАЯ ГИДРОДИНАМИКА
При движении проводящей жидкости или газа в магнитном
поле возникают дополнительные силы, действующие на
частицы жидкости со стороны этого поля. В свою очередь,
электрические токи, возникающие в движущейся жидкости, изменяют
внешнее магнитное поле. Взаимодействие между полем
скоростей в жидкости и магнитным полем приводит к ряду
специфических особенностей движения жидкости и в значительной
степени усложняет его описание. Раздел науки, изучающей это
движение в приближении сплошной проводящей среды,
называется магнитной гидродинамикой.
В природе примерами проводящей жидкости в магнитном
поле могут служить жидкое ядро Земли, ионизированные газы
(плазма) в ионосфере, на Солнце и других звездах, в
межзвездном пространстве и т. д. В последнее время интенсивное
развитие магнитной гидродинамики и примыкающей к ней физики
плазмы связано также с постановкой практических технических
задач, таких, как создание магнитогидродинамических
генераторов, осуществление управляемого термоядерного синтеза
и т. п. Отметим, однако, что в ряде важных случаев описание
поведения плазмы в магнитном поле выходит за рамки
рассматриваемого ниже приближения магнитной гидродинамики.
§47. Приближение магнитной гидродинамики
47.1. Основные уравнения. Основными уравнениями магнитной
гидродинамики являются известные уравнения гидродинамики
и электродинамики, в которых должна быть учтена связь
между движением частиц и магнитным полем. Эту связь можно
описать, если в гидродинамические уравнения движения ввести
силу, с которой магнитное поле напряженностью Н действует
на проводник с плотностью тока J. Как известно из общего
курса физики, эта сила, отнесенная к единице объема, равна
f = ljXH, (13.1)
с
где с — скорость света в вакууме. Здесь и ниже используется
абсолютная, или гауссова, система единиц СГС, которая нам
представляется наиболее удобной в физике.
С учетом силы (13.1) уравнение Навье— Стокса (8.8), в
котором можно положить а=г\, а также Ь=—2т)/3 (см.
задачу 8.1), запишем в виде
р Ц + p(v V)v = - Vp + <пДv + -2- V (V v) + J- JxH. (13.2)
dt 3 c
279

Гидродинамическое уравнение неразрывности (6.9) не
изменяется:
-^ = f- + vVp = -pVv. (13.3)
Уравнение состояния жидкости, "пренебрегая возможным
изменением энтропии, запишем так:
Р=р(р). (13.4)
В случае несжимаемой жидкости (р=const) вместо (13.3) —
(13.4) будем использовать одно уравнение: divv=0.
Для плотности тока J имеем закон Ома:
J = аЕ. == а (Е + — v к Н), (13.5)
где а — коэффициент электропроводности (проводимость)] Е —
напряженность электрического поля; Еш — аналогичная
величина в сопутствующей системе координат, движущейся вместе с
жидкостью. В магнитной гидродинамике обычно
рассматриваются немагнитные среды (магнитная проницаемость |i=l) и
достаточно медленные процессы, так что можно пренебречь
током смещения. Тогда в соответствии с уравнениями Максвелла
для полей Е и Н имеем:
rotE = -i-—, rotH=—J, divH = 0. (13.6)
с dt с
Уравнений (13.2) —(13.6) достаточно для определения
неизвестных векторных и скалярных величин р, р, v, J, Е, Н.
47.2. Магнитное давление. Вмороженное поле. Выразим из
второго уравнения (13.6) J через Н, подставим в (13.2) и
преобразуем возникающий в правой части член rotHxH,
используя известную формулу векторного анализа:
rotHXH=(HV)H—V#2/2.
В результате (13.2) запишем так:
р-^- = _V(p + Hy8n) + (HV)H/4n + r\^ + ir\V(Vv)/3. (13.7)
dt
Предположим, что градиент магнитного поля направлен
перпендикулярно направлению самого поля. Тогда (HV)H=0, и
(13.7) для перпендикулярной к Н компоненты \± переходит в
уравнение
где F± — перпендикулярная к Н компонента вязких сил. Из
этого уравнения следует, что движение проводящей жидкости
в направлении, нормальном к магнитному полю, происходит
280

таким образом, как если бы в жидкости наряду с давлением р
действовало еще и магнитное давление Н2/8л. Следовательно,
на проводящую жидкость можно оказывать воздействие сила-
ми магнитного давления: толкать магнитным поршнем, ограни
чивать магнитной стенкой и т. п. Исключим из уравнений
(13.5), (13.6) переменные Е и J. Предполагая a=const, имеем
iiL = rot(vxH)— — rot rot Н.
dt 4яа
Это уравнение можно переписать и в несколько ином виде,
если воспользоваться формулой векторного анализа rot rot=
=Vdiv—А и учесть, что div Н = 0. При этом получаем
!iL = rot(vxH) + —ДН. (13.8)
dt 4яа
Последнее уравнение позволяет найти магнитное поле Н, если
известно поле скоростей частиц жидкости v. В частности, для
покоящейся среды (v=0) имеем уравнение диффузии для
поля Н:
4—АпДН, (13.9)
01
где параметр Dm=c2/4no играет роль коэффициента диффузии.
Отсюда следует, что магнитное поле просачивается сквозь
вещество от точки к точке. Глубинупросачивания за некоторое
время t можно оценить как h~~\/Dint=rftl4no. В случае пери-
одического процесса частотой о время /~1/<о и Аа>~с/У4яасо.
Именно поэтому переменный ток течет в проводнике лишь в
тонком поверхностном слое толщиной порядка К
{скин-эффект) . Чем больше проводимость а и выше частота ю, тем
сильнее эффект, т. е. слабее диффузия поля. 1
Рассмотрим теперь предельный случай идеальной
проводимости жидкости (о-^оо). При этом (13.8) перейдет в уравнение
(?H/# = rot(vxH), Ц3.10)
тождественное уравнению для вихря скорости в идеальной
несжимаемой жидкости, которое можно, например, получить из
результатов задачи 8.2, положив там tj=0» р=р(р) и Vv=
— 0. По аналогии с линиями вихря отсюда следует, что
магнитные силовые линии жестко связаны со средой, т. е. движутся
вместе с жидкостью. Обычно говорят, что в этом случае
магнитное поле «вморожено» в вещество (вмороженное поле).
Этот результат также легко следует из общих физических
представлений. Действительно, если бы идеально проводящая
жидкость при своем движении пересекала бы силовые линии
магнитного поля, то возбуждаемая в ней электродвижущая сила
приводила бы к бесконечному току, что невозможно.
В случае идеально проводящей жидкости, как это следует
из уравнения (13.5), должно обратиться в нуль и электрическое
281

поле E#:=E+vXH/c=0 в сопутствующей системе координат,
откуда Е= — vxH/c=—Vj_XH/c. Последнее условие
накладывает определенные требования на скорости движения идеально
проводящей жидкости поперек магнитного поля, в то время как
составляющая скорости vB вдоль поля Н может быть любой.
Если теперь умножить последнее уравнение векторно на Н и
раскрыть двойное векторное произведение по известным
формулам, то с учетом v±H=0 получаем:
Vjl =сЕхН/#2 = сЕххН///2,
(13.11)
vI=\v±\^cEJH9
где Е± — проекция вектора напряженности электрического поля
на плоскость, перпендикулярную Н.
Таким образом, в скрещенных магнитном и электрическом
полях идеально проводящая жидкость должна двигаться
поперек силовых линий магнитного поля со скоростью,
определяемой выражением (13.11). Это движение называется
электрическим дрейфом, а скорость у± — дрейфовой скоростью.
Последняя всегда перпендикулярна плоскости, в которой лежат
векторы Е и Н, а ее величина пропорциональна отношению
перпендикулярной к Н составляющей вектора Е и величины
магнитного поля Н.
Мы рассмотрели два предельных случая, когда основную
роль в правой части (13.8) играет первый (конвективный) или
второй (диффузионный) член. В общем случае относительная
роль того и другого члена определяется величиной,
аналогичной числу Рейнольдса. Под последним понимают отношение
величины vD (D — характерный масштаб) к коэффициенту
диффузии. В вязкой жидкости роль коэффициента
диффузии выполняет кинематическая вязкость v, и обычное
число Рейнольдса vD/v определяет степень преобладания
конвекции над диффузией вихря. В магнитной гидродинамике
коэффициентом диффузии является Dm (эту величину иногда
называют магнитной вязкостью), а отношение Reu=vD/Dm=
=4navD/c2 называют магнитным числом Рейнольдса. При
ReM>>l доминирующей* является конвекция и во всей области
(за исключением пограничных слоев) справедливо
приближение идеальной проводимости (подробнее о безразмерных
параметрах подобия см. задачу 13.1).
47.3. Течение Пуазейля (Гартмана). Рассмотрим
стационарное ламинарное течение Пуазейля проводящей жидкости
между двумя покоящимися плоскопараллельными пластинами.
Предположим также, что внешнее однородное магнитное поле
Н0 направлено перпендикулярно плоскостям пластинок.
Примерно в такой постановке эта задача была впервые решена
Гартманом, поэтому это течение часто ' называют гартманов-
ским.
282

Направим ось х вдоль вектора скорости течения, ось у — в
направлении внешнего магнитного поля Н0, а ось 2—
перпендикулярно им. Так же и для обычного течения Пуазейля, в силу
симметрии задачи скорость v может зависеть только от у (v—
= vx=v(y))9 от координаты z ничего не зависит. В направлении
движения жидкость «растягивает» силовые линии магнитного
поля, поэтому отлична от нуля доставляющая поля Нх. Кроме
того, в жидкости возникает ток, плотность которого легко найти
из закона Ома (13.5). Причем этот ток будет направлен вдоль
оси z, так как вектор vXH/c имеет отличную от нуля
составляющую только в этом направлении. Допустив также наличие
постоянного электрического поля Е0 вдоль оси г, для плотности
тока будем иметь
J=Jt=oE=a(E9+vHJc). (13.12)
Подставив это выражение в (13.2), получаем уравнение для
скорости потока v(y):
dp , &v
-^ + Ц
дх dy'
±JEo + Jtf-)Ho = 0. (13.13)
Здесь E0, H0 — постоянные, также и др/дх=const, что легко
следует, например, если продифференцировать уравнение (13.2)
по х и учесть, что v, J и Н от х в нашем случае не зависят:
V(dp/dx)=0, др/дх = const. В результате будем иметь линейное
обыкновенное дифференциальное уравнение относительно
скорости v (у) с постоянными коэффициентами:
£l-2Lv-(£ + jleji,)U (13.130
dy* г\с \дх с ]1
Решение этого уравнения, удовлетворяющее условию равенства
нулю скорости v на пластинах y=±dt имеет вид
где безразмерное число М = —— У а/г\ называется числом
с
Гартмана*. В результате получено полное решение
поставленной задачи. При желании составляющую магнитного поля Я.
можно найти из второго уравнения (13.6):
dy "
• J2 = ™?-(E0 + H0v/c).
Выражение (13.14) показывает, что на течение Гартмана в
отличие от обычного течения Пуазейля можно воздействовать
не только изменением градиента давления др/дху но и
изменением внешнего электрического поля Ег=Е0. Профиль скорости
1 Не путать с ранее введенным числом Маха.
283

v(y) существенно зависит от значения числа Гартмана,
которое, как легко видеть из уравнения (13.13), определяет
соотношение между магнитной Fu~oH02v/c2 и вязкой FB~r)v/d2
силами: M~FJFB. Если вязкие силы значительно превышают
магнитные (Л1«с1),тоиз (13.14) находим
0 = _(!г + Т ВД>)-^0-</2/П (13.14')
что соответствует при Я0=0, y-+y+d и 2d=h выражению
(8.22) для течения Пуазейля (параболический профиль
скорости). Если же превалируют магнитные силы (Л!>>1), то
получается совершенно иной результат:
Скорость практически постоянна почти по всей ширине со
значением v0 = — L-2- + — EqH<\ ~— » и только в узких
пограничных слоях вблизи пластин, толщина которых h~d/M, она
резко меняется от значения v0 до нуля.
§ 48. Магнитогидродинамические волны
48.1. Волны Альвена. Входящая в уравнение движения
проводящей жидкости (13.2) магнитная сила JxH/c привадит к
новому типу волнового движения жидкости. Обратимся к
следующему из (13.2) уравнению (13.7). Из него видно, что эффект
магнитного поля сказывается в появлении «магнитного
давления» #2/8я и силы (НУ)Н/4я, компоненты которой по осям
запишем в виде
JLHk ^l = _L^(/W_ ±нс^± = ХЛ-{нгнк).
4я дхк 4я дхк } 4я дхк 4я dxk v '
В последнем преобразовании было учтено, что dHJdxh=
= divH=0. В результате мы видим, что действие силы
(HV)H/4n эквивалентно системе напряжений а<*=//<#А/4я.
Заметим далее, что если в произвольной точке направеть ось xt=
=х вдоль Н, то в этой точке ои = охх=Н2/4я, а12=сгХ1/=а13= ...
...=ааз = 0. Таким образом, следуя Фарадею, силу (HV)H/4n
можно рассматривать как натяжение Нг/4л, действующее вдоль
магнитной силовой линии.
В хорошо проводящей среде магнитные силовые линии, с
одной стороны подверженные кажущемуся натяжению, а с
другой, будучи вморожены в среду, обладающие инерцией
последней, могут совершать колебания, как струна. Распространение
таких колебаний происходит в виде волн, называемых волнами
Альвена.
Уравнение для этих волн можно получить, линеаризируя
исходную систему уравнений магнитной гидродинамики. При этом
284 i

будем считать жидкость невязкой Сп=0), несжимаемой (Vv=
= 0) и идеально проводящей (о-мх>). Невозмущенное внешнее
магнитное поле предполагаем однородным (Н0=const), а его
возмущение, связанное с движением жидкости, будем
обозначать через Н, так что полное поле равно Н0 + Н. В этом случае
из уравнений (13.7), (13.10), пренебрегая квадратичными
членами по Н и v, получаем:
>Т5Г=-"('+1)г) + 1>ЛН-0'
-ffi- = rot(vxH0)-(H0V)v. (13.15)
01
Применяя к первому уравнению операцию V и учитывая, что
div H = divv=0, находим
&(р+ МЛ = о. (13.16)
Ограниченное во всем пространстве решение уравнения
Лапласа может быть только постоянным, т. е. р + Н0Н/4я=const.
Учитывая это обстоятельство и направляя ось х вдоль
невозмущенного магнитного поля Н0, из (13.15) получаем два
уравнения:
(13.17)
(13.18)
(13.19)
— скорость альвеновских волн.
Выпишем решение уравнения (13.18) в виде плоской волны:
H = F(x^cJ). (13.20)
Из уравнения divH=0f поскольку д/ду=д/дг=0, следует, что
dFJdx=0t Fx=const. Для решения волнового типа надо
положить F*=0, т. е. возмущение Н в плоской альвеновскои волне
ортогонально направлению ее распространения. Аналогичное
(13.20) выражение можно получить и для поля скоростей v:
v = G(jc=fc.O. (13.21)
причем также vx=0. В силу уравнений (13.17) функции G и F,
а следовательно, v и Н в плоской волне связаны друг с другом
соотношением
v = т>.«/Я0. (13.22)
285
ан
дх
__ 4яр dv
#о dt '
из которых следуют
дх2
1 д*Н
с\ dt*
дх ~ #0
ан
dt '
волновое уравнение
и аналогичное уравнение для v.
с* =
Я0/|/4яр
Здесь

Отметим, что уравнению (13.18) удовлетворяет также и
волна более общего вида
H = F(*=fc*, у, г), (13.23)
для которой по-прежнему сохраняется соотношение (13.22).
Этот факт говорит о своеобразной дисперсии альвеновских
волн. Действительно, найдем решение уравнения (13.18) в виде
гармонической плоской волны
Н = А exp [r(kR — со/)], (13.24)
где А —постоянный вектор; k={£x, kVi kt}\ R={*, у, z}.
Подставляя волну (13.24) в уравнение (13.18), получаем
дисперсионное соотношение для альвеновских волн:
(& = $£, ю = |*,|са. (13.25)
Отсюда для фазовой и групповой скоростей имеем:
Сф = со/& = cakx/k = са cos ф, сгр = Vjfeco = са (Н0///0) sign kx.
(13.26)
Таким образом, мы видим, что фазовая скорость
альвеновских волн зависит от направления их распространения (угла ф
между волновым вектором к и направлением магнитного поля
Н0), их же групповая скорость всегда равна альвеновской и
направлена по Н0. Из уравнения divH=0 также имеем, что
направления возмущения Н и волнового вектора к ортогональны.
В силу справедливости для гармонических волн соотношения
(13.22) также и vJ_k. Следовательно, альвеновские волны
являются поперечными как в электромагнитном (HJLk), так и в
гидродинамическом (v_Lk) смысле.
48.2. Магнитоакустические волны. Рассмотрим теперь
волновые движения в сжимаемой, идеально проводящей и невязкой
жидкости, находящейся в однородном магнитном поле Н0. В этом
случае плотность жидкости р в первом уравнении (13.15)
следует положить равной ее невозмущенному значению р0.
Получающееся уравнение вместе с линейными уравнениями
неразрывности (13.3) и состояния (13.4) дает систему:
*v—v('+™)+iir<"«v>H'
■J- + p0divv = 0, p = <%>,
где ca=(dp/dpYh — адиабатическая скорость звука, которой мы
приписали индекс s, чтобы не спутать со скоростью света с.
Продифференцировав первое уравнение по t, а также учтя
второе и третье уравнения, получим
^-=vfC|divv--^^-)+-i-(H0V)^-. (13.27)
dt* \ s 4яр0 dt I 4яр, dt
286

Второе уравнение (13.15), если воспользоваться соотношением
rot(vXH0) = (H0V)v—H0divv, запишем в виде
3H/a = (H0V)v — H0divv. (13.27')
Два векторных уравнения (13.27) и (13.270 относительно v и Н
и образуют систему уравнений магнитоакустики.
Рассмотрим плоскую волну, выбрав оси координат так, чтобы
Но совпадало с осью х, а направление распространения волны,
определяемое вектором к, лежало в плоскости ху. В этом случае
от координаты z ничего зависеть не будет. Распишем уравнение
(13.27') по компонентам:
дНх_ „К »*,_ 9оу «*,„*, mM.
1Г--Н°-^' -^Г-Я°17' "аГ Я°1Г (Ш8)
С учетом этих соотношений из (13.27) легко получить
следующую систему уравнений для компонент скорости:
ач _г1*>» , *°»\
dt* $\ дх* ^ >дхду)
дхду>
_в^ + ^)+^+*Ц, (13.29)
^ = с{^, (13.30)
где сл — введенная выше (см. (13.19)) альвеновская скорость.
Отметим, что компонента vt9 перпендикулярная как
невозмущенному магнитному полю Н0, так и направлению
распространения волны, не связана с другими составляющими поля скорости
и распространяется независимо от них со скоростью са. Нетрудно
видеть, сравнивая третье уравнение (13.28) с (13.17), что это
обычная альвеновская волна.
Две другие составляющие vx и vy в общем случае связаны
друг с другом. Рассмотрим сначала некоторые простейшие
случаи.
1. Волна распространяется вдоль оси х (д/ду=0). Система
(13.29) при этом распадается на два независимых уравнения:
^Ч аЧ л^ ^
э/а s дх* а/а a*2 v '
Отсюда следует, что составляющая vx распространяется со
скоростью звука с8. Это обычная звуковая волна, на которую
магнитное поле не оказывает влияния. Возмущение магнитного поля Н
согласно (13.28) при этом равно нулю. Составляющая vv
распространяется в виде альвеновской волны.
2. Волна распространяется вдоль оси у (д/дх=0). Из (13.29)
следует:
i^L = 0, ^- = {cl + cl)^L (13.32)
dt> дР ду* '
287

В этом случае может распространяться только продольное
возмущение vv со скоростью Уса2 + сй2, т. е. волна акустического типа.
Однако в этом случае в силу первого уравнения (13.28) имеется
также возмущение магнитного поля {НхфО). Если внешнее
магнитное поле велико (са2^>св2), то эта волна, называемая
«магнитным звуком», будет распространяться с альвеновской
скоростью са, но характер движения частиц в ней существенно
отличен от альвеновских волн, поскольку последние являются
поперечными. Таким образом, в проводящей жидкости
перпендикулярно внешнему магнитному полю может распространяться
волна акустического типа, скорость которой определяется не
только силами упругости жидкости, но и магнитным давлением.
48.3. Быстрые и медленные магнитоакустические волны.
Рассмотрим теперь общий случай k= {kxy kv, 0} и будем искать
решение уравнений (13.29) в виде гармонической волны:
y=Aexp[i(kr—©*)], (13.33)
где А={ЛЖ, Ау}—постоянный вектор; г={х, у}. Подстановка
(13.33) в (13.29) приводит к однородной системе алгебраических
уравнений относительно величин Ах и Ау\
(со2 — c\kl) Ах — сШуАу = 0, c\kxkyAx - ((o2—c2sk2y—clk*) Ау=0.
(13.34)
Отсюда видно, что vx и vv находятся в фазе, т. е. траектории
частиц всегда являются прямыми линиями. Приравнивая
определитель системы (13.34) нулю, получаем дисперсионное уравнение
для магнитоакустических волн
о)4 — (cl + с\) £2соа + c\c\k* cos2 9 = 0, (13.35)
где 6=arccos (£*/£)—угол, составленный вектором к с
направлением невозмущенного магнитного поля. Два решения
последнего уравнения
о)2± = {(<£ + cl)/2 ± [(cl + £)Ч4 - del cos2 в]*} £2 (13.36)
соответствуют двум видам волн, распространяющимся с
фазовыми скоростями c±=<ujk. Учитывая, что (с2+сЛ2)*—4св2сЛ2cos20^
^(с82—са2)2, легко получить следующие соотношения между сД
с* и с±г:
cl <min{^, caa}<max{& cl}^& (13.37)
Таким образом, в общем случае в сжимаемой, проводящей
жидкости возможно распространение волн двух классов.
Фазовая скорость волн одного из этих классов не превышает ни
скорости звука в среде, ни альвеновской скорости. Этот класс волн
называется медленными магнитоакустическими волнами.
Скорость волн другого класса, называемых быстрыми магнитоаку-
288

стическими волнами, больше как скорости звука, так и альвенов-
ской скорости.
В силу уравнения divH=0 магнитоакустические волны
являются поперечными в электромагнитном смысле: divH = /kH = 0
(k±H). Однако угол между вектором скорости частиц v и
волновым вектором к у этих волн может быть разным. В задаче 13.4
рассмотрены два предельных случая: св2>са2 и са?»св2. При этом
оказывается, что в первом случае быстрая волна, для которой
с+жс8, является практически продольной, медленная волна —
поперечной, распространяющейся со скоростью c_«cacos8. Во
втором случае в быстрой волне, распространяющейся со
скоростью с+«са, частички движутся параллельно оси у. Напротив,
в медленной волне (скорость c_«c,cos8) частицы жидкости
движутся вдоль ОСИ X.
Задачи
13.1. Найти безразмерные параметры подобия, характеризующие
движение проводящей жидкости в магнитном поле.
Решение. Для уравнений магнитной гидродинамики (13.2) — (13.6)
основными размерными параметрами служат: характерная скорость t/0,
характерный размер D, внешнее магнитное поле Я0. Прежде всего, обратимся к
уравнению (13.7). По порядку величины сила инерции в этом уравнении
FH=p(vV)v~pi/o2/A вязкая, сила Fb = ,r\kv~r\VolD2 и магнитная FM~W/
/4я/). Соотношение между этими силами определяет два безразмерных
параметра: обычное число Рейнольдса
RettFJF*ttv0Dpl4
и так называемое число Альвена
A&FJFuttHoWnpvf.
Рассмотрим теперь два члена в правой части уравнения (13.8). Первый
из них, описывающий вмороженное поле, по порядку величины равен
rot (vxH)~VoHo/D. Второй, соответствующий диффузионному процессу,
имеет порядок величины с2ДН/4ясг ~ c2H0l4noD2. Отношение первого ко второму
характеризует степень вмороженности поля и называется магнитным числом
Рейнольдса:
ReK = AnavQD/c2.
При ReM > 1 поле будет вмороженным, при ReM <С 1 — диффузионным.
Введенное в п. 47.3 число Гартмана М= (HoD/c)1o/r\ выражается через*
Re, А и ReM:
M2=AReReM=(/7M/FB)Re„.
Иногда также вводится так называемое число Стюарта:
S=AReM = оНоЮ/рс^о.
13.2. Рассчитать стационарное течение проводящей жидкости между
двумя плоскопараллельными пластинами, одна из которых покоится, а другая
движется в своей плоскости со скоростью Vq (течение Куэтта). Внешнее
магнитное поле Но направлено перпендикулярно плоскости пластин.
289

Решение. Задача вновь сводится к решению уравнения (13.13'), но с
другими граничными условиями: v(—d)=0t v(d)=v<>. Кроме того, в (13.13')
положим £о=0 и, как это должно быть для течения Куэтта, др/дх=0. Тогда
решением будет
v(y)=v0sb[M(y+d)ld)]lsh2Mt
что переходит в линейную функцию при М<1 ив
v(y)=voexp [—M(\—yld)] приМ>1.
13.3. Рассчитать течение Гартмана (Пуазейля), описанное в п. 47.3, в
предположении, что по оси z канал ограничен идеально проводящими
параллельными стенками, отстоящими друг от друга на расстоянии, много большем
расстояния d между пластинами.
Решение. В этом случае выражение для скорости v(y) будет снова
определяться формулой (13.14), но здесь уже нельзя считать электрическое
поле произвольным. Его величину можно найти из условия равенства нулю
полного тока, перпендикулярного идеально проводящим стенкам:
d
Jzdy = Q.
id
Поскольку
]t„(B, + M^,--- + y ^ лм
■fo£+«4
с dp , ( с dp t _гч\ ch(My/d)
о
имеем
d
с dp
5'•«-%[
оЕ0 th М - — -f- (М - th М)
Но ох
-а
Приравнивая последнее выражение нулю, получаем
с dp М — th М
°~ аЯ0 дх thM
и с учетом (13.14)
с2 др й ch М — ch (М у Id)
v(y) = -^TxM 5^
13.4. Рассмотреть движение частиц жидкости в магнитоакустических
волнах в двух предельных случаях: а) с*>са; б) сл">св.
Решение. Если max {c»t ca}>min{ce, са}, то в выражении (13.36)
можно разложить в ряд квадратный корень:
V(«5+c2)«/4-eKcoe»e« (ci+cD/2 - i*tt%(t*+<*)} cos» е.
В результате для фазовых скоростей волн c±s—й>±2/*2 получим:
с\ « с\ +с\^ max {с , с*}, с9_ « —i-S- cos» в » min {cj, с|} cos. в.
с\ + с\
Далее, из (13.34) найдем vv = (<ui—c.2kxi)vx/(c.3kxkv).
9.90

В случае «а» (с«2>са2) имеем для быстрой волны с+2«с«2, со+2«св2&2,
vytt(ky/kx)vx или Vx/Vyttkx/ky, т. е. эта волна является продольной.
Соответственно для медленной волны с-2« са2 cos2 9, со-2« ca2fc2 cos2 в=cA2kx2t
vvtt — (kxlky)vx или kxVx+kyVyttO, следовательно, медленная волна
является поперечной.
Аналогично в случае «б» (са2>св2) имеем с+«са, ш+2«са2^2, иу«
»(cSL2k2/c92kxky)Vx=2(Cb2lce2)vx/sin2Q'>Vxt т. е. в быстрой волне частицы
жидкости перемещаются практически вдоль оси у. Дляч медленной волны
с-2 «св2 cos2 9, w_2«ce2fc2cos28==ce2£x2, иу«0— движение параллельно
оси х.
Глава 14
НЕЛИНЕЙНЫЕ ЭФФЕКТЫ
В ТЕОРИИ ВОЛН
В предыдущих главах, посвященных волновым движениям в
жидкости, описаны основные типы волн в линейном
приближении, когда справедлив принцип суперпозиции. При этом волны
каждого типа, так же как и их отдельные гармонические
составляющие, распространяются в среде независимо друг от друга.
Однако не следует забывать, что линейные уравнения для волн
в жидкости получены в результате упрощения (линеаризации)
исходных нелинейных уравнений гидродинамики. Поэтому
представляется необходимым выяснить, при каких условиях
оправдано линейное приближение для волн, а также рассмотреть
принципиально новые эффекты, обусловленные нелинейностью
уравнений. Этим вопросам и посвящена настоящая глава.
Прежде всего мы качественно оценим необходимые условия,
накладываемые на амплитуду волн, для справедливости
линейного приближения. Затем рассмотрим некоторые типичные
задачи нелинейной теории волн, такие, как генерация высших
гармоник, искажение профиля волны, солитоны в
диспергирующих средах, резонансные взаимодействия волн и т. п.
Отметим также, что основные нелинейные эффекты будут
изложены на основе простых модельных уравнений независимо от
природы волн. Такой подход хотя и может показаться
абстрактным, но позволяет освободиться от громоздких математических
выкладок, неизбежных при непосредственном анализе
гидродинамических уравнений и часто затеняющих суть явлений. Кроме
того, при таком подходе проявляется единство нелинейных
эффектов для волн любой природы, поскольку качественно эти
эффекты зависят только от типа дисперсионных зависимостей волн
и порядка нелинейности. Применение общей теории к
конкретным видам волн дано как в основном тексте, так и в задачах в
конце главы.
291

§ 49. Нелинейные одномерные волны
49.1. Параметр нелинейности. Одним из нелинейных членов,
входящих в уравнение движения (8.1), является инерционный
член (vV)v. Сравним его по порядку величины с линейным
членом dv/dt. Если vQ — амплитуда скорости, о) — частота волны и
k — волновое число, то d\/dt~(uv0t (vV)v~kv02, отношение этих
членов е=kv02/toV0 = и0/сф, где сф = co/k — фазовая скорость
волны.
Таким образом, для справедливости линейного приближения
необходимо, чтобы скорость частиц жидкости в волне была
значительно меньше ее фазовой скорости e-Cl. Параметр е
называют параметром нелинейности. Для акустических волн это число
Маха М=0о/с, где с — скорость звука.
В случае поверхностных волн на глубокой воде удобнее
вместо амплитуды скорости v0 ввести амплитуду вертикального
смещения свободной поверхности a=v0/(u. При этом для параметра
нелинейности имеем z = vQlc^=kai и требование e^Cl совпадает
с требованием малости наклонов поверхности, или, что то же
самое, малости амплитуды волны а по сравнению с ее длиной
X=2nfk. Для волн на мелкой воде, где kH<^\, Н — глубина
жидкого слоя, параметр нелинейности будет иным. Это связано с
тем, что для оценки е надо взять горизонтальную скорость
частиц vx, поскольку она в \jkH раз больше вертикальной vz: vx=
= vJkH=(dalkH=CbalH. Поэтому здесь B = vjc$=a/H, т. е.
амплитуда волны должна быть много меньше толщины слоя.
Естественно, что при этом по-прежнему ka=kH(a/H)=ekH<^
<1.
Аналогичные условия могут быть получены и для волн
других типов, например для внутренних волн е=ао/сф=£а«<1, где
а — максимальное вертикальное смещение частицы. В случае
термоклина конечной толщины d появляется также параметр е=
= аД/<1.
Условие малости параметра нелинейности е является
необходимым, но, вообще говоря, не достаточным для
справедливости линейного приближения. Нелинейные эффекты могут
накапливаться во времени или пространстве по мере распространения
волн даже при малых нелинейных членах. В какой мере эффект
нелинейности будет сказываться, сильно зависит от скорости
диссипации энергии, а также от дисперсии волн. Последняя при*
водит к расплыванию волнового пакета и к изменению
соотношения фаз между отдельными гармоническими составляющими, что
сокращает временной или пространственный интервал
эффективного взаимодействия волн.
49.2. Модельное уравнение. Генерация второй гармоники.
Поскольку нелинейные эффекты аналогичны для волн любой
природы, рассмотрим простое уравнение, описывающее одномерные
292

волны:
- + Lu = -eu- (14.1)
Здесь член иди/дх аналогичен (vV)v; е<С1—параметр
нелинейности; L — линейный оператор, соответствующий определенной
дисперсии линейных волн. Например, в случае Ь=с0д/дх
волновым решением уравнения (14.1) с е=0 будет бездисперсионная
волна акустического типа
u=u0exp[i(kx—(ut)]t (o=&(k)=c0k. (14.2)
Важную роль в нелинейной теории волн играет уравнение
(14.1) с L = с0 ЬР—-> называемое уравнением Кортеве-
га — де Вриза (КдВ) и впервые полученное при исследовании
волн на мелкой воде. Дисперсионное соотношение для линейных
волн в этом случае будет
<b=cQk—$k\ (14.3)
В задаче 14.1 показано, что этот закон дисперсии с точностью до
(kHy включительно совпадает с дисперсией волны на мелкой
воде.
д д2
Оператор L = С0 а соответствует уравнению Бюр-
дх дх2
герса, описывающему затухающую волну в среде с диссипацией
энергии:
и(х, t)=u0exp[—ak2t+ik(x—c0t)].
Из (14.1) легко получить, что в общем случае произвольного
оператора L закон дисперсии линейных волн определяется функцией
со = о (k) = о'—iV'=— i exp (—ikx) L exp (ikx). (14.4)
При этом вещественная часть этого соотношения описывает
дисперсию волн, а мнимая равна коэффициенту затухания:
и(х, /)=и0ехр[—g/7+i(kx—(u't)].
Рассмотрим теперь нелинейный волновой процесс,
описываемый полным уравнением (14.1), предполагая, что закон
дисперсии линейных волн известен. В дальнейшем для удобства будем
его записывать в виде со(&)=(оЛ. Пусть при /=0 задано
возмущение и(х, 0) = еа exp{ikx) +к. с, где символом к. с. здесь и ниже
обозначается слагаемое, комплексно-сопряженное первому. Оно
введено для учета вещественности и, что является важным в
нелинейных задачах. Ищем решение уравнения (14.1) в виде
разложения по малому параметру е: н=еи1 + е2ы2 + в3«3+ При
подстановке этого выражения в (14.1) и приравнивании членов,
содержащих первую степень е, получаем линейное уравнение
duJdt+Lu^O. (14.5)
293

Решением последнего в предположении, что при £=0 щ(ху 0) =
= а exp(ikx) +к. с, будет функция
ut (х, t)=a ехр [ i (kx—&ht) ] + к. с.
Приравнивая теперь члены с е2, получаем для и2 неоднородное
линейное уравнение
*±. + 1Щ = _ Ul ^L = _ iktf ехр [21 (kx — ®kt)] + к. с. (14.6)
at ox
с начальным условием и2(х, 0)=0. Если правая часть этого
уравнения не является решением однородного уравнения, или,
что то же, 2(ок=7^о)2л=(1)(2Л), то решение и2(х, t) имеет вид
\ka2
u2(х, t) = —- {ехр [2i (kx—<dkt)] — ехр [i (2kx— cd2*/)]}+k. с»
(И.7)
Последнее можно также записать в форме волны с удвоенным
волновым числом и модулированной по времени амплитудой:
U2 = _2^^i^exp[t-(2^-^l^)] + K.c. (14.7')
Если расстройка Дш=2й)Л—<o2h велика, то для всех моментов
времени амплитуда второй гармоники будет оставаться малой
величиной. Промежуток времени тв=я/Дсо = я/(2(оЛ— со2Л), в те-
чение которого амплитуда второй гармоники возрастает от нуля
до своего максимального значения, называется характерным
временем взаимодействия. Чем больше расстройка Дсо, т. е. чем
сильнее дисперсия, тем меньше время взаимодействия тв.
В случае До>=0, как, например, для бездисперсионных волн
о)Л=с0&, из (14.7') предельным переходом легко получить
решение, содержащее вековой член:
и2(х, t)=—ika2texp[i(2kx—(u2kt)]+K.c. (14.8)
Этот случай соответствует резонансному возбуждению второй
гармоники, когда «внешняя сила» в (14.6) является решением
однородного уравнения. При этом условие 2(оЛ=(о2Л является
частным случаем так называемых общих условий синхронизма (см.
§ 50). Вторая гармоника волны растет линейно со временем, так
что при любом как угодно малом е линейное приближение при
больших временах становится неверным. Характерное время тл„
на котором это произойдет, можно оценить, приравняв друг
другу члены etfi и г2и2: еа=е2&а2тл, тл=1/е&а. В частности, для
акустических волн еа=и0— амплитуда скорости частиц, и для
тл получаем хл=1/ки0~Т/М, где Т=2я/(о — период волны; М=
= и0/с0 — число Маха.
Заметим, что в случае бездисперсионных волн по мере роста
второй гармоники усиливается ее взаимодействие с первой,
сопровождающееся возбуждением третьей гармоники, затем чет-
294

вертой и т. д. В результате с течением времени в спектре волн
возникают все более высокие частоты, соответствующие все
более резким изменениям фронта волны.
49.3. Решение Римана. Ударные волны. Точное решение
нелинейных акустических уравнений в одномерном случае было
получено еще в прошлом веке Риманом. Найдем аналогичное
решение нашего модельного уравнения в среде без дисперсии и
диссипации. В этом случае, опуская также параметр е, имеем (см.
(14.1) при L=c0d/dx)
ди , ди ди ,ЛА m
- + Со- = -и-. (14.9)
Пусть при /=0 и(х, 0) =/(#). Покажем, что функция
u{x,i)=f[x—{c0+u)t], (14.10)
задающая и(х, t) в неявной форме, является решением
уравнения (14.9). Действительно,
dt [° dt j1 дх \ дх )'
откуда имеем выражение для du/dt=—(с0+и)/7(1+Г0 и
duldx=f'/(l+f't), подстановка которых в уравнение (14.9)
обращает его в тождество.
Решение (14.10) уравнения (14.9) имеет простой физический
смысл, а именно: возмущение в среде, соответствующее
определенному фиксированному значению и, движется с постоянной
скоростью с0+и. При этом более мощные возмущения
перемещаются с большей скоростью, «догоняя» более слабые. Это
приведет к изменению формы волны, например к укручению
переднего фронта возмущения с и>0.
Изменение профиля волны удобно анализировать графически.
Предварительно перейдем в систему координат, движущуюся со
скоростью с0, введя новую переменную %=х—c0t. В этой системе
координат решение (14.10) примет вид
u(bt)=f(l-ut). (14.100
На рис. 14.1 штриховой линией изображена форма волны £=
=g(u) в начальный момент времени, где g(u)—функция,
обратная u=f(l). В произвольный момент времени />0 из (14.100
имеем \=g(u) +ut. Следовательно, для построения решения
и(%у t) нужно сложить заданный профиль g(u) с линейной
функцией ut, наклон которой увеличивается с ростом t. На рис. 14.1
сплошными линиями показан профиль волны в два
последовательных момента времени tt и /а>Л- Точки gf и |2, в которых
возмущение равно нулю, во все моменты времени остаются на месте.
Из рис. 14.1 видно, что верхняя половина кривой |(и) с Уве_
личением t становится все круче и круче. Наконец, при
некотором t=tm один из ее участков станет перпендикулярным оси £,
295

после чего образуется разрыв. Поскольку
d%ldu=(dgldu)+t,
то время tm найдем из соотношения /m=min(—dg/du). При />
>tm возникает «перехлест» — неоднозначность функции и(%, /),
что, за исключением некоторых случаев, например морского
прибоя, не имеет физического смысла. Для акустических волн
вместо перехлеста возникает тонкий ударный фронт (разрыв), где
происходит интенсивная диссипация энергии волны. При этом
оказывается, что с течением времени профиль волны стремится
296

к треугольному (ударная волна), причем со временем
максимальное возмущение в ней уменьшается, а ее пространственная
протяженность увеличивается. Закон изменения этих величин
может быть найден на основе закона сохранения полного импуль-
00
са волны #>= Г Hdg=const, следующего из (14.9). В простей-
•-оо
шем случае треугольного начального импульса этот расчет
проведен в задаче 14.3. Последовательные изменения формы
импульса (и>0) изображены на рис. 14.2, где /i</2<^<^.
Аналогичные построения можно провести и для возмущений
с и<0, а также для знакопеременных и. В частности, любое
периодическое начальное возмущение, например гармоническая
волна, с течением времени приобретает пилообразную форму.
49.4. Диспергирующие среды. Солитон. Даже слабая
дисперсия, имеющаяся, например, в случае волн на мелкой воде и
длинных внутренних волн, препятствует образованию фронта
ударной волны. Здесь слабая нелинейность, способствующая укруче-
нию волны, и слабая дисперсия, вызывающая ее размытие,
могут как бы компенсировать друг друга. При этом возникает так
называемая стационарная нелинейная волна,
распространяющаяся без изменения формы с постоянной скоростью.
Рассмотрим этот процесс на примере уравнения КдВ (см.
п. 49.2):
*L + C. *L + pJ5Le_tt*!. (14.11)
dt ° дх к дх* дх v '
Переходя к системе координат \=х—c0t, движущейся со
скоростью с0> перепишем это уравнение в виде
*L„p*!_ai£. (14.11')
Здесь первый член в правой части описывает дисперсию волн,
второй — нелинейные процессы. Проследим качественно, как
изменяется роль этих членов по мере распространения волн. Пусть
при £=0 характерный размер возмущения /, а его амплитуда Л.
Оценивая по порядку величины дисперсионный и нелинейный
члены, имеем рд3и/д|8~рЛ//3, иди/д1~А2/1> при этом
отношение второго к первому будет q~Al2/$. Предположим, что q^>l
при /=0, это соответствует плавному длинному импульсу
протяженностью /. Тогда дисперсионный член будет относительно мал,
и основную роль будет играть нелинейность, приводящая к укру-
чению волны, т. е. к уменьшению /. При этом параметр q падает,
следовательно, усиливается влияние дисперсионного члена. Но
это приводит к расплыванию волны, т. е. вновь к росту / и вместе
с ним параметра q. Эта качественная картина указывает на
возможность существования стационарного неизменяющего своей
формы решения уравнения (14.1 V) с постоянным q~\.
297

Ищем это решение в виде u=f(\—ct), где с —некоторая
новая постоянная — скорость распространения стационарной
волны. Подстановка и в (14.1 Г) приводит к обыкновенному
дифференциальному уравнению для функции f(r\) (т] = |—ct):
-cr+ir+fr=(-cf+tr+r/2V=o,
которое один раз легко интегрируется:
р/"-с/+/2/2=0. (14.12)
Здесь постоянная интегрирования положена равной нулю, так
как заменой f=f+f0, c = c+f0 уравнение (14.12) приводится к
виду
Pr-cf+r/2 = /o(c+/0/2), (14.120
правая часть которого может быть обращена в нуль
соответственным выбором f0. Поэтому следует помнить, что к любому
решению уравнения (14.12) можно добавить произвольную
постоянную, одновременно добавив ее и к с, т. е. переходя в
движущуюся систему координат.
Обратим внимание, что (14.12) аналогично уравнению
движения тела массой р в потенциальном поле U(f):
ti".=—dU/dft U=fd/6—cf2/2. (14.13)
Ограниченное решение f(r\) существует, если уровень полной
энергии тела E=($/2)(f')2 + U находится в потенциальной яме.
На рис. 14.3, а приведена зависимость U(f) при [J>0 и с>0. При
этом ограниченное решение существует при £^0.
Сделаем подстановку /?=/', f"=dp/dr]=pdp/df. Тогда (14.13)
запишем так: d/df($p2/2 + U) =0. Отсюда находим
p=dfldr)=±y(2/$)(E-U), (14.14)
где Е=const — полная энергия.
С помощью (14.13) и (14.14) можно каждому значению f
сопоставить соответствующее значение р. Получающиеся на
плоскости (/, р) кривые при разных фиксированных значениях Е
называются фазовыми траекториями уравнения (14.14). Эти
траектории изображены на рис. 14.3, б. Особо интересен случай Е=
= 0, когда уравнение E=U(f) имеет двукратный корень fi,2=0
и однократный fa=A = 3c. При этом соответствующая фазовая
траектория будет сепаратрисой, отделяющей периодические
движения от непериодических. В этом случае, как легко проверить
подстановкой, решением (14.14) будет так называемая
уединенная волна, или солитон:
/(л)=Л/сЬ2[(л + Ло)/Л], ^=1Wc=iЩIA. (14.15)
Скорость солитона однозначно связана с его амплитудой с=А/3,
параметр Д определяет протяженность солитона. В исходной
системе координат скорость солитона v=c0 + c всегда больше фа-
298

зовой скорости гармонических волн сф=с0—$k2. Профиль
уединенной волны изображен на рис. 14.4, а.
В случае £<0 решение f (г\) заключено в пределах f2<f<fs,
где ft и fi — второй и третий по величине корни уравнения Е=
= £/(/). Поскольку к решению можно добавить произвольную
постоянную (см. (14.12')), то корень f2 может быть
отрицательным. Замкнутые фазовые траектории соответствуют
периодическим решениям, называемым кноидальными волнами.
Характерный вид этой волны представлен на рис. 14.4, б. При Е^Ь
фазовая траектория приближается к сепаратрисе, изображающая
точка при движении по этой траектории большее время находится
в окрестности /2. При этом решение приближается к
периодической последовательности солитонов.
Если £'«£/mln=[/(2c)=—2с3/3, то, разлагая правую часть
(14.13) в ряд по степеням (f—2с), получим уравнение $f"+
+ c(f—2с) =0, решением которого является гармоническая
волна, сдвинутая от невозмущенного состояния на величину 2с:
f=2c+u0sinkr), &=]/c/(J, и0— произвольная амплитуда. В
системе координат, движущейся со скоростью 2с, получаем обычное
линейное решение уравнения КдВ. Учитывая, что в этой системе
у\ = 1—ct+2ct=x— (с0—c)t, а также с=(1&2, имеем для этого
решения:
и=щ sin (kx—со/), со=k (с0—с) =kc0—$k\
Путем точного решения нестационарной задачи (уравнения
(14.11)) показывается не только наличие солитонного решения,
но и его устойчивость. Более того, оказывается, что если для
начального импульса (отрицательного при р<0 или
положительного при (i>0) параметр q>\2 (для солитона q=AA2l$=l2)t то
с течением времени он распадается на последовательность
солитонов, расположенных в порядке возрастания амплитуд. Первым
всегда бежит солитон с наибольшей амплитудой, т. е. с
наибольшей скоростью распространения.
Укажем еще на одну интересную особенность многосолйтон-
ных решений уравнения КдВ. Допустим, что имеются два
солитона. При этом если амплитуда идущего впереди солитона меньше,
то в некоторый момент времени его догонит второй солитон.
Какое-то время они будут распространяться вместе в виде
возмущения, не являющегося простой их суммой. Однако затем это
возмущение вновь распадется на два солитона той же формы, но
впереди уже будет тот, амплитуда которого больше. Таким
образом, солитоны ведут себя так же, как невзаимодействующие
линейные волны. Нелинейность проявится только в сдвиге
солитонов относительно того положения, в котором они находились бы,
если их распространение было бы полностью независимым.
299

§ 50. Резонансные взаимодействия волн
50.1. Условия синхронизма. В предыдущем параграфе на примере
среды без дисперсии было указано на важную роль резонанса в
процессах взаимодействия волн. При этом во втором
приближении метода возмущений возникают линейно растущие со
временем вековые члены. Заметим, что рассматриваемый там процесс
можно интерпретировать как взаимодействие трех волн, так как
основное условие резонанса ©(2£)=2©(£) могло бы быть
записано в таком виде: k3=ki+k2y ©з=(»>1 + ©2, где ki=k2=k, ks=
=2А,ю,= ©(*,) (/=1,2,3).
Аналогичные трехволновые резонансные процессы могут
возникнуть в общем случае неодномерных волн в среде с
квадратичной нелинейностью. В самом деле, рассмотрим некоторое
нелинейное уравнение в частных производных:
Liw=tL2(w1) + (14.16)
Здесь Li — линейный оператор, допускающий решения Liw1;=0
в виде плоских гармонических волн:
а;1=аехр[/(кг—ю/)]+к.с, (о=со(к), (14.17)
a L2(w2) —символическая запись членов второго порядка по wf
е— малый параметр нелинейности. Решение (14.16) ищем в виде
w = bWi + e2w2+. .. Пусть, далее, при /=0 заданы такие
начальные условия, что решение линейного приближения имеет вид
суммы двух волн (14.17) с ah к, и coj=a)(kj) (/=1, 2). Для функции
w2 второго приближения получим неоднородное линейное
уравнение Llw2=L2(wi2)f правая часть которого будет содержать
слагаемые, пропорциональные exp[t(ksr—©в01- При этом пары
к3, ©3 принимают следующие возможные значения: ±(km±kn),
±(©m±©„) cm, n=l,2.
Если окажется, что хотя бы для одной из этих пар ks, (о3
соответствующий член в правой части уравнения для w2f например
~exp{i[ki+k2)r—(©i + ©2)f]}, удовлетворяет однородному
линейному уравнению, т. е. является гармонической волной (14.17),
то будет иметь место резонанс и в решении w2 возникает вековой
член. Легко видеть, что необходимым условием этого будут так
называемые условия синхронизма:
К = К + К °>з = <*>(к3) = ^ + ©2 = ©(kx)+ ©(к2). (14.18)
Заметим, что в таком же виде можно записать условие
резонанса и для других комбинаций kt и k2, ©i и ©2, если, считая
частоты всех волн положительными, как это обычно и делается,
соответствующим образом перенумеровать волны из заданной
тройки. Например, если волна кз=к4—к2 и ©s=©t—©2
удовлетворяют линейному уравнению, то заменой индексов 1^*3 вновь
получаем (14.18).
В задаче 14.5 показано, что для изотропных (в дисперсионное
соотношение входит только &=|к|) волн, дисперсионная кривая
'о = (о(£) для которых монотонно возрастает (©'>()) и выпукла
300

вниз (со">0), всегда можно найти такие kt и к2, для которых
(14.18) выполняется. Если же дисперсионная кривая выпукла
вверх (о)"<0), то условия синхронизма не выполняются ни для
какой пары kt и к2. Следовательно (см. рис. 10.3 и 10.9), во втором
приближении резонансные процессы возможны для капиллярных
волн на поверхности жидкости и запрещены для
гравитационных, а также для внутренних волн в пределах одной и той же
моды.
Если же рассматривать процессы взаимодействия между
волнами различной природы или же между модами разных номеров
одного типа волн, то, как правило, появляется возможность
удовлетворить условиям синхронизма (14.18). Например, две
поверхностные гравитационные волны близких частот o)2«coi, но
почти противоположных направлений k2«—kt резонансно
возбуждают звуковую волну частотой o)s=(Oi + <dz=2toi и с
горизонтальной проекцией волнового вектора ks=k1+k2, £,<& (см.
задачу 14.9). Аналогично внутренняя волна с волновым вектором
kt и частотой ©i может быть резонансно возбуждена при
взаимодействии двух поверхностных волн: оэ2, к2 и ©3, к3. Если вновь
ПОЛОЖИТЬ G)2«G)S, ТО ИЗ УСЛОВИЙ (14.18) ПОЛУЧИМ (0i<C(02, что и
должно быть для внутренних волн.
50.2. Метод медленно изменяющихся амплитуд. Метод
последовательных приближений справедлив только на начальном
этапе развития нелинейного процесса, пока еще амплитуда
возбуждаемой волны мала. При этом время, за которое ее амплитуда
становится сравнимой с амплитудами исходных волн, обратно
пропорционально параметру нелинейности е и для е<С1
значительно превышает период исходных волн. Этот результат,
полученный для одномерных волн в п. 49.2, можно обосновать и в
общем случае, т. е. можно ожидать, что при слабой
нелинейности (е<1) амплитуды взаимодействующей тройки волн будут
медленно меняющимися со временем функциями. Это позволяет
записать выражение для волнового поля резонансной тройки
волн в виде
з
ш = ^ a/(eOexp(i(k/r —©/01 + к. с, (14.19)
т. е. ввести «медленное время» т=е/, от которого только и
должны зависеть амплитуды волн.
При подстановке (14.19) в уравнение (14.16) в левой части
появятся слагаемые, содержащие edajdx, ггй2а^йт2... Члены
вида аД,!ехр[/(к,г—со^)1 при этом будут равны нулю, поскольку
каждая волна удовлетворяет линеаризованному уравнению.
В правой части (14.19) дифференцировать afat) не следует, так
как там уже содержится одна степень е. Следовательно, в правой
части пропорциональными е будут члены, состоящие из
попарных произведений различных волн, как в п, 50.1.
301

В результате, приравнивая члены первого порядка по е,
имеющие к тому же одинаковую зависимость от г, получаем
следующую систему так называемых укороченных уравнений:
(*i = Vtala3t а2 =lV2a[as, а, = У^А- (I4 -20)
Здесь точкой обозначено дифференцирование по медленному
времени, а знаком * — комплексное сопряжение, волна номера 3
предполагается наивысшей частоты. Величины I/, (/=1, 2, 3),
характеризующие взаимодействие волн, называются
коэффициентами (или потенциалами) взаимодействия. Если нормировать
амплитуды волн таким образом, чтобы энергия /-й волны была
пропорциональна |а,|2 с не зависящим от номера /
коэффициентом, то все Vj будут чисто мнимыми и равными: Vj=mjV (/=
= 1, 2, 3). При этом (14.20) перейдет в систему уравнений:
a1=^m1Va2az, a2 = i(u2Vaxav а3 = i&3VaLa2. (14.20')
Заметим (см. задачу 14.6), что в этом случае тройка волн
удовлетворяет закону сохранения энергии в виде
£=|a1|2+|a2|2+|a,|2=const. (14.21)
В задаче 14.6 получены также еще три закона сохранения для
системы (14.200, любые два из которых являются следствием
третьего и (14.21):
M'/cot— Ы2Ло2=#12, |а1|7со1+|а3|2/(о3=Я13,
(14.22)
|а2|7со2+|аз|7о)з = Я23,
где #12, Я13, #23 — постоянные.
Отсюда следует, что энергия низкочастотных волн (o)i и о2)
изменяется в фазе (одновременно растет или падает), а
высокочастотной (о)а)—в противофазе им. Иначе говоря,
высокочастотная волна может либо приобретать энергию от.
низкочастотных волн, либо отдавать ее им. Если переписать второе и третье
выражения в (14.22) в таком виде: |а>|2—|аД0) |2 + й)/со3
(|а3(0) |2—|а3(т) |2) (/=1, 2), то становится ясным, что
энергия высокочастотной волны распределяется между
низкочастотными пропорционально их частотам.
С учетом законов сохранения можно получить общее решение
системы (14.200 в квадратурах, что и сделано в задаче 14.6.
Здесь же ограничимся несколькими замечаниями для случая;
когда амплитуда а3 высокочастотной волны поддерживается
постоянной при помощи некоторого внешнего источника энергии. При
этом, дифференцируя одно из первых двух уравнений (14.20') по
т, с учетом второго получаем
ai=o)1a)2V2|a3|2ai, /=1,2.
Отсюда следует, что амплитуды низкочастотных волн будут
нарастать экспоненциально а,~ехр(ат), где а=^У(д1(огУ\аЛ\.
302

Этот эффект, носящий название распадной неустойчивости
высокочастотной волны, часто используется для «параметрического»
возбуждения низкочастотных волн.
50.3. Многоволновые взаимодействия. Резонансную триаду
часто нельзя рассматривать изолированно от других волн. Такая
ситуация возникает, например, когда одна из волн триады
находится в резонансе с какой-либо еще парой волн. Показательным
здесь является пример генерации высших гармоник в среде без
дисперсии (<o=c0k). Единичным резонансным процессом при
этом будет взаимодействие типа kl+ki=k2, со1 + ©1=(02. В
задаче 14.7 рассмотрен процесс такого типа, но в среде с сильной
дисперсией. При t^oo имеем полную перекачку энергии во
вторую гармонику. Однако в случае бездисперсионных волн это
решение заведомо неправильно, поскольку гармоническая волна
должна переходить в периодическую ударную волну (решение
Римана). Ошибка как раз и заключается в отбрасывании
резонансных взаимодействий высших гармоник: ki=ki+k2, kk=
Проиллюстрируем на простом одномерном уравнении (14.1)
метод, позволяющий в принципе учесть многоволновые
взаимодействия. Будем искать решение (14.1) в виде разложения Фурье
по х:
оо
и(х, *)= j Ak(t)exp(ikx)dk, (14.23)
•-оо
где Ah{t)=A(ky t) и A-h=Ak* в силу вещественности и(х, t).
Удобно положить ЛА=«Лехр(—tW), где a_k=aft*; ю_ь=— юк;
G)ft=u)(&) — дисперсионное соотношение для линейных волн.
Очевидно, что d/dx=ik и в соответствии с (14.4) L = tcofc. С
учетом этого, подставив (14.23) в уравнение (14.1), получаем
следующую систему уравнений относительно амплитуд волн ah:
оо
a,k = — i— \ OLtfis ехр (— iAqskt) dq, s = k — q, (14.24)
•-00
Если при /=0 было только гармоническое возмущение
u(xt 0)=ai(0)exp[i(kix)]+K.c, т. е. ah(0)=ai(0)6{k—ki) +
+ al*(0)6(k+ki), то в последующие моменты времени спектр
и(х, t) останется дискретным, содержащим только компоненты
kn=nkit o)n=(o(*n) (n=±l, ±2,...) и afc(0 = S МО-
п
6(k—kn). При этом (14.24) переходит в бесконечную систему
обыкновенных дифференциальных уравнений:
ап = —2ятЯ/ехр(— ibmint), l = n — m, (14.25)
2 m
303

где Am/n=cDm+cDf—G)n; a-n=an*; a0=0. В случае сильной
дисперсии и резонанса между первой и второй гармониками, как
это имеет место в задаче 14.7, равной нулю будет только
расстройка Д112. Поэтому, оставляя в (14.25) только волны с
номерами 1 и 2, получим систему уравнений задачи 14.7.
Однако если отсутствует дисперсия, как в случае звуковых
волн, или имеется участок с малой дисперсией, как для
поверхностных и внутренних волн, то в системе (14.25) следует
сохранить большее число уравнений. Численное интегрирование такой
системы описывает начальный этап образования ударной волны,
а также распад гармонического импульса на последовательность
солитонов.
50.4. Нелинейная дисперсия. В заключение рассмотрим
распространение плоской гармонической волны в среде с сильной
дисперсией. При этом вторая гармоника 2kt основной волны kx
не будет удовлетворять условиям синхронизма. Из (14.25) для
амплитуд первой и второй гармоник имеем:
аг = — iek^ldz ехр (— Ш)9
(14.26)
а2 — — Uk^X ехр(£Д0-
Из-за большой расстройки А = о)2—2a)t амплитуда аг при всех /
остается малой. Поэтому решение второго уравнения (14.26)
можно искать в предположении, что а{=const, тогда
o2(t) = -5J-1 а\ (Оехр(Ш). (14.27)
Подставляя теперь a2(t) из (14.27) в первое уравнение (14.26),
получаем замкнутое уравнение для at (t) :
alW== W 4-1*1 Ni- (14-28)
Нетрудно видеть, что решением последнего уравнения будет
функция ai = ai(0)exp(—ЯМ). гДе 6<o = —B2ki2\ai\z/A. Мы видим,
что частота исходной гармонической волны изменяется
на.величину б(о, пропорциональную квадрату ее амплитуды. Этот
эффект носит название нелинейной дисперсии волн.
Отметим, что нелинейная поправка к частоте бсо получена
для идеализированного случая бесконечной гармонической
волны. В более реальном случае синусоидального цуга волн с
конечной шириной спектра следует учесть взаимодействие
отдельных гармонических составляющих в этом спектре. Это
взаимодействие также приводит к нелинейной поправке к частоте
основной гармоники, пропорциональной e2^i2|aj|2 (см. задачу
14.11).
Заметим также, что правая часть (14.28) соответствует уже
нелинейному резонансному взаимодействию третьего порядка.
304

Поэтому если в исходных уравнениях есть члены с кубичной
нелинейностью, они внесут дополнительный вклад в правую часть
(14.28).
Задачи
14.1. Показать, что закон дисперсии для поверхностных волн на мелкой
воде совпадает с дисперсионным соотношением для линеаризованного
уравнения КдВ, если пренебречь величинами порядка (кН)ъ и выше.
Решение. В случае мелкой воды разложим дисперсионное
соотношение для поверхностных волн to2=gkthkH в ряд по степеням &Я<1 и
ограничимся первыми двумя членами:
о = Vgk У kH - j(kH)* = \TgH k \\- -^-1 = c0k - fl*».
В результате получилось соотношение (14.3) cc0=ygH и &=lUc0H2.
14.2. Получить решение Римана для одномерных нелинейных
акустических уравнений.
Решение. Будем предполагать, что равновесная плотность и энтропия
постоянны во всей жидкости. Тогда уравнение состояния имеет вид р=р(р)
dp dp dp e , dp Л
и --=--—= с2 (р) —- С учетом этого соотношения уравнения неразрыв-
дх др ох ох
ности (6.9) и Эйлера (6.14) для одномерного случая примут вид:
др , ди t др ^ ди , ди , с2 др
dt ^Р дх ^ дх ' dt ^ дх ' р дх
Вместо р введем функцию Римана # (р) = Л с (р) — — = , —— =
J р dt р dt дх
с др
= — — , а также две новые функции / = 7а (Л + и) и g = Ya (Я — и), для
р ах
которых будем иметь:
df df dg dg
df дх dt дх
Эти уравнения аналогичны (14.9) и соответствуют распространению
фиксированного возмущения /0 со скоростью c+ut a go —с другой скоростью, и —с.
Но u=f—g, следовательно, скорость распространения возмущений /0 и go
будет изменяться, так как, например, /о при своем движении проходит через
точки с разными g. Если при г=0 возмущение g=0, то оно будет равным
нулю всегда. Тогда /? = ы, f=u, р=р(ы) и
ди ди
—+ (с+м) —=0, u = F[x-(c + u)t]
— волна Римана, распространяющаяся в сторону положительных х.
Аналогично при /=0 получаем волну Римана u=G[x+(c— u)t],
распространяющуюся в обратном направлении (если и<с). Если возмущения F и G не
перекрываются, то они распространяются независимо/ Однако в общем случае
они могут наложиться друг на друга и взаимодействовать. После того как
возмущения разойдутся, они вновь будут распространяться независимо.
11 Л. М. Бреховских, В. В. Гончаров 305

14.3. На основе закона сохранения импульса найти изменение во времени
пространственной протяженности /(/) треугольной ударной волны и ее
максимальной амплитуды um(t).
Решение. Предполагая, что форма возмущения останется треугольной
всегда, запишем и (£, f) в движущейся системе координат £=*—Со/:
u(t,t)=Qt если £<0, £>/(/),
«(l,0-«.(0WW. если 0<6</(г).
Это возмущение при /=0 нв момент времени f изображено на рис. 14.5,
А>«о
Полный импульс волны равен.&= \ ul%tt)d% =—ит (/) =я-2т2-, где/0=/,Оч;
»' 2 2
«о="т (0). Смещение фронта /(f), как
видно из рис. 14.5, равно/(f) =£(0,ит)+
+ Umt=(Um/Uo)l0 + Umt = (/0/«о)(1 +
+u0t/l0)um. В результате для um(t) и
/(f) получаем:
-7,
"т«
Рис. 14.5
/(/)
-('+t)"
14.4. Получить стационарное решение уравнения КдВ в неявной форме,
а также выражение для пространственного периода (длины) кноидальной
волны.
Решение. Подкоренную функцию в правой части выражения (14.14)
мржнр записать таким образом:
2 2 / /3 с/а \ 1
T(£-t/)=?(£-^- + ^) = -(/-/1)(/-/2U/,-/)>
где fi<f2<h — корни уравнения E—U(f)=0. Интегрируя теперь (14.14),
получаем искомое выражение
4
Зр Л Л° £к$-Л>(6-ЛИЛ-5)1*
Кзр
Следовательно, функция /(л) (^2=/(Ло)) выражается через эллиптический
интеграл первого рода. Пространственный период кноидальной волны будет
равен
t-*m\ S 4-уГЖк(уьЕЬ),
где K(s) —полный эллиптический интеграл.
14.5. Показать, что для изотропных волн (о)=о)(£)) с ю(0)=0 при
условиях со'(я)>0 и <d">0 всегда можно выполнить условия синхронизма (14.18),
а в случае со'>0 и о)"<0'этн условия удовлетворить невозможно.
Решение. Решение задачи вытекает из следующих очевидных
соотношений. При (о">0 дисперсионная кривая ю(£) выпукла вниз и (o(\k2—£i|)<
306

<co(&i)+u)(&2)<<«)(£i+fc2). Если положить k3=ki+k2, то при изменении угла
между векторами ki и к2 от нуля до я имеем \k2—kY\ ^fh^k\+k2.
Следовательно, частота о)3=ш(Л3) будет непрерывно изменяться от (o(ki+k2) до
(o(\k2—ki\) и в какой-то точке совпадет с ay(ki)+(o(k2). При со"<0 имеем
о) (fci)+<D(fc2)>w (^1+^2)^(0(^3)» и такое совпадение оказывается
невозможным.
14.6. Свести систему укороченных уравнений (14.20') к одному
обыкновенному дифференциальному уравнению.
Решение. Для волны aj (/=1, 2, 3) введем амплитуду и фазу
aj=i4jexp(i(pj)v i4j=|aj|. Теперь, например, первое уравнение (14.20')
запишем так: (Л1-ь/Л1ф1)=/а)1УЛ2Лзехр[1(фз—q>i—Ф2)], и аналогично другие
уравнения. Далее, введя величину я|)=фз—ф1—фг и отделяя вещественные и
мнимые части, получаем:
^i = — «hVA2A3 sin ib, фх = щУ * 3 cos -ф = — -?- ctg ty,
Ах Ах
А А А
Аг = — coalM^a sin ф, ф, = с^ V -^-J- cos \J) = — -р- ctg ф,
А2 А2
Ав = созЛИ, sin гр, <р8 = a)3V ~h^" cos if = -р- ctg г|),
A$ A3
но
«... iM2i43 + ЛаЛИз + A3AXA2 d/dx (А±А2А3)со8 г|)
* = Фз - Ф1 - Ф,= j^ Ctg*= АгА2А3 Щ'
Следовательно, система уравнений сводится к четырем вещественным:
Ёх = — 2сохУ УехЕ2Е3 sin ф, Е2 = — 2co2V K^i^^s sin if,
. d ,
£3 = 2щУ VEiE2E3 sin гЬ, —- (КЯ^Яз cos \b) = 0,
ax
где Ej=Aj2= \uj\2. Из этих уравнений с учетом условий синхронизма (14.18)
легко следуют законы сохранения (14.21) и (14.22), а также yE\E2EzCOS^>^=
= 9=const или smty=duyElE2Ez—Q2fyEiE2Ez. В результате, выражая Е\ и
Е2 через £3> например, из второго и третьего выражений (14.22), получаем
искомое уравнение для Е$:
Ё9 = ± 2(0!^^ I Е3 ((о3#13 — ^з) («зЯ23 — Е3) ■
(0x0)2 J
Последнее, как и в задаче 14.4, решается в эллиптических функциях.
14.7. В задаче 10.5 показано, что для дисперсионного соотношения
гравитационно-капиллярных волн G)=Vgfc+Yfc8 имеется соотношение 6)(2&Р) =
= 2w(fcp) =2о)р, где £p=Vg/2Y, т. е. резонанс. Предположив такую
дисперсию для волн уравнения (14.1), проинтегрировать соответствующие
укороченные уравнения с начальными условиями ak (0)=ai(0)=ao, a2k (0)=a2(0)=0-
Решение. Подставив в уравнение (14.1) решение вида
и = аг [ef) exp [i (kpx — сор/)] + а2 (et) exp [2i (k?x — a?t)] + к. с.,
получим укороченные уравнения:
*i = — ibpa{a2, Да = — /Л aj.
307
11*

Действуя, как и в предыдущей задаче, получаем:
Аг = kpAiA2 sin -ф, Л, = — kpA\ sin г|>, — (Л^Ла cos ty = 01
где а^=Л;ехр (iy3), ф=ф2—2фь Л^О^Ло, Л2(0)=0. Но тогда Л!2+Л22=
=Л02, Л^Лг cos ф=О, г|> =—я/2, sin t|>=—1. В результате для Л2 имеем
уравнение Л2=£р(Л02—Л22), Л2(0)=0, интегрируя которое, получаем Л2=
=Л0Ш(^рЛ00, Л1=Л0/сЬ(^рЛоО- Отсюда следует, что энергия
гравитационных поверхностных волн может переходить к капиллярным*
14.8. Найти решение укороченных уравнений (14.20') при условии, что
амплитуда низкочастотной волны coi поддерживается постоянной.
Решение. Дифференцируя второе или третье уравнение (14.20') с
учетом другого, получаем 5,=—o)2o)3V2|ai|2a;- (/=2, 3), откуда a^=a,cos6/+
+PiSin6f, 6=Усо2соз| V\ \а\\. Постоянные а,] и р,- определяются из начальных
условий aj(0)=ai0t а2(0)=ш2Уа1*а9оУ а3(0) = козУа^го, что дает а2=а20,
о&з = азо,
Рг = /соаУа*а3о/^» Рз = иозУвАо/в-
Если при /=0 амплитуды а^ и азо были малы, то и в последующие моменты
времени они останутся малыми. Это говорит об устойчивости низкочастотных
волн в резонансной триаде.
14.9. Найти условия, при которых две поверхностные волны при
нелинейном взаимодействии друг с другом могут излучать внутреннюю или
звуковую волну. Определить направление излучаемых волн.
Решение. Пусть ki и к2 — волновые векторы поверхностных волн, а
Oi и (о2 — их частоты. При их взаимодействии возникнут волны
комбинационных частот и волновых векторов: o) = o)i±o)j и k=k|±k2. Частота
внутренней волны должна быть существенно меньше частот поверхностных волн. Это
возможно только для разностной комбинационной волны g)b = g)i—о)2 при
условии, что (о2«Wi (также и k2&k{). При этом внутренняя волна будет
распространяться под таким углом 9В с вертикалью, что sin9B = (o)i—o)2)/W,
где N — частота Вяйсяля, предполагаемая постоянной.
Длина звуковой волны существенно превышает длину поверхностной той
же частоты. Следовательно, горизонтальная проекция волнового вектора
звуковой волны к3 должна быть малой по сравнению с ki (h<,k\). Это
возможно только для комбинационной волны в виде суммы k3=ki+k3 при k2«—kj
(o)2«<»>i), следовательно, частота звука o)3=o)i+o)2=2o)i равна
(приближенно) удвоенной частоте поверхностных волн. Для вертикальной проекции
волнового вектора звуковой волны имеем &2=Уо)32/с2—&32, где с — скорость
звука. Направление распространения звуковой волны 9Э определяется
соотношением sin 9з=с£3/2о)1.
14.10. Определить амплитуду звуковой волны, излучаемой при
взаимодействии двух поверхностных волн.
Решение. Вертикальное смещение свободной поверхности, вызванное
ловерхностными волнами, имеет вид
г*
£=S afехр [i (k/r—v^» ^ = gkf
/=1
308

Pl—= дг
При этом в соответствии с предыдущей задачей: кг=—ки o)2«<oi—
горизонтальная проекция волнового вектора звуковой волны k3=ki+k2, а ее частота
<u3=(Di+g)2. Амплитуду звукового давления будем искать методом
последовательных приближений, подставляя в нелинейные члены акустических
уравнений и граничных условий возмущения, обусловленные поверхностными
волнами, которым припишем индекс «и»: vn и ра. Поскольку поверхностные
волны не меняют плотности среды, единственным нелинейным членом
акустических уравнений будет (vnV)vn. Учитывая, что для потенциальных воли
(vnV)vn = V(vn2/2>, запишем уравнение для акустического давления
Вычисляя второе приближение динамического граничного условия (10.5) при
а=0 и пренебрегая для звукового давления» силой тяжести, получаем
£=G. Выражения для рп[и vn={un, wn] следуют из (10.32),
lz=o
где bj = —i(ujaj (/=1, 2). Опуская множитель exp [i(kj-r—coj/)], имеем:
2 со2 2 к
Рп = Ро У) — aj ехР (Л/2), ип = - i 5J vfaf exp {kfz) -±
/=i k! /=i kf
«>„ = — t#S <°/a/exP (fyO*
Вычисляя теперь правые части F и G, ограничиваясь только резонансным
членом exp [i(k3r—о)зО] и пренебрегая отношением &3/£j<l, получаем:
F = Ро I «111 <h 14Л; exp [(^ + V * + * (k3r - ^3/)],
с = - Po^i 1 fli IКI ехР U (кзг - <***>]•
Решение для р ищем в виде
<»3
р = {А ехр [(*! + k2) z] +В exp (i*2z)} exp [i (k3r - cdo*)1 % k\ = — — £*.
Подставляя /7 в уравнение и граничное условие, находим амплитуду
затухающего члена j4 = p0|ai| |a2|a)i2 и амплитуду звуковой волны
B=-2p0|a1||a2|(o12.
14.11. Найти нелинейную поправку к частоте для квазигармонического
волнового пакета конечной длины, распространяющегося в среде с сильной
дисперсией.
Решение. Пусть kx — волновое число основной гармоники пакета, а
Ыг<^кх— спектральная ширина пакета. Ввиду конечности Ak систему
уравнений (14.26) следует расширить, включив в нее взаимодействие
составляющих волнового пакета с длинными волнами, для которых волновое число
£^;Д£. Уравнение для спектральной амплитуды <х$ следует из (14.24):
% = - l*Y Г [«At+uOg^n ехР (*'А+') + «^-^«б+^+ц ехР У А-'Лd4>
309

где
rfu) I
± <oft>± ^Н (Л + I) = Ш£- *,р (*!> ? = [сф(0) - crp (A^J £ = Д5
Кроме того, а а^ ж а^^ ^ аАх, а^.^ ж а^^ « с£, следовательно,
<Ц ^ — ie£ | аЛ11» exp (iA^f) АЛ.
Временно считая здесь а^ = const, находим
«g (t) = - f- I «*, )a exp (iAs/) ДЛ = - g (Q)_Cg (j^ I c^ p exp (t A^) A*.
Этому взаимодействию соответствует следующее уравнение для а*:
ак = - fe* J аъак.г ехр (- /Д6<) dg ж g (0)_g ^ I «*, Is «* (ДАЛ
Aft
где \k—ki\^hk. Обозначив через Ai=a,kAk амплитуду основной гармоники
в пакете волн и уч'тя также член, соответствующий взаимодействию с
удвоенной гармоникой, вместо (14.28) получим уравнение
«,.»«il»i-{t+W)'<>,■,)-■
Решение этого уравнения ai=ai(0)exp(—i6(ot) соответствует волне с
нелинейной поправкой к частоте, равной
Таким образом, нелине!
член по сравнению с (14.28).
Таким образом, нелинейная поправка к частоте имеет дополнительный

ПРИЛОЖЕНИЕ
Некоторые сведения из теории тензоров
В физике встречаются величины различного типа. Простейшие
из них — скаляры, характеризующиеся одним числом (масса,
температура и др.) и имеющие одно и то же численное значение
в определенных единицах в любой системе координат.
Более сложными величинами являются векторы, которые
характеризуются как численным значением, так и направлением,
или тройкой чисел, например составляющими по осям в
декартовой системе координат. Естественно, что сам вектор, так же
как и скаляр, не изменяется при переходе от одной координатной
системы к другой, но его составляющие преобразуются по
вполне определенному закону. В простейшем случае, взяв в качестве
вектора радиус-вектор, проведенный из начала координат в
некоторую точку, этот закон легко установить. Для простоты
ограничимся прямоугольной декартовой системой координат с осями
xit х2, х3 в пространстве трех измерений и рассмотрим только
преобразования поворота системы координат. Как известно, при
поворотах новые координаты точки М */, х2'> х/ выражаются
через старые хи jc2, jc3 так:
3
Х\ = Ъ CLikxk = aikxk (П.1)
-суммирование по дважды повторяющемуся индексу в
формулах подразумевается даже при отсутствии знака суммы.
В выражении (П. 1) коэффициенты aih являются проекциями
единичного вектора (орта) оси х/ на старые оси xh: а<*=
/\
=cos(x/, xfc). Преобразование (П.1) можно также
рассматривать как преобразование компонент радиус-вектора г,
проведенного из начала координат в точку М, так как координаты точки
М и являются компонентами радиус-вектора г.
Теперь мы можем дать следующее определение
произвольного вектора: вектором В назовем совокупность трех величин Bt
(f=l, 2, 3), преобразующихся при повороте системы координат
по закону
В\ = atkBk. (П.2)
По аналогии с (П. 2) можно определить более сложные
величины, а именно: тензором второго ранга назовем совокупность
девяти величин gikJ преобразующихся при поворотах системы
координат по закону
gik = auubngtm- (П.З)
311

Соответственно тензор третьего ранга — совокупность 27
величин gijh, преобразующихся по закону g'iik=ailaigahngi,tK,... Во
всех формулах преобразования aih — та же таблица чисел, что и
в (П. 1). Ясно также, что обычный вектор можно назвать
тензором первого ранга, а скаляр (А'=А) —тензором нулевого ранга.
Не представляет трудностей обобщение наших определений
на пространство любого числа измерений п (хи х2, ..., хп)у а
также на любое линейное преобразование системы координат
(таблица чисел aik произвольная, допускающая обратное
преобразование).
При изучении законов движения сплошной среды часто
требуется установить соответствие некоторых физических величин
с формально определенными тензорами. Для этого оказываются
полезными некоторые теоремы относительно тензоров,
позволяющие установить тензорный характер каких-либо величин. Мы
приведем эти теоремы для случая тензоров не выше второго
ранга.
Предварительно выявим некоторые соотношения между
коэффициентами преобразования aih. Известно, что поворот
системы координат вполне характеризуется тремя параметрами (углы
Эйлера). У нас же имеется девять величин aih, следовательно,
между ними должно существовать шесть связей. Для
установления этих связей вспомним, что aih — проекция орта х/ новой
системы координат на ортхЛ старой, т. е.
х/ = а{1 хх -f ait х2 + сц9 х3 = aik х*. (П.4)
Аналогично Xi=ai1jLm. Найдем скалярное произведение ортов
х/х; = aaftim x*xm. (П.5)
Здесь, как и выше, по дважды повторяющемуся индексу
подразумевается суммирование. Но в силу ортогональности ортов в
прямоугольной системе координат
ВДп = Ькт> Х,'х; = 6,/, (П.6)
где бу=1 при i=j\ 6*i=0 при 1Ф\ — символ Кронекера.
Следовательно, в правой части (П. 5) нужно учитывать только члены
с k=m. © результате получим
flftflik—б« (П. 7)
— искомые шесть соотношений (а не девять в силу
симметричности левой части (П. 7) по перестановке индексов i и I: a{halh=
Соотношения (П. 7) можно записать также в другой форме,
если рассматривать систему х/ как старую, а хк как новую и
учесть, что таблица чисел ам задает обратное преобразование
/\
(jc,=cos(x{, х/)х/=амх/). Образуя хл и рассуждая
аналогична* = б«. (П. 7')
ным образом, найдем
312

Свойства тензоров
Теорема 1. Если Ак — вектор и gih — тензор второго ранга,
то величины B{=gikAk также образуют вектор.
Доказательство. Запишем это равенство в новой
системе координат Bi=g'ikAh' и применим формулы преобразования
для величин gik' и Ак: g'tk=ailaknglni, Ак'=акаА8. Тогда Я/=*
= aaakTnakaglmAaf но аЛшам = 6тв, ЬтАг=Ат. Поэтому В,' =
= CLugimAm=ciiiBh т. е. величины В{ преобразуются как вектор.
Теорема V (обратная). Если gik преобразует по формуле
Bi=gikAk произвольный вектор Ак в векторе, то gifc —тензор
второго ранга.
Доказательство. В новой системе координат имеем
В\ =g'ihAh. Подставив сюда справедливые для векторов
соотношения В/=аиВ1 и Ак'=актАт, получаем ailBl=g,ikakmAm. Умно
жая обе части последнего равенства на сцл с последующим сум-
мированием по in учтя, что a<ea«=6ei, 6.jB,=£e, находим Вв==
=g/<fcflfcma1v4m. Сравнивая это равенство с исходным Bi=gikAkt
заключаем, что g,m=ahmaiag'{k. Еще раз умножим обе части на
dnsdpm с суммированием по 5 и т и учтем, что актарт=8кр, аиапа=
=бгп, SAP6ing/tft=g/ftp. В результате получим преобразование для
тензора: g'nI> = anaaprngarn.
Совершенно аналогично доказываются еще две теоремы.
Теорема 2. Если А{ и Вк — произвольные векторы и gik —
тензор второго ранга, то величина M—gikA{Bk — скаляр.
Теорема 2' (обратная). Если величина M=gikAiBk —
скаляр, Ai и Вк — произвольные векторы, то gik~тензор второго
ранга.
Теорема 3. Сумма диагональных элементов тензора
второго ранга — скаляр, т. е. не изменяется при поворотах системы
координат.
Доказательство. Воспользовавшись преобразованием
(П. 3), запишем
g'u = auQimgim = blmglm = gmm>
что и требовалось доказать.
В теории векторов доказывается теорема Гаусса,
заключающаяся в справедливости соотношения
f^tdV = Ji4*nifcdSf (П.8)
v к S
где V — объем некоторой замкнутой области; 5 — ее
поверхность; п — вектор внешней нормали. Покажем теперь, что для
тензора второго ранга gik также имеет место
Теорема 4
\dj^dV = ^giknkdS. (П.8')
313

Доказательство. Применим соотношение (П. 8) к
вектору Ah=gihBit где В{ — произвольный постоянный вектор. При
этом (П. 8) можно записать в виде
Bt ttdjjjLdV- ^giknk ds\ = О,
откуда в силу произвольности вектора В{ и следует утверждение
теоремы.
Определение. Тензор второго ранга gih называется сим-
метричным (антисимметричным), если ghi=gik (gA<=—£,*).
Очевидно, что у симметричного тензора имеется лишь шесть
независимых компонент: giit g^ gsiy gi2=g2li gi*,=g*i, g2*=gn,
а у антисимметричного — только три: gi2=—g2i, gi3=—£л, g2s=
Теорема 5. Симметричность (антисимметричность)
тензора сохраняется при поворотах системы координат.
Доказательство.
Ski = ablaimglm = ± akiutngmi = ± g[k.
Знак минус здесь относится к случаю антисимметричного
тензора.
Определение. Величины, составленные из компонент
тензора и неизменяющиеся при переходе к новой системе
координат, называются инвариантами тензора.
Теорема 3 дает один инвариант тензора второго ранга g«=
=const. Для того чтобы найти другие инварианты, рассмотрим
вопрос о главных осях и главных значениях симметричного
тензора.
Пусть дан gih — симметричный тензор второго ранга и два
вектора А=В=г (А{=В{=х{). Тогда по теореме 2 имеем
скаляр M=gihXiXh. Будем теперь изменять х{ и xk таким образом,
чтобы М=\. Тогда равенство
gtkXiXb— guX? + g22X22 + £3з*з2 + 2£12*Л + 2giZXiXi + 2g23X2X3 = 1
будет уравнением поверхности второго порядка, называемой
тензорной поверхностью. В частном случае, когда все gik>0,
получаем уравнение эллипсоида. Известно, что поворотом осей
координат уравнение поверхности второго порядка, не
содержащее первых степеней хи можно привести к каноническому виду
v;2 + m;+v;2 = i. (п-9)
Но поскольку при этом преобразовании компоненты тензора
также преобразуются в g'^ и д'ъХ/хх=1, то в новой системе
координат g,11=X1, ^22=^2, g'»=b*> а g'<fc=0 при гфк. Другими
словами, тензор приобретает диагональный вид. При этом
направления осей новой системы координат называются главными
направлениями тензора g^, а величины Я, — главными
значениями.
314

Пусть теперь вектор А коллинеарен какому-либо главному
направлению, например первому, тогда в системе координат, оси
которой совпадают с главными направлениями тензора, очевидно,
имеем В/=Х1Л1/ (B/^=XiA/)t т. е. преобразование g'ikAk просто
удлиняет вектор А в А,4 раз. Это свойство не должно зависеть от
выбора системы координат, следовательно, для вектора Ак,
совпадающего по направлению с главным, в произвольной системе
координат справедливо равенство В{=)ыА{ (B=A,iA). Тем
самым мы получили способ нахождения главных значений и
главных направлений тензора второго ранга. Для этого нужно найти
такие значения X, при которых однородная система уравнений
Я«А=ХА, или (gik—6ikX)Ak=0 (П.10)
имеет нетривиальное решение, т. е. те значения А,, при которых
обращается в нуль определитель системы (П. 10):
821 £22 — А» &3
£31 gn gas — ^
= 0. (П. 11)
Уравнение (П.11) является уравнением третьей степени
относительно Я, три его корня h и будут искомыми главными
значениями тензора. Соответствующая каждому из найденных h
тройка чисел, являющаяся решением уравнения (П.10) Ak{i) (i=
= 1, 2, 3), определяет компоненты вектора А(1), коллинеарного
одному из главных направлений.
Нетрудно показать, что главные направления Ak(i) и Ак{2}9
соответствующие двум различным главным значениям A,i=j£h2,
ортогональны. В самом деле, поскольку -ЛА(1'2) — решение
уравнения (П. 10), то gikAh(i) =KiA{{i) и gihAk(2)=%zAi{1\ Умножая первое
равенство на Аг\ второе — на A{{i) (естественно, с
суммированием по 0 и вычитая почленно, получим с учетом симметрии
тензора gih
(Xi—ht)At^Aiw=09
что переходит (A,t—Х2ф0) в условие ортогональности векторов
А(1) и А(2): Л<(1)Л,(2)=А(1)А(2)=0. Если же какая-то пара (или
все три) главных значений совпадает, то в силу произвола в
решении уравнения (П. 10) векторы А(г) можно выбрать взаимно
ортогональными.
Теперь не составляет труда найти еще ряд инвариантов
тензора второго ранга, воспользовавшись тем, что решения
уравнения (П. 11), являющиеся главными значениями тензора, не
должны зависеть от выбора системы координат. Следовательно, не
должны зависеть от системы координат и коэффициенты
уравнения (П. 11), определяемые компонентами тензора gih. Раскры-
315

вая определитель (П. 11), получаем
коэффициенты
Я =.£21 #22 £Г23 > Ii = gu,
I £31 £32 &зз I
12 &!2 "Г bis ~Т" ©2
-Х'+ЛЛЛ-I2'l+D=0, где
" gllgw §11§33 S22&33
(П. 12)
и являются искомыми инвариантами тензора #Л.
Инвариантность Л мы уже доказывали (теорема 3). Вместо инварианта /2*
обычно используют легко запоминаемую комбинацию
инвариантов U и /2* вида
I2=Iiz + 2I2'=g\i+g222+g\s + 2g\2 + 2g\3 + 2g*
(П. 13)
— всегда положительная сумма квадратов всех элемелтов
тензора.
Основные формулы векторного анализа
Приведем ряд основных положений и формул векторного
анализа в объеме, необходимом для чтения настоящей книги.
Скалярное и векторное произведения. Пусть имеются два
вектора А={Аи Аъ А3} и В={ВЬ В2, Б3}, заданных их
компонентами А{ и В( (t=l, 2, 3) в прямоугольной декартовой
системе координат. Скалярным произведением этих векторов будет
АВ = В А = АВ cos (&Ъ) = АгВг + А2В2 + А3В3 = AkBk.
Векторным произведением АхВ этих векторов является
вектор, перпендикулярный как А, так и В. Длина этого вектора
равна ЛВ | sin(AB) |, а направление определяется таким
образом, чтобы вращение от А к В по кратчайшему пути вокруг век-
хора Ах В происходило в ту же сторону, что и вращение оси
я4 к оси х2 вокруг оси х3. В компонентах имеем
АхВ =
+ (А1В2~А2В1)хВ1
*1
л
Вг
*2
л
в»
*з
л
в3
= (А2В3 - АА) хх +(А3Вг - АгВ3) х2 +
вде х{ — единичный вектор в направлении t-й оси координат.
Часто вводят так называемый абсолютно антисимметричный
т£Нзор третьего ранга eiik, компоненты которого имеют
значения:
а) 0, когда любые два индекса равны;
б) 1, когда ijk является четной перестановкой чисел 1, 2, 3;
в) —1, когда ijk является нечетной перестановкой чисел
Ц 2, 3.
Выражение для векторного произведения может быть
записано через тензор elik следующим образом:
АхЪ = етАзВьХ<.
316

Отметим некоммутативность векторного произведения и его
ассоциативность по отношению к скалярному множителю М:
ВХА = — АХВ, (МА)ХВ = М(АХВ)=АХ(Л1В).
Двойное векторное произведение записывается в виде
Ах (ВхС) =В(АС)-С(АВ). (П.14)
Градиент. Если каждой точке т={хи х2, хл} некоторой
области пространства поставлен в соответствие некоторый скаляр
<р(г) или вектор а (г), то рассматриваемая область называется
скалярным или векторным полем. Выберем некоторую точку г
скалярного поля ф(г), проведем через нее прямую в
направлении единичного вектора s={slf s2, s3} и рассмотрим предел
1 im ф (г + s6) - ф (г) ^ _aq>_
называемый производной скалярного поля по направлению s.
Разложив <рч(|"+8в) в ряд Тейлора, получим
ds \ дхг дх2 дх3 /г dxk
Sk — gs.
Вектор g={d(p/d*i, д<р/дх2, дф/д*3} называется градиентом ср в
точке г и обозначается символом grad<p. Мы видим, что
производная скалярного поля по направлению s равна проекции
gradcp на это направление. Следовательно, grad<p направлен в
сторону быстрейшего увеличения функции ф(г), а его модуль
равен производной по этому направлению.
Для удобства и упрощения выкладок вводится так
называемый дифференциальный оператор Гамильтона (оператор «на-
бла»):
дхх дх^ дх3 dxk
При этом grad <р = Уф. Легко проверить, что
Vr = vy*12 + x21+*,2 = r/r> Vq>(r)=q>'(r)r/r, V(Cr)=C = const.
Дивергенция и теорема Гаусса — Остроградского.
Определение. Потоком вектора а через Поверхность S называется
поверхностный интеграл j an dSt где n — нормаль к S.
Выберем некоторую точку г векторного поля а, окружим ее
малым объемом AV\ вычислим поток вектора а через
замкнутую поверхность S, ограничивающую объем AV, и рассмотрим
предел
#.
2Lt\dS
lim =diva.
AV-»o AV
317

Здесь n — внешняя нормаль к S. Значение этого предела
обозначается символом diva и называется дивергенцией
(расхождением) вектора а в точке г. Этот предел существует, не
зависит от выбора объема А К и оказывается равным
diva = -^-+i^ + iEL = ^i = Va.
дх\ dxt dxz dxk
Если а=г, то divr=(dxjdxi) + (dxjdx2) + (dxjdxi)=3.
Одной из важнейших теорем векторного анализа является
теорема Гаусса — Остроградского.
Поток вектора а через замкнутую поверхность S равен
интегралу от дивергенции вектора а по объему, ограниченному
этой поверхностью:
jancfS= jdivadV.
s v
Вектор вихря и теорема Стокса. Определение.
Интеграл от вектора а вдоль кривой L, т. е. J arfr, называется ли-
L
нейным интегралом вектора а. Если кривая L замкнута, то Г =
= (р adr называется циркуляцией вектора а вдоль L.
L
Обозначим через AS некоторую поверхность, ограниченную
контуром L, и рассмотрим предел при AS-^0 (L стягивается в
точку):
lim
adr
AS
= rota.
Значение этого предела называется ротором (вихрем) вектора
а. Для компонент последнего справедливы формулы:
v п дх% дх3
(rota)2 = ^
дхз
дхх
(rot а)3 =
да*
дхх
дхз
Используя оператор V, выражение для вектора rota можно
записать в виде
rota = Vxa =
д
dxi
д
дх2
02
д
дх3
а*
dak
= е//л —- х,.
ЗХ:
Легко убедиться, что
rot grad ф=0, dlv rot а=0.
В терминах вектора вихря формулируется теорема Стокса.
31*

Циркуляция произвольного вектора а по замкнутой кривой
L равна потоку вихря этого вектора через односвязную
поверхность S, ограниченную контуром L:
ad г «= j (rota)ndS.
Векторные тождества. Используя оператор V и следуя
правилу, что этот оператор действует только на те скаляры и
векторы, которые стоят позади него, можно получить ряд форму/i
векторного анализа. При этом следует иметь в виду, что если
оператор V стоит перед произведением нескольких величин, то
нужно поступать так же, как при дифференцировании
произведения функций. А именно, сначала оператор V действует только
на первый сомножитель, оставляя остальные неизменными,
затем только на второй и т. д. Здесь удобно отмечать те
величины, которые временно считаются постоянными, каким-либо
значком, например с (const).
Следуя этому, найдем:
grad (<р\(з) = V (фф) = V (<рсф) + V (ффс) =ф grad ф+ф grad ф,
div (фа) =ф(Уа) +аУф = ф div а + а grad ф,
rot (фа) =VX (фа) = фУХа—аХУф=ф rot а—аXgrad ф..
Несколько сложнее получается выражение для вихря
векторного произведения rot(aXb)=Vx (aXbc)+VX (acxb).
Воспользуемся формулой (П. 14) для двойного векторного
произведения, записав ее так, чтобы вектор, на который действует
оператор V, стоял справа от него:
VX (axbc) = (bcV)a—b<(Va) = (bV)a—b(Va),
VX (acXb) =a.(Vb) —(acV)b = a(Vb) —(aV)b.
Складывая полученные равенства, находим
rot (axb) = (bvja—(aV)b+a div b—b div a.
Аналогичным путем получаем
div(aXb)=b(VXa)— a(VXb) =b rot a—arotb.
Вычислим градиент скалярного произведения grad(aXb) =
= V(abc)+V(acb). Положив в (П.14) сначала A=bc, B = V, С=
= а, затем Л = а<., B = V, C=b, соответственно находим:
V(bca) = (b«V)a+bcX (VXa), V(acb) = (acV)b+aeX (Vxb).
Следовательно,
grad (ab) = (bV)a+ (aV)b + bXrot a+aXrotb.
В частном случае, когда b = a, имеем
grad(a2/2) = (aV)a+aXrot a.
319
t

Операции второго порядка по V. Примером таких операций
являются
div grad q>=V (Уф) = (VV)cp = V2<p=Д<р,
где
Д = -iL + —+ —= —
дх\ дх\ дх\ дх\
— оператор Лапласа;
div (<р grad \|)) =<р div grad tf-f (grad <p) grad if;
rot rot a = V (Va) — (VV) a=grad div а—Да.
Криволинейные координаты. Рассмотрим замену переменных
£<(r)=5t(*i, *2, *з), '=1, 2, 3, допускающую обратное
преобразование Хг=х{(1и l2, Is). Поверхности g*(г) = C<=const
называются координатными поверхностями. Линии пересечения двух
координатных поверхностей |<=С* и \}=С} называются
координатными линиями. Чаще всего vпoтDeбляютcя ортогональные
криволинейные координаты, координатные линии которых взаимно
перпендикулярны. Примером таких координат являются:
1. Сферические: h^r^xf+xS+Xs2, £2=G — угол вектора
г с осью х3; £з=Ф — угол проекции вектора г на плоскость хи
хг с осью Xi. При этом хх = r sin 8 cos ф, Jt2=rsin9sir^, xs =
= rcos0.
2. Цилиндрические: £1 = р=Ул:12+*22, g2=<p — угол вектора
р={хи х2} с осью xt\ h = z=x3. Обратное преобразование: xt =
= pcos<p, л:2=р5тф, xs=l$.
В общем случае в каждой точке пространства можно ввести
единичные векторы et, е2, е3, параллельные касательным к
соответствующим координатным линиям в этой точке. Тогда для
производных функции r(gi, £2, It) имеем:
-тг^ = Hxtv —- = Н&, — = Я3е3,
0%! Ot,2 068
где #,= [ (dxjdti)l+ (dx2ldl<)2+ (дх5/дЪ)2]4* — модуль вектора
dr/d^i. Величины Н( (/=1, 2, 3) называются коэффициентами
Ламе.
В случае ортогональных криволинейных координат
справедливы следующие формулы:
grad g1 = e1//^lf grad £2=е2/#2, grad £3 = е3/#з,
(d rf = HI (<&? + HUdtf + HI (dy2>
dV=dxidx2dx3 = HMzHsdltdlzdlsy
gnidV(Elfbfb)=^erad6ik = ^^ + ^-^ + -b^Lf
div а = (ЯЛЯ.Г f«« + »<«*■"»> + aco^^i f
L d£i 3|a d£3 J
320

d(a*Hi)
аь
(го1а)1 = (Я2Я3)-1[-^М
(rot a)2 = (ВДГ [-iMi - -*&&-
(rot a)3 = (ЯгЯ2)- [^-iM
+
_L _д_ /ЯхЯа jty
' аь v я8 ai3 ;j
Отсюда для сферических координат имеем:
Н, = 1, Н» = г, Hy = r sin 0,
gradij, = е, -4*" + ввг-1 i*- + e^rsinep-^,
Л д(г2аг) rd(aftsin6) da^i
div а = г"* -i-=L + (г Sin ер *' + -*■ 1,
dr I dv dq> J
<"*•>' = ('«"en [-l -£],
(rota). = ^-0^-^-1
L дф dr J
, . ч _, Г д (raj dar -i
L ar V ar Jn ae \ дв) a<p2 J
И для цилиндрических H„= 1, //,=р, Нг=1:
gradt = eP-fL + e<pP^-fL + ^,TL.
dp дф dz
дф J. dz
dlva = plj___ + _^
да, да_
(rota) =^1-^-,
v ;<p дг dp
(rota)z = pl[^-^__^j,
T K LФ \ ap / к в»«] *'
321

БИБЛИОГРАФИЧЕСКИЙ КОММЕНТАРИИ
Для более глубокого изучения вопросов, затронутых в этой книге,
читатель может обратиться к специальным учебным пособиям и монографиям.
Классические основы механики сплошных сред изложены в книгах:
Ландау Л. Д., Лифшиц Е. М. Механика сплошных сред. М: Гостехиздат,
1954.
Ландау Л. Д., Лифшиц Е. М. Теория упругости. М.: Наука, 1965.
Зоммерфельд А. Механика деформируемых сред. М.: Изд-во иностр. лит.,
1954.
Ламб Г. Гидродинамика. М.; Л.: Гостехиздат, 1947.
Милн-Томсон Л. М. Теоретическая гидродинамика. М.: Мир, 1964.
Фейнман Р., Лейтон Р., Сендс М. Фейнмановские лекции по физике. М.:
Мир, 1966, т. 7.
Седов Л. И. Механика сплошной среды. М.: Наука, 1973, т. 1/2.
Бетчелор Дж. Введение в динамику жидкости. М.: Мир, 1973.
Желающим глубже изучить вопросы теории турбулентности можно
рекомендовать книгу:
Монин А. С, Яглом А. М. Статистическая гидромеханика. М.: Наука. Ч. I,
1965; Ч. II, 1967.
Общие вопросы теории волн хорошо изложены в книгах:
Уизем Г. Лилейные и нелинейные волны. М.: Мир, 1977.
Tolstoy I. Wave propagation. N. Y., McGraw-Hill, 1973.
вопросам распространения волн, описываемых волновым уравнением
(акустических, электромагнитных, упругих), посвящена монография
Бреховских Л. М. Волны в слоистых средах. 2-е изд. М.: Наука, 1973.
Теория волн в упругих средах также изложена в книге
Ewing W. М., Jardetzky W. S., Press F. Elastic waves in layered media.
N. Y.: McGraw-Hill, 1957.
«Современное состояние теории волн в жидкостях можно изучить по
монографии
Лайтхилл Дж. Волны в жидкостях. М.: Мир, 1981.
Физические и математические основы динамики волн в океане и атмосфере
изложены в книге
Экарт К. Гидродинамика океана и атмосферы. М.: Изд-во иностр. лит.,
1963.
Теоретическим вопросам волн в океане посвящена монография
Каменкович В. М. Основы динамики океана. Л.: Гидрометеоиздат, 1973.
Поверхностные и внутренние волны в океане, их возбуждение, спектры и т. п.
хорошо описаны в книге
Филлипс О. Динамика верхнего слоя океана. 2-е изд. Л.: Гидрометеоиздат,
1980.
Атмосферные волновые |Щ>одессы (акустико-гравитационные волны, волны Рос-
сби, магнитогидродинамические волны в ионосфере) описаны в монографин
Госсард Э., Хук У. Волны в атмосфере. М.: Мир, 1978.
Подробное исследование волн Россби содержится также в статье
Longuet-.Higgins М. S. Planetary waves and a rotating sphere.— Proc. Roy.
Soc, A, 1964, vol. 579, p. 446—473.
322

Среди многочисленной литературы по акустике прежде всего хочется
обратить внимание на фундаментальный труд
Релей. Теория звука. М.: Гостехиздат, 1955, т. 1/2.
Подробное изложение физических основг акустики имеется также в книге
Исакович М. Л. Общая акустика. М.: Наука, 1973.
Современное состояние акустики океана изложено в коллективном труде-
Акустика океана/Под ред. Брехевских Л. М. М.: Наука, 1974.
Распространение звука в движущихся средах рассмотрено в книге
Блохинцев Д. И. Акустика неоднородной движущейся среды. М.: Наука,.
Основы магнитной гидродинамики, а также физики плазмы изложены,
например, в книгах:
Каулинг Т. Магнитная гидродинамика. М.: Изд-во иностр. лит., 1959.
Франк-Каменецкий Д. Л. Лекции по физике плазмы. М.: Атомиздат, 1968.
Вопросы нелинейной теории волн, помимо уже упомянутой книги Г. Уизема^
хорошо изложены в монографии
Карпман В. И. Нелинейные волны в диспергирующих средах. М.: Наука,.
1973.
Этим же вопросам посвящен также обзор
Кадомцев Б. Б., Карпман В. И. Нелинейные волны.—УФН, 1971, т. 103„
вып. 2, с. 193—232.
В качестве учебного пособия по нелинейным волнам можно также
рекомендовать книгу
Виноградова М. Б., Руденко О. В., Сухорукое Л. Я. Теория волн. М.:
Наука, 1979.
Ряд проблем нелинейной теории волн обсуждалось на конференции по
нелинейным диспергирующим волнам, труды которой опубликованы в книге.
Нелинейная теория распространения волн/Под ред. Баренблатта Г. И. М.г
Мир, 1970.
Развитие так называемого гамильтоновского формализма для нелинейных волн,,
позволяющего, как и в классической механике, рассматривать
многочисленные нелинейные эффекты с единой точки зрения, изложено в обзорной
статье
Захаров В. Е. Гамильтоновский формализм для волн в нелинейных средах:
с дисперсией.—Изв. вузов. Радиофизика, 1974, т. 17, № 4, с. 431—453.
В последнее время получили широкое распространение точные
аналитические методы решения нелинейных уравнений типа Кортевега де Вриза,
основанные на связи этих уравнений с линейной обратной задачей теории,
рассеяния. Изложение этих вопросов можно найти в книге
Захаров В, Е., Монаков С. В., Новиков С. П., Питаевский Л. Я. Теория со-
литонов (метод обратной задачи)/Под ред. Новикова С. П. М.: Наука,.
1980.
Читателю следует иметь в виду, что приведенный здесь список литературы
весьма неполный и касается в основном общих вопросов механики
сплошных сред. Однако желающие иметь литературу по какой-либо конкретной
задаче, как правило, могут ее найти, просмотрев библиографию в книгах,
указанных выше
При написании настоящей книги авторы стремились использовать
математический аппарат, обычно хорошо знакомый читателю, прослушавшему
математические курсы в учебных заведениях по физическим специальностям.
323

© качестве математических пособий можно, например, рекомендовать
следующие книги:
Морс Я., Фешбах Г Методы теоретической физики. М.: Изд-во иностр.
лит., 1958, т. 1/2.
Конин Н. Е. Векторное исчисление и начала тензорного исчисления. М.:
Наука, 1965.
Мак-Коннел Л. Дж. Введение в тензорный анализ. М.: Физматгиз, 1963.
Шабат Б. В. Введение в комплексный анализ. М.: Наука, 1969.
Евграфов М. А. Аналитические функции. М.: Наука, 1965.
Зоммерфельд А. Дифференциальные уравнения в частных производных
физики. М.: Изд-во иностр. лит., 1950.
Тихонов А. Н., Самарский А. А. Уравнения математической физики. М.:
Наука, 1966.
курант Р. Уравнения с частными производными. М.: Мир, 1964.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Амплитуда волны 21, 203
« комплексная 21, 58
Аттрактор простой 161
— странный 161
Вектор волновой 56, 193, 203, 249
— плотности потока энергии 99
акустической 253
— смещений 41
Взаимодействие волн 294
резонансное 294, 300
многоволновое 303
Вихрь 106, 166
Вода глубокая 196
—мелкая 196
Волна акустическая 247
— Альвена 264
— антисимметричная 73, 77
— вертикально поляризованная 58, 61
— внутренняя 201
— вязкая 148
— гармоническая 21, 28, 56, 193, 203
— горизонтально поляризованная 57,
58, 65
— гравитационная поверхностная 193
— изгибиая 28, 79, 81
— инерционная 225, 231
— капиллярная 199
— кноидальная 299
— кручения 25
— линейная 188
— локально-плоская 260
— Лява 66, 67
— магнитоакустическая медленная
288
быстрая 289
— модулированная 31, 204
— неоднородная 63, 251
— нормальная (мода) 73, 207
— отраженная 22, 58, 62, 205, 244, 254
— падающая 57, 59, 244, 254
— плоская 55, 57, 203, 248
— поверхностная 64, 66, 193, 217, 275
— поперечная 55, 57, 61
— продольная 20, 55, 61
— прошедшая (преломленная) 22, 68,
256
— распространяющаяся 193, 203, 206,
266
— Релея 64
— Римана 295, 305
— Россби 234
баротропная 236
— симметричная 73, 77
— стационарная нелинейная 297
— Стонелли 276
-г-стоячая 195, 250
— сферическая 268
гармоническая 269
— ударная 297
— уединенная 298
— юнговская 78
Волновод акустический 265
— океанский 209
Время взаимодействия 294
— медленное 301
Вязкость 86, 136
— магнитная 282
— турбулентная 171
Гипотеза Ландау 160
— подобия Колмогорова 181, 182
Глубина эквивалентная 240
Граница абсолютно жесткая 22, 57,
193
мягкая 22, 57
— двух сред 22, 56, 57, 201, 221, 256
Давление 86
— акустическое 248
— магнитное 281
Движение безвихревое 96
— вихревое 104
—потенциальное 114
— частиц в волне 55, 195, 228, 290
Деформация 6
— адиабатическая 5, 46
— изгиба 13, 14, 80
— изотермическая 5, 46
— кручения И
— однородная 8, 16, 42
— сдвига 10, 43
325

Диполь 128
— акустический 272
Дисперсия волн 29, 30, 67, 293
акустических нормальных 266
Альвена 286
внутренних 203, 213, 2 И, 232
гравитационно-акустических 277
гравитационно-гироскопических
243
гравитационно-капиллярных 200
гравитационных поверхностных
193
инерционных 226, 229, 231, 242
капиллярных 199
магнитоакустических 288
нелинейная 304, 310
Россби 236, 239
Длина волны 21, 56
— пути акустическая 261
Дорожка Кармана вихревая 167
Дрейф электрический 282
Жесткость крутильная 12
— пластинки 81
Жидкость 86
—баротропная 91, 93
— идеальная 86
— несжимаемая 92, 192
Закон Гука 6, 7
дифференциальный 8
обобщенный 45, 48
— Колмогорова «2/3» 182
— Обухова «5/3» 182
— Ома 280
— подобия Рейнольдса 163
— преломления 256
— Снеллиуса 262
— сохранения импульса 101
массы 89
энергии 98, 99
Звук магнитный 288
Значение собственное 73, 207, 211
Зона волновая 269
— неволновая 269
Излучение звука 254
— плоских волн 250
Импеданс 33, 257
— входной 257
жидкого слоя 273
упругого полупространства 276
— нормальный 257
— сферической волны 271
Интеграл Коши — Лагранжа 114
Интенсивность вихревой трубки 107
Интервал инерционный 176
Источник вихревой 120
Колебание инерционное 234
— собственное 24, 29, 216
Коэффициент взаимодействия волн
302
— вязкости 136
кинематической 136
турбулентной 171
— давления 123, 129
— диффузии магнитного поля 281
— затухания 293
— истечения струи 103, 133
— отражения волны 22, 58, 61,254,
265
— прохождения (прозрачности) 23,
256, 265
— Пуассона 6
— сопротивления 141, 167
— трансформации волны 61
— электропроводности 280
Кризис сопротивления 167
Линия вихревая 106
— тока 95
Луч 261
Масса присоединенная 129, 134, 271,
272
Масштаб турбулентности внешний
176
внутренний 176
Метод медленно меняющихся
амплитуд 301
— мнимых источников 278
— разделения переменных 237
Мода внутренняя 207, 213, 231, 233
— звуковая 266
— инерционная 231, 233
— поверхностная 207, 211, 231, 233
Модуль всестороннего сжатия 9, 48
— сдвига 11, 49
326

— Юнга 6, 48
Момент диполя 128, 272
Монополь 268
Напряжение б
— сдвига 10, 12
— Рейиольдса 171
Насадок Борда 103
Натяжение магнитное 284
Неустойчивость гидродинамическая
160
— распадная 303
Область односвязная 104
— течения 121
Оператор Лапласа 115, 142
Описание движения лагранжево 87
—г — эйлерово 87
Ось диполя 272
Отражение полное 63, 258
Парадокс Даламбера — Эйлера 124
Параметр Кориолиса 225, 230
— нелинейности 292
Период волны 21, 56
Плазма 279
Плоскость падения волны 57
Поверхность свободная 190, 191, 255
Подобие гидродинамическое 124
Подслой вязкий 172
Поле магнитное вмороженное 281
Постоянные Ламе 48
— упругие 5
Потенциал векторный 53
— диполя 128
— комплексный 119
— скалярный 53
— скорости 114
Преобразование конформное 120
Жуковского 122
Приближение Буссинеска 203
— р-плоскости 235
— геометрической акустики 261
— гидростатическое 214, 239
— «твердой крышки» 207, 212
— «традиционное» 229, 235
Принцип суперпозиции 8, 291
Проводимость среды волновая 249
электрическая 280
идеальная 281
Производная локальная 88
— материальная полная 88
Производительность источника 120
Пространство фазовое 161
Прохождение полное 258, 274
Процесс статистический 168
однородный 170
стационарный 170
эргодический 169
Расстройка 294
Сечение нейтральное 14
Сила Архимеда 94
— вязкая 140
— Кориолиса 92, 224
— магнитная 279
— перерезывающая 15
— подъемная 126
— потенциальная 92
— сопротивления лобового 124
— тяжести 92
— центробежная 92
— Эйлера 18
Скин-эффект 281
Скорость альвеновская 285
— групповая 32, 73, 79, 204, 224, 244
волн Альвена 286
внутренних 204, 232, 243
звуковых (мода) 266
инерционных 226, 232, 242
поверхностных
гравитационных 194, 196, 200
капиллярных 199, 20(Т
Россби 236
— дрейфовая 282
— звука 91, 248
— истечения 97
— комплексная 121
— объемная излучателя 269, 270
— распространения волн 21, 26, 55
—солитона 298
— средняя статистическая 169
— трения (динамическая) 173
— фазовая 32, 73, 79, 193, 199,251,
266
— частиц жидкости 86, 195, 248, 251
След волны 250
Слой пограничный 147, 149
логарифмический 173
327

турбулентный 172
Солитон 298, 299
Соотношение дисперсионное 30, 73,
82, 193, 196, 199, 203, 207
Сопротивление среды волновое 249
Тело изотропное 6, 47
— упругое 5
Тензор деформаций 42
— корреляционный 174
— модулей упругости 45
— напряжений 40
вязких 138
— плотности потока импульса 101
— спектральный 179
— структурный 177
Теорема Бернулли 96
— Гельмгольца 106, 107
— о сохранении циркуляции 105
— Эйлера 102
Теория размерностей 164
Термоклин 202, 208
Течение безвихревое 96
— вихревое 104
— Гартмана 282, 290
— Куэтта 136, 140
— ламинарное 158
— плоское 115
— потенциальное 104, 114
— Пуазейля 141, 142
— сопряженное 118
— стационарное 95
— турбулентное 158
Точка узловая 24, 25
Траектории фазовые 161, 298
— частиц 196, 245
Трубка Вентури 96
— вихревая 106, 107
— лучевая 261
— тока 97, 98
Турбулентность 158
— развитая 159
— локально-изотропная 175, 177 #
Угол отражения 59, 205, 256
— падения 59, 205, 256
— прохождения 256
— скольжения 262
Уравнение Бюргерса 293
— внутренних волн 202, 203
— волновое 21, 54, 248
неоднородное 270
— волн России 235, 237
— Гельмгольца 249, 260
— гидростатики 92, 93
— гравитационно-гироскопическиж
волн 230
— движения 44, 49, 90
— диффузии магнитного поля 281
— инерционных волн 225
— Кортевега-де-Вриза 293, 297
— Лапласа 115, 116, 285
— луча 261
— Навье — Стокса 139
— неразрывности 89
обобщенное 270
— равновесия 44, 49
— С. Жермен 81
— состояния 91
— эйконала 261
— Эйлера 90
Уравнения акустики движущихся
сред 264
— акустические 248
— гидродинамики линеаризованные
189, 190
— магнитоакустических волн 286, 287
— Максвелла 280
— нелинейные 293
укороченные 302
— пограничного слоя 151
Условия граничные 22, 28, 56, 92
в вязкой жидкости 136, 142, 144„
149
динамические 191
кинематические 191
— Коши — Римана 118
— ортогональности собственных
функций 222
— синхронизма 294, 300
Фаза волны 21, 260
Флюктуации скорости 169
Формула барометрическая 93
— Лапласа 191
— Пуазейля 143
—Стокса 146
Формулы Френеля 24, 256
Фронт волновой 56, 261
ударный 294
328

Функция аналитическая 118
— корреляции 170
— собственная 207
— тока 115
Характеристика направленности 271
диполя 272
Циркуляция скорости 104
в вязкой жидкости 155
— вокруг цилиндра 125
Частота волны 21, 56, 203
— Вяйсяля 94, 202
— звука минимальная 277
— критическая 74, 266
— собственная 73, 216
Число Альвена 289
— волновое 21, 56
— Гартмана 283, 289
— Маха 165, 264
— Прандтля 165
— Рейнольдса 141, 143, 150, 165, 289
критическое 159
магнитное 282, 289
— Струхаля 165
—-Стюарта 289
— Фруда 165
Энергия внутренняя 46, 98
— волны 197, 199, 208, 252
кинетическая 197, 219
потенциальная 198, 220
— деформации 46
— диссипации 176
— излучения монополя 270
диполя 278
—кинетическая 98
—, плотность спектральная 180
— потенциальная 98
— свободная 46
— стержня деформированного 19
Энтальпия 95
Энтропия 46, 86, 91
Якобиан преобразования 87

ОГЛАВЛЕНИЕ
Предисловие
Часть первая
ТЕОРИЯ УПРУГОСТИ
Глава 1. Основные виды деформаций упругих тел в
§ 1. Законы линейной теории упругости в
1.1. Закон Гука б
1.2. Дифференциальная форма закона Гука. Принцип
суперпозиции 8
§ 2. Однородные деформации ~
2.1. Тело под действием гидростатического давления
2.2. Продольная деформация при запрещенных боковых смеще
ниях
2.3. Деформация чистого сдвига
§ 3. Неоднородные деформации *2
3.1. Кручение стержня *2
3.2. Изгиб балки *3
3.3. Форма нагруженной балки. Перерезывающая сила ^
Задачи *6
Глава 2. Волны в стержнях, вибрации стержней 20
§ 4. Продольные волны в стержне
4.1. Волновое уравнение
4.2. Гармонические волны
8
9
10
20
20
21
- 24
§ 5. Отражение продольных волн лх
5.1. Граничные условия 2*
5.2. Законы отражения волн 22
§ 6. Продольные колебания стержней . **
§ 7. Волны кручения в стержне. Крутильные колебания *5
§ 8. Волны изгиба в стержнях ^"
8.1. Уравнение для изгибных волн 2"
8.2. Граничные условия. Гармонические волны 2°
8.3. Отражение волн. Изгибные колебания 2^
§ 9. Дисперсия волн и групповая скорость 30
9.1. Распространение негармонических волн 30
9.2. Распространение узкополосных возмущений 31
Задачи . 33
Глава 3. Общая теория напряжений и деформаций 38
§ 10. Описание состояния деформированного тела 38
10.1. Тензор напряжений 38
10.2. Тензор деформаций . 41
10.3. Физический смысл компонент тензора деформаций 42
§ 11. Уравнения равновесия и движения сплошной среды 43
330

ГИДРОДИНАМИКА
11.1. Вывод уравнения движения ^3
11.2. Тензор модулей упругости *4
§ 12. Энергия деформированного тела 4S
12.1. Плотность энергии 45
12.2. Число независимых компонент тензора модулей упругости 47 ^
§ 13. Упругое поведение изотропных тел |7
13.1. Обобщенный закон Гука для изотропного тела
13.2. Связь постоянных Ламе с Е и v . *8
13.3. Уравнения движения для изотропной среды 49
Задачи J*
Глава 4. Волны в упругих средах ^3
§ 14. Свободные волны в однородной изотропной среде 53
14.1. Продольные и поперечные волны 53
14.2. Граничные условия для упругих волн . 5&
14.3. Отражение горизонтально поляризованной волны 58
§ 15. Отражение вертикально поляризованных волн 60
15.1. Коэффициенты отражения и трансформации 60
15.2. Особые случаи отражения 61
15.3. Неоднородные волны 63
§ 16. Поверхностные волны 64
16.1. Волна Релея 64
16.2. Поверхностчые волны Лява 65
16.3. Свойства волн Лява 66
Задачи 67
Глава 5. Волны в пластинках 71
§ 17. Классификация волн 71
17.1. Дисперсионные соотношения 71
17.2. Симметричные и антисимметричные нормальные волны 73
17.3. Критические частоты волн 74
17.4. Некоторые особые случаи 75
§ 18. Нормальные волны низшего порядка 76
18.1. Квазирелеевские волны на границах пластинки 76
18.2. Юнговская и изгибная волны 77
§ 19. Уравнение изгиба тонкой пластинки 79
19.1. Приближение тонкой пластинки 7$
19.2. Уравнение С. Жермен 80
19.3. Волны изгиба в тонкой пластинке 81
Задачи 82
Часть вторая
Глава 6. Основные законы гидродинамики идеальной жидкости 86
§ 20. Способы описания движения жидкости 86
20.1. Эйлеров и лагранжев способы задания движения жидкости 86
20.2. Переход от одного описания к другому 87
20.3. Субстанциональная и локальная производные по времени 88-
§ 21. Система уравнений гидродинамики 89-
331

21.1. Уравнение неразрывности 89
21.2. Уравнение Эйлера 90
21.3. Полнота системы уравнений 91
§ 22. Гидростатика 92
22.1. Основные уравнения . . 92
22.2. Условие гидростатического равновесия. Частота Вяйсяля 93
§ 23. Теорема Бернулли и закон сохранения энергии 95
23.1. Теорема Бернулли . 95
23.2. Некоторые применения теоремы Бернулли 96
23.3. Теорема Бернулли как следствие закона сохранения энергии 97
23.4. Закон сохранения энергии я нестационарном случае 98
§ 24. Закон сохранения импульса 100
24. Ь Тензор плотности потока импульса 100
24.2. Теорема Эйлера 101
24.3. Применение теоремы Эйлера 102
§ 25. Вихревое движение жидкости 104
25.1. Циркуляция скорости 104
25.2. Теорема о сохранении циркуляции скорости 105
25.3. Теоремы Гельмгольца о вихрях 106
Задачи 108
Потенциальное течение жидкости 114
Система уравнений гидродинамики для потенциального
движения 114
Потенциал скорости 114
Плоское течение. Функция тока 115
Применение теории аналитических функций в задачах
гидродинамики 118
Комплексный потенциал 118
Примеры двумерных течений 119
Конформные преобразования 120
Стационарное обтекание кругового цилиндра 122
Решение задачи методом конформного преобразования 122
28.2. Коэффициент давления 123
28.3. Парадокс Даламбера — Эйлера 124
28.4. Циркуляционное обтекание цилиндра 125
§ 29. Обтекание сферы потенциальным потоком 127
29.1. Потенциал и скорости частиц 127
29.2. Присоединенная масса 129
Задачи . 130
-Глава 8. Течение вязкой жидкости 13$
§ 30. Уравнения гидродинамики вязкой жидкости 136
30.1. Коэффициент вязкости и вязкие напряжения ^36
30.2. Уравнение Навье — Стокса 138
30.3. Вязкие силы 139
§ 31. Примеры течений вязкой жидкости ^q
31.1. Течение Куэтта 140'
31.2. Течение Пуазейля между двумя пластинками 141
31.3. Течение Пуазейля в круглой трубе 142
31.4. Обтекание сферы медленным течением вязкой жидкости 144
Глава
§
§
§
7.
26.
26.1.
26.2.
27.
27.1.
27.2.
27.3.
28.
28.1.
332

31.5. Формула Стокса 145
§ 32. Пограничный слой 147
32.1. Вязкие волны 14Т
32.2. Пограничный слой. Качественные соображения 148
32.3. Уравнения Прандтля пограничного слоя 150'
32.4. Решение уравнений пограничного слоя в простейшем случае 152-
Задачи .* 154
Глава 9. Элементы теории турбулентности 158
§ 33. Качественные закономерности. Гидродинамическое подобие 159
33.1. Переход ламинарного течения в турбулентное 159
33.2. Понятие о подобных потоках 162
33.3. Применение теории размерностей 164
33.4. Картина обтекания кругового цилиндра при различных
числах Рейнольдса 165
§ 34. Законы усредненного турбулентного движения 168*
34.1. Уравнения Рейнольдса для усредненного потока 168
34.2. Турбулентное трение 171
34.3. Турбулентный пограничный слой 172:
§ 35. Локально-изотропная турбулентность 174
35.1. Качественные соображения о структуре развитой
турбулентности 174
35.2. Статистические характеристики локально-изотропной
турбулентности 177*
35.3. Гипотезы подобия Колмогорова* 181
Задачи 183*
Глава 10. Поверхностные и внутренние волны в жидкости 18&
§ 36. Линейные уравнения для волн в жидкости 189
36.1. Линеаризация уравнений гидродинамики 189*
36.2. Линейные граничные условия 190
36.3. Линейные уравнения для гидродинамических волн 191
§ 37. Гравитационные поверхностные волны 192*
37.1. Основные уравнения 192"
37.2. Гармонические волны 193-
37.3. Приближения мелкой и глубокой воды 196
37.4. Энергия волн 197
§ 38. Капиллярные волны на поверхности жидкости 199*
38.1. Чисто капиллярные волны 199s
38.2. Гравитационно-капиллярные волны 200
§ 39. Внутренние гравитационные волны 201
39.1. Вводные замечания . 20Г
39.2. Основное уравнение для внутренних волн. Приближение
Буссинеска 202
39.3. Волны в безграничной среде 203-
§ 40. Внутренние волны в волноводе 206
40.1. Качественный анализ уравнения для внутренних волн 206-
40.2. Модель океанского волновода 209
40.3. Поверхностная мода. Условие «твердой крышки» 211
40.4. Внутренние моды 212
Задачи 215-
333

Слава 11. Волны во вращающейся жидкости 224
§ 41. Инерционные (гироскопические) волны . 225
41.1. Уравнение для волн в однородной вращающейся жидкости 225
41.2. Плоские гармонические инерционные волны 226
41.3. Волны в однородном жидком слое. Приложение к геофизике 228
§ 42. Гравитационно-гироскопические волны 230
42.1. Общие уравнения. Простейшая модель среды 230
42.2. Классификация волновых мод 231
42.3. Гравитационно-гироскопические волны в океане 232
§ 43. Волны Россби 234
43.1. Приближение Р-плоскости 234
43.2. Баротропные волны Россби 235
43.3. Совместный учет стратификации и Р-эффекта 236
43.4. Волны Россби в океане 238
Задачи 240
Глава 12. Звуковые волны 247
§ 44. Плоские волны в покоящейся жидкости 247
44.1. Система линейных акустических уравнений 247
44.2. Плоские волны 248
44.3. Излучение плоских волн. Неоднородные волны 250
44.4. Энергия звуковых волн 252
§ 45. Распространение звука в неоднородных средах 254
45.1. Отражение плоских волн на границе раздела сред 254
45.2. Особые случаи. Полнбе прохождение и полное отражение 257
45.3. Энергетические соображения. Вопросы взаимности 259
45.4. Плавно неоднородная среда. Приближение геометрической
акустики
45.5.'Уравнения акустики движущихся сред 263
45.6. Волноводное распространение звука 265
§ 46. Сферические волны 268
46.1. Сферически-симметричное решение волнового уравнения 268
46.2. Объемная скорость. Импеданс сферической волны 269
46.3. Акустический диполь 271
Задачи 272
Глава 13. Магнитная гидродинамика 279
§ 47. Приближение магнитной гидродинамики 279
47.1. Основные уравнения . 279
47.2. Магнитное давление. Вмороженное поле 280
47.3. Течение Пуазейля (Гартмана) 282
§ 48. Магнитогидродинамические волны 284
48.1. Волны Альвена 284
48.2. Магнитоакустические волны 286
48.3. Быстрые и медленные магнитоакустические волны 288
Задачи 289
Глава 14. Нелинейные эффекты в теории волн 291
§ 49. Нелинейные одномерные волны 292
49.1. Параметр нелинейности 292
49.2. Модельное уравнение. Генерация второй гармоники 292
49.3. Решение Римана. Ударные волны 295
260
334

49.4. Диспергирующие среды. Солитои 29/
§ 50. Резонансные взаимодействия волн 300
50.1. Условия синхронизма 300»
50.2. Метод медленно изменяющихся амплитуд 301
50.3. Многоволновые взаимодействия 30$
50.4. Нелинейная дисперсия 304*
Задачи 305-
Приложение 31 f
Библиографический комментарий 322
Предметный указатель
325

Леонид Максимович
Бреховских
Валерий Владимирович
Гончаров
ВВЕДЕНИЕ В МЕХАНИКУ
СПЛОШНЫХ СРЕД
В ПРИЛОЖЕНИИ
К ТЕОРИИ ВОЛН
Утверждено к печати '
Институтом океанологии
им. П. П. Ширшова АН СССР
Редактор
Ю. Г. Тихомирова
Художник
И. Е. Сайко
Художественный редактор
Т. П. Поленова
Технический редактор
Т. А. Прусакова
Корректоры
Н. Г. Васильева, Л. В. Лукичева
ИБ № 24025
Сдано в набор 29.03.82
Подписано к печати 23.08.82.
Т-12945. Формат 60X90Vie
Бумага типографская М° 1
Гарнитура литературная
Печать высокая
Усл. печ л. 21. Уч.-изд. л. 21,5. Усл. кр. отт. 21
Тираж 4800 экз. Тип. зак. 4099
Цена 2 р. 40 к.
Издательство «Наука»
117864 ГСП-7, Москва, В-485, Профсоюзная ул., 90
2-я типография издательства «Наука»
121099, Москва, Г-99, Шубинский пер., 10

СПИСОК ОПЕЧАТОК
Страница
156
205
232
242
277
310
312
Строка
14 св.
1 св.
ф-ла (11.22)
7 св.
15 сн.
3 сн.
4 св.
ф-ла (П.5)
Напечатано
А = -±
4л
Rz
(л2Л2 + *2#2)
12k =£0
exp(ixr) =
(fc2 + a2)
a aki + л
x,V
Должно быть
—4
К
(Л2Л2 + ^Я2)«
Qk=0
exp(ixr), х =
(А:2 + a2)2
a*i + H
XiV
Зак. 4099. Л. М. Бреховских. В. В. Гончаров