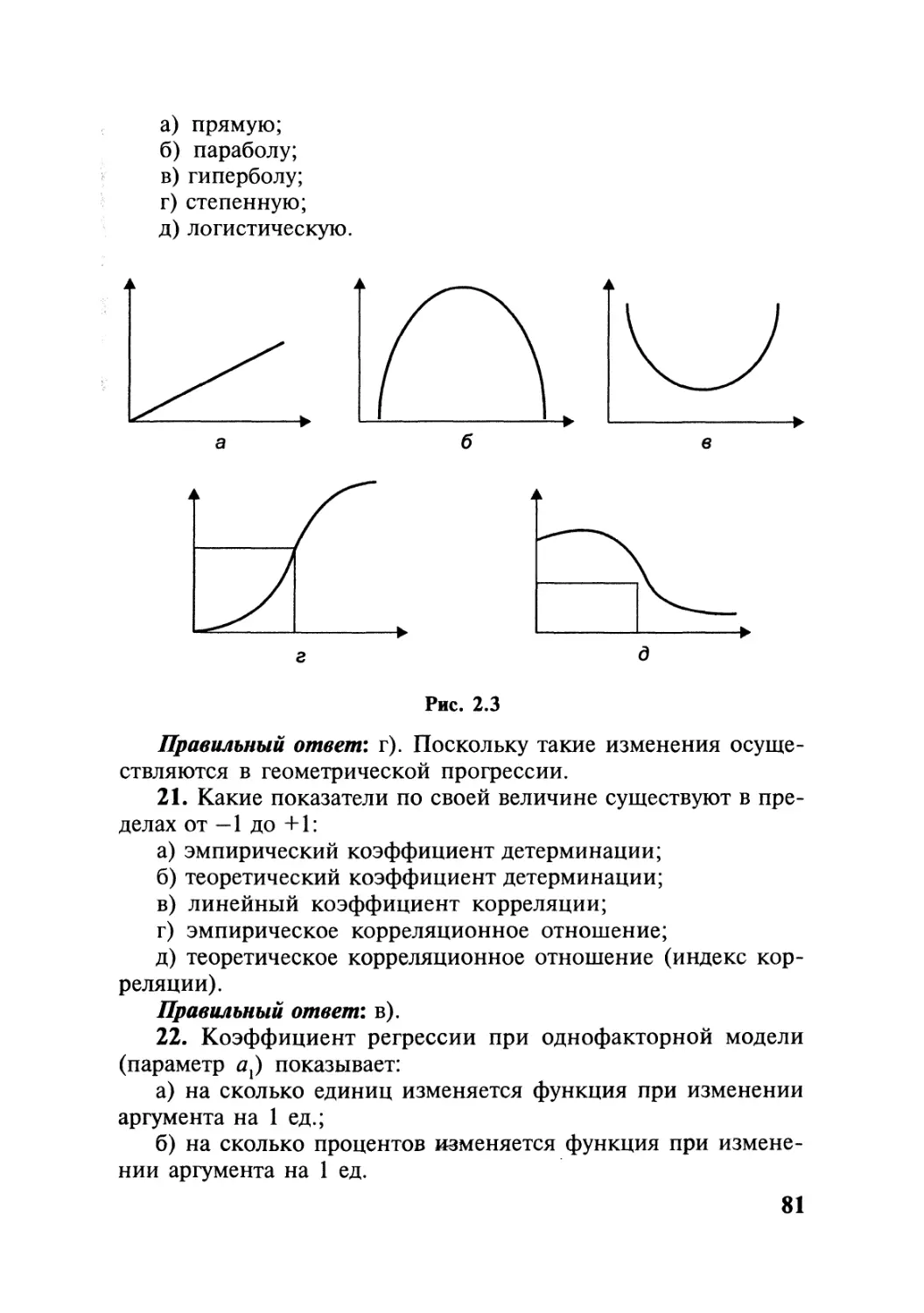
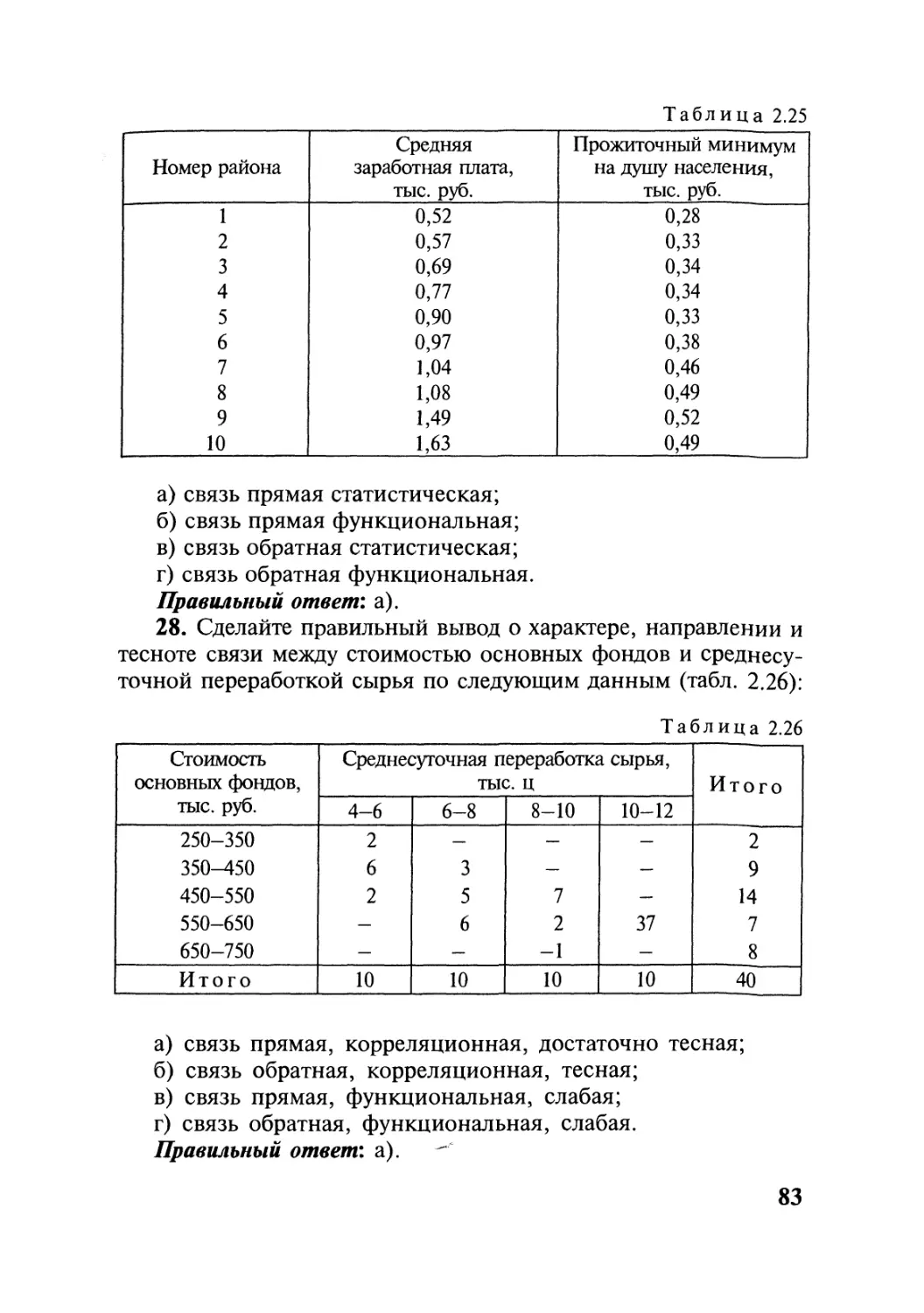
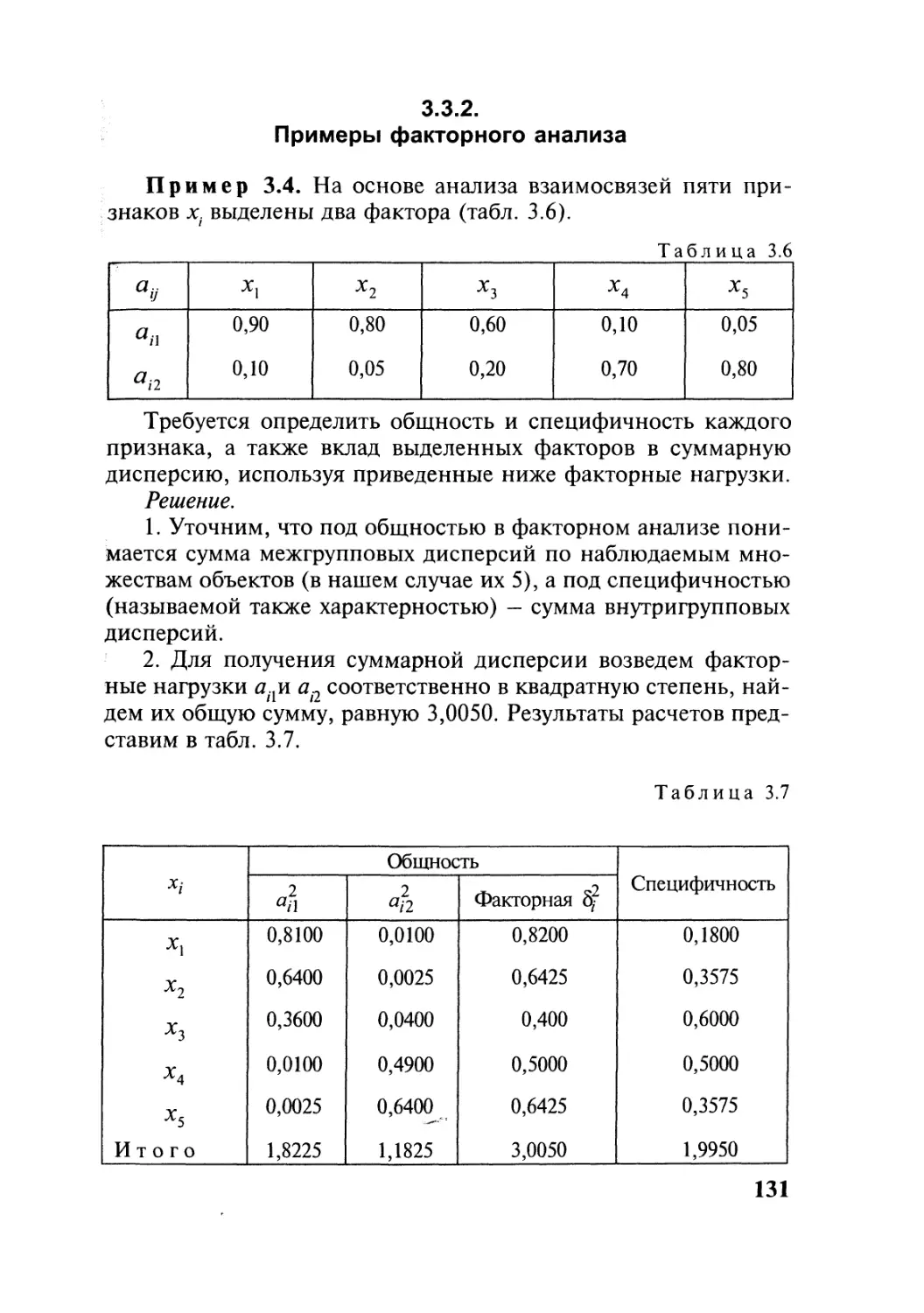
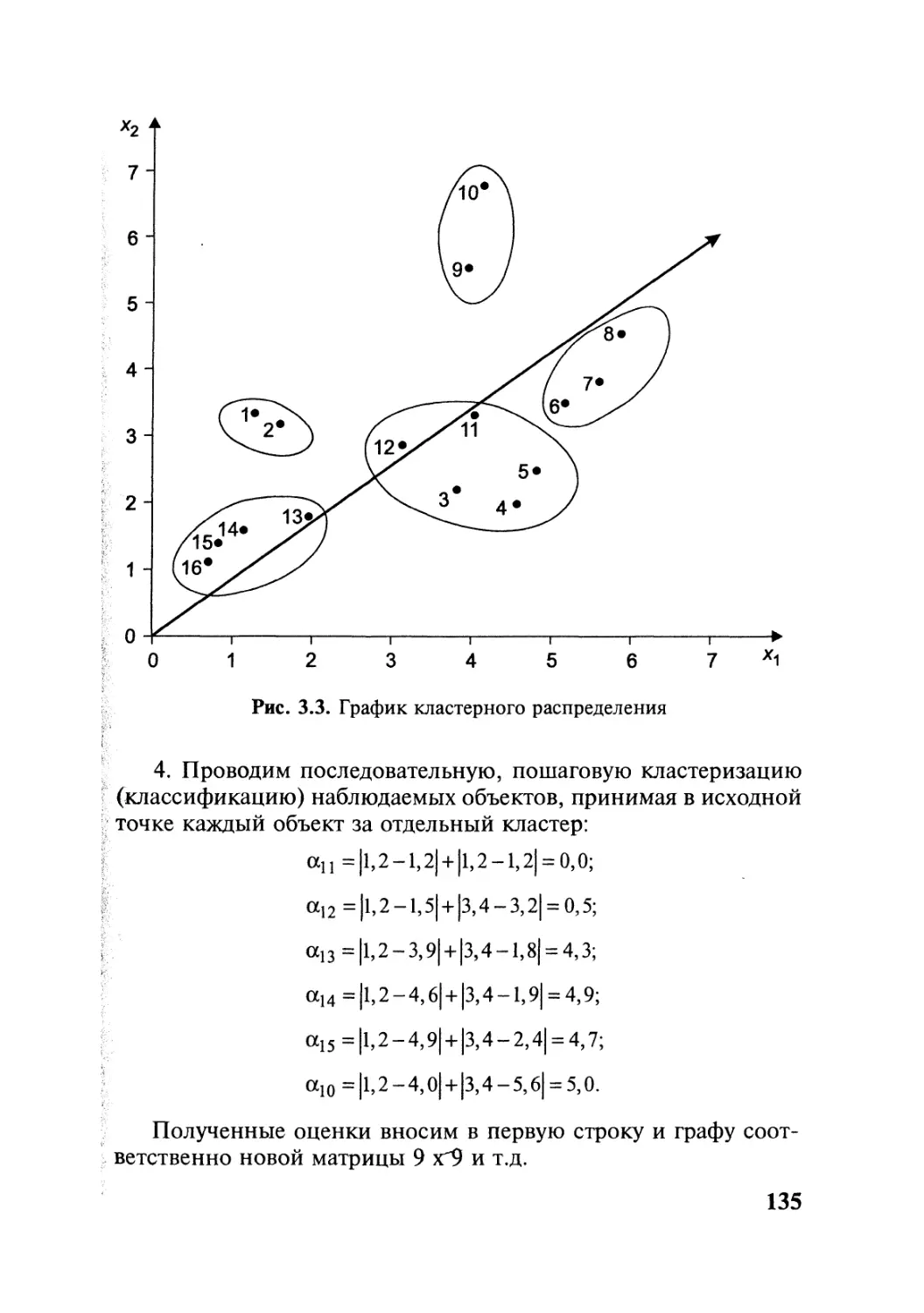
Автор: Симчера В.М.
Теги: теория вероятностей и математическая статистика теория вероятностей математическая статистика комбинаторный анализ теория графов бухгалтерский учет мировая экономика
ISBN: 978-5-279-03184-9
Год: 2008
Текст
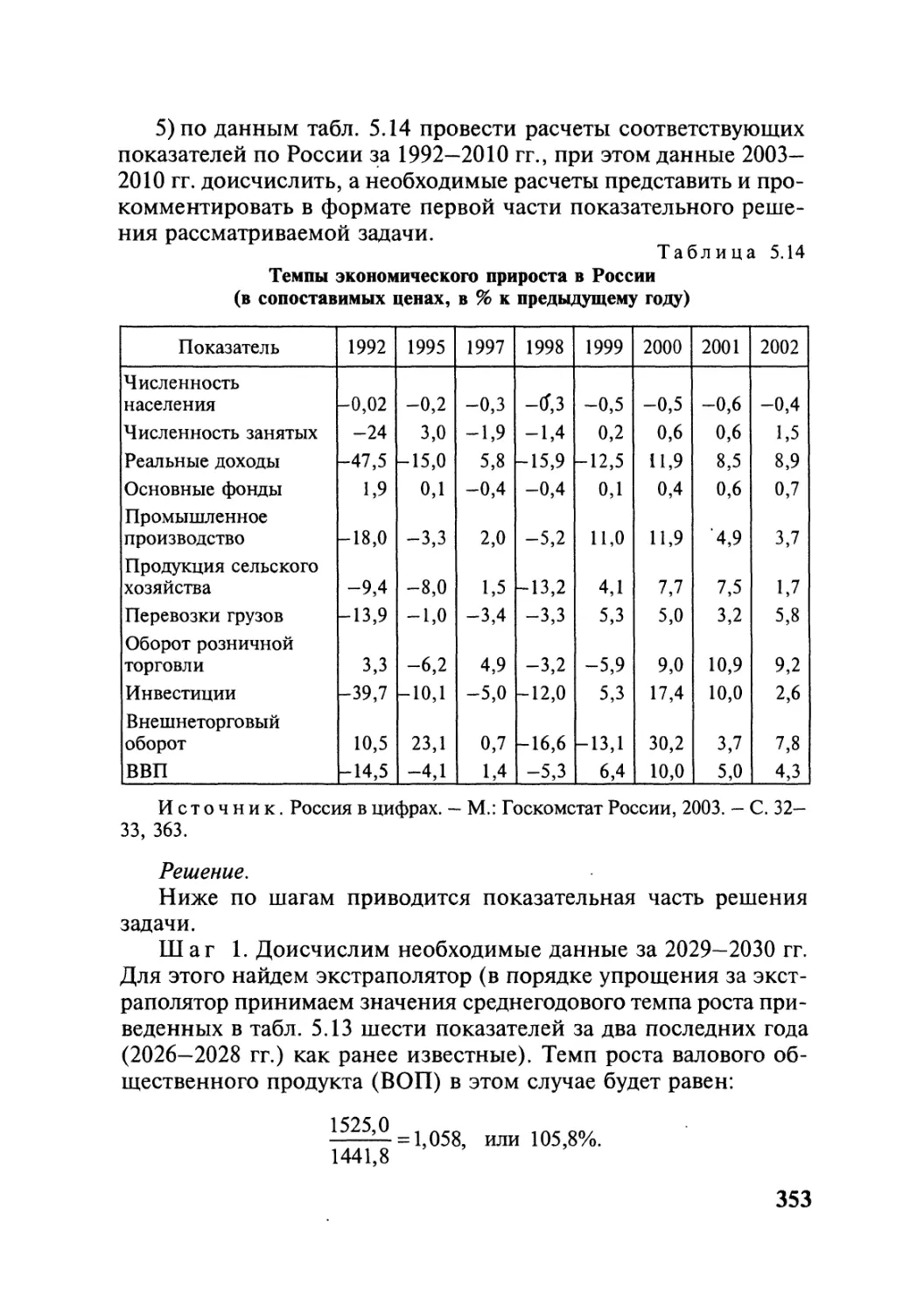
Методы В.М.Симчера
многомерного
анализа
статистических
данных
ТЕМА 1
ТЕМА 2
ТЕМА 3
ТЕМА 4
ТЕМА 5
Типология методов многомерного
анализа данных
Методы многомерного корреляционного
изучения данных
Методы многомерной обработки данных
Методы многомерного моделирования данных
Методы многомерного сопоставления данных
В.М.Симчера
Методы
многомерного
анализа
статистических
данных
Рекомендовано
Учебно-методическим объединением
по образованию в области финансов,
учета и мировой экономики
в качестве учебного пособия
для студентов, обучающихся по специальностям
“Финансы и кредит”, “Бухгалтерский учет,
анализ и аудит”, “Мировая экономика”,
“Налоги и налогообложение"
©
МОСКВА
“ФИНАНСЫ И СТАТИСТИКА”
2008
УДК 519.237(075.8)
ББК 22.172я73
С37
РЕЦЕНЗЕНТЫ:
Кафедра статистики
Финансовой академии при Правительстве РФ
(заведующий кафедрой — профессор В.Н. Салин);
Б.И. Искаков,
доктор экономических наук, профессор
На 1-й странице обложки — репродукция картины
«Демографические волны» М.А. Королева, председателя
Межгосударственного статистического комитета СНГ,
из частной коллекции ВЛ. Соколина, руководителя
Федеральной службы государственной статистики.
Публикуется с разрешения М.А. Королева и ВЛ. Соколина
Симчера В.М.
С37 Методы многомерного анализа статистических данных:
учеб, пособие. — М.: Финансы и статистика, 2008. — 400 с.: ил.
ISBN 978-5-279-03184-9
В данном пособии в отличие от аналогичных изданий процедуры при-
менения сложных методов многомерного анализа рассматриваются по ша-
гам на конкретных, а не на абстрактных примерах (их представлено в книге
более 150). Каждая из пяти тем пособия включает вводные замечания, типо-
логию решаемых задач, задачи для самостоятельных занятий, тесты и воп-
росы для самоконтроля. Примеры решения большеразмерных задач приве-
дены с применением пакетов электронной обработки данных, в частности
пакетов SAS, Statistica, Stadia, Statgraphics.
Для студентов, аспирантов и специалистов, занимающихся статисти-
ческими вычислениями повышенной сложности.
£,1602090000-125
010(01)-2008
50 - 2007
ISBN 978-5-279-03184-9
УДК 519.237(075.8)
ББК 22.172я73
© Симчера В.М., 2008
© Издательство «Финансы и статистика»,
2008
Предисловие
Методов многомерного анализа данных много, но они раз-
розненные и, как правило, несводимые в единое целое. Много-
образие этих методов обусловлено объективным многообразием
изучаемых явлений, которые данные методы призваны отобра-
жать и измерять. Ценность их определяется тем, насколько каж-
дый из них и все они адекватны изучаемым предметам, полно и
достоверно выявляют и объясняют скрытые причинно-след-
ственные связи признаков, которые не могут быть установлены
и предъявлены с помощью плоских одномерных расчетов и при-
митивных цифровых иллюстраций.
Распространенное пренебрежение этими методами, игно-
рирование их в условиях принятия сложных управленческих
решений чревато большими упущенными выгодами и потеря-
ми материальных, трудовых и финансовых ресурсов, которые
вне реализации оптимальных схем используются некомплекс-
но, а следовательно, неэффективно. Отсюда вытекает объек-
тивная необходимость изучения методов многомерного анализа
данных и, несмотря на сложные процедуры их приложения,
столь же объективная целесообразность их широкого практи-
ческого применения.
В отличие от простых одномерных методов, оперирующих
ограниченными и, как правило, однородными наборами объек-
тов наблюдения и очевидными взаимосвязями между их при-
знаками, многомерные методы имеют дело с неограниченными
и разрозненными наборами наблюдаемых объектов и неочевид-
ными и, как правило, многообразными и по преимуществу
разнонаправленными взаимосвязями между их признаками.
фундаментальное отличие состоит в том, что само множе-
ство наблюдаемых объектов и признаков, как и гипотезы и за-
кономерности распределения и изменения их значений в про-
странстве и времени, здесь неизвестны и не даны, а должны
быть найдены, выступая каждый раз не только целью определе-
ния исходных условий, но и сущностью самого исследования.
Предметом наблюдения и изучения здесь выступают как па-
раметрические, так и непараметрические (качественные поряд-
3
ковые или ранговые) связи, детерминированные и недетерми-
нированные (стохастические), массовые и робастные, реальные
и ложные, наблюдаемые и ненаблюдаемые (латентные) связи,
т.е. все виды и формы связей, недоступные для простого на-
блюдения и изучения. При этом разнородность наблюдаемых
объектов и многообразие признаков, характеризующих их,
неочевидность и разнонаправленность взаимосвязей между
ними определяются многомерной природой наблюдаемых яв-
лений, формирующих сложное матричное множество пересе-
кающихся неоднородных объектов и комплексных признаков,
выявление и изучение которых невозможны с помощью про-
стых одномерных методов. В результате возникает объективная
необходимость обращения к методам многомерного анализа дан-
ных, успех в применении которых определяется знанием при-
роды изучаемых объектов, их размерности и многообразных
форм многомерных взаимосвязей*.
* Конечно, при наличии однородных совокупностей наблюдаемых яв-
лений и однонаправленных процессов их изменения в пространстве и
времени, аппроксимируемых линейными функциями, вопрос выбора ме-
тодов анализа их связей, оценки сходимости и проверки достоверности
получаемых результатов не возникает.
Определять характер и значение факторов методами функционально-
го, дисперсионного, индексного, корреляционного или многомерного ана-
лиза при наличии линейных и однонаправленных связей — это безразлич-
но. Все эти методы обеспечивают получение относительно одинаково схо-
димых и относительно правдоподобных результатов. В этих случаях
предпочтение всегда и везде, при прочих равных условиях, отдают мето-
ду, с помощью которого искомый результат находится кратчайшим путем
и с минимальными затратами сил и средств.
Принципиальная разница появляется в случаях наличия неоднород-
ных, нелинейных и разнонаправленных данных и их связей, которых в
природе и обществе подавляющее большинство. Вот тогда приходится
обращаться к методам компонентного и факторного анализа, поскольку с
помощью всех остальных методов эти данные и связи попросту не ап-
проксимируются.
Методы одно- и многомерного факторного анализа двух показателей
и более в обиходе обычно пугают и представляют как равноценные и вза-
имозаменяемые, что не соответствует действительности.
Методы одномерного анализа, под которыми понимают методы опре-
деления общего прироста за счет отдельных факторов (в том числе и боль-
шего числа чем один-два), в частности методы функционально-стоимост-
ного (нормативного), индексного, дисперсионного и корреляционного
анализа, аппроксимируют, как правило, один-единственный тип нормаль-
4
Несмотря на актуальность и важность, многомерные мето-
ды в современной литературе (не говоря о работах прошлых
времен) представлены чрезвычайно усложненно. К сожалению,
прозрачно объединить в целое и извлечь нечто рациональное
из того, что к настоящему времени опубликовано, очень слож-
но. А студентам сегодня преподаются в качестве многомерных
методов скорее наборы некоторых усложненных счетных про-
цедур, не имеющих, как правило, ни начала, ни конца, но не
логически связанные и практически понятые и применимые
алгоритмы. Подобные материи в нормальных дидактических
средах понять нельзя, их можно только запомнить. Это объяс-
няется во многом, конечно, не отсутствием желания излагать
сложное прозрачно и просто, а сложностью и многоразмерно-
стью самого предмета анализа, объективной невозможностью
его простого представления, о чем речь шла ранее.
Нельзя объять необъятное, нельзя алгоритм, требующий
выполнения нескольких десятков и даже сотен действий, за-
менить алгоритмом из двух-трех действий. Попытка такой за-
мены — это всегда упрощенчество и, следовательно, разруше-
ние сути самого дела, а не упрощение, удача или гениальный
ход, как это иногда может показаться легковерным. И поэтому
не случайно, а скорее закономерно, что все (или почти все)
современные, и тем более старые, традиционные учебные по-
собия по статистике оперируют, как правило, одномерными
методами сбора, обработки и анализа данных, упрощая мно-
гомерные как чрезвычайно сложные, которые в рамках учеб-
ных пособий физически просто невозможно представить.
Иллюстрировать с помощью таких приемов что-то, конеч-
но, можно и нужно, доказать и объяснить практически ничего
нельзя. Столетиями, начиная с Я.Бернулли (1654—1705), про-
бовали, ничего не вышло. Не выйдет и впредь, когда доказы-
вать и объяснять приходится куда более сложные виртуальные
ных^распределений и строятся в предположении существования и вос-
производства линейных связей, тогда как методы многомерного фактор-
ного анализа аппроксимируют много различных типов распределения и
строятся в предположении существования и моделирования нелинейных
связей. Количество сопрягаемых факторов при этом не имеет значения; и
в том и в другом случае их может быть сколь угодно много.
В зарубежной литературе методы факторного анализа называются и
представляются как собственно методы факторного анализа (Factors Analysis),
а методы одномерного анализа — как One Way или Two Way Analysis.
5
вещи и нейронные связи, о существовании которых прежде
понятия не имели.
Почему? Объяснение простое. При изучении и применении
одномерных статистических методов ограничиваются обычно за-
ранее известными, как правило, упрощенными предпосылками,
допущениями и гипотезами, не требующими предварительных
доказательств и проверок. Здесь повсеместно доминируют здра-
вый смысл и принцип правдоподобия, ходячие истины типа «все
сущее — разумно, все разумное — суще», «все очевидное — верно,
все верное — очевидно», а все неочевидное — неверно, и оно,
конечно же, только от болезненного воображения или дьявола.
Словом, дело обычно представлялось (представляется и те-
перь) так, что основу основ, фундамент статистики как науки
составляют эмпирические наблюдения за окружающим нас ми-
ром, упрощенные детерминированные законы его познания, не
требующие доказательств индуктивные обобщения, а все осталь-
ное (стохастические процессы, индетерминизм, случайность,
вероятность, риски, методы проверки статистических гипотез,
ненаблюдаемые факты и т.д.) — это упражнения досужего ума.
В связи с этим в прошлом почти все ограничивалось имита-
цией и во многом воображаемыми оценками. Не отвечая свое-
му призванию и назначению, статистика была вынуждена адап-
тировать факты, представлять их в ожидаемом виде, а не как
соответствующие духу и букве праведной жизни. И так обстоя-
ло дело (продолжает обстоять и теперь) отнюдь не в одной Рос-
сии. Так оно в принципе обстоит и в других странах, включая
страны так называемой развитой демократии и экономики, от-
куда, в сущности, как раз и происходит практика формального
представления и субъективной интерпретации данных.
Причина заключается в том, что изучением неочевидных
событий и процессов, законами распределения скрытых, латент-
ных и, как правило, ненаблюдаемых явлений, сложными ги-
потезами и законами, скажем, многомерного, робастного или
биноминального распределений, распределениями Пуассона,
Байеса, Вальраса, Парето, Коши, Вейбула и т.д., изучением
случайности как сложной закономерности, словом, изучением
реального мира традиционная статистика мало интересовалась
и ограниченно не занималась. Не особо занимается она этим
по тем же соображениям сложности предмета сколько-нибудь
значимо и теперь.
6
В результате за рамками традиционных методов оставались (и
остаются) все (или почти все) приемы и процедуры статистиче-
ского эксперимента, эконометрики, актуарных вычислений, элек-
тронной обработки данных, прикладной статистики, важней-
шие гипотезы статистических распределений, критерии и при-
емы их проверки, независимые, нелинейные и непараметрические
связи и т.д. Отсюда общая ограниченность традиционной стати-
стики, убывающий коэффициент ее полезного действия, недо-
вольство ею и игнорирование ее фундаментальных ценностей.
Между тем окружающий нас мир — это мир сложных, много-
мерных и противоречивых процессов, фактов и событий, адекват-
ное познание и одномерное объяснение которого невозможно (и
никогда не было и не будет возможно) с помощью простых при-
емов, на уровне здравого смысла, эмпирически, одним лишь мето-
дом проб и ошибок. Преодолевать ограниченность современной
традиционной статистики вне апелляции и практического приме-
нения методов многомерного анализа данных далее невозможно.
Конечно, концептуальное понимание отличий многомерных
от одномерных методов сбора, обработки, анализа, моделирова-
ния и сопоставления данных необходимо, но недостаточно в
учебном процессе. Здесь дополнительно требуются знания про-
фессиональных различий, без которых осмысленно решать и
предметно объяснять решение прикладных задач проблема-
тично. В чем состоят эти отличия?
При применении одномерных методов наблюдаемые объекты
(их множество может быть сколь угодно большим; минималь-
ное множество, соответствующее требованиям малой выборки,
во всех случаях должно составлять 30 ед.; в более продвинутых
случаях — 100 ед.) характеризуются одним-единственным на-
блюдаемым признаком (например, наблюдаемые предприятия —
численностью занятых), при двумерном пространстве — соот-
ветственно двумя признаками (например, численностью заня-
тых и производительностью труда), а при применении много-
мерных методов и, следовательно, при работе в многомерных
пространствах — тремя признаками и более (например, чис-
ленностью занятых, производительностью труда и фондово-
оруженностью, фондами, выручкой, фондоотдачей и прибы-
лью. Это пример семимерной модели анализа связей).
В изложенной нами постановке задачи одномерный стати-
стический анализ представляет частный случай многомерного,
7
его отправную точку, иллюстративный стенд. И в этом пони-
мании он всегда необходим и важен.
Целью традиционных методов является по преимуществу
декларация фактов, иллюстрация конкретных случаев, фотогра-
фическая характеристика наблюдаемых объектов и их призна-
ков, а не их представление как носителей и образцов, модели-
рующих и объясняющих законы поведения целых явлений. И в
этом случае методы одномерного анализа имеют право на суще-
ствование, но только на существование в отнюдь не универ-
сальном масштабе и значении. Цель многомерных методов -
выявление именно этих законов путем установления характера
распределения и тесноты связей между многими (обычно тремя
и больше) не только очевидными, но и скрытыми признаками,
позволяющими полно и детально изучать и объяснять наблюда-
емые процессы, что в принципе невозможно сделать, оперируя
традиционными одномерными методами.
Еще более фундаментальное отличие касается теоретиче-
ских допущений и гипотез, аппроксимирующих признаки и
связи ненаблюдаемых явлений.
Практически все задачи одномерного анализа ставятся и ре-
шаются в предположении того, что в природе существует так на-
зываемый гауссовский закон распределения данных. Под этот
закон подгоняются или подстраиваются многие многомерные
статистические данные и связи. То же самое происходит, когда
речь идет о решении некоторого класса специфических много-
мерных задач, эмпирическое распределение данных в которых
сходится или хорошо согласуется с гауссовским распределением.
Других типов распределений (нелинейных, непараметрических,
робастных, нейронных и т.д.) эмпирическая статистика не знает
или почти не знает. Какой выход в этом случае? Законы одних
распределений подменяются другими, вводится сущая чехарда или,
что еще хуже, вопрос о гипотезе попросту игнорируется.
Конечно, это крайний случай. Специалисты, разумеется,
обычно обращаются к так называемым комбинаторным мето-
дам или искусственно подгоняют наблюдаемые данные, отсекая
те массивы данных, которые не укладываются в их схемы, ква-
лифицируя такого рода данные как ненормальные, случайные
или вырожденные. Это иногда дает неплохие результаты, но в
большинстве случаев находится далеко от конструктивного ре-
шения. Комбинаторика, как и подмена так называемых ненор-
мальных распределений и нелинейных связей нормальными
8
распределениями и линейными связями, в сущности, не дает
ничего: многомерный анализ остается лишенным ясных теоре-
тических оснований, а получаемые результаты — необходимого
содержательного смысла*.
* Допустим, наблюдаемые семь факторных признаков-показателей,
детерминирующих один результативный, например рост ВВП, соответствуют
семи типам разных распределений. Предположим, эмпирические данные
о численности занятых соответствуют теоретическим значениям нормаль-
ного распределения Гаусса, производительность труда — биноминально-
го, фонды — распределения Парето, фондовооруженность — распределе-
ния Вальраса, фондоотдача — показательного распределения, издержки —
распределения Пуассона, прибыль - распределения Байеса, а распределе-
ние ВВП на разных отрезках пространства и времени робастно, асиммет-
рично и разнонаправленно.
Как в этом случае установить общий закон их распределения и, следо-
вательно, общую их связь с законом распределения ВВП? Можно ли вы-
вести закон распределения ВВП как гибрид из семи других представлен-
ных типов распределений, которым следуют приведенные факторы ВВП?
Без доказательств очевидно, что нельзя, любая попытка синтеза данных
разнотипных распределений будет примитивной фикцией.
Можно ли построить на основе частично робастных, асимметричес-
ких, разнонаправленно меняющихся и по большей части хаотических дан-
ных тренд, аппроксимирующий какой-либо из известных или конструиру-
ющий какой-либо новый, неизвестный тип распределений? В принципе
можно, но проблематично. С аналогичной задачей сталкиваются практи-
чески всегда, аппроксимируя эмпирические данные по любому наблюдае-
мому показателю, но всего лишь в единичных случаях, при наличии
предельных массивов данных, когда, опираясь на закон больших чисел,
удается констатировать приемлемую сходимость эмпирических данных
с теоретическими их значениями. В подавляющем большинстве статисти-
ческих экспериментов сходимость обычно плохая или вовсе отсутствует,
что указывает на неудачную аппроксимацию данных с помощью избран-
ного типа распределений и требует либо увеличения круга наблюдаемых
данных, либо поиска нового типа и, следовательно, проведения повтор-
ного эксперимента. Именно путем такой, подчас многократной итерации
нахождение тренда в сложных случаях становится возможным.
В таких ситуациях, располагая общим трендом и опираясь на метод
дедукции, можно шаг за шагом решать задачу нахождения частных трен-
дов (УТутем построения евклидовых пространств и определения минималь-
ных парных расстояний между наблюдаемыми частными и общим трен-
дами). Впрочем, при подобных допущениях методом индукции также ре-
шается задача нахождения неизвестного общего тренда на основе известных
частных трендов.
Конечно, в данном случае речь идет всего лишь об идее решения
задачи, но идее конструктивной, заслуживающей экспериментальной про-
верки, идее, которая открывает перспективы построения единой теории
многомерных распределений.
9
Понятно, что при наличии разных типов распределений и
задач апеллировать к одним и тем же процедурам их иденти-
фикации и решения в принципе невозможно. На встречаю-
щиеся имитации здесь вообще не следует обращать внимание.
Как действовать? Разбивать сложные многомерные простран-
ства на части, вводить их типы, соответствующие типам суще-
ствующих теоретических допущений и распределений, т.е. ре-
шать задачу отдельно по каждому признаку или однородной
группе признаков, применяя разные методы. Словом, класси-
ческие многомерные данные и задачи модифицировать и пере-
водить в форму специфических данных и задач, соответствую-
щих известным и доступным методам их обработки и решения.
В сущности, это означает переход от методов многомерного
решения соответствующих классов задач к методам одномерно-
го. Понятно, что, если подобные задачи существуют в природе,
их разбиение может быть признано приемлемым и полезным,
если нет — каждый раз оно будет профанацией и пустой тратой
времени. Нельзя ведь, к примеру, матрицу 1000 х 1000 позиций
разбить на пять или десять меньших и при этом найти полно-
ценное решение искомых задач, в частности коэффициенты
полных затрат или объективно обусловленные издержки и цены.
Именно поэтому, к сожалению, приходится признавать факт
существования огромной массы нерешаемых статистических
задач и апеллировать к поиску новых теорий и статистической
идентификации новых информационных пространств.
По той же причине приходится накладывать своего рода
ограничение на существующее множество методов многомер-
ного анализа данных и в обиходе обращаться только к тем из
них, которые адекватно аппроксимируют известные законы и
гипотезы распределения данных и нашли широкое примене-
ние в статистической работе.
Среди этих методов, кроме методов корреляционного изу-
чения связей, особое значение имеют методы компонентного,
факторного, дискриминантного и кластерного анализа, моде-
лирования и сопоставления данных, которые представляют
предмет настоящего учебного пособия.
К решению задач именно этого рода с помощью представ-
ленных в пособии методов как раз и призывает автор настоя-
щей работы. И не только призывает, но и методично, шаг за
шагом показывает, как это следует делать, что заслуживает одоб-
рения и, на мой взгляд, может вызвать неподдельный интерес и
принести пользу как студентам, так и многим исследователям, а
также всем тем, кто занимается применением и развитием фун-
даментальных методов современной прикладной статистики.
Академик Н.П. Федоренко
ТЕМА 1
Типология методов многомерного
анализа данных
и.
Вводные замечания
Условием успеха любого исследования является сходимость
теоретических допущений наблюдаемым фактам, и наоборот.
И неважно, идет ли речь об индуктивном или дедуктивном
исследовании, детерминированных или индетерминированных
фактах и их причинно-следственных связях, — условие каж-
дый раз остается неизмененным.
Сходимость теории и фактов, их адекватность или неадек-
ватность устанавливаются путем идентификации теоретиче-
ских и эмпирических распределений, существующих в приро-
де и известных науке.
Сходимость на уровне необходимых и достаточных условий,
а не абстрактных идеалов проверяется по известным критериям
статистического согласия (или в случае их отсутствия) — по кри-
териям правдоподобия и здравого смысла. Именно так, как много
столетий назад, измышления и теории проверяются фактами и
практикой, а факты и практика — теорией и измышлениями.
Ничего другого человек за это время не смог или не успел при-
думать.
И там, где теория подтверждается фактами, а факты — тео-
рией, возможен и проводится статистический эксперимент, спо-
собный дать (и обычно дающий) весомые результаты, имеющие
ясный смысл и первостепенное научное и практическое значе-
ние^ а там, где не подтверждается, подобный эксперимент не-
возможен, его инициирование бессмысленно, а результаты
фальшивые.
Приходится не без сожаления констатировать, что первый
случай (и скорее не столько в общественных, сколько в есте-
ственных науках) по разным причинам, а главное, по причине
лимита самих знаний и ресурсов их реализации, ограничен и
11
конечен, и каждый удачный эксперимент воспринимается как
настоящее везение, тогда как второй случай ввиду попрания
закона предельных знаний — неограничен и бесконечен. Отсю-
да доминирование легковесных и по большей части притвор-
ных исследований, лишенных смысла и значимых результа-
тов, и как следствие — обесценение коэффициента полезного
действия самой науки и знаний в целом, их игнорирование.
Исправление общего положения дел требует не столько изме-
нения существующего ныне неудовлетворительного так называе-
мого рыночного, а в сущности откровенно пренебрежительного
отношения к фундаментальным исследованиям и трудоемким
экспериментальным их результатам, сколько повышения сис-
темного уровня продуцирования самих знаний и их приложе-
ния по точному формату идентифицируемых процессов и собы-
тий окружающего нас мира, их, так сказать, эндогенной вос-
требованности. Именно в этом здесь суть стагнирующего
научного эксперимента и науки в целом. Не критика внешних
обстоятельств, а очищение самой науки, переосмысление ос-
нов статистического эксперимента — вот с чего следует начи-
нать и что может и должно помочь современной науке.
Это означает, что не явления и события окружающего нас
мира, их состав, динамика и структура должны приспосабли-
ваться к формату научного эксперимента, а, напротив, сам
формат статистического эксперимента, весь, так сказать,
мировоззренческий потенциал должны непрерывно видоиз-
меняться и адаптироваться к окружающему нас миру, улав-
ливая тенденции его быстротекущего и противоречивого из-
менения.
Понимая именно так существующее положение дел, начи-
нать надо с теоретических гипотез современного научного экс-
перимента, фундамент которых составляют многомерные стати-
стические распределения, аппроксимирующие их функции и
законы. Насколько полно и достоверно эти функции и законы
отражают структуру и динамику окружающего нас мира, насколь-
ко они пригодны и состоятельны для того, чтобы конструктив-
но влиять на происходящие события, обеспечивая каждый раз
возможность принятия более доказательных, а следовательно,
эффективных управленческих решений?
Конструктивный ответ на вопрос требует переосмысления
всего множества одномерных и многомерных распределений,
12
их инвентаризации, адаптации и идентификации примени-
тельно к задачам производства, труда и жизни, решаемым ныне.
Первым шагом на пути получения такого ответа является ти-
пология существующих (или наиболее употребительных) функ-
ций и законов распределения наблюдаемых явлений и их си-
стематизация.
Функций теоретических распределений много, но они раз-
розненные и несводимые в единое целое. Часть этих функций
(функции линейного, нормального, степенного, показательного
и других распределений) приемлемо аппроксимируют наблюда-
емые эмпирические факты, имеют ясную предметную интер-
претацию параметров и смысла получаемых на их основе ре-
зультатов и получили широкое практическое применение.
Другая, большая их часть (функции логистических распре-
делений, максимального правдоподобия и в особенности функ-
ции нелинейных и непараметрических распределений) теорети-
чески менее обоснованна, неадекватно или вовсе не отражает
существующие эмпирические распределения и требует намно-
го больше сил и средств, затрачиваемых в ходе их идентифика-
ции и применения к решению конкретных задач многомерного
анализа.
Еще одна, своего рода забалансовая часть функций много-
мерных распределений, ориентированная на хаотические, отча-
сти робастные, а отчасти непараметрические распределения, как
правило, лишена каких-либо теоретических обоснований, пло-
хо или никак не аппроксимирует эмпирические данные и тре-
бует разработки принципиально новых подходов к ее построе-
нию. Сюда относятся комбинаторные задачи синтеза функций
распределения, конструирования неизвестных гибридных
функций на основе существующих известных. Ввиду исклю-
чительной сложности и трудоемкости эти задачи здесь только
упоминаются.
Ниже излагается суть и обобщаются формы девяти видов
многомерных теоретических распределений и их функций как
наиболее распространенных и широко применяемых в совре-
менной прикладной статистике. Цель — обоснование типологии
этих распределений и функций по разрешающим их способно-
стям, определяемым по признакам и критериям соответствия
существующим эмпирическим распределениям.
13
1.2.
Методы многомерного эмпирического
и теоретического анализа данных
Линейное распределение. Линейное распределение или близкие
к нему (распределения Пирсона) аппроксимируется функцией
где х. - эмпирические значения наблюдаемых факторных признаков-
показателей;
а0, ах — параметры линейной функции;
ух — теоретические значения моделируемого результативного при-
знака-показателя.
Параметры распределения а0, ах находятся как определите-
ли системы нормальных уравнений или методом наименьших
квадратов как
wLyx-ZxLy _ _
яХх - SxZx
В качестве широко применяемых разновидностей линей-
ного распределения в статистике рассматривают распределе-
ния Джини (Р-распределение, 1911 г.), распределение Лоренца
и др.
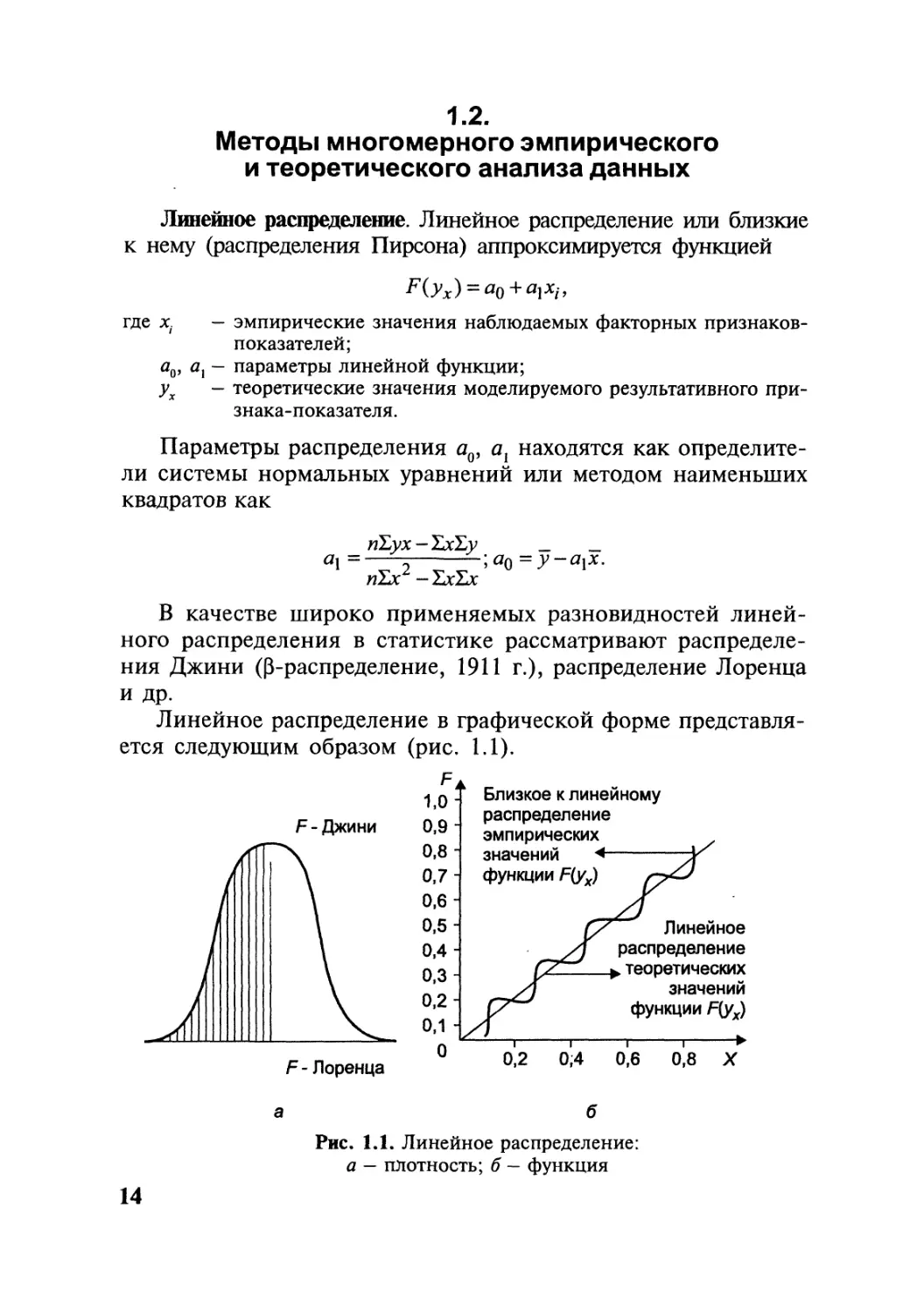
Линейное распределение в графической форме представля-
ется следующим образом (рис. 1.1).
F- Лоренца
F±
1,0
0,9-
0,8-
0,7-
0,6-
0,5-
0,4
0,3-
0,2-
0,1
0
Близкое к линейному
распределение
эмпирических
значений ◄
функции F(yx)
Линейное
распределение
> теоретических
значений
функции F(yx)
0,2 0;4 0,6 0,8 X
a б
Рис. 1.1. Линейное распределение:
а — плотность; б - функция
14
Нормальное распределение. Значения наблюдаемых показа-
телей х. имеют нормальное распределение с параметрами а и о,
если плотность их распределения задается специальными фун-
кциями типа
-(х-л)2
1 2
<pW=—7z=e 2а ;
ov2ti
_ 2 /l.dt
л/2л
где а — среднее значение распределения;
о — стандартное отклонение;
е —число Эйлера (2,71...);
я -число пи (3,141...);
t — коэффициент доверия;
dt - производная.
При этом ф(х) стремится к нулю при х —> — ©° их-» +<*>,
график функции ф(х) симметричен относительно точки а, а
функция ф(х) в точке а достигает своего максимума, который
равен 1/(л/2ло).
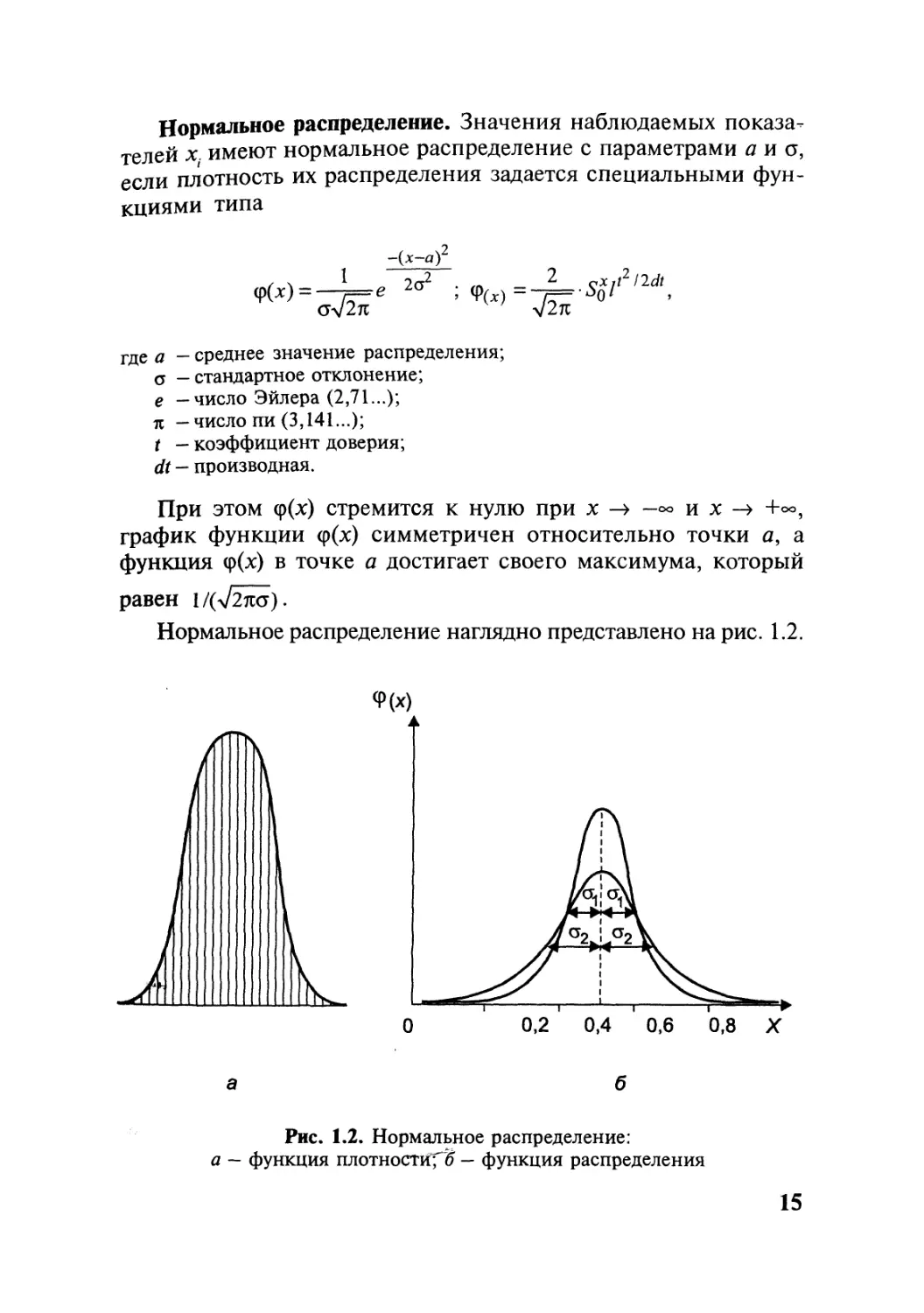
Нормальное распределение наглядно представлено на рис. 1.2.
б
Рис. 1.2. Нормальное распределение:
а — функция плотности^? — функция распределения
a
15
В статистике нормальное распределение представляют в виде
параболы первого порядка.
Разновидностью нормального распределения является рас-
пределение Лапласа, степенное или так называемое двойное
экспоненциальное распределение, представляемое в виде па-
раболы второго порядка. Оно имеет функцию плотности
= l/2b-e~^x~a^b при х ± оо5
где а — среднее значение вероятности, математическое ожидание;
b - параметр масштаба;
е — число Эйлера (2,71...).
К нормальным распределениям относятся также биноми-
нальные (бимодальные) и мультиноминальные (мультимодаль-
ные) распределения.
Классическим примером нормального распределения в ста-
тистике является возрастная пирамида распределения населе-
ния по полу.
Нормальное распределение, или распределение Гаусса, впер-
вые в статистике было введено Гальтоном (1889 г.).
Степенное распределение. Степенное распределение значе-
ний случайных величин х аппроксимируется функцией парабо-
лы второго порядка = яо*/6*1 или функцией плотности следую-
щего вида:
/(х) -1 = ^хо(2л)1 /2 ] • ехо(- [log(x) - ц]2 / 2 о2)
при 0 < х < оо; ц > 0; о > 0,
где а0 — коэффициент размерности;
— определитель функции;
р - параметр масштаба;
о — параметр (формы);
е — число Эйлера (2,71...);
л — число пи (3,141...).
Плотность и характер степенного распределения наглядно
иллюстрирует рис. 1.3.
16
Рис. 1.3. Степенное распределение:
а — функция плотности; б — функция распределения
Разновидностями степенного распределения являются лог-
нормальное, логарифмическое и другие аналогичные распре-
деления, аппроксимируемые функциями
/(х) = 1 lb• e-{x~aVb [1 + ;
У = Я [logn(x)]+Z>;ух = аоха'.
Степенное распределение впервые было введено в статис-
тический обиход Гаддумом (1945 г.).
Показательное распределение. Наблюдаемые случайные ве-
личины х имеют показательное распределение с параметром 0 > О,
если их плотность аппроксимируется функцией
F(x,0) = 0е~9х (х>-0),
где е - число Эйлера (2,71...);
О — параметр масштаба (иногда его называют параметром «отношение
риска»).
В ряде случаев вместо параметра 0 используют параметр b =
= 1/0. Тогда функция распределения представляется в виде
p(x,b) = —ex/b (х>0),
b
или
1
yx=a0 + ai-,
х
где а0 — параметр масштаба;
at — определитель функции.
17
В последних двух случаях показательные распределения на-
зывают экспоненциальными и гиперболическими.
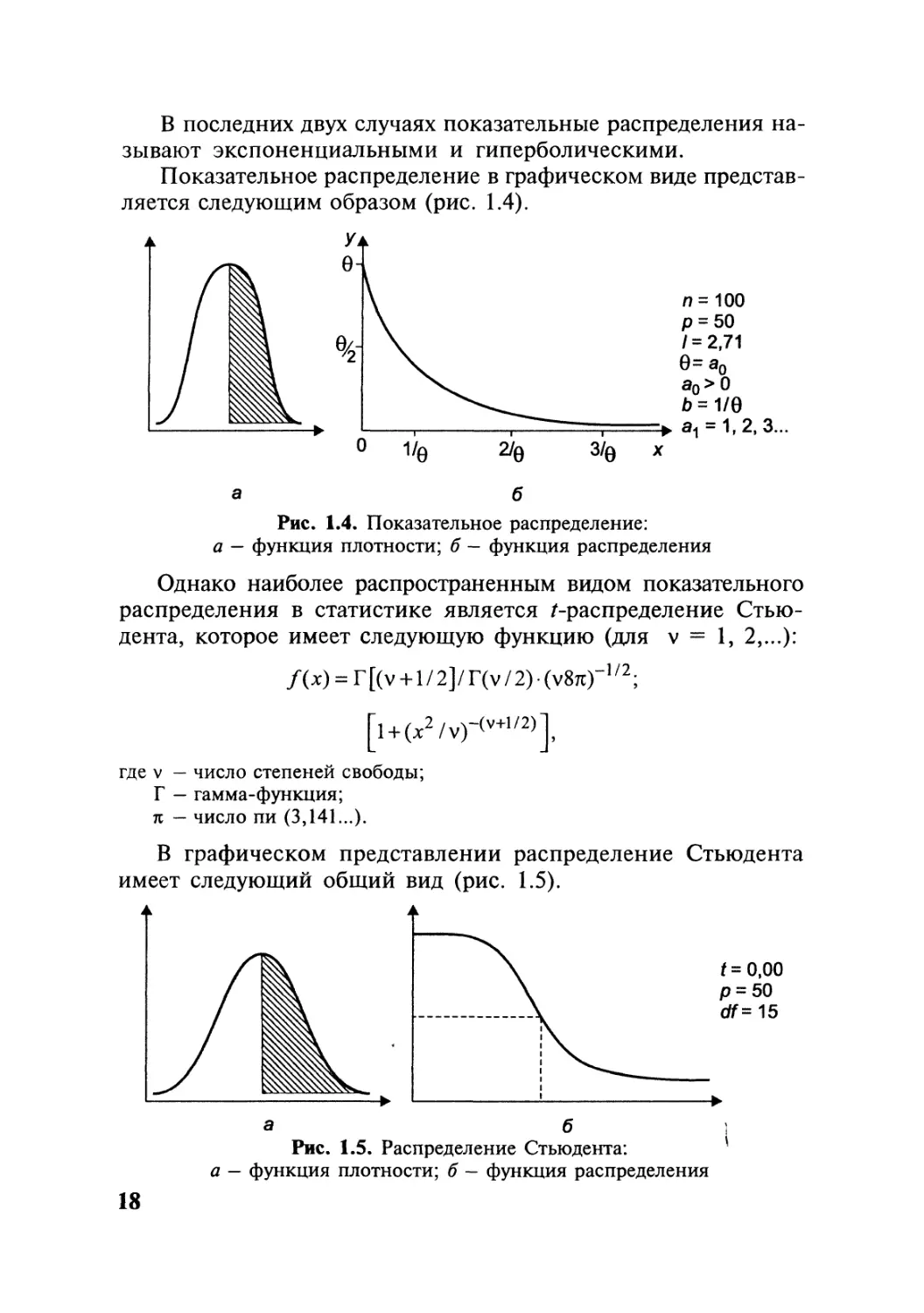
Показательное распределение в графическом виде представ-
ляется следующим образом (рис. 1.4).
п = 100
р = 50
/ = 2,71
0= а0
> 0
Ь = 1/0
а! = 1,2,3...
а б
Рис. 1.4. Показательное распределение:
а — функция плотности; б — функция распределения
Однако наиболее распространенным видом показательного
распределения в статистике является ^-распределение Стью-
дента, которое имеет следующую функцию (для v = 1, 2,...):
У(х) = Г [(v +1 / 2] / f(v / 2) • (V87t)~’/2;
[l + (x2/v)-<v+1/2)],
где v — число степеней свободы;
Г — гамма-функция;
я — число пи (3,141...).
В графическом представлении распределение Стьюдента
имеет следующий общий вид (рис. 1.5).
а — функция плотности; б — функция распределения
18
На рисунке показаны различные р-значения для распреде-
ления Стьюдента при 15 степенях свободы.
Четыре рассмотренных типа распределений имеют относи-
тельно хорошие теоретические обоснования и ясную интерпре-
тацию смысла результатов, получаемых на их основе.
Другие четыре типа распределений теоретически менее обо-
снованы и требуют намного больше сил и средств, затрачивае-
мых в ходе их идентификации и применения для решения кон-
кретных задач многомерного анализа.
Логистические распределения. Логистические распределения
представляют класс левосмещенных (асимметрических) распре-
делений, плотность значений признаков которых описывается
следующей функцией:
Ь)е~(х~а)/Ь ^\ + е~{х~а}1Ь^ 2,
где а — среднее значение распределения;
b — параметр масштаба;
е — число Эйлера (2,71...).
При параметре положения, равном нулю, и параметрах мас-
штаба 1, 2, 3 форма логического распределения имеет следую-
щий сигмоидный вид (рис. 1.6).
Рис. 1.6. Логистическое распределение:
а — функция плотности — функция распределения
19
К разновидностям логистических распределений относятся
распределения Коши и Ремея, аппроксимируемые соответствен-
но функциями
/(х) =1(0я)1+|[(х-т|/0)]2|;
при 0 < х < «J, b > О,
где ц - параметр положения (медиана);
9 — параметр масштаба;
я — число пи (3,141...);
b — параметр масштаба;
е — число Эйлера (2,71...).
С определенными оговорками сюда можно отнести также
известные распределения Лапласа и Пуассона.
Впервые в статистический обиход логистические распреде-
ления были введены Сопером (1914 г., распределения Пуассо-
на) и Успенским (1937 г., распределение Коши).
Гамма-распределения. Функция гамма-распределений значе-
ний наблюдаемых величин в наиболее общем виде представля-
ется так:
f(x}={xlbc-x е<-х/6>) [1/6Г(С)]
при 0 < х, b > 0, с > О,
где Г — гамма-функция;
b — параметр масштаба;
с — параметр формы;
е - число Эйлера (2,71...).
Функция гамма-распределения в статистике представляет-
ся также как функция максимального правдоподобия.
При изменении значений параметра формы от 1 до 6 гамма-
распределение в графическом виде представляется следующим
образом (рис. 1.7).
Наиболее старыми и широко распространенными видами
гамма-распределений являются распределения хи-квадрат,
распределение Парето и распределение Вейбулла, аппроксими-
руемые соответственно функциями:
20
Рис. 1.7. Гамма-распределение:
а - функция плотности; б — функция распределения
/(х) = {l/[2v/2r(v/2)]}[xv(2)-le^/2]
при v = 1, 2, ... О < х,
где v — число степеней свободы;
Г — гамма-функция;
е — число Эйлера (2,71...);
fM=c/xc+i
при 1 < х, с > О,
где с — параметр формы распределения;
/(х) =clb[x-blbf 1 ел {-[(х - 0) / Z>]c},
где b — параметр масштаба распределения;
с — параметр формы распределения;
0 — параметр положения распределения;
е — число Эйлера (2,71...).
Наиболее сложным является распределение Вейбулла, плот-
ность и форма которого при параметрах с = 1, 2, 3, 4, 5 и 10
имеет следующий вид (рис. 1.8).
Гамма-распределение впервые введено в статистический оби-
ход Везерберном (1946 г.), распределение Вейбулла — Вейбуллом
(1939, 1951 г.), распределение хи-квадрат — Пирсоном (1894 г.),
распределение Парето, известное так же, как закон распреде-
ления доходов — Парето (1873 г.).
21
Рис. 1.8. Распределение Вейбулла:
а — функция плотности; б — функция распределения
Нелинейные распределения. Значения наблюдаемых пере-
менных имеют нелинейное распределение с параметрами, от-
личными от гауссовских параметров а, о, 6, л, е, если они по
своей природе независимые или непараметрические и в прин-
ципе и вне необходимых преобразований не могут быть пред-
ставлены в известных или близких к ним режимах композит-
ных линейных связей. Такие распределения в статистике на-
зываются криволинейными.
Типы функций нелинейных распределений определяются
природой, составом наблюдаемых независимых переменных и
характером их связи с зависимыми переменными (результат,
отклик и т.д.), которые они детерминируют.
Если все наблюдаемые переменные независимые (в приклад-
ной статистике они называются «предикативные») и представ-
ляются как количественные величины, зависимые от них пере-
менные находятся как логарифмические, степенные или любые
другие известные функции распределения или как комбинация
этих функций, адаптивно аппроксимирующих наблюдаемые
смешанные типы распределений.
Если все наблюдаемые независимые переменные непарамет-
рические, представляются в виде порядковых шкал балльных,
рейтинговых или ранговых оценок, идентифицирующих каче-
ственные показатели, получаемые экспертным путем, то зави-
симые от них переменные находятся по так называемым непа-
раметрическим функциям R Спирмена, т Кендалла, коэффи-
циентам Соммера, кривым Джонсона и другим функциям
соответствий, аппроксимирующим наблюдаемые связи соответ-
ствующих качественных показателей.
22
Поиск функций теоретических распределений и определе-
ние степени их соответствия наблюдаемым эмпирическим рас-
пределениям необходим и достаточен в случае получения при-
емлемых оценок, удовлетворяющих известным критериям со-
гласия (в частности, критериям Пирсона, Стьюдента, Фишера
или указанным критериям Спирмена или Кендалла).
В случае получения неудовлетворительных оценок согла-
сия наблюдаемые множества независимых переменных рассмат-
риваются как неаппроксимируемые с помощью известных фун-
кций теоретических распределений и квалифицируются как
подлежащие разбиению на однородные группы или как не под-
лежащие многомерному анализу с помощью параметрических
функций и требующие обращения к функциям непараметри-
ческих распределений.
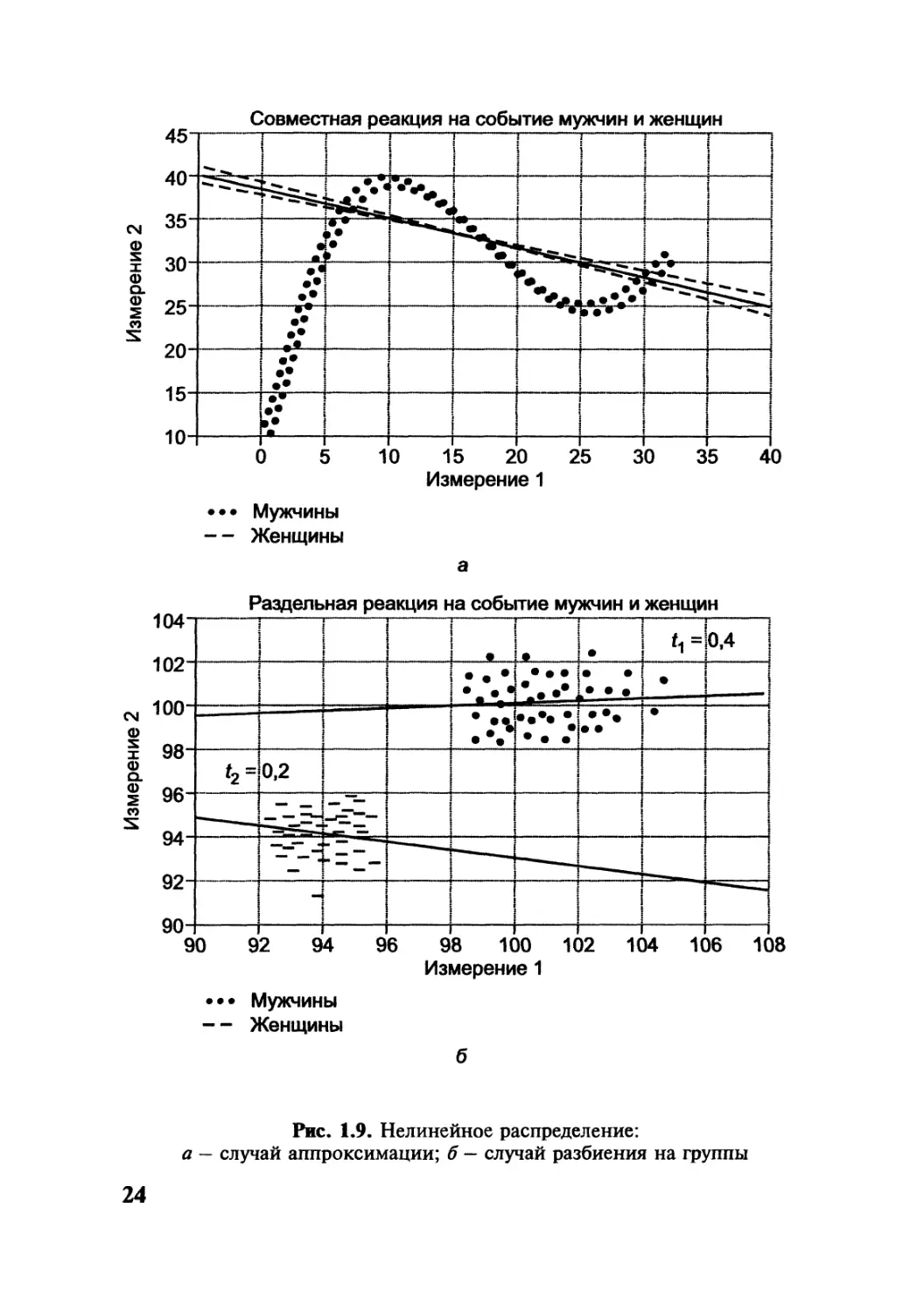
Нелинейные распределения представлены на рис. 1.9.
К классу сложных нелинейных распределений относятся
распределения Байеса и робастные распределения, в частности
распределения Тагучи (1975 г.), затрагивающие процессы кон-
троля надежности и качества.
Примером нелинейных распределений может служить мно-
жество, состоящее из семи детерминирующих переменных, от-
части зависимых, отчасти независимых, определяющих рост
национального богатства и валового внутреннего продукта
(ВВП) России за 100 лет, приведенных в книге Н.П. Федорен-
ко, опубликованной при участии автора данного пособия*.
Непараметрические распределения. Предметом непарамет-
рических распределений являются случаи асимптотического ис-
числения так называемых нечисловых, т.е. качественных, по-
казателей, например успеваемости, результатов спортивных игр,
сортов пива или, скажем, порядочности, милосердия и спра-
ведливости.
При этом используются числа-образы или дискриминан-
ты, по которым строго на альтернативной основе судят о на-
личии или отсутствии того или иного наблюдаемого качества,
например ума, денег, таланта. Понятно, что такие цифры —
Это всего лишь мнения о них, «одетые в цифры», ясность и
точность которых определяются ясностью и точностью опре-
деления и понимания самих наблюдаемых качеств.
* См.: Россия на рубеже веков. — М.: Экономика, 2003. — С. 121—243,
697—721; Симчера В.М. Развитие экономики России за 100 лет (Истори-
ческие ряды, вековые тренды, институциональные циклы). — М.: Наука,
2006. - С. 3-587.
23
Измерение 2 Измерение 2
• • • Мужчины
— Женщины
• • • Мужчины
— Женщины
б
Рис. 1.9. Нелинейное распределение:
а — случай аппроксимации; б — случай разбиения на группы
24
Непараметрические распределения аппроксимируются обыч-
но в виде тех же известных (в большинстве случаев многомер-
ных нелинейных) функций плотности наблюдаемых показате-
лей х., измеряемых в виде балльных, рейтинговых или других
ранговых оценок, что и параметрические оценки наблюдае-
мых числовых показателей. При этом сами оценки представ-
ляются в виде различных числовых шкал или полушкал (бал-
лов очков, голосов, шаров и т.д.), идентифицирующих (в
большинстве случаев - имитирующих) аналоги единиц изме-
рения действительных числовых показателей, например зат-
рат, выпуска или производительности труда.
Основным способом непараметрических измерений явля-
ются экспертные или другие аналогичные оценки, например
судебные решения, опросы общественного мнения, результа-
ты голосования и т.д., достоверность которых определяется
репрезентативностью наблюдения, а точность — величиной не-
избежных систематических ошибок, допускаемых при их про-
ведении. Известно, что чем больше наблюдаемых единиц п и
чем они однороднее (о2), тем при прочих равных условиях
меньше ошибка наблюдений (А) и, следовательно, выше до-
стоверность получаемых оценок.
Старое название непараметрических измерений — категори-
ческие исчисления номинальных (альтернативных) величин типа
«да» — «нет», «за» — «против», «виновен» — «невиновен» и т.д.
В социологии и ряде других прикладных отраслей знания
непараметрические оценки предпочитают называть индикатив-
ными, а непараметрические распределения — индикативными
распределениями.
Признаки наблюдаемых явлений (например, демократии,
равенства, справедливости, качества жизни или, скажем, духов-
ности и милосердия) имеют непараметрическое распределение,
если их значения целиком не могут быть измерены и представ-
лены.в количественном виде, т.е. параметризованы (отсюда на-
звание распределения), или могут быть измерены частично в
бедных шкалах номинальных, категорических (альтернативных)
или ранговых оценок. К непараметрическим распределениям
обращаются также в случае наличия ограниченного набора на-
блюдаемых данных, которых оказывается недостаточно для при-
менения параметрических методов.
25
В случае, когда признаки наблюдаемых непараметрических
явлений вообще не могут быть представлены в каких-либо
количественных, номинальных или ранговых оценках и, сле-
довательно, на их основе не могут быть исчислены какие-либо
элементарные обобщающие характеристики, например сред-
няя или сигма (стандартизованное отклонение), соответству-
ющие распределения называются свободными (они свободны
и от параметров, и от допущений, и от гипотез) и относятся к
разряду хаотических.
Отдельные задачи непараметрических распределений реша-
ются путем последовательной пошаговой симуляции значений
нейронных сетей (обучающих выборок), т.е. путем нахожде-
ния последующих неизвестных непараметрических значений
на основе ограниченного массива предыдущих известных, в
том числе непараметрических оценок.
Случай пошагового нахождения значений непараметричес-
ких распределений наглядно иллюстрирует график нейронных
сетей, приведенный на рис. 1.10.
Нейронная сеть
Вход Слой 1 Слой 2 Выход
Рис. 1.10. Непараметрическое распределение
26
к непараметрическим распределениям относятся также все
сложные классы распределений в области планирования экс-
перимента, оценки качества и надежности, многомерного
экспертного оценивания и анализа производственных процес-
сов изучения общественного мнения и др.
Хаотические распределения. Хаотические распределения пред-
ставляют собой тип маргинальных распределений переменных
наблюдаемых и ненаблюдаемых, в том числе вырожденных яв-
лений, отражающих предельно сложные закономерности совре-
менного мира, недоступные не только для представления, но и
понимания в категориях существующих парадигм и знаний. Это
наиболее распространенный тип распределений и вместе с тем
менее всего теоретически понятный и, следовательно, освоен-
ный в природе и обществе.
Кроме констатации факта существования хаотических рас-
пределений, современной науке о них ничего неизвестно.
Вместе с тем ложная наука и пропаганда строят о хаотических
распределениях многочисленные догадки и сочиняют мифы,
подменяя ими необходимость выявления подлинных причин-
но-следственных связей.
Классический пример хаотических распределений в приро-
де — броуновское движение, эпидемии, катастрофы и коллапсы.
Пример хаотических распределений в обществе — воюющие
страны или стихийно реформируемые политические режимы,
Вроде режима США, экономики переходных периодов, вроде
экономики современной России, предсказать исходы и судьбы
которых причинно-следственным путем невозможно.
В отличие, скажем, от сложных непараметрических распре-
делений в хаотических распределениях неизвестными являются
обычно не только количественные значения наблюдаемых пе-
ременных, но и режимы, и параметры их причинно-следствен-
ных связей, что априорно исключает выдвижение каких-либо
Р^Жхчих гипотез и построение функций распределения, ограни-
чивая каждый возможный эксперимент наблюдениями и зак-
лючениями сугубо апостериорного свойства.
* Освоенный путь моделирования хаотических распределений -
Дробление их на части и изучение каждой из них с помощью
известных распределений. Помогает здесь также обращение к
существующим аксиоматическим и асимптотическим вычис-
27
лениям, в частности к методам приближенных вычислений,
описанным автором в других работах*.
На рис. 1.11 представлены четыре типа смешанных (два лево-
и два правосторонних) хаотических распределения, наиболее
распространенных в статистике.
Хаотические симметрии
96 98 100 102 104
Класс 3
Класс 2 &
о
Класс 4
Ось абсцисс
Рис. 1.11. Хаотические распределения
Полностью хаотические распределения, в основе которых
лежит гипотеза о существовании в природе и обществе сим-
метрии хаоса (например, болезней, войн, катастроф, преступ-
лений, бед и т.д.), встречаются в статистике редко, поскольку
почти не подтверждены данными эмпирических наблюдений.
* См.: Методы приближенных вычислений. — М.: ВЗФЭИ, 1986. —
87 с.; Методы сравнительного анализа статистических данных. — М.:
ВЗФЭИ, 1987. — 72 с.; Симчера В.М. Практикум по статистике. — М.:
Финстатинформ, 1999. - С. 244—258; Как возродить экономику России. —
2-е изд. - М.: Паритет, 2000. — С. 323-351; Симчера В.М. Введение в
финансовые и актуарные вычисления. — М.: Финансы и статистика, 2003. —
С. 82-104.
28
Конечно, все (или практически все) девять типов представ-
ленных многомерных распределений пересекаются по разным
основаниям, признакам и параметрам. И поэтому понятно,
что при других допущениях, формах наблюдаемых данных и
ценностных ориентациях не исключена их иная геометрия и
топология, возможные обоснования и разработки которых
выходят за пределы настоящей работы, требуя самостоятель-
ного исследования.
Рекомендуемая литература
1. Айвазян С.А. Классификация многомерных наблюдений. —
М.: Статистика, 1974.
2. Бикел TL, Доксам К. Математическая статистика. — М.:
Финансы и статистика, 1983.
3. Ван-ден-Варден Б.Л. Математическая статистика. — М.:
Иностранная литература, 1960.
4. Гнеденко Б.В. Курс теории вероятностей. — М.: Наука,
1969.
5. Колмогоров А.Н. Основные понятия теории вероятностей. —
М.: Наука, 1974.
6. Нефедова Е.А., Узорова О. В. 200 задач и примеров по ма-
тематике. — М.: ACT, 2001.
7. Маленво Э. Статистические методы эконометрии. — М.:
Статистика, 1975.
8. Одинцов Б.Е. Обратные вычисления в формировании эко-
номических решений. — М.: Финансы и статистика, 2004.
9. Осовский С. Нейронные сети для обработки информации. —
М.: Финансы и статистика, 2004.
10. Пригожин И. Конец определенности. Время, хаос и
новые задачи природы. — Ижевск, 2001.
11. Растригин Л.А. Статистические методы поиска. — М.:
Наука, 1968.
12. Саати Т. Принятие решений. Метод иерархий. — М.:
Радио и связь, 1993.
13. Хьюбер Д. Робастность в статистике. — М.: Мир, 1984.
14. Чураков Е.П. Математические методы обработки экс-
периментальных данных. — М.: Финансы и статистика, 2004.
15. Ярушкина Н.Г. Основы теории нечетких и гибридных
систем: учеб, пособие. — М.: Финансы и статистика, 2004.
ТЕМА 2
Методы многомерного
корреляционного изучения данных
2.1.
Вводные замечания
В зависимости от масштаба и охвата наблюдаемых явлений,
характера и точности решаемых задач, границ и областей при-
менения методы многомерного анализа понимаются в широ-
ком (родовом) и узком (видовом) смыслах.
В широком смысле — это методы физического измерения и
предметного анализа любых сложных явлений в системах мно-
гомерных пространств, начиная с трехмерного, представляю-
щего в материальной форме некоторую трехмерную матрицу
значений действительных чисел, характеризующих параметры
трех различных явлений по трем различным признакам.
В узком смысле — это методы множественного (по мини-
муму — трехфакторного) измерения однородности и анализа
взаимосвязи любых наблюдаемых явлений по любому набору
измеряемых признаков.
Под такими методами в современной специальной стати-
стической литературе, как правило, понимают методы диск-
риминантного и кластерного анализа как методы многомерно-
го анализа однородности наблюдаемых явлений и методы мно-
жественного корреляционного, компонентного и факторного
анализа - как методы многомерного анализа взаимосвязей.
В отличие от изданных ранее учебных пособий, в которых
методы многомерного анализа представляются обычно в узком
смысле слова как собственно методы множественного корре-
ляционного, дискриминантного, кластерного, компонентно-
го и факторного анализа, в настоящем руководстве они пони-
маются в широком смысле слова как методы образного, в том
числе межотраслевого, оптимизационного, графического и даже
теневого и метафорического анализа любых взаимосвязанных
данных, какими в наиболее распространенном случае являют-
ся статистические данные, которые в реальных режимах про-
странства и времени сами по себе представляют в некотором
30
поде образы тех явлений, которые отражают и поэтому прак-
тически везде и всегда требуют именно такого широкого по-
нимания.
Связи между явлениями в природе и обществе подразделяют-
ся на детерминированные (закономерные) и индетерминирован-
ные (случайные). Детерминированные связи представляют обычно
как линейные, а индетерминированные - как нелинейные.
При линейных связях следствия (значения искомых функ-
ций; в статистике чаще говорят о результатах) изменяются прямо
пропорционально обусловливающим их причинам и аргумен-
там (в статистике причины и аргументы предпочитают назы-
вать факторами).
При нелинейных связях значения искомых функций под
воздействием обусловливающих их аргументов изменяются не-
однозначно и непропорционально, в том числе разнонаправ-
ленно — с изменением наблюдаемых аргументов искомая функ-
ция в одних случаях возрастает (разумеется, непропорциональ-
но), в других (в том же режиме) убывает, а в отдельных случаях
может оставаться неизменной.
При этом, если значение искомой функции обусловлива-
ется и идентифицируется одним фактором, говорят о парных
связях, а если изменение функции рассматривается под влия-
нием двух факторов и более, говорят о многофакторных, мно-
жественных или многомерных связях.
Подавляющее большинство наблюдаемых связей (и в при-
роде, и тем более в обществе) относится к нелинейным. Ввиду
чрезвычайного многообразия и исключительной сложности
нелинейных связей (и в науке, и в практической работе), в
целях упрощения подхода к их изучению и пониманию, дан-
ные связи условно приравнивают к линейным, а многофак-
торные линейные связи, в свою очередь, — к предельно упро-
щенным парным связям, где изменение функции рассматри-
вается в зависимости от изменения одного-единственного
фа^сгора-аргумента. Линейные связи при этом рассматривают
как частный случай нелинейных.
Так обстоит дело потому, что определять многообразные
многомерные нелинейные связи на уровне статистического эк-
сперимента и сегодня, при наличии мощной вычислительной
техники, представляется попросту невозможным или чрез-
вычайно затруднительным из-за отсутствия необходимой ин-
формации.
31
Линейные связи обычно рассматривают и представляют как
некоторые детерминированные, т.е. закономерные, явления,
наблюдаемые причины и следствия которых изменяются в стро-
го функциональном режиме или как аксиомы, не требующие
доказательств.
Нелинейные связи, отражающие взаимодействие множе-
ства случайных причин и следствий, эволюционирующих в
природе и обществе по спирали, рассматривают и представля-
ют как индетерминированные, которые меняются в стохасти-
ческом, т.е. вероятностном режиме, прослеживаются лишь при
наблюдении необходимого множества массовых данных, ми-
нимальное значение которых представляют данные так назы-
ваемых малых выборок (30 ед., наблюдаемых по двум призна-
кам и более).
Линейные связи, аппроксимизируемые аксиомами и есте-
ственными законами, отслеживаются и подтверждаются одно-
значными оценками. Нелинейные выстраиваются на основе
некоторых теоретических допущений и гипотез, приемлемость
или неприемлемость которых определяется эмпирически и под-
тверждается степенью их сходимости с некоторыми норматив-
ными критериями и оценками (например, известными крите-
риями оценки связи Фишера, критериями оценки однород-
ности V = 0,33 или критериями оценки достоверности f).
Линейные связи изучаются с помощью методов функцио-
нального анализа (дифференциальных и интегральных исчисле-
ний) путем построения соответствующих функций, нахождения
их дифференциалов и далее (на их основе) различного рода про-
изводных, а нелинейные - с помощью методов теории вероят-
ностей и математической статистики (в первом приближении
методов регрессионного и корреляционного анализа) путем по-
строения моделей распределения и исчисления различных коэф-
фициентов эластичности, корреляции, детерминации и др. На
этой основе линейные связи называют обычно функциональны-
ми, а нелинейные — стохастическими. Простейшими методами
изучения линейных связей являются пропорции и балансы.
В случае, если применяемые методы изучения связей бази-
руются на цифровых данных, т.е. на фактах, они называются
параметрическими, если на вербальных оценках, т.е. не на фак-
тах, а на мнениях о фактах (данных так называемых номиналь-
ных, т.е. качественных или категорических исчислений, напри-
мер альтернативных оценках общественного мнения) — непара-
32
метрическими. В случаях использования смешанных данных (в
текущей практике это наиболее распространенная ситуация)
говорят о полупараметрических методах изучения связей.
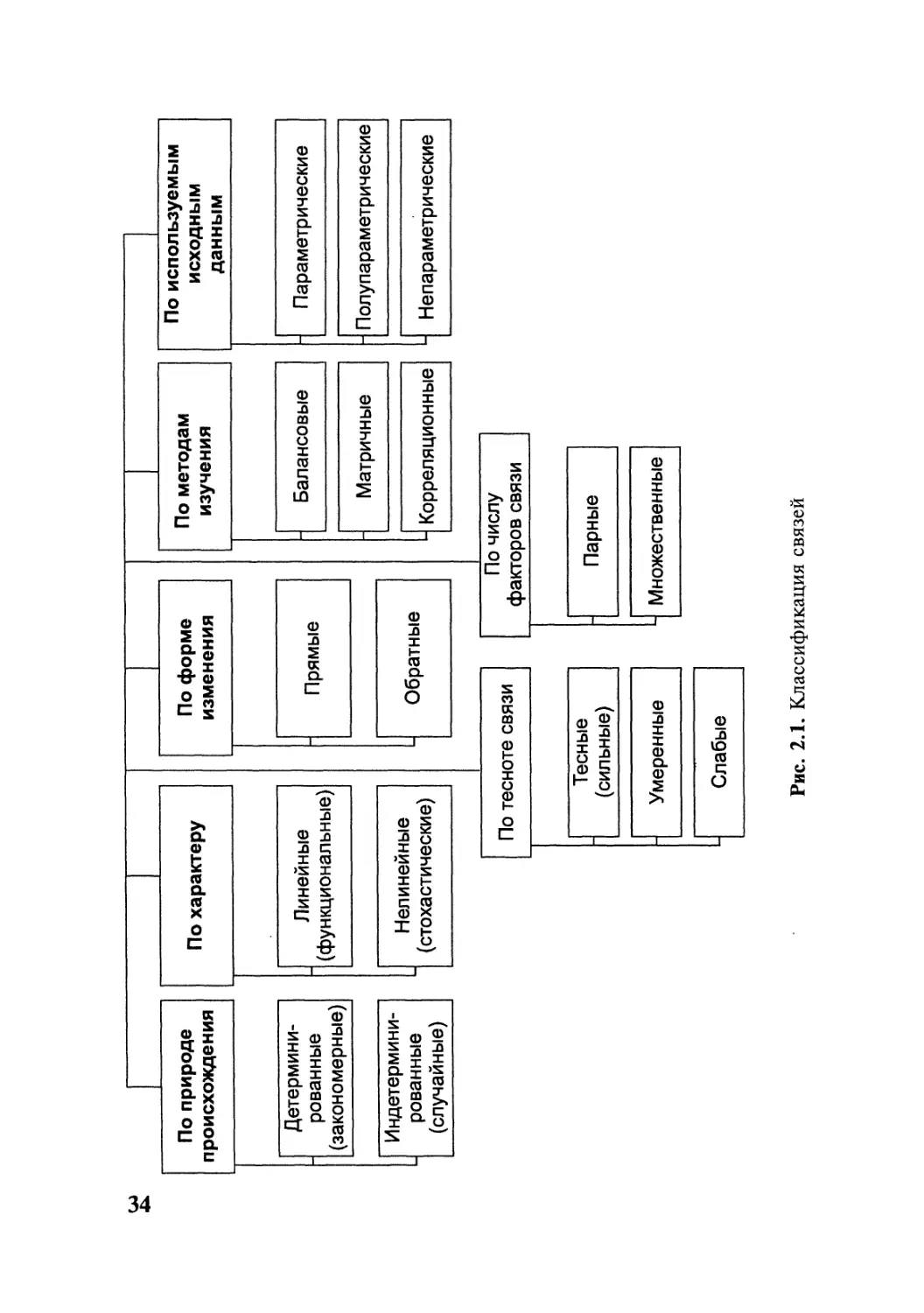
На рис. 2.1 представлена наиболее распространенная в на-
уке классификация изучаемых связей.
Классификация существующих связей и определение их
характера, идентификация методов их адекватного представле-
ния — исходное условие объективно обусловленного, целевого и
эффективного их понимания и изучения.
Как отмечалось, в текущей практике (в целях упрощения
статистического эксперимента) распространены случаи приме-
нения линейных методов для изучения нелинейных, т.е. сто-
хастических, связей. В чисто иллюстративном порядке воз-
можно также использование стохастических методов для изу-
чения линейных связей. Однако практика применения методов
детерминированной статистики к изучению стохастических свя-
зей не означает, что сами эти связи становятся детерминиро-
ванными, как и наоборот — использование стохастических
методов при изучении детерминированных связей не означа-
ет, что эти связи становятся стохастическими*.
* Понимание этих, казалось бы, простых истин на практике затруд-
нительно, особенно в общественной жизни, где детерминированные (ре-
гулируемые) и индетерминированные (нерегулируемые) связи переплета-
ются и непрестанно опрокидываются в общественном сознании, выступая
на поверхности явлений наиболее причудливо, а в практической жизни —
крайне противоречиво.
Возьмем, к примеру, рыночные связи, как якобы наиболее полно и
последовательно реализующие демократические принципы естественного
отбора, никем не направляемого и, следовательно, справедливого распре-
деления жизненных шансов, прав и свобод.
Эти рыночные права, шансы, свободы и другие ценности «никем не
регулируемые» и, стало быть, «одинаково и в равной мере доступные всем»,
в действительности распределяются, закрепляются и используются отнюдь
не по жребию и воле случая, пропорционально и адекватно закону есте-
ственного отбора без какого-либо вмешательства извне. Напротив, при
внешне демократической оболочке честной игры и справедливой борьбы
в реальной жизни происходит самый жестокий и цинично организован-
ный отбор, в основе которого сговор, направленный на удовлетворение
корыстных интересов, на фоне которого лотерея или игра в рулетку ка-
жутся самой невинностью.
Подобную подмену притворно нерегулируемых отношений жестко
регулируемыми мы называем асимметрией общественных и рыночных
отношений. Вот наглядные примеры такой подмены.
33
По природе
происхождения
По характеру
Детермини-
рованные
(закономерные)
Индетермини-
рованные
(случайные)
Нелинейные
(стохастические)
Линейные
(функциональные)
По методам
изучения
По используемым
исходным
данным
По тесноте связи
Тесные
(сильные)
Умеренные
Слабые
По числу
факторов связи
Парные
Множественные
Рис. 2.1. Классификация связей
Практически все взаимосвязи, рассматриваемые в социаль-
но-экономической статистике, являются стохастическими. Изу-
чение этих взаимосвязей предполагает обращение к соответству-
ющим стохастическим методам, среди которых наиболее распро-
странены методы корреляции. Именно поэтому в данном
пособии основное внимание уделяется изложению сути, целей,
задач и основных направлений практического применения этих
методов.
2.2-
Методические указания по изучению темы
Статистическое изучение корреляционных связей помимо
предварительного анализа его целей и идентификации факто-
ров, определения формы и выбора соответствующей теорети-
До захвата государственной собственности (в России — до приватиза-
ции) либералы всех мастей, попирая законы общественного развития, выс-
тупали против всякого рыночного регулирования и детерминирования об-
щественных отношений, против государственного плана, порядка и закона,
против защиты государственной собственности, представляя их как чудо-
вищные административно-командные методы управления. После захвата
собственности те же либералы, защищая уже свою частную собственность,
напротив, стали ратовать за регулирование общественных отношений, за
порядок и закон, выступать против бесправия, стихии и нерегулируемого
рынка. В этом классовом интересе суть общественной асимметрии, отражаю-
щей подмену понятий, фабрикацию и искусственную эксплуатацию недо-
разумений, к чему чаще всего и привлекается статистическая наука.
Другой, более яркий пример той же общественной асимметрии — вы-
боры представителей государственной власти, и прежде всего глав совре-
менных государств, которые благодаря господству грязных технологий и
административных ресурсов ныне уже немыслимы как справедливые не
только в США, но и ни в одной развитой стране.
И последний пример, имеющий отношение не только к современной
социально-экономической практике, но и к теории принятия решений в
условиях закономерного господства асимметричной информации, проти-
воречит как принципам равенства и справедливости, так и элементарным
требованиям здравого смысла. Решения, принятые на рынке на основе
симметричной информации, т.е. информации, одинаково доступной и
известной продавцу и покупателю как сторонам сделки, согласно этой
теории признаются неэффективными и нерыночными. А ведь авторами
этих теоретических моделей являются лауреаты Нобелевских премий
Д. Акелроф, М. Спенс, Д. Стиглиц (2001 г.), Д. Канэман, В. Смит (2002 г.),
Р. Энгл и К. Грэйнджер (2003 г.)!
35
ческой модели предполагает организацию и поэтапное прове-
дение конкретной эмпирической работы по подготовке ис-
ходной информации и исчислению показателей тесноты связи
наблюдаемых явлений, оценке адекватности полученных ре-
зультатов, объяснению их социально-экономического смысла
и прикладного назначения.
Основной акцент при этом делается на установление фор-
мы, расчеты параметров и измерение тесноты корреляционной
связи как наиболее сложных и трудоемких этапов работы, а
также на интерпретацию результатов корреляционного анали-
за и критерии оценки адекватности и точности их содержа-
тельного смысла и назначения.
Установление формы и расчет параметров корреляционных
связей. В современной социально-экономической статистике
корреляционные связи (кроме методов аналитических группи-
ровок) воспроизводятся наиболее широко и, следовательно,
моделируются путем построения линейных уравнений, уравне-
ний параболы и соответствующих степенных функций. При этом
к линейным уравнениям обращаются преимущественно в ими-
тирующих целях, так как они представляют технику расчетов
наиболее просто, наглядно и доступно. Ниже по шагам излага-
ются суть и алгоритм определения корреляционных параметров
на основе трех основных видов этих уравнений.
Расчет параметров корреляции на основе линейных уравне-
ний. Корреляция на основе линейных уравнений определяется
в случае наличия прямых связей между наблюдаемыми явле-
ниями, т.е. связей, при которых индивидуальный результат у
равномерно возрастает или убывает с увеличением факторно-
го признака. Такая связь обычно выражается (аппроксими-
руется) в виде следующего уравнения:
Ух=ао + а\х> (2.1)
где у - индивидуальные значения результативного признака;
х — индивидуальные значения факторного признака;
а0, — параметры уравнения; при этом а0 — параметр влияния неиз-
вестных факторов;
ух — теоретическое значение результативного признака.
Параметры яои ах формулы (2.1) определяются путем реше-
ния системы нормальных уравнений методом определителей
36
или наименьших квадратов, детерминцрующих условия нахожде-
ния пределов в отклонениях между наблюдаемыми значениями*.
Ъу - па$ + а{£х\
2
Ъух = a^Lx + a{Lx .
(2.2)
При этом параметр aQ находится как
ZyEx2 - ЪухХх
CIq ~
- ZxLx
(2.3)
или в случае, если известны другие параметры искомого урав-
нения, как v
«О = у-щх.
(2.4)
Соответственно параметр а{ находится как
nLyx — LxZy
ri£x2 -ZxEx
(2.5)
Параметр aQ интерпретируется как математический опера-
тор, коэффициент размерности, характеризующий степень влия-
ния неизвестных факторов, а параметр ах — как коэффициент
* Условия пределов, покоящиеся на свойствах взаимосвязи средней из
сумм произведений и произведением средних, как известно, выполняют-
ся, если разности между суммами и средними произведений, с одной сто-
роны, и произведениями сумм и средних двух и более наблюдаемых при-
знаков, с другой стороны, достигают максимума, а их модуль стремится к
своему пределу - разнице между произведением квадратов наблюдаемых
факторных значений и произведением их сумм.
При этих условиях остаточные отклонения будут минимальными, их
квадраты — наименьшими, а влияние ненаблюдаемых факторов и коэф-
фициент размерности — несущественными и незначительными.
Элементы уравнения наименьших квадратов и исчисляемые на их ос-
нове параметры соответственно называют еще множителями и определи-
телями, а рассматриваемые методы — методами множителей и подстано-
вок; названия, которыми предпочитают оперировать в практике матрич-
ного анализа и межотраслевых расчетов. Формулы уравнений наименьших
квадратов широко известны, а содержательное истолкование, т.е. пони-
мание их смысла — нет. Отсюда необходимость приведенных замечаний,
без которых обучение лишено предметного назначения.
37
регрессии, показывающий степень изменения результативно-
го признака при увеличении или уменьшении на единицу на-
блюдаемого факторного признака.
В случае представления наблюдаемых признаков в разных
единицах измерения для оценки параметров корреляции обра-
щаются к исчислению среднего коэффициента эластичности
Э = ах = или Э-ух—, (2.6)
У У,
где х, у - соответственно средние значения наблюдаемых признаков,
а у'х — первая производная уравнения регрессии ух.
Коэффициент эластичности, как и коэффициент регрес-
сии, показывает, на сколько процентов изменяется результа-
тивный признак при изменении факторного признака на 1%.
В случае наличия данных в виде корреляционной таблицы
параметры линейного уравнения определяются путем решения
следующей системы уравнений:
[ Ly/ = a0V + aiXxfx;
2 (27)
^Lys/Ху — a^Exfх + ajLx fx.
При этом параметр а0 находится как
Syi/b:2/-Lxy-Lx/
«0=-------5----------> (2.8)
L/Lx2/-Lx/Lx/
и соответственно параметр ах — как
sni’/.W
где f —веса соответствующих групп.
При проведении аналитических группировок параметру а{
соответствует коэффициент межгрупповой дисперсии.
Установление формы и расчет параметров корреляции на ос-
нове степенной функции. В случае изменения факторного при-
знака по отношению к результативному в геометрической про-
38
(2.13)
(2.14)
(2.15)
(2.16)
грессии связь между ними наиболее правдоподобно представ-
ляется в виде степенной функции
Ух=аОха'- (2.10)
Параметры такой функции определяются методом наимень-
ших квадратов путем приведения ее к логарифмическому виду:
Igy = lg(70+<71lgX (2.11)
Параметры указанной функции находят, решив систему нор-
мальных логарифмических уравнений вида
nlg«0+aiSlg* = Slgb (212)
IgfloZlgx + a^lgx)2 = Zlgy.lgx.
Эти же параметры можно найти также по формуле
Igxlgy-lgxlgy
a, = -—,
Igx2—(Igx)2
1g «0 = lgy-ailgx.
Соответственно а0 будет равно:
ZlgyZ(lgx)2 = Elg ylgxZlgx
*g ao -----’---5-------------
и Д 1g x) - Z 1g xS 1g x
И соответственно at будет равно:
_ «Zlgxlgy = SlgxZlg y
rcZ(lg x)2 - Z 1g xZ 1g x
Соответствующие параметры приведенных логарифмичес-
ких значений находятся по таблицам мантисс и антилогариф-
мов, готовые значения которых (с разной степенью точности
исчисления) публикуются в печати на регулярной основе*.
* Наиболее известные среди этих таблиц — таблицы В. Брадиса.
См.: Теория и практика приближенных исчислений. — М.: ОНТИ, 1995;
В.М. Симчера. Введение в финансовые и актуарные вычисления. -
С. 293-321.
39
Параметр ах логарифмической функции является коэффи-
циентом эластичности, который показывает, на сколько про-
центов изменяется результативный признак при изменении
факторного признака на 1%.
Установление формы и расчет параметров корреляции на ос-
нове уравнения гиперболы. При гармоническом изменении ре-
зультативного признака по отношению к факторному связь между
ними определяется на основе уравнения гиперболы вида
1
+ (2.17)
Параметры уравнения гиперболы находятся методом наи-
меньших квадратов путем решения преобразованной системы
нормальных уравнений. Преобразование осуществляется заме-
1
ной значения х на обратное его значение —.
Ху = па$ ;
%1 (2.18)
1 v । v 1
Xy— = aQX— + qL—.
*1 *i Xy
Параметры уравнения гиперболы можно найти так же, как
определители, по формулам:
1 1 1
ZyZ—-L—уХ—
Ху *1 Х1
«о =---г-----j--j—; (2.19)
Х1 *1 Xy
1 1
nX—y — X— Xy
4 =----J-----j--Г’ (2.20)
nX-^-X—X—
Xy Xy
Измерение тесноты корреляционной связи. Измерение тес-
ноты корреляционной связи осуществляется путем исчисле-
40
ния линейного коэффициента корреляции, теоретического кор-
реляционного отношения и индекса корреляции. При наблю-
дении двух признаков говорят об установлении так называе-
мой парной связи (один фактор — одно следствие), а при на-
блюдении трех и более признаков — множественной связи (два
фактора и больше — одно следствие и больше). Степень пар-
ной связи определяется путем исчисления линейного (парно-
го) коэффициента корреляции, а множественной связи — пу-
тем исчисления корреляционного отношения или индекса кор-
реляции.
Линейный (парный) коэффициент корреляции. Определяет-
ся только при наличии функциональной связи как отношение
двух операторов — оператора разности средней из суммы про-
изведений (ху) и произведения средних (ху) к оператору про-
изведения квадратических отклонений, т.е.
_ ху-ху
<5Х '
или как определитель (2.21), или как предельное отношение
суммы произведений линейных отклонений к произведению
сумм их квадратических отклонений (формула (2.22)), или как
скорректированное отношение корней межгрупповой и об-
щей дисперсий (формула (2.23)):
V ^Х^у
1ух--~
п
tc2-^^w2-^^
п п
Щ-х)2 S(j,-y)2
п п
(2.21)
(2.22)
(2.23)
41
Исходное условие или критерий наименьших квадратов —
равенство или минимум расхождений между операторами Еху =
= Yx Ъу, или максимум, достигаемый между двумя другими
парными операторами ху-ху = тах, о чем речь шла ранее.
Теоретическое и эмпирическое корреляционное отношение.
Исчисляется при наличии любой формы нелинейной связи
между любым количеством факторных и результативных при-
знаков. Теоретическое корреляционное отношение исчисля-
ется при наличии соответствующим образом идентифициро-
ванных уравнений регрессии (2.21), а эмпирическое корре-
ляционное отношение — при наличии соответствующих
аналитических группировок и расчетах внутригрупповых и
межгрупповых дисперсий.
Теоретическое корреляционное отношение (У?2) представля-
ется как предел отношения суммы квадратов отклонений груп-
повых средних теоретических значений результативного при-
знака (ух) от общего среднего теоретического его значения (у)
к сумме квадратов отклонений индивидуальных эмпирических
значений (у) от общего среднего теоретического значения (у),
а эмпирическое корреляционное отношение ц — как предел
^(х — х )2
отношения межгрупповой 52 = ———— и общей
р . п
ДЛ“*обш)2
8общ -------— эмпирических дисперсии, определяемых на
п
основе данных соответствующих аналитических группировок.
Теоретическое корреляционное отношение будет рассчиты-
ваться по формуле
Ду,--у)2
(2.24)
где Ъ(ух — у) — факторное отклонение результативного признака от
2 среднего его теоретического значения;
ДУ/ _ у) — общее отклонение эмпирического значения результатив-
ного признака от среднего его теоретического зна-
чения.
42
Соответственно эмпирическое корреляционное отношение
определяется как
х2
2 = °мгр
я2
^общ
(2.25)
е? ^(Амгп -^обш) ^(*мгр хобщ) f
где Омгр ~-------------- или --------v7-------- (если веса групповых
средних *Мгр неравны) — эмпирическая факторная дисперсия,
которая характеризует вариацию результативного признака под
влиянием эмпирического признака-фактора, включенного в модель;
2 ^(хмгр -^общ) ^(хмгр ^общ) f
Ообщ =--------------- или ------------------ - общая эмпириче-
п
ская дисперсия, показывающая вариацию результативного при-
знака под влиянием всех индивидуальных значений эмпири-
ческих факторов, влияющих на общую вариацию.
Теоретическое корреляционное отношение, как и эмпи-
рическое изменяется в пределах от 0 до 1: чем ближе корреля-
ционное отношение к 1, тем теснее связь между признаками.
В целях приведения как теоретических, так и эмпирических
показателей корреляционного отношения к натуральному виду,
т.е. к размерности исходных данных применяется коэффициент
детерминации или индекс корреляционной связи, которые
определяются соответственно как
L ^вгр
П=\ 1---2~^
V ^общ
(2.26)
2 2L(x,- хВГр)
где <увгр =---------— - внутригрупповая дисперсия по каждому из
р п
учтенных факторных признаков, а Е — их общая сумма; количе-
ство внутригрупповых дисперсий будет соответствовать количе-
ству наблюдаемых группв любом случае их количество не мо-
жет быть меньше двух;
43
(2.27)
I _ 2
D L *y- Хгвгр)
V Z(y-y)2
2 МЛ Лхвгр?
где y_y ------------— — сумма остаточных отклонении, характери-
зующих вариацию результативного признака под влиянием
вариации всех внутригрупповых и прочих неучтенных фак-
торов.
Построение моделей связи в виде уравнения множественной
регрессии. Изменение экономических явлений происходит под
влиянием не одного фактора, а большого числа самых разнооб-
разных факторов. Связь между результативным признаком и
двумя и больше факторами принято выражать уравнением мно-
жественной регрессии.
Уравнения множественной регрессии могут быть линейные,
криволинейные и комбинированные.
Наиболее простым видом уравнения множественной регрес-
сии является линейное уравнение с двумя независимыми пере-
менными:
Ухт = а$ +щхх+а^х^ (2,28)
Параметры уравнения множественной регрессии определя-
ются тем же методом наименьших квадратов путем решения
следующей системы нормальных уравнений:
Ъу = нац + a{Lxx + «2^2’
Хухх = + ахЪсх + #2^*1 *2 (2.29)
Ey%2 ~ ^0^2 + a\ ^lx2 + •
Параметры уравнения множественной регрессии показы-
вают изменение результативного признака при раздельном
изменении каждого факторного признака на единицу. Для
оценки влияния факторных признаков на результативный рас-
считываются частные коэффициенты эластичности и бета-ко-
эффициенты.
Частный коэффициент эластичности (Э) вычисляется по
формуле
44
Э = а^, (2.30)
У
где aj - параметр при признаке-факторе;
xh у — средние значения факторного и результативного признаков;
/= 1, 2, 3 ... п.
Частный коэффициент эластичности показывает, на сколько
процентов изменяется результативный признак при измене-
нии факторного признака на 1 % при фиксированных значениях
других факторов.
Бета-коэффициент (Р) вычисляется по формуле
₽ = (2-31)
и показывает, на какую часть сигмы изменяется результативный
признак прй изменении факторного признака на величину его
сигмы.
Сравнение бета-коэффициентов при различных факторах дает
возможность оценить силу их воздействия на результативный
признак.
Параметры уравнения регрессии можно находить также по
формулам через коэффициенты корреляции и средние квадра-
тические отклонения:
«о = у-аххх -а2х2;
_'ухх 'ух2'ххх2
1—
ххх2
ГУХ2 ГУх2Гх\х2
1-г2
Х1Х2
(2.32)
(2.33)
(2.34)
Парные коэффициенты корреляции можно вычислить по
следующим формулам:
(2.35)
45
(2.36)
r ^x2y-x2y,
yX2 OX3av
л2 У
*1*2-*1X2
axia%2
(2.37)
Средние квадратические отклонения определяются по фор-
мулам
~ V*"i (х1) ’
оу=^у2-(у)2;
I_2 _2
^х2 = уХ ~ (х2^ •
(2.38)
(2.39)
(2.40)
Статистические методы измерения тесноты корреляционной
связи в многофакторных моделях. При проведении многофак-
торного корреляционного анализа возникает необходимость рас-
чета множественных, парных и частных коэффициентов корре-
ляции. Для измерения тесноты корреляционной связи между
результативным признаком и несколькими факторными при-
знаками при линейной форме связи рассчитывается множе-
ственный коэффициент корреляции по формуле
Х1Х2
г2 + г2 - 2 rvr, rvr„ гГ1
[ yxi УХ2 УХ1 Ух2 xlx2
(2.41)
где г , г , г — парные коэффициенты корреляции.
У1 ух2 Xjx2
Множественный коэффициент корреляции изменяется от
0 до +1. Он показывает тесноту корреляционной связи между
результативным и факторными признаками, включенными в
уравнение множественной регрессии.
Парные коэффициенты корреляции вычисляются по формулам
5x1 -
nXyxi - ZyLxj
- (LX! )2 ] [«Zj2 - (Lx)2 ]
(2.42)
46
(2.43)
_ п^Ух2 “
-(Lx2)2][nZy2 -(Еу)2] ’
ГХ|Х2
Л7Хх1Л*2 “£*1^2
^[и&12 -(W][«^22 ~(W]
(2.44)
или по формулам (2.35) - (2.37).
Парные коэффициенты корреляции показывают тесноту кор-
реляционной связи как между факторными и результативными
признаками, так и между признаками-факторами.
Для исследования тесноты корреляционной связи между
признаками при построении моделей множественной регрессии
применяются частные (парные) коэффициенты корреляции,
которые характеризуют тесноту корреляционной связи между
факторным и результативным признаками при элиминирова-
нии влияния учтенных факторов.
Частные коэффициенты корреляции вычисляются по фор-
мулам
ГУХ[(х2)
Г — Y F
Ух\ х1х2
.1(1-Г2 )(1-Г2 )’
V УХ2Л *1*2 '
(2.45)
ГУХ2(*1)
ГУХ2 ГуХ2ГХ|Х2
J(l-r2 )(1~Г2 )’
\ ух2'^ х\х2'
(2.46)
гх2*1(У)
rX|X2 ryx2ryx2
J(l-r2 )(l-r2 )
V УЧ yx2'
(2.47)
Эмпирическое корреляционное отношение и совокупный индекс
корреляции. Эти показатели имеют такой же экономический смысл,
что и при парной регрессии, и определяются по формулам
(2.48)
47
(2.49)
Ду~у)2
Вместо теоретического корреляционного отношения мо-
жет быть использован адекватный ему показатель — совокуп-
ный индекс корреляции:
о2_
R= 1--------У..^1Х2 ;
v & v
(2.49*)
Ду-Ух^У2
Ду-у)2
Множественный коэффициент корреляции. Множественный
коэффициент корреляции характеризует влияние на результа-
тивный признак двух факторов и больше.
Множественный коэффициент корреляции имеет вид:
гух rух ryz rxz
\-r2z
(2.49**)
где rxy, г , rxz — парные коэффициенты корреляции.
Алгоритм нахождения множественного коэффициента кор-
реляции включает следующие расчетные операции.
Шаг 1. Сначала рассчитываются парные коэффициенты
корреляции rxy, ryz, rxz по приведенным ниже трем формулам:
_ nLyx-lLyLx
УХ ^[nlx2-(Дс)2][п^у2-(Zy)2] ’
_ riLyz - HyLz
-(Ez)2][«Sy2 -(by)2] ’
riLxz - ExEz
^[nZz2 -(Zz)2][wbc2 -(be)2]
48
Шаг 2. На основе заданных исходных значений х, у, z по
наблюдаемому множеству объектов п (в них должны вклю-
чаться 30 ед. по минимуму) находятся квадраты индивидуаль-
ных значений х, у, z и сумма этих квадратов, их средние зна-
чения, далее произведения ху, yz, xz и сумма этих произведе-
ний.
Шаг 3. По алгоритму трех приведенных формул находятся
соответствующие конкретные значения парных коэффициентов
корреляции rxy, ryz и rxz.
Ш аг 4. Подставив найденные эмпирические значения пар-
ных коэффициентов в исходную формулу, получим множествен-
ный коэффициент корреляции, по величине которого будем
судить о тесноте связи между наблюдаемыми факторами.
Ш аг 5. Делаем выводы о существенности или несуществен-
ности связи между наблюдаемыми явлениями и целесообразно-
сти дальнейшего изучения их связи на основе рассмотренного
метода.
Коэффициент ранговой корреляции. Наиболее простыми по-
казателями измерения тесноты корреляционной зависимости
являются коэффициенты ранговой корреляции. Один из них —
коэффициент корреляции рангов Спирмена, который рассчи-
тывается по формуле
6SJ2
и(и2 -1)
где р — коэффициент корреляции рангов;
d - разность между величинами рангов в изучаемых рядах;
п — количество рангов изучаемого ряда.
Ложные корреляции. Понятие «ложная корреляция», введен-
ное в свое время К. Пирсоном, относится к измерению индекс-
ных связей. При корреляции двух индексов, каждый из которых
представляет отношение одного к другому, при наличии у них
общего делителя между ними обнаруживается формальная связь,
несмотря на полное отсутствие ее в действительности. Отражая
ситуацию случайного совпадения, а не причинную связь между
наблюдаемыми индексами, такую корреляцию называют лож-
ной и отличают от сопутствующей корреляции двух наблюдае-
мых явлений с одним и тем же третьим, связь между которыми
49
рассматривается как иерархическая, а ее теснота устанавлива-
ется путем последовательного расчета соответствующих част-
ных коэффициентов корреляции.
Критерии оценки адекватности и измерения точности корре-
ляционной связи. Адекватность, или точность измерения тесно-
ты корреляционной связи, оценивается в статистике по разным
критериям. При малой выборке теснота связи оценивается по
^-критерию Фишера:
° Ух п~т
о2 т-1 ’
У-Ух
(2.50)
где п — число единиц наблюдения;
т — число параметров модели.
Эмпирическое значение критерия F3 сравнивается с крити-
ческим (табличным) F с уровнем значимости 0,01 или 0,05 и
числом степеней свободы (т — 1), (л — т). Если F > Fv то
эмпирические оценки корреляции признаются значимыми.
Значимость коэффициентов линейного уравнения регрессии
aQ оценивается с помощью /-критерия Стьюдента (п < 30):
t
«о
(2.51)
(2.52)
(2.53)
Эмпирическое значение /-критерия сравнивается с крити-
ческим (табличным) значением /-распределения Стьюдента с
уровнем значимости 0,01 или 0,05 и числом степеней свободы
(и — 2). Параметр корреляции признается значимым, если эм-
пирическое значение / больше табличного.
Аналогично проводится оценка коэффициента корреляции
г с помощью /-критерия, который определяется по формуле
50
(2.54)
где (и — 2) — число степеней свободы.
Если эмпирическое значение t оказывается больше таблич-
ного, то линейный коэффициент корреляции признается зна-
чимым.
Для оценки тесноты связи между атрибутивными признака-
ми применяются коэффициенты ассоциации Юла и Пирсона.
Для расчета этих коэффициентов строится четырехклеточная
корреляционная таблица (табл. 2.1).
Таблица 2.1
Корреляционная таблица для расчета
коэффициентов Юла и Пирсона
а b а + Ъ
с d с + d
а + с b + d а + b + с + d
Примечание, a, b, с, d ~ частоты сопоставляемых признаков.
Коэффициент ассоциации при этом определяется как
ad -be
ad + be
и соответственно коэффициент контингенции как
_ ad-be
к у/(а 4- Ь)(с 4- d^ta* c)(b 4- d)
(2.55)
(2.56)
Установленная эмпирическая связь между признаками счи-
тается существенной, если значения коэффициентов не меньше
0,5 и 0,3 соответственно. При этом коэффициент контингенции
всегда меньше коэффициента ассоциации.
Для оценки тесноты связи альтернативных признаков при-
меняются коэффициенты взаимной сопряженности Пирсона
или Чупрова.
51
Коэффициент Пирсона при этом определяется как
(2.57)
. 2 X1
где ф2 — показатель взаимной сопряженности, исчисляемый как ср =-.
N
Показатель ср2 можно находить так же, как сумму отноше-
ний квадратов частот каждой клетки таблицы распределения к
произведению итоговых частот соответствующего столбца и
строки минус единица.
Коэффициент взаимной сопряженности Чупрова равен:
' = I ф2 ~
(2.58)
где kv к2- число групп по каждому признаку.
2.3.
Примеры решения типовых задач
Пример 2.1. Имеются выборочные данные по 10 одно-
родным предприятиям (табл. 2.2).
Таблица 2.2
Номер предприятия 1 2 3 4 5 6 7 8 9 10
Электровооруженность труда на одного рабочего, кВтч 2 5 3 7 2 6 4 9 8 4
Выпуск готовой продукции на одного рабочего, т 3 6 4 6 4 8 6 9 9 5
Требуется построить однофакторную регрессионную модель.
Решение. Предположим, что между электровооруженностью
труда и выпуском готовой продукции существует линейная кор-
52
реляционная связь, которую можно выразить уравнением пря-
мого вида
Zv =<я0+Я1Х.
Факторным признаком является электровооруженность тру-
да, а результативным — выпуск готовой продукции.
Для определения формы корреляционной связи необходимо
вычислить параметры уравнения прямой путем решения систе-
мы нормальных уравнений вида (2.2). Для того чтобы заполнить
систему нормальных уравнений фактическими данными, необ-
ходимо определить Zxy, Zx1 2, Zy2.
Расчеты этих показателей приведем в табл. 2.3.
Таблица 2.3
Исходные данные Расчетные значения
Номер предприя- тия Элекгро- вооружен- ность труда на одного рабочего, кВтч X Выпуск продукции на одного рабочего, т У ху л2 у К (у - уУ
1 2 3 6 4 9 3,61 0,3721
2 5 6 30 25 36 6,01 0,0001
3 3 4 12 9 16 4,41 0,1682
9 8 9 72 64 81 8,38 0,381
10 4 5 20 16 25 5,20 0,04
Итого 50 60 343 304 400 60 5,761
В среднем 5,0 6,0 34,3 30,4 40,0 6,0 0,5761
Подставим в системы нормальных уравнений (2.2) факти-
ческие данные из табл. 2.2 и получим равенства:
1 Оац +50^1 = 60;
5Оао + ЗО4я1 =343.
Систему нормальных уравнений решим в такой последова-
тельности (по методу множителей): умножим каждый член пер-
вого уравнения на число, рапное 5. Получим:
53
5Одо +250#i = 300;
50470 + 304б7] = 343.
Затем вычтем из второго уравнения первое: 43 = 54а,, отку-
да а, = 43/54 = 0,7963.
После подстановки значения ах в первое уравнение получим
ах = 2,02.
Уравнение регрессии имеет вид ух = 2,02 + 0,796х.
С помощью определителей параметры уравнения прямой
можно вычислить по формулам (2.3) и (2.4).
Если параметры регрессионного уравнения определены вер-
но, должно соблюдаться равенство сумм теоретических и эмпи-
рических значений выпуска готовой продукции, а сумма разно-
стей между эмпирическими и теоретическими значениями вы-
пуска готовой продукции должна быть равна нулю.
Окончательную проверку правильности расчета параметров урав-
нения связи можно также провести подстановкой aQ и в систему
нормальных уравнений (рассматривая их как корни уравнения).
Используя уравнение корреляционной связи, можно опре-
делить теоретическое значение выпуска готовой продукции на
одного рабочего для любого промежуточного значения элект-
ровооруженности труда на одного рабочего (см. табл. 2.2).
В нашем уравнении регрессии параметр = 0,796 показыва-
ет, что с увеличением электровооруженности труда одного рабо-
чего на 1 кВт ч выпуск готовой продукции возрастет на 0,796 т.
Средний коэффициент эластичности исчислим по фор-
муле (2.6):
Э = 0,796-5/6 = 0,66.
Коэффициент эластичности, равный 0,66, показывает, что
с увеличением электровооруженности труда на 1% выпуск
готовой продукции возрастет на 0,66%.
Измерим тесноту корреляционной связи между произво-
дительностью и электровооруженностью труда линейным ко-
эффициентом корреляции, теоретическим корреляционным от-
ношением, индексом корреляции, которые рассчитываются по
формулам (2.23), (2.24), (2.27) (данные, необходимые для рас-
чета этих показателей, представлены в табл. 2.2):
54
343-50--60
10
7(304 - 502 /10)(400 - 602 /10)
= 0,926.
Для расчета теоретического корреляционного отношения
необходимо предварительно вычислить дисперсии
по формулам:
_^f = 400_36 = 4;
у п [ п ) 10
а2 =^-^)\У61 =0)5761;
у~у* п 10
о2 = о2-ст2 =4-0,5761 = 3,424.
Ух У У~Ух
Эмпирическое корреляционное отношение гр по формуле
(2.25) равно:
2 =М24=0 856
4
Коэффициент детерминации т| по формуле (2.26) равен
0,925. Индекс корреляции R по формуле (2.27) равен:
/? = Ji-2^1
V 4
= 0,925.
Все показатели тесноты корреляционной связи показыва-
ют тесную связь между производительностью и электровоору-
женностью труда. Коэффициент детерминации 0,856 означа-
ет, что вариация выработки рабочих на 85,6% объясняется ва-
риацией электровооруженности труда и на 14,4% — прочими
факторами.
Так как г = R = ц, можно сделать заключение, что гипотеза
о линейной форме связи подтверждена.
55
Проведем оценку адекватности регрессионной модели ух =
= 2,02 + 0,797х, выражающей зависимость между произво-
дительностью и электровооруженностью труда, с помощью
F-критерия Фишера по формуле
F3 =
0,5761 2-1
(2.59)
Табличное значение Fy с уровнем значимости 0,95 и чис-
лом степеней свободы (2 — 1), (10 — 2) равно 5,32. Так как
F3 > Ер уравнение регрессии можно признать адекватным.
Оценим значимость параметров уравнения регрессии с по-
мощью /-критерия Сьюдента по формулам (2.60) и (2.61):
/ =2,02- =7,53;
а° VO,5761
/а| = 0,796-
Ю-2 „ г оо
-------- 2,32 — 6, оо.
0,5761
(2.60)
(2.61)
Значение ох вычисляется по формуле
0 = 730,4-25 = 2,32. (2.62)
Табличное значение /-критерия с уровнем значимости 0,05
и числом степеней свободы (п — 2) равно 2,307.
Так как /э > t, параметры уравнения регрессии можно
признать значимыми.
Значимость коэффициента корреляции оценим с помощью
t-критерия по формуле
tr = 0,926-
10-2
1 -0,9262
= 6,9.
(2.63)
Эмпирическое значение t больше табличного, следователь-
но, коэффициент корреляции можно признать значимым.
Вычислим ошибку аппроксимации по формуле
56
£ = 1^1Г_Ы.1ОО;
W у
^^"^1 = 0,58;
У
ё = — 0,58 100 = 5,8%.
10
Поскольку параметры уравнения регрессии значимы, урав-
нение значимо, показатели тесноты значимы, ошибка апп-
роксимации равна 5,8%, коэффициент детерминации равен
0,856, можно сделать заключение, что построенная регресси-
онная модель зависимости производительности труда от его
электрово-оруженности ух = 2,02 + 0,796х может быть исполь-
зована для анализа и прогноза.
Пример 2.2. Имеются данные по 52 предприятиям отрас-
ли (табл. 2.4).
Таблица 2.4
Группа заводов по фондовоору- женности, млн руб. X Количество заводов f Объем продукции, млн руб. У
5—7 1 3,0
7-9 2 5,0
9—11 3 6,3
21-23 2 17,0
23-25 1 19,0
Требуется по исходным данным найти параметры линейно-
го корреляционного уравнения, характеризующего зависимость
между продукцией и фондовооруженностью.
Решение. Параметры линейного уравнения регрессии ух =
= aQ + а{х можно вычислить по формулам (2.3) — (2.5). Рас-
четные данные для вычисления параметров представлены в
табл. 2.5.
57
Таблица 2.5
X X f y,f х/ y,xf -2 г x f
5-7 6 1 3,0 3,0 6 18,0 36
7—9 8 2 5,0 10,0 16 80,0 128
9-11 10 3 6,3 18,9 30 189,0 300
21-23 22 2 17,0 34,0 44 748,0 968
23-25 24 1 19,0 19,0 24 456,0 576
Итого — 52 — 550,2 766 8641,2 11924
Расчетные данные из табл. 2.5 подставим в формулы (2.8),
(2.9) и определим параметры а0, ау:
550,2-11924-8641,2-766
йл =----------------------= -1,763;
и 52-11924-766-766
52-8641,2-766-550,2 п опо
а\ =--------------------= 0,838.
1 52-11924-766-766
Параметр а, показывает, что с ростом фондовооруженно-
сти на 1 млн руб. объем произведенной продукции увеличива-
ется на 0,838 млн руб.
Уравнение регрессии имеет вид:
ух =-1,763 + 0,838%.
Пример 2.3. Имеются следующие данные по 10 однород-
ным магазинам (табл. 2.6):
Таблица 2.6
Товарооборот, тыс. руб. 5 3 24 35 44 55 63 74 82 95
Товарные запасы, дней 18 12 8 8 8 8 7 6 8 8
58
Требуется определить уравнение регрессии (связь гипербо-
лическая) между товарооборотом и товарными запасами.
Решение. Для вычисления параметров уравнения гипербо-
1
лы вида ух - ао + а\ — необходимо построить систему нормаль-
ных уравнений (2.17), (2.18) и методом определителей вычис-
лить параметры aQ и а} по формулам (2.19) и (2.20). Расчетные
данные для вычисления параметров уравнения гиперболы со-
держатся в табл. 2.7.
Подставив значения фактических данных из табл. 2.4 в си-
стему нормальных уравнений, получим:
10^+0,6966^ =91;
0,6966^+0,1550^ =8,8631.
Вычислим параметры aQ и а{ по формулам (2.19), (2.20),
подставив расчетные данные из табл. 2.7:
91 0,1550-8,8631 0,6966 , ЛАО
а0 =---------------------= 7,448;
° 10 0,1550-0,6966-0,6966
10 0,8631-0,6966-91
сь =---------------------= 23,7.
1 10 0,1550-0,6966 -0,6966
Уравнение регрессии имеет вид
ух = 7,448 + 23,7—.
X
Пример 2.4. Имеются следующие данные (табл. 2.8) по
группе однородных предприятий.
Требуется найти уравнение логарифмической корреляцион-
ной зависимости продукции от основных фондов.
Решение. Параметры степенного уравнения можно найти
путем решения системы логарифмических уравнений (2.12) или
по формулам определителей {2.13) и (2.14).
59
Таблица 2.7
№ п/п Товарооборот, тыс. руб. X Товарные запасы, дней У 1 X 2 ух = 7,448 + 23,7- X
1 5 18 0,2000 0,0400 3,6000 12,19
2 3 12 0,3333 0,1111 3,9996 15,35
3 24 8 0,0417 0,0017 0,3336 8,44
9 82 8 0,0122 0,0001 0,0976 7,74
10 95 8 0,0105 0,0001 0,0840 7,69
Итого 480 91 0,6966 0,1550 8,8631 91,0
Таблица 2.8
(тыс. руб.)
Номер завода 1 2 3 4 5 6 7
Основные фонды 330 400 480 550 600 700 750
Продукция 9,9 10,8 11,5 12,0 12,4 12,9 13,1
Продолжение
Номер завода 8 9 10 11 12 13
Основные фонды 850 870 940 1020 1030 1200
Продукция 13,5 13,6 13,8 14,0 14,1 14,2
Определим параметры степенной функции по формулам
(2.15), (2.16) (расчетные данные для вычисления параметров
содержатся в табл. 2.9):
Таблица 2.9
№ п/п Основные фонды, тыс. руб. X Продукция, тыс. руб. У 1g X 1g У 1g X 1g у (W
1 330 9,9 2,5185 0,9956 2,5074 6,3428
2 400 10,8 2,6021 1,0334 2,6890 6,7709
3 480 11,5 2,6812 1,0607 2,8439 7,1888
12 1030 14,1 3,0128 1,1492 3,4623 9,0770
13 1200 14,2 3,0792 1,1523 3,5482 9,4815
Итого 36,9832 14,3415 40,8982 105,5631
В среднем 2,8449 1,1032 3,1460 8,1202
а1Л146°-Р032:2^ = 0,2819;
8,1202-2,84492
1g а0= 1,1032-0,2819-2,8449 = 0,3012;
а0 =2,008.
61
Уравнение корреляционной связи имеет вид:
Igy = lg2,008 + 0,28191g лг,
или 1g у - 0,3012 + 0,28191g х,
или ух = 2,0008л°’2819.
Параметр ах показывает, что с ростом основных фондов на
1% продукция увеличится на 0,28%.
Пример 2.5. Имеются следующие данные о выработке, про-
должительности внутрисменных простоев и производственном
стаже рабочих (табл. 2.10).
Таблица 2.10
Номер рабочего Выработка продукции, т Продолжительность внутрисменных простоев, мин Производственный стаж, лет
1 39,0 19 4
2 38,7 15 3
3 38,9 17 4
9 40,4 10 7
10 39,5 13 5
Требуется найти уравнение множественной регрессии, ха-
рактеризующее связь между выработкой, продолжительностью
внутрисменных простоев и производственным стажем рабочих.
Решение. Предположим, что связь между исследуемыми при-
знаками линейная и уравнение регрессии имеет вид
Уххх2 W + “2*2>
где — продолжительность внутрисменных простоев;
х2 — производственный стаж рабочих;
у — выработка изделий.
Параметры уравнения множественной регрессии определим
по формулам (2.32) — (2.34). Необходимые данные для расчета
параметров находятся так, как это показано в табл. 2.11.
62
Таблица 2.11
Исходные данные Расчетные данные
номер рабочего выра- бот- ка, т У внутри- сменные простои, мин *1 производ- ственный стаж, лет *2 У2 Х12 4 Ух2 *1*2 (У ^*1*2)
\ 1 39,0 19 4 1521,0 361 16 741 156,0 76 38,841 0,3721
2 38,7 15 3 1497,69 225 9 580,5 116,1 45 38,912 0,0001
3 38,9 17 4 1513,21 289 16 661,3 155,6 68 38,981 0,1681
9 40,4 10 7 1632,16 100 49 404,0 282,8 70 40,098 0,3844
10 39,5 13 5 1560,25 169 25 513,5 197,5 65 39,470 0,04
Итого 394 140,0 50,0 15526,1 2030 264 5506,1 1974,6 676 394,0 5,763
В сред- нем 39,4 14,0 5,0 1552,61 203 26,4 550,61 197,46 67,6 39,4 0,576
Проведем расчет параметров уравнения множественной рег-
рессии, предварительно вычислив <зх , <зх , о по данным табл. 2.11.
Подставив в формулу (2.38) данные из табл.2.11, получим
значение о :
xi
о„, = J203 -142 = 2,646 мин.
Подставив в формулу (2.40) данные из табл. 2.11, вычислим
значение о :
Л2
О,- J26,4 - 52 =1,183 года.
Подставив в формулу (2.39) данные из табл. 2.11, получим
значение
оу = 71552,61-39,42 = 0,5 т.
Вычислим коэффициенты корреляции по формулам (2.35)—
(2.37). Подставим данные из табл. 2.11 и вычисленные значе-
ния о в формулы коэффициентов корреляции (2.42) — (2.44).
Вычислим г ,г , г :
Ух1’ ух2’ ххх2
550,61-14-39,4
’------------= = -0,748;
т 2,646-0,5
19^46-5^
У 2 1,183 0,5
67,6-14 5
=-----------= -0,767.
Х}Х2 2,646 1,183
Подставив в формулы (2.32) — (2.34) найденные значения
парных коэффициентов корреляции и средних квадратиче-
ских отклонений, получим искомые параметры а0, av а2:
64
а0 = 39,4 - (- 0,07) • 14 - 0,209 • 5,0 = 39,335;
-0,748-0,777 (-0,767) 0,5
Я] = — ----------Ц< — = - О,07;
1-(-0,767) 2>646
а _0,777-(-0,748) (-0,767) 0,5
2 1 -(-0,767)2 1,183
Уравнение множественной регрессии имеет вид
= 39,335-0,07^ +0,209х2.
Параметр ах показывает, что с увеличением внутрисменных
простоев на 1 мин выработка продукции снижается на 0,07 т.
Параметр а2 показывает, что с увеличением стажа рабочего
на 1 год выработка продукции увеличивается на 0,209 т.
Вычислим частный коэффициент эластичности:
14 0
9i = -0,07 —- = -0,0248,
1 39,4
где Эх = - 0,0248 показывает, что с увеличением простоев на 1% выра-
ботка продукции снижается на 2,48%.
Вычислим коэффициенты эластичности выработки от ста-
жа по формуле (2.39):
Э2 =0,209 -^1 = 0,0265.
39,4
Коэффициент эластичности Э2 показывает, что с увеличе-
нием стажа на 1% выработка увеличивается на 2,65%.
Бета-коэффициенты вычислим по формулам:
Р1 =-0,07 •^^ = -0,37;
0,5
1 183
В2 = 0,209 == = 0,494.
- 0,5
65
Анализ бета-коэффициентов показывает, что наиболее силь-
ное влияние на производительность труда оказывает стаж ра-
бочего.
Измерим тесноту корреляционной связи между выработкой
рабочих, внутрисменными простоями и стажем работы с помо-
щью парных коэффициентов корреляции. Эти показатели, вы-
численные ранее при определении параметров уравнения рег-
рессии, равны:
Г =-0,748; = 0,777; гх^ =-0,767.
Анализ коэффициентов корреляции показывает, что меж-
ду выработкой и внутрисменными простоями существует тес-
ная обратная корреляционная связь, между выработкой и ста-
жем работы — тесная прямая связь. Коэффициенты парной
корреляции отражают влияние на результативный признак не
только исследуемого фактора, но и других, не включенных в
модель факторов, которые связаны с исследуемым фактором.
Для более точной оценки тесноты корреляционной связи
вычислим коэффициенты частной корреляции (2.45) — (2.47):
-0,748-0,777-(-0,767)
УЧ(*2) ~ I 2 2~~
7(1 - 0,7772) (1 - (- 0,767)2)
(2.64)
= -0,777-(-0,748)-(-0,767) (2.65)
УЧ! 14/ I 77 ’ ’
7(1 - (-0,748)2) (1 - (- 0,767)2)
-0,767-(-0,748)0,777 „
’х^М ~ I j Г” °>445.
7(1 - (-0,748)2) (1 - (- 0,7772)
(2.66)
Коэффициенты частной корреляции показывают, что вли-
яние стажа рабочих на выработку при исключении влияния
внутрисменных простоев меньше, чем при парной корреля-
ции. Большое влияние на выработку оказывает стаж рабочих.
Вычислим множественный коэффициент корреляции по
формуле (2.49*):
66
R - j- 0,7482 + 0,7472 - 2(- 0,748) 0,777 (-0,767) _
Ух'Х2 V 1 — 0,7672 (2.67)
= ^0,7566 =0,869.
Для измерения тесноты корреляционной связи между вы-
работкой, простоем и стажем рабочего вычислим совокупный
индекс корреляции по формуле (2.49). Для этого построим
вспомогательную таблицу (табл. 2.12), в которой приведем еще
раз исходные данные из табл. 2.11. Уравнение множественной
регрессии рассчитано по формуле
уХ|Л?2 = 39,335-0,07^ +0,209х2.
(2.68)
Для расчета индекса корреляции по формуле (2.68) предва-
2 гг2
рительно вычислим общую и остаточную Оу-Хх1х2 диспер-
сии по формулам:
gZ (2.69)
у п 10
< ^k^,-;)=0j49 = 0[|g49 (2.70)
У П 10
Индекс корреляции по формуле (2.49*) равен:
Я =11-0,0849 = ^0,659 =0,812.
V 0,25 V
(2.71)
Значения множественного коэффициента корреляции и ин-
декса корреляции 0,869 и 0,812 свидетельствуют о наличии тес-
ной корреляционной связи между выработкой, стажем и внут-
рисменными простоями, а расхождение между ними менее 0,1
подтверждает гипотезу о линейной форме связи.
67
Таблица 2.12
Номер рабочего Выра- ботка, т У Внутри- сменный простой, мин *1 Стаж, лет *2 Расчетные данные
у-у Л[Х2 (^-^,х2)2 У-УхЛ У
1 39,0 19 4 -0,4 0,16 38,841 0,159 0,025 0,004
2 38,7 15 3 -0,7 0,49 387,912 -0,212 0,045 0,0054
3 38,9 17 4 0,5 0,25 38,981 -0,081 0,007 0,0020
9 40,4 10 7 1,0 1,00 40,098 0,302 0,091 0,0074
10 39,5 13 5 0,1 0,01 39,470 0,030 0,0009 0,0007
Итого 394,0 140,0 50,0 - 2,5 394,0 - 0,849 0,0814
В сред- нем 39,4 1,40 5,0 - 0,25 39,4 - 0,0849 -
Оценим адекватность данной регрессионной модели
=39,335-0,07^+0,209х2 с помощью F-критерия Фи-
шера. Для этого предварительно вычислим факторную дис-
персию:
о2 =<5у-<52_ =0,25-0,0849 = 0,165.
Ух1х2 У УХ] Х2
F-критерий равен:
_0Д65_ 10-3
э 0,0849 3-1
(2.72)
Табличное значение FT с уровнем значимости 0,05 и числом
степеней свободы (2.2), (2.7) равно 4,74. Так как F3 > Fr, урав-
нение регрессии можно признать значимым, адекватным.
Оценим значимость параметров уравнения множественной
регрессии с помощью /-критерия Стьюдента:
-0,07 2,646 д/1-0,7672 710-3-1
0,5 л/1 - 0,8692
0,209 1,18371-(-0,767)2
‘а2 =---------------— -----------= 1,67.
0,5 л/1 - 0,8692
Табличное значение /-критерия с уровнем значимости 0,05
и числом степеней свободы 6 равно 2,447. Так как /э < /т, в
отношении значимости параметров и а2 уравнения регрес-
сии возникают сомнения.
Одной из причин такой неопределенности суждения отно-
сительно параметров ах и а2 является небольшое число наблю-
дений. Эта величина должна превышать число параметров в
6—7 раз, поэтому в данном случае она должна составлять не
менее 18 ед.
Оценим значимость коэффициента множественной корре-
ляции с помощью /-критерия Стьюдента:
0,869 710- 3 -1
1 — 0,8692
(2.73)
69
Табличное значение ^критерия с уровнем значимости 0,05 и
числом степеней свободы 6 равно 2,447. Так как t3 > ?т, коэффи-
циент множественной корреляции можно признать значимым.
Коэффициент детерминации, равный 0,659, показывает,
что вариация выработки на 65,9% объясняется вариацией внут-
рисменных простоев и стажем работы, а на 34,1% — прочими
факторами.
Вычислим среднюю ошибку аппроксимации:
- 0,0814
е =-------
10
100 = 0,8%,
где УХ'Х-2 =0,0814.
У
Пример 2.6. Имеются следующие данные (табл. 2.13).
Таблица 2.13
Семья Расход семьи на одежду в месяц, долл. США У Доход семьи в месяц, долл. США X Размер семьи, чел. Z
1 18,63 80,87 2,0
2 19,47 90,73 2,1
3 12,89 109,17 2,2
4 21,17 113,07 2,2
5 25,22 120,22 2,3
6 17,05 135,66 2,3
7 33,60 140,99 2,4
8 27,03 151,07 2,4
9 40,62 175,96 2,5
10 43,10 188,97 2,5
На основе приведенных данных самостоятельно постройте
расчетную таблицу и исчислите соответствующие коэффици-
енты парной и множественной корреляции г , ryz, rxz и Ryxz-
Пример 2.7. Измерим тесноту корреляционной связи
между прибылью туристических фирм и затратами на рекламу
с помощью коэффициентов взаимной сопряженности Пирсо-
на и Чупрова (табл. 2.14).
70
pf Таблица 2.14
Затраты Низкие Средние Высокие Итого
"Низкие 3 14 — 17
Средние 4 29 10 43
Высокие — 15 25 40
Итого 7 58 35 100
Согласно данным табл. 2.14 по формулам (2.57) - (2.58)
получаем:
2 ( З2 42 142 292 152 102 252 'I
<р = ---+------+------+------+------+-----+------- -1=0,275-
у 717 743 58 17 58-43 58-40 35-43 35-40
\ 7
0,275
С = “ ^’^64 (коэффициент Пирсона);
К = ^-^===== = 0,37 (коэффициент Чупрова).
Коэффициенты показывают, что между прибылью тури-
стических фирм и их затратами на рекламу существует замет-
ная связь.
Решение.
1. Для получения искомых коэффициентов корреляции воз-
ведем исходные значения х, у, z в степень, определим их сум-
мы, средние и произведения ух, yz, xz.
2. Результаты расчетов представляем в табличной форме.
3. Подставив полученные значения в формулу парных ко-
эффициентов корреляции, имеем:
36531,7541-258,78 1306,71
гух = ----- - - -- = 0,848;
7(1817031,951- (1306,71)2 ] [7634,4050 - (258,78)2 ]
6051,12-258,78-22,9 п о,п
ryz~ I—- 2 5 0»819;
V[526,9 - (22,9)2 ] [7634,4050 - (258,78)2 ]
30429,94-1306,71-22,9 п п,п
rxz = . rz - 0,969.
7(526,9 - (22,9)2 ][1817031,951 — (1306,71)2 ]
71
Определим множественный коэффициент корреляции, под-
ставив в его формулы значения найденных парных коэффи-
циентов:
„ /о,8482 +0,8192 -2 0,848 0,819 0,969 п о„о
У \ 1-0,9692
Значение множественного коэффициента корреляции, рав-
ное 0,848, свидетельствует о наличии тесной связи между рас-
ходами на одежду, доходом и размером семьи.
Пример 2.8. В результате наблюдения у 6800 чел. был
установлен цвет волос и глаз. Оказалось, что у разных людей
связь между цветом глаз и цветом волос разная.
Требуется подтвердить, существует ли устойчивая связь между
цветом глаз и цветом волос у людей.
Решение.
1. По данным наблюдения строим групповую таблицу (табл.
2.15).
Таблица 2.15
Цвет глаз Цвет волос Итого
светлый темный
Светлый 2814 3129 5943
Темный 131 726 857
Итого 2945 3855 6800
Определим формулу, с помощью которой рассчитаем ко-
эффициент ассоциации:
& _ ad -be
у](а + b)(b + с)(а + с)(с + d)
Определим значение коэффициента ассоциации:
2817726-3129 131 ЛО
Лд I - - - 0,0.
л/5943-857-2945-3855
Сделаем вывод о наличии или отсутствии связи между цве-
том глаз и цветом волос у людей.
Зная, что при Ка > 0,3 связь прямая и тесная, можем на основе
найденного коэффициента однозначно утверждать, что связь меж-
ду наблюдаемыми качественными признаками существует.
72
Пр имер 2.9. По приведенным ниже данным (табл. 2.16)
требуется оценить существенность связи между цветом глаз
дочерей и цветом глаз матерей с помощью коэффициентов
ассоциации и контингенции.
Таблица 2.16
Цвет глаз дочерей Цвет глаз матери Итого
светлый темный
Светлый 471(a) 148(6) 619(а+/>)
Темный 151(c) 230(d) 381(c+rf)
Итого 622(а+с) 378(6+d) 1000(a+c+Z>+rf)
Коэффициенты ассоциации и контингенции (взаимной со-
пряженности) вычислим по формулам (2.56) и (2.58) соответ-
ственно:
_ 471 230-148.151 _
Ak = ...= "• = = 0, Зоо,
>/619 381-622 378
„ 471-230-148 151 п
К„ = .. — = 0,657.
>/471 230+148 151
Так как К > 0,5 и К. > 0,3, можно сделать заключение о
а к
существовании значимой корреляционной связи между цветом
глаз матерей и дочерей.
2.4.
Задачи для самостоятельных занятий
Задача 2.1. Имеются следующие данные по 10 однород-
ным предприятиям (табл. 2.17).
Таблица 2.17
Номер предприятия 1 2 3 4 5 6 7 8 9 10
Элекгровооружен- ность труда на одного рабочего, кВт ч 10 12 14 17 24 28 30 35 40 50
Выпуск готовой про- дукции на одного рабочего, т 18 17 14 12 10 10 8 9 6 6
73
Требуется построить по исходным данным однофакторную
регрессионную модель зависимости между выпуском брако-
ванной продукции и профессиональной подготовкой рабо-
чих. Вычислите коэффициенты эластичности, показатели тес-
ноты корреляционной связи. Проверьте найденную модель на
адекватность. Сделайте выводы. Постройте графики.
Задача 2.2. Имеются следующие данные по 120 предпри-
ятиям отрасли (табл. 2.18).
Таблица 2.18
Энерговооруженность, кВтч Количество заводов Производительность труда, шт.
7-10 6 14
10-13 11 16
13-16 35 19
16-19 26 22
19-21 17 25
21-24 12 27
24-27 8 31
27-30 5 35
Требуется построить по исходным данным линейное урав-
нение корреляционной связи между энерговооруженностью и
производительностью труда. Сделайте выводы о пригодности
модели для анализа и прогноза.
Задача 2.3. Имеются следующие данные по восьми одно-
родным магазинам (табл. 2.19).
Таблица 2.19
Товарооборот, тыс. руб. 7 10 15 20 30 45 60 120
Уровень издержек об- ращения по отношению к товарообороту, % 10,0 9,0 7,5 6,0 6,3 5,8 5,4 5,0
Требуется найти уравнение корреляционной связи товаро-
оборота и уровня издержек обращения. Изобразите графически
корреляционную связь. Вычислите коэффициенты эластично-
сти, показатели тесноты корреляционной связи. Проверьте най-
денную модель на адекватность. Сделайте выводы. Постройте
графики.
74
Задача 2.4. Имеются следующие данные по 25 предпри-
ятиям отрасли (табл. 2.20).
Таблица 2.20
Номер предприятия Продукция, тыс. шт. Потребление сырья, тыс. т Объем электро- потребления, кВтч
1 24,6 3,2 2,3
2 37,4 4,1 1,7
3 45,4 2,2 0,9
4 46,7 1,6 2,0
5 50,1 4,4 2,7
6 51,3 10,5 3,7
7 55,0 2,6 1,0
8 66,5 5,7 2,0
9 68,3 9,5 2,1
10 70,8 5,0 1,6
11 86,1 2,8 2,0
12 96,9 8,1 2,3
13 99,1 6,0 1,5
14 111,9 6,2 2,8
15 122,6 10,6 4,2
16 166,9 8,3 2,6
17 171,6 6,1 2,2
18 173,8 9,8 3,5
19 177,5 9,6 8,5
20 177,6 13,3 4,2
21 171,2 12,3 4,6
22 213,0 7,7 3,9
23 257,1 13,1 6,5
24 269,3 19,5 5,3
25 359,2 21,5 7,8
Требуется найти по исходным данным уравнение корреля-
ционной связи (связь линейная) между продукцией, потреб-
лением сырья и объемом электроэнергии. Вычислите коэффи-
циенты эластичности, бета-коэффициенты, показатели тесно-
ты корреляционной связи. Оцените адекватность найденной
модели. Проведите анализ модели и сделайте заключение о
пригодности полученной модели для анализа и прогноза.
75
Задача 2.5. Имеются следующие данные по заводу,при-
веденные в табл. 2.21.
Таблица 2.21
Группа рабочих Число рабочих в группе Всего
выполнившие и перевыполнившие норму не выполнившие норму
Прошедшие техни- ческое обучение Не прошедшие тех- ническое обучение 115 15 20 50 135 65
Итого 130 70 200
Требуется определить степень тесноты связи между выпол-
нением норм выработки и технической подготовкой рабочих.
Задача 2.6. Имеются следующие данные о садовых насаж-
дениях в 100 фермерских хозяйствах (табл. 2.22).
Таблица 2.22
Фермерские хозяйства Садовые насаждения Итого
отсутствуют имеются
Отсутствуют 32 14 46
Имеются 20 34 54
Итого 52 48 100
Требуется определить тесноту связи между наличием фер-
мерских хозяйств и садовых насаждений.
Задача 2.7. Имеются данные о внесении удобрения в по-
чву и урожайности по 50 участкам (табл. 2.23).
Таблица 2.23
Степень удобрения почвы Урожайность
низкая высокая
Низкая 16 10
Высокая 6 28
Требуется установить тесноту связи между урожайностью
и степенью удобрения почвы.
76
Задача 2.8. Получены следующие данные в результате
обследования населения района (табл. 2.24).
Таблица 2.24
Семьи Число лиц, имею- щих сбережения Число лиц, не имею- щих сбережений Всего
Одинокие 480 360 840
Полные 1500 900 2400
Итого 1980 1260 3240
Требуется установить тесноту связи между семейным поло-
жением и наличием сбережений.
Тесты и вопросы для самоконтроля
Тесты
1. Индекс физического объема продаж по своей величине
находится в интервале:
а) до 0,7;
б) 0,7 - 1,0;
в) 1,0 и более.
Правильный ответ', б).
2. Значение общего индекса товарооборота:
а) больше единицы;
б) меньше единицы.
Правильный ответ', б).
3. Абсолютное снижение товарооборота (выручки от прода-
жи всех товаров), равное 11,143 тыс. руб., обусловлено:
а) средним изменением цен;
б) средним изменением физического объема продаж;
в) действием двух указанных факторов вместе.
Правильный ответ: б).
4. Найденное значение индекса производительности труда
переменного состава показывает изменение средней произво-
дительности (выработки на одного рабочего) за счет:
а) среднего изменения собственно производительности тру-
да по предприятиям;
б) изменения структуры рабочих по предприятиям;
в) действия двух указанных факторов вместе.
77
Правильный ответ: в).
5. Вычисленное значение индекса производительности труда
постоянного состава находится в интервале:
а) до 1,25;
б) 1,25 и более.
Правильный ответ: б).
6. Индекс структурного сдвига:
а) меньше единицы;
б) равен единице;
в) больше единицы.
Правильный ответ: а).
7. Абсолютный прирост средней производительности труда
за счет структурного сдвига численности рабочих представляет
собой значение:
а) положительное;
б) нулевое;
в) отрицательное.
Правильный ответ: в).
8. Индекс заработной платы постоянного состава по своей
величине:
а) отрицателен;
б) положителен, но менее 1,15;
в) положителен и более 1,15.
Правильный ответ: в).
9. Индекс заработной платы постоянного состава показыва-
ет изменение среднего заработка за счет:
а) среднего изменения собственно заработков рабочих по
цехам;
б) изменения структуры численности рабочих между цехами;
в) действия двух указанных факторов вместе.
Правильный ответ: а).
10. Индекс структурного сдвига по своей величине:
а) меньше единицы;
б) больше единицы;
Правильный ответ: б).
11. Абсолютный прирост средней заработной платы, рав-
ный 46 руб., вызван:
а) средним ростом собственно заработной платы;
б) изменением структуры рабочих по цехам;
в) одновременным действием двух указанных факторов.
78
Правильный ответ*, б).
12. По характеру различают связи:
а) функциональные и статистические;
б) функциональные, криволинейные и прямые;
в) корреляционные и обратные;
г) статистические и прямые.
Правильный ответ*, а).
13. При прямой (положительной) связи с увеличением фак-
торного признака результативный признак:
а) уменьшается;
б) не изменяется;
в) увеличивается.
Правильный ответ: в).
14. Отметьте методы, используемые для выявления нали-
чия, характера и направления связи в статистике:
а) средних величин;
б) сравнения параллельных рядов;
в) аналитической группировки;
г) относительных величин;
д) графический.
Правильные ответы: б), в), д).
15. Отметьте метод, используемый для выявления формы
воздействия одних факторов на другие:
а) корреляционный анализ;
б) регрессионный анализ;
в) индексный анализ;
г) дисперсионный анализ.
Правильный ответ: б).
16. Отметьте метод, используемый для количественной оцен-
ки силы воздействия одних факторов на другие:
а) корреляционный анализ;
б) регрессионный анализ;
в) метод аналитической группировки;
г) метод средних величин.
Правильный ответ: а).
17. Расположите по степени важности следующие формы
корреляционной взаимосвязи:
а) объем изучаемой совокупности (численность ее единиц);
б) предварительный теоретический анализ внутренних свя-
зей явлений;
79
в) фактически сложившиеся закономерности в связном изме-
нении явлений.
Правильные ответы, а), б), в).
18. Какой график (рис. 2.2) лучше всего характеризует за-
висимость урожайности от количества внесенных минераль-
ных удобрений (по линии абсцисс откладываются значения
объема внесенных удобрений, по оси ординат — урожайности).
в г
Рис. 2.2. Графики четырех видов зависимостей
Правильный ответ: г). Поскольку перенасыщение почвы
минеральными удобрениями вначале приведет к снижению уро-
жайности, а в конечном итоге — к полному ее исчезновению.
19. Если ограниченность данных (см. тест 18) позволяет ил-
люстрировать зависимость урожайности от количества внесен-
ных удобрений с помощью прямой линии, какой график пред-
почтительнее: а или 61
Правильный ответ: б). Поскольку почва без удобрений все
равно плодородна.
20. Какую форму линии регрессии (форму связи) нужно
выбрать для наилучшего отображения изменения численности
населения территории (естественного прироста) (рис. 2.3):
80
а) прямую;
б) параболу;
в) гиперболу;
г) степенную;
д) логистическую.
Рис. 2.3
Правильный ответ: г). Поскольку такие изменения осуще-
ствляются в геометрической прогрессии.
21. Какие показатели по своей величине существуют в пре-
делах от —1 до +1:
а) эмпирический коэффициент детерминации;
б) теоретический коэффициент детерминации;
в) линейный коэффициент корреляции;
г) эмпирическое корреляционное отношение;
д) теоретическое корреляционное отношение (индекс кор-
реляции).
Правильный ответ’, в).
22. Коэффициент регрессии при однофакторной модели
(параметр о,) показывает:
а) на сколько единиц изменяется функция при изменении
аргумента на 1 ед.;
б) на сколько процентов изменяется функция при измене-
нии аргумента на 1 ед.
81
Правильный ответ', а).
23. Коэффициент эластичности показывает:
а) на сколько процентов изменяется функция с изменени-
ем аргумента на 1 ед. своего измерения;
б) на сколько процентов изменяется функция с изменени-
ем аргумента на 1%;
в) на сколько единиц своего измерения изменяется функ-
ция с изменением аргумента на 1%.
Правильный ответ', б).
24. Величина индекса корреляции, равная 1,587, свидетель-
ствует:
а) об отсутствии взаимосвязи между признаками;
б) о слабой взаимосвязи;
в) о заметной или сильной (тесной) взаимосвязи призна-
ков;
г) об ошибках в вычислениях.
Правильный ответ: г). Поскольку этот показатель по своей
величине не превышает единицы.
25. Отрицательная величина эмпирического корреляцион-
ного отношения свидетельствует:
а) об отсутствии взаимосвязи;
б) о наличии отрицательной взаимосвязи;
в) о наличии положительной взаимосвязи;
г) о неверности предыдущих выводов.
Правильный ответ: г). Поскольку этот показатель не может
быть отрицательным.
26. Что является наиболее корректным при пояснении зна-
чения эмпирического коэффициента детерминации, равного
64,9%:
а) результативный признак зависит от факторного призна-
ка на 64,9%:
б) вариация результативного признака на 64,9% определя-
ется вариацией факторного признака;
в) доля межгрупповой дисперсии в общей дисперсии ре-
зультативного признака составляет 64,9%;
г) вариация результативного признака зависит от прочих
(кроме факторного) признаков на 33,1%.
Правильные ответы: б), в) и г). См. тема 4.
27. Сделайте правильный вывод о направлении и характере
связи между прожиточным минимумом и средней заработной
платой населения по 10 районам РФ, используя метод сравне-
ния параллельных рядов (табл. 2.25):
82
Таблица 2.25
Номер района Средняя заработная плата, тыс. руб. Прожиточный минимум на душу населения, тыс. руб.
1 0,52 0,28
2 0,57 0,33
3 0,69 0,34
4 0,77 0,34
5 0,90 0,33
6 0,97 0,38
7 1,04 0,46
8 1,08 0,49
9 1,49 0,52
10 1,63 0,49
а) связь прямая статистическая;
б) связь прямая функциональная;
в) связь обратная статистическая;
г) связь обратная функциональная.
Правильный ответ', а).
28. Сделайте правильный вывод о характере, направлении и
тесноте связи между стоимостью основных фондов и среднесу-
точной переработкой сырья по следующим данным (табл. 2.26):
Таблица 2.26
Стоимость основных фондов, тыс. руб. Среднесуточная переработка сырья, тыс. ц Итого
4-6 6-8 8-10 10-12
250-350 2 — — — 2
350-450 6 3 — — 9
450-550 2 5 7 — 14
550-650 — 6 2 37 7
650-750 — — -1 — 8
Итого 10 10 10 10 40
а) связь прямая, корреляционная, достаточно тесная;
б) связь обратная, корреляционная, тесная;
в) связь прямая, функциональная, слабая;
г) связь обратная, функциональная, слабая.
Правильный ответ', а).
83
29. Сделайте правильный вывод о характере, направлении
и тесноте связи между уровнем издержек обращения и уров-
нем рентабельности по 40 фирмам (табл. 2.27):
Таблица 2.27
Уровень издержек обращения, % Уровень рентабельности, % Итого
2,5-3,5 3,5-4,5 4,5-5,5 5,5-6,5
3,0-3,5 — — — 9 9
3,5-4,0 — — 6 1 7
4,0-4,5 — 3 4 — 7
4,5-5,0 2 7 — — 9
5,0-5,5 8 — — — 8
Итого 10 10 10 10 40
а) связь прямая, корреляционная, достаточно тесная;
б) связь обратная, корреляционная, тесная;
в) связь прямая, функциональная, слабая;
г) связь обратная, функциональная, слабая.
Правильный ответ*, б).
30. Выберите формулу и рассчитайте эмпирическое корре-
ляционное отношение по следующим данным, если известно,
что общая дисперсия результативного признака равна 3258,7
(табл. 2.28).
Таблица 2.28
Группы банков по объему собственных средств, млрд руб. Число банков Привлеченные средства в среднем на один банк, млрд руб.
15-30 5 85
30-45 8 135
45-60 11 180
60-75 6 220
Итого 30 160,2
а) 0,629;
б) 0,778;
в) 0,405.
Правильный ответ: б).
84
31. Выберите формулу и вычислите эмпирическое корре-
ляционное отношение, если известно, что общая дисперсия
равна 38, групповые дисперсии of =12, 02=8, 03=18, а чис-
ленность групп — соответственно 30, 50 и 20 ед.
а) 0,839;
б) 1,209;
в) 0,603.
Решение.
П= Е= = з/0,705 =0,839,
Vo2 V 38 V
где 82 =о2 — (ст,)2 =38 —(12-30 + 8-50 +18-20): 100 = 38 —11,2 = 26,8.
Следовательно, связь между признаками тесная.
Правильный ответ', а).
32. Выберите формулу и определите величину эмпирическо-
го корреляционного отношения, если известно, что общая дис-
персия результативного признака о2 = 8,4, общая средняя у = 13,0,
групповые средние у} = 10, у2 = 15, у3 = 12, численности групп —
соответственно 35,50 и 15 ед.
П =
|(о,)2.
N G2 ’
а) 0,794;
б) 0,583;
в) 0,902.
Решение.
85
ГДе g2 _ ^Xy-yf f _(10-13)2 -35 + (15-13)2 50 + (12-13)2 15 _
" Ё7 ” wo
= 530:100 = 5,3.
Следовательно, связь между признаками тесная.
Правильный ответ: а).
33. Отметьте правильную формулу линейного уравнения
регрессии:
, Я1
а) Ух=ао+—;
х
б) Ух=«о + а1х;
в) Ух = «о + а1х + а2х2;
Г) ух=аоха'.
Правильный ответ: б).
34. Связь между двумя признаками аналитически выражает-
ся гиперболой. Отметьте правильную формулу:
а) Ух = «о+—;
X
б) Ух=яо + а1*;
в) Ух =а0 +О}Х + а2х2:
г) yx=aoxai.
Правильный ответ: а).
35. Связь между двумя признаками аналитически выражает-
ся степенной функцией. Отметьте правильную формулу:
а\
а) Ух=«о+—;
X
б) Ух~а0+а1х^
в) Ух =а0 +а\х + а2х2;
г) Ух=а0*а1-
Правильный ответ: г).
86
36. Связь между двумя признаками выражается аналити-
чески параболой. Отметьте правильную формулу:
к а\
а) ух=д0- + -Ч
X
б) ух=а0+а1х;
в) Ух = а0+а1х + а2х2"’
г) Ух=аоха‘-
Правильный ответ: в).
37. Отметьте правильные высказывания:
а) коэффициент регрессии показывает, на сколько изменя-
ется в среднем значение результативного признака при увеличе-
нии факторного на единицу;
б) коэффициент эластичности показывает, на сколько про-
центов изменяется результативный признак при изменении фак-
торного на 1%;
в) коэффициент регрессии показывает усредненное влияние
неучтенных факторов на результативный признак;
г) коэффициент эластичности показывает, на сколько изме-
няется в среднем значение результативного признака при уве-
личении факторного на единицу.
Правильные ответы: а), б).
38. Отметьте правильные формулы коэффициента регрессии:
а)
а\ =---7е;
5Х2
б) «1 =Э^;
X
в)
г)
«1 =г—;
д)
=------г-.
87
Правильные ответы-, а), б), в), г).
39. Отметьте правильную формулу среднего коэффициента
эластичности:
a) 3 = O]i;
У
Э =
б)
Yd2x '
в) Э —
X
Правильный ответ- а).
40. Отметьте правильные формулы линейного коэффициен-
та корреляции: Л
______ * 1 4
ху - X у
а) г = —
Wy
б)
ху ~ X у
— -2 ’
X -х
в) г = щ —;
Л у
е)
. Uxd
д) г = -===^=г;
£ху-^—
V- ___________ П
п
Правильные ответы', а), в), г), д), е).
88
41. По следующим данным постройте линейное уравнение
регрессии, вычислите линейный коэффициент корреляции:
ху = 106; х = 11; 7 = 9; х2 =137; у2 = 85;а0 =4,8.
а) ух = 5 — 0,2х; г = 0,321;
б) ух = 4,182 + 0,438х; г = 0,875;
в) = —2 + 0,5х; г = 0,181.
Решение.
Определим;
а0=у-а1 -х = 9-0,438-11 = 4,182.
Построим линейное уравнение регрессии: ух = 4,182 + 0,438х.
Вычислим линейный коэффициент корреляции по формуле
ху - х • у
где
=а/85-92 =# = 2;
Следовательно, связь между признаками тесная.
Правильный ответ: б).
42. По следующим данным постройте линейное уравнение
регрессии:
а0 - 3; г = 0,92; о2 = 25; о2 = 36.
89
a) yx - -2 + 6x;
6) yx = 5 + 2x;
в) yx = 3 + l,104x.
Решение.
gv 6
ai=r—^- = 0,92 —= 1,104;
5
yx = 3 + 1,104x.
Правильный ответ: в).
43. По следующим данным определите параметры линейно-
го уравнения регрессии, вычислите линейный коэффициент
корреляции:
ху = 120; х = 10; v = 10;x2 =149;/ = 125;Э = 0,6.
а) «о=4,О; «, = 0,6; г = 0,571;
б) а0 = 8; 1,2; г = 0,8.
Решение.
Зная средний коэффициент эластичности, можно опреде-
лить коэффициент регрессии по формуле
- у Ю
ах = 3-4 = 0,6 — = 0,6.
1 х 10
Найдем
яо=у-#1Х = 1О-О,61О = 4,О
и, значит, уравнение регрессии будет таким:
ух =4,0 +0,6х.
Линейный коэффициент корреляции рассчитаем по формуле
г^ху-х-у
90
= у[х*-х2 = 7149~1()2 = >/49=7;
о у = ^у2-у2 = 7125-Ю2 = >/25 = 5;
120-10 10 20 л„,
г =----------= — = 0,571.
7-5 35
Связь между коэффициентами заметная.
Правильный ответ: а).
44. По следующим данным определите параметры линей-
ного уравнения регрессии:
х = 20; у = 10; 9 = 0,8.
а) я0 = 5; = 0,7;
б) aQ = 4; а} = 0,4;
в) а0 = 8; а{ = 0,8.
Решение,
Коэффициент регрессии ах определяется из соотношения
д, = 9-i = 0,8—= 0,4,
1 х 20
соответственно
ао= У~ щх = 10 - 0,4 • 20 = 4.
Линейное уравнение регрессии: ух = 4 + 0,4х.
Правильный ответ: б).
45. По следующим данным постройте линейное уравнение
регрессии:
aQ = 3,5; г = 0,85; о2 = 36; а2 = 49.
а) ух = 3,5 + 0,6х;
,.0,729
б) ух =3,5 +--;
х
в) ух = 3,5 + 0,729х.
91
Решение.
Для построения уравнения определим коэффициент рег-
рессии. В данном случае найдем а{ по г.
<5V 6
а} =г-^- = 0,85 — = 0,729.
7
Следовательно, линейное уравнение регрессии будет иметь
вид:
ух = 3,5 + 0,729*.
46. По следующим данным рассчитайте коэффициент кор-
реляции:
Хх = 70; £у = 50; Ъху = 320; Lx2 = 500; Zy2 = 500; п = 10.
а) 1,2;
б) 0,5;
в) -0,6.
Решение.
V ИХ'И,У
п
Z_(W
п п
320-
70-50
10
==зо==_зо 6
V10-250 50
Связь между признаками обратная заметная.
Правильный ответ*, в).
47. Статистическая зависимость описана теоретической рег-
рессией. Среднеквадратическое отклонение результирующей
переменной равно 5, остаточное среднеквадратическое откло-
нение равно 3. Найти теоретическое корреляционное отно-
шение.
а) 3/5;
б) 5/3;
в) 4/5.
92
Решение.
Теоретическое корреляционное отношение определяется по
формуле
где (у2 — факторная дисперсия, характеризующая вариацию результатив-
Ух ного признака под влиянием вариации факторного признака;
О2 — дисперсия результативного признака, характеризующая вариа-
цию результативного признака под влиянием всех факторов.
В данном примере факторную дисперсию можно найти вы-
читанием остаточной дисперсии из дисперсии результативно-
го признака:
о2 =а2-а2 =52 — З2 = 25-9 = 16.
Ух У У-Ух
Теоретическое корреляционное отношение будет равно:
[16 4
П_\25 5’
Связь между признаками тесна.
Правильный ответ: в).
48. Какие из приведенных чисел могут быть значениями
коэффициента корреляции: 0,4; —1; 0; —2,7; 1; -0,7; 2; 5?
Правильный ответ: 0,4; —1; 0; 1; —0,7.
49. Отметьте известные вам показатели тесноты статисти-
ческой зависимости:
а) корреляционное отношение;
б) индекс корреляции;
в) линейный коэффициент корреляции;
г) парные коэффициенты корреляции;
д) коэффициент детерминации;
е) частные коэффициенты корреляции;
ж) множественный коэффициент корреляции;
з) коэффициент вариации;
и) совокупный индекс корреляции.
93
Правильные ответы-, а), б), в), г), е), ж), и).
50. По данным табл. 2.29 найдите линейный коэффициент
корреляции между переменными х и у.
Таблица 2.29
Номер наблюдения 1 2 3 4 5
X 10 15 20 20 25
У 8 6 6 3 2
а) 0,85;
б) - 0,894;
в) - 0,56.
Решение.
Определить линейный коэффициент корреляции проще все-
го по формуле
v VXXS7
л.ух~---------
п
I И И
Для этого подсчитаем значения Ех, Ху, Хху, Хх2, Ху2 и при-
ведем их в табл. 2.30.
Таблица 2.30
X У лу № У
10 8 80 100 64
15 6 90 225 36
20 6 120 400 36
20 3 60 400 9
25 2 50 625 4
Lx = 90 Ly= 25 Ъху = 400 Lx2 = 1750 Lj2 = 149
94
400
5
902 1 _
-50
= --7= = -0,894.
?s2 A V130-24
1750-— J 149 - —
5
5
Связь обратная тесная.
Правильный ответ', б).
51. Имеются следующие данные (табл. 2.31).
Таблица 2.31
Номер рабочего Стаж, лет X Выработка, шт. У Ух
Г 1 1 7 10
2 8 29 22
3 6 16 19
4 12 26 30
5 3 17 14
Измерьте тесноту корреляционной связи между стажем и
выработкой с помощью индекса корреляции, выбрав правильно
формулы.
Индекс корреляции:
остаточная дисперсия:
__ 2 __ 2
1(у-у) . Z(t-Tx)2. Z(tx-t) .
п ’ п п
а) 0,836;
б) -0,512;
в) 0,632.
Решение.
Индекс корреляции определяется по формуле
95
I °2-
"4—9^
V
остаточная дисперсия
о2 = Ух^ = — = 18,4 (табл. 2.32).
У-У- п 5
Таблица 2.32
(у-Ух)2 (з'-з')2
9 144
49 100
9 9
16 49
9 4
Z(y-Zr)2=92 Z(y-j)2=306
Общая дисперсия:
- Уу 7 + 29 + 16 + 26 + 17 95
у - --------------=---
п 5 5
Индекс корреляции будет равен:
18 4 I—
Я =11----— = Ж7 =0,836.
V 61,2
Связь прямая тесная.
Правильный ответ, а).
Вопросы
1. Что такое корреляционная связь?
2. Для каких целей применяются метод параллельных рядов,
корреляционной таблицы, графический метод, метод ана-
литической группировки?
96
З. Для чего строится уравнение парной регрессии?
4. Чем определяется выбор типа регрессионной модели?
5. Каким методом определяются параметры уравнения регрес-
сии?
6. Всегда ли имеют экономический смысл параметры уравне-
ний регрессии?
7. Каким образом проводится проверка значимости парамет-
ров уравнения парной регрессии?
8. Какие показатели измеряют тесноту связи при линейной и
нелинейной формах связи?
9. Как проводится оценка существенности тесноты связи?
10. В чем отличие анализа многофакторных моделей связи от
однофакторных?
11. Что характеризуют парные, частные и множественный ко-
эффициенты корреляции?
12. Что показывают частные коэффициенты эластичности, бета-
и дельта-коэффициенты?
13. Какими показателями измеряется теснота связи между атри-
бутивными признаками?
Рекомендуемая литература
Айвазян С.А. и др. Прикладная статистика. Исследование
зависимостей. — М.: Финансы и статистика, 1985.
2. Андерсон Т. Введение в многомерный статистический ана-
лиз. - М.: ГИФМЛ, 1963.
3. Дубров А.М., Мхитарян В.М., Трешин Л.И. Многомерные
статистические методы. — М.: Финансы и статистика, 2000.
4. Кендалл М., Стюарт А. Статистические выводы и связи. —
М.: Наука, 1973.
5. Маслов П.П, Корреляция. — М.: Госфиниздат, 1955.
ТЕМАЗ
Методы многомерной
обработки данных
3.1.
Вводные замечания
Явления в природе и обществе связаны между собой проч-
ной цепью сложных отношений. Находясь в непрерывном взаи-
модействии, дополняя и видоизменяя друг друга, обогащая или,
напротив, нивелируя и подчас погашая и разрушая друг друга,
эти явления выступают как объективно обусловленная данность,
существование которой подчиняется общим законам эволюции
природы и общества. Представления об этих явлениях и отно-
шениях между ними в значительной мере очевидны, восприни-
маются как продукт естественной жизни и регулируются на на-
чалах природного инстинкта или общественного договора, не
требуя иных обоснований и доказательств.
Другая часть взаимосвязанных явлений природы и общества
неочевидна, законы их формирования и видоизменения скры-
ты, последствия изменения неопределенны, риски развития или
крушения велики и труднопредсказуемы, а представления о них
ограниченны и требуют каждый раз новых обоснований и дока-
зательств.
Еще одна, пожалуй, самая масштабная группа явлений, су-
ществующих в природе и обществе, современному человеку вовсе
неизвестна. Отношения и взаимосвязи этих явлений на поверх-
ности выступают как череда случайных и непостижимых собы-
тий, подчас как кошмар и хаос, о законах поведения которых
можно только догадываться или что-то мистически измышлять.
Понимать и направлять развитие сложных и неоднородных
отношений в нужное человеку русло с помощью одних и тех же
простых методов познания, включая известные методы элемен-
тарной математики и статистики, можно далеко не всегда. Бо-
лее того, попытки такого упрощенного понимания дела, равно-
значные попыткам втиснуть любое сложное явление в прокрус-
тово ложе существующих схем познания, приводят, как правило,
98
к неудачам, компрометируют науку, низводя ее до примитива
обывателя.
Выявление и познание скрытых явлений, распознавание и
истолкование случайностей как предельно сложных закономерно-
стей, отделение познаваемого от непознаваемого предполагают
обращение к более сложным методам научного исследования,
среди которых наиболее доступными являются ныне статисти-
ческие методы многомерного анализа.
Исходное условие и конечная цель успешного применения
этих методов — овладение основами активного познания их сути
и отличий от обычных методов комплексного статистического
анализа. При изучении методов многомерного анализа студент
в первую очередь должен ориентироваться в существе наблюда-
емых явлений, определять и различать их типы, владеть при-
емами адекватного и максимально быстрого и эффективного
исчисления. Одновременно студент должен уметь отбирать не-
обходимые источники информации, предъявляя такие требова-
ния к исходным данным, которые исключают дальнейшую их
неопределенность и позволяют получать однозначные стати-
стические выводы.
Именно знание основ многомерного анализа выступает га-
рантией успешного его применения, предпосылкой принятия
эффективных решений. Поэтому, приступая к изучению мето-
дов многомерного анализа, студент должен знать, что от него
требуется не только комплексное понимание целей и задач изу-
чения этих методов и умение их истолковывать, но и умение
аргументированно использовать для принятия доказательных
решений. При этом надо понимать и осознавать, что подобные
решения могут быть найдены только с помощью таких методов,
как эксклюзивные. В этом особенность и объективная необхо-
димость применения методов многомерного анализа в совре-
менной статистике.
Задачи многомерного анализа сводятся к нахождению одно-
родных неизвестных выборочных данных о наблюдаемых объек-
тах и их признаках на основе неоднородных известных данных
(генеральной совокупности или обучающей выборки) или к на-
хождению неизвестных факторов, определению их размерности
и значимости на основе и по отдельным признакам известного
общего результата.
В классической статистической постановке, как правило,
неизвестен результат, а определяющие его объекты и факторы и
99
их информационные характеристики обычно известны. В не-
классической постановке, напротив, известен результат, но не-
известно как и на базе каких данных он получен. При изучении
методов многомерного анализа решающее значение имеют два
положения: 1) идентификация подходов, обеспечивающих ов-
ладение элементарными методами анализа многомерных про-
странств, умение пользоваться ими сообразно решаемым зада-
чам и 2) наличная информация, умение строить многомерные
оценки наиболее разумным способом.
Эти положения неразрывно связаны, составляя две части
единого целого, поэтому разбор каждого метода проводится с
привлечением фактического материала, иллюстрируется конк-
ретными примерами, а предметное рассмотрение осуществляет-
ся с применением всех других доступных методов, в частности
методов группировок, классификаций и корреляционных оце-
нок связи.
Центр тяжести при этом смещается к выбору эффективных
методов, обеспечивающих сокращение размерности многомер-
ных матриц кратчайшими путями. Залог успешного освоения
этих методов — систематическая самостоятельная работа сту-
дентов, которая должна строиться по тематическим планам прак-
тических занятий и компьютерных контрольных работ на базе
регулярного изучения рекомендуемой литературы (список при-
лагается).
С основными методическими положениями и проблемами
многомерного анализа, требующими дальнейшего изучения, сту-
денты-заочники знакомятся в порядке дистанционного обуче-
ния, получая возможность беспрепятственного доступа к тексту
соответствующих учебных пособий, участвуя в проведении дис-
танционных компьютерных занятий, решая задачи в процессе
выполнения домашних заданий или проведения аудиторной или
контрольной работы.
В случае необходимости студентам предоставляются допол-
нительные компьютерные коллективные и индивидуальные кон-
сультации, которые проводят преподаватели кафедры стати-
стики Всероссийского заочного финансово-экономического ин-
ститута.
Главное при изучении методов многомерного анализа — это
в первую очередь понимание смысла и назначения многомер-
ных задач, умение корректно их формулировать и решать, и лишь
100
во вторую очередь — владение многочисленными техническими
процедурами решения этих задач, изучение которых должно рас-
сматриваться как предмет специальных факультативных заня-
тий. Овладение курсом считается удовлетворительным в том
случае, когда каждый студент умеет самостоятельно и в установ-
ленные сроки решить пакет компьютерных задач и дать необхо-
димые пояснения применительно к решению каждой задачи.
Приведем основные положения, которым нужно следовать
при изучении методов многомерного анализа.
3-2-
Методические указания по изучению темы
Предметом многомерного анализа являются сложные систе-
мы, элементы которых характеризуются множеством зависимых
между собой объектов и признаков, представляемые обычно в
виде матрицы, строки которой соответствуют наблюдаемым
объектам, а столбцы — характеризующим их признакам:
Хц Х|2 %13 ••• %\т
х2\ *22 *23 ••• х2т
*31 *32 *33 - х3т
хп\ хп2 хпЗ ••• хпт
где п — число объектов (строк);
т — число признаков (столбцов);
хпт — конкретное значение признака т у к-го элемента х п-го объекта.
Для параметрических признаков х. — числовое значение из-
меряемого свойства, для непараметрических — качественные ха-
рактеристики признаков, а для полупараметрических призна-
ков — комбинированные количественные и качественные их ха-
рактеристики.
Исходным условием приемлемого изучения многомерного
пространства является наличие в нем не менее 30 единиц на-
101
блюдаемых объектов и не менее 30 признаков, характеризую-
щих поведение этих объектов.
Обращение к методам многомерного анализа при наблюде-
нии меньшего количества объектов и признаков теряет смысл,
так как полученные многомерные оценки лишаются достовер-
ности.
С увеличением количества наблюдаемых единиц и призна-
ков точность многомерных оценок повышается, что каждый раз
выступает как важное условие улучшения параметров многомер-
ного анализа.
Технология многомерного анализа в краткой формулировке
сводится к следующему.
1. Распознавание и формирование образов существующих
однородных групп наблюдаемых объектов и связей между ними
по двум направлениям:
• выявляются группы объектов и признаков, в наибольшей
степени соответствующие типу или «образу» изучаемого явле-
ния, т.е. распознаются и представляются однородные группы
объектов;
• выделяются группы признаков, находящихся в устойчивых
и относительно тесных взаимосвязях, или, иначе говоря, рас-
познаются и выделяются однородные связи.
Обычно эти направления переплетаются.
2. Обоснование и выбор эффективных методов решения той
и другой задачи. Эффективнее при этом рассматривать методы,
требующие минимума времени и средств, а также минимума
информации для их реализации.
3. Обеспечение эффективного решения двух групп целевых
задач:
• выявления устойчивых тенденций (трендов) и далее зако-
номерностей и законов в изменении наблюдаемых явлений на
основе фильтрации путем измерения существенных их связей
во времени;
• идентификации множества наблюдаемых объектов путем
объединения их в родственные группы, кратного снижения их
размерности и представления в виде небольшого числа типов —
образов, открывающих возможность фиксировать структурные
тенденции (тренды) и далее закономерности — законы измене-
ния наблюдаемых явлений в пространстве.
102
При решении первой группы задач применяются методы
регрессионного, дисперсионного и ковариационного анализа.
При решении второй группы задач используются методы мно-
гомерного факторного и компонентного анализа, в основе ко-
торых лежит гипотеза о возможности изучения существующих
связей между наблюдаемыми явлениями косвенным путем, со-
стоящим в построении корреляционных матриц*, и распознава-
ния на их основе факторных оценок, искомые значения кото-
рых находятся методами многомерного анализа.
Следовательно, статистические методы многомерного ана-
лиза представляют некоторое комбинированное применение и
своего рода продолжение методов множественного корреляци-
онного изучения связей, предметом изучения и целью исполь-
зования которых является определение степени влияния иден-
тифицированного набора факторов на результат по заранее из-
вестной или воображаемой схеме их взаимосвязи в одномерном
режиме. В случае обращения к методам многомерного анализа
набор факторов и схема их взаимосвязи рассматриваются зара-
нее как неизвестные, существующие в двух гипотетически неод-
нородных пространствах и более, неоднозначно влияющие друг
на друга и на общий результат, образуя на поверхности явлений
своеобразный информационный хаос, информационную энтро-
пию, требующую упорядочения и преодоления.
При этом количество наблюдаемых факторов в многомер-
ном анализе будет всегда больше двух (в принципе оно рассмат-
ривается всегда как множество факторов), а предметом изуче-
ния их будут разграниченные по определенным критериям-
образам дискриминантные классы, кластеры или группы, в за-
висимости от степени существенности (закономерности) или
второстепенности (случайности) влияния не только на резуль-
тат, но и взаимного влияния друг на друга, включая ложное
влияние, измеряемое и представляемое в статистике в виде ав-
токорреляции.
Методы многомерного анализа всегда, при любом наборе
факторов, следует рассматривать как более сложную ступень
одномерного анализа, отличительным признаком которых яв-
ляется не только образное разграничение всегда сложного про-
* При наличии функциональных связей строятся линейные матрицы,
которые рассматриваются в теме 4.
103
странства факторов на существенные, менее существенные и
второстепенные, но и вращение факторов, отслеживание их влия-
ния друг на друга по спирали, многократно, в режиме прямых и
обратных связей, в чем как раз и проявляется суть их многомер-
ного представления.
Несмотря на сложности, связанные с проведением много-
мерного анализа, цель его будет та же, что и в случае примене-
ния других методов изучения однородности и связи, — установ-
ление на основе распознавания образов устойчивых зависимо-
стей между наблюдаемыми явлениями, выявление существующих
закономерностей их изменения в пространстве и времени, до-
казательное объяснение их причинно-следственной обусловлен-
ности.
Методов многомерного анализа много, поэтому они требуют
предварительного сравнительного анализа и отбора по принци-
пам адекватности представления, простоты понимания и эф-
фективности применения.
Для решения практических задач в современной статистике
наиболее часто обращаются к методам дискриминантного, кла-
стерного, факторного и компонентного многомерного анализа
как наиболее простым и экономичным по своим разрешающим
возможностям.
Ниже излагается суть каждого из данных методов на приме-
ре иллюстрированного решения конкретных задач. При этом
методы дискриминантного и кластерного анализа рассматрива-
ются как методы изучения однородности наблюдаемых объек-
тов и их признаков, а методы факторного и компонентного ана-
лиза — как методы изучения их взаимосвязи*.
3.2.1.
Методы компонентного анализа
В отличие от одномерного факторного анализа, где предме-
том изучения является выявление степени влияния одного-двух
заранее известных факторов-признаков на результат, многомер-
* В иллюстративных целях некоторые наглядные схемы и отдельные
учебные материалы взяты из методических разработок ВЗФЭИ, МЭСИ и
МФИ, с кафедрами статистики которых автор в прошлом активно сотруд-
ничал.
104
ный компонентный анализ имеет дело с множеством неизвест-
ных факторов и связей. При этом не только число таких факто-
ров и характер их взаимосвязи заранее неизвестны, многие из
них латентны и проявляются лишь опосредованно через внеш-
ние признаки или их группы. Задача заключается в том, чтобы
на основе множества внешних (и существенных, и мало суще-
ственных, и многочисленных ничтожных) признаков найти
небольшое, но значимое число их гибридов, которые, детерми-
нируя суть изучаемых процессов, коротко и ясно объясняя их
причинно-следственные связи в пространстве и времени, пред-
ставляются как компоненты, а процедуры их нахождения — как
методы компонентного анализа.
Значения искомых компонент находятся методом индукции,
т.е. объединением исходных первичных факторов в те или иные
группы по тем или иным признакам их связи. Однако те же
компоненты могут находиться также и методом дедукции, а
именно путем разложения наблюдаемых укрупненных факторов
на составляющие, и шире — путем нахождения на основе извест-
ного результата неизвестных факторов, его определяющих.
В первом случае искомые компонентные значения находят-
ся с помощью так называемого метода главных компонент или
метода максимального правдоподобия путем выбора адекватной
ортогональной системы координат в пространстве наблюдений.
При этом в качестве первой главной компоненты выбирают
фактор-признак, вдоль которого массив других наблюдаемых
признаков имеет наибольший разброс, а в качестве каждой пос-
ледующей — очередной по убывающему рангу фактор-признак с
максимальным разбросом значений наблюдаемых признаков.
Находимые компоненты на всем протяжении расчетного
процесса должны быть ортогональны по отношению друг к дру-
гу, что достигается путем их преобразования (вращения) и дове-
дения до прозрачного логического смысла.
Процедура нахождения искомых компонент путем разложе-
ния укрупненных факторов на составляющие части аналогична
процедуре разложения общей дисперсии на межгрупповые и
внутригрупповые.
Реализуя эту процедуру, в ряде случаев можно достичь более
высокого уровня идентификации и интерпретации искомых
компонент в категориях существенно и несущественно детер-
минирующих наблюдаемый процесс, представления наблю-
105
даемых причинно-следственных связей, что делает данную про-
цедуру предпочтительной при использовании ее в практиче-
ских целях.
Применяя методы дискриминантного и кластерного анализа для
нахождения однородных групп наблюдаемых явлений, исследова-
тель получает возможность идентифицировать любой наблюдаемый
объект и определить его принадлежность к одной из идентифици-
руемых групп по совокупности любого набора признаков.
В сущности, эти методы представляют собой относительно
простой, дешевый и доступный способ выявления различий или
распознавания образов, что в случае наличия противоречивых
характеристик наблюдаемых объектов (а именно такие случаи
наиболее широко распространены в практике экономико-ста-
тистической работы) имеет особое значение. По сути, методы
дискриминантного и кластерного анализа имитируют процеду-
ры нахождения эмпирического корреляционного отношения и
теоретических значений индекса корреляции. Практическое ре-
шение при выборе того или другого метода для решения одних
и тех же классов задач зависит от сложности сбора необходимых
данных и трудоемкости процедур их обработки.
Методы дискриминантного анализа как методы нахождения
своего рода «различителей» в большинстве случаев оказываются
проще и не требуют особых комментариев. Методы кластерного
анализа более громоздкие, но зато они позволяют определять
искомые однородные группы наблюдаемых объектов, которые в
данном случае называются кластерами, на более обоснованной
и доказательной базе.
Кластеры находятся индуктивным или дедуктивным спосо-
бом. В первом случае наблюдаемые единичные объекты после-
довательно, шаг за шагом объединяют в однородные (сходные
или близкие) группы (метод индукции), во втором случае, на-
против, совокупности наблюдаемых объектов разбивают на од-
нородные группы (метод дедукции). В первом случае говорят о
так называемом агломеративном (объединительном) процессе
кластеризации, во втором — о дивизивном процессе разбиения
наблюдаемых совокупностей объектов на однородные классы.
При этом приемы кластеризации зависят от способа опреде-
ления близости между наблюдаемыми объектами, применяемых
алгоритмов счета расстояний, характера распределения исход-
106
ных данных, множества наблюдаемых признаков и характера
существующих связей между ними, способа проверки достовер-
ности получаемых результатов и т.д., что делает кластерные оцен-
ки подчас тоже спорными и требующими дополнительных со-
держательных обоснований.
К методам кластерного анализа примыкают методы много-
мерного шкалирования данных, позволяющие экспертным пу-
тем оценивать степень сходства или различия между парами
наблюдаемых объектов, представлять находимые парные значе-
ния в виде многомерного точечного пространства, в котором
каждой паре значений наблюдаемых объектов соответствует одна
точка. Координаты точек рассматриваются как значения исход-
ных характеристик наблюдаемых объектов, которые в случае
упорядоченного их пространственного расположения позволя-
ют наглядно интерпретировать изучаемую совокупность объек-
тов как однородную. В случае оперирования качественными, а
не количественными характеристиками наблюдаемых объектов
и их признаков методы многомерного шкалирования представ-
ляются как неметрические, или ранговые.
Здесь главное — разобраться в моделях компонентного ана-
лиза и научиться отличать их от других внешне похожих моде-
лей многофакторного анализа. Для того чтобы делать это без-
ошибочно, необходимо разбираться в типологии компонентных
социально-экономических задач, уметь в предварительном по-
рядке, на логическом уровне, ставить, решать и истолковывать
смысл решения такого рода задач. Затем нужно обратиться к
рассмотрению его конкретных приемов, решению конкретных
классов производственных задач. Следует помнить, что надо из-
менять не социально-экономические условия применительно к
избираемым приемам компонентного анализа, а, напротив, сами
приемы. Отсюда встает самостоятельная задача отбора способов
компонентного анализа, которая должна решаться в ходе пред-
варительного качественного анализа изучаемых процессов.
Решение этой задачи требует освоения основ классифика-
ции социально-экономических компонент, изучения принци-
пов обоснования и выбора эффективных приемов их выявле-
ния, организации сбора и обработки необходимых данных.
Говоря конкретно, надо научиться определять собственные
векторы и собственные значения, весовые коэффициенты, раз-
личные формы главных компонент, двух-, трех- и конечномер-
107
ных пространств компонент. Работая самостоятельно над от-
дельными вопросами, особое внимание следует уделить моде-
лированию с помощью главных компонент нестандартных
хозяйственных ситуаций, в частности конверсии резервов и по-
терь, формированию достаточных условий эффективного функ-
ционирования рыночной экономики и т.д., закреплению основ-
ных положений на примере компонентного анализа решения
практических задач.
Овладение предметом означает, что студент умеет решать в
установленные сроки сквозную задачу по определению роли и
значения отдельных компонент эффективности и перераспре-
деления наличных ресурсов в соответствии с наиболее разум-
ным способом их использования.
Зная методы компонентного анализа, каждый студент полу-
чит ясное представление о том, как использовать современные
методы компонентного анализа для выявления резервов произ-
водства, как обеспечить более эффективное использование на
предприятиях всех видов материальных, трудовых и финансо-
вых ресурсов. Вместе с тем студент должен уметь показать, как
сами методы и модели компонентного анализа выступают до-
полнительным фактором повышения эффективности работы,
какие объемы ресурсов экономят (или могут экономить) пред-
приниматели при правильном и своевременном применении этих
методов и моделей.
Модель компонентного анализа описывается уравнением
Z = AG,
где Z — матрица (п х tri) стандартизованных значений исходных объектов
и их признаков;
А — матрица (т х г) компонентных нагрузок я.., отражающих связь
между х. и (7;
G — матрица (п х г) индивидуальных значений г скрытых признаков,
называемых компонентами.
Исходная матрица компонентного анализа для случая т х п = 4
представляется в виде следующей системы уравнений:
Z] = <7ц6| + °12G2 + °13G3 +
Z2 = a2lGt + a22G2 + «23^3 + «2464;
Z3 = a3lGt + a32G2 + <73363 + <73464;
Z^ — c?4 ] C7] + a42^2 + + ^44^4-
108
Исключим нагрузки, близкие к нулю, т.е. нагрузки, отражаю-
щие отсутствие связи между х. и G, и оставим только существен-
ные нагрузки. Это приведет к упрощению матрицы (рис. 3.1).
xz
1 2 3 4
1 2 3 4 + + + 4- + + + + + +
Рис. 3.1. Исходная матрица компонентного анализа
Каждому признаку х. свойственна своя факторная структура,
а каждой факторной структуре - свой набор признаков. Число
существенных нагрузок признака х. на факторы называют его
сложностью, а число признаков, формирующих каждую фак-
торную структуру, — компонентой. Согласно рис. 3.1 признаки
Xj и х2 имеют трехуровневую сложность, а х3 и х4 — двухуровневую,
характеризующуюся соответственно тремя и двумя признаками.
Задача компонентного анализа — определить, сколько выде-
лить компонент и каких именно, чтобы по возможности точно
воспроизвести и объяснить с их помощью наблюдаемые связи,
представляемые в виде корреляционной матрицы R.
Решение задачи предполагает поэтапное нахождение значе-
ний пяти нижеприведенных групп показателей (рис. 3.2).
I II III IV V
п п т т п
Рис. 3.2. Исходная схема компонентного анализа
Для нахождения фактических значений приведенных групп
показателей необходимо выполнить стандартную процедуру рас-
четов и комментариев, включающую формирование матрицы
признаков х/?., принадлежащих множеству наблюдаемых объек-
тов хк, исчисление на этой основе производных значений на-
блюдаемых признаков, выявление их однородных групп и про-
вести анализ их устойчивой и показательной взаимосвязи.
109
Задачи компонентного анализа решаются по шагам. Для ре-
шения любой такой задачи в обязательном порядке нужно про-
делать 17 шагов. Опишем каждый из них.
Шаг 1. Строим матрицу X:
Хц...Х17...хи
X— х^...Ху ...Xjk
Размерность матрицы (п х к), где х.. — значение у-го показа-
теля у /-наблюдения (z = 1, 2,..., и; j = 1, 2, ... , к).
Ш а г 2. Вычислим средние значения показателей
а также 5р ..., sk, GxV Gk.
Шаг 3. Построим матрицу нормированных (стандартизо-
ванных) отклонений Z:
zn...zXj...zxk
Z— Zj^...Zjj...zik
zn\’"zni",znk
\ J J
При этом
Ш а г 4. Формируем матрицу парных коэффициентов кор-
реляции R:
П2 Пз - г\к
г2\ 1 г23 - г2к
Г31 г32 1 - г3к
|Д1 гк2 г„3 ... г„к
ПО
При этом
где
1 п
Xi*e > 7, в — 1,2,..., £
J П z-1 J
Шаг 5. Преобразуем матрицу А в диагональную матрицу X
собственных значений многочлена |Х£ — Л|, где Е — единичная
матрица.
Шаг 6. Решим уравнение:
|Л£-Я = 0|,
корнями которого являются К собственных значений:
Я1 >^2
Шаг 7. Построим матрицу собственных значений:
% 0 ... О
О ... О
Х= 2
о о ...
V к 7
Шаг 8. Найдем на основе приведенной матрицы собствен-
ные значения, характеризующие вклады соответствующих глав-
ных компонент в суммарную дисперсию исходных признаков,
к
равную К, т.е. S =К.
V=1
При этом первая главная компонента оказывает наибольшее
влияние на общую вариацию, а последняя £-я — наименьшее.
Шаг 9. Определим вклад V-й главной компоненты в сум-
марную дисперсию как
^-•100%.
к-
111
Шаг 10. Определим суммарный вклад т первых главных
компонент, доля которых должна составлять не менее 60—70%:
т
S Лу
----100%.
к
Шаг 11. Построим матрицу факторных нагрузок:
л = кх1/2 =
^akl
alv ••• alk
ajv ... Qjk ,
akv ••• akk j
где V - матрица, составленная из нормированных векторов К.
Шаг 12. Определим собственно вектор £7, соответствую-
щий собственному значению Ху корреляционной матрицы R.
Значение U находим как отличное от нуля путем решения урав-
нения:
(kyE-R)Uy=0.
Шаг 13. Найдем стандартизованное значение собственного
вектора И как
Шаг 14. Исчислим матричный коэффициент а , где j = 1,2,..., к;
j = 1, 2, ... , к — коэффициенты, отражающие тесноту связи
между Xj показателем и f-fa главной компонентой, причем
-1<а7„ <1, а
Шаг 15. Интерпретируем матрицу факторных нагрузок А
как линейных функций исходных признаков. При этом в ходе
экономической интерпретации полученных функций f исполь-
зуем лишь те Хр для которых |a7-v| = 0,5.
112
Шаг 16. Построим сводную матрицу всего множества ком-
понент для каждого компонента в отдельности и для всей их
совокупности в целом:
(/и - fiv
flk
fin '
fnk
где F — матрица нормированных значений исходных показателей, на ос-
—1 —1/2
нове которой по алгоритму F = Z4 = ТУА происходит рас-
познавание главных компонент, дающих в сжатом виде представ-
ление о всей структуре наблюдаемых взаимосвязей.
Шаг 17. Интерпретируя те главные компоненты, собствен-
ные значения которых больше единицы, определяем их вклад в
п п X
суммарную дисперсию Г = Е — 5 и проводим их оптимиза-
z=l z=l т
цию. В разделе 3.1 далее на конкретных примерах иллюстриру-
ется изложенная техника компонентного анализа.
3.2.2.
Методы факторного анализа
В факторном анализе в отличие от компонентного при на-
хождении главных характеристик взаимосвязи наблюдаемых яв-
лений имеют дело не с синтезом, а с разбиением обобщающих
результативных оценок на части путем разложения вариации на-
блюдаемых признаков по образующим ее главным причинам.
Обращаясь к схемам факторного анализа, кроме техники
расчетов следует уделить особое внимание возможным подхо-
дам к получению факторных оценок и их сравнению, в частно-
сти эмпирических и теоретических. При этом точные способы
факторных оценок должны дополняться приближенными, по-
лучаемыми на основе методов распознавания образов, алгорит-
мов голосования, изучения общественного мнения и т.д.
При изучении техники расчетов должны быть рассмотрены
вопросы, связанные с оценкой отдельных факторных значений
и определением их влияния на результат, технологии построе-
113
ния факторного отображения и факторной структуры, методы
оценки главных факторов и факторных общностей.
Особое внимание необходимо обратить на комплексное мо-
делирование факторных показателей, взаимосвязь этих показа-
телей с другими, в частности, показателями компонентного и
кластерного анализа. Комплексное моделирование факторов
предполагает овладение всем набором рекомендуемых методов
и применение их, а также опору на все имеющиеся источники
данных.
Активная работа каждого студента заключается в умении
оперативно выявлять имеющиеся резервные факторы производ-
ства и грамотно определять наиболее эффективные пути даль-
нейшего совершенствования экономической работы.
Предмет применения методов факторного анализа включает
также изучение разных аспектов технологии принятия решений,
с одной стороны, и показателей эффективности принимаемых
решений, с другой стороны. В поле зрения при этом должны
находиться так называемые методы функционально-стоимост-
ного анализа, предполагающие анализ затрат и эффективности
развития системы не только в целом, но и отдельных ее функ-
ций — постановки задач, сбора и обработки данных, принятия
решений и контроля за выполнением принятых решений, под-
ведения итогов и анализа полученных результатов, в том числе
прямых и косвенных результатов. Особое внимание следует уде-
лять моделированию стандартных затрат и нормативной эффек-
тивности управления при помощи методов факторного анализа
как наиболее приемлемых в данном случае.
Суть факторного анализа сводится к идентифицированному
разложению вариации каждого из наблюдаемых признаков х. на
вариацию, происходящую под влиянием общих, специфичес-
ких и индивидуальных факторов соответственно. Такое пони-
мание дела предполагает развернутое представление общей мо-
дели факторного анализа в виде
Z=AG+Q
или
zi ^aijGj+giQ,
где а.. - нагрузки общих факторов G;
— нагрузка специфических факторов Q.
114
Соответствующим образом расщепляют и дисперсию при-
знака х. на две части: объясняемую общими факторами (общ-
ность /г?) и объясняемую специфическими факторами, пред-
ставляемую как характерность qf:
2 v11 2 . 2
s.^hi+qi.
Суммарную общность , как и специфическую характер-
ность д?, используют при определении вклада отдельных фак-
торов в общую вариацию наблюдаемых признаков х,.
Факторное решение можно рассматривать как итерацион-
ный процесс, определяя последовательно, на уровне каждого
шага итерации, факторные нагрузки ajJ9 воспроизводимую мат-
рицу R' = А'А и матрицу существенности остаточной корреля-
ции 4, = R'-R как
Процесс идентификации факторов прекращается, если оста-
точная корреляция несущественная, а след матрицы равен сум-
марной общности ZXy =
Аналогичные оценки общих и специфических факторов мож-
но находить геометрическим путем, осуществляя вращение си-
стемы координат наблюдаемых признаков в сторону угла 0 при
фиксированном расположении независимых векторов G.. В ре-
зультате находят такую матрицу преобразования Т, которая удов-
летворяет условию АТ = В, где А и В - факторные отображения
в различных системах координат.
При вращении против часовой стрелки для z = 2 соответ-
ствующая матрица имеет вид:
Г =
COS/
-smi
sinZ
cos/
115
При вращении по часовой стрелке
Т =
cos i sin i
sin i cos i
При r > 2 полная матрица преобразования будет представ-
лять произведение матриц для всех парных комбинаций фак-
торов.
Наилучшие конечные оценки факторов получают на основе
первичной факторной структуры А, корреляционной матрицы
7?j и стандартизованных переменных z :
G = A,R~XZ = (A’AY'a’Z.
Необходимым и достаточным условием получения таких ко-
нечных оценок факторов является близкое к равенству или пол-
ное равенство парных коэффициентов корреляции:
rihrsi ~~ rhiris ~
Техника применения методов факторного анализа иллюст-
рируется на конкретных примерах, приведенных в разд. 3.3.2.
3.2.3.
Методы кластерного анализа
Напомним, что кластерный анализ рассматривается как ме-
тод изучения однородности сложных, на поверхности неочевидно
взаимосвязанных объектов.
Кластер как образ при этом понимается как некоторая ре-
ально существующая общность данных объектов, обладающих
необходимыми и достаточными признаками, например показа-
ниями и свойствами, нужными для слияния, объединения, ко-
операции или поглощения одних компаний другими.
Цель применения этого метода — определение однородности
изучаемых объектов, если она не может быть установлена други-
ми более простыми методами, анализ и идентификация наблю-
даемых однородных объектов, образование их ранее неизвестных
групп как носителей новых явлений, содержательная интерпре-
тация роли и значения этих групп в преобразовании окружаю-
щей социально-экономической действительности.
116
Алгоритм кластерного анализа сводится к построению евк-
лидовых пространств 6/(XjX2), расстояния между которыми опре-
деляются как модули типа:
X (х\к ~~xzk)
к=]
В процессе проведения кластерного анализа следует сосре-
доточить внимание на вопросах комплексной классификации
объектов (единиц наблюдения), выяснении сходства и различий
между ними, объективной противоречивости классификаций
одних и тех же объектов по двум и более признакам, конвенци-
ональном характере решения этих противоречий. Студент дол-
жен понимать и помнить, что цель кластерного анализа — изу-
чение однородности наблюдаемых объектов, определяемой по
совокупности признаков, характеризующих их поведение в по-
вседневной практике, тогда как цель факторного и компонент-
ного анализа — изучение их связи по совокупности необходимого
и достаточного множества объектов как носителей этих связей.
Важно понимать, что единичные объекты, равно как и еди-
ничные признаки, их характеризующие, по определению не могут
выступать в качестве предмета кластерного анализа, как, впро-
чем, и любого другого метода многомерного анализа. Здесь во-
дораздел, обозначающий исходное условие обращения к мето-
дам многомерного анализа.
Предметом конкретного изучения являются модели класте-
ризации, в частности модели определения расстояний и харак-
теристики близости между наблюдаемыми объектами, процеду-
ры кластерного анализа и типология выбора их в зависимости
от характера решаемых задач, критерии оптимизации методов
кластерного анализа.
В кластерном анализе различают параллельные, иерархичес-
кие и функциональные процедуры, которые при изучении сле-
дует рассматривать раздельно. Особое внимание надо обращать
также на возможные варианты формирования кластерных мо-
делей, их размерность, области применения, смысловую интер-
претацию результатов, получаемых на их основе.
Наряду с освоением техники кластерного анализа присталь-
ное внимание следует уделить прикладному истолкованию клас-
терных оценок, в частности оценок стандартных классифика-
117
ций видов экономической деятельности, продукции, работ и
услуг, устойчивых социальных, политических и экономических
общностей и групп как носителей новых явлений. В связи с
этим здесь, как нигде, важен предварительный анализ социаль-
но-экономических задач, решаемых методами кластерного ана-
лиза, обоснование их типологии, идентификация связи с при-
меняемыми конкретными методами.
Прикладная суть техники кластерного анализа сводится к
следующему.
1. Адаптируются и представляются исходные данные в фор-
мате матрицы
X = К К' = i, 2,...,Л7) (7 = 1,2,..., т),
где х. — объекты (их число по минимуму должно равняться 30), характе-
ризующиеся по отдельно взятым признакам (число признаков
должно быть не менее двух).
2. Формулируется задача включения каждого из наблюдае-
мых объектов в одну и только в одну группу, в рамках каждой из
которых различия между объектами отдельно взятых и далее по
совокупности наблюдаемых признаков были бы в обязательном
порядке существенно меньшими, чем между объектами разных
групп.
Идентифицированные таким образом группы как раз и бу-
дут представлять собой кластеры Кг
3. Проводится последовательное решение сформулированной
задачи, которое предполагает выполнение следующих шагов.
Шаг 1. Выберем метод, определим масштаб и единицу из-
мерения внутригруппового сходства и межгруппового кластер-
ного различия наблюдаемых объектов. Выбор делается, как пра-
вило, между геометрическими мерами функций удаления и бли-
зости с использованием на старте разнообразных вербальных
методов определения правдоподобий и различий.
Однородными, принадлежащими одной и только одной груп-
пе считаются объекты х} и х2, наблюдаемые признаки которых
находятся в непосредственной близости друг от друга, а неодно-
родными — объекты, находящиеся, судя по тем же признакам, на
удалении друг от друга сверх установленной нормы. Норму бли-
зости или удаленности называют метрикой расстояния.
118
Ш аг 2. Выберем одну из метрик расстояний, которая в об-
щем виде представляет неотрицательную функцию d(xf, х) = d,
если для всех х. и х. d(x., х) > 0, d(x., ху) = 0 тогда и только тогда,
когда х. = ху, т.е. d(xp ху) = 0;
(7(xz,xy) = d(xj,xi); d(Xi,Xj) < d(xi,xk) +d(xk,Xj).
Ниже приведены формулы, по которым наиболее часто на-
ходится метрика расстояния.
Метрика расстояния
Евклидово расстояние
Взвешенное евклидово
расстояние
- норма
Формула
т
Э 2
<7(хг-,Xj) — £ (х;£ — Xj^)
_ь=1
1р - норма
При равномерном распределении количественных призна-
ков наблюдаемых объектов измерения проводят, как правило,
обращаясь к метрике евклидова расстояния, при криволиней-
ном распределении применяют матрицу взвешенного евклидова
расстояния, принимая (лк как априорно задаваемый вес Л-го при-
знака (0 < &>к < 1).
При наличии ранговых корреляций обращаются к метрике
хемминговых расстояний, кластеры которых представляют слу-
чаи несовпадения значений альтернативных признаков, фикси-
руемых в виде +, —, 0, 1 и т.д.
Ш а г 3. Построим матрицу расстояний по выбранной мето-
дике. Расстояния (L между парами альтернативных признаков
при этом представляются обычно в виде симметричной мат-
рицы D:
119
Неотрицательная функция s(x., х.) = s.. представляет меру сход-
ства, если
О < s{xhXj) < 1; s^x^x^ = 1, a sf^Xj) = s(xjXj).
В прикладных социально-экономических исследованиях наи-
более широкое применение получили две группы методов клас-
терного анализа:
1) метод иерархических алгоритмов и 2) центрографический
метод определения концентрации (сгущений) объектов. Ввиду
существенных различий рассмотрим технику применения тех и
других алгоритмов раздельно.
Иерархические алгоритмы — это алгоритмы последователь-
ной кластеризации (группировки) объектов по принципу от об-
щего к частному, а алгоритмы сгущений, напротив, реализуют
принцип индуктивной группировки, предполагая отслеживание
отдельно взятых объектов от частного к общему.
Иерархические алгоритмы подразделяются по количеству,
последовательности и метрике выделяемых кластеров. В после-
днем случае говорят об алгоритмах ближнего, дальнего и сред-
него соседа, которые различаются выбором метрик межкластер-
ного расстояния.
Практическая реализация любого иерархического алгоритма
предполагает выполнение следующих пяти действий:
1) представление всех последовательно наблюдаемых объек-
тов х. | i = 1, 2, ..., п | как п в виде самостоятельных кластеров Л;
2) определение пар наименьших расстояний dlm между объек-
тами i и кластерами т\
3) последовательное объединение выбранных пар и умень-
шение числа кластеров на единицу на уровне каждого шага;
4) определение расстояния drq между значением г найденно-
го и любого другого
5) последовательное применение действий пп. 2 — 4 до
момента получения одного и только одного конечного кластера.
120
Реализация любого иерархического алгоритма предполагает,
что наблюдаемые как внутригрупповые (aL), так и межгруппо-
вые (d ) расстояния нормированы или задаются заранее требуе-
мой метрикой.
Общая формула расчета расстояний между кластером г, пред-
ставляющим результат объединения кластера i и т, с кластером
q следующая:
^rq ^i^lq + ^m^mq + + Y \^lq ^mq | »
где dlq, dmq, dlm — геометрические расстояния между соответствующими
кластерами;
а., ат, р и у — параметры, определяющие конкретный алгоритм иерар-
хической кластеризации.
В табл. 3.1 приведены значения параметров, соответствую-
щие трем рассмотренным критериям кластеризации.
Таблица 3.1
Алгоритмы и параметры кластеризации
Алгоритм Значение параметра
а/ ₽ Y
«Ближний сосед» х 2 1 2 0 _x 2
«Дальний сосед» 1 2 х 2 0 x 2
Средний сосед П1 nl 0 0
nt+nm nt+nm
При использовании центрографического метода (алгоритмов
концентрации или сгущения объектов) фиксируются поля по-
вышенной плотности скопления наблюдаемых объектов, соот-
ветствующие скалярной величине Т, которая представляет ра-
диус сферы наблюдаемых признаков. Поля концентрации при
этом идентифицируются путем проведения последовательных
расчетов, схема которых включает следующие семь шагов.
Шаг 1. Определим количество точек, попавших в этот ра-
диус, на основе произвольно выбранной точки-центра xQ =
= |хор х02, x0J, при заданном радиусе Т,
Шаг 2. Рассчитаем средние значения признаков по сово-
купности объектов, попавших в первый круг наблюдения
121
Ш аг 3. Определим среднюю Для второго круга наблюда-
емых объектов, приняв х{ за очередную точку-центр при том же
заданном радиусе Т.
Ш а г 4. Представленная процедура поиска указанного рода
средних при заданных условиях будет продолжаться до момента
получения устойчивой, т.е. далее не меняющейся средней, рав-
ной средней предпоследнего круга наблюдаемых объектов.
Шаг 5. Интерпретируем полученный результат. Объекты,
попавшие в последний круг, идентифицируем как объекты пер-
вого кластера, и, следовательно, исключаем их из дальнейшего
анализа.
Шаг 6. На основе множества объектов, не попавших в пер-
вый круг наблюдения, таким же способом образуем новый мас-
сив, на базе которого по точно такой же процедуре проводится
поиск второго кластера.
Ш аг 7. Прекратим процедуру. Процедура прекращается при
условии распределения всех наблюдаемых объектов по кла-
стерам.
Примеры применения изложенных процедур кластерного
анализа приводятся в разд. 3.3.3.
3.2.4.
Методы дискриминантного анализа
Однородность изучаемых объектов определяется с помощью
как дискриминантного, так и кластерного анализа. При этом к
дискриминантному анализу обращаются тогда, когда методами
кластерного анализа задача не решается, либо для ее решения
отсутствуют необходимые исходные данные. Методы дискри-
минантного анализа предполагают построение функции
/(х) = а1х1 + fd2xi^anxn и нахождение на основе этой функции
значения искомых параметров a^gy и xiy и далее значение са-
мой функции /
Приступая к изучению алгоритмов дискриминантного ана-
лиза, нужно помнить об их связи с предыдущими и прежде все-
го с алгоритмами кластерного анализа, как родственными.
В центре внимания дискриминантного анализа — выявле-
ние, идентификация и сравнение однородности групп по общ-
122
ности наблюдаемых объектов, определяемой по эмпирическим
данным с их однородностью, устанавливаемой на основе обуча-
ющих (эталонных) оценок или выборок.
Вот почему акцент в этой работе должен быть сделан на иден-
тификации областей достаточности таких сравнений, которые
определяются по критерию сходимости результатов различных
выборок. Достаточными при этом являются области получения
однородных групп наблюдаемых объектов, например высокопри-
быльных, средних и убыточных компаний, образов положитель-
ных и отрицательных героев, здоровых и больных людей и т.д.
При дискриминантном анализе, как нигде, существенное
значение имеет определение зависимости его приемов (линей-
ный, пошаговый и др.) от характера статистического распреде-
ления данных, подготовка и отбор этих данных, процедуры их
идентификации с обучающими выборками, в частности с экс-
пертными оценками.
Главное — научиться не только технике проведения дискрими-
нантных расчетов, но и пониманию их смысла, умению распозна-
вать и отбирать на основе полученных дискриминантных оценок
образцовые объекты, представлять их как ноу-хау, своеобразные
бренды, носители будущего, заслуживающие культивирования.
Предметом дискриминантного анализа является как раз по-
иск и идентификация таких объектов.
В отличие от аналитических группировок где, по сути, ре-
шается та же задача с ограниченным количеством наблюдаемых
одномерных признаков (максимум 5—7), в дискриминантном
анализе количество наблюдаемых признаков, как правило, нео-
граничено, а измерение их — многомерно и конечно.
Ключевым моментом в дискриминантном анализе является
определение идентификационных характеристик т и 5, форми-
рование на их основе эталонных классов и обучающих выборок
и отнесение наблюдаемых эмпирических объектов к одному и
только одному классу, что невозможно сделать ограничиваясь
методами простых группировок.
Смысл работы сводится к определению для каждого эмпи-
рического объекта с фиксируемым набором признаков х. неко-
торого обобщающего признака т, находимого путем соизмере-
ния его исходных эмпирических значений х, распознаванию
принадлежности и отнесениию наблюдаемого объекта по вели-
чине т к одному из эталонных классов, назначаемых норматив-
123
но или устанавливаемых на основе альтернативных принципов
подобия и различий.
Алгоритм определения принадлежности некоторого множе-
ства эмпирических объектов к эталонным классам включает сле-
дующие классификационные и расчетные процедуры.
1. Выбор формы и построение дискриминантной функции,
простейшей из которых является линейная функция fx) = a{xv +
+ а2х2 = С, искомое значение С которой и есть дискриминант.
2. Идентификация объектов с эталонными признаками класса
5р которые при их подстановке в функцию Дх) будут давать
значения, большие С, и соответственно объектов класса S2, ко-
торые будут давать значения, меньшие С.
3. Проведение процедуры распознавания любого неизвест-
ного объекта и его принадлежности к тому или иному классу в
зависимости от величины С: еслиДх)' > С — объект относится к
классу 5р если Дх)' < С — объект относится к классу S2, если
Дх)' = С — объект не принадлежит ни одному из идентифици-
рованных классов.
Если групп больше двух, а распределение их признаков не
подчиняется требованиям приведенной функции, для анализа
привлекаются разные формы других функций.
4. Определение на основе выбранной формы дискриминан-
тной функции ее неизвестных параметров. При работе с линей-
ной функцией последовательно определяются средние значения
Xi каждого из наблюдаемых признаков для каждого эталонного
класса объектов , параметры и значение С, минимизиру-
ющие ошибку А2.
5. Решение классической системы нормальных уравнений,
отыскание параметров а..и подстановка их значений в дискри-
минантную функцию каждого объекта для получения эмпири-
ческих значений Д и Д'.
6. Квалификация найденных параметров и оценивание сте-
пени соответствия эмпирических оценок построенной функции
идентифицированным эталонным или обучающим образцам.
Правило здесь такое: если параметры Д и Д' максимально
удалены друг от друга и равноудалены от среднего их значения,
искомые дискриминанты найдены с минимальными погрешно-
стями А2, объекты разграничены и включены в соответствую-
щие классы верно, задача решена правильно.
124
И напротив, в случае обнаружения больших уклонений и
погрешностей наблюдаемые объекты разграничены неверно, за-
дача должна решаться заново, с уточнением ее общей постанов-
ки и возможным привлечением дополнительных эмпирических
данных.
Примеры дискриминантного анализа приводятся в разд. 3.3.4.
3.3.
Примеры решения типовых задач
3.3.1.
Примеры компонентного анализа
Пр и м е р 3.1. Приводится матрица R:
р
R = 0,8
0,2
0,8 0,2Л
1 0,6 .
0,6 1
Требуется определить собственные значения и собственные
вектора приведенной матрицы.
Решение. Задача решается по шагам.
Шаг 1. Найдем обобщающий определитель матрицы:
1-Х 0,8 0,2
(Л-ХЕ) = 0,8 1-Х 0,6 =0.
0,2 0,6 1-Х
Ш аг 2. Преобразуем представленный определитель в поли-
ном третьей степени:
|Л - Х£Г] = (-1)3 X3 + (-l)2gl X2 + (-l)g2X+g3 = 0.
Ш аг 3. Определим по приведенному алгоритму коэффици-
ент полинома gs: gl =^|7?|; g2=±l£(RB}),
125
где Bt = R - gtE;
gy = | tz(RB,y,
B3 = RBt - g,E.
Для матрицы R:
= 1 + 1 + 1= 3 — сумма диагональных элементов исход-
ной матрицы;
tz\RBt\ = (-1,32) + (-1,0) + (-1,60) = (-3,92) - сумма диаго-
нальных элементов произведения матриц
0,8 0,2^ г-2 0,8 0,2 А 1,32 -0,68 0,28 "
R = 0,8 1 0,6 0,8 -2 0,6 = -0,68 -1 -0,44
0,2 к 0,6 1 7 0,2 \ 0,6 -2 ^0,28 -0,44 -1,60
tz^RIty = 0,152 + 0,152 + 0,152 = 0,456 — сумма диагональ-
ных элементов произведения матриц
Ч 0,8
R= 0,8 1
0,2 0,6
0,2^ г-0,64 0,8 0,28 ' г0,152 0 0
0,6 0,68 -0,96 -0,44 = 0 -0,152 0
1 7 0,28 0,44 -0,36 ) 0 к 0 0,152 7
Отсюда:
gi =3;
g2=l(-3,93) = -l,96;
g3 =-0,456 = 0,152;
3 3
| R = ХЕ |= -X3 + ЗА.2 + 0,152 = A,3 + ЗА2 +1,96A, - 0,152 = 0.
Собственные значения равны:
%! =2,1; А2 =0,81; Х3 =0,09.
126
Ш а г 4. Проверим правильность проведенных вычислений
путем идентификации параметров X. и е:
J s
X] + Х2 + Х3 — g\ = 2,1 + 0,81 + 0,09 ~ 3;
ХхХ2 + X! Х3 + Х2Х3 = g2 = 2,1 • 0,81 + 2,1 • 0,09 + 0,81 • 0,09 = 1,96;
Х]Х2Х3 = g3 =2,1 0,81 0,09 = 0,152.
Ш а г 5. Найдем собственные вектора и компонентные на-
грузки соответствующих X. для первой компоненты. Для этого
решим систему нормальных уравнений для X, = 2,1, которая
имеет вид:
-1,1/]+0,8/2+0,2/3=0;
0,8/7] -1,1/2 + 0,6/3 =0;
0,2р ] +0,6р2 -1,1/3 =0.
При р3 = 1 получим
0,8/7] -1,1/2 +0,6/3 =0
0,2/7] + 0,6/72 — 1,1/73 =0
-3,5р2=-5 ’
Р2 =+1,42857.
Отсюда 0,8/, = 1,1 • 1,42857 - 0,6 = 0,971;
/, = 1,213.
Шаг 6. Используя найденный постоянный множитель
представим искомые факторные нагрузки в табличной форме
(табл. 3.2).
127
Таблица 3.2
РУ р? aij ~ pij^j
1,213 1,47136 0,828 0,6855
1,428 2,03918 0,975 0,9506
1,000 1,00000 0,683 0,4645
X 4,51054 X 2,1006
Шаг 7. Интерпретируем приведенные в табл. 3.2 фактор-
ные нагрузки, сумма которых равна собственному значению мат-
рицы: 2^=^ =2,1.
Факторные нагрузки для Х2 = 0,81 и = 0,09, рассчитанные
аналогичным образом, приводятся в матрице А:
0,828 -0,532 0,170
0,975 -0,052 0,221
0,683 0,723 0,109
Вывод. На основе найденных компонентных нагрузок мож-
но заключить о наличии неоднородной связи главных компо-
нент (7 с переменными х:. представленная в матрице в гр. 1
первая компонента, как видим, тесно связана со всеми тремя
переменными, вторая — с первой и третьей, а третья связана
слабо со всеми тремя переменными и далее не должна прини-
маться в расчет при объяснении изменений.
Пример 3.2. На основе корреляционной матрицы R полу-
чены следующие собственные значения (табл. 3.3).
Таблица 3.3
xi 1 2 3 4 5 6 7
3,62 1,48 1,05 0,53 0,27 0,09 0,06 7,1
Требуется определить, сколько и какие компоненты следует
выделить для получения существенных оценок.
Решение. Суммарная дисперсия т равна 7,1. Если использо-
вать критерий Ц > 1|, то для получения существующих оценок
нужно выделить три начальные компоненты, первая из которых
объясняет 50,7% (3,62/7,1) суммарной дисперсии, вторая - 20,8%
128
(1,48/7,1), третья — 14,8% (1,05/7,1). На долю первых трех ком-
понент приходится 86,3% суммарной дисперсии, что достаточ-
но для того, чтобы именно этими тремя компонентами объяс-
нить общее изменение наблюдаемого явления.
Пример 3.3. Выделенные для семи показателей три ком-
поненты имеют следующие факторные нагрузки (табл. 3.4).
Таблица 3.4
Показатель ап ai2 ai3
1 2 3 4
х\ 0,84 0,09 0,04
х2 0,92 0,15 0,11
х3 0,87 0,26 0,13
х4 0,62 0,38 0,76
Х5 0,46 0,65 0,24
Х6 0,72 0,88 0,31
х7 0,48 0,21 0,68
По приведенным данным требуется определить главные фак-
торные нагрузки и обобщенную оценку влияния, детерминиру-
ющую поведение наблюдаемых объектов в зависимости от из-
менения всех семи признаков-показателей, взятых вместе.
Решение.
ai\
1. Определяем коэффициент необходимый для нахож-
дения значения G.. Для х. имеем: т— = 0,232 ; для х * - 0,254
Kl 1 3,62 z j,oz
И т.д.
(Коэффициент Х1 = 3,62 приведен в примере 3.2.)
2. По модели Z = AG найдем главные компоненты по от-
дельно взятым объектам и всей их совокупности.
Зная, что матрица А всех т компонент обратима, имеем
G = A-'Z.
Определив Zтолько для главных компонент (Z < т), полу-
чим: G = k~'AlZ.
129
Значение j-й компоненты для к-то объекта совокупности будет
Cis:
находиться как — -zki, а для всей совокупности объектов GkJ —
V аИ
как 1—%
7=1 j
3. Полученные значения Gkj можно интерпретировать как
обобщенную оценку, детерминирующую состояние наблюдае-
мых объектов в зависимости от всех семи признаков, вместе
взятых.
Результаты расчетов zki и Gki представим в табл. 3.5.
Таблица 3.5
Коэффици- енты ал / Объект 1 Объект 2
z\i Gll z2i g2]
х( 0,232 0,846 0,196 -0,113 -0,026
х2 0,254 0,428 0,109 0,326 0,083
х3 0,240 0,242 0,058 0,553 0,133
х4 0,171 0,289 0,049 1,067 0,182
х5 0,127 -0,150 -0,019 0,111 0,014
х6 0,199 0,211 0,042 -0,065 -0,013
х7 0,133 -0,407 -0,054 0,455 0,061
Итого X X 0,381 X 0,434
4. Согласно полученным оценкам главная компонента по
объекту 2, имеющая значение 0,434 и обобщающая влияние
семи признаков Xj — х7, детерминирует его лучше, чем соответ-
ствующая компонента 0,381, найденная для объекта 1.
5. Судя по значениям приведенных факторных нагрузок и
полученным компонентным оценкам, первую из них можно
интерпретировать как определяющую, вторую - как промежу-
точную, а третью — как второстепенную.
130
3.3.2.
Примеры факторного анализа
Пример 3.4. На основе анализа взаимосвязей пяти при-
знаков х. выделены два фактора (табл. 3.6).
Таблица 3.6
ау X, х2 хз Х4 Х5
а,1 0,90 0,80 0,60 0,10 0,05
а12 0,10 0,05 0,20 0,70 0,80
Требуется определить общность и специфичность каждого
признака, а также вклад выделенных факторов в суммарную
дисперсию, используя приведенные ниже факторные нагрузки.
Решение.
1. Уточним, что под общностью в факторном анализе пони-
мается сумма межгрупповых дисперсий по наблюдаемым мно-
жествам объектов (в нашем случае их 5), а под специфичностью
(называемой также характерностью) — сумма внутригрупповых
дисперсий.
2. Для получения суммарной дисперсии возведем фактор-
ные нагрузки апи аа соответственно в квадратную степень, най-
дем их общую сумму, равную 3,0050. Результаты расчетов пред-
ставим в табл. 3.7.
Таблица 3.7
xi Общность Специфичность
41 а12 Факторная 8?
X] 0,8100 0,0100 0,8200 0,1800
х2 0,6400 0,0025 0,6425 0,3575
х3 0,3600 0,0400 0,400 0,6000
Х4 0,0100 0,4900 0,5000 0,5000
х5 0,0025 0,6400 0,6425 0,3575
Итого 1,8225 1,1825 3,0050 1,9950
131
3. Найдем общую дисперсию как 3,0050 + 1,9950 = 5,0000.
4. Найдем специфичность, вычитая из общей дисперсии фак-
торную дисперсию, т.е. 5,0000 — 3,0050 = 1,9950 (гр. 4 табл. 3.7).
5. Определим долю факторной нагрузки в общей дисперсии
как 3,0050 : 5 = 0,6010, в том числе долю дисперсий первого
фактора как 1,8225 : 5 = 0,3645.
6. Аналогично определим долю дисперсий второго фактора
как 1,1825 : 5 = 0,2365.
7. Определим долю специфичности как 1,9950 : 5 = 0,3990.
Пр имер 3.5. Известны пять парных коэффициентов кор-
реляции. Требуется построить корреляционную матрицу.
Решение.
1. Представим в виде триангулированной табл. 3.8 заданные
парные коэффициенты корреляции.
Таблица 3.8
xi X, х2 х3 х4 х5
Х1 1 0,825 0,744 0,815 0,638
*2 1 0,517 0,694 0,843
х3 1 0,748 0,575
х4 1 0,787
*5 1
2. Ранжировав приведенные коэффициенты в возрастающем
порядке и разместив их по диагонали, построим редуцирован-
ную корреляционную матрицу (табл. 3.9).
Таблица 3.9
xi *1 *2 х3 х4 х5
*1 0,825 0,825 0,744 0,815 0,638
х2 0,825 0,843 0,517 0,694 0,843
х3 0,744 0,517 0,748 0,748 0,575
х4 0,815 0,694 0,748 0,815 0,787
х5 0,638 0,843 0,575 0,787 0,843
132
3. Найдем минимальное значение усредненной корреляции
редуцированной матрицы как меньшее по отношению к диаго-
нальному значению:
,2 0,825 + 0,744 + 0,815 + 0,638 п
/г. = —--------------------= 0,756.
1 4
4. Определим общность по методу триад для этого случая:
2 = 0,8 25-0,81 5^ %9
0,694
5. Сравним найденные значения (0,756 и 0,969) и выберем
минимальное 0,756 как искомую величину.
Пример 3.6. Даны факторные нагрузки аа и аР_ для пяти
признаков (табл. 3.10).
Таблица 3.16
аУ Х1 Х2 Х3 х4 Х5
ап 0,60 0,40 -0,30 -0,20 -0,10
ai2 0,40 0,50 0,60 0,80 0,70
Требуется преобразовать факторное решение путем враще-
ния против часовой стрелки на 30°.
Решение.
1. Найдем sin 30° = 0,500, cos 30° = 0,866.
2. Строим матрицу преобразования:
Т =
0,866 -0,500
0,500 0,866
3. Исходя из равенства В = A~l Т, получаем:
А Т = в
0,60 0,40 0,866 -0,500 0,7196 0,0462
0,40 0,50 0,500 0,866 0,5964 0,2330
-0,30 0,60 = 0,0402 0,6696
-0,20 0,80 0,2368 0,7928
-0,10 0,70 0,2634 0,9062
133
4. Проведя соответствующие расчеты, получим значения
фактора = 0,725, который имеет высокие нагрузки на призна-
ки х, и х2, и значение фактора о2 = 0,584, который имеет более
низкие нагрузки на признаки х3, х4 и х5.
3.3.3.
Примеры кластерного анализа
Пример 3.7. Имеются следующие данные о 16 объектах,
наблюдаемых по двум признакам xt и х2 (табл. 3.11).
Таблица 3.11
Объект Х1 х2 Объект Х1 х2
1 1,2 3,4 9 3,7 5,2
2 1,5 3,2 10 4,0 6,0
3 3,9 1,8 11 3,9 2,9
4 4,6 1,9 12 3,0 2,4
5 4,9 2,4 13 2,0 1,6
6 5,2 2,7 14 1,0 1,6
7 5,6 3,4 15 0,8 1,4
8 5,9 3,9 16 0,7 1,2
Требуется:
1) представить расстояние между приведенными объектами
в геометрическом виде; 2) выбрать алгоритм и выделить одно-
родные классы наблюдаемых объектов.
Решение.
1. Строим график расположения объектов, используя их при-
знаки в качестве координат. По оси абсцисс откладываем значе-
ния хр а по оси ординат — значения х2 (рис. 3.3).
2. Для решения задачи выбираем так называемый алгоритм
ближайшего соседа, предполагающий использование метрики
— норма как наиболее простой, и, следовательно, адекватный
в данном случае.
Согласно этой метрике расстояние находится путем опре-
деления суммы модулей между парными значениями наблюдае-
мых признаков.
3. На основе найденных модулей строим матрицу расстоя-
ний Dq размерности, внося каждое значение аув соответствую-
щую клетку таблицы (табл. 3.12).
134
Рис. 3.3. График кластерного распределения
4. Проводим последовательную, пошаговую кластеризацию
(классификацию) наблюдаемых объектов, принимая в исходной
точке каждый объект за отдельный кластер:
ап =|1,2-1,2| + |1,2-1,2| = 0,0;
а12 = |1,2 —1,5| + |3,4-3,2| = 0,5;
а13 =|1,2-3,9| + |3,4-1,8| = 4,3;
а14 = |1,2-4,б| + |3,4-1,9| = 4,9;
а15 =|1,2-4,9| + |3,4-2,4| = 4,7;
а10 =|1,2-4,0|+|3,4—5,б| = 5,0.
Полученные оценки вносим в первую строку и графу соот-
ветственно новой матрицы 9 и т.д.
135
Таблица 3.12
Объект 1 2 3 4 5 6 7 8 9 10
1 0,0 0,50 4,30 4,90 4,70 4,70 4,40 5,20 4,30 5,0
2 0,50 0,0 3,80 4,40 4,20 4,20 4,30 5,10 4,20 4,90
3 4,30 3,80 0,0 0,80 1,60 2,20 3,30 4,10 3,60 3,90
4 4,90 4,40 0,80 0,0 0,80 1,40 2,50 3,30 4,20 4,30
5 4,70 4,20 1,60 0,80 0,0 0,60 1,70 2,50 4,00 4,10
6 4,70 4,20 2,20 1,40 0,60 0,0 1,10 1,90 4,00 4,10
7 4,40 4,30 3,30 2,50 1,70 1,10 0,0 0,80 3,70 3,80
8 5,20 5,10 4,10 3,30 2,50 1,90 0,80 0,0 3,50 3,60
9 4,30 4,20 3,60 4,20 4,00 4,00 3,70 3,50 0,0 0,70
10 5,00 4,90 3,90 4,30 4,10 4,10 3,80 3,60 0,70 0,0
Напомним, что модуль в отличие от обычного числа — это
оператор, действие над которым осуществляется без учета зна-
ка. Классификатор при этом понимается как реально существу-
ющая общность объектов, однородных по наблюдаемым при-
знакам непосредственной близости друг к другу. Модуль близо-
сти определяется по критерию минимума расстояний.
Из приведенной матрицы видно, что первой такой величи-
ной является а, 2 = 0,5, затем а5 6 — 0,6, а910 = 0,7, а}4 = 0,8 и т.д.
Принадлежность соответствующих объектов к одному клас-
теру обозначается вектором минимальных расстояний. В пер-
вом случае такими являются объекты 1, 2, во втором — 5, 6, в
третьем — 9, 10 и т.д.
5. Последовательно объединяя объекты в кластеры, строим
укрупненные матрицы, размерность которых после каждого шага
кластеризации уменьшается на 1. Процесс кластеризации пре-
кращается на уровне объединения всех наблюдаемых объектов в
кластер. На этом уровне матрица превращается в вектор, дей-
ствия по укрупнению которого по определению далее невоз-
можны.
В нашем примере необходимо сделать девять шагов, а следова-
тельно, построить девять укрупненных матриц, каждая из которых
будет отражать комбинацию одного или большего числа матрично
представленных кластеров и остаточного числа объектов.
6. На уровне первого шага это будет матрица 9x9, представ-
ляющая собственно первый кластер, объединяющий объекты 1,
2 и 8 первичных объектов, содержащихся в первичной таблице;
на уровне второго шага — матрица 8x8, состоящая из двух
кластеров (ранее найденного и кластера при а56, объединяюще-
го объекты 5 и 6) и шести некластеризированных объектов; на
уровне третьего шага — матрица 7 х 7 (3 кластера и 4 некласте-
ризированных объекта) и т.д. до шестого шага.
На уровне шестого и последующих шагов процедура объеди-
нения первичных и некластеризированных объектов с кластера-
ми заканчивается и дальше объединяются кластеры.
7. Расстояние по графам находится как
а21 = [1,5-1,2] + [3,2-3,4] = 0,5;
а23 = [1,5 - 3,9]ч- [3,2-1,8] = 3,8;
137
а24 = [1,5-4,6] + [3,2 -1,9] = 4,4;
«25 =[1,5-4,9] + [3,2-2,4] = 4,2;
«21 =[1,5-4,0]+[3,2-5,б] = 4,9.
8. Объединяем первичные объекты с кластерами и далее кла-
стеры с кластерами по формуле средней арифметической про-
стой. Соответственно на уровне первого шага получаем матрич-
ные значения
а/1,2/,3 = |а13+^а23=|/4,3+3,8/ = 4,05;
а/1,2/,4 = |а14+|а24 = |/4,9+4,40/ = 4,65.
На уровне шестого шага:
а/1,2/(3,4,5,6) = —а12(3>4) +—«1,2(5,6) =
9. Соответственно на уровне второго шага объединяем объек-
ты 5,6, третьего шага — 9, 10, четвертого шага — 3, 4, пятого —
объекты 7 и 8.
На уровне седьмого шага, со стартовым значением 1,5, на-
чинается, как отмечалось, объединение кластеров (3, 4) и (5, 6),
на уровне седьмого шага с отметкой 2,55 — кластеров (3-6) и
(7, 8), на уровне восьмого — кластеров (3—8) с кластером (9, 10),
наконец, на уровне десятого шага объединяют все объекты и
получают один-единственный кластер, на котором завершается
вся работа.
10. Для того чтобы каждый раз не переписывать пересчитан-
ную матрицу в полном объеме, строят объединенную пошаго-
вую матрицу, в которую вносят только итоговые строки объеди-
ненных объектов и кластеров с указанием стартовых точек объе-
динения (табл. 3.13).
138
Таблица 3.13
Объект Шаг
1 2 3 4 5 6 7 8 9
1 0,50 4,45 4,60 4,35 4,75 4,40 4,575 4,588
2
3 4,05 1,90 3,75 0,80 3,30
4 4,65 1,10 4,25
' 5 4,45 0,60 4,05 1,50 1,80 1,50
6 4,45 2,55 4,588
7 4,35 1,40 3,75 2,90 0,80 2,55 3,838
8 5,15 2,20 3,55 3,70
9 4,25 4,00 0,70 4,00 3,65 4,025 3,838
10 4,95 4,10
Кластеры 9 8 7 6 5 4 3 2 1
11. Принимая во внимание, что все производные матрицы
симметричны, их значения представляют обычно в триангули-
рованном виде. Соответственно матрица на уровне шестого шага,
включая четыре кластера (1,2), (3,4,5,6), (7,8) и (9,10), будет иметь
вид:
4,40
4,75
к4,60
^6 =
0
2,55 0
4,025 3,65 0
Далее матрица на уровне седьмого шага в составе трех клас-
теров (1,2), (3—8), (9,10) имеет вид Z>7:
D7= 4,575 0
^4,60 3,838 0^
12. Представим процесс объединения объектов в схемати-
ческом виде (рис. 3.4).
Средняя
расстояния 12910785 643
0,50
0,60
0,70
0,80
0,90
1,50
2,55
3,84
4,59
Рис. 3.4. Пошаговая кластеризация объектов
140
Выводы. Технический вывод: на основе приведенных 10
объектов по максимуму может быть выделено 9 различных их
комбинаций, каждая из которых без целевого содержательного
анализа не имеет прикладного значения. Содержательный вы-
вод: среди выделенных кластеров содержательное значение имеют
те, которые включают в свой состав однородные объекты. Таки-
ми являются три кластера: (1, 2), (9, 10) и (3—8), удаление коор-
динат в рамках каждого из которых минимально*.
Пример 3.8. Имеются следующие данные о 12 объектах,
наблюдаемых по двум признакам х1 и х2 (табл. 3.14).
Таблица 3.14
Объект *1 *2
1 1,75 3,25
2 2,65 5,50
3 1,80 4,47
4 2,50 4,75
5 3,00 5,00
6 3,54 4,71
7 2,82 4,22
8 2,53 4,07
9 2,25 4,04
10 2,06 3,95
11 2,75 3,75
12 3,24 3,93
Требуется найти классы однородных объектов при радиусе
круга, равном 1,10, используя центрографический метод поиска
соответствующих кластеров.
Решение.
1. Обоснуем выбор радиуса круга. Радиус круга, величина
которого обычно обозначается как Т, определяется по признаку
минимального и максимального значений расстояний между
наблюдаемыми объектами. Если принять минимальный радиус,
равный расстоянию между двумя ближайшими объектами, вы-
деляется максимальное число кластеров, тождественное числу
наблюдаемых объектов или приближающееся к нему число; если
* Более подробные пояснения применяемых здесь кластерных про-
цедур см.: Дубров А.М., Мхитарян JB. С., Трошин Л.И. Многомерные ста-
тистические методы. — М.: Финансы и статистика, 2000. — С. 251-255.
141
принять максимальный радиус, равный расстоянию между край-
ними объектами, вся совокупность наблюдаемых объектов пре-
вращается в один-единственный кластер, собственно кластер-
ный анализ которого теряет смысл. Обычно процедуру выбора
радиуса рассматривают как итерационную.
2. Представим расположение наблюдаемых объектов в гра-
фическом виде, как более наглядном (рис. 3.5), принимая за
координаты каждого значения соответствующие их признаки х(
и х2.
3. Определим шаги последовательного решения задачи по
определению кластеров. В случае нахождения первого кластера
их 10.
Шаг 1. Выбрав матрицу lt — норма в качестве меры рассто-
яния, определим точку отсчета (центр тяжести), приняв за нее
объект 2 с координатами (2,65; 5,50), представляющими центр
круга радиуса 1,10.
Шаг 2. Измерив расстояния от центра тяжести до других
объектов, определим совокупность точек, попавших в этот круг,
142
и среднее расстояние между ними (их, как видно на рис. 3.4,
три — объекты 2, 4, 5). По найденным средним расстояниям,
которые вносятся в таблицу, определяется радиус следующего
центра и т.д. (табл. 3.15).
Таблица 3.15
Объект Шаг
1 2 3 4 5 6 7 8 9 10
1 1,15 — 1,84
2 0,0 0,49 0,72 0,98 — — — — — 1,51
3 1,88 — — — — — — — 1,10 1,01
4 0,90 0,55 0,36 0,38 0,51 0,81 0,77 0,73 0,68 0,61
5 0,85 0,36 0,39 0,45 0,60 0,74 0,86 1,02 — 1,36
6 1,68 — 0,96 0,70 0,85 0,99 — — — 1,61
7 1,45 0,96 0,73 0,51 0,36 0,22 0,10 0,12 0,19 0,40
8 1,55 — 1,01 0,95 0,80 0,66 0,54 0,38 0,25 0,12
9 1,86 — — — — 0,97 0,85 0,69 0,56 0,35
10 2,141 — — — — — — 0,97 0,84 0,63
11 1,85 — — 1,05 0,90 0,76 0,63 0,52 0,57 0,66
12 2,16 — — — 1,05 0,75 0,79 0,83 0,88 0,97
Коор- 2,72 2,74 2,84 2,83 2,91 2,83 2,73 2,64 2,49 2,49
динаты центра 5,08 4,87 4,71 4,57 4,35 4,31 4,25 4,21 4,15 4,15
тяже- сти
Шаг 3. Определим по формуле средней арифметической
простой координаты центра тяжести этих точек:
хц = (2,65 + 2,50 + 3,00): 3 = 2,72;
xj2 =(5,50 + 4,75 + 5,00): 3 = 5,08.
Ш аг 4. Примем точку с координатами (2,72; 5,08) за центр
нового круга, найдем расстояния от этого центра до точек всех
наблюдаемых 12 объектов, средняя которого представляет ра-
диус данного круга. В табл. 3.15 вносим расстояния только для
объектов, попавших в этот круг, т.е. объектов 2, 4, 5 и 7.
143
Шаг 5. Далее находим центр тяжести для этой группы
объектов:
х'21 = (2,65 + 2,50 + 3,00 + 2,82) : 4 = 2,74;
^22 = (5,50 + 4,75 + 5,00 + 4,22): 4 = 4,87.
Ш аг 6. Итерационный процесс продолжается до 10-го шага,
на уровне которого совокупность объектов, попавших в круг,
становится неизменной, их центр далее не смещается (весь путь
смещения этого центра показан на рис. 3.5 пунктирной линией)
и, следовательно, не меняется, приобретая значение центра пер-
вого кластера. В образуемый круг с этим центром попадают
объекты 3, 4, 7—12, формирующие общность, которую представ-
ляет искомый первый кластер, значение которого получаем на
уровне 10-го шага.
4. Изменяя каждый раз величину радиуса круга, по той же
процедуре находят значение всех других искомых кластеров и
далее устойчивое их множество, представляющее собой конеч-
ное множество кластеров, состав объектов которых далее не
меняется в зависимости от последующей любой комбинаторики
и любого смещения радиуса их круга.
Выводы. Для обоснованного определения числа кластеров
процедуру вычисления необходимо повторять, выбирая различ-
ные значения Г и их комбинации, каждый раз уменьшая (или
увеличивая) кластерную пару на заданную величину так, это
показано на рис. 3.6. Процедура прекращается при получении
одного и того же множества кластеров на основе ряда последо-
вательного уменьшения значений Т с приближением их к ми-
нимуму, равному величине То.
Несмотря на исключительную трудоемкость расчетов, обра-
щение к процедурам кластерного анализа неизбежно в случае,
когда имеют дело с предельно сложными иерархическими объек-
тами, когда определять общности, расщеплять разнородные со-
ставы и распознавать образы которых с помощью других стати-
стических методов не представляется возможным
Пример 3.9. Даны координаты расстояния между объекта-
ми Xj и х2 (см. рис. 3.6).
Требуется определить евклидово расстояние между объекта-
ми х, и х2 по методу уменьшения величины кластер-радиуса Т.
144
Рис. 3.6. График распределения кластер-процедур Го
Решение.
1. Представим исходные данные в виде разрешающей мет-
рики
2 4
7 6
2. Выберем формулы расчета искомого расстояния а(хр х2):
а(х1,х2) - 4/ X (XU -х2к)2 - V<XH -х21)2 +(х12 -х22)•
U=1
3. Найдем искомое евклидово расстояние:
а(х] ,х2) = а/(2-7)2+(4-6)2 = 5,39.
145
3.3.4.
Примеры дискриминантного анализа
Пр и мер 3.10. Дана таблица исходных показателей (хр х2,
х3, х4) по 32 объектам (табл. 3.16).
Требуется:
1) представить графики эмпирического распределения ис-
ходных данных и дискриминантной функции /(х) в начале и
конце расчетов в целом и по каждому показателю xt к х2, х3, х4;
2) по алгоритму дискриминантного поиска найти соответ-
ствующие параметры от а до С (const) по каждому объекту, их
классам и общему множеству функции. Все результаты предста-
вить в табличном виде;
3) определить принадлежность объектов 33, 34, 35, 36 к со-
ответствующим классам;
4) на основе данных, полученных для 36 объектов, найти
принадлежность объектов 37 и 38 со следующими характеристи-
ками х., х_, X., X'
1’ 2’ 3’ 4
37 : х1 = 3,85;х2 = 4,47; х3 = 10,5; х4 = 8;
38 : х ,= 4,6; х, = 6,2; х = 8,7; х, — 9;
5) представить дискриминантную функцию Дх) в виде гра-
фика.
Для решения задачи необходимо выбрать один из методов
многомерного анализа путем проведения пошагового сравнения
методов дискриминантного, кластерного, факторного, компо-
нентного и центрографического анализа.
Мы выбрали метод дискриминантного анализа как наиболее
простой и информативный.
Решение. Необходимо сделать 15 шагов. (Общая схема реше-
ния представлена на рис. 3.7.)
Шаг 1. Найдем значение х для классов (их четыре): х( — х4
(1—12), X] — х4 (1—6), х, — х4 (1—6), х( — х4 (1—8), квадрантов (их
тоже четыре): хр х2 (1—18), х3, х4 (1—18), х,, х2 (19—32), х3, х4 (19-
32) и для всех 32 объектов, взятых вместе (рис. 3.8):
146
Таблица 3.16
Исходные и расчетные данные для нахождения четырех частных
и одной общей дискриминантных функций
№ п/п X] х2 х3 *4 5 h X] -X]
1 2 3 4 5 6 7
1 1,75 5,25 8 16 1 -1,3877
2 2,65 5,50 11 15 1 -0,4877
3 1,80 4,47 10 6 1 -1,337
4 2,50 4,75 7 9 1 —0,о377
5 3,00 5,00 12 7 1 -0,1377
6 3,54 4,71 8 6 1 0,4023
1 2,82 4,22 10” 5 1 -0,3177
8 2,53 4,07 8 5 " I 0,6077
9 2,25 4,04 12 16 1 -0,8877
10 2,06 ' 3,95 9 8 1 1,0777
11 11 2,75 3,75 9 7 1 -0,3877
12 3,24 3,93 10 8 1 0,1023
Е 30,89 53,64 114,00 108,00 -7,2670
2,5741 4,4700 9,500 9,000 +0,5046
13 4,14 3,52 12 11 2 1,0023
14 4,62 3,34 13 7 2 1,4823
15 4,27 3,11 11 8 2 1,1323
16 3,78 2,92 15 6 2 0,6423
17 4,25 2,76 14 5 2 1,1123
18 4,53 2,60 14 ‘ 5 2 1,3923
Е 25,59 18,25 79,00 42,00 +6,7638
4,2^50 3,0416 13,1666 7,000 0,5046
+7,2684
" 19 5,28 5,00 13 7 3 0,8900
20 5,21 4,54 10 5 3 0,8200
- 21 6,01 5,00 12 9 3 1,6200
22 5,25 4,23 15 8 3 0,8600
23 6,00 4,37 14 8 3 1,6100
24 5,76 3,92 15 7 3 1,3700
Е 33,51 27,06 79,00 44,00 +7,4700
5,5850 4,5100 13,1^66 7,333
’"25 3,50 2,00 8 4 4 -0,8900
26 2,77 1,54 4 4 4 -1,6200
" 27 3'51 1,40 3 6 4 - О,880О
28 4,00 1,75 7 2 4 -0,3900
29 3,03 1,00 8 2 4 -1,3600
“ 30 3’25 0,88 6 3 4 -1,4400
31 3,69 0,49 5 2 4 -0,7000
32 4,20 1,00 7 2 4 -0,1900
Е 27’95 10,06 48,00 25,00 -7,4700
3,4937 1,2^75 б,(5оо 3,1250
Е 117,94 109,01 320,0 ^19,0
3,6856 3,4(566 10,0 6,8438
33 2,30 6,11 10 14 -1
34 5,21 1,18 и- 4 -3
35 4’75 3,25 И 8 -3
36 3,13 2,50 7 3 -4
37 3,85 4,47 “1В,5 8 —
38 4,6 | (5,2 : 9 —
147
Продолжение
*2“ *2 k> х3-х3 х4 -х4 (-«1 ~*i)2 а 22 (х2-х2)2 °зз (*з_*з)2 ° 44 (х4-х4)2
8" - -9 - 10™ ~ 11 12 13 14
'СТТ -2,7’2221 7’,ШТ 1,9257“ 1,575(1” 7,4103 58,7782”
” l>62 0,2778' 6,6667 0,2378 2,2686 0,0771 44,4448
0,4762 -0,7222 -2,33’3’3” 1,7894 Щ225Г 0,3215 5,4442
0,7562 -3,7222 0,6667 0,4066 0,5718 13,8547 0,4444
1,0062 1,2778 -1,3333 0,0189 1,0124 1,6327 1,7776
0,7162 -2,7222 -2,3333 0,1618 0,5129 7,4103 5,4442
0,2262 -0,7222 -3,3333 0,1009 0,0511 0,5215 11,1108
'0>6Т -2 7222' - з,33зз 0,3692 0,0058 7,4103 11,1108
0,0462 ft277S 7^567” 0,7880 0,0021 1,6327 58,7782
-0,0438 1,7222 -0,3333 1,1614 0,0019 2,9659 0,1108
-0,2438 -1,7222 -1,3333 0,1503 0,0594 2,9659 1,777’6
—0,0638 -0,7222 -0,3333 0,0104 0,0040 0,5215 0,1108
+6,0658 -17,4990 +22,5668 7,1104 6,2947 46,9144 199,3324
-0,3514 +2,8334 2,6667’ 199,3324
25,3335
-0,4738 1,2778 2,666’7 1,0046 0,2244 1,6327 7,1112
-0,6538 2,2778 -1,3333 2,1972 0,4274 5,1883 1,7776
-0,8838 0,2778 -0,3333 1,2821 0,7811 0,0771 0,1108
-1,0738 4,2778 -2,3333 0,4125 1,1530 18,2995 5,4442
-1,2338 3,2778 —3,3333 1,2372 1,5222 10,7439 11,1108
-1,3938 3,2778 -3,3333 1,9384 1,9426 10,7439 11,1108
-5,7128 + 14,6668 -10,6663 8,0720 6,0507 46,6854 36,6652
-0,3514 2,8334 — 14,6664
"6>42" + 17,5002 —25,3329
2,3486 3,9286 2,0715 0,7921 5,5159 15,4338 4,2911
0,8886 ” 0t<J286 0,0715’ 0,672’4 3,5668 0,8622 0,0051
2,3486 2,9286 4,0715 2,6244” 5,5159 8,5766 16,577Г
1,5786 5,928s 3,0715 0,7396 2,4919 35,1482 9,4341
1,7186 4,9286 3,0715 2,5921 2,9535 24,2910 9,4341
’1,2’686 5,9286 2,0715 ”’1,8759" 1,6093 35,1482 4,2911
+ 11,1516 +24,5716 14,4290 9,2975 21,6533 119,4600 44,0326
1,0715"
13;5ОО5
-0,6514 -1,0714 -0,9285 0,7921 0,4243 1,1478 0,8621
-1,1114 -5,07 Г4 -0,9285 2,6244 1,2352 25,7190 0,8621
-1,2514 -6,0714 1,0715 0,7744 1,5660 36,8618 1,1481
-0,9014 -2,0714 -2928’5” 0,1521 0,8125 4,2906 8,5761
-1,6514 -1,0714 —2,9285 1,8496 2,7271 1,1478 8,5761
-1,7714 -3,0’714 -Г,’9285 2,0736 3,1378 9,4334 3,7191
-2,1614 -4,0714 -2,9285 0,4900 4,6716 16,3762 8,5761
-1,6514 -2,0714 -2,9285 0,0361 2,7271 417906 8,5761
-11,1504 -24,551’6 3-15,4995 8,8023 17,30’1’6 99,4662 40,8758
33,2822 51,3003 312,5260 320,906
1,0401 1,6031 9,7664 10,0283
148
Продолжение
^12 (а, а2) = = (+| -Х])Х х(х2-х2) г13 (<*1 <ъ) *14 (о, а4) *23 (о2 а3) *24 (а2 -а4) *34 (а3 <*4)
15 16 17 18 19 20
-1,7432 3,7775 -10,6390 -3,4196 9,6309 -20,8702
-0.7345” ' -0,1354 -3,2513 0,4184 10,0413 1,8520
-0,6370 0,9660 3,1212 -0,3439 -1,1111 1,6851
—0,4822 2,3736 -0,4251 -2,8147 0,5041 -2,4815
-0,1385 -0,1759 0,1835 1,2857 -1,3415 -1,7036
+0,2888 -1,0954 -0,9386 -1,9496 -1,6711 6,3517
-0,0718 0,2294 1,0589 -0,1633 -0,7539 2,4073
-0,0463 1’6542 2,0256 -0,2074 -0,2539 9,0739
-0,3608 -1,1343 -6,8057 0,0590 0,3542 9,7965
+0,0472 1,8560 0,3591 0,0754 0,0145 0,5740
+0,0945 0,6676 0,5169 0,4198 0,3250 2,2962
-0,0065 —0,00б5 -0,0340 0,0460 0,0212 0,2407
-4,2205 + 11,5243 +7,2652 +1,0646 +20,8912 +34,2774
+0,4305 -2,5475 -22,0934 -8,8985 -5,1315 -25,0553
-03748 ' 1,2807 2,6728 -0,6054 -1,2634 3,4075
-0,9691 3,3763 -1,9763 -1,4892 0,8717 3,0369
-1,0007 0,3145 -0,3773 -0,2455 0,2945 -0,0925
-0,6897 2,7476 -1,4986 -4,5935 2,8788 -9,9813
-1,3723 3,6458 -3,7076 -4,0441 4,1126 -10,9258
-1,9405 "4’5636 -4,6409 -4,5685 4,6459 -10,9258
-6,4471" 15,9285 +2,6728 + 13,0035 +3,4075
-п;пв7~ -15,5962 -1,2634 -35,4623
2,0902 3,4964 1,8436 9,2267 4,8651 8,1380
1,5486 0,7614 0,0586 1,7537 0,1350 0,0663
3,9047 4,7443 6,5958 6,8781 9,5623 11,9237
1,3575 5,0985 9,3588 4,8486 18,2096
2,7669 7,9350 4,9451 8,4702 5,2786 15,1381
1,7379 8,1221 2,8379 7,5210 2,6279 12,2810
13,3058 30,1577 18,9224 43,2075 27,3175 65,7567
0,5797 0,9535 0,82'63 0,6979 0,6048 0,9947
1,8004 8 2156 1,5041 5,6363 1,0319 4,7087
1’1012" 5>28 -0,9424" 7,5977 -1,3408 -6,5055
0’3515 ' 0,8078 +1,1421 1,8671 2,6397 6,0660
2,2459 1,4571 Х9827- Г,7603 ' 4,8361 3,1375
2,5508 4,4228 2,7770 5,4406 3,4161 5,9231
1 5129 " 2,8499 2,0499 8,7999 6,3296 11,9230
03137 о’3935 0,5564 3,4207 4,8361 6,0660
10’4561 ' 24,4430 + 12,8385 35,2295 20,6942 +38,8150
-0,9424 -l‘J40T -6,5055
13,5248 7'9,5060 7,4б"44- 55,056 74,1707 75,2375
0,4227 2,4846 0,2333 1+205 2,3178 2,3512
149
Продолжение
Лх)|2 f-f (/-/)2 /(*)34 f-f (/-/)
21 22 23 24 25 26
2,6203 2,1500 4,6225 -3,2560 -9,3559 87,5328
1,6330 1,1627 1,3519 -5,4038 -11,5037 132,3351
1,8088 1,3385 1,7916 -5,9236 -12,0235 144,5645
1,1225 0,6522 0,4254 -3,5110 -9,6109 92,3694
0,6799 0,2096 0,0440 -7,1348 -13,2347 175,1573
-0,3318 -0,8021 0,6434 -4,5800 -10,6799 114,0603
0,1817 -0,2886 0,0833 -6,0560 -12,1569 147,7659
0,4336 -0,0367 0,0013 -4,7124 -10,8123 116,9058
0,7863 0,3160 0,0999 -5,9432 -12,0431 145,0363
0,9593 0,4890 0,2391 -4,9870 -11,0869 122,9194
-0,2384 -0,7087 0,5023 -5,1194 -11,2193 125,8727
—0,6666 -1,1369 1,2925 -5,6588 -11,7587 138,2670
+8,9886 +6,3180 11,0972 -62,2860 -135,4848 1542,7865
111,46221 -2,9730
-2,2828 -2,7531 7,5796 -6,6052 -12,7051 164,4196
-3,1081 -3,5784 12,8050 -7,8066 -13,9065 193,3907
-2,8507 -3,3210 11,0290 -6,3306 -12,4305 154,5173
-2,3644 -2,8347 8,0355 -9,2826 -15,3825 236,6213
-3,1569 -3,6272 13,1566 -8,7432 -14,8431 220,3176
-3,6907 -4,1610 17,3139 -8,7432 -14,8431 220,3176
-17,4536 -20,6754 69,9176 -47,5114 -84,1108 1186,5841
6,7716 2,5186 6,3434 6,3598 10,8127 116,9145
6,3217 2,0687 4,2795 4,7610 9,2139 84,8960
7,0756 2,8226 7,9671 6,7362 11,1891 125,1960
6,0549 1,8019 3,2468 7,3120 11,7649 138,4129
6,4952 2,2422 5,0275 7,0064 11,4593 131,3156
5,9837 1,7307 2,9953 6,9710 11,4239 130,5055
38,7027 13,1927 29,8596 39,1464 65,8638 727,2405
3,2866 -0,9664 0,9339 3,8088 8,2617 68,2557
2,5619 -1,6911 2,8598 2,5864 7,0393 49,5517
2,7420 -1,5110 2,2831 2,2928 6,7457 45,5045
3,2661 -0,9869 0,9740 2,8212 7,2741 52,9125
2,1763 -2,0767 4,3127 3,1268 7,5797 57,4519
2,1581 -2,0949 4,3886 2,8566 7,3095 53,4288
1,9846 -2,2684 5,1456 2,2100 6,6629 44,3942
2,6635 -1,5895 2,5265 2,8212 7,2741 52,9125
20,8391 -13,1849 23,4242 23,1938 58,1470 424,4118
88,4576 156,344 134,2986 172,1376 343,6064 3881,0229
150
№ *1 х2 *3 *4 S
1 1
2 1
3 1
4 1
5 1
— А
6 7 *11(1-12) *21(1-12) *31(1-12) *41(1-12) 1 1
t 8 2,5741 4,470 9,50 9,00 1
9 1
10 11 1-й квадрант 2-й квадрант 1 1
12 1
13 2
14 2
15 *12(13-18) *22(13-18) *32(13-18) *42(13-18) 2
16 4,265 3,0416 13,1666 7,00 2
17 2
18 2
19 3
20 *13(19-24) *23(19-24) *33(19-24) *43(19-24) 3
21 5,585 4,510 13,1666 7,3333 □
22 3
23 3
з
Z4
3-й квадрант 4-и квадрант А
25 4
26 4
27 4
28 *14(25-32) *24(25-32) *34(25-32) *44(25-32) 4
29 3,4937 1,2575 6,00 3,1250 4
30 4
31 4
32 4
33 2,30 6,11 10 14 2
34 5,21 1,18 13 4 2
35 4,75 3,25 11 8 2
36 3,13 2,50 7 3 2
Рис. 3.7. Общая схема решения задачи
I
151
№
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Х2 хз х4
С — + а2х2^ — 0,7547 С — а3х3«|+ a4x4j — 5,7204
1-й класс
С0бщ“ а1Х11+ а2Х21 + аЗХ31 + а4Х41-28,1002
Сн = а^х^2+ а2х22 “ “ 2,9090 Си = а3х32+ а4х42 = - 8,4012
2-й класс
Собщ~ а1Х12+ а2Х22+ аЗХ32+ а4Х42-45,9099
С|||= а^х^* а2х23 = 6,4504 С|||= а3х33+ а4х43 = 6,5244
3-й класс
S
1
1
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
25
26
27
28
29
30
31
32
Собщ“ а1Х13+ а2Х23+ а3х33+ а4Х43— 61,8192
CIV= а.|Х14+ а2х24 = 2,6049 С — с?зХ34+ а^х^— 2,8992
4-й класс
Собщ= а1х14+ а2х24+ а3х34+ а4Х44= ~ 41 >2297
3
3
3
3
3
3
4
4
4
4
4
4
4
4
C,+ C,,+ C,,,+ C,v с’+С"+Cm+C,v
сх1х2=--------------= 1 ’7252; Схзх4=-------а------= ~ 1 ’1745
I fc /I О *т St
Рис. 3.8. Значение х для 32 объектов
152
а) для x 1 -го класса:
- 30,89 ___Л1 - 114,0
xi j =-----= 2,5741; Х31 =--------= 9,50,
12 12
^3,64 л - 108,0 Q п
Х21 =------= 4,470; Х41 =------= 9,0.
12 12
б) для х 2-го класса:
25,59 . - 79,0
xi2 =------= 4,2650; хз2 =--------= 13,1666,
6 6
18,25 аП/|1А - 42,0 _п
6 6
в) для х 3-го класса:
33,51 - 27,06 . С1П
xi з =-----= 5,5850; хзз =--------= 4,510;
6 6
79,0 17 1^4 ~ 44’0
Х23 =------= 13,1666; Х4з =-------= 7,3333.
6 6
г) для х 4-го класса:
27,95 ал(УГ7 " 79’° ^40^
Х14 =------= 3,4937; хз4 =--------= 3,4937,
8 6
х24 =1^ = 1,2575; *44=^ = 3,1250.
8 8
Найдем х для квадрантов:
а) для х 1-го квадранта:
56,48
*1(1-18) = = 3,1377;
1о
71,89 . 0СП8
*2(1—18) = 7—— = 3,9938.
153
б) для х 2-го квадранта:
193
X3(i-i8) ——10,7222;
1 о
150 «
*4(1-18) = —— = 8,3333.
1 о
в) для х 3-го квадранта:
61,46 л аоп
*1(19-32) = 14 =4,390;
37 12
*2(19-32) =-^- = 2,6514.
г) для х 4-го квадранта:
127
*3(19-32) = = 9,0714;
69
*4(19-32)= —= 4,9285.
Найдем значение х для общей совокупности, состоящей и
32 объектов:
а) для х 1-го квадранта:
117,94
*1(1-32) =-----= 3,68 56;
109,01 „
*2(1-32) = — = 3,4066;
320
*3(1-32) = — = 10,0;
219
*4(1-32) = — = 6,8438.
154
Ш а г 2. Вычислим по квадрантам (напомним, их у нас че-
тыре) значения линейных отклонений /,, /2, /3, /4:
а) для 1-го квадранта:
Z, =xj -xi(i-i8) = 1,75-3,1377 = -1,3877
и т.д. последовательно для объектов с 1-го по 18-й. Результаты
представляем в табл. 3.16 (гр.6);
/2 = х2 — *2(1-18) = 5,25 — 3,9938 = 1,2562
и т.д. Результаты для объектов 1—18 занесем в таблицу;
б) для 2-го квадранта:
/3 = Х3 - х3(1-18) — 8 — 10,7222 = —2,7222
и т.д. для объектов 1—18;
/4 = *4 —*4(1-18) = 16 —8,333 = 7,6667
и т.д. для объектов с 1-го по 18-й;
в) для 3-го квадранта:
=Х] -xi(i9-32) =5,28 - 4,39 = 0,89
и т.д. Результаты занесем в таблицу;
/2 = х2 - х2(19-32) = 5,0 - 2,6514 = 2,3486
и т.д. для объектов 19-32;
г) для 4-го квадранта:
/3 =х3-хз 1(19-32) =13 - 9,0714 = 3,9286
и т.д. для объектов 19—32. Данные заносим в таблицу;
/4 =х4-х4(1 9-32) =7-4,9285 = 2,0715
и т.д. для объектов 19—32. Результаты заносим в таблицу.
155
Ш аг 3. Найдем значения дисперсий по квадрантам С?п, G22,
G„.
Для этого необходимо последовательно возвести в квадрат
полученные линейные отклонения /:
(xj -xi)2 — <?11; G22 — (*2 -xi)2;
(Xj — хз) =(733; G44 = (Хд -Х4) •
Результаты вычислений представим в табл. 3.16 (гр. 10—13).
Шаг 4. Вычислим значения ковариаций И|2, И13, К14, К23,
И24, Г34 (табл. 3.16, гр. 14-18).
Для этого необходимо:
(x1-xi)(x2-X2) = Gi2,
т.е. перемножить /, • /2, аналогично и для остальных /:
Аз -h h’ l23~l2l3’
Il4=l\l4> l24=l2l4> l34=l3l4-
Результаты вводим в табл. 3.16.
Ш аг 5. Найдем параметры и д2 для 1-го квадранта по сле-
дующей принципиальной формуле матричных определителей:
а1°11 +а2°12 =ХЦ-Х12;
Й1СТ21 + йГ2ст22 =*2\~Х22',
S(X[ - xi )2(i-18) _ 15,1824 _
18 18
°12 ~ ст21 “
Дх1Х1)(х2-х2)(1_18) -10,2371 псгоп
-------------------=----------= —и, эоо /.
18 18
156
Дисперсии о12 и о21 тождественны, поскольку симметричны:
= Дх2-х2)2£м8) = 12,3454
22 18 18
12
£ = 30,89
хц = ^-----------= 2,5741;
1 12
18
£ =25,59
XI2 = —---------= 4,2650;
12 6
12
£ = 53,64
х21 = ^---------= 4,470;
21 12
18
£=18,25
х22 = --------= 3,0416.
22 6
Запишем систему уравнений с исчисленными значениями о
И X.
ах • 0,8435 - аг 0,5687 = 2,5741 - 4,2650 = -1,6909;
-а, 0,5687 - а2 • 0,6859 = 4,47 - 3,0416 = 1,4284.
Решим приведенную систему уравнений путем построения
соответствующих матриц А, А]} А2 и исчисления матричных оп-
ределителей.
Определители соответствующих матриц находим путем пе-
рекрестного (диагонального) перемножения (триангуляции) их
членов, начиная с члена, размещенного в верхнем левом углу
матрицы, и заканчивая членом, размещенным в правом нижнем
углу, с последующим вычитанием из значения первого множи-
теля значения второго. При этом число членов матрицы может
быть сколь угодно большим.
157
0,8435
-0,5684
-0,5687
0,6859
= 0,5786 - 0,3234 = 0,2552 * 0.
Следовательно, полученная система уравнений является со-
вместной, поскольку ее функция не равна нулю.
Соответствующим образом найдем частные определители для
матриц:
|Л2|-
-1,6909
1,4284
-0,5687
0,6859
= -1,1598 + 0,8123 = -0,3475;
0,8435
-0,5687
-1,6909
1,4284
= 1,2048-0,9616 = 0,2432.
Соотнося частные определители к общему, находим после-
довательно (так, как показано на рис. 3.10) далее соответствую-
щие параметры av а2, а3 и а4 для каждой из четырех частных и
одной общей дискриминантной функции. Для/' (функция пер-
вого квадранта) искомые параметры будут следующими:
«1 =
|л|.
И’
-0,3475
0,2552
= -1,3617;
0,2432
0,2552
= 0,9530.
Аналогичным образом найдем параметры а3 и для второго
квадранта (/""):
a3G33 + а4°34 - х31 - х32;
«3043+04044 = х41 -*42-
ОЗЗ
Х(хз~хз)(1-18) _ 93,5998 _ 20
18 18 ” ’ ’
Z(x3-x3)(x4“x4)(l-18) 22,8327 , _
034 = 043 =-----------------*----- =-------= -1,2685;
18 18
Z(x4-X4)2d-18) = 235,9976 = J1 р
18 18 ’ ’
158
12
£ = 114,0
х3| = ^--------= 9,50;
J 12
18
£=79,0
Х32 =—---------= 13,1666;
6
12
X =108,0
х41 = ^--------= 9,0;
12
18
Z =42,0
Х42 = -------= 7,0;
6
5,2а3 -1,2685а4 = 9,5 -13,1666(-3,6666);
-1,2686а3 +13,111а4 = 9,0 - 7,0(2,0);
। । 5,2
-1,2685
-1,2685
13,111
= 68,1772-1,6091 = 66,5681.
Поскольку найденный определитель не равен нулю, система
является совместной:
|4|=
3,6666
2,0
-1,2685
13,111
= -48,0728+2,537 = -45,5358.
|Л2|-
5,2 -3,6666
-1,2685,0 2,0
= 10,4-4,6511 = 5,7489;
-45,5358
66,5681
= -0,6840;
5,7489
66,5681 = 0,0864’
159
Далее по той же схеме вычислим параметры и а2 для 3-го
квадранта
а1ст11 + а2ст12 =*13~*14;
alc21 +«2С22 = *23~*24-
= 1(х1-..Д)2а9£32) = 18^ =
11 14 14
__ S(xt -х,)(х2 -х2)(19-32) _ 23,7619 = ]
12 14 14
= Е(х2-х2)2(19-32) = 38^9548
22 14 14
24
Z =33,51
хв -------------= 5,5850;
13 6
32
£ =27,95
хм = —----------= 3,4937;
8
24
X =27,06
Х23 = -------= 4,510;
6
32
£ =ю,об
х24 = -------= 1,2575.
8
l,2928ai +1,6973л2 =5,585-3,4937(2,0913);
1,6973»! + 2,7825а2 =4,51-2,2575(3,2525).
1,2928
1,6973
1,6973
2,7825
= 3,5972 - 2,8808 = 0,7164 * 0.
160
На этом этапе расчетов вновь фиксируем факт совместности
представленной системы:
|л|-
2,0913
3,2525
1,6973
2,7825
= 5,8190-5,5207 = 0,2983;
1,2928
1,6973
2,0913
3,2525
= 4,2048-3,5496 = 0,6552;
0,2983
0,7164
= 0,4164;
0,6552
0,7164
= 0,9146.
Наконец, тем же способом найдем искомые параметры а3 и
а4 для 4-го квадранта:
«3°33 + а4ст34 - х33 ~ х34;
йГ3°43 + ^4^44 ” х43 ~ х44*
Озз = W-^3А19.32) = 218,9262 =
33 14 14
Е(хз ~ хз)(х4 ~ х4)(19-32) 98,0702
о 1--->_ =------= 7 0050;
34 ’ ‘ 14
14
Х(х4 -х4)2(19-32) _ 84,9084 _
14 14
24
X =79,0
хзз = ------= 13,1666;
32
Е =48,0
Х34 -1=25-------—
24
Е =-44,0
1^2--------= 7,3333;
161
32
I -25,0
X44 =—----------= 3,1250.
8
15,63 76a3 + 7,005a4 = 13,1666 - 6,0(7,1666);
7,005a3 +6,0649^ =7,333-3,1250(4,2083).
и=
15,6376
7,005
7,005
6,0649
= 94,8405 - 49,070 = 45,7705 * 0.
На основе подтверждения совместности системы строим и
решаем соответствующие матрицы А, и А2 относительно поиска
их определителей и исчисления по искомым параметрам:
И1=
7,1666
4,2083
7,005
6,0649
= 43,4647 - 29,4791 = 13,9856;
|Л2|-
15,6376
7,005
7,1666
4,2083
= 65,8077 - 50,2020 = 15,6057;
13,9856
45,7705
= 0,3056;
15,6057
45,7705
= 0,3410.
Шаг 6. На основе полученных параметров:
а, = —1,3617; а2 = 0,9530 для 1-го квадранта,
а, = 0,4164; а2 = 0,9146 для 2-го квадранта,
находим функцию /= (хр х2) по отдельным объектам и группо-
вую функцию по каждому из четырех классов объектов.
Подставив найденные параметры а( и а2 в уравнение f—(.xi,x2) =
= а(х + а2х2, получим некоторую долженствующую оценку уров-
ня развития каждого из наблюдаемых объектов, соответствую-
щую значению функции.
Если, например,/соответствует объему выпуска, х{ — затра-
ты труда, х2 — производительность труда, значение 2,6203 фик-
сирует, каким должен быть объем выпуска на объекте 1 при
заданных параметрах ах и а2. Сравнивая этот объем выпуска с
эмпирическим (допустим, он равен 2,6203), средним по группе
162
12 предприятий (он равен 8,9896) и общим средним по всей
совокупности 32 предприятий (3,9445), заключаем, что ресурсы
на предприятии 1 используются с интенсивностью больше на
0,200 ед., но на 6,3683 ед. хуже, чем в среднем по классу 12
родственных предприятий, и на 1,3242 ед. хуже, чем в среднем
по всей совокупности 32 наблюдаемых предприятий.
1.-1,3617 1,75 + 0,953 • 5,25 = -2,3830 + 5,0033 = 2,6203.
2.-1,3617 • 2,65 + 0,953 + 5,50 = -3,6085 + 5,2415 = 1,6330.
3.-1,3617 • 1,80 + 0,953 + 4,47 = -2,4511 + 4,2599 = 1,8088.
4.-1,3617 2,50 + 0,953 + 4,75 = -3,4043 + 4,5267 = 1,1225.
5.-1,3617 • 3,00 + 0,953 + 5,00 = -4,0851 + 4,7650 = 0,6799.
6.-1,3617 • 3,54 + 0,953 + 4,71 = -4,8204 + 4,4886 = -0,3318.
7.-1,3617 • 2,82 + 0,953 + 4,22 = -3,8400 + 4,0217 = 0,1827.
8.-1,3617 • 2,55 + 0,953 + 4,07 = -3,4451 + 3,8787 = 0,4336.
9.-1,3617 • 2,25 + 0,953 + 4,04 = -3,0638 + 3,8501 = 0,7863.
10. -1,3617 • 2,06 + 0,953 + 3,95 = -2,8051 + 3,7644 = 0,9593.
11. -1,3617 • 2,75 + 0,953 + 3,75 = -3,7447 + 3,5063 = -0,2384.
12. -1,3617 • 3,24 + 0,953 + 3,93 = -4,4119 + 3,7453 = -0,6666.
Найдем групповую функцию X по классу первых 12 объектов
путем суммирования значений 12 частных функций. В результа-
те имеем:
Е = -42,0630 + 51,0515 = 8,9886.
Далее найдем значения частных и групповых функций для
последующих классов наблюдаемых объектов:
13. -1,3617 • 4,14 + 0,953 + 3,52 = -5,6374 + 3,3546 = -2,2828.
14. -1,3617 4,62 + 0,953 + 3,34 = -6,2911 + 3,1830 = -3,1081.
15. -1,3617 • 4,27 + 0,953 + 3,4 = -5,8145 + 2,9638 = -2,8507.
16. -1,3617 • 3,78 + 0,953 + 2,92 = -5,1473 + 2,7828 = -2,3644.
17. -1,3617 4,25 + 0,953 + 2,76 = -5,7872 + 2,6303 = -3,156.
18. -1,3617 • 4,53 + 0,953 + 2,60 = -6,1685 + 2,4778 = -3,6907.
Е = -34,8459 + 17,3623 = -17,4536.
19. 0,4164 • 5,28 + 0,9146 • 5,0 = 2,1986 + 4,5730 = 6,7716.
20. 0,4164 • 5,21 + 0,9146 • 4,54= 2,1694 + 4,1522 = 6,3217.
21. 0,4164 • 6,01 + 0,9146 • 5,0 = 2,5026 + 4,5730 = 7,0756.
22. 0,4164 • 5,25 + 0,9146 • 4,23= 2,1861 + 4,8687 = 6,0549.
23. 0,4164 • 5,76 + 0,9146 3,92= 2,3985 + 3,5852 = 5,9837.
Е= 13,9536 + 24,7489 = 38,7027.
163
25. 0,4164 • 3,50 + 0,9146 • 2,00 = 1,4574 + 1,8292 = 3,2866.
26. 0,4164 • 2,77 + 0,9146 1,54 = 1,1534 + 1,4085 = 2,5619.
27. 0,4164 • 3,51 + 0,9146 • 1,40 = 1,4616 +1,2804 = 2,7420.
28. 0,4164 • 4,00 + 0,9146 • 1,75 = 1,6656 + 1,6005 = 3,2661.
29. 0,4164 • 3,03 + 0,9146 1,00 = 1,2617 + 0,9146 = 2,1763.
30. 0,4164 • 3,25 + 0,9146 • 0,88 = 1,3533 + 0,8048 = 2,1581.
31. 0,4164 3,69 + 0,9146 • 0,49 = 1,5665 + 0,4481 = 1,9846.
32. 0,4164 • 4,20 + 0,9146 • 1,00 = 1,7489 + 0,9146 = 2,6635.
Е = 11,6384+9,2007 = 2,8391.
Представляем полученные значения в гр. 20 рабочей мат-
рицы.
На основе полученных параметров а3 = —0,6840; <з4 = 0,0864
для 3-го квадранта и а3 = —0,3056; а4 = 0,3410 для 4-го квадранта
по уравнению f = (х3, х4) = п3х3 + а4х4 вычисляем общее значение
f по всем наблюдаемым объектам и среднее значение по четы-
рем классам этих объектов.
Соответственно имеем:
1. -0,684 • 8 + 0,0864 16 = -5,472 + 1,3824 = -4,0896.
2. -0,684 • 11 + 0,0864 • 15 = -7,524 + 1,2960 = -6,2280.
3. -0,684 10 + 0,0864 • 6 = -6,840 + 0,5184 = -6,3216.
4. -0,684 • 7 + 0,0864 • 9 = -4,788 + 0,7776 = -4,0104.
5. -0,684 • 12 + 0,0864 • 7 = -8,208 + 0,6048 = -7,6032.
6. -0,684 • 8 + 0,0864 • 6 = -5,472 + 0,5184 = -4,9536.
7. -0,684 • 10 + 0,0864 5 = -6,840 + 0,4320 = -6,4080.
8. -0,684 • 8 + 0,0864 • 5 = -5,472 + 0,4320 = -5,0400.
9. -0,684 • 12 + 0,0864 • 16 = -8,208 + 1,3824 = -6,8256.
10.-0,684-9 + 0,0864-8 =-6,156 + 0,6912 = -5,4648.
11.-0,684-9 + 0,0864-7 =-6,156 + 0,6048 = -5,5512.
12. -0,684 • 10 + 0,0864 8 = -6,84 + 0,6912 = -6,1488.
Е = -77,976 + 9,3312 = —68,6448.
13. -0,684 12 + 0,0864 11 = -8,208 + 0,9504 = -7,2576.
14. -0,684 • 13 + 0,0864 • 7 = -8,892 + 0,6048 = -8,2872.
15. -0,684 • 11 + 0,0864 • 8 = -7,524 + 0,6912 = -6,8328.
16. -0,684 • 15 + 0,0864 • 6 = -10,260 + 0,5184 = -9,7416.
17. -0,684 • 14 + 0,0864 • 5 = -9,576 + 0,4320 = -9,144.
18. -0,685 • 14 + 0,0864 • 5 = -9,576 + 0,4320 = -9,144.
Е = -54,036 + 3,6290 = -50,407.
164
19. 0,3056 • 13 + 0,341 • 7 = 3,9728 + 2,3870 = 6,3598.
20. 0,3056 • 10 + 0,341 • 5 = 3,0560 + 1,7050 = 4,7610.
21. 0,3056 • 12 + 0,341 • 9 = 3,6672 + 3,0690 = 6,7362.
22. 0,3056 • 15 + 0,341 • 8 = 4,5840 + 2,7280 = 7,3120.
23. 0,3056 14 + 0,341 • 8 = 4,2780 + 2,7280 = 7,0064.
24. 0,3056 15 + 0,341 • 7 = 4,5840 + 2,3870 = 6,9710.
S = 24,424 + 15,0040 = 39,1464.
25. 0,3056 • 8 + 0,341 4 = 2,4448 + 1,3640 = 3,8088.
26. 0,3056 • 4 + 0,341 • 4 = 1,2224 + 1,3640 = 2,5864.
27. 0,3056 3 + 0,341 • 6 = 0,9168 + 2,0460 = 2,9628.
28. 0,3056 • 7 + 0,341 2 = 2,1392 + 0,6820 = 2,8212.
29. 0,3056 • 8 + 0,341 2 = 2,4448 + 0,6820 = 2,1268.
30. 0,3056 6 + 0,341 • 3 = 1,8336 + 1,0230 = 2,8566.
31. 0,3056 • 5 + 0,341 • 2 = 1,5280 + 0,6820 = 2,2100.
32. 0,3056 • 7 + 0,341 • 2 = 2,1392 + 0,6820 = 2,8212.
E= 14,6688+8,5250=23,1938.
Полученные результаты заносим в табл. 3.16 (гр. 23).
Ш а г 7. Найдем значения соответствующих субфункций и
субконстант по приведенным ниже уравнениям в формате ис-
комых однородных классов и подклассов 32 наблюдаемых объек-
тов, представленных на рис. 3.9 и 3.10.
/ - |S11 - Я1Х] 1(1-12) + 02*21(1-12) ~ С*
С1 = -1,3617 • 2,5741 + 0,953 • 4,47 = -3,5052 + -4,2599 = 0,7547.
f -1^21= а1 *12(13-18) + а2*22(13-18) = ^П;
Сп = -1,36 • 4,265 + 0,953 • 3,0416 = 5,8077 + 2,8987 = -2,909.
f = l^l = а1 *13(19-24) + а2*23(19-24) = >
с111 = 0,4164 • 5,585 + 0,9146 • 4,51 = 2,3256 + 4,1248 = 6,4504.
/ = |s4| = а1Х|4(25_32) + 02*24(25-32) =
CIV = 0,4164 • 3,4937 + 0,9146-1,2575 = 1,4548 + 1,1501 = 2,6049.
165
№
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
S
fl= a^ + a2x2=
= - 0,4665
a1^11+ a2^12= *11 " *12
a1^21+ Q2^22~ *21 ~ *22
a^-1,3617
a2= 0,9530
= a3*3 + a4*4=
= -6,6140
a3^33+ a4^34= *13 ’ *23
a3^43+ a4^44= *14 ’ *24
a3= - 0,6840
a4= 0,0864
1
1
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
19
20
21
22
23
24
25
26
27
28
29
30
31
32
*1(1-18) *2(1-18)
3,1378 3,9939
*3(1-18) *4(1-18)
10,7222 8,3333
flll = a1x1 + a2x2=
= 4,2530
flv= a3x3 + a4x4=
= 4,4528
a1^11+ a2^12~ *13 “ *14
a1^11+ a2^22= *23 “ *24
a^ 0,4164
a2= 0,9146
a3^33+ a4^34“ *33 ’ *34
a3^43+ a4^44= *43 ’ *44
a3= 0,3056
a4= 0,3410
3
3
3
3
3
3
4
4
4
4
4
4
4
4
^1(19-32) ^2(19-32)
4,390 2,6514
^3(19-32) *4(19-32)
9,0714 4,9286
Рис. 3.9. Форматы искомых однородных классов
и подклассов 32 наблюдаемых объектов
166
a
s
Ф
(0
X
co
CD
3
X
X
(0
El
(0
co
*1 *2 *3 *4
f общ = собщ- Дискриминант f общ = а1*1 + а2Х2+ а3*3+ а4х4= - 41 >0442 aAi+ а2Ь12+ а3Ь13+ а4Ь14= - х12 - х13 - х14 а1^21+ а2^22+ а3^23+ а4^24= Х21 ” Х22 “ Х23 “ Х24 а1^31+ а2^32+ а3^33+ а4^34= Х31 " Х32 ’ *33 “ Х34 а1ьм+ а2Ь42+ а3Ь43+ х41 - х42 - х43 - х44 -13,0507 а2=-1,1351 а3=-1,0337 а4=-1,0445
^1(1-32) -*2(1-32) -*3(1-32) *4(1-32) 3,6856 3,4066 10,0 6,8438 2,30(-13,0507) + 6,11(1,1351) + 10(1,0337) + 14(-1,0445) = -27,3522 5,21 (-13,0507) + 1,18(1,1351) + 13(1,0337) + 4(-1,0445) = -57,3946 4,75(-13,0507) + 3,25(1,1351) + 11(1,0337) + 8(-1,0445) = -55,2870 3,13(-13,0507) + 2,50(1,1351) + 7(1,0337) + 3(-1,0445) = -33,9085
Рис. 3.10. Заданные и искомые значения 32 наблюдаемых объектов
167
d+C11 0,7547-2,909 -2,1543 , г
= = — — 1, U / /Z — Ст I
2----------------------------2-2
/' = *1 *1 (1-18) + «2*2(1-18) = -1.3647 • 3,1378 + 0,953 • 3,9939 =
= -4,2727 + 3,8062 = -0,4665.
Cin+C,v 6,4504 + 2,6049 9,0553 . сп_. „
= = — 4, jZ /о — Стт;
2------------------------------2-2
У Ш = «1*1(19—32) + «2*2(19—32) ~ 0,4169 • 4,39 + 0,9146 • 2,6514 =
= 1,8280+2,4250 = 4,2530.
_CI + CII+CIII + CIV =С1+С11
4*1*2) ” д 2
-1,0772 + 4,5276 3,4504 ^
г “ 2 ” ’ ’
/ = |S1| - а3 -Хз1(1_12) + «4*41(1-12) -
С1 = -0,684 • 9,5 + 0,0864 • 0,0864 9,0 = -6,498 + 0,7776 = -5,7204;
У = |531 = °3 “ *32(13-18) + «4*42(13-18) = С1' •
С11 = -0,684 • 13,1666 + 0,0864 • 7,0 = -9,0060 + 0,6048 = -8,4012.
у = |s3| = а3 - Хзз(19-24) + «4*43(19-24) = С”1;
СШ = 0,3056 • 13,1666 + 0,341 • 7,3333 = 4,0237 + 2,5007 = 6,5244.
f = |S4| = а3 - *34(25-32) + «4*44(25-32) = >
С IV= 0,3056 0,341 -3,125 = 1,8336 + 1,0656 = 2,8992.
СТ+СП -5,7204+ (-8,4062) -14,1216 _ „ Л£ЛО_„
---------_------------------------_------------_ — / (JoUo — Cm.
2 2 2 111
168
—^3^3(1—18) ^*^4^4(1—18) ——0,684 • 10,7222 + 0,0864 8,3333—
= -7,3340 + 0,720 = -6,614;
Cin+Clv 6,2544 + 2,8992 9,4236
---------------------------------= 4,7118 = Crv;
2 2 2 > iv.
У* IV — 6/3X30 9—32) 4" а4х4(19-32) = 9, 3056 9,0714 + 0,341 • 4,9286 =
= 2,7722 + 1,6806 = 4,4528; '
_ С1 + СП + Сш + CIV _ Сш + CIV _
с(х3х4) ~ 4 2
_ -7,0608+4,7118 -2,349 _ ч 1745
2 2 “ ’
Шаг 8. Находим общие функции /(32) и общие константы С
по 32 объектам.
Этот шаг состоит из четырех ступеней.
Ступень 1. Строим систему уравнений по четырем клас-
сам объектов с четырьмя неизвестными:
я1/11 + «2/12 + аз/13 + «4/14 = Х11 - XI2 - X] з - XI4;
«1/21 +«2/22 +«3/23 +«4/24 -Х21-Х22-Х23-Х24;
«1/з1 +«2/32 +«з/зЗ +Л4/34 =Х31-Х32-Х33-Х34;
«1 /41 + «2/42 + аз/лЗ + «4/44 = х41 - Х42 - Х43 “ Х44 •
aj • 1,0401 + а2 • 0,4227 + а3 • 2,4846 + а4 • 0,2333 =
= 2,5741 - 4,265 - 5,585 - 3,4937;
at • 0,4227 + а2 1,6031 + а3 1,7205 + а4 • 2,3178 =
= 4,47-3,0416-4,51-1,2575;
\ • 2,4846 + а2 • 1,7205 + а3 • 9,7664 + а4 • 2,3 512 =
= 9,5-13,1666-13,1666-6,0;
а} 0,2333 + а2 • 2,3178 + а3 • 2,3512 + а4 • 10,0283 =
= 9,0-7,0-7,3333-3,1250.
1 169
aj -1,0401 + a2 0,4227 + a3 -2,4846+ a4 -0,2333 =-10,7696;'
a} • 0,4227 + a2 1,6031 + a3 -1,7205 + a4-2,3178 =-4,3394;
4 a]-2,4846 + 02 1,7205 +a3-9,7664 + o4-2,3512 =-22,8332;
ax -0,2333 + o2 -2,3178 +o3-2,3512 + o4 • 10,0283 =-8,4583.
Ступень 2. Решаем построенную систему уравнений пу-
тем вычитания из уравнения 2 уравнение 1, умноженного на
0,4064:
ах 0,4227 + а2 • 1,6031 + а3 1,7205 + а4 • 2,3178 = -4,3394
~ Q1 - 0,447 + о2 • 0,1718+о3 1,0097 + а4 0,0948 = 4,3768
а2 • 1,4313 + а3 • 0,7108 + а4 • 2,2230 = 0,0374
Соответственно из 3-го уравнения вычитаем 1-е, умножен-
ное на 2,3888:
О] • 2,4846 + «2 • 1,7205 + а3 • 9,7664 + а4 • 2,3512 = -22,8332
ах 2,4846 + а2 1,0097 + а3 - 5,9352 + о4 0,5573 = -25,7264
а2 • 0,7108 + а3 • 3,8312 + а4 • 1,7939 = 2,8932
Далее из 4-го уравнения вычитаем 1-е, умноженное на 0,2243:
ах • 0,2333 + а2 • 2,3178 + а3 2,3512 + а4 • 10,0283 = -8,4583
~а1 0,2333 + д2-0,0948+а3-0,5573 + а4-0,0523 = -2,4156
а2 • 2,2230 + а3 • 1,7939 + а4 • 9,9760 = -6,0427
ах • 1,0401 + а2 • 0,4227 + а3 • 2,4846 + а4 • 0,2333 = -10,7696;
а2 • 1,4313 + а3 • 0,7108 + а4 - 2,2230 = 0,0374;
4 а2 • 0,7108 + а3 • 3,8312 + а4 • 1,7939 = 2,8932;
а2 • 2,2230 + а3 • 1,7939 + а4 • 9,9760 = -6,0427.
Ступень 3. Из 3-го уравнения вычтем 2-е, умноженное на
0,4966:
а2 • 0,7108 + а3 • 3,812 + а4 • 1,7939 = 2,8932
~а2-0,7108 + а3-0,3530 + а4-1,1039 = 0,0186
а3 • 3,4782 + а4 0,6900 = 2,8746
170
Соответственно из 4-го уравнения вычтем 2-е уравнение,
умноженное на 1,5531:
а2 • 2,2230 + «3 • 1,7939 + «4 • 9,9760 = -6,0427
~«2-2,2230 + «з-1,1039 + «4-3,4525 = 0,0581
а3 • 0,6900 + а4 • 0,5235 = -6,1008
«! • 1,0401 + а2 • 0,4227 + а3 • 2,4846 + а4 • 0,2333 = -10,7696;
а2 • 1,4313 + а3 0,7108 + а4 • 2,2230 = 0,0374;
а3 3,4782 + а4 • 0,6900 = 2,8746;
а3 • 0,6900 + а4 • 6,5235 = -6,1008.
Ступень 4. Из 4-го уравнения вычтем 3-е, умноженное на
0,1984: «3 • 0,6900 + а4 • 6,5235 = -6,1008 ~«3 - 0,6900 + «4-0,1369 = 0,5703 #4-6,3866 =-6,6711
В результате придем к триангулированной системе уравне-
ний, решение которой найдем с конца:
аг 1,0401 + а2 0,4227 + а3 • 2,4846 + а4 • 0,2333 = -10,7696;
а2 • 1,4313 + а3 • 0,7108 + а4 2,2230 = 0,0374;
а3 3,4782 + а4 • 0,6900 = 2,8746;
а4-6,3866 = -6,6711.
6,6711
6,3866
1,0445.
а3 • 3,4782 + (-1,0445) • 0,6900 = 2,8746;
«3-3,4782 = 0,7207 + 2,8746.
«3
3,5953
3,4782
= 1,0337.
«2 • 1,4313 + 0,7108 • 1,0337 + (—1,0445) • 2,2230 = 0,0374;
171
а2 • 1,4313 + 0,7347 - 2,3219 = 0,0374;
. а2 • 1,4313 + 0,7347 - 2,3219 = 0,0374;
«2 =
1,6246
1,4313
= 1,1351.
а, • 1,0401 + 0,4227 • 1,1351 +1,0337 2,4846+
+ (-1,0445) 0,2333 = -10,7696;
1,0401 + 0,4798 + 2,5683 - 0,2437=—10,7696;
• 1,0401 = 0,2437 -0,4798 - 2,5683-10,7696;
«1 =
13,5740
1,04013
= -13,0507.
<7] =-13,0507; а2 =1,1351; а3 = 1,0337; а4 =-1,0445.
Шаг 9. По приведенной ниже формуле найдем искомое зна-
чение общей функции для 32 объектов так, как это представле-
но на рис. 3.11.
/общ = а1*1 + <*2*2 + «3*3 + «4*4 = Общ-
Соответственно имеем:
(-13,0507) • 3,6856 + 1,1351 3,4066 + 10,0 1,0337 +
+ 6,8438(—1,0445) = -48,0997 + 3,8668 + 10,337 - 7,1483 =
= -41,0442.
Шаг 10. На основе параметров общей функции вычислим
(/бщ для каждого из 4-х классов Jp
для 1-го класса 5р
f = О]Хл + «2х2| + «3*31 + «4*41 =(-13,0507);
2,5741 + 1,1351 4,47 + 1,0337 • 9,5 + (-1,0445) • 9,0 =
= -33,5938 + 5,0739 + 9,8202 - 9,4005 = -28,1002;
172
Х2,3,4
Масштаб 1:2
1а
О: *
1
1-й класс
2-й класс
3-й класс
ж
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1------
1 2 3 4 5 6 7 8 9 10 11 12131415 16...
1-й объект № 33
3-й объект № 34, № 35
4-й объект № 36
Выбросы
4-й класс
о
32-
31-
30-
29-
28-
27-
26-
25-
24-
23-
22-
21-
20-
19-
18-
17-
16-
15-
14-
13-
12-
11-
10-
9-
8-
7-
6-
5-
4“
з-
2“
1-
0
4х?
ж ж
Ж UZ
• ж*3оз
□4 4*.s
’ °°o'\
® ° \ 3
32 х1
Рис. 3.11. Эмпирические кластеры для четырех классов
173
для 2-го класса S2:
f ~ а1 Х12 + а2х22 + а3х32 + а4х42 ~ 13,0507);
4,265 + 1,1351 • 3,0416 + 1,0337 • 13,1666 + (-1,0445) • 7,0 =
= -55,6612 + 3,4525 + 13,6103 - 7,3115 = -45,9099.
для 3-го класса S3:
f = Х|з + #2x23 + a3x33 a4x34 ~ 13,0507);
5,585 + 1,1351 - 4,51 + 1,0337 • 13,1666 + (-1,0445) • 7,3333 =
= -72,8882 + 5,1193 + 13,6103 - 7,6596 = -61,8182.
для 4-го класса 54:
f-atxj4 +a2x24 +«зх34 + a4x44 =(-13,0507);
3,4937 + 1,1351 • 1,2375 + 1,0337 • 6,00 + (-1,0445) • 3,125 =
= -45,5952 + 1,4274 + 6,2022 - 3,2641 = -41,2297.
Шаг 11. Для этого подставим значения общих параметров
а2, а3, аА в эмпирические уравнения по объектам 33—36.
Соответственно получим значения функций по отдельно взя-
тым объектам;
по объекту 33:
/„ = (-13,0507) • 2,3 + 6,11 • (1,1351) + 1,0337 10 +
+ (-1,0445) • 14 = (-30,0017) + 6,9355 + 10,3370 +
+ (-14,6230) = 27,3522;
по объекту 34:
/34 = (-13,0507) • 5,21 + 1,1351 • 1,18 + 1,0337 • 13 +
+ (-1,0445) 4 = -67,9941 + 1,3394 + 13,4381 - 4,178 =
= -57,3946;
по объекту 35:
/35 = (-13,0507) • 4,75 + 1,1351 • 3,25 + 1,0337 • 11 +
+ (-1,0445) 8 = -61,9908 + 3,6891 + 11,3707 - 8,356 =
= -55,2870;
по объекту 36:
/36 = (-13,0507) • 3,13 + 1,1351 • 3,5 + 1,0337 • 7 +
+ (-1,0445) 3 = -40,8487 + 2,8378 + 7,2359 - 3,1235 =
= -33,9085.
174
Шаг 12. Определим принадлежность объектов 33—36 к
одному из четырех классов путем сравнения найденной функ-
ции для каждого объекта с исчисленным дискриминантом. Объект
относится именно к тому классу, дискриминант которого боль-
ше его функции.
Если функция объекта больше дискриминанта, объект отно-
сится к следующему классу:
33. —27,3671 > —28,1002, значит, объект принадлежит к 1-му
классу.
34. —57,3946 < —45,9099, объект принадлежит к 3-му классу.
35. -55,2870 > 61,8182, объект принадлежит к 3-му классу.
36. —33,9085 > 41,2297, объект принадлежит к 4-му классу.
Шаг 13. Для подтверждения правильности и адекватности
исчисленных дискриминантов находят предельные расстояния
между константами расстояния и субконстантами всех наблю-
даемых объектов. В случае, если найденные расстояния крат-
ные, задача поставлена и решена верно. Если эти расстояния
незначительные или совпадают, задача решена неверно.
Обычно ограничиваются исчислением парных расстояний, в
нашем случае это расстояния между хх и х2 и х3 и х4. Найдем
предельное расстояние М12 для х1 и х2 (гр. 21—22):
Л/12 -
f-f
(/-/)2
56,344
4,1968
= 13,4255;
32
(/-7)1,2=56,344;
(А7)1=1Ч2986 = 68-
32 32
И соответственно предельное расстояние Л/,, для х, и х.
(гр. 23-24): ’
^3,4 =
343,6064
121^282
175
(/-7)3,4 =343,6;
(/-7)2 _ 3881,0 ^121J
32 32
Вывод. Наблюдаемые объекты, судя по их субконстантам,
находятся на предельном удалении друг от друга: Мх 2 = 13,4255
и М34 = 2,8331 и, следовательно, определены верно.
При этом конечная принадлежность или непринадлежность
конкретно наблюдаемых объектов к тому или иному идентифи-
цированному их классу определяется по их константам: если
субконстанта по данному объекту больше общей субконстанты,
то этот объект будет принадлежать к идентифицируемому клас-
су, если меньше — к другим классам, принадлежность которых
должна устанавливаться путем проведения дополнительных эк-
спериментов.
Напоминаем, что при решении нашей задачи (шаг 8, сту-
пень 4) получено четыре групповые и одна общая константа,
всего 5, а именно:
для 1-го квадранта с матрицей 18 х 2 : С1(Х1>Х2) = -1,0772;
для 2-го квадранта с матрицей 14 х 2 : =-4,5276;
для 3-го квадранта с матрицей 2 х 18 : C2(X3jX4j =-7,0608;
для 4-го квадранта с матрицей 2 х 14 : Л > =4,7118.
Общая константа с матрицей 32 х 4 : Собщ =-41,0442.
Полученные оценки единственные, так как общая констан-
та С = —41,0442 меньше предельного удаления, что позволило
однозначно квалифицировать принадлежность всех наблюдае-
мых 36 объектов к одному из четырех идентифицированных их
классов.
Шаг 14. Наконец, найдем принадлежность объектов 37 и
38 к одному из наблюдаемых классов, для чего подставим значе-
ния общих параметров at, а2, а3, а4 в соответствующие эмпири-
ческие уравнения объектов 37 и 38.
Соответственно имеем:
176
fv = (-13,0507) • 3,85 + 1,1351 4,47 + 1,0337 • 10,5 +
+ (-1,0445) • 8 = -50,2451 + 5,0629 + 10,8539 - 8,356 =
= 15,9168 - 58,6012 = -42,6844;
/38 = (-13,0507) • 4,60 + 1,1351 6,2 + 1,0337 • 8,7 +
+ (-1,0445) • 9 = -60,0332 + 1,3626 + 8,9932 - 9,4005 =
= 10,3558 - 69,4337 = -59,0775.
По значению дискриминанта определим принадлежность
соответствующих объектов:
/ = -42,6844 > -45,9099,
объект относится ко 2-му классу;
/38 = -59,0775 > 61,8182,
объект относится к 3-му классу.
Шаг 15. Построим общий график распределения 32 основ-
ных и 6 дополнительных наблюдаемых объектов по четырем
признакам и четырем дискриминантным классам переменных
(рис. 3.12) и 24 графика (по 6 в рамках каждого класса) парной
взаимосвязи наблюдаемых объектов по признакам х(, х2; хр х3;
X], х4; х2, х3; х2, х4 и х3, х4 (рис. 3.13 — график зависимости объек-
тов первого класса; рис. 3.14 — второго, рис. 3.15 — третьего и
рис. 3.16 — четвертого классов соответственно).
Рис. 3.12 (начало)
177
Рис. 3.12. Общий график распределения 32 основных
и 6 дополнительных объектов:
а - х,х2; б - ххх2, в - ххх*, г - х2х3; д - х2х4; е - х3х4
178
б
Рис. 3.13 (начало)
179
Рис. 3.13. Графики зависимости объектов первого класса:
а - хр х2; б - Хр х3; в - хр х4; г - хр х3; д - х2, х4; е - х3> х4
180
Рис. 3.14 (начало)
181
182
б
Рис. 3.15 (начало)
183
д
Рис. 3.15. Графики зависимости объектов второго класса:
а - х,, х2; б - хр х3; в - хр х4; г - х2, х3; д - хр х4; е - х3, х4
184
Рис. 3.16. График зависимости объектов четвертого класса
3.4.
Задачи для самостоятельных занятий
3.4.1.
Задачи компонентного анализа
Задача 3.1. Имеются следующие факторные нагрузки (табл.
3.17).
Таблица 3.17
xi ап ai2 а.з ^/4 ai5
1 0,72 0,80 0,13 -0,08 -0,02
2 0,67 -0,46 -0,22 0,13 0,09
3 0,92 0,68 0,19 0,02 0,00
4 0,85 -0,21 -0,34 0,21 0,01
5 0,58 -0,47 -0,06 -0,15 -0,10
185
Требуется:
1) определить вклад каждой компоненты в суммарную дис-
персию; 2) выделить главные компоненты; 3) объяснить эконо-
мический смысл проведенных расчетов.
Задача 3.2. Имеются следующие собственные значения
семи компонент (табл. 3.18).
Таблица 3.18
1 2 3 4 5 6 7
3,21 2,60 1,96 1Д2 0,85 0,44 0,17
Требуется:
1) определить долю вариации каждой компоненты, а также
накопленную долю вариации;
2) используя сочетание критериев, ответить на вопрос, сколь-
ко компонент и какие следует выделить для нахождения суще-
ственных оценок?
Задача 3.3. Имеются семь компонент, собственные значе-
ния двух из которых больше единицы. Ниже приведены фак-
торные нагрузки этих компонент (табл. 3.19).
Таблица 3.19
Показатель «/1 «/2
Доля городского населения 0,815 0,092
Доля населения трудоспособного возраста 0,508 0,684
Плотность населения 0,463 0,142
Денежные вклады населения в сберега- тельные кассы 0,689 - 0,304
Денежные доходы населения 0,874 - 0,215
Средний размер семьи - 0,316 0,828
Доля женщин - 0,387 0,792
Требуется определить вклад каждой компоненты в суммар-
ную дисперсию и объяснить его экономический смысл.
Задача 3.4. В табл. 3.20 приведены следующие коэф-
фициенты корреляции четырех показателей бытовой инфра-
структуры.
186
Таблица 3.20
Показатель *1 *2 х3 х4
иЬ * 1 0,92 1 0,86 0,73 1 0,78 0,95 0,84 1
%! - обеспеченность городского населения жилой площадью; Хг — доля комплексно благоустроенного жилья; х3 — объем бытовых услуг на 1000 жителей; х4 — число телефонных аппаратов на 1000 жителей. \
Требуется определить собственные значения вектора корре-
ляционной матрицы и сделать необходимые экономические
выводы.
Задача 3.5. По приведенным в задаче 3.4 данным требует-
ся выделить главные компоненты и определить их факторные
нагрузки.
Задача 3.6. По данным задачи 3.4 требуется определить
значения главных компонент со следующими стандартизован-
ными значениями переменных х. (табл. 3.21):
Таблица 3.21
*1 А в С D
Xi *2 х3 х4 1 0,92 1 0,86 0,73 1 0,78 0,95 0,84 1
Задача 3.7. Имеются следующие данные по 17 объектам и
6 признакам (табл. 3.22).
Требуется построить компонентную модель с собственными
значениями X! = 2,8; Х2 = 1,3 и дать экономическую интерпрета-
цию выделенных компонент.
187
Таблица 3.22
Объект *1 х2 х3 х5 xf>
1 8,2 0,6 37,3 15,5 121,4 46,1
2 9,9 0,5 33,1 15,9 128,6 54,5
3 9,9 0,7 32,7 17,9 160,7 39,4
4 10,3 0,6 56,1 20,4 119,3 54,7
5 11,7 0,8 32,5 15,9 91,9 45,3
6 и,2 0,8 55,2 21,7 137,4 30,5
7 14,3 0,8 47,2 20,9 88,0 41,8
8 14,2 0,8 47,6 18,9 138,2 30,6
9 15,3 0,7 51,8 20,6 184,6 43,1
10 12,9 1,1 33,6 22,2 12,6 29,2
11 13,4 6,8 57,7 30,8 146,0 76,6
12 16,8 0,9 60,3 4,0 200,6 55,5
13 14,6 0,8 56,2 33,0 203,1 36,4
14 13,8 0,8 68,7 29,9 473,3 39,2
15 16,0 0,9 61,3 28,3 190,4 46,3
16 17,3 0,9 76,3 30,9 163,4 39,5
17 19,5 1,0 81,7 28,9 223,0 50,5
3.4.2.
Задачи факторного анализа
Задача 3.8. Определите вклады общих факторов в диспер-
сию z-переменной при = 0,8(7, + 0,5С?2 + 0,33(7. Прокоммен-
тируйте смысл полученных оценок.
Задача 3.9. На основе парных коэффициентов корреля-
ции (табл. 3.23) постройте редуцированную корреляционную мат-
рицу, проведите разложение вариации каждой переменной на:
а) обусловленную общим фактором; б) специфическую (харак-
терную).
Таблица 3.23
X,. 1 2 3 4
1 1 0,65 0,72 0,44
2 1 0,58 0,86
3 1 0,35
4 1
188
Задача 3.10. Получены факторные нагрузки для двух вза-
имно некоррелированных факторов (табл. 3.24).
Таблица 3.24
xi ап ai2
*1 0,60 -0,10
х2 0,40 -0,40
х3 0,70 0,30
х4 0,70 0,40
х5 0,50 -0,50
Требуется:
1) определить факторную нагрузку и специфичность при-
знаков х.; 2) найти суммарную общность.
Задача 3.11. По данным задачи 3.3 требуется определить,
какую долю общей суммарной дисперсии объясняет межгруп-
повая (факторная) дисперсия, вклад каждого фактора в общую
дисперсию.
Задача 3.12. Имеются два некоррелируемых фактора со
следующими нагрузками (табл. 3.25).
Таблица 3.25
х;- «л ai2
*1 0,40 0,70
х2 0,60 -0,50
х3 -0,30 0,80
*4 0,50 0,40
х5 + 0,70 0,50
Требуется преобразовать факторные нагрузки путем враще-
ния системы координат на 30° (sin 30° = 0,5000, cos 30° = 0,8660)
против часовой стрелки.
Задача 3.13. Имеются следующие собственные векторы и
собственные значения корреляционной матрицы (табл. 3.26).
Таблица 3.26
Л Л Л
К = 2,5 2,32 1,74 0,56 1
X, = 1,7 - 1,12 -0,46 -0,17 2
189
Требуется определить факторные нагрузки и провести
преобразование факторного решения путем вращения системы
координат на 45° (sin 45° = cos 45° = 0,71) против часовой стрелки.
Задача 3.14. Имеются следующие коэффициенты корре-
ляции (табл. 3.27).
Таблица 3.27
X;- Х1 х2 х3 х4
X] X 0,78 0,92 0,86
*2 0,78 X 0,67 0,76
х3 0,92 0,67 X 0,82
Х4 0,86 0,76 0,82 X
Требуется определить общности и с помощью критерия три-
ад проверить гипотезу о наличии одного общего фактора.
3.4.3.
Задачи кластерного анализа
Задача 3.15. Имеются следующие исходные данные (табл.
3.28).
Таблица 3.28
Объект Признак
X] х2 х3 х4
1 13,8 0,8 68,7 29,9
2 16,0 0,9 61,3 28,3
3 15,3 0,7 51,8 20,6
4 9,9 0,7 32,7 17,9
5 16,8 0,9 60,3 4,0
Требуется построить матрицу евклидовых расстояний между
объектами, стандартизуя приведенные данные по значениям
следующих общих средних и среднеквадратических отклонений
(табл. 3.29).
Таблица 3.29
Показатель Х1 х2 х3 х4
х; 13,49 0,79 52,31 22,10
О/ 3,02 0,15 15,19 7,50
190
Задача 3.16. Требуется определить группы однородных
объектов по данным задачи 3.15. Расчеты провести по центро-
графическому алгоритму «ближайшего соседа».
Задача 3.17. Требуется определить группы однородных
объектов (кластеры) по центрографическому алгоритму «даль-
него соседа» по данным задачи 3.15.
Задача 3.18. Имеются данные о 36 объектах, каждый из
которых попарно характеризуется признаками х, и х2, и х3 и х4
(табл. 3.30). Требуется определить центрографическим методом
существующие кластеры.
Таблица 3.30
Обь- ект Признак Объ- ект Признак
X, х2 *3 х4 5 Х1 х2 ' х3 х4 5
1 1,75 5,25 8 16 1 19 5,28 5,0 13 7 3
2 2,65 5,50 11 15 1 20 5,21 4,54 10 5 3
3 1,80 4,47 10 6 1 21 6,01 5,00 12 9 3
4 2,50 4,75 7 9 1 22 5,23 4,23 15 8 3
5 3,00 5,00 12 7 1 23 6,00 4,37 14 8 3
6 3,54 4,71 8 6 1 24 5,76 3,92 15 7 3
7 2,82 4,22 10 5 1 25 3,50 2,00 8 4 4
8 2,53 4,07 8 5 1 26 2,77 1,54 4 4 4
9 2,25 4,04 12 16 1 27 3,51 1,40 3 6 4
10 2,06 3,95 9 8 1 28 4,00 1,75 7 2 4
11 2,75 3,75 9 7 1 29 3,03 1,00 8 2 4
12 3,24 3,93 10 8 1 30 3,25 0,88 6 3 4
13 4,14 3,52 12 11 2 31 3,69 0,49 5 2 4
14 4,62 3,34 13 7 2 32 4,20 1,00 7 2 4
15 4,27 3,11 11 8 2 33 2,30 6,11 10 14 —
16 3,78 2,92 15 6 2 34 5,21 1,18 13 4 —
17 4,25 2,76 14 5 2 35 4,75 3,25 11 8 —
18 4,53 2,60 14 5 2 36 3?13 2,50 7 3 —
Задача 3.19. По данным задачи 3.18 из совокупности пер-
вых 18 объектов выделить второй кластер, используя центрогра-
фический алгоритм поиска однородных объектов, приняв за
начальную точку координаты 15-го объекта.
Задача 3.20. По данным задачи 3.18 из совокупности вто-
рых 18 объектов (объекты 19—36) выделить третий кластер, при-
няв за начальную точку координаты 28-го объекта.
Задача 3.21. Имеются следующие данные по 10 объектам
(табл. 3.31).
191
Таблица 3.31
При- знак Объект
1 2 3 4 5 6 7 8 9 10
X, 1 2,3 1,2 1,1 1,5 2,4 1,6 1,5 1,6 1,7
2 8 2 1 5 8 3 4 4 5
Требуется выделить множество кластеров и обосновать пред-
почтительный метод кластеризации.
3.4.4.
Задачи дискриминантного анализа
Задача 3.22. По данным задачи 3.18 требуется построить
дискриминантную функцию по признакам xY и хт При этом в
качестве обучающей выборки необходимо использовать объекты
1-18.
Задача 3.23. По данным задачи 3.18 требуется построить
дискриминантную функцию по признакам х3 и х4, используя в
качестве обучающей выборки объекты 20—36.
Задача 3.24. По данным задачи 3.18 и обучающей выбор-
ки, состоящей из первых 18 объектов, требуется построить дис-
криминантную функцию по признакам хр х3, х4.
Задача 3.25. На основе задачи 3.24 и приведенных ниже
расчетных данных табл. 3.32 постройте дискриминантную функ-
цию для 32 объектов и определите принадлежность объектов
33—36 с характеристиками, приведенными в составе данных
задачи 3.18, к одному из четырех выделенных дискриминант-
ных классов.
Таблица 3.32
Коэффициент Номер класса по признаку S
1 2 3 4
«о -58,74 -63,80 -119,13 -32,37
12,89 20,35 26,76 16,39
а2 18,86 13,41 19,71 5,94
192
Задача 3.26. В исходные данные задачи 3.18 вводятся до-
полнительно два объекта со следующими признаками. Объект
37: xt = 3,12, х2 = 4,47, х3 = 10,5, х4 = 8. Объект 38: xt = 4,6, х2 = 6,2,
х3 = 8,7, х4 = 9.
На основе общей дискриминантной функции и ранее най-
денных параметров а0, ар а2, а2 и а4 требуется определить значе-
ния дискриминантной функции для объектов 37 и 38 и отнести
рассматриваемые объекты к одному из четырех выделенных дис-
криминантных классов.
Задача 3.27. В табл. 3.33 приведены следующие фактиче-
ские данные по России за 1992—2003 гг. Требуется определить
прогнозные значения темпов экономического роста на 2004—
2010 гг. путем построения дискриминантной функции для двух
классов (данных класса 1992—1998 гг. и данных класса 1999—
2003 гг.).
3.5.
Варианты компьютерных
контрольных заданий
Представлены следующие варианты основных (1—5), допол-
нительных (6—9) и аудиторных компьютерных контрольных за-
даний (задание 9).
Варианты основных контрольных заданий выполняются на
основе обработки данных табл. 3.16 и 3.30, примера 3.18, вари-
анты дополнительных заданий — на основе обработки данных
табл. 3.34 и 3.35.
Студенты, у которых первая буква фамилии от А до Д, вы-
полняют задание 1, от Е до К — второе, от Л до П — третье, от
Р до Т — четвертое, от У до Я — пятое.
Варианты дополнительных заданий выполняются по указа-
нию преподавателя.
Аудиторное контрольное задание выполняется по решению
кафедры.
193
Таблица 3.33
Год Индексы прироста в % к предыдущему году, в сопоставимых ценах
численность населения числен- ность занятых *2 ВВП х3 основные фонды х4 промыш- ленное производ- ство *5 сельское хозяйство % инвести- ции X? класс роста
1992 -0,02 -2,4 -14,5 1,9 -18,0 -9,4 -39,7 51
1995 -0,2 -3,0 -4,1 0,1 -3,3 -9,4 -10,1 51
1997 -0,3 -1,9 1,4 -0,4 2,0 -8,0 -5,0 51
1998 -о,з -1,4 -5,3 -0,4 -5,2 1,5 -12,0 51
1999 -0,5 0,2 6,4 0,1 11,0 -13,2 5,3 52
2000 -0,5 0,6 ' 10,0 0,4 11,9 4,1 17,4 52
2001 -0,4 0,6 5,0 0,6 4,9 7,7 10,0 52
2002 -0,5 1,5 4,3 0,7 3,1 7,5 2,8 52
2003 -0,5 0,5 7,3 0,7 6,9 1,3 12,5 52
Источник. Россия в цифрах. — М.: Госкомстат России, 2003. — С. 32—33.
3.5.1.
Основные контрольные задания
Задание 3.1. Даны табл. 3.34 и 3.35.
Таблица 3.34
Валовой общественный продукт и национальный доход
по отраслям экономики (в сопоставимых ценах; млрд долл. США)
Год Валовой общественный продукт Национальный доход
Всего в том числе Всего в том числе
в промыш- ленности в сельском хозяйстве в промыш- ленности в сельском хозяйстве
1 2 3 4 5 6 7
1999 282,2 172,5 48,0 136,2 71,2 29,0
2000 303,8 189,5 49,3 145,0 75,8 29,7
2001 324,1 206,5 50,5 152,9 79,7 32,1
2002 344,4 226,8 51,1 164,6 86,1 37,0
2003 364,8 235,3 0,58 168,8 88,5 34,6
2004 388,9 249,3 63,8 181,5 97,3 38,8
2005 420,2 266,2 71,2 193,5 100,1 43,6
2006 451,0 284,0 80,0 207,4 104,6 50,3
2007 502,0 321,0 81,0 225,5 115,9 50,7
2008 550,0 356,0 87,0 244,1 127,3 52,7
2009 587,0 381,0 88,0 261,9 140,4 50,6
2010 643,5 409,0 103,0 289,9 148,3 63,1
2011 685,3 434,3 108,1 305,0 156,9 62,9
2012 717,4 458,4 108,8 313,6 163,6 59,6
2013 770,9 490,1 121,9 337,8 173,3 68,4
2014 816,7 525,6 122,1 354,0 186,3 65,6
2015 862,6 558,3 122,3 363,3 191,2 61,5
2016 903,9 578,4 132,4 385,7 199,7 66,2
2017 949,6 605,5 141,7 405,6 207,0 71,6
2018 992,1 633,1 147,0 422,5 216,2 73,6
2019 1032,4 657,1 151,9 440,6 226,5 73,2
2020 1078,5 685,5 152,6 462,2 238,1 68,9
2021 1122,8 709,0 160,0 486,7 248,0 73,1
2022 1236,0 792,7 170,3 523,4 266,8 80,3
2023 1292,7 800,0 207,9 548,1 254,1 110,1
2024 1345,8 826,7 217,0 569,6 262,2 112,7
2025 1383,6 844,6 219,6 578,5 263,1 112,8
2026 1441,8 856,0 219,7 586,0 265,0 115,4
2027 1464,5 892,3 234,9 599,6 268,6 122,6
2028
2029
2030
195
s©
Таблица 3.35
Темпы экономического прироста в России
(в сопоставимых ценах; в % к предыдущему году)
Показатель-фактор 1992 1995 1997 1998 1999 2000 2001 2002 2003 2004 2005
Численность населения (1) -0,02 -0,2 -0,3 -0,3 -0,5 -0,5 -0,6 -0,5 -0,5 -0,5 -0,5
Численность занятых (2) -24 3,0 - 1,9 - 1,4 0,2 0,6 0,6 1,0 0,5 0,4 0,8
Реальные доходы (3) -47,5 - 15,0 5,8 - 15,9 - 12,5 11,9 8,5 11,1 15,0 10,4 9,3
Основные фонды (4) 1,9 0,1 -0,4 -0,4 0,1 0,4 0,6 0,7 0,7 0,9 1,1
Промышленное производство (5) - 18,0 -з,з 2,0 - 5,2 11,0 11,9 4,9 3,1 6,9 8,3 4,0
Продукция сель- ского хозяйства (6) -9,4 - 8,0 1,5 - 13,2 4,1 7,7 7,5 1,7 1,3 3,1 2,0
Перевозки грузов (7) - 13,9 - 1,0 - 3,4 -з,з 5,3 5,0 3,2 6,8 8,0 6,5 2,7
Оборот розничной торговли (8) з,з -6,2 4,9 - 3,2 -5,9 9,0 10,9 9,3 6,8 13,3 12,8
Инвестиции (9) - 39,7 - 10,1 -5,0 - 12,0 5,3 17,4 10,0 2,8 12,5 11,7 10,7
Внешнеторговый оборот (10) 10,5 23,1 0,7 - 16,6 - 13,1 30,2 3,7 7,8 26,6 34,4 25,5
ВВП (результат) - 14,5 -4,1 1,4 -5,3 6,4 10,0 5,0 4,7 7,3 7,2 6,4
Источник. Россия в цифрах. — М.: Госкомстат России, 2003. — С. 32—33, 363; 2006. — С. 35—36.
Проведите группировку и определите по пятилетиям сред-
негодовые темпы прогнозируемого роста валового обществен-
ного продукта и национального дохода России в целом и по
отраслям экономики обычным методом и методом кластерного
анализа. Сделайте выводы.
Данные за 2028—2030 гг. при этом доисчислите, экстраполи-
руя соответствующие темпы роста за предыдущие годы.
Задание 3.2. По данным табл. 3.34 проведите группировку
и определите по десятилетиям 2001—2010, 2011—2020, 2021—2030 гг.
среднегодовые темпы роста валового общественного продукта и
национального дохода России в целом и по отраслям экономи-
ки обычным способом и методом дискриминантного анализа.
При этом обучающей выборкой считайте темпы роста нацио-
нального дохода за соответствующие годы. Сделайте экономи-
ческие выводы.
Задание 3.3. По данным табл. 3.34 определите по пятиле-
тиям темпы экономического роста России и проведите их груп-
пировку методом максимального правдоподобия и методом ли-
нейной оценки расстояний, образовав кластеры, характеризую-
щие однородные периоды экономического развития России.
Сделайте необходимые экономические выводы. Ответьте, поче-
му однородные периоды экономического развития России по
времени и масштабам не совпадают с пятилетними? При каких
допущениях и условиях такое совпадение было бы возможным?
Задание 3.4. По данным табл. 3.34:
1) определите по пятилетиям и по периодам 2001—2010, 2011 —
2030 гг. среднегодовые темпы экономического роста России и
проведите их перегруппировку методами дискриминантного и
кластерного анализа;
2) сравните полученные оценки и определите однородные
периоды предстоящего экономического развития России по тем-
пам экономического роста;
3) представьте исходные и полученные оценки экономиче-
ского роста России графически и сделайте необходимые выводы.
Задание 3.5. По данным табл. 3.34:
1) определите условные обобщенные факторные оценки за-
висимости темпов роста валового общественного продукта и
национального дохода России от темпов роста промышленного
производства и сельского хозяйства по пятилетним периодам и
в целом за 2001—2030 гг.
2) сделайте необходимые экономические выводы.
197
3.5.2.
Дополнительные контрольные задания
Задание 3.6. По данным табл. 3.35:
1) определите зависимость темпов роста ВВП России от тем-
пов изменения приведенных в ней 10 факторов, определяющих
его рост, методом главных компонент по пятилетним периодам
и в целом за 1992-2002 гг.;
2) доисчислите недостающие данные за 2003—2006 гг. мето-
дом экстраполяции;
3) выделите реальные и мнимые факторы, влияющие на темпы
роста ВВП России;
4) сделайте необходимые экономические выводы.
Задание 3.7. По данным табл. 3.35:
1) исчислите парные коэффициенты корреляции между фак-
торами и результатами экономического роста России в 1992—
1998 гг. и в 1999-2006 гг.;
2) постройте матрицы парных коэффициентов корреляции
и выделите все матрицы устойчивых коэффициентов корре-
ляции;
3) определите устойчивые циклы экономического роста, а
методами факторного анализа — главные и общие факторы, оп-
ределяющие темпы роста ВВП России в 1992—2006 гг., метода-
ми максимального правдоподобия (близости объектов), комби-
нации порядковых статистик (расстояние объектов) и методами
корреляции рангов;
4) сделайте необходимые содержательные выводы.
Задание 3.8. По данным табл. 3.35:
1) определите степень влияния каждого из 10 факторов на
темпы экономического роста России (раздельно темпы роста ВВП
и темпы роста инвестиций) тремя методами факторного и двумя
методами компонентного анализа;
2) сравните результаты, полученные в процессе использова-
ния разных методов, и ответьте на вопросы:
по какому критерию определяется и выбирается предпочти-
тельный метод?
какой из трех методов факторного анализа предпочти-
тельнее?
какой из двух методов компонентного анализа предпочти-
тельнее?
198
какой из всех пяти методов предпочтительнее?
при каких условиях и в каких областях следует обращаться к
отдельно взятым конкретным методам многомерного оценива-
ния факторов экономического роста?
3.5.3.
Аудиторные задания
Задание 3,9. По данным табл. 3.34 и 3.35:
1) постройте матрицы парных коэффициентов корреляции
между приведенными в таблицах показателями;
2) обработайте полученные матрицы парных коэффициен-
тов методами кластерного, дискриминантного, факторного и
компонентного анализа и постройте матрицы устойчивых пар-
ных коэффициентов корреляции между рассматриваемыми по-
казателями;
3) постройте модель канонических корреляций и охаракте-
ризуйте многомерную зависимость между отчетными (1992—
2006 гг.) и прогнозируемыми темпами экономического роста
России по стадиям экономического развития страны, выделив
стадии упадка, кризиса, застоя, подъема, рецессии и депрессии
экономического роста в целом за рассматриваемый период на
основе полученных данных;
4) сравните оценки, полученные на основе многомерной
обработки данных табл. 3.34 и 3.35 и сделайте необходимые со-
держательные выводы.
Задание 3.10. Имеются следующие эмпирические данные
(табл. 3.35, тема 3) по семи показателям, шесть из которых (чис-
ленность занятых, фонды, инвестиции) характеризуют динами-
ку факторов производства в России за 10 лет (1992-2002 гг.),
а восьмой показатель — динамику ВВП.
Данные по каждому из семи приведенных факторных и ре-
зультативному показателю идентифицируются восемью разны-
ми типами теоретических распределений (см. графики функций
1—8 рис. 1—8, тема 1).
На основе приведенных эмпирических данных и представ-
ленных графических иллюстраций их воображаемых теорети-
ческих значений:
1) постройте графики, иллюстрирующие распределение при-
веденных эмпирических данных по восьми наблюдаемым по-
казателям;
199
2) проведите идентификацию эмпирических и теоретиче-
ских значений наблюдаемых показателей, представленных на
рис. 1.1;
3) идентифицируйте пары относительно сходимых и несхо-
димых эмпирических и теоретических распределений наблюда-
емых показателей;
4) определите области несходимых распределений наблюда-
емых показателей. Ответьте на вопрос: можно ли преодолеть
несходимые распределения, и если можно, то с помощью каких
известных методов это целесообразно делать, а если нельзя, то
почему?
5) проиллюстрируйте расчеты примерами, а полученные ре-
зультаты сопроводите пояснениями их экономического смысла;
6) сделайте необходимые выводы;
7) ответьте на вопрос: существует ли альтернативное реше-
ние рассмотренной задачи, и если да, изложите свою идею ее
решения?
Тесты и вопросы для самоконтроля
1. Сформулируйте задачи компонентного анализа.
2. Что такое сжатое описание структурных связей?
3. Объясните понятия «компонентное отображение» и «компо-
нентная нагрузка».
4. Перечислите этапы компонентного анализа.
5. Почему в экономических исследованиях проводится стан-
дартизация исходных данных?
6. Что является исходной базой построения компонентной мо-
дели? Как она формируется?
7. Назовите основополагающее равенство компонентного ана-
лиза. Как обеспечить однозначность его решения?
8. В чем сущность принципа максимизации дисперсии?
9. Что представляет собой суммарная факторная дисперсия при-
знаков? Чему она равна и чем отличается от общей дисперсии?
10. Как определить вкладу-й компоненты в общую дисперсию?
11. По какому правилу проводится выделение главных ком-
понент?
12. Как распознаются и отбираются главные компоненты?
13. Перечислите отличительные особенности факторной модели.
200
14. Объясните понятие «общность».
15. Перечислите способы определения исходной общности.
16. Как проверить адекватность факторной модели?
17. Объясните логику факторного решения и выделения факторов.
18. Изложите суть и назначение преобразования факторного
решения методом вращения.
19. Каким образом и для каких целей проводится измерение
(оценка) факторов?
20. Сформулируйте предпосылки применения факторной моде-
ли для построения обобщающих показателей социально-эко-
номических явлений.
21. Перечислите задачи кластерного анализа.
22. Что такое меры сходства и функции расстояния?
23. Какие иерархические классификационные алгоритмы вы знаете?
24. Назовите алгоритмы кластерного анализа.
25. Что такое функционалы качества классификации?
26. Назовите области практического применения методов клас-
терного анализа.
27. Что понимают под решением задачи классификации соци-
ально-экономических объектов? Каковы основные методы
классификации?
28. В чем различие методов группировки и многомерной клас-
сификации?
29. Сформулируйте основные принципы кластерного анализа.
30. Что такое кластер?
31. Приведите примеры использования различных метрик для
классификации конкретных объектов.
32. В чем состоит принципиальная разница между иерархиче-
скими и неиерархическими алгоритмами классификации?
33. Как изменится схема алгомеративного иерархического алго-
ритма, если в качестве метрики использовать не функцию
расстояния объектов, а меру их сходства?
34. Какова взаимосвязь всех трех типов кластеризации?
35. Как связаны между собой методы классификации и другие
методы многомерного анализа (например, корреляционно-
регрессионного или факторного анализа)?
36. Назовите основные проблемы, которые возникают при клас-
сификации объектов и могут быть описаны качественными
признаками.
201
37. Каким образом можно обосновать число выделяемых клас-
сов в исследуемой совокупности объектов?
38. Как связаны методы классификации с формой выделяемых
кластеров (рассмотреть на примере двухмерного признако-
вого пространства)?
Темы для занятий
Темы для теоретических занятий
1. Роль и значение многомерного статистического анализа при
изучении общественных явлений.
2. Задачи, решаемые с помощью методов многомерного анализа.
3. Классификация многомерных наблюдений и типология ме-
тодов многомерного анализа.
4. Области практического применения методов многомерного
анализа в социально-экономических исследованиях.
5. Сравнительный анализ эффективности использования ме-
тодов многомерного анализа.
6. Этапы компонентного анализа.
7. Сущность метода главных компонент.
8. Компонентное отображение и компонентная структура.
9. Определение факторных компонент.
10. Распознавание главных компонент.
И. Измерение и интерпретация главных компонент.
12. Сравнительный анализ эффективности методов компонент-
ного и факторного анализа.
13. Цели и задачи моделирования.
14. Разложение дисперсии в факторном пространстве.
15. Определение общностей.
16. Критерий числа общих факторов.
17. Преобразование факторного решения.
18. Оценка значений факторов.
19. Применение моделей факторного анализа для построения
обобщающих показателей.
20. Задачи кластерного анализа.
21. Методы и модели кластерного анализа.
22. Области применения методов кластерного анализа.
23. Задачи дискриминантного анализа.
202
24. Методы дискриминантного анализа.
25. Перечислите основные области и направления применения
дискриминантного анализа.
26. Что понимается и как определяется расстояние между двумя
или несколькими классами объектов?
27. В чем состоит прогностическая функция дискриминантного
анализа?
28. Как используются методы дискриминантного анализа в про-
гнозировании социально-экономических процессов?
29. Взаимосвязь и сравнительная характеристика методов диск-
риминантного и кластерного анализа.
30. Графическое представление данных многомерного и диск-
риминантного анализа.
А
Темы для практических занятий
В соответствии с учебным планом и программой курса прак-
тические занятия должны быть построены так, чтобы обеспечи-
вать глубокое изучение определенных разделов курса и стать
основой для выработки у студентов навыков использования ме-
тодов многомерного анализа в ходе решения практических за-
дач. При подготовке к семинарам студенты должны использо-
вать конспект лекций, учебную основную и дополнительную
литературу, а также материалы заданий, рекомендуемых для са-
мостоятельной работы.
1. Теоретические вопросы многомерного анализа.
2. Законы статистических распределений и робастные рас-
пределения.
3. Типология условий и методов многомерного анализа.
4. Методы многомерного анализа однородности статисти-
ческих наблюдений.
5. Методы многомерного анализа взаимосвязи показателей
статистических наблюдений.
6. Приближенные методы многомерного анализа однород-
ности единиц и взаимосвязи показателей статистических наблю-
дений.
7. Условия, критерии и области сходимости методов много-
мерного анализа.
203
Темы для работ на компьютере
и контрольных работ
Компьютерные занятия должны проводиться в аудиториях,
оснащенных вычислительной техникой. Предполагается, что
студенты к этому времени имеют навыки использования ЭВМ
для реализации стандартных вычислительных алгоритмов мно-
гомерного анализа.
1. Теоретические основы и модели факторного анализа.
1.1. Методы определения общностей в факторном анализе.
1.2. Вращение общих факторов в факторном анализе. Эко-
номическая интерпретация получаемых результатов.
1.3. Формирование названия общих факторов.
1.4. Классификация признаков в факторном анализе.
1.5. Классификация объектов исследования с помощью об-
щих факторов.
2. Методы компонентного анализа и регрессия на главных
компонентах.
3. Классификация объектов иерархическими методами клас-
терного анализа.
4. Методы линейного дискриминантного анализа.
5. Методы исследования зависимости между группой при-
знаков, характеризующей эффективность производств, и груп-
пой показателей, определяющих условия и характер производ-
ства (методы канонических корреляций).
6. Компьютерные методы многомерного статистического
анализа.
Рекомендуемая литература
Основная
1. Айвазян С.А., Бежаева З.И., Староверов О.В. Классифика-
ция многомерных наблюдений. — М.: Статистика, 1974.
2. Айвазян С.А., Енюков И. С., Мешалкин Л.Д. Прикладная ста-
тистика. — М.: Финансы и статистика, 1983. — Т. 1.
3. Айвазян С.А., Енюков И. С., Мешалкин Л.Д. Прикладная ста-
тистика. — М.: Финансы и статистика, 1985. — Т. 2.
4. Дубров А.М. Обработка статистических данных методом
главных компонент. — М.: Статистика, 1978.
204
5. Иберла К. Факторный анализ. — М.: Статистика, 1980.
6. Мандель И.Д. Кластерный анализ. — М.: Финансы и стати-
стика, 1988.
7. Рябушкин Т.В., Симчера В.М., Машихин Е.А. Статистиче-
ские методы и анализ социально-экономических процессов. —
М.: Наука, 1990.
8. Смоляк С.А., Титаренко Б.П. Устойчивые методы оцени-
вания. — М.: Статистика, 1980.
Дополнительная
1. Дюран Б., Одел П. Кластерный анализ: Пер. с англ. — М.:
Статистика, 1977. \
2. Жуковская В.М., Мучник И.Б. Факторный анализ в соци-
ально-экономических исследованиях. — М.: Статистика, 1976.
3. Многомерный статистический анализ в социально-эконо-
мических исследованиях. — М., 1974.
4. Окунь Я. Факторный анализ. — М.: Статистика, 1974.
5. Репин С.В., Шеин С.А. Математические методы обработки
статистической информации с помощью ЭВМ: учеб, пособие. —
Минск: Университетское, 1990.
6. Сравнительный многомерный анализ в экономических
исследованиях. Методы таксономии и факторного анализа. —
М., 1980.
7. Харман Г. Современный факторный анализ — М.: Статис-
тика, 1972.
8. Хьюбер П. Робастность в статистике. — М.: Мир, 1984.
ТЕМА 4
Методы многомерного
моделирования данных
4.1.
Вводные замечания
В любой социально-экономической работе, как правило,
решается одна из двух целевых задач: при заданных условиях и
целях минимизируются затраты труда и капитала или при за-
данных затратах труда и капитала максимизируются прибыли
или другие аналогичные выгоды и интересы. В обиходе такие
задачи называются и представляются как задачи минимакса.
При наличии ограниченного объема информации и простых
целевых установках для решения такого рода задач привлекают-
ся соответствующие общие или упрощенные статистические ме-
тоды, основные назначения и техника применения которых рас-
смотрены выше.
Для обеспечения полномасштабного и быстрого решения тех
же минимаксных задач, связанных со сложным набором эконо-
мических целей и отношений и большими объемами и потока-
ми информации, привлекаются специальные статистические
методы, которые в обобщенном виде представляются как стати-
стические методы социально-экономического моделирования.
Многоразмерные по формату, требующие сбора и обработки
огромных массивов исходных данных, реализуемые по преиму-
ществу в компьютерном режиме и используемые главным обра-
зом при принятии решений в прогнозировании эти методы на-
зывают также методами принятия решений или прогнозиро-
вания.
Основу основ, своеобразный фундамент рассматриваемых
методов составляет сама модель. В статистике любая модель —
это ядро, матрица изучаемого объекта, схематическое его пред-
ставление в цифрах и фактах (или представление его отноше-
ний и связей с другими объектами), содержащее в предельно
сжатой форме все существенное и отсекающее второстепенное
и лишнее.
206
Модель в статистике используется там, где другие методы
научного представления наблюдаемых объектов и явлений не-
доступны или неэффективны, требуя намного больше затрат сил
и средств для их применения или намного больше места и вре-
мени для представления результатов и выводов, получаемых на
их основе.
Методов экономико-статистического моделирования, как и
методов многомерного анализа, представляющих одну из его
разновидностей, много, но они разрозненные и в разной сте-
пени пригодны для проведения статистических расчетов и вы-
водов.
Самое широкое распространение имеют методы градиент-
ного, функционального, матричного и межотраслевого анализа.
В последние годы к этим методам относят также методы техни-
ко-экономического обоснования и программирования как обоб-
щающие методы социально-экономического моделирования.
В настоящей главе кратко рассматриваются только те, кото-
рые получили непосредственное практическое применение в
статистике.
4.2.
Методические указания по изучению темы
4.2.1.
Методы градиентного анализа
С помощью указанных методов можно относительно легко и
просто находить теоретические или долженствующие значения
наблюдаемых явлений и фиксировать отклонения конкретных
случаев от них, показывая, какие практические действия надо
предпринять, какие регулирующие меры реализовать, чтобы
процесс оставался управляемым и, следовательно, чтобы затра-
ты были минимальными, потери — нулевыми, а конечные ре-
зультаты — максимальными.
Простейший случай статистического моделирования суще-
ствующих зависимостей — линейный их анализ, основу которо-
го составляют исчисления дифференциальных (разностных) по-
казателей, исходными среди которых являются коэффициенты
опережения, или градиенты.
207
Коэффициент опережения — частное от деления модулей,
абсолютных значений или приращений любых двух или боль-
шего количества показателей, отражающих те или иные отно-
шения или связи уровней, темпов и пропорций между наблюда-
емыми явлениями.
Градиент в простом представлении — это угол наклона (при
линейных зависимостях — тангенс) двух величин, точка перело-
ма, т.е. некоторая предельная величина, обозначающая измене-
ние вектора фактора-аргумента при изменении функции на еди-
ницу. Возможно и обратное истолкование градиента — как пре-
дельной точки переломного изменения функции при изменении
фактора-аргумента на единицу.
В чисто алгоритмическом смысле градиент — это некоторое
число-оператор, или мультипликатор, представляющий некото-
рую производную величину первого порядка. Ее находят как
отношение первого приращения функции к первому прираще-
нию ее аргумента.
При нахождении градиента для различных значений функции
и при работе с двумя и более факторами-аргументами, детермини-
рующими рассматриваемую функцию, появляется система гради-
ентов, изучение которых предполагает обращение к методам мно-
гомерного и матричного их анализа (см. тему 1 и разд. 2.2).
В простейшем случае градиент — это параметр фактора (фак-
торов) линейной функции, который в дифференциальном ана-
лизе находится как производная, в матричном — как определи-
тель, в анализе эластичности — как коэффициент эластичности,
в корреляционном — как коэффициент или индекс множествен-
ной корреляции; в рядах динамики — Это коэффициент опере-
жения, заменяемости, склонности или любой другой мульти-
пликатор, в частности известный мультипликатор Кейнса.
Процедуры градиентного анализа наиболее просто иллюст-
рировать графически.
Пусть функция издержек (Q имеет вид: С — 100 + 5q.
На графике она будет представлена следующим образом (рис. 4.1).
Градиент (прирост С к приросту q) равен:
АТ _125_5
ZY ” 25 ” ’
250 =5. 375
50 ~ ’ 75 ~
208
Рис. 4.1. График линейной функции издержек
т.е.
225-1001 475-225 _ 850-475 = Прирост С = 5
50-25 ’ 75-25 100-75 Прирост q
Из графика видно, что при наращивании объема продукции
(q) на 1 ед. издержки возрастают на 5 ед.
Предельные затраты при этом представляются в виде издер-
жек в расчете на единицу объема продукции q.
В приведенном случае представленная зависимость строго
линейная, что, конечно, упрощает ее понимание, но не соответ-
ствует ее поведению в реальной жизни.
На практике же функция предельных затрат обычно не яв-
ляется прямой, а имеет криволинейную форму типа С = 100 + q\
При различных режимах изменения криволинейная функция
издержек и углы (градиенты) ее наклона будут иметь различные
формы (рис. 4.2).
Как видно на рисунке, градиент и соответственно предель-
ные затраты в разных точках производства будут разными: сна-
209
Рис. 4.2. График нелинейной функции издержек
при различных режимах изменения
чала затраты с увеличением объемов производства растут (рис.
4.2, а), затем (рис. 4.2, б) понижаются (эффект эмерджентно-
сти), достигая предельного минимума в точке насыщения спроса.
Отсюда понятно, что при анализе простейших зависимостей
нельзя ограничиваться нахождением градиента для одной точ-
ки, необходимы системные оценки его значений на всем протя-
жении изменения параметров выпуска.
В связи с этим возникает необходимость обращаться к более
адекватным примерам нахождения градиентов. Вот один из них.
Пусть С = 100 + q2. Требуется найти градиент (предельные зат-
раты) по этой функции при значении q = 10, затем 11, 15 и 20
(рис. 4.3).
Искомые градиенты при соответствующих имениях, есте-
ственно, будут разными.
Рис. 4.3. График функции издержек при q = 10, 20
210
Градиент для С при увеличении количества единиц продук-
ции с 10 до 20 будет равен 30 (рис. 4.4).
Рис. 4.4. График функции издержек при q = 10, 15
При q = 10 С = 100 + 102 = 200.
При q = 20 С = 100 + 202 = 500.
Градиент равен:
£С _ 500-200 _ 300
АС ~ 20-10 “ 10
Однако градиент отрезка АВ не является градиентом каса-
тельной в точке Ф2, который нам необходимо найти.
Приближая точку В к точке А и, следовательно, сокращая
расстояние между ними, значение градиента данного отрезка
будет более близким к искомому.
При увеличении количества единиц продукции с 10 до 15
(рис. 4.5) значение градиента будет равно 25.
Рис. 4.5. График функции издержек при q = 10, 15
211
При q = 10 С = 100 + 102 = 200;
при q = 15 С = 100 + 152 = 325.
Градиент равен:
В'С _ 325-200 _ 125 _25
А'С'~ 15-10 5
Для отрезка от 10 до 11 единиц искомый градиент будет ра-
вен:
при q = 10 С= 100 + 102 = 200;
при q = 11 С= 100 +112 = 221.
Градиент равен:
В"С" _ 221-200 _ 21 _21
А"С"~ 11-10 ~ 1 “
Отрезок А'В" еще больше приблизился к линии, которая была
бы касательной в точке А'. Продолжая уменьшать длину этого
отрезка, мы в конце концов получим значение градиента в точ-
ке А, равное 20.
Соответственно для различных значений фактора q по изло-
женной схеме расчетов получим следующие градиенты:
Фактор q Градиент
10 20
15 30
20 40
25 50
30 60
Отсюда для функции С = 100 + q1 общий градиент (предель-
ные издержки) будет равен 2q.
4.2.2.
Методы линейного программирования
Нахождение градиента — это простейший случай линейного
программирования. Однако графическое решение задач линей-
ного программирования хотя и наглядно, но ограничено. Пред-
ставленные ранее решения возможны только в случае, если по-
следовательно оптимизируются отношения между двумя пере-
212
менными С и q. Если переменных больше двух, требуются более
сложные приемы, в основе которых принцип последовательно-
го приближения к искомым оптимальным значениям.
Кроме того, графические методы поиска оптимальных зна-
чений и в линейных, и особенно в нелинейных моделях громозд-
ки, требуют выполнения большого объема расчетов и чертежей.
Поэтому подобные задачи следует решать более гибкими и эко-
номными методами программирования, позволяющими нахо-
дить искомые оптимальные оценки при любой размерности рас-
пределения имеющихся ресурсов и любой комбинации воз-
можных вариантов их использования.
Для того чтобы узнать, как это делается, рассмотрим гра-
фик.
График дифференциальной функции издержек q + &q
(рис. 4.6}.
Рис. 4.6. График дифференциальной функции издержек q + Ад
Пусть q — объем производства, a Aq — величина его прира-
щения. Обозначим через Ас соответствующее изменение вели-
чины издержек. Соответственно С — это общие издержки при
объеме производства q. Отсюда уровень производства будет оп-
ределяться как q + Aq, а издержки — как С + Ас.
Представив выпуск как q + Aq и подставив это выражение в
приведенное уравнение С = 100 + qv получим:
С + Дс = 100 + (? + Д?)2.
В графическом виде имеем (см. рис. 4.6).
Для того чтобы избавиться от переменной С, вычтем из пер-
вого уравнения второе:
213
С + Дс = 100 + (4 + Д4)2-100-42.
В результате имеем:
\с = 100 + q1 + 2qkq + (\q)2 -100 - q1,
или в конечном виде:
Ас = 2gA<7 + (A#)2.
Зная, что градиент находится как “, разделим обе части
равенства на A# и получим:
Ас _ .
— = 2q + \q.
По мере того как &q уменьшается отрезок, соединяющий X и
Ас
У, становится касательной в точке X а приобретает значе-
de
ние дифференциала . Значение A# при этом становится рав-
но нулю.
Таким образом:
б/с _
— = 2^
dq
Укажем, что исходное значение издержек, равное в нашем
случае 100, рассматривается как свободный член, приравнива-
йте
ется к нулю и поэтому не влияет на дифференциал .
Поскольку градиент (т.е. дифференциал) функции постоян-
ных издержек равен нулю, в нашем примере (С = 100 + q7) имеет
смысл рассматривать только переменные издержки:
С. £ = 2,.
dq
214
В графической форме функции соответствующих издержек
аппроксимируются следующим образом (рис. 4.7).
Рис. 4.7. График функции различных составляющих издержек
Для других видов функции издержек значение дифференци-
алов определяется как:
п з
dq
c = q , — = 4^;
dq
C = q5,^ = 5q.
dq
В общем виде имеем:
C = q",^- = nq"-1.
dq
При этом показатели степени соответствующих функций
являются не чем иным, как собственно градиентами.
Дифференцируя поочередно сумму переменных со степен-
ными показателями при С = q2 + q3 + 10, имеем:
215
de у
dq
Соответственно дифференцируя функцию издержек вида
С = Зд2, получим:
de ~
— = 3 2q = 6q.
dq
При наличии функции С = 5q имеем:
t
de _ §
dq
Вообще график функции издержек С = 5q является прямой
линией, градиент которой и соответственно тангенс угла накло-
на будет равен 5.
Мы привели всего лишь пример решения простой линейной
задачи с двумя переменными.
В реальных ситуациях, когда имеют дело не с двумя, а с
десятком, сотней и тысячей переменных, когда нахождение мат-
ричных значений вручную вообще немыслимо, обращаются к
иным, более сложным процедурам, в том числе стандартным
компьютерным процедурам, примеры и техника применения
которых приведены в разд. 3.2.
4.2.3.
Методы межотраслевого анализа
Методы межотраслевого анализа, называемые еще балансо-
выми методами (методы построения межотраслевого баланса или
таблиц затраты-выпуск) представляют частный случай приклад-
ного использования методов матричного анализа, относящийся
к изучению затрат и выпуска продукции предметно связанных
между собой отраслей или видов экономической деятельности.
Применение этих методов связано с практическим интере-
сом, проявляемым к анализу многомерных межотраслевых свя-
зей, начало которому было положено в нашей стране в 1926 г.
Одним из инициаторов и авторов матричного анализа межот-
раслевых связей являлся В.В. Леонтьев (1906—1999), отечествен-
ный ученый, лауреат Нобелевской премии по экономике (1973 г.),
216
присужденной «за разработку метода «затраты-выпуск» и его
приложение к решению важных экономических проблем».
Впоследствии в нашей стране (в целом по СССР и отдельно
по РСФСР) были построены аналогичные межотраслевые ба-
лансы за 1959, 1966, 1972, 1977, 1982, 1987 гг., а в Российской
Федерации — соответственно за 1991 — 1992, 1995 гг. и проме-
жуточные балансы за 1996-1997, 1998-1999 и 2000 гг., 2003 и
2006 гг.
Размерность моделей соответствующих межотраслевых ба-
лансов колебалась в пределах от 29 х 29 (1928 г.), 83 х 83 (1959 г.)
до 157 х 157 отраслей (2003 г.)*.
Принципиальная модель баланса межотраслевых связей при-
ведена на рис. 4.8.
Выпуск-----------------------------------► Итого выпуска
Затраты
Матрица
материальных
затрат
(1-й квадрант)
Итого
затрат
Матрица
затрат труда
и капитала
(2-й квадрант)
Матрица
конечного потребления
материальных благ
(3-й квадрант)
Матрица
конечного потребления
услуг
(4-й квадрант)
Итого -------
промежуточных
затрат
> Итого
конечного
продукта
Рис. 4.8. Модель баланса межотраслевых связей (фрагмент)
Модель баланса межотраслевых связей, как видно на рис. 4.8
и в табл. 4.1, состоит из четырех матриц (эти матрицы называют
еще квадрантами). Первая из них представляет собственную квад-
ратную матрицу «затраты-выпуск», а три другие — смещенные
* Более подробно см.: Соколин В.Л., Симчера В.М. История становле-
ния и развития балансовых работ в России. — М.: ИИЦ «Статистика Рос-
сии», 2006.
217
NJ
OO
Модель баланса межотраслевых связей (в % к итогу)
Таблица 4.1
Выпуск Промышленность
д S д д X
Код S § § я S S й д о (D s
стро- ки £ V ж 2 Д Д 2 ю Д ю Д сь Q, Д д S ё о д 1 о 1 V S у X 5 s 2 § X £Х
о § V £ 2 д 03 д § ж л д 0? Д д д X 8 £ § S о
Q О е « О с*) § о л X а> д s a 5 £ л
Затраты S Ж х Й д >> Й о X X S S S
Код графы 01 02 03 04 05 06 07 08 09 10
Электро- и теплоэнергия 01 8,08 3,91 3,48 1,39 0,86 0,02 4,47 6,20 7,00 7,47
Продукты нефтедобычи 02 0,08 5,71 33,17 0,13 0,00 0,01 0,00 0,00 0,71 0,01
Продукты нефтепереработки 03 5,50 1,34 3,38 0,25 0,14 0,01 1,65 1,21 1,34 3,43
Продукты газовой промышленности 04 14,54 0,62 0,03 5,13 0,02 0,00 3,20 0,70 3,50 2,10
Уголь 05 14,15 0,62 0,03 0,02 8,26 0,01 18,28 0,68 2,18 3,87
Горючие сланцы и торф 06 22,96 0,23 0,60 0,05 0,55 2,93 1,43 0,79 0,78 4,18
Черные металлы 07 0,30 0,82 0,08 0,06 0,24 0,00 21,82 1,26 1,92 18,31
Цветные металлы 08 0,47 0,06 0,03 0,09 0,00 0,00 2,77 35,94 0,85 8,46
Продукты химической и нефтехими- ческой промышленности 09 0,45 1,71 0,14 0,30 0,58 0,01 0,73 1,26 16,47 6,57
Машины и оборудование, продукты металлообработки Продукты лесной, деревообрабаты- вающей и целлюлозно-бумажной 10 0,55 0,75 0,06 0,04 0,32 0,01 0,69 0,73 0,65 14,81
промышленности 11 0,07 0,07 0,02 0,01 0,26 0,00 0,42 0,27 2,87 2,47
Строительные материалы (включая продукты стекольной и фарфоро- фаянсовой промышленности) 12 0,21 0,44 0,01 0,01 0,14 0,00 0,44 0,22 1,04 1,35
Продукты легкой промышленности 13 0,03 0,11 0,00 0,01 0,06 0,00 0,24 0,04 0,61 0,81
Продукты пищевой промышленности 14 0,01 0,02 0,00 0,00 0,01 0,00 0,03 0,02 0,27 0,09
Прочие промышленные продукты 15 0,85 0,29 0,17 0,26 0,17 0,00 0,77 0,32 1,10 2,24
Продукты промышленности - всего 16 1,58 1,27 3,63 0,25 0,29 0,01 2,65 4,18 2,45 6,53
Продукция строительства Сельхозпродукты, услуги по обслужи- ванию сельского хозяйства и продукты 17 1,57 2,91 0,30 0,32 0,09 0,00 0,65 0,71 0,68 1,25
лесного хозяйства 18 0,01 0,01 0,00 0,00 0,00 0,00 0,02 0,00 0,04 0,04
Услуги транспорта и связи Торгово-посреднические услуги (вклю- 19 0,42 2,31 0,08 0,19 0,50 0,00 0,54 0,46 1,03 0,91
чая услуги общественного питания) Продукты прочих видов 20 0,75 0,73 0,33 1,72 0,12 0,00 0,25 3,41 0,52 1,50
деятельности Услуги жилищно-коммунального хо- зяйства и непроизводственных видов 21 1,09 2,21 0,44 0,29 0,30 0,01 0,79 0,82 1,20 . 3,25
бытового обслуживания населения Услуги здравоохранения, физической культуры и социального обеспечения, 22 0,83 0,33 0,32 0,08 0,26 0,01 0,45 0,67 0,83 2,06
образования, культуры и искусства Услуги науки и научного обслужива- ния, геологии и разведки недр, геоде- зической и гидрометеорологической 23 0,03 0,05 0,01 0,00 0,01 0,00 0,03 0,01 0,01 0,06
служб Услуги финансового посредничества, страхования, управления и общест- 24 0,20 15,24 0,24 0,23 0,23 0,00 0,27 1,34 0,46 7,86
венных объединений Прямые закупки за рубежом, совер- 25 0,20 0,68 0,05 0,07 0,03 0,00 0,38 0,43 0,13 0,35
шаемые резидентами 26 — — — — — — — — — —
Итого 27 1,35 1,15 2,68 0,22 0,18 0,00 1,59 2,17 1,43 3,56
Продолжение
Выпуск Затраты х. Код стро- ки Промышленность Промышленность — всего (сумма граф 1—15) Строительство Сельское и лесное хозяйство Транспорт и связь Торговля, посредническая деятельность и общественное питание
лесная, деревообрабатываю- щая и целлюлозно-бумажная I строительных материалов 1 (включая стекольную и фарфорофаянсовую промышленность) легкая пищевая прочие отрасли
Код графы 11 12 13 14 15 16 17 18 19 20
Электро- и теплоэнергия 01 1,88 2,42 0,85 2,14 0,90 51,Об 2,60 2,04 7,29 3,72
Продукты нефтедобычи 02 0,00 0,01 0,00 0,00 0,00 39,84 0,01 0,00 0,51 —
Продукты нефтепереработки Продукты газовой 03 1,74 0,33 0,12 2,83 0,26 24,52 6,39 4,74 10,95 8,26
промышленности 04 0,32 1,75 0,13 0,75 0,17 32,97 0,13 0,25 2,87 0,98
Уголь 05 1,39 1,08 0,36 1,20 0,33 52,46 1,69 1,17 1,03 1,46
Горючие сланцы и торф 06 2,92 3,09 0,22 0,66 0,05 41,45 21,54 16,11 0,41 0,91
Черные металлы 07 0,50 2,03 0,07 0,42 0,31 48,13 8,78 0,06 1,22 0,62
Цветные металлы Продукты химической и нефтехи- мической промышленности Машины и оборудование, 08 0,33 0,29 0,01 0,53 3,74 53,59 0,53 0,00 0,04 0,06
09 1,69 1,17 1,57 1,71 1,40 35,76 3,67 3,07 1,90 6,62
продукты металлообработки Продукты лесной, деревообраба- тывающей и целлюлозно- 10 0,64 0,32 0,07 0,82 0,21 20,67 4,84 2,33 3,63 2,80
бумажной промышленности Строительные материалы (вклю- чая продукты стекольной и фар- 11 18,67 0,80 0,11 5,18 3,98 35,20 8,19 0,27 1,51 7,77
форофаянсовой промышленности) 12 0,40 9,41 0,04 1,43 0,11 15,25 59,74 0,95 2,20 5,81
Продукты легкой промышленности 13 0,64 0,17 11,42 0,54 0,57 15,27 0,31 0,26 0,49 2,52
Продукты пищевой промышлен- ности 14 0,03 0,01 0,03 21,35 0,29 22,15 0,03 2,27 0,10 3,87
Прочие промышленные продукты 15 0,29 0,24 0,14 3,27 5,33 15,44 0,61 18,28 1,82 5,79
Продукты промышленности - всего 16 1,42 0,92 0,89 4,36 0,96 31,40 4,58 2,06 2,62 3,38
Продукция строительства 17 0,33 0,17 0,05 0,49 0,11 9,62 0,79 0,42 3,81 1,88
Сельхозпродукты, услуги по об- служиванию сельского хозяйства и продукты лесного хозяйства 18 0,01 0,00 0,24 23,54 1,39 25,31 0,00 20,66 0,00 1,81
Услуги транспорта и связи 19 0,49 0,31 0,07 0,81 0,10 8,22 2,25 1,28 4,99 30,03
Торгово-посреднические услуги (включая услуги общественного питания) 20 0,41 0,32 0,14 2,08 0,20 12,47 1,87 0,21 15,30 32,52
Продукты прочих видов деятельности 21 0,44 0,56 0,25 2,39 0,50 14,53 2,55 0,47 5,35 27,98
Услуги жилищно-коммунального хозяйства и непроизводственных видов бытового обслуживания насе- ления 22 0,29 0,36 0,25 0,84 0,18 7,76 0,92 0,27 2,18 1,94
Услуги здравоохранения, физиче- ской культуры и социального обеспечения, образования, культу- ры и искусства 23 0,01 0,01 0,00 0,03 0,02 0,27 0,03 0,01 0,11 0,11
Услуги науки и научного обслу- живания, геологии и разведки недр, геодезической и гидроме- теорологической служб 24 0,08 0,08 0,01 0,17 0,06 26,46 0,24 0,06 1,14 0,13
Услуги финансового посредниче- ства, страхования, управления и общественных объединений 25 0,14 0,04 0,03 0,25 0,03 2,80 0,22 0,08 0,78 0,88
Прямые закупки за рубежом, со- вершаемые резидентами 26 — — — — — — — — — —
Итого 27 0,84 0,58 0,48 3,79 0,59 20,62 2,84 2,43 2,59 4,53
ы * В полном объеме модель 36 х 39 отраслей опубликована в издании «Система таблиц «затраты-выпуск» России за
2000 год». — М.: Госкомстат России, 2003. — 116 с.
матрицы соответственно затрат, труда и капитала или заработной
платы и прибыли (матрица II), конечного выпуска и потребле-
ния материальных благ, или матрица реального сектора эконо-
мики (матрица III) и конечного выпуска и потребления услуг,
или матрица финансового сектора экономики (матрица IV).
Матричное представление баланса межотраслевых связей,
каждая строка которого может быть дана в формате уравнения
выпуска (использования) конкретных видов продукции, а каж-
дая графа — как уравнение затрат на выпуск этих видов продук-
ции (а вместе — в формате системы соответствующих уравнений
затрат и выпуска) позволяет решать большой круг важных при-
кладных задач.
В одной постановке задачи, располагая фактическими дан-
ными межотраслевых матриц, можно определять объем конеч-
ной продукции при заданных объемах затрат и продукции от-
дельно взятых отраслей и всех отраслей, взятых вместе. В дру-
гой постановке задачи, напротив, можно установить необходимые
объемы прямых и полных затрат в каждой отрасли в зависимо-
сти от заранее заданных объемов конечной продукции.
Возможно также решение некоторых других эксперименталь-
ных задач, например исчисления объективно обусловленных оце-
нок (ООО), установления равновесных цен, ранжирования от-
раслей производства по различным критериям затрат и эффек-
тивности.
На основе первичных данных отраслевых балансов констру-
ируются различные производные показатели и определяются их
конкретные оценки. Принципиальными среди них являются
коэффициенты прямых и полных затрат.
Коэффициенты прямых затрат, например затрат электроэнер-
гии на 1 т угля, затрат угля на 1 т чугуна, затрат чугуна на
1 т стали и т.д., определяются путем деления соответствующих
затрат одного вида продукции на выпуск другого вида. Эти ко-
эффициенты исчисляются обычно в натуральном выражении и
рассматриваются как сметные или нормативные технико-эко-
номические показатели производства.
Разновидностью коэффициентов прямых затрат являются
коэффициенты материальных, трудовых и финансовых затрат в
расчете на единицу конечной продукции. Эта наиболее распро-
страненная группа коэффициентов прямых затрат исчисляется
обычно в стоимостном выражении и представляется в виде ко-
222
эффициентов материалоемкости, трудоемкости и фондоемко-
сти производства или обратных их величин — коэффициентов
выпуска продукции и услуг на единицу материальных затрат
(коэффициенты материалоотдачи), трудовых (коэффициенты
производительности труда) или финансовых затрат (коэффициен-
ты рентабельности).
Коэффициенты полных затрат показывают, сколько расхо-
дуется данного вида материальных, трудовых и финансовых ре-
сурсов не только непосредственно, но и косвенно, опосредство-
ванно через другие, участвующие в производстве затраты сопря-
женных отраслей. Так, угля расходуется 35 кг на производство
1 т чугуна. Это прямой расход. Если же учесть расход, который
отражается коэффициентом сопряженных затрат, т.е. расход угля
через кокс, расход угля при добыче руды, изготовлении огне-
упоров и оборудования для чугунолитейной промышленности и
т.д,, то к 35 кг добавится еще более 1470 кг угля на 1 т чугуна.
Всего, таким образом, получим 1505 кг угля на 1 т чугуна. Это
будет коэффициент полных затрат.
Нетрудно видеть, что такие коэффициенты имеют огромное
значение для расчета стоимостной структуры производства. Осо-
бенно важны обобщенные расчеты прямых, сопряженных и пол-
ных материальных, трудовых и финансовых затрат, так как с их
помощью можно определить конечную цену производства, т.е.
цену, которую платит общество в целом за единицу производи-
мой продукции. Отслеживая по каждому продукту, каждому
производителю, отрасли и региону отклонение полных затрат
от прямых и соответственно объективно объединенных оценок
(ООО) от рыночных, обычно случайных и по преимуществу
субъективных цен, можно отчетливо видеть и предприимчиво
регулировать, что и почем производить и от чего и когда отка-
зываться как невыгодного или убыточного производства.
Например, при конвертируемой цене за 1 т нефти, составля-
ющей 130-150 долл. США, прямых затратах 80—90 долл. США
за 1 т ее добычи и при соответствующих полных затратах, пре-
вышающих в России ныне (2006 г.) 270 долл. США, можно сде-
лать вывод, что производство или дальнейшее наращивание про-
изводства нефти в стране должно быть признано как крайне
невыгодное и, следовательно, приостановлено, а в дальнейшем,
возможно, по этой фундаментальной причине и вовсе прекра-
щено.
223
И напротив, при цене за 1 кг продукции самолетостроения,
превышающей ныне 3000 долл. США, и при прямых затратах
1250 долл. США на условный килограмм этой продукции, зная, что
соответствующие полные затраты не превышают здесь 1800 долл.
США, можно однозначно делать вывод, что самолетостроение в
России должно быть признано как выгодное и в сравнении с
нефтедобычей максимально перспективное дело, а не наоборот,
как это ошибочно практикуется в нынешней России.
Зная аналогичные зарубежные и международные оценки
прямых и полных затрат, можно выстраивать такую прозрачную
и обоснованную стратегию экономического развития, которая
будет гарантировать предельную эффективность национального
производства. Выстроить такую стратегию на основе одних по-
казателей прямых затрат попросту невозможно. В этом незаме-
нимое практическое значение моделирования полных затрат,
возможное с использованием балансов межотраслевых связей и
невозможное без них.
4.2.4.
Методы технико-экономических обоснований
Эта группа методов представляет совокупность приемов и
процедур, связанных с технико-экономическим обоснованием
(ТЭО) затрат и эффективности различного рода инвестицион-
ных и других проектов, включая государственные. Ввиду много-
образия этих методов, равно как и многообразия объектов и
направлений их применения, Организацией промышленного
развития ООН (ЮНИДО) рекомендована стандартная процеду-
ра разработки ТЭО и компьютерная методика ее реализации*.
Цель ТЭО — минимизация затрат и максимизация эффек-
тивности разрабатываемых проектов. По определению эта рабо-
та должна быть организована и проводится до, а не в ходе или
после реализации того или иного проекта, когда какое-либо его
улучшение становится попросту невозможным и, следователь-
но, бесполезным.
* UNIDO Manual for the Preparation of Industrial Feasibility. Studies. —
Vienna, 1978, 1991; (на русс. яз. «Руководство по оценке эффективности
инвестиций». — М.: Инфра-М, 1995. — 527 с.); UNIDO Computer Model of
Feasibility Analysis Reporting. — Vienna, 1982, 1984, 1985, 1988, 1990.
224
Содержание работы заключается в проведении сравнитель-
ного анализа затрат и эффективности по каждому разделу ТЭО
и в целом по проекту.
Стандартная методика разработки ТЭО включает процедуры
проведения сравнительного анализа инвестиционных проектов
и программ по следующим 10 разделам.
1. Выводы и рекомендации по разделам проекта (результаты
экспертизы по сокращенной программе).
2. Предпосылки разработки проекта и анализ исходных данных.
3. Коммерческий и производственный потенциал (спрос-
предложение, импорт-экспорт, цены-инфляция, структура -
приоритеты, прогноз-маркетинг).
4. Производственная программа (требования и оценка про-
граммы в целом и по компонентам: производственные мощно-
сти, оборудование, сырье, полуфабрикаты, вспомогательные ма-
териалы, комплектующие, рабочая сила, услуги и т.д.).
5. Строительная программа (выбор строительной площадки,
инвестиции, проектно-сметная документация, строительные
работы, сдача в эксплуатацию).
6. Техническое обеспечение проекта (технология, оборудо-
вание, ноу-хау).
7. Организация производства и накладные расходы (схемы
организации производства, сбыта, управления, оценки наклад-
ных расходов, в том числе производственных, управленческих,
финансовых).
8. Кадры (оценка требований, штатные и внештатные рас-
писания, листы ожидания, оклады, заработная плата, доплаты и
премии, анкеты и тестирование кадрового потенциала, коэффи-
циенты «производительность — заработная плата», «заработная
плата — прибыль», «цена — полезность»).
9. Схемы реализации проекта (модели реализации проекта,
сетевой график выполнения работ, график затрат на выполне-
ние проекта, графическое представление результатов реализа-
ции проекта).
10. Финансово-экономическое обоснование проекта (общая
стоимость работ, источники финансирования, калькуляция зат-
рат и издержки производства, коэффициенты эффективности и
сроки окупаемости, социально-экономические последствия ре-
ализации проекта).
Фундамент работы составляет доказательная, опирающаяся
на статистические расчеты экспертиза самих проектов и прежде
225
всего уровня и качества технико-экономического их обоснова-
ния. Экспертиза должна проводиться на независимой базе, а
технико-экономическое обоснование любых проектов — в обя-
зательном порядке. Крупные проекты при этом должны под-
вергаться экспертизе и обоснованию по расширенной програм-
ме, а средние и мелкие — по сокращенной. Без экспертизы, ТЭО
и проектно-сметной документации о реализации какого-либо
значимого инвестиционного проекта и тем более крупной госу-
дарственной инвестиционной программы речи быть не может.
При этом любая государственная социально-экономическая про-
грамма, лишенная ТЭО, должна ставиться вне закона и рассмат-
риваться как неприемлемая для практического применения.
Мнения экспертов по каждому проекту должны представ-
ляться в виде ответов на следующие группы конкретных вопро-
сов и примерно в следующем виде (возможная формулировка
вопросов приводится на примере разработки проекта социаль-
но-экономического развития России).
1. С каким видом ТЭО вы ознакомились — разработанным
по расширенной или сокращенной программе? Какой вид ТЭО
вы согласны экспертировать?
2. Ваше мнение о том, что представлено в ТЭО избыточно
или поверхностно, чего в нем нет, но должно быть.
3. Считаете ли вы, что представленные 10 разделов ТЭО от-
ражают существо дела в полном объеме или они недостаточны.
Если недостаточны, укажите, пожалуйста, какими разделами
следовало бы дополнить ТЭО?
4. Насколько следует увеличить ресурсы России, чтобы реа-
лизовать выдвинутые программы развития России в полном объе-
ме, без напряжения и в намеченные сроки. Какие, на ваш взгляд,
предпочтительные источники финансирования этих ресурсов:
финансовые интервенции на внутреннем рынке (рост цен, по-
вышение налогов, относительное снижение заработной платы и
т.п.); компенсационная приватизация имущественных объектов;
иностранные кредиты и инвестиции; эффективное расширен-
ное воспроизводство на собственной основе; традиционные ис-
точники эволюционного развития России в 1971—1985 гг.?
5. Дополните представленные в ТЭО положительные и от-
рицательные последствия, вызванные социально-экономическим
развитием России в условиях создания рынка. Укажите оценки
масштабов этих последствий.
226
Далее должны следовать ответы на вопросы, которые выте-
кают из анализа каждого из 10 представленных разделов ТЭО.
Общая идея и конечная цель всей работы — выделение про-
ектов, пригодных для рассмотрения и запуска, создание по стан-
дартным правилам и соображениям здравого смысла статисти-
ческих доказательств и своеобразного их банка, а на этой осно-
ве — ранжирование проектов по коэффициенту эффективности,
выбор приоритетных, обладающих необходимыми и достаточ-
ными условиями для достижения предельной эффективности.
Во всем мире дело обстоит ныне именно так. Ни одна разви-
тая страна, ни одна серьезная компания, ни одно международ-
ное сообщество не позволяет себе игнорировать профессиональ-
ные экспертизы и ТЭО любого сколько-нибудь значимого про-
екта, неважно, государственного или частного.
В России к настоящему времени закончена разработка раз-
вернутой компьютерной программы экспертизы и ТЭО круп-
ных объектов. Программа по своей размерности превосходит на
порядок компьютерную программу ЮНИДО, адаптированную
применительно к условиям проектирования большемасштабных
инвестиционных проектов. При наличии необходимой и доста-
точной информации экспертиза и ТЭО любого крупного проек-
та, параметры которого описываются матрицами 100 х 100 и
выше (с предъявлением текста и графиков), реализуются с мини-
мальными затратами времени и средств, не превышающими 0,2—
0,3% его сметной стоимости. При этом основное время уходит на
сбор и форматизацию исходной информации, необходимой для
подготовки и выпуска полноценного и качественного ТЭО.
Технико-экономическое обоснование обычно разрабатыва-
ется и представляется в матричном формате, в номенклатуре
отраслей и позиций, по которым проводится предпроектное
обследование и обеспечиваются сбор и обработка необходимых
и достаточных данных.
При разработке ТЭО, кроме рассмотренных стандартных
методов социально-экономического моделирования, использу-
ются специальные методы определения затрат и эффективно-
сти, в частности нормативные методы «стандарт-кост», методы
функционально-стоимостного анализа, объективно-обусловлен-
ных дисконтных оценок и другие, позволяющие проводить срав-
нительный анализ затрат и эффективности по различным кри-
териям.
На протяжении многих лет и повсеместно фиксируемые в
мире многочисленные факты отклонений реальных параметров
внедренных инвестиционных проектов от расчетных указывают
на очевидную непрозрачность применяемых методов ТЭО и не-
обходимость их совершенствования.
В связи с этим в последнее время в ТЭО находят широкое
применение новые методы, в частности методы актуарных рас-
четов, обеспечивающие возможность оценки рисков и тем са-
мым позволяющие сравнивать будущие инвестиционные обяза-
тельства с будущими инвестиционными активами в правдопо-
добном режиме, приближенном к условиям и срокам сдачи
проектируемых объектов в эксплуатацию.
4.3.
Примеры решения типовых задач
4.3.1.
Примеры градиентного анализа
Пример 4.1. Дана функция издержек С = q1 + 2q + 10.
Необходимо определить алгоритм и найти объем предельных
издержек при значении q = 5.
de __
Предельные издержки равны ~ - 2(7 + 2 .
При значении q = 5 получаем: 2 • 5 + 2 = 12.
Пример 4.2. Дана функция R = 14# — q1. Необходимо оп-
ределить формулу и найти объем предельного дохода (выручки)
при q = 4.
dR _
Предельный объем (выручки) дохода равен:
При значении q = 4 получаем 14 - (2 • 4) = 6.
Функция дохода (выручки) при этом будет рассматриваться
как произведение цены единицы продукции на количество про-
изведенных единиц:
В условиях абсолютно конкурентного рынка цена считается
фиксированной и не зависит от объема производства. В этом
228
случае значение искомой функции дохода Л будет равно 5q. В
графической форме эта функция может быть представлена сле-
дующим образом (рис. 4.9).
Р
5--------------------- р = 5
Рис. 4.9. Функция дохода при фиксированной цене р = 5
В условиях монополии цена может определяться количеством
произведенной продукции при допущении, что вся произведен-
ная продукция будет реализована.
Пример 4.3. Дано уравнение цены: р — 28 — q.
На основе приведенного уравнения требуется найти предель-
ный объем дохода (выручки).
В этом случае объем дохода (выручки) определяется как
R = pq.
Подставив в приведенное уравнение вместо р его значение
28 - q, имеем R = (28 — q)q.
В результате
7? = 28^-д2,
при q = 4 получаем:
Л = 28-4—42 = 112-16 = 98.
Пример 4.4. Требуется определить, при каком предельном
уровне затрат и при каком максимуме дохода уровень издержек
достигает минимума?
Решить задачу, как и две предыдущие (см. примеры 4.2 и
4.3), можно графически.
Представив на графике (по оси ординат) (рис. 4.10) соответ-
ствующие значения объемов выпуска (дохода), устанавливаем,
что минимальный уровень затрат в данном случае обеспечива-
ется при q = 14, а подставив (теперь уже по оси абсцисс) значе-
ние затрат, находим максимальный уровень дохода.
229
Рис. 4.10. График нахождения максимума дохода и минимума затрат
Другой результат получим, решив уравнение R = 28q — q2.
Допуская, что в точке максимума касательная на графике
функции строго горизонтальна, поскольку тангенс наклона ка-
сательной в этой точке равен нулю, имеем:
— = 0;
dq
R = 28q-q2-
dR _
— = 28-2g.
dq
Отсюда
0 = 28-2g; 2g = 28; g = y = 14.
Соответственно максимальный объем дохода (выручки) со-
ставит:
7? = 28g-g2;
7? = (28 14)-142 =196.
Пример 4.5. Даны три функции:
издержек: С = 64 — 8g + д2;
дохода (выручки): R = 28g — g2;
цены: R = pq.
Требуется найти уравнение функции прибыли, а также объем
затрат, при котором достигается ее максимум.
230
Решение.
Прибыль л = Доход (выручка) (R) — Издержки (Q:
л = 28#-#2-(64-8# + #2);
л = -64 + 36#-2#2;
—64 + 8#- #2 . 2\
С =-------X—= (-64 - 8# + #2);
-64 + 36#-2#2
d'K _ ~ ч
— = 36-4д = 0 (в точке максимума),
J#
d'K
dq
что равнозначно возведению в степень: —64° + 361 — 292 =
= —64 • 0 + 36 • 1 + 2 • 2q, имеем:
36 — 4q = 0; q = 9.
Максимальная прибыль составит: —64 + (36 • 9) — (2 • q2) = 98.
Цена: Р = 28 - q = 28 - 9 = 19.
Известно, что максимум прибыли достигается при равенстве
предельного прироста выпуска продукции предельным издерж-
кам. Проведем расчет:
уравнение
Л = 28#-#2 :281-2#= — 28-2#;
dq
уравнение
С = 64-8#+ #2 :64 0-8-1 + 2# = - = -8 + 2#;
J#
28 - 2g =-8 +2g.
Уподобим подобные члены q и перенесем их в правую часть
уравнения:
28 + 8 — 2g + 2g;
36 = 4g;
g = 9.
231
Приведенный результат соответствует полученному ранее.
Если возьмем функцию издержек
С = ~ 4<jr2+12<j + 150,
получим график одновременных и максимумов, и минимумов q,
которые неочевидны при дифференцировании этой функции
(рис. 4.11).
Рис. 4.11. График максимумов выручки R и минимумов затрат q
а3 2
Из функции издержек: C--^-4q + 12^ + 150 находим про-
изводную (дифференциал) обычным путем, т.е. приравниваем
степени к коэффициентам, в результате имеем: — = ^2-8(7+ 12 = 0
в точке экстремума (максимума или минимума):
Q = q2-iq + \2',
(q-6)(q-2) = 0,
q = 6 и q = 2 (производные первой степени, т.е. два экстремума).
Для того чтобы определить, какое значение соответствует
максимуму, а какое — минимуму, необходимо повторно про-
дифференцировать полученные производные первой степени:
-у-2^-8.
dq
232
Если значение дифференциала отрицательное, то это озна-
чает максимум, положительное — минимум.
Для q = 2 второй дифференциал: (2 • 2) - 8 = —4 отрицатель-
ный, соответственно это максимум. Максимальное значение
издержек (Q в этой точке равно 160.
Для q = 6 вторая производная положительная: (2 • 6) — 8 = +4.
Значение издержек С равно 150.
Для решения задач максимизации или минимизации необ-
ходимо всегда проводить двойное дифференцирование. В про-
тивном случае достоверно установить тип экстремума представ-
ляется невозможным.
Пример 4.6. Предположим, что на каждую единицу про-
дукции (данные примера 4.5) введен налог в размере 4 ед. цены,
т.е. 4g. '
Теперь рассчитаем:
Прибыль = Выручка — Издержки — Налоги',
л = 28g-g2 -(64-8g + g2)-4g.
Приравняв значение q нулю и перенеся его в левую часть
уравнения, получим:
л = -64 +32g-2g2,
откуда 4“ = 32 - 4g = 0, = -4 (значение отрицательное);
dq dq2'
4g = 32; g = 8.
Максимальное значение прибыли составит:
-64 + (32 • 8) - (2 • 82) = 64 долл. США.
Цена: р = 28 — g = 28 — 8 = 20.
В случае, если вместо введения налога выделяется субсидия,
допустим, в размере тех же 4 ед., формула прибыли будет выгля-
деть следующим образом:
Прибыль = Выручка — Издержки + Субсидия.
Расчет максимума прибыли при заданной субсидии прово-
дится аналогично расчету ее максимума при заданном налоге.
233
Пример 4.7. Дано: q = 10 — 2р. Требуется вывести формулу
эластичности спроса от цены и определить ее значение для р = 3.
Эластичность спроса рассчитывается по формуле
_ Процентное изменение (приращение') величины спроса
Процентное изменение (приращение) цены товара
&р \qp Аа р
или —- — г =
р Apq Др q
bq/
/д р =р М
Ар/ q Ар q Ар'
/Р
р dq
т.е. г = — —.
q dP
В нашем случае е = —; <7 = 10—2/7.
q dp
Тогда производная (дифференциал, который можно рассмат-
ривать как параметр уравнения) будет равна:
— = -2;
dp
£л.^=р.(-2)=^.
q dp q q
Выражение г представляет коэффициент эластичности спроса
от цены.
При цене р = 3, q = 10 — 2р = 4.
2р 2-3 3 1/
Соответственно г = -^- =-= — -1 % = 1,5.
4 4 2/2
Это означает, что при увеличении цены в один раз спрос
(величина q) увеличивается в 1,5 раза:
РА = 1010-5^;
PL = 1600-4^.
При р =1 q = 10 = 2 1 = 8; е = 2 | = 0,25.
О
234
4.3.2.
Примеры линейного программирования
Пример 4.8, Имеются следующие исходные данные.
Компания изготавливает четыре вида телеметрических при-
боров. На производство этих приборов затрачивается пять раз-
ных видов сырьевых ресурсов: А, В, С, D, Е. i
Программа-максимум количества производимых продуктов
хр х2, х3 и х4 представляется в виде линейного уравнения:
Р = 203^ +215х2 + 266*3 + 195х4.
Расходу отдельных видов ресурсов при хр х2, х3, х4 > 0 соот-
ветствует следующая система линейных уравнений:
А -1 Ох] +12х2 + 15х3 + 16х4 < 1000 долл. США;
В = 8*! + 6х2 + 5х3 + 6х4 < 500 долл. США;
С = Oxj + 2х2 + 2х3 + 1х4 < 100 долл. США;
D = 5xj + 5х2 + 0х3 + Зх4 <150 долл. США;
Е - 1х] + 2х2 + Зх3 + 4х4 < 600.
Требуется:
1) определить метод решения задачи и ввести данные в ли-
нейную программу;
2) решить приведенную систему линейных уравнений и найти
оптимальные оценки хр х2, х3 и х4. Найти максимальный объем
выпуска Р;
3) рассчитать объемы избыточных или дополнительно необ-
ходимых ресурсов для выполнения намеченной программы и
найти оптимальный их размер;
4) объяснить экономический смысл и практическое назна-
чение полученных результатов, а также возможные погрешно-
сти и ошибки, которые могут быть допущены (или допускают-
ся) при подобного рода расчетах.
Решение. ,
1. Искомые значения находим методом определителей на
основе заданных исходных условий-ограничений.
Определители можно находить разными способами, в на-
шем случае выбран способ дополнительных множителей.
235
2. Решив систему приведенных линейных уравнений, най-
дем оптимальные оценки переменных: = 30,0, х2 = 0,0, х3 =
= 46,7, х4 = 0,0. Это и есть наилучшие оценки.
Оптимальными они являются потому, что именно при этих
значениях х}_4 достигается максимум выручки.
В самом деле, подставив в приведенное уравнение приведен-
ные значения х14, имеем: 203 • 30 + 215 • 0,0 + 266 • 46,7 + 195 • 0,0 =
= 18512,2 .
При любых иных значениях х{_4, которые будут получены
(в случае использования других параметров), максимум выруч-
ки будет всегда меньше, чем 18512,2 ед. Поэтому найденная ве-
личина 18512,2 по определению будет означать максимум.
3. Определим избыток или нехватку отдельных видов ресур-
сов, необходимых для выполнения заданной программы выпуска
четырех видов телеметрических приборов на сумму 18512,2 ед.
Избыточные или дополнительно необходимые ресурсы рас-
считываются как разница между наличными (см. условие зада-
чи) и оптимальными объемами, нужными для выполнения на-
меченной программы.
Оптимальные объемы при этом находят путем решения при-
веденной системы уравнений, подставляя в каждое из них зна-
чения соответствующих определителей х, 4 (подставим только
значения хх = 30 и х3 — 46,7, поскольку х2 = 0,0 и х4 = 0,0).
Отсюда получаем:
= 1000-(10,30 +15-46,7 = 1000) = 0;
S2 = 500 - (8,30 + 5 • 46,7 = 473,5) = 26,5;
S3 = 100 - (0,0 + 2 • 46,7 = 93,4) = 6,6;
54 = 150-(5-30 = 150) = 0;
55 = 600 - (1 • 3 0 + 3 • 46,7 = 170,1) = 429,9.
Устанавливаем, что для изготовления заданного объема теле-
метрических приборов компания располагает тремя видами из-
быточных ресурсов. Избытки составляют соответственно 276,5 ед.
по ресурсу Sv 6,6 по ресурсу 53 и 429,9 ед. по ресурсу 55.
Оптимальный размер каждого вида ресурсов определяется
как арифметическая сумма потребности в них по каждому из
четырех видов выпускаемых приборов. Находим, что по двум
видам ресурсов (5j и 54) он равен фактической потребности в
них, а по трем — он ниже уровня фактической потребности (ре-
сурсы 5j, 53 и 55).
236
4.3.3.
Примеры межотраслевого анализа
Решение той же задачи (пример 4.8) методами матричного
анализа приводится ниже.
Схема решения задачи двумя методами матричного анализа
Дано следующее уравнение Р
+230Xj + 215 Х2 + 266^ +195 Х4.
Требуется найти максимум для наблюдаемых единиц С.
С,: + ю а; 4- 12 Х2 + 15 У3 + 16 х4 < 1000
С2: + 8 X, + 6 Х2 + 5%3 + 6Х4 < 500
Су + 0Х, 4- 2 Х2 + 2 Х} + 1 х4 < 100
С4: + 5 X, 4- 5 Х2 + ох3 + 3 х4 < 150
С5: + 1 X, 4- 2 Х2 + 3 х3 + 4 Х4 < 150
Решение. Решая систему линейных уравнений для четырех
неизвестных (методом наименьших квадратов), находим соот-
ветствующие значения (параметры) X:
AJ = O,1;
Х2 = 0,0;
Х3 = 0,0;
Х4 = 0,0.
Подставив найденные параметры в исходные уравнения,
получим соответственно искомую объективно обусловленную
оценку (максимум) Р= 20,30000 и оценки дефицитности (slack)
или избыточности (surplus) ресурсов для переменных:
5, = 0,00000;
= 499,19998;
53 = 100,00000;
S4 = 149,50000;
55 = 599,89996.
Решение методом двойственных оценок и чувствительного
анализа приводится в табл. 4.2.
237
Таблица 4.2
Схема нахождения двойственных оценок и оценок чувствительности
Двойственные оценки Оценки чувствительности
Наблюдаемые единицы Вспомогательные переменные Оценки двойствен- ных переменных Нижний предел Исходная оценка Верхний предел
1 < 5, = 0,00 20,300 0,00 1,00 300,00
2 < S2 = 499,20 0,000 0,80 500,00 Нет
3 < S, = 100,00 0,000 0,00 100,00 Нет
4 < S4 = 149,50 0,000 0,50 150,00 Нет
5 < S5 = 599,90 0,000 0,10 600,00 Нет
Предельные коэффициенты чувствительности
Переменные Оптимальная Двойственные оценки Нижний Исходные Верхний
оценка дефицит/избьггок предел оценки предел
х, ОДО 0,00 179,17 203,00 Нет
X 0,00 28,60 Нет 2415,00 243,60
X 0,00 38,50 Нет 266,00 304,50
Л 0,00 129,80 Нет 195,00 324,80
Объясним экономический смысл полученных результатов и
определим их практическое назначение.
Общий экономический смысл нахождения приведенных оце-
нок заключается в определении оптимальных объемов затрат и
выпуска, аналогом которых является максимум выпуска и ми-
нимум затрат. Оптимальные объемы достигаются в точке рав-
новесия между затратами и выпуском. Если этого равновесия нет —
система избыточная или недостаточная. В нашем случае систе-
ма избыточна по затратам.
Говоря другими словами, при имеющихся в распоряжении
менеджеров рассматриваемой компании ресурсах и использова-
нии представленной линейной программы можно беспрепят-
ственно обеспечить заданный максимум выпуска телеметричес-
ких приборов. Но, как показывают приведенные данные, при
заданном объеме выпуска можно было обойтись меньшим объе-
мом ресурсов.
Можно ли было на базе выявленных избыточных ресурсов
провести дополнительный объем приборов? Однозначно нет,
поскольку возможности дополнительного выпуска определяют-
ся не только излишками отдельно взятых видов ресурсов, но и
комбинацией этих излишков. Излишние виды ресурсов (ресур-
сы S2, 53, 55) налицо, необходимой их комбинации из пяти ви-
дов нет. Следовательно, фактический объем выпуска в условиях
приведенной задачи тождествен оптимальному, но не факти-
ческий объем затрат, который превышал оптимальные оценки.
Какие выводы должен сделать менеджмент компании? Ме-
неджмент, обнаружив, что фактический объем затрат значительно
превышает требуемый, должен осознать, что материально-тех-
ническое снабжение компании требует корректировки. Конста-
тируя факты расхождений в цифрах, подсчитывая потери, т.е.
то, что недополучено из-за неудовлетворительной организации
использования производственных ресурсов компании, менедж-
мент вынужден коренным образом изменить действующий под-
ход к принимаемым решениям.
Для современного менеджмента подобные расчеты важны и
в другом отношении, а именно: при заданных объемах затрат
менеджмент получает альтернативу относительно легко нахо-
дить предельные значения объемов производства. Это так на-
зываемая задача программирования на максимум выпуска. Реше-
ние подобного рода задач гарантирует возможность организации
полноценного использования ресурсов, выступает инструмен-
239
том реализации безотходных технологий, а в более широком
смысле — инструментом оптимизации и, следовательно, разде-
ления всех имеющихся в стране и мире материальных, трудовых
и финансовых ресурсов.
Наконец, эти расчеты — верный путь выявления действен-
ных вариантов экономии ресурсов, их защиты и сохранения в
интересах будущих правопреемников, что также немаловажно
для менеджеров компании, особенно тех, кто стремится стать ее
владельцем.
При расчетах оптимальных оценок допустимы погрешности
и ошибки. К наиболее распространенным из них относятся сле-
дующие:
1. Неправильные или недостаточные исходные данные для
расчетов.
2. Обращение к неверно выбранным методам расчетов (об-
ращаются, например, к методу матричных определителей, тогда
как расчеты должны производиться по методу факторных оце-
нок, поскольку модель корреляционная, а не строго линейная).
3. Погрешности в расчетах, в том числе из-за различных под-
ходов к формулировке исходных допущений и применяемых
правил округления.
4. Использование разных методов с разной точностью счета
(в нашем случае методов множителей и двойственных оценок,
которые дают разные оценки выпуска).
5. Выбор неадекватных методов вычислений, искаженная
интерпретация результатов, использование недостоверных или
неполных объемов исходных данных, технические ошибки в
расчетах и др.
Пример 4.9. Проектировщики нуждаются в оптимизации
территориального размещения 10 подразделений строящегося
завода. Критерий оптимизации — это минимум расстояний.
В табл. 4.3 приводятся фактические данные о расстоянии между
подразделениями завода.
Требуется:
1) сформулировать общий смысл решения задачи и опреде-
лить усредненное расстояние между подразделениями завода.
Зафиксировать одну из возможных схем размещения под-
разделений завода как гибкую, открытую для улучшений. Затем
видоизменить выбранную схему с целью нахождения улучше-
ний, представить найденную схему и привести ее экономиче-
ское обоснование;
240
2) найти ближайшее расстояние и наилучшее размещение
подразделений завода 1—10 по критерию минимального расстоя-
ния;
3) указать, чему равно минимальное расстояние между под-
разделениями завода;
4) указать подразделения завода, непосредственно примыка-
ющие к подразделению 7;
5) перечислить подразделения завода, непосредственно при-
мыкающие к подразделению 10.
Решение.
1. Формулируем цель решения задачи.
Требуется разместить подразделения завода таким образом,
чтобы среднее расстояние между ними не превышало так назы-
ваемую евклидову норму, т.е. общее расстояние мёжду ними было
минимальным. По результатам расчетов (расчеты приводятся
далее) средним минимальным расстоянием С является 9,54. Это
расстояние найдено с помощью кластерного анализа. При дру-
гом методе расчетов, например методе пошаговых вычислений
от условного нуля, среднее расстояние будет другим, по модулю
большим, равным 12,75.
Цель работы заключается в том, чтобы найти такую схему
размещения подразделений завода, при которой расстояние меж-
ду двумя любыми подразделениями не будет превышать величи-
ну 9,54. Это и есть ответ на первый вопрос. Цель применения
метода пошаговых расстояний другая: находится такая схема
размещения подразделений завода, при которой общее расстоя-
ние между ними не будет превышать 209,0 единиц.
2. Решим задачу нахождения ближайших расстояний между
подразделениями завода для 10 объектов с 10 переменными.
Используем иерархический метод «ближайшего соседа». Рассто-
яние определим по метрике евклидовых пространств. Цель этой
части работы — проведение последовательного улучшения ис-
ходной схемы расстояний.
Строим схему размещения подразделений завода и определяем
ближайшие расстояния между соседними подразделениями завода
(см. табл. 4.3). На основе этой схемы строим таблицу данных и
определяем суммарное единичное расстояние (см. табл. 4.3). Затем
строим новую (вторая по счету) таблицу расстояний, в которой
представляется расстояние между первым кластером и остальны-
ми, не попавшими в первый кластер подразделений завода.
241
Таблица 4.3
Подразделение Расстояние между подразделениями, км
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10 5 3 3 5 5 3 2 3 5 5 5 4 4 5 4 5 4 5 5 2 5 5 2 1 3
3. Чему равно минимальное расстояние между подразделе-
ниями завода? Для того чтобы получить ответ, требуется много-
кратно повторить рассмотренную процедуру и остановиться,
когда будет найдена схема наилучшего размещения подразделе-
ний завода. Напомним, что наилучшая схема та, при которой
сумма расстояний между двумя оставшимися кластерами, ими-
тирующими два идеально размещенных подразделения завода,
будет минимальной.
В нашем случае это расстояние равно 9,1, что меньше эмпи-
рического 9,54. Другими словами, все 10 подразделений завода
следовало бы разместить в двух точках, причем так, чтобы рас-
стояние между ними не превышало 9,1 ед. Понятно, что это
размещение будет оптимальным, поскольку расстояние между
всеми другими подразделениями в данном случае будет равно
нулю.
Для того чтобы найти такое расстояние в условиях представ-
ленной задачи, по схеме, приведенной в табл. 4.4, надо постро-
ить девять кластерных таблиц, каждая из которых будет соот-
ветствовать матричному измерению интеграла расстояний девя-
ти наблюдаемых объектов от определяемого первого кластера.
Первым кластером при этом будет считаться тот, в который вой-
дут два наблюдаемых объекта, расстояние между которыми ми-
нимально.
242
Таблица 4.4
Расстояние Объект
1 2 3 4 5 6 7 8 9 10
2,045151 6
4,472136 3 5 6
5,385165 1 4 2
5,477226 4 6 10 5
5,916080 2 7 9 6
6,708204 7 8 7 5 9
6,928203 5 9 8 3 6 10 5
7,000000 8 3 2 8 8 3 6 9
9,539392 9 2 1 9 7 2 7 10 5 7
Число кластеров 9 8 7 6 5 4 2а 2 1 1
В порядке иллюстрации в табл. 4.5 представлена схема опре-
деления расстояний между объектом 1 и наблюдаемыми объек-
тами 2, ..., 10.
Таблица 4.5
Обь- ект Евклидово расстояние
1 2 3 4 5 6 7 8 9 10
1 0 10,6 7,0 5,4 7,5 9,2 11,2 7,9 9,2 9,2
2 0,6 0 6,9 10,7 9,3 7,7 11,4 6,7 5,9 8,1
3 7,0 6,9 0 9,3 5,9 4,5 12,6 7,7 7,9 4,8
4 5,4 10,7 9,3 0 7,9 10,2 9,5 9,2 9,8 9,9
5 7,5 9,3 5,9 7,8 0 6,1 10,8 8,7 10,0 5,5
6 9,2 7,7 4,5 10,2 6,1 0 13,7 8,8 8,8 2,6
7 11,2 11,4 12,6 9,5 10,8 13,7 0 11,5 11,0 13,0
8 7,9 6,7 7,7 9,2 8,7 8,8 11,5 0 7,9 8,5
9 9,2 5,9 7,9 9,6 10,5 8,8 11,8 7,5 0 8,9
10 9,2 8,1 4,8 9,9 5,5 2,6 13,0 8,8 8,0 0
Подобным же образом определяются расстояния между объек-
тами второго кластера и остальными объектами, далее между
объектами третьего кластера и остальными объектами и т.д. до
девятого кластера, который может быть образован на основе на-
блюдаемых данных. Следовательно, для конечного решения за-
дачи, кроме приведенной, в нашем случае надо строить дополни-
тельно восемь таблиц. На рис. 4.12 показано графически, какие
наблюдаемые объекты и в какой последовательности будут объе-
динены вместе для образования соответствующих 9 кластеров.
243
В графическом виде расстояния между наблюдаемыми объек-
тами можно иллюстрировать следующим образом (рис. 4.13).
Л/4
= 4
Л/ 2
Рис. 4.13. Схема кластеризации 10 объектов с 10 переменными
Какое расстояние между наблюдаемыми объектами является
минимальным?
Как видно на рис. 4.13, это расстояние между подразделения-
ми 4 и 7 (выделено скобкой). Оно равно 4, а все остальные
расстояния до подразделения 7 равны 5 и более единицам.
244
4. Какое подразделение завода непосредственно примыкает
к подразделению 7? Ответ: подразделение 4, поскольку его соб-
ственное расстояние 9,5 меньше среднего единичного минималь-
ного расстояния 9,54 (см. рис. 4.12).
5. Подразделения завода, непосредственно примыкающие к
подразделению 10, — это подразделение 6 с собственным рас-
стоянием 2,6; подразделение 3 (собственное расстояние 4, 8) и 5
с собственным расстоянием 5,5.
Менеджеру компании это важно знать. Размещая подразде-
ления завода именно так, он будет экономить на всем, начиная
с маршрутов личного общения и заканчивая маршрутом теле-
фонных связей.
4.3.4.
Примеры технико-экономического обоснования
Пример 4.10. Иностранная фирма намерена инвестиро-
вать 1,0 млрд ф.ст. в проект (строительство автомобильного за-
вода в России). Строительство рассчитано на пять лет, деньги
кредитные, процентная ставка — 12% годовых, ввод первой очере-
ди — на втором году на базе старых площадей. Предполагается, что
строительство (проект) ведется на Волжском автомобильном заво-
де. Инвестиции будут осуществляться и соответственно доходы будут
распределяться по годам следующим образом (табл. 4.6).
Требуется:
1) обосновать предпочтительный метод оценки предстоящих
инвестиций. Провести сравнительный анализ существующих
норм рентабельности и срока окупаемости;
2) определить чистую современную стоимость предстоящих
инвестиций, выручку и прибыль от реализации рассматривае-
мого проекта;
3) провести расчеты эффективности освоения рассматривае-
мого проекта двумя другими методами (методом окупаемости и
методом рентабельности) и сделать выводы, какой из методов
является наиболее точным, а следовательно, приемлемым. От-
ветить на вопрос, почему приемлемый метод, как правило, не
является одновременно самым простым и доступным?
Решение.
1) Обосновываем предпочтительный метод оценки эффек-
тивности (рентабельности или выгодности) инвестиционных
проектов.
245
Таблица 4.6
Показатель Год Всего за пять лет
первый второй третий четвертый пятый
I. Номинальные 1.1. Инвестиции 360 240 180 120 100 1000,0
(Investment) (360 0,2)= (600 0,2) = (780 0,2) = (900 0,2) = (1000 • 0,2) =
= 72 = 120 = 156 = 180 = 200 728,0
1.2. Выручка (Return) 1.3. Прибыль (доход) -288 -120 -24 +60 +100 -271
(п. 1.2-п. 1.1)
II. Дисконтированные II. 1. Инвестиции 204,6 152,9 128,5 96,0 88,1 660,1
II.2. Выручка — 188,4 218,4 225,0 112,0 743,8
II.3. Прибыль -204,6 35,5 89,9 129,0 23,9 83,7
(современная стоимость минус NP) (п. П.2-п. II. 1)
Смысл любого технико-экономического обоснования заклю-
чается в том, чтобы определить выгоды от вложения денег в
какое-либо дело (проект). Если сумма выгоды больше, чем сум-
ма затрат, тогда следует вкладывать деньги, если меньше - не
следует.
Однако часто результат зависит от того, как считать. Неред-
ко при измерении эффективности имеют дело не с истинным
результатом как таковым, а с эффектом ее измерения или счета.
Этим вызвана необходимость четко различать и выбирать
методы измерения эффективности, обеспечивающие получение
однозначных оценок. Под однозначными оценками понимают-
ся такие, которые меняются в зависимости от изменения реаль-
ных процессов и факторов роста эффективности (и только от
этих процессов и факторов) и не меняются в зависимости от
методов их наблюдения, оценки и представления.
Наиболее широко в разные годы и в разных странах для это-
го дела применялись (и применяются сегодня) следующие пять
разных методов измерения эффективности:
1) определение срока окупаемости (Pajback period — РР);
2) определение внутренней ставки дохода, или внутренней
рентабельности (Internal rate return — IRR);
3) определение учетной ставки дохода или чистой прибыли,
ожидаемой от вложений в проект (Accounting rate of return —
ARR);
4) определение дисконтированных будущих наличных зат-
рат и будущих поступлений от проекта (Discounted cash flow —
DCF);
5) определение чистой текущей стоимости проекта (Net
present value — NPV).
Считается, что метод определения чистой современной
стоимости, предполагающий рыночную оценку стоимости при-
роста денег путем вычета из текущих поступлений (выручки)
дисконтированных затрат, является предпочтительным, посколь-
ку отражает не только номинальную сумму денег, но и процен-
ты на них, т.е. рыночную цену денег.
Рыночная цена — это плавающая, непрерывно меняющаяся
цена, т.е. цена с учетом скидок или накидок, называемых дис-
контом. 1000 ф.ст. сегодня — это не 1000 ф.ст. завтра, а больше,
если курс фунта к доллару, например, завтра повысится на
1,2 п. или банковская ставка повысится на ту же величину. Зна-
247
чит, завтра, это будет, если конвертировать в долларах, 1012 ф.ст.,
или 1012, если фунты стерлингов вложить в банк под возрос-
ший процент. Более того, если умудриться на протяжении од-
ного и того же дня сделать и то и другое последовательно, это
будет уже 1024,1 ф.ст.
И наоборот, это будет меньше, если курс и ставка понизятся
на ту же величину 1,2%. Тогда 1000 ф.ст. сегодня будут равны
всего лишь 988,1 ф.ст. (точная цифра 988,142) и 976,4 ф.ст. (точ-
ная цифра 976,425) соответственно.
В переоценке номинальной стоимости (у нас это 1000 ф.ст.)
в современную стоимость (у нас это 1012 раздельно и 1025 ф.ст.)
и состоят все преимущества метода измерения эффективности в
NPV по сравнению с другими методами, оперирующими, как
правило, номинальными величинами. Но есть и трудности.
Трудность заключается в том, что надо раздельно определять
текущую стоимость издержек на проект и сумму доходов от про-
екта по разным ставкам дисконтирования, которые заранее неиз-
вестны. В результате расчеты уже из-за этого будут неточными, а
следовательно, несопоставимыми. Обычно и для затрат на про-
ект, и для будущих выгод (поступлений) от проекта применяются
одни и те же процентные ставки (как правило, средние банков-
ские ставки для инвестиций, которые сегодня колеблются в Анг-
лии и других странах Европейского союза (ЕС) в пределах 3,0 —
3
3,8% в год, в месяц это приблизительно 0,5% (—= 0,5 • 100 =
= 0,5%).
Однако если ставки в будущем повысятся, то равенство в
оценке выгод и вложений, скажем, под 3% годовых будет нару-
шено. Особенно ощущается это нарушение, когда инвестиции
осуществляются со ставками намного более высокими и в не-
устойчивую экономику, какой, например, продолжает оставать-
ся современная экономика России.
Норма окупаемости проекта в случае I (табл. 4.6) — 20%,
чистая сумма дохода определяется упрощенно как 20% от сум-
мы вложений в период окупаемости, который начинается со
второго года.
Вторая трудность заключается в том, что и инвестиции, и
выручка от них, как видно из табл. 4.6, распределяются по го-
дам неравномерно (в первые годы, как правило, больше объемы
инвестиций, а в последующие годы — выручка), что в сочетании
248
с неравномерно распределяемыми ставками процентов и окупа-
емости приводит к еще большим нарушениям равновесия в оцен-
ках их общего баланса.
Третья трудность в том, что вся выручка от проекта рассмат-
ривается обычно как некоторый общий доход, хотя в действи-
тельности это не так (из поступлений, кроме издержек произ-
водства, надо вычитать налоги, непредвиденные текущие затра-
ты, штрафы, которые, в свою очередь, следует дисконтировать
по своим процентным ставкам и т.д.).
Четвертая трудность — технология расчетов, которые надо вести
не только по дифференцированным (разным) ставкам, опреде-
лять чистую будущую стоимость (Net Future Value — NFV) и пред-
ставлять ее как текущую стоимость денег, раздельно проводить
расчеты по затратам и поступлениям, отдельно по каждому году
и кварталу, а если ставки сильно колеблются, то по каждому ме-
сяцу и, возможно, по каждому дню. Отсюда большая размерность
расчетов, но чем более развернутыми, а следовательно, громозд-
кими будут они, тем точнее будут результаты оценок.
Как правило, расчеты делаются с ориентацией на годовые
процентные ставки, что в условиях сильной их колеблемости по
месяцам предопределяет существенные неточности в оценках
чистой текущей стоимости (в России, например, ставка рефи-
нансирования в начале 2003 г. была 24, затем 18, а в конце года
даже 16%. В 1998 г. соответствующая ставка в начале мая была
30%, в середине — 50%, с 21 мая по 10 июня — 150%, с 11 июня
1996 г. — 60%). При этом в Англии такая же ставка колебалась в
пределах 6,5—6,8% годовых, а в 2003 г. — в пределах 2,5—3,5%.
Но даже в Англии и странах ЕС разница получается ощутимой
(за месяц примерно 0,35%). Отсюда необходимость определения
чистой современной стоимости (NPV) по месяцам, а не по годам.
2) Теперь покажем, как исчислять современную, т.е. реаль-
ную или текущую, стоимость и в чем состоит ее отличие от
номинальной и будущей стоимости*.
* Следует напомнить, что современная рыночная стоимость по моду-
лю будет всегда меньше будущей стоимости денег. Между тем именно бу-
дущая стоимость денег обычно представляется как аналог нарицательной
цены необходимых инвестиций, тогда как в действительности аналогом в
условиях капитализации денег она никогда не является и являться не мо-
жет. Реальным аналогом цены инвестиций является современная их стои-
мость. Распространенная подмена понятий, т. е. игнорирование необходи-
мости учета реальной цены денег, — это результат не одних только недора-
зумений, но и знак лукавых интересов и манипуляций.
249
Схема исчисления такая: вначале определяется общая за пять
лет сумма дисконтированных (значит, со скидкой) издержек или
затрат на строительство завода (шаг 1), затем точно так же вы-
ручка (сумма поступлений) от продаж автомобилей (со второго
года, когда они начнут выпускаться заводом — шаг 2) и после
этого (шаг 3) из выручки (шаг 2) вычитается сумма затрат (шаг 1),
как показано в табл. 4.6.
Ш а г 1. Находим общую сумму затрат на проект, которые тре-
буются за все пять лет. Простая сумма затрат, указанных в табл. 4.6
(п. 1.1), как сумма 360 + 240 + 180 + 120 + 100 = 1000 млн ф.ст. не
годится. Затраты надо дисконтировать. По условию задачи го-
довая ставка скидок (дисконтирования) — 12%. Тогда требуемая
сумма затрат будет намного меньше указанных в таблице
360 млн ф.ст.
Эти 360 млн ф.ст., которые вложены в первый год строи-
тельства завода, будут в действительности стоить (если они бу-
дут использоваться заводом все пять лет и будут возвращены
заводом только в конце пятого года) сумму, равную:
(1 + г)"’
где PV — текущая стоимость (Present Value);
FV — будущая стоимость (Future Value);
г — процент 0,12;
п — число лет, равное 5.
360 _ 360 ,
~17А 1 млн ф.ст. (приблизительная оценка).
I А "Т" V/j 1 ) А / V/А
Пояснение. Расчет по простым процентам:
360 _ 360 _^ОС
1 + (5-0,12)"Тб 5 млнф’ст-
Процент по простым расчетам за пять лет будет:
0,12 • 5 = 0,6; 1,6 - это 1,0 + 0,6.
По сложным процентам, как это указано в формуле, надо 1,12
умножить пять раз друг на друга — именно так считаются сложные
проценты. Значит, (1,12)5= 1,762 = 1,12 1,12 • 1,12 • 1,12 • 1,12.
250
Соответственно текущая дисконтированная стоимость будет
равна:
240 240 , п
для второго года: --------г = —— = 152,9 млн ф.ст.;
(1,0 + 0,12)4 1,572
180 180
для третьего года: -------т = —= 128,5 млн ф.ст.;
(1 + 0,12)3 1,404
120 120 пг
для четвертого года: --------т- , млнф.ст.
(1,0 + 0,12)2 1,254
100 100 оо ,
и для пятого года: -------=------ 88,1 млн ф.ст.
(1 + 0,12) 1,12 .
Запишем полученные оценки в табл. 4.6, п. П.1.
Далее найдем в целом дисконтированную сумму затрат за
пять лет как
204,6 + 152,9 + 128,5 + 96,0 + 88,1 + 660,1 млн ф.ст.
Ш аг 2. Определим сумму выручки (поступлений) от проек-
та. Напоминаем, что проект внедряется на Волжском автомо-
бильном заводе (ВАЗ), где уже производятся автомобили. Допу-
стим, что на старых площадях выручка завода в первом году
составила 72 млн ф.ст. (см. табл. 4.6, п. 1.2), а со второго года
завод получал выручку исключительно за счет строительства
нового завода, под который взял кредит в 1,0 млрд ф.ст. Уста-
новлено, что текущая стоимость этих денег — 660,1 млн ф.ст.
Полученная заводом выручка (считается со второго года ин-
вестиций) определяется с учетом будущих процентов на нее.
Предположим, что выручка завода от производства новых авто-
мобилей составила столько, сколько указано в п. 1.2 табл. 4.6;
определение физического объема этой выручки, т.е. дефлятиро-
вание — отдельная задача, которая не входит в предмет настоя-
щего решения.
Тогда номинальную выручку за каждый год, начиная со вто-
рого, умножаем на банковский процент (Л = 12%) и находим
будущую ее величину (FV), которую и сравниваем с дисконти-
рованной стоимостью затрат за соответствующий год. Соответ-
ственно имеем:
251
для второго года:
для третьего года:
для четвертого года:
для пятого года:
120 • (1+0,12)4 = 120
156 • (1+0,12)3 = 120
180 • (1+0,12)2 = 180
100 • (1+0,12) = 100
• 1,57 = 188,4 млн ф.ст.;
• 1,404 = 218,4 млн ф.ст.;
125,4 = 225 млн ф.ст.;
• 1,12 = 112 млн ф.ст.
Предполагается, что завод заключил с покупателями авто-
мобилей фьючерсные контракты и все доходы капитализировал
в начале каждого года, а не в конце.
В случае, если доходы завод будет получать в обычном режи-
ме в конце года, для второго года будем имеем: 120 • (1 + 0,12)3 =
= 168 млн ф.ст. и т.д.
Следовательно, общая будущая (FV) сумма выручки от вы-
пуска автомобилей составит: 188,4 + 218,4 + 225,0 + 112,0 =
= 743,8 млн ф.ст.
Ш а г 3. Сравнивая указанную сумму будущей суммы выруч-
ки от внедрения проекта с дисконтированной суммой текущей
стоимости затрат на проект, получим ответ на вопрос эффекти-
вен (прибыльный) или неэффективен (неприбыльный) проект.
Если сумма выручки больше суммы затрат, проект считается
прибыльным (в пределах установленного срока затрат на него и
его освоение), если меньше — убыточным в пределах этого сро-
ка, т.е. требующим большего срока окупаемости, а следователь-
но, вообще не подходящим для внедрения.
В нашем случае чистая современная стоимость (NPV) при-
были, получаемой от внедрения проекта, составляет:
743,8 (выручка, return) - 660,1 (затраты, expenditure) = 83,7 млн ф.ст.
Оценки по годам представлены в табл. 4.6 п. II.3.
Вывод. Проект выгодный, поскольку окупается за четыре года.
В случае, если дисконтировать будущую сумму выручки (FV)
и приводить ее к номиналу текущей стоимости (PV), проект и в
этом случае за четыре года почти окупается: текущая дисконти-
рованная выручка равняется 656 млн ф.ст. (120 + 156 + 180 + 200)
и оказывается лишь ненамного меньше текущей дисконтиро-
ванной стоимости издержек (660,1 млн ф.ст.).
Следовательно, чистая современная стоимость (NPV) в этом
случае хотя и будет отрицательной: 656,0 — 660,1 = —4,1 млн
ф.ст., но отрицательная величина незначительна, что дает осно-
вание рекомендовать проект к внедрению со сроком окупаемо-
сти немногим больше четырех лет.
252
3) Проводим расчеты эффективности по методам окупаемо-
сти и рентабельности или внутренней ставки доходности. Со-
вершенно очевидно, что расчеты дисконтированных показате-
лей даже в схематическом и упрощенном виде, как представле-
но выше, дело сложное и неизбежно связано с допускаемыми
субъективными оценками (например, мы субъективно допусти-
ли, что будущая норма окупаемости на заводе составит условно
20% в год, будущая процентная ставка условно будет равна 12%
в год (фактическая процентная ставка в России была установле-
на выше 60% в год, а какая будет через пять лет - никто не
знает).
Именно поэтому прежде всего в разных странах, в том числе
в России, оценки эффективности предпочитают определять бо-
лее просто, фиксируя срок окупаемости (РР 5- payback period),
внутреннюю ставку дохода (internal rate of return), учетную став-
ку (acounfing rate of return) или дисконтированные наличные
(кассовые) поступления (discounted cash flow).
Самым распространенным методом оценки инвестиций в
большинстве стран мира остается метод оценки срока окупаемо-
сти (РР).
Суть метода заключается в следующем: сумма первоначаль-
ных затрат на проект (С) (в нашем примере 1 млрд ф.ст.) делит-
ся на среднегодовую сумму доходов от проекта (Л), рассматри-
ваемых как чистая прибыль (в нашем примере 728 млн ф.ст.
п. 1.2 указанной табл. 4.6), что в расчете на год означает
145,6 млн ф.ст. (728 : 5), т.е.
__ С 1000,0 млн ф.ст. _
R 145,6 ф.ст.
Если за критерий принять окупаемость 1,0 млрд ф.ст., вло-
1000 млн ф.ст.
женных в банк под 6% годовых, т.е. ,<тттг ж = 16,6 года,
OU МЛН ф. ст.
то срок в 7 лет должен рассматриваться как очень и очень при-
емлемый, а проект — более чем в два раза выгоднее проекта
вложения указанной суммы денег в банк.
В этой связи можно сделать вывод, что имеется смысл вкла-
дывать деньги в строительство, а уже потом (если негде строить
или рискованно строить, некому продать результат построенно-
го) - в банк.
253
Хотя по сравнению с расчетами NPV расчеты срока окупае-
мости (РР) просты, тем не менее именно они наиболее широко
применяются в практике оценки инвестиций, в частности тех-
нико-экономических обоснований (Feasebibity study).
Третий метод оценки инвестиций — расчет внутренней став-
ки доходности (IRR) или нормы прибыли. Суть метода: при-
быль (Р) делится на инвестиционные затраты (Q.
В нашем случае прибыль приравнивается к доходам (7?) и
оценивается в среднем за год в 145,6 млн ф.ст., а при затратах —
1,0 млрд ф.ст. Тогда IRR или норма прибыли равняется:
Р_ 145,6 100
С~ 1000,0
14,5%.
Если внутренняя ставка дохода или норма прибыли превы-
шает рыночную ставку процента (банковская ставка в Англии и
странах ЕС, так называемая ставка LIBOR, как отмечалось, не
поднимается выше 6,0—6,7% в год. В последние годы это всего
2,1—2,5% в год) проект считается прибыльным и пригодным для
освоения.
В нашем случае норма прибыли 14,5%, а следовательно, наш
проект более чем выгодный.
По сравнению с NPV метод IRR рассматривается как менее
надежный показатель оценки эффективности инвестиций. При-
чин здесь несколько.
Во-первых, если доходы колеблются в разные положитель-
ные и отрицательные стороны (а по годам они действительно
сильно колеблются), получить среднегодовую ставку трудно, и
она будет очень условной. Во-вторых, показатели нормы при-
были в начальный период эксплуатации обычно завышаются,
даже если их чистая текущая стоимость мала. В-третьих, не-
трудно видеть, что исчисление IRR требует при точном подходе
определения чистой текущей стоимости (NPV), а при нахожде-
нии NPV нет необходимости исчислять IRR. В-четвертых, не-
трудно видеть, что если не корректировать исходные данные
для расчета IRR, то этот показатель представляет собой всего
лишь обратную величину показателя срока окупаемости, т.е.
145,6 _ 1000
Iqqq О , обратная величина = 7 лет. И в этом случае, если
известен срок окупаемости (РР), нет необходимости исчислять IRR.
254
К исчислению IRR близки также расчеты учетной (балансо-
вой) ставки доходности (ARR), определяемой как отношение
чистой прибыли от инвестиций (net profit) к балансовой сто-
имости инвестиций (Q, т.е. если прибыль по проекту будет рав-
на, допустим, 120 млн ф.ст., а инвестиции — 1,0 млрд ф.ст.,
тогда ARR будет:
120
——•100 = 12%.
1000
Нетрудно показать, что показатели окупаемости и нормы
эффективности (при их исчислении на основе одних и тех же
исходных данных) можно рассматривать как прямые и обрат-
ные величины. Следовательно, один из двух указанных показа-
телей можно каждый раз находить упрощенно, производным
путем, как обратно пропорциональную величину.
Наконец, сюда же относятся расчеты так называемых буду-
щих наличных поступлений — Discounted cash flow (DCF), суть
которых заключается в сопоставлении будущего дохода от инве-
стиционных проектов (return или revenue) и будущих инвести-
ций в эти проекты с соответствующими текущими доходами и
инвестициями (капитальными затратами). При этом считается,
что будущие поступления (доходы) стоят меньше, чем текущие,
так как на текущие поступления может быть получен процент.
С другой стороны, выгода и в том, что будущие расходы ме-
нее обременительны по сравнению с текущими расходами. Ведь
деньги, зарезервированные для будущих платежей (покупка че-
рез год-два автомобиля или строительство завода в будущем),
можно вложить на это время в банк под процент и получить
дополнительный доход, тогда как деньги для текущих расходов
надо тратить и не мечтать о проценте на них (нельзя отложить,
например, затраты на лечение или питание).
Следовательно, будущие инвестиционные поступления и
платежи (затраты (FV) приводятся к их текущей (современной)
оценке PV с учетом дисконтирующих факторов (т.е. скидок),
представляющих величину дополнительных доходов на процен-
тные вложения за соответствующее количество лет, которые
должны пройти до момента фактического платежа или поступ-
ления доходов. Расчет будущей стоимости (FV) делается так,
как в примерах на с. 253—254, а расчет современной стоимости
(PV) - так, как это показано на с. 252.
255
Вывод. Метод окупаемости, равно как и метод рентабельно-
сти при оценке эффективности инвестиций, является наиболее
простым и доступным. Однако точность и адекватность оценок
эффективности, получаемых на основе применения этих мето-
дов, являются недостаточными и лишь при прочих равных ус-
ловиях их можно рассматривать как приемлемые.
А поскольку в условиях реальной жизнедеятельности и жиз-
ни, как правило, не бывает «прочих равных условий», оценки
эффективности и технико-экономические обоснования инве-
стиционных и любых других проектов следует производить в
формате дисконтированных показателей как более точных и
адекватно отражающих непрерывно меняющиеся условия ры-
ночной обстановки.
Именно поэтому метод дисконтированных оценок рассмат-
ривается как наиболее приемлемый и рекомендуется для прак-
тического применения.
Почему же этот метод одновременно не может рассматри-
ваться как более простой и доступный? Ответ: потому, что при
его использовании приходится учитывать значительно большее
число переменных и ограничений, чем при применении любого
другого метода.
Пример 4.11. Принято решение инвестировать в проект
500 тыс. долл. США, в том числе 200 тыс. заемных, привлекае-
мых на условиях 10% годовых. Собственные средства (300 тыс.
долл. США) имеется возможность вложить в банк под 10%
годовых. Ожидаемая рентабельность проекта на основе разрабо-
танного технико-экономического обоснования - в 20% годовых.
Требуется:
1) обосновать и исчислить средневзвешенную стоимость ка-
питала;
2) определить номинальную и реальную стоимость дохода от
реализации проекта;
3) обосновать и исчислить арбитражную стоимость;
4) провести сравнительный анализ той и другой оценки ка-
питала и ответить на вопрос, являются ли они альтернативными
ДРУГ другу.
Решение.
1) Обоснуем понятие «средневзвешенная стоимость капита-
ла». Средневзвешенная стоимость капитала (СКК) — это рас-
четная средняя взвешенная величина, которая представляет со-
256
бой сумму собственного капитала (Shareholders Capital or Egulty)
и заемного капитала (Loan Assets), корректируемую (т.е. пере-
считываемую) каждый раз с учетом разных процентных ставок
привлечения заемного и использования собственного капитала.
Таких ставок минимум восемь: четыре — по процентам уплачен-
ным и четыре — по процентам (доходам) полученным.
Средневзвешенную стоимость капитала надо исчислять по-
тому, что стоимость заимствованных денег по источникам их
привлечения, определяемая через процентные ставки, как пра-
вило, разная. При ставке рефинансирования, составляющей в
России ныне (сегодня — 1 февраля 2006 г. — 12%; в мире 2—3%)
проценты по собственному капиталу (это обычно проценты,
выплачиваемые по обыкновенным акциям) примерно 16% го-
довых, текущему банковскому капиталу — 20—24% годовых (дол-
госрочному капиталу — ставка 30—36% годовых).
Тем более различаются проценты по доходам и прибыли,
рентабельность и эффективность производства в различных от-
раслях и различных видах вложений в рамках одних и тех же
отраслей.
Найдем средневзвешенную процентную ставку как
10% • 0,6 +12% • 0,4 = 10,8%,
300
где 0,6 = — доля собственных средств в общей сумме денег, необхо-
200
димых для реализации проекта, и соответственно 0,4 = —
доля заемных денег.
Словом, 10,8% — это средняя взвешенная ставка привлече-
ния денег для реализации рассматриваемого проекта. Тогда стои-
мость денег (капитала), которая необходима для реализации
проекта, будет равна не 500, а 554 тыс. долл. США:
300 • 1,1 + 200 • 1,112 = 500 • 1,108 = 554 тыс. долл. США.
Полученная величина 554 тыс. долл. США — это средневзве-
шенная будущая стоимость номинального капитала, равного 500 тыс.
долл. США современной стоимости.
2) Однако та же средневзвешенная будущая стоимость того
же номинального капитала может быть определена по-другому,
257
а именно путем деления современной стоимости капитала на
величину 100% — 10,8%, т.е. на 89,2%, или 0,892 (1,0 — 0,108):
= 560,6 тыс. долл. США.
0,892
Или в развернутом виде (с учетом разных ставок привлече-
ния денег):
300 + 200 = 333 3 + 227,3 = 560,6 долл. США,
0,9 0,88
где 0,9 -это 1,0 - 0,1, или 90% (100% - 10%);
0,88 - это 1,0 - 0,12, или 88% (100% - 12%).
Операция, в ходе которой вместо банковской используется
учетная ставка, называется дисконтированием.
Если 500 тыс. долл. США принять за будущую стоимость, то
современная их стоимость составит 451,3 тыс. долл. США (500 :
: 1,108). Отсюда следует строго и точно определять понятия «со-/
временная и будущая стоимость».
3) Определяем номинальную и реальную величину дохода от
реализации рассматриваемого проекта. Современная стоимость
капитала, исчисляемая методом дисконтирования, в исходном
случае окажется на 6,6 тыс. долл. США (560,6 — 554,0) больше,
чем та же величина, определяемая методом банковского учета.
Следовательно, реальный доход, который будет получен при
вложении денег в рассматриваемый проект, составит на самом
деле не 100 тыс. долл. США (500 1,2 — 500, или 500 • 0,2), как
это представляется первоначально, и даже не 56 тыс. долл. США
(600,0 — 544,0), а всего лишь 39,4 тыс. долл. США (600 — 560,6,
или 100 — 60,6).
Ведь 60,6 тыс. долл. США нужно возвратить за привлечение
денег в кредит; 33,3 тыс. долл. США — самому себе и 27,3 тыс.
долл. США — за действительно привлеченные деньги со стороны.
4) Определяем арбитражную стоимость. Арбитражная сто-
имость — это альтернативная стоимость, которая называется
обычно арбитражной ценой. Допустим, рассматриваемые 500 тыс.
долл. США вкладываются в приобретение акций (скажем, ак-
ций РАО Газпром, при цене одной акции 1,2 долл, против пер-
воначальной цены 1,0 долл, и годовой доходности 36%). В этом
258
случае годовой доход составит по минимуму 180 тыс. долл. США
(500 • 1,36 — 500 = 180), по максимуму — 316 тыс. долл. США
(500 1,632 - 500).
Однако спрашивается, с той ли вероятностью будет получен
повышенный доход в данном случае , что и в предыдущем слу-
чае? Гипотетическое утверждение при прочих равных условиях
выстраивается как однозначное. Но только соблюдение «прочих
равных условий» в действительности как раз невозможно.
Допустим, что риск в данном случае повышается в два раза,
поэтому доходность при вероятности ±0,5 может составить не
36% годовых, а 18% (36 0,5) и даже —18%, т.е. сумма дохода
может понизиться до 90 тыс. долл. США и до —90 тыс. долл.
США убытка. Сравнение разных вариантов вложений, цен, до-
ходности как раз и представляет собой моделирование арбит-
ражной стоимости, или арбитражной цены.
Арбитраж, по сути, — это операция, в рамках которой совме-
щаются покупка и продажа ценных бумаг или товаров (в нашем
случае вложение в проект и продажа акций). Арбитраж — это
оценка расхождений между ценой продажи (в нашем случае
минимальная цена продажи акций (текущая цена) 410 тыс. долл.
(500 • 0,82) и ценой покупки (цена, получаемая вместо цены
продажи, т.е. ожидаемая в будущем цена, или располагаемая цена
в случае реализации проекта) 600,0 тыс. долл. США.
Следовательно, выгода от арбитража по максимуму в дан-
ном случае составит
600 — 410 = 190 тыс. долл. США.
Однако, если дела на рынке акций будут идти умеренно, ар-
битражная выгода от реализации будет минимальной:
600 — 590 = 10 тыс. долл. США,
где 590 тыс. долл. США — это вложенные 500 тыс. долл. США в акции под
18% годовых.
Если дела на рынке акций будут развиваться самым успеш-
ным образом, вложение в проект будет означать потерю значи-
тельной части денег по сравнению с доходом от их вложения в
приобретение акций.
Арбитражная потеря в этом случае составит 80 тыс. долл.
США (600 - 680 = -80).
680 тыс. долл. США — это 500 тыс. долл. США, вложенные в
акции под 36% годовых.
259
Пример 4.12. На заводе в течение дня отливается по пять
золотых слитков эталонным весом 20 унций каждый. Имеются
следующие выборочные данные за 10 дней (табл. 4.7) о содер-
жании золота (в унциях) в каждом из пяти отлитых слитков.
Таблица 4.7
(в унциях)
День Содержание золота, слиток В це- лом в 4-5 слитках Средняя дневная Сред- няя без 2, 6, 10-го дней
1-й 2-й 3-й 4-й 5-й
1 19,8 20,1 20,2 19,4 20 99,8 19,96 19,96
2 19,9 19,5 19,6 19,6 19,7 98,3 19,66 —
3 20,1 20 19,9 19,8 19,9 99,7 19,94 19,94
4 20 20 20,1 19,9 19,9 99,9 19,98 19,98
5 19,8 19,8 20,1 20 20,1 99,8 19,96 19,96
6 20,3 20,2 20,4 20,2 20,3 101,4 20,28 —
7 20 20 19,9 20,1 20,1 100,1 20,02 20,02
8 19,9 19,9 20,1 20 20 99,9 19,98 19,98
9 20,2 20,1 20,1 20 19,9 100,3 20,06 20,06
10 20,5 20,1 20 19,4 19,9 99,9 19,98 —
Итого 200,5 199,7 200,4 198,7 199,8 999,1 19,982 19,985
Требуется:
1) идентифицировать данные и ввести их в файл для постро-
ения графика контроля за средней (см. рис. 4.14);
2) построить график контроля за средней (х ) на основе пра-
вила двух сигм или стандартного отклонения:
а= С*/-*)2.
N п
3) определить, в какие дни процесс изготовления слитков
выходил из-под контроля;
4) построить стандартную модель контроля за изготовлени-
ем золотых слитков по критерию допустимых отклонений от
эталона;
5) обосновать степень корректности примененных методов
и сформулировать ограничения по их применению, которые
рекомендуется знать каждому пользователю.
Решение задачи представить в обычном (ручном) и компью-
терном режимах.
260
Решение задачи в обычном (ручном) режиме следующее.
Найдем среднюю по дням дисперсию и допустимые отклоне-
ния от средней, равные 2а. Затем сравним эмпирическую сред-
нюю с эталонной в графической форме как наиболее наглядной.
Прежде всего идентифицируем исходные формулы и дан-
ные. Средняя исчисляется как
-
X -
П
где х — количество золота в каждом слитке (/), т.е. 19,8; 20,1; 20,2 и т.д.;
п — число слитков, их 50 (по 5 за каждый из 10 дней).
Дисперсия определяется по формуле:
а2 =
п
Чтимые отклонения исчисляются как
х±2а;а = >/а^.
Исходные данные для расчета (выборочная статистика):
число наблюдений (и) = 50; средняя нормативная (теорети-
ческая) величина — 20 (дается как эталон).
Далее найдем значение средней дневной фактической (эмпи-
рической) величины содержания золота в отлитых пяти слитках:
для первого дня:
- 5>/-5 19,8 + 20,1 + 20,2 + 19,7 + 20
jq = —=-----------------------------= 19,96 унции;
п 5
для второго дня:
- SX-5 19,9 + 19,5 + 19,6 + 19,6 + 19,7
*2 - ? =------------------------= 19,66 унции
п 5
и т.д. для каждого следующего дня.
Полученные расчетные оценки вносим в табл. 4.8. Затем по
найденным средним (их десять по дням и пять по слиткам) рас-
считаем общую среднюю (генеральную среднюю).
261
Таблица 4.8
№ п/п Показатель День
1-й 2-й 3-й 4-й
А 1 2 3 4
1 Средняя 19,96 19,66 19,94 19,98
2 Медиана 20 19,6 19,9 20
3 Мода 19,8 19,6 19,9 20
4 Среднее геометрическое 19,9591 19,6595 19,9397 19,9799
5 Дисперсия 0,043 0,023 0,013 0,007
6 Стандарт отклонения 0,207364 0,151658 0,114018 0,083666
7 Стандартная ошибка 0,092736 0,067823 0,05099 0,037417
8 ВКУ 19,7 19,5 19,8 19,9
9 НКУ 20,2 19,9 20,1 20,1
10 Размах 0,5 0,4 0,3 0,2
11 Нижний квартиль 19,8 19,6 19,9 19,9
12 Верхний квартиль 20,1 19,7 20 20
13 Межквартильный размах 0,3 0,1 0,1 о,1
14 Коэффициент асимметрии -0,23551 1,11808 0,404796 0,512241
15 Стандарт асимметрии -0,21499 1,02066 0,369527 0,46761
16 Коэффициент эксцесса -1,96322 1,45558 -0,17752 -0,61225
17 Стандарт эксцесса -0,89609 0,664377 -0,08102 -2,27945
Продолжение
№ п/п Показатель День
5-й 6-й 7-й 8-й
А 5 6 7 8
1 Средняя 19,96 20,28 20,02 19,98
2 Медиана 20 20,3 20 20
3 Мода 20,1 20,3 20,1 20
4 Среднее геометрическое 19,9596 20,2799 20,0199 19,9799
5 Дисперсия 0,023 0,007 0,007 0,007
6 Стандарт отклонения 0,151658 0,0836 0,83666 0,0836
7 Стандартная ошибка 0,067823 0,037417 0,037417 0,037417
8 ВКУ 19,8 20,2 19,9 19,9
9 НКУ 20,1 20,4 20,1 20,1
10 Размах 0,3 0,2 0,2 0,2
11 Нижний квартиль 19,8 20,2 20 19,9
12 Верхний квартиль 20,1 20,3 20,1 20
13 Межквартильный размах 0,3 од од од
14 Коэффициент асимметрии -0,31536 0,512241 -0,51224 0,512241
15 Стандарт асимметрии -0,28788 0,46761 -0,46761 0,46761
16 Коэффициент эксцесса -3,08129 -0,61225 -0,61225 -0,61225
17 Стандарт эксцесса -1,40641 -0,27945 -0,27945 -0,27945
262
Продолжение
№ п/п Показатель День В целом за 10 дней Средне- дневная величина Средняя без 2, 6, 10 дней
9-й 10-й
А 9 10 11 12 13
1 С редняя 20,06 19,98 199,82 19,982
2 [едиана 20,1 20 199,9 19,99
3 м [ода 20,1 19,9 199,8 19,98
4 Среднее гео- метрическое 20,0597 19,9768 199,814 19,9814
5 Дисперсия 0,013 0,157 о,з 0,03
“5“ Стандарт отклонения 0,114018 0,396232 1,469612 0,146961 0,119722286
7 Стандартная ошибка 0,05099 0,1772 0,65723 0,065723
8 ВКУ 19,9 19,4 198 19,8
9 НКУ 20,2 20,5 201,7 20,17
10 Размах 0,3 1,1 3,7 0,37
и Нижний квартиль 20 19,9 199 19,9
12 Верхний квартиль 20,1 20,1 200,5 z 20,05
13 Межквартиль- ный размах ОД 0,2 1,5 0,15
14 Коэффициент асимметрии -0,4048 -0,35687 1,234827 0,123483
15 Стандарт асимметрии -0,36953 -0,32577 1,127236 0,112724
“1F" Коэффициент эксцесса -0,17752 1,45929 -4,93365 -0,49337
17 Стандарт эксцесса 0,08102 0,666071 2,2519 -0,22519
Значение этой величины можно найти двумя способами.
Первый способ. На основе средних дневных величин:
_ Х-Ч +Х2 +... + X1Q _
общ“ и = 10
19,96 + 19,66 + 19,94 + 19,98 + 19,96 + 20,28 + 20,02 + 19,98 + 20,06 + 19,98 _
10
= 19,982-19,98;
Второй способ. На основе средних по каждому слитку:
200,5 + 199,7 + 200-,4 + 198,7 + 199,8 АО
хобщ =-----------------------------------= 19,98.
263
Эти средние будут тождественны при исчислении на основе
одних и тех данных при одной и той же точности округлений.
Тождественность оценки одного и того же явления, полу-
ченной двумя и более способами, служит прямым доказатель-
ством достоверности его оценки.
Вывод. При норме 20,0 унции изготовленные слитки содер-
жали в среднем 19,98 унции золота.
Строим график расхождений между эмпирическими и тео-
ретическими (эталонными) оценками.
В случае приведенного эксперимента по замеру содержания
золота в 50 слитках процесс будет считаться нормальным, если
отклонения будут удовлетворять требованию (правилу) двух сигм,
т.е. будут находиться в пределах: х±2а = 19,84+2о (верхний кон-
трольный уровень, ВКУ) и 19,84 — 2о (нижний контрольный
уровень, НКУ).
Стандартное отклонение о для первого дня находится как
(*1 -xQ2 __
_ п
у (19,8-19,9) + (20,2-19,96) + (20,2-19,9) + (19,7-19,96) + (20-19,96)2
= 0,207364
(см. табл. 4.8, стр. 6, гр. 1).
И т. д. за каждый день (см. табл. 4.8, стр. 6, гр. 2—10).
Стандартные отклонения в целом за 10 дней находятся как
средняя из сг за каждый день:
_ О;+О2+<7з+... + O1Q _
общ । q
_ 0,21+ 0,15 + 0,11 + 0,08 + 0,15 + 0,08 + 0,08 + 0,11 + 0 <40 _
10
= 0,146961= 0,15 (точнее, 0,146961).
Следовательно,
ВКУ = 19,98 + (2 • 0,15) = 20,38;
НКУ = 19,98 - (2 • 0,15) = 19,68.
Без учета данных за 2-й, 6-й и 10-й день имеем соответ-
ственно:
264
ВКУ = 19,93 + (2 • 0,12) = 20,23 унции;
НКУ = 19,99 + (2 0,12 ) = 19,75 унции.
Далее будет пояснено, для чего в задачу вводится расчет этих
показателей.
3) В какие дни процесс изготовления слитков выходил (если
вообще выходил) из-под контроля?
Ответ: в тот день (или те дни), когда содержание золота в
слитке оказывалось больше, чем 20,28 унции, или меньше, чем
19,68 унции.
Построим график контроля средней и по графику находим
эти дни (рис. 4.14).
Точки — это эмпирические значения (в унциях) по каждому
из 50 изготовленных слитков.
Крестики — это средние значения по дням.
Волнистая линия — это норма (теоретическая средняя).
Прямая линия — это контрольный график средней эмпири-
ческой.
Из приведенного рис. 4.14 видим, что отклонения от нормы
наиболее значительны на 2-й, 6-й и 10-й день.
Точно так же строится график (см. рис. 4.14) и находятся
значения верхнего и нижнего уровня отклонений фактического
содержания золота в слитках против нормы на основе показате-
лей размаха (табл. 4.8, стр. 12).
265
Тогда имеем:
размах ВКУ = 0,37 +(2 0,15) = 0,67;
размах НКУ = 0,37 — (2 0,15) = 0,07.
При допустимом размахе ±1 делаем вывод, что процесс из-
готовления слитков вышел из-под контроля практически толь-
ко на 10-й день.
4) На основе полученных данных строим стандартную мо-
дель контроля за содержанием золота в изготовленных слитках.
Было установлено, что в дни 2-й, 6-й и 10-й процесс выхо-
дит из-под контроля (по средней) и на 10-й день по размаху. В
связи с этим данные по перечисленным дням исключаем из рас-
четов средней, а новые (рекомендованные или прогнозные) рас-
четы проводим, используя данные только за остальные семь дней.
Расчеты (с исключением данных за 2-й, 6-й и 10-й дни) про-
водятся по той же процедуре.
В результате для семидневной средней имеем 19,985 = 20,0.
_ 19,96 + 19,94 + 19,98 + 19,96 + 20,02 + 19,98 + 20,06
----------------------------------------=
= 19,99 (точная цифра 19,985);
0,21 + 0,11 + 0,08 + 0,15 + 0,08 + 0,08 + 0,11 0,82
а7 =---------------------------------=------=
7 7
= 0,12 (точная цифра 0,119722286).
Соответственно:
ВКУ = 19,99 + (2 • 0,12) = 20,24 унции;
НКУ = 19,99 - (2 0,12) = 19,75 унции.
Точно так же проводятся расчеты для стандартного отклоне-
ния на основе данных строки 6. Имеем:
ВКУ = 0,12 + 2 0,1197 = 0,3594 (верхний контрольный уро-
вень стандартного отклонения);
НКУ = 0,12 - 2 • 0,1197 = -0,1197 (нижний контрольный
уровень стандартного отклонения).
Строим график на основе выборки за семь дней и приходим
к выводу, что процесс не выходил в эти дни за контрольные
уровни.
Вывод. Процесс изготовления слитков должен быть органи-
зован так, как проходил в эти семь дней.
266
Расчеты показывают, что эмпирическое значение средней
(среднее фактическое содержание золота (19,88 унции) в изго-
товленных 50 слитках (т.е. в первоначальной выборке уровня
доверия к расчетам (t — 2), равном при 2о 95,4%) может откло-
няться от теоретического значения (нормы, равной по условию
задачи 20 унциям) в пределах:
19,98 + 2(7 = 19,98 + (2 0,15) = 20,28 унции (верхний предел
отклонения, ВКУ);
19,98 — 2(7 = 19,98 - (2 • 0,15) = 19,68 унции (нижний предел
отклонения, НКУ).
Те слитки, которые выходят за пределы найденных значе-
ний верхнего или нижнего уровня контроля, представляют брак
(нестандарт) и должны быть исключены из производства.
Вторая часть задачи заключается в том, чтобы провести сво-
еобразную цензуру, «выбраковку» изготавливаемых слитков.
Установлено, что в дни 2-й, 6-й, 10-й изготовлялись как раз
такие слитки. Выбрасываем 15 слитков, и имеем повторную
выборку, состоящую из 35 слитков, которые вписываются в стан-
дарт.
На основе обработки данных по этим 35 слиткам (которые из-
готавливались на протяжении 7 дней) по тем же процедурам про-
водим новые расчеты, находим новые верхний и нижний конт-
рольные уровни и делаем общий вывод (строим прогноз): процесс
изготовления слитков с допусками ВКУ = 19,99 + (2 • 0,12) = 20,23
и НКУ = 19,99 — (2 0,12) = 19,75 нас устраивает.
Этот процесс может продолжаться до тех пор, пока вновь не
появятся слитки с весом, выходящим за установленные преде-
лы. Когда это произойдет, процедуру (эксперимент), которая
здесь представлена, нужно будет повторить.
Решение той же задачи в компьютерном режиме осуществ-
ляется с помощью программы Statgrahics.
5) Определяем степень корректности методов, использован-
ных в задаче, и формулируем условия и ограничения по их при-
менению, соответствующие страницам QQ (компьютерного) тек-
ста или фотокопиям соответствующих страниц.
Корректность расчетов зависит от правильного выбора типа
(закона) распределения, т.е. идентификации сути решаемой про-
блемы, определения тенденции (тренда) поведения ее основных
параметров, модели расчетов и, конечно же, формулировки са-
мой задачи, а также от характера, точности и достоверности
267
используемой информации. Все перечисленное — это общие
положения корректности применения любого метода, которые
должны быть сопровождены пояснениями и рекомендациями,
сформулированными в доступной форме в случае обращения к
ним пользователей.
6) Сформулировать рекомендации по использованию полу-
ченных результатов простым языком, доступном для рядового
менеджера, не представляющего или плохо представляющего суть
используемых методов.
Рядовому менеджеру нужно знать, что результаты, которы-
ми он пользуется, в значительной мере зависят от точности и
достоверности избираемых метода, модели, алгоритмов, про-
грамм, а также информации, привлекаемой для расчетов. Очень
часто результаты, которыми оперирует менеджер, представляют
эффект не реальных изменений, а всего лишь эффект расчетов.
Простому менеджеру рекомендуется проверять (верифицировать)
результаты, которые ему предлагают модельеры-компьютерщи-
ки, т.е. сравнивать их с какими-то гипотезами, аналогами, здра-
вым смыслом и собственными представлениями. Далее менед-
жер должен знать, на основе какой модели, какого метода полу-
чены результаты. Например^ курсы акций могут быть исчислены
на основе индексов Доу-Джонса (30 компаний), Никкеи (—300
других компаний) или курсов акций всех компаний. Достовер-
ность будет разная. Менеджерам малых компаний индекс Доу-
Джонса ни к чему, им надо интересоваться индексами курсов
акций малых компаний. Лишь тогда они будут принимать пра-
вильные решения, связанные с собственным пакетом акций, а
не только знать ситуацию вообще.
Рекомендуется также уметь сопоставить результаты, получа-
емые из разных источников и моделей, соизмерять их с ресурса-
ми, приводить несопоставимые результаты, представляемые в
разных ценах и валютах, в сопоставимый вид, вводить данные в
компьютер и извлекать необходимые результаты, понимая их
смысл и назначение.
Наконец, менеджеру рекомендуется знать ограничения от-
носительно применяемых методов, которые могли бы являться
причиной ошибочности принимаемых им решений и причиной
отказа от принятия необходимых решений. Среди этих ограни-
чений практически всегда, при использовании любого метода,
существенны следующие пять:
268
1) неадекватность применяемых методов изучаемым процес-
сам, состоящая в использовании детерминированных методов
индексного анализа для изучения эластичности спроса вместо
использования стохастических методов, например методов
корреляционного анализа;
2) неправильный выбор типа распределений. Так, номиналы
наблюдаемых величин соответствия закону нормального распре-
деления (у = а0+ ах). а моделируются на основе уравнения ги-
перболы (у = а0 + а} ) или параболы (у = aQ + а{х{ + а2х2);
3) отсутствующий, слабый или неизвестный (робастный) тип
распределения, исключающий возможность использования из-
вестных рабочих гипотез и, следовательно, требующий форму-
лировки иной модели распределения, собственного закона, либо
отказа от притворного эксперимента по изначально ложной схеме
его проведения;
4) ограниченное количество наблюдаемых единиц и призна-
ков. В случае нашей задачи 50 точек наблюдения (слитков) не-
достаточно. Малая выборка — это, как известно, минимум 100
наблюдаемых точек. Отсюда возможен и неправильный выбор
типа (закона) распределения, и неправильные результаты;
5) наконец, самая распространенная причина ошибочных
ответов — фальсификация данных, их недостоверность, случай-
ный характер, заведомая подтасовка. Обычно этим страдают в
наибольшей мере опросы общественного мнения и избиратель-
ные кампании, не свободны от этого и многие так называемые
научные эксперименты недобросовестных экспериментаторов.
Пример 4.13. Что такое эффект Паккарда? Объясните, по-
чему при росте цен спрос повышается, а при их снижении -
понижается?
Как добиться устойчивого успеха в бизнесе, к каким моде-
лям обращаться, какими рекомендациями пользоваться? Эти
вопросы встают перед менеджерами любой компании и особен-
но остро перед менеджерами старых компаний.
Как решаются эти вопросы в современном бизнесе? Инте-
ресно обратиться к разработке и анализу рекомендательных про-
цедур традиционных (старых) компаний, которых в каждом кон-
кретном случае всегда больше, чем новых. А значит, и ценность
таких рекомендаций выше, поскольку распространяется на мак-
симально большое количество компаний.
269
Рассмотрим, к примеру, одну из старых и знаменитых фирм
«Кока-Кола».
Известно, что компания «Кока-Кола» ведет жестокую кон-
курентную войну с более молодой «Пепсико», постоянно долж-
на искать новые эффективные пути своего развития.
К ним относятся:
• новые технологии менеджмента и организации производ-
ства, ориентирующие на выпуск новых продуктов (расширение
предложения);
• расширение рынков сбыта за счет освоения новых регио-
нальных рынков, в частности рынка России и других стран быв-
шего СССР, вытеснения конкурентов путем продажи более ка-
чественных товаров по прежним ценам. Успех возможен и
при обращении к иным комбинациям: производство тех же то-
варов по более низким ценам, производство большего объема в
расчете на ту же цену или производство принципиально новых
сопутствующих товаров.
Широко известен эффект, которого добилась корпорации
«Маттел», производящая популярную куклу Барби. Кукла выш-
ла на рынок в конце 1950-х гг., к ней выпускается огромное
количество предметов одежды, туалета, игрушечных домов с
предметами домашнего обихода и пр. После большого коммер-
ческого успеха Барби фирма стала выпускать и куклу-мальчика
Кена — приятеля Барби, а также других друзей и подруг.
Раньше, как известно, так делалась знаменитая кукла Пак-
карда.
И там, и здесь смысл один: сначала заманить покупателя
низкой ценой на куклу (даже такой ценой, которая иногда зна-
чительно ниже фактических затрат на производство).
Допустим, затраты на изготовление куклы условно равны
14 долл. США (цена продажи — 10 долл.). Казалось бы, бес-
смысленное производство, убыточная затея. Однако это всего
лишь на первый взгляд, убыток здесь получается «при прочих
равных условиях». При рыночной цене аналогичной куклы в
20 долл. США продажа временно по цене 10 долл, и затратах
14 долл. США при временных потерях будет означать расшире-
ние рынка, его захват.
После состоявшегося захвата цена под предлогом незначи-
тельных улучшений и добавок к товару (так называемых фишек,
а затем просто одного брэнда) мгновенно начинает расти. И в
270
итоге — баснословная прибыль, неуклонно превышающая цену
производства, многократно превысит и с лихвой окупит перво-
начальный убыток.
Вот иллюстрация.
Выходное нарядное платье для куклы: затраты на его изготовление -
7 долл. США, цена продажи - 8,4 долл., прибыль - 1,4 долл., норма
1,4
прибыли: ~~ 0,2, или 20%.
Дом для куклы: затраты на его изготовление — 15 долл. США, цена
19,5-15 = 4,5 1П_ _по/
продажи — 19,5 долл., норма прибыли: --—-----НЮ-Зи/о.
Дача для куклы: затраты на производство - 28 долл. США, рознич-
39 2 — 28 = 11 2
ная цена - 39,2 долл., норма прибыли: —’-----— 100 = 40%.
28
Автомобиль для куклы: затраты на его изготовление - 40 долл.,
60-40
цена продажи - 60 долл., норма прибыли: ——— = 0,5, или 50% и т.д.
Идея везде и всюду одна: первоначальные убытки или до-
полнительные затраты должны компенсироваться большими
доходами в последующем.
И дополнительные доходы получаются не только потому,
что растет прибыль на единицу товара, как это видно из приве-
денного примера. При таком подходе растет спрос, а следова-
тельно, объем продаж. Но при возрастающем объеме продаж,
как известно, снижаются затраты на единицу производства и
реализации товара (так называемый эффект масштабов произ-
водства, или эмерджентный эффект).
Однако почему же с увеличением цены на куклу и особенно
цены на вмененные сопутствующие товары к ней спрос повы-
шается, а не понижается, как того требует закон экономии на
масштабах производства?
То, что спрос в данном случае повышается, — дело понят-
ное. С помощью нехитрой схемы вмененных покупок родители
оказываются мгновенно в плену у детей.
Но почему же при этом цена растет, а не понижается? Ответ
находится в области психологии: родители опасаются, что при
росте спроса цена завтра будет еще выше, а рост цены завтра
271
увеличит и спрос. По этим соображениям при снижении цен
сокращается спрос. В данном случае потребитель психологиче-
ски настроен, что в последующем цена будет еще ниже.
Компания «Пепсико» сегодня в конкурентной борьбе с ком-
панией «Кока-Кола» делает в России следующее: продает 0,6 л
напитка за ту же цену, что раньше продавала 0,5 л того же на-
питка того же качества. Почему менеджеры компании рекомен-
довали эту новинку? Потому, что так они добиваются увеличе-
ния объема продаж и, следовательно, большей экономии на зат-
ратах по сравнению с потерями в цене.
Вывод. Приобретение от любого нововведения в конечном
итоге должно быть больше, чем затраты на него.
Отсюда менеджеру необходимо знание не только новых идей
и альтернатив, но и техники соизмерения затрат и результатов,
умение корректно проводить расчеты, убеждать акционеров ком-
пании расширять дело, приобретать новые акции, соглашаться
на снижение прибыли на акцию сегодня, чтобы получить боль-
шую прибыль на ту же акцию завтра.
Как все это делают менеджеры компании «Кока-Кола» се-
годня, с какими призывами они обращаются к своим акционе-
рам, какие аргументы используют, какие рекомендации дают
компаньонам по расширению объемов производства, и наконец,
к каким инвестиционным схемам прибегают при реализации своих
очередных инноваций — предмет отдельного аналитического
исследования, представляющий едва ли не самую конфиденци-
альную сторону деятельности любой компании, выдаваемый ныне
как ноу-хау.
Фундамент такого аналитического исследования составляет
технико-экономическое обоснование перспектив совершенство-
вания основных направлений деятельности современных ком-
паний, перспектив их инноваций.
Для ответа на поставленные вопросы требуется в первую
очередь провести на фоне общих показателей сравнительный
анализ основных финансовых результатов деятельности ком-
пании.
В табл. 4.9 приведен краткий анализ соответствующих
показателей компании «Кока-Кола», достигнутых за 2002—
2003 гг.
272
Таблица 4.9
Показатель 2003 г. 2002 г. Прирост к 2002 г. 2003 г. к 2002 г., %
Общая сумма приращения стоимости акций плюс ди- виденды 27,8 43,1
Рыночная цена акции (при закрытии) 66,69 52,63 Т1 —
Общая рыночная стоимость обыкновенной акции 164,766 130,575 26 —
Чистая операционная вы- ручка (доход) минус из- держки производства 18,868 18,673 1
Операционная прибыль 5,001 3,195 28 —
Чистая прибыль (после уп- латы налогов) 4,129 3,492 18 —
Чистая основная прибыль на акцию 1,67 1,40 19 —
Разбавленная чистая при- быль на акцию 1,64 1,38 19 —
Дополнительные выплаты на акцию 0,56 0,50 12 —
Средняя ... акций 2,477 2,494 (1) —
Средняя ... выручка акций с учетом разбавления 2,515 2,523 0 —
Акционерный капитал на конец года 7,311 6,156 19 —
Доход на капитал 39,4 36,7 — —
На основе цифрового анализа, который охватывает данные
за большее число лет (в пределе за весь период существования
компании), аналитики делают соответствующие выводы й вно-
сят предложения по улучшению ее деятельности.
Вот образчик кратких выводов и предложений, содержащих-
ся в ежегодном отчете компании «Кока-Кола».
1. Прежде всего менеджеры компании «Кока-Кола» обраща-
ют внимание на историю создания и развития компании, возда-
ют должное и приносят благодарность ее основателям, подчер-
кивая тем самым первейшую роль человека в любом деле. В
этой связи менеджерам не устают повторять и напоминать о
вкладе основателей в общий успех дела компании. В порядке
аргументации приводится всего несколько впечатляющих цифр
и слоганов, например: «Компании «Кока-Кола» почти 120 лет».
273
Старик Джон Пембертон в 1885 г., а затем Эйза Кэндлер и Ро-
берт Вудруф в начале и Роберто Голсуета в конце XX в. знали
что делали, чтобы компания стала не только одной из крупней-
ших, но и одной из устойчивых и быстро растущих в мире. Обо-
рот компании ныне — более 1 млрд долл. США в день (27 лет
назад это был годовой оборот), число занятых — более 50 тыс.
чел. (30 тыс. в 1997 г.), капитализации почти 200 млрд долл.
США (в 1997 г. 165 млрд долл.).
2. Проводится анализ результатов деятельности компании,
представленных в табл. 4.9. Как получены эти результаты — пред-
мет изучения курса «Operating Management».
Повторять данные расчеты здесь нет необходимости. Важно
указать, что они означают, какие рекомендации следует делать
на будущее. Среди этих результатов важно выделить один — 23%
прибыли на одну акцию, что почти в два раза выше, чем в дру-
гих компаниях, и почти в 4 раза выше, чем приносят вложения
в банковский капитал.
3. Очень важное направление — освоение компанией «Кока-
Кола» новых рынков сбыта, ибо в этой области секрет роста
общего потенциала компании. Компания ныне интенсивно про-
двигается на рынки не только Китая, России, Индии, Индоне-
зии, но и рынки арабских стран, мало доступные другим компа-
ниям.
4. Компания на всем протяжении, везде и всюду в иннова-
циях прибегает к новым подходам к расфасовке и продаже сво-
их напитков. Визитная карточка компании— это ее новые заво-
ды не только в Великобритании, Канаде, США, но и в других
странах, прежде всего Китае и других странах Азии, которые
делают все — от лучших в мире напитков до лучших в мире
бутылок и стаканов для них.
5. Нововведения, рекомендуемые менеджерами по производ-
ству и доставке напитков по точному профилю и адресу потре-
бителей.
6. Производство новых видов напитков, особенно не содер-
жащих примесей, лишенных канцерогенных веществ; напитков,
не содержащих ничего, кроме запаха.
7. Привлекают внимание социальные перспективы компа-
нии. Компания уже 75 лет спонсирует мировые олимпийские
игры и намерена делать это впредь. Компания спонсирует чем-
пионаты мира и многие чемпионаты стран и континентов по
274
футболу. Все ближайшие чемпионаты мира более чем по 50 ви-
дам спорта, включая предстоящий чемпионат мира по футболу
2006 г. Мистер Вудруф любил повторять, что каждый, кто при-
коснулся к компании «Кока-Кола», остался в выгоде, ибо полу-
чил максимум, затратив минимум, почти ничего или ровным
счетом ничего.
8. Главный вопрос, который постоянно возникает: будет ли
компания менять свой курс, свою стратегию поведения? Девиз
компании «Ни шагу влево, ни шагу вправо». Путь компании
только вперед, к освоению новых производств и рынков, сим-
патий и признательности новых миллионов потребителей. Мир
без компании «Кока-кола» уже давно не тот мир.
9. Наконец, но не в последнюю очередь, перспективы ком-
пании — это обоснованное и непрерывное улучшение ее финан-
совых альтернатив мультиплицированного привлечения и вли-
вания дополнительных ресурсов, стремление к увеличению ак-
ционерного капитала, который планируется довести к 2005 г. до
15 млрд долл, (в 1997 г. — 7,3 млрд долл.), повышению цены
акции «Кока-Колы» до 100 долл, (вместо 66,69 долл, в 1997 г.) за
единицу, перспективы аккумулирования доходов компании до
уровня 12 млрд долл, в год (в 1997 г. — 5 млрд долл.), повышения
прибыли на акцию до 4—5 долл, и денежных выплат на акцию до
2 долл, против соответственно 1,67 и 0,56 долл, в 1997 г.
К 2005 г. намечено улучшение (на 12—15%) остальных клю-
чевых показателей работы компании, в том числе увеличение
стоимости капитала и источников привлечения капитала, сис-
темы контроля производства и продаж, выбора выгодных мо-
ментов и точек продажи акций «Кока-Колы», снижения рисков,
привлечения новых технологий и специалистов, обеспечения
равновесия финансовых показателей, повышение уровня и эф-
фективности технико-экономических обоснований всех начи-
наний и разработок компании.
Особое место в деятельности компании занимает поиск прин-
ципиально новых напитков и технологий их изготовления. Преж-
де всего воды, не содержащей (кроме таинственного и приятно-
го запаха, мгновенно утоляющего жажду) ни сахара, ни пище-
вых добавок, ни красителей и канцерогенов, причиняющих вред
здоровью и искусственно стимулирующих жажду и навлекаю-
щих нарекания на «Кока-Колу^, короче говоря, напитков, спо-
собных удивить мир новым качеством жизни, а не новым всплес-
275
ком цен и проблем, в том числе цен на старый напиток «Кока-
Колу».
Вот такая компания «Кока-Кола», такие ее напитки нрави-
лись, нравятся и, несомненно, будут нравиться всем и всегда,
везде и всюду, ежедневно и ежеминутно во всем мире. Иных
целей компания не знает, другой идеологии не преследует, на
большее не претендует.
Пример 4.14. Имеются следующие данные о двух про-
ектах с равными объемами выручки и разными издержками
(табл. 4.10).
Таблица 4.10
(тыс. у.е.)
Показатель Год
1-й 2-й 3-й 4-й 5-й
Выручка 6875 9375 11250 12500 12500
Издержки — проект! 3658 4987 5985 6650 6650
Издержки — проект 2 3652 3676 3583 3469 3368
Убыточный - проект 1 3217 4388 5265 5850 5860
Прибыльный - проект 2 3323 5699 7667 9031 9132
Коэффициент безубыточ-
ности - проект 1 0,88 0,88 0,88 0,88 0,88
Коэффициент безубыточно-
сти — проект 2 0,91 1,55 2,14 2,60 2,71
Коэффициент освоения
проектов 1, 2 0,55 0,75 0,90 0,95 1,00
Требуется:
1) определить объем годовой прибыли по каждому проекту;
2) определить точку безубыточности по каждому проекту:
а) как точку во времени (в годовом масштабе);
б) как номинальную величину;
в) как координату на графике.
3) определить минимальный уровень необходимой выручки,
гарантирующий безубыточное производство;
4) представить решение задачи в графическом виде;
5) сделать выводы.
Решение.
1. Объем прибыли определяем как разницу между выручкой
и издержками.
По проекту 1 для первого года имеем:
6875 - 3658 = 3217 у.е.
276
Соответственно по проекту 2 для первого года:
6875 - 3652 = 3323 у.е.
2. Определяем точку безубыточности:
а) во времени — это момент (в нашем случае — год), когда
объем прибыли начинает превышать или превышает объем из-
держек. По проекту 1 искомого момента нет, проект на протя-
жении всех пяти лет его освоения, включая последний год пол-
ного его освоения, остается убыточным. По проекту 2 искомым
моментом является второй год. Проект с этого года и на всем
протяжении его освоения и полного ввода в эксплуатацию (пя-
тый год) является безубыточным;
б) номинальная точка безубыточности — это точка, в кото-
рой сумма прибыли больше или строго равна сумме издержек.
По проекту 1 эта точка по определению отсутствует, по проекту
2 она соответствует цифре 3676 у.е., достигнутой в начале вто-
рого года освоения проекта;
в) как координата на графике точка безубыточности нахо-
дится на пересечении кривых прибыли и издержек. На рис. 4.15
помечена знаком (•), на рис. 4.16 — знаком (х).
3. Определим минимальный уровень выручки, гарантирую-
щий безубыточное производство как точку С (см. рис. 4.15), со-
ответствующую координатам 1, 4; 7, 8. Соответственно опреде-
лим область безубыточности как пространство АБСДна рис. 4.16.
Понятно, что на рис. 4.15 точки области безубыточности нет,
поскольку проект 1 по определению убыточен, а на рис. 4.16
они появляются уже в самом начале освоения проекта.
4. Решение задачи в графическом виде представлено на
рис. 4.17.
Выводы. Точка безубыточности как показатель оценки эф-
фективности предпочтительная, поскольку ее можно найти про-
ще, чем другие оценки эффективности.
По этим же соображениям находятся и используются в прак-
тике технико-экономического обоснования точка и область бе-
зубыточного производства: выше этой точки и области освое-
ния проекта выгодно, поскольку прибыльно, ниже и за преде-
лами этой области — невыгодно.
Пример 4.15. Имеются следующие условные данные о ко-
эффициентах риска реализаций проекта (табл. 4.11).
277
Показатели, тыс. усл. ед. Выручка, издержки прибыль, тыс. усл.
~1 I I I I Т I
50 60 70 80 90 95 100
Коэффициент освоения проектных мощностей, %
Рис. 4.15. График анализа убыточности
278
Коэффициент освоения проектных мощностей, %
Рис. 4.17. График совместного анализа убыточности и безубыточности
Таблица 4.11
Фактор риска Коэффициент риска Норма рентабельности Взвешенная норма
Отсутствие реакции на проект о,1 20,0 0,20.
Вероятное снижение цен 0,4 18,5 0,74
Недостаточное стимули- рование продаж 0,3 19,0 0,57
Ограниченное стимули- рование продаж 0,2 17,5 0,35
Средние значения 0,248 18,75 1,86
Требуется:
1) определить средневзвешенную норму рентабельности про-
екта:
279
а) без учета риска,
б) с учетом риска;
2) средневзвешенный коэффициент риска;
3) пояснить смысл и назначение исчисленных показателей.
Решение.
1. Средневзвешенная норма рентабельности проекта равна:
а) без учета риска (определяется как средняя арифмети-
ческая простая):
20,0 + 18,5 + 19,0 + 17,5
4
= 0,1875, или 18,75%;
б) с учетом риска:
0,20 0,1+ 0,185 0,4 + 0,19 0,3 + 0,175 0,2 = 0,0186, или 1,86%.
2. Средневзвешенный коэффициент риска равен:
0,1 -20,2 + 0,4 18,5 + 0,319,0 + 0,217,5
20,5 + 18,5 + 19,0 + 17,5
= 0,248, или 24,8%.
Выводы. Рентабельность проекта в условиях риска понижа-
ется почти на порядок, а именно с 18,75 до 1,86%.
Повышение рентабельности требует уменьшения факторов
риска до уровня 0,5 и выше, на отметке которого освоение про-
екта целесообразно.
На уровне приведенных коэффициентов риска освоение про-
екта должно быть признано нецелесообразным, а проект непри-
емлемым.
Пр им ер 4.16. Имеются следующие исходные данные: цены
в первом году (2000 г.) в России повысились в 1,202 раза, а во
втором году (2003 г.) — в 1,12 раза. В первом году курс рубля к
доллару США понизился (девальвация) на 4,3%, а во втором —
повысился (ревальвация) на 7,3%.
Требуется:
1) исчислить индекс инфляции в России в 2000 и в 2003 гг.;
2) определить индекс инфляции с учетом девальвации рубля;
3) определить индекс инфляции с учетом индекса ревальва-
ции рубля;
4) определить рост цен в предположении, что инфляция в
2002 г. повысилась на 20% в 2002 г. и на 12% в 2003 г.;
5) ответить на вопрос: претерпят ли приведенные оценки
инфляции в России модификацию, и если да, то какого рода,
280
если корректировать их с учетом девальвации или ревальвации
рубля по отношению к евро?
6) пояснить различия между исчисленными индексами инф-
ляции, девальвации и ревальвации, их смысл и назначение;
7) ответить на вопрос: требуют ли публикуемые в России
оценки инфляции дополнения и корректировки?
Решение.
Для решения задачи нужно проделать девять шагов.
Ш а г 1. Идентифицируем индекс потребительских цен в Рос-
сии, приняв, что он исчисляется по одной и той же методике с
охватом одного и того же круга показателей и одного и того же
репрезентативного набора цен на товары, услуги и капиталы*.
Индекс роста потребительских цен в России в 2000 г., по
данным Госкомстата России, составил 120,2% (прирост 20,2%),
соответственно в 2003 г. — 112,0% (прирост 12,0%). Инфляция в
России, как отмечалось, отождествляется с увеличением потре-
бительских цен, а следовательно, фиксируется в тех же зна-
чениях.
Шаг 2. Квалифицируем принятую идентификацию инфля-
ции как неприемлемую и переформулируем схему ее расчета.
По тому же сопоставимому кругу составляющих и набору реп-
резентативных цен на товары и услуги исчислим индекс инфля-
ции как обратное значение индекса потребительских цен**.
* Положения о порядке наблюдения за изменением цен и тарифов на
товары и услуги определения индекса потребительских цен. См.: Методо-
логические положения по статистике. — Вып. 1. - М.: Логос, 1996. -
С. 429—451; Основные положения о порядке наблюдения за потребитель-
скими ценами и тарифами на товары и платные услуги и определения
индекса потребительских цен. — М.: Госкомстат России, 2002. — 47 с.
** Здесь не касаемся уточнения и расширения сопоставимого круга
составляющих и цен, в частности дополнительного включения в этот круг
опережающе возрастающих цен и тарифов на услуги образования, транс-
порта, ЖКХ, здравоохранения, недвижимость и т.д., посреднические и
комиссионные услуги малого бизнеса, которые могут на 5—6 пунктов по-
высить ежегодные значения публикуемых индексов потребительских цен.
Не рассматриваем эти вопросы потому, что не располагаем соответствую-
щей информацией, сбор которой требует организации и проведения само-
стоятельного статистического обследования. Распространенные на этот счет
экспертные оценки и догадки не могут заменить такие данные, а следова-
тельно, не могут рассматриваться как серьезные основания для пересмот-
ра публикуемых индексов потребительских цен.
281
Разумеется, все расчеты должны начинаться с определения
групповых и далее укрупненных групповых индексов потреби-
тельских цен и только затем на этой основе исчисляться общий
индекс потребительских цен.
Тогда общий индекс инфляции (с допустимыми округлениями)
в 2000 г. составит 0,833(1,0 : 1,202), а в 2003 г. - 0,893 (1,0 : 1,12).
Заключение. Инфляция (вздутие рубля, обесценение денег)
в 2000 г. составила в России не 20,2%, а 16,7%, и в 2003 г. не
12,0, а 10,7%. Разница в оценках существенна и не может быть
проигнорирована как пренебрежительно малая величина, в час-
тности в случае принятия решения о размере дополнительной
эмиссии денег.
При существующем (2003 г.) в России объеме денежного
оборота, превышающем 5,0 трлн руб. (в эквиваленте 175,4 млрд
долл. США), это означает эмиссию в оборот более 65,0 млрд
руб. или 2,3 млрд долл. США лишних денег.
Ш а г 3. Определим индексы девальвации (2000 г.) и реваль-
вации (2003 г.) рубля, получив соответственно:
2000г.;
27,00 руб./долл. J
0,927(-29,4- РУ6-/Д°ЛЛ- ]в 2003 г.
I 31,78руб./долл.
Фиксируем, что рубль по отношению к доллару США в 2000 г.
обесценился на 4,3%, а в 2003 г. вырос по стоимости на 7,3%.
Ш а г 4. Найдем индекс инфляции с учетом девальвации рубля
в 2000 г. и ревальвации рубля в 2003 г. в предположении всей
рублевой массы.
f 0,833 А
Соответственно имеем: для 2000 г. — 0,799 I’
( 0,893
для 2003 г. - 0,963 I q 927 I-
Фиксируем, что реальная инфляция в 2000 г. с учетом де-
вальвации рубля составляла 20,1%, а не 16,7%, и соответственно
в 2003 г. всего 3,7%, а не 10,7%, как это следует из формального
ее расчета без учета реальной девальвации рубля.
282
Ш а г 5. Учитывая чрезмерность допущения о возможной де-
вальвации (в 2000 г.) и ревальвации (в 2003 г.) в России всей
рублевой массы и предполагая, что под влиянием этих процес-
сов в России находилось примерно 15% общего объема рубле-
вой массы, найдем индекс инфляции с учетом ограниченной
девальвации и ревальвации рубля.
Соответственно имеем.
Для 2000 г.: 0,833 • 0,85 + 0,799 • 0,15 = 0,828.
Для 2003 г.: 0,833 • 0,85 + 0,963 • 0,15 = 0,904.
На основе полученных оценок окончательно фиксируем,
что учтенная реальная инфляция в России в 2000 г. составляла
17,2 (1,000—0,828) • 100, а не 20,2% и соответственно в 2003 г.
9,6 (1,000—0,904) • 100, а не 12%, как это официально зафикси-
ровано.
Ш а г 6. Определим рост цен в продолжении повышения ин-
фляции в 2000 г. на 20%, а в 2003 г. на 12%. Если бы в России в
2000 г. инфляция повысилась на 20%, то с учетом изложенных
соображений (т.е. с учетом частичной или полной девальвации
рублевой массы) расчетное увеличение потребительских цен в
том же году составило бы не 20%, как это, по-видимому, имело
место на самом деле и представлялось в обиходе, и не 25% (точ-
ная цифра 25,3), как это вытекает из логики счета обратных
чисел (1,0 : 0,8), а все 30% и более (точная цифра 30,6%), а
именно:
1,25 • 1,0415 = 1,306,
где 1,045 = 1,0/0,957, а 0,957 = 1,0 - 0,043.
Соответствующая цифра по минимуму (при ограниченной
доле рублевой массы, равной в валютном обращении 15%) —
1,25 • 0,85 + 1,045 • 0,15 = 1,219, т.е. общее увеличение цен
составило бы в 2000 г. не 20,2%, а 21,9%.
То же самое относится и ко всем остальным случаям, когда
инфляция сопровождается, а следовательно, усиливается деваль-
вацией национальных валют. И напротив, сделанное утвержде-
ние будет несправедливым, если инфляция сопровождается ре-
вальвацией, дефляция — девальвацией или будет иметь место
одновременный процесс дефляции и ревальвации как наиболее
желательный.
Понятно, что в рассмотренных случаях «обратный счет» не
исключается, а допускается притворная аберрация чисел. Ибо,
283
если, скажем, в 2003 г. именно инфляция составляла 12%, то
расчетная скорость увеличения цен тогда равнялась бы 13,6%, а
не 12%. В этом как раз и состоит притворная аберрация. Спеку-
лятивных рассуждений подобного рода можно выстраивать бес-
конечно много.
Шаг 7. Определим характер инфляции с учетом девальва-
ции и ревальвации рубля в евро. При котировке рубля в евро, а
не в долларах США, его девальвация будет фиксирована в 2003 г.,
а ревальвация — в 2000 г. И тогда представленные оценки пре-
терпят модификацию, мера и форма которой будут определять-
ся каждый раз конкретной долей конвертируемой рублевой массы
в соответствующих валютах и рассматриваться как комбиниро-
ванная средневзвешенная девальвация или ревальвация рубля.
По этой причине расчетные и публикуемые оценки инфляции
тоже могут претерпеть соответствующие уточнения.
Шаг 8. Поясним различия между исчисленными индекса-
ми, их смысл и назначение.
Как видно, расхождения в оценках инфляции, в зависимос-
ти от ее понимания и корректировки с учетом девальвации и
ревальвации, во всех рассмотренных случаях существенные, что-
бы ими можно было пренебречь.
Нетрудно показать и согласиться, что с учетом ныне не ох-
ватываемых составляющих инфляции, в частности чрезмерного
роста цен и тарифов на образование, услуги здравоохранения,
спорта, транспорта и связи, ЖКХ, строительство и недвижи-
мость, посреднические и т.д., полученные оценки инфляции
могут и должны быть существенно скорректированы в сторону
их повышения.
Ш а г 9. Ответим на вопрос, требуют ли публикуемые оцен-
ки инфляции дополнения и корректировки?
Ответ. Факты существования значительных различий между
расчетными и реальными оценками инфляции требуют присталь-
ного внимания. Факты эти, включая представленные, по раз-
ным причинам до настоящего времени не нашли должного от-
ражения в оценках инфляции. Отсюда эти оценки, искусствен-
но заниженные в одних случаях и по одному кругу причин и
завышенные в других случаях по другому кругу причин, продол-
жают оставаться в значительном объеме неудовлетворительны-
ми, вызывая справедливые нарекания общественности. Отсюда
все существующие оценки инфляции требуют исправления и
дополнения.
284
4.4.
Задачи для самостоятельных занятий
4.4.1.
Задачи градиентного анализа
Задача 4.1. Даны функции издержек и дохода:
R = 40q-q2;C = l-(5q + -q2).
4
Требуется определить формулу и найти объем:
а) выпуска, при котором достигается максимальный доход;
б) прибыли и на ее основе рассчитать объем выпуска, при
котором прибыль достигает максимального объема;
в) предельного дохода и предельных издержек.
Рассчитать предельный уровень выпуска продукции, при ко-
тором прибыль максимальна.
5
Ответы: а) 20, 400; б) Р= 35g— 10 - -g2, 14, 235; в) предель-
ная прибыль равна 40 — 2g; предельные издержки равны 5 + д/2;
г) 10.
Задача 4.2. Дана кривая общих издержек (д — объем про-
изводства):
C = q3/3-2q2+5q + 20,
а также кривая дохода R = 2Qq— q2.
Требуется найти объемы предельных издержек и предельно-
го дохода, а также объем производства, при котором предельная
прибыль будет равна предельным издержкам.
Ответы. Предельные издержки равны q2 — 4q + 5; предель-
ная выручка равна 20 — 29 + 5.
Задача 4.3. Производство составляет q единиц продукции
в неделю. Общие издержки производства заданы формулой
С = 30+10д + 92/2.
Производитель является монополистом, функция спроса на
его продукцию задается линейным уравнением
/> = 46—9.
285
Требуется обосновать формулу расчета дохода в зависимо-
сти от параметра q, а также доказать, что при уровне производ-
ства q = 7 прибыль будет максимальной. Исходя из приведен-
ных ниже предположений следует определить цену моно-
полиста.
Вводится налог в размере трех единиц на каждую единицу
продукции, производимой монополистом. Монополист вклю-
чил налог в стоимость своих издержек и соответственно изме-
нил выпуск и цену. Покажите, что цена продукции выросла на
1/3 от величины налога.
Ответ: R = 40q — q\ р = 21# — 30 — 3#2/2,33.
Задача 4.4. Дана кривая спроса q = 25 - р/2 и функция
издержек 40 + 1 = q + q2/2.
Требуется:
а) определить функцию дохода в зависимости от q и дока-
зать, что она будет 40# — 5#2/2 — 40;
б) определить размер выпуска, при котором прибыль макси-
мальна. Найти также соответствующий уровень цены и макси-
мальный размер прибыли;
в) выполнить условие задания п.б, но с учетом введения на-
лога в размере 10 ед. на каждую единицу продукции.
Ответ: a) R = 50# - 2#2; б) 8, 34, 120 ; в) 6, 38, 50.
Задача 4.5. Общие издержки фирмы заданы функцией
с = #2 4- 4# + 24.
Кривая спроса: р = 6 — #.
Требуется найти:
а) предельные издержки;
б) предельную прибыль.
При каком значении # предельная прибыль равна нулю и
каков экономический смысл этой величины?
Ответ: а) предельные издержки равны 2# + 4; б) предельная
прибыль равна 2 - 4#, 1/2.
Задача 4.6. Общие издержки и доход заданы функциями
/? = 20<?-g2; С = 10 + 4g + g2.
Требуется:
а) подсчитать уровень производства, при котором максими-
зируется доход, а также его значение в точке максимума;
б) найти функцию прибыли и рассчитать значение произ-
водства, при котором прибыль максимальна. Подсчитать ее;
286
в) найти функции предельного дохода и предельных издер-
жек. Показать, что объем производства в точке равенства пре-
дельного дохода и предельных издержек соответствует значе-
нию, при котором прибыль максимальна.
Ответ: а) 10, 100; б) Р= —10 + 16# — 2#2, 4,22; в) предельная
выручка равна 20 — 2#, предельные издержки равны 4 + 2q .
Задача 4.7. Общие издержки С заданы функцией:
С = х3/3 - 2х2 = 10х.
Требуется найти:
а) функцию средних издержек;
б) функцию предельных издержек;
в) выпуск, при котором достигается минимум средних из-
держек.
Покажите, что в точке минимума средних издержек предель-
ные издержки равны средним издержкам.
Ответ: а) х2/3 — 2х + 10; б) х2 — 4х + 10; в) 3.
Задача 4.8. Фирма работает в условиях совершенной кон-
куренции. Функция издержек имеет следующий вид: С= #3/3 —
— 6#2 + 45# + 10.
Покажите, что функция предельных издержек имеет вид:
#2 — 12# + 45, а функция средних издержек — #2/3 — 6# + 45.
Докажите, что минимум средних переменных издержек до-
стигается при # = 9 и что соответствующий их уровень 18. Най-
дите значение предельных издержек при # = 9, прокомменти-
руйте полученный результат.
Найдите объем производства, при котором максимизируется
прибыль при цене р = 58. Указание: в условиях свободной кон-
куренции цена неизменна, а доход равен 58#.
Ответ: 18, 13 .
Задача 4.9.
Имеются следующие условия:
а) условный недельный уровень потребления товара состав-
ляет 7 (спрос) по цене 4 ед. Если цена снизится до 2 ед., в этом
случае количество проданного товара увеличится до 19. Пред-
полагая, что зависимость линейная, найдите функцию спроса
(# — количество товара, р — его цена);
б) недельное производство (предложение) равно 5 ед. про-
дукции при цене 5 и 11 ед. при цене 8. Исходя из того что
зависимость линейная, найдите_функцию предложения (# - ко-
личество товара, р — его цена);
287
в) определите равновесные цену и количество;
г) найдите выражение зависимости дохода от количества (q)
и такое значение q, при котором достигается максимальный
доход. Найдите также соответствующую цену;
д) какова будет новая равновесная цена, если каждую еди-
ницу продукции обложить 10%-ным налогом?
Ответ:
а) = 31-бу?; б) =-5 + 2р; в) ре = 4* /2 qe =4;
г) R = 31^/6, 31/2, 2 7 /12;д) ре =4,60, qe =4,37.
Задача 4.10. В здании гостиницы расположено 70 номе-
ров. Подсчитано, что если месячная плата составит 200 ф. ст., то
они все будут заселены. Если же поднять цену на 10 ф. ст., то
один номер будет свободным. Управляющий гостиницы также
подсчитал, что стоимость обслуживания одного свободного но-
мера составляет 10 ф.ст. в месяц, в то время как заселенного —
30 ф.ст.
а) Если прибыль от аренды считать равной доходу за выче-
том издержек на обслуживание, найдите формулу для определе-
ния прибыли, где х — количество сдаваемых в аренду номеров.
б) Какова должна быть арендная плата, чтобы получать мак-
симальную прибыль?
в) От подрядчика поступает предложение на обслуживание
блока по цене 15 ф.ст. за номер, вне зависимости от того, заня-
ты все номера или нет. Будет ли это более выгодным для гости-
ницы в плане получения прибыли?
Ответ: а) р = 880х • 10 2 — 700; б) 44; в) да, потому что
прибыль составит: в случае б) 18660 ф.ст.; в случае в) 19200 ф.ст.
4.4.2.
Задачи линейного программирования
Задача 4.11. Известно, что при цене в 10 ед. в неделю
продается 16 ед. товара. При цене в 15 ед. — только 6 ед.
Также известно, что потребитель согласен покупать по 30 ед.
товара в неделю по цене 11 ед. и 15 ед. по цене 6,50 ед.
Предполагая, что зависимость линейная, найдите:
а) функцию спроса;
б) функцию предложения;
288
в) равновесную рыночную цену;
г) эластичность спроса по цене;
д) эластичность предложения по цене;
е) эластичность спроса и предложения в точке равновесия.
Ответ: a) qd = 36 —2р; б) q = —20/3 + 1О/Зр; г) р/(18 — р);
д) р/(р - 2); е) 8/|0, %.
Задача 4.12. Найдите первые производные следующих
функций:
1) С=30 + q\ 2) C=3g2; 3) С= 10 - q + 2q>; 4) С= 10 + 5g;
5) С = 3q3 - 2q2 + 4q + 60; 6) C= 10 - 2q + 4g2; T)P=4L- Z2;
8) P =30K-2K2- 9) P= 15 + 4K—3K2; 10) у = 3x2 - 4x + 2;
11) Y= 6x3 - 4x2 + 3x - 1; 12) у = (3x - 4)2.
Ответ:
^Tq^’ _ de . de , л 3) —= -l + 4g; c?g
4) —= 5; dq 5|т=’’! dq de -4g+4; 6) — = -2 + 8g; c/g
7) —= 4-2Z; dL 8) —= 30- аК dP 4K-, 9) —= 4-6/C; dK
10) —= 6x-4; dx 11) —= 18х dx 2-8x + 3; 12)^ = 18x-24. dx
Задача 4.13. По данным задачи 4.11 найдите вторые про изводные. Ответ:
°$=2; у. d2c_ dq2 d2c . .. d2c 3)j3 = 4^ 4)T3 = 0; dq dq
5)^ = 18д-4; б/2с-8- 6) —7 = 8, ^d2P „ оу2Р л 7)-^- = -2; 8)—^ = -4; <й,2 dK2
9)-^—y = -6; 10)^ = 6; ll)^-Z = 36x-8; 12)^ = 18.
dK2 dx2 dx2 dx2
Задача 4.14. Найдите максимум и/или минимум следую-
щих функций:
289
l)C = q2-6q + 30; 2) P = 18Z-2-3Z2; 3) у = ~2x2+3x + 2;
4) у = x3-9x2+15x + l 1.
Ответ:
1) минимум: q = 3, C — 21; 2) максимум: L = 3, P = 25;
3) максимум: x = 1, у = 3*/3; 4) минимум: x = 3, у = 2;
5) максимум: x = 1, у — 18; 6) минимум: x = 5, у = —14.
Рекомендуемая литература
1. Андерсен Т. Введение в многомерный статистический ана-
лиз. — М.: Физматгиз, 1963.
2. Афифи А., Эйзен С. Статистический анализ. Подход с ис-
пользованием ЭВМ. — М.: Мир, 1982.
3. Бард Й. Нелинейное оценивание параметров. — М.: Фи-
нансы и статистика, 1979.
4. Большее Л.Н., Смирнов Н.В. Таблицы математической ста-
тистики. — М.: Наука, 1983.
5. ГОСТ 23554.2—81. Система управления качеством продук-
ции. Экспертные методы оценки качества промышленной про-
дукции. Обработка значений экспертных оценок качества про-
дукции. — М.: Изд-во стандартов, 1982.
6. Демиденко Е.З. Линейная и нелинейная регрессия. — М.:
Финансы и статистика, 1981.
7. Дженкинс Г., Ватте Д. Спектральный анализ и его прило-
жения. — М.: Мир. — Вып. 1. — 1971; Вып. 2. — 1972.
8. Джонсон Н., Лион Ф. Статистика и планирование экспе-
римента в технике и науке. — М.: Мир, 1980. — Т.1; 1981. — Т. 2.
9. Енюков И. С. Методы, алгоритмы, программы многомер-
ного статистического анализа. — М.: Финансы и статистика, 1986.
10. Кендэлл М., Стьюарт А. Статистические выводы и связи. —
М.: Наука, 1973.
11. Кулаичев А.П. Средства и программные системы анализа
данных// МИР ПК. - 1994. - № 10.
12. Поллард Дж. Справочник по вычислительным методам
статистики. — М.: Финансы и статистика, 1982.
290
13. Практикум по статистике/ Под ред. В.М. Симчеры. -
М.: Финстатинформ, 1999.
14. Рао С^Р. Линейные статистические методы и их приме-
нение. — М.: Наука, 1968.
15. Симчера В.М. Методы сравнительного анализа статисти-
ческих данных. — М.: ВЗФЭИ, 1987.
16. Симчера В.М. Методы экономико-математического мо-
делирования. — М.: ВЗФЭИ, 1989.
17. Соколин В.Л., Симчера В.М. История становления и раз-
вития балансовых работ в России. — М.: ИИЦ «Статистика Рос-
сии», 2006.
18. Справочник по прикладной статистике: В 2-х т. / Под
ред. Э. Ллойда, У. Ледермана, Ю.Н. Тюрина. — М.: Финансы и
статистика, 1989, 1990.
19. Тюрин Ю.Н., Макаров А.А. Анализ данных на компьюте-
ре. — М.: Финансы и статистика, 1995.
20. Факторный, дискриминантный и кластерный анализ. —
М.: Финансы и статистика, 1989.
21. Хартман Г. Современный факторный анализ. — М.: Ста-
тистика, 1972.
22. Хикс Ч. Основные принципы планирования эксперимен-
та. - М.: Мир, 1967.
23. Холлендер М., Вулф Д. Непараметрические методы стати-
стики. — М.: Финансы и статистика, 1983.
ТЕМА 5
Методы многомерного
сопоставления данных
5.1. Вводные замечания
Методы многомерного анализа применимы не только в слу-
чае вариационных, но и детерминированных исчислений, в час-
тности в случае обработки данных временных и пространствен-
ных рядов с целью нахождения переломных точек и определения
прогнозируемых и непрогнозируемых горизонтов экономическо-
го роста, однородных типов экономических регионов, рейтингов
их деловой активности, предпринимательской уверенности, ин-
вестиционной привлекательности и т.д.
Наиболее подходящим в этом случае является использова-
ние методов дискриминантного анализа (см. тему 3, разд. 3.2.4;
3.3.4; 4.4.3). Однако техника применения методов дискрими-
нантного анализа и содержательная интерпретация получен-
ных оценок в случае многомерного регионального анализа и
прогнозирования имеют существенные особенности и поэтому
требует самостоятельного рассмотрения.
Ниже на примере массива региональных данных и таблиц их
дискриминантного анализа рассмотрены процедуры определе-
ния однородных типов сопоставляемых региональных образо-
ваний (разд. 5.2) и тесноты связи их показателей (разд. 5.3) и
методы определения многомерных рейтингов (разд. 5.4) и мно-
гомерных прогнозных оценок экономического роста регионов
России (разд. 5.5).
5.2. Методы определения однородных типов
сопоставляемых региональных образований
Пример 5.1. Имеются данные хр х2, х3 и х4 по 18 сопостав-
ляемым регионам-объектам. В табл. 5.1 приводятся данные х, и х2
по этим объектам, а также обобщенные оценки каждого объекта —
положительные 5, (объекты 1—12) и отрицательные — S2 (объек-
ты 13—18) при /= fljX] + д2х2 + о3х3 + а4х4.
292
293
Таблица 5.1
Признак Объект (S)\ *1 х2 Xi-Xi х2-х2 (*i -*t) х2-х2 (х,-Х1)2 (х2-х2)2 fi fi-f (Л-л2
1 2 3 4 5 6 7 8 9 10 11
1 1,75 5,25 -1,39 1,26 -1,751 1,932 1,588 2,847 • 3,129 9,791
2 2,65 5,50 -0,49 1,51 -0,740 0,240 2,280 1,876 2,158 4,657
3 1,80 4,47 -1,34 0,48 -0,643 1,796 0,230 2,004 2,286 5,226
4 2,50 4,75 -0,64 0,76 -0,486 0,410 0,578 1,334 1,616 2,611
5 3,00 5,00 -0,14 1,01 -0,141 0,020 1,020 0,905 1,187 1,409
6 3,54 4,71 0,40 0,72 0,288 0,160 0,518 -0,115 0,167 0,028
х 7 2,82 4,22 -0,32 0,23 0,074 0,102 0,053 0,374 0,656 0,430
8 2,53 4,07 -0,61 0,08 -0,049 0,372 0,006 0,617 0,899 0,808
9 2,25 4,04 -0,89 0,05 —<0,045 0,792 0,003 0,967 1,249 1,560
10 2,06 3,95 -1,08 -0,04 0,043 1,166 0,002 1,135 1,417 2,008
11 2,75 3,75 -0,39 -0,24 0,094 0,152 0,058 0,001 0,283 0,080
12 3,24 3,93 0,10 -0,06 -0,006 0.010 0,004 -0,484 -0,202 0,041
13 4,14 3,52 1,00 -0,47 -0,470 1,000 0,221 -2,111 -1,829 3,345
14 4,62 3,34 1,48 -0,65 -0,962 2,190 0,423 -2,940 -2,658 7,065
15 4,27 з,п 1,13 -0,88 -0,994 1,277 0,774 -2,695 -2,413 5,823
16 3,78 2,92 0,64 -1,07 -0,685 0,410 1,145 -2,219 -1,937 3,752
17 4,25 2,76 1,Н -1,23 -1,365 1,232 1,513 -3,015 -2,733 7,469
18 4,53 2,60 1,39 -1,39 -1,932 1,932 1,932 -3,554 -3,272 10,706
Среднее 3,14 3,99 0 0 -9,92 0,844 -0,283 0 3,712
Е 56,48 71,89 - - 9,470 15,203 12,346 -5,093 - 66,809
Требуется:
1) определить принадлежность каждого из объектов к одной из
двух возможных групп (труппе положительных объектов — S't и груп-
пе отрицательных — 5,) по двум наблюдаемым признакам х, и х2;
2) определить принадлежность к одной из двух указанных
групп дополнительно введенного в эксперимент нового, 19-го
объекта с признаками: xt = 2,17, х2 = 4,31;
3) объяснить, почему первоначально выделенные группы St
и S2 и расчетные группы S , и У2 и далее S" и S"2, т.е. группы
положительных и отрицательных объектов, по составу могут раз-
личаться каждый раз?
Решить задачу, используя один из известных методов диск-
риминантного анализа.
Решение.
Выполним требования первого условия решения задачи.
1. Представим расположение наблюдаемых объектов в сис-
теме координат %] и х2 в графической форме (рис. 5.1).
2. Для нахождения значения функции построим и решим
систему нормальных уравнений с двумя неизвестными:
а1ст11 + а2ст12 = х11 ~Х2Ь
а1ст21 +а2ст22 = х12 -х22-
3. Для нахождения искомых параметров и а2 определим
линейные отклонения (х{ — Х]), (х2 — х2) и их суммы, затем
ковариацию линейных отклонений (х, — х,), (х2 — х2)и их квад-
раты (для того, чтобы избавиться от нулевой суммы их ариф-
метических отклонений от средней). Далее найдем четыре
2 2 —9 у 92 2 2
групповые дисперсии Oi1,n12=—= -0,551, О2ьа22 и две об-
18
2 2 15 10
щие дисперсии о, и о2, равные соответственно = о 844 и
18
1^^ = 0 686- Определим соответствующие групповые CTi 1,^12»
18
I 2 15,19 I 1 о о с
°21>а22и общиеOi ио2как ^CTi = jg =0,844 и Jo? = =0,686 ,
равные соответственно 0,918 и 0,823.
294
Рис. 5.1. Распределение наблюдаемых 18 региональных объектов
При этом по правилу о перемене мест слагаемых дисперсия
2 2
а12 = а21, а по правилу сложения дисперсии сумма внутригруп-
повых и межгрупповых дисперсий равна общей дисперсии, т.е.
X ^внгр + ^межгр = ^общ-
295
По условию решения приведенной системы уравнений нахо-
дятся также средние значения хп, х12 для класса положительных
объектов, равные 2,57 и 4,27 соответственно, и х12 и х22 для класса
отрицательных объектов, равные соответственно 4,47 и 3,04.
4. Выберем систему уравнений, удовлетворяющую требова-
ниям нахождения искомых определителей:
2 2 — —
ajO| + а2СТ]2-Хц -х2];
2 2 — —
а1ст21 +а2а2 —-'-21 ~х22-
Подставив найденные значения ст и х в приведенную систе-
му уравнений, имеем:
0,844а] -0,551а2 =2,57-4,47;
-0,551а] + 0,686а2 =4,47-3,04.
5. Решим приведенную систему уравнейий путем вычитания
из значений первого уравнения значения второго, и, приведя ее
члены к общему виду, найдем значения искомых параметров:
aj =1,355; а2 =0,994.
В результате получим искомую функцию; f = -l,355aj +0,994a2.
6. Подставив в указанную функцию эмпирические значения
наблюдаемых признаков х„ и хд, получим искомые значения
функции f. по каждому объекту:
/1 =-1,355-1,7 + 0,994-5,25 =2,847;
/2 = -1,3 55 • 2,65 + 0,994 • 5,50 = 1,877;
/з =-1,355-1,80 + 0,994-4,47 = 2,004;
/18 = -1,355 • 4,53 + 0,994 • 2,60 = -3,554.
Полученные / представляют некоторые теоретические зна-
чения, т.е. уровни объектов, какими они должны быть, их некие
эталонные образцы.
7. Далее найдем две групповые субфункции соответственно
по двум группам наблюдаемых объектов и общую функцию по
всей совокупности 18 наблюдаемых объектов.
296
Групповые функции находятся раздельно, для положитель-
ных объектов 51 и отрицательных объектов S'2 как:
, 12
/1,12 = X Ч *11 + «2 *12 = -1,355 • 2,57 + 0,994 • 4,47 = 8,995;
Z=I
ж 18 -
/13,18= X «1*21 +«2*22 =-1,355-4,57+ 0,994-3,04 = 2,756.
/=13
Общая функция f = а^ + а2х2 находится как
18
/118 = 5>1 *1,18 + «2 х2,18 =(—1,355-3,14 + 0,994-3,99) =—0,289.
/=1
Общую функцию принято обозначать С, а групповые функ-
ции в данном случае — Си С. Тогда общую функцию представ-
ляют и находят как среднюю из групповых функций, т.е.
Л,£±/; 5дС^=0.95-2.756 = 0|
v 2 2 2
8. Проведем идентификацию и дискриминантную класси-
фикацию наблюдаемых объектов. Найденные значения груп-
повых и общей дискриминантной функции представляют со-
бой искомые критерии для проведения такой классификации.
По ним происходит идентификация и определяется принад-
лежность каждого из наблюдаемых объектов к одной из выде-
ленных групп. _
Объекты, для которых f или С' > С, равного — 0,901, клас-
сифицируются как принадлежащие к^оложительной группе
объекты, для которых f " или С < С, классифицируются как
принадлежащие соответственно к отрицательной группе 5,.
В табл. 5.1 (гр. 9) приведены значения /для каждого наблю-
даемого объекта, согласно которым объекты 1—12, имеющие
большие значения, чем С = —0,901, будут отнесены к первой
группе Sv И соответственно объекты 13—18, находящиеся ниже
отметки указанного дискриминанта С, будут отнесены ко второй
группе S".
297
Дискриминант С будет при этом идентифицировать принад-
лежность всего множества наблюдаемых объектов к одному классу
при наличии у них признаков и х2.
9. Определим предельное значение отклонений признаков
наблюдаемых объектов друг от друга. Расчет проведем по фор-
муле Маханалобиса:
„г (Г+Л2
=~~ё—’
ст/
2 дл-7)2 66>809 , п,-,
где Of = :-= 3,712.
7 п 18
В результате имеем:
^.(0,955-2,756)^
3,712
Выполним требования второго условия решения задачи.
1. Определим принадлежность 19-го объекта по тем же двум
признакам, а именно: х{ = 2,17 и х2 = 4,31.
2. Воспользуемся параметрами ах и аг построенной дискри-
минантной функции:/9 = —1,355 • х, 19 + 0,994 • х219.
3. Подставив в эту функцию фактические значения призна-
ков X] и х2, получим/;, = —1,355 • 2,17 + 0,994 • 4,31 = 1,345.
4. Определим принадлежность объекта 19 к одной из двух
идентифицированных групп.
Исходя из того, что фактическое значение /19 больше диск-
риминанта С = —0,901, указанный объект отнесем к положи-
тельной группе
5. Сделаем содержательные выводы.
• Задача будет иметь точно такое же процедурное решение,
если в условиях будут приведены данные по х3 и х4 в том же
формате объектов: 18 + 1.
• Принадлежность конкретных объектов к группам S' и S 2 в
данном случае будет определяться дискриминантой функцией Д
расстояний между признаками х3 и х4 по определению может
разойтись с принадлежностью объектов, определяемой по фун-
кции f х.
XjA2
298
• Принадлежность конкретных объектов по четырем при-
знакам, взятым вместе (определяется по более сложной процеду-
ре, см. тему 1), по определению будет другой, поскольку вклю-
чает другое множество признаков, которые формируют новое
измерение наблюдаемых объектов и поэтому могут сконструи-
ровать новые общности и новые образы представления этих
объектов. Лишь в частном случае, когда полученные парные груп-
пы образов S' и (первая пара) и S\ и 5* (вторая пара) сольют-
ся вместе, т. е. 51 = S" и S2 = S"2, и будут представлять один
образ, состав групп парных и множественной дискриминанты
будет идентичным.
В этом случае крайне сложную процедуру множественной
дискриминации правомерно заменять процедурой простой пар-
ной дискриминации.
Пр и м е р 5.2. Имеются соответствующие пространственные
данные xt и х2 по 32 сопоставляемым объектам, объединенным в
четыре разные группы S2 S3 и S4 с теми ее характеристиками,
которые приведены ранее в табл. 3.16.
Требуется:
1) построить дискриминантную функцию, исчислить соот-
ветствующие дискриминантные оценки, определить необходи-
мые критерии и на этой базе подтвердить или опровергнуть пра-
вильность включения каждого из наблюдаемых объектов в одну
из четырех эмпирически образованных групп: 5, S2 S3 и S4;
2) определить принадлежность дополнительно включенных
в эксперимент объектов 33, 34, 35 и 36 с характеристиками х, и
х2, приведенными в табл. 3.1.
Расчеты необходимых показателей провести, используя одну
из существующих компьютерных программ дискриминантного
анализа.
Решение.
Выполняем требования первого условия задачи.
1. Для проведения необходимых расчетов обратимся к про-
грамме Comstat.
2. Используя известную дискриминантную функцию / = at xs +
+ а2 х2 + ... + ап хп, построим и решим систему соответствую-
щих уравнений с двумя неизвестными, получив в результате
следующие оценки параметров групповых дискриминантных
функций:
299
fl =l2,9xi +18,9x2 "58,7;
/2 = 20,4x] +13,4x2 -63,8;
/3=26,8х1 +19,7x2-119,1;
/4 = 16,4xi + 5,9х2 -32,4.
3. На основе построенных функций найдем соответствую-
щие групповые дискриминанты:
fl -fi = -7,5х] +5,5х2 +5,1;
f -f3 =-13,9xj -0,9х2 +60,4;
/] - /4 = -3,5xi +13,0х2 - 26,3;
/2 ~/з = -6,4х, -6,3х2 +55,3;
/2-/4 =4,0X1+7,5х2-31,4;
/з -/4 = 10,4х( +13,8х2-86,7.
4. По найденным дискриминантам определим принадлеж-
ность каждого наблюдаемого объекта к одной из четырех рас-
сматриваемых групп, фиксируя существование факта неравен-
ства значений построенных функций:
/!(*)>h{x), /1(х)>/3(х) и /1(х)>/4(х).
5. На пересечении соответствующих прямых найдем облас-
ти расположения объектов каждой группы, первая из которых
определяется пересечением прямых —7,5 xt + 5,5 х2 + 5,1 = 0;
—13,9 х, — 0,8 х2 + 60,4 = 0 и —3,5 xf + 13,0 х2 + 26,3 = 0 и т.д.
Выполним требования второго условия решения задачи.
1. По общему алгоритму решения данной задачи найдем зна-
чения соответствующих функций для объектов 33—36.
2. Установим, что при/j = 12,9 х( + 18,9 х2 — 58,7 искомое
значение/ для объекта 33 будет равно 86,45,/ = 65,0, / = 65,0
и / = 41,37. Точно так же находятся соответствующие значения
групповых f для объектов 34, 35 и 36.
3. Определим принадлежность каждого из вновь введенных в
эксперимент объектов 33—36 к одной из четырех рассматривае-
мых групп. Фиксируя, что / > / при f = 2,3,4, объект 33 при
300
ft = 86,45 относим к первой группе, объекты 34 и 36 — к четвер-
той, а объект 35 — ко второй группе.
Имеются следующие исходные данные (табл. 5.2).
Таблица 5.2
(в сопоставимых ценах; млрд долл. США)
Год Валовой региональный продукт Добавленная стоимость
Всего в том числе Всего в том числе
в промыш- ленности в сель- ском хо- зяйстве в про- мыш- ленности в сель- ском хо- зяйстве
1 2 3 4 5 6 7
Исходные показатели
1 2,82 1,72 48,0 1,36 0,71 0,29
2 3,03 1,89 49,3 1,45 0,75 0,29
3 3,24 2,06 50,5 1,52 0,79 0,32
4 3,44 2,26 51,1 1,64 0,86 0,37
5 3,64 2,35 0,58 1,68 0,88 0,34
6 3,88 2,49 63,8 1,81 0,97 0,38
7 4,20 2,65 71,2 1,93 1,00 0,43
8 4,51 2,84 80,0 2,07 1,04 0,50
9 5,02 3,21 81,0 2,25 1,15 0,50
10 5,50 3,56 87,0 2,44 1,27 0,52
11 5,87 3,81 88,0 2,61 1,40 0,50
12 6,43 4,09 1,03 2,89 1,48 0,63
13 6,85 4,34 1,08 3,05 1,56 0,62
14 7,17 4,58 1,08 3,13 1,63 0,59
15 7,70 4,90 1,21 3,37 1,73 0,68
16 8,16 5,25 1,22 3,54 1,86 0,65
17 8,62 5,58 1,22 3,63 1,91 0,61
18 9,03 5,78 1,32 3,85 1,99 0,66
19 9,49 6,05 1,41 4,05 2,07 0,71
20 9,92 6,33 1,47 4,22 2,16 0,73
21 10,32 6,57 1,51 4,40 2,26 0,73
22 10,78 6,85 1,52 4,62 2,38 0,68
23 11,22 7,09 L60 4,86 2,48 0,73
24 12,36 7,92 1,70 5,23 2,66 0,80
301
Продолжение
Год Валовой региональный продукт Добавленная стоимость
Всего в том числе Всего в том числе
в промыш- ленности в сель- ском хо- зяйстве в про- мыш- ленности в сель- ском хо- зяйстве
1 2 3 4 5 6 7
25 12,92 8,00 2,07 5,48 2,54 1,10
26 13,45 8,26 2,17 5,69 2,62 1,12
27 13,83 8,44 2,19 5,78 2,63 1,12
28 14,41 8,56 2,19 5,86 2,65 1,15
29 14,64 8,92 2,34 5,99 2,68 1,22
30 15,25 9,12 2,59 6,30 2,69 1,43
Экстраполированные показатели по регионам
31 15,67 9,42 2,34 6,54 2,71 1,59
32 16,13 9,72 2,59 6,79 2,74 1,77
Требуется:
1) провести группировку наблюдаемых регионов по данным
табл. 5.2.
2) определить факторные оценки для однородных групп ре-
гионов и показателей одним из методов многофакторного ана-
лиза взаимосвязанных показателей;
3) объяснить экономический смысл полученных оценок и
сделать необходимые выводы;
4) доисчислить данные по регионам 31—32 путем их экстра-
поляции по данным регионов 29—30.
Решение.
Ниже по шагам приводится решение задачи.
Шаг 1. Доисчислим необходимые данные по регионам 29—
32. Для этого найдем экстраполятор (в порядке упрощения за
экстраполятор примем коэффициенты приращения данных по
региону 30 к региону 28 как наиболее репрезентативные). Иско-
мый экстраполятор валового регионального продукта (ВРП) в
этом случае будет равен:
15 25
—2— = 1,058, или 105,8%.
14,41
302
Аналогично найдем экстраполяторы для остальных пяти по-
казателей.
Тогда абсолютные значения соответствующих показателей по
региону 32 будут равны (млрд долл. США):
ВРП — всего:
15,25 • 1,058 = 16,135.
В промышленности:
9,12 • 1,066 = 9,725;
В сельском хозяйстве:
2,59 • 1,182 = 3,070.
Добавленная региональная стоимость (ДС) — всего:
6,30 1,076 = 6,790.
В промышленности:
2,69 1,017 = 2,741.
В сельском хозяйстве:
1,43 • 1,242 = 1,779.
Искомые показатели для расчета значений экстраполируе-
мого региона 31 найдем путем исчисления соответствующих
среднегеометрических значений.
Для ВРП искомый показатель составит:
71,058 = 1,028, или 102,8%.
Соответствующим образом по региону 31 найдем экстрапо-
ляторы для других рассматриваемых показателей.
На основе полученных экстраполяторов определим абсолют-
ные объемы соответствующих показателей в регионе 31:
15,25-1,028 = 15,67;
9,12-1,032 = 9,42;
2,59-1,087 = 2,82;
6,30-1,037 = 6,54;
303
2,69-1,008 = 2,71;
1,43-1,114 = 1,59.
Шаг 2. Проведем группировку полученного полного мно-
жества первичных исходных данных по семи группам регионов:
регионам с годовым размером ВРП от 2,7 до 3,1 млрд долл. США,
от 3,1 до 4,3; от 4,4 до 6,5; от 6,6 до 8,9; от 9,0 до 10,9; от 1,0 до
13,9; от 14,0 до 15,3 млрд долл. США соответственно. При этом
первую группу, в состав которой входят всего два наблюдаемых
региона, снимем с дальнейшего рассмотрения как неполную и
недостаточную для сопоставления.
В пределах каждой из выделенных шести групп исходных
данных исчислим исходные показатели средних (х) и линей-
ных отклонений (раздельного от средних групповых; х( — х^ и
общей средней для 30 регионов; х. — х^), внутригрупповой
Цх.-Х™)2 х2 _£(хгр~*общ)
^внгр =-- 5 Р’ межгрупповои °межгр “ “ И об-
„ r2 _ ~ хобщ)
щей дисперсии °общ--------------. Исчислим также соответству-
ющие групповые коэффициенты квадратических отклонений
Х(х-х)2
V т
и коэффициенты вариаций V = -.
п
Результаты этой части расчетов представим в табл. 5.3.
Всего на базе наблюдаемых содержательных показателей дол-
жно быть исчислено соответственно по 36 групповых и по 6
общих средних, линейных и квадратических отклонений, по 36
внутригрупповых, 6 межгрупповых и 6 общих дисперсий, а так-
же соответствующее количество коэффициентов квадратичес-
ких отклонений и коэффициентов вариации.
Шаг 3. Весь массив расчетных исходных показателей (а их
в общей сложности набирается 192) выстроим для оценки одно-
родности выделенных семи групп каждого из шести наблюдае-
мых содержательных показателей и однородности всего массива
наблюдаемых показателей.
304
Таблица 5.3
Реги- он Xi у. _ у i Л сргр (^7 ^сргр) ^общ (*/-*обШ)2
1 282,20 0 0 -591,7 350105,2
2 303,8 21,6 466,6 -570,1 325010,4
%сргр =282,20
3 324,1 -33,6 1129,0 -549,8 302276,6
4 344,4 -13,3 176,9 -529,5 280366,9
5 364,8 7,1 50,4 -509,1 259179,6
6 388,9 31,2 973,4 -485,0 235222,0
7 420,2 62,5 3906,3 -453,7 205840,9
^сргр = 357,7 ОвНГр = 1247,2
8 451 -74,6 5567,6 -422,9 178841,8
9 502 -23,6 557,7 -371,9 138307,3
10 550 24,4 594,5 -323,9 104909,2
11 587 61,4 3767,9 -286,9 82309,8
12 643,5 117,9 13896,5 -230,4 53082,7
Zcprp= 525,6 °вн гр =4876,9
13 685,3 -64,1 4108,8 -188,6 35570,0
14 717,4 -32 1024 -156,5 24492,3
15 770,9 21,5 462,3 -103 10609
16 816,7 67,3 4529,3 -57,2 3271,8
17 862,6 113,2 12814,2 -п,з 127,7
Хсргр =749,4 °вигр =4587,7
18 903,9 -66,0 4349,4 30 900
19 949,6 -20,3 410,1 75,7 5730,5
20 992,1 22,3 495,1 118,2 13971,2
21 1032,4 62,6 3912,5 158,5 25122,3
22 1078,5 108,7 11804,8 204,6 41861,2
%сргр =969,9 Овнгр =4194,4
23 1122,8 -120,4 14504,2 248,9 61951,2
24 1236 -7,2 52,3 362,1 131116,4
25 1292,7 49,5 2447,0 418,8 175393,4
26 1345,8 102,6 10519,9 471,9 222689,6
27 1383,6 140,4 19702,8 509,7 259794,1
А-сргр =1243,2 Овнтр =9445,2
28 1441,8 -57,6 v 3312,0 567,9 322510,4
29 1464,5 -34,9 1214,5 590,6 348808,4
30 1525 25,7 657,9 651,1 423931,2
31 1567,7 68,4 4671,7 693,8 481358,4
32 1613,5 114,2 13030,2 739,6 547008,2
*сргр =1499,4 авн гр =9577,3
^обш = 873,9 7 45Щ =176614,7
305
Продолжение
Реги- он Xi ^сргр (^i ^сргр) ^общ (*/-*общ)2
1 172,5 0 0 -373,5 139502,3
2 189,5 17 289 -356,5 127092,3
jrcprp= 172,5
3 206,5 -22,4 503,3 -339,5 115260,3
4 226,8 -2,1 4,6 319,2 101888,6
5 235,3 6,4 40,5 -310,7 96534,5
6 249,3 20,4 414,8 -296,7 88030,9
7 266,2 37,3 1388,8 -279,8 78288,0
^сргр = 228,9 °внгр =470,4
8 284 -52,2 2724,8 -262 68644
9 321 -15,2 231,0 -225 50625
10 356 19,8 392,0 -190 36100
11 381 44,8 2007,0 -165 27225
12 409 72,8 5299,8 -137 18769
JTcprp =336,2 авнгр ~ 2131,0
13 434,3 -45,0 2023,5 -111,7 12476,9
14 458,4 -20,9 436,1 -87,6 7673,8
15 490,1 10,8 117,0 -55,9 3124,8
16 525,6 46,3 2145,2 -20,4 416,2
17 558,3 79,0 6243,6 12,3 151,3
Хсргр =479,3 авнгр ~ 2193,1
18 578,4 -41,3 1701,6 32,4 1049,8
19 605,5 -14,2 200,2 59,5 3540,3
20 633,1 13,5 180,9 87,1 7586,4
21 657,1 37,5 1402,5 111,1 12343,2
22 685,5 65,9 4336,2 139,5 19460,3
ХСргр =619,7 свнгр = 1564,3
23 709 -67,4 4545,0 163 26569
24 792,7 16,3 265,1 246,7 60860,9
25 800 23,6 556,2 254 64516
26 826,7 50,3 2528,4 280,7 78792,5
27 844,6 68,2 4649,0 298,6 89162,0
*сргр =776,4 °внгр = 2508,7
28 856 -47,3 2237,3 310 96100
29 892,3 -11 121 346,3 119923,7
30 912,4 9,1 82,8 366,4 134249,0
31 942 38,7 1497,7 396 156816
32 972,5 69,2 4788,6 426,5 181902,3
Хсргр =903,3 авнгр = 1745,5
^общ “ ^46 собщ ~ 63271
306
Продолжение
Реги- он X. V. _ V Л1 сргр ^сргр) %i ^общ (*г-*общ)2
1 48 0 0 -90 8100
2 49,3 ^сргр ~ 48 1,3 1,7 -88,7 7867,7
3 4 5 6 50,5 51,1 58,3 63,8 -6,9 -6,3 0,9 6,4 47,2 39,3 0,9 41,4 -87,5 -86,9 -79,7 -74,2 7656,3 7551,6 6352,1 5505,6
7 71,2 ^сргр = 13,8 191,4 авнгр = 64,0 -66,8 4462,2
8 9 10 И 80 81 87 88 -5,0 -4,0 2,0 3,0 25,3 16,3 3,9 8,8 г«О wn IT) Illi 3364 3249 2601 2500
12 103 Хсргр = 85,0 18,0 322,8 авнгр = 75,4 -35 1225
13 14 15 16 108,1 108,8 121,9 122,1 -6,3 -5,6 7,5 7,7 39,6 ' 31,0 56,8 59,8 -29,9 -29,2 -16,1 -15,9 894,0 852,6 259,2 252,8
17 122,3 *сргр = 114,4 7,9 62,9 ствнгр = 50,0 -15,7 246,5
18 19 20 21 132,4 141,7 147 151,9 -8,9 0,4 5,7 10,6 79,5 0,1 32,3 112,0 -5,6 3,7 9 13,9 31,4 13,7 81 193,2
22 152,6 *сргр= 141,3 н,з 127,3 авнгр ~ 70,3 14,6 213,2
23 24 25 26 160 170,3 207,9 217 -27,9 -17,6 20 29,1 778,4 309,8 400 846,8 22 32,3 69,9 79 484 1043,3 4886,0 6421
27 819,6 ^сргр ~ 187,9 31,7 1004,9 авнгр = 668,0 81,6 6658,6
28 29 30 31 219,7 234,9 259,7 282,4 -34,2 -19,0 5,8 28,5 1168,5 360,4 33,8 813,2 81,7 96,9 121,7 144,4 6674,9 9389,6 14810,9 20851,4
32 307 Хсргр= 253,9 53,1 2821,4 свнгр = 1039,5 169 28561
-^общ ~ 138 аобщ ~ 5096
307
Продолжение
Реги- он Xi ^cprp (^-Xcprp)2 ^общ (*/-*общ)2
1 136,2 0 0' -239,8 57504
2 145 8,8 77,4 -231 5336
Zcprp = 136,2
3 152,9 -14,8 219,5 -223,1 49773
4 164,6 -3,1 9,7 -211,4 44690
5 168,8 1,1 1,2 -207,2 42931
6 181,5 13,8 190,0 -194,5 37830
7 193,5 25,8 664,8 -182,5 33306
*cprp= 167,72 авнгр ~ 217,0
8 207,4 -29,7 879,1 -168,6 284426
9 225,5 -11,6 133,4 -150,5 22650
10 244,1 7,1 49,7 -131,9 17397
11 261,9 24,9 617,5 -114,1 13018
12 289,9 52,9 2793,1 -86,1 7413
-¥сргр = 237,05 авнгр = 894,6
13 305 -22,3 495,8 -71 5041
14 313,6 -13,7 186,8 -62,4 3893,8
15 337,8 10,5 111,0 -38,2 1459,8
16 354 26,7 714,7 -22 484
17 363,3 36,0 1298,4 -12,7 161,3
JCprp= 327,27 авнгр = 361,3
18 385,7 -27,6 762,7 9,7 94,1
19 405,6 -7,7 59,5 29,6 876,2
20 422,5 9,2 84,3 46,5 2162,3
21 440,6 27,3 744,4 64,6 4173,2
22 462,2 48,9 2389,6 86,2 7430,4
Xcp jp =413,32 авнгр ~ 808,1
23 486,7 -41,4 1712,6 110,7 12254,5
24 523,4 -4,7 21,9 147,4 21726,8
25 548,1 20,0 400,7 172,1 29618,4
26 569,6 41,5 1723,6 193,6 37481,0
27 578,5 50,4 2541,8 202,5 41006,3
Xcprp= 528,08 ствнгр = 1280,1
28 586 -35,4 1253,2 210 44100
29 599,6 -21,8 475,2 223,60 49997,0
30 630,8 9,4 88,4 254,80 64623,0
31 654,5 33,1 1095,6 278,50 77562,3
32 679 57,6 3317,8 303 91809
%cprp= 621,40 °внгр = 1246,0
^общ = 376 стобщ ~ 28267
308
Продолжение
Реги- он Xi ^сргр (Хг- ^СрГр) ^общ (Л-^общ)2
1 71,2 0 0 -110,8 12276,6
2 75,8 4,6 21,2 -106,2 11278,4
^сргр ~ 71,2
3 79,7 -8,2 67,5 -102,3 104465,3
4 86,1 -1,8 3,3 -95,9 9196,8
5 88,5 0,6 0,33 -93,5 8742,3
6 97,3 9,4 88,0 -84,7 7174,1
7 100,1 12,2 148,4 -81,9 6707,6
^сргр ~ авнгр = 61,5
8 104,6 -18,2 330,0 -77,4 5990,8
9 115,9 -6,9 47,2 -66,1 4369,2
10 127,3 4,5 20,6 -54,7 2992,1
И 140,4 17,6 310,9 -41,6 1730,6
12 148,3 25,5 652,0 -33,7 1135,7
*срп> =122,8 авнгр - 272,1
13 156,9 -13,0 169,9 -25,1 630,0
14 163,6 -6,3 40,1 -18,4 338,6
15 173,3 3,4 и,з -8,7 75,7
16 186,3 16,4 267,9 4,3 18,5
17 191,2 21,3 452,3 9,2 84,6
Хсргр =169,9 ствнгр = 188,3
18 199,7 -13,4 180,0 17,7 313,3
19 207 -6,1 37,4 25 625
20 216,2 3,1 9,5 34,2 1169,6
21 226,5 13,4 179,1 44,5 1980,3
22 238,1 25,0 624,2 56,1 3147,2
-?сргр =213,1 авнгр = 206,0
23 248 -7,4 54,5 66 4356
24 266,8 11,4 130,3 84,8 7191,0
25 254,1 -1,3 1,6 72,1 5198,4
26 262,2 6,8 46,5 80,2 6432,0
27 263,1 7,7 59,5 81,1 6577,2
^сргр = 255,4 авнгр ~ 58,5
28 265 -3,7 13,6 83 6889
29 268,6 -0,1 0,0 86,6 7499,6
30 269,5 0,8 0,7 87,5 7656,3
31 271,8 3,1 9,7 89,8 8064,0
32 274,1 5,4 29,3 92,1 8482,4
Хсргр = 268,7 авнгр = Ю’7
^общ = 182 о аобщ = 4962
309
Продолжение
Реги- он X' ^сргр (^-А-сртр)2 ^общ (^-^общ)2
1 29 0 0 —46 2116
2 29,70 0,7 0,5 -45,3 2052,1
^ср.гр = 29
3 32,10 -3,9 15,0 -42,9 1840,4
4 37 1,0 1,1 -38 1444
5 34,60 -1,4 1,9 -40,4 1632,2
6 38,80 2,8 8,0 36,2 1310,4
7 43,60 7,6 58,3 -31,4 986,0
*срлр =35,97 авнгр = 16,8
8 50,30 -1,5 2,4 -24,7 610,1
9 50,70 -1,1 1,3 -24,3 590,5
10 52,70 0,9 0,8 -22,3 497,3
11 50,60 -1,2 1,5 -24,4 595,4
12 63,10 11,3 126,9 -11,9 141,6
Хсрлр= 51,83 авнгр = 26,6
13 62,90 -0,6 0,4 -12,1 146,4
14 59,60 -3,9 15,3 -15,4 237,2
15 68,40 4,9 23,8 -6,6 43,6
16 65,60 2,1 4,3 -9,4 88,4
17 61,50 -2,0 4,1 -13,5 182,3
^ср.гр = 63, $2 авнгр = 0,6
18 66,20 -3,0 8,8 -8,8 77,4
19 71,60 2,4 5,9 -3,4 11,6
20 73,60 4,4 19,7 -1,4 2,0
21 73,20 4,0 16,3 —1,8 3,2
22 68,90 -о,з 0,1 -6,1 37,2
-^ср.гр =69,17 авнгр =10,1
23 73,10 -19,9 395,3 -1,9 3,6
24 80,30 -12,7 160,9 5,3 28,1
25 110,10 17,1 293,0 35,1 1232,0
26 112,70 19,7 388,7 37,7 1421,3
27 112,80 19,8 392,7 37,8 1428,8
^ср.гр =92,98 авнгр = 326,1
28 115,40 -23,2 539,0 40,4 1632,2
29 122,60 -16,0 256,5 47,6 2265,8
30 143,30 V 21,9 68,3 4664,9
31 159,70 21,1 444,5 84,7 7174,1
32 177,90 39,3 1543,2 102,9 10588,4
Jcprp = 138,62 авнгр = 561,0
^общ = 75 о <4щ = 1409
310
В расчетных табл. 5.4 и 5.5 приведены соответствующие дан-
ные, полученные для валового регионального продукта, добав-
ленной стоимости. Полученные оценки значений расчетных по-
казателей представим в тех же табл. 5.4 и 5.5.
Шаг 4. Делаем заключение об однородности наблюдаемых
показателей, наличии или отсутствии устойчивой закономерно-
сти в их изменениях.
Известно, что чем меньше дисперсия, квадратическое от-
клонение и соответственно коэффициент вариации, тем, при
прочих равных условиях, наблюдаемые регионы однороднее, а
изменение их показателей закономернее, и наоборот.
По значениям полученных оценок можно судить, что выде-
ленные группы регионов по наблюдаемым показателям в целом
однородные, коэффициент вариации у каждой из них ниже 0,3,
тогда как наблюдаемые 30 регионов, вместе взятых, по ВРП и
ДС в целом (и тем более по отдельно взятым отраслям промыш-
ленности и сельского хозяйства) неоднородны и, следовательно,
на их основе нельзя строить общие прогнозные или рейтинго-
вые экстраполяторы-оценки.
То же самое подтверждают полученные оценки дисперсий и
квадратических отклонений как более простых измерителей од-
нородности, пригодных для оценивания в случае наличия на-
блюдаемых явлений одной размерности.
Содержательный вывод, который следует из представленных
оценок, заключается в том, что на основе групповых значений
рассматриваемые показатели по наблюдаемым группам регио-
нов можно сопоставлять и далее прогнозировать и использовать
как рейтинговые оценки, тогда как на основе итоговых оценок
по всей совокупности, состоящей из 30 регионов, — нельзя.
Следовательно, показателей вариации, несмотря на их уни-
версальность, недостаточно для надежной оценки однородно-
сти и устойчивости экономического положения регионов, в ча-
стности сопоставления уровней их экономического развития,
необходимо обращаться к более адекватным и чувствительным
методам получения соответствующих оценок, т.е. к методам
дискриминантного анализа.
Ниже на примере тех же данных описана процедура расчета
дискриминантных оценок, необходимых для получения обоб-
щенных весовых коэффициентов однородности наблюдаемых
шести групп регионов по шести показателям. Эта процедура
состоит из следующих семи шагов.
311
312
Таблица 5.4
Группа ВРП в целом В промышленности В сельском хозяйстве
регионов (по размеру ВРП), (млрд долл. США 2 авг авг V, % 2 авг авг И, % 2 авг авг И, %
Первая от 3,1 до 4,3 1247,2 35,3 9,9 470,4 21,7 9,5 64,0 8,0 13,9
Вторая 4,4—6,5 4876,9 69,8 13,2 2131,0 46,2 13,7 75,4 8,7 10,2
Третья 6,6-8,9 4587,7 67,7 9,03 2193,0 46,8 9,7 50,0 7,1 6,1
Четвертая 9,0-10,9 4194,4 64,8 6,6 1564,3 39,6 6,4 70,3 8,4 5,9
Пятая 11,0-13,9 9445,2 97,19 7,8 2508,7 50,1 6,5 668,0 25,8 13,8
Шестая 14,0-15,3 4577,3 67,7 4,5 1745,5 41,8 4,6 1039,5 32,2 12,7
= 176614,7 овг = 63271,0 Овг = 5096,0
овг = 420,3 овг = 251,5 °вг = 71,4
И, % = 48,1 И, % = 46,1 V, % = 51,7
Таблица 5.5
Группа регионов ДС в целом В промышленности В сельском хозяйстве
2 авг свг V, % 2 авг авг V, % 2 авг °вг V, %
Первая 217,0 14,7 8,8 61,5 7,8 8,9 16,8 4,1 11,4
Вторая 894,6 29,9 12,6 272,1 16,5 13,4 26,6 5,2 10,0
Третья 561,3 23,7 7,2 188,3 13,7 8,1 9,6 3,1 4,9
Четвертая 808,1 28,4 6,9 206,0 14,4 6,7 10,1 3,2 4,6
Пятая 51280,1 35,8 6,8 58,5 7,6 2,9 326,1 18,1 19,4
Шестая 1246,0 35,3 5,7 10,7 3,3 1,2 561,0 23,7 17,1
<4 = 28267,0 ОвГ = 4962,0 2 _ авг 1409,0
овг = 168,1 оВг = 70,4 авг ~ 37,5
И, % = 44,7 Г, % = 38,7 Г, % = 50,0
313
Шаг 1. Выбор формы и определение параметров дискри-
минантной функции.
Как правило, обращаются к прямолинейной форме этой
функции/= а, X] + а2х2+ ... + апхп и нахождению ее параметров
путем решения системы нормальных уравнений с ограничен-
ным числом неизвестных.
В нашем случае необходимо построить и решить уравнение
с шестью неизвестными.
Шаг 2. Проведем парное разбиение исходных данных и
ограничим функцию двумя параметрами, приведя ее к виду
f= а^- а2хг
Шаг 3. Для нахождения параметров at и а2 воспользуемся
фрагментом данных х (в целом и в сельском хозяйстве) по двум
группам регионов, использованных для построения дискрими-
нантной функции/= «]%, + а2х} (табл. 5.6).
Ш а г 4. Используя приведенные данные, решим систему урав-
нений с двумя неизвестными методом множителей.
30,3 + а2 684,7 = 327,27- 63,52;
аг30,3 + я2 9,9 = 413,32-69,17;
«2 684,7-я2 9,9 = -80,40;
«2 =-0,12;
at 30,3 + (-0,12) • 684,7 = 263,75;
^30,3 = 345,91;
я, =11,42.
Шаг 5. Найдем значения функции для каждого региона, в
каждой из двух наблюдаемых их групп и общее значение функ-
ции для двух групп регионов, вместе взятых. Представим эти зна-
чения в табл. 5.7. Значение функции для 13-го региона будет:
/13 =11,42-305,0 + (-0,12-62,9) =3475,6;
/общ = а1х10 + а2х10 = Q
fl 3-22 = 11,42 • 379,0+( -0,12 •67,2) = 4320,1.
Шаг 6. Определим дискриминанты:
/' = 3734,7 = С';
314
Таблица 5.6
ы
н-*
СП
Группа регионов ха ха -X . (Ха-Х) Xi2 xi2-x (Xi2-X)2 (Xa-X)(Xi2-X)
289,9 63,10
305 -22,3 495,8 62,90 -6 0,4 13,73
Третья 313,6 -13,7 186,8 59,60 -3,9 15,3 53,53
337,8 10,5 111,0 68,40 4,9 23,8 51,44
354,0 26,7 714,7 65,60 2,1 4,3 55,69
363,3 36,0 1298,4 61,50 -2,0 4,1 -72,67
*5 327,27 561,3 63,52 9,6 20,3
385,7 -27,6 762,7 66,20 -з,о 8,8 81,93
Четвертая 405,6 -7,7 59,5 71,60 2,4 5,9 -18,78
422,5 9,2 84,3 73,60 4,4 19,7 40,71
440,6 27,3 744,4 73,20 4,0 16,3 110,04
462,2 48,9 2389,6 68,90 -0,3 1 -13,04
*5 413,32 808,1 69,17 10,1 40,2
*10 379,0 684,7 67,2 9,9 30,3
U)
I—*
Таблица 5.7
Группа регионов ^•1 ^•2 fi fifi" fi-f (Л-/)2
305,0 62,9 3475,6 -1371,2 1880189,4
Третья 313,6 59,6 3574,2 -1272,6 1619510,7
337,8 68,4 3849,5 3734,7 -997,3 994607,3
354,0 65,6 4034,8 -812,0 659344,0
363,3 61,5 4141,5 -705,3 497448,1
385,7 66,2 4396,8 -450,0 202500,0
405,6 71,6 4616,5 -230,3 53038,09
Четвертая 422,5 73,6 4816,1 4711,8 -30,7 942,49
440,6 73,2 5022,9 176,1 31011,21
462,2 68,9 5270,1 423,3 179182,9
Среднее 7 = 4846,81 569695,7
/' = 4711,8 = С';
С = ^- -= 4223,3;
5/
Ит ОЧД = (3734,7 + 4711,8)^ = 23 =
g2 569695,7
Выводы. Дискриминант для образования третьей группы
регионов — значение 3734,7, для четвертого — 4711,8, для двух
групп, вместе взятых, — 4223,3.
Значение функции ниже дискриминанта (с поправкой на
т = 125,23} будет принадлежать другим группа^ экономическо-
го развития.
Сравнивая значения полученных функций, можно заметить,
что третья группа относится к плохому типу регионов по показа-
телям уровня добавленной стоимости в целом и в сельском хо-
зяйстве, тогда как четвертая группа — к типу благоприятного эко-
номического развития.
Аналогичные дискриминантные оценки по тем же процеду-
рам получим на основе фрагментарных данных добавленной
стоимости в целом и в промышленности по тем же двум груп-
пам регионов (табл. 5.8, 5.9), а именно: а{ = 0,26, а2 = —0,09,
/13_22 = 0,26 • 379,0 - 9,09 • 195,9 = 80,9 = С:
/' = 69,8 = С";
/' = 88,3 = С*;
lim^--/^- = 122,5 = т.
5/
Расчеты параметров ах и аг проведем по прежней процедуре:
364,9aj + а2 684,7 = 327,27 -169,9;
364,9^ +а2197,2 =413,32 -213,1;
317
Таблица 5.8
CM
и-*
00
Группа регионов ха fi fifi fi-f (Л-/)2
305,0 156,9 65,2 -25,6 655,4
Третья 313,6 163,6 66,8 -24,0 576,0
337,8 173,3 72,2 69,8 -18,6 346,0
354,0 186,3 75,3 -15,5 240,3
363,3 191,2 77,3 -13,5 182,3
385,7 199,7 82,3 -8,5 72,3
Четвертая 405,6 207,0 86,8 -4,0 16,0
422,5 216,2 90,4 88,3 -0,4 0,16
440,6 226,5 94,2 3,4 11,56
462,2 238,1 98,8 8,0 64,0
Среднее 7 = 90,81 204,6
Таблица 5.9
319
Группа регионов */1 xzl-x (Ха-Х) xi2 xi2-x (Xi2-X)2 (Xn-X)(Xi2-X)
289,9 148,3
305 -22,3 495,8 156,9 -13,0 169,9 290,21
Третья 313,6 -13,7 186,8 163,6 -6,3 40,1 86,56
337,8 10,5 111,0 173,3 3,4 н,з 35,46
354,0 26,7 714,7 186,3 16,4 267,9 437,54
363,3 36,0 1298,4 191,2 21,3 452,3 766,31
*5 327,27 561,3 169,9 188,3 323,2
385,7 -27,6 762,7 199,7 -13,4 180,0 370,52
Четвертая 405,6 -7,7 59,5 207 -6,1 37,4 47,20
422,5 9,2 84,3 216,2 3,1 9,5 28,32
440,6 27,3 744,4 226,5 13,4 179,1 365,14
462,2 48,9 2389,6 238,1 25,0 ' 624,2 1221,27
Х5 413,32 808,1 213,1 206,0 406,5
х10 379,0 684,7 195,9 197,2 364,9
а2 684,7 - а2197,2 -157,37 + 200,22 = 0;
487,5а2 =-42,85;
а2 = -0,09;
364,9^ +(-0,09)-684,7 =157,37;
364,9^ =157,37-61,62;
364,9а! =95,75;
а\ =0,26.
Соответственно значение дискриминантной функции по двум
рассматриваемым группам регионов находим как
/10 = «1^10 +^2*10;
/ю =0,26-379,0-0,09-195,9 =80,9 = С
Следует заметить, что наиболее благоприятный уровень по-
казателей по добавленной региональной стоимости в целом и в
промышленности приходится на четвертую группу регионов.
Правда, регионы третьей группы по характеру исходных усло-
вий однороднее, если рассматривать показатели коэффициен-
тов вариации, которые в рассматриваемой третьей группе ниже,
чем в четвертой.
Аналогичная схема расчетов будет действительной и для всех
других фрагментов приведенных исходных данных, как и для
всего их массива. При этом расчеты в целом будут сравнитель-
ным фоном, поэтому их процедуру следует каждый раз рассмат-
ривать не только как желательное, но и обязательное условие
проведения целостного статистического эксперимента.
Общий вывод при этом будет всегда один: на основе отдель-
но взятых измерителей, в частности показателей дисперсии и
вариации, однозначно судить об однородности наблюдаемых
регионов нельзя, на основе дискриминантных оценок — всегда
и вполне можно.
Отсюда объективная необходимость исчисления этих оце-
нок при попытках организации и проведения любого рода серь-
езных межрегиональных сопоставлений.
320
5.3. Методические рекомендации
по определению однородности
и тесноты взаимосвязи сопоставляемых
региональных показателей
Регионы России характеризуются огромным многообразием
сложных отношений и показателей. Находясь в постоянном вза-
имодействии, дополняя и видоизменяя друг друга, обогащая или,
напротив, нивелируя и подчас погашая и разрушая друг друга,
региональные явления и их показатели выступают как объек-
тивно обусловленная данность, существование и изменение ко-
торой подчиняются требованиям общих законов экономическо-
го и социального развития. Представления об этих показателях
и отношениях между ними очевидны, воспринимаются как про-
дукт территориального разделения труда и регулируются в по-
вседневной жизнедеятельности на началах функционирования
взаимосвязанных систем, не требуя иных обоснований и дока-
зательств.
Другая, гораздо большая часть региональных, как и любых
других явлений, неочевидна, законы их формирования и видоиз-
менения скрыты, последствия изменения неопределенны, рис-
ки развития или крушения велики и труднопредсказуемы, а пред-
ставления о них ограничены и требуют каждый раз дополни-
тельных и новых обоснований и доказательств.
Выявление и познание этих явлений, распознавание и истол-
кование их в предельном многообразии региональных и нереги-
ональных отношений предполагают обращение к более сложным
методам познания, чем те, которые применяются в обыденной
практике.
Среди данных методов сегодня находятся статистические
методы многомерного анализа как наиболее адаптированные к
этим целям.
При использовании методов многомерного анализа в целях
регулирования региональных отношений в первую очередь сле-
дует считаться с особенностью самих регионов как предельно
неоднородных и, следовательно, сложно сопоставимых объек-
тов наблюдения, оперирование которыми с изменением обыч-
ных приемов идентификации, типологии и моделирования не
обеспечивает получения адекватного и максимально быстрого и
эффективного результата. Одновременно необходимо считаться
321
с крайней ограниченностью источника информации, необходимо-
стью ее непрерывного расширения, дополнения и модификации,
без чего исключается возможность принятия эффективных реше-
ний по всей совокупности необходимых региональных образова-
ний. И это касается практически всех без исключения современ-
ных типов региональных образований и прежде всего муниципаль-
ных образований как наиболее многочисленных и наименее всего
изученных в России.
При этом очень важно выбрать эффективные методы, обес-
печивающие минимизацию или сокращение формата такого рода
предметно-территориальных многомерных матриц кратчайши-
ми путями. Здесь речь идет о матрицах, предельные размеры
которых превышают 30 тыс. различного рода региональных об-
разований, существующих в России на 14,5 тыс. показателей,
которыми характеризуется их развитие, а минимальные эмпи-
рические размеры 7x258 (матрица 7 федеральных округов Рос-
сии на 258 основных показателей, характеризующих их разви-
тие) и 88x258 (88 субъектов Российской Федерации на 258 регу-
лярно публикуемых основных показателей, характеризующих их
развитие).
Цель при этом состоит в нахождении таких минимальных на-
боров показателей и однородных групп региональных образова-
ний, на основе которых можно было бы находить конечные, не
меняющиеся далее оценки уровней и темпов социально-эконо-
мического развития регионов, обеспечить их сопоставимость на
объективно доказательной и устойчивой основе, освобождаясь от
нынешней практики произвольного сопоставления случайных
показателей и манипуляции ими в популистских или спекуля-
тивных и узкокорыстных целях. Решение данной задачи в иной
постановке — это оптимизация системы региональных социально-
экономических показателей и их межрегионального сопостав-
ления.
Ниже излагаются основные положения, которыми следует
руководствоваться при решении этих задач.
Предметом многомерного анализа являются сложные систе-
мы, элементы которых характеризуются множеством зависимых
между собой объектов и признаков. Они представляются обычно в
виде матрицы, строки которой соответствуют наблюдаемым объек-
там (в нашем случае — регионам России), а столбцы — характери-
зующим их региональным признакам-показателям.
322
*11 *12 *13 ... х\т
Х21 х22 х23 - х2т
*31 х32 хзз ••• х3т
хп\ хп2 хпЗ ••• хптп
где п — число регионов;
т — число признаков;
хк. — значение первого признака у к-го элемента.
Для параметрических признаков х. — числовое значение из-
меряемого свойства, для непараметрических — качественные
характеристики признаков, а для полупараметрических призна-
ков — комбинированные количественные и качественные их
характеристики.
Исходным условием изучения такого сложного предмета, как
многомерные региональные пространства, является наличие в
этих пространствах не менее 30 единиц наблюдаемых регионов
и такое же число признаков, характеризующих поведение на-
блюдаемых регионов.
Обращение к методам многомерного анализа при наблюде-
нии за меньшим количеством регионов и признаков теряет
смысл, лишая полученные многомерные оценки даже минималь-
ной достоверности.
С увеличением количества наблюдаемых регионов и призна-
ков точность многомерных оценок повышается, что каждый раз
выступает как важное условие улучшения параметров многомер-
ного анализа.
Технология многомерного анализа в краткой формулировке
сводится к следующему.
1. Распознавание и формирование образов существующих
однородных групп наблюдаемых регионов и взаимосвязей меж-
ду ними по двум направлениям:
• выявление группы регионов и признаков, в наибольшей
степени соответствующих типу или «образу» регионального раз-
вития, т.е. распознаются и представляются однородные группы
регионов;
323
• выделение группы показателей, находящихся в устойчи-
вых и относительно тесных взаимосвязях, или, иначе говоря,
распознаются и выделяются однородные связи.
Обычно эти направления переплетаются и представляются в
формате различного рода предметно-пространственных матриц.
2. Обоснование и выбор эффективных методов решения той
и другой задачи. Эффективными при этом являются методы, тре-
бующие минимальных затрат времени, средств и информации для
их реализации.
3. Обеспечение эффективного решения двух групп целевых
задач:
• задач выявления устойчивых тенденций (трендов) и далее
закономерностей и законов в изменении наблюдаемых регио-
нальных явлений на основе и путем фильтрации и измерения
существенных их связей во времени;
• идентификации множества наблюдаемых регионов путем
проведения их типологической группировки в родственные ре-
гиональные образования, кратного снижения их размерности и
представления в виде небольшого числа типов — образов, от-
крывающих возможность фиксировать структурные тенденции
(тренды) и далее закономерности — законы изменения наблю-
даемых региональных явлений в пространстве и времени.
При решении первой группы задач используются методы дис-
персионного, вариационного, регрессионного, дискриминантного
и кластерного анализа. При решении второй группы задач исполь-
зуются методы многомерного факторного и компонентного ана-
лиза, в основе которых гипотеза о возможности изучения суще-
ствующих региональных связей между наблюдаемыми явления-
ми косвенным путем — путем построения корреляционных
матриц* и распознавания на их основе факторных оценок, значе-
ния которых находятся с помощью методов многомерного ана-
лиза.
Следовательно, статистические методы многомерного ана-
лиза — это комбинированное применение и своего рода про-
должение методов множественного корреляционного изучения
связей, предметом и целью которых является определение сте-
* При наличии функциональных связей строятся линейные матрицы,
процедура и техника работы с которыми более простая и поэтому шире
представлена в статистической литературе.
324
пени влияния идентифицированного набора факторов на ре-
зультат по заранее известной или воображаемой схеме их взаи-
мосвязи в одномерном режиме.
В случае обращения к методам многомерного анализа набор
факторов и схема их взаимосвязи рассматриваются как заранее
неизвестные, существующие в двух и более гипотетически неод-
нородных пространствах, неоднозначно влияющие друг на дру-
га и на общий результат, образуя на поверхности явлений свое-
образный информационный хаос, информационную энтропию,
требующую упорядочения и преодоления. Именно этими харак-
теристиками обладают современные региональные и межрегиональ-
ные отношения и связи.
При этом количество наблюдаемых факторов в многомерном
анализе будет больше двух (в принципе оно рассматривается всегда
как множество факторов), а предметом изучения — их разграниче-
ние по определенным критериям-образам на дискриминантные клас-
сы, кластеры или другие однородные группы в зависимости от сте-
пени существенности (закономерности) или второстепенности (слу-
чайности) однородного влияния не только на результат, но и друг
на друга, включая ложное влияние, измеряемое и представляемое
в статистике в виде автокорреляции.
Методы многомерного регионального анализа всегда, при
любом наборе факторов объектов-регионов следует рассматри-
вать как более сложную ступень одномерного анализа, отличи-
тельным моментом которых является не только образное разгра-
ничение множества сложных факторов по однородным объек-
там, равно как и всегда сложного пространства объектов (регионов)
по однородно взаимосвязанным показателям на существенные,
менее существенные и второстепенные, но и вращение факто-
ров, отслеживание их влияния друг на друга по спирали, много-
кратно, в режиме прямых и обратных связей, в чем проявляется
суть их многомерного представления.
Несмотря на сложный характер, цель многомерного региональ-
ного анализа будет та же, что и в случае применения других мето-
дов определения однородности и изучения связи - установление
на основе распознавания образов устойчивых зависимостей между
наблюдаемыми явлениями, выявление существующих закономер-
ностей их изменения в пространстве и времени, доказательное
объяснение их причинно-следственной обусловленности.
Методов многомерного регионального анализа много, по-
этому они требуют предварительного сравнительного анализа и
325
отбора по принципам адекватности представления, простоты
понимания и эффективности применения.
Для решения практических задач в современной региональ-
ной статистике наиболее часто обращаются к методам дискри-
минантного, кластерного, факторного и компонентного много-
мерного анализа как наиболее простым и экономичным.
В теме 3 изложена суть каждого из этих методов. При этом
методы дискриминантного и кластерного анализа рассмотрены
как методы изучения однородности наблюдаемых объектов и
регионов с набором характеризующих показателей, а методы
факторного и компонентного анализа — как методы изучения
их взаимосвязи по группам наблюдаемых однородных регионов.
5.4. Методы определения многомерных
рейтингов деловой активности,
предпринимательской уверенности
и инвестиционной привлекательности
регионов России
Рейтингов экономического развития и деловой активности, а
также и их аналогов в виде индексов и барометров предпринима-
тельской уверенности и инвестиционной привлекательности раз-
личных отраслей и секторов экономики, рынков банковских, фи-
нансовых, страховых и других видов активов и капиталов много,
но они разрозненные и как следствие несводимые в единое целое.
Этим обусловливается ограниченное значение, низкий или
недостаточный КПД, использование рейтингов по преимуще-
ству как орудия манипуляции и спекуляции общественным мне-
нием, а не как мощного средства предсказания и преобразова-
ния окружающей действительности, каким оно, по существу,
должно являться.
Вышеуказанное относится и к международным, и к большин-
ству национальных и корпоративных рейтингов и их аналогов.
Для того чтобы переломить эту ситуацию, требуется переос-
мыслить и сформулировать новую методологию построения и
анализа исходных данных, а также практику присвоения и веде-
ния мониторинга рейтинговых брендов.
Особую актуальность и значимость при этом имеет обоснова-
ние рейтинговых оценок деловой активности, предприниматель-
326
ской уверенности и инвестиционной привлекательности регио-
нов, которые сегодня мало пригодны как инструменты принятия
решений, обеспечивающих рост предпринимательской уверенно-
сти, инвестиционной привлекательности, социально-экономичес-
кой стабильности регионов России с гарантированной эффектив-
ностью.
В изложенной постановке вопрос рассматривается на приме-
ре построения рейтингов деловой активности, предпринима-
тельской уверенности и инвестиционной привлекательности
регионов Российской Федерации как важных и вместе с тем
менее всего обоснованных и продвинутых в современной миро-
вой и национальной социально-экономической практике.
Предметом конкретного рассмотрения являются методологи-
ческие рекомендации по разработке системы показателей и опре-
делению необходимых и достаточных условий и алгоритмов для
построения объективно обусловленных рейтингов деловой актив-
ности, предпринимательской уверенности и инвестиционной при-
влекательности трех различных категорий регионов России —
7 федеральных округов, 88 субъектов Российской Федерации, бо-
лее 15,0 тыс. сельских администраций и свыше и 10,5 тыс. город-
ских и поселковых муниципальных образований.
Разработка системы рейтинговых показателей, определяющих
необходимость и целесообразность совершенствования и реорга-
низации существующих систем регионального управления как
решающих факторов повышения деловой активности, предпри-
нимательской уверенности и инвестиционной привлекательнос-
ти регионов России, требует формирования единых подходов,
стандартов и нормативов определения научно обоснованной си-
стемы показателей, обеспечивающей возможность выявления ос-
новных факторов, их детерминирующих и конструирующих и
построения в последующем системы надежного управления эти-
ми факторами.
Цель заключается в построении объективно обусловленных
рейтингов, в обеспечении их адекватности решаемым задачам и
вместе с тем в их упрощении, обеспечении понятности и дос-
тупности в каждом регионе страны.
В настоящее время таких рейтингов нет. В результате сегодня
невозможно доказательно, на основе нормативно-правовых, со-
циальных и экономических оценок и методик научно обоснован-
но определять эффективные векторы развития регионов, стимули-
327
ровать их концентрацию и специализацию, осуществлять перс-
пективную реорганизацию производственных мощностей, продук-
тивно, с гарантированной отдачей наращивать их производствен-
ный потенциал.
Без такой разработки не приходится и говорить о технико-
экономических обоснованиях эффективности развития наблю-
даемых регионов, их инвестиционной привлекательности, ре-
альной возможности привлечения каких-либо кредитных ресур-
сов и прежде всего каких-либо иностранных кредитов.
Решать эти задачи призвана во многом современная региональ-
ная статистика. В реальном контексте от региональной статисти-
ки, адекватной решению изложенных задач, требуется не только
качественное расширение существующей системы региональных
показателей, но и полноценное обеспечение их сопоставимости
по всему множеству и на всех уровнях существующих региональ-
ных образований (на уровне федеральных округов, субъектов Рос-
сийской Федерации, местных органов управления и муниципаль-
ных образований). Одновременно требуется их параметризация и
приведение этих показателей (их более 14,5 тыс.) в единую систе-
му предельной матрицы 29,6 х 14,5 тыс. позиций (29,6 тыс. регио-
нальных образований, в том числе 7 федеральных округов,
88 субъектов Российской Федерации и более 29,5 тыс. органов
местного самоуправления). На основе такого подхода только и воз-
можно решение тех задач, которые решает современная региональ-
ная статистика развитых стран — задач построения единой рей-
тинговой системы деловой активности и предпринимательской уве-
ренности и инвестиционной привлекательности различных
регионов России, разработки и присвоение им рейтинговых наци-
ональных и международных брендов, ведение их мониторинга на
регулярной основе, обеспечивающего подъем ныне отсталых реги-
онов и дальнейшую их равноправную интеграцию в единое сооб-
щество эффективно организованных и устойчиво-развивающихся
регионов Европы и мира.
Эмпирических решений этой задачи много, но все они не
только разрозненные, но и беспомощные. Доказательных реше-
ний, отвечающих на вопрос, какой должна быть конечная, да-
лее не меняющаяся система рейтинговых показателей и конеч-
ная, далее не меняющаяся система их весов, нет и не было.
Отсюда необходимость сравнительного моделирования сис-
темы показателей и весов региональных рейтинговых оценок, пред-
328
полагающая одновременное решение двух указанных основопола-
гающих задач, а именно:
1) задачи обоснования и разработки системы показателей,
необходимых и достаточных для получения устойчивых оценок
межрегиональных социально-экономических сопоставлений;
2) задачи обоснования и определения весов, необходимых и
достаточных для исчисления интегральных показателей и пост-
роения рейтинговых оценок объектов Российской Федерации.
При этом и в том, и в другом случае под необходимыми и
достаточными показателями и весами понимаются конечные их
наборы и структуры, любое дальнейшее расширение и уточне-
ние которых не изменяет и не влияет на получаемые рейтинго-
вые оценки и, следовательно, гарантирует их независимость и
достоверность как объективно обусловленных оцендк.
Решая первую задачу, для практического применения при
построении объективно обусловленных региональных рейтингов
рекомендуется трехуровневая система показателей, а именно:
• система показателей, характеризующих сопоставимые уров-
ни и темпы развития федеральных округов Российской Федера-
ции (система включает 380 показателей);
• система показателей, характеризующих сопоставимые уров-
ни и темпы развития субъектов Российской Федерации (730 по-
казателей);
• муниципальных образований (790 показателей).
Для целей углубленных рейтинговых социально-экономичес-
ких сопоставлений дополнительно рекомендуется:
• система рейтинговых показателей деловой активности, пред-
принимательской уверенности и инвестиционной привлекатель-
ности регионов России (200 показателей);
• международная система рейтинговых показателей, харак-
теризующих сопоставление уровней и темпов развития регио-
нов России с аналогичными показателями регионального раз-
вития других стран Европы и мира (505 показателей).
Приведенные системы исходных показателей рассматрива-
ются как необходимые и достаточные, применение которых
обеспечивает получение устойчивых оценок и рейтингов наблю-
даемых регионов, независимо от возможного пополнения их
дополнительными показателями.
На основе представленных систем исходных показателей стро-
ятся соответствующие системы однородных, групповых и блоч-
329
ных показателей, рекомендуемые для индикативной оценки ук-
рупненных и сводных (интегральных) уровней, темпов и рейтин-
гов социально-экономического развития наблюдаемых регионов.
Исчисленные групповые и сводные (интегральные) оценки и рей-
тинги рассматриваются как конечные, объективно обусловленные
оценки, т.е. оценки, которые не меняются, независимо от увели-
чения набора показателей, на основе которых рассчитываются.
Для межрегиональных рейтинговых сопоставлений федераль-
ных округов, субъектов Российской Федерации и муниципаль-
ных образований рекомендуется следующая унифицированная
трехуровневая система показателей:
• шестиблочная система интегральных показателей, характе-
ризующих обобщенное социально-экономическое положение и
развитие регионов России, включающая семь интегральных по-
казателей: человеческого потенциала (среднегодовая численность
населения в расчете на 1 км2 территории региона, среднегодовой
уровень занятости, технический прогресс; производственная база
и ресурсный потенциал региона; уровень развития экономики;
ВРП и национальное богатство региона); уровень развития фи-
нансового сектора экономики; уровень развития социальной сфе-
ры региона, уровень охраны окружающей среды и безопасности
региона, уровень интеграции региона в российскую и междуна-
родную экономику и пять дополнительных показателей (уровень
качества развития человеческого потенциала региона, уровень
деловой активности региона, уровень предпринимательской уве-
ренности и инвестиционной привлекательности региона, уровень
издержек и потерь в регионе, уровень эффективности развития
региона);
• система рейтинговых оценок уровней развития федераль-
ных округов Российской Федерации, включающая 15 укрупнен-
ных натуральных и 15 групповых стоимостных показателей;
• система пяти групповых и одного сводного рейтинга уров-
ней развития субъектов Российской Федерации;
• система показателей, характеризующих деловую активность,
предпринимательскую деятельность и инвестиционную привле-
кательность регионов (11 укрупненных показателей);
• стандартная система международных показателей, характе-
ризующих уровень и темпы развития регионов России в сравне-
нии с аналогичными регионами других стран Европы и мира.
Основу и конечную цель работы по построению региональ-
ных рейтингов составляет оценка и сравнение деловой акгивно-
330
сти, предпринимательской уверенности и инвестиционной при-
влекательности регионов России.
В современных эмпирических разработках деловая активность
регионов сравнивается с данными регулярных выборочных об-
следований деловой активности предприятий трех различных от-
раслей региональной экономики (промышленность, строитель-
ство и торговля), проводимых Росстатом по методологии Центра
экономической конъюнктуры при Правительстве РФ, дополнен-
ные данными, в том числе расчетными данными Совета по изу-
чению производительных сил Российской академии наук и На-
учно-исследовательского института статистики Росстата.
Обследования проводятся по международной методологии
путем анкетного опроса руководителей наблюдаемых предприя-
тий и организаций.
Смысл работы заключается в сравнении полученных анкет-
ных оценок с их нормативными значениями. При этом и те и
другие оценки определяются респондентами и экспертными груп-
пами как репрезентативные выборочные оценки. Оценкам со-
стояния активности присваиваются категории «Выше», «Соот-
ветствующие» и «Ниже нормального» уровня, а оценкам изме-
нения активности — категории «Увеличение» («Улучшение»), «Без
изменения», «Уменьшение» («Ухудшение») активности.
Результаты выборочных оценок деловой активности распро-
страняются на генеральную совокупность по общим правилам
экстраполяции соответствующих оценок. Полученные оценки
представляются в виде простых (индивидуальных) и обобщен-
ных индикаторов деловой активности.
В качестве простых используются сальдовые оценки, опреде-
ляемые (в процентах) как разность долей респондентов, зафик-
сировавших «Увеличение» или «Уменьшение» показателя по срав-
нению с предыдущим периодом, или как разность долей респон-
дентов, оценивших уровень активности «Выше нормального» или
«Ниже нормального». Результаты обследований представляются
в виде временных рядов сальдовых оценок.
Сальдовые оценки являются обобщенным выражением мне-
ний экспертов об уровне и динамике наблюдаемых показателей.
На основе индивидуальных оценок рассчитываются обобщен-
ные сальдовые оценки деловой активности, в частности индексы
предпринимательской уверенности и инвестиционной привлека-
тельности, характеризующие состояние предпринимательского
331
климата в том или ином регионе или отрасли экономики соот-
ветствующего региона.
При этом в промышленности индекс предпринимательской
уверенности и инвестиционной привлекательности определяется
как среднее арифметическое значение сальдовых оценок факти-
чески сложившихся уровней спроса (портфеля заказов), запасов
готовой продукции (полученное значение принимается с обрат-
ным знаком) и ожидаемого изменения выпуска продукции. Соот-
ветственно в строительстве индекс предпринимательской уверен-
ности определяется как среднее арифметическое значение саль-
довых оценок фактического состояния портфеля заказов и
ожидаемого изменения численности занятых, а в торговле — как
среднее арифметическое значение сальдовых оценок фактическо-
го экономического состояния торговых организаций, уровня склад-
ских запасов (принимается с обратным знаком) и уровня ожида-
емого их экономического положения.
При определении эффективных регионов все три указанных
индекса корректируются с учетом так называемых коэффици-
ентов их реорганизации, перепрофилирования, слияния, при-
соединения и расформирования.
Оценки и сравнение деловой активности регионов прово-
дятся в формате следующей системы показателей:
1. Общий индекс предпринимательской уверенности региона
(определяется путем взвешивания по численности занятых в
соответствующих отраслях экономики региона индексов ожида-
емого выпуска основных видов продукции, состояния портфеля
заказов, уровня запасов готовой продукции и собственно уров-
ня занятости в регионе). Положительные изменения индекса
означают, что предпринимательская уверенность в регионе рас-
тет, отрицательные — падает.
2. Выпуск основных видов продукции.
уровень: выше нормального, нормальный, ниже нормального,
сальдо;
изменение: увеличение, без изменений, уменьшение, сальдо;
перспективы изменения в ближайшие три месяца0: увеличе-
ние, без изменений, уменьшение, сальдо*.
* Знаком ° здесь и далее отмечены показатели, на основе которых
определяется индекс региональной предпринимательской уверенности.
332
3. Спрос на продукцию (портфель заказов)'.
уровень0: выше нормального, нормальный, ниже нормаль-
ного, сальдо;
изменение: увеличение, без изменений, уменьшение, сальдо.
4. Запасы готовой продукции'.
уровень0: выше нормального, нормальный, ниже нормаль-
ного, сальдо;
изменение: увеличение, без изменений, уменьшение, сальдо.
5. Уровень экономическая ситуации'.
благоприятный, удовлетворительный, неудовлетворительный,
сальдо.
6. Уровень загрузки производственных мощностей (в процента).
7. Цены реализации готовой продукции'.
изменение: увеличение, без изменений, уменьшение, сальдо.
8. Численность занятых'.
уровень0 выше нормального, нормальный, ниже нормаль-
ного, сальдо;
изменение: увеличение, без изменений, уменьшение, сальдо.
9. Обеспеченность собственными финансовыми средствами'.
изменение: увеличение, без изменений, уменьшение, сальдо.
10. Факторы, ограничивающие деловую активность'.
неопределенность экономической обстановки;
недостаточный спрос на продукцию предприятий внутри
страны;
недостаточный спрос на продукцию предприятий за ру-
бежом;
высокая конкуренция со стороны зарубежных производителей;
отсутствие надлежащего оборудования,
недостаток денежных средств.
11. Показатели технико-экономического обоснования эффек-
тивных границ региональных образований'.
• реорганизация и перебазирование непрофильных произ-
водственных мощностей и перепрофилирование региональных
образований;
• укрупнение региональньсеобразований, обладающих совокуп-
ными признаками и потенциалом самодостаточного развития;
• присоединение неэффективных региональных образований;
• слияние несамодостаточных региональных образований;
• расформирование безнадежных региональных образований;
333
• создание принципиально новых, как правило, укрупненных
региональных образований, обладающих, очевидно, самодоста-
точными признаками и потенциалом устойчивого роста с гаран-
тированной эффективностью.
Фиксируемые значения по каждому из перечисленных показа-
телей представляют доли (в процентах) соответствующих катего-
рий предприятий в общей численности наблюдаемых предприя-
тий. Средние значения оценок и изменения уровня соответствую-
щих показателей за год определяются по результатам ежемесяч-
ных и квартальных конъюнктурных обследований активности пред-
приятий региона, проводимых Росстатом, и экспертных оценок
специалистов региональных исследовательских центров и инсти-
тутов.
Общая оценка деловой активности предпринимательской
уверенности и инвестиционной привлекательности регионов
определяется как средняя взвешенная арифметическая величи-
на, исчисляемая на основе оценок деловой активности ведущих
отраслей их развития и ключевых показателей реорганизации
(слияния, присоединения, укрупнения и образования новых
групп отраслей и регионов).
При определении региональных индексов деловой активнос-
ти в качестве весов используются данные о численности занятых
в соответствующих отраслях экономики региона, а при определе-
нии общерегиональных индексов — данные о численности заня-
тых в целом в соответствующих регионах.
Индексы исчисляются на месячной, квартальной и годовой
основе. Расчеты ведутся начиная с данных за 1998 г.
Эмпирическая работа по построению и мониторингу регио-
нальных рейтингов деловой активности является, безусловно,
необходимой, но недостаточной, она требует не только расшире-
ния исходной базы, но и более доказательных обоснований.
В настоящее время в соответствии с принятыми в 2004 г. феде-
ральными законами по изменению принципов организации уп-
равления в субъектах Российской Федерации и организации мест-
ного самоуправления начата работа по сбору и обработке данных,
необходимых для исчисления указанных показателей и построе-
ния на их основе рейтингов деловой активности наблюдаемых ре-
гионов с учетом показателей технико-экономического обосно-
вания и пересмотра границ устойчиво неэффективных и безна-
дежно убыточных и отсталых региональных образований страны.
334
В табл. 5.10 и 5.11 приводится система рейтинговых оценок
деловой активности федеральных округов, а в табл. 5.12 — субъек-
тов Российской Федерации, построенная с учетом указанных
корректировок.
Однако изложенных соображений и представленной систе-
мы региональных рейтинговых показателей недостаточно, и не
только для полноценной и комплексной оценки деловой актив-
ности, предпринимательской уверенности и инвестиционной
Таблица 5.10
Рейтинговые оценки развития федеральных округов
Российской Федерации в 2001 г., Россия = 100%
Индикатор Федеральный округ
Северо- Запад- ный Цент- раль- ный Юж- ный При- волж- ский Ураль- ский Си- бир- ский Даль- невос- точный
Ожидаемая про- должительность жизни 98,4 99,9 102,9 100,5 99,9 97,9 99,7
Уровень занятости 101,5 103,3 94,7 100,6 99,8 97,5 98,8
Обеспеченность жильем 94,0 96,9 165,0 85,4 84,5 81,5 83,0
Численность учащихся в обще- образовательных учреждениях 91,3 89,6 109,5 103,5 102,5 106,0 106,1
Число студентов на 1000 чел. 102,5 110,3 82,2 95,9 99,4 105,7 97,4
Численность врачей на 10 тыс. чел. 94,5 96,6 162,2 84,5 74,7 88,1 94,0
Численность среднего мед- персонала на 10 тыс. чел. 88,3 90,5 153,7 94,9 91,0 88,1 87,5
Число больнич- ных коек на 10 тыс. чел. 86,2 94,7 149,8 91,6 89,1 89,4 96,4
Мощность вра- чебных АПУ на 10 тыс. чел. 103,1 100,7 136,6 82,5 98,6 92,0 86,5
335
Продолжение
Индикатор Федеральный округ
Северо- Запад- ный Цент- раль- ный Юж- ный При- волж- ский Ураль- ский Си- бир- ский Даль- невос- точный
Индекс безо- пасности 100,4 136,3 67,7 117,5 86,7 92,0 89,3
Доля малых предприятий в общем числе 119,5 97,8 80,1 103,4 89,5 104,4 115,3
Плотность автодорожной сети 128,9 90,2 79,7 101,4 77,2 119,4 130,5
Удельный гру- зооборот авто- транспорта 107,6 79,5 85,7 112,8 135,2 99,4 114,6
Относитель- ный пассажиро- оборот 138,5 109,7 59,8 120,0 107,3 73,6 65,1
Обеспеченность телефонами 136,7 122,7 77,7 88,2 95,1 82,7 86,0
Поступления в бюджетную си- стему РФ 91,7 141,4 45,6 78,4 205,1 63,4 80,1
Плотность инвестиций 112,9 94,7 71,3 78,1 261,0 60,0 115,6
Среднедуше- вые денежные доходы 91Д 134,0 110,5 69,0 114,8 75,8 94,6
Среднемесяч- ная заработная плата 113,4 101,2 66,6 79,9 160,6 99,5 132,9
ВРП на душу населения 96,0 132,0 53,8 79,2 178,2 78,1 97,7
Плотность про- мышленного производства 117,5 84,5 42,9 106,9 218,4 86,4 112,2
Плотность сель- скохозяйствен- ного производ- ства 60,1 86,3 132,7 121,0 75,2 111,7 70,4
Плотность строительного производства 102,1 106,2 71,7 81,7 220,8 65,8 114,5
336
Продолжение
Индикатор Федеральный округ
Северо- Запад- ный Цент- раль- ный Юж- ный При- волж- ский Ураль- ский Си- бир- ский Даль- невос- точный
Душевой оборот розничной торговли Душевые плат- 93,0 165,9 66,7 72,8 87,6 77,2 82,0
ные услуги 99,3 159,5 72,5 65,2 91,6 73,9 122,2
Бюджетная обеспеченность 99,4 118,7 54,6 82,1 169,0 78,1 159,9
Налоговая нагрузка Удельные 95,5 107,1 84,9 9,1 115,1 81,3 82,0
инвестиции 117,6 71,7 132,7 98,6 146,5 76,9 118,3
Наполнение душевых доходов Наполнение 93,6 123,7 131,3 79,7 113,0 80,7 76,1
розничного товарооборота 95,6 153,1 79,2 84,2 86,3 82,2 66,0
Источник. Регионы России в 2001 г. — М.: Госкомстат России, 2002.
Таблица 5.11
Рейтинговые оценки развития федеральных округов
Российской Федерации в 2003 г., Россия = 100%
Индикатор Федеральный округ
Северо- Запад- ный Цент- раль- ный Юж- ный При- волж- ский Ураль- ский Си- бир- ский Даль- невос- точ- ный
Ожидаемая про- должительность жизни 99,0 100,4 103,4 100,8 100,2 97.9 97,9
Уровень заня- тости 105,2 103,3 91,2 100,8 99,8 96,7 102,3
Обеспеченность жильем 106,5 110,5 95,0 97,0 95,5 92,0 93,5
337
Продолжение
Индикатор Федеральный округ
Северо- Запад- ный Цент- раль- ный Юж- ный При- волж- ский Ураль- ский Си- бир- ский Даль- невос- точ- ный
Число студентов на 1000 чел. 85,0 90,8 90,8 112,7 112,1 108,7 108,1
Численность врачей на 10 тыс. чел. 107,1 109,6 93,1 95,0 84,8 99,8 106,1
Численность среднего меди- цинского пер- сонала на 10 тыс. чел. 98,9 100,9 90,9 105,3 102,4 99,3 98,0
Число больнич- ных коек на 10 тыс. чел. 96,0 105,3 91,5 100,3 98,4 100,3 106,7
Мощность вра- чебных АПУ на 10 тыс. чел. 113,6 110,6 83,9 90,3 106,6 100,4 95,6
Доля малых предприятий в общем числе 121,8 99,1 82,1 111,8 86,0 92,6 98,7
Плотность авто- дорожной сети 125,0 581,3 343,8 384,4 62,5 56,3 16,6
Удельный гру- зооборот авто- мобильного транспорта 56,9 307,7 210,2 221,2 66,3 27,6 9,5
Обеспеченность телефонами (город) 126,0 117,4 84,3 92,7 91,3 81,9 81,3
Поступления в бюджетную систему РФ 80,0 108,7 89,1 106,9 114,4 85,9 72,1
Плотность инвестиций 101,3 90,1 61,5 74,3 239,0 56,4 121,2
Среднедушевые денежные доходы 98,9 142,5 66,8 75,6 119,6 82,7 106,1
338
Продолжение
Индикатор Федеральный округ
Северо- Запад- ный Цент- раль- ный Юж- ный При- волж- ский Ураль- ский Си- бир- ский Далъ- невос- точ- ный
Среднемесячная заработная плата 116,3 101,7 68,2 78,3 151,1 98,8 137,1
ВРП на душу населения 96,9 128,9 51,7 81,4 177,6 78,9 102,6
Плотность про- мышленного производства 10,6 515,3 153,0 326,9 158,8 34,2 12,3
Плотность сельскохозяйст- венного произ- водства 64,0 595,2 565,2 429,0 61,5 51,4 9,8
Плотность строительного производства 103,0 671,3 302,6 255,2 187,0 26,7 15,7
Душевой оборот розничной торговли 92,4 158,8 71,4 74,9 91,2 78,8 84,5
Источник. Регионы России в 2003 г. — М.: Госкомстат России, 2004.
Таблица 5.12
Групповые и сводный рейтинги субъектов Российской Федерации
в 2000 г.
Регион Групповые рейтинги Свод- ный рейтинг
население и труд уровень жизни ВРП торговля и услуги фи- нансы
Россия 100,0 100,0 100,0 100,0 100,0 100,0
Республика Карелия 98,9 99,4 89,2 75,9 80,0 88,9
Республика Коми 99,4 102,9 134,1 91,0 124,4 111,0
339
Продолжение
Регион Групповые рейтинги Свод- ный рейтинг
население и труд уровень жизни ВРП торговля и услуги фи- нансы
Архангельская обл. 99,0 99,5 87,4 66,9 77,5 86,5
Вологодская обл. 99,0 93,8 127,0 67,1 101,8 98,6
Калининград- ская обл. 98,8 88,9 65,2 83,3 71,0 81,3
Ленинградская обл. 95,8 78,3 128,6 52,1 77,8 87,4
Мурманская обл. 107,7 108,9 97,3 115,7 96,0 104,8
Новгородская обл. 98,5 91,9 86,3 73,0 60,9 82,3
Псковская обл. 94,4 84,6 61,3 54,4 52,0 69,5
г. Санкт-Петер- бург 113,8 124,1 101,4 137,7 111,1 117,1
Белгородская обл. 99,7 98,9 96,5 61,6 55,8 82,9
Брянская обл. 96,8 87,7 56,6 53,9 42,2 67,6
Владимирская обл. 101,7 86,0 67,4 45,9 53,4 71,3
Воронежская обл. 95,9 99,7 68,3 60,0 45,1 74,0
Ивановская обл. 102,8 94,8 45,8 47,0 44,8 67,3
Калужская обл. Костромская 100,7 86,4 76,9 52,7 69,0 77,6
обл. 96,9 90,4 76,9 46,9 49,8 72,6
Курская обл. 94,9 90,1 75,7 48,5 49,4 72,1
Липецкая обл. 97,7 98,6 108,2 67,2 87,3 92,4
Московская обл. 104,2 95,2 89,7 93,6 101,6 96,9
Орловская обл. 96,2 92,7 86,4 55,1 80,4 82,8
Рязанская обл. 98,1 99,8 79,1 47,4 60,3 77,5
Смоленская обл. 97,2 93,3 77,6 67,7 51,4 77,5
Тамбовская обл. 94,1 87,6 55,6 58,5 41,9 67,6
340
Продолжение
Регион Групповые рейтинги Свод- ный рейтинг
население и труд уровень жизни ВРП торговля и услуги фи- нансы
Тверская обл. 99,2 90,6 68,5 49,7 51,7 72,3
Тульская обл. 102,8 93,0 80,7 53,4 56,1 77,6
Ярославская обл. 104,3 96,2 87,6 65,2 80,8 87,2
г. Москва 115,7 171,4 176,5 498,7 303,4 247,7
Республика Адыгея 91,5 89,2 52,3 50,5 \ 46,1 66,1
Республика Дагестан 82,2 82,6 27,8 32,5 36,4 52,5
Республика Ингушетия 82,6 51,2 21,7 14,6 71,0 48,8
Кабардино- Балкарская Республика 91,9 90,4 68,3 52,5 50,2 71,0
Республика Калмыкия 82,8 93,4 87,7 28,3 97,5 79,2
Карачаево- Черкесская Республика 84,8 87,6 46,8 44,0 37,3 60,3
Республика Северная Осе- тия-Алания 92,2 96,1 50,5 79,4 57,0 74,8
Краснодарский край 91,0 90,6 103,0 88,8 56,3 85,8
Ставрополь- ский край 92,0 83,7 70,9 82,0 45,3 74,5
Астраханская обл. 96,5 101,7 93,2 68,3 69,5 86,2
Волгоградская обл. 101,1 96,7 77,1 59,7 63,8 80,0
Ростовская обл. 96,3 92,3 72,0 77,5 45,4 76,6
Республика Башкортостан 96,8 105,6 109,1 72,3 122,9 102,1
Республика Марий Эл 94,3 86,3 63,6 40,1 38,9 65,1
341
Продолжение
Регион Групповые рейтинги Свод- ный рейтинг
население и труд уровень жизни ВРП торговля и услуги фи- нансы
Республика Мордовия 94,8 96,0 70,5 44,4 67,5 75,2
Республика Татарстан 102,3 101,4 142,3 66,5 160,1 115,9
Удмуртская Республика 99,1 102,6 97,0 56,7 80,8 87,9
Чувашская Республика 95,8 93,6 65,3 50,5 50,0 71,4
Кировская обл. 100,2 96,8 64,5 56,6 51,9 74,2
Нижегородская обл. 103,1 97,5 72,2 67,5 61,2 80,5
Оренбургская обл. 92,0 98,2 101,4 51,1 81,7 85,7
Пензенская обл. 96,3 96,6 58,3 51,0 40,4 68,8
Пермская обл. 100,0 102,4 104,8 83,8 101,4 98,9
Самарская обл. 102,8 102,0 113,3 123,6 95,0 107,0
Саратовская обл. 100,1 97,4 74,9 57,4 52,2 76,7
Ульяновская обл. 101,9 93,9 64,0 58,1 47,6 73,3
Курганская обл. 90,7 79,4 54,9 46,5 43,2 63,2
Свердловская обл. 105,8 100,6 85,7 83,8 76,0 90,4
Челябинская обл. 104,2 98,5 94,1 69,5 88,3 91,4
Тюменская обл. 102,2 126,1 433,7 118,7 464,2 253,7
Республика Алтай 75,1 85,9 50,0 28,8 108,2 70,5
Алтайский край 90,9 87,6 68,1 52,8 45,3 69,2
Кемеровская обл. 104,7 97,0 85,3 73,0 72,8 86,8
Новосибирская обл. 99,8 104,0 79,0 110,4 57,3 89,5
342
Продолжение
Регион Групповые рейтинги Свод- ный рейтинг
население и труд уровень жизни ВРП торговля и услуги фи- нансы
Омская обл. 96,6 99,5 62,7 63,8 37,9 72,1
Томская обл. 96,5 107,4 99,9 81,7 100,1 97,5
Республика Бурятия 89,7 86,5 58,3 52,8 51,1 67,9
Республика Тыва 79,5 91,5 28,6 29,9 43,0 54,9
Республика Хакасия 97,5 88,9 71,8 74,9 ' 48,8 76,3
Красноярский край 98,7 108,1 141,4 97,9 125,5 114,9
Иркутская обл. 100,6 98,9 83,8 80,7 69,1 86,6
Читинская обл. 92,2 87,3 61,0 35,9 46,8 65,-2
Республика Саха (Якутия) 95,3 121,5 170,8 124,9 210,1 145,4
Приморский край 100,9 94,4 68,7 91,1 60,6 82,8
Хабаровский край 101,9 104,6 100,6 128,2 81,7 102,8
Амурская обл. 94,4 95,5 67,8 61,8 49,6 74,0
Камчатская обл. 100,8 115,0 105,1 143,3 124,7 117,2
Магаданская обл. 107,7 108,7 113,9 109,5 130,6 114,2
Сахалинская обл. 104,3 100,1 147,9 97,1 113,3 113,1
Еврейская авт. обл. 94,0 88,9 49,5 52,0 52,6 67,6
Чукотский авт. округ 98,8 118,1 78,2 77?1 188,6 113,0
ЛЭМОЯГ
Источник. Регионы России в 2001 г. — М.: Госкомстат России, 2001.
привлекательности регионов России, но и, это главное, для тех-
нико-экономического обоснования и объективного определения
их однородности, оптимальных территориальных границ.
343
Для решения этой важной и сложной проблемы современных
межрегиональных социально-экономических сопоставлений, пред-
ставляющей ключ к избавлению нынешних развитых (донор-
ских) регионов от необоснованной иждивенческой нагрузки, ко-
торую они насильственно несут, в явном и неявном виде, упла-
чивая дань безнадежным дотационным регионам, требуется до-
полнительная оценка взаимозависимых, а следовательно, взаи-
мосвязанных ресурсов и резервов тех и других групп регионов. В
частности, оценка внутренних резервов и фактов подъема отста-
лых регионов страны на базе собственных материальных, трудо-
вых и финансовых ресурсов, избавления от многочисленных ре-
гионов-реципиентов, в том числе путем расформирования, слия-
ния или присоединения безнадежно отсталых их групп к
самодостаточным и емким, успешно развивающимся регионам
страны и, следовательно, по-настоящему организованного и обес-
печенного выравнивания уровней их развития с регионами.
Необходима также аналитическая оценка миграции и пере-
лива ресурсов отсталых и мнимо развитых регионов, на основе
которой только и возможно выстроить объективные рейтинги
регионов России.
Этим обусловливается исключительное значение определе-
ния роли и значения отдельно взятых регионов страны в сово-
купно взятых показателях, характеризующих их положение и
развитие, предполагающее решение второй основополагающей
задачи региональных рейтинговых сопоставлений.
Для практического решения этой второй задачи определе-
ния удельных весов, необходимых для построения групповых и
интегральных рейтинговых показателей развития регионов Рос-
сии, рекомендуется применять двухуровневую систему взвеши-
вания соответствующих индивидуальных показателей.
При построении рейтингов на основе стоимостных данных,
в частности рейтингов уровня развития экономики региона, в
качестве весов рекомендуется использовать удельные значения
(доли) отдельно взятых показателей в совокупности их объема,
соответственно доли в ВРП и национальном богатстве региона.
При построении рейтингов на основе смешанных систем
натуральных, стоимостных и других показателей, несводимых к
единому стоимостному основанию (например, сквозного рей-
тинга развития регионов на основе показателя «Население —
344
труд», «Уровень жизни», ВРП, «Торговля и услуги», «Финан-
сы»), веса рекомендуется определять на основе факторных оце-
нок, получаемых путем исчисления частных коэффициентов
эластичности или корреляции.
И на основе простых, и на основе факторных весов соответ-
ствующие групповые и интегральные показатели и сводные рей-
тинги развития регионов находятся как средневзвешенные оцен-
ки по общей формуле:
(РС) = Р,У1,
где Рс — сводный рейтинг;
Р, — рейтинг отдельно взятого индивидуального или группового по-
казателя; >
У, — удельные веса (доли) отдельно взятых индивидуальных или груп-
повых показателей в совокупных их объемах.
Например, совокупный рейтинг Республики Карелии, опре-
деленный на основе пяти групповых интегральных показателей
(см. табл. 5.3), исчислен как
98,9 • 0,26 + 99,4 • 0,21 + 89,2 • 0,4 +
+ 75,9 0,09 + 80,0 • 0,14 = 88,9.
При этом удельные веса соответствующих смешанных пока-
зателей определены как стандартные факторные оценки. Соот-
ветственно рейтинг Москвы на основе стандартных факторных
весов определен как
115,7 0,26 + 171,4 0,21 + 178,5 • 0,4 +
+ 498,7 • 0,09 + 303,4 • 0,14 = 247,7.
Для решения второй фундаментальной задачи наряду с суще-
ствующими разрозненными рейтингами необходимо выстра-
ивать совокупный (интегральный) рейтинг эффективности и эф-
фективных региональных образований России (ИР), представля-
ющий среднеарифметический взвешенный индекс рейтингов де-
ловой активности (Рд), предпринимательской уверенности (Рп),
инвестиционной привлекательности (Ри), социальной защищен-
ности (Рсз), экономической безопасности (Р6), региональной реор-
ганизации (Рр) и экономической эффективности (Рэ) наблюдае-
мых регионов как
345
ИР = Рд^ + Рп.у2 + Р^з + Рсэу4 + Р&у5+ РрУ6+ Р^7;
где у}^ — удельные веса.
Возможно и целесообразно построение сводного рейтинга с
набором большего числа частных показателей, предельное мно-
жество которых представлено в табл. 5.10.
Удельные веса при этом определяются как факторные оцен-
ки, получаемые путем построения условно линейных регресси-
онных моделей типа
yxi ~ а0 + а\х\ + а2х2 + аЗхЗ + а4х4 + <^*5 + + а7х7» У~ aj^} ’
1 1 1
lg^ = a0+ailgx; Ух=ао+Ч —
xi
или комбинированных типов линейных и нелинейных моделей
типа производной функции Кобба—Дугласа: Y— А • La • К\ или
многофакторной производственной функции:
Y = A-La-K* ег*,
где Y - ИР;
- Р^К^Р^Р^,
А — коэффициент масштаба или размерности;
er'Q — остаточный член;
а, р, rt — коэффициенты эластичности или доли каждого фактора в ко-
нечном результате, на основе которых проводится интегриро-
вание рассматриваемых рейтингов.
В качестве удельных весов можно рассматривать также ран-
жированные коэффициенты эластичности типа е = д!^- или
Л
ранжированные частные индексы корреляции типа
* Логарифмически дифференцируя приведенную функцию, имеем: у =
= а/ + (1 — а) к + г, где у — прирост ВРП; / - прирост труда, к - прирост
капитала, г — прирост прочих факторов (остаточный прирост или прирост за
счет факторов эффективности).
Допуская (по Коббу—Дугласу), что а = 0,75, 1 — а = р = 0,25, при 1= 3%,
к =1%, значение ert будет 1,5% (0,04 - (0,03 • 0,75 + 0,01 • 0,25)400), а
искомая функция у = 0,03 4- 0,75 • 0,01 • 0,25 + 0,015 — 0,04.
346
гух{ 'ух2 'л~1Х2
ГУ*\(Х2)
/ \ Ух2 Ух\ х\х2
7(1-^2)(1-^х2)’ УХ2 1 ^(1-гД )(1-гх2 )’
где г (2), г у (х), г v (у) — частные коэффициенты корреляции;
ЛХ1 "ХЭ Х|ХЭ
соответствующие значения частных рейтингов.
уХ1' " х,х2
7, Х3’ Х4, Х5,Х6 1
В рассматриваемом нами случае системная квалификация од-
нородности наблюдаемых регионов, необходимая для определе-
ния их обоснованных рейтингов, осуществлялась путем пошаго-
вой итерационной их группировки с применением методов вариа-
ционного и дискриминантного анализа.
Нетрудно заметить, что приведенные значения аир, представляющие, по
сути, фиксированные доли фонда потребления и фонда накопления, вклю-
чая амортизацию, в общем объеме ВРП являются условными и требуют
каждый раз пересчета в реальные, складывающиеся между факторами,
которые следует находить путем исчисления коэффициентов эластичности е,
производных —;-----...--, или (в случае равновесного развития) простых
day da2 dan
коэффициентов удельного прироста отдельных факторов в общем прирос-
те ВРП.
При этом указанные производные величины определяются путем на-
хождения дифференциальной функции: у = F(av а2, ..., ап) , а доли приро-
А/ АЛ
ста отдельных факторов — как —; —.
Ау Ау
На основе данных приведенного цифрового примера доли отдельных
факторов в общем приросте в двухфакторной модели будут равны:
Ы 0,03 лп, АЛ 0,01 „
— =------= 0,744, или 74,4%; — =-----= 0,248, или 24,8%. Показатель
Ау 0,0403 Ау 0,0403
прироста 0,0003(1,0403 — 1,04) и соответственно доли прироста 0,008, или
0,8%, в представленной схеме расчета называют также неразложимой до-
лей прироста, принадлежащей остаточным или неидентифицированным
факторам общего прироста.
Соответственно в представленной трехфакторной модели производ-
ственной функции искомые доли будут:
А/ 0,03-0,75 Л Ы 0,01-0,25
— = _2------= 0,5625, или 56,25%; —=—--------=0,0625, или 6,25%
Ау 0,04 Ду 0,04
и — = = 0,375, или 37,5%.
Ду 0,04
347
На первом шаге однородными признавались регионы, сово-
купный коэффициент вариации которых не превышал значение
0,33 (совокупный коэффициент вариации определялся как сред-
няя индивидуальных коэффициентов вариации семи рассматри-
ваемых исходных показателей), а на втором шаге — как дискри-
минант, значение которого находилось так, как представлено на
с. 169—177 соответствующего раздела.
Параметры а. в представленной условно линейной модели
определялись по-разному в зависимости от характера взаимо-
Заметим, что при коэффициенте масштаба (размерности) А, близком к
1,0, отношение значений а/p или а/r рассматривают как коэффициенты
взаимозаменяемости. Тогда при а = 0,75 и р = 0,25 или ос = 0,744 и р =
= 0,248 и тем более при а = 0,5626, р = 0,0625 и г = 0,375 единица вложе-
ний или единица прироста труда будет в три раза больше 0,75/0,25 или
0,744/0,248, чем единица вложений, или единица прироста капитала, и
соответственно в 1,5 раза больше (0,5626/0,375), чем единица вложений в
другие факторы экономического роста.
Добавим также, что в еще одной экономической интерпретации со-
пряженные коэффициенты взаимозаменяемости рассматривают как пре-
дельные величины взаимозаменяемости в категориях, где одни и те же
суммы вложений в разных условиях, в разные сферы или в разные перио-
ды времени не равны друг другу. В этом случае в банковском или актуар-
ном деле указанные сопряженные коэффициенты представляют как дис-
контные ставки, эффективные проценты или предельные коэффициенты
эффективности, на основе которых принимают предпочтительные эконо-
мические решения, выстраивая надежные приоритеты и рейтинги пре-
дельной окупаемости осуществляемых вложений.
Еще более наглядной иллюстрацией взаимозаменяемости служат из-
вестные показатели долей богатых и бедных в национальном продукте и
его потреблении, сопоставляемые с показателями их долей в общей чис-
ленности населения (коэффициенты Джини). Сегодня иррациональным,
противоречащим здравому смыслу остается не только само это так назы-
ваемое золотое сечение, но и еще более иррациональным, граничащим с
абсурдом его изменение в сторону ухудшения положения в мире 5 млрд
бедных и улучшение положения «золотого миллиарда».
Дело не только в том, что, например, в России 5% богатых сегодня
принадлежит 75% национального имущества страны, дело в том, что это
крайне опасное антисоциальное положение стремительно усугубляется.
В приросте ВВП 2004 г. уже 97% долей принадлежит 5% богатым и
лишь 3% остальным слоям населения. В переводе на простой язык это
означает, что от прироста ВВП на 1% простой человек получает сегодня
всего 6 коп., а богатый — 2 руб., т.е. в 33 раза больше, тогда как в прежние
годы богатый в России получал «всего» в 14 раз больше (в США эта норма
составляет 9 раз, а в Белоруссии, например, 5 раз).
348
связи между общим результативным показателем и отдельно
взятыми семи показателями-факторами, его определяющими.
При этом в качестве результативного показателя принимался
ВРП по 88 наблюдаемым регионам.
Веса регионов по отдельно взятым показателям находились
по их абсолютному натуральному или стоимостному модулю, а
веса разнородных показателей, в частности веса указанных семи
смешанных показателей, необходимые для построения совокуп-
ного рейтинга экономического развития наблюдаемых регио-
Многие современники склоняются к тому, что исправить эту коренную анти-
социальную несправедливость трудящимся массам нигде не удается. Изме-
нить положение ныне пытаются глобалисты, голоса которых раздаются в мире
все громче. Возможно, таким образом учение о взаимозаменяемости будет не
только наиболее понятным, но и полезным всему человечеству.
Коэффициенты взаимозаменяемости, или доли факторов производ-
ства, — это своего рода то, что мы понимаем под значением «1 % прирос-
та». При коэффициентах взаимозаменяемости, например, труда и капита-
ла, равных соответственно 0,75 и 0,25, для того чтобы заместить единицу
труда, необходимо иметь 3 ед. капитала, а чтобы заменить единицу капи-
тала — всего 1/3 ед. труда.
Вместе с тем коэффициенты взаимозаменяемости можно понимать как
своеобразные лимиты, превышение которых ведет к снижению эффектив-
ности роста. Известно, что равновесный уровень эффективного роста до-
стигается при коэффициентах взаимозаменяемости труда и капитала или
при их долях в производстве, равных 0,75 и 0,25 соответственно. Что озна-
чает, однако, рост этих коэффициентов? Их пропорциональный рост, по-
нятно, означает пропорциональное удорожание стоимости единицы про-
изводства, разнонаправленный рост — повышение доли одного и умень-
шение доли другого фактора производства. При опережающем приросте
коэффициента взаимозаменяемости труда, т. е. увеличении доли труда,
цена единицы прироста производства, при прочих равных условиях, будет
в 3 раза выше цены единицы прироста капитала, а цена единицы капита-
ла — в 3,3 раза дешевле. Поэтому понятно, что выгодно заменять капита-
лом, фондовооруженностью или техническим прогрессом труд, а не капи-
тал — трудом. Именно поэтому безработица труда во все времена и во всех
странах мира превышает «безработицу» капитала.
Одновременно взаимозаменяемость, особенно в социологии, рассмат-
ривается и как своего рода лимит, своеобразный порог, значение цены
факторов ниже которого рассматривается как потери, и разными способа-
ми ограничивается. В этом смысле понижение коэффициента взаимоза-
меняемости труда ниже значения 0,75, представляющее адекват пониже-
ния доли труда в экономическом росте, рассматривается как посягатель-
ство на права трудящихся, а понижение доли капитали — как посягатель-
ство на права собственников.
349
нов, — как факторные оценки методами многомерного корреля-
ционного и компонентного анализа, представленными в темах
2 и 3 настоящего пособия.
На основе этих моделей проводилось ранжирование факто-
ров по степени их влияния на общие результативные показате-
ли, характеризующие конечное, далее не меняющееся, положе-
ние и место наблюдаемых регионов в общей системе межрегио-
нальных связей в Российской Федерации.
Представленные модели и получаемые на их основе оценки —
это та база, на которой только и можно выстраивать и принимать
вразумительные управленческие решения, избавившись тем са-
мым от множества манипулятивных рейтингов, которые практи-
чески полностью затемняют истинное положение дел и публику-
ются преимущественно в популистских целях.
Общая система рейтингов технико-экономического обосно-
вания эффективных региональных преобразований существую-
щих регионов России представлена ниже.
Интегральный рейтинг
Рейтинг деловой активности
Рейтинг инвестиционной привлекательности
Рейтинг предпринимательской уверенности
Рейтинг социальной защищенности населения
Рейтинг экономической безопасности
Рейтинг региональной реорганизации
Рейтинг экономической эффективности
Индекс качества развития человеческого потенциала
Рейтинг экологической безопасности регионов
Индекс социальных и межнациональных конфликтов в регионе
Рейтинг устойчивого развития регионов
Рейтинг эффективного использования ресурсов
Рейтинг самодостаточности региональных образований
Коэффициент целесообразности пересмотра региональных границ
Рейтинг необходимых преобразований
Степень соответствия региона эффективному стандарту
Индекс роста потенциала региона
Дотации из бюджета и отчисления в бюджет
Рейтинг приоритетности региональных преобразований
350
Рейтинги потерь и упущенных выгод в регионах России в 1992—2003 гг.
(потери в виде снижения объемов производства, упущенные выгоды от не-
эффективной приватизации, ущербы, причиненные населению и хозяйству
региона ростом правонарушений и преступлений на почве обострения меж-
региональных конфликтов и национальных и социальных протестов)
Рейтинги различий в уровнях социально-экономического развития
регионов России за 100 лет
Рейтинг инфляционных, валютных, фондовых и инвестиционных ухуд-
шений
Рейтинг погодно-климатических условий
Приведенная система показателей представляет возможность
объективно обусловленно решать любые задачц региональных
преобразований, в том числе совершенствования и реорганиза-
ции органов управления регионами России*.
5.5. Методы многомерного прогнозирования
региональных темпов экономического роста
Имеются следующие исходные данные (табл. 5.13).
Таблица 5.13
Валовой общественный продукт и национальный доход
по отраслям экономики (в сопоставимых ценах; млрд долл. США)
Год Валовой общественный продукт Национальный доход
Всего в том числе Всего в том числе
в про- мыш- ленности в сельском хозяйстве в про- мыш- ленности в сельском хозяйстве
1999 282,2 172,5 48,0 136,2 71,2 29,0
2000 303,8 189,5 49,3 145,0 75,8 29,7
2001 324,1 206,5 50,5 152,9 79,7 32,1
* Эти задачи сформулированы в принятых в России в 2004 г. феде-
ральных законодательных актах «Об общих принципах организации зако-
нодательных (представительных) и исполнительных органов государствен-
ной власти субъектов Российской Федерации» и «Об общих принципах
организации местного самоуправления в Российской Федерации» и соот-
ветствующих изменениях в более чем 200 других законодательных актах
Российской Федерации.
351
Продолжение
Год Валовой общественный продукт Национальный доход
Всего в том числе Всего в том числе
в про- мыш- ленности в сельском хозяйстве в про- мыш- ленности в сельском хозяйстве
2002 344,4 226,8 51,1 164,6 86,1 37,0
2003 364,8 235,3 0,58 168,8 88,5 34,6
2004 388,9 249,3 63,8 181,5 97,3 38,8
2005 420,2 266,2 71,2 193,5 100,1 43,6
2006 451,0 284,0 80,0 207,4 104,6 50,3
2007 502,0 321,0 81,0 225,5 115,9 50,7
2008 550,0 356,0 87,0 244,1 127,3 52,7
2009 587,0 381,0 88,0 261,9 140,4 50,6
2010 643,5 409,0 103,0 289,9 148,3 63,1
2011 685,3 434,3 108,1 305,0 156,9 62,9
2012 717,4 458,4 108,8 313,6 163,6 59,6
2013 770,9 490,1 121,9 337,8 173,3 68,4
2014 816,7 525,6 122,1 354,0 186,3 65,6
2015 862,6 558,3 122,3 363,3 191,2 61,5
2016 903,9 578,4 132,4 385,7 199,7 66,2
2017 949,6 605,5 141,7 405,6 207,0 71,6
2018 992,1 633,1 147,0 422,5 216,2 73,6
2019 1032,4 657,1 151,9 440,6 226,5 73,2
2020 1078,5 685,5 152,6 462,2 238,1 68,9
2021 1122,8 709,0 160,0 486,7 248,0 73,1
2022 1236,0 792,7 170,3 523,4 266,8 80,3
2023 1292,7 800,0 207,9 548,1 254,1 110,1
2024 1345,8 826,7 217,0 569,6 262,2 112,7
2025 1383,6 844,6 219,6 578,5 263,1 112,8
2026 1441,8 856,0 219,7 586,0 265,0 115,4
2027 1464,5 892,3 234,9 599,6 268,6 122,6
2028 1525,0 912,4 259,7 630,8 269,5 143,3
2029 1567,7 942 234,4 654,5 271,8 159,7
2030 1613,5 972,5 259,0 679,0 274,1 177,9
Требуется:
1) провести группировку данных, приведенных в табл. 5.13;
2) определить взаимосвязь между исчисленными показате-
лями методами многомерного анализа;
3) объяснить экономический смысл полученных оценок и
сделать выводы;
4) данные за 2029—2030 гг. доисчислить путем экстраполя-
ции данных за предыдущие годы;
352
5) по данным табл. 5.14 провести расчеты соответствующих
показателей по России за 1992—2010 гг., при этом данные 2003—
2010 гг. доисчислить, а необходимые расчеты представить и про-
комментировать в формате первой части показательного реше-
ния рассматриваемой задачи.
Таблица 5.14
Темпы экономического прироста в России
(в сопоставимых ценах, в % к предыдущему году)
Показатель 1992 1995 1997 1998 1999 2000 2001 2002
Численность населения -0,02 -0,2 -о,з —tf,3 -0,5 -0,5 -0,6 -0,4
Численность занятых -24 3,0 -1,9 -1,4 0,2 0,6 0,6 1,5
Реальные доходы -47,5 -15,0 5,8 -15,9 -12,5 11,9 8,5 8,9
Основные фонды 1,9 0,1 -0,4 -0,4 0,1 0,4 0,6 0,7
Промышленное производство -18,0 -3,3 2,0 -5,2 11,0 11,9 4,9 3,7
Продукция сельского хозяйства -9,4 -8,0 1,5 -13,2 4,1 7,7 7,5 1,7
Перевозки грузов -13,9 -1,0 -3,4 -3,3 5,3 5,0 3,2 5,8
Оборот розничной торговли 3,3 -6,2 4,9 -3,2 -5,9 9,0 10,9 9,2
Инвестиции -39,7 -10,1 -5,0 -12,0 5,3 17,4 10,0 2,6
Внешнеторговый оборот 10,5 23,1 0,7 -16,6 -13,1 30,2 3,7 7,8
ВВП -14,5 -4,1 1,4 -5,3 6,4 10,0 5,0 4,3
Источник. Россия в цифрах. — М.: Госкомстат России, 2003. — С. 32—
33, 363.
Решение.
Ниже по шагам приводится показательная часть решения
задачи.
Шаг 1. Доисчислим необходимые данные за 2029—2030 гг.
Для этого найдем экстраполятор (в порядке упрощения за экст-
раполятор принимаем значения среднегодового темпа роста при-
веденных в табл. 5.13 шести показателей за два последних года
(2026—2028 гг.) как ранее известные). Темп роста валового об-
щественного продукта (ВОП) в этом случае будет равен:
=1 058, или 105,8%.
1441,8
353
Аналогично находим соответствующие темпы роста для ос-
тальных пяти показателей.
Тогда абсолютные значения соответствующих показателей в
2030 г. будут (млрд долл. США):
ВОП — всего:
1525,0 • 1,058 = 1613,5.
В промышленности:
912,4 • 1,066 = 972,5;
в сельском хозяйстве:
259,7 • 1,182 = 307,0.
национальный доход (НД) — всего:
630,8 • 1,076 = 679,0.
В промышленности:
269,5 • 1,017 = 274,1;
в сельском хозяйстве:
143,3 • 1,242 = 177,9.
Общий экстраполятор для расчета значений соответствую-
щих показателей в 2029—2030 гг. находим как среднегодовой темп
роста.
Для ВОП среднегодовой темп роста за два указанных года
будет:
05 8 =1,028, или 102,8%.
Соответствующим образом находим экстраполяторы для дру-
гих рассматриваемых показателей.
На основе полученных экстраполяторов определим абсолют-
ные объемы соответствующих показателей в 2029 г.:
1525,0 • 1,028 = 1567,7;
912,4 • 1,032 = 942,0;
259,7 • 1,087 = 282,4;
354
630,8 • 1,037 = 654,5;
269,5 • 1,008 = 271,8;
143,3 • 1,114 = 159,7.
Шаг 2. Проводим группировку полученного полного мно-
жества первичных исходных данных по пятилетним периодам:
2001-2005 гг., 2006-2010 гг., 2011-2015 гг., 2016-2020 гг„ 2021 —
2025 гт., 2026-2030 гг. На этой основе по каждой из выделенных
шести групп исходных данных исчислим необходимые для диск-
риминантного анализа расчетные исходные показатели средних
(х) и линейных отклонений (раздельного от средних групповых
— х(. — х^ и общей средней для 30 лет - х — х^), внутригруп-
« о 2 -^гр) - о2 ^Х^гр ^общ)
повои: 3»нгп =------——, межгрупповои: 8„РЖГП =-------“----=— и
ОП1 J л. * MVflU JJ
общей 32бщ
Дх. -Хобш)2 . ,
—' Зд — ; коэффициентов
g_ IZ(x-x)2
V т
квад-
ратических отклонений и вариаций шести показателей: и = - •
п
Результаты их расчетов представим в табл. 5.15.
Всего на базе наблюдаемых содержательных показателей дол-
жно быть исчислено соответственно по 36 групповых и по 6
общих средних, линейных и квадратических отклонений, по 36
внутригрупповых, 6 межгрупповых и 6 общих дисперсий, а так-
же соответствующее количество коэффициентов квадратичес-
ких отклонений и коэффициентов вариации.
Шаг 3. Весь массив расчетных исходных показателей (а их в
общей сложности 228) выстраивается для оценки однородности
выделенных шести групп каждого из шести наблюдаемых со-
держательных показателей и однородности всего массива на-
блюдаемых показателей.
В табл. 5.16 и 5.17 приводятся данные, полученные для ВОП
иНД.
Шаг 4. Делаем заключение об однородности наблюдаемых
показателей, наличии или отсутствии устойчивой закономерно-
сти в их изменениях.
355
Таблица 5.15
Расчет значений средних, дисперсии и вариации ВРП и ДС
Год ^сргр (Z,-%cprp)2 ^общ
1999 2000 282,20 303,8 0 21,6 0 466,6 -591,7 -570,1 350105,2 325010,4
Jcprp= 282,20
2001 2002 2003 2004 2005 324,1 344,4 364,8 388,9 420,2 -33,6 -13,3 7,1 31,2 62,5 1129,0 176,9 50,4 973,4 3906,3 -549,8 -529,5 -509,1 -485,0 -453,7 302276,6 280366,9 259179,6 235222,0 205840,9
Jcprp =357,7 °внгр = 1247,2
2006 2007 2008 2009 2010 451 502 550 587 643,5 -74,6 -23,6 24,4 61,4 117,9 5567,6 557,7 594,5 3767,9 13896,5 -422,9 -371,9 -323,9 -286,9 -230,4 178841,8 138307,3 104909,2 82309,8 53082,7
^сргр ~ 525,6 авн гр =4876,9
2011 2012 2013 2014 2015 685,3 717,4 770,9 816,7 862,6 -64,1 -32 21,5 67,3 113,2 4108,8 1024 462,3 4529,3 12814,2 -188,6 -156,5 -103 -57,2 -и,з 35570,0 24492,3 10609 3271,8 127,7
*сргр =749,4 ствнгр = 4587,7
2016 2017 2018 2019 2020 903,9 949,6 992,1 1032,4 1078,5 -66,0 -20,3 22,3 62,6 108,7 4349,4 410,1 495,1 3912,5 11804,8 30 75,7 118,2 158,5 204,6 900 5730,5 13971,2 25122,3 41861,2
Jcprp =969,9 °внгр =4194,4
2021 2022 2023 2024 2025 1122,8 1236 1292,7 1345,8 1383,6 -120,4 -7,2 49,5 102,6 140,4 14504,2 52,3 2447,0 10519,9 19702,8 248,9 362,1 418,8 471,9 509,7 61951,2 131116,4 175393,4 222689,6 259794,1
Хсргр = 1243,2 авнгр =9445,2
356
Продолжение
Год X, %i "^сргр (^/ ^сргр) ^общ (*,-*общ)2
2026 2027 2028 2029 2030 1441,8 1464,5 1525 1567,7 1613,5 -57,6 -34,9 25,7 68,4 114,2 3312,0 1214,5 657,9 4671,7 13030,2 567,9 590,6 651,1 693,8 739,6 322510,4 348808,4 423931,2 481358,4 547008,2
%сргр = 1499,4 «внгр =4577,3
Хобщ =873,9 =176614,7
Год Xi ^сргр (^-*сргр)2 %i ^общ
1999 2000 172,5 189,5 0 17 0 289 -373,5 -356,5 139502,3 127092,3
Хсргр= 172,5
2001 2002 2003 2004 2005 206,5 226,8 235,3 249,3 266,2 -22,4 —2,1 6,4 20,4 37,3 503,3 4,6 40,5 414,8 1388,8 -339,5 319,2 -310,7 -296,7 -279,8 115260,3 101888,6 96534,5 88030,9 78288,0
Хсргр= 228,9 авнгр = 470,4
2006 2007 2008 2009 2010 284 321 356 381 409 -52,2 -15,2 19,8 44,8 72,8 2724,8 231,0 392,0 2007,0 5299,8 -262 -225 -190 -165 -137 68644 50625 36100 27225 18769
Хср1р= 336,2 ствнгр = 2131,0
2011 2012 2013 2014 2015 434,3 458,4 490,1 525,6 558,3 -45,0 -20,9 10,8 46,3 79,0 2023,5 436,1 117,0 2145,2 6243,6 -111,7 -87,6 -55,9 -20,4 12,3 12476,9 7673,8 3124,8 416,2 151,3
^сргр = 479,3 ствнгр = 2193,1
357
Продолжение
Год Xi Y. ~ Y ^1 лсргр (%/ Л^сргр) ^общ
2016 2017 2018 2019 2020 578,4 605,5 633,1 657,1 685,5 -41,3 -14,2 13,5 37,5 65,9 1701,6 200,2 180,9 1402,5 4336,2 32,4 59,5 87,1 111,1 139,5 1049,8 3540,3 7586,4 12343,2 19460,3
Jcprp =619,7 авнгр =1564,3
2021 2022 2023 2024 2025 709 792,7 800 826,7 844,6 -67,4 16,3 23,6 50,3 68,2 4545,0 265,1 556,2 2528,4 4649,0 163 246,7 254 280,7 298,6 26569 60860,9 64516 78792,5 89162,0
%cprp =776,4 °внгр ~ 2508,7
2026 2027 2028 2029 2030 856 892,3 912,4 942 972,5 -47,3 -11 9,1 38,7 69,2 2237,3 121 82,8 1497,7 4788,6 310 346,3 366,4 396 426,5 96100 119923,7 134249,0 156816 181902,3
Jcprp= 903,3 авнгр = 1745,5
*общ=546 Оцбщ = 63271
Год Xi V. _ V лсргр (X/ ^сргр) ^общ (TG-^общ)2
1999 48 0 0 -90 8100
2000 49,3 1,3 1,7 -88,7 7867,7
^сргр ~ 48
2001 50,5 -6,9 47,2 -87,5 7656,3
2002 51,1 -6,3 39,3 -86,9 7551,6
2003 58,3 9 9 -79,7 6352,1
2004 63,8 6,4 41,4 -74,2 5505,6
2005 71,2 13,8 191,4 -66,8 4462,2
^сргр=57,4 авнгр ~ 64,0
358
Продолжение
Год Y — X лсргр ^срГр) ^общ ( -^общ )
2006 2007 2008 2009 2010 80 81 87 88 103 -5,0 -4,0 2,0 з,о 18,0 25,3 16,3 3,9 8,8 322,8 -58 -57 -51 -50 -35 3364 3249 2601 2500 1225
*срп>=85,0 авнгр ~
2011 2012 2013 2014 2015 108,1 108,8 121,9 122,1 122,3 -6,3 -5,6 7,5 7,7 7,9 39,6 31,0 56,8 59,8 62,9 -29,9 —29,2 —16,1 -15,9 -15,7 894,0 852,6 259,2 252,8 246,5
*срп> = НМ °внгр = 50,0
2016 2017 2018 2019 2020 132,4 141,7 147 151,9 152,6 -8,9 4 5,7 10,6 11,3 79,5 1 32,3 112,0 127,3 -5,6 3,7 9 13,9 14,6 31,4 13,7 81 193,2 213,2
^срп, =141,3 авнгр = 70,3
2021 2022 2023 2024 2025 160 170,3 207,9 217 819,6 -27,9 -17,6 20 29,1 31,7 778,4 309,8 400 846,8 1004,9 22 32,3 69,9 79 81,6 484 1043,3 4886,0 6421 6658,6
*срп>= 187,9 ствнгр = 668,0
2026 2027 2028 2029 2030 219,7 234,9 259,7 282,4 307 -34,2 -19,0 5,8 28,5 53,1 1168,5 360,4 33,8 813,2 2821,4 81,7 96,9 121,7 144,4 169 6674,9 9389,6 14810,9 20851,4 28561
=253,9 авнгр = Ю39,5
^общ ~ !38 аобщ = 5096
359
Продолжение
Год X. ^сргр (Kj ^сргр) ^общ ^общ)
1999 136,2 0 0 -239,8 57504
2000 145 8,8 77,4 -231 5336
Хсргр= 136,2
2001 152,9 -14,8 219,5 -223,1 49773
2002 164,6 -3,1 9,7 -211,4 44690
2003 168,8 1,1 1,2 -207,2 42931
2004 181,5 13,8 190,0 -194,5 37830
2005 193,5 25,8 664,8 -182,5 33306
Хсргр= 167,72 °внгр ~ 217,0
2006 207,4 -29,7 879,1 -168,6 284426
2007 225,5 -11,6 133,4 -150,5 22650
2008 244,1 7,1 49,7 -131,9 17397
2009 261,9 24,9 617,5 -114,1 13018
2010 289,9 52,9 2793,1 -86,1 7413
Jcprp= 237,05 °внгр ~ 894,6
2011 305 -22,3 495,8 -71 5041
2012 313,6 -13,7 186,8 -62,4 3893,8
2013 337,8 10,5 111,0 -38,2 1459,8
2014 354 26,7 714,7 -22 484
2015 363,3 36,0 1298,4 -12,7 161,3
Jcplp =327,27 °внгр = 561,3
2016 385,7 -27,6 762,7 9,7 94,1
2017 405,6 -7,7 59,5 29,6 876,2
2018 422,5 9,2 84,3 46,5 2162,3
2019 440,6 27,3 744,4 64,6 4173,2
2020 462,2 48,9 2389,6 86,2 7430,4
xcprp =413,32 °внгр = 808,1
2021 486,7 -41,4 1712,6 110,7 12254,5
2022 523,4 -4,7 21,9 147,4 21726,8
2023 548,1 20,0 400,7 172,1 29618,4
2024 569,6 41,5 1723,6 193,6 37481,0
2025 578,5 50,4 2541,8 202,5 41006,3
Jrcprp= 528,08 °внгр = 1280,1
2026 586 -35,4 1253,2 210 44100
2027 599,6 -21,8 475,2 223,60 49997,0
2028 630,8 9,4 88,4 254,80 64623,0
2029 654,5 33,1 1095,6 278,50 77562,3
2030 679 57,6 3317,8 303 91809
Хсргр =621,40 °внгр = 1246,0
^общ ~ 376 ^общ — 28267
360
Продолжение
Год %i ^сргр (^7 Aqjpp ) ^общ (2^/ 'Гдбщ)
1999 71,2 0 0 -110,8 12276,6
2000 75,8 4,6 21,2 -106,2 11278,4
^сргр = 71,2
2001 79,7 -8,2 67,5 -102,3 104465,3
2002 86,1 -1,8 3,3 -95,9 9196,8
2003 88,5 6 3 -93,5 8742,3
2004 97,3 9,4 88,0 -84,7 7174,1
2005 100,1 12,2 148,4 -81,9 6707,6
*сРП,=87.9 2 °внгр = 61,5
2006 104,6 -18,2 330,0 —77,4 5990,8
2007 115,9 -6,9 47,2 -66; 1 4369,2
2008 127,3 4,5 20,6 -54,7 2992,1
2009 140,4 17,6 310,9 -41,6 1730,6
2010 148,3 25,5 652,0 -33,7 1135,7
*сргр = 122,8 авнгр ~ 272, 1
2011 156,9 -13,0 169,9 -25,1 630,0
2012 163,6 -6,3 40,1 -18,4 338,6
2013 173,3 3,4 11,3 -8,7 75,7
2014 186,3 16,4 267,9 4,3 18,5
2015 191,2 21,3 452,3 9,2 84,6
%Сргр =169,9 ствнгр =188,3
2016 199,7 -13,4 180,0 17,7 313,3
2017 207 -6,1 37,4 25 625
2018 216,2 3,1 9,5 34,2 1169,6
2019 226,5 13,4 179,1 44,5 1980,3
2020 238,1 25,0 624,2 56,1 3147,2
Jcprp =213,1 °внгр ~ 206,0
2021 248 -7,4 54,5 66 4356
2022 266,8 11,4 130,3 84,8 7191,0
2023 254,1 -1,3 1,6 72,1 5198,4
2024 262,2 6,8 46,5 80,2 6432,0
2025 263,1 7,7 59,5 81,1 6577,2
%сргр= 255,4 авнгр ~ 58,5
2026 265 -3,7 13,6 83 6889
2027 268,6 -1 0 86,6 7499,6
2028 269,5 8 7 87,5 7656,3
2029 271,8 3,1 9,7 89,8 8064,0
2030 274,1 5,4 29,3 92,1 8482,4
%Сргр =268,7 °внгр =10,7
^общ = 182 7 аобщ ~ 4962
361
Продолжение
Год X. ^сргр (^,-Хсргр)2 ^общ
1999 29 0 0 -46 2116
2000 29,70 7 5 -45,3 2052,1
^сргр =
2001 32,10 -3,9 15,0 -42,9 1840,4
2002 37 1,0 1,1 -38 1444
2003 34,60 -1,4 1,9 -40,4 1632,2
2004 38,80 2,8 8,0 36,2 1310,4
2005 43,60 7,6 58,3 -31,4 986,0
Jcpi-p =35,97 авнгр = 16,8
2006 50,30 -1,5 2,4 -24,7 610,1
2007 50,70 -1,1 1,3 -24,3 590,5
2008 52,70 9 8 -22,3 497,3
2009 50,60 -1,2 1,5 -24,4 595,4
2010 63,10 и,з 126,9 -11,9 141,6
*сргр =51,83 2 °внгр ~ 26,6
2011 62,90 -6 4 -12,1 146,4
2012 59,60 -3,9 15,3 -15,4 237,2
2013 68,40 4,9 23,8 -6,6 43,6
2014 65,60 2,1 4,3 -9,4 88,4
2015 61,50 -2,0 4,1 -13,5 182,3
Лсргр= 63,52 авнгр = 9,6
2016 66,20 -3,0 8,8 -8,8 77,4
2017 71,60 2,4 5,9 -3,4 11,6
2018 73,60 4,4 19,7 -1,4 2,0
2019 73,20 4,0 16,3 1 -1,8 3,2
2020 68,90 -3 -6,1 37,2
*сргр =69,17 °внгр = Ю, 1
2021 73,10 -19,9 395,3 -1,9 3,6
2022 80,30 -12,7 160,9 5,3 28,1
2023 110,10 17,1 293,0 35,1 1232,0
2024 112,70 19,7 388,7 37,7 1421,3
2025 112,80 19,8 392,7 37,8 1428,8
1ср1р =92,98 2 °внгр = 326,1
2026 115,40 -23,2 539,0 40,4 1632,2
2027 122,60 -16,0 256,5 47,6 2265,8
2028 143,30 4,7 21,9 68,3 4664,9
2029 159,70 21,1 444,5 84,7 7174,1
2030 177,90 39,3 1543,2 102,9 10588,4
Гсргр= 138,62 2 авнгр = 561,0
^общ ~ 75 7 ^общ ~ 1409
362
Таблица 5.16
Оценки расчетных показателей средних дисперсий и вариации ВОП
Годы Расчетные показатели
в целом в промышленности в сельском хозяйстве
2 ^в.г ав.г И, % 2 ав.г ав.г И, % 2 ав.г ав.г к %
2001- 2005 1247,2 35,3 9,9 470,4 21,7 9,5 64,0 8,0 13,9
2006— 2010 4876,9 69,8 13,2 2131,0 46,2 13,7 75,4 8,7 10,2
гои- гои 4587,7 67,7 9,03 2193,0 46,8 9,7 50,0 7,1 6,1
2016— 2020 4194,4 64,8 6,6 1564,3 39,6 6,4 70,3 8,4 5,9
2021— 2025 9445,2 97,19 7,8 2508,7 50,1 6,5 668,0 25,8 13,8
2026— 2030 4577,3 67,7 4,5 1745,5 41,8 4,6 1039,5 32,2 12,7
2 ав.г ав.г ~ И, % = 176614,7 420,3 48,1 2 _ ав.г ав.г ~ И, % = = 63271,0 = 251,5 46,1 2 _ ав.г ав.г “ к % = : 5096,0 = 71,4
Таблица 5.17
Оценки расчетных показателей средних дисперсий и вариации НД
Годы Расчетные показатели
в целом в промышленности в сельском хозяйстве
2 ^в.г ав.г К, % 2 ав.г ав.г К, % 2 ^в.г ^в.г К %
2001— 2005 217,0 14,7 8,8 61,5 7,8 8,9 16,8 4,1 И,4
2006— 2010 894,6 29,9 12,6 272,1 16,5 13,4 26,6 5,2 10,0
2011— 2015 561,3 23,7 7,2 188,3 13,7 8,1 9,6 3,1 4,9
2016— 2020 808,1 28,4 6,9 206,0 14,4 6,7 10,1 3,2 4,6
2021— 2025 51280,1 35,8 6,8 58,5 7,6 2,9 326,1 18,1 19,4
2026— 2030 1246,0 35,3 5,7 10,7 з,з 1,2 561,0 23,7 17,1
2 _ ^в.г ав.г ~ к % = : 28267,0 168,1 44,7 2 _ ^в.г ^в.г “* И, % = : 4962,0 70,4 38,7 2 - ав.г ав.г “ И, % = = 1409,0 37,5 50,0
363
Известно, что чем меньше дисперсия, квадратическое откло-
нение и соответственно коэффициент вариации, тем, при прочих
равных условиях, однороднее наблюдаемые явления, а измене-
ние в их поведении и составе закономернее, и наоборот.
По значениям полученных оценок можно судить, что выде-
ленные группы по темпам роста в целом однородные, коэффи-
циент вариации у каждой из них ниже 0,3, тогда как в целом
наблюдаемый рост (и ВОП, и НД) неоднороден, и, следователь-
но, на его основе нельзя строить общие прогнозные экстраполя-
торы-оценки. То же самое подтверждают полученные оценки
дисперсий и квадратических отклонений как более простых из-
мерителей однородности, пригодных для оценивания в случае
наличия наблюдаемых явлений одной размерности.
Содержательный вывод заключается в том, что на основе груп-
повых значений темпы экономического роста можно прогнози-
ровать, тогда как на основе итоговых оценок в целом за 30 лет
прогнозировать нельзя.
Общий вывод: показателей вариации, несмотря на их уни-
версальность, недостаточно для надежной оценки однородно-
сти и устойчивости темпов экономического роста. Необходимо
обращаться к более адекватным и чувствительным методам по-
лучения соответствующих оценок, в нашем случае — к методам
дискриминантного анализа.
На примере тех же данных рассмотрим процедуру получе-
ния дискриминантных оценок, которая включает следующие
шаги.
Шаг 1. Выбор формы и определение параметров дискри-
минантной функции.
При простейшем подходе к делу обычно обращаются к пря-
молинейной форме этой функции:/= а{хх + а2х2 + ... 4- апхп и
нахождению ее параметров путем решения системы нормаль-
ных уравнений с ограниченным числом неизвестных.
В нашем случае необходимо строить и решать уравнение с
шестью неизвестными.
Шаг 2. Для упрощения проведем парное разбиение исход-
ных данных и ограничим функцию двумя параметрами, приведя
ее к виду f = а{ х. + а2 х..
Шаг 3. Для нахождения параметров а{ и а2 воспользуемся
фрагментом данных х (см. табл. 5.5).
364
Шаг 4. Используя приведенные данные, решим систему
уравнений с двумя неизвестными методом множителей:
30,3+а2 684,7 = 327,27- 63,52;
а]30,3+а29,9 = 413,32- 69,17;
а2684,7-а29,9 = -80,40;
а2 =-0,12;
^30,3+(-0,12)-684,7 = 263,75;
^30,3 = 345,91;
at =11,42.
Шаг 5. Найдем значения функции для каждого года, в каж-
дой пятилетке и общее значение функции для двух пятилеток
вместе. Эти значения представим в табл. 5.6. Значение функции
для 2001 г. будет:
/20,, = 11,42 • 305,0 + (-0,12 • 62,9) = 3475,6;
/общ = а1х10 + а2х10 = ^>
/2011-2020 = 11,42 379,0 + (-0,12 • 67,2) = 4320,1.
Шаг 6. Определяем дискриминанты:
/' = 3734,7 = С';
/' = 4711,8 = С';
(f' + Г*)2
С= ——/-^- = 4223,3;
83-
(/+/Y (3734,7 + 4711,8)2
lim——/-2- = ------’-----= 125,23 = т.
бЗ 569695,7
Выводы. Дискриминантом для первого пятилетия является
значение 3734,7, для второго — 4711,8, для десятилетия — 4223,3.
Значение функции ниже дискриминанта (с поправкой на
т = 125,23) будет принадлежать другим группам роста.
365
Сравнив значения полученных функций, можно заметить,
что пятилетие 2011—2015 гг. относится к плохому типу роста НД
в целом и в сельском хозяйстве, тогда как следующие пятиле-
тие — к типу благоприятного экономического роста.
Аналогичные дискриминантные оценки по тем же процеду-
рам получим на основе фрагментарных данных сельского хо-
зяйства и промышленности за те же 2011—2020 гг. (табл. 5.16—
5.18), а именно:
=0,26; я2 = ~0,09;
/2011-2020 = 0,26 • 379,0 - 0,09 • 195,9 = 80,9 = С;
f' = 69,t = C';
f" = SS,3 = C";
цт£/±/)._ = 122,5 = m.
3}
Расчеты параметров at и а2 проводим по прежней процедуре:
Я] 364,9 + а2 684,7 = 327,27 -169,9;
а]364,9 + а2197,2 = 413,32-213,1;
а2 684,7 - а2197,2 -157,37 + 200,22 = 0;
я2 487,5 =-42,85;
а2 = -0,09;
а} 364,9 + (-0,09) • 684,7 = 157,37;
01364,9 = 157,37-61,62;
Я] 364,9 = 95,75;
а} =0,26.
Соответственно значение дискриминантной функции за две
пятилетки находим как
/10 =al^io+a2^io;
/ю = 0,26-379,0-0,09 195,9 = 80,9 = С.
366
Заметим, что наиболее благоприятный экономический рост
показателей по национальному доходу в целом и в промышлен-
ности приходится на пятилетие 2015—2020 гг. Правда, пятиле-
тие 2011—2015 гг. по характеру исходных условий однороднее,
если рассматривать показатели коэффициентов вариации. И в
этом можно убедиться, если сравнить, что коэффициенты вари-
ации, которые в рассматриваемом пятилетии ниже, чем в пре-
дыдущем и последующем.
Аналогичная схема расчетов будет действительной и для дру-
гих фрагментов приведенных исходных данных, равно как и для
всего их массива. При этом расчеты в целом будут сравнитель-
ным фоном, поэтому их проведение следует каждый раз рассмат-
ривать не только как желательное, но и обязательное условие
проведения целостного статистического эксперимента.
Вопросы для самоконтроля
1. В чем заключается сущность многомерного сопоставления
данных?
2. Перечислите основные цели и задачи многомерного сопос-
тавления данных.
3. В чем состоят общие черты и основные отличия одномерно-
го и многомерного сопоставления данных? В единицах и чис-
ленном составе наблюдаемых объектов или наблюдаемых при- •
знаков, законах распределения значений наблюдаемых при-
знаков, детерминированной и стохастической природе
исходных данных, параметрическом или непараметрическрм
их представлении, методах обработки-данных, интерпрета-
ции полученных результатов и т.д.?
Ответ иллюстрируйте примерами одномерного и многомер^
ного сопоставления данных.
4. Перечислите основные направления и методы многомерного
сопоставления данных. Правильно ли определять региональ-
ные показатели в расчете на душу населения, а не на семью? ,
5. В чем заключаются основные особенности многомерного со-
поставления региональных данных? Можно ли игнорировать
при таких сопоставлениях региональные дифференциалы в из-
менениях цен, инфляции, курсов валют, социальных, природ-
ных и других факторов, влияющих на региональное развитие?
367
Если нет, как учитывать эти дифференциалы? Если да, то по-
чему их можно игнорировать?
6. Изложите принципы типологии и приемы определения реп-
резентативности сопоставляемых многомерных региональных
образований и показателей. Какова достоверность сопостав-
ляемых региональных показателей? Равномерно ли распре-
деляются по регионам нелегальные, латентные, фиктивные
и другие неучитываемые современной статистикой данные?
Общественное мнение в регионах и экспертные оценки не-
наблюдаемых региональных явлений. Можно ли на их осно-
ве проводить региональные сопоставления? Региональные
субсидии, льготы и другие трансферты. Действительно ли
они содействуют выравниванию регионального развития
России или усугубляют неравенство и бедность наблюдае-
мых регионов?
7. Сформулируйте условия для обоснования и выбора необхо-
димой и достаточной многомерной системы сопоставимых
региональных показателей. Существует ли в природе и мож-
но ли найти конечную систему сопоставимых показателей,
дальнейшее изменение и пополнение состава которой не будет
влиять на устойчивость исчисляемых на ее основе обобщаю-
щих показателей?
8. Сформулируйте необходимые и достаточные условия опре-
деления и выбора адекватных многомерных весов сопостав-
ляемых систем региональных показателей.
9. В чем заключаются особенности определения и анализа мно-
гомерных рейтингов?
10. Перечислите процедуры определения и особенности анали-
за многомерных рейтингов деловой активности, предприни-
мательской уверенности и инвестиционной привлекательно-
сти регионов России.
11. В чем заключаются особенности и отличия одномерного и
многомерного прогнозирования экономических показателей?
12. Для чего строятся эмпирические системы показателей и од-
номерные рейтинги? Почему они преобладают в экономи-
ческой практике?
13. Приведите примеры манипулирования одномерными рей-
тингами.
14. Почему искажают реальное положение дел практически все
современные рейтинги деловой активности, включая рей-
тинги «Стандарт энд Пурс», «Мудс», «Форбс», индексы Доу-
368
Джонс, Насдак и другие корпоративные и биржевые рей-
тинги и индексы?
15. Как, по вашему мнению, можно и следует преодолевать изъя-
ны и манипуляции современными рейтингами? В частности,
как следует поступать в случаях, когда одно и то же однона-
правленное изменение дел представляется различными рей-
тингами в разнонаправленных оценках? Например, почему
на систематической основе рейтинги отрицательных измене-
ний подменяются рейтингами положительных изменений, в
частности, рейтинги продолжающегося падения темпов мате-
риального производства - рейтингами мнимого их роста, рей-
тинги понижения качества жизни во вногих регионах Рос-
сии — рейтингами их роста, рейтинги донорских регионов —
рейтингами регионов-реципиентов и т.д.?
Рекомендуемая литература
1. Айвазян С.А. Анализ синтетических категорий качества
жизни населения субъектов РФ: их измерение, динамика, ос-
новные тенденции // Уровень жизни населения регионов Рос-
сии. — 2002. — № 11.
2. Айвазян С.А. Россия в межстрановом анализе синтетичес-
ких категорий качества жизни населения // http://www.hse.ru/
journals/wldross/vol l-4/ivaianl.htm // ЭММ. — Т. 39. — 2003. —
№ 2,3.
3. Бабашкина А.М. Государственное регулирование нацио-
нальной экономики: учеб, пособие. — М.: Финансы и статисти-
ка, 2005.
4. Бизнес-план. Методические материалы / под ред. Н.А. Ко-
лесниковой, А.Д. Миронова. — 3-е изд., доп. — М.: Финансы и
статистика, 2004.
5. Большакова О.В. Российская империя: система управле-
ния. Библиографический обзор. — М.: ИНИОН, 2003.
6. Гранберг А.Г. Основы региональной экономики: учебник
для вузов. — 4 изд. — М.: ГУ ВШЭ, 2004.
7. Гранберг А.Г, Зайцева Ю.С. Валовой региональный про-
дукт: межрегиональные сравнения и динамика. — М.: СОПС,
2003.
8. Иванова В.Н., Гузов Ю.Н., Безденежных Т.И. Технологии
муниципального управления: учеб, пособие. — М.: Финансы и
статистика, 2005.
369
9. Измерения региональной асимметрии и системные оцен-
ки возможностей и последствий ее снижения (2003—2005 гг.). —
М.: Отделение общественных наук РАН, 2003—2005.
10. Караванова Б.П. Мониторинг финансового состояния
организации: учеб.-метод, пособие. — М.: Финансы и статисти-
ка, 2006.
11. Карминский А.М., Пересецкий А.А., Петров А.Е. Рейтинги
в экономике: методология и практика. — М.: Финансы и стати-
стика, 2005.
12. Кистанов В.В., Копылов Н.В. Региональная экономика
России: учебник. — М.: Финансы и статистика, 2006.
13. Колесникова Н.А. Финансовый и имущественный потен-
циал регионов: опыт регионального менеджмента. — М.: Фи-
нансы и статистика, 2000.
14. МВФ. Специальный стандарт на распространение дан-
ных. — Вашингтон, 1996.
15. Межрегиональные экономические сопоставления // Все-
российская научно-практическая конференция. — М.: СОПС,
4—5 декабря 2003 г.
16. Методология регионального прогнозирования. — М.:
СОПС, 2003.
17. Общеэкономические и отраслевые проблемы стратегии
территориального развития России. — М.: СОПС, 2003.
18. Общий стандарт распространения данных. — Вашингтон,
1999.
19. Оценка бизнеса: учебник / под ред. А.Г. Грязновой,
М.А. Федотовой. — 2-е изд., перераб. и доп. — М.: Финансы и
статистика, 2006.
20. Проблемы теории и практики реформирования регио-
нальной экономики. - М.: Институт региональных экономи-
ческих исследований, 2004. — Вып. 5.
21. Проект методики распределения финансовых средств
из фонда регионального развития. Сайт Министерства эконо-
мического развития и торговли Российской Федерации
www.economy.gov.ru.
22. Региональные процессы в современной России. Эконо-
мика. Политика. Власть. — М.: ИНИОН, 2003.
23. Регионы России // Стат. сб. — В 2-х т. — М.: Госкомстат
России, 1996, 2004.
370
24. Рейтинги инвестиционной привлекательности регионов
России // Эксперт, 1999—2005. www.expert.ru.
25. Социально-экономическое положение регионов Российс-
кой Федерации в 2003 г. // Российская газета. — 2004. — № 46. —
6 марта (см. также РГ. — 2003. — № 49. — 15 марта, РГ. — 2002. —
№31.-16 февр.).
26. Стандарты на распространение странами экономической
и финансовой статистики: проект для обсуждения. — Вашингтон,
1996.
27. Стратегия социально-экономического развития субъек-
тов Российской Федерации. — М.: СОПС, 2003.
28. Суспицын С.А. Барометры социально-экономического
положения регионов России. — Новосибирск, ИЭОПП СО РАН,
2004.
29. Ткачев А.Н., Луценко Е.В. Качество жизни населения как
интегральный критерий оценки эффективности деятельности
региональных организаций // Научный электронный журнал
КубГАУ. - 2004. - № 2(4).
30. Трансформационная экономика России: учеб, пособие /
под ред. А.В. Бузгалина. — М.: Финансы и статистика, 2006.
31. Уткин Э.А. Сборник ситуационных задач, деловых и пси-
хологических игр, тестов, контрольных заданий, вопросов для
самопроверки по курсу «Менеджмент». — М.: Финансы и стати-
стика, 2001.
32. Федеральный бюджет и регионы. Опыт анализа финансо-
вых потоков. Институт Восток—Запад. — 2-е изд. — М.: МАКС-
Пресс, 1999.
33. Шелковников В.Е., Зуев В.М. Политическая система и ре-
гиональная экономика переходного периода. — Ростов н/Д, 2001.
34. Яндиев М.И. Финансы регионов. — М.: Финансы и стати-
стика, 2002.
35. IMF. Fund Politicizes — Data Provision to the Fund for
Surveillance and Standards to Guide Members in the Publication of
Data. — Washington, 1996.
36. Standards for the Dissemination by Countries of Economic
and Financial Statistics: A Discussion Draft. — Washington, 1996.
37. World Competitiveness Yearbook Lausanne. 2004 Institute
for Management Development. Switzerland, 2004, 1015 p. Internet:
http://www.imd.ch/wcy; e-mail: wcy.info@imd.ch.
--------- Русско-английский
словарь терминов
по многомерному анализу
статистических данных
Анализ
второго порядка
гетерогенного (или неоднородного)
распределения
главных компонент
данных
дискриминантный
дисперсионный
иерархический кластерный
кластерный
ковариационный
многомерный (множественный)
многомерный статистический
множественного фактора
нормальных координат
параллельных линий
последовательный
ридитивный
углового коэффициента (прямой);
тангенса угла наклона (кривой)
факторный
чувствительности
Блоки пересекающиеся
Блокировка
Вероятностные нейронные сети
Взаимная (перекрестная)
ковариация
Всевозможные регрессии
подмножества
Выборочное обследование;
многостепенная выборка;
последовательный выбор;
последовательная выборка
Analysis
second-order
dissection (of heterogeneous
distributions)
general components
data
discriminant; discriminatory
of dispersion; multivariate of variance;
manova
hierarchical cluster
cluster
of covariance; ancova; covariance
multivariate
multivariaate statistical
multiple factor
principal coordinates
parallel line assay
sequential
ridit (ralative to an identified
distribution)
slope ratio assay
component
sensitivity
Linked blocks
Interblock
Probability neural network
Cross-covariance
All-possible-subsets regression
Cluster sampling;
multi-stage sampling;
sequential selection;
sequential sampling
372
Выделение кластеров по
соседним элементам
Выделение признаков (при
распознавании образов)
Выпадание
Главный фактор
Горизонт (для нейронных сетей)
Градиентный спуск
Графики взаимосвязи
Декартовы координаты
Декомпозиция
Делящиеся значения
Деревья классификации
Дисперсия
внутригрупповая
межгрупповая
общая
остаточная
по факторам
стохастическая
Иерархическая классификация
Иерархическая модель
Интерпретация таблиц частот
с многомерными откликами
Кардиоидное распределение;
косинус-распределение
Каскадный процесс
Категоризация, группировка,
разбиение на подмножества
Квадратичное сглаживание
Кластер
Кластеризация, выделение
кластеров; объединение в
кластеры
Кластерный рандомизированный
критерий
Ковариантность
Ковариационная матрица;
дисперсная матрица
Nearest-neighbour clustering;
single-linkage clustering
Feature selection
Dropout
General factor
Horizon for neural network
Grade ascending
Graph of relationship
Cartesian coordinates, orthogonal
coordinates, rectangular coordinates
Decomposition
Dividing value
Classification trees
Variance
intragroup
intergroup
general
residual
by factors
stochastic
Hierarchical classification;
nested classification
Hierarchical model
Interpretation of frequency tables
with multidimensional response
Cardioid distribution;
cosine distribution
Cascade process
Categorization, grouping,
division by subset
Quadratic smoothing
Cluster
Clustering
Cluster randomized trial
Covariance
Covariance matrix;
dispersion matrix
373
Ковариационный анализ
Ковариация
Ковариация с запаздыванием
аргумента
Ковариация, зависящая от
времени
Коваримин (метод)
Когерентная система;
монотонная структура
Компактная (серийная) группа
Корреляционная(ое, ые)
зависимость
связь
таблица
исчисления
отношение
уравнение
эллипс
Корреляция
асимметричная
взаимная (перекрестная)
внутригрупповая
индекс
криволинейная
линейная
ложная
множественная
нормальная
отрицательная
переменная
положительная
рангов
рядов динамики
совокупная
частная
частная (парная)
четырехклеточная
Коэффициент
ассоциации
взаимной сопряженности
детерминации
дисперсии Лексиса (критерий
устойчивости)
доверия
корреляции (парный) частный
корреляции множественной
374
Analysis of covariance; ANCOVA;
covariance analysis
Covariation
Lag covariance
Time-dependent covariates
Covarimin
Coherent structure;
monotonic structure
Compact (serial) cluster
Correlation
interdependance
relationship
table
calculus
ratio
equation
ellipse
Correlation
skew
cross
inteigroup
index
curvilinear
linear
spurious
multiple
normal
negative
variable
positive
grade
dynamic series
aggregate
partial
partial
two-by-two table
Coefficient
association
cross-conjugation
of determination
Lexis dispersion (stability criterion)
confidence
of partial correlation
multiple correlation
корреляции рангов
парной (частной) корреляции
поправочный
ранговой корреляции Джини
ранговой корреляции Спирмана
регрессии
регрессии; вес регрессии
совокупной корреляции
согласия; согласия Кенделла;
ранговый согласия
сопряженности признаков
частной множественной корреляции
Критическая линия
Кросс-перекрестная проверка
Кросс (перекрестная) энтропия
Матрица корреляции,
корреляционная матрица
Метод
полурасщепления; испытание
на расщепление
принятия множественных решений
простого суммирования
(в факторном анализе)
пяти точек (для оценки кривой
эффекта)
сопряженных градиентов
Тагучи
усреднения критического значения
Многократность, повторяемость
Многокритериальная
оптимизация
Многомерная(ое)
выборка
геометрия
группировка
нелинейная корреляция
расслоение
случайная величина
Ф-распределение
шкалирование
бета-распределение
биноминальное распределение
Л1 -среднее распределение
мультиноминальное распределение
of ranks correlation
of partial correlation
correction factor
Gini’s index of cograduation
Spearman’s rho; Spearman’s p;
Spearman’s rank correlation
regression
regression coefficient; regression weight
of correlation aggregated
of concordance; Kendall’s
of concordance; rank concordance
of contingency
of multiple partial correlation
Rejection line
Cross-test
Cross-entropy
Correlation matrix
Method(s)
split half; split test
multiple decision
centroid
five-point assay
conjugate gradients
Taguchi
average critical value
Repetition
Multi-objective optimization
Multiple
sampling
geometry
classification
nonlinear correlation
stratification
random value
F-distribution
dimensional scaling
Multivariate
beta distribution
binomial distribution
LI-mean
multinomial distribution
375
нормальное распределение
обратное гипергеометрическое
распределение;
отрицательное гипергеометрическое
распределение;
отрицательное факториальное
мультиноминальное распределение
отрицательное биноминальное
распределение; отрицательное
мультиноминальное распределение
рапределение Паскаля
распределение Бурра
распределение Парето
распределение Поля
распределение Пуассона
распределение степенного ряда
Многомерное распределение;
совместное распределение
Многомерное экспоненциальное
распределение, распределение
экспоненциального типа
Многомерные(ный)
анализ таблицы дисперсий
введения дополнительных
данных
временные ряды
дихотомии
изменения
контроль за качеством
коэффициент корреляции R
критерий размаха выборки
неравенства Чебышева
отклики
относительный ранговый критерий
процесс Маркова
процесс Пуассона
процессы (характеризуемые
несколькими переменными)
сравнения
фазовый процесс
Многомодальное распределение
Многообразие
Многослойные персептроны
Многостепенная оценка
дисперсии Дурбина
Многостепенной план
непрерывного выборочного
контроля
normal distribution
inverse hypergeometric distribution;
negative hypergeometric distribution;
negative factorial multinomial
distribution
negative binomial distribution;
negative multinomial distribution
Pascal distribution
Burr’s distribution
Pareto distribution
Polya distribution
Poisson distribution
power series distribution
Multivariate distribution;
joint distribution
Multivariate exponential distribution
Multiple
analysis of variance table; manova table
imputation
time series
dichotomy
changes
quality control
correlation coefficient R
range test
Tchebyshev inequalities
Multidimensional responses
signed rank test
Markov process
Poisson process
processes
comparisons
phase process
Multi-modal distribution
Variety; diversity
Multilayer perceptrons
Durbin’s multistage variance
estimator
Multi-level continuous sampling
plans
376
Многоугольник Дэлфиэла;
многоугольник Вороного;
многоугольник Тиссена
Многоугольник частот
Многофакторный план
Многочлен Бернулли
Многочлен Чарлиера
Многочлены Хермита
Многоэтапная выборка
Многоэтапная оценка
Множеств теория
Множественная выборка
Множественная задача
принятия решений
Множественностепенной
Множественность
Множество
Множество трансформаций
латинского квадрата
Множители, увеличивающие
дисперсию (VIF)
Множитель Лагранжа тест;
Множитель Лагранжиана тест;
тест множества
Моделей теория
Момент-бисериальная
корреляция
Момент нецентральный
Момент производящей функции
Мультиколлинеарность
Мультипликативная повторная
перепись
Мультипликативная сезонность,
демпфированный тренд
Мультипликативная сезонность,
с исключенным трендом
Мультипликативная сезонность,
экспоненциальный тренд
Мультипликативная система
записи (регистрации)
Мультипликативные
произвольные старты
Delthiel polygon;
Voronoi polygon;
Thiessen polygon
Frequency polygon
Multi-factorial design
Bernoulli polynomial
Charlier polynomials
Hermite polynomials
Multi-stage sample; multi-stage
sampling
Multi-stage estimation
Set theory
Bulk sampling
Multiple decision problem
Heterograde
Multiplicity
Multitude
Transformation set of Latin squares
Variance inflation factors
Lagrange multiplier test;
Lagrangean multiplier test;
score test
Models theory
Point Biserial correlation
Crude moment
Moment generating function
Multicollinearity
Multiple recapture census
Multiple seasonality,
damped trend
Multiple seasonality, with excluded
trend
Multiple seasonality,
exponential trend
Multiple record system
Multiple random starts
377
Мультифазовая выборка
Мультиэквациональная модель;
модель системы уравнений
Мягкое колебание функции
между пределами
Наблюдаемая информационная
матрица
Наиболее мощная критическая
область
Наиболее мощный критерий
Наиболее мощный критерий ряда
Наиболее строгий критерий
Наиболее эффективная оценка
Наилучшая постоянная
асимптотически нормальная
оценка
Наилучшее соответствие
Накопленная (суммарная)
ошибка
Накопленная инцидентность
Накопленное отклонение
Накопленный процесс
Нейронная кривая
Нейронная сеть
Нелинейная корреляция
Нелинейная регрессия;
нелинейная модель;
асимметрическая регрессия
Нелинейное оценивание
Нелинейный тренд
Ненаблюдаемое смешивание
Неограниченно случайное
разностное уравнение
Неодинаковые подклассы
Неоднородность
Неоднородный процесс Пуассона
Неортогональные данные
Неортогональный фактор
Непараметрическая
доверительные интервалы
допустимые пределы
достаточность
максимальная вероятность
статистика
Multi-phase sampling
Multi-equational model;
simultaneous equations model
Relaxed oscillation
Observed information matrix
Most powerful critical region
Most powerful test
Most powerful rank test
Most stringent test
Most efficient estimator
Regular best asymptotically normal
estimator
Best fit
Cumulative error
Cumulative incidence
Accumulated deviation
Accumulated process
Neural curve
Neural network
Nonlinear correlation; curvilinear
correlation
Nonlinear regression;
nonlinear model; curvilinear
regression; skew regression
Nonlinear estimation
Curvilinear trend
Unobserved confounder
Explosive stochastic difference
equation
Unequal subclasses
Heterogeneity
Inhomogeneous Poisson process
Non-orthogonal data
Oblique factor
Non-parametric
confidence intervals
tolerance limits
sufficiency
maximum likelihood
statistics
378
Непараметрический дельта-метод
Непараметрический метод .
Неполная рандомизация
Неполноблочный план деления
групп
Неполное обследование
Неполные данные
Неполный блок
Неполный латинский квадрат;
квадрат Юдена
Неполный момент
Неполучение данных
Непосредственно наблюдаемая
переменная
Непосредственный (прямой)
выбор
Непосредственный метод
отыскания производной
Неправдоподобное отношение
Непрерывная случайная
переменная (см. Множественный
анализ)
Непрерывность
Непрерывный вероятностный
закон
Непрерывный во времени
процесс
Непрерывный процесс
Неприведенный план
Неприводимая цепь Маркова;
неприводимая цепь
Неравенство Чебышева
Неравенство Шварца
Неслучайная выборка
Несмещенная критическая
область
Несмещенная оценка
Несмещенная оценка уравнения
Несмещенные доверительные
интервалы
Несмещенный критерий
Non-parametric delta method
Distribution-free method
Restricted randomisation; restricted
randomization
Group divisible incomplete block
design
Incomplete census
Incomplete data
Incomplete block
Incomplete Latin square;
Youden square
Incomplete moment
Non-response
Observable variable <
Direct sampling
Delta method
Unlikelihood ratio
Continuous random variable
Continuity
Continuous probability law
Temporally continuous process
Continuous process
Unreduced designs
Irreducible Markov chain;
irreducible chain
Tchebychev inequality
Schwarz’s inequality
Non-random sample
Unbiased critical region
Unbiased estimator
Unbiased estimating equation
Unbiased confidence intervals
Unbiased test
379
Несобственное распределение
Несобственный процесс
Несовершенное сплошное
наблюдение (Метод основного
массива)
Несогласованная выборка
Несоответствие
Несоразмерное число
(наблюдений) в подгруппе
Несущая переменная
Несущественные параметры
Несходство, несходимость
Неупорядоченные изменения
Неупорядоченные распределения
Неустойчивые гамма-модели
Неустранимое смещение
Нечистое распределение
Неэффективная оценка
Неявный слой
Нижний квартиль
Нижний контрольный предел;
нижний предел регулирования
Нижняя дисперсия
Новое использование выборки
Новое распределение лучше,
чем старое
Нуклеотидное разнообразие
Нулевое возвратное состояние;
переходное (во времени)
состояние
Нулевое различие
Нулевые выборки
Нулевые структуры
Область
безразличия
вида А
вида Б
вида Д
вида Е
вида С
Область изучения
Область приемлемости
Improper distribution
Dishonest process
Imperfect continued observation
(General data method)
Discordant sample
Non-compliance; non-adhere nee
Discordance
Disproportionate subclass numbers
Carrier variable
Incidental parameters
Discrepancy
Abrupt change
Abrupt distribution
Gamma-frailty models
Inherent bias
Contaminated distribution
Inefficient estimator
Implicit strata
Lower quartile
Lower control limit
Underdispersion
Sample reuse
New distribution is better than old
one; NDBO distribution
Nucleotide diversity
Null recurrent state;
transient state
Difference of zero
Sampling zeros
Structural zeros
Region
of indifference
Type A
Type В
Type D
Type E
Type C
Domain of study
Acceptance region
380
Область сферического среднего
Обобщенная
авторегрессивная модель, зависящая
от другой случайной величины
аддитивная модель
классическая линейная оценка
линейная модель
линейная скрытая и смешанная
модели
максимальная оценка вероятности
оценка наименьших квадратов
смешанная модель (факторного
эксперимента)
Обобщенное
биноминальное распределение;
биноминальное распределение
Пуассона
двумерное экспоненциальное
распределение
линейное интерактивное
моделирование
мультиноминальное распределение
нормальное распределение;
одномерное распределение Каптейна
правило решения Бейеса
распределение
распределение Парето
распределение степенного ряда
распределение Т2
распределение экстремального
значения
расстояние
Обобщенные
гамма-распределения; обобщенное
гамма-распределение Криди
и Мартина
оценочные уравнения
поликеи
Обратимая цепь скачков Монте-
Карло Маркова
Обрезка ветвей
Общий фактор-вариации;
относительная дисперсия
простых факторов
Общий фактор-пространство
Spherical mean direction
Generalised
autoregressive conditional
heteroscedasticity model
additive model
classical linear estimators
generalized linear model
Linear Latent and Mixed Models
maximum likelihood estimator
least squares estimator
mixed model
binomial distribution;
Poisson binomial distribution
bivariate exponential distribution;
generalized bivariate exponential
distribution
Linear Interactive Modelling
multinomial distribution
normal distribution;
Kapteyn’s univariate distribution
Bayes’ decision rule
distribution
Pareto distribution
power series distribution
T2 distribution
extreme-value distribution
distance
gamma distributions;
Creedy and Martin generalised gamma
estimating equations
polykays
Reversible jump Markov chain
Monte Carlo
Tree-pruning
Common factor variance;
communality
Common factor space
381
Однократный отборочный контроль; единичная ступенчатая выборка;, однократная выборка Ожидаемый критерий нормальных меток Оптимальное распределение (объектов в выборке) Оптимальное расслоение Ортогональные полиномы Чебышева Ортогональные таблицы Ортогональные функции Ортогональный план Ортогональный процесс Ортонормированная система Ослепляющий Основные компоненты Остаточный эффект условий эксперимента; остаточный эффект, последействие; отсроченный эффект Отрицательное гипергеометрическое распределение Отрицательное распределение Отрицательные моменты Отсечение Отсечение (для деревьев классификации) Оценка вариации путем расщепления Оценка просеивания Оценка смешанной регрессии Тейла Single sampling; unit stage sampling; unitary sampling Expected normal scores test Optimum allocation Optimum stratification Tchebychev orthogonal polynomials Orthogonal arrays Orthogonal functions Orthogonal design Orthogonal process Orthonormal system Blinding Principal components Residual treatment effect; residual effect; cany over effect; treatment- period interaction Negative hypergeometric distribution Inverse distribution Negative moments Cut-off Cut-off (for classification trees) Jackknife variance estimator Sieve estimator Theil’s mixed regression estimator
Параллельное распределение Парная кросстабуляция переменных с многомерными откликами Парный критерий-т Перекрывающий элемент выборки Переменная сопутствующая; ковариация Matching distribution Paired crosstabulation of variables with multidimensional responses Paired t-test Overlapping sampling units Concomitant variable; covariate
382
Пересекающиеся факторы
План когортной выборки
План непрерывного выборочного
контроля Доджа
План отсеивающего
эксперимента
Поверхность (двумерного)
распределения
Повторное обследование,
повторный сбор информации,
повторная выборка
Повторный выбор (из одной и
той же совокупности)
Повторный план измерений
Повторяемая игра
Погрешность метода
Подгонка центрированных
полиноминальных моделей
с помощью множественной
регрессии
Подтверждающий факторный
анализ
Поликей (семейство
симметричных многочленов)
Поликросс-методы
Полилинейный (многолинейный)
процесс
Полиноминальная регрессия
Полиноминальный
(многостепенной) тренд
Полиноминалы Лагуэрра
Полиноминалы Легендре
Полиномы (многочлены)
Чебышева—Хермита
Полиспектр
Полная корреляция
Полная оценка
Полная регрессия
Полнодостаточная статистика
Полностью пропавшие случайно
Полностью сбалансированный
решетчатый квадрат
Crossed factors
Case-cohort design
Dodge continuous sampling plan
Screening design
Frequency surface
Repeated survey
Rotation sampling
Repeated measures design
Recurrence game,
Procedural bias
Fitting of centered polynominal
models by means of multiple
regression
Confirmatory factor analysis; CFA
Polykay
Polycross designs
Multilinear process
Polynomial regression
Polynomial trend
Laguerre polynomials
Legendre polynomials
Tchebychev—Hermite polynomials
Polyspectra
Total correlation
Overall estimate
Complete regression; Total
regression
Complete sufficient statistics
Missing completely at random;
MCAR
Completely balanced lattice square
383
Полный класс решающих
функций
Полный класс тестов
Полный латинский квадрат
Полный набор латинского
квадрата
Полуразмах квартилей;
семиинтерквартильная широта
Полураспределение Каучи
Полустационарный процесс
Полуширина; полуразмах
Полярные координаты
Помеха, шум
Понижение размерности
Попарная независимость
Попарное удаление пропущенных
данных
Попарное удаление пропущенных
данных и подстановка среднего
Поправка Йейтса
Поправка на группировку
Поправка на группировку
Шеппарда
Поправка на крайнее значение
Поправка на недоучет
Поправка на ненулевую
плотность распределения
в конечной точке
Поправка Шеппарда
Поправочный коэффициент
Поправочный множитель
на конечность совокупности
или выборки; корректировка
конечной совокупности;
корректировка выбора из
конечной совокупности
Порог
Порядковая шкала
Порядок стационарности
стохастического процесса
Последовательная область
допустимых значений
Complete class (of decision
functions)
Complete class (of tests)
Complete Latin square
Complete set of Latin squares
Quartile deviation;
semi-interquartile range
Half-Cauchy distribution
Semi-stationary process
Half-width; semi-range
Polar coordinates
Noise
Dimension lowering
Pairwise independence
Pairwise removal of missing data
Pairwise removal of missing data
and mean substitution
Yates correction
Correction for grouping; Grouping
corrections
Sheppard’s corrections
End corrections
Deficit corrections
Corrections for abruptness
Sheppard’s corrections
Correction factor
Finite multiplier; finite population
correction;
finite sampling correction
Threshold
Ordinal scale
Stochastic process stationarity order
Sequential tolerance region
384
Последовательная процедура
Джирина
Последовательная статистика
линейного ранга
Последовательная схема
выборочного контроля
Последовательная схема;
перекрывающий план
Последовательно
цензурированная выборка
Последовательное оценивание
Последовательность
Последовательность выборочных
средних
Последовательный кластер
Последовательный критерий
Последовательный критерий Т2
Последовательный ряд
Последующая корреляция
Послойное сжатие
Поствыборочное обследование
Постепенное (плавное)
изменение
Постепенное устойчивое
воздействие
Постоянная (систематическая)
ошибка
Постоянно несмещенная оценка
Постоянный множитель первого
рода
Постсинаптическая
потенциальная функция (PSP)
Продольное обследование
Произвольное начало отсчета;
рабочее среднее; рабочее начало
отсчета; предполагаемое среднее;
принятое среднее
Произвольный порядок;
случайный порядок
Пространственно-временная
кластеризация
Пространственный точечный
процесс
Jifina sequential procedure
Serial linear rank statistics
Serial sampling inspection schemes
Serial design;
overlap design
Progressively censored sampling
Sequential estimation
Coherency, consistency
Progressive average consistency
Serial cluster
Sequential test
Sequential T2 test
Series queues
Trace correlation
Layered pressure
Post cluster sampling
Gradual changes
Gradual stable effect
Non-sampling error; Systematic
error
Uniformly unbiased estimator
Alpha factoring
Post-synaptic potential function
(PSP)
Longitudinal survey
Arbitrary origin;
working mean; working origin;
provisional mean;
assumed mean
Random order
Space-time clustering
Spatial point process
385
Пространство решений
Пространство событий;
выборочное пространство,
пространство выборок; описание
выборочного пространства
Профильный анализ; анализ
дисперсии продольных данных
Процедура стохастической
аппроксимации
Процедуры кумулятивных сумм
Процесс нахождения значения
(точки) кластера
Процесс объединения
Процесс с неограниченно
возрастающими средними
Распознавание образов
Распределение
анизотропное
асимметрическое многомерное бета
асимметрическое многомерное Ф
мультимодальное
сдвоенное
сложное гипергеометрическое
сложное отрицательное
мультиноминальное
четырехнормальное
частное
Расстояние
Бернулли
Бхаттачарииа
Евклидово кодовое
Кука
Махал ан обиса
Фречета
Харриса
Хэллингерса
Регрессия
множественная
полная
гребневая
полиноминальная
частная
Рекурсивный алгоритм
Рекурсивный остаток
Множественное решение
386
Decision space
Event space;
sample space;
sample description space
Profile analysis; analysis of variance
of longitudinal data
Stochastic approximation procedure
CUSUM procedures
Cluster (point) process
Coalescent process
Explosive process
Pattern recognition
Distribution
anisotropic
asymmetric multivariate beta
asymmetric multivariate F
multimodal
twinned
compound hypergeometric
compound negative multinominal
quadri-normal
marginal
Distance
Bernoulli
Bhattacharyya’s
Euclidean
Cook
Mahalanobis
Frechet
Harris
Hellinger’s
Regression
multiple
complete
ridge
polynomial
partial
Recursive algorithm
Recursive residual
Multi-valued decision
Решетка Риманг. геомехрия многообразие поверхность Робастная оценка Ротатабельный план Grid Riemann geometry manifold; variety surface Robust estimators Rotatable design
Сгруппированные данные Седельная точка Симметричная матрица Сингулярное разложение Склонное к выбросу распределение Скошенное распределение, несимметричное распределение Скрытая переменная, ненаблюдаемая переменная Скрытая структура Скрытый анализ класса; скрытый анализ особенностей Слабая (медленная, плохая) сходимость Сложное гипергеометрическое распределение Сложное отрицательное мультиноминальное распределение Сложное распределение Вишорта Гауссово Пуассона Сложный эксперимент Случайное поле Маркова (случайный процесс с многомерным временем или параметром) Случайное распределение Случайное самоизбегающее блуждание Смешивание Сокращение объема выборки без смещения (поисковый графический анализ) Integrated data Saddle point Symmetric(al) matrix Singular decomposition Outlier prone distribution Skew distribution Latent variable Latent structure Latent class analysis; latent trait analysis Weak convergence Compound hypergeometric distribution Compound negative multinomial distribution Complex distribution of Wishart Gaussian Poisson Complex experiment Markov random field Random distribution Self-avoiding random walks Confounding Reduction of sample volume without displacement (searching graphical analysis)
387
Сопряженные задачи
Сопряженные распределения
Сопряженный латинский корень
Среднее квадрата по условиям
испытаний (факторного
эксперимента)
Статистика
D2
классификаций Андерсона
меченых правдоподобий
основанная на рангах
рангов;
порядковая
Статистический уровень
значимости (р-уровень)
Тест
Зигеля-Таки
на двумерную симметрию
Холландера
на логарифмические ряды;
Мантела—Хаенжела
на разбиение на равные промежутки
на расхождение Таки
на симметрию Гупты
на улучшение
на ускорение
на экстремальный размах суммы
наименее значимого различия
пси-квадрата Неймана
пустая клетка
ранговой суммы Вилкоксона;
Вилкоксона; Вилкоксона—Манна-
Уитни; Манна—Уитни; Ю
реверсивного фактора
сконцентрированной вариации
совместного дисперсионного
отношения
Таки
Фишера—Ятса; Фишера—Ирвина
Ходжеса-Эйнса
Хотллинга (зависимые корреляции);
Т-тест
Тестирование групп
Тесты на рандомизацию;
критерий перестановки
Тесты ранговой рандомизации
Congestion problems
Conjugate distribution
Conjugate Latin squares
Treatment mean square
Statistics
D2
Anderson’s classification
Signed likelihood ratio
based on ranks
order
Statistical significans level (r-level)
Test
Siegel—Tukey
Hollander’s bivariate symmetry
Log-rank;
Mantel-Haenszel
Equal spacings
Tukey’s gap
Gupta’s symmetry
bootstrap
accelerated
extreme rank sum
least significant difference
neyman’s psi square; Neyman’s T2
empty cell
Wilcoxon rank sum; Wilcoxon's;
Wilcoxon- Mann—Whitney;
Mann-Whitney; U
factor reversal
lumped variance
simultaneous variance ratio
Tukey’s
Fisher—Yates; Fisher—Irwin test
Hodges-Ajne’s
Hotelling’s (dependent correlations);
T-test
Group testing
Randomisation tests; randomization
tests; permutation tests
Rank-randomisation tests; rank-
randomization tests
388
Тетрахорическая (четырех-
клеточная) функция
Тетрахорическая корреляция
Техника выпавшей делянки
Техника Дулиттла
Ти-тест замкнутой
последовательности
Толерантное распределение
Точечный процесс
Точка двумерного распределения;
двумерное распределение двух
дискретных переменных
Точка достижимости
Точка максимума; значение
точки максимума
Точка первого ввода
Точка разрыва; точка перехода
Точная идентифицируемая
модель
Точная матрица
Трансвариация
Трансформация Бокса-Кокса
Треугольные (одно- или
двукратно) блоки
пересекающиеся
Треугольный критерий
Треугольный план
Трехкомпонентная модель Бокса
Трехмерная решетка
Трехстадийные наименьшие
квадраты
Тригонометрические переменные
Тригонометрическое
преобразование; арксинус
преобразование
Триномиальное распределение
Тройная решетка
Тройное сравнение
Т-счет
Убывание
Убывающая интенсивность
отказов
Tetrachoric function
Tetrachoric correlation
Missing plot technique
Doolittle technique
Closed sequential t-tests; wedge
plans
Tolerance distribution
Point process
Point bivariate distribution;
bivariate distribution of two discrete
variables
Hitting point
Peak; peak value
Point of first entry
Preak point; change point
Just identified model
Precision matrix
Transvariation
Box—Cox transformation
Triangular (singly or doubly) linked
blocks
Triangle test
Triangular design
Bock’s three component model
Three-dimensional lattice
Three-stage least squares
Angular variables
Angular transformation; arc sine
transformation
Trinomial distribution
Triple lattice
Triple comparisons
T-score
Attenuation
Decreasing failure rate; Decreasing
hazard rate
389
Убывающая переменная
функция
Увеличение седельной точки
Увеличивающий фактор
Уровень фактора
Усеченная оценка наименьших
квадратов
Усечение справа
Усеченное нормальное
распределение Пуассона
Усиленная итерация
Ускорение посредством
усиления
Ускоренная стохастическая
аппроксимация
Ускоренное падение
временной модели
Ускоренное тестирование
времени
Факториальный анализ
Факториальный момент
Факториальный семиинвариант
Факторизационная теорема
Неймана
Факторная матрица; матрица
факторных коэффициентов
Факторная нагрузка; тест
коэффициента
Факторная таблица
Факторный анализ Була
Факторный эксперимент;
факторный план
Фидуциальная вероятность
Фидуциальный вывод
Фильтр
Фильтр Калмана
Функция среднего объема
выборки
Функция статистического
решения
Slowly varying function
Saddle point expansion
Raising factor
Level of a factor
Trimmed least squares estimator
Right-truncation
Poisson truncated normal
distribution
Iterated bootstrap
Acceleration by powering
Accelerated stochastic
approximation
Accelerated failure time model
Accelerated life testing
Factor analysis
Factorial moment
Factorial semiinvariant,
factorial culmilant
Neyman’s factorisation theorem;
Neyman’s factorization theorem
Factor matrix
Factor loading; test coefficient
Contingency table
Boolean factor analysis
Factorial experiment;
factorial design
Pistimetric probability (Fiducial
probability)
Fiducial inference
Filter
Kalman filter
Average sample number function;
ASN function
Statistical decision function
390
Циклические (нетранзитивные)
тройки; круговые триады
Частичная замена
Частичная ранговая корреляция
Частичная связь
Частичная сопряженность
Частично сбалансированная
решетка
Частично сбалансированные
планы
Частично сбалансированный
неполноблочный план
Частично сбалансированный
план сцепленного блока
Частично совместные
наблюдения
Частично среднеквадратический
Частичный план сцепленного
блока
Частная коррелограмма
Четырехкратная таблица;
четырехклеточная таблица
колебаний
Четырехугольник
Шкала отношений
Эволюционирующий спектр
Эволюционное планирование
(эксперимента)
Эволюционный процесс
Эквивалентная выборка
Эквивалентная доза
Эквивариантная оценка
Эквивариантная оценка
регрессии
Эквилибриум
Экспоненциальное
распределение; отрицательное
экспоненциальное распределение
Экспоненциальное сглаживание
Эксцесс, превышающий эксцесс
нормального распределения
Эффект Rm Хадсона
Ядро ковариации
Circular triads
Partial replacement
Partial rank correlation
Partial association
Partial contingency
Partially balanced lattice
Partially balanced arrays
Partially balanced incomplete block
design
Partially balanced linked block
design
Partially consistent observations
Partial least squares; PLS
Partially linked block design
Partial correlogram
Four-fold table;
two-by-two frequency table
Quad
Ratio scale
Evolutionary spectrum
Evolutionary operation
Evolutionary process
Equivalent samples
Equivalent dose
Equivariant estimator
Regression equivariant estimator
Equilibrium
Exponential distribution; negative
exponential distribution
Exponential smoothing
Leptokurtosis
Hudson's Rm
Covariance kernel
------------ Публикации В.М. Симчеры ----------------------
по методам многомерного анализа
статистических данных
1. Многомерные экономические классификации и группиров-
ки: учеб, пособие. — М.: Университет дружбы народов им. П. Лу-
мумбы, 1967.
2. Экономико-математические методы в зарубежных исследо-
ваниях. — М.: Статистика, 1974 (в соавторстве).
3. Межотраслевой анализ и эффективность производства. — Киев:
Наукова думка, 1974.
4. Статистические публикации в СССР. — М.: Статистика, 1974
(в соавторстве).
5. Проблемы экономической информации. — М.: Наука, 1975
(в соавторстве).
6. Очерки международной статистики. — М.: Наука, 1981 (в со-
авторстве).
7. Группировка и корреляция в экономике-статистических ис-
следованиях. - М.: Наука, 1982 (в соавторстве).
8. Развитие статистической науки в СССР. — М.: Наука, 1985.
9. Теоретические концепции в отечественной статистике. — М.:
Наука, 1986.
10. Статистические методы и анализ социально-экономических
процессов. — М.: Наука, 1990 (в соавторстве).
11. Методы экономико-математического моделирования. — М.:
ВЗФЭИ, 1989.
12. Многомерные статистические методы. — М.: ВЗФЭИ, 1990.
13. Практикум по статистике: учеб, пособие. — М.: Статинформ,
1999 (в соавторстве).
14. Энциклопедия статистических публикаций. — М.: Финансы
и статистика, 2001 (в соавторстве).
15. Финансовые и актуарные вычисления: учеб.-практич. посо-
бие. — М.: Маркетинг, 2002.
16. Введение в финансовые и актуарные вычисления. — М.: Фи-
нансы и статистика, 2003.
17. Организация государственной статистики в Российской Фе-
дерации. — М.: Госкомстат России, 2004 (в соавторстве).
18. Статистика: учеб, пособие. — М.: Финансы и статистика,
2005 (в соавторстве).
19. Развитие экономики России за 100 лет, 1900—2000 гг. Исто-
рические ряды. — М.: Наука, 2006.
Содержание
Предисловие...................................................3
Тема 1. Типология методов многомерного анализа данных........11
1.1. Вводные замечания..................................11
1.2. Методы многомерного эмпирического
и теоретического анализа данных.........................14
Рекомендуемая литература................................29
Тема 2. Методы многомерного корреляционного изучения данных...30
2.1. Вводные замечания...................4..............30
2.2. Методические указания по изучению темы.............35
2.3. Примеры решения типовых задач......................52
2.4. Задачи для самостоятельных занятий.................73
Тест ы и вопросы для самоконтроля......................77
Реко мендуемая литература..............................97
Тема 3. Методы многомерной обработки данных..................98
3.1. Вводные замечания..................................98
3.2. Методические указания по изучению темы...........101
3.2.1. Методы компонентного анализа................104
3.2.2. Методы факторного анализа...................113
3.2.3. Методы кластерного анализа..................116
3.2.4. Методы дискриминантного анализа.............122
3.3. Примеры решения типовых задач......................125
3.3.1. Примеры компонентного анализа..............125
3.3.2. Примеры факторного анализа.................131
3.3.3. Примеры кластерного анализа................134
3.3.4. Примеры дискриминантного анализа...........146
3.4. Задачи для самостоятельных занятий................185
3.4.1. Задачи компонентного анализа................185
3.4.2. Задачи факторного анализа...................188
3.4.3. Задачи кластерного анализа..................190
3.4.4. Задачи дискриминантного анализа.............192
3.5. Варианты компьютерных контрольных заданий.........193
3.5.1. Основные контрольные задания................195
3.5.2. Дополнительные контрольные задания..........198
3.5.3. Аудиторные задания..........................199
Тесты и вопросы для самоконтроля..................... 200
Темы для занятий.......................................202
Рекомендуемая литература...............................204
393
Тема 4. Методы многомерного моделирования данных...........206
4.1. Вводные замечания..................................206
4.2. Методические указания по изучению темы ............207
4.2.1. Методы градиентного анализа..................207
4.2.2. Методы линейного программирования............212
4.2.3. Методы межотраслевого анализа................216
4.2.4. Методы технико-экономических обоснований.....224
4.3. Примеры решения типовых задач......................228
4.3.1. Примеры градиентного анализа.................228
4.3.2. Примеры линейного программирования...........235
4.3.3. Примеры межотраслевого анализа................ 237
4.3.4. Примеры технике-экономического обоснования...245
4.4. Задачи для самостоятельных занятий.................285
4.4.1. Задачи градиентного анализа..................285
4.4.2. Задачи линейного программирования............288
Рекомендуемая литература.................................290
Тема 5. Методы многомерного сопоставления данных..............292
5.1. Вводные замечания..................................292
5.2. Методы определения однородных типов сопоставляемых
региональных образований............................292
5.3. Методические рекомендации по определению
однородности и тесноты взаимосвязи сопоставляемых
региональных показателей............................321
5.4. Методы определения многомерных рейтингов деловой
активности, предпринимательской уверенности
и инвестиционной привлекательности
регионов России.....................................326
5.5. Методы многомерного прогнозирования
региональных темпов экономического роста................351
Вопросы для самоконтроля................................367
Рекомендуемая литература................................369
Русско-английский словарь терминов
по многомерному анализу статистических данных................372
Публикации В.М. Симчеры
по методам многомерного анализа статистических данных........392
----------------------------- Contents -----------------------------------------
Foreword......................................................................3
Topic 1. Typology of multivariate data analysis methods......................11
1.1. Introductory remarks............................................11
1.2. Methods of multivariate either empirical
and practical data analysis......................................14
Recommended literature for further studying of topic..................29
Topic 2. Methods of multivariate correlation data analysis...............30
2.1. Introductory remarks.......................................... 30
2.2. Methodological directions on topic studying.....................35
2.3. Examples of routine problems solving............................52
2.4. Exercises.......................................................73
Tests and questions...................................................77
Reco mmended literature for further studying of topic..............97
Topic 3. Methods of multivariate data processing.............................98
3.1. Introductory remarks............................................98
3.2. Methodological directions on topic studying....................101
3.2.1. Methods of component analysis...........................104
3.2.2. Methods of factorial analysis...........................113
3.2.3. Methods of cluster analysis.............................116
3.2.4. Methods of discriminant analysis........................122
3.3. Examples of routine problems solving...........................125
3.3.1. Examples on component analysis..........................125
3.3.2. Examples on factorial analysis..........................131
3.3.3. Examples on cluster analysis............................134
3.3.4. Examples on discriminant analysis.......................146
3.4. Exercises......................................................185
3.4.1. Problems on component analysis..........................185
3.4.2. Problems on factorial analysis........................188
3.4.3. Problems on cluster analysis............................190
3.4.4. Problems on discriminant analysis.....................192
3.5. Variants of computer control problems..........................193
3.5.1. Variants of main control problems.......................195
3.5.2. Variants of additional control problems.................198
3.5.3. Variants of audit problems..............................199
Tests and questions............................................................................... 200
A topics for classes.................................................202
Recommended literature for further studying of topic.................204
395
Topic 4. Methods of multivariate data modeling........................206
4.1. Introductory remarks.......................................206
4.2. Methodological directions on topic studying................207
4.2.1. Methods of gradient analysis........................207
4.2.2. Methods of linear programming.......................212
4.2.3. Methods of inter-branch analysis....................216
4.2.4. Methods of feasibility studies......................224
4.3. Examples on problems solving..............................228
4.3.1. Examples on gradient analysis.......................228
4.3.2. Examples on linear programming......................235
4.3.3. Examples on inter-branch analysis...................237
4.3.4. Examples on feasibility studies.....................245
4.4. Exercises.................................................285
4.4.1. Problems on gradient analysis.......................285
4.4.2. Problems on linear programming......................288
Recommended literature for further studying of topic...........290
Topic 5. Methods of multivariate data comparisons..................292
5.1. Introductory remarks.......................................292
5.2. Determination methods of uniform types of regional formations
being compared..................................................292
5.3. Methodological recommendations on determination
of homogeneity and closeness relations of regional indicators
being compared..................................................321
5.4. Determination methods of multivariate ratings
(by the example of rating determination of business activity,
business confidence and investments attractiveness
of Russian regions).............................................326
5.5. Methods of multivariate forecasts on economic growth rate..351
Questions.......................................................367
Recommended literatuue..........................................369
Russian-English Glossary of widely used terms
on methods of multivariate analysis of statistical data.........372
Others books by Professor Vasily M. Simchera
on methods of multivariate analysis of statistical data.........392
Methods of multivariate analysis
of statistical data
Vassily M. Simchera
Moscow, Financy i Statistica Publishers, 2007, 400 p.
Unlike simple methods which operate with limited and as a rule
uniform sets of observations as well with as obvious relationships between
their characteristics, the multiple methods deal with unlimited and as a
rule separate and not obvious sets of observations as well as with multi-
directional and diverse relationships between their characteristics.
The subjects of observation and study in this book are as parametric
as non-parametric (qualitative, ordinal and rank) relations, deterministic
and non-deterministic (stochastic), mass and robust, true and false,
observable and non-observable (latent) phenomena, i.e. all kinds and
types of statistical combinations and relations which are inaccessible for
direct survey and study.
At the same time the diversity of objects being observed and multiplicity
of their properties, unobviousness and multi-direction of relations between
them are defined by multi-dimensional nature of phenomena being
observed which form the complex matrix multitude of intercrossed multi-
dimensional objects and features reflecting their relations which one cannot
explore and study using simple methods.
This book contains five topics referring to methods of multivariante
data analysis representing the subject of scrutiny and application of modem
statistics success ful application of which became possible because of
knowledge of subbjects nature beins studyed, their dimensions and manifold
types of multivariante relations.
There are methodological instructions for studying each topic, typology
of tasks being solved and examples of solving typical tasks as well as
exercises for practice presented in brief.
The solving big dimensional problems is made with appliance of
modem packages of electronic data processing in particular Statistica,
Stadia and Statgrafhics.
This book is intended for students, post-graduates and experts engaged
in application of multi dimensional methods for solving.big dimensional
applied statistical tasks problems.
Учебное издание
Симчера Василий Михайлович
МЕТОДЫ МНОГОМЕРНОГО АНАЛИЗА
СТАТИСТИЧЕСКИХ ДАННЫХ
Заведующая редакцией Л.А. Табакова
Ведущий редактор Н.А. Кузнецова
Младший редактор Н.А. Федорова
Художественный редактор Ю.И. Артюхов
Технический редактор Т.С. Маринина
Корректоры Т.М. Васильева, Г.Д. Кузнецова
Компьютерный набор И. В. Витте,
Е.Ф. Тимохиной, О. В. Фортунатовой
Компьютерная верстка И.В. Витте, Е.Ф. Тимохиной
Оформление художника Н.М. Биксентеева
ИБ № 5081
Подписано в печать 12.10.2007. Формат 60x88/16
Гарнитура «Таймс». Печать офсетная
Усл.п.л. 24,5. Уч.-изд. л. 22,7
Тираж 1500 экз. Заказ 692 «С» 125
Издательство «Финансы и статистика»
101000, Москва, ул. Покровка, 7
Телефоны: (495) 625-35-02, 625-47-08
Факс (495) 625-09-57
E-mail: mail@fmstat.ru http://www.fmstat.ru
Отпечатано в типографии
издательско-полиграфического комплекса
СтГАУ «АГРУС»,
г. Ставрополь, ул. Мира, 302.
Тел./факс: (8652) 35-06-94.
E-mail: agrus@stgau.ru; http:// agrus.stgau.ru
Василий Михайлович
СИМЧЕРА
Директор научно-исследовательского института статистики
Федеральной службы государственной статистики, доктор
экономических наук, профессор, Заслуженный деятель науки
Российской Федерации, действительный член Международного
статистического института и ряда других отечественных
и зарубежных научных обществ и академий, вице-президент
Российской Академии экономических наук. Автор более
50 монографии и учебных пособий по экономике и статистике.
Опытный педагог и профессиональный переводчик, организатор
и редактор энциклопедических изданий. Его оригинальные идеи
получили широкое признание научной общественности и высшей
школы. Настоящее издание представляет собой продолжение
учебного пособия ‘Статистика (М.: Финансы и статистика, 2006),
подготовленного с участием и под редакцией В.М.Симчеры.