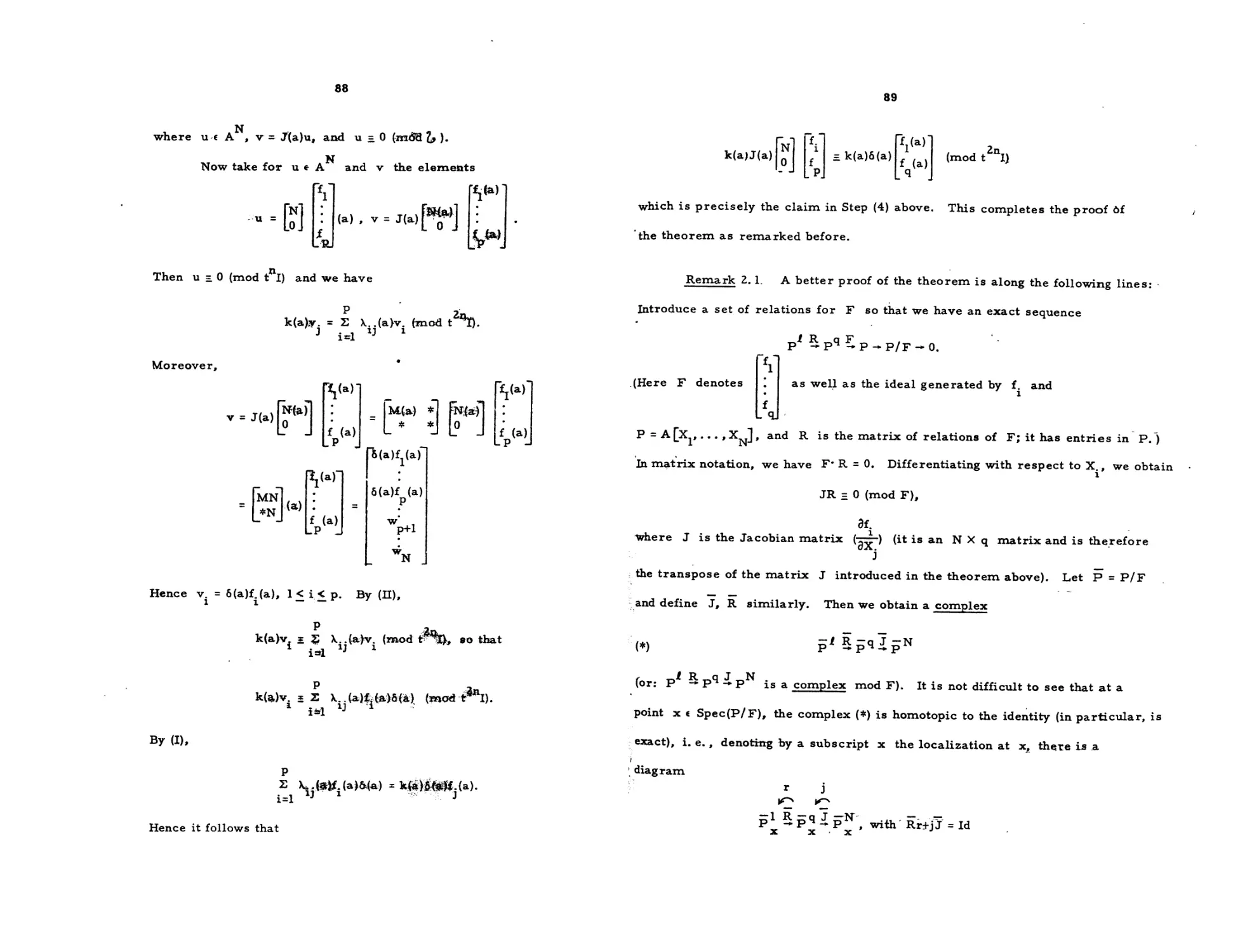
Текст
Lectures on
DEFORMATIONS OF SINGULARITIES
By
MICHAEL ARTIN
Notes by
C. S. Seshadri
Allen Tannenbaum
TATA INSTITUTE OF FUNDAMENTAL RESEARCH
BOMBAY
1976
TATA INSTITUTE OF FUNDAMENTAL RESEARCH, 1976
No part of this book may be reproduced
in any form by print, microfilm or any
other means without written permission
from the Tata Institute of Fundamental
Research, Colaba, Bombay 400 005
PRINTED IN INDIA
BY
AWL D. VED AT PRABHAT PRINTERS. BOMBAY 400 004
AND PUBLISHED BY
THE TATA INSTITUTE OF FUNDAMENTAL RESEARCH.
CONTENTS
Page
Introduction i
Part I: Formal Theory and Computations 1
1. Definition of deformations 1
2. Iarrobino's example of a O-dimensional scheme which is not a
specialization of d distinct points 4
3. The meaning of flatness in terms of relations 7
4. Deformations of complete intersections 11
5. The case of Cohen-Macaulay varieties of codimension 2 (Hilbert,
S chaps) 16
6. First-order deformations of arbitrary X: Schle s singer1 s T. ... 25
7. Versal deformations and Schles singer1 s theorem. 34
8. Existence of formally versal deformations. 40
9. The case that X is normal. 46
1Q. Deformation of a quotient by a finite group action 51
11. Deformation of cones. 52
12. Theorems of Pinkham and Schles singer on deformation of cones. 60
13. Pinkham1 s computation for the cone over a rational curve in IP . 67
Part II: Elkik1 s Theorems on Algebraization. 80
1. Solutions of systems of equations 80
2. Existence of solutions when A is t-adically complete 82
3. The case of a henselian pair (A,0C). 93
4. Tougeron1 s lemma. 100
5. Existence of algebraic deformations of isolated singularities. .... 104
Introduction
These notes are based on a series of lectures given
at the Tata Institute in January-February, 197 3. The lectures are centered
about the work of M. Schlessinger and R. Elkik on infinitesimal deformations.
In general, let X be a flat scheme over a local Artin ring R with residue
field k. Then one may regard X as an infinitesimal deformation of the closed
fiber Хл = X X/Dx Spec(k). Schlessinger1 s main result proven here in part
0 Spec(R)
(for more information see his Harvard Ph.D. thesis) is the construction, under
certain hypotheses, of a "versal deformation space" for X . He shows that
-j a complete local k-algebra A = limA/m and a sequence of deformations
X over Spec(A/m ) such that the formal A-prescheme 3Cs HmX is versal
in this sense: For all Artin local rings R, every deformation S/Spec(R) of
XQ may be obtained from some homomorphism A -• R by setting
Note that by 'versal deiormation11 we do not mean that there is in
fact a deformation of X_ over A. The versal deformation is given only as a
formal scheme. However, Elkik has proven (cf. "Algebrisation du module formel
d'une singularite isolee" Se'minaire, E. N. S. , 1971-72) that such a deformation
of X over A does exist when XQ is affine and has isolated singularities. We
give a proof of this result in these lectures.
Finally, some of the work of M. Schaps, A. Iarrobino, and H.
Pinkham is considered here. We prove Schaps1 s result that every Cohen-
Ma caul а у affine scheme of pure codimension 2 is determinantal. Moreover,
we outline the proof of her result that every unmixed Cohen-Macaulay scheme
{ of codimension 2 in an affine space of dimension < 6 has nonsingular deforma-
deformations. For more details
see her Harvard Ph. D. thesis, "Deformations of Cohen-Macaulay schemes
of codimension 2 and non-singular deformations of space curves". We also
reproduce Iarrobino's counterexample (cf. "Reducibility of the families of 0-
dimensional schemes on a variety", University of Texas, 1970) that not every
0-dimensional projective scheme (in IP for n > 2) has a smooth defor-
deformation. Finally, we give some of Pinkhamfs results on deformations of cones
over rational curves (cf. his Harvard Ph. D. thesis, "Deformations of algebraic
varieties with <E action),
m
There is of course much more literature in this subject. Two papers
relevant to these notes are Mumford's "Pathologies IV" (Amer, J. Math. , Vol.
XCVII, p. 847-849) in which expanding onlarrobino's methods he proves that
not every 1-dimensional scheme has nonsingular deformations, and M. Artin' s
"Versal deformations and algebraic stacks" (Inventiones mathematicae, vol. 2 7,
1974), in which is shown that formal versality is an open condition.
Thanks are due to the Institute for Advanced Study for providing
excellent facilities in getting this manuscript typed.
DEFORMATIONS OF SINGULARITIES
part I. Formal Theory and Computations.
$1. Definition of deformations.
We work over an algebraically closed field k.
Let X be an affine scheme, X«^* А.П. Let A be a finite (i.e., finite-
dimensional/k) local algebra over k, so that A~ k[t^ . . . , t^] /0L with
J&C = (t , . . . ,t ). Let T = Spec A.
Definition 1.1. An infinitesimal deformation X (or X ) of X is a
scheme flat/T together with a k-isomorphism X X^, Speck — X.
More generally, suppose we are given a commutative diagram
where R is a ring of finite type over к and X is a scheme with closed fiber
isomorphic to X. We then say that X is a family of deformations or a deforma-
deformation of X over R.
Remark 1. 1/ X is necessarily affine. In fact J a closed immersion
X ^а!1 ( = Spec A [X, . . . ,X ]) such that its base change with respecf to the
morphism Speck-* T (representing the closed point of Spec A) is the immersion
Let &= coordinate ring of X and <У= к [XJf . . . , Xj /I, with xi the
II
canonical images of Xi in &. To prove the remark, it suffices to prove
that if Xе-* A is an affine scheme (over A) imbedded in АП, A' is
A A A'
a finite local algebra/k such that
0-*J—A'—A — 0 is exact
with J = 0 (J is an ideal of square 0) and X , is a scheme/A» such that
XA' XSpecA' SPecA:rxA> then the immersion Xе-* A** can be lifted to an
immersion XA,^-~ A*, . (This reduction is immediate since the maximal ideal
is nilpotent. Say that m^t = 0, and take J = m^",1. . . ). We have an exact .
sequence
where
x
XA«
denotes the structure sheaf of X . Now I2 = 0 since J2 = 0.
A
This implies that I, which is a priori a(sheaf of) & module(s), is in fact
XA'
a module over & /I, i. e. , it acquires a canonical structure of coherent
A1
Crx -module. Since Хд is affine, it follows that н\х ,, I) = 0 (for it is
A a
= h\xa,I)). Hence
0-H°(XA,,I)-H°(XA,.
X
is exact, i.e., in particular H°(X GT )-* H°(X, cT )-0 is exact Let x
XA' XA ' Ц
be the coordinate functions on Хд which define Хдс-~ 1°, The x. can be lifted
to |. € H (XA, , &x ). Then the g. define a,morphism ? :X , - АП . It
A' A
follows at first that ^ is a local immersion; for this it suffices to prove that'
| generate the local ring & at every closed point x of X , . Let
1 A',x
1 be the stalk of the ideal sheaf I at a closed point x of X. We have
x
0 — I -+ & % — &* -~ Q (&* , , &\ represent the local rings at x
x A ,x A#x A ,x ' A, x
of XAI and XA respectively). We have I =J- сУ . Now j- 8 =j* 8
.A A xa,x it.
for j € J аш? 8., 8_ in & , such that their canonical images in & are
1 c, A f X A, X
the same. Let S be the subalgebra of & t generated by g. over A1.
A $ x l
Then we see that I = JS. Since J(^A' it follows that I C S. Since S maps
onto & t given X € & t , J s € S such that X-s € I . This implies that
Ay X А у X X
X « S. This proves S = & . We conclude then that ^ :X ,^1 , is a local
A x A A
v x
X ,^1 ,
A A
immersion. But ? is a proper injective map (since X
е-* A»
A A
is a closed im-
mersion). From this it follows that 4 is a closed immersion. This proves
the Remark.
Note that in the above proof we have not used the fact that XA, is
flat/A' .
Given the closed subscheme Xе-* Ж, let us define the following two
functors on the category of finite local algebras over k.
(Def. X) : (Finite local alg) - (Sets)
II
{Deformations of X /a}i- {isom. classes (over A) of schemes X flat/A and
such that XA ® к-
A
(Emb. def. XH -{Finite local alg.) — (Sets)
{Embedded deformations/A ь* {closed subschemes X of 1 flat/A, such that
of X} . A A
Xе—A by base change is the given X*~ A., }.
These should be called respectively infinitesimal deformations of X and
infinitesimal embedded deformations of X. Then we have a canonical morphism
of functors
(Emb. def. X) - (Def. X).
The above Remark says that f is formally smooth; that is, if A1 -*A -* 0
• is exact in (Finite local alg.), we have
(Emb. def. X)(Af) - (Def. X)(A')
I i
(Emb. def. X)(Af) -* (Def. X)(A)
(by definition of a morphism of functors), and the canonical map
(Emb. def. X)(Af) - (Def. X)(A!) X (Emb. def. X)(A)
\jjei. ада;
is surjective.
§2. Iarrobino's example of a O-dimensional scheme which is not a specialization
of d distinct points.
Given X as above, we can ask whether it can de "deformed" into a
nonsingular scheme. Here by a deformation we do not mean an infinitesimal
one, but a general family of deformations. Let us consider the simplest case
of Krull dimension 0. Then X = Spec & where & is a k-algebra of finite dim-
dimt2)
ension d. If d = 1, e^k. If d = 2, O'srk X к or ©^*k[t]/(t ). If d = 3,
we have
(k3 or к X k[t]/t2
or k[t]/t3 or k[X,Y]/(X,YJ
In our particular case the question is whether X can be deformed into d
distinct points of A. . Now A. C-*JP~ and we see easily that this deformation
implies a "deformation" of closed subschemes of IP , i. e. , if. X can be de-
deformed into d "distinct points" we see (without much difficulty) that this can
be done as an "embedded deformation" in A. and in fact as an embedded de-
deformation in IP . Let Hilb denote the Hilbert scheme of 0-dimen-
d
sional subschemes ZeL-* IP such that if Z = Spec В then В is of dimdoverk.
Then it is known that Hilb, is projective/k. Let U, denote the open sub-
a a —
scheme of Hilb corresponding to d distinct points, i. e. , those closed sub-
subschemes of IP corresponding to points of Hilb , which are smooth. We see
a
that U is irreducible; in fact, it is the d-fold symmetric product of IP minus
the "diagonals". Now if every O-dimensional subscheme can be deformed into
a nonsingular one, then U, is dense in Hilb , and it would follow that Hilb ,
ad a
is irreducible.
We shall now give the counterexample (due tolarrobino) where Hilb
d
is not irreducible. It follows therefore that a O-dimensional scheme cannot
in general be deformed to a smooth one.
Theorem 2.1. Let Hilb, denote the Hilbert scheme of closed 0-
- d,n
dimensional subschemes of IP of length d. Then Hilb, is irreducible
d, n
for n < 2. For n > 2, Hilb. is not in general irreducible.
~ d, n
Proof. We give only the counterexample for the case n > 2. Let
СГ1 =k[x.,...,X ]/(X.,...,X )r+1. Let I be the ideal in (Х)Г/(Х)Г+1 (where
u 1 nJ 1 n
(X) = (Xy . . . ,XJ). Then I is a vector space over к and
Rank of i/k = Polynomial of degree (n-1) in r
Rank of (У/к= " " " n in г.
Now I is an ideal in &x and in particular an &% module. Moreover, if
X с max ideal of &% then X-1 = 0. Hence &' operates on I through its
residue field. In particular, it follows that any linear subspace (over k) of
I is an ideal in 6Г' and hence defines a closed subscheme of Spec &x . Take
now 9 = j Rank I or j Rank I-\ according as Rank I is even or odd and
d = Rank(#"/V), where V is a subspace of I of rank 9. Hence 9= Polynomial
of degree (n-1) in r and d = Polynomial of degree n in r. Let us now
count the dimension of the set L of all linear sub spaces of I of rank = 9.
9
Then it is a Grassmannian and dimL = (j Rank I) or (j Rank I~j)(j Rank I+j)
9
according as Rank I is even or odd = (Polynomial of degn-1) in
r = Polynomial of degree Bn-2) in r. Now if П is the subscheme of Hilb
—- a d
of "d distinct points" as above, then
dimU, = d*n = n (Polynomial of degree n in r).
Now if r » 0, we see that
dimL > dimU,.
9 d
Since L can be identified as a subscheme of Hilb ,, it follows now that U,
9 ad
is not dense in Hilb,. To see that L_ is a subscheme of Hilb,,, note that
a 9 a
Spec &/1 as a point set consists only of one point. The family of subschemes
of IP parametrized by L as a point is given by (x XL ). It suffices to
9 о 9
check that on (x X L ), we have a natural structure of a scheme Г such that
9
IP Г is a closed subscheme of IP XL and p" (x) is
if the subscheme of Spec QT/l defined by the linear
subspace of I corresponding to x. Then we see that p : Г — L is flat, for
p is a finite morphism over L such that Ф" *s a sheaf of & -algebras;
9 1 LQ
in particular, <Э" becomes a coherent sheaf over С . At every X€ L ,
1 LQ 9
for &— ® <Э"Т , x/maxideal ( = &— ® k), the rank is the same. Since L_
Г Le Г 9
is reduced, this implies that & is locally free over & . In particular,
Г is flat/L..
§3. Meaning of flatness in terms of relations.
A module M over a ring A is said to be flat if the functor N^M ®
is exact.
<=> TorA(M,N) = 0 \/N/A.
q
<=> Tor^(M, N) = 0 V finitely generated N/A.
Let us now consider the case when A is a finite local k-algebra. Then
if N is an A-module of finite type, there is a composition series
N = Nq JNX D. . . D^ = 0, such that N./N^l ^k.
From this it follows immediately that
M flat/A <=5> Tor (M,k) = 0 (if A finite local alg/k).
Let X = Spec & , A finite local algebra and & an A-algebra of
iinite type so that we have
exact with P = A [x] (X = (X , . . . ,X )). Tensor this vrith k. Then we have
Let X = Spece;, X%X 0k, I ideal of X in A . Then
к A.
XA is flat/A <=> Tor.(e\ ,k) = 0,
A 1 A
<=> I ® к = I.
A
Take a presentation for the ideal I in P , i. e. , an exact seque
A A
IA
(*)
Then we have (because of the above facts): & }± A-flat <=> the above pre-
1 —— ———- ————— — ——— ——— ^
sentation for I tensored by k, gives a. presentation for I, _L je. , tensored
by к gives again an exact sequence
that its ®A к is the given exact sequence Pm — P -» & -* 0. Note that this
need not imply that I ® к = I if I = Ker(PA - &A and I = Ker(P-c^).
A A A A
Suppose we are now given a "complete set of relations" (or a presen-
presentation for I) between ?\s, i. e. , an exact sequence
Then giving a^ lifting of these relations to that of f! ¦ s (or I ) is to give
1 A
A A A A
which extends the exact sequence РШ -* P - & - 0, which is a complex
A A A
at PA, i.e., ImPACKer(P^-PA) and such that (**) lifts (*). In this
situation we have the following
Proposition 3. 1. Suppose
k
/\
0 0
(**) is exact and
<**>
is a complex such that the part
Suppose we are given!
<ЭГ= Kfxi/tf,,. . .,f ) and liftings (f!) of (f.) to elements in A.[x]. \
u J 1 m li
m
Let I = (f1f . . .,f ), IA = (f!,. . . , f ) and €ГД = A [x] / (?\ , . . . , f! ). These ? A "* A "* A "*
1 m A 1 m A x m .; \
data are equivalent to giving a lifting P™ - Рд - &A - 0 of the exact sequence V,, ^^ ^ (^} y = {^ Then & ^ ^^
-¦ CC -* 0, i. e. , to giving an exact sequence P -* P -* & -*• 0 such
Proof. Suppose first that
10
и
(**)
is exact not merely a "complex at Pm". Then we claim that the flatness of
A
& over A follows easily. For then (**) can be split up as:
Corollary Let &= k[x]/(f . , f ) and & = A [x]/(f' . . , f )
l m A 1 m
where f! are liftings of f.. Then
is A-flat <=> every relation among (f.,. . . , f ) lifts to a relation
1 m
among
exact.
Therefore P* ® к - L. ® к-* 0 and L ® к - Pm ® к - I ® к -* 0 are exact.
А А А л л
This implies that 1Д 0 к = Coker(k ® P^ - к ® P™), i. e. , cokernel is pre-
preserved by к ® . On the other hand, I = Coker(P — P ). Hence 1Д ® к = I.
From this it follows that & is flat/A as remarked before. Now the hypotheses]
of our proposition amount to the fact that all relations in I can be lifted to I .
Given a relation in I , i.e., an m-tuple (X?, . . . , X' ) such that SX!f' =0,
A -i m l i
this descends to a relation in 1 by taking the canonical images of X^ in P.
Take a complete set of relations for I , i. e. , an exact sequence
A
f' m
U)
(i1 need not be I),
then from our above argument this descends to a complete set of relations for
I, i. e. , tensoring (i) by к we get an exact sequence
(ii) Pi? -*Pm-P-(^-0.
Consequently, we have already shown in this situation that we must have ©*"
to be A-flat. q. e. d.
Remark 3. t. It is seen immediately that
O: flat/A => I flat/A.
A A
For, the exact sequence 0 — I — P — €f -* 0 by tensoring by к gives
A A A
0 0 0
II II II
Tor (У -k)-Tor (I k)-Tor1(P.,k)-*Tor.(©'..kJ-l-P, -^-0.
?• ¦"> LA 1A 1A к
This implies that Tor (I ,k) = 0, hence that I is flat/A, by a previous
1 A A •
Remark. Repeating the procedure for <Э^А, we see by successive reasoning
' A
that any resolution for & lifts to one for <У .
A
$4. Deformations of complete intersections.
Let Xе- A. be a complete intersection. Let d = dimX (Krull dim)
and I = (fx, . . . , fQ_d) the ideal of X. Let & = P/l, where P = P = к [x ,. . . , X ]
Then it is well known that the "Koszul complex" gives a resolution for & , i. e. ,
the homomorphisms being interior multiplication by the vector
The criterion for flatness can again be formulated as follows:
12
13
{iy . . .|»f ,) « P » (e. g. , P — P is the map (\ ,. . . , X .) *~ L.X.f.).
The image of ЛрП" in Pn" gives the relations in I, which shows that the
relations among the f. are (generated by) the obvious one-s, i. e. , f.z.-f.z. = 0.
Let A = k[t]/(t ) (which we write A = k+kt with t = 0). Then
deformations of X over A are called first order deformations. Let I be
the ideal in /К Гх,,. . . , X 1
iA =
where g. « P.. We claim that for arbitrary choice of g. « P., & =PA/IA
1 к -—-_ — 1 К А A A
is flat over A (of course we have seen that any deformation X of X can be
defined by I for suitable choice of g.). This is an immediate consequence of
the fact that the above explicit relations between f. can obviously be lifted to
relations between (f.+g.t). This proves the claim.
Thus to classify embedded first order deformations it suffices to write
down conditions on (g.)# (g!. ) in P so that in P the ideals ((f.+g.t)) and
l 1 A 1 1
((l+g[t)) are the same. We claim;
((f.+gjt)) = ((f.+g! t)) <=> g.-g« € I.
To prove this we proceed as follows:
(r X r) matrices (a..) and (p..) with coefficients in P such that
, i.e.. (a..-Id)C ) = @), and
(a)
(о.
.)
J
V
f
=
Y
f
(b) (a..)
+ (P..)
Since the coordinates of the relation vectors are in I it follows from (a)
above that the elements of (a..-Id) are in I, i. e. , (a) => (a..) = (Id)(mod I).
Then (b) implies that
(mod I).
Hence ((f.+g!t)) С ((f.+g.t) => (g.-g!) € I. Hence ((f.+g.t)) = ((f.+g!t)) => (g.-g^c I.
Conversely, suppose that (g.-g!)c I. Then there is a matrix (p..) such that
(P..)
•
•
f
_ г
=
.
gi
g
tf.+g! t)) С ШЛЯЛ)) <=>
(Set r = n-d.)
Hence, (Id)
V
\
gr
+ (pjj)
Y
\
gi"
_g'r_
г
= (Z Q;;
Г Г
tB a..g. + 2
Taking (а_) = Id we see that the conditions (a), (b) are satisfied, which implies
that ((f.+g.t)) = ((Г+g! t)). This proves the claim and thus we have classified
14
15
all embedded (in A. ) first order deformations of X.
Now to classify first order deformations of X we have only to write
down the condition when two embedded deformations X , X1 are isomorphic
A A
over A. Let в be an isomorphism X. 'X X\ . By assumption, X в к =
X' в к = X, i. e. » their fibres over the closed point of Spec A are
We denote {of course) by X the canonical coordinate functions of X «-» A. =
Soec A [X ,..., X J. Let X^ = 6*(Xy). Then we have
x;=xv+?v(x)t
for some polynomials <P (X). Hence to identify two embedded deformations of
X we have to consider the identification by the above change'of coordinates.
Then
By Taylor expansion up to the'first order, we get
= f (X) + t {g.(x)
{g.(
v=l
Hence (f.+g.t) and (f.+g! t) define the same deformation of the first order
up to change of coordinates above, which is equivalent to the fact that there
exists (CD ,,. . , <pn) such that
V
У
эх, эх
1 n
9f 9f
г ... г
ЭХ, ЭХ
_ 1 n
"9 Г
(*)
Recall that &- P/l and X = Spec &. Then embedded first order deformations
are classified by Ф =©'Э...9<У (n-d times), which is an &- module .
To classify all deformations, consider the homomorphism of P modules
T
Jac.
, di. 3f. 3f.
& whose matrix is fef-)j "ггг* the images of 3V in P/I.
dX. dX. dX.
Let us call the quotient & " /imC by this map T. This is an
С-module and we see that its support is located at the singular points of X.
In particular, if X has isolated singularities, T is a finite dimensional vector
space/k.
For example, consider the case that X is of codimension one, i. e. ,
defined by one equation f. Then
'¦"МЦ э5Г>-
1 n
The cone in 3-space has equation f = Z -XY, and if char к f 2,
T = к [X, Y, Z] / (f, - Y. -X, 2Z) 3- k.
Thus a universal first order deformation is given by
Z2-XY+t = 0.
16
17
$5- The case of Cohen-Macaulay varieties of codim 2 in A (Hilbert, Schaps).
The theorem that we shall prove now was essentially found by Hilbert.
This has been studied recently by Mary Schaps.
Let P be as usual the polynomial ring P = k[X ,. . . , X ]. Let
(g..) be an (r X r-1) matrix over P
elr-l
r,r-l
Then F^ ...,6r)
. Let 6. = (-1I det((r-l) X (r-1) minor with ith row deleted).
r,l'** gr,r-l
= 0; for, det
T,l'- gr,r-l' gr,l
= 0, etc.
is exact, i. e. , it gives a resolution for P/J.
2) Conversely, suppose given a Cohen-Macaulay closed subscheme
Xе-* АП of codim 2. Let X = V(J); then P/J has a resolution of length 3
r-l(gii) rV'-'V
which will be of the form 0 - P —±*+ P * P -* P/ J -* 0, because
hdpP/J = 2. (Depth P/j+hdpP/j = n, depth P/J .= n-2, => hgP/J = 2. ) Note
that f. need not be 6. as defined above. Then we claim that we have an iso-
isomorphism
О
0 -*
r'6l'---'6r>
P
ist.
This implies that the sequence
V Fi V
(g..) has rank (r-1), or equivalently, J some x € A such that (g..(x )) is
of rank (r-1).
Theorem 5. 1 (Hilbert, Schaps).
1) Let (g..) be an r X (r-1) matrix over P and 6. its minors as
defined above. Let J be the ideal F^ . . . , б ). Assume that V(J) = VF.,. . . , б )
is of codim > 2 in A , Then X = V(J) is Cohen-Macaulay, precisely of
codim 2 in A . Further, the sequence
r
Fl
,6 )
i. e. , J a unit u € P such that f. = иб..
3) The map of functors (Deformations of (g..)) — (Def. X) is smooth,
i.e., (i) deforming (g..) gives a deformation of X, (ii) any deformation of
X can be obtained by deforming g.., and (iii) given a deformation X of X
ij A
defined by (g..) over A[x], A1 -*A-*0 exact and a deformation X , of X
inducing XA, 4 (g1..) over A1 [xl which defines Хд| and the canonical
A —' ij L J A1
image of (g|L) in A is (g ).
that
Proof. A) Let (g..), 6., etc., be as in A). " We shall first prove
o-p-Vp.
is exact, assuming codimX> 2. - This will complete the proof of A). For, it
follows hd P/J<2. On the other hand, since codimX>2, depth P/j<(n-2).
18
19
But depth P/J+hd P/J = n. This implies that. dimP/j = depthP/J = (n-2)
and hd P/J = 2, which shows that X. is Cohen-Macaulay of codim 2 in A .
Since V(J) к A , the 6.'s are not all identically 0, hence
0 —P " -* P is exact. Further we note that at any x / V(J), (g. .(x )) is
о ij о
of rank (r-1) and in fact one of (б.,. . . , 6 ) is nonzero at x and hence a
1 г о
unit locally at x . This implies that РГ" — рГ -* P is split exact locally at
—___ Q _________
x (i. e. , if В is the local ring of A. at x , then tensoring by В gives a
о о
split exact sequence). Because of our hypothesis that codim V(J) > 2, if x
is a point of Ж represented by a prime ideal of height one and В its local
ring, then tensoring by В makes P — P — P exact (i. e. , the sequence
is exact in codim 1). Let К = Кег(РГ-Р). We have KQ P* such that
0 — P " — K, and, 0 - K— P — P exact. Tensoring by В as above, it follows
that P 0 В —К ® В is an isomorphism (tensoring by В is a localization);
i.e. , the inclusion P С К is in fact an isomorphism in codim 1. Since рГ~ is fre$
sections of P defined in codimension 1 extend to global sections. Moreover,
К is torsion-free. Therefore, the fact that P С К is an isomorphism in
codimension 1 implies that it is an isomorphism everywhere. Therefore,
P " -* P ¦* P is exact, and this completes the proof of A).
B) Let I = (f ,. . . ,fy) be a Cohen-Macaulay codim 2 ideal in P.
Since hd P/l = 2, there is a resolution
(*)
"'•••'V
(Here we should take the warning about using free resolutions instead of using projec-
tive resolutions. ) Let the complex (*#) be defined by
(**)
r
0 -» РГ
-^P-P/J-O,
6. being as before.
The sequence (*) is split exact at every point x / V(I). This
implies that some 6. is a unit at x, and hence by direct calculation that
(**) is also split exact, and P/J = 0, at x. This means
V(J)CV(I),
hence codim V(J) > 2. Hence by A) it follows that (**) is exact.
We shall now show that
a unit u such that
Take the
dual of (*) and (**) (dual: Homp(M, P) = M ), i. e. ,
(*)
(**)*
<pV
) F.)
We claim that these sequences are exact. The required assertion about the
* {?)Л * г
existence of и is an immediate consequence of this. For then P * (P )
3 (S.) # r % r
and P * (P ) are injective maps into the same submodule of (P ) of
rank 1 which implies that (f) and F) differ by a unit. We note that
{1±?
l ff!
P and
-> Р
5r. P are split exact in
codimension 1. Consequently, it follows from this and the fact that
Horn (P/I,P) = Horn (P/J, P) = 0 that we have sequences
20
21
О -* р
Conversely, let X be an infinitesimal deformation of X = VF ,. . . , 6 ).
Lift the generators for I to I say (f , . . . ,f ). Then as we remarked before
A 1 Г
the exact sequence (*) can be lifted to an exact sequence
г*
and we must prove exactness at the P module. But we have that
bnf. CKer(g..) and ImF.) CKer(g..) with equality at the localization of
each prime ideal of height 1. Consequently, bnf. = Ker(g..) , ImE.) = Ker(g..)
(same argument as was used above). This completes the proof of B).
C) Let A be an Artin local ring over k, and P = A[X , . . . , X ].
Let (gl.) be an r X (r-1) matrix over P and (g..) the matrix over P such
ij A lj
that g!.*-*g.. by the canonical homomorphism A [x] -»k[xj. Define 5| analo-
analogous to 6.. Suppose that codimVF! ) in 1 is of codim >^ 2 <=> codimVF.)
1 1 A l
in A is of codim ]> 2 <=> codimVF.) = 2 because of A). Consider
(**)
0 -
г (б!)
? —-— Р — Р /I — О
А А А А
(**)¦
r-l^lj» r(fi>
р J— p — р — р /I
А А А А' А
[Note that f. need not be (a priori) the determinants of minors of (gl.). J
Let 6'. be the minors of (g!.), J the ideal F', . . . , 5' ). Then as we saw above
l ij A 1 г
(**)
is exact and PA/JA is A-flat. Taking the duals of (**) and
———— A. A
)' as before,
it follows that there is a unit u in P . such that f. = u6! . This shows that
A li
I = J . Thus any deformation is obtained by a diagram of type (**). The
A A
assertion of smoothness also follows from this argument. This completes the
proof of the theorem.
E.)
(*)
0-]
•P-*P/I-*0.
Now (#*) is lifting of (#). Of course (*) is exact and P* — P -*PA/JA"*°
A A A. A
is exact. Besides, (**) is a complex. This implies by Proposition 3.1 that
PA~ -* PA — PA -* Рл /JA — 0 is exact and PA/IA is A-flat and by Remark 3. 1
A A A A A A A 7
(**) is exact. (The exactness of (**) can also be proved by a direct argument
generalizing A).) This shows that any (infinitesimal) deformation (g!.) of (g..)
as in A) gives a (flat) deformation X of X = SpecP/l and that X is "pre-
A A
sented" in the same way as X.
Remark 5.1. Any Cohen-Macaulay Xе-
of codim 2 is defined
by the minors of an r X (r-1) matrix (g..) (this is local, note the warning about
using free modules instead of projective ones). The g..1 s define a morphism
пФ Mr(r-1)
Let Q=k[x..], l<i<r, i< j< r-1, so that АГ^Г"^ = Spec к [Х..].
Then Ф (X..)=g... Consider (X..) as an r X (r-1) matrix over Q, and let
Д. = (-1I det(minor of X.. with i* row deleted). Then the variety
22
23
V = V(A , . . . , Д ) -* A is called the generic determinantal variety defined
by г X (r-1) matrices. It is Cohen-Macaulay and of codim 2 in A
Then ф" (x) = X. This means that any Cohen-Macaulay codim 2 subscheme
is obtained as the inverse image by A -»1 of the generic determinantal
variety V of type r X (r-1).
<f € Hom(A , A. " ) and (V € X , then im Gf> is a k-dimensional space. Hence
Ф is determined by an arbitrary k-dimensional subspace of A. { = kerfl?)
an (r-k)-dimensional subspace of A { = Im CD) and an arbitrary linear
map of an (r-k)-dimensional linear space onto an (r-k)-dimensional linear space.
Hence
Remark 5. 2. Other simple examples of codim 2, Cohen-Macaulay
dimX =
= (r-k)k+(r-k)(k-l)+(r-kJ.
X are
(a) any 0-dimensional subscheme in A ,
(b) any 1-dimensional reduced X in A , and
(c) any normal 2-dimensional X in A .
More about the generic determinantal variety.
Now let
denote the determinantal variety У(Д.) = V defined
above. Then any infinitesimal deformation X of X is obtained by the minors
of a matrix (X. .+m..) where m.. € mA Гх. Л, where mA is the maximal ideal
of A. Set X|. = X. .+m... We see that X.. »-» X!. is just change of coordinates
4 4 4 lJ 4
in A^, i.e., A[X..] =A[X!.]. This implies that X is rigid, i.e., every de-
formation of X is trivial.
The singularity of X: X can be identified with the subset of
Ж = Horn.. (A , A ) of linear maps of rank < r-2. Now
linear r -
G = GL(r) X GL(r-l) operates on A ~ in a natural manner. Let X
к.
denote the subset of A of linear maps of rank equal to (r-k). We note
that X is an orbit under G and hence is a smooth, irreducible locally closed
subset of A To compute its dimension we proceed as follows: If
Suppose к = 2, i. e. , consider linear maps of rank (r-2). Then X is obviously
open in X and
dimX2 = (г-2J+(г-2)+(г-вГ = (r-2J+l+(r-s) = (r-
It follows that codim X = 2.
It is clear that X is dense in X (easily seen that every x € X is a
? , . о
specialization of some x tf. X ). This implies that X is irreducible. Further-
Furthermore, X is smooth, and in particular reduced. By the unmixedness theorem,
since X is Cohen-Macaulay, it follows that X is reduced. Hence X is a
subvariety of АГ*Г~1}.
Let X1- = X UX ... be the s.$t,p|?all linear maps of rank ? (r-3).
Clearly X' is a closed suoset of X. To compute its dimension it suffices
to compute dimX-, as we see easily that X. is a dense open set in X' Now
dimX3 = (r-3K+(r-3J+(r-3J = (r-3)(r+2).
Hence codimX^ (in АГ*Г~ ') = 6, for r > 3. (If r = 2 it is a complete inter!-*
section; X is the intersection of two linear spaces and hence X is smooth. )
24
25
Hence codirnX. in X is 4. We claim also that every point of X' is
———— j — — j
singular on X. To prove this, suppose for example 0 € X . Since G acts
transitively on X-, we can assume it is the point
9 =
1 0 0
0 10
0 0 1
ЭД.
Then
= 0 Vk, 1. Thus 9 € X is smooth <=> 9 € X .
Thus the generic determinantal variety has an isolated singularity if
and only if r = 3, in which case dimX = 4, XC A6 ( = A**1"*). We thus
get an example of a rigid isolated singularity (a 4-dimensional isolated Cohen-
Macaulay singularity).
Proposition 5.1 (Schaps). Let X c-* A (d _< 5) be of codim 2 and
Cohen-Macaulay. Then X. can be deformed into a smooth variety.
Proof. We give only an outline. Since X. is determinantal, it
0
is obtained as the inverse image of X in A by some map
Now codimX in
A -¦ A
is 6. "Perturbing" (g..) to (g!.)=<p!, the map
, defined by (g!.) can be made "transversal" to X. This implies
that qp1 (A )PlSingX = 0 [ Sing X is of codim 6] and in fact that q> ' ~\x)
is smooth.
Remark 5. 2. It has been proved by Svanes that if X is the generic
determinantal variety defined by determinants of (r X r) minors of an (m X n)
matrix, then X is rigid, except for the case m = n = r.
$6.. First order deformations of arbitrary X and Schlessinger1 s T .
Let X = V(I) and A=k[t]/(t2). Let I = (f ,. . . , f ). Fix a presenta-
presentation for I, i. e. , an exact sequence
(*)
Let I = (f' ..,f ) where f| = (f.+tg.), g. € P. Then X. = V(I) is A-flat
Aim iiii AA
if (*) lifts to an exact sequence
(**)
, (r!.) (f!)
A A A A A
In fact we have seen (cf. Proposition 3.1) that in order that (**) be exact it
suffices that (**) be a complex at Pm, i. e.,
_ A
X = V(I ) is A-flat iff there is a matrix (r!.) over P extending
(г„), such that
Set r!. = r..+ts.., where s..€ P. Then X is A-flat iff J (s..) over P
such that the matrix product
(f+gt)(r+st) = fr+t(gr+fs) = 0,
27
where f = (f.),. . . , г = (г..). Now fr = 0 since (*) is exact. Thus the
flatness of X over A is equivalent with the existence of a matrix s = (s..)
A ij
over P such that
<*)
(gr)+(fs) = 0.
j : (First order def. of X) -* H°(X, N__)
is injective, which implies, since j is surjective, that j is indeed bijective.
The proof that I = J is immediate; from the computation in §4 we see that
A A
Consider the homomorphism
<=> J (m X m) matrices (a..) and (p..) over P such that
<g):Pm-*P
defined by (g..). Then condition (*) implies that (g) maps Imp under the
homomorphism (г..) : P -¦ P into the ideal I. Hence (g) induces a homo-
homomorphism
(g) : РШ/1ш(г) = I - P/I,
i. e. , g is an element of Homp(I, P/I) - Homp/l<I/l2, P/l) = Hom^ (I/I2, &x) =
X
the dual of the coherent Cv module I/I on X. The sheaf Horn— (I/I ,& ) =
X <3"х X
Nv is called the normal sheaf to X in A . Thus g is a global section of N.
Conversely, given a homomorphism g : Horn (I, P/I) and a lifting of g to
g : P -* P, then (g) satisfies (*). This shows that we have a surjective map
of the set of first order deformations onto H (X, N ). Suppose we are given
X
two liftings (f+tg ) and (f+g_t) such that g , g define the same homomorphisms
1 ?* 12
of I/I into P/I, i.e., ~g ="g . We claim that if I = ((f.+tg1 .) and
ic, A i 1, i
J = ((f.+tg .)), then I = J , i. e. , the two liftings define the same sub-
A 1 ut 1 A A.
scheme of A . This will prove that the canonical map
A
5l,m
As was done in §4, if (g^ = (g2), i. e
gli"g2i ~
Then there exists (p..) such that (a) and (b) are satisfied with (a..) = Id.
This implies that J QlA* In a similar manner I Q J , which proves that
A A. A A
J = I . Thus we have proved
Theorem 6.1. The set of first order embedded deformations of X
in Ж is canonic ally in one-one correspondence with N (or H (NY))--the
X X
normal bundle to X of ([
Remark 6.1. Suppose now we are given
0 - eA1 -*Af -*A-0 exact
2В
where A1 , A are finite Artin local rings such that rk, (cA1 ) = 1 (in particular
it follows easily that t is an element of square 0). We see easily that eA1
has a natural structure of an A-module and in fact eA1 ~A/m as A-module.
"""" A
(Given any surjective homomorphism A1 -* A of Artin local rings by successive
steps this can be reduced to this situation. ) Suppose now that X. is a lifting
of X defined by V(I ), I = (f' . . . , f' ) with f! s as liftings of f., X = V(I),
A A l m i l
I = (fj,. . . , f^). We observe that even if A is riot of the form k[t]/t , in order
that X be flat/A andbe a lifting of X it is neccessary and sufficient that
A
there exists a matrix (r!.) such that
l' * '' ' fm)(rij) = ° (fl are liftings of f ).
Suppose now we are given two liftings X^, and X|, of Хд, flat over A defined
by V(I^,) and V(l|,):
Now XA is defined by an exact sequence
(*)
such that 0 к gives the presentation for X. An easy extension of the argu-
argument given before (cf. Proposition 3. 1) for characterization of flatness by lifting
of generators for I shows that X' and X are flat/A. They are presented
respectively by
(a)
exact
29
p
A'
such that (a 0 , A) and (p 0 A) coincide with (*) and in fact it suffices
A A
that (g)(s) and (g1 )(s' ) are zero and s, s1 are liftings of r. We can write
g! = g.+eh., with h. с Р, and
g! = g..,
s!. = s..+et.., with t.. с P.
ij iJ ij ij
Then (g1 )(s' ) = 0 iff (g.)(t..) + (h.)(s..) = 0, and by the remark about eA1 as
an A-module (or A' -module) it follows that the right hand side above is 0 if
and only if
(t)
.)(..)
О(г..)
0,
i.e., j (t..) and (h.) over P such that this holds. Conversely, we see that
given XAt flat/A1 and (-{-), we can construct X , flat/A1 by defining
A A
g! = g.+eh. and lifting of relations by s!. = s..+et... Now ("(¦) gives rise to
N as before. Thus fixing an X1 flat/A1 which is a lifting of X flat/A
л А А
the set of flat liftings X , of X over A are in one-one correspondence with
A A
Nv (or H°(N_J) or in other words the set of flat liftings X , over X. is
X X A A
either empty or is a principal homogeneous space under N (ojr H (N )).
In the case A = k, A! =k[t]/(t ) (or more generally A1 = A [~e~)) we us e
X. , = X 0, A1 (resp. Хд| =ХА 0Д А1 ) as the canonical base point, and using
А1 к ь A? A A ^ a
this base point the set of first order deformations gets identified with Nv or
H°(NX).
Remark 6. 2. Compare the previous proof (cf. 5 4) for the calculation
ai
зо
of first order (embedded) deformations of X--a complete intersection in A .
In that proof we required the knowledge of the relations between f.1 s where
X = V(I), I = (f., . . . ,f ) whereas this is not required in the present proof (we
1 m
assume X arbitrary). This is because in the proof for the complete inter-
intersection we obtained a little more, namely, (First order embedded deformations
of X) *¦-* {g.}, g. « CVr* The previous proof gives also the fact that N i^
i i X X
free over <5^ of rank = codimX. Hence a better proof for the case of the
X
complete intersection would be to prove first the general case and then show that
i/l is free of over & of rank = codimX (in A ) (this implies that N =
X X
Hom^ (I/I2, C_J is free of rank = codimX).
Remark 6. 3. The above proof also generalizes to the computation for
first order deformations of the Hilbert scheme or more generally the Quotient
scheme (in the sense of Grothendieck) as well as the consideration of Remark
6.1 above.
Schlessinger' s T :
We have computed above the first order embedded deformations of X.
Now to compute the first order deformations of X (as we did in §4) we have
to identify two first order embedded deformations X , X , (Cl") A = k[t]/(t2)
A A A
when there is an isomorphism 9 : X ~ X1 which induces the identity auto-
A A
morphism X — X. As we saw before, the isomorphism 9 is induced by a
change of coordinates in A , i. e. , if X are the canonical coordinates of
A v
A we started with and 9 (X ) = Xf then we have
If a first order embedded deformation of X = V(I), I = (f.) vis given by
A+g.t), then
= fi(X)+t{S-^(|)v(X)} + tg.(X)
i
n df.
= f.(x) + t{g.(x) + s -a5T<
N and X1 the canonical image of
are arbitrary elements of the
n df.
Let X be the canonical image of (g.) in N
i л.
n Ы.
'l*^»™ ^ NX* N°W ?1" •-
coordinate ring of A , and the canonical image of Б -
v=l
precisely the image under the canonical homomorphism
where в n represents the tangent bundle of A and |x denotes its restriction
to X. We have a natural exact sequence
¦nx-°
where О denotes the Kahler differentials of order one on a scheme X/k.
The dual of this exact sequence gives an exact sequence
=X
32
33
where в n -¦ N__ is the homomorphism defined above. We define T
Ж X X
X
to be the cokernel of this homomorphism, so that we have
-* N -*• T -*• О
X ХХ *
Thus we have proved
Theorem 6. 2. The first order deformations of X are in one-one
correspondence with T .
X
Remark 6. 4. Suppose that A1 = A[e] (i. e. , A1 = А в ек). Then
the argument which is a combination of that of the theorem and Remark 6.1 above
shows that
Def(A' ) = Def(A) X Def(k[c]),
i. e., the set of deformations of X over A1 which extend a given deformation
over A are in one-one correspondence with the first order deformations of
X. For the proof of this, we remark that a similar observation has been proved
above for embedded deformations. Now identifying two embedded deformations
XA, and X* which reduce to the same embedded deformation X4 over A,
A1 A1 A
the argument is the same as in the discussion preceding Theorem 6. 2, and the
above remark then follows.
Remark 6. 5. Deformations over A1 which extend a given deformation
over A form a principal homogeneous space under Def(k[e]), or else form
the empty set.
Remark 6. 6. Note that if X is smooth, then T = 0. This implies
that any two embedded deformations' X , X1 (A=k[e])c>f X are isomorphic
over A (in fact obtainable by a change of coordinates in A.).
Rema rk 6. 7. If X has isolated singularities, T as a vector space
over к has finite dimension. For, it is a finite С -module with a finite set
as support.
Proposition 6.1. Suppose that X = X . Then
tL - ExtL, (SI*
X — "._ л
л.
Proof. Let X = V(I). Then the exact sequence
i/i2 -
can be split into exact sequences as follows:
(i)
(H)
0-c -I/I-F-0
_ _ .1
Since X = X ,, the set of smooth points of X is dense open in X, so that
e, being concentrated at the nonsmooth points, is a torsion sheaf, in particular,
Hom-ь, {t,&') = Q, Writing the exact sequence Hom(»,(9^Yl for (i), we get that
crx x x
0 -Horn., (F, ©'„) - Hom(l/I2, &) - 0 is exact.
^x X || X
N
X
34
35
Writing the exact sequence Hom(« , С ) for (ii), we get that
- F* -
, &x) - 0 is exact
(since Ext {Q\ n I ,
x Ix
being free). Now
T = coker(9 n I -*N__), and coker(9 n -* F ) =
A A. I А А.
Ix x
above F ^-N__, and so
A v
t (Q
A A
. But as
§7. Versal deformations and Schlessinger* s theorem.
Let R be a complete local k-algebra with к as residue field (k-alg.
closed as before). We write R =
П
where W. =Ъ1 is the maximal
К
_ where W.
К К
ideal of R. We are given a closed sub scheme X of А.П (note that definitions
similar to the following could be given for more general X).
Definition 7.1. A formal deformation X of X is: (i) a sequence
¦ xv.
{X }, X = X where X • is a deformation of X over R , and (ii) iso-
n n R JR. n
n n
morphisms X ®_ R , ~~ X , for each n.
* n R n-1 — n-1
n
Suppose that A is a finite-dimensional local k-algebra. Then a
k-algebra homomorphism Cp : R-*A is equivalent to giving a compatible
sequence of homomorphisms q? : R -* A for n sufficiently large. This is
so because a (local) homomorphism Cp : R -» S of two complete local rings
R, S is equivalent to a sequence of compatible homomorphisms
<P : R/7K* -S/7fc!!, and in our case %,* = 0 for n » 0. Given a formal
• n xv. о А
deformation X_ of X and a homomorphism Q»:R-*A;X ®_ A (via
К 'ПК
n
Q : R — A as above) is up to isomorphism the same for n » 0. It is a
• n n
deformation of X o
by Spec A-* Spec R).
• n n
deformation of X over A. We define this to be X ® A (base change of X
"~~~~ XV. XV.
Definition 7.2. A formal deformation X of X is said to be versal
if the following conditions hold: Given a deformation X of X over a finite
A
dimensional local k-algebra A, there exists a homomorphism Qf : R -* A and
an isomorphism X ® A ~~X ; in fact, we demand a stronger condition as
xv. A ,
Д
follows: Given a surjective homomorphism A1 -* A of local k-algebras, a
deformation X , over A1 a homomorphism 0?:R-»A and an isomorphism
X О A ~ X , ® A, there is a homomorphism О' :R-*A' such that OP1
A. R "*~ A. '
lifts Cp and X 0 A1 is isomorphic to X , . (Note that it suffices to assume
* xv. xv. A
the lifting property in the case ker 0 is of rank 1 over k. )
Let F : (Fin. loc. k-alg. ) — (Sets) be the functor defining deformations
of X, i. e. , F(A) = (isomorphism classes/A of deformations of X/A). Given
a formal deformation X of X, let
R
G : (Fin. loc. k-alg. ) -* (Sets)
be defined by G(A) = Horn, (R, A). Then we have a morphism j : G -¦> F
K-alg.
of functors defined by
That a. formal deformation i? versal i_s equivalent to saying that the functor
36
j is formally smooth.
Theorem 7.1 (Schlessinger). Let F : (Finite, local, k-alg. ) ~+ (Sets)
be a (covariant) functor. Then there is a formally smooth functor (as above),
i.e.,
Horn, (R,-)-F(-),
it—axg.
where R is a complete local k-algebra with residue field k, if
A) F(k) = a single point.
B) Given (е)-А1 -*A-»0 with A1 , A finite local к-algebras and
(e) = Ker(Al -*- A) of rank 1 over к and a homomorphism (V : В — A let
B1 = A1 X В = {(a, P) € A1 X В such that their canonical images in A
A>
are equal}. (SpecB* is the "gluing" of Spec В and Spec A' along Spec A
by the morphisms SpecA-*SpecB and Spec A -* Spec A1. If Ф is surjective,
i. e., Spec A -*• Spec В is also a closed immersion, this is a true gluing. ) Then
we demand that the canonical homomorphism
(*)
is surjective. (Note that B1 is also a finite-dimensional local k-algebra. )
C) In B) above, take the particular case A = к and A1 = k[fi] (ring of dual
numbers), then the canonical map defined as in (*) above
F(B') -F(k[?]) X F(B)
II II (>
(F(B0])-F(k(>]) X F(B))
is bijective, not merely surjective.
37
D) F(k[c]) is a finite-dimensional vector space over k.
Remark 7.1. One first notes that F(k[*]) has a natural structure
of a vector space over к without assuming the axiom D) above: Given с с к,
we have an isomorphism k[c] -*k[c] defined by e — с* г {of course 1-*1)
which defines a bijective map
By this we define "multiplication by с с к" on F(k[cJ). By the third axiom
we have a bijection
F(k[e x, с J) ~ F(k[e J ) X^ F(k[c J )
e
(k[c.,t?] being the 4-dimensional k-algebra with с = e = 0 and basis 1, с
с , e1?7)« We have a canonical homomorphism kfe ,?_]-¦ к [с] defined by
€-¦?, €2"*e which gives a map F(k [c , ? ]) — F(k [z] ), so that we get a can-
canonical map
F(k[?]) XptF(k[?j)
Here we use the fact that
F(k[c] ek
This follows by axiom C), and
We define addition in F(k[e]) by this map, and then we check that this map
is bilinear. This gives a natural structure of a k-vector space on
38
39
if axioms A), C) hold.
Remark 7. 2. The versal R can be constructed with Ъ1 /Ж ~ F(k[-]).
Then with this condition R is uniquely determined up to isomorphism. (Note:
We do not claim that given X the homomorphism R-*A is unique. ) The
A
functor represented by R on (finite local k-alg. ) is called the hull of F which
is therefore uniquely determined up to automorphism.
Proof of Schlessinger' s Theorem. Let <? denote the full subcategory
_________ _______________ т jj
of (fin. loc. k-alg. ) consisting of the rings A such that Ъь = О. This category
A
is closed under fibered products. We will show the existence of R by finding
j D J Dm
n-1 n n-i
a versal R for FJ? , for all n inductively.
Take the case n = 1. <? is just the category of rings of the form
A = к © V where V is a finite-dimensional vector space. So, (Jf is equivalent
to the category of finite-dimensional vector, spaces. Let V be the dual space
to F(k[e]), and put R = к © V. Then a map R_-*k[c] is given by a map
V-»ck, i.e., an element of F(k[e]). So, Hom(R , k[_] ) = F(k [e] ). Since,
by axiom C), F is compatible with products of vector spaces, R represents
Suppose now that R is given, versal for F/C ., and let u , €
n-l n-1 n-1
F(R .) be the versal element. Let P be a power series ring mapping onto
R
n-1
Choose an ideal J ,
n
0-*J -*p-*R
n-1 n-1
which is minimal with respect to the property that u ., lifts to u^ € F(P/Jr
and put R = P/J . We test (R ,u ) for versality. Let A1 -*A be a
r n n n n
surjection with length 1, kernel in Cn» and let a test situation be given:
A1
I
> A , u
а1 с F(A! )
Form R1 = R X A' :
П A
Since P is smooth, a dotted arrow exists. By axiom B), there is a u1 € F(R' )
mapping to u and a1 . Since J was minimal, R1 cannot be a quotient of
P. Hence im(P -> R1 ) % im(P -» R ) = R , and so R' -* R splits:
n n n
Let v1 be the element of F(R' ) induced from u by the splitting. The versality
n
will be checked if u1 = v1 , for then the map R^ -* R' —A1 is the required one.
We can still change the splitting, and the permissible changes are by
elements of Hom(Rn,k[>]) = Нот^,к[-]) = F(k[c]). By axiom C), F(R' ) =
F(R ) X F(k[c]). Both u1 and v! have the same image un in F(Rn>. So,
we can make the required adjustment. This completes the proof of Schlessinger' s
theorem.
40
41
$8. Existence of formally versal deformations.
Theorem 8.1. Let X(^A be an affine scheme over к with isolated
singularities. Then for the functor F = Def. X =Def the conditions of Schles-
singer1 s theorem are satisfied. In particular X admits a versal deformation.
Proof. Since X has isolated singularities, we have ranK (Def. X) [k [e]] =
ranlc (Т„) < oo. Hence it remains only to check the axioms B) and C).
Axiom B): driven (e ) •* A1 -¦ A, q>x : В -* A a deformation X of X and two
T A
deformations X , ,
over Хд
^Al
V"
Let В1 = А1 X В. We need to find a deformation X . over B1 inducing
А В
the given deformations X , and X over A1 and В respectively. As usual
we write (У__ = &. ,,..., etc. We now set & - & X_, ©1. We have
X | А В А СГ В
canonical homomorphisms B1 -*• В and B1 -• A1 . It is easily seen that
^ni ®T>t в % &o and ^>i ®tji A' % ^Ii • The оп1У serious point to check
в а в а а а
is that ©, is flat/B1 . Since B1 = A1 XA B, we have a diagram
J3 A
о-*(о-в' -B-o
0-(?)-A' -A-0
with exact rows, (c) is of rank 1 over k, so (e) «** к as B' modules. Similarly,
II I
It follows easily that the exact sequence 0 -* с & -* &' -*> & '-* 0 is obtained
by tensoring 0-*(e)-*B! -*B-*0 with & , , and that с • & s% & . Now
the flatness of Cf over B1 is a consequence of
В
Lemma 8.1. Suppose that 0 -* (e ) — В1 -* В -> 0 is exact with В' , В
finite local к-algebras and rK(^) =1 (so that (e)^k as B1 module). Suppose
that X_, = Spec O" is a scheme over B1 such that &. ®та1 В = <^та is
В В В В В
flat over В, with X = Spec <У a deformation of X = Spec & , and that
В В к
кег(Ф, -* & ) is isomorphic to & (as c7 module). Then & , is B1
В В к В В
flat; in particular, X , = Spec Ol, is a deformation of X over B1 .
В В *
Conversely, if Ф^,, is B1 flat giving a deformation of X = Spec &* ,
В к
^Rt has an exact sequence representation as in the lemma .
Proof. We have an exact sequence
with e ОС ~ &. . We claim that this is obtained by tensoring
(*) 0 -* (e)-^B' -* В -*0
by & t and in fact that it remains exact because of our hypothesis that
is 5; ©: as B1 -module. For, tensoring (*) by &' , we have
к В
42
43
^0 exact-
But с ® & , % е • с?, *» &. . It follows then that the canonical-homomorphism
В л. К
с & сУ_, -* OL, is injective, i. e. , (*) remains exact when tensored by & , .
Consider
(R2)-\ 0-(e)- B1 -B-O
Tensoring (Cl) by 0%,, (over B1 ) and using the Tor sequence we find that
В
B!
Tor. (©%,• »k) = 0 iff Gf , is B1 flat iff the canonical homomorphism
IB В
^в! ®b« ^в1 ** °в' ®в« в' = ^в1 is inJective- <We use the fact
B1
Tor. (Ф'-,, i B1 ) = 0. ) Now (C2) is an exact sequence of B-modules, and tensoring
1 В
it by O"^ (over B1 ) amounts to tensoring it by 0" (over B). Hence
в а
(C2) ®_. ©'_, stays exact since & is B-flat. Finally
В В В
(И) вв,
(R2)
"в1
11
в,
-0 exact
, В -0 exact.
(R2) ®_., ©*_, is
В 13
exact as we observed above. To prove that С_,t is B1 flat, it
15
В
is equivalent to proving that a1 is injective, i. e. , Ker a1 = 0. Note that
and
~ &
в
в- Since
is B"flat' a
в в
is injective, and from the diagram it follows that q1 is also injective.
Further discussion of Axiom B) а,щЗ*Axiom pj: Suppose we are given .
0-»(?)-* A1 -*A-*0 with rlc(?)=l and a k-algebra homomorphism (p:B-*A.
Set В1 = В X A1 . Let us consider the canonical map (*) in Axiom B) of Schles-
singer1 s theorem for the functor Def. (X) in more detail, (i. e. , the map
Def. (B1 ) -*• Def. (A1 ) xDef ,A) Def- (B))- Suppose we are given deformations
(not merely isomorphism classes) X , over B1 , X , over A1 and X
В А В
over В and isomorphisms
Now v# induce isomorphisms
1а
, A.
But now there is a canonical isomorphism
Hence the v# determine an isomorphism
(*>
By the universal property of the "join11, we get a morphism
where Z = Spec(C X _, QT )(X = Spec fr is chosen to be one of the
44
, . ре _> Cf & -* & are then defined
objects in (*) and the homomorphisms '^ A' A' A
uniquely but the fibre product
is independent of the choice for
, is in p
X : It is the fibre product of 5Г and &^ by
A
«ъ
\
and thus well defined). We claim that f is an isomorphism. From this claim
it follows as a consequence that given deformations X and X , of X such .
that X_ ®__ A is isomorphic to X , ®A, A, i. e. , given a point
Jj В А A
|€ (Def. X)(B) XD (Def. X)(A'), a deformation Xfi, which lifts Xfi and
X , depends (up to isomorphism) only on the choice of the isomorphism
A.
X ® A %X ® A, so in particular, we have a surjective map
В В А А
(*)
l8om(X
J
(Def. X)(A' ) is the canonical '
VB ~B ~ "А1 ~
where \ : (Def. X)(B' ) - (Def. X)(B) *{DeL х)(д)
map of Axiom B). ((Def. X)(B) by definition = isomorphism classes of defor-
deformations of X, i. e. , all deformations of X , of X over B1 modulo isomorphisms
15
which induce the identity map on X. ) Take the particular case A = k, A1 =
к [el, (p: В-A; then X ® A - X, X. , ® . ,* A - X and then the left
L J T В В can A' A1 can
hand side of (*) consists of a unique element, namely, the one induced by the
identity map X -* X. This implies that \ (|) consists of a unique element,
and completes the verification of Axiom C). Thus, finally it suffices to prove
that the morphism f : X_. -* Z_, is an isomorphism as claimed above. Note
45
that (f ® k) is the identity map X — X and that X_. , Z , are flat over B.
В В
Hence our claim is a consequence of
Lemma 8. 2. Let X = Spec^. and X = Spec^ be two deforma-
A A . A A
tLons of X = Spec<^. and f : Хл -*X. (f : & . — &K a homomorphism of k-
r к А А А А
algebras) a morphism such that f 0k is the identity (f ®k is the identity). Then
•is an isomorphism. (In the proof, it would suffice to assume & flat/A).
Proof. The & can be realized as embedded deformations of
________ j^
X = Spec &., so that we have a diagram
Let X1 = f(X ) where X are the variables in PA. We have X1 = X + <P
v v v A v v I v
where CP « *7^A (X ,. . . ,X ) (Жд = max. ideal of A). It follows easily since
7 v A 1 n A.
A is finite over к (as we have seen before) that X и- X1 is just a change of
v v
coordinates in A , so that 1 is induced by an isomorphism P "•'P.. We can
A A A
assume without loss of generality that this is the identity. Then it follows that
f is induced by an inclusion I. C ** • This implies that f is surjective. Let
A A
J = Kerf so that
r1 -+GrZA -0 is exact.
A A
Since <У\ is A-flat, it follows that
A
0- J
k->0 is exact.
47
Since i ®k is the identity, it follows that (J ® k) = 0. Since 7?t is in the radical
of О A, by Nakayama1 s lemma, it follows, that J = 0; hence f is an iso-
A
morphism.
This completes the proof of the theorem.
§9. The case that X is normal.
Let Х^*ЖП be normal of dimension > 2. Let U = X-SingX (Sing X =
Singular points of X). We use the well-known
Proposition 9.1. Let Z be any smooth (not necessarily affine) scheme
over k. Then the set of first order deformations of Z is in one-to-one cor-
correspondence with H (Z, 9 ), i.e.,
(Def. Z)(k[e]) * h\z, 9 ) (9 tangent bundle of Z).
Proof. If Z is affine, we have seen that any first order deformation
of Z is trivial, i. e. , it is isomorphic to base change by k?e] (this was a con-
consequence of the fact that when Ze-* A and Z is smooth, T = @)), Hence
any first order deformation of Z is locally base change by k[e]. Hence if
{U.} is an affine covering of Z, a first order deformation of Z is given by
(p. : (U.PlU.) ® k[c] - (U.PlU.) ® k[c],
{(P..} being automorphisms of (U.PlU.)®k[c] satisfying the cocycle condition.
It is easy to see that first order deformations correspond to cohomology classes.
Now it is easy to see that for an affine scheme W/k, (W = Spec B)
AuU ..(W ® к[ф = Derivations of B/k ( = H°(W, в^).
The proposition now follows.
Lemma 9.1. Let X , X be two deformations of X (not necessarily
A A
of the first order, A = local, finite over k). Let U1 = X* |U and let
@: U -+ U be an isomorphism over A. Then CP extends to an isomorphism
(unique) X* - X\ .
A A
Proof. If X is a deformation of X as above, we shall prove
(*)
The proposition is an immediate consequence of (*), for <f induces a homo-
mo rp his m
,аг , ).
XA
This implies that CP is induced by a morphism ф ; X -¦ X . It is easily seen
* A A
that {ф 0 к) is the identity, and this implies easily that ф is an isomorphism.
To prove {-^, we note first that if A = k, it is well known. In the
general case, we have a representation
0-MO—A-* A —0 exact,
= 1.
48
49
By induction it suffices to prove (*) assuming its truth for
Then we have
0 - с & •*
- О exact,
lemma again by an induction as in the previous proposition. This induces an
exact sequence of sheaves by flatness
0 -* ^ -¦
—0
with e • & % ft . This is because X is flat over A. As a sheaf its
A
restriction to U is also exact. Then we get a diagram
о - н°(х, ay - н°(хА, &A) - н°(хА , erA ) - о
л I Л °
о -* н°(и, ©y - н°(иА, ^A) - h°(ua , <^A ).
о о
The first and the last vertical arrows are isomorphisms, and it follows then
that the middle one is also an isomorphism. This proves the proposition.
Remark 9.1. The proposition is equivalent to saying that the morphism
of functors
(Def. X) - (Def. U)
obtained by restriction to U is a monomorphism.
Lemma 9. 2. Suppose that X has depth >¦ 3 at all the points (not
merely closed points) of Sing X (e.g., dimX>^3 and X is Cohen-Macaulay)
(X necessarily normal). Then every deformation U of U extends to a
A.
deformation XA of X.
A
Proof. Define X. by X. = Spec <5"v with &. = <Э"„ = H°(UA , <2"A ).
A'A^X. AXA AA
A A
Suppose we have a presentation 0 — (e)-*A-*A -* 0 rlc (e) = 1. We prove this
Since depth of &„ at x € Sing X >; 3, by local cohomology the maps
X, x
are isomorphisms.
The isomorphisms iTfX,^ )~ rT(U,^, ) follow from Theorem 3. 8, p. 44, in
Hartshorne1 s Local Cohomology. Indeed, we have the following exact sequence
0 — С -* & — 7f-*- 0. We must prove that H Cf) = гГСЗО = О. Theorem 3. 8
(loc. cit. ) states that for X a locally Noetherian prescheme, Y a closed pre-
scheme and JS a coherent sheaf on X, the following conditions are equivalent:
(i) Н^.(Л) =0, i < n. (ii) depth #]>n. Taking # = & and Y = Sing X, the
fact that H°C0 = H C*) = 0 follows immediately. In particular, НГAГ,<У ) = 0.
Hence we get
(*) 0 - H°(U, Or) - H°(U, (TTT ) - H°(U, e-TT ) - О is exact.
Now H°(U, & ) = H°(X, Ck) = &y and
H (V, O^ ) = & flat/A by induction hypothesis.
Ao
50
. 51
Hence
О - С. -+ &. - ©- -0 is exact
к о
and & flat/A . By Proposition 3.1 it follows that 0* is flat/A
А о
о
and so X represents a deformation of X.
A
Proposition 9. 2. Let X— АП be such that X is of depth > 3 at
\/x € Sing X. Then the morphism of functors
Def(X) - Def(U) , U = X-SingX
obtained by restriction is an isomorphism, i. e. ,
(DefX)(A) -* (DefU)(A) is an isomorphism VA local finite over k.
Proof. Immediate consequence of the above two lemmas.
Remark 9. 2. Suppose Х-АП is normal (with isolated singularities).
Then if ex is of depth > 3 at V* « Sing X, X is rigid. For, it suffices to
prove that first order deformations of X are trivial and by the preceding to
prove this for U. We have an isomorphism
Н*(и, 6 ) - ri (X, 6X)
because of our hypothesis. But H*(X, 9^ = 0 since X is affine. This implies
the assertion.
510. Deformation of a quotient by a finite group action.
Theorem 10.1 (Schlessing-e-r--Inventiones f 70). Let Y be.a smooth affine
variety over к with char к = 0. Suppose we are given an action of a finite
group G on Y such that the isotropy group is trivial except at a finite number
of points of Y, so that the normal affine variety X = Y/G has only isolated
singularities ( at most the images of the points where the isotropy is not trivial).
Then if dimY = dimX>^ 3, X is rigid. (It suffices to assume that the set of
points where isotropy is not trivial is of codim >^ 3 in Y. Of course, the
singular points of X need not be isolated, but even then X is rigid. )
Proof. Let U = X-SingX, and V = Y-(points at which isotropy is not
trivial). Then the canonical morphism V -¦ U is an etale Galois covering with
Galois group G. From the foregoing discussion, it suffices to prove that
H (U, 6 ) = 0. We have the Cartan-Leray spectral sequence
where ^(®у) denotes the G-invariant subsheaf of the direct image of the sheaf
of tangent vectors on V. We have 0 = f^ (в ). Hence the above spectral
sequence gives the spectral sequence
hp(g,h4(v, ey)) => Hp+q(u, ви).
Now HP(G,Hq(V, 6y)) = 0 for p>^l since G is finite and the characteristic
is zero. Hence the spectral sequence degenerates and we have
isom.
H°(G, HqtV, в» Hq(U, 0TT).
52
53
In particular, H*(U, 6^ - H°(G, hV, By)). Now 6y is a vector bundle, and
since dim Y > 3 and (Y-V) is a finite number of points, 6y is of depth > 3
at every point of (Y-V) (or because codim(Y-V) > 3). Hence rT(V, 9у) =
H^Y, в ) = 0. It follows then that H*(U, Q^) = 0, which proves the theorem.
Remark 10.1. Let Y be the (x,y)-plane, G = X /2 operating by
(x> y) и. (_x> „y)e Then X = Y/G can be identified with the image of the (x, y)-
plane in 3 space by the mapping (x, y) i- (x2, xy, у ), so that X can be identified
with the cone v = uw in the 3 space (u, v,w). It has an isolated singularity
T
at the origin, but it is not rigid (cf., the computation of
done for the case of a complete intersection, §4 and §6).
which has been
$11. Deformations oi cones.
Let X be a scheme and F a locally free &^~ module of constant
rank r. The vector bundle V(F) associated to F is by definition SpecS(F),
i. e. , "generalized spec" of S(F)--the sheaf of symmetric algebras of the Ф^
module F. We get a canonical affine morphism p : V(F) - X. The sections
of V(F) over X (morphisms s:X-*V(F) such that p« s = Idx can be
identified with
Homex-alg(S(F), 0^) % Hom^-mod , (F,
H°(X, F ),
where F* is the dual of F. With this convention, sections of the vectg? bundle^
V(F) considered as a scheme over X are % sections of F over X.
Let 1PN+1 - @, . . . , 0,1) ¦? IPN be the "projection of IP onto P
from the point @,. . . , 0,1)", i. e. , ir is the morphism obtained by dropping the
last coordinate. Let L = IP - @,... y 0,1). Then we see that L has a natural
structure of a line bundle over IP , and in fact
L^Spec( Ф & N(-n)).
n=0 P
Proof that L ^ Sp^c( © & xj(-n)): We first remark that in general
n=0 PN
given F a locally free & -module of constant rank r, the vector bundle
V(F) = Spec S(F) associated to F (in the definition of Grothendieck) is such
that the geometric points of V(F) correspond to the dual of the vector bundle
IF associated to F in the "usual" way, that is, F becomes the sheaf of sections
oo
of IF. Consequently, in order to prove that L ^Spec( © & M(-n)) we must
n=0 IP
N
show that the invertible sheaf corresponding to L -» P is & N(l)- We do
IP
this by calculating the transition functions. If we denote the standard covering
of P by uQ,. . . , u , then we see for P - @, 0, . . ., 0,1) -* P we have
v ((Xq, . . . , X )) is of the form (X , . . . , X , X.) and hence the patching data
-1 xi/xi 1
is of the form тг (и.Пи.) ~ С X (u.Plu.) * С X (u. OuJ^T *"" (u.Plu.) (where
X. are the standard coordinate functions on P ). This is precisely the patching
data for &"
P
Consequently, QT M(l) is the invertible sheaf associated to
PN+1 - @, . . . , 0,1) * IPN. The set of points IPN % S = (*,...,*, 0) С IPN+1
N
give a section of L over IP ; we can identify this as the 0-section of the line
N+l ^ N+l
bundle L. We have a canonical isomorphism Jk, ¦¦ (IP -S) sending
@, • . . , 0) ^ @,. . . , 0,1), and hence L-(O-section) - A.N+1-@, . . . , 0). Further-
more, it is easily seen that L-(O-section) = Spec( Ф fir „
— ¦" ¦ ^
-oo IP
and it is the
54
55
—1
(
bundle associated to L.
Suppose now that Y is a closed sub scheme of IP . Let L = x (Y).
Then Ь„ is a line bundle over Y and from the preceding we have
00
L =S?ec( О СГ (-a)).
1 n=0 x
Let С be the cone over Y, i. e. , if p is the canonical morphism
p : (A -@,. . . , 0)) — TP induced by the isomorphism A — (IP -S)
defined above, we define C1 = p (Y) and then C1 = C-@,. . . ,0). The point
@,. .., 0) is the vertex of the cone С So, С = closure of C1 in A
before we have
As
-@-section) = Spec(
П=-00
— N+l N+l
Let С be the closure of С in IP (C being identified in IP as above).
Then we see that
С = LyU @,..., 0,1) , С = Ly - @-sectioxi).
We call @, 0,.. . , 1) the vertex of the protective cone C, for @,. .., 0,1)
N+l N+l
goes to the vertex of С under the canonical isomorphism (IP -S) -* A,
If Y is smooth, С is smooth at every point except (possibly) at the vertex.
N
Consider тг : L -* IP . Let T denote the line bundle on L -consisting
N
of tangent vectors tangent to the fibres of L -» ]P . Then we have
(*)
T - 0T - tt*0 -* 0 exact.
L N
я- : L — Y be the canonical morphism. Then we have a similar exact
sequence. Let T denote the bundle of tangents along the fibres of L — Y,
so that we have a commutative diagram
0 0 0
0—T
(A)
j i
Г —-—•¦ 6
Y L,
I i
o-tL -
0 N
N+l
where N = normal bundle for the immersion L *-• JP , N = normal
L Y Y
N
bundle for the immersion Y^ IP . We have T 2; Т| from which it
Y Ly
follows that
l. e. ,
CokerFL -©LIL- )- Сокег[(тгу(ву))-*т (^L)L. ] ,
N %w*(N ).
LY Y
Let U = C-(vertex). Then if N is the normal bundle for U** AN+1, it is
*
immediate that N = j (N ) where j : U -* L is the canonical inclusion.
U L Y
If we denote by the same ж the canonical morphism л* : U -* Y, we deduce
that N = тг (N ). Then restricting the bundles in (A) to U we get
Let us now suppose that Y is a smooth closed subscheme of IP . Let
57
(Bi)
(вг> о -'
(В)
I
О
ir*(Ny)
The exact sequence (B2) is obtained by restriction to U of the exact sequence
H°(A ,© N .) is a free module M over P = k[z ,...,Z ] with basis
A
-—
az
JN+1J
. We see easily that h is defined by restriction to A -@) of
ZN+1
: P-M
Cf:
where Cj>(l) = 2z. -r— A is generator of P over P). Hence Cf> is a graded
i
¦homomorphism, and is therefore defined by a homomorphism of sheaves on
N *
JP . We see indeed Cf> = 7Г {q> ), where
(**)
where T
0-T
N+l
N+1
is the bundle of tangent vectors tangent to the fibres of
lA^-(O)
jt : A -@) -» IP . We shall now show that we have
{& NU) is defined by homogeneous elements of degree ^ 1 in P considered
P
as a module over P). From this the assertion (C) follows easily, and we leave
these details to the reader.
Let J be a coherent <У __ module. Then we have
(C)
IP
IP
where the second row is the pull-back ir of the well-known sequence
,*
Now it 3* is defined by the sheaf of & ^ modules
IP
oo
on P (the middle term
of this exact sequence is the direct sum of & A)
JP
taken (N+l) times). Let us exam:
ine the canonical homomorphism h : Т| -*
N+l
Let (z ,. . . , z ) be the coordinate of A . Then
considered as a sheaf of modules over G & (-n)), so that we find
0 P
* °°
Jr J = ® 3^("n) anc* hence
HP(L, 7Г 3f) = ® HP(P ,
58
59
Similarly, if 3* is at coherent (^.-module, we get
HP(U,
(U = C-(
and
N
Let us now suppose that Y is ji smooth closed subvariety of IP
(of dimension >^ 1) and that it i^ projectively normal, i_. e_. , С is normal.
We have then
But since С is normal (of dimension.> 2)
Now from (B) we get
H°(U,
Hence T1 = Cokera = Coker(Imp? H°(U, T*Ny)). Now p is a graded homo-
morphism of graded modules over Э H°(Y,CY(n)), namely, the gradings are
n=0
From(C). identifying в |тт*ж {СГ N(i)) *We get
A -@)tU IP
For, в I is a trivial vector bundle and hence this follows from the
^n+11 C
fact H°(U,e*TT) = H°(C, CTJ. Now
U L»
N_ is a reflexive ©'.-module since
L ————— ^
TT
U
N_ = Horn (I/I ,Or ), where I is the defining ideal of С in
C ^C C
of this it follows that
H^U.lty =H°(C,NC).
Hence we have
AN+1. Because
and then Ъу (С), р is also a graded homomorphism. Hence (Imp) is a graded
submodule of H°(U, ж (в
- From *bis il follows that T has a canonical
structure of a graded module over k[z ,...,
quotient of the graded module
and in fact that it is a
H°(Y,Nv(n)).
Thus we get
Proposition 11.1. Let Y be a smooth projective subvariety of IP
N
60
61
(of dimension^ 1) such that the cone С over Y is normal. (we have only to
suppose that С is normal at its vertex). Then T has a canonical structure
of a graded module over k[jz ,. . ., z Л , in fact it is a quotient of the graded.
module Ф H°(Y,Ny(n)).
S12. Theorems of Pinkham and Schlessinger on deformations of cones.
Theorem 12.1. Let Y be as above, i. e., Y is smooth closed-* IP
and dimY>l. Then
A) (Pinkham). Suppose that T _ is negatively graded, i. e. , T^(m) = 0,
m > 0. Then the functor
Hilb(C)-Def(C)
1 .
is formally smooth.
B) (Schlessinger). Suppose that T_ is concentrated in degree 0. Then
we have a canonical functor
Hilb(Y)-Def(C),
and it is formally smooth. In particular, every deformation of С is a cone.
Recall that Hilb(C) is the functor such that for local finite k-algebras A
Hilb(C)(A) = <ZClPn+ XA, z closed subscheme, Z is flat over A and Z
represents an embedded deformation of С over A}.
Proof. A) Given 0 —(e) —A1 -* A-* 0 exact with rk(e) = 1 and
A1 , A finite local over k, we have to prove that the canonical map
(*) Hilb(C)(A' ) - Def(C)(A» ) *Def(c)(A) Hilb(C)(A)
is surjective. Take the case A1 =k[c], A = k. In particular (*) implies that
(a) HUb(C)(k[c]) -Def(C)(k[?]) is surjective, and
(b) given i с Hilb(C)(A), let ?* be the canonical image of ? in Def(C)(A).
Then, if % can be extended to a deformation of С over A' , then
Jtj € ffilb(C)(A' ) such that -r\»— % (the difference between this and (*) above
is that we do not insist that r\ *¦ ?).
We claim now that (a) and (b) => (*). (In particular, to prove A) it
suffices to check (a) and (b). ) Given % as above,the set of all ^ € Hilb(C)(A' )
such that т]*-* ? (provided there exists an r\ such that t] »— ?) has a structure
of a principal homogeneous space under Hilb(C)(k[c]) (see Remark 6.1).
[This can be proved in away similar to proving that Hilb(C)(k[e]) ~
H°(C,Hom%,Cr~)), where I is the ideal sheaf defining С in IPN+\ cf.
Remark 6. 2. J Similarly, all deformations т^ which extend ? form a principal
homogeneous space under Def(C)(k[c]), provided there exists one. Hence,if
(b) is satisfied and T] is a deformation extending ?, because of (a) there
exists in fact r\,t\ *+ ? and tj »¦* "Л* This completes the proof of the above claim.
Now Hilb(C)(k[?]) = H°(C,N~). We have С = L U (vertex) and С
is normal at its vertex. Hence
H°(C,N~) =H°(Ly,NL )= Э H°(Y,Ny(-n)).
If T is negatively graded,it follows that the canonical map
С
Ф HO(Y,Ny(-n))C ® H°(Y,Ny(n))
n=0 I n=-oo
62
63
is surjective. Hence wr. have checked that
ffilb(C)(k[?])- (Def C)(k[cl)
is surjective. It remains to check (b). Given ? с ffilb(C)(A), suppose tihat
' N+l
? is locally extendable, i. e., given ? : С — IP , (i) ? can be extended
A. A.
locally to a deformation over A1 at every point of С , and (ii) this exten-
A.
sion can be embedded in P , , so as to extend ? locally. We observe that
it is superfluous to assume (ii), for we have seen that in the affine case
(Embedded Def)(X)-* Def(X)
is formally smooth. Then we see that to extend ? to an *i с Ш1Ь(С)(А1), we
get an obstruction in H (C, N—) (this is an immediate consequence of the fact
already observed, that extensions form a principal homogeneous space, cf.
Remark 6. 5). We observe that for ? the property (i) is satisfied. Since there
is an ^ € Def(C)(A' ) with ^»- ? (? < Def(C)(A), ? -*I), the condition (i) is
satisfied for all x с С. But now G is smooth at every point of C-G. In this
case we have already remarked before that (i) is satisfied (cf. , Proof of Propo-
Proposition 9.1). Since G is normal, С is of depth >^ 2 at its vertex, so that by
local cohomology we get
We have
Now by hypothesis ? € Def(C)(A) can be extended to r\ € Def(C)(A! ); in
particular, x| I gives an extension of ? I . Hence the canonical image
of this obstruction in H (U, N ) is zero. (We see that as above, extending
an embedded deformation of U gives an obstruction in H (U,N ). ) This
implies that there is an -p с Hilb(C)(A' ) such that т\*+?. This checks (Ъ),
and the proof of A) is now complete.
B) Given a deformation ot Y, we get canonically a deformation of U = C-@).
To get a canonical functor Hilb(Y) -*• Def(C), it suffices to prove that a de-
deformation of U can be extended to a deformation (which is unique by an
earlier consideration). If depth of С at its vertex is > 3 this follows by an
.earlier result, but we shall prove this without using it. Let
A1
0—(e)--A1 -*A —0 be as usual, and let Y
N
in IP . Then we have an exact sequence of sheaves.
• Y be deformations of Y
A
0-0- -er -е- -о, е-
Y Y Y Y
YAf
&L. being A1 flat, etc. Similarly for Y = IP . Then we get a commuta-
YA!
tive diagram
H°(JPN,
IP
A
A
• H (Y, <ry(n)) - 0
Y., ,
A
,N )= © H*(Y,N (-
Y 4 n=D Y
A
(n))
0
(Cl)
A'UY
j
1
0
(C2)
(n)) -0
64
65
where n ^ 0. It is immediate that (Cl) and (C2) are exact. From this com-
commutative diagram, by induction on rk A1 , it follows that
°
hV*. , & „ (n)) - H°(Y , fr (n)) - 0
A IP*, A'
is exact because (Cl) and (C2)'are exact and the first and third rows are exact.
Then as an easy exercise it follows that the second row is exact. Then it
follows that H°(YAl,<yv , (n))-H°(Y 9 СГ (n)) - 0 is exact. Define
A YA, л хА
00
Of = 0 H°(Y ,,C (n)) (resp. & ). Then we get an exact sequence
C A Y
CA« n=0
с cA, cA
-o,
Ч.'
Again by induction on rkA1 it follows that & is A1 -flat (for, &^ is
A A
A-flat by induction hypothesis and by, an earlier lemma (Lemma 8.1) this
claim follows). Hence Spec ?T provides a deformation of C, i. e. , it
CAl
extends the deformation of U = C-@) which is given by the deformation Y^,
of Y in IP . This proves the required assertion. Since depth of С at its
vertex is >. 3 by an earlier result this is the case. Hence we get a canonical
functor •
Hilb(Y)-*Def(C).
From this stage the proof is similar to A) above. As before it suffices to
check assertions similar to (a) and (b) above. We see that Hilb(Y)(k[e]) 2Г
H°(Y,Ny). We have
oo
HO(Y,Ny)C Ф H°(Y,NY(n))
n=-oo i
The hypothesis that T consists only of degree 0 elements, implies that
С
H (Y, N ) — T is surjective, i. e. ,
i С
ffilb(Y)(k[c])-* (Def C)(k[e])
is surjective. This checks (a). To check (b), take 0 — {t) — A1 — A — 0 as-
usual, |€ Hilb(Y)(A), I^tic (DefC)(A). Suppose we are given л' e (Def C)(A
extending t], then we have to find |! € HLlb(Y)(Af ) extending §. Since Y
is smooth, the condition for loca] extension over A is satisfied as above,
and hence we get an obstruction element X. с H (Y, N ). We have
In a similar way, the element t^l defines an obstruction element
1 °° J
Ц « H (U, Ny) = © HT(Y,NY(n)). But by hypothesis this bbstruction
is zero.
1 1
By functorially and the fact that H (Y, Ny)^ Q H^(Y,N (n)) it follows that
-oo
X. = 0. This proves the existence of ?» and the theorem is proved.-
Examples where the hypothesis ?f the above theorem are satisfied.
N
Lemma 12.1. Let Y*5- IP be a smooth projective variety such that
ГН {Y, (^y(n)) = 0, Vn / 0, n € Z
, ©Y(n)) =0, \/n t 0, n €
66
67
and Y is protectively normal. Then tJ, consists only of degree 0 elements
(dim Y >, 2, follows from the hypothesis).
The hypothesis H^Y, QT (n)) =0, n h 0 implies that
TC =
[as graded modules modulo elements of degree 0]. To prove this we have
only to write the cohomology exact sequence for (B2) of §11 as well as use (C)
of §11. To compute Сокег(я- F .. ) -*j (NY)), use the exact sequence
о -
N|Y)-»*(Ny)-o.
Now н\тг*(еу)) = © H^Y, еу(п)). Since by hypothesis hV, 0y(n)) = 0 for
-oo
n k 0, it follows by writing the cohomology exact sequence for the above, that
* * 1
Сокег(тг @ ._ __) — л- (N )) = T has only degree 0 elements. This proves
jpN Y Y С
the lemma.
Lemma 12. 2. Let YC & be a smooth projective variety such that
^ -y(n)) = 0, \/n > 0
=0, Vn> 0.
Then T has only elements in degree ? 0.
Proof; The proof is the same as for B) above.
Remark 12.1. Given a smooth projective Y and an.ample line bundle
L on Y the conditions in A) (resp. B)) above are satisfied for the projective
embeddings of Y defined by nl., n» 0 if dimY> 1 (resp. dimY.> 2).
Exercise 12. L
Let Y = 3 collinear points in IP and
Y = 3 non- collinear points in P. Take a deformation
of Y to Y_, which obviously exists. Show that this deformation cannot
о 1
be extended to a deformation of the affine cone С over Y to the affine cone С over Y.
О О ¦ JL 1
[For, if such a deformation exists, we see in fact that J a deformation of
С to С , closures respectively of С and C- in IP . We have a (finite) morphism^:C-*C
which is an isomorphism outside the vertex and not an isomorphism at the
vertex. We have
This implies that the arithmetic genus of C_ = (arithmetic genos of С +1), but
if there existed a deformation, they would be-equal. J
$13.
1 g computation for deformations of the cone over a- rational
curve in JP .
Lemma 13.1. Let
be a- connected curve of degree n, not
contained in any hyperplane. Then Y = Y-U...UY where Y. are smooth
rational curves of degree n. such that n =2n., each T. spans a linear sub-
space of JP of dimension n. and the intersectionstof Y. are transversal.
Proof. Let Y be an irreducible curve of. degree < n in JP . Then
we claim that there is a hyperplane H such that YCH- Choose n distinct
68
points on Y. There exists a hyperplane H passing through these n points.
We claim that H contains Y for if H does not contain Y it follows that
deg(H • Y) > n, contradicting the fact deg Y < п.'-Щ% then follows that if Y
is an irreducible curve of degree r, r < n, then there is a linear subspace
H2:JPS in,Fn such that УСН^Б?8.
Now let Y be a curve in IP of degree • n- not contained in any hyper-
hyperplane. Let Y. A <^ i ? r) be the irreducible components of Y. Then if
n. = deg Y., we have n = Sn.. By the foregoing, if H. is the linear subspace
of IP generated by Y., then dimH. <^ п.. Since. Y.1 s generate IP , _a
fortiori the H.1 s generate IP . Since Y is connected, UH. is also connected,
НПн ? 0 We find
i. e. , we can write a sequence H ,. . . , H such that Н.Пн.
.
0. We find
then
i. ,
easily that if L. is the linear subspace generated by H.,. . ., H..,
J r J
dimL. < n, + . . . + п.. Since n = 2 n. and dimL = n it follows that
dimL. = n + . . . + п.. It follows in particular that dimH. = n. and that
L.OH. = one point. It remains to prove that Y. is smooth and rational (the
assertions about transvereality are immediate by the foregoing), and this is
a consequence of the following
Lemma 13. 2. Let Y be an irreducible curve in IP of degree n not
contained in any hyperplane. Then Y is a smooth rational curve, in fact
parametrized by t и- A, t, t ,...,t ).
Proof. Let x. be a singular point of Y. Choose n distinct points
x ,. . . ,x on Y. Then there is a hyperplane H such that x. € H. Now x
cannot be smooth in HOY, {or if it were so it would follow that x is also
smooth-on Y. Frdtn this itfollows easily
Deg(H • Y) > n
which is a contradiction. Hence every point of Y is smooth.
To prove the assertion about parametric representation and ratiorality
of Y, project Y from a point p in Y into IP (see $11). We get an
irreducible curve У С Д3 • °* degree (n-1). Then it is smooth and by-
induction hypothesis Y1 ca~n be parametrized as A, t,. . .., t ). The pro-
projection can be identified as the mapping obtained by dropping the last coordinate.
Hence the parametric form of Y can be taken as A, t,. . . , t ,f(t)) where
f(t) is a polynomial. Take the hyperplane H as x =0; then by the hypothesis
>
that Y is of degree n, it follows that f(t) polynomial of degree n. Then by
change of coordinates we see easily; that thef parametric form of Y is
t*4l,t,t2,...,.tn>.
Lemma 13. 3. Let Y be an irreducible curve in IP of degree n,
not contained in any hyperplane, or equivalently, a (smooth) curve parametrized
by A, t,. . . , t ). Then Y is projectively normal.
Proof. Let L = & ПШ| у ^ is wel1 known that projective normality
of Yd IP is equivalent to the fact that the canonical mapping
Cfv : Н°AРП, & n(v))-H°(Y,LV) is suxjective.
IP
This follows from the following
Sublemma 13.1. Let X be a normal projective variety. Then X
70
71
is projectively normal, i. e.
L =
over X) is normal if and only if
. " > 0. 1
*>" JP" -
Proof. In general we have A = {functions on X-@)} = в H°(X,LV)
о v
(see discussion in ? 11). Now since L is ample we have H (X, L ) = 0,
v < 0, and therefore A = Э H (X, L ). Now suppose X is normal. Then
v>0
{functions on X-@)} = {functions on X}. Also, XC^P = A » and using
the same Teasoning as before В = {functions on A } = 0 H (JP ,C (v)).
v>0 JP
But any function on X can be extended to Ж which implies the natural
map B^A is surjective. Therefore H°(Jpn, & (v)) — H°(X, L ) is sur-
jective Vv >. 0-
In general we have H°(JPtt, QT (v)) — H°(X, 1?) is surjective for v
JPn
large. Also 0Н°(Х,М is normal since X is. Thus в Н°(Х,1/) is
v>0
the integral closure of bn v. Hence if we assume H°(JPtt. QT Jy)) - H°(X, Ъ)
JPn
is surjective Vv >^0, we have that Ф H (X, L ) is normal. This means X
is normal.
Now returning to the proof of the lemma, Y ~ JP and L ~ & ЛЫ
JP
so that L 2: & i(nV)- I* is clear that Cf is injective if and only if Y is
not contained in any_Jiyperplane. On the other hand, we have
A)) =
n
An))
1
Hence Q is an isomorphism, i. e. , Y*-* JP is the immersion defined by
ociated to С (n). It is seen easily that
IP
Any)) is surjective. This implies that CP
the complete linear system associated to С .(n). It is seen easily that
IP
SW(H°AP1, & .Wj-
IP
is surjective for all v, and the lemma is proved.
Lemma 13. 4. Let Y be as in the previous lemma. Then
h\y,
L ) = 0 , v > 0
n+1.
H1(Y,eY(v)) = 0 , v > 0
(the conditions in Lemma 12.1 are satisfied).
Proof. It is well known that eL_^<r Al) and H*(jp\ О А*)) = 0,
Y" JP1 IP1
v >_ 0. This proves the lemma.
Proposition 13.1. Let Y be the nonsingular rational curve in JP
of degree n parametrized by tn-(l,t, ...,t ). Let С be the cone in Ж
over Y and С its closure in IP . Then the functor
Hilb(C) - Def(C)
is formally smooth. (Note by Hilb(C) we mean the restriction of the usual
Hilb to (local alg. fin./k) and defining deforjnation of C.)
Proof. This is an immediate consequence of Lemma 12.1.
Let R be the complete local ring associated to the versal deformation
of. С (with tangent space = Def (C) (k [e ]) and R1 the completion of the local
ring at the point of the scheme Hilb(C) corresponding to C. Let p : R -» R1
73
be the k-algebra homomorphism defined by Hilb(C) — Def(C) to define this
homomorphism we need not use the representability of Hilb(C), it suffices
to note that Hilb(C) also satisfies Schlessinger1 s axioms). From the above
proposition it follows that the homomorphism p is formally smooth. Hence
we can conclude that R is reduced (resp. integral, etc. ) iff R1 is reduced
(integral, etc. ).
To study Hilb(C) we note that С is of degree n in P and that
it is smooth outside its vertex.
Proposition 13. 2. Let Xе-* 3P be a smooth projective surface of
degree n in IP , not contained in any hyperplane. Then X specializes
to C, jl.?. , there is a 1-parameter flat family connecting X and C.
Proof. Let H be the hyperplane at oo, with equation x = 0
oo n+1
(coordinates (x ,...,x )). Let X be any closed subscheme of IP .
о n+1
it is easy to see that X "specializes set theoretically1 to the cone over
X * H (with vertex @,. . . , 0,1) and base X * H ) ; in fact we define the
о oo
Then
and that ф is indeed a morphism outside the point x = (@,. . . , 0,1), 0).
1 о
Let us denote by Qo the morphism (resp. rational for t = 0)
Then for all t ? 0, O? is an isomorphism. Let Z1 = (f (X) (scheme theo-
theoretic inverse image). We see that Z' is a closed subscheme of IP X (A -x ).
о
There exists a closed subscheme Z of IP X A which extends Z' aad
such that Z is the closure of Zf as point set. It is easy to see that
Z = Z1 LJ @,. . . , 0,1) (as sets). Let p : Z -* A denote the canonical morphism.
Then Vt с A , t ? 0, p" (t) ~XA and for t = 0, p" @) - cone over X * H (as
t oo
sets).
The map (X ,. . ., x ) — (x ,. . . , x , tx ) (t к 0) define s an auto -
О П+1 О П Пт1
morphism of IP , the image of X under this is denoted by X . The scheme
X specializes to a scheme X c-* IP (this follows for example by using the
fact that Hilb is proper). From the above discussion it follows that X =
r i -v v - y v - orm*» nvpr X • H (as point set) as follows.
1-parameter family Xt. Xj - X, Xq - cone over ^ (a p cone over H- X^ (as point sets). It follows f*om this argument that we can
This family is obtained as follows: Consider the morphism
n+2 v 1
A X A —
defined by ((* xn+1), t) ^ <xq x^ t*a+1). We see that it defines
rational morphism
choose Z so that p : Z -* A is flat (and then Z is uniquely determined).
Suppose now that X is smooth, X • H is smooth and that the cone
00
отег Н • X (scheme theoretic intersection) is normal. Then we will show
oo
that p @) = X = (cone over X • H ) scheme theoretically. For this, let
о oo
I be the homogeneous ideal in к [x ,. . . , x Л of all polynomials vanishing
on X. Let I = (f ,. . . ,f ) where f. = f.(x , . . . , x .) are homogeneous poly-
i q l l о n+1
aornials. Then Xt = V(Ifc) where Jt = (^(хо» • • • »^n, txn+1)) for t к 0. Let
74
75
X'o=V(I'o) where I"q is the ideal ^ = (f^, . . . ,xq, 0)). Let Iq be the ideal
of X . Then clearly I! С IQ- Also it is easy to see X^ is the scheme
theoretic cone over X! • H^. This means (X^red = (XQ)red. For, since
I1 Г I we have Xf I)X . But by assumption X! is normal hence in parti-
o о о о о
cula* reduced. Therefore X1 = Xq as required.
Let us now return to our particular case, where X is a smooth pro-
projective surface in РП+1 of degree n not contained in any hyperplane. Then
we can choose a suitable hyperplane and call it H^ such that H^ • X is
smooth (Bertini) of degree n in 1РП, and not contained in any hyperplane.
(The ideal defined by ХПН is C__(-l). We have
is exact. This gives
0 *Н°(Х,ё-х)
Н°(СГХA)) Н
surjection
I I
injective
+1)
Pn+1
IP
U»
exact
exact-
The second row is exact, and the first vertical arrow is a surjection. The
second vertical line is injective. This implies (via diagram chasing) thatthe third^
arrow is an injection which implies ХПН^ is not contained in any hyperplane.
(We make this fuss because a priori degree does not imply having the same
Hilbert polynomial. ))
Then by the preceding lemmas it follows that H^ • X is a rational
curve in 1РП parametrized by A, t, . . . , tn) and then by the above discussion
it follows that there is a 1-parameter flat family of closed subschemes de-
deforming X to С (С is the closure in 1РП of the cone associated to X * H ).
oo
This completes the proof of the proposition.
Remark 13.1. Let P be the Hilbert polynomial of C^* IPn+1. Let
H denote the Hilbert scheme of all closed subschemes of jpn with Hilbert
polynomial P. Then H is known to be projective. The ring associated with
Hilb(C) above,is the completion of the local ring of H at the point corresponding
to C. Let H be the open subscheme of H of points h с Н such that
(a) the associated subscheme X, of IP is smooth and (b) X, is not
n n
contained in any hyperplane in IP .It is easy to see that (a) and (b) define
an open condition; that (a) defines an open condition is well known, and that
(b) also defines an open condition is easily checked. The foregoing shows that
as a point set H corresponds to the set of smooth surfaces in 1РП of
degree n not contained in any hyperplane and further H contains points
associated to projective cones over smooth irreducible rational curves of
degree n in IP .
The varieties in IP corresponding to points of H have been
classified by the following
Theorem 13.1 (Nagata). Let Xе-* jpn+ be a closed smooth (irreducible)
surface of degree n, not contained in any hyperplane. Then either (a) X is a
rational scroll, i. e. , it is a ruled surface where the rulings are lines in
P and it is P bundle over P ; in fact X % F .; where F we denote
n- 2 r
a IP bundle over IP with a section В having self-intersection (B) = -r,
76
77
and then it is embedded by the linear system | B+(n-l)L|, where L denotes
the line bundle corresponding to the ruling, or
{ti) n = 4 and X = IP given by the Veronese embedding of IP in IP , i. e.
the embedding defined by &
IP B)
v v 4
b or
(c) n = 1, X = IP .
Remark 13. 2. Let X = IP , and take the Veronese embedding, with
-4v*°."i
=XlX2' V1=X
2V
Then X is a determinantal variety, defined by BX2) minors of the matrix
U V, V.
о 2 1
V, U. V
2 1 о
v, v и.
The cone С over the rational quartic curve has a determinantal representa-
representation defined, for instance, by letting U specialize to V , i. e., substituting
V for U? in the above matrix.
Remark 13. 1 The general scroll can be checked to be theydetermin-
antal variety defined by BX2) minors of the B X n) matrix
x .. . (x +x )
0 n-1 n+1'
X. ... X
1 n
and the cone С is obtained by setting x = 0 in this matrix.
n+1
Let us now take the case n = 4. Any two scrolls (resp. Veronese
surfaces) in IP are equivalent under the projective group. Hence H split.
up into two orbits under the projective group: say, H = К UK . We note
S x Ci
also that there exists no flat family of closed subschemes of IP connecting
a scroll and a Veronese. For if there existed one, the Veronese would be
topologically isomorphic to a scroll (say, we are over <C). This is not the
case: One can see this,for example,by the fact that H (scroll, 2?) = Z ,
H (IP , Z) = Ж. Since K. are orbits under PGLE), they are locally closed
in H , and the nonexistence of a flat family connecting a member of К to
К shows that K. (i = 1, 2) are in fact open in H , so that H is the union
Cm \ S S
of disjoint open sets K_ and К ; in particular, H is reducible. Let % be
the point of H determined by С [we fix a particular C, namely, the cone
in IP with vertex @,. . . , 0,1) and base the rational curve in IP paramet-
parametrized by A, t, t ,. . . , t )J . We saw above that the closure of H contains ?.
This implies that H is reducible at ?.
We shall now show that any "generalization11 of С is again a projective
cone over a smooth rational curve in IP not contained in any hyperplane. In
other words, consider a 1-parameter flat family of closed subschemes whose
special member is С and whose generic member is W. Then W has only
isolated (normal) singularities, is of degree n and not contained in any hyper-
hyperplane. We shall how prove more generally that a surface W in IP (which
is not smooth) having these properties is a cone of the type C. . To prove this
let б be a singular point of W. Then we can find a hyperplane L through 9
79
such that (L • W) is smooth outside в (Bertini1 s theorem). Now L%IP ,
L • W is connected, (L • W) is not contained in any hyperplane (same argu-
argument as for XPlH in the proof of Proposition 13. 2), and it is of degree n.
Since it has only one singular point , it follows by Lemmas 13. 1 and 13. 2 that
(L • W) consists of n lines meeting at в. This happens for almost all
hyperplanes L passing through 9. We take coordinates in IP so that
в = @,. . . , 0,1) and take projection on the hyperplane M = {x = 0}. We
can suppose that the choice of L is so made that L • W is smooth and not
contained in any hyperplane, so that L • W is the rational curve parametrized
by A, t, ...,t ) with respect tQ suitable coordinates in L%IPn. Let В be
the projected variety in M. It follows that almost all the lines joining 9
to points of В are in W from which it follows immediately that in fact all
these lines are in W. In particular, we have В = W • M and W is the cone
over B. This proves the required assertion.
Thus any "generalization" of С is either a cone of the same type as
C, a scroll, or a Veronese. It follows then that in the neighborhood of ?,
H consists of only (parts) of three orbits under PGLE), namely, К , К
and Д, where Д is the orbit under PGLE)
determined by С In a neighborhood of ?,
K. and K- are patched along Д.
H
Remark 13. 4. It has been shown by Pinkham that R is reduced,
that the irreducible component corresponding to scrolls is of dimension 2
and the one corresponding to Veronese is of dimension 1, that they are
smooth, and that they intersect at the unique point corresponding to С having
normal crossings at this point.
Remark 13. 5. The above argument can be extended to show that
SpecR for n>4 is irreducible. Pinkham shows Spec R has an embedded
component at the point corresponding to С and outside this it corresponds to
scrolls.
Remark 13. 6. The reason that for n = 4 we have got two components'
is that in this case the cone over the rational quartic is a determinantal variety
in two ways, namely, it can be defined by BX2) minors of
or of
Xo X2 X4
X4 X3
Remark 13. 7. Case n < 4. Exercise: Discuss.
It follows that SpecR where R is the complete local ring defined
by Def(C) is again reducible and has only two irreducible components.
80
ai
Part II. Elkik1 s Theorems on Ajgfebraiaation.
§1. Solutions jaf systems of equations.
Let A be a commutative noetherian ring with 1 and В a commutative
finitely generated A-algebra, i. e., В = A[X , . . . , X ]/ (f ,. . . , f ), F = (f^ . . . , f ).
Then finding a solution in A to Т{ц) = 0, i. e. , finding a vector
x = (a.,. . . , a ) € A such that
f.(x) =0 A < i < q) ,
is equivalent to finding a section foif Spec В over Spec A.
Let J be the Jacobian matrix of the f.1 s defined by
J =
ЭХГ* *XN
dt
nJ
(q X N) matrix ,
We recall that at a point z € Spec B^-* &. represented by a prime ideal
in A[X ,. . . , X ], Spec В is smooth- over Spec A at z if and only if:
There is a subset (a) = (a ,. . . , a ) of A, 2, . . . , q) such that
(iy there exists a (pXp) minor M of the (p X N) matrix
a.
di
a.
-r—^ such that M Д 0 (mod-p ), and
j
(ii) (f.,. . « ,f ) and (f ,...,? ) generate the same ideal at z.
i q ai °p
If the conditions (i) and (ii) are satisfied at z, then Spec В is of
relative codimension p in A (i.e., relative to Spec A).
Let F. . bte Шэ ideal (f ,. . :,f ). The condition (ii) above is
equivalent to the following: There is a g € A[X ,. .. , X ] such that z I V(g)
and
- (FV
(The subscript g means loeelfessation with respect to the multiplicative set generated by g
This implies that g (F)C (F. ,) for some r. Conversely suppose given a
g€ A[Xr-...ay, such that
«'r>CF(e)
(i.%. , g с conductor of F ic F JH&. . : F)).
or (a)
Then at all points z € Spec В such that g(z) k 0, (F) and F. generate the
same ideal (since F С F). Hence the condition (ii) above: can be expressed as:
(ii) There is an element g с К. = conductorof W in Ъ% v (i. e. , tbe set
(a-) (a)
of elements g such that
. .
) such that g(z) MO.
Let Д = ideal generated by the determinants of the (p X p) minors
of the (p X N) matrix tgg-). Let H be the ideal in A [x^ . . . , X ] defined by
H = 2 К. .Д, ,
(a) (a) (a>
i.e., the ideal generated by tfee ideals {K. .A. .} where Ш ranges over
(a) (a)
all subsets of A, . . . , q). Then we see that at a point z € Spec 3е-* A, ,
Spec В is smooth over Spec A <=> H generates the unit ideal at z <=> z / V(H).
Hence we conclude *
z € Spec В is sjmooth over Spec A if and only if z / V(H)nSpecB.
82
83
§2. Existence of solutions when A is t-adically complete.
With the notations as in the above §1, we have
Theorem 2.1. Suppose further that A is complete with respect to the
(t)-adic topology, (t) = principal ideal generated by t « A (i. e. , A = limA/(t) )
Let I be an ideal in A. Then there is a positive integer q such that
whenever
F(a) = 0 (mod Л) , n > n , n > r
(i. e. , f.(a) = 0 (mod Л), \/1 < i < q, n > n , n > r) and
x — — — о
tr с H(a)
(H(a) is the ideal in A generated by H evaluated at a, or equivalently, the
closed subsclieme of Spec A obtained as the inverse image of V(H) by the
s N
section Spec A — A defined by (a.,. . . , a )),
N
then we can find (a' ,. . . , a' ) « A such that*
F(a' ) = 0 and a' = a (mod tn'ri).
Remark 2.1. The condition tr € H(a) implies that V((t)) DV(H(a)).
N
So the section s : SpecA^-
defined by (a ,. . . , a ) does not pass through
V(H) except for the points t = 0. Roughly speaking, the above theorem says
N
that a section s of A over Spec A which is an approximate section of
A
Spec В over Spec A and not passing through V(H) except over t = 0 can
be approximated by a true section of Spec В over Spec A.
Proof of Theorem 2.1. A) We claim that it suffices to prove the
—i N
following: j h« A (represented as a column vector) such that
<*>
F(a) = J(a)h(mod t2n"rl), and
h=0(tn"rl).
To prove this claim we use the Taylor expansion
F(a-h) = F(a)-J(a)h+O(h ) (error terms quadratic in h).
Now h2 с t2(n"r)L We note further that
• 2n~ г
We have F(a)-J(a)h с t I and hence
I F(a)-J(a)hc t2n'2rl,
f i. e., (*) implies
F(a-h) с t2(n"r)I, and
Set
a. = a-h, a = a. Then this gives
1 о
с t2(*-r>I,
Hence by iteration we can find a. € A such that
(i)
(ii)
i
F(a.) € XT (n'r)I, i> 0, and
Now by (ii), a1 = lima, exists, and a1 = a (mod t " I). Further (i) implies
that F(a' ) = 0. This completes the proof of the claim.
N
B) We claim that it suffices to prove that there is a z € A such that
84
2n
trF(a) = J(a)z (mod t I), and
For,we see easily that there is an h с A . such that t h = z and h с t I.
Then, if J = J denotes the Jacobian for F, we have
tr(F(a)-JF(a)h) = 0 (mod Л),
h = 0 (mod tn"rl).
Set t F = G; then these relations can be expressed as
G(a)-J_(a)h = 0 (mod t2ni), and
G
h =.0 (mod tn"rl).
In particular we certainly have
(**)
G(a)-J_(a)h = 0 (mod t2n"rl)f and
G
h = 0 (mod tn"rl).
These are just the same as the relations (*) as in Step A) above, with F
replaced by G. Hence we conclude (as for F) that there is an a' such that
G(af ) = 0, and
tn"rI
a1 = a (mod t" *I).
Thus we conclude that there is an a1 such that
• trF(a! ) = 0, and
a' = a (mod tn"ri).
Note that F(a') € tn"ri since
F(a' ) = F(a)+JF(a)(a« -a) (mod t2(n"r)I)
and F(a) с Л. Thus we have
85
trF(a') = 0, and F(aT ) с tn'rI.
We would like to conclude that F(a' ) = 0; this may not be true; however, we have
Lemma 2.1. Let T = {a € A|tqa = 0} and let q be an integer such
q ^o
that T = T +1 = T +2 = .. . ,etc., (note that T С T , for q1 >q and
A being noetherian, the sequence T CT _. .. terminates). Then
T П (tm)A = @) for m > q .
q na-q
Proof. Let ас Т ПЛ. Then a = tma' =t °(t °a'). Since
Чо П+Чо
t a = 0, we have t a' = 0. But by the choice of q , we have in fact
q q xn-q m-q q
t °a' = 0. Hence a = t °t °af = t °t °a* = 0. This proves the lemma.
By the lemma if (n-r) > q , then trF(af ) = 0, and F(a' ) « tn"rl
implies that F(af ) = 0. Thus the claim B) is proved.
C) Let (P) = (P,,...,|3 ) denote a subset of p elements of A,. . . , N).
p Э?<ч
Given (a) - (a_, .. . , a ) С (h • • • # Я)> let 6 _ be the pXp minor (-zrz—)
I p a, p с А
of the Jacobian matrix J. Then we claim that it suffices to prove the following:
Given к с K, * and 6 € A F defined as above) then there exists
(a) ap a ap
a z = 0 (mod t I) such that
k(aN A(a)F(a) = G(a)z (mod t2ni).
. Forwe have t = S X. _k (aN _(a). Then by hypothesis, given к
a ap a ap a
afnd|6 ,^г we have, z such that z fl = 0 (mod t I) and
(mod Л);
86
87
then we see that if we set z = 2 X. _z . we have
tr • F(a) = J(a)z (mod t2ni), and
z = 0 (mod t I),
which is the claim B).
D) We can assume without loss of generality that (a) = A,. . . , p) and
F) = A,. . . ,p) so that б _ = detM where
ap
df. 1 < i ? p
Then we have
J =
Let N be the matrix formed by the determinants of the (p-1) X (p-1) minors
of M so that we have
MN = б • Id , б = б л , a, p as above.
We denote by If the (N X p) matrix by adding zeros to N.
Let к € К, ., (a) as above and б be as above. Then we claim that
if z is defined by
Pal
-CT
, Z is an (NX 1) matrix;
then if z = Z(a), we have
k(aN(a)F(a) = J(a)z (mod t2nl), and
z = 0 (mod Л).
By the foregoing, if we prove this claim, then the proof of the theorem would
be completed. .«
To prove this claim, we observe that the relation z = 0 (mod t I) is
immediate. Since к € К. v, (a) as above, we have
(I)
This gives
kf = Z X f, 1< j<q.
1 i=l 3
d? p Bt
= S X .. -r— (mod F), 1 < j < q.
1 i=l lj3Xl
Substituting (a), we get
Э?. р Ы.
k(ah-f(a) = S X.. -~r(a) (mod F(a))
i
= S X..(ah~-(a) (mod Л).
i=l Ч ЭХ1
Let u с A be an element such that u 5 0 (mod *2я)# where Ъ is some ideal
of A. Let v = J(a) • u с AN. Then
N 3f
k(a)v = k(a)
1=1
N p
= S (S
1=1 i=l
3f.
N oi.
X..(a) ' ( 2 ~-(a)u.) (mod
lj 1=1 ЭХ1 l
X..(a)v. (mod t
1J x
In other words,
(И)
k(a)v. = 2 \. .(a)v. (mod t lb), for 1 < j < q,
J i=l 1J '
88
89
where u € A , тг =¦ J(a)u, and u = 0
TNT
Now take for u e A and v the elements
-Id
Then u = 0 (mod t I) and we have
k(a),y. « 2 \..(a>v. (mod t
И
Moreover,
v = J(a)
[mn]
*nJ
L1.
:] [r]
(a)
6(a)fp(a)
Hence v. = 6(a)f.(a), 1 < i < p. By (П),
k(a)J(a)
= k(aN(a)
(modt
which is precisely the claim in Step D) above. This completes the proof 6f
the theorem as remarked before.
Remark 2.1. A better proof of the theorem is along the following lines:
Introduce a set of relations for F so that we have an exact sequence
(Here F denotes
f
L qj
as well as the ideal generated by f. and
P = A[X ,.. . »XN]» and R is the matrix of relations of F; it has entries in P.)
In matrix notation, we have F* R = 0. Differentiating with respect to X., we obtain
JR = 0 (mod F),
3f.
where J is the Jacobian matrix (д ) (it is an N X q matrix and is therefore
j
the transpose of the matrix J introduced in the theorem above). Let P = P/F
and define J, R similarly. Then we obtain a complex
By (I),
k(ayv, ? ^ X..(a)v. {mod
P
1J
P
2
Hence it follows that
, »o that
Tor: P S pq -* p is a complex mod F). It is not difficult to see that at a
point x с Spec(P/F), the complex (*) is homotopic to the identity (in particular, is
exact), i. e. , denoting by a subscript x the localization at x, there is a
}
' diagram
p 1 5 p Я J -1
p Я J 1
X X
=
90
91
if and only if Spec(P/F) is smooth at x. For example, suppose that Spec(P/F)
is smooth at x. Then we can assume without loss of generality that
di. 1 < i < p
det(-rrr-) , . . . . , is a unit in P . From this it follows easily that there
dX. 1 <¦ j <_ p x
is a direct summand Qf~~Pq, Q %PP such that ImfJ) = Im(jfQ ) and
j|Q- : Q -*Im(J) is an isomorphism (JJQ. denotes the restriction to Q ).
Indeed, we can take О to be the submodule generated by the first p-coordinates.
n af.
(Note we have J(e.) = 2 ^pL, with (e.) a basis of P4, and (?.) a basis
1 i=l dXl l г г
~"N —
of P ). We see also that Im(R) is of rank (q-p) and is a direct summand
in P , In fact the relations
give elements of the form
in bnR. Suppose now S $i,I. is a relation; then as we have seen before
i=l * X
(on relations for a complete intersection), ц. с (f , . . . , f.) so that /i. = 0.
Hence we conclude that (bnR) is precisely the submodule generated by
P _ _
(e. - 2 X. .e.), j >^ p+1, which shows-that ImR is of rank (q-p) and is a
direct summand in P 4. Now we see easily that the .complex (*) jjs homotopic
to the identity at x if and only if, (i) (*) is exact and (ii)ImR is a direct
summand which admits a complement Q such that J|Q, is an isomorphism
and Im J ^ImfJlQ^). Now we have checked these conditions when Spec(P)
is smooth at x. Conversely if (i) and (ii) are satisfied (at x), it can be
checked that Spec(P) is smooth at x.
Suppose more generally that we are given a complex
(we keep the same notation). Then we can define an ideal Ifb in P which
measures the nonsplitting of the complex as follows: *K *s tne ideal generated
by elements h such that there are maps r, j:
p1 5: pq J p
such that
It can be shown that J? is the following ideal: Take a (pXp) minor M in
J and a "complementary" (q-p) X (q-p) minor К in R (involving "comple-
"complementary indices11); then ft is the ideal generated by the elements (detM)(detK).
In our case, SpecP - V(}?) is the open subscheme of smooth points.
It follows then that 7t and the ideal H (H is the ideal defined before and H
denotes the image of H in В = P/F) have the same radical. In our case we
have then
Rr+j J = h (mod F), for some h с P with image h in If.
Multiplying by F (where F is a vector now), we have
FRr+FjJ = Fh (mod F2).
Since FR = 0, this gives
FjJ = Fh (mod F ).
'.t t
We have used the transposes of the original J; setting z = j F and taking
92
93
"evaluation at a11, we get
h(a)F(a) = J(a)z~(mod t2ni).
Now a power of h is contained in H since H and ft have the same radical.
This is the crucial step in the proof of the theorem above. Hence from this
the proof of the theorem follows easily.
Before going to the next theorem, let us recall the following facts
about Ot-adiс rings (cf. Serre, Algebre Locale, Chap. П, A). Let (A,01) be
a Zariski ring, i.e. , A is anoetherian ring, is an ideal contained in the Jacobson radic
RadA of A, and A is endowed with theOL-adic topology, i. e. , a fundamental
system of neighborhoods of 0 is formed by ОЬ . Since О Л = @), it follows
n
that this topology is Hausdorff. Let A denote the<7t-adic completion. Then
A is noetherian. If M is an A-module of finite type we can consider the
01-adic topology on M and similarly it is Hausdorff and i/ M denotes the
<Jt-adic completion of M, we have M = M 0 A. In fact the functor МкМ
is exact. Suppose now that M = M. Then we note that any submodule N of
M is closed with respect to the Л-adic topology (for, the quotient topology
in M/N is the fft-adic topology and since M/N is of finite type and
ObQ RadA, this topology is Hausdortf and hence N is closed). If A = A, i. e.,
A is complete, then any module of finite type is complete for the adic topology
so that we don1 t have to assume further that M = M.
Let A = A, M be as usual and t € OL. Then M/tM is complete for
the tft/tdt-adic topology, for this is simply the/Tt-adic topology on M/tM.
Let A = A and 2*Ъе an ideal in A. Given an r, suppose that the
relation СП Qlf + OL , m» 0, holds. Then <Я-ГСЪ» for our relation implies
that <гГ(А/МСПЛт(А/Ы. Since A/Z» is Hausdorff for the Ot-adic topology.
m
it follows that CL А/Ь = @), which implies CL С Ъ*
$3. The case of a henselian pair (A,0t).
Theorem 3.1. With the same notations for А, В as in the pages
preceding Theorem 2.1, suppose further that (A,OL) is a henselian pair
(in particula-r CLQ RadA), and that A is the JC-adic completion of A. Suppose
we are given a € A such that F(a) =0 (i. e. , a formal solution) and CL * A
(or briefly Ob )C H(a) for some r. (This means that the section of Spec В
over Spec A where B=A|x|/(f.) represented by a passes through smooth
points of the morphism Spec В -* Spec A except over V{av). ) Then for all
N
n >. 1 (or equivalently for all n sufficiently large) there is an a € A such
that F(a) = 0, and a = a (mod a~L ).
Proof. il) Reduction t? the case ОС principal.
Let CL = (t ,. . ., V). Let us try to prove the theorem by induction on
k. If «k = 0, then the theorem is trivial. So assume the theorem proved for
(k-1). We observe that the couple (A/t , (t ,. . . ,t )) is again a henselian
pair Vi >1 (here t , ...,t denote the canonical images of t. in A/t ).
Definition. By a henselian pair we mean a ring A and an ideal 0"CC RadA
( = Jacobson radical of A) such that given F = (f ,. . . , f ), N elements of
A[Xr . . . , XN] and x° € АП, x° = (x? . .., x^) such that F(x°) = OmodfcrU
and such that det( ) 1 is invertible modffl», then HxcA ,x = x mod@L)
ax. |xo
with F(x) = 0.
94
95
Set t = t. and A = A/(t ). We note also that the OTL-adic topology on A is
tHe same as the (t ,. . . , t .) = fft -adic topology. If A, A. denote the cor-
corresponding completions, we get a canonical surjective homomorphism
A-*A whose kernel is t *A. Let b be the canonical image of a in A .
Then we have F(b) = 0. Besides,we see that Ot С H(b) for some s (this
follows from the fact that V(H)PlSpec В = locus of nonsmooth points for
Spec В -• Spec A and the set of smooth points behaves well by base change and
for us the base change is A — A . We cannot say that s - r, for the ideal H
(or rather H(modB)) which we have defined using the base ring A does not
behave well with respect to base change. The ideal 7 does behave well
with respect to base change, and if we had used this ideal we could have got
the same integers). Hence by induction hypothesis, for all m^ t, there exists
a b с A™ such that F(b) =0, and b = b (mod<7tm).
N
Lift b to an element а. с A and choose / so that f >_ m. Then
we see that
a = a (modtfL ), and
F(ax) =0 (mocKt1)).
(The fact that b = b (mod<7Lm) implies (a -a) + x с <Я,Ш with x € Ker(A - A ) =
(t ). Now t € CTL, and if i >; m, (t ) € at. ) We claim that if m » 0 (and
consequently / » 0), we have СП QH{oi ). By hypothesis we have
OL С H(a), and from the relation a = a (mod 0ЪШ), we get
(as ideals in A; to deduce this we use the Taylor expansion). Then, as we
remarked before the theorem for m*>> 0, this implies that Ob Q Ща^.
Since t с at it follows that t € H(a ).
Let A denote the t-adic completion. Then the following -relations
in A,
for all / > 0,
= 0 (mod(t ))
N г
there exists a € A such that t €
hold a fortiori in A , and hence by Theorem 2.1 we can find a1 A such that
— ¦ t
F(a! ) = 0, and
Note that the pair (A, (t)) is.also henselian. Hence if the theorem were true .
for к = 1, we would have
\/n,
such that
a) = °» and
a = a1 (mod tnA).
But we have
a1 = a (moid(tS)At), for s sufficiently large, and
a = a @L.m- A), m sufficiently large.
These imply a=I(mod<Jon) (since t € cjc and AtC A), which implies the
theorem. Hence we have^only to prove the theorem in the case к = 1, i- e. ,
OL principal.
B) A general lemma:
Lemma 3. 2. Let А, В be as in the pages preceding the theorem,
i.e., В = A[Xr ...,XN]/(fr...,f ), F = (fj,...,^). Let С be the symmetric
96
97
algebra on F/F over B, so that Spec С is the conormal bundle' over
Spec В (F/F as a B-module is the conormal sheaf over Spec B). Let
f, g, h denote the canonical morphisms
Spec С — Spec В — Spec A, g = h - f.
f h
Let V be the open subscheme of Spec В where Spec В -» Spec A is smooth
and V1 = f" (V). Then we have the following:
(a) g : Spec С-* Spec A is smooth and of relative dimension N (over
A) on V1 and
(b) J an imbedding Spec С*— Ж q (A-morphism) such that the
A
restriction of the normal sheaf (for this imbedding) to every affine open subset
U^* Vf is trivial.
Proof of Lemma 3. 2. We set
,I), К =
On V we have the exact sequence
(i)
O-F/F -
(This is an abuse of notation; strictly speaking we have to write (F/F ) I . . . , etc. )
On V we have the exact sequence
(ii)
0-*f
nc/B*f*(F/F2).
Taking f^* of the first sequence,we get sequences
0 - f*(F/F2) - (Free) -
- 0
which are exact on any affine open set U in V1 . These exact sequences are
split on U, so that we conclude
fl i is free on U.
On V we have the exact sequence
c-oc/A-o.
Thus it follows that on U
K/K2 Q (Free) = (Free),
of rank N
(From the exact sequence (ii) it follows that &C#A is °* rank N over С
and this implies the assertion (a). ) If we introduce N more indeterminates
Zr...,ZN, then
•(*)
С = A[X, Y, Zr . . . , Zj/(K, Z^
Let K1 = (K, Z ,. . ., Z ). Then we see easily that
; К1 /К1 2 = К/К2 Ф (Free of rkN).
It follows that K1/K1 is free on U. Thus fo.r the embedding Spec O*A-A q,
the restriction of the normal bundle К1 /К1 to U is trivial. This completes
the proof of the lemma.
98
99
C) We. saw in A) above ,that for the theorem it suffices to prove it in the
case oc= (t). The condition Ся/лСШа) becomes t* € H(a). (Note that
H(a) is the ideal in A generated by evaluating at a elements of H and H
is an ideal in A^, ...,XN] not in A-fX^ . . . , 3^]. )
"We' claim now that there jls_ an h € H such that
h(a) = (unit) • tr.
A priori it is clear there is an h € H'A[x] such that h(a) = tr. Since A is
the t-adir completion of A, we can find an h с Н such that
h = h (mod(tr+1))
(i. e., the coefficients of h and h differ respectively by an element of
(tr+ )). This implies that
h(aL) - h(a) = *tr+\ hence
h(I) = tr(l+*t).
Now (l+*t) is a unit in A. This proves the required claim.
D) The final step.
Since Spec С is a vector bundle over Spec B, we have the 0-section
Spec С*?Spec B. We are given I € AN such that FG) = 0. Now a determines
a section of Spec(B ® A) over A, or equivalently a morphism
A
s : SpecA -» Spec В forming a commutative diagram
Spec A -*- Spec В
SpecA
Using the 0-section, s can be lifted to a morphism s : SpecA — Spec C:
~ Sl
SpecA — Spec С
\
SpecA
Now By C), s carries (SpecA-V(t)) to Spec С [l/h], where h is as in C)
(here h denotes the canonical image in С of the h in C)). NWe observe that
Spec С [l/h] С V1,
(V1 = f (V), V = locus of smooth points of Spec B —SpecA) and V1 is contained
in the locus of smooth points of the map Spec С -* SpecA. We have
С = A[X, Y, Z] /K1 where K1 = (F, I, Z ,. .. , Z ). The section s defines
a solution K1 (a1 ) = 0, where а1 с А Ч (a1 extends the section 7). We
have t с H(a! ) for a suitable k. Hence the conditions,similar to those of
Spec В — SpecA, are now satisfied for the map Spec С — SpecA. It is immediately
seen that it suffices to solve for the case Spec С — SpecA, in fact if we get a solution
.- a1 « A , we have to take for a the first N coordinates of a1 .
Let U = Spec С [l/h]. Then the restriction of the normal bundle of
the imbedding Spec О- А. Ч is trivial on U and, U being smooth over A,
, it follows easily that U is open in a global complete intersection. By this we
mean there exist g ,. . . , g € A [X, Y, Z] such that V(g ,. . . , g ) has
dimension N and we have an open immersion
(SpecC[l/t]) = SpecC[l/h]^*SpecA[x,Y,
Let G = (g1,. . . , gN+ ). Then we have
K;=ct.
n+q'
100
101
(We denote the localization with respect to t by a subscript. Note that
localizationwith respect to t is the same as localization with respect to b. ) The given
solution a' in A q is such that K' (a' ) gives rise to a solution G(a' ) = 0
by changing the g., multiplying them by suitable powers of t. Conversely,
suppose we have solved the problem for G, i. e. , we have found a' € A
such that G(a ) = 0 and a' = a (mod t ). Then we see easily that there is a
8 such that
t9 • F(a' ) = 0.
Since F(a) =0 by Taylor expansion, it follows that F(a' ) = 0 (mod t ). Now
if n» 0, by Lemma 2.1, it follows that F(a' ) = 0. Thus it suffices to solve
the problem for G, i; e. , for the morphism
Spec С -SpecА, С = A[X, Y, Z]/G.
We have seen that a1 defines a section of this having the required properties.
Further, Spec C1 is a global complete intersection and smooth over A in*
A , i. e. , we have reduced the theorem to the following lemma.
§4. Tougeron1 j5 lemma.
Lemma 4.1. Let (A,Ob) be a henselian pair and f. € aTy., . . . , Y__] ,
Э? l N
К i < m. Let J = (т~) be the Jacobian matrix, 1 < i < m, 1 < j < N.
— — Ox — — — —
(т)
Ox.
J
Suppose we are given у = (у ,. . . >У^) « A such that
f(Y°) ?0 (mod Д2Ь)
where V(k) = V(tft) (or <=> Ъ is also a defining ideal for (A, G1)) and Д
is the annihilator of the A-module С presented by the relation matrix
(i. e., С is the cokernel of the homomorphism A -* A whose matrix is
N
J(y )). Then there is а у с A such that
f(y) = 0 and у = y° (mod Д^).
Proof. The henselian property of (A,?7L) is used in the following
manner: Let F = (F-,... , F ) be N elements of A[Y., . ¦., Y ] and
У = (Yj # • • • # YN) « A such that
(P)
(i) F(y") = 0 (modOl)
ar
(ii) detfr^-) is a unit (mod OL),
oY, о
J У=У
Then there is а у € A such that F(y) = 0 and у = y° (mod Ob).
Let 5.,..., 6 generate the annihilator of A. This implies that
there exist N X m matrices such that
Write
m components.
We try to solve the equations
f(y° + 2 6.U.) = 0
for elements U. = (U ,. . ., U ) « A (we consider vectors in A to be
J02
103
column matrices). Expansion by Taylor1 s formula in vector notation gives
0 = f(y°) + J- B6.U.) + 2 6.6.Q..,
ii uj i J iJ
where
and
Expanding, we get
J is an (m X N) matrix,
f(y ) is an (m X 1) matrix,
U. is an (N X 1) matrix (not A X N) matrix as it is written),
Q..,?.. are (m X1) matrices.
where M is an Nr X Nr matrix of polynomials in Z and every m has
no constant term.
Let z° с A represent the vector @,... ,0); then we have
F(z ) = 0 (modi?) since с..у с Ъ .
Without loss of generality we can suppose 1j -CL since }j is also a defining
ideal for (A, CC)
F(Z°) =0 (modJL).
0 = J-(S 6.U.) + 2 6.6. (Q. .+?..),
isli i ui i J ч и
(m XN)(N XI) matrix (m XI) matrix
= 2 6.(JU.) + 2 6. • JN.
i=l i j
= 2 F.J) • U. + 26.JBN.(Q. .+?..))
i=1 i i . i j J ч U
Thus it suffices to solve the r equations
(*) 0 = U + SN^Q^+
j J iJ
F .Id = JN.)
F. are scalars).
К i < r.
This is an equation for an (N XI) matrix. Thus (*) gives Nr equations in
the Nr unknowns U. , 1 < i < r, 1 < v < N.
lV _ _ __ _
We note that Q.. are vectors of polynomials in U. all of whose
terms are of degree >. 2. Let F = F ,. . . , FNR 6 A[uiv] represent the right
hand side of (*). Write Z, ...,Z for the indeterminate s U.y. Then
, M = (m J , (Nr X Nr) matrix
ap
k
Further, we have (^_ )_ o is a unit in A/OL. Hence by the
henselian property of {A,oL)9 w^e have a solution z of (*) in A such that
z = z (mod GL), i. e., z = 0 (mod OL) since z = @). Set
о
у = у +z.
Then we have
о
у = у (mod A0L) and f(у) = 0,
which proves the lemma.
; Remark 4.1. It is possible to take Ъ such that Ъ Q.OL ', for if
(A,(Jl) is a henselian pair, the henselian property is true for 2p , &
< Then the above proof also goes through for this case.
Corollary. Let (A,0L) be a henselian pair and
and CD the canonical mo rphism
Cp : Spec A [yr . ..,
, fm> - Spec A
104
Suppose that Cf is smooth and a relative complete intersection. Then
given у € A ((Jt-adic completion of. A) such that
f (У) = 0,
there is а у с A such that f(y) = 0 and
у = у (mod (Я*
for any given с >^ 1.
Proof. We can take с = 1 for Ot is also a defining ideal for (A,crc).
We can a^ fortiori find у « A such that
f(y°) = 0 (mod ОЦ { <= f(y) = 0)..
y° then defines В a section of Spec(B) over SpecA/ot. The morphism is
a complete intersection and smooth at points of this section. This implies
that the Ideal generated by canonical images in A/Ob of the determinants
of the (m X m) minors of J(y ) is the unit ideal in A/OC, i. e., the canonical
о
image of Д in A/<7L is the.unit ideal. Since OX is in the Jacobsoa radical,
it follows that Д is itself the unit ideal. Indeed Д being the unit ideal in
A/tft implies there exists a u « Д such that u = 1 (mod0L), hence u-l с OL,
hence u = 1+r, г с 0L. Since OLQUadA, u is a unit in A.
§5. Existence of algebraic deformations of isolated singularities.
Definition 5.1. A family of isolated singularities is a scheme
X^S over S = Spec A, A a k-algebra such that (i) v is flat, of finite pres-
presentation and X is affine, X = Spec & and (ii) if Г is the closed subset of
X where ir is not smooth, then Г — S is a finite morphism (for this let us
say that Г is endowed with the canonical structure of a reduced scheme). -\
Definition 5. 2. We say that two families X — S and X1 — S of
isolated singularities are equivalent or is ото гр hi с if there is a family of
isolated singularities X"-* S (note that S is the same) and etale morphisms
X'UX', X"-X such that
(i) the following diagram is commutative
Y»
etale у j\etale
X X1
and (ii) these maps induce isomorphisms
Г Г1 .
An equivalence class of isolated singularities represented by X -*- S
is therefore the henselization of X along Г.
r. Consider in particular a one point "family11 X -* Speck with an
isolated singularity. (We could also take a finite number of isolated singu-
singularities. ) We see easily that the formal deformation space of X (in the sense
о
of Schlessinger defined before) depends only on the equivalence class of X .
Let A be the formal versal deformation space associated to X (we can .
speak of the versal deformation space of X by taking Zariski tangent space
of A = dimT ), i. e., A is a complete local ring, and we are given a sequence
:{X } of deformations over A
* n n
n+1
X = Spec Cf , A = A/m" , Q- ® A , -
n r n n A ' ^n n-1 =
•r satisfying the versal property mentioned before. Note that by a versal
106
107
deformation it is not meant that there is a deformation of Xq over A. The
following theorem,proved by Elkik, asserts that in fact a deformation of Xq
over A does exist (i. e. , in the case of isolated singularities). It is the
crucial step for the existence of "algebraic" versal deformations for X~.
Theorem 5.1. Let X = Spec <У , & = k[X ,. . . , X ] /(f),
о о о 1 m
(f) = if ,. . . ,f ). Let X = Spec & be as above, but we suppose moreover
that X is equidimensional of dimension d. Then there is a deformation
X1 over A such that Xf ® A ^ & , and if X1 = Spec &x then 6" is an
n n
A-algebra of finite type. (We do not claim that &x has the same presentation
as <3T .)
о
Proof. Let С-ИтО", & = A [x . . , X ]/(f(n)), where
- «- n n n1- 1 mJ
ffn) с A [X] is a lifting of f. € k[x]. Let A[x]A denote the m-adic
(m = m ) completion of A[x]. We see that A[x] is the set of formal power
A
series Sa.X*1' such that a. - 0 in the m-adic topology of A. Then
7. = limf. is in A[x] and we see easily that
& =A[X]A/G).
(For, we see that we have a canonical homomorphism
o:A[X]A/(f)-5>
obtained from the canonical homomorphism A[x]A/(f) —A [x]/(f ). It is
easy to see that a is an isomorphism. )
The proof of the theorem is divided into the following steps:
A) It is enough to find a (flat) deformation Xм over A of Xq such that
O" 8. А, ^вГл, where X" = Speed'" (recall that A. = A/m ).
For, given a (flat) deformation X" over A we get deformations
{X*1} = Xn ® A over A . For each n, we get then by the versal property
of A, a homomorphism
a : A-A .
n n
Note that a is defined by
n
(a ) : A — A , m » 0,
n m m n
so that X ® A ^X!l. These {a } are consistent and hence {a } patch
m A n n n n
m
up to define a homomorphism of rings
a : A-A.
The hypothesis that ©"' ® A « & ' implies that
A 1 1
a = Id (mod m ).
A.
This condition on a implies that a is an isomorphism; for it follows that a
induces an isomorphism on the Zariski tangent spaces, so that Ima contains
a set of generators of m , hence a is surjective; further, this condition
* A
implies that the induced homomorphisms a : A/m -¦ A/m are surjective,
n A. A
and these vector spaces being finite-dimensional, it follows that a is an
n
isomorphism for all n (in particular injective). It follows easily that
KeraC ^mA = №)» i. e. , a is injective. Hence a is an isomorphism,
n
Now define the deformation X! over A as the pull back of Xй over
A by the isomorphism a-1. It is easily checked that X1 8>A A ^;X , and
An n
this proves A). _
Let us set X = SpecC. Consider the Jacobian matrix J =
эх
108
109
l<.i?r, l<J<m ((f) = (f ,.. . ,f )). Let Г denote the locus of points in
X = Spec С where rk J < (m-d). Then Г is a closed subscheme in X. (We
эт
aote that f.« А[х]л and -ттр « А[х]л so that the Jacobian matrix J is a
matrix of elements in A[x]A.) Hence if x € SpecA[x]A (in particular if
x € Spec©" = Xе-* Spec A [x]), we can talk of the rank of J at x, i. e. , the
matrix J(x) whose elements are the canonical images in k(x) (residue field
at x) of the elements of J. It follows then easily that the locus of points x
of X where J(x) is of rank < (m-d) is closed in X; in fact we see that
Г = V(I) where I is the ideal generated by the determinants of all the
(m-d) X (m-d) minors of J1 where J1 is J with elements replaced by
their canonical images in Cf. It is clear tjiat ГПХ is precisely the set
о
of singular points of X , which is by our hypothesis a finite subset of X .
It can then be seen without much difficulty that Г is finite over А (Г is
endowed with the canonical structure of a reduced scheme or a scheme
structure from the ideal I introduced above). The proof of this is similar
to the fact:quasifinite implies finite in the "formal case11, i. e. , in the situation
A -* В where А, В are complete local rings and В is the completion of a
local ring of an A - algebra of finite type.
Let Г = Spec ©7 Д and let A be tne ideal in & defined by A
о о
(i. e. , the canonical image of A 0 к in СГ ). By the No ether Normalization
lemma we can find y. ,. . . , у in A such that СГ is a finite kfy, ,. . . , у ,1
1 а о о 1 a.
module such that the set of comiaon zeros of y. is precisely the set of
singular points of X . Lift y. to elements y_,. . . ,y• in A so that
y_,.. . ,y vanish on Г. Then we have
1 d
B) СГ is a finite А [у]л module (and Г is precisely the Iqcus of y. =0).
This is again obtained by an argument generalizing^quasifinite implies
finite in the "formal11 cases. "
C) The open subscheme Х-Г of X is regular (over А) (ь^е., Х-Г is
flat over A and the fibres are regular).
This is a generalization of the Jacobian criterion of regularityto
the adic and formal case.
D) Outside'the set {y = 0} in SpecA[y]A (this is a section of SpecA[y]A
over SpejcA and Г lies over this set), Cf is locally free over A[y]A say
of rank r, i._e. , pj& ) is a locally free sheaf of ^SpecA Гу"|Л-{у -о}
X —1 1
modules (p : X ~* Spec A [y] A canonical morphism).
For, p^O" ) is finite over SpecA[y]A. Now SpecA[y]A is regular
X
over Spec A. We have seen that Х-Г is regular over SpecA, so that it is
in particular Cohen-Macaulay over SpecA. Now a Cohen-Macaulay module
:M (of finite type) over a regular local ring В is free (cf. Serre1 s "Algebre
I locale") and from this D) follows. (We can use this property only for the
•corresponding fibres, but then the required property is an easy consequence
of this. )
E) Set P=A[y]A. Then for & considered as a P module we have a rep-
resentation of the form
Am ir An — л
p —i»p — &-~ 0 (exact as P modules)
with rk(a..) <^ (n-r) (i. e. , determinants of all minors of
rk(n-r+l) of (a..) are zero).
110
111
More generally, let us try to describe an R-algebra В having a rep-
representation of the form
(a .)
Г R —¦="*¦ R -» В -* 0 exact sequence
(*) < of R-modules
a..)< (n-r).
Then we have
Lemma 5.1. J an affine scheme V (of finite type) over Spec Ж
such that every R-algebra of the form (*) is induced by an R-valued point of V.
Proof of Lemma. To each R we consider the functor
_ Г set of all commutative R-algebras B'l
" J^with a representation of the form (#) J .
One would like to represent the functor *3* by an affine scheme, etc. We
don11 succeed in doing this, but we will represent a functor G such that we
have a surjective morphism G -¦ 3^
An algebra structure on В is given by an R-homomorphism
В Ф_ В -* В.
XV.
Then in the diagram
31
the homomorphism R
R ® R R
R — R factors via a homomorphism
R ® R -* R (of course not uniquely deterinined). Now the following sequence|
(R
Rn) 9 (Rn в Rm) t Rn в Rn -. в 0 в - 0
is exact where ф = (a..) 0 Id Q Id ® (a..). [We have
(Ker(Rn-* B) ® Rn) В (Rn ® (KerRn- В)) °аП ОП^ Ker(Rn ® Rn - В ® В) - 0.
This implies exactness of the given diagram.] Again there exists a lifting
of the above commutative diagram
(RmeRn)e<RneRm)^RneRn-B®B B-0
XV.
•0 .
R 1 „ R * В
On the other hand, giving a commutative diagram
(Rm в R°) О (R° в Rm) t Rn S Rn
Vм
where ф - (a..) (8> Id Q Id ® (a..) determines the commutative diagram (I ).
The algebra structure on В induced by (I ) is associative if the diagram
Id»b\
and the map
|ЬвИ1я° factorizes through Rm-Rn, i.,
(U)
or, b» (Id в b) - b- (b ® Id) is zero in B.
112
113
Let b:RnXRn-*Rn be the homomorphism obtained by changing
b : Rn X Rn — Rn by the involution defined by x®y^y ®x in R 0 R. Then
the algebra structure is commutative if there is a homomorphism
6 : Rn ®та Rn :* Rm such that
R
such that the following diagram is commutative:
(Rm В Rn) О (Rn
(I)
-R"
К.
(Ш)
commutes.
Finally the identity element 1 « В can be lifted to an element e « R
(determines a homomorphism R — R ) and there is a map e : R -* R such
n e®b-Id n
—R
(IV)
а..)
commutes, i. e. , e ® b-Id = 0 in B.
Let us then define the functor G : (Rings) -* (Sets) as follows:
G(R) = (i) Set of homomorphisms a : R — R
such that rka <_ (n-r) (i. e. , determinants of all
minors of a of rk(n-r+l) vanish), together with
(ii) Set of homomorphisms b, с
Rn 0 R° , (Rm 0 Rn) © (Rn S> R1")
@)
together with
(iii) an R-homomorphism a:R 0R ®R -*R such that the
following is commutative
0 Rn
(ID
and
(iv) an R-homomorphism 6 : R 0 R -* R such that
(Ш)
commute s, and
(v) an R-homomorphism • e : R -* R and e : R -*• R such that
n e0b-ld л
(IV)
\/
commutes.
It is now easily seen that G(R) can be identified with a subset S*-* R
such that there exist polynomials F.(X_,. . . ,X ) over Ж such that
l 1 p
s = (s^ . . ., s ) « S iff F.(s ,. . ., s ) =0, and the set {F.} and p are
114
115
independent of R. From this it is clear that G(R) is represented by a scheme
V of finite type over Ж and since G(R) -* F(R) is surjective, Lemma 5.1
follows immediately.
It follows in particular that & is represented by a homomorphism
Cp:.SpecP-V (P = A{yy . .'. ,ym]' ).
(^) The image of SpecP-{y = 0} in V lies in the smooth locus of V over
Spec Z.
We have a representation
(*>
~+& -* о
(homomorphisms of rings and homomorphisms a-s P modules). Now
P[z, ...,z] is regular over A and Х-Г is regular over SpecA-{y = 0}.
Hence the immersion Xе-* SpecP?z ,. . . , z ] ^T-^- » being an A-morphism, is
S P
a local complete intersection at every point of Х-Г (we use the fact that a
regular local ring which is the quotient of another regular local ring is a
complete intersection in the latter; we use this fact for the corresponding local
rings of the fibres and then lifting the m-sequence, etc. ). Now codimX
in A. is s. Now take a closed point x « SpecP-{y = 0}. Then tensoring
P
(*) by k(xQ) we get
k(xQ) [zr . .., zg] - & 0л k(XQ) - 0 exact.
л __
Now Spec & 0Д k(x ) ib precisely the fibre of X over x for the morphism
— л —
Xе-* Spec P. We claim that Spec С ®л к(х ) is also a local complete inter-
intersection in k(x )[z , ...,z ] wherever x € SpecP-{y = 0} (it is a
0-dimensional subscheme of Speck(x ) [z ,.. ., z Iе-* ^L ) and in fact
О 1 о К\Х /
о
that Spec С 0A R*=-* SpecR fz., . .., z "I is a morphism of local complete
A p О U 1 SJ
intersection over R for any base change Spec R — SpecP-{y = 0} (i. e. ,
-—; о
flat and the fibres of the morphism over Spec R is a local complete intersection).
To prove this we note that (T 0Д Rq is locally free (pf rank r) (SpecR -*
SpecP-{y = 0}) and SpecR [z ,. . . , z ] -¦ SpecR is a regular morphisra. in
particular a Cohen-Macaulay morphism. Now the claim is an immediate con-
consequence of
Lemma 5. 2. Let B, C, R be local rings such that В, С are R-
algebras flat over R and В is Cohen-Macaulay over R. Let f : В -» С
be a surjective (local) homomorphism of R-algebras such that С is a complete
intersection in B. Then for all R-*R -* 0, the surjective homomorphism
о
B0R -*C0R -*0
о о
(the morphism Spec(C 0 R )c* Spec(B 0 R )) is a morphism of complete inter-
intersection over SpecR .
Proof. Since the flatness hypothesis is satisfied, it suffices to prove
that С 0 к is a complete intersection in В 0 к (к = R/m ), Now we have
XV.
0-I-B-C-*0 exact,
I = ker В -* С, and I = (f ,. .. , f ), f. is an m-sequence in B. Now the co-
dimension of C, Spec(C 0 k) in Spec(B 0 k), is equal to the codimension of
Spec С in Spec B, which is s. (This follows by flatness of В, С over R
116
117
and the fact that flat implies equidimensional. ) Let f. denote the canonical
images of f. in В 0 к. We have then. (B ® k)/G , . . . ,7 ) = С ® к. Now
i Is
(B ®4c) is Cohen-Macaulay and the codimension of Spec(C ® k) in Spec(B ® k)
is s. It follows by Macaulay1 s theorem that f ,. ¦ . , f is an m-sequence
in В ® к. This implies that С ® к is a complete intersection in В ® к,
and.proves Lemma 5. 2.
The complete intersection trick. We go back to the proof of E). Let
X : SpecR — Spec P be a morphism such that R is Artin local and
MSpecR )CSpecP-{y = 0}. Consider the morphism (CD » \) : SpecR —V.
Then {'CP о \) defirles an R algebra В which is a free R -module of
' о о
rank r (in particular flat over R ), and B* is a mbrphism of local complete
intersection over R (B is of relative dimension 0 over R ). Let
о о
R-» R —0 be such that SpecR is an infinitesimal neighborhood of SpecR .
о о
Then the assertion E) follows if we show that (Q> о X.) : SpecR — V factors
1 о
through SpecR-*V.
Now В is defined by
where a = (a..). Now Spec В -*• SpecR is a morphism of local complete
intersection for a suitable imbedding and Spec B. It is clear that Spec В—
SpecR is in fact a morphism of global complete intersection for the cor-
corresponding imbedding, for it is easily seen that a 0-dimensional closed sub-
scheme of A which is a local complete intersection's in fact a global
intersection. We have seen in §4, Part I, that the functor of global deforma-
deformations of a. complete intersection jljs unobstructed, i_. je. , formally smooth.
Hence there is a flat R-algebra 31 such that В1 ® R ^B. Hence th.e
mao R °
sequence R —- R — В — 0 can be lifted to an exact sequence
R -* R -* B1 — 0; the proof of this is in spirit analogous to imbedding a.
deformation (infinitesimal) of Xе-* Ж in the same affine space. A hoirio-
morphism (Rn — B) over R is given by n elements in B. Hence this
homomorphism can be lifted to R -* B1 and it becomes surjective. Now
it is seen easily that Rm -> R can be lifted to R -> R . It follows that
о о
determinants of all minors of a of rank (n-r+1) vanish. Thus the relations
@) above can be lifted to K.
Consider the relations (I). We are given b , с such that the following
о о
diagram is commutative:
a ®Id©Id®a_=0_
(Rm 0 Rn) 0 (R*0 Rm) °
With the above lifting of (aj to a we get
(Rm 0 Rn) 0 (Rn ® Rn
в'
(A)
-0
¦ 0.
The two rows are exact. We claim that there is a b which lifts b^, and
such that the square (A) is commutative. In fact this is quite easy, .for it is
clear that we can find V : R ® R -* R such that (A) is commutative. Let
b1 be the reduction mod R of b1. Then we see that the composition of
о о r
118
119
the canonical map R — В with b -b1 is zero. Hence
c о о о
b (z)=b!(z) (modlma , or KerRn-*B).
о о о о
Now b (z)-b' (z) can be lifted to elements in Ima, so that taking for {z }
о о a
a canonical basis in R -¦ R we define b : R ® R — R
b(zQ) = v
ea,
where 9 с Ьпа lifts b (z)-b' (z). It is now clear that b lifts b and the
а о о о
square (A) is commutative. This proves the claim.
By a similar argument as above there is а с such that с reduces
to с and the square (B) is commutative. (Я necessary we can prolong to
о
the left the exact sequence of the second row in the diagram (*). ) Thus it
follows that the relations in I can be lifted to R.
/*"
A similar argument shows that a , б , e and e which are given
о о о о
representing the point Spec R -*• V can be lifted to R so that the diagrams
(II), (III) and (IV) are still commutative. This means that the Spec Rq — V
can be lifted to an R-valued point of V. As we remarked before, the
assertion E) now follows.
We go back to the usual notations in the theorem. Then:
G) _Let CL = m (y , . . . , у ) ideal m A [y] . Then P = А [у] А is_ also the
Ql-adic completion of A[y] (of course P is also the m • (A[y"])-adic
completion of A [y 1).
The proof of this assertion is immediate for a convergent series
Zf.,f. € A[y] in the Ot-adic topology is precisely one such that the coefficients
i
of f, tend to zero in the m -adic topology and the degree of the monomials — oo
1 A
This implies that a convergent series is precisely a formal power series
in {y.} such that the coefficients (in A) tend to 0 in the m -adic topology,
l - ~." A.
л . ч:
This is the description of P we had and G) improved.
л -
(8) Now for the morphism Op : SpecP -* V we have that the image of
SpecP-{y = 0} is in the smooth locus of V over Ж. We note that
V{6b) = (Speck[y])U{y = 0} (k residue field of A), i. e. , V(<Jl) contains
{y = 0} so that the image of. SpecP-V(JL) (by Cf ) is also in the smooth, locus
л ^
of V over Z. Now the ffL-adic completion of A|_yJ is P. Let P denote.
the henselization of (P,tft), P = A[y]. Now apply Theorem 2 proved above.
Hence we can find an etale map SpecR-* SpecP which is trivial over V@t)
and a morphism CP' : SpecR-* V (note that P is also theOC-adic completion
of P ) such that
N
Cf* = Cp (mod ), for any given N.
(Note that the OT.-adic (i. e. , G1R-adic, OL is not an ideal in R) completion of
R is also A|y|A). Let &x be the R-algebra defined by y1. Then we have
& E&{modOL ) (i. e. , еЧсЬ =&/CTL ). Now Qr* becomes an A-algebra
and then we have
Ol =& (mod m"^)
A
N N
br (m^R) 2)OO '. Take in particular N = 2. Thus we can find an R-algebra
O1 of finite type and consequently of finite type over A such that
О-1 =.& (mod Шд).
A.
Thus to conclude the proof of the theorem, it suffices to prove that (Э*1 is
flat over A.
120
(9) Choice of Ort such that a-1 is flat/A.
We had a presentation of С as follows:
We claim that we have a presentation such that
(*)
where
л I
P
a . 0 = 0 and РШ ^ РП -> & -* 0 is exact, and
88>k ' a®kA
-*0 is exact,
where k. = A/m .
A A
This follows if we prove that Q is flat over A (cf. , §3, Part I).
However, (*) can be established directly as follows: We can find an exact
sequence of the form
A
A
• P
'kA~'
kA - 0.
A
(Note that Spec С ® kA = X = Spec & is the scheme whose deformation
А о о
we are considering and that X = ^ ® A/m = Spec & are infinitesimal
n A n
deformations of X . ) The above exact sequence can be lifted to an exact
sequence
121
such that a • 9 = 0, and P -^ Pn — С-* 0 is exact. This proves the existence
of (*).
Now define a functor G1 which is a modification of G as follows:
G! (P0 = Set of {8, a, b, с, а, б, е, с where а, Ъ, с, а, б, е, е are as
in the definition of G(R); and 0 is defined by R1 -2 Rm t Rn with
a- 8 = 0}.
Then as in the case of G(R), we see that G1 is represented by a scheme
V1 of finite type over Ж. The given representation for Cf as in (*) above
gives rise to a morphism ф : SpecP -*- V . We claim that as in the case of
> V, the image of SpecP-{y = 0} lies in the smooth locus of V1 . With the
same notations for R, R as in the proof of this statement for the case V,
о
it suffices to prove the following: Given
в е а
R'-J>R™_°R*-.B_0
о о о
a
such that а о 8 = 0 and Rm —2- Rn — В -> 0 is exact, and a flat lifting B1
о о о о
over R (hence free over R), we have to lift this sequence to R (the proof
of the lifting of the quantities involved is the same as for G(R)).. As we have
seen before, for G(R) we have a lifting
P ®A/m.
A
** * / n+1 n^n . n+1 -~
®A/mA —* P ®А/тд — & — 0
A An
since Cf is Hat over A/m . Passing to the limit, we have an exact
П A
sequence
л/
- Now bn 0 are a set of relations. Since B1 is flat over R these relations
о
can also be lifted, i. e. , we have a lifting
such that а о 9 = 0 and Rm ^ Rn — B1 ¦* 0 is exact. This proves the required
122
123
claim and hence it follows ф (SpecP-{y = 0}) lies in the smooth locus
(over Ж) of V1 .
Applying Theorem 2, we can find an etale Spec R -¦ Spec P, P = A[yJ
and a morphism фх : Spec R -* V such that
у = ф (mod OX. ).
Let erx be the R-algebra defined by ф\ Then as we have seen
before, we have
&* = & (mod m*).
A.
We claim that &x is flat over A. For this we observe that we have a fortiori
(mod m ).
A.
This impHes that &% /m •#' =0/mK& ^ <y . Let
А А о
(Г)
. в' =0, Pm-$>n~ff. ^
exact
be a representation of €fx . Recall we have the representation for &
(I)
л i e ?m a An js,
P -* P -* P -* 6" -» 0, and а о 6 = 0.
exact
Now tensoring (I1 ) with А/т** yields
A.
л. 6' BA/m" a1 B>A/m°
А ^m8A/ ^n®A/"-*a" в A m" - 0,
A A
and
exact
(a1 8> A/m*) о (в1 ® A/m^) = 0.
We have (I1 ) 0 A/m = (I) ® A/m , as a consequence of the fact that
A. A
б% = Ъ (mod m ). By (I) I ® A/m is exact. This implies that (I1 ) 0 A/m
A. Ai ——i—— . ji
is exact. So
property, (a1
is exact. So we have that (Г ) ® A/m is exact, and (Г ) ® A/m has the*
A • A
(91
A.
= 0 and
®A/m*-
- РП 8> А/тпПл - Cl' 0 A/m11 - 0,
A A
for all n. This implies, as we saw in the first few lectures,that &x 0 A/m
A.
is flat over A/m for every n.
Now 0X is an A-algebra of finite type and so С1 ® A/m flat over
A.
A/m for all n implies that ?T! is flat over A (cf. SGA exposes on flatness).
A.
The proof of the theorem is now complete.
Remark 5.1. The fact that &' is flat over A can also be shown in
a different manner. This can be done using only the functor G (i. e. , V),
but a better approximation (i. e. , better than N = 2) for Ori may be needed.
' This uses the following result of Hironaka: Let В be a complete local ring,
b С rn an ideal in В and M a finite В-module locally free (of rank r)
outside V(b). Then there is an N such that whenever M1 is a finite B-
N
module locally free of rank r outside V(b) and M1 ? M (mod b ), then
M1 ~ M. Take in our present case В = А [[у]] so that we have
R etale over A[y] such that A [y] Id ~ R/Ot and that all the extensions are
faithfully flat. Take a coherent sheaf on Spec R; to verify that it is flat over
124
125
A it suffices to verify that its lifting to Spec A [[y]] is flat over A. Take
b to be Ob- A[[y]], Then by taking a suitable approximation for &x it
follows that the liftings to A[?y]] of &x and & are isomorphic. This
implies that & 0 A/m % ffl 0 A/m , hence that O'1 is flat over A, sincel
Spec( & 0 A/m11) = X is flat over A.
TATA INSTITUTE OF FUNDAMENTAL RESEARCH
LECTURES ON MATHEMATICS AND PHYSICS
General Editors: K.G. RAMANATHAN and B.V. SREEKANTAN
MATHEMATICS
1. On the Riemann Zeta-function. By K. Chandrasekharan*
2. On Analytic Number Theory. By H. Rademacher*
3. On Siegel's Modular Functions. By H. Maass*
4. On Complex Analytic Manifolds. By L. Schwartz*
5. On the Algebraic Theory of Fields. By K.G. Ramanathan*
6. On Sheaf Theory. By C.H. Dowker*
7. On Quadratic Forms. By C. L. Siegel*
8. On Semi-group Theory and its application to Cauchy's problem in
Partial Differential Equations. By K. Yosida*
9. On Modular Correspondences. By M. Eichler*
10. On Elliptic Partial Differential Equations9 By J. L. Lions*
11. On Mixed Problems in Partial Differential Equations and Representation
of Semi-groups. By L. Schwartz*
12« On Measure Theory and Probability. By H.R. Pitt*
13. On the Theory of Functions of Several Complex Variables. By
B. Malgrange*
U. On Lie groups and Representations of Locally Compact Groups.
By F. Bruhat*
15.. On Mean Periodic Functions. By J.P. Kahane *
16. On Approximation by Polynomials. By J.C. Bur kill*
17. On Meromorphic Functions. By W.K. Hayman*
18. On the Theory of Algebraic Functions of One Variable.
By M. Deuring*
126
127
19. On Potential Theory. By M. Brelot
20. On Fibre Bundles and Differential Geometry. By J.L. Koszul*
21. On Topics in the Theory of Infinite Groups. By B.H. Neumann
22. On Topics in Mean Periodic Functions and the Two-Radius Theorem.
By J. Delsarte *
23. On Advanced Analytic Number-Theory. By C. L. Siegel *
24. On Stochastic Processes. By K. Ito
25. On Exterior Differential Systems. By M. Kuranishi*
26. On Some Fixed Point Theorems of Functional Analysis. By F.F. Bonsall*
27. On Some Aspects of p-adic Analysis. By F. Bruhat*
28. On Riemann Matrices. By C.L. Siegel
29. On Modular Functions of one complex variable. By H. Maass
30 On Unique Factorization Domains. By P. Samuel*
31. On The Fourteenth Problem of Hilbert. By M. Nagata
32. On Groups of Transformations. By J. L. Koszul
33. On Geodesies in Riemannian Geometry. By M. Berger
34. On Topics in Analysis. By Raghavan Narasimhan
35. On Cauchy Problem. By Sigeru Miz-ohata
36. On Old and New Results on Algebraic Curves. By P. Samuel
37. On Minimal Models and Birational Transformations of Two Dimensional
Schemes. By I.R. Shafarevich
38. On Stratification of Complex Analytic Sets. By M. -H, Schwartz
39. On Levi Convexity of Complex Manifolds and Cohomology Vanishing
Theorems. By E. Vesentini
40. On An Introduction to Grothendieck's Theory of the Fundamental
Group. By J. P. Murre
41. On Topics in Algebraic К-Theory. By Hyman.Bass
42. On The Singularities of the three-body problem. By C.L. Siegel
43. On Polyhedral Topology. By J.R. Stallings
44. On Introduction to Algebraic Topology. By G. de Rham
45. On Quadratic Jordan Algebras. By N. Jacobson
46. On The Theorem of Browder and Novikov and Siebenmann's Thesis.
By M.A. Kervaire
47. On Galois Cohomology of Classical Groups. By M. Kneser
48. On Discrete subgroups of Lie groups. By G.D. Mostow
49. On The Finite element method. By Ph. Ciarlet
50. On Disintegration of measures. By L. Schwartz
51. On Introduction to moduli problems and orbit spaces. By P. E. Newstead
52. On Numerical methods for time dependent equations - Application to
Fluid flow problems. By P. Lascaux
53. On Optimisation - Theory and Algorithms. By Jean Cea
,54. On Deformations of Singularities. By M. Artin
I
.55. On Sieve Methods. By Hans E. Richert
* Not available