Текст
ОПТИМИЗАЦИЯ
И ИССЛЕДОВАНИЕ
ОПЕРАЦИЙ
В. Ф. ДЕМЬЯНОВ
Л. В. ВАСИЛЬЕВ
Недифференцируемая
оптимизация
к
ОПТИМИЗАЦИЯ
И ИССЛЕДОВАНИЕ
ОПЕРАЦИЙ
Редактор серии
И. Н. МОИСЕЕВ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
198 1
в. Ф. ДЕМЬЯНОВ, Л. В. ВАСИЛЬЕВ
НЕДИФФЕРЕНЦИРУЕМАЯ
ОПТИМИЗАЦИЯ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1981
22.18
Д 82
УДК 519.6
Демьянов В. Ф., Васильев Л. В. Недифференцируемая
оптимизация. — М.: Наука, Главная редакция физико-математиче-
ской литературы, 1981 (Оптимизация и исследование операций).—
384 с.
Многие задачи, возникающие в технике, экономике, в самой ма-
тематике, приводят к необходимости нахождения экстремальных
значений негладких функций.
Книга посвящена систематическому изложению начал теории
оптимизации недифференцируемых функций. Приводятся необходи-
мые сведения из теории точечно множественных отображений, изуча-
ются свойства некоторых классов недифференцируемых функций,
устанавливаются условия оптимальности. Подробно рассматриваются
численные методы минимизации выпуклых недифференцируемых
функций, а также функций максимума как при наличии, так и при
отсутствии ограничений.
Книга предназначена для широкого круга научных работников
и инженеров, специализирующихся в области теории управления,
оптимизации и проектирования, а также студентов и аспирантов со-
ответствующих специальностей.
Библ. 172. Илл. 55.
♦
Владимир Федорович Демьянов
Леонид Васильевич Васильев
НВДИФФЕРЕНЦИРУЕМАЯ ОПТИМИЗАЦИЯ
Редактор И. В, Морозова
Техн, редактор Н. В. Вершинина. Корректор Л. Н. Ворована
ИВ № 11644
Сдано в набор 28.10.80. Подписано к печати 04.12.81. Т-27790. Формат 84Х1081/э>.
Бумага тип. № 1. Литературная гарнитура. Высокая печать. У с ловя. Печ. Л. 20,16.
Уч.-изд. л. 19,47. Тираж 6800 экз. Заказ № 968. Цена 2 р. 10 к.
Издательство «Наука». Главная редакция физико-математической литературы.
117071, Москва, В-71, Ленинский проспект, 15
Ленинградская типография № 2 головное предприятие ордена Трудового Крас-
ного Знамени Ленинградского объединения «Техническая книга» им. Евгений
Соколовой Союзполиграфпрома при Государственном комитете СССР по делам
издательств, полиграфии и книжной торговли.
198052, г. Ленинград Л-52, Измайловский проспект, 29.
д WWKB-8*81-8b 1702070000
© Издательство «Наука».
Главная редакция
физико-математической
литературы. 1981
ОГЛАВЛЕНИЕ
Предисловие................................................ '
Глава I. Элементы выпуклого анализа и смежные вопросы 13
§ 1. Выпуклые множества. Выпуклые оболочки. Теорема
отделимости............................................13
§ 2. Точечно-множественные отображения................22
§ 3. Выпуклый конус. Конус возможных направлений. Со-
пряженный конус........................................31
§ 4. Выпуклые функции. Непрерывность и дифференцируе-
мость по направлениям..................................40
§ 5. Субградиент и субдифференциал выпуклой функции 54
§ 6. Расстояние от множества до конуса. Условия миниму-
ма ....................................................70
§ 7. 8-субдифференциал................................77
§ 8. е-производные по направлению. Непрерывность 8-суб-
дифференциального отображения.........................87
§ 9. Некоторые свойства и неравенства для выпуклых функ-
ций ..................................................99
§ 10. Условный е-субдифференциал......................109
§ 11. Условные производные по направлениям. Непрерыв-
ность условного 8-субдифференциального отображе-
ния ...................................................119
§ 12. Задание выпуклого множества с помощью неравенств 130
| 13. Нормальный конус. Коническое отображение . . .137
§ 14. Дифференцируемость по направлениям функции суп-
ремума ...............................................143
§ 15. Дифференцируемость выпуклой функции.............150
§ 16* . Сопряженные функции..........................163
§ 17. Вычисление 8-субградиентов некоторых классов вы-
пуклых функций........................................177
Глава II. Квазидифференцируемые функции...................183
§ 1. Определение и примеры квазидифференцируемых
функций...............................................183
§ 2. Свойства квазидифференцируемых функций. Основные
формулы квазидифференциального исчисления . . .189
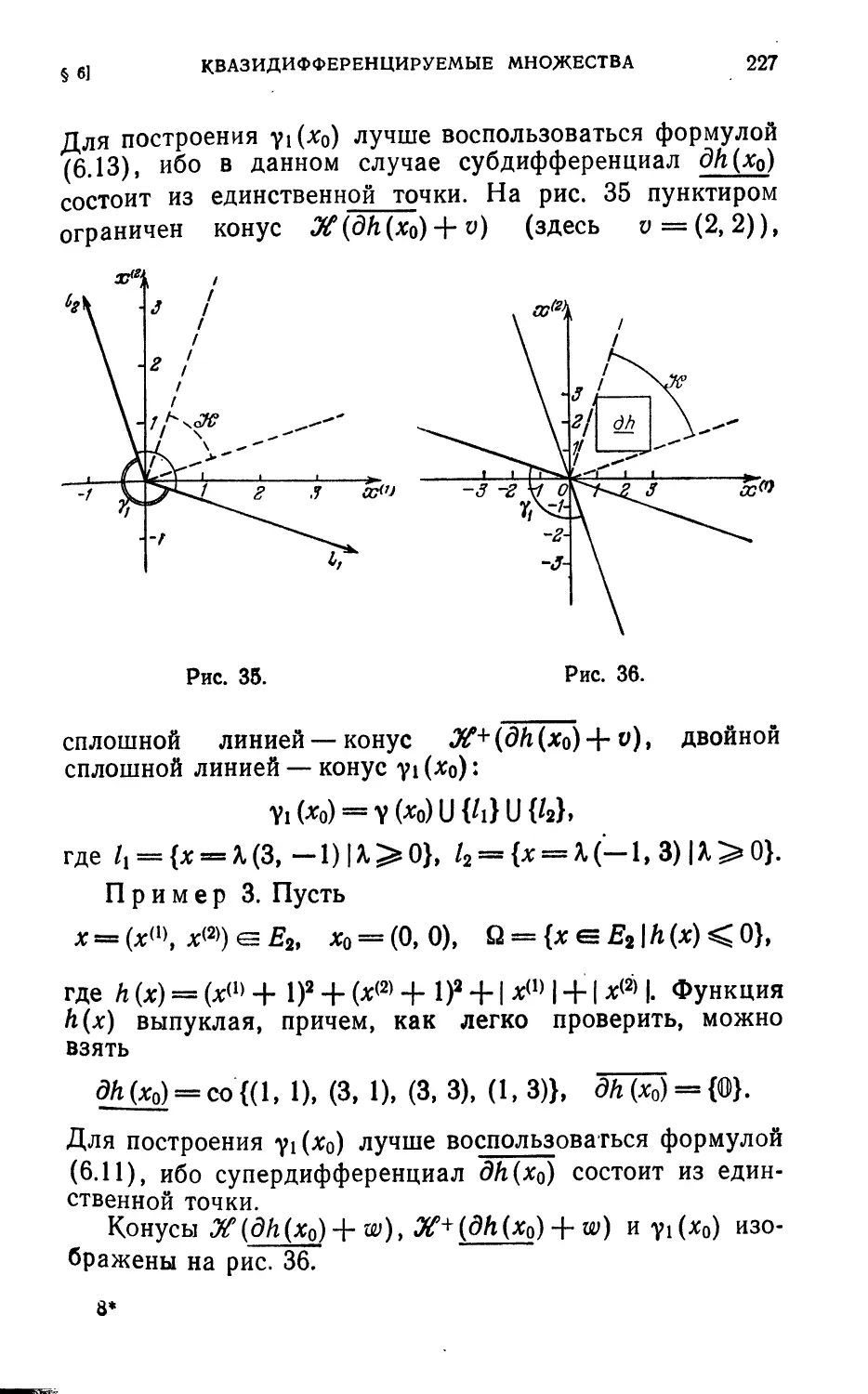
§ 3. Примеры вычисления квазидифференциалов .... 198
§ 4* . Квазидифференцируемость выпукло-вогнутой функции 207
§ 5. Необходимые условия оптимальности квазидифферен-
цируемой функции на Еп................................214
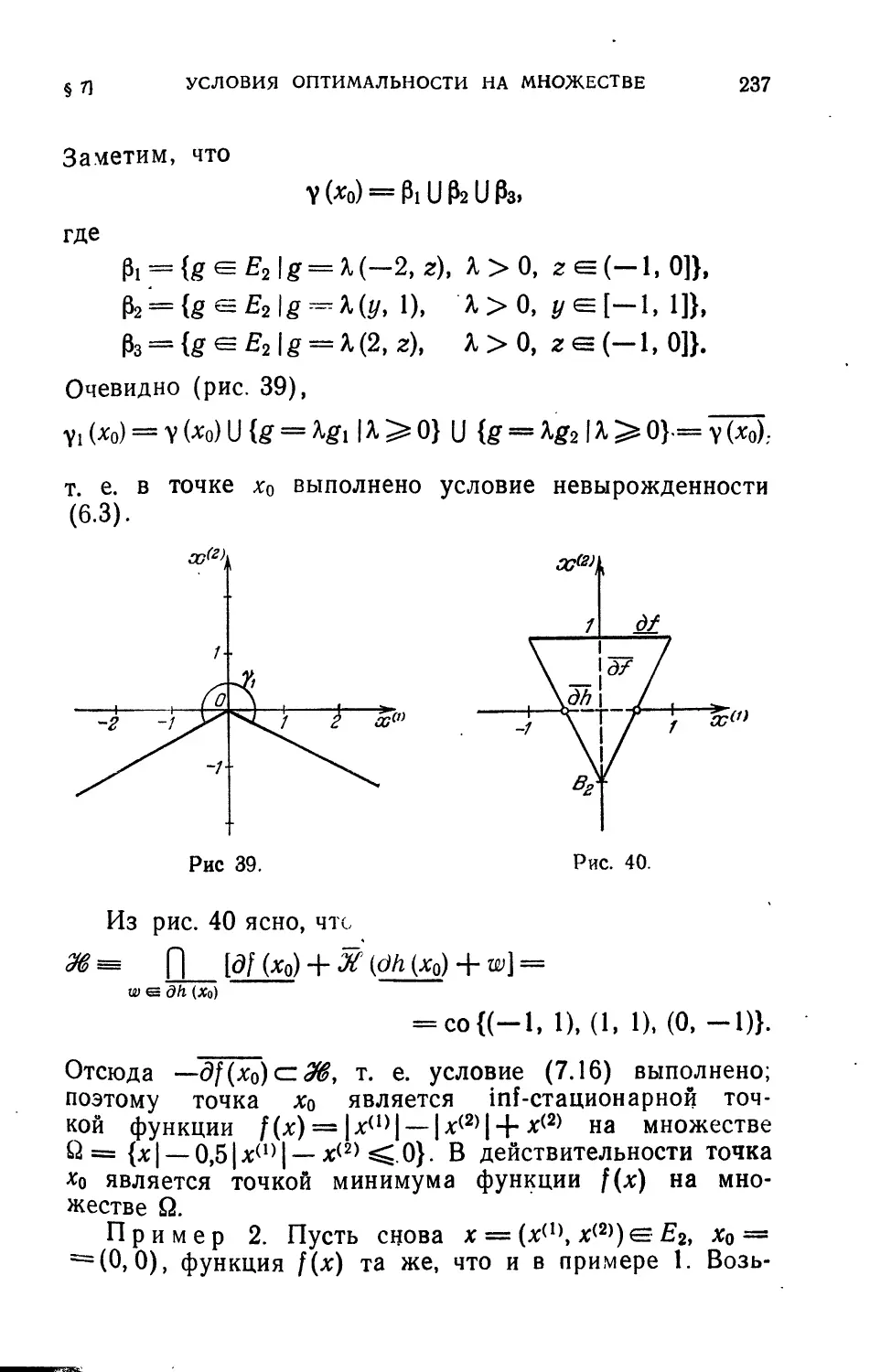
§ 6. Квазидифференцируемые множества.................220
§ 7. Необходимые условия оптимальности квазидифферен-
цируемой функции на квазидифференцируемом множе-
стве ...............................................229
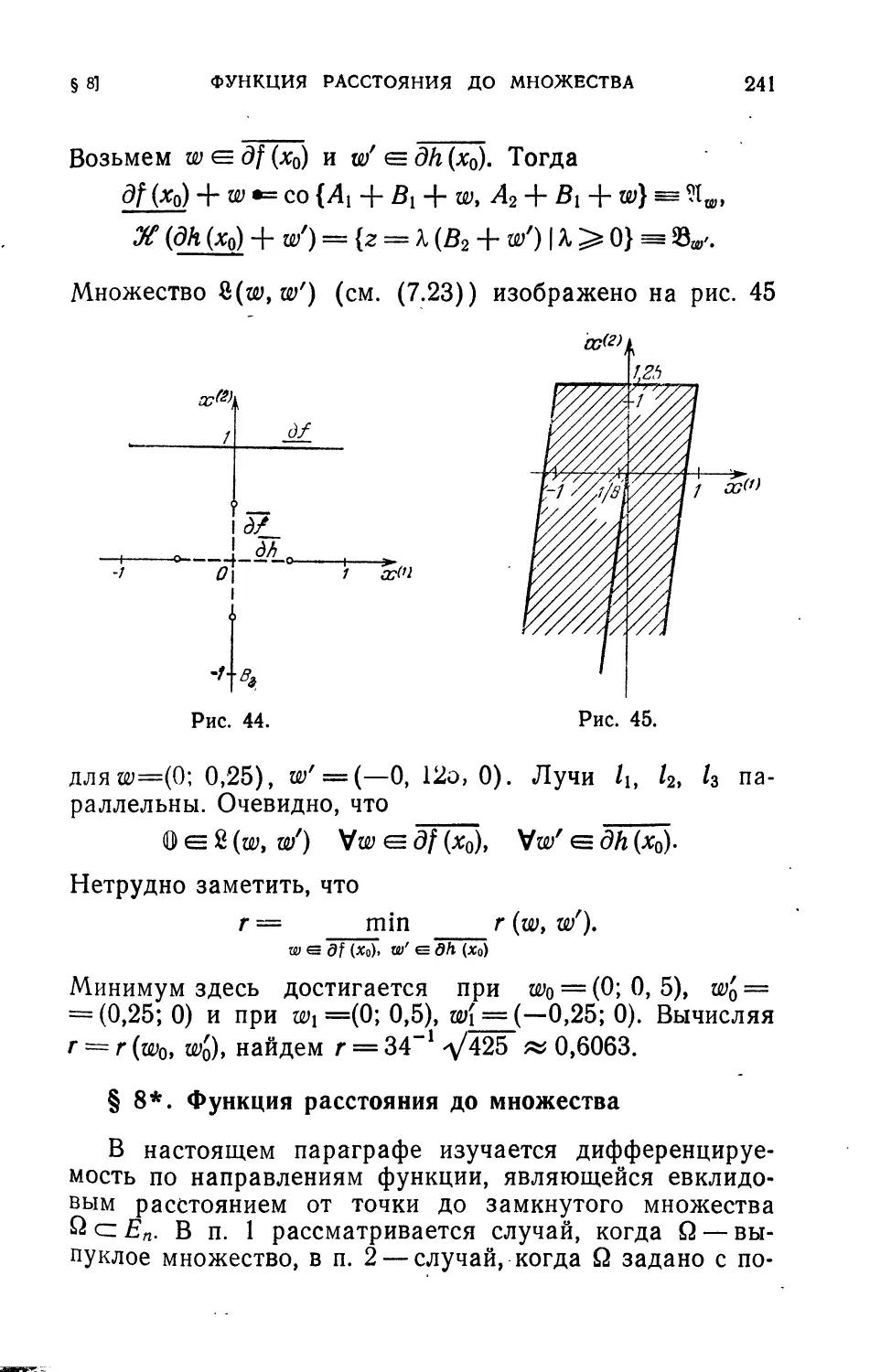
§ 8*. Функция расстояния до множества...................241 '
§ 9. Неявные функции...................................251
в
ОГЛАВЛЕНИЙ
Глава III. Минимизация на всем пространстве . i i . . . 254
f 1. Необходимые и достаточные условия минимума вы-
пуклой функции на Ёп......................................254
§ 2. Минимизация гладкой функции....................256
§ 3. Метод наискорейшего спуска.....................258
§ 4. Субградиентный метод для минимизации выпуклой
Йгнкции..........................................265
ногошаговый субградиентный метод...............277
§ 6. Релаксационный субградиентный метод............286
I 7. Релаксационный е-субградиентный метод . . s . .301
5 8. Метод Келли....................................310
§ 9. Минимизация функции супремума..................315
§ 10. Минимизация выпуклой функции максимума. Метод
экстремального базиса.................................318
Глава IV. Минимизация при наличии ограничений .... 326
§ 1. Необходимые и достаточные условия минимума вы-
пуклой функции на выпуклом множестве..................326
§ 2. e-стационарные точки............................334
| 3. Метод условного градиента........................33?
§ 4. Методы наискорейшего спуска для минимизации вы-
пуклых функций........................................342
§ 5. (в, ц)-субградиентный метод при наличии ограниче-
ний ..................................................348
| 6. Субградиентный метод с постоянным шагом .... 352
$ 7. Модифицированный (8, р,)-субградиентный метод при
наличии ограничений ................................ . 355
в 8. Метод негладких штрафных функций.................359
$ 9. Метод Келли для минимизации на выпуклом множе-
стве .............................................366
§ 10. Релаксационный субградиентный метод при наличии
ограничений ..................................... 869
Библиографический комментарий.............................373
Литература................................................376
ПРЕДИСЛОВИЕ
Термин «недифференцируемая оптимизация» (НДО),
сравнительно недавно вошедший в научный оборот,
включает в себя широкий круг вопросов, связанных с
нахождением экстремальных значений недифференци-
руемых функций. Задачи минимизации или максимиза-
ции негладких функций естественным образом возни-
кают как при решении практических задач, так и в
самой математике. В качестве примера достаточно со-
слаться на задачи чебышевской аппроксимации. Везде
далее, не теряя общности, мы будем обсуждать задачи
минимизации. Среди негладких задач минимизации наи-
более изученными являются минимаксные и выпуклые
задачи (монографии [31], [36], [57], [НО], [120]). Ин-
терес к НДО особенно возрос в последние годы. Различ-
ным аспектам негладкой оптимизации посвящены ра-
боты [30], [81], [127], а также многочисленные сбор-
ники и статьи (см., например, [14], [20], [87] — [89],
[98], [130], [135], [140] —[142], [152], [153], [160]).
Для решения любой задачи минимизации необхо-
димо:
1. Исследовать свойства минимизируемой функции,
в частности ее дифференцируемость и дифференцируе-
мость по направлениям.
2. Установить необходимые (а при возможности идо-
статочные) условия глобального или локального мини-
мума.
3. Найти направления спуска (наискорейшего или
просто «подходящего» в некотором смысле).
4. Разработать методы последовательных приближе-
ний.
В книге рассматриваются задачи минимизации не-
гладких функций конечного числа переменных.
Следует отметить принципиальную важность не-
обходимых условий экстремума (их исследованию.
8
ПРЕДИСЛОВИЕ
посвящены, например, работы [24], [45], [57], [73], [74],
[103], [159], [163], [167], [168]).
Известно значение понятия градиента в случае глад-
кой функции. У негладких функций уже не существует
градиента. Для функции максимума и выпуклой функ-
ции аналогом градиента служит субдифференциал: с
каждой точкой хо связан некоторый выпуклый компакт
df(x0), называемый субдифференциалом функции f(x)
в точке х0- Любой элемент uedf(xo) называется суб-
градиентом функции f (х) в точке хо.
С помощью субдифференциала можно:
1. Найти производную функции f(x) в точке хо по на-
правлениям:
ff (x0) а |im or1!/(Xo + ag) —Н*о)]= max (v, g).
° 8 а->+0 vedf(x0)
2. Проверить необходимое условие минимума: для
того чтобы точка х* была точкой минимума функции
/(х) на Еп, необходимо, чтобы
0 е df (х*).
3. Найти направление наискорейшего спуска: если
O§fedf(xo), то направление
g (хо) == — о (х0) || v (х0) 1Г1,
где || v («о) II== min || v ||, и (х0) <= df (хо), есть направле-
VGdf(x0)
ние наискорейшего спуска функции f(x) в точке х0.
Такая важная роль субдифференциала привела к по-
пыткам расширить понятие субдифференциала на класс
липшицевых функций (работы Ф. Кларка [133], [134],
Дж. Варги [9], [168], Б. Н. Пшеничного [104],
Н.З. Шора [126], [127], А. Голдстейна [139], [140]
и др.).
Используя субдифференциалы и субградиенты, уда-
лось построить ряд методов последовательных прибли-
жений для минимизации выпуклых функций, функций
максимума и некоторых других классов функций ([30],
[36], [51], [91], [127], [149] —[151], [155], [156],
[170], [171]).
Задача минимизации гладкой функции f(x) на мно-
жестве
Q = {х е= Еп\ht (х) < 0 Vi s 1: N},
ПРЕДИСЛОВИЕ
9
где ft/(xj—гладкие на Е„ функции, тоже является за-
дачей НДО, ибо множество Q можно задать так:
Q {х е Еп | h (х) < 0},
где Л(х)= max hi (х) —• негладкая уже функция.
Цель настоящей книги — дать систематическое изло-
жение начал теории оптимизации недифференцируемых
функций конечного числа переменных. В гл. I приводят-
ся необходимые сведения из теории выпуклых функций,
выпуклых множеств и точечно-множественных отображе-
ний. Большое внимание уделено е-субдифференциалам и
свойствам в-субдифференциального отображения. Вы-
пуклые функции важны не только потому, что это бога-
тый класс негладких функций, но и потому, что аппарат
теории выпуклых функций позволяет исследовать и дру-
гие классы негладких функций.
Мы уже говорили о некоторых обобщениях субдиф-
ференциала. Это понятие для выпуклых функций и функ-
ций максимума органично связано с производной по на-
правлениям. Большинство из упомянутых выше авторов
в своих обобщениях субдифференциала использовали не
производную по направлениям, а какую-нибудь другую
конструкцию. Для целей оптимизации, однако, представ-
ляется более естественным и полезным опираться на
производную по направлениям.
В гл. II описан новый класс недифференцируемых
функций — квазидифференцируемые функции. Для та-
ких функций существенную роль играет понятие квази-
дифференциала, тесно связанное с производной по на-
правлениям. Оказывается, каждой точке соответствует
пара выпуклых множеств (квазидифференциал). Квази-
дифференциал является обобщением понятия производ-
ной (для гладкой функции) и субдифференциала (для
выпуклой функции). С помощью квазидифференциала
удается достаточно просто описать необходимые условия
экстремума, найти направления наискорейшего спуска
и подъема. Установлены основные формулы квазидиф-
ференциального исчисления, являющегося обобщением
классического дифференциального исчисления. Класс
квазидифференцируемых функций представляет собой
линейное пространство, замкнутое относительно всех
10
ПРЕДИСЛОВИЕ
«алгебраических» операций, а также операций взятия
поточечных максимума и минимума (напомним, что
класс выпуклых функций, как и класс функций макси-
мума, не является линейным пространством, а представ-
ляет собой выпуклый конус). Введено понятие квази-
дифференцируемого множества. Получено необходимое
условие экстремума квазидифференцируемой функции
на квазидифференцируемом множестве в терминах ква-
зидифференциалов, что значительно расширяет класс
задач, которые можно аналитически исследовать. Для
широкого класса квазидифференцируемых функций мож-
но алгоритмизировать процесс проверки необходимых
условий экстремума и нахождение направлений наиско-
рейшего спуска и подъема. Тем самым открыт путь к
численному решению подобных задач, хотя методы на-
хождения экстремума квазидифференцируемых функций
требуют еще своей разработки.
Численным методам решения задач НДО посвящены
главы III и IV, в которых излагаются основные методы
и идеи, используемые при минимизации выпуклых функ-
ций и функций максимума. Методы последовательных
приближений делятся на релаксационные и нерелакса-
ционные. Метод называется релаксационным, если зна-
чение функции на очередном шаге меньше, чем на пре-
дыдущем. Среди излагаемых методов есть как релакса-
ционные, так и нерелаксационные. Мы воздерживаемся
от обсуждения преимуществ одного метода перед дру-
гим, поскольку у дракона оптимизации много голов и
против каждой из них нужен свой меч. Так, метод субгра-
диентного спуска весьма прост в реализации, но очень
медленно сходится. Многое зависит от поставленной
цели и имеющихся ресурсов. Иногда можно ограничить-
ся достаточно грубым приближением к оптимальному
решению, но получить его нужно быстро; в другом слу-
чае необходима высокая точность, а время счета практи-
чески не имеет значения.
Большинство описанных методов являются методами
первого порядка, поскольку в них используются аппрок-
симации первого порядка (производная, субградиент,
субдифференциал). Можно надеяться, что дальнейшее
развитие теории НДО приведет к появлению методов
й более высокого порядка.
ПРЕДИСЛОВИЕ
И
Часть материала вынесена в задания для самостоя-
тельного изучения. Мы совершенно не затрагиваем
вероятностных подходов (отсылая читателя к моногра-
фиям [51], [83], [107], [117]), а также вопросов, свя-
занных с теорией игр ([21], [58], [63], [64]) и много-
критериальной оптимизацией ([95]), в которых возни-
кают задачи НДО.
В книге отражены результаты исследований по не-
гладкой оптимизации, проводимых в последние годы на
факультете прикладной математики — процессов управ-
ления ЛГУ и в НИИ Вычислительной математики и
процессов управления ЛГУ.
Часть результатов докладывалась на VII и VIII Все-
союзных школах по оптимизации в Жукине (1977 г.) и
Шушенском (1979 г.).
Авторы искренне признательны Н. Н. Моисееву, ко-
торый способствовал возникновению замысла настоящей
монографии и поддерживал работу над ней на различ-
ных ее этапах.
А. Б. Певный и А. М. Рубинов внимательно и кри-
тически прочли рукопись. Ряд замечаний, сделанных
Е. Ф. Войтоном, М. К. Гавуриным, Ю. М. Ермольевым,
С. С. Кутателадзе, В. Н. Малоземовым, Б. Н. Пшенич-
ным, В. М. Тихомировым, способствовал улучшению
книги. Большую помощь в оформлении рукописи ока-
зала Э. В. Демьянова. Наконец, авторы благодарны
всем, кто своими замечаниями, вопросами, советами по-
могал работе.
В книге пп. 1, 2 § 13 гл. I и § 5 гл. II написаны
Л. Н. Поляковой, §§ 15, 16 гл. I — А. М. Рубиновым,
§ 14 гл. I и пп. 1, 2 § 4 гл. IV — В. К. Шомесовой, § 9
гл. I, §§ 5, 7 гл. IV — Л. В. Васильевым, В. Ф. Демья-
новым.
Л. В. Васильевым написаны п. 6 § 4, § 6, пп. 5, 6 § 8,
§ 17 гл. I, §§ 1, 3, 6, 7 гл. III, §§ 1—3, п. 3 § 4, §§ 6,
8—10 гл. IV.
В. Ф. Демьянов написал §§ 1—3, пп. 1—5 § 4, §§5, 7,
пп. 1—4 § 8, §§ 10—12, п. 3 § 13 гл. I, §§ 1—4, 6—9
гл. II, §§ 2, 4, 5, 8—10 гл. III.
В книге используются стандартные обозначения и со-
кращения.
12
предисловие
Выражение т({/(х)|хаЛ) есть то же самое, что и
inff(x).
хе А
Запись
Q = {о €г Е„| Эа0 > 0: Хо + аоеЛ Vae[0, cto]}
читается так: Q есть множество таких точек и <= Еп, для
которых существует ао > 0 такое, что хо + av е А для
всех аеа[0, ао].
Символ означает конец доказательства.
Множество целых чисел от р до q обозначается р: q.
Нижний и верхний пределы соответственно обозна-
чаются 11m и Игл.
Количество элементов множествах обозначается |А|.
Символ ss означает «равно по определению».
Звездочкой отмечены параграфы и их части, чтение
которых не обязательно для понимания последующего
материала.
В. Ф. Демьянов
Л. В. Васильев
ГЛАВА I
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
И СМЕЖНЫЕ ВОПРОСЫ
§ 1. Выпуклые множества. Выпуклые оболочки.
Теорема отделимости
1. Далее рассматривается n-мерное евклидово про-
странство Еп векторов х = (х(1), .... х(п)). Пространство
Еп является линейным. Обозначим 0rt == 0 = (0, ..., 0) s
&Вп>хквМ}...........4П))> (*р *2) = S/M0- 11*Иет
= V(X, х) , X2 = (х, х).
Имеет место неравенство Коши — Буняковского:
Цхь х2)К||х,||.||х2||.
Векторы Xi, ..., хг называются линейно независимыми,
Г
если равенство возможно тогда и только
А-1
тогда, когда все коэффициенты a*, k е 1: г, равны нулю.
Если то векторы Хь .... хГ линейно зави-
Г
симы, т. е. найдутся числа 61..рг такие, что У, в2 > 0
Л-1
(т. е. они не все одновременно равны нулю) и
= (1.1)
Если г п + 2, то одновременно с (1.1) можно добиться
выполнения равенства
Ур4 = 0. (1.2)
«-1
Докажем это. Введем векторы
***=(1, х’*1».....х^)®£я+1, й®1:г, г>«4-2.
14
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
В любые п + 2 вектора линейно зависимы, т. е. су-
г
ществуют числа Pfe, У, > 0, такие, что
(1-3)
Из (1.3) следует
У Ра^а “ ®л» Ра = О
А-1 А-1
(приравняли нулю отдельно первую координату и п
оставшихся).
Множество, не содержащее ни одного элемента, на-
зывается пустым и обозначается 0.
Положим
(х0) == {х Еп 11| х — х0 IK 6}, б > 0.
Множество Se(xo) называется 8-окрестностью точки х0.
Точка х0 называется внутренней точкой множества G,
если существует б > 0 такое, что Se (х0) с: G. Множество
внутренних точек множества G обозначим int G (это
множество может оказаться и пустым).
Множество GcE„ будем называть открытым, если
для любого х0 существует б > 0 такое, что Sd(xo)czG.
Очевидно, что в этом случае G = int G.
Замыканием множества G cz Еп называется множе-
ство точек х, допускающих представление х= lim xk,
k->oa
где хк е G V/? в 1 : оо. Замыкание G будем обозна-
чать G.
Множество 6сЕ„ будем называть замкнутым, если
из соотношений xk хо> xk^G 4k е 1 : оо, следует
х0 е G. Очевидно, что для замкнутого множества G = G.
Точка хо называется граничной точкой множества
Gc.En, если ее б-окрестность Se(x0) при любом б > О
содержит хотя бы одну точку, не принадлежащую О, и
хотя бы одну точку, принадлежащую G (при этом хо
может и не принадлежать G). Множество граничных то-
чек множества G обозначим Gfr.
Множество G называется ограниченным, если суще-
ствует такое число К. •< -f- оо, что || х || К. Ух е G.
ВЫПУКЛЫЕ МНОЖЕСТВА
15
$ 11
Множество О будем называть неограниченным, если
для любого К > 0 найдется такое x s G, что ||х|| > К.
Очевидно, что объединение, пересечение, сумма и раз-
ность двух ограниченных множеств есть снова ограни-
ченное множество.
Пересечение двух множеств, одно из которых ограни-
чено, есть ограниченное множество.
Если А и В — замкнутые множества, то их объеди-
нение и пересечение — снова замкнутые множества. Но
для суммы, разности и алгебраической разности это уже
не так.
Пример 1. Пусть
Л = (х = (х<‘», х<2>)е£2|х<2)>Дп-, х® >о),
I ' J
В = {х = (х®, х®) 6= Е2 | х<‘> = 0, х® < 0}.
Очевидно, что А и В — замкнутые множества и не яв-
ляются ограниченными.
Множество
С = Л + В = {х = (х®, х®) | х® > 0, х® е (- оо, оо)}
не является замкнутым, ибо
С = {х = (х®, х®) |х® > 0, х<2> е (- оо, оо)} С.
Однако если множества А и В замкнуты и хотя бы
одно из них ограничено, то сумма (и алгебраическая
разность) тоже замкнута.
Компактом или компактным множеством называется
множество, обладающее тем свойством, что из всякой
последовательности его элементов можно выбрать схо-
дящуюся подпоследовательность, предел которой при-
надлежит тому же множеству. Хорошо известно, что в Еп
множество компактно тогда и только тогда, когда оно
замкнуто и ограничено.
Определение 1. Множество QaE„ называется
выпуклым, если вместе с любыми двумя точками хь х2
оно содержит отрезок, соединяющий эти точки, т. е.
[xi, x2]cz Q, где
[хь x2]=={xe£„|x=«axi+ (1 —а)х2, ае[0, 1]}.
Выпуклое множество Q называется строго выпуклым,
если для любых xi, x2eQ, Xi «?^х2, и любого as(0,1)
точка ха = axi + (1 — a) х2 е int Q.
16
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
Существует другое определение выпуклого множе-
ства.
Определение 1*. Множество йс£л называется
выпуклым, если вместе с любыми двумя точками xb xj
оно содержит точку 2—1 (xi лег), т. е. если середина от-
резка, соединяющего точки xj и х2, принадлежит £2.
Ясно, что если множество £2 выпукло в смысле опре-
деления 1, то оно выпукло и в смысле определения 1*.
Обратное неверно.
Пример 2. Пусть £2 есть множество рациональных
чисел из [0,1]. Очевидно, что это множество выпукло
в смысле определения 1*. но не является выпуклым в
смысле определения 1.
Задание 1.1. Доказать, что если множество Q замкнуто н
выпукло в смысле определения 1*, то оно выпукло и в смысле опре-
деления 1.
Замечание 1. Везде далее, говоря о выпуклом
множестве, имеем в виду выпуклость в смысле опреде-
ления 1.
Лемма 1.1. Пусть Q с Еп — замкнутое множество и
для любых хь х2е £2 найдется ае(0, 1) (а зависит от
X] и хг) такое, что ха = axi + (1 — а)х2 е £2. Тогда мно-
жество £2 выпуклое.
Доказательство. Допустим противное. Тогда
существуют xb х2е£2, Xi ¥= х2, и такое aos(0,1), что
Положим
Gj = £2 fl [*р х0о], G2 — £2 П [хао, х2].
Эти множества замкнуты, причем хао ф Gb xao ф G*
Найдем _
min II X — Xa0 II = IIX — Хао ||,
хе Gi
min || X — Хв0 || = || X — Xao ||,
xeGj
где_xe Gb xe G2, в частности, хе £2, хе £2. При этом
на (х> Хао] и tx«o> •*) нет точек £2, что противоречит усло-
вию леммы (здесь (х,у] = [х, г/]\{х), [х,у)—.
ВЫПУКЛЫЕ МНОЖЕСТВА
17
2. Пусть О cz Еп. Выпуклой оболочкой множества G
назовем множество
coG = )x = Z “Л xk<=G, аА>0, £aft = l,
I ft-i fe-i
г — любое натуральное число?.
Теорема 1.1 (теорема Каратеодори). Любой век-
тор х е со G может быть представлен в виде выпуклой
комбинации не более чем п + 1 векторов множества G.
Доказательство. Пусть х <= со G, т. е.
х=£ал, aft>0, £a*==l.
Без ограничения общности считаем, что все ак > 0. До-
пустим, что г п + 2. По доказанному выше (см. (1.2))
существуют такие числа Pfe, У, Р£ > 0, что
£₽л=о, i₽*=o.
fe-l A-l
(1.4)
Положим 8 = min P^'«fe > 0 и ak = ak — ер., k<=l:r.
Здесь е > 0, ибо в силу (1.4) среди коэффициентов р*
существуют и положительные, и отрицательные (хотя бы
по одному). Теперь ясно, что
х=У aftXfe, Sa*=l, V6.
Очевидно также, что хотя бы одно из чисел а* обра-
щается в нуль, т. е. х может быть представлен как вы-
пуклая комбинация уже не более чем г— 1 векторов из
G. Продолжая далее аналогично, придем к представле-
нию, в котором Г < /I + 1.
Лемма 1.2. Если G cz Еп — ограниченное замкну-
тое множество, то со G — ограниченное замкнутое вы-
пуклое множество.
18
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
1
Доказательство. Пусть хе со О, т. е.
х = akxk = (х<», ..., х(п)). «4 > О, Д ak = 1, xk (= G.
Если Q ограничено, то для любого вектора из G все его
компоненты ограничены по модулю одним и тем же
числом М. Тогда для вектора х будет
Д
|х«> | =
< Д I х»> | < М Д aft = М,
т. е. компоненты вектора х (см. (1.5)) из со G ограни-
чены тем же числом М, т. е. со G — ограниченное множе-
ство.
Докажем выпуклость со G. Пусть х е со G, у е со G.
Без ограничения общности (добавив, если нужно, сла-
гаемые с нулевыми коэффициентами) можно считать,
что
y=^^kXk,
fe-1
г г
Xk<=G, aft>0, a*>0, £<^ = £(4=1,
a-i 4-1
Возьмем
xa = ax + (l — a) y, a<=[0, 1],
xa = E (aafe + (1 — a) a'k) xk = E a*xft>
4-1 s-i
где afc — actfc + (1 ~~ a)a£- Ясно, что
г г г
a*>0, £ a* = a Е +(1 — a) Е <4= 1,
4-1 А-1 4—1
т. е. xaecoG при любом а® [0,1]. Значит, множество
со G — выпуклое.
Покажем замкнутость множества со G. Пусть х5->х*,
Xs е со G. Тогда
rs rs
Xs = Е ^skXskt ^sk 0, E ®s4 “ I >
4—1 4=1
xrteG, Ael:rs, sel:x. (1.7)
1 И
ВЫПУКЛЫЕ МНОЖЕСТВА
19
По теореме Каратеодори можно выбрать такие пред-
ставления xs, что rs^n-j-l. Будем считать, что га *=
s= п + 1 (пополнив для этого, если нужно, представле-
ния (1.7) произвольными векторами из G с нулевыми
коэффициентами). Так как G — ограниченное множество
и as*e[0, 1], то можно выбрать последовательность
{$/} такую, что
ХаЛ > Ход, Я»,Д ®0А.
I к < s(->oo
Из (1.7) ясно, что
«4-1 «4-1
х*“°£ ОодХод, Хще(7, «о* > О, Е «ол=1.
т. е. х* е со G. Лемма доказана полностью.
Задание 1.2. Доказать, что если О — выпуклое множество, то
со О = О.
Замечание 2. Очевидно следующее свойство:если
Ai с.Еп — выпуклые множества, j's / s 1: N, то
со [J Л = {х!=Е cifX*Iх<еЯо а/>0, S а/—П-
i&I ( i&I I i s/ J
Теорема 1.2 (теорема отделимости). Пусть йс
cz£n — замкнутое выпуклое множество и xo^Q. Тогда
найдутся вектор g0^En, ||goll = 1, « число а>0 такие,
что для любого хе Q будет
(x — xo,go)^ — a. (1.8)
Доказательство. Найдем
где ро = 11хо — Zoll. Нетрудно убедиться в том, что наи-
меньшее значение здесь достигается. Так как x0^=Q, то
Ро > 0. Положим
во=*-(>о1(го-хо)- (1-9)
Покажем, что для всех хе й будет
(х — х0, go)< — Ро- (1.10)
Допустим противное. Тогда найдется хеЙ такое, что
(х — х0, go) == — *>о > — Ро. (1.Н)
so
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
Пусть
ха = ах + (1 — а) z0 = г0 + а (X — яь), а е [0, 1].
Ясно, что ха э [z0, х]. Тогда
(х0 — ха)2 — (х0 — 20)2 — 2а (х — z0, х0 — я0) + а2 (f — z0)2 =
= р2 - 2а [(х - х0, х0 - z0) - (z0 - х0, х0 - z0)] +
+ а2 (х - z0)2.
Учитывая (1.9), имеем
(*о ~ *а)2 “ - 2а [- Ьоро + р2] + а2 (Я — г0)2. (1.12)
Так как из (1.11) Ро —60Р0>0, то из (1.12) следует,
что при достаточно малых ае(0, 1) будет (х0 —ха)2<
< Pq, что противоречит определению точки zq.
Итак, (1.10) эквивалентно (1.8). Теорема доказана.
Замечание 3. Из доказательства теоремы выте-
кает, что если QczEn — замкнутое выпуклое множество
и хо s Еп, то существует единственная точка го е й та-
кая, что (г — Хо, г0 — Хо) > || Zo — Хо If2- VzeQ.
Следствие 1. Если йс£п— замкнутое выпуклое
множество и Хо — граничная точка множества й, то су-
ществует вёктор g0<=En, ||goll = 1, такой, что
(х — х0, go)^O Ухай. (1.13)
Доказательство. Пусть хо — граничная точка й.
Тогда найдется последовательность {xk} такая, что xk ф
ф. й, Хй->Хо. Так как х*^й, то по теореме 1.2 для всех
х е й будет
(X — xk, gk) < — ak, (1.14)
где
aft==min||xfc —z|| = ||xft —zft||> 0,
z e □
gfe==-||Zfe —Xfeir’fo-x*), IlgJI—l.
Ясно, что ak>0 и == min|| — z ||<||x0 — xj|, t. e.
z e Q
a*->0. Можем без ограничения общности считать, что
gk-^go, llgoll= 1. Переходя к пределу в (1.14), получим
(х — х0> go) <0 Vx е й,
что и требуется.
ВЫПУКЛЫЕ МНОЖЕСТВА
21
$ 11
Замечание 4. Условие (1.8) означает, что пло-
скость
(х —Хо, go) = O, (1.15)
проходящая через точку Хо, обладает тем свойством, что
все множество Й лежит по одну сторону от этой пло-
скости, причем на расстоянии, не меньшем чем а.
Условие (1.13) означает, что все множество й лежит
по одну сторону от плоскости (1.15).
Следствие 2. Пусть QcEn — выпуклое множе-
ство и х0^й. Тогда существует вектор go&En, IIgo 11 =
= 1, такой, что
(х — х0, go) < О Vx ® й.
Задание 1.3. Доказать следующие теорему и следствие.
Теорема 1.3. Пусть й] и й2 — замкнутые выпук-
лые множества и хотя бы одно из них ограничено. Если
множества Й1 и й2 не имеют общих точек, то существуют
такие вектор go, точка Хо е Й] и число а > 0, что
(х — х0, go) СО Vx <— й),
(х —хо, go)>a Ух®й2.
Указание. Надо найти
min ||х —//|р = ||х0—1/о1Р-
xaQi,
Следствие. Пусть й] и й2 — замкнутые выпуклые
множества, причем хотя бы одно из них ограничено.
Если эти множества не имеют общих внутренних точек,
т. е.
int Й1 flint Й2= 0, (1.16)
то существуют такие вектор go и точка Хо s Qi, что
(х — хо, go)СО Vx sйь
(х —Хо, go)>O Vxefi2.
Замечание 5. Утверждение в следствии можно
усилить, заменив (1.16) одним из условий:
int£J1f|Q2=0, Qif)intfi2 = 0. (1.17)
22
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
§ 2. Точечно-множественные отображения
1. Пусть Q — некоторое множество. Совокупность
всех непустых подмножеств множества Q обозначим
П(£)). Пусть Qi и — некоторые множества конечно-
мерных пространств. Отображение Л(х), которое перево-
дит каждую точку в некоторое подмножество
множества Q2, называется точечно-множественным ото-
бражением (т. м. о) Qi в Q2 или отображением Qi в
П(£2а). Будем обозначать это так: А: Й]->П(О2).
Пусть А Еп, В с: Еп. Положим
р(Л, В)== sup inf || v — оу 11 + sup inf ||v —ш||. (2.1)
шеЛчеВ vgBwgA
Число р(Л,В) называется расстоянием между мно-
жествами А и В в метрике Хаусдорфа (или расстоянием
Хаусдорфа).
Величина sup inf Г v — w || называется уклонением
w е A v е В
множества А от множества В (в смысле Хаусдорфа),
а величина sup inf ||о — ау|| называется уклонением
и е В w<= А
множества В от множества А (в смысле Хаусдорфа).
Задание 2.1. Показать, что если А и В — замкнутые множе-
ства пространства Е„, то равенство р(А, В) = 0 эквивалентно соот-
ношению А = В.
Замечание 1. Требование замкнутости в зада-
нии 2.1 существенно, что видно из следующего примера.
Пусть
А = {х = (х(1), х®) <= Е2 |х® — рациональные числа,
Iх®К1, let :2),
В = {х = (х®, х®) е Е211 х® |< 1, I е 1:2}.
Множество А не является замкнутым. Ясно, что
р(Л, В) = 0, но Л =£ В.
Отображение Л (х) называется непрерывным по
Хаусдорфу (Н-непрерывным) в точке х0, если
р(Л(х), Л(хо))—->0. (2.2)
Т. м. о. Л: Qi->n(Q2), где Qic:£4, Q2 a Em, назы-
вается полунепрерывным сверху (п. н. св.) в точке х0 SS
<= Qi, если из того, что xs->x0, vk^A(xk), сле-
дует иоеЛ(хо).
§ 23
точечно-множественные отображения
28
Отметим, что существуют разные определения полу-
непрерывности сверху [86], которые совпадают, если Qa
ограничено.
Графиком отображения 4(х) называется множество
Z = {[х, у] £= Qj X Q2I* е= Qb у (= А (х)}. (2.3
Задание 2.2. Доказать, что отображение А (х) полунепре-
рывно сверху на Qi тогда и только тогда, когда график Z (см. (2.3))
замкнут в Qi X ^2.
Задание 2.3. Пустьт. м. о. А: А
Qj -+ П (Q2) полунепрерывно сверху
на Qi. Доказать, что тогда для лю-
бого х е Q; множество А (х) замк-
нуто.
Обратное неверно, что видно из
следующего примера.
Пусть Qi =» Q2 = El,
Рис. 1.
Л(х) =
[0,1], х=/=0,
[о, 2-1]. х = 0.
При любом х множество Д(х)
не является п. н. св. в точке х0 = О
замкнуто, но отображение Л(х)
(рис. 1).
Отображение A: Qi~>II(Q2) называется полунепре-
рывным снизу (п. н. сн.) в точке если для вся-
кого и0 е А (х0) и любой последовательности {хь}, Хь~+
->х0, найдутся такие что Vk-^vn.
Отображение Д(х) называется непрерывным по Ка-
кутани (К-непрерывным) в точке х0, если оно полуне-
прерывно в этой точке и снизу, и сверху.
Следующий пример иллюстрирует полунепрерыв-
ность сверху и снизу.
Пример 1. Пусть Qi = Q2 = Рассмотрим ото-
бражения
( [х, 1 +х], х=£0,
Л (х) = < г
I [0, 2"'], х = 0,
__ ( [х, 1 -I- х] х =£ О,
Л2(х) —| {0) 2], х = 0.
В точке хо = 0 отображение Л^х) полунепрерывно
снизу, но не полунепрерывно сверху, а отображение
А2(х) полунепрерывно сверху, но не полунепрерывно
снизу (рис. 2, 3) .
24
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Отображение Д(х) называется ограниченным на Я1,
если для любого ограниченного подмножества G cz Я]
найдется ограниченное подмножество В с Яг такое, что
А (х) с В Vx е G.
Отображение А (х) называется замкнутым в точке х0,
если множество А (х0) замкнуто.
Теорема 2.1 [78]. Если отображение Д(х) ограни-
чено в некоторой окрестности точки х0 и замкнуто в
точке хо, то из непрерывности А (х) по Хаусдорфу в точ-
ке х0 следует непрерывность Л(х) по Какутани в точке
х0) и наоборот, т. е. понятия Н-непрерывности и К-непре-
рывности в этом случае эквивалентны.
Доказательство. Пусть т. м. о. А (х) непрерывно
по Хаусдорфу в точке х0, т. е. имеет место (2.2). Пока-
жем, что тогда Д(х)— п. н. св. Пусть х*.->хо, и* е
еД(Хй), vk-*-v0.
Допустим, что Vo&Afxo). В силу замкнутости Д(х0)
существует а > 0 такое, что при достаточно больших k
inf ||v —v*ll= min ||o — vft||>a > 0.
o e A (Xa) v e A (xo)
Тогда (см. (2.1)) тем более
p (Д (xft), A (x0)) > inf || v — vk || > a > 0,
V e A (Xo)
что противоречит (2.2). Итак, т. м. о. А (х) является
п. н. св.
Установим теперь, что т. м. о. А (х) полунепрерывно
снизу.
§ 2)
точечно-множественные отображения
28
Пусть Vo s А (х0)' и хк ->х0. Положим
Ьк — inf || о —Poll.
OSA(^)
Поскольку ft* < рИ(хо), А(хк)), а Д(х) непрерывно по
Хаусдорфу, то р(Д(х0), Д(х<!))->0. Отсюда 6*->0.
Тогда для любой последовательности {у4 такой, что
+ найдутся Vk^A(Xk) такие, что ||о* — voll^
т. е. уа->Оо, а это и означает (в силу про-
извольности Vo е А (х0) и последовательности {х*}), что
А (х) полунепрерывно снизу. Отсюда и из установленной
выше полунепрерывности сверху вытекает /(-непрерыв-
ность.
Пусть теперь т. м. о. А (х) является /(-непрерывным
в точке Хо- Допустим, что оно не является //-непрерыв-
ным в этой точке. Тогда найдутся число а > 0 и после-
довательность {хк} такие, что
хк Хо, р (А (хк), А (х0)) > 2а > 0. (2.4)
В этом случае (см. (2.1)) для каждого фиксированного
k либо
sup inf || v — w || а, (2.5)
®<sA(*ft) оеЛ(х0)
либо
sup inf || v — w || а. (2.6)
oeA(jf0) weA(xk)
Без ограничения общности можем считать, что для всей
последовательности {х*} имеет место либо, (2.5), либо
(2.6). Рассмотрим каждый из этих случаев подробно.
В случае (2.5) найдутся wk е А (хк), такие, что
inf || v — wk |О2~'а. (2.7)
о 6 А (хо)
По предположению т. м. о. А (х) ограничено в окрестно-
сти точки Хо, поэтому последовательность {wk} тоже ог-
раничена. Выделим сходящуюся подпоследовательность
{wfcs}, wks -> wo- Из (2.7) ясно, что wo ф А (х0), а это
противоречит полунепрерывности А(х) сверху в точке
х0. Итак, случай (2.5) невозможен.
В случае (2.6) для каждого k найдутся vk е А (х0)
такие, что
inf || vk — w И > 2~ а. (2.8)
weA(xk)
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. 1
26
Так как множество А(хо) замкнуто и ограничено, то су-
ществует подпоследовательность {А,} такая, что
—► иое А(х0). Из (2.8) при достаточно больших kt
inf || »о — а»||>4-1а,
швЛ(хМ
что противоречит полунепрерывности снизу отображения
А (х) в точке х0. Я
Следствие. Если А(х) Н-непрерывно и замкнуто
в точке х0, то оно и К-непрерывно.
Если же А(х) К-непрерывно в точке Хо и ограничено
в некоторой окрестности точки х0, то оно и Н-непре-
рывно.
Замечание 2. Требования в условиях теоремы яв-
ляются минимальными. Действительно, замкнутость
А (х0) следует из полунепрерывности сверху т. м. о. (см.
задание 2.3). Приведем пример, показывающий, что ог-
раниченность А(х) в окрестности точки х0 (и, естествен-
но, в самой точке хо) существенна. Пусть Qi = Gfo = Е\,
.. . Г [— 1 + х, 1 4-x]U{x-1}, х=/=0,
,=0.
Отображение А(х) не является ограниченным в окрест-
ности точки хо = 0. Ясно, что в точке хо = 0 отображе-
ние А(х) полунепрерывно снизу, ибо для любого vqG
е[—1, 1] и любой последовательности {х/г} такой, что
х*->0, найдется последовательность {«4 такая, что
Vk = (uo + xk) е А (хк), Vk -> vo-
С другой стороны, если х^->-0, l-f-x»,
1 4-xft]c:A(Xfe), Vk-+v0, то voe[—1, 1], т.е. »оеЛ(хо);
значит, отображение А (х) полунепрерывно сверху.
Итак, А (х) является п. н. св. и п. н. сн., т. е. ./(-непре-
рывно в точке хо = 0.
Но при | х~11 — | х | > 1
р(А(х), А(х0))>|х-Ч-1-|х| + |х| = |х-Ч-1-> + оо,
т. е. т. м. о. А (х) не является //-непрерывным в точке
Хо = 0.
2. Пусть 4 с£л, В с Еп.
Лемма 2.1. Если
sup (v, g) = sup(v, g) (2.9)
osA v&B
5 2)
ТОЧЕЧНО-МНОЖЕСТВЕННЫЕ ОТОБРАЖЕНИЯ
27
для всех g е Еп, то
со А —со В. (2.10)
Доказательство. Допустим противное. Пусть
со Д =/= со В. Тогда найдется либо точка vo е со А такая,
что vo & со В, либо точка WqScoB такая, что Wo ф. со 4.
Пусть, например, нашлась точка ОоесоД, и0^соВ.
Тогда по теореме отделимости существуют число а > 0
и вектор go, llgoll = 1, такие, что
(w — Vq, goX — a Vow s co В. (2.11)
Так как о0есоД, то (см. теорему 1.1)
Vo — lim vk, о* = Е QkiVkb
>->оо /«*1
vki<szA, а«>0,
i-i
Тогда
(o*> go) == E («kb go) < E a« sup (v, go) = sup (u, go).
овЛ оеЛ
Переходя к пределу, имеем
(ро, go)<sup(v, go). (2.12)
оеЛ
Поскольку В а со В, то из (2.11) и (2.12) следует
sup (w, go) < (t»o, go) — a < sup (v, go) — a,
weB v«A
что противоречит (2.9). Лемма доказана.
Следствие. Если А и В — замкнутые выпуклые
множества, то (2.9) эквивалентно соотношению Ага* В.
Легко показать, что
sup (u, g)== sup (v,g)== sup (v, g). (2.13)
oeA аесоА oecoA
Замечание 3. Рассуждая, как при доказательстве
леммы 2.1, можно показать, что если
sup (о, g) sup (v, g) Vg e En,
veA oeB
то co X э co B,
28
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
3. Пусть множество. А (х) замкнуто, выпукло и огра-
ничено при каждом
х int Зб (х0),
где
б > 0, Зб (хь) — {х э Еп HI х — х0 II < 6}.
Положим
h (х, g) = max (v, g).
v e A (x)
Лемма 2.2. Если функция h(x, g) непрерывна на
S6(x0yXEn, то отображение А(х) Н-непрерывно в
точке хо-
Доказательство. Установим вначале, что ото-
бражение А (х) является полунепрерывным сверху в точ-
ке Хо. Пусть хА—*-х0, Vk е А(х*), vA->t>o- Надо показать,
что
t»0«=A(x0). (2.14)
Допустим противное. Пусть Уо^А(хо). По тедреме
отделимости найдутся число а > 0 и вектор go е Еп,
llgoll™ 1. такие, что
(go, v — ооХ — а. < 0 Vo Q А (х0).
Отсюда
Шо. go) = max (v, go) ^(fo. go) —а. (2.15)
v e A (Xo)
Ho h (xk, go) max (v, g0) (vk, go)- Переходя здесь
к пределу при Л-*оо и учитывая непрерывность h(x, go)
по х и неравенство (2.15), имеем
h (хо, g0) > (»о, go) > max (о, g0) + а — h (х0, go) + а,
V е А (Хо)
что невозможно, ибо а > 0. Полученное противоречие
доказывает полунепрерывность сверху т. м. о. А (х) в точ-
ке Хо-
Установим теперь полунепрерывность снизу А(х).
Пусть vo е А (х0). Возьмем произвольную последова-
тельность {х^, х*->хо. Надо показать, что найдутся та-
кие Vk s A (Xk), что Vk -> Vo- Допустим противное. Без
ограничения общности можно считать, что
р (А (хА), vQ) = min || v — vo || = || оА — о0 II > а > 0.
ТОЧЕЧНО-МНОЖЕСТВЕННЫЕ ОТОБРАЖЕНИЯ
29
§ 2]
В силу необходимого условия минимума функции <р(и) =
= ||р— voll2 на множестве Л(хЛ) (см. замечание 3 § 1)
(||v* — foir1^ — Vo), V — v0)>a Vv<aA(xk). (2.16)
Положим
gk = — II Vk — vo 1Г1 (v* — Vo).
Без ограничения общности можем считать, что gk-+go-
Тогда из (2.16)
h (хк, gk) = max (t>, gk) < (v0, gk) — a <
< max (v, gk) — a = h(xOy gk) — a.
v e A (Xo)
Переходя здесь к пределу при k -+ оо и учитывая непре-
рывность h по х и g, получим
h (х0, g0) < h (х0, go) — а,
что невозможно, так как а > 0. Противоречие и доказы-
вает полунепрерывность снизу т. м.о. А(х). Ранее уже
установлена полунепрерывность сверху. Значит, А (х)
является /(-непрерывным. Так как А(х) ограничено в
окрестности точки х0, то по теореме 2.1 Д(х) //-непре-
рывно. Лемма доказана.
Замечание 4. Ограниченности А (х) можно и не
требовать, она будет следовать из непрерывности h(x,g)
по g. Правда, тогда надо определить h(x, g) так:
й(х, g) = sup (v, g). (2.17)
o e A (x)
Лемма 2.3 Пусть на £2i задано полунепрерывное
сверху т.м.о. А: £21->П(£22), где £2г— компакт из Ет,
а на Qi X задано полунепрерывное сверху т.м.о. В:
Qi X Й2-*П(£Р). Тогда точечно-множественное ото-
бражение С(х)== U В(х, г) полунепрерывно сверху
z е А(х)
на £2ь
Доказательство. Пусть £2i,x*->x*, Vfe-> u*,
vssC(xj). Так как о^еС(х4), то при каждом k най-
дется такая точка глеД(хл), что В(хк, гк). Выде-
лим из последовательности {zk} сходящуюся подпосле-
довательность Zks -> z*. В силу того, что А (х)
полунепрерывно сверху, будет z* е А (х*).
80
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Имеем
г*,) -► (х*. х*), Vks -* v', Vka s В (xkft zkf).
Поскольку В (x, z) полунепрерывно сверху, то v* &
& В (х*, , т. е. v* е С(х*). Лемма доказана.
Лемма 2.4. Пусть точечно-множественное отобра-
жение
Qt Qj -* П (Q2), Й1 cz Еп, й2 Ет,
полунепрерывно сверху и ограничено на Qi. Тогда со
G(x) полунепрерывно сверху на Qi.
Доказательство. Пусть
х3-+х*, vs-+v*, со G(xs).
Требуется установить, что v* е со G(x*).
По теореме Каратеодори (теорема 1.1) при каждом в
справедливо представление
т±1
4^ askvskt
jfc-M
m+1
где aSft>0, X asfe1 > vske G(xs) 1: (m + 1). Так
как G(x) ограничено, то можно выделить такую после-
довательность {$/}, что
аМ 6 ® 1: (m + 1).
» l->oo I
Тогда
лН-l m+1
V*“ Z Ea* = l,
A-l k-1
и поскольку
XtiT^x*' ^eG(4)>
a G (x) полунепрерывно сверху, то vl es G (x*) при каж-
дом что завершает доказательство.
Задание 2.4. Доказать, что если Gi(x) и G2(x) полунепре-
рывны сверху и ограничены на Qi, то отображение co{Gi(x) U Ga(x))
полунепрерывно сверху на Qb
КОНУС ВОЗМОЖНЫХ НАПРАВЛЕНИИ
31
§ 3. Выпуклый конус. Конус возможных
направлений. Сопряженный конус
1. Определение 1. Множество ГсЕп называется
конусом, если вместе с точкой х оно содержит и точку
и Кх для любого X > 0.
Пусть QdEn — замкнутое выпуклое множество и
хо е й. Рассмотрим множество
у (х0) = {v — k(x — х0) I А. > 0, х g Q}.
Ясно, что у(хо)—конус, причем 8 s у(хо).
Замыкание конуса у(хо) называется конусом возмож-
ных направлений множества й в точке хо и обозначается
Г(х0).
Замечание 1. Если XoSintQ, то очевидно, что
у (х0) == Г (х0) = Еп.
Лемма 3.1. Если £2 — замкнутое выпуклое множе-
ство и х0 е й, то Г (хо) — замкнутый выпуклый конус.
Доказательство. То, что Г(хо) — замкнутый ко-
нус, видно из определения замкнутого множества. Для
доказательства выпуклости Г(хо) достаточно убедиться
в выпуклости у(хо). Пусть оь о8еу(х0), т. е. v\ =
= %i(xi — хо), 1>2 = Мхг — хо), где Xi > 0, Х2 > 0,
Xi, х2 е й. Надо показать, что
оа = aoi + (l — a)t)2sy(xo) при а е [0, 1].
Положим
X = aZt + (l—а)Л2>0, a0 = X~1aA1, O^ao^l.
В силу выпуклости й точка х = aoXi + (1 — ао)хг s й.
Тогда
va » a%i (х, — х0) + (1 — а) Л2 (х2 — х0) =
«= X [ао (Х1 — Хо) + (1 — ао) (х2 — х0)] = X (х — х0) е у (х0),
что и требовалось доказать.
Определение 2. Пусть Г cz Еп —• конус. Сопря-
женным ему конусом Г+ называется множество
Г+ =» {а» €= Еп | (w, v) 0 Vo s Г).
32
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
ГГЛ. J
Примеры. >
1. Если Г = Еп, то Г+ = {0}. i
2. Если Г = {х — (х(1), .... х (п))1х<0 0 Vt е 1 : п), то |
г+ = г. ?
3. Если Г = {хе Е„| (Д, х) 0}, где А е Еп, то Г+== -
= {х = — М|Х>0}.
4. Если Г = {®}, то Г+ = Еп.
5. Если Г(хо) — конус возможных направлений мно-
жества Q в точке х0ихоб intQ, то, как уже отмечалось, ।
Г(х0) = Еп, и тогда Г+ (х0) = {0}. I
Задание 3.1. Пусть Г = {х е Е„| (А, х) — 0}. Показать, что »
Г+ = {о = I % е (— <х>, оо)}.
Лемма 3.2. Если Г с: Еп — конус, то Г+ с: Еп яв-
ляется замкнутым выпуклым конусом.
Доказательство следует из определения сопря- |
женного конуса.
Задание 3.2. Показать, что если Г(хо)—конус возможных
направлений множества й в точке х0, то справедливо соотношение |
Г+ (х0) = (ш е Еп | (х — х0, ш)>0 Vx s UJ. (3.1) »
Теорема 3.1. Пусть Г с: Еп — замкнутый выпуклый
конус, G сЕп — выпуклый компакт. Для того чтобы Г
и Q не имели общих точек, т. е. ;
ГПС=0, (3.2) |
необходимо и достаточно, чтобы нашелся вектор ayos 1
<= Г+ такой, что |1
max (w0, х) < 0. (3.3) i
хеО I
Доказательство. Достаточность. Так как |
te»o е Г+, то по определению сопряженного конуса |
(w0. »)>0 УоеГ. (3.4)
По предположению (см. (3.3))
(w0, х) < 0 VxeG. (З.б)
Неравенства (3.4) и (3.5) означают, что Г и G не имеют Г
общих точек. ?
$ 3]
КОНУС ВОЗМОЖНЫХ НАПРАВЛЕНИИ
33
что
Необходимость. Пусть Г и G не имеют общих
точек. Найдем (рис. 4)
р= min || х — v || = || х0 — »о11- (3.6)
х е G, v е Г
В силу условия (3.2) Цх^— Ыо11 > 0. Возьмем go =
= ||о0 —Xoll-^oo — Хо). Покажем вначале, что
(vo,go) = O. (3.7)
Допустим противное, т. е. что (и0> go) — а =/=0. Тогда
vot^O- Рассмотрим точки 1»х=А^о. При к > 0 будет
рхеГ (ибо Г — конус).
Имеем
(пл — *о)2 = («о — *о +
+ (А-1)и0)2 =
— II Хо — По Ц2 4*
+ 2 (А — 1) а || Vo — Хо || +
4- (А — I)2 Vo-
При А, достаточно близких
к единице и таких, что
sign (А — 1) = sign а,
будет ||ох — xoll2< ||х0 — Voll2,
Так же как и при доказательстве теоремы 1.2 (не-
равенство (1.10), показывается, что
(х, go) < —1| х0 — Vo II Vx <= G. (3.8)
Установим, что
(v,g0)>0 Vos Г. (3.9)
Действительно, с учетом (3.7) имеем
(v, go) = (и — х0, go) +
4- (Хо — Vo, go) 4- (t»0, go) > Р — Р == 0. (3.10)
Положим w0 = go- Тогда из (3.8) вытекает (3.3), а из
(3.9) заключаем, что a’o = gosr+. Теорема доказана.
Теорема 3.2 Пусть YcEn — замкнутый выпуклый
конус, GcEn — выпуклый компакт. Для того чтобы
intrf)G = 0, rfiintG=0, (3.11)
2 В. Ф. Демьянов, Л. В. Васильев
84
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
необходимо и достаточно, чтобы нашелся вектор
е Г+ такой, что
max(wo, х)<0. (3.12)
хе G
Задание 3.3. Доказать теорему 3.2.
2. Лемма 3.3. Если Г с.Еп — замкнутый выпуклый
конус, то
Г++ = Г. (3.13)
Доказательство. Пусть ццеГ. Тогда по опре-
делению сопряженного конуса для любого w е Г+ будет
(w, Оо) 0, т. е. Оо s Г++; значит, Г с Г++.
Докажем обратное включение. Допустим противное.
Пусть ОоеГ++, но оо^Г. Положим G = {oo}. По тео-
реме 3.1 существует Woe Г+ такой, что (w0, Оо) •< 0, т. е.
оо ф Г++, что противоречит предположению.
Следствие 1. Если ГаЕп— выпуклый конус и
Г — его замыкание, то
Г++ = Г. (3.14)
Доказательство. Г — замкнутый конус, и по
(3.13) Г++ = Г. Но Г+ = Г+.
Следствие 2. Если ViCzEni i е 1 : $, — выпуклые
конусы и
S ( S
£ Г, = {о = z о,
Z-1 I /-1
vt <=ГЬ lEl: sr,
то
/ S \+ S
(,5, г‘) - ОЛ
(3.15)
Это следует из определения сопряженного конуса и
того факта, что 0 е Г/, i <= 1 : s. Я
Следствие 3. Если ViciEn, i^i:s,— замкнутые
выпуклые конусы, то
f s \ + ~
(nrz)=Zrr. (3.16)
\Z-1 / /-1
Доказательство.
/ s \ + / s , \ + / s \ + +
Co.r-) =(дМ ЧИ
S 31
КОНУС ВОЗМОЖНЫХ НАПРАВЛЕНИЙ
35
Задание 3.4. Доказать, что если Xi, ..., Жт — замкнутые
конусы в Еп, то либо 3ti + ... + — замкнутый конус, либо су-
ществует нетривиальное представление нуля. Последнее означает,
что найдутся Xi е У?1 такие, что Xi +... + Хт = ® и не все xt рав-
няются нулю.
Замечание 2. В (3.16) знак замыкания существен.
Приведем пример, из которого следует, что сумма двух
замкнутых выпуклых конусов может не быть замкнутым
множеством.
Пример 1. Рассмотрим два конуса в Е3:
= {х = (х®, х®, х<3») | х® =» х® = 0, х® < 0},
Х2 = {х = (х®, х®, х®) | (х®)2 + (х®)2 < 2х®х®, х® 0}
(образующей конуса Хг является окружность (x®)2-f-
-(-(х<3>)2 = 2х<3) в плоскости х<2> =1). Очевидно, что Xi
и Хг — замкнутые выпуклые конусы. Однако их сумма
Xi + Х2 = {х <= Е3 |х® > 0} U {х |х® = х® = 0}
не является замкнутым конусом.
Задание 3.5. Доказать, что если множества Qi, ...» Qs мно-
гогранные (т. е. каждое из них задано конечным числом неравенств
вида (xr < bt \fi е 1: /и), то их сумма (множество Qi + ...
... + Qs) является замкнутым множеством.
3. Пусть G — произвольное множество из Еп. Через
Jif(G) обозначим выпуклый конус, натянутый на G:
X (G) = Iv = £ vk 6= G, > 0,
I
k 1 : r, r — любое натуральное число}.
Конус JJf(G) называется выпуклой конической оболоч-
кой множества G.
Задание 3.6. Показать, что если Г — выпуклый конус, то
+ Г = Г. Почему важна выпуклость?
Лемма 3.4. Любая точка v^W(G) может быть
представлена в виде
v = Е vk G, ak > 0, k е 1 : г,
ы
где и векторы Vk, kz\:r, линейно незави-
симы.
2»
36
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
Доказательство. Пусть yeJif(G); тогда
о=£а*о*, o*sG, а*>0.
к-1
Можем считать, что ak > О 1 :г. Если Vk линейно
зависимы, то существуют р*, k е 1 : г, такие, что
£й>0, S fV.-e. (3.17)
Й"1
Можем также считать, что среди {р*} есть положитель-
ные (из (3.17) следует, что среди {р*} есть хотя бы один
ненулевой коэффициент, будем считать его положитель-
ным, изменив для этого, если необходимо, знаки всех
Р* на противоположные; при этом (3.17) останется спра-
ведливым). Положим
е= min РГ’яа» й* = а* —ер*, 6е1:г.
Г
Ясно, что akvi и среди {а*} есть хотя бы один
нулевой коэффициент (а остальные неотрицательны).
Таким образом, если в представлении вектора v е (G)
имеются линейно зависимые и*, то можно получить но-
вое представление, в котором участвует меньше векто-
ров. Продолжая так далее, в конце концов придем к
лредставлению, в котором все о* линейно независимы.
При этом ясно, что их число не более п. Лемма дока-
зана.
Лемма 3.5. Пусть G с. Еп — ограниченное замкну-
тое множество м 0 со G. Тогда Ж (G)— замкнутый вы-
пуклый конус.
Доказательство. Ясно, что Jf(G) — выпуклый
конус. Докажем его замкнутость. Прежде всего заметим,
что, как легко проверить,
Х(О) = {о = Ло'|%>0, o'ecoGJ. (3.18)
Пусть теперь p*->u*, o*e^(G). Надо доказать, что
p*eX(G). В силу (3.18) имеем
ц* = Л*о*, Х*>0, u*ecoG. (3.19)
$ 3
КОНУС возможных НАПРАВЛЕНИИ
37
Так как G — ограниченное множество, то и со G — огра-
ниченное множество; кроме того, по условию 0 ф со G.
Отсюда
0<т<||о'||<Л1 < оо Vu'ecoG.
Из (3.19) заключаем, что {%*}—ограниченная последо-
вательность. Последовательность {v'k} тоже ограничен-
ная, ибо v'k е со G. Поэтому можно выбрать подпоследо-
вательность {ta} такую, что
tas~>V
Ясно, что о* = Х*1>', V 0, o'ecoG. Значит, о*<=
е J$f(G), что и требовалось доказать.
Замечание 3. Условие 0 ф со G в лемме 3.5 суще-
ственно, что видно из следующего примера.
Пусть
G = {х = (х®, х®) е= Е2| (х® - I)2 + (х®)2?< 1).
Здесь Oe=coG = G, X(G) = {®}U{x = (x(1), х<2>) |х<‘> >
> 0}, т. е. JSf(G) не является замкнутым множеством.
Но если G состоит из конечного числа точек, то усло-
вие 0 ф со G в лемме 3.5 может быть опущено.
Лемма 3.6. Если множество G состоит из конечного
числа точек, то W(G) является замкнутым выпуклым
конусом.
Доказательство. Пусть Vk-^v*, Vk^ffl(G).
Требуется доказать, что о* е Jif (G). При р* — €> sw оче*
видна^&дедует по .onpoa<WKiinnn-
rk
По лемме 3.4 vk = У. \kt > 0, o^eG. По-
Z — 1
скольку G состоит из конечного числа точек, можно
выбрать подпоследовательность наборов содер-
жащую одни и те же векторы, т. е.
Vk “ Z K,iVi, Vi > О, vt<=G, r<n.
® Ь1 о
- .ЛЛЛИЛиИО Си (н
Докажем, что последовательность {tas = (tap, ...
• • • > tasr) Ег] ограничена. Допустим противное. Пусть
это не так. Без ограничения общности можем считать,
38
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. 1
что воп' пооладсватольпоо№ puj npojipaitiwona) тГ"~о.-
Г •
Vks= X 00 (напомним, что все X*g/> 0). Тогда
Г
о [ 1 о о о
где
°* = £ Ч ivi< Kt = Vs г > °-
<S I sb 1 о о о о
Так как
X Kst = 1>
/-1 1
то
JjLoелмтал X X: *^£>0, • =
Множество со G ограничено, поэтому o/g—>0, т. е.
2= 0. что противире^т^О^^етию^Итак, — ог-
раниченная последовательность. Выбирая сходящуюся
Г
подпоследовательность, получим, что v* = где
Z-1
Vi &G, Xj > 0, т. е. о* е X (О). Лемма доказана.
4. Выше для xeQ были определены точечно-множе-
ственные отображения -у(х), Г(х)г=у(х) и Г+(х).
Лемма 3.7. Отображение у (х) полунепрерывно
снизу на Q.
Доказательство. Пусть Xo^Q. Надо показать,
что если vosy(xo) и х;->х0, х,<= й, то найдется после-
довательность точек {о/}, Vi^y(xt), такая, что Vi-+Vq.
Если t»o = O, то утверждение очевидно. Предположим,
что оо¥=0. Так как Оо^у(хо), то у0=^о(х — Хо), где
Хо > 0, xeQ, х х0. Тогда ш = Хо(х— Xi)ey(xi).
Очевидно, что Vt -> Vo-
Лемма 3.8. Отображение Г+(х) полунепрерывно
сверху на О.
Доказательство. Пусть xosfi и х*-»-Хо, «/»-*
->г/о, х^еЙ, ^еГ+(х4). Надо показать, что у0 е
е Г+ (хо) •
Так как уk е Г+(х*), то (см. задание 3.2)
(х-хк, yk)^0 Vxe=Q.
КОНУС ВОЗМОЖНЫХ НАПРАВЛЕНИИ
39
§ 3]
Переходя здесь к пределу при фиксированном xg Q,
имеем (х— х0, Уо)^ 0. Это неравенство справедливо для
любого хей, а это и означает, что у о <= Г+(х0). Лемма
доказана.
5. Пусть А с Еп — компакт, и пусть
Г = {пе=£„|(г, п)<0 Vz е= Д}.
Легко проверить, что Г — выпуклый конус.
Лемма 3.9. Справедливо соотношение
Г+ = —3?(соД), (3.20)
где JJf(G)—выпуклая коническая оболочка множе-
ства G.
Доказательство. Правую часть (3.20) обозна-
чим В. Пусть w е В, т. е.
w = lim wk, wk = — Kkzk,
Z?-»oo
rk
i-1
rk
aAt>0, E<xft/=1, zkl^A Viel.T*.
z—i
В силу леммы 3.4 без ограничения общности можно счи-
тать, что
rk = г п Vk.
Возьмем любое о еГ. По определению множества Г бу-
дет
(о, zfc/)<0 Vi е 1: г.
Поэтому
(v, wk) = — Kk Ё aki(zki, t»)>0 VusI’,
t=l
а это и значит, что Wk & Г+ Так как Г+ — замкнутое
множество, то w е Г+, т. е.
йсГ+. (3.21)
Докажем теперь, что .
Г+сй.
(3.22)
40
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
1ГЛ- I
Допустим противное. Тогда найдется такое Wo е Г+,
что wo Ф В. По теореме отделимости существует g е
е Еп, ||g||= 1, такое, что
(w0, g) < 0, (3.23)
(о, £)>0 VoeB. (3.24)
Так как для любого геА будет —zeB, то из
(3-24)
(г, g)<0 Vz е Л.
Значит, geT. Но ®о е Г+. Следовательно, (g, w0) 0,
что противоречит (3.23). Итак, (3.22) установлено.
Соотношение (3.20) вытекает теперь из (3.21) и
(3.22).
§ 4. Выпуклые функции. Непрерывность
и дифференцируемость по направлениям
1. Пусть на выпуклом множестве ScEn задана
функция f(x). Везде в дальнейшем, если не оговорено
противное, функция f(x) предполагается конечной в об-
ласти своего определения, т. е. принимающей конечные
значения в любой точке области определения.
Графиком функции /(х) называется множество
{[Р, х]е=Е„+1 |xe=S, ре£ь р==/(х)}.
Надерафиком функции f(x), определенной на мно-
жестве S, называется множество
epi f“ {[Р, ® En+i I х & S, р е Еи р > f (х)).
Функцию /(х) будем называть выпуклой на S, если
/'(ах1 + (1 — а)х2)<
(xi) + (1 — a)f(xa) Vxb x2<=S, Vae[0, 1]. (4.1)
Надграфик выпуклой функции — выпуклое множество.
Функция f(x) называется строго выпуклой на S, если
f (ах! 4- (1 — а) х2) < а/ (хО + (1 — a) f (х2)
Vxi, xg sS, Xi #= x2, Va e (0, 1).
§4]
ВЫПУКЛЫЕ ФУНКЦИИ
41
Функция f(x) называется сильно выпуклой на S,
если существует т > 0 такое, что
f (axi + (1 — а) х2)< af (х,) + (1 — а) f (ха) —
— а(1 — а)т||х, — х2II2 Vx,, x2eS, Va е [0, 1]. (4.3)
Функция f(x) называется вогнутой на S, если
f (ax, + (1 — a) х2) > af (х,) + (1 — a) f (x2)
Vx,, x2eS, Vae[0, 1].
Аналогично определяются строго вогнутые и сильно вог-
нутые функции. Заметим, что линейная функция f(x)==
= (А, х) 4- Ь, где А е Еп, b (=(—со, <х>), является одно-
временно, и выпуклой, и вогнутой. Из определения так-
же ясно, что если ft (х), i е 1 : N, — выпуклые на S
функции, то и функция
N
f (х) = £ aifi (х), а, > О, i е 1: N,
i—l
тоже выпуклая. В частности, выпуклой является и функ-
ция F(x) = Af(x), если А > 0, а f(x) — выпуклая функ-
ция.
Задание 4.1. Доказать, что если функция f(x) выпуклая,
xi в 3, а< 0, i е 11 р, а, “ 1, то
1-1
/(f аДхг). (4.4)
Неравенство (4.4) называется неравенством Йенсена.
Задание 4.2. Доказать, что если f (я) —непрерывная на S
функция и
f (2-1 (х, + х2)) < 2-1 [f (х,) + f (х2)] Vx,, х2 ® 3, (4.6)
то функция f(я)—выпуклая на S.
Утверждение перестает быть верным, если f(x) не является не-
прерывной.
Замечание 1. Очевидно, если i<= 1 :7V,— вы-
пуклые функции и хотя бы одна^из них сильно (строго)
выпуклая, то и функция f(x) = £ ft(x) является сильно
(строго) выпуклой.
42
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Задание 4.3. Доказать, что если f(x) — выпуклая на S функ-
ция и f(x)>0 VxeS, то функция ft(x)= f2(x) тоже выпуклая.
Отметим, что условие f (х) > 0 в этом задании существенно, что
видно из примера.
Пример 1. Пусть xeEt, f(x) = x2—1, fi(x) —
= f2(x). Ясно, что fi(x) не является выпуклой функ-
цией.
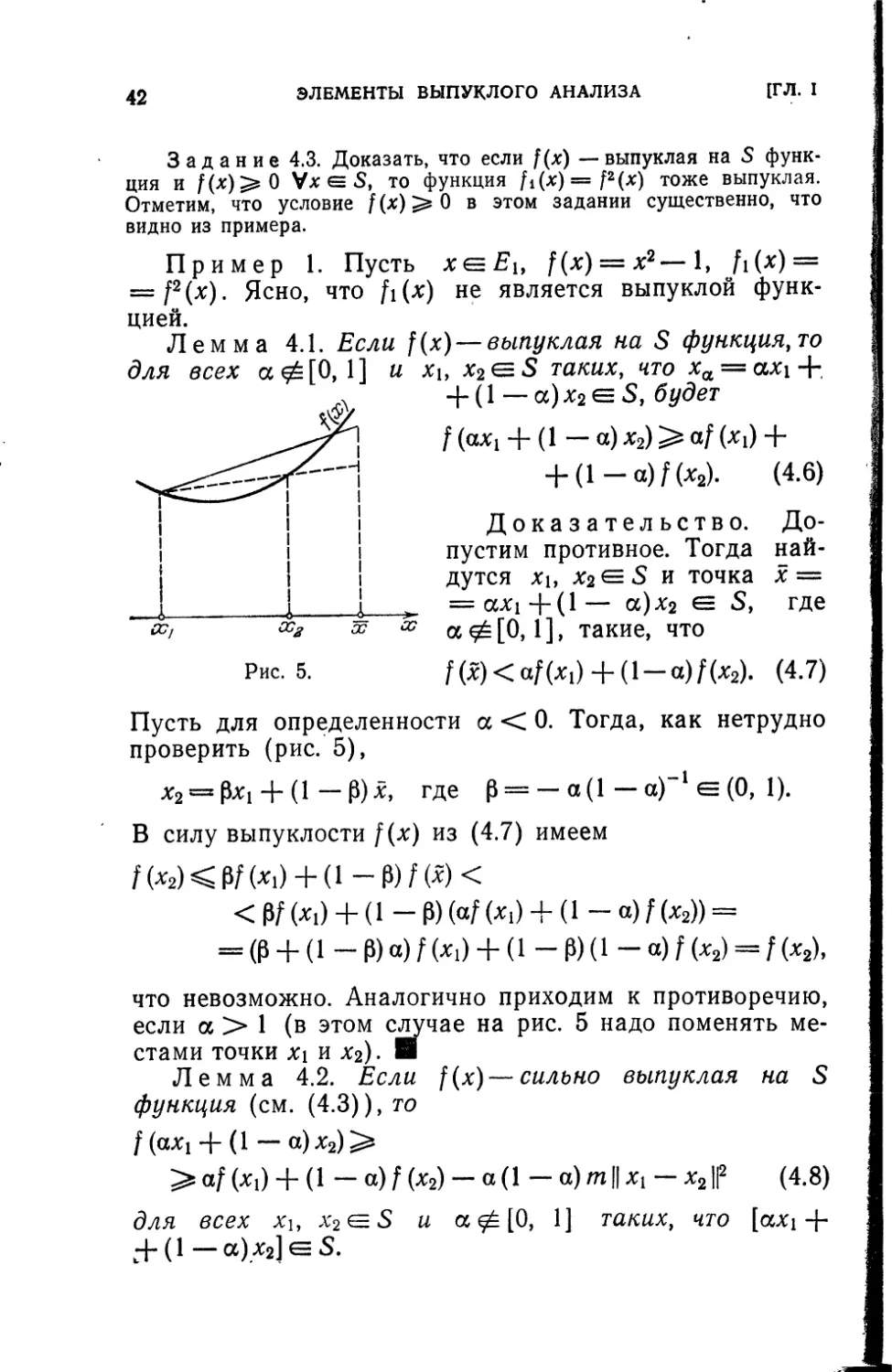
Лемма 4.1. Если f(x) — выпуклая на S функция, то
для всех а ^[0,1] и
%1, х2е$ таких, что ха — axi +
+ (1 — a)x2eS, будет
f (ах( + (1 — а) х2) > af (*i) +
+ (1 — a) f(x2). (4.6)
Доказательство. До-
пустим противное. Тогда най-
дутся хь x2gS и точка х =
= a%i+(l— a)x2 е S, где
а ^[0,1], такие, что
f(x)<af(x1) + (l — a)f(x2). (4.7)
Пусть для определенности a < 0. Тогда, как нетрудно
проверить (рис. 5),
х2 = 0X1 + (1 — 0)х, где 0 = — а(1—а)~*е(0, 1).
В силу выпуклости f(x) из (4.7) имеем
f(x2)<0f(x1) + (l-0)f(x)<
< 0/ (Xi) + (1 - 0) (af (Xj) + (1 - a) f (х2)) =
= (0 + (1 - 0)a)f (х,) + (1 - 0)(1 - a) f (x2) = f(x2),
что невозможно. Аналогично приходим к противоречию,
если а > 1 (в этом случае на рис. 5 надо поменять ме-
стами ТОЧКИ Х1 и х2).
Лемма 4.2. Если f(x) — сильно выпуклая на S
функция (см. (4.3)), то
/(axj + (l — a)x2)>
(xj + (1 — a)f (х2) — a(l — a) m || Xj — x2 Ц2 (4.8)
для всех xi, х2е$ и a^[0, 1] таких, что [axi+
(1 — a) x2] e S.
ВЫПУКЛЫЕ ФУНКЦИИ
43
Доказательство аналогично доказательству
леммы 4.1. Допустим противное; тогда найдутся xj,
х2 е S, Xi хз, а & [0,1 ] такие, что
f(x)<af(xi) + (l— a)f(x2) — a(l — a) m || xt — x21?, (4.9)
где X — axi + (1 — a) x2 e S.
Пусть для определенности a < 0. Тогда снова
x2 = pXi + (l-р)х, р= —a(l-a)“lG=(0, 1).
Из (4.3) и (4.9) имеем
f(x2)<pf(x1) + (l-p)f(x)-p(l-p)m||x1-x||2<
< Pf (*i) + (1 - Р) [af (х,) + (1 - а) / (х2) -
— а(1 — a)m||xi — ХгЦ2] — Р(1 — Р) тЦх! — х||2 =
— f (х2) + т (1 — Р) [— а (1 — а) || Х] — х21|2 —
-PUi-xll2]. (4.10)
Но Xi — х = (1—a) (xi — х2), поэтому выражение в по-
следних квадратных скобках в (4.10) равно нулю. Тогда
из (4.10) следует f (хг) < f (хг), что невозможно. Ана-
логично приходим к противоречию при a > 1.
Задание 4.4. Показать, что если f(x)—строго выпуклая на5
функция, то
f (axi + (1 — a) xt) > af (x,) + (1 — a) f (x2) (4.11)
при Xt Хз, а ф [0, 1] и таких, что axi +(1 — а)хг s S.
2. Пусть функция f(x) — выпуклая на выпуклом мно-
жестве S а Еп.
Теорема 4.1. Функция f(x) непрерывна в любой
внутренней точке множества S.
Доказательство. Пусть х0е intS. Через ei,
i е 1 : п, обозначим координатные орты: ei = (0.0,
1, 0...0). Поскольку XoGintS, то найдутся fh > 0
такие, что х0 ± gi е S, где gi = р,е(. Положим gn+i =
— —gi. Пусть х xq. Точку х можно представить в виде
2п
x — Xo + ^digi, где щ > 0, причем min {az, ai+n} — 0
2п
для всех te 1 :п. Тогда £ а/->0 при х->-хо (ясно, что
44
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
2п
а» зависят от х\. Пусть уже at < 1. Так как
i«1
2л / 2п \ 2п
х » Хо + Д atgi в «< ) х0 + а< (х0 + gt),
то в силу выпуклости f[x) имеем
f (х)< (1 — Д oQ f (х0) + atf (х0 + g{),
ИЛИ
f (х) - f (Хо) < g at (f (x0 + gt)-f (Xo)). (4.12)
Точку xo можно представить в виде Хо = 0,5 (х + х'),
где
, yi , , ( ai+n>
x'-=Xo+2Ja/^> „ />д
Ясно, что Поэтому
f(xo)<O,5[f(x) + f(x')l.
Отсюда
f(x0)-f(x)<Z x')-f(x0)<
<jg»; 1Ж+«<)-/«]• nW
Непрерывность функции f(x) в точке Xo следует теперь
из (4.12) и (4.13), ибо
2/1 2п
at 0, a't 0, У а{ — a't--------------► 0.
i.i /-1 «-**>
3. Пусть geEn, S — выпуклое множество, Хо е S,
существует ао > 0 такое, что Хо + <xog е 5, и пусть на S
задана функция f(x).
Функция f(x) называется дифференцируемой в точке
хо по направлению g, если существует конечный предел
lim сГ‘[/(хо + а#) — /(х0)].
a-> +0
ВЫПУКЛЫЕ ФУНКЦИИ
Число называют в этом случае производной
функции /(х) в точке х0 по направлению g. Очевидно,
что
f (*о + ag) == / (х0) + а + о (х0, g, а),
будем
О (Хо, g, а)_ п
где---------------> и.
м а а-»+о
Если функция f(x) дифференцируема
любому направлению g^En, то
она дифференцируема в точ-
ке Хо по направлениям. Из
определения ясно, что если
gi = ₽£> где Р > 0, то
#(*«)
dg, ~Р
Заметим, что из
цируемости по
ниям не следует
ность функции в
в точке Хо по
говорить, что
dg
дифферен-
направле-
непрерыв-
точке.
Пример 2. Пусть х =
= (x<f>, х(2>)е£2. Через G
обозначим (рис. 6) множество, ограниченное осью Е£ =
= {(х<1), х(2)) |х<» 0, х<2) = 0} и кривой
Jif = |(x(l), х(2)) |х(1) — cos <р cos -j-;
х(2) = sin ф cos -у;
Ф е [0, 2л
Положим
fl, xeff,
0, x^G.
Возьмем Хо = (0,0) = в. Ясно, что для любого g =
= (g(1), g(2)) существует =0, однако функция
f(x) разрывна в точке хо.
Функция f(x) называется дифференцируемой в точке
XoeintS, если существует такой вектор о(хо), что
/ + ag) = f (х0) + a (g, v (х0)) + о (х0, g, а)
Vge£e, ||g||==l,
46
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. 1
где ° о равномерно по g. Если функция
f(x) дифференцируема в точке х0, то она дифференци-
руема в этой точке по любому направлению g, причем
~dg°^ ° (*<>))• Кроме того, в этом случае функция
f(x) имеет частные производные первого порядка в точ-
ке Хо, причем
„(г\— д1 <*») —fdf («о) df (х0) \
О(х°)- дх dxW ............. dxW J.
Вектор v (хо) = д^д*0>> называется градиентом функции
f(x) в точке Хо. Для функции f(x) в примере 2 имело
место представление
f (х0 + ag) = f (х0) 4- о (х0, g, а),
но функция f(x) не является дифференцируемой в точке
Хо = (0, 0), ибо ° д) -> 0 неравномерно по g,
llgll=i.
Теорема 4.2. Пусть f(x) — выпуклая на S функция,
точка XoGintS. Тогда функция f(x) является диффе-
ренцируемой в точке Хо по любому направлению g е Еп.
Доказательство. Требуется доказать существо-
вание конечного предела
Нт Л (а),
dg а->+о
где й(а)= a-1[f(xo + ag) — f(x0)]. Поскольку хое
е int S, то существует б > 0 такое, что интервал (хо —
— 6g, х0 + bg)с 5. Пусть ао е (0, б). Для а е (0, а0]
будет
f (х0 + ag) = f (₽х0 + (1 — Р) (х0 + aog)),
где р==а^!(а0— а)е(0,1]. В силу выпуклости f(x)
f (хо + ag) < Р/ (хо) + (1 — Р) f (х0 + aog).
Отсюда
h (а) = а~1 [f (х0 + ag) — f (х0)] <
< а-1 (1 — Р) (f (х0 + aog) — f (х0)) =
= «о-1 [f (*о + «<£) - f (*о)] s h (ао)-
ВЫПУКЛЫЕ ФУНКЦИИ
47
§ 4]
Таким образом, /г (а) не возрастает при а-> + 0. С дру-
гой стороны,
f (хо) = f ((а Н" ао) 1 во (*о + а5*) + (а + ао) 1 а (xq ccog))
< (а + ао)-1 aof (х0 + ag) + (а + ао)-1 af (х0 — aog).
Поэтому
f (х0 + ag) > %-1 (а + а0) f (х0) - а~ *df (х0 - aog).
Отсюда
h (а) > а"1 [f (х0) - f (х0 - aQg)],
т.е. функция /г(а) ограничена снизу при а-*4-0. Су-
ществование конечного предела = lim h (а) еле-
a5 a->4*0
дует теперь из монотонности и ограниченности функции
h(а). Теорема доказана.
Следствие. Из доказательства теоремы ясно, что
dfdXsa~ = inf a-1 [f (x0 4- ag) — f (x0)].
us a>0
Лемма 4.3. Если f(x) выпукла на открытом вы-
пуклом множестве S и дифференцируема там, то
ftxo + g^f (х0) 4- (Г (х0), g)
для всех Хое S и g^En таких, что х0 4-g &S. Здесь
(v\_ df (х0) _ fdf (хр) df (xo)\
' 1 dx “I dx^ ’ dxM)’
Доказательство. Положим xj = Xq 4- g. В силу
выпуклости f(x)
f (*o 4- ag) == f (ax! 4- (1 — a) XoX
< af (xi) 4- (1 — a) f (x0) Va (= [0, 1].
Отсюда
[f (Jfo 4- ag) — f (xo)] < f (xi) — f (x0).
Переходя к пределу при a->4*0, имеем
(/' (л^о). g) < f (Xi) — f (x0) = f (Xo 4- g) — f (Xo),
что и требовалось доказать.
4. Пусть
f (х) = sup <р (х, у), (4.14)
48
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
1ГЛ. I
где х е Q с £л, Q — выпуклое множество, G — произ-
вольное множество любого пространства, функция
<р(х, у) — выпуклая по х на Q при каждом фиксирован-
ном y^G. Будем также предполагать, что функция
f(x), заданная соотношением (4.14), конечна на Q.
Легко убедиться, что тогда f(x) тоже выпукла по х
на Q. Действительно, положим ха = axi + (1 — а)х2, где
xi, х2 е Q, ае[0, 1].
Так как в силу выпуклости <р(х, у) по х
ф (ха, у) < а<р (хь у) + (1 — а) <р (х2, у),
то отсюда
f (ха) = sup <Р (ха, у) <sup [а<р (хь у) + (1 — а) <р (х2, у)] <
ye=G y&G
С a sup q> (хь у) + (1 — a) sup ф (х2, у) =
у е Q у (= G
= af(xi) + (l — a)f(x2),
а это и означает выпуклость f(x) на й. S
5. Пусть теперь
f(x) = inf ф(х, у), (4.15)
це О
где г е й с Еп, й — выпуклое множество, G — выпук-
лое множество произвольного пространства, функция
Ф(х, у)— выпуклая по совокупности переменных [х, у]
на QXG. Предположим также, что функция f(x), за-
данная (4.15), конечна на й.
Лемма 4.4. Функция f(x), заданная соотношениями
(4.15), выпукла на й.
Доказательство. Возьмем любые хь х2 е Й, и
пусть последовательности {уи} и {у2*} таковы, что
уik sй VZ е 1: 2, V/ге 1: оо,
Ф (хь у«) —> f (xt) = inf ф (xz, у). (4.16)
y&Q
Положим
Xa^axj+ (1 — a)x2, ya4 = ayu + (l — a)y2A, ae(0, 1].
§ 4]
ВЫПУКЛЫЕ ФУНКЦИИ
49
Поскольку функция ф (х, у) выпукла по совокупности
переменных, то
Ф (ха, yak) == Ф (axi + (1 — а) х2, ayik + (1 — а) y2k) <
< аф (хь ylk) + (1 — а) ф (х2, y2k).
Поэтому
f (ха) = inf ф (ха, у) < ф (ха, yaft) <
< аф (хь уik) + (1 — а) ф (х2, t/2J.
Отсюда и из (4.16) получаем, переходя к пределу,
f М < af (хО 4- (1 - a) f (х2) Va е [0, 1],
а это и означает, что функция f(x) выпукла по х на
Й. Я
Замечание 2. Для выпуклости функции (4.14)
не требовалась выпуклость множества G, а для выпук-
лости функции (4.15) это условие существенно. В усло-
вии леммы предполагалось, что функция ф(х, у) вы-
пукла по совокупности переменных х и у. Приводимый
ниже пример показывает, что выпуклости по каждой из
переменных х и у недостаточно для выпуклости по со-
вокупности переменных.
Пример 3. Пусть хеЕь y&Ei, <р(х,у) = ху.
Функция ф(х, у) является выпуклой по х при каждом
фиксированном у и выпуклой по у при каждом фиксиро-
ванном х. Положим xa = axi + (1 — a)x2, уа = ау\
+ (1 — а)«/2, где ае[0,1]. Для выпуклости ф(х, у) по
совокупности переменных необходимо, чтобы для всех
хъ хг, t/ь у2 и ае[0,1] выполнялось неравенство
Ф (ха, уа) < аф (Xi, г/i) + (1 — а) ф (х2, у2). (4.17)
Имеем
F (a) s ф (ха> уа) — аф (хь уй — (1 — а) ф (х2, у2) =
= (axi + (1 — а) х2) (ауг + (1 — а) у2) — ах1у1 —
— (1 — а) х2у2 = а (1 — а) (^ — у2) (х2 — х^.
Очевидно, что если ае(0,1), xi=#x2, yi^y2 и
S1§n(!/i—у2) = sign(х2 — Xj), то F(a)>0, а тогда нера-
венство (4.17) не выполняется, т. е. функция ф(х, у) не
является выпуклой по совокупности переменных.
so
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Замечание 3. Вообще говоря, операция inf не со-
храняет выпуклости, т. е. если функция <р (х, у) выпукла
по х при любом фиксированном y^G, то функция f(x),
заданная (4.15), не обязательно выпукла.
Пример 4. Пусть хе£|, <р(х, 1) = х,
Ф (х, 2) — —х. Тогда
х, х>0,
Л, Л V.
Очевидно, что функция /(х) не является выпуклой. Та-
ким образом, в то время как операция sup сохраняет
свойство выпуклости (см. п. 4), операция inf, вообще го-
воря, его не сохраняет
Задание 4.5. Пусть функция f(x) задана на Еп и непрерывно
дифференцируема там. Доказать эквивалентность следующих утвер-
ждений:
1. f^x)—выпуклая на Еп функция.
2. f (х2) — f (Х1) > (Г (xt), х2 — Xi) Vxb х2 €= Еп.
3. (f'(x0 + ag), g)—неубывающая при увеличении а функция
при любых фиксированных х0 и g.
4. Пусть f(x)—дважды непрерывно дифференцируемая на Еп
функция. Матрица вторых производных f"(x) неотрицательно опре-
делена. т. е.
(f"(x)g,g)>Q Vx,g<=En.
Здесь
/ d2f
I
Г(*) = | .......
I d*f
t V дх^дх^
d2f d2f
dx^ dx^ dx^ dx^
d2f d2f
dx^ dx<® dx^ dx^
3 а д а н и e 4.6. Пусть f(x) — непрерывно дифференцируемая на
фунодияЛДекаэать эквивалентность следующих утверждений:
1, f(x)— строго выпуклая функция.
2. f (х2) — f (xi) > (/' (xi), х2 — Xi) Vxb х2 е Еп, xi х2.
3. (f'(x + ag),g) —возрастающая при увеличении а функция а.
4. Пусть f(x)—дважды непрерывно дифференцируемая на Еп
функция. Матрица вторых производных f"(x) положительно опреде-
ленная, т. е. (f" (х) g, g) > О Vx, g Еп, g Ф О.
Задание 4.7. Доказать, что если f(x)— сильно выпуклая
дважды непрерывно дифференцируемая на Еп функция, то суще-
ствует т> 0 такое, что
(f" М g, g)^m\\g ||2 Vx, g €= En.
Задание 4.8. Доказать, что для квадратичной функции
f(x) = 2~I(Ax, x) + (b, х).
ВЫПУКЛЫЕ ФУНКЦИИ
51
§ 4]
г$е а — (п%п)-матрица, b г Еп, понятия строгой выпуклости и
сильной выпуклости совпадают (т. е. всякая сильно выпуклая функ-
ция является строго выпуклой, и наоборот).
Задание 4.9. Показать, что если непрерывная на Еп
функция и
+ + — Vxit Хг^Еп,
где у > 0 одно и то же дм всех xt, xieE„, то функция f(x)
сильно выпукла на Е„, и наоборот.
6. Квазивыпуклые функции. Пусть на выпуклом мно-
жестве SczEn определена функция f(x). Будем считать,
что она конечна.
Функция f(x) называется квазивыпуклой на S, если
f (ах 4- (1 — а) z/X max {f (х), f (у)} (4.18)
Vae=[0, 1], Vx, z/eS.
Если при as(0,1), х=£у неравенство (4.18) стро
гое, то функция f(x) называется строго квазивыпуклой.
Очевидно, что любая выпуклая функция является
квазивыпуклой.
Если функции f<(x), iel:m, квазивыпуклы на S, то
функция f(x) = max f((x) также квазивыпукла на S.
I е 1 :т
тп
Из (4.18) вытекает, что если x(gS, а(^0, 2}а<=1,
г-1
Т0 maX
/ i е 1: m
Лемма 4.5. Функция f(x) квазивыпукла на S тогда
и только тогда, когда при любом ceEt множество S)c =
= {х s S | f (х) с} выпукло.
Доказательство. Необходимость. Зафик-
сируем с е Е\. Если х е 3)с и у s S)c, то из (4.18)
f (ах + (1 — а) у)< max {f (х), f (у)} < с
Vas[0, 1],
а это означает, что множество St)c выпукло.
Достаточность. Пусть при любом ce£i мно-
жество выпукло. Возьмем любые точки х s S и у s S.
Положим со = max{f (х), f (у)}. Тогда xs^(1,
52
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
и, следовательно, -
ах + (1 — а)г/е^Со Vae[0, 1],
т. е. выполнено (4.18).
Точку х е S назовем точкой действительного локаль- Ц
ного минимума функции f(x) на S, если из того, что
х Е S и f (х) < f (х), вытекает, что£на отрезке [х, хунай-
дутся такая точка уГчто f («/) > f(x), и такое б > О, что
VxeSJx). I
Положим JI* = {хеS|f(x) = inff(y)}. x
у eS f
Следствие. Если функция f(x) квазивыпукла $
на S, то множество Л* выпукло и любая точка дейст-
вительного локального минимума функции f(x) на S
есть точка глобального минимума f(x) на S. 1
Доказательство. Выпуклость множества Л* \
вытекает из леммы 4.5.
Пусть хе S — точка действительного локального
минимума функции f(x) на S, а х^.Л*. Пусть хфЛ*.
Поскольку Л* выпукло, то f(x)</(x). Поэтому най-
дется такое as[0, 1 ], что
f(ax + (l-a)x)>f(x). (4.19) J
В силу квазивыпуклости функции f(x) намножествеЗ 1
f (ax + (1 — a) х) < max {/ (х), f (х)} = f (х), j
I
а это противоречит (4 19) j
Замечание 4. Точка х.)ЕS называется точкой ло- <
кального минимума функции f(x) на S, если существует
такое г > 0, что -
f(xY^f(x0) Vx<=(x<=S|||x —х0||<г). (
Отметим, что точка локального минимума f(x) на S
может оказаться точкой глобального максимума f(x) на
S, чего не может случиться с точкой действительного ;
локального минимума f(x) на S, если только f(x) от- J
лична от постоянной на S. • |
Лемма 4.6. Пусть функция f(x) выпукла на S, a J
функция g(x) линейна на S Тогда функция h(\) = |
= f (х) (g(x))~l квазивыпукла на множеаве £2 — {х е я
eS|£(x)>0}. I
I
§ 41
ВЫПУКЛЫЕ ФУНКЦИИ
88
Доказательство. Зафиксируем y&Q и
ае[0,1]. Очевидно, что ах + (1— а)</ЕЙ, ибо мно-
жество Й выпукло. Имеем
ft(ax + (l —а)^) =
= /(ах + (1 — a}y)/g(ax + (l — а)у)<
< [af (х) + (1 — a) f (у)] [ag (х) + (1 — a) g (у)]-1 «
- [ag W (f (x)/g (x)) + (1 - a) g (y) (f (y)/g (у))] X
X[ag(x) + (1 — a)g(y)]<
< max {f (x)/g (x), f (y)/g (y)} = max {h (x), h (y)J.
Следствие. Множество точек минимума функции
й(х) на S выпукло.
Пусть квазивыпуклая на Еп функция f(x) дифферен-
„ . df (х)
цируема по направлениям. Тогда функция квази-
выпукла по g^En. Действительно, пусть хое£п, g~
== Pgi + U —Р)#2, gi, g2^En, Ре[0,1]. Имеем
^=. lim a-4f(xo + <ig)-f(xo)]«=
= lim а-1 [f (Р (хо + agj) + (1 — Р) (х0 + ag2)) — f (х0)] <
а->4-0
< lim a-1 [max { f (х0 + ag,)» f (х0 + ag2)} — f (x0)] =
a~>0
= max ( lim a-1 [f (x0 4- agi) — f (x0)],
U-»+o
Jim a-1 [f (x0 + agz) — f (*o)l}. H
Положим
f (x) = inf {g e Ei | (и, x) e co epi f}.
Ясно, что функция f(x) выпукла на Еп и inf J W =
• с c x^Bn
e lnf I (x). Это означает, что в принципе задача нахожде-
иия минимума квазивыпуклой функции f(x) сводится к
задаче нахождения минимума выпуклой функции /(х).
54
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
1ГЛ. I
Важным примером квазивыпуклой задачи (но не вы-
пуклой) является задача наилучшей равномерной дроб-
но-линейной аппроксимации
У, xlai (t)
max а0 (0 — ---------► min,
fes[a, V* а /а xss&n
>. x{bt (0 n
i-1
где a0(t), ai(f), ie 1:n, — непрерывные на [a, 6]
функции.
§ 5. Субградиент и субдифференциал
выпуклой функции
1. Пусть функция f(x) выпукла и конечна на Еп,
Хо е Еп. Множество
df (х0) = {» еЕп| f (х) — f (х0)>(у, х — х0) Vx sЕп} (5.1)
называется субдифференциалом функции f(x) в точке хо.
Элемент сед/(х0) называется субградиентом (или обоб-
щенным градиентом) функции f(x) в точке х0.
Теорема 5.1. Множество df(x0) непусто, выпукло,
замкнуто и ограничено.
Доказательство. Введем множество
2. = {[р, х] s £„+1 |р е Еь х <= Ея, р> f (х)}.
Множество Z выпуклое, замкнутое и непустое (это над-
график функции f(x)). Точка [f(x0), х0] — граничная
точка множества Z. По следствию 2 из теоремы 1.2 су-
ществуют такие число с и вектор и, одновременно не
равные нулю, т. е.
с2 + о2 > 0, (5.2)
что _
ср + (о, х) > cf (х0) + (о. Хо) V [р, х] е Z. (5.3)
При х = хо имеем с(Р — f(xo))^O Vp^sf(xo). Отсюда
с 0. Но при у = 0 из (5.3)
(v, х — х0) > 0 Vx е Еп. (5.4)
Из (5.4) следует v = 0, что противоречит (5.2). Итак,
с > 0. Полагая в (5.3) р = f(x), получим
f (х) — f (хо) > (— c~lv, х — х0) Vx s Еп,
$ 5)
СУБДИФФЕРЕНЦИАЛ ВЫПУКЛОЙ ФУНКЦИИ
55
т е. Vo =—c~1v^df(x0). Значит, множество df(x0) не-
пусто. Выпуклость и замкнутость df(xo) очевидны. Оста-
лось показать ограниченность.
Допустим противное. Тогда существует последова-
тельность. {ук} такая, что vk<=df{xo), ||цл||->оо. Поло-
жим Xk = xo + zk, где Zk = бо1|ол1|-’1>А. Из (5.1)
f (хк) — f (х0) (vk, xk—x0)=(vk, z*)=do|| vk Ц-* +oo. (5.5)
Поскольку ||x* — x0||=||z*|| = б0> a f(x) — непрерывная
функция в силу выпуклости, то f(x) ограничена на мно-
жестве <$б0 (х0), что противоречит (5.5). Полученное про-
тиворечие и доказывает теорему.
Следствие. Отображение df(x) ограничено на лю-
бом ограниченном множестве.
Доказательство аналогично доказательству тео-
ремы.
Замечание 1. Из определения (5.1) ясно, что ото-
бражение df(x) является полунепрерывным сверху в лю-
бой точке х0 е Еп. Однако, как будет показано ниже,
оно, вообще говоря, не является полунепрерывным снизу.
Лемма 5.1. Пусть хо^Еп, f(x) — выпуклая на Еп
функция. Для любого е > 0 найдется такое 6 > 0, что
df(x)<=df(x0) + Se(ft) Vx6=Se(x0). (5.6)
Доказательство. Допустим противное. Тогда
найдутся число е0 > 0 и последовательности {хк}, {ук}
такие, что
хк->х0, vkf=df(xk\
Р (»ь df (х0)) = min || vk — v || > e0.
uedf (Xo)
Поскольку множества df(x) ограничены в совокупности,
то последовательность {vk} ограничена. Без ограничения
общности можем считать, что vk-*~vo. Из (5.7) тогда
следует, что vo^df(xo), а это противоречит полунепре-
рывности сверху отображения df(x) в точке х0.
Теорема 5.2. Справедливо соотношение
df (хо) / ч
max (о, g).
VG=df (хо)
Доказательство. Дифференцируемость f(x) по
направлениям установлена в теореме 4.2. Положим
(5.7)
66
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. 1
Л(а)= oHfffxo + ag)— f(*o)] и найдем lim h (а).
СС“^ +о
В силу (5.1) для любого и е df(x0)
f (х0 + ag) — f (x0) > (», ag).
Отсюда
555 lim Ma)> max (v> g)- (5.8)
°s a-> +0 vesdf (x,)
Введем множества
Z = да, x] €= En+i | X e En, p > f (x)},
2’={[P, x]|p = f (Xo) + a - gg °- , x = Xo + ag, a>o|.
При доказательстве теоремы 4.2 было показано, что
h(a) не возрастает при а->4~0; поэтому
lim A(a')<ft(a) Va>0, (5.9)
a'->+0
t. e.
f (xo + ag) > f (x0) + a .
Луч Z и множество Z не имеют общих точек. Действи-
тельно, в противном случае существовала бы точка
[pi, xi]&Z(]Z, т. е.
P1>f(x1), Pi = f(xo) + a1-^-,
Х1 = Хо + ад
где ai > 0. Отсюда
f (хо) + a] - g(g0-- > f (х0 + atg),
что противоречит (5.9). Образуем множество
P = Z — 3^ — {w — v — v'jv^Z, о'е ^}.
Очевидно, что Р — выпуклое множество и 0 ф Р.
По следствию 2 из теоремы отделимости существует
точка [с, a] е En+i такая, что
с2 + v2 > 0,
ср 4- (V, x)^c(f (х0) + + (V, ХО + ag) (5.10)
$ 6)
СУБДИФФЕРЕНЦИАЛ ВЫПУКЛОЙ ФУНКЦИИ
57
и при
для всех а, 0, х таких, что 0>f(x), а > 0. Как
доказательстве теоремы 5.1, устанавливаем, что
При 0 = f(x), а = 0 будет
f (х) — f (х0) > — с-1 (v, х — х0) Vx е £„,
т е. Vo = —c~rv е df (хо). Из (5.10) следует
f (х) — f (хо) > (v0> х — х0) + а ( — (t»o. g)
ПрИ х = х0 и а> 0 получим
< (t>0, g)< max (о, g).
°s v^dfM
Отсюда и из (5.8) следует утверждение теоремы.
Следствие. Пусть — — а < О и oiSdf(x0)
таково, что
(«ь g) = max (0, g)=^2L.
oedf (Хо) °S
Тогда для gi = —g будет
-^7= max (v, gi)>(vb ^)==-(ui, g)=-^^=a>0,
т. e. если в каком-то направлении функция f(x) убывает,
то в противоположном направлении она непременно*
должна возрастать.
Замечание 2. В дальнейшем будет использоваться
следующее представление выпуклой функции:
f (х) = max [f (z) + (и (z), x — z)], (5.11)
tl
где y(z)—произвольный вектор из df(z).
Докажем (5.11). Если u(z)edf(z), то
f(x)>f(z) + (t»(z), х —z).
Это неравенство справедливо для всех z&En. Поэтому
f (х) > sup [f (z) 4- (v (z), x — z)]. (5.12)
zeEn
Соотношение
sup [f (z) + (о (г), x — г)] > f (x)
S8
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА '
1ГЛ. 1
очевидно. Отсюда и из (5.12) и следует (5.11) (вместо
супремума можно написать максимум, ибо супремум до-
стигается при z — х). Ясно также, что
f (x) = max[f (z) + (v(z), х — z)], (5.13)
z<=S
где S c£„ — любое множество, содержащее х в качестве
своей внутренней точки.
Итак, выпуклая функция есть максимум линейных
функций.
Замечание 3. Из теоремы 5.1 следует, что если
f(x)—выпуклая функция, то для любого хое£п суще-
ствует такое Оо = о(х0)е Еп (возможно, даже и не
одно), что
f (х) — f (х0) > (v (хо), х — х0) Vx е £„.
Докажем, что верно и обратное. Именно, если для
любого Хо е Еп существует и (х0) s Еп такое, что выпол-
нено приведенное выше неравенство, то функция f(x)—
выпуклая.
Возьмем произвольные хь Хъ<=Еп и ае[0, 1]. Поло-
жим х0 = аХ1 + (1 — а)х2. По предположению найдется
v0 = v (х0) такое, что
f (х) — f (хо) > (оо, х — хо) Vx <= Еп.
«При х = Xi отсюда следует
f (-«О > f (х0) + (1 — а) («о. Xi — х2).
При х = х2 аналогично имеем
f (х2) > f (х0) — a (v0, Х1 — х2).
Умножая первое из последних двух неравенств на а, а
второе — на (1 — а) и складывая, получаем
f (хо) = f (axi + (1 — а) х2)< af (xi) + (1 — а) f (х2).
Это и значит в силу произвольности Xi, х2 е Еп и ае
е[0,1], что f(x) — выпуклая функция, что и требовалось
доказать. Установленное только что свойство может
быть взято в качестве определения выпуклой функции.
2. Субдифференциал суммы и функции максимума.
Пусть fi (х) и f2(x) — выпуклые на Еп функции. Функция
f(x) = A(x) + f2(x) (5.14)
тоже выпуклая.
. И СУБДИФФЕРЕНЦИАЛ ВЫПУКЛОЙ ФУНКЦИИ 69
Лемма 5.2. Имеет место соотношение
df (х) = dfi (х) + df2 (х). (5.15)
Доказательство. Для любого g е £ ,
т- = max (о, g). (5.16)
°S oeflf (х)
С другой стороны, из (5.14) ясно, что
lim a-1 [f(* + «g)“ f(x)] =
dg а->+0
•= lim а'1 (А (х 4-ag) — f1 (х)] +
(Х~^ 4-0
+ lim a-4f2(x4-ag)-A(x)]--^- + ^-. (6.17)
а->4-0 s »
Но
max (о, g), max (о, g).
vesdfj (x) uedf2 (x)
Отсюда, из (5.16) и (5.17) имеем
max (v, g) — max (v, g) + max (u, g) =
vedt (x) vsdfi (x) vedf2 (x)
= max (v, g).
oe[dfi (x)+df2 (x)]
Поскольку это равенство имеет место для всех
ge£n, а множества df(x) и dfi(x)+ df2(x) замкнутые
и выпуклые, то по следствию из леммы 2.1
df(x) = dfl(x) + df2(x),
что и требовалось доказать.
Задание 5.1. Доказать, что если f(x)—выпуклая на Е„ функ-
ция, Л > 0, fi(x) = Af(x), то
dfi(x) = Adf(x). (5.18)
Лемма 5.3. Пусть f(x) — выпуклая непрерывно диф-
ференцируемая на Еп функция. Тогда
df(x0)=‘{f'(x0)}. (5.19)
Доказательство. Зафиксируем xosEn. В лем-
ме 4.3 показано, что в этом случае
f (х) — f (х0) > (А (х0), х — х0) Vx е Еп.
Значит, 0 = /'(xo)€=df(xo).
60
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
Пусть v е df (х0), т. е.
f (х) — f (х0)>(о, х — х0) VxеЕп. (5.20)
Тогда Л(х) ^f(x) — f(x0) +(v, х0 —х)— непрерывно
дифференцируемая на Еп функция, причем из (5.20)
ft(x)> О Ух&Еп. Но поскольку h(x0)= 0, то точка х0 —
точка минимума функции h(x) на Еп. По необходимому
условию минимума й'(хо) = О, т. е. f'(x0)—f = 0, или
и = f'(x0), что и требовалось доказать. Я
Лемма 5.4. Пусть f,(x), \:N,— выпуклые
на Еп функции. Пусть также f (х) = max ft (х). Функция
isl
f(x) является выпуклой, причем
df (х) = со {dfz(x) |i е/?(х)}, (5.21)
где
R (х) = {/ е 11 f t (х) = f (x)J.
Доказательство. Правую часть в (5.21) обозна-
чим £>(х). Выпуклость функции f(x) очевидна. По тео-
реме 5.2
max (v,g). (5.22)
°S (x)
С другой стороны, при фиксированных х и g
f (X 4- ag) = f (х) + а + О (а) =
= max [f i (х) 4- а 4- ot (а)] •
где а~’о(а)-----► 0, а *oz(a) -----> 0 Vie/.
' а->+0 ‘' а->+0
При достаточно малых а > 0 будет
f (х 4- ag) = max ft (х 4- ag) =
(x)
= max Гfi (x) 4- а 4- oz (a)l =
i<=R (Xi L og J
= /(x) + amax -4-o(a)<
jeg (x) °S
СУБДИФФЕРЕНЦИАЛ ВЫПУКЛОЙ ФУНКЦИИ 61
где
а“’о (а)
а->+0
о (а) е [б (а), о (а)],
б (а) = min О/ (а), о (а) = max о, (а).
/eR (х) ieR (х)
Поэтому
#(*) „1ДТ dfi^ _
— =—max д ——
dg ieR (X)
= max max (vt, g) — max (o, g).
ieR (x) v^df^ (x) vt=D (x)
Отсюда и из (5.22) следует
max (», g)= max (v, g).
vedf (x) veD (x)
Поскольку это соотношение справедливо для всех
п, то по следствию из леммы 2.1 получаем <3/(х) =
= £)(х), что и требовалось доказать.
Пример 1. Пусть хе£,, f(х) = |х| = max{/i(x),
/2(х)}, где ft(x) = —х, fi(x) — х. Здесь 7 = 1:2. Так как
функции fi(x) и /г(х) линейные (а потому и выпуклые),
то и функция/(х) выпуклая, п—— «
ад=1,
f {!},
ад=4 {2},
I (1, 2),
Поскольку fI (x) = — 1,
x = 0,
то по формуле (5.21) и лемме 5.3
т. е.
df (х) = со {f'i (х) 11 г 7? (х)},
Для этой же функции теперь покажем, что отобра-
жение df(x) не является полунепрерывным снизу. Вы-
берем точки х0 = 0, ио = 0,5 и последовательность {х,}
такую, что х,^- — 0. Функции f\(x) и f2(x) дифферен-
цируемы. Ясно, что vo^df(Xo), так как
^(0) = со{/((0), /НО)} ~со {-1, !} = [-!, 1].
62
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Однако для выбранной последовательности {xj имеем
= = V/.
Поэтому не существует последовательности {oj,
edf(Xi), которая сходилась бы к Vo — 0,5. Это и озна-
чает, что отображение df(x) не является полунепрерыв-
ным снизу в точке Хо = 0, а тем самым оно не является
непрерывным по Какутани.
Пример 2. Пусть
х = (х<1>,
f (х) = тах| х(0 | м max ft (х),
где f/(x) = |x(/)|. Из примера 1 следует, что
— е(,
dh(x) = {
et,
со {ег, — е J,
если
если
если
х<‘> < 0,
х<» > 0,
х<« = 0,
где ei — единичные орты, ei = (0, ..., 0,1, 0, ..., 0).
По формуле (5.21)
df (х) = со {Wi | i s R (x)J,
/?(x) = {Ze 1 :n||x<«l = f(x)},
{elt если x(i)^0,
— ei, если x<« 0.
При этом df (0) = co{±e/|Ze 1 :n}. Отметим, что f(x) =
= (w, x), где w e df(x).
Задание 5.2. Доказать формулу, аналогичную (5.21), для
случая, когда
f (х) = шах <р (х, у), (5.23)
уеО
где GcE„— компакт, функция ф(х, у) непрерывна по у и выпукла
по х при любом фиксированном у ей.
3. Лемма 5.5. Выпуклая функция является липши-
цевой на любом выпуклом ограниченном множестве, т. е.
для любого ограниченного О cz.En найдется L < оо та-
кое, что
|f(x)-f(z)|<L||x-z|| VxeG, VzeG.
§ 5] СУБДИФФЕРЕНЦИАЛ выпуклой ФУНКЦИИ 63
Доказательство. По определению df(z) имеем
f(x) — f (г)>(о, х — z), где v еdf (z).
В силу следствия из теоремы 5.1 найдется такое L < оо,
|| v ||< L Vv<=df (z), Vz е G.
Отсюда
f (х) — f (z)> —L||x —z||.
Поменяв ролями z и х, имеем
f (?) — f (х) > — L || z — x ||.
Из последних двух неравенств вытекает
| f (х) — f (z) К L || х — z || Vx <= G, Vz<=G,
а это и означает, что функция f(x) является липшице-
вой на G. Лемма доказана.
Зафиксируем хое£„ и g<=En. Пусть 0(a)—произ-
вольная вектор-функция такая, что
0(a)6=£„, a-i(|0(a)|| —0.
Лемма 5.6. Если функция f(x) липшицева в окре-
стности точки х0 и дифференцируема в точке Хо по на-
правлениям, то
Дт V <х° + а£ + ® («)) — f <хо)1 =
lim a-‘[f(xo + ag)-f(xo)].
иё а-» 4-0
Доказательство. Поскольку f(x)—липшицева
функция, то
I / (х0 + ag + 0(a)) — f (х0 + ag) |<L||0(а) || = L| о (а) |,
т. е. f(xo + ag + O(a)) —f(x0 + ag) = o(a),
где о (а) = || 0 (а) ||, а-1о(а)0.
Отсюда
alimo а~> [f (х0 + ag + 0 (а)) - f (х0)] =
= lim [a-1 [f (х0 + ag) — f (х0)] + а~1о (а)] ==
-|-0
= lim а-> f/ (х0 + ag) - f (х0)] + lim а-’о (а) = ,
а-»+0 а->+0 aS
что и требуется. В
64
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Отметим, что лемма 5.6 справедлива и для любой
выпуклой функции, ибо выпуклая функция дифференци- )
руема по направлениям и липшицева в окрестности лю-
бой точки хо (см. теорему 4.2 и лемму 5.5).
Определение. Функция одной переменной ф(г)?
заданная на [О, Т], Т < оо, называется абсолютно не-
прерывной там, если для любого е > 0 найдется S > О
. такое, что
jv
Е 1Ф(^)~ Ф (**) I < »>
/г-1
как только
N
Е - t'k) < ъ,
k-i
где 0 < fM,
N— любое натуральное число.
Пусть f(x) — выпуклая на Еп функция, x(t)— непре-
рывная n-мерная вектор-функция, заданная на [О, Г] и
удовлетворяющая там условию Липшица, т. е. сущест-
вует Ki > 0 такое, что
II х (П - х (Г) IK Ki | f — t" | Vf, t" e= [О, Т].
Положим ф(/) = f(x(t)). В силу леммы 5.5, выпук-
лая функция f(x) является липшицевой по х на любом
ограниченном множестве GcEn. Функция ф(0 является
липшицевой на [0, Г], ибо
( ф (/') - ф (/) I = | f (X (t')) - f (X (/)) I <
<K||x(f)-x(/)||<KKl|f-/| V/', t s [0, T],
поскольку f(x) и x(t) является липшицевым по x и t со-
ответственно.
Нетрудно отсюда видеть, что ф(/)—абсолютно не-
прерывная на [0, Г] функция.
Как известно (см., например, [115]), тогда суще-
ствует суммируемая на [0, Т] функция ©(/) такая, что
t
ф (/) = ф (0) + ^ © (т) dx. (5.24)
о
СУБДИФФЕРЕНЦИАЛ ВЫПУКЛОЙ ФУНКЦИИ 65
Интеграл понимается в смысле Лебега. При этом почти
для всех t е [О, 7]
о) (/) — lim А-1 (ф (t + А) — ф (/)) es ip' (/), (5.25)
т. е. функция ф(/) является почти везде дифференцируе-
мой. Если вдобавок x(t) — дифференцируемая вектор-
функция, т. е. х(/ + А) = х(/)ф- Ах(0 + ®(А), где
д-i1|® (А) || 0, то из (5.24), (5.25) и лёммы 5.6 сле-
дует f
f (X (/)) = f (X (0)) + J dr. (5.26)
Лемма 5.7. Пусть Sc En — выпуклое открытое мно-
жество, и пусть fi(x) и f2(x)— выпуклые на S функции.
Если
dfi (х) = df2 (х) Vx е S,
то fi(x)—f2(x)=C, где С — постоянная величина.
Доказательство. Возьмем любое Хо е S. Из
(5.26) для произвольного хе$ будем иметь
А(*) = А(х0)+$-^Ц^^т,
о
f2(x) = f2(xo)+<j-^(^-Tg-)dT,
6
где g — х — Хо. Но
af-(X+tg) - max (a, g).
v^df2(Xo^.T;S)
Поскольку df i (x) = df2 (x) Vxe S, to
fi W — /2 W = fl (*o) — f2 (*o) s c,
ЧТО и требовалось доказать. И
Таким образом, выпуклая функция определяется
своим субдифференциальным отображением с точностью
ио постоянного слагаемого.
8 В. Ф. Демьянов, Л. В, Васильев
66
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
1
[ГЛ. I '
Лемма 5.8. Пусть f(x) — выпуклая на Еп функция. ;
Пусть также Xi =/= х2. Для того чтобы ' *
df(Xl) Л df(x2)^ 0, (5.27)
необходимо, чтобы для всех ae(0, I), и достаточно,
чтобы хотя бы для одного ае(0,1) было выполнено ра-
венство
f (ах, + (1 — а) х2) = af (хх) + (1 — а) f (х2). (5.28)
Доказательство. Необходимость. Пусть
uedf(x2). По определению субдифферен-
циала
f(z) — f(xi)>(f, Z — Xi) Vz<=En, (5.29)
f(z) — f (x2) >(o, z — x2) Vz g (5.30)
Подставляя в (5.29) z = x2( а в (5.30) z = Хь имеем
f (X2) — f (x,) = (v, x2 — Xi). (5.31)
Возьмем любое ае(0,1) и положим xa=axi +
+ (1 —a)x2. Из (5.29) и (5.31)
f M — f (xi)>(1 — a)(v, x2 - Xj) = (1 - a) (f (x2) — f (xj),
t. e.
f (xa) > af (xj) + (1 — a) f (x2). (5.32)
Но функция f(x) выпуклая, поэтому
f (xo) < af Ui) + (1 — a) f (x2) Va G [0, 1].
Отсюда и из (5.32) следует (5.28).
Достаточность. Пусть для некоторого aG(0,1)
имеет место (5.28). Возьмем любое vedf(xa). Тогда
f (z) > f (ха) + (о, z — xa) Vz G £•„.
Отсюда и из (5.28)
f (z) > af (xj) + (1 — a) f (x2) + (v, z — axi — (1 — a) x2) =
= a [f (xi) + (z — xi, y)] +
+ (1 - a) [f (x2) + (z - x2, o)] Vz g En. (5.33)
При z = xi
f (Xi)>af(x1)+ (1 — a) [f (x2) + (xi — x2, o)], |
T. e. -A
(1 — a)[f Сч) — f (x2)]>(1 — a) (xi — x2, v). |
§ б]
СУБДИФФЕРЕНЦИАЛ ВЫПУКЛОЙ ФУНКЦИИ
67
Так как 1 — а > 0, то
f U1) — f (х2) > (xt — хя, v).
Аналогично при z = х2 из (5.33) получаем
f (Х2) — f (Xj) >(х2 — хи V).
Отсюда и из предыдущего неравенства
f (xi) — f (х2) = (х, — х2, о). (5.34)
Из (5.33)
f(z) — f(xt)Xz — xi, v) +
+ (1 — a) If M — f Ui) + (xi — x2, о)] Vz e £„. (5.35)
В силу (5.34) выражение в квадратных скобках в (5.35)
равно нулю. Поэтому
f(z) — f (xj>(z — xb v) VzеЕп,
т. е.
v е df (xi). (5.36)
Аналогично из (5.33)
f(z) —f(x2)>(z —х2, v) +
+ a If (*i) — f (x2) — (xi — x2, v)] Vz <= En,
и снова из (5.34) получаем
f (z) — f (x2)>(z — x2, v) Vz s En,
t. e. oedf(x2). Отсюда и из (5.36)
df (xa) <= [df (xi) fl df (x2)].
Тем самым (5.27) установлено. Лемма доказана.
4. Зафиксируем хо&Еп. Тогда для любого g, ||g|! =
= 1, имеем
f (Хо + ag) = f (Хо) + а-^- + о (a, g), (5.37)
где
а"'° 7ТЙ °' (5-38)
Покажем, что стремление к нулю в (5.38) равно-
мерно по g, ||g||= 1. Действительно, из (5.26)
f (хо + ag) = f (хо) + $ + dx. (5.39)
3*
68 ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА [ГЛ. I
По теореме 5.2
df W / \
= max (у, g).
°S veaf (x)
Отсюда и из (5.39)
f (х0 + ag) — f (х0) < a max (v, g), (5.40)
ueB (а)
где В(а)= U df (х). Поскольку отображение df(x)
||х-х||<а
полунепрерывно сверху (см. замечание 1), то
max (о, g) max (о, g) + q (а) =
иеВ (а) vedf (х0)
“-^-+<7 (а), (5.41)
где q (а) 0, причем q (а) не зависит уже от g,
||g||= 1. В силу (5.1)
f (х0 + ag) — f (х0) >
Отсюда, из (5.40) и (5.41) получаем
0 < f (х0 + ag) — f (х0) — а < aq (a),
Так как q(a) не зависит от g, ||g|| = 1, то из (5.37)
следует равномерность соотношения (5.38) по g, ||g||= 1.
Отметим, что функция о (a, g) = о (a, g, х0) не яв-
ляется, вообще говоря, даже непрерывной по х0.
5. Пусть f(x)—вогнутая конечная на Е„ функция,
т. е.
f (axi + (1 — a) х2) > af (xi) + (1 — a) f (x2)
Vxb x2eE„, Vae[0, 1]. (5.42)
Множество
df (x0) =
= {o e En | f (x) — f (x0) < (a, x — x0) Vx <= En} (ЪАЗ)
называется супердифференЦиалом функции f(x) в точке
Хо, а элемент v^df(xo) называется суперградиентом
f(x) в точке хо- Поскольку функция Д(х) = —f(x) яв-
ляется выпуклой, то ясно, что
df (Хо) = - dfi (х0).
§ 5]
СУБДИФФЕРЕНЦИАЛ ВЫПУКЛОЙ ФУНКЦИИ
69
Поэтому для супердифференциалов и суперградиентов
справедливы утверждения, аналогичные доказанным для
выпуклых функций:
Множество df(x0) непусто, выпукло, замкнуто и огра-
ничено.
Вогнутая функция f(x) дифференцируема по любому
направлению, причем
d</*o) = min (5.44)
S uedf (Xo)
Задание 5.3. Доказать формулу, аналогичную (5.15), для
суммы вогнутых функций.
Задание 5.4. Найти супердифференциал функции
f (х) = min f. (х),
Где / = 1 : W; fi(x) — вогнутые на Еп функции.
Задание 5.5. Доказать, что для вогнутой функции f(х) и не-
прерывно дифференцируемой вектор-функции x(t) справедливо пред-
ставление
t
f (х (/)) - f (X (0)) + J dx. (5.46)
о
Интеграл в этом равенстве понимается в смысле Лебега.
Замечание 4. Смысл названия субградиент (и
субдифференциал) станет ясным, если обратить вни-
мание на то, что (см. определение (5.1)) плоскость
& (*о) = {[р, X] <= En+i | X €= Еп, fi = f (х0) + (v, х — х0)}.
где v^df(x0), проходит через точку [f(x0),x0] и лежит
«под» графиком функции f(x) (рис. 7):
В = {[0, х]|хе=£„, р = /(х)}.
70
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
Аналогично для суперградиента вогнутой функции пло-
скость S’(xo), где uedf(xo), лежит «над» графиком
функции f(x) (рис. 8) и тоже проходит через точку
1/(*о), х0].
Замечание 5. Пусть f(x) — выпуклая на Ei функ-
ция. Имеет место следующая геометрическая интерпре-
тация субдифференциала в точке х0. Через точку (f(x0),
Хо)е2?2 проведем опорную прямую к надграфику функ-
ции f(x). Пусть а — тангенс угла наклона этой прямой
к оси Ох. Тогда аед/(х0). Обратно, если aedf(x0),
то существует прямая, проходящая через точку (f(x0),
Хо), являющаяся опорной к надграфику функции /(х) и
такая, что тангенс угла ее наклона к оси Ох равен а.
§ 6. Расстояние от множества до конуса.
Условия минимума
1. Пусть на выпуклом множестве SczEn задана вы-
пуклая конечная функция /(х). В § 4 было установлено,
что функция f(x) дифференцируема по любому направ-
лению в каждой внутренней точке множества S. Пусть
й az int S — выпуклое замкнутое множество.
Лемма 6.1. Для того чтобы в точке х* е й функция
f(x) достигала наименьшего на й значения, необходимо
и достаточно, чтобы
min (6.1)
еде Г(х*)—конус возможных направлений множества й
в точке х*.
Доказательство. Необходимость. Пусть
х*е й — точка минимума f(x) на й. Допустим, что (6.1)
не выполняется. Тогда, поскольку Г(х*) = у(х*), сущест-
вует вектор
go е у (х*) э {о = % (z — х*) | А > 0, z s й),
II go 11= 1,
такой, что
af (х*)
dg»
— a < 0,
(6.2)
§ 61
УСЛОВИЯ МИНИМУМА
я
Так как t
f (X* + ago) = f (О + a + о (a),
o(a)-a-—->0 (6.3)
Ц» TV
и при достаточно малых а > 0 будет х* + ago е й, то
из (6.2) и (6.3) вытекает существование такого ао > О,
что
f (х* + ago) < f (х*), х* + ago е Q Va е (0, ао].
Это противоречит тому, что х*—точка минимума f(x)
на £2.
Достаточность. Пусть выполнено (6.1). В силу
определения df (х*) имеем для х ф х*
f(x)>f(x*)+ max (о, x-x‘) = f(x*)-Hlx-x’||^,
v е df (х*) W
где g(x) = ||x — x*||-1(x— x*). Отсюда и из (6.1)
f(x)>/(x*) + l|x-x*|| min -^->f(xf)
5бГ(Л llgll-1 °S
\fx e Q,
что и требовалось доказать. И
Следствие. Условие (6.1) эквивалентно условию
df (х*) л
min - ' лл ~ =0.
gem II g II <1
Замечание 1. Необходимым условием минимума
для любой дифференцируемой по направлениям функ-
ции является условие
int ДЩ.>0,
ge у(х*), || g Ц-I °S
где y(x*) = {g = 1(х —х*) |A > 0, хе £2}.
Задание 6.1. Доказать это утверждение.
Замечание 2. Отметим, что в (6.1) фигурирует
минимум, ибо (см. п. 4 § 4) функция max (v, g) вы,
v е df (х*)
пУкла по g. Очевидно, она конечна, и, следовательно,
непрерывна по g на Еп, и достигает минимума на лю-
бом компакте из Еп, в частности на множестве
еГ(х*)| ||g||= 1}.
72
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. 1
2. Приведем несколько лемм геометрического харак-
тера, которые будут часто использоваться в дальней-
шем.
Пусть BczEn — выпуклый компакт, Г с: Еп — выпук-
лый замкнутый конус, Г+— конус, сопряженный конусу
Г. Положим
С = В-Г+, Cfr = C\intC,
ф== min max (о, g), <р— inf sup (v, g),
|| g || = 1, ger v e В llgll- lose
p= inf || o||, d= inf || о ||.
v e Cfr v e C
Поскольку множества В и Г+ замкнутые, а В ограни-
чено, то инфимум в определении р и d достигается, т. е.
р= min || о ||, d== min||o||.
v е С^г v е С
Если d> 0, то р = d, т. е. р — расстояние от начала
координат до множества С (или, что то же самое, рас-
стояние от множества В до конуса Г+), а если d = 0, то
р есть радиус максимального шара с центром в 0, содер-
жащегося в С.
Лемма 6.2. Справедливо равенство
ф = ф. (6.4)
Доказательство. Покажем, что при любом
gfs.En
( max (о, g), если g е Г,
sup (о, g) — < о ® в (6.5)
оеС I 4-со, если g^T.
Действительно,
sup (о, g) == sup (ui + v2, g) =
0, s B, o2e |-r+]
= max (oi, g) + sup (o2, g).
01 e В о,е[-Г+]
Если g e Г = (Г+)+, to (— v2, g) > 0 Vo2 e [— Г+], а по-
скольку ЭеГ+, то sup (v, g) —0. Если же g^T,
v e [ —Г"Н
то найдется такой v2 e [— Г+], что (— v2, g) < 0, а так
$ 6]
УСЛОВИЯ МИНИМУМА
73
как Г+ — конус, то sup (v, g) = + оо. Итак,
«е[-Г+1
( 0, если g е Г,
.Л-5-Л s)=i +“>•
(6.6)
Отсюда вытекают (6.5) и (6.4), ибо (6.5) справедливо
для любого g е Еп. Лемма доказана.
Из доказательства следует, что инфимум в определе-
нии <р достигается, т. е. <р — min sup (v, g).
II g II -1 v e= C
Лемма 6.3. Условие ф 0 эквивалентно условию
d = 0-
Доказательство. Пусть ф 0. Тогда в силу
(6.4) ср > 0. Допустим, что d > 0. Пусть vq^C и
||u0||==d. Как было установлено при доказательстве тео-
ремы Г.2 (см. неравенство (1.10)),
(v, Vo)>l|folP. (6.7)
Положим go = —IIi»oll-1Uo. Из (6.7) имеем
<р = min sup (u, g)^
|| g Ц-l v e C
< sup (v, go) = —1| Vo || = — d < 0. (6.8)
о s C
Получили противоречие, т. e. из условия ф 0 вытекает
d = 0.
Предположим теперь, что d — 0. Это означает, что
С. Тогда
ф = Ф= min sup (о, g)^ min (0, g) = 0,
II g Я-los С llgll-1
т. e. из условия d = 0 следует ф 0. Лемма доказана
полностью.
Следствие. Условие ф <Z 0 эквивалентно тому, что
d>0.
Лемма 6.4. Справедливо соотношение
( — р = — d, если d> 0,
Ф= 1 р если d — о (6.9)
Доказательство. Рассмотрим сначала случай,
к°гда d > 0. Учитывая (6.8) и то, что в этом случае
74
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. 1
р = d, имеем ф — р. Установим справедливость нера-
венства противоположного знака. Пусть »оеСи ||uoll =
= d = р. Положим go = —IIПо11-1ио- Покажем, что для
любого gs Еп, llgll = 1, g #= go, будет
sup (и, g)> —1| п01| = — d. (6.10)
»cC
Действительно, пусть g<^En, ||g||= 1, g=£go- Тогда
II t»o II > (— Vo> g) > — sup (n, g).
t>e C
Из (6.4) и (6.10) заключаем, что
ф = min sup (о, g) > — р.
llgll—IvsC
Отметим, что в силу (6.5) go е Г. Итак, если d > 0, то
ф — —р = —d. Пусть теперь d = 0. Тогда по лемме 6.3
ф 0. В этом случае, как уже отмечалось, р есть ра-
диус максимального шара с центром в начале коорди-
нат, содержащегося в С, т. е. Sp(0)czC. Для любого
S > 0 такого, что Se(0) с С, будет
6= max (о, g)< sup (и, g) Vge£„, ||g||=l.
v s (®) v e= C
Отсюда б <p. В частности, p ф. Из (6.4)
р<Ф = ф. (6.11)
Установим теперь, что
S^(0)czC. (6.12)
Допустим противное. Тогда найдется вектор voeEn та-
кой, что t»o s (®), но по 0 С. Очевидно,
II По || <ф. (6.13)
По теореме отделимости существуют вектор goe£n,
||go||=l, и число а>0 такие, что (и, go) С (vo. go).— а
Упе С. Поэтому
ф = Ф= min sup (п, gX sup (п, goX(u0, go) —а.
|| g ll-l V e== C v e= C
Отсюда и из (6.13) ф ||по11—а ф — а < ф. Получили
противоречие. Итак, включение (6.12), а вместе с ним
и неравенство
Ф<Р (6.14)
УСЛОВИЯ МИНИМУМА
76
$ «1
установлены. Объединяя (6.11) и (6.14), приходим к вы-
воду, что если d == 0, то ф = р. Лемма доказана пол-
ностью.
Следствие 1. Пусть ф < 0. Тогда, если вектор
goe Г, ||goll = 1> такой, что
max (о, g0) = ф,
о е В
ТО
(о, go)=C~P VoeB,
(w, go) 1^0 Vay <= Г+. '
Замечание 3. Вектор для которого Цоо11 =
r=d, единствен. Это вытекает из того, что сильно вы-
пуклая функция (о, v) достигает минимума на любом
выпуклом замкнутом множестве в единственной точке.
Следствие 2. Если С — выпуклое замкнутое мно-
жество (не обязательно ограниченное),
ф = min sup (о, g), d — min || v ||, p=min||t>||,
||g||-1 t>eC v e C v^Cfr
то условие ф 0 эквивалентно условию d — Q,
( —p>= — d, если d > 0,
ф = < , л
( p, если d^O.
Кроме того, вектор vq&C, для которого ||t>ol|— d,
единствен.
Следствие 3. Пусть множество В состоит из един-
ственной точки Ь. Тогда, если b Г+, то
min || b — v || — max (b, g) — max (b, g).
oer+ g в [-Г], I g I—1 gst-Г]. Sg|<l
Это очевидным образом следует из (6.9), Ясно также,
что
min || b — о || ™ max (b, g) ЧЬ е Еп.
овГ+ gs [- Г], || g Ц<1
3. Геометрическая интерпретация условий минимума.
Теорема 6.1. Условие (6.1) эквивалентно условию
5/(х‘) П Г+(х*) =/= 0. (6.16)
Доказательство. Заметим, что (6.16) эквива-
лентно тому, что
О «= [<?/ (х‘) - Г+ (х‘)]. (6.17)
76
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. 1
Пусть выполнено (6.1), т. е.
min max (к, g)^0. (6.18)
gs Г (x*). II g ll-l v e df (x*)
Положим B = df(x*), Г = Г(х*). Из (6.18) тогда
ф 0. По лемме 6.3 заключаем, что d = min ||t»|| =
V е В-Г+
= 0, т. е. имеет место (6.17) и тем самым (6.16).
Пусть теперь выполнены (6.16) и (6.17), тогда d — Q
и по лемме 6.3 ф 0, что и требовалось доказать.
Следствие. Если Q — En, то условие (6.16) экви-
валентно условию
0<=<Э/(х*). (6.19)
Если же вдобавок f(x)— непрерывно дифференцируе-
мая функция, то (6.16) превращается в классическое
условие
f(x*) = ®. (6.20)
4. Направление наискорейшего спуска. Пусть хо е Q.
Положим
d(x0) — min || о —w ||- (6.21)
V е= df (Хо)
w е Г+ (х0)
Тогда существуют такие точки
и(х0) <= д/(х0) и w(x0)e
е Г+(х0), что
d(xo) = ||t»(xo) — да(х0)||. (6.22)
Вектор 1»(х0) — w (х0), удовлет-
воряющий (6.22), единствен
(см. замечание 3), хотя точки
о(х0) и пу(х0) могут быть и
неединственными (рис. 9)'.
Если tZ(xo) = O, то по теореме 6.1 точка Хо — точка
минимума функции f(x) на Q.
Рассмотрим случай d(x0)> 0. Положим
g (*о) = II w (х0) — v (х0) || 1 (w (х0) — v (х0)). (6.23)
Определение. Пусть d(xo)>0. Вектор
llgoll= 1> такой, что
df (х0) _ jnf df (х0)
dgo ge г (x,). Ilgll-l dS
go€=r,
(6.24)
§ 71
6-СУБДЙФФЕРЕНЦИАЛ
77
(6.25)
называется направлением наискорейшего спуска функ-
ции j(x) на множестве Q в точке xQ.
Теорема 6.2. Если d(x0)>0, то вектор g(x0) яв-
ляется направлением наискорейшего спуска функции
f(x) на множестве Q в точке х0, при этом
‘ dg (х0) v и/
Это направление единственно.
Доказательство. Положим В = д/(х), Г =
= Г(хо)- Тогда из (6.22), (6.23) и (6.8) имеем
sup (t», g (х0)) = —1| v (х0) — w (х0) || = — d (х0).
v е С
Поскольку d(%o) < + оо, то из (6.5) заключаем, что
§(х0)еГ, — d(x0) = max (v, g(xt)) = & . (6.26)
v e df (Xo) OS (*0/
Из (6.10) и (6.5) для всех §еГ(х0), 11^11=1, получаем
т. е. направление g’(xo)—направление наискорейшего
спуска функции f(x) на £2 в точке х0. Из (6.10) выте-
кает также и единственность направления наискорей-
шего спуска. Равенство (6.25) следует из (6.26). И
Замечание 4. Направление g(x0)e Г(х0), но мо-
жет оказаться, что g(x0)^v(x0), т. е. это направление
может выводить из множества Q.
Задание 6.2. Пусть Л* — {х е Еп | f (х) = inf f (z)}. Пока-
г е
зать, что если Л* 0 и int Л* 0, то
df (х) = {©} Vx е int Л*.
§ 7. е-субдифференциал
1. Пусть f(x)—выпуклая конечная на Еп функция.
Зафиксируем хое£,, е^Ои положим
(Хо) = {v е= Еп | f (х) — f (х0) >
>(о, х —х0) —8 Vxe£„}. (7.1)
Множество def(xo) называется е,-субдифференциалом
функции /(х) в точке х0. Элемент vedef(x0) называется
ь-субградиентом функции f(x) в точке Хо.
78
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. 1
Теорема 7.1. Для любых фиксированных хГ1еЕп
« е>0 множество dtf(x0) непусто, замкнуто, выпукло и
ограничено.
Доказательство. Поскольку df (х0)с: dtf(x0)
Уе>0, то множество dtf(x0) непустое. Замкнутость и
выпуклость очевидны из определения. Докажем ограни-
ченность. Зафиксируем 6 > 0. В силу непрерывности
функции f (х) найдется такое с < оо, что
6_1I/W-Hxo) + e]<c
VxeESe(x0)s{xe£„|||x — х0||<6). (7.2)
Возьмем любое ti6dj(xo) и точку Х\ = х0 + 6t>||v||-1.
Тогда
f (Xi) > f (х0) -г (v, Х1 — Хо) — в = / (х0) + 6|| о II — е. (7.3)
Отсюда
IIУ II<а-1 [/(*1) — f(x0) + e]<c е= (х0), (7.4)
что и требовалось доказать. В
Следствие. Отображение def: [0, оо)ХЕ„-+ЩЕп)
ограничено на любом ограниченном множестве из
[0, оо)Х-Е«.
Доказательство аналогично доказательству ог-
раниченности в теореме 7.1.
Пример 1. Пусть f(x) = 6(x— а)2, где аеЕп,
6>0 фиксированы. Найдем dtf(x). Пусть ое<?е/(х).
Представим v в виде v = f(x)-|- г = 26 (х — а) + г. По
определению
f(z)-f(x)^(v, г — х) —е VzsEn,
т. е.
6 (ж — а)2 — 6 (х — а)2>(26(х — а) + г, z — х) — a
V* Q Еп. (7.5)
Отсюда
6 (ж — х)2 — (г, z — х) + е > 0 Уж ® £п. (7.6)
Найдем минимум в левой части этого неравенства. Он
достигается при ж* » х 4- 0,56-1г. Из (7.6) при ж = ж*
имеем —0,256-1г2 + в > 0. Значит, || г || 2 -у/гб. Это ус-
ловие является необходимым и достаточным для вы-
полнения (7.6). Таким образом,
dtf (х)« {о = 26 (х - а) + г |г е Еп, || г || < 2 Уеб}. (7.7)
§71
8-СУБДИФФЕРЕНЦИАЛ
79
Задание 7.1. Построить множество def(x) для функции
х), где А — симметричная положительно определенная
п X п-матрица.
Пример 2. Пусть f (х) — (а, х) + Ь, где а<=Еп, Ь<=
e£i. Возьмем v&def(x). Тогда
— f (х)>(о, z — х) — в,
или
(а — v, z — х) — в Vz е Еп. (7.8)
Ясно, что v — а; поэтому дЁ[(х) = df(х) = {а}.
2. Зафиксируем хо <= Еп и 8 0. Положим
Be/(xo) = {fS^nl3xeEn: ve=df(x), f(x) —f(x0)>
(и, x — x0) — в}. (7.9)
Лемма 7.1. Справедливо соотношение
def (x0) = Bef (x0).
(7.10)
Доказательство мы опускаем, ибо соотноше-
ние (7.10) является частным случаем доказываемой
ниже теоремы 10.1 при
Q = Еп.
Из (7.10) вытекает
Следствие. Пусть
Хо зафиксировано. Тогда
для любых хеЕп и v е
edf(x) найдется е > 0
такое, что v&def(x0).
Замечание 1. Из
(7.10) получаем следую-
щую геометрическую ин-
терпретацию 8-субдиффе-
ренциала: субградиент v
функции f(x) в точке х
принадлежит dtf(xo), если линейная функция 1(у)'=
~(v,y— x) + f(x), задающая опорную гиперплоскость
к множеству epi f в точке х, принимает в точке Хо зна-
чение ^f(xo)—е (рис. 10).
Приведем пример, показывающий, что замыкание в
(7.10) существенно,
80
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Пример 3. Пусть xe£i. Рассмотрим функцию
I. X *, X^l.
Нетрудно проверить, что f(x) — выпуклая функция. Возь-
мем точку Хо = 2 и е — 0,5. Имеем
( 3 — 2х — 0,5, х< 1,
f«-f(2)={ л.,_06 х>, (МП
Ясно, что
f(x)-f(2)>-0,5 = (0, х-2)-0,5 Vx<=£b
Отсюда следует, что
0e<W(2).
С другой стороны,
(7.12)
{2}.
df(x) = < [-2, -1],
х= 1
Поэтому не существует такого хе£ь что Oedf(x).
Вспоминая определение множества Bef(x0) (см. (7.9)),
заключаем, что Оф B0,bf(2), хотя, конечно, 0 е Bo,sf(2).
Таким образом, знак замыкания в (7.10) убрать нельзя.
Однако, как будет сейчас показано, в некоторых слу-
чаях это можно сделать.
Лемма 7.2. Если f(x) — сильно выпуклая (см. п. 1
§4) функция, то
dJ(x0) = Btf(x0). (7.13)
Действительно, включение
Bef(x0) az dtf (х0) (7.14)
очевидно из (7.10).
Докажем справедливость противоположного включе-
ния. Пусть ysdef(xo), т. е.
f(z) — f (хо)>(t», z — хо) — s VzеЕп. (7.15)
Положим h(z) = f(z)— f(xo) + (t», xq — z). Поскольку
f(x) — сильно выпуклая функция, то и h(z)—сильно
выпуклая функция, и потому она достигает своего
s-СУБДИФФЕРЕНЦИАЛ
81
§ Л
минимального значения в некоторой точке х' е Еп:
h\x')~ min/г(г). Тогда h(x’)^h(z) Vz<=En, т. е.
zs Еп
f(x') — (v, х')^ f(z)— (о, г) или f(z) — f(x')^(v, z — х')
\/z<=En, а это и означает, что v^df(x'). Из (7.15)
(и, х0 — х') + f(х') — f(x0)^ — е, т. е. v е Bef(x0),
значит,
def(xa)cBef(x0). (7.16)
Отсюда и из (7.14) следует (7.13).
3. Пусть fi(x) и fi(x) — выпуклые конечные функ-
ции. Положим f(x)— fi(x) + [г(х). По лемме 5.2
#(х) = <?Мх) + <?/2(х). (7.17)
Для е-субдифференциалов аналогичное соотношение уже
не имеет места.
Теорема 7.2. Справедливо представление
и [V.W+y.WJ Р-18)
Bl *г82=*8
8l > О, 82 > О
Доказательство. Выражение в правой части
(7.18) обозначим 3). Включение
0ад№) (7.19)
очевидно. Возьмем y<=dj(xo). По лемме 7.1 существует
последовательность {у*} такая, что
vk^°- (7-20)
По определению Bef(x0) для каждого Vk найдется х* та-
кое, что Vk^df(xk), (Vk.Xo — Xkj + Kxnj — ^xoj^—e.
Из (7.17)
= < + (7-21)
где о' е df, (xft), v" е df2 (xft), и при этом из (7.20)
[«• хо - xk) + fi (Л) - fi (*о)] +
“Ь [(ул > хо ~ xk) “Ь ^2 (Х*) fi (^о)] е- (7.22)
Поскольку выражения в квадратных скобках в левой
части (7.22) неположительны, то (7.22) возможно лишь
82
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
тогда, когда существуют такие 8*1 0 и 8*2 0, что
8*1 8*2 = 8,
(а*’ Х0 Xk) f 1 (Х*) f 1 (Хо) ®*1»
(У* > Х0 ~ Х*) "Ь ^2 (Х*) h (хо) — 8*2’
т. е. v'k <= В^ (х0), t/''eBEfe2f2(x0). Поскольку/,(х) и
f2 (х) — конечные функции,
BEkifi (х0) cz deklfi (х0) с dsfi (хо),
Btk2f2 Uo) <= dtk2f2 (х0) <= dj2 (хо),
множества defi(xQ) и def2(xQ) ограничены, то, не теряя
общности, можем считать, что
и*-**''’ 8ftl->8'>0, eft2->8">0.
При этом в'+е" = в. Так как и'«= (х0), то
f 1 (z) (х0) (ufe, z х0) 8ftl Vz e En.
Переходя здесь к пределу при каждом фиксированном
ге£л, получим fi(z)— fi(x0)^ (v', г — х0) — г', т. е.
v' е de'f 1 (х0). Аналогично v" е de«f2 (хо). Поэтому из
(7.20) и (7.21)
и = v' + v" е [<Vi (хо) + de"f2 (х0)] с:
Значит, dgf(x0)c:S). Отсюда и из (7.19) следует
(7.18).
Следствие 1. Если fi(x), ie/ 1:N, — конечные
выпуклые функции, то
2 У,
i el 1 1
Следствие 2. Если f2(x) — линейная функция, то
def {x) = defl (x) + df2(x).
Это вытекает из того, что для линейной функции
f2(x) = (а, х) + b (см. пример 2)
dj2 (х) = df2 (х) = {а}.
Задание 7.2. Построить множество дгЦх) для функции
f (х) = (Ах, х) + (а, х),
где А — положительно определенная п X ^-матрица, а е
s n
eСУВДИФФВРЕНЦИАЛ
B3
Замечание 2. Отметим очевидное соотношение
ae[JfW]-Mrt->f(x).
Здесь f(x) — выпуклая функция, b > 0.
Замечание 3. Положим
fe (х) == sup [f (г) + (ие (г), х — z)j, (7.23)
геЕп
где v»(z)edgf(z) (для каждого z выбирается один, все
равно какой, вектор vt(z) из dtf(z)). Из определения
def (z) очевидно, что
0<fe(x)-f(x)<e ’ (7.24)
(ср. с (5.11)).
4. Найдем е-субдифференциал функции максимума.
Пусть fi(x), I э 1 :N, — выпуклые на Еп функции.
Положим
f (х) == max ft (х). (7.25)
i s I
Возьмем Xo e En, e > 0 и построим множество
^e(Xo)
V = £ alvl> ai >
i S /1
У, 1, hczl,
i s /1
У 8/ -f- 8q = 8, 8/ 0, 8q 0,
i -/i
E aJi(x0)>f (x0) —80-
i s 7i
Теорема 7.3. Для функции максимума (7.25) имеет
место представление
деЦх0)~Же(х0). (7.27)
Доказательство. Возьмем любое v s ^Се(х0).
Тогда
X Wi, I, vtsd -ifi (xa).
I e h i i
Значит,
fi(z) — fl (Xo) z — x0) — sta-1 Vz s Ea, VZ e= .
(7.28)
84
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
Умножая обе части (7.28) на ai и складывая, получим
£ a-ifdz)— £ а/Л(хо)>(У, z — х0) — £ ez (7.29)
I е h i^h i е: h
Vz е En.
Поскольку £ aJi (z) f (z), то из (7.26) и (7.29)
i 6 Л
f(z) — f (x0)>(v, z — x0)~ £ ez —e0 =
Z e /i
= (v, z~ x0) — e Vz e En.
Отсюда • v e def(x0). Итак, доказано, что ЛС8(х0)с:
czde/(x0). В силу замкнутости def(xo) отсюда вытекает,
что
^(zo)cdJW. (7.30)
Пусть теперь v edj(xo). Тогда по теореме 7.1 ое
е Bsf(x0), т. е.
v = lim wk, wk <= Bef (хо). (7.31)
По определению fief(x0) для каждого k найдется точка
xk е Еп такая, что
wk <= df (xk), (wk, xa — Xk) + f (xk) — f (-vo) > — e. (7.32)
По формуле (5.21)
df (xft) = co {df i (xk) |Z <= 7? (x*)},
где
R (Xk) --={iG= lift (xk) = f (xft)}.
Отсюда
Wk= £ OkiVkb Vkt^dfi{xk),
£ <W=1, aAZ>0,
t. e.
fi (z) — fl {xk) (Vki, z — xk) \fz e E„. (7.33)
Пусть
/^=={i<=/?(xA)|a4Z>0).
Из (7.33) для каждого i e Rk имеем
fi (z) — fi (xo) > {vkl, z — xo) +
+ [Л (xA) — fl (Xo) 4- (vkt, Xo — x*)J Vz. (7.34)
§ л
е-СУБДИФФЕРЕНЦИАЛ
Положим
Nkl в fi (Xk) - fl (xo) + (Vki’ xo ~xil) = - akKi- (7-35)
Тогда из (7.34) для каждого i е Rk получим
fi(z) ft (xQ) (yki’ Z Xo) aki&ki (7.36)
T’ e' vHe5e_ie Л(ХО). (7.37)
kt ki
Из (7.36) при z = x0 получаем
°- <7-3S)
Отсюда
E aklNkl — ~ E eM~
UzRk
= {Wk, x0 — Xk) 4- E UkifM— E <Lkifi(xo). (7.39)
Так как
E <hifi(*ii=IM<
i^Rk
E akifi W< f Oo)>
то из (7.39) и (7.32)
E akiNkt—~ E
Итак,
> (Wk, Xo - Xk) 4- f (xk) — f (Xq) > — 8.
e.
(7.40)
Из (7.38) также вытекает
ем >0. (7.41)
Умножая (7.35) на а*/ и суммируя, получаем
f (хк) — Е akift (х0) + (wk, х0 - хк) = - £ гк{,
ieRk i^Rk
т. е.
Е <*kifi (Хо) = f (хк) + (Wk, ХО — Хк) + Е 8/.
86
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. 1
Положим eM в 8 — Z еА/. Из (7.40) ясно, что
i&Rk
8М>0. (7.42)
Из (7.32)
S akifi (х0) > f (х0) — 8 4- £ 8fti -= f (х0) — ew. (7.43)
i^Rk
При этом
S &kl 4- 8*0 = S &kl 4" 8 — 2 6ki = 8.
i^Rk i&Rk
Из (7.37), (7.40), (7.43) и определения (7.26) следует
ВУй к (хо).
Отсюда и из (7.31) вытекает v е Же(хо), т. е.
де/(х0)<=^№). (7.44)
Утверждение теоремы следует из (7.30) и (7.44),
Задание 7.3. Найта вид dj(xi>) для функции /(*) =
е=тах<₽(х, у), где <р(х, у) выпукла по х при любом y^G, непре-
ysG
рывна по х и у на Еп X G, G — компактное множество.
Пример 4. Проиллюстрируем применение формулы
(7.27). Пусть, хе£b f(x) = |x|. Найдем dtf(x), где
8>0.
Так как 1х| = тах{х, —х}, то f(x)= max fz(x), где
i е 1 :2
/j(x)ex, f2(x) =—x. В примере 2 было показано, что
dtft (х) = {4-1} Ve > 0, Vx е£ь
W*) = {-1} Ve>0, Vxe£(.
В (7.26) в качестве Ц могут выступать множества:
1) />={!}; 2)Л = {2}; 3)/(-{1,2}.
Поэтому из (7.45)
Jife(x) = ^tUX2U^3. (7.46)
где
v = l, х>|х| —е0, 8ое[О, е]},
^’2=,{»е£1| у = — 1, —х>|х| —е0, 80^(0, е]},
Ха•= {о ® £i| v == а 4-(1—а)(—1)“2а—1, ае(0, 1),
ах(1 — а)х^|х| — е0, ейе[0, в]}.
5 8]
• ПРОИЗВОДНЫЕ ПО НАПРАВЛЕНИЮ
87
Если х > 0, то |х| = х и потому
( {—1}, если х^О.бв,
если х>0^
jf3 = {u<=Eil о = 2а— 1, ае(0, 1), а>1 —
8о^ [0, в]}-
Отсюда ясно, что
------------ ( [1 — &x~l, 1], если х>0,5в,
dtf (х) = Кя (х) = | j , jесли 0 х 0 5е (7.47)
Аналогично в случае х < 0 имеем |х| = — х и потому
{{1}, если х^> — 0,5в,
п \
0, если х < — 0,5в,
= fveE1|o = 2a—1, ae(0, 1),
Отсюда
{[—1, 1], если О^х^— 0,5в,
г 1 1 -и л к (7.48)
[— 1, — 1— вх-*], если х< — 0,5в. ' '
Из (-7.47) и (7.48) окончательно получаем
f [1 — вх"1, 1], если х>0,5в,
[—1, 1], если |х|<0,5в,
[—1, — 1 — вх-1], если х< —0,5в.
dj(x) =
§ 8. 8-производные по направлению. Непрерывность
8-субдифференциального отображения
1. Пусть f(x) — выпуклая конечная на Еп функция.
Зафиксируем 8^0. Величину
(8Л)
оеаеГ(х0)
будем называть ^-производной функции f(x) в точке Xq
по направлению g.
88
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Теорема 8.1. Справедливо соотношение
= inf а"1 (х0 + ag) “ f (*о) + в]. (8.2)
°S а>0
Доказательство. Положим
/i(a) = a-1[/Uo + ag) —fUo) + e], inf h (a). (8.3)
a>0
Поскольку по определению
f (х0 + ag) — f (x0) > (о, ag) — e
Vo <=<V(x0), Va>0,
TO
(v,g)^h(a) Va>0, Vo edj(xo).
Следовательно,
== max (v, g) inf h (a)ȣ25. (8.4)
aS v e d£f (x0) a>0
Из (8.4) следует, что 3) > — co.
Зафиксируем x0 и g. Введем множества
Z = {[0, х]е£„+1|хе£„, 0>f(x)},
3£ = {[0, х] еВ„+1 |х = х0 + ag,0 = f (хо) + а£> — е, а > 0}.
Покажем, что
2’nZ = 0. . (8.5)
Допустим противное, т. е. что при некоторых ось 01 и xj
окажется
₽i> f(xi), Pi = /(х0) 4-ai^> — 8,
Xi == х0 + Oig, at > 0. '
Из (8.6), в частности, имеем
f (хо) + аф — 8 > f (xi).
Поэтому
^>-^[f(X1)-/(Xo)+8] =
= [f (Хо + aig) — f (хо) 4- 8] = h (a(). (8.7)
Но (8.7) противоречит (8.3). Таким образом, (8.5) дока-
зано. Образуем множество Р = Z — 3?. Ясно, что оно вы-
S 81
в-ПРОЙЗВОДНЫЕ ПО НАПРАВЛЕНИЮ
89
пукло, причем 0 ф. Р. По следствию 2 из теоремы отде-
лимости существует такая точка [с, 1']еЕп+1, что
сеЕь геЕЛ1 с2 + о2>0, (8.8)
ср + (f> х) > с (f (х0) + а^> — в) + (о, х0 + ag)
Vp, х, a: p>f(x), а>0. (8.9)
Покажем, что с > 0. При а = 0, х = х0 из (8.9) имеем
c(₽-f(xo) + 8)>O Vp>f(x0).
Отсюда с > 0. Если бы оказалось
с = 0, (8.10)
то из (8.8) было бы
II о II >0. (8.11)
При а = 0 из (8.9) и (8.10) получаем
(о, х — х0) 0 Vx е Еп,
что возможно лишь при о = 0, а это противоречит
(8.11).
Итак, с > 0. Тогда из (8.9) при р = f(x), а = О
f (х) — f (хо) > (— с-1», х — х0) — в Vx е Еп,
т. е.
о* = (— c-’t>) е def(x0).
Из (8.9) при р = f (х)
f(x) — f (хо) > (о*, х — х0) — е + а (3> — (о*, g)).
При х = х0
3) (о*, g) + a-I8 Va > 0.
При а->4-°° получаем
< (v*> g) < max (о, g) = -^*о) .
Отсюда и из (8.4) следует {8.2). Теорема доказана.
Замечание 1. При 8 = 0 функция h(a) =
==a-1[f(xo + ag’) — f(x0)l является, как следует из до-
казательства теоремы 4.2, невозрастающей при a->-f-O;
поэтому
в Дто a-1 [f (хо + ag) — f (x0)] =
= inf a-1 [f (xq + ag) — f (x0)J,
a>0
ЧТО совпадает с (8.2) при 8 = 0.
90
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
2. Пусть f(x)—конечная выпуклая функция. Рас-
смотрим отображение def: [0, оо)Х Еп-+ЩЕ„).
Теорема 8.2. Отображение dtf(x) Н-непрерывно по
ей х на (0, ooJX-En.
Доказательство. Зафиксируем любые во > 0 и
хо&Еп. Вначале рассмотрим случай, когда f(x)—силь-
но выпуклая функция, т. е. существует такое m > 0, что
f(0,5(x + i,))<0,5|fW + fto)l - 0,25тЛх — 91Р
V.r.veE,. (8Л2)
Возьмем v е df(x), т. е.
f (z) > f (х) + (V, z - х) Vz e £„. (8.13)
Положим z = 0,5(x + у). Из (8.12) и (8.13)
0,5 (f (x) + f (y)) - 0,25m || x - у II2 > f (0,5 (x + y)) = f (z) >
>f(x) + (u, z — x) = f(x)4-0,5(v, y — x) Vye=£„.
Отсюда
f(y)>f(x) + (v, у — x) 4-0,5m || x — у II2 Vy<=En. (8.14)
(В действительности здесь можно вместо 0,5m поста-
вить m, как будет показано в § 9 (см. (9.4)).)
В теореме 8.1 установлено, что
max (v, g) = inf a-1 [f (x + ag) — f (x) + e] =s
pedJU) a>0
. sb inf h (x, g, а, г),
_L a>o
где X**4S
h (x, g, a, e) = МД (x + ag) — f (x) + e].
Заметим, что при в > 0
h(x> g> «> 8)^ + °°-
Поскольку во > 0, а f(x)—непрерывная функция, то су-
ществуют ао > 0 и 0 > 0 такие, что
inf h (х, g, а, е) = inf h (х, g, а, г) Vx е S» (хо),
a>0 a>a0 ₽
Ve:|e-8ol<₽, Vs:||g||=l.
4 8)
8-ПРОИЗВОДНЫЕ ПО НАПРАВЛЕНИЮ
91
С другой стороны, из (8.14) вытекает, что
h(x., g, + <»; поэтому существует ои > ао та-
кое, что
inf ft(x, g, a, e)== inf ft(x, g, а, в) Vx eSe(x0),
а>0 аэ<а<а1 р
Ve: |е —воКР, Vg: ||g||= 1.
Поскольку h — непрерывная по всем переменным функ-
ция, то
max (о, g)= min h (х, g, а, в) Н (х, g, в).
оеве/И а0<а<а1
Функция Н(х, g, е)® max (v, g) тоже непрерывна
о s 5gf U)
no x, в и g. Отсюда, по лемме 2.2, следует, что отобра-
жение def(x) Я-непрерывно по 8 и х в точке [е0, х0],
если /(х) — сильно выпуклая функция.
Пусть теперь /(х)—выпуклая (но не обязательно
сильно) функция. Образуем функцию #"е(х) = f(x) +
-f-S(x — хо)2 ® f (х)4- fe(x), где 6 > 0. Эта функция яв-
ляется сильно выпуклой, поэтому отображение да&~&(х)
Я-непрерывно по в и х в точке [е0, х0]. По теореме 7.2
U [М(х) + Мв(х)]. (8.15)
81+82-8
81 >0, 83>0
Поскольку (см. (7.7))
def6 (х) = {и = 2d (х — х0) + г 11| г IK 2 ,
то отсюда и из (8.15) ясно, что при 6->0
def(x))-+O, (8.16)
.где р(Л,В)— расстояние между множествами Л и В
в метрике Хаусдорфа (см. (2.1)). Поскольку отображе-
ние де^в(х) Я-непрерывно по в и х, то из (8.16) заклю-
чаем, что д8/(х) тоже Я-непрерывно по в и х в точке
[во, Хо]. Теорема доказана.
3. Определение. Пусть 8^:0. Точку хоеВя бу-
дем называть г-стационарной, если
OsdJ(xo). (8.17)
Лемма 8.1. Соотношение (8.17) эквивалентно соот-
ношению
(8 18)
92
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
где
Г = inf f(x).
xsEn
Доказательство. В силу определения def(xo)
(8.17) эквивалентно неравенству
f(x)>/(x0) +(0, х — х0) — e = f(x0) — 8 Vx &Еп,
что и требовалось доказать.
Пусть точка х0 не является е-стационарной. Тогда
(см. доказательство теоремы 6.2)
inf = min max (v, g) = max (v, g)<0.
lgl-1 ag Jgll-l »sdef(x0) aedef(x0)
При ЭТОМ
go = — II Vo 1Г1 v0, где II Vo 11= min ||v||.
oe<?g(fr0)
Направление go = g(xo) называется направлением
е-наискорейшего спуска функции f(x) в точке х0. Оно
единственно. Это доказывается так же, как доказыва-
лась единственность в теореме 6.2 (см. замечание 4 § 6).
Из (8.2) имеем
inf а-1 [/ (х0 + ago) — f (х0) + в] < 0.
а>0
Отсюда следует существование ао > 0 такого, что
f (хо + aogo) — f (х0) + в < 0,
т. е.
inf f (х0 + ago) < f (х0) — 8. (8.19)
a>0
Значит, в направлении go функция /(х) может быть
уменьшена не меньше, чем на 8.
Это свойство справедливо для любого g&En такого,
что
def (хо) п
dg
4. Пусть Ос£л — выпуклое замкнутое множество,
f(x)— выпуклая на Q функция. Было доказано (тео-
рема 6.1), что для того чтобы в точке х'ей функция
f(x) достигала своего наименьшего на Q значения, необ-
ходимо и достаточно, чтобы
<?/(х*)Г|Г+(х*) =£ 0, (8.20)
е-ПРОИЗВОДНЫЕ ПО НАПРАВЛЕНИЮ
93
§ 8]
где Г+(х*)— конус, сопряженный конусу возможных на-
правлений.
Лемма 8.2. Если х0Ей и
сУ(хо)ПГ+(хо)=/= 0, (8.21)
ТО
0<f(x0)-r^e, (8.22)
где
Г = inf f (х).
xsQ
Доказательство. Из (8.21) следует, что най-
дется такое vo^def(xo), что у0еГ+(хо), т. е.
(х — х0, t»o) О Vx е й. (8.23)
Из определения def(x0)
f (х) — / (х0) Хи, х — х0) — 8 Vx е £„. (8.24)
Отсюда и из (8.23)
f (х) — f (х0) > — 8 Vx <= £2.
Последнее неравенство эквивалентно (8.22).
5. Пусть на Еп задана линейная функция g(x), а на
множестве £2 = {х е Еп | g (х) > 0} — выпуклая функция
f(x). Положим
/г (х) = f (х) g~l (х) (здесь g~l (х) = 1/g (х)),
h* = inf h(x), JT* = {xe£2|/i(x) = ft‘}.
xsQ
Лемма 8.3. Всякая точка локального минимума
функции h(x) на £2 является точкой ее глобального ми-
нимума на £2. Множество Jt* выпукло.
Доказательство. Пусть хое £2 — точка локаль-
ного минимума функции h(x) на £2. Это означает, что
найдется такое S > 0, что 39 (х0) с: £2, ибо £2 открыто, и
/г(х)>й(х0) Vx<=S9(x0). (8.25)
Надо показать, что /г(х) й(х0) при всех хе £2.
Возьмем произвольную точку х е £2\39(хо). Пусть пря-
мая, проходящая через точки х и хо, пересекает сферу
св(^о) = {х|||х —Хо||=6) в точках xt и х2. Тогда из
(8.25) следует
f (*i)>g(*i)A(*o), f(x2)^g(x2)h(x0). (8.26)
94
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
Ясно, что найдется такое р^[0, 1], что x=Pxi4:.
+ (1—Р)Х2. В силу выпуклости функций f(x) и —g(x)
будет (см. лемму 4.1)
f (х) Pf (Xi) + (1 — Р) f (х2), g (х) < pgr (Xj) + (1 — р) g (х2).
Отсюда и из (8.26) получим f (х) Pg(xi)ft(xo)4“
+ (1 — Р)^(х2)й(х0) = (Pg(xj) + (1 — P)g(x2))ft(x0)>
gf (х) Я (хо), т. е. Я(х)^Я(хо). Поэтому, так как х —
произвольная точка из Q\S6(xo) и выполнено (8.25), то
Я(х)>Я(х0) = Я* VxeQ. (8.27)
Из (8.27) вытекает, что хо — точка глобального ми-
минимума функции й(х) на множестве £2. Так как й(х)
квазивыпукла, то множество Л* выпукло (см. п. 6 § 4).
Лемма доказана.
Возьмем Хо еЕп, v еЕп, ||о|| = 1, и е ^О.
Следствие. Любой локальный минимум функции
h(a) = a-1[f(xo + at») — f(x0)4-e] на (0, oo) является
глобальным минимумом функции h(a) на (0, оо), при-
чем множество этих минимумов выпукло.
в. Лемма 8.4. Пусть х0, g е Еп. Для того чтобы
f (хо + ag) = f (Хо) + а Va > 0, (8.28)
необходимо, чтобы для любого в > 0, и достаточно, что-
бы хотя бы для одного е > 0 было
- f . (8 29)
ag ag ' '
Доказательство. Необходимость. В силу
теоремы 8.1 из (8.28) имеем
= inf a-11/ (х° + aS) — f (xq) 4- e] =
a>0
e-^r~ + lnf а-*е = -^^-.
dS a>0 dg
Достаточность. Покажем, что если выполнено
(8.29), то множество О = {а > 01 f (х0 + ag) = f (х0) +
Ц-а ---------е} пусто. Допустим противное. Пусть
при некотором X > О
f (Хо 4- Kg) - f (х0) 4- <8-30)
5 8J
8-Производные по направлению
95
Для любого v (== df (х0)
f (х0 + «g) — f (хо) > (о, ag).
Отсюда
f (х0 + ag) — f (х0) > a max (v, g) = a . (8.31)
Из (8.30) и (8.29) имеем
= деЩо) = А-1 [f (Хо + Kg) _ f (х0) + е] >
> V1 [f (Хо) + - f (хо) + е] = 4- V*8,
что невозможно. Итак, G = 0, следовательно,
%(g*o) = Ит a"1 [f (x0 + ag) - f (x0) + в]. (8.32)
a->4-00
Предположим, что (8.28) не имеет места, т. е. нашлось
такое у > О, что
f (Хо 4- Yg) > f (хо) 4- Y • (8.33)
Для любого v е dffxo 4- yg) будет
f (хо) — / (х0 4- Yg) > ~ Y («> g).
Отсюда
Y-1 [f (хо 4- Yg) — f (хо)] < max (о, g) = ^^°±Vg) .
vedf (Xo + Yg) °"
(8.34)
Из (8.33), (8.29) и (8.34) получаем
df (x0 + yg) df (x0) def (xo)
—rg-------> ~дГ~ =—дГ' • <8-35)
Как и при выводе (8.31), при a > у получаем
f (х04- ag) — f (х04- Yg)>(a — Y) — (8.36)
Из (8.32) и (8.36)
9go) = ,im a-1 If (Хо 4-ag) — f (х0) 4-8] >
a->+oo
> lim a"1 [f (x0 4- Yg) + (a - y) Yg) - f (x0)4-el=-
a->+oo L °8 J
__ df (xp + Yg)
dg
9Й
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
что противоречит (8.35). Полученное противоречие и до-
казывает достаточность. Лемма доказана.
Следствие. Если при некоторых xs,geE„ и е > О
df(x0) _ def(x0)
dg dg
mo
inf f(x) — — <x>.
Замечание 2. Если нашлось хотя бы одно в > О,
при котором выполнено (8.29), то (8.29) справедливо
при всяком е > 0.
Лемма 8.5. Для любых хо, g^En и е > 0 найдется
такое р > 0, зависящее от х0, g и е, что
/(хо + а^)</(хо) + а-Ц^ Va<=[0, р]. (8.37)
ГТ Т7 М df (х0)
Доказательство. Если ' j-- = —, то по
лемме 8.4 р = + оо. Поскольку
def М df (xQ)
dg dg ’
то остается рассмотреть случай, когда
def (*о) _________________ df (хр) । ® /о qq\
dg — dg + °’ (8.38)
где
6 > 0. (8.39)
Допустим, что утверждение леммы не имеет места. По-
кажем, что тогда
f (Хо + ag) > f (Хо) + a Va > 0. (8.40)
Действительно, в противном случае нашлось бы такое
Ро > 0, что
Hxo + Po^XfW + Po^F21- (8-41)
Так как f(x)— выпуклая функция, то для [>е[0, 1]
/ (*о + Y₽og) = f (Y (xq + Pog) + (1 — Y) ХоХ
< Yf (Хо + Pog) + (1 — Y) f (xo)
5 8J
•-ПРОИЗВОДНЫЕ ПО НАПРАВЛЕНИЮ
9Г
Из (8.41)
f (хо + Y₽og) < f (хо) + Ypo VY «I°> Н’
т. е. нашлось р0 > 0 такое, что
f (Хо + ag)^f(x0) + а^Уг- Va S [0’ М’
что противоречит предположению. Итак, если утвержде-
ние леммы не имеет места, то должно быть выполнено
(8.40). Из (8.40) и (8.38)
a-'[f(xo + a^)-f(xo)]>^^- + d Va > 0. (8.42)
Так как (см. следствие из теоремы 4.2)
= inf a"1 [f (х0 -f- ag) — f (x0)],
a>0
то из (8.42) 6^0, что противоречит (8.39). Лемма до-
казана.
Геометрически лемма 8.6 означает, что прямая
Z = {(a, z) е Е21 г - f (х0) + а -2^-}
является либо секущей графика функции h(a)*=*
= f(xo + ag), либо совпадает с ним при а 0.
Лемма 8.6. Пусть х0, g^En, s > 0. Положим
G = {a > 01 f (хо + ag) - f (х0) + a - в },
е[ ---------> если G ограничено,
X ““ ' | л
+ оо, если и пусто или
неограничено.
Тогда
f(xo + ag)<f(xo) + a^sI Vae[0, X]. (8.43)
Доказательство. Если G #= 0 и у е G, то,
в силу выпуклости функции f (х), при а е [0, у] вы-
полняется (8.43). Поэтому, если G неограничено, то
(8.43) справедливо при любых X 0. В случае же,
4 В. Ф. Демьянов, Л. В. Васильев
68
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. 1
когда множество G ограничено, для любых у Q О полу«
чим
f(x0) + y^^-&^f(x0 + yg)^f(X<i)i-y^-.
Отсюда вытекает
,,^оГ^(х0) #(Хо)Г* ?
-------3F"J k
Обратимся теперь к случаю, когда множество 0 = 0.
Прежде всего заметим, что тогда
[/ (Хо + ag} ~ f {Хо} + 81 ”
= lim а-1 [/ (х0 + ag) — f (х0) + в]. (8.44)
а->оо
Допустим, что в рассматриваемом случае утвержде-
ние леммы неверно, т. е. для некоторого у > 0 оказа-
лось
< V’1 [/ (*о + yg)-f (Хо)]. (8.45)
Из (8.34) тогда
def (хо) < df (х0 + Yg) /о лох
dS dg \ /
Из (8.36)
f (х0 + ag) — f (х0 + Yg)>(а — у) Va> у.
Отсюда и из (8.44) и (8.45)
• ~41Хо) = lim a-1[f(xo + ag) — f(x0)4-e]>
a->4-oo
> lim a'1 [7 (x0 + Yg) + (a - Y) df (*&~ ~ f (*o) +
a->+oo L
> lim «-[a a'^+ ' +v (A^>- W )+.]-
a->4-oo L ue \ J
df (Xo + yg)_
“ dg
что противоречит (8.46). Лемма доказана.
«4
СВОЙСТВА ВЫПУКЛЫХ ФУНКЦИИ
99
§ 9. Некоторые свойства и неравенства
для выпуклых функций
1. Пусть f(x) —выпуклая конечная на Еп функция,
т. е.
f (axi + (1 — a) х2) < af (х,) + (1 — a) f (x2)
Vxb x2g=£„, Vae[0, 1]. (9,1)
В силу леммы 4.1, для любых Xi, х2е£„ и a^[0, 1]!
будет
f (ax, + (1 — a) x2) > af (xO + (1 — a) f (x2). (9.2)
Определение. Пусть XoeEn. Множество
0(Xo) = {x€= En |f (x)< f (Xo)} (9.3)
будем называть лебеговым множеством функции f(x)
в точке хо.
Очевидно, что это множество непусто, ибо Хо ей) (х0),
выпукло и замкнуто.
Возьмем любое vedf(x0). Тогда по определению
f (х) — f (х0)>(и, х — хо) Vx е Еп.
Для хей)(х0) будет (v,x — хо)^О, т. е. гиперпло-
скость Р(х0) = {х е £п| (х — Хо, и) = 0}—опорная к мно-
жеству й) (хо) в точке Хо. Положим
jr* = {xeEn|f(x)<f(z) Vze£J. (9.4)
Множество Я* является множеством точек минимума
функции /(х) на Еп. Это множество может быть и пу-
стым (см. пример 1 ниже).
Лемма 9.1. Если множество Л* непусто и ограни-
чено, то для любого х0&Еп лебегово множество й)(х0)
(см. (9.3)) является ограниченным.
Доказательство. Выше уже отмечалось, что
множество й)(х0) непустое, замкнутое и выпуклое.
Покажем, что (рис. 11) для любого е > О
ф8 s= min фе (х’) — min min > 0. (9.5)
Действительно, допустим противное. Тогда для неко-
торых в > 0, и g^En, ||g||=l, будет
(9.6)
4*
100
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
Tart как df(x*)c: def(x*) и х*еЯ*, то
def (х*) df (х*) А (Q7.
dg dg ^U- , (V-7'
Из (9.6) и (9.7) заключаем, что де^ ~ = 0.
Отсюда, в силу леммы 8.4,
f(x* + ag) = f(x*) + a-^- = f(x*) Va>0,
что противоречит ограниченности множества *#*.
Для любых х е Еп, х* е Я* и е > 0 имеем
f (х) — f (х*) max (v, х — х*)~^
>гМ**)11*~**11-8. (9.8)
Пусть в = f(x0)— f*. Тогда из (9.5) и (9.8) получаем,
что
s>(xo)c=srom
где г0 = 28'ф“1. Лемма доказана.
Следствие 1. Для того чтобы множество точек
минимума выпуклой функции было ограничено, необхо-
димо, чтобы для любого х0 Еп лебегово множество
£2)(х0) было ограничено, и достаточно, чтобы хотя бы
для одного Хо^Еп это множество было ограничено.
Необходимость только что доказана, а достаточность
очевидна.
Положим
0е = (хеДЛ(х)<Г + е}.
В силу леммы 8.1 3)е есть множество 8-стационарных
точек функции f (x) на Еп.
«я
СВОЙСТВА ВЫПУКЛЫХ ФУНКЦИЙ
км
Следствие 2. Если множество Л* непусто и огра-
ничено, то множество ограничено для любого фикси-
рованного е > 0.
Положим ae=maxp(x, Л*}, где р (х, Л} =
= min || х — и ||.
v е <М
Следствие 3. Если множество Л* непусто и огра-
ничено, то ае > 0.
Действительно, допустим противное, пусть найдутся
число b > 0 и последовательность {х*} такие, что
xAs0eft, еА-> + 0, р(хй, Л*)^Ь. Поскольку при
е ео множества £)е ограничены, то, не умаляя общно-
сти, можем считать, что х*->-х*. При этом
р(х‘, Л*)^Ь.
(9.9)
С другой стороны, xk<=s>ek, т. е. f(x*Xf* + e*. Пере-
ходя здесь к пределу, получим f(x*) = /*, что противо-
речит (9.9). Н
Следствие 4. Если множество Л* непусто и
ограничено, то для любого а > 0 найдется такое
е = е(а) > 0, что 3)t cz 8а(Л*) = {хе £п|р(х, Л*} а}.
Лемма 9.2. Если множество Л* непусто и ограни-
чено, то для любых 8^0 и г > 0 существует сег >• 0 та-
кое, что
||o||>cer>0 Vv@def(x), Xfx&Sr (£>,). (9.10)
Доказательство. Положим
Ger = {х s £„ | р (х, 0е) = г).
По следствию 2 из леммы 9.1 множество ограничено.
Тогда ограничено и множество Ger. Так как
== 0, то
fer= min /(х)>Г+е. (9.11)
хеОгг
Зафиксируе^м x* а Л* и возьмем любое х §4 Sr (^Z)e).
Пусть Xi == Xi (x) a Qzr П co {x*, x}. По лемме 4.1
/(*)-/ (Л > || х, - *• Ц -Ч| x - x* || (/ (xj - f (x’)) >
102
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
1ГЛ. 1
Так как v^def(x), то f(х‘) — f(х)>(о, х* — х) — е>
>—||и||||х* — х||—в. Отсюда и из(9.12) ||u||>||xi—х*||-1Х
Х(Л>г — f*)—||х —х’Ц-'е. Поскольку ||х — x*||>||xi— х*||,
то Holl^ll^-xT^fer-r-e). но llxj-xMKde
== diamSr(3)e). Поэтому, учитывая (9.11), имеем
|| v ||> d~x (ftr — f* — e)^cer>0
\/х ф Sr т, Vv е= dj (х). (9.13)
2. Если f(x) — строго (или сильно) выпуклая функ-
ция на замкнутом выпуклом множестве £2 с: Еп, то из
неравенства
/ (-ЧР-) < I to) + f to)] VX„ x2 e= Q, Xj Ф x2, (9.14)
заключаем, что функция f(x) достигает своего наимень-
шего на £2 значения не более чем в одной точке.
Лемма 9.3. Если f(x)— сильно выпуклая на £2
функция, то она достигает своего наименьшего значе-
ния на множестве £2 (причем в единственной точке).
Доказательство. Единственность отмечена выше.
Выберем любую точку хо<=£2. Из (8.14) вытекает, что
для любого v е df(x0) будет
3) (-«о)s {х е £2 | f (х) < f (хо)} с:
с {хе=£2|0> —IIц||-||х —x0||4-m||x —Xolf).
Отсюда заключаем, что S)(x0)—компакт. Так как функ-
ция f(x) непрерывна, то она достигает своей нижней
грани на 0(хо). В
Замечание 1. Для строго выпуклых функций ин-
фимум может и не достигаться. Так, функция f(x) — е~х,
заданная на Eit является строго выпуклой и inf f(x)=
= 0, однако этот инфимум не достигается.
3. Получим некоторые оценки для сильно выпуклых
функций. Пусть f(x) — сильно выпуклая на Еп функция
с константой сильной выпуклости пг > 0, т. е.
f (axi 4- (1 — a) х2)
<a/(xj) +(1 — a)f (х2) — a(l — а)/и || Xi — х2 II2 (9.15)
Vxb x2s£„, Vae[0, 1].
$ я)
СВОЙСТВА ВЫПУКЛЫХ ФУНКЦИЙ
103
Лемма 9.4. Если f(x)— сильно выпуклая на Еп
функция с константой сильной выпуклости пг>0, то
для произвольных
х, х0^Еп, v (х0) s def (х0), в>0, ае(0, 1]
справедливо неравенство
f(x)-f(x0)>
>(»(хо), х —х0) —ва-1+ (1 —а)/п||х0 —xll2. (9.16)
Доказательство. Пусть х0е Еп и а е (0, 1 ]
фиксированы. Возьмем любое у(х0)е def(x0). По опре-
делению е-субградиента
/(«)>/ (х0) + (о (х0), z — х0) — в Vz е Еп.
Положив z = ax + (l — a)x0, отсюда и из (9.15) имеем
af (х) + (1 — a) f (х0) — a (1 — а) /п || х0 — х II2 >
>f (<хх + (1 —а)х0) sf(z) = f (х0 +а (х — х0))>
> f (х0) + а (у (х0), х — Хо) — 8.
Неравенство (9.16) теперь очевидно.
Следствие 1. Для любых хаеЕп и v(xo)sdf(xo)
справедливо неравенство
f(x) — f (хо) > (о (х0), х — х0) + /п || х — х0 IP Vx е Еп. (9.17)
Справедливость (9.17) следует из (9.16), если поло-
жить там в = 0 и перейти к пределу при а-> -|- 0.
Следствие 2. Для любых xi, Xt^En, s
sdf(xi), vz&df(Xi) справедливо неравенство
(t»i — t>2. Хх — x2) > 2/n || Xi — x21|2. (9.18)
Доказательство. Для любых Xi, x2sEn в силу
(9.17)
f (x) — f(xl)>(ob x — Xi) + mllx — Xi IF Vxe£rt,
f(x) — f(x2)>(o2, x — x2) + m||x — xjp Vxs£„,
где 0! e df(xi), o2 e df (x2).
Подставляя в первое неравенство х == х2> а во вто-
рое х = xi и складывая получившиеся неравенства, по-
лучим (9.18).
104 ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА {ГЛ. I Я
Из (9.18) ясно, что <
ll^i ~ V211>2т||Х1 —х21|.
Отсюда, в частности, вытекает, что если f(x) — сильно
выпуклая функция, то любой вектор v е Еп может быть
ее субградиентом не более чем для одной точки.
Задание 9.1. Доказать, что этот результат справедлив и для
строго выпуклых функций, т. е. если f (х) — строго выпуклая функ-
ция, то любой вектор может быть ее субградиентом не более чем
для одной точки.
Следствие 3. Пусть х #= х0. Максимум по а вы-
ражения___в правой части (9.16) достигается при
ct = V8m-1llx—хоИ-1, « тогда, если ||х — xolls> Ve/n-1,
то из (9.16)
f(x) — f (хь) > __
> (v (х0), х — Хо) + m || х — Хо ||2 — 2 Ve/n || х — Хо II2.
Таким образом, для сильно выпуклой функции вы-
полнено (9.17). Оказывается, справедливо и обратное
утверждение.
Лемма 9.5 Пусть на Еп задана функция f(x). Если
для любого хо е Еп найдется о (х0) е Еп такое, что имеет
место (9.17), то функция f(x) является сильно выпуклой
на Еп с константой сильной выпуклости т.
Доказательство. Возьмем произвольные Х|,
х2 е Еп и ае[0,1]. Положим x0 = axi-|-(l — a)x2. По
предположению найдется о(х0)е£п, для которого выпол-
нено (9.17). При х = X] из (9.17) следует
f (xj> f (х0) + (1 — а) (ц (х0), Xi — х2) + т (1 —а)21| Xi —х2 II2.
(9.19)
Полагая теперь х = х2, аналогично имеем
f (xz) f (х0) — а (о (хо), Xi — х2) 4- та21| Xi — х2 II2. (9.20)
Умножая (9.19) на а, а (9.20) на (1—а) и складывая,
получим
f (хо) = f (axi + (1 — a) х2)<
<af(xi) + (1 — a)f(x2) — a(l — a) m || Xi — x2 If.
J 9] СВОЙСТВА ВЫПУКЛЫХ ФУНКЦИИ 105
Поскольку здесь хь хз е Еп и ос <= [0, 1 ] произвольные,
то, сравнивая с (9.15), заключаем, что f(x)— сильно вы-
пуклая функция с константой сильной выпуклости т.
Лемма доказана.
Замечание 2. Если для некоторых х0Еп и
v(xo)^En имеет место (9.17), то ясно, что v(xo)e
е df(xo).
4. Пусть f(x) — сильно выпуклая функция с констан-
той сильной выпуклости т > 0. Положим f* — inf f (х).
х s
Как установлено в лемме 9.3, значение f* достигается
(причем в единственной точке), т. е. существует точка
х*^Еп такая, что = Возьмем любые хоеЕл,
8>0 и положим
<4 = de (хо) m min (| v || = || ve (х0) ||.
osV(xo)
Лемма 9.6. Справедливы неравенства
0 < / (*0) “ Г < е + (d2e + 4de V^) (4m)-1, (9.21)
||x0 — x*IK(de + 2 д/ёйг) (2/n)-1. (9.22)
Доказательство. Установим вначале справедли-
вость неравенства (9.21). При de = 0 оно очевидно из
леммы 8.1. Пусть dt > 0. Возьмем v edef(x0). Из (9.16)
для всех х <= Еп и 0 е (0, 1] будет
f(x)>f(x0) +
+ max (о, х —Хо) —80“*+ (1 — p)m||xo—xlp^s
oeiM(xo)
>||х —хо|| min max (v, в} — 80-1 + (1 — 0)/n||x—Xoll2.
Il g Ц-1 Osdef (х0)
По следствию 2 из леммы 6.4
— min max (о, в).
II g Ц-1 v е 9&f (Жо)
Поэтому
f(x) -/(Хо)> - d8||x- ХО|| + (1 - 0)т||х-ХоН2-80-*
Vxe£„, V0s(O, 1].
106
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Отсюда
f = inf f(x)>
Еп
>/(xo)+ inf [(1 — P)m||x —XqH2 —de||x —x0||] —8P~‘ =
*sBn
«= f (x0) 4- inf [(1 - ₽) ma2 - dea] - e0-1 Vp €= (0, 1].
a> 0
(9.23)
Инфимум здесь достигается при a = 2-1/n"‘1(l — P)_1de
и равен — d2[4m(l — р)]-1. Отсюда и из (9.23)
0 < f (х0) - Г < ер’1 + dl [4т (1 - р)]"1. (9.24)
Это неравенство справедливо при всех ре (0,1]. Най-
дем минимум функции
/г(р) = ер"1 + d2[4m(l - ₽)]’*.
Так как й'(Р) = [dip2 — 4/пв(1 — P)2][4mp2(l — Р)2] \ то
h' (Р) = 0 при
Pi = 2 Vme(de + 2 тъ) ', р2 = 2 д/тв(2д/те —de)- .
Поскольку Рг^(0,1), то в (0,1) существует единствен-
ная точка Pi, в которой /г(Р) достигает экстремума. Не-
трудно проверить, что /г"(Р1) > 0, т. е. Pi — точка мини-
мума функции /г(Р). При этом, как легко подсчитать,
h (Pi) = (4m) “1 (d8 + 2 Vem)2 = 8 + (4m) “1 (d2 4- 4dg Ve/n).
Отсюда и из (9.24) получаем (9.21).
Осталось доказать (9.22). Из (9.17) для точки ми-
нимума х*
f (хо) — f (X*)>(о, х — х*)4- т||хо — х*|р Vv еdf (х*).
Поскольку х* — точка минимума f(x) на Е„, то по необ-
ходимому и достаточному условию минимума Oedf(x*).
Поэтому
f (х0) — f (х*) > т || х0 — х* Ц2.
Отсюда и из (9.21) сразу получаем (9.22). Лемма дока-
зан$.
§ 91
СВОЙСТВА ВЫПУКЛЫХ ФУНКЦИЙ
107
Следствие. При г = 0 имеем
0 < f (х0) - Г < (4m)"‘ d\ || х0 - х* || <(2/n)"1 dt
где d = dQ = d0(x0) = min || v ||.
V s df (Xo)
При de — 0 (т. e. если Xo — е-стационарная точка)'
из (9.21) и (9.22) получаем
О</(*о) —Г<е, ||х0 — х*||< Ует“*.
Таким образом, для сильно выпуклых функций можно
оценить, насколько значение функции в точке хо отли-
чается от минимального (неравенство (9.21)), а также
расстояние от точки хо до точки минимума (неравен-
ство (9.22)).
5. Пусть QaEn— выпуклый компакт, f(x) — выпук-
лая на Еп функция.
Лемма 9.7. Если функция f(x) не является постоян-
ной на й, то она достигает наибольшего на й значения
только на границе множества й.
Доказательство. Предположим противное,
пусть х0 е int й,
f (хо) > f (х) Vx е й, (9.25)
т. е. х0 — точка максимума f(x) на й. Так как хоет1й,
то существует г>0 такое, что 5г(х0)с=Й. Возьмем лю-
бое ХЕЙ, X ф Хо. Положим
х = Хо — г (х — Хо) || х — Хо 1Г *• (9.26)
Так как хе5,(х0), то хей, и поэтому из (9.25)
f(x)<f(x0). (9.27)
С другой стороны, для любого v е df (хо)
f (х) > f (хо) + (», X — Хо). (9.28)
Поэтому из (9.27) и (9.28) (о, х — хо)^0. Отсюда и из
(9.26)
(о, х —х0)>0. (9.29)
Так как по определению субградиента f(x)>f(x0) +
+ (о, х — хо), то из (9.29) f(x)^f(x0). Отсюда и из
(9.25) следует
f(x) = /(x0).
(9.30)
108
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. 1
Поскольку %— произвольная точка й, то из (9.30) по-
лучаем
f (х) = f (х0) Vx е й,
что противоречит условию леммы. Лемма доказана.
Замечание 3. Из доказательства леммы очевидно,
что если множество Й не является ограниченным и функ-
ция f(x) отлична от постоянной, то ее наибольшее зна-
чение на й может достигаться разве лишь на границе
множества й (но может и не достигаться, если функция
/(х) не является ограниченной на й).
Лемма 9.8. Если функция f(x) сильно выпукла на
Еп, то для любого veEn найдется единственная точка
х^.Еп такая, что v е df (х).
Доказательство. Возьмем произвольное vo s Еп.
Так как функция f(x) сильно выпукла на Еп, то и функ-
ция й(х) = /(х) — (по, х) тоже сильно выпукла, как сум-
ма сильно выпуклой и линейной функций. По лемме 9.3
существует единственная точка хо е Еп, в которой функ-
ция й(х) достигает своего наименьшего на Еп значения.
По условию минимума функции й(х) на Еп будет Ое
^dh(xo). Но dh(x0) = df(х0)—{»о} (так как й(х) есть
сумма двух выпуклых функций, то по лемме 5.2 dh (х0) =
= df(x0) +dF(xo), где F(x0) — — (о0, х)). Отсюда о0е
ед/(хо). Таким образом, для любого v0^En нашлась
точка хо&Еп такая, что vo^df(xo). Единственность точ-
ки хо вытекает из следствия 2 леммы 9.4.
Замечание 4. Условие сильной выпуклости функ-
ции /(х) в лемме 9.8 существенно, что видно из следую-
щего примера.
Пример 1. Пусть xe£i, f(x)==e*. Функция f(x)
строго выпукла и дифференцируема. Поэтому
df (х) = {/' (х)} Vx®£].
Очевидно, что не существует точки х0®£1 такой, что
f'(х0) = еХо = О, т. е. для уо = О нельзя найти соответ-
ствующей точки Xq.
Задание 9.2. Пусть f(x)—строго выпуклая на Е„ функция.
Доказать, что верна следующая
Лемма 9.9. Если f(x) строго выпукла на Еп, то для
любых х0^Еп и v(х0)df (х0) cnpaвedлuвo неравенство
f (*) — f (хо) > {v (Хо), х — Хо) Vx ® Еп, х=7^Хо. (9.31)
УСЛОВНЫЙ 8-СУБДИФФЕРЕНЦИАЛ
109
| 10!
Обратно, если для любого xQ^En найдется v(xo)&En
такое, что имеет место (9.31), то функция f(x) является
строго выпуклой.
§ 10. Условный 8-субдифференциал
1. Определение и свойства условного субдиффе-
ренциала и условного 8-субдифференциала. Пусть
Qczfn — выпуклое множество. Через Г (я) обозначим
конус возможных направлений множества й в точке я@
s Й, являющийся замыканием множества
у (я) = {ц = X (z — я) | X > 0, гей).
Пусть на множестве Й определена выпуклая конечная
функция /(я). Положим для фиксированных яоей и
0
d*f (я0) == {и Еп | f (z) — f (я0) >(v, з — я0) Vz ® й),
dff (я0) = {v е Еп | f (z) — f (я0)>(и, z — я0) — в Vz е й}.
Множества dQf (я0) и def(x0) назовем соответственно
условным субдифференциалом и условным ъ-субдиффе-
ренциалом функции f(x) в точке я0ЕЙ по множеству й.
Элемент v^dQf(x0) назовем условным субградиен-
том, а элемент v е dff (яо) — условным г-субградиентом
функции /(я) в точке яоей по множеству й.
Если функция f(x) определена и выпукла на Еп, то
множества dEnf (я0) = df (я0) и df nf (я0) s dj (я0), как
обычно, называются cyбduффepeнцuaлoм и ъ-субдиффе-
ренциалом функции f(x) в точке яо по Еп.
Очевидно, что если Qi zo й2, то при е 0 будет
d°‘f(x)<=$3f(x) VxeQ2. (10.1)
Отметим еще одно свойство условного е-субдиффе-
ренциала: если й— замыкание выпуклого множества й
и /(я) непрерывна на й, то
dff(x) = dlf(x) VxeQ, е>0.
Лемма 10.1. Пусть функция f(x) конечна и выпукла
Ёп. Если Яо ш int Й, то бля любого фиксированного
по
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
8^0 множество d®f (х0) непусто, выпукло, замкнуто и
ограничено.
Доказательство. Непустота, выпуклость и замк-
нутость множества d®f (х0) очевидны. Доказательство
ограниченности аналогично доказательству ограничен-
ности def(x0) в теореме 7.1. И
Лемма 10.2. Если функция f(x) конечна и выпукла
на Еп, то
dQf(x0) = df(x0)-r+(x0), (10.2)
где Г+(х0)— конус, сопряженный конусу возможных на-
правлений множества Й в точке х0 е Й.
Доказательство. Правую часть в (10.2) обозна-
чим S). Пусть о = + t/г, где t>i @ df(xo), — о2 е Г+(хо).
Тогда с и
f (х) — f (Х0) > (vi, х — х0) Vx е Еп,
(— о2, х — х0) 0 Vx е й.
Складывая эти неравенства, получаем
f(x) — f (х0) > (vi + v2, х — Хо) Vx е й.
Значит, v в daf (Хо), т. е.
0сд°/(хо). (10.3)
Пусть теперь о ® dQf (х0). Тогда
f (х) — f (хо)>(с, х — хо) VxsQ. (Ю.4)
Положим /г(х) = /(х)—f(x0) — (v, х — хо). Очевидно,что
функция /г(х) выпукла на й, а из (10.4) следует, что
А(х)> 0 для всех хе й, причем й(хо) = 0. Значит, хо —
точка минимума функции й(х) на множестве й. По не-
обходимому и достаточному условию минимума функции
/г(х) на й будет (см. теорему 6.1)
dh (хо) П Г+ (х0) 0.
Но dh(x0) = df(хо) — {о}. Поэтому найдутся t>oedf(xo)
и да0еГ+(х0) такие, что t>o — v = Wo, т. е. v = vo — Wo-
Отсюда
dQf (Xo) a: £>. (10.5)
Из (10.3) и (10.5) следует (10.2). Лемма доказана.
$ 10]
условный «-субдифференциал
111
Следствие 1. Если xoeintQ, а функция f{x) ко-
нечна и выпукла на Еп, то
dQf (x0) = df (х0). (10.6)
Действительно, для х0 г int Q имеем
Г(х0) = £„, Г+ (хо) = {0}.
Таким образом, условный субдифференциал функции
f(x) во внутренних точках множества Q совпадает с суб-
дифференциалом функции
f(x). Положим
s= Si (х0)!=
= {х |||х — xolKd}, б>0.
Тогда по доказанному выше
df(xa) = d 6f(xQ).
Отсюда ясно, что субдиффе- ___ :__
ренциал функции f{x) опреде- °°а
ляетсялишь локальными свой- Рис j2.
ствами функции f(x).
Замечание 1. Вообще говоря, при в>0 может
оказаться
(х0) т^= d&f (xq).
Это видно из следующего примера. Пусть f(x) =
= (а, х)+ Ь, где а, хе Еп, Ъ е Е\. В примере 2 § 7было
показано, что в этом случае (рис. 12)
<3ef(x) = ^(x) = {a) Vxe£„, Ve > 0.
Пусть Q = {zeE„ |||z —XolK 1). Покажем, что
(x0) = {v = a + r |re£n, ||r ||<e}. (10.7)
По определению def (x0) для любого v e d®f (x0) будет
f(z) — f (x0) = (a, z — x0)>(o, z — Xo) — e VzeQ,
T. e.
(t> — a, z — Xq) e Vz e Q.
(10.8)
112 ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА (ГЛ. I
Но
max (о — а, г — х0) = (о — a, г0 — х0), 1
z е Q
где zQ — Хо = || v — а ||-1 (о — а). Отсюда и из (10.8) имеем
max (о — а, z — хо) = || и — а ||=С 8 Vo е де/(хо).
z е Q
Из последнего неравенства и следует (10.7).
Таким образом, при в > 0 для линейной функции
8-субдифференциал и условный 8-субдифференциал мо-
гут не совпадать.
Следствие 2. Если функция f(x) конечна и вы-
пукла на Еп, то из формулы (10.2) ясно, что
^) = дХ^М,
где
^q(xo) = {x = Xo+ v |о ® Г (хо)}, Г (хо) = у(х0),
у (х0) = {о = % (х — Хо) IX >0, х е й}
(г. е. Ж а (х0) — это конус возможных направлений мно-
жества Й в точке Хо, перенесенный в точку х0).
Следствие 3. Если geГ(х0), то
—ъ(*о) = ma^ (v> S)= sup (v, g) = max (v, g).
° v e df (Xi) о e daf (Xo) о s da f (Xo)
Если же цфГ (x0), to sup (v, g) = + oo.
о e dfy (xi)
Действительно, пусть v e da/(x0), g e Г(х0). Тогда
по лемме 10.2 v = vi — w, где t>ied/(x0), weT+(xo).
Так как (w, g) 0 для всех gs Г(х0), то
(V, g) = (vi, g)—(w, g) < (vi, g).
Отсюда
sup (v, g) max (u, g).
v e dQf (Xo) vedf (Xo)
Поскольку dQf(xo)ZD df(xo), то справедливо неравенство
max (a, g)< sup (fl, g).
oGdf(Xo) oeaQf(vo)
Таким образом,
sup (fl, g)= max (a, g).
p.G dQf (Xo) V в df (Xo)
$ 10] УСЛОВНЫЙ s-СУБДИФФЕРЕНЦИАЛ 113
В силу компактности множества df(x0) супремум в по-
следнем равенстве достигается, а следовательно, дости-
гается и супремум по множеству dQf (х0) •
Пусть теперь #9*-Г(х0). Тогда найдется шо®Г+(хо)
такое, что (g, Wq) = —а <. 0. Возьмем любое t»o s df(xo).
По лемме 10.2 для произвольного X > 0 будет
vK “ [vo — Mi] е dQf (х0).
Но
(fк> 8) = (Ро, 8) + Ьа ——> + оо.
А-> -Г°О
Следствие 3 доказано полностью.
Следствие 4. Если функции fi(x) и f2(x) конечны
и выпуклы на Еп, точка хоей, то для функции f(x)**
= fi (*) + h (х) справедливо соотношение
0Qf (х0) = dQf, (хо) + daf2 (хо). (10.9)
Действительно, поскольку (см. лемму 5.2)
df (хо) = df 1 (х0) + df2 (х0),
то получаем
daf (Хо) = df (Хо) - г+ (Хо) = дк (х0) + df2 (х0) - г+ (Хо) -
= [<?fi (хо) - Г+ (хо)] + [<% (хо) - Г+ (х0)] =
==^Л(хо) + д%(хо).
Здесь использовано равенство (см. задание 3.6)
Г+ (хо) = Г+ (хо) + Г+ (хо),
которое справедливо, так как Г+(х0)—выпуклый ко-
нус.
Замечание 2. Из доказательства формулы (10.9)
ясно, что справедливы соотношения
daf (хо) = dQft (хо) + df2 (хо) = dfi (хо) + dQf2 (хо), (10.10)
т.е. для одной из функций f i (х) или f2(x) можно рас-
сматривать субдифференциал по Еп.
2. Представление условного 8-субдифференциала.
Пусть в > О фиксировано. Положим для х0 е Q
Ве/ (х0) = (о <= Еп I Эх г Q; os dQf (х), f (х) - f (х0) >
> (и, х — хо) — ej.
114
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. 1
Теорема 10.1. Имеет место соотношение
д^(х0) = В^(х0). (10.11)
Доказательство. Возьмем v е Bgf (х0). Тогда
v — lim Vk, Vk е Bgf (x0) Vk.
В силу определения множества B®f (xq) найдутся xjgQ
такие, что Vk е dQf (x*),
f (xk) — f (Xq) > (14, Xk — xo) — 8.
Поскольку Vk^cFftXk), TO
f(z) — f (xk) > (vk, z — Xk) Vz e= □.
Складывая два последних неравенства, имеем
f (z) — f (x0) > (vk, z — Xo) — e Vz s Q.
Переходя здесь к пределу по k при любом фиксирован-
ном zefi, получаем
f (z) — f (хо) (о, z — хо) — в Vz е Q.
Значит, Следовательно,
(10-12)
Пусть теперь о е d~f (х0), т. е.
f (z) — f (хо)^(и, z — Хо) — 8 Vz е Q. (10.13)
Положим h(z) = f(z)—f(xQ) — (v, z — xq). Тогда из
(10.13)
ft(z)>-8 VzeQ. (10.14)
Зафиксируем любое б > 0 и построим функцию
Лб (z) = h (z) + б max | z(i) — x^Z) | at h (z) + i>q (z),
где z=(z(I)...z(n)), x0=(x*)1), .... x(on)), q (z)=max |z(,)—x^>|.
Функции h(z), h6(z), q(z) — выпуклые на Q. Из (10.14)
следует, что Ae(z)-> + оо при ||z||-»-4- оо. Поэтому при
любом фиксированном б > 0 функция h6 (z) достигает
Сиоего наименьшего на Q значения в некоторой точке ze.
УСЛОВНЫЙ е-СУБДИФФЕРЕНЦИАЛ
118
$ 10]
По необходимому и достаточному условию минимума
функции Ae(z) на множестве £2 будет (см. теорему 6.1)
dh6(z&) П Г+(2в)#= 0. (10.15)
Но
dh6(z) = dh(z) + t>dq(z), (10.16)
где (см. пример 2 § 5)
dh (z) = df (z) — {u}, dq (z) = co {w, | i e (z)},
R (z) = {i <= 1 : n 11 z<z> — x</> | = q (z)},
' co {e/( — ej, если z(l> — x^ =* 0,
Wl = . ep если zW~ xo°>0,
— е{, если z(i) — x^* < 0,
ei — единичные орты. Из (10.15) и (10.16) следует су-
ществование w6 е dq(z&) такого, что
= (v - бдав) е= (z6) - Г+ (ze)J = (z6). (10.17)
* Ясно, что
ue->v при б->0. (10.18)
Из (10.14) следует h6(z6) :> h(z6) > — в. Отсюда
f(z6) — f(x0) + (v — bw6, х0 —ze)> —в, (10.19)
так как (см. пример 2 § 5)
max | z(i) - х<о | = (w6, z6 - х0).
Из (10.17) и (10.19) ясно, что v6 е Bff (х0), а из (10.18)
вытекает, что v е Bff (х0). Таким образом,
(10.20)
Из (10.12) и (10.20) получаем (10.11). Теорема дока-
зана.
В лемме 7.2 показано, что в случае сильно выпуклой
функции f(x) справедливо соотношение
dj (х0) = BJ (х0).
Аналогично показывается, что если функция f (x) сильно
выпукла на множестве Й, то
W- »№)
lie
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Задание 10.1. Доказать, что если функция f(x) конечна и
выпукла на Еп, а множество Й есть гиперплоскость в Еп, то спра-
ведливо равенство
(*о) = <*0> - г+ (*о) Ve > 0. (10.21)
3. Условный е-субдифференциал суммы функций.
Пусть функции fi(x) и f2(x) выпуклы на Еп. Положим
f(x) = /i(x)+ fz(x). Возьмем хоей.
Теорема 10.2. Справедливо соотношение
ВД- и py.w+^^wi- о»-22)
81+82—8
81>0, 82>0
Доказательство. Правую часть в (10.22) обо-
значим SD. Включение
0с<$(хо) (10.23)
очевидно. Докажем противоположное включение. Пусть
v ^d^f (х0). По теореме 10.1 существует последователь-
ность {Vk} такая, что
^sB^(xo), (10-24'
т. е. для каждого Vk найдется такое х* е Q, что
vk <= dQf (xfe), f (хк) — f (х0) + (vk, х0 — xk) > — е.
Из (10.10) следует, что о* =• к* + v'k, где
v'k е dfi (xfe), v'k <s дй/2 (xfe). (10.25)
Поэтому из (10.24) имеем
[(Vk, хо — хк) + fi (xk) — fi (xo)] +
+ [{v'k, Xo — Xk) + f2 {Xk) — fz (xo)] > — 8. (10.26)
Выражения в квадратных скобках в (10.26) неположи-
тельны. Поэтому неравенство (10.26) возможно лишь
тогда, когда существуют e*i 0, е*2 0 такие, что
8fel + е*2 8 и
(v'k, Хо — Xk) + fl (Xk) — fl (Xo) — e*l,
(v'k, XO — Xk) 4- fz (Xk) — f2 (Xo) > — 8».
Отсюда и из (10.25) вытекает
<4 S (х0), v'^ е B^kif2 (х0).
5 10] УСЛОВНЫЙ е-СУВДИФФЕРЕНЦИАЛ ttf
Последовательность (о*) ограничена, так как
BRklfi (х0) <= deklft (х0) с defi (х0),
а множество defi (х0) — компакт в Еп. Из (10.24) сле-
дует, что ограничена и последовательность {р*}. Без
ограничения общности можно считать, что
ра-*р', Рй-*р", 8fti->е' >0, вм-*в">0,
при этом в' + е" в. Поскольку v'k ® deklfi (хо), а р£ е
е^24(хо)> то
h (х) — fl (Хо) > (Ofe, х — Хо) — 8fei Vx <= Еп,
fi (z) — f2 (хо) > (о*, z — Хо) — 8*2 Vz s й.
Переходя в этих неравенствах к пределу по k при фикси-
рованных хе Еп, гей, убеждаемся в том, что v' е
®Vi(xo)> v" s (xo)- Поэтому из (10.24) и (10.25)
будет
« = (»-+»"),= р.7, (X,) + д=г, (*„)] с
=РУ, (*.)+<%(*.)].
т. е. <?2f(x0)c=^. Отсюда и из (10.23) следует (10.22).
Теорема доказана.
Следствие. Из доказательства теоремы 10.2 ясно,
что вместо (10.22) можно написать
<w«)= и РУ. W + ад (*»)]=-
eiT”C2eB
81 0, £2 0
- и [ад.м+адм]. (ю.27)
Bl
£1>0, £2>0
Т.е. для одной из функций, ft(x) или fs(x), можно рас-
сматривать не условный, а обычный 8-субдифференциал
по Еп.
4. Распространение выпуклой функции. Пусть
— выпуклое множество, G cz int £2 — выпуклый
компакт, и пусть на Q задана выпуклая функция f(x).
Образуем функцию
SF(х) = sup (z) + (р (z), х — z)], (10.28)
zgeG
118
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
«г где v(z)— произвольный (но фиксированный для каж-
дого г) вектор из dQf(z).
Лемма 10.3. Функция &"(z) выпукла и конечна на
Еп и совпадает на G с функцией f(x), т. е.
^-(x) = f(x) Vxe=G. (10.29)
Доказательство. Выпуклость &~(х) очевидна.
Докажем (10.29). Пусть xsG. Тогда тем более xgQ,
и по определению множества daf(x) будет
f(x) — f (z) (w (2), х — z) Vz ^G.
Значит,
f (x) > sup [f (z) + (u (z), x — z)J s ST (x).
Zf=G
Отсюда вытекает конечность &~(x). Ho &~(x) f(x). Из
предыдущих двух неравенств следует (10.29). И
Таким образом, любая выпуклая конечная на й
функция может быть распространена (с сохранением
выпуклости и конечности) на Еп, причем на G эта функ-
ция совпадает с f(x), при этом супремум в (10.28) до-
стигается, т. е.
У (х) = max [f (z) 4- (о (z), х — z)].
Замечание 3. В лемме 10.3 предполагалось, что
функция /(х) задана на множестве й, а множество Gc
ед int й замкнуто и ограничено. Это условие нельзя от-
бросить, что видно из следующего примера.
Пусть хе £|, f (х) = 1 — -y/l — х2, G = [0, 1 ]. Функ-
ция f(x) дифференцируема на [0, 1). Поскольку
f" (х) = (1 - х2)"3/2 >0 Vx е [0, 1),
то функция f(x) выпукла. Она ограничена на [0, 1]. Од-
нако f'(x) не является ограниченной на [0, 1), поэтому
функция
& (х) = sup [f (z) + (f (z), x — z)]
ze|0, 1)
уже не является конечной при х>1, ибо для любого
фиксированного х > 1 имеем Зг(х) = оо.
§ Ill
УСЛОВНЫЕ ПРОИЗВОДНЫЕ ПО НАПРАВЛЕНИЯМ
119
§ 11. Условные производные по направлениям. Не-
прерывность условного 8-субдифференциального
отображения
1. Пусть функция f(x) выпукла и конечна на Еп,
Qc:En — выпуклое множество. Пусть х0 е Q, е О,
п, ||g|| = !• Положим
^(*о) . v ^(*о) , ч
—дГ~ = sup (V. g), = sup (о, g).
ved f(x0) oe<5ef (xq)
Величину назовем условной производной
функции f(x) в точке х0 по9направлению g по множеству
д?} (х0)
£2, а —— назовем условной s-производной функции
f(x) в точке х0 по направлению g по множеству Q.
Из (6.5) имеем (при C = daf(xo), B — df(Xo))
g @ Г (х0),
(11.1)
g <£ Г (х0).
dQ(xo) 7 J если
dg I I
<4-оо, если
Поскольку имеет место включение d®f (х0) с: d®f (x0)t то
defdgX(^ = + °° при g <£ Г (х0).
Лемма 11.1. Если У£ — выпуклый конус, содержа-
щий точки g и —g, причем geintJlf, то
Ж — Еп. (11.2)
Доказательство. Поскольку gеintX, то най-
дется г > 0 такое, что
xq = g + q^.X
Так как X — выпуклый конус, gi = — g е Jtf, то
yq = [0,5g! + 0,5xJ e Ж Vq^Sr (0). (11.3)
Ho yq = O,5<7, поэтому из (11.3) S0,er (0) cz Jif. Итак, шар
радиуса 0,5r с центром в начале координат содержится
в конусе Ж Отсюда и вытекает (11.2). Ц
120
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. 1
Ф(х
dg
Следствие. Пусть х — граничная точка множе-
ства fl, g^En, ||gl|= 1. Если ge int Г(х), то
gi = -g^T(x). (11.4)
Действительно, допустим противное. Пусть gi е
еГ(х). Тогда из леммы 11.1 следует, что
Г(х) = £„,
что невозможно, поскольку х — граничная точка.
Теорема 11.1. Если хоей, gey(xo), ||g|| = 1, то
: sup (о, g) =
Q
oe=def(x0)
= inf а“‘[/(xo + ag) —/ (хо) + е]. (11.6)
a>0
xo + ag e fi
Доказательство. Прежде всего заметим, что
если инфимум в (11.5) достигается при некото-
ром ai, то ой > 0, ибо й(а) —+ оо, где Л(а) =
= a-1 [f (хо + ag) — f (х0) + в].
Из определения <5gf(x0) имеем
f (ха) - f (*о) > а (о, g) - в Vt? е d%f (х0), Vxa е Q,
где ха = хо + ag. Отсюда
inf ft(a)^s sup (о, g). (11.6)
а>0, xaefi .
“ oedef(xo)
Установим противоположное неравенство. Поскольку
dg/(x) = dff (х) VxeQ и h*Q==h^= inf _й(а),
а>0, xaefi
то далее без ограничения общности считаем, что мно-
жество Q замкнуто.
Напомним (см. следствие из леммы 8.3), что если
ai — точка локального минимума функции h (а) на
(О, оо), то
Л* inf й (а) = Л (ai). (П.7)
а>о
Возможны два случая:
а) h*^hU (11.8)
6) Л*</Й, (11.9)
, И] УСЛОВНЫЕ ПРОИЗВОДНЫЕ ПО НАПРАВЛЕНИЯМ 181
Рассмотрим случай а). Согласно (8.2)
h* == max (о, g). (11.10)
oedef (xq)
Из того, что def (х0) cz d^f (х0), и из (11.8), (11.10)
имеем
sup (о, g),
ae<5ef(x0)
что вместе с (11.6) дает (11.5).
Обратимся к случаю б). Пусть
tt = A(ai), (11.11)
причем xaeQ при всех aE(0, ai). Тогда xa<£Q при
всех а > ai, ибо если допустить противное, то, с учетом
выпуклости множества й, точка ои будет точкой ло-
кального минимума функции h (а) на (0, оо) и поэтому,
в силу (11.7) и (11.11), будет выполнено (11.8), что
'противоречит (11.9).
Таким образом, ха, — граничная точка множества й.
Поскольку /i(a0= min h(a), то, в силу замечания
as(0, ai]
1 § 6, должно быть
h'_ (си) s lim a-1 [h (си + а) — h (cti)] 0.
а-» -0
Но, как нетрудно подсчитать,
(“,) = “Г1 + -Г" [/ (*,) - f («,) + е],
где
gi^ — g, xi = xat.
Следовательно, существует vo^df(xi) такое, что
»г’ [(«». S,) + 1 (/ м - f (*») +«)] > 0.
т. е.
«ГЧЛ'О-?(*о) + «]>(*о. ё)- 01.12)
Предположим вначале, что xoeintn. Тогда -ge
s inly (xj) и, в силу следствия из леммы 11.1, ^^Г(Х1).
Значит, найдется даеГ+(Х1) такое, что (w,g)<ZQ. По-
скольку r+(xi)—конус, то существует X 0 такое, что
w0 = Xw s r+(xi), и вместо (11.12) будет
f (*1) — f (х0) = СЦ (Со — Wo, g) — 8. (11.13)
122
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
Учитывая, что
»i = (уо - wo) s (xi)> е = аг1 (*i — хо)>
из (11.13) получим f(xi)— f(xo) = (t»i, Xi — х0)—в. По-
этому по определению множества B®f (х0) и по теореме
10.1 будет Vj е Bff (х0) a: d®f (х0). Таким образом, из
(11.11) и (11.13) имеем
hos=h(ai) = (vl,g)^, sup (v, g). (11.14)
oedgf (x0)
Пусть теперь Xo— граничная точка множества О.
Положим
Qe = со {Q (J Se (х0)}, йо.= inf й(а), б>0.
a>0,xueQj
В этом случае (рис. 13) Qef|{x = х0 + ag|a > 0} =
= [хо, хи], где xie = x0 + aieg. Покажем, что
*1» ГГн xi = xo + aig.
Поскольку g^y(xi), то при любом фиксированном
а > ai точка ха — х0 -j- ag Ф- Q- По теореме отделимости
(теорема 1.2) найдутся go^Bn и число а > 0 такие, что
(х — ха, go) < — a Vx<= □.
При достаточно малых б > 0 будет
(х — ха, go) < — 0,5a Vx е Q U (x >),
а тогда справедливо неравенство
(х — xa, go) < — 0,5a Vx e Qe,
t. e. xa e Qe и Хц e [xi, xa] при достаточно малых б > 0.
Итак, х1а б^+> *1, а в СИЛУ непрерывности h (а) и
ha6-^ha. Отсюда и из (11.9) вытекает, что при доста-
точно малых б будет й* < йа6. Значит, снова находимся
в условиях случая б), но уже для множества йв. Тогда
вместо (11.14) соответственно имеем
Йй.< sup (п, g).
re58°f(x0)
§ и]
УСЛОВНЫЕ ПРОИЗВОДНЫЕ ПО НАПРАВЛЕНИЯМ
123
Отсюда и из того, что d°ef (*0) (х0), ибо QcQt,
следует
< sup (v, g).
oe5gf(x0)
Переходя здесь к пределу по б->4-0, снова получаем
(11.14).
Таким образом, в случае б) независимо от того, яв-
ляется точка Хо граничной или внутренней точкой мно-
жества й, имеет место (11.14). Из (11.14) и (11.6) сле-
дует (11.5). Теорема доказана.
Следствие 1. Для любого е > О
___ ,
dg "Г
оо Vg^y(xo).
Действительно, пусть х0 е й, ъ > 0, g <= Г(хо)\у(хо)
(рис. 14), т. е. g<£v(x0), но£= limg*, gkt=y(x0). Рас-
смотрим множества йв = co{Q U Se(xo)}^> й, где 6 > 0.
Тогда geye(x0). где
Уб(*о) = {f = ~х0)|Л>0, №Йв}.
В силу теоремы 11.1 имеем
inf h(a)— sup (»,§)< sup (v,g). (11.15)
a>0, xoeSe vesd®if(Xo) v<sd®f(x0)
Ho h6 = inf ft (а). Поскольку g у (x0), to a*----> 0,
as(0,ae) 6-» 4-0
dQf(x )
поэтому ft6 4-oo. Из (11.15) получаем-8^07 =4-oo.
124
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Выше было показано, что при g ф Г (х0)
ffi(*o)
dg
= + оо. а
Следствие 2. Если для некоторого g0^En, ||g|| =
га 1, оказалось
^<0, (Н.16)
ТО
inf f (х0 + ago) < f (х0) — е. (1117)
а>0,хвеЙ
Действительно, в силу (11.6) найдется ои > 0 такое,
h (а,) = аГ> [f (х0 + alffo) - f (х0) + в] < О, (11.18)
причем Хо + aigo ® £2. Поскольку ai > 0,- то из (11.18)
f (хо + digo) — f (х0) + е < О,
откуда и следует (11.17).
Следствие 3. Если f(x) сильно выпукла и
то
Ogo
inf f (Хо + ago) < f (х0) — е.
а>0, xoWos^
П Г* - ffl(*o)
Доказательство. Случаи -—<0 рассмот-
рен в следствии 2. Пусть теперь
Q
Тогда найдутся последовательности {«а}, {0а} такие,что
«*>0, xo + aftgoeQ, A(afc)<0A, 0*->О,
где
h (а) == а-1 [f (х0 + ago) — f (х0) + в].
В силу сильной выпуклости функции f(x) существует
ао > 0 такое, что а* ао для всех k. Поэтому
/ (хо + akgo) — f (xq) + е < аА0* < Оо0*
$ 111 УСЛОВНЫЕ ПРОИЗВОДНЫЕ ПО НАПРАВЛЕНИЯМ 125
Отсюда
inf f (х0 + ago) — f (*о) + в < О,
a>0, x0+agoeQ
что и требовалось доказать.
Заметим, что условие сильной выпуклости существен-
но, что видно из следующего примера.
Пусть f(x) нз const, Q = Еп- Тогда для любого
go^En, ||g|| = 1, будет
inf a-1 [f (x0 4* ago) — f (x0) + в] = inf a-’e = 0,
a>0 a>0
но уменьшить функцию f(x) нельзя.
2. Рассмотрим точечно-множественное отображение
d*f: (0, оо)ХЙ-*П(£„),
где при фиксированных хай и в>0 по определению
d®f (х) “ {f е Еп I ft2) ~ f (х) z — x) — e Vz& Q}.
Отображение d^f(x), как и отображение dQf(x), не яв-
ляется ограниченным.
Пусть функция f(x) конечна и выпукла на Еп.
Теорема 11.2. Если Q с: Еп — замкнутое выпуклое
множество, то отображение d^f (х) непрерывно по Каку-
тани по х и г на множестве (0, оо)ХЙ (т. е. полунепре-
рывно и сверху, и снизу).
Доказательство. Полунепрерывность сверху
отображения d®f (х) следует непосредственно, из опреде-
ления. Докажем полунепрерывность этого отображения
снизу.
Пусть даны во >0, х0 е Q, о0 е d®f (х0) и произволь-
ные последовательности {е*}, {х*} такие, что е* > 0,
е&->е0, х*®й, xft->xo. Надо показать, что найдутся
vk-G f (x*) такие, что Vk-^Vo. Допустим противное.
Тогда существует а > 0 такое, что
inf || v — 1>о11“Н vk~ > 0 Vk, (11.19)
vsdekf(xk)
Инфимум в (11.19) достигается, поскольку множества
f (х*) замкнуты. Без ограничения общности можно
считать, что
Vk-^V*, gft^lluo — о*И"’(оо — vk)-^go, II go II “I.
126
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА [ГЛ. I
В силу (11.19)
(у - ёk) < (oft “ о0. Vu е ду (xfe).
Значит,
Зе f(xk)
~^g----soup (°> Sk)=^(vk, gk) (11.20)
k
и (vk, gs)^(vo, gk)~ а. Отсюда и из (11.20) ясно, что
найдется номер К такой, что
^fa)
------(Vk, gk) < (Vo, go) - о,ба \fk > К. (11.21)
Поэтому
<5?f(x0) deJ(xk)
“^>_^r+0,5a vk>K- <11-22)
По теореме 11.1
^J(xk)
— = inf a-1 [f (xk + agk) — f (xk) + s] *
u*k a>0,
— inf h(xk, gkTa,ik).
a>0, «j+ogjsO
Из (11.21) ясно, что существует a0>0 такое, что
&J(xb)
—-------= inf h(xk, gk, a, eft). (11.23)
uBk a>a0, Jt4+egjsO
Предположим вначале, что функция f(x) сильно вы-
пукла. Тогда при каждом k инфимум в (11.23) дости-
гается в некоторой точке а*, т. е.
дУ(хк)
~"'dg~ = h (х*> Sb, Uk, 8ft), (11.24)
причем а* Ро, где 0 < р0 < 4-оо, р0 одно и то же для
всех k. Можем считать, что а*-> а' ао. Тогда из
(11.22) и (11.24) имеем
^J(xft) ^*Чхо)
—---------► h (х0, go, а', е0) < —---0,5а. (11.25)
§ Ill
УСЛОВНЫЕ ПРОИЗВОДНЫЕ ПО НАПРАВЛЕНИЯМ
127
Так как хк + akgk е Q, то и Хо + a'go е Поэтому
~ n inf Л(*о, £о, а, 8о)<М*о, go, <*'> бо),
^so а>а0, Xo+agoeQ
что противоречит (11.25). Полученное противоречие и
доказывает полунепрерывность снизу отображения
d%f(x) в точке [е0, хо].
Пусть /(х)—произвольная выпуклая конечная функ-
ция. Построим функцию 3re(x) = f(x) + 6(x — хо)2, где
б > 0. По доказанному выше отображение d^Fe(x) по-
лунепрерывно снизу в точке [ео, х0] в силу сильной вы-
пуклости функции ^в(х). По формуле (10.22) имеем
<W*) = U [<W + <VeW]>
8i4-e2-e
81 >0, 8?^0
где /в(х) = б(х— хо)2. Как следует из примера 1 § 7
(см. (7.7)),
<VdW = {o = 2fl(* —*o) + d геЕп, IIг||<2^/ей].
Возьмем произвольные о0 s d®f (х0) и последователь-
ности {е*} и {х*} такие, что eft->e0, х^->х0. Поскольку
Oedefe(xo), то p0e5f^e(x0) для любого б > 0. Из по-
лунепрерывности снизу отображения в точке
[во, х0] найдется последовательность такая, что
°k& S ^efe^"e (Х/г)’ VM “* °0-
При этом, в силу представления д®ЗГ6(х), будет nfte =
где v'M е d®kf (xft), v'm ® d&kfi (xk). Так как
||»£б|| 0, то можно выбрать подпоследовательности
{Ы и {v'k6k} такие, что бА +0, v'kok »о. Значит,
отображение d^f (х) полунепрерывно снизу в точке [s0, х0].
В силу произвольности точки [е0, х0] отображение (х)
пдлунепрерывно снизу на множестве (0, оо) X Q. Теорема
доказана.
Следствие. Если xoeintQ, во > 0, то отображе-
ние d°f(x) непрерывно по Хаусдорфу в точке [е0, х0].
Доказательство следует из леммы 10.1.
128
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
1ГЛ. I
3. Необходимые и достаточные условия миниму-
ма в задаче с ограничениями. Пусть Qcz£n — замкнутое
выпуклое множество, и пусть на множестве Q задана вы-
пуклая функция f(x). Рассмотрим задачу минимизации
функции f(x) на множестве Q.
Справедливо следующее очевидное утверждение.
Лемма 11.2. Для того чтобы в точке функ-
ция f(x) достигала своего наименьшего на множестве Q
значения, необходимо и достаточно, чтобы
(11.26)
Замечание. Если функция f(x) конечна и вы-
пукла на Еп, то по лемме 10.2
daf(x*) = df(x*)-r+(x*),
и условие (11.26) эквивалентно соотношению (см.
(6.16))
^(Х*)ПГ+(Х’)=54 0.
Если Q = Еп, то условие (11.26) имеет вид
О ед/(А
Пусть 8^0. Точка хей называется 8-стапионарной
точкой функции f(x) на множестве Q, если
Oed“f(x). (11.27)
Лемма 11.3. Соотношение (11.27) эквивалентно не-
равенству
(11.28)
где f* = inff(x).
xeQ
Доказательство. По определению соотношение
(11.27) эквивалентно тому, что
f (*) > f (*) + X — х) — 8 = f (х) — 8 Vx е Q,
что и требовалось доказать.
Пусть х G Q. Положим
§ 11]
УСЛОВНЫЕ ПРОИЗВОДНЫЕ ПО НАПРАВЛЕНИЯМ
129
Согласно следствию 1 теоремы 11.1
*фе (х) = min
llgll-l, gsy(x)
dg
Следствие 1. Условие (11.27) (или, что то же,
условие (11.28)) эквивалентно тому, что
ф8 (X) 0.
Это вытекает из следствия 2 леммы 6.4.
Следствие 2. Если 0 ф. d^f (х), то существует на-
правление go^^(x), ||g’oll= 1, такое, что
<%(*)
&go
При этом (см. следствие 2 из теоремы 11.2) имеют место
неравенства
inf f (X + ago) < f (х) — в.
a>0, x+agos Q
что
Пусть x0 <= £2, e > 0 и ф8 (x0) < 0.
Определение. Вектор go<=En, ||goll= 1,
такой,
Фе(Хо),
назовем направлением условного е,-наискорейшего (наи-
скорейшего, если 8 = 0) спуска функции f(x) в точке
хоей.
Оно, согласно следствию из леммы 6.3, существует и
единственно. Более того, если для v (х0) Q dff (х0) имеем
lp(xo)|“ min 11°И> то вектору =-||и(хо)||-1ц(хо)
° saeC(*o)
является направлением условного e-наискорейшего спуска
функции f(x) в точке х0<= £2.
Отметим также, что, в силу следствия 1 из теоремы
11.1 и формулы (11.1),
(х0)
ф8 (х0) = min , go е= у (Хо),
llgll-1. gs Y(xo) й
а если 8 =• 0, то
daf (x0)
Ф (Xo) фо (Xo) = min —Д—g0sl'(x0).
ten-1» ger(xo)
5 В. Ф. Демьянов, Л. В. Васильев
130 ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА (ГЛ, 1
Наконец, на основании следствия 2 из теоремы 11.1
заключаем, что если
dgo ’
ТО
inf f (х0 + ag0) < f (х0) — в. (11.29)
а>0, Хо 4-ago ей
§ 12. Задание выпуклого множества
с помощью неравенств
1. Пусть йсз£я— выпуклое замкнутое множество.
Для любого Хо €= й рассмотрим нормальный конус
yr(x0) = {oe£„|(v, х —хоХО Vxe=Q). (12.1)
Если xoeintQ, то ясно, что Лс’(х0) = {0}. Если же х0—
граничная точка й, то Л9(х0)\{О}^ 0 (см. следствие!
из теоремы 1.2). Положим
ф — {х е Еп | (о (х0), х — хоХ 0
Vo (х0) е Л5 (х0), Vx0 s й). (12.2)
Замечание 1. Очевидно, что если й =£ Еп, то
& — {х <= Еп |(t> (хо), х — хоХ 0
Vo(х0)е Jf (х0), ||и(х0)||=1, Ух0(=й(г},
где й{г — множество граничных точек й.
Лемма 12.1. Имеет место соотношение
Q = 0>. (12.3)
Доказательство. Пусть хеЙ. Из (12.1) ясно,
что х е т. е.
Й <= 0>. (12.4)
Пусть теперь 2Е#1. Покажем, что хей, Допустим
противное. Предположим, что г ф й. Тогда
min||x — z|| = ||x0 — z||> 0. (12.5)
х е Q
Ясно, что хо — граничная точка й. Положим g =
== ||z — xoll-1(z — хо). Из доказательства теоремы 1.2 вы-
текает, что
(х — Хо, gX 0 Vx е й,
§ 12] ЗАДАНИЕ ВЫПУКЛОГО МНОЖЕСТВА НЕРАВЕНСТВАМИ
131
т. е. geAf(x0). Из (12.5) (g, z — х0) = ||z — х0||> 0, а
это противоречит тому, что ге^1. Значит, в действи-
тельности ге^1, т. е. ^cQ. Отсюда и из (12.4) и сле-
дует утверждение леммы. Н
В определении множества Ф в (12.2) участвовали все
векторы множества Л’(хо). Установим условия, при ко-
торых для каждого х0 достаточно взять лишь один не-
нулевой вектор из (хь) • Пусть
' = {х е=Еп |(4(х0), х — хо)<0 Vx0 е= Qfr}, (12.6)
где Of г — множество граничных точек Q, А (х0)е Л’(хо),
||Д (х0) || = 1 (т. е. в каждой точке х0 е Й(Г выбираем
только один — все равно какой — единичный вектор из
Л’(хо)).
Лемма 12.2. Если int й =/= 0, то
Q = ^i. (12.7)
Доказательство. Включение
Q<=0>i (12.8)
очевидно. Пусть теперь zs^i. Надо показать, что
ZE Q. Допустим противное. Пусть zф й. Возьмем хе
eintQ. Тогда существует г>0 такое, что Sr(i)cQ.
На отрезке [х, z] найдем граничную точку xi е й{г (она
существует и единственна). Тогда (A(xi), х —Xi)^0
Ух ей. В частности, (A(xi), х —xiXO VxeSr(j?).
Тогда
(A(xi), х + v — х0<0 VxеSr(0).
Значит,
(А(хО, х — хХ(—о, A(xi)) Vt>®Sr(O). (12.9)
Возьмем о=:гА(Х1). Имеем из (12.9) (A(xi), х —xiX
—г < 0. С другой стороны, z —Xi = —а(х —aj),
где а > 0. Отсюда
(A (xi), z-Xi) = — a(A(xi), Л — xj)>ar > 0. (12.10)
Неравенство (12.10) противоречит тому, что ze^i. Из
полученного противоречия следует z&Q, т. е. ^’1 а: Й,
что вместе с (12.8) завершает доказательство леммы.
Замечание. 2. Требование наличия внутренних
точек в лемме 12.2 (это условие Слейтера) существенно,
что видно из следующего примера.
5*
132
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Пусть х = х<2>, х(8>)е Е3. На плоскости Q =
= {х е Ез | х(3) = 0} возьмем многоугольник й. Это мно-
жество выпуклое, но внутренних точек в пространстве Е3
* оно не имеет. В данном случае вектор е3 = (0,0, 1)<=
еЛ’(хо) Для всех хоей. Следовательно, можно взять
А (х0) = е3 для всех х0 е йи, поэтому
^>1 = {х е Е3 |(е3, х — х0)<0} — {х <= Е3 |х® < 0}.
Однако ясно, что ф й.
Из лемм 12.1 и 12.2 вытекает
Следствие. Справедливо представление
й = {хеЕ„|й(х)<0},
где
hi (х), если int й = 0,
hz(x), если intfi
hi (х) = sup sup (А (хо), х — х0),
*oe“fr л(хо)е^(хо)
||А (Хо)Ц- 1
hi (х) — sup (А (хо), х — х0).
*ое “fr
Л(х) =
В определении hz(x) для каждого Хоейи выбирает-
ся только один (все равно какой) вектор А (х0) из Л’(хо), !
причем ||А(х0)||=1. Функция й(х) определена на Еп.
Очевидно, что А(х)— выпуклая конечная на й функция,
и если й — ограниченное множество, то й(х) — выпуклая ;
конечная на Еп функция.
2. Пусть
Й = {хе=Еп|/г(х)<0), (12.11) ;
где h (х) — некоторая выпуклая функция. Очевидно, что
множество Й, заданное (12.11), всегда является (если
оно непустое) выпуклым и, если Л(х)—конечная функ-
ция, то и замкнутым.
Рассмотрим множество
й = {хе£л |Л1(х, у)<0 Vye<»}, (12.12) ;
где (nczEp — ограниченное замкнутое множество, a i
функция hi(x, у) выпукла на Еп по х при любом у^ч>.
ЗАДАНИЕ ВЫПУКЛОГО МНОЖЕСТВА НЕРАВЕНСТВАМИ
133
Множество Q, заданное (12.12), тоже выпукло, причем
его можно представить в виде (12.11), если положить
ft(x) = maxfti(x, у). При этом функция й(х) является вы-
уе®
пуклой.
Итак, пусть Q задано в виде (12.11), где й(х) —ко-
нечная выпуклая на Еп функция. Ниже будем предпола-
гать, что выполнено условие Слейтера: существует х&Еп
такое, что
ft(j?)<0. (12.13)
Возьмем Хо s П и положим
у(хо) = {це£„|о = Л(х-Хо), Л>0, xefi},
rw=5W. (12J4)
Множество у(Хо) можно представить и в виде, эквива-
лентном (12.14):
|Эаот
— ао(о) > 0: h (х0 + av) < 0 Va е [0, ао]}. (12.15)
Множества Г(хо) и Г+(х0) изучались в § 3.
Положим
если h (х0) < 0,
В (хо) == <
(t»e£n|(w, р)<0 Vw<=5ft(x0)},
если Л (хо) = 0
где dh (хо) — субдифференциал функции й(х) в точке х0,
г. е.
5ft(х0) = {пу е Еп |Л(х) — h(х0)>(&', х-х0) Vx еЕп}.
Очевидно, что если ft(xj)<0, то xoe=intQ. Из (12.13)
следует, что если х0 <= Q, но х0 ф int Q (т. е. h (х0) = 0),
ТО
0<£5ft(x0), (12.16)
ибо хо не является точкой минимума ft(x) на Еп.
Лемма 12.3. Если выполнено условие Слейтера
(12.13), то
Г(хо) = В(хо). (12.17)
134 ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА [ГЛ. I
Доказательство. Соотношение (12.17) очевидно,
если h (хо) < 0. Пусть теперь
й(хо) = О. (12.18)
Вначале покажем, что Г(х0)с: В(х0). Пусть оеГ(хо);
тогда найдется последовательность {t>4 такая, что
lim vk, о*б=у(х0).
£~>ОО
Фиксируем произвольное k. Тогда (см. (12.15)) су-
ществует ао(Пй)>О такое, что й(хо + ап*)^О Voe
е(0, a0(vk)). Отсюда и из определения dh(x0) для всех
w^dh(xo) будет
(w, vk) < a-1 [Л (х0 + avk) — h (х0)] < О,
ибо в силу (12.18) А(хо)=О. Фиксируя произвольное
toedft(xo) и переходя к пределу при А-*оо, имеем
(to, о) 0 Vto е dh (хо),
т. е. Г(х0)с: В(х0).
Пусть теперь t>sB(x0). Вначале предположим, что
max (а/, о) = — a < 0. (12.19)
w е dh (хо)
Тогда
h (хо + ao) = h (хо) + a dh^ + о (а) =
= a max (to, о) + о (а) = — аа + о (а).
w е dh (хо)
Очевидно, при достаточно малых а > 0 будет h (хо 4*
+ ап)<0, т. е. Хо4-аое0. Значит, о е у(х0)с: Г(х0).
Если же max (to, о) = 0, то возьмем вектор ое = v +
w г dh чхо)
4-в(х — Хо), где е > 0, х — точка, удовлетворяющая ус-
ловию Слейтера (12.13). Из определения dh(x0) имеем
h (х) —• h (х0) (to, х — Хо) Vto е д/г (х0),
т. е. (to, х — хо) Л (х) < 0. Поэтому
(to, ое) = (to, о) + е (to, х — х0).
Отсюда
max (to, ve) < max (to, v) +
w e dh (xo) w ен dh (x0)
4- e max (to, x — x0) &h (x) < 0.
w e dh (xp)
§ 12]
ЗАДАНИЕ ВЫПУКЛОГО МНОЖЕСТВА НЕРАВЕНСТВАМИ
135
Итак, для ve. имеет место (12.19), и по доказанному
цееу(х0). При е-»0 имеем vt-+v, цееу(х0). Значит,
кеГ(хо)- Лемма доказана.
Пусть снова Хо £= & Положим
( {0}, если h (х0) < 0,
( {u = Xa>|A^O, wedft(xo)}, если й(хо) = О.
Лемма 12.4. Если выполнено условие Слейтера
(12.13), то
Г+(хо) = ^(хо). (12.20)
Доказательство. Утверждение очевидно, если
/г(х0) < 0. Рассмотрим случай
й(хо) = О. (12.21)
Тогда по лемме 12.3
Г(х0) = {о е Еп| (да, «)<0 V® е д/г(х0)}.
Согласно (12.15) для любого оеу(х0) существует
ао(о)> 0 такое, что
/г(хо + ао)<0 Va е [0, ао(о)]. (12.22)
Для любого а>ед/г(х0) по определению субдифферен-
циала
h (х0 + at») — h (Хо) > a (w, о).
Учитывая (12.22) и (12.21), имеем (w, ц)< 0. Поэтому
(Kw, о) 0 VX 0, Vo е у (х0).
Так как Г(хо) = у(х0), то отсюда
(fav, о)^0 УиеГ(х0),
а это и значит (см. определение сопряженного конуса
в § 3), что Хаг <= Г+(х0). Итак,
JJf (х0) а: Г+(х0). (12.23)
Пусть теперь и е Г+(х0), т. е.
(v, g)>0 У§еГ(хо). (12.24)
Рассмотрим луч2’ = {а;=—ao|a>0}. Если 2W(Xo)^=
то существует а0 такое, что w = —аооед/г(х0).
136
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Очевидно, что ао >• 0, ибо в случае ао = 0 имеем 0 е
ед/г(х0), что противоречит (12.16). Тогда — a^kiy,
а это и значит, что о Q УС (хо), ибо А = — а~‘ < 0.
Покажем, что всегда
^П<5/г(х0)=^ 0. (12.25)
Допустим противное, пусть S>f]dh(x0) — 0. Как и при
доказательстве леммы 6.2, получаем, что существует г,
||г||= 1, такое, что
(г, р)-0, (г, g) = -a<0 Vg6=dA(x0). (12.26)
В силу (12.26) (рис. 15) найдется z' такое, что
(«'. g) < ~ 0,5а Vg 6= dh (хь), (12.27)
(г', о) < 0. (12.28)
Из (12.27) и леммы 12.3 заключаем, что г'бГ. Но тогда
(12.28) противоречит (12.24).
Итак, всегда имеет место (12.25), а тогда, как уже
установлено, veJ$f(x0), т. е. Г+(х0)сз Jf(xo). Отсюда
и из (12.23) получаем
(12.20). Лемма доказана.
3. Рассмотрим случай,
когда множество Q имеет :
вид
ah(aie)
О_______
\
\
\
\
г'1
С
(12.29)
Рис. 15.
где
h (х) «=» max hi (х), / = 1: <
1&I
(12.30) ‘
функции hi(x) выпуклы И j
непрерывно дифферент»- 5
руемы на Еп. Предположим, что выполнено условие
Слейтера (12.13): существует точка хеЕп такая, что
й,(*)<0 VZeZ. (12.31) :
Очевидно, что х е int Q, и поэтому int О =# 0.
Задание 12.1. Доказать, что условие Слейтера эквивалентно г
условию: найдутся такие точки х/е Q, i s /, что |
$ 13]
НОРМАЛЬНЫЙ КОНУС
137
Пусть х е Й. Положим Q(x) = {iе / |hi(х) — 0}. Оче-
видно, что hi (х) < 0 Vi ф. Q (х).
Заметим, что если Q(x) = 0, то xeintQ. Обратное
неверно, так как из того, что х е int й, еще не следует
Q(x) = 0.
Из лемм 5.4 и 12.3 вытекает
Лемма 12.5. Если хоей, множество й задано со-
отношениями (12.29), (12.30) и выполнено условие Слей-
тера (12.31), то
Г(хо)”В(хо),
(12.32)
где
В (х0) ='
Ец, если Q (xq) 0,
{v s £„ |(v, h'i (x0)) <0 Vi e Q (x0)}>
если Q(xo)=/=0.
(12.33)
Из лемм 5.4 и 12.4 вытекает
Лемма 12.6. В условиях леммы 12.5
Г+ (х0) = А (х0), (12.34)
где
{0}, если Q(xo)“0,
<4 (хо) = •"
0=- Е
I GE Q (Хо)
(хо) I 0 V/ s
если Q(xo)=/=0.
(12.35)
§ 13. Нормальный конус.
Коническое отображение
1. Пусть QaEn — выпуклое замкнутое множество.
Для х0 G= й в § 12 был введен нормальный конус:
•4’(xo) = {v <=£„|(о, х —х0)<0 VxeQ}. (13.1)
Пусть теперь хо — произвольная точка Еп (не обяза-
тельно из Й).
Лемма 13.1. Для любого ха^Еп множество Л®(хо)
является непустым, выпуклым, замкнутым конусом. Если
Хо ф int й, то
^(xo)\{®}^=0. (13.2)
Если х0 е= int Й, то Л’(Хо) = {0}.
138 ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА [ГЛ. 1
Доказательство. Все свойства, кроме (13.2), г
очевидны. Соотношение (13.2) вытекает из теоремы 1.2
(если хо^й) или из ее следствия 1 (если Хо— гранич-
ная точка О). И I
Теорема 13.1. Если х0 не является граничной точ-
кой множества £2, то точечно-множественное отображе- -
ние Л°(х) непрерывно по Какутани в точке х0. =
Доказательство. Если xeintQ, то, как уже
отмечалось в п. 1 § 1, Л’(х) = {0} и непрерывность в
точке хо <= int й очевидна. Пусть теперь х0 ф int й. Не-
обходимо установить полунепрерывность Л’(х) в точке .1
Хо сверху и снизу. Для любых последовательностей {х*}
и {у*} таких, что х*->х0, у*->Уо, о*^Л’(х*), из (13.1)
следует, что vo^.JV’(xo), т. е. отображение Л?(х) полу-
непрерывно в точке Хо сверху.
Возьмем произвольное у0^Л’(х0) и любую- по-
следовательность {хк} такую, что х*->х0. Найдем
min||z— xft|| = ||zft — х*|| Без ограничения общности мож-
zsQ
но считать, что хк ф й и
l|zft-xA||>o>0, (13.3) •
где 2а = min || z — х0||. Как следует из замечания 3 § 1,
(х — X*, zk — Xfe)>||zft — Xfelp УхеЙ. (13.4) 1
Положим
dft = 2||zft — xjr’Koo, хо — х*)I, .
-i . (13.5)
= + —Zft|| (Xk — Zk).
Ясно, что 6k ->0. Тогда для x s й имеем
(x xk, Vk)=s (x - Xk, Vk ~b 6k || Xk — Zk II* (Xj Zk)) ==
= (x — Xo, Vo) + (Xo — Xk, Vo) +
+ (x — xk, || Xk — Zk 1Г1 (xk — Zj)).
Поскольку по^Лс’(хо), то
(x — Xo, Vo) 0 Vx s Й.
Из (13.4) — (13.7) получаем
(x — Xk, — | (Vo> Xo — Xk) к 0 Vx s Й,
(13.6)
(13.7)
(13.8)
§ 13]
нормальный конус
139
т.е. Vk^^(Xk)- Так как 6л->0, то н*-*-По, а это и зна-
чит, что отображение Л’(х) полунепрерывно снизу в
точке Хо- Итак, отображение Л’(х) полунепрерывно и
сверху, и снизу в точке хо^й. Теорема доказана.
2. Пусть /(х)— выпуклая на Еп функция. В простран-
стве En+i рассмотрим множество (см. п. 1 § 4)
G = epif = {х = [р, х] |Pe=£b P>f(x), х (= Е„}.
Это выпуклое замкнутое множество. Возьмем точку
xo = [f(xo) — во, Хо], где во>0. Ясно, что x0&G. По до-
казанному в теореме 13.1 отображение Л°(хо) = {й е
<= En+i I (й, х— хо) 0 VxeG} непрерывно по Каку-
тани (или К-непрерывно). Положим
Q(x0) = {i»g=£„|[-1, u]e^(x0)}.
Лемма 13.2. Имеет место соотношение
Q(xo) = <?eof(xo). (13.9)
Доказательство. Возьмем любое ио(х0).
Тогда
f (х) — f (х0) > (п0, х — х0) — во Vx е Еп.
Для р f (х) тем более
(P — [f(x0) —80])(—!) +(по. х —х0)<0 Vxe£n.
Положив йо = [—1, По], х = [р, х], отсюда имеем
(и0, х —х0)<0 VxeG, (13.10)
ибо x = [p,x]eG при p>f(x). Из (13.10) следует,что
иоеЛ’(хо), и потому noeQ(xo), а значит,
<9ef(x0)<=Q(x0). (13.11)
Теперь пусть иое Q(хо),тогда й0 = [—1, и0]е Л9(х0), т. е.
(й0, х — ХоХО VxeG. (13.12)
Так как
х = [р, х], р > f (х), хь = [f (х0) — в0, х0],
то из (13.12)
I (— 1) (Р — f (х0) + е0) + (ио, х — х0)] < 0 Vx е= Еп.
При р = f(x) будет
f W — f (х0) > (п0, х — х0) — е0 Vx s Еп,
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
14»
а это значит, что о0 ® deJ (*о). Итак, Q (х0) <= (х0). От-
сюда и из (13.11) получаем (13.9).
Из только что доказанной леммы и теоремы 13.1 вы-
текает
Следствие. Отображение дJ(х) К-непрерывно по
в и х на (0, оо)Х£л.
Действительно, полунепрерывность сверху отображе-
ния def(x) очевидна. Покажем полунепрерывность его
снизу. Пусть X/1-^Xg, vo&def(xo) = Q(%o), ец-^е и^ =
= [/(•**) —е*» хк]. Так как Лк-*-хо& G и v0 =• [—1, о0]е
е.Т(хо), то в силу полунепрерывности снизу отображе-
ния Л’(Я) найдется такая последовательность {tfj, что
ОкеЛ^Лк), бк-*б0. Поскольку о*] ® Л’(Лк), то и
<>;-ip»r‘5,-[-i. iM_4W уд
причем Тогда < —" v^sQfa),
что и требовалось доказать.
Отображение dtf(x)— ограниченное, замкнутое, и по
теореме 2.1 оно является и //-непрерывным, т. е. непре-
рывно по Хаусдорфу. //-непрерывность отображения
<?8f(x) уже была установлена в § 8 другим способом.
Замечание. Если функция f(x) определена лишь
на выпуклом замкнутом множестве Q, то, положив
G = {x==[p, x]&En+i\x&Q, P>f(x)}
и рассуждая так же, как при доказательстве леммы 13.2,
устанавливаем, что для £0 = [/(х0) — в0, *о]> где во > О,
х0 в Q, будет
(13.13)
Из (13.12) и теоремы 13.1 следует /(-непрерывность ус-
ловного 8-субдифференциала. Этот факт также был уста-
новлен другим способом в § 11.
3. Пусть JSf: G-*-H(En)— точечно-множественное ото-
бражение, заданное на G<zEn, причем при каждом хе
eG множество Ж(х)— выпуклый замкнутый конус с
вершиной в начале координат. Такое отображение назо-
вем коническим.
Обозначим 3?+(х) сопряженный конус:
(х) ^{we Еп |(о, w) >0 Vo е= Ж(х)}.
$ 13]
НОРМАЛЬНЫЙ КОНУС
141
Свойства сопряженных конусов изучались в § 3. В част-
ности, там было установлено, что J$f+(x)— выпуклый
замкнутый конус, причем
О+ (х))+ « Ж++ (х) =» Ж (х). (13.14)
Очевидно, что отображение Jf+(x) тоже является кони-
ческим.
Лемма 13.3. Если т.м.о. Ж(х) полунепрерывно
сверху в точке Хо е G, то т. м. о.
Ж+(х) является полунепрерыв-
ным снизу в этой же
точке. о -------
Доказательство. Пусть i
woe J4f+(xo), и пусть последо- !
вательность {х*} такова, что
xk <= О, xh-+х0. Надо дока-
зать, что найдутся х*вЛ!’+(х*) Рис. 16.
такие, что х*-»-иУо.
Допустим, что это не так. Тогда без ограничения
общности можно считать, что существует а > 0 такое,
что
mln || w — w01| || Wk — t®o || ak a > 0 VA.
v s X+ (x^)
Заметим, что ||a>ft|| ограничены, ибо (рис. 16) ||ш||^
^||ш»о11- По необходимому и достаточному условию ми-
нимума (см. замечание 3 § 1)
(wk — wo, w — wo) > al > a2 > 0 Va> e + (xft). (13.15)
Положим Vk = Wk — o>o- Как и при доказательстве
теоремы 3.1 (см. (3.7)), имеем (v*, а>л) = 0. Поэтому из
(13.15)
(vk, w) = (Vft> w _ tt,0) _|_ (Vft, Wq — Wk) _|_ (t,A>
>a2 —a2 = 0 Vte/eJf+(xft),
т. e. в силу (13.14)
vk e (JT+ (xft))+ . Ж++ (Хк) = Ж (xk).
Без ограничения общности можем считать, что
Поскольку Ж(х) полунепрерывно сверху в точке х0, то
142
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. !
vo&M’fxo). При w = 0 из (13.15) получим (vk, а»0)<
— а2 < 0. Переходя к пределу, имеем
(»о, WoX-a2. (13.16)
Но ао&Ж(хо) и (13.16) противоречит тому, что
sJ$f+(xo). Полученное противоречие и доказывает лемму.
Лемма 13.4. Если т.м.о. Ж(х) полунепрерывно
снизу в точке Хо® G, то т.м.о. <Ж°+(х) является полуне-
прерывным сверху в точке хо.
Доказательство. Допустим противное. Тогда
найдутся последовательности {хк} и {wk} такие, что
xk ^G, xk~*Хо, wk ® Ж* (xk),
Wk -> W но Ф Ж+ (х0).
Найдем
mln || w — wo || = || г® — w0 II и || v ||.
аеХ+ (Хо)
Тогда
|| о || = а > 0, (S, w — w0) а2 > 0 V® ея Ж+ (хо),
т. е. v & (Ж+ (х0))+ = Ж (х0). При этом
(б, w)e_||6|F = _a2<0.
(13.17)
Поскольку т. м. о. Ж (х) полунепрерывно снизу в точке
хо, то для точки v и последовательности {х*} найдутся
о*®Ж(хЛ) такие, что и*-»-#. Тогда
(о*, w)^0 Уго^Ж+ (хк).
В частности, для №к&Ж+(хк) отсюда получаем
(vk, wk) > 0.
Переходя здесь к пределу, имеем (5, Wo) 0, что проти-
воречит (13.17). Лемма доказана.
Из лемм 13.3 и 13.4 вытекает
Следствие. Если Ж(х)—коническое отображение,
непрерывное по Какутани в точке Хо, то и т.м.о. Ж+(х)
тоже является непрерывным по Какутани в точке х0.
§ 14)
ФУНКЦИЯ СУПРЕМУМА
143
§ 14. Дифференцируемость
по направлениям функции супремума
В § 5 уже рассматривался пример функции макси-
мума конечного числа выпуклых функций и была уста-
новлена формула для производной по направлениям и
вид субградиента. Ниже, в п. 1, более подробно изучает-
ся задача дифференцируемости по направлениям функ-
ции супремума дифференцируемых, не обязательно вы-
пуклых функций, а затем в п. 2 рассматривается функ-
ция супремума выпуклых функций.
1. Пусть
f (х) = sup <р (х, у), (14.1)
уеО
где х& Еп, у^.Ер, G cz Ер — произвольное множество.
Параметрические семейства функций ф(х, у) иф'х(х, У),
где — параметр, предполагаются равностепенно
непрерывными по х в точке х0, т. е. для любого е > О
найдется S > 0 такое, что
I Ф(х, y) — q(xQt z/)|<e,
?/)-Фх(хо> f/)|<e Vx: IIx - xo II < VysG.
Кроме того, предполагается, что
|ф(*о> К)|<^о< °°- К(*о> ^)||<^<°° Vy<=G.
(14.2)
Легко убедиться, что f(x) —непрерывная в точке х0
функция. Возьмем в > 0. Введем множества
= — ф(х, z/)<e},
(х) == {и е Еп 13 е( -> + 0, yt е= (х): <р' (х, yt) и).
Заметим, что множество /?е (х) не обязательно замкнуто.
Множество <Э^(хо) непусто, замкнуто и ограничено. То-
чечно-множественное отображение <9$(х) полунепре-
рывно сверху в точке Хо, т. е. из того, что u(ej#(xz),
Xi -+ хо, Vi -> v, следует v е Ж (хо).
Теорема 14.1. Функция f(x), заданная соотноше-
нием (14.1), является дифференцируемой по любому на-
правлению g^En в точке Хо, причем
max (v, g). (14.3)
144
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Доказательство. Положим
h (а) = а-1 (/ (х0 + ag) — f (х0)].
Пусть последовательность {а,} такова, что а<->-|-0,
h (а,)-------------------> lim h (а). /14
а->+0 ' ‘ '
Для любого существуют последовательности
{е/} и {г/,} такие, что
е, -* + 0» yt е (х0), ф' Оо» -► о. (14.5)
Без ограничения общности можем считать, что
-гЧтй-0- (14-в>
Тогда
f (*о + atg) > ф (х0 + atg, yt) ==
= Ф Оо» + «< (Фх Оо + е<£» ^)> S),
где 0/е(О, ai). В силу равностепенной непрерывности
семейства функций ф' (х, у) в точке хо имеем
f Оо + “/£) > Ф Оо» У{) + ai (Фх Оо» 8) + о{ (а,), (14.7)
о,
где - ► 0. Поскольку yt е /?е, (*о), то
f Оо + aiS) > f Оо) - 8< + ai (Фх Оо» У/)’ е) + ot (aj.
Отсюда
А(аО>(фхОо» Уд> g)+ 0<-(а^
Учитывая (14.4) — (14.7), получаем lim A(a)^(o, g).
а-> 4-0
Это неравенство справедливо для всех о е Ж (х0). По-
этому
lim Л(а)> max (о, g). (14.8)
а^>+0 о е Ж (хо)
Для любого е > 0 существует а0 > 0 такое, что для
всех а е [0, а0] будет
) (х0 4- ag) = sup ф (х0 4- ag, у).
«еЛв(*о)
ФУНКЦИЯ СУПРЕМУМА
146
§ MJ
Так как
Ф (х0 + ag, у) = Ф (х0, у) + а (ф' (х0, у), g) + o (а, у),
где .° (а* - > 0 равномерно по у е О, то
f(x0 + ag)< sup Ф(хо> у) +
4 У е К8 НО)
+ « % /<(хо>4*)+о(а)-
(*о)
Но sup ф(х0, y)^f(x0), поэтому
»e«eW
h(а)< 1 &(х°г g)+(14-9)
0 s «е (*о)
Пусть аг-> + 0 и ft(ar)-> lim й(а). Отсюда и из (14.9)
а->4-0
получаем
Пт Л(а)< sup (<р' (х0, у), g). (14.10)
а->+0 уеДе(х0) 4 4 7 7
Неравенство (14.10) справедливо для всех е > 0.
Пусть в» ->• 4-0 и ук <= /?е (х0) таковы, что
sup, х (Ч (хо> У)> 8) < («Pi (х0. yk\ 8) +
(*о)
где ~Ь 0- Поскольку в силу (14.2) множество
{ф' (х0, у) | у е О) ограничено, то без ограничения
общности можем считать, что ф'(х0, уА)~*й. Очевидно,
йе<2^(хо). Из (14.10) заключаем, что
lim Л(а)<(о, g)< max (о, g). (14.11)
а->+0 tis»(xt)
Объединяя (14.8) и (14.11), получаем
max (о, g)^ lim Л(а)^ lim Л(а)^ max (v, g).
9tsni(xi>) d^+0 a->+0 ve«(x)
Отсюда следует существование s lim ft (a) и
O’
формула (14,3). Теорема доказана.
146
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Замечание 1. Из доказательства ясно, что доста*
точно равностепенной непрерывности функций <р и ср' по х
в точке Хо относительно у е (х0), где > 0 — любое
фиксированное число.
Замечание 2. Ясно, что в формуле (14.3) можно
написать
2. Пусть
= max (о, g).
V е со Ж (Хо)
f (х) = sup ф (х, у),
y^G
где х е Еп, у еЕр, О czEp — произвольное множество,
функция ф(х, у) выпукла по х при любом фиксирован-
ном у & G. Возьмем g е Еп, Хо е Еп. Тогда
ф (хо + ag, у) = ф (х0, у) 4- а 0 (а> g> y)t (14.12)
o.(a, g, у)..-
м а а->+о
max (».g),
V е дф (Хо, у)
а множество
(14.13)
дф(*о> {/) = {» е Еп |ф(г, у)>
> ф (Хо, у) 4- (V, Z —• Хо) Vz е £„}
есть суб дифференциал функции ф (х, у) в точке х0 е Еп
при фиксированном ye G.
Предположим, что множества дф(хо, у) ограничены в
совокупности, т. е.
1М<К<оо Уоедф(хо, у), Vy^G. (14.14)
Допустим также, что выполнено условие: в (14.12)
"° gY+o 0 равномерно по у е /?е, (х0), где во > 0
фиксировано.
Легко видеть, что функция f (х) является выпуклой
и потому (см. § 4) дифференцируемой по всем направ-
лениям. Возьмем 8 > 0, в в0. Введем множества
(х0) = {у е G | f (х0) — Ф (х0, у) < 8},
(Хо) = {и е Еп | 3ef -* 4- 0, yt е /?ег (х0),
ц.(=<Эф(х0, у(): v^v}.
i 14]
ФУНКЦИЯ СУПРЕМУМА
147
При сделанных предположениях множество Зё(х<д не-
пусто, замкнуто и ограничено.
Теорема 14.2. Функция f(x) является дифференци-
руемой по любому направлению g в точке хо, причем
= max (v.g). (14.15)
О<=Я?(х0)
Доказательство. Дифференцируемость f(x) по
направлениям вытекает, как уже отмечалось, из выпук-
лости функции f(x). Нам остается лишь найти вид про-
изводной по направлению. Положим
h (a) = a~'[f (х0 + ag) — f (х0)].
Для любого ие$(хо) найдутся последовательности
{ej, {th}’ W такие, что е;-> + 0, yt е RS{ (х0),
(=д<р(х0, t/z), vt-+v. Возьмем последовательность {а,}
такую, что а/-»- + 0. Как и в п. 1, считаем, что
(14.16)
Тогда в силу определения дф(хо, уд
f(x0 + atg) > <р (х0 + a{g, уд ф (х0, уд + ai (v{, g). (14.17)
Так как yt е= /?е, (х0), то f (х0 + atg) f (х0) — ez + at (vh g).
Поэтому Л («,)>(»,, g) —а"’ег Отсюда и из (14.16),
(14.17) следует -^^>(о, g). Поскольку это неравен-
ство справедливо для всех и еЖ (х0), то
шах (и, g). (14.18)
°S пеХ to)
Докажем неравенство противоположного знака.
Для любого е > 0 при достаточно малых а > 0 бу-
дет
f (х0 + ag) *=* sup ф (хо + ag, у).
«sRe. (*о)
Из (14.12) имеем
fUo + ag)^ Sup ф(х0, у) + а sup --ф -|-о (а).
</s*e(*o) д8
148
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. 1
Но sup <р(х0, г/)™/(х0), поэтому
0вМ*о)
М«)< sup Л£1дЛ+££1.
»елв(хо) °8
Переходя к пределу при а-> + 0, получаем
df (х0) ___ <Эф (х0, у)
Т*„Л“РЛ)
Пуоть ->+ 0 и yksRSk(x0) таковы, что
d<f(x0,y) d<f(x0,yk)
(14.19)
где 6ft -—► 4- 0. Поскольку
9<f(xo>.Vk) , х , ,
—V — max (о, g) = (о*, gft),
* oa3<p(x0. yk)
то, 6es ограничения общности, в силу (14.14) считаем,
что Очевидно, us^(z0). Поэтому из (14.19) за-
ключаем, что
g)< max (о, g). (14.20)
Из (14.18) и (14.20) следует (14.15). Теорема доказана.
Введем множество 8(хо) = соЗё(хо).
Следствие 1. Имеет место равенство
df(x0) = 2(x0).
Действительно, из (14.15) видно, что
max (v, g). (14.21)
v Q s (Хо)
С другой стороны,
max (о, g), (14.22)
v & df (хо)
где df(x0) = {t>«=£n|f(x) — f(x0) > (о,х—х0) Vx<=
е £4}—субдифференциал функции f(x) в точке xq. По-
скольку (14.21) и (14.22) справедливы для любых
g^En, а множества 8(хо) и df(x0) — выпуклые ком-
пакты, то (см. следствие из леммы 2.1) <5f(xo) = S(xo).
ФУНКЦИЯ СУПРЕМУМА
149
S 14]
Следствие 2. Если f (х) =« max ф (х, у), где G —
y&G
компакт, а функция f(x,y) выпукла по х при любом
фиксированном у&О и непрерывна по х, то
df (х)« со {<р' (х, у) | у <= R (х)},
R(х) == {у е Q If (х) = <р (х, у)}.
Пример 1. Пусть хе£ь f(x)= max ft(x), где
i s 1:2
A(x) = (x—I)2, fz(x) = (x-j- l)2. Возьмем точку x0 = 0.
Так как f(x) —функция максимума, то (см. пример 2 § 5)
= 8>>’
где R (хо) = {t е 1:21А (хо) == f (Хо)} = 1 : 2. Значит,
-2^ = max {-2g, 2g}.
Здесь ||g||=l. Но в Е\ только два таких направления:
gi+ 1, £г = — !•
Поэтому
-^^-=- + 2 (14.23)
и для g == gi, и для g = g2.
С другой стороны, поскольку f(x)—выпуклая функ-
ция, то (см. (5.11))
f (х) = max [/ (у) + (v (у), х —у)], (14.24)
где v(y)&df(y) (для каждого у берется один o(g) из
W)). Но
f . ( если х<0,
/ W в | (Д если х Q
Поэтому
( {2(я- 1)}» если х<0,
/W | |2 (х + 1)}, если х>0,
и для х = 0 имеем df(O) = [—2, 2].
160 ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА [ГЛ. 1
В формуле (14.24) возьмем v(0) = 0. Очевидно, что
в (14.24) /?(0) = {0}, поэтому max (о (у), g) = 0. От-
У в R (0)
сюда ясно, что формула
= max (v(y),g)
°s уецм
неверна, ибо противоречит (14.23).
В формуле (14.15) будет <3^(хо) = {—2,2}.
§ 15. Дифференцируемость выпуклой функции
1. В настоящем параграфе изучается вопрос о диф-
ференцируемости выпуклой функции, заданной на Еп.
Оказывается, что множество точек, в которых эта функ-
ция имеет дифференциал, достаточно массивно. Вначале
рассмотрим случай, когда п = 1.
Пусть функция f(x) задана на прямой Ei, хоеЕь ’
Пределы
Г+(х,)=а11т «-Щхо+«)-Цхо)]
и
Г_(*о) = lim а~* [f (х0 + а) — f (х0)]
4 7 а->-0
называются соответственно левой й правой производ-
ными функции f(x) в точке xQ. На прямой Ei существует
лишь два направления. Одно из них задается вектором
gi = -|- 1, другое — вектором g2 = —1. Понятно, что
f'+ (х0) == lim а-1 (х0 + agi) — f (х0)] = ,
7 а->+0
f- (Хо) = Йоа’*[/ (Хо) “ Нх° + = ~
Если функция f(x) выпукла, то, как следует из тео-
ремы 4.2, производные по направлениям и
существуют. Точнее, справедлива
Лемма 15.1. Если f(x) — выпуклая функция, задан-
ная на Ех, то в каждой точке x0<=Ei существуют левая
и правая производные, причем
ff (.. \________df (х0) с/ df (хо)
'+(хо)=-а^-« 1-(.хо)^------
еде gi = + 1, — 1.
§ 15]
ДИФФЕРЕНЦИРУЕМОСТЬ ВЫПУКЛОЙ ФУНКЦИИ
151
Приведем неравенства, связывающие левую и пра-
вую производные выпуклой функции.
Лемма 15.2. Пусть f(x) —выпуклая на Ех функция,
х0> xi е Ei, причем Xi > х0. Тогда
f'+ (х0) < (х, - х0)"‘ (f (х,) - f (хо)) < f'_ (х,).
Доказательство. По следствию из теоремы 4.2
4^ = inf a"1 [f (хо + а) - f (х0)].
^l=inf а-1[/(х1-а)-Пг!)\
^2 а>0
где gi = 4-1, gz = — 1.
Полагая а = xi — Хо, получим
f'+ W=< “1 If w - f < - TJT -(*)>
что и требовалось доказать.
Лемма 15.3. Если f(x) — выпуклая функция на Е\
и хое Е\, то
Доказательство. При gi = + 1, gz = — 1
имеем
ff (v\— dfM t _
W l-(,xo)— dgi “T dg2 ~
— max о + max (—max (t» + (—1>)) = 0.
v e df (Хо) V e df (x0) v g= df (Xo)
Выясним теперь основные свойства односторонних
производных.
Теорема 15.1. Если f(x) — выпуклая на Е^ функ-
ция, то ее односторонние производные не убывают. При
этом для всех х^Е\ справедливы равенства
lim f+(t/) = f+(x), lim f'_ (у) = f' (x), (15.1)
lim f'+ (z) = (x), lim f'_ (z) = f'_ (x). (15.2)
2->X-0
Доказательство. Пусть у > x. Из лемм 15.2 и
15.3 вытекают соотношения
Г- W < f'+ (X) < (у - X)-1 (f (у) - / (X)) < f'_ (у) < f'+ (у).
(15.3)
152
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ, I
Отсюда ясно, что функции f'+ (х) и f'_ (х) не убывают.
Из непрерывности функции f(х) следует
Так как по лемме 15.2
при у > t, то
(/(!/) lim f'+(t)
<->х+0 т
(существование предела гарантируется монотонностью
функции f'+ (х)). Поэтому
f'+(x)= lim (у — x)~l(f(y) — f(x))> lim f+(/).
y + x+Q /->x+0
Заменив в последнем пределе t на у, получим оконча-
тельно
f+(x)> lim r+(f/). (15.4)
y->x+0
С другой стороны, как следует из (15.3),
Г+(х)<Г_(1/)<Г+(р),
и потому, переходя к пределам, которые существуют
вследствие монотонности f'+ и f'_, имеем
f+(x)< lim f'_(yX Hm f'+(y). (15.5)
Из (15.4) и (15.5) вытекают равенства (15.1). Анало-
гично устанавливаются и равенства (15.2). Теорема до-
казана.
Как известно, существование производной в некото-
рой точке равносильно (для функции одной переменной)
тому, что правая и левая производные в этой точке сов-
падают (существование односторонних производных сле-
дует из леммы 15.1). Положим
y(x) = f'+(x) — f'_(x}.
В силу леммы 15.3 ф(х)^0 при всех х. Из сказанного
выше следует, что функция f(x) не дифференцируема в
точке хо тогда и только тогда, когда ф (х0) > 0.
§ 16]
ДИФФЕРЕНЦИРУЕМОСТЬ ВЫПУКЛОЙ ФУНКЦИИ
153
Будем говорить, что f(x) не дифференцируема в точ-
ке Хо с точностью до г (где 8 > 0 фиксировано), если
ф(х0)^ в. Геометрически это означает, что разность тан-
генсов углов наклона правой и левой касательных в точ-
ке Хо не меньше в.
Лемма 15.4. На любом ограниченном интервале
(а, Ь) при каждом в > О множество точек, в которых
f(x) не дифференцируема с точностью до е, либо пусто,
либо конечно.
Доказательство. Предположим, что указанное
множество бесконечно. Тогда из его элементов можно
выбрать монотонную последовательность {х*}, сходя-
щуюся к некоторой точке хое[а, £>]. Определенности
ради считаем, что последовательность {х*} убывает.
Тогда, в силу теоремы 15.1,
lim (f' (xj - f'_ (xj) = lim f' (y) — lim f'_ (y) «= 0,
что противоречит неравенству
r+(xft)-f'_(xfc)>8 Vk.
Лемма доказана.
Теорема 15.2. Выпуклая функция f(x), заданная
на Ei, дифференцируема во всех точках £ь за исклю-
чением, быть может, не более чем счетного множества.
Если функция f(x) дифференцируема в некоторой точке
Хо, то и правая, и левая производные непрерывны в
этой точке. В частности, если f(x) дифференцируема на
некотором интервале, то ее производная непрерывна
там.
Доказательство. Положим
Amk m {х @ [— т, т] | ф (х) > fe-1}.
Тогда множество А — {х <= £\ | ф (х) > 0}, состоящее из
всех точек, в которых f(x) не дифференцируема, пред-
ставимо в виде
оо оо
А *= U U Amk.
т*=1 k«l
В силу леммы 15.4 каждое из множеств Атк конечно или
сю
пусто. Поэтому при каждом т множество Лт= U Amk
t-i
154 ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА [ГЛ. 1
являющееся счетным объединением множеств Amk, не
более чем счетно. По тем же причинам множество j
оо >
А = J Ат не более чем счетно.
т—1
Если f(x) дифференцируема в точке хо, Tof+(x0) =
= Г_ (*о)’ и потому все четыре предела, участвующие
в формулировке теоремы 15.1, совпадают. Из этого, в i
частности, следует непрерывность левой и правой про- j
изводных в точке х0. Если f(x) дифференцируема на ин- j
тервале, то ее производная совпадает с правой (или ле- (
вой) производной на всем интервале и потому непре-
рывна. Теорема доказана.
2. Перейдем теперь к общему случаю. Пусть функ-
ция f(x) задана на Еп (п — произвольное натуральное
число). Как известно, функция f(x), определенная на
Еп, называется дифференцируемой в точке х0 е Еп, если •
существует вектор А е Еп, при котором |
lim || х — х0 Г* [f (х) — f (хо) — (Л, х — х0)] = 0 -
Х->Хо 'I
или, что то же самое,
f (х) = f(x0) + (Л, X — Хо) + о( ||х —ХоН). '
При этом вектор Л называется градиентом функции f(x)
в точке хо и обозначается /'(хо). Хорошо известно, что
.....
где
х = (х(1), .... х(п>),
d^t) — частная производная функции f(x) по i-й пере-
менной. Таким образом, из дифференцируемости следует
существование частных производных. Обратное неверно:
из существования частных производных еще не следует
дифференцируемость функции. Как известно из курса
анализа, наличие непрерывных частных' производных
уже влечет дифференцируемость. Покажем, что в случае |
выпуклой фУнкц.ии дифференцируемость равносильна
существованию частных производных. Предварительно
§ 15]
ДИФФЕРЕНЦИРУЕМОСТЬ ВЫПУКЛОЙ ФУНКЦИИ
155
равен-
отметим, что справедливы следующие очевидные
СТВа ’ df (х) df (х) _ df (х) e df (х)
dxw det ’ dx^ d (— ez) ’
где ei — i-й орт пространства Еп.
Теорема 15.3. Пусть f(x)— выпуклая на Еп функ-
ция. Функция f(x) дифференцируема в точке х0&Еп в
том и только в том случае, когда она обладает частными
л df (х0) df (х0)
производными .....
Если f(x) дифференцируема в точке х0, то
#(хо) = {Г(хо)}.
Доказательство. Если функция f(x) дифферен-
цируема, то она обладает частными производными. При
этом для g^En
f (хо + ag) = f (хо) + a (f (х0), g) 4- о (а).
Из леммы 5.3 теперь получаем
df(x0) = {f'(x0)}.
(15.6)
Пусть существуют частные производные , ...
дх[1>
• • •’ • Покажем, что вектор f'(x0) = (, ...
dx[n> г \ dxw
‘ ‘ является субградиентом функции f (х)
в точке х0. Для v = (v(1), .... о|л|)е^(х0) имеем
df (х0) • df (х0) . .___
— /. = _L5..JV — тах (ау>е/)>
dx det tt> <= df (ж»)
^4 _ д/(х0) _
dxw д (— е{) wedf (х0)
(v, ez) = и<г> VZ <= 1 : п,
Таким образом, . и, следовательно,
Г(хо) — субградиент. Более того, df[x0)== {/'(хо)}.
166
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
При всех и е Еп выполняется неравенство
п
ffo + «)>f(xo) + g-^«w.
(15.7)
Здесь и = («<», ..., u<">).
Проверим, что функция f(x) дифференцируема в точ-
ке х0. Рассмотрим векторы gi, gn, gn+i.......g2n, где
gn+l = —ei Vi s 1 : n, gi = ei Vi e 1: n. Положим
( max 0), i s 1: n,
™ (. max (— M(f), 0), i s (n + 1): 2n;
/+ = {ie 1
Тогда
и = X = У uwet 4- У, uwet =•
i = 1 i e IbI_
П 2n tyt
=‘L^i)gi+ Ё
Z-l /-П4-1 Z«1
2n n
Обозначим Х(ы) сумму У zw== У uw. Из определения
сразу следует, что 2иТ(ЛГ” 1- Крометого, [Х(и)]^’г(0>
Z-1
0. Поэтому для любых векторов vi, .... vsn будет
/ 2п \ 2п
f ( У S 1М«)Г1г(<)т (15.8)
М-1 / /-1
Нам понадобятся величины Oz(a), определяемые в точке
xq из равенства
f (хь + agt) = f (Хо) + а + ot (а). (15.9)
Так как f(x) — выпуклая функция, то о,(а)^0. Оценим
теперь величину /(хо + и), считая вектор и отличным от
$ 14 ДИФФЕРЕНЦИРУЕМОСТЬ ВЫПУКЛОЙ ФУНКЦИИ 167
нуля Воспользуемся соотношениями (15.8) при vi =
== х04-Х(и)^' и (15.9) при а = %(«). Имеем
f(Xo + «) = f( Xo + Xz<^) =
\ /
= f 4“ Mw) 2^ 1Л (w)] =
\ /“1 /
- f [Л («)]' zW (хо + л (ц) g,)) <
< £ [шг12U)f (х°+ш =
= («)]* ZU> (f (Хо) + Л («) 4г1 + °1 (Л (и))1 =
= f (Хо) + 2У> 4^- + £ Ot (Л (и)) [Л (а)]-1 (15.10)
г=1 1 1-1
Покажем, что последнее из трех слагаемых полученной
суммы стремится к нулю при ||ы||->-0 быстрее, чем ||и||.
Действительно,
11«Г*£1[Л(И)]-1?%,(Х(«))»
= 2 [Л(и)]-101 (Л(««Hair1?0<
( = 1
2п
Здесь воспользовались очевидным соотношением z(i)
С |«(;)| <||ц|| и неотрицательностью величины oz(%(«)).
Среднее слагаемое рассматриваемой суммы имеет
вид
V-in ^(х0) _у ш df(Xo)
Lz д§1 Lu dxw •
158 ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА [ГЛ. I
Это следует из равенств (15.6) и определения z(/). По-
этому из (15.10) вытекает
п <
/(хо + и)<Нхо) + Уы<г)4^Г- + °(«)- (15.11) ;
Ь дх |
i
Дифференцируемость функции f(x) следует теперь из >
(15.7) и (15.11). Теорема доказана. • |
Теорема 15.4. Выпуклая функция f(x) дифферен-
цируема в точке хо^Еп тогда и только тогда, когда ее Р
субдифференциал df(xo) состоит из единственной точки.
Доказательство. Если функция f(x) дифферен-
цируема, то
<№) = {№)}
состоит из единственной точки. Пусть df(xo) = {v}, u =
= (о(1).. у(п)). Тогда
lim а"1 [f (х0 + ае<) — f (х0)] =
а->+0
= ' =* max (“>» ^) = (р, e/) = v’O, $
оеЧ w&df (хо) Ъ
lim сГ1!/(%о +ае/)“ f (*о)] =
а->-0 (.
“ lim r'[f(xo)-f(xo + P(-ei))] = —!
₽>+о et)
= — max (w, —е{) = — (v, — е{) = о(г).
w е df (Хо)
Таким образом, существуют частные производные
= lim а-1 (х0 + aei) — f (х0)],
dxw а->0
и, как следует из теоремы 15.3, функция f(x) дифферен-
цируема в точке х0. Теорема доказана.
Опишем структуру множества, на котором выпуклая
функция f(x) не дифференцируема. Обозначим это мно-
жество А и рассмотрим пересечение Ат множества А
с открытым кубом
= {х е= Е„ I |x<z> I < m Vi «= 1: п),
где т — натуральное число. Обозначим А^т (k^l:n) |
множество тех точек хеХт, в которых не существует »
§ 151
ДИФФЕРЕНЦИРУЕМОСТЬ ВЫПУКЛОЙ ФУНКЦИИ
159
частная производная . Из теоремы 15.3 следует
Ат == Ajm U ^2/п U • • • U Апт.
Соотношение
оо оо П
А= U Ат= U U Akm
т=1 fe«l
сводит изучение множества А к изучению множества
Акт- Расщепим, в свою очередь, эти множества на про-
сто устроенные части. Рассмотрим правую и левую част-
ные производные f'+k (х0) и f'_k (х0) функции f(x) в точ-
ке хо по k-й переменной. По определению
Гн W= (*• + “»>)-/ (*•)]
Г_. W = Jim a-1 [f (х, + №,) - f (x,)].
Если функция й(а) одной вещественной переменной оп-
ределена соотношением ft(a) = f (хо + авк), то
/«(х,)-Л'+(0), Д,(хо)-Л'.(О).
Из выпуклости f(x) сразу следует выпуклость Я(сс), и
потому по лемме 15.3
f-k (хо) f+k (хо)-
Положим
(хо) ~ f+k (хо) f-k (хо)-
Тогда фл (х0) > 0, причем существование частной произ-
водной эквивалентно равенству ф*(хо)=0. Иными сло-
вами,
Akm = {х <= Жт | фй (х) > 0}.
Положим
Akmi ’ т I *Фй 00 1 1 * °°.
Тогда
оо
Akm= U Akmi-
Структуру множества Akmi проще всего описать, выяс-
нив, как устроено пересечение этого множества с каж-
дой прямой, проходящей в направлении ек. Для этого
160
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. I
рассмотрим гиперплоскость — {х е Еп | (х, ек) а 0} и
пересечение 2ёкт этой гиперплоскости с кубом У£т.
Пусть
х = (х(»....х**-1', О, х<»+«)..
и Пх = {х + Ъвк | — оо < X < оо}— прямая, проходящая
через х в направлении ек. Положим <р(Х) = f(xx), где
хх = х + Хей = (х(1).x(ft-1), X, x(fe+l).х<»>).
Тогда
Ф+ (М = f+k (хх)> Ф_ W = f_ft(xx),
и потому, как нетрудно проверить, пересечение множе-
ства Акт/ с прямой Пх совпадает с совокупностью точек
хх, для которых
Ф'+(А)-Ф/_(А)>Г1.
В то же время пересечение всего куба с прямой
Пх представляет собой интервал {хх11X | < т}. Из лем-
мы 15.4 следует, что множество чисел X из интервала
(—т, т), в которых функция ср (х) не дифференцируема
е точностью до е = i~*, конечно либо пусто. Отсюда
сразу вытекает, что множество точек хх на интервале
{хх| |Х|< т}, в которых
ф'+ т - ф'_ w=w - r.t w > г',
также конечно или пусто. Иными словами, пересечение
множества Akmi с прямой IL для любого x&a^km ко-
нечно или пусто.
Итак, множество Akm представимо в виде счетного
объединения множеств Akmi, пересечение каждого из ко-
торых с любой прямой, параллельной вектору ek, ко-
нечно или пусто. Указанное свойство множеств Akmi по-
казывает, что они в некотором смысле «малы», яв-
ляются разреженными, «тощими».
Совокупность множеств {Akmi | k s 1: n, tn e 1 : oo,
/el:00} является счетной. Поэтому множество А =
П оо оо
"= U U U Akmlточек, в которых функция f (х) не диф-
/?=«1 m-1 Z-l
ференцируема, можно рассматривать как счетное объе-
динение множеств, «малых» в указанном выше смысле.
§ 151
ДИФФЕРЕНЦИРУЕМОСТЬ ВЫПУКЛОЙ ФУНКЦИИ
161
' v 1 »-k ' Qek
TO
Bb/ = (xeE-l max
Счетное объединение «малых» множеств и само «не
слишком велико». В этом смысле совокупность точек,
в которых функция f(x) дифференцируема, достаточно
«массивна».
Отметим еще, что если функция f(x) дифференци-
руема на некотором открытом множестве, то ее гра-
диент непрерывен на этом множестве.
3. Уточним приведенные выше рассуждения для чи-
тателя, знакомого с теорией меры (см., например [85]).
Рассмотрим множества
Bkl = {х <= Еп | f'+k (х) — W > <-1}, k е= 1: п, I е 1: оо.
Поскольку
f/ fv\ _ f' I и == <*) I dl (*) _
= max (v, ek) + max (v, — e4),
v&dito vGdHx)
............ (v,ek)+ max (v, — eA)>Z-1}.
V s df (x) V e d; (x)
Из этого равенства и полунепрерывности сверху ото-
бражения df(x) легко следует замкнутость Вы. Действи-
тельно, пусть Xj&Bkt, Xj-+xQ. Найдем такие векторы
t>, е df (xj и v" е df (х^, чтобы выполнялись соотно-
шения
max (v, = еХ
max (у, — ek\ = (v"., — еХ
V<=df(xf)K Ы
По следствию из теоремы 5.1 отображение df(x) ограни-
чено в окрестности точки х0. Поэтому, не умаляя общно-
сти, считаем, что существуют пределы
o' — lim V/, v" = lim v'!.
/->«> 1 /->oo 1
При этом v's df (x0), v" <= df (x0). Так как
«•O+W'.-O»'-’.
TO
P2X >(v’ + тлаЛ ,(u’ “ +
u or (xo) и & df (xo)
6 В. Ф. Демьянов, Л. В. Васильев
162
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. 1
т. е. Xo^Bki. Таким образом, В*,- — замкнутое и тем бо-
лее измеримое множество. Равенство Akmi = Вы fl
показывает, что и множество Акт1 измеримо. Найдем
его меру. Пусть
Alimi W = Akrnl П Пж Vx е a^km-
Как показано выше, множество Akmt(x) конечно или
пусто, и потому мера рЛлт((х) этого множества равна
нулю. Равенство
pAkmi= $ nAkmi(x)dx,
xkm
восстанавливающее меру Akmi по мере его сечений
Akmi(x), показывает, что и множество Akmi имеет нуле-
вую меру. Так как множество точек недифференцируе-
мости А представимо в виде счетного объединения мно-
жеств Akmi, то и |ъ4 == 0. Таким образом, доказана сле-
дующая
Теорема 15.5. Пусть f(x)—выпуклая на Еп функ-
ция. Тогда f(x) дифференцируема почти всюду на Еп.
4. Теперь можно получить следующий интересный ре-
зультат. Пусть функция f(x) задана на Еп. По тео-
реме 15.5 функция f(x) дифференцируема почти всюду
на Еп. Как и выше, обозначим А множество точек, в
которых функция f(x) не является дифференцируемой.
Теорема 15.6. Имеет место представление
df (х0) = со {z е Еп | z = lim f' (xft),
fe“>oo
Xft->xo, xk& A}. (15.12)
Доказательство. Множество в правой части
(15.12) обозначим В. Включение
Bczdf(x0) ' (15.13)
очевидно из полунепрерывности сверху отображения
df(x), ибо для ХкфА по теореме 15.3 будет df(xk) =
= {f'(xk)}. Установим включение противоположного зна-
ка. Пусть t»edf(x0). Надо показать, что иеВ. Допу-
стим противное. Тогда найдутся такие число а > 0 и
вектор g0<=En, ||goll= 1. что
(u —z, g0)>a>0 VzsB. (15.14)
СОПРЯЖЕННЫЕ ФУНКЦИИ
163
$ 16]
По следствию из теоремы 5.1 отображение df(x) ограни-
чено на любом ограниченном множестве. Поскольку для
х&А будет df(х) = {/'(х)}, а мера множества А равна
нулю, то найдутся последовательность {х*} и точка
zq е В такие, что
xk = x0 + akgk, aft-> + 0,
, , „ (15.15)
х4<£Л, zk — f (x^^zq^B.
Так как v&df (х0), то
f (х) — f (х0)>(о, х — х0) VxгЕп.
Отсюда и из (15.14) при достаточно больших k в силу
ограниченности В (ограниченность В очевидна из
(15.13))
А (aJ s akl (f (*о + akSk) ~ f (*o)) >
> (v, gk) > (z, gk) + 0,5a Vz e B.
В частности, Н(ак) >(z0, g*) + 0,5a. Из (15.15) при до-
статочно больших k имеем
Ма*)>(гъ gft) + 0,25a. (15.16)
Так как {z*} = df(xk), то
f(x) — f (xft) > (zft, x — xk) Ух e £„.
Отсюда
>(-*» «.)•
t. e.
»(“*)> °;' (I (*«+зд.) - f (*«))=
что противоречит (15.16). Итак, ней, т. e. df (x0)c: B.
Отсюда и из (15.16) вытекает утверждение теоремы.
§ 16*. Сопряженные функции
Удобным аппаратом для исследования свойств вы-
пуклых функций и выпуклых множеств являются сопря-
женные функции. Многие изложенные ранее результаты
можно получить на языке этих функций. Ниже приво-
дятся первоначальные сведения из теории сопряженных
функций.
6*
164
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. 1
Выпуклая функция f, определенная на выпуклом мно-
жестве Q cz Еп, называется замкнутой, если ее надгра-
фик
epif = {(X,
является замкнутым множеством. Нетрудно проверить,
что каждая непрерывная выпуклая функция, определен-
ная на замкнутом выпуклом множестве, является замк-
нутой. Обратное, однако, неверно. В частности, замкну-
тая функция может быть определена и на незамкнутом
множестве. В качестве примера приведем функцию
f(x) = tgx, определенную на промежутке [0, л/2). От-
метим, что
lim tgx = + co.
X->Jl/2-0
Как показывает следующая ниже лемма, подобным
свойством обладают все замкнутые функции, определен-
ные на незамкнутом множестве.
Лемма 16.1. -Пусть f — выпуклая замкнутая функ-
ция, определенная на множестве Q, и х — предельная
точка Q, причем хф. Q. Тогда
lim f (у) = + оо.
Доказательство. Предположим, что лемма не-
верна. Тогда найдется последовательность ук -> х, у* е£2,
такая, что для некоторого числа А выполняется неравен-
ство
/(#*)< X \fk.
Это означает, что (%, yfe)eepif. Так как (X, х)
и множество epi f замкнуто, то (%, x)eepif. Отсюда по
определению надграфика получаем x s Q, что противо-
речит условию леммы. S
Задание 16.1 Показать, что выпуклая функция f, определен-
ная на выпуклом множестве Q, замкнута в том и только в том слу-
чае, когда она обладает следующими свойствами: a) f полунепрерыв-
на снизу в каждой точке xeQ, т. е. f (х) < lim f (xfe), если xfe е Q,
х*->х; 6) lim f (у) = +.°°, если x — предельная точка Q, не вхо-
у-*х
дящая в Q.
Напомним, что если Q имеет непустую внутренность, то f непре-
рывна во внутренних точках Q. В граничных же точках замкнутая
функция может иметь разрывы.
Задание 16.2. Привести пример выпуклой незамкнутой функ-
ции, определенной на сегменте [0, 1] czEj.
S 1<я
СОПРЯЖЕННЫЕ ФУНКЦИИ
165
Пусть f — выпуклая функция, определенная на вы-
пуклом множестве й. Множество
.^«{(р, 1) е= Ei X En\(l, x) — n^f(x) VxsQ)
называется опорным множеством функции f. Можно ска-
зать, что элементы опорного множества определяют ли-
нейные функции h(x) = (I, х) — р, не превышающие
функцию f. Отметим, что для каждого субградиента v
функции f в некоторой точке х0 е й найдется число р
такое, что (р, v)^Uf. В самом деле, по определению
субградиента
f(x) — f (х0) > (о, х) — (о, х0),
т. е. при р^(о, хо)—f(x0) выполняется (о, х)—р^
sg:f(x). Это и означает справедливость включения
(р, v)f=Uf.
Установим связь выпуклой замкнутой функции f и
ее опорного множества Uf.
Лемма 16.2. Если f — выпуклая замкнутая функ-
ция, определенная на выпуклом множестве Q cz £\, то
f(x) = sup {(Z, х) — ц) (16.1)
(ц, \
Доказательство. Для любого в >• О рассмотрим
точку (/(х) — е, х) пространства EtXEn. Так как эта
точка не входит в замкнутое множество epi f, то, при-
меняя теорему отделимости, можно указать вектор
(с, й) е £\ X £,,, при котором выполняется неравенство
с (f (х) — в) -J- (й, х) < сЛ + (h, z) V (^, ?) е epi f. (16.2)
Полагая здесь z = х, l = f(x), получим —се < 0, т. е.
с>0. Поэтому из (16.2) при k = f(z) вытекает нера-
венство
f (z) > (— c~'h, х) + f (х) — е + с"1 (й, х) \jz <= й.
Положим —c-lh= lo, f (х) — е 4-с-1 (й, х) — —р0. Тогда
(й, г) > (Zo, z) — ро Vz е й,
т. е. вектор (р0, /0) входит в Uf.B то же время (1о,х) —
— Но = f (х)— 8. Поэтому
sup {(/, х) — р) > (Zo, х) - р0 = f (х) - 8,
168
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
1ГЛ. 1
Ввиду произвольности г получаем sup (/, х) — р >
(ц, DsUf
^/(х). Противоположное неравенство вытекает непо-
средственно из определения опорного множества. Лемма
доказана.
Замечание 1. Если Хо— внутренняя точка мно-
жества й, то найдется такой элемент (р,0> /о) опорного
множества, что /(х0) = (/о, *о) —Цо, т. е. супремум в фор-
муле (16.1) реализуется. Это сразу следует из формулы
(5.13). Если хо — граничная точка й, то такого эле-
мента может и не найтись.
Задание 16.3. Пусть Q = {х = (х(*>, *<2>)s Е2|х<»> О,
О}, / (х) «= — Vх<1)х(2) • Показать, что для точки х» = (1, 0)
не существует такого элемента (|io, lo)eUf, при котором выпол-
няется равенство f(xo) = (/o, Хо)—До.
Для дальнейшего понадобится вычислить супремум
по опорному множеству при любом элементе х е Еп, не
обязательно входящем в й.
Лемма 16.3. Пусть f—выпуклая замкнутая функ-
ция, определенная на выпуклом множестве й. Тогда,
воли х й, то
sup {(/, х) — ц} = + оо.
(ц, l)^Uf
Доказательство. Рассмотрим отдельно два слу-
чая.
1. Пусть х — предельная точка й. Возьмем некоторое
число %. Поскольку, как установлено в лемме 16.1,
lim/(^)== + оо, то найдется выпуклая окрестность V
точки х, для элементов у которой (у г й) выполняется
неравенство /(#)>Л. Возьмем точку у0 е V Q й и рас-
смотрим в пространстве ЕгХ^л отрезок 8 с концами
в точках (X, х) и (%, у). Покажем, что этот отрезок не
пересекается с надграфиком epi f функции /. Действи-
тельно, если (v, »)е 8, то v = X, v = ах + (1 — а)у при
некотором а > 0. Так как х е V, у е V, то и v е V, по-
этому Это означает, что (%, v) ф epi/. Так как
множества 8 и epi / не пересекаются и замкнуты и, кроме
того, отрезок 8 ограничен, то, применяя теорему отде-
лимости, найдем вектор (с, ft) в Е1 %Еп, обладающий
S 161
СОПРЯЖЕННЫЕ ФУНКЦИЙ
16?
следующими свойствами:
cv + (й, z) > сЛ + (й, х) V(y, z)eepif, (16.3)
cv + (й, г) > ск + (й, у) у (v, z)eepif. (16.4)
Полагая в (16.4) z = у, v = f(y), получим cf(y)>ck,
откуда вытекает неравенство с > 0. Полагая в (16.3)
v = f (z), придем к неравенству
f (z) > (— c~lh, z) + к + (с-1й, х) уz s й.
Пусть l0 — —c-'h, — go = к + с-1 (h, х). Тогда f(z)>'
>(/0, z) —цо, т. е. (р.о, /о)<= Uf- В то же время (to, х) —
— р,0 = к. Таким образом,
sup {(/, х) — g) (/о, х) — Ро = А,.
(Н, l)e=Uf
Ввиду произвольности к получаем отсюда, что
sup {(/, х) — р) = + оо.
(ц, l)<=Uf
2. Пусть х^й, где й— замыкание й. Зафиксируем
некоторую точку у е й и рассмотрим отрезок {ах +’
+ (1—а)У1ае:[0,1]} с концами в точках х и у. Так
как х^й, то найдется число аое[О, 1] такое, что точки
ах + (1 — а) у не входят в й при а > ао- Возьмем те-
перь некоторое число к и покажем, что найдется такое
число б, при котором отрезок 8 в пространстве Е\ X Еп
с концами в точках (к, х) и (б, у) не пересекается с над-
графиком epi f функции f. В качестве б можно взять лю-
бое число, меньшее
бо= inf (1 — ос)-1 [/ (ах + (1 — а) у) — аЛ]
0<а<а0
(заметим, что б0 > — оо). Действительно, если 8f|
hepif^=0, то найдется такое аб[0, ао], при котором
ак + (1 — а) б f (ах + (1 — а) у).
Отсюда следует, что б бо. Итак, существует число б,
при котором множества 8 и epi f не пересекаются. При-
меняя теорему отделимости, найдем вектор (с, й)е£1Х
X Еп, обладающий теми свойствами, что
cv 4- (й, z) > ск + (й, х) V (v, z) е epi f, (16.5)
cv + (й, z) > cd + (й, у) V (v, z) <= epi f. (16.6)
168
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Полагая в (16.6) z — y, получим c(v— б)>0. Так как
v — б > О при достаточно больших v, то с > 0. Пусть
1о — —с-Чг, —ро = % х). Тогда, полагая, в (16.5)
v = f(z), получим f(z)>(Z0, z) — go, т. е. (ц, l0)<=Uf.
В то же время (1о,х)— ц — к. Таким образом,
sup^ {(Л х) ~ и} > Л, что ввиду произвольности % и до-
казывает лемму.
Леммы 16.2 и 16.3 показывают, что удобно рассмат-
ривать выпуклые замкнутые функции, определенные на
всем пространстве и принимающие, возможно, значение
4-оо. В самом деле, для таких функций равенство
f (х) = sup {(/, х) — ц} справедливо при всех х.
(н.
Введем соответствующие определения. Функция /,
определенная на всем пространстве Еп и принимающая
значения в полурасширенной числовой прямой (—оо,
.4-со], называется выпуклой, если
f (ах 4- (1 — а) #)< af (х) 4- (1 — а) f (у)
для всех х, у&Еп, ае[0, 1]. Предполагается, что
О - (4~ °°) = + °°- Множество
dom f = {х е Еп | f (х) < 4- 00}
называется эффективным, множеством функции f. Если
dom f Ф 0, то / называется собственной выпуклой функ-
цией. Как и для функций, принимающих конечные зна-
чения, множества
epi/ = {(%,x)eE1X5„lf(x)>M
C/f = {(p, l)^EvXEn\(l, x)-n^f(x) yxe=En}
называются соответственно надграфиком и опорным
множеством функции f. Если надграфик epi/ замкнут,
то функция f называется замкнутой.
Пусть f — выпуклая функция, определенная на мно-
жестве Я и принимающая лишь конечные значения. По-
ложим
(4-00, x^Q.
Тогда dom/ — Q, epi/= epi f, Uj—Uf. Понятно, что
изучение функции f сводится к изучению функции J. Так
СОПРЯЖЕННЫЕ ФУНКЦИИ
169
$ 1Я
как epi J = epi f, то замкнутость функции f эквивалентна
замкнутости функции f.
Всюду ниже в этом параграфе, говоря о функции f,
считаем, не оговаривая этого особо, что f определена на
всем пространстве и принимает, возможно, значение
оо, однако f не равна тождественно + т. е. f — соб-
ственная функция.
Леммы 16.2 и 16.3 выражают основное свойство рас-
сматриваемых функций. Сформулируем его в виде тео-
ремы.
Теорема 16.1. Пусть f — выпуклая замкнутая
функция. Тогда для всех х^Еп выполняется равенство
f (х) = sup {(Z, х) — ц}.
(ц, l)(=Uf
Верно и обратное утверждение, которое приведем в
следующем виде.
Теорема 16.2. Пусть функция f обладает тем свой-
ством, что для некоторого множества U cz Ei^En и всех
хе Еп выполняется равенство
f(x)= sup {(/, х) —р}.
(И. nsU
Тогда функция f выпукла и замкнута.
Доказательство. 1. Функция f выпукла. Дей-
ствительно, если х, у е Еп, а е [0,1], то
f (ах 4- (1 — а) у) =
= sup {(/, ах4-(1 — а) у) — р}==
(и, 1)&и
= sup {а[(/, х) — р] + (1 — а)[(/, у) — р]} <
(ц, 1)&U
<а[ sup {(/, х) — р}] +
(ц, 1)<=и
4-(1—а)[ sup {(/, у) — p}] = af(x)4-(l — a)f(y).
(Ц, D&U
2. Функция f замкнута. Для каждого элемента (р, /)
множества U рассмотрим подмножество
= {(А, х) е £, X Еп | (/, х) - Л < р)
пространства EiX,En. Понятно, что ^/ — замкнутое
множество (на самом деле — полупространство^.
170
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
Покажем справедливость равенства
epif = Л (16.7)
(Ц, 1)еУ
Из этого равенства и будет следовать справедливость
теоремы, ибо пересечение замкнутых множеств замкнуто.
Перейдем к доказательству (16.7). Пусть (X, х)е
е epi f и (р, /) <= U. Тогда
X / (х) (/, х) — р Vх s -Ей,
откуда вытекает включение (X, х)еЖц|. Так как
(X, х) — произвольный элемент epi/, то epi/cz^gz. Так
как (р, /)—произвольный элемент U, то
epi f <= Л
(ц, 1)&U
Пусть теперь (Хо, х0)е^р.( при всех (р,/)<=£/. Тогда
Хо > sup {(/, х) — р) = f (х0)
(и, 1)^и
и, следовательно, (Хо, х0) е epi f. Теорема доказана.
Задание 16.4. Пусть множество U <z. Ei X Еп обладает тем
свойством, что f (х) =« sup {(/, х) — р}. Показать, что в этом
(ц, ПеО
случае выпуклая замкнутая оболочка U совпадает с опорным мно-
жеством Uf функции f.
Перейдем к определению сопряженной функции.
Предварительно докажем следующую лемму.
Лемма 16.4. Множество U в пространстве Е\У^Еп
является надграфиком некоторой выпуклой замкнутой
функции f в том и только в том случае, когда U непусто,
выпукло, замкнуто, с каждой своей точкой (X, х) содер-
жит «вертикальный» луч {(X', х) | X' X} и, кроме того,
не содержит вертикальных прямых {(X, х) | — оо < X <
< + При этом для всех хеЕ„ выполняется равен-
ство
/ (х) = inf {X | (X, х) е £/}. (16.8)
(Как обычно, считаем, что inf пустого множества равен
гЬ °°-)
Доказательство. То обстоятельство, что над-
график epi f выпуклой замкнутой функции f обладает
указанными в лемме свойствами, очевидно. Пусть теперь
множество Ц обладает этими свойствами. Определим
СОПРЯЖЕННЫЕ ФУНКЦИИ
171
функцию f формулой (16.8). Так как U не содержит
вертикальных прямых, то f(x)> — оо при всех х. Не-
посредственно проверяется, что надграфик epi f совпа-
дает с U. При этом эффективное множество dom f совпа-
дает с совокупностью таких х<=Еп, что прямая {Хх|%®
е(—оо,4- °0)} пересекает множество U. Поэтому из
непустоты U следует, что dom f 0. Из выпуклости
и замкнутости множества U = epi f вытекает выпуклость
и замкнутость функции f. Лемма доказана.
С каждой выпуклой замкнутой функцией f связано
два множества — надграфик epi f и опорное множество
Uf = {(и, I) еX£„| f (х)>(Z, х)-ц vxs£„}.
Непосредственно из определения следует, что множество
Uf выпукло и замкнуто. В силу теоремы 16.1 это множе-
ство непусто. Если (р, Z)eZ/f, р' р, то и (ц',1)еУ|.
Кроме того, Uf не содержит вертикальных прямых. Дей-
ствительно, если Хо s dom f и (р, /) s Uf, то р (Z, х0) —
— f(xo)>—оо. Как следует из леммы 16.4, опорное
множество Uf является надграфиком некоторой выпук-
лой замкнутой функции. Эта функция называется со-
пряженной к f и обозначается f*. Итак, сопряженная
функция f* определяется равенством
epir = £7f. (16.9)
Приведем явное выражение этой функции. Используя
формулу (16.8), имеем
f(Z) = inf{p|(p,z)<=t/f} =
= inf {р | (/, х) — р < f (х) ух е Еп} =
= inf{p|p>(/, х) — / (х) ух<=Еп}.
Если множество чисел {(Z, х) — f(x) |х е Еп} ограничено
сверху, то f* (Z) = sup [(Z, х) — f (х)]. В противном случае
множество {p|p^(Z,х) — f(x) УхеЕ„) пусто и потому
inf{p|p>(Z, х) — f(x) ух<=Еп} =
= 4- оо = sup {(Z, х) — f(x)| х е= £„}.
Таким образом, во всех случаях справедливо равенство
Г(0*== sup [(Z, х) - f (x)]. (16.10)
172
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. X
Непосредственно из (16.10) вытекает следующее ут-
верждение (неравенство Юнга*)); для любых х, 1еЕп
справедливо соотношение
(l,x)^f(x) + f*(l).
Так как функция f* выпукла и замкнута, то имеет смысл
говорить о сопряженной к ней функции, которая обозна-
чается символом /** и называется второй сопряженной
к f. Одно из основных утверждений теории сопряженных
функций заключено в следующей теореме, называемой
обычно теоремой Фенхеля — Моро.
Теорема 16.3. Если f— выпуклая замкнутая функ-
ция, то f** = f.
Доказательство. Пусть (ц.', l')sUf. Тогда
х) — f (х) ц' при всех х е Еп и потому f* (I') =
sup [(/', x) — f (x)] p'. Отсюда следует, что
Г (X)- sup [(/, X) - Г (01 > (/', X) - Г (П > (/', X) - [Г.
Привлекая теорему 16.1, имеем
f*(x)> sup [(/', x) — p'] ™ f (x).
С другой стороны, как непосредственно следует из нера-
венства Юнга,
Г(Х)= sup [(/,x)-f(/)]<f(x).
гав„
Теорема доказана.
Замечание 2. Из доказанной теоремы и (16.9) вы-
текает, что
t/f. =— epi /** = epi f.
Таким образом, если U — множество в X Еп, удовлет-
воряющее условиям леммы 16.4, то его можно тракто-
вать двояко: либо как надграфик некоторой выпуклой
замкнутой функции f, либо как опорное множество дру-
гой выпуклой замкнутой функции f*. При этом по мно-
жеству U определяется сопряженное ему множество V,
*) Иногда это неравенство называют неравенством Фенхеля.
СОПРЯЖЕННЫЕ ФУНКЦИИ
173
$ 1<я
которое является опорным к f и одновременно надграфи-
ком f*. Можно сказать, что в некотором смысле теория
выпуклых замкнутых функций совпадает с теорией неко-
торых специальных выпуклых множеств, а именно мно-
жеств, описанных в лемме 16.4.
Замечание 3. Пусть f — произвольная, вообще го-
воря, невыпуклая и незамкнутая функция, определенная
на Еп и принимающая значения в (—оо, Н~оо). Фор-
мула (16.10) определяет функцию /*, которая и в этом
случае называется сопряженной к f. Положим
U = {(р, х) е £[ X Еп\х е dom f, n = f (х)}.
Так как f*(/) = sup [(/, х) — р], то в силу теоремы 16.2
(ц,
f* является выпуклой замкнутой функцией и в данном
случае. Легко проверить, что функция f** совпадает в
рассматриваемом случае с «замкнутым овыпуклением»
функции f, а именно с наибольшей выпуклой функцией,
не превышающей f. Иными словами, надграфик epi /**
функции f** есть выпуклая замкнутая оболочка надгра-
фика epi / = {(х, 1) | Л > f (х)} функции f.
Приведем несколько примеров.
1. Пусть f—постоянная функция, f(x) = c для всех
х <= Еп. Тогда
Г (/) = sup 1(/, х) - f (х)] =
*^Еп
ги х 1 ( — С> /“О»
= sup [(/, Х)-С] = ] ’
(4-00, Z^=0.
В частности, если f = 0, то
1 v' (4-00,
2. Пусть f — линейная функция, f(x) = (h, х) для
х е= Еп. Тогда
Г (0 = sup [(/, х) — (ft, х)] «=
п
= sup[(/-ft,x)] = f °’ '==*’
t “F оо, • h*
174 ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА (ГЛ. 1
3. Пусть U — выпуклое замкнутое подмножество про-
странства Еп. Введем в рассмотрение следующие две
функции, связанные с U:
( 0, xe=U,
Мх)=1+», хфи,
Рц W = sup (/, х).
1&U
Обычно би называется индикаторной функцией множе-
ства U, а Ри — опорной функцией этого множества. По-
нятно, что бу и Рц — выпуклые замкнутые функции.
Найдем
бу (I) = sup [(/, х) — bv (х)] = sup (Z, х) — Ру (/).
Таким образом, В силу теоремы 16.3
Задание 16.5. Рассмотрим следующие выпуклые замкнутые
функции, определенные на £i: fi(x)== (Р > 1),
е / ч f — 0,5 — In %, х > 0,
,,м-1 +<». ,<0.
Показать, что
1 In 1 -1, />о,
0, Z = 0.
+ °°> КО,
й=г 1111’, где р"‘4<7_1 = 1,
/з(0 = (3(- ~ °>б -ln(-Z), КО,
4-00, Z>0.
Сопряженные функции представляют собой удобный
аппарат для изучения выпуклых функций. На их языке,
в частности, удобно изучать субдифференциалы. При
этом основную роль играет следующее утверждение. ]
Теорема 16.4. Пусть f — выпуклая замкнутая функ-
ция, хо, 1о е Еп. Следующие условия эквивалентны:
a) l0<=df(x0)-,
б) хое<Э/*(/о);
в) (/о, Хо) = /(х0) + /*(/о)
(соотношение в) показывает, что на элементах xq и /о Я
в неравенстве Юнга реализуется равенство}, *
СОПРЯЖЕННЫЕ ФУНКЦИИ
175
5 Ifl
Доказательство. Пусть lo&df(xo). Тогда по
определению субградиента имеем
(/о. хо) — f (х0) > (/, х) — f (х).
Отсюда следует, что
Г (/) = sup [(/, х) — f (х)] = (/о, Хо) - f (х0).
Наоборот, равенство /*(/) = (/о. х0) —/(х0) влечет соот-
ношение (/о,хо) — f(x0)X/,x) — f(x). Это означает эк-
вивалентность утверждений а) ив). Рассуждая таким
же образом относительно функции /*, получим, что вклю-
чение хо е df* (/о) равносильно равенству
Г(хо) = (/о,Хо)-Г(/о).
Поскольку в силу теоремы 16.3 f** = f, то условия б)
и в) тоже эквивалентны. Теорема доказана.
В терминах сопряженных функций удобно формули-
ровать экстремальные свойства выпуклой замкнутой
функции f. Отметим прежде всего, что
Г (0) = sup (— f (х)) = — inf f (х).
п п
Таким образом,
inf f(x) = -m
Отсюда следует, что f ограничена снизу в том и только
в том случае, когда 0 е dom f*. Пусть
& = {х е= Еп | f (х) = - Г (0)} = {х е Еп | f (х) - inf f (у)}
УеЕп
— множество минимумов функции f.
Соотношение хе® равносильно тому, что для пары
элементов х, 0 реализуется равенство в неравенстве
O«(x,O) = f(x) + f(O).
Поэтому, как следует из теоремы 16.4, соотношение
хе® равносильно включению ®edf(x), и мы прихо-
дим к известному условию минимума (см. § 6).
176
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[ГЛ. I
С другой стороны, в силу той же теоремы соотноше-
ния Oedf(x) и xedf*(0) равносильны. Следовательно,
множество минимумов Ф выражается через сопряжен-
ную функцию /• следующим образом:
Отсюда следует, в частности, что функция f достигает
минимума в том и только в том случае, когда сопряжен-
ная функция f* имеет непустой субдифференциал в нуле
(это можно гарантировать, например, в том случае,
когда 0 — внутренняя точка эффективного множества
dom /*).
Дальнейшие применения сопряженных функций осно-
ваны на теоремах, позволяющих вычислять сопряженные
функции от суммы, произведения на число, максимума
выпуклых замкнутых функций и т. п. При этом прихо-
дится рассматривать не обязательно замкнутые функ-
ции, а также функции, принимающие, возможно, значе-
ние — оо. С помощью указанных теорем на языке сопря-
женных функций можно изучать практически все задачи
выпуклого анализа. Проиллюстрируем это на примере
условного субдифференциала.
Пусть f— выпуклая замкнутая функция и Q — вы-
пуклое замкнутое множество, содержащееся в domf.
Рассмотрим индикаторную функцию ба множества Q
А , х f °> хе Q,
а Х I + оо, X(£Q,
и положим fi = f -|- ба. Понятно, что
( f (х), х е Q,
( + оо, х 9= Q,
т. е. dom fi = й. Вычисление условного субдифферен-
циала функции f на множестве Q сводится поэтому к
вычислению обычного субдифференциала суммы fa =
= f 4- ба, которое можно провести, используя технику
сопряженных функций.
Подробное изложение многих результатов выпуклого
анализа на основе теории сопряженных функций содер-
жится в книге Р. Рокафеллара [НО], а также в работах
[57, 76].
ВЫЧИСЛЕНИЕ в-СУБГРАДИЕНТОВ
177
§ 17. Вычисление е-субградиентов
некоторых классов выпуклых функций
Вычисление всего множества dgf(x), е > 0, — задача,
несомненно, очень трудная, ибо, в силу определения
def(x), для этого необходима информация о глобаль-
ном поведении функции f(x) на всем пространстве Еп.
Что же касается вычисления отдельных е-субградиентов
функции /(х), то, вообще говоря, эта задача более про-
стая, чем вычисление субградиентов функции f(x), по-
скольку df (x)cz def(x) и множество def(x) может ока-
заться богаче, чем df(x). Но и она достаточно трудная,
ибо опять же требует знания поведения функции f(x)
на всем пространстве Еп. Ниже будет показано, как вы-
числять е-субградиенты сильно выпуклых гладких функ-
ций и функций максимума сильно выпуклых гладких
функций.
Лемма 17.1. Пусть функция f(x) сильно выпукла
на Еп с константой сильной выпуклости tn и пусть е 0.
Справедливо включение
df(x) + S2^(&)cdef(x), (17.1)
где
Se(0) = {OeE„|||p||<d}, 6>о.
Доказательство. Пусть и(хо)е df(x0), геЕ„.
Получим условия, при которых
(ц (х0) + г) г dj (х0). (17.2)
В силу определения def(x0) для того, чтобы выполня-
лось (17.2), необходимо и достаточно, чтобы
f(2)-f(x0)>
> (и (Хо), z — Хо) + (г, z — х0) — е s A (г) У/z <= Еп. (17.3)
Так как функция /(х) сильно выпукла на Еп, то (см.
(9.24))
— f (хо) > (»(х0), z — х0) + m || z — х0 IP = В (z) \/z^ Еп.
Отсюда вытекает, что (17.3) справедливо тогда, когда
Л(г)<В(г) Vze=£„, (17.4)
т. е. когда
пг||г — х0If2>(r, z — х0) — е VzЕп.
178
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
[гл. I
Перепишем последнее неравенство следующим образом:
h (г, z) = (г, z — х0) — т || z — х0 II2 < е Vz е Еп.
Теперь видно, что (17.4) будет выполнено, если
max h (г, z) е. (17.5)
геВп
Найдем max h (г, z). Для этого приравняем нулю про-
zeE„
изводную функции h(r, z) по z. Имеем г — 2т (z— х0)==
= ®. Следовательно, (z— х0) = г-2~'т~1. Поэтому
max h(r, z) = ||r II2 • 4-1/п-1. Отсюда ясно, что неравен-
zeE„
ство
|| г || < 2 а/ып
влечет за собой последовательно (17.5), (17.4), (17.3) и
(17.2). Таким образом, включение (17.1) доказано.
Из леммы 17.1 следует, что у сильно выпуклой функ-
ции f(x) любой субградиент и(х) е df (х) вместе со своей
' е-субдиф-
окрестностью радиуса 2^мп принадлежит
ференциалу def(x).
Следствие 1. Пусть х, g<=E„, ||g||= 1.
df <х) 4- 9 л/^7 def (х)
-^- + 2д/ет <—§£-•
Тогда
Действительно,
тах (о, g)> max (a, g)==
°g oeag f W vedf M+52^8Й7 ®
= max (v, g) + max (v, g) = Д^-4-2а/ъгп.
vedf(x) veS /_(©)
2-yem
Следствие 2. Пусть f(x) = 0,5(Ax, х) + (а, x), где
a^En, A — n X п-матрица, причем матрица А симмет-
рична, положительно определена и m — ее минимальное
собственное число. Тогда
(2Ах + а + г) <= def (х) Vr е S2 (0).
Лемма 17.2. Пусть функция f(x) дифференцируема
на Еп и ее производная f'(x) удовлетворяет на Еп усло-
вию Липшица с константой L < оо, т. е.
ИШ-Г(х)1|<и</-х11 Vx,ge£4.
ВЫЧИСЛЕНИЕ B-СУБГРАДИЕНТОВ
179
|«1
Тогда
f(y)<f(x) + (f'(x), y~x) + 0,5L\\y — х|р Vx, t/6=£„.
Доказательство. Для гладкой функции f(x)
справедливо разложение
1
f (У) = f W + J (Г (x + t(y — х)), у - x)dt.
о
Отсюда
f(y)-f W ~ У — х) =
1
= J (f'(x 4-/{if — x)) — f (х), y — x)dt^
О
1
< $ Ilf'(х-Н(у — *)) — f'(x)Il-Ill/ — x||d/<
О J
<£ № - х|р J tdt = 0,5L ||у - х|р. В
о
Пусть функция f(x) сильно выпукла и дифференци-
руема на Еп и ее производная f'(x) удовлетворяет на Еп
условию Липшица, т — константа сильной выпуклости
функции f(x), L — константа Липшица производной
функции f(x). Положим
vo} == (К(хо + Ч) “ fv(О) • А"*’ 1 е 1 : п> (17.6)
где ei — i-й координатный орт, h > 0, v 0 — точность
вычисления функции f (х), т. е.
f (х) — v < fv (х) < f (х) + V.
Лемма 17.3. Деды
0,5L/i + h~l • 2v < 2 , (17.7)
то вектор v0=*(y^, .... у*п)) с координатами (17.6) яв-
ляется Е-субградиентом функции f(x) в точке Xq, т. в.
Vosdef(xo).
180 ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА [ГЛ. I
Доказательство. Из леммы 17.2 следует
| f (х + Дх) — f (х) — (/' (х), Дх) | < 0.5L || Дх II2 Vx, Дх<= Еп.
(17.8)
Пусть Г(хо) = (-^тг-............) — градиент функ-
ции f (х) в точке х0. Учитывая, что
^ = (Г(хо),е/) V/ei:n,
оценим | и(0° — - I • Имеем (см. (17.6))
I и дх'11 |
|(fv (хо + het) - fv (Хо)) h~x - (Г (Хо), et) | <
<1 f (х0 + het} — f (х0) — h (f' (Xo), et) |Л-1 + 2vA-1.
Отсюда, согласно (17.8), получаем
(г) _ д[(х^_I 0 5Lh 2 A-i
0 дх'1' I
Поэтому в силу (Г7.7)
II »о - f' (хо) II < (0,5L/i + 2vA-1)2 = _ ___
= (0,5Lh + 2vh~l)^/n < 2 Vет.
Теперь из леммы 17.1-вытекает, что vosdef(xo). Лемма
доказана.
Таким образом, в лемме 17.2 дается способ построе-
ния е-субградиента функции f(x) в точке хо при исполь-
зовании приближенных значений функции f(x) в точках
Хо и хо + hei, i е 1 :п. Отметим, что конструкция, опи-
санная в лемме 17.2, весьма часто употребляется во мно-
гих практических вычислениях, когда нахождение ана-
литического вида градиента функции f(x) оказывается
сложным.
Остановимся теперь на вопросе вычисления е-субгра-
диента функции максимума выпуклых функций. Пусть
f (х) = max <р(х, у), (17.9)
где GczEp — замкнутое ограниченное множество, функ-
ция ф(х,у) непрерывна вместе с на Eny^G и
выпукла по х на Еп при каждом y^G.
$ Ifl
ВЫЧИСЛЕНИЕ в-СУБГРАДИЕНТОВ
181
Введем обозначения:
R^x) = {y^G\f(x) — ф(х,1/)<е), е>0, 7?(х) = Я0(х),
у (х) е R (х), уй (х) 6= /?е (х),
S’sp (х) = со {du<p (х, у) | у е /?е (х)},
в > О, ц > О, S’ (х) — S’oo (х).
Известно (см. § 5), что df(x) = S’(x). Поэтому, если
экстремальная задача max <р (х, у) является достаточно
сложной, то для вычисления функции f(x) требуется
бесконечный процесс последовательных приближений.
Тем более это касается вычисления субградиентов функ-
ции f(x), поскольку для нахождения а<||>^-^ в общем
случае также требуется бесконечный процесс последова-
тельных приближений.
Лемма 17.4. Справедливо включение
^eil(x)c=de+llf(x) Vxe=E„, Ve>0, ц>0. (17.10)
Доказательство. Зафиксируем 8^0, ц 0,
хое£„. Пусть уе(х0)е Re(x0), т. е. <р (х0, у, (х0)) >
>f(xo)— в и Оц(х0)уе(х0))е<Э1Лф(х0,уе(х0)).
Нужно показать, что
/ (г) — f (х0) > (Цц (х0, уе (х0)), г — х0) — (в 4- ц) Vz е Еп.
Используя определения f(x) и дцф(х, у), получаем
/ (z) — f (х0) > ф (г, у (z)) — ф (х0, у г (Хо)) — 8 >
> ф (Z, у г (х0)) — Ф (х0, Уе (х0)) — 8 >
> (Рц (Хо, Уь (Хо)), z — х0) — ц — 8 Vz е= Е„.
Лемма доказана.
Из лемм 17.2 и 17.3 вытекает следующий способ вы-
числения (в 4-р)-субградиентов функции f(x), опреде-
ляемой соотношением (17.9). Зафиксируем е > 0, ц>0
и х0. Найдем t/e(xo)e Re(x0). Для этого достаточно ре-
шить задачу максимизации функции ф(х0, у) по у на G
с точностью е, что в общем-то может быть осуществлено
за конечное число шагов некоторой бесконечной про-
цедуры вычисления значения f(xo).
182
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
(ГЛ. 1
Построим вектор и0 — (pw, ...» о^п)) с компонентами
°о ’ = h~l [Vv (хо + het, уе (х0)) - <pv (х0, у, (х0))], /«=!:„.
(17.11)
Теорема 17.1. Предположим, что функция у(х,у)
сильно выпукла по х на Еп при каждом y^G с кон-
стантой сильной выпуклости m и что
LЦ х _ х,Ц
II дх дх || 11 "
Vx е Еп, Vx' е Sh (х), у у е G.
Если
0,5Lh + 2vh 1 2 V цтп 1,
то для вектора vo с компонентами (17.11) справедливо
соотношение
v0 de+llf (х0). (17.12)
Доказательство. Действительно, в силу лем-
мы 17.3 вектор и0 е (х0, г/е (х0)), откуда, на основа-
нии леммы 17.4, следует (17.12).
ГЛАВА II
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
§ 1. Определение и примеры
квазидифференцируемых функций
1. В гл. I мы познакомились с рядом негладких
функций. Подробно были изучены выпуклые функции.
В частности, было установлено, что если f(x)—конечная
выпуклая на выпуклом открытом множестве S cz Еп
функция, то она дифференцируема по направлениям в
любой точке хо S, причем
= max (v,g), (1.1)
oedf(x)
где df(x0) — субдифференциал функции f(x) в точке xq.
Множество df(x0)c.En является выпуклым компактом.
В § 14 гл. I при некоторых предположениях была
установлена дифференцируемость по направлениям
функции супремума и формула (см. замечание 2 § 14
гл. I)
max (v, g), (1.2)
v&df (Xo)
где df(xQ) = co5^(xo)cz En — выпуклый компакт. Это
множество df(xo) будем тоже называть субдифференциа-
лом функции f (х) в точке хо.
Таким образом, с каждой точкой х0 у функции f(x),
являющейся выпуклой функцией или функцией супре-
мума, связано множество df(x0) — субдифференциал.
При этом оказывается (для выпуклой функции это было
установлено в гл. I, но справедливо также и для функ-
ции супремума), что:
1. Производная по направлениям выражается с по-
мощью df(x0) по формулам (1.1) и (1.2).
2. Необходимое условие минимума на Еп имеет вид
0е5/(х*), (1.3)
где х* —точка минимума f(x) на Еп,
184
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
[ГЛ. П
3. Если O^=df(xo), то направление
g(x0) = — v(x0) 1|о(хо)1Г1,
где || о (хо) 11 = min || v ||, является направлением наиско-
оед! (Хо)
рейшего спуска функции f(x) в точке х0.
В следующих главах будет показано, как можно ис-
пользовать направление наискорейшего спуска для по-
строения численных методов для минимизации f(x).
Отсюда видно, что понятие субдифференциала по-
лезно для исследования функций, в частности для реше-
ния задач оптимизации.
Эти соображения привели к попыткам найти более
широкий класс функций, для которых можно было бы
построить нечто, аналогичное субдифференциалу. Среди
этих попыток следует выделить работы Ф. Кларка [133],
Б.Н. Пшеничного [104], Н. 3. Шора [126]. Еще в мо-
нографии [103] Б. Н. Пшеничный предложил рассмат-
ривать функции (он назвал их квазидифференцируе-
мыми), для которых в каждой точке хо существует мно-
жество df(x0) такое, что производная по направлению
вычисляется по формуле (1.1). Пример выпуклых функ-
ций показывает, что класс таких функций не является
линейным пространством (уже функция ft(x) =—f(x)
не является квазидифференцируемой по Пшеничному).
Ф. Кларком [133] было введено понятие верхней суб-
производной. Пусть f(x) — непрерывная в окрестности
Хо функция. Положим
5C[f (Хо) — f (х' 4- ggr) — f (х')
а-»+0
5g
а
Эту величину, если она существует и конечна, назовем
верхней субпроизводной (или производной Кларка)
функции f (х) в точке хо по направлению g и будем го*
ворить, что функция f(x) дифференцируема по Кларку
в точке Хо-
Было установлено, что если функция f(x) липшицева
в окрестности точки х0, то она дифференцируема по
Кларку в точке Хо, причем существует такой выпуклый
компакт dcif(xo)c: Еп, что
5С1/ (х0)
~ дд -= тах
vg oeaciHx»)
§ 1] ОПРЕДЕЛЕНИЕ КВАЗИДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ 185
Множество dcif(Xo) называется субдифференциалом
Кларка. A(f)c:S обозначим множество точек, в которых
функция f(x) дифференцируема. Ф. Кларк [133] пока-
зал, что
дс1/(х0) = со {о | 3 {xft}: xft->x0, xk(=Mf), f'(xk)-+v}.
(1.3)
При этом, если S = Еп, то для того, чтобы точка
была точкой минимума функции f(x) на Еп, не-
обходимо, чтобы
Ое<Эс/(х*). (1.4)
Субдифференциал Кларка обладает рядом важных и
интересных свойств (см. обзор [165], а также работы
[9,65,136,140]).
Пример 1. Пусть х = (х('>,х(2>)е£2, х2 = 0 =
= (0, 0). Рассмотрим функции
А (х) = | х<‘> | +1 х® |, f2 (х) = | х® | -1 х® |,
А (х) = -1 х® I - I X® I, А (х) = — | X® I + I X® I,
f8 (х) = max {f2 (х), А(х)}.
Нетрудно показать, что для всех функций Д(х), te 1:5,
справедливо следующее свойство: плоскость Ё2 можно
разбить на четыре части, в каждой из которых функция
А(х) совпадает с одной из функций:
х® + х®, X®—X®, — х® + х®, — X® — X®.
Так, для функции fi (х) будет
fl (х) = •
Z X® + X®,
х® - х®,
- X® 4- X®,
к- х®-х®,
если х®; &.0,
если х®; >0,
если х®« S0,
если х®« so,
х®>0,
х®<0,
х®>0,
х® < 0.
Поэтому из (1.3) заключаем, что
Mi(xo) = co{(l,l), (1,-1), (-1,1) (-1,-1)} VZ<= 1:5.
В точке хо = О для всех функций Д(х), ie 1:5, вы-
полнено необходимое условие минимума (1.4), хотя точ-
ка х0 является точкой минимума только для функций
и(х) и /5(х).
186
КВАЗИДИФФЕРЕНЦИРУЕМЫЁ ФУНКЦИИ
(ГЛ. II
Отметим, кроме того, что субдифференциал Кларка
не годится ни для вычисления производных по направ-
лениям (ибо производная Кларка не всегда равна про-
изводной по направлению), ни для нахождения направ-
ления наискорейшего спуска. Так, даже для вогнутой
на Еп функции (см. п. 4 § 5 гл. I) оказывается, что
dci/(X0) = df(x0), но
= min (v, g) = min (v, g),
g vs-дЦх^ osdcif(*o)
т. e. уже не имеет места формула вида (1.1).
В настоящей главе изучен класс функций не такой
обширный, как класс липшицевых функций, однако до-
статочно богатый и обладающий «хорошими» свой-
ствами.
2. Пусть на открытом множестве ScE„ задана ко-
нечная функция f(x). Будем говорить, что функция f(x)
квазидифференцируема в точке х0 s S, если она диффе-
ренцируема в точке хо по любому направлению
если существуют выпуклые компакты df(x0)cz Еп и
df(xo)czEn такие, что
нв lim а-‘ [f (хо + ag) - f (х0)] =
а->+о
= max (о, g) + min (w, g). (1.5)
psaf(xo) a>e5f(xo)
Пару множеств
&>f (*o) = Pf (xp), 5Hx7)]
назовем квазидифференциалом (КВД) функции f(x)
в точке х0, а множества df(x0) и df(x0) — соответственно
субдифференциалом и супердифференциалом функции
/(х) в точке хо.
Из формулы (1.5) видно, что КВД определяется не-
однозначно: пара множеств
А (хо) = [#(хо) + В, дГМ - В],
где ВаЕп—произвольный выпуклый компакт, тоже
является квазидифференциалом.
i Л
ОПРЕДЕЛЕНИЕ КВАЗИДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ 187
Если среди квазидифференциалов функции f(x) в
точке Хо есть элемент вида
= WWff(xo), 0],
то функцию /(х) будем называть субдифференцируемой
в точке хо. Аналогично, если среди квазидифференциа-
лов функции f(x) в точке хо есть элемент вида
0f(xo) = [{O}. Msfo, W7)L
то функцию f(x) будем называть супердифференцируе-
мой в точке х0.
Пусть QcS. Если функция f(x) квазидифференци-
руема в каждой точке Хо е й, то она называется квази-
дифференцируемой на множестве й.
Приведем простейшие примеры квазидифференцируе-
мых функций.
Пример 2. Пусть функция f(x) непрерывно диф-
ференцируема на S с£„ и Хо е S. Поскольку
^ = (/'(Хо), g),
то ясно, что f(x) является квазидифференцирумой функ-
цией на S, причем в качестве КВД функции /(х) в точке
хо можно взять пару множеств
0П*о) = [Г(хо),
т. е.
df(x0) = {r(x0)}, dfto) = {0}.
Очевидно, что пара множеств
[О, /'(хо)]
тоже является КВД функции f (х) в точке хо.
Таким образом, функция f(x), дифференцируемая в
точке хо, является и субдифференцируемой, и супердиф-
ференцируемой в этой точке.
Пример 3. Пусть f(x)—конечная выпуклая на вы-
пуклом открытом множестве S с Еп функция, хо е S.
рем^З^^ диФФеРендиРУема по направлениям. По тео*
= max (v, g),
Где df (х0) s {(, s । _ f (Xo) (0> x _ Xo) yx e
188 КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ [ГЛ. Ц
Отсюда ясно, что функция f(x) является квазидиф-
ференцируемой в точке хо, причем в качестве КВД
можно взять
^/(х0) = [5/(х0), 0],
т. е. df(x0) = df(xQ), dfM = {0}.
Поскольку df(x0) = {()}, то выпуклая функция суб-
дифференцируема в точке хо (и на S).
Пример 4. Пусть f(x)—конечная вогнутая на вы-
пуклом открытом множестве S с Еп функция и
Функция f(x) дифференцируема в точке х0 по направле-
ниям. В п. 4 § 5 гл. I было показано, что
== min (w, g),
& w&df (ха)
где
df (x0) = {w<=En\f(x) — f (x0) < (w, x — xo) Vx e S).
Отсюда очевидно, что функция f(x) квазидифферен-
цируема в точке х0, причем в качестве КВД можно взять
0f(xo) = [®, WT)J.
Так как здесь df(xo) = {<0}, то вогнутая функция су-
пердифференцируема в точке хо(и на S).
Пример 5. Пусть
f(x)= sup <р (х, у),
y^G
где х е ЕПу у&Ер, G cz Ер — произвольное множество.
Семейства функций qp(x, у) и фх(х, у), где y^G> равно-
степенно непрерывны по х в точке хо- Также предпола-
гается, что
|ф(*о, #)1<к< ОО, I <pi(x0> у) К К < оо Vy«=G.
Как показано в теореме 14.1 гл. I, функция f(x) суб-
дифференцируема, а тогда она тем более квазидиффе-
ренцируема. В качестве ее КВД можно взять пару мно-
жеств
0f(xo) = [co^(xo), {0}],
где 3^(х0) определено в п. 1 § 14 гл. I.
в 2>
СВОЙСТВА КВАЗИДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИИ
189
§ 2. Свойства квазидифференцируемых функций.
Основные формулы
квазидифференциального исчисления
1. Вначале установим простейшие свойства квази-
дифференцируемых функций. Пусть по-прежнему все
рассматриваемые функции заданы на открытом множе-
стве S az Еп.
1. Если fi(x)—квазидифференцируемая в точке хое
eS функция, то и функция f(x) = cfi(x), где с :> О,
тоже квазидифференцируема в точке х0.
Действительно, так как
#(х0) .. (*о) -
~~dg dg ~
= сГ max (о, g)+ min (w, g)1 =
[osSMxo) w^dhi^) J
= max (o, g) -f- min (w, g),
о s led fi (x0)l we[c df, (Xo)]
то ясно, что функция f(x) квазидифференцируема в
точке хо, причем
^f(x0) = [df(x0),
где df (х0) — с dfi (х0), df (х0) «= с afi (х0).
2. Если fi(x) — квазидифференцируемая в точке
Хо е $ функция, то и функция f(x) = —ft (х) тоже квази-
дифференцируема в точке Хо-
Действительно, имеем
df (хр) dh (хр) l .
dg dg
= —Г max (о, g)4- min (w, g)l. (2.1)
we-dhM J
Поскольку
— max (o, g)= min (— v, g)~ min (w, g),
v e dfi (xi) v e dfi (x») w e [ —df, (Xo)]
~ min (“’> 8) = max (— w, g) = max (u, g),
w e df, (xt) о e df, (Xo) v e (- df, (x0)l
то из (2.1)
<*o) = max (v, g) + min (w, g).
dg oel-dfi(xo)] te>s[-df,(xo)]
190
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
[ГЛ. И
Таким образом, функция f(x) квазидифференцируема
в точке хо, причем
£>f(x0) = [df(x0), df(x0)],
где _____ _______
df(xp) = — <?Л (х0), df (х0) = — dfi (х0).
3. Если функции fi(x) и f2(x) квазидифференци-
руемы в точке zosS, то и функция f(x) = fi(x)-j- f2(x)
тоже квазидифференцируема в точке Хр.
Действительно, поскольку
df (xp) _ dfi (х0) . df2 (хр) _
dg dg dg
*= max (v, g) + min (w, g) + max (v, g) +
t>s5fi (xo) wsdf,(xo) pedfoto)
+ min (ay, g)— max (o, g) +
®«=№(xo) csiafi(xo+df,(xo)]
+ min____ (w, g),
we[dfi (Xo)+dft (Xo)]
то ясно, что f(x)—квазидифференцируемая в точке хр
функция, причем
^(хр) = [^(х0), JWL
где _____ ________ ________
df (х0) = [dfi (х0) + df2(xQ)], df (х0) = [df, (х0) + df2 (х0)].
4. Если функции fi(x), ..., f*(x) квазидифференци-
k
руемы в точке х0 е S, то и функция f (х) = Z (х), где
Ci^Ei, тоже квазидифференцируема в точке хр.
Это очевидным образом следует из свойств 1—3. Не-
трудно выписать и формулы для субдифференциала и
супер дифференциала функции /(х).
Из свойств 1—4 теперь следует
Лемма 2.1. Множество квазидифференцируемых
функций является линейным пространством.
2. Пусть ft(x), — квазидифференцируе-
мые в точке XpeS функции. Образуем функцию
f (х) = max ft (х). (2.2)
5 21
СВОЙСТВА КВАЗИДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ
191
(2.3)
Прежде всего заметим, что если функции fi(x) диф-
ференцируемы в точке х0 по направлению geEn, то и
функция f(x) тоже является дифференцируемой в точке
Хо по направлению g, причем
^(*о) max dft(Xo)
где R(x) = {i^I\ fi(x) = f (x)}.
Действительно, поскольку
fi (xo T ag) = fi (xo) + a + ot (a), (2.4)
rn(1 --------->. О, то при достаточно малых a > О
lAC a a-»+0
f (xo + ag) = max ft (x0 + ag) = max f t (x0 + ag).
i&I Ze^(Xo)
Отсюда и из (2.4)
f(x0 + ag) —f(x0)= max [a-^*^4-of (a)].
<eR(xo)L J
Теперь имеем
о(a)< f (xo + ag) — f (x0) — a max —<o(a), (2.5)
~ i<=R(Xo)
где
о (a) = min ot- (a), d (a) = max (a),
— ieZ itsl
^-—.0, »0.
a a->+0 a a-»+0
Положим h (a) = a-1 [f (x0 + ag) — f (x0)]. Из (2.5)
h(a)— max —4^- --------->0,
isR(x4) ag a-*+o
а это и означает, что справедливо (2.3).
Лемма 2.2. Если функции fi(x), I е / == 1 : N, ква-
Зидифференцируемы в точке xQ е S, то функция
f(x) = max ft (х)
i&I
является квазидифференцируемой в точке х0, причем
^f(x0) = [df(x0), дЖ)1,
192
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
(ГЛ. II
где
df(,х0) = со ( dfk(х0) — £ дЛ(х0)1 kе= R(xq)), (2.6)
----- 1 (
I l^k )
df(x0) = £ dfk (хй). (2.7)
4<=№)
Доказательство. Функции fi(x) квазидиффе-
ренцируемы в точке х0, т. е.
= max (v, g)+ min (u>, g). (2.8)
8 as^(*o) ®edf7(x7)
Обозначим
A i = df f(x0), Bt = df^). (2.9)
Без ограничения общности можем считать, что /?(xo)sa
в 1 :т, где т N. Из (2.3) и (2.8) имеем
= max [max (о, g) 4- min (w, g)l (2.10)
weBi J*
Рассмотрим вначале случай tn — 2. Пусть a, b, c, d,
r — вещественные числа. Поскольку
max {a 4- b, c + d} — max {a + b — r, c 4* d — r} 4- r,
то, полагая r = b 4- d, имеем
max{a4-&. c 4-J} = max {a — d, c — b} 4- (b 4- d).
Отсюда и из (2.10)
/72втах [max (v, g)4- min (w, g)l =
weB{ J
= max ( max (v, g) — min (w, g), max (o, g) —
( u’e Ai w e B2 v e A2
— min (ay, gH 4-[ min (w, g)4- min (w, g)]. (2.11)
we Bi J IwsBi weB3 J
Так как
— min (ay, g)— max (—ay, g)= max (v, g), Ze 1:2,
weB^ veB^
то из (2.11)
Zf2 = max ( max (о, g)4- max (o, g), max(o, g)4-
4- max (», g) I 4- min (w, g) 4- min (w, g). (2.12)
c>gs[-Bi) J we Bi we Bi
СВОЙСТВА КВАЗИДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИИ ЮЗ
Но
max (о, g) 4-max (о, g) = max (о, g),
ue A veB оеЦА+В]
min (w, g) + min (w, g) = min (to, g).
w^A w&B we[4+B]
Поэтому ИЗ (2.12)
#, = max( max (o, g); max (u, g)\ 4- min (w, g).
loe-M-BJ oq[A,-Bi] J we[Bi+Bi]
Поскольку
max ( max (v, g), max(v, g)l — max (v, g),
I vsA osB J osco{AU£}
TO
H2 = max (v, g)4- min (w, g), (2.13)
o e Qn we <?22
где (?21 — C0 {^1 — ^2> ^2 — BJ, G22 — Bl 4“ B2.
Далее доказываем по индукции. Пусть уже установ-
лено, что
//( = тах Гтах (о, g)4- min (w, g)l =
i e 1:1 Lu e Ai J
= max (0, g)4- min (to, g), (2.14)
weG|2
где
Gn — cofAk — £ Bz|6<=l:/L (2.15)
I isl-.l, i+к )
(2,16)
i = l
Найдем
H1+1 sss max Г max (v, g) + min (w, g)l =
i e 1: (/+1) L» ® A^ w^B^ J
= max f Ht, max (0, g) 4- min (w, g) 1 =
I osAut wsBi+i )
= max ( max (0, g) + min (to, g), max (v, g) +
(ueG^ weGi2 ueAj+1
4- min (to, g)l.
weB/+1 J
7 В. Ф. Демьянов, Л. В. Васильев
194
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
[ГЛ. II
Рассуждая, как при выводе (2.13), получим
Hw = max (о, g) + min (w, g),
v e A w&B
где 4 = co{G/i—В/+ь A+i — G/s}, В = G# + Bz+i.
Осталось заметить, что
A = co f Ak — У*, Bi | k s 1 ’ (I -p 1) 1 s G/+j i,
5 Zg=1:(Z + 1) f
\ Z )
z+l
6 = Bi e G/+i, 2*
Z = 1
Итак, доказано, что
Hm= max (v, g)+ min (w, g).
vsGmi wsOmi
Справедливость леммы теперь вытекает из (2.15), (2.16),
(2.9) и (2.10). Я
Лемма 2.3. Если функции i&I s 1 : N, квази-
дифференцируемы в точке х0 s S, то функция
f(x)~=mln ft(x)
l<al
является квазидифференцируемой в точке х0, причем
^f(xo)^[dfCxo), №)],
еде
df(x0)^ S dfk (х0),
k&Q (Xq) *
df (x0) == co( dfk (x0) — E dfi (xQ) |fe eQ (x0) ),
1 J (2.17)
Q (x) = {i s 11 f i (x) — f (x)},
co{4J/?g=Q}sco(U {AH k e Q}}.
Доказательство. Поскольку f(x) = —тахйДх),
i e I
где /i,(x) = —fi(x), то, используя лемму 2.2 и свойство 2
п. 1, сразу получаем утверждение леммы. И
Из лемм 2.2 и 2.3 вытекает
§ 2]
СВОЙСТВА КВАЗИДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИИ
195
Следствие. Если функции
квазидифференцируемы в точке х0 е S, то и
f(x) = max min fu(x)
функция
(2.18)
последо-
(х)
тоже квазидифференцируема в. точке х0.
Аналогично устанавливается, что функция
вательного максимина вида
f(x) — max min max ... minf,,b ,
i / k i ‘
является квазидифференцируемой, если fuk... i(x)-—
квазидифференцируемые функции.
Задание 2.1. Получить вид квазидифференциала функции
(2.18).
Пример 1. Пусть f(x) — квазидифференцируемая
на S функция. Тогда и функция
1, если f (х) > 1,
Дх), если - 1<Дх)< 1, (2.19)
1, если f (х) < — 1,
F (х) = sat f (х) =
является квазидифференцируемой на S.
Действительно,
F (х) = max {Л (х), —1},
где fi(x) = min{f(x), -f-1}.
Функция fi(x) квазидифференцируема по лемме 2.3,
а функция F(x) теперь квазидифференцируема по
лемме 2.2.
Задание 2.2. Найти квазидифференциал функции (2.19).
3. Пусть функция fi (х) квазидифференцируема в точ-
ке xoeS и непрерывна в окрестности точки х0.
Лемма 2.4. Если ft (х0) ф 0, то функция] (х)=|Г1 (х)
квазидифференцируема в точке Хо, причем S)f(xo) =
= [df(x0), df(x0)], где
df (Хо) = — f г2 (Xo) dfi (xo), df (Xo) = — f Г2 (Xo) dfi (x0).
Здесь и ниже ff1 (x) = (h (x))”1, f~2 (x) = (fj (x)')~2.
7*
196
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
(ГЛ. II
Доказательство. Заметим, что
-£о)- Е Hm a-1 [f (хо + ag) — f (х0)] =
°* а-> +0
— lim a“1[fr1(x04-ag) — /Г‘(хо)]==
а->+0
= Пт [Л-1(хо)А'?(хо4-а^)а"’(/1(хо) —
а->+0
- fi (Хо 4- ag))] --f г2 (хо) .
Теперь осталось воспользоваться свойствами 1 и 2
п. 1.
Лемма 2.5. Если функции fi(x) и fi(x) квазидиф-
ференцируемы в точке xoeS, то и функция f(x) =
= fi(x)fz(x) тоже является квазидифференцируемой в
8той точке, причем
0f(xo) = [df(xo). Wo)],
где fidfi + fidfi, если fie 5=0,
fi>0,
df(x0)=* fi dfi + fjdfj, если fi<0, fi'* >0,
fidfi + fidfu если fi<0, fi 5 ^o,
fidfi + fidfi, если fi>0, fi SO,
fidfi 4- fzdfi, если fi>0, fi^ so,
fidfz + fidK, если fi<0, fi^ SO,
df (x0) = fi dfi + fidf^, если fi<0, fi^ so,
[ fi dfs-f- fidfi. если fi>0, fi<0.
Здесь везде значения функций fi(x) и f2(x) и их суб-
и супердифференциалов вычислены в точке хо.
Доказательство. Очевидно, что
- fi (Хо) + f2 (Хо) • (2.20)
Поскольку
df, (ХО)
- д\..= max (о, g)+ min (w, g), iel: 2,
8 °65 dfj (*o) we ^77^)
§2]
СВОЙСТВА КВАЗИДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ
197
то из (2.20)
df(Хо) = ft(Хо) шах (ц, g) + fi(xQ) min (w, g) +
dg v s e dfi (Xo)
+ f2 (x0) max (v, g) + f2 (x0) min (w, g).
v e dfi to) w s (Xo)
Осталось воспользоваться свойствами 1 и 2 п. 1.
4. Пусть F(y\,yz.....У*} — непрерывно дифференци-
руемая на йс£5 функция, и пусть fi(x), iel:s,—
квазидифференцируемые в точке Хо функции. Предполо-
жим, что
УО = (У(О1)..y^(fM, .... f,(xb))eQ.
Лемма 2.6. Функция f(x) — F(fi(x), f$(x)) ква-
зидифференцируема в точке Xq.
Доказательство очевидно, если учесть, что
df (х0) _ dF (уо) dft (хо) .
dg dy(1) dg "Г
dF (у0) df2 (х0) . . dF (у0) dfs (х0)
<Эу(2) dg ”' dy(s} dg
Далее рассуждаем, как при доказательстве леммы 2.5. М
Таким образом, множество квазидифференцируемых
функций представляет собой линейное пространство,
замкнутое относительно всех «алгебраических» опера-
ций, операций взятия поточечного максимума, мини-
мума, последовательного максимина.
Замечание. Пусть S) = [А, В] — пара множеств
из Еп. Определим операции умножения на вещественное
число X и сложения:
( [АЛ, АВ], если А>0,
^ = ([АВ, АЛ], если А<0.
Если ^>1 = [Л1, Bi], &>2 = [А2,В2], то S)i -^3^2=a
= [Л1 -|- А2, В\ Вг].
Тогда формулы для квазидифференциала линейной
комбинации, произведения и частного квазидифференци-
руемых функций можно записать в более компактном
198
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
(ГЛ. И
виде:
Ф [ Е М/ (Хо)] = Е U®fl (Хо),
0 [fl (Хо) f2 (Хо)1 = fl (Хо) 0f2 (Хо) + f2 (Хо) 2>f 1 (Хо),
0 Гтгт1 = 127-Т V* W - f' <хоЛ
U2(*o)J W)
(в последней формуле предполагается, что f2(xo)^O).
Эти выражения являются обобщением обычных фор-
мул дифференциального исчисления.
§ 3. Примеры вычисления квазидифференциалов
Приводимые ниже простейшие примеры вычисления
квазидифференциалов играют чисто иллюстративную
роль, и подготовленный читатель может считать их
упражнениями, которые ему следует выполнить само-
стоятельно.
Пусть
X = х<2>) €= Е2, х0 = (0, 0) = О,
А = (1,0), л2 = (—I, 0),
В, = (0,1), В2 = (0, -1),
С, = (1,1), С2 = (-1, -1).
Пример 1. Пусть f(х) = f(х(1), х<2>) = |х(1)|. Имеем
I х(|) | = max {х(1), — х(1>} = max (fi (х), f2 (х)},
где /1(х) = х<’>, f2(x)==—х(1). Функции fi(x) и f2(x) не-
прерывно дифференцируемы, и потому (см. пример 2 § 1)
&>fi (хо) = [dfi (х0), dfi (хо)],
где dfi (х0) = {Л J, dfi (х0) = {0},
^f2(xo) = [^f2(xo), df2 (х0)],
где df2(x0) = {А2}, df2(х0) = {0}.
По лемМе 2.2 имеем (рис. 17)
0f(Xo) = [df(Xp), Э/W],
где df (хр) = со{Д|, Д2}, df (х0) = {0}.
§ 3] ПРИМЕРЫ ВЫЧИСЛЕНИЯ КВАЗИДИФФЕРЕНЦИАЛОВ 199
200
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
(ГЛ. п
Пример 2. Пусть f(x) =— ]xi| = — fi(x). Из пре-
дыдущего примера и свойства 2 п. 1 § 2 ^f(x0) =
= [df(xo), д/(х0)],где df(xo) = {O},df(xo) = —со[Л1,Л2).
В данном случае (рис. 17)
— со{Ль Л2} = со{Л1, Л2}.
Пример 3. Пусть f(x) = |x(2)|. Как и в примере 1,
получаем
&f(x0) = [df(x0), df(x0)],
где df(x0) = со {Bi, В2), df (х0) = {0}.
Пример 4. Пусть f(x) ——|х<2)|. Как в примере 2,
имеем
0f(xo) = [df(xo)], «ЭТИ,
где df (х0) = {0}, df (х0) =« со {Вь В2).
Пример 5. Пусть f(x) = |x(1)|— |х(2)|.По свойству3
п. 1 § 2 из примеров 1 и 4 имеем
2>f(x0) = [df(x0), W)l,
где (рис. 18) df(x0)= со{Л], Л2}, df(x0) = co{Bb В2).
Пример 6. Пусть f{x) = |х(1)|-|-|х(2)|.
По свойству 3 из п. 1 § 2 имеем
&>f (х0) = [df(x0), df(x0) ],
где (рис. 19) <?/(х0) = со{Л1, Л2}-|-со{В1, В2), df(x0) =
= {0}.
Пример 7. Пусть fi(x) = |x(,)|— |х<2>|, f2(x) =
= |х(2>|— |х(1)|. Положим f(x) = max{fi(x), f2(x)} =
= | |х(Ь|—Ix(2)|J.
Из примера о
&>fi (x0) = [df! (x0), dfi (x0)l,
где dfi(x0) = со{Ль Л2}, dfi(x0) = co{Bb B2).
Из свойства 2 п. 1 § 2
^>fz (x0) = [df2(x0), df2(x0)],
где df2(x0) = — dfi(xo), dfs(x0) =—dft(x0).
§ 3J
ПРИМЕРЫ ВЫЧИСЛЕНИЯ КВАЗИДИФФЕРЕНЦИАЛОВ
201
В нашем случае (рис. 18)
df2 (х0) = — со {Вь В2} = со (Вь В2},
df2 (х0) == — со {Л 1, А2} = со {Ль Л2).
Применяя лемму 2.2, получим 3)f(x0) — [df(x0), df(x0)J,
где
<j/(x0) = co {dA — dfa, — dfi} =
= co {co (Ль Л2}Н-со{Ль Л2}, co {Вь В2} + со{Вь B2}}, *
^) = ^T+^=co{Bb B2} + co {Ль Л2).
Множества df(x0) и df(xp) изображены на рис. 20, где
сплошной жирной линией обозначена граница df(x0),
а пунктирной линией — граница df(xp).
Пример 8. Пусть Д(х) = |х(1)|4-|х(2)|, fi(x) =
= | х< 01 — | х(2) |. Положим
f (х) = max {fi (х), f2(x)}.
Из примеров 5 и 6 по лемме2.2<Z>f(х0) = [^(хр),д/(хо)],
где (рис. 21)
df(x0) = co {dfi — df2, dk — dfi} —
— со {со {Ль Л2), со {Ль Л2} + со{Вь В2} — со{Вь В2}},
df (х0) = со {Вь В2}.
202
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
[ГЛ. И
Пример 9. Пусть fi(x) = |x(l>|4-|x<2)|, f2(x) =
= |х(1)|— |х<2>|. Положим
f (х) = min {Л (х), f2 (x)J.
Из примеров 5 и 6 и леммы 2.3 S)f (х0) = [df (хр), df (хр) ],
где
df (х0) «= dfi + df2 = со {Ль Л2}4-со{Ль Л2}4*со{Вь В2},
af^) = co{df1-df2, df~2 — dfi} =
= со {со {Bi, В2} —со{Ль Л2} —со{Вь В2), со {Ль Л2}} =
= со {со {Bi, В2) + со {Ль Л2) + со {Вь В2), со {Ль Л2}}
(последнее равенство справедливо в силу того, что
со {Ль Л2} = — со {Ль Л2},
со {Вь В2} == — со {Вь В2}).
Множества df(x0) и df(xQ) изображены на рис. 22.
Пример 10. Пусть f(х) — | |х(1>|4-х<2>|. Имеем
f (х) = max {fi (х), f2 (х)}, где
f 1 (х) = | х<>) | + х®, f2 (х) = -1 х<» | - х<2».
Так как для функции f3 (х) = х(2) будет 3)f2 (х0) =
= [df3(x0), df3(x0)], где df3(x0) = {ВJ, df3(x0) = {<D}, то
из примеров 1 и 2
&>fi (*о) = [dfi (хр), df, (хр)],
где ______
dfjxp) = со {Ль Л2} + Вь df 1 (х0) == {©},
0/г (*о) = [df2 (*о), df2 (JCo)],
где _______
df2(x0) = {©}, df2 (х0) = — со {Л,, Л2} — Вь
По лемме 2.2 ^>f (х0) = [df(xp), df(x0)], где (рис. 23)
dfM = со{df,-df2, dh-dfi}^
«= со {со {Ль Л2} 4- Bi со {Ль Л2) 4" Вь ®),
df (х0) = df? 4- df^ = — со {Ль Л2) — Bi = со {Ль Л2) — Вь
$ 3]
ПРИМЕРЫ ВЫЧИСЛЕНИЯ КВАЗИДИФФЕРЕНЦИАЛОВ
203
Пример 11. Пусть f(x) = |х(1) + х(2>|. Так как
f(x) = max{fi(x),f2(x)}, где fi(х) = х<!>+ х<2>, f2(x) —
= —х<1) — х(2), то (рис. 24)
0Ихо) = РИхо), <V(x0)],
dHxo)=co{cb с2), тео={©}.
Пример 12. Пусть fi(x)= 1 +|х(1>|, f2(x)=l-f-
+ |х(1) + х<2>|. Положим f(x) = fi(x) -f2(x).
Если с—константа,то 2>[f(x) + с] = S)f(x). Поэтому
0Щ) = Ш*о). <ЭЛ(хо)],
dfi (х0) = со {Ль А2}, dfi (хо) = {0},
0/г (х0) — [д/2 (х0), ^(хр)],
df2 (хр) = со {Сь С2}, о/2 (х0) = {0}.
Отсюда и по лемме 2.5 2)f (х0) = [df (х0), <5/(х0)], где
(рис. 25)
df (хр) = fi (х0) df2 (х0) + f2 (xo)dfi(x0) =
= со{Ль А2} 4-со{Сь С2},
дЖ) = {0}.
204
КВАЗИДИФФфЕНЦИРУЕМЫЕ ФУНКЦИИ
(ГЛ. П
Пример 13. Пусть Л(х) = |х(1) 1 + х(2>+ 1, f2(x) = I
= /з (х) = I Х<‘> I — I Х(2> 1+ 1. Положим f(x) =
= Л(х)-/2(х). i
Так как SDfi (х) = 2Dfi (х), где f< (х) = | х(1) | + х(2), то
(см. пример 10)
dfi(x0) = со{Ль Л2) + Вь dfi(х0) = {©}.
Поскольку S>f3(x)*=*2>fs(x), где Ых)=|х(,)| —|х® |, 1
то (см. пример 5)
0/з(хо)и[д/з(хо), df 3(х0)],
dfs (хр) = co {Ль Л2), df3 (x0) = co {Bb B2}. i
По лемме 2.4
&>f2(xo) = [df2(xQ), df2(x0)],
где
dh (x0) — — df3(x0) = — co {Вь B2) = co (Bb B2),
df2 (x0) “ — df3 (xq) «=» — co {Ль Л2} = co {Ль Л2}.
По лемме 2.5 окончательно получаем (рис. 26)
£>fM = [df(x0), dTMl
<-
at
$ Я
ПРИМЕРЫ ВЫЧИСЛЕНИЯ КВАЗИДИФФЕРЕНЦИАЛОВ
205
где
df (хр) = fi (xo) df2 (хр) + ft (х0) dfi (хр) —
“ со {В1, В2} + со {Ль А2} + Bji
df (хр) “ fi (*о) df2(xt) + f2 (x0)dfi(x0)—
= со{Ль Д2) 4" {®}co {Л[, Л2},
Пример 14. Пусть А (х) = 1 +1 х(1) | + х(2). Образуем
функцию f (х) [fi (х)р. В предыдущем примере уже
отмечалось, что ^А (х0) — РА (х0), dfi (х0)], где dfi (х0) -
= со{Л1, A2} + Bi, <ЭА(хо)в{О}.
По лемме 2.5 3>f (х0) = [df (хр), df (х0)], где (рис. 27)
df(x0) = fi (хр) dfi (хр) + А (хр)дА(хо)п
= df 1 (хр) + dfi (хр) = со {Ль Л2} + Bi + со {Ль А2} + Ву
df (х0) = fi (х0) dfi (х0) 4- fi (х0) df 1(х0) = {0}.
а?#-)
4
^-2 / ^| ' i ‘
Рис. 28.
Пример 15. Пусть А (х) =* 2 4-1 х(1> | + *(2>. Положим
f (х) = [А (х)]2. Поскольку (см. пример 13) &)fi (хр) =*
“ tdfi (*о)» dfi (х0)], где dfi (х0) = со {Ль Л2) + Вь ЭА(х0) —
= {0}, то по лемме 2.5 $>f (х0) = [<9f (х0), д/(х0)]. Здесь
(рис. 28)
df (х0) = А (х0) dfi (х0) + fi (х0) dfi (х0) =
= 2df|(xp) + 2dfi(x0) =» 2 со {Ль Л2) 4- 2Bi 4-
-1-2 со {Ль Ла)4-2Вь
дЙ^) = fi (хр)« + fi (х0) df^>) = {0}.
206 КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ [ГЛ. И >.[
П р и м е р 16. Пусть f (х) = || х ||, где || х ||=V(xll))2+(x<2*)2.
Очевидно, что = limber1 [f (х0 + ag) — f(x0)] =
= <х • a-1||g|| = ||gi|. Значит, = max (v, g), где
°S v Si (0)
{t> e E21II v || !}• Поэтому функция f(x) является
квазидифференцируемой (даже субдифференцируемой),
причем £)f (х0) = [df (x0), df(x0)], где df (x0) = Si (0), |
I
Замечание 1. Если x = (x(1), ..., x(n)) e En, f(x)— (
= || x ||, где || x || = VS то аналогично показывается,
ЧТО I
0f (x0) = [df (x0), df(Xp)], 1
где I
df(x0) = S1(O)^{u sEJIlolK 1}, dfW={0}.
Замечание 2. Везде выше для каждой функции
был построен один из возможных квазидифференциалов.
Функция в примере 8 совпадает с функцией в примере 6,
а функция в примере 9 — с функцией в примере 5, хотя
квазидифференциалы у совпадающих функций получены ।
разные.
Задание 3.1*. Пусть А с:Еп — выпуклый компакт. Определим
отображение Ж: Ел-*-П(£л):
(£) = {» ^ 4 | (о, g) = max (z, g)}.
zs A {
Ясно, что Зв a (®) = А и что достаточно рассматривать Зв а на еди-
ничной сфере Ci я» {g е£я||| g || =s 1}, ибо
^4(Xg)«^(g) VX>0.
Можно показать, что почти для всех g е Ci множество Зв a (g) со-
стоит из единственной точки.
Пусть f(x)—квазидифференцируемая в точке х0 функция, и
пусть ^f(xo) *= [df (хр), df(xo)] — ee квазидифференциал в точке xq. 1
Введем отображение Q: С1->П(ЕЯ) следующим образом:
Q(g)=^f<xo)(g)-^-—Jg)-
Множество Q (g) почти для всех g е Ci тоже состоит из един-
ственной точки. Через Ci обозначим множество тех g е Ci, для ко-
торых Q(g) состоит из единственной точки.
л I
____—1
§ 4]
ВЫПУКЛО-ВОГНУТЫЕ ФУНКЦИИ
207
Доказать или опровергнуть следующее утверждение:
Если функция f(x) липшицева и квазидифференцируема в
окрестности точки %о, то для субдифференциала Кларка (см. (2.3))
этой функции имеет место представление
^Glf(^o) = co{Q(^)I^^C1}. (3.1)
Проверить, что во всех рассмотренных в настоящем параграфе
примерах соотношение (3.1) выполняется.
§ 4*. Квазидифференцируемость
выпукло-вогнутой функции
1. Пусть функция f(x)s= f(y,z) задана и конечна на
S =Si XSzCzEn, где х = [у, z]<=En, n = n1 + n2,
Si с ЕП1 и S2 cz ЕП1 — выпуклые открытые множества в
соответствующих пространствах. Функция f(x) назы-
вается выпукло-вогнутой на S, если функция f(y,z) вы-
пукла по у на Si при каждом фиксированном ze=S2 и
вогнута по z на S2 при любом фиксированном
Положим
dfy (Уо, z0) = {у 6= ЕП1 | f (у, z0) — f (Уо, zo) >
>(v, у — уо) yy^Si}, (4.1)
dfg (yo, z0) = {w €= En, | f (y0, z) — f (y0, z0) <
(w, z — z0) Vz e S2}. (4.2)
Множество dfy(y0, z0) является субдифференциалом вы-
пуклой функции h\(y) = f {у, Zo) в точке уо, а множество
dfzG/o, Zo) — супердифференциалом вогнутой функции
hi(z) = f(y0, z) в точке zq. Эти множества непусты, вы-
пуклы, замкнуты и ограничены.
Установим непрерывность выпукло-вогнутой функции
f(x) по совокупности переменных (непрерывность f(x)
по каждой из переменных у и z следует из свойств вы-
пуклых и вогнутых функций). Вначале докажем лемму,
представляющую самостоятельный интерес.
Лемма 4.1. Если функция f(y,z) выпукла по у на
Si при любом фиксированном zeS2 и непрерывна по z
на S2 при каждом фиксированном y^S\, то f{y,z) не-
прерывна по совокупности переменных.
Доказательство. Пусть х0 = [t/o, z0] s S и й =
= £2i X й2, где QicSi, Q2cS2 — выпуклые компакты
такие, что уо <= int £2Х, zoeintQ2- Вначале установим, что
208
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
(ГЛ. п
функция f(x) ограничена на И. Для этого рассмотрим
функцию ср (у) = sup f (у, z). При каждом фиксирован-
zgQ2
ном y&Si функция f(y, z) непрерывна по г на й2 и,
поскольку й2— компакт, то и ограничена там. Поэтому
<р(у) — конечная функция, причем можно написать
Ф (у) = max f (у, z). Нетрудно теперь проверить, что
2 6 02
<р(у)— выпуклая на Si функция. Действительно, по-
скольку f(y, г) — выпуклая по у функция, то
ф (a</i + (1 — а) У2> = max f (ayi -f- (1 — a) y2, z) <
z e Q2
< max [af (yh z) + (1 — a) f (y2, z)] <
Z <= Й2
a max f (ylt z) + (1 — a) max f (y2, z) =
2 6 02 ' z s 02
= аф(#1) + (1 — а)ф(у2) Va<=[0, 1],
а это и означает выпуклость ф(у) на Si. Но конечная
выпуклая функция (см. § 4 гл. I) является непрерывной
на Si, а тогда она и ограничена на любом компакте
Q'czSi. Отсюда заключаем, что f(y,z)— ограниченная
на £2' X $2 функция. Зафиксируем любое й' с Si такое,
что
Й1 с: int й'. (4.3)
Покажем теперь, что множество субдифференциалов
dfv z) ограничено на й = й] X й2. Допустим против-
ное, пусть найдется такая последовательность {aft}, что
vk^dfy(yk, zfc), ||vfcl|-> +оо, хк = [ук, zft] <= й. (4.4)
По определению (см. (4.1))
f (У, zk) — f (ук, zk) > (vk, у - yk) Vу g= Sb (4.5)
В силу (4.3) найдется р > 0 такое, что
^в=^ + Р°*||0*Г1 eQ'c=Si Vk.
Из (4.5)
f (У» zk) > f (Уь> zk) + 01 vk I- (4-6)
Так как значения f(yk,zk) ограничены на й'Хй2, то из
(4.4) и (4.6) f(y'k, z*)-> 4'.o°, что противоречит ограни-
§ 4] ВЫПУКЛО-ВОГНУТЫЕ ФУНКЦИИ 209
ченности f(y, z) на £2' X йг- Итак, найдется такое L < оо,
что
||v||<L Vo s=dfy(y, z), V[i/, z]sQ. (4.7)
Пусть теперь x'->x0, x' ей, х' = (/, z'), хо — (уо, z0).
Имеем
|f(x') —Ж)1 = 1Ж, z') — f(y0, z0)| =
= I f (y\ z') — f (yQ, z') + f (y0, z') — f (y0, Zo) I <
z')-f(y0, z')\ + [f(y0, z')-f(y0, z0)|. (4.8)
Из (4.5) и (4.7)
f (у', z') — f (y0, z') (o0, y' — y0)> — L|| у' — Уо ||, (4.9)
где oo e dfy (y0, z'). Аналогично
f (Уо, z') — f (y', z')^(v', у о — y')> — 1Лу' — уо II, (4.10)
где о' е dfy (у', z'). Из (4.9) и (4.10)
1Ж> z')-f(y0, г')\^Ц\у'-уо\]. (4.11)
Функция f(y0, z) непрерывна по z. Поэтому
Ж, z')—+f(y0, z0).
Отсюда, из (4.11) и (4.8) имеем f (x')->f (х0), т. е. функ-
ция f(x) непрерывна по совокупности переменных. В
Теорема 4.1. Если f(y,z)—выпукло-вогнутая на S
функция, то она и непрерывна на S по совокупности пе-
ременных.
Доказательство. Функция f(y,z) вогнута по z
на S2 при любом фиксированном у е Si, а потому она
и непрерывна по z при фиксированном у. Утверждение
теоремы теперь следует из леммы 4.1.
Следствие. Выпукло-вогнутая функция f (у, z)
является липшицевой на любом множестве й = Й1 X й2,
где Qi cz Si, й2 с S2, Й1 и й2— выпуклые компакты.
Действительно, как и при доказательстве леммы 4.1,
можно установить, что множество супердифференциалов
dfz(y,z) ограничено на й, т. е. существует Ц < оо та-
кое, что
IIW||< Ц Vw <= dfz (у, z), V [у, z] <= й. (4.12)
Из (4.8), (4.11) и (4.12) теперь заключаем, что функ-
ция f (у, z) является липшицевой по совокупности пере-
менных на множестве й = Й1 X ^2. В
210
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
[ГЛ. II
Лемма 4.2. Пусть функция f(y,z) выпукла по у
на Si при любом фиксированном ге S2 и непрерывна по
z на S2 при каждом фиксированном у <= S,x0 = [у о, zo] е
е S = Si X 5г. Тогда для любого в >• 0 найдется б > 0
(зависящее от х0) такое, что
dfy (у, z) az dfy (у0, z0) + SJe V [у, z] az Se (y0, z0), (4.13)
где
Sie = {v^En, |||v||<e},
S6(y0, z0) = {[y, z]<=S|||y — yoll + llz — z0||<6}.
Доказательство. Предположим противное.
Тогда найдутся во > 0 и последовательность {о*} такие,
что
vk s dfy (yk, zk), \yk, Zkl -> [Уо> zo] = x0,
P (vk, dfy (y0, zo)) = min || vk — v || > во. (4-14)
zo)
Поскольку множества dfy(y,z) ограничены в совокуп-
ности (это было установлено при доказательстве лем-
мы 4.1), то без ограничения общности можем считать,
что
. (4.15)
Из (4.14) очевидно, что
Vo Ф df у (уо, Zo). (4.16)
Так как Vk е dfy(yk, zk), то
f (У, zk) — f (Ук< zk) > (vk, у — yk) Vу 6= Sb
Отсюда
f (У, Zo) — f (уо, zo) > (vk, У —Уо) + (vk, Уо — Ук) +
+ f (у, Zo) — f (у, zk) + f (yfc, Zk) — f (Уо, Zo) Vy<=Si. (4.17)
Зафиксируем любое z/eSi. По лемме 4.1 функция
f(y,z) непрерывна по совокупности переменных. По-
этому из (4.17) и (4.15) при £->оо имеем
f (у, Zo) — f (Уо, Zo) > (Оо. У — Уо).
Так как полученное неравенство справедливо для каж-
дого y&Si, то отсюда и из (4.1) и0 dfy (yQt z0) > что
противоречит (4.16). Лемма доказана.
ВЫПУКЛО-ВОГНУТЫЕ ФУНКЦИЙ
211
§ 4]
Следствие 1. Пусть f(y,z)— выпукло-вогнутая на
S = SiXS2 функция, Хо = [у0, zo] е S. Тогда для лю-
бого 8 > 0 найдется 6 > 0 такое, что при всех [у, г] е
<= Se (уо, zo)
dfy (у, z) с: dfy (уо, z0) + Sle,
dfAy, z)<=dfz(y0, z0) + S2e> (4J8)
где
Sie = {v^Eni HI v ||<8}, S2e = {ayeE^|||a>||<e},
Se (y0, zo) = {[y, z] e S| ||у — y01| +1|z — ZolKd).
Доказательство аналогично только что прове-
денному.
Следствие 2. Отображения dfy(y,z) и dfz(y,z)
полунепрерывны сверху на S.
2. Найдем теперь производную по направлениям вы-
пукло-вогнутой функции. Пусть
Хо == [уо, ZO] е S = Si х «$2, g = [gi, g2] e= En, x ЕПг.
Теорема 4.2. Функция f(x)esf(y,z) дифференци-
руема в точке Хо по любому направлению g = [g1( g2] е
<=Eni ХЕп„ причем
-^^- = max (о, gi) + min (w, g2). (4.19)
8 0 e dfy (yv Zo) w e dfz (y0. z0)
Доказательство. Правую часть в (4.19) обо-
значим В. Положим
h (а) == а-1 [f (у0 + agb z0 + ag2) — f (у0, z0)]. (4.20)
Надо установить существование предела
lim h(a)^-^L (4.21)
a->+0
и найти его вид. Имеем
f (Уо + ago zo + ag2) — f (Уо, z0) =
= (Уо + agi. Zo + ag2) — f (y0 + agb z0)] +
4" I/ (Уо + agi> Zo) — f (Уо, Zo)] = Xi + A2. (4.22)
Так как функция f(y, Zo) — выпуклая по у, то
Л2 s f (Уо + agi, zo) — f (Уо, zo) == a Oj (a)t (4.23)
1
212
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ -ФУНКЦИИ
[ГЛ. II
= Нт а 1 [f (у0 + agb z0) — f (у0, z0)] “ max (o,gi).
а>+0 vedfy (у0, z0)
Поскольку f(y,z)— вогнутая по z функция, то из соот-
ношения (5.45) гл. I
f (Уо + agb zo + ag2) =
* а
- / (й + «8,. «.) + $ + «•+№! Л, (4.24)
О
где
dfj’ 555 lim a~4fG/.z + ag2) —f(jGz)] =
^«2 a->4-0
— min (w, g2). (4.25)
w&Of2(y, z)
Зафиксируем e>0. Из (4.18) следует, что найдется
такое а (в) > 0, при котором
dfz (Уо + ag,, z0 4- Tg2) с= dfz (уй, z0) 4- S2e
Vt s [0, a (в)], Va @ [0, a (в)]. (4,26)
Если О a Gi 4? G2, to min (w, g2) > min (w, g2) —
weGi . weGt+Gi
“ min (w, g2) 4- min (w, g2). Поэтому из (4.24) и (4.26)
w e Gi w&Qi
Ai в f (yo 4- a£i, zo 4- ag2) — f (Уо 4- agb Zo) >
>a min (w, g2) — ae||g2||.
w ® 9fz го)
Поскольку min (w, g2) = — e||g2||, то из (4.22) и (4.23)
t»sSu
ft(a)> max (v, gi)4- min (w, g2) — e||g21| =
э = ^(»о-2о)
= B-e||g2||.
Значит,
lim /i(a)>B — e||g2||.
a->+0
В силу произвольности e отсюда
lim ft(a)>B. (4.27)
a-> 4-0
S 41
ВЫПУКЛО-ВОГНУТЫЕ ФУНКЦИИ
213
С другой стороны,
f (Уо + aSi> го + ag2) — f (у0, z0) =
, e [/ (Уо + agi, z0 + agz) — f (Уо, «о + ag2)] +
+ [/ (Уо, zo + ag2) — f (Уо, го)]s Л + Л4. (4.28)
Так как f(yo, г) —вогнутая функция, то
Д4 а f (у0, zo + ag2) — f (уо, zo) = a --(|^г<>)- + o2 (a), (4.29)
где o2(a)<0,
df(yo,zo).B, lim a-i[;(^0> zo + ag2) ~ f (Уо, z0)] =
ogt a->+o
min (w, g2).
m^^fz(4o-zo)
Функция f(y, Zo + ag2) выпукла по у, поэтому из
формулы (5.26) гл. I
A3 = f [(г/о + agb Zq + ag2) — f (y0, Zo 4- ag2)] =
df (ya + Tgi, z0 + ag2)
dgi
При этом
df (Уо + Tgl, Zq + ag2) M
(P, gl). (4.30)
° s dfy го+“в2)
Возьмем в > 0. По лемме 4.2 найдется такое а(в)>0,
что
dfy (Уо 4- Tgi, Zo 4- a^2) dfy (у0, z0) 4- $ie
Vtg=[0, a(e)J, Vas[0, a(e)].
Так как для G cz Gi 4- O2 будет
max (о, giX max (v, gi) = max(p, gi) + max(o, gi),
oeG DsOi+G2 t»eGi oeG2
то из (4.30)
поскольку
A3<a max (0,^1)4-0811^11,
Oe<5fj,(y0. г0)
max (v, gi) = e||gl||.
v s Sjg
214
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
1ГЛ. ц
Отсюда и из (4.29)
Л(а)< max (t>, gr) Ч- min (w, g2) + e||g21| =s
os^(y0. Zo) wsdfz(y0,z0)
s в + «II g2||.
Поэтому
lim h (a) < В + e || g2||.
a->+o
В силу произвольности e имеем
lim h (a) < B. (4.31)
a-»+0
Сопоставляя (4.27) и (4.31), заключаем, что существует
lim h (а) и lim h (a) = ~f = n
a->+0 a->4-0 dg
что и требовалось доказать.
Следствие. Выпукло-вогнутая на S функция ква-
зидифференцируема там, причем
0H*o) = [Wo), Wo)L
еде df (х0) = [<Э/У (у0, z0), OJ. df (х0) = [0ftl, dfz (у0, г0)].
Это следует из формулы для производной по направ-
лениям (формула (4.19)).
§ 5. Необходимые условия оптимальности
квазидифференцируемой функции на Еп
1. Пусть f(x)—квазидифференцируемая на Еп функ-
ция. Установим вначале необходимые условия минимума
и максимума.
Теорема 5.1. Для того чтобы квазидифференцируе-
мая на Еп функция f(x) достигала в точке х*е Еп своего
наименьшего на Еп значения, необходимо, чтобы
-dftf)<=df(x*). (5.1)
Доказательство. Если функция f(x) дифферен-
цируема по направлениям в точке х*, а х* — точка ми-
нимума функции f(x) на Еп, то (см. лемму 6.1 гл. I)
^>0 (5.2)
НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ НА 215
Поскольку в рассматриваемом случае
= max (о, g) + min (да, g), (5.3)
s о г df (х*) wedf (х*)
то из (5.2) и (5.3) имеем
inf [ max (у, g) + min (да, g)] = 0, (5.4)
gsSi v^df (x*) wedffx*)
где (здесь и далее в этом параграфе)
Si = {ge B„|||g||< 1).
Из (5.4)
min min max (v + да, g) =
g e Si w e Of {x*) v e df(x*)
= min min max (v, g) = 0. (5.5)
g S Si w e df (x*) V e [df (x*)4-t0]
Так как множества Si и df(x*)— выпуклые ком-
пакты, то из (5.5)
min min max (о, g) = 0,
wedf (x‘) 8eS1 psl^f (х*На1]
т. e. ______
min max (o, g) = 0 Уда e df (x*). (5.6)
geSi V s [df (x*)+w]
По следствию из леммы 6.1 гл. I и по следствию из
теоремы 6.1 гл. I получаем, что условие (5.6) эквива-
лентно условию
Oe=df(x*) + tt> УдаедЙР).
Но это и означает, что
— да е df (х*) Уда е df (х*),
т. е. — df (х*) с: df (х*)> что и требовалось доказать.
Аналогично доказывается
Теорема 5.2. Для того чтобы квозибифференци-
руемая на Еп функция f(x) бостигала в точке х?*&Еп
своего наибольшего на Еп значения, необхобимо, чтобы
- df(x**) с dfTjrj. (5.7)
Определение. Точку х*еЕп, удовлетворяющую
(5.1), будем называть inf-стационарной точкой функции
216
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
[ГЛ. II
f(x) на Еп, а точку х**е£я, удовлетворяющую (5.7),
будем называть sup-стационарной точкой функции f(x)
на Еп-
Очевидно, что если для некоторой точки х0 е Еп ока-
зал ось, что — df(xo) = df(x0), то точка х0 является од-
новременно и inf-стационарной, и sup-стационарной.
2. Пусть х* — inf-стационарная точка функции f(x)
на Еп, т. е. имеет место (5.1). По определению
f (х* + ag) - f (х*) + a + о (a, g), (5.8)
где
Теорема 5.3. Если x* — ini-стационарная точка
функции f(x) на Еп и при этом
-df^)'<= intdf(x*), (5.10)
а соотношение (5.9) имеет место равномерно по g^S\,
то точка х* — точка строгого локального минимума функ-
ции f(x).
Доказательство. Из (5.10) следует, что най-
дется г > 0 такое, что
с:[df(х*) + «>] YwtsdfW),
где 5г = {геЕ„|||г||<г}.
Тогда
шах (о, g)>r Yw s df (х*), Yg: ||g||=l.
Из (5.5)
min mln max (о, g)>r,
eeEn wsdf (x*) v^[df(x*)+w]
Ugll-l
t. e.
-^->r VgeE„: ||g||=l. (5.11)
Поскольку (5.9) имеет место равномерно по geSi,
то из (5.8) и (5.11) найдется ао > 0 такое, что
f (х* + ag)^f (х*) + аг2"‘
Vae[0, ао], Vg<=£„: ||g||=l,
5 5] НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ НА Еп 217
а это и означает, что х* — точка строгого локального ми-
нимума функции f(x).
Аналогично доказывается #
Теорема 5.4. Если х** — ^-стационарная точка
функции f(x) на Еп, при этом
. -W^crintW5) (5.12)
и соотношение (5.9) имеет место равномерно по geSi,
то точка х**—точка строгого локального максимума
функции f(x).
В качестве примеров рассмотрим некоторые функции,
изученные в § 3. Точка х0 — (0, 0) является inf-стацио-
нарной (а в действительности и точкой минимума) для
функций, описанных в примерах 1, 3, 6, 7, 8, 10, 11, 12,
13 § 3. Точка хо является sup-стационарной для функ-
ций, описанных в примерах 2, 4. Точка хо является точ-
кой строгого локального минимума для функций, опи-
санных в примерах 6 и 8.
3. Пусть точка Хо не является inf-стационарной, т. е.
условие (5.1) не выполнено. Тогда не выполнено и усло-
вие (5.2), т.е.
infdf^-------а<0 (5.13)
g е Si
Отсюда и из (5.3)
min min max (о + w, g) =
в®31 (Xo) оesdf (xo)
= min min max (v + w, g) = — a. (5.14)
wedfC^) gsS1 p 65 <*«>
Как и при доказательстве теоремы 6.2 гл. I, показы-
вается, что
min max (о + w, g) = — min || о + w ||.
geSt о s df (xo) p e df (xQ)
Отсюда, из (5.13) и (5.14)
a — — max min || v + w ||. (5.15)
wedfM Q&dfM
Выберем ay0Gd/(x0) и vp s df (x0) так, чтобы
max min ||v + a)|| = min || v + w0 II = II Vp + Wp ||.
w® df (Xo) VQdf (Xo) о e df (xo)
218
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
(ГЛ. II
Тогда направление go =—(v0 + ^о) l|fo + Well-1 является
направлением наискорейшего спуска функции f (х) в точ-
ке Хо- Оно может оказаться не единственным.
Аналогично показывается, что если точка х0 не яв-
ляется sup-стационарной, т. е. — df (х0) df (х0), то
а = sup = max min [| v-j-w ||. (5.16)
geSi v e df (X») w eafTxJ
Если a > 0, то направление g\ = (t>i + a>i)|| Ui + W[ Ц-1»
где min ||t>i+tt'|l= max min ||o + tt’||, || t»i+wi ||=
w e df (Xo) v s df we df (xo)
= min || t>i + w ||, является направлением наискорей-
w edf (Xo)
шего подъема функции f(x) в точке x0. Оно тоже мо-
жет оказаться не единственным.
Найдем расстояние между множествами df (х0)
и — df(x0) в метрике Хаусдорфа (см. (2.1) гл. I):
P(df(x0), — df (х0))»
max min || v + w || + max min || v + w ||.
t»edf(xo) ° g df cedf(Xo)
Первое слагаемое здесь есть уклонение множества
—df(xo) от множества df(x0) (в смысле Хаусдорфа), а
второе слагаемое есть уклонение множества df (х0) от
множества —df(x0).
Поэтому из (5.15) и (5.16) получаем, что сумма аб-
солютных величин скоростей наискорейшего спуска и
наискорейшего подъема функции f(x) в точке х0 равна
расстоянию между множествами df(x0) и —df(x0) в мет-
рике Хаусдорфа.
Пример 1. Пусть х = (х(1),х<2»)е Е2> хо = (О,0).
Возьмем функцию
f (х) = min{| х(1) 1 +1 х(2> |, |х<»|-|х<2>|}.
Эта функция рассматривалась в примере 9 § 3. Там
было показано, что df (хр) есть (рис. 29) прямоугольник
с вершинами (2, 1), (—2,1), (—2,—1), (2,—1), а мно-
жество df(xp) есть прямоугольник с вершинами (1, 2),
j я НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ НА Еа 219
(—1,2), (—1,—2), (1,—2). Очевидно, что в силу сим-
метричности df(x0)= —df(x0). Применяя формулы
(5.15) и (5.16), найдем, что существует два направления
наискорейшего спуска go = (O, 1) и go = (O, 1) и два на-
правления наискорейшего подъема gi = (1, 0) и =
= (—1, 0). Очевидно также, что
df (х0) _ df (ха) _ _ j af (х0) _ dfM_ = j
dgQ dg'o ’ agl dg{
Пример 2. Пусть теперь
x = (x*1», x<2>) e E2, xo = (0, 0),
f(x)= ||X<» l + x® I.
Эта функция рассматривалась в примере 10 § 3. Там
было показано, что (рис. 30)
df (х0) = со {(0, 0), (2, 2), (-2, 2)},
дП77) = со{(1, -1), (-1, -1)}.
Тогда -57йГ) = со{(1,1), (-1,1)}.
Точка хоявляется inf-стационарной, т. е. fnf —
== 0. Очевидно, что существует два направления наиско-
рейшего подъема
\ 2 ’ 2 )’ \ 2’2/
220
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
[ГЛ. И
и при ЭТОМ
_11П df(xo) _ df(x0)
geSi dg dg{
df (xq)
dgi
2.
Таким образом, проверка необходимых условий ми-
нимума сводится к разысканию уклонения множества
—df(x0) от множества df(xQ) (в смысле Хаусдорфа), а
проверка необходимых условий максимума сводится к
разысканию уклонения множества df(xp) от множества
—df(x0). При решении этих задач одновременно нахо-
дятся направления наискорейшего спуска или наиско-
рейшего подъема (в зависимости от того, какое условие
проверялось — минимума или максимума).
§ 6. Квазидифференцируемые множества
1. Пусть QcE„— замкнутое множество,
Вектор vsEn назовем возможным в широком смысле
направлением множества £2 в точке Хо, если существуют
число % 0 и последовательность {х<} такие, что
Xi s Q, ¥= х0, Xi -> Хо,
, \ и п-i л (6-0
ог = (х/ —Хо)||Х( —х0|| » = Ло0.
Очевидно, что множество возможных в широком смысле
направлений образует замкнутый конус с вершиной в
начале координат. Обозначим его через Г(х0) и будем
называть конусом возможных в широком смысле направ-
лений множества £2 в точке Хо.
Рассмотрим случай, когда £2 имеет вид
£2 — {хгЕп |h(х)<0},
где h (х) — непрерывная квазидифференцируемая на Еп
функция. Предположим, что £2 =/= 0. Будем говорить, что
множество £2 имеет квазидифференцируемую границу,
или просто называть его квазидифференцируемым. Оче-
видно, что £2 — замкнутое множество. Пусть хо е £2. По-
ложим
Y(x0) = {ge£„|^l<0},
Yi(xo) = {^s Еп О}.
5 61
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ МНОЖЕСТВА
221
Очевидно, что если h (х0)' = 0, то
у (х0) «= Г (х0). (6.2)
Пусть й(хо)=О. Будем говорить, что в точке хо вы-
полнено условие невырожденности, если
Y (хо) = Yi (хо)- (6.3)
Здесь у—замыкание множества у. Нетрудно построить
пример, показывающий, что условие (6.3) выполнено не
всегда.
Лемма 6.1. Если /i(x0)<0, то Г(хо) = Еп. Если же
h (хо) = 0 и в точке хо выполнено условие невырожден-
ности (6.3), а функция Л(х) является липшицевой в ок-
рестности точки Хо, то
Г (х0) = Yi (хо). (6.4)
Доказательство. Если h(хо)< 0, то Г(х0) = Еп,
и все доказано. Пусть теперь Л(х0) = 0. Из (6.2) и (6.3)
вытекает
У1(хо) = у(хо)с=Г(хо). (6.5)
Осталось установить обратное включение. Возьмем
#еГ(х0). Тогда существуют число X > О и последова-
тельность {х,} такие, что
X/ е Q, хг х0, X/ -* х0,
gi = (х/ — х0) || xz — х0 |Г' -* go, ga hgo. (6‘6)
Если 1 = 0, то g = 0 и, очевидно, g = 0 е yi (х0). Пусть
теперь X > 0. Тогда
lim а-1 [й(х0 + ag) — ft(x0)]s lim Н (а),
°® а-»+о а-»+0
где Н (а) = a-1 [h (хо + ag) — h (хо) ]. Возьмем
сЧ — Х_11|х(-х0||. (6.7)
Ясно, что а,----► 0. Имеем
1 Z->oo
Н Ч) = аг‘ Р (*о + М - h (х0)] =
= а-1 [Л (х0 + a(Xg0) — h (х0 + a,Xgz) +
+ h (х0 + a<Xg/) - h (xo)] = ap1 [A (x0 + a;Xg0) -
- Л (x0 + a^g,)] + af1 [Л (x0 + a^Xg,) - h (x0)]. (6.8)
222
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
[ГЛ. II
Функция й(х) липшицева в окрестности точки Хо, т. е.
существуют числа б > 0 и L <Z оо такие, что
| h (х) — h (х') К L || х — х' || Vx, х' е S6 (х0).
Значит, при достаточно больших I
I h (х0 + а№о) — Л (х0 + UiKgt) I < ЛаД || gt — gQ ||. (6.9)
Так как из (6.7) хо + ahgt = х- е Q, то h (хо + aihgi)
Л (х0) = 0. Отсюда, из (6.8) и (6.9)
н (ai) < “Г* [Л (*о + а№о) - h (х0 + <*№)]-* о,
т. е. ' = lim Н (<xz) 0, а это значит, что g е yi (х0).
°S Z->oo
Таким образом,
Г (х0) с у( (х0). (6.10)
Утверждение леммы теперь вытекает из (6.5) и (6.10).
Лемма 6.2. Справедливо соотношение
У1(х0)= Ц [-Х+(дА(х0) + и>)]- (6.11)
wsdh (хо)
Доказательство. По определению
у1(х0) = {^е£„|^!!Г<0}.
Так как
dffi- » max (о, g) + min (w, g) =
&& v e dh (xo) wEdh (x0)
= min [ max (v, g)],
w еЗй(Хо) ° s [aft (Xo)+a>]
TO
Yi(xo)= и Гю, (6.12)
w e dh, (xo)
где
= Vu s[dA(x0) + ar']}.
По лемме 3.9 гл. I
rZ^{q^En\(q, g)>0 V^eTw} =
== - (co (dA(x0) + w)) = - Х(<9/г(х0) + да).
§ 6j КВАЗИДИФФЕРЕНЦИРУЕМЫЕ МНОЖЕСТВА 223
Поскольку Гцу — замкнутый выпуклый конус, то (см.
лемму 3.3 гл. I)
Г^+ = ГШ, т. е. Гш = - Ж*- (д/г(х0) + w).
Отсюда и из (6.12) вытекает (6.11).
Лемма 6.3. Имеет место соотношение
у(х0)—Еп\ (J X+(dhM) + v). (6.13)
v^dh (хр)
Доказательство. Обозначим 2) множество в
правой части (6.13). Возьмем любое gey(x0); тогда
д/г (*о) < Q, т е max min < q значит>
S vedh (х») [5h(xo)+t>]
min (w, g) <0 Vo e dh(xQ).
w e [dft (Xo)+o]
Поэтому
g^X+(lM^) + u) VoedA(xo).
Отсюда
g& И ^+{dh^+v),
vEdh (Xo)
g6=£„\ U W+(dh(b) + v)^8>.
v&dh (Xo)
Поскольку g— произвольный вектор из у(х0), то
y(x0)cz^. (6.14)
Возьмем теперь g&3>, т. е. g [J JSf+0Л (x0) + и).
v g dh (xo)
Тогда
g ф X+ (dhM + v) Vv едЛ(хр).
Отсюда
min (w, g) < 0 Voedft(xo). (6.15)
w e [dh (xo)+u]
Множество dh(x0) — компакт, поэтому из (6.15)
max min (w, g) < 0,
o e dh (xo) w e [dft(xo)4-vl
224
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
[ГЛ. П
т. е# .д^°^ < 0, а это и значит, что g е у (х9). Итак
S)czy(xo). Отсюда и из (6.14) получаем (6.13).
2. Проиллюстрируем введенные в п. 1 определения
множеств Г(хо), у(хо) и yi(xo)..
x2 = (—1,
x5 = (0, 2),
Пример 1. Пусть
точки
Х! = (1, 1),
Х4 = (1, -1),
и построим функции
hi (х) — (х — %])2 — 2,
Ы*) = {х — *з)2 — 2>
h5 (х) = (х — х5)2 — 4,
Л7 (х) = max {hi (х), h2 (х)},
hn (x) = max {h5 (x), й9 (x)},
х = (х<1 >, х(2>) s Е2. Возьмем
1), х3 = (—1, -1),
х6 = (0, -2)
h2 (х) = (х — х2)2 — 2,
Л4 (*) = (х — х4)2 — 2,
А6(х) = (х —х6)2 —4,
ft8(x) = max{/i3 (х), h4(x)},
Лю(*)в —М*)>
h12 (х) = max {h6 (x), hw (x)},
h (x) = min {hn (x), hi2 (x)}.
Образуем множество
Q = (x e E21 h (x) < 0}.
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ МНОЖЕСТВА
225
§ 6)
Это множество изображено на рис. 31. Возьмем точку
Хо = (О, 0) и найдем 3)h(x0), конусы у(хр), yi(x0), Г(х0).
Прежде всего, заметим, что
0Л1 (хь) = [— 2хь 0]» (х) — [— 2х2, 0],
(*о) = [—2х3, 0], (х0) = [—2х4, 0],
S)h5 (х0) = [—2х5, 0], 3)h6 (х0) = [— 2х6, 0]
(точнее говоря, надо писать ^5/i1(x0) = [{—2xi}, {0}]|
и т. д.). По лемме 2.2
S)h7(x0) = [со {—2Х], —2х2}, ®] = [—со {2xi,'2х2), 0]»
2£>hs (хр) = [со {—2х3, —2х4), 0] = [—со {2х3, 2х4}, 0].
Так как /г9(х) =—h7(x), Ню(х) = —hs(x), то'
3)h9 (х0) = [®, Л], 3)hl0 (х0) = [О, В],
где
Л = со {2хь 2х2}, В —со {2х3, 2х4).
Снова по лемме 2.2
(х0) = [С, D], &)hi2 (х0) = [F, G],
где
С — со {—2х5 — А, ®}, D = А,
F==co{— 2х6 — В, ®}, G = B.
Множества Л, В, С, F изображены на рис. 32 (мно-
жества Л и В — отрезки, множества С и F— треуголь-
ники). Теперь по лемме 2.3 имеем
£)h (х0) = [dh (х0), dh (х0)],
где
dh (хр) = dhu (Хр) + dh\2 (хр) = С 4- F,
dh (х0) = со {dhi 1 — dhl2, dh12 — dhn} =
= co{£>-F, (? — С} = co{Л — F, B-C).
Множества dh(x0) и dh(x0) изображены на рис. 33
(множество dh (хр) ограничено сплошной жирной ли-
нией, а <3й(хр) — пунктирной). Так как
= max (о, g) + min ' (w, g),
о ve dh (xo) w dh (Xo)
8 В. Ф. Демьянов, Л. В. Васильев
226
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
1ГЛ И
ТО
Y (Хо) = {V - Kg | Л > 0, g = (1, а), а е {(О, 1)} U {(0, - 1)}}U
U {« = Kg |1>О, g-H, а), ае={(0, 1)}U{O, -1}),
Yi (хо) = {о = Kg |Л> 0, g==(l, а), а€=[— 1, 1]} U
U{t’“A,g|A>0> g — (— 1, а), as[-l, 1]}.
Очевидно, что Yi (хо) = у(хо), т. е. в точке хо выпол-
нено условие невырожденности, а тогда по лемме 6.1
Г(х0) = Yi(xo)-
Рис. 34.
Пример 2. Пусть х = (х*1*,х<2>)(=Е2, х0 == (О,0),
Q = {х е= Е21 h (х) < 0),
где А (х) = (х<«> + I)2 Н-(х<2> + I)2 — | x<i> | — | лг<2> |. Ясно,
что х0ЕЙ. Поскольку Л(х)== hi(x) + h2(x), где
/г|(х) = (х<1>+ 1)« + (х<2>+ I)2,
й2 (х) = — I Х(1) I —-1 Х(2) I,
функция Л1(х) гладкая, а функция h2(x) вогнутая, то
можно взять (рис. 34)
______ дй(хо) = {(2,2)},
дЛ(х0) = со{(1, 1), (-1, 1), (-1, -1), (1, -1)}.
5 6]
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ МНОЖЕСТВА
227
Для построения yi(x0) лучше воспользоваться формулой
(6.13), ибо в данном случае субдифференциал dh (х0)
состоит из единственной точки. На рис. 35 пунктиром
ограничен конус У£ (dh (х0) + о) (здесь v = (2,2)),
сплошной линией — конус W+(dh(xo)-}-v), двойной
сплошной линией — конус yi (хо):
Vi (*о) = Y (хо) U {/J U {/2}.
где /1 = {х = Л(3,-1)|Л>0}, /2 = {х = Л(-1,3)|Л>0).
Пример 3. Пусть
х = (х<», х<2>) е= Eit х0 = (0, 0), Q = {х е= Et | h (х) < 0},
где h (х) = (х<>> + I)2 + (х<2> + I)2 +1 х*» | +1 х<2> |. Функция
h(x) выпуклая, причем, как легко проверить, можно
взять
d/t(x0) = co {(l, 1), (3, 1), (3, 3), (1, 3)}, ЭГ(^) = {0}.
Для построения yi(xo) лучше воспользоваться формулой
(6.11), ибо супердифференциал dh (х0) состоит из един-
ственной точки.
Конусы X(dh(x0) + w), (dh(x0) -f- w) и ?i (x0) изо-
бражены на рис. 36.
8*
228
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
(ГЛ. ц
Задание 6.1. Пусть
х = (х(1\ х(2)) е Е2, хо = (О,О), х1==(1, 1), х2 —(—1,1),
Х3 == (-1, -1), х4 - (1, -1), х5 = (2, 2), х6 - (-2, 2),
х7 = (-2, -2), х8 == (2, -2).
Образуем множества
S2 = {x|(x-x2)X2(
З3 = {х | (х - х3)2 < 2}, S4 = {х | (х — х4)2 < 2},
S5 = {х | (х - х5)2 < 8}, S6 = (х | (х — хб)2 < 8},
S7 = {x|(x-x7)2<8}, 38 = {х|(х-х8)2<8}
Построим множество Q = Qi U й2, где Qi = Q3 \Q4, Q2 »
□з = 35 П Se, П4 = 3i Л 32, Qg = 37 Л 38, Qe = З3 Л 34. Множество
Q изображено на рис. 37.
Найти функцию h(x) такую, что
Q = {х <= Е21 h (х)< 0}:
построить ^)Л(хо), у(хо), Yi(*o), Г(хо) Проверить, выполнено ли в
точке Хо условие невырожденности.
§ я
УСЛОВИЯ ОПТИМАЛЬНОСТИ НА МНОЖЕСТВЕ
229
§ 7. Необходимые условия оптимальности
квазидифференцируемой функции
на квазидифференцируемом множестве
1. Пусть на открытом множестве S cz Еп задана ко-
нечная непрерывная функция f(x), и пусть Йс5—
замкнутое множество.
Лемма 7.1. Пусть функция f(x) липшицева в окре-
стности точки х* е Й ы дифференцируема в точке х? по
направлениям. Для того чтобы функция f(x) достигала
в точке х* своего наименьшего на й значения, необхо-
димо, чтобы
-^->0 У£<=Г(х*), (7.1)
где Г(х*)— конус возможных в широком смысле направ-
лений множества й в точке х* (см. § 6).
Доказательство. Допустим противное; тогда су-
ществует go е Г (х*) такое, что
^---<.<0. (7.2)
Из (6.1) следует, что найдутся число Л > 0 и последова-
тельность {х,} такие, что
Х/«=й, ХгУ=Х*, Xz->X*,
Vi — (Xi — X*) II Xi — X* 1Г1 -> Vo, go = to0.
Поскольку
f (Xi) = f (x* + xt — x*) = f (x* + II xt — x* II Vi) = f(x* + aiVi),
где a, = ||x< — x*||, то по лемме 5.6 гл. I
limar'[f(x,)-fU’)] =
= a‘ ' (*’ + f «Л - •
Отсюда
f(Xi) = f(xo) + ai^p- + o(ai). (7.3)
Ho °
= Илу a~1 [f (x* + ao0) — f (**)] =
= V1 lim Xa"V (x* + aV1 (too)) - f (x*)] = Г1 .
a->4-0
230
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
(ГЛ. И
Из (7.2) и (7.3) теперь получаем, что при достаточно
больших i будет f(xi) < f(x*), что противоречит предпо-
ложению о том, что х*— точка минимума функции f(x)
на множестве Q, ибо Xi е й. Лемма доказана.
Пусть теперь йс£я — квазидифференцируемое мно-
жество, т. е.
й = {х е Еп | h (х) 0},
где Л(х)— непрерывная квазидифференцируемая на Еп
функция. По-прежнему предполагаем, что й с: S. Везде
далее в этом параграфе функция /(х) квазидифференци-
руема на S.
Теорема 7.1. Пусть функция f(x) липшицева в ок-
рестности точки х* е й. Если h (х*) = 0, то предпола-
гается, что функция h(x) липшицева в окрестности точ-
ки а в точке х* выполнено условие невырожденности
(6.3). Для того чтобы функция f(x) достигала в точке
х* своего наименьшего на Й значения, необходимо, чтобы
— df(x*)czdf(x*), если Л(х’)<0, (7.4)
и для всех w^df (х*), w' s dh (х*)
(df(x*) + w) П [- (dh(x*) + а/')] =£ 0, если h (х*) = 0.
(7.5)
Здесь, как обычно, Jf(A)— коническая оболочка мно-
жества А.
Доказательство. В случае й(х*)<0 условие
(7.4) следует из теоремы 5.1. Пусть теперь Л(х*)= 0. По
лемме 7.1.
VgG=r(x*).
Конус Г(х*) по лемме 6.1 есть
Г (х*) = у, (х*) = { g е= Еп | =
= max (o', g) + min (w', . (7.7
v's W e dh (x*) J
УСЛОВИЯ ОПТИМАЛЬНОСТИ НА МНОЖЕСТВЕ
231
Из (7.6) и (7.7)
min max (t>, g) > 0 Vg s Г (x*), (7.8)
weSHx1) ° g tdf U*)+tfl
r(x*)=* (g sE„| min max (t»',f)<01. (7.9)
t Iw'cSSTF) v’aldh^+w'] f
Из (7.9)
Г(х*)~ U_IV, (7.10)
w' e dh (x*)
где rw-“(?s£J max (v',g) <01. Из (7.8) и
I I o' a [Oh (x*)+wz) J
(7.10) получаем для любых w^df(x*) и w' e dh (x*)
max (t», g)>0 Vger„-. z7 in
о a [3f (x*)4-tol У1’**/
Положим
F®(g) = max (v, g), HW'(g) = max «g).
v <s [<9f (x*)4-w] o' & [dh <x*)+w']
Тогда ГЮ' — {g ® En IHW' (g)< 0}. Функции Fw(g) и
HW'(g) выпуклые. Найдем
= min ЛЛя)- <7-12)
£ s Где'
Из (7.11) следует, чтофв щ,==0, т. е. g* ™ 0 —решение
задачи (7.12). По теореме 6.1 гл. I должно быть
5Fw(g*)n^(g*)¥=0, (7.13)
где 0~w'(g*) — конус, сопряженный конусу возможных
направлений множества Г®.. Функция Fw(g)—функция
максимума, поэтому по следствию 2 из теоремы 14.2
гл. I
^„,(0) = ^) + ®. (7.14)
Поскольку конус возможных направлений множества
Г®, в точке g* = 0 имеет вид
IF®' = {q е Еп | (g, v') < 0 Vu' ® [дй (х*) + &']},
то по лемме 3.9- гл. I
(0) = - Ж (со (д/г (х*) + да')) = - Ж (д/г(х*) + а/). (7.15)
232
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
[ГЛ. 11
Из (7.13), (7.14) и (7.15) получаем
(df(x*) + w) П [- % (dh(x*f + w')\^ 0
Vayedf(x*), Xfw' ed/i(x*),
а это и есть (7.5). Теорема доказана.
Теорема 7,2. Условие (7.5) эквивалентно условию
П [df (**) + Ж (dh (х*) + w)]. (7.16)
w е dh (х*)
Доказательство. Пусть выполнено (7.5). Возь-
мем любые wsdf(x*) и о/<= <Э/г(х*). Из (7.5) следует
существование вектора v е df(x*) такого, что
v + w «= \-%(dh(x*) + да')].
Отсюда
- w е [о + ^(дЖ) + «О] с= df (х*) + Ж (Oh (х*) + w^.
В силу произвольности w' е dh (х*) имеем
П pf(x*) + J?(dft(x‘)4-w')].
w' е dh (х*)
Так как вектор w^df(x*) произволен, то отсюда полу-
чаем включение (7.16), Пусть теперь имеет место (7.16).
Тогда для любых w^df(x*) и w'&dh(x*) будет
- w «= [df(x*) + Ж (dh(x*) 4- о>')].
Отсюда
О G= [df(x*) ч- W + Ж (dh (х*) 4- ®')].
т. е.
[df(x*) 4- ш] П [-Ж(dh(x*) 4- ш')]#= 0,
а это и есть (7.5). Теорема доказана.
Следствие. Пусть h(х*) = 0, в точке х* функция
h(x) cyбduффepeнцupyeмa и выполнено условие невы-
рожденности. Toeda
- df(7) с df(x*) - Г+ (х*).
233
УСЛОВИЯ ОПТИМАЛЬНОСТИ НА МНОЖЕСТВЕ
§ П
Это вытекает из (7.16) и того, что
дЖ) = {0}, Ж (dh(x*)) = - Г+ (х‘),
где Г(х*)—конус возможных направлений множества
Q в точке х*.
Аналогично устанавливаются необходимые условия
максимума.
Теорема 7.3. Пусть функция f(x) липшицева в ок-
рестности точки х*‘ей. Если h(x**) = 0, то предполо-
жим, что функция h(x) тоже липшицева в окрестности
точки х** и в точке х** выполнено условие невырожден-
ности (6.3). Для того чтобы функция f(x) достигала в
точке х** своего наибольшего на Q значения, необхо-
димо, чтобы
-д{(х**)сдПх^, (7.17)
если h(x**) < О,
- df (х**) с П I~ Ж(дЬ (х~) + да)], (7.18)
w g= dh (х**)
если /г(х**) = О.
Задание 7.1. Доказать теорему 7.3 и показать, что если
h(x) — выпуклая функция, то из (7.18) вытекает условие
— df (х**) <= df (х*“) + Г+ (х**).
2. Пусть Предположим, что функция f(x)
липшицева в окрестности точки хо- Если Л(хо) = 0, то
будем также предполагать, что функция й(х) липши-
цева в окрестности точки хо и в точке хо выполнено ус-
ловие невырожденности (6.3).
Определение. Точку х0ЕЙ, для которой выпол-
нено соотношение (7.4), если й(хо)<0, и соотношение
(7.5), если й(хо) = О, назовем ini-стационарной точкой
функции f(x) на множестве £2. Точку хоей, для кото-
рой выполнено условие (7.17), если /г(хо)<О, и (7.18),
если /г(хо) = О, назовем sup-стационарной точкой функ-
ции f(x) на множестве Q.
Рассмотрим подробнее случай, когда h (х0) = 0. Пусть
точка хо не является inf-стационарной, т. е. не выпол-
234
КВАЗИДИФФЕРВНЦИРУЕМЫВ ФУНКЦИИ
[ГЛ. II
нено условие (7.16) (или, что то же, (7.6)). Найдем
Р(*о)“ max min || 2 4-х'11 =
w е Of (х,) * <=Jdf (xo)+w)
w' e J/i(x0) zz г X (dh (Хо)4-а>Э
s max d (a>, w') d (a>0, wq), (7.19)
w s у (Xo)
w' &bh(xo)
где
d (w, w') — min || 2 4-z' H.
2 68 [df (Xo)+W]
2' e Ж (Qfc (Xq)4-wz)
Поскольку (7.5) не имеет места, то р(х0) > 0.
Пусть d (w0, w'o) = || z0 4- z'o || (при этом || z0 4- z'o ||«=p (x0)).
Положим
go = — («0 + z'o) II «0 + z'o 1Г1.
Лемма 7.2. Если h (x0)e 0 и в точке xo выполнено
условие невырожденности (6.3), то направление g0 есть
направление наискорейшего спуска функции f(x) в точке
Хо по множеству Q, а величина p(x0) = ||zo4-zo|l есть
скорость наискорвйшвео спуска, т. е.
min ------------р(х0). (7.20)
гшГ(жо) °g
Ш-1
Доказательство. Как и при доказательстве
леммы 6.4 гл. I, устанавливается, что
gog[-^+(dft(x0)4-^)],
а тогда (см. (6.4) и (6.11)) £о^Г(хо). Осталось дока-
зать (7.20). Допустим, что (7.20) не выполнено. Тогда
существует gi е Г(х0), llgdl® 1, такое, что
-^-<-р(х0). (7.21)
Так как
= min max (и, g0,
wsdfixi) P«[3f M+ail
5 71
УСЛОВИЯ ОПТИМАЛЬНОСТИ НА МНОЖЕСТВЕ
235
то найдется вектор е df (х0) такой, что
= max (v, gi). (7.22)
°°l v s [af (Xo)4-Wil
Так как gi £ Г (x0), то (см. (6.4) и (6.11)) существует
такое w'i е dh (х0), что
gle[-X+(d/7(x0) + H)].
Найдем
d(wt,u>'i)= min ||z + z'|| = ||zi+ «il|.
z €= [df (Xo)+a>i]
z €= &(dh (x0)+tt»i)
Как и при доказательстве леммы 6.4 гл. I, показывается,
что
— IIZ14- zf || = min max (о, g) <
йе[-ж+(ал(хо)+ш0] Pepf(x0)4-tPt]
< max (о, gi) .
Отсюда и из (7.21) имеем
d (wi, w'i) > — > P (x0),
что противоречит (7.19). Лемма доказана.
Замечание. Направление наискорейшего спуска
может быть и не единственным.
Задание 7.2. Доказать результат, аналогичный лемме 7.2, для
направлений наискорейшего подъема.
Пример 1. Пусть х == (х(п, х(2)) е Е2, хо=(О, 0), f (х)=
= I X(1) I _ I Х(2) I + x(2)t h(x) = — 0,51 х(1> | — х<2>. Тогда
f (х) “ fi (х) + f2 (х) + f3 (х), h (х) => Л, (х) + h2 (х),
где fi (х) = | х<‘> |, f2(x) = —|х(2> |, f3(x) = x<2>,
hl (X) = - 0,51 х'1» |, Л2 (х) = - х<2>.
Образуем множество (рис. 38)
Q = {х е Е21 h (х) 0}.
236
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
1ГЛ. П
Поскольку'(см. примеры 1—4 § 3)
= со{Л1; А2}, dfi (х0) = {©},
^2(ХО) = д/г(хо) = со {В,; В2},
dfM = {Bl}, dhx (х0) = {©}, dh2 (х0) = {В2}, ^з(Хр)={®}, dhi (хр) = со {0,5Дь 0,54J, dh2 (х0) = {0},
ГДе Д1 = (1,0), Л2 = (-1,0), В1 = (0, 1), В2 = (0,-1), то
df (х0) = со {Дь А2} + {BJ, df (х0) = со {Bf, В2},
dh (х0) — {В2}- dh(xa) — со {0,5Л; 0,5Д2}
Рис. 38.
Прежде всего проверим, что в точке хр выполнено усло-
вие невырожденности. Имеем
= (В2, g) + min {(0,5Лд; g), (0,5Д2; g)}.
Найдем те g<=.E2, ||g||=l, для которых = 0.
Очевидно, что
dh (хо) _ dh (х0) _п
dgt dg2
где
( 2 —1 \ / —2 -1 \
gl к л/Г ’ V5" Л ~~ IV5" ' д/Г)'
§ л
УСЛОВИЯ ОПТИМАЛЬНОСТИ НА МНОЖЕСТВЕ
237
Заметим, что
Y (х0) = ₽! U Р2 U Рз>
где
= {& е £2 lg = 2, ?), А > О, ге(-1,0]},
p2 = {geE2|g=-A(i/, 1), Z> 0, z/e[-l, 1]},
03 = {ge=E2|g = A(2, г), к > 0, z е= (— 1, 0]}.
Очевидно (рис. 39),
Yi (*о) = Y (*о) U {g = |Л > 0} J {g = kg2\k^ 0} = у (*о).-
т. е. в точке х0 выполнено условие невырожденности
Из рис. 40 ясно, чтс
"И п______[df (*о) + % (dfl (*о) + О’] =
w е dh, (Хо)
= со{(-1, 1),(1, 1), (0, -1)}.
Отсюда —df(xo)cz3@, т. е. условие (7.16) выполнено;
поэтому точка Хо является inf-стационарной точ-
кой функции f(x) — |х(1>| — |х(2)| + х(2) на множестве
Q= {х| — 0,5|х(1)| — х(2) ^ 0}. В действительности точка
Хо является точкой минимума функции f(x) на мно-
жестве Q.
Пример 2. Пусть снова х = (х(1), х(2)) е Е2, Хд =
==(0,0), функция f(x) та же, что и в примере 1. Возь-
238
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
(ГЛ. II
мем множество (рис. 41) Q = {х е Е2|/г(*) 0}, где
h(x) = —|х(1)|— х(2). Имеем (см. пример 1)
df (х0) = со {Ль Л2} + {BJ, df (х0) = со {Вь В2}.
Легко видеть, что
dh (х0) = {В2}, dh (х0) = со (Ль Л2}.
Как и в примере 1, проверяется условие невырожден-
ности в точке хр. Множество Ж изображено на рис. 42:
= П [Wo) +WMx0) + w)]~
w е dh (Хо)
= со{(-1, 1), (1, 1), (0, 0)}.
Очевидно, что
— df (хр) — — со {Вь В2} =* со {В1( В2} ф 28.
Найдем направления наискорейшего спуска. Имеем для
w^df (х0), w's Sh (х0)
df (х0) + w == со {Л1 + Bi + w, Л2 + Bt + w) = 91ц,,
-X!(dh(x0) + а/) =
= {z = % (- B2 - w')« X (Bi - w') | % > 0} =
Множества SU есть отрезки, параллельные отрезку
со{Ль Л2} и заполняющие прямоугольник с вершинами
S 71
УСЛОВИЯ ОПТИМАЛЬНОСТИ НА МНОЖЕСТВЕ
239
(__1,0), (—1,2), (1,2), (1,0). Множества есть лучи
с центром в начале координат, проходящие через точки
отрезка, соединяющего точки (—1, 1) и (1, 1). Найдем
р(х0) (см- (7.19)):
р (Хо) = max d (w, w') — d (wo, wo) =* d (wi, w[),
w e df (Xo)
w' e dh (xi)
где
®o = (O, 1), u»o = Xi, = ад (0, 1), w'i = Az.
Имеем два направления наискорейшего спуска (рис. 43):
g0=(4. -4), -4)^
При ЭТОМ
— max (о, go) + min (w, gQ) = — .
Аналогично я _ . Очевидно, что =
dg0 2 dg0
3. Установим достаточные условия локального мини-
мума функции f(x) на множестве Q.
Пусть хое£2 — inf-стационарная точка функции f(x)
на множестве й. Теорема 5.3 устанавливает достаточ-
240
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
[ГЛ. II
ные условия минимума, если /г(х0)< 0. Рассмотрим слу-
чай, когда /г(хо) = О. Предполагаем, что в точке xq вы-
выполнено условие невырожденности (6.3) и функции
f(x) и h(x) липшицевы в окрестности точки хр. По тео-
реме 7.1 для любых w&df(xQ) и w'sdft(xo) имеет ме-
сто (7.5), т. е.
® е= [df(xQ) + w + Ж (д/г(х0) + ^')] = 2 (w, ш'). (7.23)
Через r(w, w'} обозначим радиус максимальной сферы
с центром в начале координат, вписанной в 8(ш, ш')«
В силу (7.23) a(w, w') 0. Положим
г — min г (w, w').
wedf (Хо), w' е dh (Хо)
Напомним, что
f (хо + ag) = f (х0) + а -(д*о) + о (а, g). (7.24)
Теорема 7.4. Предположим, что в (7.24) ° -» 0
равномерно по g&En, ||g|| = 1. Если г > 0, то точка хй
является точкой локального минимума, причем
df (х0) *
min А; - = г.
ger (хо), ||g||-l
Доказательство очевидно.
Пример 3. Пусть
х — (х<*>, х<2>) е Е2, х0 — (0, 0),'
f (х) = | х<!) I- 0,51 х<2> 1 + X®,
и пусть множество Q задано так: '
£2 = {хеЕ21h(х)<0},
где ft(x) = —0,251x0) | — х<2>.
Как и в примерах 1 и 2, получаем (рис. 44), что
^Нхо) = со{Л1( А2} + {BJ==co{(l; 1), (-1; 1)},
df(x0) = со {0,5Bi; 0,5В2) = со {(0; 0,5), (0; -0,5)},
dh (х0) = {В2},
dh(x0) = со {0,25^4j; 0,25Л2} = со {(0,25; 0), (-0,25; 0)}.
§ 8J
ФУНКЦИЯ РАССТОЯНИЯ ДО МНОЖЕСТВА
241
Возьмем w <^df (х0) и w' ^dh (х0). Тогда
df(xQ) + да •= со {Д1 + В] 4- w, А2 + В{ + w} =
У£ (дЛ(х0) + w') = {z = К (В2 + w') | к 0} = 3V
Множество 8(w, w') (см. (7.23)) изображено на рис. 45
а?®,
/
<2| ° 5 х(ч
I
Рис. 44.
для ш>=(0; 0,25), w' = (—0, 12а, 0). Лучи /1, 12, 1з па-
раллельны. Очевидно, что
О е 2 (да, w') Vw е df (х0), Va>' е dh (х0).
Нетрудно заметить, что
г — min г (w, w').
we df (Xo), w' e dh (xo)
Минимум здесь достигается при wq — (0; 0, 5), w'o =
= (0,25; 0) и при =(0; 0,5), w'i = (—0,25; 0). Вычисляя
г = г (w0> ^о)> найдем г = 34-1 V425 « 0,6063.
§ 8*. Функция расстояния до множества
В настоящем параграфе изучается дифференцируе-
мость по направлениям функции, являющейся евклидо-
вым расстоянием от точки до замкнутого множества
Q с Еп. В п. 1 рассматривается случай, когда Й — вы-
пуклое множество, в п. 2 — случай, когда й задано с по-
242
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
[ГЛ. Ц
мощью квазидифференцируемой функции. Такие функ-
ции интересны сами по себе и естественным образом
возникают при решении практических задач.
1. Пусть Q cz Еп — выпуклое замкнутое множество.
Образуем функцию
f (x) = min ||х — g|| = ||x — if (х)||.
У<= й
Очевидно, что если xeQ, то f(x) = O. Заметим прежде
всего, что f(x) — выпуклая на Еп функция. Действитель-
но, возьмем точки xi е Еп и х2 е Еп. Пусть
f (х,) = || xi — yi ||, f (х2) = || х2 — у2 И,
где i/i eQ, г/2ей. При осе [0,1] в силу выпуклости
£2 будет
г/а = аг/1 + (1 — а)«/2^О.
Поэтому
f(axi + (l — о^ХаХИах! + (1 — а)х2 — g„|| =
= ||а(Х1 — #i) + (1 — а) (х2 — у2) ||<
<a||xi — yi ||4-(1 — а)||х2 —^2|| = af(x1) + (l — a)f(x2),
а это и означает, что f(x) — выпуклая функция.
Наша цель — найти субдифференциал этой функции.
Пусть х0 е Еп. Если Хо е int й, то
» lim a-1 [f (х0 + ag) — f (x0)] = 0
a->4-0
Vg e En.
Следовательно,
<5f(x0) = {®}. (8.1)
Если xo ф й, то
f(x) = min||g — x||=>min V(y —x)2 =min <p(x, y).
y&Q yeQ yaQ
Функция q>(x, g) = V(y — x)2 непрерывно дифференци-
руема по x в окрестности точки х0. Так как
min q> (х, у) = — max (— ф (х, у)),
y&Q у<= Q
то выполнены все условия теоремы 13.1 гл. I и поэтому
$ 81 ФУНКЦИЯ РАССТОЯНИЯ ДО МНОЖЕСТВА 243
где Q(xo)= {#<=й|ф(хо, y) = f(x0)}. Но в данном слу-
чае множество Q(xo) состоит из единственной точки
у(х0). Поэтому
^- = (о, g), (8.2)
где
-------- * (х0 - у (хо)) = . (8.3)
V(y (Хо) — х0)2 f (х0)
т. е. функция f(x) непрерывно дифференцируема в ок-
рестности ТОЧКИ Хо.
Осталось рассмотреть случай, когда хо — граничная
точка множества Q. Имеем
= Нт Я (а),
dg а->+о
где Я(а)= a-*[f(xo + a£) —f(x0)]. Так как xosQ, то
f(x0) = 0, т. е.
Н (а) = а~7 (х0 + ag) = a-1 min || х0 + ag — у ||.
Для любого у е Q
II Xo+ag—у ||=|| xo-f-ag—(х0 + (у—х0)) || =а || g—а-1 (у—х0) ||.
Поскольку а > 0, то v (у, а) = а-1 (у — Хо) е у (хо) =
= {[i = X(x — x0)|xeQ}. Поэтому
II х0 + ag — у || = а|| g — v {у, а) ||> a min ||g — v || ss аР,
иеГ (Хо)
где Р = min llg —oil, Г (хо) = у (х0) — конус возмож-
иеГ (х0)
ных направлений множества □ в точке хо- Так как Р
не зависит от у, то min || х0 + ag — у || аР, т. е.
Я(а)>Р. (8.4)
Возьмем теперь любое иву (х0). При достаточно ма-
лых а > 0 будет х0 + ao е Q. Поэтому
f (хо + ag) = min ||х0 + ag — у ||<
у s Q
<||x0 + ag — х0 — av || = a||g — v||.
244
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
[ГЛ. Ц
Отсюда
Я(а)<и-р||.
Поскольку это неравенство справедливо для любого
v е у (х0), то
Н (а) С inf || g — v || = min || g — v || = P. (8.5)
V e= у (X.) У e Г (Xo)
Так как Р не зависит от а, то из (8.4) и (8.5) имеем
^L = P= min ||g-p||.
°S v s Г (x,)
По следствию 3 из леммы 6.4 гл. I имеем (поменяв ро-
лями Г и Г+)
min Ilf— V11= max (w, g),
оеГ(Хо) ше[-Г+(xs)]
Dv| < 1
т. e.
-o) = max (w, g). (8.6)
® W s [~r+ (Xo)]
IIwll < 1
Значит,
^(x0) = {a>eEn|||a>||< 1, ше=[— Г+(х0)]} =
= (- Г+(х0)) П Sb
где
Si= {®eEn||M< 1).
Так как в случае й(х0)<0 будет Г+(х0) = {0}, то из
(8.1), (8.2) и (8.6) окончательно получим, что справед-
лива
Лемма 8.1. Функция f (х) дифференцируема по на-
правлениям на Еп, причем
^Г- = max (у, g), (8.7)
и e=df (хс)
еде
(I ! если
#(х0) = Ц f(Xo) > (8.8)
’ (— Г+ (х0) П Si), если Xq е Q.
ФУНКЦИЯ РАССТОЯНИЯ ДО МНОЖЕСТВА
245
§ 8]
Задание 8.1. Найти субдифференциал функции
{(х)= min II х— г/II ,
у s Q
где ||х — у|| = max { | х(0 — y(i} | }> х = (х(1).х(п)), У —
т i е 1 : п
= (у™...» у^)’ Q cz Еп-— выпуклое замкнутое множество.
2. Пусть й с. Еп — замкнутое множество (уже не
обязательно выпуклое). Рассмотрим снова функцию
f (х) = min || х — у ||. (8.9)
у е й
Положим
Q(xo) = {0 = Q| II*-Я = /(*)}. (8.Ю)
Ясно, что множество Q(x) может состоять более чем из
одной точки. Функция f(x) уже не обязательно выпук-
лая.
Пусть хо е Еп. Если Хо е int й, то
^21 = 0 Vge£„. (8.11)
Если х0^й, то f (х0) == min || у — х ||. Как и в п. 1,
уей
= min (<р£ (х0, у), g),
°S y<=Q (х0)
где <р(х, у) = -у/(у — х)2 . Значит,
-^- = min (о, g), (8.12)
где
Л = со { *| t/sQ(x0)|.
Пусть теперь Хо — граничная точка множества й.
Предположим, что множество й имеет вид
й = {х е Еп I h (х) 0),
где /г(х)—квазидифференцируемая на Еп функция.
Предположим также, что в окрестности точки хо функ-
ция /г(х) липшицева и в точке х0 выполнено условие не-
246
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
• [ГЛ. II
вырожденности (6.3). Поскольку х0— граничная точка
множества й, то й(хо) = О. По лемме 6.1
Г (х0) = Yi (х«) = Y (х0),
где
Y(x0) = {geE„|^^-<0}. (8.13)
Положим
Н (а) = а-1 [f (х0 + ag) — f (х0)] =
= а-1/ (х0 + ag) = а-1 min || х0 + ag — у ||.
(/ей
Пусть последовательность {а*} такова, что
аА->+0, //(а*)-* lim Н (а) (8.14)
а->+0
(такая последовательность существует), и пусть
f (хо + akg) » min ||х0 + akg — у || = ||х0 + akg — yk || =
Уа-*о
ак
= а*
„ 11Уа~ *о11 =
II Ук ~ х0 II ak
==a*llg — ^aZaII, (8.15)
Ук~хо
где
. Уа~*о _ ||Уа-М
k 11уа-хо|Г k %
Поскольку
f(xo + akg)^O, ||z*||=l,
Л* ограничено. Можно считать, что Ла-*Л^
то в (8.15)
0, za->z0. Из (8.14) тогда
lim Н (а) = lim Н (ак) «= || g — Zz01|.
а->+0
Так как здесь 2оеГ(хо), zi = Лг0еГ(х0), то
lim /7(a) = ||g —zJO min ||g — z||esP (8.16)
а->+0 г s Г (Хо)
(выше неявно предполагалось, что ук Ф Хо, в случае
yk ss х0 соотношение (8.16) очевидно).
§ 81
ФУНКЦИЯ РАССТОЯНИЯ ДО МНОЖЕСТВА
247
Возьмем теперь последовательность {с^} такую, что
аЛ->+0, Я(аЛ)-> Пт Н (а). (8.17)
а->+0
Зафиксируем любое zsy(xo). Тогда из (8.13) следует,
что при достаточно малых а > 0 будет ха = х0 + az е
е Q; поэтому
f (Хо + akg) = min || Хо + akg — У IK
yeQ
< | Xo + akg — Xak II = ak II g — z ||.
Отсюда и из (8.17)
IIS Я (a)- lim H (ak) < ||g - z||.
a->4-0 &->oo
Это неравенство справедливо для всех zey(x0). По-
этому
lim Н (а) inf || g — z ||.
a-> +0 z s y (x4
Так как Г(х0) = у(х0), то отсюда
Йт tf(a)< min ||g-z|| = P. (8.18)
a->4-0 z e Г
Из (8.16) и (8.18) получаем, что существует lim Я (a),
a-Ц-О
причем
lim Я(а) = Р^ min ||ff-z||, (8.19)
°S a->+0 г«Г(х.)
т. e. функция f(x) дифференцируема в точке хо по на-
правлениям. Так как Г(х0) = ?i(Xo), то
Г(х0)=(ге£п| max (v, z)+ min (w, z)< 0 X =
X | о « dh (Xo) a> s dh (x.) f
= fz<=£„| min Г max (v, z)l<0) =
I | m saTirJ ° eJ J
= Ц f max (v, z)<01 =
m 1 p s [Эй W+wi f
“ HJ- X'+ (^o) + “>)]’
w s dh (x9)
248
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
[ГЛ. И
где Jf(A)—коническая оболочка множества А, $£+—
конус, сопряженный конусу Ж Из (8.19)
= min min II g — z||.
“ w е dh (х ) z e [ -Я’+ (dh (xQ+tti)]
По следствию 3 из леммы 6.4 гл. I
min II g — z||= max (v, g).
ze[-X+ (dh (x0)+w)] о e X (dh (x-)+tt>)
Окончательно имеем
= min max (°* £)• (8-20)
w e dh (x ) v <= УС (dh (x3)+w)
IMI < 1
Из (8.11), (8.12) и (8.20) вытекает
Лемма 8.2. Функция f (х), заданная соотношением
(8.9), дифференцируема по направлениям для всех хое
е int £2, для всех х0 ф £2 и в тех граничных точках мно-
жества £2, в окрестности которых функция Л(х) липши-
цева и в которых выполнено условие невырожденности
(6.3). При этом производные по направлениям вычис-
ляются соответственно по формулам (8.11), (8.12) и
(8.20).
Замечание. Из (8.11) и (8.12) заключаем, что
f(x) квазидифференцируема для х0 е int £2 и х0^£2.
Формула (8.20) показывает, что в граничных точках
функция f(x) уже не является квазидифференцируемой
(по крайней мере из (8.20) нельзя сделать вывод о
квазидифференцируемости функции f(x)). Приведем
пример, показывающий, что условие невырожденности
в граничной точке хо существенно для дифференцируе-
мости в точке хо по направлениям.
Пример 1. Пусть
х = (х<‘>, х®) е= £2, £2 = {0} U П
fe-0
где 3)k — выпуклая оболочка точек 4*, Bk, Ck,
Ak = (2~k, 0), 5ft = (2*-ft, 0), Ck = (2~k, 2~k).
Множество £2 изображено на рис. 46. Положим хо =
= (0,0), go = (0, 1). Ясно, что для точки х0 конус воз-
§ 8]
ФУНКЦИЯ РАССТОЯНИЯ ДО МНОЖЕСТВА
249
можных в широком смысле направлений Г(х0) есть
(рис. 47)
Г(х0) = (о = %г|Л>0, г = (1, а), а <= [0, 1]}.
Рассмотрим последовательности чисел {«*}, где
а* = 2-*, и точек хк — х0 + akg = (0, 2~к) Очевидно, что
f (хк) s min|| хк — у || —1| хк — Cfe_i || ==
__ л i ( 1 А I ( 1________L.V ___л/9~ .
— Д/ 2k)
т. е.
// (аА) = ак 1 [f (хо + aftgo) — f (х0)] =
== V2’.2fe-2~<*+1) = ^L Vfe.
260
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
[ГЛ. II
Пусть теперь
' 1 (-L _1_ 1 ч _ 3
2 ' 2ft+1 ) 2^а
Для точек x'k = хо + <4go “ (о, бУДет
f (x'k) = min || х'к — у || = || x'k — Ck-г II =
У €= Q
H («4) - (<!)' [f (a + algo) - f (a)] = VS" 3-‘ Vk.
Таким образом, пределы функции Н (а) по последова-
тельностям {а*} и {а*} не совпадают (они равны со-
ответственно V2 -2 1 и V5 *3 *), т. е. функция f(x) =
= min || х — у || в точке хо = (0, 0) не является дифферен-
У е Q
цируемой по направлению g0.
Задание 8.2. Пусть х *= (х(1)> х(2>) s Et. Рассмотрим функции
Г1 (х) = (х — xi)’ — 2, гз (х) — (х — xs)2 — 2,
г, (х) = (х — х8)3 — 2, г4 (х) = (х — х4)3 — 2,
где х, = (1. 1), х2 = (1, — 1), х3 = (—1, 1), х4=»(— 1, — 1).
НЕЯВНЫЕ ФУНКЦИИ
251
§ 81
Положим
hx (х) =я max {/4 (х), r2 (х)}, h2 (х) = max {г 1 (х), г4 (х)},
h3 (х) == max {гз (х), r4 (х)}, h4 (х) = max {г2 (х), г8 (х)}.
Пусть
h (х) «ш min h{ (х).
i<=l:4 1
Образуем множество Q = (хе E2\h(x) <0} и функцию f (х) =
= min || х — у ||. Множество Q изображено на рис. 48. Для точки
у s Q
Хо = (0,0) найти (надо воспользоваться формулой (8.20),
для этого найти dft(x0) и дЛ(х0)). Множество Q также называют
пропеллером Карлсона — Пшеничного.
§ 9. Неявные функции
Пусть f(z) = f (х, у) — функция двух переменных,
z = (х, у)е Е2, и пусть Zo = (хо, уо)— решение уравнения
f(z) = 0, т. е.
/(Хо, г/о) = 0. (9.1)
Предположим, что функция /(г) квазидифференци-
руема в окрестности точки Zo- Зафиксируем любое
ge£i, ||g|| = 1 (таких g в Ei может быть только два:
gi = 4-l и gz = —1), и рассмотрим функцию F(a, у) =
= f (х0 + у), где а > 0, у е Еь
Требуется найти условия, при которых существуют
число ссо>О и непрерывная функция у (а), заданная
на [0, ао], такие, что
F (а, у (а)) s f (х0 + ag, у (а)) = 0 Va <= [0, ао]. (9.2)
Так как /(z)—квазидифференцируемая в окрестно-
сти точки zo функция, то
/ (zo+at])=f (zo) + а Г max (о, n) + min (a>, т))]+о (a).
Lo s dt (Zo) w & df (Zo) J
(9.3)
Здесь n=(£, q)- Допустим, что существует qo&Ei та-
кое, что
ss max (о, т)0) + min (w, По) = 0, (9.4)
О'По о <= (г,) w s df (Zo)
где i)o = (g, <7o) • Предположим, что функция о (а) =
252
КВАЗИДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
(ГЛ. II
— o(a,q) в (9.3) такова, что 0 равномерно
по q в некоторой окрестности точки qo е Ех. Положим
V = (о1,а2), w = (wi,w2) и рассмотрим функцию
h(q) — max (щ§ + о2<7) + min (wtg + w2q). (9.5)
о e df (z») ®edf<z)
Из (9.4) следует, что
Ш) = 0. (9.6)
Теорема 9.1. Пусть h(qo) — Q. Если функция h(q)
строго монотонна в окрестности точки qo, то существует
функция у (а), заданная и непрерывная при ае[0, а0],
где а0 > О, “ такая, что выполнено (9.2). При этом
у (а) имеет производную справа в точке а = 0 иу'+(О)=
-Яо-
Доказательство аналогично доказательству
теоремы о неявных функциях в гладком случае и предо-
ставляется читателю.
Замечание 1. Факт существования неявной функ-
ции устанавливается рассмотрением функции (9.5),свой-
ства которой определяются лишь квазидифференциалом
функции f(z) в точке z0. В частности, может оказаться,
что qo, удовлетворяющее (9.6), неединственно.
Пример 1. Пусть f(z) = |x| — |jf|, го = (0,0). Оче-
видно, что f(zo) = 0. Эта функция изучалась в примере 5
§ 3. Возьмем g=4-l. Из рис. 36 ясно, что уравнение
(9.5) имеет два решения qo — +1 и q0 = — 1. Ясно так-
же, что функция h(q) в окрестности точки q0 строго убы-
вает, а в окрестности точки q0 — строго возрастает, по-
этому выполнены условия теоремы и, значит, существует
два решения уравнения | а | — |g| = 0 (при а > 0) у (а)
и у (а), причем (0) — +1, у\ (0) —— 1. Аналогично
из рис. 36 ясно, что при g = — 1 уравнение (9.5) тоже
имеет два решения: q0 = + 1 и q0 = —1, а функция h(q)
строго монотонна в окрестности этих точек.
Пример 2. Пусть f(z) = | |х| + у\, г0 — (0, 0).
Ясно, что f(z0) = 0. Эта функция изучалась в примере 10
§ 3. Из рис. 41 ясно, что при g= +1 уравнение (9.5)
имеет решение q0 = —1, однако функция h(q) не яв-
ляется строго монотонной. Тем не менее решение урав-
нения ||аЦ-*/| = 0 существует, причем ^(0) = — 1.
НЕЯВНЫЕ ФУНКЦИИ
253
§ 9]
Задание 9.1. Изучить случай, когда f(z) является суб- или
супердифференцируемой функцией в точке г0, для которой f(zo)=O.
Замечание 2. Рассмотрим систему уравнений
Ь(г)в/((х,?) = 0 Vzs/==l:n. (9.7)
Здесь х <= Ет, у<^Еп. Пусть известно решение z0 — [х0, z/0]
системы (9.7): fz(zo) = O У/1&1. Возьмем и рас-
смотрим систему
fi (х0 + ag, у) = О V/ «= 1.
Функции fi(z) предполагаются непрерывными и квази-
дифференцируемыми в точке гй. Наша задача — выяс-
нить, существуют ли число сс0 > 0 и непрерывная век-
тор-функция у (а) такие, что
У (0) = Уо, fi (х0 + ag, у (а)) = 0 Vae [0, -а0], Vz <= /. (9.8)
Из квазидифференцируемости функций fi(z) имеем
fi (х0 + ag> Уо + а?) =
== ft (Хо. Уо) + a I max ((ou, g) + (v2t, <?))4-
pzsdfz (г0)
+ min g) 4- (w2t, <?))] 4- ot (a) Vz e= 1, (9.9)
wie dfi (zo)
где Vi = [olf, t»2i] «= Em X En, wt = [a>H, w2t] e EmX En.
Рассмотрим систему
max ((ци, g) + (v2l, <?)) 4-
azg#z(*o)
4- min ((wu, g) 4- (w2i, q)) = 0 Vz e I. (9.10)
e dh (*o)
Здесь неизвестным является вектор q^En.
Из (9.9) следует, что вопрос о существовании неяв-
ной функции нескольких переменных сводится к изуче-
нию свойств решений системы (9.10). Эти системы, сле-
дуя Веллману и Калабе, будем называть квазилиней-
ными.
ГЛАВА III
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
§ 1. Необходимые и достаточные
условия минимума
выпуклой функции на Еп
Пусть f(x) — выпуклая на Еп функция. Напомним
(§ 6 гл. I), что, для того чтобы в точке у? выпуклая
функция f(x) достигала своего наименьшего на Еп зна-
чения, необходимо и достаточно, чтобы
0<=#(х’).
Пусть е 0. Точка хе е Еп называется г-стационар-
ной точкой функции f(x), если
О <= dj (хе)
или, что то же самое,
0<f(xe)-r<e, (1.1)
где f = inf f(x).
хаЕп
Напомним также, что если O&def(xo) и ~
= max (о, go) < 0, где g0 s Еп, то (см. п. 3 § 8 гл. I)
vsd6f(x9)
f (х0) — inf f (х0 4- ago) > 8. (1.2)
a>0
Введем обозначения:
фе(х) = min max (v, g);
||g||-l v€=dgf(x4
pe (x) = min II v ||,
(x)]fr
P(-v) = Po(x), de(x)= min ||p||, d(x) = d0(x).
u eagf (X)
J 1] УСЛОВИЯ МИНИМУМА выпуклой функции НА вп 255
Ясно, что если de (х)> 0, то p8(x) = de(x), а если
de (х) == 0, то ре (х) есть радиус наибольшего шара с
центром в начале координат, содержащегося в def(x).
Связь между ф8(х), р8(х) и de(x) устанавливает
Лемма 1.1. Имеет место следующее соотношение-.
( — Ре (*) = — dt (х), если de (х) > О,
р8(х), если d8(x) = 0.
Доказательство получаем, применяя лемму 6.4
гл. I для случая В = def(x), Г+ = {0}.
Лемма 1.2. При любых х, уеЕпи 6^0 справед-
ливо неравенство
f(y)~ f(x)>^e(x}\\y — *11 — в. (1.3)
Доказательство. В силу определения def(x) и
а|з8(х) имеем
f(F) — f(*)> тах («. У — *) — 8>||1/ — хНе(х)—8.
iia»ef(x)
Лемма 1.3. Пусть е > 0, х8 — г-стационарная точка
функции f(x) на Еп и -ф 8 (хе) > 0.
Тоеда f* > — оо, множество JC* = {х е 5л|/(х) = f*Y
есть непустой выпуклый компакт,
f(xt)-r<&, (1.4)
и если f* < f(xt), то
(Г (Хе) - Г) (Р (Хе))"1 СII х* - X. || < (f*-f (х.) + в) (р, (х.))~1
(1.5)
где х*—точка минимума функции f(x) на Еп, р(х) =
= ро(х).
Доказательство. Так как ф8(х,)> 0, то Ое
е def(Xe) И ИЗ (1.1)
/(х8)-Г<в; (1.6)
следовательно, f* > — оо.
В силу (1.3) для любого хе Еп будет
f (х) — f (Xg) > 'Фе (xe) II X — Хе II — в.
Поэтому
|| X — X, II < (f (х) — f (хе) + е) (1|)8 (х8))~1. (1.7)
256
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. IH
Из (1.7), в частности, следует, что лебегово множе-
ство 3>(xe) — {x&En\f(x)^.f(xe)} ограничено, более
того,
Ф (х8) с: S« (х8), где 6 — е (-фе (х8))-1.
Тем более непусто и ограничено множество Ж* сг
cz£Z5(x8). Замкнутость и выпуклость множества Ж* оче-
видны.
Допустим теперь, что
f(x8)-/* = e. (1.8)
Полагая в (1.7) х = х* и учитывая (1.8), получаем
хе = х*, а это противоречит (1.8). Таким образом, ра-
венство (1.8) невозможно. Теперь (1.4) вытекает из
(1.6).
Далее, из леммы 1.1 следует, что ф8(х8) = р8(х8),
ибо </8 (х8) = 0, и ф (х8) = — р (х8), ибо d (х8) > 0. Теперь
неравенство в правой части (1.5) получаем, полагая в
(1.7) х = х*, а неравенство в левой части (1.5) следует
из того, что согласно (1.3)
f-f(x8) = f(x*)-f(xe)>
> Ф (х8) II X* — х8 II =- — р (х8) IIX* — х81|. Н
Замечание. Условие f* < f(xe) требуется только
для справедливости левостороннего неравенства в (1.5).
§ 2. Минимизация гладкой функции
Ряд методов негладкой оптимизации, обсуждаемых
ниже, В идейном плане тесно связан с методами, разра-
ботанными для минимизации гладких функций.
Пусть f(x)—непрерывно дифференцируемая на Еп
функция, не обязательно выпуклая. Для того чтобы f(x)
достигала в точке х*еЕп своего наименьшего на Еп
значения, необходимо, а если f(x) — выпуклая на Еп
функция, то и достаточно, чтобы
f(x‘)=0. (2. В
Точка х*, удовлетворяющая (2.1), называется стацио-
нарной точкой функции f(x) на Ей. Если f'(xo)#=O, то
§ 2]
МИНИМИЗАЦИЯ ГЛАДКОЙ ФУНКЦИИ
257
направление g(x0) =—Г(хо)/11/'(хо) II является направ-
лением наискорейшего спуска функции f(x) в точке Хо,
Напомним, что в этом случае -Hp). = (Г (хо)> g\
Многие методы оптимизации используют условие
(2.1).
1. Метод непрерывного спуска. Рассмотрим систему
обыкновенных дифференциальных уравнений
х(/) = -Л(х(/))/'(*). (2.2)
х(О) = хо, (2.3)
где Д(х)— непрерывная на <2>(x0)ss{xeEn|f(x)sg:
f(x0)} матричная функция размерности «Хп, при-
чем существует т > 0 такое, что
(А (х) z, z) > m || z Ifi Vz e En, Vx^2) (x0). (2.4)
При наложенных условиях решение x(t, Хо) системы
(2.2) — (2.3) существует на [0, оо). Отметим также, что
х(/, xo)e0(xo) V/>0. (2.5)
Лемма 2.1. Если множество S)(xq) ограничено, то
всякая предельная точка решения х(/, х0) является ста-
ционарной точкой f(x) на Еп.
В качестве дискретных аналогов непрерывного ме-
тода (2.2) можно получить метод наискорейшего спуска,
метод наискорейшего спуска с постоянным шагом и ме-
тод Ньютона (см. [16], [59], [61], [105], [114]).
2. Метод наискорейшего спуска. В качестве началь-
ного приближения выберем произвольное х0 е Еп. Пусть
уже найдено хк^Еп. Если f'(Xs) = O, то точка хк—
стационарная, и процесс прекращается. Если же
Г(хй)^=0, то положим gk = f'(Xk) и рассмотрим луч
{x<=En\x = xka^xk — agk, а>0}.
Найдем min f (х*о)=/(предполагаем, что inf f(x*a)
достигается). Положим xk+i = xkak.
В результате строим последовательность {хк}. Если
эта последовательность состоит из конечного числа то-
9 В. Ф. Демьянов, Л. В, Васильев
258
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. 111
чек, то последняя полученная точка является стационар-
ной по построению. В противном случае справедлива
Теорема 2.1. Если множество 3)(хо) ограничено,
то всякая предельная точка последовательности {хк} яв-
ляется стационарной.
Оказывается, что при весьма естественных предпо-
ложениях скорость сходимости метода наискорейшего
спуска — геометрическая.
Замечание. В качестве gk можно выбирать лю-
бой вектор такой, что
(gk, f'M)>\\gk\\-\\f'(xk) ц.е,
где g*=#0, 9е(0,1] фиксировано.
3. Метод наискорейшего спуска с постоянным ша-
гом. Пусть f'(x) удовлетворяет на Еп условию Лип-
шица: существует L <Z оо такое, что ||f'(x)— f (z)||
<5 L||x —z||Vx, zeE„.
Зафиксируем A e (о, . Выберем Xq e En. Пусть
уже найдено x*e^5(x0). Если f(xs)==0, то точка x* —
стационарная, и процесс прекращается. Если же^'(хА)У=
то полагаем xk+i — хк— Af'(x*). Для последова-
тельности {xs} справедлива теорема 2.1.
§ 3. Метод наискорейшего спуска
1. Пусть f(x) — выпуклая на Еп функция. В § 8 гл. I
было введено понятие e-производной выпуклой функции
f (х) в точке хо по направлению g:
max (о, g).
°8 o«aef(x0)
Если Oed8f(xo), то точка х0 — е-стационарная, и
тогда
0</(х0)-Г<8,
где inf f(x).
Если 0 def (х0), то вектор ge (х0) = — ve (х0) || ve (х0) Ц-1.
вде ие (х0) <= def (х0), || ve (хо) || = min || v || = de (х0), яв-
(х0)
5 31
МЕТОД НАИСКОРЕЙШЕГО СПУСКА
259
ляется направлением e-наискорейшего спуска, т. е.
df (х0) _ . dj (х0)
dge(xj ~ J™ dg ’
Направление gt (х0) единственно.
В § 8 гл. I было также показано, что если для неко-
r> dfj (Хо) (\
торого g^En оказалось - < 0, то
inf / (х0 + ag) < f(x0) — в, • (3.1)
а>0
т. е. в направлении g функция f(x) может быть умень-
шена не меньше чем на е.
2. 8-алгоритм. Зафиксируем е > 0 и выберем про-
извольное начальное приближение хо е Еп. Пусть уже
найдено k-e приближение х4е£п. Если Обdsf(х*), то
xk является 8-стационарной точкой функции f(x) на Еп.
Если же 0фд^{хк), то найдем такой вектор gk^En,
||^||= 1, что
4JXk> = max (v,gk)<0. (3.2)
dgk v^det(xk)
После этого на луче {х*(а) = х* + а£*|а 0} най-
дем точку Xft+i = Xk(a,k), в которой
f(xft+i)</(xfe)-e. (3.3)
Из (3.1) следует, что такая точка хк+1 обязательно най-
дется.
На основании (3.3) заключаем, что либо за конечное
число шагов будет получена е-стационарная точка функ-
ции f(x) на Е„ (это произойдет, если f* > — оо), либо
/* = —оо.
Поясним, как в случае ® &.dtf(xk) находить вектор
gk, удовлетворяющий (3.2). Очевидно, что в качествен
может быть взят вектор ge(Xk) — направление в-наиско-
рейшего спуска функции f(x) в точке хк. Действительно,
пусть
®<£def(xk), v.EdJlxJ, \\ve(xk)\\ = dt(xk),
gi (хк) = — ve (хк) II vt (x^ 1Г1.
9’
260
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. Ill
Тогда
8
Если в качестве gk брать ge(Xk)—направление 8-наи-
скорейшего спуска функции f(x) в точке хк, то полу-
чающийся при этом метод назовем методом е-наискорей-
шего спуска.
Для нахождения vt(Xk) требуется решить следую-
щую задачу: найти vt(Xk)<3 dtf(Xk) такой, что
II ».(**) IIе min ||о||. (3.4)
Если в процессе решения задачи (8.4) найден такой
вектор Vk е def(xk), что Vk
(о, v^ > 0 (vk, ок) Vo & dj (xk), (3.6)
где 6s(0, 1], то вектор gk =—v*l|o*ll_* будет удовлет-
ворять (3.2).
Замечание 1. Если вместо направления gk такого,
что < 0, брать направление, для которого
df (ч) *
- , < 0, то метод может не сходиться (среди всех
® k
предельных точек последовательности {х^ может не
оказаться точки, минимума функции f(x) на Еп). Это
объясняется тем, что в этом случае нет оценки типа
(3.1) — гарантированного убывания функции f(x) на
каждом шаге.
3. В изложенной схеме е-алгоритма для построения
точки Xk+i, удовлетворяющей (3.3), в общем случае не-
обходимо прибегать к одномерной минимизации функ-
ции f (xk + agk) по а > 0, в процессе которой может по-
требоваться вычислять функцию f(x) в достаточно боль-
шом числе точек. Если £* =—ОлНМ-1, где о* удовлет-
воряет (3.5), то можно выбирать длину шага из точки
хк в направлении gk, вычисляя функцию f(x) на луче
{х*(а)|а^0} лишь один раз. Одним из способов та-
кого выбора чисел а» является следующий:
а4 = е
Wk) dKxk)l
d«k dSk J
i з)
МЕТОД НАИСКОРЕИШЕГО СПУСКА
261
Если числа а* выбирать таким образом, то в силу
леммы 8.6 гл. I при каждом k будут выполняться нера-
венства
f(xA+1)<f(xft) + aft-^l. (3.6)
Если лебегово множество 3) (х0) = {х е Еп | f (х)
^f(xo)} ограничено, то любая предельная точка после-
довательности {хь+1 = хк + akgk} будет е-стационарной
точкой функции f(x) на Еп. Действительно, если допу-
стить, что существует подпоследовательность {xAi} такая,
что Xks~*x*, но ®^dtf(x*) (тогда </е(х*)> 0), то при
достаточно больших k3, в силу полунепрерывности сверху
def(x), окажется (см. (3.5))
д f(х, <
ks
Отсюда, из (3.6) и вида as имеем
f (*fes+i) < f (*ss) — у (x*)«
где b = max max || v ,
x<=s>(xo) 0Sdef(x)
Следовательно, f(xk) — оо, а это противоречит
ограниченности f(x) на 3>(x0).
4. Покажем теперь, как применять е-алгоритм для
нахождения точек минимума функции f(x) на Е„.
Выберем произвольным образом точку х0 е Еп и чис-
ло ео > 0. Применяя 8-алгоритм п. 2 с 8 = во из началь-
ного приближения Хоо = Хо, либо выясняем, что f* =
“— оо, либо за конечное число шагов t0 находим точку
x\ = xotc, которая является ео-стационарной точкой функ-
ции f(x) на Еп. Далее рассматриваем случай, когда
f* > — оо. Положим Хю = X! и выберем ei < во. Из
точки хю, двигаясь с помощью е-алгоритма с 8 = 8], за
конечное число шагов t\ найдем точку х2 = х1/1, которая
будет 81-стационарнбй точкой функции f(x) на Еп.
Продолжая аналогично, построим последователь-
ность {х*}, каждая точка х* которой является ва-гста-
ционарной точкой функции /(х) на Еп.
262
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. Ш
Теорема 3.1. Пусть f* > — со, в*->0. Тогда
= (3.7)
/?->оо
и если множество 3)(хй) ограничено, то любая предель-
ная точка последовательности {х*} является точкой ми-
нимума функции f(x) на Еп.
Доказательство. Так как при каждом k точка
Xk есть Bk-i-стационарная точка функции f(x) на Еп, то
0<f(Xk)-r^ek^. (3.8)
Из (3.8) и того, что е* -> 0, вытекает (3.7). Если
S)(x0) ограничено, то, поскольку Xk^S)(x0) при каж-
дом k, последовательность {х*} имеет предельные точки.
Пусть xks ->х*. Тогда, в силу (3.7), f(x*) = f*. Теорема
доказана.
5. Опишем еще одну модификацию е-алгоритма для
отыскания точек минимума функции f(x) на всем про-
странстве.
Выберем произвольным образом начальное прибли-
жение х0<=Еп. Если Oedf(xo), то х0 — точка минимума.
Пусть O^df(xo). Найдем такое число во>0, что
®sdeJ(x0), т. е. f(x0)—Г во- В качестве во можно
взять, например, f(x0)—f*.
Заметим, что если при любом е > 0 будет
®<£<V(x0), (3.9)
то f* = — оо. Действительно, условие Oedef(xo) экви-
валентно условию f(xo) — f*^e. Поэтому (3.9) равно-
сильно тому, что f (хо) — f* > е. Поскольку это неравен-
ство справедливо для всех в > 0, то f* = — оо.
Предположим, что f* > — оо.
Будем перебирать числовую последовательность
= 2_<?ео, q = 1, 2, ..., до тех пор, пока не окажется,
что при некоторых qQ 1 и е, = 0 ф. deJ (х0), причем
ei <12-1в0 и
Oe<?2e,f(xo), f(x0) — Г<2в,. (3.10)
Теперь найдем такой вектор g0&En, ||g0||= 1, что
< °’ и на лУче {*о (°0 = хо + а£о Iа найдем
такую точку Xi = хо(ао). что
/(Xi)-f(xo)<-ei. (3.11)
$ fl
МЕТОД НАИСКОРВИШЕГО СПУСКА
263
Согласно (3.1) такая точка xi обязательно найдется. Из
(3.10) и (3.11) вытекает, что
f (*1) f W — 8] f* 4* 81.
Следовательно, Oed8J(xi) и точка xi является ei-ста-
ционарной точкой функции f(x) на Еп.
Продолжая аналогично, построим последователь-
ность {х*}, которая либо конечна (тогда найдена точка
минимума), либо каждая ее точка х* есть ^-стационар-
ная точка функции f(x) на Еп, где еА = 2-‘?А-|еА_1,
0^f(xk)-r<2-^->e/t_l^2-kSo Vk. (3.12)
В этом случае справедлива следующая
Теорема 3.2. Пусть f* > — оо. Тогда
lim f (xft)==f,
£->оо
причем скорость сходимости геометрическая, и если мно-
жество S)(x0) ограничено, то любая предельная точка
последовательности {х*} является точкой минимума
функции f(x) на Еп.
Доказательство аналогично доказательству
теоремы 3.1. Неравенство (3.12) означает, что скорость
сходимости геометрическая.
6. Для нахождения f* можно поступать также сле-
дующим образом. Выберем произвольно начальное при-
ближение х0^Еп. Зафиксируем положительные числа
а и Ь, а < Ь.
Предположим, что множество 2>(х0) ограничено ’и
S) — его диаметр.
Пусть уже найдено Л-е приближение х* е S) (хо).
Возьмем такое ел > 0, что
(**)• (3.13)
В силу непрерывности def (xk) по е > 0 и того, что
(*л) —0, такое е» существует.
' °° де J (**)
Найдем gkeEn, ||g*||=l, такой, что —-------< 0, и
на луче {х*(а) = xk + ag*|a > 0} найдем точку хк+1 =
= xk(a,k) такую, что
f {xt+1) / ixk) вц. (3.14)
264 МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ (ГЛ. II1
Продолжая аналогично, построим последовательность
{xk}. Теорема 3.2 справедлива и в данном случае. Кроме
того,
f (xft+i) - Г < (1 - а (1 + &)-*) (f (хк) - П V*. (3.15)
Действительно, в силу лемм 1.1 и 1.2 имеем
+ (3.16)
Объединяя (3.13), (3.14) и (3.16), получаем (3.15).
Замечание 2. Если функция f(x) сильно выпукла
или если она строго выпукла и множество 2)(х0) огра-
ничено, то последовательности {хк} из теорем 3.1 и 3.2
сходятся к единственной-точке минимума функции f(x)
на Еп.
7. Рассмотренные в этом параграфе модификации
8-алгоритма, как и сам 8-алгоритм, представляют в ос-
новном теоретический интерес, ибо на каждой итерации
необходимо знать все соответствующее множество <5ef(x).
К сожалению, класс функций, для которых е-субдиффе-
ренциалы эффективно вычисляются, недостаточно широк.
Таким образом, 8-субдифференциалы, с одной сто-
роны, очень удобны и обладают рядом важных и полез-
ных свойств (непрерывность def(x), гарантированная
оценка (3.1) уменьшения функции на 8, если O^=def(x),
возможность получения геометрической скорости сходи-
мости последовательности {/(хА)} к f* без предположе-
ния о сильной выпуклости функции f(x)), которых не
имеют их аналоги в нелинейном программировании и
минимаксных задачах. С другой стороны, в-субдиффе-
ренциалы трудно вычисляемы, ибо являются глобальной
характеристикой функции, что делает методы, изложен-
ные в этом параграфе, практически малоприменимыми.
Пример. Пусть f(x) = (Ах, х)4~(а,х), где А —
симметричная положительно определенная п X «-мат-
рица.
Тогда
<V (х) — {2А (х 4- v) + а |(Av, v) < в),
т. е. даже для такой «простой» функции, как квадратич-
ная, для нахождения def(x) необходимо знать все мно*
жество решений нелинейной системы (Аи, у)^е.
$ 4J СУБГРАДИЕНТНЫЙ МЕТОД 265
Далее, метод наискорейшего спуска в данном случае
состоит в построении последовательности {ха} по фор-
муле
х*+1 = хк- (Г М, Г (xft)) (2ЛГ (xft), Г (Ха))-1 f' (хД
А для нахождения только направления в-наискорей-
шего спуска функции (Ах, х) + (а, х) в 8-алгоритме на
каждом шаге требуется решить задачу
min || 2А (х + о) + а ||.
(Л», U) <8
В результате оказалось, что вспомогательная задача,
которую необходимо решать при применении метода в-
наискорейшего спуска, сложнее, по крайней мере фор-
мально, исходной задачи минимизации.
§ 4. Субградиентный метод
для минимизации выпуклой функции
1. Субградиентный метод. Пусть f (х) — выпуклая
конечная на Еп функция. Выберем произвольные точку
Хо е Еп и последовательность чисел {£а} такую, что
*А-* + 0, IX = + <*>• (4.1)
А-0
Пусть уже найдено хк^Еп. Возьмем любое Vk^df(xk).
Если ик = 0, то Oed/(xj.) и точка хк— точка минимума
f(x) на Еп, и процесс прекращается. В противном случае
положим
Ха+1 = ха — Ma II vk |Г‘" xk + zk, (4.2)
где
za = —МаИМЛ IIzaII = %a.
Таким образом строим последовательность {ха}.
Если эта последовательность состоит из конечного числа
точек, то по построению последняя полученная точка —
точка минимума функции f(x) на Еп. Рассмотрим слу-
чай, когда последовательность {ха} бесконечна. Как
и выше,
^* = (xsE„|f(x) = f},
266
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
1ГЛ. Ш
где
f*= inf f(x), р(х, = min ||z —x||
x e En ze
(множество Л* может оказаться пустым).
Теорема 4.1. Если множество Л* непусто и огра-
ничено, то при k-+ оо
p(xft, лГ)->0, f(xfe)-*f. (4.3)
Доказательство. Покажем вначале, что
lim р(хъ ЛГ) = О. (4.4)
А-»ОО
Допустим противное, пусть существуют а > 0 и Ki < со
такие, что
p(xbjT)>2a>0
(4.5)
Поскольку Л*— ограниченное множество, то, согласно
следствию 4 из леммы 9.1 гл. I, найдется с > 0 такое,
что
^ = {х|Нх)<Г + ^}с5а(Л (4.6)
где
Sa(JT) = {x|p(x, jT)<a).
Существует такое г > 0, что
$г(х)==з{х| Hx-jeiKrJcz^ VJe<=Jf. (4.7)
Зафиксируем любое (рис. 49). Из определения
df(xk) имеем
f(x)— f(xk)^(vk, х — хк) Vx(=En. (4.8)
Из (4.5.) и (4.6) получаем f(xk)>f* + c Vk > Ki, и по-
тому из (4.8)
(vk, х — xft) < 0 Vx е= £>в,
(zk,xk — x)<0 Vxt=3)c. (4>9)
Возьмем хк = х — rz*||zft|J-1. Из (4.7) следует %к&Фс,
и поэтому из (4.9)
(zk, xk — xk)=‘(—Xkvk\\vk\\~i, xk — x + rzk\\zk\r')<0,
т. е.
(zft, Хк — х) < — гКк.
8 4j
СУБГРАДИЕНТНЫЙ МЕТОД
267
Далее,
||xft+i — x|p = ||x* + z4 — х\? =
= I— X||2 4- 2 (zk, Xk - x) + Z2 < ||xft - x|2 - + 4
Поскольку X*->4-0, то при достаточно больших k
II Xft+1 — XII2 < II xft — X If2 — гЛ*.
Продолжая аналогично, получим
II хк+з — * II2 < II хА — х II2 — г Z h+i-
/-0
(4.10)
В силу (4.1) отсюда следует ||xft — х|Н—00. что невоз-
можно. Полученное противоречие и доказывает (4.4).
Зафиксируем 6 > 0. Как и выше, найдем гд > 0 та*
кое, что
llx^-xl^llxfe-xll2-^ VxeJf* (4.11)
для всех достаточно больших k и таких, что р(х*,
>6. Из (4.11)
Р2 (xfc+i, ЛГ) < р2 (xft, JT) - гЛ. (4.12)
В силу (4.4) существуют k такие, что
р(хьлГ)<б. (4.13)
Поскольку Xk+\ — Xkгк, l|z*||=Xfe, то, учитывая (4.1),
можно считать, что p(x*+i, Л'*) < 26 для k, удовлетво-
268
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
(ГЛ. Ill
ряющих (4.13). Если при этом оказалось р(х*+ь Л*) >
> б, то в силу (4.12)
Р (хк+а, Л*) < р (хк+и Л*) < 26.
Далее рассуждаем аналогично. Итак, если р (xk+i, Л*) <;
<6, то p(jfi»+i+i, Л*) < 26; если же 6 < р (хк+1, Л*} <
< 26, то p(Xb+i+i, Л*) < р(хл+1, Л*) < 26. Окончательно
для всех i^l имеем р(хк+г, Л*) < 26. В силу произ-
вольности 6 отсюда следует р(хк, Л*)->-0, а тогда
f(xk)-+f*, что и завершает доказательство теоремы.
Следствие. Если intЛ* =£ 0, то последователь-
ность {хй} конечна, т. е. для некоторого k будет vk = 0.
Доказательство. Допустим противное. Предпо-
ложим, что Vk Ф 0 для всех k\ тогда последовательность
{xk} бесконечна. Возьмем любое ieintJP*. Найдется
г > 0 такое, что Sr (х) cz Л*. Построим точку хА = х —
— rzkllzkll-1. Ясно, что хк е Sr (х) с Л*, и потому f(i*) =
= f*. По определению субградиента
f (Xk) — f (xk) > (vk, Xk — Xk).
Так как f (xft) f(Xk), то отсюда
(vk, Xk — XkXf (Xk) — f (xk) < 0,
t. e.
(vk, X — xt) < r (vk, Zk II Zk Г ')•
Так как zk ——Xftt>*llv*ll_то отсюда («*, xs — Х)^.
—гХй. Рассуждая далее, как при доказательстве тео-
ремы, получаем
Цх*+1 - i||2<||xft - ill2-гХ*. (4.14)
Значит, || Хй+^ — i || — оо, что невозможно. Полу-
ченное противоречие и доказывает конечность последо-
вательности {хА}.
Замечание 1. После получения неравенства (4.14)
доказательство можно завершить и иначе: из (4.14) вы-
текает, что расстояние До точки х убывает, и из (4.14)
заключаем, что за конечное число шагов найдем точку
Хй+t такую, что Хй+s s int Л*. Но если х ® int Л*, то (см.
задание 6.2 гл. I) df(x) = {0}. Значит, и про-
цесс прекратится, т. е. последовательность {хй) конечна.
$ 4]
6УВГРАДИЕНТНЫЙ МЕТОД
269
Замечание 2. Описанный субградиентный метод
часто называют методом обобщенного градиентного
спуска (ОГС-методом).
2. е-субградиентный метод. Множество е-субградиен-
тов (е-субдифференциал), вообще говоря, богаче множе-
ства df(x). Поэтому найти элемент из def(x) может ока-
заться проще, чем найти элемент из д[(х). В связи с
этим естественным образом возникает следующий метод
для нахождения е-стационарных точек.
Зафиксируем 8 > 0. Пусть числовая последователь-
ность {%*} удовлетворяет (4.1). Возьмем произвольное
хо е Еп. Предположим, что уже найдено х* е Еп. Возь-
мем любое Vk&def(xk).
Если оа = 0, то def(Xk), и точка х*— е-стацио-
нарная точка функции f(x) на Еп, и, как показано в п. 3
§ 8 гл. I, 0 < f(xft) — f* < е, где /**= inf f (х).
Если же v* =£ 0, то полагаем
xk+i e xh — Xkvk || vk И"1 ав xk + zk. (4.15)
Теорема 4.2. Если множество М* непусто и огра-
ничено, то
ИтР(х„Ж.)-0, p(vSs(^)T^-0, (4.1в)
где
&e’Ba{xlf (х) < f* + е}, ае = max р (х, JT),
*в<?8
Qe”{x|f(x) = f* + 8}.
Доказательство. Вначале покажем, что
lim p(xft, ®е) = 0. (4.17)
Допустим противное, пусть существуют а > 0 и Ki < оо
такие, что
р (хА, Фе) > 2а > 0 \fk > Ki. (4.18)
Так как Л*— ограниченное множество, то и множество
тоже ограничено, и потому найдется с > 0 такое, что
0.+. -{* If (*)< Г + * + •}<= $« Ш (4.19)
270
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. Ill
Тем более с Sa(0e)- Существует г>0 такое, что
Sr (х) = {х 11| х— x\\^r}cz2)c 'ix^JC. (4.20)
Зафиксируем любое хе/*. Из определения де/(х*)
имеем
f (х) — f (xft) > (vk, x — xk) — e Vx e En. (4.21)
Из (4.18) и (4.19) следует f (x*) > f* + 8 + с, и потому
из (4.21)
(vk, x — x*)<f (x) — f (xft) + e < f (x) — f* — c. (4.22)
Для x e S)c будет f (x) f* 4- с. Теперь из (4.22) полу-
чаем
(vk, x — xk) < 0 Vx e &><• (4.23)
Возьмем xk = x — rz*||z*ll-1. Из (4.20) Зна-
чит, из (4.23) и (4.15)
(zft, xk — xk) < 0.
Отсюда
(zft, xk — x) < — rXk.
Повторяя далее дословно рассуждения, проведенные при
доказательстве теоремы 4.1, устанавливаем, что ||х* —
— х||->—оо, что невозможно. Итак, (4.17) доказано.
Выше фактически показано, что для любого б > 0
будет
р(х*+1, JC)<(>(Xk, JT)
при достаточно больших k таких, что р(х*, > б. Рас-
суждая теперь так же, как при доказательстве второй
части теоремы 4.1, получаем, что p(xft, Sag(J7*))->0.
Итак, существует подпоследовательность {&s} такая,
что хк s->- х*, где f (х*) /* + 8. Далее, для любого б > 0
найдется К6 < оо такое, что
р(хъЛГ)<ае + б V*>Ke.
Ранее (см. следствие 3 из леммы 9.1 гл. I) уже отме-
чалось, что а,----{• 0.
’ 8 е-»+0
3. вй-субградиентный метод. Наконец, опишем еще
один метод последовательных приближений, в котором
§ 41
СУВГРАДИЕНТНЫЙ МЕТОД
5ГГ1
на каждом шаге используются вл-субградиенты, причем
е*---->0.
* fe->OO
Пусть снова последовательность {Л*} удовлетворяет
условию (4.1). Выберем такую последовательность {в*}»
что
вА-> + 0. (4.24)
Возьмем произвольную точку х0^Еп. Пусть уже най-
дена точка Хь е Еп. Выберем любое vk s dSkf (xk) и по-
ложим хл+1 = Xk + Zk, где
( 0, если
zk = i i (4.25)
I \ если
Теорема 4.3. Если множество Я" непусто и огра-
ничено, то при k -> оо
p(xk, ЛГ)->О, f(xft)->f. (4.26)
Доказательство. Вначале установим, что
lim р(хъ JT) = O. (4.27)
fe->OO
Допустим противное. Тогда найдутся а > 0 и Ki < оо
такие, что z
р (xk, JT) > 2а > 0 Vk > К,. (4.28)
Без ограничения общности можно считать, что Vk 0,
ибо если таких k, для которых ок — 0, бесконечно много,
то можно найти подпоследовательность {xfts}, для кото-
рой p(Xfes, •<*)—>0. (Пользуемся ограниченностью
Как и при доказательстве теоремы 4.1, существует
с > 0 такое, что
^ = {x|f(x)<f + c)cSem
При этом можем считать, что
inf f (х) — f* d > с : x^s2a(M>) >0. (4.29)
Существует г > 0 такое, что Sr(x) = {х 11|х — х||<= Vx е ЛГ. (4.30)
Зафиксируем любое Тогда f(x)-f (хА) > (vk, x-Xk) — еА Vx e En. (4.31)
272
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
1ГЛ. HI
Из (4.28) и (4.30) имеем f (х*) > f* -|- d, и потому из
(4.31) при достаточно больших k таких, что 8* < d — с,
будет
(vk, х — xk) < / (х) — f (xk) + e* < f + c — Г — d + 8ft < 0.'
Теперь, дословно повторяя доказательство теоремы 4.1,
получаем (4.26).
4. Субградиентные методы с почти полной релакса-
цией. Все три метода, описанные в этом параграфе, не
являются релаксационными, т. е. значение функции не
обязательно убывает при переходе из точки хк в точку
Хк+1- Отличительной особенностью субградиентных мето-
дов является их чрезвычайная простота, ибо при их ис-
пользовании на каждом шаге требуется лишь найти ка-
кой-нибудь субградиент (или е-субградиент). Однако
существенным недостатком этих методов является очень
медленная сходимость. Для преодоления этого недо-
статка можно использовать различные идеи, некоторые
из которых будут обсуждаться ниже. Опишем, напри-
мер, следующий вариант субградиентного метода. Пусть
по-прежнему последовательность {А.*} удовлетворяет
условию (4.1). Последовательность {х*} строим так:
Хк+i = Хк — а^к II vk Г* s xk + akgk,
где а* е[0Х*, уХ*], числа 0>О и у>0 фиксированы.
Правило выбора а* из отрезка [0Х*, уХ*] может быть
любым, например:
1) ак — произвольное число из [0Х*, уХА];
2) f (хк + akgk) == min f (xk + agk);
3) f(xk + akgk)= min +
где
1п = 0Аь P<0b 0/ = 2<-10i....... 0„ = 2"->01<у.
При использовании последних двух правил субгра-
диентный метод становится методом с почти полной ре-
лаксацией, если взять маленькое 0 и большое у, напри-
мер: 0 = 10_ 10, у = 10’°. Сходимость при этом сохра-
§ 41
СУБТРАДИЕНТНЫЙ метод
273
няется, ибо последовательность {а*} по-прежнему удов-
летворяет условию
оо
а*-* + 0, Еа* = + °°-
А-0
Аналогичный подход можно применить к е-субградиент-
ному методу и к вА-субградиентному методу.
5. Субградиентный метод с постоянным шагом. Вы-
берем произвольные хоеЕп и % > 0. Пусть уже по-
строено Найдем любое и положим
Xk+i = xk — Aojlojr1. (4.32)
Если оказалось о* = 0, то процесс прекращаем, ибо
Xk — точка минимума.
В результате строим последовательность {хк}. Если
эта последовательность конечна, то по построению по-
следняя полученная точка — точка минимума. Пусть по-
следовательность {ха} бесконечна, а множество Л* ог-
раничено.
Положим
г = 2-1Л, Sr (Л*) = {х | р (х, Л*) < г},
max f (х) — f* + сг.
Заметим, что максимум здесь достигается на границе
(см. лемму 9.7 гл. I) и что сг > 0,
&>сг — (х If (х)< f* + cj, rt = maxp(x, .(Г\.
ХеЯ>Сг
Теорема 4.4 Если последовательность {xk} беско-
нечна, то
Р (ха> (*^*)) °’
при этом
lim р (хА, 0Сг) = 0. (4.33)
£-»оо
Доказательство. Вначале установим (4.33).До-
пустим противное. Тогда существуют а > 0 и Ki <Z оо
такие, что
р(хк,3>Сг)>а (4.34)
274
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
(ГЛ. 1П
Найдутся с' > ст и г' > г такие, что (рис. 50)
Зт(Л’)<=^. <4-35>
Возьмем любое х е Л'*. Ясно, что
Sr' (х) = {х | IIX — х II < г'} CL S)e. (4.36)
Из определения <9f(x*) имеем
f(x) — f (xk) (vk, х — xk) Ух е= £„. (4.37)
Так как из (4.34) и (4.35) f(xk) > f* 4- с', то из (4.37)
при k Ki будет
(vk, х — хк) < 0 Vx е ФС’. (4.38)
Положим Xk — X 4-r'v*||Oftir‘. Ясно, 4TOXfee^V, и по-
этому из (4.38)
(— Kvk II vk 1Г1, xk — X*) < 0.
Отсюда
(— Kvk II vk 1Г1, xk — x) + (10ft II vk 1Г1, r'vk II vk 1Г1) < 0,
t. e.
(— Kvk II vk 1Г1, xk — x) < — V.
Далее,
II Xk+1 — % II2 = II Xft — Kvk II Vk 1Г1 — X ||2 ==
= II xk - XII2 + 2 (- Kvk II Vk IF1, Xk - + %2 <
< II xk - x II2 + a [- 2/ + Л]. (4.39)
» fl
СУ В ГРАДИЕНТНЫЙ МЕТОД
275
Так как г’ > г = Л/2, то из (4.39) следует ||хк — х|| ->
_> — оо, что невозможно. Полученное противоречие и до-
казывает (4.33).
Возьмем любое б > 0. Как и выше, найдется < оо
такое, что для k > и таких, что p(xft, > 6, будет
выполнено (4.39). Из (4.33) следует, что существуют k
такие, что р (xk, < 6- Поскольку xk+i = хк —
— то ||Xft+i — хАЦ = %, и поэтому Хк+i е
«= Зх+д (0Сг). Если при этом р(хА+1, 0С(.) > б, то в силу
(4.39) при достаточно больших k (при k будет
Р (*k+2> < Р (х*+1, ^*) Л + Г1 + б.
Если же р(хА+1,^Сг)<б, то снова p(xfe+2, ^Сг)<Х + б,
т. е. Vfe+2 s -$л+в Далее продолжаем аналогично.
В силу произвольности б > 0 отсюда вытекает
Р (xk, SK+ri (Л*)) 0.
Теорема доказана.
Замечание 3. Из формулы (5.26) гл. I следует
1
f (х + z) = f (х) + \ max (и, z) dx.
J v&df (x+tz)
Отсюда, если ||z|| г, то cr rB — XB/2, где
В = max max || о ||.
v e Sf (o40) v&df (x)
Очевидно, что за счет X можно добиться сколь угодно
малого сг.
Замечание 4. С практической точки зрения удобно
использовать следующий вариант описанного метода.
Пусть Л > 0 фиксировано. Строим последовательность
{х4 по формуле
Xft+1=sf II «а Г1, если || vk || > Л, (44())
( xk — если || vk II Л.
Для гладкого случая (см. § 2) этот метод обеспечи-
вает сходимость последовательности {х*} к точке мини-
мума.
276
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. Ш
Задание 5.1. Исследовать е-субградиентный метод с постоян-
ным шагом (последовательность {х*} строится по формуле (4.32) или
(4.40), а g= d&f(xk)).
6. Рассмотрим снова субградиентный метод, описан-
ный в п. 1. Пусть последовательность {X*} удовлетво-
ряет (4.1) и, кроме того,
£4 = Л<оо. (4.41)
ft-0
Теорема 4.5. Если множество Л* непусто, то по-
следовательность {хь} сходится к точке множества Л*.
Доказательство. Возьмем любое х* е Л*. Как
и в п. 1, имеем
Ь+. - Г - к» - Г+рп (’.• - *.)+4 <4-42)
Так как vk^d](xk) и х* е Л*, то
0 > f (х*) - f (xj > (vft, x* - xft). (4.43)
Отсюда
(vk, x*-xfc)<0 V£. (4.44)
Поэтому из (4.42)
k-i
llx.-x’lPOIxo-x’IP+Zlf.
i-0
Из (4.41) следует ограниченность последовательно-
сти {х*}. Значит, и последовательность {Vk} тоже огра-
ничена, т. е. существует число L < оо такое, что
11М<Ь V£. (4.45)
Покажем теперь, что существует такая подпоследо-
вательность {xfts}, что
= (%’ х* ~ X*s) °- <4-46)
Допустим противное. Тогда из (4.44) вытекает, что
найдутся b > 0 и К < оо такие, что
ak^-b Vk>K. (4.47)
Из (4.42), (4.45) и (4.47) получаем ||х* — х*||2-> — оо,
что невозможно. Итак, существует подпоследователь-
§ б]
МНОГОШАГОВЫЙ СУБГРАДИЕНТНЫЙ МЕТОД
277
ность для которой выполнено (4.46). Из (4.43),
(4.44) и (4.46) следует
(4.48)
Так как последовательность {х^ ограничена, то без ог-
раничения общности можем считать, что xk$-*x. Из
(4.48) заключаем, что х е Л*. Покажем теперь, что вся
последовательность {хк} сходится к точке х. В (4.42) и
(4.44) можно вместо х* взять точку х. Для любого е > О
найдется Ki <Z оо такое, что
Vfe > Ki.
Из (4.42) и (4.44) для таких ks
ks+N-l
K+v-*lT<IK-*ll2+ s ^<8
а это и означает, что
Замечание 5. Таким образом, при выполнении
дополнительного условия (4.41) последовательность
{xk}, построенная с помощью субградиентного метода,
имеет единственную предельную точку, и эта точка —
из множества Л*. При этом множество Л* может быть
и неограниченным. Примером последовательности {X*},
удовлетворяющей (4.1) и (4.41), может служить после-
довательность {у- Условие (4.41) может быть ис-
пользовано и в методах пп. 2 и 3 настоящего параг-
рафа.
§ 5. Многошаговый субградиентный метод
При минимизации гладких функций весьма эффек-
тивными являются многошаговые методы, т. е. методы,
в которых при нахождении очередного (k + 1)-го прибли-
жения используется информация не только о значении
функции и ее производных на данном k-м шаге, но и на
одном или нескольких предыдущих шагах. К таким ме-
тодам относится, например, метод сопряженных гра-
диентов. Можно надеяться, что и в негладких задачах
278
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. III
многошаговые методы будут эффективными. Если . в
гладких задачах градиенты в близких точках не очень
отличаются друг от друга в силу непрерывной диффе-
ренцируемости функции, то в негладких выпуклых зада-
чах по какому-нибудь субградиенту в одной точке еще
трудно судить обо всем субдифференциале, даже в этой
точке. Поэтому знание субградиентов в нескольких со-
седних точках может дать ббльшую информацию о суб-
дифференциале, а потому и о направлении спуска. Ниже
описывается многошаговый субградиентный метод.
1. Пусть f(x)—конечная выпуклая на Еп функция.
В § 5 гл. I было показано, что
f(x)=max [f (z) + (v (г), x — z)], (5.1)
z e= E„
n
где y(z) — любой фиксированный элемент из df(z).
Пусть дан набор точек x = {yit ..., ур}, yi^En, где
р 1. Положим
Ф (х) = max [f (у) + (о(у), х — г/)],
ует
Отсюда
Ф (х0 + z) = max [f (у) + (v (у), х0 — у) + (о (у), г)].
ysx
Найдем
min ф (хо + z) = ф (х0 + zo (а)).
11г||=а
Кривую {х|х = хо +го(а), а 0} назовем аппроксими-
рующей кривой функции f(x), построенной в точке х0по
множеству т. Если р=1 и т=={х0}, то аппроксимирую-
щая кривая — луч {х|х = х0 — ао(хо), а^О}. Опишем
следующий метод последовательных приближений. Вы-
берем число N > п + 2 и невозрастающую последова-
тельность чисел {X*} такую, что
оо
X* -* + 0, X ~ + 00• (5.2)
k-о
Возьмем любую точку хо^Еп и зафиксируем произволь-
ное А > f (хо). Положим Оо = {хо}. Пусть уже найдены
точка xk <= Еп и множество ст*, причем
°* = {xZjft, .... х,^ J, /и <jik< ... < jSkk,
— h*|==s*<n + i.
МНОГОШАГОВЫЙ СУВГРАДИЕНТНЫИ МЕТОД
279
5 Ч
Напомним, что | о | — число элементов в множестве ст.
Возьмем произвольное v (хк) е df (хк). Если v(x*) = 0, то
хк — точка минимума функции f(x) на Еп, и процесс
прекращается. Рассмотрим случай п(х*)^=0. Если
f(xk) > А, т0 полагаем
°k {xs}- (5-4)
Если же f (хк) А, то возьмем
°k = °k U {хь}- (5-5)
В силу (5.3)
|<|<« + 2. (5.6)
Найдем
min <р* (z) = Ф* (zft), (5.7)
где
ФА (z) = max В (хк + z, у), (5.8)
в (х, у) =*f(y) + (x — y,v (у)).
Заметим, что в случае (5.4)
г* = -Х*ММЛ (5.9)
где Vk — v (хк). Введем множества
~ {У е ak I & (xk + zk’ У) = Фй (za)}> = со U »(у)-
Так как /?^а:ст', то из (5.6) имеем | Rk I =£= п + 2. По не-
обходимому и достаточному условию минимума функции
Фл(х) на множестве {z |||z||2 < К2к} будет (см. § 6 гл. I):
1. Если |]zft|| < Xk, то
ОеЛ- (5.10)
Если Zk = 0, то xk — точка минимума, и процесс пре-
кращается.
2. Если ||zft||=Z,A, то существует ук > 0 такое, что
-2yftz*e^. (5.11)
280
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
(ГЛ. III
По теореме Каратеодори (теорема 1.1 гл. I) суще-
ствует множество Rk cz Rk такое, что | Rk | п + 1 и
Os со U = в случае (б. 10),
»eR'k
— 2yftzft s 2*к в случае (5.11).
В частности, если [Я* | < п 4- 2, то можно взять Rk = Rk.
Положим теперь
Хм=хк^гк,
( Rk> если xk_N_x Rk,
*+1 t \ {x*_jy_i}> если xk_N_x s Rk.
Таким образом, базис <y*+i есть некоторое подмножество
множества точек {хк, Xk-i..хк-п}. Пусть
Г= inf f(x), jr = {z<=Entf(z) = r},
хеЕп
р(х, Ж*) = min || z — x||.
Теорема 5.1. Если множество Ж* непусто и огра-
ничено, то
р(хА, Ж*)-+Ь, fM-f*. (5.12)
Доказательство. Из ограниченности Ж* выте-
кает (см. § 9 гл. I) ограниченность множества
^Л1 = {хе£п|Г(х)<Г + Л1}, где Л1 = Л~Г.
Кроме того (см. леммы 9.1 и 9.2 гл. 1), существуют
b > 0 и В < оо такие, что
II v || >6 Vt»sdf(x), х^ё^А, (5.13)
|| v || < В Vosdf(x), хе®л,.
Докажем вначале, что
lim p(xft, JT) = O. (5.14)
fe->0O
Допустим противное. Покажем, что тогда найдется d > 0
такое, что
min ||t»|| = ||nft||>t/> 0 V6. (5.15)
§ 5] МНОГОШАГОВЫЙ СУБ ГРАДИЕНТНЫЙ МЕТОД 331
Действительно, предположим, что это не так. Тогда су-
ществует такая подпоследовательность индексов {Л$}>
что
min || v Н = |%||—Г °> (5.16)
где vks^&ks.
Без ограничения общности можно тогда считать, что
Xks~^х* ибо если допустить противное, то в силу
(5.13) получим противоречие с (5.16).
Так как + 2, то можно также считать, что
при всех ks
И
уkai~^Ур aksi~>ai VZ е 1: tn,
гдет<п4-2, £ ам=1.
I е 1: т
Из полунепрерывности сверху отображения df(x)
следует, что о* = <3/(г/*). Так как |Я^| — т> то
Ф*, (Ч) “ тах, 5 (хмь У) =
= f (*h) + (vksb Xks - yksi} + (Vkst, z*e) (5.17)
VZ e 1: tn.
Поскольку xk e 0^, то из определения qpftj (z) вытекает
ФлД^,+1) > f (О + (° (4)’ Ч)- <5-18>
Кроме того,
f(xAs + zAs)><pfts(zfts), (5.19)
ибо
f (x + z) — max В (x + z, y) >
VsEn
> max В (x + z, y) = <p* (x + z) Vx, z^En, VA:.
282
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. III
Переходя в (5.17) — (5.19) к пределу при £s->oo, по-
лучим
f (х*) > max, [/= («/}) + (0; х* - > f (X*),
f(x*)= max,[f(z/;) + (4 х* — (6.20)
При этом из (5.16) вытекает
О <= со {t>J 11 е 1: т), (5.21)
а из (5.17)
f (**) = f (1/3 + (v;> X* - у^ Vi<=V. tn. (5.22)
Соотношения (5.21) и (5.22) означают, что функция
Ф* (х) == .max, Д (z/*) + (о*, х — z/‘)]
в точке х* достигает своего наименьшего на Еп значения,
которое в силу (5.20) равно Дх*). Но
f (х) = max [/ (у) + (о (у), х — г/)] > ф* (х),
»s£n
где v (у) е df (у). Поэтому
inf f(x)^ min ф* (x) — f (x*),
xeEn xeEn
что и означает справедливость (5.14).
Итак, если имеется такая подпоследовательность ин-
дексов {&з}, что выполнено (5.16), то выполняется и
(5.14).
Таким образом, для некоторого d > 0 выполнено
(5.15). По предположению (5.14) не имеет места, т. е.
существует а > 0 такое, что
p(xft, JT)>2a Vk. (5.23)
Из (5.11) и (5.15) вытекает, что
2» = -а1г S S <(г/)=1.
veRk (5.24)
а4>°, <(^)>0, У^Як.
§ 51 МНОГОШАГОВЫЙ СУБГРАДИЕНТНЫИ МЕТОД 283
Так как vk t=2?k и ||vft||> d, a ||zft|| = Кк, то а* sg d-'b*.
Отсюда
таха4(#)т—>0, (5.26)
v&Rk ®-*°°
где a.k (У) — <хка'к (у).
В силу ограниченности Я* найдется с > 0 такое, что
&c = {x\f(x)^f* + c}czSa№),
где
SaMO = (x|p(x, jT)<a}.
Возьмем произвольное х е Я*. Очевидно, что х s int 5ЬС,
т. е. существует г > 0 такое, что
Sr(x)<=S)c.
Из определения df(xk) имеем
f W — f (хк) > (о (xft), х — xk) Ух e= En. (5.26)
Поскольку в силу (5.23) f(xk)> f* + с, то из (5.26)
(о (хД х — хк) < 0 Vx е Фс. (5.27)
Если f(xk)>A, то по построению zk=—%*о(х*) ||и(х*) Ц-*,
и потому из (5.27)
(zk, хк — х) < 0 Vx е Фа. (5.28)
Рассмотрим случай [(хк)^А. Возьмем у <= a'k. Из
(5.13) имеем || v (у) || В. Существует i^k — N такое,
что у = Xi. Так как
(«(у). У — хк) = (о (у), Xt — xk) ==
3==(^(у)> (xi — *<+i)4"(x<+i — *j+2)+ ••• 4-(-*a-i — хк)),
то
k
(V (у), У — XkX В £ Цх/_/ — X/\\^BNXkN,
/и i 4" 1
где ккы= max А,,-. Заметим, что KkN->0. Отсюда и
i.<= (й-ЛГ): ft
из (5.27) для У^о'к имеем
(»(У), х — хА) =
= (v (у), х — у) + (о {у), у — хк)^ BNXkN Ух е= 3>с. (5.29)
284
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
1ГЛ. Ill
Из (5.24) и (5.29)
(z*. хк — х) =
= Z а* (У) (V (У)> х — хк) < BNXkNak ж ЛАлгу* (5.30)
Vx е Фс.
Здесь у* = BNak. Из (5.24) получаем у* -> 0.
Неравенство (5.30) установлено для случая f(xft)<
< А. Для случая f(xk)>A имеет место (5.28). Поэтому
можно считать, что неравенство (5.30) справедливо для
всех k.
Возьмем хк = х — rz*||z*||-1. Тогда из (5.30)
(zk, хк — х + rzk || гк И-1) < ykKkN,
т. е.
(zk, хк — х)<[— rXk +
Но
1|х*+1 —ЛР = ||хА + гА —х||2 =
=1х.-*1!+2(А’
<k»-il! + [-2rt. + 2vA«] + 4-
Поскольку 1*-> + 0 и у*->0, то при достаточно боль-
ших k
II хк+1 — х II2 < II хк — х II2 — гкк.
Продолжая аналогично, получим
S-1
l|xft+s — xlPdlXft — x|p-r £ Kk+i.
je=0
В силу (5.2) Их* — x||->—оо, что невозможно. Итак,
(5.14) установлено.
Возьмем произвольное 6 > 0. Рассуждая, как и
выше, заключаем, что найдется такое г6 > 0, что для
всех х <= Jt* будет
II xk+i — X II2 <|| Хк — X II2 — Г6\к
при всех достаточно больших k и таких, что р(х*, Л*) >6.
Отсюда
p2(xt+1, ЛГ)<р2(х*, Л‘)-г6Кк. (5.31)
В силу (5.14) существуют k такие, что р(х*, ^*) < 6.
Так как xk+i = хк -|- zk, ||z&|| < Хл, то можно считать, что
»я
МНОГОШАГОВЫЙ СУБГРАДИЕНТНЫЙ МЕТОД
285
р (хл+ь *^*) < 26. Если оказалось при этом p(x*+i, М*} >
>. 6, то в силу (5.31)
р(** +2» ^‘)<p(xfe+i, JT)<26.
Далее рассуждаем аналогично. Итак, если p(xk+t, Ж*) <.
< 6, то p(xfc+<+i, Ж*) < 26; если же 6 < p(xft+/, Л’*) <
< 26, то
Р(хл+/+ь < p(%k+t> < 26.
Окончательно получаем, что р (х*+г, Л"*) < 26 npni^l.
В силу произвольности 6 отсюда следует, что р (хк, Ж*} —
—> 0, а тогда и /(х*)->/*, чем и завершается доказатель-
ство теоремы.
Следствие. Как и при доказательстве следствия
из теоремы 4.1, можно показать, что если int^*=#0,
то последовательность {хк} конечна.
Замечание. Задача (5.7) является задачей ли-
нейного программирования, если вместо евклидовой нор-
мы в (5.7) взять /n-норму: ||z|| = max | z(l) |. Здесь z =
I <= 1: п
«(zW, .... z<«>).
2. Многошаговый е-субградиентный метод. Как и в
п. 2 § 4, в описанном выше методе можно выбирать
о(х»)е де[(хк); где 8>0 фиксировано. В результате
строим последовательность {хк}. Если эта последова-
тельность конечна, то по построению последняя получен-
ная точка является е-стационарной, ибо по построению
процесс прекращается, лишь когда 1>(х&) = 0, т. е. Оа
sdef(xk). Если же последовательность {хк} бесконечна,
то справедлива
Теорема 5.2. Если множество Ж* непусто и огра-
ничено, то
Hm р (хъ -> 0, р (хъ Sat (Ж*)) О,
где
0e = {xe-EJf(x)<r + e},
ае — max р (х, Ж*),
ле <эе
<2в = {хИ(х) = Г + е}.
Доказательство аналогично доказательству
теоремы 4.2.
286
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. III
§ в. Релаксационный субградиентный метод
Метод, излагаемый в этом параграфе, идейно бли-
зок, с одной стороны, к методу 8-наискорейшего спуска
для минимизации произвольной выпуклой функции f(x),
а с другой — к методу сопряженных градиентов для ми-
нимизации непрерывно дифференцируемой выпуклой
функции. Причем если в методе е-наискорейшего спуска
для нахождения направления движения требуется знать
все множество dtf(x), то в релаксационном субградиент-
ном методе для построения направления спуска исполь-
зуется некоторое конечное число точек изdj(x),аппрок-
симирующих это множество.
1. Принципиальная схема. В этом пункте предпола-
гается, что функция f(x) строго выпукла на Еп и что
могут быть точно выполнены операции вычисления са-
мой функции f(x), ее субградиентов и операция нахож-
дения минимума функции f{x) на луче.
Положим d (х) = min || v ||. Сначала опишем релак-
v s д f (х)
сационный субградиентный метод для нахождения та-
ких точек хо^Еп, что d(x0)^e, где г > 0, а потом по-
кажем, как его применять для нахождения точек мини*
мума функции f(x) на Еп.
Зафиксируем положительные числа ео, б и целое
число то п.
Выберем произвольно начальное приближение XqS
Предположим, что множество 2)(х0) = {хб
eEn\f(x)^ f(x0)) ограничено.
Пусть уже найдено k-e приближение хк е Еп. Пере-
ход к (/?-{- 1)-му приближению хк+\, который назовем й-м
циклом, осуществляется следующим образом.
Положим хко — хк и вычислим произвольный вектор
vko^df(xko). Если ||as,.JI < е0, где vk, -i = vk, о, то
полагаем 4 = 0, xk+i = xktk, и на этом й-й цикл за-
канчивается (через tk будем обозначать число шагов на
А-м цикле). Если ||£>*._i||> е0, то на луче {х*0(а) = хко —
— avso|a^O} находим точку хк\ — x*o(a*o) такую, что
f Ufti) = min f (x*o (a)).
РЕЛАКСАЦИОННЫЙ СУБГРАДИЕНТНЫй МЕТОД
287
Обратим внимание на то, что возможен случай, когда
хк\ = хм- Это будет, если —иА0 не является направле-
нием спуска f(x) в хк0.
Если ||х*1 — хм||>б или f(xfto)—-f(Xfti) > 6, то пола-
гаем /л = 1, = и на этом k-w. цикл заканчи-
вается. В противном случае вычислим такой вектор
vko^df(Xki), что
(им, vk0) < 0.
Такой вектор vko е df(xk\) обязательно найдется, ибо,
в силу необходимого условия минимума функции
f(x*o(cc)) по а, должно быть
df
л-(_ /у = шах (ц, — vkQ) 0.
Если llt^oll^eo, то полагаем /*=1, xk+i = xktk, и
на этом й-й цикл заканчивается. Если же ||ом|| > ео, то
найдем такой вектор vk\, что
Vki — + (1—₽ао)«м> s (0, 1),
и
II vki II = min II ₽vft0 + (1 — ₽) Vko II,
₽ «[0, 1]
t. e. Vki есть ближайшая к началу координат точка от-
резка [ц*о, й*о].
Нетрудно убедиться в том, что
vkl = UkO — (»W, vk0 — vM) IIVM — Vko Г2 (vk0 — vk0).
Теперь на луче {xki (a) = хк1 — avki | a > 0} найдем та-
кую точку xk2 = xki(aki), что
f (x*2) = minf(xH(a)).
a>0
Далее продолжаем аналогично до тех пор, пока не
будет сделано такое число шагов tk, что выполнится по
крайней мере одно из следующих условий:
а) tk т0',
Ь> К tk-x - <бЛ)
с) (в-2)
288
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
(ГЛ. III
Теперь за (£+1)-приближение xft+i принимаем точ-
ку xktk. На этом £-й цикл заканчивается, причем если
выполнено условие d), то заканчивается и весь процесс
последовательных приближений, ибо d(x*+i)^e0.
Заметим, что по построению
V/G=0:/ft, (6.3)
где Ik = tk— 1.
Доказательство сходимости релаксационного субгра-
диентного метода опирается на неравенства (6.3) и сле-
дующую лемму.
Лемма 6.1. Пусть функция f(x) строго выпукла на
Еп, множество 2>(х0) ограничено, а последовательность
{хл}"-о такова, что
f(xk+i)= min f(xk + a(Xk+1—Xk)). (6.4)
as[0, 1J
Тогда lim || xk+i — xk || = 0.
/г->оо
Доказательство. Допустим противное. Тогда
найдутся такие число h > 0 и подпоследовательность
что
Vs.
Так как f(x*+i)^ f(х*), то хк^Ф(х0) при каждомk.
В силу ограниченности S){xo), не_ умаляя общности,
можно считать, чтох^->х, xks+i~+х, причем ||х — х||>
h. Поскольку f(xk+i) /(**) и f(x) ограничена снизу,
то
f(x) = f(x). (6.5)
Так как функция f(x) строго выпукла, то
f(2-lx + 2-1x)<f (х).
В силу (6.4) имеем
f ОЧ+i) = а min } f (xks + a (xfts;t - xfes)) < .
^/(г-'х^ + г-'х^!).
/
$6] РЕЛАКСАЦИОННЫЙ субградиентный МЕТОД 284
Переходя в этом неравенстве к пределу, получаем
f(x)^f(2-‘x + 2-4)<f(x),
а это противоречит (6.5). Лемма доказана.
Отметим, что лемма’ 6.1 справедлива и для непре-
рывной строго квазивыпуклой функции f(x).
Перейдем теперь к обоснованию сходимости релакса-
ционного субградиентного метода. Если последователь-
ность {xk} конечна, то для последней полученной точки
Xk по построению будем иметь d(x*)^80. В противном
случае справедлива
Теорема 6.1. Пусть функция f(х) строго выпукла
на Еп, множество 3)(хй) ограничено.
Тогда, если х* — предельная точка последовательно-
сти {х*}, то
d (х*) < max {е0, bqmi>~1} as d0,
где b= max max ||v||, ? = [1+(e06-1)2] 1/2.
x s S (Xo) v e df(x)
В частности, если mo + 1 > [In ^]-11п(ео6-1). to
d(x*)^80.
Доказательство. Существование предельных то-
чек последовательности {х*} следует из ограниченности
£Z)(xo) и того, что Хйе^(хо). Допустим, что утвержде-
ние теоремы не верно: предположим, что xftj->x*, но
d(x*) — 3. > do.
Так как функция /(х) строго выпукла, множество
2>(хо) ограничено и на каждом шаге выполнено (6.4),
то по лемме 6.1 при достаточно больших k окончание
й-го цикла невозможно вследствие (6.1), а в силу рав-
номерной непрерывности функции f(x) на £Z>(x0), и
вследствие (6.2). Поэтому при достаточно больших k,
скажем при k К, будет
th=*mo. (6.6)
Положим в = 2-1 (5 — do). Поскольку d (х*) = d> do,
то, в силу полунепрерывности сверху точечно-множе-
ственного отображения df (х), найдется такое 6 > 0, что
df (х) с Se [df (х*)) -Vx е= S6 (х*), (6.7)
10 В. Ф. Демьянов, Л. В. Васильев
290
МИНИМИЗАЦИЯ НА ВСЁМ ПРОСТРАНСТВЕ
(ГЛ. III
т. е. при х, достаточно близких к х*, все множества д[(х)
будут содержаться в некоторой выпуклой окрестности
множества д/(х*), расстояние от которой до начала ко-
ординат больше d0 (на рис. 51 эта окрестность показана
пунктиром). Поскольку эта окрестность выпукла, то
вместе с любыми двумя точками на этой окрестности
ей будет, очевидно, принадлежать и весь отрезок, сов’
диняющий эти точки.
Таким образом, из (6.6) и (6.7) следует, что при
достаточно больших ks будем иметь
|| vkst | > d0 > в0 V/ <= 0 : (то - 1). (6.8)
Из (6.8) и определения числа b вытекает, что (рис. 51)
КИ°К<| /l|g 'p+L ,.-<1ч1|(л/1+(в.ь-)а)~‘,
VIIМ +гмг
где vkst — точка, лежащая на отрезке [ё^, такая,
что угол между vkst и vkst равен л/2. Поэтому
|%.<+11|< 1|K+1 <bqt+x V/€= 0: (m0- 1).
Отсюда и из (6.6) заключаем, что
|| vks, mo_! || = j vksiks j < (6.9)
в частности, если то > т, то || 11| е0, где т —
— 1 + In (eoiH) (In^)-1. Но (6.9) противоречит (6.8). Тео-
рема доказана.
релаксационный сувградиентный метод
291
I в)
Замечание 1. Проверка условий (6.1) и (6.2) про-
изводится для того, чтобы избежать лишних вычисле-
ний в начале процесса последовательных приближений.
Замечание 2. Если оказалось, что xkt = хко при
всех t е 1 : tk и tk = т0, то, как следует из доказатель-
ства теоремы 6.1, d(xft)^d0, и в таком случае процесс
последовательных приближений можно закончить.
Назовем Л-й цикл полным, если = то. Из лем-
мы 6.1 вытекает, что при достаточно больших k будет
tk s= /по, т. е. все циклы будут полными, и, следова-
тельно, й-й цикл будет заключаться в построении точек
х*0. xki, .... хкто, субградиентов 9*,m0_2.
vkt&df(xk,t+i) и векторов vkl, vk2, .. .,.vkt mo_i таких,
что при каждом t е 0: (т0 — 2) вектор v*. /+/ есть бли-
жайшая к началу координат точка отрезка [о*/, б*<],
причем (оkt, Vkt) 0 и при каждом fsO:(mo—1)
должно быть f (хк, /+1) == niin f (xkt (a)).
С помощью релаксационного субградиентного метода
строим последовательность {хк}. Для любой ее предель-
ной точки х* по теореме 6.1 будет d(x*)^2 d0 и согласно
лемме 1.2
0</(х*)-Г<<Ш0, ' (6.10)
где Ф — диаметр множества 3> (х0), f* == inf f (х).
Из (6.10) следует, что для любого 3 > dQ за конеч-
ное число шагов будет получена точка х* такая, что
Изложенный метод можно применить и для нахож-
дения точек минимума функции f(x) на Еп. Схема ме-
тода при этом сохраняется. Изменяются лишь условия
а) и d) на следующие:
a) tk = mk, d) Цг^ЦСвь
причем переход к (^4-1)-му циклу происходит после
выполнения любого из условий а)—d).
Теорема 6.2. Пусть функция f(x) строго выпукла,
множество 3>(х0) ограничено и ел->0, /и*->оо.
Тогда любая предельная точка последовательности
(х*) является точкой минимума функции f(x) на Ея.
10*
292
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. III
Доказательство. Допустим противное: предпо-
ложим, что xks —> х* и для некоторого do > 0 оказалось
d(x*) > d0.
Так как отображение df(x) полунепрерывно сверху,
то при достаточно больших ks все множества df (х^) бу-
дут содержаться в некоторой выпуклой окрестности мно-
жества df(x*), удаленной от начала координат больше
чем на do.
Рассмотрим теперь такие ks, что eks < dQ, tks = n4s
(см. аналогичную часть доказательства теоремы 6.1) и
mks > 1 + (In «у)-1 In (do&-1),
где
b= max max || v ||, </ = (1 + cW»-1)
xg'S (xo) v e df (x)
Тогда при достаточно больших ks, с одной стороны,
1),
а с другой (см. доказательство теоремы 6.1),
Получили противоречие. Теорема доказана.
2. Связь релаксационного субградиентного метода с
методом сопряженных градиентов. В этом пункте будем
считать, что длина всех циклов релаксационного субгра-
диентного метода одинакова и равна т п, т. е. усло-
вия b), с), d) не проверяются (это будет, если 8о = О,
б = оо).
Кратко релаксационный субградиентный метод мож-
но описать следующим образом:
хое£„, v0edf(x0), ₽о=1./^ st£
=*хк — акрк,
f (хк+1)== min f(xk — арк),
a>0
Pk = Pk-l + ₽*(«* — Pk-l), VkG=df(xk),
(vk, p*_i)<0,
(6.11)
JI, если k кратно m,
(Pk-i,vk—pk-i)[\vk—Pk-iT2 в противном случае.
§ 6] релаксационный субградиентныи МЕТОД 293
Нетрудно заметить, что такая запись релаксацион-
ного субградиентного метода формально напоминает ме-
тод сопряженных градиентов. И на самом деле между
этими двумя методами имеется тесная связь: релакса-
ционный субградиентный метод превращается в метод
сопряженных градиентов, если он применяется для ми-
нимизации гладкой функции.
Методы сопряженных градиентов с восстановлением,
так же как и релаксационный субградиентный метод,
носят циклический характер (длина цикла — число т’—
есть число шагов, через которое производится спуск в
направлении ацтиградиента функции f(x), т' >п).
Напомним, что метод сопряженных градиентов Флет-
чера— Ривса для минимизации непрерывно дифферен-
цируемой на Еп функции f(x) заключается в построении
последовательности {х'^ по следующим правилам:
х'о^Еп> «о = Л(хо)> Рь“0»/^
x'k+laXk-akPk>
= < +
\ ь) ’ дх^ / *
( 0, если k кратно т',
II°*if ’Pa-jJ-2 в противном случае.
Теорема 6.3. Пусть множество Sb (х0) = {х е
s 5л|^(х) f(xo)} ограничено и функция f(x) выпукла
и непрерывно дифференцируема на Еп-
Тогда, если релаксационный субградиентный метод и
метод сопряженных градиентов Флетчера — Ривса на-
чаты из одной и той же точки (хо = х'о^, длина циклов
в обоих методах одинакова (т = т'), то при любом k
xk==xh> (6.12)
Рк = М> (6-13)
т- е. оба метода генерируют одни и те же последователь-
НЫе приближения.
294
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. Ill
Доказательство проведем по индукции. При
k = 0 равенства (6.12), (6.13) справедливы по условию
теоремы и построению методов, ибо для выпуклой диф-
ференцируемой функции f(x) имеем df (х) = {f'(х)}.
Предположим, что равенства (6.12), (6.13) выпол-
нены при любом k е 0 :1, где I 0, и покажем, что они
выполняются и при k — I 4- 1.
Поскольку xz — х' и pt — fitp\, то
{xz — ар, | а 0| = {xz — ар' | а^ 0)
и, следовательно, xl+i — x't+t в силу условий выбора
точек xz+l и x'i+l как доставляющих минимум функции
f(х) на лучах {xz — apJa^O) и {х'—• ap'|a^0) соот-
ветственно.
Если /4-1 кратно т, то pz+l = l, Pz+1=0 и pz+l =
~ Р1+1Р/+1 = (xi f-i)’
Рассмотрим случай, когда / 4- 1 не кратно т. Если
функция f(x) выпуклая и гладкая, то для направлений
в релаксационном субградиентном методе вместо (6.11)
будет
(»а, Pa-i) = 0 Vfe, (6.14)
и, кроме того, если k не кратно т, то
Ра = II Pk |ГII vk Г2 (о* 4- II vk ||21| р4_( |Г2 Pa-i). (6.15)
Действительно, поскольку
Pk = Ра»а 4" (1 — Ра) Ра-1, (Ра, Ра-i) = (Ра, »а) = 11 Ра I’2. (6.16)
то в силу (6.14) имеем
(Ра> »а) = Ра(»а- »а)4-(1 — Pa)(Pa-i. »а) = Ра II vk Ц2,
(рА. Pa-i) = Pa(®a> Pa-i)4-(1 — Ра)(Ра-ь Ра-1) =
= (1 - Pa)II Pa-i IF.
откуда
Ра = II Ра II2 II vk 1Г2, 1 - Ра = II р* II2II Pa-i Г2-
Теперь (6.15) очевидным образом следует из полу-
ченного представления чисел и 1—Р* и (6.16).
& 61
РЕЛАКСАЦИОННЫЙ субградиентныи метод
295
Воспользуемся равенством (6.15) при k = /4-1 и
тем, что
Получим
pl+l - II Рш 11211 «ж1Г2 («ж + II V<+, II2 II Pl 1Г2 Р1) -
=|| pl+i II2 II vi+i Г2 (рж + II II21 Pi Г21 Pi II2 II vi Г2 р'д -
= ₽Ж («Ж + || <+1 fl V'l Г2 Р0 - h+lP'l+l.
Итак, pl+i = ₽жр,+1 (рис. 52). Теорема доказана.
Замечание 3. Прерывание цикла по выполнении
условий, эквивалентных условиям (6.1), (6.2), полезно
и при применении метода сопряженных градиентов, ибо
далеко от минимума градиентный метод работает доста-
точно хорошо.
3. В п. 1 был рассмотрен релаксационный субгра-
диентный метод с полной релаксацией, т. е. метод, в ко-
тором на каждом шаге минимум в направлении дви-
жения отыскивается точно. Понятно, что в большинстве
случаев осуществление полной релаксации невозможно,
ибо для этого требуется вспомогательная бесконечная
итерационная процедура. Поэтому ближайшей нашей
целью будет построение такого варианта релаксацион-
ного субградиентного метода, в котором не требуется
точного решения задач одномерной минимизации. За-
одно избавимся и от ограничительного условия строгой
выпуклости целевой функции f(x).
При доказательстве теоремы о сходимости релакса-
ционного субградиентного метода существенную роль
296
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. Ill
играла лемма 6.1; поэтому первое, что необходимо сде-
лать,— это получить некоторый аналог леммы 6.1.
Лемма 6.2. Пусть функция f(x) определена на Еп
и последовательность {х^ такова, что
xk+i = xk + akgk, f(x*+i)<f(xt) —d2aft||oj|,
gk = — v JI Vk 1Г1. I|fjl>eo>
где 8o > 0, 62 > 0 — фиксированные числа.
Если последовательность {f(*/?)} ограничена снизу,
то последовательность {xk}—сходящаяся.
Доказательство. В силу условий леммы имеем
k
f (*4+1) < f (Xfl) — 6260 Z II Х|_1 — Xt II,
откуда
k
ДII Xt_I — xt II < (80ба)"1 (f (Хо) — inf f (х J) < 00 VAt,
а это означает, что последовательность {х*} сходится.
Таким образом, установлено, как выбирать длину
шага так, чтобы норма разности между соседними при-
ближениями стремилась к нулю, более того, так, чтобы
последовательность {xj сходилась.
Другим важным требованием, обеспечивающим схо-
димость релаксационного субградиентного метода, явля-
лось получение векторов Vkt, Vkt, удовлетворяющих (6.3),
т. е. таких, что угол между ними не меньше прямого.
Если последовательность {xj строить так, как это тре-
буется в лемме 6.2, то точка x*+i не обязательно будет
близка к точке, в которой функция /(х) достигает ми-
нимума на луче {х* -f- agja > 0}. Поэтому необходимо
ослабить условие (6.3).
Лемма 6.3. Пусть f(x)—выпуклая на Еп функция.
Если при некоторых a > 0 и Si > О
f(x + ag)>f(x)-Sia||0||, (6.17)
где g = — vlloir1, v&En, то
(о, 0XSi||v|p Vo е df (x + ag). (6.18)
Доказательство. Действительно, для любого
б е df(xag) имеем с учетом (6.17)
f(x)^f(x + ag) — a(g, v)>f(x) —Si<x||t»|| —a(g, tJ),
т. e. — (g, 6)<6il|o||, откуда следует (6.18). S
§ 6]
РЕЛАКСАЦИОННЫЙ СУВГРАДИЕНТНЫИ МЕТОД
297
Замечание 4. Совершенно аналогично показы-
вается, что если f(x + ag) f(x), то (v, 6)^0 V6e
edf(x-|-ag).
Перейдем теперь к описанию релаксационного суб-
градиентного метода для минимизации выпуклой (не
обязательно строго) функции /(х) на Еп, в котором вспо-
могательные задачи одномерной минимизации можно ре-
шать приближенно.
Зафиксируем положительные числа а, ео, б, бь 62.
О < б2 < б! < 1.
Выберем произвольно начальное приближение xoS
е Е„, число vo > 0 и целое число то > 1.
Пусть уже найдено k-e приближение xk е Еп. Опи-
шем й-й цикл метода, т. е. процесс перехода от х* к х*+ь
Выберем число v* > 0 и целое число m* > 1 — макси-
мальную длину k-ro цикла.
Положим х*о = хк и вычислим любой субградиент
Vko^df(xko)- Если ||t>feoll<8o, то полагаем tk = 0,хк+1 =
= xktk, и на этом k-й цикл заканчивается. В противном
случае найдем на луче {х*0(а) = х*о +agsoja 0}, где
gko = — vwIIvmII-’, точки Xki = xfto(a*o) и xki = xft0(aft0)
такие, что (рис. 53)
f (xki) < f (xft0) — 62afe01| Vko II, (6.19)
f (xki) min {/ (x* 1), f (xA0) — 6iaA0 II vka ||), (6.20)
298
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. Ill
причем
v*<a*0<v* + (a+1)а*0. (6.21)
Опять обратим внимание на то, что хк\ может ока-
заться равным Xko. Заметим также, что не исключен
случай, когда хщ = Хм.
Если ||х*о — б или f(xk0)—f(x*i)>6, то пола-
гаем 4=1, хк+1 = Хщ, и на этом k-й цикл заканчи-
вается. В противном случае вычисляем любой (и в этом
также существенное отличие от метода с полной релак-
сацией) субградиент ик0^ df(xki).
В силу (6.20) и леммы 6.3 должно быть (vko, vko)
<6il|vft0||2. Более того, если меньшим в (6.20) является
число f (хк\), то по замечанию 4 (vk0, б*о)^ 0.
Теперь находим вектор vki — ближайшую к началу
координат точку отрезка z>*o], т. е.
+ (1 — ₽м) Vkt), Р*о [0, 1],
||»м11в min ||₽о*о + (1 — Р)уао11.
₽е[0.11
Если HomIK е0, то полагаем 4 = 1, xk+i = xktk, и на
этом k-й цикл заканчивается. Если же е0, то,
имея точку хк1 и направление gki — —vkillosill-’, выпол-
няем второй шаг k-vo цикла, который, как и все после-
дующие шаги А-го цикла, делается по тем же правилам,
что и первый. В результате будет сделано такое число
шагов tk тк, что выполнится по крайней мере одно
из условий:
a) 4 = m*; b) #ft_j — Хщ\ >б;
с) —f(xft(J>6; d)
После этого полагаем xk+i = xktk, и на этом k-й
цикл заканчивается, причем если xkt = хк0 Vt&O:tk и
цикл прерывается вследствие выполнения условия d),
то заканчивается и весь процесс последовательных при-
ближений — получена такая точка хк, что d (хк) vktk |<
<8q.
Отметим, что по построению на основании леммы 6.3
должно быть
(i»*p V/. (6.22)
* 6]
РЕЛАКСАЦИОННЫЙ СУБГРАДИЕНТНЫЙ МЕТОД
299
Теорема 6.4. Пусть
+ 0, mk -> оо. (6.23)
Тогда, если последовательность (f(x»)) ограничена
снизу, то последовательность хк сходится к такой точке
X*, что
d (Z) =
min || v ||< 8q.
р e df (%*>'
(6.24)
Доказательство. Поскольку последовательность
{f(xk)} ограничена снизу, то согласно лемме 6.2
xk-► х*, xkt^x* Vt^O: tk. (6.25)
Из (6.23) и (6.25) вытекает, что при достаточно боль-
ших k, скажем при К, окончание А-го цикла вслед-
ствие выполнения условий Ь), с) невозможно.
Согласно (6.21) имеем при всех /еО:(/*—1)
II Xk. f+i — Xkt IK vk + a || Xk, /+1 — Xkt ll-
откуда, в силу (6.23) и (6.25), следует
Xkt~*X* Vt<=l-.tk,
(6.26)
ибо IIXkt — X*IKIIXkt — XA(|| + llx« — X*||.
Таким образом, все точки xkt, xkt, / е 1 :/*,
VA принадлежат некоторому компакту, который обозна-
чим X. Поскольку отображение df(x) ограничено на X,
то
b = max max || v || < оо.
х @ X и е dt (х)
Следовательно,
IKJK&.
IKrIKb V/, VA.
(6.27)
Возьмем целое число m > 1 + (1п§)~‘ • 1п(е0&-1), где
q2 ~ 1 — (1 — 6i)2[l — 2б| + (beo"1)2]-1- Не ограничивая
общности, считаем, что тк > т при всех
Покажем, что тогда tk т < тк.
йоо
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
(ГЛ. 111
Действительно, допустим, что tk > т. Тогда с учетом
(6.22), (6.27) и того, что ||оА<||> е0 при всех fe
е 0 '.(tk— 1), имеем
ll»ft.«+ill2= min ||₽о« + (1 - P)vw|F =
Ре [0,1]
= IIW2 min Г₽24у4 +
P e [0, 1] L |РйИГ
+ 2₽(l-P)^^- + (l-₽)2]<
<1°«1Г₽^1][Р2(Ч-1)2 + 2₽(1 - P)6, + (1 - ₽)2] =
= II II2 (1 - ”v*‘IF F-
\ \beo ) — 2°1 + 1 J
Отсюда вытекает, что
l|v«ll<ll^oll?4^ V/eO :(/*-!),
и, значит, II vk, m_j IK^m-*< 80. Ho || vkf ||>в0 V/eO : (tk— 1).
Следовательно, tk tn.
Итак, если последовательность {f(xk)} ограничена
снизу, то все циклы конечны и длина их не превосхо-
дит числа т, причем при всех k К окончание &-го
цикла происходит только вследствие выполнения усло-
вия d):
(6.28)
Предположим теперь, что (6.24) не верно. Тогда
е0 < min || v || в в.
V е df (х*)
Так -как отображение df(x) полунепрерывно сверху,
то найдется такое б > 0, что
df(x)<=Se(df(x'))^0 VxsSe(x*),
где в = 2-1 (ё — 80).
Таким образом,
II V II > 80 Vo s S).
Но в силу (6.25) и (6.26) при достаточно больших k
будет vktk^^>, и поэтому || vktk | > в0, что противоре-
чит (6.28). Теорема доказана.
5Л
РЕЛАКСАЦИОННЫЙ в-СУБГРАДИЕНТНЫЙ МЕТОД
301
Метод, изложенный в настоящем пункте, можно при-
менить и для нахождения точек минимума функции
f(x) на Еп. Для этого вместо условия d) || vktk || 8j сле-
дует проверять условие d) | причем е*->0.
В этом случае справедлива
Теорема 6.5. Пусть
е*-*0, vA—>0, mk-+oc.
Тогда либо
ffe)—* —оо,
/?->ОО
либо при некотором k и соответствующем t
f(xkt + agkt)—+ — <x>,
(Х-> со
либо любая предельная точка последовательности {хк}
является точкой минимума функции f (х) на Еп.
Задание 6.1. Доказать теорему 6.5.
Замечание 5. В методе с полной релаксацией в
точке Xk,t+i вычисляется vkt <= df (xft, ж) такой, что
(v kt, 6kt) 0, причем такой субградиент существует.
В методе настоящего пункта в точке хк, ж вычисляется
любой vkt^df(vk, ж)., причем будет (vkt, vkt)^ 6i||t>ftdl2.
Поскольку выпуклая функция почти всюду дифференци-
руема, т. е. почти всюду df(x) состоит из единственной
точки — градиента функции f (x), то может показаться,
что конструкция «любой v^df(x)» немногим предпоч-
тительней конструкции «существует oedf(x)». Но если
функция f(x) не является гладкой, то зачастую в про-
цессе точной одномерной минимизации происходит попа-
дание именно на то множество меры нуль, на котором
df(x)— выпуклый компакт с непустой внутренностью, и
поэтому в конструкции «существует uedf(x)» необхо-
димо действительно организовывать поиск «того, что су-
ществует». Это соображение указывает еще одно пре-
имущество по простоте реализации метода настоящего
пункта перед методом с полной релаксацией.
§ 7. Релаксационный е-субградиентный метод
В § 6 предполагалось, что могут быть точно вычис-
лены целевая функция f(x) и ее субградиенты. При рас-
четах на ЭВМ, однако, такая возможность отсутствует,
802
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ, ш
ибо, во-первых, ЭВМ оперирует только с рациональными
числами, а во-вторых, для вычисления самой целевой
функции и тем более ее субградиентов может потребо-
ваться бесконечный итерационный процесс. Примером
такой функции является функция максимума /(*)=»
= maxq)(x, у) (см. § 17 гл. I).
у е= G
Поэтому важно построить такой вариант релакса-
ционного субградиентного метода, в котором допуска-
лось бы приближенное вычисление целевой функции и
ее субградиентов, т. е. в котором вместо целевой функ-
ции f(x) использовалась бы некоторая функция ft(x)
такая, что
f(x)-8<fe(x)<f(x) + e, (7.1)
а вместо субградиентов v е df(x)—s-субградиенты v, ®
е def(x).
Такой вариант релаксационного субградиентного ме-
тода и построен в настоящем параграфе.
1. Сначала получим аналог леммы 6.3 в рассматри-
ваемом случае. Возьмем положительные числа 61, с, v,
в, во и 62, причем Si s(0, 1), 62 <6ь 8 <(с +2)~I(6i—
— 62) 80V.
Положим xi — Хо + ао£о, где go — —v0||foil-1, о0 s En.
Лемма 7.1. Если || v0 II ео, «о v и
Н 33 f е 01) — [fa to) — б2Оо II Vo II1 > о, (7. i)
то
(Оо, Оо) < 61II Оо IP V60 е dct+ilf to). (7.3)
Доказательство. Согласно (7.2) имеем
ft (xi) e ft to) — 6iOo II оо II + (6i — 62) Оо II о011 + и >
> ft (*о) — 6|<Хо IIЦ0 II + (с + 2) 8 + р.
Отсюда, в силу (7.1), получаем
/ to) > A, to) — 8 > ft to) — 6100 II Оо II + (с + 1) 8 + И >
> f to) — 610о II t>0 II + C8 + g.
Теперь справедливость (7.3) вытекает из того, что для
любого во е дсе+nf (xi) должно быть
f to) > f to) — Cto (go, 60) — (08 + p).
5 Л
РЕЛАКСАЦИОННЫЙ 8-СУБГРАДИЕНТНЫЙ МЕТОД
303
Лемма 7.1 показывает, какой должна быть точность
вычисления функции f(x) для того, чтобы из (7.2) сле-
довало (7.3).
2. Переходим к описанию релаксационного в-субгра-
диентного метода.
Зафиксируем положительные числа а, с, v, е, 6, во, 6/,
i е 1 : 3, такие, что 6iS(0, 1), 0 < 63 < 62 < Si,
(с 4- 2)-1 (Si — 62)eov. Выберем произвольно началь-
ное приближение хо е Еп и целое число то. Пусть уже
найдено k-e приближение хк е Еп. Переход к (k + 1)-му
приближению Хь+1 (k-й цикл) осуществляется следую-
щим образом.
Выберем целое число т*. — максимальную длину й-го
цикла.
Положим хка = Х£ и вычислим fe(xft.) и произвольный
се-субградиент vko еdctf (х*о). Если ||vaoII< во, то пола-
гаем tk = 0, Xk+i — xbtk> и цикл заканчивается.
Если же || о*0П > е0, то на луче {хм (а) =*хм + agk0 |а>0),
где gko = — vwllffeoir1, найдем точки xkl = xkoM и
Xki = Xko(&ko) такие, что (при / — 0)
akt>akt, v<aft(<v + aat/, (7.4)
причем либо ctkt = 0, либо ош v, и
fe(xk, <+1) II Vkt II» (7.5)
h (xk, /+1) — min {fe (xk, f+i), fe (xkt) — S2aft| || vkt II} > 0. (7.6)
Если же (7.5) выполняется при любом ам 0, то
fe(-v«(a))^> — 00, следовательно, f(xkt(a))-^+ —00,
и процесс последовательных приближений заканчи-
вается.
ЕСЛИ ||Xjto —Xftlll >6 либо ft(xko)— fe(Xki)^ 6, то
полагаем 4=1, xk+i = xktk, т. е. k-й цикл закон-
чен. В противном случае вычислим произвольный св-суб-
градиент vko s dctf(xkt). Так как ||о*о11>е0, v<
'Ми, е (с + 2)-1 (Si — 62)e0v и выполнено (7.6), то
согласно лемме 7.1
(v/л, би) < 6i II vM Iй.
После этого находим вектор Vki — ближайшую к на-
чалу координат точку отрезка [о*о, бло].
304
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
(ГЛ. III
Если ||i>aiII< во, то полагаем /А=1, xft+i = xftfft, и на
этом k-й цикл заканчивается. Если же || Vkt II > во, то на
луче {xftl(a) = x*i + ag*i|a > 0}, где gk\ == — v*ill»*ill—
находим такие точки x*2 = xAi(aAi) и х*2 = **i(ctfei).
что при /=1 выполняются соотношения (7.4) — (7.6).
Далее продолжаем аналогично до тех пор, пока не
будет сделано такое число шагов tk, что выполнится по
крайней мере одно из следующих условий:
а) tk*=mk\ b) ||xft,<A_i —
с) fe (xk. tk-\) — ft (хщ) > 6; d) J vktk || < «о-
Теперь полагаем Xk+i = xktk, и на этом &-й цикл за-
канчивается, причем если k-й цикл прервался вследствие
выполнения условия d) и Xkt = хко при всех t е 1 : tk, то
весь процесс последовательных приближений также за-
канчивается.
В результате будет построена последовательность
{%*}.
Положим Vk,-i = Vko,
( tk — 1, если /г-й цикл прерван вследствие d),
k~~ (, tk — 2 в противном случае.
Отметим, что по построению на основании леммы 7.1
будет
(vkt, vkt) < 6i II vM II2 V/ е 0 : 1к.
Теорема 7.1. Пусть
пгк-+<х>. (7.7)
Тогда либо
либо при некотором k и соответствующем t
f(xkt + agkt)^-co,
либо процесс последовательных приближений заканчи-
вается в такой точке хк, что
f(z)-f(Xk)>-eo\\z-Xk\\-(c + 2)e-(l+i>2)vbo (7.8)
Vz <=
еде bo= max ||сЫ|.
5 Л
РЕЛАКСАЦИОННЫЙ е-СУБГРАДИЕНТНЫЙ МЕТОД
805
Доказательство. Рассмотрим сначала случай,
когда последовательность {хк} бесконечна. Покажем, что
тогда найдется такая подпоследовательность {xfts}, что
¥= xks Vs. (7.9)
Допустим, что это не так. Тогда, начиная с некото-
рого К, при всех k К должно быть
~ == ••• = Xktfr ~ xk+it (7.10)
и, следовательно,
eo<l|v«ll<* V/еЩ, ||о„||<& Vte=-l-.lk, (7.11)
где b < max || v |( < оо.
vsdcJ(xk)
Так как последовательность {х*} бесконечна, то из
(7.10), (7.11) вытекает, что при любом k /< будет
tk = mk.
В силу (7.7), не ограничивая общности, можно счи-
тать, что тк > т, где целое число т таково, что
т> 1 + 1п-1^-1п(ео&-1)>
« = [1 - (1 - *.)’(’ - 2»1 + (Ч-'Л’Т-
Тогда так же, как и при доказательстве теоремы 6.4,
показывается, что || vk, m-i II во, а это противоречит
(7.Н).
Итак, если последовательность {х*} бесконечна, то
найдется такая подпоследовательность {xfcj}, для кото-
рой выполняется (7.9). Тогда на основании (7.4) и (7.5)
заключаем, что
fe(Xfes+i)<fe(xfes) — Мео Vs,
откуда и из того, что fe(xft+i)^ fe(xk), вытекает
fe (xk)—’—оо, а это, в силу (7.1), означает, что
fe->oo
f U*)—— оо.
fe->oo
Обратимся теперь к случаю, когда последователь-
ность {х4 конечна. Предположим, что процесс закан-
чивается в точке хк+1 = хА. Тогда выполняется (7.10) и
ИМ1<е0-
306
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. III
Так как i>k,-i — Vko^dcef(xko), то
f(z) — f (xk)(vk. _i, z — xk) — ce Vz <= En. (7.12)
Согласно (7.4) и (7.10), имеем
xk — xkt = — vgk. t_i = vvk. t_i|| vk. Г* V/ <= 1: tk. (7.13)
Поскольку при любых t e 1 : tk и z e En
f(z) — f(xkt) (vk, Z — Xkt) - C8 =
= (vk. t-ъ Z — xk) — ce + (vk. t_i, xk — xkt),
то, с учетом (7.13) и того, что Цу*. <_i l|^bft, получим
f(z) — f (xkt) > (Vk. t-1, z — xk) — ce — vbk (7.14)
Vz s Vt s 1: tk.
В силу (7.10), (7.6) и (7.13) будет
f (Xkt)~ t(xk)>
> — 2e —б2т||о*,(_111> —2e —62v&fe V/e 1 : tk,
откуда и из (7.14), (7.12) следует
f (Z) - f (Xk) > (Vk. t-i.z- xk) - (c + 2) e-(l +d2) vbk (7.15)
VzsE„, V/e0:/s.
Очевидно, что vktk e co {vk, *_i 10 : tk}, T. e.
‘k lk
Vktk = t^tVkt, ,1,^ = 1. (7.16)
0 V/ — 1 • lk*
Умножим теперь каждое из неравенств (7.15) на со-
ответствующий коэффициент \t из представления (7.16)
вектора vktk и сложим полученные при этом tk +1 не-
равенств. Тогда
f(z) — f(Xk)>(Vktk, z — xk) — (c-f-2)e — (1 -f-62)v&fe>
— II^J-llz —xj| — (с 4-2)в —(1 4-62)v&a vze£„,
откуда с учетом того, что j vktk | в0, следует (7.8). Тео-
рема доказана.
3. Теорема 7.1 и, в частности, оценка (7.8) показы-
вают, как можно применить метод, изложенный в п. 2,
J n
РЕЛАКСАЦИОННЫЙ е-СУБГРАДИЕНТНЫЙ МЕТОД
307
который для краткости назовем 8-алгоритмом, для на-
хождения точек минимума функции f(x) на Еп-
Возьмем последовательности {еОл}, {е*} и {vj поло-
жительных чисел, стремящиеся к нулю. Выберем произ-
вольным образом начальное приближение х0 s Еп- При-
меним 8-алгоритм при во = 8oi, в = 81, v = Vi, начиная
из точки хо = хо. В результате его работы либо устано-
вим, что f = inf f(x)== —оо, либо найдем точку х*,
х ®
удовлетворяющую (7.8). Положим xi = х*. Применим
8-алгоритм, начиная из точки х0 = Хь при во = в02, в =
= е2, v = v2h либо установим, что [* = —оо, либо най-
дем точку Xk, удовлетворяющую (7.8), но уже при изме-
ненных 8о, 8, V. Положим Х2 = Хк-
Продолжая далее аналогично, либо установим, что
J* = — оо, либо построим бесконечную последователь-
ность {х*}, каждая точка которой удовлетворяет, в силу
(7.8), соотношению
f(z)-f(xk)>
> — Во*|| z — h II — (с + 2) в» — (1 + d2) vkbk-i Ух <= Е,.,
Отсюда ясно, что если множество 0(хо) — {х<=
s E„|f(x) < f(x0)} ограничено, то f(x*)->-/*> причем лю-
бая предельная точка последовательности {х*} будет
точкой минимума функции /(х) на Еп.
4. Во всех рассмотренных вариантах релаксацион-
ного субградиентного метода направление движения оп-
ределялось из решения простейшей задачи квадратич-
ного программирования — нахождения ближайшей к на-
чалу координат точки отрезка [w, €>*/]. Если размер-
ность пространства Еп не слишком велика и позволяют
возможности используемой ЭВМ, то эффективность ре-
лаксационного субградиентного метода значительно по-
вышается, если ввести в процесс последовательных при-
ближений более сложную вспомогательную задачу вы-
бора направления движения, заключающуюся в нахож-
дении ближайшей к началу координат точки многогран-
ника, натянутого на множество Зёы — {5». -i, Vko, ...
..., Gk, r-i} или его некоторую часть.
В этом случае векторы Vk, <+i, t е 1 : tk, строятся сле-
дующим образом: выбирается некоторое подмножество
308
МИНИМИЗАЦИЯ нА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. ш
множества Ж^_и находится вектор Vk, ж где
Zm = со{и*<, vkt, 2^kt}, такой, что
||v*,/+1||= min ||v||. (7.17)
vs*kt
При такой модификации релаксационный субгра-
диентный метод становится близким к. методу е-наиско-
рейшего спуска и в идейном плане, и по эффективности.
Поскольку [Vkt, Vkt]<=.3?kt, то все теоремы, доказан-
ные в §§ 6, 7, остаются справедливыми, если находить
вектор о*,ж из условия (7.17).
Зная размеры исходной задачи минимизации функ-
ции f(x) на Еп, можно подсчитать максимально допусти-
мый на используемой ЭВМ размер задачи квадратич-
ного программирования (7.17). Чем больше векторов из
2^kt включается в 2ffikt, тем более точно множество S’*,
будет аппроксимировать множество def(xk,t+\) и тем
реальнее значительно уменьшить функцию f(x), дви-
гаясь из точки х^ ж в направлении
gfe.t+l “ ~ vk, f+l II fft, i+l II *•
5. В заключение остановимся на вспомогательной за-
даче одномерного поиска точек хк, ж = **/(«**) и
хл, <+1 = Xftf(Sft/), удовлетворяющих (7.4) —(7.6). Оче-
видно, поиск этих точек можно производить многими
способами. Покажем здесь, как это делается по методу
золотого сечения. Отметим, что обычно метод золотого
сечения применяют для одномерной минимизации на от-
резке. Ниже приводится вариант метода золотого сече-
ния для поиска на луче.
Введём обозначения: x(a)=xkt(a), x—Xkt, х+=хй)<+1,
x+ = Xk,t+i, f (а) = fe (х (а)), (а5)—f(as_I) + d3as||t»ft/||,
Us =» f (as) — min{f (as_i), f (oq) — d2as II vki ||}.
Положим ao = 0, «[ —v, q = 2 '(1 + V^) > 1.
Вычислим f (a0), f (a^ и щ. Если щ 0, то пола-
гаем х+ = х, х+~ х((Х1), иначе вычислим f(a2), ц,2 и £а>
где a2 = v(l t?) = v E q‘.
<-о
5 fl
РЕЛАКСАЦИОННЫЙ 8-СУБГРАДИЕНТНЫИ метод
309
5-1
Пусть уже найдены f (as), и gs, где as = v £ql.
s
Если < 0, то полагаем ai+1 = v £ ql и вычисляем
i-0
f («s+l)> Hs+1> Bs+1-
Пусть hs>0. Если £s_i<0 и as<v + aas_i или
gs <: 0, то полагаем x+ = x (as),
( x+, если Is^O,
X+~l <(as_i), если gs > 0, gs_,<0, as<v + avs_b
В противном случае (по-прежнему рассматриваем
случай ps 0) продолжаем поиск на отрезке [a$-2, as]
методом золотого сечения. Заметим, что a$-i есть золо-
тое сечение отрезка [as-2, а$].
Действительно, как известно, золотым сечением от-
резка называется такое деление его на части, что отно-
шение длины меньшей части к длине большей части рав-
но отношению длины большей части к длине всего от-
резка. Имеем
5-3 5—2 5 — 1
i-0 i-0 i-0
«8~«8~I <7*~‘ e
a, — a,-, qs~l + q3"2 1+?’
«8-1-98-» - q3~2 _ 1
—....1 Г . —Я5 Г I » ZSS t
a, - a,-! q*~' q
« « a 1
а одним из корней уравнения t , =у является число
2"*(1+V5).
На отрезке [а5-2, а,] поиск продолжается следую-
щим образом. Положим a*+i = as, as = as_2 + a5+i —
— as_j и вычислим f(as), p,s и gs.
Случай 0 рассматривается так же, как и выше.
Пусть < 0. Тогда, если as+i v + aas, то пола-
гаем x+ = x(as), x+ = x(as+i), в противном же случае
полагаем as_2 = «s-ь as-i == as, as = as+i и продол-
жаем поиск на отрезке [as-2, as].
810
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВА
[ГЛ. Hi
Ясно, что такой процесс либо конечен, либо
Замечание 1. Если k-ti цикл прерван по выпол-
нении условия а) и xkt = хк Vt е 0: tk, то на самом деле
это означает, что число т* выбрано неудачно, и, увели-
чив его, следует продолжить £-й цикл.
Замечание 2. С вычислительной точки зрения
наиболее удобен случай, когда хы — xkt, поскольку за
следующую точку принимается точка Хщ и субградиент
Vk, /-1 вычисляется также в точке xkt и нет необходимо-
сти хранить в памяти ЭВМ лишнюю точку. Если а*, е-i
v, то всегда можно добиться того, чтобы Xkt — Хм,
причем затратив на это конечное число вычислений
функции. Но специально на это много усилий затрачи-
вать не стоит.
§ 8. Метод Келли
1. Метод Келли. Пусть / (х)—выпуклая конечная
на Еп функция. Тогда (см. (5.11) гл. I)
f (х) = max [/ (z) + (о (z), х — z)] в max В (z, х), (8.1)
где v(z)i=df(z) (для каждой точки z выбирается один
произвольный вектор из df(z)). Требуется найти
min f (х),
где Qc=.En— замкнутое ограниченное множество. Выбе-
рем произвольный набор о0 конечного числа точек из
Еп. Пусть уже найдено множество о*. Образуем функ-
цию
и найдем Если то точка xk — ft W = max В (z, x) mln fk (x) «= fk (xfc). x e <» fk(xk)~f(xk), точка минимума функции f(x) (8.2) (8.3) на fi. Дей-
§ 81
Метод келли
311
ствительно, fs(x) f(x), и потому
fk (,xk) = min fk (x) < min f (x) — f* < f (xk).
x e U x e Q
(8.4)
Отсюда и из (8.3) f* = f(xk).
Если же fk(Xk) < f(Xk), то полагаем Ok+i = ок(]{хк}
и далее поступаем аналогично. Заметим, что хк е й,
fk+l (Xk+l)^ fk(Xk),
В (хк, xk) = f (xk).
(8.5)
В результате строим последовательность множеств {а*}
и точек {хк}.
Теорема 8.1. Всякая предельная точка последова-
тельности {xk} является точкой минимума функции f(x)
на й.
Доказательство. Существование предельных то-
чек вытекает из ограниченности и замкнутости множе-
ства й. Пусть хк -*-х* ей. Надо показать, что
f(x*) = f*. (8.6)
Заметим вначале, что f (xAs) -* f (х*) по непрерывности
функции f(x). Зафиксируем любоеks<>. Тогда при ks> kSt
в силу (8.4)
r>fks(xks}>B(xksa, xAs) =
Учитывая ограниченность v(z) на й (отображение df(z)
ограничено на любом ограниченном множестве) и пере-
ходя к пределу по ks„ ks-*<x>, при ks > kSa, получаем
из (8.7)
f*>f(x*). (8.8)
Очевидно, что
f(x*)> inf f(x)=*f*. (8.9)
х е Q
Из (8.8) и (8.9) следует (8.6). Теорема доказана.
Замечание I. Если оказалось f(xk) — 1ь(хк)^е,
то из неравенства fk(x) f(x) имеем
min fh (х) = fk (Xk) < min f (x) - f.
312
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. Ill
Отсюда f(xfe) — 8 f*, т. е. точка х*— в-стационарная
точка функции f(x) на й.
Замечание 2. Рассмотрим теперь задачу миними-
зации функции f(x) на всем пространстве Еп. Предпо-
ложим, что множество
ЛГ = {хеЕя|/(х)== inf f(x)}
хаЕп
непусто и ограничено. Выберем компакт QczEn такой,
что v^*czintQ (естественно выбрать й попроще, напри-
мер, заданное линейными неравенствами). Применяем
изложенный выше метод Келли. При этом из теоремы 8.1
следует, что при больших k будет
min fk (х) = min fk (х),
х е= Q X е Еп
т. е. множество й играет вспомогательную роль и ис-
пользуется лишь в начале процесса. Если заранее мно-
жество й неизвестно (но известно, что Ж* ограничено),
то можно взять произвольное множество Йо с Еп и сде-
лать несколько шагов; если на некотором шаге ko ока-
жется, что
xftoeintQo. (8.10)
то дальше при k > kQ можно, в силу (8.4), вместо за-
дачи (8.2) решать задачу
min fk(x).
xsEn
Если же включение (8.10) долго не имеет места, то
можно попробовать взять новое Йо гэ й0.
Замечание 3. Положим
Rk = {z е= crft | fk (xj == В (г, xk)}.
Легко заметить, что в этом случае задача (8.2) эквива-
лентна задаче
min f k (х),
где
fkW — max В (z, x).
§ 8J
МЕТОД КЕЛЛИ
813
Предположим, что f(x)— сильно выпуклая функция, и
пусть х*— точка минимума функции f(x) на й. По тео-
реме 8.1 последовательность {х*} сходится к точке х*
(у сильно выпуклой функции существует единственная
точка минимума). Покажем, что любая точка х^=х* мо-
жет встретиться в лишь для конечного числа k. Дей-
ствительно, допустим противное, Пусть х е Rks, ks-+ оо.
Имеем
5 (*> х*5) = Их) + (v (х), хкз — х) = fks (х*а).
Так как xAj->x*, то из (8.9)
f(x) + (a(x), х’-х) = /(х*).
Но функция f(x)—сильно выпуклая, и поэтому сущест-
вует т > 0 такое, что (см. (9.17) гл. I)
f (х*) = f (х+(х*—х)) > f (х) + (ц (х), х* — х) + т || х* — х ||2.
Поскольку х=^х*, то отсюда f(x*) > f(x) + (v(x),
х* — х). Получили противоречие с предыдущим равен-
ством.
Итак, всякая точка х* х* является «существенной»
лишь конечное число раз. Этот факт может быть исполь-
зован при практической реализации метода Келли.
2. е-метод Келли. Для каждого zsEn выберем ка-
кой-нибудь вектор t/(z)<= d8/(z) и положим
F(x) — sup [f (z) + (о(z), x —z)]. (8.11)
Из определения def(z) имеем
f (x) — f (z) > (v (z), x — z) — e Vx e En.
Отсюда
f (x) < sup [f (z) + (t> (z), x — z)] ж F (x) < f (x) + e. (8.12)
Функция F(x) тоже является выпуклой, как супремум
выпуклых функций. Пусть ЙсЕ, - произвольное замк-
нутое ограниченное множество. Требуется найти
minf(x)sf*. Напомним, что если x*eQ и /*^f(x*)<.
f* + е, то точка х* называется 8-стационарной точкой
314
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
(ГЛ. Ш
функции f(x) на £2. При этом оказывается (см. лемму 8.1
гл. I), что если х* е int £2, то
О <= dj (х*).
Напомним, что множество J dgf(z) ограничено.
zeQ
Опишем обобщение изложенного в п. 1 метода Келли
для нахождения 8-стационарных точек. Пусть ао — про-
извольный конечный набор точек из Еп, и пусть уже
найдено множество а*. Образуем функцию
fk (*) = тах (2» *)>
где
В (z, х) = f (z) 4- (р (z), X — z), V (z) <= dtf (z),
и найдем
fк(хк) = min fk(x), (8.13)
x e U
Если fk(xk) > f (хь), то из (8.12)
f* < f (Xk) < fk (xft) == min fk (x) < min f (x) + e = f + e.
(8.14)
Значит, f* f(xk)^. t. e. x* — e-стационарная
точка функции f(x) на £2, и процесс прекращается.
Если же fk(xk) < f(xk), то полагаем ohi = (I*UW
и далее продолжаем аналогично. В результате строим
последовательности множеств {а*} и точек {х*} таких, что
хк е= £2, fk (xft) < fk+i (xk+i). (8.15)
Отметим еще, что если при некоторых k и н > 0 ока-
жется
(8.16)
то из (8.14) получим
(8.17)
Учитывая (8.16), имеем
f М — H<fk (хк) < Г + е,
т. е. f* f (хк) f* -|- |л + е, а это значит, что хк яв-
ляется (в 4: нестационарной точкой функции /(х) на £2.
§ 9)
МИНИМИЗАЦИЯ ФУНКЦИИ СУПРЕМУМА
315
Теорема 8.2. Всякая предельная точка последова-
тельности {хл} является ^стационарной точкой функ-
ции f(x) на Q.
Доказательство. Существование предельных
точек следует из ограниченности множества Q. Пусть
хъ-*хеЙ. Так как f*s(x*s)> B(xkso, **,) = f (х*,0)+
+ (v (х*«о)’ x*s ~ -%) ПРИ < ks’ т0’ переходя к пределу
при ks, k -+ео, при условии ks > kSQ и учитывая огра-
ниченность vks и (8.14), получим
Г + е>/(х)>Г, (8.18)
а следовательно, х—е-стационарная точка f(x) на Й.
Замечание 4. Если множество Й задано линей-
ными неравенствами, то задача (8.13) есть задача ли-
нейного программирования.
Замечание 5. При е = 0 получим «чистый» метод
Келли.
Замечание 6. В пп. 1, 2 выпуклость множества й
не предполагалась. Требуется лишь уметь решать за-
дачу вида (8.2).
§ 9. Минимизация функции супремума
Пусть X—линейное нормированное пространство,
G с: Ер — ограниченное множество, й с X. На ЙХ<? за-
дана непрерывная функция ф(х, у), причем
— оо < inf sup qp (х, у) » f* < 4- оо.
X е Q у е G
Положим
f(x)= sup ф(х, у). (9.1)
р® О
Требуется найти inf f(x).
Предположим, что существует конечное множество
Go е G такое, что
inf тахф(х, у)> — оо. (9.2)
х е Q у е
Пусть функция ф(х, у) удовлетворяет условию Липшица
по у, т. е. существует L < оо такое, что
| ф (х, у') — ф (х, у") | < L || у' — у" || (9.3)
Vx € й, у', у" е G.
316
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. ш
Лемма 9.1. Если {х*} (xk <= Q V&) — произвольная
последовательность, а последовательность {yk} (yk&G
VA) такова, что
ф(*ь yk+i)> max <f(xk, yt), (9.4)
TO
lim [<p(xb yk+l) — max q>(xk, yt)] = 0. (9.5)
/г-> оо 0 i k
Доказательство. Предположим, что (9.5) не
имеет места; тогда из (9.4) следует, что найдутся по-
следовательность индексов {£s} и число е0 > 0 такие, что
Ф(xks, yks+i)—omaxk <р(xks, у^ >е0.
Отсюда и из (9.3), (9.4)
Во < ф (xks, yks+i) — ф (xkat yt) < i jykt+i — y{ I Vie 0: k„
t. e.
что противоречит ограниченности множества G (всякое
ограниченное множество конечномерного пространства
можно покрыть лишь конечным числом шаров заданного
радиуса в). Лемма доказана.
Выберем и зафиксируем в 0, б 0.
Возьмем произвольное множество оо е G, удовлетво-
ряющее (9.2). Пусть уже найдено о* <= G. Построим
функцию
ФА(х) = тах ф (х, у)
»sek
и найдем точку хк в £2 такую, что
Фл (хк) < inf фй (х) + б, (9.6)
т. е. инфимум функции ф*(х) находим с б-точностью.
Теперь найдем точку yk+i е G такую, что
ф(*й, yk+i)>f(xk) — е, (9.7)
Ч(хк, ук+1)^<рк(хк), (9.8)
т. е. задачу (9.1) решаем с 8-точностью.
§ 9]
МИНИМИЗАЦИЯ ФУНКЦИИ СУПРЕМУМА
317
Полагаем а*+1 = и далее продолжаем ана-
логично.
Теорема 9.1. Имеют место соотношения
0< lim f (xfe)-f<8 + d,
fe->oo
0 C lim f (xk) — f* <1 e + 6.
k->OO
Доказательство. Из (9.6) и (9.7)
/ХЖХфХ !/a+i) + 8>
f*= inf sup ф(х, г/)>
xgQ yE G
inf max ф(х, y)— inf <p* (x) <pft (xk) — 6.
x&Q у ~ xeQ
Отсюда
0 < f (xk) — <p(xft, ^+i) + e —
< Ф (xk, yk+l) — Ф* (xA) + 8 4- d. (9.9)
Из леммы 9.1 следует, что ф(х*, yk+i)— Фй(Хй)->0. По-
этому из (9.9) вытекает, что для любого ц > О найдется
такое К < оо, что
0</(х,)-Г<8+.д + ц Vk>K. fi
Следствие. Если вместо (9.6) и (9.7) точки хк и
Ук+\ удовлетворяют неравенствам
ФаХ< inf Фа(*) + 6ь
х е Q
фХ yk+i)>f(xk) — &k,
еде dk —> + 0, еА -► + 0, го
lim f (xk) = Г
fe->oo
и любая предельная точка последовательности {xk}t
если таковые существуют, является точкой минимума
Функции f(x) на множестве Q.
Замечание 1. Выше функция ср(х, у) не предпо-
лагалась выпуклой по х, множество й тоже не обяза-
тельно выпукло.
Замечание 2. Поскольку любая выпуклая функ-
ция есть функция максимума (формула (5.11) гл. I),
318
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. III
то изложенный выше метод можно применить и для на-
хождения минимума выпуклой функции, в результате
получится метод Келли (см. § 8).
§ 10. Минимизация выпуклой функции максимума.
Метод экстремального базиса
1. Пусть
/(х) = тахф(х, у),
где О — компактное множество, функция ф(х, у} непре-
рывна вместе с <р'х (х, у) по х и у на Еп X О и сильно вы-
пукла по х с константой т > 0 при каждом фиксирован-
ном у е О, т. е.
Ф(х4-Д, у)>ф(х, у) + (ср'х(х, у), Д) + т||Д(10.1)
V[x, y]c=EnXG, VAe£n.
Возьмем любое Хо е Еп. Положим
b = min ф (х0, у), Ki = maxIIф' (х0, у\||.
уеО «еО11 4 711
Из (4.1) ясно, что
ф(х, У)>Ъ — Killx — Xoll + mllx — xo|pv[x, y]^EnXG.
Поэтому
Ф (х,у)> f(x0), (10.2)
если
||х — х0J > z, где з= [у Ki + (у K2i+m(f (хо) — Ь))2] т~\
Положим Кe max ||ф'(х, у)||. Требуется найти
х«Зж(х0). * 711
min f(x).
хе Еп
В § 1 было показано, что для того, чтобы точка
х*еЕл была точкой минимума функции f(x), необхо-
димо и достаточно, чтобы
0s^(x*), (Ю.З)
где
S (х) = со^ (х), 96 (х) = {ф' (х, у) | у @ Е (х)},
R (х) = {у е О |ф (х, у) «= f (x)L
§ 10] МЕТОД ЭКСТРЕМАЛЬНОГО БАЗИСА 319
С каждой точкой хо е Еп связано множество S’(xo). Если
O^^Uo), то направление
g Uo) = — z (х0) || z (х0) Г1,
где ||z(x0)|| = min || z ||, является направлением наиско-
г е <е (хо)
рейшего спуска функции f(x) в точке х0. Умение вы-
числять направление наискорейшего спуска или близ-
кие к нему направления дает возможность разработать
численные методы для минимизации (см. § 3). Однако
при этом необходимо учитывать все точки множества
/?(х) и производить минимизацию функции f(x) на луче
(в направлении спуска). На практике множество G,если
оно содержит бесконечное количество точек, дискретизи-
руют (заменяют конечным множеством точек), но более
точная аппроксимация f(x) требует учета большого ко-
личества точек множества G. Было бы желательно раз-
работать метод минимизации функции f(x), при реали-
зации которого можно было бы обойтись сравнительно
небольшим количеством точек множества G.
Опишем вначале «принципиальный алгоритм» (по
терминологии Э. Полака [96]). Выберем произвольный
набор из п + 2 точек множества G:
ао = {Уо1....Уо, п+г}> У01 s G Vi s 1: (ti + 2).
Набор <т0 назовем базисом.
Пусть уже построены точки хо, >.., х*_] и базис
aft=={z/fci> • • • > У к, п+2}, yki^-G Visl:(n-}-2)
Определим функцию
fk (х) = max ф (х, у^
Iе 1: (п+2)
и найдем точку х* такую, что
fk (xk) = min fk (x). (10.4)
* e En
Решение задачи (10.4) проще, чем минимизация
функции f(x), ибо для нахождения функции fk(x) тре-
буется вычислить значения функции f(x,y) в п + 2 точ-
ках. По необходимому условию минимума функции fk(x)
®G2&k, (Ю.5)
320
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. III
где
г, - со жк, - {<₽' (х„ 9„) | г е я,),
Я, — I ф (X*, Ни) = fk (*»)}
Так как по теореме Каратеодори (теорема 1.1 гл. I)
любая точка множества S’* может быть представлена
в виде выпуклой комбинации не более чем п + 1 точек
множества <9$*, то существует по крайней мере один ин-
декс I* е 1 : (п + 2), без которого «можно обойтись», т. е.
либо ik^Rk, либо начало координат в (10.5) можно
сформировать и без вектора <р* (хк, У kl^y Пусть ук е
s G — такая точка, что
Ф (Ч, ук) = f (xk) => max ф (х*, у), (10.6)
yes О
т. е. у к е R (хн). Построим теперь новый базис <y*+i ™
= {«М+1, ь .... Уь+ъ л+г} так:
_ ( Ум, IФ 4.
1-4..
Базис 04+1 отличается от базиса о* одной точкой и тоже
содержит «4-2 точки. Если f(x*) = ^(х*), то хк — точка
минимума функции f(x), ибо в этом случае <р (х*, ум) —
= f{Xk), т. е. yki^R(xk), и в силу (10.5) выполнено
необходимое и достаточное условие (10.3). Если же
f (хь) > fk(Xk), то, исходя из базиса o*+i, строим функ-
цию fk+i (х) и далее продолжаем аналогично.
В результате имеем последовательность точек {х*}.
Если эта последовательность конечна, то последняя по-
лученная точка по построению является точкой мини-
мума функции f(x). Если же последовательность {х*}
бесконечна, то справедлива
Теорема 10.1. Последовательность точек {хк} схо-
дится к точке минимума функции f(x).
Доказательство. Отметим прежде всего, что
последовательность {х*} ограничена, ибо из (10.2) сле-
дует, что fk W > f (*о) > fл (*о). если || х — х0 II > z. Поэтому
Us —х0||<г, (10.7)
поскольку fk(xk)— min f*(x)^/*(x0),
5 10)
МЕТОД ЭКСТРЕМАЛЬНОГО БАЗИСА
321
Обозначим Д* = х*+1 — xk. Из (10.1) имеем
Ф (xk+i, Ум) — Ф (xk + да> Ум) >
> Ф (*а> Ум) + (Ф* (хм УмУ да) + т || Дй IP. (10.8)
Для i е Rk будет ф (xk, ум) = fk (хк).
В силу (10.5) существует такое ум^ок, что
«(хмУм)>^)>°- (10.9)
Из (10.8) для такого i имеем
<Р(ха+1>^)>/Дха) + /иДа.
т.е.
A+i) ® mzax ф (*а+р yk+l. i) > fk (*fe) + пЦ- (Ю-10)
Отсюда следует, что
Aft->0. (10.11)
Л->ОО
Действительно, допустим противное. Пусть существуют
число а> 0 и подпоследовательность {Ага} такие, что
Тогда из (10.10) имеем /а(ха)->4-оо, но
f(xk)^ 1к(хк), поэтому f(х*)->4- оо, что невозможно,
так как {**}—ограниченная последовательность, а
f(x)—непрерывная функция.
Итак, (10.11) доказано.
Из (10.6) имеем
H*k) = fk+dXk)- (10.12)
Так как
Ф(А+р^)г=Ф(Л + Да’ у) =
= Ф (хм У) + (ф; (хк + &А» У)> Да)«
где s (°> 0. то
IF (W-Ч (xj К КII Да II,
1/а+1(ха+1)-/а+1(ха)1 = /(||Да11
и из (10.12) получаем
I Fa+i (*a+i) — f (xa+i) I
^1 fk+i (Xfe+i) — Fa+i (ха) I +1 Fa+i (xa) — f (xa+i) 1 =
QI Fa+1 (Xa+1) — f A+l (Xa) I + I f (Xa) — f (Xa+1) I 2ЛII II.
(10.13)
11 В. Ф. Демьянов, Л. В. Васильев
322
МИНИМИЗАЦИЯ нА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. Ill
Из (10.5) получим 0 есо {<₽; (xft+1, yft+1>z) | i е= Rk},
где 1ф (xk+l, yk+i, i)=fk+i (Xfe+i)}. Отсюда и из (10.13)
(хл+1),
где ел = 2Я||М> (х) = со (х),
<^е (*) = {Ч\ (х, У) \y^G: f (х) — <р (х, у) < е).
Значит, х*+1 является е^-стационарной (см. § 1) точ-
кой функции f (х) на Еп.
Так как е*->0, то последовательность вл-стационар-
ных точек сходится к единственной точке минимума
функции f(x) на Еп. И
Выше предполагалось, что функция ф(х, у) сильно
выпукла по х. Это условие существенно, что видно из
следующего примера.
Пример 1. Пусть хе Е{, G = 1 :4,
ф (X, 1) аа 1, Ф (X, 2) — х2, Ф (х, 3)=2 — х, ф (х, 4) — 2 + х. |
Положим
f (х) — max ф (х, у) = max ф (х, i).
уев 1-1:4
Так как п = 1, то базис должен состоять из трех точек.
Положим <Уо= {1, 2, 4). Ясно, что
min f0(x) = minmax{l, х2, 2 + x) = f0(— 1)= 1,
т. e. x0 = — 1. При этом
/?о = {1.2,4),
= ф;(-1,2),ф;(-1,4)} = {0,-2, 1}.
В качестве /о можно взять /о = 4. Поскольку
f (х0) — max ф (хо, у) = Ф (х0, 3) = 3,
y<sl : 4
то уо = 3, поэтому oi — {1, 2, 3).
Теперь имеем ft (х) — тах.{1, х2, 2 — х}, и поэтому
min fi (х) = fi (+ 1) = 1, т. е. Xi — 1. При этом Ro =
= {1,2, 3}, = {0, 2,-1}. Можно положить ц = 3. Так
5 10]
МЕТОД ЭКСТРЕМАЛЬНОГО БАЗИСА
323
как f(xi)= ф(хь 4) = 3, то yi = 4. Снова имеем 02 =
= {1,2,4} = оо- Далее аналогично получаем
ст3 — °Ъ • • •» G2 k — а0> ^2k + l~°l’
Таким образом, случилось зацикливание.
Очевидно, что min f(x) = ЦО) = 2.
Зацикливание произошло вследствие нарушения ус-
ловия сильной выпуклости функций ф(х,у) (функции
ф(х, 1), ф(х, 3), ф(х, 4) не являются сильно выпуклыми).
2. Вспомогательная задача (10.4) в изложенном
выше методе, вообще говоря, не решается за конечное
число шагов, поэтому практически метод п. 1 неосу-
ществим. Ниже будет изложено еще три метода, два из
которых позволяют реально осуществить изложенный
выше метод последовательных приближений. Доказа-
тельство сходимости можно найти в [20], [33].
Вначале опишем е-метод. Выберем последователь-
ность {ej такую, что
оо
8а->4-0, Zeft<oo. (10.14)
*=а
Возьмем произвольную точку и произвольный
(п -|-2) -точечный базис
cro = {yoi...Уо,п+2}, yoi^G VZ s 1 : (п 4-2).
Пусть уже построены точка х* е Еп и базис
^k = {yki....Ук.п+2}> Ум^С VZ«=l:(n + 2).
Положим
fk(x)= max ф(х, ykl) (10.15)
fel :(n+2)
и найдем точку x*+i такую, что
(10.16)
где
— со 3^kSk, a@ke,k «= {ф£ (Xfe+1, уы) | Z е= Rkt
1 “Ь 2) | ф (Xfe4-1, ykl) f k (Xfe + 1)
?°(x^a *A+l является ^^'Стационарной точкой функции
U*
324
МИНИМИЗАЦИЯ НА ВСЕМ ПРОСТРАНСТВЕ
[ГЛ. II1
Теперь строим новый базис cik+i так же, как в п. 1.
Если f(x*+i) == fk(x/i+i) и при этом имеет место (10.5),
то точка x*+i—точка минимума функции /(х), и процесс
прекращается. В противном случае, исходя из точки
xft+i и базиса о*+ь строим функцию /*+1(х) и находим
8А+1-стационарную точку этой функции. Если построен-
ная таким образом последовательность точек {х*} ко-
нечна, то последняя полученная точка является точкой
минимума функции f (х). В противном случае имеет место
Теорема 10.2. Последовательность точек {х*} схо-
дится к точке минимума функции f(x).
3. К сожалению, е-метод, изложенный в п. 2, еще не
вполне устраивает нас, ибо нахождение е-стационарных
точек в ряде случаев требует осуществления бесконеч-
ной процедуры. От этого недостатка свободен излагае-
мый ниже р-метод.
Пусть последовательность {р*} такова, что
оо
Pk (10.17)
fe=»0
Пусть уже найдены точка хь и базис о* и определена
функция fk(x) (см. (10.15)). Найдем точку Xk+i такую,
что
min 1И1<Р*-
Здесь S’* — множество, определенное после соотношения
(10.5). Новый базис o*+i строим, как и в п. 1. В резуль-
тате имеем последовательность {х*}.
Теорема 10.3. Последовательность точек {х*} схо-
дится к точке минимума функции f(x).
4. Наконец, изложим (е, р) -метод, являющийся ком-
бинацией е-метода и р-метода.
Пусть последовательности {е*} и {р*} удовлетворяют
соотношениям (10.14) и (10.17). В качестве х*+1 выби-
раем точку, для которой
min ||z||<p*, . (10.18)
где 3?k&k — множество, определенное после включения
(10.16). Смена базиса происходит, как и выше. Нахож-
дение точки х/г+1, удовлетворяющей неравенству (10.18)/
МЕТОД ЭКСТРЕМАЛЬНОГО БАЗИСА
326
5 1<Ч
производится тоже в конечное число шагов. Для полу-
чающейся таким образом последовательности также
справедлива теорема о сходимости.
Замечание 1. Изложенные выше методы обоб-
щаются на случай, когда минимизация производится на
множестве, заданном неравенствами ([20], [33]).
Замечание 2. Поскольку любая выпуклая, функ-
ция может быть представлена в виде функции макси-
мума своих опорных функций (т. е. всякая выпуклая
функция есть функция максимума линейных функций, а
всякое выпуклое множество представимо в виде пере-
сечения полупространств), то описанный выше метод
экстремального базиса можно применять для решения
задачи минимизации выпуклой функции на выпуклом
множестве, причем на каждом шаге необходимо решать
задачу линейного программирования небольшой раз-
мерности. Для устранения возможного зацикливания,
вызываемого тем, что линейные функции не являются
строго выпуклыми, могут быть разработаны специаль-
ные методы (см. [20]).
. Итак, в отличие от метода Келли (см. § 8), количе-
ство ограничений во вспомогательной задаче линейного
программирования не увеличивается.
ГЛАВА IV
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИИ
§ 1. Необходимые и достаточные условия
минимума выпуклой функции
на выпуклом множестве
1. Пусть ScEn— открытое множество, QczS — вы-
пуклое замкнутое множество и на S определена выпук-
лая функция f (х).
Требуется найти такую точку х* <= й, что
f*^f(x*) = inf f(x). (1.1)
В исследовании задачи (1.1) важную роль играют
необходимые и достаточные условия минимума функции
j(x) на множестве й. Напомним их (см. §§ 6, 10 гл. I).
Положим у(х0) — {t> = %(z— Хо) |X > 0, гей}.
Множество Г(хо) = у(хо) называется конусом воз-
можных направлений множества £2 в точке х0. Обозна-
чим Г+(хо) конус, сопряженный конусу Г(х0).
Множество у(хо) есть выпуклый конус, а Г(х0) и
Г+(хо) — выпуклые замкнутые конусы, Оеу(хо)Л Г+(х0)
(см. § 3 гл. I).
В § 6 гл. I была доказана следующая
Теорема 1.1. Для того чтобы в точке х* е й функ-
ция f(x) достигала своего наименьшего на множестве й
ёначения, необходимо и достаточно, чтобы
df(x*) Л Г+(х*)^0. (1.2)
Если воспользоваться понятием условного субдиф-
ференциала функции f(x) на множестве й в точке х0:
daf (х0) = (у <= Еп | f (z) — f (х0) >(u, z — х0) Vz е й),
то, учитывая соотношение (см. лемму 10.2 гл. I)
д£7(х0) = ^(х0)-Г+(х0), (1.3)
5 1] НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ МИНИМУМА 327
условие (1.2) можно записать в следующей форме:
О е= <Э'7 (х*). (1.4)
Пусть хо s Q. Положим
Ф(х0) = min - д, ф(х0) = min --А(ХА,
(1вН-1 lUfO-i. e«rw ds
d(x0) = min || v ||, p (x0) = min || v ||.
o«=dQf(x0) u<=[dQf (xt)]fr
Если ®edsf(x0), то p(x0) есть радиус наибольшего
шара с центром в начале координат, содержащегося в
<9af(xo); если же O^<9Qf(xo), то р(х0) = min ||t»|| =
vedaf (Хо)
= d(x0), т. е. р(хо) — расстояние от множества dQf(x0) до
начала координат.
Условие (1.2) эквивалентно тому, что (см. лемму 6.3
гл. I)
ф(х*)>0.
Лемма 1.1. Пусть хоей. Справедливы соотноше-
ния
ф(х0)«ф(х0), (1.5)
, f — Р (хо) = — rf (хо), если d(x0)>0,
Ф(хо) = < , . . Л (1.6)
I р (х0), если d (хо) = 0.
Доказательство. Применим леммы 6.2 и 6.4
гл. I для множеств B = df(x0) и Г+ = Г+(х0). Получим
требуемое.
Возьмем х0ЕЙ. Если ф(х0)<0, ||ц(х0) ||= р(х0),
w(x0)e<3a/:(x0), то вектор £osg(xo) = —t'(xo)||t>(xo)||-1
есть направление наискорейшего спуска функции f(x)
на множестве Q в точке хо и из (1.5) следует (см.
§ 6 гл. I)
__ 0 к _ df (хо) _ m!n df (хо) _ . dQf (х0)
Р (х0) = — = min —=-— = min —т-—.
д8л llgll-l.garwo) OS №||-i Og
Введем обозначения:
(х) == {о е= — Г+ (х) 11| v || = л}-
<?ч(х) = со {<ЭНх)и7\,(х)},
где т]>0 — произвольное фиксированное число.
328
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
[ГЛ± IV
Заметим, что если Г+(х)= {0}, то <2\(л') =
Лемма 1.2. Для того чтобы выполнялось условие
(1.2), необходимо и, если множество Q имеет внутрен-
ние точки, достаточно, чтобы
0е^п(х*). (1.7)
Доказательство. Необходимость. Пусть
выполнено (1.2). Тогда существуют oedf(x*) и ®е
еГ+(х*) такие, что v = w. Если w = 0, то и v = 0, а
значит, (1.7) выполнено. Если же то вектор
g = —т]аг||wII-1 s Л) (х*), и поскольку v — w — 0, то
tl^Hwir1 + g = ®. (1.8)
Из (1.8) для a^q||ffii|r‘(l + т]||гг»|Г1) * получаем
с„ = ас4-(1 — a)g = 0.
Так как а е (0,1], v е df (х*), g (х*), то va е (х*),
и поэтому (1.7) справедливо.
Достаточность. Если 7\)(х*)=0, то из (1.7)
следует, что 0<=df(x*). С другой стороны, 0еГ+(х*),
а значит, (1.2) выполнено.
Пусть теперь Тп(х*)^=0. Из (1.7) вытекает, что
найдутся такие t»e<9f(x*), g есоТп(х*) и число as
е[0,1], что
ao + (l-a)g = (0>. (1.9)
Так как множество Q имеет внутренние точки, то 0 &
^со7\(х*). Поэтому в представлении (1.9) число а>
> 0. Тогда в силу (1.9) имеем
t>==(a — l)a-,g.
Но (a— IJoHgeГ+(х*), ибо a-1 (а— 1)<0. Сле-
довательно, (1.2) выполняется и в данном слу’Де. Лем-
ма 1.2 доказана.
Пусть хо е Q и ф (хо) < 0. Тогда
f (хо) — f (х)< d (х0) |j x — xo || VxeQ. (1.10)
Положим d„ (x0) = min || v ||.
(*o) •
Для получения оценки f(x0) — f* через dn(x0) уста-
новим связь между d (х0) и (х0).
} 1] НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ МИНИМУМА 329
Пусть A,BczE„ — выпуклые компакты. Положим
S — со {Д (J В}, d = min || v ||,
р= min || о ||, ф= min max (v, g).
II «11-1
Пусть О^Л. Положим Г+= —Ж (А), где ^(Д) =
= {Хп|Х 0, v^A}. Множество Г+ в силу леммы 3.5
гл. I будет замкнутым выпуклым конусом.
Лемма 1.3. Пусть
||»||>а>0 VseX, || v ||< b Vv <= В. (1.11)
Тогда
5<3<(1+ 26а-1)Я, (1.12)
где d = minj. v ||.
оеВ-Г+
Доказательство. Возьмем произвольное Хе
е(0, 1). Если 3 > Ха, то, поскольку ОеГ+, В cz В — Г+
и выполнено (1.11), будем иметь
d— min || v ||min|| v ||^b ^b(Ха)-1 d,
оеВ—г+ сев
т.е.
3<6(Ха)-15. (1.13)
Рассмотрим теперь случай, когда 3 Ха. Пусть
асе^ и ||оо11 = 3. Вектор Уо можно представить в виде
t>o = a»i + (l—a)t»2> ae[0, 1], t»i e A, v2& B.
В силу (1.11) имеем
Xa d —1| aai + (1 — a) v21|
> all th II —(1 — a)l|t»2||>aa —(1 — a)b,
откуда
a<(Xa + b)(a + b)-1 < 1,
ибо Xe(0,1).
Так как oe[0, 1), то a(l — a)-1aie—Г+, и поэтому
3«=||aol + (l — a)o2|| = (l — a)||a(l — a)-^ + v21| >
>(1 -a)3>a(l — X) (a + &)-13.
330
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
(ГЛ. IV
Следовательно, если 3 Ха, то
й<(а + &)[(1-A)a]-1d. (1.14)
Из (1.13), (1.14) получаем
min max {(а + b) [(1 — Л) а]”1, b (Аа)-1}й =
Ле(0,1)
= (1 +2ba~l)d.
Докажем теперь неравенство в левой части (1.12).
Пусть d =||t»i 4- 02II, Vi s—Г+, О2^В. Так как Г+=
= —Jif(A), то найдутся такие wi^=A и М>0, что
vi — kjWi. Тогда
d — (1 + %i)j (1 + Ai) 1 W\ + (1 + Ai) 11»2 II
(1 + Ai) J > J.
Лемма 1.3 доказана.
Предположим теперь, что множество Q ограничено
(следовательно, b ai max max II о II < ©о).
хеЙ v^df(x)
Пусть D — диаметр множества Q, г — радиус наи-
большего шара, содержащегося в й, г > 0.
Тогда для любой точки хо е Q сопряженный конус
Г+(х0) содержится в телесном угле 2л— а, где
sin(a/2) = D~{r, и поэтому (рис. 54 и 55)
min min II v II > т)г£>~*.
xeQ veco (x)
Отсюда, из (1.10) и леммы 1.3 вытекает
0 < f (х0) - Г < D (1 + 2bD (nr)’1) d, (хо). (1.15)
$ 1] НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ МИНИМУМА 331
2. Рассмотрим случай, когда множество й имеет вид
Q = {xeE„|ft(x)<0),
где h (х) — выпуклая на Еп функция.
Предположим, что выполнено условие Слейтера, т. е.
что для некоторого х е Еп будет h (х) < 0.
Пусть хоЕЙ. В этом случае (см. § 12 гл. I)
+ | {О}, если й(х0)<0,
Х° t — Ж (dh (х0)), если h (х0) = 0,
где X (Л) = {ш = Аи |А 0, v е А}.
В частности, если h(x) = тахйДх), J — 1 :m, hj(x) —
j G J
выпуклые непрерывно дифференцируемые на Еп функ-
ции, то
dh (х0) = со {Л; (х0) | / <= Q (х0)},
где Q(xo)= {/е У|й/(хо) = А(х0)}_, и поэтому
Г+(х0) =
Г {0}, если Л(х0)<0,
{о = — Е Kjh't (х0) | Л./>0 V/ е Q (х0)}, если h (хо)=О.
' /eQ (х«)
Для любого хо е й введем множество
ср, х ( df (хо), если h (х0) < 0,
Х° t со {df (хо) U dh (хо)}, если h (х0) — 0.
Теорема 1.2. Пусть выполнено условие Слейтера.
Для того чтобы в точке х* ей функция f(x) достигала
своего минимального на множестве Й значения, необхо-
duMo и docTaroHHO, чтобы
0е^(х*). (1.16)
Доказательство. Необходимость. Тре-
буется показать, что из (1.2) вытекает (1.16). Пусть
выполнено (1.2). Это значит, что нашлись такие и<=
е df (х*) и w <= Г+(х*), что
и — = (1.17)
Если /г(х*)<0, то Г+(х*) = {0}, w=0 и из (1.17)
следует, что v = 0, т. е. 0 е of (х*)с: ^(х*).
Пусть /г(х*) = 0. Поскольку выполнено условие Слей-
тера, то Г+(х*) = —X(dh(x*)\. Поэтому найдутся та-
f
332 МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИИ [ГЛ, IV |
кие Х>0и ze5/!(z*), что 'W = —Xz, и из (1.17) по-
лучим v + Xz — <0>. Следовательно, (1 4- %)-1 v + X (1 +
+ X)~1z = O. Но (1 + Х)->1» + Х(1 + X)-‘zе= &(х*)-, зна-
чит, Ое^(х*), что и требовалось доказать.
Достаточность. Нужно показать, что (1.2) яв-
ляется следствием (1.16). Если /г(х*)<0, то это оче-
видно.
Пусть й(х*) = 0. Включение (1.16) означает, что най-
дутся такие vedf(x*), wedh(x*) и число ае[0, 1],
что
av + (1 — а)до = 0. (1.18)
Число а в (1.18) не может быть равно 0, ибо, в силу
условия Слейтера, 0^д/г(х*).
Поделив (1.18) на а, получим
v = (а — 1) а~ lw,
но (а—1)а-1да е Г+(х*), и, следовательно, df(x*)f) I
ПГ+(х*)#=0. ’
Теорема 1.2 доказана.
Пусть хо е П. Положим I
ф (х0)= min max (о, g), d (х0) = min || о Ц, '
|| g 11-1 ve<t (x«) veil (xo)
p(xo)== min ||o||. i
velz (xo)]fr
Если 0> e 9? (xo), то p (xo) есть радиус максимального
шара с центром в 0, содержащегося в S’(xo), а если
O^S’(xo), то р(хо) = 3(хо), т. е. р(х0)—расстояние от
множества 2? (х0) до начала координат.
Применяя леммы 6.2—6.4 из гл. I для множеств
В — S’(xo), Г+ = {0}, получаем, что условие (1.16) экви-
валентно тому, что ф (х*) 0, а также, что
_ [ — р (х0) = — d (хо), если d (х0) > 0,
- ,Ф(*о) = 5 ... . п
I р (х0), если а(хо) = 0.
Пусть -ф(х0) <0 и б(хо)е2’(хо), ||б(х0) || = р(хо). Век-
тор go = g(xo) — —v(xq) II v (хо) ||-1 называется направле-
нием квазинаискорейшего спуска функции f(x) на мно-
жестве Q в точке Хо ([36, стр. 201]).
Пусть /г(хо)= О и 3(хо)>О. Обратим особое внима-
ние на то, что если g(xo) и g (х0) есть направления наи-
§ 13 НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ МИНИМУМА 333
скорейшего и квазинаискорейшего спуска функции f(x)
на множестве Q в точке хо, то может оказаться, что
х0 + ag (*о) Q Va > 0,
но всегда найдется такое число ао > 0, что
Xq -|- ag (xq) Q Va g= [0, ао].
Это объясняется тем, что 4^ ^0, а < 0.
dg(*o) dg(xo)
Таким образом, направление g(x0) является направ-
лением убывания функции f(x) в точке хо, и, кроме
того, в этом направлении можно двигаться из точки хо,
оставаясь при этом в множестве Q. Действительно, спра-
ведливо разложение
f (х0 + ag (х0)) = f (х0) + a -Шту + о (a), ----->0.
\хо) & а->+0
При достаточно малых а будет
Поэтому при таких a
f (хо + ag (х0)) < f (х0) — ap (Хо).
Аналогично показывается, что при достаточно ма-
лых a
h (х0 4- ag (х0)) < — ap (x0).
Отметим также, что p(x0)^p(x0). В самом деле,
пусть
р (х0) = II оо + hw0 II,
где
о0 е df (х0), ®о е dh (х0), Хо > 0.
Если Хо = 0, то р(х0) = р(хР). Если же Хо > 0, то
Р(х0) = (1+ Хо)1|оо(1+М ' 4-XotOo(l 4-А-о)
>(1+Mp(xo).
Из того, что ₽ (Хо) < р (Хо), следует .
Более того, если р(х0)=-р(х0), то g(x0) = g(x0), а
если р4х0) < р(х0), то g (x0)¥=i (х0) и .
334
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИИ [ГЛ. IV
Предположим теперь, что
max || v |К b, min || v || > a.
vedf(xo) vedh(x-)
Тогда из (1.10) и леммы 1.3 вытекает
0 ^Цх0) — f (х)<||х — х0||(1 + 2а&-1) d (х0) Vx<=Q.
(1-19)
Задание 1. 1. Пусть Q, = {хе £л| hi (х) < 0}, где hi (х) =
= max hif(x), hiJ(x)-=(Al,x) + bj,\\Ai\\>Q
/е/1
Доказать, что для того, чтобы в точке х* е Q Г) функции f (х)
достигала своего наименьшего на множестве Q П Qi значения, необ-
ходимо и достаточно, чтобы
^(хЭЛГ^ (х*)¥=0,
где
„ . . = Г df (х), если h (х) < 0,
(со {df (х) U dh (х)}, если h (х) = 0,
/ {ДО}, если h\ (х) < 0,
rf (*) = < (р = _ £ V/SQ^X)}, если Л!(х)=0,
( /eQi (х)
Qi (x) = {jeJilhn (x) = Mx)}.
§ 2. е-стационарные точки
Пусть выпуклая функция f(x) задана на некотором
выпуклом открытом множестве, содержащем выпуклое
замкнутое множество Q.
1. Возьмем хоей и е^О. Положим
фе (х0) — min sup (v, g)>
«в»-1 OeaeQf(x0)
de (x0) = min || v ||,
Pea(xo)= min II v||, Pa(xo) = Po(xo)»
H^(*o)]fr
d~ (xo) — do (xo), ф"’ (xo) = фо (xo), f* = inf f (x).
§ 2]
е-СТАЦИОНАРНЫЕ ТОЧКИ
335
Ясно, что если 0 0 def (х0), то pf (х0) = d? (х0), а если
до <= деf (хо), то ре (Хо) есть радиус наибольшего шара
с центром в начале координат, содержащегося в def (хо).
Применив следствие 1 из леммы 6.4 гл. I для множе-
ства В = def (хо), приходим к выводу, что
Фе(Хо) = {
—р? (Хо) = — de(x0),
Ре (Хо),
если de (хо) > 0, (2
если de (хо) = 0.
Точку хое£2, в которой (хо) 0 или, что то же
самое, O^f(xo) — f* е, назовем е-стационарной точ-
кой функции f(x) на множестве £2.
Очевидными обобщениями лемм 1.2 и 1.3 гл. III яв-
ляются
Лемма 2.1. Для любого х0 е £2 имеет место оценка
f(y)-f(x0)>\\y-x0\\^ (х0)-е Vy<=£2. (2.2)
Лемма 2.2. Пусть х8ей, е> 0 utff (хе) > 0. Тогда
/• >—оо, множество S)* = {х <= £2|f(x) = /*} есть не-
пустой выпуклый компакт,
и, если f(xe)> f*, то
f (Хе) ~ Г
Р°(*е)
Г-Нхе) + в
Ре (л'е)
(2.3)
где х* — точка минимума функции f(x) на множестве £2.
Пусть функция f(x) сильно выпукла на £2, tn—-кон-
станта ее сильной выпуклости. Так же, как и в лемме 9.6
гл. I, показывается, что для любого хое £2
f (хо) - f (х‘) < (4m)’1 (d? (хо) + 2 V^T)2, (2.4)
|| хо — х* || < (2m) “1 (de (Хо) + 2 -y/em ), (2.5)
f (хо) - f (х*) < (4m)-‘ [dQ Ы2, (2.6)
||х0-х*1К(2т)-* rfs(xp). (2.7)
336
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИИ (ГЛ. IV
2. Пусть /(х) и Л(х)— выпуклые на Еп функции. За-
фиксируем хо е Еп. Допустим, что существует такая
точка х е Еп, что
/z(x)</i(x0)-a, (2.8)
где а > 0.
Лемма 2.3. Если при некоторых е^О и ц@[0, а)
оказалось, что
О е со {def (хо) U d^h (х0)}, (2.9)
го
(2.Ю)
где
Ц»-л (х0) = {х е Еп | h (X) < h (х0) - и}.
Доказательство. Из (2.9) вытекает существо-
вание о0^ dtf(xQ), w0 е дц/i (Хо), aie[0,1] таких, что
а^оЧ-(1 — а>)^о = ®- (2.11)
При этом ой > 0, ибо в противном случае te»o = ®> что
невозможно в силу (2.8) (если wo = О, то это противо-
речит (2.8)). Поэтому (2.11) можно переписать в виде
1>о + Оо^о = о» (2.12)
где а0 = (1 — а^ар*.
В силу определения де[(х0) и dyjifxo) имеем
f (х) — f (х0) > (t»0 > х — х0) — е Vx е Еп,
ft (х) — h (хо) (шо> х — Хо) — р Vx s Еп.
Отсюда и из (2.12)
f (х) — f (х0) + а0 (h (х) — h (х0)) > (и0 + «о®о> х — х0) —
— (е + аоц) = — (е + аоН) Vx е Еп. (2.13)
Для х <= 4i-ft(x0) будет й(х)^й(х0)—ц. Тогда из (2.13)
f W f (^о) 8 Vx е (Хо)»
а это и означает, что
f (Хо) /ц-Л (Жо) Ч~ 61 Я
»3!
МЕТОД УСЛОВНОГО ГРАДИЕНТА
337
Следствие. Предположим, что существует такая
точка х&Еп, что f(%)^f(x0)—b, причем Ъ>ъ.
Если выполнено (2.9), то
A(x0)<Cf(x.) + H,
где h*e_. м = inf {h (х) | f (х) < f (х0) — в}.
§ 3. Метод условного градиента
В этом параграфе будем предполагать, что Qc£, —
произвольный выпуклый компакт.
1. Сначала получим необходимые и достаточные ус-
ловия минимума выпуклой функции f(x) на множестве
й, которые используются в методе условного градиента;
Введем функции
Фе(х) = пнп max (о, г — х),
где в^О — произвольное число,
Ф(х) = Ф0(х).
Заметим, что
Фе(х)<0 ¥хе=Й, Ve>0. (3.1)
Теорема 3.1. Для того чтобы в точке х’ей функ-
ция f(x) достигала своего наименьшего на множестве й
значения, необходимо и достаточно, чтобы
Ф(х*) = пнп max (о, г — х*) = 0.
zeQ v&df (х*)
Доказательство. Необходимость. Допу-
стим противное; тогда найдется такая точка г* е й, что
(поскольку в силу (3.1) Ф (z) 0 Vz <= Q)
max (о, z* — х*) < 0.
v^df(x*)
Положим g = z* — х*. В силу полунепрерывности
сверху отображения dtf(x) по 8 на [0, оо), найдется та-
кое во > 0, что *
— = max (о, g) < 0.
338
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ [ГЛ. IV
Тогда согласно (8.19) гл. I
f (х*) — inf f (х* + ag) > во.
а>0
Следовательно, при достаточно малых <хе(0,1] будет
х* + ag е= Q, f (х* + ag) < f (х*).
Получили противоречие, ибо х* есть по предположе-
нию точка минимума функции f(x) на множестве Q.
Достаточность. Пусть ф(х*) = 0. Согласно оп-
ределению df(x*) для любого гей имеем
f(z)>f(x') + max (v,z-x*)>f(x*) + O(x*) = f(x*),
vedf(x*>
что и требовалось.
Положим f = min f (х).
Лемма 3.1. Для любых хо е Q и е> 0 справедлива
оценка
О</(хо)-Г<8-Ф8(хо).
(3.2)
Доказательство. Из определения def(x0) имеем
f(z)>f(xo) + max (о, г —х0) —в,
oe<V(xo)
min f (z) f (x0) + min max (a, z — x0) — e,
zeQ zgQ oedef(x0)
откуда и следует (3.2).
Следствие. Если Фе(х0) = 0, то из (3.2)
O<f(Xo)-f<8.
(3.3)
2. Опишем теперь метод условного градиента для на-
хождения точек, в которых выполнено (3.3), т. е. для
нахождения 8-стационарных точек функции f(x) на мно-
жестве £2.
Зафиксируем число в > 0. Выберем произвольным
образом начальное приближение xos Q.
Пусть уже найдена точка х*ей. Если Фе(х*) = 0,
то в точке Xk выполняется (3.3), и процесс на этом за-
канчивается.
5 3j МЕТОД УСЛОВНОГО ГРАДИЕНТА 339
Если же Фе (хк) == max (у, z* — xk) < 0, то за
0S<Wfe)
(A+ l)e приближение принимаем такую точку xk+i =
= хк 4- (zk — xk), что
f(x*+i)= min f(Xk+>a(zk — Xk)).
a s [0, 1]
Отметим, что и f(xk+i) <f(xk).
Далее процесс последовательных приближений про-
должается аналогично.
Если последовательность {хк} конечна, то последняя
ее точка по построению является е-стационарной. Если
же последовательность {хк} бесконечна, то справедлива
следующая
Теорема 3.2. В любой предельной точке х* после-
довательности {хй} будет ф8(х*)== 0 и
Доказательство. Допустим противное, предпо-
ложим, что Xks —> х*, но Ф8(х*) = —а < 0.
Тогда, в силу полунепрерывности сверху отображе-
ния d9f(x) по х, при достаточно больших ks окажется
• 8 \ KS/
где gks = Zks-xks.
Возможны два случая:
1) min f (xk (a)) = min f{xk (a));
a>0 as [0, 1]
2) inf f (хк (a)) < min f (xk (a))
a>0 as [0, 1]
(здесь xk (a) = xk + a (zft — xk)).
В случае 1) согласно (8.19) гл. I имеем
f (Xft+i)< f (x^ - e.
Рассмотрим случай 2). На основании леммы 8.6 гл. I
при всех
340
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ [ГЛ. IV
будет
f (Хк + agk) <f(xk) + а , (3.5)
где gk = гк — хк.
Тем более (3.5) будет выполнено при
а = — е ( ) = — в (Ф (х*))-1.
Следовательно, в случае 2)
f (xft+i) < f (xk) + min {1, — 8 (Ф (xft))-'} Фе (xft).
Положим b = max | Ф (x) |. Число b конечно в силу того,
х ей
что отображение д[(х) ограничено на й. Тогда
f (xk+i) < f (xk) + ₽Фв (x*),
где
P = min{l, 8&-1}.
Таким образом, в обоих случаях
f (х*+1) < f (х*) + max {— 8, ₽ФЬ (xft)) V/г. (3.6)
Из (3.4) и (3.6) заключаем, что при достаточно боль-
ших ks
f(xks+i)<f(Xks) — min{e, у₽а},
откуда вытекает, что f(xft)-> — оо, а это противоречит
ограниченности функции /(х) на множестве Й. В
Отметим, что применять метод условного градиента
целесообразно тогда, когда множество й имеет доста-
точно простую структуру, например задается линейными
неравенствами, и можно эффективно вычислять в-суб-
дифференциал функции f(x).
Замечание 1. Вместо того, чтобы находить точку
х*+1 из условия минимума функции f(x) на отрезке
[Xk.Zk], можно поступать следующим образом: при
1 = 0, 1, 2, ... проверять выполнение неравенства
t (х* + 2"' (г* - х*)) С / (х*) - 2~‘Фе (х*). (3.7)
»3J
МЕТОД УСЛОВНОГО ГРАДИЕНТА
341
Пусть при i = ik первый раз выполнилось (3.7),
тогда полагаем
Xk+\ = xt + 2~‘k (zk — Хк)« Xt + at (Zt — Xt).
На основании леммы 8.6 гл. I число ik конечно, более
того,
aft>min{l, 8[2(<De(xft) —Ф(хл))Г*}.
Задание 3.1. Доказать теорему 3.2 для метода условного гра-
диента с только что описанным вариантом одномерного поиска.
3. Укажем теперь модификацию метода условного
градиента для нахождения точек минимума функции
f(x) на множестве £2.
Зафиксируем некоторые е0 > 0 и So > 0. В качестве
начального приближения возьмем произвольную точку
х0 •== х00 е Q. Применяя метод условного градиента с
е — во, в конечное число шагов (это следует из тео-
ремы 3.2) найдем точку xoi,ей, в которой
Фе, (xOt„) > — до.
Положим ei = е0/2, Si = до/2, xi = хю = %о«,.
Взяв в качестве начального приближения хь снова
применим метод условного градиента, но уже с в = еь
В конечное число шагов получим точку хк, такую, что
Фе. (Х1/,)> — дь
Продолжая описанный процесс, строим последовав
тельность {хк}, для которой
Фе6 Uft+l) — dft, (3.8)
где ек = ео/2*, — 60/2*. k = 0, 1,2, ...
Очевидно, что f (x*+t) f(xk) и х^ей при всех k.
Теорема 3.3. Любая предельная точка последова-
тельности {хк} является точкой минимума функции f(x)
на множестве Q.
Доказательство. Допустим противное, предпо-
ложим, что хкз—*-х*, но ф(х*) = —a < 0. В силу полу-
непрерывности сверху отображения де[(х) по х и е на
Д>Х[0, оо), найдется такое е > 0, что при достаточно
больших ks будет
(3.8)
342
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
[ГЛ. IV
Рассмотрим теперь такие ks, что выполнено (3.9) и,
кроме того,
ess<8, 6ks<a/2.
Тогда из (3.9) следует
что противоречит (3.8).
Замечание 2. Можно не требовать ограниченно'
сти множества й, если вместо функции фе(х) использо-
вать функцию
Ф8(х)== min max (v, z — x).
zefi, uedef(x)
§ 4. Методы наискорейшего спуска
для минимизации выпуклых функций
1. В настоящем параграфе рассмотрены методы, свя-
занные с направлением наискорейшего (или близкого к
нему) спуска. Вначале обсуждаются непрерывные мето-
ды минимизации, или методы дифференциального спуска.
Хотя непрерывные методы минимизации не могут
быть непосредственно реализованы на ЭВМ, но на их
основе могут быть построены дискретные алгоритмы
(один из них изложен ниже, в п. 3).
Пусть функция f(x) конечна и выпукла на Еп. Тогда,
как доказано в лемме 5.5 гл. I, функция f(x) является
липшицевой на любом выпуклом ограниченном множе-
стве G с: Еп.
Пусть вектор-функция x(t) непрерывно дифференци-
руема на [О, Т], где Т > 0. Тогда
t
х (0 = хо + х (т) dx,
о
где Хо = х(О), х(т)—непрерывная на [0, Г] вектор-
функция. Из (5.26) гл. I для t е [0, Т] будет
t
f (х (/)) = f (х0) + J -^^-dx. (4.1)
о
Здесь интеграл понимается в смысле Лебега.
«41
МЕТОДЫ НАИСКОРЕЙШЕГО СПУСКА
343
Пусть йсЕ„— замкнутое выпуклое множество. Как
было установлено в теореме 11.2 гл. I, отображение
dgf (х) непрерывно по в и х на (0, оо)ХЙ по Какутани.
Обозначим о8(х) ближайшую к началу координат точку
множества d®f (х), т. е.
||ое(х)||= min ||v||. (4.2)
Лемма 4.1. Вектор-функция ог(х) непрерывна по в
и х на множестве (0, оо)ХЙ.
Доказательство. Пусть ео>О, хое£2. Так как
def (х) с: dlf (х)
для любых t > 0 и x s Й, то
О min || v ]' < min || о ||.
Функция h(x,e)= min || и || ограничена в окрестно*
v е def (х)
СТИ ТОЧКИ [ео, Хо] • Поэтому и функция
Н (х, е) = min || v ||
v <= t (х)
при хе5{(хо)ПЙ, ве£в(ео)= {е > 0| |в —80| С б},
где б > 0,- ограничена. Обозначим ое (х0) = о0. Пусть
е*-»-8о, х*->Хо. В силу полунепрерывности снизу ото-
бражения dtf (х) существует последовательность {о*}
такая, что vk е d^f (xft), и0. Значит,
Ц% (л*)|= min || v IK|| vk||. (4.3)
° e <£/(**)
Последовательность {vek (xft)J ограничена. Поэтому
можно считать, что
v4(xk)^v. (4.4)
Так как отображение d°f(x) полунепрерывно сверху,
то б е (х0). Из (4.2)—(4.4) следует
,11 f КII foil. (4.5)
344
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
[ГЛ. IV
Поэтому из (4.2) и (4.5) заключаем, что v == Vq. Лемма
доказана.
Рассмотрим систему дифференциальных уравнений
х(/) = — Ve (/)(х(0),
х(О) = хоеЙ, (4’6)
где е(/) — непрерывная на [0, оо) функция, причем
8 (/) + 0. По лемме 4.1 вектор-функция ve(x) непре-
рывна по 8 и х на множестве (0, оо)ХЙ. По теореме
Пеано решение x(t, х0) системы (4.6) существует, при-
чем х(/,хо)—непрерывно дифференцируемая функция
на [0, оо). Снова обозначим
II о8 (х) || = min || v ||.
v в <5g f (х)
Пусть х е й. Если 0 & d^f (х), то
Ssf (х)
di = sup (о, х) = — mirt (о, — х) =
о s dg f (х) о е dg f (х)
= — min (v, o8(x)) = —1| oe (x) IP < 0. (4.7)
oed®f(x)
Отсюда ясно, что если хей не является г-стационар-
ной точкой функции f на множестве й, то
1) направление х — —vt (х) е у(х) = {v = X (z —
— х) |Х > 0, zefl}, причем ge =—Ve(x)||vt(x)||-1 есть
направление е-наискорейшего спуска функции f в точ-
ке хей (по множеству й). Поэтому существует та-
кое Г == Т(х) > 0, что
x + tg^Q V/ е= [0, Г];
2) справедливо неравенство
inf f (х + age) < f (х) — в, (4.8)
а>0, x+a?gsQ
г. e. в направлении ge функцию f можно уменьшить не
меньше чем на в, не покидая множество й.
Если для некоторой точки хе й оказалось ое (*) = 0,
т. е. Oed’f(x), то х—е,-стационарная точка функции
f на множестве й,
§ fl
МЕТОДЫ НАИСКОРЕЙШЕГО СПУСКА
345
Положим
0(xo) = {x<=Q|f(x)<f(xo)}.
Теорема 4.1. Если множество 125 (х0) ограничено,
то любая предельная точка решения x(t,x0) системы
(4.6) является точкой минимума функции f(x) на мно-
жестве £2.
Доказательство. Поскольку
t
x(t)==X (t, Xq) = Хо + X (T) dx,
то из (4.1) и (4.7) имеем
t
/ М’)) — / W + j <
< f м+j (т)> а,, (г®
0
так как max (v, x(r))< sup (v,x(t)).
5х(т) osaf(x(t)) osdat)f(x«))
Из (4.2) и (4.6) следует
sup (v, X (т)) = — II Vs (t) (x (т)) Ц2. (4.10)
Поэтому
t
f (X (t)) < f (Xo) — (II Ve (t) (x ft)) II2 dx.
Отсюда ясно, что f(x(/)) f(xo) V/ 0, t. e,
x(/)e0(xo) VZ>0.
В силу ограниченности множества 2)(х0) предельные
точки решения x(t) существуют. Пусть х* — предельная
точка. Это значит, что найдется последовательность
{/»} такая, что
4->оо, х(4)-»х*.
346
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ [ГЛ, IV
Ясно, что / ей, Надо показать, что х*— точка мини-
мума функции f(x) на Q, т. е. Оеда/(х*). Допустим
противное, пусть ||t>0(^*) 11= а > 0. Из полунепрерывно-
сти сверху отображения d®f (х) следует, что найдутся
ео > 0 и 6>0 такие, что ||ие(х)||^ а/2 Vee[0, е0],
VxeSs(x*). Значит, существует К\ < оо такое, что
Кроме того, в силу непрерывности z(t) и x(t) суще-
ствуют число А >0 и номер Кг Ki такие, что
II ve (0 (х (/)) II > а/4 Vt е [4 - A, ik + A], V6 > К2.
Без ограничения общности можно считать, что
4+1 — 4>2А V£>/<2.
Из (4.9) имеем
t
f (X (0) < f (Хо) — 5 II fe (т) (X (т)) IP dx < f (хо) — a2 &т (0/8,
0 (4.11)
где m(t) — такой номер, что Ясно,
чтот(/)у^>оо. Поэтому из(4.11)следует
что противоречит ограниченности непрерывной функ-
ции /(х) на компакте 0(хо). Теорема доказана.
2. Рассмотрим систему
где
ge (х (0) = |
х(/) = —ge(x(/)),
х (0) = х0 s й,
veWII ve wir1,
о,
если
если
(4.12)
Ve(x)=^&,
ое (х) == 0,
8 > 0 фиксировано. Функция в правой части системы
(4.12) непрерывна, пока ое (х) =/= 0, и по теореме Пеано
решение системы существует. Как и выше, можно дока-
зать, что x(t)^ 2)(xq) V/>0 и что любая предельная
точка решения является е-стационарной. Более того,
справедлива
§41
МЕТОДЫ НАИСКОРЕЙШЕГО СПУСКА
347
Теорема 4.2. Если множество 2&(хй) ограничено,
а функция f(x) сильно выпукла на Еп, то найдется та-
кое Т<.оо, что у8(х(7')) = 0, т. е. система приходит в
^-стационарную точку за конечное время.
Доказательство. Пусть /(х)— сильно выпуклая
на Еп функция с константой сильной выпуклости пг > 0.
По следствию 1 из леммы 17.1 гл. I будет
(4.13)
Так как def (х) cz def (х), то из (4.13)
dfM d°f(x) _.. .. /— ...
-----2||g||Ve/n. (4.14)
Если »8(х(/))#=® (из определения £е(х(/)) и системы
(4.12) тогда ое(х(т))#= <0> для всех те[0, /]), то из (4.9),
(4.10) и (4.14) имеем
t
f (X (/)) < f (х0) — § II Ое со (х (т)) II d% — 2/ -yjem. (4.15)
Предположим, что утверждение теоремы неверно; тогда
при любом 1>0 будет ое (х (/))¥= 0. и в силу (4.15)
/(х(/))->—оо, что противоречит ограниченности множе-
ства S>(xo). Теорема доказана.
Замечание 1. Из (4.12) следует, что если
»е(х(7’)) = 0, ТО ge(x(t)) = ® При t Т, И ПОТОМу
x(f) = х(Т).
Замечание 2. В системе (4.6) правую часть тоже
можно пронормировать.
3. Теперь можно описать следующий дискретный ме-
тод минимизации выпуклой функции /(х) на выпуклом
замкнутом множестве й.
Выберем произвольное хоей. Если ®sdaf(x0), то
Хо — точка минимума функции f(x) на множестве Q, и
процесс прекращается. Если O^dQf(x0), то найдем та-
кое число ео > 0, что Oe<?e0f(xo). Если <0>^dgf(xo) при
любом е > 0, то f*s= inf f(x) = — оо. Поэтому в даль-
х е Q
нейшем предполагается, что /* > — оо.
348
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИИ
(ГЛ. IV
Перебирая числовую последовательность eOq = 2-’,
9=1,2, .... найдем такое qo 1, что <0^ де,/(х0),
Ое «Д/(х0), где в! = во,, = 80/24 Тогда е^уво и
/(Хо)-Г<2вь
(4.16)
Теперь
^,/(х0)
dgo
найдем такой вектор g0 е у(х0), llgoll= 1, что
< 0, и на множестве {х0(а) = х0 + ago|a > 0}f)
П Q найдем такую точку xi = х0(а0), что
f(Xi) — f(x0)< — 81.
(4.17)
Из (4.8) следует, что такая точка обязательно найдется.
Из (4.16) и (4.17) имеем f (хО f (х0) — 8t f* -|- ei =
= f* + е0/2'7&. Значит, 0 g= de,f (хО, т. е. точка xi является
81-стационарной точкой функции f(x) на множестве £2.
Продолжая аналогично, построим последователь-
ность {xft}, которая либо конечна, либо каждая ее точка
является е*.-стационарной точкой функции f(x) на £2,
где 84+1 = е*/2Ч 9ft>l, т. е.
f(^+i)-r<eft/2^<8o/2ft Vfe. (4.18)
Из (4.18) вытекает
Теорема 4.3. Пусть — оо. Тогда lim f (хк) = f *,
&->оо
причем скорость сходимости f(x) к f* геометрическая,
и если множество М* = {х е £21 f (х) = /*} ограничено, то
любая предельная точка последовательности {х*} яв-
ляется точкой минимума функции f(x) на множестве £2.
§ 5. (в, |л)-субградиентный метод
при наличии ограничений
1. Пусть G cz Еп — выпуклое замкнутое множество,
имеющее внутренние точки.
Возьмем произвольную точку хо е Еп. Найдем такую
точку уо ss у(хо), что
min II у — х01| = || у (х0) — хо ||. (б. 1)
уе а
(в, ц)-СУБГРАДИЕНТНЫЙ метод
349
§ S]
Точка уо^у(хо) (она единственна для любого
хо е ибо норма в (5.1) евклидова) называется про-
екцией точки хо на G. Отметим, что если для некоторых
Хо е G и ид е Еп оказалось
У(х0 + и0) = х0,
то
(х — х0, t»o) 0 Vx е G.
Поэтому oi = —о0<=Г+(хо). Отсюда, в частности,
ясно, что если оо=/=®, то х0 — граничная точка множе-
ства G (ибо для внутренних точек будет Г+(х0) = {0}).
2. Пусть на Еп заданы выпуклые функции f(x) и
ft(x). Положим
Q1 = {xe£n|/i(x)<0}, Q = GQQi.
Требуется найти min f (х)« f*.
Возьмем числа в > 0, ц > 0 и последовательность
{k*} такую, что
^т-> + 0, = <5-2)
k-0
Предположим, что существует такая точка х е int G, в
которой
Л(х)< —ц. (5.3)
Это, в частности, означает, что int #= 0, где =
= {хе G|ft(x)^ — р}. •
Предположим также, что f*> — оо.
Опишем следующий метод последовательных при-
ближений. Возьмем произвольное х0 е G. Пусть уже
найдено хк <= О.
Если h(xk)s^.O, то вычислим произвольное
<=dtf(xk). Если t>* = 0, то
0<f(x*)— inf f(x)<e, (5.4)
х s Еп
и в этом случае процесс прекращается.
Если h(xk)>Q, то вычислим произвольное wke
^dllh(xlt). В силу (5.3) и леммы 9.2 гл. I обязательно
350
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ [ГЛ. IV
Положим
f — М1МГ1. если /i(xft)<0,
Sk I и ir1 \a (^.5)
( — wk || wk || , если h (xk) > 0,
и найдем (см. (5.1))
xk+i = y(xk + kkgk). (5.6)
Отметим, что если G = Еп или хк + \kgk е G, то
^Л+1 = Хк -|- 'kkgk.
Далее продолжаем аналогично. В результате строим
последовательность {хк}. Если эта последовательность
конечна, то по построению последняя полученная точка
хк принадлежит £2 и удовлетворяет (5.4). Рассмотрим
теперь случай, когда последовательность {хк} содержит
бесконечное число точек. Образуем множество
^ = {xeQ|f(x)<f; + e + c}, (5.7)
где f* = inf f(x).
Поскольку f* > — оо, то множество 3)с непусто при
любом с 0.
Теорема 5.1. При любом, с > 0 последовательность
{xft} содержит бесконечное число точек, принадлежащих
множеству
Доказательство. Допустим противное. Тогда
найдутся такие с > 0 и К < оо, что
хкф£>с (5.8)
В силу (5.3) int {х е= | f (х) < f* + с} =Д 0. Поэтому
существуют точка xeQu и число г > 0 такие, что
xeG, f(x)<f* + с, й(х)< —р. VxsSr(x). (5.9)
Если /i(xftX0, то согласно (5.5) g* = —о*По*||-1,
где vk&dtf(xk). Следовательно,
f (х) — f (хк)>(оь х — хк) — е Vxe=E„. (5.10)
Из (5.9), (5.7) и того, что h(xk)^.Q, вытекает, что
?(хь) > "Ь 8 "Ь с- Отс1°Да и из (5.9), (5.10) имеем
(ук, х —xA)<f(x) + s —f(xft)<
< С + с + е~(С + 6 + с) = 0 VxeSr(x).
$$)
(в, |Л)-СУБГРАДИЕНТНЫЙ МЕТОД
351
Поэтому
(gk, Xk — х) < О Vx <= Sr (х). (5.11)
Если Л(хА)>0, то согласно (5.5) gk =—a’JIwll-1,
где a>k е d^h. (xft). Тогда
h (х) — h (xfe) > (wk, х — хк) — ц УхеЕ,
и с учетом (5.9)
(wk, х — xj< h (x) + ц — h (xk) < — p. — 0 + H = 0
Vxe Sr(x).
Поэтому снова имеет место (5.11).
Возьмем точку х^ = х — rgk. Очевидно, что хц. s
eSr(x). Из (5.11) вытекает (gk, хк — Хи) < 0, т. е.
(gk, xk — x)<—r Vk. (5.12)
В силу (5.1) и (5.6)
II хк+1 — х II2 = II у (хк 4- Kkgk) — X Ip < II хк + hgk — XII2 <
< || xft — х ||2 + 2Л6 (gk, хк — х) + Ц.
Отсюда и из (5.12) следует, что при достаточно боль-
ших k будет
II хк+1 — X IP <|| Хк — X IP — гКк.
Тогда из (5.2) получаем || х* — х||^^>-— оо, что невоз-
можно. Теорема доказана.
Следствие 1. Существует такая подпоследова-
тельность {x*s}, что
xh &G, h(х )< 0, lim f (xft ) < + e.
* ' s/ *s->~ s
Доказательство получаем, устремляя в (5.7) в
к -j-0.
Следствие 2. Предположим, что множество
0- = {xe=Q1df(x)<Q
ограничено. Тогда
p(xft, Sa(^‘))^0,
sde а = maxр(х, S)*), Sb = (х е Q|/ (х)<Ц 4- е).
ле®
352
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ [ГЛ. IV
Доказательство основывается на тех же рас-
суждениях, что и доказательство соответствующей части
теоремы 4.1 гл. III.
§ 6. Субградиентный метод с постоянным шагом
Пусть f(x) и й (х) — выпуклые на Еп функции и
Q — {х е £л|й(х) 0}. Предположим, что при некого*
ром ро > 0
Йц0 =/= 0 ,
(6.1)
где й* = {х 6= Еп | h (х) < - ц0}.
Рассмотрим следующий метод последовательных при-
ближений для минимизации функции f(x) на множе-
стве й.
Зафиксируем числа 8^0, X > 0, 0 >0 и р. е [0, Цо).
Выберем произвольное Хо е Ея. Пусть уже получено
х* е Ея.
Если й(х*)^0, то вычислим произвольное
ed8f(x*). Если = 0 и й(х*)^0, то процесс прекра-
щается. При этом точка х* <= Й и является е-стационар-
ной точкой функции /(х) на Ея.
Если й(хл)>0, то вычислим произвольное
е dyji (xk). Так как цо, то, в силу (6.1) и леммы 9.2
гл. I,
Положим
если й(х*)<0,
I — vok || wk Г1, если h (xk) > 0,
и возьмем
хл+1= xk + (6.3)
Далее продолжаем аналогично. В результате строим
последовательность {хь}. Если эта последовательность
конечна, то последняя полученная точка по построению
принадлежит множеству й и является в-стационарной
точкой функции Цх) на Е„. Рассмотрим случай, когда
последовательность {х*} содержит бесконечное число
точек.
§ 6]
СУВГРАДИЕНТНЫИ МЕТОД С ПОСТОЯННЫМ ШАГОМ
353
Положим
d*= inf f(x), 0* = {x€=QJf(x) = f*},
djj2 = sup h (x) + ц, &v — inf h (x),
x e SV2 (2ц)
0c = {x«=Q_b |f(x)<c}, cx = sup f(x),
71 J x e SK/2 (®‘)
Г1 =»= sup p(x, 2)*), Qc — {x — En\h(x)^c}.
x s ®e+ti
Л
Предположим, что множество Q ограничено. Тогда
max {сх, Ьъ dw} < оо.
Теорема 6.1. Пусть dM2 < ₽^&v. Тогда
lim р (xfe, 0e+cJ = 0, (6.4)
Ит р(хъ Sri+^0‘)) = °. (6.5)
Доказательство. Установим вначале справед-
ливость (6.4). Допустим противное. Это означает, что
найдутся такие а > 0 и К < оо, что
xk&Sa(0e+C)) Vk>K. (6.6)
Ясно, что существует такое с > ск, для которого
®г+с Sa (6.7)
Нетрудно увидеть, что
SV2(0’)c0e. (6.8)
Выберем такое г > Х/2, при котором
$г (£) с (]$,(□„). (6.9)
dr = max й(х) + 1х<р, (6.10)
хеЗг(Яи)
где х е S)*. Из (6.8) и того, что dx/2 < Р, следует, что
такое г обязательно найдется.
Если /г(х*)^р, то в силу (6.2) gk = — v*|]o*||—где
Vk е d&f (хк). Поэтому
f(x) — f (х^ > (Vk, x-^Xk) — e Vx e En. (6.11)
12 В. Ф. Демьянов, Л. В. Васильев
354
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ [ГЛ. IV
Если Л(х*)>р, то в силу (6.2) gu = — a’*lla’*ll~l, где
wk е d^h (Xk). Поэтому
h (х) — h (xk) > (wk, x — xk) — ц Vxe En. (6.12)
Пусть х*ей_6у< Тогда согласно (6.6) и (6.7)
f(Xk)> е + с, и если /i(x&)^p, то с учетом (6.9)
для любого xeSr(x) будет f(x) — f(xft)<—е. Отсюда
и из (6.11) (Vk, х — Xj)<0h
(gk, xft-x)<0 VxeSJx), V£>/C (6.13)
Если же Х4е£1_^и Л(х*)>р, то с учетом (6.10)
для любого xeSr(x) будет ft(x) — h(Xk)<dr — у,—
— P —у. Значит, согласно (6.12) (wk, x— xk)<.0, и
снова имеет место (6.13).
Наконец, если хк ф Q_6v, то /г(х*) > Ьх р, и опять
будет выполнено (6.13).
Итак, во всех случаях имеет место (6.13).
Положим хк = х — rgk. Ясно, что x*eS,(x). По-
этому из (6.13) вытекает (gk, х* — xft)<0, т. е.
(gk.Xk-x)<-r Vk>K. (6.14)
Согласно (6.3)
II Xfe+l — XII2 = II Xk + Kgk — XII2 =
= l|xft — XIP-ь2Л,(fif*. xk — X) + A2.
Отсюда и из (6.14) следует, что
llxft+i-x||2<||xft-x||2-2V + A2. (6.15)
В силу (6.15) || х* — х II — °°, а это невозможно. По-
лученное противоречие доказывает справедливость (6.4).
Покажем теперь, что справедливо (6.5). Возьмем
любое б > 0. Согласно (6.4) существует бесконечное
число таких k, что
Р (Xk> ^е+с^)
Для таких k, поскольку ||х^+1 — х*|| = Л, будет
Xk+i ^Х+6 (,^е+с^) *— ^гц-Х+б (^ )•
Если при этом р(х4+1, ^е+сх) > б, то для k, больших
некоторого /С4, окажется выполненным (6.15), и поэтому
xk+2 е $r1’+x+J (ЗУ). (6.16)
МОДИФИЦИРОВАННЫЙ СУБГРАДИЕНТНЫЙ МЕТОД
355
Если же p(Xft+b ^е+сх) < то снова будем иметь
(6.16), поскольку ||xft+2 — лг*+1|| = X.
Рассуждая далее аналогично, приходим к выводу,
Xk s •Sr^x+e (^*) Vfe
В силу произвольности 6 отсюда вытекает (6.5).
Задание 6.1. Пусть G cz Еп — выпуклое замкнутое множество.
Описать субградиентный метод с постоянным шагом и проектирова-
нием на множество G для минимизации функции f(x) на множестве
G (] {х &En/h(x) 0}. Доказать теорему 6.1 для такого метода.
§ 7. Модифицированный (в, ц)-субградиентный
метод при наличии ограничений
Пусть f(x) и Л(х)— выпуклые на Еп функции. Тре-
буется найти f = inf f(x), где £2 = {х е En\h(x) 0}.
х е Q
Предположим, что существуют такие х е Еп и у > 0, что
h (х) = — у < 0.
(7.1)
Зафиксируем числа е 0, d\ Z> 0, це[0, у),
е (0, у — ц) и возьмем последовательность положитель-
ных чисел {X*.} такую, что
>0, Х&— оо.
(7.2)
В качестве Хо возьмем произвольную точку Еп. Пусть
уже найдена точка хк е Еп.
Если hfxkl^dj' то вычислим произвольное Vk е
^д^(Хк), и если Vk = 0 и /i(xft)^ 0, то на этом процесс
прекращается, ибо точка xk е £2 и является е-стационар-
ной точкой функции f(x) на Еп (и тем более на £2).
Если Л(х*)^—d2> то вычислим произвольное
е dyJi^Xk). В силу (7.1) и того, что Й2 + ц<у. должно
быть Wk 0.
Положим
Г — KVk II Vk II *, если h (xft) < — d2,
t — || ayA II-’, если h(xk}>dx.
12*
856
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ (ГЛ, IV
Если же —di h(xk) di, то z* определим так,
чтобы
llzdK^, min ФА (z) = Ф* (zft), (7.3)
где Ф4(г) = max ((о*, z), A(xft) + (ayft> z)}.
Заметим, что если aft=0, то z* =—ш*||~
Если оказалось, что ||z*|| < %* и h(xk) 0, то процесс
прекращается. В этом случае Ф*(г*) = min Ф*(г) и по
г s
необходимому условию минимума функции Ф*(г) на Еп
будет Ое coft»*, Wk}- Тогда Ое co{def(x*)U дцй(х*)} и
в силу леммы 2.3
/(^)<Гц + 8. (7.4)
Ясно, что если ||z*||< %* и й(х*)>0, то z*=/=0.
Теперь полагаем
xi+i = xA + zft. (7.5)
Далее продолжаем аналогично. В результате строим
последовательность {х*}- Если она конечна, то по по-
строению последняя полученная точка принадлежит
множеству Q и либо является е-стационарной точкой
функции /(х) на Еп, либо удовлетворяет (7.4). Рассмот-
рим случай, когда последовательность {х*} содержит
бесконечное число точек.
Для любых ci 0, е [0, di] положим
Сц+Ca = {Х S Еп I h (х) (И 4” Cfi)}>
Q_Cj = {х <= Еп |h(х)<с2}>
Z^ = xJ"f f(x)t
н*® и м </;«,+«+
SDa - {x e Q.„| f (x) + 8} - 2>0.
Предположим, что f* > — оо; тогда множества
Ci и непусты. Отметим, что так как с2 d2i то
int 0 •
S п
модифицированный субградиентныи метод
357
Предположим также, что
sup sup || v || < оо, (7.6)
x<=Q vadgf(x)U9llh(x)
где Q = {x<=En\ — dz^.h(x)^di}t
Теорема 7.1. Если найдется такая подпоследова-
тельность индексов {М- что 1Ы1<Ч’ то пРи лк>б°м
c2e(0, di] множеству 2DC, принадлежит бесконечное
число точек последовательности {х*}. В противном слу-
чае при. любых Ci >0, Ci <= (0, di] бесконечное число то-
чек последовательности {х*} принадлежит множеству
^Ci, Сг*
Доказательство. Пусть нашлась такая подпо-
следовательность индексов {&J, что Цг* В этом
случае из (7.3) вытекает
и по необходимому условию минимума функции Ф*4(г)
на Еп будет
О е со {vk., wkf) с со {dj (xks) U dji (x*s)}.
Тогда в силу леммы 2.3
На основании (7.2), (7.6) и того, что | zkg || < за-
ключаем
Поэтому при достаточно больших ks будет
~h(xks)^c2t
йц+са Йи-Л (xksy fu—hj < fu+e^
Из (7.7) и (7.9) получаем
(7.8)
(7.9)
(7.Ю)
Итак, при достаточно больших ks будут выполнены
(7.8) и (7.10), и для рассматриваемого случая утверж-
Дение теоремы доказано,
368
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ [ГЛ. IV
Далее, не ограничивая общности, можем считать, что
l|zj|=ta при всех k. Тогда, в силу необходимого усло-
вия минимума функции Ф^(г) на множестве {зе
е Еп | ||z|| М, при каждом k
Zk = 4gk, gk = — + $kwk),
Ш1=1, a*>0, fo>0. (7.11)
Допустим, что утверждение теоремы неверно и на-
шлись такие ci > 0, с2 е [0, d2) иК< оо, что
xt<£0Cl,C1 (7.12)
Можно считать, что с2 di. Рассмотрим множество
Так как с2 d2 и d2 + ц < у, то и с2 + ц < у.
Поэтому int^,С2т^0 и найдутся такие число г>0 и
точка хеАц+с, что Sr (х) с: ЗУС1, Сг. Это значит, что
h (х) С — (ц + с2), f (х) < /*+Сг + cl Vx <= Sr (х).
(7.13)
Если h(xk)^c2, то в силу (7.12), (7.13) для любого
х е Sr (х) будет f (х) - f (xk) < /‘+С2 + с1-(^*+С2+е+с1)=
= — е. Поэтому
(о,х — хл) < 0 VxeSr(x), V£>/C, Vo е def (xk). (7.14)
Если /1(х^)>—с2, то в силу (7.13) для любого хе
^Sr(x) будет й(х) —Л(х*)<—(р + с2) —(—с2) = —Ц.
Поэтому
(w,x — xk)<0 У/х^8г(х), yfk~^K, V® е^й(хД
(7.15)
Если /г(х*)< — с2, то нетрудно видеть, что при до-
статочно больших k, скажем при k Ki К, должно
быть хь = — XaMoJ-1, где Vk<^d^(Xk). Тогда из (7.14)
имеем (os, х — хА)<0ииз (7.11)
{gk, *к — х) < 0 VxeSr(x). (7.16)
Если h{xk)> с2, то при достаточно больших k, ска-
жем при k К2 Ki, должно быть zk = — ^kwk|| wk||_ 1 =1
s= %kgk, где wksdlxh(xk). Тогда из (7.15) имеем
5 8]
МЕТОД НЕГЛАДКИХ ШТРАФНЫХ ФУНКЦИЙ
359
(да*, х — х*)<0, и, следовательно, (7.16) выполнено и
в этом случае.
Пусть, наконец, —с2 h(xk) с2. Тогда согласно
(7.П)
& = -(ад + Ш > °. II gk 11=1-
Подставим Vk в (7.14), а wk в (7.15) и умножим
(7.14) на а*, а (7.15) на (3*. Сложив полученные нера-
венства, снова, убеждаемся в справедливости (7.16).
Итак, при всех k :> К2 имеет место (7.16).
Пусть x.k = x — rgk. Ясно, что Xk^Sr(x). Тогда из
(7.16) (gk,xk — Xk)<Q. Отсюда
(gk,xk-x)<-r Vk^K2. (7.17)
В силу (7.5) и (7.11)
jxft+I - xf = ||xft - х|2 + 2Xk (gk, Xk - x) + X2.
Отсюда с учетом (7.17) имеем
II Xft+1 - x IP < II xk - x II2 - (2r - Л*) Kk.
Из (7.2) теперь следует ||x* —x||£-q^-> — оо, что не-
возможно.
Следствие. Если множество 2D — {х е Q | f (х)
5^f*+e} ограничено, то существует предельная точка
последовательности {х*}, принадлежащая множеству 2D.
Действительно, в этом случае множество Фс„ е,
ограничено при любых щ 0, с2 <= [0, d2). Поэтому в
силу теоремы 7.1 предельные точки последовательности
{х*} существуют, а то, что они принадлежат множеству
3), вытекает из полунепрерывности сверху отображения
0С|, с, по ci > 0, с2 е [0, d2) •
Задание 7.1. Построить (е, и)-субградиентный метод с проек-
тированием для минимизации функции f(х) на множестве СПЯ, где
G с Еп — произвольный компакт такой, что int {xeGj/i(x)
С —у < 0} непусто. Доказать теорему о сходимости.
§ 8. Метод негладких штрафных функций
Все методы минимизации выпуклой функции на вы-
пуклом множестве, рассмотренные в предыдущих параг-
рафах настоящей главы, решали непосредственно исход-
360 МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ [ГЛ. IV
ную задачу. Можно, однако, свести исходную задачу ус-
ловной минимизации к некоторой задаче безусловной
минимизации либо к задаче минимизации на множестве
простой структуры. Один из способов состоит в исполь-
зовании методов штрафных функций. В этом параграфе
будет показано, как задача минимизации выпуклой
функции f(x) на множестве Й={хеЕл|/г(х)^0} мо-
жет быть сведена к решению конечного числа некоторых
задач минимизации на всем пространстве Еп.
1. Пусть f(x) и h(x)— выпуклые конечные на Е„
функции. Требуется найти
г= inf f(x), (8.1)
х s Й
где £2 = {/s Еп | h (х) 0}.
Предположим, что задача (8.1) разрешима, т. е. что
существует точка х*е£2 такая, что f(x*) = /*, и, кроме
того, что множество ^0(х*) = {хе En|f(x) f*} ограни-
чено. В силу непрерывности f(x) множество J£o(xT)
замкнуто.
Положим
(х) = max {h (х), 0),
F (х, X) = f (х) + Хй+ (х),
Ф (Л) = min F (х, X),
fi (1) «= (х е Еп\F (х, X) = Ф (%)}.
Заметим, что inf F (х, %) достигается при каждом фик-
х s Еп
сированном X 0, поскольку множество Жо(х?) ограни-
чено.
Пусть
дх, BF (х, X) «= {и <= Еп\F(z,K)-F (х, X) >
J>(n, z —х) —е VzeFn).
dxF (х, X) = dx. 0F (х, X), dKF (х, X) = {h+ (x)}.
В силу леммы 5.2 гл. I
( df (х), если h (х) < 0,
dxF (х, X) = s ,
I df (х) + X dh+ (х), если h (х) 0.
S 8]
МЕТОД НЕГЛАДКИХ ШТРАФНЫХ ФУНКЦИИ
361
Здесь использован тот факт, что если й(х)<0, то
(х) = {©}. Отметим также, что
dh (х) = dh+ (х), если h (х) > О,
dh (х) cz dh+ (х), если h (х) = 0.
Справедливы следующие утверждения.
1. Функция ф(Х) вогнута на [0, со).
Это следует из того, что функция F(x, X) линейна по
%, и, следовательно, вогнута, а операция взятия мини-
мума сохраняет вогнутость.
2. Ф(Х)< min/(x) VX>0. (8.2)
Действительно, при любом имеем
Ф (Л) = min F (я, Л) < min F (я, Л) = min f (я).
х&Еп х е £2 х е £2
Положим Ф* = тахФ(Х).
Х>0
3. Пусть хое/?(Ло)> Хо^О. Если Л+(хо) = О, то
/(хо) = Г = Ф(М==Ф‘. (8.3)
В самом деле, поскольку Ф (Хо) = f (х0) 4- (х0) =
= /W, то
f (х0) = min F (х, Хо) < min F (х, Хо) = min f (х)< f (х0).
х&Еп х е У х е £2
Отсюда и из (8.2)
Ф*« max Ф (X) < f х= f (х0) = Ф (Ао).
х>о
А это означает, что (8.3) справедливо.
4. Пусть ф(Х0) = Ф*, Хо >> 0. Tozda Ф(Х)=Ф(Х*)
VX > Хо.
Действительно, если Xi Хо, то для любого
х е Еп, в силу того что /г+(х) 0, должно быть F(x, XJ
>F(x,X0).
Поэтому
Ф*>Ф(Х1)>Ф(ХО) = Ф‘. Я
362
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ [ГЛ. IV
5. Для производной функции Ф(Х) по любому на-
правлению g справедлива формула
~Фд^ = min (h+ (х), g). (8.4)
°s X <= R (M
Действительно (см. § 5 гл. I), так KaKF£(x, A)==
= h+ (x) и
min F (x, A) = — max [— F (x, A)],
x<=£„
TO
= — max (— h+ (x), g) = min (й+ (x), g).
x <= R (A.) x e R (A.)
На основании формулы (8.4) заключаем, что если
при каждом А > 0 множество /? (А) состоит из одной
точки (/?(А) = {х(А)})> то
^- = U+(x(A)),g) Vg,
и в этом случае функция Ф(А) непрерывно дифференци-
руема по А > 0. В частности, /?(А) = {х(А)}> если функ-
ция /(х) строго выпукла на Еп. И
6. Пусть Ф(А0)=Ф*, Ао 0. Тогда для некоторого
хое/?(Ао) будет
х0 е Q, f (х0) = /*,
а при любом Ai > Ао
^еЙ, f(xi) = f* Vx!S/?(Ai).
В силу свойства 3 достаточно показать, что
min h+ (х) = 0, max h+ (х) = 0.
X<=R (М xeR (М)
Так как согласно свойству 4 Ф(А0 + а) — Ф(Ао) при
любом а 0, то
Ф'+ (Ао) = lim = о,
а->+0 а
а по свойству 5 Ф+(Ло)= min h+ (х). Таким образом,
• X G R (М
min h+ (х) = 0.
K&R (Хо)
§ 8]
МЕТОД НЕГЛАДКИХ ШТРАФНЫХ ФУНКЦИЙ
363
Пусть теперь %i > %о- Тогда, опять же используя
свойства 4 и 5, получаем
П \ lim ® (%» — а) — Ф (%1)
О = Ф- (Xi) = lim --------------------------=
а-»+0 а
— min [— h+ (х)] — — max h+ (х).
х е R (Л.,) х <s R (ХО
Достаточные условия существования А* О такого,
что Ф(А*) = Ф*, сформулированы в следующем свой-
стве.
7. Предположим, что задача (8.1) разрешима и вы-
полнено условие Слейтера: при некотором х<^Еп
/г(х) = -у<0. ' (8.5)
Если х*ей есть точка минимума функции f(x) на
множестве £2 и 0 = 1»* + %*®*, где А* О, v*&df(x*),
w* е dh (х*), то
х* <=/?(%*), Ф(А*) = Ф*
и для любых Ai > А* и Xi будет
x,«=Q, f(x1) = f*. (8.6)
Доказательство. Отметим прежде всего, что
%* < оо, ибо выполнено (8.5) и /г+(х*) = 0.
Равенство Ф(А*) = Ф* будет, в силу свойства 3, вы-
полнено, если показать, что х*е /?(%*).
Если А* = 0, то, с одной стороны, 0 = v* е df(x*) и
поэтому х*—точка минимума функции f(x) на Еп, а с
другой, F(x, %*) = f (х) и, следовательно, R (А*) = {х 6=
е Еп | f (х) = min f (z)} и х* е= R (А*).
Пусть %* > 0. Тогда А(х*) = 0, а значит,
д/г(х*)сдЛ+(х*). (8.7)
Условие (П)=и* + А*®* означает, что ®edf(x*) +
+ A*d/i(x*). Отсюда и из (8.7) имеем
0> е dxF (х\ А*) = df (х*) + A* dh+ (х*),
т. е. х* — точка минимума функции F(x, А*) на Еп и
х*е/?(%*).
364
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
(ГЛ. IV
В силу свойства 6 при любых М > %* и Xi
выполняется (8.6).
8. Пусть 0 е dXt е/?(х0, А,о), е > 0, Хо > 0. Тогда
Ф* < F (х0, Ао) + (h+ (х0), X* - Хо) + в, (8.8)
где К* таково, что Ф (X*) = Ф* = max Ф (X).
Х>0
В самом деле,
Ф (Х‘) < Ф (Хо) + (₽, X* - Хо) + в Vp е д8Ф (Хо). (8.9)
Но (см. § 17 гл. I)
со {h+ (х) | х е /?е (Хо)} <= деФ (Хо).
Так как 0 е дх, tF(x0, Хо), то
0 < F (х0, Хо) — min F (х, Хо) < в.
хе £2
Это значит, что 0 F(x0, Хо) — Ф(Хо)^е, т. е. хое
eftJXo)- Тогда Л+(х0)е <ЗеФ(Хо). Теперь (8.8) следует
из (8.9):
Следствие. Если 0едж, е/?(х0, Хо) и хоей, го
Ф (X*) < F (хо, Хо) + в.
9. Если Хо X* и О е дх> eF (х0, Хо), го
f (х0) + Хой+(х0) — min f (х)<е; (8.10)
в частности, для х0 имеем
0<Нх0)-Г<г.
Действительно, из того, что Хо X*, вытекает,
что Ф(Хо)=Ф(Х*), а поскольку Ое дх> tF(x0, Хо), то
f (х0) + Хой+ (х0) — f* — F (х0, Хо) - Ф (Хо) < в.
2. Перейдем теперь непосредственно к самому ме-
тоду штрафных функций.
Опишем «принципиальный» алгоритм.
. Возьмем произвольное Хо >• 0. Каким-либо из мето-
дов гл. III найдем точку хо = х(Хо) е/? (Хо), т. е. такую,
что
F (х0, Хо) “ min F (х, Хо).
МЕТОД НЕГЛАДКИХ ШТРАФНЫХ ФУНКЦИИ
365
§ 8]
Если h (хо) = 0, то в силу свойства 3 точка х0 есть
точка минимума функции f(x) на множестве Q. Если же
ft(xo) > 0, то положим 11 = + 2max{lo, Л+(х0)} и най-
дем точку хь в которой
F(xb ^i)= min F {х, 11).
Еп
Далее продолжаем аналогично.
Если задача (8.1) разрешима и выполнено условие
Слейтера (8.2), то в конечное число шагов будут най-
дены число Xk> 0 и точка хк е Еп такие, что хк е й
(т. е. h(xk) ^0) и
Ф(^) = Ф‘, f(xft) = f.
Докажем это утверждение. Пусть х* — точка мини-
мума f(x) на Q.
Если Л(х*)<0, то 0s df(х*) = dxF(^, 0) и, значит,
х*е/?(0). В силу свойства 3 Ф(0) = Ф*.
Отсюда для точки хо, найденной на первом же шаге,
будет выполнено
xoeQ, f(x0) = f= min f(x)
(по свойству 5).
Пусть теперь /i(x*)=0. Тогда в силу необходимого
условия минимума существуют 1*^0, o*edf(x*),
w* е dh(x*) такие, что 0 — и* 4- l*w*. По свойству 6
Ф (1‘) = ф* = max Ф (1),
и для первого 1*, большего 1*, будет выполнено
x.eQ, f(xk) = r.
Более того, пусть 6 = 1* — 10. Поскольку 1* 1о 4*
4- 2fel0, то для того, чтобы получить 1* 1*, необхо-
димо будет сделать не более 6(21о)-1 шагов. Н
Замечание. Все результаты этого параграфа спра-
ведливы и для случая, когда
Q = {х <= Еп |Л/(х)<0 V/sЛ-
где ft/(x), /е/=1 :т, — выпуклые на Еп функции.
366
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ [ГЛ. IV
При этом под X следует понимать вектор X =
= (Xi, Хг, ..., Хт) и по определению
{Х>О} = {Х|Х/>О V/g= 1 : т},
{X > X*} = {X |Х/ > X/ у/ е= 1 : т},
т
h (х) = max hj (х), Х/г+(х) = £ Х//г* (х),
/-1
т
U+ (х), g) == Z Л/+ (х) gr
§ 9. Метод Келли для минимизации
на выпуклом множестве
Пусть f(x) и й(х)—выпуклые на Еп функции. Тре-
буется найти
Г = inf f(x),
X е Q
где Q = {хе En\h(x) 0}.
Предположим, что множество й ограничено и удов-
летворяет условию Слейтера: существует точка х&Еп
такая, что
Ш)<0. (9.1)
Пусть S а Еп — произвольный компакт, содержа-
щий Q.
Зафиксируем в>0и це[0,—Л(х)). Выберем про-
извольную ТОЧКУ X(|SS И ПОЛОЖИМ СИ ={хо}. Вычислим
любые а(хо)е dtf (хо) и w(x0)& дцН(хо). Положим
Ф1 (х) = max Bf (х, z) «= f (х0) + (о (х0), х — х0),
z е Qi
©j = {х s S | Bh (х, Z) < 0 Vz е Oi) =
s= {х <= S | й (х0) + (да (х0), х — х0) < 0},
где
Bf (х, z) = f (z) + (v (z), x — z), V (z) e dj (z),
Bh (x, z) = h (z) + (да (z), x — z), да (z) s d^h (z).
Пусть уже построены множества cts-i, и функ-
ция ф*_1(х), и пусть
х*_1®о&_1, Фа-1(х*_1)>= min Ф*_1(х).
МЕТОД КЕЛЛИ
367
§ 91
Вычислим произвольные v(x>t-i)edsf(xfl-l) и a^x^Je
е dixh(Xk-i).
Положим
OA = Or4-lU{^-l}> (9.2)
фк (х) = т“х (х> z)>
Z!3ak
&k — {х е S |Bh(х, z)< О Vz е <М
и найдем точку х* е со*, в которой
Ф (хА) = min ф* (х). (9.3)
Из (9.2) вытекает, что
<9.4)
Тогда из (9.3) и (9.4) имеем
Ф*_i(x*_i)= min max Bf(x, z)^.
xe<ak-i zsok-i
< min max Bf (x, z) = ф* (xft). (9.5)
Если оказалось, что хк <= Q и
Ф* (xk) > f (xk), (9.6)
то процесс прекращается. В этом случае
f(xft)<ft + e, •• (9.7)
где Гц = min f (х), = {х <= Еп I h (х)< — ц}.
Действительно, по определению def (z)
fix') — f (z) > (v (z), X — z) — 8
Vx, z e= En, V» (z) e def (z).
Поэтому
f (x) + 8 sup Bf (x, z) max Bf (x, z) = ф* (x). (9.8)
zeEn zsoft
Из определения дц/г(х) имеем
h (х) — h (z) (w (z), x — z) — p
Vx, z e En, Vw (z) e d^h (z),
368
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
[ГЛ. IV
Следовательно,
□и = {х е S \h (х) — ц) cz
<=. {х s S | Bh (х, z)< 0 Vz е £„} CZ
cz {х е S |Bh(х, z)<0 Vz еak} = ®*.
Отсюда и из (9.8) заключаем, что
/ц + е = min f (х) + е > min Фй (х) >
> min Фй (х) = Фй (xft). (9.9)
Теперь (9.7) вытекает из (9.6) и (9.9).
Если (9.7) не имеет места, то строим o*+i, <0*4-1 и
Ф*+1(х) и продолжаем аналогично. В результате полу-
чаем последовательность {хй}. Если она конечна, то по-
следняя ее точка по построению принадлежит множе-
ству Q и удовлетворяет (9.7). В противном случае спра-
ведлива
Теорема 9.1. Если х* — предельная точка последо-
вательности {хй}, то х* <= й и
f(x*)</; + e. (9.10)
Доказательство. Существование предельных
точек последовательности {хй} следует из ограничен-
ности множества S.
Пусть Хй —► х*. В силу (9.2) и того, что xft_ есгй.
при ks > ks„ будет
h (хч) + (w (хч)’ х^ ~ х*^ 0 > k*v (9-11)
Поскольку d^h(x) ограничено на S, то, переходя в
(9.11) к пределу по ks, ks,-* сю при условии, что ks > kSl>,
получим й(х*) 0, т. е. х* е £2.
Последовательность {Фй(хй)} монотонно возрастает
и, в силу (9.9), ограничена сверху числом /ц + е. При
ks > ks, будем иметь
Гя + е > Ф^ (xks) > f (хй4о) + (о*,,, xks - xftJ. (9.12)
Поскольку dtf(x) ограничено на S, то, переходя в
(9.12) к пределу по ks, ks,-*00 при условии, что ks>
> kst, получим (9.10). М
РЕЛАКСАЦИОННЫЙ СУБГРАДИЕНТНЫЙ МЕТОД
369
§ 10]
§ 10. Релаксационный субградиентный метод
при наличии ограничений
В этом параграфе часть результатов § 6 гл. III рас-
пространяется на задачу минимизации выпуклой функ-
ции на выпуклом множестве.
1. Минимизация на произвольном выпуклом замкну-
том множестве. Пусть й az Еп — выпуклое замкнутое
множество и f(x)—выпуклая на некотором выпуклом
открытом множестве, содержащем й, функция. Требует-
ся найти inf f
х е Q
Предположим, что множество Q имеет внутренние
точки. Тогда (см. лемму 1.2), для того чтобы в точке х*
функция f(x) достигала своего наименьшего на множе*
стве Q значения, необходимо и достаточно, чтобы
где 2’1i(x) = со {df(x)U7\i(*)}, Tv(x) = {v^—-Г+(х)|||о|| =
= т]}, т] > 0 — произвольное фиксированное число.
Нетрудно убедиться в том, что отображение 7\)(х)
полунепрерывно сверху на й. Поэтому, в силу лемм 2.3
и 2.4 гл. I, полунепрерывно сверху отображение
Кроме того, оно ограничено на любом ограниченном
множестве из й, ибо этим свойством обладают df(x)
и 7\(х).
Положим d (х) = min || v ||. Опишем релаксацион-
о е (х)
ный субградиентный метод для рассматриваемого слу-
чая.
Зафиксируем положительные числа т], во, б и целое
число т0. В качестве начального приближения возьмем
произвольную точку Хо е й.
Предположим, что множество £Z>(x0) = {хе й|f(х)
-Cf(xo)} ограничено.
Пусть уже найдено k-e приближение хк е й. Пока-
жем, как выполняется й-й цикл — построение (&+1)-го
приближения x/i+i е й.
Положим Хцо — хк и возьмем произвольный вектор
vk0<= 2\(хы). Если ||у*.-Л < е0, где vk,-\ = то по-
лагаем ^ = 0, xk+i=xkt., и на этом k-a цикл заканчи’
л?
370
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИИ [ГЛ. IV
вается (через tk будем, как и раньше в §§ 6 и 7 гл. Ш,
обозначать число шагов на &-м цикле).
Если же ||ti*, -ill > во, то на луче {х*о(а) = **о—
— ао*о|а^0} найдем такую точку х*о(а*о), в которой
f(**o(aw)) = min f (xfe0 («)) (10.1)
Xko (a)eQ, a>0
(может оказаться, что a*o = 0).
Положим теперь x*t = хм. Очевидно, что f(Xkt)^
Cf(xso) ихиеЙ. Если ||х*о — x*ill> б или f(Xko) —
— f(xki)^b, то полагаем /* = 1, Xk+i — xktk, и на этом
k-ft цикл заканчивается. В противном случае возьмем
такой вектор vM е 2% (x*i), что
(Vko> t'fto) 0.
(10.2)
В силу (10.1) такой вектор Vko •S’u (*н) обязательно
найдется. Действительно, если в точке x*i = х*о(а*о) вы-
полнено (10.1), то это может произойти по двум при-
чинам:
а) либо -%-. \ — тах (о, —• t>*o)^ 0, и тогда
vk0> o<sdf(xkl)
найдется субградиент Vko е df(xk\), для которого имеет
место (10.2);
Ь) либо хк1 — при любом р > 0, т. е.—
&y(Xk\) = {v = X(z — х*1) |Х > 0, гей}, а тогда най-
дется такой вектор vM е — Г+(х*1), [|v*oll = П> что имеет
место (10.2).
Если ||й*о11^ во, то полагаем 4=1, xk+\=Xktk, и
на этом &-й цикл заканчивается. Если же ||v*oll> е0) то
найдем вектор Vki такой, что (см. п. 1 § 6 гл. I)
^kl — PfeoffeO + (1 — Р*о) Vk0> Р&0 е (0, 1),
|| ofti ||= min IIPt»*o + (l — 0)v*oll.
P e [0, 1]
Теперь на пересечении луча {x*i (a) = xft] — ao*i | a :>
0} и множества Q найдем такую точку х*2 = x*i(a*i),
в которой
f(xk2)= min f(x*i(a)).
(a) eU a>0
I 10]
РЕЛАКСАЦИОННЫЙ СУБГРАДИЕНТНЫЙ МЕТОД
371
Далее продолжаем аналогично до тех пор, пока не
будет сделано такое число шагов tk zn0, что выпол-
нится по крайней мере одно из условий:
а) tk = m0; (10.3
*k
Ь) II xk, t-i~ xkt 11^6; (Ю.4)
с) f W — f (xktk) >6; (10.5)
d) II vk, ^ill<80. (10.6)
После этого полагаем xk+\ = %ktk, и 6-й цикл закан-
чивается, причем если выполнено (10.6), то заканчи-
вается и весь процесс последовательных приближений.
Отметим, что
(»иА)<0 V/e0:(4-l). (10.7)
В результате построим последовательность {%*}•
Если она конечна, то для последней полученной точки
Xk по построению будет d(xft)^e0. В противном случае
справедлива
Теорема 10.1. Пусть функция f(x) строго выпукла
на множестве й, имеющем внутренние точки, множе-
ство 3)(хо) ограничено.
Тогда, если точка х* является предельной точкой по-
следовательности {х*}, т0 х*е
d (х*) max {е0, fo?"1»-1} s tZ0, (10.8)
где q = (1 + (вод-1)2) */2, b = max {л, max max || о ||).
(х0) v е df (х)
В частности, если /по > 1 + (In «у)-11п(ео&-1), то
d(x*) sC е0.
Доказательство проводится аналогично дока-
зательству теоремы 6.1 гл. I, с учетом того, что точечно-
множественное отображение .2\(х) = co{df(x)(J 7\(х)}
полунепрерывно сверху на й и выполнены неравенства
(10.7). Я
Пусть D — диаметр множества 3)(х0), а г — радиус
наибольшего шара, содержащегося в Й. Тогда в силу
(1.15) и (10.8) для любой предельной точки х* последо-
вательности {xk} будет справедлива оценка
f(x‘)-r<D(14-2&P(nrr‘)d0.
372
МИНИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
[ГЛ. IV
Изложенный метод можно применить и для нахож-
дения точек минимума функции f(x) на множестве Q.
Схема метода при этом остается прежней, только вместо
условий (10.3) и (10.6) проверяются условия tk = гпк и
соответственно, причем 8/?->0, т^->оо.
Теорема 10.2. Пусть функция f(x) строго выпукла
на множестве Q, имеющем внутренние точки, множество
£>(х0) ограничено и >0, >оо.
Тогда любая предельная точка последовательности
{х^ является точкой минимума функции f(x) на мно-
жестве Q.
Задание 10.1. Доказать теоремы 10.1 и 10.2.
2. Пусть множество Q имеет вид
Q — {х е Еп | h (х)< 0},
где h(x)—выпуклая на Еп функция.
Предположим, что выполнено условие Слейтера: су-
ществуют такие у > 0 и х е Еп, что
h (х) — — у < 0.
Тогда множество Q имеет внутренние точки.
Используя специфику • задания множества Q, можно
конкретизировать метод п. 1
Положим
'df(x),
£ (х) =4 со {df (х) (J dh (х)),
dh (х),
если
если
если
h (х) < 0.
Л (х) = 0,
h (х) > 0.
Для того чтобы в точке x*eQ функция f(x) дости-
гала своего наименьшего на множестве Q значения, не-
обходимо и достаточно, чтобы (см. теорему 1.2)
0се2*(х*).
Последовательные ппт^дижения строятся аналогично
тому, как это делало/ь ъ п. 1 только вместо векторов
о kt е 2\(*а, <и) = со}д/\х*. ж)и Гт1(х/е, ж)} берем век-
торы vkt <^&{Xkt n).
БИБЛИОГРАФИЧЕСКИЙ КОММЕНТАРИЙ
Глава 1
К §§ 1, 3. Более подробно с материалом можно ознакомиться
по монографиям В. Ф. Демьянова, В. Н. Малоземова [36], И. И. Ере-
мина, Н. Н. Астафьева [49], А. Д. Иоффе, В. М. Тихомирова [57],
С. Карлина [60], В. Л. Макарова, А. М. Рубинова [78], Б. Н. Пше-
ничного [103], Р. Т. Рокафеллара [110].
К § 2. Изложение основано на работе [78, гл. I]. Свойства то-
чечно-множественных отображений изучались в [57], [99], [111],
[137], [144], [146], [162], [165].
К §§ 4, 5. Свойства выпуклых функций и их субдифференциа-
лов можно найти в [56], [57], [67], [68], [69], [70], [71], [77],
[110], [111], fl 19], [166].
К § 6. Лемма 6.4 имеется, по существу, в [80]. Необходимым
Условиям экстремума посвящена обширная литература* [6], [22],
24], [26], [32], [39], [45], [57], [73], [74], [82], [102], [147],
[158], [159], [163].
К § 7. Леммы 7.1, 7.2 опубликованы в [43], [44]. Теорема 7.3
является частным случаем соответствующей теоремы из работы
С. С. Кутателадзе [66]. Пример 4 предложен В. М. Тихомировым.
К § 8. Соотношение (8.2) установлено в [ПО, стр. 237], где и
введено понятие е-субдифференциала. На непрерывность 8-субдиффе-
ренциала по х при фиксированном в > 0 первым обратил внимание
Е. А. Нурминский [90]. Теорема 8 2 опубликована в [43], [44].
Лемма 8.1 и оценка (8.19) получены в [132].
К § 9. Оценки (9.21) и (9.22) обобщают соответствующие оцен-
ки из [37].
К §§ 10, 11. Основные результаты имеются в [43], [44].
К § 13. Изложение пп. 1, 2 следует работе [100].
К § 14. Результаты изложены в [42]. Близкие вопросы изуча-
лись в работах [5], [27], [62], [116], [143].
К § 15. Принятое здесь изложение близко к [НО]. Дифферен-
цируемость выпуклой функции одной переменной рассмотрена в [8],
[121]. Случай многих переменных изучался в [109]. Существование
почти везде второго дифференциала выпуклой функции установлено
в [2].
К § 16. Изложение следует монографии С. С. Кутателадзе,
А. М. Рубинова [68]. Доказательство леммы 16.3, по-видимому, но-
вое. Сопряженные выпуклые функции и другие аспекты двойствен-
ности изучались в работах [57], [ПО], [128], [138], [156], [157],
[169].
§ 17, за исключением леммы 17.2, публикуется впервые. При
ц = 0 включение (17.10) отмечалось в [92].
374
БИБЛИОГРАФИЧЕСКИЙ КОММЕНТАРИЙ
Глава 11
Материал этой главы является новым. Квазидифференцируемые
функции были введены в [38], [41]. Там же, а также в [40], [101]
указаны основные свойства этих функций. В работе Б. Н. Пше-
ничного [104] введено понятие верхней выпуклой аппроксимации
(в. в. а.) для исследования на минимум весьма широкого класса
функций (в частности, липшицевых). Между квазидифференциалом
и в. в. а. имеет место следующая связь: если 0f(xo) — [Of (xp), df (хо)],
то для любого w s df(Xo) множество [ш + df (*о)} есть в. в. а. функ-
ции /(х) в точке Хо.
Теоремы 5.1—5.4, 7.2, 7.3 и лемма 6.3 установлены Л. Н. Поля-
ковой. Ею же получены необходимые условия экстремума квазидиф-
ференцируемой функции на множестве, заданном квазидиффсренци-
руемым равенством. §§ 6, 7 написаны на основе [40]. Лемма 8.1
установлена Б. Н. Пшеничным.
Недавно А. М. Рубинов, используя один результат А. Я. За-
славского, доказал теорему о квазидифференцируемости компози-
ции квазидифференцируемых функций и нашел вид ее квазидиффе-
ренциала.
Для квазидифференцируемых функций нетрудно установить
связь с «шатрами» В. Г. Болтянского [6].
Глава 111
Различным вопросам математического программирования посвя-
щены работы [16], [22], [49], [61], [84], [93], [55], [105], [112],
[114], [129], [145], [164], [172].
К § 1. Лемма 1.3 новая.
К § 2. Непрерывные аналоги итерационных процессов, по-види-
мому, впервые рассмотрены в [23]. Подробно с методами миними-
зации гладких функций можно ознакомиться по монографиям
М. Аоки [3], Ф. П. Васильева [16], Л. В. Канторовича, Г. П. Аки-
лова [59], В. Г. Карманова [61], Э. Полака [96], Б. Н. Пшеничного,
Ю. М. Данилина [105].
К § 3. Методы наискорейшего спуска для минимизации функции
максимума (не обязательно выпуклой) разработаны в [36]. Там же
показано, что при е = 0 метод наискорейшего спуска может расхо-
диться. Относительная свобода в выборе направления спуска при
использовании 8-субдиффсренпиалов была замечена в работе [132],
на основе которой написан п. 5.
К § 4. Субградиентный метод (первоначальный вариант с по-
стоянным ненормированным шагом) разработан в [125]. Близкая
идея использована в [47]. Сходимость к множеству точек минимума
при выборе шага (4.1) обоснована в работе [50]. Следствие из тео-
ремы 4.1 замечено в [124]. е-субградиентный метод для достаточно
широкого класса негладких функций (включая выпуклые) предло-
жен в [92] — это, по-видимому, одна из первых попыток создания
конструктивных методов минимизации. Идея п. 4 высказана
М. 3. Хенкиным.
Обобщение субградиентного метода на задачи стохастического
программирования систематически изучено в монографии Ю. М. Ер-
БИБЛИОГРАФИЧЕСКИЙ КОММЕНТАРИЙ
375
мольева [51]; см. также монографии [30], [91], [127]. В [30] раз-
работана схема применения субградиентного метода для минимиза-
ции локально липшицевых функций на основе операции сглажива-
ния. Дальнейшему развитию и совершенствованию субградиентного
метода посвящены работы [4], [28], [58], [124], [127].
К § 5. Изложение основано на работе [34].
К § 6. Впервые метод этого параграфа в несколько отличных
формулировках был предложен в [149], [150] и [170]. В [171] по-
казано, что при точной одномерной минимизации метод [170] пре-
вращается в метод сопряженных градиентов, если целевая функция
квадратичная. Для произвольной гладкой функции эта связь уста-
новлена в [И].
К § 7. Результаты этого параграфа ранее не публиковались.
К § 8. Первоначально метод Келли был предложен в [148] для
минимизации линейной формы на выпуклом множестве. Достаточно
обширное исследование различных модификаций метода Келли про-
ведено В. П. Булатовым [7]. Здесь изложение следует работе
Н. К. Храмовой [122].
К § 9. Метод этого параграфа разработан в [1] (см. также [39]).
К § 10. Изложение основано на работе [33]. Идея метода тесно
связана с работами [1], [108], [148].
Глава IV
К § 1. Лемма 1.2 установлена в [12], а лемма 1.3 — в [20,
стр. 49]. Теорема 1.2 есть очевидное обобщение теоремы 3.1 гл. V
из [36].
К § 2. Лемма 2.3 получена в [13].
К § 3. Метод § 3 является обобщением метода из [36, § 6,
гл. IV].
К § 4. Результаты пп. 1, 2 принадлежат В. К. Шомесовой.
К § 5. При 8 = ц — 0 метод § 5 предложен в [97]. В [52] ме-
тод из [97] обобщен на случай квазивыпуклых функций. Приводи-
мый здесь вариант при G = Еп опубликован в [13].
К § 7 Изложение основано на работе [13].
К § 8. Ключевым в этом параграфе является свойство 6, уста-
новленное в [48]. Методу штрафных функций посвящены монографии
Ю. Б. Гермейера [25], Б. С. Разумихина [106], В. В. Федорова [120].
К § 10- Метод п. 1 разработан в [12] и является, по существу,
обобщением методов из [149] — [151] и [170], [171] на задачи с
ограничениями. В [155] предлагается подобный метод для миними-
зации полугладких [154] функций.
§§ 6 и 9 публикуются впервые.
ЛИТЕРАТУРА
1. Акилов Г. П.» Рубинов А. М. Метод последовательных
1П)иближений для разыскания полинома наилучшего приближения. —
ДАН СССР, 1964, т. 157, № 3, с. 503—505.
2. Александров А. Д. Существование почти везде второго
дифференциала выпуклой функции и некоторые связанные с ним
свойства выпуклых поверхностей. — Уч. записки ЛГУ. Сер. матем.,
1936, вып. 6, с. 3—35.
3. Аоки М. Введение в методы оптимизации. — М.: Наука,
1977.
4. Б а ж е н о в Л. Г. Об условии сходимости метода минимиза-
ции почти-дифференцируемых функций. — Кибернетика, 1972, № 4,
с. 71—72.
5. Береснев В. В. Необходимые условия экстремума в вы-
пуклой задаче максимина на связанных множествах. — Кибернетика,
1972, № 2, с. 87—91.
6. Болтянский В. Г. Метод шатров в теории экстремальных
задач. — УМН, 1975, т. 30, вып. 3, с. 3—55.
7. Булатов В. П. Методы погружения в задачах оптимиза-
ции. — Новосибирск: Наука, 1977.
8. Бурбаки Н. Функции действительного переменного. — М.:
Наука, 1965.
9. Варга Дж. Оптимальное управление дифференциальными
и функциональными уравнениями. — М.: Наука, 1977.
10. Васильев Л. В. Выравнивание максимумов. Теорема
о квадратичной скорости сходимости. — В кн.: [20], с. 34—40.
11. Васильев Л. В. О связи релаксационного метода обоб-
щенного градиента с методом сопряженных градиентов. — В кн.:
[123], ч. I, с. 45—49.
12. Васильев Л. В., Демьянов В. Ф. Релаксационный ме-
тод для минимизации выпуклой функции на выпуклом множестве. —
В кн.: Численные методы нелинейного программирования: Тезисы
II Всесоюзного семинара. — Харьков, 1976, с. 100—102.
13. Васильев Л. В., Демьянов В. Ф. Метод (е, ц, т)-об-
общенного градиентного спуска при наличии ограничений. — Вести.
ЛГУ, 1979, № 19, с. 19—23.
14. Васильев Л. В., Демьянов В. Ф., Лисина С. А.
Минимизация выпуклой функции с помощью 8-субградиентов.—
В кн.: Управление динамическими системами. — Л.: Изд-во ЛГУ,
1978, с. 3—22.
15. Васильев Л. В., Тарасов В. Н. Об одном методе ре-
шения задач на минимакс. — В кн.: Оптимизация. — Новосибирск,
1977, вып. 9 (36), с. 53—57,
ЛИТЕРАТУРА
377
16. Васильев Ф. П. Лекции по методам решения экстремаль-
ных задач. — М.: Изд-во МГУ, 1974.
17. Войтон Е. Ф. О методах решения некоторых экстремаль-
ных задач синтеза электрических цепей. — В кн.: Исследование опе-
раций (модели, системы, решения). — М.: Изд-во ВЦ АН СССР,
1976, с. 16—23.
18. В о й т о н Е Ф. Одна задача со связанными ограничениями.—
В кн.: Г20], с. 106—114.
19. Войтон Е. Ф., Полякова Л. Н. Об одном классе за-
дач при связанных ограничениях. — В кн.: Оптимизация. — Новоси-
бирск, 1973, вып. 10, с. 41—46.
20. Вопросы теории и элементы программного обеспечения ми-
нимаксных задач. — Л.: Изд-во ЛГУ, 1977/Под ред. В. Ф. Демья-
нова, В. Н. Малоземова.
21. Воробьев Н. Н. Современное состояние теории игр.—
УМН, 1970, т. 25, вып. 2 (152), с. 81—140.
22. Г а б а с о в Р., Кириллова Ф. М. Методы оптимиза-
ции.— Минск: Изд-во Б ГУ, 1975.
23. Г а в у р и н М. К. Нелинейные функциональные уравнения и
непрерывные аналоги итеративных методов. — Изв. вузов. /Матема-
тика, 1958, № 5, с. 18—31.
24. Г а м к р е л и д з е Р. В. Необходимые условия первого по-
рядка и аксиоматика в экстремальных задачах.—Тр. МИАН СССР
им. В. А. Стеклова, 1971, т. 112, с. 152—180.
25. Г е р м е й е р Ю. Б. Введение в теорию исследования опе-
раций.— М.: Наука, 1971.
26. Г и р с а н о в И. В. Лекции по математической теории экс-
тремальных задач. — М.: Изд-во МГУ, 1970.
27. Гольштейн Е. Г. Теория двойственности в математиче-
ском программировании и ее приложения. — М.: Наука, 1971.
28. Гольштейн Е. Г. Обобщенный метод отыскания седловых
точек. — Экономика и матем. методы, 1972. т. 8, вып. 4, с. 569—579.
29. Горелик В. А. Приближенное нахождение максимина с
ограничениями, связывающими переменные. — ЖВМ и МФ, 1972,
т. 12, № 2, с. 510—517.
30. Г у п а л А М. Стохастические методы решения негладких
экстремальных задач. — Киев: Наукова думка, 1979.
31. Д анскин Дж. М. Теория максимина и ее приложения
к задачам распределения вооружения. — М..: Советское радио, 1970.
32. Демьянов В. Ф. Минимакс: дифференцируемость по на-
правлениям — Л.: Изд-во ЛГУ, 1974.
33. Д е м ь я н о в В. Ф. К методу экстремального базиса. — ДАН
СССР, 1976, т. 229, № 2, с. 272—275.
34. Демьянов В. Ф. Многошаговый метод обобщенного гра-
диентного спуска.— ЖВМ и МФ, 1978, т. 18, № 5, с. 1112—1118.
35. Демьянов В. Ф. Модифицированный метод обобщенного
градиента при наличии ограничений. — Вести. ЛГУ, 1978, № 19,
с. 25—29.
36 Демьянов В. Ф.. Малоземов В. Н. Введение в ми-
нимакс. — М.: Наука, 1972.
37. Д е м ь я н о в В. Ф., П е в н ы й А. Б. Некоторые оценки в
минимаксных задачах. — Кибернетика, 1972, № 1, с. 107—112.
378
ЛИТЕРАТУРА
38. Демьянов В. Ф., Полякова Л. Н., Рубинов А. М.
Об одном обобщении понятия субдифференциала. — В кн.: Всесоюз-
ная конференция «Динамическое управление»: Тезисы докладов. —
Свердловск: 1979, с. 79—84.
39. Д е м ь я н о в В. Ф., Рубинов А. М. Приближенные ме-
тоды решения экстремальных задач.— Л.: Изд-во ЛГУ, 1968.
40. Демьянов В. Ф., Полякова Л. Н. Условия минимума
квазидифференцируемой функции на квазидифференцируемом мно-
жестве. — ЖВМ и МФ, 1980, т. 20, № 4, с. 849—856.
41. Демьянов В. Ф., Р у б и н о в А. М. О квазидифферен-
цируемых функционалах. — ДАН СССР, 1980, т. 250, № 1,
с. 21—25.
42. Д е м ь я н о в В. Ф., Ш о м е с о в а В. К. Дифференцируе-
мость по направлениям функции супремума. — Вести. ЛГУ, 1978, №7,
с. 15—20.
43. Демьянов В. Ф., Ш о м е с о в а В. К. Условные субдиф-
ференциалы выпуклых функций.— ДАН СССР, 1978, т. 242, № 4,
с. 753—756.
44. Д е м ь я н о в В. Ф.., Ш о м е с о в а В. К. Условные субгра-
диенты и условные субдифференциалы выпуклых функций. — В кн.:
Современное состояние теории исследования операций/Под ред.
Н. Н. Моисеева. — М.: Наука, 1979, с. 311—335.
45. Дубовицкий А. Я., Милютин А. А. Задачи на экс-
тремум при наличии ограничений. — ЖВМ и МФ, 1965, т. 5, № 3,
с. 395—453.
46. Евтушенко Ю. Г. Численный метод отыскания наилуч-
ших гарантированных оценок.— ЖВМ и МФ, 1972, т. 12, № 1,
с. 89—104.
47. Еремин И. И. Итеративный метод для решения чебышев-
ских приближений несовместных линейных неравенств.— ДАН СССР,
1962, т. 143, № 6, с. 1254—1256.
48. Еремин И. И. О методе штрафов в выпуклом программи-
ровании. — Кибернетика, 1967, № 4, с. 63—67.
49. Е р е м и н И. И., Астафьев Н. Н. Введение в теорию
линейного и выпуклого программирования. — М.: Наука, 1976.
50. Е р м о л ь е в Ю. М. Методы решения нелинейных экстре-
мальных задач. — Кибернетика, 1966, № 4, с. 1—17.
51. Ермольев К). М. Методы стохастического программиро-
вания. — М.: Наука, 1976.
52. 3 а б о т и н Я. И., Кораблев А. И., X а б и б у л л и н Р. Ф.
О минимизации квазивыпуклых функционалов. — Изв. вузов. Мате-
матика, 1972, № 10, с. 27—33.
53. За б о т и н Я. И., К р е й н и н М. И. О сходимости методов
отыскания минимакса. — Изв. вузов. Математика, 1977, № 10 (185),
с. 56—64.
54. 3 а н г в и л л У. И. Нелинейное программирование. Единый
подход. — М.: Советское радио, 1973.
55. Зойтендейк Г. Методы возможных направлений. — М.:
ИЛ, 1963.
56. И о ф ф е А. Д., Левин В. Л. Субдифференциалы выпуклых
функций.— Тр. Моск, матем. об-ва, 1972, т. 26, с. 3—73.
ЛИТЕРАТУРА
379
57. Иоффе А. Д., Тихомиров В. М. Теория экстремальных
задач. — М.: Наука, 1974.
58. Итеративные методы в теории игр и программировании/Под
ред. В. 3. Беленького и В. А. Волконского. — М.: Наука, 1974.
59. К а н т о р о в и ч Л. В., Акилов Г. П. Функциональный
анализ. —М.: Наука, 1977.
60. Карлин С. Математические методы в теории игр, програм-
мировании и экономике. — М.: Мир, 1964.
61. Карманов В. Г. Математическое программирование. — М.:
Наука, 1975.
62. К и р и н Н. Е. Методы последовательных оценок в задачах
оптимизации управляемых систем. — Л.: Изд-во ЛГУ, 1975.
63. К р а с о в с к и й Н. Н., Субботин А. И. Позиционные
дифференциальные игры. — М.: Наука, 1974.
64. К у р ж а н с к ий А. Б. Управление и наблюдение в условиях
неопределенности. — М.: Наука, 1977.
65. К у с р а е в А. Г. О необходимых условиях экстремума для
негладких векторнозначных отображений. — ДАН СССР, 1978, т. 242,
№ 1, с. 44—47.
66. К у т а т е л а д з е С. С. Выпуклое 8-программирование.—
ДАН СССР, 1979, т. 245, № 5, с. 1048—1050.
67. Кутателадзе С. С. Выпуклые операторы. — УМН, 1979,
т. 34, вып. 1 (205), с. 167—196.
68. Кутателадзе С. С., Рубинов А. М. Двойственность
Минковского и ее приложения. — Новосибирск: Наука, 1976.
69. Лебедев В. Н., Ты ня некий Н. Т. Теория выпукло-вог-
’ нутых игр. — ДАН СССР, 1967, т. 174, вып. 6, с. 1264—1267.
70. Левин В. Л. О субдифференциалах выпуклых функциона-
лов. — УМН, 1970, т. 25, вып. 4 (154), с. 183—184.
71. Левин В. Л. Субдифференциалы выпуклых отображений
и сложных функций. — Сибирский матем. ж., 1972, т. XIII, № 6,
с. 1295—1303.
72. Л е в и т и н Е. С. Об одном методе минимизации для не-
гладких экстремальных задач. — ЖВМ и МФ, 1969, т. 9, № 4,
с. 783—807.
73. Левитин Е. С., Милютин А. А., Осмоловский Н. П.
Об условиях локального минимума в задачах с ограничениями. —
В кн.: Математическая экономика и функциональный анализ. — М.:
Наука, 1974, с. 139—202.
74. Левитин Е. С., М и л ю т и н А. А., Осмоловский Н. П.
Условия высших порядков локального минимума в задачах с огра-
ничениями. — УМН, 1978, т. 33, вып. 6 (204), с. 85—148.
75. Лисина С. А. Минимизация е-выпуклой функции. — В кн.:
[123], с. 122—124.
76. Лоран П.-Ж. Аппроксимация и оптимизация. — М.: Мир,
1975.
77. Л уд ер ер Б. Задачи на минимакс и выпуклый анализ.—
Вести. МГУ, 1975, № 6, с. 25—31.
78. Макаров В. Л., Рубинов А. М. Математическая теория
экономической динамики и равновесия. — М.: Наука, 1973.
79. М а л о з е м о в В. Н. О выравнивании максимумов. — ЖВМ
и МФ, 1976, т. 16, № 3, с. 781—784.
380
ЛИТЕРАТУРА
80. Малоземов В. Н. О достаточных условиях локального
минимакса. — Вести. ЛГУ, 1976, № 7, с. 55—59.
81. Малоземов В. Н., П е в н ы й А. Б. Выравнивание макси-
мумов. — В кн.: [20], с. 27—34.
82. Моисеев Н. Н. Элементы теории оптимальных систем. —
М.: Наука, 1975.
83. М о ц к у с Й. Б. Многоэкстремальные задачи в проектирова-
нии. — М.:Наука, 1975.
84. Мухачева Э. А., Рубинштейн Г. Ш. Математическое
программирование. — Новосибирск: Наука, 1977.
85. Натансон И. П. Теория функций вещественной перемен-
ной.—М.: Наука, 1974.
86. Н и к а й д о X. Выпуклые структуры и математическая эко-
номика. — М.: Мир, 1972.
87. Н о р к и н В. И. Нелокальные алгоритмы минимизации не-
дифференцируемых функций. — Кибернетика, 1978, № 5, с. 57—60.
88. Нурминский Е. А. К дифференцируемости многознач-
ных отображений. — Кибернетика, 1978, № 5, с. 44—48.
89. Нур ми нс кий Е. А. Квазиградиентный метод решения за-
дачи нелинейного программирования. — Кибернетика, 1973, № 1,
с. 122—125.
90. Н у р м и н с к и й Е. А. О непрерывности 8-субградиентных
отображений. — Кибернетика, 1977, № 5, с. 148—149.
91. Нурминский Е. А. Численные методы решения детермини-
рованных и стохастических минимаксных задач. — Киев: Наукова
думка, 1979.
92. Нурминский Е. А., Желиховский А. А. е-квазигра-
диентный метод решения негладких экстремальных задач. — Кибер-
нетика, 1977, № 1, с. 109—113.
93. Ортега Дж., Рейнболдт В. Итерационные методы ре-
шения нелинейных систем уравнений со многими неизвестными. —
М.: Мир, 1975.
94. П е в н ы й А. Б. Дифференцирование функции максимина. —
ЖВМ и МФ, 1971, т. 11, № 2, с. 510—514.
95. П о д и н о в с к и й В. В. Об относительной важности кри-
териев в многокритериальных задачах принятия решений. — В кн.:
Многокритериальные задачи принятия решений. — М.: Машинострое-
ние, 1978, с. 48—92.
96. Полак Э. Численные методы оптимизации. Единый под-
ход. — М.: Мир, 1974.
97. П о л я к Б. Т. Один общий метод решения экстремальных
задач. —ДАН СССР, 1967, т. 174, № 1, с. 33—36.
98. П о л я к Б. Т. Минимизация негладких функционалов. —
ЖВМ и МФ, 1969, т. 9, № 3, с. 509—521.
99. П о л я к Р. А К отысканию неподвижной точки одного клас-
са точечно-множественных отображений.—ДАН СССР, 1978, т. 242,
№ 6, с. 1252—1255.
100. П о л я к о в а Л. Н. Непрерывность нормальных конусов. —
Вести. ЛГУ, 1979, № 7, с. 112—113.
101. Полякова Л. Н. Минимизация одного класса недиффе-
ренцируемых функций. - В кн.: [123], с. 145 — 148.
ЛИТЕРАТУРА
381
102. П о н т р я г и и Л. С. и др. Математическая теория опти-
мальных процессов. — М.: Наука, 1961.
103. Пшеничный Б. Н. Необходимые условия экстремума.—
М.: Наука, 1969.
104. Пшеничный Б. Н. О необходимых условиях экстремума
для негладких функций. — Кибернетика, 1977, № 6, с. 92—96.
105. Пшеничный Б. Н., Данилин Ю. М. Численные ме-
тоды в экстремальных задачах. — М.: Наука, 1975.
106. Разумихин Б. С. Физические модели и методы теории
равновесия в программировании и экономике. — М.: Наука, 1975.
107. Растригин Л. А. Статистические методы поиска экстре-
мума. — М.: Наука, 1968.
108. Ремез Е. Я. Основы численных методов чебышевского
приближения. — Киев: Наукова думка, 1969.
109. Решетник Ю. Г. Обобщенные производные и дифферен-
цируемость почти всюду. — Матем. сб., 1978, т. 75, с. 323—334.
ПО. Рокафеллар Р. Выпуклый анализ. — М.: Мир, 1973.
111. Рубинов А. М. Сублинейные операторы и их приложе-
ния.— УМН, 1977, т. 33, вып. 4 (196), с. 113—174.
112. Рубинштейн Г. Ш. Конечномерные модели оптимиза-
ции. — Новосибирск: Изд-во Новосибирск, ун-та, 1970.
113. Рудин У. Основы математического анализа. — М.: Мир,
1966.
114. Се а Ж. Оптимизация. Теория и алгоритмы. — М.: Мир,
1973.
115. Смирнов В. И. Курс высшей математики, т. V. — М.:
Физматгиз, 1959.
116. Соте ко в А. И. Необходимые условия минимума для од-
ного класса негладких задач.— ДАН СССР, 1969, т. 189, №> 2,
с. 261—264.
117. С т р о н г и н Р. Г. Численные методы в многоэкстремальных
задачах. — М.: Наука, 1978.
118. Тарасов В. Н. Ускорение сходимости при решении не-
линейных минимаксных задач. — В кн.: [20], с. 76—81.
119. Т ы н я н с к и й Н. Т. Сопряженные вогнуто-выпуклые функ-
ции в линейных топологических пространствах и их седловые точ-
ки.— Матем. сб., 1969, т. 78 (120), № 4, с. 512—541.
120. Федоров В. В. Численные методы максимина. — М.: Нау-
ка, 1979.
121. Харди Г. Г., Литтльвуд Д. Е., Полна Г. Неравен-
ства. — М.: ИЛ, 1948.
122. Храмова Н. К. Некоторые обобщения метода секущих
плоскостей. — Вести. ЛГУ, 1979, № 7, с. 116—117. .
123. Численные методы нелинейного программирования: Тезисы
III Всесоюзного семинара. — Харьков, 1979.
124. Шепилов М. А. О методе обобщенного градиента оты-
скания абсолютного минимума выпуклой функции. — Кибернетика,
1976, № 4, с. 52—57.
125. Шор Н. 3. Применение метода градиентного спуска для
решения сетевой транспортной задачи. — В кн.: Материалы научн.
семинара по теоретическим и прикладным вопросам кибернетики и
382
ЛИТЕРАТУРА
исследования операций. — Киев: Институт кибернетики АН УССР,
1962, вып 1, с. 9—17.
126. Шор Н. 3. О классе почти-дифференцируемых функций и
одном методе минимизации функций этого класса. — Кибернетика,
197-2, № 4, с. 65—70.
127. Шор Н. 3. Методы минимизации недифференцируемых
функций и их приложения. — Киев: Наукова думка, 1979.
128. A u s 1 е и d е г A. Methodes et theoremes de dualite. — C. R.
Ac. Sci. Paris, 1968, v. 267, p. 1—4.
129. Auslender A. Optimization. Methodes numeriques.— Pa-
ris: Masson, 1976.
130. Auslender A. Differentiable stability in non convex and
nondifferentiable programming. — Math. Progr. Study, 1979, v. 10,
p. 29—41.
131. Bertsekas D. P. Nondifferentiable optimization via ap-
proximation. — In: [153], p. 1—25.
132. Bertsekas D. P., Mi t ter S. K. A descent numerical
method for optimization problems with nondifferentiable cost func-
tionals. — SIAM J. Control, 1973, v. 11, N 4, p. 637—652.
133. Clarke F. H. Generalized gradients and applications.—
Trans. Amer. Math. Soc., 1975, v. 205, p. 247—262.
134. Clarke F. H. A new approach to Lagrange multipliers.—
Mathematics of Oper. Research, 1976, v. 1, N 2, p. 165—174.
135. Cullum Jane, Donath W. E., Wolfe P. The minimi-
zation of certain nondifferentiable sums of eigenvalues of symmetric
matrices. — In: [153], p. 35—55.
136. Ekeland Ivar. Nonconvex minimization problems.—
Bull. Amer. Math. Soc., 1979, v. 1, N 3, p. 443—474.
137. Ekeland I., Valadier M. Representation of set-valued
functions. — J. Math. Anal. Appl., 1971, v. 35, p. 621—629.
138. Fen ch el W. On conjugate convex functions. — Canad. J.
Math., 1949, v. 1, p. 73—77.
139. Goldstein A. A. Optimization with corners. — In: Nonli-
near programming. — New York: Academic Press, Inc., 1975, v. 2,
p. 215—230.
140. Goldstein A. A. Optimization of Lipschitz continuous
functions. — Math. Programming, 1977, v. 13, p. 14—22.
141. Halkin H. Mathematical Programming without differenti-
ability. — In: Calculus of variations and control theory/Ed. D. L. Rus-
sel. — New York: Academic Press, 1976, p. 279—288.
142. Hiriart-Urruty J. B. On optimality conditions in non-
differentiable programming. — Math. Programming, 1978, v. 14,
p. 73—86.
143. Hogan W. W. Directional derivatives for extremal values
functions. — West. Manag. Sci. Inst., Working paper. — Los Angeles,
1971, N 177.
144. Hogan W. W. Point-to-set maps in mathematical program-
ming.— SIAM Review, 1973, v. 15, 591—603.
145. Hua rd P. Resolution of mathematical programming pro-
blems with nonlinear constraints by the method of centres. — In: Non-
linear programming/Ed. J. Abadie. — Amsterdam: North-Holland, 1967,
p. 206—219.
литература
383
146. Hua rd P. Optimization algorithms and point-to-set maps.—
Math. Programming, 1975, v. 8, p. 308—331.
147. Ioffe A. D. Necessary and sufficient conditions for a local
minimum. 1—3. — SIAM J. Control and Optimization, 1979, v. 17,
N 2, p. 245—288.
148. Kelley J. F. The cutting-plane method for solving convex
problems. — SIAM J. Appl. Math., 1960, v. 8, N 4, p. 703—712.
149. Lemarechal C. Note on an extension of Davidon methods
to nondifferentiable functions. — Math. Programming, 1974, v. 7, N 3,
p. 384—387.
150. Lemarechal C. An algorithm for minimizing convex func-
tions.— In: Proc. IFIP Congress-74. — Amsterdam, 1974, p. 552—556.
151. L e m a r e c h a 1 C. On extension of Davidon methods to
nondifferentiable problems. — In: [153], p. 95—109.
152. Mangasarian O. L. Pseudo-convex functions. — SIAM J.
Control, 1965, v. 3, N 3, p. 281—290.
153. Mathematical Programming Study 3. Non-differentiable optl-
mization/Eds. M. L. Balinski, P. Wolfe. — Amsterdam: North-Holland,
1975.
154. Mifflin R. Semismooth and semiconvex fuctions in con-
strained optimization. — SIAM J. Control and Optimization, 1977,
v. 15, N 6, p. 959—972.
155. Mifflin R. An algorithm for constrained optimization with
semismooth functions. RR-77-3, IIASA. — Laxenburg, Austria, 1977.
156. Moreau J. — J. — Fonctionelles sous-differentiables. — C. R.
Ac. Sci. Paris., 1963, v. 257, p. 4117—4119.
157. Moreau J.— J. Convexity and duality. — In: Functional
analysis and Optimization/Ed. E. R. Caiancello. — New York: Academic
Press, 1966, p. 145—169.
158. Neustadt L. W. A general theory of extremals. — J. Com-,
put System. Sci., 1969, v. 3, p. 57—92.
159. Neustadt L. W. Optimization: A theory of necessary con-
ditions. — Princeton, N. J.: Prinston Univ. Press. 1976.
160. Nonsmooth optimization Proceedings of a IIASA Workshop.
28 March —8 April 1977/Eds. C. Lemarechal, R. Mifflin — Oxford:
Pergamon Press, 1978.
161. Osborne M. R., Watson G. A. An algorithm for mini-
max approximation in the non-linear case. — Comput. J., 1969, v. 12,
N 1, p. 63—68.
162. Robinson S. M., Meyer R. R. Lower semicontinuity of
multivalued linearization mappings. — SIAM J. on Control, 1973, v. 11,
N 3, p. 525—533.
163. Robinson S. M. First-order conditions for general non-
linear optimization. — SIAM J. on AppL Math., 1976, v. 30, p. 597—
603.
164. Rockafellar R. T. Augmented Lagrangian multiplier
rule and duality in nonconvex programming. — SIAM J. Control and
Optimization, 1974, v. 12, N 2, p. 268—285.
165. R о с к a f e 11 a r R. T. The theory of subgradients and its
applications to problems of optimization. — Lecture Notes, Univ, of
Montreal. — Montreal, 1978.
384 ЛИТЕРАТУРА
166. Vai a diet М. Sous-differentiels d’une borne superieure et
d’une somme continue de fonctions convexes. — C. R. Ac. Sci. Paris,
1969, t. 268, p. 39—42.
167. W arg a J. Necessary conditions without differentiability
assumptions in optimal control. — J. Diff. Equations, 1975, v. 18,
p. 41—62.
168. Warga J. Derivative containers, inverse functions and con-
trollability. — Calculus of Variations and Control Theory, 1976,
p. 13—45.
169. Weiss E. A. Konjugierte Funktionen. — Arch. Math., 1969,
Bd. XX, S. 538—545.
170. Wolfe P. Note on a method of conjugate subgradients for
minimizing nondifferentiable functions. — Math. Programming, 1974,
v. 7, N 3, p. 380—383.
171. Wolfe P. A method of conjugate subgradients for minimi-
zing nondifferentiable functions. — In: [153], p. 145—173.
172. Wolfe P. Convergence theory in nonlinear programming.—
In: Integrer and nonlinear programming/Ed. J. Abadie. — Amsterdam:
North-Holland, 1970, p. 1—36.
2 р. 10 к.
2Р- Юк