Л.А.КАЛУЖНИН, В.И.СУЩАНСКИИ
ПРЕОБРАЗОВАНИЯ
И ПЕРЕСТАНОВКИ

22.141
K17
Калужнин Л. А., Суданский В. И.
К17 Преобразования и перестановки: пер с укр.-М. Наука. Главная
редакция физико-математической литературы» 1979» 34 илл., 112 с
В книге рассматриваются важные частные виды отображений —
преобразования и перестановки конечных множеств Детально изу-
изучаются свойства операции суперпозиции функций применительно
к преобразованиям и перестановкам, вводятся понятия группы пере-
перестановок и полугруппы преобразований. Рассказывается о простейших
применениях теории групп для решения комбинатор!
перечисление, классификации многочленов со многими
исследования корней уравнений высших степеней, мат
анализа игры «в пятнадцать»
Книга может быть использована как для само
изучения учащимися старших классов средних школ, так
в качестве основы факультативного курса
к ъЁвяг •"*17О2в30в9в
Лее Аркадьевич Калужнин, Виталий Иванович Сущанский
ПРЕОБРАЗОВАНИЯ И ПЕРЕСТАНОВКИ
М, 1979 iv 112 стр с илл
Редакторы А И Фалин, М М Горячая
Техн редактор Н В'Вершинина
Корректор Л С Сомова
ИБ № 11456
Сдано в набор 0204 79 Подписано к печати 29 1079 Т-17ДО Бумага 84 х КЮ'/зз» тип № 3
Гарнитура Тайме
Высокая печать.
Условн печ л 5,88
Уч-изд. л 5,92
Тираж 125 000 экз Заказ № 585* Цена книги 20 коп
Издательство «Наука»
нматематическ
, Ленинский проспект, 15
Главная редакция физико-математической литературы
117071, Москва, В-71, Г
Ордена Октябрьской Революции, ордена Трудового Красного Знамени Ленинградское
производственно-техническое объединение «(Печатный Двор» имени А М Горького «Союз-
полиграфпрома» при Государственном комитете СССР во делам издательств, полиграфии
и книжной торговли 197136, Ленинград, П-136, Чкаловский пр, 15
© Главная редакция
физико-математической
литературы
20202 — 173 издательства «Наука»,
К У 2vL79 86-79 1702030000 1^вод с Украинского,

ПРЕДИСЛОВИЕ К РУССКОМУ ПЕРЕВОДУ
Цель книги — ознакомить учащихся с началами тео-
рил групп. Понятие группы нашло широкое приме-
дение в современной математике, а также в ядерной
физике, кристаллографии, теории относительности и
I*. д. Математическая глубина и необычайно широкая
сфера применений теории групп сочетаются с простотой
ее основных положений — цонятие группы, целый ряд
й&жных теорем можно сформулировать и доказать,
обладая начальными представлениями в области теории
множеств. Поэтому теория групп как нельзя лучше
цодхо дит для того, чтобы показать школьникам образец
довременной математической теории.
Из педагогических соображений при этом важно
избегать крайней степени абстракции и общности.
Кроме того, цонятие группы будет в достаточной
Мере оправдано, только если применения его будут
разнообразны и интересны. Именно поэтому теоретико-
*#удповые понятия и результаты в книге излагаются
Ь рамках теории групп перестановок конечных множеств.
Этот подход имеет еще и то преимущество, что посто-
постоянная работа с отображениями конечных множеств
позволяет лучше усвоить центральные в современном
курсе школьной математики понятия множества и
функции.
В процессе написания книги авторы использовали
опыт изложения основ теории групп школьникам на
кружках и факультативных занятиях в республиканской
з

физико-математической школе при Киевском универси-
университете.
Текст предлагаемого перевода отличается от украин-
украинского оригинала тем, что в нем существенно расширен
материал, касающийся приложений групп перестановок.
Добавлены новые параграфы «Группы симметрии»,
«Теорема Лагранжа», «Орбиты группы перестановок.
Лемма Бернсайда» и «Комбинаторные задачи». Пере-
Переработан параграф о решении уравнений в радикалах.
Добавлен ряд задач, сводящихся к вычислениям с
перестановками
Авторы искренне признательны Г. И. Фалину, кото-
который в процессе работы над переводом улучшил и до-
дополнил ряд примеров и доказательств, исправил
некоторые неточности и опечатки, имевшиеся в украин*
ском издании.
Киев, 1978 г. Л. А. Калужшп
В. И. Сущанский

§ 1. СУПЕРПОЗИЦИЯ ФУНКЦИЙ
Действие (или, иначе, операция) суперпозиции функций
имеет ряд интересных свойств и много важных применений.
Напомним определение и простейшие свойства суперпозиции
для функций действительной переменной (функций, области
определения и множества значений которых являются под-
подмножествами множества действительных чисел).
Пусть /(х) и д(х) — произвольные функции действитель-
действительной переменной. Суперпозицией этих функций (именно
в том порядке» в котором они записаны) называется такая
функция h(x), что:
а) область определения h(x) образована теми числами
х0 из области определения функции /(х), для которых /(х0)
принадлежит области определения функции д(х);
б) значение функции п(х) в какой угодно точке х0 из
области ее определения связано со значениями f(x) и д(х)
равенством
Таким образом, чтобы найти значение функции h(x) в
точке х0, нужно найти/(хо) = у09 а затем д(у0). Число д(уо)
и есть значение функции h(x) в точке х0.
Если функция- и(х) в точке х0 принимает значение и09 то
это будем изображать так:
X0 iU(X0) = U0.
Читается такая схема одним из следующих способов:
«функция и (х) в точке х0 принимает значение м0», «функция и (х)
точке х0 ставит в соответствие точку и0», «точка и0 является
образом точки х0 под действием функции м(х)». Для суперпо-
суперпозиции h(x) функций у^Дх) и z — g(x) такая схема будет
5

иметь вид
/ 9
I * Т
(если функция /(х) точк^е х0 ставит в соответствие точку
Уо» а фУнкЦия #(х) точке у0 — точку z0, то функция h(x)
точке х0 ставит в соответствие точку z0).
Пример. Пусть f(x) — х2, д (х) = sin x. Чтобы найти значение
суперпозиции h(x) этих функций в некоторой точке х0, нужно
возвести х0 в квадрат,
v _JL v _ Х2
Ло * У о — -Х-о»
и найти значение д(х) в тoчкe^>'0:
Объединяя эти две схемы, получаем
д
—->
Хо —:-> у0 = Xq
Таким образом, функция h (x) каждой точке х0 ставит в соответствие
число sin(xo), т. е. h(x) можно задать формулой
Рассмотрим теперь суперпозицию fei(x) функций д(х) =
= sin х и f(x) = х2, т. е. суперпозицию тех же самых функций,
но в обратном порядке. Получим
sin . . (. .J , • ч2
х0 —> sin х0 > (sin х0)
L 1. j
Это означает, что суперпозиция функций д (х) = sin х и/(х) = х2
есть функция
hx (х) = (sin хJ = sin2 х.
Таким образом, сур ер позиция функций зави-
зависит от порядка, в котором записаны функции.
Будем обозначать суперпозицию функций у =/(х) и
z = g(x) так: {f*g)(x), т. е.
L f°9
Следовательно,

Особую роль относительно операции суперпозиции играет
функция у = х, которую будем обозначать е{х). Схема этой
функции такая: е
Xq ~+ Xq
каждого числа Xq. Очевидно, для какой угодно функции
у а? Дх) выполняются равенства
или схематично
> Уб /(*) > У х^ х0
Т L
J
Дадим отдельное обозначение и для функции у = - х,
а именно: е'(х).
Мы будем рассматривать множества функций, которые
имеют следующее свойство:
Если функции /(х) и # (х) принадлежат заданному мно-
множеству функций, то и суперпозиция {f°g)(x) этих функций
Также принадлежит этому множеству.
О таком множестве говорят, что оно замкнуто относи-
относительно действия суперпозиции функции или, иначе, что супер-
погиция является внутренним действием для такого множе-
множества.
Найдем, например, суперпозицию двух линейных функций.
Пусть/(х) = 2х + 5, #(х) = Зх + 1. Для произвольного числа
Хо имеем
х0—^2хо + 5 = уо—^-3 Уо + 1 =3Bхо + 5)+ 1,
т. е.
Хо-^ 3Bх0 + 5) +Л = 6х0 + 16,
$ следовательно, {f о д)(х) = 6х + 16. Отсюда суперпозиция двух
заданных линейных функций снова есть линейная функция.
Легко доказать, что это верно и в общем случае:
<?сли/(х) = ах + b,ag(x) = сх + d, ro{f°g)(x) = c{ax + b) +d =
#• асх + Ьс + d = axx + Ьь т. е. снова функция линейная. При
Этом коэффициенты этой функции выражаются через коэф-
коэффициенты /(х) и g (x) с помощью равенств
«j = ас, bx = be + ^.
' Следовательно, множество всех динейных функций вместе
С каждыми двумя функциями содержит и их суперпозицию,
.у. е. суперпозиция является внутренним действием для мнд-
*жества всех линейных функций.
1

Результат суперпозиции для линейных функций также
зависит, вообще говоря, от порядка их написания. Напри-
Например, еслиДх) = 2х + 3, а д(х) == Зх + 2, то (f°g)(x) есть функ-
функция alx + bl, причем ах —2-3 = 6, bj =3-3 + 2 = 11,
a (goj)(x) - это фушадая а2х + Ь2, где а2 =* 3-2 = 6, Ь2 =
= 2-2 + 3 = 7. Следовательно, (/"°0)(х) = 6х + 11, а (?о/)(х) ч*
= 6х + 7, т. е. для заданных функций {f°g){x) ф (g°f}(x).
Другим примером'множества функций, замкнутого отно-
относительно взятия суперпозиции, есть множество всех много-
многочленов вида
~аохп + аххп~1 +... + ап_& + ап
с целыми коэффициентами. Действительно, пусть
f(x) = С0Х* + С^" 1 + . . . + Ск- jX + Сь
g(x)=boxm + blXm+l + ... +bm_1x + ^т
— два таких многочлена. Тогда суперпозицией (f°g){x), как
легко убедиться, является такое выражение:
+ bt (cox* + CtX*""J + ... + ck)m~l + ... + bm.
Это есть многочлен степени тк, который имеет вид
doxmk + ^у**~ 1 + ... + 4а_ jX + J^,
где коэффициенты d0, dly..., #mk выражаются определенным
способом через коэффдщиенты/(х) и #(х).
Общее правило для нахождения чисел d0, du ..., d^ no
известным коэффициентам с0, ..., сь Ьо, ..., Ьт довольно
громоздкое, но в каждом конкретном случае коэффициен-
коэффициенты d{ удается вычислить без особых трудностей. Например»
пусть
Дх) = х2 + 2х + 2, д(х) = 2х2 + х + 2.
Тогда
tfog){x) « 2(х2 + 2х + 2J + (х2 + 2х + 2) + 2 =
-2х4 + 8х3 + 17х2 + 18х+ 12;
ig*j)(x) = Bх2 + х + 2J + 2Bх2 + х + 2) + 2 =
= 4х4 + 4х3 + 13х2 + 6х + 10 Ф tf°g)(x).
В рассмотренных прцмерах множества функций, замкну-
замкнутые относительно суперпозиции, были бесконечныг'Однако
это условие не является необходимым для замкнутости. Для
множества, которое состоит тшь из двух функций у = х и
8

¦» — #, которые мы обозначили е(х) Ш е'{х), суперпозиция
будет етутреюнйй действием. Действительно,
Г. е. условие замкнутости выполняется
Даже ш приведенных примеров видно, что множества» для
которых суперпозиция является внутренним действием, MorjT
быть очень разными. Далее мы рассмотрим строение таких
множеств для функций, определенных на конечных мно-
множествах.
УПРАЖНЕНИЯ
1. Найти суперпозиции tf°g){x) и (g°j)[x), где у = Дх) и
у <* д(х) — соответственно функции:
а) у-*= 2х + -3, у =5 3-х + 4;
бK 52 23
" ! Зх+2' '- х-Г
2. Будут ли замкнуты относительно взятия суперпозиций-:
множества функций.
а) множества всех функций вида у = лх, где а — произвольное
действительное число;'
б) множество всех функций вида у = х + а, где а — произвольное
рациональное число;
в) множество функций у =* х, у = 1/х, у = — 1/х, у = — х, каждая
ш которых рассматривается на множестве всех действительных
чисел без нуля;
г) множество многочленов степени-не выше чем 3;
д) Множество функций у — у~—, у — ~* ,:,.t ^ 3 i - х, >?=»-,
i х х х
| 2. ПРЕОБРАЗОВАНИЯ
Как известно, отображением множества А в мно~
жество В называется соответствие, по которому каждому
шменту множества А сопоставляется однозначно окре*
деленный элемент множества В; этот элемент Ъ называ-
называется образом элемента а; элемент а9 в свою очередь,
называется прообразом элемента Ь.
9

Отображения одного множества в другое обозначаются
маленькими буквами греческого алфавита. Если задано ото-
отображение ф множества А в множество В, то это обозначается
при письме одним из способов:
<р: А >В, А-^-*В.
Образ элемента а е А при отображении ф будем обозначать
так: (а)ц> (знак отображения будем записывать справа
от символа элемента).
Отображение одного множества в другое можно задавать
описательно, указывая правило, по которому каждому эле-
элементу какого-то множества А ставится в соответствие его
образ из множества В, а также с помощью таблиц,
графиков, стрелочных схем.
Остановимся на указанных способах задания отображений
произвольных множеств (как числовых, так и нечисловых).
Строя таблицу отображения ф: Л->Б, в нее записывают
все возможные пары вида {а, (я)ф), аеА:
X
(Х)ф
<-.)ф
а2
Ыф
ап
(«„)ф
Такая таблица полностью задает отображение лишь тогда,
когда множество А конечно и исчерпывается элементами
аи а2,...,ап.
Построение графиков отображений нечисловых множеств
А, В несколько отличается от построения графиков числовых
функций, с которым читатель хорошо знаком. Оно осущест-
осуществляется так. Проводят два взаимно перпендикулярных луча,
которые выходят из одной точки, — «оси координат». На
горизонтальном луче произвольным способом (например,
через одинаковые промежутки) отмечают точки, которые
отвечают элементам множества А, а на вертикальном —
точки, которые отвечают элементам множества В. Через эти
точки проводят соответственно вертикальные и горизонталь-
горизонтальные прямые, которые образуют прямоугольную сетку. Чтобы
построить график отображения ф: А-+ Б, нужно поставить
точки в тех вершинах сетки, «координатами» которых
являются всевозможные пары вида (а, (а) ф), где а — произ-
произвольный элемент множества А.
10

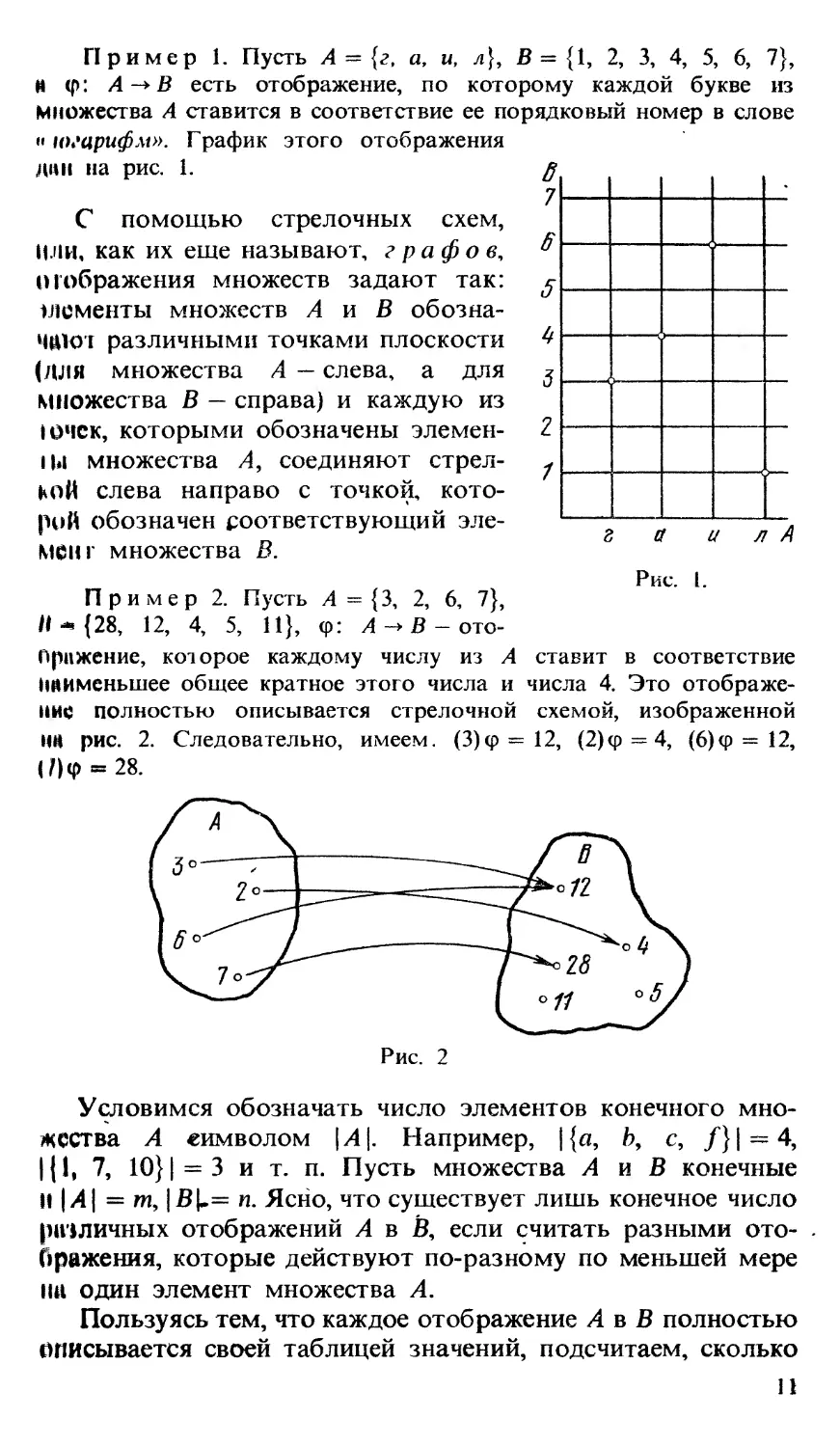
Пример 1. Пусть А = {г, а, и, л), В = {1, 2, 3, 4, 5, 6, 7},
И (р: А-* В есть отображение, по которому каждой букве из
множества А ставится в соответствие ее порядковый номер в слове
«шгарифм». График этого отображения
Hun на рис. 1.
С помощью стрелочных схем,
ИДИ, как их еще называют, графов,
отображения множеств задают так:
элементы множеств А и В обозна-
обозначают различными точками плоскости
(для множества А — слева, а для
множества В — справа) и каждую из
ючск, которыми обозначены элемен-
IM множества А, соединяют стрел-
стрелкой слева направо с точкой, кото-
которой обозначен соответствующий эле-
элемент множества В.
а
Рис. I.
и
л А
Пример 2. Пусть А = {3, 2, 6, 7},
II ¦* {28, 12, 4, 5, 11}, <р: А -> В - ото-
Прцжение, которое каждому числу из А ставит в соответствие
Наименьшее общее кратное этого числа и числа 4. Это отображе-
отображение полностью описывается стрелочной схемой, изображенной
Hit рис. 2. Следовательно, имеем. C)(р = 12, B)ф=4, F)ф = 12,
Рис. 2
Условимся обозначать число элементов конечного мно-
множества А символом \А\. Например, \{а, Ь, с, /}| = 4,
|{1, 7, 10} | = 3 и т. п. Пусть множества А и В конечные
И |Л| = т, |В|*= п. Ясно, что существует лишь конечное число
рмличных отображений А в В, если считать разными ото-
Ьражения, которые действуют по-разному по меньшей мере
па один элемент множества А.
Пользуясь тем, что каждое отображение А в В полностью
описывается своей таблицей значений, подсчитаем, сколько
11

именно существует разных отображений множества А в мно-
множество В.
Обозначим элементы множества А символами аи а2, ...
..., ат. Тогда таблицу каждого отображения А в В можно
будет записать так:
«1
ь,
а2
Ъг
ьп
где bu bl9 ..., bm — обозначения некоторых, не обязательно
разных элементов множества В. Верхний ряд таблицы оди-
одинаков для всех отображений А в В, а нижний — меняется,
потому что разным отображениям отвечают разные -таблицы.
При этом разньдх отображений А в В будет столько,
сколькими разными способами можно заполнить второй ряд
рассмотренной таблицы. В каждую клетку второго ряда
таблицы можно записать обозначение какого угодйо элемента
множества В. Таким образом, каждую из т клеток нижнего
ряда таблицы отображения можно заполнить п разными
способами независимо от способа заполнения других клеток.
А это означает, что в таблице отображения можно образо-
образовать всего m
. п-п-... • п = п
разных нижних рядов. Следовательно, существует пт разных
отображений А в В.
Выделяется и отдельно изучается несколько важных
классов отображений одного множества в другое.
1. Отображение на. Отображение ср: А-*В называется
отображением на все множество В или сюръек-
цией, если для каждого элемента be В найдется такой
элемент ае А, что (а) (р = Ъ.
Примеры. 3. Пусть А — R, В —*R+ есть соответственно
множество всех действительных и множество всех положительных
действительных чисел. Зададим отображение <р: R-+R+, положив
(х) ф = х2 для каждого х е R. <р будет сюръекцией, потому что для
каждого числа yeR+ существует по меньшей мере одно число
xeR такое, что (х)<р = у. Достаточно положить х = уу. Даже
больше, для каждого yeR* существует точно два прообраза:
]/у, -]/у-
4. Пусть А = Г— множество всех прямоугольных треугольников
на плоскости, B = R+. Определим. отображение <р: T-*R+ так:
12

поставим в соответствие каждому прямоугольному треугольнику
Hi T число, которое является его площадью при фиксированной
единице измерения, ф есть сюръекция, так как для произвольного
%щЯ* существует прямоугольный треугольник (с катетами
ух й 2j/x), который имеет площадь х. Существует даже беско-
бесконечно много прямоугольных треугольников, которые имеют площадь
* (например, треугольники с катетами ]/х/к, 2кух, к — 1, 2, 3, ...).
Следовательно, тут каждый элемент xeR+ имеет бесконечно много
прообразов.
5. Пусть S — множество трехзначных простых чисел, a L—
Множество цифр. Отображение <р: S -> L определим так: поставим
t соответствие каждому трехзначному простому числу его вторую
Цифру. Например;
A79)ф = 7, (821)ф = 2, (907) ф = 0.
. Непосредственной проверкой убеждаемся, что ф — сюръекция,
Т. 0. для каждой цифры найдется трехзначное простое число, в
котором эта цифра стоит посередине. Тут множества S и L
конечны, и для каждого элемента из L существует лишь конечное
число элементов из S, которые на него отображаются.
Если множества А и В конечны и ф: А -> В есть сюръ-
сюръекция, то в нижнем ряду ее таблицы встречаются все элементы
И'1 В. Йа каждой горизонтальной прямой графика сюрьекции
обязательно есть обозначение вершины сетки. На стрелочной
схеме сюръекции в каждую точку, которая обозначает
элемент множества В, входит по меньшей мере одна стрелка.
Сюръекция конечного множества А на /множество В
существует не всегда. Очевидно, для этого необходимо, чтобы
множество В также было конечно и выполнялось нера-
нсиство \А\ > \В\. ~ 0
2. Взаимно однозначное отображение. Отображение
ф: А-* В называется взаимно однозначным или
инъекцией, если разные элементы множества А перевод ят-
сн этим отображением в разные элементы множества В:
для каждых хи х2еА из ххФх2 вытекает (х1)ф^(х2)ф.
П р и м е р ы. 6. Отображение <р множества целых чисел Z в мно-
множество всех четных чисел 2Z определим так: положим (z)<p = 6z
для каждого zeZ. Это отображение — инъекция, так' как из
ft j* z2 вытекает bzx Ф 6z2.
7. Пусть А — множество всевозможных двухэлементных под-
подмножеств множества действительных чисел R, В — множество
приведенных квадратных уравнений. Каждому элементу {а, Ь} мно-
множества А поставим в соответствие уравнение из В, для которого
числа а, Ъ являются корнями. Как вытекает из теоремы Виета, такое
отображение будет инъективным.
13

В нижнем ряду таблицы инъективного отображения
Ф: А-> В в отличие от таблиц произвольных отображений,
каждый элемент множества В встречается лишь один раз.
Следовательно, на каждой горизонтальной прямой графика
инъекции обозначено не более одной вершины сетки, а при
стрелочном изображении инъекпии в каждую точку, которой
обозначается элемент множества В, входит не более чем
одна стрелка.
Если множества А и В конечны и существует инъекция
множества А в множество В, то, очевидно, должно выпол-
выполняться неравенство
3. Взаимно однозначное отображение на. Если отображение
Ф множества А в множество В является одновременно
инъективным и сюръективным, то оно называется взаимно
однозначным отображением множества А
на множество В или биекцией А на В.
Примеры. 8. Пусть А — В — П — множество точек плоскости.
Тогда биекцией является каждое из следующих известных из
школьного курса геометрии отображений множества П на себя:
симметрия относительно фиксированной точки, симметрия относи-
относительно фиксированной прямой, параллельный перенос, поворот
вокруг фиксированной точки, гомотетия.
9. Отображение q>: х-+2х, где xeZ, есть, очевидно, биекция
множества Z на множество 2Z четных чисел.
Если существует биекция конечного множества А на
конечное множество В, то должны выполняться неравенства
|^4|^|Б|и|у4|^|Б|. Следовательно, для конечных множеств
А и В биекции А на В существуют тогда и только тогда,
когда выполняется равенство \А\ = \В\.
Подсчитаем, сколько существует разных биекции мно-
множества А = {аи а2, ..., ап) на множество В = {Ьи Ь2, ..., Ь„}.
Каждая биекция ср: А-+В полностью описывается своей
таблицей:
X
ь.
а2
Ь2
о»
К
Верхний ряд таблицы не меняется, а в нижнем ряду могут
стоять произвольно размещенные обозначения элементов
множества В, причем обязательно разных. Следовательно,
14

первое (например, слева) место нижнего ряда таблицы можно
1*полнить п разными способами. Если первое место уже
Шнолнено, то независимо от того, каким элементом оно
Шполнено, на второе место можно поставить обозначение
какого угодно из тех элементов множества В, которые
остались. Аналогично третью клетку, независимо от того,
какие элементы поставлены в первые две клетки, можно
шполнить п — 2 способами и т. д. Для предпоследнего
моста остаются лишь две возможности его заполнения, а для
последнего — только одна. Поскольку каждая клетка заполня-
заполняется независимо от остальных, существует
п(п~ 1)(л-2)...2-1 =п\
разных способов одновременного заполнения клеток. Следова-
Следовательно, можно составить п\ разных таких таблиц, т. е. су-
существует п\ разных биекций А на В.
Очень часто приходится рассматривать отображения
некоторого множества М в себя. Такие отображения назы-
называются еще преобразованиями множества М. Читателю
морошо известны, например, разные типы геометрических
Преобразований, которые уже упоминались в примере 8.
Для преобразований произвольного множества также
можно рассмотреть введенные выше классы отображений:
инъекции, биекций и сюръекции. Но для конечных множеств,
ки? легко понять, эти три класса преобразований совпадают,
г. е. каждая инъекция конечного множества в себя будет
также и сюръекцией, а каждая сюръекция есть одновременно
и инъекция. А поэтому для конечных множеств выделяется
лишь класс биективных преобразований.
Изучая преобразования произвольного конечного множе-
множества, удобно придерживаться определенных стандартных
обозначений. Природа элементов множества М при изучении
©го преобразований несущественна. Следовательно, мы
можем занумеровать все элементы множества М и опериро-
оперировать не с самими элементами, а с их номерами. Поэтому,
рассматривая преобразования конечных множеств, мы будем
япредь иметь в виду множество
М = {1, 2, 3, .... п}
первых п натуральных чисел.
Задавая преобразования таблицами, будем записывать их в
таком упрощенном виде:
А 2 3 ...в\
\ai az a3 ... aj

Ясно, что такое обозначение однозначно характеризует преоб-
преобразование и не вызывает недоразумений. Например, если
М = {1, 2, 3, 4, 5}, то:
а) А 2 3 4 5\. б) Л 2 3 4 з\. в) Л 2 3 4 5\
\2 2 4 2 5/' \3 2 1 5 4/' \5 4 3 2 1/
есть таблицы разных преобразований на множестве М.
Читать такую таблицу, например^), следует так:
«Преобразование <р, заданное таблицей а),
1 переводит в 2,
2 переводит в 2,
3 переводит в 4,
4 переводит в 2,
5 переводит в 5».
Порядок записи элементов верхнего ряда такой таблицы
не существен. Например, преобразование, заданное таблицей
б), можно обозначить также таблицами:
(l 1 3 4 5\ E 4 1 2 3\ Л 3 2 5 4\
V2 3 1 5 4/' \4 5 3 2 1/' \3 1 2 4 5/
Поскольку каждое преобразование конечного множества
полностью описывается своей таблицей, мы часто будем
обозначать одинаковыми символами само преобразование и
его таблицу.
Некоторые преобразования множества М имеют специ-
специальные названия.
а)-Тождественное преобразование. Это пре-
преобразование е, которое все элементы из М оставляет на месте,
т. е. (а)г = а для каждого аеМ. Если М — конечное мно-
множество, это преобразование будет иметь таблицу
Л 2 3 ... п-1 п\
\1 2 3 ... n-i и/
б) Постоянное преобразование. Преобразова-
Преобразование называется постоянным, если оно каждому эле-
элементу из М ставит в соответствие некоторый фиксиро-
фиксированный элемент этого множества. Если М — конечное
множество, постоянное преобразование характеризуется таб-
таблицей вида
(l 23 ... п-1 п\
\а а а ... а а;

V) Перестановки. Перестановкой будем на-
Шштъ биекцию конечного множества на себя. Следо-
РАТёЛЬНО, ф есть перестановка на М тогда ц только тогда,
НОГД& для произвольных элементов а, ЪеМ, аФЪ, имеем
(и) ф ф (Ь) ф. А это означает, что перестановка определяется
i aft Лицей вида
е2 3 ...п-1
« а2 аъ ... «„_!
М$ Л|> в^, ..., «и - разные элементы из М.
УПРАЖНЕНИЯ
1. Построить графики и стрелочные схемы для отображений
множества {1, 2, 3, 4, 5} в множество {а, Ь, с, d), заданных
ткнми таблицами:
а) А 2 3 4 sY б) А 2 3 4 5Y в) А 2 3 4 5\
\а Ъ с Ъ а) \с а а с а/ \а Ъ а Ъ с)
2. Пусть А и В — конечные множества, причем \А] = т, |В| = п.
i колысо существует разных инъекций множества Л в множест-
йн 0?
3. Пользуясь решением предыдущего упражнения, найти, сколь-
Hi существует • m-элементных подмножеств множества из п эле-
элементов.
4. Будет ли сюръекцией отображение ф: S -* L из множества
I «ШОВ русского языка в множество L букв русского алфавита,
которое каждому слову ставит в соответствие его первую букву?
5. Какие свойства отличают графики и стрелочные схемы
Аиекций от графиков и стрелочных схем произвольных отображе-
отображений?
6. Сколькими способами можно расположить п одноцветных
лчлей на шахматной доске с п2 клетками так, чтобы никакие
лие из них не били друг друга?
7. Сколько существует разных перестановок на множестве
ht т {1, 2, 3, 4, 5}, которые ни один элемент из М не оставляют
на месте (т. е. для таких перестановок <р имеем (а) ф ф?. для
каждого деМ)?
8. Сколькими способами можно расположить на шахматной
доске 8 одноцветных ладей так, чтобы никакая из них: не стояла
!Ш белой диагонали и никакие две не били друг друга?
9. Сколько можно составить разных шестизначных чисел из
цифр 0, 1, 2, 3, 4, 7, 9?
10. Сколько существует разных перестановок ф на множестве
A, 2, 3, ..., и}, для которых A)ф - B)ф > 1?
11. Доказать, что при п ^ 4 существует перестановка
*оства М = {1, 2, ..., и}, для которой при любых i
Нйстся условие \(i)q> -(/)<Pl = U ~j\-

12. Доказать, что при п ^ 4 существует размещение и одноцвет-
одноцветных ферзей на шахматной доске с п2 клетками, при котором ника-
никакие 2 ферзя не бьют друг друга.
13. Сколькими способами можно разместить 8 одноцветных
ферзей на шахматной доске так, чтобы никакие 2 из них не били друг
друга?
§ 3. УМНОЖЕНИЕ ПРЕОБРАЗОВАНИЙ
В § 1 мы рассмотрели действие образования суперпо-
суперпозиции функций, заданных на множестве действительных
чисел. Аналогично можно строить новое преобразование
по двум данным и для произвольных множеств.
Пусть М — произвольное множество, ф и \|/ — некоторые
преобразования этого множества. Произведением
преобразований ф, \|/ называется такое преобразование со
множества М, которое на каждый элемент аеМ действует
так:
т. е. чтобы найти образ произвольного элемента аеМ под
действием преобразования со, нужно сначала найти образ Ъ
элемента а под действием преобразования ф, а потом — образ
с элемента Ъ под действием преобразования \|/. Элемент с и
есть образ элемента а под действием преобразования со.
На языке стрелочных схем действие преобразования со на
элемент аеМ можно выразить так:
1 * Т
Произведение преобразований <р, \|/ будем обозначать далее
через фо\|/.
Примеры. 1. Пусть М — множество людей, которые когда-
либо жили на Земле, ф — преобразование множества М, которое
каждому человеку ставит в соответствие его отца, а \(/ — преобра-
преобразование множества М, которое каждому человеку ставит в соот-
соответствие его мать. Тогда
а) ф о \|/ — преобразование множества М, которое каждому чело-
человеку ставит в соответствие бабушку по отцовской линии;
б) ф о ф - преобразование множества М, которое каждому чело-
- веку ставит в соответствие дедушку по отцовской линии;
в) ^° ф - преобразование множества М, которое каждому че-
человеку ¦^гадйт^соответствие его дедушку по материнской линии;

(В)(фо<р)
\) фоф — преобразование множества М, которое каждому чело-
человеку ставит в соответствие его бабушку по материнской линии.
2. Пусть М = П — множество точек плоскости, ф — поворот
Ншодости вокруг фиксированной точки О на угол тс/2 по часовой
нр#лке, а \|/— поворот плоскости
Httipyr точки на угол 2тс/3 против
чт имой стрелки. Тогда и ф ° ф и
ф а Ф — поворот на угол я/6 против
жижой стрелки (рис. 3).
3. Пусть ф: х-*х + 3- преоб-
|пИ(»ипние множества действитель-
действительным чисел R, которое числу х ста-
вн» W соответствие число х + 3,
а ф: х->х + 2 — преобразование
мню множества, которое каждое
ЧН1ЛО х переводит в число х + 2. Тогда ф ° ф = ф °ф — преобра-
которое каждое число х переводит в число х + 5 (рис. 4).
Очень легко находить произведения двух преобразований,
1ЙЦШШЫХ стрелочными схемами. Поясним это на примере.
Пусть ф и \|/ — преобразования множества М = {а, Ь, с, d9 1},
и (блочные схемы которых изображены на рис. 5. Чтобы
Я7 Ф
Рис. 5.
•
настроить стрелочную схему преобразо-
иания фо\(/, нужно соединить стрелками те точки правой
чаети стрелочной схемы ф и левой части стрелочной схемы \[/,
которые обозначают одинаковые элементы из М (на рис. 5
ми стрелки изображены пунктирными линиями). Получаем
единую схему, по которой образ произвольного элемента
19

из М при преобразовании ф ° ф находим так: из каждой точки
левой части стрелочной схемы преобразования ф проходим
вдоль стрелок до соответствующей точки правой части стре-
стрелочной схемы преобразования \|/.
Будем иметь
Следовательно, преобразование фо\|^ имеет стрелочную
схему, изображенную на рис. 6.
Таблицу произведения
перестановок
i «2
Vi 72 Уз ••• Л/
Рис. 6. находят по такому удобному пра-
правилу:
а) переставляют столбцы в таблице \|/ так, чтобы ее
верхний ряд совпадал с нижним рядом таблицы ф, и
получают
ф' = Ml «2 «3 • • ht \ .
\ki к2 къ ... kj9
б) строят новую таблицу, первым рядом которой явля-
является первый ряд таблицы ф, а вторым — второй ряд
таблицы \|/.
Построенная таблица и будет таблицей преобразования
Ф ° \j/.
Пример 4. Пусть
Имеем
А 23 45б\ +1А 23 4 5б\
\3 4 1 6 2 5/ \6 5 4 3 2 1/
,Л 2 3 ^5 6Vf 1 2 3 4 5
\3 4 1 6 2 5/ \6 5 4 3 2
= /1 2 3 4 5 б\/3 4 1 6 2 5\ Л 2 3 4 5 б\
\3 4 1 6 2 5/Д4 3 6 15 2/ \4 3 6 1 5 2/
В предыдущем параграфе были рассмотрены три класса
преобразований произвольного множества: инъекции, сюръ-
екции и биекции. Оказывается, что каждый из этих классов
20

у относительно действия умножения преобразований,
т $ч произведение инъекций снова инъекция, произведение
— сюръекция и, наконец, произведение биекций —
нЦЫА*
Действительно, пусть преобразования ср и \|/ являются
ННАКЦИЯМИ множества М в себя и со = ф°\|/. Тогда для
пары элементов а, ЬеМ, а Ф Ь, будем иметь:
Подействуем преобразованием со на элементы а и Ь. Па
произведения преобразований имеем
(Ь)со =
i #it^ «1 * (а)ф, bi = (Ь)ф. Поскольку ф — инъекция, то
<ii f* Ь|* В свою очередь, поскольку \|/ — инъекция, имеем:
I11! )Ф f* (bi)^. Значит, для каждой пары а,ЪеМ9аф Ь, имеем:
и) to Ф (Ь)со и со является инъекцией.
Пусть теперь преобразования ф и \|/ сюръективны. Убе-
нимбЯ, что для каждого элемента аеМ найдется такой элемент
ЬфМщ для которого (Ь)со = я. Поскольку v|/— сюръекция,
найдется такой элемент сеМ, что (с)\|/ = а, а из сюръектив-
ф вытекает, что существует такой элемент ЬеМ,
которого (Ь)ф = с. Элемент Ь искомый:
Следовательно, преобразование со - сюръекция.
Отсюда сразу же получаем, что произведение биективных
преобразований — преобразование биективное. В частности,
1ЩЯ конечных множеств все три класса преобразований совпа-
совпади Ют, т. е. произведение произвольных двух перестановок
Ш1 множестве М снова является перестановкой на мно-
ми>ствё М. Это вытекает также из описанного нами
Правила нахождения произведения перестановок.
Как известно, действия сложения и умножения чисел ха-
|щктеризуютря рядом свойств. Например, действие сложения
чисел имеет такие свойства (именно действие сложения,
и не сами числа):
a) Ассоциативность. Для каждых трех чисел а, Ь, с
справедливо равенство
а + (Ь + с) = (а + Ь) + с,
b) Коммутативность. Для каждых двух чисел а, Ъ
выполняется равенство
a + b = b + а.
21

в) Существует нейтральный элемент (нуль)
такой, что для любого числа а
г) Для каждого числа а существует против о по-
ложное к нему число — а такое, что
а + (- а) = 0.
Выясним, справедливы ли отмеченные свойства для
действия умножения преобразований произвольного множе-
множества М.
а) Умножение преобразований произвольного множества М
имеет свойство ассоциативности. Это означает, что
для каждых трех преобразований а, Р, у множества М
справедливо равенство
(аср)оУ=.ао(роу). B)
Оно свидетельствует о том, что на любой элемент аеМ
преобразования ср = (а ° р) ° у и \j/ = а ° (р ° у) действуют оди-
одинаково :
(я) «а о р) о у) = (fl) (а о (р о у)). C)
Действительно, возьмем произвольный элемент аеМ, и
пусть (а) а = Ь, (Ь)Р = с, (с) у = d. Тогда по определению A)
(*)<р = ((л) (а о Р))у = (((а)а)р)у = «Ь)р)у = (с) У = *
(я)ф = ((fl)a)(poy) = (Ь)(Роу) = ((Ь)Р)у = (с) у = А
Таким образом, равенство C) выполняется для произвольно-
произвольного аеМ, и, следовательно, справедливо равенство B).
aoJS
i
I—I- ..
c-Wfi \
Рис. 7.
На рис. 7 изображено схематично действие произведения
преобразований на элемент аеМ. Произведению а°(Роу)
отвечает путь, обозначенный линией из жирных точек, а
произведению (а ° р) ° у — путь, обозначенный пунктирной ли-
22

\
мири Обе линии заканчиваются в точке, которая отвечает
</еМ, т. е. преобразования ф и v|/ действуют на
а одинаково. Следовательно, действие умножения
Н|н1иб|ппований множества М ассоциативно.
О) Умножение преобразований произвольного множества
ц § комму та тив но. Это означает, что существуют
преобразования ф и vj/ заданного множества М, для
ф о \|/ ф \|/ о ф#
Гйкими преобразованиями на соответствующих множест-
множества! Ийляются преобразования ф, v|/, приведенные в примерах
1 и 4.
Mi следует думать, что произведение преобразований
в v • 1 Л а зависит от порядка, в котором записаны сомножи-
19 ми, Например, произведение преобразований, определенных
i примерах 2 и 3, не зависит от порядка сомножителей.
Ириишсдение перестановок
• ф = Л23 4 56>)И11/ = Л 2 3 45б\
\2 3 1 6 5 4/ \3 1 2 4 5 6/
не зависит от порядка их записи:
2
2
3 4 5 б\
3 6 5 4/
И) Особую роль при умножении преобразований игра-
играми юждественное преобразование г и посто-
постоянные преобразования 5Х, хеМ (напомним, что
(if) и ¦¦ fl и (а) 6Х = х для каждого а е М). Преобразование е
выполняет для действия умножения преобразований ту же
i цмую роль, что и единица при умножении чисел (или нуль при
i тшении чисел), т. е. для каждого преобразования ф мно-
*1ЧП na M имеем
ф о е = s о ф = ф. D)
Действительно, положив (а) ср = Ь, по определению произве-
произведения A) для каждого элемента аеМ будем иметь
= Ь.
'fro и означает, что справедливо равенство D).
Легко понять, что 8 — единственное преобразование,
i) m которого выполняются равенства D); Действительно,
допустим, что существует другое преобразование г' ф е
23

такое, что для каждого ф имеем
е' о ф = ф о ?' =
Тогда произведение г ° г' = е' ° г, с одной стороны, должно
равняться г' (когда роль единицы выполняет г), а с другой -
s (когда роль единицы выполняет г'). Следовательно,
а потому 8 = 8', и мы пришли к противоречию, которое
свидетельствует о том, что наше допущение неверно.
Преобразования Ъх (их столько, сколько элементов имеет
множество М) для действия умножения выполняют роль
«нулей», т. е. для любого преобразования ср имеем
Но
(проверьте!).
Пример 5. Пусть
Тогда
4,.82-f12345U12345Wl234i\
V5 4 3 2 1/ \2 2 2 2 2/ \2 2 2 2 2/
52°<р = Л 2 3 45\ Л 2345\ /123 45^
V2 2 2 2 2/ \5 4 3 2 1/ \4 4 4 4 4/
(тут 4
Следовательно, если произвольное преобразование умножить на
«нуль» справа, то получим тот же самый «нуль», а если слева,-
«нуль», вообще говоря, будет другой.
г) Обратным для преобразования а произвольного мно-
множества М называется такое преобразование C этого множе-
множества, что справедливы равенства
ао|3 = |3оа = 8.
Это преобразование выполняет ту же роль, что и проти-
противоположное число для действия сложения чисел или обратное
число для действия умножения чисел. Так же, как и об-
обратное число а (которое существует только для а ф 0),
преобразование, обратное к данному, может существовать,
а может и не существовать. Например, обратным к
преобразованию
(\ 2 3 4 5\
\3 4 1 5 2]
24

преобразование
/i 2 3 4 5\
\3 5 1 2 а)9
§ #н< нпуюкнных преобразований обратных преобразований
№ tlriilfUTiyor. Но в тех случаях, когда обратное преобра-т
v у ще стелет, .оно единственно.
, допустим, что для некоторого преобразо-
миищ ф множества М существует два обратных преоб-
I мнриннШ фх и ф2, 9i # фг, т. е. одновременно выполня-
! >пч равенства
фоф4 = ф1°ф = г, ф °ф2 = Фг°Ф = е.
ill пик равенств и свойства ассоциативности действия
f - жнфгчшя преобразований последовательно имеем
и мы пришли к противоречию, которое свидетельствует
» him, что наше допущение неверно.
I цимспгвенное преобразование, обратное к преобра-
ф, далее будем обозначать ф.
же существует обратное преобразование? Исчер-
i ННЦИ1ЩИЙ ответ на этот вопрос дает такая теорема.
I § о р С м а. Преобразование, обратное к преобразованию а
чтпнества М, существует тогда и только тогда, когда а
*ш \ншея биекцией множества М.
Доказательство. Необходимость. Пусть для
|||<м}брцэования а существует обратное к нему преобразо-
В4ИИР р, т. е. а°р = р°а = г. Тогда для каждого уеМ
нмргм: у = (у)в = (у)(Р°а) = (ООР)а = (z)a, где z = (у)р. Сле-
«нйнгельно, для каждого уеМ существует элемент zeM
tiiotl, что (z)a = у, и a - сюръекция.
Покажем, что преобразование а будет также инъекцией.
Мннустим, что это не так. Тогда найдутся различные элемен-
i t=i м, ЬеМ, для которых (a) a = (b) a = с. Поэтому будем иметь
(a) e = (b) e и a = fe.
Мы пришли к противоречию, которое и доказывает,
и €К — инъекция.
25

Достаточность. Пусть а — биективное преобра-
преобразование. Тогда для каждого хеМ существует единственный
прообраз — такой элемент уеМ, что (у) ос = х. Поэтому можно
определить такое преобразование Р множества М, которое
ставит в соответствие каждому элементу хеМ его прообраз у
при преобразовании а:
> если у >х, то х >у.
р действительно является преобразованием, так как, по-
поскольку а — сюръекция, оно определено для каждого элемента
из М. Из самого определения р вытекает, что выполняются
равенства
(
для каждого х е М. Это означает, что а ° Р = р ° а = е, т. е.
р — преобразование, обратное к а.
Теорема доказана.
Пользуясь этой теоремой, легко решить вопрос о суще-
существовании обратной функции. Обратной для функции
fix) называется такая функция g (х), что (/° д) (х) ==
= @°Я(*) = х.
Для того чтобы функция Дх) имела обратную, необходи-
необходимо и достаточно, чтобы она осуществляла биективное отоб-
отображение области своего определения на множество своих
значений.
Очевидно, преобразования ос и а взаимно обратны,
т. е. каждое- из них обратно к другому. Следовательно,
(а) -а.
Примеры. 6. Пусть ср — поворот плоскости на угол 2л/3
против часовой стрелки вокруг точки О. Поскольку ср — биекция,
Ф существует. Легко понять, что ф -поворот плоскости на
угол 2л/3 по часовой стрелке вокруг точки О.
7. Функции у = 2 х + 3, у — х3 - биективные преобразования
х~» 2х-ЬЗ, х-*х3
множества действительных чисел R на себя. Поэтому для них
существуют обратные преобразования, а именно:
х-3 J/
2
Г*-.
Следовательно, функции у — —=— и у — ух обратны соответст-
соответственно к функциям у - 2 х 4- 3, у = х3.
Функции у = х2, у — sin х — преобразования
х -> х2, х -> sin х
26

множества R, которые не биективны. А поэтому для них не
существует обратных. Однако можно рассмотреть ограничение
функции у = х2 на множество Л+ (J {0} неотрицательных дейст-
ШИтельных чисел. Это функция, область определения которой есть
Множество R+ (J {0}, причем во всех точках области определения
Она совпадает с функцией у = х2. Это ограничение будет биектив-
биективным преобразованием множества Rf (J {0}, т. е. для него существует
Обратное преобразование х -> j/x. Таким образом, функция у = ]/х
рбратна к ограничению функции у — х2 на множество R+ \J {0}
(а не к функции у = х2, как часто говорят).
Вполне аналогично можно рассмотреть ограничение функции
у т sin х на промежуток [ — я/2, я/2]. Это ограничение является
биективным отображением множества [ - л/2, л/2] на множество
[—1, 1]. Следовательно, для него существует обратное — функция
у щ arcsin х.
8. Пусть преобразование ф множества точек плоскости явля-
является параллельным переносом в заданном направлении на рас-
расстояние d. Ясно, что ф — биективное преобразование, следовательно,
для него существует обратное. Это также параллельный перенос
на то же самое расстояние, но в противоположном направлении.
Для преобразования конечного множества М существует
обратное преобразование тогда и только тогда, когда оно
является перестановкой. Пусть дана перестановка
= A
23
тогда обратная к ней перестановка, как вытекает из правила
умножения перестановок, будет такая:
\1 2 3 ... п)'
Ее столбцы можно переставить так, чтобы числа верхнего
ряда были расположены в порядке возрастания. Например,
Обратной к перестановке
ф = (\ 2 3 4 5 6 7\
\4 2 1 5 7 6 3/
будет перестановка
фм=/421 5763^/1 234567^
\1 2 3 4 5 6 7/ \3 2 7 1 4 6 5/
Для преобразований произвольного множества можно со-
составлять и решать уравнения. Как пример рассмотрим
уравнения первой степени. Пусть <р, \j/ — произвольные
Преобразования множества М. Существуют ли такие преоб-
27

разования х, у этого множества, для которых иыполнялиа/бы
равенства ф.. х - i|r. E)
Если такие преобразования существуюi, 10 единственны ли
они? Подчеркнем, что елсдусг рш-тмтришггь оба урав-
уравнения, так как действие умножении мрсобрпювшшй неком-
некоммутативно и эти ура пне н и n могут иметь
разные решения.
Довольно легко ответил» ни пощнк о существовании и
единственности решении дли уравнений E) и F), в которых
«коэффициент» ср ~ п с р с с i а и о и н и /I шом случае реше-
решения обоих уравнении существуют и &)инстп$нны.
Доказывает си jtoi фпп i tic дующим образом. По-
Поскольку ф — биекция, дли iici о с у щ о v г щ у с т обратное
преобразование <р *. Можно но пому рассмотреть преобразо-
преобразования ф"! м)/ и v|/ »ф 1 (оi мб i им, *ло, вообще говоря,
Ф о \|/ ф v|/ о ф 1 так как операции умножения преобразований
некоммутативна). Покажем, <п<> ф ' \|/ будегг решением урав-
уравнения E). Для пою вычислим нроипкщенис фо(ф"о^).
Используя ассоцишивносп* дейепшм умножения преобразо-
преобразований и определение обришот преобразования, получим
А это и о»11ичис1, 41 о ф ' м|/ -- решение уравнения E).
Аналогично докаii.imicген, чго преобразование vj/оф -ре-
-решение уравнении F).
Теперь докажем, ч го у на питые решения уравнений E) и F)
единствен и м. Дойсгвиюлыю, если преобразования а и
Р - решения уравнений E) и F) соответственно,
Ф-ог-ф, ХУ)
то, умножая равенство G) слепи па ф~!, а равенство (8)
справа на ф, получим
Ф »(ф«а) -: ф 4 »ф,
(Р°~Ф)°Ф ' » ф»ф"',
т. е.
(ф " Х о ф) о а = ф ! « \|/э
Р°(Ф°Ф~1) = Ф°Ф~1,
28

Эти равенства означают, что никаких других решений, кроме
отмеченных ранее, уравнения E) и F) не имеют.
Пример 9. Пусть М = {1, 2, 3, 4},
2 3 4 \) \2 1 4 3/
Нетрудно проверить, что решением уравнения E) будет перестановка
\Ъ 2 1 4
а решением уравнения F) - перестановка
•--С.
Если преобразование ср в уравнениях E) м F) — не
становкагто эти уравнения могут иметь решения, а могут и
не иметь их (см. упражнения 8 — 11).
УПРАЖНЕНИЯ
1. Доказать, что произведение параллельных переносов снова
будет параллельным переносом.
2. Изобразить преобразования, заданные таблицами, с помощью
стрелочных схем и найти произведения этих преобразований:
v А 2 3 4 5\ Л 2 3 4 5V
' \4 2 3 2 4/' \3 1 2 1 2/'
^ч /^л Ь с J е\ | а Ь с d e\.
}\аЪаЪс)' \с d с а Ь/'
, А 2 3 4 5 б\ Л 2 3 4 5 б\
j \2 3 1 2 1 2/' \2 3 1 2 1 б/.
3. Доказать, что произведение симметрии относительно прямых,
которые пересекаются, является поворотом.
4. Преобразования <р, \|/ заданы графиками. Указать правило
нахождения графика <р°\|/.
5. Если произведение ср ° \|/ преобразований ф, \|/ конечного
множества — перестановка, то ф и ф - перестановки. Доказать это.
6. Если для заданного преобразований <р существует такое
число и, что <ри — тождественное преобразование, то ф — биекция.
Доказать это (определение <ри см. в § 6).
29

7. Решить уравнения:
? \ 4
Ч ";?;)¦
6) л (
\4
8. Какие решения имени уршмн мни и i ннц,ки?
/I 2.\AS\ ч /I Л ^
б) vY ^
V I ^ Л -I/ \ I .» 4 I J
I I ) i r»
9. Пум». Af ii|xnttuniihiiMP Miio«#t iио, ф М > М некоторое
нрсоПрп toiiiiinir Л/ II fat я ы м ( 11 в м и ) I» Л /»н ж м ы м к ф назы-
ваепнч такое щнч*1)\ч1иттш> и 5iM^wt*«»w<i M, мто ф»а = ?
((Чя>то('ШGМг1гммм fv ((I - и) Диии*1М^, 'по преобриювание ф тогда и
только Ю1ДЙ оПнммцр! мрннмм A№»ым) обритым, когда ф инъек-
гивно (coomeu IU0IMHI «lopb^kiMHito)
10. \Wrni <р iniitPiiiifHiio (норм»*i инно), ю ураниснис E) (соот-
ветственно @)) при ншбпм н^иАршомвмии ф имеет решение (но,
вообще м>ж>рч, иг ii/tini) Дощ|*1Н# но, иеиольтуя упражнение'9.
11. Мус и. ф (Hip^HiiiHiio (инй§Г1Инно) Докажите, что если
уравнение (S) (соошги темно Щ) имеет решение, то оно единст-
единственно.
12. 2м фи 1куим Уринсон hbnipofiiw м шеренгу по одному.
Рассчигивншсь ни нрртн о шпрщ о, они i д шиит юг ряды. Стоящие
во втором риду, начшшн i Hmhiiipi о неиофипж оного, делают
«обходной мансир>' и ncprxo/iMi ни нрйиый край так, что левофлан-
левофланговый обращается в прннофтми оною (рис. К). Считая, что номера на
I'm 8
майках физкультурников соогвегсгвуюi перед пера руппировкой их
порядковым номерам в шеренге, найги персе шпонку, характеризую-
характеризующую расположение фю культурников в шереше после трехкратной
перегруппировки.
30

§ 4. ГРУППА ПЕРЕСТАНОВОК
И ПОЛУГРУППА ПРЕОБРАЗОВАНИЙ
Как было установлено, действие умножения преобразова-
преобразований произвольного множества М имеет ряд свойств, которые
не зависят от природы элементов множества М. Эти свойства
могут быть разными для разных совокупностей преобра-
преобразований множества М. Например, в множестве всех преобра-
преобразований не для каждого преобразования существует обратное,
а в множестве биективных преобразований это имеет место.
Действие умножения произвольных преобразований некомму-
некоммутативно, а действие умножения (последовательного выпол-
выполнения) параллельных переносов на плоскости коммутативно.
Изучать свойства отдельных классов преобразований отно-
относительно действия умножения бывает нужно очень часто.
А потому удобно разработать определенную общую схему
изучения таких свойств.
* Кроме действия умножения преобразований, приходится
иметь дело и с другими операциями, которые задаются на
разных множествах. Например, рассматривается действие
сложения действительных чисел, действие умножения в мно-
множестве рациональных чисел, действие возведения в степень
в множестве целых чисел и т. д.
Это наводит на мысль рассмотреть общее понятие
операции. Из приведенных примеров видно, что опера-
операция, заданная на некотором множестве D, произвольной
паре элементов из D ставит в соответствие определенный
элемент из D (результат применения операции). Напри-
Например, действие сложения целых чисел паре B, 3} ставит в
соответствие число 5, а паре ( — 2, 1) — число —1; действие
умножения перестановок на множестве {1, 2, 3} паре пере-
перестановок
F?!)-
ставит в соответствие перестановку
12 3\
I 3 2У
и т. д.
Следовательно, естественно дать такое определение:
Операцией на множестве D называется соответствие,
при котором с каждой парой элементов из D сопоставлен
определенный элемент этого оке множества.
31

Операций обозначают разными символами, например
+ > х, •, °, * и т. д. Если операция на множестве D
обозначена символом ¦ и паре (a, h) элементов из D она
ставит в соответствие элемент с, то коротко тго записывают
так:
а * h = с.
Элемент с называют композицией или, чаще, произведением
элементов a, b, a действие ¦ и тгом случае называют
умножением (это оправдано тем, что очень часто действие
* понимают как действие умножения перестановок).
Примерами множеств с операциями являются множество
целых чисел с операцией сложения, множество параллельных
переносов на плоскости с операцией их последовательного
выполнения, множество положи цельных действительных чи-
чисел с операцией возведения в степень (паре положительных
чисел (а, Ь) ставится в соответствие число аь), множество
перестановок первых 100 натуральных чисел с операцией
умножения перестановок.
Рассматриваются множества с операциями, которые име-
имеют определенные свойства. Из сказанного в предыдущем
параграфе вытекает, что естественно выделять две совокуп-
совокупности преобразований - множество всех преобразований и
множество перестановок. Запишем отдельно свойства дейст-
действия умножения произвольных преобразований и свойства
действия умножения перестановок на множестве М. Будем
обозначать совокупность всех преобразований множества М
символом Р(М)Ч а совокупность всех перестановок на этом
множестве — символом 5(М).
А. Свойства действия умножения преобра-
преобразований из Р(М).
Ai. Произведение двух преобразований множества М^-
снова преобразование этого же множества:
Если ф, \|/еР(М), то и ф"ф*Р(М).
Или иначе: множество Р(М) замкнуто относительно
действия умножения преобразований.
А2. Действие умножения преобразований имеет свойство
ассоциативности, т. е. для каждых ф, \|/, соеР(М)
справедливо равенство
(ф°\|/)°@ = ф ° (v|/ ° О)).
А3. Существует единственное преобразование ееР(М)
такое, что для каждого ц>еР{М)
32

Б. Свойства действия умножения переста-
перестановок из S(M).
Бх. Если ф, \|/eS(M), то и ф ° \|/е S (М).
Б2. Действие умножения перестановок ассоциативно.
Б3. Существует единственная перестановка zeS(M) та-
такая, что для каждой перестановки фе5(М) имеем
Б4. Для каждой перестановки фе5(М) существует такая
перестановка \|/eS(M), что
фО\|/=:\|/Оф=?.
Общая схема, по которой изучаются совокупности пре-
преобразований с действием умножения, должна как-то учиты-
учитывать серию свойств А или серию свойств Б. Это достига-
достигается введением общих понятий группы и полугруппы.
Определение. Произвольное множество D с заданным
на нем действием * называется полугруппой, если
а) для каждых at beD произведение а*Ъ принадле-
принадлежит D;
б) для каждых трех элементов a, b, ceD выполняется
равенство
c = a*(b*c), A)
т. е. действие умножения, заданное на D, ассоциа-
ассоциативно;
в) существует такой элемент eeD, что для каждого
aeD имеем
Элемент е называется нейтральным для дейст-
действия*.
Примеры. 1. Множество Z всех целых чисел для действия
сложения — полугруппа.
Действительно, сумма целых чисел - снова целое число. Дей-
Действие сложения целых чисел имеет ассоциативное свойство. Нейт-
Нейтральным элементом для действия сложения целых чисел служит
число 0, потому что для каждого aeZ имеем
2. Множество Q+ всех положительных рациональных чисел
для действия умножения — полугруппа.
3. Множество преобразований Р(М) для действия последователь-
последовательного выполнения преобразований — полугруппа.
2 Л. А. Калужнин, В. И. Сущанский 33

Множество R+ положительных действительных чисел с задан-
заданной на нем операцией а*Ъ = аь не будет полугруппой, так как
эта операция не ассоциативна, т. е. для чисел из R+ не всегда
выполняется равенство A). Например,
B*3)*2v*2*C*2)
(потому что B3J =64, а 23' = 512).
Определение. Множество D с шданцой на нем опе-
операцией * называется группой, если удовлетворяются
требования а) — в) определения полугруппы и, кроме того, такое
требование:
г) для каждого элемента а< I) существует такой элемент
ЬеД что
a* b ~ b* a - е.
Примеры. 4. Множество Z всех целых чисел для действия
сложения — группа.
Действительно, в примере 1 было проверено выполнение
требований а) - в). Кроме тою, для каждою числа aeZ суще-
существует такое число heZ (противоположное к а), что а + Ь —
= Ъ + а — 0. Следовательно, выполняется и последнее требование
определения группы.
5. Множество R * положительных действительных чисел
для действия умножения - группа.
Действительно, ироишедснис положительных чисел — снова
положительное число; действие умножения чисел ассоциативно;
нейтральным элементом является число I; для каждого числа aeR+
существует обратное к нему число а ~'.
6. Множество всех поворотов плоскости вокруг фиксирован-
фиксированной точки на произвольные углы для действия последовательного
выполнения поворотов - группа.
Действительно, произведение поворотов плоскости вокруг точки
О на углы аир является поворотом вокруг этой точки или
на угол а + Р, или на угол |а — Р|; действие умножения поворотов
ассоциативно, так как таковым является действие умножения произ-
произвольных преобразований; нейтральный элемент — тождественное
преобразование плоскости, которое можно рассматривать как по-
поворот вокруг точки О на 0 радианов; обратным к повороту на угол
а будет поворот на угол - а.
Совокупность S(M) всех перестановок на множестве
М = {1, 2, 3, ..., п} для действия умножения перестановок
образует группу. Эта группа называется симметриче-
симметрической группой перестановок на множестве М. Выполнение
всех требований определения группы вытекает из свойств
34

Каждая группа будет также и полугруппой, но не на-
наоборот. Например, множество целых неотрицательных чисел
для действия сложения — полугруппа, но не группа.
Действия сложения и умножения чисел имеют свойство*
коммутативности. Однако требование коммутативности не
включено в определение полугруппы и группы. Это объясня-
объясняется тем, что действие умножения преобразований не комму-
коммутативно, а исторически понятие группы возникло именно
на основе изучения свойств действия умножения перестано-
перестановок на конечных множествах (понятие полугруппы появилось
значихельно позднее). Отдельно рассматриваются группы, для
которых выполняется требование коммутативности. Они
называются абелевыми (в честь норвежского математика
Н. Г. Абеля A802 — 1829), установившего роль таких групп
в теории разрешимости алгебраических уравнений в ра-
радикалах).
Для множеств с заданными на них операциями проверять
выполнение свойств группы бывает довольно тяжело. Если
множество конечно, для faKofi проверки можно воспользо-
воспользоваться так называемой таблицей умноэгсения группы. Эту
таблицу составляют подобно таблице умножения целых чисел.
Строят ее так. Пусть qu q2, ..., qn — все элементы группы G.
Запишем их в первом ряду и в первом столбце подготов-
подготовленной таблицы.
Зйтем заполним клетки таблицы, записывая в них произ-
произведения соответствующих элементов первого ряда и первого
столбца в указанном порядке. В результате получим:
g\
#2
g\
gl*g\
g2*g\
gn*g\
Si
g\*g2
gi*gi
gft*g2
gn
g\*gn
g2*gn
gn*gn
Примеры. 7. Пусть G - множество перестановок
2 3\ „ Л 2 3\ „ Л 2
/
35

Непосредственно перемножая их, легко убеждаемся, что таблица
умножения элементов из G будет такая:
а,
а2
аз
а1
а2
а2
'*2
Я*
аз
«1
а2
8. Пусть И — множсстко прсобраюпаний
\гг
и .
P V2 2 2J/
/1 2 3\
Нзз)
Перемножая эти нрсобраюпания, получим такую таблицу:
е
a
Р
Y
С
\.
a
Р
У
a
г/
a
a
7
Р
Р
Р '
СО.
1*
Y
У
У
У
Y
Пользуясь двумя последними шблицими, легко убедиться,
что множества G и Я для действия умножения преобразований
образуют соответственно группу и полугруппу. Убедимся, например,
что G — группа. Поскольку все клетки первой из отмеченных
таблиц заполнены только символами ab a2, ал, множество G
замкнуто для действия умножения заданных перестановок. Условие
ассоциативности действия умножения элементов из G выполняется
автоматически, потому что оно выполняется для умножения
произвольных преобразований. Перестановка at является нейтраль-
нейтральным элементом группы. Из таблицы также видно, что каждый из
элементов аь а2, а3 имеет обратный, а именно: af1 = ось а^1 = а3,
1
36

УПРАЖНЕНИЯ
1. Образуют ли полугруппы такие множества с заданными в них
операциями:
а) множество натуральных чисел с операцией, которая каждой
паре чисел ставит в соответствие их наибольший общий делитель;
б) множество всех многочленов произвольной ненулевой степени
для суперпозиции многочленов; ^
в) множество нечетных целых чис§л для действия умножения?
2. Являются ли группами такие множества с заданными в
них операциями:
а) множество действительных чисел для действия умножения;
б) совокупность функций у = х, у = — х, у =? 1/х, у — — 1/х,
определенных на множестве действительных чисел без нуля, для су-
суперпозиции функций;
в) множество функций у = х, у = — х для суперпозиции функций;
г) множества с операциями из упражнения 1?
3. Доказать, что в каждом ряду и в каждом столбце
таблицы умножения для группы перестановок обозначение каждой
из перестановок встречается точно два раза.
4. Какое свойство таблицы умножения абелевой группы не имеет
места для таблиц умножения неабелевых групп?
5. Составить таблицу умножения:
а) для группы 5(М), где М = {1, 2, 3};
б) для группы из упражнения 2,6);
в) для полугруппы Р(М), где № = {1, 2}.
6. Сколько можно составить разных таблиц умножения для
четырехэлементного множества перестановок, которые были бы
таблицами группы?
§ 5. ГРАФЫ ПРЕОБРАЗОВАНИЙ. ОРБИТЫ.
ЦИКЛИЧЕСКАЯ ФОРМА ЗАПИСИ ПЕРЕСТАНОВОК
Стрелочные схемы — графы преобразований заданного
множества можно строить иначе, чем схемы произвольных
отображений. Обозначим каждый элемент множества М
точкой на плоскости так, чтобы разным элементам отвечали
разные точки. Точки обозначим теми же самыми символами,
чтр и соответствующие элементы множества М. Две точки
соединим стрелкой в направлении от а к Ъ тогда и
только "Тогда, когда для элементов ах Ь выполняется условие
(а) ф = Ъ. Так получим граф преобразования <р. Ясно, что он
определяет преобразование однозначно. Наоборот, если не
обращать внимание на форму стрелок и размещение точек
на плоскости, то каждому преобразованию будет отвечать
вполне определенный граф.
37

Примеры. 1. Пусть преобразование ф множества М = {1, 2,
3, 4, 5, 6} задано таблицей
Ф \3 4 2 5 6 2
Обозначим каждое число из М точкой на плоскости, например
так, как на рис. 9. Поскольку A)<р = 3, точки / и 3 соединим
стрелкой в направлении от точки / к точке 3. Аналогично
построим стрелки, которые выходят и* тчек 2, 3, 4, 5, б (рис. 10).
Это и есть граф преобразования <р.
Рис. 9.
2. Пусть ф г. юждес! пенное преобразование множества
М = {1, 2, 3 п\. No определению, для каждого аеМ,
(д)е = а. Так что i раф прсобраюнания п будет такой, как на "рис. 11.
<0
Рис. П. Рис. 12.
3. Пусть ф = фв - постоянное преобразование множества
М = {1, 2, ..., и}, которое каждому шементу ЬеМ ставит в соот-
соответствие фиксированный элемент ае М, г. с. ;и«я каждого ЬеМ имеем
В этом случае на графе преобразования ip каждая точка Ь
соединена с фиксированной точкой а стрелкой, которая заканчи-
заканчивается в а (рис. 12).
4. Пусть М = Z, ф — преобразование множества Z, которое
каждому целому числу х ставит в соответствие число х + 3: (х) ф =
= х + 3. В этом случае граф преобразования полностью построить
38

не удается, но можно изобразить определенную часть его так, чтобы
стало понятным строение графа в целом (рис. 13).
/ 1 5 4 5 б 7 6 3
Рис. 13.
5. Если М — конечное множество и преобразование ф является
перестановкой на множестве М, то из каждой вершины графа ф
выходит одна и только одна стрелка и в каждую вершину
обязательно входит стрелка, причем только одна.
В частности, если М = {1, 2, 3, 4, 5, 6, 7} и ф — перестановка
на множестве М:
^241365
то ее граф будет такой, как на рис. 14.
Граф произвольного преобразования ф состоит из одной
(рис. 10, 12) или нескольких (рис. 14) не связанных между
собой частей, каждая из которых составляет одно целое.
При этом отдельная связная часть графа преобразования ф
может состоять лишь из одной точки с «петлей», т. е. со
стрелкой, которая выходит из этой точки и заканчивается
в ней. Если а — такая точка, то для соответствующего
элемента аеМ справедливо равенство
Такие элементы называются неподвижными точками
преобразования ф. Если для элемента аеМ выполняется
условие
(а) ф ф а,
то а называется подвижной точкой преобразования ф.
На графе подвижные точки — это точки без петель.
Например, на рис. 14 точки 1, 2, 3, 4, 5, 6 - под-
подвижные, а точка 7 — неподвижная точка преобразования ф.
Количество подвижных точек преобразования является
одной из важных его характеристик, которая называется
39

степенью этого преобразования. Единственным преобразо-
преобразованием степени нуль является тождественное преобразование;
постоянное преобразование множества из п элементов имеет
степень и_— 1.
Пусть ф — некоторое преобразование множества Мий-
произвольный элемент из М. Последовательность
а0 = а, (а)(р = аи (д^ф = я2,..., (яп)ф = ап+и ... A)
элементов из М называется орбитой элемента а для
преобразования ф. В общем случае множество О (а, ф) ==
= {а0, аи ..., апу ...} элементов орбиты A) является под-
подмножеством множества М. В частности, может случиться, что
О(а9 ф) = М.
Рассмотрим детально строение орбит, когда М-конеч-
н о е множество, О (а, ф) = М и | М | = т. Очевидно, в этом
случае элементы в последовательности A), начиная с неко-
некоторого места, будут повторяться. Пусть к ~~ наименьшее
число такое, что
Ясно, что элементы ак, ,, ак, 2, •.. также встречаются среди
элементов а0, аи а2, ..., ак. Поэтому к = т — 1 и легко
понять, что граф преобразования ф будет такой, как на рис. 15.
Рис. 15. Рис. 16.
Если / Ф 0, преобразование ф не является перестановкой,
потому что в точке ах заканчиваюкя дне стрелки. Для I = О
преобразование имеет граф, коюрый называется циклом
(рис. 16), и в этом случае оно, очевидно, будсч перестановкой.
Эта перестановка действует на элементы из М так:
(«о)Ф = аи («i) ф = а2, ..., (ат-2) Ф = ат .,, (ат -1) ф = а0.
Такая перестановка называется циклической или просто
циклом, и обозначается
ф =(Д(ь «1, U2> •••> ат-\У
40

Число т есть длина цикла. Циклы длины 2 называются
транспозициями.
Если элементы орбиты О (а, <р) не исчерпывают все мно-
множество М, то графы (рис. 15, 16) не полностью характери-
характеризуют преобразование. Тогда нужно рассмотреть орбиты
других элементов, которые не вошли в О (а, <р). Разные орбиты
для заданного преобразования могут иметь общие вершины
(рис. 12), но для перестановки разные орбиты очерчи-
очерчивают не связанные части ее графа.
Действительно, пусть Ох = {аи а2, ..., ат} и О2 =
= {&ь &2, •••'>&«} ~ разные орбиты перестановки <р. Допустим,
что Ох и О2 имеют общие элементы. Идя в порядке
возрастания номеров, выберем первый элемент аке0и
который равняется определенному элементу bje02- Тогда
ак_х Ф bi-t. Значит, (flk-i)cp = ак = bt = (Ь1_1)ф и преобразо-
преобразование ф не является перестановкой. Мы пришли к проти-
противоречию, которое и доказывает сформулированное утвер-
утверждение.
Теперь можно подробнее охарактеризовать графы пере-
перестановок на конечном множестве М. В этом случае мно-
множество М распадается на отдельные части без общих
элементов. На каждой из этих частей перестановка ф
образует цикл. Поэтому граф каждой перестановки состоит
из определенного числа не связанных между собой циклов.
Поскольку граф перестановки распадается на отдельные,
не связанные между собой циклы, перестановки на конеч-
конечном множестве удобно записывать так, чтобы по этой записи
сразу же можно было строить отдельные части графа —
циклы. Соответствующая запись перестановок называется
циклической. Прежде чем рассказать про такую форму запи-
записи перестановок, сделаем несколько общих замечаний.
Пусть ф — произвольная перестановка на множестве М и
Р — такое подмножество множества М, что для каждого эле-
элемента аеР имеем
По перестановке ф на множестве М можно определить
преобразование \|/ на множестве Р, положив для каждого
ЪеР
Ясно, что \|/ является перестановкой на Р. Будем назы-
называть ее ограничен и ем перестановки ф на подмножество
Р множества М.
41

Пример 6. Пусть
М = {1, 2, 3, 4, 5, 6J, Р = {1, 2, 3, 4},
/
4 3 2 16 5
Непосредственно видно, что (а)(реР для каждого а е Р, поэтому
можно рассмотреть ограничение <р на Р. Это будет перестановка
Л234\
\4 3 2 I/
Обратно, если имеем перестановку \|/ на множестве РсМ,
то можно определить перестановку ср на множестве М, по-
положив для каждого элемента аеМ:
J(fl)i[/, если аеР,
\а, если а^Р.
То есть на элементы из Р перестановка (р действует
так же, как перестановка \|/, а все остальные элементы из М
оставляет на месте. Будем называть перестановку ф
расширением перестановки \\f на множество М.
Пример 7. Пусть Р - A,2,3,4,5), М = {1.2, 3,4, 5, 6, 7, 8} и
¦ --С123451
\2 3 1 5 4/
Тогда расширением i|/ на М янпясюя персегаиовка
(\ 2 3 4 5 6 7 8\
Ф \2 3 15 4 6 7 8/
Назовем две перестапонки па множестве М взаимно
простыми, если^их множества подвижных точек не имеют
общих элементов.
Взаимно простыми буду?, например, перестановки
(\ 2 3 4 5 6 7 Х\ /| 2 3 456 78\
\3 4 2 1 5 6 7 8/ V I 2 3 4 5 7 6 8/'
ибо множеством подвижных foncK для (р является {1, 2, 3, 4},
для \)/ - {6, 7}.
В отличие от перестановок общего вида, произведение
взаимно простых перестановок не зависит от порядка
множителей.
Действительно, пусть (р и \)/ — взаимно простые
перестановки и а — произвольный элемент множества М. Если
а — подвижная точка для перестановки ср, то положим
(а)ц> = Ь; элементы а, Ь — неподвижные точки для \|/, ибо
42

(а) ф ф а и (Ь)<р ф Ь, Поэтому имеем
(аЩо ф) = ((а)\|/)ф = (а)ф = Ь,
т. е. в этом случае (а) (фG v|/) = (а) (\|/ ° ф).
Если а — неподвижная точка перестановки ф, то
положим (а) \|/ = с (если а является неподвижной точкой и
для перестановки \[/, то а = с) и аналогично получим, что
элементы а, с не меняются под действием перестановки ф,
а поэтому
(а) (фо \|/) - ((а) ф) vj/ = (а) v|/ == с,
(а) (\|/ о ф) = ((а) \|/) ф = (с) ф = с.
Так что и в этом случае перестановки ф°\|/ и \|/°ф
действуют на элемент аеМ одинаково, а это и означает,
что
ф о V}/ = 1|/ о ф.
Таблицу произведения двух взаимно простых перестановок
Ф, \J/ составить очень просто. Для этого во втором ряду таб-
таблицы ф о \|/ нужно записать на своих местах (т. е. на тех местах,
на которых они стоят в таблицах для ф, \|/) все подвижные
точки перестановок ф, \|/, а остальные места заполнить
неподвижными точками. Например,
(\ 2 3 4 5 б\Л 2 3 4 5 в\ Л 2 3 4 5 б\
1 2 4 5 6/1 1 2 3 4 6 5/ \3 1 2 4 6 5/
Пусть теперь ф — произвольная перестановка на множест-
множестве М. Разобьем М на разные части Мь М2, ..., Ms,
каждая из которых является орбитой некоторого элемента
из М. Это разбиение имеет такие свойства:
а) каждый элемент из М принадлежит одному из
подмножеств М, (/ = 1, 2, ..., .s); .
б) если i ф j, то Мг и М,- не имеют общих элементов;
в) для каждого аеМг (i есть один из номеров 1, 2, ..., s)
элемент (а)ф также принадлежит М?.
По последнему свойству можно рассмотреть ограничение
Ф^ перестановки ф на каждое из подмножеств Mt; (pt есть,
очевидно, циклическая перестановка на Mf. Она определя-
определяется перестановкой ф однозначно.
В свою очередь каждую из перестановок <pt можно
расширить на все множество М. Обозначим это расширение
через (pi (i — 1, 2, ..., s). Далее такие перестановки также
будем называть циклическими и обозначать их так, как и
43

обычные циклы. Следовательно, перестановка будет цикличе-
циклической в этом понимании тогда и только тогда, когда она имеет
граф такого вида, как на рис. 17.
0000
Рис 17.
Очевидно, множество подвижных ючск каждой из переста-
перестановок ф; совпадает с множеством M-t\ по свойству в) пере-
перестановки (pi и (рр / #7, взаимно просты. Пользуясь приве-
приведенным выше правилом для умножения взаимно простых
перестановок, получаем
Ф = ФГ1 Ф2 "... (l\v
Поскольку перестановки <(>,, ф2 t,o, попарно взаимно
простые, это4 произведение не зависит от порядка множи-
множителей. Таким образом, доказана такая
Теорема. Каждую перестановку на конечном множе-
множестве М можно разломить в и ротведение вшимно простых
циклов, причем это разложение однозначно с точностью до
порядка множителей.
Набор чисел /сь к*щ ..-., /сЛ, являющихся длинами
циклов, на которые разложена д;шпая перестановка, называет-
называется ее типом и обозначается <&,, к2, ..., ks}.
Пример 8. Разложи 1ь и произведение никлой перестановку
/I 2 34 5 67К
\2 3 1 6 7 4 5 К
Находим разные орбиты для <р. Имеем:
A) ф = 2, B) ф = 3, C) ф = 1; D) Ф 6, F) ф --- 4;
E)Ф = 7,
Так что орбиты определяют подмножссиш •{!, 2, 3}, {4, 6},
{5, 7}, {8}. Ограничениями перестановки ф на тги множества
будут такие перестановки:
/ 2 3\ /4 б /
44

Расширениями этих перестановок на множество М будут
перестановки
B34567
1 4 5 6 7
- ,А ~
= A2
\2 3
ф Ef7).A23 45678\
\1 2 3 4 7 6 5 8/
2 3 4 5 6 7
Поэтому можно записать:
Ф = Ф1оф2оф3оф4=A,2,3)оD,6)оE,7)о(8)=A, 2, 3)оD, 6)»E, 7).
Последняя запись однозначно определяет перестановку
лишь тогда, когда известно, на каком множестве она действует.
УПРАЖНЕНИЯ
1. Может ли произвольный граф быть графом какого-нибудь
преобразования?
2. Перестановка задана графом. Как построить граф обратной
перестановки?
3. Указать правило для нахождения графа" произведения
преобразований, каждое из которых задано своим графом, не строя
таблиц этих преобразований.
4. Построить графы преобразований, заданных таблицами:
v (\ 234567 8\~ Л 234567 8V
\5 6 I 8 3 7 2 47' ' \6 8 5 4 3 7 I 3/'
v Л 2 3 4 5 6 7\. v Л 2 3 4 5 6 7 8 9\
\6 4 3 7 5 1 2/' \6 4 1 8 4 3 4 9 9/
5. Каждая перестановка, граф которой связан, циклична. До-
Доказать это.
6. Длиной орбиты называется число ее элементов. Найти наи-
наибольшее и наименьшее значение сумм длин разных орбит для
преобразований множества из п элементов.
7. Преобразование ф множества М будет перестановкой тогда
и только тогда, когда сумма длин разных ее орбит равняется
|М|. Доказать это.
8. Пусть ф — произвольное преобразование множества М. Су-
Существует такое множество Р а М и такое натуральное число к,
что (а)<ркеР для каждого аеР, и ограничение фк на Р есть
перестановка. Доказать это.
45

9. Разложить в произведение взаимно простых циклов и найти
типы таких перестановок:
2 3 4
3 2 5 1;
Л 2 3 4 5 б\
\5 6 1 4 3 2/'
/123456789
v \7 9. 3 1 5 8 4 2 6
10. Описать общий вид графа произвольною преобразования
(так, как это сделано для перестановок).
11. Сколько существует перестановок па множестве из т эле-
элементов, которые имеют заданный тип <»,, н2, ..., wk>, где пх <
< п2 < ... <пк (ясно, что пх + п2 + ... + пк - т).
12. В группе 54 = 5{1, 2, 3, 4}) наГпи число перестановок
каждого возможного типа.
13. Определить тип персстаноики, характеризующей располо-
расположение тридцати физкультурников после двукратной перегруппировки
(см. упр. 12 § 3).
§ 6. ПОРЯДОК НКРКСТЛНОВКИ
Для каждого преобразования ф можно рассмотреть его
степени; п-й степенью преобразования ср называется произ-
где п — натуральное число. Далее будем обозначать
ее фи.
Из определения степени преобразования вытекают такие
равенства:
а) фи»фж = ф"' ж; б) (ч>")т = фт
ти
Положим также для каждого преобразования ф
ф" -= П.
Для перестановок (произвольных биекций) понятие
степени можно обобщить и на случай целых отрица-
отрицательных чисел, положив
Равенства а) и б) в этом случае будут верны для
произвольных целых показателей.
Если ф — некоторая перестановка на множестве М,
|М | < оо, то ф" для каждого целого п также есть переста-
46

новка на М. Таких перестановок лишь конечное число, т. е.
в последовательности ср, ф2, ф3, ф4, ... не все перестановки
разные.
Пусть для некоторых натуральных чисел к, 1(к < I) выпол-
выполняется равенство ц>к = ф'. Тогда
(ф*)~1 = ц>-\ (ф*)~ ^ф^ (ф*)-1 оф'5
откуда ф/-Л = 8, т. е. для каждой перестановки фе5(М),
где М — конечное множество, найдется по меньшей
мере одно натуральное число s такое, что ф* = 8. Наи-
меньшееиз таких натуральных чисел называется порядком
перестановки ф.
Степени циклической перестановки (ах а2 ... ап) на-
находят по формуле
(аи а2, ..., an)k = (ak, ak+u ... ат аи ..., afc_i).
Это равенство можно толковать так. Если какая-нибудь
шестерня, которая имеет п зубцов, поворачивается вокруг
своего центра, то, занумеровав зубцы числами 1, 2, 3,..., п и
зафиксировав некоторое начальное положение зубцов, ее
повороты можно однозначно описывать перестановками на
множестве {1, 2, ..., п}. Циклическая перестановка
/12 3...п-1 п\
\2 3 4 ... п \у
очевидно, описывает поворот на угол 2п/п (зубец с номером
1 встает на место зубца с номером 2 и т. д.).
Не нарушая общности, будем считать, что шестерня
поворачивается по часовой стрелке. Чтобы повернуть
шестерню на угол 2кп/п, надо к раз осуществить поворот
на угол 2п/п в одном направлении, так что перестановка
а\ к > 0, отвечает такому положению шестерни, когда
на месте первого зубца стоит /с-й, на месте второго (к + 1)-й
и т. д. Если шестерню повернуть п раз вокруг центра
на угол 2п/п, то она займет начальное положение. Таким
образом, для каждого цикла (ах, а2, ...; ап) выполняется
равенство
(аи а2, ..., ап)п = е.
При этом для натуральных чисел, меньших п, это равенст-
равенство невозможно. Для к < 0 перестановки а* описывают по-
повороты шестерни на углы 2пк/п против часовой
стрелки.
47

По доказанному в предыдущем параграфе произвольную
перестановку можно разложить в произведение попарно
взаимно простых циклов:
ф = ф^ о ф2 о t m # о фз>
Для каких угодно номеров i, j произведение перестановок
Ф,-, q>j не зависит от порядка множителей. Пользуясь
этим, i-ю степень перестановки ф для каждого целого п
можно записать так:
ф" = (ф 1 ° Ф2 ° • • • Фз) ° • • • ° (ф 1 ° Ф2 ° • - • ° Фл) ^
; A)
Это равенство также допускает механическое толкование.
Поскольку циклы фь ср:, ..., фЛ, взаимно просты, их степе-
степени описывают поворота нокру! центров s шестеренок с
соответствующими количествами зубцов, причем эти- шес-
шестерни не связаны одна с другой. Поэтому степенями
перестановки ф описываются повороты целой системы шес-
шестеренок. Зубцы каждой ю шестеренок можно занумеровать
так, чтобы все повороты осуществлялись в одном направ-
направлении.
Порядок является очен!» важной характеристикой пере-
перестановки. Чисел п таких, что ф" - е, для произвольной
перестановки ф существует мною. Но все они делятся на
порядок nepecmauoeicu.
Докажем это методом от противного. Допустим, что
существует такое натуральное число /с, для которого спра-
справедливо равенство
ф* = е,
причем к не делится на порядок г перестановки ф. По
определению порядка перестановки, к > г, поэтому
к = /г + 5, 0 < s < г.
Тогда имеем ф* = ф*г+я = <p!ro(psm Но
ф*' = (ф'У = (гI = s.
Таким образом,
4S

Однако 0 < s < г, и мы пришли к противоречию, которое и
доказывает сформулированное утверждение.
Выведем теперь правило для нахождения порядка про-
произвольной перестановки. Прежде всего заметим, что произ-
произведение нескольких взаимно простых перестановок
может равняться тождественной перестановке лишь тогда,
когда каждая из перестановок единична. Это вытекает из
того, что произведение ср взаимно простых перестановок
Фь Ф2> •••> 4>s действует на каждую свою подвижную
точку так, как действует на нее та перестановка срь для
которой эта точка является подвижной. Поэтому из равенства
A) получаем, что ф" = е тогда и только тогда, когда
одновременно
ф" = е, Ф2 = е, •-., Ф? = е. B)
Если перестановки фь ф2, ..., ф8 есть циклы длины
/сь къ ..., ks соответственно, т. е. имеют порядки ки к2, •••
..., /cs, то наименьшее число п, для которого одновременно
выполняются все равенства B), равняется, очевидно, наимень-
наименьшему общему кратному чисел ки к2, ..., ks. Следовательно,
мы доказали, что порядок перестановки ф, которая расклады-
раскладывается в произведение циклов длиною ки к2, ..., kSi есть
наименьшее общее кратное чисел /сь /с2, ..., ks:
пор. ф = К(пор. фь пор. ф2, .-., пор. ф5).
Пример. Пусть
Л 23 45678\
\3 6 4 1 8 7 2 5/
Разложим ф в произведение циклов:
Ф = A, 3, 4)оB, 6, 7)оE, 8).
Отсюда пор. ф = КC, 3, 2) = 6.
УПРАЖНЕНИЯ
1. Найти порядок каждой из перестановок
v Л 2 3 4 5 6 7 8 9\ gv Л 2 3 4 5 6-7 8 9 10\
} \3 5 7 9 6 8 12 4/' \3 54678921 10/
2. Найти порядки всех перестановок на множестве из 6
элементов.
3. Какой наивысший порядок могут иметь перестановки на
множестве из 10 элементов?
4. Найти перестановку, обратную к циклу (аи а2, ..-, а„).
49

5. Если произведение перестановок <р и \|/ не зависит от
порядка записи множителей, то порядок ф°ф есть делитель
наименьшего общего кратного порядков <р и ф. В общем случае
нельзя утверждать, что пор. (<р ° ф) = К (пор. (р, пор. ф). Привести
примеры.
6. Сколько существует перестановок 15-го порядка на множестве
из 8 элементов?
7. Вывести формулу для нахождения порядка перестановки*
пользуясь механическим толкованием действия возведения в степень.
8. Если п — простое число, то для каждого /с, 0 < к < п^ пере-
перестановка (аи а2, ..., а„)к есть цикл длины п. Если число и —
составное, то'эта перестановка будет циклом для чисел к, взаимно
простых с п, и произведением циклов одинаковой длины в ином
случае: Доказать это.
9. Доказать, что для каждой перестановки ф, которая раскла-
раскладывается в произведение / циклов одинаковой длины s, найдется
цикл ф длины Is и натуральное число к такое, что ф = ф*. Един-
Единственный ли такой цикл?
10. 12 мальчиков перебрасываются разноцветными мячами,
каждый из них бросает свой мяч всегда одному и тому же
партнеру, все мячи бросаются одновременно и никакие два мальчика
не бросают мяч одному игроку. Через какое наименьшее число
ходов игры все мячи окажутся в руках тех же мальчиков, что и в
начале?
11. Колода из 36 карт тасуется следующим образом. Колода
берется лицевой стороной вниз в левую руку и карты сверху по
одной перекладываются в правую руку, причем в правой руке
они поочередно кладутся то сверху, то снизу тех карт,
которые к этому моменту уже скопились в правой руке. Сколько
раз нужно повторить такую перетасовку, чтобы в колоде был
восстановлен первоначальный порядок?
12. Какое наименьшее число перегруппировок тридцати физ-
физкультурников (см. упр. 12 § 3) нужно осуществить, чтобы в шеренге
был восстановлен начальный порядок? Какой ответ получится в
случае, когда физкультурников 36?
§ 7. ОБРАЗУЮЩИЕ СИММЕТРИЧЕСКОЙ ГРУППЫ
Задача. На стенах круглого зала картинной галереи
висели картины. Как-то решили разместить их в другом
порядке, меняя местами картины, которые висят рядом. Всегда
ли можно с помощью таких перемещений разместить картины,
как задумано?
Решение. Занумеруем картины в* первоначальном
порядке числами 1, 2, ..., п. Пусть на место первой
"картины нужно повесить картину с номером jb на место
второй — картину с номером i2 и т. д., наконец, на
место n-й картины — картину с номером in (ix, i2,..., i« — раз-
50

ные числа из множества {1,2,...,«}). Перемещаясь вдоль стены
обозначенным способом в одном направлении картина
последовательно занимает все места, на которых висят кар-
картины. Поэтому картину с номером
*! можно повесить на место
первой картины (рис. 18). Выбирая
направление перемещения картины
с номером i2 так, чтобы не двигать
картину с номером ib картину
с номером i2 можно повесить на
место второй. Аналогично, вы-
выбирая такое направление пере-
перемещения, чтобы не двигать карти-
картины с номерами ^ и \ъ картину
с номером i3 можно повесить на
место третьей. Продолжая этот рис щ
процесс дальше, каждую картину
можно повесить на нужное место.
Следовательно, ответ на вопрос, поставленный в задаче,
утвердительный.
Сформулируем теперь эту задачу на языке перестановок.
Занумеруем места, на которых висят картины, так, чтобы
нумерация мест совпадала с нумерацией картин в перво-
первоначальном положении. Размещение картин, при котором
картина с номером ix висит на первом месте, картина с
номером i2 — на втором и т. д., картина с номером in — на
/7-м месте, однозначно описывается перестановкой
A)
в частности, первоначальное размещение картин характе-
характеризуется тождественной перестановкой. Если в положении,
которое описывается перестановкой A), поменять местами
картины, которые стоят на /с-м и (к + 1)-м местах A < к ^ п\
то перестановка аь которая будет характеризовать это
новое положение, будет результатом умножения перестановки
а слева на транспозицию (к, к + 1):
(\ 2 ... к- 1 к к 4- 1 fc + 2 ...
Vi h ••• h~i h+i h h + 2 •••
Л 2 ... к-1 к к+ 1 к -f 2 ... п\
\1 2 ... к- 1 /с+1 к к + 2 ... п)
Л 2 ... к-
V*! /2 ... ik_i
к к+ 1
ik ik+l
... п\
... V
51

Если переход от первоначального положения к желаемому,
которому отвечает перестановка ср, осуществляется за s шагов,
то можно записать:
6j 062°... °6s°e = ф,
где 8Ь 82, ..., 8S — некоторые транспозиции. Следовательно,
вопрос задачи можно сформулировать так:
Можно ли разложить произвольную перестановку в
произведение транспозиций?
Аналогичные вопросы интересно решать не только для
транспозиций, но и для произвольных множеств переста-
перестановок.
Определение.Подмножество Тмножества всех пере-
перестановок называется системой образующих заданной
симметрической группы S, если каждую перестановку из S
можно разложить в произведение перестановок из Т.
В § 5 было установлено, что сисгемой образующих
является совокупность всевозможных циклов. Каждый цикл
(аи а2> •••> as) можно разложить в произведение транспо-
транспозиций:
{аи а2, -.., л,) = (аь a2)»{ai9 а3)<> ...°(aiK as)
(проверьте!). Пользуясь этим, каждую перестановку, разложив
ее сначала в произведение циклов, можно представить в
виде произведения транспозиций.
Пример 1. Разложить в произведение транспозиций пере-
перестановку
Л 2 34 5 6 7 8\
V \8 7 2 I 6 5 3 4/
Раскладываем <р в произведение циклов:
Ф = A, 8, 4) о B, 7, ЗИ5, 6).
Далее имеем
A, 8, 4) = A, 8)оA, 4);
. B, 7, 3) = B, 7)оB, 3).
Следовательно,
Ф=A, 8)оA,4)оB, 7)оB, 3)оE, 6).
Из этого примера видно, что в разложении перестановки
в произведение транспозиций порядок множителей является
существен ным.
52

Далее будем обозначать символом Sn симметрическую
группу перестановок на множестве М = {1, 2, ..., п}. В этой
группе будем выделять системы образующих, которые будут
складываться только из транспозиций определенного вида.
Например, последовательности транспозиций
I A, 2), B, 3), C, 4), ..., (и-1, и),
II A, 2), A, 3), A, 4), .... A, и),
как легко убедиться, будут системами образующих для Sn.
Действительно, перестановку (i, j) можно разложить в произ-
произведение транспозиций системы II так:
(U) = (i, 0°(l, /И1, 0. * B)
(Убедитесь, что перестановки, которые стоят справа и слева в
этом равенстве, одинаково действуют на каждый элемент из
М.) Поскольку какую угодно перестановку ф можно разложить
в произведение транспозиций вида (i, ;), то, заменив в этом
разложении все транспозиции в соответствии с равенством B),
получим разложение ф в произведение транспозиций сис-
системы П.
В свою очередь произвольную транспозицию из после-
последовательности II можно разложить в произведение переста-
перестановок системы I по равенству
A, *) = A, 2)оB, 3)o...o(fc-i, fc)o(fc-l, *-2)о...оB, 1).C)
Проверим, правильно ли равенство C). Пусть 6$ = (i, i + 1).
Перестановка ф = 6Х °52О.. . °§*-i °6fc_2o...°6i действует на
элементы 1 и к так:
*k
Ф
Sfc-2
k-
k-
>.
- 1
5t-2>
^k
T
Si
+ 1
T
L 'L
Остальные элементы множества будут неподвижными точ-
точками для ф. Следовательно, ряд I также есть система
образующих для Sn.
Наиболее интересными системами образующих являются
такие, из которых нельзя выбросить ни одной перестановки,
чтобы новая система снова была системой образующих.
Эти системы называются неприводимыми. Они могут состоять
из разного количества перестановок. В частности, сущест-
существуют системы образующих, которые состоят из двух
53

перестановок (они всегда неприводимы). Например, такой
будет система
III а = A, 2), р = A, 2, 3, ..., л).
Действительно, если I ^ j'^ л — 2, то A)PJ ~ / + 1, B) (У =
= 7 + 2, а поэтому
^'оао(^)-1 =(/+ 1,./ f 2).
Таким образом, каждая перестановка системы I расклады-
раскладывается в произведение перестановок а, р, потому что
элемент [У имеет конечный порядок, например /, так что
УПРАЖНЕНИЯ
Разложить перестановки
2 3 4 5 6 7 8\ « /l 2 3 4 5 6 7\ \ Л 2 3 4 5
J; 6)(j62l 4з 5р В) [s 1 3 2 6
в произведение элементов системы I, II, III.
2. Будут ли системы образующих I и II неприводимыми?
3. Доказать, что все циклы длины 3 вместе с какой-нибудь
транспозицией образуют систему образующих симметрической
группы Sn. *
4. Образуют ли систему образующих симметрической группы
S9 перестановки A, 2, 3), A, 2, 3, ..., 9)?
5. Каждое подмножество из 5П, которое состоит более чем из
и!
—х- элементов, образует систему образующих Sn. Доказать это.
§ 8. ПОДГРУППЫ СИММЕТРИЧЕСКИХ ГРУПП
Как мы уже видели на примерах, некоторые подмно-
подмножества множества Sn сами образуют группу для действия
умножения перестановок. Такие подмножества играют важную
роль для изучения строения группы Sn.
Определение. Подмножество Т множества Sn на-
называется подгруппой группы Sn, если оно является
группой для действия умножения перестановок.
Часто, если это не вызывает недоразумений, под-
подгруппы симметрической группы Sn называют просто группами
перестановок надмножестве {1, 2, 3, ..., и}. В частности,
само множество Sn также является своей подгруппой,
которую называют несобственной. Кроме того, множество,
54

которое состоит лишь из одного элемента е, также явля-
является подгруппой, как это вытекает из равенств
8°? = S, б = 8.
Она называется тривиальной подгруппой группы Sn. Для
каждой другой подгруппы G группы Sn, очевидно, выполня-
выполняется неравенство
1 < \G\ <n\
Для каждого подмножества множества Sn, которое явля-
является подгруппой, должны выполняться все требования опреде-
определения группы. Но проверять все эти требования не нужно.
Точнее, справедлива такая теорема:
Теорема. Подмножество Т группы Sn, которое содер-
содержит по меньшей мере одну перестановку, является подгруп-
подгруппой группы Sn тогда и только тогда, когда:
1) вместе с каждыми двумя элементами ос, Р в него
входит и их произведение а°Р;
2) если аеТ, то и а~1еТ.
Действительно, если Г- подгруппа группы 5„, то она
замкнута относительно, действия умножения перестановок,
которые принадлежат Т, т. е. выполняется условие 1).
Каждый элемент из Т имеет обратный, следовательно,
выполняется условие 2).
Обратно, пусть для множества Т перестановок выпол-
выполняются условия 1), 2). Проверим, имеет ли множество Т
все свойства группы. Условие 1) означает, что множество Т
замкнуто относительно действия умножения своих элементов,
следовательно, удовлетворяется первое требование определе-
определения группы. Ассоциативность действия умножения переста-
перестановок Т имеет место, так как умножение произвольных
перестановок (в частности, и тех, которые принадлежат Т)
имеет такое свойство. Тождественная перестановка также
должна принадлежать множеству Т. Действительно, Т содер-
содержит хоть одну перестановку, например а, а тогда Т при-
принадлежит по условию 2) и перестановка а. Поэтому по
условию 1) Г принадлежит перестановка а о а — е. Наконец,
условие 2) показывает, что каждый элемент из Т имеет
обратный, который также принадлежит Т. Следовательно, Т
является подгруппой группы Sn.
Примеры. 1. Пусть Я — множество перестановок
8 Л23 4\ а=A2 3 4\ р = Л 2 3 4\ = /1 2 3 4\
\1 2 3 4/ \2 1 4 3/ Н \3 4 1 2/ \4 3 2 1/
55

Проверим, является ли Н подгруппой группы S4. Имеем: а * = а,
Р~1=:Р, Y"^?» следовательно, для множества Я выполняется
условие 2) только что доказанной теоремы. Кроме того,
ОѰР= Р°О1 = у, a°Y — У ° 01 = Р, poy = yop = (x,
а2 = р2 = у2 = е, а°е = а, Р°е = р, у°е = У
(проверьте!). Следовательно, произведение каждых двух элементов
множества Н является элементом того же множества, т. е. для
Н выполняется и условие 1) упомянутой теоремы. Из записанных
нами равенств вытекает, что группа Н а 6 е л с в а.
2. Пусть G — множество перестановок
2 3 4 5\ „ (Х 2 3 4 5\ R Л 2 3 4
2 3 4 5\ о (\ 2 3 4
Тогда а =8, р =у, 8 = а, у"* = Р; следовательно, выполня-
выполняется условие 2) теоремы о подгруппах группы Sn. Кроме того,
выполняются равенства
а о р = р о a = у, р о у = у.. р = бэ а2 = Р, 82 = у,
a о у = у о a = б, р ¦ 5 = б о р = а, р2 = 8, у2 = а,
(проверьте!). Как видим, произведение каждых двух элементов
множества G является элементом из G, следовательно, выпол-
выполняется и условие 1). Поэтому множество G является подгруппой
группы S5, причем из приведенных равенств вытекает, что группа G
а б е л е в а.
3. Пусть Т— множество перестановок
a /1234\ /1234\р /1234\
\2 3 1 4J' \1 2 3 4/' 1 \3 1 2 л)'
1 \2 4 1 3
Это множество не является подгруппой группы S4, так как для
него не выполняется ни одно из условий 1), 2). Действительно,
Симметрическая группа 5И имеет много разных под-
подгрупп, причем их число очень быстро возрастает с увели-
увеличением числа п. Ряд примеров мы приведем в следующем,
параграфе. Полностью описать все подгруппы группы Sn
56

удается лишь для небольших и, а для п больших изучаются
лишь общие свойства таких подгрупп.
Задача. Описать все подгруппы симметрической груп-'
пы S3.
Решение. 1) Опишем сначала подгруппы, которые со-
состоят из двух элементов. Если Н — такая подгруппа, то в нее
входит элемент s и еще какой-то другой элемент а. Элемент
обратный к а не может совпадать с s, поэтому ос~* = а.
Последнее равенство можно записать так: а2 = s. Сле-
Следовательно, а — перестановка второго порядка, т. е. цикл
длины 2. Таким образом, существует не больше трех подгрупп
ш второго порядка группы S3. Это такие подмножества
множества S3:
А = {е, A, 2)}, В = {е, B, 3)}, С = {е, A, 3)}.
Теперь, пользуясь сформулированной выше теоремой, легко
убедиться, что подмножества А, В, С действительно явля-
являются подгруппами, так как для каждого из них выполняются
условия-1), 2) этой теоремы.
2) Опишем подгруппы, которые состоят из трех элементов.
Если G = {s, а, р} — такая подгруппа, то элементы а, р
должны иметь порядок 3. Действительно, если один из них,
например а, имеет порядок 2, то а = а~1, и, поскольку
каждый элемент имеет лишь один обратный, отсюда полу-
получаем, что и Р = р, т. е. р2 = 6. Но легко проверить
непосредственно, что произведением любых двух элементов ср,
\|/, Ф / \|/, второго порядка является элемент, который име-
имеет порядок 3. Следовательно, при таких предположениях
произведение а ° р не принадлежит G и G не есть подгруппа.
Рассмотрим теперь случай, когда перестановки аир имеют
порядок 3, т. е. G == {е,- A, 2, 3), A, 3, 2)}. Имеем
а =р, Р =а, аор = роа = 89 а2 = р, р2 = а,
т. е. подмножество G множества S3 действительно явля-
является подгруппой группы 53.
Легко убедиться непосредственно, что подмножества
множества S3, которые состоят из 4 или 5 элементов,
подгрупп не образуют. Оставляем это читателю.
Таким образом, симметрическая группа 53 имеет шесть
разных подгрупп.
Рассмотрим еще один общий пример группы перестано-
перестановок. Пусть а Ф s — произвольная перестановка из Sn, которая
имеет порядок к. Тогда перестановки
а, а2, а3, ..., а*, а* = е
57

отличны одна от другой. Убедимся, что множество С
этих перестановок является группой. Действительно, по опре-
определению действия умножения, для произвольных переста-
перестановок ос1', <xjeC имеем
К
ol1+j \ если i +j ^ к.
Обратной к перестановке ос'еС является перестановка ос*~1,
так как а1°ак~1 = ак = ?. Таким обраюм, произведение
произвольных двух перестановок т множества С снова есть
элемент множества С, и персе книжка, обратная к про-
произвольной подстановке из Г, шкже принадлежит С. Сле-
Следовательно, С — группа. Такие i руины называются цикли-
циклическими.
Циклической будет, например, подгруппа из примера 2;
каждая подгруппа группы Sb также циклическая. Но под-
подгруппа из примера 1 не циклическая.
J УПРАЖНЕНИЯ
1. Описать все подгруппы i румпы Л'4, которые состоят из
трех перестановок. Сколько их?
•2. Сколько подгрупп второю порядка имеет группа S51
3. Доказать, что множесюо всех элементов группы Sn, которые
оставляют без изменения искоюрос число /сэ образую группу.
4. Говорят, что перестановки а, Р коммутируют, если
аор = роа. Множество всех \>лемешов произвольной группы, ко-
которые коммутируют с каждым ее элементом, называется центром
группы. Найти центр группы S4.
5. Какого наибольшего порядка может быть циклическая"
подгруппа группы S9?
6. Доказать, что подмножество К множества Sn образует
подгруппу, если произведение произвольных двух элементов из К
принадлежит К.
§ 9. ГРУППЫ СИММЕТРИИ
Одним из наиболее употребляемых примеров групп и, в
частности, групп перестановок являются группы, которыми
«измеряется» симметричность геометрических фигур
как плоских, так и пространственных. В этом параграфе
мы приведем соответствующие примеры.
Рассмотрим сначала симметрию плоских фигур. Плос-
Плоская фигура может иметь ось симметрии (одну или несколько) —
58

прямую, которая разбивает ее на две части (рис. 19),
каждая из которых является зеркальным отражением другой.
В этом случае фигура называется симметричной относи-
относительно данной прямой.
Рис. 19.
Рис. 20.
Другим типом симметрии является симметрия относи-
относительно точки (рис. 20), которая называется центром сим-
симметрии, а фигура — централъносимметричной. Это понятие
естественным образом обобщается. А именно, будем говорить,
что точка О есть центр симмет-
симметрии п-го порядка для фигуры М, если фи-
фигура М совмещается -с собой при по-
поворотах на углы, кратные 2к/п. Напри-
Например, на рис. 21 изображена фигура,
имеющая центр симметрии порядка 3.
Каждому типу симметрии соответ-
соответствует преобразование симметрии —
преобразование множества точек пло-
плоскости, определяемое этим типом. Так,
если О - центр симметрии и-го по-
порядка, то соответствующим преобра-
преобразованием симметрии является преобразование вращения всех
точек плоскости вокруг точки О на угол 2к/п (см. пример 8
§ 2). Для определенности будем считать, что поворот осуще-
осуществляется против движения часовой стрелки. А то, что неко-
некоторая фигура симметрична, означает, что она самосовмещает-
самосовмещается при соответствующем преобразовании симметрии. Таким
образом, обозрение всех симметрии данной фигуры равно-
равносильно обозрению всех тех преобразований плоскости, при
которых она самосовмещается. Понятно, что эти преобра-
преобразования являются бйекциями. Поэтому множество всех
таких преобразований относительно умножения преобразова-
преобразований образует группу, которая является как бы мерой
59
Рис. 21.

степени симметричности данной фигуры. Преобразования
симметрии многих плоских фигур естественно описываются
перестановками, т. е. их симметричность «измеряется» не-
некоторыми группами перестановок. Опишем эти группы в
случае, когда рассматриваемая фигура является правильным
многоугольником.
1. Группа симметрии правильного тре-
треугольника. Занумеруем вершины правильного треуголь-
т ника числами 1, 2, 3 (рис. 22) и
будем характеризовать каждое его
самосовмещенис ф перестановкой на
множестве вершин треугольника
Vi h
где ik - (к) ф — номер места, кото-
которое после выполнения преобразова-
преобразования ф заняла вершина к, к = 1,
2, 3. Цритр правильного тре-
треугольника О является центром сим-
симметрии порядка 3, т. е. попороты ф0 = с, фь ф2 на углы 0, 2я/3,
4тс/3 соответственно вокруг точки О против часовой стрелки
переводят треугольник в себя. Кроме того, имеется три
осевых симметрии ф3, Ф4, Ф5> определяемых осями симметрии
/, m, n соответственно, проходящими через вершины правиль-
правильного треугольника и середины его противоположных сторон
(рис. 22). Принятое нами соответствие между самосовме-
самосовмещениями треугольника и перестановками множества вершин
треугольника дает
Фо
(\ 2 з\ т (\ 2 3\ п -
4l2 3> Ф1Ч2 3 1ГA'2'
Ф2'
2 3
3 г
= B,
Таким образом, группа симметрии правильного треуголь-
треугольника — это симметрическая группа S3.
2. Группа симметрии квадрата. Все самосов-
самосовмещения квадрата являются либо вращениями ос0 = в, ось
ос2, а3 на углы 0, я/2, п9 Зя/2 соответственно вокруг центра
квадрата, либо симметриями а4, ос5, сх6, а7 относительно осей
к, I, m, n соответственно, проходящих через середины про-
60

тивоположных сторон и через противоположные вершины
(рис. 23). Соответствие между самосовмещениями квадрата
и перестановками на множестве вершин квадрата при приня-
принятой на рис. 23 нумерации вершин
квадрата имеет вид
а, -A, 2, 3,4), а2-A, 3)оB, 4),.
а,-A, 4, 3, 2), а4-A, 2)оC, 4),
*« Ml, 4).B, 3), а6~ B, 4), а7 - A, 3).
Таким образом, группа симмет-
симметрии кпадрата является собственной
подгруппой симметрической группы
S4. Она обозначается символом ZL. Рис. 23.
3. Группа симметрии пра-
в и л ь н о г о и-у i о л ь н и к а состоит
из и вращений на углы 0, 2тс/п, 4тс/п, ..., 2(п — 1)п/п
вокру! центра п-угольника и п симметрии относительно
прямых. Положение осей симметрии зависит от четности
числа п. При п четном имеется п/2 осей симметрии,
проходящих через середины противолежащих сторон и п/2
осей-, проходящих через противолежащие вершины (и центр)
многоугольника. При п нечетном осями симметрии являются
прямые, проходящие через вершины (и центр) п-угольника и
середины противолежащих сторон. Таким образом, группа
симметрии правильного п-угольника состоит из 2 п преобразо-
преобразований. Если эти преобразования описывать перестановками
множества вершин правильного п-угольника, то соответ-
соответствующая группа перестановок является подгруппой симмет-
симметрической группы Sn. Эта группа перестановок называется
группой диэдра и обозначается Dn.
¦f
I
Рис. 24.
-т
4. Группа симметрии многоугольника, изо-
изображенного на рис. 24, состоит из тождественного
преобразования а0 = 8, симметрии аг и а2 относительно
61

осей / и т соответственно и центральной симметрии а3
с центром О. Они описываются такими перестановками
множества {1, 2, 3, 4, 5, 6}:
а, ~A, 2)оC, 6)оD, 5), а2 -A, 5)оB, 4),
а3~A, 4) о B, 5)оC, 6).
Для пространственны х тел можно говорить о
следующих типах симметрии:
а) зеркальная симметрия (симметрия относительно
плоскости); *
б) осевая симметрия (симметрия относительно прямой);
в) центральная симметрия (симметрия относительно
точки).
По аналогии с плоским случаем понятие осевой симметрии
естественно обобщается. Прямая называется осью симметрии
п-го порядка, если тело совмещается с собой при вращениях
вокруг прямой на углы, кратные 2к/п. Каждому типу сим-
симметрии соответствует свое преобразование пространства,
и симметричность тела означает, что оно самосовмещается
при соответствующем преобразовании пространства. Мно-
Множество всех тех преобразований, при которых тело совмеща-
совмещается^ с собой, образует группу симметрии данного тела.
Симметрии многогранников и
некоторых других тел можно
характеризовать перестановка-
перестановками множества их вершин.
В этом случае группа симметрии
также является некоторой груп-
группой перестановок. Приведем
один пример такого описания.
5. Группа симметрии
тетраэдра. Тетраэдр (рис. 25)
имеет 4 оси симметрии /ь /2,
/3, /4 3-го порядка, проходя-
проходящие через его вершины 1, 2, 3, 4
и центры Ои 02, 03, 04 про-
противолежащих граней. Вокруг
каждой оси, кроме тождественного, возможны еще два вра-
вращения. Им соответствуют такие перестановки:
2 3 4\ Л 2 3 4^
3 4 2Г VI 4 2 Зу
вокруг оси
вокруг оси 12
\ Л 2 3 4)
)У U 4 2 3/'
А 2 3 4\ Л 2 3 4\
\4 2 1 3/' V3 2 4 1/'
62

вокруг оси /з A 2 3 4
УУ 3 \2 4 3
4\ Л 2 3 4V
1/' \4 1 3 2)
вокруг оси /4 Л 2 34\ Л 2 3 4\
Р>У 4 \Ъ 1 2 4/ \2 3 1 4/*
Кроме того, имеется 3 оси симметрии 2-го порядка, про-
проходящие через середины А, В, С, D, E, F скрещиваю-
скрещивающихся ребер. Поэтому имеется еще 3 (по числу пар
скрещивающихся ребер) нетождественных преобразования,
которым соответствуют перестановки:
вокруг оси АВ A 2 3 4)
1 \4 3 2 1/
вокру! оси Сб ( 1 2 3 4V
** \3 4 1 2/' '
вокруг оси EF
Итак, вместе с тождественным преобразованием получаем
12 перестановок. Группа симметрии тетраэдра в таком
описании является подгруппой группы S4. Аналогично можно
определять группы симметрии и других многоугольников
и многогранников (не обязательно правильных). Они будут
подгруппами соответствующих симметрических групп. Уже из
этого видно, что симметрические группы очень богаты
подгруппами. Более того, имеет место такой важный факт,
что любая конечная группа по существу является подгруппой
симметрической группы Sn при подходящем п. Однако на до-
доказательстве этого утверждения мы останавливаться не будем.
УПРАЖНЕНИЯ
1. Определить порядки всех элементов группы Х>8.
2. Являются ли группы Ц, абелевыми?
3. Понятие системы образующих можно рассматривать для
произвольных групп перестановок, а именно, подмножество Т
группы перестановок G называется системой образующих, если
любую перестановку из G можно записать в виде произведения
перестановок из Т. Аналогично определяются и неприводимые сис-
системы образующих. Укажите неприводимую систему образующих
группы Dn. Существует ли неприводимая система образующих группы
Цр состоящая из перестановок порядка 2? Существуют ли непри-
неприводимые системы образующих, состоящие из разного количества
перестановок?
63

4. Описать группу симметрии звезды, изображенной на рис. 26.
Каков порядок этой группы?
5. Доказать, что группа симметрии куба состоит из 48 пере-
перестановок.
Рис. 26. Рис. 27.
6. Опишите все вращения куба вокруг всевозможных осей
симметрии. Сколько их?
7. Отличаются ли группы симметрии плоских фигур, изображен-
изображенных на рис. 27.
§ 10. ТЕОРЕМА ЛАГРАНЖА
Пусть G и Я — группы перестановок, причем Я <= G,
т. е., как принято говорить, Я является подгруппой группы
G. Одной из первых теорем теории групп является теорема,
устанавливающая связь между порядками групп G и Я,
доказанная в несколько иных терминах Лагранжем еще в
конце XVIII столетия. Эта простая по идее доказательства
теорема очень часто применяется как в самой теории групп,
так и во всех приложениях, одно из которых мы рассмотрим
ниже.
Теорема Лаг ран ж а, Если Я — подгруппа группы G, то
ее порядок является делителем порядка G.
Доказательство. Пусть е, аь а2, ..., оси_х — все
перестановки, содержащиеся в группе G, р0 = ?> Рь • • •» Pm-1 —
все перестановки из Я (т. е. т ^ п). Если Я = G, то утвержде-
утверждение теоремы справедливо, поэтому предположим, что
Я ф G (Я — собственная подгруппа G). В силу этого предпо-
предположения существует перестановка jieG такая, что у^Я.
Рассмотрим ряд перестановок
Po°Yi =Yi. Pi°Yb ..., Pm-i°Yi. A)
Все перестановки этого ряда различны: если бы для
64 ¦ .

каких-то U j имело место равенство Pi°Yi = Pj°Ti> то,
умножив его правую и левую части на yj~ *, мы получили бы
равенство рг = Pj. Кроме .того, ни одна из них не содержится
в подгруппе Н: если бы для какого-то номера i имело место
включение ^i°yleH9 то это означало бы, что Pj°Yi = Pj для
какого-то у. Из этого равенства имеем ух = РГ1 ° Р> а так как
Н — группа перестановок, то у1 е Я, что противоречит выбору
этой перестановки.
Если перестановками группы Я и ряда A) исчерпаны все
перестановки из G, то | G | = 21Н], и все доказано. В против-
противном случае найдется такая перестановка у2 е G, что у2 Ф И и
у2 не содержится в ряде A). Определим для нее ряд переста-
перестановок
Po°Y2=Y2, Pl°Y2, .-., Pm-1OY2- B)
Аналогично проверяется, что: а) все перестановки ряда B)
различны; б) они не содержатся в Я; в) ни одна из них
не встречается среди перестановок ряда A).
. Если перестановками из подгруппы Я и рядов A) и B)
исчерпываются все элементы группы G, то | G \ = 31Н \, и все
доказано. В противном случае продолжаем процесс выбора
перестановок у^ и построения рядов вида A) и B) даль-
дальше. Так как группа G конечная, то на каком-то, например,
на k-м шаге все перестановки из G будут исчерпаны.
Иными словами, все их можно расположить в такую
таблицу:
Ро, Рь Рг> •••> Рт-ь
Po°Yi> Pi°Yi, P2°Yb •••, P«-i°Yi, C)
Po°Y2, Pl°Y2, P2°Y2, •-., Pm-1°Y2,
Po°Yk> Pl°Yk, P2°Yk, ••-, Pm-l°Yk,
при этом все перестановки в каждой из строк этой таблицы
различны и любые 2 строки не имеют общих элементов.
Поскольку общее число элементов в таблице равно п
(порядок группы G\ а число элементов в заждой строке
равно т (порядок группы Я), то имеем равенство п = тк9
т. е. т является делителем п, и теорема доказана.
Число к называют индексом подгруппы Н в группе G и
обозначают [G: Я]. Из доказательства теоремы Лагранжа мы
получаем, что имеет место равенство
3 Л. А. Калужнин, В. И. Сущанский 65

Так как порядок циклической подгруппы, порожденной пе-
перестановкой oceG, совпадает с порядком перестановки а, то
из теоремы Лагранжа получаем,, что порядок любой переста-
перестановки из G — делитель \G\.
Теорема Лагранжа позволяет также существенно упро-
упростить решение задачи описания всех подгрупп данной
группы. Например, если порядок \ G \ группы G есть простое
число, то, согласно этой теореме, в G нет собственных
подгрупп*
Собственные подгруппы из 53 могут состоять из двух и трех
перестановок (делители числ'а 3! =6), поэтому непосредст-
непосредственную проверку, о которой идет речь в задаче из § 8, можно
опустить. А ведь эта проверка длинная, так как есть
Cj + Cj = 21 подмножество из 53, состоящее из 4 или 5
элементов. Даже на этих двух примерах видно, насколь-
насколько существенным может быть применение теоремы
Лагранжа.
УПРАЖНЕНИЯ
1. Множества перестановок, стоящие в рядах таблицы C)
называются правыми (так как yt умножается справа)
классами смежности, а таблицу C) естественно назвать таблицей
разложения группы G на правые классы смежности по подгруппе Н.
Вполне аналогично можно построить таблицу разложения группы G
на левые классы смежности по подгруппе Я. Построить таблицы
разложения группы 53 на классы смежности как правые, так и левые
по подгруппе А = {е, A, 2)}; по подгруппе В = {е, A, 2, 3), A, 3, 2)}.
2. Доказать, что вращения правильного шестиугольника вокруг
центра на углы, кратные тс/3, образуют подгруппу в группе всех
его симметрии. Составить таблицы разложения на правые и ле-
левые классы смежности группы симметрии шестиугольника по под-
подгруппе всех вращений. Обобщить это на случай произвольного
«-угольника.
3. 1;сли Н — подгруппа индекса 2 в группе G, то правые
и левые классы смежности по этой подгруппе совпадают. Дока-
Докажите.
4. Пусть kl9 к2, ..., К — решение (kt — натуральные) уравнения
*1 + *2 + • • • + хп = т
(т — произвольное натуральное). Тогда ki! • к2 !¦...• кп! является
делителем ml. Докажите.
5. Выпишите все числа, которые, согласно теореме Лагранжа,
могут быть порядками элементов в группе D12. Существуют ли в
группе Х>12 перестановки таких порядков?
6. Тот же вопрос для группы S4.
66

§ 11. ОРБИТЫ ГРУППЫ ПЕРЕСТАНОВОК.
ЛЕММА БЕРНСАЙДА
Рассматривая группы перестановок, мы ограничивались
изучением их действия на элементы некоторого мно-
множества. Но ведь если такое действие определено, то
перестановки поэлементно «передвигают» и подмноже-
подмножества данного множества. При изучении свойств действий на
подмножествах первым шагом является, естественно, описа-
описание тех подмножеств, которые данная группа перестановок
в целом не передвигает. В связи с этим возникает понятие
орбиты группы перестановок на данном множестве.
Пусть G — группа перестановок на множестве М =
••= {1, 2, ..., п}. Подмножество О с М называется орбитой
группы G, если:
а) (а) сне О для любого oleG и любого аеО\т..е. действие
перестановок из G на элементы О не выводит за пределы О;
б) любые два элемента из О молено перевести друг в
друга некоторой перестановкой из G.
Всякая группа перестановок G = {е = а0, аь ..., ак_х}
имеет орбиты. Для доказательства выберем произвольный
элемент аеМ и, рассмотрим множество О (а) = {а = (а) а0,
(а)аь ..., (a)oik-i}. Оно будет орбитой группы G, так как:
а) если a,EG и Ь = (а)а;еО(а), то (b)ai = (a)(oijooLi)eO{a)9
так как ajoa^GG (ведь G — группа);
б) если b =(а)аги с = (а) О; — произвольные элементы из
0(а\ то fe=(fl)ai=(a)Foai) = (a)(aJoar1oa.) = (c)a-1oa.; и
при этом a) l°<XjEG, так как G — группа.
Оказывается, что орбитами подобного вида исчерпываются
все типы орбит. Более точно, если О — орбита группы G и а е О,
то О = О (а). Справедливость этого утверждения вытекает
непосредственно из определения орбиты группы.
Ясно, что любые две орбиты О (а) и О (Ь) либо совпадают
(если be О (а)), либо не пересекаются (если ЬфО(а)). Отсюда
(почти так же как и при доказательстве теоремы Лагранжа)
следует, что множество М распадается в объединение непере-
непересекающихся подмножеств — орбит группы G. В частности,
может случиться, что единственной орбитой группы G будет
само множество М, как это имеет место для групп Dn
(проверьте!). Группы с таким свойством называются тран-
транзитивными. Таким образом, группа перестановок G на
множестве М транзитивна, если любой элемент аеМ может
быть получен из любого другого элемента ЬеМ под
действием подходящим способом выбранной перестановки
3* ' - 67

oleG: (a) = (Ь)а. Все другие группы перестановок называются
интранзитивными.*
В связи с разбиением множества М на орбиты группы
перестановок G возникают следующие два вопроса:
1) Сколько орбит имеет группа G на множестве М?
2) Какова длина каждой из этих орбит, т. е. из скольких
элементов они состоят?
~ Сформулируем вначале утверждение, позволяющее выяс-
выяснить ответ на второй вопрос. Оно формулируется с использо-
использованием понятия стабилизатора элемента из М. А имен-
именно, для любого элемента аеМ можно рассмотреть
множество Ga всех перестановок из G, для которых
точка а является неподвижной. Это множество, очевидно,
является группой (еще один способ образования групп'
перестановок!), которая и называется стабилизатором
точки а.
Теорема. Длина орбиты О (а) равна индексу стаби-
стабилизатора Ga в группе G, т. е.
\O(a)\ = \G\:\Ga\.
Доказательство. Пусть G = {а0 = 8, аь ..., а*^},
Ga = {Ро = е, Рь..., Ps-1}« Для подсчета различных элементов
в последовательности а, (а)аь ..., (q)oLk-\ удобно особым
образом расположить в* ряд элементы группы G. Для этого
вспомним примененное при доказательстве теоремы Лагран-
жа разложение группы G в правые классы смежности по
подгруппе Ga. Существуют перестановки у0 = е, уи ..., у(_!
из группы G такие, что все перестановки ряда
<*о =Ро°Уо = е, «1 = р1оу0, ..., ocs_! =Ps-i°Yo,
<xs =Po°Yi,
попарно различны и исчерпывают всю группу G, Для любого
i = о, ..., /—1 применение s перестановок ais, ais+i, ...
..., a(l-+ 1)s_ ь образующих i-ю строку таблицы A), к элементу
а дает один и тот же элемент (а)уг. Все / элементов
(a) yt попарно различны. Действительно, если бы (a) yt = (a) Yj
для некоторых i, j, то a = (a)jj°y(rl9 т. е. перестановка
Yj ° Y»~х 6 &а- Но это возможно только тогда, когда yt и Yj
содержатся в одном правом классе смежности группы G
по подгруппе Ga, чего быть^ не может.
68

Таким образом, длина орбиты О (а) равна /, т. е. числу
строк в таблице A). А это число в § 10 и было названо
индексом подгруппы в группе.
Проиллюстрируем понятие орбиты группы и доказанную
теорему на примере 4 из § 9, где рассматривалась группа
перестановок G = {е, а, р, у}, действующая на множестве
М = {1, 2, 3, 4, 5, 6}. Имеем, A)е = 1, A)а = 5, A)Р = 2,
A)у = 4, т. е. 0A) ={1, 2, 4, 5}. Выбирая какой-нибудь
элемент из М, не принадлежащий 0A), скажем 6, получим
FN = 6, F)<х = 6, F)р = 3, F)у = 3, т. е. 0F) = {3, 6}. Таким
образом, группа перестановок G на множестве М имеет две
орбиты ОA) = {1JL,5}, 0F) = {3,6} •
и поэтому является интранзитивной. .
Стабилизатор Gj точки 1 из 0A) состоит из одной
перестановки е. Поэтому [G :GX] = 4 = |0A)|. Стабилизатор
G6 точки 6 из 0F) состоит из перестановок 8 и а. Разложение
группы G на правые классы смежности по подгруппе
G6 = {e, а} имеет вид
б, а, еор = р, а°р = у.
Поэтому [G : G6] = 2 = 10F)|.
Докажем теперь утверждение, чисто исторически называе-
называемое леммой Бернсайда по имени английского математика-
алгебраиста В. Бернсайда A852 —1927), который, по-видимому,
первый опубликовал его доказательство в своей книге по
теории конечных групп A911 г.) Это простое утверждение
является основой теории перечисления, разработанной Д. Пойа
и рядом других математиков, — теории, нахбдящей широкие
применения в кибернетике, технике, органической химии, био-
биологии и т. д.
Пусть х(°0 — число неподвижных точек перестановки ос,
t(G) — число орбит группы перестановок G = {а0 = 8, ocl5 ...
..., ак_х}, действующей на множестве М = {1, 2, ..., и}.
Лемма Бернсайда. Для любой группы перестановок
имеет место равенство
¦'(GLlxD
1 ' aeG
Доказательство. Рассмотрим отношение «переста-
«перестановка а сохраняет неподвижным элемент т>> между пере-
перестановками группы G и элементами множества М. Сопоставим
парам (a, m), aeG, meM, вершины прямоугольной сети
69

и отметим те из них, для которых соответствующая пара
(а, т) находится в указанном отношении, т. е. (т) ос = т
(рис. 28). Иными словами, построим график указанного
отношения. Число отме-
М
1
1
ченных точек (точек, при-
принадлежащих графику)
можно подсчитать двумя
способами: определить чи-
число отмеченных точек на
каждой вертикали и про-
просуммировать полученные
величины или же опреде-
определить число таких точек
по каждой горизонтали и
затем вычислить их сумму.
Согласно определению
отношения на каждой вер-
. тикали отмечаются все
точки, сохраняемые пере-
перестановкой а, соответств>-
ющей этой вертикали. Их число равно х(°0- Поэтому
число всех точек графика равно
а
1 "г
Рис. 28.
aeG
С другой стороны, на каждой горизонтали отмечаются
все перестановки! сохраняющие элемент теМ9 отвечающий
этой горизонтали. Мы знаем, что они образуют группу Gm —
стабилизатор элемента m-иих число, согласно предыдущей
теореме, равно*
\Gm\ = \G\:\O(m)\.
Поэтому при втором способе подсчета числа отмеченных
точек графика рассматриваемого отношения получаем выра-
выражение
|G1| + |G2| + ...+ |GB|= ? |GJ. B)
теМ
Однако если элементы i, jeM содержатся в одной орбите,
то О@ = О0% и поэтому |G,| = \G\ :|O(i)| = \G\ :\0<j)\ = \Gj\.
Пусть Оu O2, ..., O| — все орбиты группы G такие, что
М = Oi (J 02 U • • • U 0" и слагаемые в этом объединении не
пересекаются. Разобьем сумму B) на части так, чтобы внутри
каждой из частей суммирование шло по элементам некоторой
70

орбиты:
I |GJ= E IGJ+ I IGJ + ...+ ? |Gm|.
meM meOi meO2 meO,
Каждое из t слагаемых в правой части этого равенства
можно преобразовать следующим образом:
Поэтому
Таким образом, при втором способе подсчета мы получили
t\G\ отмеченных точек графика. Приравнивая величины,
полученные при первом и втором способах, получим
т. е.
Лемма доказана.
В частности, если группа G транзитивная, т. е.
r(G) = 1, то по лемме Бернсайда
|G|= Zx(a).
aeG
УПРАЖНЕНИЯ
1. Пусть G — группа симметрии куба. Найдите порядок стабили-
стабилизатора некоторой вершины в этой группе. Какие перестановки
в нем содержатся?
2. Проверьте правильность утверждения леммы Бернсайда на
примере группы G (пример 4 § 9).
3. Перестановки аи р из группы G сопряжены в ней, если в
G найдется такая перестановка у, что у~1°а°у = р. Доказать,
что: а) каждая перестановка сопряжена сама с собой; б) если
перестановка а сопряжена с перестановкой р, то и, наоборот,
перестановка р сопряжена с перестановкой а; в) если а сопряжена
с р, а р — с у, то а сопряжена с у.
4. Из свойств а), б); в) упражнения 3 следует, что множество
G разбивается в объединение непересекающихся подмножеств пере-
перестановок, попарно сопряженных между собой, которые называются
классами сопряженных перестановок, группы G. Докажите это.
71

5. Если перестановки аир сопряжены, то х(а) = х(Р)> т- е.
функция % постоянна на классах сопряженных элементов G.
6. Используя предыдущую задачу, показать, что формулу для
определения числа орбит группы G можно переписать в виде
где %i — общее значение х(а) Для перестановок i-ro класса со-
пряженных перестановок, \|/? — число перестановок в i-м классе
сопряженных перестановок, 5 — число классов сопряженных пере-
перестановок.
7. Доказать, что сопряженные перестановки имеют одинако-
одинаковый тип.
8. Группой вращений куба называется подгруппа группы всех
его симметрии, состоящая из всевозможных вращений куба вокруг
центра или осей симметрии. Доказать, что она транзитивна и,
пользуясь леммой Бернсайда, определить ее порядок.
9. Группа вращений куба естественным образом определяет
группу перестановок на множестве его ребер. Определить типы
всех перестановок *из этой группы.
10. Каждое вращение куба естественным образом переставляет
его грани, т. е. группа вращений куба определяет группу пе-
перестановок на множестве его граней. Доказать, что эта группа
транзитивна. Определить стабилизатор одной из точек (граней куба)
в этой группе.
§ 12. КОМБИНАТОРНЫЕ ЗАДАЧИ
Рассмотрим два простых примера, иллюстрирующих воз-
возможности применения леммы Бернсайда при решении комби-
комбинаторных задач на перечисление. Ряд примеров читатель
найдет также в упражнениях к этому параграфу.
1. Раскраска вершин куба. Сколькими способами можно
раскрасить вершины куба в три цвета (например, красный,
синий и зеленый).
На первый взгляд может показаться, что задача совсем
простая. Поскольку каждую из восьми вершин куба можно
раскрасить тремя способами, причем независимо от того,
как раскрашены другие вершины, то множество всех вершин
куба можно раскрасить З8 = 6561 различными способами.
Однако при таком подходе к решению задачи молчаливо
предполагается, что мы умеем различать вершины куба
перед окраской, т. е., скажем, куб жестко закреплен или его
вершины занумерованы. При этом полученный ответ можно
интерпретировать следующим образом: можно так раскра-
раскрасить З8 абсолютно одинаковых, жестко закрепленных кубов,
72

что все они будут различаться. Для З8 4- 1 кубов этого сделать
уже нельзя.
Ситуация существенно меняется, если мы откажемся от
предположения о том, что кубы жестко закреплены, так
как по-разному окрашенные кубы можно повернуть так,
что в новом положении их окраски совпадут (рис. 29).
(
/
/
6
д
7
1 if
о-сити цдет
• - красный цбет
* - зеленый
Рис. 29.
Естественно считать, что два куба раскрашены одинаково,
если их раскраски совпадают вплоть до способа размещения
кубов в пространстве, т. е. вплоть до некоторого вращения
одного из кубов. Будем говорить, что такие раскраски
кубов геометрически неотличимы. Поэтому естественным
уточнением задачи о раскраске является следующая задача:
сколькими геометрически различными способами можно рас-
раскрасить вершины куба в три цвета.
Переформулируем теперь эту задачу так, чтобы стала
понятной ее связь с леммой Бернсайда. Пусть М —
множество всевозможных по-разному раскрашенных кубов
одного размера^ положение которых в пространстве фикси-
фиксировано, \М| = З8, G — группа всех вращений куба, состоящая
из 24 перестановок. Группа G естественным образом
определяет группу перестановок на множестве М. Именно,
если aeG — некоторое вращение, то каждому кубу из М
можно сопоставить некоторый, вообще говоря, другой куб,
который получается из первого при вращении а. Это соот-
соответствие является, очевидно, перестановкой на множестве М,
которую будем обозначать &. Группу всех таких перестановок
множества М, определяемых перестановками из G, мы будем
73

обозначать G. Ясно, что \G\ = |G|. To, что два куба Кх и
К2 из М раскрашены геометрически одинаково, означает, что
один из них можно перевести вращением в такое положение,
в котором они неразличимы. Иными словами, существует
такая перестановка oceG, что (К1)й = К2 т. е. Кг и К2
содержатся в одной орбите группы, G, действующей на
множестве М. Таким образом, для того чтобы определить
•число геометрически различимых способов раскраски вершин
куба, нужно найти количество орбит группы G на мно-
множестве М.
Считая вершины кубов занумерованными числами 1, 2, 3,
4, 5, 6, 7, 8, раскраску каждого из З8 кубов можно
однозначно охарактеризовать «словом» из 8 букв, каждая из
которых есть либо к, либо с, либо з. То, что i-я буква
слова равна к (или с, или з) означает, что i-я вершина
при выбранной нумерации окрашена в красный цвет (или
в синий, или в зеленый соответственно). Например, для кубов
изображенных на рис. 29, имеем соответственно последова-
последовательности ссззсскк, ссссккзз. Перестановки из группы G
переставляют такие последовательности. Например, если а =
= A, 2, 3, 4) о E, 6, 7, 8)eG, то перестановка а слово
сссссссз переводит в ссссзссс, слово ссззсскк переводит в
сззссккс, слова сссссссс, кккккккк, зззззззз оставляет не-
неизменными и т. д. Выписать всю таблицу значений для
перестановки а затруднительно, поскольку она состоит из З8
строк!
Для того чтобы применить лемму Бернсайда, необхо-
необходимо определить число неподвижных точек каждой переста-
перестановки из G. Последовательность букв к, с, з будет непод-
неподвижной для перестановки а е G тогда и только тогда, когда
при разложении соответствующей перестановки а е G в произ-
произведение циклов вершины куба, номера которых входят в один
и гот же цикл, окрашены одним цветом. Например, если а =
= A, 2, 3, 4) о E, 6, 7, 8), то неподвижными относительно а
будут слова, составленные целиком из одной буквы и слова,
составленные из двух разных букв, причем одна из них
стоит на первых четырех местах в слове, а вторая —
на четырех последующих. Поэтому имеется 9 неподвижных
точек перестановки а на множестве М. Уже на этом
примере видно, что подсчет числа неподвижных точек
перестановок из G сильно упрощается, если известны разло-
разложения в произведение циклов соответствующих переста-
перестановок из G. Если перестановка aeG разложена в произве-
произведение к циклов, то число ее неподвижных точек равно 3*
74

A ^ к ^ 8). Поэтому сначала мы опишем разложения в произ-
произведение циклов для всех перестановок из группы G враще-
вращений куба.
а) Вокруг каждой из трех осей соединяющих центры
противоположных граней имеется три нетождественных вра-
вращения на углы я/2, я, Зя/2. Им соответствуют перестановки
A, 5, 8, 4) о B, 6, 7, 3), A, 4, 3, 2) с E, 8, 7, 6),
A, 8)»B, 7)оC, 6)°D, 5), A, 3)оB, 4)°E, 6)«F, 8),
A, 4, 8, 5) о B, 3, 7, 6),; A, 2, 3, 4) о E, 6, 7, 8);
A, 5, 6, 2)оC, 4, 8, 7),
A, 6)оB, 5)оC, 8)оD, 7Х
A, 2, 6, 5)°C, 7,'8, 4).
б) Вокруг каждой из четырех диагоналей, т. е. осей, соеди-
соединяющих противоположные вершины куба, имеется по два не-
нетривиальных вращения. Им соответствуют перестановки
A)°B, 5, 4)оC, 6, 8)оG), A)оB, 4, 5)»C, 8, 6)°GХ
B)оA, 3, 6)сD, 7, 5)о(8), B)оA, 6, 3)оD, 5, 7)о(8Х
' C)оA, 6, 8)оB, 7, 4)оEХ C)оA, 8, 6)оB, 4, 7)° E),
D)оA, 3, 8) о B, 7, 5) ° F), D)сA, 8, 3)оB, 5, 7) о F).
в) Вокруг каждой из шести осей, соединяющих середины
противоположных ребер имеется одно нетривиальное враще-
вращение. Им соответствуют перестановки
A, 5)°B, 8)оC, 7)оD, 6), A, 7)оB, 6)°C, 5)°D, 8),
A, 2)оC, 5) с D, 6) о G, 8), A, 7) о B, 8)°C, 4) о E, 6), .
. A, 7)°B, 3)°D, 6)оE, 8), A, 4)оB, 8)оC, 5)оF, 7).
Вместе с тождественной получаем 24 перестановки —
все элементы группы G. «Итак, в группе G вращений куба
имеется ,
1 перестановка типа <1, 1, 1, 1, 1, 1, 1, 1>
6 перестановок типа D, 4>,
9 перестановок типа <2, 2, 2, 2>,
8 перестановок типа <1, 1, 3, 3>.
Перестановка первого типа имеет З8 неподвижных точек,
любая из перестановок второго типа — З2, третьего и чет-
четвертого типов — З4 неподвижных точек. Поэтому, согласно
75

лемме Бернсайда, имеем
t(G) = -^-(З8 4- 6- З2 + 9 • З4 4- 8 • З4) = 333.
Таким образом, число геометрически различимых способов
раскраски вершин куба в три цвета равно 333.
2. Составление ожерелий. Сколько различных ожереАий
из семи бусин молено составить из бусин двух цветов —
красного и синего2
Для того чтобы стала понятной аналогия этой задачи с
предыдущей, переформулируем ее следующим равносильным
образом: . ,
Сколькими геометрически различными способами молено
раскрасить вершины правильного семиугольника в два цвета?
Здесь два способа раскраски неотличимы, если один из
них можно получить из другого, применяя к семиугольнику
либо преобразования вращения, либо симметрии относитель-
относительно осей, т. е. перестановки из группы диэдра D7. Если
вершины семиугольника пронумерованы, имеется 27 = 128
различных вариантов их раскраски, так как каждую вер-
вершину независимо от других можно раскрасить двумя спо-
способами.
Снова будем описывать раскраски словами длины 7,
составленными из букв к (вершина окрашена в красный цвет)
и с (вершина окрашена в синий цвет). На множестве N
всех таких слов действует группа ?O перестановок, зада-
задаваемых перестановками из ?>7. Например, если а = A, 2, 3, 4,
5, 6, 7), то перестановка а последнюю букву каждого
слова переставляет в его начало, а остальные буквы не
изменяет. Для того чтобы определить число орбит группы
D-j на множестве N, необходимо найти типы перестановок
из D1. Эта задача гораздо проще аналогичного вопроса
для группы G из примера 1. Группа ZO состоит из 14 пе-
перестановок множества {1, 2, 3, 4, 5, 6, 7}, которые распре-
распределены по возможным типам так:
1 перестановка имеет тип <1,4, 1, 1, 1, 1, 1>, ч
6 перестановок имеют тип <7>,
7 перестановок имеют тип <1, 2, 2, 2>.
Слово неподвижно относительно перестановки осе/^тог-
осе/^тогда и только тогда, когда буквы», стоящие на местах с номера-
номерами из одного, цикла в перестановке а, совпадают. Поэтому
тождественная перестановка имеет-27 неподвижных точек на
ЛГ, перестановки второго типа — по 2, а перестановки третьего
76

типа — по 24. Применяя лемму Бернсайда, получаем
t(D7) - -1_B7 + 6-2 + 7-24) = 18.
Итак, из бусин двух цветов можно составить 18 семибусен-
ных ожерелий.
УПРАЖНЕНИЯ
1. Грани куба можно раскрасить: а) все в белый цвет; б)
все в черный цвет; в) часть в белый, а остальные в черный.
Сколько имеется разных способов раскраски?
2. Сколько различных. ожерелий можно составить из двух
синих, двух белых и двух красных бусин?
3. Сколькими геометрически различными способами три" аб-
абсолютно одинаковые мухи могут усесться в вершинах
правильного пятиугольника?
4. Использовавшееся нами ранее понятие графа является одним
из основных в современной прикладной математике. В достаточно
общей ситуации (ориентированный) граф можно определить как
систему точек на плоскости, некоторые из которых соединены стрел-
стрелками. Точки называются вершинами графа, а стрелки — дугами.
Рассматриваются также графы неориентированные, т. е. такие, дуги
которых не имеют указателя направления. Сколько существует
различных ориентированных графов с тремя вершинами?
5. Сколько существует разливных неориентированных графов с
четырьмя вершинами?
6. Сколькими способами можно раскрасить вершины куба в два
цвета так, чтобы вершин каждого цвета было поровну?
7. Сколькими различными способами можно грани куба раскра-
раскрасить в четыре цвета?
§ 13. ДЕЙСТВИЕ ПЕРЕСТАНОВКИ НА МНОГОЧЛЕН
Напомним, что многочлен — это сумма каких-то одно-
одночленов. Если все одночлены многочлена / образованы из
символов хь х2,..., хп, то будем обозначать такой многочлен
f(xl9 х2, ..., х„) и говорить, что это многочлен с п перемен-
переменными. Например,
/(хь х2) = х\х2 + 2xiX2 4- 5xj
— многочлен с двумя переменными, а
д(хи х2, х3) = 2х?х2Хз + 5х?х2 4- 6х3
— многочлен с тремя переменными.
77

Пусть f(x\9 х2, ..., хи) — некоторый многочлен с л
переменными, М = {1,- 2, ..., и} — множество индексов при
переменных. Для произвольной перестановки а е 5И определим
действие а на многочлен/(хь х2, ..., хи), положив
Пример li а) Если /(хь х2, х3, х4) =
+ xfx2x3x4 + xt + x2 + 1, а
\2 3 1 47'
то
J \Xi> Х2, Х3, Х4^ =: X2X3XjX4 "г X2X3XjX4 "т" Х2 "т" Х3 ¦
б) Для многочлена
1» ^2» ^3» Х4) = XjX2X3X4 ¦
и перестановки а из предыдущего примера имеем
д°(хи х2. х3, х4) = х|х3Х!Х4 + х2х|х!Х4 + x2x3xfx4 = д(хи х2, х3, х4).
Из этого примера видно, что многочлен /°(х1} х2,..., хи).
может отличаться от Дхь х2, ..., хи), а может и совпадать
с ним.
Если /а(хь х2,..., х„) =/(хь х2,..., хи), то говорят, что
многочлен / не изменяется под действием перестановки а,
или, иначе, инвариантен относительно действия а. Понятно,
что каждый многочлен от п переменных инвариантен отно-
относительно действия тождественной перестановки:
/? (хь х2, ..., х„) = /(хь. х2, ..., х„).
Поскольку действие умножения двух перестановок
означает их последовательное выполнение, то для любых
перестановок а, т и произвольного многочлена/(хь х2,..., хи)
имеем %
•<(/(хь х2, ..., хи))Т=/СО1(*ь х2, •• •,'*¦).
Отсюда вытекает, что когда многочлен /(хь х2, ..., хи)
не изменяется под действием перестановок а и т, то он будет
инвариантен и относительно их произведения. Кроме того,
каждый многочлен/(хь х2, ..., х„), инвариантный относи-
относительно перестановки а, будет инвариантным и относительно
перестановки а. Поэтому множество всех перестановок
которые не меняют заданный многочлен /(хь х2, ..., хи),
образует группу. Эта группа называется группой инерции
многочлена /(хь х2, ..., хи).
*78

Пример 2. Найдем группу инерции многочлена
А(хи х2, х3) = (х! - х2)(х! - х3)(х2 - х3).
Имеем:
А{1> 2)(хи х2, х3) = (х2 - Xi)(x2 - х3)(хх - х3) = - Л(хи х2, х3),
А{2' 3)(ХЬ Х2, Х3) = (ХХ - Х3)(Х! - Х2)(Х3 - Х2) = - A(XU Х2, Х3),
ЛA'3)(хьх2, х3) = (х3 -х2)(х3 -х^(х2 - хх)= - А(хих2, х3),
ЛA'#2' 3)(*i,x2, х3) = (х2 -х3)(х2 -X!)(x3 -х1) = Л(х1, х2, х3),
А{и 3- 2)(хь х2, х3) = (х3 - Xi)(x3 - x2)(xj - х2) = А (хь х2, х3).
Следовательно, группой инерции многочлена А(хи х2, х3) является
множество {е, A, 2, 3), A, 3, 2)}.
Из этого примера видно, что многочлен А(хи х2, х3)
меняет знак под действием любой транспозиции.
Этот результат обобщается на многочлены такого вида с
большим числом переменных.
Многочлен А (хь х2, х3) является произведением разностей
Xi — Xj для i <j, i, j = 1, 2, 3; поэтому многочлен такого
вида с п переменными будет такой:
A(XU Х2, ..., Xn)=(Xl -Х2)(Х! -Х3)(Х! -Х4)...(Х! - Х„) X
X (^2 ~ Х3)(Х2 - Х4) ... (Х2 - Хи) X
х (х3-х4)...(х3-хп) х
Он содержит (п - 1) + (п — 2) + ... 4- 1 = п(п - 1)/2 сомножи-
сомножителей. Пусть (i, Д i <j — произвольная транспозиция. Она
действует лишь на те сомножители хк — хь к < I, в которых
по меньшей мере один из индексов к, I совпадает с i.
или j. Под действием транспозиции (i, 7) знак сомножителя
х, — xj меняется на противоположный:
(Xt - X/' Л = Xj -Xt=- (Xt - Xj)
Для других сомножителей, которые изменяются под дейст-
действием транспозиции (*', Д имеем:
а) если i, j < к, то xt — xk переходит в Xj — xk и наоборот,
не меняя знака;
б) если ij > к, то xk — xt переходит в хк — х;- и наоборот, не
меняя знака;
в) если i < к < j, то xt — хк переходит в х^ — х^ =
= — (хк — Xj), a xfc — Xj переходит в хк — хг = — (Х| — хк), т. е.
79

произведение (xt — хк)(хк — xj) под действием (ij) не. изменяет .
знака.
Следовательно, произведение всех сомножителей много-
многочлена А(хи х2, ..., хи), кроме Xi — Xj, под действием (i, j)
не изменяет знака, а сомножитель xt — Xj изменяет знак на
противоположный. Поэтому произведение всех сомножите-
сомножителей—многочлен A(xt, х2, ..., хп) — также изменяет знак:
AiU Л (хь х2,..., хп) = - Л (хь х2,..., х„).
Поскольку каждую перестановку можно разложить в
произведение транспозиций, то под действием любой пере-
перестановки многочлен А(хи х2, ...., хп) может лишь изменить
знак. Именно поэтому этот многочлен называется знакопере-
знакопеременным многочленом с п переменными.
Пусть /(хь х2, ..., х„) — некоторый многочлен. Дей-
Действуя на него всевозможными перестановками из Sm получим,
вообще говоря, какой-то набор разных многочленов:
fi(xux2,...,xn), /2(xi,x2,...,xn), ..., /s(xbx2,...,xw).
Сам многочлен/(хь х2, ..., хи) в этом ряду обязательно
встретится, так как /Е *=/. Многочлен
/!(хь хъ ..., х„)+/2(хь х2, ..., х„) + ... 4-/s(xb х2, ..., хя)
будем называть орбитальным для/(хьх2,... ,хи). Орбиталь-
Орбитальный многочлен, как легко понять, инвариантен относительно
произвольной перестановки из Sn.
Пример 3. а) Для одночлена х\ орбитальным многочленом
с п переменными будет многочлен
sfc = Xi + *2 + • • • + *t
Такие многочлены называются степенными суммами от п пере-
переменных. В частности, степенными суммами с двумя переменными
будут многочлены
SX = Xi + Х2, S2 = X? 4- Х|, S3 = X? + х\.
б) Для одночлена Xix|x3 орбитальным многочленом с тремя
переменными будет многочлен
х\х\хг + х\х2х\ + х?х|х3
Орбитальный многочлен с п переменными для одночлена
x'jx^ ... х^ будем обозначать оп (xl[xl\ ... х'|). Например,
о2 {ххх2) = хгх2 4- xix2,
^3(^1^2) = -^1^2 + Xl*3 + XiX2 + х\хъ + Х2Хз + Х2Х3.
Легко убедиться, что для любого п многочлен оп(х\х12)
выражается через степенные суммы. Проверим это для случая
80

и = 3. Имеем
эд = (х* 4- х* 4- х%){х\ + xl2 + х'з) = х5+| + х*2+' +
= sk+l
Следовательно, о3(х\хг2) = ад — sk+i-
- Интересным является вопрос о нахождении количества
слагаемых в орбитальных многочленах. Понятно, что коли-
количество одночленов в многочленах on(x\xli ... х1/) не может
превышать и! Максимальное количество одночленов будем
иметь только тогда, когда все переменные будут входить в
одночлен с разными степенями, а если показатели перемен-
переменных в одночлене будут повторяться, то оно будет меньше.
УПРАЖНЕНИЯ
один из многочленов:
1 ГТ Л 2 3 4\ Г
1. Пусть <7 = 12 1 3 4 Г а^~
aj Х^Х2Х^Х4. I ^Х^Х2ХзХ4.
_ б) Х1Х2Х3Х4 + х? + х3;
В) Х\ + Х2 + Х3 + Х4.
Найти /°.
2. Найти группу инерции многочлена
1, Х2, Х3, Х^./ ^ Х^Х2ХзХ^. Т ^ Х^Х2ХзХ^. i Э Х\ т J X2
3. Из какого числа перестановок состоит группа инерции много-
многочлена Л(хи х2, х3, х4)?
4. Для произвольной группы перестановок существует много-
многочлен, для которого эта группа является группой инерции. Доказать
это.
5. Сколько одночленов содержит многочлен о4(х1Х2ХзХ4). За-
Записать этот многочлен.
6. Доказать, что многочлен о„(хкх1) выражается через степенные
суммы для любого п.
7. Сколько одночленов содержит многочлен вида ои(х1х2 ... xt)
для разных п, 11
{§ 14. ЧЕТНЫЕ И НЕЧЕТНЫЕ ПЕРЕСТАНОВКИ.
ЗНАКОПЕРЕМЕННАЯ ГРУППА
Разложение перестановок из Sn в произведение транспо-
транспозиций, вообще говоря, не однозначно, например:
A, 2, 3) = A, 3)оB, 3) = A, 2)оA, 3).
4 Л» А. Калужнин, В. И. Сущанский 81

Все-таки определенную характеристику, которая остается
одинаковой для каждого из таких разложений, указать
можно. Такой характеристикой является четность числа
сомножителей в разложений. Точнее, справедлива такая важ-
важная теорема:
Теорема. Если otj ° ос2 °... ° ocs и Pj о р2 о ... о рг — разложе-
разложения перестановки в произведение транспозиций, то числа
s и t имеют одинаковую четность.
Доказательство. Пусть <р — некоторая перестановка
на множестве М — {1, 2, ..., п}, аг ° ос2 °... ° ocs, Pi ° P2 ° • • • ° Pr ~
разложения ф в произведение транспозиций. Подействуем
перестановкой ф на знакопеременный многочлен А (хи х2, ...
..., хп). Как было установлено в предыдущем параграфе,
А и у4ф могут отличаться лишь знаком, причем, если а
транспозиция, то А* = — А. Рассмотрим две последователь-
последовательности многочленов:
A, A«* = Fl9F«l> = F2,...,F:-1=Fs,
В каждой из них два соседних выражения отличаются
лишь знаком. А поэтому
С другой стороны, Fs = Gt = Лф. Следовательно, (- If A =
= (— 1)*А, т. е. s и t — числа одинаковой четности.
Теперь можно дать такое определение:
Перестановка называется четной, если она расклады-
раскладывается в произведение четного числа транспозиций. В про-
противном случае перестановка называется нечетной.
Таким образом, четными будут те и только те пере-
перестановки, которые, оставляют без изменения знакоперемен-
знакопеременный многочлен А (хь х2,..., хп). Обозначим через Ап множество
всех четных перестановок из Sn, а через Вп — множество всех
нечетных. По доказанной теореме каждая перестановка
<peSn принадлежит одному из этих множеств, причем Ап
и Вп не имеют общих элементов.
Покажем, что множества Ап и Вп состоят из одинакового
количества подстановок, т. е.
\Ап\ = \Вщ\. A)
Для этого построим взаимно однозначное отображение *Р
множества Ап на множество Вп. Зафиксируем некоторую транс-
транспозицию а и поставим в соответствие каждому элементу
82

соеД, перестановку ю°а:
*F: со -> со о а.
Перестановки со и со о а — разной четности, т. е. со ° а е Вп
и отображение Ч? определено правильно.
" Убедимся в том, что отображение Ч0 биективно.
Если Р, уеАп и C Ф у, то и Р°ос^у°а, потому что
равенство Р ° а = у ° ос можно было бы сократить на а и полу-
получить, вопреки условию, что Р = у.
Для каждой перестановки РеВ„ существует перестановка
уе ЛП9 а именно у = poor1 =роа такая, что (у) Ч* = р. Следо-
Следовательно, отображение Ч? является одновременно и инъек-
инъекцией, и сюръекцией. Отсюда вытекает справедливость
равенства A).
Каждая транспозиция — нечетная перестановка. Равенство
B) § 7 показывает, что цикл нечетной длины — перестанов-
перестановка четная. Четной будет также тождественная перестанов-
перестановка 6. Понятно, что произведение четных перестановок —
перестановка четная, произведение двух нечетных перестано-
перестановок - также четная, а произведение четной на нечетную (или
наоборот) — нечетная.
Если перестановка ср разложена в произведение транспо-
транспозиций
то обратной к ср будет перестановка
ф1 — Ss°5s_i °... °5
так как из равенства
вытекает, что ср~ * —Ъ~х о 5~Д o,..o5^o5f1, а для транспо-
транспозиций 8j~l = Ъ{..
Отсюда получаем, что множество Ап образует под-
подгруппу группы Sn. Эта подгруппа называется знакопере-
знакопеременной группой перестановок. Она играет очень важную роль
в теории групп перестановок и в ее применениях.
Заметим, что четность перестановки можно определить,
не раскладывая ее в произведение транспозиций. Достаточ-
Достаточно лишь разложить перестановку в произведение циклов и
прдсчитать количество циклов четной длины. Если найденное
число будет четным, то перестановка четная, в противном
случае — нечестная (см. упр., 11).
4* 83

УПРАЖНЕНИЯ
1. Какую характерную особенность имеет граф четной
перестановки?
2. Какой наивысший порядок могут иметь элементы группы А51
3. Составить таблицу умножения группы >44.
4. Какая из описанных нами в § 8 подгрупп S3 будет знако-
знакопеременной?
5. Найти центр группы А„ (см. упр. 4 § 9).
6. Доказать, что Ап — максимальная подгруппа Sm отличная от
Sm т. е. каждая подгруппа, которая содержит Ат совпадает или с
Ат или с 5„.
7. Доказать, что каждую четную перестановку можно разложить
в произведение циклов длины три.
8. Можно ли разложить каждую четную перестановку из Sm
где п нечетно, в произведение циклов
A, 2, 3), A, 4, 5), ...,A,и-1, и)?
9. Говорят, что пара чисел i, j образует инверсию, если
i>j\ Доказать, что перестановка
Л 2 3 ... п\
Vi h (з ... U
будет четной тогда и только тогда, когда количество инверсий,
образованных элементами ее второго ряда,— число четное.
10. Сколько имеется перестановок H3,S10, в которых элементы
второго ряда образуют ровно 6 инверсий?
11. Пусть </сь fe2, ..., /с3> —тип перестановки фе5и. Разность
п — s называется декрементом этой перестановки. Доказать, что
четность перестановки совпадает с четностью ее декремента.
§ 15. СИММЕТРИЧЕСКИЕ И ЧЕТНОСИММЕТРИЧЕСКИЕ
МНОГОЧЛЕНЫ
Многочлен f(xu х2, ..., хи) называется симметрии е-
ским, если он является инвариантным относительно дейст-
действия любой перестановки из Sn, т. е. группой инерции такого
многочлена является вся симметрическая группа Sn.
Например, симметрическими будут такие многочлены с и
переменными:
а^Хь х2, ...,хп) = Х! +х2 + ... + хи,
a2(xl5 х2, ...,хи) = Х!Х2 4-ХхХз + ... + хп-1хт
2> •••> хп) — *iX2X3 + ХхХ2Х4 + ... + Хи_2Хи_1Хт
qn(xi, x2,..., хи) = Х!Х2 ... хп.
84

Д@ЙС1 нитслыю, орбитальный многочлен любого одночлена —
симметрический, а
П| (Х|. хг хя) = оя(хх)9 а2(хь хг,..., х„) = ои(*1*2), •••
..., ст„(*ь х2,..., xn) = on(xtx2 ... х„).
Многочлены сть а2,- ..., ап называются элементарными
симметрическими многочленами. Запишем их полностью
для п « 2, п = 3:
"I (*Ь *г) = *1 + *2, СУ! (ХЬ Х2, Х3) = X! + Х2 + Х3,
"а (Х|. х2) = Х!Х2, -a2(xls х2, х3) = xtx2 + xtx3 + х2х3,
Непосредственно видно, что: а) сумма симметрических
многочленов — симметрический многочлен; б) произведение
симметрических многочленов — симметрический многочлен.
Полому, если в произвольный многочлен д(уи Уг> • ••» Уп)
с н переменными подставить вместо уи у2, .. •, уп элемен-
i мрные симметрические многочлены ab a2,..., а„, то получим
некоторый многочлен от хьх2, ..., хи, который будет
симметрическим. Например, если
д(УиУ2) = У1У2 + 5у2 +2,
ТО
и а2) = (хх + x2JXiX2 + 5xiX2 + 2 =
2х\х\ + ххх\ + 5ххх2 + 2
— симметрический многочлен.
Оказывается, что так можно получить каждый симметри-
симметрический многочлен.
Теорема. Каждый симметрический многочлен является
многочленом от элементарных симметрических многочленов.
Эта теорема называется основной теоремой о симметри-
симметрических многочленах. Мы докажем эту теорему лишь для
многочленов с тремя неизвестными. Рассмотрение этого
случая даст нам возможность обозреть все этапы полною
доказательства.
Понятно, что каждый симметрический многочлен с произ-
произвольным числом .переменных является суммой орбитальных
многочленов. А потому для доказательства теоремы в случае
п = 3 достаточно убедиться, что многочлены вида ол(к*).
0з(*1*2)| °з(*1*2*з) можно представить в виде многочленом
от ab a2, a3.

1) Убедимся методом математической индукции по числу к,
что каждая степенная сумма sk = Xi + х\ + х% выражается
через элементарные симметрические многочлены. Действи-
Действительно, sx = Xj + х2 + х3 совпадает с аь s2 = х2 + х2 + х2* =
= (хх + х2 + х3J - 2(XiX2 + х2х3 + XiX3) = а? - 2а2, s3 =
= а? — Заха2 4- За3. Выразим теперь sk для произвольного
к через многочлены sf, i < к. Имеем
fc-! = (х, + х2. + х3)(х*ГJ + 4"J + х3"J) = sk + о3(хкГ гх2).
Отсюда
Аналогично
O2Sk- 2 = О3 (Xfci ~ JX2) + О3 (Xfci " 2Х2Х3), CT3Sk_ 3 = О3 (х\ ~ 2Х2Х3).
Определяя из двух последних равенств многочлен о3 (х\ ~ хх2)
и подставляя его в предыдущее, будем иметь
В соответствии с предположением индукции степенные
суммы sfc-i, sk_2, sk_3 можно записать в виде многочленов
от элементарных симметрических многочленов, следова-
следовательно, через них можно выразить и сумму sk.
2) В § 13 было установлено, что любой орбитальный
многочлен вида о3(х\х2) выражается через степенные суммы.
По только что доказанному о3(х\х12) можно представить
в виде многочлена от элементарных симметрических много-
многочленов.
3) Пусть о3(х^х2хз) — некоторый орбитальный много-
многочлен, и пусть, например, число т — наименьшее из чисел fc,
/, т. Тогда имеем:
= х™х2х3оъ(х\~тх12т) = о3о3(хк1~тх2~т).
o3(xkl~lxl2~m) — орбита одночлена с меньшим числом перемен-
переменных, т. е. этот случай сводится к предыдущим.
Основная теорема о симметрических многочленах для
п — 3 доказана. Для п = 2 доказательство будет вполне ана-
аналогично, но значительно проще. Предлагаем читателю про-
провести его самостоятельно.
Рассмотрим несколько примеров применения основной тео-
теоремы о симметрических многочленах.,
1. Решить систему
(х + ху + у = 7,
\
86

Выразим симметрические многочлены в левых частях обоих
уравнений через а, = х 4- у и а2 = ху и введем новые неизвестные
и - х 4- у, v = ху. Получим вспомогательную систему
(и + v = 7,
{и2 -у= 13.
Она имеет два решения:
(и = _5, |w = 4,
\v = 12, [и - 3.
Значит, множество решений исходной системы A) равно объединению
множеств решений следующих двух систем:
(х + у=-5, |х4->> = 4,
\ху = 12; |х>> = 3.
Множество решений первой из них пусто, а множество решений
второй - {A; 3), C; 1)}. Следовательнр, множество решений исход-
исходной системы A) есть
0 U {A; 3), C; 1)} = {A; 3), C; I)}.
2. Доказать, что при а + b 4- с = 0 справедливо тождество
а3 + Ь3 + с3 = 3 abc.
Выразим симметрический многочлен а3 + Ь3 + с3 - 3 abc через
элементарные симметрические многочлены at = а + 6 4- с, a2 = ab +
+ ас + be, a3 = abc. Как было уже установлено при доказательстве
теоремы о симметрических многочленах, многочленом от аь ст2,
ст3, который совпадает с суммой s3 = a3 4- b3 4- с3 является ст3 —
— 3CTta2 + Зст3. Поэтому получим
а3 + Ь3 + с3 - 3 abc = aj - 3 atCT2 + 3 ст3 - 3ст3 = aj - .
Поскольку по условию а, = 0, то с/3 + Ь3 4- с3 — ЗаЬс также рав-
равняется 0, откуда и вытекает правильность доказываемого тож-
тождества.
3. Составить квадратное уравнение с корнями хь х2, если
{*! + х2 = 2,
Ixf + х* = 82.
Такое уравнение можно составить, использовав теорему Виета.
Для этого нужно найти, чему равняется произведение корней.
Выражая х\ + х\ = s4 через элементарные симметрические многочле-
многочлены, получим s4 = ст? — Аа\а2 4- 2а|. Если в это равенство подста-
подставить вместо s4 и стх их значения, то будем иметь квадрат нос
уравнение для ст2
2о22 - 16а2 +66 = 0.
Отсюда aBn = 11, о22) = -3. Следовательно, искомыми уравнениями
будут
х2-2х + 11=0, х2-2х-3 = 0.

Наряду с симметрическими многочленами часто прихо-
приходится иметь дело с четносимметрическими многочленами.
Четносимметрическими называются многочлены,
инвариантные относительно всех четных перестановок.
Следовательно, группа инерции четносимметрического мно-
многочлена будет содержать знакопеременную группу. Поскольку
в симметрической группе S2 четной будет лишь тождествен-
тождественная перестановка, то каждый многочлен с двумя неизвест-
неизвестными четносимметрический, т. е. в этом случае понятие
четносимметричности излишне. Однако уже среди многочле-
многочленов с тремя неизвестными есть нечетносимметрические,
например X!-b2x2-b3x3 (группа инерции этого многочлена
единичная).
Понятно, что каждый симметрический многочлен четно-
симметрический, но не наоборот. Например, знакопеременный
многочлен, A(xl9 x2, ..., хи) четносимметрический для
любого и, но не симметрический. Четносимметрическим
будет, в частности, каждый многочлен, который под дей-
действием произвольной транспозиции меняет знак. Многочлены
с таким свойством называются антисимметрическими. Как
было установлено в § 13, многочлен А(хи х2, ..., хи)
антисимметрический. Вполне понятно также, что произве-
произведение симметрического многочлена на произвольный анти-
антисимметрический многочлен снова антисимметрический
мнргочлен. В частности, антисимметрическими будут много-
многочлены вида
р(хи х2, ..., хп)Л(хь х2, ..., х„),
где р(хь х2, ..., хп) — любой симметрический многочлен.
Можно доказать, что каждый антисимметрический многочлен
записывается в виде такого произведения (см. упр. 7). Ясно,
что произведение двух антисимметрических многочленов —
многочлен симметрический.
Л е м м а. Действуя на произвольный четносимметриче-
четносимметрический многочлен /(хь х2, ..., хи) нечетными перестановками,
будем получать один и тот же многочлен, т. е.
/а(хь х2,..., xn) =/p(xj, х2,..., хя)
для любых нечетных перестановок ос, р.
Действительно, в этом случае ос ° а и |3°ос-четные
перестановки, и, следовательно,
уаоос __ Л}°а
Действуя на обе части этого равенства перестановкой а,
88

получим
Поскольку (TY ^Z01 для любых перестановок а, т, то
Используя ассоциативность умножения перестановок, полу-
получим
В силу определения обратной перестановки имеем
/аОЕ=/ро?, т.е.
/а=/р.
*
Теорема. Каждый четносимметрический многочлен
может быть представлен и притом единственным обра-
образом в виде суммы симметрического и антисимметрического
многочленов.
Доказательство. Единственность. Пусть за-
заданный четносимметрический многочлен/представлен в виде
f = 9 + K A)
где g — некоторый симметрический, h — антисимметрический
многочлены; Подействуем на обе части этого равенства
какой-нибудь нечетной перестановкой а:
Однако в силу предположений о д и Л, да = д, ha — — h,
т. е.
f* = 9-h. B)
Складывая и вычитая почленно равенства A) и B), получим
Отметим, что в силу ранее доказанной леммы правые части
равенств C) не изменятся, если вместо а взять какую-
нибудь другую нечетную перестановку р.
Проведенные рассуждения доказывают, что если разложе-
разложение A) возможно, то обязательно для д и h справедливы
формулы C), т. е. д и h, если существуют, то
определены однозначно.
Существование. Для доказательства существования
разложения A) необходимо проверить, что:

/ + /"* 1 — f1
1) / = :— h '-—-—, где а — некоторая (безразлично
какая) нечетная перестановка;
f+Г
2) G — -— симметрический многочлен;
f—fa
3) Н — антисимметрический многочлен.
Но I) очевидно, а для доказательства 2) и 3) достаточно
заметить следующее. Если р — четная перестановка, то
f^—f> (Г*)р =/а р =/° в силу леммы, так как а°Р~не-
четная перестановка. Поэтому Gp = G, Яр = Н. Если же Р —
нечетная перестановка, то /р =/а в силу леммы, а
(ГУ =/а°р =/, так как ос°Р будет четной перестановкой.
Поэтому f f
Теорема доказана.
В частности, любой многочлен с двумя неизвестными
является суммой симметрического и антисимметрического
многочленов.
УПРАЖНЕНИЯ
1. Выразить через элементарные симметрические многочлены:
а) х? + х52; б) х\ + х$ + xj; в) о3(х?х2).
2. Решить системы уравнений
[x2 + у2 + xy = 19.
в) '
fх + у = 4,
[х4 + / = 82.
3. Найти площадь треугольника, зная его периметр, сумму
квадратов длин его сторон и сумму кубов длин его сторон.
4. Если некоторый многочлен f(yl9 y2) обращается в нуль при
подстановке х1 + х2 вместо у\ и ххх2 вместо у2, то он тождест-
тождественно равен нулю. Доказать это.
5. Теорема единственности: для произвольного симметрическо-
симметрического многочлена /(хь х2) существует только один многочлен
д(Уи Уг) такой, что/(хь х2) = 0(сгь ст2). Доказать это утвержде-
утверждение, используя упражнение 4.
6. Если/(хь х2) — антисимметрический многочлен, то/(хь xt) =
= 0. Доказать это. Сформулировать и доказать аналогичное
утверждение для многочленов с тремя переменными.
90

7. Используя предыдущее упражнение доказать, что произволь-
произвольный антисимметрический многочлен/(хь х2) с двумя переменными
имеет вид (xt — x2)g(xl9 x2), где #(хь х2) — симметрический мно-
многочлен.
8. Функция /(хь х2, .-., х„) от'П переменных называется
симметрической, если она не изменяет значений при произволь-
произвольной перестановке аргументов, т. е. для любой перестановки
oeSn имеем ДхA)о, хB)о, ..., х(и)о) =/(хь х2, ..., х„). Докажите,
что функция
/(хьх2, хэ) = ||х! -х2| 4-Х! +.y2 - 2.v3 | + |Xi -х2| + Xi + х2 + 2х3
симметрическая.
§ 16. РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
1. Алгебраическим уравнением степени п называется урав-
уравнение вида
аохп 4- агхп~1 + ... 4- ап- ^х 4- ап = О,
где старший коэффициент а0 ф 0.
Простейшие виды алгебраических уравнений - уравнения
1-й и 2-й степени и даже некоторые специальные виды
уравнений 3-й степени — математики могли решать еще в
Древнем Вавилоне примерно 4000 лет тому назад. Правда,
в те далекие времена ученые еще не знали современной
математической символики и записывали и само уравнение
и процесс его решения словами, а не формулами.
2. Произвольное уравнение первой степени
ах 4- Ъ = 0
всегда имеет и притом единственное решение х — — Ь/а.
В школьном курсе алгебры доказывается следующая
теорема о решении произвольного квадратного урав-
уравнения * ,
ах2 4- Ъх 4- с = 0.
Если число D = Ъ2 — 4 ас > 0, то уравнение имеет ровно
два корня, которые даются формулой
_ -Ъ±]/Ъ
Xl'2 2a
Если D = 0, то корень только один: им является число
Ъ
Х~ 2а'

Если же D < 0, то корней среди действительных чисел
нет.
Математики всегда стараются избежать подобного раз-
разделения случаев — их число только увеличилось бы при
переходе к уравнениям более высокой степени. Желательна
была бы, конечно, формулировка: «Уравнение второй сте-
степени имеет два корня». Ее можно достичь, если, с одной
стороны, так расширить понятие числа, что стало бы воз-
возможным извлекать квадратные корни из отрицательных чисел,
а с другой — считать некоторые корни «несколько раз»
(ввести понятие кратного корня). И то и другое можно акку-
аккуратно сделать.
Сейчас же поговорим об уравнениях 3-й степени.
3. Общее уравнение третьей степени имеет вид
Ах3 + Вх2 + Сх + D = 0.
Разделив обе части этого уравнения на старший коэффициент
А — решения от этого, очевидно, не меняются — приходим
к уравнению вида
х3 + ах2 + Ъх 4- с = 0.
Введением новой неизвестной величины z = х 4- — можно
избавиться от слагаемого, содержащего неизвестную во
второй степени, т. е. привести уравнение к виду
z3 + pz + q = 0, A)
называемому редуцированным уравнением третьей степени.
Сведения об истории открытия формулы корней кубиче-
кубического уравнения неполны и противоречивы. По-видимому,
первым (около 1515 г.) нашел метод решения кубических
уравнений профессор университета в Болонье С. Ферро
A465 — 1526). Независимо от него (около 1535 г.) этот метод
открыл Н. Тарталья A500—1557). Однако первым опублико-
опубликовал формулу корней кубического уравнения Дж. Кардано
A501 — 1576) (его-работа вышла в 1545 г.), и поэтому эта
формула носит его имя. Отметим, что, возможно, Кардано
был знаком с работами Тартальи и Ферро.
В современных обозначениях метод решения уравнения
A) состоит в следующем.
Введем две новые неизвестные и и v; положив z = и + v,
имеем
(и + г;K + р(и + v) + q = 0,
м3 + и3 4- (и + v)Cuv + p) + q = 0.
92

Если неизвестные м, v удовлетворяют системе
| —f C)
( и3 +. v3 = — <ь
то они также удовлетворяют уравнению B). Решить систему
C) очень просто. Возведем первое уравнение в куб и подставим
вместо v3 его выражение из второго уравнения; получим,
что и3 — у удовлетворяет квадратному уравнению
Следовательно,
и, наконец,
-4- /-V + -ST- D)
Это и есть формула Кардано для решения редуцирован-
редуцированного кубического уравнения A).
Сразу возникают вопросы:
1) Что делать, если выражение -?—+ -^—<0?
2) Сколько корней имеет кубическое уравнение?
3) Дает ли формула Кардано D) все решения уравне-
уравнения A)?
Вопросы эти взаимосвязаны. Легко, например, убедиться,
что уравнение
х3-19х + 30 = 0
имеет решения —5, 2, 3, а как раз в этом случае
~т 27"""'
так что квадратные корни в формуле Кардано теряют
смысл и три указанных корня этой формулой не выра-
выражаются.
Все говорит о том, что здесь еще больше, чем в случае
квадратных уравнений, нельзя обойтись без введения каких-то
«новых чисел», для которых извлечение квадратного корни

всегда возможно. Такие числа были постепенно введены на
протяжении XVI — XIX веков. Они называются комплексными
числами. В поле комплексных чисел любое алгебраическое
уравнение n-й степени имеет ровно п корней*).
Рассмотрим в качестве примера уравнение
хп - 1 = 0. E)
Оно играет важную роль в теории и понадобится нам в
дальнейшем. В поле комплексных чисел это уравнение имеет п
различных решений, которые называются корнями п-й степени
из единицы:
2% . . 2к
Ро = 1, Pi = cos h i sin ,
F)
2к(п- 1) . . 2тф- 1)
р„_ i = cos — + г sin — -.
n n
Для записи решений кубического уравнения нужны корни
3-й степени из 1. В соответствии с формулами F) это будут
следующие комплексные числа:
Ро = 1, Pi = cos -^- + isin -^- = - — -f — i,
4л; ... 4л; 1 |/3
р2 =cos-j-+isin-y-= ~~2~ —2~1-
Можно показать, что три корня редуцированного куби-
кубического уравнения z3 4- pz 4- q — 0 есть
*) Прочесть о комплексных числах можно в книгах:
К у р о ш А. Г. Алгебраические уравнения произвольных степе-
степеней: Популярные лекции по математике.—М.: Наука, 1975.
Курош А. Г. Курс высшей алгебры.— М: Наука. 1975.
(Прим. пере в.)
94

Здесь буквой р обозначен рг — корень 3-й степени из 1;
р2, как нетрудно видеть, равно р2. Это и есть окончатель-
окончательные формулы Кардано.
4. В случае уравнений 1-й, 2-й и 3-й степени нам
известны формулы, выражающие корни через коэффициенты
уравнения при помощи рациональных операций +, —,
х, :, операции у извлечения квадратного корня (в случае
квадратного уравнения), операций |/~ и ]/~ извлечения квад-
квадратного и кубического корней (в случае кубического уравне-
уравнения). Подобные же правила были указаны и для уравнений
4-й степени учеником Дж. Кардано итальянским алгебраистом
Л. Феррари A522—1565). В них также участвуют лишь
рациональные операции и операции у , у . Все попытки
на протяжении почти трех веков (XVI — XVIII) найти подоб-
подобные правила для уравнений 5-й и более высоких степеней
при помощи рациональных операций и операций у не
увенчались успехом. Постепенно стали подозревать, что,
возможно, вообще нельзя выразить корни уравнения и-й
степени для п ^ 5 через коэффициенты лишь при помощи
тг~
операций +, —, х, : хи у для произвольных
натуральных т, т. е. что нельзя свести решение таких
уравнений рациональными операциями к последовательному
решению уравнений специального вида У" = А. Корни уравне-
уравнений уГ = А, т. е. то, что обычно обозначают через
|Л4, принято называть радикалами, и поэтому задачу о воз-
возможности сведения нахождения корней произвольного урав-
уравнения к нахождению уравнений вида уГ = А принято называть
задачей о выражении корней уравнения радикалами.
Попытки доказать или опровергнуть эту гипотезу особенно
участились во второй половине XVIII столетия и привели в
начале XIX столетия к доказательству невозможности ре-
решения общего уравнения 5-й и более высоких степеней в
радикалах.
% Среди работ XVIJI столетия в отмеченном направлении
ясностью мысли выделяется мемуар знаменитого француз-
„ского математика Ж. JI. Лагранжа A736—1813), озаглавлен-
озаглавленный «Рассуждения об алгебраическом решении уравнений»
A771 — 1772). В нем автор подробно и внимательно про-
проанализировал известные методы решения уравнений 2-й, 3-й
и 4-й степени в радикалах, чтобы выяснить, как и почему
в этих случаях такое решение удается. При этом он отметил
следующее обстоятельство: во всех указанных случаях име-
95

ются некоторые функции от корней, которые удовлетворяют
уравнениям более низкой степени и про которые уже
известно, что они решаются в радикалах. Корни исходного
уравнения в свою очередь могут быть найдены из этих
промежуточных функций опять-таки из уравнений, решаемых
в радикалах.
Далее Лагранж исследует вопрос, каким образом находят-
находятся подобные функции от корней в известных случаях. Ока-
Оказалось, что это полиномы q>(?i, ?2» •••» 5и) от корней ?ь
^2» • • • 9 %ю которые при всевозможных перестановках корней —
а их число, как известно, равно п\ — принимают не и!, а
меньшее число значений, и даже меньшее, чем и (и — сте-
степень исследуемого уравнения). Это произойдет тогда, когда
Ф(?ь %2> • • •» ?п) не меняется при некоторых пере-
перестановках корней.
Вот каким образом перестановки появились в вопросе
о решении уравнения в радикалах!
Если функция <p(?i, ..., ?п) от корней принимает только
к различных значений <рь..., <рк, то коэффициенты многочлена
по одной известной уже давно теореме — это так называемая
основная теорема о симметрических функциях — должны
рационально выражаться через коэффициенты исследуемого
уравнения
аохп + а^"'1 + ... + ап = 0.
Приведем примеры:
1) Пусть А(?ь ..., ?„) = А — знакопеременная функция
- А = П fe - U '
1<т
от корней уравнения n-й степени. Она принимает при
всевозможных перестановках корней лишь два значения А
и —А в зависимости от того, будет ли перестановка четной
или нечетной. Следовательно, дискриминант^ уравнения
D=J±2 не меняется при всевозможных перестановках и выра-
выражается рационально через коэффициенты исследуемого урав-
уравнения. Для квадратного уравнения ах2 + Ъх 4- с = 0
для редуцированного кубического уравнения х3 4- рх + q = 0
Знакопеременная функция А от корней удовлетворяет
96

уравнениям
у2 _ ^2 _ 4яс) « 0 и у2 + Dр3 + 27 я2) = О
соответственно. Мы узнаем выражения под квадратным кор-
корнем в формуле для решения квадратного уравнения и — с
точностью до постоянного множителя — в формуле Кардано.
2) Другой пример появился в упоминавшейся выше работе
Лагранжа. Это так называемые резольвенты Лагранжа. Мы
их рассмотрим, как и сам Лагранж, для случая уравнения
3-й степени. При~ помощи кубических корней из 1
1, Р, Р2
они определяются следующим образом:
Ло = $1 + ^2 + 5з,'
Л1-^1 + Р^2 + рЧз, G)
Л2 = 5l + Р^2 + Р^З-
Здесь %и ^2» ^з — корни исследуемого кубического уравнения.
Обратим внимание на вторую и третью резольвенты. Как
нетрудно видеть, при циклической перестановке корней
(?ь &2» ?з)->(?2, 5з, 50 они лишь умножаются на р2 ц р
соответственно. Следовательно, ц? и ц\ выдерживают цикли-
циклические перестановки и поэтому выражаются рационально
через коэффициенты уравнения и через А. Соответствующие
представления можно подсчитать. Извлечением кубического
корня можно получить г|! и г|2. По теореме Виета
?i + \г + ^з ~~ это коэффициент при z2 с обратным знаком,
т. е. . в случае редуцированного кубического уравнения
110=0. Зная г|о, Ль Лг» из системы линейных уравнений
G), можно получить ?ь ^2> ^з- Если осуществить указанные
вычисления, то можно убедиться, что ?ь ^2> ^з вычисляются
по формулам Кардано.
Аналогично, только технически более сложно, можно полу-
получить решение в радикалах уравнения 4-й степени. Что же ка-
касается уравнения 5-й степени, то аналогичное сведение к
уравнениям низших степеней получить не удалось. Однако
Лагранж не исключал его возможности.
Что такое понижение принципиально неосуществимо,
. показал в 1799 г. в работе «Общая теория уравнений, в
которой доказывается невозможность алгебраического реше-
решения общих уравнений выше четвертой степени», итальянский
математик П. Руффини A765-1822). Однако в его доказав
тельстве содержались пробелы, которые ему не удалось
97

устранить. Аккуратное доказательство было дано лишь в
1826 г. в работе норвежского математика Н. Г. Абеля
A802 — 1829) «Доказательство невозможности алгебраической
разрешимости уравнений, степень которых превышает чет-
четвертую».
Глубокую причину несуществования функций от корней,
удовлетворяющих уравнениям более низкой степени, чем
рассматриваемое (исключение составляет всегда знакопере-
знакопеременная функция, удовлетворяющая квадратному уравнению),
вскрыл гениальный французский математик Эварист Галуа
A811 —1832). Галуа сопоставил каждому уравнению группу тех
перестановок его корней, которые не меняют значения
всех полиномов от корней с коэффициентами, зависящими
рационально от коэффициентов заданного уравнения. Эту
группу называют теперь группой Галуа рассматриваемого
уравнения. По свойствам этой группы можно определить
будет ли данное уравнение разрешимо в радикалах или нет.
Полученный признак содержит в виде частных случаев все
ранее известные сведения о разрешимости или неразреши-
неразрешимости в радикалах алгебраических уравнений.
Но не исключается, что некоторые уравнения с число-
числовыми коэффициентами разрешимы в радикалах. Возможно
это или нет, устанавливается опять-таки на основании
признака, найденного Галуа.
§ 17. ИГРА «В ПЯТНАДЦАТЬ»
Теория перестановок нашла применение и при матема-
математическом анализе многих популярных игр. Например, в
течение одного времени очень популярной была почти забы-
забытая теперь игра «в пятнадцать». И «виноваты» в том, что
она забыта, математики, потому что они строго доказали,
что определенные позиции этой игры являются выигрыш-
выигрышными, а все остальные — нет. Здесь мы приведем доказатель-
доказательство этого факта, использовав теорию перестановок.
Сначала коротко опишем смысл игры.
В плоской квадратной коробке размещены 15 одинаковых
фишек квадратной формы, одно место остается свободным.
Фишки занумерованы числами от 1 до 15 и размещены в
определенном порядке (например, так, как на рис. 30, а).
Не вынимая фишек из коробки, а лишь передвигая друг
. за другом на свободное место, нужно разместить их в порядке
возрастания номеров так, как на рис. 30,6.
98

Оказывается, что прийти к такому размещению фишек —
будем называть его стандартным — можно не всегда. Су-
Существуют позиции, от которых этот переход осуществить
нельзя. ч.
Рис. 30.
Договоримся называть начальными те размещения фишек
в коробке, в которых свободное место остается в правом
нижнем углу. В другом случае будем говорить просто про
позицию игры.
С каждым размещением фишек в коробке можно связать
определенную перестановку на множестве М = {1, 2, 3, ...
..., 15, 16}, считая, что свободное место — это фиктивная
фишка с номером 16. Для этого занумеруем места, которые
могут занимать фишки, числами от 1 до 16 так, чтобы
порядок нумерации совпадал с порядком стандартного разме-
размещения фишек. Следовательно, каждое размещение фишек
однозначно характеризуется перестановкой на множестве
М, первый ряд которой составляют номера мест, а второй —
номера фишек, которые на этих местах стоят. Например,
размещение фишек на рис. 30, а описывается перестановкой
Л 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1б\
\9 6 3 13 1 5 7 2 14 4 8 11 10 15 12 16/'
а размещение фишек на рис. 30, б — единичной перестановкой.
Начальные размещения можно однозначно описывать
перестановками на множестве Af\ = {1, 2, ..., 15}, так как
для них фиктивная фишка «стоит» на месте с номером 16.
Переход от позиции, которая характеризуется перестановкой
Ф, к позиции, которая характеризуется перестановкой \|/,
если он возможен, осуществляется за несколько «ходов»,
причем каждый ход — это передвигание на свободное место
какой-нибудь соседней «фишки. Если свободным является
i-e место, а фишка, которая будет передвигаться, имеет
99

номер aj и стоит на ;-м месте, то после перемещения
эта фишка будет стоять на i-м месте, a j-e место освобо-
освободится. Значит, за один ход от размещения
ф Л 2 ...i ...j ... 16 \
y*i а2 ... 16 ... dj ... а16/
мы переходим к размещению
ф Л 2 :.., ..^...16 N .
Следовательно, перестановку ф мы умножаем на транспо-
транспозицию
и имеем равенство
Если от позиции, которая описывается перестанойкхш фь
можно перейти к новой за один ход, то найдется такая
транспозиция 52, что перестановка ф2, которая отвечает
новой позиции, будет связана с фх равенством
ф2 =ф1°82.
Допустим теперь, что для перехода от позиции ф к
позиции \|f нужно сделать к ходов. Это означает, что су-
существуют такие транспозиции 6Ь 62, ..., 6к вида (i, 16), для
которых справедливо равенство
ф = фо51о52о... о5к.
На свободное место каждый раз передвигается соседняя
фишка, а это накладывает определенные ограничения на
произведение 8Х ° 82 °... ° дк. Если от начального размещения ф
удается перейти к стандартному, то можно подобрать
такие транспозиции 8Ь 62, ..., 8S отмеченного вида, чтобы
выполнялось равенство
ф ° §s ° Ss-1 °. •. ° §i = е,
откуда ф = 8^1 о 82 1 о... о 5~ * = 8i ° 82 °... ° 8Я. Но такое про-
произведение не может быть произвольным, так как последова-
последовательности транспозиций 8Ь 82,..., 8S отвечает последователь-
последовательность ходов, причем на свободное место каждый раз передви-
передвигается соседняя фишка.
Покажем сначала, что когда от начального положения ф
можно перейти к стандартному, то перестановка ф — ч е т -
на я.
100

B,5)
Занумеруем ряды и столбцы, составленные из фишек
так, как на рис. 31. При каждом перемещении фишки на
свободное место (переставлении ее с фиктивной) сумма
номеров ряда и столбца, в которых стоит фиктивная
фишка, увеличивается или уменьшается на единицу. Действи-
Действительно, место каждой фишки одно-
однозначно характеризуется парой чисел 1 I Ь Ь
(i, j) (i, j — 1, 2, 3, 4). Если фиктив- /
ная фишка «стоит» на месте (ц Д
то очередной ход можно сделать
четырьмя способами:
ft/)->(!+ 1,/) (i#4),
(U)->(U-D (/#0, рис31.
или лишь двумя или ^тремя из них, если фиктивная
фишка «стоит» возле стенки коробки. В каждом из этих
случаев сумма i + j заменяется на i + j + 1 или на i + j — 1,
т. е. увеличивается или уменьшается на единицу.
Пусть теперь задана некоторая начальная позиция <р.
Пустое место в этой позиции по нашей нумерации имеет
«номер» D, 4). Если после некоторого количества передвиже-
передвижений фишек на свободное место перейдем к стандартной
позиции, то фиктивная фишка вновь будет иметь такой
номер. Поскольку на каждом шаге (при" каждой транспо-
транспозиции) четность суммы номеров ряда и столбца, в которых
«стоит» фиктивная фишка, изменяется» она может вернуться
- на место D,4) лишь через четное число ходов. Следовательно,
, перестановка <р раскладывается в произведение четного числа
транспозиций, т. е. она четна.
Оказывается, что условие четности перестановки, которая
характеризует начальное расположение фишек, является и
достаточным для того, чтобы от этой позиции можно
было перейти к стандартной. Доказывать это утверждение
для всех четных перестановок не нужно, потому что, как
легко понять, когда от каждой из позиций, которые описы-
описываются перестановками <р и \|/, можно перейти к стандартной,
то это удается осуществить и от позиции <р°\|/. Поэтому
достаточно убедиться в этом лишь для таких перестановок,
в произведения которых раскладывается каждая четная
перестановка. Возьмем, например, перестановки
A, 2, 3), A, 2, 4), A, 2, 5), ..., A, 2, 15). A)
101

7
b
«
1Ъ
1
6
u
1T
ъ
г
4
15
Рис. 32.
Все фишки в коробке, кроме тех, которые стоят на первом
и втором местах, можно «связать» в одну цепь, которая
может двигаться так, чтобы взаимное размещение звеньев
цепи не изменялось (если не учитывать свободного места,
которое может двигаться вдоль цепи).
Для этого достаточно представить себе,
что в коробке поставлены внутренние
стенки, например так, как это сделано на
рис. 32. Фишки могут двигаться вдоль
«стенок» по часовой стрелке или про-
против нее. Каждая фишка, которая входит
в цепь, после определенного числа ша-
шагов может стать на место с номе-
номером 3.
Пусть размещение характеризуется
циклом A, 2, к)9 т. е. в коробке фишка с номером
2 стоит на первом месте, фишка с номером к —
на втором месте, фишка с,' номером 1 — на к-м
месте C < к < 15), а все остальные — на своих местах.
Делая определенное число перемещений звеньев цепи, мы
можем фишку с номером 1 поставить на 3-е место. После
этого, перемещая фиктивную фишку вдоль цепи в противопо-
противоположном направлении, освободим место с номером 7. Теперь
можно, переставляя лишь фишки, что стоят на местах с
номерами 1, 2, 3, 5, 6, 7, достичь тоге, чтобы фишки с но-
номером 1 и 2 стали на свои места, с номером к — на третьем,
а остальные не изменили - позиций. Это видно из схемы
последовательного перемещения фишек, приведенной на
рис. 33. На этой схеме ° и х обозначают фишки, номера
которых для нас несущественны.
В результате таких перемещений изменился порядок разме-
размещения лишь трех фишек. Фишку с номером к можно теперь
1
X
к
о
/
г
X
О
к
1
X
О
2
1
к
X
О
/
г
к
1
X
2
о
к
Рис. 33.
включить в цепь. Перемещая по цепи, поставим ее на место
с номером /с. При этом все остальные фишки из цепи
займут начальное положение. Осталось лишь поставить фик-
фиктивную фишку на последнее место, и мы получим стандарт-
стандартное размещение.
Докажем теперь, что каждая четная перестановка раскла-
раскладывается в произведение циклов из ряда A). Действительно,
102

каждая четная перестановка а раскладывается в произведение
четного числа транспозиций
(X = 51o52o...o52k_1o52k. B)
Если а = A, 2), то в силу равенства а2 = е можно написать
<х = 51°а°сто52о5зост°сто54.о ...о52fc_i°o°o°62fc =
= (Ь1 о а) о (<j о 52) о E3 ° а) ° (а ° 54) ° ... ° (Ь2к-1 ° cj) о (а о 52к).
Для завершения доказательства достаточно показать, что для
любой транспозиции (i, j) оба произведения (i, j)°(l, 2)
и A, 2)°(i, j) можно разложить в произведение циклов из
ряда A). А этот факт действительно имеет место, как пока-
показывают следующие легко проверяемые равенства:
A, 2)p(i,;) = (/,;)o(l, 2) = (l,2,;)o(l,2,0°(l,2,0o(l,2,7),
если i, j > 2,
A,2)оA,;) = B,;)оA, 2) = A, 2, Д если ; > 2,
A, 2)оB, j) = A, /)оA, 2) = A, 2, /)оA, 2, Л если ; > 2.
Если одно из 6к в разложении B) равно A, 2), то соот-
соответствующее произведение на а будет тождественной пере-
перестановкой и его можно не учитывать.
УПРАЖНЕНИЯ
1. Как практически осуществлять переход к стандартной позиции
от размещений, которые характеризуются четной перестановкой?
2. Доказать, что каждая четная перестановка на множестве
М = {1, 2, ..., п} раскладывается в произведение таких циклов
длины 3: A, 2, 3), B, 3, 4), ..., (п - 2, п - 1, п).
3. Разложить в произведение циклов вида A, 2, к) такие
перестановки:
Ф = A, 2, 3)оG, 5)оD, 6,9, 8),
х|/ = A, 2, 3, 4) о (8, 7, 5, 6).
. 4. Можно ли перейти к стандартному размещению от начальных
позиций, заданных перестановками
/12 3 4 5 6 7 8 9 10 11 12 13 14 1в\
\8 7 6 5 1 2 4 3 13 15 11 10 14 12 9/'
/12 3 4 5 6 7 8 9 10 И 12 13 14 15\?
\6 3 4 5 2 1 15 10 13 12 11 14 9 8 7 /
5. Если позиция характеризуется нечетной перестановкой, то от
нее можно перейти к размещению, которое отличается от стан-
стандартного порядком двух последних фишек. Доказать это.
103

6. На фишках для игры «в пятнадцать» вместо чисел написаны
буквы и, г, р, а, в, п, я, т, н, а, д, ц, а, т, ь. Перемещая
фишки, как в игре «в пятнадцать», от каждого размещения можно
перейти к такому, когда
буквы на фишках образуют
фразу «игра в пятнадцать».
Доказать это.
7. Игра «хамелеон» про-
проводится на «доске» с девя-
девятью клетками, которые сое-
-динены прямолинейными от-
отрезками {рис. 34). На восьми
фишках выписаны буквы х, а,
м, е, л, е, о, н. Фишки
в случайном порядке рас-
расставлены на клетках, распо-
расположенных в вершинах много-
многоугольника. Цель игры со-
состоит в том, чтобы, перед-
передвигая фишки по соединитель-
соединительным отрезкам, разместить их
в правильном порядке, т. е.
так, чтобы при чтении по часовой стрелке, начиная с клетки I,
получилось слово «хамелеон». Докажите, что прийти к правильному
размещению фишек можно при любом их начальном расположении.
8. Доказать, что теория игры «в пятнадцать» остается в силе
и для игры «в восемь», правила которой такие же, как и
при игре «в пятнадцать», но здесь 8 фишек с номерами 1, 2, 3,
4, 5, 6, 7, 8 перемещаются в квадрате с 9 клетками.
9. Пусть на фишках для игры «хамелеон» вместо букв выписаны
числа 1, 2, 3, 4, 5, 6, 7, 8. Правила игры остаются прежними.
Доказать, что полученная таким образом игра в точности
совпадает с игрой «в восемь».
10. По аналогии с игрой «в 15» проведите исследование игры «в
двадцать четыре».
Рис. 34.

ОТВЕТЫ, УКАЗАНИЯ, РЕШЕНИЯ
1. a) tfog)(x) = 6х + 13, ig°J)(*)= 6х + 11; б) tf°g)(x) = х6 +
+ 10х5 + 25 х4 + 3, igof)(x) = х6 + 14 х4 + 57х2 + 72; в) (Л>0)(х) =
= х6 + 6х4 + 13х^+ И, (goj) = х6 + 2х4 + 2х3 + х2 + х + 3.
{
{х+11 ^3
| —, если х Ф - —, х Ф 1,
1-х • 2
не определена, если х = —=- или х = 1;
{^-—г-, если хФ -2, хф 1,
не определена, если х = — 2 или х = 1.
2. а) Замкнуто; б) замкнуто; в) замкнуто; д) незамкнуто.
. §2
2. При т ^ п существует п(п — 1) ... (п — т + 1) разных инъек-
инъекций множества А в множество В.
3. Решение. Пусть В есть /г-элементное множество. Зафикси-
Зафиксируем произвольное множество А, \А\ = т. Образ множества А при
любом инъективном отображении А-+В будет некоторым т-эле-
ментным подмножеством множества В, причем так можно получить
каждое m-элементное подмножество В. Множество А будет иметь
тот же самый образ А' а В при разных инъекциях тогда и только
тогда, когда они будут отличаться на некоторую биёкцию множества
А в себя. Поскольку |А'| = |А| = т, то существует т! различных
биекций А на себя. А поэтому есть
т\
различных m-элементных подмножеств множества В. *
5. На каждой вертикальной или горизонтальной прямой графика
биекций отмечена одна и только "одна вершина сетки. При стре-
— 105

л очном изображении биекции А-* В из каждой точки, которой
обозначен элемент множества А, выходит точно одна стрелка и в
каждую точку, которая является обозначением элемента множества В,
входит одна и только одна стрелка.
6. 44. Указание. Сначала нужно найти количество перестаг
новок, которые оставляют без изменения по меньшей мере
один элемент множества М.
7. 6-75.
8. Пусть Gt и G2 — множества перестановок ф, которые удов-
удовлетворяют соответственно условиям A) ф - B) ф > 0 и A) ф —
— B) ф < 0. Понятно, что каждая перестановка содержится в одном
из этих множеств. Поскольку отображение множества Gj на мно-
множество G2, в соответствии с которым каждой перестановке
Ф = (* 2 3 ...
\ii i2 *з ••¦
из множества Gy ставится в соответствие перестановка
б, (аЬс4 е\. , А 2 3 4 5 б\
6){cdcdc)' ВЧз 12323|
из множества G2, биективно (проверьте), то |Gi| = |G2| =
п\
= —-. Для (п — 1)! перестановки множества Gt справедливо равен-
п\
ство A)ф-B)ф = 1. Следовательно, существует -^— (п — 1)!
перестановок, которые удовлетворяют условию упражнения.
§ 3
234 '
1 2 1
4. Вершина (а, Ь) координатной сетки при построении гра-
графика преобразования ф°\]/ обозначается тогда и только тогда,
когда существует такое число сеМ, что на графике преобразования ф
обозначена вершина сетки (а, с), а на графике преобразования ф —
вершина (с, Ь).
5. Допустим сначала, что ф — не перестановка. Тогда найдутся
.элементы а, ЬеМ, а ф Ъ такие, что (а)ф = (Ь)ф. Для них имеем:
(а) (ф о \|/) = ((а) ф) \|/ = ((Ь) ф) v|/ = (Ь) (ф ° ф), что противоречит условию
задачи. Если ф — не перестановка, то множество образов элемента М
при действии ф является собственным подмножеством множества
М. Следовательно, элементы вида (а) (ф ° ф) = ((а) ф) ф, ае М, не
исчерпывают все множество М, т. е. преобразование ф ° ф — не
сюръекция, а это противоречит условию задачи.
6. Указание. Воспользоваться утверждением, сформулирован-
сформулированным в предыдущем упражнении.
^5 4 126 3/ \4 3 1 2
106

8. а) Уравнение не имеет решений; б) уравнение имеет четыре
решения:
(\ 2 3 4 S\ Л 2 3 4 5\ (l 2 3 4 5\ Л 2 3 4 5\
\1 2 5 4 2/' \1 3 5 4 2/' \1 2 5 4 3/' \1 3 5 4 3/'
в) уравнение не имеет решений; г) уравнение имеет единственное
решение
\2
2 2 2
§4
2. а) Нет; б) да; в) да.
2. а) Нет; б) да; в) да; г) ни одна из этих полугрупп группы
не образует.
4. Таблица умножения абелевой группы симметрична относи-
относительно оси, которая проходит из левого верхнего ее угла к правому
нижнему.
§5
1. Нет. Если граф задает преобразование, то из каждой его
вершины выходит одна и только одна стрелка.
3. На графе произведения <р ° \|/ преобразований <р, \|/ множества
М точки, которыми обозначены элементы а9 ЬеМ, соединяются,
стрелкой в направлении от а к b тогда и только тогда, когда
существует такая точка с, что на графе преобразования <р точки
а, с соединяются стрелкой в направлении от а к с, а на графе
преобразования \|/ точки с, b соединены стрелкой в направлении от
с к Ь.
§ 6
1. а) 12; б) 9.
2. 1, 2, 3, 4, 5, 6.
3. 30.
4. (ап, ап-и ..., а2, ах).
5. Указание. Рассмотреть перестановки
А 2 3 4 з\ Л 2 3 4 5\
\3 4 5 1 2/' \4 5 1 2 3/
Of
6. ~-^~. Указание. Воспользоваться решением упражнения
И, § 5.
9. Если перестановка <р имеет разложение
107

то цикл ф определяется так:
Ф = («i».bb ..., сь аъ Ьъ ..., с2,..., а„ Ь„ ..., cs).
Убедиться, что справедливо равенство ф' = ф.
§7
1. а) A, 3, 4, 7) = A, 3)оA, 4)оA, 7) = A, 2)° D, 5)°E, 6)°(б, 7)-
оF, 5)оE, 4)оD, 3)оC, 2)°B, 1) = A, 2)оA, 2, 3, 4, 5, 6, 7)о
оA, 2)оA, 2, 3, 4, 5, 6, 7)оA, 2)оA, 2, 3, 4, 5, 6, 7Г1оA, 2)о
сA, 2, 3, 4, 5, 6, 7)"ML 2)o(l, 2, 3, 4, 5, 6, 7)оA, 2)о
сA, 2, 3, 4, 5, 6, 7)оA, 2)оA, 2, 3, 4, 5, 6, 7)оA, 2)<>A, 2, 3, 4, 5, 6, 7)о
°A, 2).
2. Да.
3. Из равенства (i, 7, /с) = (i, 7') ° & fc) вытекает, что (i, j) ="(i, j9 к) о
°(i, /с). При фиксированных U к получаем, что транспозиции вида
(i, j) (i — фиксированный; j — произвольный) можно, выразить через
отмеченные перестановки. Осталось убедиться, что множество таких
транспозиций является системой образующих Sn.
4. Нет.
§8
1. Группа S4 содержит 4 трехэлементных подгруппы:
{е, A, 2, 3), A, 3, 2)}, {8, A, 2, 4), A, 4, 2)},
{8, A, 3, 4), A, 4, 3)}, {е, B, 3, 4)~ B, 4, 3)}.
2. С§ + С§-С§ = 40.
4. Центром S4 является тривиальная подгруппа {г}.
5. 20.
6. Указание. Для произвольной перестановки а е К существу-
существует натуральное число / такое, что а' = е (например, порядок пере-
перестановки а). Отсюда а =а*~1.
§ 13
2. Группой инерции многочлена f(xu *2> *з» х4) являбтся
циклическая группа порядка 2: {е, B, 4)}.
3. Группа инерции многочлена А(хи х2, х3, х4) состоит из 12
перестановок.
4. Доказательство. Рассмотрим многочлен /(хь х2, ...
...,хп) = х1 + 2 х2 + ... + пх„. Его группа инерции тривиальна. Кроме
того, для каждой перестановки osSm а Ф б имеем f° Ф /. А поэтому
для произвольной подгруппы G = {а!, а2, ..., аЛ} группы 5И
многочлен У**1/*2 .../a* = fi(x1, x2, ..., хи) инвариантен относительно
действия тех и только тех перестановок, которые входят в под-
подгруппу G.
108

5. оА(х\хгх\х^ содержит шесть одночленов.
7. о„ (x2x2 ... х,), / < и, содержит q\ _ w? одночленов.
" l\(n —1)\
§ 14
2. 5.
4. Подгруппа, которая содержит три элемента.
5. Центром группы Л„ является тривиальная подгруппа (п > 3).
Указание. Доказать, что каждая четная перестановка, которая
коммутирует со всеми циклами длины 3, тождественная.
7. Указание. Воспользоваться равенствами (i, j, к) = (i, j)о
o(i, к), (i, j)°(k, /) = (*, /, k)o(i, j9 k\ где i, j, /, /с-разные
элементы множества {1, 2, ..., n}.
8. Да.
9. Указание. Доказать, что при умножении перестановки на
транспозицию четность числа инверсий ее второго ряда изменяется.
10. Указание. Воспользоваться тем, что число 1\ перестановок
множества из п элементов, вторые ряды которых содержат ровно
к инверсий, удовлетворяет соотношению
где Т{ = 0 для j < 0 или j > —-—
11. Указание. Разложить каждый цикл в циклической форме
записи перестановки в произведение транспозиций и подсчитать
число транспозиций. *
§ 15
1. a) s5 = erf — 5а?ст2 4- 5аха2; б) * s4 = о\ — 4olo2 + 2а2 +
+ 4o"iCT3J в) О3 (&iX2) = G\&2 — 3 СТ3.
2. а) {D; 16), A6; 4)}; б) {B; 3), C; 2), B; -5), -5; 2)};
в) {A; 3), C; 1)}.
3. Указание. Выразить сумму попарных произведений длин
сторон треугольника и произведение длин всех его сторон через
данные числа и воспользоваться тем, что в формуле Герона под
знаком корня стоит симметрический многочлен.
4. Указание. Для многочлена /{хь х2) рассмотрите одно-
одночлен ах\х12, у которого показатель степени к наивысший. Если таких
одночленов несколько, то нужно взять тот, у которого показатель
I наивысший. Докажите, что одночлен с такими свойствами не может
уничтожаться при переходе от Дхь х2) к f(x% + х2, Х!Х2).
6. Действительно, если в многочлене /(хь xt) поменять
местами Xi и хь то он, с одной стороны, не изменится, а с
другой, изменит знак на противоположный. Значит, /(хь xt) =
= — f(xl9 хД т. е. /(хь хх) тождественно равен 0.
8. Указание. Докажите, что Дхь х2, х3) = 4тах(хь х2, х3).
109

§17
4. а) Да; б) нет.
5. Указание. На каждой фишке напишем новый номер по
следующему правилу. Если старый номер 14 A5), то новый 15
(соответственно 14). На всех остальных фишках новый номер совпа-
совпадает со старым. Сами же фишки передвигать не будем. Размещение
фишек с новыми номерами характеризуется четной перестановкой
и поэтому от него можно перейти к стандартному относительно
новых (!) номеров. Но стандартное размещение относительно
новых номеров -*¦ это требуемое размещение относительно старых
номеров.
6. Указание. Занумеровать буквы в том порядке, в котором
они стоят в фразе «игра в пятнадцать». Учесть, что среди этих
букв есть одинаковые — буква «а», и воспользоваться решением
предыдущего упражнения.

ЛИТЕРАТУРА
Подробное обсуждение понятий отображения и преобразования
можно найти в книге
Кемени, Снелл, Томпсон. Введение в конечную матема-
математику.-М.: Мир, 1966.
Много комбинаторных задач, связанных с понятием преобра-
преобразования и перестановки, есть в книгах:
Ежов И. И., Скороход А. В., Ядренко М. И.
Элементы комбинаторики.—М.: Наука, 1977.
Виленкин Н. Я. Популярная комбинаторика. — М.: Наука,
1975.
Калбертсон. Математика и логика цифровых устройств.—
М.: Просвещение, 1965.
Подробнее ознакомиться с теоретико-групповыми понятиями
можно из книг:
КострикинА. И. Введение в алгебру. — М.: Наука, 1977.
Гроссман И., Магнус В. Группы и графы. — М.: Мир, 1971.
К а л у ж н и н Л. А., Введение в общую алгебру. — М.: Наука,
1973.
О применениях теории групп можно узнать из книг:
Вей ль Г. Симметрия.—М.: Наука, 1968.
Болтянский В. Г., Виленкин Н. Я. Симметрия в алгебре. —
М.: Наука, 1968.
Постников М. М. Основы теории Галуа. — М.: Физматгиз,
1960.
Алексеев В. Б. Теорема Абеля в задачах и решениях. —
М.: Наука, 1976.
Теория многочленов подробно изложена в книге:
Курош А. Г. Курс высшей алгебры.—М.: Наука, 1975.

ОГЛАВЛЕНИЕ
Предисловие к русскому переводу 3
§ 1. Суперпозиция функций 5
§ 2. Преобразования ; , . 9
§ 3. Умножение преобразований 18
§ 4. Группа перестановок и* полугруппа преобразований 31
§ 5. Графы преобразований. Орбиты. Циклическая форма
записи перестановок ^ ' 37
§ 6. Порядок перестановки 46
§ 7. Образующие симметрической группы 5&
§ 8. Подгруппы симметрических групп , . . •. 54
§ 9. Группы симметрии 58
§ 10. Теорема Лагранжа 64
§ 11. Орбиты группы перестановок. Лемма Бернсайда ... 67
§ 12. Комбинаторные задачи 72
§ 13." Действие перестановки на многочлен 77
§ 14. Четные и нечетные перестановки. Знакопеременная
группа 81
§ 15. Симметрические и четносимметрические многочлены 84
§ 16. Решение алгебраических уравнений 91
§ 17. Игра «в пятнадцать» 98
Ответы, указания, решения . . " 105
Литература 111

20к.