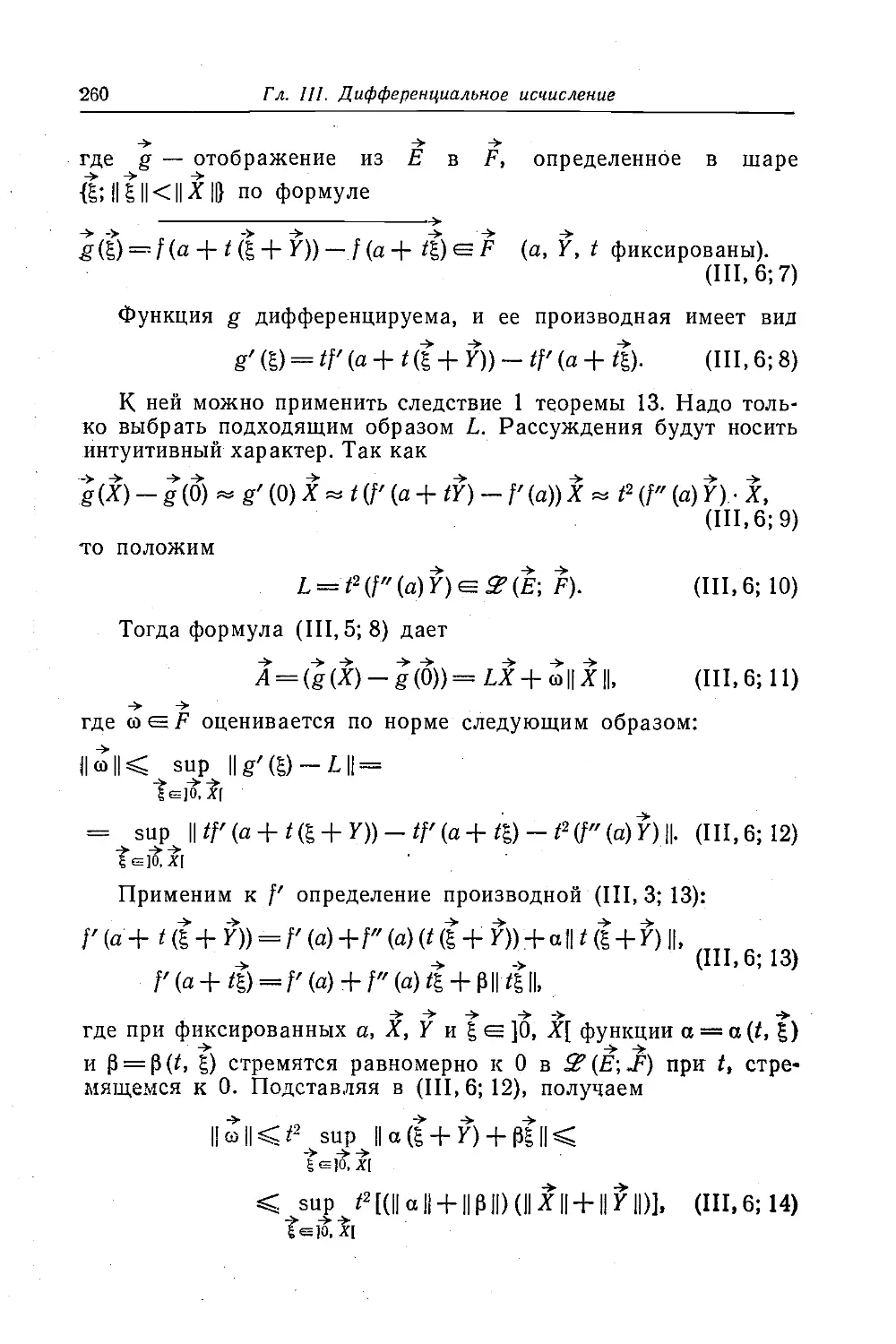LAURENT SCHWARTZ
Professeur a l'Ecole Polytechnique
et a la Faculte des Sciences de Paris
ANALYSE
MATHEMATIQUE
COURS
PROFESSE A L'ECOLE POLYTECHNIQUE, PARIS
I
HERMANN
1967

ЛОРАН ШВАРЦ
АНАЛИЗ
Том I
ПЕРЕВОД С ФРАНЦУЗСКОГО
В. П. ПУГАЧЕВА
ПОД РЕДАКЦИЕЙ
С. Г. КРЕЙНА
ИЗДАТЕЛЬСТВО «МИР»
МОСКВА 1972

УДК 517.43+519.55
Имя Лорана Шварца — одного из крупнейших
математиков современности — хорошо известно советским
специалистам.
Его двухтомный курс существенно отличается от
всех имеющихся книг по анализу. Изложение
характеризуется глубоким взаимопроникновением методов
классического и функционального анализа, современной
алгебры и топологии. Следует отметить также
блестящий стиль курса, умение автора выделить основное,
объяснить значение тех или иных идей.
Первый том включает теорию множеств, топологию,
дифференциальное и интегральное исчисление.
Книга Л. Шварца, несомненно, заинтересует
преподавателей математики, научных работников в области
математики, физики и механики, а также инженеров и
будет весьма полезна студентам университетов,
педагогических институтов и высших технических учебных
заведений с углубленным изучением математики.
Редакция литературы по математическим наукам
ЛОРАН ШВАРЦ
АНАЛИЗ
том I
Редакторы Д. Ф. Борисова, А. А. Бряндинская
Художник А. В. Шипов
Художественный редактор В. И. Шаповалов
Технический редактор Т. А. Максимова
Сдано в набор 29/Х 1971 г.
Подписано к печати 2/VIII 1972 г.
Бумага тип.- N» 2 6OX907ie = 25,75 бум. л. 51,50 усл. печ. л. Уч.-
изд. л, 47,58. Изд. № 1/5722. Цена 3 руб. 51 коп. Зак. 1339
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2
Ордена Трудового Красного Знамени
Ленинградская типография № 2 имени Евгении Соколовой
Главполиграфпрома Государственного Комитета Совета
Министров СССР по делам издательств, полиграфии и книжной
торговли. Измайловский проспект, 29
2-2-3
34-72

ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Мы предлагаем вниманию читателей двухтомный курс
анализа, написанный известным французским математиком
Лораном Шварцем. Задачи, которые ставил перед' собой автор при
написании курса, достаточно ярко описаны в его предисловии.
Формально для чтения книги предварительных знаний не
требуется, однако, по существу она доступна лишь тем, кто знаком
с обычным курсом математического анализа и имеет
определенную математическую культуру.
В курсе Л. Шварца излагается ряд математических
дисциплин, которые по установившейся в нашей системе преподавания
традиции изучаются раздельно. Мы считаем, что объединение
всех этих дисциплин в единый курс вполне отвечает духу
современной математической науки. Заметим, что на самом
деле — это возврат на новом уровне к старым традициям:
достаточно вспомнить классический курс математического
анализа Э. Гурса или курс математики В. И. Смирнова.
В первой главе курса излагается элементарная теория
множеств. Вторая глава содержит основы
теоретико-множественной топологии и элементы функционального анализа, которые
в дальнейшем широко используются. В третьей главе
развивается аппарат многомерного дифференциального исчисления.
Здесь же вводятся понятия, связанные с дифференцируемыми
многообразиями. Последний параграф этой главы посвящен
основам вариационного исчисления.
Четвертая глава содержит развернутое изложение теории
интеграла и меры. После краткого изложения теории интеграла
Римана вводится понятие меры Радона как непрерывного
функционала на пространстве финитных непрерывных функций,
которое лежит в основе всей теории интеграла. В главе, кроме
общей теории, имеются и приложения интегрального исчисления.

6
Предисловие редактора перевода
Сравнительно небольшая пятая глава посвящена теории
дифференциальных уравнений. В ней содержатся общие
теоремы и теория линейных уравнений. (В русском издании в целях
более равномерного распределения материала она перенесена
из первого тома во второй.)
Большое место в курсе занимает изложение внешнего
дифференциального исчисления (глава шестая). Это весьма
отрадно, так как важный аппарат дифференциальных форм
незаслуженно медленно пробивает себе дорогу в нашу учебную
литературу. Здесь же освещены связи между теорией
дифференциальных форм и алгебраической топологией.
В последней, седьмой главе изучаются функции
комплексных переменных. Преимущественно исследуются функции одной
комплексной переменной, правда, со значениями в банаховом
пространстве, в связи с чем затрагивается ряд вопросов
функционального анализа. Заметим, что в этом отношении седьмая
глава не составляет исключения: всюду, где только возможно,
автор рассматривает векторнозначные функции.
Лоран Шварц является превосходным лектором, и
академический стиль его книги часто прерывается живой речью. Мы
старались, чтобы эта эмоциональная речь автора не потерялась
при переводе. Мы надеемся, что его курс будет Весьма
полезным пособием для студентов математических и физических
факультетов университетов, для аспирантов и преподавателей
вузов, а также для студентов технических вузов, желающих
более глубоко изучить математику.
С. Г, Крейн

ПРЕДИСЛОВИЕ
Как часто говорят, для физиков и инженеров «нет
математики без слез». Физикам и современным инженерам нужны
необъятные математические познания в самых разнообразных
областях. Абсолютно исключено, чтобы эти «прикладники»
знали все нужные им результаты со всеми доказательствами
на уровне строгости, принятом в математике. И вот сложилась
такая ситуация. Имеются краткие курсы, содержащие
сравнительно немного результатов, но доказанных весьма
обстоятельно,— эти книги удовлетворяют математиков, но не
физиков. Имеются также краткие курсы, богатые результатами, но
с доказательствами, либо едва намеченными, либо вовсе
отсутствующими,— эти книги не удовлетворяют читателей,
воспитанных в декартовом духе.
Мы избрали третью возможность. Курс, который мы
предлагаем, велик (пожалуй даже слишком велик), он содержит
много теорем, и притом с достаточно полными
доказательствами. Это, собственно говоря, не учебник, а книга, содержащая
фактический, документальный материал.
Лекции, основанные на этой книге, должны сводиться лишь
к кратким резюме. Студентам же для обязательного изучения
следует каждый раз выбирать строго определенную часть
книги, которая содержит много формулировок, но мало
доказательств.
Учащиеся должны научиться схватывать новые идеи и
структуры, понимать суть теорем и применять их там, где
нужно, хотя бы с книгой в руках. Это не так легко, как кажется,—
тот, кто никогда не думал над теоремой, не сможет и сразу
применить ее, даже если у него есть книга. Подробно изучать
нужно лишь те доказательства, которые являются наиболее
типичными и поучительными.

8
Предисловие
Кроме того, учащиеся могут (и мы активно это
рекомендуем) выбрать для факультативного изучения какой-либо из
разделов курса в соответствии с собственными вкусами или
рекомендациями преподавателей. При этом можно удовлетворить
различные вкусы и учесть разные уровни подготовки. Если
студенты одного потока изберут не совсем одинаковые разделы, это
можно только приветствовать.
Лоран Шварц

ГЛАВА t
Теория множеств
§ 1. МНОЖЕСТВА. ЭЛЕМЕНТАРНЫЕ ОПЕРАЦИИ
Множеством называется совокупность некоторых объектов.
Примеры: Множество учащихся одного выпуска,
множество точек плоскости,
множество невырожденных поверхностей 2-го
порядка в трехмерном пространстве,
множество N неотрицательных целых чисел,
множество Z произвольных целых чисел,
множество Q рациональных чисел,
множество R вещественных чисел,
множество С комплексных чисел.
Части множества
Запись х^Е означает: «х является элементом множества
Е1)». Если множество А состоит из элементов, принадлежащих
некоторому другому множеству Е, то оно называется частью
или подмножеством этого множества. Множество эллипсоидов,
например, является частью множества поверхностей второго
порядка.
Частями множества Е являются: оно само; его пустая часть,
обозначаемая через 0; часть, сводящаяся к одному элементу а,
обозначаемая через {а}; часть, образованная тремя элементами
я, Ь, с, обозначаемая через {а; Ь; с). Не следует смешивать а
как элемент Е и [а] как часть Е, состоящую из одного
элемента а. Для того чтобы обозначить множество элементов,
обладающих некоторым свойством Р, часто пользуются такой
записью; {х; х обладает свойством Р). Например, {х; х е R, х^О}
означает множество вещественных чисел ^0, {arctg*; x e R,
е^С#<12е} означает множество значений arctg*, когда х
принимает все вещественные значения между е и 2е включительно.
Через ty(E) обозначают множество всех частей множества
£• Это некоторое новое множество, которое можно образовать,
') Множество иногда называется также пространством, а его элементы
часто называются точками.

10
Гл. 1. Теория множеств
исходя из множества Е. Можно затем рассмотреть *p(9(S(£))
и т. д.
Если £ содержит п элементов, то $(£) содержит 2П
элементов ').
Отношение включения. Дополнение
Пусть X и Y— две части множества Е. Говорят, что X
содержится в Y, или что Y содержит X, если каждый элемент из
X является элементом из У; при этом пишут X cz Y или YzdX.
Так, например, QczXczE, &az&, EczE. Если X cz Y и YczZ,
то X cz Z.
Множество элементов Е, не принадлежащих некоторой его
части А, называется дополнением к Л в £ и обозначается
через СЕЛ или просто СМ, когда это не может привести к
путанице. Очевидно, ССЛ = А, и если A cz В, то CM zz> СВ. Если
А и В — две части множества Е и AzdB, то через А — В
обозначают иногда множество элементов из А, не
принадлежащих В.
Объединение. Пересечение
Объединением некоторого множества частей из Е называют
часть £, состоящую из элементов, принадлежащих по крайней
мере одной из этих частей. Объединение частей А, В, С
записывается в виде A U В U С.
Объединение семейства частей .4{, занумерованных с
помощью некоторого множества индексов /, обозначается через
Пересечением множества частей Е называется часть Е,
состоящая из элементов, принадлежащих одновременно всем
этим частям. Для пересечения применяются аналогичные
обозначения: А(]В{]С, П Л«-
>) Через С£, или лучше ( I, обозначается число частей, содержащих
по р элементов некоторого множества, состоящего из п элементов. Если
теперь подсчитать все части £ (не пропуская ни 0, ни самого £), то получим:
(:)+(;)+(;)+•••+(.:.)+(:)-«■•
Действительно, если £„ = {1,- 2 я}, то ty(E„) для и ^ 1 можно считать
состоящим из двух различных множеств: множества частей, содержащих
элемент и, и множества частей, не содержащих его. Количество элементов
в каждом из них такое же, как и в множестве 5P(£„_i). Если ty(En)
содержит Ап элементов, то Ап = 2/4„_,, и поскольку А0 == 1 (£0 — пустое
множество, имеющее ровно одну часть 0), то Л„=2".

§ 2. Отображения. Функции
11
Две части называются непересекающимися, если их
пересечение пусто.
Дополнение пересечения некоторого семейства частей
совпадает с объединением их дополнений, и дополнение
объединения семейства частей есть пересечение их дополнений:
С(ЛЛВ) = СЛиСВ и С(ЛиВ) = СЛПСВ. (I, 1; 1)
Преобразование, которое каждой части из Е ставит в
соответствие ее дополнение, является, следовательно, соответствием,
переводящим с в э, э в с, U в П, П в U.
Произведение множеств
Произведением Е X F двух множеств Е и F называется
множество всевозможных упорядоченных пар (х, у),
образованных из элементов х множества Е и элементов у множества
/•'. При этом пары (х, у) и (у, х) с хфу считаются
различными. Это особенно важно иметь в виду, когда множества Е и F
совпадают.
Точно так же можно определить произведение нескольких
множеств или произвольного семейства множеств. Множества
(Е X F)\G, E\(F\ G) и Е X F X G отождествляются, так
что произведение ассоциативно.
Произведения £ X Е, £ X Е \ Е и т. д. обозначаются также
через Е2, Ег и т. д. Отсюда возникло обозначение R" для
произведения п множеств, идентичных множеству R всех
вещественных чисел. Точка из R" является, следовательно,
упорядоченной системой произвольных п вещественных чисел
(х\, х2, ..., хп).
§ 2. ОТОБРАЖЕНИЯ. ФУНКЦИИ
Пусть заданы два множества Е и F. Отображением Е в F,
или функцией, определенной на Е. со значениями в F,
называется соответствие /, которое каждому элементу х из Е
относит некоторый элемент из F, обозначаемый через f(x).
Обозначение E—+F будет означать, что f является
отображением Е в F. Множество Е называется исходным множеством,
а множество F конечным множеством отображения. Следует
различать отображение f и элемент /(*),- соответствующий х
при этом отображении. Однако по чисто практическим
соображениям при изложении это различие иногда не принимается
во внимание. Так, например, неправильно (но удобно)
говорить «функция sin x», хотя следовало бы читать «функция sin»,
поскольку sin а: является значением этой функции в точке х.
Эту неточность обычно исправляют, говоря, что «задана

12
Гл. I. Теория множеств
функция x->sinx», или «функция f, определенная равенством
f (х) = sinx».
Отображение множества в себя называют также оператором.
Примеры отображений
1°) Функция f, определенная формулой f(x)=l/x, является
отображением множества отличных от нуля элементов
вещественной прямой R в R. Будет неточным говорить, что это —
функция вещественной переменной, поскольку здесь
переменная не может принимать все вещественные значения. Однако
вполне возможно рассматривать отображение R в R,
определенное соотношениями g(x)=\/x для х ф О и g(0) = 2. Эта
функция g отлична от функции f, так как имеет иную область
определения. Можно также рассматривать отображение h,
определенное как h(x)= \/х для х Ф 0 и /г(0) = +оо,
множества Е = R в множество F, образованное из R и некоторого
дополнительного элемента, обозначаемого -f-oo.
2°) Если Е — множество вещественных функций ф(х),
определенных и интегрируемых на вещественном интервале [а, Ь],
ъ
то интеграл ф —> q>(x)dx является отображением Е на веще-
а
ственную прямую R.
3°) Если Е является множеством кривых конечной длины
на евклидовой плоскости, то можно определить отображение
Е на полупрямую R+ (множество элементов ^0 из R),
которое каждой кривой ставит в соответствие ее длину.
Отображение f множества Е в Е, определенное равенством
f(x) = x, называется тождественным.
Если Е составляет часть F, то отображение Е в F,
определенное равенством f(x) = x, называется канонической
инъекцией Е в F.
Если Е X F — произведение двух множеств, то отображение
Е X F'в Е, ставящее в соответствие каждой паре (х, у) е Е X F
элемент х е Е, называется проекцией на Е. Точно так же
определяется проекция на F.
Пусть Е, F, G — три множества. Отображение f множества
Е X F в множество G каждой паре (х,у) = z^EX_F ставит
в соответствие некоторый элемент из G, обозначаемый через
f (z) = f ((х, у)). Обычно двойную скобку заменяют на простую
f(x,y) и говорят, что f является функцией двух переменных.
Например, если Е является множеством вещественных функций
вещественной переменной, интегрируемых на каждом конечном
интервале, то интеграл \к{х)йх определяет некоторое ото-
а

§ 2. Отображения. Функции 13
Сражение Е X R X R в R, поскольку это отображение является
функцией трех переменных: фе£,оеРи6еР.
Рассмотрим теперь отображение Е в F'X G. Оно имеет вид
x-*(f(x),g(x)), где / (соответственно g} является
отображением Е в F (соответственно в G). Задание такого отображения
эквивалентно заданию системы двух функций. В общем случае
задание отображения некоторого произведения £j X ^2 X • • •
... X Еп в произведение F\ X F2 X ... X Fm равносильно
заданию системы m функций от п переменных.
Отображение / множества Е в множество F называется
постоянным, если f(x) для всех х^Е является одним и тем же
элементом из F.
Инъекции, сюръекции, биекции
Говорят, что отображение / множества Е в множество F
инъективно, или является инъекцией, если два различных
элемента из Е имеют образами при отображении / два различных
элемента F. Каноническая инъекция некоторого подмножества
в само множество является инъективным отображением.
Отображение ■/ называют сюръективным, или сюръекцией,
если каждый элемент из F является образом при отображении
/ по крайней мере одного элемента из Е.
Отображение / называют биективным, или биекцией, если
каждый элемент F является образом при отображении /
некоторого, и притом единственного, элемента из Е. Отображение
биективно тогда и только тогда, когда оно одновременно
инъективно и сюръективно. Биекция множества на себя
называется также перестановкой, или преобразованием.
Пусть / — некоторая биекция, и пусть y^F. Обозначим
через /_I (у) единственный „элемент х из Е, такой, что f(x) = y.
Тем самым мы определили некоторое отображение f~l
множества F в Е. Это — снова биекция. Ее называют обратным
отображением, или обратной биекцией к /. Часто ее также
называют просто обратной функцией.
Образ и прообраз подмножества
Пусть / — отображение Е в F и А— подмножество Е.
Обозначим через f(A) подмножество F, образованное из всех
элементов f(x), лгееЛ. Очевидно, /(0) = 0. Исходя из отображения
U мы тем самым определим некоторое отображение A—*-f(A)
множества ty(E) в множество $(f). Это отображение
сохраняет символы с, id, U в том смысле, что
если А<=В, то f(A)czf(B),
f(A[)B) = f(A)[}f{B). {1'2'Ц

14
Гл. I. Теория множеств
Однако символы П, с при этом отображении не
сохраняются, так как имеет место лишь включение
f(A{\B)^f{A)(\f{B)% (1,2; 2)
Часть f(A) называется образом части А при отображении f.
Пусть теперь В является некоторой частью множества F.
Будем обозначать через f~l{B) часть Е, образованную из всех
таких элементов х, что |(х)еВ2). Очевидно, f~'(0) = 03). Мы
связали с отображением f отображение В—*f_1(B) множества
$(/*") в множество ty(E).
Это отображение сохраняет 5 символов с, гэ, U, П, С
в том смысле, что:
если А<=.В, то Г'(Л) с Г1 (В),
Г1 (A U В) = Г1 (Л) U Г' (В), Г1 (Л П В) = Г1 (А) П Г' (В), (I, 2; 3)
Г'(СЛ) = СГ'(Л).
Мы видим, следовательно, что так определенное отображение
/_1 проще описанного выше отображения f. Часть f~l(B)
называется прообразом множества В при отображении f. Уместно
заметить, что это определение вовсе не предполагает биектив-
ности f. Во всяком случае, если у е F, то можно говорить о
/~'({#}). но это — некоторая часть Е, а на элемент Е. Эта часть
может содержать более одного элемента, если f не является
инъективным, и может оказаться пустой, если f не сюръективно4).
Если f биективно, то f~l{{y}) = {f~i(y)}-
Символ f_1(B), кроме того, может иметь два возможных
одинаковых значения: это прообраз В при отображении f или
образ множества В при биективном обратном отображении
f_1. Естественно, если отображение f биективно, то образ также
сохраняет все 5 символов: сг, гэ, U, П, С. Кроме того, имеем:
r'(fG4))=M для А*=ЩЕ),
f{f-l(B))czB для fi«=$0F). (' ' 2)
') Пусть {— постоянное отображение, т. е. f(x)=b при любом х е Е.
Пусть А и В — непересекающиеся части Е. Так как А П В = 0 то f(A f| В) =
что не совпадает с множеством f~(A)f\ f(B) = {b}.
2) Согласно кратким обозначениям, введенным на стр. 9,
r'(B) = fefWefi), f(A)-{f(x);x(=A).
3) Может оказаться, что f-'(B)=0 при В =з£ 0. Если, например, /
является отображением х-*■ х2 множества R в R, то f*1({— 1}) =0.
4) См. примечание 3.

§ 2. Отображения. Функции 15
Множество отображений. Семейства. Последовательности
Если Е и F — два множества, то можно говорить о
некотором новом множестве — множестве отображений Е в F. Если
Е имеет только 2 элемента а\ и а2, то множество отображений
Е в F может быть биективно отображено на квадрат F2, ибо
каждое отображение Е в F полностью определяется парой
(x,y)^F2 образов х, у элементов а\, а2 из Е. Если Е состоит
из п элементов а\, а2, ..., ап, то множество отображений Е
в F можно биективно отобразить на /•"", ибо каждое такое
отображение эквивалентно заданию системы {Х\, х2, •••. xn)^Fn
образов элементов ах, а2, ..., а„ при этом отображении.
Поэтому множество отображений Е в F принято обозначать
через FE.
Естественно в дальнейшем рассматривать различные
подмножества множества FE: множество непрерывных
отображений Е в F, если Е и F—метрические пространства; множество
линейных отображений Е в F, если Е и F — векторные
пространства и т.д. Семейство (#г)г<=/ элементов из Е,
снабженных индексами из множества I, можно рассматривать как
отображение I в Е. Множество семейств элементов из Е,
снабженных индексами из /, является не чем иным, как множеством
Е1 отображений I в Е.
В частности, последовательность элементов из Е можно
определить как семейство элементов из Е, снабженных
индексами из множества N целых чисел ^0, или же как
отображение N в £. Множество всех последовательностей элементов из
Е является множеством EN . Можно также говорить о
последовательностях с индексами из множества Ni целых чисел ^1,
или о конечной последовательности, снабженной индексами из
конечного множества целых чисел 1, 2, ..., п. Всегда будет
важным уточнять смысл слова «последовательность», когда
множество индексов не совпадает с N.
Композиция отображений
Пусть Е, F, G — три множества, и пусть / — некоторое
отображение Е в F, a g — отображение F в G. Композицией gof
называется отображение Е в F, определенное формулой
g°f(x) = g(f(x)). Заметим, что запись gof. производится в
порядке, обратном тому, в котором производятся операции:
E-t+F-S+G. (1,2; 4)
Таким образом, в математике принято правило, согласно
которому в композиции операций gof надо начинать с
операции f, расположенной справа.

16
Гл. I. Теория множеств
Если А— часть Е, то g °f(A) = g(f(A)). Если В— часть G,
то (g °f)~l(B)==f~l(g~l(B)). Композиция отображений
ассоциативна, т.е. если f, g, h — отображения Е в F, F в G и G в Н
соответственно, то (hog) °f = k° (g °f), что проще
записывается в виде ho g of.
Если f'1 является биекцией, обратной к биекции f
множества Е на F, то f~1of = JEt где 1е — тождественное отображение
Е, и fof~l=IF, где If — тождественное отображение множества/7,
Обратно, если отображение f множества Е в F и отображение
g множества F в Е таковы, что g о f = fE и f og = IF, то f
является биекцией, a g — его обратной биекцией.
Если f—биекция Е на F, a g — биекция F на G, то g о f
является биекцией Е на G, а ее обратной биекцией будет f_1°g_I.
Пусть f — отображение Е в F и А — некоторая часть Е.
Отображение fA множества А в F, определяемое формулой
fA(x)=f(x) для леД называется сужением f на А и часто
обозначается через f\A. Говорят также, что f является
продолжением на Е отображения fA множества А в множество F.
Чаще всего в этом случае продолжают писать f вместо fA.
Точно так же, если f — некоторое отображение Е в F и если
f(E)aB, то f определяет некоторое отображение fe множества
Е в множество В, задаваемое формулой f_B (x) = f (х).
Практически вместо fs всегда пишут f.
Замена переменных и замена функций
Пусть f — функция, определенная на Е, со значениями в F.
Если и является отображением некоторого множества Е\ в
множество Е, то можно построить новую функцию fi = f««,
определенную на Е\, со значениями в F. Говорят, что тем самым
совершена замена переменной и или замена исходного
множества £[ — •> Е и что /i является прообразом f при этой замене
переменных. Производя в выражении f(x) подстановку х =
= и(х\), получают выражение h{x\)- Часто, если не
указывается сама замена переменной и, функция f\ обозначается
через u*f или даже через f*. Таким образом,
u"f (Xi) = f (и (*,)) или Г (х,) = f (и (х,)). (I, 2; 5)
При беглом изложении, допуская вольность речи, иногда
отождествляют ft и f, говоря, что это та же самая функция
(sicl), представимая через переменную х\ вместо переменной
х, но такое упрощение изложения опасно, так как может
привести к серьезным противоречиям.
Если теперь v является некоторым отображением F в
множество F2, то можно определить новую функцию f2 = v о f,
определенную на Е, со значениями в F2. Говорят, что произве-

§ 3. Отношения эквивалентности. Фактормножество 17
дена замена v функции или замена множества значений
F: F —> F2 и что /г является образом f при этой замене.
Можно произвести одновременно и замену функции,
рассматривая /3 = Vofou. Здесь /з является образом f при замене
переменной и и замене функции v.
§ 3. ОТНОШЕНИЯ ЭКВИВАЛЕНТНОСТИ. ФАКТОРМНОЖЕСТВО
Говорят, что на множестве Е определено некоторое
бинарное отношение, если задано множество всех пар (х, у)
элементов из Е, удовлетворяющих этому отношению. Так, например,
отношения х = у, х г^ у, х>у, х2 = у3, (х2-\-у2=1, х Ф 0)
являются бинарными отношениями между вещественными
числами. Очевидно, бинарное отношение на Е есть не что иное,
как подмножество R произведения Е X £•
В этом и следующем параграфах мы будем изучать
бинарные отношения, имеющие особые значения.
Бинарное отношение R называется отношением
эквивалентности, если оно обладает следующими тремя свойствами:
a) рефлективность: (х, x)^R при любом xgE,
b) симметричность: из (x,y)^R следует (y,x)^R, (1,3; 1)
c) транзитивность: если (х, у) ее R и (у, z)ge R, то (х, z)^R.
Вместо того чтобы писать (х, y)^R часто пишут х^ у или
x = y(modR) (читается: «х конгруэнтно у по модулю Я») или,
проще, х ~ у и х = у, если нет необходимости каждый раз
указывать, что речь идет об одном и том же отношении R.
Примеры. Отношения, приведенные в начале параграфа,
кроме первого, отношениями эквивалентности не являются.
Легко доказать, что все перечисленные ниже бинарные
отношения являются отношениями эквивалентности.
1°) Будем исходить из множества Z целых чисел
произвольного знака. В качестве множества Е возьмем подмножество
множества Z X Z пар (р, q), у которых q Ф 0.
Отношение эквивалентности определим формулой
(р, q) = (р', q% если pq' - p'q = 0. (I, 3; 2)
2°) Возьмем в качестве Е множество вещественных
неотрицательных функций вещественной переменной, т. е. множество
отображений R.b R+ = {х; xgR, x^O}. Отношение
эквивалентности выберем таким, в котором f = g тогда и только тогда,
когда fug «эквивалентны» при х -*■ + оо, т. е. если, каково бы
ни было е > 0, существует х0, такое, что для всех х ^ хо имеют
место неравенства f(x)(l — е) ^ g(x) ^ f(x) (1 + е).
3°) Определим на множестве целых чисел Z отношение
эквивалентности так, чтобы р == q тогда.и только тогда, когда

18
Гл. I. Теория множеств
р — q делится на заранее заданное число т. В теории чисел
такое отношение записывается в виде р == ^(modm).
4е) Пусть Е — множество прямых на плоскости. Определим
отношение эквивалентности для прямых D и D', считая D s=D',
когда эти прямые параллельны или совпадают.
5е) Пусть Е — множество всех векторов АВ на плоскости.
Определим в Е отношение эквивалентности А'В'~АВ, если
векторы А'В' и АВ параллельны, одинаково направлены и
имеют одинаковую длину.
6е) В том же самом множестве Е установим отношение
эквивалентности, согласно которому А'В' ~ АВ, если А'В' и АВ
лежат на одной прямой, одинаково направлены и имеют
одинаковую длину.
Классы эквивалентности. Разбиения
Пусть для элементов множества Е определено некоторое
отношение эквивалентности R. Часть Е, образованную из всех
эквивалентных между собой элементов, будем называть
классом эквивалентности.
Теорема. Два класса эквивалентности всегда либо
совпадают, либо не пересекаются.
Доказательство. Пусть А и В — два класса
эквивалентности. Предположим, что они пересекаются, и х — некоторая
точка пересечения. Класс А образован из элементов,
эквивалентных одному из своих элементов а, но, так как х и а
эквивалентны, то из свойства с) следует, что А образован также из
элементов, эквивалентных х. Однако тогда по той же причине
В обладает тем же свойством, и, значит, А и В совпадают.
Из проведенного доказательства, кроме того, вытекает, что
класс эквивалентности является множеством всех элементов,
эквивалентных произвольному элементу из этого класса. Таким
образом, классы эквивалентности определяют некоторое
разбиение множества Е, т. е. некоторое множество непустых попарно не
пересекающихся частей Е, объединение которых равно Е. Если
известны эти части, то известно и отношение эквивалентности,
ибо хну эквивалентны тогда и только тогда, когда они
принадлежат одному классу эквивалентности. Обратно, всякое
разбиение множества Е: Е= (J Л*, где Л{ не пусты и попарно не пере-
секаются, определяет некоторое отношение эквивалентности,
а именно: х = у, если существует такой индекс i е /, что х е Аи
y^Ai. В этом случае множества At являются классами эквива-

§ 3. Отношения эквивалентности. Фактормножество 19
лентности в этом соотношении. В частности, если / — некоторая
сюръекция множества Е на множество F, то отношение f(x) = f(y)
является отношением эквивалентности на £ и множества f~]({z}),
.z e Л являются классами эквивалентности.
Фактормножество
Фактормножеством множества Е по отношению
эквивалентности R называется множество, обозначаемое через E/R,
каждый элемент которого является одним из классов
эквивалентности. Если через х обозначить класс эквивалентности эле-
мента х, то х является элементом фактормножества h^gi
Отображение, ставящее в соответствие каждому элементу х
из Е класс эквивалентности х, называется канонической сюръек-
цией Е на E/R. Действительно, отображение сюръективно.
Обратно, мы видели выше, что всякая сюръекция / множества Е
на F определяет некоторое отношение эквивалентности R.
Отображение, ставящее в соответствие каждому z^F класс
эквивалентности f~l({z}), является биекцией множества F на EJR,
что позволяет рассматривать F как некоторую «модель»
фактормножества E/R.
Можно дать простую интерпретацию фактормножества на
примерах отношений эквивалентности, приведенных ранее на
стр. 17—18.
В нервом примере фактормножество является множеством Q
рациональных чисел, поскольку рациональное число обычно
определяется как семейство пар (р, q), q Ф О, где при pq' — p'q =
= 0 две пары (р, q) и (р', q') определяют одно и то же
рациональное число.
В третьем примере фактормножествами являются
множества целых чисел, сравнимых по модулю.т.
В четвертом — фактормножество есть множество
направлений прямых на плоскости.
В пятом — фактормножеством является множество
свободных векторов на плоскости. При этом свободным вектором
называется как раз класс всех эквивалентных векторов.
В шестом примере фактормножеством является множество
«скользящих векторов» плоскости, применяемых в механике.
Факторгруппа по инвариантной подгруппе
Пусть G — некоторая группа, закон композиции которой
записываем мультипликативно: (х, у)—>ху. Заданная композиция
является отображением С X С в С.

20
Гл. 1. Теория множеств
Пусть Г — некоторая инвариантная подгруппа1). Будем
рассматривать следующее бинарное отношение: «л: == у, если
существует элемент йеГ, такой, что у = ах, или, что то же самое,
если ух'1 е Г». Можно проверить, что такое отношение есть
отношение эквивалентности. Классами эквивалентности
являются «правые классы смежности» в G по подгруппе Г.
Поскольку Г инвариантна, то отношение эквивалентности «х = у,
если существует элемент а е Г, такой, что у = ха, или если
x~ly e Г», идентично предыдущему и правые классы смежности
являются также левыми классами смежности. Пусть а, р—два
из этих классов. Какими бы ни были х е а, */ е р,
произведение ху всегда принадлежит одному и тому же классу. Будем
обозначать его через ар. Закон композиции (а, р)—► ар
превращает фактормножество в новую группу, обозначаемую через
G/T и называемую факторгруппой группы G по инвариантной
подгруппе Г.
Факторпространство векторного пространства
по векторному подпространству
Пусть Е.— векторное пространство над полем К, и пусть
F—некоторое векторное подпространство. Рассмотрим
бинарное отношение на Е «разность х — у принадлежит F». Это —
некоторое отношение эквивалентности. Впрочем, относительно
сложения Е является абелевой группой, a F — ее подгруппой.
В абелевой группе всякая подгруппа инвариантна.
Следовательно, рассматриваемое отношение является частным случаем
предыдущего. Пусть E/F — факторгруппа. Эта факторгруппа
абелева, и закон композиций в ней мы записываем аддитивно.
Пусть Х^К— некоторый скаляр и а — некоторый класс
эквивалентности. Если х — произвольный элемент из а (х = а), то
Хх всегда принадлежит одному и тому же классу
эквивалентности, обозначаемому через Ха. Закон сложения на E/F и
закон умножения на скаляры (X, а)-»-^а превращают E/F в
векторное пространство, называемое факторпространством
векторного пространства Е по векторному подпространству F.
Согласно определению векторных операций в E/F, для х е Е,
• • • • •
у е £, X е К имеем (х + у) = х + У, (Хх) = X х- Другими
•
словами, каноническая сюръекция х ->• х пространства Е на E/F
является линейным отображением.
Каноническая сюръекция не биективна (кроме случая, когда
F = {0}). Однако, если G является векторным подпростран-
') Подгруппа Г называется инвариантной, если из a^G, хеГ следует,
что сша-1 е Г.

§ 4. Отношения порядка
2t
ством Е, дополнительным ') к. F, то сужение на G канонического-
отображения является биекцией G на E/F. В самом деле:
a) Это сужение инъективно, ибо если х и у — два эле-
• •
мента G, таких, что х = у, то х — у^Е. Так как G —
векторное подпространство, то х — у е G. Поскольку F a G
дополнительны друг другу, то их пересечение сводится к нулевому
элементу, а, значит, х = у.
b) Рассматриваемое сужение сюръективно, ибо если а
является некоторым классом эквивалентности и если х есть
некоторый элемент этого класса» то х записывается в виде х =
= х' + х", х' <= F, х" <= G (значит, х — х' <= G), а, следователь-
• •
но, х" = х = а, где х" е G, что доказывает сюръективность
рассматриваемого отображения.
•
Итак, отображение х-*х подпространства G на E/F
является линейной биекцией, т. е. биекцией, сохраняющей
векторную, структуру. Оно позволяет считать G моделью векторнога
факторпространства E/F. В частности, G имеет ту же
размерность, что и E/F2).
§ 4. ОТНОШЕНИЯ ПОРЯДКА
Бинарное отношение R на множестве Е называется
отношением порядка, если оно обладает следующими свойствами:
a) рефлективность: (х, jc) е= #;
b) транзитивность: если [х, у)^ R и (у, z) e R, то (jc, z) e R;
(I, 4; 1>
c) антисимметричность: если (jc, у)е/?и (у, х) е R, то х — у.
Вместо того чтобы писать (х, у) е R, пишут также х ^ Ryy
или х =^ у, если отношение порядка было указано заранее и нет
необходимости его повторять.
В этом случае у^=х означает х^.у. Отношения (1,4; 1)
теперь можно записать в виде:
a) х я^ х;
b) если х ^. у и у ^ z, то х ^ z;
c) если х я^ у и у^х, то х — у.
') Каждый элемент Е представляется единственным образом как сумма
некоторого элемента из F и некоторого элемента из G.
2) Факторпространство EJF существует всегда, поскольку мы его явно/
определили. Однако всегда ли существует дополнение G к F в £?
Существование такого дополнения очевидно, если Е конечномерно. То же
справедливо и во всех других случаях. Этот факт мы примем без доказательства-

22
Гл. I. Теория множеств
Примеры отношений порядка
Г) В множестве N неотрицательных целых чисел, в
множестве Z всех целых чисел, в множестве Q рациональных чисел и
в множестве R вещественных чисел отношение «(.if,y)e^
тогда и только тогда, когда х ^ у» является отношением
порядка.
"7 Уместно заметить, что отношение «(х,у)^ R тогда и только
^- тогда, когда х ^ у» является также отношением порядка, назы.
ваемым противоположным предыдущему.
Символ =^ был использован по аналогии с символом ^. По
этой же аналогии можно рассматривать отношения:
х<#, х<#, */>х и у Ух,
читаемые соответственно как «х предшествует' у», «.х строго
предшествует у», «.у следует за х», «у строго следует за х»,
а символ х<^ у означает «х <J у и х ф у».
Заметим, что мы порываем здесь с принятыми определе-
7 ниями, говоря «х предшествует у» вместо обычного «предше-
^" ствует или совпадает» и «строго предшествует» вместо
«предшествует». Причина этого изменения, полностью оправдываемая
в дальнейшем, заключается в том, что чаще всего используется
отношение <J и его следует называть короче. Следует всякий раз,
когда это возможно, вместо символа <^ применять символ =^.
Когда пишется строгое неравенство с -^ , то это должно
являться предупреждением для читателя в том, что здесь
требуется осторожность, что неравенство ^ не подходит.
Например, непрерывность вещественной функции / вещественной
переменной в точке а следует записывать следующим
образом:
«каково бы ни было е > 0, существует ц > 0, такое, что из
\х — а| ^ т] следует \f(x) — /(а) | ^ 8».
Мы употребили знак более широкого неравенства там, где
это было возможным, и применили строгое неравенство > О
только там, где это было абсолютно необходимо.
Использованная аналогия между произвольным -отношением
порядка =Sj и его частным случаем ^ в множестве
вещественных чисел может создать некоторые затруднения, поскольку
можно писать х <С у и говорить «г предшествует у» даже в том
случае, когда отношение порядка определено неравенством
х ^ у.
2°) В множестве слов существует отношение порядка,
называемое алфавитным (если договориться отождествлять
омонимы).
3°) В множестве E = ty(F) частей множества F существует
естественное отношение порядка: X <J Y, если ХсУ.

§ 4. Отношения порядка
га
4°) В множестве Е = RF функций, определенных на
множестве F, с вещественными значениями также существует
естественное отношение порядка: f ^ g, если при любом xef
выполняется неравенство f(x)^g(x). Заметим, что здесь
отношение / <^g означает, что, каково бы ни было х, f{x)^Cg{x) и что,
по меньшей мере для одного х, f(x)<g(x). Рассматриваемое
отношение вовсе не означает, что при любом х имеет место
неравенство f(x)<g(x).
5°) В множестве N.i целых чисел ^ 1 существует отношение
порядка, применяемое в арифметике: а <С Ь, если а является
делителем Ь.
6°) В произвольном множестве Е отношение «х <С у, если
^ = у» является отношением порядка. Говорят, что это —
хаотический порядок на Е.
Говорят, что отношение порядка является полным или что
множество Е вполне упорядочено, если для любых двух
элементов х, у из Е необходимо имеем: или х <( у, или х = у, или
х>У-
Это справедливо для естественных порядков в множествах
N, Z, Q, R в алфавитном порядке слов, но это не так для
отношений порядка, рассмотренных в примерах 3°)—5°).
В каждом из таких случаев, если х и у не удовлетворяют
никакому из трех указанных соотношений, говорят, что они. не
сравнимы. В примере 3°) две непустые не пересекающиеся
части F не сравнимы; в 4°) — не сравнимы функции 0 и х; в 5°) —
не сравнимы целые числа 2 и 3; в хаотическом порядке
примера 6°) два произвольных не совпадающих элемента не
сравнимы.
Мажорируемые части, мажоранты, максимум,
точная верхняя грань
Говорят, что некоторая часть упорядоченного множества £,
мажорируема, если существует по крайней мере один элемент
из Е, следующий за всеми элементами этой части. Каждый
такой элемент называется мажорантой этой части.
Аналогичное определение дается для минорируемой части и
миноранты.
Часть, одновременно мажорируемая и минорируемая,
называется «ограниченной».
Говорят, что некоторая часть Е имеет максимум, если
существует мажоранта этой части, ей принадлежащая.
Часть не обязана иметь максимум, однако, если она его
имеет, то этот максимум единствен. В самом деле, если а и
b — два максимума одной и той же части, то одновременно
имеем: а ^ b и Ъ <С а, откуда а = Ь. Максимум некоторой.

24
Гл. I. Теория множеств
части Л, если он существует, обозначается через max x или
же А
тах(Л).
Аналогичное определение дается для минимума,
обозначаемого через min.
Говорят, что некоторая часть Л множества Е имеет точную
верхнюю грань, если множество ее мажорант имеет минимум, и
этот минимум называется точной верхней гранью
рассматриваемой части.
Точная верхняя грань является, следовательно, наименьшей
из мажорант. Любой элемент, мажорирующий часть А,
мажорирует также и ее точную верхнюю грань.
Часть не обязана всегда иметь точную верхнюю грань, но
если она ее имеет, то эта грань единственна. Точная верхняя
грань некоторой части А, если она существует, обозначается
через sup х или sup Л.
хе А
Если точная верхняя грань принадлежит Л, то она является
максимумом, и обратно. Аналогичное определение дается для
точной нижней грани, обозначаемой через inf.
Теорема 2. Всякая непустая мажорируемая часть
вещественной прямой R, снабженной отношением естественного,
порядка, имеет точную верхнюю грань, и всякая непустая минори-
руемая ее часть ') имеет точную нижнюю грань. Кроме того,
точная верхняя грань Ь мажорируемой части А характеризуется
соотношениями
a) при любом хеЛ,л</);
b) каково бы ни было bi <. b, существует по крайней мере
одно число х е А, такое, что Ь\ ^ х ^Ь.
Доказательство этой теоремы общеизвестно.
Естественно, что не мажорируемая часть не имеет точной
верхней грани. Прямая R ни мажорируема, ни минорируема.
В множестве Е частей множества F при отношении порядка
X a Y (пример 3°) каждая часть имеет точные верхнюю и
нижнюю грани. В самом деле, любая часть из Е является
некоторым множеством частей F. Точной верхней гранью будет
объединение этих частей, а точной нижней гранью — их
пересечение.
В множестве Е вещественнозначных функций, определенных
на множестве F (пример 4°), всякая мажорируемая часть имеет
точную верхнюю грань и всякая минорируемая часть имеет точ-
') Условие «непустая» существенно. Часть 0 мажорируема, так как
любая точка R является мажорантой для 0. Множество мажорант
совпадает с R, не имеющим минимума. Хотя 0 и ограничена, она не имеет ни
точной верхней, ни точной нижней граней.

§ 4. Отношения порядка
25
ную нижнюю грань. Действительно, если А — эта часть, то ее
точной верхней гранью будет функция f0, задаваемая формулой:
f0(x) = supf(x) для всех x^F. (I, 4; 2)
Заметим, что имеется два совершенно разных, но полезных
понятия. С одной стороны, точная верхняя грань части А в
упорядоченном множестве RF. Это вещественная функция,
называемая верхней огибающей функций f ^ А. С другой стороны,
точная верхняя грань в R множества всех значений этих функций,
sup f(x), которая является, если она существует, некоторым
вещественным числом — точной верхней гранью функций f <= А.
Если А состоит из одного элемента f, то говорят о точной
верхней грани f, supf(x),— вещественном числе, являющемся точ-
ной верхней гранью множества значений функции f. Если она
достигается для некоторого значения х, то ее называют
максимумом.
Аналогичное замечание можно сделать для нижней
огибающей и точной нижней грани. Эти часто употребляемые понятия
в силу своей близости таят в себе некоторую опасность.
В множестве Ni целых чисел ^1 с отношением делимости 5°)
всякая конечная часть имеет точную верхнюю грань — общее
наименьшее кратное и точную нижнюю грань — общий
наибольший делитель чисел, входящих в эту часть.
Возрастающие функции
Пусть Е и F— два упорядоченных множества.
Отображение /множества Е в F называется возрастающим, если
из л;<*/ следует f(x)*^f(y). (I, 4; 3)
Если, сверх того,
из х<у следует f{x)<,f{y), (I, 4; 4)
то отображение называется строго возрастающим.
Соответствующим образом измененное определение дается
для убывающего и строго убывающего отображений.
Если Е вполне упорядочено, то всякая одновременно
возрастающая, и убывающая функция на Е постоянна. В самом деле,
пусть х и у — произвольные элементы Е. Для них либо х ^ у,
либо х^у. Так как f — одновременно возрастающая и

^26
Гл. I. Теория множеств
убывающая функция, то /(*)</(#) и /(*)>/(#), а, значит,
f(x) = f(y), т. е. / постоянна ').
Замкнутым интервалом [а, Ь], а ^ Ь, упорядоченного
множества Е называется множество элементов х из Е,
удовлетворяющих неравенствам а ^ х ^ Ь. Открытым интервалом ] а, Ь [
называется множество элементов х, удовлетворяющих
отношениям а^х^Ь. Через [а, Ь[ обозначается множество
элементов х, удовлетворяющих неравенствам а^х^Ь, а через ]а,Ь]—
множество элементов х, для которых а -^ х ^ Ь. Последние
множества называются также полуоткрытыми интервалами. Во
всех случаях а является началом, а Ь — концом интервала.
Иногда нам придется рассматривать интервалы с началом а и
концом b без уточнения того, являются ли они открытыми,
полуоткрытыми или замкнутыми. Мы их будем обозначать через | a, b \.
Множество таких элементов х, что а ^ х, называется
правым замкнутым сечением [а, —►), а множество таких х, что
а ^ х, называется правым открытым сечением ]а, ->).
Аналогичное определение дается для левых сечений (<—, а]
и (<-, а [.
В случае вещественной прямой R с естественным
упорядочением такие сечения называются полупрямыми. Эти сечения, так
же как и все множество Е в целом, принято считать
интервалами.
Пополненная прямая
Пополненной прямой R называется множество, образованное,
с одной стороны, из элементов вещественной прямой R и, с
другой стороны, — из двух элементов, обозначаемых —оо и +°°-
На R устанавливается отношение порядка, обозначаемое
через sg: и определяемое следующим образом: а ^.Ь, если а и Ь
конечны и если они удовлетворяют неравенству < в R, или же
■если а=—оо или й =+оо. Множество R вполне упорядочено
и имеет, кроме того, минимум —оо и максимум +°°. Любая,
часть R ограничена, и теорема 2 справедлива в R без
предположения мажорируемости части А, поскольку эта мажорируе-
мость всегда имеет место2). Интервал из R вида [а, +°°[ при
aeR содержится в R, поэтому его часто называют полупря-
!) Мы замечали, что отношение х=у является таким отношением
порядка в Е, при котором два различных элемента не сравнимы. Если F —
некоторое упорядоченное множество, то любое отображение Е в F является
одновременно возрастающим и убывающим, не являясь необходимо
постоянным. Таким образом, предположение о полной упорядоченности^ не излишне.
2) Точная верхняя грань пустой части 0 есть минимум R (см.
примечание на стр. 24), т. е. —<», точной нижней границей является +°°. Для
непустой части А всегда sup (А)^ inf (А). Это оказывается неверным для
пустого множества.

§ 5. Мощности. Счетные множества
27
мой [а, —+) в R. Точно так же, если Л — некоторая не
мажорируемая часть R, то часто пишут sup(/l)= + 00, это приводит
к тому, что А лучше рассматривать как некоторую часть R.
§ 5. МОЩНОСТИ. СЧЕТНЫЕ МНОЖЕСТВА
Рассмотрим отображение N в N, ставящее в соответствие
каждому целому числу удвоенное число. Это отображение
взаимно однозначно и позволяет таким образом в некотором
смысле считать, что существует столько же четных чисел,
сколько существует целых. Отсюда следует также, что в
случае бесконечных множеств может существовать биективное
отображение некоторого множества на его часть, отличную от
самого множества.
Может показаться слишком смелым, несмотря на сказанное
выше, пытаться сравнивать между собой бесконечные
множества. Тем не менее, благодаря понятию биективного
отображения такое сравнение возможно.
Теорема 3 (Бернштейн). Пусть Е и F — два произвольных
множества. Тогда
1°) либо существует инъекция Е в F, либо существует
инъекция F в Е (оба обстоятельства не исключают друг друга);
2°) если существуют одновременно инъекция Е в F и
инъекция F в Е, то существует также биекция Е на F.
Мы примем эту теорему без доказательства.
Следствие. Для заданных множеств Е и F имеется
только три возможности:
a) Существует инъекция Е в F и не существует инъекции
F в Е. В этом случае говорят, что F имеет мощность, строго
большую мощности Е, или что Е имеет мощность, строго
Меньшую F.
b) Существует инъекция F в Е и не существует инъекции
Е в F. Тогда Е имеет мощность, строго большую, чём F, или F
по мощности строго меньше, чем Е.
c) Существует биекция Е на F. В этом случае говорят, что
Е и F имеют одинаковую мощность; или равномощны 1).
Мощности. Кардинальные числа
Отношение «Е равномощно F» является отношением
эквивалентности между множествами2). Класс эквивалентности,
') Доказательство теоремы Бернштейна сложно, и мы его не приводим.
Следствие вытекает непосредственно из этой теоремы. Если Е равномощно
с F или мощность его строго меньше, чем F, то говорят, что Е имеет
мощность, меньшую, чем мощность F.
2) Мы намеренно не останавливаемся на логических трудностях,
связанных с понятием множества всех множеств.

28
Гл. I. Теория множеств
т. е. класс всех множеств, равномощных данному множеству,
называется мощностью, или кардинальным числом. Конечные
кардинальные числа являются классами эквивалентности
конечных множеств. Эти числа по определению являются целыми
натуральными числами 0, 1, 2 ... . (Заметим, что мы приняли как
первичное понятие целые натуральные числа, но их строгое
математическое определение полно сложностей. В частности, не
легко a priori определить конечные множества. Часто по
определению считают множество конечным, если оно не равномощно
никакой из его частей, отличных от самого множества, а затем
доказывают, что кардинальные конечные числа обладают
свойствами целых натуральных чисел.) Бесконечное кардинальное
число, т. е. мощность бесконечного множества, называется
трансфинитным кардинальным числом, или трансфинитным числом.
В классе кардинальных чисел существует отношение
порядка: «.если а является кардинальным числом некоторой части
множества мощности р, то а ^ р». Согласно теореме 3, это
отношение обладает антисимметрией, а, значит, действительно
является некоторым отношением порядка. Из этой же теоремы
следует, что это отношение порядка является полным, т. е.
любые два кардинальных числа сравнимы.
Заметим, что если существует сюръекция f множества Е на
множество F, то мощность F меньше мощности Е. В самом
деле, прообраз каждой точки F не пуст, и если в каждом из
этих прообразов мы выберем по одному элементу, то получим
некоторую часть Е, равномощную F1). Например,
фактормножество множества Е по некоторому отношению эквивалентности
всегда имеет меньшую мощность, чем Е.
На множествах кардинальных чисел можно определить
операции сложения, умножения, возведения в степень точно так
же, как и в множестве натуральных чисел.
Г) Пусть а и р— два кардинальных числа, а £ и F —
множества мощности соответственно а и р. Через а + р
обозначается мощность «суммы» Е и F, т. е. всякого множества,
допускающего разбиение, образованное из двух множеств, равно-
мощных Е и F соответственно.
2°) Через ар обозначается мощность произведения Е X F.
Это — кардинальное число объединения а непересекающихся
частей, каждая из которых имеет мощность р.
3°) Через ар обозначается мощность множества EF всех
отображений F в Е.
') Нетрудно выбрать по одному элементу в каждом из конечного числа
множеств. Производить подобный выбор в случае бесконечного числа
множеств не легко. После больших споров в начале нашего века было признано,
что • возможность такого выбора может быть введена как аксиома теории
множеств — аксиома выбора, или аксиома Цермело.

§ .5. Мощности. Счетные множества 29
Теорема 4. Предыдущие операции, определенные на
множестве кардинальных чисел, обладают следующими свойствами:
ассоциативность и коммутативность сложения,
ассоциативность и коммутативность умножения,
дистрибутивность умножения по отношению к сложению,
и, сверх того, имеют место соотношения
(о») (ov) = oP+v, avpv = (ap)v> (aP)V = aPv_ (I5; 1}
Доказательство. Не очевидны лишь равенства (1,5; 1).
Пусть Е, F, G — множества мощностей а, р, у
соответственно. Тогда мощности множеств EF и EG равны ар и av. Для того
чтобы определить отображение множества F -f- G в Е,
достаточно определить сужение этого отображения на F и на G, т. е.
произвольное отображение F в Е и произвольное отображение
G в Е. Общий элемент EF+G получается, таким образом, как
пара, состоящая из произвольного элемента EF и произвольного
элемента EG. Каждая такая пара является произвольным
элементом EF X EG> а следовательно, EF+G равномощно EF y^EG и
aP+v = aPav.
На стр. 13 мы видели, что всякое отображение G в Е X F,
т.е. любой элемент (Е X F)G, является парой, состоящей
из'некоторого отображения G в Е и некоторого отображения G в F,
т. е. элемента EG и элемента FG. Такая пара является произ-'
вольным элементом EGy^FG, а, следовательно, (Е X F)G рав-
номощно множеству EG X FG и (aP)v = aYPv.
Пусть теперь f — некоторое отображение F X G в Е.
Отображение х—*f(x, у) множества F в Е при фиксированном у
из G называется частным отображением fy, так что по
определению fv(x)=f(x,y). Таким образом, f из EFXG определяет
некоторое отображение у—*fy множества G в множество EF
отображений F в Е, т.е. элемент (EF)G. Обратно, если y-*gy
является отображением G в EF, то оно порождается с помощью
предыдущего процесса из отображения g множества F X G в Е,
определяемого по формуле g(x,у) —*-gy(x). Тем самым нами
установлена биекция EFXG на {EF)G, откуда aPv=(ap)v.
Эти формулы могут убедить читателя в том, что
кардинальные числа, даже трансфинитные, обладают всеми свойствами
обычных натуральных целых чисел, но это не так, как
показывает приводимое ниже удивительное свойство, которое мы
примем без доказательства.
Теорема 5. Если а и р^—два кардинальных числа фО и
если по крайней мере одно из них трансфинитно, то сумма а+р
и произведение ар равны наибольшему из них1).
) Доказательство весьма замысловато:

30
Гл. I. Теория множеств
Отсюда, в частности, вытекает, что для кардинальных
бесконечных чисел определить вычитание невозможно, ибо среди
чисел, прибавление которых к а дает а, фигурирует не только 0,.
но и любое конечное число и даже само а.
Теорема 6. Каково бы ни было множество Е, множества
его частей имеет мощность, строго большую мощности Е.
Эта теорема показывает, что последовательность
кардинальных бесконечных чисел не ограничена.
В самом деле, предположим, что существует сюръекция f
множества Е на множество частей ty(E). Тогда, для Jte£, f(x)
является элементом $(£), т.е. некоторой частью Е. Обозначим
через Л часть Е, образованную из таких ie£, что x^f(x).
Так как A czty(E), то в Е существует по крайней мере один
элемент у, такой, что f(y)—A. Если г/е/(г/)=Л, то, по
определению множества Л, у ф. Л, что невозможно. Если у ф.1(у)=А,
то (/ е Л. В обоих случаях мы приходим к противоречию.
Поскольку, однако, существует инъекция Е в ty(E), а
именно х—► {*}, то Е имеет мощность, меньшую мощности ty(E),
а значит, строго меньшую мощности ty(E).
Замечание 1. Если Е бесконечно, то множество ^/(f)
конечных частей Е равномощно множеству Е. Это легко
доказывается с помощью приводимой ниже теоремы 7. Отображение
(х\, х2, ..., хп)~*{х\, х2, ..., хп}, ставящее в соответствие
каждому элементу (хи х2 хп) из Еп (п ^ 1) часть Е,
образованную из этих элементов (не обязательно различных),
является некоторой сюръекцией Еп на множество tyn{E)
непустых частей Е, образованных не более чем из я элементов. Но
тогда card^„(£') ^ card £" = card£ (теорема 5), и поскольку
cardan (Я) ^ card£, то card tyn(E) = card E. Пусть теперь
fn'. x->fn{x)—некоторая биекция Е на tyn{E). Положим /о(х) ф 0
для всех х^Е. Тогда (п, х) —► /„ (х) будет некоторой
сюръекцией N X Е на fyf(E), а значит, card %(E)< card (N X Е) =
==v card E=cardE (в силу теоремы 7, неравенства v ^ card E
и теоремы 5). Поскольку обратное неравенство очевидно,
окончательно получаем: card $/(Я) = card E.
Замечание 2. Характеристической функцией некоторой
части Л множества Е называется функция <рА, определенная на
Е, со значениями в двухэлементном множестве, {0, 1}, такая, что
Фд(*) = 1, если *еЛ, и фл(л:) = 0, если хф.А. (1,5; 2)
Задание этой функции однозначно определяет часть Л.
Впрочем, всякая функция на Е, принимающая значения 0 и
^единственным образом определяет некоторую часть Е. Существует,
таким образом, некоторая биекция множества %{Е) частей Е

§ 5. Мощности. Счетные множества
31
на множество отображений Е в множество {0, 1}. Отсюда
следует, что кардинальным числом множества ^(Е) является
ocard E
Предыдущую теорему теперь можно сформулировать
следующим образом:
Каково бы ни было кардинальное число ос, 2а>ос').
Мы сейчас изучим две наиболее важные трансфинитные
мощности: мощность счетного множества и мощность
континуума.
Счетные множества
Мощностью счетного множества v называется мощность
множества N целых натуральных чисел. Всякое множество, равно-
мощное N, называется счетным2).
Теорема 7. .v является наименьшим трансфинитным
кардинальным числом.
Это означает лишь, что всякое бесконечное множество Е
содержит по меньшей мере одну счетную часть. Предположим, что
для некоторого бесконечного множества, Е соотношение
card£>v не имеет места. Согласно теореме 3, это означает,
что существует биекция Е на некоторую бесконечную часть Р
множества N. Отображение п^-хп, где хп есть (п + 1)-й (в
порядке возрастания) элемент Р, определяет биекцию N на Р.
Окончательно получаем, что card£=v.
Теорема 8. Для любого конечного числа m^ 1
выполняются равенства tn\ = v и vm = v.
Результат непосредственно вытекает из теоремы 5, согласно
которой mv=v при n^vn v2=vv=v, а следовательно, по
индукции vm=v. Однако мы приняли теорему 5 без
доказательства, в то время как равенство vv = v, из которого вытекает
теорема 8, доказывается элементарно.
') В частности, для любого целого п ^ 0 имеем 2П > п.
2) Сказать, что некоторое множество счетно, означает сказать, что оно
Допускает по крайней мере одну биекцию на N. Однако это не значит, что
такая биекция задана. Это означает также, что возможно расположить
элементы данного множества в некоторую последовательность Ха, хи х2, ...,
хотя сама эта последовательность не задана. Часто кардинальное число
множества обозначают через № (к—«алеф» — первая буква древнееврейского
алфавита). Во многих работах счетными называют множества, кардинальные
числа которых <v. Множество Е конечно или счетно (cardE^v) тогда
« только тогда, когда существует инъекция Я в N, или, если положить Еф 0,
тогда и только тогда, когда существует сюръекция N на Е.

32 Гл. I. Теория множеств
Покажем, что N X N равномощно N. Если элементы N X N
перенумеровать в порядке, определяемом последовательными
линиями, параллельными диагонали квадратной таблицы:
(0.
(1.
(2,
(3,
К-,
то получится последовательность (0, 0), (1, 0), (0, 1), (2, 0),
(1, 1), (0, 2), ..., определяющая биекцию N на N X N.
Следствия. 1°) Объединение конечного или счетного мно~
жества конечных или счетных частей множества Е конечно или
счетно.
В самом деле, пусть /—некоторая часть N и Ait i^I,-—
некоторые части Е. Можно предположить, что ни одна из них
не пуста, так как пустые множества ничего не изменяют в
объединении. Пусть fi — некоторая сюръекция N на Ai% Тогда
(i, n)-*fi(n) будет являться сюръекцией / X N на (J At.
Поскольку / X N счетно (или пусто, если / пусто), то (J Ai
конечно или счетно.
2°) Множество Z всех целых чисел счетно (как объединение
двух счетных множеств). Множество Q рациональных чисел
счетно.
В самом деле, отображение, ставящее каждой паре (р, q),
q ф 0, множества ZXZ в соответствие рациональное число p/q,
является сюръекцией подмножества Z X Z на Q. Значит, Q не
более чем счетно, но так как оно содержит N, то Q счетно.
3°) Множество алгебраических вещественных чисел счетно.
Алгебраическим вещественным числом называется
вещественный корень некоторого не равного тождественно нулю
полинома с целыми коэффициентами.
Поскольку не равный тождественно нулю полином степени
^.пг с целыми коэффициентами имеет т + 1 коэффициентов,
которые являются произвольными целыми числами и не все равны
нулю, то мощность множества этих полиномов равна vm+1 = v.

§ 5. Мощности. Счетные множества 33
Каждый такой полином имеет не более m алгебраических
вещественных корней, а следовательно, множество алгебраических
чисел, корней полиномов степени <:/п, можно рассматривать
как объединение счетного множества конечных множеств.
Такое множество не более чем счетно, а так как оно бесконечно,
то оно счетно. Поскольку m принимает все значения, то
.множество всех алгебраических чисел получается как объединение
счетного множества счетных множеств, а значит, является
счетным множеством.
4°) Множество всех точек R" с рациональными или
алгебраическими координатами счетно, ибо его кардинальное число-
равно vn=v.
Мощность континуума
Теорема 9. Множество всех вещественных чисел несчетно.
Доказательство. Покажем, что даже множество Е
вещественных чисел, удовлетворяющих неравенствам 0 ^ х < 1,
несчетно. Допустим, что Е счетно и существует некоторая биек-
ция Ni на Е, т. е. элементы Е могут быть записаны в виде
попарно различных элементов некоторой последовательности
Х\, Хч, Х3, .
Кроме того, рассмотрим вещественное число £,
определяемое следующим образом: перед запятой мы поставим 0, затем
в качестве /-го десятичного знака выберем произвольное целое
число между 1 и 8, отличное от /-го десятичного знака числа Xj.
Таким путем мы образуем бесконечную дробь, определяющую
некоторое число £. Поскольку п-й десятичный знак числа £
отличен от п-го десятичного знака числа хп и все десятичные
знаки числа | отличны от 0 и 9, то | Ф хп. (Применение
десятичных знаков 0 и 9 может создать затруднения, поскольку
число, в десятичном разложении которого, начиная с
некоторого места, стоят только нули, допускает иное десятичное
разложение, содержащее с некоторого места одни девятки,
например 0,102000 ... =0,101999 ... .) Итак, мы пришли к
противоречию: множество {х\, я2, х3, • • •} не содержит числа,
расположенного на отрезке [0, 1[.
Трансцендентные числа
Вещественные числа, не являющиеся алгебраическими,
называются трансцендентными. Поскольку множество
алгебраических чисел счетно, а множество вещественных несчетно, то
существуют трансцендентные числа и даже «большинство»
вещественных чисел трансцендентны. Однако, несмотря на это, не
так легко указать явно трансцендентные числа. Можно
2 Зак. 1339

34
Гл. I. Теория множеств
доказать (но это вовсе не очевидно!), например, что числа е и я
трансцендентны.
Замечание. Часть множества £=[0, 1[, образованная из
чисел, в десятичном разложении которых имеются лишь
цифры 1, 2, 3, 4, 5, 6, 7, 8, является множеством, равномощным
множеству {1, 2, 3, 4, 5, 6, 7, 8}N, т. е. имеет мощность 8V.
Что же касается самого множества Е, то его мощность
sg:10v (мы пишем ^, а не = из-за указанного выше двоякого
десятичного представления чисел). Поэтому 8V ^ card-E ^ 10v,
откуда 2v<card£< 16v = (24)v=24v=2v, а значит, card£=
=2V. Только что доказанная теорема является лишь частным
случаем теоремы 6. Впрочем, приведенное доказательство
является лишь частным случаем доказательства теоремы 6
(небольшое усложнение возникло в силу двойственного
десятичного представления чисел).
Будем обозначать через у мощность множества £=[0, 1] и
называть его мощностью континуума. Мощность континуума —
это мощность множества R вещественных чисел (ибо х —*>
—»-logx/(l — x) является биекцией ]0, 1[ на R).
Теорема 10. Имеют место равенства my=vy=^yy=ym=
=YV=Y, где m^l—произвольное целое конечное число.
Доказательство. Все эти кардинальные числа ^yv и
^у, поэтому достаточно доказать, что yv=Y- Легко видеть, что
Yv= (2v)v=2v2=2v=y-
Следствия1). 1°) Множество комплексных чисел имеет
мощность континуума (поскольку оно равномощно R2).
2°) Любое векторное пространство конечного числа
измерений п над полем вещественных или комплексных чисел имеет
мощность континуума.
Действительно, зафиксировав базис, легко определить биек-
цию такого пространства на R", имеющего, согласно равенству,
Yn_Y> мощность континуума. Отсюда, в частности, вытекает
парадоксальное следствие о существовании биекции R на
плоскость R2, поскольку множества R и R2 равномощны. Когда
сравнивают семейства точек, кривых, поверхностей, зависящих
от некоторого числа параметров, то часто говорят, что одно из
этих семейств больше другого, поскольку его элементы зависят
от трех вещественных параметров, в то время как элементы
другого зависят лишь от двух параметров. Такое рассуждение
') Эти следствия, точно так же как и многие другие элементарные
свойства счетных множеств и континуума, могут быть доказаны учащимися
младших курсов непосредственно, т. е. без применения принятых нами без
доказательства больших теорем 3, 4, 5.

«5 5. Мощности. Счетные множества
35
не является строгим, поскольку R2 и R3 равномощны. Во второй
главе, посвященной топологии, мы познакомимся с другими
типами сравнений, но ни в коем случае не следует сравнивать
бесконечности в описанном смысле.
3°) Множество всех последовательностей вещественных
чисел и последовательностей комплексных чисел имеет мощность
континуума, ибо их кардинальное число равно yv—y.
4°) Множество Я непрерывных вещественных функций
вещественной переменной имеет мощность континуума. В самом
деле, каждой такой функции можно поставить в соответствие
последовательность вещественных чисел — значений функции
в точках с рациональными абсциссами. Можно считать также,
что эти точки находятся во взаимно однозначном соответствии
с N, поскольку Q счетно. Конечно, последовательность этих
значений не произвольна: если бы значения функции в
рациональных точках выбирались произвольно, то невозможно было
бы ее продолжить непрерывно на всю вещественную прямую.
Однако последовательность вещественных чисел,
соответствующая непрерывной функции, ее полностью определяет.
Следовательно, можно установить биекцию множества непрерывных
функций на часть множества последовательностей
вещественных чисел. Значит, это множество Я имеет мощность, не
большую мощности континуума. А так как отображение, которое
каждой непрерывной функции ставит в соответствие ее
значение в одной точке, например, в начале координат, является
сюръекцией Е на R, то Е имеет мощность, не меньшую
мощности континуума. Отсюда следует, что Я имеет, мощность,
в точности равную мощности континуума.
5°) Множество всех вещественных функций вещественной
переменной или даже множество всех функций, принимающих
только значения 0 и 1, имеет мощность, строго большую
мощности континуума, ибо их мощности равны соответственно у* и
2\ a YV=(2V)"'=2V''=2Y > у. Из 4°) и 5°) вытекает, что
«большинство» функций имеет не менее одной точки разрыва.
Континуум-гипотеза
Согласно этой гипотезе, 2V является кардинальным числом,
непосредственно следующим за v. В общем случае обобщенная
континуум-гипотеза заключается в предположении, что при
любом кардинальном числе а кардинальное число'2™
непосредственно следует за а.
Недавно доказано (П. Коэн, 1963), что континуум-гипотеза
неразрешима — ее невозможно ни доказать, ни опровергнуть,
можно лишь принять ее или противоположное ей утверждение
как аксиому.
2*

.36
Гл. I. Теория множеств
§ 6. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ ЛОГИКИ
Всякая теорема заключается, вообще говоря, в том, что
задается некоторое свойство А, называемое условием, из которого
выводится свойство В, называемое заключением.
Коротко выражение «Л влечет В» записывается формулой
А =ф В. Обратная теорема, которая не всегда справедлива,
запишется тогда в виде В =ф А.
Если данная теорема и ей обратная обе справедливы, то
свойства А и В эквивалентны, и такую теорему можно записать
в виде А^В, что также выражается в форме: «Для того
чтобы А . .., необходимо и достаточно, чтобы В ...».
Утверждение, противоположное некоторому свойству А,
записывается «неЛ», или ~\А. Если х не принадлежит множествуЕ,
то пишут х ф. Е. Если X и У — части Е и если X не содержится
в У, то пишут X ф. У (что вовсе не означает, что X содержит У).
Во всех случаях «не не Л» = Л, и справедливо утверждение:
«или Л, или не Л» (принцип исключенного третьего).
Теорема 11. Предложение А =#> В справедливо тогда и
только тогда, когда верно предложение ~[ В =#> ~~| Л.
Доказательство. 1°) Предположим, что Л =ф В верно
и в то же время имеет место ~\В. Тогда свойство Л невозможно
без того, чтобы не было справедливым В, что противоречит
свойству ~\В, Мы имеем, следовательно, свойство ~\А, что
доказывает справедливость предложения ~] В =#> ~~| Л.
2°) Если справедливо предложение ~~| В =#> ~~| Л, то, согласно 1°),
справедливо ~~| ~| Л =#> ~| ~]В. Так как -)_М = Л и ~|~|iJ—В,
то справедливо предложение Л=фВ.
Пример. Эквивалентными являются следующие
предложения: «Любая вещественная функция, непрерывная на
конечном вещественном интервале [о, Ь], ограничена» и «Любая
вещественная функция, определенная на [а, Ь] и не ограниченная
на нем, разрывна по крайней мере в одной точке».
Когда некоторый объект обладает свойством Л или
свойством В, то пишут, что он удовлетворяет AV В или еще «Л или
В». В математике связка или никогда не относится к событиям,
обязательно исключающим одно другое. «Л или В» вовсе не
исключает одновременного выполнения Л и В. Например, если Л
означает х-^.0, а В означает х^-0, то имеет место Л или В. Эти
два свойства не исключают друг друга, поскольку возможно,
что *=0.
Если имеют место одновременно свойства Л и В, то это
записывается в виде А А В или же «Л и В».

§ в. Некоторые основные понятия логики
37
В математических теоремах часто используются выражения:
«Для всех ...» и «Существует .. . такое, что ...». Их
обозначают соответственно ч'ерез V и 3 и называют кванторами.
Предложения «Для всех ...» и «Существует . ..» часто
сопровождаются некоторыми ограничениями. Эти ограничения
обычно записываются в круглых скобках.
Предположим, что для некоторой вещественной функции f
вещественной переменной мы хотим сформулировать свойство
быть, непрерывной в каждой точке. Непрерывность функции
в точке а означает, что, каково бы ни было е > 0, существует
ц > 0, такое, что неравенство \х— а\ ^ ц влечет за собой
неравенство \f{x) —f{a)\ ^ е. Иначе говоря, каково бы ни было
е > 0, существует ц > 0, такое, что для любого «gR, такого,
что \х — а\ ^ т), имеет место свойство Р: \f (х) —г f (a) | г£С е.
Для того чтобы теперь выразить, что функция, непрерывна
в любой точке, мы должны записать:
(Для всех aeR) (для всех е > 0) (существует ц > 0,
такое, что) (для всех neR, таких, что ' |лс — а|^т)) имеем
P:\f(x)-f(a)\^s.
Эта фраза коротко записывается в виде:
(Va s'R) (Ve> 0) (Эл>0) (V* e R, | х - а | <л): I f (х) - f (a) | <е-
(1,6; I)
Теорема 12. Отрицание свойства, содержащего некоторое
число кванторов V, 3 и свойство Р, получается заменой
каждого квантора V на 3 и 3 на V и свойства Р на его
отрицание ~~]Р.
Так, например, свойство вещественной функции
вещественной переменной не быть всюду непрерывной, т. е. иметь разрыв
хотя бы в одной точке, может быть записано в одну строку
(ЗаеК)(Эе>0)(Ул>0)(Эхе#, \x-a\Kn)-\f(x)-f (а)\>е.
(1,6; 2)
Этот метод отрицания свойства применяется так же
автоматически, как и правило знаков в умножении или при
раскрытии скобок.
Доказательство. Предположим, что имеется один
квантор, например V. Наше свойство имеет тогда вид:
(V*, удовлетворяющий 5) : Р.
Его отрицание очевидно: существует некоторое х,
удовлетворяющее S, но не обладающее свойством Р, т.е.
,(Э*, удовлетворяющий 5) : IP.

38 Гл. I. Теория множеств
Теорема для данного случая доказана. Аналогичное
доказательство имеет место для случая, когда имеется только кванг
тор Э. Для завершения доказательства теперь достаточно
применить индукцию по произвольному числу кванторов.
Предположим, что теорема доказана в том случае, когда
имеется п — 1 квантор, и докажем ее для случая, когда их
имеется п. Пусть рассматриваемое свойство записано,
например, в виде
(Ух, удовлетворяющее 5) : Q,
где Q — свойство, содержащее п — 1 кванторов. Тогда, в силу
доказанного выше, его отрицанием будет свойство:
(Эх, удовлетворяющий S) : ~!Q.
Однако 1Q можно получить, используя теорему, поскольку Q
содержит только п — 1 квантор. Итак, теорема для этого
случая верна. Тот же самый результат получится, если первым
квантором является Э, а следовательно, теорема имеет место
в общем случае.
Замечание Каждый раз, когда квантор Э предшествует
некоторому числу других кванторов, следующая за ним буква
может оказаться функцией всех букв, фигурирующих в
предыдущих кванторах.
Например, в свойстве функции быть всюду непрерывной
т] зависит от а и от е. Может случиться, что tj можно выбирать
в зависимости только от е, а не от а. В этом случае говорят, что
функция равномерно непрерывна. Свойство функции быть
равномерно непрерывной более сильное, чем свойство быть
непрерывной. Его можно записать следующим образом:
(Ve > 0) (Эч > 0) (Va e R) (V« e R, | х - а |< ц): | / (х) - f (а) | < е.
(1,6; 3>
Очевидно, перестановка кванторов существенно изменяет
заданное свойство. Непосредственно видно, что самым сильным
является такое свойство, в котором символ Э поставлен как
можно раньше. Производя, например, еще одну перестановку,
получим:
(Эл > 0) (Va е= R) (Ve > 0) (V« e R, | х - а |< ц): \ f (x) - f (а) |< е.
(1-6; 4)
Фиксируем ц, о котором говорится в самом начале, что оно
существует. Для любого х из интервала [а — ц, а + tj] имеет
место неравенство \f(x) — f(a) | ^ e, Ve>0, что означает
\f(x) — /(a) | = 0. Яо тогда f(x) = f(a) для любого а и любого х
из интервала [а — tj, a +ti]. Выбирая в качестве а все числа

§ 6. Некоторые основные понятия логики
39
вида р/10ь, где целое р изменяется от—оо до +°° и выбрано
так, что pllOb <; т), ..., получаем: предложение (1,6;4)
означает, что f постоянна. Получаем еще большее усиление
свойства непрерывности!
N. В. Мы рассматривали теорию множеств и логику с
«наивной» точки зрения. Слова: множество, равный, каков бы ни
был, существует, влечет и т. д. ... употреблялись в том смысле,
какой они имеют в разговорном языке. Совершенно ясно, что
при этом не проводилось никакого серьезного математического
обоснования смысла этих понятий. Символы V, 3, е, —, =ф
должны были быть только знаками, подчиняющимися
некоторым «правилам игры», как конь и ладья в шахматах являются
фигурами с определенными правилами передвижений, не
совпадающими с теми, какими обладают настоящие конь или ладья.
Точно так же евклидова плоскость — это не поверхность воды,
а сфера — это не апельсин. Математическая логика
(содержащая теорию множеств) является ветвью современной
математики. Заметим, что еще не доказана ее непротиворечивость.
Логическая теория называется противоречивой, если существует такое
предложение Р.для которого можно одновременно доказать как
Р, так и ~\Р. В этом, случае будет справедливым любое
предложение Q (а также и 1Q). В самом деле, соотношения Р=ф'
=ф(Р или Q) и ({Р или Q) и 1P)^>Q дают (Р и 1P)=#>Q.
Однако если современная теория множеств противоречива, то это
еще не означает, что мы находимся в безнадежном положении.
Надо лишь уменьшить число аксиом теории, что, без сомнения,
не изменит заметно математики в целом!

ГЛАВА II
Топология
§ 1. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА. ЭЛЕМЕНТАРНЫЕ ПРИМЕРЫ
Множество Е называется метрическим пространством, если
для его элементов определено понятие расстояния, т. е.
определено некоторое отображение множества Е X Е в полупрямую
R+ = {х, хе R, х ^ 0}, которое каждой паре (х, у) из Е~ХЕ
ставит в соответствие некоторое число d(x, */) ^ 0, называемое
расстоянием между х и у.
Расстояние должно обладать следующими тремя свойствами:
1) симметрия: d {х, у) = d {у, х);
2) положительность d(x,y) > 0, если х ф у,
и d(x,x) = 0; ' ■ m 1- \\
3) неравенство треугольника: \11' ' /
d(x, z)^L d\x,y)-\-d(y,z) (каждая сторона
треугольника не превосходит суммы двух других сторон).
Из неравенства треугольника как следствие вытекает, что
каждая сторона треугольника не меньше разности двух других
сторон:
d(x,z)^\d(x,y)-d(y,z)\. (II, 1; 2)
Из этого же неравенства вытекает также, что для
произвольных п точек множества имеет место неравенство
d(xlt *„)<</(*„ x2) + d(x2, х3)+ ... +'d(*n_„ хп). (II, 1;3)
Приведем сразу же ряд важных примеров метрических
пространств:
1°) Вещественная прямая R и комплексная плоскость С, с
расстоянием d(x, y) — \x — у\. Эту метрику называют
естественной метрикой в R и .С. Всюду, где специально не оговорено
противное, в пространствах R и „С, метрика считается
естественной.
2°) Вещественная прямая R, для точек которой расстояние
определено формулой d(x,y) = \F(x) —F(y)\, где F —
произвольная вещественная строго монотонная функция вещественной
переменной.
3°) Евклидово вещественное пространство R" или
унитарное комплексное пространство С" п измерений, расстояние

§ 1. Метрические пространства 41
между точками (хих2,...,хп) и {уиу2,... ,уп) в котором опре-
/ " у/2
делено формулой I 2 ! xt — yt |2J .
Несколько позже мы строго докажем, что здесь действительно
определено метрическое пространство (стр. 43). Введенную
метрику называют естественной метрикой R" и С". Если не
оговорено противное, то метрика в пространствах R" и „G"
всегда будет считаться естественной.
4°) В произвольном множестве можно ввести дискретную
метрику, положив d(x,y)= 1, если х ф у, и d(x,x) — 0.
Сферы. Шары
Сферой с центром а конечного радиуса R > 0 называется
множество точек х из Е, таких, что d(a, x) = R. Из определения
вовсе не следует, что такая сфера не пуста или что две сферы
с различными центрами не совладают (пример: в дискретной
метрике все сферы радиуса 2 совпадают и пусты).
Множество точек х из Е, таких, что d(a, x)<R
(соответственно =^/?), обозначается через B0(a,R) (соответственно В (a, R))
и называется открытым (соответственно замкнутым) шаром с
центром в а и конечным радиусом R > 0 '). •
Когда говорят о шаре без каких-либо пояснений, то имеют в
виду замкнутый шар. В дискретной метрике замкнутый шар
радиуса < 1 сводится к его центру. Шар (замкнутый)
радиуса ^ 1 совпадает со всем пространством. (Для R = 0 открытый
шар пуст, сфера же и замкнутый шар сводятся к их центрам. Мы
будем всегда предполагать, даже если это специально не
оговорено, что радиусы сфер или шаров конечны и > 0.)
Часть метрического пространства называется ограниченной,
если существует шар (как всегда, конечного радиуса), в
котором она содержится. Множество R и часть N множества R не
ограничены. Однако если в Е введена дискретная метрика, то
Е ограничено.
Нормированные векторные пространства
Пусть Е — векторное пространство над полем К
вещественных или комплексных чисел. Нормой в векторном пространстве
Е называется любая функция, обозначаемая через х-*~ \\х\\2),
■) Мы делаем строгое различие между понятиями сферы и шара. В
случае плоскости R2 говорят окружность вместо сферы и круг вместо шара.
2) Договоримся всегда ставить, стрелку над элементами векторного
пространства. При этом мы будем строго различать число 0 и нуль 0 векторного
пространства.

.42
Гл. II. Топология
обладающая следующими свойствами:
1) положительность: ||л:||>0 для х Ф О и ||0|| = 0;
2) преобразование при гомотетии: || Ял; || = | Я |||л; ||Де/С; i (П,1;4)
3) условие выпуклости: || х + г/||^|| л; || -\-\\у II-
Из 2) и 3) легко выводится обобщенное условие выпуклости
\\* + х2+ ... + *П1К11*, 11 + 11*211 + ••• + IKII. (Н,.1;5)
а также неравенство
\\х-у\\>\\\х~\\-\\у\\\- (". 1; 6)
Если в векторном пространстве £ введена норма,
обладающая указанными выше свойствами, то его называют
нормированным векторным пространством.
Символ || ||, естественно, можно употреблять лишь тогда,
когда речь идет о некоторой раз и навсегда определенной
норме. Если в одной и той же задаче для одного и того же
векторного пространства вводится несколько различных норм, то их
следует обозначать различными символами.
Пусть Е — нормированное векторное пространство. В этом
пространстве можно определить расстояние между элементами,
удовлетворяющее всем аксиомам расстояния, по формуле:
-»-»-»-»■
d(x,y)= \\x — у\\. Таким образом, любое нормированное
векторное пространство является автоматически метрическим
пространством. Расстояние в нем обладает дополнительными свойствами,
совместимыми с его векторной структурой: расстояние инва-
-> ->->.->
риантно относительно сдвига, иначе говоря, d (х — а, у — а) =
-> -»
= d(x, у), а гомотетия с коэффициентом гомотетии Я приводит
-> -> -> ->
к умножению расстояния на |Я|, т. е. d(Xx, Xy) = | Я \d(x, у).
Обратно, легко видеть, что любое расстояние в векторном
пространстве, обладающее двумя этими свойствами, определяет
в нем некоторую норму, а именно: ||je|| = d (0, х).
Под открытым шаром радиуса R в векторном пространстве,
если не указан его центр, мы будем понимать шар радиуса R
с центром в нуле векторного пространства. Аналогично
определяется замкнутый шар. Они обозначаются соответственно
через B0(R) nB(R).
В частности, единичный открытый (соответственно замкну-
->
тый) шар есть открытый (замкнутый) шар с центром в 0
радиуса 1. Единичный шар без каких-либо уточнений означает
просто единичный замкнутый шар.

§ 1. Метрические пространства
43
Отрезком с концами а и Ь в векторном пространстве над
полем вещественных или комплексных чисел называется множе-
ство всех точек вида ta-\-(l—l)b, 0 ^t ^.l. Его обозначают
через [а, Ь] точно так же, как и замкнутый интервал в
упорядоченном множестве. Говорят, что некоторая часть
множества Е выпукла, если вместе с любыми двумя различными
точками этого множества она содержит и весь отрезок,
соединяющий эти точки. Из условия выпуклости следует, что всякий шар
нормированного векторного пространства является выпуклым
множеством. В самом деле, если \\х\\ ^ R и \\у\\ ^ R, то
l\tx + {l^t)y\\<\\tx\\ + №-t)y\\ =
= [t\\\x\\ + \l-t\m<[t + (l-t)]R = R. (П, 1;7)
Приведем примеры нормированных векторных пространств:
1°) Функция х—*\х\, определенная над полем R или .С,
является нормой. Она определяет упоминавшуюся ранее (1°,
стр. 40) естественную метрику.
2°) Функции
п In N1/2
t*i, х2 хп)-+ max |л;,-], :ли 2U(|,- или 2 I xt Р
f=i п i=i \i=i I
в векторных пространствах R" или С" определяют некоторые
нормы. Для первых двух норм это очевидно. Проверим
выполнение аксиом нормы в третьем случае. Пусть (*ь *2, .-.., хп),
(Уи У2, ■ ■ ■, Уп) — две системы п комплексных чисел. Для
доказательства условия выпуклости
(2|*(-Н-ЫГ<(2|*ЛГ + (2|^2Г (H,l;8)
заметим, что левая часть этого неравенства не превосходит
Qj (|*г|-г-|#г|)2)'/2, а значит, достаточно доказать, что
2(ил-1^1)2<2игРН-2|^12н-2(2|^Р)1/2(21^Р)1/2(п,1;б)
2UJI^K(2l^P)1/2(2l^P)I/2. (II. 1; 10)
Это — известное Неравенство Коши — Буняковского — Шварца1)'.
Норма х = (х1г ..., хп)-> 1/ 2 I Х{ р называется естествен-
Г (=1
ной нормой в R" или С".
Позже мы познакомимся с другими важными примерами
векторных нормированных бесконечномерных пространств.
') См., например, книгу И. М. Гельфанда «Лекции по линейной алгебре»,
«Наука», 1966, стр. 35. — Прим. ред.^

44
Гл. П. Топология
§ 2. ОТКРЫТЫЕ И ЗАМКНУТЫЕ ЧАСТИ. ОКРЕСТНОСТИ.
ВНУТРЕННОСТЬ. ГРАНИЦА. ЗАМЫКАНИЕ.
ПЛОТНЫЕ ПОДМНОЖЕСТВА
Открытые части
Пусть Е— метрическое пространство. Часть А
пространства Е называется открытой, если вместе с каждой своей
точкой она содержит некоторый открытый шар (радиуса > 0)
с центром в этой точке1).
Открытые части пространства Е обладают, очевидно,
следующими свойствами:
a) само пространство Е и его пустая часть 0
открыты 2);
b) пересечение конечного числа открытых мно- ,,, ~ . >
жеств открыто; - \ > > г
c) объединение конечного или бесконечного числа
открытых множеств открыто.
Докажем, например, свойство Ь).
Пусть О и Ог, ■ ■-, Оп — открытые подмножества Е и х—
произвольный элемент их пересечения. Для каждого i
существует такое число Ri > 0, что шар B(x,Ri) полностью
содержится в Оi. Если теперь положить R = min (Ri), то шар
г=1, 2 л
B(x,R) будет содержаться в рассматриваемом пересечении, а,
значит, пересечение открыто.
Имеет место интересное четвертое свойство, называемое
аксиомой отделимости Хаусдорфа.
d) Каковы бы ни были различные точки а и Ь пространства
Е, существуют две открытые непересекающиеся части Е,
содержащие соответственно а и Ь.
В самом деле, если взять открытые шары с центрами в
точках а и Ь радиуса d/З, где d — расстояние d(a,b), то эти шары
'')< Короче: А является открытой частью в Е, если (V* е А) (Эр > 0) (Уг/ S
<= £, d(х, у)<р):у <= А, или еще короче: (V* <= А) (Эр>0): В0 (х, р) с: А.
Естественно, р зависит от х. В определении можно «открытый шар» заменить
на «замкнутый шар», поскольку замкнутый шар радиуса р содержит открытый
шар радиуса р, а открытый шар радиуса р содержит замкнутый шар радиуса р/2.
2) Множество А открыто, если для любого х е А существует шар с
центром в х, содержащийся в А. Если /4=0, то найти точку х^А невозможно,
а потому указанное свойство выполняется и 0 открыто. Приведем другой
пример того же самого логического рассуждения. Будем говорить, что
человек обладает свойством (Р), если его рост больше роста его детей. Тогда
люди, не имеющие детей, будут, очевидно, обладать свойством (Р). Можно,
впрочем, исходить из отрицания рассматриваемого свойства. Некоторая
часть А не является открытой, если найдется хотя бы один элемент х е А,
для которого не существует шара с центром в х, содержащегося в А.
Множество 0 не может не быть открытым, так как элементов х е 0 не
существует. Пустое множество, таким образом, открыто.

§ 2. Открытые и замкнутые части. Окрестности
45
не будут иметь общей точки, так как в противном случае для
такой точки с из неравенства треугольника d(a, b) =£^ d(a, с) -f-
-\-d(c, b) получилось бы неравенство d(a,b)^.2d/3, которое
неверно.
Примеры. Открытые шары являются открытыми, и это
оправдывает их название. В частности, при введении
естественной метрики на прямой R открытые интервалы являются
открытыми множествами. Легко проверяется от противного, что
замкнутые или полуоткрытые интервалы открытыми
множествами не являются.
Для того чтобы некоторая часть Е была открытой,
необходимо, согласно определению, чтобы она была объединением
открытых шаров. Однако это условие и достаточно, поскольку
каждый открытый шар открыт, а объединение открытых частей
открыто (свойство с)). Приведенное условие является,
следовательно, необходимым и достаточным для того, чтобы некоторое
множество было открытым.
В пространстве R", снабженном метрикой, которая
определяется одной из указанных на стр. 43 норм, открытый
параллелепипед, т. е. множество
{х = (хи х2, ..., хп); ai<Xi<bi, i=U 2, ..., п},
является открытой частью.
В любом метрическом пространстве множество точек х,
удовлетворяющих неравенству d{a,x)> R, открыто.
В дискретной метрике (пример 4°), стр. 41) все части Е
открыты.
Замкнутые части
Замкнутой называется любая часть пространства Е,
дополнение к которой в Е открыто.
Переходом к дополнениям в свойствах а), Ь), с) открытых
частей непосредственно получаются эквивалентные свойства
замкнутых частей:
а') £ и 0 замкнуты;
Ь') объединение конечного числа замкнутых
частей замкнуто; } (II, 2; 2)
с') пересечение конечного или бесконечного числа
замкнутых частей замкнуто')..
Переход от открытых множеств к замкнутым в аксиоме
Хаусдорфа интересного результата не дает.
') Следствие из теоремы 15 дает наилучший практический критерий для
определения замкнутости множества.

46
Гл. II. Топология
Примеры. Всякая часть, сводящаяся к одной или
конечному числу точек, замкнута. Замкнутый шар является
замкнутой частью. В частности, каждый замкнутый интервал
вещественной прямой R с естественной метрикой замкнут, в то время
как полуинтервал или открытый интервал не замкнуты.
Множество {х : d(a,x)^ R} замкнуто. Любая сфера замкнута.
В пространстве Rn с одной из введенных метрик, указанных
на стр. 43, замкнутый параллелепипед, определенный
неравенствами {х = (хи Хъ, .. . , хп), at sg: х{ ;£[ bt, i = 1, 2, . . ., n},
является замкнутой частью.
В дискретной метрике все части Е замкнуты.
Замечания. 1°) Рассматривая объединение и пересечение
семейств открытых или замкнутых частей, очень важно
тщательно различать случаи, когда рассматриваемое семейство конечно
или бесконечно.
Например, на вещественной прямой R с естественной
метрикой часть, сводящаяся к точке, замкнута, но не открыта, и в то
же время она является пересечением счетного множества
открытых интервалов. Точно так же открытый интервал не замкнут, и
в то же время он является объединением счетного множества
вложенных в него замкнутых интервалов.
2°) Существуют части Е, не являющиеся ни открытыми, ни
замкнутыми; например, полуоткрытые интервалы в R.
3°) Как показывает пример дискретной метрики, кроме 0 и
Е, могут существовать и другие множества, являющиеся
одновременно и открытыми, и замкнутыми1).
Окрестности
Окрестностью точки а множества Е называется любая
часть Е, содержащая по крайней мере одно открытое
множество, содержащее точку а (или же содержащая открытый или
замкнутый шар с центром в точке а).
Кроме свойства включать в себя точку а, окрестности
точки а обладают следующими свойствами:
а") всякая часть, содержащая окрестность а,
является окрестностью а;
V) пересечение конечного числа окрестностей
точки а является окрестностью а; \ (II, 2; 3)
с") аксиома отделимости Хаусдорфа: каковы бы ни
были различные точки an b множества Е, существуют
не пересекающиеся окрестности точек а и Ь.
') Сравните с изложенным в § 9.

§ 2. Открытые и замкнутые части. Окрестности
47
Следует заметить, что слово «окрестность» может ввести в
заблуждение: создается впечатление, что окрестность точки а
является множеством, весьма близким к а, и что чем меньше
множество, тем вероятнее, что оно является окрестностью
точки а. В действительности свойство а) окрестностей
показывает, что, напротив, чем часть А множества Е больше, тем
скорее она может быть окрестностью точки а. Все
пространство Е является окрестностью точки а, и, кроме
исключительных случаев, таких, как случай дискретной метрики, часть,
сводящаяся к самой точке а, не является окрестностью точки а.
Говорят, что некоторая точка Е изолирована, если часть Е,
сводящаяся к этой точке, является ее окрестностью, т. е.
является открытой частью. В дискретной метрике каждая точка
изолирована. В множестве R изолированных точек нет.
Пусть А — часть Е. Окрестностью части А называется всякая
часть Е, которая содержит открытую часть, содержащую А. Если
задано некоторое е > О, то окрестностью А порядка е
называется объединение всех шаров радиуса е с центрами в точках
из А. Это множество является окрестностью, так как оно
содержит объединение всех отрытых шаров радиуса е с центрами в
точках из А, которое открыто и содержит А.
Теорема 1. Для того чтобы некоторая часть А
пространства Е была открытой, необходимо и достаточно, чтобы она
являлась окрестностью каждой своей точки.
Доказательство. Пусть А является окрестностью
каждой своей точки. Тогда вместе с каждой своей точкой
множество А должно содержать некоторую открытую часть Е,
содержащую эту точку, т. е. А должно содержать некоторый
шар с центром в рассматриваемой точке. Это означает,-что А
является открытой частью. Обратно, если часть А открыта и
а£ А, то А всегда содержит некоторое открытое множество,
содержащее а, а именно: саму часть А. Это означает, что Л
является окрестностью точки а.
Пусть задано семейство (^i)is/ окрестностей точки а в Е.
Говорят, что это семейство является фундаментальной системой
окрестностей точки а, 'если любая окрестность точки а
содержит одну из окрестностей У{. Например, в метрическом
пространстве Е открытые шары (или замкнутые шары) с центром
в а или шары с центром в а и рациональными радиусами
образуют фундаментальную систему окрестностей точки а.
Внутренность
Пусть А — некоторая часть метрического пространства.
Внутренностью А называется объединение всех открытых частей

48
Гл. II. Топология
из Е, содержащихся в А. Внутренность множества А
обозначается через А. Множество А есть открытое множество,
содержащееся в А (свойство с), стр. 44) являющееся, очевидно,
наибольшим открытым множеством, содержащимся в А. Конечно,
А может быть пусто (см. пример на стр. 50 при Е = R, А = Q).
Теорема 2. Внутренность А части А является множеством
точек из Е, каждая из которых является центром по крайней
мере одного шара, содержащегося в А, или, иначе, это
множество точек Е, у которых имеются окрестности, целиком
лежащие в А, или, иначе, это множество точек Е, для которых А
является окрестностью.
Доказательство. В самом деле, пусть а является
центром некоторого открытого шара, содержащегося в А. Этот
шар является открытым множеством, содержащимся в А, а,
значит, он содержится в А и тем более а^А.
Обратно, если а е А, то в силу того, что А открыто,
найдется некоторый шар с центром в а, содержащийся в Л и тем
более в А.
Внешность
Внешностью А называется внутренность его дополнения.
Это — наибольшее открытое подмножество Е, не пересекающееся
с А. Внешность А является множеством всех точек Е, каждая
из которых есть центр по крайней мере одного шара радиуса >0,
не пересекающегося с А. Внутренность и внешность А,
очевидно, не пересекаются.
Граница
Множество точек Е, не принадлежащих ни внутренности, ни
внешности А, называется границей А и обозначается через А.
Поскольку дополнение к границе, являясь объединением
двух открытых частей, открыто, граница А замкнута.
Из свойств двух этих частей непосредственно вытекает
Теорема 3. Для того чтобы точка а принадлежала
границе А множества А, необходимо и достаточно, чтобы любая
окрестность а содержала бы одновременно как точки А, так и
точки его дополнения.
Доказательство. Прежде всего, если любая
окрестность У точки а пересекается одновременно с частями А и СА,
то она не содержится ни в одной из них. Но тогда а не лежит
ни во внутренности, ни во внешности А и, следовательно, при-

§ 2. Открытые и замкнутые части. Окрестности 49
надлежит границе Л. Обратно, пусть а принадлежит границе
и У— некоторая окрестность а. Окрестность У пересекается
с Л, так как в противном случае она лежала бы в СЛ и точка а
принадлежала бы внешности. Точно так же видно, что
окрестность У пересекается с СЛ, ибо в противном случае она
лежала бы в Л, а, значит, а принадлежала бы внутренности Л.
Внутренность, внешность и граница части Л попарно не
пересекаются, а их объединение совпадает с Е.
Замыкание
Замыканием А части Л называется пересечение всех
замкнутых частей Е, содержащих Л. Оно замкнуто (свойство с'),
стр. 45). Это — наименьшая замкнутая часть, содержащая Л.
Точка, принадлежащая замыканию, называется точкой
прикосновения части А.
Теорема 4. Замыкание множества А является
объединением его внутренности и границы, иначе говоря, это дополнение
к внешности А. Можно сказать также, что замыкание есть
множество всех точек Е, каждая окрестность которых
пересекается с Л 4).
Доказательство. А является наименьшей замкнутой
частью, содержащей А. Это утверждение эквивалентно тому,"
что СА является наибольшей открытой частью, содержащейся
в СЛ, т. е. С А является внешностью Л, а это как раз то, что
требовалось доказать.
Пусть а — некоторая точка прикосновения части А. Тогда
любая окрестность У точки а пересекается с Л. В самом деле,
в противном случае при У с СЛ нашлось бы открытое
множество О, содержащее а и содержащееся в У, которое входит в
С Л. Но тогда О, а вместе с ним и а принадлежали бы
объединению всех открытых частей, содержащихся в СЛ, которое
является внешностью Л, что противоречит предположению qgJ.
Обратно, если точка а такова, что каждая из ее окрестностей
пересекается с Л, то а не может лежать во внешности Л, ибо
в противном случае эта внешность была бы некоторой
окрестностью а, не пересекающейся с Л. Отсюда следует, что а
принадлежит замыканию А.
Мы доказали тем самым, что а является точкой
прикосновения части А тогда и только тогда, когда любая ее
окрестность пересекается с А.
Приведем несколько примеров. Пусть А — некоторый
открытый или замкнутый шар с центром а и радиусом, R > О
') В теореме 15 будет указана другая существенная характеристика
замыкания.

50
Гл. II. Топология
в нормированном векторном пространстве. Его внутренностью
является соответствующий открытый шар, его замыканием —
соответствующий замкнутый шар, его внешностью — множество
{х\ d(a, х) > Щ, а его границей — сфера с центром в а
радиуса R. (Заметим, что, вообще говоря, это не всегда так. Если
в Е введена дискретная метрика и А— замкнутый шар
радиуса 1, то он совпадает с Е и, следовательно, со своей
внутренностью, в то время как его граница и внешность пусты.
Открытый шар радиуса 1 в этом случае вырождается в центр.)
Пусть А — множество рациональных чисел вещественной
прямой R. Тогда А = 0, А = А = R.
Для того чтобы некоторая часть А пространства Е- была
открытой, необходимо и дЬстаточно, чтобы она совпадала со
своей внутренностью.
Для того чтобы она была замкнутой, необходимо и
достаточно, чтобы она совпадала со своим замыканием.
Плотные подмножества
Часть А метрического пространства Е называется плотной
в Е, если каждая точка Е является для нее точкой
прикосновения, т. е. если ее замыкание совпадает с Е. Это означает также,
что любая открытая часть пространства Е пересекается с А.
Метрическое пространство Е называется сепарабельным, если оно
конечно или если оно содержит в себе некоторую счетную всюду
плотную часть.
Примеры. В пространстве R с естественной метрикой
множество А рациональных чисел и множество В иррациональных
чисел плотны. Поскольку множество рациональных чисел
счетно, то R сепарабельно.
Подпространства. Индуцированная метрика
Пусть F — некоторая часть метрического пространства Е,
Сужение функции расстояния, определенной в Еу(Е, на F X F
превращает множество F в новое метрическое пространство.
Его называют метрическим подпространством Е, а
определенную в нем метрику — «индуцированной» метрикой.
Пусть А — подмножество F. В этом случае следует четко
различать свойство А быть открытым или замкнутым в F от
аналогичного свойства в Е. Так, например, множество F само
по себе одновременно открыто и замкнуто, но если
рассматривать F как подмножество Е, то это утверждение, вообще говоря,
не верно.

§ 2. Открытые и замкнутые части. Окрестности 51
Теорема 5. Для того чтобы некоторая часть А множества
F была открытой (соответственно замкнутой) в метрическом
пространстве F, необходимо и достаточно, чтобы она была
пересечением F и некоторой открытой (замкнутой) части
метрического пространства Е.
Для того чтобы некоторая часть А в метрическом
пространстве F была окрестностью точки а е F, необходимо и
достаточно, чтобы она была пересечением F и некоторой окрестности а
в Е.
Доказательство. Обозначим через В шары
пространства Е и через р— шары пространства F.
Пусть А—часть F, являющаяся пересечением F и
некоторой открытой части А\ из Е. Если a^F лежит в А, а, значит,
и в А\, то существует некоторый шар В0(а, R), принадлежащий
А\. Но тогда Ро(я, R)=B0(a, R) Г) F содержится в А. Это
означает, что А открыто в F.
Обратно, пусть часть А открыта в F. Тогда А является
(стр. 45) объединением некоторого семейства р(а,-,/?,), i'e/,
открытых шаров, причем а,- еЛ и /?* > 0. Объединение шаров
Bo(Oi,Ri) является открытым множеством А] из Е и A =A\\\F.
Таким образом, свойство, относящееся к открытым
множествам, доказано.
Пусть теперь А\—некоторая замкнутая часть Е. Пусть
С\—ее дополнение в Е. Части А\ и С\ разбивают F на два
взаимно дополнительных подмножества Л и С множества F.
Так как С открыто, то Л=Л1 (") F замкнуто.
Обратно, пусть А — некоторая замкнутая часть F. Пусть
С — ее дополнение в F, Так как С открыто, то в £ существует
такая открытая часть С\, что С\{\ F=C. Пусть А\ —
дополнение к С\ в Е. Множество At замкнуто. Поскольку А\ и G
взаимно дополнительны в Е, то их пересечения с F будут
взаимно дополнительными в F. Так как Сх (") F=C, то Л=А\ ("I F.
Из замкнутости А\ теперь следует замкнутость А. Теорема
доказана и в этом случае.
Пусть, наконец, Т\ — некоторая окрестность точки а е F
в Е. Она содержит некоторую открытую часть А\, содержащую
а. Но тогда Т=Т\ Г) Л содержит открытую часть А=А\ П F
пространства F, содержащую а. Эта часть является
окрестностью а в F. Обратно, пусть У — некоторая окрестность а в F.
Она содержит некоторую открытую часть А из F, содержащую
а. В этом случае существует открытая часть А\ из Е, такая, что
А=А\ П F. Поскольку множество Т\^=А\ \]У содержит
открытую часть А\, содержащую а, оно является некоторой
окрестностью а в Е, причем T=Ti Г) F.
Из доказанного вытекают два следствия:

52
Гл. II. Топология
1°) Открытые, замкнутые части и, следовательно,
окрестности метрического пространства F полностью определяются
соответствующими множествами в Е; для их определения не
нужно знать функцию расстояния. В важности этого замечания
мы убедимся позже (см. § 4).
2°) Какова бы ни была часть F из Е, если некоторая часть А
из F открыта (соответственно замкнута) в метрическом
пространстве Е, то она открыта (замкнута) в метрическом
подпространстве F; если А является окрестностью точки йе F в Е, то она
заведомо является окрестностью точки а в F.
Обратное утверждение, вообще говоря, не верно, как
показывает рассмотренный ранее случай A = F. Однако имеет место
Теоремаб. а) Если F — открытая часть Е, то любая часть
А из F, открытая в метрическом пространстве F, также открыта
в метрическом пространстве Е.
b) Если F — замкнутая часть Е, то любая часть А из F,
замкнутая в метрическом пространстве F, также замкнута в
метрическом пространстве Е.
c) Если F является окрестностью точки а в Е, то любая
часть А из F, являющаяся окрестностью точки а в F, есть
окрестность точки а в Е.
Доказательство, а) Пусть часть F открыта в Е. Если
А — открытая часть F, то, согласно теореме 5, существует часть
Аи открытая в £ и такая, что A=A\ f| F. Поскольку А\ и F
открыты в Е, то часть А=А\ П F также открыта в Е. Отсюда
сразу же вытекает утверждение с).
Ь) Доказательство аналогично. Достаточно всюду заменить
открытые части на замкнутые.
§ 3. НЕПРЕРЫВНЫЕ ФУНКЦИИ. ГОМЕОМОРФИЗМЫ
Пусть / — отображение метрического пространства Е в
метрическое пространство F. Говорят, что отображение f
непрерывно в точке а е Е, если, каково бы ни было е > 0,
существует такое х\ > 0, что неравенство d(a, x) ^ г\ влечет за
собой неравенство d(f (a), f(x)) <; е.
Можно также сказать иначе: каким бы ни был шар с
центром в f(a), существует шар с центром в а, образ которого при
отображении f содержится в предыдущем шаре.
Можно также сказать, что, какова бы ни была окрестность
У точки f(a), существует такая окрестность Щ точки а, что
}(<И)аГ.
Можно также сказать, что прообраз при отображении f лю-
~бой окрестности точки f(a) является окрестностью точки а.
Отображение Е в F называется непрерывным, если оно
непрерывно в каждой точке а пространства Е.

§ 3. Непрерывные функции. Гомеоморфизмы
55
Первое определение непрерывности существенно использует
метрику. Напротив, два последних определения используют
только открытые множества и окрестности, а не саму метрику.
Важность этого замечания будет ясна в дальнейшем (см. § 4).
Пример. Функция 1/х, т.е. отображение х-+1/х
метрического пространства Е, дополнительного к началу координат
вещественной прямой, в метрическое пространство F—R
(вещественная прямая) всюду непрерывно.
Теорема 7. Для того чтобы отображение f метрического
пространства Е в метрическое пространство F было
непрерывным, необходимо и достаточно, чтобы прообраз при
отображении f любой открытой части F был открытой частью в Е.
Доказательство. Докажем сначала, что это условие
необходимо. Предположим, что отображение / непрерывно.
Пусть В — открытая часть F и A=f~l(B). Пусть а^А. Так как
отображение / непрерывно в точке а и В является окрестностью
/(а), то часть А будет окрестностью точки а. Итак, А является
окрестностью каждой своей точки, а это значит, что А
открыто (теорема 1).
Докажем теперь его достаточность. Предположим, что
прообраз при отображении / любой открытой части F открыт в Е.
Пусть а — произвольная точка Е и У° — окрестность точки f(a)
в F. Тогда У3 содержит некоторую открытую часть В,
содержащую точку b=f(a). Прообраз f~l(T) содержит открытую часть
р!(В), содержащую а. Значит, /_1(F) является окрестностью
точки а, что доказывает непрерывность отображения / в точке а.
Теорема 8. Для того чтобы отображение f метрического-
пространства Е в метрическое пространство F было
непрерывным, необходимо и достаточно, чтобы прообраз при
отображении f каждой замкнутой части F был замкнут в Е.
Доказательство повторяет доказательство предыдущей
теоремы. Надо лишь везде заменить открытые части из Е и F
на их замкнутые дополнения и применить формулу (I, 2;3).
Замечание. Если в двух предыдущих теоремах заменить
прообразы на прямые образы, то можно прийти к неверным
результатам. Рассмотрим, например, постоянное отображение Е
в F. Такое отображение, очевидно, непрерывно. Однако, образ
любой открытой части Е, в том числе и самого множества Е,
сводится к единственной точке F, а подмножества,
вырождающиеся в точку, вообще говоря, не являются открытыми. Если
рассмотреть функцию \/х из разобранного выше примера, то
образ всего множества Е, т. е. некоторого замкнутого
множества при этом отображении, является в множестве F = R.

54
Гл. 11. Топология
дополнением к началу координат, не являющимся замкнутым
в R.
Теорема 9. Норма в нормированном векторном
пространстве Е, рассматриваемая как отображение Е в прямую R с
естественной метрикой, является непрерывной функцией.
Доказательство. Из (II, 1; 6) вытекает, что для
заданного е > 0 достаточно выбрать л —е> чтобы из неравенства
\\х — а\\ ^ т) вытекало неравенство | ||х|| — ||а|| | ^ е.
Теорема 10. Композиция двух непрерывных отображений
непрерывна.
Доказательство. Пусть Е, F, G — три метрических
пространства и h=g°f—композиция отображения f
пространства Е в F и отображения g пространства F в G. Будем
считать, кроме того, что функция f непрерывна в точке а е Е,
а функция g непрерывна в точке b—f(a) пространства F.
Пусть c=g(b)=h{a) и W — окрестность точки с в G. Так
как функция g непрерывна в точке Ь, то прообраз T=g~l(W)
является окрестностью Ь в F. Поскольку f непрерывна в а, то
прообраз cU=f'1 (T) является окрестностью а в Е. Из того, что
<M=f~l(g~iW:')) совпадает с прообразом trl(W), следует
непрерывность h в точке а1). Отсюда, очевидно, вытекает, что
если fug всюду непрерывны, то h тоже всюду непрерывна.
Этот факт можно было бы получить непосредственно, если
применить теорему 7 или теорему 8.
Гомеоморфизмы
Гомеоморфизмом метрического пространства Е на
метрическое пространство F называется любая биекция Е на F,
непрерывная вместе со своей обратной биекцией.
Теорема 11. Для того чтобы биективное и непрерывное
отображение f пространства Е в F было гомеоморфизмом,
необходимо и достаточно, чтобы образ при отображении f каждой
открытой части Е был открытым в F; необходимо и достаточно
также, чтобы образ при отображении f каждой замкнутой
части Е был замкнутым в F.
В самом деле, эти образы есть не что иное, как прообразы
относительно обратной биекции g=f~l, и предыдущие условия
совпадают с условиями непрерывности f_1, указанными в
теореме 7 и теореме 8.
') В качестве упражнения проведите другое доказательство, пользуясь
лервым (метрическим) определением непрерывности с помощью Ve, Зт), ..i.

§ 4. Метрические и топологические пространства
55
Замечание. Не надо думать, что любая непрерывная
биекция является заведомо гомеоморфизмом. Так, например,
если Е является прямой R с дискретной метрикой, a F — пря-
Z. мой R с естественной метрикой, то тождественное отображение
£ в F непрерывно и биективно, но не является
гомеоморфизмом.
Говорят, что два метрических пространства Е и F
гомеоморфны, если существует по крайней мере один гомеоморфизм
Е на F. В этом случае оба пространства обладают
одинаковыми топологическими свойствами, т. е. свойствами,
относящимися к открытым, замкнутым множествам и окрестностям.
Пример. Внутренность круга и внутренность треугольника
в евклидовой плоскости являются гомеоморфными
метрическими пространствами. Полуплоскость у > 0, область у > х2,
расположенная над параболой у=х2, область у < х2, лежащая
под этой параболой на плоскости R2, гомеоморфны ').
Два метрических пространства, определенных кривыми,
изображенными на следующем ниже рисунке, гомеоморфньк
Рис. 1.
Z Однако внимание! Это вовсе не означает, что существуег
гомеоморфизм первой плоскости на вторую, переводящий
первое подпространство на второе!
Вещественная прямая с естественной метрикой и
вещественная прямая с дискретной метрикой не гомеоморфны потому, что
в последнем случае все подмножества открыты, а в первом
случае это не так2).
§ 4. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
И ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Используя лишь понятие расстояния,.мы смогли определить
в метрическом пространстве Е понятия открытого и замкнутого
множеств, окрестности, замыкания, внутренней и внешней
части множества, его границы, плотного множества, непрерывного
') В качестве упражнения укажите в каждом случае гомеоморфизм
соответствующих гомеоморфных метрических пространств.
2) Мы показали выше, что в данном случае тождественное
преобразование не является гомеоморфизмом между двумя рассматриваемыми,
пространствами. Здесь же мы показали, что между ними не существуег
никакого гомеоморфизма, — это более сильное утверждение.

г56
Гл. //. Топология
отображения. Все эти понятия могут быть определены, исходя
из понятия открытого множества.
Может случиться, что две различные метрики в одном и
том же пространстве Е определяют одну и ту же систему
открытых множеств. Тогда они определяют одинаковые системы
замкнутых подмножеств, окрестностей каждой точки и т. д.
Пусть, например, в метрическом пространстве Е расстояние
•определяется функцией d и функцией 2d, т. е. такой функцией,
при которой расстояние между двумя элементами х и у
считается равным 2d(x, у). Эти функции определяют одни и те же
открытые множества.
Две метрики в пространстве Е называются эквивалентными,
если они определяют одну и ту же систему открытых множеств.
Говорят также, что они определяют одну и ту же топологию
в Е. Можно также сказать и иначе: тождественное
отображение множества Е, снабженного 1-й метрикой, на множество Е,
■снабженное 2-й метрикой, является гомеоморфизмом.
В векторных пространствах две нормы называются
эквивалентными, если соответствующие им метрики эквивалентны.
Теорема 12. Две нормы || IIi и \\ \\% на некотором
векторном пространстве эквивалентны тогда и только тогда, когда су-
ществуют такие постоянные k', k" > 0, что для всех х из Е
имеют место следующие неравенства:
l|x|b<ft,||x||1 и IU||,<£"|UII2. (11,4; 1)
Доказательство. Обозначим через B\(R)
(соответственно через Bi{R)) замкнутый шар с центром в нуле
пространства и радиусом R в смысле первой нормы
(соответственно второй нормы). Предположим, что обе нормы эквивалентны,
т.е. определяют одни и те же открытые множества.
Шар В\(\) содержит некоторое открытое в смысле 1-й
метрики подмножество Е, содержащее нуль пространства. Но
тогда В\(1) содержит также некоторое множество, открытое в
смысле 2-й метрики, содержащее этот нуль. Существует,
следовательно, число l/k", такое, что В\(\) ^> B2(\lk"), С помощью
гомотетии с множителем k"R отсюда получается включение
Bx(k"R) zd B2(R), означающее, что соотношение \\х\\% ^ R вле-
чет за собой неравенство ||x||i =s^ k"R. Так как первое неравен-
ство остается верным при R = \\х\\%, то второе неравенство дает
-> ->
-при этом |U||i<.£" ||лг||2.
Меняя ролями нормы || ||] и || ||2, мы можем доказать
необходимость условия теоремы. Покажем теперь, что оно и до-

§ 4. Метрические и топологические пространства
57
статочно. Если это условие выполнено, то из неравенства
ЦхЦг ^ R/k" будет вытекать неравенство ||x||i ^ R, а значит,.
B2(R/k") <^ Bi(R). Отсюда следует, что любой шар в первой
метрике заведомо содержит некоторый шар во второй метрике,,
и обратно. С помощью параллельного переноса легко
убедиться, что все только что доказанное для шаров с центром в нуле
остается верным для произвольных шаров1).
Поскольку в топологии каждое открытое множество является
таким множеством, которое вместе с любой точкой содержит
некоторый шар с центром в этой точке, то из свойств,
установленных нами для шаров, вытекает, что открытые множества в обеих
метриках совпадают.
Замечание. Пусть d\ и d2 — расстояния,, определяемые
двумя эквивалентными нормами. Тогда найдется такая
постоянная k, что при любых х и у имеют место неравенства
d\ (х, у) < kd2 (x, у) и d2 (x, у) < kdx (x, у).
Это обстоятельство является характеристическим для
эквивалентных метрик, определенных эквивалентными нормами на
векторных пространствах.
Пусть теперь d — расстояние, определенное некоторой
метрикой на множестве Е. Легко проверяется, что d'=\ni(d, 1),
определяемое через d'(x, y)=m\n(d(x, у), 1), также является,
некоторым расстоянием (проверьте свойства (II, 1;1)).
Метрика, определяемая с помощью d', очевидно, эквивалентна
исходной метрике (шары радиусов ^1 одни и те же). Далее,,
если d изменяется от 0 до +оо, то d' изменяется от 0 до 1. Это
означает, что неравенства типа (11,4; 2) для расстояний d и d'
не имеют места. Если Е— векторное пространство и d —
расстояние, определенное в нем некоторой нормой, то расстояние
d' таким уже не будет. Этот пример показывает, что при любой
заданной метрике в Е всегда можно найти эквивалентную
метрику, относительно которой Е будет ограниченным.
Следствие. Все три нормы, определенные в пространстве
R" в начале этой главы, эквивалентны.
') Доказательство необходимости. Если бы не существовало такого-
числа k", то для любого целого числа п ^ О нашлась бы точка хп Ф 0, та--
кая, что ||jcra|| 1 ~^п \\xnh- Используя при необходимости гомотетию, можнс
всегда предполагать, что ||xra|li —1. При этом \\хп\\2^1/п. Таким образомг
последовательность хп сходится к нулю по 2-й норме и не сходится к нулю-
no 1-й норме, а это означает, что нормы не эквивалентны. (Это
доказательство использует сходящиеся последовательности, которые будут рассмотрены»
позже.)

58
Гл. II. Топология
Это утверждение вытекает из неравенств:
п п
1 V
tEi*'I^ max I*<kXi*<I'
/ n \l/2 /ix
<=1 / '• \i=I
Имеет место следующее более общее утверждение, которое
мы примем без доказательства '):
Теорема 13. В конечномерном векторном пространстве
над вещественным или комплексным полем любые две нормы
эквивалентны. Существует единственная система открытых
множеств, замкнутых множеств и т. д. для любых введенных в нем
норм.
Здесь уместно заметить, что, как мы увидим далее на
примерах, это свойство не переносится на бесконечномерные
векторные пространства.
Итак, мы пришли к тому, что для метрических пространств
определяются два рода свойств: метрические свойства,
зависящие явно от самой метрики, такие, как расстояние между двумя
точками, свойство сторон треугольника или фигуры,
образованной из нескольких точек, сферы и т. д., и топологические
свойства, не зависящие явно от самой метрики, а зависящие только
от множества открытых, замкнутых 2) и т. д. частей. Становится
ясным, что топологию можно ввести, не используя в качестве
посредника метрику.
Топологическим пространством Е называется множество Е,
в котором выделено семейство частей, называемых открытыми
в этой топологии.
Это — совершенно произвольное семейство частей, которые
должны обладать лишь свойствами а), Ь), с), d), указанными
на стр. 44 3).
') Доказательство можно найти на стр. 72 (см. теорему 23).
2) Ограниченность части А из Е (см. определение на стр. 41) является
метрическим, а не топологическим свойством: множество N i целых чисел ^ 1
не ограничено в метрике d(p, q) = \р— q\, но оно станет ограниченным, если
метрику в нем определить по формуле d (p, q) = , в то время
как эти две метрики эквивалентны. Однако, в нормированных векторных
пространствах две эквивалентные нормы приводят, согласно теореме 12, к
одним и тем же ограниченным частям (см. замечание на стр. 57).
3) Вообще говоря, на открытые множества в топологии налагаются лишь
требования аксиом а), Ь), с). Если, кроме того, они подчиняются требованиям
аксиомы d), то топологическое пространство называется отделимым.
Неотделимые пространства в анализе используются очень редко, и нам они не по-

§ 4. Метрические и топологические пространства
59
Мы видим, что метрическое пространство является частным
случаем топологического пространства. Существуют
топологические пространства, которые нельзя определить, исходя из
какой-либо метрики.
Говорят, что топологическое пространство метризуемо, если
существует метрика, порождающая его топологию.
Подавляющее большинство топологических пространств,
с которыми мы встретимся в будущем, метризуемы.
Заметим, что почти все рассмотренные нами определения и
теоремы относительно метрических пространств служили для
введения в них топологии, а не самой метрики. Легко
проверить, что они имеют место для произвольных топологических
пространств. Однако теоремы 2, 9, 12 и 13 справедливы только
для метрических пространств, ибо они существенно используют
метрику даже в своих формулировках.
Каждая точка всегда имеет фундаментальную систему
открытых окрестностей (поскольку в любой окрестности точки а
содержится открытое множество, содержащее а, которое
является открытой окрестностью этой точки). Однако такой
системы замкнутых окрестностей может и не быть.
Топологическое пространство называется регулярным, если каждая его
точка обладает фундаментальной системой замкнутых
окрестностей. Метризуемое пространство регулярно. С другой
стороны, пересечение замкнутых окрестностей точки а сводится
к точке а. Следовательно, пересечение всех окрестностей
точки а тем более сводится к а. В самом деле, если Ьфа, то,
согласно аксиоме Хаусдорфа, существуют открытые
непересекающиеся множества s4- и 3§, содержащие точки а и Ь. Из того,
что s4- является замкнутой окрестностью точки, а и s&czC3t,
следует, что бФ с: С$, а, значит, s4- не содержит Ь. Точка Ь,
таким образом, принадлежит не всем замкнутым окрестностям
точки а.
Теорему 5 можно использовать для определения
индуцированной топологии. Пусть Е — некоторое топологическое
пространство, a F — часть Е. В множестве F можно ввести
топологию, принимая за открытые множества в F пересечение с F
открытых множеств в смысле топологии Е. В этом случае
говорят, что F является топологическим подпространетвом Е или
же что его топология индуцирована топологией Е.
В дальнейшем всякий раз, когда это будет возможно, мы
будем рассматривать теоремы в топологических пространствах.
требуются. Поэтому мы всегда будем предполагать, что топологическое
пространство отделимо, а его открытые множества удовлетворяют аксиоме А).
В неотделимом пространстве часть, вырождающаяся в точку, не является
необходимо замкнутой, и сходящаяся последовательность может иметь
несколько различных пределов (см. теорему 14)1

«60
Гл. П. Топология
Однако мы не постесняемся проводить доказательства только
для случая метрических пространств, если это может привести
к упрощению рассуждений.
Топология пополненной прямой R (см. стр. 26 гл. I)
В R можно ввести топологию, определяя открытые множе*
ства следующим образом. Часть U множества R считается
открытой при выполнении следующих условий:
a) если U содержит точку х из R, то она содержит также по
крайней мере один открытый интервал, содержащий х;
b) если U содержит точку —со, то она содержит также по?
крайней мере один интервал вида [—со, А[;
c) если U содержит точку +со, то она содержит также пб'
крайней мере один интервал вида ]А, +со].
Можно доказать, что определенные таким образом открытые
множества удовлетворяют всем аксиомам, необходимым для*
того, чтобы R было топологическим пространством. Легко
видеть, что в этой топологии R метризуемо, а несколько позже-
мы приведем бесконечное множество эквивалентных метрик,
порождающих эту топологию (теорема 38, стр. 99), но ни одна
из них естественным образом не выделяется среди других. R
является подпространством R, и в этом подмножестве топология,
порождаемая топологией R, совпадает с топологией, определяе-
.мой естественной метрикой.
§ 5. ПОСЛЕДОВАТЕЛЬНОСТИ. ПРЕДЕЛЫ. СХОДИМОСТИ
Существенным свойством топологических пространств яв-
.ляется возможность рассматривать в этих пространствах
сходящиеся последовательности.
1°) Пусть х0, х\, х2, ..., х„, ... — некоторая
последовательность точек метрического пространства Е. Говорят, что эта
последовательность сходится к точке I из Е, или что она имеет
пределом точку I1), если последовательность вещественных чи-
•сел d(l, x0), d(l, x\), ..., d(l, xn), ... сходится к нулю.
Это означает следующее: каково бы. ни было г > 0,
существует такое целое число п0, что из неравенства п ^ й0 следует
неравенство d(l, хп) ^ г. Можно также сказать так: какова бы
ни была окрестность jf точки I, существует такое целое число
щ, что для п ^ п0 все хп принадлежат У. Можно также ска-
') Подразумевается: «при п, стремящемся к +оо».
Если хп — вещественные числа; то можно считать, что / е [—оо, +оо].
Яоследоватёльность при этом рассматривается в R.

5. Последовательности. Пределы. Сходимости
61
зать иначе: какова бы ни была окрестность Т. точки I, все хп
принадлежат У, за исключением конечного числа значений и1).
Последние два определения пригодны и в том случае, когда
Е — топологическое пространство. Однако если даже Е —
метрическое пространство, то сходимость последовательности в нем
является свойством топологическим, а не метрическим.
Существуют и другие определения пределов, не относящиеся
к последовательностям.
2°) Рассмотрим двойную последовательность хт< „, где т и
п — целые неотрицательные числа, т. е. отображение Ц X N в Е.
Говорят, что эта двойная последовательность сходится к
элементу I из Е при тип, стремящихся к бесконечности, если,
каково бы ни было е > 0, существуют такие целые числа пг0, п0,
что из неравенств m ^ m0, n ^ п0 вытекает неравенство
d(xmyn, I) ^ е2).
3°) Говорят, однако, что хт< п сходится к /, когда m или п
стремятся к бесконечности, если, каково бы ни было е > 0,
существуют целые числа пг0 и п0, такие, что из неравенства m ^
:=s m0 или п ;> п0 вытекает неравенство й{хт<п, I) ^е3).
4°) Если f является отображением вещественной прямой R
в Е, то выражение «f(x) стремится к /, когда х стремится к а
справа», означает, что, каково бы ни было е > 0, существует
такое т) > 0, что из (\х — а|-Ст), х > а) следует d(f(x), J)-Се.
5°) В тех же самых условиях выражение «f(x) стремится к /
при х, стремящемся к -f-co». означает, что, каково бы ни было
е > 0, существует такое вещественное число А, что из х ^ А
вытекает d(f(x), I) ^ е.
Все эти пределы легко определяются, если Е является
топологическим и не обязательно метрическим пространством. Они
входят в рамки следующего более общего определения.
Пусть X — топологическое пространство, А — некоторая
часть X, а — точка X, принадлежащая замыканию А, и f —
отображение А в Е. Говорят, что f(x) сходится к 1-при х,
стремящемся к а по значениям из Л4), если, какова бы ни была
') Это определение показывает, кроме того, что сходимость
последовательности не зависит от порядка ее членов. Изменить порядок членов
последовательности х0, хи х2, ..., хп, ... — это значит заменить ее
последовательностью х„ , х„ , ..., х„ , ..., где соотношение п -*■ рп является биек-
цией N на себя. Если исходная последовательность сходится к /, то это
будет верно и для преобразованной последовательности.
2) Короче: (Ve>0) (3m0eN)(3«0eN) (Vm>m0, Vn>n0):d {xm, „, /)<e.
3) Короче: (Ve>0)(3mGeN)(3n0eN)(V(ffl, n) e= N X N, m>ma или
n >rt0): d{xm% n, /)< e. _
4) Очень часто аеЛ, но афА. Именно это имеют в виду, подчеркивая,
что «когда X стремится к а, то предполагается, что хфа>. Здесь мы не хотим
ограничивать се'бя этим условием. Можно считать, что а е А или афА.

62
Гл. П. Топология
окрестность У точки / в Е, существует окрестность <U точки с
в X, такая, что ^{°U П А) аУ. Так, например, в случае после
довательностей (случай 1°)): X = R, Л = М, а —+ оо. В случае
4°): X = R, A = {x<=R, х>а). В случае 5°): X = R, A = R, a =
= +оо.
Сказать, что некоторое отображение f топологического
пространства Е в топологическое пространство F непрерывно в
точке а из Е, — то же самое, что сказать: f(x) сходится к f(a),
когда х стремится к а.
Теорема 14. Если последовательность имеет предел, то
этот предел обязательно единствен.
Доказательство. Предположим, что некоторая
последовательность х0, Xi, x2, ... элементов из Е имеет два
различных предела а и Ь из Е. Согласно аксиоме отделимости Хаус-
дорфа, существует окрестность °U точки а и окрестность У
точки Ь, не имеющие общих точек. Тогда, с одной стороны,
должно существовать такое целое число пг0, что хп е °U нри
п ^ т0, а с другой — такое целое число п0, что хп е У при
п>-я0. Для п >• max (m0, п0) получим xn^1i Г\У, а это
невозможно, так как пересечение °U и У пусто.
Теорема 15. Для того чтобы точка а метризуемого
пространства Е принадлежала замыканию части А из Е,
необходимо и достаточно, чтобы существовала последовательность
элементов из А, сходящаяся к а1).
Д о к а з а т е л ь с т в о. Условие, очевидно, достаточно, так
как если такая последовательность существует, то любая
окрестность У точки а содержит хотя бы одну точку этой
последовательности, т. е. хотя бы одну точку А, а это означает, что а
принадлежит замыканию А (см. теорему 4).
Обратно, пусть а принадлежит замыканию А. Выберем
какую-либо метрику, определяющую топологию Е. Тогда шар
с центром в точке а радиуса 1/л содержит по крайней мере
одну точку хп, принадлежащую А. Образованная таким
образом последовательность х0, хи а:2, ... принадлежит А и
сходится к а. _
Итак, замыкание А множества А является множеством
пределов последовательностей из А, сходящихся в Е.
Следствие. Для того чтобы некоторая часть
топологического метризуемого пространства Е была замкнутой,
необходимо и достаточно, чтобы она содержала пределы всех своих
последовательностей, сходящихся в Е.
') Если Е — топологическое, но не метризуемое пространство, то
указанное условие будет достаточным, но не будет необходимым.

§ 6. Топологическое произведение 6$
Теорема 16. Для того чтобы отображение f метризуемого
пространства Е в метризуемое пространство F было
непрерывным в точке а е F, необходимо и достаточно, чтобы образ при
отображении f любой сходящейся к а последовательности точек
из Е был последовательностью точек из F, сходящейся к f(a)1).
1°) Условие необходимо. В самом деле, пусть отображение f
непрерывно в точке а и х0, Х\, х2, ... — сходящаяся к а
последовательность из Е. Тогда, какова бы ни была окрестность У
точки f(a) в F, ее прообраз при отображении / является
некоторой окрестностью <U точки а в Е. Но тогда для всех целых га,
кроме конечного числа, хп лежат в °U и, следовательно, f(xn)
находятся в У, что доказывает сходимость последовательности
/(*„) к f(a).
2°) Условие достаточно. Предположим, что указанное в
теореме условие выполнено и что в Е выбрана некоторая метрика,
определяющая его топологию. Если бы отображение / не было
непрерывным в а, то нашлось бы такое число е > 0, что при
любом выборе ц > 0 существовала бы точка х, такая, что
d(x,а)<^.ц и в то же время d(f(x), /(a))>e.
В частности, при таком выборе е для каждого целого га
найдется хотя бы одна точка хп, такая, что d(xn, a)<C 1/га и
d(f(xn),f(a))>-B.
Последовательность хп, очевидно, сходится при этом в £ к а,
в то время как последовательность f(xn) в F к f (а) не сходится,
что противоречит предположению.
§ 6. ТОПОЛОГИЧЕСКОЕ ПРОИЗВЕДЕНИЕ
Обозначим через d\ и d2 соответственно расстояния,
введенные в двух метрических пространствах Ех и Е2. На множестве
произведения Е\ X Е2 с помощью формулы
S((*i> х2), (уи y2)) = max(d1(xl, г/,), d2{x2, у2)) (И,6;1)
можно определить метрику, которую мы будем записывать
в виде 6 = max (с?!, d2). Точно так же по формуле
{d\ + d2) {xux2), {yuy2))=dl(xuyl)-\-d2(x2,y2) можно ввести
метрику, записываемую в виде d\ + d2, или же метрику
Vd\-\- d\, определяемую выражением у d\ + d2((xu х2), {у\,у2)) =
= V{dx{xu yi)f + {d2(x2, y2)f '. Очевидно, ни одна из этих
метрик не выделяется среди других. Впрочем, легко видеть, что
эти метрики эквивалентны, т. е. они определяют в Ег X Е2 одну
и ту же топологию. Это рассуждение подчеркивает
равноценность метрик: ни одна из них существенно не выделяется среди
') Если Е и F — топологические, но не метризуемые пространства, то
условие остается необходимым, но не достаточным.

64
Гл. 11. Топология
других метрик на произведении. С другой стороны, легко опре*-
делить естественную топологию на произведении двух тополо-*
гических пространств:
Рассмотрим в пространстве £t открытую часть Ль а в
пространстве Е2 открытую часть Л2 и определим произведение
j4iX^2, т. е. множество пар (х, у) из fi X £2, таких, что
х<=Ах и у<=А21).
Говорят, что некоторая часть Е\ X Е2 открыта в топологии;
произведения, если вместе с любой точкой произведения она
содержит хотя бы одно произведение открытых множеств АхУ^А2,
содержащее эту точку.
Легко проверяется, что выделенные таким образом на
Ei У.Е2 системы множеств удовлетворяют всем аксиомам,
которым должны удовлетворять открытые множества некоторой
топологии. При этом произведение открытых частей открыто, но
имеются и другие открытые множества. Определенная таким
образом топология на Ех X ^2 называется произведением
топологий, заданных на Ei и Е2- Точно так же определяется
топология, произведения нескольких пространств. (Например, если
Ei = Е2 = ... = Еп = R, то их произведение является
известным топологическим пространством R", определенным,
например, с помощью естественной метрики.) Из самого определения
этой топологии вытекает, что канонические проекции Ех X Е2 на
£, и Е2 непрерывны. В самом деле, если f является проекцией
£iX?2 на Ei и если Ai есть некоторая открытая часть Е\, то
ее прообразом будет множество f-1(i4i) =Л1Х^2, которое
открыто в Ех X ^2 и даже есть произведение открытых множеств.
Сходящиеся последовательности в произведении
Теорема 17. Для того чтобы последовательность (хо, у0),
(хиУ\), (Х2,У2), ...2) элементов из Е X F сходилась к точке
(а, Ь) относительно произведения топологий, необходимо и
достаточно, чтобы последовательность хп сходилась к а в Е, а
последовательность уп сходилась к b в F.
Предположим сначала, что последовательность (хп, уп)
сходится к (а, Ь). Из теоремы 16, в силу непрерывности проекций
(х, у)-+х и (х, у)-* у, вытекает, что последовательность хп
сходится к а, а последовательность уп сходится к Ь.
Обратно, предположим, что последовательность хп сходится
к а в Е, а последовательность уп сходится к b в F. Пусть У —
окрестность (а, Ь) в Е X F. Она содержит некоторое открытое
') Ах X А2 иногда называют открытым прямоугольником по аналогии
с прямоугольником в R2, являющимся произведением интервалов из R.
2) Мы обозначили здесь через Е и F топологические пространства,
чтобы сохранить нумерацию 1, 2, ... элементов последовательности.

§ 6. Топологическое произведение
65
множество, содержащее (а, Ь), а, значит, согласно определению
открытых множеств в Е X F, содержит некоторое открытое
произведение А X В, a е= A, b е= В. Согласно предположению о
сходимости последовательностей хп и уп в этом случае существуют
такие целые числа П\ и п2, что х„еЛ для я ^ П\ и j„e В для
н ^ «2- Но тогда при п^ max(ni,n2) пара (х„, уп) е= Л X ^ с=-
czT, что означает сходимость последовательности (х„,уп)
к (a,b).
Пусть G — топологическое пространство. Отображение h
множества Е в множество F X G задается парой отображений f и g
множества Е в F и G соответственно, таких, что Л(х) = (f(x), g(x))
(гл. I, стр. 13). Для того чтобы это'отображение было
непрерывным, необходимо и достаточно, чтобы каждое отображение f и g
в отдельности было непрерывным. Доказательство очевидно.
Непрерывные функции многих переменных
В математике часто встречается понятие непрерывной
функции двух переменных.
Пусть f —функция двух переменных: (х, y)-+f{x, у). Это —
отображение произведения пространств Е X F в пространство G.
Предположим, что все три пространства являются
топологическими. Выясним, когда можно утверждать, что функция f
непрерывна в точке (а, Ь)?
В случае метрических пространств непрерывность означает,
что, каково бы ни было е > 0, существует такое г\ > 0, что из
неравенств d(x, a) ^ ц и d(y, b)^r\ следует неравенство
d(f (x,y),f(a,b))^el).
Однако это означает лишь, что отображение f пространства
E~XF в G непрерывно в точке (а, Ь) в смысле произведения
топологий на Е X F. Именно так мы и будем определять
непрерывность функции двух переменных в общем случае. Задание
непрерывного отображения произведения Ех X Е2 X ■ • • X Еп
в произведение Fx X F2 X ... X Fm равносильно заданию
системы m непрерывных функций п переменных.
Теорема 172. Если Е — метрическое пространство, то
функция расстояния d, отображающая Е X Е в вещественную
прямую R, непрерывна.
В самом деле, каково бы ни было е > 0, из неравенств
d(x, а) ^ е/2 и d(y, b) ^ e/2 вытекает неравенство
\d(x, у)—d(a, b)\^d(x, d)-\-d(y, b)^.e, означающее, что
функция d непрерывна.
') Расстояния в Е, F, G для простоты мы обозначим тем же
символом d.
3 Зак, 1339

66 Гл. II. Топология
Топологические группы.
Топологические векторные пространства
Топологической группой называется множество G, имеющее,
с одной стороны, групповую структуру и наделенное, с другой
стороны, такой топологией, что основные отображения, опреде-.
ляющие групповую структуру, т. е. отображение (х, у)-*ху
множества GX G в G и отображение х-+х~1 множества G в G,
являются непрерывными.
Топологическим векторным пространством называется
множество Е, имеющее, с одной стороны, структуру векторного
пространства над полем вещественных или комплексных чисел
и обладающее, с другой стороны, такой топологией, относи-
тельно которой сложение {х, у) —> х + у является непрерывным
отображением Е X Е в Z:1), а умножение на скаляры (Х,х)-*-.
—* Кх является непрерывным отображением К X Е в Е, где
К — поле скаляров с естественной топологией. Легко видеть, что
нормированное векторное пространство является
топологическим векторным пространством. В самом деле,
||£+£)-(а+6)||<||х-а|| + ||£-Н
||Кх — аа|| <|Я. — а||| х|| + | а||| х — а\\.
Отсюда вытекает, что для \\х — а|| ^ е/2, \\у — b\\ ^ е/2
справедливо неравенство || (х + у) — (а + Ь) || ^ 8, выражающее
непрерывность сложения. Далее, если последовательность (Хп, хп)
сходится к (а, а) в К X Е, т. е. если последовательность хп схо-
дится к а и если последовательность Х„ сходится к а (теоре-
-> -> ->■-*■
ма 17), то || х„ — а||, а вместе с ним и | a ||| хп— а ||, сходится к
нулю. С другой стороны, \Хп — а| стремится к нулю и ||*„||
ограничена, а, значит,\k„ — a ||| хп\]сходится к нулю. Из второго
->• ->
неравенства вытекает, что %nxn сходится к аа. Согласно тео-
-> -*■
реме 16, это доказывает непрерывность отображения (К, х)—*Кх
множества К X Е в Е.
Теорема 13 обобщается следующим образом: в
конечномерном векторном пространстве существует только одна топология
топологического векторного пространства.
') Непрерывность сложения означает, что предел суммы двух векторов
является суммой пределов этих векторов.

§ 7. Компактные пространства
67
Раздельная непрерывность функции двух переменных
Пусть f — некоторое отображение Е X F в G и (а, Ь) —
точка Е X F. Зафиксировав х = а, мы получим отображение F
в G: y-+f(a,y), определяемое с помощью / и а. Это
отображение часто обозначают через /„, так что fo(y) = f(0, у)- Иногда
его обозначают через f{a, ), опуская переменную у. Может
случиться, что это отображение непрерывно в точке у = Ь. В этом
случае говорят, что отображение f раздельно непрерывно по у
в точке b для фиксированного х = а. Такое же определение
дается для отображения fb~. x—*f(x, b), обозначаемого также
через К ,Ь), и для понятия раздельной непрерывности в.
точке а по х при фиксированном у = Ь.
В обоих случаях речь идет о том, что сужение отображения
/ на подпространство {а} X F или подпространство Е X {Ь}
непрерывно в точке (а, Ь). Говорят, что / раздельно непрерывно
в точке (а, Ь), если оно раздельно непрерывно по обеим
переменным в указанном выше смысле. Отображение называется
раздельно непрерывным на Е X F, если оно раздельно
непрерывно в каждой точке (а, Ь) произведения Е X F.
Непрерывная функция является, очевидно, раздельно
непрерывной, однако обратное, вообще говоря, не верно.
Рассмотрим, например, функцию двух вещественных переменных,
определенную формулой:
/ (*. У) = ^f^2 Для (х, у) Ф (О, 0) и / (0, 0) = 0.. (II, 6; 3)
Эта функция, очевидно, непрерывна, всюду на дополнении
к началу координат в R2. Она непрерывна на оси х'х и на
оси у'у, где она = 0. Следовательно, она раздельно непрерывна
в начале координат, а значит, и во всей плоскости. Однако, эта
функция не является непрерывной по совокупности обеих
переменных в начале координат, ибо на прямой у = пгх вне начала
координат она принимает значение пг/(1 + пг2)Ф0 и не
стремится к нулю, когда (х, у) стремится к началу координат.
§ 7. КОМПАКТНЫЕ ПРОСТРАНСТВА. ЭЛЕМЕНТАРНЫЕ СВОЙСТВА
Пусть Е — некоторое топологическое пространство.
Множество частей Е, таких, что каждая точка Е принадлежит по
крайней мере одной из этих частей, называется покрытием
множества Е. Подпокрытием покрытия называется покрытие,
образованное из част&й первого покрытия. Покрытие называется
конечным, если оно состоит из.конечного числа частей Е.
Покрытие называется открытым, если все части этого покрытия от:
крыты в Е. Так, например, множество интервалов ]п—1,я+ 1[
при п, пробегающем Z, образует открытое покрытие R. В этом
3*

68
Гл. //. Топология
случае у этого покрытия других подпокрытий не существует,
так как достаточно удалить какой-либо интервал ] п — 1, п + 1 [,
как соответствующая точка не будет покрыта1).
Определение. Свойство Гейне — Бореля — Лебега.
Топологическое пространство называется компактным, если из
любого его открытого покрытия Е можно выделить хотя бы одно
конечное подпокрытие. Это означает, что для любого покрытия
пространства Е множеством открытых частей существует
конечное множество этих частей, покрывающее Е.
Заметим, что до настоящего момента мы изучали
топологические свойства лишь некоторых частей Е относительно самого
множества Е, например свойство части А из Е быть открытой,
замкнутой и т. д. Свойство же компактности является свойством
7 самого топологического пространства. Однако можно говорить
*— о компактности части А топологического пространства Е, если
в смысле топологии, индуцированной в А топологией из Е,
часть А является компактным пространством. При этом само Е
не обязано быть компактным! Всякая часть Е, замыкание
которой компактно, называется относительно компактной
частью Е.
Легко видеть, что объединение конечного числа компактных
частей Е компактно.
В самом деле, пусть А\, А2, ..., Ап ■— компактные части Е и
Я— некоторое открытое покрытие объединения А = А\ U
U A2 U ... U Ап. Так как пересечение открытого множества из Я
с А\ является открытым множеством в А\, то Я определяет
открытое покрытие множества А\. Поскольку часть А\ компактна,
то ее можно покрыть конечным числом , открытых множеств
из Я. То же самое верно и для А2, ■ ■ ■, Ап. Значит, выбирая
одновременно эти п конечных систем открытых множеств из Я,
можно покрыть все А, конечным числом открытых множеств
из Я, а это означает, что А компактно. В силу тех же
соображений объединение конечного числа относительно компактных
множеств относительно компактно.
Примеры. Пространство, содержащее только конечное
число точек, компактно. Вещественная прямая R, векторное
пространство R™, векторное нормированное конечномерное или
бесконечномерное пространство не компактны. В самом деле,
рассмотрим множество открытых шаров с центром в нуле и
радиусом >0. Они образуют, очевидно, покрытие пространства.
') Множество интервалов \п—j, n + -j- также является открытым
покрытием R. Оно образовано из открытых частей, меньших, чем
предыдущие части.' Однако это — не подпокрытие рассматриваемого покрытия, так
как оно является множеством частей, существенно отличных от первых.

§ 7. Компактные пространства
69
Далее, любое конечное число этих шаров содержится в одном
шаре конечного радиуса и, следовательно, не покрывает всего
пространства. Более общо, любое неограниченное подмножество
метрического пространства, т. е. не содержащееся хотя бы в
одном шаре (конечного радиуса), не компактно.
Теорема 18. Замкнутый ограниченный интервал [а, Ь]
вещественной прямой является компактным пространством.
Доказательство. Пусть 91— открытое покрытие
интервала [а, Ь], и пусть с — середина [а, Ь]. Предположим, что из 91
невозможно выбрать конечного числа частей, покрывающих
полностью [а, Ь]. Тогда это невозможно сделать по крайней мере
для одного из подинтервалов [а, с] или [с, Ь], например для [а, с].
Обозначим этот интервал через [аи Ь{\. Разделив его на два, мы
можем найти подинтервал [а2, Ь2], в два раза меньший
интервала [fli,- bi] и обладающий тем же свойством. Таким образом
можно построить бесконечную последовательность [а0, bo] =
= [а, Ь], [аи Ь{\, [а2, Ь2], ... подинтервалов [а, Ь], обладающих
общим свойством: ни один из них не может быть покрыт
конечным числом частей, принадлежащих 91.
Возрастающая ограниченная сверху последовательность ап
сходится к некоторому пределу а. В свою очередь убывающая
ограниченная снизу последовательность Ьп сходится к
некоторому пределу р, а так как длина отрезка [ап, Ьп] равна
(Ь — а) /2™, то необходимо а = р. Согласно определению
предела последовательности, любой открытый интервал,
содержащий а = р, содержит все ап и Ьп с достаточно большими
номерами, а значит, содержит и все интервалы [ап, Ьп] с этими
номерами.
Далее, в покрытии 91 существует открытое множество У,
содержащее точку а = р. Поскольку У открыто, то существует
открытый интервал ] а', Ь' [, содержащийся в У и содержащий
эту точку. Для достаточно больших п интервал [ап, Ьп] будет
находиться в ]а', Ь'[, а значит, и в У. Мы пришли к
противоречию: по построению интервал [ап, Ьп] не может быть покрыт
конечным числом частей из 91, и в то же время он покрывается
одной из них, а именно У. Это противоречие доказывает
компактность [а, Ь].
Более общо, в пространстве Rm замкнутый ограниченный
параллелепипед, т. е. множество точек (хх, х2, ..., хт),
определенных системой неравенств «,^^[^6,, а2^х2<^.Ь2, ..., ат^.
^ хт ^ Ьт, где аи а2, . .., ат и bi, b2, ..., bm — конечные числа,
является компактным пространством. Этот факт доказывается
тем же методом деления с той лишь разницей, что вместо
Деления на две части на каждом шаге операции приходится

70
Гл. II. Топология
разбивать параллелепипед на 2т частей, деля на два каждую
из т координат.
Теорема 19. Пополненная прямая R, снабженная
естественной топологией, является компактным пространством.
Доказательство. Пусть 91— открытое покрытие R-
Точка —оо принадлежит хотя бы одному открытому
множеству, скажем У-, из 91, и точка + оо принадлежит хотя бы
одному открытому множеству, скажем У+, из 91. Отсюда, в
частности, вытекает, что дополнение к объединению этих двух
открытых множеств содержится в достаточно большом замкнутом
ограниченном интервале [А, В]. Поскольку в этом случае
существует конечное число открытых множеств из 91, покрывающих
[А, В] (теорема 18), то это конечное число открытых множеств,
дополненное открытыми множествами У- и У+, покрывает все
R, откуда и следует компактность R.
Замечания. 1°) Из определения компактности вытекает
следующее свойство:
Пусть компактное пространство Е является объединением
возрастающей последовательности открытых множеств У\,У2,...
. . ., Уп, . • - . Тогда при некотором п открытое множество Уп
совпадает с Е.
2°) Если два пространства гомеоморфны и одно из них
компактно, то второе также компактно. Из предыдущих примеров;
следует, что R и R не гомеоморфны (не существует
гомеоморфизма одного множества на другое). Замкнутый ограниченный
интервал [а, Ь] из R не гомеоморфен R (в то время как
открытый интервал гомеоморфен R: x-*tgx является, например,
гомеоморфизмом ] л/2, л/2 [ на R). Критерии, позволяющие
установить негомеоморфность двух пространств, слишком сложны;
доказать же, что два пространства гомеоморфны, обычно проще
всего путем установления соответствующего гомеоморфизма.
Теорема 20. Для того чтобы топологическое пространства
Е было компактным, необходимо и достаточно, чтобы из любого
множества замкнутых частей Е, пересечение которых пусто,
можно было выбрать конечное множество частей с пустым
пересечением.
Доказательство. Для доказательства достаточно в
формулировке теоремы заменить части их дополнениями.
Объединение при этом перейдет в пересечение, а открытые части
перейдут в замкнутые.
Следствие 1. Если Е — компактное пространство, a F0, F\+
F2, ■ ■ • — убывающая последовательность замкнутых подмно-

§ 7. Компактные пространства 71
жесте Е, пересечение которых пусто, то существует такое п, что
Fn пусто.
Заметим, что указанное свойство, очевидно, не верно для
вещественной прямой R, и это подтверждает отмеченный ранее
факт некомпактности R. В самом деле, если мы рассмотрим
убывающую последовательность замкнутых интервалов [п, +оо[,
то их пересечение пусто, в то время как ни один из них не пуст.
Замечание. Если воспользоваться теоремой 11 гл. I, то
можно заметить, что предыдущее следствие эквивалентно
следующему:
Следствие 2. Если Е — компактное пространство, a F0, F\,
F2 • • • — убывающая последовательность замкнутых подмножеств
Е, ни одно из которых не пусто, то их пересечение также не
пусто.
Теорема 21. Пусть Е — топологическое пространство,
•a F — компактная часть Е. Тогда заведомо F является
замкнутой частью Е ').
Доказательство. Для простоты при доказательстве мы
ограничимся тем случаем, когда Е является метрическим
пространством. Пусть а — точка прикосновения F. Нам надо
доказать, что а е F. Если мы через Fn обозначим пересечение F и
замкнутого шара с центром в а радиуса 1/л, п — целое ^ 1, то
мы увидим, что Fn образуют убывающую последовательность
замкнутых частей F (теорема 5). Ни одно из Fn не пусто, ибо а
является точкой прикосновения F (теорема 4), а так как F, по
предположению, компактно, то их пересечение не пусто. Однако
пересечение рассматриваемых шаров сводится к точке а.
Следовательно, а — единственная точка пересечения всех F„. Отсюда
вытекает, что а принадлежит всем Fn, а значит, и множеству F,
что доказывает замкнутость F в Е.
Очевидно, что обратное утверждение к этой теореме, вообще
говоря, не верно. Произвольное замкнутое множество
топологического пространства не обязательно компактно, так как в
противном случае пространство, являясь замкнутым, всегда было
■бы компактным. Однако имеет место следующее обратное
утверждение:
Теорема 22. Всякая замкнутая часть компактного
пространства является компактным пространством.
Доказательство. Пусть Е — компактное пространство,
F— замкнутая часть Е. Пусть (^г)ге/—некоторое семейство
') Внимание! Эта теорема сравнивает внутреннее свойство F — свойство
быть компактным (в индуцированной топологии) — со свойством множества F.
относительно Е быть замкнутым в Е.

72
ГА И. Топология
частей F, замкнутых в F, пересечение которых пусто. Поскольку
Fi замкнуты в F и пространство F, по предположению,
замкнуто в Е, то Ft замкнуты в Е (теорема 6,Ь)).Так как Е, по
предположению, компактно, то существует конечное число частей Fu
пересечение которых пусто, а это, согласно теореме 20,
обеспечивает компактность F.
Из теорем 21 и 22 следует, что в компактном пространстве
компактные подмножества совпадают с замкнутыми
подмножествами. Так, например, для того чтобы некоторое подмножество
пополненной прямой R было компактным, необходимо и
достаточно, чтобы оно было замкнутым в R.
Теорема 22г. Всякое компактное пространство регулярно:
любая его точка обладает фундаментальной системой
компактных окрестностей.
Доказательство. Пусть У—некоторая окрестность
о о
точки а и У— ее внутренность. Тогда К = СУ замкнуто и, в
силу теоремы 22, компактно. Пусть Ж— замкнутая (и,
следовательно, компактная) окрестность точки а. Тогда Ж Л К
является замкнутым подмножеством К. При всевозможных W
эти замкнутые подмножества из К имеют пустое пересечение,
поскольку пересечение всех Ж сводится к точке а (стр.59),
которая не принадлежит К. Так как К компактно, то из
множества замкнутых окрестностей Ж можно выбрать конечное
число множеств Жи Жг, ■ ■ ■, Жп, таких, что пересечение всех
Wif]K пусто. Множество Ж0 = ЗГ4 П ЗГ2 Л ... П Жп является
такой компактной окрестностью точки а, что Же Л К пусто; при
этом ЖоаЖ. Таким образом, любая окрестность У точки а
содержит компактную, окрестность Жо, что и требовалось
доказать.
Более общо, тем же самым методом доказывается, что в
компактном пространстве каждая компактная часть имеет
фундаментальную систему компактных окрестностей.
Теорема 23. Для того чтобы часть конечномерного
векторного нормированного пространства Е была компактной,
необходимо и достаточно, чтобы она была замкнутой и
ограниченной.
Доказательство. 1°) Указанное условие необходимо.
Как мы видели вначале, компактная часть всегда ограничена,
и в силу теоремы 21, она заведомо замкнута.
2°) Условие достаточно. Если даже полем скаляров
является .О, мы можем рассматривать л-мерное векторное
пространство над С как векторное пространство над R размерности 2л.
Поэтому можно предполагать, что полем скаляров является R,

§ 7. Компактные пространства
73
a) Предположим сначала, что пространством Е является Rn
и что норма в нем определена функцией (хи х2, ..., хп)~*
-> max \xi\.
i=\, 2 п
Любая ограниченная часть содержится в некотором шаре,
являющемся в нашем случае замкнутым ограниченным
параллелепипедом, т. е. содержится в некотором компакте.
Поскольку рассматриваемая часть предполагается замкнутой, она
является замкнутой частью компактного множества, и потому
для доказательства достаточно будет применить теорему 22.
(Более общо, если в метрическом пространстве любой
замкнутый шар компактен, то любая его ограниченная замкнутая часть
будет также компактной.)
b) Пусть теперь Е является произвольным нормированным
n-мерным векторным пространством над R.
Докажем сначала утверждение теоремы 13. Выберем в Е
какой-либо базис еъ е2, ..., еп. Тогда каждая точка х может
быть выражена через свои координаты хи х2> ■••> хп. Обозна-
чим через \\х\\ заданную норму в Ей положим |*|= max \xt\.
2=1. 2, ..., п
-У
Тогда || х \\
2*ifif <Sl*illleill<2l|eill max |*,|=2lle,ll|*|.
I i i 2=1, 2 n i
Если положить fe = 2 IIе» ll> то получим неравенство
t=i
||jc||<fe|Jc|. (11,7; 1)
Нам нужно получить противоположное неравенство. Из
неравенства (II, 7; 1) следует, что тождественное преобразование
Е с нормой \xt\ в Е с нормой ||*|| непрерывно. (В самом
деле, каково бы ни было е > 0, полагая r\ = e/k для всех х,
таких, что \х — а\^.г\, получим Цд: — а||^^|лг — а|^fer| = 8
а это — определение непрерывности преобразования в точке а.)
Но тогда прообраз любого замкнутого множества замкнут
(теорема 8). Другими словами, любая часть F пространства Е,
замкнутая в метрике || II, замкнута и в метрике | |. В частности,
шар ||*|| ^ R, будучи замкнутым в метрике || ||, замкнут и в
метрике | |. Обозначим через Q сферу (полый куб) |*|=1.
Это — некоторая замкнутая и ограниченная в Е часть по метри- ,
ке | | и, следовательно, компактная часть в силу того, что мы
видели в начале доказательства. Пусть FR — пересечение Q с

74
Гл. II. Топология
шаром ||*|| •</?, замкнутое по метрике | |. Это — некоторая
замкнутая часть компакта Q. Так как пересечение всех шаров
||*|| ^ R содержит лишь одну точку — начало координат, не
принадлежащую Q, то пересечение всех рассмотренных
замкнутых подмножеств пусто. Согласно теореме 20, из них можно
выбрать конечное число с пустым пересечением. Другими
словами, существует такое число р > 0, что шар ||*|| ^ р с
множеством Q не пересекается. Но тогда из ||*|| ^ р следует
|*| < 1 (в противном случае нашлась бы точка *о,
удовлетворяющая неравенствам II *01Кр и | *0|^ 1, и тогда для Я,=
= 1/|*о | мы получили бы ||А,*0 |К Хр < р и |А,*0|=1, что
противоречит изложенному выше). С помощью гомотетии с
отношением ц отсюда получаем, что неравенство ||*||^ цр влечет
за собой неравенство |*|<ц и тем более -<ц. Первое неравен-
ство справедливо при Ц = ||*||/р> но тогда второе принимает вид
1*1<£Й. (И, 7; 2)
что вместе с (11,7; 1) доказывает эквивалентность норм | | в
II II, т. е. теорему 13.
Теорема 23 теперь доказана во всех случаях, ибо понятия
«замкнутый, ограниченный, компактный» одни и те же для двух
эквивалентных норм (см. примечание2) на стр. 58), а то, что
доказано в п. а) для специальной нормы в Е, определенной с
помощью базиса, сохраняется и для данной нормы, эквивалентной
ей по теореме 13.
Локально компактные пространства
Говорят, что топологическое пространство Е локально
компактно, если каждая его точка имеет по крайней мере одну
компактную окрестность. Так, например, любое конечномерное
нормированное векторное пространство локально компактно,
поскольку локально компактен замкнутый шар такого
пространства.
Можно доказать, что бесконечномерное нормированное
векторное пространство локально компактным быть не может
(теорема 45г). Замкнутый шар в таком пространстве не
компактен. Для того чтобы некоторая часть пространства была
компактной, необходимо, но не достаточно, чтобы она была
замкнутой и ограниченной.
Если два топологических пространства гомеоморфны и одно
из них локально компактно, то таким же будет и второе. Это

§ 7. Компактные пространства
75
дает нам новый критерий, позволяющий выяснить, когда два
пространства не являются гомеоморфными. Например,
конечномерное и бесконечномерное векторные нормированные
пространства гомеоморфными быть не могут.
Любое локально компактное пространство регулярно, и
каждая точка в нем обладает фундаментальной системой
компактных окрестностей. В самом деле, если У является компактной
окрестностью точки а, то, согласно теореме 222, точка а имеет
в У фундаментальную систему компактных окрестностей.
Остается заметить, что каждая окрестность точки а в У
является также окрестностью точки а во всем пространстве
(теорема 6, с)). Более общо, каждый компакт локально
компактного пространства обладает фундаментальной системой
компактных окрестностей.
Точка сгущения последовательности 1)
Пусть лго, хи Хг, ... — некоторая последовательность
элементов топологического пространства Е. Говорят, что точка а
является точкой сгущения этой последовательности, если для
любой окрестности У точки а найдется бесконечное множество
значений п, таких, что хпеГ Если последовательность
сходится к а, то а для нее является точкой сгущения.
Теорема 24. Пусть Е — метризуемое пространство и а —
точка сгущения последовательности лг0, xit хг, ... элементов Ё.
В этом, и только в этом случае, из этой последовательности
можно выбрать подпоследовательность, сходящуюся к а.
Доказательство. Подпоследовательностью
последовательности лго, xit Хг, ... называется последовательность вида
Хра, Xpt, Хрг, ..., где п-*-рп является строго возрастающим
отображением N в N2). Исходя из определения, теперь легко
проверить, что если существует подпоследовательность,
сходящаяся к а, то точка а является точкой сгущения для исходной
последовательности (и это так даже в том случае, когда Е — не-
метризуемое топологическое пространство). Докажем теперь
обратное, предполагая, что в Е выбрана некоторая метрика,
определяющая ее топологию. Пусть а — точка сгущения
исходной последовательности. Тогда для каждого шара В(а,1/п)
существует бесконечное множество значений р, таких, что
') Ее часто называют также точкой прикосновения последовательно-
■сти. Однако это может привести к ошибочному отождествлению с понятием
точки прикосновения множества. По этой причине мы используем различные
слова.
2) Полагая рп = п, получаем, что последовательность является подпосле-,
довательностью самой себя.

76
Гл. II. Топология
хр е В {а, 1/п). Возьмем сначала такое целое число pit что
хр е В (а, 1). Выберем затем такое целое рг > р\, что
Хр2 е В (а, 1/2), затем такое целое рз > рг, что хРг е В (а, 1/3)
и т. д. Шаг за шагом таким методом мы образуем
подпоследовательность я-*- хр исходной последовательности, которая,
очевидно, сходится к а.
Теорема 25 (свойство Больцано — Вейерштрасса). Для
того чтобы метризуемое пространство Е было компактным,
необходимо и достаточно, чтобы любая последовательность
элементов из Е имела по крайней мере одну точку сгущения1).
Доказательство. 1°) Пусть Е компактно и Хо, Xi, Хг,... —
некоторая последовательность его элементов. Обозначим через
Ап множество {хп, хп+и ■■■}, а через Ап — его замыкание.
Множества Ап образуют убывающую последовательность замкнутых
множеств. Так как ни одно из этих множеств не пусто, то их
пересечение не пусто. Пусть а — точка этого пересечения. Сказать,
что а принадлежит Ап или что а является точкой прикосновения
Ап, означает сказать, что каждая окрестность точки а содержит
хотя бы одну точку из Ап, а так как это верно при любом п, то
мы получаем, что а является точкой сгущения исходной
подпоследовательности.
2°) Доказательство обратного утверждения не просто. Мы
его получим, предварительно рассмотрев две леммы.
Лемма 1. Пусть Е — метрическое пространство, каждая
последовательность которого имеет по крайней мере одну точку
сгущения. Пусть 31 — открытое покрытие Е. Тогда существует
такое число е > 0, что любой шар с произвольным центром
радиуса ^ е будет полностью содержаться хотя бы в одном из
открытых множеств покрытия.
Предположим, что это не верно. Тогда для каждого целого п
можно будет найти в Е такую точку ап, что шар с центром в ап
радиуса 1/п не лежит целиком ни в одном из открытых множеств
покрытия. Образуем таким образом бесконечную
последовательность а4, аг, ... элементов Е. Эта последовательность имеет
по крайней мере одну точку сгущения а. Поскольку Я —
покрытие, то существует открытое множество У из 91, содержащее а.
Само это множество содержит некоторый шар с центром а ра-
риуса а. Однако существует бесконечное множество значений а
и, значит, хотя бы одно такое значение-, что одновременно
выполняются неравенства 1/п ^ а/2 и d(an, а)^Са/2. Теперь видно, что
шар с центром ап радиуса 1/п ^ а/2 целиком лежит в шаре
В (а, а) и тем более в открытом множестве У покрытия, что про-
') Если Е — топологическое, но не метризуемое пространство, то условие
останется необходимым, но не будет достаточным.

§ 7. Компактные пространства 77
тиворечит сделанному предположению относительно
последовательности ап. Тем самым лемма доказана.
Лемма 2. Пусть Е— метрическое пространство, каждая
последовательность которого имеет по крайней мере одну точку
сгущения. Тогда, каково бы ни было е > 0, множество Е может
быть полностью покрыто конечным числом шаров радиуса е.
В самом деле, пусть «о — любая точка Е. Если Во («о, е) = Е,
то лемма доказана. Если же это" не так, то существует хотя бы
одна точка аи не принадлежащая шару В0(а0, е). Если В0(а0, е) U
U B0{aite) == Е, то лемма доказана. Если же это не так, то
можно найти точку а2, не принадлежащую В0 {а0, е) U В0 (аи е).
Продолжая рассуждать таким образом далее, мы сможем образовать
последовательность В0(а0, е), В0(аи е), Bo(az, e), ... шаров
радиуса е. Если такое построение мы не Сможем закончить, то
придем к бесконечной последовательности точек ао, аи az, ...,
"взаимные расстояния между которыми ^ е. Но это невозможно,
так как эта последовательность, как любая бесконечная
последовательность, должна иметь точку сгущения а. Последнее
означает, что существует бесконечное множество значений п,
а значит, хотя бы два различных значения р и q, таких, что
d(a, ap)^e/3 и d(a,aq)^.e/3. Полученное противоречие
показывает, что исходные построения закончатся при некотором
целом п, а это означает, что Е может быть покрыто п + 1
открытыми шарами радиуса е.
С помощью этих двух лемм без труда доказывается вторая
часть теоремы 25. Выберем некоторую метрику, определяющую
топологию в Е. Для доказательства компактности Е рассмотрим
некоторое открытое покрытие Я.. Согласно лемме 1, существует
число е > 0, такое, что каждый шар радиуса ^ е полностью
лежит по крайней мере в одном из открытых множеств
покрытия 91. Согласно лемме 2, множество Е может быть полностью
покрыто конечным числом шаров B0,Bi,B2, ..., Вп радиуса е.
Поскольку каждый шар В,- целиком- содержится в некотором
открытом множестве Ух покрытия Я., мы получаем, что для
покрытия Е достаточно иметь лишь конечное число открытых
множеств То, У и У г, ... ,Тп покрытия Я.
Замечание 1. Леммы 1 и 2 определяют свойства
компактных метрических пространств1).
Замечание 2. Теорема Больцано — Вейерштрасса,
очевидно, не верна для прямой R: последовательность целых поло-
') Слово «компактность» означает некоторую уплотненность и хорошо
отражает суть дела. Лемма 2 отмечает, что если даже шары имеют
маленький радиус, все равно Е может быть покрыто конечным числом этих шаров.
Множество Е, таким образом, весьма уплотнено.

78
Гл. II. Топология
жительных чисел не имеет точки сгущения. Напротив, в Д, з
силу ее компактности, такая последовательность сходится
к -f-oo.
Теорема 26. Топологическое произведение двух
компактных пространств компактно.
Доказательство. Ограничимся доказательством для
случая двух метрических компактных пространств Е и F. Пусть
(*о, Уо), (xi,yi), (*2, #2), ■-. — некоторая последовательность
элементов из Ey^F. Согласно теореме 25, последовательность
хо,хиХг, ... имеет по крайней мере одну точку сгущения а в Е.
Согласно теореме 24, из этой последовательности можно извлечь
подпоследовательность хРа, xPl, xPt, ..., сходящуюся к а. Под-'
последовательность ур,, yPl, yp„ ... в свою очередь имеет хотя
бы одну точку сгущения b в F, и в силу той же теоремы 24 из
нее можно извлечь подпоследовательность и„ , и„ , и„ , .. .,
"я» p<?i "я>
сходящуюся к Ь.Окончательно,подпоследовательность^ ,ур \,
(х„ , у„ \, (х„ , у„ \, ... исходной последовательности схо-
\ ря\ ря0 V РЯ' pw
дится к (а, Ь). Отсюда вытекает, что исходная произвольная
последовательность имеет точку сгущения, что полностью
доказывает компактность произведения.
Теорема 27. Пусть Е — компактное пространство. Для
того чтобы последовательность элементов из Е сходилась к
точке а, необходимо и достаточно, чтобы точка а для нее была
единственной точкой сгущения.
Доказательство. Условие это очевидным образом
необходимо. Если последовательность сходится к а, то точка а
для нее является точкой сгущения. Другой точки сгущения b
■быть не может. В самом деле, существуют окрестность %1
точки а и не пересекающаяся с ней окрестность У* точки Ь, такие,
что для всех п, кроме конечного числа их, xn^°U и в то же
время «„ef для бесконечного множества значений п, а это
бессмысленно. Докажем теперь, что указанное условие
достаточно. Пусть х0, Xi, х2, ... — последовательность элементов Е,
для которой точка а является единственной точкой сгущения.
Если бы эта последовательность не была сходящейся, то
существовали бы по крайней мере одно открытое множество Т,
содержащее а, и подпоследовательность хРп данной
последовательности! такие, что все хр находились бы в дополнении
к Т. Поскольку это дополнение замкнуто, то оно, согласно
теореме 22, компактно. Подпоследовательность хРп должна тогда
иметь в ОТ хотя бы одну точку сгущения, которая также
является точкой сгущения для исходной последовательности, а это

§ 8. Свойства непрерывных функций
79
противоречит тому, что данная последовательность имеет лишь
одну точку сгущения.
Замечание. Приведенное в теореме утверждение,
очевидно, не верно для случая вещественной прямой R. Например,
последовательность 1, 1, 2, 1/3, 3, ..., п, 1/п, ... имеет
единственную точку сгущения 0; однако, эта последовательность не
сходится.
Верхний и нижний пределы вещественной последовательности
Пусть Хо, Хи Хг, ... — последовательность элементов R.
Поскольку R компактно, то множество ее точек сгущения не пусто.
Это — некоторая часть F множества R. Множество F как
пересечение замкнутых множеств Ап, где Ап = {хп, хп+\, ...}, всегда
замкнуто (см. стр. 71). Следовательно, F является компактным
множеством в R. В нем имеется максимальный элемент L и
минимальный элемент /; L называется верхним пределом
последовательности, а / — ее нижним пределом. Они обозначаются через
L =' lim sup хп и I— lim inf xn соответственно. Верхний пре-
дел характеризуется следующим свойством: какие бы ни были
Lx и Z-2, такие, что Lx <c L <c L2, все хп, кроме конечного их
числа, <; Z-2, и имеется бесконечное множество значений п, для
которых хп ^ L].
Не надо смешивать верхний предел и точную верхнюю грань.
Например, 1 является точной верхней гранью
последовательности 1, 1/2, 1/3, .... Но эта последовательность сходится к нулю,
который будет ее единственной точкой сгущения и,
следовательно, ее верхним пределом. .
Для того чтобы некоторая последовательность из R
сходилась, необходимо и достаточно, чтобы ее верхний предел
совпадал с ее нижним пределом (ибо это условие выражает
единственность точки сгущения).
§ 8. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ
НА КОМПАКТНЫХ ПРОСТРАНСТВАХ
Теорема 28. Образ компакта при непрерывном
отображении является компактом.
Доказательство. Пусть f — непрерывное отображение
компактного топологического пространства Е в топологическое
пространство F. Конечно, мы не хотим доказать, что F
компактно. Надо доказать, что образ f(E) пространства Е при
отображении f, как подпространство пространства F с
индуцированной на нем топологией, компактен.

80
Гл. If. Топология
Пусть 91— открытое покрытие 1(E). Прообразы f~l(Ti)
открытых множеств Ти составляющих 91, образуют открытое
покрытие Е. В самом деле, если х — некоторая точка Е, то ее
образ f(x) принадлежит хотя бы одному из открытых множеств
покрытия 91, например Ti и, следовательно, х принадлежит
элементу f~l(Ti)'. Множества f~l(Ti) открыты в силу
непрерывности f.
Поскольку Е предполагалось компактным, то для его
покрытия достаточно конечного числа открытых множеств f~l (Ti),
например f~l (У\), f-1 (Т2), ••-, f~l(Tn)- Но это значит, что
открытые множества Уи Тг, ..., Тп образуют покрытие образа
f(E). В самом деле, для y^f(E) прообраз f"'({#}) не пуст. •
Пусть х — некоторый элемент этого прообраза. Хотя бы одно из
открытых множеств f-1 (Т\), f~l (Т2), ..., f-1 (Уп)> например
f~l (У°к)> содержит х, и, следовательно, Ук содержит y = f(x),
что доказывает сказанное выше. В итоге получаем, что f(E)
удовлетворяет определению компактных пространств: из любого
открытого покрытия можно выделить конечное подпокрытие.
Следствие. Всякая непрерывная■ биекция компактного
пространства Е на топологическое пространство F является
гомеоморфизмом.
В самом деле, согласно теореме 22, образ каждой замкнутой
части Е является образом компактной части и, следовательно,
по доказанному выше, компактен, а значит, согласно теореме 21,
замкнут. Согласно теореме 11, любое биективное и непрерывное
отображение, переводящее замкнутые множества в замкнутые,
является гомеоморфизмом.
Замечание. Не следует думать, что прообраз компакта
при непрерывном отображении является компактом. Пусть,
например, f — постоянное отображение некомпактного
пространства Е в некоторое пространство F. Образ всего множества Е
является подмножеством, сводящимся к точке Ь из F, т. е. к
некоторому компакту, тогда как прообраз {Ь} при отображении /
не компактен, поскольку прообразом является всё Е. Заметим
также, что если / — непрерывное отображение Е в F, то
прообразы открытых (или замкнутых) частей открыты (или
замкнуты), а образы компактных частей компактны. Здесь имеется
существенное различие между образами и прообразами
множеств при отображении. Объединяя же два рода утверждений,
можно получить следующий результат: если Е компактно и если
f— непрерывное отображение Е в F, то образ любой замкнутой
части Е при этом отображении замкнут в F. В самом деле,
поскольку £ компактно, то его замкнутая часть также компактна, а,
следовательно, ее образ компактен в F, а значит, и замкнут в Р.

§ 8. Свойства непрерывных функций 81
Теорема 29. Непрерывное отображение непустого
компактного пространства в R достигает своего максимума и
минимума.
Доказательство. Напомним, что точной верхней гранью
функции, определенной на-множестве Е, со значениями в R
называется точная верхняя грань ее значений. Эта грань
называется максимумом функции, если она достигается для
некоторого значения переменной. Пусть / — непрерывное отображение.
компактного пространства Е в пополненную прямую R.
Согласно предыдущей теореме, образ f(E) является непустым
компактом в R. Согласно теореме 23, это непустое замкнутое
множество в R. Непустое множество в R, согласно теореме 2 гл. I
(измененной так, как указано на стр. 26), имеет точную
верхнюю грань, и, кроме того, согласно той же теореме, эта грань
является точкой прикосновения рассматриваемого множества.
Поскольку оно замкнуто, точная верхняя грань принадлежит
этому множеству и, следовательно, является максимумом
функции. Аналогичное доказательство имеет место и для минимума
функции.
Теорема 29 имеет важное значение. Поэтому полезно в
качестве упражнения дать различные ее доказательства.
Доказательство, основанное на свойстве Гейне — Бореля — Лебега,
будет дано на стр. 86. Приведем еще одно доказательство. Пусть
М — точная верхняя грань функции /; М0, Ми М2,... — возрас-,
тающая последовательность чисел < М, стремящихся к М. Для
каждого п множество Fn: {x; x^E, Mn ^Zf(x)^.M} не пусто
(теорема 2 гл. I) и замкнуто как прообраз замкнутого
интервала [Мп, М] из R при преобразовании / (теорема 8).
Последовательность Fn является убывающей последовательностью
непустых замкнутых подмножеств компакта Е. Согласно
следствию из теоремы 20, их пересечение не пусто. Это некоторое
множество точек х из Е, в которых f(x) = M. Таким образом,
в множестве Е существует хотя бы одна точка, в которой /
достигает своего максимума М.
Можно рассуждать иначе. Сохраняя предыдущие
обозначения, заметим, что при любом п существует хотя бы одна
точка хп из Е, такая, что Мп ^ f(xn) ^ М. Последовательность
точек хп имеет хотя бы одну точку сгущения а (теорема Боль-
цано — Вейерштрасса), а следовательно, из нее можно
извлечь подпоследовательность хРа, хРх, ..., сходящуюся к а
(теорема 24). Так как /непрерывна в а, то последовательность
f(xPn) сходится к f(a) (теорема 16). Поскольку MP/j</(*рп) =С
<М, то 7 (хРп) сходится к М, а, значит, f(a) — M, где М —
максимум функции /.

82
Гл. II. Топология
Следствие 1. Вещественная (т. е. со значениями в R)
функция f, непрерывная на компакте Е, ограничена. Если во
всех точках х из Е функция f (х) > 0, то существует такое число
б > О, что f (х) ^ б для всех х из Е. '
В самом деле, можно считать, что значения f принадлежат R.
Ее точная верхняя грань М, точнее максимум, достигается в
некоторой точке а из Е: М = f (а) <1 -\- оо. Таким образом, f
ограничена сверху. Точно так же она ограничена снизу. Если f
повсюду > 0, то ее минимум б достигается в некоторой точке Ь и,
следовательно, б > 0. Итак, f(x)^ f(b)— б при любом х из Е.'
Следствие 2. Пусть f — вещественная непрерывная
функция, определенная на метрическом пространстве Е, и пусть К —
компакт в Е. Тогда существует такая окрестность компакта Кг
на которой f ограничена. Если f (х) > 0 для всех х из К, то
существуют такое число б > 0 и такая окрестность К, на которой
f(x)>8.
В самом деле, согласно следствию 1, f(K) является
ограниченным подмножеством R. Поэтому существует такое число М,
что f(K)c]-M,+M[. Тогда К ср(]-М, +M[). Так как f
непрерывна и интервал ] —М, -\-М [ открыт, то множество
/~'(]—М, +М[) открыто. Это множество содержит К, и f на
нем ограничена ло модулю числом М.
Пусть теперь f(X)>0 для всех х из К- Из следствия 1
вытекает, что существует такое число б'> 0, что f(x)^8' для
всех ле/(. Положим б = б'/2. Тогда f(K)<^]6, + °° [, а,
значит, /(cf_l(]6, -f-oo[), где /_|(]б,+ °°[)—открытое
множество, содержащее К, на котором f(x)^ б.
Замечание. Эти результаты, естественно, не верны для
разрывных функций. Разрывная функция может быть всюду
конечной и тем не менее не быть ограниченной; такой будет,
например, функция 1/х, определенная на дополнении к началу
координат в компактном интервале [0, 1] и принимающая
значение 0 в начале координат. Это вещественная функция,
определенная в компактном пространстве, но имеющая точку разрыва.
Она повсюду конечна, но не является ограниченной. Впрочем,
указанные результаты будут не верны и для непрерывной
функции, но определенной на некомпактном пространстве. Например,
на вещественной прямой функция х непрерывна, но не
ограничена, функция arctgjc непрерывна и ограничена, но не достигает
своей точной верхней грани, т. е. не имеет максимума. Конечно,
точка максимума может быть не единственной, как показывает
пример постоянной функции.
Приложения. Пусть Е — метрическое пространство, F —
замкнутая часть Е, а — некоторая точка. Расстоянием d(a, F)

§ 8. Свойства непрерывных функций
83
от точки а до множества F называется точная нижняя грань
расстояний от а до точек множества F. Поскольку все эти
расстояния ^ 0, то расстояние от а до F само ^ 0.
Если а е/% то, очевидно, d(a, F) = 0. Если же aqEF, то
d(a, F) ;> 0. В самом деле, если бы это было не так, то любой
шар с центром в а содержал хотя бы одну точку F, а,
следовательно, точка а была бы точкой прикосновения F и, в силу
замкнутости F, принадлежала бы этому множеству, что
противоречит исходному предположению.
Покажем, что a-*-d(a, F) является непрерывным
отображением Е в R, т. е. расстояние от некоторой точки до замкнутого
множества меняется непрерывно с изменением точки.
Действительно, пусть а и а' — две точки. Согласно свойству
точной нижней грани (теорема 2 гл. I), каково бы ни было
б > 0, существует точка х из F, такая, что d(a, x) ^ d(a, F)-{- 6.
Так как d(a', x) < d(a, x) + d(a, a') < d(a, F) + d(a, a') + 6, то
d(a', F)^Ld(a', x)^L d(a, F)+d(a, a') +6. Поскольку б
произвольно, d(a', F)^.d(a, F)+d(a, а'). Меняя ролями а и а',
точно так же получаем, что d(a, F)^. d(a', F)-\- d(a, а'), откуда
окончательно вытекает неравенство
\d(a',F)-d(a,F)\^d(a,a'). (II, 8; 1)
Из d(a, а') ^ е следует \d(a', F)— d(a, F) | ^ е, что доказывает
непрерывность отображения a-* d(a, F).
Можно поставить вопрос: будет ли точная нижняя, грань
d = d(a, F)=inid(a, x) при заданной точке а минимумом;
другими словами, существует ли точка с е F, такая, что
d(a, c)=d? Покажем, что это действительно так, если все
замкнутые шары в F компактны (согласно теореме 23 этот
случай имеет место тогда, когда Е—конечномерное
нормированное векторное пространство).
Рассмотрим шар В радиуса d -f 1 с центром в а. По
предположению этот шар замкнут и компактен. Его пересечение
с замкнутым множеством F, являясь замкнутой частью
компактного шара В (теорема 5), компактно (теорема 22). Отсюда
следует, что непрерывная на компакте В Л F функция х—>d{a, x)
достигает своего минимума. Точка с, в которой достигается этот
минимум, является решением поставленного вопроса. В самом
деле, d(a,c)<Cd(a,х) для любой точки xeBflf. Кроме того,
d(a, с) :g: d(a, х) для любой другой точки х из F, поскольку все
другие точки F находятся на расстоянии ^ d -f 1 от точки а, и
d(a, c)<d-f l.
Из неравенства d(a, с) <; d(a, x), имеющего место для всех
JteF, следует, что d(a, с) действительно является минимумом
функции d(a, х) при х е F (и d(a, с) = d).

84
Гл. II. Топология
Пусть теперь Е — некоторое метрическое пространство, a F\
и F2— замкнутые части Е. Расстоянием d(Fu F2) между
множествами F\ и F2 назовем точную нижнюю грань расстояний
d(x{,x2) при Х\ е Fu x2^F2. Если даже F{r\F2 = &, может
случиться, что d(Fu Fz) = 0, как видно из примера гиперболы и
ее асимптоты в евклидовой плоскости. Этот пример также
показывает, что точная нижняя грань не является минимумом.
Покажем, что если F\ компактно и если F\ Г) F2 = 0, то d =
= d(F\, F2) > 0. Кроме того, если замкнутые шары из Е
компактны, то эта точная нижняя грань является также и
минимумом.
В самом деле, d= inf d {хь F2). Мы знаем, что функ-
ция х\ H»d(xi, F2) непрерывна. Так как на компакте F\ она
всегда > 0, то она имеет минимум, т. е. существует точка
C\ e F\, такая, что d = d(c\, F2) > 0. Предположим теперь, что
все замкнутые шары из Е компактны. Мы видели ранее, что
в этом случае существует точка с2 е F2, такая, что d{c\, c2) =
= d(cu F2), а, значит, d(cu c2) = d = d(Fu F2) действительно
является минимумом.
Часто оказывается полезным такое утверждение: если Q —
открытое множество метрического пространства Е и
К—компакт, содержащийся в Q, то d = d(K, CQ) > 0. Этот факт
вытекает из^того, что К является компактом, не имеющим общих
точек с замкнутым множеством CQ.
Теорема 30 (Даламбера). Каждый полином комплексной
переменной степени m с комплексными коэффициентами имеет
m комплексных корней.
Доказательство. Когда мы говорим пг корней, то
предполагаем, естественно, что каждый корень считается столько
раз, какова его кратность.
Для доказательства этой теоремы достаточно показать, что
каждый полином при т>1 имеет по крайней мере один
корень а. Действительно, если мы затем разделим данный полином
на z — а, то сведем его к полиному степени пг + 1, к которому
снова можно применить то же самое утверждение. Тогда
теорема будет доказана индукцией по степени полинома. Итак,
предположим, что полином
P(z) = aQ + alZ+ ... +amzm (H, 8; 2)
не имеет корней, и попытаемся прийти к противоречию.
Известно, что j73(г) | стремится к + °° ПРИ \z\< стремящемся
к + оо. Но тогда, существует число R, такое, что вне
окружности радиуса R с центром в 0 комплексной плоскости
выполняется неравенство \P(z) | ^ \Р(0) |. Обозначим через ц
минимум > 0 (следствие из теоремы 29) непрерывной функции \Р\

§ 8. Свойства непрерывных функций
85-
на компакте |z|^/?, а через z0 такую точку, в которой
|Р(.го)|=ц. Поскольку \P(z) |>|Р(0) \>ц для |z|>/?, то-
неравенство |^(z)| ^ ц справедливо для всех z. Значит, ц
является минимумом модуля полинома на всей комплексной
плоскости.
Рассмотрим разложение Тейлора полинома Р в точке zo:
P(z) = P (z0) + ck(z- z0)k + ck+l (z - z0)k+l +...+Cm(z- z0)m.
(П, 8; 3)
Заметим, что первый член этого разложения отличен от нуля:
|P(zo)|= ц. Далее, существует настолько малое число р, что
на окружности Г с центром в точке Zo радиуса р имеет место
неравенство
|Cft+1(z-z/+1+ ... +cm(z-z0)m\<\ck(z-z0)k\ = \ck\pk.
(П,8; 4>
Можно считать р столь малым, что |cft|pft<;n.
Если z пробегает окружность Г, точка Ch(z — z0)h пробегает
окружность с центром в начале радиуса |cft|pft и, значит,
P(z0)-\-ck(z — z0)h пробегает всю окружность с центром в
P(z0) радиуса |cft|pft. Следовательно, существует точка z\ e Г,
такая, что P(z0) + ch(z1 — z0)h находится на отрезке [0, P(z0)\
комплексной плоскости. Имеем:
l^(«o) + cfc(z1-z0)*| = |i-|cfc|p*. (11,8; 5)
В результате мы получаем оценку
\P(zl)\<\P(z0) + ck(z1-z0)k\ +
+ \ck+1 (z, - z0)ft+1 + ... + cm(z, - z0)m I<
< (I* — I сЛ I p*) +1 сЛ ] p* = i*. (II, 8; 6)
Полученное неравенство |P(zi)|<n противоречит тому, что
ц является минимумом модуля полинома.
Обобщение теоремы 29. Пусть /—функция на
топологическом пространстве £ со значениями в R. Говорят, что
эта функция полунепрерывна сверху в точке а е Е, если,
каково бы ни было Ь\ >• f (а), в пространстве Е существует такая
окрестность У" точки а, что из хеГ следует f(x)^.b{.
Говорят, что она полунепрерывна снизу, если, каково бы ни было
b2<.f{a), в пространстве Е существует такая окрестность Т"
точки а, что изхе Т" следует f (х) ^ b2.
Вещественная функция непрерывна тогда и только тогда,
когда она одновременно полунепрерывна сверху и снизу,
Теорему 29 теперь можно обобщить следующим образом:

«6
Гл. П. Топология
Теорема 30г. Всякая функция, полунепрерывная сверху
(снизу) на компактном пространстве, достигает на нем
максимума (минимума).
Доказательство. Пусть М — точная верхняя грань в R
функции f, которая, по предположению, полунепрерывна сверху
на компакте Е. Предположим, что она не является максимумом.
Тогда f (х) <с М для любой точки х из Е. В силу
полунепрерывности сверху функции f на Е, для любого 0 < ех < М — f(x)
можно найти такую открытую окрестность Тх точки х, в
которой функция мажорируется числом Mx^=f (x) -f ex <. M. При
всевозможных значениях х получаем систему открытых
окрестностей Тх, покрывающих Е. Поскольку, пространство Е
компактно, из этого покрытия можно выбрать конечное покрытие.
Другими словами, существует конечное множество точек Х\, Хч\ . .
,.., хп из Е, такое, что Е будет- объединением множеств
Ухх, Ух, •••> У* . Поскольку в каждом множестве Тх
функция f мажорируется числом МХ.<М, то во всем пространстве Е
она мажорируется максимальным из чисел Мх , ..., Мх,...
• ••> Мхп,которое само < М. Однако это противоречит тому, что
М является точной верхней гранью f. Мы видим, что М
действительно является максимумом функции f.
Равномерная непрерывность
Свойства, которые мы сейчас рассмотрим, относятся только к
метрическим пространствам и не могут быть распространены на
общие топологические пространства. Впрочем, даже две
эквивалентные метрики могут привести к различным результатам ').
Определение. Пусть Е и F — два метрических
пространства. Говорят, что отображение f пространства Е в
пространство F равномерно непрерывно, если, каково бы ни было е > 0,
существует ц > 0, такое, что из неравенства d (х', х")-^ ц следует
d(f(x'),f(x"))<e.
Короче,
<Ve > 0) (Зл > 0) (Vx' e= E, Vx" e= E, d (х', х") < г,):
d(f(x'), f (*"))< е. (II, 8; 7)
Каждая равномерно непрерывная функция, очевидно, непрерыв-
') Другими словами, отображение метрического пространства Е в
метрическое пространство F может быть равномерно непрерывным и перестать
быть таковым, когда метрика заменяется другой эквивалентной метрикой.
Тем не менее, если эти метрики определены нормами в векторных
пространствах, то в силу теоремы 12 равномерная непрерывность сохранится при
.замене норм на эквивалентные.

§ 8. Свойства непрерывных функций
8?
на, но обратное не верно. Если функция / всюду непрерывна,
то для любой точки а <= Е при любом е > 0 существует ц > О,
такое, что d(x, a) sg: r\ влечет за собой d(f(x), f(a)) <; е;
однако так определенное число ц зависит одновременно и от а, и
от е. Когда же говорят, что функция равномерно непрерывна,
то это означает, что ц можно выбрать в зависимости только от
е (см. по этому поводу гл. I, стр. 38).
На вещественной прямой функция х равномерно непрерывна,
однако функция х2 этим свойством не обладает. В самом деле,
\(x + h)2 — x2\ = \2hx + h2\^2hx при h ^ 0 и х ^ 0. Для
того чтобы при заданном е найти h так, чтобы |2/гх + /г2| ^ е,
необходимо взять 1/г| ^ е/2|х|. Выбрать при этом условии h
независимо от х невозможно.
Говорят, что отображение / метрического пространства Е
в метрическое пространство F удовлетворяет условию Гёльдера
или условию Липшица порядка а, 0 ■< ос ^ 1 '), если существует
такая постоянная k, что при любых х' и х" из Е
а (/(*'), f (x")) <k[d (х\ х")]а. (Н,8; 8)
При а = 1 говорят просто, что / удовлетворяет условию
Липшица (не уточняя, что ее порядок равен 1).
Функция, удовлетворяющая условию Гёльдера порядка а и
тем более условию Липшица, равномерно непрерывна. Обратное
утверждение не верно, как показывает пример функции,
равной 1/lnx на интервале ]0, 1/2] и нулю в точке х=0. Она
непрерывна, а, следовательно, как будет показано в теореме 31,
равномерно непрерывна. Однако \f(x)—/(0) | = 1/1In x\ не может
быть, мажорируема выражением вида й|х|а.
Теорема 31. Всякое непрерывное отображение
компактного метрического пространства Е в метрическое пространство
F равномерно непрерывно.
Доказательство. Предположим, что отображение / не
равномерно непрерывно, и покажем, что это приведет к
противоречию. То, что / не является равномерно непрерывным,
означает, что
(Зе>0)(Ул>0)(Зл;'е£) Э*"е£, d(x',x")<4) ■ d(f(x'),f(x"))>e.
Пусть е—число, стоящее в начале этого соотношения.
Тогда, каково бы ни было целое число п ^ 1, можно найти две
точки х'п, х", такие, что d{x'n, х")<1//г и d(/(x'n), f (д£))>е..
а > 1 из
) Случай а > 1 не представляет интереса. Например, для E=F=R при.
< k | А |а_ следует, что функция / всюду имеет
f(x + h)-fjx)
h
производную, равную нулю, а это означает, что эта функция постоянна.

«8
Гл. II. Топология
Поскольку Е компактно, из последовательности х'п можно
выделить подпоследовательность п—> х' сходящуюся к некото-
рой точке х (теоремы 24 и 25). Из соотношения d(x'n, x"^ ^ 1/п
-следует, что подпоследовательность х" также сходится к х.
Поскольку отображение f непрерывно, то последовательности
j (х'р \ и f(x'p \ заведомо сходятся к f(x) (в силу теоремы 16).
Тогда для достаточно больших п имеем d (f (xpJ, f (x)~j ^ e/2,
■d(f(x'£\, f(x)\<e/2, а, следовательно, d (f lx'p )> f (*" )) ^ e. что
противоречит условию построения точек х' и/.
рп рп
Как мы только что видели на примере функции на
вещественной прямой R, функция может быть непрерывной на
метрическом некомпактном пространстве и не быть равномерно
непрерывной на нем.
§ 9. СВЯЗНЫЕ ПРОСТРАНСТВА
Интуитивно ясно, что некоторые топологические
пространства можно рассматривать как нечто целое, как, например,
сферу, шар в пространстве R™, в то время как другие пространства
состоят из нескольких различных «кусков». Таким будет,
например, пространство, являющееся объединением двух сфер, не
имеющих общих точек, или дополнение к некоторой сфере в R".
Уточним это интуитивное понятие.
Определение. Топологическое пространство называется
связным, если его невозможно разбить на две
непересекающиеся открытые части, или иначе: если его невозможно разбить
на две непересекающиеся замкнутые части, или иначе: если в Е
не существует одновременно открытых и замкнутых
подмножеств, кроме самого пространства Е и пустого множества 0.
Эквивалентность этих трех определений следует из
определения замкнутых множеств как дополнений к открытым. Как и
компактность, связность является внутренним свойством самого
топологического пространства; однако, говорят, что F является
■связной частью Е, если F, рассматриваемое как пространство
с индуцированной топологией, связно.
Теорема 32. Для того чтобы часть Е пополненной
вещественной прямой R была связным топологическим
пространством, необходимо и достаточно, чтобы она была открытым,
полуоткрытым или замкнутым интервалом.
Доказательство. Пусть Е — связная часть R, а х и
у — две любые различные точки Е. Покажем, что весь замкну-

§ 9. Связные пространства
89>
тый интервал [х, у] содержится в Е. Если бы это было не так,,
то на этом интервале можно было бы найти хотя бы одну
точку z, не принадлежащую Е. Тогда открытые в R множества
[—оо, z[ и ]z, +00], пересекаясь с Е, делили бы Е на два
открытых непересекающихся (поскольку z ф Е) множества, а,
значит, Е не было бы связным. Если мы теперь обозначим через а
(соответственно через Ь) точную верхнюю (соответственно
нижнюю) грань Е, то, как мы только что видели, Е будет совпадать
с одним из четырех интервалов [a, b], [a, b[, ]a, b], ]a, b[.
Обратно, пусть Е — некоторый интервал в R. Пусть Л—
некоторое непустое подмножество Е, одновременно открытое »
замкнутое в Е. Для доказательства связности Е достаточно по-
казать, что А=Е. Пусть с — некоторый элемент А. Рассмотрим
множество Н всех х ее £, таких, что [с, x]czA, и пусть у —
точная верхняя грань Н в R. Для каждого у', такого, что с ^ у' <
< у, существует элемент Я, мажорирующий у'. Следовательно,.
у'еЛ и [с, у'] с А. Поскольку А замкнуто, отсюда вытекает,,
что у ее А и [с, у] с Л, кроме того случая, когда у = Ь м Ьф Е.
Если бы элемент у был <Ь, то в силу того, что А открыто,
существовал бы элемент у" > у, такой, что [у, у"] с А, а,
следовательно, [с, у"] cz А и у" еЯ, а это невозможно, так как у
является точной верхней гранью Н. Поэтому у=Ь, [с, Ь[ с А и,
кроме того, 6 ее Л, если b ее Е. Проводя слева от точки с
рассуждения, аналогичные только что проведенным справа от этой:
точки, мы получаем точно так же, что ]а, с] с: Л и а ее Л, если
а ее Е. Окончательно получаем, что А=Е и, следовательно, Е
связно.
Следствие. Множество Q рациональных чисел не связно^
Теорема 33. Образ связного топологического
пространства при непрерывном отображении является связным.
Доказательство. Пусть f—непрерывное отображение
связного пространства Е в F. Речь, естественно, идет не о том,
чтобы доказать связность F; мы докажем, что образ f(E)
пространства Е в F является связным. В самом деле, если бы это
было не так, то f(E) можно было бы разбить на две открытые
непересекающиеся части Л и В. Тогда их прообразы образуют
разбиение Е (согласно (I, 2; 3)), причем их пересечение пусто.
Если х ее Е, то f(x) принадлежит либо Л, либо В, т.е. х
принадлежит либо f_1 (Л), либо f_1(B), а, значит, Е является
объединением f"'(i4) и f'^B). Ни одно из этих множеств не пусто.
В самом деле, Л, например, не пусто и содержится в f{E),
а значит, его прообраз не пуст и открыт (согласно теореме 7),
что противоречит предположению о связности Е.

90
Гл. II. Топология
Следствие. Если f — непрерывная функция, определенная
на связном пространстве Е, со значениями в R, то множество ее
значений является открытым, полуоткрытым или замкнутым
интервалом в R.
Доказательство. В самом деле, это множество должно
быть связным подмножеством R и остается лишь применить
предыдущую теорему..
Это свойство часто формулируют для частного случая,
когда Е само является открытым, полуоткрытым или замкнутым
интервалом R. Наконец, часто просто говорят, что
вещественная непрерывная функция, заданная на связном пространстве,
вместе с любыми двумя значениями принимает и все
промежуточные. Это так называемое свойство промежуточных значений.
Уместно заметить, что оно не является характеристическим
свойством непрерывных функций. В связных пространствах
существуют разрывные функции, обладающие тем же самим
свойством. Например, функция, заданная формулами f(x) — sin \jx
для хф® и /(0)=0 и определенная на всей вещественной
прямой, разрывна в точке 1 = 0 и все же обладает тем свойством,
что множество ее значений образует замкнутый интервал
[—1, 1]; в любом интервале \а, Ь\ она вместе с двумя
значениями принимает и все промежуточные.
Однако можно привести следующую обратную теорему:
Теорема 34. Если топологическое "пространство Е таково,
что любая, определенная на нем вещественная непрерывная
функция вместе с любыми своими двумя значениями принимает
также и все промежуточные значения, то Е связно.
Доказательство. Пусть Е не связно. Тогда его можно
разбить на две открытые части А и В, не имеющие общих точек.
Вещественная функция, равная 0 на Л и 1 на В, будет
непрерывной, поскольку прообраз любого открытого в R множества
является одним из четырех открытых множеств 0, А, В, Е. Эта
функция принимает значения 0 и 1, не принимая никаких
промежуточных значений, что противоречит условию теоремы.
Следовательно, Е связно.
Линейно связные пространства
Полезно иметь некоторый критерий, позволяющий
определять связность пространства. В связи с этим введем понятие
линейно связного пространства.
Дугой, или путем, соединяющим точку а и точку b
топологического пространства £, называется такое непрерывное
отображение / интервала [а, р] вещественной прямой R в простран-

§ 9. Связные пространства
9t
ство Е, что /(а)=а и /(р)=6. Точки а и b называют при этом
началом и концом пути.
Не следует смешивать отображение, входящее в определение
пути, с образом интервала [а, р], который при этом отображении
называется образом пути.
Если, например, отображение постоянно, то этот образ
сводится к точке. Можно, впрочем, сказать в этом случае, что путь
сводится к точке, но путь — это нечто иное, чем множество
точек, полученных при отображении.'
Точно так же лемнискату Бернулли можно «обойти» в двух
различных направлениях, тогда как рассматриваемая как
множество она остается одной и той же в обоих случаях. Два способа
обхода соответствуют двум, различным путям, т. е. двум
различным отображениям интервала из R на плоскость:
оооо
Рис. 2.
Говорят, что путь / проходит через точку с из Е, если образ
f([a, p]) содержит с. Говорят также, что путь пересекает часть Л
множества Е, если f ([а, р]) П Аф®.
Непосредственно видно, что если две точки а и b могут быть
соединены некоторым путем и в свою очередь точки b и с
могут быть тоже соединены некоторым путем, то точки а и с
также могут быть соединены путем.
Теорема 35. Если любые две точки топологического
пространства Е могут быть соединены некоторым путем, то Е.
связно.
Доказательство. Предположим, что это не так. Тогда
Е можно разбить на два непересекающихся открытых
множества А и В. Пусть а и b — элементы множеств А и В
соответственно. По предположению, точки а и b можно соединить
некоторым путем. Пусть К — образ этого пути. Тогда К П А и К П В
будут открытыми дополнительными подмножествами К
(теорема 5), и ни одно из них не пусто, поскольку а и b
принадлежат соответственно первому и второму множествам. Мы
получим разбиение К на два открытых непересекающихся
множества, что противоречит теореме 33, в которой утверждается, что
образ связного пространства [а, р] при непрерывном
отображении связен. Противоречие доказывает связность множества Е.
Обратное утверждение к этой теореме, вообще говоря, не
верно. Если, например, мы рассмотрим в евклидовой плоскости
R2 множество Е, являющееся объединением кривой, опре-

92
Гл. II. Топология
деляемой функцией t/ = sin \]х, хфО, и вертикального отрезка
х = 0, \у\ ^ 1, то легко проверить, что Е связно, и тем не менее
точки (0, 0) и (a, sin 1/а) соединить путем невозможно.
Говорят, что пространство линейно связно, если две его
произвольные точки могут быть соединены некоторым путем. Это
свойство более сильное, чем обычная связность.
Пример. Любое нормированное векторное пространство
линейно связно. В самом деле, любые две его точки могут быть
соединены отрезком с началом и концом в рассматриваемых
точках.
Точно так же проверяется, что шар и сфера в нормирован-
яых векторных пространствах линейно связны.
Теорема 36 (о переходе через таможню). Пусть А — часть
топологического пространства Е. Любой путь, соединяющий
внутреннюю точку А с точкой ее внешней части, пересекает
границу А.
Доказательство. Поскольку образ К, согласно
теореме 32, является связным множеством, то эта теорема является
частным случаем следующего утверждения:
Любое связное подмножество В а Е, имеющее общие точки
с внутренней и внешней частями А, заведомо пересекает его
границу. Это свойство очевидно. В самом деле, если бы это было
не так, то В содержалось бы в объединении внутренней и
внешней частей А, пересечение В с обеими этими частями определяло
•бы в этом случае разбиение,В на два непересекающихся
открытых множества, что невозможно.
| 10. ДОПОЛНЕНИЕ ПО ОБЩЕЙ ТОПОЛОГИИ СВЯЗНЫХ ПРОСТРАНСТВ
Теорема 36г- Объединение А любого семейства (Лг), ie/,
связных частей топологического пространства Е, имеющих
попарно непустые пересечения, связно.
Доказательство. Допустим, что это не так. Тогда А
можно рассматривать как объединение двух непересекающихся
и открытых относительно А частей В' и В". Для каждого под-
множества-Лг множества Л, [~| В' и Ai f| В" не пересекаются,
являются открытыми относительно Л; и в объединении дают Л,-.
Поскольку Лj по условию связны, одна из этих двух частей
необходимо пуста, а другая совпадает с Лг. Таким образом, At
целиком содержится в В' или в В". Поскольку пересечение
любых двух частей Л* и Л;- не пусто, то обе они заведомо
содержатся либо в В', либо в В", так что, окончательно, все части Л,-
содержатся в В' или же все лежат в В", а, значит, А с В' или

§ 10. Общая топология связных пространств 93
A с В". Это противоречит предположению, согласно которому
А является объединением непустых непересекающихся частей
В' и В". Полученное противоречие доказывает связность
множества А.
Теорема 363. Замыкание А связной части А в
топологическом пространстве Е связано.
Доказательство. Пусть это не так, т. е. пусть А
является объединением двух непустых непересекающихся частей В' я
В", каждая из которых замкнута относительно А. Поскольку А
замкнуто в Е, то они замкнуты относительно Е (теорема 6). Мы
получаем, что А является объединением двух непересекающихся
частей А Л В' и А Л В", замкнутых относительно А. Поскольку
часть А предполагалась связной, то одно из этих пересечений
должно быть пустым, так что мы имеем, например, А Л В'=0 и
А—А Л В" : А а В". Отсюда, в силу замкнутости В в Е,
получаем A с В", а это противоречит предположению о том, что А
является объединением непересекающихся непустых частей В'
и В"^ Полученное противоречие доказывает связность
замыкания А.
Определение. Две точки топологического пространства
Е называются связанными, если существует связное
подмножество Е, содержащее эти точки. Две точки, которые можно
соединить некоторым путем, связаны.
Теорема 364. Отношение «х и у связаны в Е» является
отношением эквивалентности в Е.
Доказательство. Это отношение, очевидно,
рефлексивно и симметрично; поэтому достаточно доказать его
транзитивность. Итак, пусть х и у связаны. Если, кроме того, связаны
точки у и z, то существует, с одной стороны, связное
подмножество, содержащее х и у, и, с другой стороны, связное
подмножество, содержащее у и г. Так как оба подмножества связны и
их пересечение не пусто, то по теореме 362 их объединение
связно. Так как точки х и z содержатся в общем связном
подмножестве, то они связаны.
Определение. Класс эквивалентности Е по отношению
эквивалентности «х и у связаны в Е» называется связной
компонентой Е. Пространство Е является объединением связных
попарно не пересекающихся компонент. Связной компонентой
точки х из Е называется содержащая ее связная компонента Е.
Теорема 364. Связная компонента точки х из Е
совпадает с множеством точек Е, связанных с х, и является
наибольшей связной частью Е, содержащей х. Связные компонен~
ты Е замкнуты.

94
Гл. //. Топология
Доказательство. 1°) По определению классов
эквивалентности, связная компонента Ех точки х в Е является
множеством точек Е, связанных с х. Каждая связная часть Е,
содержащая х, полностью лежит в Ех, поскольку все ее точки
связаны с х. Обратно, если точка у е Ех, то она связана с х, а,
следовательно, содержится хотя бы в одной связной части Е,
содержащей х. Таким образом, Ех является объединением всех
связных частей Е, содержащих х. Так как все эти связные
части содержат х, то попарное пересечение их не пусто. Из
теоремы 362 вытекает, что это объединение Ех связно. Это —
связная часть Е, содержащая х, а также любую связную часть,
содержащую х. Таким образом, Ех является наибольшей
связной частью Е, содержащей х. _
2°) Согласно теореме 363, замыкание Ех множества Ех в Е
связно. Поскольку Ех является наибольшей связной частью Е,
содержащей х, то ЁХ=ЕХ и, следовательно, Ех замкнута.
Определение. Пространство Е называется локально
связным, если, какова бы ни была точка а из £ и окрестность^
точки а в Е, существует связная окрестность У" точки а,
содержащаяся в У. Как показывает сам выбранный нами термин,
свойство некоторого пространства быть локально связным
является локальным свойством, в то время как обычная
связность носит глобальный характер. Эти два свойства совершенно
не связаны друг с другом').
1°) Рассмотрим, например, в плоскости R2 множество Е,
образованное двумя прямыми, определяемыми уравнениями у=0
и у = 1. Это множество, как подмножество R2, не связно. Однако
оно локально связно, так как любая окрестность У точки а из
Е содержит некоторый горизонтальный интервал с центром
в точке а, являющийся связной частью. Этот пример
показывает, что пространство может быть локально связным, не
будучи связным.
2°) Обозначим через Е множество точек плоскости R2,
состоящее из всех прямых, параллельных оси Ох и имеющих
рациональные ординаты, и всей оси Оу. Это топологическое
пространство не является локально связным: если рассматривается
произвольная точка Е с координатами (а, Ь), где а Ф О, и
некоторый шар с центром в этой точке радиуса <|а|, то эта
окрестность не содержит никакой связной окрестности. Однако
множество Е связно и даже линейно связно. Любые две его точки
можно соединить путем, составленным из трех отрезков:
первый и третий отрезки параллельны оси Ох, а второй отрезок
') Не следует проводить аналогий с понятием компактности: любое
компактное пространство является и локально компактным (обратное не верно),
тогда как связное пространство не обязано быть локально связным.

§ 10. Общая топология связных пространств
95
расположен на оси Оу. Поэтому рассмотренное пространство
связно, но не локально связно.
Теорема 366. Если топологическое пространство Е
локально связно, то каждая его связная компонента
одновременно открыта и замкнута в Е.
Доказательство. В самом деле, пусть Ех — связная
компонента х в Е и у — некоторая точка Ех. Так как у
обладает некоторой связной окрестностью, то все точки z этой
окрестности связаны с у, а, следовательно, и с точкой х.
Отсюда следует, что Ех содержит всю эту окрестность. Итак, если
Ех содержит точку у, то она содержит и некоторую ее
окрестность. Значит, Ех открыто. Согласно теореме З65, Ех
одновременно и замкнуто. "
Замечания. 1°) Обратное утверждение, вообще говоря,
не верно. Так в приведенном выше примере, где Е связно, но
не локально связно, имеется лишь одна связная компонента Е.
Эта компонента одновременно открыта и замкнута, и тем не
менее Е не локально связно.
2е) Если Е является открытым множеством нормированного
векторного пространства Е0, то Е локально связно. В самом
деле, каждая окрестность точки а из £ заведомо содержит не.-
который шар с центром а в Е0, который, как известно,
является связным, и даже линейно связным. В этом случае
применима сформулированная теорема. Связные компоненты Е
заведомо одновременно открыты и замкнуты в Е. Они тогда также
открыты и в Eq.
3°) Отметим еще один замечательный случай, когда все
связные компоненты одновременно открыты и замкнуты: это
случай, когда Е имеет только конечное число связных
компонент. Каждая из этих компонент, будучи уже замкнутой,
является дополнением к объединению других компонент. Далее,
так как конечное объединение замкнутых подмножеств само
замкнуто, то рассматриваемые компоненты открыты.
Определение. Топологическое пространство называется
локально линейно связным, если, каковы бы ни были точка а
и ее окрестность У, существует линейно связная окрестность У"
точки а, содержащаяся в Т. Поскольку линейно связное
пространство связно, локально линейно связное пространство
является локально связным. Открытое множество
нормированного векторного пространства локально линейно связно.
Теорема З67. Пусть Е — локально линейно связное
топологическое пространство. Если оно связно, то оно линейно связно.

96
Гл. II. Топология
Если оно не связно, то каждая, его связная компонента
открыта, замкнута и линейно связна.
Доказательство. Пусть х—некоторая точка Е.
Обозначим через Fx множество точек Е, которые могут быть
соединены с точкой х некоторым путем. Если у — такая точка, то
существует окрестность у, все точки z которой могут быть
соединены с у некоторыми путями. Поскольку у может быть
соединена с х некоторым путем, то z также может быть соединена
с х некоторым путем. Другими словами, если Fx содержит
точку у, то оно содержит целую ее окрестность. Это означает, что
Fx открыто.
Докажем теперь, что множество Fx замкнуто. Для этого
достаточно показать, что его дополнение открыто. Предположим,
что у принадлежит этому дополнению, т. е. не принадлежит Fx.
Существует окрестность У точки у, все точки которой могут
быть соединены с у некоторым путем. Тогда никакая точка z
из У не принадлежит Fx. Действительно, если бы можно было
соединить путем точки х и z, то можно было бы соединить
точки х и у, что противоречит нашему предположению. Итак, если
дополнение к Fx содержит точку у, то оно содержит и
некоторую окрестность этой точки. Это означает, что дополнение к Fx
открыто, а, значит, само Fx замкнуто.
Пусть Е связно. Множество Fx одновременно открыто,
замкнуто и не пусто, поскольку оно содержит х. Это означает, что
FX=E, и, значит, Е линейно связно.
В любом случае, если даже Е не связно, для связной
компоненты Ех точки х в Е мы получаем следующий
результат. Поскольку Fx, будучи линейно связным, связно, то Fx с Ех.
Так как Ех связно, a Fx одновременно открыто и замкнуто в Е-,
а, значит, и в Ех, то FX=EX. В итоге получаем, что Fx открыто,
замкнуто и линейно связно.
Замечания. 1°) Две предыдущие теоремы будут
применяться, в частности, когда Е является некоторым
многообразием (см. далее гл. III, § 9). В самом деле, каждая
окрестность точки содержит тогда некоторую окрестность, гомеоморф-
ную сфере, и, следовательно, локально связна.
2°) Легко доказываются и другие теоремы этого рода.
Предположим, например, что Е является открытым
множеством нормированного векторного пространства. Тогда оно
локально связно по ломаным в том смысле, что каждая
окрестность У точки а содержит другую окрестность У (например,
шар с центром в а), две произвольные точки которой могут
быть соединены ломаной линией (т. е. путем, последовательно
образованным из конечного числа отрезков прямой; для шара
достаточно одного отрезка). То же самое доказательство, что

§ 10. Общая топология связных пространств 97
и выше1), показывает, что если Е связно, то оно локально
связно по ломаным, и что, даже если Е не связно, каждая его
связная компонента является связной по ломаным.
Если Е является открытым множеством конечномерного
нормированного векторного пространства с введенной в нем
системой координат, то точно так же доказывается, что любая
связная компонента Е является связной «по ломаным линиям с
отрезками, параллельными осям координат»; другими словами,
любые две точки связной компоненты Е могут быть соединены
путем, последовательно образованным из конечного числа
отрезков, параллельных осям координат.
Некоторые применения понятия связности.
Критерии негомеоморфности
Так же как и понятие компактности, рассмотренное выше
понятие связности позволяет нам установить в некоторых
случаях, являются ли два данных топологических пространства го-
меоморфными. В самом деле, если два пространства гомео-
морфны и одно из них связно, то связным также должно быть
и второе. Рассмотрим, например, вещественную прямую R и
плоскость R2. Мы знаем, что эти множества имеют одинаковую
мощность, значит, существует некоторая биекция одного из них
на другое. Легко видеть также, что существует непрерывное'
сюръективное отображение плоскости на прямую. Это —
проекция (х, у) -*х плоскости R2 на R. Довольно сложным путем
Пеано доказал, что существует непрерывное сюръективное
отображение прямой R на плоскость VR2. Но эти отображения, как
это ни кажется парадоксальным, не могут быть биективными:
всегда существуют точки плоскости, имеющие несколько
прообразов! Довольно просто можно доказать, что
гомеоморфизма прямой на плоскость не существует. В самом деле,
согласно теореме 32, прямая обладает следующим свойством:
если из нее удаляют точку, то оставшееся дополнение,
рассматриваемое как топологическое пространство, не связно.
Напротив, плоскость этим свойством не обладает: дополнение к точке
безусловно связно и даже линейно связно2). Отсюда
непосредственно вытекает, что прямая и плоскость не могут быть гомео-
морфными. Точно так же, несмотря на то что интервал [а, Ь]
прямой R и окружность плоскости R2 компактны, они не гомео-
морфны. В самом деле, если из интервала [а, Ь] выкинуть его
середину, то дополнение этой точки не будет связным, в то
') То есть нужно рассмотреть множество точек Fx, которые можно
соединить с х ломаной линией.
2) Две произвольные точки могут быть соединены путем, образованным
из двух прямолинейных отрезков плоскости.
4 Зак. 1339

98 Гл II. Топология
время как удаляя любую точку окружности, мы всегда
получаем связное дополнение.
Можно доказать (но это не просто!), что два
нормированных векторных пространства разной размерности не могут быть
гомеоморфными. Сфера в Rm и сфера в R" при тфп не го-
меоморфны.
Существование и непрерывность обратной функции
для строго монотонной непрерывной функции
Теорема 37. Пусть f — некоторое непрерывное строго
возрастающее отображение интервала^ \а, Ь\ (открытого,
полуоткрытого или замкнутого) из R в R. Тогда рбраз f(\a,b\) лот
ляется интервалом |а, р| того же вида, a f есть гомеоморфизм
\а, Ь\ на |а, р|. Продолжение f отображения f, определенное
с помощью равенств f(a) = а, f(b) = р, является
гомеоморфизмом [а, Ь] на [а, р].
То, что образ является интервалом |а, р|, вытекает из
следствия теоремы 33. Иньективность / вытекает из того, что это
отображение строго возрастающее. Следовательно, / является
непрерывной биекцией \а, Ь\ на |а, Р|. Поскольку / сохраняет
отношение порядка и a = inf(|a, b\), a=inf(|a, p|), то а
принадлежит образу тогда и только тогда, когда интервал \а, Ь\
содержит а. То же самое справедливо для точек b и р. Поэтому
интервал |а, р| имеет тот же вид (открытый, полуоткрытый
или замкнутый), что и интервал \а, Ь\. Образ любого
интервала \с, d\ из \а, Ь\, открытого в \а, Ь\-, является интервалом
того же вида, а, следовательно, является открытым множеством
в |а, р|. Образ любого открытого множества из \а, Ь\ при
отображении / является открытым множеством из |а, р|, а,
следовательно, / является гомеоморфизмом \а, Ь\ на |а, р|
(теорема 11). Обратное отображение, будучи, очевидно, строго
возрастающим, является также биективным и непрерывным
отображением |а, р| на \а, Ь\.
Когда х стремится к а строго справа, то f(x) стремится к a
(см. стр. 61). В самом деле, каково бы ни было а' > а,
прообразом интервала ]а, а'[ является интервал ]/ад, fwl,
являющийся пересечением некоторой окрестности точки а в R с
интервалом ]а, Ь[. Следовательно, если положить f(a)=a и,
точно так же f(6)=P, то f будет продолжением /, являющимся
строго возрастающим непрерывным отображением, а, значит,
гомеоморфизмом [а, Ь] на [а, р]. Если а==—оо, Ь = -\-оо, а а и р
конечны, то f определит некоторый гомеоморфизм R на
замкнутый ограниченный интервал в R.

§ 10. Общая топология связных пространств
99
Замечание. Предположение о строгой монотонности f
естественно: непрерывное и инъективное отображение f
интервала \а, Ь\ из R в R заведомо строго монотонно. В самом деле,
предположим, что это не так. Тогда в \а, Ь\ будут существовать
точки хи х2, х3, Х\ < х2 < х3, такие, что f(Xi) < f(x2) и f(x2) >
>f(x3), или такие, что f(x{) > f(x2) и f(x2) <.f(x3).
Рассмотрим, например, первый случай. Пусть у — общая точка
интервалов ]/(*i), f(x2)[ и ]f(x3), f(x2)[. Тогда, согласно теореме о
промежуточных значениях (следствие из теоремы 33), существуют
точка х' e]JCi, x2[ и точка х" ^]х2, х3[, в которых f принимает
значение у. Это означает, что f не является инъекцией, а это
противоречит исходному условию.
Применение: метрики, определяющие топологию в R
Теорема 38. Пространство R метризуемо. Если f — строго
возрастающее непрерывное и ограниченное отображение R в R,
го метрика
d(x,y) = \f(x)-f(y)\, xeR, j,eR, (НЛО; 1)
где f — продолжение отображения f до отображения R в R,
определяемое равенствами f (— оо)= inf f(x) и f(-{-oo) =
= sup/ (x), задает топологию в пространстве R.
ieR
Согласно теореме 37, f является гомеоморфизмом R на
интервал ]ос, р[ из R. Так как f ограничено, то а > —с», р < +оо.
Кроме того, а= inf f(x), $=supf(x) и продолжение f отоб-
хs R же R
ражения f, такое, 4Tof(—оо)=ос и f(-|-oo)=p, является
гомеоморфизмом R на [а, р] с: R.
Поскольку топология в [а, р] с= R определяется естественной
метрикой прямой R, то топология в R определяется метрикой,
перенесенной от естественной метрики в [а, р] отображением f-1,
т. е. такой метрикой, в которой расстояние между JteR и je
е R является естественным расстоянием между f (x) nf(y), т. е.
\f(х)—f(y)\, или (II, 10; 1), что и требовалось доказать.
Например, можно взять
/(jc) = arctgjc, где f(-oo) = -|, f(+oo)=|, (II, 10; 2)
у
что, по существу, сводится к метрике d(x, у)= | е?|/(1 + |2)
4*

100
Гл. П. Топология
Более общо, если h является непрерывной функцией >0,
интегрируемой на R, то можно положить
d(x, у)
\h{l)dl
(II, Ю; 3)
Здесь можно принять
f{x) = \hx и f(-oo) = -l, f(+oo)= + l. (II, 10; 4)
Можно положить
/W = TTT7T и f(-~)==-l- f(+°°)=l (И, Ю;5)
и т. д. Все эти весьма различные метрики эквивалентны в R
(а следовательно, в R), поскольку они определяют одну и туже
топологию.
§ 11. ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
Пусть в метрическом пространстве Е задана
последовательность точек. х0, Х\, х2 сходящаяся к х. Тогда эта
последовательность обладает следующим свойством '):
(Ve>0)(3peN)(Vm<=N, VneN, m>p, n^p):d(xm, x„)<e
(П, И; 1)
или же
d(xn,xm) стремится к 0, когда тип стремятся к + °о.
(П, 11; 2)
Последовательность, обладающую этим свойством, называют
последовательностью Коши (или фундаментальной
последовательностью).
Из общего курса анализа известно, что если х0, Х\, х2, ... —
последовательность Коши в поле вещественных или
комплексных чисел, то она сходится.
Это свойство является основным, поскольку оно позволяет
выяснить, является ли последовательность сходящейся, даже
если мы не знаем предела, к которому она может сходиться;
общее определение сходимости не дает такой возможности.
Именно это свойство приводит к построению различных критериев
сходимости рядов и позволяет решить, сходится ли ряд,
составленный из вещественных или комплексных чисел, даже если
мы ничего не знаем о его сумме, что очень важно в анализе.
Однако это свойство, справедливое в поле вещественных и
комплексных чисел, не имеет места в произвольных метрических
') Его часто называют критерием Коши.

§ И. Полные метрические пространства
101
пространствах. Изучению этого вопроса мы и посвятим этот
параграф.
Рассмотрим прежде всего некоторые общие свойства
последовательностей Коши.
Теорема 39. Любая подпоследовательность
последовательности Коши также является последовательностью Коши.
Каждая последовательность Коши ограничена.
Доказательство. Первое свойство очевидно. Докажем
второе. Ясно, что существует целое р, такое, что из m ^ р,
n~$i p следует d(xm, хп) ^ 1. Но тогда все хп с п ^ р
содержатся в шаре В(хр, 1) и, следовательно, вся
последовательность находится в шаре В(хр, R), где
R = max[d{xp, x0), d{xp, хх) d(хр, хр^), 1].
Теорема 40. Если последовательность Коши х0, xt, х2, ... в
метрическом пространстве Е~ имеет точку сгущения а, то эта
последовательность сходится к а.
Доказательство. При заданном е>0 существует
такое р, что для m ^ р и п~^ р имеет место неравенство
d{xm,хп)^. е/2. Существует, кроме того, бесконечное множество,
а, значит, по крайней мере одно такое т, что d(xm, а)^. е/2 для
пг^р. Отсюда получаем, что d(xn, a) ^ d(xn, xm)-{-d(xm, a) ^
^ е при п^ р.
Следствие 1. Всякая последовательность Коши либо не
имеет точек сгущения, либо имеет только одну такую точку, и
тогда она сходится.
Следствие 2. Если последовательность Коши такова, что
одна из ее подпоследовательностей сходится, то и сама
последовательность сходится.
В самом деле, из предположения следует, что данная
последовательность имеет точку сгущения.
Определение. Метрическое пространство Е называется
полным, если любая последовательность Коши в нем сходится.
Мы уже видели, сколь важным является понятие полноты.
Необходимо поэтому найти критерии, позволяющие выяснить,
является ли данное метрическое пространство полным.
Заметим здесь же, что понятие полного пространства не
имеет смысла в случае неметрических топологических
пространств. Впрочем, легко видеть, что для двух эквивалентных,
метрических пространств последовательности Коши не
обязательно должны быть одинаковыми и что одно из таких
пространств может быть полным, а второе — нет. Понятие полного

102
Гл. II. Топология
пространства является метрическим, а не топологическим
понятием.
Рассмотрим в качестве примера вещественную прямую R.
Если на ней ввести естественную метрику, то, как мы увидим
позже, она будет полной (это известно и из общего курса
математического анализа). Последовательность N целых чисел в
этой метрике не является последовательностью Коши.
Напротив, если мы рассмотрим на пополненной прямой R одну из
метрик, определенных на стр. 100, то она индуцирует на
прямой R некоторую метрику, эквивалентную естественной. Однако,
в этой метрике R не полно. В самом деле, последовательность
целых чисел является последовательностью Коши на R,
поскольку она сходится к +°°. а, значит, она является
последовательностью Коши на R, где она вовсе не сходится.
Теорема 41. Любое метрическое пространство Е, все
замкнутые шары которого компактны, полно. В частности, полно-
любое метрическое компактное пространство и любое
конечномерное нормированное векторное пространство.
Доказательство. Согласно теореме 29, каждая
последовательность Коши Хо, Хи Хг, ... ограничена, а, следовательно,
содержится в некотором замкнутом шаре В, т. е. в некотором
компакте. По теореме Больцано — Вейерштрасса она имеет хотя
бы одну точку сгущения. Согласно теореме 40,
последовательность сходится, а, следовательно, Е полно.
Замечания. 1°) Из условий теоремы следует, что Е
локально компактно. Однако в локально компактных
метрических пространствах замкнутые шары не обязательно
компактны1). Рассмотрим, например, пространство R, снабженное
одной из метрик, указанных на стр. 100. Подпространство R в этой
метрике локально компактно, однако, как было замечено выше,
оно не полно. Легко проверить, что все замкнутые шары в нем
не компактны. В самом-деле, в силу компактности пополненной
прямой R она ограничена. Следовательно, для достаточно
большого р шар радиуса р в R совпадает со всей прямой R.
Тогда шар радиуса р в R совпадает с некомпактным
множеством R.
2°) Бесконечномерные нормированные векторные
пространства могут быть как полными, так и неполными. Позже мы
приведем примеры тех и других пространств. Наиболее
интересными, естественно, будут полные пространства.
') Локальная компактность метрического пространства Е является
топологическим свойством. Свойство компактности замкнутых шаров является
метрическим свойством.

§ П. Полные метрические пространства 103
3°) Существуют не локально компактные метрические
пространства, которые являются полными. Именно об этом
говорится в замечании 2°).
4°) Точно так же как и свойство компактности, свойство
полноты метрического пространства является внутренним
свойством самого пространства. Однако если F является
подмножеством некоторого метрического пространства Е, то мы будем
говорить, что F полно, если оно полно как метрическое
пространство с индуцированной метрикой.
Теорема 42. Полнее подмножество F метрического
пространства Е замкнуто в Е.
Доказательство. Пусть а е Е является точкой
прикосновения F. Согласно теореме 15, существует последовательность
точек Xq,Xi,Xz, ... из F, сходящаяся к а. Это —
последовательность Коши в Е, а, следовательно, и в F. Поскольку F полно,
последовательность имеет предел а' в F, а значит, и в Е.
Последнее означает, что а = а' е F. Так как а е F, то F замкнуто.
Следствие 1. Пусть Е — метрическое пространство. Плот'
ное подмножество F, не совпадающее с Е, не обязательно полно.
В самом деле, замыканием F в Е является Е Ф F.
Следовательно, F не замкнуто. Отсюда следует, например, что поле -Q
рациональных чисел с естественной метрикой не полно. Легко,
впрочем, образовать несходящуюся последовательность Коши
в Q. Достаточно взять последовательность из Q, сходящуюся
в R к иррациональному числу. Необходимость расширения
поля рациональных чисел и- введения поля вещественных чисел
диктуется двумя важными причинами: каждое ограниченное
непустое множество должно иметь точную верхнюю грань и
каждая последовательность Коши должна быть сходящейся.
Следствие 2. Конечномерное подпространство F
нормированного векторного пространства Е замкнуто в Е.
В самом деле, согласно изложенному перед теоремой 41,
подпространство F полно. Можно доказать, что этот результат
сохраняется, если Е — всего лишь векторное топологическое
пространство.
Естественно, обратное утверждение к предыдущей теореме
не верно. Например, F = Е всегда замкнуто в Е, а тем не менее
не обязательно полно. Однако имеет место
Теорема 43. Любое замкнутое подмножество F полного
метрического пространства Е полно.
Доказательство. Пусть х0, xlt х%, ... — последователь-,
ность Коши из F. Она является также последовательностью
Коши в £ и, так как Е полно, сходится к некоторой точке

104
Гл. II. Топология
а е £. Поскольку все хп лежат в F, то а является точкой
сгущения для F (теорема 15) и, в силу замкнутости F,
принадлежит ему. Итак, любая последовательность Коши в F сходится
в F, т. е. F полно.
Из теорем 42 и 43 следует, что если Е полно, то его полные
и замкнутые подмножества совпадают. Отметим сходство
между этими свойствами и соответствующими свойствами
компактных пространств.
Теорема 44. Пусть £4 и Е2 — два полных метрических
пространства. Тогда произведение £4 X Е2 будет также полным в
смысле какой-либо из метрик, указанных на стр. 63.
Доказательство. Обозначим через d\ и d2 расстояния
в Ei и Ег, и пусть б — расстояние в произведении £4 на Е2,
обладающее следующими свойствами:
1°) б определяет в £4 X Е2 топологию произведения
топологий, в Ei и Е2, определенных расстояниями di и d2;
2°) существует такое число k, что для каждой пары (xi,x2),
(УиУг) элементов £4 X Е2 имеют место неравенства:
kb\(xx, х2), (ух, y2))^dx (хх, ух) и >d2(*2. у2). (Н, П;3)
Докажем, что в так определенной метрике пространство'
£iX^2 полно. В самом деле, пусть ({xi)n, {х2)п)—некоторая
последовательность Коши этого пространства. Из условия 2°)
следует, что (хх)п является последовательностью Коши в Ех, а
последовательность (х2)п — последовательностью Коши в Е2.
Поскольку пространства £i и Е2 полны, эти последовательности
сходятся соответственно к элементам ai е £4 и а2 е Е& Но
тогда в топологии произведения, т. е. в рассматриваемой
метрике б, последовательность ((xi)п, (х2)п) сходится к (ai,a2) в
EiY.E2, что означает полноту этого пространства.
Продолжение равномерно непрерывных отображений
Теорема 45. Пусть Е и F — некоторые метрические
пространства, Ei — подпространство, плотное в Е, a fi — отбраже-
ние Ei в F. Предположим также, что fi равномерно непрерывно
на Еи a F полно.
Тогда существует, и притом единственное, непрерывное
отображение f пространства Е в F, являющееся продолжением fu
Это отображение, кроме того, равномерно непрерывно.
Доказательство. 1°) Если даже fi только непрерывно,
a F не полно, то не может существовать более одного
отображения, обладающего указанными свойствами. В самом деле,
пусть имеется некоторое такое отображение /. Пусть х — точ-

§ 11. Полные метрические пространства 105
ка Е. Так как £i плотно в Е, то, согласно теореме 15,
существует последовательность х0, хи х2, ... в Е\, сходящаяся к х.
В силу теоремы 16, из непрерывности / вытекает, что
последовательность f(xn) — fi(xn) сходится к f(x) в F, Следовательно,
f(x), являясь пределом /i(*n)> полностью определена, что
доказывает ее единственность.
2°) Для доказательства существования необходимо
предполагать, кроме того, что / равномерно непрерывна и F полно.
Пусть теперь снова х—некоторая точка Е и x0,Xi,X2, ... —
последовательность в Ei, сходящаяся к х. Тогда это
последовательность Коши в Е. Отсюда немедленно вытекает, что
последовательность fi(xn) является последовательностью Коши в F.
В самом деле, для любого заданного е > 0, в силу
равномерной непрерывности, существует такое число ц > 0, что из
x'e=Ei, x*e£,, d(x',x")<4 следует d^MJi^Xe.
Поскольку Хо, Xi, X2, ... является последовательностью Коши,
существует такое целое р, что из m ^ р, п ^ р следует d(xm, xn) ^
^ т), а, следовательно, и d(f(xm),f(xn)) ^ е, что полностью
доказывает наше утверждение.
Поскольку F по предположению полно, последовательность
fi(xn) имеет предел в F. Обозначим его через f(x). Надо
доказать прежде всего, что f(x) полностью определяется заданием
х, т. е. не зависит от выбора последовательности хп.
Рассмотрим с этой целью какие-либо две последовательности х'п и д£,
сходящиеся к одному и тому же х. «Смешанная»
последовательность х'0, *ц, х\, х", х'2, х", ... является некоторой
последовательностью из Ei, сходящейся к х. Но тогда последователь-
ность f(*J), f«), f«), f«), ..., f(x'n), f«), ... должна
сходиться к некоторому элементу F и это полностью
доказывает тот факт, что обе последовательности f(*Q и /(л£) имеют
один и тот же предел в F.
Показав это, мы определили некоторое отображение f
пространства Е в пространство F. Это отображение является
тривиальным продолжением fi, ибо для любого х^Е{ можно взять
последовательность х, х, х, ... , сходящуюся к х. При этом образ
f(x) является пределом последовательности fi{x),fi(x),fi(x),...,
т. е. совпадает с fi(x). Остается, следовательно, доказать
равномерную непрерывность отображения /. Пусть е > 0 — заданное
число, а т) > 0 — соответствующее ему число, входящее в
определение равномерной непрерывности fi. Пусть х и у—
произвольные точки Е, такие, что d(x, y)^ ц/2. Докажем, что тогда
d (f (х), f (у))-^ г, что обеспечит равномерную непрерывность /.
Пусть хп и уп — последовательности из Еи сходящиеся
соответственно к х и у. В силу непрерывности функции расстояния
Хтеорема 172), существует такое целое число р, что для п~^р

106
Гл. II. Топология
имеем с!(хп,*/n)«S d(x, у)-\-ц/2. Отсюда вытекает, что для п ^ р
выполняется неравенство d(xn, уп) ^ т) и, следовательно,
d(fi(xn), fi(yn))-^> е. Поскольку в F функция расстояния
непрерывна, а последовательности f\(xn) и }\{уп) сходятся
соответственно к f(x) и f(y), то d(fi(xn), fi(yn)) сходится к d(f(x),f(y)).
Следовательно, d(f(x), f(y))^e. Доказательство теоремы
закончено.
Замечания. 1°) Предположение относительно полноты
пространства F существенно. Если, например, мы возьмем F =
= Ei, а в качестве fi возьмем тождественное отображение £i в
Еи то оно не может быть продолжено до непрерывного
отображения f пространства Е в Et.
В самом деле, пусть х — некоторая точка Е, не
принадлежащая Ei. Пусть хп — последовательность из Еи сходящаяся к х.
Тогда, если бы существовало непрерывное продолжение f,
последовательность fi(Xn) = Xn сходилась бы к f(x) в Еи а,
значит, и в Е, и мы имели бы f(x) = x, что невозможно, так как
х ф.Еи
2°) Недостаточно предполагать, что f\ только непрерывно.
Рассмотрим, например, пространство £ = R и снабдим его
одной из метрик, указанных в теореме 38; положим Ei = R. В
качестве F выберем прямую R с естественной метрикой. Тогда F
полно. Легко видеть, что тождественное отображение fi
пространства Ei в F непрерывно, но не равномерно непрерывно.
Его, очевидно, нельзя продолжить до непрерывного
отображения f пространства £ = R в f =R. В самом деле, точка х —
= +оо из Е — R является пределом в Е последовательности
целых чисел N. Однако образ этой последовательности, т. е.
само N, не сходится в F = R, тогда как он должен был бы
сходиться к f(-j-oo), если бы отображение f существовало.
Частные свойства конечномерных топологических
векторных пространств
Мы уже отмечали некоторые такие свойства: теорема 13,
теорема 23, следствие 2 из теоремы 41. Остается доказать
свойство, указанное на стр. 74:
Теорема 45г (Фредерик Рисе). Для того чтобы
топологическое векторное пространство было локально компактным,
необходимо и достаточно, чтобы оно было конечномерным.
Доказательство. Для простоты мы будем считать, что
Е является нормированным векторным пространством.
Незначительное видоизменение доказательства даст общий результат.
Мы уже знаем, что из конечномерности Е вытекает его
локальная компактность. Нам же надо доказать обратное утвержде-

§ 12. Теорема о неподвижной точке
107
ние. Предположим, дто в Е имеется некоторая компактная
окрестность У точки 0. В дальнейшем мы будем пользоваться
следующими обозначениями. Если А— некоторая часть Е, то ХА,
где X— скаляр, является множеством точек Хх, где х^А. Если
А и В — две части Е, то через А + В обозначается множество
точек х-\-у, х^А, у^В. (Внимание! 2Л содержится в А +.4,
но, вообще говоря, с ним не совпадает.) Векторное
подпространство М пространства Е характеризуется следующими
свойствами: М + М = М и ХМ а М для любого X. Далее, 2У являет-
о
ся окрестностью 0 и а-\-У является открытой окрестностью
точки а. Когда а пробегает множество 2У, множества а + У
образуют открытое покрытие множества 2У. В силу
предположения о компактности, существует конечное число точек
аи &г, ••-, о.п, таких, что аг- + У покрывают 2У. Пусть М —
векторное подпространство, порожденное векторами а*. Оно
конечномерно, а М-\-У покрывает 2У.
Имеем: М + У=М + М + У=>М + 2У. Умножая на 2,
получаем: М + У => М + 2У = 2М + 2У = 2 (М + У) => 2 (М + 2У) =
= 2М-\-4У = М-\-4У. Для любого я имеют место
включения М + У id M + 2пУ id 2пУ. Так как объединение всех 2пУ
дает все пространство, то М + У совпадает со всем
пространством Е. Отсюда можно получить, что М также совпадает с £,
а, значит, Е конечномерно. Если бы это было не так, то
существовала бы точка аф.М. Так как М замкнуто (следствие 2
теоремы 41), то тогда существовал бы шар с центром в а, не
пересекающийся с М. Этот шар можно представить в виде а + В,
где В — шар с центром в нуле пространства. Тогда М + В не
будет содержать а. Для произвольного р > 0 множество М +
Ч- рВ = рМ + рВ не содержит ра, и мы получаем ра ф М + рВ.
Однако окрестность У компактна, а, значит, ограничена. При
достаточно большом р она содержится в рВ, и тогда рафМ+У,
что противоречит ранее полученному результату М + У = Е.
§ 12. ТЕОРЕМА О НЕПОДВИЖНОЙ ТОЧКЕ
Определение. Отображение f метрического
пространства Е в Е называется сжатием, если существует такая
положительная постоянная k<L\, что для любой пары элементов
х и у из Е имеет место неравенство
d(f(x),f(y))^kd(x,y). (II, 12; 1)
Отсюда, очевидно, вытекает, что отображение f
удовлетворяет условию Липшица и, следовательно, равномерно
непрерывно.
Точка а называется неподвижной точкой отображения f,
если f(a) = a.

108
Гл. II. Топология
Теорема 46. Каждое сжатие полного метрического
пространства в себя имеет неподвижную точку, и притом
единственную.
Доказательство. Единственность неподвижной точки
очевидна, даже если Е не полно. В самом деле, если а и b —
две неподвижные точки, то
d(a, b)^.kd(a, b)<d(a, b), если только d(a, b) ф 0. (II, 12; 2)
Поэтому d(a, b) = 0, т. е. а и b совпадают.
Докажем теперь существование неподвижной точки. Мы
применим для этого метод, называемый методом
последовательных приближений.
Пусть х0—произвольная точка Е. Положим
*i = f (*о)> Ч = f (*i). • • • > xn = f (*„_,). (II, 12; 3)
Мы образовали некоторую бесконечную последовательность
Хо, Х\, х2, ... элементов из Е. Докажем, что она является
последовательностью Коши. Поскольку f — сжатие, мы можем
записать последовательность неравенств:
d(x2, XiX.kd(xlt x0),
d{x3, x2)<:kd{x2, xl)<:k2d(xl, x0), 12. 4.
d(xa+l, x„)<fe"d(x„ x0),
а, следовательно,
« (xn + p> xn) ^= " \xn+p> xn+p-l) "T " \xn + p-[> xn+p-2) ~T • • •
... +d (xn+l, xn) < (feP"1 + kP-z + ... + k + 1) knd (xu x0) <
. <-jTrjd(*i.*o)- (II, 12; 5)
Отсюда получаем, что d(xn+P, xn) стремится к 0, когда п
стремится к +°°- Таким образом, последовательность хп
является последовательностью Коши. Так как Е по условию
полно, то эта последовательность сходится к некоторому пределу а.
В силу непрерывности f последовательность xn+i — f(xn)
сходится к Да), а так как xn+i также сходится к а, то f(a) — а
является неподвижной точкой отображения f. Описанная
процедура не только позволяет установить существование неподвижной
точки, но и является практическим методом ее вычисления.
Неравенство
kn
d {хп, а) = lim d (хп, хп+р) < ттгт d (*„ х0) (II, 12; 6)
р-»оо ' к
дает оценку быстроты сходимости последовательности л:„ к а.

§ 12. Теорема о неподвижной точке 109
Замечания. 1°) Предположение k < 1 необходимо, ибо
условие k ^ 1 не является достаточным ни для существования,
ни для единственности неподвижной точки.
Тождественное отображение метрического пространства в
себя удовлетворяет неравенству (II, 12; 1) при k = \\ все
точки пространства являются для него неподвижными. Сдвиг
х-*-х+1 на прямой также удовлетворяет неравенству
(11,12; 1) с k = 1, но он не имеет ни одной неподвижной точки.
29) Пусть f — отображение Е в Е, не обязательно
являющееся сжатием. Если одна из его итераций fp является сжатием,
то отображение f имеет неподвижную точку, и притом
единственную.
Напомним, что итерации отображения f множества Е в себя
определяются формулами:
f2 = f°f, fz = f°f°f, ■■■, fp = f°fp-l=fP-l°f- (H. 12; 7)
Пусть а — неподвижная точка /. Она является неподвижной
точкой для любой из итераций /, среди которых имеется
итерация fP, являющаяся сжатием, а, следовательно, имеющая
только одну неподвижную точку. Отсюда следует, что само f может
иметь только одну неподвижную точку. Для доказательства
существования будем исходить из того, что сжатие fP имеет
единственную неподвижную точку а. Элемент fp+i(a) может быть
записан двумя способами: либо f(fP(a)) =f(a), либо fP(f(a)).
Равенство fP(f(a)) = fP+i(a) = f(a) означает, что f(a) является
новой неподвижной точкой итерации fp. Поскольку fp, будучи
сжатием может иметь только одну неподвижную точку, то
f(a)=a, т. е. а является неподвижной точкой отображения /.
Таким образом, f имеет единственную неподвижную точку а.
Мало того, ее можно получить теми же последовательными
приближениями, так как последовательность Хо, хи х2, .. . ,
определенная формулами (II, 12; 3), сходится к а. В самом деле,
каждая из последовательностей
Xq, Xр, Х2р, • • • > Хпр, • . . ,"
■*1> -^р + 1» -^2р + 1> •••> ХПр^\, ...', Хр-.\, Х2р — \, • ••■> -^лр + р-1> •••
сходится к а, поскольку она определяет последовательные
приближения для итерации fp. Последнее означает, что вся
последовательность xQ, X[, Xi, ... сходится к а. (Отметим следующее:
предположение о том, что отображение \р является сжатием, не
влечет за собой непрерывности /.)
Предположим теперь, что сжатие f достаточно хорошим
образом зависит от некоторого параметра X. Тогда для каждого
значения К оно имеет, и притом единственную, неподвижную
точку а%. Отыщем условия, при которых неподвижная точка ак
непрерывно зависит от параметра К.

по
Гл. II. Топология
Теорема 46г. Пусть Е— полное метрическое пространство,
Л — топологическое пространство, a f — отображение Е X Л в Е.
Предположим, что для каждой фиксированной точки х из Е
частное отображение X->f(x,X) пространства Л в пространство Е
непрерывно и что для каждого А, е Л отображение fx: x-+f(x, X)
является сжатием Е в Е, соответствующим числу k <. 1
(формула (II, 12; 1)), не зависящему от к.Тогда единственная
неподвижная точка ах отображения fk непрерывно зависит от параметра X,
иначе говоря, отображение А,-»-а*, пространства Л в Е
непрерывно.
Доказательство. Обозначим через Ае какую-либо
точку Л. Тогда
d(av aj = d(f%(ak), f^iaj) <d(f^(aj, /\(aj) -f d(fx(aj, f^iaj) <
< kd (ax, a J + d(f K, X), f (ab, X0)), (II, 12; 8)
откуда
(1 — k) d K, a J < d (f (ab, X), f {au, XQ)).
Зададим е>0. В силу непрерывности f по X при
фиксированном х = аи существует в Л такая окрестность Т точки А0,
что соотношение AeF влечет за собой d(f(au, X), f {au, X0)) <|
<^е(1 — k). Тогда из соотношения Х^Т следует также
неравенство d (ax, аи)^.е, доказывающее непрерывность
рассматриваемого отображения в точке Х0 пространства Л.
§ 13. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ НОРМИРОВАННЫХ ВЕКТОРНЫХ
ПРОСТРАНСТВ И ПРОСТРАНСТВ БАНАХА
Пусть Е и F — два векторных нормированных пространства
над полем К, которое мы всегда будем предполагать полем
вещественных или полем комплексных чисел1). Пусть и —
некоторое отображение Е в F. Напомним, что и называется
линейным, если
->-»■-»■->• -> ->
и (х + у) = и (х) + и (у), и (Хх) = Хи (х),
-> ■>
X е К, х^Е, у^Е.
') Любое векторное пространство над полем комплексных чисел является
также векторным пространством над полем вещественных чисел. Поэтому,
если заданы'два векторных пространства Е и F, одно над полем
вещественных, другое над полем комплексных чисел, то оба их можно рассматривать
как векторное пространство над полем вещественных чисел.
Принято одним и тем же символом 0 обозначать нейтральные элементы
(вообще говоря, различные) пространства Е и F. Очевидно, ы(0)=0. Одним
и тем же символом II II принято часто обозначать нормы в Е и F.

§ 13. Нормированные векторные пространства
111
Если Е конечномерно, то линейное отображение Е в F
заведомо непрерывно и даже удовлетворяет условию Липшица, а
значит, равномерно непрерывно. В самом деле, поскольку все
нормы в конечномерном пространстве эквивалентны
(теорема 13), то для доказательства непрерывности, а также и
равномерной непрерывности') достаточно ввести в Е некоторый ба-
->->-> ->
зис ех, е2 еп и определить норму любого элемента х
через его координаты в этом базисе хи хг хп по формуле
||х|| = max\х,\. При этом
|| «(*')-«(>) II = || «(*'-*'') 11 =
и ( 2 (*{ - х'!)\ | = || 2 (*; - х'!) и (е{) | <
<(2||"Й)|) max \х'г-х';\^к\\Р-х"\\,
\(=1" ч ""/ 1=1, 2 л1 '
что полностью доказывает наше утверждение.
Если же, напротив, мы будем считать Е бесконечномерным,
то высказанное утверждение будет неверным. Как это ни
кажется странным, существуют линейные разрывные
отображения.
Приведем пример. Возьмем в качестве Е векторное
пространство полиномов с вещественными коэффициентами над полем
вещественных чисел2). Норму в Е введем по формуле
IIP||= max \P(x)\. (II. 13; 1)
0<х<1
В том, что это действительно норма, легко убедиться, ибо все
необходимые для нормы неравенства проверяются без труда.
(Существование максимума вытекает из непрерывности Р и
теоремы 29.) Очевидно, ||А,Р|| = |Х\ \\Р\\ для любого
вещественного К, а для любых полиномов Р и Q имеет место неравенство
WP + QW < \\Р\\ + IIQII. Если Р Ф-О, то \\Р\\ > 0; если же \\Р\\ =
') Непрерывность является топологическим, а не метрическим свойством,
чего нельзя сказать относительно равномерной непрерывности; однако
теорема 12 утверждает, что в определении равномерной непрерывности
некоторого отображения нормированного векторного пространства в другое
пространство нормы можно заменить эквивалентными нормами.
2) Сложение и умножение на вещественное число является обычным
сложением полиномов и обычным умножением их на число. При этом Е будет
векторным пространством, нулевым элементом которого является
полином s=0. Векторное пространство полиномов степени ^т имеет размерность
"*+ 1. Один из его базисов составляют полиномы 1, х, х2, ..., хт. Векторное
пространство всевозможных полиномов поэтому бесконечномерно.

112
Гл. П. Топология
= 0, то полином Р, равный нулю на [0, 1], тождественно равен
нулю.)
Выберем в качестве и вещественную функцию над Е, которая
каждому полиному Р ставит в соответствие его значение в
точке х — 3: и(Р) = Р(3). Это, очевидно, некоторая линейная
форма над Е. Покажем, что она разрывна. Для этого достаточно
рассмотреть последовательность полиномов, определенных
формулами:
Pn(x) = (j)n. (II, 13; 2)
Очевидно, \\Рп(х) II = 2~п, и, следовательно, эта последова-
->
тельность сходится к 0 в Е. Тем не менее Р„(3) = (3/2)п, и
потому последовательность значений и(Рп) стремится к +оо, а
это означает, что отображение и разрывно.
Теорема 47. Всякое линейное отображение
нормированного векторного пространства Е в нормированное векторное
пространство F, непрерывное в нуле пространства, непрерывно
всюду. Это отображение, кроме того, удовлетворяет условию
Липшица, а, следовательно, равномерно непрерывно. Для того
чтобы отображение обладало этим свойством, необходимо и
достаточно, чтобы существовало такое постоянное число k^-0,
что
|| и (х) ||< k|| х || для всех х из Е. (II, 13; 3)
Доказательство. Докажем прежде всего, что если
отображение и непрерывно в нуле пространства Е, то существует
число k, при котором имеет место неравенство (II, 13; 3).
Непрерывность и в нуле влечет за собой существование такого числа
-> ->• .
г\ > 0, при котором из ||х|| ^ т] следует ||«(х)|| ^ 1. В силу ли-
-»
нейности и, с помощью гомотетии получаем, что из ||х|| ^ Кг\
-»
следует ||«(х) II =SS А,. Так как первое из этих неравенств всегда
->
выполняется, если взять К = ||х||/т], то будет всегда выполнять-
-> ->
ся и второе неравенство ||и(х)|| ^ ||х||/т], и мы получим искомое
неравенство с k = 1/т). Обратно, предположим, что существует
некоторое число k, при котором имеет место неравенства
(II, 13; 3). Тогда отображение и не только будет непрерывным
в нуле пространства Е, но будет также непрерывным всюду и
даже удовлетворяющим условию Липшица, ибо, в силу
линейности и, имеет место неравенство
|| и (х') - и (х") || = || и {Р - х") ||< k || х' - х" ||. (II, 13:4)

§ 13. Нормированные векторные пространства
113
Замечание. Это теорема включает в себя, как частный
случай, теорему 12. В самом деле, утверждение «две нормы а
векторном пространстве Е эквивалентны» равносильно
утверждению «тождественное отображение пространства Е,
снабженного одной из двух норм, на пространство Е, снабженное
другой нормой, является непрерывным». Но тогда из (II, 13; 3)
следует (11,4; 1).
Ядро и образ непрерывного линейного отображения
Пусть Е и F — векторные пространства над полем Каи—,
линейное отображение Е в F.
Ядром отображения и называется множество таких х из Е,
■> -*■ .
что и(х) = 0. Это множество является также прообразом
и~1{0}. Ядро является векторным подпространством в Е, ибо
■> ■> ->->->->
для любых х и у, принадлежащих ядру, и (х) = О, ы(г/) = 0, а
■> ■> ■> ■> ■> -> ->
так как ы (х + у) = и (х) + ы (г/) = 0, то х+г/ также принадле-
->■ ->.->. ■>
жит ядру; и(Хх) = Хы(х) = 0 для любого скаляра X, т. е. Кх
также принадлежит ядру.
Образом отображения и называется образ и(Е)
пространства Е при отображении и. Это также некоторое векторное
подпространство в F. Размерность этого подпространства
называется рангом отображения и. Напомним, что если Е и F
конечномерны и если в рассматриваемых пространствах выбраны
базисы, то и выражается с помощью некоторой матрицы. Ранг
отображения и является наибольшим порядком отличных от
нуля миноров этой матрицы. Напомним, что ранг является
также разностью размерности Е и размерности ядра
отображения и.
Если пространства Е и F нормированы, а и непрерывно, tq
ядро является замкнутым векторным подпространством, ибо
оно является прообразом подмножества F, сводящегося к точке,
которое замкнуто (теорема 8). Образ же не обязательно
замкнут 4) .
Определение. Точная нижняя грань таких чисел k, при
которых выполняется неравенство (II, 13; 3), называется нормой
линейного отображения и2). Эта норма обозначается через \\и\\
') Образ замкнутого подмножества при непрерывном отображении
вовсе не обязан быть замкнутым!
2) Норму можно определить и тогда, когда линейное отображение и
разрывно. В этом случае следует положить ||ыЦ=+о°. Заметим, что эта
точная нижняя грань является минимумом.

114
Гл. 11. Топология
и определяется следующими соотношениями:
II и 11= sup^i^^= sup ||«WH= sup || u(x) ||. (II, 13; 5>
1сфо 11*11 ntii<i |й=1
хфО
Заметим, в частности, что для любого х
ll«(*)IKII"IIIUI|. (И, 13; 6)
Теорема 48. Множество & (Е; F) линейных непрерывных
отображений векторного нормированного пространства Е в
векторное нормированное пространство F имеет структуру
нормированного векторного пространства с нормой, определенной
формулой (II, 13; 5). Кроме того, если G— третье нормированное
векторное пространство, ue^(E; F), a ne^(F; G), та
v о и е & (Е; G) и имеет место неравенство
II о о и || <|| о ЦП и ||. (II, 13; 7)
Доказательство. Докажем сначала, что &(Е; F) имеет
структуру векторного пространства над полем К. Пусть «i и
«2 — два линейных непрерывных отображения Е в F. Определим
отображение «i + "г формулой:
(и1 + и^{х) = и1(х) + и2(х). (П> 13'>8>
Легко проверить, что так определенное отображение
является новым линейным отображением Е в F. С другой стороны,
неравенство (полученное из (II, 13; 6)):
||(u, + U2)(*)ll<ll"i(3lH-ll"2(3ll<(ll"ilH-ll"2ll)ll*ll (И. 13; 9)
показывает, что оно непрерывно, т. е. иГ+ «2 ^ 3? {Е; F), и,
кроме того, согласно (II, 13; 5), имеет место неравенство
II и. + «2II < II "ill+ 11 "я И- (II, 13; 10)
Мы видим, что в SE(E\F) определено сложение элементов*
превращающее его в абелеву группу. Нулем этой группы
является нулевое отображение 0, т. е. такое отображение,
которое каждому элементу из Е ставит в соответствие нулевой век-
тор 0 пространства F. Пусть теперь К—некоторый скаляр. Для
любого u^3?(E;F) определим отображение Хи по формуле
(Ки)(х) = К(и{х)). (II, 13; 11)

§ 13. Нормированные векторные пространства
115
Легко проверяется, что это снова некоторое линейное
отображение. Кроме того, это линейное отображение непрерывно, т. е.
%u^2?(E\F). В самрм деле,
|[ (Хи) (х) || = I Я ||| и (х) || <| Я ||| и ЦП х ||. (II, 13; 12)
Кроме того,
|| UII = sup || (Яи) (х) || = | Я | sup || и Й ||; (II, 13; 13)
№=i n*ii=i
другими словами,
||Яи|| = |Я|||и||. (И, 13; 14)
Таким путем в множестве 2 (Е; F) мы определили
умножение на скаляры. Легко видеть, что это умножение обладает по
отношению к сложению элементов из 9? (Е; F) всеми
свойствами, необходимыми для того, чтобы можно было считать S' (Е; F)
векторным пространством над полем К. Кроме того, из
(II, 13; 10) и (11,13; 14) следует, что отображение u-»-||u||,
действительно, определяет некоторую норму в 3? (Е; F) (тот факт,
что из ||и|| = 0 следует и = 0, очевидным образом вытекает из
(II, 13; 6)). Таким образом, %{E;F) является нормированным
векторным пространством. Далее, если кей'^Р) и ое
eS'I^G), то, очевидно, v о и е 2?(Е\ G)1). С другой стороны,
-> ■ -> ->
из неравенства || (v о и) (х) || < \\v\\ \\и(х)\\ < ||t>|| ||ы|| ||х|| следует,
что ||о о ы|| ^ ||о|| Hull — неравенство (II, 13; 7), указанное в
формулировке теоремы.
В частности, когда F является полем скаляров К, то
линейное отображение Е в К называется линейной формой на Е.
Пространство линейных непрерывных форм обозначается через Е'
и называется сопряженным к Е. Оно является векторным
нормированным пространством2).
-> ->
Обозначения. Если ttexj^F) и х е Е, то через и°х
-> -> ->
(или даже их) удобно обозначать образ и(х) вектора х при
') Композиция двух линейных отображений линейна, а композиция двух
непрерывных отображений непрерывна (теорема 10).
2) В курсах алгебры и геометрии сопряженным к векторному
пространству Е обычно называют векторное пространство линейных форм на Е. Это
определение совпадает с нашим, если Е конечномерно, так как в этом
случае при любой норме на Е каждая линейная форма непрерывна (стр. 111).
Если же пространство Е бесконечномерно и нормировано, то существуют
разрывные линейные формы, но они не представляют интереса, и термин
«сопряженный» предпочтительно оставить за пространством непрерывных
лилейных форм.

116
Гл. II. Топология
отображении и. Если, кроме того, имеется отображение v e
ei?(F; G), то через v-u или vu часто обозначают композицию
-> ->
Vou. Тогда соотношение (v ° и) (х) = v{u{x)) может быть запи-
-> -> -> ->
сано так: (v о и) о х, или v°{u<>x), или v°uox, или vux. Если
F = Е и и^ 2 (Е; Е) ,то « о и обозначается через и2, «он»«
обозначается через и3 и т. д.
Теорема 49. Пусть Е и F — нормированные векторные
пространства, Ei — плотное векторное подпространство Е и и{ —
линейное непрерывное отображение £\ в F, Если F полно, то
существует, и притом единственное, непрерывное .продолжение
и отображения и\ в Е. Это отображение Е в F линейно, и
норма и в 2' (Е; F) равна норме их в 2? (Ей F).
Доказательство. Поскольку отображение «i линейно и
непрерывно, оно равномерно непрерывно (теорема 47).
Следовательно, согласно теореме 45, существует, и притом
единственное, непрерывное отображение Е в F, являющееся продолже-
-> ->
нием «1. Докажем сначала, что и линейно. Пусть х и у — эле-
->->-> ->■ ->
менты Е, а X—некоторый скаляр. Пусть х0, хх, х2, . . . и у0,ух,
->
у2, ... — последовательности элементов из £ь сходящиеся со-
-> ->
ответственно к х и у. В силу того, что Е является
топологическим векторным пространством (стр. 66), последовательность
-> -> -> -> ->
хп + уп сходится к х + у, а последовательность Кхп сходится
->
к 1х.
Имеем
" (х + У) = lim "l (хп + Уп) ') = Пш [ы, (хп) + щ (уп)]2) =
""" . Г" * -> (И, 13; 15)
= lim щ (хп) + lim щ (уп) 3) = и (х) + и (у) 4);
Л->оо л->оо
->- -> -> -> ->
и (1х) = lim щ (kxn) = lim Ли, (хп) = X lim и{ (хп) = Ки (х),
Л->оо л->оо л->оо
что говорит о линейности отображения и.
Покажем теперь, что норма ив 2 (Е; F) равна норме и{ в
S?(EuF). Из определения нормы (формула (II, 13; 5))
очевидным образом следует, что ||«ill ^ ||«||. Впрочем, если х^Е яв-
-> -> > -*
') Поскольку Хп + уп сходится к х + у и и является функцией,
непрерывно продолжающей и\.
2) Потому, что щ линейно.
s) Так как F является .топологическим векторным пространством.
*) Поскольку и непрерывно и является продолжением ut.

§ 13. Нормированные векторные пространства 117"
ляется пределом последовательности хп е Еи то и(х) является
-> -> ->
пределом «i(x„). Из неравенства ll«i(x„) || ^ ||«i|| ||х„||
и.непрерывности нормы (теорема 9), переходя к пределу, находим, чта
||и(х)|| ^ ||«ill IWI- Это означает, что ■ |l"ll ^ ll«ill, а
следовательно ||«|| = \\ui\\.
Следствие. В условиях теоремы, т. е. если £4 плотно в Е
и F полно, векторные нормированные пространства 3? (Е; F) и
Sg (Ei, F) можно отождествлять.
В самом деле, поставим в соответствие каждому линейному
непрерывному отображению и пространства Е в пространство F
его сужение «4 на Е\. Теорема утверждает, что так
определенное соответствие н->«1 пространств 2?(Е; F) и 9?(E\\F)
является биекцией, сохраняющей структуру векторного просгран-
ства и нормы. Это означает, что два векторных нормированных
пространства S?(E;F) и S (E^; F) могут быть отождествлены.
Определение. Векторное нормированное полное
пространство над полем вещественных и комплексных чисел
называется банаховым пространством.
Из изложенного ранее на стр. 102 (теорема 41) вытекает,,
что всякое конечномерное нормированное векторное
пространство является банаховым.
Т е о р е м а 50. Если Е и F — нормированные векторные
пространства^ и F банахово пространство, то пространство 3? (Е; F)
также банахово. В частности, сопряженное пространство Е' к
пространству Е банахово.
Доказательство. Достаточно доказать первое
утверждение. Поскольку поле скаляров К является банаховым, то
второе утверждение немедленно вытекает из первого (£' =
= &(Е; К)). Итак, пусть и0, ии и2, ... — некоторая
последовательность Коши в &(Е; F). Это означает, что при тип,
стремящихся к +оо, норма \\ит — «яII стремится к нулю.
Неравенство \\ит(х)— ип(х)\\ г=: ||ыт —ы„|| ||х||,
справедливое для каждого фиксированного х, доказывает, что последова-
тельность ип{х) является последовательностью Коши в F.
Поскольку F по предположению полно, то эта последовательность
сходится к некоторому элементу F, который мы будем
обозначать через и(х). Тем самым мы определили отображение-
u: x-*-u(x) Е в F. Покажем, прежде всего, что отображение и
линейно. Пусть х и у — элементы £ и Я—-некоторый скаляр.

118
Гл. II. Топология
Тогда
и (х + у) = Нт и„ (х + у) ') = lim (ы„ (ж) + ип (у)) 2);
rt-»oo rt-»oo
= lim ы„ (х) + lim ы„ (г/) 3) = и (х) + и (у),
Я->оо Я->оо
■> -> ->
и (Хх) = lim un (Хх) J) = lim Хип (х) 2) =
Я->оо Я-»оо
= Я lim ип (х) 3) = Хи (х),
(II, 13; 16)
что означает линейность отображения ы.
Докажем теперь, что отображение и непрерывно. Согласно
критерию Коши, существует такое целое число р, что из
неравенств tn^p и п^р следует неравенство \\ит — «nll^e.
Отсюда получаем, что для т > р, и> р \\ит\\ ^С ||«„|| + е.
Кроме того, выполняются также неравенства
11"тЙ-"»(3|Ке||х||, (И, 13; 17)
ll"m(*)IK(ll"»H + e)IU||. (И, 13; 18)
->
Фиксируя в (11,13; 18) п^р н вектор х и устремляя т к
+оо, получаем:
И"(*)1К(11"»11 + в)||х||, (И, 13; 19)
откуда следует непрерывность отображения и. Таким образом,
и является элементом пространства 3?{E;F).
->
Если теперь при фиксированном х и п ^ р в соотношении
(II, 13; 17) устремить т к +°°, то получим
II и (ж)-«„(*) ||<е || ж ||, (И, 13; 20)
а, следовательно,
||«-«„1Ке. (И, 13; 21)
Полученное неравенство показывает, что ип стремится к и
в нормированном пространстве & (Е; F) при п, стремящемся к
+ оо, а это означает, что SB (E\ F) полно.
Произведения нормированных векторных пространств
Пусть Ei и Ег — два векторных пространства над полем К.
Известно, что их произведение Е{ X Е2 может быть снабжено
') По определению и.
2) В силу линейности и„.
3) Так как F является топологическим векторным пространством.

§ 13. Нормированные векторные пространства 119*
структурой векторного пространства. В самом деле, если
(х\, ^2) и (У\> У2) — Два элемента этого произведения, то можно
положить
(*ь *2> + {уи у2) = (*, + 2/1, *2 + у2)- (И, 13; 22>
Если X—некоторый скаляр, то можно считать
M*i, х2) = (А,*,, Я*2). (II, 13;23>
Введенные операции на Et X £2 превращают его в векторное
пространство над полем К.
Векторное пространство R" (соответственно С") является
не чем иным, как векторным пространством произведения п
пространств, тождественных R (соответственно С),
рассматриваемых как векторные пространства над самим- R (или С).
В этом векторном пространстве существует два особых
подпространства: пространство Ai = Ei'X{0} элементов вида
-> -> -v ■> ->
(х\, 0) и пространство А2 = {0} X ^2 элементов вида (0, х2). Эти
пространства являются дополнительными в том смысле, что
-> ->
каждый элемент {хи х2) произведения единственным образом
записывается в виде суммы одного элемента из первого про-
-> ->
странства и одного элемента из второго, так что {хи х2) =
= (*„ 0) + (0, *2).
Когда два векторных подпространства некоторого векторного
пространства являются дополнительными, исходное
пространство может быть представлено в виде прямой суммы этих
подпространств, и эта прямая сумма обозначается знаком ф.
Поэтому мы можем записать
ЕХХЕ2 = Ех Х{О}0{6} X Е2. (II, 13; 24>
Если Ei и Е2—два нормированных векторных пространства
с нормами || Hi и || ||2, то на произведении Е\ X Е2 не существует
нормы, которая была бы предпочтительнее других. Можно
взять, например, какую-либо одну из следующих эквивалентных
норм:
II (*„ х2) ||=тах (|| Xi ||,, || х2 %), или || *, ||, + II х21|2, или V\\ *\ %М\ х21.
(II, 13; 25)
Для каждой из этих норм топология пространства £\ X Е2
является топологией произведения. Дополнительные
подпространства Ei X {0} и {0} X Ег замкнуты в Е. Если не будет
оговорено противное, пространство £\ X Е2 всегда будет снабжаться

120 Гл. II. Топология
одной из этих норм и один и тот же символ || || будет
обозначать нормы в Еи Е2 и Ei X Ег-
Теорема 51. Пусть £\ и Е2— два нормированных
векторных пространства. Всякое линейное непрерывное отображение
и из Е\ X Е2 в векторное нормированное пространство F
выражается, и притом единственным образом, в виде
-> -> -> ->
и(хх, х2) = их (xt) + и2 (х2), (II, 13; 26)
где «1 (соответственно и2) является линейным непрерывным
отображением Ei (соответственно Е2) в F. Обратно, если «4
(соответственно иг) является линейным непрерывным
отображением Ei (соответственно Е2) в F, то отображение и,
определенное формулой (II, 13; 26), яЪляется линейным непрерывным
отображением Ei X £2 в F.
Доказательство. При заданном и определим отобра-
->
жение «1 следующим образом: значением их на элементе Х\ из Ех
-> -> ->->->
будет значение и на элементе (xx,Q) из Ех X Е2: их (хх) = и(х, 0).
Таким же образом определим отображение и2 из Е2 в F.
Отображения «1 и «2, очевидно, являются линейными. Они
непрерывны, если на Е\ X Е2 с помощью формулы (II, 13; 25) ввести
одну из эквивалентных норм, т. е. если на Ех X Е2 ввести
топологию произведения.
В самом деле, в этом случае имеем неравенство
II". £.) 11 = 11 "&. 0)||<||«||||(^, 0).||=||ы||||£||, (II, 13;27)
которое доказывает наше утверждение и показывает в то же
время, что имеют место неравенства
11",1К11"11, ll«2ll<ll"l|. (II, 13; 28)
Непосредственно видно, что
->-> ->-> ->-> -> ->
и(хх, х2) = и{хи 0) + «(0, х2) 1) = их(х1) + и2(х2), (II, 13; 29)
а это доказывает, что и представлено в указанном выше виде.
Непосредственно видно, что других отображений «i и и2,
обладающих тем же свойством, не существует, потому что, если
бы vx и v2 были бы такими линейными отображениями, что
-> -> ->->->
.и (хх, х2) = vx (хх) + v2(x2), то мы имели бы и (хх, 0) = и, (хх),
•а следовательно, vx = их и точно так же v2 = и2.
Обр'атно, если щ (соответственно иг) является линейным
непрерывным отображением £\ (соответственно Е2) в F, то ото-
') В силу линейности и, а также потому* что (хх, хг) = (*i, 6) + (б, х2).

§ 13. Нормированные векторные пространства
121
бражение ы, определенное формулой (II, 13; 26), очевидно,
линейно и, кроме того, непрерывно, ибо
||И(*1, *2)IKII"l5l)ll+ll«2(*2)IKII"lllll^ll + ll"2llll*2lK
<(||«ill+ll«2lDmax(||*I||,||*2||K(||u,||+||U2|D||(*„J!)||.(II,13;30)-
Отсюда сразу же получаем, что оно удовлетворяет
неравенству
ll"ll<ll",ll + ll«2ll- (II, 13; 31)
Мы предоставляем читателю определить структуру
нормированного векторного пространства произведения п
векторных нормированных пространств ЕиЕ2, ..., Еп и обобщить
теорему 51 на линейные непрерывные отображения Е\ХЕ2Х ...
... X Еп в F.
Билинейные непрерывные отображения произведения
нормированных векторных пространств
в нормированное векторное пространство
Пусть Е, F, G— векторные пространства над полем К. Мы
изучили линейные отображения векторного пространства Е X F
в пространство G. Теперь рассмотрим совершенно новое
понятие билинейного отображения Е X F в G.
Отображение и пространства Е X F в пространство G
называется билинейным, если при фиксировании одной из
переменных оно линейно относительно другой переменной. Если мы
зафиксируем х, то и определит некоторое частное отображение
-> -> ->
у->и(х, у) пространства F в G. Это отображение обозначается
через «->., так что
X
и+(у) = и(х,у). (II, 13; 32)
->
Удобно также обозначать это отображение через и(х, ), опу-
->
екая переменную у ').
Если и — билинейное отображение, то и-> должно быть
линейным отображением F в G; другими словами, должны выпол-
') Если Е и F различны, обозначение u_>. для данного элемента х из Е
х
не вызывает недоразумений. Но если E=F и и является билинейным
отображением Е X Е в G, то обозначение u_>. для элемента л: из £ не имеет точ-
X
ного смысла, ибо непонятно, о какой из частных функций идет речь — о
первой или второй. В этом случае следует писать и(х, ) или и( , х).

122
Гл. II. Топология
няться равенства:,
и(х, у1 + у2) = и(х, у{) + и(х, у2),
> -> -> -> Щ. 1-3; 33)
и(х, Ху) ~Хи(х, у).
-> -> ■> ->
Аналогично, частное отображение «-> или и( , у): х -> и (л:, г/)
должно быть линейным отображением Е в G; другими
словами,
и(х{ + х2, y) = u(xi, y) + u(x2, у),
-> -> -> -> (И. 13; 34)
и (Ял:, у) = Яи (х, г/).
Имея в виду соотношения, относящиеся к сложению,
говорят, что и дистрибутивно по отношению к сложению. Из двух
предыдущих формул легко получить соотношения:
■>->->-> ->-> ->-> ->-> ->->
и (*i + х2> г/, + г/2) = и (хи ух) + и(хи у2) + и (х2, ух) + и (х2, у2) '),
(II, 13; 35)
■> ■> ■> ■>
и(Хх, цу) = Хци(х, у).
Например, скалярное произведение векторов является
билинейным отображением R3 X R3 в R; векторное произведение
является билинейным отображением R3 X R3 в R3. Прототипом
билинейных отображений являются обычные произведения
вещественных или комплексных чисел. Это — билинейные
отображения R X R в R или С X С в .С'. Впрочем, любое
билинейное отображение R X R в R имеет вид (х, у) —> сху, где с —
некоторая вещественная постоянная, в то время как линейное
отображение R X R B R имеет вид (х, у) —► ах + &#, где а и
6 — вещественные постоянные.
Теорема 52. Всякое билинейное отображение
произведения нормированных векторных пространств Е X Fв
нормированное векторное пространство G, непрерывное в нуле
пространства Е X F, непрерывно всюду (но не равномерно
непрерывно). Для того чтобы оно было таким, необходимо и
достаточно, чтобы существовала такая постоянная k ^ 0, что для
*■ > -
всех х из Е и всех у из F имело место неравенство
\\u(t,y)\\^k\\x\\\\y\\2). (П, 13; 36)
') Если бы и было линейным на Е X F> то в правой части равенства
■> ->' ■> -> ■> ■> -> ■>
мы бы имели либо u(xlt yi) + u(x2, у2), либо и(хи у2) + и(х2, у{).
2) Для линейного отображения правая часть имеет, например?-такой вид:
k (IU|| + IMI).

§ 13. Нормированные векторные пространства 123
Доказательство. Пусть Е, F, G — векторные
нормированные пространства, и пусть и — билинейное отображение Е X
X F в G, непрерывное в нуле. Тогда, согласно определению
топологического произведения, должно существовать такое чис-
-*• ->
ло Л > 0, что из неравенств || х || <! т), || у || ^ ti следует нера-
-*• -*•
венство || и (х, у) || ^ 1. Если мы теперь произведем гомотетию
с отношениями К и ц ^ 0, то из второй формулы (II, 13; 35) по-
-> -> ->■ ->
лучим, что из || х || <; 1ц, \\у || <! цт) следует || и (х, у) || <! Хц.
Так как первые неравенства будут выполнены при X—
= IUII/t). Н- = Н#Н/л> то мы всегда будем иметь неравенство
II и {х, #)||*^(1ЛгОН х\\\\у\\, являющееся формулой (II, 13; 36)
с й=1/т)2. Обратно, пусть и является билинейным
отображением, удовлетворяющим неравенству вида (II, 13; 36).
Докажем, что тогда оно непрерывно всюду. Пусть задана точка
> ->
(а, Ь) пространства - Е X F и число е > 0. Имеет место формула
-> -> -> -> ->->-> ->->->
«(*> У) — и(а, Ь) = и{х — а, у) + и{а, у — Ь), (II, 13; 37)
из которой вытекает оценка
\\u(t,y)-u(a, b)\\^k\U -a\\\\y\\+ k\\a\\\\y - b\\. (II, 13; 38)
4 Положим т)2=е/(2&||а||). Из неравенства || у — b ||^ть следует,
очевидно, неравенство д|| а |||| у — b ||<!e/2. Выберем затем
t)i =e/[2k(\\b\\+ Лг)]- Очевидно, для || у — b ||< т)2 имеет место
-> -> ->■ ->
оценка || у || <! || b || + ц2> откуда получаем, что из \\х — а||^т),
вытекает неравенство k\\ x — а |||| у\\ s^e/2.
■> ->
Полученные оценки показывают, что из || х — a||<Tii>
-> -> ->->->->
\\У — b ||<; т)2 следует неравенство \\и{х, у) —и {а, 6)||^е, а это
является определением непрерывности отображения и в точ-
ке (а, Ь).
Заметим, напротив, что если билинейное отображение и не
является тождественно нулевым, то оно не может быть и
равномерно непрерывным. В самом деле, предположим, что суще-
-> ->■ -> ->
ствует хотя бы одна пара (а, Ь), для которой и (а, Ь) ф 0.
Рассмотрим теперь в пространстве £ X F последовательность
точек Хп==(па, nb) и последовательность точек Yn = ((n-\- \/n)a,
{п+ \/п)Ь). Из неравенства || Хп — Yn IK(||a|| + || b \\)/n следует,

124
Гл. П. Топология
•что эта величина стремится к нулю при п, стремящемся к -f- оо.
-> ->
Тем не менее норма разности и (Хп) — и (Yn) — (п2 — (п -f- 1/«)2) X
■*■"*" "*" "*"
Х"(я. Ь) = —- (2 + 1/п2)и(а, Ь) при п, стремящемся к +°о, стре-
-> ->
мится к 21|«(а, 6)||=^=0, а это означает, что функция и
равномерно непрерывной быть не может ')•
Определение. Точная нижняя грань таких чисел k, при
которых имеет место неравенство (II, 13; 36), называется
нормой билинейного отображения и обозначается через ||«||. Таким
образом, по определению,
-> ■>
||и ||= sup ""i*'^" = .» sup^ ||(*. J) ||. (II, 13; 39)
■%фХуФо Л*ШИ i*i<i.i»Ki
Заметим, что всегда
11"(*, S/)IKII"llll*llllJll- (II, 13; 40)
Теорема 53. Множество 3!г{Е, F; G) билинейных
отображений произведения нормированных векторных пространств
Е X F в нормированное векторное пространство G будет иметь
структуру нормированного векторного пространства, если в нем
определить норму по формуле (II, 13; 39). Если, кроме того, G
.является банаховым пространством, то S,2(E,F;G) также
будет банаховым пространством. В частности, выбирая в
качестве G поле скаляров, получаем, что векторное пространство
билинейных непрерывных форм на произведении нормированных
векторных пространств является банаховым пространством.
Доказательство аналогично доказательствам теорем 48 и 50.
Рассмотрим теперь непрерывное билинейное отображение и
•пространства Е X F в пространство G. Мы видим, что для фик-
сированного х оно определяет линейное отображение и-> из F
в G. Это отображение, очевидно, непрерывно и его норма
;< || «|| || х || в силу (II, 13; 40), а значит, «^принадлежит
пространству &(F; G). Тем самым мы нашли отображение, кото-
рое каждому элементу х из Е ставит в соответствие некоторый
элемент «> из S(F\ G); другими словами, мы определили
отображение U пространства Е в пространство 3' (F; G). Оба
пространства Е и 3?(F; G) являются нормированными векторными
') Впрочем, известно, что произведение (х,у)^>-ху не является
равномерно непрерывным отображением R X R в R и что функция х-ух2 не
Лвляется равномерно непрерывной функцией из R в R.

§ 13. Нормированные векторные пространства 125
пространствами. Докажем, что U является линейным
непрерывным отображением Е в &(F; G) и что норма \\U\\ этого
линейного отображения есть не что иное, как норма ||и||
рассматриваемого билинейного отображения.
Докажем прежде всего линейность отображения U; для этого,
естественно, не требуется использовать топологию. Нам надо
показать, что
ыч> -> —ы-> + "ч>- и ы-> = Яы->. (II, 13; 41)
Хх+Хг X, Хг АХ X
Все выписанные элементы являются элементами
пространства 3?{F\ G), т.е. линейными отображениями F в G. Согласно
определению суммы двух линейных отображений или
произведения линейного отображения на скаляр, эти равенства озна-
->
чают, что для каждого элемента у из F имеют место
равенства:
->->-> ->-> ->-> ->-> ->->
и (л;, + х2, у) —и (х„ у) + и (х2, у) и (кх, у) = Ки (х, у). (II, 13; 42)
Но эти равенства справедливы, ибо они означают лишь то,
что частное отображение и^> пространства F в пространство G
v ->
для каждого фиксированного у линейно.
Докажем теперь непрерывность отображения U. Норма ли-
->
нейного отображения U(x) = u^. пространства F в G не пре-
восходит величины ||и|| ||х||. Из этого неравенства следует, что
U является линейным непрерывным отображением Е в 2? (F; G)
и что \\U\\ < ||u||. Так как II U (x) ||<|| U \\\\х\\, то || и (х, у)\\ =
= \\U(x)\\\\y\\<\\U\\\\x\\\\y\\, откуда ||ы||< ||£/||, а, значит,
\\и\\ = \\Щ.
Обратно, будем исходить из линейного непрерывного отоб-
ражения U из Е в 3? (F; G). Для каждого х из Е, U(x)
является элементом &{F\ G), т.е. линейным непрерывным
отображением F в G, и, следовательно, для каждого элемента у из F
-> ■*• -> ■*■
и (х) ■ у является элементом G. Если мы положим и (х, и) =
= U(x)-y, то получим, что и: (х, у)-*и(х, у) есть
отображение Е X F в G. Без труда проверяется, что оно билинейно, а из
неравенств \\и(х, у) ||<|| U (х) |||| ylKII U ||||*||||J ||, ||ы||< ||£/Ц
следует его непрерывность.
Частное отображение и>, соответствующее и, для каждого
. ■> ->
фиксированного х является не чем иным, как U(x), а линейное

126
Гл. II. Топология
непрерывное отображение Е в 3(F;G), соответствующее и,
есть не что иное, как исходное отображение U. Установленное
соответствие между отображениями и и U является биекцией
пространства 3i(E, F; G) билинейных непрерывных
отображений из Е X F в G на пространство 3 (Е; 3(F; G)) линейных
непрерывных отображений Е в 3(F; G), и эта биекция
сохраняет векторные структуры и нормы. Существует, естественно,
аналогичная биекция 3i(E,F; G) на 3(F; 3(E, G)).
Теорема 54. Пусть Е и F — нормированные векторные про-
-*■ -*■
странства. Тогда отображение (и,х)-^>и-х пространства
3 (Е; F) X Е в пространство F является билинейным
непрерывным и имеет норму, равную 1 (за исключением того случая,
когда Е или F сводится к нулю).
Если Е, F, G — три нормированных векторных пространства,
то отображение (и, v)-*Vou пространства 3 (Е; F) y^3(F; G)
в пространство 3? (Е; G) билинейно, непрерывно и имеет норму,
равную 1 (за исключением того случая, когда Е, F или G
сводятся к нулю).
Доказательство. Билинейность рассматриваемого
отображения очевидным образом вытекает из определения суммы
двух линейных отображений и умножения линейного
отображения на скаляр1). Непрерывность'этих билинейных
отображений и тот факт, что их норма ^1, сразу вытекает из оценок
||и-*||<||и||||*||, II о-и II <|| и НИ «II (формулы (11,13; 6) и
(II, 13; 7)). Далее, при заданном и и любом заданном е > О,
согласно определению нормы и, существует по крайней мере
-*■-*■ -*■ ->
один элемент х ф О из Е, такой, что || и ■ х\\^ (1 — е)||ы |||| х ||,
откуда следует, что норма первого билинейного отображения
^1 — е. Так как е может быть выбрано сколь угодно малым,
то эта норма ^1, и, следовательно, "она равна 1.
Тот факт, что норма второго билинейного отображения
также равна 1, мы примем без доказательства.
Мультилинейные непрерывные отображения
Пусть Е\, Е2, ..., Еп, F — нормированные векторные
пространства над одним и тем же полем К (полем
вещественных или комплексных чисел). Отображение и пространства
') Билинейность этих отображений позволила ввести
мультипликативные обозначения их, vu и и" на стр. 115.

§ 13. Нормированные векторные пространства
127
Е\ X Е2 X .. • X Еп в пространство F называется мультилиней-
ным (или п-линейным), если при фиксировании п—1
переменных в произвольных п—1 векторных пространствах это
отображение является линейным относительно п-й переменной.
Например, обычное произведение (xi, х2, . .., хп)-+х1х2... хп
является п-линейным отображением К" в К. В пространстве R3
смешанное произведение трех векторов определяет
трилинейное отображение R3 X R3 X R3 в R.
Пространство п-линейных непрерывных отображений из
Ei X Е2 X • • • Х^п в F можно наделить структурой векторного
нормированного пространства. Его тогда обозначают через
9?п{Еи Ег, ..., Еп; F). Если F является банаховым
пространством, то и рассматриваемое пространство также будет
банаховым.
Изложенное перед теоремой 54 может быть обобщено
следующим образом:
Теорема 542. Между пространствами
^п\Е\, Е2, •••> Еп; *")» *ь\ \Е\'> °bn-\\Efr • ••> Еп; г)),
ic2 \Ь\, Ь2, £сп-2(Ь3, ••■> Еп', г)), ,.,, tcn-i (С], Ь2, ..., £n_ii zc 1 (сп; г))
и пространствами, полученными перестановкой индексов,
существуют биекции, сохраняющие векторную структуру и норму.
Элемент U в 9?Р{Е{,Е2, ..., Ер; 2Vp(£p+I En;F)),
соответствующий элементу и е 9?п{Е\, Е2, ..., Еп; F), задается
формулой
->-> ->-> -> ->-> ->-> ->
U \Х\, Х2, . • • , Хр) • \Xp + i, • • •, Хп) = U \Xit Х2, . . ., Хр, Хр + \, . . ., Хп).
(II, 13; 43)
Алгебры. Нормированные алгебры
Алгеброй зФ над полем К называется векторное
пространство над полем К, в котором определено билинейное
отображение s& X s& B «s^, называемое умножением и обозначаемое че-
■» -> ->-> ->-> -> -> ->->
рез (л:, у)—*-ху. Это умножение ассоциативно: (xy)z = x(yz) и
-> -> ->-> ->-> ->
имеет единицу 1ф0 (xl = lx для любого л:). Поле К само
является алгеброй. Нормированной алгеброй называется
алгебра, представляющая собой такое нормированное векторное
пространство, в котором
II/11=1, И5Г|КИ*|1П?11- (II, 13; 44)
Полная нормированная алгебра называется банаховой.
Пусть Е — нормированное векторное пространство. Простран?

128 Гл. II. Топология
ство 2? (Е; Е) будет нормированной алгеброй, если в нем
определить умножение элементов через их композицию: (и, v) —*■
—*uov. Эта алгебра банахова, если пространство Е банахово.
§ 14. РЯДЫ В НОРМИРОВАННЫХ ВЕКТОРНЫХ ПРОСТРАНСТВАХ
Пусть задана некоторая последовательность и0, и,, и2, ...
элементов нормированного векторного пространства Е. Сумма
5„ = «o + «i+ ••• +«/г= 2 ит (И, 14; 1)
00 ->
называется частной суммой с индексом п ряда 2 "*• Частная
сумма Sn является элементом пространства Е. Говорят, что
ряд 2л Uk сходится и имеет сумму S, если последовательность
-> -*
Sn сходится и имеет своим пределом S [). Понятие ряда
сводится, таким образом, к понятию последовательности.
Впрочем, верно и обратное: последовательность в нормированном
векторном пространстве можно выразить через ряд. Последо-
■> ■> ■> >
вательность хй, х{, хъ ... сходится и имеет пределом число а
тогда и только тогда, когда сходится ряд х0 + (jcj — *0) +
-> -> -> ->
-f(*2 —*i) + ... +(*п — *n-i) + ■■■ и имеет сумму,
равную а.
Если пространство Е конечномерно и если в нем выбран
некоторый базис, то, вспоминая результаты, полученные нами ра-
нее для последовательностей, можно утверждать, что ряд 2л ип
п
является сходящимся и имеет своей суммой S тогда и только
тогда, когда каждый ряд из координат 2 (un)i сходится к не-
п
>
которой сумме S,-, где («п)г есть i-я координата элемента и„,
a S{ есть i-я координата S.
Преимущество банаховых пространств заключается в том,
что в них, как и в поле комплексных чисел, можно судить о
сходимости ряда, не зная заранее о существовании суммы S.
Для того чтобы ряд в банаховом пространстве Е был
сходящимся, необходимо и достаточно, чтобы он удовлетворял кри-
') Сходимость или расходимость ряда сохраняется, если одну норму
заменяют другой, ей эквивалентной, ибо сходимость является топологическим
свойством.

§ 14. Ряды в нормированных векторных пространствах 129
->
терию Коши: при тип, стремящихся к +°°. II 5„ — 5т ||
стремится к 0, или же
-> -> ->
(Ve>0)(3«eN)(Vm>«)(VAeN):||Mm + Mm+1 + ... + Mm+fe||<e,
(П, 14; 2)
Отсюда получается основная теорема, дающая наиболее
важный критерий сходимости векторных рядов:
°° ^
Теорема 55. Пусть S чп — ряд из элементов банахова
№=0
пространства Е. Если ряд, составленный из норм, 2 II"nil
сходится, то и сам ряд также сходится и, кроме того,
->
II S«» IKS II и» II- (Н,14;3)
Доказательство. Проверим выполнение критерия Коши.
Так как ряд, составленный из норм, по условию сходится, то
для любого е > 0 можно найти такое п, что для всех m ^ n и
-> -> ->
любого k l|«m|| + IIWm+ill+ ... +ll«m+felKe- Отсюда тем бо-
-> -> ->
лее для m ^ пи любого k имеем, что ||Mm-f-"m+i ~Ь • • • + «m+ftll ^
^е, т. е. что заданный в Е ряд удовлетворяет условию
Коши, а так как пространство Е предполагалось полным, то
рассматриваемый ряд сходится. Кроме того, для конечного чис-
ла членов имеет место неравенство || Sn || ^- 2л II "mil, 0Т-
куда, переходя к пределу при п, стремящемся к +°°, и учиты-
-> -> ->
вая, что сходимость Sn к S влечет за собой сходимость ||S„|| к
->
||5|| (теорема 9), получаем искомое неравенство (II, 14; 3).
Определение. Говорят, что ряд элементов банахова
пространства Е нормально сходится, или абсолютно сходится1),.
если сходится ряд из норм, являющийся числовым рядом с
положительными членами. Ряд называется условно сходящимся,
если он сходится, не являясь нормально сходящимся.
Полнота пространства Е является весьма существенным
фактом. Впрочем, можно доказать следующее обратное
утверждение:
Теорема 56. Пусть Е — нормированное векторное
пространство. Если в этом пространстве сходится любой ряд 2«ш
ы„е£\ у которого сходится ряд из норм 2л II"»II» то
пространство Е полно.
') В силу теоремы 12, нормальная сходимость сохраняется, когда
норма Е заменяется на другую, ей эквивалентную.
5 Зак. 1339

130
Гл. 11. Топология
Доказательство. Нам надо доказать, что любая
последовательность Коши из Е является сходящейся.
Пусть «0, и,, «2, ... — некоторая последовательность Коши.
Тогда, каким бы ни было целое число k ^ 0, всегда можно
найти такое целое число Pk, что из tn ^ pk, п^ pk следует не-
•> •> .
равенство || ит — ип || ^ 1/2 .
Будем выбирать одно за другим целые числа ри таким
образом, чтобы последовательность ръ. была строго возрастающей,
и рассмотрим ряд ира + (ир_ — uj + (ирг — ир) +... . Ряд,
составленный из его норм, мажорируется числовым рядом
||« 1+1 + 1/2+1/4+ ..., сходящимся в силу известных
свойств числовых рядов с положительными членами. Но тогда,
в силу предположения относительно Е, рассматриваемый ряд
сходится, что означает сходимость подпоследовательности и .
Рассматриваемая последовательность Коши «„ имеет, таким
образом, сходящуюся подпоследовательность. Согласно
следствию 2 из теоремы 40, она должна сходиться, а, значит, Е
полно.
Перестановка членов ряда
Пусть «0 + «j + «2 + ... — ряд, составленный из
векторов Е. Изменить порядок членов последовательности означает
рассмотреть биекцию п-*рп из N на N и заменить данный ряд
новым «„+«„+«„+ ....
Теорема 57. Если ряд и0 + и, + щ + ... в
нормированном, векторном пространстве Е сходится и вместе с ним схо-
дится ряд, составленный из норм \\ и01| + || щ || + || и21| + ...,
то перестановка его членов не отражается на сходимости ряда
и, кроме того, не меняет его суммы.
->
Доказательство. Пусть S — сумма данного ряда. При
любом заданном е > 0 существует т, такое, что 2 ||ипН^в/2.
п>т
Далее, существует такое целое число т', что множество целых
чисел [pQ, pv р2, ..., рЛ содержит множество {0,1,2, ..., т].
-> ->
Тогда для п' ^ т' частная сумма ип + и + ... + и пре-
-> -> ->
образованного ряда равна ча'стной сумме щ-\-их-\- ... + ит,
дополненной на некоторую конечную сумму членов с
индексами >т.

§ 14. Ряды в нормированных векторных пространствах 131
Норма суммы этих дополнительных членов может быть
промажорирована суммой 2 II"nil, где р — наибольшее из
т<п^р
целых чисел р0, рх, ..., рп,\ тем более она не превосходит
->
2 II"nil. а, значит, и е/2. Таким образом, для п'^т' имеем:
п>т
|| (иРо + «р, + ... + «„„,) — («о + «1 + ... + ит) | <у. (II, 14; 4)
Поскольку
||(^0 + ",+ ...+«J-S 11 = 1 2 "»N 2) H"»IKf • (И, 14; 5)
II n > m || n>m
то окончательно для n' ^ m' получаем неравенство
f («Po + uPl+ ... + up„,) - S J < e, (II, 14; 6)
доказывающее, что преобразованный ряд сходится и имеет
сумму S.
Следствие. Если ряд с вещественными положительными
членами сходится, то его сходимость и сумма сохраняются при
любой перестановке членов.
Определение. Пусть / — счетное множество индексов и
("')*<=/— семейство векторов некоторого нормированного
векторного пространства Е. Говорят, что ряд 2 "г безусловно
сходится и имеет сумму S, если, какова бы ни была биекция
п-*-рп множества N на множество /, обычный ряд 2 «р схо-
дится и имеет суммой вектор S, не зависящий от выбора
биекции.
Пусть m — вещественные числа ^ 0. Обозначим через S
точную верхнюю грань в R (конечную или равную +°°) сумм
Sj— 2 "/, Соответствующих всем конечным подмножествам /
множества индексов /. Если S конечна, то ряд безусловно
сходится и имеет сумму S. В самом деле, пусть п-+рп — некоторая
биекция N на /. Тогда uPo + uPi + ... +uPn^.S. С другой
стороны, при заданном е > 0 существует конечное
подмножество / из /, такое, что Sj ^ S — е. Если m является
наименьшим из целых чисел, при которых множество {ро, Рь • • •, рт)
содержит множество /, то для п^ т ир<> + uPi + ... + "р„ *>

132
Гл. 11. Топология
^ Sj~^t S — е. Следовательно, ряд ы„о+ «/>,+ ••• + «р„ + • • •
оо
сходится и имеет сумму S. Если S = +оо, го ряд 2 "р„
расходится для любой биекции п-*- рп множества Ы на
множество I, ибо если бы он был сходящимся для некоторой частной
биекции и имел суммой число а, то тогда для любого / имели бы
место неравенства Sj =sj а и S =sC а, что противоречит нашему
предположению. В этом случае можно сказать, что ряд
безусловно расходится, и писать 2 и* = + °°.
Для рядов с положительными членами нет необходимости
говорить о безусловной сходимости. Она будет такой
автоматически, и поэтому имеет смысл говорить лишь об обычной
сходимости.
Если / является бесконечным подмножеством /, то всегда
имеют место следующие соотношения: Sj= 2 ut^.S = 2j «£•
Теорема 57 показывает, что если 2 «г является рядом из
векторов банахова пространства Е и если ряд из норм его чле-
нов 2л II «г II сходится, то сам ряд является безусловно сходя-
щимся. К этому результату можно добавить следующее:
1°) Если речь идет о вещественных числовых рядах, то
имеется обратное утверждение к предыдущему результату:
Числовой вещественный ряд может быть безусловно
сходящимся только в том случае, когда он абсолютно сходится, т. е.
когда сходится ряд 2j\ui\-
В самом деле, рассмотрим ряд из вещественных чисел.
Выберем некоторую биекцию N на /, или, что по существу то же
самое, предположим, что / = N. Члены ряда будем выбирать
следующим образом.
Выпишем сначала из данного ряда подряд все
положительные члены до тех пор, пока их сумма не превзойдет 1. Затем
возьмем первый отрицательный член данного ряда. После этого
из оставшихся положительных членов выберем подряд столько,
чтобы получить сумму, большую 2. Затем снова добавим
следующее отрицательное число из данного ряда (если оно есть)
и будем продолжать добавлять положительные числа, пока
сумма не превзойдет 3 и т. д.
Если подпоследовательность, составленная из
положительных членов ряда, расходится, то проводимое нами построение
можно продолжать неограниченно. Получаемый такой
перестановкой ряд расходится, так как при любом и^О существуют его

§ 14. Ряды в нормированных векторных пространствах 133
частные суммы, превосходящие п. Поэтому, если ряд,
составленный из положительных членов, расходится, то данный ряд
безусловно сходиться не может. Точно такие же рассуждения
можно провести и в том случае, когда расходится
подпоследовательность, составленная из отрицательных членов ряда.
Таким образом, данный ряд может безусловно сходиться только
тогда, когда сходятся подпоследовательности положительных
и отрицательных членов ряда, т. е. когда данный ряд
абсолютно сходится.
2°) Такое же обратное утверждение имеет место, если Е —
нормированное конечномерное векторное пространство.
Поскольку векторное пространство размерности k над полем С
является пространством размерности 2k над полем R, то можно
считать, что рассматривается конечномерное векторное
пространство над полем R. Поскольку, кроме того, результат не
зависит от выбранной нормы (в силу эквивалентности всех норм
(теорема 13)), то можно считать, что в пространстве выбран
базис, и отождествить Е с пространством Rm, и в этом случае
в качестве нормы взять ||(*,, х2, ..., хт)\\= 2 1*П на Rm.
Если теперь ряд безусловно сходится, то непосредственно видно,
что каждая из компонент ряда представляет собой безусловно
сходящийся ряд вещественных чисел и, следовательно, согласно
результату, полученному для рядов с вещественными членами,
каждая из компонент ряда должна быть абсолютно сходящейся.
Окончательно, по определению выбранной нормы, получаем, что
данный ряд абсолютно сходится.
3°) Напротив, с помощью весьма тонких рассуждений можно
доказать, что в любом бесконечномерном нормированном
векторном пространстве Е можно найти безусловно сходящийся
ряд, не являющийся абсолютно сходящимся1).
Если ряд безусловно сходится, то его сходимость и сумма
не зависят от порядка членов. Естественно предположить, что,
как и в случае рядов с положительными членами, можно дать
определение безусловно сходящегося ряда и его суммы, не
выбирая определенную биекцию N на /.
В самом деле, можно доказать следующее:
') Пусть 2 ип — ряд из векторов некоторого банахова пространства.
п=0
Тогда для него возможны следующие случаи:
a) ряд сходится абсолютно и, следовательно, безусловно;
b) ряд сходится безусловно, но не абсолютно (только тогда, когда Е
бесконечномерно);
c) ряд сходится, но не безусловно;
d) ряд расходится.

134 Гл. II. Топология
->
vi "*
Теорема 58. Ряд 2i ui безусловно сходится и имеет
сумму S тогда и только тогда, когда для любого е > 0 существует
такое конечное подмножество J индексов из множества
индексов I, что для любого конечного подмножества К
множества I, содержащего J, имеет место неравенство
II SK - S ||=|| 2 Щ -Щ <в. (II, 14; 7>
Читатель может доказать эту теорему в качестве
упражнения.
Суммирование по блокам безусловно сходящегося ряда
Теорема 59. Предположим, что счетное множество
индексов I является объединением семейства непустых и
непересекающихся подмножеств Ia, cted:
'= U 7». /аП/р = 0 дЛЯ а^Р').
аеА
->
Тогда, если ряд 2 «г "3 векторов банахова пространства Е
> „ ->
безусловно сходится к S, то каждый из частных рядов , 2i ut
"а
->
->
безусловно сходится; если их суммы мы обозначим через Sa,
- VI "* ■*
то ряд 2j Sa будет безусловно сходиться и иметь сумму S. Дру-
гими словами, имеет место формула суммирования по блокам:
2 Щ= 2 / 2 ut). (II. И;8)
«е/ a&A\iela J
Доказательство. Ограничимся доказательством
теоремы для случая, когда данный ряд абсолютно сходится.
Положим М— 2 II ut ||. Тогда, очевидно, 2 II "«II ^М; это
означает, что каждый из рядов 2 «г является безусловно схо-
дящимся (теоремы 55 и 57). Следовательно, если рассматривать
некоторое конечное множество В элементов из множества ин-
дексов А, то мы получим неравенство 2л IISa||^ 2i II"гII^М,
') Множество А конечно или счетно, и каждое множество 1а конечно ила
«четно.

§ 14. Ряды в нормированных векторных пространствах 135
которое показывает, что ряд 2 Sa является также
безусая А
ловно сходящимся. Остается доказать формулу 2j Sa — S.
Прежде всего при заданном е > 0 можно найти такое
конечное подмножество / индексов из /, при котором имеет
место неравенство
2j II "г 11^ у • а> следовательно, \\S — SyH^y.
1-е СУ
Пусть теперь п-+рп — некоторая биекция множества N на
множество А в случае, когда А счетно, или же подмножества
{О, 1, ..-, гп) множества N на Л в случае, если А конечно.
В обоих случаях существует такое целое т, что объединение
множеств /„ , /Р , ..., /р содержит /. Тогда для я ^ m част-
ная сумма 5Po+5Pi-t- ... + SPn является суммой Sj и
некоторого безусловно сходящегося ряда, образованного из тех чле-
нов ии индексы i которых принадлежат дополнению /.
При этом имеем неравенство
-> -> -> ->
е
|(SPo+SP|+ ... +SPn)-S/j<f, (II, 14; 9)
из которого вытекает неравенство
||(5Ро+ SPl + • • • + К) ~ 5||<е, (II, 14; 10)
доказывающее искомую формулу 2i Sa = S.
asit
->
Замечания. 1°) Если / = N и если заданный ряд 2 "л
№=0
сходится, но не безусловно, то такое утверждение будет
неверным. Например, если ип — вещественные числа и если ряд
2 ип является условно сходящимся, то частный ряд,
Составлю
ленный из членов ^ 0, и частный ряд, составленный из
членов < 0, расходятся!
2°) Рассмотрим обратное утверждение к этой теореме. Пусть
(/а)а(_л —некоторое разбиение множества индексов У на
непересекающиеся подмножества. Предположим, что для каждого а
v "*■ *
из А ряд 2j ut безусловно сходится и имеет сумму Sa;
с другой стороны, предположим, что ряд 2 Sa является
ае=Д

136
Гл. 11. Топология
безусловно сходящимся и имеет сумму S. Можем ли мы тогда
утверждать, что исходный ряд 2 "г также безусловно сходится
ге/
и имеет сумму S?
Если он безусловно сходится, то из теоремы следует, что его
■*
сумма заведомо равна S, но ничто не говорит о том, что этот
ряд должен быть безусловно сходящимся. В самом деле,
достаточно рассмотреть пример, в котором / равно множеству Z всех
целых чисел, А является множеством N всех целых чисел ^ О
и в котором для каждого а, т. е. для каждого целого п ^ О,
/а совпадает с множеством {+я, —л}1). Тогда если мы
рассмотрим ряд, в котором «г=', то увидим, что формула 2 I 2 "<) =
•= 2 (n — n) дает безусловно сходящийся ряд с суммой, рав-
ной 0, в то время как ряд 2 г не является безусловно
сходящимся / 2 I'■ I = + °°\ •
3°) Напротив, если все и{ — вещественные положительные
числа и если 2 / 2 "А дает в результате S, то ряд 2 "ь
конечно, сходится (потому что все его частные суммы,
составленные из конечного числа членов, ограничены) и,
следовательно, имеет ту же сумму S.
Если в случае рядов с положительными членами
договориться через + оо обозначать сумму расходящегося ряда, то
без всяких дополнительных предположений имеет место
равенство (II, 14; 8), обе части которого либо являются конечными
числами, либо равны + оо.
4°) Отсюда, наконец, следует, что если Е является
пространством Банаха и если сходится ряд 2 (2 ||«г||), то можно
утверждать, что ряд 2 II "г II сходится, и, следовательно, ряд
2 "г является безусловно сходящимся, а, значит, применима
теорема 59 и имеет место формула (II, 14; 8).
Действие линейного непрерывного отображения на ряд
Теорема 60. Пусть Е и F — два нормированных
векторных пространства и L — линейное непрерывное отображение Е
') Сводящимся к одному элементу, если п = 0.

§ 14. Ряды в нормированных векторных пространствах 137
в F. Если 2j "n является сходящимся рядом в Е, то ряд
со _^
2 L • ип сходится в F; при этом
2(L-«J==L-(2"J. (II, И; 11)
Такое же утверждение имеет место для безусловной и
абсолютной сходимости в случае, когда Е и F являются
пространствами Банаха. Кроме того, справедливо неравенство
2llL-"JI<ll£||-2ll"JI- (П. И; 12)
п=0 п=0
Доказательство. В силу линейности L,
L-C2, «„)= 2 (£■«„). (II, 14; 13)
При m, стремящемся к + °°, сумма 2 «я сходится к сумме
5; следовательно, в силу непрерывности L, левая часть послед-
него равенства сходится к L ■ S. К тому же пределу стремится
правая часть, а это означает, что ряд 2 L, • ип сходится и
->
имеет сумму L-S, откуда мы получаем (II, 14; 11).
Из (II, 13; 6) следует, что
2 \\L-un\\ <||L|| 2 II «„II, (II, 14; 14)
откуда, переходя к пределу при т, стремящемся к "+"оо, мы
получаем (II, 14; 12). (Написанные выражения могут быть коцеч-
ными или равными -f- оо.) Таким образом, если 2 ип абсо-
°° -=►
лютно сходится, то то же самое будет верно и для ,2 L, ■ «„.
Произведение двух числовых рядов. Применение
билинейного непрерывного отображения к двум рядам
Напомним, что самым простым билинейным непрерывным
отображением является произведение — непрерывное
билинейное отображение R X R в R.

138
Гл. II. Топология
В общем курсе математического анализа показывается, чта
для представления произведения двух рядов в виде ряда
необходимо предполагать, что ряды абсолютно сходятся. По этой
причине здесь также не будет теорем, относящихся к просто
сходящимся рядам.
Теорема 61. Пусть В — билинейное непрерывное
отображение произведения Ey^F банаховых пространств в банахова
пространство G. Пусть 2 «г " 2 0/ — ^ва абсолютно схо-
VI "^ "*
дящихся ряда с элементами из Е и F. Тогда ряд 2j В (ы,-, о Л
абсолютно сходится в G и имеет место формула
2 fl(«i,oy) = fl(2«i. So/V (И, 14; 15)
(«\/)е/х/ We/ /е/ /
-> >
Доказательство. Обозначим через U и У соответ-
VI "* V! "*
ственно суммы 2j"( и 2j Vj- Пусть К — некоторое конечное
подмножество / X 1- Существуют такие конечные
подмножества L из / и М из /, что L X М содержит К и при этом имеют
место оценки:
2 и я («I, о/) и < 2 II в ни и, ни о, ц=
HI SII (.2j!",-!!)( 2jl^<llfl||(^ll^(^flo/ll). (И.14; 16)
Эти неравенства показывают, что все частные суммы конеч-
vi ■*■"*■
ного числа элементов ряда Zi \\B(ut, V/)\\ ограничены и
a, j)(=i xj
VI -> ->
что, следовательно, ряд 2и B(u{, Vj) абсолютно сходится.
(«, /) е / х /
Мы можем применить к нему теорему 59 о суммировании по
блокам. Произведение / X / допускает разбиение на
непересекающиеся части — объединение множеств {£} X Л когда i
пробегает /. При этом
2 в(щ, о,)= 2 (2 в(и„ *,)).
(I, fle; х/ «е/\/е/ I
VI -> ->
Рассмотрим сначала сумму 2i В(щ, vp для фиксирован-
'е/
ного значения Л При фиксированном ы{ отображение и->
-> ->
—*-B(Ui, v) является линейным и непрерывным отображением /*
в G. Поэтому к абсолютно сходящемуся в F ряду 2 Vj и

§ 14. Ряды в нормированных векторных пространствах 139
к этому линейному непрерывному отображению можно
применить теорему 60 и записать формулу
2 В (и], о/) = В («„ 2 оЛ = В («,, У). (II, 14; 17)
Но точно так же мы можем затем рассмотреть линейное и
■> ■> ■>
непрерывное отображение и->В(и, V) пространства Е в G и
применить к этому отображению и ряду 2 «г теорему 60. На
этот раз мы получим следующее:
2 В («„ У) = В ( 2 ",-, Ю = В (U, V), (II, 14; 18)
■и, следовательно, ^ В (и{, vA= В (U, V), что совпадает
<*, I) е / х /
с (II, 14; 15).
В случае, когда / и / являются множеством N целых
чисел ^ 0, удобно положить
ш„ = В («„, о0) + 5 ("«-г. у.) + ... + В («о, vn) (II, 14; 19)
В («г, у,) как ряд 2j ^n-
<*, /) е N X N п=0
Замечание. Из доказательства вытекает следующее: если
заранее известно, что ряд 2 В (и{, vt) безусловно сходится, то
i. I
нет необходимости предполагать ряды абсолютно сходящимися.
Обратимые отображения в банаховых пространствах
Определение. Пусть и — линейное непрерывное
отображение нормированного векторного пространства Е в
нормированное векторное пространство F. Говорят, что отображение и
обратимо, если оно является биекцией и если обратная биек-
ция и~1 (очевидно, линейная) также непрерывна. Если Е — F,
то это означает, что элемент и в алгебре j?(£;£) имеет
обратный. Учитывая соотношение «и °и~1 = тождественное
отображение» и формулу (II, 13; 7), между нормами этих двух обратных
биекций можно установить соотношение:
1=11 тождественное отображение || ^|| и |||| и-1 ||, или || и-1 Ц-1 ^11" II-
(II, 14; 20)
Свойства рядов в банаховых пространствах позволяют
доказать, что отображение, достаточно близкое к обратному
отображению, само обратимо. Точнее, имеет место такое утверждение;

140
Гл. П. Топология
Теорема 62. Пусть и — линейное непрерывное обратимое
отображение банахова пространства Е в банахово
пространство F, и пусть v — линейное непрерывное отображение Е в Fr
удовлетворяющее неравенству
ЫКИи-ЧГ1. (И, 14; 21)
Тогда линейное непрерывное отображение и + v
пространства Е в пространство F также обратимо, и при этом
!(« +игЧ< \ .
Пи"1 1Г1—1о]|
Доказательство. Рассмотрим сначала случай F — En
и = 1, где / — тождественное отображение Е в Е. Тогда v
будет линейным непрерывным отображением Е в Е,
удовлетворяющим неравенству ||и|| < 1. Знак < не может быть заменен
знаком <С, ибо для и = —/ отображение / — / = 0 не
обратимо.
Произведем сначала чисто формальные выкладки. Мы будем
вычислять (/ + и)-1 как вычисляют (1 + г)-1 = 1/(1 + г),
записывая сумму в виде ряда геометрической прогрессии
1 — z + z2 — .... Напишем
(/+„)-' = /_ u + t)2-u3+ ... +(_1)"и"+ .... (И, Н; 22)
В этой формуле отображение vn является композицией
you о ... о и, составленной из п отображений, совпадающих с v.
Теперь обоснуем написанную формулу.
Ряд, стоящий в правой части, нормально сходится в
пространстве Банаха 9? (Е\ Е) (теорема 50), ибо ||и2|| ^ ||i>°u|| ^
<: IMP, \\vz\\ ^ IMP, ... и т. д. и по условию ||и|| < 1. Согласно
теореме 55, этот ряд сходится и представляет собой элемент w
из %{Е;Е).
Согласно теореме 54, функция, и —*■ uv является линейным
непрерывным отображением пространства 3? {Е\ Е) в
пространство 2'(Е; Е). Теперь можно к этому отображению и ряду,
стоящему в правой части (II, 14; 22), применить теорему 60, что
дает:
w{I-\-v) = w-\-w-v =
= (/-у + и2-и3+ ...) + (v — v2+v3— ...) = /. (II, И; 23)
Такое же рассуждение показывает, что (I-\-v)w = I. Тогда,
в силу изложенного на стр. 16 гл. I, отображение I + v будет
являться биекцией, а отображение w — его обратной биекцией.
Поскольку meS'tf; £). то /+и обратимо, и для
рассматриваемого случая теорема доказана. Кроме того, имеем оценку:
||ш|Ы(/+1>Г1|<1-НМ|-Н|И|р+ •••=T=W- (H,14;232>

§ И. Ряды в нормированных векторных пространствах
141
Заметим, что обратимость I -\- v вытекает также из теоремы
о неподвижной точке. Пусть у — некоторый элемент Е. Прове-
-> -> ->
пим, существует ли такая точка х из Е, что (I -{■ v) х = у, или
4. > > -> > ->
x + v-x — у, или х =s—v-x-\-y? Рассмотрим отображение
> >
f: х—*—v-x-\-y пространства Е в Е. Это отображение — сжатие,
ибо W—v-(х1 — х2)\\^Ы\\\х1 — х2\\ и IIу||< 1. В силу полноты
->
Е, существует, и притом единственный, элемент х, такой, что
_> -> -> ->
х = f(x) или (I -г v)x = у (теорема 46). Следовательно,
отображение / + v является биекцией. Поскольку эта биекция
линейна, ее обратная биекция также линейна. Кроме того, теоре-
ма 4Ьг показывает, что решение х непрерывно зависит от у;
следовательно, отображение (/ + у)-1 непрерывно, а
отображение / + v обратимо.
->
Заметим, что выражение для х может быть получено из
->
элемента у по методу последовательных приближений. Исходя
->-> -> -> -> -> ->->->
из х0 = 0, получаем хх = у, х2 = — v • хх + у = — v ■ у + у, х3 =
->->->-> ->
= — v • х2-{- у = у — v ■ у + v • У> ••• и в пределе находим х =
-> -> ->
= 1/ — v '• у + v2 ■ у — v3 • у + .... Это новый способ записи
равенства (/ — v)~ = I — v + v2 — v3 + ....
Рассмотрим теперь общий случай произвольных пространств
Е и F, обратимого отображения и и II и II < || и~1 ||-!. Поскольку
отображение и обратимо, можно записать, что
u + v = u(I + u-]v). (II, 14; 24)
Здесь u~]v и / + ы~'у — линейные непрерывные отображения
пространства Е в Е. В силу предположения, сделанного
относительно v, ||и-1у|| ^ ||«-11|||w|| < 1. Теперь, в силу доказанного
частного случая, / + u~]v обратимо и его обратное отображение
может быть записано в виде
(/ + ы~'у)-1 = / — u~lv + u~lvu~h — u~xvu~{vu-{v + ... .
(II, 14; 25)
Но тогда, согласно (11,14; 22), и -f- v можно представить
в виде композиции двух обратимых отображений, а, значит,
обратимо само это отображение и его обратное отображение
является композицией обратных отображений, взятых в обратном
порядке:
(и + у)-1 ==(/.+и~'р)-1 u~l = u~l — u~xvu-{ + u-lvu~lvu~[ —
-u-]vu-hu-lvu-] + (II, 14; 26)

142
Гл. II. Топология
Кроме того, имеет место оценка:
I (« +о)-'| < | (/ч-ы-м-1 lii"-1 н <
< llf Я < ««-'J! = ^ . (IIil4;27)
1 —1| и—1» II I —II и—1 IIИ о У || и-"1 |Г - II о II'
Замечание 1. Пусть °U — множество обратимых
элементов пространства 3?{E\F) и °и~^ — множество обратимых
элементов пространства 3?{F\E). Если ио е °U, то любой элемент
пространства 9?{E;F), принадлежащий открытому шару с
центром и0 радиуса Цы^'Ц-1, лежит в °U. Следовательно,
множество °U является открытым подмножеством пространства
9?{E\F), а если поменять ролями Е и F, то мы получим, что
таким же будет множество °U~X. Предыдущие неравенства
позволяют легко доказать, что и—+и~1 является гомеоморфизмом
°U на <U~X. Это можно проверить в качестве упражнения. С этим
фактом мы встретимся в теореме 27 гл. III.
Замечание 2. Пусть si- — банахова алгебра. То же самое
рассуждение показывает, что если элемент х^зФ обратим, т. е.
имеет в алгебре обратный, а у является таким элементом S4-,
что || у || < || х-11| , то элемент х-\-у обратим и обратный
к нему элемент выражается формулой
(£+ J)-1 = х-1 - х-'ух-1 + х-^ух-1 - ... . (II, И; 272)
Если °U является множеством обратимых элементов алгебры
Ы-, то °U является открытым подмножеством s4-, а отображение
> ■>
х-*х~1 является гомеоморфизмом °ll на себя.
Критерий условной сходимости
->■
Говорят, что последовательность щ, щ, и2, ■■■, ип, ...
элементов банахова пространства Е имеет ограниченную вариацию,
если ряд
II и, - «о 11 + II "2 - «III + II «з - «2II + ■ ■ • (И, 14; 28)
сходится. Сумма (II, 14; 28) называется полной вариацией
последовательности. Ограниченность вариации
последовательности приводит, естественно, к ее сходимости. В самом деле, схо-
->■
димость последовательности равносильна сходимости ряда и0 +
->■->■ ->■->■
-4-(«1 — «о) + ("г — ui) + •••.а сделанное выше предположение
равносильно абсолютной сходимости этого ряда. Таким образом,

§ 14. Ряды в нормированных векторных пространствах 143
последовательность с ограниченной вариацией является
сходящейся, так как абсолютно сходящийся ряд сходится. Если
последовательность вещественных чисел ип монотонна и
ограничена, то она ^имеет ограниченную вариацию^ В самом деле,
например, если последовательность возрастающая и
ограниченная, то
|И, — «ol + l"2 — «ll+ ••• = («1 — "о) + («2 — "l) + ••• =
= - u0 + lim u„ < + oo. (II, 14; 29)
Я-»оо
Впрочем, Жордан доказал, что и, обратно, если некоторая
последовательность вещественных чисел имеет ограниченную
вариацию, то она может быть записана в • виде и„ = ап — Ьп,
где ао, аи аг, ... и b0, b\, b2, ...— две возрастающие и
ограниченные последовательности ').
Дадим теперь наиболее важный критерий условной
сходимости рядов, к которому практически можно свести все наиболее
употребительные критерии (в особенности теоремы о
знакопеременных рядах).
Теорема 63 (Абель). Пусть Е, F, G — три пространства
Банаха. Пусть ип — некоторая последовательность векторов из
Е с ограниченной вариацией, стремящихся к 0 при п —► оо, и
vn — последовательность векторов из F с ограниченными
частными суммами, т. е. такая, что нормы величин
<V» = »m+ »«+!+ ••• +о». n>mt (II, 14; 30)
ограничены. Тогда, если В является билинейным непрерывным
отображением пространства Е X F в пространство G, то ряд
с общим членом wn = В (ип, vn) сходится.
Кроме того, если положить Un = || um+, — um || + II um+2 —
— um+1|| + ... и Vm= sup ||am,„||, то сумма S и остаток Rm =
-*■ ->
= wm+l + wm+2+ ... могут быть оценены следующим образом:
1|£0<ЦЯЦВД> и \\%т\\<\\В\\ит+1Ут+Л (II, 14; 31)
') Это почти очевидно. Достаточно положить а0 —»(ио)+. а\ = ("о) +
+ («i — "о)+, а2 = (и0)+ + (ui — uo)+ + («2 —"i)+, ..-, где х+ —х для х>0
и х+ — О для х<0. Затем Ь0 = (и0)~, Ь, = (и0)~ + {щ — и0)~, Ь2 = (и0)~ +
+ («, — и0)~ + ("г — "i)~. ..., где х~ = 0 для х>0 и х~ =\ х\ для х<0.
Ясно, что х = х+ — х~ и | х | = х+ + х~.
2) Эти величины стремятся к нулю при т, стремящемся к +°°,
потому что Vm+i остается ограниченным, а ит+\ стремится к нулю как
остаток сходящегося ряда с положительными членами.

144
Гл. П. Топология
В большинстве приложений Е = F = G = .С,—* поле ком-
->
плексных чисел, а В— произведение. Величины ат, „ тогда за-
ведомо ограничены, если ряд Zi vn сходится.
Доказательство. Имеем;
-> ->-> ->-> ->->
5„ = В (и0, v0) + В (и,, vi)+ ... + В («„, i>„) =
= В (и0, а0,0) + В («„ а0,, — а0,0) + ... + В («„, а0, „ — а0, „_,) =
= В(и0, а0,0) + [В(щ, a0,i) — B(Ui, а0,0)]+ ...
... + [В («„, а0, „) — В («„, а0, „.J] =
= В(ы0 —«!, а0,0) + В (и, — «2. сг0,,)+ ...
...+ В («„_, — «„, а0, „_,) + В («„, а0, „). (II, 14; 32)
-> ->
Отличный от других член В (ип, а0, „) мажорируется по норме
величиной || В |||| ип \\V0, а так как при п, стремящемся к + оо,
ип стремится к 0, то эта величина стремится к 0.
Остается доказать, что сумма
В(щ — и,, а0,0)+ В{щ — «2. cr0, i)+ ... + В («„_,-— «„, а0,„_,)
(II, 14; 33)
имеет предел при «, стремящемся к +оо, т. е. что ряд с общим
членом
zn = B(un — un+l, а0, „) (11,14; 34)
сходится. Ряд же из норм этих членов сходится, поскольку
\\Zn\\<\\B\\\\un-un+l\\V0 (П. 14; 35)
->
и последовательность «„ по предположению имеет
ограниченную вариацию. Так как пространство G по предположению
полно, то в силу теоремы 55 сходимость данного ряда
доказана. Доказав сходимость, мы можем, исходя из неравенства
II Sn || < || В ЦП ип || V0 + || В || U0V0, (H, 14; 36)
переходом к пределу при п, стремящемся к бесконечности, полу-
чить оценку для суммы 5 = w0-\- a>, + w2-\- ...:■
HS|K||B||£/0VV. (II, 1.4; ЗГ)

§ 14. Ряды в нормированных векторных пространствах 145
->
Те же самые рассуждения', начатые с члена wm+l с учетом
->->■-*
того, что Rm = wm+l -f wm+2 + .... дадут оценку остатка
(11,14; 31).
Примеры. Iе) Теорема о знакопеременных рядах. Рассмо-
оо
трим вещественный ряд 2 (— 1)""п, B котором последователь-
ность чисел Ыо, щ, и2,... ^ 0 является убывающей и сходящейся
к 0 при п, стремящемся к -f- оо. В этом случае применима
доказанная теорема, если положить о„ — (—l)n, Um = um, Vm==
= 1. Она же дает известное неравенство
\Rm\<um+l. (II, И; 38)
Известно также, что в этом случае остаток имеет знак
первого отброшенного члена.
2°) Случай тригонометрических рядов. Рассмотрим ряд
оо
2 ипепШ, в котором предполагается, что последовательность
комплексных чисел и0, щ, и2, ... имеет ограниченную вариацию
и сходится к 0 при п, стремящемся к + оо, и что 0 является
вещественным числом1). Примем vn — enie. По формуле суммы
членов геометрической прогрессии при 0 Ф 2kn получаем
равенство
етю _|_ym+i) т + тшш +eni9 = i е_ (ц, 14; 39)
6 — 1
и, следовательно, оценку
■I cfm „ К ■
|в'°^1
(II, 14; 40)
Напротив, если 0 = 2ftjt, то мы получаем величину emie-(-...
... + e",e = п—' т + 1, которая не является ограниченной. От-
оо
сюда вытекает, что для 0 ф 2kn ряд 2 tinenie сходится и
имеют место оценки
|5|<f/°le*>?_ij' \Rm\<Um+([ete2_ir (II, 14; 41)
Аналогичный результат, конечно, имеет место и для рядов
оо оо
2 u„cosn0 и 2 u„sinn0. Последний же ряд. сходится и при
0 = 2kn, поскольку все его члены при этом обращаются в нуль.
') Если и„ вещественны, убывают и стремятся к 0 и если 6 =-я, то мы
получаем знакопеременный ряд.

146
Гл. П. Топология
§ 15. НАИБОЛЕЕ УПОТРЕБИТЕЛЬНЫЕ ПРИМЕРЫ
ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВ.
СХОДИМОСТЬ ПРОСТАЯ И РАВНОМЕРНАЯ
Функциональные пространства
Под функциональным пространством понимают
пространство, элементами которого являются функции, т. е. отображения
одного множества в другое.
Пусть Е и F — два множества. В гл. I (стр. 15) через /**
мы обозначали множество всевозможных отображений Е в F.
Если F обладает некоторой структурой (векторного
пространства, топологического пространства и т. д.), то, вообще говоря,
и в FE можно ввести аналогичную структуру.
1°) Предположим, что F является векторным пространством
над полем К. Тогда, очевидно, в FE можно также ввести
структуру векторного пространства над полем К. В самом деле, если
fug — два отображения Е в F и % — некоторый скаляр, то
можно определить сумму f + g и произведение Xf как новое
отображение из Е в F по формулам:
(7+ g) (х) = Т(х) + g (х) для любого х (= Е, (II, 15; 1}
(Xf) (х) = xj(x) для любого х <= Е. (II, 15; 2}
Таким образом, на FE мы определили закон сложения и
закон умножения на скаляр из К. Без труда проверяется, что эти
законы удовлетворяют всем аксиомам, превращающим FE в
векторное пространство над полем К ').
Например, если F является полем скаляров К, а последнее
является полем вещественных или комплексных чисел, то
множество КЕ вещественных или комплексных функций,
определенных на Е, является векторным пространством над полем
вещественных или комплексных чисел.
2°) Предположим теперь, что F является метрическим
пространством. Если f и g — два отображения £ в F, то
расстоянием между этими функциями будем называть величину,
обозначаемую через d(f, g) и определяемую по формуле:
d(f, g)=supd(f(x), g(x)). (II, 15; 3)
х е= £
Это расстояние не обязательно конечно; точную верхнюю
грань следует брать в пополненной прямой R. Отсюда вытекает,
') Если Е состоит из двух элементов, то FE может быть отождествлено
с F2 = F X F. Структура полученного при этом векторного пространства
совпадает со структурой пространства произведения, рассмотренного на
стр. 119 (формулы (II, 13; 22) и (II, 13; 23)).

§ 15. Примеры функциональных пространств 147
что в множестве FE невозможно непосредственно ввести
естественную структуру метрического пространства. Поэтому мы
ограничимся рассмотрением подпространства (FE)b
пространства FE, состоящего из ограниченных отображений Е в F.
Говорят, что отображение f множества Е в F ограничено, если
область значений f(E) — образ множества Ё — является
ограниченной частью F. В этом случае расстояние между любыми
двумя ограниченными отображениями f и g из Е в F заведомо
конечно. (В самом деле, пусть, например, f(E) содержится в
шаре с центром а радиуса a, a g(E) лежит в шаре с центром b
радиуса Р и тем более в шаре с центром а радиуса p + d(a, b)
множества F. Очевидно, для всех х из'Е имеет место неравенство
d(f(x), g(*)X a + р + d(a, b) и, следовательно, d(f, g)
конечно.)
Проверим теперь, что отображение d: (f,g)-+d(f,g)
действительно определяет расстояние в пространстве (^Н1). Для
этого необходимо проверить все три свойства определения
(II, 1; 1). Симметрия очевидна. Положительность также
очевидна, ибо, с одной стороны, d(f,g)^-0, а, с другой стороны, для
различных f и g найдется хотя бы один элемент х из Е, такой,
что d(f(x),g(x))>0, и тогда тем более d(f,g)>0.
Остается проверить неравенство треугольника.
Пусть /, g, h — три отображения Е в F. Для любого х из Е
имеем:
d (f (x), h (x)) < d (f (x), g (x)) + d (g (x), h (x)) <d(f,g) + d (g, h).
(1Ы5; 4)
Поскольку это верно для любого х, то получаем искомое
неравенство:
d(f,h)^d(f,g) + d(g,h). (И, 15; 5)
Замечание. Только что введенные понятия являются
метрическими, а не топологическими. Легко доказывается, что
если в F заменить данную метрику на эквивалентную, то
полностью изменяется в первую очередь пространство (FE)b, ибо
ограниченность функции зависит от метрики, а не от топологии
(см. стр. 57), и, кроме того, если даже это пространство не
изменится, то новая метрика в (FE)b не будет эквивалентна
первой.
') Если Е состоит лишь из двух элементов, то F* может быть
отождествлено с Fi — Fy^F. Только что установленное расстояние в (FE)b (кото-
Рое в нашем случае совпадает с FE) является одним из расстояний, которое
мы в свое время выбирали для произведения на стр. 119:
d((xu xt), {yi, y2)) = sup [d(xi, у{), d(x2. Уз)].

148
Гл. 11: Топология
3°) Предположим теперь, что F имеет структуру
нормированного векторного пространства. Тогда в пространстве (FE)b
также можно ввести структуру нормированного векторного
пространства, положив
||| f |||= sup \\Ш II1). (II, 15; 6)
х <s Е
Методы, аналогичные предыдущему, показывают, что мы
определили некоторую норму. Кроме того, метрика, определяемая
этой нормой, - является метрикой, которую мы определили
вп. 2°):d(f,g)=|||f-g|||.
Если, например, F является полем вещественных или
комплексных чисел, то пространство вещественных или
комплексных ограниченных функций, определенных на некотором
множестве Е, является нормированным векторным пространством2).
Векторные пространства, полученные в п. 1°) и 3°),
практически всегда бесконечномерны. В самом деле, предположим, что
Е является некоторым множеством из п элементов, которые для
удобства мы обозначим через 1, 2, ..., п. Тогда множество FE
в частном случае, когда F = R, является
пространством-произведением Rn, а норма, введенная в п. 3°), имеет вид
|| (*i, х2, .... х„) || = sup (I*! |, |х21,:. • •• \xn\)- (H. 15; 71-
Каждый раз, когда Е содержит бесконечное множество
элементов (а во всех практически важных случаях в качестве Е
берется вещественная прямая или некоторый интервал этой
прямой), рассмотренное выше пространство FE
бесконечномерно.
Теорема 64. Если метрическое пространство F полно, то
■Метрическое пространство (FE)b ограниченных отображений Е
в F также полно3).
Доказательство. Пусть fQ, fi, h, • ••—
последовательность Коши из (FE)b- Из определения расстояния следует, что
.d(fm(x), fn(x))^d(fm, fn), а, значит, для любой точки х из Е
') Через II II мы обозначаем норму элемента F и через III III норму
ограниченного отображения Е в F для того, чтобы избежать смешения
нормированных векторных пространств F и (FE)b. Таким образом, II / II означает
функцию х-> || f(x) |, которая >0, в то время, как 1||/||| означает
точную верхнюю грань этой функции, т. е. число 2^0.
• 2) В поле скаляров К норма совпадает с модулем, обозначаем через | |.
Поэтому, если /е (КЕ)ь, то \f\ является функцией х-»- |f(x)|, которая ^0.
Здесь будет уместным через II / II обозначать точную верхнюю грань этой
функции, т. е. норму f в (КЕ)ь-
3) В силу примечания на стр. 147, эта теорема содержит как частный
случай теорему 44.

§ 15. Примеры функциональных пространств 149
последовательность точек fn(x) является последовательностью
Коши в F.
Поскольку пространство F по предположению полно, то эта
последовательность сходится к некоторой точке F, которую мы.
обозначим через f(x). Тем самым мы определили
отображение f множества Е в пространство F.
Докажем прежде всего, что это отображение ограничено.
Зададим е > 0. Тогда существует целое число р, такое, что при
m ззг Р, п ^ Р имеет место неравенство d(fm, f„)^. e, а,
следовательно, d(fm(x), fn(x))^ е для всех х из Е. Зафиксировав х
из Е, перейдем в последнем неравенстве к пределу при ш,
стремящемся к + оо, и, учитывая непрерывность функции
расстояния в F, получим неравенство d(f(x), fn(x))^. е для п ^ р. Так
как fp ограничено, то множество fp(E) содержится в некотором8
шаре с центром av радиуса Rp. Из неравенства
d (ap, f (x)) < d (ap, fp (x)) + d (fp (x), f (x))
следует, что множество f(E) содержится в шаре с центром av.
радиуса Rp + e; тем самым ограниченность f полностью
доказана. Отображение f, таким образом, также является элементом:
(FE) й. Остается убедиться, что fn сходится к f при п,
стремящемся к + оо. Действительно, при заданном е и выбранном-
р для вс«х х^Е и п^р имеем неравенство d(f(x), fn(x))^. е„
из которого следует неравенство d(f,fn) ^ е, означающее
сходимость /„ к f. Окончательно получаем, что (FE)b является:
полным метрическим пространством.
Следствие. Если F является пространством Банаха, то
нормированное векторное пространство (FE)b также является
пространством Банаха. В частности, пространство (КЕ)ь
ограниченных функций, определенных на множестве Е, с
вещественными или комплексными значениями является пространством
Банаха.
Было бы полезным использовать полученные результаты при
исследовании сходимости последовательностей функций, чтобы
иметь возможность сказать, что некоторая последовательность-
функций fn сходится к предельной функции f, если эти функции
как точки fn некоторого топологического пространства сходятся'
в этом пространстве к точке f.
Простая сходимость последовательности функций
Говорят, что последовательность функций fn, т. е.
последовательность отображений множества Е в метрическое
пространство F, просто сходится при п, стремящемся к + оо, к предель-

150
Гл. II. Топология
ной функции f, если для любого х из Е последовательность
точек fn{x) из F сходится при я, стремящемся к -f се, к точке f(x)
пространства F.
С помощью логических знаков можно это определение
записать так:
(V* е= Е) (Ve > 0) (3m ее N) (Vn >m): d (f„ (x), f (x)) < 8.
(II, 15; 8)
Отметим, что, как мы видели ранее (в гл. I, стр. 38), выбор
т зависит в действительности одновременно от е и от х.
Возникает вопрос: можно ли в пространстве F? отображений Е в F
ввести топологическую структуру таким образом, чтобы
элементы этого топологического пространства /„ сходились к
элементу f тогда и только тогда, когда функции fn просто сходятся
к функции f в указанном выше смысле? Это в действительности
возможно, но не просто. Получаемое при этом топологическое
пространство не метризуемо, и мы его здесь рассматривать не
будем.
Равномерная сходимость последовательности функций
Говорят, что последовательность функций fn сходится
равномерно к функции f при п, стремящемся к + со, если целое
число т, указанное в (II, 15; 8), может быть выбрано
независимо от х, т. е. если оно является лишь функцией е; другими
словами, если
(Ve > 0) (3m e= N) (Vx e= E) (Vn > m): d (/„ (х), f (x)) < e.
(II, 15; 9)
Это же можно записать короче:
(Ve>0)(3m€=N)(Vn>m): d(fn,f)<e. (II, 15; 10)
Последнее означает, что расстояние между fn и f стремится
к нулю при п, стремящемся к бесконечности.
Очевидно, равномерная сходимость влечет за собой простую
сходимость, но, как мы сейчас увидим, обратное не верно.
Равномерная сходимость является гораздо более сильным
свойством, чем обычная сходимость.
Пример 1. Рассмотрим вещественную функцию веществен-
лой переменной, определенную формулой
£(*) = -пЬ-- (II. 15; 11)

§ 15. Примеры функциональных пространств 151
Назовем сдвигом этой-функции на h функцию, полученную
перемещением графика данной функции параллельно оси х на
расстояние Л, т. е. отображение {х, у)-*(х -{- h, у). Другими
словами, значениями новой функции Xhg в точке х являются
значения старой функции g(x) в точке * — Л:
так что
(***) (х) = g (х- К),
(4g)(x)= l + {x_h)*
(II, 15; 12>
"(II, 15; 13)
Рассмотрим теперь последовательность сдвигов xng, neN.
Непосредственно видно, что эта последовательность функций
*-х
Рис. 3.
Рис. 4.
сходится к тождественно нулевой функции при п, стремящемся
к + оо. Действительно, для фиксированного х
lim . . , Г5-
„->«. 1 + (*-я)2
= 0.
(II, 15; 14)
Впрочем, это означает лишь, что последовательность
значений функции g в точках х — п стремится к 0 при п,
стремящемся к + оо, что очевидно.
Однако, последовательность функций xng при п,
стремящемся к + °°, равномерно сходиться к 0 не может, ибо
расстояние от xng ДО 0, будучи всегда равным 1, не зависит от п.
Пример 2. Рассмотрим вещественную функцию /„(и ^ 1)
вещественной переменной, определенную следующим образом:
она равна 0 для х ^ 0 и х ^ 1/п, она равна па, а > 0, для
х = 1/(2«), а в каждом из интервалов [0,1/(2и)],[1/(2и), 1/«]она
аффинно линейна '). График этой функции изображен на рис. 4^
') Аффинно линейной, или аффинной, мы называем функцию у = ах + Ь.
Слово «линейная» в соответствии с общим определением линейного отобра»
жения векторных пространств мы сохраняем за функцией у = ах.

152
Гл. II. Топология
Как это ни кажется странным, но последовательность fn
сходится к функции, тождественно равной 0, при п,
стремящемся к -f- <х>. В самом деле, при любом х > О для достаточно
большого а выполняется неравенство 1/га <С х, а, следовательно,
fn(x) — 0. Для всех х ^ 0, fn(x) — 0, откуда и следует наше
утверждение. Однако расстояние от fn до 0 равно па; эта
величина стремится к бесконечности, а, значит, fn не сходится
равномерно к 0 при п, стремящемся к -f- оо. Мы видим, что понятие
простой сходимости на самом деле является не столь уж
естественным, как это кажется с первого взгляда. В самом деле,
тот факт, что две рассмотренные выше последовательности
функций стремятся к 0 при п, стремящемся к + оо, выглядит
довольно странным. Для последовательности функций понятие
равномерной сходимости является более естественным, чем
понятие простой сходимости.
Из сказанного выше о связи между равномерной
сходимостью и расстоянием между функциями видно, что
топологическим пространством, приспособленным к равномерной
сходимости, является метрическое пространство (/гя)ь. Сказать, что
некоторая последовательность ограниченных отображений fn из £
в F сходится равномерно к ограниченному отображению f из Е
в F, означает сказать, что последовательность точек fn
метрического пространства {FE)b сходится к точке f этого метрического
пространства.
Другие применения выражения «равномерная сходимость»
Рассмотрим последовательность элементов хп(Х)
метрического пространства F, зависящих от параметра X, пробегающего
множество Л. Говорят, что эта последовательность элементов
сходится к некоторому пределу х(Х) из F (зависящему,
очевидно, также от параметра X) равномерно по X, пробегающему
множество Л, если
(Ve > 0) (3m е= N) (V*. е= Л) (Vra > m): d {хп {X), х {X)) < е.
Это, по существу, равносильно утверждению, что
последовательность функций X —* хп {X), определенных на Л со
значениями в F, сходится равномерно к функции X—*х(Х). Это
понятие сводится, следовательно, к предыдущему, но с
психологической точки зрения мы находимся в разных ситуациях, когда
рассматривается последовательность функций или когда мы имеем
дело с последовательностью точек, зависящих от параметра X.
Рассмотрим теперь последовательность отображений fn
вещественной прямой R в метрическое пространство F. Что
означает выражение: последовательность fn сходится при п,
стремящемся к -f- оо, к предельной функции f равномерно на каждом

§ 15. Примеры функциональных пространств
153:
ограниченном интервале R? Очевидно, это значит, что каким
бы ни был ограниченный интервал [а, Ь] прямой R,
последовательность сужении fn в этот интервал сходится равномерно к
сужению f; другими словами, это означает, что
(Va е R) (V6 е= R, 6 > a) (Ve > 0) (3m е= N)
(Vxe=[a, b]){Vn>m): d(fn(x), /(*))<е. (II, 15; 15)
Входящее в это определение число m не зависит от х, но
является функцией, с одной стороны, числа е, а с другой, —
интервала [а, Ь]. Здесь можно, естественно, заменить прямую R и
ограниченные интервалы на пространство R" и ограниченные-
подмножества R". Более общо, если заданы множество Е,
метрическое пространство F и семейство частей (А{). е/
множества Е, то можно говорить о последовательности отображений
fn множества Е в F, которая при п, стремящемся к +00,
сходится к отображению f равномерно на каждой части Лг- данного
семейства. Если мы вернемся к примеру функций xng из
формулы (II, 15; 13), то увидим, что последовательность функций
x„g сходится к 0 равномерно на каждом ограниченном
интервале R и даже равномерно на всей полупрямой ] — оо, Ь[. В
самом деле, при п~^Ь для всех х ^ Ь имеем: 1/[1-|-(* — я2)]^
=£= 1/[1 -\-(Ь — и)2], а эта величина стремится к 0 при п,
стремящемся к + оо. Если мы рассмотрим теперь второй пример
(стр. 151), то увидим, что последовательность функций fn
сходится к функции, тождественно равной нулю, равномерно на
дополнении к любому интервалу [—6, +6], 6 > 0, с центром
в начале, но она не сходится равномерно ни на каком
интервале ] 0, 6 [.
Наконец, если Е является топологическим пространством, то-
говорят, что последовательность функций fn сходится к f
локально равномерно на Е, если каждая точка а из Е имеет
окрестность Та, на которой fn сходится равномерно к f. Это
можно записать следующим образом:
(Ча<^Е)(ЭУ, окрестность a) (Ve > 0) (Зи е N)
(V*e=3n(V«>m): d(f„(*), f (*))<e. (II, 15; 15^
Если Е локально компактно, то локально равномерная схо~
димость эквивалентна равномерной сходимости на каждом
компакте Е. В самом деле, если функции fn сходятся к функции f
равномерно на каждом компакте, то, поскольку каждая точка а
из Е имеет компактную окрестность, на которой fn сходятся
равномерно, рассматриваемая сходимость является локально
равномерной. Обратно, предположим, что сходимость локально
равномерна, и пусть К — некоторый компакт Е. Для любого а
из К существует окрестность Уа точки а, на которой сходимость

154
Гл. II. Тспслогиящ
равномерна. Компакт К покрывается конечным числом
окрестностей Та', следовательно, сходимость является равномерной
на К.
Впрочем, все то, что было сказано по поводу простой или
равномерной сходимости .последовательности функций,
распространяется на сходимость множества функций в смысле,
указанном на стр. 61. Например, если ft для любого feR является
отображением Ев метрическое пространство F: x^>ft(x), то
можно говорить о простой или равномерной сходимости
отображения /( к отображению / из Е в F, когда t стремится к 0 по
положительным значениям или стремится к -f- оо и т. д.
Пространства, порожденные структурами пространств Е и F
До настоящего времени мы вводили функциональные
пространства, исходя только из алгебраических или топологических
структур на F. Но если Е и F уже наделены такими
структурами, то можно определить новые пространства. Например,
если Е и F оба являются векторными пространствами над
одним и тем же полем К, то можно рассмотреть пространство
линейных отображений Е в F. Это векторное подпространство
пространства FE всех отображений Е в F. Если Е и F —
топологические пространства, то можно ввести пространство (FE)C
непрерывных отображений Е в F. Если F — метрическое
пространство, то это пространство не является подпространством
\(FE)b, ибо непрерывное отображение не обязательно
ограничено. Однако можно рассмотреть подпространство (FE)bC
пространства (FE)b, образованное непрерывными ограниченными
отображениями Е в F. Предположим, наконец, что Е и F
являются нормированными векторными пространствами. Тогда
можно ввести, как мы это делали на стр. 1,14, пространство
S {E\ F) линейных непрерывных отображений Е в F. Оно не
является подпространством (FE)bc, так как линейное
отображение, если только оно не является тождественно нулевым,
ограниченным быть не может '). Обозначим через Е0 единичный шар
из Е. Если линейное отображение Е в F задано на шаре Е0, то
-> ->
в силу гомотетии и (кх) = Хи (х) оно определено всюду на Е.
Впрочем, если задано некоторое отображение единичного шара
£о в F, то можно выяснить, является ли оно сужением
линейного отображения Е в F. В самом деле, достаточно продолжить
его на Е, полагая и(х) = Цх\\и(х/\\ х[\) для ||л:||>1, и прове-
') В самом деле, если а есть-некоторый вектор Е, такой, что и(а)фО,
-> -> •>
то последовательность и (па) = пи (а) не ограничена, ибо || пи (а) || =
и=п|1 и (а) || стремится к +°° при п, стремящемся к +°°.

§ 15. Примеры функциональных пространств
155
рить, является ли полученное отображение линейным. Согласно
теореме 47, для того чтобы линейное отображение и из Е в F
было непрерывным, необходимо и достаточно, чтобы образ
единичного шара Е0 при отображении и был ограниченным в F. Мы
видим, следовательно, что пространство линейных
отображений Е в F можно отождествить с некоторым подпространством
пространства всех отображений Е0 в F, а именно с
подпространством Отображений, являющихся сужением линейных
отображений Е в F. Пространство линейных непрерывных
отображений Е в F, т. е. 9?(E;F), можно отождествить с некоторым
подпространством пространства (F °)ь ограниченных
отображений шара Е0 в пространство F. Учитывая определение, которое
мы дали для нормы линейного непрерывного отображения Е в F
и для нормы ограниченного отображения шара Е0 в F, можна
пространство &' (Е; F) отождествить также с некоторым
нормированным векторным подпространством нормированного
векторного пространства (FE°)b.
Легко видеть, что 9?(E\F) отождествляется с некоторым
замкнутым подпространством (F£o)*- Если F полно, то, по
теореме 64 {FB')„ также полно. Поэтому & (Е; F) как замкнутое
подпространство полного пространства полно (теорема 43). Мы
получили новое доказательство теоремы 50.
Непрерывность локально равномерного предела
последовательности непрерывных функций
Теорема 65. Пусть Е и F — два метрических
пространства и /о, /ь /г, ,.., /я, • •. — последовательность отображений Е
в F, локально равномерно сходящаяся к f. Если все функции /„
непрерывны в точке а из Е, то и предельная функция
непрерывна в точке а. Если функции fn непрерывны всюду, то f
также непрерывна всюду. Если сходимость равномерна на Е и
все fn равномерно непрерывны на Е, то f также равномерно
непрерывна на Е.
Доказательство. Пусть сходимость равномерна в
окрестности Та точки а. По определению, для заданного s > 0
существует такое пг, что для всех х из Уа имеет место неравенство-
d(L(x), /(*))<у. (II, 15; 16)
Зафиксировав т, заметим, что функция fm предполагалась
непрерывной в точке а. Следовательно, существует окрестность
Т сг Та точки а, такая, что для всех х е Т имеет место
неравенство
d(fm(x), fm(a))<j. (II,15;J.7>

^6
Гл. П. Топология
Но тогда для любого х е.Т
d {f (x), f (a)) < d (f (x), fm (x)) + d (fm (x), fm (a)) + d (fm (a), f (a))<e,
(II, 15; 18)
т. е. функция f непрерывна в точке a.
Из доказательства следует, что если fn всюду непрерывны,
то f также всюду непрерывна ').
Предположим теперь, что fn равномерно непрерывны, а
сходимость равномерна на Е. Зададим е > 0 и выберем т так,
чтобы для всех х из Е выполнялось неравенство (II, 15; 16).
Функция fm равномерно непрерывна. Следовательно, существует
такое число т] > 0, при котором из d(x', x") ^ г\ следует
неравенство d(fm(x'), fm{x")) ^ е/3. Для d(xf, x") ^ у\ при этом
имеем
d (f (*'), f (*")) < d (f (x'), fm {x')) + d (fm (*'), fm {x")) +
+ d(fm(x"),f(x"))<e, (II, 15; 19)
что и доказывает равномерную непрерывность f.
Замечание. Напротив, последовательность непрерывных
•функций fn вполне может сходиться просто к разрывной
функции f. Так, например, если взять fn(x)= хп для 0 ^ х ^ 1, то
'fn непрерывны для всех п и сходятся к разрывной функции f,
равной 0 для 0 ^ х <. 1 и 1 для х = 1.
Следствие 1. В пространстве (FE)ь ограниченных
отображений Е в F, снабженном метрикой, определенной формулой
(11,15; 3), подпространство (FE)bc ограниченных непрерывных
отображений Е в F замкнуто.
Это утверждение является другой формулировкой теоремы.
Следствие 2. Если F полно, то пространство (FE)Ьс
ограниченных непрерывных отображений Е в F, снабженное
метрикой (II, 15; 3), является полным метрическим пространством.
В самом деле, так как оно замкнуто в полном метрическом
пространстве (FE)b (теорема 64), то для доказательства
достаточно применить теорему 43.
Следствие 3. Если F является пространством Банаха, то
пространство (FE)bC непрерывных ограниченных отображений Е
в F, снабженное нормой, определяемой по формуле (II, 15; 6),
является пространством Банаха.
Особенно важен следующий частный случай. Возьмем в
качестве F поле скаляров К. Тогда пространство вещественных
') Что касается первых двух результатов, то Е может быть
топологическим не обязательно метризуемым пространствой.

§ 15. Примеры функциональных пространств 157
или комплексных функций, ограниченных и непрерывных на ме-.
чрическом пространстве Е, является пространством Банаха.
В частности, пространство вещественных или комплексных
непрерывных и ограниченных функций одной вещественной
переменной является пространством Банаха.
Если Е компактно (в большинстве практических приложений
это будет замкнутый или открытый интервал вещественной
прямой), то, согласно теореме 29, получаем, что всякая векторная
функция, непрерывная на Е, заведомо ограничена1). Тогда
пространство (FE)C функций, непрерывных на некотором компакте
Е, со значениями в банаховом пространстве F и с нормой
(II, 15; 6) является пространством Банаха.
Некоторые контрпримеры
Мы теперь в состоянии дать контрпримеры, о которых
говорилось в предыдущих параграфах.
1°) Обозначим через ФЦа, Ь]) векторное (бесконечномерное)
пространство вещественных или комплексных функций,
непрерывных на замкнутом ограниченном интервале [а, Ь], а < Ь,
множества R2). Покажем, как в этом пространстве можно
определить не эквивалентные друг другу нормы. Об этом мы
говорили после теоремы 13. В качестве первой нормы возьмем ту,
которая была определена формулой (II, 15; 6). Вторую норму
определим, используя понятие интеграла:
ь
N(f) = j\f(x)\dx*). (II, 15; 20)
а
Эти нормы не эквивалентны. В самом деле, с одной стороны,
мы имеем оценку
tf(f)<(6-a)|||f|||. (П, 15; 21)
С другой стороны, очевидно, не существует оценки вида
lllflll ^ kN(f), где k — не зависящая от непрерывной функции f
') Мы это утверждали только для вещественной функции. Однако
если f является векторной непрерывной функцией, то ее норма || f || является
непрерывной вещественной, а, значит, и ограниченной функцией.
2) *& ([а, Ь]). можно записать также в виде (К'"' b')c, где К — поле
вещественных или комплексных чисел.
3) Это число, очевидно, >0. Неравенство треугольника и соотношение
Л'(Xf) = \X\N(f) очевидны. Есля f Ф 0, т. е. если / *й 0, то существует по
крайней мере одна точка с на [а, Ь], в которой 1(с)Ф0. Тогда, в силу
непрерывности, существует некоторый интервал, окружающий с, где |/(х)|>0,
а, значит, и N(f)> 0.

158
Гл. //. Топология
постоянная. В самом деле, рассмотрим случай [а, Ь] = [0, 1] и
последовательность функций, указанных в примере 2 на стр. 151,
Для этих функций имеем следующие нормы:
Ш|| = л°, tf(/„) = i-n«-', откуда Щ^- = 2п, (II, 15; 22>
что и доказывает наше утверждение. Если, например, 0 < а <
< 1, то fn стремится к 0 при п, стремящемся к + °°> по норме
N, но не по норме ||| |||. Легко доказывается, что в векторном
пространстве ^([о, Ь]) существует бесконечное множество
других попарно не эквивалентных норм.
2°) Покажем теперь, что в пространстве ^([0,1]), снабженном
нормой ||| HI, единичный шар не компактен. Для этого достаточно
рассмотреть последовательность функций /„, определенных
формулой fn(x) — xn (см. замечание на стр. 156). Имеем:
f„(x) = xn, HI /„|||=1 для л>1. (II, 15; 23)
Поскольку эта последовательность просто сходится к функции,,
равной 0 для 0<д:< 1 и 1 для х = 1, то любая ее равномерно
сходящаяся подпоследовательность должна сходиться к этому
же пределу» но этого не может быть, так как пределом
является разрывная функция. Мы нашли некоторую
последовательность, принадлежащую единичному шару в ^([0, 1]),
никакая подпоследовательность которой не сходится. Согласно
теореме Больцано — Вейерштрасса (теорема 25), единичный шар
не компактен. Итак, пространство ^([0, 1]) не является
локально компактным. Как мы видели (теорема 45г), это верно
для любого бесконечномерного нормированного векторного
пространства.
Теорема 66. Пусть Е и F — два метрических
пространства, А — некоторая часть Е и fo, fi, ■ ■ ■, fn, ... ■
—последовательность отображений А в F, равномерно сходящаяся к f. Пусть
а^Е — точка прикосновения А1). Если для каждого п
функции fn (x) имеют предел при х, стремящемся к а по значениям
в А, и если F полно, то f(x) имеет предел при х, стремящемся
к а по значениям в А, и, кроме того,
lim/(jc)= lim[lim/„(*)]■ (II, 15; 24)
х-+а n->oo х-¥а
хеА 1еЛ
Доказательство. Рассмотрим для каждого п функцию
/„, определенную на объединении A U {а} следующим образом:
fn(x) = fn{x) для хфа и f„(a)= lim/„(*). По определению,
4 х->а
х'г- А
') Никакого предположения относительно принадлежности точки а
к множеству А не делается. ' •

§ 15. Примеры функциональных пространств
159
функция fn непрерывна в точке а. С другой стороны, каким бы
ни было е > О, существует такое целое р, что из неравенств
ш^ р и n I^ p следует неравенство d(fm(x), fn(x))^ е, а также
неравенство d(f(x), fn(*))^e для ie/1, х ф а. Устремляя х
к а, в пределе получаем d(fm(a), fn(a))^.e. Это означает, что
fn(a) образуют последовательность Коши в F, а так как F по
предположению полно, то она имеет предел, который мы
обозначим через f(a). Функция f, определенная формулой f(x) =
= f(x) для х^А, х ф а, и принимающая только что
определенное значение f(а) в точке а, является функцией,
определенной на множестве A U {а}, со значениями в F. При п,
стремящемся к +оо, fn(x) стремится к f(x) для х Ф а. Но fn(a)
стремится к f(a) по определению f(a), а, следовательно, f„
сходится просто к f. Однако, f„ сходится, кроме того, и
равномерно, ибо для т^ р, п~^ р при х Ф а имеем d (f (x), fn (x)) =
= d (f (x), fn (*))< е, а также d(fm(a), f„(a))<e. Поэтому,
устремляя m к +оо и переходя к пределу, получаем неравенство
d(f(a), f„(a))^e, т. е. окончательно d(f, f„)<e.
Так как fn непрерывны в точке а, то из теоремы 65 следует,
что f также непрерывна в точке а, т. е. f(x) имеет предел
при х, стремящемся к а по значениям из А, и что этот предел
равен f (a)= lim fn(a)— lim [lim fn(x)]. Теорема доказана.
n->°° re->°° x-*a
Пример. Если fn н f являются вещественными
непрерывными функциями на вещественной прямой R, если fn сходится
равномерно к f при п, стремящемся к + оо, и если при любом п
существует lim fn(x) = ln, то существует lim f-(x) = l и /„ схо-
ДЯТСЯ К /.
Ряды функций со значениями в нормированном
векторном пространстве
->■-*■ ■>
Пусть ы0, Ы[, ..., ы„, ... — отображения множества Е в
нормированное векторное пространство F. Тогда можно рас-
смотреть ряд 2 "п- Говорят, что этот ряд сходится и имеет
№=0
сумму S (отображение Е в F), если для каждого * из Е ряд
оо
векторов 2 «п (*) из F сходится в нормированном векторном
«=■0
пространстве F к сумме S(x). Это означает еще, что последова-
•>->-> ■>
тельность частных сумм 5n = M0 + Mi+ ••• + ип является по-,
следовательностью функций на Е со значениями в F, сходя-

160
Гл. II. Топология
щейся просто к S. Говорят, что ряд равномерно сходится, если
последовательность частных сумм Sn является равномерно
сходящейся.
Если F является пространством Банаха, то при
использовании понятий, связанных с абсолютной сходимостью или
нормальной сходимостью, можно допустить некоторую неточность.
Когда речь идет о рядах из векторов нормированного
векторного пространства, мы можем не различать термины «ряд
абсолютно сходится» или «ряд нормально сходится». Однако этого
нельзя делать в случае, когда речь идет офункциональных рядах.
Говорят, что ряд просто абсолютно сходится, если для
каждого х ряд из норм в банаховом пространстве F, т. е. ряд
°° -> °° ->
2 II "л (•*) Н> сходится. Это означает, что ряд S II "nil1), СОСТаВ-
nM) п=0
ленный из функций, определенных на Е, с вещественными
положительными значениями просто сходится. Говорят, что ряд
нормально сходится, если ряд из норм в нормированном век-
торном пространстве (FB)b, а именно 2|||"п-|||. является схо-
п=0
дящимся рядом с положительными членами. Последнее
понятие, очевидно, более сильное. Всякий нормально сходящийся
ряд является и просто абсолютно сходящимся. Обратное же,
вообще говоря, не верно. В каждом из этих случаев ряд просто
сходится (F предполагается полным!). Кроме того, если ряд
сходится нормально, то он сходится и равномерно. Нормальная
сходимость является наиболее важным критерием равномерной
сходимости рядов векторных функций. Этот факт часто
выражают следующим образом.
°° -»
Пусть задан ряд 2 ип функций, определенных на Е, со зна-
ге=0
чениями в пространстве Банаха. Если существует такой ряд,
составленный из положительных вещественных чисел ап ^ 0, что
оо
|| и„ (х) || ^ а„ для любого х из Е и 2ап<°°> то данный ряд
ге=0
нормально, а, значит, и равномерно сходится. Этот критерий
может быть полезен также и как критерий равномерной услов-
ной сходимости. В общем случае функционального ряда 2 ип
п=0
доказательство его равномерной сходимости можно начать с до-
') Напомним, что ||и„|| является функцией х-> ||ип{х)|| и что Шн„||| =
«= sup || ип (х) ||.

§ 15. Примеры функциональных пространств 161
казательства сходимости для каждого х из Е. Затем вычис-
ляется остаток /?т = ит+1 + «т+2 + ••• ряда и доказывается,
что последовательность функций Rm равномерно сходится к О
при т, стремящемся к + сю. С этой целью используется
подходящая оценка остатка.
Приведем пример, представляющий интерес с точки зрения
теории рядов Тейлора.
Теорема 67. Если ряд Тейлора (с комплексными коэффи-
со
циентами) 2 ctnxn сходится в точке х = R своего круга сходи-
га=0
мости, то он равномерно сходится на всем интервале [О, R].
В частности, его сумма является непрерывной функцией на
интервале [О, R].
Доказательство. В самом деле, имеет место формула
апхп =(anRn)(x/R)n. Поэтому для каждого х из [О, R [ мы
можем применить критерий сходимости Абеля1). Действительно,
если положить ип = (x/R)n, vn = anRn и за билинейное
отображение В принять произведение, то мы увидим, что эти
величины удовлетворяют условиям Абеля и формула (II, 14; 31)
дает оценку остатка:
"~.<Ч(*ГЧ*П+1(*Г-(*П+•••-
-((С('-т))('+^+(т)'+-)-(тГ-<"•*«»
Vm+1(*) = Vm+1= sup \am+iRm+i+ ... +anRn\,
ix\m+i " , ., (".15:27)
Rm+i(x)< 4 sup am+lRm+l+ ... +anRn\.
\K/ n>m+l
Тот же самый критерий Абеля не применим при х = R, так
как последовательность l-p-l =1, имеющая постоянную
ограниченную вариацию, к нулю не сходится. Однако ряд
предполагался сходящимся, и оценка остатка сохраняется по
определению остатка. В результате получаем, что эта оценка справедлива
для всех х из интервала [О, R]. Поскольку при т,
стремящемся к '-+- оо, величина Vm+i стремится к 0, в силу критерия
') Может показаться бессмысленным применять критерий, относящийся
к условно сходящимся рядам, в области, где степенной ряд, мажорируемый
геометрической прогрессией, абсолютно сходится! Но мы хотим доказать
равномерную сходимость; и, поскольку при х = R ряд не предполагается
абсолютно сходящимся, другими методами мы не располагаем.
6 Зак. 1339

162
Гл. //. Топология
Коши сходимости числового ряда 2аХ и Um+l<~\, то
видно, что остаток Rm+i сходится равномерно к 0 при т,
стремящемся к + °°- Тем самым доказана равномерная сходимость
ряда Тейлора. Непрерывность суммы теперь вытекает из тео^
ремы 65.
Доказанная теорема часто используется в различных
областях математики. Рассмотрим, например, разложение Тейлора
1п(1+*) = !-4+ ••• +(-1Г'-7Г+ ••• Для |*|<1.
(II, 15; 28)
При х = 1, согласно теореме о знакопеременных рядах, этот
ряд сходится. Следовательно, он представляет некоторую
непрерывную функцию в интервале [0, 1], а его сумма равна
lim In (1 + jc) == In 2. При х = 1 отсюда получаем следующую
х<\
формулу:
1п2=1-4+|- .... + (-'пГ~' + ... '). (II, 15; 29)
Точно так же, рассматривая разложение в ряд функции
arctgrx-f-4 + T-- ... +(-1Г^г+ •••
и проводя те же самые рассуждения для ж = 1, получаем
формулу:
7в|-{ + Г ••• +(-!)"^ГТТ+ •••• (п'15;30)
§ 16. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ ВЕЩЕСТВЕННЫХ
ИЛИ КОМПЛЕКСНЫХ ЧИСЕЛ И ФУНКЦИЙ
Определение. Пусть и0, ии и2, ... — последовательность
вещественных или комплексных чисел. Говорят, что бесконечное
оо
произведение Ц ип сходится, если при п, стремящемся к + °°.
сходится к некоторому конечному числу ф О
последовательность частных произведений П„= Ц ит.
0<т<ге
') В этом частном случае можно непосредственно воспользоваться тео?
ремой о знакопеременных рядах. Для каждого х е [0, 1] эта теорема
применима; значит, остаток Rm+l(x) мажорируется по модулю первым отброшен-
ным членом I ■ ^ I . и потому действительно сходится равномерно
кО.

§ 16. Бесконечные произведения 163
Во всех других случаях произведение называется
расходящимся. Кажется довольно странным считать расходящимся
произведение, в котором частные произведения П„ сходятся
к нулю. Но это вызвано, как мы увидим позже, многими
причинами. Если хотя бы один из сомножителей ип является нулем,
то произведение, конечно, расходится. Если все числа ип
вещественны и ^з 1, то Пп образуют возрастающую
последовательность, а, значит, мы имеем предел, конечный или равный + оо,
оо
В том случае, когда произведение расходится, пишут Ц ип =
■ = -J- оо. Точно так же каждый раз, когда Пп стремится к О,
оо
для расходящегося произведения пишут Ц «„ = 0.
л=0
Теорема 68. Для того чтобы бесконечное произведение
со
Д ип было сходящимся, необходимо, чтобы его общий член ип
стремился к 1 при п, стремящемся к + оо.
Доказательство. В самом деле, если бесконечное
произведение сходится и его значением является П ф 0, то
произведения П„ и П„_, оба сходятся к II, откуда следует, что их
отношение ип при п, стремящемся к + оо, сходится к П/П = I.
Заметим сразу, что это свойство не сохраняется для
бесконечных произведений, частные произведения которых П„ сходятся
к 0. Например, если мы рассмотрим бесконечное произведение
(1) (1/2) (1/3).. .(1/п)..., частные произведения которого,
очевидно, стремятся к G, то его общий член 1/п к 1 не сходится.
Замечание. В случае сходящегося бесконечного
произведения остатком Rm называют произведение Ц ип. Остаток Rm
стремится к 1 при т, стремящемся к +оо.
Для того чтобы бесконечное произведение было сходящимся,
необходимо и достаточно, чтобы выполнялся критерий Кошт
отношение П„/Пт должно стремиться к 1, когда, тип стремятся
к -f- оо (все члены ип предполагаются Ф 0). Сходящееся
произведение, очевидно, удовлетворяет этому критерию. Обратно,
пусть бесконечное произведение удовлетворяет критерию Коши.
Тогда существует целое р, такое, что при я ^ р выполняется
неравенство | Пр — П„ |<| Пр |. Из неравенства |П„К|П„ —
■— Ир | + 1 Upl ^21 Пр j следует, что все П„ ограничены. Пусть
М — их точная верхняя грань. Тогда для заданного е >.0.
г*СМ/2, можно определить q так, чтобы при любых т~^- q и
« > <7 выполнялось неравенство |Пт —П„ |^-гг |Пт|^е. По-
б»

164 Гл. //. Топология
следовательность чисел П„ является, следовательно,
последовательностью Коши в поле комплексных чисел С. Посколько это
поле полно, то П„ имеет предел П. Устремляя в последнем
неравенстве я к + оо, получаем
inm-ni<^-inmi<i-inmi,
т. е. П ф О, а значит, бесконечное произведение сходится.
Бесконечные произведения и логарифмические ряды
При изучении сходимости или расходимости бесконечного
произведения представляется заманчивым вычислить логарифм
его членов с тем, чтобы заменить произведение рядом. Если
члены вещественны, то логарифмы можно вычислить, начиная
с того момента, когда все ы„ > 0.
Если такого номера, начиная с которого все ы„ > 0, не
существует, то это означает, что общий член ип при я,
стремящемся к -f- оо, к 1 не сходится. Но тогда сразу ясно, что
произведение расходится, и его изучение заканчивается.
Если же при я, стремящемся к -f- оо, общий член ы„
стремится к 1, то, начиная с некоторого номера, все ип строго
положительны, и можно вычислять их логарифм.
Предположим, что ип комплексны. Известно, как сложно
брать логарифм комплексного числа, ибо каждое комплексное
число имеет бесконечное множество логарифмов. Если
положить z = reie, то мы получим общую формулу: Ln z = In r -f- id,
где 9 определено с точностью до сомножителя, кратного 2я.
Предположим, однако, что г изменяется в полуплоскости х =
= Re z > 0. Тогда можно выбрать его аргумент между —я/2
и я/2 и затем определить по соответствующей формуле его
логарифм. Так определенный логарифм является непрерывной
функцией. Его называют главным значением логарифма и
обозначают через In1).
В частности, если v — такое вещественное число, что |у|<1,
то 1 -f- v находится в предыдущей полуплоскости, и ранее
определенный логарифм можно записать в виде разложения
Тейлора
ln(l + o) = -f--£+ ... +(_l)»-iil+ .... (II. 16; 1)
оо
Пусть теперь 1J ип — бесконечное произведение комплекс-
п=0
ных чисел. Если ип не стремится к 1 при я, стремящемся к +оо,
') Можно также определить главное значение логарифма в дополнении
к полупрямой ^0 в плоскости. Тогда —л < arg г < +л и —«л < Im (In г) <
< «л.

§ 16. Бесконечные произведения 165
то произведение расходится. Если же ип стремится к 1 при п,
стремящемся к + оо, то, начиная с некоторого п, числа ы„
находятся в полуплоскости Re ы„ > 0 и, опустив конечное число
членов, можно взять логарифмы. При этом мы сразу же получаем
такую теорему:
Теорема 69. Для того чтобы бесконечное произведение
оо
YI ип, для всех членов которого Re ы„ > 0, било сходящимся,
оо
необходимо и достаточно, чтобы сходился ряд "^Ыи^
ге=0
Предположим сначала, что бесконечное произведение
сходится. Обозначим через П„ частные произведения и через S„
частные суммы ряда логарифмов. Не обязательно lnIIn = S„,
и нельзя даже утверждать, что Re П„ > 0. Однако, согласно
критерию Коши, существует такое целое число р, что при « ^ р
имеем |П„/ПР—1|<1, а, следовательно, Re(II„/IIp) >0,
а также Re(II/IIp)>0. Зафиксируем такое р. Тогда
In (П„/Пр) = S„ — Sp + 2knin. Поскольку П„/Пр сходится
к П/Пр, то из непрерывности главного значения логарифма
следует, что S„ — Sp + 2k„in при п, стремящемся к +, оо,
сходится к пределу, а, значит, ряд с общим членом In ы„ -J-]
+ 2(&„ — kn-i)in является сходящимся и его общий член
стремится к нулю. Однако, так как ы„ в силу того, что
произведение сходится, стремится к 1, то 1пы„ также сходится к 0.
Начиная с некоторого значения п, мы получаем kn-i = kn, а, значит,
ряд с общим членом 1п ы„ является также сходящимся.
Обратно, если ряд сходится, то S„ сходится к некоторому
пределу S. В силу непрерывности показательной функции
получаем, что числа Un = eSn сходятся к II = es=^=0. Теперь видно,
почему в доказательстве было существенным предположение
П ф 0. Впрочем, если ы„ вещественны >0 и П„ стремятся
к 0, то 1пм„ будет являться общим членом расходящегося ряда
с суммой — оо. Говорят, что бесконечное произведение, которое
по предположению сходится, абсолютно сходится
(соответственно условно сходится), если ряд из логарифмов его членов
(который будет определенным начиная с некоторого места)
является абсолютно сходящимся (соответственно условно сходящимся).
Естественно, что здесь используется весьма вольный оборот
речи. Сказать, что произведение абсолютно сходится, вовсе не
значит сказать, что произведение П1ы„| сходится. (Поскольку
оо оо
ПI "п I = П ип , то произведение абсолютно сходится, если
п=0 и=0
оно сходится.) Если все ы„ вещественны и >1 или заключены

166
Гл. П. Топология
между 0 и 1, то сходимость является синонимом абсолютно»
сходимости.
Т е о р е м а 70. Для того чтобы бесконечное произведение-
оо
Ц(1 + о„), vn ф—1')> было абсолютно сходящимся, необхо-
со
димо и достаточно, чтобы был сходящимся ряд 2 1 vn |.
Доказательство. Если произведение абсолютно
сходится, то оно сходится просто, а, следовательно, 1 + о„
стремится к 1, и для достаточно больших п ^ р можно вычислять
логарифм членов произведения. Ряд 2 |1п(1 + о„)1 по пред-
л>р
положению сходится. В сходящихся же рядах с положительными
членами При исследовании сходимости общий член ряда можно-
заменять на эквивалентный ему. При п, стремящемся к + со,
v-„ стремится к 0, а тогда In (1 -j- vn) ~ vn и, следовательно, ряд
оо
2" I Чп I также сходится, а вместе с ним и ряд 2 I vn |.
rt>P tt=0
Обратно, предположим, что ряд 21 °п I сходится. Тогда
л=0
vn стремится к 0, а, следовательно, для п^р, при достаточно
большом р, Re (1 -f- o„)>0 и можно вычислить логарифмы чисел
1+"о„. Так как при га, стремящемся к + °°. Un(l + vn) |~| vn:\y
то ряд 2 |1п(1 + о„)| сходится. Следовательно, сходится ряд
2 In (1 + »■„),; а, значит, согласно теореме 69, сходится произ-
л>Р
ведение XI 0 + »п)- Поскольку все о„=^=—1, то произведе-
п>р
оо
ние П(1+»„):, не имеющее нулевых членов, также сходится..
л=0
оо
Поскольку Ц (1 + vn) сходится и сходится ряд 2 11п(1 + Vn) \*
рассматриваемое произведение сходится абсолютно.
Пример. Бесконечное произведение
П(*+£) илиП(1-£)' <п>16;2>
') Если не налагать ограничения vn Ф—1, то может случиться, что»
2 I a" I < "Ь °°> а бесконечное произведение имеет нулевой член, т. е. расхо~
дится!

§ 16. Бесконечные произведения
167
сходится, если а> 1, и расходится, если а ^ 1. В частности,
оно расходится при а = 1. Заметим, что последний случай
практически очевиден, ибо здесь легко вычисляются частные
произведения
('+т)('+т)('+1)-('Н)-"+ь
('4)('--9('--a--;('-*)-f <II,1M)
Можно даже сказать, что поскольку расходимость произ-
оо оо
ведения II (l Н—) или II (l 1 более очевидна, чем рас-
п=1 л=»2
оо
ходимость ряда V —, то с помощью теоремы 70 можно дока-
зать расходимость этого ряда!
Бесконечные произведения вещественных
или комплексных функций
Пусть Uo, Hi, ..., н„, ... — последовательность функций,
определенных на множестве Е с вещественными или комплекс-
°о
ньши значениями. Бесконечное произведение Ц ип называется
просто сходящимся, если для любого х из Е сходится бесконеч-
оо
ное произведение Ц ип (х) вещественных или комплексных чи-
п=0
сел. Это означает, что последовательность функций П„ =
= Д ип просто сходится к нигде не равной нулю предельной
0<т<л
функции.
Произведение называется абсолютно просто сходящимся,
оо
если для любого х из Е числовое произведение IIип(х) абсо-
л=Ю
лютно сходится.
Выражение «равномерная сходимость» для произведения
функций не ясно. Фраза о том, что произведение комплексных
оо
функций XI ип на Е сходится равномерно к функции П, может
п<=0
означать, что П„ и П нигде на Е в нуль не обращаются и что
функции П„ равномерно сходятся к функции П. Та же самая
фраза может также означать, что П„ и П нигде на Е в нуль
не обращаются и что ' отношение П„/П равноМерЙ'о сходится

168
Гл. II. Топология
к 1. Как легко видеть, эти два понятия не обязательно
совпадают. Однако они совпадают, если предел П имеет на Е
равномерные оценки снизу и сверху такого вида: 0 < а ^ П (х)^
^ Ь < + °°- В самом деле, в этом случае из неравенства
| П„ — П ] <; е следует неравенство | П„/П — 11 ^ е/а, а из
неравенства | П„/П — 11 <; е следует неравенство | Ця — П | ^
^ be. Только в этом случае мы можем позволить себе говорить
о.равномерной сходимости бесконечного произведения функций.
Однако всегда можно говорить о локальной равномерной
сходимости бесконечного произведения функций, непрерывных на
некотором топологическом пространстве Е' (и тогда предел П
будет также непрерывным). В самом деле, если функции Г1„
сходятся! локально равномерно к функции П, то, согласно
теореме 65, функция П будет непрерывной. Так как рна везде
отлична от 0, то для каждой точки а существует окрестность Т'а,
в которой | П | органичена сверху и снизу некоторыми
фиксированными положительными числами. Но тогда во всякой
окрестности TaczTa, в которой функции П„ сходятся равномерно
к функции П, отношение П„/П равномерно сходится к 1.
Обратно, предположим, что П„/П локально равномерно сходится
к 1. Тогда для каждого а из £ существуют окрестность Т'а и
число п, такие, что | П„(х)/П (х)—1|^ 1/2 для х<^Т'а. От-
сюда следует 1/2 sg; | П „ (х) /П {х) | < 3/2, а, значит, ^-1 П„ {х) | <
^| П {х) |«£^2| Цп{х) |. Поскольку функции Пп непрерывны и
П„ (а) Ф О, то существует окрестность Т" cz Ta точки а, в
которой функции |П„| ограничены сверху и снизу
положительными постоянными. При этом функция | П (х) [ также будет
ограниченной. Если теперь Та cz T"a является окрестностью, на
которой П„/П сходится равномерно к 1, то П„ будут на ней рав-.
номерно сходиться к П.
Применение к функции £ Римана
Функция Римана £ определяется формулой
оо
£(S> = S-?F- (И, 16; 4)
№=1
Пусть s = о"+ it и б — вещественное число > 0. Тогда
данный ряд, рассматриваемый как ряд функций, определенный
в области а ^ 1 -h б комплексной плоскости, является
нормально сходящимся. В самом деле,
= 4r<-rir- (Н,16;5>
1
„а "^ „1+а

§ 16. Бесконечные произведения
169
Так как для любого п функция s —*■ l/ns непрерывна в
полуплоскости а ^ 1 + 6, то видно, что сумма, т. е. функция £,
также непрерывна в этой полуплоскости, а поскольку это верно
для любого б > 0, функция £ непрерывна во всей
полуплоскости а > 1.
Рассмотрим теперь бесконечное произведение, в котором р
пробегает множество всех простых чисел
G(s) = II(t^W)- (И. 16; 6)
р
Любой член этого произведения всегда ф 0. Впрочем,
знаменатель 1 — l/ps ф 0 для а > 0. Кроме того, в этом случае
при о > 0 модулем числа l/ps является число \1р° < 1 и,
следовательно, применима теорема 70.
Бесконечное произведение абсолютно сходится тогда и
только тогда, когда сходится ряд 2 1/ра- Последнее же, ко-
р
нечно, будет иметь место для а > 1, поскольку сумма этого
оо
ряда мажорируется суммой сходящегося ряда 2 1/па.
Теорема 71. При а> 1 имеет место равенство G(s) = £(s).
Доказательство. При доказательстве этой теоремы
естественно считать s раз и навсегда фиксированным. Поскольку
оо
ряд 2 1/па и произведение G сходятся, то для любого 8 > 0
можно найти целое число т, обладающее следующими
свойствами:
a) остаток 2 1/па мажорируется числом е/2;
п>т
b) если через Gm(s) обозначить частные произведения,
образованные из т первых множителей бесконечного
произведения, то \Gm(s) — G(s) |< е/2.
Для каждого простого числа р имеет место разложение в
абсолютно сходящийся геометрический ряд:
1 ,,1,1,1, v^ 1
1+^+^ + ^+-=Si- «I. 16; 7)
l-l/ps ps p» • p*s АЛр
k=0
В силу правила относительно произведения нескольких
абсолютно сходящихся рядов (теорема 61), можно записать:

170
Гл. II. Топология
где р\ = 2, р2 = 3, р3 = 5, ..., рт суть т первых простых
чисел и k\, k2, .,., йт — целые числа ^ 0. Отсюда следует, что
0т(5)=У4. (И, 16; 9)
V
где v пробегает последовательность всех целых чисел, которые
в разложении на простейшие множители содержат только
простые числа ри р2, ..., рт. Рассмотрим теперь разность
Gm(s)—£(s); она состоит из части членов ряда V—т, соот-
п
ветствующих индексам п > т, и потому
I Gm (s) - с (s) | < У 4 <|. (". 16; ю>
п>т
откуда вытекает неравенство
|G(s)-E(s)|<|G(s)-Gm(s)| + |Gm(s)-C(s)l<e. (II, 16; 11)
Поскольку е произвольно, то получаем, что G(s)=t,(s).
Следствие. При а > 1 функция £ в нуль никогда не
обращается.
Это очевидно, так как она равна, значению сходящегося
бесконечного произведения. Предыдущие результаты, очевидно,
оо
не верны для <т= 1. В частности, расходится ряд 2 1/я- До-
да=Г
кажем точно так же следующее утверждение:
Теорема 72. Бесконечное произведение JJL 1 — 1/р ряс~
р
Заметим для этого, что для произвольного числа А > 0
можно найти такое целое ш, что
1+Y+ ■•• +~Ь>А- (И. 16; 12)
Рассмотрим теперь частные произведения Gm. Примененные
выше разложения в геометрический ряд имеют смысл и,
следовательно, Gm является суммой 2V_1> B которой v пробегает все
цель1е числа, разложение которых на сомножители состоит
только из простых чисел ри р2, ..., рт. Отсюда, в частности,
вытекает, что имеет место неравенство
Got(1) = 2]t>1 +T + •••• +i>A (".16; 13)

§ 16. Бесконечные произведения
\7\
Поскольку А произвольно, из этого неравенства следует, что
рассматриваемое бесконечное произведение (сомножители
которого > 1) расходится: G(l)= + °°-
Следствие. Множество простых чисел бесконечно; кроме
того, ряд 2 Ур> составленный из простых чисел, расходится.
р
В самом деле, расходимость этого ряда эквивалентна
расходимости бесконечного произведения Д (1 —- \/р) = 1/G (1).
р
Замечание. Рассмотрим знакопеременный ряд
Ъа \&) [J 2s ~т~
+ (-1Г"'^+ .... (И, 16; 14)
Как мы только что видели, этот ряд сходится для о > 0. Мы
сейчас покажем, что он даже равномерно сходится на каждом
компакте открытой полуплоскости а > 0 комплексной
плоскости. Пусть К — такой компакт. Заметим прежде всего, что на К
функция \s\ в силу ее непрерывности ограничена сверху
некоторым числом S. Точно так же непрерывная всюду
положительная функция а на К ограничена снизу некоторым числом б > 0.
Применим теперь теорему Абеля (теорема 63). Имеем:
-*—-s— = unvn, где »„=■(—1)ге , ип
1
Величины |<хт,„| мажорируются числом 1. Покажем, что
последовательность чисел ип имеет ограниченную вариацию. Имеем:
ге+1
1 1 Г dx ')
..s+l
откуда
("+D5" SJ
1
re+l
("+1Г
dx
o+l
(II, 16; 15)
(II, 16; 16)
l
("+DS
+
l
(n+l)° (n + 2)s
+°°
(II, 16; 17)
') Это общий метод для оценки разности; полагают f (п + 1) — f(n) =
- ге+1
= f f'{t)dt.

172
Гл. 11. Топология
Следовательно, ряд сходится, а формула (II, 14; 31) дает
для остатка следующую оценку:
JiJ=^<^W. (".№18)
Так как при этом |/?m|^ S/[6(m-\- l)e], где правая часть не
зависит от s и стремится к 0 при т, стремящемся к -f- с», то
сходимость ряда равномерна на К.
Если считать, что а > 1, то можно указать простую связь
между функциями £, и £,а. В самом деле, из формулы
Us) = G(s)-25J(^*-
\2п)
п=1
получаем:
Ce(s) = S(s)(l--^=r). или №=* Sa(5i • (И, 16; 19)
Свойство равномерной сходимости, доказанное для £а,
показывает, что эта функция непрерывна на каждом компакте К
открытой полуплоскости от > 0. Следовательно, она непрерывна
всюду в этой полуплоскости. В частности, при s, стремящемся
к 1, £a(s) стремится к ^,(1)= In 2. Тогда из формулы (II, 16; 19)
следует, что при s, стремящемся к 1, £(s) эквивалентна
In 2 In 2 _ 1
1-е(1-*)1п2~(5-1)1п2 s~\'
В результате формула (II, 16; 19) позволяет продолжить
функцию £ в полуплоскость от > 0 ').
Другие способы продолжения позволяют определить
функцию £ во всей комплексной плоскости и показать, что это
голоморфная комплексной переменной s, т. е. непрерывная функция
с непрерывной первой производной по отношению к этой
комплексной переменной в дополнении к точке s = 1 комплексной
плоскости. Эта точка s = I является полюсом, £(1) = с».
Продолженная функция обращается в нуль в точках s =
= —2, —4, —6, .... Исследование этой функции дает сведения
о распределении простых чисел, как мы это уже видели на
простом примере. Риман высказал гипотезу, до сих пор еще не
доказанную, о том, что продолженная функция £ имеет все нули,
') Это продолжение, естественно, не имеет больше ничего общего с сум-
оо
мой ряда 2 1/л*» не имеющей смысла для s < 1.
Л=1

§ 16. Бесконечные произведения
173
кроме предыдущих, на вертикальной полупрямой а = 1/2.
Доказательство этого утверждения дало бы исключительно
важные сведения о распределении последовательности простых
чисел. Во всяком случае, уже известные в настоящее время
свойства функции £ позволяют показать, что п-е простое число
эквивалентно при п, стремящемся к бесконечности, числу п In n, или
что число простых чисел, заключенных между 1 и N,
эквивалентно при N, стремящемся к +оо, числу N/\nN.
Теория простых чисел является одной из самых интересных,
но и самых трудных математических теорий.

ГЛАВА III
Дифференциальное исчисление
§ 1. АФФИННЫЕ ПРОСТРАНСТВА
Более или менее интуитивное представление о пространстве
дается еще в средней школе. В элементарной геометрии
пространство рассматривается как совокупность его элементов,
называемых точками. Исходя из точек — элементов этого
пространства, — можно с помощью отношения эквивалентности
ввести понятие свободных векторов, как это было сделано на
стр. 19. Пространство свободных векторов является векторным
пространством, обладающим обычными свойствами.
Однако пользоваться далее этими, недостаточно изученными
понятиями невозможно, так как пространство в элементарной
геометрии не было определено строго. В математике
принимается такая схема.
На основе общей теории множеств корректно определяется
понятие множества N целых чисел 1>0, а затем множество Z
целых чисел произвольного знака. Далее, исходя из отношений
эквивалентности, вводится поле Q рациональных чисел, как об
этом говорилось на стр. 19. В полных математических курсах,
опираясь на понятие сечения и исходя из поля Q рациональных
чисел, со всей строгостью определяется поле R вещественных
чисел и, наконец, поле С комплексных чисел. После этого
можно ввести общее понятие абстрактного векторного
пространства над некоторым полем (которое будет чаще всего полем
вещественных или полем комплексных чисел).
Понятие векторного пространства и его свойства уже были
получены нами ранее. Исходя из этого понятия, введем со всей
строгостью пространство элементарной геометрии, которое
является аффинным евклидовым пространством. Оно очень близко
к векторному пространству, но его нуль не обладает никакими
свойствами, выделяющими его среди других элементов
пространства. В дальнейшем элементы векторного пространства мы
будем всегда обозначать буквами с проведенной над ними
стрелкой и будем называть их векторами.
О п р е де л е н и е. Аффинным пространством Е над полем К
вещественных или комплексных чисел называется непустое
множество (его элементы называются точками), которому, с одной

§ 1. Аффинные пространства
175
стороны, сопоставлено векторное пространство Ё над полем
вещественных или комплексных чисел, называемое векторным
пространством, присоединенным к Е (элементы которого мы
будем называть векторами), а, с другой стороны, — некоторое
отображение множества Е X Е в пространство Е (его свойства
мы уточним ниже).
Если а и b — две точки Е, то элементом, соответствующим
паре (а, Ь)е£Х£ при рассматриваемом отображении, яв-
-> —>
ляется некоторый вектор из Е. Его обозначают через ab и
называют вектором с началом в а и концом в Ь. Отображение
Е X Е в Е должно обладать следующими свойствами:
Г) Соотношение Шаля: каковы бы ни были точки а, Ь, с
множества Е, должно выполняться равенство
—> —> —> -> -> • ->
ab-j- bc-j- са = 0, где 0 — нулевой вектор Е. (III, 1; I)
Из этого свойства вытекает, в частности (если считать все
три точки совпадающими с а), что, какова бы ни была точка
—>■ ->
а е Е, вектор аа является нулевым вектором пространства Е.
Если положить b = с, то мы получим, что ab и Ьа являются
противоположными векторами.
2°) Какой бы ни была фиксированная точка а, отображение
х —► ох должно быть биекцией Е на. Е. Мы примем следующие
обозначния.
Прежде всего, вектор ab с началом в а и концом в Ь может
>•
быть записан в виде b — а. Соотношение Шаля при этом
* * > _>
примет такой вид: b — a-j-c — b-j-a — c = 0. Принятое
обозначение согласуется с обычными свойствами вычитания. С другой
стороны, если а — точка £ и А — вектор пространства Е, то из
свойства биекции, определенной в 2°), следует, что в Е суще-
>• ->
ствует, и притом единственная, точка Ь, такая, что b — а = А.
Эту точку удобно обозначать через а + к. При этом, в силу
-> -> -> ->
соотношения Шаля, получаем а + (А + k) = (а + h) + k.
Таким образом, новое понятие согласуется с привычными
свойствами сложения. Размерность присоединенного векторного
пространства называется также размерностью аффинного
пространства Е. Пустое множество можно рассматривать как афг
финнов пространство, не имеющее присоединенного векторного
пространства.

176
Гл. III. Дифференциальное исчисление
Векторное пространство является частным случаем аффин--
ного. Достаточно считать оба пространства совпадающими и
поставить в соответствие любым двум элементам а и Ь вектор-
ного пространства вектор ab — b — а. В частности, поле
скаляров К само есть аффинное пространство размерности 1.
Общей, или аффинной, системой координат аффинного
конечномерного пространства Е называется система, образованная
точкой 0 (началом) пространства Е и некоторым базисом
-> ->
(ei)/e/1) присоединенного векторного пространства Е. Рассмо-
>
трим теперь произвольную точку х из Е. Вектор х — О имеет
-> ->
координаты (xt)ieBl в выбранном базисе Е. Эти координаты
называются координатами точки х в выбранной системе
координат, при этом имеет место формула
* = 0+2*^. (III, 1;2)
Аффинные многообразия
Пусть F — непустое подмножество аффинного
пространства Е, обладающее следующим свойством.
Существует такое векторное подпространство F векторного
пространства Е, что для каждой пары (а, Ь) из F X F вектор
b — а принадлежит F и для любой пары (a, h) из F X F точка
-> •->
а -\- h принадлежит F. Если такое векторное подпространство F
существует, то оно единственно, поскольку является множе-
->
ством всех векторов Ъ — а для всевозможных пар (а, Ь) из
F X F- При этих условиях говорят, что F является аффинным
подпространством или аффинным многообразием (часто даже
линейным многообразием пространства Е) и что F является его
присоединенным векторным подпространством.
Пространство F обладает структурой аффинного
пространства, имеющего F в качестве присоединенного векторного
пространства, а в качестве отображения F X F в F — сужение за-
->
') Если £ имеет размерность п, то / является множеством «индексов», to-
->
стоящим из некоторых п элементов, а (еЛ является «семейством» п век-
торов из Е. Чаще всего / = {1, 2, ..., п) — это множество п первых целых
положительных чисел, а базисом является «последовательность» п векторов
из Е.

§ 1. Аффинные пространства
177
данного отображения Е X Е в Е. Условимся считать пустую
часть множества Е аффинным многообразием, не имеющим
присоединенного векторного пространства. Пространство Е само по
себе является аффинным многообразием. Точка является
аффинным многообразием размерности 0. Прямой называется
аффинное многообразие размерности 1, плоскостью — аффинное
многообразие размерности 2. Векторное подпространство F про-
странства Е называется гиперплоскостью, если его
дополнительные векторные подпространства имеют размерность 1.
Аффинное многообразие F из Е называется гиперплоскостью, если его
присоединенное векторное подпространство является
гиперплоскостью. Если Е конечномерно размерности п, то
гиперплоскость представляет собой аффинное многообразие
размерности п — 1.
Два аффинных многообразия из Е одной и той же размер»
ности называются параллельными, если они имеют одно и то же
присоединенное векторное пространство1). В частности, два
совпадающих многообразия параллельны. Легко видеть, что при
таком построении теории аффинных пространств так
называемый постулат Евклида является теоремой, к тому же очевидной:
через каждую точку пространства можно провести аффинное
многообразие, параллельное заданному многообразию, и притом
единственное. Это означает, что если F — векторное
подпространство Е и а — точка из Е, то существует, и притом
единственное, аффинное многообразие, состоящее из точки а и при-
->
соединенного векторного пространства F: это множество точек
■> ■*■■*■
вида a -f- h, где Ag F.
Пересечение конечного или бесконечного числа аффинных
многообразий аффинного пространства является аффинным
многообразием. Отсюда вытекает, что если А является некоторой
частью аффинного пространства, то существует наименьшее
аффинное многообразие, содержащее А. Это — пересечение всех
аффинных многообразий, содержащих А. Его называют
аффинным многообразием, порожденным множеством А. Если
размерности двух аффинных многообразий равны р и q, через i
обозначена размерность их пересечения, а через s размерность
аффинного многообразия, порожденного их объединением, то легко
доказать, что в случае когда пересечение не пусто, имеет место
формула: р -\- q = i -\- s.
') Если Е является плоскостью (аффинное пространство двух измерений),
то две различные прямые параллельны тогда и только тогда, когда они не
пересекаются.

178
Гл. 111. Дифференциальное исчисление
Произведение Е1У(Е2 двух аффинных пространств
обладает, очевидно, Структурой аффинного пространства, имеющего
Е{ХЕ2 в качестве присоединенного векторного пространства,
->■ > >
если положить (&,, Ь2)— (а{, а2) = (Ь[—аи Ь2 — а^.
Линейные отображения. Аффинные отображения
Пусть Е и F— два аффинных пространства. Отображение
и пространства Е в пространство F называется аффинным,
если существует такое линейное отображение и из Е в F, что
и(Ь)-и(а) = и(Ь-а). (III, 1; 3)
->
Отображение и, очевидно, единственно, поскольку его зна-
->
чение на произвольном векторе из Е известно'). Пусть Е и
F — два конечномерных аффинных пространства с выбранной
в них системой координат, т. е. известно начало а в Е и базис
(е/)/е/ в Е и начало b в F и базис (/i)ie/ в F. Аффинное
отображение и будет полностью определено, если известны
координаты (с/)/е/ точки и(а) в аффинном пространстве F и ко-
-> ->
ординаты Uij, i^I, каждого вектора и (ej), j e /, в
векторном пространстве F. Отображение и при этом определяется
формулой
и(а) = Ь+ 2 cjt,
*+ „ iei (НЫ;4)
Можно также сказать, что каждой точке х = а-\- 2 Я/б/
из £ с координатами (*/),е/ ставится в соответствие точка
«/=6+2 #//< из F с координатами (г/(). по формуле
#i = с/+ 2 "</*/, «е/. (III, 1;5)
Если, в частности, F является полем вещественных или
полем комплексных чисел, снабженным своей канонической
системой координат, состоящей из нуля и единичных векторов,
') Очень часто стрелка над линейным присоединенным отображением не
ставится и через и одновременно обозначается как аффинное отображение, так
и присоединенное к нему линейное. Обозначение и может привести к ошибоч-
ному представлению о том, что и является вектором из Е или F.

§ 1. Аффинные пространства
179
то можно говорить о вещественной или комплексной аффинной
функции. Это функция, которая (если в Е выбрана система
координат) каждой точке х с координатами (*/)/s/ ставит
в соответствие вещественное или комплексное число:
и(х) = с + Zi UjXj, c = u(a), U} — u(ej). (Ill, 1;6)
Как видно, то, что часто называют линейной функцией,
следует называть аффинной функцией, а то, что часто
называют линейной однородной функцией (Е — векторное простран-
-> ->•
ство, а = О, с = 0), следует называть просто линейной
функцией. Функция у = ах-\-Ь является аффинной функцией, а у=
= ах — ее линейной присоединенной функцией.
->•
Если А является вектором из векторного пространства,
присоединенного к аффинному пространству Е, то биекция х -у
->x + h пространства Е на себя называется переносом на век-
тор А. Это, очевидно, аффинное преобразование,
присоединенное линейное отображение которого является тождественным
преобразованием. Обратно, каждое аффинное преобразование,
имеющее в качестве присоединенного линейного тождественное
>■
преобразование, является переносом. В самом деле, и (Ь) — и (а)—
->- > > -»•
= Ь — а; следовательно, и (b) — b = u(a) — а, т. е. и(х) — х не
-»•
зависит от х. Обозначив через А значение этой разности, полу-
чим и(х) = х + А.
Аффинные нормированные пространства
Говорят, что аффинное пространство нормировано, если
нормировано его присоединенное векторное пространство.
Подчеркнем, что норма является функцией, определенной в
присоединённом векторном пространстве, а не в самом аффинном
пространстве. Можно говорить о норме вектора, а не о норме
точки.
Аффинное нормированное пространство обладает метрикой,
определенной естественной функцией расстояния: d (x, у) =
■ >•
==11* — у\\. Эта функция расстояния инвариантна относительно
переноса в том смысле, что d(x-\-h, у + А) == d(x,y). С
другой стороны, при гомотетии с центром в нуле и отношением к
>
(определяемой отображением х -*■ х' = 0 + Я (х — 0) простран-

180
Гл. HI. Дифференциальное исчисление
ства Е в себя) расстояние умножается на \Х\ (в том смысле,
что d(x',y') = \X\d(x,y)). Если £ является аффинным
нормированным пространством, то отображение (х,у)^>у — х иа
-у ->->■->
ЕУ.Е в Е и отображение (х, Л)->х+Л из ЕУ,Е в Е
непрерывны.
Если Е и F—аффинные нормированные пространства и Е
конечномерно, то любое аффинное отображение Е в F
заведомо непрерывно. Для доказательства достаточно повторить
рассуждения, проведенные на стр. 111. Напротив, если Е и F
бесконечномерны, то это утверждение не всегда справедливо.
Из изложенного на стр. 111 следует, что линейное отображение
одного векторного нормированного пространства в другое
может не быть непрерывным.
Теорема 1. 1°) Аффинное нормированное пространство
полно тогда и только тогда, когда полно его присоединенное
векторное пространство.
2°) Аффинное подпространство F аффинного пространства
Е замкнуто тогда и только тогда, когда его присоединенное
-У -У
векторное подпространство F замкнуто в Е (в частности,
конечномерное аффинное подпространство всегда замкнуто).
3°) Для того чтобы аффинное отображение и аффинного
нормированного пространства Е в аффинное нормированное
пространство F было непрерывным, необходимо и достаточно,
чтобы присоединенное линейное отображение было
непрерывным '). В этом случае и равномерно непрерывно.
Доказательство. 1°) Пусть а — точка, выбранная за
-у -> -у
начало в Е. Отображение X—>а-\-Х является биекцией Е на
Е, сохраняющей расстояние, т. е. сохраняющей структуру
метрического пространства. Но тогда Е будет полным одновре-*
-у
менно с Е.
-> -у
2) Пусть a^F. Тогда Х->а-\-Х является гомеоморфизм
-> -»■
мом Е на Е, а образом F является F. Значит, F замкнуто в Е
-У -У
тогда и только тогда, когда F замкнуто в Е.
3°) Если и является аффинным непрерывным отображе-
-у
нием Е в F, то линейное присоединенное отображение и опре-
1) Напомним, что линейное отображение непрерывно тогда и только
тогда, когда оно непрерывно в нуле пространства (теорема 47 гл. И).

§ 1, Аффинные пространства
18Г
деляется формулой
>
и(Х) = и(а + Х)-и(а), (III, 1;7>
где а — некоторая фиксированная точка. Это отображение,.
очевидно, непрерывно. Обратно, если и непрерывно, то из
неравенства
II и(х)-и[у) II = II и (х- у) || < || и ЦП х- у\\ (Ш, I; 72>
следует, что отображение и удовлетворяет условию Липшица и,,
следовательно, равномерно непрерывно.
Теорема 2. Пусть Е — аффинное нормированное
пространство^- непостоянная скалярная аффинная функция над Е.
Тогда уравнение f(x) = 0 определяет некоторую аффинную
гиперплоскость Н.
Обратно, любая аффинная гиперплоскость определяется
бесконечным множеством уравнений этого вида. Bqe
соответствующие аффинные функции пропорциональны одна другой.
Каждая аффинная гиперплоскость Н замкнута или плотна
в Е. Она замкнута тогда и только тогда, когда аффинные
функции f, определяющие уравнение этой плоскости,
непрерывны.
Доказательство. 1°) Пусть / — непостоянная
скалярная аффинная функция, а /о — линейная форма на
присоединенном пространстве Z:1).
Пространство Е содержит по крайней мере две точки а и Ь,
такие, что f{a) Ф}(Ь). Формула
f(a+t(b^-a)) = f{a) + tf0(b^), f0(b^)^0,
показывает, что можно всегда выбрать t так, чтобы /
обращалась в нуль хотя бы в одной точке с из Е. Выбирая с в каче-
стве начала, мы установим биекцию Х~*с-\-Х из £ на Е,
которая позволит нам проводить рассуждения над простран-
-> ■>
ством Е вместо пространства Е. Пусть Н — множество, опре-
■> _. ■>
деленное уравнением /о(1) = 0, или, иначе, множество /о ({0})>-
или, иначе, ядро линейной формы /0- Пусть, с другой стороны,.
Н — множество из Е, определяемое уравнением f(x) = 0.
') См. примечание на стр. 178. Если мы будем писать f, то можно поду«
мать, что f (X) является вектором, в то время как это лишь скаляр.

182
Гл. III, Дифференциальное исчисление
Поскольку f(c) = О, то лёЯ тогда и только тогда, когда
■> -» .>
х — с еЯ; другими словами, мы имеем Я = с -f- Я.
■>
Если мы покажем, что Я является векторной
гиперплоскостью, то тем самым докажем, что Я является аффинной
гиперплоскостью. Поскольку f не постоянна, то /о не равна
тождественно нулю. Следовательно, существует такой элемент
->->.-* ■ ■>■
е из Е, что /о (е) ф0, а, заменяя при необходимости вектор е
на кратный ему вектор, мы можем всегда считать, что f0(e) =
-» ■>
= 1. Любой элемент X из £ тогда запишется единственным
образом в виде
X==Y + Xe, Я е= К, ГеЯ (где /0 (У) = 0), (III, 1;73)
Эта формула эквивалентна равенству
Я = Ы*)> Y = X-f0(X)t
Это равенство показывает, что векторное подпространство
Я и векторное одномерное подпространство, порожденное век-
-» -» -»
тором е, дополнительны в £, т. е. что Я является
гиперплоскостью.
2°) Обратно, пусть Я— гиперплоскость в Е. Ее
присоединенным векторным подпространством Я является по опреде-
-»
лению некоторая гиперплоскость в Е.
-» ■■-■*■
Пусть теперь е — некоторый вектор, дополнительный к Я
в Е (е ф. Я). Всякий вектор X из Е допускает тогда
единственное разложение вида (111,1; 73). Скаляр К зависит от X,
■ '..'■*■ , ■*■
и мы можем обозначить его через k = fo(X). Функция f0: Х-+
-> ->
-*f0(X) является линейной формой на Е. Она не является
тождественно нулевой (например, /о(е)=1), а множество ее
нулей совпадает с Я.
Всякая линейная форма g0, такая, что уравнение go(X) = 0
определяет гиперплоскость //, пропорциональна /.В самом
-» -» -»-»-»
деле, если k = g0(e), то g0W — kfo(x) Для ^ = е (по опре-
-» ->
делению) и для X е Я, поскольку в этом случае справа и
■> ■>
слева стоят нули, а, следовательно, g0 (X) = kf0 (X) для про-
-*•->„
извольного Х^Е. Если теперь взять произвольную точку с

§ 1. Аффинные пространства
183
из Н, то множество Я будет определено одним из уравнений
>
вида g(x) — 0, где g(x) = g0(x — с). Мы видим, что все
соответствующие аффинные функции g пропорциональны одна
другой.
3°) Если f непрерывна, то множество Я, прообраз
замкнутого множества {0} поля скаляров относительно отображения
f, замкнуто в Е. Пусть теперь функция f, а вместе с ней и
функция f0 разрывны. Согласно теореме 47 гл. II, для каждого
целого п можно найти такой вектор ап из Е, что \fo(an)\^
-* ->
~^ п\\ап\\. Умножая ап на соответствующий скаляр, можно до-
"*■ "*■
биться того, чтобы ||а„|К1/га и одновременно /0(а„) = 1.
Пусть х — любая точка из Е. Рассмотрим последовательность
•> - ■> ■
точек xn = x — f(x)a„. Так как f(x„) = f(x) — f(x)f0(an) = 0,
•> •>
то точки х„ принадлежат Я. Поскольку f(x)an сходится к 0, по-
■>■
следовательность хп сходится к х, когда п стремится к
бесконечности. Мы видим, что каждая точка х' из Е является точкой
сгущения Я, т. е. что Я плотно в Е, чем и заканчивается
доказательство теоремы.
Эта теорема выявляет в некотором смысле удивительный
факт, непривычный для тех, кто занимается изучением
конечномерных пространств: может случиться, что некоторая
гиперплоскость плотна в рассматриваемом пространстве. В
дальнейшем нам представится случай встретиться с плотными
векторными подпространствами векторных нормированных
пространств (знаменитая теорема Вейерштрасса говорит, что
подпространство полиномов плотно в пространстве ^[0,1]
непрерывных комплексных функций на [0,1]).
Выпуклые множества в аффинных пространствах
Пусть а и b — две точки аффинного пространства Е над
полем К вещественных или комплексных чисел. Множество
>
точек, которые можно записать в виде а + tb — а, где /
вещественное число, 0 <; / ^ 1, называется отрезком с концами а
и Ь. Этот отрезок обозначают через [а, Ь] и называют также
замкнутым отрезком. Через [а, Ь[ (соответственно через ]а, Ь]
и через ]а,Ь[) обозначают тот же самый отрезок без точки b
(соответственно без точки а и без обеих точек а и Ь). Здесь
применяются выражения «полуоткрытый отрезок» или
«открытый отрезок», хотя они не являются открытыми множествами,
если аффинное пространство нормировано.

184 Гл. 111. Дифференциальное исчисление
Часть аффинного пространства Е называется выпуклой,
■если вместе с любыми двумя своими точками она целиком
содержит весь отрезок с концами в этих точках.
В аффинном пространстве без труда определяется понятие
•барицентра1). Часть А аффинного пространства Е выпукла
тогда и только тогда, когда вместе с конечным числом точек
юна содержит их барицентр при любой системе масс ^0. Это
легко проверить, заметив, что барицентр нескольких точек
может быть построен с помощью последовательного построения
'барицентров двух точек и что барицентры системы двух точек
с произвольными массами ^0 находятся на соединяющем их
•отрезке.
Пустое множество, множество, сводящееся к одной точке,
само аффинное пространство Е и, более общо, любое аффинное
многообразие из Е являются выпуклыми. Если Е нормировано,
то всякий открытый или замкнутый шар является выпуклым.
Любое пересечение конечного или бесконечного числа выпуклых
частей является выпуклой частью. Можно доказать, что
внутренняя часть и замыкание выпуклой части аффинного
нормированного пространства выпуклы.
Евклидовы векторные и евклидовы аффинные пространства
■>
Пусть Е — векторное пространство над полем вещественных
'чисел R. Евклидовым скалярным произведением в Е назы-
вается билинейная форма (X, Y)-*B(X, Y) gR, которая яв-
') Пусть А[, Аг Ап— точки аффинного пространства Е, снабженные
п
такими коэффициентами at, Ог a„ e R, что 2 ai ^ 0- Тогда точка G =
£=1
=0'+j2a/) 2 аР'^1 пРостРанства £. гДе О' — некоторая точка Е, назы-
вается барицентром системы точек Ai. Если числа a,- ^ 0, то их называют
массами точек /4,-, а барицентр G — центром тяжести системы точек.At.
Точка G не зависит от выбора точки О' из Е. Необходимым и достаточным
условием того, что G является барицентром системы точек Ai, снабженных
/ п \
-коэффициентами ( а{ 2 ai ^ 0) > является выполнение равенства
п ^
apAi = 0. Барицентр системы точек не меняется, если часть этих точек
4=1
заменить их барицентром (если он существует), снабженным коэффициентом,
равным сумме коэффициентов соответствующих точек. — Прим. ред.
S

§ 1. Аффинные пространства
185-
ляется симметричной, т. е. В (X, Y) = В (У, X), и положительно-
определенной, т. е.
В(Х, Х)>0 для ХФО. (111,1;8)
-> -> ->
Два вектора X и У из Е называются ортогональными от-
-> ->
носительно скалярного произведения В, если В(Х, У) = 0.
Векторное пространство, снабженное евклидовым
скалярным произведением, называется евклидовым векторным
пространством. Аффинное пространство, присоединенное векторное-
пространство которого евклидово, называется евклидовым
аффинным пространством. То, что в элементарной геометрии
называют трехмерным пространством, является просто
евклидовым аффинным пространством трех измерений*).
-»■
Теорема 2г. Пусть Е — векторное пространство над R,.
-> ->
В — некоторая билинейная симметричная форма на Е~ХЕ, та-
-> -> -> •>
кая, что В (X, X) ^ 0 для всех X из Е. Тогда имеет место
неравенство KouiU'—Шварца
\В(Х, Y))<\^B(X,X)'\^B(Y, У) (III, 1;Э)
и неравенство Минковского
/b(X + Y, Х + У) </"в(Х, X) + /"я(У, У); (Ш,1;10>
кроме того, если В — положительно определенная форма, т. г.
В (X, X) > 0 для X Ф О, го в обеих формулах стоит всегда,
знак строгого неравенства <, кроме тех случаев, когда в
формуле (III, 1; 9) векторы X uY пропорциональны и когда
в формуле (III, 1; 10) эти векторы пропорциональны с
положительным коэффициентом пропорциональности2).
-> •>
Доказательство. Для любых векторов X, У и числа
Я имеем
В(Х + ЯУ, Х + ЯУ)>0, (III, 1; 11)
') Это не совсем точно: в элементарной геометрии еддница длины
необязательно фиксирована. Пространство становится аффинным евклидовым
лишь после выбора в нем единицы длины.
-> ->
2) Если X или У являются нулевыми векторами, то можно
считать, что они пропорциональны с коэффициентами пропорциональности gsO..

186
Гл. III. Дифференциальное исчисление
ИЛИ
В(Х,Х) + 2ХВ(Х, Y) + X2B(Y, Y)>®- (Ш, 1; 12),
Вещественный трехчлен неотрицателен лишь в том случае,
когда его дискриминант ^0, откуда и получается неравенство
(III, 1; 9). Пусть теперь билинейная форма В положительно
-> -> -> ->
определена. Если Y ф О, то В(Y, Y)>0 и трехчлен не вы-
-> •> ->-*..
рожден. Если X не пропорционален Y, то вектор X -{- XY
отличен от 0 для любого вещественного X. Следовательно, левая
часть соотношения (III, I; II) всегда >0. Но тогда трехчлен
(III, I; 12) больше нуля при любом X, т. е. не имеет
вещественных корней. Это означает, что его дискриминант <0 и
соотношение (III, I; 9) имеет место со знаком <. Таким образом,
в (III, I; 9) всегда имеет место знак <;, кроме случая, когда
К = 0 или Y Ф О, но X^=X0Y, т. е. если X и Y
пропорциональны. Что же касается неравенства Минковского, то оно
эквивалентно неравенству
B(X + Y, X + Y)<B(X,X) + B(Y, Y) + 2/b(X, X)-B<y,Y),
(III, I; 13)
или
В (X, X) + 2B (X, Y) + B(Y, Y) <
<B(X, X) + B(Y, Y) + 2/b(X,X)-B(Y, Y)- (HI, I; 14)
Последнее же неравенство следует из (III, 1; 9). Если В
положительно определена, то равенство справедливо только
в том случае, когда В(Х, Y)^0 и когда (111,1; 9) имеет ме-
-> ->
сто со знаком =, т. е. если X и Y пропорциональны с
неотрицательным коэффициентом пропорциональности.
Отсюда вытекает, что если аффинное пространство Е евкли-
дово, то функция X—*-У В(Х, X) является нормой в Е.
Именно она служит для определения расстояния в элементарной
геометрии. Евклидово пространство, векторное или аффинное,
является нормированным. Скалярное произведение в „евклйдо-
вом векторном пространстве принято обозначать через (X\Y),
а через У^(Х\Х)~ норму || Х\\.

§ 1 Аффинные пространства
187
Эрмитовы векторные и эрмитовы аффинные пространства1)
-> ->
Пусть Е и F — векторные пространства над полем
комплексных чисел Q. Отображение и из Е в F называется
полулинейным, если оно удовлетворяет следующим условиям:
u(X + Y) = u(X) + u(Y) для Х^Е, Y <=-£,
-> _ -> .> ^ (III, 1; 15)
и(ХХ) = Ки(Х) для Ie£j AeC.
Если F == С, то и является полулинейной формой.
-> ->
Полуторалинейной формой2) на ЕУ^Е называется функ-
-> -> -> -> ->
ция (^f, K)-*B(^, К)еС, линейная по Jf при фиксирован-
ном Y и полулинейная по У при фиксированном X. Другими
словами,
В (1, + Х2, Y) = Я (*„ К) + В (Х2, Y),
В (X, Yy + Y,) = B (X, Yi) + В (X, Y2),
В {XX, Y) = XB(X, Y), ЯеС,
B(X, цК) = ДВ (X, Y), р е= С.
(III, 1; 16)
Эрмитовым скалярным произведением в векторном про-
->
странстве Е над полем комплексных чисел называется полу-
-> -> -> ->
торалинейная форма (X, Y)->B(X, Y), которая является эрми-
-> -> 5 5
товой, т. е. такой, что B(Y,X) = B(X, Y), и положительно
определенной, т.. е. удовлетворяющей неравенству (III, 1; 8).
Векторное пространство над полем С, снабженное эрмитовым
скалярным произведением, называется эрмитовым векторным
пространством. Аффинное пространство над полем .О,
присоединенное векторное пространство которого эрмитово,
называется эрмитовым аффинным пространством.
Теорема 23. Заключения теоремы 22 сохраняются, если в
ее условии заменить R на С и «билинейная симметричная» на
«полуторалинейная эрмитова».
') В русской литературе вместо слова «эрмитово» принято использовать
термин «унитарное». — Прим. ред.
2) Полтора = один с половиной! полуторалинейная =ц линейная + полу,
линейная.

188 Гл. 111. Дифференциальное исчисление
Доказательство. В самом деле, вместо (III, 1; 12) на
этот раз для любого комплексного Я, получаем:
В(Х, X) + IB(Y, X) + lB(X, Y) + XXB(Y, Г)>0. (Ill, 1;17)
Пусть В {X, Y) = ре'9, где р = | В {X, Y) |. Положим А, =
— teie, где t — вещественное число (не обязательно ^0). Из
(III, 1; 17) следует, что для любого вещественного t имеет
место неравенство
В(Х, Х) + 2\В{Х, Y)\t + B(Y, Y)P>% (III, 1; 18)
яз которого снова следует (III, I; 9).
Неравенство (III,1; 10) эквивалентно неравенству
В(Х, Y) + B(Y, *)<2/я(*, X)B(Y, Y), (111,1; 182)
или
Re (В (X, Y))') </"в (X, X) В (Y, Y), (III, 1; 183)
что вытекает из (III, 1; 9).
Если В положительно определена, Yф0 н X не пропор-
->
ционален- Y, то (III, I; 18) будет >0 для любого
вещественного t; следовательно, неравенство (111,1; 9) будет
справедливым со знаком <• Равенство возможно лишь в том случае,
-У -У
когда X и Y пропорциональны. Равенство в соотношении
(111,1; 10) может иметь место только в том случае, если, кроме
-> -> -> -> -> ->
того, ЯеВ(Х, Y) = \B(X, Y)\, т. е. если В(Х, Y) вещественно и
^0, а, значит, если коэффициент пропорциональности ^0.
Таким образом, эрмитово векторное или аффинное
пространство нормировано.
Приведем теперь результаты, пригодные как для
евклидовых пространств над полем R, так и для эрмитовых
пространств над полем О. Мы их будем излагать для эрмитовых
лространств. Конечно, в евклидовом случае скаляры будут
считаться вещественными, полулинейность будет означать
линейность, полуторалинейность—-билинейность, а Я будет
заменяться на Я.
') Re = вещественная часть.

§ 1. Аффинные пространства 189
Изоморфизм (или полуизоморфизм) конечномерного
евклидова (или эрмитова) пространства
и его сопряженного пространства
Через Е' будем обозначать пространство, сопряженное
к некоторому векторному пространству Е над полем К1).
<■ <■
Если а является элементом из Е', то это линейная форма на
.> -><--> <- ->
Е, т. е, отображение Х-+а(Х). Вместо а{Х) удобнее писать
<--><--> <-
а-Х или (а, X). Известно, что Е' гакже является векторным
пространством, а функция (а, X)—>(а, X) е К — некоторой би-
линейной формой на Е' X Е, которую называют
фундаментальной билинейной формой. Ее называют также скаляр-
ным произведением ае£ и X е Е, но это скалярное
произведение не имеет никакого отношения к скалярному произве-
дению в евклидовом или эрмитовом пространствах, ибо а и X
не принадлежат одному и тому же векторному пространству2).
При этом следует строго различать обозначения (а, X) и
.-> -> ->
W|y). Однако если Е является евклидовым или эрмитовым
пространством, то оба скалярных произведения существуют
одновременно.
-> ->->->
Для фиксированного У функция X—* (X\Y) является линей-
->
ной формой на Е. Следовательно, ей соответствует некоторый
->
элемент у сопряженного пространства, такой, что
(y,X) = (X\Y) для любого X из Е. (III, 1; 19)
<- ->
Этот элемент у зависит от У, и поэтому мы будем обозна-
<- * ->
чать его через v-> или Y (Ю- Тогда полулинейность правой
->
части равенства (III, 1; 19) по отношению к У для каждого
') Сопряженное пространство и его элементы удобно обозначать
символами, снабженными сверху противоположно направленной стрелкой (тем
более, что векторы из Е называются ковекторами).
2) Кроме того, скалярное произведение ( , ) всегда билинейно, а не
полуторалинейно.

190
Гл. HI. Дифференциальное исчисление
->• <- -у
фиксированного X означает, что у± полулинейно зависит от У:
у+ -> = y^- + Y->>
"'Г' Y; Y" (III, l;20)
Таким образом, Y->y+ является полулинейным отобра-
->• <■
жением y пространства £ в его сопряженное пространство Е'.
Это отображение инъективно, ибо равенство y->-=0 означает,
■*■->->-> -> ->
что (y^-, Я) = (Я| У) = 0, каким бы ни был вектор Z из £. По-
лаг'ая Z = 7, получаем (У|У) = 0, откуда К = 0, что
доказывает инъективность отображения y- Если Е конечномерно, то
-> ■«-
Е w E' имеют одну и ту же размерность, а это означает, что
-> <-
у является биекцией Е на Е'. Отсюда следует, что задание
евклидовой структуры определяет изоморфизм между
пространством и его сопряженным; задание эрмитовой структуры
определяет полуизоморфизм между ними.
Воспользуемся только тем фактом, что y является сюръек-
<-
цией. Если а является элементом сопряженного пространства,
т. е. некоторой линейной формой на Е, то существует, и при-
->• ->
том единственный, элемент У из Е, такой, что
-> -> «- -> ^- ->
(X\Y) — {a, X) для всех X из Е.
>
-> <-
Элемент У является не чем иным, как у~ (а). Таким образом,
получаем следующий результат:
<-
Теорема 24. Если а является линейной формой над ев-
->
клидовым или эрмитовым конечномерным пространством Е, то
~>
существует, и притом единственный, вектор У, такой, что фор-
<- ->->->•
ма а является скалярным произведением X->(X\Y).
Ортонормированные базисы
->
О ртонор миро ванным называется базис (е,)ге/ евклидова
->.
или эрмитова конечномерного пространства Е, элементы
которого попарно ортогональны и имеют длину 1.

§ 1. Аффинные пространства 191
Теорема 2s. Любое евклидово или эрмитово конечномер-
ное векторное пространство имеет ортонормированные
базисы.
Доказательство. Это очевидно, , если размерность п
равна I1), ибо если {/J является базисом, то {е, = /1/||/111}
будет ортонормированный базисом. Предположим теперь, что
существование ортонормированного базиса доказано для
любого евклидова или эрмитова пространства размерности
<:/i—1, и докажем его существование в пространстве Е раз-
мерности п. Пусть f{ — некоторый вектор ФО и el = fl/\\fl\\.
Множество векторов, ортогональных еь является гиперплос-
-> -> ->
костью Я. в £. В самом деле, это множество векторов X,
удовлетворяющих линейному уравнению у+(Х) = (Х\е1) = 0,
где линейная форма Y-> не равна тождественно нулю, поско-
^i
-> -> . -> ->
льку е, Ф 0, и, кроме того, у инъективно. Так как (е1|е,)>0,
-> ->
то эта гиперплоскость не содержит ву, а, следовательно, Н[ и
->
прямая, порожденная вектором еи являются дополнительными;
•> ■>
Hi называется гиперплоскостью, ортогональной ел, и является
евклидовым или эрмитовым пространством размерности п—\.
По предположению индукции она должна иметь хотя бы один
-> ->
ортонормированный базис е2 еп- При этом система векто-
-> -> ->
ров е,, е2> •■••> еп образует ортонормированный базис
пространства Е, что и требовалось доказать.
-> ->
Если (ef)ie/ является некоторым базисом в Е, то скалярное
произведение двух векторов X— 2и X^i и Y = Zi Y&i записы-
вается в виде
(Х|Г)= 2 (еД)*,^ 2 g,./*,F/, (Ш,1; 21)
гДе gi, i — {ei\ej)- Здесь gi,i = gt,i, а неравенство (Х|Х)>0для
ХфО записывается в виде
2 gi.jXiX^O, (III.1; 22)
') Индукцию можно даже начинать с п = 0. В векторном пространстве
размерности 0 базис пуст и его можно считать артонормированным!

192
Гл. 111. Дифференциальное исчисление
кроме случая, когда Xt = 0 для всех i e /. Матрицу,
составленную из элементов g», j, называют эрмитовой положительно
определенной матрицей.
Рассматриваемый базис ортонормирован тогда и только
тогда, когда матрица из g^j является единичной:
(Х\ У)= 2 XiY,, ||Х|Р= 2 \Xif. (Ill, 1;23)
Обобщенные евклидовы или эрмитовы пространства ')
В специальной теории относительности возникает
необходимость в обобщении евклидова или эрмитова пространства,
пространстве Лоренца или пространстве Минковского. Это —
конечномерное векторное пространство Е (в физике это
четырехмерное пространство над полем R), снабженное
обобщенным скалярным произведением, т. е. полуторалинейной не
положительно определенной эрмитовой формой. Будем ее, как
обычно, обозначать через (X\Y). Для Х=£0 не обязательно
должно выполняться неравенство (Х\Х)>0. Может случиться,
что для некоторых векторов X =ф 0 произведение (X, X) = 0.
Эти векторы называются изотропными, а их объединение —
изотропным конусом2). При этом вводится существенное
условие: полуторалинейная форма не вырождений; иначе говоря,
не существует вполне изотропного вектора X =ф 0, т. е.
ортогонального ко всем векторам пространства. Разумеется, здесь
не выполняются неравенства Коши — Шварца и Минковского
и такая структура не определяет норму. Однако отображение
у пространства Е в Е' всегда полулинейно и инъективно, ибо
■*" *■ ^
равенство y+ — Q означает, что вектор У ортогонален всем
->• ->•
векторам X из Е, т. е. вполне изотропен, а, значит, равен
нулю. Отображение у биективно. Линейной форме а над Е
соответствует, как и ранее, некоторый вектор У из Е, и притом
<•->->-> •> •>
единственный-, такой, что {a, X) = (X\Y) для любого Хе£-
•>
это вектор у-1 (<*)•
') Эти пространства называют также псевдоевклидовыми и
псевдоэрмитовыми. То, что мы здесь называем ортонормированным базисом, носит
также название псевдоортонормированного базиса.
2) Это понятие отличается от принятого в физике: там рассматривается
векторное пространство над R и вещественное скалярное произведение.

§ 1. Аффинные пространства
193
Ортонормированным базисом обобщенного евклидова или
->
эрмитова пространства называется базис (^).s;, элементы
которого попарно ортогональны и скалярные квадраты которых
равны ±1. Такие базисы всегда существуют. Для
доказательства можно применить, только с некоторой осторожностью,
построения по индукции, проведенные при доказательстве
теоремы 2$.
-> ->
При rt=l исходят из произвольного вектора fi^O. При
->
п = 1 все векторы пространства пропорциональны вектору fit
поэтому утверждение «Д не является вполне изотропным» рав-
->
носильно тому, что «fi не является просто изотропным». Если
-> -> / / ^> ~^~ -> ->
взять теперь el — f1/y |(fi,/i)|, то получим (ei|e1)='±l.
Однако при переходе от п — 1 к п требуются более тонкие
рассуждения. Покажем прежде всего, что существует по
крайней мере один вектор fi, не являющийся изотропным. Если бы
каждый вектор был изотропным, т. е. ортогональным самому
себе, то из равенства
(X+Y\X + Y) = (X\Y) + <y\Y) + 2Ke{X\Y) ЦП, 1;24)
-> -> ->
следовало бы, что Re(X|F) является нулем для любых X и
> -> ->
Y. Так как в случае К = С имеет место равенство Re(X|tY) =
-> -> -> -> -> ->
= lm(X\Y), то мы получили бы (X|F) = 0 для любых X и Y.
Каждый вектор оказался вполне изотропным, что
противоречит нашему предположению. Следовательно, всегда можно
найти не изотропный вектор fi и положить ei = f\/y |(/i,fi)|.
Гиперплоскость Н\, ортогональная е\, не содержит eit- по-
скольку е\ не изотропен. Следовательно, Hi является
дополнением к прямой, порождаемой вектором в\. С другой стороны,
скалярное произведение на Hi не вырожденно. В самом деле,
-> ->
если бы в Hi существовал вектор т^О, ортогональный всем век-
-> ->
торам из Hi, то поскольку он ортогонален также и еи он был
бы ортогонален всем векторам из Е, т. е. был бы вполне
изотропным, что невозможно. Следовательно, #i является
обобщенным евклидовым или эрмитовым пространством
размерности п-1 и, значит, имеет ортонормальный базис е2 еп.
7 Зак. 1339

194
Гл. III. Дифференциальное исчисление
Так как ехфНх, то е{, е2 еп является ортонормированным
■>
базисом в Е.
-»■
Пусть теперь (б()ге/ является ортонормированным базисом
в Е. Если положить {ei\e^ = zi= ± 1, то скалярное
произведение векторов Х= ZiXfii и Y= 2jY2е2 запишется в виде
(*|Г) = 2 BtXiYt и (ВД = Ц е«|*, р. (III, 1;25)
Можно доказать, кроме того, важную теорему, называемую
законом инерции: число р чисел ег- > 0 и число q чисел ы < О
не зависят от выбора ортонормированного базиса. В самом
деле, рассмотрим фиксированный базис {ei)is-,, и пусть /
(соответственно К) — подмножество в /, образованное теми i, для
которых 8г=-(-1 (соответственно —1). Пусть р
(соответственно q)—число элементов в / (соответственно в К).
Существует, по крайней мере одно, векторное подпространство F из
Е размерности р, на котором скалярное произведение
является положительно определенным, а именно то подпростран-
ство, которое порождено векторами ег-, ie/. Векторного под-
пространства G размерности ~>р, обладающего тем же
свойством, не существует. В самом деле, если G— любое
векторное подпространство размерности i>p, то оно пересекается
с подпространством размерности п — р, порожденным векто-
рами е{, i^K, по некоторому не сводящемуся к 0
подпространству, поскольку сумма размерностей этих подпространств
■> ■>
>«. Если X Ф 0 — вектор этого пересечения, то необходимо
-> •>
имеем {Х\Х)<0, а, значит, скалярное произведение на G не
может быть положительно определенным. Итак, числа р и
q = п — р определяются независимо от первоначально
выбранного базиса. Число р (соответственно q) является максимальной
размерностью векторных подпространств из Е, на которых
скалярное произведение положительно определено (соответственно
отрицательно определено).
В итоге мы получаем такой результат:
Теорема 2б. Каждое обобщенное евклидово или эрмитово
пространство имеет ортонормированные базисы. Число векторов
такого базиса, скалярный квадрат которых равен +1
[соответственно— 1), не зависит от выбора базиса. Это — максималь-

§ 2. Вещественные функции вещественной переменной 195
пая размерность векторных подпространств, на которых
скалярное произведение является положительно определенным
(соответственно отрицательно определенным).
В физике, в специальной теории относительности, физическая
вселенная пространства-времени является аффинным
четырехмерным пространством Ец над полем вещественных чисел. Его
присоединенное векторное пространство £4 снабжено
скалярным произведением, для которого р = 3 и «7=1. Галилеева
система координат в Е4 является системой координат, образо-
ванной началом пространства Е4 и четырьмя векторами еи е2,
-> -> •>
е3, е0, образующими ортонормированный базис Е^ и такими,
что ei = e2 = 63= 1 и ео = — 1. Вектор 1е£4 пространства-
времени имеет 4 координаты Х\, Xz, Х%, Х0 = сТ, где Т —
координата времени в рассматриваемой галилеевой системе
координат и с — скорость света. Скалярный квадрат этого вектора
о о о 2229 г
равен Х]-{- Х2+ Хз — Xq — L —сТ, где L —
пространственная длина вектора в рассматриваемой галилеевой системе
координат.
§ 2. ВЕЩЕСТВЕННЫЕ ФУНКЦИИ ВЕЩЕСТВЕННОЙ ПЕРЕМЕННОЙ.
НЕПРЕРЫВНОСТЬ СПРАВА И СЛЕВА
Пусть Q — некоторая часть вещественной прямой R и F —
произвольное топологическое пространство. Говорят, что
отображение / части Q в F непрерывно справа в точке йеД
если f(x) стремится к f(a) при х, стремящемся к й в Q по
значениям ;з=а. Если точка а изолирована справа в Q, т. е. если
существует такое число ц > 0, что интервал ]а, а-\-ц[ не
содержит ни одной точки Q, то любое отображение Q в F
непрерывно справа в а. Отображение / непрерывно справа в точке
и тогда и только тогда, когда сужение / на часть х ^ а
множества Q непрерывно в точке а.
Такое же определение дается для непрерывности слева.
Отображение / непрерывно в точке а тогда и только тогда,
когда оно одновременно непрерывно справа и слева. Если
точка а изолирована слева, то ее непрерывность в точке а
эквивалентна непрерывности справа в этой точке. В дальнейшем
все утверждения сделаны в предположении, что Q является
открытым множеством в R. Такое предположение оставляет
в стороне важный для практики случай, когда Q является
полуоткрытым или замкнутым интервалом. Большинство теорем
будут справедливыми, вообще говоря, и в этом случае.
Небольшие необходимые изменения читатель сделает сам.
7*

195
Гл. 111. Дифференциальное исчисление
Разрывы первого рода. Правильные функции
Говорят, что точка а является точкой разрыва первого
рода функции f(x), если при х, стремящемся к а по
значениям, строго большим а, существует предел f(x),
обозначаемый через /(а + 0), при х, стремящемся к а по значениям,
строго меньшим а, существует предел f(x), обозначаемый
через f(a — 0), и эти пределы одновременно не равны значению
функции f в точке а. Если / непрерывна или имеет разрыв
первого рода в точке а, а пространство F метрическое, то
величина
max[d(f(a), f(a-0)), d(f(a), f(a + 0)), d(f(a-0), f(a + 0))]
называется колебанием функции / в точке а. Оно равно нулю
тогда и только тогда, когда / непрерывна в точке а. Если F
является аффинным пространством, то можно вычислить раз-
>
ность / (а + 0) — f (а — 0), которая является элементом
присоединенного векторного пространства F. Эта разность
называется скачком функции f в точке а. В определение скачка не
входит значение f(a) функции / в самой точке а. Поэтому он
может быть нулем даже в том случае, когда / разрывна:
значения /(а + 0) и f{a — 0) могут быть равны между собой, но
не равны f(a).
Функция /, разрывная в точке а, естественно, не обязана
иметь в этой точке разрыв первого рода в том смысле, что
пределы lim f(x) и lim f(x)- не обязательно должны
х>а,х-*а х<а,х-*а
существовать. Например, функция, равная sin l/x для х Ф 0
и 0 для х = 0, разрывна в начале координат, но не имеет
в этой точке разрыва первого рода.
Теорема 3. Если отображение f некоторого открытого
множества Q вещественной прямой R в метрическое
пространство F имеет лишь точки непрерывности и точки разрыва
первого рода, то оно непрерывно всюду, кроме не более чем
счетного множества точек множества Q.
Доказательство. Ограничимся доказательством для
случая Q = R. Пусть с — произвольная точка R. Колебание
ю (с) в точке с может быть каким угодно, но колебание а>(х)
в точке х стремится к 0, когда х стремится к с по значениям,
отличным от с. В самом деле, по определению /(с + 0), для
любого е > 0 существует такое г\ > 0, что из неравенства
с < х < с + 11 следует неравенство d(f(x), /(c-j-0) ^; е/2.
Тогда для любых у и z из интервала ]с, с + г\[ имеем
d(f(y), №)<.d(f(y), f(c + 0)) + d(f(c + 0), f(z))<e. Полагая

§ 2. Вещественные функции вещественной переменной 197
У = х и устремляя z к х по значениям, строго большим я, а
затем по значениям, строго меньшим х, получим d(f(x + 0), f(x))4^.e
и d(f(* — 0),f(*))^e. Устремляя г/< я и z>x к я, получим,
что d(f(x — 0), f(* + 0))^e, откуда окончательно находим
и(х)-^е для с < х < с + г). Действуя точно так же слева от
точки с, можно убедиться, что утверждение верно и в этом
случае. Рассмотрим теперь интервал [—л, -\-п]. Множество точек
этого интервала, в которых колебание ^-1/£, необходимо
конечно. В самом деле, если бы это было не так, то можно было
бы найти бесконечную последовательность точек разрыва в этом
интервале, в которых колебание было бы ^-l/k. Поскольку
интервал компактен, из рассматриваемой последовательности
можно извлечь такую подпоследовательность, которая сходилась бы
к некоторой точке с этого интервала и состояла бы из точек,
отличных от точки с (теорема 25 гл. II). Согласно только что
доказанному, колебание в этих точках всюду ^>1/£ и должно
стремиться к 0, а это невозможно. Таким образом, множество точек
интервала [—п, +п], в которых колебание >1/£, заведомо
конечно. Если взять объединение этих особых точек для k = 1, 2, 3,...,
то мы увидим, что множество точек х интервала [—п, п], в
которых колебание со(л:)>>0, не более чем счетно и, следовательно,
на всей числовой прямой R множество таких точек, являясь
объединением счетного множества не более чем счетных
множеств, не более чем счетно. В каждой другой точке х, не
принадлежащей этому не более чем счетному множеству, <»(*) =
= 0 и f непрерывна.
Функцию, определенную на части прямой R со значениями
в топологическом пространстве F и имеющую только точки
непрерывности или точки разрыва первого рода, мы будем
называть правильной. Согласно доказанному, если пространство
F метризуемо, то такая функция непрерывна всюду за
исключением, быть может, не более чем счетного множества особых
точек.
Замечание. Это бесконечное счетное множество точек
разрыва может встретиться в действительности. Рассмотрим,
например, вещественную функцию f вещественной переменной,
определенную следующим образом:
f(x) = 0, если х иррациональна,
f (—) = — , если х = —— несократимая дробь {q > 0).
Легко видеть, что если х стремится к а по значениям,
отличным от а, то f(x) стремится к нулю. В самом деле,
зададим е > 0. Пусть <7о — целое число ^ 1/е. На [а—\, a-f-1]

198 Гл. III. Дифференциальное исчисление
имеется лишь конечное число рациональных чисел,
знаменатели которых <<7о- Следовательно, существует такое
т] > 0, что каждое рациональное число из интервала [а — ц,
а + ц] имеет знаменатель ^<7о, кроме, быть может, самой
точки а, если она рациональна. Но тогда из неравенства
\х — a|^Ti, хфа, следует, что /(*)<е, — тем самым наше
утверждение доказано. Мы видим, что / непрерывна в точке а
тогда и только тогда, когда а иррациональна. Если а
рациональна, то / имеет в точке а разрыв первого рода, причем
f(a + 0) = f(a — 0) = 0. Следовательно, рассматриваемая
функция правильная и имеет счетное (и плотное) множество
точек разрыва. Ее скачок (но не колебание!) повсюду равен
нулю.
Если F является топологическим не метризуемым
пространством, то функция, определенная на R со значениями в F, может
быть правильной и всюду разрывной.
Производная вещественной функции
вещественной переменной
Пусть / — отображение открытого множества Q из R
в F — R. Производной отображения / в точке йей
называется предел, если он существует, отношения [f(a-\-h) —
— f(e)]/h при h, стремящемся к 0 по значениям =^0, таким,
что а -\- h принадлежит Q. Поскольку Q является открытым
множеством, то а + h при достаточно малом \h\ принадлежит
Й. Если этот предел существует только при h, стремящемся
к 0 по значениям >0, то его называют производной
отображения f справа. Можно точно также говорить о производной
отображения f в точке а слева. Производная отображения /
в точке а существует тогда и только тогда, когда существуют
производные справа и слева и обе они равны между собой1).
Функция, имеющая производную в точке а, непрерывна
в этой точке. Если она имеет производную в а справа, то она
непрерывна справа в а. Существование и значение
производной функции f в йё£1 зависят от значения / в окрестности
а. Производная / в точке а обозначается обычно через f'(a),
или -г~(а)> или Df(a). Если производная существует
всюду в Q, то функция х -> fr(x) называется производной функ-
') Если вместо открытого множества в качестве £2 берут замкнутый
интервал [а, Ь], то говорят также, что f имеет производную в точке а
(соответственно в точке Ь), если она имеет производную справа (соответственно
слева) в этой точке. Впрочем, это полностью соответствует общему
определению производной, поскольку рассматриваются значения h, при которых
а + h (или b -f h) принадлежат Q.

§ 2. Вещественные функции вещественной переменной 199
ши f, или просто производной. Ее обозначают через f, или
М- или Df. В свою очередь можно исследовать, имеет ли
dx '
сама эта функция производную, что приводит к понятию
второй производной, третьей производной и т. ,д. Производная по-
dmf
рядка m в точке а обозначается через /(т) (а), или -т~У (а),
или -г-) f(a), или Dmf(a). Производная функции порядка m
dmf I d \m
обозначается через pm), или -^, или l-j-j f, или Dmf.
Важно заметить, что о производной m-го порядка в точке
оей можно говорить лишь в том случае, когда существуют
все производные порядков ^Zm — 1 в множестве Q или, по
крайней мере, в некоторой окрестности точки а в О,.
Говорят, что I дифференцируема m раз в Q, если она имеет
производную порядка m в каждой точке множества Q. При
этом она заведомо k раз дифференцируема для всех k-^m,
и ее производные порядков <; m—1 непрерывны в Q. Говорят,
что f непрерывно дифференцируема m раз, или принадлежит
классу Ст, если она имеет непрерывные производные до т-го
порядка включительно. При этом она заведомо принадлежит
классу Ch для k <; т. Функция, дифференцируемая т раз,
наверняка принадлежит классу Ст~К Говорят, что
/бесконечно дифференцируема или принадлежит классу С°°, если она
имеет последовательные производные всех порядков. Все они
непрерывны.
Однако в некоторых случаях принятые обозначения могут
привести к ошибкам. Что означает, например, обозначение
/'(2л:)? Означает ли оно производную функции х—>f(2x) или-
же значение производной /' функции f в точке с абсциссой 2х?
Мы будем понимать эти обозначения лишь во втором смысле.
Если мы пожелаем записать производную функции х—>f(2x)
в точке а, то мы будем писать (f (2х))'х=а, а производную
функцию функции х—>f(2x) будем записывать в виде (f(2x))'.
Таким образом, имеем: (f(2x))' = 2f'(2x), (/(2x))<m> =
= 2mf(^)(2x). Следует отличать также Dmf(2x), или (Dmf) (2x) =
= f(m> (2х), от Dm (f(2x)) = (f (2x)) <m>.
Можно, естественно, говорить о производной, принимающей
значения -f-oo или —с», и то же самое для производной слева
или производной справа. Однако, если это специально не
оговорено, под производной мы всегда будем понимать
производную, принимающую конечное значение.
Пусть f — некоторая вещественная функция, определенная
на интервале [а, Ь] прямой R. Будем говорить, что эта функция
кусочно m раз непрерывно дифференцируема, или кусочно
принадлежит классу С™, если она правильна и существуют

200 tA. tit. Дифференциальное исчисление
такие точки а0 = а, аи ..., ап_ь а„ = Ъ, а, < ai+i, что
функции ft, равные f в ]a{,ai+i[, f(a, + 0) в a, и f(ai+I —0)
в Oi+ь принадлежат классу Ст на интервале [a,, ai+{\.
Например, если график функции y = f(x) представляет собой
ломаную линию, то f непрерывна, не дифференцируема, но кусочно
принадлежит классу С°°.
Теорема 4 (Ролля). Пусть вещественная непрерывная
на замкнутом ограниченном интервале [а, Ь] функция f имеет
в каждой точке открытого интервала ]а, Ь[ производную,
конечную, или равную +°°, или равную —оо. Если при этом.
f(a) =f(b) =0, то существует по крайней мере одна точка с
в ]а,Ь[, такая, что f'(c) = 0.
Доказательство. Если функция f тождественно равна
нулю, то результат очевиден. Если же эта функция не
является тождественным нулем, то она принимает по крайней
мере одно значение > 0 или хотя бы одно значение < 0.
Рассмотрим, например, первый случай. Так как f непрерывна на
компакте [а, Ь], то существует хотя бы одна точка с из ]а, Ь[,
в которой она достигает своего максимума. В этой точке
производная справа необходимо ^0, в то время как производная
слева ^ 0. Поскольку функция в любой точке ]а, Ь[
предполагалась дифференцируемой, то эти производные справа и слева в
точке с равны между собой, и, следовательно, производная f'(c)
равна нулю.
Замечание. Хорошо видно, почему нет необходимости
ни предполагать f дифференцируемой в точках а и Ь, ни
считать производную конечной. Напротив, существование
производной, а не только производной справа и производной слева
является существенным. Функция f(x)=l~-\x\ на интервале
{•— 1,-f-l] непрерывна, равна нулю на его концах и в каждой
точке имеет производную справа и слева. В точке л: == 0, где
ь
1
Рис. 5. у=\ - \х\, 1*|<1.
/ достигает своего максимума, производная справа равна — 1,
а производная слева равна +1. Ни в одной точке ни производи
ная справа, ни производная слева не обращаются в нулЪ.
Если предполагать только, что f имеет в интервале ]а,Ь[ про-

§ 2. Вещественные функции вещественной переменной 201
изводную справа f'n, то можно доказать существование такой
точки ci из ]а, Ь[, в которой f'n (с,) ^ 0, и существование такой
точки сг-из того же интервала ]а,Ь[, в которой /Цс^^О1).
Теорема 5 (формула конечных приращений). Пусть
вещественная непрерывная на замкнутом интервале [а,Ь]
функция имеет в каждой точке открытого интервала ]а, Ь[
производную, конечную или равную +оо, или равную —оо. Тогда
на ]а, Ь[ существует по крайней мере одна точка с, такая, что
Г{с) = 1Щ=Шт (ш>2;1)
Формула конечных приращений часто записывается в
следующем виде
f(x + h)h~Hx) =Г(х + Щ, где .ее] 0, 1 [. (III, 2; 2)
Замечание. Если предполагать только существование
производной справа f'n, то можно доказать существование
такой точки ср что f'n (с,) ^ [/ (Ь) — f (a)]/(b — а), и такой точки с2,
что ГП(с2)>[f (b)-f(a)]/(b-а).
Теорема 6 (формула Тейлора). Пусть функция f
является m раз непрерывно дифференцируемой в интервале [а, Ь]
и в каждой точке открытого интервала ]а, Ь[ имеет производную
(т+\)-го порядка, конечную, или равную + оо, или равную
—оо. Тогда существует хотя бы одна точка с в ]а, Ь[, такая, что
f(b)-f(a)-(b-a)r(a)-^^f''(a)-...-^f^f<mHa)^
==((Яг+)1В)Г/(т+|)(с)- (Ш,2;3)
Эта формула часто записывается в следующем виде:
f(x + h) = f{x) + hV (x) + ^ f"(x)+ ... +~f{m)(x) +
/.ГИ + 1 . . ,.
+ J^TWf {x+m' (ш-2;4>
где 8 — некоторое число из ]0, 1[.
Формула конечных приращений является, очевидно, частным
случаем формулы Тейлора. Формула же Тейлора доказывается
') Доказательство этого утверждения более тонкое. См. также
замечание, следующее за леммой теоремы 13.

202
Гл. III. Дифференциальное исчисление
следующим образом: вводится вспомогательная функция
gM-f№)-/M-(*-*)f'M- ...
...-.St=£.niA-!!£g.l. (III.2; 5)
где число % определено так, что g(a) =? 0.
Поскольку g(b) = 0, то к этой функции применима теорема
Ролля. Это дает некоторую точку с из ]а, Ь[, в которой g'(c) =
= 0, а, значит, fm+l(c) — 'k. Отсюда и вытекает нужный
результат.
Монотонные функции
Говорят, что вещественная функция, определенная на
открытом множестве ficR1), монотонна, если она является
возрастающей или убывающей на этом множестве.
Монотонная функция не обязательно непрерывна, однако, согласно
известной теореме математического анализа, она заведомо
обладает пределом справа /(а + 0) и пределом слева f(a — 0)
в каждой точке aeQ2). Оба эти предела не обязательно
равны между собой или равны f(a).
Монотонная функция, следовательно, является правильной.
Применяя теорему 3, получаем, что такая функция всюду
непрерывна, за исключением не более чем счетного множества
точек.
Небесполезно привести простой пример строго
возрастающей функции, имеющей счетное плотное множество точек
разрыва. Пусть h—некоторая функция > 0, определенная на
множестве рациональных чисел Q и такая, что 2 h (r) ко-
r (=Q
нечна (речь идет о сумме счетного множества положительных
чисел, не заданных в определенном порядке, смысл которой
был определен на стр. 131). Рассмотрим теперь функцию. /,
определенную следующим образом:
f(x)= 2 h (г). (01,2; 6)
reQ, r < х
') Как было сказано на стр. 195, Q также может быть неоткрытым
интервалом.
2) Если, например, / возрастает, то } (а + 0) = inf (/ (*)) и / (а — 0) =
х> а
= sup (/ (*)). При этом /(a-0)<f(a)<f(a+ 0); скачок f в точке а не
х < a
отрицателен.

§ 2. Вещественные функции вещественной переменной 203
Она всюду определена, >0 или возрастает. Это даже
строго возрастающая функция, поскольку имеет место
формула
f(x)-f(y)= 2 А (г) для у<х. (III, 2; 7)
Пусть а — произвольное вещественное число. Зададим
е >■ 0. Поскольку сумма 2 h(r) сходится, то существует ко-
нечное число рациональных точек г0, гь ..., г„, таких, что
2 А(г)<в. (III, 2; 8)
При этом существует такое число ц > 0, что
хфг0, ги ..., гп для а — т)<*<а + т), х ф а. (III, 2; 9)
В силу (III, 2; 7) имеют место следующие два неравенства:
f(a)>f(x)>/» —e для а —т)<х<а,
f(a)+A(a)<f(x)<f(a) + A(a) + e для a<x<a+T) ( ' ' >
при условии, что Л(а) = 0 в случае иррационального а. Из
этих неравенств следует, что f(a — 0) = f(a) и f(a + 0) =
= f(a) + A(a).
Функция f, таким образом, всюду непрерывна слева. Она
непрерывна справа и, следовательно, просто непрерывна
в каждой иррациональной точке. В каждой рациональной
точке она разрывна и имеет скачок, равный h(a). Она имеет
счетное плотное множество точек разрыва первого рода, а именно
множество рациональных точек.
Возрастающая функция не обязательно дифференцируема,
однако для дифференцируемых функций имеется очень
важный критерий возрастания.
Теорема 7. Пусть f — вещественная функция,
определенная на некотором интервале (открытом, замкнутом или
полуоткрытом) прямой R и имеющая всюду производную,
конечную или равную +°° или —°°- Для т°г° чтобы она была
возрастающей, необходимо и достаточно, чтобы ее производная
была всюду ^0.
Доказательство. Если функция возрастает, то,
очевидно, \J{x-\-h)—f(x)]/h^0 и, следовательно, предел этого
отношения, который по предположению существует, также
>0.
Обратно, предположим, что f непрерывна,
дифференцируема и имеет производную (конечную или нет) всюду ^ 0. Тогда,
согласно теореме о конечных приращениях, всюду имеем

264
Гл. III. Дифференциальное исчисление
[f(x-\-h) — f(x)]/h — f'(x-\-Qh)^0, а это говорит о том, что
/ — возрастающая функция.
Замечания. 1°) Точно такое же рассуждение показывает,
что если производная f > 0, то f строго возрастает. Однако
может случиться, что f строго возрастает, а ее производная не
будет всюду >0. Такой будет, например, функция f(x) = x3,
производная которой повсюду ^0 и равна нулю в начале
координат.
2°) Используя замечания, приведенные после теорем 4 и 5,
можно доказать такую же теорему с производной справа (или
производной слева) вместо обычной производной.
Дифференцируемые функции и теоремы
о промежуточных значениях
Производная функции не обязательно непрерывна. В этом
можно убедиться на примере функции, определенной
следующим образом: f (х) = л:2 sin l/x для х Ф 0 и f(0) = 0. Она всюду
непрерывна и в любой точке хфд имеет производную /'(*) =
= 2jcsinl/jc — cos 1/jc. Производная этой функции в начале
координат равна нулю. Таким образом, ее производная
определена всюду в R, но разрывна в точке х = 0, ибо cos l/x не
стремится к 0, когда х Ф 0 стремится к 0. Однако, если некоторая
функция определена на интервале и дифференцируема, то ее
производная функция обладает, как и все непрерывные
функции, тем свойством, что вместе с любыми двумя своими
значениями она принимает и все промежуточные значения. Для
простоты предположим, что функция определена на R. Пусть
f'(a) = a, /'(&) = 6 и y — число, лежащее строго между
а и В. Тогда, выбирая достаточно малым число ft, получим
[f(a + h)-f(a)]/h = a'<y и [f(b + h) — f(b}]Jh = p> у. Если
зафиксировать одно из таких значений ft, то мы получим
непрерывную функцию х—y\f (x -f- ft)—f(x)]/h. В силу
непрерывности эта функция вместе со значениями а' и В' принимает и
все промежуточные значения и, в частности, значение у, т. е.
существует такая точка х, что [f{x-\-h)—f(x)]lh = y. Если
теперь к интервалу [х, х -f- А] применить формулу конечных
приращений, то мы придем к тому, что существует такая точка с,
в которой f (с) = у.
Выпуклые функции
Вещественная функция f, определенная, на интервале /
вещественной прямой R, называется выпуклой, если она
обладает следующим свойством;

§ 2. Вещественные функции вещественной переменной 205
каковы бы ни были точки Ai = (ai, f{a\)) и А2 = (а2, f{a2))
графика функции / на плоскости R2, хорда А\А2 лежит над
дугой графика кривой /, соединяющей точки А\ и А2. Это можно
записать в виде следующего неравенства:
f(tai+(l-t)a2)^tf(al) + (\-t)f(a2), 0<*<1. (III, 2; 6)
Этот же факт эквивалентен тому, что множество точек
(х,у), удовлетворяющих неравенству y^zf(x), является
выпуклым множеством плоскости R2 (см. определение выпуклых
множеств на стр. 184).
Учитывая сказанное ранее о барицентрических свойствах
выпуклых множеств, из соотношения (111,2; 6) можно получить
более общее соотношение
, / ai*i + . •. + апхп \ «^ aif(xi)+ ... + «J (*n) (Ш 2*7)
для xx, x2, ..., xn e / и ai, a2, ..., a„ ^ 0.
Теорема 72. Для того чтобы вещественная функция f,
определенная на интервале /cR, была выпуклой, необходимо
и достаточно, чтобы она обладала следующими свойствами:
о
1°) Функция f непрерывна во внутренности I интервала I,
и, кроме того, если I полуоткрыт или замкнут, она
удовлетворяет в соответствующих концах I интервала I соотношению
Нт /(*)</(/)'). (III, 2; 8)
о
х е /, х->1
о
2°) В каждой точке х из I функция f имеет производную
слева f'n и производную справа f'n. Эти производные совпадают
о
всюду, кроме не более чем счетного множества точек из I, при
этом имеют место такие неравенства:
Г*<Ъ W<f(t-*(r}^№) для *,<*2. (III,2;9)
Отсюда, в частности, вытекает, что если f является
дифференцируемой функцией, то она выпукла тогда и только тогда,
когда ее первая производная является возрастающей функцией.
Если же функция f дважды дифференцируема, то она выпукла
тогда и только тогда, когда ее вторая производная f"(x)^ 0.
Доказательство. 1°) Предположим вначале, что /
выпукла. Если 0 < h < k и [х, x-\-k\aI, то точка {x-\-h, f{x-\-h))
) То есть / полунепрерывна на концах интервала /,

206
Гл. III. Дифференциальное исчисление
лежит вне отрезка прямой [(x,f(x)), (х + k, f (х + ■ k))]. Отсюда
получаем следующее неравенство:
f{x + h) — f(x) ^ f(x + k) — f (х) ,jjj 2-Ю)
Это неравенство показывает, что функция A —*[f(х + А)—■
— f(x)]/h является возрастающей при Л > 0. Следовательно,
она имеет предел при А, стремящемся к 0. Другими словами,
о
/ в каждой точке / имеет производную справа, конечную или
равную —оо.
Кроме того,
f'n(x)< f{x + k)k-fM , (Ш, 2; И)
что дает левую часть второй системы неравенств (III, 2; 9) при
X = Хи X + k = Х2.
Аналогичное рассуждение мол<но провести с числами А и
о
k <С 0 и проверить, что / в каждой точке / имеет производную
слева f'n, конечную или равную +оо, и что справедлива правая
часть второй системы неравенств (III, 2; 9).
Если в (111,2; 10) положить x-\-h — y, x-\-k = y-\-l, то
мы получим
m-ny-h)^f(y + o-fb-H)t (Ш(2;12)
и аналогичное рассуждение, проведенное с отрицательными
приращениями, дает
f(y + t)-+f(y-b)<f(y + ')-f(y). (ш(2;13)
Заметим только, что
fiy-h)-f(y) ^f(y + l)-f(y) ^ (III, 2; 14)
Устремляя А и / к 0, получаем f (у) ^ f'n (у), чем и
заканчивается доказательство неравенств (III, 2; 9). Заметим, кроме
того, что обе эти производные конечны.
о
- Функция f является, таким образом, возрастающей в /, а,
значит, имеет не более чем счетное множество точек разрыва.
Если х не является точкой разрыва функции ,-', то при А > 0
необходимо имеем: f'B {х — А) </^ {х) </^ (х), откуда, устремляя А

§ 2. Вещественные функции вещественной переменной 207
к нулю, находим Ул(х) — УП(х). Таким образом, / имеет
производную всюду, кроме не более чем счетного множества точек.
Далее, функция /, будучи дифференцируемой справа и
слева в каждой точке, непрерывна справа и слева, а, следователь-
но, непрерывна всюду во внутренности / интервала /. Посколь-
о
ку f'n возрастает, то она либо везде <;0 на /, либо всюду ^0,,
либо ^0 строго слева от некоторой точки с и ^0 строго
о
справа от с. Поэтому функция / либо возрастает в /, либо
убывает в / или же убывает слева от с и возрастает справа от с.
Так как эта функция непрерывна, то в точке с она достигает
своего минимума. Во всех случаях она необходимо имеет
предел справа на левом конце интервала / и предел слева на
правом его конце.
Рассмотрим, например, случай правого конца b и
предположим, что бе/. Если Ь' <. х <С Ь, то точка (х, f(x)) будет
лежать под хордой [(b', f(b')), {b, f{b))]. Переходя к пределу
при х, стремящемся к Ь, мы получим то же соотношение в точке
(b,f(b — 0)), а это означает, что имеет место неравенство
f(b — 0)^f(b). Тем самым заканчивается доказательство всех
свойств функции /, указанных в теореме.
2°) Предположим, обратно, что / обладает всеми
указанными в утверждении теоремы свойствами, но вместо второй
системы неравенств (III, 2; 9) нам достаточно будет иметь
неравенство f'n (л:,) ^ Сл (я2). Докажем, что она выпукла во внутренности
о
/ интервала /, а тогда из неравенства (III, 2; 8) будет
следовать, что она такова же во всем интервале /, если он полуот-
о
крыт или замкнут. Итак, пусть a, b — две точки из /, а<.Ь.
Функция g, определенная формулой g{x)=f (x) —f(a)—
, ч f(b)-f(a)
—(х—а) I , удовлетворяет всем перечисленным условиям
в / и, кроме того, g(a) — g(b) — 0. Для доказательства
выпуклости / нам достаточно показать, что g(x)^.0 для а <; х ^ Ь.
Если бы это было не так, то функция g имела бы в интервале
]а, Ь[ максимум >0 в некоторой точке с. Рассуждения,
проведенные в теореме 4 (Ролля), показывают, что g'B (с) ^ 0 и
g'n(c)<^0. Из неравенства (III, 2; 9) (1-я система) следует, что
обе эти величины равны нулю. Однако, поскольку g'n, согласно
(111,2; 9), возрастает, она заведомо !>0 в интервале [с,Ь].
Максимум g(c)>0 должен быть, следовательно, scgr(6) = 0, а это
невозможно. Тем самым выпуклость функции /доказана.
Если / дифференцируема в /, то предыдущие условия
сводятся к тому, что у является возрастающей, а если же она
дважды дифференцируема, то к тому, что /" ^ 0.

208 Гл. III. Дифференциальное исчисление
§ 3. ПРОИЗВОДНАЯ ОТОБРАЖЕНИЯ ОДНОГО АФФИННОГО
ПРОСТРАНСТВА В ДРУГОЕ.
ПРОИЗВОДНЫЙ ВЕКТОР ФУНКЦИИ СКАЛЯРНОЙ ПЕРЕМЕННОЙ
Рассмотрим отображение / открытого множества поля
скаляров К в аффинное нормированное пространство F1). Для
аеЙ можно придать смысл формуле
F(3= Htn M« + »)W(«Tg£ (ш>з;1)
ft ф 0,ft-»0, a+fteQ n
В правой части мы имеем, прежде всего, разность
i ->.
f{a-\-h) — f{a) двух точек из F, которая является некоторым
вектором присоединенного векторного пространства F. Этот
вектор можно делить на скаляр h ф 0 и искать предел получен-
->
ного вектора в F, когда h стремится к 0, поскольку векторное
-> >
пространство F предполагалось нормированным. Если /'(а)
существует, то его называют производным вектором
отображения / в точке а. Существование производной и ее значение
зависят не от нормы, а только от топологии пространства F,
поскольку понятие производной связано с понятием предела. Если
К = R, то можно точно так же говорить о производной слева
и производной справа. Если производная существует всюду
в Q, то можно рассматривать производную функцию J': х->
->/'(*). Это — некоторое отображение Q в векторное
нормированное пространство F. Можно затем вычислить последующие
производные при тех же условиях, что и в § 2. Они
обозначаются так же, как и в случае вещественных функций, а имен-
но: f", у", ... ,/(т>, ..., и т. д. Все эти производные, если только
они существуют, являются отображениями Q в F. Заметим, что
/ принимает свои значения в аффинном пространстве F, а ее
производные [', f", ... принимают свои значения в присоеди-
■>
ненном векторном пространстве F. Если положить Е — F =R,
то мы вернемся к обычной производной вещественной функции
вещественной переменной.
Теперь можно говорить о классах С1, С2, ..., Ст, ..., С°°
функций, непрерывно дифференцируемых 1 раз, 2 раза, ..., т
раз или бесконечно дифференцируемых со значениями в F.
') В качестве К берется R или С. Пространство предполагается
аффинным над полем К. Если К = R и F задано как аффинное пространство над
полем С, то ограничиваются рассмотрением F как аффинного пространства
над полем R.

§ 3. Производная отображения. Производный вектор 209
Здесь, как и в § 2, дифференцируемая функция непрерывна, и
о второй производной в точке аей говорят лишь в том
случае, когда первая производная определена всюду в Q или, по
крайней мере, в некоторой окрестности точки а. Важный
пример такого отображения имеется в механике. В этом случае
f< = R, переменная х есть переменная времени t, а
пространство F является обычным трехмерным аффинным
пространством. Движение частицы в этом пространстве задается
функцией времени t-*M(t) — функцией вещественной переменной t
со значениями в F. Ее первая производная dM/dt является век-
->
тором скорости, а вторая производная d2M/di2 — вектором
ускорения. Обе они принадлежат F.
Если пространство F конечномерно и в нем выбрана система
->
координат, состоящая из начала Ь и некоторого базиса (fi)teI
->
из F, то положение каждой точки пространства F определяется
через ее координаты {yt). e;, а задание функции /,
определенной на йсК со значениями в F, эквивалентно заданию
скалярных функций {F{)ieI по формуле:
f{x) = b+ S F{(x)% где yi = Fi(x). (III,3;2)
При этих условиях производная функции задается
формулой:
П3=2^ад. (III,3; 3)
i е /
Для того чтобы функция со значениями в конечномерном
аффинном нормированном пространстве была
дифференцируемой, необходимо и достаточно, чтобы ее компоненты в
некоторой системе координат были скалярными дифференцируемыми
функциями. Компоненты производной являются производными
соответствующих компонент.
Общий случай. Частная производная вдоль вектора
Пусть теперь / — отображение открытого множества Q
аффинного нормированного пространства Е в аффинное
пространство F. Очевидно, теперь нельзя говорить о производной в
предыдущем смысле. Поэтому мы вначале введем понятие произ-
водной или частной производной вдоль вектора X из Е. Пусть
а — некоторая точка Q: Производной / в точке а вдоль вектора
X называется производная, если она существует, функции

210
Гл. III, Дифференциальное исчисление
t-+f(a-\-tX) при t = 0. Эта производная обозначается через
—> ->
D+f(a)^F. Таким образом, имеем:
DMa) = {i(f(a + tX))\ = lim /(« + '*>-/(«). (III,3;4)
Здесь t — скаляр, пробегающий множество К -> элементов
a, X
из К, для которых й + IXeQ. Функция /—► /(а + /Х) является
отображением К -> в F. Множество К -> является прообра-
Г а, X а,Х К К
зом открытого множества Q при непрерывном отображении
t-*-a-\-tX множества К в Е. Это — открытое подмножество К,
содержащее нуль, что позволяет вычислить производную в
точке t = 0.
Существование и значение производной вдоль X в точке а
зависит исключительно от топологии пространства F, а не от
его нормы, поскольку понятие производной связано лишь с по-
> >
нятием предела. Если X = 0, го производная существует в
каждой точке Q и равна нулю. Если К = R и если задано напра-
>
вление полупрямой, то существует вектор X, и притом
единственный, с нормой, равной 1, имеющий это направление.
Производная вдоль такого вектора X называется производной по
рассматриваемому направлению. Она зависит, очевидно, от
нормы в пространстве Е. Например, если Е— евклидово
конечномерное пространство, S — регулярная гиперплоскость,
содержащаяся в Q, а — некоторая точка из S, v — ориентированная
>
нормаль к S в точке а, то нормальная производная d/dv в точке
а является производной вдоль единичного вектора v.
■*■
Если Е — поле скаляров и X — единица этого поля, то про-
->•
изводная вдоль X является обычной производной в смысле
определения (Ш,3; 1): D~3f{a) = пЗ- Если D3(х) существует
X X
для всех х, то можно рассматривать производную функцию
->• ->•
вдоль X функции f или просто производную функцииf вдоль X.
—->■ —* ->
Это будет функция D+f: x-+D+f{x). Для фиксированного X
X X
это — отображение Q в F. Затем можно, в свою очередь, искать
—>
производную (если она существует) функции Dff в точке а

§ 3. Производная отображения. Производный вектор 211
вдоль вектора У (отличного или нет от вектора X). Ее обозна-
>
чают через £>->£)->/(а) и называют частной производной вто-
Y К
рого порядка. Точно так же определяются производные высших
порядков.
Матрица Якоби. Якобиан
Если пространство F конечномерно и Ь, (Гг)ге/ образуют
систему координат в F, то имеют место формулы:
f (x) = b + 2 Ft (x)7t, ~Dff (x) = 2 DtFt (х)Ъ ')• (Ill, 3; 5)
Предположим теперь, что Е также конечномерно и а,
(е,-).е;—система координат в Е. Тогда производные по век-
торам в/ базиса Е являются тем, что обычно называют
частными производными функции f. Другими словами, по
определению:
->
-> ff —> f(x + te)-f(x)
dif(x) = -g-(x) = D+f(x)= lim -i lj . (111,3; 6)
axl ej t ф o, /-»o l
Наконец, если Е и F — конечномерные пространства и если
в Е выбрана система координат, то производная djf=-L-^-
выражается следующим образом:
4--%Ш (Ш.3;7)
1 Is/ '
ар,
Матрица, составленная из элементов -=-*-(х), в частном
случае при / = {1,2 т}, / = {1, 2, ..., п}
dxi v ' дх2 v ' дхп
(Ш,3; 8)
dFm , , dFm /Л dF„
(X) %SL(X) ... ^f-(x)
дх{ v ' dx2 v ' d.Cn
называется производной матрицей, или матрицей Якоби,
функции / в точке 1ЕЙ. Если m — п, то ее определитель называется
') Поскольку Fi.—г скалярные функции, D+Fi (л) являются скалярами.
х

212
Гл. III. Дифференциальное исчисление
якобианом функции / в точке х по отношению к
рассматриваемой системе координат. Часто через п; '"' 'ы[ обозначают
и (Х\, ..., хп)
якобиан функции y — f(x), определенной в заданной системе
координат скалярными функциями «/,■ = /%■(*) — Ft(xi, ..., хп),
1 = 1, 2, ..., п. Говорят также, что это якобиан п функций
Hi = F{ от п переменных хи х2, ..., хп. Для п = 1 якобиан
сводится к обычной производной.
Недостатки понятия производной вдоль вектора
Понятие производной вдоль вектора обладает рядом
недостатков. В самом деле:
1°) Функция может в каждой точке иметь производную
вдоль любого вектора и в то же время не быть непрерывной.
Рассмотрим, например, скалярную функцию, определенную на
R2 формулой
[О для (*, у) == (0, 0),
""•НТР^ для (,^,о,о, <"'•*«
Эта функция является отношением двух полиномов.
Правила дифференцирования суммы, произведения и частного для
производной вдоль вектора те же, что и для производной
функции скалярной переменной, поскольку она сводится к
производной некоторой функции от t при £ = 0 (формула (111,3; 4)).
Так как знаменатель функции / в каждой точке ф (0, 0) в нуль
не обращается, то эта функция дифференцируема в каждой
точке. Вычислим ее производную в начале координат вдоль
вектора (X, Y). Если Y Ф 0, то для 1ф0 имеем
f (tX, tY) = t2Y?+ „.=§■ '3 + • • • • (HI, 3; 10)
Поскольку функция / в начале координат равна нулю, то
при t = 0 ее производная вначале координат вдоль
рассматриваемого вектора равна нулю. Если У = 0, X Ф 0, то для t Ф 0
f(tX, tY)= ж+ ... =tX+ •••• (111,3; 11)
Так как f в начале координат равна нулю, то при t = 0 ее
производная вдоль вектора (X,0) равна X. Производная же
вдоль вектора (0, 0) всегда равна нулю. Таким образом,
функция f дифференцируема вдоль любого вектора. Однако она
разрывна в начале: на параболе у — X2 — 0 имеем f{x,y) =
= х5/х8 = 1/х3 для х Ф 0, и это выражение стремится к оо,
когда х Ф 0 стремится к 0.

§ 3. Производная отображения. Производный вектор 213
2°) Если не делать никаких предположений о
непрерывности частных производных, то может оказаться, что никакой
связи между производными вдоль различных векторов из Я в
одной и той же точке области Q не существует. Конечно, если
_—■■>
D^f(a) существует, то для скалярного X будет существовать
Л
п ->! (а), и при этом
кх
!T+f(a)==kD+f(a). (111,3; 12)
В самом деле, это очевидно, если X = 0. Если же X ф 0, то
>
> ->
при (еК и а + tXX e Q отношение [/ (а + tXX) — f (a)]/t имеет
>
вид l[f(a+ sX) — f(a)]/s, где s = ueK, a + sXeQ и
s ф 0 стремится к 0, если t ф 0 стремится к 0. Отсюда мы
получаем (111,3; 12). Однако нам бы хотелось, чтобы для фикси-
—> ->
рованного а производная D->/ (а) линейно зависела от X. Но
это не так, как показывает тот же пример (111,3; 9), в котором
производная в начале координат вдоль вектора (X, 0) равна X,
тогда как производная вдоль вектора (X, У), У Ф 0, равна нулю.
Недостатки понятия частной производной вдоль вектора
вытекают из того, что при ее вычислении в точке а используется
поведение функции только на прямых аффинного пространства
Е, исходящих из той точки, тогда как было бы полезнее учесть
глобальное поведение функции / во всей окрестности точки а.
Поэтому мы введем новое понятие производного отображения.
Полная производная, или производное отображение
Пусть / — отображение открытого множества Q аффинного
нормированного пространства Е в аффинное нормированное
пространство F. Говорят, что / имеет в точке йё£2
производное отображение, или полную производную L, или
дифференциал, или полный дифференциал Lh, если L является линейным
-> -> >
непрерывным отображением Е в F и если для а -\- h e Q имеет
место равенство
f(a + h)=f(a) + Lh + <( (А) || А ||, (III, 3; 13)
■* ->->-> ->
где ф (К) стремится к 0 при h Ф 0, стремящемся к 0. Это
равносильно утверждению, что приращениеЛ/ = / (а + h)—f (a)
может быть представлено в виде линейного непрерывного

214 Гл. III. Дифференциальное исчисление
отображения L-h с погрешностью, которая является бесконечно
малой более высокого порядка, чемЦЛЦ, когда h стремится к
О в Е. Заметим, что ф(0) может выбираться произвольно и не
представляет никакого интереса, но Ф (к) для h Ф О
определяется единственным образом по формуле
y(h) = [f(a + h)-f(a)-L-h]/\\h\\.
То, что L является производной отображения f в точке а, оз-
-> -> ->
начает, что вектор ф (h), определенный для таких h ф О, что
-> •>•>.->
а + h е й, стремится к 0, когда h стремится к 0. Обычно до-
—-*■ -> ->
говариваются считать ф(0) = 0, чтобы функция ф была бы не-
->
прерывной в начале пространства F и чтобы можно было снять
-> ->
ограничение h Ф 0.
В силу теоремы 12 гл. II, существование и значение
производного отображения зависят только от топологии пространств
Е и F, а не от их норм.
Теорема 8. Если отображение f имеет производную в
точке а, то эта производная единственна. В этом случае f
непрерывно в а. Кроме того, отображение f имеет в точке а произ-
водную вдоль любого вектора X из Е, а отображение X-+
—•> -> ->
—> /)->/ (а) есть линейное непрерывное отображение Е в F,
-являющееся не чем иным, как самим L, т. е.
Kj(a) = L-X. (Ш,3; 14)
Таким образом, существование производного отображения
L в точке а влечет за собой существование производной в точке
->■ -*
а вдоль любого вектора X из Е.
Доказательство. Поскольку отображение L предпола-
■> -> •>
галось непрерывным, то, когда h стремится к 0, Ыг также стре-
■+ —•> -*
мится к 0. То же самое будет верно и для y{h)\\h\\, а потому
->■ ->
отображение / непрерывно в точке а. Пусть 1е£. Полагая
-> ->
в (Ш,3; 13) h = IX и замечая, что для достаточно малого 1/1
->
точка а + (А лежит в открытом множестве й, получаем
следующую формулу:
>•
f(a + tb-f(a =^ + Жф(/^||. (10,3; 15)

§ 3. Производная отображения. Производный вектор 215
Так как выражение L-X определено для любого вектора X
из Е, то, устремляя / ф О к нулю, из (111,3; 15) получаем
(111,3; 14) и одновременно устанавливаем единственность
производной. Если через / обозначено отображение Q а Е в F, то
через Г (а), или -—(а), можно обозначить производное отобра-
-> ■>
жение функции / в точке а, так что f (a) e SB (E; F). Чере,
/' (а) X, или -^- (а) • X е F, можно будет обозначить значение
-> •>
этого отображения на векторе X из Е.
Таким образом, имеем формулу:
~Dtf(a) = f'{a)Xt=F. (111,3; 142)
Замечания. 1°) Пусть Е и F—аффинные пространства
над полем С. комплексных чисел. Тогда они заведомо являются
аффинными над вещественным полем R. Отображение L про-
странства Е в F линейно, когда Е и F рассматриваются как
векторные пространства над полем .С, и a fortiori обладает
этим свойством, когда Е и F рассматриваются как векторные
пространства над полем R. Значит, отображение f множества
Qc£ в F имеет производную Lg2"(£; F) в точке ugQ,
когда Е и F рассматриваются как аффинные пространства над
полем С, и a fortiori имеет отображение L в качестве
производной, когда Е и F рассматриваются как аффинные пространства
над полем R. Обратное, вообще говоря, не верно, в чем мы
убедимся позже в теории аналитических функций комплексной
переменной.
2°) Из определения производной вытекает, что f'(a) не есть
вектор пространства F, а линейное непрерывное отображение
■*■ •> ->->•>
пространства Е в пространство F. Это f'(a) ■ X для X е Е яв-
-> ->
ляется вектором из F. Однако предположим, что Е является
полем скаляров К. Тогда мы можем определить производный век-
>■ -у
тор f (a) e F по формуле (III, 3; 1) и производное
отображение f'(a) ei?(K; F) по формуле (111,3; 13). Между этими
двумя понятиями имеется простая связь. Если существует
производный вектор, то существует производное отображение, и
наоборот; при этом
}'(a) = f'(a)-l, Is К. (Ш(3;152)

216 Гл. III. Дифференциальное исчисление
В самом деле, если существует полная производная f'(a) ее
eS'JK; F), то из теоремы 8 следует, что существует производи
—-» —-» _>
ный вектор f (a) — D^f (а), равный /"(a) • 1. Обратно, если су-
ществует производный вектор f (а), то для каждого Ле К
f(a+A) = f(a) + An3 + a|A|,
-> -»
где а стремится к 0, когда h стремится к 0. Это означает, что
->-
существует производная f'(a) ee5'(K; F), являющаяся отобра-
>
жением X—*f'(a)-X. Впрочем, так как X ее К, мы можем пи-
>
сать или f'(a) -X, или f (a) X.
Слово производная неоднозначно, поскольку оно может
обозначать как производное отображение f'{a), так и производ-
—> -»
ный вектор f (a) = f (а) ■ 1. Эта неоднозначность почти не
мешает на практике. Если Е = F = К, то производный вектор
является обычной производной f (а) ее К, а производное
отображение является гомотетией X—*f'(a)X из К в К.
3°) Если пространство Е конечномерно и в нем выбрана
-> -> ->
система координат а, (£/),-<=;, то производная f' (х) ge j? (E; F)
связана с частными производными f (х) • ej = -^—(x)
следующим образом:
Г (х)-Х = Г (х) ■ ( 2 Х/1Л = 2 Xlf W et = 2 X, -§L (хУ
\j(=J J je=J j<=J '
(111,3; 153)
Пусть теперь оба пространства Е и F конечномерны и в ка-
->
ждом из них выбрана система координат, а именно: а, (е/),е/
->
в Е и b, (fi)t e j в F. Тогда каждая точка из Е и F
полностью определяется своими координатами и отображение f из Q
в F может быть определено системой m функций от п
скалярных переменных, а именно: yt = F i((xi)j(= j), i e/. (Если /=
={1, 2, . .., m) и /={1, 2, . . ., п}, то это будут функции yt=
= Fi(xi, X2, ..., хп) для i=l, 2, ..., т.) В этом случае
производное отображение в точке х, если оно существует, опреде-
ляется следующим образом: полагают X = 2л Xfi\ и обозна-

§ 3. Производная Отображения. Производный вектор 21?
чают через Y = 2j Yili его образ при производном отображе-
нии. Тогда
2 у1=v (*) • * = S -£: w */=21г w *Л ^п. з; »б)
откуда
Полученная формула показывает, что матрица производного
отображения f'(x) no отношению к рассматриваемым системам
координат является матрицей Якоби (111,3; 8). Как всегда,
столбцы матрицы линейного преобразования представляют со-
->•
бой векторы, являющиеся образами векторов базиса Е при этом
->
преобразовании; другими словами, f (х) • et=-~{x).
Существование производного отображения f (х) влечет
существование dfldxj, а, следовательно, существование dFJdXj и
существование матрицы Якоби, но обратное не верно, как показывает
пример (III, 3; 9). Если Е и F имеют одинаковую размерность,
то якобиан в х является определителем отображения f (x) e
-> ->
е 3? (Е; F) по отношению к рассматриваемым системам
координат.
Напомним, что можно также говорить об определителе ли-
->•
нейного отображения конечномерного пространства Е в себя, не
выделяя при этом какого-либо базиса (поскольку определитель
отображения, вычисленный в некоторой базисе, не зависит от
этого базиса). Таким образом, можно говорить о якобиане f
в точке х, или определителе отображения f'(x), для отображе*
ния f открытого множества из Е в Е без выделения какого^
либо базиса в пространстве Е.
Понятие дифференциала
Вместо того чтобы через х, у и т.д. обозначать точки,
пространств Е и F, а через X, Y и т. д. — векторы пространств
Е и F, часто оказывается удобным, оставляя для точек про-
странств Е и F обозначение х и у, векторы пространств Е и F
обозначать через dx, dy. Тогда выражение для производной
отображения / множества Q в F-запишется в виде
'dx-*dy = f''{x)-'dx. (111,3; 17)

218 Тл. III. Дифференциальное исчисление
В частности, если пространство Е конечномерно и в нем
выбрана система координат, то эта формула запишется
следующим образом:
d%= '£dxlel-*dy = f'(x)-dx== J] -JTdxl- (Ш.З; 18)
Когда / является функцией над полем К2, т. е. функцией
двух скалярных переменных х, у, то ее часто обозначают через
z, а через р и q обозначают ее частные производные по х и у.
Полная производная в дифференциальных обозначениях
запишется в виде
—*■ -> ■ ->
(dx, dy)-*dz = pdx + qdy. (111,3; 19)
Последняя формула из (III, 3; 16) после замены Xj, Уг на
dXj, dyi примет такой вид
dyt= ^4r^dxi' <е/* (Ш,3; 19А)
Геометрическая интерпретация производного
отображения: дифференцируемое многообразие
и линейное касательное многообразие
Пусть / — отображение открытого множества Q
пространства Е в пространство F. Его графиком называется множество
<S точек (л:, /(*)). * е й, из Е X F- Если / дифференцируемо
в каждой точке Q, то говорят, что 8 является
дифференцируемым, многообразием с уравнением y=f(x). Если, например, Е=
= R2, F=R, то & является поверхностью в R3, задаваемой
уравнением z=f(x,y). Если E=R, F—R2, то 8 есть кривая
в R3, описываемая уравнениями y=g(x), z=h{x) ').
Выясним, какой смысл следует придать понятию линейного
многообразия, касательного к графику & в точке A —(a, /(a))?
Рассмотрим произвольное множество & аффинного
нормированного пространства G. Пусть А — точка из <$. Говорят,
что вектор X из G является касательным в точке А к
множеству <%, если существуют последовательность точек М0, Мг, ...
..., Мп, ... из &, стремящаяся к А при п, стремящемся к
бесконечности, и последовательность вещественных скаляров Ко,
') Вместо х и у мы пишем х, у, г, поскольку Е X F = R3- Конечно,
фраза «уравнением множества & является у = \(х)у> ничего не означает. Она
является очевидным сокращением фразы: «.8 есть множество пар (х, у) из
Е X F, удовлетворяющих равенству У = 1(х)ъ, или ««? = {(х, у) : х е Q,

§ 3. Производная отображения. Производный вектор 219
%и . . •, Я,п, • • • ^ 0, такие, что векторы %пАМп стремятся к X
при п, стремящемся к бесконечности. Вектор 0 всегда является
касательным. Если X — касательный вектор, то при веществен-
ном Я ^ 0 вектор XX тоже является касательным. Если X Ф О—
касательный вектор, то %п заведомо стремится к +°°- Как и
само понятие предела, касательные векторы в точке А к
множеству <§? зависят лишь от топологии, а не от нормы про-
странства G. Множество касательных векторов в точке А к
множеству 8 называется векторной контингенцией множества 8
-*■ ->
в точке А. Множество точек А -\- X, где X пробегает векторную
контингенцию, называется аффинной контингенцией множества
8 в точке А.
Теорема 8А. Пусть f — отображение открытого
множества Q из Е в F, дифференцируемое в точке а е Q: Векторной
(соответственно аффинной) контингенцией в точке А = (a, f (а) =
= 6) множества 8, определяемого уравнением y—f(x) в Е X F,
-*■ -*.
является векторное подпространство в E~X.F, определяемое
уравнением
Y = f'(a)X (III,3;192)
(соответственно аффинное подпространство из Е X F,
определяемое уравнением
у — \ = ?{а)-х — а). (1П,3;193)
Доказательство. Второе утверждение тождественно
первому, поэтому достаточно доказать первое. Пусть х0, хи ■■■
..., хп, ... ■— последовательность точек из Q, сходящаяся к а, и
Яо, A,i, ..., "Кп, ■■■ — последовательность вещественных скаляров
-*■ ->
^0, таких, что %п(хп — о) стремится к некоторому пределу X.
По определению (III, 3; 13) производного отображения имеем:
f (xn) -b = f'(a)-xn-a + an\\x~^a||, (III, 3; 194)
-> ->
где ап стремится к 0 при п, стремящемся к бесконечности.
Отсюда
К (f (ха) ~ Ь) = V (а) ■ К (хп - а) + апХп || ~х~^а ||. (III, 3; 195)
Так как отображение f'(a) по условию непрерывно, а
л-п(хп — о) сходится к X, то при п, стремящемся к
бесконечности, первый член правой части последнего равенства стремится

220
Гл. 111. Дифференциальное исчисление
к f'(a)-X. Поскольку \\кп(хп— а)\\ сходится к \\Х\\, а ||а„||
стремится к 0, то второй член сходится к 0. Таким образом,
получаем, что левая часть этого равенства при п, стремящемся к бес-
-> ->
конечности, сходится к Y=f'(a) -X. Отсюда вытекает
утверждение теоремы. В самом деле,
-> •>■
1°) Пусть вектор (X, У) касателен в точке А к множеству*?,
и пусть М0, Mi, ... ,Мп, ... — последовательность точек (x„,f (х„))
из <В, сходящихся к А е Е X F, а ко, ки ..., к„, ... —
последовательность скаляров ^0, таких, что к„АМп имеет своим пре-
-*■-*■-*■-*■ *■
делом (X, У) в £ X F- Последнее означает, что кп(хп — а)
сходится к X, а кп (f (хп) — Ь) сходится к Y. Мы только что
видели, что тогда имеет место равенство (III, 3; 19г).
2°) Обратно, пусть (X, У) — некоторый вектор из Е X F,
удовлетворяющий условию (III, 3; 19г). Рассмотрим
последовательность точек х„ из Q, определенных равенством хп = а +
+ tnX, где числа t„ вещественны, положительны и стремятся к 0
при п, стремящемся к бесконечности, и последовательность кп,
определенную равенством kn = l/tn. Тогда кп(хп — а)=Х. Сле-
■ >
довательно, как мы видели выше, kn(f(xn)—b) стремится
к f'(a)-X, т.е. к У. Последовательность Мп=(хп, f(xn))
принадлежит к <5 и стремится к Л, а кпАМп сходится к вектору
(X, У), являющемуся касательным вектором к множеству <£
в точке А.
-> •>■
Векторное подпространство пространства Е X F,
определяемое уравнением (111,3; 19г) (соответственно аффинное
подпространство из E'XF, определяемое уравнением (III, 3;193))
называется векторным подпространством, касательным к
многообразию <§ в точке А (соответственно линейным многообразием,
касательным к многообразию & в точке А). Аффинная функ-
>
ция (аффинное отображение из Е в F) х —► b -f- f (a) ■ (х — а)
называется аффинной функцией, касательной в точке а к
функции f. Итак, аффинное линейное многообразие, касательное
в точке А = (a, f(a)=b) к дифференцируемому многообразию,
определяемому уравнением y=f(x) в E^F, получается заме-
->
ной dx на х — а и dy на у — b в дифференциале dy = f '(a) ■ dx.
Так, например, если £ = R2, F = R, то касательная плоскость
в точке (а, Ь, с) к поверхности, определяемой уравнением z=

§ 3. Производная отображения. Производный вектор 221
=f{x,y), имеет уравнение
г_с = -|^(а, b) (х — а) +-^-(а, Ь){у — Ь) = р(х — а) + q{y — Ь).
(Ш,3; 196)
Если E — R, F=R2, то касательная в точке (а, Ь, с) к
кривой, определяемой уравнением y—g(x), z=h(x), имеет
уравнение
у — b = g' (а) {х — а),
г — c = h' (a){x — а).
(III, 3; 197)
Градиент вещественной функции
в евклидовом пространстве
Пусть Е — конечномерное аффинное евклидово пространство
над полем вещественных чисел. Пусть f — вещественная функция,
определенная в открытом множестве Q пространства Е. Если
в некоторой точке х из Е функция f имеет производную f (я), то
эта производная является линейным отображением £ в R, т.е.
линейной формой или элементом из Е'. Согласно сказанному
в теореме 24, существует вектор Y из Е, и притом
единственный, такой, что
у (Х). X = (X\Y) для любого X из Е. (III, 3; 20)
Этот вектор называется градиентом f в точке х и
обозначается через gradf{x). Заменяя X на dx и f' (x) ■ dx на
df e R, согласно определению дифференциала, получаем
->
ZHf(*) = (gradf(*)|*),
л
(Ш,3; 21)
df = (grad / {х) | Ле).
Пусть (ei)le.j — ортонормированный базис в £. Тогда,
учитывая выражение скалярного произведения в ортонормирован-
ном базисе, формулу (III, 3; 21) можно записать в виде
df = 2 Yidxi, (III.3;22)
l e/
где У,- — компоненты градиента. Учитывая (III, 3; 18), имеем:
Yt = te^df{x))t = -g-. (Ill, 3; 23)

222
Гл. III. Дифференциальное исчисление
Координатами градиента f в ортонормированном базисе яв
ляются частные производные df/dx{.
Это же утверждение остается справедливым в случае обоб
щенного евклидова пространства, но только тогда следует вое
пользоваться формулой (III, 1; 25). При этом (III,3; 22) заме
нится на
df = 2 n,Yt dxit (III, 3; 24)
t e/
а, следовательно, координатами градиента будут ег -г—(х).
ах{
В частности, в специальной теории относительности это будут
величины
df df df д£_==_±_д/.
дх^ ' дх2 ' дхъ ' дх0 с dt
Если градиент определен на всем Q, то функция х—>
>
-^gradf (х) называется векторным полем над Q, или отображе-
-> —->
нием Q в Е. Это отображение обозначают через gradf.
Теорема 82 (производная постоянной, производная
аффинной функции). Постоянное отображение дифференцируемо и
производная является присоединенным линейным
отображение f из Е в F дифференцируемо в каждой точке а из Е, и его
производная является присоединенным линейным
отображением: f (а) =Т <=[& ф; F)-
Производная функция (которую мы определили на стр. 213)
является, следовательно, постоянным отображением Е в
-> -> ->
3S. (Е; F) '. х -> г (х) = f. Этот результат обобщает тот факт, что
производная аффинной функции у = ах-\- р является постоянной.
Доказательство очевидно.
Теорема 83 (дифференцирование является линейной опе-
->
рацией). Если f — отображение из QcE в F и g — отображе-
■> ->
ние из Q в F и -если fug имеют производные в точке aeQ,
то функция f + g- x-*f(x) -\- g(x) имеет производную в а,
равную сумме производных:
(f + gY(a) = f'(a) + g'(a). (Ill, 3; 25)
.> —->
Если X — постоянный скаляр, то функция Xg: x—>Xg(x)
имеет производную в а, равную %g'(a).
Доказательство очевидно.

§ 3. Производная отображения. Производный вектор 223
Случай, когда F является произведением
аффинных пространств
Предположим, что f является отображением множества
Q cz E в произведение F\ X F2 X ■■ ■ X Fm аффинных
нормированных пространств. Оно определяется заданием отображений
/,- пространства Е в F{, i — 1, 2, ..., m (см. стр. 13). Известно, что
отображение / непрерывно тогда и только тогда, когда
непрерывны функции fi (теорема 17 гл. II и следующие за ней).
Отображение f аффинно тогда и только тогда, когда аффинны f,.
Теорема 84. Пусть Е и Fit t = l, 2, ..., m, — аффинные
нормированные пространства. Пусть f — отображение открытого
множества £lc£e ^ = Л X ^2 X • • • X Fm, определенное
отображениями fi множества Q в Ft. Для того чтобы f было
дифференцируемым в точке aeQ, необходимо и достаточно, чтобы
fi были дифференцируемы в а, и тогда f (а) является линейным
непрерывным отображением пространства Е в F = F{ X F2 X • • •
->■
... X Fm> определенным линейными отображениями /£(а) из
-> ->
Е в Ft.
Другими словами, компоненты производной являются
производными компонент, и при этом
f (a) = (f[ (a), f2 (a), ...,f'm (a)), df = (dfv tf2, ..., 7fm). (Ill, 3; 26)
Доказательство. Предположим, что отображения fi
дифференцируемы в точке а. Для приращения dx аргумента х
имеем приращения Аг/, функций yi=fi(x), такие, что
3, = №<** + ? Il^ll, (III.3; 27)
-♦ ■* —>
где а, стремятся к 0 вместе с dx. По определению аффинного
произведения
Д(г/„ у2, ..., ут) = (Дг/„ Аг/2. •... Аг/т) =
= (f[(a)dx,r2(a)d^, ..., f'm{a)dx) +
+ (a, || dx ||, a2|| dx\\, ..., am || dx\\) —
->■ ->■
= (f[(a), f'2{a),..., f'm{a))dx + {av a2, ..., affl)||d*||, (111,3; 28)
где, согласно определению топологического произведения,
/*■-*■->. ->->-> •* —>
(a., a2, ..., am) стремится к 0 в FiXF2X ■-• X Fm, когда dx

224 Гл. 111. Дифференциальное исчисление
стремится к 0. Это говорит о том, что f дифференцируема в а
и что f>(a) = (f[(a),f'2(a) f'm{a)).
Обратное утверждение доказывается аналогично, но в
обратном порядке.
Случай, когда Е является произведением
аффинных пространств. Частные производные отображения
Если Е является произведением аффинных пространств
Е\ X -^2, то отображение f множества ficfiX^ в F
становится функцией двух переменных. Мы будем записывать ее
в виде y—f(xu х2). При фиксированном Х\ в точке ах можно
рассматривать частное отображение fa: x2->f(xi,x2) и искать,
если оно существует, производное отображение в точке а2. Если
это возможно, то полученное производное отображение
является отображением из Е2 в F. Его называют частным
производным отображения f по х2 в точке (аи а2) и обозначают одним
из следующих символов: d2f(au a2) или -^-(аи а^. Точно так
же можно рассматривать частное отображение fa2 и
соответствующее ему частное производное отображение -з—{аи а2)
в той же самой точке (аи а2). Как и ранее (пример (111,3; 9)),
тот факт, что f имеет частные производные в некоторой точке,
не влечет за собой с необходимостью того, что оно имеет полное
производное отображение в этой точке (и даже того, что оно
там непрерывно)1). Верным будет лишь обратное утверждение.
Точнее, имеет место
Теорема 9. Если Е является произведением двух
аффинных пространств Е—Е{у(Е2 и f имеет производное
отображение f (а{, а2) в некоторой точке а—(аи а2) открытого
подмножества Q произведения Е[ X Е2, то оно имеет в этой точке
частные производные отображения и его полное производное
отображение задается формулой:
jL {au а2) $it £2) = ^L (flp a2) £ + Л. {а[> fl2) f 2. (Ш) 3; 29)
Доказательство. Из теоремы 51 гл. II мы видим, что
df ■>■>■>
линейное непрерывное отображение -j-{ai,a2) из Е1У,Е2 в F
определяет линейные непрерывные отображения L\ и L2 про-
') Однако из теоремы 15 будет видно, что существование непрерывных
частных производных влечет за собой существование полной производной
функции, которая в этом случае будет непрерывное

§ 3. Производная отображения. Производный вектор 225
странств Ei и Ё2 в F и что оно задается формулой
-g- (а„ а2) (Хи Х2) = lX + L2X2. (Ill, 3; 30)
_ „ ■>■*■->
Если теперь переменной придать приращение Л=(0, Л2), то,
согласно определению производного отображения, приращение
выразится формулой
--»•
-> -> ->
f (а„ а2 + h2) - f (alf а2) = L2 ■ h2 + ф (0, Л2) || Л21|, (III, 3; 31)
где ф (0, Л2) стремится к 0, когда h2 стремится к 0. Но это
как раз означает, что L2 является частным производным
отображением отображения / по второй переменной в точке (ai, a2).
Мы предоставляем читателю перенести результат на
произведение Е\ X Е2 X • • • X Еп аффинных пространств. В
дифференциальных обозначениях получим, что
п
df = fr(x)a^=^i-^-(x)dxl, (III, 3; 32)
где на этот раз -g-J—{x) е &{E{; F), dXj^E/ и dx = (dxlt
—> —> ->■>■> ■>
dx2, ..., dxn) <= Е = Ех X Е2 X • • • X Еп.
Если множители £;- совпадают с полем скаляров, то мы
возвращаемся к формуле (III,3; 18) (с отождествлением
производного вектора и производного отображения, указанным в
замечании 2°) на стр. 215).
Производная билинейного непрерывного отображения
Классическая формула d(xy)'=y dx -f- xdy для дифферент
циала произведения обобщается следующим образом:
Теорема 92. Пусть В — билинейное непрерывное отображе-
■>->■■> -> ■>
ние EiY,E2e F. Тогда В дифференцируемо в каждой точке (аи а2)
-*■ ■> дВ ■* "*
из Е1 X Е2. Его частная производная -=— (ар а2) является част-
-> ->
ным отображением В-> е 3? (Ех\ F), определенным формулой
(см. стр. 122)
Bt{Xi) = B{Xl, i)eJF. (111,3; 33)
8 Зак. 1339

226
Гл. 111. Дифференциальное исчисление
Точно так же, его частная производная -%— (а,, а2) является
частным отображением В-» е 9? (Е2; F), определенным формулой
В%(Х2) = В(аиХ2)<=Р. (111,3; 34)
Его полная производная равна
Я'(а„ a2).(Z1,Z2) = B(Z1, а2) + А(а„ Х2), (111,3; 35)
или в дифференциальных обозначениях:
dB = B (Лс„ х2) + В(хи dbc2). (Ill, 3; 36)
Доказательство. Результаты, относящиеся к частным
->
производным, очевидны: частное отображение В-»: хх-*-
-э-В^, а2) является линейным и непрерывным, а, следовательно,
его производная в ai совпадает с самим отображением (теоре-
■*■ . ■*■ ->
ма 82), т. е. с отображением X,-»- В(Х{, а2). Если отображение В
дифференцируемо, то формула (111,3; 35) вытекает из
формулы (III, 3; 30). Однако частная дифференцируемость
отображения В не влечет за собой его полной дифференцируемости и,
следовательно, ее надо доказывать ').
Дадим хх, х2 приращения dxu dx2, и пусть ДВ является
приращением отображения В. Тогда
—> -> —> -> —> -> ->
ДВ = В(а{-{- dxb а2 + dx2) — В (а^ а2) =
= В (^ + die,, d%2) + В (Лс„ а2). (III, 3; 37)
Теперь имеем
ДВ — В (dxi, а2) — В (alt dx2) = В (dt,, djc2). (Ill, 3; 38)
Правая часть оценивается по норме величиной
IIBIIII^.IIIIdJslKIIBIKIId^lH-lldJCall)2, (III, 3; 39)
бесконечно малой более высокого порядка, чем- \\dxi\\ -f- Ц^ХгН,
—> —> ->->-> -> ->
когда (dje,, dx2) стремится к 0 в Е{у^Е2. Если в £,Х£г
взять норму II Hi + II ||2, то, согласно определению производного
-> ->
отображения (111,3; 13), производная В в (а,, а2)- существует
') Теорема 15 позволила бы нам от этого избавиться, ибо частные
производные непрерывны.

§ 3. Производная отображения. Производный вектор 227
и задается формулой (III, 3; 35), чем и заканчивается
доказательство теоремы.
Оставим читателю заботу о распространении этого
результата на произведение п нормированных векторных пространств.
На этот раз
>. —>• -> ->■ ->• —> ->
dB = B (dxu x2, ..., хп) + В (*„ dx2, ..., хп) + ...
... +.В{хих2, ..., Тхп). (111,3;40)
Замечание. Отображение В', ставящее вектору х=(хх, х2)е
^Е1'Х.Е2 в соответствие производную В' (х) = В {ху, х2) е
-» ->• ->■
eS'ff, Х^г; И> определенную по формуле (111,3; 35), является
->■ -> ->.->-»•
линейным и непрерывным отображением £[ Х^г в & {Е\ X ^ Л-
Оно очевидным образом линейно, и имеет место оценка
|| В' (х) -Х\\ = \\В' (хи х2) ■ (X„ f 2) || <|| Я (f „ х2) || +
+ ||В(х1Д)||<2||В||||х||||1||, (Ш,3;402)
а, следовательно,
|| В'(х) ||= sup ||B'(x)f||<2||B|||U||, (III, 3; 40а)
откуда и вытекает, что В' непрерывно; кроме того,
B'e^(£, X Е2, 2? (£, X £2; П) и
II В'II < 21| В Ц.1). (Ш,3;404)
Дифференцируемые функции.
Непрерывно дифференцируемые функции
Если / имеет производную f'{x) в каждой точке из Q, то она
называется дифференцируемой в Q. Отображение x—+f'(x)
является ее производной функцией. Оно обозначается через /', или
-> ->
df/djc, или Df и является отображением й в 3? {Е; F). Функция/
называется непрерывно дифференцируемой, или принадлежащей
классу С1, если производное отображение /' множества Q
в 3? (E;F) непрерывно.
Теорема 10. Если / является непрерывно дифференцируе-
■*■ ■>
мым отображением Q в F, то отображение (х, X) -+f'(x)-X из
■> ->
Q\E в F непрерывно. Обратно, если это отображение непрерывно
') Если считать Ы = IU,II, + IU2II2 и \\Х\\ = ШЬ + ШЬ, то
коэффициент 2 в формулах (III, 3; 402) — (III, 3; 404) не появляется. — Прим, ред,

228
Гл. 111. Дифференциальное исчисление
и если Е конечномерно, то отображение f непрерывно
дифференцируемо.
Доказательство. Предположим, что f является непре-
-> ->
рывным отображением Q в 9?(Е\ F). Пусть х0, xit х2,...— по-
следовательность, сходящаяся к х в Q, и Х0, Хь Х2, ... — по-
следовательность, сходящаяся к X ъ Е. Тогда, в силу
непрерывности f, последовательность f {хп) сходится к f (x) в 2?(E;F).
->
Далее, в силу теоремы 17 гл. II, последовательность {f'{xn), Xn)
-> ->->-»
сходится к (f'(x),X) в 3?(Е; F)\E. Поскольку канониче-
->• -> ->->->
ское отображение (и, Х)~*и-Х пространства SB {E; F)"X.E
->
в пространство F непрерывно (теорема 54 гл. II), то последова-
-> -> ->
тельность f (хп) • Хп сходится к f' (х) ■ X в F, что и доказывает
->• -> . ->
непрерывность отображения (х, X)-+f {х) • X множества Q Х^
->
в F.
Обратно, предположим, что это отображение непрерывно.
Выберем какой-либо базис (е/),е/ в Е. Высказанное
предположение тем более влечет за собой непрерывность каждой част-
->
ной производной x—>f (х) • в/ = ■—-{х). Позднее мы увидим
(теорема 15), что даже без предположения дифференцируемо-
сти f существование и непрерывность частных производных
>
df/dXj влечет за собой существование и непрерывность полной
производной. Этим будет доказано обратное утверждение
(легко убедиться, что следующие далее теоремы, вплоть до
теоремы 15, не опираются на теорему 10).
Примеры непрерывно дифференцируемых функций
Поскольку производная аффинной функции постоянна
(теорема 8г), такая функция непрерывно дифференцируема.
Билинейная непрерывная функция также непрерывно
дифференцируема, поскольку ее производная является непрерывной
линейной функцией (см. замечание, следующее за теоремой 92).
Отображение множества Q в произведение F\ X F2 X • • • X
X Fm непрерывно дифференцируемо тогда и только тогда,
когда каждая из его компонент непрерывно дифференцируема
(теорема 84).
В дальнейшем нам встретится много других примеров таких
функций (теорема 15).

§ 3. Производная отображения. Производный вектор 229
Пространства дифференцируемых функций
В гл. II на стр. 146 мы видели, что если Е является
произвольным множеством, a F— векторным пространством, то мно-
-> ->
жество FE всевозможных отображений Е в F является
векторным пространством. Если же F является аффинным
пространством, то FE также является аффинным пространством с присо-
->
единенным векторным пространством FE. Если f и g— два ото-
>
бражения Е в F, то формулой g(x) —f(x) определяется отобра-
-> ->
жение g — f множества Е в F1). Если F является
нормированным аффинным пространством, то пространство (FE)b
ограниченных отображений Е в F является нормированным аффинным
пространством с присоединенным векторным пространством
->
(FE)b. Это пространство полно, если полно F (теорема 64
->
гл. II). То же самое имеет место для {FE)Cb и {FE)cb, если Е
является топологическим пространством.
Пусть, далее, Е, F—аффинные нормированные
пространства и Q — открытое множество в Е. Договоримся через (FQ)b;i
(и соответственно (FQ)C6;i) обозначать пространство функций,
заданных в Q, со значениями в F, дифференцируемых и
ограниченных вместе со своими производными (соответственно
непрерывно дифференцируемых, ограниченных вместе со своими
производными)2). Это аффинное пространство с присоединен-
-> ->
ным векторным пространством (FQ)b;i (соответственно (FQ)Cb;i)-
Образуем теперь нормированное аффинное пространство,
вводя в присоединенном векторном пространстве норму
||| ЛИ, = max (||?(*) ||, || Г (х) II) = max (|||?|||, |||? |||) (III, 3; 41)
(где ||?(х) || —норма в F, a ||f (x) || - норма в S ф\ F))-
Позже мы увидим (теорема ИЗ гл. IV), что эти
пространства полны, если полно F. Сказать, что последовательность
дифференцируемых функций fn сходится при п, стремящемся к
бесконечности, к некоторой дифференцируемой функции f в смысле
(^я)ь;1, означает сказать, что функции /„ сходятся равномерно
к f, а функции fn сходятся равномерно к f. Эта сходимость
более сильная, чем сходимость в (Fa)b- Если Е является полем
') Если Е является двухэлементным множеством {1,2}, то можно
убедиться в том, что F2 = F X F является аффинным пространством с присо-
единенным векторным пространством F2 = F у, F.
2) Причина, по которой приписывается индекс 1, выяснится на стр. 267.
Речь идет о пространстве функций, один раз дифференцируемых.

230
Гл. III. Дифференциальное исчисление
вещественных чисел R, F— полем R или полем С, a Q —
компактным интервалом [а, Ь]') (соответственно всей вещественно?:
прямой R), то пространство (FQ)cb;l является векторным про
странством непрерывно дифференцируемых и ограниченных вме
сте со своей производной функций на [а, Ь] (соответственно нг
R) с вещественными или комплексными значениями. Это
пространство очень важно для приложений.
Теорема Юг. Отображение, ставящее в соответствие
каждой функции f ее производную f, является линейным и непре-
->
рывным отображением с нормой =g:i пространства (FQ) b- i (со-
ответственно '(FQ)Cb;i) в пространство ((& (Е\ F))Q)b (соответ
ственно в ((2 (Е; F))Q)cb).
Доказательство очевидно. (Напомним, что если f является
->
функцией на Q со значениями в F, то f является функцией на
-> ->
Q со значениями в & (Е; F) и, кроме того, III/'III ^ III f Hli-)
§ 4. ТЕОРЕМА О СЛОЖНОЙ ФУНКЦИИ
Теорема 11. Пусть Е, F, G — нормированные аффинные
пространства, Q — открытое множество из Е, Q' — открытое
множество из F. Пусть f — отображение Q в Q', a g —
отображение Q' в G. Если отображение f имеет в точке йей произ-
-> ->
водную f (а) е 9? (Е; F), а отображение g имеет в точке Ь =
->■ ->
= f (а) из Q' производную g'(b)t= &(F; G), то композиция
отображений h = g°f имеет производную в точке а и эта
производная является композицией производных отображений
h'(a) = g'(b)°f'(a) = g'(f(a))of'(a). (III,4;1)
Доказательство. Перед доказательством заметим, что
если положить E=F=G=K, то производные отображения
будут умножением на числа, являющиеся обычными производны-
ми, а написанная формула является формулой дифференциро-
вания сложной функции в том виде, в каком она обычно
пишется: (g(f(x)))'=g'(f(x))f'(x). Удобство принятых нами
общих обозначений заключается в том, что для аффинных
пространств произвольного числа измерений, конечно- или
бесконечномерных, они дают нам тот же самый формальный
аппарат, что и для вещественной функции вещественной переменной.
Выберем приращение dx таким образом, чтобы точка а -\- dx
принадлежала Q. Соответствующие приращения переменных у
') Интервал [а, Ь] не открыт; см. стр. 198, начало § 2.

§ 4. Теорема о сложной функции
231
и z будем обозначать через Лг/ и Az. Тогда можно написать
формулы
ЬУ = f(a + dx) — f (a) = р (а) • dx + a|| dx ||, (III, 4; 2)
-> • —> -*.
где || а || стремится к 0 при dx, стремящемся к 0, и
->■
л£ = £(& + л5-£(&) = ^)-Л# + Р1|Лу11, (III, 4;3)
где IIPII стремится к 0, когда Лг/ стремится к 0. Из написанных
равенств получаем:
~£=д'(Ь).р(а)-£+д'(Ь).а\\£\\+МАу\\- (III, 4; 4)
Разность
te-g'(b) ■ ff(a) • dx~=g'(b) • а|| d^|| +||| А? II (III, 4; 5)
по норме не превосходит
||/(6)||||a||||^||+||p||(||f'(a)||||^|| + ||a||||dt||) =
= 11^11(11^(&)1П1а|| + ||Г(а)||||Р1| + ||а||||Р||). (III, 4; 6)
Так как отображение f дифференцируемо в точке а, то оно
непрерывно в а. Поэтому если dx стремится к 0, то вместе с ним
—> -*■ -> -> ->
и Ау стремится к 0, а, значит, аир стремятся к 0, и мы
заключаем, что последняя скобка стремится к 0. Поскольку
отображение g'(b) о f'(a) непрерывно (как композиция двух непрерывных
отображений), полученный результат означает, что
отображение h=gof дифференцируемо в а и его производная равна
g'(b) of (a).
В дифференциальных обозначениях предыдущий результат
выражается следующим образом. Дифференциал f задается
выражением
dy = p(x)-dx. (Ill, 4; 7)
В свою очередь дифференциал g задается формулой
Tz = g'{y).dy*. (Ill, 4; 8)
Теперь дифференциал сложной функции получается из
дифференциала функции g, если заменить у на f(x), a dy на
дифференциал P(x)-dx. Таким образом, непосредственно получаем:
dz = h'(x)-dx = g'{f (x)) ■ (Г (*) -dx). (Ill, 4; 9)

232 Гл. 111. Дифференциальное исчисление
Следствие 1 (перестановочность дифференцирования и
непрерывного линейного отображения). Если f является
отображением Q с Е в F, имеющим производную f (а) в точке аей,
и если g — непрерывное аффинное отображение F в G, то
сложное отображение g °f из Q в G имеет производную в а,
определенную формулой:
(g°fY(a) = g°f'(a). (III.4; 10)
Это утверждение вытекает из теорем 11 и 82 (впрочем, оно
очевидно).
Предположим, в частности, что Е является аффинным
пространством над полем вещественных чисел, a F — векторным
пространством над полем комплексных чисел. Во всей этой
теории следует оба их рассматривать как аффинные пространства
над вещественным полем. Тем не менее, умножение на Я е С
сохраняет смысл в F и его можно рассматривать как линейное
непрерывное отображение F в себя. Поэтому, если / есть неко-
->■
торое дифференцируемое отображение й в f, то же самое мож-
-> -> ->.
но сказать и о Я/ и при этом (А/)' = А(/'). Например, из того,
что в R функция cosx является производной функции sinx,
вытекает, что производной функции isinx является icosx.
Следствие 2. Пусть Е, F, G — конечномерные аффинные
пространства с выбранными в них системами координат. Тогда
матрица Якоби отображения h=g°f в точке а равна
произведению матрицы Якоби отображения g в точке b=f(a) на
матрицу Якоби отображения f в точке а.
Это утверждение вытекает непосредственно из того факта,
что матрица композиции двух линейных отображений равна
произведению матриц. Мы это запишем в следующей форме.
Пусть точка в Е (соответственно в F, в G) определяется своими
координатами (Xft)fte^, (Уу)/е/, {Zi)i(=r Для простоты возьмем
/={1, 2, ..., /}, /={1, 2, ..., пг}, К={1, 2, .... я}. Тогда f
определяется с помощью m функций от п переменных: г/3=
=Fj(xi, X2, ..., хп), /=1, 2, ..., m, g определяется с помощью
I функций от m переменных: Zj=Gj(«/i, у2, ..., ут), *'=1, 2, . ..
..., /, a h=gcf определяется с помощью / функций от п
переменных: zi=Hi{x1, х2, ..., хп), t'=l, 2, .... /. Кроме того,
можно написать
Нi\X\y х2, •■■> хп) ==
-=Gi (Fi (ДГ[, Х2, • • •> хп)> F% \х1> х2> • • •> хп)> • • •> Fm\xU х2> • • •> *«))•
(Ш,4; 11)

§ 4. Теорема о сложной функции 233
Тогда имеем:
дх\
откуда
3*2
дЯ;
3*2
(а)
<3</i
ас/
<fyi
дхп
дН2
дхп
дНь
дхп
ЛЬ)
ЛЬ)
(а)
(а)
(а)
дуг
dG2
ду2
dGi
ду2
ЛЬ)
ЛЬ)
ЛЬ)
X
dF
L(a)
dxi
dF2 , л
IJxfW
dF„
дх.
(а)
дх2
dF2
дх2
dFm
dx»
(а)
(а)
dHt v dGt ...
a I ml '
Точно так же имеем
dF' ( \
6G
ду,
1(Ь)
дуп
ЛЬ)
dGi
дут
(Ь)
dF
(а) ...
X
дхп
dF2
дхп
dFm
Ча)
дхп
(а)
(а)
(III, 4; 12)
ге/, k<=K. (111,4; 13)
dxh
(a)=S
<Э(/:
■<»-й:<«>.
fee/С- (III. 4; I3a)
Последнюю формулу можно записать короче, введя не
совсем корректные, но очень удобные обозначения. Отождествим
прежде всего h и g, считая, что речь идет об одной функции g,
выражающейся либо через переменную х, либо через
переменную у. Затем будем писать частные производные, не уточняя,
в какой точке они вычислены. Конечно, при этом
предполагается, что производная f вычисляется в точке а, а производная
g вычисляется в точке f(a)=b. Далее, если не указывать
функцию f, то вместо ее частных производных dFj/dxh можно писать

234 Гл. III. Дифференциальное исчисление
частные производные dyj/dxh. Тогда рассматриваемая формула
примет широко применяемую форму:
dG, жп dGi ду,
-Ь^=Ъ^-Ш-к' 'е/, Ае*. (Ш.4; 14)
Можно даже позволить себе заменить g на текущую
переменную z пространства Н или полностью удалить g. При этом
получим:
tei _ \л dzi dyj
дх
или
PSW i^J.k^K. (III.4; 15)
д v dyi д
дх
k M dxk ду '
R jej R i
ke=K. (Ill, 4; 16)
Следствие З. Если в условиях следствия 2
пространства Е, F, G имеют одну и ту же размерность п, то якобиан
сложного отображения h в точке а равен произведению
якобиана отображения f в точке а на якобиан отображения g
в точке f(a) =b, так что имеет место формула
D (ги г2, . ■ ., гп) _ D(zu z2 г„) D{yit Уз Уп) /jjj 4- Ifi >
D(xi,x2 хп) D(yuy2 уп) D(xi, x2, .... хп) ' ( ' ' 2f
По существу, именно эта формула оправдывает
применение обозначения п, ' У2 Уп\ для якобиана функции и=
D(xlt х2 хп) ^J *
=f(x) в выбранной системе координат. .
Следствие,4. Пусть Q — открытое множество
пространства Е, Q' — открытое множество пространства F, a f —
некоторая биекция Q на Q', дифференцируемая в каждой точке
вместе со своей обратной биекцией f~l. Тогда производное отобра-
жение г(а) является биекцией Е на F, а его обратная биекция
является производной в точке b=f(a) обратной биекции f'K
Другими словами, имеет место формула
(Г (а)Г'= (/"')>)■ (Ш,4; 17)
В частности, если Е и F конечномерны, то их размерности
одинаковы 1).
') Из линейной алгебры известно, что если существует линейная биекция
конечномерного векторного пространства на другое пространство, то они
имеют одинаковую размерность. Мы здесь получили нечто более сильное: если
существует биекция некоторого открытого множества конечномерного
аффинного пространства Е на открытое множество конечномерного аффинного
пространства F, дифференцируемая вместе со своей обратной биекцией, то •£

§ 4. Теорема о сложной функции 235
В самом деле, применим теорему о сложной функции к
отображениям f и f~l, удовлетворяющим равенствам: fof-i = IF,
/_1 о/= /fi. Поскольку производное отображение тождественного
отображения является тождественным отображением, получаем:
f'(a) о (f-l)'(b)=I+ и (f~')'(6) of'(a)=/->, чем и доказывается
тот факт, что f'(a) является биекцией и что ее обратной биек-
цией будет (f~')'(6). В частности, если Е и F конечномерны, то
их размерности одинаковы, и если в них выбраны системы
координат, то матрица Якоби обратной биекции f~l в точке Ь =
= f(a) является обратной матрицей матрицы Якоби
отображения f в точке а. Якобиан обратной биекции f~l в точке Ъ обратен
якобиану f в точке а. Последнее записывается в сжатой форме:
D(yuy2, ..., уп) 1В(Хъ Xi, ..., Хп)у\ (Ш)4;18)
Следствие 5. Композиция двух непрерывно
дифференцируемых отображений является непрерывно дифференцируемым
отображением.
Надо доказать, что отображение х —>• h'(x) =g'(f(x)) of'(x)
-> ->
является непрерывным отображением Qc£ в 2'(Е; G).
Отображение x-*f'(x) является, по условию, непрерывной функцией
}'. Отображение х —> g' (f (х)) есть функция g'°f. Здесь g'
непрерывна по предположению, а / непрерывна в силу
дифференцируемое™. Следовательно, согласно теореме о сложной
функции, функция g' of непрерывна (теорема 10 гл. II). Отсюда
следует, что x—*(f(x), g'{f(x))) является непрерывным отображе-
нием Q в произведение {3?(Е; F) X 3? (F; G)) (замечание,
следующее за теоремой 17 гл. II). Но отображение х—>h'(x)
является композицией рассмотренного отображения и
билинейного непрерывного отображения (и, v) —>v°u пространства
3£ (Е; F) X 3? (F; G) в пространство g (Ё; и). Из той же самой
теоремы 10 гл. II следует, что это отображение непрерывно.
Примеры вычисления обычных производных
Пример 1. Пусть и — отображение открытого множества
О, нормированного аффинного пространства Е на прямую R.
Применим после него отображение х—► arctgx из R в R.
Тем самым мы определим новое отображение Q в R, которое
и F имеют одинаковую размерность. С помощью методов, напоминающих
примененные на стр. 98, можно доказать большее: если существует
гомеоморфизм некоторого открытого множества Е на открытое множество F, то Е
и F имеют одну и ту же размерность. Здесь не требуется никакого
предположения о дифференцируемое™.

236
Гл. III. Дифференциальное исчисление
обозначается просто через arctgu. Если отображение и
предполагать дифференцируемым, то, учитывая, что функция arctgx
дифференцируема и что ее производная равна . 2 (напомним,
что для вещественных функций вещественной переменной
производное отображение является умножением на скаляр —
обычную производную; замечание 2, стр. 215), согласно теореме
о сложной функции получаем, что отображение arctgu имеет
производное отображение, определяемое формулой
(arctg»)'(a) = i + (u(a)Y ' или (arctg»)'= x + ut, (Ш,4;19)
или в дифференциальных обозначениях:
^(arctgw)--^^. (Ill, 4; 20)
Точно такие же рассуждения можно провести, если вместо
arctg рассматриваются другие функции. Взяв, например, In,
получаем (считая и(х) >0 для xeQ) следующие формулы1):
(\пи)' (а) = Щ^-, или (1пи)' = —, или d(\nu) = —. (Ш,4;21)
Пример 2. Производная произведения. Классическая
формула производной произведения функций (ну)' = u'v + uv'
является частным случаем производной билинейного
непрерывного отображения.
-> ■>•
Теорема 12. Пусть и, v — дифференцируемые
(соответственно непрерывно дифференцируемые) отображения
открытого множества Q нормированного аффинного пространства Е
в нормированные векторные пространства Fi и F2, и пусть В —.
• •> -> ->
билинейное непрерывное отображение F,y^F2 в G. Тогда ото-
->- -> -> -> ->
брожение В(и\,и2): х—*В(щ (х), и2(х)) -из Е в G
дифференцируемо (соответственно непрерывно дифференцируемо) и его
производное отображение для хе£ определяется следующей
формулой:
(Я(и„ и2)У(а)-Х = В(и[(а)-Х; и2(а)) + В(и^а); и'2(а)-Х), (III,4;22)
или
D+B («„ и2) (а)=В (D+Ul (a), u2 (a))+fi («, (a), D+u2 (a)), (III, 4; 23)
■) Во второй формуле (III, 4; 19) или (III, 4; 21) правые части являются
линейными непрерывными отображениями Е в R, т. е. элементами
сопряженного пространства Е'.

§ 4. Теорема о сложной функции
237
или в дифференциальных обозначениях
d (В (Ир ы2)) = В (и\ (а) ■ dx, и2 {а)) + В (и1 (а), и'2 (а) ■ dx) =
^B{dux,t2) + B{ux,~cUi2). (Ill, 4; 24)')
Доказательство. Рассматриваемое отображение
является композицией двух отображений: сначала берется
отображение пространства Е в Fx X F2, определяемое формулой
> >
х-> (Ui(x), и2{х)), а затем — отображение В пространства
Fx X F2 в G. Каждое из этих двух отображений
дифференцируемо (соответственно непрерывно дифференцируемо)
(теоремы 84 и 92), и остается лишь применить теорему о сложной
функции (соответственно ее следствие 5).
В качестве непосредственного применения предположим,
что в некоторой механической задаче и и и представляют
собой векторы ориентированного трехмерного евклидова
аффинного пространства, являющиеся дифференцируемыми функция-
-> ■>
ми времени t с производными и'(1) и v'(t). Тогда скалярное
произведение и векторное произведение этих двух векторов
также являются дифференцируемыми функциями времени и
имеют место формулы 2)
-> -> -> -> -> ->
(и 1 v)' = {и' | и) + («| и') (скалярное произведение),
-> -> ->->_>.>. (Ш,4; 32)
(и Л v)' = и' Л v + и Л v' (векторное произведение).
То, что нами было получено для билинейного отображения,
естественно, годится и для мультилинейного отображения: если
задано т дифференцируемых отображений ии и2, ..., ит
открытого множества Qc£ в нормированные векторные про-
странства Flt F2, ..., Fm и если В есть m-линейное непрерыв-
-> -> -> ->
ное отображение ЛХ-^гХ ••• X Fт в G, то функция В =
-> -> -> -*• > >
= В (и{, и2, ..., ит): х-> В («! (х), и2 (х), ..., um(x))
дифференцируема и ее производное отображение задается формулой
В*' (a) •X=^B(ui {a), ...,«,_, (а), и'}{а)-Х, и/+1(а\ ..., ит(а)).
(Ш, 4; 33)
') Здесь и далее нумерация формул соответствует оригиналу. — Прим. ред.
2) Поскольку t пробегает вещественную прямую к, вместо производных
отображений в смысле (III, 3; 13) мы имеем производные векторы в смысле
(III, 3; 1). Для этого достаточно в (Ш,4;22) положить X = 1 eR.

238
Гл. 111. Дифференциальное исчисление
-*.
Например, если три вектора и, и, w ориентированного
трехмерного евклидова аффинного
пространства-—дифференцируемые функции времени, то их смешанное произведение
■>->->
(и, v, w) является дифференцируемой скалярной функцией
времени и его производная вычисляется по формуле
->->-> ■>->-> ■>->-> ■>->->
(и, и, да)' = (и', и, ю)+(". и', w) + («. t>, йу')- (III, 4; 34)
->
Пусть Я — нормированное векторное пространство.
Рассмотрим отображение и—*и°ио...0и = ит пространства
-> ->
3! (Я; Я) в себя. Это отображение является композицией ото-
-> -> ->
бражения и —> (и, и, ..., и) из £ = 3? (Я; Я) в пространство
ЛХ^Х ••• XFm = 3?(H; H)X2?(H; Я) X • • • Х^(Н;Н) и
мультилинейного непрерывного отображения (ui, «2, •••, «ш) —*
■> -> ->
•>«i о «2 ° ... ° «т пространства ^i X ^2 X • • • Х'Лп в пространство
.■ -> ->
G = S'(H; Я) (теорема 54 гл. II). Применяя теорему 12,
получаем
d (ит) = du°u°...ou-\-uoduouo...ou-\-...-\-u°uo...odu =
= d« о и"1"1 + и ° du° ит-2 + ... + «m_1 ° du. (Ill, 4; 35)
-> ■> ->
Если Я является полем скаляров К, то 9?{Н;Н) —
коммутативное поле скаляров и мы возвращаемся к классическому
случаю дифференцирования степенной функции:
d (хт) = тхт~х dx.
Пример 3. Производная отношения. Пусть и есть
отображение открытого множества Q аффинного нормированного
пространства Е в векторное нормированное пространство F, и
пусть v — скалярная функция, определенная на Q и всюду =£0.
Тогда можно определить отношение и/и: х -> и (х)/v (x). Если и
и v — дифференцируемые функции, то это отношение также
дифференцируемо и его производная определяется формулой
d(l)= °^-*>". (Ill, 4; 36)
Доказательство очевидно. Отображение и/и является ком-
-> ->
позицией отображения х—*(и(х), l/v(x)) множества Q в F X KI
->- •> -> ■>
и билинейного отображения (и, ^) ->^« пространства F X К в f.

§ 4. Теорема о сложной функции
239
)dx
Поскольку, согласно примеру -1, d(-) = — -^- = — ^~^г{х) ,
то по формуле (III, 4; 24) получаем (III, 4; 36).
Применение к замене переменных. Пусть g— некоторая
функция переменной х, т. е. некоторое отображение открытого
множества Q нормированного аффинного пространства Е в
нормированное аффинное пространство G. Практически эти
пространства обычно конечномерны и в них заданы системы
координат. Предположим теперь, что g удовлетворяет некоторому
уравнению в частных производных или системе уравнений в
частных производных, и мы хотим сделать замену переменной
у = f(x). Если речь идет о некоторой биекции, то g станет
функцией переменной у, т. е. отображением некоторого открытого
множества из F в пространство G. Теперь g будет
удовлетворять новому уравнению или новой системе уравнений в частных
производных относительно у, и наша задача состоит в том,
чтобы найти эту систему уравнений. Такая постановка
предполагает заранее известным, что дифференцируемость g по х
эквивалентна ее дифференцируемости по у. Предполагается также,
что / дифференцируема вместе с обратной биекцией /_1. Будем
называть х старой переменной, у —новой переменной и будем
искать новое уравнение в частных производных исходя из
старого. Поскольку старое уравнение содержит производную dgjdx,
достаточно выразить ее через производную dg/dy, что делается
, de ds t/ / \
по формуле -j- = -v-»/ (х), а затем подставить результат в
рассматриваемое уравнение в частных производных. Так получается
новое уравнение, содержащее только производную dg/dy,
являющееся искомым уравнением, конечно, при условии, что оно
содержит лишь переменную у, т. е. что повсюду переменная х
заменена на переменную у через ее выражение х = /"'(</)>
требующее введения обратной биекции f'K
Пример 1. Уравнение колебания струны. Так называют
уравнение')
f)2U 1 iW/ ->
45--v4^=°- (ш.4-.37>
где х — пространственная вещественная переменная,/ —
временная вещественная переменная и 0 — векторная функция двух
переменных х и t, т. е. отображение R X R в F.
') Мы должны были бы дать этот пример лишь после изучения
производных порядка >1. Однако они уже прежде изучались. Необходимое
обоснование будет дано в § 6; см. теорему 19.

240 Гл. 111. Дифференциальное исчисление
Это уравнение имеет следующее физическое происхождение.
Рассмотрим однородную струну с закрепленными концами А и
В, способную совершать поперечные колебания в окрестности
своего положения равновесия. Точка струны, занимавшая в
равновесии положение М0, во время движения занимает
положение М. Ее перемещение в каждый момент времени определяется
-*■ —->
вектором U =М0М. Если точка М0 струны имеет на ней абсциссу
->•
х, то U является функцией двух переменных х и t.
Существенно заметить, что речь идет о малых колебаниях в некоторой
окрестности положения равновесия, т. е. струна предполагается
сильно натянутой, почти прямолинейной между А и В. Без этих
предположений уравнение движения не будет таким простым,
как указанное выше. Функция U принимает свои значения в
двумерном векторном подпространстве, перпендикулярном АВ.
Величина v в уравнении — скорость распространения
поперечных колебаний вдоль струны, определяемая по формуле
*=1/т' (HI, 4; 38)
где Т — среднее натяжение струны и р — линейная плотность,
т. е. масса единицы длины струны. Заметим, что уравнение
физически однородно, ибо размерность величины v,
вычисляемой по последней формуле, в единицах массы, длины и времени
равна 1/ m =U~l, т. е. является размерностью скорости ').
У ml
Выполним теперь замену переменных
l = x + vt, r\ = x — vt. (Ill, 4; 39)
Здесь речь идет о некоторой биекции, дифференцируемой
вместе со своей обратной биекцией, олределяемой линейными
дифференцируемыми функциями
х = Ц±. * = -Ц^-. (Ш, 4; 40)
->•
Если в функции U мы заменим х и t их значениями, то по-
->
лучим сложную функцию U*, определенную соотношениями
I, 4]-*U-(t,r\) = u(^p-,^). (III, 4; 41)
->•
Коротко ее можно обозначить через U, «считая выраженной
через | и тр.
') Разумеется, предполагается, что во время колебаний длина струны
изменяется пренебрежимо мало.

§ 4. Теорема о сложной функции
241
Обратно, имеет место формула
U(x, t) = U*{x+vt, x— vt). (Ill, 4; 42)
Вычисляя старые производные с помощью новых, получаем
формулы
dU dU , dU SU "(dU 3U
дх dl ' дц ' dt
=Лж-^У (ш-4=43)
которые позволяют найти формулы для частных производных
второго порядка
d2U _ d2U , с, д2д . д2Ц 1 д2Ц _ дЮ ? д2Ъ ■ д2Ц
дх2 dl2 ~Т~ д\дч\ "*" дц2 ' v2 dt2 ~~ dl2 l д\ дц "*" дц2 '
(III, 4; 44)
Отсюда теперь получаем, что
d2U 1 d2U _ . d2U тт .„
дх2 Ъ2 dt2 ~~q д$дг\' Щ1,4,40)
-> ->
В этой записи смешаны функции U и U*. В действительности
эту формулу надо было бы записать так1):
d2U , J4 I d2U , Л , д2д'
дх2
(х, t)--^^-(x,t) = 4 -^щ (х +vt,x- vt). (Ill, 4; 46)
Полученное новое уравнение относительно переменной U,
выраженной как функция от t и т] (в действительности
относительно U*), является значительно более простым уравнением
в частных производных
я2 и
:0. (111,4:47)
д\дт\
Нетрудно решить это уравнение. В самом деле, если мы рас-
дд
смотрим частную производную -=|~» т0 заметим, что ее
частная производная по т] равна нулю. Отсюда следует, что она
постоянна по т], т. е. является «произвольной» функцией- |. Но
теперь видно, что U является суммой какой-либо
первообразной этой функции |, которая сама является «произвольной»
') Правые части равенства являются функциями от х и t. Как обычно,
d2U\ . . ,, d2U* . , - ..
д> , (x+vt, х — vt) — это значение д д в точке (х + vt, х — vt).

242 Гл. 111. Дифференциальное исчисление
функцией |, и некоторой постоянной относительно |, т.е.
«произвольной» функции ц. Окончательно получаем формулу
U=7(l) + g(4)> (Ш,4;472>
дающую искомое решение уравнения колебания струны:
б (х, 0 = Т(х + vt) + g(x - vt), (III, 4; 48)
-> ->
где / и g— «произвольные» функции вещественной переменной.
Выражение «произвольные функции» не точно. Надо, чтобы
были обоснованы все вычисления при замене переменных.
(см. теорему 19), для чего необходимо, чтобы функция U имела
полную производную 2-го порядка, а это в свою очередь озна*
чает, что функции / и g дважды дифференцируемы.
Упражнение. Решить тем же самым методом уравнение
колебания струны с правой частью:
д*и 1 д*д -> Л /rrr . .„«
-to?— -jr -рг = g(x, t), (III,4; 49)
где правая часть является заданной непрерывной функцией х
и t. Это уравнение возникает в том случае, когда струна, кроме
натяжения, подвергается действию других сил, поперечно
направленных и зависящих только от х и t.
Пример 2. Частные производные в декартовых и
полярных координатах на плоскости.
1°) Выражение производных в полярной системе координат
через производные в декартовой системе координат.
По формулам замены переменных
* = rcoscp, y — rs'my, (III, 4; 50)
пользуясь указанными ранее краткими обозначениями,
получаем формулы:
д д , . д д . д , д
(Ш,4;51)
Каков же точный смысл этих формул?
Пусть g — отображение плоскости R2 в аффинное
пространство над полем вещественных чисел. Его можно записать в виде
(x,y)-+g(x,y).
Пусть, с другой стороны, Р — отображение плоскости R2
в себя, определенное формулами
(г, ф) -> (х, у), x = rcosq>, y = rsinq>. (Ill, 4; 52)

§ 4. Теорема о сложной функции
243
(Внимание! Через (г, ф) обозначена точка плоскости R2, для
которой г и ф — ее обычные декартовы координаты. Ее образ
Р(г, ф) имеет декартовы координаты х, у, определяемые по
формулам (III, 4; 52), а, следовательно, (г, ф) являются полярными
координатами этого образа.)
Отображение Р дифференцируемо, и его матрица Якоби
определяется формулой
дх \
Зф~ \ = /со5ф -rsinqA^
ду I ^эшф гсоэф/ ' ' '
дФ /
Отсюда вытекает, что если g является дифференцируемой
функцией, то сложное отображение g* = g ° P также
дифференцируемо и имеют место формулы
-^-(г, ф)=-^|-(гсозф, гз1пф)со5ф + -^|-(гсо5ф, г sin ф) sin ф,
(Ш, 4; 54)
-gf-(r> Ф) = —-57 (г cos ф, гвтф^тф + ^гсоэф, г sin ф) г cos ф,
которые, пользуясь принятыми краткими обозначениями, можно
записать в виде.
^«созф^ + зтф^, g = _rsinq>|f + rcosq>g (III, 4; 55)
(как обычно, g* и g отождествлены). Отсюда получаются
формулы (III, 4; 51).
2°) Выражение производных в декартовых координатах
через производные в полярных координатах.
Можно попытаться выразить частные производные по х и
и, исходя из частных производных по г и ф. Однако следует
заметить, что отображение Р не является биекцией. Отображение
Р сюръективно, но не инъективно, ибо точка (х, у) имеет
бесконечное множество полярных координат. Поэтому следует
ожидать, что производное отображение отображения Р не будет
линейной биекцией. Тем не менее в окрестности точки (г, ф),
') Из теоремы 84 следует, что если обе скалярные функции (г, ф)->-гсоз ф,
(г, ф) ->- г sin ф дифференцируемы, то отображение Р также дифференцируемо.
Каждая из этих двух функций дифференцируема, если дифференцируемы
сомножители. Итак, остается показать, что дифференцируемы . функции
(г, ф)->-г и (г, ф)->-со5ф или sin ф. Далее, функция (г, <р)-»-г линейна, а
функция (г, ф)->-со5ф является композицией отображений (г,ф)->-ф и
Ф ->- cos ф, из которых первое линейно, а второе известно как
дифференцируемая вещественная функция вещественной переменной.
Можно также применить следствие 2 теоремы 15: (г, ф)->-г cos ф и
(л, ф)->-г sin ф имеют непрерывные частные производные.

244 Гл. III. Дифференциальное исчисление
СОЭф —ГБШф
в которой якобиан преобразования Р:
sinq) гсоэф
отличен от 0, т.е. в точке (х, у) Ф (О, 0), уравнения (III, 4; 54)
разрешимы1), и, исходя из частных производных dg*/dr, dg*/dq>,
можно вычислить частные производные dg/дх, dg/dy.
Непосредственными вычислениями получаем:
(III, 4; 56)
dg , . , дв* , , sin ш дв* , ,
-^(ГСОБФ, Г51Пф)=С05ф-^-(г, ф) Г^"^"^ ф)>
dg 1 • \ • dg* i ч , cos Ф дв" , ■,
-^-(ГСОБФ, Г51Пф)=51Пф-^г(г, ф) + —f- -£- (г, ф).
Заметим, что в этой формуле можно заменить г и ф
соответствующими функциями от х и у.
Можно также посмотреть на вышеизложенное с другой
точки зрения. Пусть (г0, фо) — некоторая точка R2, г0 > 0, и пусть
(х0, г/о) ее образ при отображении Р. Если Р сузить на
открытое множество Q из R2,. определенное неравенствами г > 0,
Фо — я < ф < фо + я, то получим некоторую биекцию Pq. (и
даже гомеоморфизм) множества Q на P(Q), имеющую
обратную биекцию Р~К Когда точка (х, у) изменяется в P(Q), ей
можно отнести единственную непрерывно изменяющуюся
систему полярных координат, т. е. единственный прообраз в Q, и
мы будем иметь: g — g*Po~. При этом формулы (III, 4; 56),
в которых г и ф заменены их выражениями в виде функций от
х и у, будут иметь тот же смысл, что и формулы (III, 4; 54).
Запишем эти формулы:
|S- (х, у) = 17== ^-(V^+?, Ф (X, У)) -
дх У х2 + у2 дг
(III, 4; 56j)
#<*■ ^тНЬт^МР+Т". ф(х, */)) +
Аналогичные формулы можно получить для г о < 0, если
взять г<0 и r =—V^x2 + y2- Что же касается непрерывной
функции ф: (х,у) ->ф(х,у), то у нее нет простого аналитиче-
') Мы применили здесь непосредственно очевидный частный случай
теоремы о неявной функции (§ 8; см., в частности, замечание на стр. 311).

§ 4. Теорема о сложной функции
245
ского выражения. Очевидно, ф (х, у) = arc tg yjx + kn, где k
зависит от х, у и не всегда одно и то же для (х, j)eP(Q).
Можно было бы для решения обеих задач применить
дифференциальные обозначения. В самом деле, запишем
дифференциал в виде
dg = ^dx + ^dy, (III, 4; 57)
а затем воспользуемся формулами
dx = cos ф dr — г sin ф dq>, dy = sin ф dr + r cos ф dq>, (III, 4; 58)
которые дадут новое выражение дифференциала
dg* = [cos ф -£ + sin ф -^j dr + [—r sin cp ~ + r cos ф -^-) dq>.
(Ill, 4; 59)
Коэффициенты при dr и йф являются частными
производными dg'/dr и dg*jd(f, что снова дает решение 1-й задачи и
формулу (111,4; 54).
Для того чтобы снова получить выражение (III, 4; 56),
можно провести то же самое рассуждение, исходя из формулы
dg' = -^-dr + &-d<f. (Ш, 4; 60)
Затем dr и dcp следует выразить как функции от dx и dy
путем решения системы (111,4; 58), т. е. положить
dr = cos ф dx + sin ф dy и dtp — s'mcpdx-\—cos ф dy,
(III, 4; 61)
откуда подстановкой в (III, 4; 60) получается:
T*" ( dg* sin ф dg* \ j . I . dg* . cos ф dg* \ ,
dg=(coscp-§-r JL-±-^dx + ^mv-Kr + -JL^dy.
(Ill, 4; 62)
Отсюда снова находится решение 2-й задачи и формула-
(III, 4-, 56).
В качестве применения вычислим, например, лапласиан в
полярных координатах.
Лапласиан функции g переменных х и у определяется
формулой
А* = И+-§- (Ш, 4; 63)
Для частных производных 1-го порядка уже имеются
формулы (III, 4; 56). Вычисляя частные производные 2-го порядка

246
Гл. Ilh Дифференциальное исчисление
как производные от производных 1-го порядка:
#- (-»li-*?"k) Н * f" - ^ f) ■ СП. 4-. 64)
получаем выражение вида
асоэ2ф + рэтфсоэф + узт2ф. (III, 4; 65)
От частных производных по х к частным производным по у
я
можно перейти, заменяя ф на ф х- , т. е. соэф и simp на sincp
и —соэф соответственно. Выражение для d2g/dy2 при этом по-
-> -> ->
лучит вид азт2ф— рэтфсоэф + усоз2ф, а лапласиан будет
-»• -»•
равен а + у, т.е. будет суммой коэффициентов при соэ2ф и
sin2q> в выражении (111,4; 65). Непосредственное вычисление
дает
Г*"/ ч ^8* i ч i I dg* 1 ч i 1 д*8* , ч
Ag(rcosq>, rsm<t)=r-0pr(r, ф) + 7-|г(г> ф' +Т2"-^^' ^'
(III, 4; 66)
что можно коротко записать в виде:
^Ы «ЭЛ2 ' л «Эл ' л2 <Эф2 '
или (III, 4; 67)
._ д2 . 1 д 1 д2
Л <Эл2 . ' г <Эл ' л2 <Эф2 *
Замечания. 1°) Эта формула удовлетворяет правилу
однородности. Если величины х, у, г имеют размерность длины
—*■■
I, а ф безразмерна, то размерность Ag равна gl~2 и то же самое
имеет место для членов правой части.
2°) Во всех вычислениях предполагается, что g имеет
полную производную 2-го порядка (см. § 6, теорема 19).
Пример 3. Вычисление лапласиана от функции,
определенной в R" и зависящей только от расстояния до начала
координат.
Пусть g—-отображение полупрямой R+ (множество
вещественных чисел ^0) в нормированное аффинное пространство
.G. Рассмотрим отображение г пространства Rn в полупрямую
R+, определенное по формуле
г(*,, х2 *„) =Vx\ + x\+ ..: + х\. (III,4;68)
Сложное отображение g* = g°r, которое будет кратко
записываться в виде g(r), является отображением R" в G, зави-

§ 5. Формула конечных приращений
24?
сящим только от расстояния исходной точки до начала
координат. Если g дважды дифференцируемо и (xit Хг ..., хп)ф
ф(0, 0, ..., 0) (для того, чтобы г также было дважды
дифференцируемым), то для отображения g* в точке {х\,Х2, ..., хп)
существует лапласиан Ag*= /.—%-. Этот лапласиан может
быть вычислен предыдущими методами. Прежде всего
dxt s dxt s r '
9*9 9
д в ->• x, ->• 1 ■*■ x.
(Ill, 4; 69)
Складывая затем результаты, полученные для i= l, 2, ..., «,.
находим:
дг>,. % ..., *„)=J"(V*; + *?+ ... + 0+
что можно коротко записать в виде
А| = 1" + -^11' = # + ^1#. (Ш.4;71>
При п = 2 эта формула является частным случаем
формулы (111,4; 66), в которой g n g* поменялись ролями. (Если в
(III, 4; 66) предположить, что g* зависит только от г, то
2 =0 и мы получим Ag = , 2 И д—, что эквивалентно
(III, 4; 71) при я = 2.) Легко проверяется правильность мно-
—> ->
жителя п—1: при п= 1 получаем Ag* = g". Можно заметит
также, что формула удовлетворяет правилу однородности:
правая и левая части имеют размерность gl~2 (см. конец
примера 2°).)
§ 5. ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ
Предположение, что / имеет производную в точке A6Qf
>.
->•
означает, что приращение f(a-\-h) — f(a) для бесконечно
малого h выражается по формуле (III, 3; 13), и в этом смысле
формулу (III, 3; 13) можно было бы назвать формулой

248 Гл. III. Дифференциальное исчисление
бесконечно малых приращений. Однако формула (III, 3; 13) не
^ •*
дает никакой оценки для приращения f{a -f- h) —f(a) функции/
при определенном приращении аргумента h. Этой цели будет
-служить формула конечных приращений, использующая
производную функции / в точках, близких к точке а.
Формула (III, 2; 2) непосредственно обобщается на
отображения Е в F в том случае, когда F является полем
вещественных чисел.
Теорема 13А. Пусть f — вещественная непрерывная
функция, заданная на открытом множестве Q аффинного
нормированного пространства Е над полем вещественных чисел. Если
->
отрезок [х, х + h] целиком содержится в Q и если функция f
имеет производное отображение в каждой точке открытого ин-
->
тервала ]х, х + h [, то
f(x + h) — f(x) = f'(x + Bh)he=R, где 0<6<1. (III,5; 0)
Доказательство. Рассмотрим отображение Ф: t—>
->
—*f(x-\-th) вещественного интервала [0,1] в F = R. Это ото-
->
бражение является композицией отображения t.~>x-\-th
.отрезка [0, 1] в множество Q и отображения / множества Q в R.
Согласно теореме о сложной функции, это отображение
непрерывно на отрезке [0, 1] (теорема 10 гл. II) и дифференцируемо
на интервале ]0, 1[ (теорема 11 гл. III) и его производная
вычисляется по формуле
<3>'(t) = f'(x + th)h(BR. (Ш,5;02)
Поскольку. Ф(1) — Ф (0) = / (х + h) — f{x), для получения
необходимого результата достаточно к функции Ф на отрезке
[0, 1] применить формулу (III, 2; 2).
' Напротив, формула (III, 2; 2) в том виде, какой она имеет,
' не может быть обобщена, если размерность F больше 1 или же
если речь идет об аффинных пространствах над комплексным
полем. Она не верна уже для комплексной функции
вещественной переменной1). Рассмотрим, например, комплексную
функцию х-+е2Ых, определенную на отрезке [0,1] из R. Эта
функция принимает одно и то же значение при х = 0 и х = 1. Если
бы формула конечных приращений была верна в виде (III, 2; 2),
то должна была бы существовать точка с интервала ]0, 1 [,
в которой производная рассматриваемой комплексной функции
') То ерть отображения прямой R в комплексную плоскость С, где R
.и С рассматриваются как векторные пространства размерности 1 и 2 над
полем вещественных чисел.

§ 5. Формула конечных приращений
24»
обращалась бы в нуль. Однако ее производная — функция х —*
->2ine2inx — нигде в нуль не обращается.
Приведем формулу конечных приращений для общего
случая в форме, несколько отличной от предыдущей:
Теорема 13. Пусть f —непрерывное отображение
открытого множества Q аффинного нормированного пространства Е
в аффинное нормированное пространство F. Тогда, если отре-
->•
зок [х, х + п] целиком принадлежит Q и если f имеет производ-
->
ное отображение в каждой точке открытого интервала ]х, x-\-h\
и его норма не превосходит М, то имеет место неравенство
||/(х+А)-/(х)||<Л1||А||. (III, 5; 1>
Доказательство. Предварительно докажем одну лемму.
Лемма. Пусть f— отображение отрезка [0, 1]
вещественной прямой R в аффинное нормированное пространство F и
g— вещественная функция на отрезке [0, 1]. Предположим, что-
функции fug непрерывны на замкнутом отрезке [0, 1] и
дифференцируемы на открытом интервале ]0, 1[. Если при этих
условиях имеет место неравенство
ll/'MIKg'M для 0<х<1, (111,5; 2)
то справедливо также неравенство
ll/(i)-/(0)ii<g(i)-g(0). (ш, 5; 3)
Докажем эту лемму. Пусть задано е > 0. Обозначим через Лв
множество точек х интервала [0, 1], для которых
II /(*)-/ (0) \\<g(x)-g (0) + вх + е. (Ill, 5;4>
Функция
x->\\f(x)-f(0)\\-g(x) + g(0)-ex-e (Ш,5;42>
непрерывна. Множество Ле точек, в которых эта функция =^0,
замкнуто. В частности, Ле содержит свою точную верхнюю-
грань р, которая тем самым является максимумом. Заметим,
что р не может быть = 0. В самом деле, точка х = 0
принадлежит множеству Ле, так как функция (III, 5; 42) при л:=0
принимает значение —-е < 0. Из непрерывности fug следует,
что Ле содержит некоторую окрестность нуля. Однако
неравенство 0 < р <. 1 также невозможно. Действительно, по
определению производной (формула (III,3; 13)), если 0<Р<1, то

250 Гл. III. Дифференциальное исчисление
существует число б > 0, при котором справедливы неравенства:
е
ШР + б)-/(р)11<11Г(Р)11б + тб<£'(Р)б + 4б,
г(Р + в)-г(Р)>г'(Р)в--|в,
откуда
(III, 5; 5)
llf(P + fi)-f(P)IKg(P + fi)-fir(P) + e*. (Ill, 5;6)
Однако, поскольку реЛг, то
ll/(P)-/(0)||<g(P)-g(0) + ep + e, (III, 5; 62)
а, следовательно, после сложения,
ll/(P + 6)-f(0)ll<g(P + 6)-g(0) + e(p + 6) + e. (111,5;63)
Отсюда следует, что р + беЛе, что невозможно, поскольку
{$ является максимумом для множества Ае.
Таким образом, Р=1. При этом (III, 5; 6г) запишется в виде
II /(!)-/ (0) || < g (1) - g (0) + 2е. (Ill, 5; 64)
Так как это неравенство справедливо при любом ё, отсюда
следует справедливость неравенства (III, 5; 3), и лемма
полностью доказана.
Замечания к лемме. 1°) Вместо того чтобы
предполагать функции fug дифференцируемыми, можно ограничиться
дифференцируемостью справа и соответственно условием
->
1^п!^£п- Это видно непосредственно из доказательства. Если
заменить /(х), g(x) на —/(I —х), —g{\ —х), то можно
обойтись дифференцируемостью слева.
2°) Предположим сверх того, что в интервале ]0, 1[ имеется
хотя бы одна точка с, в которой выполняется строгое
неравенство \Wfi)\<g'a(c). Тогда ||f(l)-f(6)||<g(l)-g(0). В са-
>
мом деле, если & = g'n (с) — |f£ (c)|>0, то для достаточно малого
Л>0 имеем:
II WTh^fic) II < 1ТМ || h + -i h = g'n (с) - \йй,
g(c + h)-g{c)^g'a(c)-±h,
з
з

§ 5. Формула конечных приращений 251
откуда
|| f(c + h)-f{c)\\^g{c + h) - g(c) -^h<g(c + h)-g (с).
(Ш,5;65)
Однако лемма, примененная к интервалам [0, с], [с-\-h, 1]
вместо интервала [0, 1], дает
\\f(c)-f(0)\\<g(c)-g(0),
>. (Ш,5;66)
||/(1)-/(с + й)|Кг(1)-£(с + й).
Результат получается сложением (III, 5; 65) и (III, 5; 66).
3°) Если функция / также вещественна, то можно
предполагать, что она всюду на [0, 1] имеет производную, конечную
или равную —оо, и что имеется только неравенство вида f' ^
s^g^. Тогда справедливо неравенство /(I)—/(0) ^ g{\)—
— g(0), а если хотя бы в одной точке се]0, 1[ имеет место
строгое неравенство f'n (с) <g'n (0), то /(1) —/(0) < g(l) — g(0).
4°) Отсюда вытекают обобщения, указанные в замечаниях
после теорем 4, 5, 7. Рассмотрим теорему 4 (Ролля), из
которой следуют остальные. Неравенство f'n(x)<0 не может
выполняться всюду. В самом деле, если положить g=0, то /(1) —
— /(0) < 0, что противоречит условию. По той же причине не
может всюду выполняться и неравенство f'n{x)>0.
Следовательно, существует точка сь в которой ffn(cx) ^0, и точка с2, где
Вернемся теперь к доказательству теоремы. Рассмотрим
отображение Ф: t-->f(x + th) отрезка [0,1] в F, введенное при
доказательстве теоремы 13А. Его производная записывается
в виде
Ф' (0 = /'(* + ih) h. (Ill, 5; 7)
Отсюда вытекает, что в условиях теоремы норма этой
производной не превосходит М||Л||. Если теперь применить лемму,
->
выбирая в качестве g линейную функцию t-*M\\h\\t, то
получим неравенство (III, 5; 1).
Теорема о конечных приращениях допускает следующее
интересное дополнение:
Следствие 1. Пусть L — линейное непрерывное отобра-
-> ->
жение Е в F. Тогда при условиях теоремы 13 имеет место

252
Гл. III. Дифференциальное исчисление
неравенство
■>
\\f(x + h)-f (х) - Lh ||< со|| Л ||, (III, 5; 8)
где со — точная верхняя грань величины ||/'(g) —L|| при |,
изменяющемся в интервале ]х, х + Л[. Часто предполагают, что
функция f имеет производную в х, и тогда полагают L = f'(x).
Доказательство. Достаточно применить теорему к функ-
>
ции |-*-f(i) — L-(l — х), производная которой в точке | равна
Следствие 2. Если Q является открытым выпуклым')
множеством аффинного нормированного пространства Е и если
f есть дифференцируемое отображение Q в F, производная
которого в каждой точке Q по норме не превосходит некоторой
постоянной М, то функция f удовлетворяет условию Липшица и,
следовательно, равномерно непрерывна.
Доказательство. Из выпуклости множества Q следует,
что если х' и х" — любые две точки Q, то весь отрезок [х', х"\
принадлежит Q. Следовательно, к нему можно применить
формулу конечных приращений, и мы получим неравенство
|| f (х') - f (x") || < М|| х' - х" ||, (III, 5; 9)
чем и доказывается теорема.
Следствие 3. Пусть f — дифференцируемое отображение
■аффинного нормированного пространства Е в аффинное
нормированное пространство F. Предположим, кроме того, что его
производная f является равномерно непрерывным отображе-
нием пространства Е в пространство 2:' (Е; F). При этих усло-
, f(x + h)-f{x)-f'(x)h ,
зиях функция х->——!—-—-^—■ ■ равномерно сходится
IIАII
к О при h¥=0, стремящемся к 0.
Доказательство. В силу предположения о равномерной
непрерывности производной f, по заданному е >- 0 можно ука-
■>
зать такое ч > 0, что из неравенства || я'— *"1Кч будет
следовать неравенство Wf'(x') —f (х")\\<Се. Но тогда, как только
1|А|Кч> величина со, входящая в формулу (III, 5; 8),
соответствующую L=f'(x), будет по норме не больше е, что и
доказывает высказанное утверждение.
') Условие выпуклости весьма существенно.

§ 5. Формула конечных приращений
253
Замечания. 1°) Пусть Е — поле скаляров. Тогда, согласно
>
-> ->
следствию 3, функция x->(f(х + h) — f(x))/\\h\\ сходится равно-
-> -> ->
мерно к производной функции f при пфО, стремящемся к 0.
В этом случае говорят, что f равномерно дифференцируема.
2°) Эту теорему часто применяют в следующем случае.
Предположим, что f определена лишь в открытом множестве Q из
Е (возможно, на полуоткрытом или замкнутом интервале, если
-> ->
£ = R). Тогда функция х-* —1 "~' w t очевидно,
IIЛ ||
не определена на всем множестве Q. Ограничимся рассмотре-
->
нием множества значений п, норма которых не превосходит
некоторого фиксированного числа б > 0. Тогда все
рассматриваемые функции будут определены на одном и том же открытом
множестве Q6 точек из Е, расстояние которых до С Q больше б.
Если производная f равномерно непрерывна, то отсюда полу-
>
„ . f (x+t) - f (х) - f (x)t
чаем, что на множестве Q6 функция х—>■ — —-^—-— ■
\\Ц
равномерно сходится к 0, когда пфО стремится к 0.
Теорема 14. Пусть Q — открытое множество аффинного
нормированного пространства Е. Пусть с — некоторая точка Q
и Q0 — дополнение к с в Q. Пусть f — непрерывное отображение
Q в F, всюду дифференцируемое в Qo. Если производная f'(x)
-> ->
стремится к некоторому пределу L в SE' (Е; F) при х е Q0,
стремящемся к с, то f дифференцируема в точке с и ее производная
в точке с является линейным непрерывным отображением L.
Доказательство. Достаточно применить к х=с
неравенство (III, 5; 8). Результат вытекает из того, что, в силу вы-
->
сказанных предположений, со стремится к 0, когда h стремится
->
к 0. Теперь видно, почему в теореме 13 и ее следствии 1 было
существенным не предполагать f дифференцируемой на концах
интервала.
Полная дифференцируемость и частная дифференцируемость
Теорема 15. Пусть Elt E2> F — аффинные нормированные
пространства, f — отображение открытого множества Q
пространства Ei X Ег в F. Для того чтобы отображение f было

254
Гл. III. Дифференциальное исчисление
непрерывно дифференцируемым в Q, необходимо и достаточно,
чтобы оно имело частные производные -jj-1 _L (
непрерывные в Q.
Доказательство. Если отображение / дифференцируемо
в множестве Q, то из теоремы 9 следует существование
частных производных и формула (III, 3; 29). Кроме того,
неравенства (II, 13; 28) и (II, 13; 30) говорят о том, что если линейное
непрерывное отображение и пространства Е{Х,Е2 в F пред-
ставимо по формуле (II, 13; 26) в виде суммы двух линейных
-> ->
непрерывных отображений щ, иг пространств Еи Е2 соответ-
->
ственно в F, то
ll«ill<ll"ll. ||н2|К||и||,
11«1К11",|| + 11«2||. (ш>ь,ш)
(х)--^-Ы
Если отображение f непрерывно дифференцируемо, то при х,
стремящемся к х0, норма \\f'(x) —f'(x0)\\ стремится к 0 и из
первого неравенства (III, 5; 10) следует, что -^~(х) — -s—
(t = l, 2) стремится к 0, а это означает, что частные
производные f непрерывны.
Обратно, пусть существуют частные производные функции/.
Мы уже знаем, что отсюда еще не следует существование ее
полной производной1) (пример (III, 3; 9)). Однако
существование непрерывных частных производных влечет за собой
существование и непрерывность полной производной (а значит, и
непрерывность /).
-> ->■ ->->_,
В самом деле, пусть заданы hl^El и п2<^Е2. Если а =
= (ai,02)sQ, то, поскольку множество Q открыто, существует
-> ' -> -*■
такое число р > 0, что при Ц^ ||<р, ЦЛ2|Кр точка (а, + Л,»
->
а2 + h2) e Q. При этом
/(а, + Л,, a2+h2) — f(au a2) =
= / (а, + А„ а2 + п2) — f (а, + А,, а2) + / (а, + ft,, a^ — f(au a2).
(111,5; 11)
J) И даже непрерывность /.

§ 5. Формула конечных приращений
255
Применим следствие 1 теоремы 13 к непрерывно
дифференцируемой функции x2-+f(al + Л], х2) с L=-jr—{ax, а2):
■ ►
/ (а, + Л,, а2 + Л2) — / (а, + Л„ а2) = ^- (а,, a2) Л2 + со || Л21|,
(111,5; 12).
где
|| to |K sup J-=7-(a,+Л„ a2-f 6Л2) —-^-(a,, a2) . (111,5; 13)
о < e < l II °*2 0*2 ll
->->-> ->
Если Л = (Л[, /г2) стремится к 0, то в силу непрерывности
—- в точке (а,, а2) последнее выражение стремится к 0.
0X2
С другой стороны, по самому определению производного
отображения (III, 3; 13)
>
/(a, + /i„ a2) — /(alf a2)=-^-(a„ а2)Л, + a|| Л, ||, (111,5; 14)
■> -> >
где а стремится к 0 вместе с Ль
Окончательно получаем
>
/(а, + Л„ а2 + /г2) —/(а,, а2) =
= (^-(а„ а2)Л1Ч--^-(а„.а2)Л2) + (а||Л,|| + ш||Л2||), (111,5; 15)
-> ■> -> ■>
где а и со стремятся к 0 вместе с h.
Первая скобка определяет линейное непрерывное отобра-
-> -> ->
жение и пространства Е{ X Е2 в пространство F с помощью ли-
нейных отображений и\ и и2 пространств Ех и Е2 в F. Вторая
скобка по норме не превосходит (||а || + || со ||)|| h ||, где || а || + || со ||
стремится к 0 вместе с ||/i||. Следовательно, / имеет полную
■> ■> ->
производную /'(a) c= j? (£, X £2; ^) в точке а, определяемую
с помощью -^-(а„ а2)е2'(£,; f) и -^-(а,, а2) (=^(£2; £).
гт ' df df2
Покажем, что из непрерывности -^ и -^— следует
непрерывность /'. Если х стремится к х0 в Q, то -~t-'^ '-
мится к 0 (i = 1,2), и тогда из второго неравенства (111,5; 10)
следует, что \\f'(x) — f'(xo)\\ стремится к 0, чем и заканчивается
доказательство.
дх.^-^Щ0^-

256
Гл. 111. Дифференциальное исчисление
ас
Замечания. 1°) Непрерывность -^— и только существо-
вание -^— достаточны для существования f , как это видно
непосредственно из доказательства (но не достаточны для
непрерывности /').
2°) Теорема, доказанная для произведения двух пространств
Е\ и Е2, очевидно, справедлива для произведения п пространств
Ei, Е2, ..., Еп (доказать это можно или непосредственно, или по
индукции). Кроме того, непрерывность всех частных
производных, кроме, может быть, одной, и только существование этой
производной достаточны для того, чтобы повлечь за собой
существование полной производной.
3°) Пользуясь теми же самыми неравенствами (III, 5; 10),
можно показать, что, если функция / зависит от параметра X,
пробегающего некоторое топологическое пространство Л, и если
-J—(xu Хп, X), -5—(х\, х2, X) непрерывно зависят от х\, х2, X, то
ОХ\ ОХ%
тоже самое верно и для f'(xi, x2, X).
Следствие 1. Пусть Е, F — аффинные пространства,
причем пространство Е конечномерно и в нем выбрана система ко-
->
ординат 0, (et)i^j. Для того чтобы отображение f открытого
множества Я из Е в F было непрерывно дифференцируемым,
необходимо и достаточно, чтобы оно имело частные производ-
ные -=J—, непрерывные в П.
Результат вытекает из того, что введение системы координат
отождествляет Е с KJ.
Сказанное выше объясняет, почему в математических курсах
для применения теоремы о -сложной функции (теорема 11)
всегда требуют, чтобы рассматриваемые функции имели
непрерывные частные производные. В действительности такое
предположение слишком сильно, поскольку оно влечет за собой
существование и непрерывность полной производной, в то время
как требуется установить лишь ее существование. Однако
непрерывность частных производных обеспечивает существование
полной производной, а одно лишь существование их этого
обеспечить не может.
Следствие 2. Если, кроме того, в условиях следствия 1
пространство F конечномерно и в нем выбрана система
координат 0, (К)ге/> т0 отображение /, определенное функциями
Fi (ie/) переменных Xj (/е/)1), непрерывно дифференци-
Jj Обозначения формулы (III, 3; 16).

§ 6. Производные высших порядков
257
руемо тогда и только тогда, когда функции Fi имеют
непрерывные обычные частные производные ~^--
§ 6. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
Пусть / — отображение открытого множества Q аффинного
нормированного пространства Е в аффинное нормированное
пространство F. Если это отображение всюду дифференцируемо,
то его производная функция f является отображением Q в век-
торное нормированное пространство 9? (Е; F). Естественно
изучить, будет ли в свою очередь дифференцируемым это
отображение. Если это так, то его производная в точке а, обозна-
чаемая Г (а), будет элементом пространства i? (£; 9£{Е; F)), и
если такая производная существует всюду в Q, то производная
функция \": х->/"(х) является отображением £1ъ9?{Е; 9?(Е; F)).
Пусть теперь л — некоторый вектор из Е. По определению
> ■ -> >
f"(a), f (а)Х является элементом 9? (Е; F), т. е. линейным не-
прерывным отображением Ь в F. Если взять другой вектор У
-> -> ■>
из Е, то можно говорить о (f"(a)X) -Y, являющемся вектором
из F. Дадим сейчас иную интерпретацию этому вектору.
■*■ •>
Для фиксированного У отображение и~*uY является линей-
-> •> ■»•
ным непрерывным отображением пространства 9£{Е; F) в F
(теорема 54, гл. II). Следовательно, согласно следствию 1 из
теоремы 11, это отображение перестановочно с частной
производной £)->. вдоль вектора X. Иначе говоря:
((/у) (a)) Y = (Dt (f (х) Y)) e F, (III, 6; 1)
где правая часть существует каждый раз, когда существует
левая часть равенства. Однако если существует f"(a), то Z)->/'(а)
является не чем иным, как f"(a)X, а, следовательно, левая
часть является рассмотренным выше вектором (f"(a)X)-Y.
С другор стороны, f'(x)Y — это D+f(x), поэтому правая часть
существует и равна (/)->.(D+f\\ (а).
9 Зак. 1339

258 Гл. III. Дифференциальное исчисление
Окончательно, если существует Г'(а)> т0 существует
Dt(Dff){a) и
{f"(a)X)-Y = Dt(Dff)(a). (Ill, 6; 2)
Правую часть называют также частной производной второго
порядка D^-D^-f (а) — Д->■>/ (а) (конечно, при частном диффе-
X Y л, Y
ренцировании £)->£).> сначала вычисляют частную производную
Л Y
£)->, а затем частную производную £)•>).
Впрочем, согласно теореме 54г гл. II, линейное непрерывное
•> -> •>
отображение £ в & [Е; F) можно отождествить с билинейным
непрерывным отображением £ X £ в F. Согласно определению
этого отождествления, это означает, что линейному непрерыв-
-> • -> ->
ному отображению U пространства Е в 9? (Е; F) ставится в
соответствие билинейное непрерывное отображение и простран-
ства Е X Е в F, определенное равенством
u{X,Y)=(UX)-Yl). (Ill, 6; 3)
Вторая производная часто рассматривается именно в этой
форме.
-> ->
В этом случае выражение (/" (а) X) ■ Y может быть записано
в виде \" (а) {X, Y), \" (а) становится, элементом пространства
2?2{Е> Е; F) или 3£^Е2\ F) билинейных непрерывных отобра-
жений Е X Е = Е2 в F, и если \" {х) существует для всех х е Q,
то \": x-*-f"(x) является функцией, определенной на Qc£,
со значениями в 3?2(Е2; F). При этом (III, 6; 2) принимает вид
f"(a)(X,Y)=DtDff(a), (III,6;32)
где правая часть существует, если только существует левая,
т. е. существует f" (а) г).
') Если ЁхфЁъ то имеется лишь единственный возможный способ
отождествления S (£,; S (£2; F)) с S2 (Е{, Е2; F). Поскольку здесь Е1=Е*2 = Е,
то возможны два варианта отождествления, и мы выбрали один из них.
2) Напомним еще раз, что существование f"(a) влечет за
собой'существование /' если и не во всем Q, то по крайней мере в некоторой окрестности
точки а.

§ 6. Производные высших порядков 259
Определение. Билинейное отображение и произведения'
Ё X Е в векторное пространство F называется симметричным,
если, каковы бы ни были элементы X и Y из Е, мы имеем:
u(X,Y)=u(Y,X)i (III, 6; 4)
Теорема 16. Пусть f — отображение открытого множества
Q аффинного нормированного пространства Е в аффинное
нормированное пространство F. Предположим, что оно имеет
вторую производную f"(a) в точке neQ. Тогда f"(а) является би-
линейным непрерывным симметричным отображением Е X Е в F:
f"(a)(X, Y)-f"(a)(Y, X). (Ill, 6; 5)
->■ ■->
Если Е — К", то, выбирая в качестве X и Y векторы базиса,
получаем известное соотношение
d2f d2f
дх. дх. * ' дх, dxi * ''
Доказательство, Рассмотрим выражение
■ >
A = f(a+ t(X + Y)) ~ f(a + tX)-f(a + tY) + f(a)<=F. (Ill, 6; 52>
-*■ > ■*■ ^
Предположим, что a e Q, Ie£ и Fg£ фиксированы, и
заставим скаляр t=?=Q стремиться к 0. Предположим также, что
X Ф0 и У=7^=0, так как в противном случае (III, 6; 5) очевидно.
Поскольку множество Q открыто, оно содержит некоторый шар
с центром в точке а некоторого радиуса р > 0. Мы можем
ограничиться такими значениями t, |/|<^—-——, при которых
II ЛГ || + II Y ||
-V -> -> ^>-
точки а, а-\-tX, а-\-tY, a -\- t(X -\- Y) находятся в этом шаре,
а, следовательно, и в Q. В силу выпуклости шара, множеству Q
будет принадлежать весь отрезок, Соединяющий эти точки, и
мы сможем применить формулу конечных приращений
(теорема 13).
•>
Выражение А можно записать в виде разности
A = g(X)-g(0), (III, 6; 6)

260
Гл. III. Дифференциальное исчисление
-у -> ->
где g — отображение из £ в г, определенное в шаре
{|;|||||<||Z|ft по формуле
g(t)=--f(a + t(l + Y))-f(a+me=F (a,Y,t фиксированы).
(Ill, 6; 7)
Функция g дифференцируема, и ее производная имеет вид
g'(l) = tf'(a + t(i+Y))-tf'(a + tb. (Ill, 6; 8)
К ней можно применить следствие 1 теоремы 13. Надо
только выбрать подходящим образом L. Рассуждения будут носить
интуитивный характер. Так как
I(X) - |(б) - g' (0) X ~ t (/' (а + tY) - f (а)) X ~ t2 (/" (а) У),- X,
(111,6; 9)
то положим
L = t2(f"(a)Y)^&(h F)- (Ш,6; 10)
Тогда формула (III, 5; 8) дает
A = (g(X)-g(0))= LX + a\\X\\, (Ш,6; 11)
где мер оценивается по норме следующим образом:
IMK sup ||g/(|)-L|| =
l^io, xi
= sup \\tf'(a + t(l + Y))-tf'(a+tl)-t2(f"(a)Y)\\. (Ill, 6; 12)
Те]ВД[
Применим к /' определение производной (III, 3; 13):
i4a+ti+Y)) = f'(a)+f"(a)(t(i+Y)) + a\\t(& + Y)\\, /ттт е'
_>. ->.->. (Ill, b; 13)
/'(а+^) = /'(а) + /"(а)^ + Р11^11,
где при фиксированных а, X, У и | е ]0, Х[ функции <х = <х(/, |)
и р = Р(^, |) стремятся равномерно к 0 в 3?{E;J?) при *,
стремящемся к 0. Подставляя в (III, 6; 12), получаем
1!«!Кг2 sup ||а(| + У) + р|||<
■>->->
1^}0,Х[
< sup P [(|| а 11 + ||р ||) (|| Х|| + || У ||)], (III, 6; 14)
|е]0, Х[

§ 6. Производные высших порядков
261.
где последняя скобка стремится к 0 вместе с /. Учитывая
значение L, из (111,6; 11) теперь получаем, что -w- стремится
к (f"(a)Y)-X = f"(a)(Y, X) при /, стремящемся к 0.
Так как А симметрично относительно J и У, то таким же бу-
->
А
дет предел -у, чем и заканчивается доказательство теоремы.
Замечания. 1°) В видоизмененной форме
DtDtf{a) = DfDtf(a) (II 1,6; 17)
получаем соотношение, в которое входит лишь сужение f на
пересечение множества Q с линейным многообразием, проходя-
> ->-
щим через а параллельно векторам X, Y. Поэтому нет
необходимости предполагать само / дважды дифференцируемым.
Достаточно предполагать, что сужение f на это многообразие имеет
вторую производную в точке а.
2°) Имеется вариант этой теоремы, в котором
существование I"(а) не предполагается, но в котором говорится, что если
> >
D+D+f и D->D->c существуют в каждой окрестности точки а и
X У У XI
непрерывны в а, то они равны в а.
Такая формулировка не сильнее и не слабее того, что мы
привели, но имеется различие: если мы возьмем для простоты
E==R2, то существование полной второй производной в точке
влечет за собой существование д ' и д L в этой точке, но
из него не следует ни их существование в ее окрестности, ни их
непрерывность. Обратно, непрерывность этих частных
производных недостаточна для того, чтобы обеспечить существование
второй полной производной I включающей в себя еще частные
производные -j-y , -д-Ы- Известно, что одно только предположе-
Щ d~*f
ние о существовании производных g , , , ' недостаточно
для того, чтобы обеспечить их равенство.
Последовательные производные
Точно таким же образом определяются производные более
высоких порядков. Производная порядка m в точке аей
(которая определена только тогда, когда все производные
порядков =£1т — 1 существуют во реей окрестности точки а) может

262
Гл. III. Дифференциальное исчисление
быть отождествлена с некоторым m-линейным отображением
Ет в F. Если / {х) существует для каждого j;eQ, to
/(т): х —>/(т) (х) является отображением множества .Q в простран-
ство &т{Ет; F) этих m-линейных непрерывных отображений.
Точнее, /<m> определяется следующим образом. Пусть /(т-') —
производная порядка т ■—1, отождествляемая с некоторой
->т_] -*■
функцией на Q со значениями в ЗЕт-х {Е ; F). Тогда ее
производная в точке a: (/(m_1>)'(a) = /(m)(a) является линейным не-
прерывным отображением Е в 3!т-\ {Е ; F); оно отождествляет-
-> ->
ся с некоторым элементом из 2'т(Ет; F), обозначаемым через
/<т'(а), так что
1(т) (а) (Хи Х2, ..., Хт) = ((/""""У (а) X,) -(Х2,..., Хт). (111,6; 18)
По индукции теперь доказывается, что:
1°) Если р ^ т и если рассматривать fW как функцию на
-> ->
Q со значениями в 3!р (Ер; F), то ее производная {т — р)-го
порядка в а, если она существует, является элементом про-
-*■»,_„ ->п -*■
странства Sm-P(E , 9?Р(Е; F)). Этот элемент можно
отождествлять с некоторым элементом /(т) (а) из i?m (£ ; F),
если он существует. Оба этих элемента существуют
одновременно, и при этом
(/<">)<"-" (а) = /(») (а) е= Я>„ (F>; F),
f((/("»)(m-p) (а)) (*„ Х2, ..., Хт/Р)] ■ (*„_■„+„ ..., Хт) =
= /<т> (в)№, *2, ..., fjeF. (111,6; 19)
2°) Если существует /<m) (а), то существует
D^D* ... D^ f(a)e=F и
*1 X2 Xm
/(m) (а) (*„ Х2, ..., XJ = dZdZTTTdZ) (a) eF. (Ill, 6; 20)
Определение, m-линейное отображение « Пространства
£Х£Х ••• У(Е = Ет в пространство F называется
симметричным, если при любой перестановке о: k-*0h множества
->•->• -> ->.
{1,2, ...,т} и любой системы векторов Xi, X2, ..., Хт из Я
имеет место формула
■и(Ха, Хо2, ..., XaJ = u(xlt Х2, ..., *J. (Ill, 6; 21)

§ 6. Производные высших порядков
263
Теорема 16 теперь может быть обобщена на производные
произвольных порядков:
Теорема 162. Если отображение f множества QczE
в пространство F имеет производную порядка m в точке
лей, то эта производная f(m) (а) является m-линейным не-
->
прерывным симметричным отображением Ет в пространство
->
F, т. е. для любой перестановки с множества {1,2 т\ и лю-
-> -> -> ->
бой системы векторов {Х{, Х2, ■■■, Xm) s Em имеют место
равенства
/<"•> (а) (Хи Х2,...,Хт) = Г> (а) (*„,, Ха2, .... XaJ,
->
£>->£>->...£>-> f (a) = £>-> £>-> ...£>-> f (a).
(III, 6; 22)
Доказательство. Эта теорема была доказана для
производных второго порядка. Предположим, что она справедлива
для производных порядка ^т—1, и докажем ее для
производных порядка т ^ 3. Предположим прежде всего, что
Oi = 1 и что а переставляет только числа 2, 3 т. Тогда
*■ >
функции £)-> ... £)-> f и £)-> ... £)-> f, определенные в Q,
х2 хт ха2 хат
->
со значениями в F по предположению индукции совпадают.
-> ->
Следовательно, их производные в а вдоль вектора Х1 = Х„1
одинаковы и мы имеем равенство (III, 6; 22).
Предположим теперь, что oi = 2, 02 = 1- и что а сохраняет
> —>
каждое из чисел 3,4 т. Тогда £)-> ... D+ f = £)-> ... £)-> /
Хз хт Хо3 Хот
является функцией, определенной в Q и имеющей первую
производную всюду и вторую производную в точке а.
Следовательно, к ней можно применить теорему 16 относительно произ-
водных вдоль Хх и Х2 и снова получить (III, 6; 22).
Так как каждая перестановка чисел {1,2 т) является
композицией перестановок этих двух типов (это очевидно, если
Gi = 1; в любой перестановке можно от 1, 2, ..., т перейти к
1, Gi, ..., т, затем от 1, од, ..., т к а и 1, ..., т и, наконец, от
Oi, 1, ..., т к ai, G2, ..., От), то теорема будет справедливой
в общем случае.
Упражнение. Шаг за шагом можно доказать
следующее. Пусть L есть /л-линейное непрерывно симметричное
-> ->
отображение Ет в F. Оно определяет некоторое р-линейное

264
Гл. III. Дифференциальное исчисление
непрерывное симметричное отображение Lv пространства Ер в
пространство 2?т-р{Ет~р\ F).
Тогда k-я производная функция «одночленной» функции
->- ■> -*■-*■
x-+Lx™, действующей из Е в F, является функцией вида ')
х-> т (т - 1) ... (т - k + 1) Lm-kxm~k e= Sk (Ek; P). (Ill, 6; 222)
Полагая Е — F = К, получаем элементарную формулу
дифференцирования одночленов.
Замечание. Теорема 83 (о линейности производной),
теорема 84 (о дифференцировании функции со значениями в
произведении пространств) и следствие 1 теоремы 1] (о
перестановочности производной и линейного непрерывного
отображения) с помощью индукции по т непосредственно обобщаются
на производные порядка т.
Случай, когда Е = Кп. Рассмотрим наиболее часто
встречающийся на практике случай, когда пространство Е конечномерно
и в нем выбрана система координат 0, (e,)ie/. Тогда для
второй полной производной при X = 2л XiCi и Y — 2а Yiei имеем
следующую формулу:
f"{a){X,Y)= J XtY,f"(a)(et,e,)= £ *'Г/аЛг(e) e ^
(III, 6; 23)
Для третьей производной'получаем
/"' (а) (X, Y,Z)= Yi х?11* дх дхдх {а)- (Ш' 6; 24)
i. i,ke=I l ' k
1] ^'y/z*li7
/,
Более общо: если / = {1, 2, ..., т), то
/C")(a)(X„ Хг, ...., Хт) =
= S ах,ах.!..дх, М*'■'.*»•/, • • • х".imeF- ("1.6;25)
') Lm и Z-o по условию совпадают с L, а х° есть 1бК, Через Lpxp
-> -> ->
будем обозначать Z.p (дг, х х).
р

§ 6. Производные высших порядков
265
где Ха, р является р-й координатой вектора Ха (а = 1,2, .. ., т;
Р= 1,2, ..., п) и где / пробегает множество всевозможных
отображений a—*-ja множества {1, 2, ..., т) в множество
{1,2,..., л).
Если Е = К — поле скаляров, то производный вектор по-
■*■' ч>-
рядка т, f(m) (a) e F, определенный на стр. 208, связан с
производным отображением порядка т, f(m) (a) e 3?m (Km; F),
формулой
■f(m)(a) = f«m>(a)(l, 1, ..., 1), (III, 6; 25а)
Для частных производных можно ввести сокращенные обо-
д
дхк
д "*"
значения, объединив одинаковые производные -^—. Пусть р 1)
некоторый элемент из N", т. е. система п целых чисел Р\,рч, ...
.-., Дп^О. Тогда через Dp или 1-^—I будем обозначать
частную производную
Например, если п = 3, д = (1,0,2), то Dp будет означать
производную -^—l-g—J . Если р = 0 = (0,0,...,0), то Dpf = f.
Величина М = Pi + Дг + ••• + Рп называется порядком р
или порядком частной производной. Если q — некоторый дру-
•» •»
гой элемент из N™, то через р-\-q обозначается элемент
>■ >
(Pi + ЯиР2 + Я2,...,р* + Яп), так что D*+*f = I?(D*f).
Говорят, что p^q, если р\^а.\, Р2^Я2, ■■■, Рп^Яп (это
некоторое отношение порядка в N"). В этом случае через
•» •»
р — я обозначается элемент (р1~ЯиР2— Я2,---,Рп — Яп) и
->■»••>•>
р = я + {р — ч).
') Хотя Nre не является векторным пространством, удобнее писать р
вместо р для того, чтобы напомнить, что это не целое число, а система п
целых чисел.

266
Гл. III. Дифференциальное исчисление
В дальнейшем нам понадобятся также следующие
обозначения:
p\ = Pl\p2\ ... Рп\,
Л= Xf'X2p* ...^»еК для f е= К", ?е= N".
Определение. Говорят, что функция f является m раз
непрерывно дифференцируемой, или принадлежит классу С™>
в Q, если она имеет производные порядков ^ пг, непрерывные
ей. Каждое m раз дифференцируемое в Q отображение
принадлежит по крайней мере классу Cm_I.
Случай произведения пространств.
Полная и частная дифференцируемость
Теорема 15 может быть обобщена следующим образом:
Теорема 17. Для того чтобы отображение f некоторого
открытого множества Q произведения Et X Е2 X • • ■ Х^п в F
принадлежало классу С™, необходимо и достаточно, чтобы оно
имело непрерывные в Q частные производные порядков =g: m.
Доказательство. 1°) Поскольку каждый элемент и из
2?(E;F) эквивалентен системе элементов щ пространств
S[Ei\ F), i=l, 2, ..., п, то тем самым определяется взаимно
однозначное соответствие между 3? {Е; F) и произведением
пространств 9?(Ei,F), сохраняющее векторную структуру.
л
С другой стороны, из неравенств || ы,-||^||и 11^ 2 I!"/ ll> i=K
1, ...,п, следует, что норме в пространстве 2?{E\F)
соответствует в произведении пространств 3? (£*; F) некоторая
норма, эквивалентная одной из их естественных норм.
Поэтому, согласно замечанию на стр. 264 (обобщение теоремы
84), отображение множества fi cr E в пространство 3?{E;F)
принадлежит классу Ch тогда и только тогда, когда
отображения множества й в пространства 2?{EuF), определяющие
это .отображение, принадлежат классу Ch.
2°) Теорема 17 верна для m = 1 (теорема 15). Докажем
ее справедливость для любого m методом математической ин-
1) Напомним, что |.= С? =——. ;
\s ) Г s\ (г — s.

§ 6. Производные высших порядков
267
дукции. Предположим, что она верна для т ^ 2. Пусть /
принадлежит классу Ст. Тогда f принадлежит классу С"1-1. По-
скольку /' является отображением Q в 3?{E\F), определенным
отображениями df/dxt множества Q в 9?{Ei\F), каждое
отображение df/dxi, согласно 1°), принадлежит классу О1-1. По
индуктивному предположению отображение df/dxt имеет
непрерывные в Q частные производные порядка ^.т—1 и,
следовательно, отображение / имеет непрерывные в Q частные
производные порядка ^.т. Обратно, если отображение / имеет
частные производные порядка ^.т, непрерывные в Q, то
отображения df/dxi существуют и имеют частные производные
порядка ^.т— 1, непрерывные в Q. Поэтому, согласно
индуктивному предположению, они принадлежат классу О-1.
В частности, эти отображения непрерывны, а,
следовательно, согласно теореме 15, существует f. Это — функция в Q со
->■ ->
значениями в &(Е\ F), определенная при помощи функций df/dxi
-> ->
на Q со значениями BS'ff,-; F). Поскольку df/dxt принадлежат
классу О"1, то /', согласно 1°), принадлежит классу Cm_1 и,
следовательно, отображение / принадлежит классу Ст.
Пространства т раз дифференцируемых функций
Обобщая понятия, введенные в конце § 3, мы будем
обозначать через (Fa)b.m (соответственно через (Fa)cb. Л
пространство т раз дифференцируемых (соответственно т раз
непрерывно дифференцируемых) ограниченных вместе с
каждой производной порядка ^.т отображений множества Q
в F.
Это пространство является аффинным, имеющим
присоединенное векторное пространство (^а)ь-т (соответственно
->
{FQ)cb.m). Его можно считать аффинным нормированным
пространством, если в присоединенном векторном пространстве
ввести норму
III fill» = sup (||/<*>(*) II). (Ill, 6; 27s)
xe=Q
0<fe<m
где ||/<*>(*> II-норма в &h (Ek; F).
Отсюда видно, зачем введен индекс 1 в обозначениях
(FQ)b. j и (Fa)cb. j. В этих обозначениях (Fab (соответственно
(FQ)cb) можно записать в виде (Fa)b. 0 (соответственно (Fa)cb. Л
и ||| Г ||| в виде IH/lllo.

268
Гл. III. Дифференциальное исчисление
Теорема 17г. Отображение, ставящее в соответствие
каждой функции f ее производную функцию порядка k <g; m,
есть линейное непрерывное отображение пространства (FQ)b;m
(соответственно {FQ)cb.m) в пространство {(£k (Е"; F)) )b. m_fe
соответственно ({3?k(Ek; F)) )сь-т-ь) с Н0Рм°й ^1.
Несмотря на несколько пугающую формулировку,
утверждение это очевидно.
Очень часто в предыдущих пространствах рассматривают
другие эквивалентные нормы, например определяют ||| f||]m как
т
2 (sup||f(ft) (х)||). Если пространство Е я-мерно и если в нем
ft=0 xefl
выбрана система координат, то в качестве нормы часто берут
числа
> >
\\\Ь\т= sup \\D*f(x))\ или |||flL= 2 (sup || Zn Ml».
->. \p |<m
\P\<m
Производная произведения (формула Лейбница)
Теорема 18. Пусть Е — аффинное нормированное прост-
-> -» ->
ранство, Fu F2, G— векторные нормированные пространства.
-> ->
Пусть В — билинейное непрерывное отображение Fxy^F2 в G.
-> ->
Если щ (соответственно и2) является m раз
дифференцируемым или m раз непрерывно дифференцируемым
отображением открытого множества Q а Е в F4 (соответственно в F2),
->. -> -> ->
то таким же будет отображение В(ии и2): х-> В(их(х), и2(х))
множества Q в G. Производные этой функции вычисляются
по формуле Лейбница.
Доказательство. Воспользуемся обозначениями
теоремы 92. Тогда формула (III, 4; 22) запишется в виде
(В(«,, и2))' (х) X = В^ (и[ (х) X) + В* w (и'2 (х) X) е G, (III, 6; 28)
и, следовательно,
(В (и., иЛ)' (х) = В-у о и' (х) + В-> о и' (х) е= 2 (Е; G). (III, 6; 29)
v V ' *•>' и2 (х) ' и, (х) z
Воспользуемся теперь индукцией по т. При т = 1 теорема
верна (теорема 12). Предполагая ее справедливой для
производной порядка т—1, докажем, что она верна для
производной порядка т.

§ 6. Производные высших порядков
269
Пусть их и и2 т раз дифференцируемы или т раз
непрерывно дифференцируемы. Тогда х -> и\ {х) есть т—1 раз
дифференцируемая или непрерывно дифференцируемая функция со
значениями в 9? {Е; F). С другой стороны, функция х-+В> у
и2 (х)
определенная на Q, со значениями в 9?(F\\ G) является
композицией т раз дифференцируемой или непрерывно
дифференцируемой функции x-*Ui(x) из множества Q в пространство
^> ->
F2 и линейного непрерывного отображения v2-+B+
пространен
-> ■> ■>
ства F2 в пространство 3?{F\\G). В силу перестановочности
производной и линейного непрерывного отображения
(следствие 1 теоремы 11), функция х-+В+ со значениями в
Ыг (х)
^(FijG) является т раз дифференцируемой или непрерывно
дифференцируемой. Поскольку (Ui, U2)—* Ui° U\ является би-
-> ■>
линейным непрерывным отображением пространства S (E; Fi)X
-> -> ■ ->■ ■>
yi 9? {F\\G) в пространство i?(£; G), индуктивное
предположение позволяет утверждать, что х-+В+ ° и', (х) является
m—1 раз дифференцируемым или непрерывно дифференци-
-> ■>
руемым отображением Q в 9?(E;G). Поскольку то же самое
имеет место для отображения х-* В-> °и'(х), функция
«I (X) г
(B(ui,u2))' является т—1 раз дифференцируемой или
непрерывно дифференцируемой, а, значит, т раз дифференцируема
или непрерывно дифференцируема функция В(щ,и.2)1).
В общем случае формула Лейбница является бесполезным
усложнением полученного результата; поэтому мы ее приведем
') Обычно Е конечномерно, и в нем можно выбрать некоторую систему
координат. По теореме 17, для того чтобы показать, что В(щ, щ)
принадлежит классу Ст, когда щ и и2 принадлежат этому классу, достаточно
доказать, что их частные производные по xlt х2, ..., хп порядка ^.т
непрерывны. Но это легко проверяется по индукции. Утверждение верно при т = 1.
Предполагая его справедливость для т—1, докажем, что оно верно для
/п>2. Имеем: — (В („„ „2)) = В J—, ия} + В\иу ^-j. Здесь -g-
и и2 имеют непрерывные частные производные порядка eg:m—1, а, следова-
тельно, по индуктивному предположению такой же будет В -г—, «2
То же самое можно сказать и о функции В[щ, ■д-^)- Но тогда В(«ь«2)
имеет непрерывные частные производные порядка ^т.

270 Гл. III. Дифференциальное исчисление
лишь для частного случая конечномерного пространства Е
с системой координат 0, ей в2, ..., еп- Если воспользоваться
обозначением (III, 6; 26), то формулу Лейбница можно
записать в виде
D?(B (ы„ и2)) =^(РЛв (D\, D*-%). (Ill, 6; 36)
Наиболее важен тот случай, когда F\ = F2 = G = К —
поле скаляров и fi(«i, «2) = "i«2 — обычное произведение. Тогда
Я'«1"2 =У(ЙD%D'~\. (Ill, 6; 362)
-> ->\<7/
q=SP
Применяемые здесь обозначения таковы, что в случае
n-мерного пространства формула сохраняет точно такой же вид, как
и в случае функции одной переменной.
Доказать эту формулу очень просто. В случае одной
переменной (п = 1) она записывается в виде
(Ы1Ы2Г> = J] (")«(,*Цт-*>. (Ш,6; 363)
fe<m
Эта формула известна для т = 1 и по индукции легко
доказывается для любого т. В самом деле, предположим, что
она верна для т— 1. Тогда
\fc'<m-l /
= Yi [(т 1'l) "i*'+4m-*,-,>+(m fe~') «w*0]=
" ft'<m —I
-Si-4r-»((:i,,)+(";,))-S(:)'W"-
fc<m fe<m
Теперь проведем индукцию по числу п переменных.
Предположим, что формула доказана для п—1 переменных, и
докажем ее справедливость для п. Имеем:
D*{uxu2) = (-^-)"' £>*' (Uiu2), где р' = (р2, .... р„) е N"-1.

§ 6. Производные высших порядков
271
Функция Гг' (ы^г) Для фиксированного Х\ является
производной по п—1 переменным х2,х3, ..., хп, в то время как
-г—I —производная по первой переменной. Поэтому
-> ->
~'«2-
->
Теорема 19. Пусть E, F, G — три аффинных
нормированных пространства, Q и Q' — открытые множества в Е и F
соответственно. Пусть f—'отображение Q в Q', a g—
отображение Q' в G. Если fug являются m раз дифференцируемыми
или m раз непрерывно дифференцируемыми, то таким же будет
сложное отображение h = g о f.
Доказательство. Теорема Берна для производной 1-го
порядка (теорема 11 и ее следствие 5). Предполагая ее
справедливой для производных порядка ^.ш— 1, докажем, что она
верна для производных порядка m, m ^ 2,
Перепишем формулу (III,4; 1):
h'(x) = g'(f(x))of'(x). (Ill, 6; 37)
Согласно предположению, функция f дифференцируема
m раз, а, следовательно, функция f дифференцируема m—1
раз. С другой стороны, так как функции fug' обе m — 1 раз
дифференцируемы, то функция g'-f: x—*g'(f(x)) также m — \
раз дифференцируема. Но тогда отображение х—*f{x) множе-
ства Q в пространство 9?(E\F) и отображение х —*g' (f(x))
множества Q в пространство 3?(F;G) дифференцируемы m — }
раз, а (и, v) —* v о и является билинейным непрерывным
отображением &(E\P)X&(F;G) в &(Ё;б) (теорема 54 гл. II). Из
теоремы 18 следует, что х—*g'(f(x)) of(x) также т—1 раз
дифференцируема. Таким образом, отображение И'
дифференцируемо m—1 раз, а это означает, что отображение h
дифференцируемо m раз.
Замечания. 1°) Теоремы 18 и 19 можно было бы
доказать, проводя индукцию одновременно для обеих теорем.

272
Гл. 111. Дифференциальное исчисление
В самом деле, теорема 19 для числа т опирается на
утверждение теоремы 18 только для т—1. С другой стороны, при
доказательстве теоремы 18 для т—1 следует учесть, что
функция x-*B(ui(x),u2(x)) является композицией функции
х-* (ui(x),u2(x)) класса Ст~1 и билинейной непрерывной, а,
следовательно, бесконечно дифференцируемой функции
(ui,U2)-*B(ui, u2), и, значит, можно воспользоваться
теоремой 19 для т — 1.
Далее, теоремы 18 и 19 доказаны для т=\. Отсюда
можно получить теорему 19 для т = 2, а, следовательно,
теорему 18 для т = 2, затем теорему 19 для т = 3, а,
следовательно, теорему, 18 для т = 3, и т. д.
2°) Вычислять последовательные производные функции
h — gof можно по явным формулам, но они довольно сложны.
-> -> ■>
Так, например, если X и Y— векторы из Е, то
h" (х) (X, Y) = g" (/ (х)) (/' (х) X, f (x) Y) +
+ ё' (f (*)) (/" (*) (*. У)) е G. (111,6; 38)
Если E, F, G — поля скаляров К и если выбрано Х =
= У = 1, то получается элементарная формула
h" (х) = g" (f (x)) f'2 (x) + g' (f (x)) f" (x). (Ill, 6; 39)
Иногда полезно иметь выражение производной порядка т
для функции h = gof в частном случае Е = F = G = К. Мы
его приведем в теореме 213.
§ 7. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМ И МИНИМУМ
Так как производная /<т) (а)- порядка т является
га-линейным отображением, то можно вычислить ее значение на си-
-> -> -> ->
стеме векторов (X, X,..., X) е Ет, определенной одним векто-
ром X из Е. Выражение рт)(а){Х, X, ..., X) удобно
записывать кратко в виде
/<») (а) Хт = /<т> (а) (Х,Х X). (III, 7; 1)
Имеется столько формул Тейлора, сколько существует
формул конечных приращений.
Теореме 13А соответствует формула Тейлора, обобщающая
теорему 6:
Теорема 20А. Пусть f — вещественная m раз
дифференцируемая функция, определенная на открытом множестве
Q cz Е. Предположим, что замкнутый отрезок [х, х + h] пол-

§ 7. Формула Тейлора
273
ностью лежит в Q. и что f имеет производную (пг-\-1)-го
порядка во всех точках открытого отрезка ]x,x-\-h[.
Тогда имеет место формула
f (x+h) = f (x) + Ц^-h + ^Р-Р +
I f{m)(x)tm | f(m+1>(*+9t) tm+1
где 0 — вещественное число и 0 < 6 < 1.
Доказательство. Обозначим через Ф вещественную
функцию на [0,1], определенную формулой Ф: t-*f(x + th).
По индукции проверяется, что на [0,1] существует производная
порядка k ^ m и на ]0, 1[ — производная порядка т+1,
причем
->• ->•
Ф<*>(*) = /<*>(х+*Л)Л*. (Ш,7; 13)
Теперь достаточно к этой функции применить теорему 6
(формула Тейлора для вещественной функции от одной
вещественной переменной7) на отрезке [0,1J, чтобы получить
требуемый результат.
Далее, теореме 13 соответствует следующая формула
Тейлора:
Теорема 20. Пусть f есть m раз дифференцируемое
отображение открытого множества QczE в F. Предположим, что
замкнутый отрезок [х, х -\- h] полностью лежит в Q и что f
имеет производную порядка m + 1 в каждой точке открытого
-V
отрезка ]х, x-\-h[, не превосходящую по норме числа М. Тогда
имеет место формула
J\}=\f(x + h)-f(x)-f'(x)h-^P-
fim) (*) ftm
ml
<^П]Г- (Ш'7;2)
Доказательство. Это утверждение при m = 0 было уже
доказано в теореме 13. Поэтому мы можем воспользоваться
индукцией. Предположим, что это неравенство доказано для
m — 1, и докажем его справедливость для m, m ^ 1.
->•
Рассмотрим функцию g, определенную формулой
■ (0 = / (х + th) - f (x) - /' (х) th - ... - J—p- (th)m. (Ill, 7; 3)
f<m> (x\ >■
m\

274
Гл. III. Дифференциальное исчисление
Это отображение отрезка [0,1] из R в F, и А = g(l) — g(Q).
Оно непрерывно на этом отрезке и, кроме того, имеет
непрерывную производную на всем отрезке, определенную формулой
g' (0 = f (x+ th)h-V (x) h- ... --±—^fW{x)hm. (Ill, 7; 4)
Согласно 2-й формуле (III,6; 19),
pk)(x)hk = W~14x)P~1)-h. (Ш,7;5>
Поэтому (III, 7; 4) можно записать в виде
/' (х + th)-f'(x)-...- у_ 1)г (*) {th)m-x\ h^F,
(III, 7; 6)
где выражение, стоящее в квадратных скобках, является эле-
■> -> ■> •>
ментом из i? (£; Т7). Будучи примененным кАе£, оно дает эле-
^>
мент пространства /\
Найдем теперь оценку нормы этой производной. Мы видим,
->
что выражение в скобках является аналогом выражения А, но
-*■
относящимся к приращению th, порядку т.— 1 и функции /'„
определенной на Q, со значениями в ^(f;/7). В силу
индуктивного предположения, учитывая, что (/')<m) = /(W+1), Мы сможем
написать следующую оценку, пригодную для 0<1 / <; 1:
||75|1<м1^||Л|| = М||Л|Г+1-2. (Ш, 7; 7)
Пользуясь теперь леммой, приведенной в связи с теоре-
мой 13 [заменяя там f (х) на g(x) и g(x) наМЦАЦ ,,.,),
-*■
мы можем убедиться, что для функции g на отрезке [0, 1]
выполняется неравенство
II g О) - 2(0) II <М-1^1_, (III, 7; 8)
и тем самым справедлива формула (III, 7; 2).
Следствие. Пусть L есть lm + 1)-линейное непрерывное
■> ->
отображение Ет+1 в F. Тогда при условиях теоремы имеет, ме-

§ 7. Формула Тейлора
275
СТО
Ьх
формула
:+А)-/(д)
fir.
У А»
_/"(*) £
2! "
(т+1)! я !
|<(0
1|Л|Г+'
(т+1)! '
(III, 7; 9)
где w является точной верхней гранью ||/(т+1)(£)—Ц, когда £
пробегает интервал ]х, х + А[.
Доказательство. Утверждение легко сводится к
случаю, когда L является (т + 1)-линейной симметричной
формой. Впрочем, это единственный случай, представляющий
интерес. Затем теорему следует применить к функции | —>/(£) —
— /От1 [41 (£~ x)m+ , производные которой вычисляются по
формуле (111,6; 222).
В заключение заметим, что существует формула Тейлора,
соответствующая определению производной (111,3; 13),
которую можно назвать формулой Тейлора для бесконечно малых
приращений. Здесь только удобнее заменить т+1 на т.
Теорема 21. Если f имеет в Q производные порядка
^ m — 1 и производную порядка m в точке а, то
f(a + h) = f(a) + f'(a)h+ ... + ^Лр-1т + «11 А|Г. (Ш,7;10)
где а стремится к О вместе с h.
Будем доказывать эту формулу снова индукцией по т. Она
верна для т=1. Предполагая, что она верна для целого
m— 1, докажем ее справедливость для т>2. Функция
g(S) = /(a + !)-/(a)-/'(a)!- ... —Q^ lm. (Ш.7;11)
определенная в некоторой окрестности точки 0 в Е, со значе-
->
ниями в F дифференцируема. Согласно (1П,6;222), ее
производная имеет вид
g'® = f'(a + t)-f'(a)- ... -(f(OT-l)l I h^Z{E;F).
(Ill, 7; 12)

276
Гл 111. Дифференциальное исчисление
Применим к g' формулу (111,7; 10) для т—\:
,,т-1
g'(t)=$(l)n\\ , (111,7; 122)
■> ■> ■> ■>
где ($(|) стремится к 0 вместе с |.
Тогда формула конечных приращений (теорема 13) дает
соотношения
llg(A)|| = ||g(AJ-g(0)|K||A|| sup ||g'(f)ll<
■?■ ■>->
<||Л|| sup IIPffiJIIHgir-'^ellAir, (Ш,7; 123)
N]0, ft[
где е стремится к 0 вместе с ||Л||, что и дает требуемый
результат для т.
Применение формулы Тейлора для вычисления производных
Иногда легче получить разложение Тейлора, чем
вычислить последовательные производные. Тогда эти производные
можно получить из готового разложения. Другими словами,
имеет место теорема, обратная к теореме 21:
Теорема 2Ь. Пусть f есть m раз дифференцируемое
отображение открытого множества Q cr Е в F. Если найдены
k-линейные непрерывные симметричные отображения Ьь про-
-> ->
странств Eh в F, k = 1, 2, ..., m, и некоторый элемент L0 из
F, такие, что
f(a + h) = L0 + Llt + ±f-h2 + .... + is. А™ + а || А|Г, (Ш,7;124)
■>->-> ■> ■>'
где а = а (Л) стремится к 0 вместе с Л, то всегда имеют место
равенства
Lk = f(k){a), k = l,2,...,m, и L0 = f(a).
Доказательство. Из теоремы 21 вытекает, что если
мы положим
Ak = f^{a)-Lh^Seh{Ek;F), A0 = f(a)-L0^F, (III,7;125)
ТО
m
^■^hk=$\\h\\m, (Ш,7; 126)
-> ■> ->
где р стремится к 0 вместе с Л.

§ 7. Формула Тейлора
277
-»■->■ ->
Устремляя Л к 0, мы увидим, что .40 равно нулю.
Предположим, что А0, Аи Аг, ..., Au-i — нули для k ^ т, и докажем,
что тогда Ah также будет нулем. Отсюда будет вытекать, что<
все Ah, k = 0, I, 2, ..., m, — нули, и теорема будет доказана.
Положим h = ^Х, где X фиксирован, и устремим скаляр t
к 0. Тогда величина
tk[^j-Xk+t ^ ^-t'-^X1) (III,7;127>
является бесконечно малой более высокого порядка, чем tm, и
тем более чем tk, когда t стремится к 0. Это означает, что ее
отношение к lh стремится к 0, а, следовательно, AhXk = 0 для
любого Хб£. Доказательство по индукции будет закончено^
если мы докажем такую лемму:
Лемма. Пусть А есть k-линейное симметрическое отобра-
■-*■ -*■ -*■ -*■
оюение Ek в F. Если для любого X из Е
AXk = 0^F, (III, 7; 13)
то А равно нулю.
Эта лемма хорошо известна для m = 2, ибо тогда для лю-
->->■->->
бых Хб£и Fef в силу симметричности А имеем:
А (X + Y, X + Y) - А (X, X) - A (Y, Y) = АА (X, Y),
и условие (III,7; 13) влечет за собой обращение в нуль левой
части равенства, а значит, и его правой части, откуда следует,,
что А равно нулю. Распространим это доказательство на
общий случай.
Рассмотрим для фиксированных Х\, Х2, ..., Xk функцию h
OTt=(tUt2,...,th)^Rk.
h(t) = A (f,X, + t$a +...'+ tkXk)k. (Ill, 7; 132)
По условию она тождественно равна нулю. Эта функция
является полиномом от t\, fc. •••, h. Следовательно, каждый
коэффициент этого полинома равен нулю. В силу симметрич-
->■ ->■ ->•
ности А коэффициент при tit h, ..., th равен klA (Xt, Xz, ..., Xk),.
откуда и следует утверждение леммы.
Замечание. Мы должны были предполагать функцию f
дифференцируемой до порядка т. Это существенно. Тот факт,
что в окрестности а функция / имеет разложение вида

278 Гл. III. Дифференциальное исчисление
(III, 7; 124), вовсе не влечет за собой существование
производных порядка >1. Например, вещественная функция /
вещественной переменной, определенная формулами / (0) = 0, f(x) =
= xm+1sin m+i для х ф 0, имеет рассматриваемое разложе-
7ние в начале координат "с Lh = 0. Она имеет производные
всех порядков в дополнении к началу координат.
Поскольку \f(x) —/(0)| = \f(x)\ ^ |xm+1|, в начале координат ее
первая производная равна нулю. Но эта первая производная,
равная (т + 1) л: sin '- ,, cos—хг, в точках х ф 0
х х хт
принимает сколь угодно большие значения в любой
окрестности 0. Следовательно, она разрывна в начале координат и,
значит, рассматриваемая функция не имеет там второй производной.
Применим теорему 21г к вычислению последовательных
производных сложной функции.
Теорема 213. Если g и f — дифференцируемые т раз
скалярные функции скалярной переменной, то производная
порядка m функции h = gof в точке а задается следующей
формулой, в которой /(р) означает f(p)(a) и g^> означает
Л(т> (а) _ у ^ ^
Ai+2fe2+.fJ+mAm=mfe,U2!...W(l!)ftl(2!)ft2...(m!)*'"
Xg(W-+y(/f,(|")*= ... (/<m>)*m. (Ш,7; 133)
Доказательство. Воспользуемся разложением
Тейлора
h(x) = g(f(x))= 2 {Пх)~пПа))V'+frn- (1П,7;134)
0<(<m
Так- как
f{x)-f(a)= J 1^1-*/(*) + рт1 (111,7; 135)
то с точностью до членов высшего порядка малости по
сравнению с (х— а)т, когда х стремится к а, имеем:
(/(x)-/(a))W J. "Т^^У- (1".7; 136)
Vl<ft<m /
Можно написать формулу возведения в степень суммы /
слагаемых, обобщающую формулу бинома Ньютона (см. ниже

§ 7. Формула Тейлора
27»
формулу (III, 7; 26)). Согласно этой формуле,
(f(x)-f(a))l = У —i! (* ка) „ 5-Х
*1+*1+<rr+*frt-»*i«*.l...*»l (I!) '(2!)2...(/n!)m
X (Р)*'(Г)** ... (f<m>)V (111,7; 137)
По этой формуле вычисляется Ti ' а затем'-
с. точностью до бесконечно малых более высокого порядка, чем
(х— а)т, при х, стремящемся к а, находится выражение для
Цх):
AW~ o<fem *"il*«! ...*m!(l!>*» (21)*» ... (/n!)*m •
Х(П*'(Г)** • • • (f(m))km g{l). (Ill, 7; I38>
Поскольку известно, что h дифференцируема т раз
(теорема 19), величина Л<т>(а) должна равняться произведению
т\ и коэффициента при (а- — а) т в предыдущем разложении.
Отсюда и вытекает высказанное утверждение.
На этом примере видно, какую большую роль может
сыграть разложение Тейлора в вычислении производных порядка
> 1 при условии, что существование искомых производных
доказано другими путями.
Формула Тейлора относительно некоторой системы координат
Теорема 214. Если пространство-Е конечномерно, в нем
выбрана система координат и вектор И имеет координаты h\,
h2, ..., Л„, то, пользуясь обозначениями (III,6;26—27), вы-
vi f{k) (х) ■*»
ражение V—ь^~п ' входящее в правую часть формулы
k\
k=0
Тейлора, можно записать в виде
V t(k) (х)
-А*= J/J ШМ-h'^F. (Ill, 7; 14)
Доказательство. Согласно формуле (III,6;25),
/<ft)w t*_ i v ^
/,./2 /ft '' '* 'h
. (Ill, 7; На)-
-> ->
') В формулу (Ш,6;25) входили векторы Х\, Х2 которые здесь.
равны Л.

•280
Гл. III. Дифференциальное исчисление
В этой формуле /i, /2, ..., Ik — индексы, принимающие
независимо друг от друга всевозможные значения из множества
{1,2,... ,п). Объединим между собой все конечные
последовательности /i,/г, ..., /ft, у которых р\ индексов равны 1, р2
индексов равны 2, ..., рп индексов равны п. В сумме (111,7; 14г)
они дадут элемент, который запишется в обозначениях
(III, 6; 25 и 27) в виде
D~Pf(x)hP [ д \pit д \"» I д \рп h^hl* ... h"nn ■>
-Ш"Ш"-Ш"<^
F.
(Ш,7;143)
Членов этого вида имеется столько, сколько существует
отображений / множества {1,2, ...,k) в множество {1,2,..., «},
где {1} имеет прообраз, состоящий из р{ элементов, {2} — из р?
элементов, ..., {/г} — из рп элементов, \р\ — pi -j- рг + ...
.... -f- pn = k. Это число y =Y-> называется числом
-«перестановок с повторениями» п объектов {1, 2, ..., /г}, где
объект 1 берется pi раз, объект 2 берется р2 раз, ..., объект п
берется р„ раз. Существуют разные способы вычисления этого
числа. Для того чтобы определить интересующее нас
отображение /, нам надо сначала выбрать часть из {1,2, ...,&},
состоящую из р\ элементов, которая и будет составлять /_1{1}.
Число возможных выборов равно числу подмножеств, содер-
жащих по р\ элементов из {1,2, ...,&}, т. е. , ^ ,, _ .. .
Сделав этот выбор, надо в дополнении {1, 2,..., к} — /_1{1},
состоящем из k — р{ элементов, выбрать произвольно рч элементов,
•составляющих /_1{2}- При этом число возможных выборов
равно—,,, ~ р—гг- Так можно продолжать далее. Число та-
v РгЦк — Pi — Рг)!
ких отображений / равно
_ fe! (fe — Pi)! (k — Pi — Рг— ■•• — Pre-i)! _
'p" p,! (k — Pi)! ' Рг' (Ь — Pi — Рг)! " ' Pre! (* — Pi — Рг — • • ■ — Pre)!
kl fe! (111,7; 15)
Pi'Pz! ... Pre! ^ '
а, следовательно,
p L
й! р!
(HI, 7; 16)
и теорема доказана.
В принятых обозначениях полученная формула совпадает
с формулой, соответствующей функциям одной переменной.
В левой части формулы Тейлора f(x-{-h) лежит в аффинном
лространстве F, все члены правой ее части принадлежат век-

§ 7. Формула Тейлора
28 Г
торному пространству F, кроме первого f(x), соответствую-
щего р = О и лежащего в аффинном пространстве F.
Следствие. Если при выполнении условий теоремы найдены
такие элементы с-> (c+^F для рфО, c+^F\, \p\^.m, что
р \ р о /
/(а+й) = ^ с>-^-+о||А|Г, (Ш,7; 17)
I p"l<m .
-» -> -> ->
где а е F стремится к О вместе с h, и если известно, что f
дифференцируема m раз в а, то имеют место равенства
с* = £>*/(а). (111,7; 18)
■*■ -** ->
Доказательство. Положим а+ — Dpf(a) — с+ (здесь
р р \
->■ ->
также а->е/Л. Тогда, составляя разность, можно убедиться,
что норма «полинома» *) (с векторными коэффициентами)
относительно hi, hi, ..., hn:
•> ->т -n ->
I Pl <m
ath"=^aPvP2 *№ ... ftj- (П1.7; 19)
является бесконечно малой более высокого порядка, чем
||ft||m, при h, стремящемся к 0. Полагая h = tX и устремляя t
к 0, с помощью индукции, аналогичной той, которая
применялась при доказательстве теоремы 212 (но без использования
леммы), можно убедиться в том, что однородные части
полинома 2 а+Х? степеней 0, 1, 2, ..., m тождественно равны
•> р
\Р\<гп
нулю. Но у тождественно равного нулю полинома все
коэффициенты равны нулю2), чем и заканчивается доказательство
следствия.
Упражнение. Применяя следствие, получите новое
доказательство формулы Лейбница (III, 6; 36) в духе теоремы 213.
Теорема 22. Для того чтобы отображение f открытого
связного множества Q сг Е в пространство F имело производ-
') См. далее замечание о полиномах к теореме 22.
2) Это обычно доказывается при помощи индукции по числу п
переменных Хи Хг Хп только для полиномов со скалярными коэффициентами.
Но этот результат остается верным для векторных коэффициентов, причем
сохраняется то же самое доказательство.

282
Гл. III. Дифференциальное исчисление
ную порядка т-\-\, равную нулю в Q, необходимо и
достаточно, чтобы отображение f было полиномом степени ^.т.
Доказательство. Пусть сначала т = 0. Мы уже
видели, что производная постоянной равна нулю, даже если Q
не связно. Нам надо доказать, что в случае связного
множества Q отображение f множества Q в■ F, имеющее всюду
равную нулю производную, постоянно.
Пусть х — произвольная точка Q. Существует такое число
Par > 0, что открытый шар Вх с центром в х радиуса о* це-
> ->
ликом лежит в Q. При l!/iil<px можно на отрезке [х; х + Л],
лелощем в Q, применить теорему о конечных приращениях и
получить неравенство
\\f(x+h)-f(x)\\^^ sup llf (6)11 = 0, (III,7;20)
I s= }x, x+t\
из которого следует, что f (х) постоянна в Вх.
Пусть теперь а — произвольная фиксированная точка
множества Q. Обозначим через А множество точек | из Q, таких,
что f(l) = f(a). Так как А является прообразом множества
{f(a)}^F при непрерывном отображении f, то оно замкнуто.
Это множество также и открыто, ибо для х е А любой
указанный выше шар принадлежит А. Поскольку Q связно и А
непусто, А совпадает со всем Q, что и доказывает теорему для
т = 0.
Предположим теперь, что m^l. Прежде всего надо дать
определение полинома на Е со значениями в F. Мы
ограничимся частным случаем, когда Е п-мерно.
->•->• -*■
Если выбрана система координат 0, е\, е2, ..., еп, то
полином относительно Х\, х%, ..., хп степени ^.п со значениями в F
определяется как функция вида
f(*)= 2 £>/= S ар р *?'#••• <".
(Ш,7;21)
где а-> принадлелот F, кроме а-*, лелощего в F.
р о
Эта функция имеет тот л<е вид в любой другой системе
координат и называется полиномом на Е степени ^т со
значениями в F. Ее производная порядка т+1 равна нулю
независимо от того, связно или нет мнол<ество Q, поскольку,
согласно (Ш,7;21), ее частные производные порядка т + 1
равны нулю.
Обратно, пусть Q связно, и пусть / — отображение
множества Q в пространство F, (т + 1)-я производная которого

§ 7. Формула Тейлора
283
равна нулю. Пусть aeQ. Формула Тейлора порядка т
относительно любой системы координат имеет нулевой остаточный
член Rm и, значит, отображение f в указанном шаре Ва
является полиномом Р степени sg: т. Обозначим теперь через
k такое целое число, что (f — P)W == 0 в Q. Такое целое k
существует, например к = т-\-\. Тогда, если k~^\, то
(/ — P)(h-i) является функцией, первая производная которой
равна нулю в связном множестве Q. Значит, она постоянна
в Q. Но в Ва она равна нулю и, следовательно, она равна
нулю в Q. Таким образом, k—1 обладает тем же свойством,
что и k. Шаг за шагом спускаемся до k = 0 и получаем f = P
в Q, что и завершает доказательство теоремы.
Замечания. 1°) Конечно, это заключение не верно, если
множество Q не связно. Достаточно взять в качестве Q
дополнение к началу координат на вещественной прямой R и
положить т = 0. Вещественнозначная функция, определенная
на Q, имеющая всюду равную нулю производную, не
обязательно постоянна в Q. Она может быть равной некоторой
постоянной на полупрямой ]—оо,0[ и другой постоянной на
полупрямой ]0, + °°[.
2°) Предположим, что у нас нет формулы (111,7; 15),
определяющей v->. Ее можно очень просто получить следующим
р
образом.
Не считая у+ известным, напишем формулу Маклорена для
р
полинома степени т:
> ->
П3= S Y*-^?= S с+»Ш-?. (Ш, 7; 22)
\pl<m \р\<т
Р' 1
где c-> = -tt-y->> и покажем, что с->=1.
д \"п хпп
дхп I рп]-
q<P%
(III, 7; 23)
') Отношение порядка q ^ p в N" является частичным, а не полным:
->
q^p вовсе не означает, что q > р. Так, например, при п = 2 мы имеем
(1,1)^(0,2), но при этом не выполняется и неравенство (1, 1)>(0,2).

284
Гл. III. Дифференциальное исчисление
Теперь дифференцирование Dq выражения (III, 7; 22) для
■1 q К т дает:
Л*/М= Е C.^g-^4 (III, 7; 24)
|р|<т
->l ->
Р><?
->
Положим * = 0. Тогда *р а —О для р ^= q и лг а=1 для
p = q. Поэтому
D*f(0) = c+rff(0), (III, 7; 25)
откуда с->=1, что и требовалось доказать.
Положим, в частности, /(*) —(*i + *2+ ••• + *n)ft.
Теорема о сложной функции говорит о том, что любая
частная производная порядка / этой функции равна k(k—1)...
... (k — / + 1) (xi + х2 + • • • +xn)h~l. При xi = хг —
... =хп = 0 эта производная равна нулю, кроме случая / = k,
когда она равна k\. Поэтому формула Маклорена дает:
(Xl + x2+ ... + *„)* = У у+Р= У Щ-1?. (III, 7; 26)
■» р * Р1
1р1=* |pl=fc
Итак, vp о ... р =——?2 , —, есгь коэффициент
при *р1*£2 • • • *£" в разложении (х{-\- х2-\- ... + дг„)"1+р2+ '" +р",
чго является обобщением формулы, бинома Ньютона. Это,
впрочем, очевидно, если воспользоваться комбинаторным
определением y-»> данным после (III, 7; 14).
р
Коэффициенты бинома имеют очень простой вид, что
позволяет сразу написать формулу Маклорена для функции двух
скалярных переменных хну. Полагая
; = JJ(0,.0), ;=^-.(0,0), f= |i,(0, 0), (Ш,7;262)
« = Ц(°'°Ь Р = Д*(0.0), ?=а||.(0.0). 6 = Ц(0,0),

§ 7. Формула Тейлора
285
получим:
/ (х, у) = f (О, 0) + px + qy + ± (Тх2 + Uxy + Ту2) +
+1 (ах3 + 3$х2у + Зуху2 + ty3) + ... . (Ill, 7; 263)
Применение к изучению максимумов и минимумов. Определения
Пусть / — еещественнозначная функция, определенная на
топологическом пространстве Е. Говорят, что / имеет в точке
а е £ относительный максимум1), если существует некоторая
окрестность Т точки а е Е, такая, что сужение / на эту
окрестность имеет в точке а максимум, т. е. если для любой точки
х кз У имеет место неравенство f(x)^.f(a). Относительный
максимум называют строгим, если можно выбрать Т таким
образом, чтобы для хф а из Т имело место строгое
неравенство /(*)< \{а).
Аналогичное определение дается для относительного
минимума и строгого относительного минимума.
Конечно, максимум функции /, т. е. ее абсолютный
максимум, является одновременно и относительным максимумом,
в то время как противоположное утверждение, вообще говоря,
не верно.
Говорят, что функция f имеет в точке а экстремум, если
она имеет в этой точке относительный максимум или
относительный минимум.
Необходимые условия экстремума
Теорема 23. Пусть f — еещественнозначная функция,
определенная на открытом множестве Q аффинного
нормированного пространства Е и дифференцируемая на нем.
Необходимым условием существования в точке aefi относительного
максимума или минимума является обращение в нуль
производного отображения f (а) е 2? (Е; R) = Е.
Доказательство. Заметим прежде всего, что если Е
конечномерно и в нем выбрана система координат 0, (е^ е/, то
это необходимое условге выражается в общеизвестной форме:
для того чтобы f в точке а имела относительный максимум или
минимум, необходимо, чтобы частные производные df/dxt
') Вместо того чтобы говорить, что функция f имеет в точке а максимум
или относительный максимум и т. д., иногда говорят, что точка а является
для f максимумом или относительным максимумом и т. д. Это не верно, так
как максимум равен f{a), а не а\

286 Гл. 111. Дифференциальное исчисление
в точке а были равны нулю или чтобы дифференциал в
точке а: V -~- (a) dxi был тождественно равен нулю.
Докажем теперь теорему в общем случае. Если f в точке а
имеет относительный максимум или минимум, то функция
/—*f(a + tX) при фиксированном X в Е определена для (eR
при достаточно малом |/| (поскольку Q — открытое
множество) и имеет в точке / = О относительный максимум или
минимум. Тогда доказательство, аналогичное доказательству
теоремы Ролля (теорема 4), показывает, что ее производная
■>
в точке t равна нулю при t = 0. Эта производная равна f'(a)X,
Так как f'(a)X = 0 для любого Хе£, то f (а) = 0.
Замечания. По многим причинам теорема 23 не решает
задачи об отыскании экстремума функции f.
1°) Чаще всего вещественная функция f задается не на
открытом, а на замкнутом множестве F (например, на
сегменте [а, Ь] из R или в Замкнутом шаре из Е). Она может и
не иметь никакого экстремума, если множество, на котором
она определена, не компактно (например, f(x) = x не имеет
экстремума на R). Если она и имеет экстремум, то он может
не удовлетворять теореме, которая применима только к
открытым множествам. Естественно, если f дифференцируема во
о
внутренности Q = F множества F, то каждая точка
экстремума а, находящаяся в Q, будет найдена из условия f'(a) = 0,
но экстремальные значения могут достигаться на границе
множества F (например, если f есть функция х2, определенная
на отрезке [—1,1], то ее минимум при х = 0 находится
приравниванием нулю производной, поскольку 0 лежит внутри
отрезка [—1,1], но точки максимума х = ±1 теореме не
удовлетворяют, поскольку они находятся на концах этого интервала,
где производная в нуль не обращается) ').
2°) Обратно, уравнение f'(a) — 0 зачастую определяет точки,
не являющиеся точками экстремума. Другими словами,
необходимое условие f'(a) — Q далеко не достаточно. Чтобы узнать,
как ведет себя функция в точке а, надо изучить ее разложение
Тейлора в окрестности этой точки.
') В начале § 2 на стр. 195 мы говорили, что большинство теорем,
сформулированных для открытого множества Q из Е, применимы также и к
другим множествам, в особенности к неоткрытым интервалам R. Теорема 23 —^
одна из тех, которые в этих условиях неприменимы. Ее доказательство
опирается на доказательство теоремы Ролля (теорема 4), в котором существенно
используется тот факт, что экстремальное значение достигается во
внутренней точке интервала.

§ 7. Формула Тейлора
287
Исследуем подробнее эту проблему. Иногда факт
обращения в нуль производной f'(a) более важен, чем свойство
экстремальности. Например, если рассматривается
гиперповерхность y = f{x) в пространстве Q X R. то условие f'(a) = 0
означает, что касательная гиперплоскость, проведенная к
поверхности в точке А = (a,f(a)), горизонтальна. Это
необходимое условие экстремума ординаты геометрически более важно,
чем само свойство экстремальности. Поэтому независимо от
того, имеется или нет в точке а экстремум функции, мы будем
называть точку а стационарной точкой функции f, если в ней
/'(«) = 0.
Нахождение необходимых и достаточных условий
экстремума функции
Теорема 24. Пусть f — вещественная функция,
определенная на открытом множестве Q аффинного нормированного
пространства Е и m раз дифференцируемая. Если
производные функции f порядка 1, 2, ..., m—1 равны нулю в точке
йеО, а /(т>(а)=^=0 и если в точке а функция f имеет
относительный максимум, то m четно и справедливо неравенство
/<т>(а)Хт<0 для любого 1ё£. (III, 7; 27)
Обратно, если f дифференцируема m раз в Q, все
производные f порядка 1, 2, ..., т — 1 равны нулю в точке зей
и если /<т) (а) л ограничено сверху некоторым числом
—б •< 0 для всех X из единичной сферы \\Х\\ = 1 пространства
Е, то f имеет в точке а строгий относительный максимум.
Доказательство. Г) Докажем сначала первую часть
теоремы, предполагая, что / имеет в точке йей
относительный максимум. В этом случае функция g: t-*f(a + tX),
определенная в окрестности точки t = 0 на вещественной прямой
R, имеет относительный максимум в точке ^ = 0. Ее
производная порядка k при / = 0 имеет вид f(k)(a)Xk. При ^ = 0
производные порядков ^.т— 1 равны нулю, а производная
порядка т равна /<т) (а) Хт. Поэтому для t, близких к нулю,
имеем:
g (0 - g (0) = (f(m) (a) Xm) -iL- + ettm, (HI. 7; 28)
где ei стремится к 0 вместе с \t\. Отсюда следует, что либо
/<т) (а) Хт — 0, либо разность g(t) — g{0) в окрестности
точки t — 0 имеет тот же знак, что и (/<m) (a) Xm) tm. Поэтому,

288
Гл. III. Дифференциальное исчисление
окончательно, при любом Jfe£ и вещественном t имеет место
неравенство
(fW(a)Xm)tm^0. (Ill, 7; 29)
При четном т это неравенство эквивалентно (III, 7; 27). Для
доказательства первой части остается показать, что т не
может быть нечетным. В самом деле, при нечетном т, полагая
последовательно f=+l и t = —1, из (III, 7; 29) получаем
f<m)(a)Xm = 0 для любого fel. (III, 7; 30)
Согласно лемме, относящейся к теореме 2b, это
соотношение влечет за собой равенство
/(m>(a)(l„ Х2, ..., Хт) = 0 для любых (Хи Х2, ..., Хт)^Ет,
(III, 7; 31)
или /<т>(а) = 0, что противоречит исходному предположению.
Замечание. Перед тем как перейти ко второй части
теоремы, заметим следующее: может показаться, что если / имеет
в точке а строгий относительный максимум, то форма порядка
m: f{m) (a) Xm является отрицательно определенной, т.е. имеет
место неравенство
/<m> (a) Xm < 0 для ХфО. (III, 7; 35)
Но это не так (за исключением, очевидно, случая, когда Е
одномерно). В самом деле, рассмотрим вещественную функцию
двух переменных х, у:
f(x, г/)=-(л:2+г/4). (III, 7; 36)
В начале координат она имеет строгий максимум.
Поскольку это полином, его разложение по степеням хну является
>
разложением Маклорена, так что, обозначая через (X, Y)
вектор из Е = R2, получаем, что
-jj-HO, 0)(X~J)2=-X2 (III, 7; 37)
всегда -СО, но не является отрицательно определенной (это
■ > >
выражение обращается в нуль на векторах (0, У)=£(0, 0)).
2°) Докажем теперь вторую часть теоремы. Заметим
прежде всего, что условия второй части более сильные, чем
заключение первой. Иначе не может и быть. Если предположить, что
/<*)(а) = 0 при fe=l, 2, ..., m—1, /(m> (а) ф 0 и что
выполняется неравенство (III, 7; 27), то этого вовсе не достаточно для

§ 7. Формула Тейлора 289
того, чтобы обеспечить функции / относительный максимум
в точке а.
В самом деле, рассмотрим функцию f двух вещественных
переменных х, у.
f(x,y)=-x2 + y*. (Ill, 7; 38)
Как мы видели для (III, 7; 36), имеет место соотношение
(III, 7; 37), т.е. неравенство (III, 7; 27). Однако f(0, 0) = 0 и
f(0. У) > 0 Для у ф 0, а, следовательно, f в начале координат
относительного максимума не имеет. Поэтому мы ставим более
сильные условия, указанные в формулировке теоремы:
^т){а)Хт мажорируется на единичной сфере числом—б < 0.
Это влечет за собой, в силу однородности, неравенство
f<m>(a)r"<-6||X If". (Ш, 7; 39)
Последнее, в свою очередь, влечет за собой (III, 7; 35):
f(m) (a) отрицательно определена. Если Е конечномерно, то
неравенство (III, 7; 39) эквивалентно неравенству (III, 7; 35).
Действительно, в этом случае единичная сфера компактна и
непрерывная функция X->"f<m) {a)Xm, отрицательная в силу
(III, 7; 35) на этой сфере, достигает на ней максимума,
являющегося некоторым числом —б < 0. Одйако для
бесконечномерного пространства Е это условие более сильное, чем (III, 7; 35).
Запишем разложение Тейлора порядка m в виде (111,7; 10):
f(a + h) = f(a) + -^^tm + a(h)\\h\r, (Ш,7;40)
где ос(А) стремится к 0 вместе с А. Тогда (III, 7; 39) дает
f(a + A)<f(a)-fi||Air + a(A)||Air. (Ш,7;41)
•> ->->■>
Так как а стремится к 0, то для А ф 0 с достаточно малой
нормой f(a-f-A) — f(a)<0 и, следовательно, в точке а функция
f имеет строгий относительный максимум.
Естественно, аналогичная теорема имеет место для
минимума. Отсюда получается правило, позволяющее выяснить,
имеет ли f в точке а относительный максимум или минимум.
Правило. Прежде всего необходимо, чтобы f'(a)=0.
Затем ищется первое целое число /п, такое, что ft™) (а) Ф0. Если
m нечетно, то в точке а нет ни относительного максимума, ни
относительного минимума. Если m четно, то рассматривается
знак формы степени m: X->f(m) (a)Xm. Если она может
принимать значения разных знаков, то в точке а нет ни относительного
Ю Зак, 1339

290
Гл. III. Дифференциальное исчисление
максимума, ни относительного минимума1). Если она
всегда ^0 (соответственно 1>0), не будучи отрицательно
определенной (соответственно положительно определенной), то без
изучения производных порядка \>ш ничего определенного
заключить нельзя. Если же она отрицательно определенная
(соответственно >0) и Е конечномерно или же если имеет место
более сильное условие sup (f<п?) (а) Хт) < 0 (соответственно
inf (f(m) (a)Xm)>0) для бесконечномерного Е, то а является
II £ц=1
точкой строгого относительного максимума (соответственно
минимума) .
Из всего изложенного следует, что не существует простого
условия, одновременно необходимого и достаточного для того,
чтобы вещественная функция, определенная на Йс£, имела
в точке а относительный максимум или минимум.
Замечания. 1°) Если функция f имеет в точке а все
последовательные производные, равные нулю, и не является
тождественно нулевой функцией, то изучение разложения Тейлора
не позволяет выяснить вопроса о существовании в точке а
относительного максимума или относительного минимума.
2°) Предположим, что в точке а функция имеет седло.
Тогда можно попытаться узнать, в какой части области Q в
окрестности точки а имеет место неравенство f(x) ^f(a) и в какой
части f(x) ^.f(a). Здесь применимы те же правила. Если на
"*" "*■
множестве В единичной сферы \\Х\\ = \ величина /<ш) (а) Хт не
-> -»■
превосходит —6 < 0, то во всем конусе {а + XX; ХеВ, Я > 0
вещественно} в окрестности точки а имеет место неравенство
f(x)<f(a).
Частный случай вещественной функции f
двух вещественных переменных х,у
При исследовании такой функции на экстремум надо пре-
df
жде всего найти точки, в которых частные производные р = -^-
и q=-J- равны нулю. Пусть (а, Ь)—такая точка. Рассмот-
') В этом случае говорят, что в точке а функция / имеет седло.
Типичный пример такого седла дает функция двух вещественных переменных
f(x,y) = xy. Ее графиком в R3 служит гиперболический параболоид г — ху.
В начале координат функция / имеет седло. Сужением / на прямую у = kx
является функция x^>-kx2, имеющая строгий максимум в начале координат
при k < 0 и строгий минимум при k > 0. Можно также говорить о седле
и в том случае, когда m нечетно.

§ 7. Формула Тейлора
291
рим теперь разложение функции f по формуле Тейлора по
степеням х— а=Х и у — b = Y. Это разложение начинается с
у (rX2 + 2sXY + tY2). (111,7; 42)
\-й случай: rt — sz>0, r (и t) < 0. Квадратичная форма
(III, 7; 42) в этом случае отрицательно определенная, а,
значит, f имеет в точке (а, Ь) строгий относительный максимум.
2-й случай: Н — s2 > 0, г (и t) > 0. Функция f имеет в
точке (а, Ь) строгий относительный минимум.
3-й случай: Н — s2 < 0. Квадратичная форма (III, 7; 42)
принимает значения разных знаков, и, следовательно, мы имеем
дело с седлом. Уравнение rX2-\- 2sXY -f- г?У2==0 задает две
прямые D и D' на плоскости R2, определяющие 4 попарно
вертикальных угла. Обозначим их по порядку обхода через (1), (2),
(3), (4). Предположим, например, что рассматриваемая
квадратичная форма ^0 в углах (1) и (3) и ^С0 в углах (2) и (4).
Пусть угол (1) определен в полярных координатах
неравенствами р^О и а^ф^р. Тогда каждый угол a' =Sj ф ^ Р',
где а' > а и р' < р, пересекает «единичную сферу» из R2, т. е.
окружность, по компактной дуге, на которой квадратичная
форма имеет минимум б > 0. Следовательно, существует такое
число е > 0, что если положить х=а + р совф, у = Ь + р sin ф,
р > 0, а' ^ ф ^ Р', то для 0 < р ^ е имеет место неравенство
f(x,y)>f(a,b).
Однако это число е зависит от а' и р'. Поэтому невозможно,
не привлекая к изучению производные f порядков >2 в точке
(а, Ь), делать какие-либо выводы при р, стремящемся к 0, если
одновременно с этим ф стремится к а или р. Тот же результат
имеет место в угле (3). В углах (2) и (4) имеет место
аналогичный результат, но с заменой неравенства f(x, у) > f(a,b) на
f(x,y) <f(a,b).
Области плоскости R2, в которых f(x,y) ~>f(a,b) и f(x,y)<.
"<.f(a,b), разделены кривой f(x,y)—f(a,b). Эта кривая в
точке (а, Ь) имеет две ветви, касательные соответственно к D и D'.
Однако, не привлекая к рассмотрению производные функции f
порядков >2 в точке (а, Ь), невозможно сказать, в каком из
углов находятся эти кривые.
4-й случай: rt — s2 = 0, г или t < 0. Квадратичная форма
равна квадрату некоторой линейной формы =^=0, взятому с
противоположным знаком. Она <0, но обращается в нуль на
некоторой прямой D. Пусть ф=фо-(-&л; — полярный угол этой
прямой. Если л;=а + рсозф, y=b -f- рэшф, р ^ 0, а' < ф «^ Р',
где а' и р' фиксированы, а' > ф0 и р' < ф0 + л, то существует
такое число е > 0, что для 0 < р ^ е имеет место неравенство
10*

292 Гл. 111. Дифференциальное исчисление
f(x,y) < f (a. b). Аналогичный результат справедлив для а' >
> фо + я, р' < фо + 2я.
К сказанному ничего добавить нельзя. В частности, без
привлечения производных порядков >2 нельзя сказать, имеет или
нет функция f в точке (а, Ь) относительный максимум.
5-й случай: rt— s2 = 0, г или t > 0. Результат аналогичен
предыдущему, надо только заменить f (х, у) < f (a, b) на
f(x,y) >f(a,b).
6-й случай: г = s = t = 0. Без привлечения производных
функции f в точке {а, Ь) порядка >2 никакого вывода о поведении
функции f в точке (а, Ь) сделать невозможно.
Заключение. Проведенные исследования показывают,
что различных вариантов поведения функции более одной
переменной значительно больше, чем это имеет место для функции
одной переменной.
Применение формулы Тейлора к изучению
расположения гиперповерхности по отношению
к касательной гиперплоскости
Пусть f — дифференцируемая вещественная функция,
определенная на Q с= Е. Тогда y=f(x) является уравнением
дифференцируемого многообразия пространства EXR. Такое
многообразие называют дифференцируемой гиперповерхностью. Ее
касательная гиперплоскость в точке А=(а, f(a)) определяется
уравнением (111,3; 19з). Расположение гиперповерхности по
отношению к касательной гиперплоскости в окрестности точки А
определяется знаком разности
f(x)-f(a)-f(a)(7^a) (III, 7; 43)
для х, близких к а.
>
Но x-*f(x)—f'(a)(x — а) является дифференцируемой
вещественной функцией, производная которой в точке а равна
нулю. Все сводится к тому, чтобы выяснить, имеет ли эта
функция в точке а экстремум какого-нибудь типа или седло. Тем
самым мы возвращаемся к теореме 24. В силу приведенного
выше заключения, наличие седла является обстоятельством
частым, а не исключительным и, следовательно, кроме случая
одномерного Е, гиперповерхность обычно пересекает свою
касательную гиперплоскость, даже если 1"{а)фЬ. В частном случае
функции f двух переменных х, у поверхность локально
расположена с одной стороны от касательной плоскости, если rt-=s2 >?!
> 0, и пересекает ее, если rt — s2^C. 0.

§ 8. Теорема о неявной функции
293
§ 8. ТЕОРЕМА О НЕЯВНОЙ ФУНКЦИИ. ПОСТАНОВКА ЗАДАЧИ
Пусть / — отображение множества Е в множество F. Тогда,
если Ь — некоторая точка F, можно поставить задачу
отыскания множества тех х из Е, для которых f(x)=b, т.е. задачу
отыскания прообраза f~l({b}). Поставленная задача называется
задачей о решении уравнения f(x) = b. Пусть теперь / —
отображение произведения множеств Е X F в множество G, и пусть
с — некоторая точка множества G.
Рассмотрим уравнение
f(x,y) = c. (Ш,8;1)
Может случиться, что для заданного х уравнение f(x,y)=c
относительно у имеет решение, и притом единственное, при
любом заданном значении х. В таком случае это уравнение
определяет у как некоторую функцию g(x) переменной х. Эта
функция называется неявной функцией, определенной предыдущим
уравнением. Она характеризуется следующим свойством:
f(x,g(x))=*c. (Ill, 8; 2)
Можно еще сказать, что для (х, у) ^Ey^F соотношение
(III, 8; 2) равносильно соотношению у=g(x).
Естественно, это такие счастливые совпадения случаются
редко. Чаще всего для некоторых значений х решения
относительно у не существует, для других же значений х имеется
несколько решений, а то и бесконечное множество их. Мы
изучим следующий частный случай: Е, F, G — топологические
пространства. Имеется частное решение рассматриваемого
уравнения: х = а, у = Ь. Предлагается выяснить, существует ли и
притом единственно ли решение данного уравнения
относительно у для х, достаточно близких к а, при условии, что это
решение достаточно близко к Ь. Если это так, то можно будет
определить неявную функцию y—g(x), исходя из данного
уравнения, по крайней мере,в некоторой окрестности точки (а, Ь).
Геометрический смысл рассматриваемой задачи станет
особенно понятным, если мы предположим, что каждое из пространств
Е, F и G является полем вещественных чисел. В этом случае
уравнение f(x, y)=0 определяет некоторую кривую в R2, и мы
хотим выразить эту кривую в обычной форме, представив у как
функцию от х по крайней мере в некоторой окрестности точки
') Легко видеть, почему такие сужения на окрестности неизбежны:
кривая f(x,y)=0, вообще говоря, не может быть полностью задана в виде
y = g(x).

294
Гл. III. Дифференциальное исчисление
Существование неявной функции
Теорема 25. Пусть Е — топологическое пространство, F и
G — аффинные нормированные пространства, Q — открытое
множество из Е X F и (а,Ь) — точка Q. Пусть f — непрерывное
отображение Q в G и f(a, b)=c. Предположим, что при каждом
фиксированном х функция f имеет частную производную
-fi-{x, y)^3?(F; G) и что частная производная функция -~-
является непрерывным отображением Q в 2' (F;, G).
Предположим, кроме того, что Q = -^-(a, b) является обратимым отоб-
> у >
ражением пространства F на пространство G, т. е. является
биекцией, имеющей обратную биекцию Q~l, линейную и
непрерывную. Предположим, наконец, что F полно. Тогда существуют
такие открытые множества А и В в пространствах Е и F,
содержащие а и Ь соответственно, что для любого х из А уравнение
(III, 8; 1) относительно у имеет решение в В, и притом
единственное. Это решение у является функцией х, и так
определенная функция y=g{x) является непрерывным отображением
А в В.
Доказательство. Напомним сначала бегло условия
теоремы. Ищется решение уравнения относительно у, налагаются
некоторые ограничения на частную производную по у,
пространство F переменной у предполагается полным. Подвергнем
уравнение трем последовательным преобразованиям:
> ' >
1°) Пусть Qi — множество точек (х, у — Ь), где (х, у) ей.
Положим г/=6 + У и обозначим через /i отображение множе-
-> >
ства Qi в пространство G, определенное формулой
М*. Y) = f(x, b + Y)-c '). (Ill, 8;3)
Уравнение (III, 8; 1) эквивалентно уравнению
М*,.У)=0 (III, 8; 4)
в окрестности частного решения (а, 0).
') На практике F не обязательно должно быть векторным
пространством, в то время как G — почти всегда векторное пространство. Обычно
рассматривается уравнение f{x, у) = 0. Мы считаем G аффинным
пространством, а с произвольным для того, чтобы сохранить симметрию между F
и G. Во всяком случае, можно всегда перейти к случаю векторных F и G с

§ 8. Теорема о неявной функции
295
2°) Рассмотрим функцию /2, определенную формулой
Q-1 о £: (х, Y) -> Q-1 (h (х, Y)). (Ill, 8; 5)
-> ->-
Это некоторое отображение Qi в F, обладающее свойствами,
аналогичными свойствам отображения /. Его частная
производная по второй переменной в начале координат, в силу следствия
теоремы 11, определяется формулой
-Щг(а, 0) = Q-loQ = I<=g(F; F), (Ш,8;6)
dY
где / — тождественное отображение. Уравнение (III, 8; 1)
эквивалентно новому уравнению
/2(х, ?) = 0, (III, 8; 7)
ибо от (III, 8; 4) к (III, 8; 7) можно перейти с помощью Q-1, а от
(III, 8; 7) к (III, 8; 4) с помощью Q.
->■■
3°) Рассмотрим, наконец, функцию Ф, определенную
формулой
ф(Х, Y) = Y-f2&, П (Ш, 8; 8)
■*■ -> ->
Ф является отображением Qi в F, обладающим свойствами,
аналогичными свойствам / всюду, кроме одной особой точки: его
частное производное отображение по второй переменной в
начале координат равно нулю, так как / — /=0. Уравнение
(111,8; 1) теперь эквивалентно уравнению
Ф(Х, Y) = Y, *, = *, Y = y-b, (Ш,8;9)
->■ ->■
которое нужно решать в окрестности Я=а, У=0.
Теперь видно, что мы находимся в условиях, напоминающих
условия теорем 46 и 462 гл. II {теоремы о неподвижной точке).
■*■" -> ■>
Пусть А\ и Bi — такие окрестности точек а и 0 в Е и F соот-
-> ->
ветственно, что А\ X В\ с: Qb Если пространства £ и Л из тео-
-> ■ ->
ремы 462 заменить соответственно на В\ и А\, то функция Ф
будет непрерывной и тем более раздельно непрерывной ка
Л] X #г. Однако для применения этих теорем нужны условия,
которые здесь нельзя непосредственно проверить и которые
требуют еще некоторого изменения исходных данных задачи.

296
Гл. III. Дифференциальное исчисление
1 ) Отображение Ф должно быть отображением A\Y.B\
> -»•-»• ->
в В\\ однако оно отображает А{ X^i B F и не обязательно вВь
+
Именно это вынуждает нас заменить А{ и В{ на две меньшие
-> >
окрестности А2 и В2 точек а и 0 с тем, чтобы сужение Ф на
■> +
^2 X ^2 отображало это множество в В2.
2°) Теперь надо проверить, что для фиксированного Я в А%
->*>->■ ->
отображение Ф^: г—>Ф(Я, У) окрестности В2 в себя является
сжатием с коэффициентом сжатия k < 1, не зависящим от
выбора Я в Л2.
3°) Надо, чтобы метрическое пространство В2 было полным.
Займемся сначала условием 2°). Поскольку частная произ-
водная -^г непрерывна и равна нулю в (а, 0), можно найти
дУ
такую окрестность Л2 точки а в А\ и такой замкнутый шар ')
-> ■>
В2 в В] с центром в нуле радиуса Р > 0, что из соотношений
, -> ->
Я е Л2 и У ^ В2 следует неравенство
-^(£,у)
<|. (Ш,8; 10)
дУ *■
Применим теперь теорему о конечных приращениях. Это
возможно, поскольку шар В2 выпуклый, и, следовательно, если
-> ->
У и Y" лежат в этом шаре, то в нем лежит и весь отрезок
-> ->
[У, Y"]. Получим неравенство
||Ф(Я, У')-Ф(Я, У")||<-±-||У'-У"||. (Ш,8:11)
Таким образом, условие 2°) выполняется с &=1/2 для шаров
Л2 и В^ или для меньших множеств.
Займемся теперь условием 1°). Нам надо выбрать Л2 и В2
так, чтобы Ф было отображением А2у^В2 в В2. Окрестности
А2 и В2 уже выбраны. Учитывая непрерывность функции Ф и
тот факт, что Ф(а, 0) =0, мы можем найти такую окрестность
Лг с: Л2 точки а, в которой имеет место неравенство
IIФ(*, 0)||<4 для ЯеЛ2. (III,8; 12)
') Мы увидим несколько ниже, почему В2 должно быть замкнутым.

§ 8. Теорема о неявной функции
297
При этих условиях для 1еЛ2 и ||У|| ^ р имеет место
неравенство
||Ф(Л, У)1К1|Ф(А,, 0)|| + ||Ф(Я;, У) -Ф(Я., 0)||<|- + y||F||<p.
(111,8; 13)
>
Это неравенство доказывает, что функция Ф отображает
А2 X ^2 в В2. Наконец, условие 3°) теперь выполнено,
поскольку, в силу теоремы 43 гл. II, В2, как замкнутая часть полного
метрического пространства F, является полным метрическим
пространством. Итак, мы находимся в условиях применимости
теорем 46 и 46г. Следовательно, для заданного К в А2 имеется,
и притом единственное, решение уравнения (III, 8; 9) относи-
> -> ->
тельно Y, такое, что ||У|| ^ р и Y является непрерывной
функцией Я,, Y=${K).
Уравнение (111,8; 1) эквивалентно уравнению (III, 8; 9) и,
следовательно, имеет, и притом единственное, решение
относительно у в шаре В2 пространства F с центром в b радиуса р
для любого заданного х из А2. Кроме того, если мы обозначим
через g отображение, которое каждой точке х из А2 ставит в
соответствие единственное решение у из В2, y=g{x), то g{x) =
= b-\-W{x) и, следовательно, g является непрерывным
отображением А2 в В2.
Заметим, что определение окрестностей А2 и В2 проводилось
в два приема. Сначала были найдены достаточно малые А2 и
В2. Естественно, их можно по желанию еще уменьшить. Однако,
как только В2 фиксировано, достаточно малое множество А2
выбирается уже в зависимости от В2. Результат a posteriori
представляется очевидным, поскольку функция g непрерывна. Из
непрерывности функции g следует также, что если В является
о
внутренностью В2 множества В2, то существует открытое
множество ') в Е, содержащее а, такое, что из х е А следует g (x) e
е В, и теорема доказана.
Замечание. Рассмотрим уравнение более общего вида:
f(x,y) = z, (III, 8; 14)
в котором ищется у, близкое к Ь, как функция х и г, близких
к токам а и с, таким, что /(а, Ь) = с.
') Для проведения доказательства мы были вынуждены брать
замкнутый шар Вг, ибо нам нужна была замкнутость шара Вг для того, чтобы он был
полным! Но удобнее формулировать теорему для открытых множеств А к В.

298
Гл. 111. Дифференциальное исчисление
Это уравнение сводится к уравнению теоремы 25:
7\({х, г), у)=0, где % ((х, z), y) = f (х, у) — г; (Ш,8;15)
fi является отображением некоторого открытого множества из
->■
(Е X G) X F в G и ищется у, близкое к Ь, как функция точки
-> ->
{x,z), близкой к точке (а, с), такой, что fi((a, с), Ь) = 0.
Дифференцируемость неявной функции
Предположим теперь, что функция f дифференцируема, и
выясним, влечет ли это за собой дифференцируемость неявной
функции g, определенной заданной функцией }. При этом мы
несколько изменим условия теоремы: мы будем предполагать,
что неявная функция существует и непрерывна, даже если
существование и непрерывность не следуют непосредственно из
теоремы 25 (мы предполагаем существование производной
только в точке (а, Ь)). Кроме того, пространство Е будет
предполагаться аффинным для того, чтобы можно было говорить о
дифференцируемое™ функции g.
Теорема 26. Пусть Е, F, G — три аффинных
нормированных пространства, Q — открытое множество из Е X F, f —
отображение Q в G. Пусть А и В — открытые множества
пространств Е и F соответственно, А X В с: Q и g является
отображением А в В, тождественно удовлетворяющим соотношению
(III, 8; 2). Пусть, далее, отображение f дифференцируемо в
точке (a, b), b—g(a), и его частные производные Р и Q в
рассматриваемой точке являются линейными непрерывными отоб-
->■->■-»•
ражениями Е и F в G соответственно, причем отображение Q
обратимо. Тогда, если отображение g непрерывно в точке а, то
оно дифференцируемо в точке а и его производное отображение
задается формулой
g,(a) = -Q-ioP = -{^L(a, b))~]o(-g-(a, b)). (111,8; 16)
Доказательство^ Если заранее предположить
существование производной отображения g, то формула (111,8; 16)
получается сразу. В самом деле, мы можем
продифференцировать тождество (111,8; 2), пользуясь теоремой о сложной
функции, и получить уравнение
-g- (a, b) + ^ (a, b)°g>(a) = 0^3? (E; G), ^ ^ ^
или P + Q°g'{a) = Q,

§ 8. Теорема о неявной функции
299
откуда путем композиции слева с Q-1 вытекает (III, 8; 16). Но
доказательство получается более сложным, так как мы не
знаем заранее, дифференцируема ли функция g в точке а. Пусть
dx=x — а — некоторое приращение х, а Дг/— соответствующее
приращение y=g(x). Из того факта, что g является неявной
функцией, определенной рассматриваемым уравнением, и что
функция / дифференцируема в (а, Ь), следует формула
0=-A/ = Pdt+QAj+a(||d^|| + |!Aj||). (111,8; 18)
Вектор а зависит от dx и Дг/, т. е. в конечном счете только
от dx. Он стремится к 0, если dx и Дг/ стремятся к. О, т. е.
—> ->
при dx, стремящемся к 0, ибо, в силу непрерывности g
в точке а, Дг/ стремится к 0 вместе с dx. Отсюда вытекает
следующий результат для Дг/:
Q^=-pTx-l{\\Tx\\ + \\£)\\),
или
^=_(Q-1oP)dt-(Q-1a)(||dt|| + ||^||). (111,8; 19)
Теперь необходимо избавиться от Дг/ в правой части. Это
можно сделать с помощью некоторых оценок. С этой целью
напишем сначала неравенство
l|AjlKlQ",|ll/>llll^ll + lQ",|lla||||d^||+lQ-,ll|a||||4j||,
(III, 8; 20)
—> ■> •>
Мы видели, что при dx, стремящемся к 0, а также стремится
к 0. Следовательно, можно выбрать dx настолько малым,
чтобы коэффициент ||Q ||||<х|| не превосходил 1/2. Перенося
затем налево последний член, получим следующее неравенство,
имеющее Место для всех достаточно малых \\dx\\:
или
или
||Ajfl^(2 8Q-I|lll/>IH- 1)||Лж||, (»Ь8;21)
№ll + l|Ajll<2(|Q-,|||P||+l)||d^|| = A||rfx||,

300
Гл. 111. Дифференциальное исчисление
где k—некоторая постоянная. Используя теперь эту оценку для
последнего члена правой части равенства (111,8; 19),
окончательно получаем
Ay = -(Q-1°P)^+P№l, где IIPIlOlQ-'IllaH. (Ill, 8; 22)
-> -> —> ■*
Здесь р стремится к 0, когда dx стремится к 0, чем и
заканчивается доказательство теоремы.
Замечание. В дифференциальных обозначениях без
труда приходим к следующему правилу:
Правило. Для нахождения дифференциала функции у как
функции х, неявно определяемой уравнением f(x,y)=c, следует
продифференцировать это уравнение, что дает
Pdx + Qdy = 0, (III, 8; 23)
а затем разрешить полученное соотношение относительно dy:
dy=-(Q-l°P)dx. (Ill, 8; 24)
Дифференцируемость функции и-*и-1 на Jg(F;G)
Для того чтобы иметь возможность в полной мере исполь
зовать теоремы 25 и 26, надо знать, как изменяется (-^— (л:, у)\
при изменении (х, у). Точно так же, как при обосновании диф-
ференцируемости сложной функции (теорема 19) была
использована дифференцируемость произведения (теорема 18), для
обоснования дифференцируемости неявной функции будет
нужна производная обратной функции.
■> > ■
Теорема 27. Пусть F, G — векторные нормированные
пространства, и пусть °IL (соответственно <%6~1) —множество обра-
тимыхэлементов пространства 3? (F; G) (соответственно 9?(G; F)).
Тогда:
Iе) Биекция и-*и~1 множества °И на множество °U,-X
является гомеоморфизмам.
+ +
2е) Если пространства F и G полны, то множества <%6 и °U'1
открыты, а .биекция и —► итх дифференцируема вместе со своей
обратной биекцией и ее производная в точке u^3?(F;G)
является отображением
du -> — и-1 о du о и"1 (III, 8; 25)
пространства S£(F; G) в пространство Я?(G; F).
-I

§ 8. Теорема о неявное/ функции
301
Первое доказательство. Для простоты во всех слу-
чаях будем предполагать пространства F и G полными. Тогда,
как мы видели в теореме 62 гл. II, если и0 е °U, то всякий эле-
мент из 2'(F; G), принадлежащий открытому шару с центром
в «о радиуса Цы-'Ц-1, будет находиться в 11, а, следовательно,
ац открыто. Точно такие же рассуждения можно провести для
множества <2/~1, меняя ролями F и G.
Покажем теперь, что отображение и -> wl дифференцируемо
в точке «о ^ 'U- Это отображение непрерывно и, поскольку
обратное к нему отображение также непрерывно (стоит лишь
поменять ролями F и G), оно является гомеоморфизмом,
дифференцируемым вместе с обратным гомеоморфизмом. Формула
(II, 14; 26) дает (для || du\\<\\u-'fl)
(«о+ du)~ — u^1 —«(7 йищ + щх йищ{ duu^x — ... . (Ill, 8; 26)
Отсюда получается неравенство
|((ы0 + du)~ — и^1) + «о"1 du и^11 ^
^\\u-1f\\du\?(l+\\u-i\\\\du\\ + (lu^\\\\du\\Y+ ...) =
_ КТ— _ „~0^.~-. (111,8;27)
<-' Р \\duf Iv'lfll^ll2
_ l-l^-'lll^ll "Ц^-'Ц-'-ц^ц '
При \\du\\, стремящемся к 0, это выражение мажорируется
постоянной, умноженной на ||d«||2, и, следовательно, является
бесконечно малой более высокого порядка, чем \\du\\. Поскольку
d«—»• — н~' duii*1 является линейным непрерывным отображе-
нием S?(F\ G) в 9?[G\ F), оно, в силу определения (III,3; 13)'),
является производной отображения ы—►и-1 в точке и0.
Второе доказательство. Ограничимся снова случаем,
когда F и G полны. Тогда такими же будут пространства
->- ->
') Заметим, что если F и G произвольны, то °U и Щ~х могут оказаться
->- -> ->-
пустыми! Например, если F и G конечномерны, то обратные отображения F на
> > -у
О существуют лишь в том случае, когда F и G имеют одинаковую
размерность.
Заметим также, что если <U не пусто, то F не может быть полным, если
не полно G, и обратно, ибо каждый элемент из <U устанавливает взаимно
однозначное соответствие между F и G, сохраняющее сходимость и.
последовательности Коши.

302
Гл. 111. Дифференциальное исчисление
g(f\ G) и S{G\ F) (теорема 50 гл. II). Пусть u0(=1t. Эле-
■> -У
мент v из S'(G; F) называется обратным справа к элементу
u^S(F\ G), если u°v=I. Такой элемент v существует не
всегда (например, для « = 0 не существует обратного справа
элемента). Может существовать бесконечное множество таких
элементов. Однако, если элемент и обратим, то существует лишь
один такой элемент, а именно и~\ ибо из «»t)=/ умножением
слева на и~1 получаем v = u~i.
Поиски элемента, обратного справа к элементу и, приводят
к решению уравнения uv = I относительно v. Мы можем,
следовательно, применить теорему о неявной функции. Отображение
(и, v) —► uv, как билинейное непрерывное отображение,
непрерывно дифференцируемо (теорема 9г). Его частная
производная по у в точке («о, v0), v0 = u~l, является линейным непре-
рывным отображением V —*W=u0V ') пространства & (G; F)
в пространство 9?(G\~G) (формула (11,3; 34)). Это
отображение обратимо, и обратное к нему отображение является непре-
> ■>
рывным отображением W->l/ = «~'W пространства 9?(G; G)
-*■ ■>
в пространство 9?(G\F). Теорема 25 показывает, что тогда
существует открытая окрестность (Ф/о)п элемента и0 в простран-
"*■ "*■ —1—1
стве 5?(F;G) и открытая окрестность С^о)„ элемента и0
■> ■>
в пространстве S?(G\F), такие, что каждый элемент и
окрестности C%io)n имеет единственный обратный справа элемент
ий1> лежащий в (<М0)~ ■ Кроме того, согласно теореме 26,
отображение и->и~х является непрерывным отображением (<U0)
в {aU^~ > дифференцируемым в точке и0. То же самое
рассуждение можно провести для обратного слева элемента w e
^9?(G\F) к элементу и е & {F;G), удовлетворяющего
условию wu=I. Точно так же определяются открытые множества
(<U^n и (^о)Г' и отображение и-*и~1 множества Ш0)л в (<U^j~{-
Обозначим теперь Ф/0 — (^о)п П СЦ>)Л- Это некоторая открытая
окрестность точки и0. Если и е <Мо, то одновременно существует
обратный слева элемент и~1 ъ (Ш^~ и обратный справа и~1
в (<%i0)~l- Однако, если некоторый элемент имеет
одновременно обратный справа и обратный слева, то они совпадают и
') В дифференциальных обозначениях d(uv) = du v0 + u0dv, и частная
производная по и в точке (и0, л0) есть отображение dv -> и0 dv.

§ 8. Теорема о неявной функции
303
рассматриваемый элемент обратим, ибо из ««"' = / и и~хи — 1
следует u~xuu~l = («J1«) и~1 = «"' и точно так же "J1 (""J1) —
-1
Мы видим теперь, что каждый элемент окрестности Щй
обратим. Отсюда следует, что <U является окрестностью каждой
своей точки, т. е. является открытым множеством. Меняя
ролями F и G, получаем тот же результат для множества аЫ-х.
Далее, отображение и-* и-1, совпадающее в окрестности <%
точки «о с отображением и-^-ий > непрерывно в точке «о, а,
следовательно, и всюду на <U. Его обратное отображение
обладает тем же свойством (в чем легко убедиться, меняя ролями
-> ->
F и G), а, значит, мы имеем гомеоморфизм ^ на с2^~1.
Наконец, по той же самой причине, это отображение
дифференцируемо вместе с обратным отображением.
Вычисление производной выполняется по правилу (III, 8; 23).
Дифференцируя uv — I, получаем
du°v + u°dv = 0. (Ill, 8; 31)
Умножая слева на и-1, находим
dv = — «-1 о du о v = — «-1 о du о«-'. (Ш, 8; 32)
Третье доказательство. Это доказательство пригод-
-> ->
но лишь в случае конечномерных пространств F и G. Тогда их
следует считать пространствами одинаковой размерности и1).
Выберем в каждом из них систему координат. Тогда их можно
-> -> -> ->
отождествить с пространством К", а 3? (F; G) и 3?(G; F)
отождествить с векторным пространством К,п квадратных матриц
из п строк и п столбцов. Пусть Ш—такая матрица, а тц, г =
= 1, 2, ..., п, J = 1, 2, . .., п, — ее элементы. Функция Ш ->
-*Д9Й) принадлежит классу Ст тогда и только тогда, когда
она является функцией п2 скалярных переменных т^-,
принадлежащей классу Ст. Определитель Ш -* det Ti является
полиномом относительно т.ц и, следовательно, является скалярной
бесконечно дифференцируемой функцией от Ш. Множество °U
обратимых матриц является прообразом множества СО при
этом непрерывном отображении, ибо матрица обратима тогда
и только тогда, когда ее определитель фО. Так как множество
СО открыто в К, то °U также открыто.
Матрица 9Й-1, обратная к матрице Ш, состоит из элементов
[' где Mji — алгебраические дополнения матрицы Ш; М^
') См. примечание на стр. 301,

304
Гл. 111. Дифференциальное исчисление
являются полиномами относительно т^, а, следовательно,
~, является скалярной бесконечно дифференцируемой
функцией на °U. Соответствие 9М —► 9М-1 является отображением
множества обратимых матриц °U вКш, составляющие которого
являются скалярными функциями класса С°°, и, следовательно,
оно само принадлежит классу С°°. Поскольку оно совпадает со
своим обратным отображением, мы имеем гомеоморфизм
класса С°°. Тем самым мы доказали нечто большее, чем
утверждалось в теореме: по этому поводу см. замечание к приведенному
ниже следствию.
Для того чтобы подсчитать производную отображения и -*
—► и-1, лучше всего воспользоваться концом второго
доказательства. Заметим, что в конечномерном случае, если и имеет
обратный справа элемент и~1, то, переходя к матрицам,
получим ЖШй1 — 1. Отсюда следует, что (det Ж) (det 3№^') = /. а,
значит, det 3M =7^=0, и мы получаем, что элемент и обратим (и его
обратным является элемент и"1).
Следствие. Пусть х-+и(х) — дифференцируемое
отображение открытого множества Я йффинного пространства Е в про-
-> -*■ -> -*■ ^
странство 9? (F\ G) (F и G —пространства Банаха).
Если для каждого )tsQ отображение и(х) является обра-
-> ->
тимым элементом пространства 3?{F; G), то х->и~х{х) является
дифференцируемым отображением О, в 9?{G\F) и его производ-
ная для 1е£ задается формулой
(и-уОе) • Х = - и-1 (х)о(и'(х) • X) »«"' (*) e=#(G; F). (111,8; 33)
В частности, если 9М является квадратной матрицей из
п строк и п столбцов, зависящей от скалярного параметра / и
дифференцируемой по /, и если она обратима для каждого /, то
производная обратной матрицы ЗМ-1 может быть вычислена по
формуле
d^=_m-i<m_m-i (III, 8; 34)
Для доказательства достаточно применить следствие к £=
-> ->
= К, F=G = Kn. При п=1 мы возвращаемся к производной
обратной функции для заданной скалярной функции /, нигде не
обращающейся в нуль:
(j)' = -f- (III, 8; 35)

§ 8. Теорема о неявной функции
305
Теперь можно применить полученные результаты к
дифференцированию неявных функций.
Теорема 28 (теорема о неявной функции). Пусть Е, F,
G — три аффинных нормированных пространства, f —
непрерывно дифференцируемое отображение открытого множества Q cz
cEXF в G.
1°) Пусть А и В — открытые множества в пространствах Е
и F соответственно, А X В cz Q, и пусть g — непрерывное
отображение А в В, удовлетворяющее условию (III,8; 2). Если для
каждого х из А частная производная -~ (х, g (x)) является об-
-» -»
ратимым элементом пространства 2?(F; G), то g является
непрерывно дифференцируемым отображением А в В.
2°) Пусть (а, Ь) — некоторая точка Q, f(a, b)=c. Если
-эМа» Ь) является обратимым элементом пространства 3?(F;G)
и пространство F полно, то существуют открытые множества А
и В в пространствах Е и F, содержащие соответственно а и Ь,
А X В cz Q, такие, что для каждого х^А уравнение (111,8; 1)
относительно у имеет, и притом единственное, решение в В и
определяемая им функция y=g(x) является непрерывно
дифференцируемым отображением А в В, а ее производная задается
формулой (III, 8; 16).
Доказательство. 1°) Из теоремы 26 вытекает, что g
дифференцируема в каждой точке А и что ее производная в точ-
ке х е А является элементом 3?(E;F), задаваемым формулой
g'(x) = -(^-(x,g(x))yl o^-(x,g(x)). (Ill, 8; 37)
Отображение x^>g(x) предполагается непрерывным в А,
а функции -J- и -г^ непрерывными в й. Следовательно,
х -> -^- (х, g (х)) и х ->• -J- (x, g (x)) являются непрерывными
отображениями А в пространства 3 (Е; G) и 3 (F; G)
соответственно. Так как и-* и-1 является непрерывным
отображением <U в <U~X (теорема 27), то функция х-> l-J-(x, g (х))\
-» -»
является непрерывным отображением А в 3{G;F).
Поскольку сложная функция (и, v)-*v°u является непре-
-» -» -» -» -» -»
рывным отображением 3? {Е; G) X 3? (G; F) в 3 (Е; F)
(теорема 54 гл. II), g' является непрерывным отображением
множества А в пространство S (E; F), а, значит, функция g
непрерывно дифференцируема на множестве А,

306
Гл. III. Дифференциальное исчисление
2°) Поскольку на этот раз пространства F. и G полны (см.
примечание на стр. 301: G полно, так как известен обратимый
df ■* ■*■
элемент -рг-(а> Ь) из 5?{F;G)), то множество %L обратимых эле-
ментов из &{F\ G) открыто. Так как (х, у)->-г~-(х, у) предпола-
-> J
гается непрерывным отображением Q в S"{F; G), то прообраз %1
при этом отображении является открытым подмножеством Qi
множества Q, содержащим (а,Ь). Теорема 25 применима к
сужению / на Q\ (поскольку F полно). Поэтому можно определить
такие открытые множества А и В в Е и F, содержащие
соответственно а и b, A X В cz Qi, что для каждого х^.А найдется,
и притом единственный, элемент у^В, являющийся решением
уравнения (111,8; 1) и такой, что определяемая при этом
функция y=g(x) из А в В непрерывна. Поскольку тогда (я, g(x)) <=
еДхйсЙ| для каждого х из А, то мы находимся в условиях
пункта 1°), а, следовательно, функция g непрерывно
дифференцируема, и по теореме 26 получаем (111,8; 16).
-> ->
Следствие. Если F и G — пространства Банаха, °и — от-
-> ->
крытое множество обратимых элементов пространства 3?(F;G),
то отображение и —► и-1 множества °и на °игх непрерывно
дифференцируемо вместе со своим обратным отображением.
Для доказательства достаточно применить теорему 28, п. 1°)
к уравнению uv = I (см. теорему 27, второе доказательство).
Можно также непосредственно доказать непрерывность
производной в теореме 27.
Частный случай, когда £=F=G= К—-скалярное поле
Напомним, что если через q=-^-(a,b) обозначить обычную
частную производную скалярной функции / двух скалярных
переменных, то ее частным производным отображением Q будет
умножение на q. Следовательно, оно обратимо тогда и только
тогда, когда частная производная q отлична от нуля. Отсюда
вытекает, что если функция f имеет непрерывные обычные
частные производные df/дх, df/dy (тогда, согласно теореме 15,
функция /дифференцируема) и q=-^~(a, Ь)ф0, то мы находимся
в условиях применимости теоремы 28 существования,
единственности и дифференцируемости неявной функции. Именно
при этих условиях дается обычно теорема о неявной функции

§ 8. Теорема о неявной функции
307
в математическом анализе. Формула (III, 8; 16) принимает вид
g'(a) = —§* . (Ill, 8; 38)
Предположим теперь, что -^- (а, 6) = 0, но -^- (а, Ь) Ф 0.
Тогда в окрестности точки (a, b) можно выразить х как
функцию у, x=h(y). Поскольку /*'(&)—0, кривая, определяемая
уравнением f(x,y) = c, имеет в точке (a, b) вертикальную
касательную, и невозможность выразить у как функцию х
становится очевидной.
Предположим, наконец, что -~(а, b) = -^-(a, b) = 0.
Кривая имеет в (а, Ь) особую точку. Эта точка может быть
изолированной особой точкой (например, если K=R, (a, b) = (0,0),
f(x,y)—x2 -f- у2). Тогда кривой в окрестности (a, b) не
существует. Однако, если кривая имеет, например, «двойную точку
с различными касательными», то можно в окрестности^(a, b)
попытаться разделить кривую на две различные ветви и для
каждой из них вычислить у как функцию от х или наоборот. Для-
простоты будем считать, что / принадлежит классу С3 и a=i=
= с=0. Вместо переменных х и у введем переменные х и т—
=у/х. Данное уравнение примет вид F(x, m)—f(x,tnx)=0.
Посмотрим теперь, позволяет ли это уравнение найти т как
функцию х. При х=0 функция F равна нулю при любом т и даже
в том случае, когда df/dx и df/ду не обращаются одновременно
в нуль в начале координат. Здесь, кроме того, производная
-^— = -J- + т-^- равна нулю при х — 0 и любом т. Позже
(теорема 119 гл. IV) мы убедимся, что отсюда вытекает
принадлежность к классу С функции G (х, т) — — 2 (значение этой
функции при х=0 определяется переходом к пределу).
Предположим, что разложение Тейлора функции / в начале
координат имеет вид
f(x,y) = ±(rx2 + 2sxy+ty2)+ .... (III,8;382)
Тогда в точке х=0, т=то имеем
G (0, т0) = lim Щр^- = ±(r + 2sm0 + tm§. (111,8; 383)
Если трехчлен т —► r -f- 2stn -f- trrfi имеет, два различных
корня m—rtii и tn=tn2 в К, то G(0, m^—O, G(0, m2)=0. Для

308
Гл. 111. Дифференциальное исчисление
уравнения G(x, m)=0 мы имеем два частных решения (0, т{) и
(0,т2). Если -^-(0, тг) и -^-(0, т2) отличны от нуля, то
теорема о неявной функции позволяет нам разрешить уравнение
G(x, т) = 0 в окрестности этих точек и получить две
функции т=щ(х) и т=ц2(х) класса С. Две ветви искомой кривой
будут определены уравнениями класса С1: у = хц\ (х), у=
=х\х.2(х). Касательные в начале координат к этим ветвям имеют
угловые коэффициенты mt и т2.
Производные -^(0, т) в корнях т\ и т2 трехчлена G(0, m)
не могут быть равными нулю, так как по условию эти корни
различны, а
-§§-(0,m0) = s + m0*. (Ш,8;384)
Итак, теорема о неявной функции может применяться даже
в тех случаях, когда ее условия непосредственно не
удовлетворяются.
Случай, когда Е, F, G конечномерны
Пусть Е, F, G — аффинные конечномерные пространства.
Пусть в присоединенных векторных пространствах Е, F, G вы-
браны базисы (е*)*ек> (f/)/e/. (gt)'tei> а в качестве начал
координат взяты начала пространств Е, F, G. Тогда
отображение fH3Qc£XfeG определяется формулами
Zi = Ft((Xk)keK,(y,)leJ), <е/. (III, 8; 39)
Непрерывность f выражается в том, что скалярные функции
F{ являются непрерывными функциями своих аргументов xh и
У). Сказать, что f имеет непрерывную частную производную по
второй переменной, означает сказать, что Ft имеют
непрерывные частные производные первого порядка по переменным у,
(теорема 15). Обратимость частного производного отображения
Q в точке (а, Ь, с), где c=f(a,b), означает следующее.
Прежде всего, G и F должны иметь одинаковую размерность, т. е.
должно быть /=/. Тогда рассматриваемая обратимость будет
иметь место тогда и только тогда, когда якобиан, состоящий из
элементов -~-(а, Ь), являющийся определителем матрицы ли-
оу J
нейного отображения Q, отличен от нуля. Если эти условия
выполнены, То в окрестности точки (а, Ь) можно (теорема 25)
определить у как функцию g(x), т.е. выразить у, в виде
У1 = 0,((хк\^к), /е/ = /. (III, 8; 40)
Если теперь функции F{ имеют частные производные не
только по переменным yit но также и по переменным xh, непрерыв-

§ 8. Теорема о неявной функции
309
ные в Q, то можно утверждать, что отображение / принадлежит
классу С1. Тогда можно применить теорему 28 и формулу
(III, 8; 16) и найти производную матрицу отображения g, т.е.
матрицу, составленную из частных производных функций r/j по
переменным xh, в виде отношения двух матриц. Если /=/=
= {1,2, ..., т}, ЛС={1,2, ..., л}, то
dO, dGl АО,
(III, 8; 41)
Вместо того чтобы производить вычисления с матрицами,
dGj
можно также найти частные производные -=— для фиксиро-
°xk
ванного k и /.е/, придавая х приращение ^.определенное
условиями dxk'= dxk, если k' = k, и 0, если k' Ф k, и вычисляя
дифференциалы dyit /е/, путем решения системы т линейных
уравнений с т неизвестными и отличным от нуля
определителем (ибо он является якобианом):
1г *** + Е if *У1=°' ' ^ L (1П'8; 42)
Обратная функция как неявная функция
Найти обратную функцию x=g(y) для некоторого
гомеоморфизма y=f(x) означает решить относительно хъ уравнение
/(х)=г/ для каждого заданного у. Эта задача является задачей
отыскания неявной функции.
Теорема 29. Пусть Е и F — аффинные полные
нормированные пространства и f —: непрерывно дифференцируемое
отображение некоторого открытого множества Q cr Е в F.
1°) Если а — точка множества Q и f (a)—обратимый
элемент пространства 9? (Е; F), то образ каждой окрестности
точки а при отображении f является окрестностью точки b=f(a)
и образ каждого открытого шара с центром в точке а при этом
отображении содержит некоторый открытый шар с центром
в точке Ь. Существуют такие открытые множества А и В в

310 Гл. 111. Дифференциальное исчисление
пространствах Е и F, содержащие соответственно а и Ь, что f
является гомеоморфизмом А на В, непрерывно
дифференцируемым вместе со своим обратным гомеоморфизмом.
Кроме того, имеем:
(Г1)' {Ь) = (Г (а)Г1. (111,8:43)
2°) Если для каждого jgQ производная f'(x) является
обратимым элементом из S' (Е; F), то образ каждого открытого
множества из Q при отображении f является открытым
множеством и, в частности, /(Q) является открытым множеством в F.
Если, кроме того, отображение f инъективно, то оно является
гомеоморфизмом множества Q на f(Q), непрерывно
дифференцируемым вместе со своим обратным гомеоморфизмом.
Доказательство. Мы видели, что обратное отображение
g' = f~l является неявной функцией х == g(у),определяемойурав-
->■
нением fi(x, у) =f (х) — у=6, где fi—отображение Q X F B F-
Применим предыдущие теоремы с неизбежным изменением
обозначений: мы будем искать х как функцию у, а не наоборот.
Поэтому необходимые предположения будут относиться к
частной производной относительно х: -^- = ——. Здесь Е полно, a f i
непрерывно дифференцируемо на Q X Л поскольку его частные
производные -—• (х, у) — f (х) и — = — / непрерывны
(теорема 15).
Докажем утверждение 1°). Условия, необходимые для
применения теоремы 28, 2°), выполнены в (а, Ь). Следовательно,
можно найти такие открытые множества А0 и й, а е 4 с Е,
b^BcF, что уравнение f{x)=y для у^В имеет в А0
единственное решение х и таким образом определенная функция
x=g(y) есть непрерывно дифференцируемая функция из В
в Ао. Однако эти открытые множества Ло и В не отвечают
непосредственно требуемым условиям. Образ f(A0) «покрывает В
один и только один раз», но он слишком велик: f (Ао) => В. Нам
надо взять А=А0 ()f~l(B). Тогда f будет отображать А в В.
Впрочем, для у^В точка g(y) множества А0 заведомо лежит
в прообразе ^(В) (поскольку f(g{y)):=y^ В), а,
следовательно, в А. Таким образом, g отображает В в А. Итак, f и g — два
взаимно обратных отображения А в В и В в А, где В открыто
по построению и А открыто как пересечение двух открытых
множеств. Отображение f непрерывно дифференцируемо по
определению, a j по теореме о неявной функции. Следовательно,
мы имеем два непрерывно дифференцируемых взаимно
обратных гомеоморфизма. Пусть теперь У— некоторая окрестность
точки а в Q. Тогда У П А является окрестностью точки а в А,

§ 8. Теорема о неявной функции
311
и так как f — гомеоморфизм А на В, то множество f(Tf]A)
является окрестностью точки Ь в В, а, значит, ив/7, поскольку
В — открытое множество в F. Множество \{Т) тем более
является окрестностью точки Ъ в пространстве F. Множество У
может быть, в частности, некоторым открытым шаром с
центром в точке а. Множество f(T), как окрестность точки Ъ,
содержит некоторый открытый шар с центром в точке Ъ. Таким
образом, утверждение 1°) доказано. Производная функции g
в точке Ъ вычисляется по правилу (III, 8; 23): надо решить
относительно dx уравнение
f (a)dx-dy = 0, (III, 8 44)
что дает
dx= (f'(a)fldy, (III, 8; 45)
откуда и вытекает (111,8; 43).
Докажем теперь утверждение 2°). Пусть О — открытое
множество из Q. Множество О является окрестностью для каждой
своей точки х. Так как f'(x) обратима, то, согласно Г), f{0)
является окрестностью точки f(x), а, следовательно, множество
ЦО) открыто. В частности, открыто множество f(Q). Если,
кроме того, отображение f инъективно, то оно является
биективным и непрерывным отображением множества Q на множество
f(Q), и образ каждого открытого множества открыт. Согласно
теореме 11 гл. II, отображение f является гомеоморфизмом.
Если а — произвольная точка Q, то в открытом множестве В,
определенном в Г), функция f"1 совпадает с функцией g, и,
следовательно, непрерывно дифференцируема в В, а, значит,
во всем множестве f(Q).
Замечание. Теорема 29, Г) приводит к той же формуле,
что и следствие 4 теоремы 11. Но две эти формулировки до
некоторой степени обратны одна другой, поскольку, с одной
стороны, для обратимости f'(a) нужны два дифференцируемых
взаимно обратных гомеоморфизма, а, с другой стороны, для
нахождения двух взаимно обратных дифференцируемых
гомеоморфизмов нужна обратимость f'(a). Очевидно также, что
условие 29, 2°) носит более тонкий характер.
Если Е и F конечномерны и если в них выбрана система
координат, то обратимость f'(a) означает, что Е и F имеют одну
и ту же размерность и что якобиан функции f в точке а в
выбранной системе координат отличен от нуля.
Теорема 29 приводит к следующему определению:
Определение. Пусть Q и F — два топологических
пространства и f — непрерывное отображение Q в F. Говорят,
что f является открытым отображением, если образ каждого

312 Гл. 111. Дифференциальное исчисление
открытого множества из Q при отображении f является открытым
множеством в F. Говорят, что f является локальным
гомеоморфизмом пространства Q в пространство F, если для любой
точки а е= Q существует открытое множество А в Q, содержащее а,
и открытое множество В в F, содержащее Ь, такие, что f
является гомеоморфизмом А на В.
Теперь легко проверяются следующие утверждения:
A) Для того чтобы отображение f было открытым,
необходимо и достаточно, чтобы для каждой точки aeQ образ любой
окрестности точки а при отображении f был окрестносФью
точки f(a), или чтобы для каждой точки а образ любого открытого
шара с центром в а при отображении f содержал некоторый
открытый шар с центром в точке f(a). (Достаточность была
установлена при доказательстве теоремы 29,2°), а необходимость
очевидна.)
B) Всякий локальный гомеоморфизм является открытым
отображением. Этот факт мы установили при доказательстве
теоремы 29, 1°): когда f — локальный гомеоморфизм, для любой
точки х е= Q и любой окрестности У точки х множество \{У)
является окрестностью точки f(x), а, следовательно, согласно А),
отображение /открыто.
C) Если f — непрерывно дифференцируемое отображение
некоторого открытого множества Q полного аффинного
нормированного пространства Е в аффинное нормированное
пространство F и если для каждого ^ей производная f'(x) обратима,
то f является локальным гомеоморфизмом Q в F. Это
устанавливает теорема 29. В частности, f является открытым
отображением, a f(Q) является открытым множеством в F.
D) Открытое инъективное отображение f является
гомеоморфизмом Q на образ f(Q). Этот факт установлен нами при
доказательстве теоремы 29, 2°).
Следующая схема подводит итог полученным результатам.
Предполагается, что f является непрерывным отображением
топологического пространства Q в топологическое пространство/7.
E,F — полные
аффинные нормированные
пространства, Q —
открытое множество из
Е, f непрерывно
дифференцируемо, f (х)
обратимо для
каждого гей
f является
локальным
гомеоморфизмом
f
открыто
ф
образ каждой
окрестности точки х при
отображении f является
окрестностью точки f(х)

§ 8. Теорема о неявной функции
313
Необходимо иметь в виду, что здесь нельзя заходить
слишком далеко и что, в частности, обратные утверждения к
указанным выше следствиям не верны.
Рассмотрим С). Если f является непрерывно дифференци-
груемым локальным гомеоморфизмом Q в F, то его производная
f'{x) не обязательно обратима для каждого х е Q. Например,
х-+х3 является дифференцируемым гомеоморфизмом R на R,
но его производная равна нулю в начале координат а,
следовательно, его обратный гомеоморфизм у—>Yу не
дифференцируем в начале координат.
Z Рассмотрим В). Открытое отображение не обязательно
является локальным гомеоморфизмом. Например, всякая
проекция произведения топологических пространств на пространства-
сомножители открыта, как это следует из определения
окрестностей, но, вообще говоря, не является локальным
гомеоморфизмом (проекция (х, у)—>х пространства R2 на R не
является локальным гомеоморфизмом!).
Наконец, в D) условие «отображение / инъективно»
необходимо точно так же, как в теореме 29,2°). Например,
отображение z-+z2 пространства С в С, суженное на открытое
множество Q, дополнительное к началу координат, удовлетворяет
условию «f'(z)=2z^=0 обратимо для каждого 2еЕ1». Значит,
оно является локальным гомеоморфизмом и открытым
отображением, но не является гомеоморфизмом, поскольку оно не
инъективно.
Вернемся к теореме 29. Предполагая f'(a) обратимой, мы
доказали свойство гомеоморфности. Отсюда как следствие
вытекает менее сильное свойство открытости отображения. Это
последнее свойство связано с менее сильным свойством, чем
обратимость f'(a), а именно с сюръективностью:
Теорема 30. Пусть f — непрерывно дифференцируемое
отображение открытого множества Q нормированного
аффинного пространства Е в конечномерное аффинное
пространство F.
Г) Если а — точка Q и если f'{a) —сюръективное отобра-
-> ->
жение Е на F, то образ любой окрестности точки а при
отображении f является окрестностью точки f(a), а образ каждого
открытого шара с центром в точке а содержит некоторый ОТ'
крытый шар с центром в f(a).
2°) Если f'(x) для любого х е Q является сюръективным
-> ->
отображением Е на F, то образ каждого открытого множества
из й при отображении f является открытым множеством в F.
В частности, f(Q) является открытым множеством. (Другими
словами, f является открытым отображением.)

314 Гл. 111. Дифференциальное исчисление
Предположение о том, что F конечномерно, очевидно,
слишком ограничительно. От него можно избавиться, предполагая
Е и F полными.
Доказательство. Докажем утверждение 1°). Пусть
ifi), i= 1,2, ..., т,— некоторый базис в пространстве F. По-
скольку отображение f'(a) сюръективно, существуют векторы Хи
-*■ •> ->■->■
Xi, ..., Хт, имеющие образами векторы f,-. Векторы Х{ линейно
независимы, поскольку линейно независимы их образы при
отображении f'(a); поэтому сужение f (а) на m-мерное векторное
-> ->
подпространство Е0, порожденное векторами Хи является сюръ-
->■->■ ■>•-».
ективным отображением Е0 на F. Но так как Е0 и F имеют
одинаковую размерность, то f'{a) является биективным отображе-
-> ->
нием Е0 на F; другими словами, рассматриваемое как линейное
-*■-*■■ ->
отображение Е0 в F, оно обратимо. Пространство Е0, в силу
конечномерности, полно (теорема 41 гл. II). Сужение
отображения f на аффинное подпространство Е0, проходящее через а
параллельно Е0, имеет в точке а обратимую производную, а само
Е0 полно. Применяя к нему теорему 29, получаем
утверждение 1°). Мы видим, что если Т является окрестностью точки а,
то не только образ f(Y) является окрестностью f(a), но даже
f (Т П £о) есть окрестность точки f(a).
Переход к 2°) производится точно так же, как при
доказательстве теоремы 29, т. е. С использованием критерия А) для
открытых отображений. Естественно, здесь не возникает вопроса
о том, является ли f локальным гомеоморфизмом, так как f (x)
не предполагалось инъективным.
Вычисление производных высшего порядка неявной функции
Теорем а 31. Если при условиях теоремы 28 функция f
непрерывно дифференцируема m раз в Q, то неявная ■ функция g
непрерывно дифференцируема m раз в А.
Доказательство. Поскольку эта теорема уже доказана
для т=1 (теорема 28), рассуждения будем проводить по
индукции: предположим, что она доказана для ■ производных
порядка m — 1, и докажем ее для производных порядка m ^ 2.
Заметим сначала, что уравнение uv — I, рассматриваемое во
втором доказательстве теоремы 27, входит сюда в виде уже
изученного случая, ибо функция (и, v) —> uv билинейна и
непрерывна, а, следовательно, бесконечно дифференцируема.
Отображение «—*«"', в силу индуктивного предположения,
принадлежит классу Cm_1 на Щ. Рассмотрим теперь формулу

§ 8. Теорема о неявной функции
315
(III, 8; 37). Функция g непрерывна, поскольку, в силу
индуктивного предположения, она принадлежит классу Cm_1.
Функция df/dx принадлежит классу Cm_1, так как f принадлежит Ст.
Поэтому, согласно теореме 19, отображение х -> -^- (х, g (х))
принадлежит классу Cm_1. To же самое имеет место для
отображения х->-^-(х, g{x)). Поскольку, как мы только что видели,
функция и—►«"' также принадлежит классу О-1, из теоремы 19
следует, что функция х ->i~-(x, g(x))) принадлежит классу
О-1. Наконец, {и, v)-+vou является билинейным непрерыв-
ным отображением 2?(Е; G) )>(9?(G\F) ъ 2! (Е; G) (теорема 54).
Из теоремы 18 следует, что g' принадлежит Ст~\ а, значит, g
принадлежит классу Ст.
->
Следствие 1. Если F и G—пространства Банаха, а %1
(соответственно Щ~у) — открытое множество обратимых элемен-
-> ->- ->->■
тов из 3?(F\ G) (соответственно из 3? (G\ F)), то u->wl является
гомеоморфизмом <и на И'1, бесконечно дифференцируемым
вместе со своим обратным гомеоморфизмом.
Это дополняет теорему 27. По существу мы уже доказали
это следствие по индукции во время доказательства теоремы 30.
Определение. Если биекция вместе со своей обратной
биекцией принадлежит классу Ст, но она называется
^-диффеоморфизмом. Так, например, отображение и->и-1 является
С°°-диффеоморфизмом 1С на li'1.
->
Следствие Ь- Если и является m раз дифференцируемым
отображением (соответственно принадлежит классу Ст)
открытого множества О. аффинного нормированного пространства Е
-> -* -*■
в пространство 9?(F\G) и если и(х) для каждого xgQ яв-
> ->
ляется обратимым элементом пространства 9?(F; G), то х-*
-*■ и~1 (х) является m раз дифференцируемым (соответственно
принадлежащим классу Ст) отображением Q в 3?(G\F).
Это вытекает из следствия 1 и теоремы 19, примененной
к композиции отображений х —>и(х) и и—►и-1.
Отметим важный частный случай: функция l/f, обратная
-> -> -> ->
к скалярной функции f (F=G= K=3?(F; G)), m раз
дифференцируемой или принадлежащей классу Ст на Q cr E и всюду
=7^=0, также m раз дифференцируема или принадлежит
классу Ст.

316
Гл. III. Дифференциальное исчисление
Если t-*M(t) является дважды дифференцируемой
функцией, определенной на К, со значениями в пространстве
квадратных матриц и если Ш(1) обратима для каждого t, то
вторая производная -^(W1) получается непосредственным
дифференцированием (III, 8; 34):
•^(fflrV 2а»-1-^ эг1 -f^r1 - эг1 ^эг1.
Следствие 2. Если в условиях теоремы 29,1°)
отображение f принадлежит классу Оп, то обратная биекция /_I
отображения I является отображением В в А класса Cm: f является
Ст-диффеоморфизмом А на В.
Вычисление в самом общем случае производной функции g
порядка т, исходя из частных производных функции /
порядков ^т, приводит к чрезвычайно сложным алгебраическим
выражениям.
Мы ограничимся рассмотрением частного примера. Пусть
/ — функция трех вещественных переменных. Будем считать,
что уравнение
f(x,y,z) = 0 (III, 8; 46)
определяет z как функцию переменных х и у в окрестности
точки, в которой частная производная df/dz отлична от нуля.
Вычислим в этой точке частные производные р, q, r, s, t
функции z, исходя из частных производных функции /. В (111,8; 16)
мы уже получили формулы
(Ш, 8; 47)
dz
dx
df
дх
df '
dz
Я
dz
ду
df
ду
df
dz
Остается теперь с помощью теоремы о сложной функции
продифференцировать предыдущие выражения по х и у и
получить следующие выражения:
_ d*z
r~~ dx2
дЧ (dff d2f df df d2f I df \2
dx2\dz) "*" dx dz dx dz dz2 \ dx )
№
d2f (dfy d2f df df 32f df df d2f df df
d2z dx dy \dz) "*" dx dz dy dz dy dz dx dz dz2 dx dy
S~~ dxdy~~ /д[\я
d*t ( df у d2f df df d*f I df \2
. __d2z _ dy2 \dz ) ~* dydz dy dz dz* \ dy ) mT R. AK,
l~~dY~ /df\3 ' \ln'°' *°)
\дг)

§ 8. Теорема о неявной функции
317
Можно поступить иначе. Соотношение, дающее р,
записывается в исходном виде
■Ш+РШ-0- <ш.8;4в)
Затем полученное равенство дифференцируется по х и у с
одновременной заменой dz, dp, dq на pdx-\-qdy, rdx+sdy,
sdx-\-1 dy. Таким путем получается соотношение
&dx + ^dy+-£&<Pdx+qdy) + -ILirdx + 8dy) +
+ P-£kdx + Pwkdy+Pwr(Pdx + (ldy)==0- ("1.8; 50)
Приравнивая затем пулю коэффициенты при dx и dy,
получаем некоторые равенства, из которых находятся частные
производные г и s. Аналогичные вычисления проводятся исходя из
df , df _
соотношения ~^- + q ■^г_ = 0 Для нахождения sat.
Существует другой метод, использующий разложение
Тейлора (см. теоремы 212 и 213).
Запишем разложение Тейлора функции / в окрестности
точки х, у, г до 2-го порядка:
0^f(x + X,y + Y,z + Z)-f(x,y,z) = -^X + ^Y+^Z+.
+ 2^УгХ + 2жкХ¥}+-' (И1.8;Б1)
Если в этой формуле Z заменить его разложением Тейлора
в точке X, Y, т. е. положить
Z = pX + qY + ±(rX2 + 2sXY + tY2) + ..., (Ill, 8; 52)
то получится тождественный нуль. Приравнивая нулю
коэффициенты при X, Y, X2, XY, Y2, получим 5 уравнений, дающих р,
q, r, s, t. Прежде всего, приравнивая нулю коэффициенты при
X и Y, получаем соотношения для определения р и q.
Приравнивая затем нулю коэффициенты при X2, XY, Y2, находим
dz l + dy* + dz* q + ^ ду дг Ч U'
откуда и получаются выражения (III, 8; 48).

318
Гл. III. Дифференциальное исчисление
В этом методе, использующем разложение Тейлора, можно
провести другой вариант преобразований: вычислить первые
производные р и q, перейти к вычислению вторых, приравнивая
нулю соотношение (III, 8; 51) и выражая в нем Z как функцию
других величин, т. е. X, Y, X2, XY, У2, XZ, YZ, Z2. При этом
получится формула
df df df y_JT^L У2,^[_ V2,il 72,
"dz — ~~дх~Л ду \ 2LWA +^' ^ dz*^ ^
в которой переменная^ выражена через XZ, YZ и Z2. Однако
для того чтобы иметь приближение второго порядка, можно
удовлетвориться заменой в этом выражении Z на рХ-\-qY, где
р и q были вычислены ранее. Таким путем получим выражение
дг*-~ дх ду1
~i[uX2 + 2l^XY+^Y2 + 2l^XW + M +
+ 2^¥(РХ + М + Т?(РХ + №2]+--- (И1,8;бб)
Вычисляя коэффициенты при X2, 2XY, Y2 в разложении Z,
1 1 1 ,
снова получим у г, —s, у г.
Техника замены переменных и замены функций
С заменой переменных мы встречались ранее до теоремы
о неявной функции, но теперь эта теорема позволяет
производить значительно более важные замены.
Предположим, что задано уравнение в частных производных
второго порядка относительно скалярной функции z двух
скалярных переменных х и у:
F (х, у, Z, р, q, r, s, 0 = 0. (III, 8; 56)
Необходимо выполнить в нем одновременно замену^
переменных и замену функции по формулам
X = X(x,y,z), Y = Y{x,y,z), Z = Z(x, у, z) l). (Ill, 8;57)
Мы хотим узнать, как преобразуется рассматриваемое
уравнение в частных производных при такой замене переменных.
Она законна лишь в том случае, когда (III, 8; 57) определяет
С2-диффеоморфизм некоторого открытого множества из К3 на
открытое множество в К3 и поверхность z = z(x,y), определяе-
1) X, Y, Z имеют, очевидно, не тот смысл, какой им придавался ранее.

§ 9. Дифференцируемые многообразия
319
мая уравнением (III, 8; 56), преобразуется в поверхность Z =
= Z(X,Y) так, что обе написанные функции принадлежат
классу С2. Следуя обычному методу, надо выразить р, q, r, s, t
как функции новых частных производных Р, Q, R, Ss Т. Можно
начать с производных первого порядка и затем перейти к
вычислению производных второго порядка. Для производных первого
порядка можно начать с соотношения dZ = PdX + QdY,
заменяя dX, dY, dZ их дифференциальными выражениями,
найденными из (III, 8; 57), и получая таким путем соотношение между
dx, dy, dz. Это соотношение, представленное в виде dz — pdx +
+ qdy, позволит выразить р и q через х, у, z, P, Q.
Дифференцируя полученное соотношение, затем находим dp как функцию
от dx, dy, dz, dP, dQ. Заменяя dz, dP, dQ на pdx + qdy, Rdx-\-
+ Sdy, SdX + TdY, затем р и q их значениями, найденными
прежде, dX и dY — их значениями, полученными из (III, 8; 57)
(где dz должно быть заменено на pdx + qdy с уже найденными
р и q), мы выражаем dp как комбинацию dx и dy, которая,
будучи представленной в виде dp = rdx + sdy, дает г и s как
функции от х, у, z, P, Q, R, S, Т.
Точно так же вычисляется t. Полученные результаты
подставляются в (III, 8; 56).
Полученное уравнение относительно Р, Q, R, S, Т содержит
в действительности величины х, у, z, а не X, Y, Z. Поэтому, если
эти переменные входят в уравнение, следует еще выразить
(х, у, г) через (X,Y,Z), решая систему уравнений (III, 8; 57)'),
§ 9. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ
В теореме 8А мы рассматривали множество <5 в
произведении аффинных пространств Е X Л определенное уравнением
y = f(x). Оно называется дифференцируемым многообразием,
если f является дифференцируемой функцией. Это множество
называется пг раз дифференцируемым многообразием, если
функция f дифференцируема m раз; непрерывно
дифференцируемым многообразием или пг раз непрерывно
дифференцируемым многообразием, если f непрерывно дифференцируема или
пг раз непрерывно дифференцируема; бесконечно
дифференцируемым многообразием, если f бесконечно дифференцируема.
Вместо того чтобы говорить, что многообразие пг раз непрерывно
') Вместо (III, 8; 57) могут быть заданы старые координаты как функция
Новых или заданы три неразрешенных соотношения между старыми и
новыми переменными. Имеется много возможных вариантов. Вместо того
чтобы начать сразу применять стандартную замену, надо сначала подумать!
В математическом анализе можно встретить, например, такую замену
переменных, когда кривизна кривой у = у(х), выраженная через у' и у в
декартовой системе координат, вычисляется как функция от г, г', г" для кри«
вой г=_г{<р), заданной в полярных координатах.

320
Гл. III. Дифференциальное исчисление
дифференцируемо, говорят, что оно принадлежит классу Ст.
Вместо того чтобы говорить, что многообразие бесконечно
дифференцируемо, говорят, что оно принадлежит классу С°°. Чаще
всего встречаются многообразия, принадлежащие классам Ст
и С°°. Если т = 0, то многообразие называется топологическим.
Оно определяется уравнением y — f(x), где функция / непрег
рывна. Топологические многообразия играют очень важную
роль, но мы ограничимся изучением многообразий класса Ст
при т ^ 1.
Очевидно, что такое определение многообразия не является
самым общим. Так, например, в евклидовом аффинном
пространстве размерности N естественно рассматривать сферу как
бесконечно дифференцируемое многообразие размерности N—1.
Однако если выбрать в нем систему координат, то невозможно
описать полностью всю сферу, выражая одну из координат
как бесконечно дифференцируемую функцию остальных1).
Придется разделить сферу на достаточно малые области, так
чтобы в каждой из этих областей можно было одну из
координат выразить как бесконечно дифференцируемую функцию
остальных. Это обстоятельство приводит' к общему понятию
многообразия класса Ст.
Определение многообразия путем выражения некоторых
координат как функции остальных. Пусть Е — аффинное
пространство размерности N над полем К вещественных или
комплексных чисел и V — некоторое подмножество Е. Множество
V называется многообразием размерности п, принадлежащим
классу Ст, если для каждой точки а множества V
существуют: система координат 0, е\, е%, ..., eN пространства Е,
открытое множество & в подпространстве, натянутом на п
первых координатных осей, система Л; — п скалярных
функций Ck, k = 1,2, ..., N — п, класса Ст, определенных на Jf,
открытое множество У пространства Е, содержащее а,
проекция которого на подпространство, натянутое на п первых
осей, совпадает с <%, такие, что пересечение V П У° является
в точности множеством точек х = (хи ..., xN) из Е,
удовлетворяющих уравнениям
Xn+k = Gk(xu ..... xN)2), fc==l,2 N-n. (Ill,9; 1)
') Уравнение сферы с центром в начале координат радиуса J) в R"
имеет вид хп = ± УR —Х\ — ... — *„_q. Из-за наличия знаков ± это не
одна функция (и даже если выбрать знак +, то не получится функция,
дифференцируемая при хп = 0).
2) Согласно указанному свойству проекции множества Т., точка
(х\, х2, .,., хп) лежит в Ш, где определены функции 0\.

§ 9. Дифференцируемые многообразия 321
Итак, в Т последние N— п координат хп+и . .. , xN на
многообразии V выражаются как функции класса О первых
координат хи Хг, ..., хп, которые можно выбирать в $} произвольно.
(В том, что первые координаты играют особую роль, нет ничего
удивительного, поскольку для рассматриваемой точки а из V мы
выбираем систему координат в Е. Если эту особую роль играют
другие координаты, то изменением порядка векторов в системе
координат можно добиться того, чтобы это были первые п
координат.)
Позже мы дадим (следствие теоремы 32) эквивалентное
определение, в котором первые п координат не играют
никакой особой роли, поскольку раз и навсегда выбирается
определенная система координат в Е.
Можно еще сказать, что разделение системы из N
координат на п первых и N — п остальных равносильно
представлению Е в виде произведения Kn X KN~n и что, если обозначить
через g отображение открытого множества 38 из Кп в KN~n,
определенное формулами (111,9; 1), то g принадлежит классу
С™, а множество V Г) У является в точности множеством точек
х = (у, z) из Е = Кп X KN~n, удовлетворяющих уравнению
z = g{y)-
Таким образом, мы вернулись к частному случаю,
рассмотренному в теореме 8А, но для того, чтобы это стало
возможным, мы в окрестности точки а специальным образом выбрали
систему координат.
Определение многообразия при помощи
его параметрического представления
Пусть V — множество N-мерного аффинного пространства
Е. Истинным ') параметрическим представлением множества V
размерности п, принадлежащим классу Ст, называется
отображение Ф: ы->Ф(ы) открытого множества О из Кп в Е,
обладающее следующими свойствами:
1°) Ф является гомеоморфизмом О на V;
2) Ф является отображением множества О в
пространство Е, принадлежащим классу Ст;
3°) в каждой точке а= (ai, аг, •.., ап) е С? производное
отображение Ф'(а) е 9?(Кп; Е) имеет ранг п. Иначе говоря,
образ векторного пространства Кп при этом отображении
является векторным подпространством в Е размерности п, т. е.
частные производные векторы -з—(а), /— 1, 2, ..., п, являются
линейно независимыми векторами в Е, т. е. хотя бы один из
') В дальнейшем слово «истинное» часто опускается. — Прим. pedt
11 Зак. 1339

322
Гл. III. Дифференциальное исчисление
определителей ранга п производной матрицы (матрицы, со-
ставленной из элементов -=— (а)) отличен от нуля.
Можно подумать, что многообразия размерности п класса
Ст из Е будут единственными множествами, допускающими
такое параметрическое представление. С другой стороны,
совершенно очевидно, что многообразие, вообще говоря, может
и не иметь такого параметрического представления. В самом
деле, для параметрического представления необходимо, чтобы
рассматриваемое многообразие было гомеоморфно некоторому
открытому множеству из Кп. Пример сферы, являющейся
компактным множеством, показывает, что многообразие может не
быть, вообще говоря, гомеоморфным открытому множеству из
Кп. Мы снова убеждаемся, что только достаточно малые
области многообразия могут иметь такие параметрические
представления.
Конечно, в задание Ф входит задание открытого
множества О из К" и его образа Ф((У) в V, но их обычно
указывают, когда пишут Ф : О —>Ф((У).
Теорема 32. Для того чтобы множество V некоторого
аффинного пространства Е размерности N было
многообразием класса С™ размерности п, необходимо и достаточно,
чтобы для каждой точки а е V существовала такая открытая
окрестность Т точки а в Е, чтобы пересечение V П Т
допускало параметрическое представление размерности п,
принадлежащее классу Ст.
Доказательство. 1°) Предположим, что V является
многообразием размерности п, принадлежащим классу Ст.
Пусть а — некоторая точка V. Определим открытые множества
$ и Т, как это было сделано в определении. Тогда для того,
чтобы получить параметрическое представление искомого
вида, достаточно положить О = $ и при помощи функций Gk
из (111,9; 1) определить отображение и—*х = Ф(и)
формулами
Х\ = М[, . . ., Хп = Un, -Кя+1 ==: "I \Цц • • • 1 Мц), . . ., Xм =
— Gjv-n("i. ■■■> "«)• (HI.9;2)
Г) (х х \
Здесь якобиан „, ' —Ц- отличен от нуля ').
2°) Предположим теперь, что V есть некоторое множество
пространства Е, обладающее указанными свойствами. Дока-
') То, что мы здесь проделали, напоминает «хитрый» прием
первокурсника, который для исследования кривой у =■ f(x) предпочитает записывать
ее в виде х = t, у = /(/).

§ 9. Дифференцируемые многообразия
323
жем, что тогда V является многообразием размерности т,
принадлежащим классу Ст.
Пусть а — некоторая точка V и Ф — истинное
параметрическое представление, т. е. гомеоморфизм некоторого
открытого множества О из Кп на окрестность а в V. Выберем
произвольно систему координат в Е. Тогда отображение Ф будет
иметь в точке а = Ф~'(а) некоторую производную матрицу по
отношению к системам координат в К™ и Е. Эта производная
матрица по предположению имеет ранг п, и по крайней мере
один из ее определителей п-то порядка фО. Изменяя при
необходимости порядок векторов базиса Е, мы можем
предполагать, что этот определитель является якобианом
г., ' —Ч-. Таким путем построенная система координат
D(ui и„) J l t
в Е отождествляет это пространство с пространством KN,
а разделение на систему из п первых координат и N — п
остальных отождествляет его с K"XKJV_n. Поэтому каждую
точку х из Е мы будем представлять как пару (y,z), г/еКп,
геК5""". Пусть а = (Ь,с). Отображение Ф является
отображением открытого множества О в произведение К"ХК^"
и, следовательно, разлагается на систему двух отображений X
и W множества О соответственно в пространства К™ и К"-",
а именно: г/ = Х(ы), z = x¥(u). Но тогда якобиан
отображения X множества (У а Кп в точке а отличен от нуля.
Следовательно, согласно теореме 29, существует открытое множество
s4- в множестве О, содержащее точку а, и открытое
множество $ в пространстве К™, содержащее точку Ь, такие, что X
является гомеоморфизмом s4- на $, непрерывно
дифференцируемым вместе со своим обратным гомеоморфизмом. Кроме
того, отображение X принадлежит классу Ст, а следствие 2
теоремы 31 говорит о том, что его обратный гомеоморфизм
также принадлежит классу Ст. Обозначим этот обратный
гомеоморфизм ^ на rf через Х-1. Образ s£ при отображении Ф
является открытым множеством в V, поскольку Ф есть
гомеоморфизм множества О на его образ, являющийся открытым
множеством в V. Следовательно, существует такая открытая
окрестность У точки а в Е, что Ф($&)= V [)У. Поскольку
Ф(.5#) проектируется в пространство Кп на множество $,
можно считать, что множество У также проектируется на !Й
(в противном случае можно взять его пересечение с
открытым множеством {х; (х\,х2, ■.. ,хп)^Щ пространства К*"'). Для
того чтобы точка х = (у, z) принадлежала пересечению ]/[)У,
необходимо и достаточно, чтобы она была образом некоторой
точки из s4- при отображении Ф, т. е. чтобы точка у
принадлежала <%, а точка z была связана с точкой у формулой z =
= W(X~i(y)). Эта композиция g = 4foX"1 двух отображений
11*

324
Гл. III. Дифференциальное исчисление
класса Ст, по теореме 19, сама является отображением класса
Ст. Итак, нам удалось найти окрестность У точки а в
пространстве Е и некоторую систему координат в Е, такие, что
пересечение V Г) У представляется с помощью уравнения z =
= g(y), где g- —отображение 98 в Е класса Ст. Поскольку
это верно для любой точки а из V, то V является
многообразием размерности п класса Ст.
Одновременно мы доказали, что если заранее выбрать
определенную систему координат в Е, то для каждой точки а
из V достаточно соответствующим образом изменить порядок
векторов базиса для того, чтобы получить систему координат,
обладающую свойствами, указанными в определении
многообразия. Это изменение, очевидно, зависит от выбора точки а.
Таким образом, можно сформулировать
Следствие 1. Пусть V — некоторое множество
аффинного пространства Е размерности N. Для того чтобы V было
многообразием размерности п класса Ст, необходимо и
достаточно, чтобы при произвольно выбранной системе координат
в Е для каждой точки йе1/ выполнялись следующие
условия: найдется такая перестановка а = {сть сгг, ..., on} множества
1,2, ..., N, что существуют некоторое открытое множество 98
в подпространстве, порожденном началом координат и базис-
-*■-*■ ■>
ными векторами е^, ва2 е0п, и открытое множество
У czE, содержащее а, проекция которого на предыдущее
подпространство совпадает с 98; кроме того, существует система
N — n скалярных функций Gk, k=l, 2, ..., N — п, класса С'п,
заданных на 98 и таких, что пересечение V Г\У определяется
уравнениями
Xen+k = Gk(xai, ха2, ..., Хап), k=l, 2 N — п. (III, 9; 3)
Следствие 2. Пусть Е и F — два конечномерных
аффинных пространства одной и той же размерности, Н —
диффеоморфизм класса Ст некоторого открытого множества Щ
из Е на открытое множество Н (Щ) из F. Тогда если V
является многообразием размерности п класса Ст в множестве
<U, то его образ H(V) является многообразием размерности п
класса Ст в Н(°и).
Это следствие говорит о том, что многообразия класса Ст
сохраняются при Ст-диффеоморфизмах.
Доказательство. Пусть Ф : (У
—*Ф((У)—параметрическое представление открытого множества Ф(0) из V. Тогда
отображение Ноф является гомеоморфизмом О на Н(ф(0)),
т. е. отображением класса Ст множества О в пространство F.
Пусть а е О. Так как ранг отображения Ф'(а) равен п, а ото-

§ 9. Дифференцируемые многообразия
325
бражение #'(Ф(а)) является линейной биекцией, то ранг
(Яоф)'(а) = #'(Ф(а)) оФ'(а) также равен п (следствие 4
теоремы 11, примененное к отображению Н). Значит,
отображение #°Ф является параметрическим представлением
размерности п класса Ст. Можно выбрать семейство
представлений, подобных Ф, так, чтобы их образы покрывали V; тогда
образы Н °Ф покрывают H(V), чем и заканчивается
доказательство следствия.
Следствие 2г. Для того чтобы множество V аффинного
пространства Е размерности N было многообразием
размерности п класса С™, необходимо и достаточно, чтобы для
каждой точки aeV существовал Ст-диффеоморфизм Ф открытого
множества СУ czKN на такую окрестность Т точки а в Е, что
V0T является образом при отображении Ф пересечения О
и векторного подпространства К", порожденного первыми п
векторами базиса KN.
Это следствие говорит о том, что с помощью
^-диффеоморфизма можно локально свести многообразие класса Ст
размерности п в Е к векторному подпространству размерности
п в пространстве KN.
Доказательство. 1°) Предположим сначала, что
множество V обладает требуемым свойством. В каждой точке ос
из Ф-,(У) производная Ф'(а) является линейной биекцией К^
на Е (следствие 4 теоремы 11). Следовательно, она вместе со
своим сужением на рассматриваемое подпространство К™
является инъекцией, и, значит, это сужение имеет ранг п.
Сужение Ф отображения Ф на О = б ПК" является
параметрическим представлением размерности п класса С™, и, поскольку
каждая точка V имеет некоторую окрестность, допускающую
такое параметрическое представление, V действительно
является многообразием размерности п класса С™.
2°) Обратно, пусть V является многообразием размерности
п класса Ст. Согласно определению, если а е V, то существует
система координат в £ и некоторая окрестность У точки а
в Е, в которой V может быть определено формулами (III, 9; 1)
с (xi,x2,...,xn)^&. Обозначим через 38* открытое множество
из KN, образованное точками, первые п координат которых
определяют точку из 38: 38* = \х\ (хи х2, ...,х„)^38}. Тогда
формулы
*, = И/, /=1,2, ..., п,
*n+ft = "n+ft+ Gk(uu u2, .. ., иа), k= 1, 2, ..., N — п, ' ' 2
определят некоторое отображение Ф множества 38* в KN,
совпадающее с Е, причем Ф(38*) = 38*. Отображение Ф является

326
Гл. I'll. Дифференциальное исчисление
биекцией с обратной биекцией ф-1, определяемой равенствами
Uj — Xj,j—l,2 п,
un + k == xn + k — "А \х\< х2 xnh К = 11 £ Л/ — П.
Так как Gk принадлежат классу С"1, то оба отображения
Ф и Ф-1 принадлежат классу С™. Следовательно, Ф является
гомеоморфизмом класса С™ вместе со своим обратным
гомеоморфизмом. Если через О обозначить прообраз Ф'{(Т), то
О является открытым множеством в KN, а сужение Ф на О
обладает теми же свойствами. Но тогда Vf]T определяется
уравнениями (111,9; 1) и, следовательно, является образом
подпространства un+h = 0, k = 1, 2 jV — п, при отображении
Ф, чем и заканчивается доказательство следствия.
Если V является многообразием размерности п класса С™,
то всякое параметрическое представление Ф класса С™
открытого множества V[\T этого многообразия называется также
локальной картой класса С™, или просто картой, если нет
опасности путаницы. Множество Ф(С)= 1/flF называется
образом этой карты, а Ф называется также картой множества
V П Т. Если Ф(0) содержит точку а е V, то говорят также,
что карта покрывает эту точку. Атласом многообразия V
называется множество карт открытых множеств из V, образы
которых покрывают V. Универсальным атласом V называется
множество всех карт (размерности п класса Ст) открытых
множеств из Vм).
Слова «карта» и «атлас», очевидно, взяты из картографии.
Земная поверхность приближенно представляет собой сферу,
и ее можно рассматривать как некоторое многообразие V
размерности 2. Глобального параметрического представления
этого компактного многообразия, заданного в некотором
открытом множестве из R2, не существует. Однако существует
покрытие V системой открытых-множеств, каждое из которых
является образом некоторой карты. Поскольку V компактно,
существует, естественно, конечный атлас для V, т. е. атлас,
содержащий конечное число карт2). Каждая «страница»
атласа является прямоугольником, который мы будем
рассматривать как открытый прямоугольник из R2. Около тех или
иных точек этого прямоугольника отмечается название
соответствующего места на Земле, т. е. некоторых точек
множества V. На идеальной с математической точки зрения карте
') Универсальный атлас есть множество карт, имеющее мощность
континуума.
2) Географические атласы содержат конечное число карт. Универсальный
атлас по причине, указанной в предыдущем примечании, был бы очень
громоздким и рбошелся бы слишком дорого.

§ $. Дифференцируемые Многообразия
32?
каждой точке прямоугольника ставится в соответствие
некоторая точка Земли, т. е. определяется отображение Ф
открытого прямоугольника на некоторое открытое множество
многообразия V. Из того факта, что карты являются открытыми
множествами, немедленно вытекает, что некоторые точки V
покрываются несколькими картами атласа (мы требуем, чтобы
каждый город мира был представлен внутренней точкой хотя
бы одной из прямоугольных карт). Если бы каждая точка
покрывалась не более чем один раз, то V было бы объединением
конечного числа >1 открытых непересекающихся множеств,
т. е. было бы несвязным. Однако хотим мы этого или нет,
Земля, как и всякая сфера, связна.
Примеры многообразий. Г) Каждое линейное
многообразие размерности п является бесконечно
дифференцируемым многообразием. Оно содержит атлас, состоящий из
одной карты, получаемой при выборе системы координат
в этом многообразии, — системы координат, которая
определяет некоторую линейную биекцию Ф пространства Кп на это
многообразие, обладающую всеми требуемыми свойствами.
В частности, пространство Е само является многообразием.
2°) Мы неявно предполагали, что п^1. Можно
рассматривать как многообразие размерности 0 каждое множество V
изолированных точек Е. Картой некоторой окрестности точки
аеУ является отображение 0 —* а множества К0 = {0} в
множество {а}.
Можно также рассматривать пустое множество 0 как
многообразие размерности —1, вовсе не имеющее карт.
Многообразие размерности 1 называется кривой,
многообразие размерности 2 — поверхностью, а многообразие
размерности jV — 1 называется гиперповерхностью. Однако эти
слова использовались и используются в столь различных
смыслах, что надо быть осторожными при их применении.
Принято рассматривать лемнискату Бернулли как «кривую»;
однако из-за своей особой точки она не является многообразием.
Говоря «кривая класса О1», следует уточнить, что речь идет
о «многообразии размерности 1 класса С™», и лемниската
будет исключена.
3°) Многообразие V размерности N аффинного пространства
Е размерности N — это просто некоторое открытое множество
из Е. (В самом деле, здесь jV — п — 0. Если обратиться к
определению, можно убедиться, что уравнение (III,9; 1)
отсутствует, а V [)У = У° = $! является открытым множеством в Е,
содержащим а. Определение выражает просто тот факт,
что каждая точка аеУ имеет окрестность У в Е,

32$ Гл. ///. Дифференциальное исчисление
принадлежащую V, т. е. что V открыто.) Каждое такое
открытое множество является многообразием класса С°° и имеет атлас
из одной карты, определяемой тождественным отображением
VczE в V, где Е отождествляется с KN с помощью некоторой
Системы координат.
Каждая часть многообразия V из Е, являющаяся
открытым множеством в V, будет многообразием того же класса
и той же размерности.
Обратно, если W и V—некоторые многообразия из Е
одной и той же размерности п и W с: V, то W является просто
некоторым открытым подмножеством из V. В самом деле,
пусть а е W. Согласно следствию 22 теоремы 32, существует
Ст-диффеоморфизм Ф некоторого открытого множества 0 а
с KN на открытое множество из Е, содержащее точку а,
такой, что множество Ф_1(У) является пересечением О с
некоторым векторным подпространством К" пространства KN.
Следствие 2 показывает в свою очередь, что Ф_1(№)
является также многообразием из KN размерности п, заведомо
содержащемся в К". Из того что мы видели в' начале пункта
3°), следует, что Ф-1(№) является открытым множеством
в пространстве К" и, значит, Ф_1(№) является окрестностью
точки Ф-1(а) в множестве Ф_1(У), а, следовательно, W
является окрестностью а в V. Так как это утверждение
справедливо для любой точки а из W, то W является открытым
множеством в V.
4°) Покажем, что в аффинном евклидовом Af-мерном
пространстве над R сфера является (N—1)-мерным бесконечно
дифференцируемым многообразием. Для простоты выберем
некоторую систему координат и в качестве сферы S возьмем
единичную сферу с центром в начале. Обозначим через У^ +
открытое множество из Е, определенное неравенством х, ~> О,
а через 3S, — открытое множество из KN~\ определенное
неравенством х\ + х\ + ... + x2^t + x2l+l + ... + x2N < 1. Тогда в
Tj,+ сфера S будет определяться уравнением
(xiy ..., Xj-i, X/+\, ..., xN)&3$/,
X = l/l— X2— ^Л-2 ^Х2 — ^~Х? (Ш'9;4)
Точно так же можно рассуждать для открытого множества
Tj, _, определенного неравенством Xj <. 0. Так как все
рассуждения можно провести для /—1, 2, ,.., N, то исходное
утверждение Доказано полностью. Кроме тогб, мы видим, что
сфера S покрывается атласом, состоящим из 2N карт класса
С°° размерности N— 1.

§ 9. Дифференцируемые многообразия
329
Рассмотрим классическое параметрическое представление
двумерной сферы в R3:
x = sin 8coscp,
у = sin 8 sin qv (Ш,9;5)
г = cos 8.
Здесь в качестве О можно взять,. например, открытое
множество 0 < ф < 2я, 0 < 8 < я пространства R2. Отображение
(III, 9; 5) дает карту открытого множества сферы, определяв'
мого неравенствами у Ф О или у = 0, х < О (дополнение к
замкнутому полумеридиану ф = 0, 0 4^9-^ я). Обычно предыдущим
представлением пользуются для всей сферы, допуская значения
0^ф^2я, О^б^я, но тогда это представление не будет
истинным параметрическим представлением. Другими словами,
одна эта карта, как мы уже видели, не может составлять атлас
всей сферы. С помощью стереографической проекции легко
показать, что существует атлас сферы, состоящий только из двух
карт. В самом деле, рассмотрим обратное отображение к
стереографической проекции, т. е. отображение R^-1 на сферу,
определяемое формулами
*«=*-!■' , '=1,2 N-1, хя = в£± . (III, 9; 10)
При е = +1 (соответственно —1) эти формулы
определяют карту класса С°°, образом которой служит открытое
множество сферы, дополнительное к северному полюсу
(соответственно к южному полюсу) (т. е. к точке 0, 0, ..., е1)). Мы
имеем, таким образом, атлас сферы, состоящий из двух карт.
Из доказательства теоремы 32 вытекает, что отображение
в: (у, z)->X~](y) является отображением У в S4-, сужение
которого на многообразие УГ\У является также сужением
обратного гомеоморфизма Ф-1 к Ф. Таким образом, получаем
такую теорему:
Теорема 33. Если Ф: 0^+Ф(0) является
параметрическим представлением размерности п класса С™ открытого
множества многообразия V из Е и если ф(а)= а, то существуют
открытое множество зФ в О, содержащее а, открытое
множество У в Е, содержащее а, такие, что V Г) У = Ф {s4-), и,
наконец, существует отображение в множества У в $£ класса Ст,
') В качестве упражнения можно проверить выполнение всех
необходимых свойств карты.

330
Гл. III. Дифференциальное исчисление
сужение которого на V П Т совпадает с сужением обратного
гомеоморфизма Ф-1. В частности, в бФ имеем: 0 о ф = /.
Однако равенство Фо0 = / не выполняется, поскольку
если исходить из точки Т, не принадлежащей V, то ее образ
при отображении 0 лежит в s4- и потому образ при
отображении Ф находится в V, а, значит, отличен от исходной точки.
Напротив, можно сказать, что отображение Ф ° 0, будучи
отображением (у, г) -»• (у, g(y)) множества Т на V \ЛТ, является
своего рода «проекцией Т на V П Т».
Следствие 1. Пусть Ф^ и Ф2 — два параметрических
представления класса С™ одного и того же открытого
множества V [}Т многообразия V из Е. Пусть d и Ог — открытые
области определения функций Ф{ и Ф2, такие, что Ф1(С1) =
= Ф2((^2)- Если через Ф^ обозначить обратный
гомеоморфизм к Ф2, являющийся отображением V П Т в 02, то
отображение Ф2 ° Ф1 множества 0\ в 02 является гомеоморфизмом
класса С™, так же как и его обратный гомеоморфизм ФГ' °Ф2.
Доказательство. Пусть aiGC, и Ф!(<Х1)=а.
Рассмотрим отображения 0] н 02, определенные, согласно
теореме, на двух окрестностях Т\ и Т2 точки а в Е. Пусть Т0 =
= Т\ П Т2. Обозначим через s4-\ и s4-'2 прообразы То при
отображениях Ф) и Фг. Тогда на множестве s&\ отображение
ФГ 0Ф( совпадает с отображением 02оф], поскольку Ф\{и)
для UEi[ лежит в V [)Т0,и на V П Т0 а V Г) Т2 отображение
Фг-1 совпадает с 02. Следовательно, согласно теореме 19, эта
композиция отображений класса С™ сама принадлежит
классу Cml). Таким образом, каждая точка oci множества 0\
имеет некоторую открытую окрестность, на которой ФТ °Ф\
принадлежит классу С™, а, следовательно, это отображение
принадлежит классу С™ на 0\.
Следствие 2. Если V является многообразием
размерности п, то оно не может быть многообразием размерности
п' ф п.
Доказательство. В самом деле, предположим, что для
некоторой точки иеУ имеется карта размерности п
некоторой открытой окрестности точки а и карта размерности п' дру-
') Проводить то же самое рассуждение непосредственно для Ф^'"©!
нельзя, ибо 1>2 является отображением некоторого открытого множества
из V, а не открытого множества аффинного пространства в К", и,
следовательно, утверждение, что Ф^~ принадлежит классу Сп, не имеет смысла.
Позднее на стр. 336 мы узнаем, какой смысл можно ему придать.

§ 9. Дифференцируемые многообразия
331
гой открытой окрестности этой точки. Тогда для пересечения
этих окрестностей будут существовать две различные карты
размерностей п и п'. В рассуждениях, проведенных в
предыдущем следствии с параметрическими представлениями, не
предполагалось, что размерности п и п' должны быть
равными. Однако ФГ'оф, должно быть Ст-диффеоморфизмом
множества 0\ на Оч; поэтому из следствия 4 теоремы 11
вытекает, что размерности карт должны быть равными.
В противоположность этому многообразие класса Ст тем
более принадлежит классу С* для любого k ^ m.
Определение многообразия с помощью неявных уравнений
Теорема 33г. Для того чтобы множество V аффинного
пространства Е размерности N было многообразием
размерности п класса С™, необходимо и достаточно, чтобы для
каждой точки а е V в Е существовала окрестность Т этой точки
и система N — п скалярных функций Fh, k = О, 1, 2, ..., N—п,
определенных на У, класса Ст и обладающих следующими
свойствами:
<-
1°) производные F'k (а)') образуют N — п линейно неза-
^*-
висимых форм над Е;
2°) пересечение V П У в точности определяется
уравнениями Fh(x) = 0.
Говорят, что такая система уравнений является
нормальной системой N — п уравнений множества V в окрестности
точки а.
Заметим, что если положить n—'N, то уравнений не
будет, а V будет некоторым открытым множеством из Е. Если
же положить п = 0, то получится N уравнений, и в
некоторой окрестности точки а других решений, кроме самой точки
а, не будет. В этом случае а является изолированной точкой
множества V, а V будет множеством изолированных точек Е,
или многообразием размерности 0.
Доказательство. 1°) Предположим, что V является
многообразием. По определению это многообразие задается
уравнениями Fft(x)=0, где Fh определяются равенствами
Fk(xu x2, ...,xN) = xn+k — Gk(xh x2, .. ., х„). (III, 9; 11)
Поскольку в точке а (или в любой точке из У) dFh
содержат dxp+h с коэффициентом 1 и не содержат ни одного из
dxn+j для j = 1, 2, ..., N — п, то dFh линейно независимы.
') F'k (а) е= 2 (Е; К) = £".

332
Гл. III. Дифференциальное исчисление
2°) Предположим теперь, что V является множеством,
обладающим указанными в теореме свойствами. Утверждение
<-
о том, что система линейных форм /*! (а) независима,
означает, что если в Е выбрать какую-либо систему координат, то
по крайней мере один из миноров порядка N — п матрицы,
составленной из частных производных функций Fh, отличен от
нуля. Предположим для определенности, что отличен от нуля
D (F , F , ..., F _ )
якобиан п. ''—2' —N . (а) (к этому случаю можно все-
U(Xn + V Хп + 2' •"•' XN)
гда перейти, изменив при необходимости порядок нумерации
векторов базиса Е). Положим, как и ранее, у = {х\, х% ..., хп)
и z = (xn+i,xn+2,...,xN), так чтобы точку ле£ можно было
отождествить с парой (у, z) пространства К™ X К^-™. Теперь
можно считать, что множество функций F^ определяет функ-
цию f на К" X К^-" со значениями в KN~n, такую, что f{a) —
=J(b,c)=t
Предположение относительно якобиана означает, что
частная производная -Ц- (a) = -g-(6, с) eS^K"-"; К"-") этой
функции обратима. Из теоремы о неявной функции (теорема 29)
следует, что существуют окрестность 3S точки Ь в К™ и окрестность
<& точки с в KN~n, такие, что 3S X ®* сг У, а уравнение f(y, z) =
= 0 имеет, и притом единственное, решение в 9? для точек у,
заданных в окрестности 3S. Кроме того, определяемая таким
способом неявная функция z = g(y) является непрерывным
отображением <% в ^. Из теоремы 31 следует, что если f принадлежит
классу Ст, то g также будет принадлежать классу Ст. Мы
видим, что пересечение V с 3S X ^ определяется в точности
уравнением z — g(y) и что, поскольку это утверждение
справедливо для любой точки а е V, множество V является
многообразием размерности п класса Ст.
Приведем другое доказательство утверждения 2°).
Обозначим через W отображение множества У в пространство K'v,
определенное соотношением (х.\, Х2, ..., xN)->(ui, и2, ..., uN), где
«,-*,. «, = *.... «--** (III)9;Il2)
и будем исходить, как и в первом доказательстве, из случая
D (F , F , ..., F _ )
—7w—~ '—^Г~ (а) ^ 0- Поскольку этот якобиан является
и(хп+\' ••■• xn)
якобианом отображения V в точке а и отличен от нуля, суще-

§ 9. Дифференцируемые многообразия
333
ствует такое открытое множество Т\ с: У, содержащее а, что
сужение W на Т\ является гомеоморфизмом класса С™, точно
так же как и его обратный гомеоморфизм Ф множества Т\
на некоторое открытое множество s4-u содержащее W(a) = <х
(теоремы 29 и 31). Но тогда Ф является
^-диффеоморфизмом множества si\ на Т\, а V Г) У°\ есть образ векторного
подпространства Кп пространства KN при отображении Ф:ип+к =
= 0, k= 1, 2, ..., N — п. Из следствия 22 теоремы 32 теперь
вытекает, что V — многообразие размерности п класса С™.
Следствие 1. Для того чтобы множество V
пространства Е было гиперповерхностью (т. е. многообразием
размерности N—1) пространства Е класса Ст, необходимо и
достаточно, чтобы для каждой точки а е V существовали
окрестность Т точки а в Е и скалярная функция F, определенная
в Т, класса Ст, производная которой F'(a)^Ol), такие, что
множество V [)У в точности определяется уравнением F(x)=0.
Теперь становится очевидным, что сфера евклидова
пространства является многообразием, поскольку сфера с
центром в точке а радиуса R определяется в Е уравнением
-> ->
(х — а\х — а) = R2.
Этот пример показывает, что в то время как, вообще
говоря, многообразие нельзя полностью задать с помощью
разрешенных уравнений или же с помощью параметрического
представления, возможность определить его целиком с помощью
неявных уравнений указанного в теореме вида значительно
более вероятна. ^
Естественно, условие, что F'k (а) независимы или, в слу-
чае одного уравнения, что производная F' (а) отлична от
нуля, абсолютно необходимо. Например, конус второго
порядка, определенный в пространстве R3 уравнением х2-\-у2—
— г2 = 0, не является многообразием. Он не удовлетворяет ни
одному из определений из-за особой точки в начале координат.
Вещественные и комплексные многообразия
До сих пор в качестве поля К можно было брать поле
вещественных или поле комплексных чисел. В соответствии
с первым или вторым случаем говорят, что V является
вещественным многообразием или комплексным многообразием.
') Напомним, что F'(а) Ф 6 в некоторой системе координат означает,,
dF
что -г— (а), ( = 1, 2, ..., N, не обращаются в нуль одновременно.

334
Гл. III. Дифференциальное исчисление
Любое аффинное пространство над полем комплексных чисел
является также аффинным пространством удвоенной
размерности над полем вещественных чисел. Точно так же Сп,
рассматриваемое как векторное пространство над полем вещественных
чисел, может быть отождествлено с R2™. Так как каждое
отображение, дифференцируемое по отношению к полю комплексных
чисел, тем более дифференцируемо по отношению к полю
вещественных чисел, то каждое многообразие V размерности п
класса Ст по отношению к полю комплексных чисел можно
рассматривать как многообразие размерности 2« того же класса Ст
по отношению к полю вещественных чисел. Если нет
специальных указаний, будем считать размерностью многообразия его
размерность по отношению к полю вещественных чисел.
Абстрактные многообразия ')
Для определения многообразия нет необходимости вести
рассмотрение только в аффинном пространстве. Например,
множество страниц географического атласа дает полное
описание поверхности Земли, и при этом нет необходимости
представлять себе Землю как двумерное многообразие,
погруженное в аффинное пространство трех измерений. Можно ввести
понятие абстрактного многообразия.
Определение. Абстрактным многообразием V
размерности п класса С™ (не обязательно лежащим в некотором
аффинном пространстве) называется топологическое
пространство V, снабженное некоторым атласом или системой карт,
обладающих следующими свойствами:
1°) Каждая карта является гомеоморфизмом Ф некоторого
открытого множества О пространства Кп на открытое
множество Ф((У) пространства V. (Говорить, что этот гомеоморфизм
принадлежит классу С™, не приходится, поскольку речь идет
об отображении открытого множества аффинного
пространства в топологическое пространство, не лежащее в аффинном
пространстве.)
2°) Пусть Ф| и Фг — две произвольные карты атласа
множества V. Если образы Ф{{0{) и Фг{02) имеют непустое
пересечение Q, то прообразы Qi и Q2 множества Q при
отображениях Ф1 и Фг являются открытыми множествами в 0\ и <У2.
Сужения Ф! и Ф2 на Q, и Q2 имеют один и тот же образ. Они
должны обладать следующим свойством, аналогичным
утверждению следствия 1 теоремы 33: отображение Ф-Г °Ф) откры-
') Здесь мы приводим лишь беглый набросок теории. Абстрактные
многообразия подробно изучаются в других курсах.

§ 9. Дифференцируемые многообразия
335
того множества BicK" на открытое множество Ог с К™
принадлежит классу С™. Эта фраза имеет определенный смысл,
ибо речь идет об отображении открытого множества аффинного
пространства в аффинное пространство. Именно этим условием
определяется принадлежность многообразия V классу Ст.
3°) Множество образов карт должно составлять покрытие
пространства Vм).
Изучение абстрактных многообразий играет большую роль
в математике и во многих разделах физики. Рассмотрим,
например, механическую систему, имеющую конечное число
степеней свободы, например гироскоп с одной закрепленной
точкой оси вращения. Положение этой системы «может быть
определено с помощью конечного числа вещественных
параметров qu Q2, • • •, q„». В действительности эта система
параметров весьма произвольна,.и очень редко удается все без
исключения положения механической системы эффективно
выразить через значения конечного числа параметров. Так,
например, если положение гироскопа определяется углами
Эйлера \р, 6, ф, то множество всех положений гироскопа не имеет
параметрического представления.
В действительности множество положений механической
системы может быть определено как абстрактное
многообразие, которое в случае гироскопа является трехмерным много?
образием V класса С°°. Но это многообразие является
абстрактным и, естественно, не погружено в аффинное
пространство. Когда говорят, что 3 угла Эйлера выбираются для
определения положения гироскопа, то это означает, что
рассматривается частная карта, представляющая только некоторое
открытое множество многообразия, являющегося множеством
положений гироскопа2).
Тем не менее теория абстрактных многообразий приводит
в некоторых вопросах к значительно большим усложнениям,
чем теория многообразий, погруженных в аффинные
пространства. Если это не будет приводить ни к каким усложнениям,
мы будем рассматривать абстрактные многообразия. Каждый
') Разрешается, вообще говоря, дополнить первоначально заданный
атлас. Для этого добавляются все карты, не нарушающие принадлежность
классу С™, т. е. все гомеоморфизмы Ф открытых множеств О из К" на
открытые множества из V, обладающие следующим свойством: для каждой
карты Ф* заданного атласа, такой, что Ф((У) ПФ,(0{) = Q ¥=0,
отображение ф-'о Фг является С™-диффеоморфизмом Ф^ (fi) на Ф~'(П).
2) Для получения параметрического представления надо ограничиться,
например, открытым множеством 0 < г|з < 2я, 0 < 8 < я, 0 < <р < 2л,
которое не исчерпывает множества всех положений гироскопа. Впрочем,
многообразие здесь компактно и для полного представления достаточно
конечного числа (>1) карт.

336 Гл. III. Дифференциальное исчисление
раз, когда это может привести к упрощению, мы будем
предполагать, что многообразия лежат в аффинных
пространствах.
Определение. Пусть V и W—многообразия класса Ст
размерностей р и q над одним и тем же полем К, и пусть
Н — непрерывное отображение V в W. Говорят, что Н
принадлежит классу Ch, если, каковы бы ни были точка а <= V,
Н(а) = Ь, карта Ф окрестности Т точки а в V и карта W
окрестности Ж точки Ь в W, сложное отображение Чг~ °Н°Ф,
определенное на открытом множестве Ф~*(У) Г) Ф~1(Н~1(Ж))
пространства Кр, со значениями в К9 принадлежит классу Ch
в обычном смысле. Очевидно, если многообразие принадлежит
классу С™, то определить отображение класса Ст для т' ~> т
невозможно. Очевидно также, что любое отображение
класса Ch принадлежит классу С для k' ^ k. Всегда можно
ограничиться случаем k — т, поскольку если V и W принадлежат
классу С™, т ^ k, то они тем более принадлежат классу Ch.
Если U, V, W — три многообразия класса Cm, H —
отображение класса С™ множества U в У, К — отображение класса
О множества V в W, то К ° И является отображением U в W
класса С™. В самом деле, если Ф (соответственно W) является
картой некоторой окрестности °U точки а (соответственно W
точки с = (К ° Н) (а)) в множестве U (соответственно W) и
если через X мы обозначим карту некоторой окрестности У
точки Ь — Н(а) в V, то на множестве Ф"1 (<U) f\ ф-1 (я-1 (Т)) [)
?Чо/(о//оф = (Г1о/(оХ)о(Х-|а//оф); (Щ, 9; 12)
каждое из двух отображений правой части принадлежит, по
предположению, классу О, а, значит, согласно теореме 19,
их композиция также принадлежит классу С™. Гомеоморфизм
V на W, принадлежащий классу О вместе со своим обратным
гомеоморфизмом, называется Ст-диффеоморфизмом. Если
такой диффеоморфизм существует, то, согласно следствию
теоремы 11, V и W имеют одинаковую размерность.
Теорема 333. Пусть V и W — многообразия класса С™ и
Н — непрерывное отображение V в W. Для того чтобы Н
принадлежало классу С™, необходимо и достаточно, чтобы для
каждой точки аеУ существовали хотя бы одна карта Фа
некоторой окрестности точки а в У и хотя бы одна карта Ч^
некоторой окрестности точки Ь = Н(а) в W, такие, что отображение
Ч?£ °Н°Фа принадлежит классу С™,

§ 9. Дифференцируемые многообразия
337
Доказательство. Необходимость этого условия
очевидна. Надо доказать лишь его достаточность. Для этого мы
должны показать, что если Ф и Ч7— произвольные карты
окрестностей точек а и Ъ в V и W, то ^¥~ °Н°Ф принадлежит
классу Ст. В окрестности точки а = Ф-1 (а) имеем
Ч'-1 о Я о ф = (¥-1 о Wa) о (Ч'-1 о Я о фа) о (ф"1 о ф). (Ш, 9; 13)
Средний член правой части предполагается принадлежащим
классу С™. Крайние члены, согласно аксиоме 2°) на стр. 334
о картах многообразия, также принадлежат классу С™. Это и
доказывает теорему, которая имеет многочисленные следствия.
Приведем наиболее важные из них:
Следствие 1. Если V и W являются открытыми
множествами аффинных пространств Е и F, то отображение Я
множества V в W принадлежит классу Ст тогда и только тогда,
когда оно принадлежит классу Ст в смысле, определенном на
стр. 266.
В самом деле, возьмем для V и W тождественные карты.
Тогда Ч7-1 ° Н о ф сведется к Я.
Следствие 2. Пусть V — многообразие класса Ст
аффинного пространства Е. Тогда каноническая инъекция Я
многообразия V в W = Е также принадлежит классу Ст.
Для доказательства достаточно взять произвольную карту
Ф для V и тождественную карту для W=E. Тогда Ч'-1 оЯоф=
= Ф, где Ф — отображение класса Ст.
Следствие 3. Пусть V лежит в аффинном пространстве
Е. Тогда любое отображение Я множества V в W, являющееся
сужением на V некоторого отображения Я класса Ст
открытого множества Йс£ a W, является отображением V в W
класса Ст.
В самом деле, в этом случае Н является композицией H°J,
где / — каноническая инъекция V в Е, которая, согласно
следствию 2, принадлежит классу Ст.
Следствие 4. Пусть V — многообразие размерности п
класса С™, а Ф — карта некоторого открытого множества У"
многообразия V. Тогда Ф является Ст-диффеоморфизмом
множества Ф-1(ЗН на Т.
В самом деле, возьмем для множества Ф-1 (У)сКт
тождественную карту, а для множества У карту Ф. Для Я = Ф или
Ф-1 отображение вида Чг~ о#оф, является тождественным
отображением множества Ф~1(Т), принадлежащим тем самым

338
Гл. III. Дифференциальное исчисление
классу Ст. Следствие 1 теоремы 33 очевидным образом
вытекает теперь из следствия 4, однако мы уже неоднократно
использовали его для получения предыдущих результатов.
Следствие 5. Предположим, что многообразие W
размерности q погружено в аффинное пространство F. Для того
чтобы отображение Н многообразия V в W было класса С™,
необходимо и достаточно, чтобы для любой карты Ф для V
отображение #оф принадлежало классу Ст или чтобы для
любой точки оеУ существовала карта Ф„ некоторой окрестности
точки а в V, такая, что отображение Н ° Фа принадлежит
классу Ст.
В самом деле, пусть W—карта некоторой окрестности
точки b = H(a)<^W. Уменьшая при необходимости эту
окрестность, можно сделать так, чтобы отображение W'1
продолжалось в отображение в класса Ст некоторой окрестности точки
def в К?. Теперь мы должны показать, что для каждой
карты Ф (или для некоторой частной карты) W~ °#оф
принадлежит классу Ст тогда и только тогда, когда #оф принадлежит
классу О. Так как Н °Ф = W о(Ч,~1 о Н °Ф) и Чг_1оЯоф =
= 0° (#°Ф), где отображения W и 9, определенные на
открытых множествах аффинных пространств, принадлежат классу
Ст, то результат вытекает из теоремы 19.
Это следствие можно сформулировать следующим образом:
если W a F, то отображение Н множества V в W принадлежит
классу Ст тогда и только тогда, когда это отображение,
рассматриваемое как отображение V в F, принадлежит классу Оп.
Векторное пространство, касательное в точке
к многообразию аффинного пространства Е размерности N
Теорема 334. Пусть V — многообразие размерности п
класса С1 в аффинном пространстве Е. В каждой точке ае^
векторная (соответственно аффинная) контингенция в смысле
теоремы 8А является векторным подпространством в Е
(соответственно аффинным подпространством в Е) размерности п.
Это подпространство называется векторным (соответственно
аффинным) пространством, касательным в точке а к многооб-
->
разию V, и обозначается через Т(а; V) (соответственно Т(а; V)).
Если п = N, то векторным (соответственно аффинным) ка-
сательным пространством является само пространство Е
(соответственно Е). Если п — 0, то им будет {0} (соответственно {а}).

§ 9. Дифференцируемые многообразия
339
Доказательство. Для доказательства достаточно
обратиться к определению многообразия. Выбирая соответствующую
систему координат в Е, это пространство можно отождествить
с пространством К" X КЛ'~П и определить многообразие
в окрестности точки а уравнением z = g(y). Мы приходим
теперь к теореме 8А и, учитывая формулу (111,3; 19о), видим, что
векторное подпространство, касательное в точке а = (Ь,с),
определяется в выбранной системе координат уравнением
Z = g'{b)Y (III, 9; 14)
или что линейное многообразие, касательное в точке а,
определяется (в той же системе координат) уравнением
7^c = g'(b)(^%). (111,9; 15)
Следствие 1. Пусть V — многообразие класса С1
размерности п аффинного пространства Е. Пусть Ф — некоторая
карта, т. е. отображение открытого множества (7 с: К" на открытое
множество из V. Пусть а — некоторая точка из О и а = Ф(а).
Производное отображение Ф'(а) является линейной биекцией
К" на векторное пространство, касательное в точке а к
многообразию V.
Доказательство. Предположим сначала, что Ф
—отображение класса С1 множества О в V, которое может и не быть
истинным параметрическим представлением (Ф'(а) не обяза-
->
тельно имеет ранг. п). Пусть X — некоторый вектор из К™.
Рассмотрим последовательность точек хп = Ф(а + tnX), где tn
образуют последовательность положительных вещественных
чисел, стремящуюся к нулю при п, стремящемся к бесконечности.
Точки хп принадлежат V и стремятся к а. С другой стороны,
1 , %
векторы -г- {хп — а), которые можно также записать в виде
Ф [а ■+■ t„A — Ф [а „ , .
—i т1 i—, сходятся к производной отображения Ф в
точке а по вектору X, т. е. к Ф'(а)Х. Этот вектор принадлежит
векторному пространству, касательному к V в точке а. Отсюда
вытекает, что образ К" при отображении Ф'(а) содержится в
касательном векторном пространстве. Если теперь мы учтем,
что по предположению Ф'(а) имеет ранг п, то получим, что этот
образ является векторным подпространством размерности п и,
следовательно, совпадает со всем касательным пространством
в точке а, а отображение Ф'(а) есть линейная биекция
пространства К" на это касательное векторное пространство.

340
Гл. III. Дифференциальное исчисление
Отсюда вытекает, что векторы -^— (а) образуют базис
векторного пространства, касательного к V в точке а, и что
линейное многообразие, касательное к V в точке а, задается
параметрическим уравнением
П >
* = «+2*/|г(а), ^/еК')- (ПЬ 9; 16)
Следствие 12. Пусть V и W — два многообразия класса
С в двух аффинных пространствах Е и F. Пусть Н — такое
отображение Е в F класса С1, что H(V)czW. Тогда для
каждого a^V при b = H(a)^W образ касательного векторного
-*■ -> ->
пространства Т(а; V) при отображении Н'(а)^2'(Е; F) содержится
-> ->
в касательном векторном пространстве T(b; W): H'(a)T(a; V)cz
czf(b; W).
Доказательство. Пусть Ф — карта ((7сК")-»Ф(С)
некоторой окрестности Ф((У) точки а в V и Ф(а) = а. Тогда
Я.оф является отображением класса С множества О в WaF.
В начале доказательства предыдущего следствия мы видели,
->
что (#оф)'(а)Кп с T(b; W). Согласно теореме о сложной
функции, (Н оф)'(а) = Н'(а) оф'(а), а по следствию 1,
->
Ф'(а) К" = Т(а; V), откуда и вытекает доказываемое
утверждение.
Следствие 2. Пусть выполнены условия следствия {.Если
(У —такое открытое множество пространства К", содержащее
а, что сужение Ф на О допускает обратное слева отображение
G, удовлетворяющее условиям теоремы 33, то линейная биек-
->-
ция Ф'(а) пространства К" на Т(а; V) имеет в качестве обрат-
->-
ной биекции сужение на Т(а; V) производного отображения
©'(а).
Доказательство. По теореме 11 о сложной функции из
Тождества Ооф = / получается тождество 8'(а)»Ф'(а) = /,
из которого следует, что сужение & (а) на образ К" при ото-
->
бражении Ф'(а), т.е. на Т(а; V), является обратной биекцией
для Ф'(а).
') В весьма частном случае, когда V — поверхность пространства R3,
заданная параметрическим представлением (и, о)-*- М(и, v), касательная
плоскость в некоторой точке порождается частными производными дМ/ди, дМ/ди
в этой точке.

§ 9. Дифференцируемые Многообразия 341
Следствие 3. Пусть <Di и Ф2 — отображения открытых
множеств 0\ и О г пространства К" в V, определяющие карты
с одним и тем же образом в многообразии V, погруженном в Е.
■>
Пусть X — вектор, касательный к V в точке a, a = <Di(ai) =
■> ->
= Фг(а2). Если gi и |2 — два таких вектора пространства К",
->■
для которых вектор X является образом при отображениях
■> ■>
Ф{(аЛ и Ф£(а2), то |2 является образом £i относительно
производной отображения Ф<Г °Ф1 класса С в точке ац.
В самом деле, достаточно заметить, что
1-(тЫ)~'°^Ы)1- (Ш, 9; 17)
Точнее, согласно предыдущему следствию, обратное
отображение к O£(o2) является также сужением отображения Щ (а)
на векторное подпространство в точке а. Поэтому можно запи-
-> ■>
сать зависимость между £2 и gi в виде
^(едоф^а,))?. (Ш, 9; 18)
На этот раз Ф1 и вг являются отображениями открытого
множества некоторого аффинного пространства в аффинное
пространство. Поэтому можно применить теорему о сложной
функции (теорему 11) и заменить предыдущее равенство
равенством
|2 = (в2°Ф,)'(«>)!>. (Ш, 9; 19)
Наконец, из свойств отображения вг следует, что вг°Ф1
совпадает с Фг~ °Ф1 и, следовательно, можно написать
|2 = (ф2-1оф1)'(а1)|1( (III, 9; 20)
чем и заканчивается доказательство следствия.
Следствие 4. Пусть V — многообразие класса С1
размерности п аффинного пространства Е. Пусть а — некоторая точка
V, и пусть Ри(х) = 0, k = 1, 2, ..., N— п, — нормальная
система уравнений многообразия V в некоторой окрестности точки
а в Е. Тогда векторное подпространство, касательное к V в
точке а, определяется в Е уравнениями
F'k(a)X = 0, 6=1, 2, ..., N-n, (III, 9; 21)
а линейное многообразие, касательное к V в точке а,
определяется в Е уравнениями
F'k(a)(x-a) = 0, k= 1, 2, ..., N-n. (III,9;22)

342 Гл. III. Дифференциальное исчисление
Доказательство. Пусть хп— последовательность точек
многообразия V, стремящаяся к а, и К„ — такая
последовательность положительных вещественных чисел, что последователь-
-> -> ->
ность векторов Кп{хп — о) стремится к вектору I из £ при п,
стремящемся к бесконечности. Поскольку тогда Fh(xn) = 0 и
Fh(a) = 0, из определения производной (формула (III,3; 13))
следует, что
р№(ЪГ-а) + ап1*^-а1 = 0' (Ш, 9; 23)
где ||а„|| стремится к 0 при п, стремящемся к бесконечности.
Отсюда, умножая на Х„, получаем:
П (а) К (хп - а) + "„К \\ \ ~ а || = °- (Ш- 9; 24)
Поскольку Хп(хп — а) сходится к X, a F'k (а) является не-
прерывной линейной формой, то каждый вектор X,
касательный в точке а к многообразию V, удовлетворяет N— п
линейным уравнениям (III, 9; 21). Поскольку эти N — п линейных
уравнений предполагаются независимыми, они определяют не-
->
которое я-мерное векторное подпространство пространства Е.
Это подпространство является векторным пространством,
касательным к V в точке а. Отсюда непосредственно вытекает
утверждение, относящееся к касательному линейному
многообразию.
Следствие 5. Пусть Е — аффинное евклидово
пространство размерности N над полем вещественных чисел и V —
гиперповерхность, определяемая уравнением F(x) = 0, где F —
вещественная функция класса С1, градиент которой в точке а
отличен от 0. Этот градиент нормален к V в точке а, а вектор
grad F (а) , ,,
,——— является единичным вектором нормали к V в
II grad F (а) ||
точке а').
') Если в Е выбрать ортонормальный базис, то
grad F (а)
II grad F (а)
dF dF . , dF
Жу(а) -дГ2(а) dTN(a)
i=l i=l i=l

§ 0. Дифференцируемые многообразия
343
Следствие 6. Пусть V — многообразие размерности п
класса С1 аффинного пространства Е. Пусть Ф — карта,
отображающая открытое множество О'сК" на открытое множе-
ство многообразия V. В этом случае отображение (и, U) -*
-*(Ф(«), Q)'(u)U), ставящее в соответствие каждой паре (и, U),
где и — точка, a U — вектор из К", пару, составленную из
-*■
образа Ф(«), являющегося точкой V, и вектора Ф'(и)11,
касательного к многообразию V в этой точке, является
гомеоморфизмом С? X К" на свой образ.
Доказательство. Рассматриваемое отображение
непрерывно (теорема 10) и биективно. Для доказательства того, что
это отображение является гомеоморфизмом, достаточно
выяснить, что его обратное отображение непрерывно. Впрочем,
поскольку непрерывность является локальным свойством,
достаточно ограничиться сужением обратного отображения на мно-
жество пар (х, X), для которых х пробегает некоторую
окрестность точки а в V. Пользуясь теперь теоремой 33 и выбирая
эту окрестность так, как указывается в этой теореме, можно
убедиться (следствие 2), что обратное отображение является
-> -> ->
сужением отображения (х, Х)-+(<д(х), в' (х) X) из Т\Е в
К" X К". Это отображение непрерывно также и в силу
теоремы 10.
Векторное пространство, касательное
к абстрактному многообразию в точке1)
Пусть V—абстрактное многообразие размерности п класса
С и а е V. Как определить касательный вектор к У в точке
о? Пусть Ф: О—*Ф{0)—карта некоторого открытого
множества Ф(0) из V, содержащего точку а, и пусть ае К" — такая
точка, что Ф(а)=а. Интуитивно кажется ясным, что если | —
произвольный вектор К", то можно с помощью отображения Ф
поставить ему в соответствие вектор X, касательный к
многообразию V в точке а. Пусть Ф^ 0\ -*Ф\ (б\) и Ф2: 02->Фг(Ог) —
две карты открытых множеств многообразия V, содержащих
точку а. Пусть gi и £2— два вектора из Кп. При каком условии
им будет соответствовать при отображениях Ф! и Фг один и
->
тот же вектор А', касательный к У в точке а? Пусть Q —
пересечение Ф,(С\)П Ф2(<?2), и пусть Й1 = ФГ'Р и Й2 = Ф2_1(^)-
Тогда Ф^" о ф, будет Ст-диффеоморфизмом Qi на Q2. В точке
') См. примечание на стр. 334.

344 Гл. III. Дифференциальное исчисление
ai e Qi он имеет производное отображение (ф2 '.оФ^' (а{). Мы
условимся, что векторы gi и £г представляют при отображениях
Ф[ и Фг один и тот же вектор X, касательный к многообразию
V в точке а, если имеет место соотношение
|2 = (ф-1оф1)'(а1)|;. (Ш,9;242)
Такое определение оправдывается следствием 3 теоремы 334.
Мы приходим к следующему определению: касательным
вектором к многообразию V в точке а называется такое семей-
ство (ь*)(е=/ векторов из К™ (где / — множество индексов
всевозможных карт Ф{ многообразия V, для которых Ф*(Сг)
содержит а), что выполняются соотношения (Ф/~ °Фг/ (<хг) 1г = |/>
/,/е/. Однозначно определяется сумма двух касательных
-> -> -> ->
векторов (У,.е/, Ы(<=/ по формуле (|г + %),•<=/• Точно так же
-> .
определяется произведение касательного вектора (|г);е/наЯ,е
->
еК: (Я,|г).е/. Векторы, касательные к многообразию V в точке
а, образуют векторное пространство, имеющее размерность п,
т.е. размерность самого многообразия V. Через Т(а; V)
обозначается векторное пространство, касательное к многообразию V
в точке а. Следует заметить, что если а и b — две различные
точки V, то между касательными векторными пространствами
-> ->
Т(а; V) и Т(Ь; V) нет никакой простой связи. Эти векторные
пространства не являются подпространствами одного и того же
заранее заданного векторного пространства, как в случае
многообразия в аффинном пространстве.
Пусть V и W — два многообразия класса С1 размерностей
соответственно р и q. Пусть Н— отображение V в W класса С1
и 6 =//(а). Примем обозначения, введенные в определении
на стр. 336: Ф является картой некоторой окрестности точки а
в V, Ф(а) = а, a W является картой окрестности b в W. Пусть
| — некоторый вектор пространства К?, определяющий с по-
->
мощью отображения Ф вектор X, касательный к V в точке а.
Его образ при производном отображении (Ч*""1 о// °ф)'(<х) яв-
->
ляется некоторым вектором г\ из К', определяющим с помощью
->
отображения \F вектор Y, касательный к W в точке Ь. Легко
-> ->
доказать, что У зависит только от А' и а и не зависит от
выбранных карт ФиТ, Можно сказать, что задание Н определяет ли-
-> ->
нейное отображение Т(а; V) в T[b\ W). Это отображение назы-

§ 9. Дифференцируемые многообразия
345
вают производным отображением отображения Н в точке а и
обозначают через Н'{а). Это производное отображение
является обобщением рассмотренных выше производных
отображений для отображений класса С1 аффинных пространств.
В самом деле, если V и W—некоторые открытые множества
пространств Кр и К?, то в качестве Фи? можно взять
тождественные отображения. Векторное пространство, касательное
к У в точке а, тогда совпадает с Кр, а векторное пространство,
■> ■>
касательное к W в точке а, совпадает с К4; при этом А" = | и
■> ■>
У = т]. Определенное выше производное отображение является
отображением Н'(а) из Кр в К?. Без труда проверяется, что
так определенное обобщенное производное отображение
удовлетворяет теореме о сложной функции (теорема 11). Впрочем,
это определение отображения Н' (а) е 3? (Т (а; V); Т (b; W))
является естественным результатом следствия 1г теоремы ЗЗ4.
С другой стороны, если V есть многообразие, содержащееся
в аффинном пространстве Е, то в качестве отображения Н
можно взять инъекцию V в Е. Производное отображение Н'(а)
■> ■> . ->
определяет тогда линейное отображение Т(а; V) в Т(а; Е) = Е.
Можно проверить, что это линейное отображение является инъ-
->
екцией. Оно дает возможность отождествить Т(а; V) с его об-
->
разом, т.е. с некоторым векторным подпространством из Е, и
это подпространство есть найденное нами ранее векторное
подпространство, касательное к многообразию V в точке а,
лежащему в аффинном пространстве Е.
Мы не настаиваем на том, чтобы читатель сразу усвоил это
довольно сложное понятие векторного пространства,
касательного к абстрактному многообразию. Оно приведено здесь лишь
для иллюстрации того, что построения, проведенные нами ранее
в случае аффинных пространств, допускают обобщение на
произвольные дифференцируемые многообразия.
Теорема о постоянном ранге
Теорема ЗЗ5. Пусть О — открытое множество простран'
ства К", и пусть Ф: и—*и — ф^и)—такое отображение класса
С™ множества О в аффинное пространство Е, что в каждой
точке аеС производное отображение Ф'(а) имеет один и тот
же ранг I ^ п. Тогда для каждой точки аеС существует от^
крытое множество s&, содержащееся в О и содержащее а, об<
раз которого при отображении Ф является многообразием V cz
cz Е размерности I, принадлежащим классу Ст.
Доказательство. Выберем в Е некоторую систему
координат. Сказать, что ранг Ф'(а) равен /, означает прежде

346 Рл. til. Дифференциальное исчисление
всего, что по крайней мере один из определителей с I строками
и I столбцами производной матрицы отображения Ф в точке а
отличен от нуля. Изменяя при необходимости порядок векторов
базиса Е, мы можем предположить, что этот определитель яв-
- D{xv *2 xi) , \
ляется якобианом п ; — ~ (а).
D(uv "2 ui)
D (x , х х )
Так как Ф принадлежит классу С1 якобиан „ ; ''— —^т-
является непрерывной скалярной функцией на С и
существует окрестность s&o точки а, в которой этот определитель не
обращается в нуль. Поскольку в О и, следовательно, в s£u ранг
производного отображения всюду равен /, в s4-o каждый минор
производной матрицы, содержащий предыдущий определитель,
равен нулю. Разложим К" в произведение К1 X Кп~1. Точку
«бК" мы будем обозначать через (v, да), где v= (ии ..., щ)
и да — (Ы(+ь ..., ип). Пусть а = (р, у). Тем же самым
способом разложим Е в его системе координат в
произведение К'ХК^-' и положим х = (у, z), где у = (xt, х% ..., xt)
и z = (xi+i, ...,xN). Пусть а = Ф(а) = (Ь, с), и пусть у =
= Х(у, да), z = xF(y, да) определяют х = Ф(и) при этом
разложении. Согласно предположению, сделанному относительно
якобиана, из теоремы о неявной функции (теоремы 28 и 31) ')
следует, что существуют открытые множества S4-' и si-" в
пространствах К' и Кп~1, содержащие соответственно р и у, s&' X
X s&" с: s&oi и открытое множество 9& в пространстве К1,
содержащее точку Ь, такие, что для произвольно заданных точек да
и у в $$■" и 9& существует единственный элемент v e s&', для
которого X(v,w) = у. Кроме того, таким образом определенная
функция v = A(y,w), действующая из & X S&" в s&',
принадлежит классу Ст. Поскольку, в силу непрерывности Л, всегда
можно, не изменяя $$■', заменить Я и зФ" меньшими
окрестностями, мы можем взять в качестве $Ф" некоторый шар с
центром в точке у. Обозначим через s4-i произведение s4-'y^s4-"y
а через W — его образ при отображении Ф. Если х = (у, z)
принадлежит W и если, кроме того, у принадлежит ^, то v =
— Л(г/, да) и, следовательно, z = х¥(А(у, да), w) = g(y, да).
Покажем, что в действительности g не зависит от да. Для этого
вычислим дифференциал dg в некоторой точке (у, да).
Для выполнения этих вычислений надо начинать с
дифференцирования отображения X по формуле
dy = -^ (v, да) dv + -^ (v, w) dw . (Ill, 9; 25)
') Здесь решается уравнение X{v,w)= у относительно v при заданных
way.

§ 9. Дифференцируемые многообразия
347
D Ix., х„ хЛ
Тот факт, что якобиан ■ г ф О, означает, что
и (иу и2, ..., «,)
частная производная -у- (и, aijeS'fK'; К') обратима.
Предыдущее уравнение можно разрешить относительно dv:
fo=(°£-(v,w)\ Ту- {{~(v, w)\ ■ -£-(о, да)) d^ =
du v ' V v \\ dv v 'У day
= -|^(j,, a,)dj + |£(0. «O^- (Ill, 9; 26)
Подставляя найденный результат в дифференциал W:
—> дуу —> ^ijf —>
dz =~fo-(v, w) ■ dv +-g^(v, w) ■ dw, (111,9; 27)
получаем искомый дифференциал. Тот факт, что все миноры
ранга >/ производной матрицы отображения Ф равны нулю
в зФ'У^зФ", означает, что dxi+h, k—1, 2, ..., N — I, зависят
только от dx\, dxi dxL и не зависят от йщ+\, ..., dun.
Другими словами, в развернутом выражении
+-^-•^(111, 9; 28)
7* дЧ'
dz = -V-
5Х\-1 т* / ах\~1 <зх
-т— • ^ — -з- ■-^—■ dw
dv ) \ dv / aw
величина dz в действительности зависит только от dy и не
зависит от dw. Иначе говоря, функция g, определенная на $y^s4<",
со значениями в $Ф' имеет тождественно равную нулю частную
производную dg/dw. Поскольку в качестве бФ" мы выбрали
шар, т.е. связное множество, для фиксированного у можно
к функции w —* g(y,w), определенной на s4<", применить
теорему 22 и убедиться в том, что при фиксированном у величина
g{y,w) постоянна, т.е. что g не зависит от w. Это — некоторая
функция только переменной у, определенная на <М. Отсюда
вытекает, что множество точек (у, z), принадлежащих W, для
которых у лежит в $, является многообразием V размерности /
класса Ст, определенным уравнением z = g(y). Это множество
V точек Е является образом при отображении Ф пересечения
s4-\ и множества Х-1 (.$) точек и, таких, что Х(«)е^, т.е.
образом пересечения двух открытых множеств и, следовательно,
образом некоторого открытого множества $Ф из s&\, содержащего
а. В силу сказанного, образ Ф(яФ) является многообразием V
размерности / класса Ст, и теорема доказана.
Замечания. 1°) Если даже отображение ф является
биекцией и I — п, будет ошибкой считать, что образ при
отображении Ф всего открытого множества О окажется
многообразием в Е.

348
Гл. III. Дифференциальное исчисление
У
1 3
г
4
„_ «(1+«2)
Х 1 + «4
«(1 -и2)
у 1 + «4
Рассмотрим, например, на плоскости R2 лемнискату Бернул-
ли. Выберем на этой лемнискате направление обхода 1, 2, 3, 4,
указанное на рис. 6 стрелками. Всегда можно найти такую
биекцию Ф; и—*Ф(и) класса С°° вещественной прямой R
в плоскость R2, чтобы Ф(К) была в точности этой лемнискатой,
Ф(0) — двойной точкой лемнискаты и чтобы при и, стремящемся
к —оо (соответственно + °°), Ф(") стремилась к двойной точке
по ветви 1 (соответственно 4):
(Ш, 9; 29)
Рис. 6.
Производная Ф'(а) имеет ранг, равный 1, в каждой точке
aeR. Другими словами, х'(и) и у'(и) одновременно в нуль не
обращаются. Кроме того, Ф является биекцией1). Тем не менее
Ф не является, очевидно, гомеоморфизмом, ибо можно найти
последовательность точек лемнискаты, сходящуюся к двойной
точке, для которой последовательность и, вместо того чтобы
сходиться к 0, сходится к -j100 или —°°- Впрочем, это видно и
из того, что лемниската является компактным множеством, в то
время как R этим свойством не обладает. Итак, образ Ф^)
не является многообразием, так как он имеет особую точку
в начале координат. Однако для точки а = 0 можно найти
такую окрестность, например интервал ]—А, А[, где А —
произвольное положительное число, что образ этой окрестности при
отображении Ф является многообразием.
2°) Предположим, что п ^ N и I = N. Предположение
о том, что Ф'(а) для любого ае(7 имеет ранг, равный l = N,
означает просто, что Ф'(а) является сюръекцией К" на Е. Но
тогда Ф(^), как многообразие размерности W аффинного
пространства размерности N, есть открытое множество в Е.
Поэтому если Q — некоторое открытое множество из (У, то Ф^)
будет окрестностью каждой из своих точек, т. е. открытым
множеством, и мы снова убеждаемся, что Ф — открытое
отображение (теорема 30). Отсюда вытекает также первая часть
теоремы 30. Если известно лишь, что Ф'(ао) имеет ранг, равный
N, в некоторой точке оо. то имеется по крайней мере один минор
ранга N производной матрицы (в некоторой системе координат
пространства Е), отличный от нуля в точке схо. В силу его
1) Двойная точка получается лишь при и = 0.

§ 9. Дифференцируемые многообразия
349
непрерывности, он отличен от нуля во всех точках а некоторого
открытого множества 0\а0, содержащего а0- Но Ф является
открытым отображением множества С\ в Е, и, следовательно,
образ любой окрестности точки ао является окрестностью
точки ао = Ф(а0) в Е.
3°) В случае / <С п. отображение Ф, естественно, не инъек-
тивно и каждая из точек многообразия V — (D(s£) является
образом бесконечного множества точек из s£. В самом деле,
если xo = (yo,Zo)—некоторая точка V, то можно произвольно
выбрать точку w в st-", затем вычислить v = A(yo, w), и тогда
рассматриваемая точка х0 будет образом точки и = (и, до) =
= (Л (г/о, w), до). Если рассматривать сужение отображения Ф
на s&, то прообразом х0 будет множество точек (и, до) из si/-,
для которых w^l$&" и v = A(yo, w). Это множество является
многообразием класса Ст размерности п — /в пространстве Кп,
определенным предыдущим явным соотношением. Напротив,
если / = п, то Ф — инъекция (для достаточно малого si).
4°) Из последней теоремы снова вытекает теорема 32. В
самом деле, если для каждой точки аеУ существует
параметрическое представление Ф: 0-*-Ф{0), Ф(ос) = а, всюду имеющее
ранг / = п, то из теоремы 33s следует существование такой
открытой окрестности s& точки а в 0, что Ф(^)= W является
многообразием. Но Ф, кроме того, является гомеоморфизмом
б на открытое множество в V. Поэтому Ф(^) является
открытым множеством в V, и значит, существует такая открытая
окрестность Т\ точки а в Е, что W— V Г\Т\. Но если для
каждой точки аёУ найдется такая открытая окрестность Т\ в Е,
что V П У\ — многообразие, то по определению V само является
многообразием.
5°) Если ранг отображения Ф не постоянен, то не
существует никакой теоремы, позволяющей утверждать, что образ
окрестности точки а при отображении Ф имеет простую
структуру. Рассмотрим, например, отображение Ф плоскости R2
в пространство R3, определяемое формулами (г, ф) —► (х, у, г),
где
X = Г COS ф,
# =/-sirup, (III, 9; 30)
Z == Г.
Так как в точке а = (0, ф0) производная дФ/дф равна нулю,
то ранг производного отображения равен 1. Однако в близких
точках этот ранг равен 1 или 2. Образом R2 при отображении
Ф является конус в R3, определяемый уравнением хг-\-уг—z2=0,
для которого отображение Ф не определяет параметрического
представления. Образ каждой окрестности рассматриваемой

350
Гл. 111. Дифференциальное исчисление
точки а при отображении Ф является окрестностью
вершины конуса, которая не является многообразием из-за
наличия особой точки в вершине.
Сформулируем по этому поводу следующее свойство:
Если Ф является отображением класса С1 открытого
множества (У пространства Кп в Е, то ранг 1(a) производного
отображения Ф'(а) является полунепрерывной снизу функцией а.
В самом деле, покажем, что если ао^(У, то существует
такое открытое множество s40 из О, содержащее а0, что /(а)^
^г/(а0) для каждого а <= s&o- Действительно, выберем в £
некоторую систему координат. Согласно определению ранга,
существует по крайней мере один минор порядка 1(ао)
производной матрицы отображения Ф в точке а0> отличный от нуля.
Однако, поскольку Ф принадлежит классу С, этот минор
является непрерывной функцией а, а, следовательно, существует
окрестность s&0 точки а0> во всех точках которой этот минор
ф 0. Значит, в каждой точке а^М-0 ранг Ф'(а)>/(а0)-
Зависимые и независимые функции
Пусть Ф], Фг, ..., Ф]у суть N скалярных функций класса С1
от п переменных щ, и2, ..., ип. Они определяют отображение
Ф: и-*х = Ф(и) класса С открытого множества (УсКп в KiV.
Посмотрим, в каких случаях эти функции являются
зависимыми или независимыми в окрестности точки ae(J. Пусть
а = Ф(а).
1-й случай. Независимость. Предположим, что ранг
отображения Ф'(а) равен ./V — числу функций. Другими словами, один
из миноров ранга N производной матрицы, состоящей из
элементов -~-(а), t= 1, 2, ..., N, /= 1, 2, ..., п, отличен от
нуля. Для этого, очевидно, необходимо, чтобы п > N, т. е. чтобы
число переменных было не меньше числа функций. Тогда
теорема 30 (или 335) говорит нам о том, что образ всякой
окрестности а при отображении Ф является окрестностью точки а.
Функции CDi(m), Ф2(и), •••, Ф]у(«) могут принимать
произвольные значения, лишь бы только эти значения были достаточно
близкими к а\, а2, ..., aN. Следовательно, если между
функциями Ф{ имеется соотношение вида
R{Oi{ult и2, ..., и„), Ф2(«!,и2, .. .,«„), ...,Фы(иии2, ..., ип))=0,
(III, 9; 31)
где R— некоторая функция N переменных, то R должна быть
тождественным нулем в окрестности точки (а\, а2, ..., ап), т.е.
по существу никакого соотношения нет.

§ 9. Дифференцируемые многообразия 351
В этом случае естественно говорить, что N функций Ф*
независимы в окрестности точки а.
2-й случай. Зависимость. Предположим теперь, что Ф'(а)
для каждой точки а имеет один и тот же ранг / ■< N. Тогда из
теоремы 33s следует, что существует окрестность точки а,
образ которой при отображении Ф является многообразием V
размерности / класса С1 пространства К^. Изменяя при
необходимости порядок заданных функций Фг, можно прийти к
случаю, когда это многообразие задается уравнениями вида
xt+k = Gk{xu х2, ..., Xi), k=l, 2, ..., N-l. (Ill, 9; 32)
Тогда в окрестности а функции Ф, удовлетворяют N — I
нетривиальным соотношениям
Ф/+й(ы„ ..., ип) =
==Gft(Q,("i. ..., ип), Ф2{щ, ..., ип), ..., Ф[(ии ..., ип)),
А = 1, 2, ..., N-1. (III, 9; 33)
На этот раз это настоящие соотношения, поскольку при
заданных значениях Фь Ф2, ..., Ф; они определяют функции Фг+Й.
Последние N — / соотношений независимы, так как функции
х -> Xi+h — Gh(xi,x2, ..., xt) независимы в смысле 1-го случая.
В самом деле, их дифференциалы dxi+h—dGk таковы, что
dX[+k входит с ненулевым коэффициентом лишь в k-й из них.
Следовательно, для фиксированного х не существует линейного
соотношения между ними с постоянными коэффициентами. Ранг
системы этих Л/ — / дифференциалов равен N — / для любого х,
близкого к точке а. Естественно говорить в этом случае, что
функции Фь Ф2, . .., On зависимы и удовлетворяют N — /
независимым соотношениям.
Существуют, конечно, и другие, не рассматриваемые нами
случаи, когда ранг производной не постоянен в окрестности
точки а. В этих случаях результаты будут гораздо более сложные,
чем те, которые мы получили выше. Поэтому утверждение
такого рода: N функций Фь Ф2, ..., Ф^ от л переменных щ, и%, ...
. . ., ип с непрерывными частными производными первого
порядка независимы тогда и только тогда, когда производная
матрица функций Ф< имеет ранг N, и зависимы тогда и только
тогда, когда производная матрица имеет ранг <Л/,—не является
точным и в конечном счете неверно.
Рассмотрим, например, представление (III, 9; 30) конуса
х2 + у2 — z2 = 0. Три функции F, G, Н двух вещественных
переменных г, ф удовлетворяют соотношению F2 + G2 — Н2 = 0.
Но в окрестности точки (0, ф0), представляющей начало
координат x=y = z=0, из этого соотношения невозможно выразить

352 Гл. III. Дифференциальное исчисление
одну из этих трех функций как непрерывно дифференцируемую
функцию двух других, как это делалось во 2-м случае.
Можно столкнуться со значительно более сложными
фигурами, чем конус, для которых невозможно придать никакого
«утилитарного» смысла понятию зависимости или
независимости. Поэтому разумно ограничиться только рассмотренными
выше случаями.
Особые, или параметрические, многообразия
Вводимое здесь новое понятие является обобщением
понятия пути, введенного в гл. II на стр. 90.
Особым, или параметрическим, многообразием размерности
п класса Ст в аффинном пространстве Е размерности N
называется отображение Ф класса Ст некоторого многообразия
V размерности п класса Ст (абстрактного или погруженного
в аффинное пространство) в пространство Е. Образ ф(У) = №
называется образом параметрического многообразия. Не
следует путать его с самим параметрическим многообразием,
которое является отображением Ф многообразия V в W.
Например, если Ф постоянно: Ф(У)—{а}, а^Е, то образом является
точка, но параметрическое многообразие — это постоянное
отображение Ф. Лемниската Бернулли в R2 не является
многообразием, но она есть образ некоторого параметрического
многообразия при V=R (см. формулу (III, 9; 29)); в этом примере
отображение Ф инъективно. Она является также образом
параметрического многообразия, для которого V — окружность,
причем можно построить параметрическое многообразие так,
что, когда V пробегается в некотором заданном направлении,
лемниската будет пробегаться в направлении 1, 2, 3, 4, указан-
Р и с. 7.
Рис. 8.
Ном на рис. 7, а можно так, что она будет пробегаться в
направлении 1, 2, 3, 4 на рис. 8. Наконец, она является образом
параметрического многообразия, для которого V представляет собой
систему двух отдельных окружностей, которые при
отображении Ф переходят в две петли лемнискаты. Все это — различные
параметрические многообразия.

§ JO. Условные максимумы и минимумы 353
Если вместо V взять замкнутый отрезок [а, Ь] из R, то
отображение Ф класса Ст отрезка [а, Ь] в Е называется кривой
класса Ст из Е с началом Ф(а) и концом Ф(Ь). Если Ф(а) = Ф(Ь),
то говорят, что это замкнутая кривая (хотя это никак не
связано с топологическим понятием замкнутого множества).
Два параметрических многообразия Фь Vtr+E, ф2: Уъ-*-Е
называют Ст-эквивалентными, если существует
^-диффеоморфизм Я многообразия Vi на V%, такой, что. Ф\ = Ф<1°Н (тогда
ф2=ф,оЯ-1).
Такие многообразия имеют одни и те же образы. Это
соответствует тому, что называется в математике изменением
vпараметрического представления кривой или поверхности.
Рассмотренные выше различные параметрические представления
лемнискаты не являются эквивалентными параметрическими
многообразиями.
§ 10. УСЛОВНЫЕ МАКСИМУМЫ И МИНИМУМЫ
Пусть Q — открытое множество аффинного нормированного
пространства Е над полем R, и пусть f, git g2 gm суть m+1
непрерывно дифференцируемых вещественных функций на Q.
Займемся изучением экстремумов, т. е. максимумов или
минимумов, функций f на подмножестве А с Q, определенном
уравнениями
*i(*) = 0, &(х) = 0 gm(x) = 0. (Ill, 10; 1)
Мы будем искать, следовательно, максимумы или минимумы
функции f не Ha'Q, а только на некотором замкнутом, а не
открытом подмножестве множества Q. В этом случае говорят об
условном максимуме или условном минимуме.
Теорема 34. Пусть f, glt g2 gm — вещественные
непрерывно дифференцируемые функции, определенные на
открытом множестве Q аффинного нормированного пространства Е.
Пусть а — некоторая точка Q, удовлетворяющая уравнениям
gi(a) =g2(a) = ... =gm{a) = 0. Если линейные дифференциаль-
ные формы g[(a), g'2{fl)T..., gfm(a)^E' независимы, то
необходимым условием того, что точка а является точкой условного
максимума или минимума функции f на подмножестве А
множества Q, определенном уравнениями gi(x) = g2(x) — ...
• ■ ■ = gm(x) =0, является наличие таких m вещественных
постоянных К\, Кг Km, при которых имеет место соотношение
Г (а) = Кё[ (а) + K,g'2 (а)+ ... + Kmg'm{a). (Ill, 10; 2)
Величины Kt называются множителями Лагранжа,
соответствующими экстремальной точке а.
12 Зак. 1339

354 Гл. III. Дифференциальное исчисление
Перед доказательством этой теоремы укажем ее
геометрический смысл. В открытом множестве Q уравнения gi(x)=Q
определяют в окрестности точки а некоторое дифференцируемое
>
многообразие. Уравнения g't (а) (х — а) = 0, t=l, 2, ...., т,
являются уравнениями касательного линейного многообразия.
Соотношения (III, 10; 2) выражают тот факт, что гиперплоскость
>•
f'(a)-(x— а), касательная к гиперповерхности f(x)=f(a) в
точке а, содержит это линейное многообразие.
Доказательство. Проведем сначала доказательство для
конечномерного пространства Е. В этом случае можно выбрать
некоторую систему координат 0, ех, е2, ..., еп и выразить
точку х е Е в этой системе через ее координаты Х\,, х2, .... хп-
Предположение, что в точке а дифференциалы dgi являются
независимыми линейными формами, означает, что Существует
т координат, например Х\, х2, ..., хт, таких-, что якобиан
■п, " g2'-'' " gm/ (а) ф 0. Для этого, очевидно, необходимо, что-
бы п~^ т. Тогда в окрестности этой точки а, согласно теореме
28, переменные хи х2, .. ., хт можно выразить как функции от
gi, gz, • • ■. gm, xm+i, ..., xn. Найденные значения можно
подставить в f и получить новую непрерывно дифференцируемую
ФУНКЦИЮ F(gi, gi, ... , gm, Xm+i, . . . , Xn).
Запишем теперь, что функция F имеет экстремум в точке а
при условии, что Хт+и ■ ■ ■, хп изменяются, в то время как
gi, gz, •••. gm остаются нулями. Необходимым условием этого
является равенство нулю частных производных функций F по
Xm+i, • •., хп в точке а. Это означает, что дифференциал dF в
точке а имеет вид
dF = Я, dgl + k2dg2 + ... + Кdgm, (III, 10; 3)
где Х\, %2, ..., %т — вещественные постоянные. Поскольку
дифференциал df, выраженный через dxu dx2, ..., dxn, получается
заменой в дифференциале dF, записанном относительно
переменных dgu dg2, ..., dgm,dxm+h ..., dxn, дифференциалов dgi
их выражениями через dx\, dx2, ..., dxn, этот дифференциал df
удовлетворяет соотношению
df = \ldgl + Xidgi+ ... +Kdgm, (III, 10;4)
что приводит к (III, 10; 2), и теорема доказана.
Предположим теперь, что пространство Е бесконечномерно.
Поскольку g't (а) по предположению независимы, они могут
принимать произвольные заданные значения. Для каждого i можно
-*■-*■ -*■
найти такой вектор ^е£, что g't {а) • Xt = Ьц — 0 для \ф{ и

§ 10. Условные максимумы и минимумы
355
1 для /=»'. Построенные так векторы Хи Х2 Хт, очевид-
но, независимы, ибо если положить 2^Л = 0. то мы получим
£=1
g'i (я) • ^j A,(Jff = Я./ = 0. Положим теперь Xi=f'(a) -Хи Линейная
форма {'(а)—Zi^-ig'iia) равна нулю на векторах Хи Х2, ...
..., Хт, а, следовательно, на порождаемом ими векторном про-
-> ->
странстве. Пусть X — произвольный вектор пространства Е,
-*■ ■*
Обозначим через Е0 подпространство пространства Е,
порожденное векторами Хи Х2 Хт, X. На аффинном простран-
стве Е0, проходящем через а параллельно Е0, функция / должна
иметь экстремум в точке а на множестве /40=Л Л Е0,
определенном уравнениями gt{x)=0. Однако пространство Е0 имеет
конечную размерность т или т + 1. Следовательно, существуют
такие постоянные ць ц2, ..., цт, что производная {'(а) —
— 2 Pig'(a) равна нулю на Е0- Если записать, чтоонаобращает-
*■ ■*■ ->
ся в нуль на Xi, Х2, ..., Хт, то мы получим, что \ц = Ки Отсюда
т
следует, что f (a) — 2 ^.g' (а) равна нулю на произвольном век-
£=1
-> ■*■ ->
торе X пространства Е, а, значит, обращается в нуль на всем Е,
чем и заканчивается доказательство теоремы
Из доказательства вытекает, что множители Лагранжа Кг
определяются единственным образом, что, впрочем, ясно было и
заранее, поскольку g'i (а) предполагались независимыми.
Замечание. Пусть g—некоторая функция класса С1,
определенная на й сг Е, со значениями в пг-мерном аффинном
-*■ -*■
пространстве G, такая, что ее производная g'(a)^S'(E; G)
имеет ранг пг. Для того чтобы f имела в точке а экстремум на
подмножестве А множества й, определенном уравнением
g(x) =g(a), необходимо, чтобы существовал такой элемент К
из G' = 3?(G; R), при котором имеет место равенство
Г(а) = ко§'(а)<=Ё' = 2(Ё; R). (Ш,10;42)
В самом деле, выберем в G некоторую систему координат
с началом в точке g{a). Таким путем G отождествляется с Rm.
Теперь составляющие функции g — это m скалярных функций
12*

356
Гл. III. Дифференциальное исчисление
gu i = 1, 2, .. ., т, и множество Л определяется уравнениями
gi(x) = 0. То, что g'(a)e 3? (Е; G) имеет ранг т, означает,
что g\ (а) е 3? (Е; R) независимы. Мы находимся в
условиях применимости теоремы. Существование таких
множителей Лагранжа Ки i = 1, 2, ..., т, при которых имеет место
соотношение (III, 10; 2), эквивалентно существованию такого эле-
мента % е G', при котором имеет место соотношение (III, 10; 42).
Однако результат, записанный в виде (III, 10; 4г), вовсе не
зависит от выбора системы координат в G. Заметим, что в
(III, 10; 4г) производная g'{a) является элементом простран-
■> ■>
ства 9?(Е; G), а К есть некоторый элемент пространства
->
j?(G;R), последовательно, %°g'(a) является элементом
пространства 2'(Е; R).
Практический способ вычисления условного
максимума или минимума
Предположим для определенности, что Е имеет размерность
п, что в нем выбрана некоторая система координат и что
каждая точка х е Е задана своими координатами х\, х2, ..., хп.
Будем искать точку а= (аи аъ, ..., ап) условного экстремума
функции f при условии gi(x)=0, i=l, 2, .. ., т. Прежде всего
должно удовлетворяться уравнение (III, 10; 2), эквивалентное
системе п уравнений
^(а) = 2а,,-|г(а), /=Ь2, ..., п. (III, 10;5)
Если сюда добавить систему т уравнений (III, 10; 1) (где х
должно быть заменено на а), то получится система т-\-
«уравнений относительно т -\- п неизвестных, а именно, относительно
координат cij точки а и множителей Лагранжа %{. Нет
необходимости полностью решать эту систему. Можно при.желании
исключить множители Лагранжа %i и свести данную систему
к системе из п уравнений относительно п неизвестных а.).
Замечание. Хотя практически предыдущие уравнения
записывают, не проверяя, что в рассматриваемой точке а
производные функций g{ независимы, это является существенным
условием применимости теоремы.
Предположим, например, что f—некоторая вещественная
непрерывно дифференцируемая функция п вещественных
переменных Xi, х2, ..., хп и g есть функция х\ + х\ + ... +х\_г

§ 10. Условные максимумы и минимумы
357
Что же можно сказать о точке а, в которой функция f
достигает своего максимального или минимального значения на
подмножестве А, определяемом уравнением £(#)=() в R"? Это
уравнение эквивалентно системе уравнений Xi—Xz= ...
... =л:п_1=0, и, следовательно, рассматриваемое подмножество
J\ является осью Хп- Для того чтобы функция f имела в
точке а оси х„ условный максимум или минимум, необходимо
лишь, чтобы ее частная производная dfjdx„ равнялась нулю
в точке а без каких-либо условий, относящихся к другим
частным производным. Если же, напротив, учесть существование
множителя Лагранжа К, при котором -^— (а) = К -^- (a), i=
= 1,2 п, то мы получим, чго все частные производные
функции f в точке а равны нулю! Но в этом случае теорема 34
неприменима, так как в точке а оси хп дифференциал функции g
равен нулю.
Заметим, кроме того, что, как и для безусловных
максимумов и минимумов, этот метод не позволяет утверждать, что
данная функция имеет максимум или минимум в точке а,
поскольку нами использованы лишь члены первого порядка в
разложении Тейлора функции f в точке а. Заметим также, что этот
метод совсем не затрагивает условные экстремумы функции,
которые могут соответствовать граничным точкам множества F,
если оно не является открытой частью Е.
Этим методом можно воспользоваться для того, чтобы
определить оси некоторой поверхности 2-го порядка в евклидовом
я-мерном аффинном пространстве, отыскивая точки этой
поверхности, в которых расстояние от центра экстремально. Точно
так же можно искать оси сечения такой поверхности
плоскостью. В общем случае ищется точка х гиперповерхности,
заданной уравнением
g{xux2 xn) = 0 (g непрерывна) (III, 10; 6)
в пространстве R", евклидово расстояние от которой до
заданной точки b=(bi, b2, ..., bn) минимально. Поскольку
поверхность является замкнутым множеством (как прообраз нуля при
непрерывном отображении g пространства R" в R), то, согласно
изложенному на стр. 83,' существует хотя бы одна точка этой
поверхности, расстояние от которой до точки b минимально. Мы
должны искать точку х, реализующую минимум величины
f(x)=I1(xi-bi)2, (III, 10; 7)
среди всех точек, удовлетворяющих уравнению поверхности.
Если х удовлетворяет этому условию и если в этой точке
дифференциал dg не равен нулю, т. е. п частных производных

358
Гл. 111. Дифференциальное исчисление
dg/dXi не обращаются одновременно в нуль, то существует
такой множитель Лагранжа X, при котором имеют место
равенства ,
Х{-Ь{ = Х-^-(х), /=1, 2, .... п. (Ш,10;8>
Исключая отсюда X, можно будет определить искомую точку х,
выписывая п уравнений с п неизвестными:
dxt _.dxi _ _ дхп g(x) = 0. (Ill, 10;9)
xt — b, x2 — b2 " ' xn — b„ '
Эти уравнения выражают тот факт, что искомая точка, если она
не особая, является основанием нормали к гиперповерхности,
проведенной из точки Ь. Это согласуется с геометрической
интерпретацией, данной после формулировки теоремы 34:
в искомой точке х гиперповерхность касательна к сфере с
центром Ь, проходящей через эту точку. При таком решении
задачи необходимо иметь в виду следующее:
1°) Точка поверхности, являющаяся основанием нормали,
проведенной через точку Ь, не обязательно определяет минимум
расстояния. Она может определять относительный минимум,
относительный максимум или седло.
2°) Может случиться, что основания нормалей не дают
эффективно абсолютный минимум расстояния и что такой
минимум реализуется в особой точке поверхности, т. е. в точке, где
все п частных производных dg/dxi одновременно равны нулю и
где, следовательно, техника множителей Лагранжа не пригодна.
Впрочем, заметим, что если для получения (III, 10; 9)
исключается параметр ?., то тем самым вводятся эти новые решения.
Если поверхность не имеет особых точек, то, как мы видели,
минимум обязательно существует. Отсюда следует, что через
каждую точку b можно провести к этой поверхности по крайней
мере одну нормаль. Если, сверх того, поверхность компактна,
то расстояние от точки поверхности до точки Ь, будучи
непрерывной функцией на компакте, имеет максимум, и в этом
случае, считая, что на поверхности нет особых точек, можно из
точки b провести еще по крайней мере одну нормаль,
основание которой даст максимум расстояния от точек поверхности
до точки Ь.
Применение теории условных максимумов.
Неравенства Гёльдера и Минковского
Пусть Си С2, ..., с„ — п заданных и фиксированных
положительных чисел. Пусть задано, кроме того, некоторое р > 0.
Для каждой точки Х= (Хи Х2, . .., Х„) из С" положим
ll*llP = (c1U1|p + c2|*2rD + ... + ся\ХяГ)ир (III, 10; 10)

§ 10. Условные максимумы и минимумы
359
и назовем эту величину нормой X порядка р относительно
коэффициентов Ci > 0. Очевидно, это число ^0. С другой стороны,
-> ->
тривиально проверяется, что ||Ял|| = \К\ \\Х\\. Наконец, равенство
-> -> ->■
11X11=0 эквивалентно равенству Х=0. Для того чтобы
обосновать название нормы, остается доказать неравенство
выпуклости.
Позже мы увидим, что это неравенство выполняется только
для р~^\. Только в этом случае будет оправдано название
нормы. Тем не менее мы будем продолжать говорить о норме
порядка р и обозначать ее тем же самым образом, даже если
р<1.
Конечно, отображение (X, р) —»■ \\X\\V является непрерывным
отображением С"Х^+ в R, где R+ есть множество
вещественных чисел >0. Посмотрим, что происходит с этой нормой,
когда р стремится к +оо. Пусть Af=sup (|Xi|, \Хг\, ..., |^п|),
и предположим для определенности, что i является тем
индексом, при котором |Х,|=М. Тогда имеют место неравенства
II*H,<(2jC,J M и ||Х||р>с'/*М. (III, 10; 11)
Правые части этих неравенств при р, стремящемся к +оо,
стремятся к М. Отсюда следует, что для фиксированного X при
р, стремящемся к бесконечности, \\Х\\Р стремится к М.
Поэтому обычно полагают
ll*L = sup(|X,|> l*2l \ХЯ\). (Ill, 10; 12)
Заметим теперь, что рассмотренные на стр. 43 три нормы
над С" являются нормами \\Х\[„, \\Х\\и \\Х\\2. Посмотрим, что
происходит с \\X\\V при р, стремящемся к 0. В общем случае
характер поведения нормы не представляет интереса: Это инте-
п
ресно лишь в частном случае, когда сумма 2<Y равна 1.
j=t
В этом случае норма называется средним порядка р чисел \Х^\,
\Хг\, ..., \Хп\ по отношению к коэффициентам с*.
Здесь речь идет о взвешенном среднем.
Обычное среднее арифметическое соответствует Ci = l/n и
р = 1. Для С{=\/п и произвольного р средним порядка р
является число, р-я степень которого есть среднее арифметическое
р-х степеней \Х{\.

360 Гл. 111. Дифференциальное исчисление
Положим Zi с{— 1 и будем искать предел \\Х\\Р при р, стре-
мящемся к 0. Предположим сначала, что ни одно из чисел Х$
не равно нулю. В этом случае можно написать разложение
.\X,f = eeinlx'l=l+pln\X,\ + .... (111,10; 13>
откуда
2сл^г=2с< + р2с<1п|Л'<|+ ... =
i—l *=1 «=1
= l + p2iciln\Xi\+ ...; (Ш,10;14>
л,
учитывая, что 2^=1, получаем разложение
ln(Sc,|^n = p2c,lnUj|+ .... (Ill, Ю; 16)
\J—1 / *— 1
Отсюда видно, что при р, стремящемся к 0, In || J4T Ц^, =^
= — In I V Ci\Xi\p J стремится к Vc/lnl-X^I, и, следовательно.
w=
->
|| X ||р стремится к
IIlAYf'. (Hl,l0;i6>
<=i
Эта величина является взвешенным средним геометрическим
чисел 1 А"; | с весами ct.
Если все с,- равны 1/п, то мы получаем обычное среднее
геометрическое У\ XtX2 ... Х„ |. Легко проверить, что результат
остается верным, если некоторые А',- равны нулю. Предел \\Х\\Р
будет тогда равен нулю.
л
Мы приходим к тому, чтобы при 2 с<= 1 положить
\\Xh=f[\Xi\\ (III, Ю; 17)
<=i

§ 10. Условные максимумы и минимумы
361
Теорема. 35 (неравенство Минковского). Для р ^ 1')
имеет место неравенство выпуклости:
\\X + Y\\P<\\X\\P + \\Y\\P, (III, 10; 18)
причем для 1 < р < се имеет место строгое неравенство, за ис-
ключением случая, когда векторы X и Y пропорциональны с
некоторым коэффициентом пропорциональности ^ 0.
Доказательство. Неравенство очевидно для р=1 и р —
= -)-оо. Остается, следовательно, изучить случай конечного р >
>1 и при этом, естественно, провести доказательство для слу-
чая, когда оба вектора X и Y отличны от нуля. При этом можно
ограничиться случаем, когда Xi, Yt вещественны и ^ 0. Однако
множество точек Rn, координаты которых Г^О, не является
открытым -множеством в векторном нормированном
пространстве и, следовательно, теоремы об экстремумах не
применимы. Поэтому мы докажем неравенство для всего векторного
-*• -*• -*•-*•
пространства Rn. Положим \\Х\\р = а, ||У||р = В и \\Х-\-Y\\p=y.
-> -*•
Рассмотрим множество А точек (X, У) из R2n = RnXR'\ для
которых аир принимают заданные отличные от нуля
значения ао и Ро- Это, очевидно, некоторая компактная часть
пространства R2". В самом деле, это множество А замкнуто как
прообраз точки (ао, Ро) ^ R X R при непрерывном
отображении {X, У) — (\\Х\\Р, \\Цр) пространства R" X R" в R X R. Оно
ограничено, ибо-задание ао и Ро определяет мажоранту для всех
координат векторов X и У. Согласно, теореме 23 гл. II, это
множество компактно. Поскольку у является непрерывной функ-
-*• ->
дней точки {X, У) из R"XRn> она принимает на компакте А
-*• -*•
максимум или минимум. Обозначим через (X, У) точку, в
которой этот минимум или максимум достигается. Это будет точка
условного экстремума. В самом деле, в этой точке непрерывная
на RnXR" функция уР достигает своего максимума или
') Для р < 1 результат не имеет места. Возьмем, например, р = 1/2,
« = 2, с1 = с2=1, Хи Х2, Yu К2>0. Тогда (III, 10; 8) означает, что
{УХТТг + VxThT2)2 < (УХ + УХ)2 + {VT, + УГ,)2,
или /№ + К,)(^2 + К2) <УХГ, + УПГь
или (Xi + Г,) (Х2 + Y2) < XtX2 + YJi + 2 Vx^Yjl,
или XlYi + XiYisZ2Vx1X2YiY1,
в то время как в силу неравенства о + Ь ^ 2 У ab должно иметь место
неравенство вида ^.

362 Гл. 111. Дифференциальное исчисление
минимума среди точек, связанных двумя соотношениями:
а"(Х, Г)=ав(Х) = а0р и рр (1 Y) = рр (У) = р0Р •
Все гры функции ар, Рр, yp непрерывно дифференцируемы.
Рассмотрим, например, функцию а*\ Она имеет частную
производную по Х{ в открытом множестве Х{Ф0, равную
-^{ap) = pcfit\Xtr\ в, = sign X,. (Ill, 10; 19)
При X,-, стремящемся к 0, эта производная имеет равный
нулю предел. Согласно теореме 14, примененной к функции а*\
если изменяется только Xiy существует также частная
производная на гиперплоскости Xt=0 и эта производная равна
нулю1). Следовательно, производная ар по Xt всюду
существует. Производная функция определена соотношением
(III, 10; 19). Эта функция непрерывна во всем R"XR". %
следовательно, аР, имеющая непрерывные частные производные
первого порядка, согласно теореме 15, непрерывно
дифференцируема. То же самое имеет место для функций р? и уР,
производные которых имеют вид
д <P,) = pcmi\Yir1'. Ti^signy,, (III, 10; 20)
dYi
д
Ж(Y'P) = -Щ {уР) = P°ili\X'+Y' ' ' «i = sign (X; + Yt).
(Ill, 10; 21)
(Очевидно, предыдущие результаты не были правильными для
-> ->
р^.1.) Теперь в той точке (X, Y), где реализуется либо
максимум, либо минимум, существуют два множителя Лагранжа
% и ц, такие, что 2)
d (yp) = Ы (а") + [id {§,"), (111,10; 22)
или
pc&,t\Xt + Yt\'-x=*\pcfit\Xt\'-\. г=1, 2, /.., п,
pc&l\Xl + Yir1 = lipclrUlYirl, /=1, 2, ...', п.
(III, 10; 23)
Если для некоторого индекса i координата Xf равна нулю,
то первое уравнение из (III, 10; 23) для этого индекса
превращается в равенство Х{ -\- У<=0, откуда в свою очередь У*=0.
•) Непосредственная проверка показывает, что в тех точках, где Хг = 0,
производная d/dXt равна нулю!
2) При условии, что дифференциалы d(oC) и d(Pp) независимы. Однако
один из них зависит только от dXu а другой только от dYt. Они могут быть
зависимыми только тогда, когда один из них равен нулю, т. е. когда X = 0
или У = 0, что мы исключили, положив oto Ф 0 и Ро Ф 0.

§ 10. Условные максимумы и минимумы 363
Точно так же, если Yt = 0, то второе уравнение даст Х, = 0.
Следовательно, в той точке, в которой имеет место максимум или
минимум, если одна из координат Хи Yt обратилась в нуль, то и
другая также обратится в нуль.
Если ни одна из координат не равна нулю, уравнения
(III, 10; 23) для индекса i эквивалентны уравнениям
£(|1+^-|"_1 = еД, £.|i+!l|p"' = T№. (Ш, Ю; 24)
Во всяком случае множество этих уравнений, после
исключения X и jj., можно записать в эквивалентной форме
-£- = £- = ••• =TL- (Ш,Ю;25)
Л1 л2 Лп
Некоторые из отношений могут оказаться неопределенными,
вида 0/0 (но не все, поскольку X и Y не нули). Пусть s — общее
значение этих отношений. Тогда Ро = I s | ссо и, следовательно,
y-^CiW+snXifj =|1 + S|a0. (Ill, 10; 26)
Отсюда с необходимостью вытекает, что максимум у равен
ссо + Ро и достигается при s > 0 и что его минимум равен
| ссо — Ро| и достигается при s < 0. Теперь получаем, что всегда
имеет место неравенство y ^ a + Р. являющееся неравенством
выпуклости (III, 10; 18). Кроме тех точек, в которых
реализуется максимум, везде имеет место строгое неравенство у <
< a + р. В точках максимума имеет место (III, 10; 25)
с общим значением отношений s > 0. Иначе говоря, векторы X
и Y пропорциональны с коэффициентом пропорциональности
^0'). Конечно, это доказывает вторую часть теоремы лишь
->• ->•
в том случае, когда векторы X и Y имеют вещественные
координаты. Однако точно так же в общем случае комплексных
координат получается последовательность неравенств
/ п \Чр
IIX +У !|РЦ2 ^(1^1 + 1^1)') <||Х||Р + !|К||Р. (III, Ю;27)
Первое из них является строгим неравенством, кроме случая,
когда все отношения Xf/Yj вещественны и ^0, чем и
доказывается теорема в общем случае.
') Мы пишем >0 вместо >0 для того, чтобы вернуться к
отложенному ранее очевидному случаю, когда по крайней мере из двух векторов
->■ ->
X и У равен нулю.

364 Гл. Ш. Дифференциальное исчисление
Теорема 36 (неравенство Гёльдера). Если при произволь~
ных числах р и q и таком числе г, что 1— = —, обозначить
через XY точку с координатами Х{Уи X2Y2, ..., XnYn, то
WXYH^WXWpWYW,. (III,m;28>
Кроме того, если 0 < р < Ч-°°> О < Я < +°°, то всегда имеет
место строгое неравенство, за исключением случая, когда
jY1^_=\Y1^_ =\Хп1_ ail 10-29V
Докажем прежде всего теорему для случая, когда все три
числа р, q, r больше 1 и конечны. Как и в теореме 35, мы
воспользуемся методом множителей Лагранжа. Положим
а = ИЛ!р, Р = ||У||,, y = \\XYl.
Если мы рассмотрим точку, в которой достигается либо
максимум, либо минимум функции у, когда аир принимают
заданные значения ао и ро=й=0, то существуют два таких множителя
К и ц, что d(yr) —Xd(aP) + \id($<i), или
rcfltlXtr^Yj^kpcfitlXtr1, t=h 2 п, _
rcmAXtrpj-^vLqcmtiYtf-*, i=i,x...,n. ' ''
Отыскание минимума производится без труда. В самом деле,
если для каждого i хотя бы одна из координат Х{, Yt равна
нулю, но таким образом, что одновременно а=ао и р = ро
(например, если Х1 = —j^- и Х2=Х3= ... =Хп = 0 и далее
6 ■ ■*■■*
Yi = 0, Y2 — -777. Y3=... — Уп = 0), то XY равняется нулю и
минимум у также равен нулю. Мы не будем касаться этого
случая и будем искать только максимум.
Если для некоторого индекса i координата Xt равна нулю,
то второе уравнение для этого индекса дает У,=0 или ц.— 0.
Однако если ц=0, то при любом i хотя бы одна из двух
координат Х{, Y{ равна нулю, и мы приходим к случаю минимума,
уже исключенному из рассмотрения. Таким образом, \1ф0 и,
следовательно, из ^, = 0 следует У,= 0. Точно так же из У| = 0
следует Х{—0. Если Xt и У, обе =^=0, то уравнения (III, 10; 30)
дают соотношения
p%\Xi\t' = q[i\Yt\q, /==1,2 я, (III, 10; 31)
а, следовательно, (III, 10; 29),

§ 10. Условные максимумы и минимумы
365
Некоторые из этих соотношений, но не все, могут представиться
в неопределенной форме 0/0.
Положим | Kj|9=s|Xi\р. Тогда р^ = saj. Отсюда получаем
га ,_рг_ га
уг = snq 2 с. IX. I 1 = s"« 2 с. | Л", I" = s"«aj?, (111,10; 32)
что дает \г = аоРо, или v=aoPo. Отсюда вытекает, что для ка-
ждой точки (X, У)ек"ХК" имеет место неравенство \^
^ аоРо, что совпадает с неравенством (III, 10; 28).
Кроме того, везде имеет место строгое неравенство у < одРо,
за исключением отдельных точек, где реализуется максимум, и
в этих точках имеют место равенства пропорциональности
(III, 10; 29).
Теорема была доказана лишь для конечных р, q, г,
больших 1. Однако если мы будем считать теорему доказанной для
1.1 1
индексов р, q и числа г, определенного равенством 1 = — ,
и если мы положим |Xj| = |gj|fe, | У,| = |iii|fe, 0 < k < 4-°°, то
будет иметь место неравенство
\\Ш1<\\КРЫС (III,10;33)
откуда следует, если возвести обе части равенства в степень
l/k, что теорема доказана для показателей kp, kq, kr, таких, что
kp ' kq kr ■'
Отсюда вытекает, что доказательство теоремы для
произвольных конечных показателей >0 можно свести к уже
изученному случаю показателей вида p/k, qjk, выбирая k таким
образом, чтобы числа p/k, qjk, rjk были >1, Это, однако, не дает
возможности доказать теорему, если показатели р, q, r равны
га
+°° или 0 при 2с;=1. Если, например, р=-\-оо, то q=r и
неравенство (III, 10; 28) запишется в виде
ll*n,,<ll*Llinir (III, Ю; 34)
Это неравенство тривиально, даже если q также равно +°°-
Ва всяком случае оставшиеся неравенства могут быть
доказаны предельным переходом.
Следствие 1. Два показателя р, р' ^ 1 называются
сопряженными, если имеет место соотношение
± + ±=1, или Р' = у?гт- (III, Ю; 35)

366
Гл. III. Дифференциальное исчисление
В этом частном случае неравенство Гёльдера имеет вид
2 с,Х,У|< ИЛИ У И,. (III, 10; 36)
(=1
Кроме того, для рф\ и фоо имеет место строгое неравенство,
за исключением случая, когда выполняется соотношение
пропорциональности
_ I Yn |"'
\У,\"
\хп
\р •
(III, 10; 37)
где все произведения Х{У{ имеют один и тот же аргумент1).
Для доказательства достаточно применить общее
неравенство, в котором г—\. Из него тогда получится соотношение
->-> -> ->
|| XY ||, <!|| Х||р||У Ир- и, следовательно, тем более соотношение
(III, 10; 36). Однако
2 c,X,Yt
<\\XY\
(III, 10; 38)
кроме случая, когда все комплексные числа ХгУ; имеют один и
тот же аргумент. Очевидно, что, кроме случая, указанного в
условии, неравенство (III, 10; 36) будет строгим.
Следствие Ь (неравенство Коши
сто неравенство
2'с^»у»
(=1
Шварца). Имеетме-
<||!||2||У|Ь (III, 10; 39)
со знаком строгого неравенства <, кроме того случая, когда
векторы X и У пропорциональны.
Достаточно применить следствие 1 к сопряженным
показателям р=р'=2. Аргумент А^У,- совпадает с аргументом XilYit
а все числа УгДг- имеют общий модуль и общий аргумент тогда
и только тогда, когда векторы X и У пропорциональны. Мы
давали ранее другое доказательство (формула (111,1; И)). Для
получения (III, 10; 39) достаточно применить формулу (Ш, 1; 11)
к положительно определенной полуторалинеинои эрмитовой
форме
В(Х, У)
2 ctXtYt.
(III, 10; 40)
') Если все Xt отличны от нуля, то соотношение (III, 10; 37) означает,
что существует такая постоянная k, что |К;| = k\Xi\»-1.

§ JO. Условные максимумы и минимумы
367
Следствие 2. Если сумма весов 2 с« равна 1, то для
-> -»-
фиксированного X среднее порядка p. \\X\\V является
непрерывной возрастающей функцией р. Эта функция строго возрастает,
кроме случая, когда \ Х\ | = | Х21 = ... = | Хп \, в котором она
постоянна.
В самом деле, достаточно применить неравенство Гёльдера
к случаю, когда Y\ = Y2— ... =У„ = 1. Если учесть, что
" ->
2j Ci= 1, то ||У||9=1. Это дает при любом q ^ 0 и, следова-
<=1
тельно, при любом г ^ р неравенство
ЦХ||,<1|Х||Р. (III, 10; 41)
Более того, здесь будет всегда иметь место строгое
неравенство, кроме случая, когда
I Хх \р ^ | Х2 \р = •" = | х„ \р ' (III, 10; 42)
т.е. когда все \Xi\ равны. При этом среднее очевидным
образом будет постоянной, равной общему значению этих чисел.
Следствие 2г. Среднее геометрическое конечного числа
неотрицательных чисел не превосходит их среднего
арифметического и всегда строго меньше его, за исключением случая,
когда все эти числа равны между собой.
Для доказательства достаточно применить (III, 10; 41) при
/■=0 и р = 1.
Доказательство неравенств Гёльдера и Минковского с
помощью теории выпуклых функций. Функция х—* Xs, s ^ 1,
выпукла для х > 0. В самом деле, она непрерывна, а ее вторая
производная для х > 0 существует и равна s(s — l)xs~2 > 0
(теорема 7г). Следовательно, для zu zz, ..., zn ^ 0 и а±, аг, ..., ап^0
имеем:
/„,„+,.. +„,,\' аА+ +аЛ
\ а, + ... + а„ / ^- а, + ... + а„ v '
или, умножая на (а, + ... + a„)s и возводя в степень 1/s:
(a,Z| + .. • + «„*„) <(«,*?+...+ a,**)1" (a, + ... + aj1"1".
(Ill, 10; 44)
Положим теперь для Х„ У*>0, c,->0, p, q > 0, — + 7 = 7
«1 = ^, \^Х\Г-\ s = £. (Ill, 10; 45)

368 Гл. III. Дифференциальное исчисление
Тогда
I = -L, 1-1--I (ибо ^- + -1=1),
s Р ' s q \ р ' q )'
aizi = cl(XlYly, (III, 10; 46)
■ рч
«,< = c№?' <'-<" = ctX>tY*+q~ - *,**.
Возводя теперь (III, 10; 44) в степень 1/r, получаем
неравенство Гёльдера
(cl(XlYl)r + ... +cn(XnYnY)Ur^
<(сХ+ ••• +«Л"Р(?Л+ ••• + СЛ'"- (Ш'Ю;47)
Функция я->(1 — jc''p)p, /?:> 1, выпукла на [0, 1], ибо ее
вторая производная на ]0, 1[ равна
(1 —х1'")"""2 (l --) jc'/p-2 > 0.
Следовательно, для 0^2,, г2, ..., zn<S 1 и щ, а2, ..., а„^0
имеем
/ _ /а,Я|+ ...+«.,,,,, у/'У1 «д(1-«1/У+ ... +«И(1-»УУ
\ \ а, + ... +а„ / / "~-- а, + ... +а„
(III, 10; 48)
Возводя в степень 1/р, а затем умножая на (а{ + ... + а„)1/р,
получаем
(а,+ ... +а„)"р<(а12:1+ ... + anzn)l,p +
+ (а, (1 - г\*у + ... + а„ (1 - z'">)p)"P. (III, 10; 49)
Для си Xiy Yt^0 положим
o.l = cl(Xl + Yi)p, ■ а,>0,
-.-/ Xt у 0<г<1 (Ш, 10; 50)
Отсюда
at(l-zl'y^cfi. (Ш, 10; 51)
Теперь (III, 10; 49) принимает вид неравенства Минковского:
(cl(Xt+Yly+ ... +cn(Xn + Yny)l,P<
<№+ ... +caXff»(ClY!+ ... +cX)!l°. (Ill, Ю;52>

§ //. Вариационное исчисление
369
Неравенство Минковского можно также получить из
неравенства Гёльдера. В самом деле,
£ (Xt + Yt)p= 2 (Xt+ Yl)p-lXl+ 2 (^| + У|)"-,Т/. (Ill, 10;53)
t=\ i=i *=i
Согласно неравенству Гёльдера, написанному относительно
показателей р, р', —+ —г=1 \Р' — р — i ) > имеем:
п I n \1/Р' / гг \'/Р
/ гг \!/Р' / „ \1/Р
+ (S№ + Ki)(p-,)p'j (2/fj • (Ш, Ю; 54)
Поскольку (р— 1)р' = р, достаточно обе части равенства умно-
/ п \-i/p'
жить на I 2 № + ^»)р) и получить
/ гг \1-(1/Р') / „ \1/Р / „ sl/p
(S (** + ^«)PJ < (S *Р) + (2 ГР) ., (HI, Ю; 55)
что совпадает с неравенством Минковского, так как 1 - = —.
Р Р
§ 11. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Постановка задачи
Рассмотрим следующую задачу механики:
Пусть в трехмерном пространстве заданы две точки А и В
и некоторая кривая Ч? класса С1, соединяющая эти точки. По
этой кривой без трения и под влиянием своего веса свободно
скользит некоторая материальная точка.
Выходя из точки А с нулевой начальной скоростью, она
попадает в точку В через время t. При заданных точках А а В
это время является функцией рассматриваемой кривой.
Спрашивается, как следует выбрать эту кривую, чтобы время / было
минимальным? Кривая, обладающая таким свойством,
называется брахистохроной («кривой наискорейшего спуска»).
Будем пока считать очевидным, что кривая, реализующая этот
минимум, располагается в вертикальной плоскости, проходящей
через отрезок АВ. Выберем в этой плоскости горизонтальную
ось х и вертикальную ось г, направленную вниз. Пусть z—a,
х=а и z=b, х=р — координаты точек А и В. Классическая
теория падения тел говорит, что в заданной точке кривой при

370
Гл. III. Дифференциальное исчисление
отсутствии трения скорость v материальной точки задается
формулой
v2 = 2g(z — a). (Ill, 11; 1)
Отсюда получается дифференциал времени как функция
дифференциала криволинейной абсциссы: <jt =—г так что
V2g(z — a)
окончательно -время, необходимое для перехода от Л к В,
задается интегралом
f VTT72 А с У"' + г2 (?) А " riII ,, ov
г — dz — лгп , ==■ dz, (III, 11; 2}
J V2e (z - a) J ng(z-o) v '
a a
в котором предполагается, что кривая определяется с пом.ощьк>
х как функции z: x=f(z) '). Мы приходим к следующей
математической задаче: найти такую вещественную функцию f
вещественной переменной z, для которой интеграл (III, 11; 2) при
заданных a, b, g, f(a)=a, f(6)=p принимает возможно
меньшее значение.
Можно поставить общую задачу следующим образом. Пусть
[а, Ь] — вещественный интервал, F — аффинное нормированное
пространство над полем вещественных чисел, °U — открытое
->•
множество из F X F. Пусть, с другой стороны, задана непре-
->• ->•
рывная вещественная функция L: (х, (у, У)) —* L(x, у, У),
определенная на [a, b]y^°U. Пусть, наконец, f: x-*y=f(x)
—непрерывно дифференцируемая функция, определенная на [а, Ь] со
значениями в F, ^акая, что для х е [а, Ь] все (f (x), f'(x)) лежат
в<Ш2).
При этих условиях сложная функция х—*L(x, f(x), f'(x))
является непрерывной функцией на [а, Ь] со значениями в R.
При этом можно вычислить интеграл
ь
J№=\ L(x,f(x),f(x))dx, (III, 11; 3)
a
являющийся некоторым вещественным числом.
') Возможность выразить х как функцию z спорна: см. рассуждения,
приведенные на стр. 386.
2) Поскольку речь идет о функции на R, {'(х) является производным
вектором в точке х, т. е. элементом F, определенным с помощью формулы
(111,3; 1). Он равен f'(x)-l, если f(A;)G^(R;f) является производным
отображением. С другой стороны, [а, Ь] не является открытым множеством
в R; см. по этому поводу начало § 2, стр. 195.

§ П. Вариационное исчисление 371
Это вещественное число зависит от выбора функции /. Тем
самым определяется некоторая функция /: f-*J(f). Требуется
при фиксированных а, Ь и L среди всех функций f,
принимающих фиксированные значения а, р* на концах а, Ъ, найти ту,
которая обеспечивает интегралу /(/) максимум или минимум.
Если F является /n-мерным пространством, то введением
системы координат его можно отождествить с Rm, и тогда
функция, определенная на [а, Ь] со значениями в F, является
системой вещественных функций /{, i=l, 2, ..., т, определенных на
[а, Ь], а производная функция является системой т производных
функций f'r В этом случае L есть вещественная функция
2т + 1 независимых переменных х, уи Yu i=l, 2 т, и
среди всех систем непрерывно дифференцируемых на [а, Ь] и
принимающих заданные значения в а и Ъ функций /*, i=l, 2 т,
отыскиваются те, которые обеспечивают экстремум интегралу
h
1 (/, У =] L (х, /, (х) fm (х), f[ {x) /'„ (х)) dx.
(1П,И;4)
Напомним, что пространство Е = (Яа-Ь])с6;1 непрерывно
дифференцируемых функций, определенных на [а, Ь] со значениями
в F, является аффинным нормированным пространством с
присоединенным векторным нормированным пространством
->
(Яа'ь!) сь;,!). Расстояние между двумя элементами fug
аффинного пространства Е задается формулой (111,3; 41):
III/~JIII. = sup (\\f(x)-g(x)\\, llfM-s'WII). (Hl,ll;5)
Мы рассмотрим здесь сначала некоторое подмножество
аффинного пространства Е — множество Q, образованное такими
функциями /, что образ при отображении (f,f) интервала [а, Ь]
содержится в открытом множестве Ш из F X Е.
Теорема 37. Пусть: [а, Ь] — отрезок в R, F — аффинное
нормированное пространство над полем вещественных чисел и
->
<U — открытое множество из F X Е. Множество Q функций f,
определенных на [а, Ь] со значениями в F, таких, что (f(x), f'(x))
для всех х е [а, Ь] лежит в Щ, является открытым множеством
в пространстве Е = (Ла>ь') сь; i непрерывно дифференцируемых
функций, определенных на [а, Ь] со значениями в F.
') Поскольку [о, Ь] компактно, непрерывная на [о, &1 функция ограничена
и символ cb, означающий непрерывность и ограниченность, может быть
заменен символом с, обозначающим непрерывность.

372
Гл. III, Дифференциальное исчисление
. В самом деле, пусть fo — некоторая точка этого множества.
Образ компактного интервала [а, Ь] при отображении (f0, f„)
является компактом К в °U (теорема 28 гл. II). Согласно
показанному на стр. 84, расстояние от К до СШ является
некоторым числом б > 0. Рассмотрим теперь в Е открытый шар
с центром fo радиуса б, образованный всеми функциями f,
>
удовлетворяющими неравенству III f — fo III < б. Мы видим,
->
что для каждой такой функции f отображение (f, f) принимает
все свои значения в °U. Иначе говоря, каждый такой шар
принадлежит множеству Q и множество Q открыто в Е.
Множество функций f e E, удовлетворяющих заданным
равенствам f(a)=a, f(b)=P, является некоторым аффинным
подпространством Е0 из Е. Его присоединенное векторное подпро-
странство является множеством Е0 функций из Е,
обращающихся в нуль в точках а и Ь. Множество Q отсекает на Е0
некоторое открытое множество Q0 из Е0. Далее, J: f —* /(f) является
вещественной функцией, определенной на открытом множестве
Q0 аффинного нормированного пространства Е0, и мы ищем
максимум или минимум этой функции. Теорема 23 должна нам
дать необходимое условие. Мы видим здесь, что теорема 23 и
все теоремы дифференциального исчисления представляют
интерес для случая бесконечномерных нормированных пространств.
В самом деле, если даже F конечномерно, если даже это,
например, вещественная прямая R, входящее сюда пространство Е
бесконечномерно.
Для облегчения формулировок мы не будем повторять
данные [a, b] cz R, F, Ш, Q, L, J, если в этом не будет особой
необходимости.
Дифференцируемость /
Для изучения дифференцируемости функции / мы будем
рассматривать общий случай аффинного пространства Е
и рассматривать производную /'(fo) на элементе f0. Сужение /
на Е0 имеет производной в fo^Eo сужение производной /'(fo)
-> —>■
на Е0. Обозначим через 6f заданное приращение f. Это
некоторый элемент из Е, т.е. функция х-*б[(х), определенная на
[а, Ь] со значениями в F. Мы будем искать «главную часть» б/
приращения А/ функции /, когда f0 заменяется на fo + 6f.
Обозначение df, которое в том случае, когда f является
отображением [а, Ь] в F, означает дифференциал этого отображения:

§ 11. Вариационное исчисление
373
df—f(x)dx<=F, применять опасно. Поэтому мы применяем
обозначение 6/ и по аналогии 6/.
Теорема 38. Вещественная функция J, определенная на
Q формулой (III, И; 3), непрерывно дифференцируема, и ее
<- -> <-
производная /'(/о) eS'^; R) = Е' в точке /0 определяется
формулой
->
6/-*6/ = /'(/о)-6/о =
= { (Z/ (jc, /о (jc), /о (jc)) • (0, 6/ (jc), 6/' (jc)) ) dx =
а
Ь
= \{b\L (jc, /0 (jc), f'0 (x)) ■ 6~ftc)+dJ. (x, f0 (x), f'0.(x)) • Щх)) dx,
(III, П; 6)
где U — полная производная, a d2L и d3L — частные
производные функции L (определенной на открытом множестве в
->
[a, b]X,F)>(F) no 2-й и 3-й переменным.
Заметим, что вместо d2L и d3L можно было бы писать
дЦду и dL/dY, поскольку мы через у и Y обозначили пере-
->
менные в пространствах F и F.
Вместо L(x, f(x), f'(x)) коротко пишут также L(x,y,y');
поэтому вместо d2L и d3L можно также писать дЦду и дЦду'. Это
-> ->
производные функции (х, у, y')->L(x, у, у'), когда х е [а, Ь],
-> ->
у е= F, у' е F рассматриваются как независимые переменные.
После того как они вычислены, следует заменить у на /0 (х) и
? на % (х).
Так как y~>L(x, у, У) является отображением пространства F
■*— -> ->
в R, то d2L(x, у, Y) является элементом пространства 2' (F', R)=
<- -> ч
— /*■', сопряженного к F, откуда следует выбор стрелки d2L.
<—
То же самое имеет место и для d3L. Далее, для каждого jce
<= [а, Ь] имеем d2L(y, fo(x), /о(jc)) е F' и 6/(х) е F, откуда
следует, что d2L(x, fo(x), fo(x))-6f(x) в (III, 11; 6) является
вещественным числом; (III, 11; 6) является интегралом от некоторой
вещественной функции на [а, Ь].

374
Гл. III. Дифференциальное исчисление
Доказательство. Вариация Л/ интеграла,
соответствующая вариации б/ функции /, задается формулой
h
Л/ = J [L (jc, /о (JC) + б/ (х),~?0 (х) + б?' (jc) )-L (x, h (jc),7o (*)) \dx.
(Ш, И; 7)
Формула конечных приращений (следствие 1 теоремы 13) для
фиксированного х дает
L (х, /о(дс) + 6?(jc), Ш + 6?(х) )-L(x, /0(jc),7T(jc) ) =
= V (х, /о (jc), f (jc) ) • (0, 6?(х), 6Г(х) ) + #(*) =
= oKh(jc, /о(jc), ft (jc))-6f(x) + o\L(x, /o(jc),t(x))-bf'(x) + R (jc),
(III, 11; 8)
где R (x) допускает оценку
Ш*)К sup ||L'(jc, /0(Jc) + f, /f(*) + ?)-
iifii<iie'f<*)ii
nfii<ii6n*)ii
-L(jc,/0(jc),^(jc))|| • II (0, ^ (jc); бТ'М)!!1). (HI, 11; 9)
Воспользуемся теперь усиленной теоремой (теорема 31 гл. II)
-о равномерной непрерывности2). Функция U предполагалась
непрерывной на [а, Ь]у_еи. Множество точек (jc, /0(jc), /q(jc)),
jc e [a, b], содержится в компакте [a, ft] X К множества [a, b] X
X 'U (в обозначениях, принятых при доказательстве
теоремы 37).
') На RXFXF мы выбрали норму ||(Х, Y, Z)\\ = sup( | X |, ||Щ, Щ\).
2) Речь идет о следующей теореме: Если f является непрерывным
отображением метрического пространства Е в метрическое пространство F и если К
является компактом в Е, то, каково бы ни было е > 0, существует такое
т) > 0, что из d(x',x") sg т), х' е.К, следует d(f(x'), f(x")) =g; е. Теорема 31
относится к Е = К- Доказательство остается прежним. Если бы это было не
так, то можно было бы найти две такие последовательности хп е К, хп е
s £, что<*(л:^, *")<!/« и d (/ (д:^), f (х") )> е. Поскольку К является
компактом, можно из хп извлечь подпоследовательность, сходящуюся к
некоторому элементу сеК. Тогда хп тоже стремились бы к с в Е. Так как f
непрерывна в с, то f(x'n) и f(x") стремятся к [(с), а, значит,d(f(x'^, f(x'n))
«тремится к 0, и мы получили противоречие.

§ И. Вариационное исчисление
375
Итак, при заданном е > 0 существует число ц, О ■< ц < 6*
такое, что из х^[а, Ь], ||g|| s$ r\, |||'|| sg; г\ следует
\\L'{x, f0(x) + l ]t(x)+t)-L'(x, f0(x),.t(x))\\<-b~-
(III, 11; Ю)
Далее, из ||| 6f llli ^ Л следует, что
l#WI<-^-|||6fl||,. (Ш, И; И)
Таким образом, имеем:
ъ ь
Ы= ${d^L-6f + c&-6?')dx+$ R(x)dx, (III, 11;112)
где каждая из функций х->d2L(x, f0(x), f'Q(x)) bf (x), jc->
-+d3L(x,f0{x), f'u{x)}bf {x), а, следовательно, также и *->/?(*)
непрерывны. В самом деле, d2L является непрерывным отоб-
ражением [a, b] X <U в F', поскольку L непрерывно
дифференцируема. Функции f0, f0, 6f непрерывны как функции из [а, Ь\
■* ->• ■*— —>
в F, F, F соответственно. Следовательно, x^-d2L(x, f0 {x), f'0{x))
<-
является непрерывной функцией из [а, Ь] в F' и, поскольку
<- -> <- -> <- ->
{и, Х)-+и-Х = (и, X) есть непрерывное отображение из
(F' = 3?(F;R))'XF в R, то х-+д£{х, f0(x), f0{x)) ■ bf{x)
есть непрерывная функция из [а, Ь] в R.
-> х
Второй интеграл при |||6f |||, <Iri мажорируется величиной
е ||| 6f HI,. Следовательно, он является бесконечно малым па
-> ->
сравнению с |||6f|||i, когда |||6f|||i стремится к 0.
Первый интеграл определяет некоторую линейную форму,,
непрерывную на Е. В самом деле,
ь
$ (%L • 6f+ $£•$) dx
ь
j (Z/(x, f0(x), fQ(x)). (0, fif (*), ?' (x))dx
<
< (b - a) M HI tf |||„ где M = sup IIU (x, f0 (x), ?0' (x) )||.
(III, li; Из)-

376 Гл. III. Дифференциальное исчисление
Тем самым мы доказали, что функция / дифференцируема
b|0eQ и что ее производная задается формулой (III, 11;6).
Покажем теперь, что функция / непрерывно
дифференцируема на Q. Рассмотрим элементы /0 и / из Q. Имеем:
ь
= J (L'(x,f(x), Пх))-и(х, f0(x), fftx)))- (0, tf (x), 6p(x))dx.
(in. 11; H4)
■>
Согласно (111,11; 10), из |||/ — /0|||i <t] следует, что
|(/ЧЙ-/^).в?Кв|Цв7|||, (III, 11; 12)
и
II/'(/)-/'(/о) 11= sup | (/'(/)-/'(/о))-6f |<е. (Ш,11;122)
П1^111,<1
Итак, /'{/) — /'(/о) сходится к 0 в Е', когда / стремится к /0
в £, и, следовательно, / принадлежит классу С1.
Пример. Небесполезно бегло рассмотреть простой случай
F=R и %L=\a, 6] X R X R- Будем предполагать,
следовательно, что L является функцией класса С1 трех вещественных
переменных х, у, у', х^[а, b], jieR, //'eR. Рассматривается
функция /, определенная на (Rla,b])cb;i формулой
ь
J (f) = J L (x, I (x), Г (x)) dx. (Ill, 11; 123)
a
Функции / дается приращение б/, являющееся также
некоторой функцией класса С1 на [а, Ь]. Приращение Д/
функционала / в этом случае записывается в виде
ь
Л/ = { (L(х, /0 + б/, /; + б/') - L (х, /0, /Q) dx. (Ill, 11; 124)
a
Его «главной частью» является" дифференциал
ь
(III, 11; 12в)
Обоснование этой формулы вытекает из оценки вида
|в;-Д/|<в|||в/|||, для |||в/|||,<т| (стр. 375), (1П,11;126)

§ И. Вариационное исчисление
377
получающейся применением к L формулы конечных
приращений.
Преобразуем теперь (III, 11; 6), вводя для L и элемента
f0eQ, в котором мы вычисляем производную /, упрощающее
предположение: L и /о взяты из класса С2.
Теорема 39. Если в условиях теоремы 38 функция L
принадлежит классу С2 на [a, b)y^<U и если f0^Q принадлежит
классу С2 на [а, Ь], то производная J'(fo) может быть записана
в виде
61 = PJo) ■ б/ = [$■ (*• h W. /fW ) • &f (*)]Sa +
6
+ J [#£(x, f0(x), fQ(x)) - -^$Z (x, fQ(x), fax))] . 6?W «fc.
(Ill, 11; 13)
Квадратная скобка [ ]*IIa означает разность значений для
х = b и х = а.
Доказательство. Достаточно в формуле (III, 11; 6)
применить интегрирование по частям. В этой формуле d/dx
является производной отображения х ~> d3L {x, f0 (x), %(*)) отрезка
->
[а, Ь] в F. Это, следовательно, не частная производная djL =
<-
= д/дх, а полная производная, которая учитывает, что fQ и /j
являются функциями х. Выполняемое здесь интегрирование по
частям является более общим, чем то, которое обычно
употребляется в математическом анализе. Оно производится по
формуле
ь ь
J" В(и*(х), %'(x))dx = [B{u(x), Нх))}^1- J" B(u'(x), P(x))dx,
(III, И; И)
где В — непрерывная билинейная форма. Эта формула
непосредственно вытекает из того факта, что производной функции
х^>-В(и(х), v(x)) является функция х^-В(и'(х), v(x)) -}-
r^B(u(x), v'(x)) (теорема 12). Здесь речь идет (относительно
В) о непрерывном билинейном отображении (и, v)~*u-v или
<- -> <- ->
{и, v) из F' X F в R. Естественно, это интегрирование по
частям можно выполнить только в том случае, когда
рассматриваемые функции и и v непрерывно дифференцируемы. Поэтому
мы предполагали, что /о принадлежит классу С2. Поскольку L
принадлежит классу С2, d^L принадлежит классу С1, Так как

378
Гл. III. Дифференциальное исчисление
f0, f'Q принадлежат классу С1, то и: x-*d3L(x, f0(x), f'0(x)),
согласно следствию 5 теоремы 11, также принадлежит классу С1.
-Пример. Если F = R, <U==RX^-, то формула
(III, 11; 12s), полученная в соответствии с теоремой 39, дает
частный случай формулы (III, 11; 13):
ъ
+1 [%(*• fоw. пi*))—h(w(*• f°(х)' г°(х)))]6/wrf*•
Необходимые условия экстремума
Вернемся к первоначально поставленной проблеме
экстремума. Необходимое условие того, что точка /о ^ Qo (т. е. /о ^ Q
при заданных f0(a) = a и Ы^)=Р) доставляет экстремум
функции / на открытом множестве Q0 из Е0, заключается в том,
что /'(/о) должна равняться нулю на £о (теорема 23).
Теорема 40. Пусть [а, Ь] — некоторый отрезок в R, F —
аффинное нормированное пространство, °И — открытое множество
->
из Fy^F, Q—множество непрерывно дифференцируемых
отображений f из [а, Ь] в F, таких, что (/(*), f (x))^.°U для всех
х е [a, b], Q0 — подмножество Q, образованное функциями f,
удовлетворяющими заданным условиям f(a) = a, f(b) = р, и
L — функция класса С2 на [а, 6] X ^-
Для того чтобы функция /0 ^ &о класса С2 доставляла
максимум или минимум на множестве Q0 интегралу J,
определяемому формулой (III, 11; 3), или, более общо, являлась для него
стационарной точкой, необходимо, чтобы функция f0 была
решением дифференциального уравнения %-го порядка
fc{xj0(x),?0(x))-±(dj.(x,f0{x), /J(*)))= 0, (111,11; 15)
(^г) = 0. (Ш, 11; 16)
Это уравнение называется уравнением Эйлера, а его
решение называется экстремалью интеграла J или функции L.
или
tL </_/л7\ •*-
ду dx
Доказательство. Если 8f ^ Е0, то б/(а) = 6/(6) = 0.
Поэтому в равенстве (III, 11; 13) скобка t ]x==b равна нулю>
х=а

§ 11: Вариационное исчисление
379
Необходимое условие экстремума б/ = О теперь говорит
о том, что интеграл, фигурирующий в правой части равенства
(III, 11; 13), равен нулю, какова бы ни была функция б/ е Еа.
Для того' чтобы отсюда получить, что функция /о удовлетворяет
дифференциальному ■ уравнению (III, 11; 15), достаточно
применить к функции Ф:
х-*Ф(х) = д^(х,Цх), H(x))-^(XL(x,f0(x), ?й(х)))
(Ш, И; 17)
лемму Хаара.
Лемма Хаара
<-
Если Ф является непрерывной функцией на интервале [а, Ь]
<-
со значениями в сопряженном пространстве F' некоторого век-
■>
торного нормированного пространства F и если для каждой
->•
непрерывно дифференцируемой функции ц, определенной на
■>
[а, Ь] со значениями в F, обращающейся в нуль на концах этого
интервала, имеет место равенство
ь
|(Ф(*), л(*)><** = О, (HI, 11; 18)
а
то функция Ф тождественно равна нулю на [а, Ь].
■*-
Предположим, что Ф не является тождественным нулем, и
покажем, что тогда мы придем к противоречию. Пусть х0 — точка,
<-
в которой Ф(л:о) ФО. Всегда можно считать точку Хо отличной
от концов а и Ь, ибо если непрерывная функция Ф будет
тождественно равна нулю в открытом интервале ]а, Ь[, то она будет
тождественным нулем и в замкнутом интервале. Утверждение
<- >
«непрерывная линейная форма Ф(хо) отлична от 0 на F » равно-
-> ->•
сильно существованию такой точки е е F, что значение этой ли-
> ->
нейной формы на е отлично от 0. При этом е можно выбрать так,
->
чтобы значение рассматриваемой линейной формы на е было
> 0 (в противном случае можно заменить е на —е). В ситу не-
<-
прерывности Ф, существует настолько малое число ос, что
интервал [х0 — а, Яо-г-ос] содержится в [а, Ь] и непрерывная скалярная
функция х-*-(Ф{х),е) на нем положительна

380
Гл. III. Дифференциальное исчисление
Пусть теперь ф — непрерывно дифференцируемая скалярная
функция, положительная в ]х0 — а, Хо + а[ и равная нулю вне
этого интервала. Можно взять, например, функцию (рис. 9)
[0, если хф.]хй — а, x0-j-a[,
Ф (х) = j cos2 (Jt- (x - х0)) или (а2 - (х - xuff, (Ш, 11; 19)
если х е= ]х0 — а, х0 + а[.
У
1.
а
У*9>(.х)
а *„-<* *„ *„*« Ъ
-*- х
Рис. 9.
->• ->•->•
Возьмем в качестве т) функцию ц(х) =еу(х). Она, очевидно,
непрерывно дифференцируема в [а, Ь] и обращается в нуль на
<- ->•
обоих концах. Функция х —>• (Ф(х), г\(х)) непрерывна, >>0 в
интервале ]х0 — а, х0 + <х[ и равна нулю вне этого интервала. Ее
интеграл, очевидно, >>0.
Мы пришли к противоречию: Ф должна быть тождественно
равной нулю, чем и заканчивается доказательство леммы.
Пример. Для того чтобы функция f0 доставляла экстремум
интегралу / среди всех функций f е Rfa>bl, принадлежащих
классу С1 (см. пример, приведенный после теоремы 38) и
удовлетворяющих заданным граничным условиям /(a) =a,f(b) = (3,
необходимо и достаточно, чтобы, если f0 принадлежит классу С2,
для любой функции б/ е= Ria- bl класса С1, удовлетворяющей
условиям 8f(a) = 6f(b) = 0, имело место равенство
ь
j* [^ (х, /0 (*), f'0 (*))--£ (4? (х, f0 (х), f'0 (х)))] 6f (х) dx = 0.
(Ill, 11; 19а)
Лемма Хаара утверждает, что для этого необходимо и
достаточно, чтобы функция f0 удовлетворяла равенствам fo(a) = а,
fo(b) = р и являлась решением дифференциального уравнения
Эйлера
т!-ад-»- он. Hi и»
Следствие. Пусть fo — некоторая функция, определенная
на [а, Ь] и доставляющая при условиях теоремы 40
стационарное значение функционалу J. Тогда при at ^ a, b\. ^ b функция

§ 11. Вариационное исчисление
381
fo доставляет также стационарное значение интегралу
/,(/)= $L(x,.f(x), f{x))dx (III, 11; 19а)
на множестве всех функций f класса С1, определенных на
->
[аь bi] со значениями в F, таких, что пара (f, f'-) отображает
[аи Ь^ в °ii и удовлетворяет условиям f(ai) = ai = fo(ai),
f(bt) =pi = fo(fti).
В самом деле, уравнение Эйлера не использует концы
интервала.
Этот результат не очевиден даже для случая абсолютного
максимума или минимума. Предположим, например, что fo
является точкой минимума для /. Тогда для заданной на [аи bi]
функции f с описанными выше свойствами обозначим через f
функцию, равную f в [аи bt] и f0 в [а, а^ и ]ЬЬ Ь]. Эта функция
непрерывна, поскольку f(ai) = fo(fli), f(bi) = fo(bi). Если она
принадлежит классу С1, то, в силу свойства минимальности,
J(f) ^/(fo), а, следовательно, вычитая из двух интегралов их
а, Ь
общую часть + ] , получим Ji(f) ^/i(fo) и f0 по-преж-
а Ь,
нему будет доставлять минимум функционалу J\. Однако f
в точках ui и bi имеет не обязательно равные правые и левые
производные, а, значит, f не принадлежит классу С1 и
проведенное рассуждение не применимо. Для того чтобы сделать его
пригодным, необходимо воспользоваться приближением f с
помощью функций класса С1 и выполнить предельный переход,
который мы здесь не уточняем, но который показывает,
независимо от уравнения Эйлера, что f0 остается точкой минимума
для Ji.
Замечания. 1°) Заранее мы не можем быть уверенными
в том, что функция fo, для которой интеграл достигает своего
максимума или минимума, действительно существует. В самом
деле, Qo — открытое некомпактное множество (см. замечание
1°) к теореме 23).
2°) Если даже можно доказать, что элемент fo
рассматриваемого открытого множества Q0, на котором интеграл
достигает своего максимального или минимального значения,
существует, то это еще не означает, что этот элемент дважды
непрерывно дифференцируем, а вторая производная может не
быть связана с рассматриваемой задачей. В то время
как на функцию L, входящую в условие задачи, можно
наложить ограничения, относительно функции f0 это сделать нельзя,
поскольку она является неизвестной. Несколько более сложное

382 Гл. 111. Дифференциальное исчисление
доказательство, чем проведенное нами выше, позволяет обойти
эту трудность и показать в большинстве случаев, что функция
класса С1, доставляющая функционалу J стационарное
значение, заведомо принадлежит классу С2.
3°) Практически обычно пишут дифференциальное
уравнение (III, 11; 16) и ищут решение этого уравнения,
удовлетворяющее краевым условиям f(a) = a, f(b) — р. Относительно f
получается дифференциальное уравнение второго порядка.
Вместо того чтобы писать, как обычно, что функция f и ее
производная У принимают в некоторой заданной точке заданные
начальные значения, пишут два условия другого рода, а
именно что функция f принимает в двух заданных точках
заданные значения. Ничто не доказывает в общем случае ни
существования решения, обладающего этими свойствами, ни его
единственности.
Возвратимся к формуле (III, 11; 4). Здесь б/ является
системой m приращений (bfu bf2, ..., 6/m). Частная производная
-тг-(х, y,Y), как вектор из /=v = Rm, является системой m
fil
производных j^ix, уи у2 ym, K„ Y2 YJ, i= 1 т.
dL -*■
В свою очередь =>- (х, у, Y) есть система т производных
ду'
аг аг
—г или ^г(*' У\ Ут> У\ YJ, /=1, 2, .... т.
ду, dYt
*■ -> <- -> *
Наконец, скалярное произведение (а, X) или а-Х для et =
— (а,, а2, ..., О, Х = (Хи Х2 Хт) равно а,Х, +а2Х2+ .. .
... -\-атХт. Уравнение Эйлера, относящееся к функции
f — (fi, U fm), эквивалентно системе т составляющих
уравнений:
dL--r(-rr) = 0' /=1'2 т- (Ш, И;20)
4i dx \дУ1 1
ду{
или
dL diL V dL , V dL t, n /ttt ii oi\
i~- -гут- - У, A,я y]-2u~r^^y=Q- ("I. u;2i)
dyt дУ;дх £?\дУ1дУ1 jTJ дУ{ду; '
Решение этой системы зависит от 2т произвольных
постоянных. Они должны удовлетворять 2т условиям fi(a) = at>
fi(b) =• Pi, ( = 1, 2, ..., m. Полезно переписать выражение
для б/ прл 6/ е £о в виде
6/:
-/ §(t-^(f))*г- a,u,i21,>

§ И. Вариационное исчисление
зва
4е) Мы записали условия для вариации первого порядка, не
налагая никаких условий на вариации высших порядков
(формула Тейлора). Поэтому остается неизвестным, идет ли речь
о максимуме, минимуме или седле (см. замечание 2°) к
теореме 23).
Простые случаи интегрируемости уравнений Эйлера
1е) Предположим, что L не зависит от у. Тогда ~g- = 0.
Уравнение сводится непосредственно к дифференциальному
уравнению 1-го порядка
дЧ. ■*"■*"
ут(х, у') = постоянная cef (III, 11;213)
(если F = R, то -^-г(х, у') —с — вещественная постоянная\.
2е) Предположим, что L не зависит от х. Уравнения Эйлера
в частном случае (III, 11; 21) запишутся в виде
т т
dL \\ d2L , VI d2L „ Л . , „ т
~л 2l^~T^yl~U я'*' yi =0' г=1'2 т.
дУ1 j~l дУ\ дУ1 /S дУ1 дУ\
(ш, И;214)
Умножая 1-е уравнение на y't и суммируя, получаем:
mm m
Я дУ1 ^ дУ\ дУ1 ' i^Lx дУг дУ\
или
4~x{L-l-§;yf)-0- (111.11:21.)
Отсюда находим первый интеграл
m <-
L~S^-^ = C' или "L-|^' = c, (III,11;217)
£.i~dyl ду
который, как мы увидим ниже, имеет интересную
интерпретацию в задачах механики (формула (III, 11; 96)).
В частности, если m = 1, то мы приходим к уравнению
первого порядка
Ь-Щгу' = е, (III, 11; 22)

384 Гл. III. Дифференциальное исчисление
в котором из-за умножения на у введено постороннее решение
у = const.
Пример. Брахистохрона. Вернемся к примеру,
рассмотренному в начале этого параграфа. Требуется найти минимум
интеграла (III, 11; 2). В нем г— независимая переменная,
х = /(г)—вещественная функция вещественной переменной г,
а х' — ее производная. Уравнение Эйлера здесь запишется
в соответствующих обозначениях в виде (формула (III, 11; 213)):
dL х' ' = const = -±L, (Ш, И; 23)
дх
Vl+x'2 V2g(z-a) Vlgc
где с >• О — некоторая произвольная постоянная. Мы отбросим
случай постоянной, равной 0, которую невозможно записать
±1
в виде г Такая постоянная дает х = const = а. Это со-
V\gc
ответствует случаю, когда В лежит на одной вертикали с Л и,
конечно, решение дается вертикальным отрезком АВ.
Рассматриваемое уравнение можно записать в виде
^^0 + П «ли х>*{х-^-) = ^. (in, 11:24)
Если сделать замену переменной (законную в силу
неравенства 0^ 2~ а ^2)
с /
z = a + c(l — cos u), (III, 11;25)
то мы получим новое уравнение
dx -. /" г — а -. f 1 — cos и
dz~ — V 2c — (z — a)~~~V 1 -f cos м '
dx , . _ / 1 — cos и , r, • 9 и . /1 \
ж = ± с sin и y l+cosu =±2с sin2— = ±с (l - cos и),
(III, ll;26)
для которого без труда найдем решение
z = a + c(l — cosu), х— ±с(и — sin и) + const. (Ill, ll;27)
Постоянная с и дополнительная постоянная в (III, И; 27)
должны быть выбраны так, чтобы кривая прошла через А и В.
Возьмем для простоты точку А в начале координат. Тогда для
Н = 2Ая имеем z = а = 0. В силу периодичности (замена и
на и — 2kn) можно считать, что это условие выполняется при
и = 0; при этом мы получим х = 0, если const из (III, И; 27)
возьмем равной нулю. В соотношениях (III, И; 27) можно

§ 11. Вариационное исчисление 385
взять знак +, ибо знак — может быть скомпенсирован заменой
и на —и.
Итак, мы видим, что брахистохроной является циклоида Г,
имеющая в исходной точке А точку возврата с вертикальной
касательной. Постоянная с должна быть определена так,
чтобы кривая проходила через точку В. Поскольку с изменяется,
мы имеем семейство циклоид Гс, гомотетичных кривой ГЛ,
соответствующей с = 1. Постоянная с геометрически может быть
определена следующим образом: прямая АВ пересекает Г4 в
конечном числе точек Си Сг, ... (кроме случая, когда АВ
горизонтальна и имеется бесчисленное множество решений). Если
d — одна из них, то гомотетия кривой Г4 с центром гомотетии
А и коэффициентом AB/Ad проходит через В и является
решением поставленной задачи (рис. 10).
Кривая Г,
Рис. 10.
В этом примере сосредоточены почти все трудности
вариационного исчисления.
1°) , Когда мы ставили задачу в самом начале параграфа,
мы предположили, что кривая находится в вертикальной
плоскости, проходящей через А и В. Это ограничение может быть
легко устранено. Выберем произвольно три координаты в R3,
считая ось z направленной вертикально вниз. Будем искать
брахистохрону как дугу параметрической кривой класса С2,
представленной тремя функциями x(w), y(w), z(w). Будем
предполагать, что точки А а В соответствуют фиксированным
значениям w = оч и w = wt. Тогда время, необходимое для
движения от точки А к В, выразится в виде
t= -r , =■ = ■./■ ==—dw, (III, 11; 28)
где функции х, у, z принимают заданные значения (координаты
точек А а В) при w'= wit w = w2.
Поскольку имеется 3 неизвестные функции, то мы имеем 3
уравнения Эйлера. Двумя первыми, в силу (III, 11; 2Ь),
13 Зак. 1339

386
Гл. III. Дифференциальное исчисление
являются
х' 1
—, . =■ = const,
/^+и.У5й^Г (ШЛ1;29)
— — - = const.
Vx'2 + y'2 + z'2 V2g{z-a)
Отсюда получается соотношение с постоянными
коэффициентами кх' + \iy' = О, а затем кх + \ху + v = 0. Таким образом,
кривая заведомо находится в вертикальной плоскости,
проходящей, конечно, через Л и В, и выбор двух новых координат
8 этой плоскости вполне законен.
Впрочем, ничего не зная о вариационном исчислении, в этом
результате можно было убедиться непосредственно. Возьмем
произвольную кривую Г, но систему координат выберем так,
чтобы плоскость xz была вертикальной плоскостью,
проходящей через А и В. Ортогональная проекция Го кривой на эту
плоскость определится функциями x(w), 0, z(w). Она пройдет
также через Л и В. Время падения to вдоль этой проекции
задается тем же самым интегралом (III, 11; 28), что и t, если
заменить у' на 0: это время строго меньше t, если y'(w) не
равно тождественно нулю, т. е. если кривая Г не лежит в
плоскости у = 0. Таким образом, минимум t может быть
реализован только на кривой, лежащей в вертикальной плоскости,
проходящей через А и В.
2°) С самого начала- мы допустили, что брахистохрона
может быть представлена при помощи функции х переменной z.
Это предположение ничем не оправдано, как это видно из
окончательного результата. В самом деле, получив, уравнение
Эйлера, мы преобразовали его, совершив соответствующую замену
переменной (III, 11; 25). Решениями преобразованного
уравнения оказались циклоиды, в которых х не обязательно
выражается как функция от z\ Если повторить построение,
проведенное н стр. 385, то АВ может пересечь Ti в единственной
точке С, расположенной на первой поднимающейся дуге циклоиды.
При этом имеется единственное решение, соответствующее
точкам А и В, и для этого решения х не выражается Как функция
от z. Как же исправить это положение? Мы можем действовать,
как в п. 1°), отыскивая Г в вертикальной плоскости,
проходящей через А и В, как параметрическую кривую,
принадлежащую классу С2.
Получается два уравнения Эйлера относительно х и z:

§ 11. Вариационное исчисление
387
или
—г „ ' —, = = COnst,
V х' + г'2 V2g(z- a)
(III, 11; 30)
VV' + z'2 и , * , , = 0
2 VTg{z-af12 dw \V^T^ V2g(z-a)
При заданных А и В существует бесконечное множество
решений этих уравнений, ибо уравнения (III, 11; 30) не являются
независимыми. В самом деле, мы находимся в условиях п. 2°)
на стр. 383 и существует комбинация х'Х + z'Z левых частей
уравнений (III, 11; 30), приводящая к уравнению (III, 11; 21е):
, дЬ , дЬ \ п
dw \
Поскольку функция L однородна и первой степени относительно
х', г', то тождество Эйлера х'-s-т- + z'-zp- = L показывает, что
эта комбинация тождественно равна нулю. Впрочем, это и не
удивительно: главное — это сама кривая Г, а не ее
параметризация. Все параметризации, эквивалентные одной и той же
кривой Г, дадут одно и то же время падения, и если одна из
кривых экстремальна, то такими же будут и остальные. Это
неудобство можно устранить следующим образом. Считать, что
w представляет криволинейную абсциссу s для всех кривых
невозможно, поскольку концы А и В всех этих кривых должны
соответствовать одним и тем же значениям Wi и w%
переменной w, а кривые могут иметь разную длину. Однако удобно
считать, что параметр w является криволинейной абсциссой s
искомой экстремальной кривой Г. Тогда, не имея возможности
заменить в (III, 11; 28) Ух' +2' на 1, это можно сделать
в (III, 11; 30). Получится два упрощенных уравнения. Каждое
решение первого уравнения обращает также в нуль
комбинацию х'Х + z'Z, а значит, и z'Z и, следовательно, удовлетворяет
также и второму уравнению, за исключением того случая,
когда z=const (z=const, x'= 1 является решением первого, а не
второго уравнения). Итак, исключая постороннее решение z =
=const, получаем, что (III, 11; 30) эквивалентно уравнению
dxlds =const> (III, 11; 31)
У 2g (z — a)
что совпадает с (III, 11; 23) и снова дает, после
соответствующей замены переменной, циклоиды. Таким образом, несмотря на
ложное допущение в самом начале, окончательный результат
оказывается верным. Замена переменных (III, 11; 25)
восстанавливает положение.
13*

388
Гл. III. Дифференциальное исчисление
Считая х функцией от z, мы только отбрасываем кривые
z = const, которые не являются решениями задачи.
3°) Вспомним замечание 1°) к теореме 40. Мы говорили, что
существование максимума или минимума может быть не
обеспечено. В самом деле, рассмотрим задачу минимизации
интеграла (III, 11; 2) функцией x = f(z) класса С1. Единственные
возможные решения — это найденные циклоиды. Если в
условиях, указанных в п. 2°) на стр. 386, через Л и В не проходит ни
одна циклоида, позволяющая выразить х как функцию z, то
искомый минимум не существует. Интеграл (III, 11; 2) на
изученном множестве QoczEo будет иметь точную нижнюю грань >0,
но не минимум.
4°) В замечании 3°), стр. 382, мы говорили, что краевые
условия у (а) — а, у(Ь) = р не обеспечивают единственности
решения уравнения Эйлера. Возможно, что решений нет вовсе (в
этом мы только что убедились) или этих решений имеется
конечное или бесконечное (стр. 387) множество.
5°) Для брахистохроны не выполняются условия, при
которых можно применить теорему 40, поскольку рассматриваемая
функция L = V 1 + х'21У2g(z — а) имеет особенность в точке
z = а, являющейся одной из границ интегрирования! К
несчастью, с подобными фактами часто приходится сталкиваться
в математике. Доказываются прекрасные общие теоремы,
которые почти не применимы к встречающимся частным случаям.
6°) Выше мы говорили, что если кривая удовлетворяет
дифференциальному уравнению Эйлера, то она является
экстремальной для интеграла с совершенно произвольными пределами.
Это кажется противоречащим найденным результатам, а
именно тому, что кривая заведомо имеет вертикальную касательную
в начальной точке (это, впрочем, видно непосредственно из
дифференциального уравнения: для z = а имеем х' = 0).
Объясняется это просто: кривая действительно является экстремалью
для интеграла
i'vrer*2' (ш'11;33)
каким бы ни были начало аЛ и конец Ьи но всегда с одной и
той же подинтегральной функцией, т. е. с одной и той же
постоянной я в выражении Y2g(z — a).
Не обязательно рассматривать поставленную механическую
задачу только при условии, что начальная скорость равна нулю.
Та же циклоида с концами в Ai и В и где Ах уже не является
точкой возрата с вертикальной касательной, минимизирует
интеграл (III, 11; 28), определяющий время падения т.очки вдоль

§11. Вариационное исчисление
389
кривой, когда начальная скорость в точке А{ равна Y2g(a{ — а)
ai > а. Эта величина соответствует скорости 0 в точке А. Эти
замечания не должны обескуражить читателя. Они показывают
только, что, рассматривая уравнения Эйлера, можно решить
лишь небольшую часть поставленной проблемы о максимуме
или минимуме. Чтобы справиться со всеми трудностями в
полной общности, необходимо привлечь очень мощные методы,
использующие теорию пространств Гильберта, теорему ЗОг гл. II,
алгебраическую топологию, теорию дифференциальных
уравнений и т. д.
Уравнение геодезических на поверхности
Пусть Vn — многообразие размерности п над полем
вещественных чисел в аффинном евклидовом пр&странстве En
конечной размерности N. Пусть 'iP.— параметрическая кривая ка
V класса С1. Говорят, что она является геодезической между
точками А и В, если длина дуги АВ кривой <& минимальна или
по крайней мере стационарна среди всех кривых класса С1,
соединяющих Л и В на многообразии V1). Согласно следствию
из теоремы 40, такая кривая остается геодезической между
любыми двумя точками Аи Bt дуги АВ и поэтому окончательно
геодезической можно назвать кривую, сохраняющую это
свойство для любых двух своих точек. Она является экстремальной
относительно длины, т. е. является решением некоторого
уравнения Эйлера.
Пусть Ф: б—*Ф((У)—карта многообразия V. Здесь О —
некоторое открытое множество из R™. Обозначим через
и—>М(и) отображение, определяющее эту карту. Будем
предполагать, что V — многообразие класса С3, а, следовательно, М
также принадлежит классу С3. Несколько позже мы покажем,
что элемент дуги на V можно записать в таком виде:
= V (24SJ"du< Yi^ukdui)= У 2 gti{u)dutdu„
где
(ill, И; 34)
*''<и>Ч1|Н1|(и))- ("Ml,35)
n
Максимум длин кривых, соединяющих две точки, не существует:
точная верхняя грань этих длин равна +оо.

390
Гл. Ш. Дифференциальное исчисление
является вещественной функцией класса С2, определенной н
множестве О. Параметрическая кривая класса С1 на '
представляется функциями w-*-Ui(w). Так как функция
L=y 2 gtj (и) и\ • u't принадлежит классу С2, то применима
теорема 40, а уравнениями Эйлера будут являться уравнения
ди
Ц/2*и«)«1«/)-^(-4-/2*«(«)«м)в0--
(III, И; 36)
В частном случае поверхности в евклидовом пространстве
трех измерений после замены щ и н2 на и и у получаем:
ds = ]/Edu2 + 2Fdudv + G dv2,
где
F_\\dMf р_(дМ\дМ\ г_||сШ|р /ттт Ц.07Ч
Е==\\-ди-\\ > р=\-ш-\-шг)> 0=\-дг\' (П1'П;37>
Если искать кривую V, представляя v как функцию и, то урав~
нение Эйлера запишется в виде
-^ Ve (h, v) + 2F (и, v)v' + G (и, v) v'* -
-Ил/ F{U'V) + G{U'V)V' Л-0. (Ш,11;38)
аи \ VЕ (и, v) + 2F (и, v)v'+G (и, v) v I
Это — дифференциальное уравнение 2-го порядка с решением,
зависящим от двух произвольных постоянных. Если ищется дуга
геодезической кривой, соединяющей две точки А и В, то для
определения этих двух постоянных имеются два уравнения.
Может случиться, что через две точки А и В не проходит
никакой геодезической кривой. Так, например, если в R2
многообразие V представляет собой открытое множество х2-{-у2~> 1,
то через точки А = (2,0 и В=(— 2,0) не проходит ни одной
геодезической _в этом многообразии. (Если заменить V его
замыканием V, представляющим собой множество точек
х2 + У2 5= 1> то найдется параметрическая дуга класса С1,
соединяющая А и В в V и реализующая минимум длины, и даже
имеются две дуги, симметричные относительно АВ и дающие ту
же минимальную длину. Каждая из этих дуг составлена из от>
резка касательной АС, проведенной из точки А к окружности
х2-\-У2 — 1, дуги CD этой окружности и отрезка касательной
DB, проведенной из точки В. Однако эти кривые лежат в V,
а не в V, а V не является многообразием. По этой причине
теорема 40 не применима, так как мы имеем дело не .с открытым

§ J J. Вариационное исчисление
391
множеством Е0, а с замкнутым. Дуга CD окружности
уравнению Эйлера не удовлетворяет, ибо его решениями в данном
случае являются прямые на плоскости R2.) Можно показать,
что если многообразие V компактно или, более общо, полно по
евклидовой метрике, то любые две его точки могут быть всегда
соединены хотя бы одной геодезической, обеспечивающей
абсолютный минимум длины. Вообще говоря, имеется бесконечное
множество геодезических, соединяющих Л и 5, и можно
показать, что те из них, которые не дают абсолютного минимума
длины, дают по крайней мере относительный минимум.
Рассмотрим, Например, цилиндр вращения в R3,
определяемый уравнением
х2 + у2 = а2. (III, 11; 39)
Его можно «развернуть» на плоскость, т. е. можно найти
параметрическое представление цилиндра, сохраняющее длины.
Это — отображение Н плоскости R2 на цилиндр: (и, v) -*■
-^ (х, у, г), где
x = acos —,
а '
y = asin^,
- z = v. (Ill, 11;40)
Отображение Н сохраняет длины в том смысле, что ds2 =
= dx2 -f- dy2 -\-.dz2 = du2 -\- dv2. Поэтому длина дуги кривой
класса С1 на плоскости R2 равна длине ее образа при
отображении Н, а геодезические цилиндры — это образы геодезических
в R2 при отображении И, т. е. прямых на плоскости R2.
Однако Н не является биекцией. Если А — некоторая точка
цилиндра, то ее прообразом является множество точек Ап =
= А0-\-2л an i, где i — единичный вектор оси Ох в R2. Если А
и 5 — две точки цилиндра, то каждый отрезок прямой ApBq,
p^Z, ?eZ, будет иметь образом геодезическую дугу,
соединяющую точки А и В. Поскольку ApBq и Ap+kBq+k имеют
один и тот же образ, можно будет ограничиться выбором
отрезков прямой А0Вп, neZ. Это также дает бесконечное
множество геодезических дуг класса С1, соединяющих А и В. Только
одна из них (за исключением двух симметричных) дает
минимум длины. Все другие дают относительный минимум.
Властности, если В = А, определяется бесконечное множество
геодезических с началом и концом в А. Одна из них длины 0 Дает
минимум длины. Та же, которая является образом прямой
А0А„, имеет длину, равную 2яа|п|. Она определяет
относительный минимум и даже абсолютный минимум длин кривых

392 Гл. III. Дифференциальное исчисление
класса С1, соединяющих А с самой собой, причем
алгебраическое число оборотов этих кривых вокруг оси Ог равно п (это
термин из алгебраической топологии).
В качестве примера рассмотрим решение уравнения Эйлера
для задачи о геодезических.
Пусть в R3 определена поверхность, образованная вращением
вокруг оси Ог кривой, заданной уравнением Z = F(r) $
полуполярных координатах. Элемент дуги на этой поверхности
определяется формулой
ds = Vdr2 + г2 Жр2 + F'2 (r) dr2. (Ill, 11; 41)
Если при этих условиях ищут геодезическую, выбирая ф как
функцию г, то длина дуги кривой АВ записывается в виде
'г (В)'
Vl + F'2 (г) + rV2 dr. (Ill, 11; 42)
г (А)
Дифференциальное уравнение Эйлера имеет вид
r2m'
а его решение находится в квадратурах:
Г ф . = const = k, (III, 11; 43)
,-J
i^JU + Ф.. (»i,..;44>
Уравнение (III, 11; 43) можно записать также в виде
r2^ = k, или r(1jf) = k, или rcos<P = fe, (III, U;45)
где Ф — угол между касательной к параллели
(ориентированной в сторону возрастающих значений ф) и касательной к
геодезической (ориентированной в направлении возрастания
длины дуги). Этим формулам можно придать следующий
геометрический смысл. Пусть точка описывает геодезическую кривую
с единичной скоростью. Тогда производная по времени момента
ее скорости по отношению к оси Ог равна моменту ее
ускорения. Поскольку скорость равна 1, то ускорение направлено по
главной нормали к кривой, т. е., как это мы увидим позже в
силу геометрического свойства геодезических, по нормали к
поверхности. Это значит, что вектор ускорения пересекает ось Ог
и, следовательно, его момент относительно оси Ог равен нулю.
Значит, момент скорости относительно оси Ог постоянен, что и
выражается формулой (III, 11; 43).

§ П. Вариационное исчисление
393
Относительный экстремум
Теорема 41. Пусть в обозначениях теоремы 40 Mi, i —
= 1, 2, ..., m, — функции, обладающие теми же свойствами,
что и функция L) a kt — заданные вещественные числа. Пусть
Ki — функции, заданные на Qo соотношениями:
ь
f->Ki(f)=JMi(x,f(x),P(x))dx. (Ill, П;46)
а
Предположим, что в точке fo^Qo производные /С/ (fo)
независимы, a Ki (fo) = ki- Для того чтобы функция f0 обеспечивала
максимум или минимум функции J на Q0 в множестве таких
функций f из Qo, что Ki (f) = ki, i = 1, 2 m, необходимо
и достаточно, чтобы существовали такие вещественные числа
ki, i= l, 2 m, при которых справедливы уравнения
Эйлера
#-£(#Н£Ч#-£(#))-№П;47>
Для доказательства достаточно применить теорию
множителей Лагранжа (теорема 34).
Если F является n-мерным, то мы получаем систему п
дифференциальных уравнений 2-го порядка, решения которых при
известных %i зависят от 2п произвольных постоянных. Однако
%i не известны. Поэтому общее решение этой системы зависит
от 2п-\- m произвольных постоянных, которые нужно выбрать
так, чтобы удовлетворить 2п краевым условиям и m условиям
Ki = h, i = 1, 2 m.
Пример. Среди всех кривых класса С1, соединяющих
точки Л и б и имеющих заданную длину I, найти такую кривую,
которая вместе с отрезком АВ ограничивает максимальную
площадь. Будем искать эту кривую, выражая у как функцию х и
выбирая АВ в качестве оси х. Тогда длина выразится
интегралом
х (S)
/= j V1 + у'2 dx, (III, 11;48)
х(А)
а площадь 4) будет вычисляться с помощью интеграла
х{В)
S= J ydx. (III. 11;49)
х (А)
') Так называемая «алгебраическая площадь». Для получения обычной
Площади можно ограничиться случаем у ^ 0.

394 Гл. 111. Дифференциальное исчисление
Согласно сказанному выше, должен существовать такой
множитель Лагранжа К, при котором справедливо уравнение
Эйлера
-%-U ^---Wl, ИЛИ - Лу//г,з;2=1- (Ш, Hi 50)
Мы показали, что кривизна кривой должна быть постоянной,
т. е. кривая является дугой окружности. Ее центр и радиус не
известны, а следовательно, она зависит от трех произвольных
постоянных. Если считать, что дуга искомой окружности
проходит через точки А и В, находится над осью х (у ^ 0) и имеет
заданную длину /, то окружность определится однозначно. Если
окажется, что 1>-^\АВ\, то искомая дуга окружности будет
больше полуокружности и она не может быть явно
представлена уравнением, выражающим у как функцию х. См. по этому
поводу изложенное на стр. 386. Можно, естественно,
предположить, что А и В совпадают, и тогда мы придем к следующему
утверждению:
Среди всех замкнутых кривых заданной длины I класса С*
максимальную площадь ограничивает окружность.
Радиус этой окружности равен, очевидно, //2я,. и,
следовательно, ее площадь определяется формулой S = Р/4п, что
позволяет утверждать следующее:
Любая замкнутая кривая длины I класса С1 ограничивает
площадь, удовлетворяющую неравенству
S<^, (III, 11;51)
при этом всегда имеет место строгое неравенство, за
исключением того случая, когда кривая является окружностью.
Обратно, если некоторая замкнутая кривая класса С1
ограничивает площадь S, то ее длина удовлетворяет неравенству
/>2У^5, (III, 11;52>
причем всегда имеет место строгое неравенство, за
исключением того случая, когда кривая является окружностью.
Повторяем еще раз, что мы не дали строгого решения
задачи. Так, например, неравенства (III, 11; 51) и (III, 11; 52)
полностью не обоснованы.
Замена переменных
Пусть Fi — аффинное нормированное пространство, h —
отображение [a, b] X Fi в F, принадлежащее классу С1. Если
теперь ^ — функция класса С1, определенная на [а,Ь] со значе-

§ 11. Вариационное исчисление
395
ниями в Fit то сложная функция /
x-^f(x) = h(x,fl(x)) (III, 11; 53)
является функцией класса С1, определенной на [а, Ь] со
значениями в F. Таким образом, h определяет отображение fi-*f
пространства Е\ = (F["' 6))с6; : в пространство £ = (р(а* ь,)с6.,. Мы
сейчас убедимся в том, что если h принадлежит классу С2, то
это отображение дифференцируемо.
Теорема 42. Отображение f\-*f пространства £, =
= [Fi"' ь,)с6; 1 в пространство Е = (F[a'Ь])сЬ;,, определенное
формулой (III, 11; 53), в которой h — отображение [а, Ь] X Л 0 Z7
класса С2, дифференцируемо, а его производная в точке /i
пространства (Fi )сЬ. j определяется по формуле:
6/,^6f> (III, U; 54)
где
6f(x) = d2h(x,fl(x))-tfl(x).
Доказательство. Следует доказать два утверждения.
1°) Формула (III, 11; 54) для фиксированного f\ определяет
некоторое линейное непрерывное отображение 6/i-»-6/
пространства Ei в пространство Е. Поскольку h взято из класса
С2, то дф. принадлежит классу С1, и из следствия 5 теоремы 11,
с одной стороны, и теоремы 12, с другой, сразу же вытекает,
—> •->•-> ->
что если б/i лежит в Еи то 8f принадлежит Е. Отображение
—> ->
б/i -> б/ очевидным образом линейно, а его непрерывность
следует из оценок
III Л <( sup 11<УФ,/,(*))||)|||б/,|||0>
III tf |||0 < |up_^ || ^ (x, /, (*)) + dJA (x, /, (x)) • f{ (x) || HI бТ, |||0 +
+ *uO№.M*>) Illicit OH. H; 66)
дающих неравенство
->
| б/HI, < const HI б/, HI,. (HI, 11; 56)
2°) Для приращения б/i функции /i приращение А/ функции
f определяется формулой:
tf (x) = h(x, /, (x) + 6/, (x)) - Л (a:, /, (x)). (Ill, 11;57)

396
Гл. 111. Дифференциальное исчисление
Естественно аппроксимировать его приращением б/,
определяемым формулой (III, И; 54). Считая приращение б/
определенным формулой (III, И; 54), можно рассмотреть Д/— б/,
а также Д/' — б/'. Для каждого из этих двух выражений можно
применить формулу конечных приращений для фиксированного
х, как это делалой> при доказательстве теоремы 38, и
одновременно применить усиленную теорему о равномерной
непрерывности (см. примечание1) на стр. 374). Можно показать также,
что при заданном е > 0 можно найти такое ti > 0, что из
I||S/iIIIi<ti следует |||Д/ —fi/llli < elllfif Н^. Это говорит о том,
что |||Д/ — б/llli является бесконечно малой более высокого
порядка по сравнению с нормой || |6ДII 1ь когда последняя
стремится к нулю, а это означает, что б/ является искомым
дифференциалом.
Доказанная теорема обобщается следующим образом:
Если к принадлежит классу Cm+h на [а, Ь] X Л, то
отображение /j -* f пространства (F1"' b])cb; m в пространство (F[a' b])cb.
принадлежит классу СК
Приложение к задаче о геодезических
Пусть Vn — многообразие размерности п евклидова
аффинного пространства En размерности N. Рассмотрим
параметрические кривые класса С1, соединяющие точки Л и В и
расположенные или не расположенные на V. Будем предполагать, что
такая кривая определяется отображением w^>-M(w)
фиксированного отрезка [a, J]eR в £#. Если через х\ обозначить
координаты точки М в некотором ортонормированием базисе
EN, то Xi будут функциями w, а длина дуги АВ кривой & будет
определяться интегралом
ь
/= J/Sxj1 dw. (Ш. И;58)
а
Определим некоторую кривую ^о функцией M(w), а
соседнюю кривую 92 функцией M(w) + 8M(w). Дифференциал 81
длины в условиях теоремы 39 определяется выражением
n ь / ' \
6/==£ \—L\ Г1—^ Wi(w)dw. (III,11;59)

§ И. Вариационное исчисление
397
Здесь величины x't/т/ ^x't являются направляющими
косинусами полукасательной к ?( в направлении возрастания дуг (или
возрастания w). Пусть t(w)—единичный вектор этой
полукасательной. Формула (III, 11; 59) может быть записана в виде
Ь -у
ы = - j(-~\6M(w))dw. (111,11:60)
а
Согласно формуле Френе, Ha,d?o
1 = 1- (Ш.11;61)
Эта формула, доказываемая в соответствующих разделах
дифференциальной геометрии в аффинном евклидовом трехмерном
пространстве, пригодна и для произвольного числа измерений
-> ->
./V: из равенства (t\t) = 1 дифференцированием получаем
->
:0, з, следовательно, dtjds является вектором норма-
im-
ли к кривой, а, значит, его можно обозначить через n/R. Здесь
->
п — единичный вектор направления, называемого главной
нормалью, a R > 0, по определению, — радиус кривизны. Этот
радиус можно рассматривать как коэффициент растяжения при
сферическом отображении; плоскость (t, n) (двумерная) обычно
называется соприкасающейся.
Итак,
Ь -> s(b) ->
bl = -j(^\6M)-^dw = - $ (±\6M)ds. (Ill, 11;62)
a s (a)
Здесь кривая ff расположена на многообразии V, а,
следовательно, ЬМ не является произвольной вариацией функции
w—*M(w). Рассмотрим настолько малую дугу геодезической
ф
кривой, чтобы она находилась в образе карты О—*-Ф((У)
многообразия V (в обозначениях, принятых на стр. 389).
Кривая на О будет определена отображением w—*■ u(w) отрезка
[а, Ь] в О, а образ кривой в V будет определяться сложной
функцией w —► M(u(w)). Теорема 42 утверждает, что если V
принадлежит классу С2, то дифференциал 8М, соответствующий
вариации 6и кривой, проведенной в О, задается равенством
п —>
Ш(ш) = М'(и(ш)) ■6u{w) = ^l-~-(u{w))6u1(w). (Ill, 11;63)

398
Гл. III. Дифференциальное исчисление
Но тогда теорема о сложной функции (теорема 11)
утверждает, что дифференциал Ы по отношению к приращениям 8uj
получается из дифференциала (III, 11; 62) заменой в нем 8М
на дифференциал (III, И; 63) по отношению к 8iij. Поэтому
искомый дифференциал запишется в виде
s ф) п -у —>
б/==- J 2(i|lr)6"'ds' (I".ll;64)
s (a) /=1 V '
где на этот раз 8uj являются произвольными скалярными
функциями w -* 8iij(w), определенными на [а, Ь] класса С1 и
принимающими нулевые значения в точках а и Ь. Другими сло-
->
.вами, бы = (б«ь б«2, • • •, б«п) является произвольной
функцией, определенной на [а, Ь], со значениями в Rn класса С1,
обращающейся в нуль в точках а и Ь.
Теорема 40 (или лемма Хаара) теперь показывает, что
геодезическая класса С2 на V характеризуется уравнениями Эйлера
(п|4^) = 0, /=1,2 п, (Ш,11;65)
выражающими тот факт, что главная нормаль к геодезической
кривой в каждой из своих точек является нормалью к
многообразию или что соприкасающаяся плоскость перпендикулярна
к многообразию.
Для произвольной кривой <!Ро на V дифференциал часто
оставляют с небольшими видоизменениями в виде (III, 11; 62).
Обозначим через у угол между главной нормалью к Ч?о и
нормалью к поверхности, отсчитываемый от 0 до п. Если теперь
->
через nY обозначить единичный вектор ортогональной проекции
главной нормали на касательную гиперплоскость, то проекция
-> . -> —>
вектора п будет равна /^siny. Поскольку 8М в каждой точке
кривой 'ё'о является вектором касательной гиперплоскости
2
->
-д—б«/, то его скалярное произведение на п равно ска-
лярному произведению на nysmy. Отсюда
б/=- \\jt-\bM)ds, (III, 11;66)
s{a) V
где Ry = R/s'm у является радиусом геодезической кривизны
кривой ЧРо- Это — радиус кривизны ортогональной проекции
кривой на касательную гиперплоскость. Геодезические линии —
это кривые с бесконечным радиусом геодезической кривизны^
или кривые с нулевой геодезической кривизной: l/Ry=0.

§ 11. Вариационное исчисление
399
Поставим теперь такую задачу: на поверхности V2
аффинного евклидова трехмерного пространства найти кривую Фо
заданной длины I, соединяющую две заданные точки А, В и.
вместе с заданной кривой Го, проходящей через эти точки,
ограничивающую участок поверхности наибольшей площади.
Пусть кривая $? представляется функцией параметра до,
принимающего в точках А и В заданные значения. Тогда можно
определить дифференциал б/ при переходе от кривой ffo к
соседней кривой 9!?, соответствующей приращению &M(w).
Дифференциал 8S рассматриваемой площади является главной
линейной частью «алгебраической» площади, заключенной между
ЧРо и <&. Произведем интуитивную оценку 8S. Пусть М0 и Р0 —
две соседние точки кривой ffo, соответствующие параметрам
ш0 и Доо -+- dw, с дугой М0Ро длины ds. В результате
перемещения кривой они перейдут в точки М и Р: М = М0 + 8М(до0),
Р = P0+bM(w0 + dw).
Рис. 11.
Если считать М0РоРМ «параллелограммом», то его площадь
будет равна произведению ds проекции &М на нормаль в точке
М0 к ffo, лежащую в плоскости, касательной к рассматриваемой
поверхности. Единичный вектор этой нормали, с точностью до
знака, совпадает с вектором, обозначенным нами через пу.
Площадь параллелограмма равна, следовательно,
± (ny\8M)ds, а вариация искомой площади 8S есть
s(b)
±(ny\m)ds, (III, 11; 67)
s(a)
где знак Ц- или — в каждой точке ffo выбирается в
зависимости от того, повернута ли кривая выпуклостью к Го или нет
•>
(нормаль пу направлена всегда в сторону вогнутости).
Согласно теории множителей Лагранжа (теорема 41),
должна существовать такая вещественная постоянная X, что
8S — Х81 равна нулю на ffo, где
| (±l-^)(^Y|6M)ds = 0. (Ill, П;68)
6S= {

400 Гл. III. Дифференциальное исчисление
Естественно, Ш не является произвольным приращением.
Если (и, v) — параметры, определяющие карту поверхности, то
согласно формуле (III, 11; 63)
6M=-^г6" + 47~бt'• (111,11; 69)
где би и 8v — произвольные приращения, равные нулю в Л и
В. Уравнениями Эйлера (см. лемму Хаара) будут
(*>-£)р.|#)-°. (=t'-ir)P'l#)=°-
(Ш,11;70)
Поскольку вектор пу не может быть одновременно
ортогональным к двум независимым векторам дМ/ди и dM/dv, эти
уравнения эквивалентны уравнению
+ 1_А=о. (Ш,П;71)
ку
Так как i?Y ^ 0, а К постоянно, то сохраняется один из
знаков + или —. Таким образом, Wo является кривой постоянной
геодезической кривизны, что обобщает результаты, полученные
на стр. 394, и следующие за ними. Замкнутая кривая заданной
длины, охватывающая максимальную площадь, имеет
постоянную геодезическую кривизну.
Переменные концы. Условия трансверсальности
Предположим, что вместо того чтобы искать кривую
класса С1, соединяющую точки Л и В многообразия V некоторого
аффинного евклидова пространства Е и имеющую наименьшую
длину (отыека'ние геодезической), мы бы начали искать
кривую минимальной длины, соединяющую заданные точки
подмногообразий зФ и & многообразия V. Эта задача является
более общей, чем предыдущие, поскольку концы а и Ь интервала
интегрирования и значения аир функции / в этих точках в этом
случае не заданы, а должны лишь удовлетворять некоторым
соотношениям. Функция / теперь является функцией не только /,
но также и точек а и Ь, относительно которых мы будем
предполагать, что они описывают некоторый заданный компактный
отрезок Ri множества R.
Теорема 43. Пусть R4— некоторый компактный отрезок
из R, F — аффинное нормированное пространство над полем ве-
щественных чисел, °Ы — открытое множество из Fy^F, L —
вещественная функция на Ri X ^ класса С2. Если Q является

§ 11. Вариационное исчисление
401
открытым множеством из Е = (FR,)cb. ,, образованным такими
функциями /, при которых (/,/') отображает Ri в °U, то
функция J, определенная на Q X Ri X Ri rt0 формуле (III, 11; 3), не-
прерывно дифференцируема и ее производная в /о, а0, 6о, где fo
принадлежит классу С2, определяется соотношением
(бГ,ба,б6)>)-б/ = /(§-^(§))^^ +
а
+ (-^ (ь, /о (6). fiW) • б/ W +1 (6. U Ф), Т0{Ь))ьь) -
- (|£-(а, /0 (а), % (а)) • б/ (а) + L (а, /0 (а), \ (а)) ва). (III, 11; 72)
Доказательство. Функция 1 в точке / имеет частную
производную dJ/df, определяемую формулой (III, 11; 6). Значит,
-<—
■щ (/о. ао< ьо) • в/ =
ъ +- <-
= J (-Sf- (*• /о w. Го W) •б/ w + -^ (*. A. w. Й W) •б/' м)<**•
(III, 11; 73)
Частные производные / по а и 6 известны: это частные
производные определенного интеграла по границам интервала
интегрирования;
U (/о> ао> Ьо) = — L (a< fo (fl). /о ("))•
а/ -> (ИЫ1;74)
Для того чтобы получить отсюда, что / непрерывно
дифференцируема на Q X Ri X R1» достаточно применить теорему 15.
Частная непрерывность dJ/df по / для фиксированных а и Ъ была
доказана в теореме 38. Дополняя соответствующим образом
доказательство, легко убедиться (мы будем это считать
доказанным), что dJ/df непрерывна по /, а, Ъ.
') 6а и 66 являются вещественными числами и можно было бы их
обозначить через da и db. Но поскольку по причинам, указанным на стр. 372,
вариацию / мы обозначили через б/ и, по аналогии, дифференциал /
через б/, мы будем также обозначать через ба и 66 приращения для а и Ь.
2) Здесь a, b, J(f,a,b)—вещественные числа. Поэтому dJ/да и dJ/db —
обычные производные вещественной функции вещественной переменной.

402
Гл. 111. Дифференциальное исчисление
Другие типы непрерывности очевидны. Если /, a, b
стремятся в Е, Rj, Rj соответственно к /0, «о, Ь0, то
f (b) - /о Фо) = f(b)- /о (Ь) + /о Ф) - fo(b5 (III, И;75)
стремится kObFb силу равномерной сходимости / к /о в
первом члене правой части (вытекающей из сходимости f к /0
в пространстве Е) и непрерывности /о в точке &о во втором
члене. ТочЧю так же, в силу равномерной сходимости у к Уй и не-
прерывности у0 в Ь0, разность Г {b) — f'u{b^ стремится к 0.
Поскольку L непрерывна в точке (b0, f0(b0), ff0(b0Jj пространства
R1 X F X F, то разность L (b, f (b), ? (Ь)) - L(b0, f0 (b0), % (b0))
стремится к 0, чем и доказывается непрерывность dJ/db в точке
(/о, а0, b0)^ Q X Ri X Ri- Непрерывность dJ/da доказывается
аналогично.
Полный дифференциал б/ в (/о, Яо, ^о) вычисляется теперь по
формуле
«-J(#-9+!"*)*+
ft,
+ L(Ь0, f0(Ь0), % (b0))bb-L (aQ, f0 (а0), ?0(а0))Ьа. (III, 11; 76)
Если теперь в интеграле правой части полученного
равенства выполнить интегрирование по частям, как это делалось
в (III, 11; 13), то,, поскольку б/ не обязательно обращается
в нуль в точках а<> и 60. мы получим формулу (III, 11; 72).
Изменим это выражение, введя вместо б/(а0), б/(bo)
дифференциалы ба, бр значений / в точках а и Ь.
Теорема 44. Пусть Rt — некоторый интервал R, F —
аффинное нормированное пространство, | — отображение Е =
= (FR')cb. j X Ri в F, определенное равенством
l(f,x) = f(x)z=F, (III, 11; 77)
где f(x) — значение f ex1). Это отображение непрерывно
дифференцируемо, и его производная определяется по формуле
Г(/о. х0) ■ ($, 6^0) = b(f(x))^tf(x0) + f{x0) ■ 6x0€=F. (Ill, 11;78)
') Функция | подобна билинейному каноническому отображению
(и,Х)-+и-Х пространства 3?(ЕХР)ХЕ в %

§ 11. Вариационное исчисление
403
Доказательство. Для фиксированного х отображение
f-*f(x) gF является аффинным непрерывным отображением £
в F, а его линейным присоединенным отображением является
f-*J(x). Следовательно (теорема 8г),. £ имеет частную
производную по /, которая определяется формулой
-^-(Л *) •?=?(*) е£ (Ш, П; 79)
Эта частная производная непрерывно зависит от / и х. В
самом деле, из формулы конечных приращений (теорема 13)
||6FM-^Uo)IKlll^llloU-^ol<lll6FllliU-^ol (Ш, 11; 80)
следует неравенство
(/, Х)-Щ- (/о, Х0) || = _SUP || (-Ц- (/, Х)-Щ- (/о, Хо)) ■ tf || =
5/ ....
"«flll.<«
= sup ||6/(*)-6/(*-0)||<|*-*0|, (IH,11;81)
доказывающее требуемую непрерывность. Для фиксированного
/ отображение |: д:—>-/(д:) является самой функцией /. Она
дифференцируема, поскольку / принадлежит классу С1. Значит,
отображение \ имеет частную производную по х, определяемую
формулой
f(f,x)=fWsh (III,11;82)
->
Производная функция д%1дх непрерывно зависит от / и х,
поскольку при /, стремящемся к /0 в {F 1)сЬ.,, ид:, стремящемся
к jc0, /'(*) стремится к /о(*0) (это рассуждение уже было
проведено на стр. 402 с b, bo вместо х, Хо). Таким образок, | имеет
непрерывные частные производные, и требуемый результат
вытекает из теоремы 15.
Согласно (III, 11; 78), формулу (III, 11; 72) можно изменить,
-> -> ■> —> —> ■>
заменяя в ней б/(Ь) на 6f$— f^b^bb и б/(а) на ба — ff0(a0^6a.
Тогда мы получим такой результат:
') Поскольку х пробегает поле вещественных чисел, то производный век-
тор можно взять в виде -г— = ~3"^* '• См. замечание 2°) после теоремы 8.

404
Гл. III. Дифференциальное исчисление
Следствие 1. Если в условиях теоремы 43 значения f
в точках а и Ь обозначить через а и р, то производная J в
точке (f0, a0, b0) определится формулой
б/ = J [-f- (*• fo <*>• I w) ---t (w (*• fo w• Го w))] • 5 w ^+
+ [fKV ш. ад) • (вр-Г5(*,ов*)+L(vw to И -
- У? (e0> fo Ы> То Ы) • (*a - fo Ы ba) + L (ao> fo Ы> % Ы) H
(III, 11; 84)
Следствие 2. Предположим, что выполнены условия
теоремы 43. Пусть а, Ь, а, р — заданные функции параметра t,
пробегающего некоторое открытое множество аффинного
нормированного пространства Т, со значениями в Rj, Rt, F, F
соответственно. Для того чтобы интеграл J(f,a(t), b(t)) среди всех
значений t eF и всех f e Q, таких, что f(a(t)) — a(t), f(b(t)) =
= Р(0> достигал своего максимального или минимального
значения при f0, to, где f0(a(t0)) = a(t0) и fo(b(t0)) = р(/0),
необходимо, чтобы функция была решением ■ уравнения Эйлера
(III, 11; 16), а точка t0, кроме того, удовлетворяла так
называемым условиям трансверсальности, т. е. обращала в нуль обе
квадратные скобки выражения (III, 11; 84), в которых 8а, 66,
бос, бр являются дифференциалами функции а, Ь, а, р,
соответствующими произвольному приращению Ы параметра t в
точке t0.
Доказательство. Проведем беглое нестрогое
рассуждение. Прежде всего, среди всех функций fefi,
удовлетворяющих условиям f(a(t0)) = a(t0) и f(b(t0)) — Р(/о), функция f0
обеспечивает максимум или минимум значения функции
J(f,a(t0), b(to)), соответствующего фиксированным пределам
a (t0) и b(to). Следовательно, по теореме 14, она должна
удовлетворять уравнению Эйлера (111,11; 16). При этом
дифференциал б/ в (III, 11; 84) не содержит интеграла и сводится к
выражению, заключенному в квадратные скобки. Надо, кроме того,
заметить, что в силу соотношений f(a(t)) =«(/), f(b(t)) =
= р(0. переменные f и t не являются независимыми. Однако
мы можем рассматривать t как независимую переменную. Для
фиксированного t функция f подчиняется некоторым
соотношениям и потому остается в некотором аффинном
подпространстве Et пространства Е (которое меняется-вместе с t).
Поскольку t является независимой переменной, а дифференциал б/
> . ->
в (III, 11; 84) зависит только от приращения Ы (через величины

§ 11. Вариационное исчисление 40!>
ба = a'(U) ■ 8t, 8b, ба, бр) и не зависит от 8f (поскольку f0
удовлетворяет уравнению Эйлера), то необходимое условие
экстремума сводится к тому, что б/ = 0 при любом 8t, откуда а
вытекает утверждение следствия.
Применение к геодезическим кривым
Пусть (да, t) —>M(w, t)—отображение класса С2 множества
[U, 1] X Т в многообразие V класса С3 евклидова аффинного
пространства EN конечной размерности N. Здесь [0,1] —
отрезок прямой R, Т — открытое множество аффинного
нормированного пространства (практически Т = R и £е Т — время). Для-
каждого /еГ частное отображение w —*M(w, t) определяет
параметрическую кривую fft класса С2 на V с концами At —
= M(0,t) и Bt = M(\,t).
Выясним, как изменяется длина /( кривой в зависимости от t.
Дифференциал б/, соответствующий приращению 8t в точке t0,
задается формулой (III, 11; 84). Интеграл же сводится
к (III, 11; 66). С другой стороны, здесь a(t) =0, b(t) ==1, zy
следовательно, 8а = 8b = 0, a(t) = At и р(/) = Bt. Положим
Wo = ffn, Ao = Au, B0 = B(0. Известно, что если в EN выбрать-
некоторый ортонормированный базис, то компонентами дЬ/дуг
Vh'
в этом базисе будут x't{w) I/ Zi х\ (да), /=1, 2, ..... W, т. е.
направляющие косинусы cos Ф* (да) полукасательной / (в
направлении возрастающих да) к кривой Wo1) в точке да. Если
через а*, р» мы обозначим координаты точек Л и Б, то первое
выражение, заключенное в квадратные скобки в формуле
(III, 11; 84), будет равно
2 (со8Фг)ш=1 • брг = (Т(Б0)|6Б). (III, 11;85>
Аналогичный результат имеет место в точке А. Поэтому
окончательно получаем:
s(B) -■>
(III, 11;86>
sW)
ш) ds + (?(В0) 18В) - (Г(Л0)! М).
') Не следует путать параметр t с единичным вектором t
касательной к 'So,

406
Гл. 111. Дифференциальное исчисление
В этой формуле 6М равен -^-(w, t0) • 6t, в то время как
ЬА, ЬВ соответствуют частным значениям w = 0, w — 1.
В частности, если кривая является геодезической кривой из
V, зависящей от параметра t, или, проще, если для t = tu
кривая Wo является геодезической кривой из V, то имеет место
соотношение
6/ = (Т(В0) | №) - (Т(Л0) | (6Л)). (III, 11;87)
Нами получен замечательный результат:
Вариация длины геодезической удовлетворяет той же самой
формуле, что и вариация длины отрезка прямой в евклидовом
пространстве.
Пусть, например, на V отыскивается кривая минимальной
длины, соединяющая точку А из si- и точку В из 9$, где s4- и
& — заданные подмногообразия V (см. стр. 400).
Многообразия si- и 38 можно представить параметрически, по крайней
мере локально, с помощью двух параметров |,. т), пробегающих
открытые множества аффинных пространств Н и Н. Тогда Т
будет представлять собой множество Н X Н, a t—пару (|, х\).
Согласно следствию 2, кривая, прежде всего, должна быть
геодезической, а ее концы А и В должны быть выбраны на si- и
М так, чтобы (III, 11; 87) обращалось в нуль при любом Ы,
т. е. при любых 6|, бт). Это означает, что геодезическая кривая
должна быть нормалью к si в точке А и нормалью к <% в
точке В.
Канонические уравнения Гамильтона
Рассмотрим такие задачи вариационного исчисления, в
которых F является пространством Rm, так что функция f
эквивалентна системе m функций ft, fz, ..., fm переменной х. Вводя
вспомогательные функции zl = yfi, можно уравнения Эйлера
записать в виде 2т дифференциальных уравнений первого
порядка. Рассматривая L как заданную функцию 2т + 1 переменных
х, у и Zi, получаем:
y', = z,, i= 1, 2, ..., т.,
», и,яг\ (Ш,11;88)
Произведем теперь следующую замену неизвестных
функций: вместо функций yt и Z{ введем новые неизвестные функ-
дии <7г и ри где <7t = Уи a pi заданы как функции от х, yt и

§ Л. Вариационное исчисление
407
Zi формулой
Pi = ^T.' (Ш,П;89>
Будем считать, что здесь речь идет о настоящей замене
функций, т. е. формула (III, 11; 89) позволяет выразить каж~
дую из переменных 2,- как функцию х, г/, и р^. С другой
стороны, вместо заданной функции L переменных х, г/* и г,- введем
функцию Н по формуле
т
H(x,quq2 qm, pu p2, ..., pj = 2 р(г{ — L. (III, 11;90>
(=1
Функцию Н переменных х, qt и /?,• называют функцией
Гамильтона1). Ее дифференциал выражается следующим образом
(частные производные L берутся по х, yt, zt):
dH^^i(pidzi-\-z,dpi)~'^rdx — y^l-I~-dyi-^i-^rdzi =
;=i г=1 ' ■ i=i '
m m
= ^izidpl-^ij^-dql-^dx. (Ill, 11;91>
Эта формула верна как в старой системе переменных (х, у и г,),
так и в новой (x,qi,pi). Это показывает, что частные
производные Н по х, qu pi определяются .равенствами:
дН 31.2) дН dL дН ,ттт .. oov
-дГ = --дх-> -щ = --дГг ~^=г" (1»'";92>
При этих условиях дифференциальные уравнения Эйлера
(III, 11; 88) выражаются для функций <?,• и pf переменной х.
в следующей простой форме:
4 = -щ- р,^~^' (Hi."ii:93>
Итак, имеет место
Теорема 45. Если в условиях теоремы 40 F является
пространством Rm, произведена замена переменных и функций
(x,yi,Zi) -> (x,qupi) no формулам (III, 11; 89) и введена
функция Гамильтона Н по формуле (III, 11; 90), то, предполагая, что
II является функцией х, <?,•, pit уравнения Эйлера для функций
') В то время как функция L, выраженная через х, yt, г,-, называется
функцией Лагранжа.
2) Заметим, что dL/dx является частной производной в системе
переменных (x,yi,Zt), в то время как дН/дх является частной производной в система
переменных (x,qi,pi).

•408 Гл. III. Дифференциальное исчисление
Cfi и pi переменной х можно записать в виде (III, 11; 93). Эти
уравнения называются уравнениями Гамильтона относительно
функции Н.
Замечание. Мы положили F = Rm только ради
простоты. Предположим, что F конечномерно. Всегда можно вместо
функций у и z = у', определенных на [а, Ь], со значениями в F
и F соответственно взять новые неизвестные функции q = у и
р = dL/dz, определенные на [а, Ь], со значениями соответствен-
но в F и F\ Функция Гамильтона Н является вещественной
функцией на [а, 6]Х^Х^' и определяется равенством
Н(х, q,p) = (p,z)-L(x,y,z), (III, И; 94)
где (р, 2)gR — скалярное произведение р е=F' на zgF. При
этом предполагается, что у и z заменены их значениями как
<-
•функции q и р.
<-
Для неизвестных функций q и р переменной х уравнения
Гамильтона будут иметь вид:
# = ■?■ ■§ —Ф- (1П>11;95)
д* dp ax dq
<-
При фиксированном р, Н является вещественной функцией
^e=F, а, следовательно, =^г(х, <7, /?) е ^(F; R) = (F')'; при
<?<? ^_
этом требуется, чтобы выражение было равным dpfdx.
дН <■<-<-■
Точно так же -+=г{х, q, р) е= Я? {F', R) = (F')'. Так как про-
др
странство (/*")'» сопряженное к F, совпадает с F, то
дИ ■*■ ■*
-^=-(лс, (7, p)e=F и требуется, чтобы последнее выражение было
.Эр
-> <-
равным dqfdx. Функция р называется «сопряженным моментом»
функции q. Это название объясняется тем, что q принимает зна-
<- <-
чения в F, а р — в Г.
Предположим, в частности, что L явно не зависит от х.
Тогда Н не будет явно зависеть от х, и предыдущие уравнения
означают, что величина

§11. Вариационное исчисление
409-
тождественно равна нулю. Другими словами, Н является
первым интегралом для экстремальных кривых. Вдоль любой
экстремальной кривой функция Н постоянна. На это мы
указывали в (III,1;217).
Применения к механике
Уравнения Гамильтона имеют исключительно важные
приложения как в механике, так и в теоретической физике.
Рассмотрим для простоты механическую задачу о движении
системы материальных точек с наложенными на нее
определенными идеальными связями, находящейся под действием поля
потенциальных сил, не зависящих от времени. В этой задаче
положение системы может быть, например, описано с помощью-
конечного числа параметров qit q%, ..., qm. Для этой системы
точек можно подсчитать потенциальную энергию U,
являющуюся известной функцией параметров. С другой стороны,
всегда возможно вычислить кинетическую энергию 1 = V — г
являющуюся квадратичной формой относительно первых
производных q[, q'2>..., q'm [q'i = dqiJdt'), коэффициенты которой
сами зависят от qu qz> • • • ■ qm- Решение этой задачи дает
«траектории», каждая из которых определяется некоторыми
функциями t: t-*qi(t). Траектории рассматриваемой задачи
являются решением некоторой экстремальной задачи. Для двух
определенных моментов ti и t% вдоль действительной
траектории или произвольных «фиктивных» траекторий можно
рассмотреть интеграл
и и
J L(qp q't)dt= J (T(qt, qfi-U (qt))dtl). (Ill, 11;97>
и и
Нетрудно доказать, что среди всех траекторий, проходящих
в заданные начальный и конечный моменты ti и t2 через одни и
те же точки qi(ti), qi(h), реальной траекторией является таг
при которой интеграл (III, 11; 97) достигает своего
стационарного значения.
Другими словами, каждая траектория является некоторой
экстремалью, а уравнение, определяющее траектории
рассматриваемой механической задачи, является системой уравнений
Эйлера:
^--Ht^\=q' /=i'2 m' ("Ui;98>
dqt dt \dqi)
J) L(qt,qfl здесь означает L(qx, q2, .... qm, q\, q'2, .... q'm).

410
Гл. III. Дифференциальное исчисление
лли
дТ _ d_ I дТ\ _ dU_
dqt dt [dq'J dq{ '
В этом случае они называются уравнениями Лагранжа,
■а функция L — Т — U — функцией Лагранжа. Переход к
переменным Гамильтона определяется формулами
P^ir^lTT- (III, 11; 99)
dqt dqt
Функция Гамильтона Н принимает вид
m
ff(^Pi)=S^I^-^- а", и; loo)
i=i
dq
Однако если учесть тот факт, что Т является квадратичной
формой относительно q\, то тождество Эйлера относительно
однородных функций приведет к формуле
m
5V|^ = 27\ (III, 11; 101)
£f д(Ч
Если теперь выразить Н в виде
Я = 2Г-(Г — U) = T+U, (III, И; 102)
то мы увидим, что Н является энергией системы (сумма потен-
. циальной и кинетической энергий), выраженной как функция
<7г и р^ Если Н выразить как функцию <^.и ри то уравнения
Гамильтона механической задачи будут являться системой
уравнений (III, И; 93).
Функция Гамильтона Н не зависит от времени и,
следовательно, является первым интегралом системы. Иначе говоря,
вдоль траектории системы энергия Н, сумма кинетической и
потенциальной энергий, остается постоянной — это один из
основных законов классической механики.
Вариационное исчисление для кратных интегралов
Изучим следующую задачу. Рассмотрим компактную кривую
Ч? класса С1 в аффинном евклидовом трехмерном пространстве
над полем вещественных чисел и среди всех поверхностей У
класса С1, ограниченных этой кривой1), будем искать поверхность
•) Мы здесь не будем пытаться уточнять смысл выражения
«поверхность 9", ограниченная кривой ■<?». Оно определено в гл VI. Скажем только,
что 9" и 92 являются многообразиями (в смысле § 9) размерностей 2 и 1, что
у них нет общих точек и что 9f _= 9? U "&.

§ И. Вариационное исчисление
4U
наименьшей площади (задача на минимальную площадь). Если
координаты точек пространства обозначить через (л:, у, z) и
считать, что искомая поверхность выражается в виде функции г
от х и у, то площадь рассматриваемой поверхности выразится
в виде двойного интеграла:
5==Я Vl + P2 + q2 dxdy, P = %, q = $j, (III.U; 103)-
распространенного на область S плоскости ху, ограниченную
кривой Г, где 2 — проекция на плоскость ху поверхности 5^,
а Г — проекция кривой <В. Мы пришли к задаче об отыскании
функции z = f(x,y) класса С1, принимающей заданные
значения вдоль контура Г Плоскости R2 (для того чтобы поверхность
9> проходила через кривую %?) и такой, что выписанный выше
интеграл принимает минимальное значение.
Рассмотрим в пространстве R" открытую область О,
ограниченную компактной гиперповерхностью Г класса С1. Пусть F —
аффинное нормированное пространство и %L — открытое множе-
->
ство из FXf" Пусть теперь L — вещественная функция,
определенная на О X ^ класса С21). Мы будем обозначать ее
через
-*■ -> •>
Х# {Х^) Х2> » • •» Xni Z)
Pi. Р2> •••> Рп)-
Если f является отображением класса С1 области 0 в F, то
оно имеет частные производные pi = df/dxit являющиеся
функциями, определенными на О, со значениями в F. Если обраа
_ ■* ->
области О при отображении (f, р\,..., рп) принадлежит откры-
->
тому множеству °U в Fy^Fn, то можно рассмотреть кратный
интеграл
/(/)={{ ••• J L(xu ..., хп, f(xu ..., хп), р^х^ ..., хп), ...
о
..., рп(хи ..., *„))<**, ... dxn =
= J" J ... J L (xt, f, pd dxt... dxn (III, 11; 104>
о
l) О является некоторым компактом, а не открытым множеством R".
В начале § 2, стр. 195, определялась производная функции на компактном
в R интервале [а,_Ь]. Точно так же это можно сделать для функции,
заданной на компакте О с Rn. В дальнейшем в теореме 28 гл. VI мы определим
смысл выражения «открытое множество О, ограниченное компактной гипер»
поверхностью Г класса С»,

412 Гл. III. Дифференциальное исчисление
и поставить следующую задачу: среди всевозможных функций
/, принимающих вдоль контура Г заданные значения, найти ту,
при которой интеграл J принимает наименьшее или
наибольшее значение.
Для решения этой задачи достаточно провести
рассуждения, весьма близкие к тем, которые проводились в случае
простого интеграла. При этом получается следующий результат:
Теорема 46. Функция J: f —>Jf принадлежит классу С1,
а ее дифференциал задается формулой
I <г~ П <— \
б/ = J J" • • • J" (4г •6f+S^- • 6Р{\***■■• - ■ dx*>
(III, 11; 105)
Если L и f0 принадлежат классу Cz и рассматривается
подмножество функций f, принимающих заданные значения на
контуре Г, то этот дифференциал запишется в виде
*/== Я ••• j(#-E^(|^))tf**«■■•. dxn, (III, 11; 106)
где -j.— l-g—J означает частную производную по xt сложной
функции
\х\ хп)~*■
> I Q„ \\ Х\> • • • I ХП' 10 \Х1' • • • > Xn)'~Q^' \Х1' • • •' ХП/' • • ■> Q^~\X1' •"•' Хп)\ •
Для того чтобы среди всех функций f класса С1,
принимающих на контуре заданные значения, функция f0 класса С2
минимизировала или максимизировала интеграл J, необходимо,
чтобы f0 удовлетворяла дифференциальным уравнениям Эйлера
в частных производных 2-го порядка:
Е£(#)-°- OIU1;107)
dL V d. I dL
dz
Доказательство. Единственное место в доказательстве,
не являющееся полностью аналогичным тому, что было сделано
дляпростых интегралов, — это переход от формулы (III, 11; 105)
к формуле (III, 11; 106).

§ И. Вариационное исчисление
413
Запишем (III, 11; 105) в виде
«-jj-j(lM+isr(£-3)-
Эта формула совпадает с (III, 11; 106), если только
Если воспользоваться формулой Остроградского (VI, 7; 53),
которая будет доказана позже, то интеграл по объему
(III, 11; 1073) можно заменить интегралом по поверхности
п <—
J ... {S(|r-^cosa')dS- (1"Л1;1074)
Поскольку рассматривается подмножество функций f,
принимающих заданные значения на Г, то 6f равен нулю на Г, а,
следовательно, последний интеграл действительно равен нулю."
Переход от формулы (III, 11; 106) к уравнению Эйлера
(III, 11; 107) требует применения леммы Хаара для случая
многих переменных, доказательство которой не является
существенно более сложным, чем то, которое нами было проделано для
функции одной переменной.
Вернемся, например, к задаче об отыскании минимальных
поверхностей. Минимальная поверхность, в которой z выражено
в виде функции от х и у в R3, удовлетворяет уравнению в
частных производных:
МутФтг) + И7тФтг) = 0" (Ш'";108)
которое может быть записано в виде
r(l+p2 + q2)-p(pr + qs) ■ t(l + p* + q*)-q(ps + qt)
(\ + р2 + q2)'1' {\+P2 + q2)'h
(III, 11; 109)
или
(г + t) (1 + р2 + q2) - (rp2 + 2spq + tq2) = 0. (Ill, 11; 110)
Если ввести понятие средней кривизны, то можно увидеть,
что предыдущее уравнение эквивалентно равенству Ri -f- R2 =
= 0: минимальная поверхность является поверхностью нулевой

414
Гл. 111. Дифференциальное исчисление
средней кривизны, т. е. поверхностью, в каждой точке которой
главные радиусы кривизны имеют противоположные
значения. Конечно, при строгом решении этой задачи вариационного
исчисления мы встретимся с теми же трудностями, с которыми
нам приходилось сталкиваться до сих пор, но они значительно
более сложные, поскольку речь идет о задаче с кратными
интегралами. Мы знаем, что для поверхностей 91, ограниченных
контуром <<Р, существует точная нижняя грань их площади >0,
но не знаем, достигается ли она, и тем более не знаем (в
случае когда этот минимум существует), достигается ли он
поверхностью, для которой переменная z может быть
представлена в виде функции х и у класса С2. В этом заключаются
основные трудности экстремальных проблем, связанных с кратными
интегралами.' Предположим даже, что .выполнимость
перечисленных выше условий проверена и что функция г
удовлетворяет уравнениям в частных производных (III, 11; ПО). Тогда
остается найти еще то решение уравнения в частных
производных, для которого поверхность 9? проходит через заданный
контур <<Р, т. е. является такой поверхностью, для которой г
принимает заданные значения вдоль проекции Г контура ^ на
плоскость ху. Задача отыскания минимальной поверхности,
ограниченной заданной кривой, называется задачей Плато. Она
была решена Дугласом. Ее решение слишком сложно, и потому
мы не будем на нем останавливаться.
Рассмотрим другую задачу. Задано открытое множество
0czRn, ограниченное гиперповерхностью Г класса С1.
Требуется найти вещественную функцию / на б класса С1,
принимающую заданные значения на контуре Г и минимизирующую
значение кратного интеграла (называемого интегралом
Дирихле) :
о \<=i' ' У о \i=\ }
(III, 11; 111)
Здесь / должна быть (если она принадлежит классу С2)
решением уравнения Эйлера
£^Г = 0> (III, 11; 112)
т. е. решением уравнения Лапласа
п
A/=Svt==0- (III, П; 113)
и?х дх*-

§ П. Вариационное исчисление
415
Говорят также, что f должна быть гармонической функцией.
Таким образом, мы приходим к необходимости решения задачи
Дирихле: в классе С2 функций, определенных на О, найти
гармоническую функцию, принимающую заданные значения на
контуре Г. Существует много физических проблем, приводящих
к необходимости решения задачи Дирихле. В этих проблемах
интеграл (III, 11; 111) представляет собой некоторую энергию,
и задача заключается в отыскании функции, реализующей
некоторое равновесное состояние, которое дает минимум
энергии. Риман в XIX веке решал задачу Дирихле этим методом,
предварительно доказав существование минимyмa^ интеграла.
К несчастью, решение Римана содержало ошибки. С одной
стороны, как это мы указывали в п. 1°) на стр. 381, нет никакой
гарантии, что минимум существует, а дополнительные
замечания Римана, на которых строилось доказательство
существования, были основаны на неверной теореме компактности1).
С другой стороны, как мы видели в п. 2°) на стр. 381, ничто
не доказывает, что этот минимум, если он существует,
реализуется функцией f класса С2. В решении этих задач имеется
много существенных трудностей, как мы это уже не раз
отмечали. В дальнейшем при изучении гармонических функций
будет показано, как можно устранить затруднения,
возникающие в методе Римана, и как методами этого типа эффективно
решается задача Дирихле.
1) Метод Римана основывался на том предположении, что единичный
шар в бесконечномерном банаховом пространстве компактен, как и в случае
конечномерного пространства. Однако мы видели, что это не верно
(теорема 45г гл. II).

ГЛАВА IV
Интегральное исчисление
§ 1. ИНТЕГРАЛ РИМАНА НА ПРЯМОЙ
->
Пусть заданы пространство Банаха F над полем К веще-
->
ственных или комплексных чисел и функция / со значениями
в f на интервале [а, Ь] вещественной прямой R. Мы
намереваемся определить интеграл
J f{x)dx<=F. (IV, 1; 1)
la.b]
Мы видим, почему необходимо предположение о том, что
->
функция / должна принимать значения в некотором банаховом
пространстве. Ведь, как известно, интеграл- можно
рассматривать как предел конечных сумм вида
2(с*+1-с<) ?(&<), (IV, 1; 2)
i==0
где Со, Си ...,с„ — возрастающая последовательность п+1
точек интервала [a, b],.Cq = a, сп — Ь и |,- е [й, c,-+i]. Однако для
того чтобы можно было рассматривать такую сумму, надо
прежде всего иметь возможность-, определять каждый член
(ct-+i — Ci)/(|i) этой суммы, а для этого надо уметь строить про-
изведение элемента /(|,-) из F на вещественный скаляр
d+i — Сг. Затем надо иметь возможность рассматривать сумму
таких элементов из F, а, следовательно, F должно быть
векторным пространством над полем вещественных чисел. Кроме
того, интеграл — не сумма, а предел сумм. Поэтому надо иметь
право рассматривать в пространстве F пределы, а значит,
естественно, предполагать, что F является .векторным
нормированным пространством над полем вещественных чисел.
Теоретически этого должно быть достаточно для определения
интеграла. Однако если не предполагать полноту F, то невозможно
будет найти практически применимые критерии существования
этого интеграла, ибо только в этом случае можно будет
доказать существование предела, не зная его заранее.

§ 1. Интеграл Римана на прямой
417
Поэтому в дальнейшем, если не оговорено противное, мы
будем предполагать, что F — банахово пространство. Естественно,
можно также рассматривать банаховы пространства над
полем комплексных чисел, поскольку их можно трактовать как
банаховы пространства над полем вещественных чисел.
Функцию f мы будем считать всегда ограниченной. Другими
словами, при х, пробегающем [а, Ь], будем считать ||Дл:)|| не
лревосходяшей некоторого фиксированного числа. Впрочем, как
это делалось на стр. 148, через || f || мы будем обозначать функ-
цию ^ 0: а:-* ||Да:) ||, определенную на [а, Ь], в то время как
HlfMIII будет представлять собой точную верхнюю грань этой
функции 4).
Кроме того, мы будем рассматривать функции f,
определенные на всей числовой прямой, и интегрировать их на всей
прямой, считая всегда, что эти функции равны нулю вне
некоторого ограниченного интервала.
Таким образом, мы будем писать выражения
J f(x) dx, или просто J f(x) dx, или J J. (IV, 1; 3)
R
Тогда, по определению, символ (IV,1; 1) является интегра-
-> ->
лом на всей прямой от функции f, равной f в интервале [а, Ь]
У
f\jc "
Рис. 12.
-> _
и 0 в дополнении к этому интервалу. Замыкание точек х топо-
->
логического пространства X, в которых функция f,
определенная в пространстве X, со значениями в векторном простран-
стве F отлична от 0, называется носителем функции f. По оп-
->
ределению, носитель всегда замкнут. Носитель функции f
является наименьшим замкнутым множеством X, на дополнении
-> -»•
к которому функция f тождественно равна 0. Например, для
вещественной функции, график которой изображен на рис. 12,
•>
■') Если/7 — поле скаляров, то II II заменится на | | и'тогда III III можно
будет заменить на 11 II.
14 Зак. 1339

418
Гл. IV. Интегральное исчисление
множество точек, в которых f(x) Ф 0, представляет собой
открытый интервал ]а, с[ с удаленной точкой Ь. Однако носителем
этой функции будет замкнутый интервал [а, с].
Если / — вещественная функция, равная 0 во всех
иррациональных точках R и 1 во всех рациональных точках, то
множество точек, в которых она отлична от нуля, является
множеством рациональных точек Q, в то время как ее носителем будет
вся вещественная прямая R.
Если f и g— две функции, определенные на X, со значе-
ниями в векторном пространстве F, то носитель функции f -f- g
содержится, очевидно, в объединении носителей / и g. В самом
деле, точка х, в которой f(x) -\-g(x).=£0, принадлежит либо
->
множеству точек А, в которых f ф 0, либо множеству точек В,
-> •>
в которых g ф 0. Обе эти возможности не исключают друг
друга. Но тогда эта точка принадлежит объединению А Ц В и,
следовательно, носитель содержится в замыкании A U В, которое
содержится в объединении A U В носителей. Мы будем
интегрировать на R функции f, определенные на R и имеющие на нем
компактные носители.
Ступенчатые функции
Функция f, определенная на вещественной прямой R, со
значениями в произвольном множестве F называется ступенчатой,
если существует такая конечная возрастающая
последовательность точек Со, Си с2, . .., с„ из R., что на каждом из открытых
интервалов ]— оо, с0[, ]с0, Ci[, ..., ]сп-и сп[, ]сп + оо[ функция /
постоянна. (Никаких дополнительных предположений
относительно значений функции в самих точках с,- не требуется.)
Такая последовательность точек с0, й, с2, ..., с„ называется
разбиением Д прямой R, допустимым для ступенчатой функции f.
Естественно, существуют «наилучшие» разбиения, связанные
с f, т. е. такие, при которых число точек с* будет наименьшим.
Для одной и той же ступенчатой функции f существует
бесконечное число допустимых разбиений R. Разбиение Д' прямой R
называется измельчением разбиения Д, если последовательность
с' содержит последовательность Cj. Всякое измельчение
допустимого разбиения для функции f является допустимым
разбиением для этой функции. Существует по крайней мере одно
разбиение, являющееся измельчением двух заданных разбиений
Д' и А" прямой R. Оно может быть получено объединением
точек разбиений, относящихся к Д' и Д", и перенумерацией их
в порядке возрастания. Если значения ступенчатой функции

§ 1. Интеграл Римана на пряной
419
изменятся в конечном числе точек, то она останется ступенча-
•>
той функцией. Если множество F является векторным
пространством, то произведение ступенчатой функции на скаляр и
сумма двух ступенчатых функций будет ступенчатой функцией.
Рассмотрим внимательнее последнее утверждение. Если / и
g — две ступенчатые функции, то им соответствуют некоторые
разбиения А' и А" прямой R, а, значит, и измельчение А этих
разбиений. Разбиение А является допустимым разбиением R
•> •> ■> •>
для каждой из функций f и g, а потому и для суммы f -f- g этих
функций.
Определим теперь интеграл Римана ступенчатой функции
с компактным носителем и значениями в векторном простран-
•>
стве F над полем К (не обязательно нормированном) по
формуле
J7= £ <с<+' - с<) fed. h e ]c„ с,+,[, (IV, 1; 4)
где Со, Си ..., сп — допустимое разбиение для данной
ступенчатой функции').
Следует проверить, что введенное определение корректно,
т. е. что правая часть равенства (IV, 1; 4) не зависит от
выбранного разбиения. Пусть А' и А" — два допустимых
разбиения для функции / и А — измельчение каждого из этих
разбиений. Тогда непосредственно видно, что выражения (IV, 1;4),
относящиеся к А' и А", оба дадут тот же результат, что и
(IV, 1; 4) относительно А. В самом деле, если ]cj, c\+\[ —
интервал разбиения А', то в разбиении А он будет разбит на
некоторое конечное число интервалов ]dj, dj+i[, ]dj+i, dj+Ж, ...
..., ]dk-u dh[. В каждом из этих интервалов, как и в исходном
•>
интервале ]сг, cj+i[, функция f является одной и той же
постоянной /,, и, следовательно, имеет место равенство
, , 2 ь , (<*,+, - d{)l - «+1 - <$%, (IV, 1; 5)
1=1,1+1,.... я—1
откуда следует тождественность сумм, соответствующих А' и А.
Если X — произвольный скаляр и если f и g — ступенчатые
функции с компактным носителем, то имеют место очевидные
•>
') Поскольку предполагалось, что функция { имеет компактный
носитель, она необходимо равна нулю в ]—оо,с0[ и в ]с„,+оо[. Заметим, что
значения функции / в точках ci в рассуждениях не принимаются во
внимание.
14*

420
Гл. IV. Интегральное исчисление
формулы
{ Я?=Я { Г и { (Т+2)= { Г+ { J. (IV, 1;6)
Это очевидно для умножения на скаляр. Что же касается
суммы функций, то достаточно выбрать разбиение А, общее для
->• ->• ->• ->
f и g и, следовательно, для суммы f -\-g.
Таким образом, получаем следующую теорему:
Теорема 1. Множество ступенчатых функций с
компактным носителем, определенных на R, со значениями в векторном
пространстве F над полем вещественных или комплексных
чисел К само является векторным пространством над полем К, а
интеграл f -> \ f является линейным отображением этого век-
торного пространства в F. Если F = к и f ^ 0, то \f ^ 0.
->•
Если, кроме того, F является векторным нормированным
пространством, то имеют место следующие неравенства:
\{Т\< jllftl = ГII f Wild*. I |Г||<(6-а) sup lift*) ||.
Ha,b] I (IV, 1; 7)
Если значение ступенчатой функции с компактным
носителем изменить в конечном числе точек прямой R, то она
останется ступенчатой функцией с компактным носителем, а ее
интеграл не изменится.
Конец теоремы был доказан перед ее формулировкой.
Неравенства (IV, 1; 7) очевидны на разбиении Д, допустимом для
функции f:
"S^I + l-Cl)?! <П2(С|+1—C|)llTllK(6-fl)sUP||?;||
i=0 II i=0 I i
при cQ — a и c„ — b.
->• ->
Пусть теперь f и g— две ступенчатые функции с
компактными носителями, отличающиеся лишь на конечном числе
точек R. Эти точки необходимо находятся -среди точек с{ разбие-
-> ->
ния Д, допустимого одновременно для функций f и g, а в
интеграл не входят значения функции в самих точках с,-
разбиения Д.
Для определения интеграла от произвольной функции
придется воспользоваться предельным переходом.

§ 1. Интеграл Римана на прямой
421
Верхний интеграл Римана от ограниченной функции f > О
с компактным носителем
Определение. Пусть / ^ О — вещественная ограниченная
функция с компактным носителем, определенная на прямой R.
Верхним интегралом Римана Г / функции f называется
точная нижняя грань интегралов от ступенчатых функций с
компактным носителем fi^f.
Таким образом, по определению
П= inf (ff,)>0, (IV, 1; 8)
fi—ступенчатая ^ J '
h>f
Легко понять причины предыдущих ограничений, в силу
которых функция f предполагается ограниченной и имеющей
компактный носитель. Если бы этих ограничений не было, то не
существовало бы ступенчатой функции с компактным
носителем, мажорирующей функцию f. Конечно, в том случае, когда
функция f сама ступенчатая, в качестве fi можно взять ее саму
и.тогда J f — \f-
Теорема 2. Если f < g, то \ f < J g. Для
положительных ограниченных функций f и g с компактными носителями
и неотрицательного скаляра К имеют место формулы
J'tf-Xj'f, I'V + gXft + l'g- (IV, 1; 9)
Говорят также, что верхний интеграл положительных
функций обладает свойством выпуклости. Верхний интеграл функции
не изменяется при изменении значений этой функции в
конечном числе точек из R.
Доказательство. Высказанные утверждения почти
очевидны. Докажем, например, свойство выпуклости.
Пусть fi н gi — ступенчатые ограниченные функции с
компактным носителем, мажорирующие функции f и g
соответственно. Тогда f + g^fi + gu и мы имеем
f(f + g)<j(h + gi)=lfi+jgi. (IV, 1; 10)
Левая часть этого соотношения не превосходит точной
нижней грани его правой части, равной J f + J g, откуда и
следует (IV, 1; 9).
Пусть теперь fug совпадают всюду, кроме конечного числа
точек R, и fi ^ f — ступенчатая функция с компактным
носителем. Всегда можно найти такую ступенчатую функцию gi^ g

422 Гл. IV. Интегральное исчисление
с компактным носителем, которая всюду совпадает с fit кроме
конечного числа точек. При этом Г g ^ J gi = J fi. Переходя
справа к точной нижней грани, получим неравенство J g ^
< Г f. Заменяя в предыдущих рассуждениях f на g и g на f,
точно так же получим Г f ^ \ g, откуда и следует равенство
JV-/V
Замечания. Г) Можно было бы точно так же определить
нижний интеграл Римана Г f как точную верхнюю грань
интегралов ступенчатых функций, не превосходящих f. Однако
этот нижний интеграл обладал бы тогда свойством вогнутости,
а именно:
!t(f + e)>jj + ltg> (IV. 1; 11)
практически почти не применяемым.
2°) Можно было бы подумать, что имеет место равенство
/ Г (f + g) — Г f + | g- Однако это не так. В самом деле,
рассмотрим функцию f, равную нулю в дополнении к [0, 1] и во всех
иррациональных точках отрезка [0, 1] и равную 1 во всех
рациональных точках этого отрезка. Пусть /i — ступенчатая
функция ^ f. В каждом интервале ]с,, c,+i[ любого допустимого
разложения А для функции fi имеются рациональные точки.
Следовательно, постоянные значения fi наверное ^1. Но тогда
fi не меньше характеристической функции отрезка [0, 1].
Обратно, характеристическая функция является ступенчатой и
мажорирует f. Поэтому J f = 1. Если через g мы обозначим
функцию, полученную аналогично функции f, но со взаимной
заменой значений в рациональных и иррациональных точках, то
мы также получим \ g = 1. Однако f + g является
характеристической функцией отрезка [0, 1] и I (f + g) = \ (f + g) =
= 1<1 + 1.
Из этого примера видно, что если ввести нижние интегралы,
указанные в замечании Г), то мы получим: |f= f g = 0 и
]t(f + g)=j(f + g) = i>o + o.
3°) Изменение функции на счетном множестве точек R
может привести к изменению его верхнего Интеграла. Так, напри-

§ 1. Интеграл Римана на прямой
423
мер, функция / из замечания 2°) отлична от нуля в
рациональных точках, а ее интеграл равен 1, а не 0.
4°) Условие выпуклости естественным образом обобщается на
сумму конечного числа функций, но не обобщается на сумму
счетного числа их. Другими словами, если /о, fi, ..., fn, • • • —
последовательность неотрицательных ограниченных функций
с носителями в одном и том же отрезке [а, Ь] прямой R и если
оо
ряд 2 /„ {х) при каждом х сходится к пределу f{x), где функ-
ция / ограничена (а ее носитель, очевидно, лежит в [а, Ь]), то не-
оо
равенство | /^ Л. | /„ моокет не выполняться.
ге=0
Рассмотрим, например, множество рациональных чисел
отрезка [0, 1]. Их можно расположить в последовательность
а0, а\, а2, ... . Обозначим через /„ характеристическую функцию
оо
множества {ап}. Тогда f—^Eifn является функцией, рассмот-
оо
ренной в замечании 2°), причем | /=1>^j | fn = ®-
В теории интеграла Лебега-мы введем также понятие
верхнего интеграла, который будет обладать свойством выпуклости
оо оо
и в случае счетных сумм j \fn^^ij fn> и это будет су-
П=0 №=0
щественным превосходством интеграла Лебега над интегралом
Римана.
Интегрируемые функции со значениями в пространстве Банаха
Определение. Пусть / — функция, определенная на
вещественной прямой R, со значениями в банаховом пространстве
Р. Говорят, что функция / интегрируема по Риману, если она
ограничена, имеет компактный носитель и если для любого
->
е > 0 существует такая ступенчатая функция g с компактным
носителем и значениями в F, что
fllf-llKe. (IV, 1; 12)
Это эквивалентно существованию такой последовательности сту*
пенчатых функций f0, fi, ;.., fn, ■•■ с компактными носителями
и значениями в F, для которых верхние интегралы J \\f — fn\\

424
Гл. IV. Интегральное исчисление
сходятся к 0 при п, стремящемся к бесконечности. Такая
последовательность функций называется аппроксимирующей
последовательностью функции / для интеграла Римана1),
Если две функции отличаются только в конечном числе
точек и если одна из них интегрируема, то другая также будет
интегрируемой (и будет иметь ту же самую аппроксимирующую
последовательность).
Замечания. 1°) Пусть f — ограниченная функция,
определенная на R, с компактным носителем и значениями в ба-
-*■
наховом пространстве F. Если, каково бы ни было е > 0, су-
-*■
ществует такая интегрируемая по Риману функция g, что
<•*->-> ->
\\f — g\\ =Ss e, то сама функция f интегрируема.
В самом деле, при заданном е > О мы можем сначала вы-
-*■ с* -> ■>
брать такую интегрируемую функцию g, что \\f— g\\ ^ е/2.
-*■
В силу интегрируемости g можно найти такую ступенчатую
•*■ ./•*>-*■
функцию h с компактным носителем, что \\g — h\\ ^ е/2. Тог-
/•*-*■ ■>
да, в силу неравенства выпуклости (IV, 1; 9), \\f — h\\ ^ е,
а это, по определению, означает, что /интегрируема.
Точно так же, если задана такая последовательность инте-
■> ■> -*■ /••->->
грируемых функций f0, ft /„,..., что J \\f — f„\\ стремит-
-*■
ся к 0 (в частности, если функции fn сохраняют свои носители
-*■ -*■
на одном и том же компакте и равномерно сходятся к f), то f
интегрируема. В этом случае говорят, что последовательность
fn функций (не обязательно ступенчатых) является
аппроксимирующей последовательностью в интегральном смысле для
функции f.
-*■
2°) Если f — интегрируемая функция, то, каково бы ни бы-
ло е > О, существует ступенчатая функция g с компактным
носителем и ступенчатая функция h с компактным носителем и ве-
-*■-*■ с
щественными значениями ^0, такие, что ||f — g\\ ^ h и /i^e,
и обратно.
') Не следует думать, что такая последовательность f„ сходится про-
"^ -> ->
сто к /. На стр. 550 мы приведем пример, в котором fn(x) не сходится к f(x)
ни при каком значении х.

§ 1. Интеграл Римана на прямой 425
Обратное утверждение очевидно; поэтому мы докажем лишь
прямое утверждение.
Прежде всего найдем ступенчатую функцию g с компактным
носителем, такую, что J \\f — g||<^e/2. Тогда, по
определению верхнего интеграла, найдется такая неотрицательная
вещественная ступенчатая функция h с компактным носителем,
что |f— III <Л и j"/i<e.
3°) Если / — вещественная интегрируемая по Риману функ-
ция, определенная на R, то, каково бы ни было е > 0, можно
найти две такие ступенчатые функции gt и g2 с компактными
носителями, что gi ^ / ^ g2 и \ g2 — gi^e> и обратно.
Обратное очевидно; поэтому докажем лишь прямое
утверждение. Пусть / интегрируема. Определим, согласно замечанию
2°), вещественную ступенчатую функцию g и ступенчатую
функцию А ^0 с компактными носителями так, чтобы |/ — g|^A
и [А ^ е/2. Если теперь положить gi = g — Л и g2 = g + Л, то
gi и g2 будут удовлетворять указанным условиям.
Интеграл от интегрируемой функции
->
Теорема 3. Пусть f — интегрируемая по Риману функция
-> -> > ->
со значениями в'банаховом пространстве F, и пусть fo,fuf2,..-—
аппроксимирующая функцию f последовательность ступенчатых
функций. Тогда величины \ Jn e F сходятся к некоторому пре-
->
делу в F и этот предел не зависит от рассматриваемой
аппроксимирующей последовательности.
Доказательство. Из неравенства
Ц* L- J* Ц<[ II?» ~Тп\\< f\\7-L\\+ J**ll?-?«ll (IV, 1; 13)
следует, что при тип, стремящихся к бесконечности,
\\im ~ /п стремится к 0. Это означает, что
последовательность J Jn является последовательностью Коши в F. Поскольку
F полно1), эта последовательность имеет предел L.
Остается убедиться, что этот предел не зависит от выбора
>
') Именно здесь существен тот факт, что F полно.

426
Гл. 1V. Интегральное исчисление
аппроксимирующей последовательности. Если мы рассмотрим те»
перьдве такие аппроксимирующие последовательности fo, A. ta.;,
и go>gi> 82, .-., то из них можно образовать последовательность
t "*" t "** t "*"
/о> go, /i> 8u /2> g2> •••> которая также является аппроксими-
-*■
рующей для f. Это значит, что последовательность величин
/ Jo. / !о. / Ти / li. / Г2. { |2. • • • Должна иметь предел;
другими словами, последовательности Г J.„ и Г g„ действительно
имеют один и тот же предел.
Определение. Значение предела, указанного в теореме 3,
называется интегралом Римана интегрируемой функции f и
обозначается через \J(x)dx или просто через Г f e F:
Если две интегрируемые функции fug отличаются лишь
в конечном числе точек R, то они имеют один и тот же интеграл,
поскольку они имеют одни и те же аппроксимирующие
последовательности.
-*■
Говорят, что f интегрируема на отрезке [а, Ь] из К.если функ-
ция /, равная f на [а, Ь] и 0 вне его, интегрируема, и в этом
случае полагают
{ Г= J f. (IV, 1; 13j)
Замечание. Если f является ступенчатой функцией, то
данное сейчас определение f соответствует первоначальному
определению (IV, 1;4). В самом деле, в качестве аппроксимирующей
последовательности для функции f надо взять последователь-
-*■->->->
ность f, f, f, ...(f, ..., и мы придем к исходному интегралу.
-*■ -*■
Теорема 4. Если К — скаляр, a f и g — две интегрируемые
-*■-*■->-*■
функции со значениями в F, то Kf и f -f- g интегрируемы и имеют
место формулы
J4f =Л J £ " \<f+ g)=j f+ J g. (IV, 1; 14)
Иначе говоря, множество интегрируемых по Риману функций
(необходимо ограниченных с компактным носителем) является
векторным пространством над полем К, а интеграл является ли-
нейным отображением этого векторного пространства в F,

§ J. Интеграл Римана на прямой 427
Доказательство. Утверждение, относящееся к
умножению на скаляр, очевидно; поэтому достаточно рассмотреть
случай суммы. Пусть /„ и gn — две аппроксимирующие последова-
->■ ->•
тельности для функций / и g. Тогда имеет место неравенство
J'llff+S-fn + J^Kj'llT-fnB+J'll?-?»!!, (IV, 1; 15)
-> •>
из которого следует, что последовательность /„ -f- gn является
•> ->•
аппроксимирующей для функции / -f- g, а, следовательно,
функция f-\-g интегрируема. Это неравенство означает, что |(7+g)
является пределом величин Г (/„ -f- gn) = | Тп + | gn> т- е.
равняется Т/+ J g-
Следствие. Пусть а, Ъ, с, а^Ь ^ с, — три точки прямой
R. Пусть f — функция, определенная на [а, с] со значениями в F.
Для того чтобы она была интегрируемой на [а, с], необходимо и
достаточно, чтобы она была интегрируемой на [а, Ь] и на [Ь, с],
и в этом случае
J Т= { f+ { Г- (IV. 1; 16)
[о, с] [о, Ь] lb, с]
Доказательство. Пусть f — функция, определенная на
R, равная / на [а, с] и 0 вне этого отрезка. Пусть ф[0. ь\, Ф[ь, с]
и ф[о, с] — характеристические функции интервалов [a,b], [b,c] и
[а, с]. Если функция / интегрируема на [а, Ь]и[Ь,с],то интегрируе-
мыми будут функции /-ф[о, ь] и /• ф[ь. С], а значит, и /-ф]б, с\- Но тог-
да интегрируема сумма / • (ф(0, *]+ Фг», е]) = /. а, значит,
интегрируема на [а, с] функция / и из (IV, 1,14) следует (IV, 1; 16).
Обратно, если / интегрируема на [а, с] и если /„ является
аппроксимирующей последовательностью функции / для
интеграла на [а, с], то интеграл ,11/ —/nil стремится к нулю.
J [а, с]
Вместе с ним стремятся к нулю интегралы ||/—/„ || и
J {а, Ь]
I II J—Jn, II- Это означает, что /„ является аппроксимирующей
J lb, с]
последовательностью функции / для интегралов,
распространенных на [а, Ь] и [Ь, с], а / интегрируема на этих интервалах.

428
Гл. IV. Интегральное исчисление
-г
Теорема 5. Если функция /, определенная на R, со значе-
-> •> •>
ниями в F интегрируема, то функция ||/||: х —► || / (л:) || является
вещественной интегрируемой неотрицательной функцией и имеет
место неравенство
llfflkfimi. (IV, 1; 17)
Доказательство. В самом деле, пусть /„ является
аппроксимирующей последовательностью для функции f,
составленной из ступенчатых функций. Тогда имеет место неравенство
lll?ll-l?»lll<ll?-jU (IV, 1; 18)
из которого следует, что I |||/||—-||/„||| сходится к нулю, и, сле-
•>
довательно, последовательность ступенчатых функций ||/„||
является аппроксимирующей последовательностью для функции
11/11. Эта функция, таким образом, интегрируема и Г ||/„||
стремится к ||/||. При этом для любого п имеет место неравенство
J fn <J||/nl|. При п, стремящемся к бесконечности, Г /„
стремится к Г / по определению, а, значит, в силу
непрерывности нормы (теорема 9 гл. II) | Г /„ стремится к Г / , а Г ||/„||
стремится к II/H, откуда и следует неравенство (IV, 1; 17).
Следствие 1. Интеграл вещественной интегрируемой
неотрицательной функции / неотрицателен.
В самом деле, так как |/| =/, то, применяя (IV, 1; 17), полу-,
чаем J/>| j/|>0.
Следствие 2. Если / и g —такие вещественные
интегрируемые функции, что f ^ g, то Г / ^ | g.
Действительно, достаточно к положительной функции g — /
применить следствие 1 и учесть, что \ {g — f) = \ g — \ f
(теорема 4).
->
Следствие 3. Для интегрируемой на [а, Ь] функции / имеет
место неравенство
I f 7 <(Ь-а) sup \\7(x)\\. (IV, 1; 19)

§ 1. Интеграл Римана на прямой
42$
В самом деле, прежде всего имеет место неравенство (IV, 1; 17)
относительно интеграла | : 1 Г J ^ Г ||/||. Так как функция
(а, Я 1а, Ь] 1а,Ь)
||7ll на [а, Ь] не превосходит постоянной Af = sup ||/(*))||, то,
согласно следствию 2, - имеет место неравенство Г Ц/1К
[а.Ь]
< J M = M{b-a).
[0,6]
Следствие 32. Если f интегрируема на [а, Ь], вещественна
и m < f (*)< М, то
tn(b-a)^ J f<Af(ft-a). (IV, 1;20)
[а, И
Это утверждение непосредственно вытекает из следствия 2.
Следствие 4. Интеграл вещественной неотрицательной
интегрируемой функции f совпадает с ее верхним интегралом.
Действительно, пусть fn— аппроксимирующая функцию f
последовательность, состоящая из вещественных ступенчатых
функций с'компактными носителями. Можно считать, что fn^0.
В противном случае f„ можно заменить функциями |fn|,
образующими аппроксимирующую последовательность. Тогда
f<fn + \f-fn\,
откуда (согласно теореме 2)
и точно так же
а" потому
откуда
j'f<JL+f\f-fn\ (IV, 1;202)
L<f + \L-f\, (IV, 1;203)
lL<ff+j'\f-fn\,
\ff- jfn\<j'\f-fnl (IV,1;204)
Правая часть стремится к нулю при п, стремящемся к
бесконечности, а ( /„ стремится к Г f, откуда и вытекает требуемый
результат.
Следствие 5. Пусть fn является последовательностью
интегрируемых функций, J— ограниченная функция с компактным
носителем, а I . || / — /„ \\ при п, стремящемся к бесконечности,

430
Гл. IV. Интегральное исчисление
стремится к нулю (это будет иметь место, в частности, если fn
равномерно сходятся к функции f и сохраняют свой носитель
на фиксированном компакте). Тогда функция f интегрируема,
я J in сходятся к \ J.
Мы уже видели ранее (замечание Г) на стр. 424), что функ-
ция / интегрируема, а из неравенства
j J 7- { Ц< J llT-f„ll = J'llT-T«ll (IV, 1;21)
следует, что J Jn сходится к J f,
Теорема 6 (о перестановочности интеграла и линейного
непрерывного отображения). Пусть L — линейное непрерывное
отображение банахова пространства F в банахово пространство
-> ->
G. Пусть f — интегрируемая по Риману функция, определенная
->
на прямой R, со значениями в пространстве F. Тогда функция
- > ->
L°f; определенная на R, со значениями в G интегрируема по
Риману и имеет место соотношение
jLof=L(jT)eG. (IV, 1;22)
Доказательство. Рассмотрим сначала ступенчатую
->
функцию g с компактным носителем, определенную в R, со зна-
-> ->
чениями в F. Функция Log является ступенчатой функцией
с компактным носителем, и имеет место соотношение
J W= J](ci+1-ci)LoJi=L 5](c/+,-с*)|,) = /,(]" g).
(IV,1;23)
-> ^
Пусть теперь / — произвольная интегрируемая по Риману
функция. Пусть Jo, It ы> • ■ • — аппроксимирующая /
последовательность ступенчатых функций с компактными
носителями. Покажем, что функции Lof п составляют
аппроксимирующую последовательность для функции L»/., В самом деле,
так как
|| (L ° Т- L о f„) IKH-L || || f~fn ]|,
то (IV, 1; 24)
j'HLof)-(Lofn)\l^}\L\\ j'\\J-fn\\.

§ 1. Интеграл Римана на прямой
431
Отсюда видно, что левая часть последнего соотношения
стремится к нулю при п, стремящемся к бесконечности, что и дока-
зывает интегрируемость функции L°f.
Соотношение (IV, 1; 23) имеет место для g = Jn. Так как
L°fn является аппроксимирующей последовательностью для
функции L°f, то при п, стремящемся к бесконечности, левая
часть этого соотношения стремится к \ L°f.
С другой стороны, fn в правой части равенства стремится
к Г 7 и, в силу непрерывности отображения L, эта правая часть
стремится к L( м, что и доказывает соотношение (IV, 1; 23)
■> ■>
для случая g = f.
-> ■>
Теорема 7. Пусть fug — две интегрируемые по Риману
■> ■>
функции со значениями в банаховых пространствах F и G. Пусть
■> ■>
В — билинейное непрерывное отображение пространства F X G
■> ■> ■>
в банахово пространство Н. Тогда функция В (f, g):
х —► B(f (x), g(x)) интегрируема по Риману и имеет место
неравенство
[J B(f, |)|<||В|| lllflll J" |||||. (IV, 1;242)
Доказательство. Пусть f0, fu f2, ... и g0, gu g2, ...—
последовательности ступенчатых функций с компактными носи-
■> ■>
телями, аппроксимирующие функции fag. Заметим, прежде
всего, что всегда можно предполагать выполненным неравенство
III gn III ^3 HI g |||. (В самом деле, предположим, что в одном из
интервалов разбиения функция gn равна некоторому (постоян-
■*■ ■>
ному) вектору из G с нормой >3|||g|||. Тогда во всем этом ин-
■> ■> ■>
тервале разность \\g — gn [| не меньше постоянной 2 ||| g-1||.
Заменим в каждом интервале такого вида постоянный вектор gn на
пропорциональный ему постоянный вектор g' с нормой, равной
||| J |||. Так как \g -*g'n\ <|| g|| + ||g;|| < 2|||S|||, a. 2|||g||l<
■*■■*■ ■*■■*■■■*■■*■ • ->
<|g — gj> т0 11^ — ^1 <||^ — ^„|- Функции^, заменяющие
функции gn, удовлетворяют неравенству I \\g — g'n\\<^\ \\g — gn\\,

432 Гл. IV. Интегральное исчисление
а, следовательно, последовательность g'n также является ап-
проксимирующей для функции g. На этот раз все
аппроксимирующие функции ограничены числом 3|||g|||.) При этих
условиях функция В (fn, gn) является ступенчатой функцией с
компактным носителем и имеет место неравенство
\\B<fn,gn)-B(f, g)\\^\\B(fn-T,gn)\\ + \\B(T, |„-J)||<
<IIB|llir«-iTll3|||J|||+.||B||l|iri|lll|«-?ll. (IV,1;25)
а, значит,
f\\B(Jn,gn)-B(tg)l\<
<l|B||(3|j|Ji||J,|lT«-flH-|||?ll|J*llJ«-Jll). (IV,1;26)
Отсюда следует, что функции В (/„, gn) образуют аппрок-
-»■ ->
симирующую последовательность для функции B(f,g), а,
значит, эта функция интегрируема по. Риману. Поскольку
IIВ (Г, !) || < IIВ || ||| fill II? II. (IV, 1;27)
то после интегрирования получаем неравенство (IV,1; 24).
Следствие 1. Если fug — интегрируемые по Риману
комплексные функции, то функция-произведение fg интегрируема по
Риману и- имеет место неравенство
//*|<11Л|/|£|- (IV, 1;28)
Следствие 2. Если fug — вещественные интегрируемые
по Риману функции, то функция fg интегрируема по Риману,
а в том случае, когда для всех х функция g ^ 0 и m ^
^в / (•*) =^ Л1, имеет место неравенство
>njg<jfg<MJg. (IV, 1; 29)
В самом деле, так как fg интегрируема по Риману и для
всех х выполняются неравенства
mg (x) <f(x)g (x) < Mg (x), (IV, 1; 30)
то, интегрируя эти неравенства, получаем (IV, 1; 29)1).
Замечание. Если / является непрерывной функцией, то
любая промежуточная величина между минимумом и максй-
') Конечно, эти неравенства не имеют места, если для функции g(x) не
выполняется условие g(x)^0. Пусть, например, / (х) = g (х) = х, а
интегрирование ведется на [—1, +1]. Здесь М = 1. Однако неравенство

§ 1. Интеграл Римана на прямой
433
мумом функции / может быть записана в виде /(£), где |eR
(теорема о промежуточных значениях, являющаяся следствием
теоремы 33 гл. II). Значит, в этом случае при g ^ 0, а также
при g ^ О имеет место соотношение
jf(x)g (x) dx = f(l)lg (x) dx, (IV, 1; 31)
называемое теоремой о среднем.
Примеры интегрируемых по Риману функций
Основные примеры вытекают из следствия 5 теоремы 5.
Теорема 8. Для того чтобы функция, определенная на
замкнутом интервале [а, Ь] прямой R, со значениями в полном1)
метрическом пространстве F была бы правильной, необходимо и
достаточно, чтобы она была пределом равномерно сходящейся
последовательности ступенчатых функций, определенных на
[а, Ь], со значениями в F.
Доказательство. 1°) Пусть /о,/ь/г. ••• —
последовательность ступенчатых функций, определенных на [а, Ь], равномерно
сходящаяся к функции /. Пусть с — точка [а, Ь].
Так как /„ являются ступенчатыми функциями, то при х,
стремящемся к с строго сверху, каждая из этих функций имеет
предел. Поскольку пространство F предполагалось полным, то из
теоремы 66 гл. II следует, что функция / обладает тем же
самым свойством. Аналогичное рассуждение показывает, что
функция / имеет преДел при х, стремящемся к с строго снизу.
Отсюда видно, что любая точка с является или точкой разрыва
первого рода или точкой непрерывности рассматриваемой функции
/, т. е. что функция / правильная.
2°) Обратно, пусть / — правильная функция со значениями
в метрическом пространстве F, Здесь нет необходимости
предполагать его полным. Покажем, что, каково бы ни было число
е > 0, можно найти такую ступенчатую функцию, определенную
на [а, Ь], со значениями в F, что d(f,g) ^ е. Полагая затем
последовательно е=1, 7г, ?/з, Vt, -.., мы сможем образовать
нужную нам последовательность ступенчатых функций.
Пусть х — произвольная точка [а, Ь]. Если точка х отлична ог
точки а, то, учитывая, что f(y) имеет предел при у, стремящемся
i 1
2/3 = \ х2 dx ^ 1 * dx = 0 не справедливо. Опыт показывает, что, не-
-1 -1
смотря на предостережения, эга ошибка очень живуча.
') Для того чтобы выполнялось необходимое условие, не нужно
предполагать пространство полным.

434
Гл. IV, Интегральное исчисление
к х по значениям <.х, можно найти такой интервал ]х—а, х],
а > О, для любых двух точек которого | и т), отличных от х,
имеет место неравенство d(f(%),f(r\)) ^ е.
Точно так же, если точка х отлична от точки Ь, можно найти
интервал [х, х -\- р[, обладающий таким же свойством.
Объединяя полученные результаты, получаем, что на отрезке [а, Ь]
всегда можно найти такой открытый в [а, Ь]1) интервал,
содержащий х, в котором для двух точек | и т), отличных от х и
расположенных по одну сторону от х, имеет место неравенство
d(f(t),f(4))^z.
Поскольку отрезок [а, Ь] компактен, то по свойству Гейне—Бо-
реля — Лебега его можно покрыть конечным числом таких
открытых множеств. Обозначим чер'ез с0 = сц, Си Сь ■ ■ ■, сп = b
множество точек, образованное из всех начал и концов этих
открытых интервалов, и включим в него точки х, для которых
были построены эти покрытия. Теперь мы можем следующим
образом определить ступенчатую функцию g: в каждой точке С;
она равна значению f в этой точке, а на каждом из интервалов
]ct, ci+i[ она равна постоянной f(li), где |г- — произвольная точка
этого интервала. Тогда, учитывая способ выбора интервалов, для
любой точки х получаем неравенство d(f(x), g(x))^. е, чем и
заканчивается доказательство теоремы.
Следствие 1. Любая непрерывная функция, определенная
на замкнутом интервале [а, Ь] прямой R, со значениями в
метрическом пространстве F является пределом равномерно
сходящейся последовательности ступенчатых функций.
Заметим, что доказательство для случая непрерывной
функции значительно проще, чем для случая произвольной
правильной функции. Достаточно заметить, что f равномерно
непрерывна на компакте [а, Ь] (теорема 31 гл. II). Тогда для любого
заданного е > 0 найдется такое ц > 0, что из d(x', x") ^ т] будет
следовать неравенство d(f(x'),f(x")) ^ е.
Если теперь ввести на отрезке [а, Ь] такое разбиение
Со = а, си с2, .. ., сп = Ь, при котором c*+i — с, были бы ^т], и
если выбрать функцию g равной Д|г) в [с,, ci+i[, где |, е [й, ci+l]
и g(b) = f(b), то мы получим d(f,g) sg: e.
Следствие 2. Всякая правильная функция, определенная
на прямой R, с компактным носителем и значениями в банахо-
вом пространстве F интегрируема по Р'иману. В частности, инте-
') Для х ф а и х Ф Ь это будет множество ]х — а, х + РГ При х = а
получим множество [а, а + Р[, а для х = Ь — множество ]Ь — а, Ь]. Во всех
случаях это открытые множества топологического пространства [а, Ь]. В то
же время это и интервалы. Поэтому мы их предполагаем открытыми в [а, Ь]
интервалами. Конечно, они не обязательно открыты в смысле определения,
данного на стр. 26.

$ 1. Интеграл Римана на прямой
435
грируема по Риману любая непрерывная функция с компактным
носителем.
Следствие 3. Любая вещественная функция, определенная
на интервале [а, Ь] прямой R и монотонная на этом интервале,
интегрируема.
Это справедливо, ибо монотонная функция правильна.
Конечно, имеются неправильные интегрируемые функции.
Например, функция, равная sin l/x на интервале ]0, 1] и 0 вне его,
интегрируема по Риману, хотя ее разрыв в начале координат не
является разрывом первого рода.
Теорема 9. Ограниченная функция с компактным носите-
■*■
лем и значениями в банаховом пространстве F, непрерывная
всюду, кроме конечного числа точек, интегрируема по Риману1).
Доказательство. Для доказательства теоремы
достаточно воспользоваться замечанием 1°) на стр. 424 и показать,
что для любого е^О найдется такая интегрируемая функция
|, что J" ||7— g||<e.
Пусть М — максимум ||f||, а N — число точек разрыва функ-
ции j. Рассмотрим функцию g, равную f вне объединения
интервалов [с, — ц, Ci + ц], где Ci — точки разрыва f, ц — г1(2ЫМ),
и равную нулю в этих интервалах. Тогда g будет всюду
непрерывной функцией, кроме конечного числа точек, в которых она
имеет лишь разрывы 1-го рода, а, следовательно, согласно след-
ствию 2 из теоремы 8, она интегрируема. Функция II f — g\\ не
превосходит ступенчатой функции, равной постоянной М в
каждом из N интервалов [cf — тьсг + л] и равной 0 вне их, так что
имеет место неравенство J ||/ — g||^M • 2iVri = e.
Вычисление интеграла функции
с помощью сумм Коши — Римана
Пусть f — определенная на интервале [а, Ь] прямой R со
значениями в банаховом пространстве F и интегрируемая по
Риману функция. Предлагается следующий способ вычисления ее
интеграла.
') Не следует думать, что функцию, обладающую этим свойством, можно
сделать непрерывной, изменяя ее значения в конечном числе точек RI Это
видно из предыдущего примера.

436
Гл. IV. Интегральное исчисление
С помощью точек с0 = а, си с%, ..., с„ = b производится
разбиение А интервала [а, Ь] на частичные интервалы. Для ка-
->■
ждого i через 0,- обозначается произвольный вектор простран-
■> ->
ства F, принадлежащий замыканию множества значений f
в замкнутом интервале [е,-, cj+i]. Затем строится сумма Коши —
Римана 2 (ci+1 — cf) 6г. В какой же мере эта сумма является
(=0
приближением к интегралу?
Покажем, что если взять произвольную последовательность
разбиений До, Ль Аг, . . ., такую, чтобы длина наибольшего из
интервалов разбиения Д„ стремилась к нулю при п, стремя-
->■
щемся к бесконечности, то предыдущая сумма (где 6*
произвольны в каждом интервале разбиения Ап) будет стремиться
к / при п, стремящемся к бесконечности.
->■
Теорема 10. Пусть f — функция, определенная на
ограниченном интервале [а, Ь] прямой R, со значениями в банаховом
-У
пространстве F и интегрируемая по Риману. Тогда по любому
е > 0 можно найти число ц > 0, обладающее следующим
свойством: для любого разбиения А интервала [а, Ь], определенного
такой возрастающей последовательностью точек с0 = a, cit
сг, • • •, Сп — b, что наибольший из интервалов [с,-, ct+i] имеет
длину г^г), при любом выборе вектора 6,- в замыкании
множества значений функции f на интервале [cit ci+i] имеет место
неравенство
J 7- 2 (С|+1 _ СД
<е. (IV, 1;32)
Доказательство. Прежде всего, согласно замечанию 2°)
на стр. 424, можно найти такую ступенчатую функцию g,
определенную на [а, Ь] - со значениями в г, и такую ступенчатую
функцию h с вещественными неотрицательными значениями, для
которых ||/ — gli^/г и J А^е/4. Обозначим через do = а, йи
d-z, ..., cLn = b точки разбиения, являющегося общим для обеих
->■
ступенчатых функций g и /г. Покажем теперь, что ц = e/(8MN),
где М =|||/||1> обладает необходимым свойством. В самом деле,
пусть А — произвольное разбиение отрезка [а, Ь] точками си
/=1,2,... п, такое, что наибольшая из длин отрезков [с,-, C{+i]
не превосходит ц. Выберем 0„ как было сказано выше, и обозна-

§ 1. Интеграл Римана на прямой
437
чим через 0 ступенчатую функцию, имеющую с* точками
разбиения, которая равна 0, в каждом из интервалов [с,-, ci+1[ и
' * V ■>
равна f(b) для л; = Ь. Сумма Римана 2j (ci+1 — c{)Q{ в этом
1=0
случае будет равна Г 8. Найдем теперь оценку функции
[а, Ь]
-> ->
\\f(x) — Q(x)\\ на каждом из интервалов [с,-, сц.\[.
1°) Предположим прежде всего, что интервал [си с*+1[
содержится в одном из интервалов ]dj,dj+i[. В этом интервале имеет
место неравенство
\\ftx) -д(х) \\=\\f(x) - е,|КН?М -g(x)\\+1| g(x) - eiil-
(IV, 1;33)
Первая норма здесь не превосходит h{x). Что же касается
второй нормы, то по определению 0, она не превосходит
sup ||JW-f(|)||. (IV,1;34)
->
Однако поскольку на интервале ]dj, dj+i[ функция g постоянна,
то в этой формуле можно заменить g(x) на g(%). Следовательно,
->■->.
\\g(x) — 0*11 не превосходит величины sup h(Q, которая
Ci<Kci+l
в силу постоянства h на интервале ]dj,dj+i[ равна h(x).
Окончательно в рассматриваемом интервале имеет место оценка:
\\f{x)-Q{x)\\^2h(x). (IV, 1;ЗБ)
Сумма интегралов от функции \\[—0|| по всем интервалам не
превосходит 2 Г Л^е/2.
2е) Предположим теперь, что интервал [с*, cj+i[ содержит
одну из точек разбиения dj. Поскольку 8г является точкой
прикосновения множества значений f, то можно утверждать, что
\\f(x)—Q(x)\\ не превосходит в этом интервале постоянной 2М.
Поскольку таких интервалов имеется не более 2N, а длина
каждого из них не больше т), то сумма интегралов от функции
||f—0|| по всем этим интервалам не превосходит 4MNr\ = е/2.

438
Гл. IV. Интегральное исчисление
Окончательно лолучаем неравенство
| \\f(x)-e(x)\\dx^e, (IV, 1;36)
[а, Ь]
и теорема доказана.
Следствие. Пусть f — интегрируемая по Риману
вещественная функция, определенная на ограниченном интервале [а, Ь]
прямой R. Тогда, каково бы ни было число е > О, существует
число т) > 0, обладающее следующим свойством: если для
каждого такого разбиения Д отрезка [а, Ь] возрастающей
последовательностью точек с0 = а, сх, с2, ..., сп = Ь, при котором
наибольшее из чисел Ci+i — с,- не превосходит ц, положить Mi =
= sup f(x) и ml= inf f (x), то будут иметь место
неравенства
n—\ n—\
2 (ci+l-c,)mt*Z { f(*)d*< J (<:,+,-с,)М, (IV,-1;37)
«=0 [a, b) 1=0
U
2 (сш-с,){М,-.т,Хг. (IV,1;38)
«=o
Это утверждение- непосредственно вытекает из теоремы,
поскольку на [Ci, Ci+i] имеют место неравенства т{ ^ f(x) ^ М,-,
где Mj и т,- являются точками прикосновения множества
значений функции /.
Замечание. Следствие уточняет замечание 3°) на стр. 425.
В качестве функций gi и g2 можно взять функции, принимающие
в интервалах [с{, ci+i[ соответственно значения т, и Mt и
значение /(6) в точке Ь.
Среднее значение функции на интервале
•> ■
Пусть / — функция, определенная на интервале [а, Ь] прямой
•>
К, со значениями в банаховом пространстве F, интегрируемая
по Риману на [а, Ь]. Средним значением f на интервале [а, Ь]
называется величина
51 £ [«> &]) = Т^ J T{x)dxef*). (iv,l;39)
la. 6]
') Если а = b, то договариваются считать средним значением вели»
чину /(a).

§ 2. Меры Радона
439
Из неравенств (IV, 1; 19) и (IV, 1; 20) вытекает, что это
среднее не превосходит |||/||| и что в вещественном случае оно
заключено между точной нижней и точной верхней гранями
функции /. Это среднее 'значение может быть вычислено с
помощью предела по следующей формуле:
п
ЗК(£[я. Ь])= lfr^-L^ f{a+ *(-Ц^)). (IV. 1;40)
fc=0
В самом деле, рассмотрим разбиение интервала [а, Ь] на п
интервалов длины (Ь — а)/п и вычислим сумму Коши — Ри-
мана:
%icM-cdticd = ^^t(a+k(^)). (IV,I;4I)
Из теоремы 10 вытекает, что, поскольку f интегрируема по
Риману, эта сумма необходимо сходится к Г J.
[а, 6]
Соотношение (IV, 1; 40) получается из (IV, 1;41) после умно-
п 1 1
жения его на выражение , . • -j——» стремящееся к . _ •
при п, стремящемся к бесконечности, и добавления слагаемого
■ . J (b), стремящегося к 0.
Если / является вещественной непрерывной функцией, то из
теоремы о промежуточных значениях (следствие теоремы 33
гл. II) следует, что Tl(f;[a,b]) равна /(с), где с — некоторая
точка отрезка [а, Ь].
§ 2. МЕРЫ РАДОНА НА ЛОКАЛЬНО КОМПАКТНОМ ПРОСТРАНСТВЕ
Меры Радона на компактном пространстве
Пусть X — компактное топологическое пространство.
Обозначим через ^{Х) пространство непрерывных на X функций со
скалярными значениями,обозначенное нами ранее через {Кх)е1)-
Согласно теореме о максимуме (теорема 29 гл. II),
непрерывная скалярная функция, определенная на компакте X,
ограничена. Как отмечалось ранее, функция <р->||| ф||| = sup |ф(*) |
х<=Х
') Это изменение обозначений может показаться странным. Но в
дальнейшем нам придется рассматривать случай, когда X не является
компактным, и мы тогда введем пространство Ч?(Х), не совпадающее с (К )с. Почти
всегда в качестве К будет браться поле комплексных чисел С.

440
Гл. IV. Интегральное исчисление
является нормой в ^(Х). Сходимость в смысле этой нормы
является равномерной сходимостью функций ф. В следствии
теоремы 64 гл. II говорится о том, что Ф(X) является банаховым
пространством.
Пространство, сопряженное к этому пространству, в
соответствии с общими обозначениями записывается в виде (ё"(Х).
Элементы этого сопряженного пространства называются мерами
Радона в пространстве X. Таким образом, если ц есть мера
Радона, то она определяет некоторое отображение, которое
каждому элементу ф из 'S'(X), т. е. каждой непрерывной скалярной
функции ф на X ставит в соответствие число ц(ф).
Определенное таким образом отображение линейно в том
смысле, что
n(<Pi + q>2) = M'(<Pi) + M'(<P2). n(k<f) = kn{q>) Для fee К. (IV, 2; 1)
Кроме того, оно непрерывно. Этот факт может выражаться
различными способами: либо он означает, что для каждой
последовательности скалярных непрерывных функций ф0, фь фг, ...,
равномерно сходящейся на X к 0, числовая последовательность
ц(фп) сходится к нулю, либо он означает, что мера ц обладает
такой нормой Цц,||, при которой справедливы соотношения
Ыф)К1Ы1111фИ1 и ||(i ||= sup |ц(<р)|. (IV,2;2)
111ФП1<1
С другой стороны, пространство %"(Х), будучи сопряженным
к банахову пространству, само является банаховым
пространством (теорема 50 гл. II). Его векторная структура
определяется следующим образом.
Если ц и v — две меры, то мера ц + v определяется по
формуле
(ti + v)(<p) = M«P) + v(«P). (IV, 2; 3)
Если fe — скаляр, то мера k\i определяется равенством
(*ti>.(<p) = *ti(q>). (IV, 2; 4)
Норма меры ц определяется по формуле (IV, 2; 2).
Согласно общим обозначениям, выражение ц(ф) может быть
также записано в виде ц-ф или (ц, ф).
Примеры мер Радона
1-Й пример. Мерой Дирака в точке аеХ называется мера,
определенная формулой
в(а)(ф) = ф(а). (IV, 2; 5)

§ 2. Меры Радона
441
Говорят, что эта мера определена единичной массой в точке
а множества X. Если X является векторным конечномерным
пространством, то мерой Дирака (без уточнения точки а) называют
меру, относящуюся к нулю пространства X.
Пусть теперь заданы счетная последовательность точек
Оо, fli, a2, ... пространства X и счетная последовательность
комплексных чисел с0, Си с2, ... . Тогда через2 cvbia \ обозначается
мера ц, определяемая формулой
(2 cvfyav)) • Ф = 2 cv<P Ы. (IV, 2;6)
Это выражение, наверное, будет иметь смысл, если сходится
ряд 2 |cv|, что мы будем всегда предполагать выполненным.
V
Эту меру называют атомической и говорят, что она определена
счетным множеством масс cv, расположенных в точках av
пространства X.
Докажем, что в том случае, когда все av различны, норма
этой меры равна сумме числового ряда
Scvfi(ev)l=2|cv|. (IV, 2; 7)
V
Прежде всего, если функция ср по модулю не превосходит 1,то
1Мф)1<2кД (IV,2;72)
V
откуда вытекает неравенство ||ц||^ 2 I О- С другой стороны,
v
по определению суммы сходящегося ряда с положительными
членами существует такое конечное подмножество / множества
индексов, при котором сумма V | cv | будет j>( V| cv |]—к •
V6/ \ V /
Обозначим теперь через ср непрерывную комплексную
функцию над X, не превосходящую по модулю 1 и принимающую в
каждой из точек av, ve/, значение cv/|cv|'). Теперь видно, что
МФ)= 2KI+ 2 С^Р(4 (IV, 2; 8)
ve/ v £ J
') Пусть X, например, является интервалом [а, ft] прямой R. Тогда,
очевидно, можно найти комплексную непрерывную функцию <р, не
превосходящую по модулю 1 и принимающую в конечном числе точек из X данные
значения, равные по модулю 1. Пусть d\, d.2 di — эти точки. Тогда
достаточно взять функцию ф аффинной в каждом из интервалов [a, d{\, [du d2], ...
..., [di, ft]. Эта возможность вовсе не очевидна, если X является
произвольным компактом. Однако это существенно в нашем доказательстве. В
дальнейшем мы убедимся, что это возможно (следствие 3 теоремы 11).

442
Гл. IV. Интегральное исчисление
откуда следует оценка снизу
Ыф)1>(£К1-!)-ЕК1>Е|с*1-е- (IV, 2; 9)
Так как || ф II = 1, то
Ы1>||*(ф)1>2|<\|-е. (IV, 2; 10).
V
Поскольку б > 0 произвольно, получаем || ц || ^ 2 I Cv I, откУДа
v
и вытекает требуемый результат.
Заметим также, что обозначение 2, написанное ранее без
обоснования, может быть теперь строго обосновано: речь идет
о нормально сходящемся ряде векторов банахова пространства
^"(Х). В самом деле, так как |cv6(av) 1 = 1 cv | и 2lCvl<+°°>T0
ряд 2jCv6(a ) нормально сходится к некоторому элементу из ^'(Х).
v
Пусть (ii — этот элемент. Поскольку для фиксированного ф
функция v->v^) является линейной непрерывной формой над
^'(Х), то из теоремы 60 гл. II получаем
И) (ф) = ( 2 cvS(av)j • ф■ = 2 (Cv6(av) • ф) — 2 Cv(() (av) = (i (ф) Х).
(IV, 2; 11)
Следовательно, ц — \ii можно записать в виде 2 cv6/av).
2-й пример. Возьмем в качестве X компактный интервал [а, Ь]
прямой R. Тогда интеграл ф-> | y(x)dx определяет некото-
[а, Ъ]
рую меру Радона над X. Из неравенства (IV, 1; 19) видно, что
норма этой меры ^ b — а. Впрочем, если вычислить значение
этой меры на функции ф==1, то мы получим неравенство
1с I ■
Ф '= Ъ — а. Итак, норма такой меры равна Ь — а.
[а, Ь]
Более общо, если р является интегрируемой по Риману ком-
плекснозначной функцией, определенной'на [а, Ь], то она
определяет меру по формуле
1*(ф)«= J p{x)(f(x)dx. (IV,2; 12)
[е. Я
') По определению.

§ 2. Меры Радона
443
Норма этой меры, очевидно, ^ Г \p(x)\dx. Позже мы
покажем, что норма в точности равна этому интегралу.
Определенные таким образом меры, в противоположность
атомическим мерам, называются рассеянными в том смысле, что
они не содержат точечной массы.
Говорят также, что эта мера является мерой с плотностью р
по отношению к мере dx, и записывают ее через pdx или р (х) dx1).
В силу обозначения dx, принятого для меры ф-> Г ф, произ-
[0.6]
вольная мера вместо ц обозначается через dp,, а выражение
ц(ф) называется интегралом от функции ф по мере jx или djx и
вместо |х(ф) часто.обозначается через
Г ф (х) d[i (х), или |ф<2|х, или Г ф|х. (IV, 2; 13)
х хх
Естественным образом можно образовать меру как сумму
двух мер, изученных в примерах 1 и 2, т. е. определить ее по
формуле
H(<P) = 5]<VP(av)+ J" p(x)<f(x)dx. (IV, 2; 14)-
v [a, 6]
Говорят, что эта мера является суммой точечных масс cv,
расположенных-в точках av интервала [а,Ь], и рассеянной меры
плотности р по отношению к мере dx. Ее обозначают через
|1 = Ц cv6(av) + p dx. (IV, 2; 15)
') Обозначение для меры <р-> ip(x)dx совершенно корректно. Обо-
[а.61
значение dx логически противоестественно, ибо х фигурирует в интеграле как
переменная интегрирования, которую можно обозначить или у, или /, или
другим символом. Точно так же более корректно обозначать меру через
p(x)dx, а не в виде pdx, подчеркивая этим двойным введением переменной х
ее промежуточную роль. При этом р(х) dx может быть заменена на р(у) dy
или p{t)dt. Эта некорректность аналогична той, которая отмечалась при
употреблении выражения «функция хН вместо «функция д:-»-д:2» (см. стр. 11).
Однако, как и в случае функций, часто допускают вольность речи. Если
возникает сомнение, то говорят «мера \(x)dx-» вместо «мера dx», поскольку
здесь речь идет о мере p(x)dx, где р(х)= 1 для всех х, т. е. р(х)= I.
Можно так же для dx, как и для pdx, писать полностью «мера
ф-> у(х) p(x)dx*>
[Я. Ь|

444
Гл. IV. Интегральное исчисление
Норма этой меры, очевидно, оценивается сверху числом
%\су\+ J \p(x)\dx. (IV,2; 16)
v [а, Ь]
Покажем, что если все av различны, то норма в точности равна
этой величине.
Зададим е > 0 и определим конечное множество индексов /
так, чтобы 2 |cvKJe/6. Поскольку р интегрируема по Рима-
ну, то можно найти такую ступенчатую на [а, Ь] функцию q, для
которой имеет место неравенство
J \p(x) — q(x)\dx^l.
(IV,2;162)
to. Я
Обозначим теперь через d0 = a, dx, d2, ..., dn = b
множество точек разбиения, соответствующего .функции q, и точек av,
ve/. Для каждого t'= 0, 1, 2, ..., п—1 можно теперь найти
такой интервал[dbd"i+i]c=]^'>'d/+1[,при котором имело бы место
неравенство
2 I qi I № - di) + (dw - d'i + i)) <~ (qi = q в R, dt+l[).
1=0
(IV,2;163)
Определим теперь функцию ср следующим образом. В
каждом из интервалов [di, d'i+\] будем считать.ее равной постоянной
qi/\Qt\. В каждой из точек di, i=l, 2, ..., п, совпадающей
с точкой av, ve/, положим ее равной числу cv/|cv|. В
интервалах, где она еще не определена, определим ее как аффинную
функцию. Очевидно, модуль <р всюду не превосходит 1.
С другой стороны, имеют место неравенства
2 cv<P (av) — 2 I cv I < 2 cv<P («v) — 2 cv<p (av)
+
+
S ^(av)- 2kvl + 2.1 cv I—21 c
(IV, 2; 164)
Второй член правой части равен нулю, поскольку <p(av) =
-р-^-г для v е /. Первый и третий члены не ппевосходят е/6.
Поэтому
~ ~ (IV, 2; 16Л)
2 CV<P (Оу) — J] | Cv
^ 6 ~~' 3 '

§ 2. Меры Радона
445
Далее,
\ Р М Ф (#) dx— \ \р (х) | dx
[а, Ь) [а, Ь)
<
+
<
\ р (х) ф (х) dx — Г q (х) ф (х) dx
[а, Ь] [а, Ь]
4
J* q {х) ф {х) dx — J* \q(x)\dx +
la, Ь) [а, 6]
+
J* \q(x)
[а,Ь]
d* — J \p{x)\c
(a, 6]
/jc
. (IV, 2; Г66)
Согласно (IV, 2; I62), первый и третий члены правой части не
превосходят е/6. Поскольку в интервале [d\, d'l+x] функция ф
равна qil\qi\, то, в силу (IV,2; 16з), второй член не больше
2е/6 = е/3. Поэтому
Г р (х) ф (х) dx — \ \р (х) | dx
[а,Ь] [а,Щ
<ТГ + 4 = ^Г- (IV.2; 167)
Добавляя сюда (IV,2; 16s) и учитывая (III,2; 14), для
построенной функции ф получаем неравенство
и(ф) -( J \p(x)\dx+y^l\cv\\
\[а, 61 v /
<е,
(IV, 2; 16а)
равна
доказывающее наше утверждение, а именно то, что
(IV, 2; 16).
Важно подчеркнуть, что мера с плотностью р не изменяется,
■если функция р меняется в конечном числе точек.
Плотность определяет меру, но различные плотности могут
дать одну и ту же меру.
3-й пример. Хотя мы еще не знакомились с кратными
интегралами, мы можем, однако, заметить, что если X является
замкнутым параллелепипедом в R'n, т, е. множеством, определенным
неравенствами ах ^ Xi ^ Ьи i = 1, 2, ..., и, то на X можно
определить меру dx = dxi dx2... dxn no формуле
Ф —" J" J" ... Jf(*i хп) dxi dx2 ... dxn. (IV, 2; 17)
Норма этой меры равна объему параллелепипеда X, т. е;
П (bi - ^).

446
Гл. IV. Интегральное исчисление
Меры на локально компактном пространстве
Множество X = R не компактно. Тем не менее линейные
формы ф->-ф(а) и у-+\ у (х)dx продолжают сохранять смысл
по крайней мере в том случае, когда на ф налагают некоторые
ограничения, например условие, заключающееся в том, что ф
имеет компактный носитель. Поэтому имеет смысл дать
следующее определение.
Пусть X — локально компактное топологическое
пространство. Обозначим через 9>?{Х) векторное пространство
непрерывных скалярнозначных функций ф, определенных на X и имеющих
компактный носитель4) (этот носитель, естественно, не
уточняется; каждая из функций ф этого пространства имеет
компактный носитель К, но К зависит от ф). Заметим, впрочем, что
ни в коем случае не следует смешивать функцию ф,
определенную и непрерывную-на всем X и имеющую компактный носитель,
с функцией, определенной и непрерывной на некотором
компакте из X.
Например, функция, изображенная на рис. 13, определена и
непрерывна на интервале [а, Ь]. Эта функция не является
функцией, определенной на всей числовой прямой R и имеющей
[а, Ь] в качестве носителя. Если ее продолжить на R, положив
вне [а, Ь] равной нулю, то она не будет непрерывной на R,
поскольку точки а и Ь являются ее точками разрыва.
а Ь
Р и с. 13.
**\э—*
Рис. 14.
Напротив, функция, изображенная на рис. 14, определена
на R, непрерывна, имеет компактный носитель, а,
следовательно, принадлежит пространству "^(R).
Если К является компактом X, то через 'ё'к(Х) будем
обозначать векторное подпространство пространства 'ё'(Х),
образованное функциями ф, носители которых лежат в компакте К.
Функция ф из 'ё'(Х) принадлежит Ч?к(Х) тогда и только тогда,
когда она равна нулю на С К- Отсюда следует, что она равна
') Ф(Х) является подпространством {Кх)сь\ см. примечание на стр. 439.

§ 2. Меры Радона
447
нулю не только на С К, но также и на границе компакта К,
поскольку каждая точка этой границы является пределом точек
множества СК, а функция ер непрерывна. Не следует
смешивать 'ё'к(Х) и ^{К). Функция ф1 (см. рис. 13) принадлежит
^([а,Ь]). Функция ф2 (см. рис. 14) принадлежит пространству
^1а,ы(-К).
Пространство 'ё'(Х) является объединением векторных
пространств ^РК(Х), когда множество К пробегает все компактные
подпространства X.
Если в пространстве 'ё'к (X) ввести норму ||| ф ||| — sup | ф (л:) |,
то оно станет банаховым пространством. В самом деле, (Кх)сь
является в этой норме банаховым пространством (следствие 3
теоремы 65 гл. II), а 'ё'к(Х). является в нем замкнутым
векторным подпространством. (§ самом деле', если при п, стремящемся
к бесконечности, последовательность ц>п^'^'к(Х) сходится к гр
в (Кх)сь, т. е. сходится равномерно и тем более просто, то в
силу равенства фп(л:) = 0 для xeW получим также ф(л:) = 0,
откуда фЕ?я(Х).) Из теоремы 43 гл. II теперь следует,
что 'ё'к(Х) является банаховым пространством. Естественно,
такую же норму можно ввести и на пространстве 'ё'(Х). Однако
можно показать, что тогда оно не будет банаховым. Во всяком,
случае это не та норма, которая нас будет интересовать в
дальнейшем.
Определение. Мерой Радона на локально компактном
пространстве X «азывается линейная форма ц, определенная на
векторном пространстве 'ё'(Х), сужение которой на каждое
подпространство Ч?К{Х), где К является компактом X,
непрерывно.
Выясним точный смысл этого определения.
Мера ц определяет некоторое отображение, которое каждой
функции ф, принадлежащей пространству 'ё'(Х), т. е. каждой
скалярной непрерывной функции ф, определенной на X,
имеющей компактный носитель, ставит в соответствие скаляр ц(ф).
Это соответствие должно быть линейным в смысле (IV,2;1).
Однако мы не говорим, что это соответствие непрерывно на
'ё'(Х), поскольку в этом векторном пространстве мы не вводим
ни топологию, ни норму. Мы можем сказать только, что
сужение этого отображения на 'ё'к(Х) должно быть непрерывным.
Теперь, каким бы ни был компакт К из X и какова бы ни была
последовательность непрерывных функций ф0, ф4) ф2, .. . с
носителями в К, равномерно сходящаяся к 0 при п, стремящемся
к +оо,. последовательность комплексных чисел ц(ф„) сходится
к нулю. Мы получаем, что каждому компакту К из X можно
поставить в соответствие норму меры относительно К, а именно

448
Гл. IV. Интегральное исчисление
такую норму, при которой имеет место формула
1ц(ф)1<Ии1И11ф111 Для <pe«V(*), (IV, 2; 18)
где || ц Ik e sup |ц(ф)|.
111Ф11К1
Примеры мер Радона
Пример 1. Мера б(а), определенная по формуле (IV,2;5),
также является некоторой мерой Радона на X. Аналогично,
сумма 2 cv6(a ) будет некоторой мерой Радона при условии, что
ряд 2 I cv I является «локально сходящимся», т. е. частичная
v
сумма 2 lcvl сходится для любого компакта К из X. Фор-
мула (IV, 2; 6) в этом случае определяет линейную форму на
'S'(X). С другой стороны, для каждого компакта /(для любой
фе^к^) имеет место неравенство 2<VP(flv)|^s/ 2 I су1)111ф|11>
v ' I \ave=K /
из которого вытекает непрерывность рассматриваемого
отображения. Отсюда следует также, что ИцИ^-^ 2 lcvl>
Однако можно получить более точное утверждение об этой
норме. В самом деле, в каждой точке av границы К множества
К функция ф из 'ё'к(Х) необходимо равна нулю
(каждаяокрестность этой граничной точки содержит точки дополнения
к К, где функция ф равна нулю и, кроме того, ф непрерывна
(см. по этому поводу стр. 447). Поэтому при оценке суммы
2 cv(av) точки av границы К можно не учитывать, так что имеет
место неравенство ||ц||#<^ 2 |cv|, где К — внутренность К.
Теперь, пользуясь методом, примененным на стр. 443, нетрудно
доказать, что |||л||я в точности равна 2 lcvl-
Пример 2. Мера Г или dx на R, как и в случае
компактного интервала [а, Ь] прямой R, определяется точно так же с
помощью отображения ф->-Гф. Ее называют канонической мерой
прямой R или мерой Лебега на R. Для каждого интервала [а, Ь]
ее норма ||ц||(а Ь) равна b — а.
Если р является функцией, определенной на R, комплексно-
значной и локально интегрируемой по Риману, т. е.
интегрируемой на каждом ограниченном интервале, то она определяет
меру Радона ц по формуле (IV, 2; 12); мы обозначаем ее через

§ 2. Меры Радона
449
pdx или p(x)dx и называем р плотностью по отношению к мере
Лебега.
Норма относительно компактного интервала [а, Ь] равна
при этом ||ц||(а b] = \p{x)\dx. Заметим, что это утверждение
\а, Ь]
не вытекает непосредственно из утверждения, полученного из
формулы (IV, 2; 16). В самом деле, функция ф из 9V ы (R)
в противоположность функциям из ^ {[а, Ь]) (см. стр. 447) равна
нулю в точках а и Ъ.
Если же выбрать а', Ь\ а < а' < Ь' < Ь, так, чтобы
Г \p{x)\dx-\- \p{x)\dx?C^r, и если непрерывная на ин-
[а, а') [Ь', Ь]
тервале [а', Ь'] функция ф определена так, что
J" p(x)y(x)dx— J \p(x)\dx <-|,
la'. b'\ \a', b')
согласно тому, как это было сделано на стр.444, то можно
продолжить функцию ф на интервал [а, Ь] таким образом, чтобы
она была аффинной в интервалах [a, a'], [b, b'] и принимала
нулевое значение в точках а и Ъ. Представляя теперь интервал
интегрирования [а, Ь] в виде объединения трех интервалов [а, а'],
[а', Ь'], [Ь', Ь], получаем следующее неравенство:
J" р (х) ф (х) dx — j \p(x)\dx < -~- + -|- = в,
\а, Щ [а, Ь]
доказывающее предыдущее утверждение. (Затем можно,
естественно, ввести меры вида 2 cv<bta ) + pdx.)
В силу того что функции ф имеют компактные носители, мы
смогли ввести меры предыдущего типа, где функция р может
возрастать на бесконечности с произвольной скоростью.
Например, р может быть функцией е%г или функцией ее* , и она
вполне определит меру Радона pdx.
Нормой меры ц называется точная верхняя грань чисел
|| ц \\к по всем компактам К из X. Эта норма, обозначаемая
через II ц ||, неотрицательна, конечна или равна +°° (и,
следовательно, несмотря на свое название, не является нормой).
Очевидно, ее можно определить по формуле
||ц ||= sup 1 |х (ф) |. (IV, 2; 19)
1ИФ11К1
Хотя пространство мер невозможно рассматривать как
сопряженное к пространству 'ё'(Х), его, однако, обозначают
через Ч?'(X). Это множество является, естественно, векторным-
пространством с тем же самым определением суммы и умноже-
15 Зак. 1339

450
Гл. IV. Интегральное исчисление
ния на скаляр, что и в том случае, когда X компактно. Однако
оно не нормировано. Напротив, подпространство пространства
^'(Х), образованное из таких ц, для которых || ц || конечна,
является векторным нормированным пространством. Легко
видеть, что это пространство является банаховым.
Применения к механике и физике
В механике часто приходится рассматривать распределение
масс в пространстве. В свою очередь в физике сталкиваются
с распределением электрических зарядов. Меры Радона над
аффинным евклидовым трехмерным пространством Е дают
хорошие модели для этих распределений масс и распределений
зарядов. То, что в механике называется точечной массой ш,
помещенной в точке а, или в физике — электрическим зарядом е,
расположенным в точке а, является не чем иным, как мерой
Радона mb(a) ИЛИ еб(о).
Если в физике рассматривается распределение масс или
зарядов, определенных с помощью плотности р{х), то это
означает, что рассматривается мера Радона p(x)dx, где dx является
мерой трехмерного объема в Е. В случае прямоугольной
системы координат это будет мера p(x,y,z) dxdydz.
В механике и физике часто рассматривается распределение
масс или зарядов, расположенных на замкнутой поверхности 2,
принадлежащей классу С1, в трехмерном евклидовом
пространстве с «поверхностной плотностью» р{х). Эта величина
является мерой Радона, определенной равенством
И (ф) = J" Ф .(*) Р (х) dS»). (IV, 2; 20)
Ее удобнее будет обозначать через pdS. Точно так же
распределение зарядов или масс, расположенных на замкнутой
кривой L класса С1, линейнойнлотности р относительно дуги ds
определяется по формуле
Vto)=j<t(x)p{x)ds (IV, 2; 21)
L
и может быть обозначено через pds.
Векторные меры
Рассмотренные выше меры были скалярными.
Пусть теперь Е — векторное нормированное пространство.
Мерой ц на X со значениями в Е будем называть линейное ото-
) Такие «поверхностные интегралы» будут определены позже в § 10.

§ 2. Меры Радона
451
бражение 'ё'(Х) в Е, сужение которого на каждое
подпространство 9?к(X), где К является компактом X, непрерывно. Таким
-> ->
образом, здесь для фе'йР(Х) величина ц(<р) или ц-<р является
-> -> ->
элементом Е. Как прежде, определяются нормы \\\i\\K и ||ц||.
-> -> _ ->
В качестве примера мер при полном Е можно взять ц = 2i cv6/a ь
где cvfe£, или d\i= p(x) dx, где р является функцией,
определенной на R, со значениями в £ и локально интегрируе-
мой по Риману. При этом 2i cv<p (av) e E (предполагая, как
ранее, что на любом компакте К множества X 2i l|cv||<oo,
vi ■*
получим, согласно теореме 55 гл. II, что ряд 2i MP («v) cxo"
V
. -> ->
дится) и р{х) <р (х) dx-е £. Для норм имеют место неравенства
|2**К)[-<Е Ikvll и \\^dx\\lab]< j" f|p(Jc)||rfjc'). .
la.b]
->
') Мы всегда писали 92 (X) без уточнения поля скаляров. Пусть Е—
векторное нормированное пространство над комплексным полем. Тогда С-ме-
-> ->
ра ц со значениями в Е для поля скаляров К = С является отображением
пространства 92 (X; С) комплексных непрерывных функций ф с компактным
-> ->
носителем в пространство Е, линейным относительно С. R-мера ц со зна-
->
чениями в Е для поля скаляров К = R является отображением пространства
92 (X; R) вещественных непрерывных функций ш с компактным носителем
-> ->
в Е, линейным относительно R. Мера ц для поля С определяет меру цр
->
для поля R. Мера Цр является лишь сужением на 92(Х; R) функции
ц: 92 (Х\ С)-»-£.
■*" ' "*"
Так, например, если Е = С, то ц является "скалярной мерой, однако ц^
является уже векторной мерой со значениями в векторном пространстве С
размерности 2 над R.
Пространство скалярных К-мер (или К—сопряженное пространство
к 92 (X; К)) обозначается через 92' '
Рас
,-мер (нл
?'(Х; К).
JacCMOTpHM теперь при тех же условиях векторное нормированное про-
-> ->
странство Е над полем С, и пусть v является некоторой мерой
относительно R, т. е. является некоторым R-линейным отображением пространства
->
92(X; R) в Е. Тогда возможно единственным образом продолжить ее на не-
-> ->->->
которую меру vc относительно С, полагая vg (ф] + «Фг) = v (ф|) + ^(Фг).
->->-> ->
При этом (vc)R = v и (цк)с = ц.
-> -> -> ->
Заметим, что нормы ц и цк («ли v и vc) люг(/т быть различными.
Рассмотрим, например, скалярную меру ц = б(0) + (' бц,). Ее норма относительно
15*

452
Гл. IV. Интегральное исчисление
Разложение единицы
Приведем одну теорему относительно вещественных
непрерывных функций на локально компактном пространстве X,
которой мы будем пользоваться в теории мер.
Теорема 11. Пусть X — локально компактное
пространство, «счетное в бесконечности», т. е. являющееся объединениеч
счетного множества компактов. Пусть, кроме того, (Qi)imI —
покрытие (конечное или нет) пространства X открытыми
множествами. Тогда существует система вещественных
непрерывных функций он, зависящих от того же множества индексов I,
такая, что О ^ он ^ 1, он имеет носитель в Q,, каждая точка X
имеет окрестность, в которой лишь конечное число функций осг
не равно тождественно нулю, сумма 2 °Н тождественно равт
is/
на 1 на X. Если X является многообразием класса Ст (т
конечно или = +оо) над полем вещественных чисел R, то
функции он можно брать из класса Cmi).
Замечания. 1°) По-видимому, вместе с образованием
суммы 2 ai возникает задача обоснования ее сходимости, тем
ie=/
более досадная, что / может не быть счетным. Однако в
условии указывается, что в каждой точке хе!и даже во всех
точках окрестности х эта сумма конечна, поскольку все ее члены,
кроме конечного числа их, равны нулю.
При локально компактном X мы приходим к тому, что на
каждом компакте из X все он, кроме конечного числа их, равны
тождественно нулю. В этом случае говорят, что система он
локально конечна.
2°) Хорошо видно, почему функции он определяют
разложение единицы: имеет место разложение 1 в сумму функций сн
•с носителями в заданных открытых множествах fi4.
Если Qi компактны, то он имеют компактные носители и,
следовательно, принадлежат V(X). Говорят, что разложение
единицы (аг)г s ; подчинено покрытию (Ог)г s;.
скалярного поля С равна sup|<p(a) +*<p(&)|, где sup берется по всем,
комплексным функциям ф, не превосходящим по модулю 1. Величина эта
равна 2. Норма этой же меры в поле скаляров R вычисляется как тот же sup,
взятый по вещественным функциям ф, не превосходящим по модулю 1, и
равна V~2- Почти всегда берут К = С.
') Это улучшение (переход в класс Ст) в интегральном исчислении не
играет никакой роли. Однако оно нам понадобится в теории распределений.
Существенным здесь является то, что рассматривается
многообразие С™ по отношению к полю вещественных чисел. Утверждение неверно в
■случае поля комплексных чисел. Далее мы увидим, что при доказательстве
леммы 1 будет применяться поле вещественных чисел.

§ 2, Меры Радона
453
3°) Если X локально компактно, но не является счетным
в бесконечности, то результат не верен. Однако имеет место
более слабое утверждение, достаточное для некоторых
приложений, которое мы здесь приводить не будем (оно основывается
на леммах 1 и 2, верных для произвольного локально
компактного пространства X).
Нормированное векторное конечномерное пространство ло-
каоТьно компактно и счетно в бесконечности, поскольку оно
является объединением шаров || х || ^ п, п е N.
А°) Пространство X, для которого справедлива теорема о
разложении единицы, называется паракомпактным
пространством. Локально компактное, счетное в бесконечности
пространство паракомпактно. Можно показать, что метризуемое
пространство паракомпактно.
Для доказательства мы предварительно рассмотрим три
леммы.
Лемма 1. Пусть Q — открытое множество локально
компактного пространства X и а — точка Q. Тогда существует
непрерывная функция у. удовлетворяющая условию О ^ у ^ ' >
с компактным носителем в Q, такая, что \(а)^>0. Если X
является многообразием класса С™, то у можно брать в классе Ст.
Естественно, что лемма тем интереснее, чем меньше
окрестность Q точки а.
1°) Пусть Х-—произвольное локально компактное
пространство. Теорема верна в общем случае, но мы ее докажем только
для того случая, когда локально компактное пространство X
метризуемо. Итак, предположим, что в нем введена некоторая
метрика. Поскольку Q является открытым множеством,
содержащим а, а X — локально компактно, то найдется компактный
шар В(а, ц) с центром в точке а и радиуса ц > 0,
содержащийся в Q1). Обозначим теперь через F вещественную функцию,
непрерывную на полупрямой R+ (вещественные числа 35=0),
удовлетворяющую неравенствам 0 =£Г F ^ 1 и такую, что F(Q) >
>0и F(t) = 0 для t ^ т). Можно будет, например, взять
функцию, определенную по формуле
fW = {4!/ ZZ nV^„ (IV, 2; 22)
ДЛЯ *>Т1,
для о <; t <; т).
Функция x-+F(d(a,x)) обладает требуемыми свойствами.
Она непрерывна как суперпозиция двух непрерывных функций.
') В самом деле, а имеет компактную окрестность V. Так как Q П V
является окрестностью точки а, то существует такое г\ > 0, что замкнутый
шар В (а, т)) лежит в Q П V. Этот шар лежит в Q и, будучи замкнутым в
компакте V, компактен.

454
Гл. IV. Интегральное исчисление
Поскольку d{a, а) — О и F(0) = т), то при X = а она принимает
значение т). Она равна нулю вне шара В (а, т)), поскольку вне
этого шара d(a, х)>т), и F(£) = 0 при t ^ ц. Отсюда следует,
что ее носитель содержится в этом шаре, являющемся
компактом в fi. Понятно, почему метризуемость пространства является
существенным упрощением задачи. В самом деле, метрика опре-;
деляет бесконечное множество вещественных непрерывных
функций в метрическом пространстве, а именно, функции x—*d(a,x).
Напротив, если мы знаем только, что X является
топологическим пространством, то, кроме постоянных функций, мы не
знаем а priori других вещественных непрерывных функций наХ.
2°) Предположим теперь, что X является многообразием V
размерности п над полем вещественных чисел класса С™
(возможно,, пг = -j-oo)1). Пусть Ф является некоторой картой V
с образом, содержащим точку а. Карта Ф является
гомеоморфизмом класса О некоторого открытого множества (Ji из Rn
на 0(<7i) с= V. Пусть fii = ф-!(0) ио, = Ф~1(а).
Предположим, что лемма доказана в Rn для функции
класса О. Другими словами, предположим, что найдена некоторая
функция yi класса О на Rn с компактным носителем К\,
содержащимся в fii, удовлетворяющая неравенству 0 ^ yi ^ 1 и
такая, что Yi(«i)>0- Тогда лемма будет доказанной также и
в У. В самом деле, определим у на У следующим-образом: у~
= yi о Ф~1 в множестве Ф(й4) с fi и у = 0 вне его.
Функция Ф-1 является обратной биекцией для Ф, т. е.
отображением множества Ф (Oi) на (Ji. Функция у принадлежит
классу О. Действительно, пусть Ь е V. Если йеф(£2,), то у
равна yi ° Ф-1, и поскольку Ф является картой класса О, а yi—
функцией класса О на Ои то y принадлежит классу О в
окрестности точки Ь (теорема 333 гл. III). Если Ь'фФ{^), то Ъ
лежит в открытом множестве ОуФ{К\) многообразия V,
дополнительном к компакту Ф(/(1). Функция y равна нулю в этом
множестве и, следовательно, принадлежит классу О в
окрестности точки Ь. Мы только что видели, что y равна нулю в
дополнении к компакту Ф(/С4), а, следовательно, ее носитель лежит
в компакте Ф^^аФ^^а®. Эта функция удовлетворяет
неравенствам 0 ^ y ^ 1 и у(а) = Yi (ai) > 0-
Остается решить задачу для функции Yi> принадлежащей
классу Ст на Rn. Поскольку число т может быть
произвольным, то мы должны найти функцию Yi класса С°°. Введем в R™
обычную евклидову метрику. Тогда функция Xi-*/- = d(a\,x\) не-
') Поскольку каждая точка многообразия имеет окрестность, гомеоморф-
ную некоторому открытому множеству из R", то существует также меньшая
компактная окрестность. Многообразие является локально компактным
пространством.

§ 2. Меры Радона
455
прерывна, но не дифференцируема в точке аи однако ее
квадрат л2, являясь .полиномом 2-й степени относительно своих
координат, принадлежит классу С°°.
Пусть T)i > 0 — такое число, что компактный шар B(aUf\i)
лежит в множестве Qi. Если вместо F рассмотреть
вещественную функцию G, определенную на R+ по формуле
О ДЛЯ S^T)*,
G(s) =
i
(IV, 2; 23>
Il2-s
1 ДЛЯ S<T)2,
то получим, что она удовлетворяет неравенствам O^G^l,
что G(0) > 0, что G(s) равна нулю для $^ц\ и что G
непрерывна (ибо, когда s->T)uS<T)b lime"l'\r>i~s) = e~oa = 0).
Более того, G принадлежит классу С°°. В самом деле,
последовательным дифференцированием можно убедиться, что для s<T)2
производные G имеют вид
1
G{k)(s) = Pk(-^—\e "•-*, (IV, 2; 24)
-*ш
где Ph — полином от одной переменной. При s, стремящемся
к rfi по значениям <т)?. функция Gw(s) стремится к нулю
(поскольку показательная функция растет быстрее любого
полинома). Для s>tfx имеем G(fe)(s)==0. Следовательно, GW {s)
стремится к 0 при s, стремящемся к т^ по произвольным
значениям Ф- tf{. Теорема 14 гл. III, примененная шаг за шагом к
последовательным производным, дает, что G бесконечно
дифференцируема, а все ее производные при s=?r^ равны нулю.
Вот график этой функции G:
У
1 »-С(#)
s.vf
Р и с. 15
(Разложение Тейлора порядка m для функции G в окрестности
точки s = г)? сводится к остаточному члену. Ряд Тейлора
функции G по степеням s — vfi сходится, поскольку все его члены
равны нулю, но он не представляет функцию для s<t)J.)

456
Гл. IV. Интегральное исчисление
Функция y{(xi)= G((d(auxi))2)= G(r2) принадлежит
классу С°° как композиция двух функций G и г2 класса С°° и Yi(ai) =
= G(0)>0.
Так как O^G^I.toO^y^^- Наконец, для d(au xi) ^t\i
функция yi равна нулю, поскольку G(s) равна нулю для s^y\2.
Лемма 1 доказана.
Лемма 2. Пусть X— локально компактное пространство и
(Qг). s { — открытое покрытие X. Пусть К — некоторый компакт
пространства X. Тогда существует система непрерывных
функций Вг- ^ 0, зависящих от того же множества индексов I, равных
нулю, кроме конечного их числа, имеющих компактные
носители, содержащиеся 'в Q*, и таких, что сумма 2 Pi положи-
тельна на К. Если X является многообразием класса Ст, то
функции В; можно выбирать из класса С™.
Пусть |— некоторая точка К- Точка | может принадлежать
нескольким открытым множествам Q*. Выберем произвольно
одно из них и обозначим через t(|) соответствующий ему
индекс, такой, чтобы |eQf(5). Пусть теперь yg: х-*~Уъ(х)
—функция, удовлетворяющая условиям леммы 1 относительно
открытого множества Qf(y и. точки | этого множества. Обозначим
через щ множество точек х, в которых у%(х)> 0. При |,
пробегающем К, множества tog образуют некоторое открытое
покрытие К- В самом деле, они являются открытыми множествами и
£ е tog. Последнее означает, что эти открытые множества
полностью покрывают К.. Поскольку К является компактом, для него
существует конечное подпокрытие. Иначе говоря, существует
конечное число точек |i, |г, •••, Ь> таких, что cog при v' —
= 1,2,...,./ образуют открытое покрытие К. Обозначим теперь
через Вг функцию 2 Ys • Функция Вг- непрерывна и ^=0.
*(5V)=' Ц
Если X является многообразием класса Ст, то эта функция
принадлежит классу С™. Ее носитель содержится в объединении
носителей функций Yp > i'(iv)==i'' T- е- является компактом и
содержится в Q*. Для каждой точки jceK существует хотя бы
одна из точек |v> такая, что х е cogv, ибо щ образуют
покрытие К- Соответствующая функция у^ в точке л: положительна.
Следовательно, соответствующая функция Вг- (i = i(|v))
положительна в точке х. Отсюда вытекает, что функция 2 Р; положи-
ie/
тельна на К, чем и завершается доказательство леммы1).
') Носитель функции 2 Эг == Э. содержащийся в объединении
носителе/
лей функций §i, является некоторым компактом Н, содержащим открытое

$ 2. Меры Радона
457
Лемма 3. Пусть X — локально компактное, счетное в
бесконечности пространство. Тогда существует последовательность
компактов Кп и открытых множеств Un с компактными
замыканиями, таких, что /Си с: U„, Кп образуют покрытие X и любой
компакт пересекается лишь с конечным числом U„.
Так как X счетно в бесконечности, существует
последовательность компактов Ап, объединение которых дает X. Каждый из
Ап имеет компактную окрестность Вп (см. примечание1)).
Внутренности Вп эЛ„ в объединении дают X. Положим С„ =
= В0 U By U B2 U ... U Вп. Множества С„ образуют возрастаю-
о
щую последовательность компактов, и множества Сп =э Ап
в объединении дают X. Кроме того, для каждого компакта из X
о
существует такое целое число п, что Сп =э К. В самом деле, по-
о
следовательность С„ П К является возрастающей
последовательностью открытых множеств на компакте К, объединение
которых равно К. Следовательно, одно из них совпадает с К.
о о
Положим затем Dn = Сп — C„_! = Cn[) CCn_4. Множество
Dn замкнуто (как пересечение двух замкнутых множеств),
содержится в компакте Сп и, следовательно, компактно.
Объединение Dn снова дает X. Действительно, если х е X и если л-
является таким первым числом, при котором х е С„ и х ф. Cn-i,
о
то х ф Сп-\ и, следовательно, х е Dn.
Пусть теперь р(п) —наименьшее целое число р, такое, что
о
CpZ2Cn. Пусть q(n) — наибольшее целое число q, такое, что
о о
Cq a C„_i. Положим Еп = СР(П) — Cq(n)- Множество Еп
компактно по той же причине, что и рассмотренное выше множество
Dn; En является окрестностью Dn. В самом деле, если xgD„,
о о
то х е Сп, а, следовательно, х е Ср(п). Далее, так как х ф Cn-i,
, о о
то хфСд(П), а значит, xeCpW-C,w. Поэтому Ср(„) — CqW —
множество U точек, в которых (5 > 0, и содержащим само К- Отсюда
следует, что Н является компактной окрестностью К. Можно доказать
непосредственно следующее свойство: в локально компактном пространстве X любой
компакт К имеет компактную окрестность Н и даже фундаментальную систему
компактных окрестностей.
В самом деле, пусть U — некоторая окрестность К- Поскольку каждая
точка х ^ К имеет фундаментальную систему компактных окрестностей в X
(стр. 75), то существует некоторое открытое множество Qx в X,
содержащее х, с компактным замыканием Qx в U. Множества £2* образуют
некоторое открытое покрытие компакта К- Из него можно выбрать конечное
подпокрытие Q,, Q2, ..., Й„. Множество Qi U &2 U ... U Qn является
компактной окрестностью К, содержащейся в U.

458
Гл. IV. Интегральное исчисление
— Ср(П) Л С СЯ(п) является открытым множеством, содержащим
Dn и, конечно, содержащимся в Е„. Наконец,
последовательность Еп локально конечна. В самом деле, пусть К —
некоторый компакт. Тогда существует такое q, что Сд гэ К (и
о о
даже СдГэ/С). Затем существует такое п, что C„_i гэ Сд. Тогда
о
q(n) ^ q, а, значит, для m ^ п имеем: q{m) ^ q и Cq(m) ^>
Z2 Со гэ К. Отсюда вытекает, что Сщ с К не пересекаются.
о
Очевидно, Кп = Dn и Un = Еп удовлетворяют условиям
леммы 3').
Докажем теперь теорему 11, используя множества Кп и Un-
Для каждого п рассмотрим покрытие компакта Кп из X
открытыми множествами Q* П Un- К нему можно применить лемму
2 и найти непрерывные-функции р,-, „ ^ О класса С™ (если
только X является многообразием класса С"), равные нулю, кроме
конечного их числа, и такие, что pi, n имеют носители в Й, Л Un
(компактные, поскольку Un компактно), а сумма 2 Pin поло-
is/
жительна на Кп-
оо
Обозначим теперь через р, функцию 2 р; п. Хотя эта сумма
п=0
и бесконечна, она локально конечна. В самом деле, если К
является некоторым компактом X, то существует лишь конечное
число п, при котором К пересекается с Un. Для каждого из
таких п имеется только конечное число отличных от нуля функций
Pi,„. Для всех других п функции р,, „ с носителем в Un равны
нулю на К. Отсюда следует, что функция р, непрерывна на X, а
в случае, когда X является многообразием класса С™, функция
Pi принадлежит классу С™. Действительно, свойство
непрерывности и дифференцируемости в точке множества X может быть
доказано, если вести рассмотрения только в некоторой
окрестности этой точки, которая может быть выбрана компактной.
Тогда сумма, определяющая Pi, конечна в этой окрестности.
Носитель функции Pi содержится в замыкании объединения
носителей функций рг-,„, п = 0, 1, 2, ... . Это объединение локально
конечно, т. е. лишь конечное число носителей пересекается
с любым компактом пространства X. Отсюда непосредственно
вытекает, что объединение этих носителей замкнуто и что
') Это построение лучше понять на примере векторного нормированного
пространства X. Возьмем в качестве Ап шар \\х\\ ^ п. В качестве В п МОЖНО
.будет взять шар ||х|| ^ п-\- 1, а вместо Сп взять Вп. Множество D„ = Кп
будет представлять собой шаровой слой п sg ||х|| г£ п + 1; для любого п
р(п) = п + 1 и q(n) = п — 2. Множество Еп теперь будет шаровым слоем,
a Un является открытым множеством п — 1 < \\х\\ < п + 1. Все построение
в этом случае становится очевидным.

§ 2. Меры Радона
459
оно является носителем Pi1). Этот носитель, следовательно,
содержится в Я{.
Положим теперь Р= 2 Рг = 2 Р.,л- То же самое рассуж-
*б=/ i,n
дение показывает, что р непрерывна и принадлежит классу О,
если X является многообразием класса Ст. Каждая точка X
принадлежит хотя бы одному Кп, и, следовательно, в этой
точке 2 Ргп>0, так как больше нуля по крайней мере одна
из функций pi, „. Последнее означает, что р > О всюду в X.
Но тогда функция щ = Pt/P непрерывна на X, принадлежит
классу Ст, если X является многообразием класса О, и имеет
носитель в Я*. Так как система Pi локально конечна, то система
cti ^ 0 также локально конечна. Далее, сумма 2 «г равна
2Рг/Р=1>чем и заканчивается доказательство теоремы.
Следствие 1. Пусть X — локально компактное, счетное в
бесконечности пространство, F — замкнутое множество из X, а
Q — открытое множество, содержащее F. Тогда существует
непрерывная вещественная функция а на X, принадлежащая
классу Ст, если X — многообразие класса О, имеющая носитель
в Я, удовлетворяющая неравенству 0 ^ а ^ 1 и равная 1 на
некоторой окрестности множества F.
В самом деле, для доказательства достаточно применить
теорему к покрытию X, образованному множествами Я и OF,
Если через аир обозначить функции, соответствующие этому
покрытию, то or-j- р = 1. Носитель р лежит в CF, его
дополнение является открытым множеством, содержащим F, на
котором р равна нулю, а следовательно, а= 1.
Заметим, что если F компактно, то, согласно примечанию на
стр. 456, можно взять Я с компактным замыканием и тогда а
имеет компактный носитель. Впрочем, в этом случае нет
необходимости предполагать X счетным в бесконечности (см.
замечание 3°) после формулировки теоремы 11).
Следствие 2. Пусть X — локально компактное, счетное
в бесконечности пространство, А и В — два замкнутых
непересекающихся подмножества X. Тогда существ-ует вещественная
непрерывная функция а, принадлежащая классу Ст, если X —
') Объединение F бесконечного семейства замкнутых множеств Fn не
замкнуто. Однако оно замкнуто, если это семейство локально конечно. В
самом деле, пусть х е X принадлежит замыканию множества F, а Т —
компактная окрестность х. Пусть п — такое целое число, что Fm П У = 0 для
т > п. Тогда х является точкой замыкания множества U Fm. Это множе-
т<«
ство замкнуто как объединение конечного числа замкнутых множеств. Отсюда
следует, что х е U Fm с F, т. е. следует, что F замкнуто.

460 Гл. IV. Интегральное исчисление
многообразие класса Ст, равная 1 всюду на некоторой окрест*
ности А и равная 0 всюду на некоторой окрестности В.
Действительно, для доказательства достаточно к
пространству X, замкнутому множеству А и открытому множеству Q =;
= СВ применить следствие 1. Тот факт, что функция а имеет
носитель в СВ означает, что она равна нулю всюду на
некоторой окрестности В.
Следствие 3. Пусть X— локально компактное, счетное в
бесконечности пространство, Fu F2, ..., Fn — семейство замкну-
->
тых попарно непересекающихся частей X, Е — банахово прост-
->->-> -> •
ранство и ех, е2 еп— произвольные векторы из Е. Суще-
-> -> -
ствует непрерывная на X функция f(x) со значениями в Е,
равная ег- в окрестности множества Fi.
Доказательство. Пусть / = {1,2,..., п}. Обозначим
через F\ объединение множеств Fj, j Ф i, а через Q, — дополнение
множества F\. Поскольку пересечение F\ ' пусто, то
объединение Q,- равно X. Множества Йг- образуют некоторое открытое
покрытие X. Пусть" (a,), ie/, — соответствующее разложение
единицы. Тогда носитель функции а* лежит в Q*, a, значит, а,
равна нулю в некоторой окрестности F\. Поскольку сумма 2 "г
i
равна 1, то мы получаем, что функция аг- равна 1 в некоторой
окрестности Ft. Функция
1(х)= 2 ei^i(x) или f= 2 ег«г (IV,2; 25)
iej i s /
удовлетворяет неравенствам || f (х) || ^ (max|| e{\\) 2j o«W =
is/ is/
= max||ei||. Отсюда |||/ ||| ^ max|| et\\. Однако поскольку на F{
is/
функция J равна et, то имеют место обратные неравенства,
-> ->
а, значит, |||/ ||| = max|| et\\.
Следствие 4. Пусть X — локально компактное, счетное
в бесконечности пространство, F — замкнутое подмножество X.
->
Пусть g— непрерывная функция на F со значениями в банахо-
->
вом пространстве Е. Предположим, что каждая точка а е F,
->
имеет такую открытую окрестность Та в X, что сужение g на
F П Уа можно продолжить на Уа до некоторой непрерывной
->
функции Ga (соответственно принадлежащей классу Ст, если
->
X является многообразием класса Ст). Тогда функцию g,
определенную на F, можно продолжить на X до непрерывной функ-

§ $. Меры Радона
461
ции G (соответственно принадлежащей классу Ст) со
значениями в Е.
Доказательство. Множество всех Уа и CF образует
открытое покрытие X. Ему можно поставить в соответствие
разложение единицы, образованное функциями аа с носителем в Уа
и функцией ао с носителем в CF: ( 2оа] + о0=1.
■>
Рассмотрим теперь функцию aaGa. Эта функция определена
только в Та. Однако ее можно определить на всем X, придавая
ей значение 0 вне У°а. При этом она останется непрерывной
(соответственно принадлежащей классу Ст). В открытом
множестве У*а она совпадает с функцией aaGa, которая непрерывна
(соответственно принадлежит классу Ст). Если хф.Та, то она
совпадает с 0 (в открытом дополнении носителя аа). Рассмотрим
теперь сумму G = 2j ®aGa- Так как эта сумма локально ко-
нечна, то она определяет на X некоторую непрерывную
функцию (соответственно функцию класса Ст).
В каждой точке х е F для любого ае? имеет место ра-
венство Ga (х) = g (x), ибо каждое Ga является
продолжением g. Поэтому для каждого jceF имеем: 2aaGa(x) =
aeF
= &(*) 2 aa(*). Поскольку a0 (x) равна нулю на F, сумма
равна 1, а, следовательно, G(x) = g(x), так что функция G
является продолжением функции g.
Заметим, что это следствие содержит как частные случаи
все предыдущие следствия. Если, например, мы обратимся к
следствию 3, то увидим, что в нем на X продолжают лишь функ-
цию g, определенную на \JFi и равную постоянной et на
каждом Fi.
Следствие 5. Пусть X является многообразием класса С"\
m ;>: 1, размерности N и V — замкнутое подмногообразие клас-
са С™ многообразия X размерности п. Пусть g — функция,
определенная на V, со значениями в пространствеЕ класса Ст.
Тогда эту функцию можно продолжить в X до функции G
класса С™ со значениями в Е.
Доказательство. Достаточно обратиться к условиям
предыдущего следствия. Для точки aeV можно найти откры-

462
Гл. IV. Интегральное, исчисление
тую окрестность Та точки а в X и некоторую карту Фа, т. е.
Ст-диффеоморфизм некоторого открытого множества Оа из RN
на Та. Кроме того, если записать R^ в виде произведения RnX
XR""" и представить каждую из его точек х как пару (у, z),
yeR", zeR""", to можно считать, что отображение Фа
переводит- пересечение Оа П R" на пересечение Та П V (следствие 2з
теоремы 32 гл. III)1).
Задача продолжения g из Vf]Ta на Та сводится к задаче
продолжения функции Л —£°Фа, определенной в Оа П R™, на
открытое множество Оа или, по крайней мере, на некоторую
окрестность точки а=Ф^ (а) в этом открытом множестве.
Такое продолжение в RN очевидно. Оно определено функцией
-*■
(у,z) —*h(y), что и требовалось доказать.
Следствие 6. Пусть X — локально компактное, счетное в
бесконечности пространство и Fit F2, Fn — замкнутые
попарно непересекающиеся подмножества. Тогда существуют
попарно непересекающиеся окрестности подмножеств Fi, Fz, ..., Fn.
В самом деле, построим, согласно следствию 3, функцию G
с вещественными значениями, соответствующую значениям е{=
=±= J, i=l, 2, ..., п. Открытые окрестности Ti = {x^X;
i — 1/2 < G(x) < i -+- 1/2} множеств Ft удовлетворяют
утверждению леммы.
Пространство, обладающее этим свойством, называется
нормальным. Локально компактное счетное в бесконечности
пространство нормально. Более общо, паракомпактное пространство
нормально. Однако обратное утверждение не верно.
Следствие 7. Пусть X — локально компактное счетное в
бесконечности пространство. Пусть (й»)^/ является открытым
покрытием X. Тогда найдется локально конечное покрытие
(й');^/. зависящее от того же множества индексов и такое,
что Q'i с= fi,-.
В самом деле, для непосредственного применения теоремы 11
достаточно в качестве fij взять множество таких х, чтобы сц(х) >
> 0; Q'i являются открытыми множествами.- Так как fii
являются носителями ai, то они содержатся в fii. В каждой точке
') Это следствие было доказано для подмногообразия V размерности п
некоторого аффинного пространства размерности N, например Rw. Здесь X
является абстрактным многообразием размерности Лг, V — некоторым
подмногообразием X размерности п. Однако с помощью карты окрестности а в ЛГ
приходят к открытому множеству из R" ик подмногообразию этого
открытого множества. Следствие применено именно в этих условиях.

§ 2. Меры Радона
463
х^Х сумма 2 а* (х) равна 1, а, следовательно, одна из <*,(*)
i<BI
положительна и х лежит в соответствующем множестве QJ. Тем
самым множества Q't образуют некоторое покрытие. Это
покрытие локально конечно, поскольку локально конечна
система а*.
Укажем, наконец, без доказательства результат, частично
обобщающий следствие 5 (но относящийся к непрерывным
функциям, а не к функциям класса О). Перед этим введем
->■ >
новое понятие. Пусть F — банахово пространство и / —
непрерывная функция с компактным носителем в X и со значениями
в F. Говорят, что эта функция разложима, если она
выражается в виде
->'■&-> t «♦
/ (х) = 2i g№i (х) или / = 2j £Л>г.
i=i i=i
где gi — постоянные векторы из F, а <р* — скалярные
непрерывные функции с компактным носителем. Множество значений
такой функции лежит в векторном конечномерном подпростран-
+ ■>
стве пространства г, порожденном векторами gi. Обратно,
->
пусть f — непрерывная функция с компактным носителем,
принимающая свои значения в векторном конечномерном подпрост-
ранстве G пространства F. Пусть gu g2, ..., g^ — базис G. Для
каждого х еХ, fix) является вектором G, а следовательно, его
можно единственным образом записать в виде f(x)= "Si gift (x),
и, значит, функция / является суммой 2j gff>{. Функция <р*: Х--*
t=\
-v'C! является композицией функции /: X-*-G и непрерывного
отображения и-*-С, которое каждому вектору из G ставит
в. соответствие его i-ю координату в выбранном базисе. Такая
функция непрерывна. Ее носитель, поскольку он содержится
-> ■ -> >
в носителе f, компактен, а сама функция f разложима. Таким
образом, непрерывные разложимые функции с компактным
носителем можно назвать непрерывными функциями с
компактным носителем конечного ранга. Их множество является под-
->•
пространством векторного пространства 'S'iX; F) непрерывных
■>
функций с компактным носителем и значениями в F. Можно
показать, что это множество изоморфно тензорному произведению

464
Гл. IV. Интегральное исчисление
Ф(Х) на F, которое кратко обозначают через W (X) <8> F. Это
множество совпадает с W(X; F), если F конечномерно.
Следствие 8, Пусть К является некоторым компактом
X и / — непрерывная функция на К со значениями в банаховом
-> ■■
пространстве F. Тогда, каково бы ни было е > 0 и какова бы
ни была окрестность У множества К, существует на X такая
->
непрерывная разложимая функция fE с компактным носителем
<zT, что III/ —/Е||| ^е. Можйо даже эту функцию выбрать
в виде /е == 2j gityi, где ср, ^ 0, и так, чтобы было справедли-
вым неравенство
Illfll-Sllftlki <e.
Доказательство. Для любой точки а е К существует
такая открытая окрестность TaCzT точки а в X, что для
каждой точки х из этой окрестности имеет место неравенство:
«?(*)-?(а) || < е.
Множество К покрывается конечным числом окрестностей
Уа'-Уа^ Уа2, • .., У aN- ПуСТЬ ttl, «2, ..., O.N, ССо — НвКОТОрое
разбиение единицы в X относительно покрытий Та и С К. Тог-
да разложимая функция /е = 2 / (я*) <*< удовлетворяет условию
следствия. В самом деле, поскольку ао(*) отлична от нуля
только в СК, где f(x) равна нулю; то f(x)ao{x) равна нулю, а,
N ^
следовательно, f (х) = 2 «г (*)/(*)•
i=I
Теперь имеем
S(fw-/(a*))a;w
<=1
Точно так же
fl/(3l|-2ll/(^)l|af(*H<
2>(\\Йх)\\-\\Ш)\\)<и(х)
^ 2 еа,-(х)^е').
i=l
<
i=l
'С 2 еаг (л:) ^ е.
i=l
') II / (*) - П<Ч) ||<8 длядге Гаг и а; (ж) = О для х ф. Уа

§ 2. Меры Радона
465
Теорема 12. Пусть X — произвольное метрическое
пространство, У — замкнутое подмножество X, g — непрерывная
функция на Y со значениями в нормированном конечномерном,
векторном пространстве Е. Тогда существует на X непрерывная
функция G со значениями в Е, являющаяся продолжением g
(т. е. совпадающая с g на У) и удовлетворяющая условию:
sup||G(x)|| = sup||g(s/)||<+oo. (IV, 2; 26)
X^X yesY
Если g вещественна, то и G можно брать вещественной и,
сверх того,
sup G (х) = sup g (у), inf G (х) = inf g (у). (IV, 2; 27)
X(=X y(=Y xe=X y(=Y
(Эти величины могут быть равны ± оо.)
Если X локально компактно и является объединением
счетного множества компактных подмножеств, аналогичный резуль-
->
тат имеет место, если Е является бесконечномерным
банаховым пространством.
Носитель меры Радона
Интуитивно под носителем распределения масс в механике
или распределением электрических зарядов в физике понимают
наименьшее замкнутое множество, содержащее всю массу или
весь заряд.
Определение. Пусть X — локально компактное
пространство, ц — мера Радона на X со значениями в векторном
нормированном пространстве Е, Я — некоторое открытое множество
X. Говорят, что ц равна нулю в Я, если для каждой функции <р
из ^{Х) с носителем в Я ц(<р)равна нулю1).
Интуитивно это значит, что в открытом множестве Я нет
массы или заряда.
-> ->
Точно так же говорят, что две меры ц4 и ц2 на X совпадают
■> •>
или равны в Я, если их разность hi— ,иг равна нулю в Я.
Теорема 13. Пусть X — локально компактное
пространство и (Яг)геЕ/ — произвольное семейство (конечное или нет)
') Здесь надо обратить внимание на то, что носитель ср является
компактом, a Q открыто. В дальнейшем мы увидим, почему надо выбирать Q
открытым.

466
Гл. IV. Интегральное исчисление
открытых множеств этого пространства. Тогда, если мера Ра-
->
дона ц на X равна нулю на каждом из множеств Qi, то она
равна нулю в их объединении Q.
Доказательство. Пусть q> является некоторой
функцией из 'S'(X) с компактным носителем К в Q. Нам надо дока-
->
зать, что ц(ф) равна нулю. Поскольку К компактно, то его
можно покрыть конечным числом множеств Q,-. Пусть это будут
(Q<)ie/. Пусть (at)isJ и a0— разложение единицы относительно
покрытия (^<)<е/> СК пространства X. Поскольку 2а<=1
на К, то на всем X имеет место тождество ф = 2 «W1).
Так как ц линейна, то ц (ф) = 2i И (а<ф). Каждый из членов
правой части этого равенства равен нулю, ибо а,ф имеет носи-
тель в Qu а ц предполагалась равной нулю в Q,-, и,
следовательно, ц(ф) также равна нулю. Теперь мы видим, для чего
нужно разложение единицы, — чтобы разложить ф, имеющую
носитель в объединении Q множеств Q,-, в сумму конечного
числа функций ф{ = а,ф, имеющих носители в Q{.
Следствие. Пусть ц, — мера Радона на локально
компактном пространстве X. Тогда среди всех открытых множеств
существует наибольшее, в котором мера ц равна нулю.
В -самом деле, рассмотрим все открытые множества, в кото-
рых мера ц равна нулю. Объединение этих множеств открыто,
а, согласно теореме, ц на нем равна нулю. Это объединение,
очевидно, является наибольшим открытым множеством, в кото-
->
ром ц равна нулю.
Определение. Замкнутое множество F, являющееся
дополнением к наибольшему открытому множеству Q, в котором
мера Радона ц на X равна нулю, называется носителем ц.
Пустой носитель имеет единственная мера, равная нулю
(ц(ф) = Ое£ для любой функции ф).
Из этого определения вытекает, что если ф является
функцией из &(Х), ц — мерой Радона и если носитель ф и носи-
') Это верно как для любой точки х е К (поскольку тогда- 2 а» (*) = *)
1е/
так и для хфК (поскольку тогда оба члена равны нулю).

§ 2. Меры Радона
467
тель а не имеют общих точек, т. е. если ф обращается в нуль на
некоторой окрестности носителя \и, то ц,(ф) = 0. В самом
деле, носитель функции ф в этом случае лежит в дополнении
-у
к носителю ц, т. е. по определению носителя лежит в открытом
■*■
множестве, в котором \i равна нулю.
Отсюда следует, что если две функции ф! и ф2 из ^(Х) рав-
■> > -*■
ны на всей окрестности носителя ц, то ц.(ф1) и ц,(фг) равны
между собой. В самом деле, функция ф1 — ф2 равна нулю на от-
крытом множестве, содержащем носитель ц, а, значит, носитель
Ф1—<Рг и носитель ц не пересекаются, откуда и следует наше
утверждение. Однако можно доказать более точный результат:
■>
Тео^гема 13г. Если ф обращается в нуль на носителе \i, то
->■ '■>■>■*■
ц(ф) = 0. Если ф1 и ф2 равны на носителе ц, то ц(ф0 = ц(фг).
>■
Доказательство. Пусть F — носитель ц, и К — носитель
■>
<р. Зададим е > 0. Поскольку мера \и непрерывна на *&к(Х), to
найдется такое т) > 0, что для функции ^^<&К{Х), такой, что
■>
llifll ^ т), имеет место неравенство Hnfij>)|| ^ еТ Поскольку ф
непрерывна и равна нулю на F, существует такая окрестность
Щ множества F, в которой |ф|^т)-
Пусть а — непрерывная вещественная функция на X, 0 ^
^cz^l, имеющая компактный носитель a°U, равная 1 в
окрестности компакта К Л F (следствие 1 теоремы 11).
Рассмотрим носитель функции аф—q>= (а—1)ф. Прежде
всего, он содержится в носителе К функции ф. Поскольку а — 1
равна нулю в окрестности множества К Л F, то он содержится
в С (К П F) = С К U С F. Поскольку этот носитель лежит в К,
то он находится в CF, т. е. в дополнении к носителю и. По-
этому ц(аф — ф) = 0 или |г(аф) = ц(ф).
Теперь аф£?к№ и ||аф|| ^ т) (поскольку |ф|^т) на °U и
носитель а лежит в °U). Значит, ||и(аф)|| ^ е и, следовательно,
11м(Ф)||<в.
■> »•
Поскольку е произвольно, отсюда следует, что ц,(ф) = 0.
Следствие. Для того чтобы мера \i на X имела носитель,
лежащий в множестве А, образованном конечным числом
точек ai, 02, .. ., ап, необходимо и достаточно, чтобы она была
линейной комбинацией мер Дирака:
■>-»•-> ->
ц = Ci6(a,) + с2б(Й2) + ... + спд(ап). (IV, 2; 272)

468
Гл. IV. Интегральное исчисление
Доказательство. Легко видеть прежде всего, что есл»
>
мера ц имеет указанный вид, то она обязательно имеет
носитель в А, поскольку на дополнении к А она равна нулю. Нам
остается доказать обратное утверждение. Пусть ц — мера,
имеющая носитель в А. Пусть Oi — функция из ^(Х), равная 1
в точке Ог и равная 0 в точках uj, / Ф i (следствие 3 теоре-
■* ->
мы И). Положим теперь ц,(6г)—с* для всех г. Тогда для
любой функции ф имеет место соотношение
Ф=2ф(а*)ег + Х> (IV,2;273)
где х является функцией, равной нулю на А. Из теоремы
получаем, что ц(х) = 0. так что
£ (Ф) = 2 Ф (ад it (в,) - S сгФ (ад, (IV, 2; 274)
чем и заканчивается доказательство следствия.
->
Теорема 14. Пусть р — мера Радона на локально
компактном пространстве X. Точка оеХ принадлежит'носителю F
меры ц тогда и только тогда, когда для любого открытого мно'
окества w пространства X, содержащего а, мера ц в этом
множестве отлична от нуля.
Точка а не принадлежит носителю F тогда и только тогда,
когда существует открытое множество и, содержащее а, в кото-
ром мера [I равна нулю.
Доказательство. Из эквивалентности соотношений
Л=ф5 и ~]В=^ ~]А(теорема И гл. I) следует, что обе части
теоремы эквивалентны. Поэтому, достаточно доказать,
например, вторую часть. Точка а не принадлежит F тогда и только
тогда, когда она лежит в й= С/7. Поскольку Q является наи-
большим открытым множеством, в котором ц = 0, то точка а
не принадлежит F тогда и только тогда, когда существует та-
-> . ->
кое открытое множество ©, содержащее а, в котором ц = 0.
Пример 1. Пусть [i= 2л cv6(a \— атомическая мера Ра-
дона. Точки av no условию различны, а сумма 2 l|cv|| для
ovsJC
каждого компакта К из X конечна (см. стр. 448). Носитель
этой меры Радона является замыканием объединения av.

§ 2. Меры Радона
46»
Доказательство. Обозначим через А объединение av,
через А его замыкание и через Q—дополнение к А. Очевидно,
■> ->
что если носитель ф лежит в Q, то ц(ф) = О- Следовательно,
■>
носитель F меры ц содержится в А. Остается показать, что
каждая точка aj объединения А принадлежит носителю F. Тогда
A cz F, или, в силу замкнутости носителя F, Л cz F, или,
окончательно, А = F. Итак, пусть точка й,еЛ и У— компактная
окрестность а;-. Ряд 2 II cv || сходится. Значит, существует ко-
а
v
нечное подмножество / множества индексов /, такое, что
2u lrv"^ 2
•> 1 •>
I cv || ^-^ || Су ||. Поскольку / конечно, существует откры-
чф-J
тое множество со, содержащее aj, лежащее в У и не содержащее
никаких других точек ah с k е /. При этом имеет место
следующая оценка:
^IkvIK"!11^11- (IV,2;28>
Пусть теперь Q — произвольная открытая окрестность точки
o.j. Покажем, что ц не может обратиться в нуль в Q, а это
будет свидетельствовать о том, что а;- принадлежит носителю F
меры ц. Согласно лемме 1 к теореме 11, существует
вещественная непрерывная функция о? с компактным носителем в со П Qv
удовлетворяющая неравенствам 0 <; ср ^ 1 и такая, что ф(а^)—-
= 1. При этом имеют место соотношения
£ (ф) = с) + 2 cvq> (flv), (IV, 2; '29)
откуда
|£(ф)И>ИМ- ^Ы>\
jii ч
vgfc/
а, значит, ц(ф) ф 0, чем и заканчивается доказательство
утверждения.
->•
Пример 2. Пусть р — интегрируемая по Риману,
определенная на R функция со значениями в банаховом пространстве
-*■ •> •>
£. Тогда носитель меры pdx плотности р относительно меры dx
лежит в носителе функции р и в случае непрерывности р совпа-
-*■
дает с носителем р.

470
Гл. IV. Интегральное исчисление
Это свойство устанавливает связь между понятиями
носителя функции и носителя меры.
Прежде всего, в силу предыдущей теоремы, носитель ц
содержится в носителе р. В самом деле, если носитель ф находит-
ся в дополнении носителя р, то интеграл J qpdx, очевидно,
равен нулю. Покажем, что в случае непрерывности р носитель
->■ -> »•
(х совпадает с носителем р. Пусть а — такая точка, что р(а) ф
Ф0. Покажем, что а принадлежит носителю ц. Отсюда будет
вытекать, что носитель ц содержит все точки, х, в которых
р(х) =^= 0, и, следовательно, содержит также замыкание
множества этих точек, т. е. носитель функции р. Отсюда мы получим,
что носитель ц совпадает с носителем р. Поскольку
функция р непрерывна в точке а, то существует такое открытое
множество со, содержащее а, что для любого л: еЕ со имеет место
неравенство
II ?(*)-? (а) || <11|? (а) ||. (IV, 2; 30)
-*■
Теперь видно, что обращение в нуль меры ц в любом
открытом множестве Q, содержащем а, невозможно. В самом деле,
выберем произвольную функцию ф Г^ 0 из ^{Х) с носителем
в ш П Й- Тогда будут справедливы соотношения
\\{p(x)-p{a))<t{x)dx\^\Cp{a)\\[<v. (IV, 2; 31)
Следовательно,
j J" Р(ж)Ф(*)dx >\jp(а)Ф{x)dx — ±||р(а)IIJ" ф =
= ^-||р(а)1|/ф>0, (IV, 2; 32)
-> >
откуда следует, что ц(ф) =^=0 и, значит, мера ц не равна нулю
в Q.
-> ->
Замечание. Если р не непрерывна, то носитель меры pdx
■> •>
не обязательно является носителем р. Например, если р всюду,
кроме точки aeR, равна нулю, то носителем р является {а}.
Однако мера pdx равна нулю и ее носитель пуст.

§ 2. Меры Радона
471
Пример 3. Пусть ц является мерой Радона, определенной
■*•_•>■>
на R по формуле ц = 2и сМа ) + р dx, где все точки av различ-
ны, сумма 2л II cv II локально сходится, а функция р непрерыв-
v
на. Тогда носитель ц, является объединением носителя А,
функции р и замыкания множества av-
Этот результат сразу же вытекает из предыдущего. Дейст-
->■
вительно, легко видеть, что носитель ц содержится в
рассматриваемом множестве. Поэтому достаточно последовательно
показать, что этот носитель содержит каждую из точек av и,
кроме того, каждую такую точку а, не принадлежащую замы-
-> ->■
канию av, в которой р(а) Ф 0. Рассмотрим точку а). Повторяя
построение из примера 1, выберем в качестве о> открытый
интервал, такой, что
j\\-p(x)\\dx<±\\c,\\.
(0
Построим затем для каждой окрестности Q точки а$ такую же
функцию ф, что и в примере 1, для которой на этот раз имеег
место соотношение
И (ф) = Cj + 2 cv(f (av) + J p (x) ф (x) dx.
Отсюда
II it (g>) II > ИМ-у II*/ || -1ц 5ii = -fH*y II'
чем и доказывается первое утверждение.
Рассмотрим теперь точку а, не принадлежащую замыканию-
множества точек av и такую, что р(а) Ф 0. Построим такое же
открытое множество о), что и в примере 2, но так, чтобы оно не
содержало точек av- После этого рассуждения, проведенные при
доказательстве примера 2, повторяются без изменения.
Объединяя результаты, указанные на стр. 443, с
доказанными в примерах 1—3, получим следующую теорему:
->■
Теорема 15. Пусть av — различные точки X, cv— такие
векторы банахова пространства Е, при которых для любого
компакта К из X сумма 2а ||cv|| конечна. Тогда можно
определить на X меру \и.= 2j сФ(а \ со значениями в Е

472
Гл. IV. Интегральное исчисление
по формуле
■*
2 Cy\av)\ • ф = 2 MP (flv)- (IV,2; 322)
Для каждого компакта К имеет место неравенство
2?А<о| < 2 || J || (IV,2;323)
v \K
av<sK
и, кроме того,
2?Aav) < 2 IK II- (IV,2;324)
V V
(Если Е является полем скаляров, то эти неравенства
переходят в равенства *).)
Пусть X является прямой R и р — функция на R со
значениями в Е, локально интегрируемая по Риману. Тогда эта функ-
ция определяет меру р dx со значениями в Е по формуле
рdx ■ ф = I р (х) ф (х) dx . (IV, 2; 325)
Для каждого интервала [а, Ь] прямой R
\}pdx\[aib[^ J \\}>{x)\\dx, (IV,2;326)
[a, b\
где неравенство переходит в равенство, если Е является полем
скаляров.
') Однако ничего такого не получится, если Е является векторным
пространством размерности п ^ 2. Возьмем, например, Е = R™ с введенной
/ п \!/Р
в нем нормой Минковского || (х,, х2 хп) Ир = 2 I *< \Р ) ' ' < Р ^
^ +оо. Пусть а(, аг ап суть п точек компакта Л", и пусть
cv есть точка R", v-я координата которой равна 1, а все остальные рав-
•> ~> II £. ■* I
ны нулю (сv образуют канонический базис Rn). Тогда || ц(ф) II = 1^, ф (av) cv =
/ п у/Р
= ( ^j ! Ф (^v) l^ ) • Точная верхняя грань этого выражения для ||<р|| ^ 1
\v=l - /
" ■>
достигается при ф = 1. Она равна п'/з\ Итак, ^^ I! cv || = /г и для п ^ 2
v=l
.пЧр < п.

§ 2. Меры Радона
47S
Для суммы мер на всем компактном интервале [а, Ь] прямой
R имеет место неравенство
^v6(av) + pdx < ^ 11^11+ J II ?(*)№* (IV,2;327>
v [й| щ av^[a, b] [a, b]
переходящее в равенство, если Е является полем скаляров.
Носитель меры 2 cv6ta \ является замыканием объединения
V
av. Носитель меры 2j cv^(av) + Р dx при непрерывном р яв-
v
ляется объединением замыкания множества av и носителя р.
Продолжение меры на непрерывные функции ф
с некомпактным носителем
Интуитивно кажется возможным придать смысл выражению
> ->
(j (ф) в том случае, когда ц является мерой Радона с носителем
А, а ф — скалярной непрерывной функцией с носителем В даже
в том случае, когда В некомпактно, лишь бы только А и В
имели компактное пересечение К.
Действительно, пусть а является некоторой функцией из
^(Х), равной 1 на всей окрестности компакта К (согласно
следствию 1 теоремы 11, такие функции существуют). Тогда
носитель функции аф, поскольку он находится в пересечении
носителей функций а и ф, компактен.
Положим по определению
Иф) = ИаФ) (IV, 2; 33)
— соотношение, имеющее смысл, поскольку a(p^W(X). Для
■ обоснования этого определения достаточно показать, что правая
часть не зависит от выбора а. Итак, пусть сц и аг — две
функции, равные 1 в некоторой окрестности компакта К. Функ-
ция ос1ф — ос2ф и мера ц имеют непересекающиеся носители.
(Если некоторая точка принадлежит носителю ц, то она лежит
в А. Если же она принадлежит носителю функции (а1^аг)ф,
то она содержится в носителе функции ф, т. е. в В и в носителе
функции at — 0С2, а значит, лежит в С К. Рассматриваемое
пересечение содержится в А Л В f] С/С = К П С/С = 0.) Тогда
■* -> ■ -> ->
ц (а(ф — а2ф) = 0 или ц (ед) = ц (а2ф).
В частности, если ц имеет компактный носитель, то для
непрерывной функции ф с произвольным носителем можно

474
Гл. IV. Интегральное исчисление
определить ц(ф), полагая ц(ф)=ц(аф), где ае^(^) и равна 1
в некоторой окрестности носителя ц.
Например, если ц== 8(a), то для непрерывной скалярной
функции ф с произвольным носителем получаем формулу
(IV, 2; 5). Отсюда следует, что в случае ц == б(0) можно
вычислить ц(ф) даже для разрывных функций ф, что мы и сделаем
в§3.
Пусть и, — мера с компактным носителем. Вектор ц(1) из
-> ->
Е называется «полной массой». Например, если Е полно и
-> „ ->
р, == 2j cv6ta \, где av содержатся в одном компакте и
ZjII^vIK00» то полная масса равна ^cve£. Если Х = R и
V V
-> -> ->
4ц = р dx, где р имеет компактный носитель, то полная масса
равна /7 (х) dx e £. Легко видеть, откуда возникло выражение
«полная масса». Если ц принимает вещественные значения и
представляет собой распределение зарядов (вфизике),то
рассматриваемое выражение действительно даёт «полный заряд»
(естественно, заряд алгебраический — полная масса б(а> — дф)
равна нулю). >
Определенное только что продолжение (д, обладает
следующими очевидными свойствами.
Теорема 16. Пусть А и В — замкнутые множества из X
->
с компактным пересечением К. Для меры Радона ц на X со
->
значениями в векторном нормированном пространстве Е и
носителем в А и для непрерывной скалярной функции а> с носите-
-> ->
лем в В можно определить ц(ф)е£ с помощью формулы
(IV, 2; 33), где а — функция из & (X), равная 1 на некоторой
окрестности пересечения К. Результат не зависит от выбора а. Если
<Pi и фг обладают теми же свойствами, что и ф, "и если k яв-
-> ■> ->
ляется некоторым скаляром, то ц(ф1 + ф2) = ц(фО +ц(ф2) "
у, (&ф) = k\i (ф). Если непрерывные функции фп с носителем в В
равномерно сходятся к 0 при п, стремящемся к бесконечности,
то ц(фп)е Е сходятся к 0. Кроме того, имеет место оценка
llJ(q>)IKIl£llsup|q>(jc)(. (IV, 2; 33,)
х<=Х
Замечание. В условии теоремы достаточно было считать,
что существует окрестность компакта К, на которой ф„
равномерно сходятся к 0 при п—*оо. Отсюда уже следует, что ц(фп)
сходятся к 0.

§ 2. Меры Радона 47S
Принцип кусочной склейки мер
Теорема 17. Пусть X — локально компактное
пространство и (^)ie/— произвольное семейство открытых множеств,
-*•
образующих покрытие X. Пусть (ц,)/е/ — семейство мер,
зависящих от того же семейства индексов. Предположим, что ц,
является мерой, определенной на локально компактном
пространстве Qj1) со значениями в одном и том же нормированном
пространстве Е, и что в каждом из пересечений Q» Л Qj двух
•> ->■
открытых множеств меры \ц и ц,- равны. Тогда на X существует,
и притом единственная, мера ц со значениями в Е, которая
->
в каждом открытом множестве Q» равна мере \ц.
-*■ -*■
Доказательство. Единственность ц очевидна: если Ц]
-*•
и Ц2 — две меры, обладающие указанными свойствами, то
-*• ->■
ц>— цг равна нулю в каждом Q», а, следовательно, по
теореме 13 равна нулю в их объединении, которое совпадает с X.
-*■ ■*■
Значит, hi = Ц2-
Доказательство существования можно было бы провести
с помощью модифицированной теоремы 11 (см. замечание 3е))
без какого-либо предположения о счетности X. Однако для
простоты мы предположим, что X является объединением счетного
множества компактов, и применим разложение единицы.
Итак, пусть (аг)ге/—непрерывное разложение единицы,
подчиненное покрытию (Qi)/e/ пространства X. Пусть ф —
некоторая функция из 'S'(X). Функция ссг<р принадлежит ^(Qj).
-*■
Поэтому к ней можно применить меры щ и рассматривать
-*• ->■
^г(агф). Определим теперь меру ц по формуле
M<P)=.2j Мед)- (IV,2;333>
ie/
Эта формула имеет определенный смысл. В самом деле,
носитель функции ф компактен, и на этом компакте все функции
а», кроме конечного их числа, равны нулю, так что предыдущая
сумма конечна. Она, очевидно, определяет линейное
отображение пространства 'ё'(Х) в банахово пространство Е. Из
неравенства
IIJ (ф) II < 2 II2, II* II ед и < (2II ?, II*) II ф II. (iv, 2; зз4>
ie/ Vie/ /
') Открытое множество локально компактного пространства локально
компактно.

476
Гл. IV. Интегральное исчисление
где / — такое конечное множество индексов, при которых а, не
равны тождественно нулю на К, следует, что это отображение
непрерывно на Фц (X).
Введенное отображение определяет, очевидно, некоторую
меру на X со значениями в Е. Остается доказать, что в множест-
-> ->
вах Qj имеет место равенство ц — \ij. Если компактный
носитель функции ф лежит в Qj, то для каждого i носитель ссгф
содержится в Qj П &i- Поскольку в этом открытом множестве
■> -> ->
(j,j = (j,j, то в формуле (IV, 2; 333) можно заменить |л,г(<Хгф) на
М;(^гф) и получить равенство
Ц (ф) = S Ц/ (а*ф) = Щ (2 atq>) = ц, (ф), (IV, 2; 335)
ге/ lie; /
из которого следует утверждение теоремы.
Комплексные и вещественные меры
Определение. До сих пор мы не уточняли характер поля
-скаляров К, которое можно было отождествлять либо с R, либо
с С;. Через %'(X) мы обозначали пространство непрерывных
скалярных функций на X с компактным носителем. Оба
возможных случая поля К рассматривались нами одновременно.
Однако очевидно, что в некоторых задачах целесообразно
уточнять, о каком поле скаляров идет речь.
Пусть W (X; .С) = W (X) — пространство комплексных
функций, и пусть ц— комплексная мера на X, ц ^W'iX).
Говорят, что мера ц вещественна, если |л(ф) —
вещественна1) для любой вещественной функции ф.
Для того чтобы мера Радона ц была вещественной,
необходимо и достаточно, чтобы для любой комплексной функции ф
из W (X) имело место равенство
ц(ф) = 1Ж (IV, 2; 34)
другими словами, чтобы |л(ф) и |j.(<p) были комплексно
сопряженными.
В самом деле, пусть ц является вещественной мерой. Любая
комплексная функция ф может быть представлена единственным
') Вот другая интерпретация. Пусть ц — комплексная мера, т. е. С-ли-
нейное отображение &(Х; С) в поле скаляров С. Онп определяет (см.
примечание на стр. 451) некоторую меру \i% относительно R со значениями в С,
т. е. определяет некоторое R -линейное отображение Ч? (X; R) в двумерное
векторное пространство С над R. При этом ц вещественна тогда и только
тогда, когда цк будет принимать свои значения в подпространстве R
пространства С,

§ 2. Меры Радона 477
образом в виде <р = qpi + ирг, где ф( и ф2 — вещественные
функции. Эти функции необходимо непрерывны и имеют компактный
носитель. Так как м-(ф) = M.(<pi) -Мм^фг) и ц(ф) = ц.(пл) —
—ф(фг), a n.(qpi), м-(фг) вещественны, то получаем соотношение
(IV, 2; 34). Обратно, если это соотношение справедливо, то это
говорит о том, что для каждой вещественной функции ф число
ц (ф) совпадает со своим сопряженным, т. е. вещественно.
Пусть теперь ц, — произвольная мера Радона. Обозначим
через р комплексно сопряженную меру Радона, определяемую
формулой
р (ф) = ц (ф) для фе^(Х), или Иф) = Мф). (IV, 2; 35)
Прежде всего, это настоящая мера Радона. В самом деле,
формула определяет некоторую комплексную функцию на ^(Х).
Функция эта линейна, поскольку
Й (Ф1 + Фг) = Ч (Ф1 + Ф2) = Ч (ф[) + Ч (ф2) = И (Фг) + V- (Фг) =
__ ___ =^) + ^ (IV)2;36)
р (&ф) = ц (&ф) = k\x (ф) = k\x (ф) = &р (ф)'),
и она непрерывна на каждом Я$к{Х), где К — компакт из X.
Конечно, комплексно сопряженной мерой для р будет д,
т. е. имеет место обратимость, согласно которой можно
говорить, что меры ц и р комплексно сопряжены друг другу. Две
меры ц и р комплексно сопряжены тогда и только тогда, когда
их значения на двух комплексно сопряженных функциях ф и ф
соответственно комплексно сопряжены [вторая формула
(IV, 2; 35)), или, иначе, когда, для любой вещественной функции
<р, ц(ф) ир(ф) комплексно сопряжены. Отображение \х —* р
является полулинейной биекцией пространства 'F'(X) на себя, т. е.
*+ *-*' + *» (iv, 2; 37)
k\i = &р.
Мера вещественна тогда и только тогда, когда она
совпадает со своей комплексно сопряженной (формула (IV, 2; 34)).
Соотношение между (д, и р можно еще выразить в следующей
форме:
любая комплексная мера Радона \х может быть записана, и
притом единственным образом, в виде \х = ц! + щ2, где ц, и
ц2 — вещественные меры Радона; при этом р = щ — г'рг-
') Следует внимательно рассмотреть эту последовательность равенств;
здесь существенно используется тот факт, что правая часть равенства
(IV, 2; 35) дважды содержит символ сопряжения. Функция ф->-ц(ф)
полулинейна и не является линейной точно так же, как и функция ф->-ц(ф).

478
Гл. IV. Интегральное исчисление
В самом деле, если такое разложение возможно, то, учиты*
вая (IV, 2; 37) и то, что вещественная мера совпадает со своейР
сопряженной, получаем р, = ц,1 — i\i2 и, следовательно, имеет
место единственное представление
■Ъ = Ц±.- H2 = ^- (IV,2;38>
Обратно, обе меры, определенные этой формулой, совпадают
со своими сопряженными и являются, следовательно,
вещественными. При ЭТОМ |Д, = Ц.1 + /|Д.2-
Будет полезным собрать все полученные результаты в
общую таблицу:
Ф = Ф! +гф2, Ф = ф] —гф2; <Pi = —2~, Фг= 2i '
Мф) = ц(ф),..ц(ф) = МФ); (IV, 2; 39)
i • - • ц + £ д -— £
ц = |xt + г|х2, (j, = Ц1 — гц2; Мч =——' ^2 = 2i '
Вещественные положительные меры
Говорят, что С-мера Радона ц на X положительна, если
для любой неотрицательной функции ф е ^(Х) имеет место
неравенство ц(ф) ^0. Это записывается так: ц, ^ 0. Очевидно,
для такой меры из ф1 ^ фг следует ц.(ф1) ^ ц(фг)-
Из определения следует, что положительная мера
обязательно вещественна.
Мера Радона ц называется отрицательной (в обозначениях:
ц ^ 0), если ц (ф) ^ 0 для любой функции ф ^ 0.
Для того чтобы мера была отрицательной, необходимо и
достаточно, чтобы она была противоположной по знаку к
некоторой положительной мере.
Если ц и v — две вещественные меры на X, то говорят, что
ц, ^ v, если ц— v ^ 0. Это означает, что для любой функции
Ф ^ 0 из ^(Х) имеет место неравенство ц,(ф) ^ у(ф).
Если ц ^ v ^ 0 и ф ^ -ф ^ 0, то ц (ф) ^ v (\|5) ^ 0.
Замечание. Пусть ц — некоторая мера ^0. Для любой
вещественной функции ф имеет место неравенство —|ф|^ф^
^|ф|, а, значит, — М-(|<р|) < Ц.(|ф|) =^М.(|ф|), или
I Мф) КМ М)- (IV, 2; Зад
Это соотношение сохраняется и для комплексной функции ф,
однако его доказательство в этом случае значительно сложнее.
Пусть К — носитель ф и У—компактная окрестность К- Пусть
ty — функция, построенная по функции ф согласно следствию 8

§ 2. Меры Радона
479
теоремы 11 и такая, что
где 1|)(>0и имеют носитель в Т. Тогда
ЛГ
Ф (*) — 2 gtfi (х)
1—\
<
ф(*)1 —]£)lg<l*M*)
*—1
<
2 II И ||, '
2 II Ц ||, '
(IV, 2; 39а)
(IV,2;394)
(IV, 2; 39g)
Первое и второе неравенства последовательно дают
ЛГ
. 1|*(ф)1<-2|й1и(+«)+-!<1*(1ф1) + е. (IV, 2; Зад
«=1
Отсюда вытекает справедливость неравенства (IV, 2;39г),
поскольку в произвольно.
Позже мы укажем другой метод, использующий теорию
продолжения Лебега. Будем рассматривать ц как некоторую
R-меру (R-линейное отображение ^(.XjR) в . R). Функция
■>
<ре?(1;С) является функцией с векторными значениями
в двумерном пространстве С над R. Поэтому (IV, 2; 39г)
перейдет в формулу (IV, 3;27).
Из (IV, 2; 39г) следует, что для вычисления ||ц||к можно
ограничиться рассмотрением вещественных неотрицательных
функций ф, при этом
|[ц||,= sup |1(ф) и |||i||= sup ц(ф). (IV, 2; Зад
фЕУ/fffl фе?и)
0<ф<1 0<ф<1
Используя понятия, введенные в примечании на стр. 451,
можно сказать, что если ц является вещественной
положительной .С-мерой, то меры ц и fiR имеют одинаковую норму.
Позже (см. замечание на стр. 488) мы увидим, что это
утверждение остается справедливым, если ц является произвольной
вещественной С-мерой. Но это, конечно, неверно, когда ц
является произвольной комплексной .С.-мерой (это видно из примера
в примечании на стр. 451). Можно также сказать, что в формуле
flll*lLf = sup | ц(ф) | следует брать всевозможные комплексные
1фК1
«функции ф. Если fi вещественна, то можно ограничиться
вещественными функциями ф. Если |.i ^ 0, то достаточно брать ф ^ 0.

480
Гл. IV. Интегральное исчисление
Бинарное отношение ц, ^ v определяет на множестве
вещественных мер на X некоторое отношение порядка. Для
обоснования этого утверждения достаточно доказать единственное
нетривиальное свойство: из неравенств (i^vn ц, ^ v всегда
следует равенство ц, = v. Для ф>0 из этих неравенств следует
равенство n((p) = v((p). Но всякая вещественная функция
из ^ (X) может быть представлена в виде разности двух
неотрицательных функций из %(X) (например, ф= |ф| — (|ф| —ф)),
а, следовательно, равенство справедливо для любой
вещественной функции ф, а значит, и для комплексной функции ф = ф1 +
+/фг, откуда ц, = v. Отношение порядка «совместимо с R
-векторной структурой пространства вещественных мер» в том
смысле, что:
из ц,, < v.! и Ц2 < v2 следует Hi + ц,2 < ^ + v2,
из n=S^\> при й^О следует kn^ikv.
Векторное пространство над {?, снабженное структурой
порядка, обладающей этими свойствами, называется
полуупорядоченным векторным пространством. Первое соотношение
выражает тот факт, что ц ^ v эквивалентно неравенству ц — v ^ 0
и что ц ^ 0, v ^ 0 влечет за собой ,u + v ^ 0. Второе
означает, что при k 2> 0 из (.1^0 следует k\a ^ 0. Заметим, что
в этом случае из ц<^ v следует —v ^ —ц,, т. е. следует
неравенство k\i ^ kv при k ^ 0.
Пример. Рассмотрим, меру, определенную на R формулой
(IV, 2; 15). Ее сопряженная мера равна
2cve(„v)+£d*. (IV, 2; 40)
Мера ц вещественна тогда и только тогда, когда мера
2 (cv — cv) 6ia \ + (р — р) dx равна нулю. Эта мера будет равна
V
нулю, если все числа cv вещественны и вещественна функция р.
Обратно, если эта мера равна нулю, то ее носитель пуст.
Отсюда по теореме 152 в случае непрерывной функции р можно
получить, что все величины cv — cv равны нулю и что равна
нулю функция р — р, иначе говоря, что вещественны cv и
вещественна функция р. Этот результат, естественно, может быть
неверным, если функция р не является непрерывной. Конечно,
cv вещественны, но функция р не обязательно вещественна.
Однако можно утверждать, и это существенно, что не
обязательно равные р и Re р определяют одну и ту же меру р dx =
— Repdx поскольку (р — Re p) dx = \Р 2 ) dx = 0\ и что,
следовательно, в том случае, когда р не вещественна, можно
заменить ее вещественной частью Rep без изменения меры!
(IV, 2; 398)

§ 2. Меры Радона 481
Мера (х, определенная формулой (IV, 2; 15), при cv ^ 0 и р > О
положительна. В случае непрерывной функции р можно
доказать и обратное утверждение1).
В самом деле, если точки av считать различными и
один из коэффициентов cv отрицательным или если в
некоторой точке а непрерывная функция р принимает значение
р(а) < О, то без труда доказывается, что функция ф Г5г 0,
построенная в примерах 1—3 на стр. 468—471, удовлетворяет
неравенству \x(q>) ■< 0, и мы получили противоречие.
Решетки
Полуупорядоченное множество Е называется решеткой, если
любая его часть, образованная из двух элементов, имеет точную
верхнюю грань (т. е. наименьшую из мажорант) и точную
нижнюю грань. То же самое будет и для любого конечного
непустого подмножества Е. Например, вещественная прямая R
является решеткой. Полуупорядоченное множество Rx функций
на X с вещественными значениями (см. стр. 23) есть решетка
так же, как и множество (Rx)c вещественных непрерывных
функций на топологическом пространстве X. Напротив,
множество полиномов на R с вещественными коэффициентами
относительно обычного отношения порядка, очевидно, не является ре--
шеткой. Если Е — полуупорядоченное векторное
пространство (что имело место в предыдущих примерах), то для того
чтобы оно были решеткой, достаточно, чтобы для любого е е £
существовал элемент е+ = sup (e, 0). В самом деле, пусть е и
/ — два произвольных элемента из Е. Тогда элемент е + (f —
— е)+ мажорирует элемент е = е + 0 и e -\- (f — е) = f. Если g
мажорирует е и f, то g — е мажорирует е — е = 0 и / — е, т. е.
мажорирует (f — е)+. Значит, g мажорирует элемент e-\-(f—е)+,
являющийся, таким образом, точной верхней гранью ей/.
С другой стороны, е и /имеют точную нижнюю грань, а именно
—sup(—е,—f). Наконец, всегда имеет место равенство
sup(e, f) -j- inf(e, f) = e + f. Действительно, очевидно, что
sup(e — Л, / — Л) = sup(e,/)—h. Полагая h = e-\-f, получаем
нужную формулу. Положим e"" = sup(—е, 0) = (—е)+. Тогда
е = е -\- 0 = sup (e, 0) + inf (e, 0) = е+ -\-е~. Элементы е+ и е~
называются положительной и отрицательной частью е.
Несмотря на свое название, е-^ 0, а не ^ 0, и скорее —е-
заслуживает названия отрицательной части2). Теперь видно, что каждый
') Если р не является непрерывной, то на те же вопросы дают полный
ответ теоремы 52—54.
2) Точно так же а и Ъ называются вещественной и мнимой частью
комплексного числа а + Ы, хотя скорее Ы заслуживает названия мнимой части.
1Q Зак. 1339

482 С л. /V. Интегральное исчисление
элемент е из Е является разностью двух неотрицательных
элементов: е+ и е~. Такое представление возможно бесконечным
числом способов, поскольку можно положить е = в\ —е2, где
ej = е+ + а и е2 — е~ + а, а ^ 0. Однако е+ и е~ являются
наименьшими элементами ^0, разность которых дает е. В самом
деле, если е=е( — е2, е{ и е2^0, то е( мажорирует е и 0, а,
следовательно, и е+, е2 мажорирует —е и 0, а значит, и е~. Мы
возвращаемся к прежней форме: в\ = е+ + а, е2 = е~ + а,
а ^ 0. Элементы е+ и е- являются «дизъюнктными» в том
смысле, что единственным элементом ^0, минорирующим оба
элемента, является 0. Мало того, каждый элемент g, минорирую-
щий одновременно е+ и е~, не больше нуля. В самом деле,
высказанное утверждение означает, что inf (е+, е~) = 0. Далее,
e+ + inf(0, tr — е+) = e+ + inf(0, — е) = е+— sup(0, е) = е+ —
— е+ = 0. Наконец, абсолютной величиной е называют точную
верхнюю грань элементов е и —е: \е\= sup(e, — е).
Так как \е\ + е = sup(2e, 0) = 2е+, то |е|=2е+— е =
= 2е+ — (е+ — е~) = е+ + е-. Поскольку inf (е+, е-) = 0, то е+ + е~
также равен sup(e+, е~).
Говорят, что полуупорядоченное множество является полной
решеткой, если любая его непустая мажорируемая часть имеет
точную верхнюю грань, а любая непустая мннорируемая часть
имеет точную нижнюю грань (из первого условия, впрочем,
следует второе, ибо если некоторая непустая часть А минорируема,
то множество ее минорант мажорируемо и не пусто, а значит,
имеет точную верхнюю грань, являющуюся точной нижней
гранью части А. Вещественная прямая R, является полной
решеткой точно так же, как и множество R-* функций на X с
вещественными значениями. Однако если X является
топологическим пространством, то множество (Rx)c вещественных
непрерывных на X функций является решеткой, но не полной.
Например, пусть X — вещественная прямая R и А — часть
множества (R )с, образованная из непрерывных функций,
мажорируемых характеристической функцией отрезка [—-'1,1].
Точная верхняя грань множества А в полуупорядоченном
множестве R всевозможных вещественных функций на R является этой
характеристической функцией. Так как характеристическая
функция отрезка [—1, 1] разрывна, то А не имеет точной
верхней грани в множестве (R )с непрерывных функций.
Теорема 18. Полуупорядоченное векторное пространство
вещественных мер Радона на локально компактном
пространстве X является полной решеткой. Если ц является некоторой
вещественной мерой, |х+ = sup((x, 0), fj,- = sup(—ц, 0), "|ц| =
.= sup (ц,—(х) = sup((x+, ц-) = ц+ + ц-, то имеют место еле-

§ 2. Меры Радона 483
дующие формулы:
ц+(ф)= sup ц(г|з) для ф>0, (IV, 2; 41)
II ji II = II И+ 11 + II Ji- II. (IV,2;412)
где нормы вычислены на X или на некотором компакте К
пространства X;
| и. | (ф) = sup |л (-ф) для ф ^ О
1Ф Кф
*sVm (IV,2;413)
11Ы11 = Ы1 = 11и+11 + 11ц-Ц
на X или на некотором компакте К из X.
Таким образом, для ф ^ О, ц(ф) ^ ц.+ (ф), —и(ф) ^S И_(ф)
и, для произвольного ф, | ц (ф) | ^ | ц | (| ф |).
Доказательство. Обозначим через Ф+(Х) множество
функций ф ^ 0 из Ф{Х). Определим на (&+{Х) функцию ц+ со
значениями в R+ по формуле (IV, 2; 41).
Она дает конечное значение, поскольку если К является
носителем функции ф, то имеет место неравенство |u.(if>)|^
< II ц II к II ^ II < II V II к II Ф II- Неравенство ц+(ф) ^ 0 следует из
того, что среди функций if> имеется функция 0. Покажем, что
эта функция (д,+ на Ф+(Х) обладает следующими свойствами
«линейности»:
^+ (Ф1 + Ф2) = И+ (Ф|) + И+ (Ф2).
|д,+(Яф) = Я(д,+(ф) при Л^г»0.
Второе свойство очевидно. Поэтому достаточно доказать лишь
первое. Каковы бы ни были функции if>i и if>2, такие, что 0 ^
^^1^ф1 и 0 ^ г|52 ^ фг, имеют место неравенства 0 ^ if>! -f-
+ %<ф1 + ф2, откуда m.(i|5i) + m-(^2)= |Д.(гр1+%Х ц+(ф1+
+ ф2). Переходя к точной верхней грани относительно if>i и if>2,
отсюда непосредственно получаем:
И+ Ы + И+ (ф2) < V+ (Ф1 + Фг)-
Впрочем, если ф^Ф+{Х), 0 ^ if ^ ФГ+.ф2, то можно найти
такие две функции % и if>2, которые удовлетворяли бы
соотношениям:
0*^^1^Ф1. 0^\{12^ф2 и if), + \\>2 = if).
Для этого достаточно взять
if, = inf (if, ф,) И lf2 = lf —if,.
Из определения следует, что имеют место соотношения 0 ^ if, ^
^ фь 0 ^ if2 и if, -+- if2 = if- Пусть теперь х е А". Если if(x)=s;
г^ф1(х), то ifi(#) = if(#) и, следовательно, if2(х) = 0 ^ ф2(х).
16*
(IV, 2:414)

484
Гл. IV. Интегральное исчисление
Если же, напротив, ty(x) > ф) (х), то -фi (х) = ф) (х), откуда
*|>2 М = "ф (X) — ф, (X) < ф! (X) + ф2 (*) — ф, (X) = ф2 (*).
Во всех случаях получаем 0 ^ г]з2 ^ фг-
Теперь будет справедливо неравенство
И Ы>) = И Ш + V Ш < Ц+ Ы + И+ (Фа)-
откуда, переходя к точной верхней грани относительно -ф,
получаем неравенство ц+(ф1 + ф2) ^ ц+(ф1)+|а+(ф2),
заканчивающее доказательство соотношения (IV, 2; 4Ц).
Пусть теперь задана вещественная функция ф из 'S'(X)
произвольного знака. Ее можно бесконечным числом способов
записать в виде разности ф = ф1 — ф2 двух функций ^0 из ^{Х).
Достаточно, например, положить ф = ф+ — ф_, поскольку обе
непрерывные функции ф+ и ф~ имеют компактный носитель.
Определим теперь ц.+ (ф) по формуле
ц+ (ф) = ц+ (q>j) — ц+ (ф2).
Такое определение будет обоснованным лишь в том случае,
когда мы докажем независимость ц+(ф) относительно разложения
Ф = Ф1 — фг1). Итак, если ф = ф3 — ф4 — другое разложение, то
ф1 + ф4 = ф2+Фз, откуда, согласно (IV, 2;414), Ц.+ (ф0 +
+ ц+(ф4)= ц.+ (фг)+ ц+(фз) и, следовательно, ц+(ф1) — |л+(ф2) =
= |л+ (фз) — ц+(ф4), что полностью доказывает эту
независимость. Мера ц+ теперь определена как некоторая функция на
Ч? {X; R) со значениями в R. Очевидно, кроме того, что эта
функция ц+ линейна на этом векторном пространстве. В самом
деле, формула |д+(Лф) =Л|д+(ф) очевидна и достаточно лишь
доказать аддитивность. Если ф и ф — две вещественные
функции из <ё'(Х),~то можно их записать в виде ф = ф1 — ф2 и -ф ===
== ф 1 — tyz, где фь ф2, фь ф2 ^ 0. Теперь можно записать
разложение ф + ф = (ф1 + -ф i) — (фг + Фг), из которого с
помощью (IV, 2;4Ц) следует формула
ц+ (ф Н- гр) = ц+ (ф, + ФО — ц+ (ф2 + ф2) =
= Ц+ Ы + И+ Ы - И+ (Фг) - И+ Ш = И+ (ф) + И+ (ф),
заканчивающая доказательство линейности \х+.
Проверим теперь свойство непрерывности, которое нам
позволит утверждать, что \х+ является некоторой скалярной R-мерой.
Пусть А" —некоторый компакт и а — функция ^ 0 из ^(Х),
равная 1 в некоторой окрестности компакта К (следствие
теоремы 11). Положим u+(a) = k. Тогда для вещественной функ-
') Если пользоваться только ф4 и ф-, то это доказательство не нужно.
Однако тогда мы не сможем доказать линейности ц+, так как (ц> + ^)+ф

§ 2. Меры Радона
485
ции ф имеют место неравенства
-||ф||а<ф<||ф||а, (IV,2;415)
а, следовательно,
-||ф||^+(а)<^+(ф)<||ф|!и+(а) или | .и+ (Ф) | <£||Ф||,
из которых следует непрерывность ц+ на ^(XjR) и
справедливость неравенства ||ц+|1к ^ k = ц^а)1). Этим заканчивается
доказательство того, что ц+ является некоторой R-мерой. Мера
эта, очевидно, ^ 0.
По определению, ц+ ^ ц. Кроме того, каждая мера v ^ 0,
мажорирующая меру ц, т. е. мажорирующая ц и 0, для любой
функции Ф^О и 0 «£ ^ =£S ф удовлетворяет неравенствам
v(<p) ^ v(i|j) ^ h(i|j), а, следовательно, после перехода к
точной верхней грани относительно if), — неравенству v(<p)^ Ц+(ф),
из которого вытекает соотношение v ^ ц+. Последнее означает,
что ц+ является точной верхней гранью ц и 0 в
полуупорядоченном векторном пространстве вещественных мер на X. Значит,
это пространство является решеткой.
Для произвольного компакта К имеет место неравенство
II ц IIк -^ II Ц+11к + II Ц.- \\к- Покажем, что на самом деле здесь
имеет место равенство. Каково бы ни было е > 0, существует
такая функция (pi^'S'K(X), при которой имеет место неравенство
\\p+\\>vi+toi)>U+\\K--j, о<ф1<1.
(Можно взять ф! ^ 0, поскольку ц+ ^ 0. См. формулу
(IV, 2; 39т).)
Существует теперь функция -фi e'S'k(X), O^ifi^qpi^l,
такая, что
^Ы>^+(ф1)-1->11^+11^-1-
Точно так же существует такая функция я^г s ^к{Х), 0^
^ ^2 ^ 1. при которой
— иЫ>Ни-11/г — -f-
Функция 0 = ifi — 1J32 лежит в 'ё'к(Х) и удовлетворяет
условиям |0| ^ 1 и ц(8) ^ 11ц+11к + И м-—II к: — е. Наше утверждение
следует из того, что е произвольно. Тот же результат имеет
место для норм, рассматриваемых на пространстве X.
Рассмотрим теперь меру | ц \ = ц+ -f- ц~ и покажем, что она
может быть определена по формуле (IV, 2;413). Прежде всего,
так как для \р = if>+ — if>; ц(^) = ц(*1>+)— М'(Ч'_)^ |ы+(^+) +
') Мимоходом мы доказали общее свойство: любая линейная форма на
(ё'(Х)^0 над <S'+(X) является мерой, т. е. непрерывна на каждом 'ё'к(Х),
где К — компакт, содержащийся в X.

486
Гл. IV. Интегральное исчисление
+ ц~(ф~) ^ и+(ф) + Ц~(ф) = | ц| (ф), то левая часть формулы
(IV, 2; 413) не меньше правой, ее части. Однако существуют
такие функции фь г|)2, 0 ^ ф( <; ф, 0 ^ фг ^ Ф, для которых
v(b)>v+(ч>) — j. — иШ>р~(ч>)— у-
Функция 0 = гр! — г|>2 удовлетворяет неравенству |0|^ф.
При этом ц(0) ^ ц+(ф) + ц~{ц>) — е = |ц| (ф) —е. В силу
произвольности е>0 отсюда получаем соотношение (IV, 2; 413),
которое говорит о том, что
III Ц Ilk = SUp |ц|(ф)= SUp | Ц (ф) | = || Ц ||jf,
0<ф<1 1Ф|<1
а, следовательно, || |ц| || к = || ц+ IU + II м- II к.
Мы определили ц+, ц-, |ц| как скалярные R-меры (R-ли-
нейные отображения Ч?(Х;к) в R). Полагая ц+(ф] +/ф2) =
= (г+(ф1) +1ц+(фг) и т- Д-> можно определить их как скалярные
С-меры, вещественные, ^0 в смысле, указанном на стр. 476—
478.
Согласно формуле (IV, 2; 397), для С-меры ^0 норма
вычисляется, исходя из ее значения на функциях ^ 0. Откуда
получается, что формула || ц || = || |ц| || = || ц+ || -+- || ц~ ||
сохраняется для вещественных С-мер. Кроме того, для комплексных
функций ф (и, конечно, ф ^ 0) сохраняется формула (IV, 2; 413)
вместе со своим следствием (для комплексной ф) |ц(ф)
<М(|ф|) (поскольку , |м-(ф) I < 1и+(ф)| + |и~(ф)
<|1+(|ф|)+1*-(|ф|) = |1*|(|ф|)).
Остается, наконец,, показать, что пространство вещественных
мер является полной решеткой. (Это замечательно! Напомним,
что пространство Ч?{X; R) не является полной решеткой.) Итак,
пусть (Иг)ге/—произвольное мажорируемое семейство
вещественных мер. Для него существует такая мера v, что для всех i
fit ^ v. Для каждого конечного цепустого подмножества /
множества / обозначим через (ij точную верхнюю грань мер щ,
i е /. Очевидно, цк ^ \ij, если K^>J- Надо лишь доказать, что
множество [ij имеет точную верхнюю грань. Пусть ф ^ 0.
Положим
M<P) = sup.ny(<P)- (IV,2;416)
(Внимание! Написанное вовсе не одно и то же, что -эирц^ф).
Это дает совсем другой результат, ибо уже для двух
мер щ и ц2 равенство (sup(m, ц2)) (ф) = sup(ni^), ц2(ф)) не
справедливо. Например, для ц и 0 равенство ц+(ф) =
= зир(ц(ф),0) = (^(ф))+ места не имеет.) Эта величина
конечна, так как она мажорируется величиной v^).

§ 2. Меры Радона
487
Таким путем определяется некоторая функция на ff+(X).
Докажем, что эта функция «линейна» в смысле формулы
(IV, 2;4Ц). Относительно умножения на скаляр это очевидно.
Поэтому достаточно рассмотреть свойство аддитивности. Из
неравенства
Ну (<Pi + Фг) = Ну (<Pi) + Ну (фг) < Но (Ф1) + Но (Ф2)
переходом к точной верхней грани относительно / получаем
Цо(ф1 + фг) ^ ИоСфО + ИоСфг)- Однако существует такое
конечное множество J а I, при котором иЛфО 5= р,о (фО — е/2, и такое
конечное множество К, что ця(фг) ^ Ио(фг) —е/2. Поэтому,
обозначая L = J U К, получим:
Но (Ф1 + Фг) > И£ (Ф1 + Фг) = И£ (ф|) + И£ (фг) > Ну (ф|) + И* (Ф2) >
> Но (фО + Но (Фг) — е>
откуда и вытекает искомый результат. Затем можно определить
цо на W(X;R) тем же самым способом, какой был использован
при определении ц+ из ц в начале доказательства этой
теоремы. Мера цо будет представлять собой R-линейную форму на
ff(X;R). Надо лишь доказать ее непрерывность на <S'K(X;R).
Применим способ, использованный прежде для ц+. Выберем
произвольный индекс и Тогда для ie/ из неравенства \ij <; v
следует н/^'v"1", а из неравенства —Ну ^—И* следует ну ^иГ-
Поэтому для любой вещественной функции ф
Ну (Ф) = Ну (ф+) - Ну (Ф~)^+ (Ф+) + цГ (qr) < v+ (|Ф |) + цГ (|Ф|).
Точно так же
— Ну (ф) = — Ну (ф+) + Ну (ф"~) <
<иг (ф+) -i- v+ (Ф-) < v+ (| Ф1) + цг (I ф I )•
Окончательно: |и7(ф)| ^(v+ -+- иГ)( 1Ф D» или' переходя к
точной верхней грани относительно /, |и0(ф) | ^(v+ + и,-) ("J ЧРI )■
Отсюда сразу же вытекает непрерывность цо и, кроме того,
неравенство
|HoL<llv+ll^ + ||Hr|r
Теперь цо является R-мерой (ее можно, очевидно,
продолжить в W(X; С) до некоторой вещественной С-меры). Она
очевидным образом мажорирует все меры \iJ и по определению
(IV, 2; 416) является наименьшей мерой, обладающей этим
свойством. Следовательно, ц0 является точной верхней гранью мер
Hj и, значит, множество вещественных мер на X является
полной решеткой.

№
Гл. tV. Интегральное исчисление ■
Замечание. Мы видели (формула (IV, 2;397)), что норма
.С-меры ц ^ 0 может быть вычислена с помощью fi(cp), где ф —
вещественные функции S>0. Теперь мы можем сказать, что
норма вещественной С-меры ц может быть вычислена с
помощью ц((р) с вещественными функциями ф (и что она,
следовательно, равна норме ^R;см. примечание на стр. 451). Это как
раз то, что мы видели во время доказательства теоремы.
Конечно, формула (IV, 2; 397) не верна. Однако, в силу
соотношения (IV, 2; 413), для вещественной или комплексной ф всегда
имеет место неравенство |{|(ф) | ^ |ц| (|ф|)-
Говорят, что векторная мера ц на X абсолютно мажорируема
«вещественной мерой X ^ 0, если Для любой вещественной
неотрицательной функции ф ^.^{Х) имеет место неравенство
' ||?(ф)||<Мф). (IV, 2; 42)
Если ф —вещественная функция произвольного знака, то
II Иф) 11 = 11 МФ+) - ?(<Р-) 1Ю(ф+) + Я.(Ф-) = Х (|Ф |). (IV, 2; 422)
С помощью разложения единицы (см. доказательство
соотношения (IV, 2;392)) можно показать, что это неравенство
сохраняется и для комплексной функции ф. Если ц является
вещественной С-мерой, то из формулы (IV, 2;413) следует, что
наименьшей мерой, мажорирующей по модулю меру ц, является
мера \ц\.
Пусть Е— конечномерное векторное пространство, и пусть
-> -> -> ->
е, е2, ..., еп — базис Е как векторного пространства над
полем R. Для каждой вещественной функции ф можно написать
разложение
+ .* +.
Мф) = 2 И/ (ф) et,
где щ\ ф->{г<(ф) являются R-линейными формами на #(X;R),
непрерывными на WK{X;R) (К — компакт пространства Х),т.е.
скалярными R-мерами на X. Так как для каждого ф^О
||Мф)||< max || е,|| 2 | ц, |(Ф),
<=1. 2 п i=l
То ц абсолютно мажорируема положительной мерой
max || et || 2j I Hi I- Но тогда она имеет наименьшую абсо-
/==1, 2, .... п i=l
лютную мажоранту. Более общо, любая мера со значениями
в банаховом пространстве Е, обладающая абсолютной мажо-

§ 3. Продолжение положительной меры 489
рантой, имеет наименьшую абсолютную мажоранту, а именно:
точную нижнюю грань минорируемого нулем непустого
множества абсолютных мажорант (множество вещественных мер
является полной решеткой).
Однако мера со значениями в бесконечномерном банаховом
пространстве, вообще говоря, не имеет абсолютной мажоранты.
Рассмотрим, например, случай компактного пространства X.
Пусть Е = <ё'{Х)—пространство с обычной нормой.
Тождественное отображение ф -*■ ф определяет на X меру ц со
значениями в Е=<$(Х). У этой меры нет абсолютной мажоранты
(кроме случая, когда X конечно). В самом деле, пусть X— ее
абсолютная мажоранта. Тогда для любой функции ф ^ О
II ф II = II ц(ф) || ^ Мф)- Если X — бесконечное множество, то
для любого п можно найти п попарно не пересекающихся
открытых множеств (следствие 6 теоремы 11, применённое к а
замкнутым множествам, сводящимся к отдельным точкам).Для
каждого из них можно найти непрерывные функции <х\, 0^аг-^
^ 1, с носителями в этих множествах, принимающие значение 1
не менее чем в одной точке (лемма 1 к теореме 11). Так как
1 = IIос,-1| 5^А,(а,-), то я<^ 2 Ма*) = М 2 а< ^М0> что невозг
можно, поскольку ^,(1) конечно. Мы получаем, что ц абсолютной
мажоранты не имеет.
.Замечание. Мы определили \ц\ для вещественной
С-меры (х, но не для комплексной С-меры. Теперь возможно сделать
и это. Более общо, если ц является мерой со значениями в ко-
нечномерном векторном пространстве Е над полем R или С, то
в качестве \ц\ можно взять ее наименьшую абсолютную
мажоранту.Эта мажоранта является некоторой мерой ^0 и ||ц(ф) ||^
^ IH (|ф|)- В соотношении |||х|| <:|| | ц| || в случае скалярной
меры (вещественной R-меры или комплексной С-меры) имеет
место равенство. Равенство не будет выполняться в общем
случае векторной меры (см. примечание к теореме 15), а, значит
в частности, для R-меры со значением в С.
§ 3. ПРОДОЛЖЕНИЕ ПОЛОЖИТЕЛЬНОЙ МЕРЫ. ТЕОРИЯ ЛЕБЕГА
Пусть ц — некоторая мера ^0 на локально компактном
пространстве X. Постараемся определить меру ц(ф) для
функций ф, отличных от непрерывных функций с компактным
носителем. Точно так же в случае меры р. = dx с помощью теории

490
Гл. IV. Интегральное исчисление
Римана мы могли определить (pdx для функций ф, отличных
от непрерывных функций, имеющих компактные носители.
Впрочем, если |х = 8(a), то совершенно естественно положить |х(ф) =
==6(а)(ф) =ф(а) для любой комплексной функции ф на X.
Излагаемая здесь теория Лебега является значительно более
общей, чем теория Римана. Даже в случае меры |х = dx
множество интегрируемых по Лебегу функций шире, чем
множество функций, интегрируемых по Риману. Однако эта теория
сложнее, тоньше и зачастую скучнее. Поэтому мы позволим
себе принять некоторые из теорем без доказательства1).
Раз и навсегда предположим, что X является локально
компактным, счетным в бесконечности пространством, т. е.
пространством, являющимся объединением счетного множества
компактов2). Это будет, например, случай конечномерных
векторных пространств, поскольку их всегда можно рассматривать как
счетное объединение замкнутых шаров, т. е. компактных частей.
Все локально компактные пространства, обычно встречающиеся
в анализе, обладают этим свойством. Поэтому вводимое
ограничение не является особо существенным. Оно не является
необходимым для всей теории, но потребуется для нескольких
фундаментальных теорем. С другой стороны, мы всегда будем
считать, что на X задана мера Радона |х ^ 0. Говорят, что X
является пространством с мерой, если X локально компактно, счетно
в бесконечности и снабжено мерой |х ^ 0. Тот факт, что ц ^ 0,
существен.
Внешние меры открытых множеств
Пусть О — открытая часть X. Внешней мерой открытого
множества О относительно меры ц называется норма \\[i\\o
сужения |х на это открытое множество, т. е. точная верхняя грань
|х(ф) на всех функциях ф из Ч?('Х) с носителем в О,
удовлетворяющих неравенству 0^ф^1. Эта мера будет обозначаться
через |х*(С). Число ц*(С) неотрицательно, конечно или
бесконечно.
Для мер открытых множеств можно доказать ряд свойств.
Некоторые из этих свойств очевидны.
') Приводимый здесь метод изложения теории Лебега не является ни
самым кратким, ни самым лучшим. Однако: 1) будет введено минимальное
число новых понятий, а именно: не будет необходимости в изучении
полунепрерывных снизу функций; 2) одновременно получатся интегралы от
векторных функций; 3) все, что здесь вводится, во всяком случае постоянно
применяется в анализе.
2) Мы повторим это условие, если оно будет существенным для
справедливости теоремы. Такое ограничение уже вводилось в теореме 11.

§ 3. Продолжение положительной меры
491
Например, если 0\ и 02— два открытых множества и если
OiCzOz, то в силу положительности \х, получаем: \i*(Oi) ^
С ДРУГОЙ СТОРОНЫ, (Л* (0) = О И \Х* (X) = |||Л||.
Приведем два примера не столь элементарных свойств.
1°) Пусть Со, Ci, <?2, ••• — возрастающая последовательность
открытых множеств X. Их. объединение О является открытым
множеством, и имеет место формула
И* (О) = V ({J О Л - Пт ji* {0п)- (IV, 3; 1)
\ п I "-»°°
Докажем эту формулу. Прежде всего, имеет место
очевидное неравенство ц*{(3) ^ ц*{Оп).
Пусть теперь М — такое произвольное конечное число, что
М < ц*{0). Нам достаточно доказать, что существует такое
целое число п, что \i*(On) ^ M. Согласно определению ц*((У),
существует такая функция ф£?(X) с носителем в О, что О <J
^.ф ^ 1 и ]x((f)~^ M. Открытые множества Оп пересекают
компактный носитель К функции ф по открытым множествам
этого компакта. Тем самым определяется возрастающая
последовательность открытых множеств этого компакта. Поскольку
объединение О множеств Оп покрывает К, то существует такое
целое число п, при котором Оп покрывает компакт К. Функция
ф принадлежит 'ff(X), имеет носитель в Оп и удовлетворяет
неравенству 0^ф^1, так что, по определению меры ц*(0„),
имеет место соотношение ц,(ф) ^|а*(С„). Отсюда получаем
неравенство \i*{On) Г> М, доказывающее наше утверждение.
2°) "Пусть О является объединением последовательности
открытых множеств О0, О и О г, • • • • Тогда
оо
И* «?)< 2 И* (<?„)• (IV, 3; 2)
В самом деле, пусть ф£?(X) имеет носитель К в О и 0 ^
=д; ф ^ \. Множества Оп образуют открытое покрытие К.
Поскольку К является компактом, то достаточно конечного числа
этих множеств (Сг)ге/ для покрытия К. Пусть (а,)ге/ является
разложением единицы, подчиненным покрытию {0\}ie/.
компакта К. Тогда а*ф принадлежит ^(Х), имеет носитель в 0% и
О ^ <х,ф <; 1, а, значит, |а(агф)^ \x*(Oi). Отсюда
со
И (Ф) = 2 И (а/ф) < 2 И* {Од < 2 И* (Оп)- (IV, 3; 3)
i е / i<=l п=0
Переходя в левой части к точной верхней грани по всем
рассматриваемым функциям ф, получаем соотношение (IV, 3; 2).

492
/"л. tV. Интегральное исчисление
Замечания. 1°) Предположим, что ц, является
атомической мерой 2 cv^(av)> гДе все cv^0. Из теоремы 15 вытекает,
что v
(Г(С0 = 1Ы1а= 2 cv<+<x>. (IV, 3; 4)
2°) Пусть Jf = R и ц является мерой р dx, где р ^ 0 —
локально интегрируемая по Риману функция. Если, кроме того, О'
является открытым ограниченным интервалом ]а, Ь[, то
ц'(]а, b[)= J p(x)dx. (IV, 3; 5)
[а, 61
В самом деле, неравенство и.*(]а, &[)<! Г p(x)dx очевидно.
la, Ь)
Однако легко найти а' и Ь', а < а! < Ь' < 6, такие, что
f p(jc)djc'+ f p(x) dx <{{а' — а) + (&' - Ь)) sup |р(*)|<в.
(а, а'1 [6, 6'|
Если теперь взять функцию ф, равную 1 в [а', Ь% 0 вС]а", &"[,
где а" = (а + а')/2, 6"= (6 + 6 )/2, и аффинную там, где она
еще не определена, то получим:
Ц (ф) ^ \ p{x)dx^ \ p {х) dx — е.
[а', 6'] \а, 61
Искомый результат получается в силу произвольности е.
3°) Если мера ц, равна нулю в открытом множестве О (см.
определение на стр. 465), то \л*{<У) = О, и обратно. Мера
дополнения к носителю меры ц, равна нулю.
4°) Если замыкание открытого множества О компактно, то
мера \х*(р) конечна. В самом деле, найдем, согласно следствию 1
теоремы 11, функцию 0е?(I), >0 и =1 на О. Тогда для
всех функций ф, служащих для определения \л*((У), необходимо
имеет место неравенство ц,(ф)^ ц,(0) и, следовательно, ц,*(6?)^
<ц(в).
Внутренняя мера компакта
Пусть К — некоторый компакт из X. Внутренней мерой
компакта К относительно меры ц, называется точная нижняя грань
ц,(ф) по всевозможным функциям ф ^ 0 из ^{Х) и ^ 1 на
окрестностях компакта К- Эта мера обозначается через ц,*{К).
Она всегда конечна, поскольку, согласно следствию 1 теоремы 11,
существует хотя бы одна функция ф0, обладающая указанными

§ 3. Продолжение положительной меры
493
свойствами и, следовательно, искомая точная нижняя грань
< ц(фо)-
Предположим, что К является некоторым компактом,
содержащимся в открытом множестве О. Покажем, что тогда ц*(/()^
По следствию 1 теоремы 11, существует функция-ф е 'S'(X),
удовлетворяющая неравенствам О^ф^ 1, равная 1 в
некоторой окрестности К и имеющая носитель в О. Теперь, по
определению ц*(/С) и \х*((У), имеют место неравенства ц*(/С) ^ ц(ф)
и ц(ф) ^ц*(С?), из которых вытекает наше утверждение.
Примеры. 1°) Если ц является атомической мерой
2 cvVv), где Cv ^ °- т0
МЮ = 2 Cv (IV,3;52)
В самом- деле, для любой функции ф ^ О, такой, что ф>,1 в
некоторой окрестности К, имеет место неравенство 2<VP(av)^
v
^_2 cv> a значит, и ц*(/()= 2 cv. С другой стороны, пусть
(7 — некоторая окрестность К с компактным замыканием (см.
примечание на стр. 456). Тогда 2 cv< + oo. Следовательно,
существует такое конечное множество У, что 2 cv ^ е.
Обозначим через 6?' открытое множество, полученное из О
удалением точек av, v e J', ауф К. Тогда
МЮ< И* (<?')= 2 cv< 2 cv + e. (IV,3;53)
Поскольку е произвольно, ц, (/() ^ 2 cv, а, значит, ц„ {К) =
= 2 Cv.
av<=K
2°) Пусть ц является мерой рЛс на R, где р ^ 0, и пусть К —
ограниченный интервал [а, Ь]. Тогда
П. ([а. *])= J />(*)dx. (IV,3;54)
[а, 6]
Рассуждения остаются теми же, что и в примере 1°). Прежде
всего непосредственно видно, что ц„ ([а, Ь]) > Г р(*) Ле. Выбе-
рем затем такой открытый интервал ]а', Ь'[, а' < а < b < fr',

494 Гл. IV. Интегральное исчисление
чтобы р (х) dx + р (х) dx^e. Тогда
[о, о'] [Ь, Ь'\
И. ([а, Ь]) < ц* (К, 6'[) = J /? (x) dx < J /? (*) rf* + е,
(о', Ь'\ [о, Ы
откуда и вытекает требуемый результат.
Измеримые множества. Мера множеств
Определение. Внешней мерой подмножества А
множества X относительно ц называется точная нижняя грань внешних
мер открытых множеств, содержащих А. Эта мера обозначается
через ц*(А).
Внутренней мерой подмножества А относительно ц
называется точная верхняя грань внутренних мер компактов,
содержащихся в А. Внутренняя мера обозначается через ц*(А).
Поскольку для компакта К, содержащегося в открытом множестве
О, справедливо неравенство ц*(К) ^ ц*(0), то ц*(А) ^ №*№)•
Если А а В, то ц*(А)< р*(В) и ц.(Л)< ц.(Д).
Если А является объединением конечного или счетного
семейства множества Ап, п = О, 1, 2, ..., то имеет место
неравенство
И*И)<2и*(А,). (IV, 3; 6)
Это неравенство очевидно, если одно из чисел ц*(А„) равно
+ оо. Предположим поэтому, что все они конечны.
Для каждого и, можно найти такое открытое множество Оп^>
zdA„, что ц* (Оп) ^ Ц* (An) + ~7г+Т • Если 0 = {JOn, то получаем
ц* (А) < ц* (О) < 2 (*• «?«) < 2 И* (А,) + е <)• (IV, 3; 62)
п п
Поскольку е произвольно, мы получаем отсюда (IV, 3; 6).
Предположим теперь, что множества Л„ не пересекаются.
В этом случае неравенство (IV, 3; 6) вовсе не обязано перейти
в равенство (оно станет равенством, если Ап измеримы; см.
формулу (IV, 3;73)). [Подчеркнем, однако, что неравенство
перейдет в равенство тогда, когда не только А„, но и А„ не будут
пересекаться. Мы воспользуемся этим только после теоремы 19,
а докажем с помощью этой теоремы.
Для заданного N можно найти открытые непересекающиеся
множества Оп zd Ап, п = О, 1, 2,..., N (следствие 6 теоремы 11).
Для каждого открытого множества О zd А имеет место включе-
!) Согласчэ (IV, 3; 2).

§ 3. Продолжение положительной меры
495
ние С=э {J{0(]On). Так как множества О [\Оп открыты, а зна-
rt=0
чит, измеримы и не пересекаются, то по теореме 19 получаем
rt=0 rt=0
Переходя к точной нижней грани по всем О, получаем нера-
N
венство ц*(А)^ 2 и'Ип). откуда, устремляя N к +оо, ПОЛу-
с» оо
чаем ц* (А) ^ 2 И* (^п) и> следовательно, ц* (А) = 2 И* Ип)-
Замыли n=0
кания Лп не пересекаются.] С другой стороны, при
непересекающихся Ап для внутренних мер имеют место неравенства.
Ограничимся, как и ранее, случаем конечных ц,*(Л„),так как в
противном случае рассматриваемое свойство очевидно. Для каждого п
можно найти такой компакт Кпа Ап, при котором ц*{Кп) ^
^ цД^п) — е/2п+2. Затем для заданного N можно найти
непрерывные функции а„, п=0, 1,2,..., N, 0^ап^1, принимающие
значение 1 в некоторой окрестности Кп и имеющие попарно
пересекающиеся носители (пользуясь следствием 6 теоремы 11, мы
можем взять попарно не пересекающиеся открытые множества^,
содержащие Ки i = 0, 1, 2, . .. , N, и применить следствие 1 этой
теоремы к каждой паре Ki cr Шг)- Пусть теперь задана функция
y^.W{X), ф ^ 0, равная 1 в окрестности множества Ко U Ki U ...
... U Kn и така-я, что ц (ф) < ц, (Ко U K\ U • • • U Кп) + е/2. Так как
апф ^ 0 и равна 1 на окрестности множества Кп, то ц,(а„ф) ^
^ ц*(Кп)- Однако поскольку носители функций а„ не
пересекаются, то ф ^ аоф + ••• + а^ф. а, следовательно, ц(ф) ^
^ 2 Мапф)^ 2 И,(/<«)> что дает неравенство
rt=0 rt=0
^ и *» pSmkj-i .
Окончательно,
/ N \ f N \ N N
\>ла)>\>.[ S л„ Ы*. U *» >£ »*.(/cn)—f-^Jji.Mj-e.
V rt=0 / \ rt==0 / rt=0 rt=0
(IV, 3; 7)
Поскольку это неравенство справедливо при любом е > 0, то
N
\xt (A) ^ 2 Ц. (Л„), и поскольку последнее соотношение верно
rt=0
при любом N, то для попарно не пересекающихся Ап, дающих

496
Гл. IV. Интегральное исчисление
в объединении множество А, получаем
оо
МЛ)>2МЛ,). (IV,3;72)
Говорят, что подмножество А множества X псевдоизмеримо
по \х, если его внутренние и внешние меры (конечные или нет)
равны между собой. Их общее значение называется мерой А
и обозначается через ц(Л). Мы ввели название
псевдоизмеримого, а не измеримого множества, поскольку, как мы увидим
позднее, это определение слишком широко: измеримым следует
назвать часть псевдоизмеримых множеств, для которых
справедливо свойство аддитивности.
Докажем некоторые свойства так определенной меры
множеств.
Iе) Открытые множества псевдоизмеримы. В самом деле,
пусть О — некоторое открытое множество и М — такое конечное
число, что \1*{(У) > М. Тогда существует такая функция фе
е <&* (X), 0 ^ ф ^ 1, с носителем в О, что ц (ф) ^ М.
Пусть К — компактный носитель ф. Для каждой функции
\р^&(Х), ^0 и ^1 на некоторой окрестности ^справедливо
неравенство ц(г|)) ^ ц(ф) ^ М. Переходя к точной нижней
грани по всевозможным таким \|э, получим \1*{К)^ М. Поскольку
это справедливо для любого М, то \it {О) = sup \xf (К) = \i* {О),
что означает псевдоизмеримость открытого множества О.
2°) Компактные множества псевдоизмеримы. Пусть К —
произвольный компакт. Пусть ф —функция из 'ё'(Х), ^0 и ^1
в окрестности К и такая,'что \х(ц>) ^ ц*('^0 + е. Пусть О —
открытое множество гэ К, на котором ц>(х) ^ 1. Так как для
любой функции \|э ^Ч?(X), 0 ^ i|; ^ 1, с носителем в О имеет
место неравенство ty ^ ф, то ц(\|;)^ц(ф). Переходя к точной
верхней грани по всем \|э, получим неравенства ^*((^)^ ц(ф)^
=£=М*(^0 + е. Отсюда, поскольку е произвольно, получаем
равенство \i* (К) = inf \x* (0) = \xt(K), означающее псевдоизмери-
мость компакта К-
3°) Пусть А является объединением конечного или счетного
числа псевдоизмеримых непересекающихся множеств Ап. Из
неравенств (IV, 3; 6) и (IV, 3;72) непосредственно следует, что А
псевдоизмеримо и что
И(Л)= S ц(/4„). (IV,3;73)
4е) Пусть С и D — два непересекающихся подмножества X.
Мы уже знаем, что
ц*(СиД)<ц*(С) + И*Ф). (IV, 3; 7<)

§ 3. Продолжение положительной меры 497
Пусть О — открытое множество zd(C {] D) и К — некоторый
компакт с: С. Тогда О — К является некоторым открытым
множеством, содержащим D, а, значит, \i(0 — К) ^\i*{D). С
другой стороны, О является объединением двух псевдоизмеримых
непересекающихся подмножеств К (компакт) и О — К
(открытое множество). Из 3°) следует, что
|х (О) = |х (К) + \i (О - К) > |х (К) + v (D).
Переходя теперь по всевозможным К при фиксированном О
к точной верхней грани, получаем: \i{0) ^ц*(С) + \i*{D).
Точная верхняя грань по всевозможным О дает замечательное
неравенство:
|ЛСиЯ)>МО + И*(Я)- (IV,3;75)
(Здесь, очевидно, можно переставлять множества С и D.)
В частности, если С псевдоизмеримо, то из (IV, 3; 74) и
(IV, 3; 75) можно получить замечательное равенство
(замечательное потому, что редко удается получать равенства, в
которых участвуют не псевдоизмеримые множества):
|ЛСи/» = |1(С) + |1*(Я)- (IV,3;76)
Что же касается внутренних мер, то, согласно (IV, 3;72),
прежде всего имеем:
]i.(C[)D)>]it(C) + ]i.(D). (IV,3;77)
Пусть К — некоторый компакт c(C[]D) и О — открытое
множество zdD. Компакт К Л 0(У содержится в С, а,
следовательно, его мера ^\i%(C). Так как множество К U О является
объединением двух псевдоизмеримых непересекающихся
множеств О (открытое множество) и К П С О (компакт), то оно
псевдоизмеримо и из 3°) получаем
li (К) < ii (К U О) = ii {О) + ji (К Л 00) < |х (О) + jx. (С).
Переходя последовательно к точной верхней грани по всем К,
а затем к точной нижней грани по всевозможным О, получаем:
МсияХМО + иЧЯ)- (iv,3;78)
(Здесь можно, очевидно, переставлять С и D.)
Меняя ролями С и D, затем применяя соотношения (IV, 3; 77)
и (IV, 3;78), для псевдоизмеримого С можно получить
замечательное равенство:
МСиЯ) = |х(С) + МЯ)- (IV,3;79)
Из соотношений (IV, 3; 7«) и (IV, 3; 79) следует, что если
множества С и О не пересекаются, множества Си С [} D
псевдоизмеримы, а множество С имеет конечную меру, то.

498
Гл. IV. Интегральное исчисление
множество D псевдоизмеримо, поскольку
»r(D) = pt(D) = MCUD)-p(C\
В том случае, когда ц(С) = (д,(С U D) = -{-оо, этот
результат не сохраняется, так как разность при этом не определена.
Впрочем, легко привести и контрпример. Позже (стр. 503) мы
приведем пример не псевдоизмеримого по (д, = dx множества D,
содержащегося в ограниченном интервале [а, Ь] прямой R. Пусть
. С = С {[а, Ь\). Тогда оно открыто и имеет меру, равную -\- оо.
Поскольку (С U D) Z3 С, это множество псевдоизмеримо, имеет
меру -|-оо, но тем не менее множество D не является
псевдоизмеримым.
Если положить A = CUOhS = C, то полученный
результат можно записать в другом эквивалентном виде. Если А и В
псевдоизмеримы, A zd В и если В имеет конечную меру, то
множество А — В = Л П СВ псевдоизмеримо и ц(А — В) =
= ц(Л)-ц(В).
Полученное соотношение не Сохраняется, если ц(В) = +00-
Полагая А = X, получаем, что если В ■• псевдоизмеримо и
имеет конечную меру, то С В также псевдоизмеримо (вообще
говоря, это неверно, если ц,(В) = + оо).
5°) Пусть А является объединением конечного числа псевдо-
N
измеримых множеств: A=[JAn. Тогда А псевдоизмеримо (и
N.
в силу (IV, 3; 6) имеет место неравенство ц.(Л)^ 2 у^{Ап)).Сле-
дует подчеркнуть, что п. 5°) отличается от п. 3°), так как
множества Ап здесь не предполагаются непересекающимися. Это
свойство очевидно, если одно из множеств Ап имеет бесконечную
меру, так как тогда и множество Л будет иметь бесконечную меру.
Предположим поэтому, что все меры ц(Л„) конечны. Пусть
Оп — открытое множество, содержащее Л„ и такое, что
\у{Оп)^ n{An) + e/[2{N + 1)], и пусть Кп—такой компактс=Л„,
N
что м(^п)2г ц(Л„) — el[2{N+ 1)]. Тогда 0= (J Оп является
N
открытым множеством, содержащим Л, и К=\^Кп является
№=0
компактом с=Л. Из неравенств ц* (Л) — ц, (Л) < ц (О) — и. (К) =
= р(0-К)< 2ш(0*-Ю ибо (О-К) a (J (Оп-Кп) <■
/V
S
N
< 2 ((д. (Оп) — И {Кп)) ^ е- так е произвольно, следует, что
п==0
Л псевдоизмеримо.

§ 3. Продолжение положительной меры
499
6°) Пусть А является объединением счетного множества
псевдоизмеримых множеств Ап. Пусть Вп = А0[] А^ [) ... [)Ап.
Согласно 5°), множества Вп псевдоизмеримы, и Ап является
объединением возрастающей последовательности Вп. Если Вп
имеют конечные меры, то, согласно 4°), множества Сп = Вп —
— Вп-\ также псевдоизмеримы.
Наконец, согласно 3°), множество А, являющееся
объединением непересекающихся множеств В0, d, С2, С3, ...,
псевдоизмеримо. Результат сохраняется и в том случае, когда одно из
множеств Ап имеет бесконечную меру, так как тогда
бесконечную меру будет иметь множество А. Таким образом, мы
доказали, что любое конечное или счетное объединение
псевдоизмеримых подмножеств псевдоизмеримо. Если Вп является
возрастающей последовательностью псевдоизмеримых множеств,
объединение которых равно В (здесь В — А), то (согласно
предыдущему, В псевдоизмеримо) имеет место равенство: ц(В) =
= lim (х (Вп). В самом деле, согласно 3°), ц(В) — ц(В0)-\-
П-> оо
+ ц(С1)-\-ц(С2)-\-... и, согласно 4°), ц(Сп)= (х(Вп)— ц(£„_,),
если только эти величины конечны. Отсюда в случае конечных
величин ii(Bn) получаем \i (В) = lim \i(Bn). Для случая, когда
Л-> оо
одна из этих величин бесконечна, этот результат очевиден.
7°) Пусть А является конечным пересечением псевдоизмери-
N
м.ых подмножеств Ап с конечными мерами: Л = О Ап. Тогда
А будет псевдоизмеримым.
Для доказательства будем рассуждать, как в п. 5°), с теми же
N N
обозначениями, но полагая на этот раз (3 = f\ Оп и К = f] Kn-
л=0 л=0
Тогда (х* (А) - ц. (А) < ц (О) - (х (К) = (х (О - К) < 2 (х {0п-Кп)
N \ N
так как О - К с= (J «?„ - /С») = 2 (ц (Оп) - (х (*„)) < в, что
в силу произвольности е доказывает наше утверждение. Однако
здесь, в противоположность п. 5°), результат не сохраняется, если
мера одного из множеств Ап бесконечна. В самом деле, пусть
D — не псевдоизмеримое множество, содержащееся в
ограниченном интервале [а, Ь] прямой R (см. стр. 503). Так как А =[а,Ь]
псевдоизмеримо, то множество В = D U С [а, Ь], содержащее
С [а, Ь], псевдоизмеримо и имеет бесконечную меру. Здесь
А П В = D не является псевдоизмеримым.
8°) Пересечение конечного или счетного числа псевдоизмери
мых множеств конечной меры псевдоизмеримо.

500 Гл. IV. Интегральное исчисление
В самом деле, пусть А = (") Ап и Вп = А0 П А\ П - - ■ П ^п.
Тогда, согласно 7°), каждое множество Вп является
псевдоизмеримым, последовательность Вп убывающая и ее пересечением
является множество А. Далее, Вп = В0 — (В0 — Вп). Так как по-
следовательность В0 — Вп является возрастающей, то к ней
можно применить 6°), откуда вытекает, что Во — (So — А) =А
псевдоизмеримо и, кроме того, ц. (В0 — А) = lim ц. (В0 — Вп). Та-
ким образом, если Вп является убывающей последовательностью
псевдоизмеримых множеств конечной меры с пересечением,
равным В (здесь А), то ц.(В)= lim ц.(В„). Полученные результаты
П -> оо
можно было бы считать весьма удовлетворительными, если бы
не имели места следующие факты:
Если А и В псевдоизмеримы и А =э В, но ц(В) = +оо, то
А — В может оказаться не псевдоизмеримым. Пересечение двух
псевдоизмеримых множеств может оказаться не
псевдоизмеримым, если одно из этих множеств имеет бесконечную меру.
Эти недостатки можно устранить, если ввести более сильное
определение.
Множество А называется измеримым, если для любого
компакта К пересечение А П К псевдоизмеримо (оно необходимо
имеет конечную меру). Измеримое множество псевдоизмеримо,
т. е. свойство измеримости сильнее свойства
псевдоизмеримости. Действительно, множество X можно представить как
объединение последовательности компактов Кп- Следовательно, если
А(\Кп псевдоизмеримы, то, согласно 6°), А также будет
псевдоизмеримым. С другой стороны, всякое псевдоизмеримое
множество конечной меры измеримо. Это следует из того, что в этом
случае, согласно 7°), псевдоизмеримо множество А П К. Однако
псевдоизмеримое множество бесконечной меры не обязательно
измеримо. Например, если D не псевдоизмеримо и содержится
в [а, 6] cr R, то множество D\JC[a, b] псевдоизмеримо, имеет
бесконечную меру, но не измеримо, так как его пересечение-
с компактом [а, Ь] не является псевдоизмеримым. Очевидно
также, что если А и В измеримы, А =э В, то А — В всегда
измеримо, поскольку (А — В)Г\ К = (Л П К) —(В П К). Однако
формула \к(А — В) = \к{А) — ц(В) теряет смысл при \х,{В) = -j-oo.
С другой стороны, объединение или пересечение А конечного
или счетного множества измеримых множеств Ап измеримо,
поскольку в этом случае А П К является объединением или
пересечением множеств Ап П К. Впрочем, дополнение С А
измеримого множества А измеримо и от объединения к пересечению
можно перейти через дополнение. Напротив, формула ц,(В) =
= lim \i(Bn) для убывающей последовательности измеримых
П->оо

§ 3. Продолжение положительной меры
501
множеств Вп, пересечение которых равно В, всегда
предполагает, что В„ имеют конечные меры (это видно из доказательства
этой формулы). Если, например, мы возьмем меру dx на R, то
последовательность множеств Вп = {х е R; \х\^ п) является
убывающей, каждое из множеств имеет бесконечную меру, их
пересечение пусто, а, значит, имеет меру 0.
Добавим еще, что каждое замкнутое множество F измеримо,
поскольку в том случае, когда X является объединением
компактов Кп, это множество является объединением компактов
F П К я. Переходом к дополнению отсюда легко получить, что
каждое открытое множество измеримо даже в том случае, когда
оно имеет бесконечную меру.
Повторим определения, введенные в процессе изложения
материала.
Определение. Множество A cz X псевдоизмеримо, если
|л*(Д) = ц.*(Л). Это общее значение называется мерой
множества и обозначается через ц(А). Множество Л-называется
измеримым', если оно псевдоизмеримо и если, кроме того, для
каждого компакта К множество А {] К псевдоизмеримо.
Нами была доказана следующая теорема:
Теорема 19. 1°) Все открытые и замкнутые множества
измеримы.
2°) Если А и В — два измеримых подмножества X и А гэ В,
то множество А — В измеримо и \i(A — В) — |д,(Д) — Ц.(В), если
только ц,(Д) и ц,(В) не равны +оо. В частности, если А
измеримо, то С (А) Также измеримо.
3°) Если А является объединением конечного или счетного
семейства измеримых множеств, A=\jAn, то А измеримо и,
п
кроме того, имеет место неравенство
V- (Л) < 2 И (Ап), (IV, 3; 8)
п
переходящее в равенство, если множества Д„ попарно не
пересекаются.
3°) Пересечение конечного или счетного семейства
измеримых множеств измеримо.
4°) Пусть До, Ai, Аг, ... — возрастающая последовательность
измеримых множеств. Тогда их объединение А измеримо и,
кроме того, имеет место формула
*{А) = ^{Ап)- (IV,3; 9)
5°) Если До, Ai, Аг, ...— убывающая последовательность
измеримых множеств, то их пересечение А измеримо. Кроме того,
если все множества Д„ имеют конечную меру, то имеет место

502
Гл. IV. Интегральное исчисление
формула (IV, 3; 9). Эта формула не верна, если все \i(An)
бесконечны.
Замечание 1. Позже мы получим новую формулу для
внешних мер: если Ап является возрастающей последовательностью
произвольных подмножеств X, объединение которых равно А, то
ц* (А) = lim ц*(Л„) (см. следствие 0 теоремы 36).Однако сейчас
надо будет доказать это равенство в частном случае,
который нам вскоре понадобится: для любого ЛсХ Ц*(Л) =
= вирц*(Л Л К), где sup берется по всевозможным компактам
К множества X. Это действительно частный случай
высказанного выше общего утверждения, поскольку X является
объединением возрастающей последовательности компактов Кп-
Предположим прежде всего, что ц*(Л) < -f-oo. Тогда существует
открытое множество Oz^A, имеющее конечную меру.
Пересечения О [\СКп образуют убывающую последовательность
непересекающихся измеримых множеств, имеющих конечные меры.
Согласно п. 5°) теоремы 19, при п, стремящемся к бесконечности,
ц (О Л СКп) стремится к 0. Так как (А {] СКп) <= (О Л С/У, то
ц* (А Л СКп) также стремится к 0. Поскольку А = (А Л Кп) U (А Л
ЛС/Cn), то ц* (Л)< ц* (Л Л #п) + ^*(^Л СКп)' а, следовательно,
ц*(Л Л^пХ ц*(^) стремится к ц*(Л) при п, стремящемся
к бесконечности.
Предположим теперь, что ц*(Л) = -\-оо. Допустим для
простоты, что X метризуемо и что рассматриваются замкнутые
компактные шары (в противном случае можно провести
рассуждение, аналогичное проведенному на стр. 457).
Положим Ап=А Л {х е X; п ^ d(x, а) ^ п -р 1}. Положим
затем В0=Л0 U Л2 U Л4 U .. . и А,=Д| U Л3 U Л5 U . ... . Тогда
А = В0 О Вй поэтому ц*(Л)^ ц*(В0) + n*(Bi), а, значит, хотя
бы одно из слагаемых, например ц*(В0), равно +оо. Так как
Во является объединением непересекающихся замкнутых
множеств, то (см. стр. 494) + оо = ц*(В0) = ц*(Л0) + ц*(Л2) +
+ ц*(Л4) +... . Полученный ряд оказался расходящимся. Но
тогда
ц'(ЛЛ{*еХ; d(xta)^2N+l})^vr{A0\}A2\}...\}A2t) =
= VL'(Aa) + VL'(Aa)+...+.Vim(A2fl)
стремится к +'оо = ц*(Л) при N, стремящемся к бесконечности.
Замечание 2. Не может быть и речи о распространении
теоремы 19 на объединение или пересечение несчетных семейств
подмножеств. Например, по мере dx любое множество А с R
(измеримое или нет, конечной меры или нет) является
объединением своих точек, которые представляют собой измеримые
множества нулевой меры.

§ 3. Продолжение положительной меры 503
Различные примеры. 1°) Пусть ц. — атомическая мера
Vcv6/a \ где все cv ^ 0. Из замечаний на стр. 492—493 сле-
V
дует, что все подмножества А множества X измеримы и имеет
место формула
1*04)= .2 cv<+oo. (IV.3; 10)
2°) Для меры р dx на R всегда существуют неизмеримые
подмножества, кроме того случая, когда мера р dx равна нулю.
Приведем пример неизмеримого множества. Пусть X
представляет собой тригонометрическую окружность. На ней можно
определить, естественную меру Радона ц == dQ, называемую
угловой мерой. Эту меру можно определить, например,
следующим образом.
Поскольку каждая точка X определяется некоторым
вещественным числом с точностью до 2я, то пространство 'S'(X)
непрерывных функций на X (так как X компактно, то они имеют
компактный носитель) можно отождествить с пространством
непрерывных периодических функций на вещественной прямой
с периодом 2я. Обозначим через ^2я(К) пространство этих
функций, нормированное по формуле || <р|| = тах| ф (х) \.
Определять меру на X или определять линейную
непрерывную форму на ^2n(R)—это, в сущности, равносильно.
Поэтому мера |i = dQ может быть задана формулой
ц(ф)= J Ф(jc) djc, ?e^(R), (IV, 3; 11)
[a, a+2n]
где точку а можно выбрать произвольно. Результат от выбора
■а не зависит, поскольку все функции ф периодичны с периодом
2л1). Эта мера инвариантна относительно вращения (с центром
в начале координат) множества X. Это означает, что при любом
а имеет место формула
|i(<P(*)) = |i(<P(*-a)), Фе^2я(К). (IV, 3; 12)
Отсюда также естественно вытекает, что ц-мера множеств X
инвариантна относительно вращения. Если А является
некоторым подмножеством А' и если Аа есть множество, полученное из
А вращением на угол ос, то справедлива формула \л.*(Аа) =
= li*(А), и.*(Ла) '= Ц.*(Л). Кроме того, Аа измеримо тогда и
•) Мы привели эту меру к известному понятию интеграла Римана на R.
Однако не представляет никакого труда построить теорию интеграла Риманя
Ф (8) dQ на тригонометрической окружности X.
X

504
Гл. IV. Интегральное исчисление
только тогда, когда измеримо множество А, и при этом
ц(Ла)=ц(Л).
Обозначим теперь через а число, несоизмеримое ели
выбранное раз и навсегда. Будем говорить, что точки х, у множества
X конгруэнтны, если у — х целое кратное а. Тем самым в
множестве X мы определим некоторое отношение эквивалентности.
Пусть X — фактормножество. Следует ожидать, что
фактормножество X, как и само множество X, имеет мощность
континуума. В самом деле, .с одной стороны, существует сюръекция
X на X, а, значит, card X ~^ card X. С другой етороны, каждый
класс эквивалентности счетен и потому card X ^ v card X, и,
поскольку card X ^Э5 v (противоположное означает, что
существует лишь конечное число классов; так как каждый из них
счетен, то и X будет счетным, что невозможно), то, согласно
теореме 5 гл. I, card X ^ cardX Окончательно получаем, что
card X = card X = у — мощность континуума. Пусть теперь А
является подмножеством X, содержащим по точке из каждого
класса эквивалентности. (Очевидно, в классе эквивалентности
ни одна из точек не выделяется среди других и выбор точки не
регламентируется никаким правилом. Мы вынуждены для этого
континуального числа выборов пользоваться аксиомой выбора
Цермело (см. примечание на стр. 28).)
Докажем теперь, что множество А не является ц-измеримым.
В самом деле, так как множество А содержит не более одной
точки из каждого класса эквивалентности, то множества
Апа, neZ, попарно не пересекаются. С другой стороны,
поскольку А содержит не менее одной точки из каждого класса
эквивалентности, то объединение множеств Апа дает все
множество X. Впрочем, А и Апа могут быть преобразованы одно
в другое с помощью вращения па, и, следовательно, их внешние
и внутренние меры совпадают. Если А измеримо, то множества
Апа измеримы и имеют ту же самую меру; при этом
выполняется равенство +оо +оо
2л = ц(х)= 2 ц(л„а) = ц(Л) 2 1.
Однако этЪ равенство невозможно. В самом деле, если А
имеет нулевую меру,, то отсюда следует, что X также будет
иметь нулевую меру, в то время как его мера равна 2л. Если
мера А больше нуля, то X имеет бесконечную меру.
Итак, А неизмеримо. Кроме того, из неравенства (IV, 3; 7г)
следует, что +0о +со
2л = ^(А')> 2 МД.«) = МЛ) 2 1,

§ 3. Продолжение положительной мери 505
т. е. что нижняя мера множества А равна нулю. Однако это
множество неизмеримо, и, следовательно, его внешняя мера
> 0. Приведенный здесь пример кажется неестественным.
Можно отметить общий факт относительно всех ненулевых мер
вида pdx на прямой R или pdQ на тригонометрической
окружности (р — интегрируемая по Риману функция): неизвестно, как
явно образовать неизмеримые множества. Можно лишь с
помощью аксиомы выбора доказать их существование. Это
означает, что все множества, которые встречаются в приложениях
и которые обычно всегда определены явно, измеримы.
Открытый, полуоткрытый или замкнутый интервал \а, Ь\ измерим, и
его мера равна р {х) dx.
[a. b]
3°) Теорема 19 позволяет указать очень широкую категорию
измеримых множеств.
Назовем а-алгеброй частей множества X совокупность 3~ его-
частей, обладающую следующими свойствами:
a) если А е Т, тоСЛ е Т;
b) любое объединение или пересечение конечного или
счетного множества частей, принадлежащих 3~, принадлежит 0~^).
Вот некоторые примеры сг-алгебр: прежде всего это пустая
а-алгебра, не содержащая ни одного множества; затем:
о-алгебра, состоящая лишь из некоторого подмножества и его>
дополнения, и, наконец, 0-алгебра всех частей множества X.
Если <7~i и 3~г — две сг-алгебры, то части X, принадлежащие
одновременно обеим а-алгебрам, образуют некоторую а-алгебру,
которая называется пересечением сг-алгебр &~i П &~г- Точно так
же определяется пересечение f) 3~t конечного или бесконечного!
is/
семейства сг-алгебр. Отсюда, в частности, вытекает, что если Э9'
является произвольным множеством частей X, то существует
наименьшая а-алгебра, содержащая это множество, а именно —
пересечение всех содержащих его а-алгебр. Пусть теперь X —
топологическое пространство. Тогда борелевской называется
наименьшая а-алгебра, содержащая все открытые в смысле
топологии X части (и, следовательно, содержащая также все
замкнутые части). Часть множества X называется борелевской, если
она принадлежит борелевской а-алгебре. Борелевская а-алгебра
из X зависит только от топологии X. Например, пересечение
счетного множества открытых частей (которое не обязательно
открыто) и объединение счетного множества замкнутых частей
(которое не обязательно замкнуто) являются борелевскими.
Имеются и другие примеры. Борелевская часть «универсально
') Автор вместо термина а-алгебры использует термин «tribu» (племя).—
Прим. ред.

506 Гл. IV. Интегральной исчисление
измерима» в том смысле, что она измерима по любой из мер
Радона ц, на X.
В самом деле, по теореме 19 множество всех ^-измеримых
частей X является а-алгеброй, зависящей, естественно, от ц. Это
множество заведомо содержит открытые подмножества и,
следовательно, содержит борелевскую а-алгебру. Весьма тонкие
теоремы позволяют показать, что существуют и другие
универсально измеримые части А", отличные от борелевских.
Множества нулевой меры
Теорема 20. Для того чтобы часть А множества X имела
нулевую меру относительно ц, необходимо и достаточно, чтобы,
каково бы ни было г > 0, существовало такое открытое
множество О из X, содержащее А, что \а((У)^ е. Любое объединение
конечной или счетной совокупности множеств меры нуль имеет
нулевую меру.
Доказательство. Первое"условие означает, что внешняя
мера \i*(A) равна нулю. Поскольку тогда меньшая внутренняя
мера неизбежно также равна нулю, рассматриваемое множество
А измеримо и имеет нулевую меру. То, что касается конечной
или счетной совокупности множеств, вытекает из теоремы 19 и
из того факта, что сумма ряда с нулевыми членами равна нулю.
Следствие. Всякое счетное множество на вещественной
прямой R по мере р dx имеет нулевую меру.
Следствие вытекает из теоремы_20 и из того факта, что
множество, состоящее из одной точки, имеет нулевую меру.
Замечания. 1°) Мера всей вещественной прямой R или
отрезка с несовпадающими концами не равна нулю по мере dx.
Отсюда вытекает новое доказательство того факта, что прямая
или отрезок не являются счетными множествами. Эти примеры
еше раз показывают, что объединение бесконечной несчетной
совокупности множеств нулевой меры, в частности совокупность
точек, не обязательно должно иметь меру, равную нулю.
2°) Глядя на следствие, можно было бы подумать, что на
вещественной прямой R не существует других множеств нулевой
меры по мере dx, кроме счетных "множеств. Однако это неверно.
Мы сейчас построим на интервале [0, 1] множество,
называемое совершенным множеством Кантора, имеющее мощность
континуума и нулевую меру. Рассмотрим сначала множество Еи
являющееся объединением интервалов 0, -^\ и -=-, 1 .
Разделим каждый из этих интервалов на три равные части,
оставим из них лишь первую и третью части и обозначим образован-

§ 3. Продолжение положительной меры 507
ное таким образом множество через Е%. Множество Е2 является
объединением 4 интервалов I 0, -g-l, I j , -g- I, I -g , -g-1, l-g-, 1 .
Разделим снова каждый из этих 4 интервалов, составляющих Е2,
на 3 равных интервала, выбросим средний из них и полученное
множество, являющееся объединением 8 интервалов, обозначим
через Ез. Продолжая так далее, мы получим убывающую
последовательность замкнутых множеств Е\, Е^ £„, .... Мера
множества Е„ равна, очевидно, (—) , а, значит, пересечение Е
всех множеств Еп имеет нулевую меру. Докажем, однако, что
множество Е имеет мощность континуума. В самом деле,
любая точка Е может быть определена единственным образом
с помощью произвольной последовательности а.\, аг ап
где at является одним из двух слов: «первый» или «второй».
Пусть х е Е. Слово й\ будет первым или вторым в
зависимости от того, находится ли х в первом интервале 0, -=- или во
втором -г-, 1 , объединение которых составляет множество Et.
Пусть, например, а1 = «первый». Слово йг будет первым или
вторым в зависимости от того, находится ли х в первом пбдинтер-
1"
вале 0, -Q-
интервала
или же во втором подинтервале \-к, ~к\ разбиения
0> -о- > входящего в множество £2- Так можно
продолжать неограниченно. Положим теперь Ьп = 0, если а„ =
— «первый» и 6„=2, если ап = <свторой». Непосредственно
видно, что соответствие между х и последовательностью Ьп = 0 или 2
оо
полностью определяется равенством х= V -ф и что эта фор-
п=1
мула определяет некоторую биекцию между Е и множеством
{0,2}N отображений N в {0,2} или множеством
последовательностей элементов 0 или 2. Из результатов гл. I следует, что
card Е = card^{N} = 2V = у, т. е. мощность континуума.
Впрочем, множество Е можно определить, воспользовавшись
представлением точек интервала [О, 1] не в десятичной, а в
троичной системе счисления, т. е. системе счисления по основанию 3.
Множество Е тогда будет множеством точек, в троичном
разложении которых применяются только числа 0 и 2 и не
используется число 1 (элемент, имеющий два троичных разложения
принадлежит Е тогда и только тогда, когда одно из этих
разложений может быть записано только с помощью чисел 0 и 2).
Множество Е, описанное впервые в прошлом столетии Кантором,
обладает, кроме того, следующими свойствами: оно совершенно.
Это означает, что оно замкнуто в R и что ни одна из его точек

508
Гл. IV. Интегральное исчисление
ке является изолированной. Любая окрестность каждой из eras
точек содержит даже, как это легко доказать, бесконечное мнсЦ
жество точек Е мощности континуум.
Приведем еще один поучительный пример. Пусть а0, а^
а2, ■ • • — плотная последовательность точек прямой R (например,
множество рациональных чисел, упорядоченных в
последовательность) . Пусть Со, Си Сг, ... — такая последовательность положи-
оо
тельных чисел, что 2 с„<+оо. Обозначим через Ее множе-
ге=0
оо
ство Ег = (J {x e R; \х — ап\<есп}. Это множество открыто
ге=0
(как объединение открытых множеств), и его мера естественным
оо
образом мажорируется числом 2е 2 сп. Обозначим теперь
через Е пересечение множеств Ее, соответствующих
всевозможным е > 0. Мера этого множества равна нулю. Можно было бы
подумать, что оно счетно и сводится к последовательности точек
а„. Однако мы рекомендуем удивленному читателю самому
доказать, что в действительности это множество имеет мощность
континуума.
Если в качестве меры на R™ взять меру dx\, dx2, .. ., dxn,
то мера множества будет соответствовать его объему, и,
следовательно, как мы увидим позже, дифференцируемое
многообразие размерности <С« будет необходимо иметь нулевую меру.
Здесь мы получаем очень простые примеры множеств нулевой
меры, имеющих мощность континуума.
3°) Множество С {а} по мере Дирака б(0) имеет нулевую
меру.
4°) По мере, тождественно равной 0, любое множество имеет
меру, равную нулю.
Свойства, выполняющиеся почти всюду
Пусть Р — свойство, относящееся к точкам локально
компактного пространства X, снабженного мерой Радона ц^О1).
Это свойство определяется заданием множества А точек X,
обладающих данным свойством.
Говорят, что это свойство выполняется ц-почти всюду, или
|.1-почти все точки X обладают этим свойством, если дополнение
С Л множества А имеет нулевую меру относительно меры ^.
Можно было бы ограничиться словами «почти всюду», если бы
') Свойство Р относительно точек X можно определить как отображение
множества X в двухэлементное множество {да, нет}. Говорят, что х ^ X
обладает свойством Р, если Р(х) = да.

§ 3. Продолжение положительной меры
509
мера |j, была задана раз навсегда и если бы это не приводило
к недоразумениям. Заметим, однако, что при мере |j, = dx
понятие «почти всюду» вполне соответствует нашей интуиции. Это не
так для других мер. Например, для меры ц = 6(a) — единичная
масса в точке а — некоторое свойство выполняется почти всюду,
если оно выполняется в точке а. Для нулевой меры |j, любое
свойство выполняется почти всюду (так же точно, впрочем, как
и отрицание этого свойства). Вот что означает для функции f,
определенной на метрическом пространстве X со значениями
в метрическом пространстве F, свойство быть почти всюду
непрерывной:
(ЗА 6= Щ (X), ц (СА) = 0) (Va e A) (Ve > 0)
(Эт) > 0) (V* е X, d (а, х) < т)) : (d (f (a), f (x)) <e),
или иначе: множество точек, в которых f разрывна, имеет'отно-
->
сительно ц меру, равную нулю. Если F является векторным про-
->
странством, то утверждение «некоторое отображение f простран-
->
ства X в F почти всюду равно нулю» означает, что множество
-> ->
точек х е X, в которых f(x) 7^=0, имеет меру, равную нулю.
На вещественной прямой по мере ц = dx почти все точки
являются иррациональными и даже трансцендентными.
Теорема 21. Пусть Р0, Рь Р2, ... — конечное или счетное
множество свойств, относящихся к точкам X. Если каждое,из
этих свойств выполняется почти всюду, то свойство Р —
= Pi Л Рг Л Рз Л . .. , состоящее в том, что одновременно
должны выполняться все свойства Рп, само выполняется почти
всюду.
Это фундаментальная теорема теории вероятностей.
Доказательство. Пусть Ап — множество точек,
обладающих СВОЙСТВОМ г п- Тогда Л = Р)Л„ будет множеством точек,
п
обладающих свойством Р. Его дополнение (J(Ci4„) имеет нуле-
п
вую меру как объединение счетного множества множеств
нулевой меры.
Конечно, аналогичного утверждения для несчетного
множества свойств не существует. Например, для меры ц, = dx на R
свойство «я обладает свойством Ра, если х Ф а» верно почти
всюду. Здесь Р = А Ра является следующим свойством: «х не
а
совпадает ни с одной точкой R». Этим свойством не обладает нр
одна точка.

510 Гл. IV. Интегральное исчисление
.а*
щ-измеримые функции со значениями в метризуемом
сепарабельном пространстве
Предварительное определение. Пусть F — метрия
зуемое пространство. Говорят, что это пространство сепара*
бельно, если в F существует счетное плотное множество.
Пусть / — отображение локально компактного пространству
X, снабженного мерой ц ^ 0, в метризуемое сепарабельное проч
странство F. Говорят, что / ц-измерймо или просто измерима
(когда это не приводит к недоразумению), если прообраз при
отображении / каждой открытой части F является ц-измеримой
частью X.
В этом определении причина, из-за которой мы
предположили F сепарабельным, непосредственно не видна. Можно
определить измеримые функции со значениями в произвольном
топологическом пространстве, но тогда надо будет дать более
сложное определение, эквивалентное предыдущему в том случае,
когда F метризуемо и сепарабельно1). Из этого определения
вытекает, что каждое непрерывное отображение X в F измеримо,
ибо прообраз каждого открытого множества из F является
открытым множеством, а, следовательно, согласно п. 1°)
теоремы 19, измерим.
Естественно, переходом к дополнению можно было бы в
определении заменить открытые подмножества на замкнутые.
Впрочем, множество частей F, прообраз которых при
отображении / ц-измерим, является некоторой о-алгеброй (см. стр. 505).
Если / измеримо, то эта о-алгебра содержит открытые, а, значит,
борелевские множества, и прообраз каждого борелевского
множества из F является ц-измеримым.
Пусть А — некоторая ча"сть X и ф — ее характеристическая
функция. Эта функция, рассматриваемая как отображение X
в топологическое сепарабельное пространство R 2) или
дискретное пространство {0, 1}, измерима тогда и только тогда, когда А
измеримо, поскольку прообраз каждого открытого множества
при этом отображении равен либо 0, либо X, либо А, либо СМ.
Теорема 2Ь. Пусть f и g — два отображения X в F. Если
эти отображения почти всюду равны и одно из них измеримо, то
другое также измеримо.
Доказательство. Пусть А — множество точек х, в
которых f(x) = g(x). По условию, СМ является множеством меры
') См. следствие теоремы 33.
Мы здесь не повторяем, вообще говоря, что F сепарабельно, кроме тех
случаев, когда это существенно для справедливости теоремы.
2) R сепарабельно, поскольку счетное множество Q рациональных чисел
плотно в R.

§ 3. Продолжение положительной меры 511
нуль. Следовательно, все множества, входящие в СЛ, имеют
нулевую меру, а, значит, измеримы. Предположим теперь, что
отображение f измеримо, и покажем, что тогда отображение g
также измеримо. Пусть О — открытое подмножество F.
Перейдем от f~l{0) к g~l (О) с помощью двух следующих операций:
добавим сначала множество элементов, принадлежащих g'^iO),
но не принадлежащих f~ ((У).Это множество является частью
С А, а, значит, представляет собой измеримое множество. Далее,
вычтем множество точек, принадлежащих f_1((7), но не
принадлежащих g'l(0). Это множество снова является частью С А и,
значит, измеримо. Это означает, что g~^{0) измеримо и что,
следовательно, функция g измерима.
Теорема 22. Пусть F и G — два метризуемых
пространства, f —измеримое отображение X в F и g — непрерывное
отображение F в G. Тогда сложное отображение g °f множества
X в G измеримо.
Доказательство. В самом деле, пусть О — открытое
множество из G. Тогда прообраз (g °f)~' (О) = f~ {g~ (О))
является прообразом при отображении f открытого множества
g~l(0) и, следовательно, измерим.
Теорема 23. Пусть X — локально компактное
пространство, снабженное мерой \\. ^ 0, и пусть F — метризуемое
пространство. Тогда любое отображение f пространства X в F,
являющееся \1-почти всюду пределом последовательности f0, fu
f2, ... ^-измеримых отображений X в F, измеримо. В частности,
каждое отображение, являющееся почти всюду пределом
последовательности непрерывных отображений, измеримо.
Когда мы говорим, что f является почти всюду пределом
последовательности fn, то хотим этим сказать, что Эта
последовательность является почти всюду сходящейся и имеет пределом
функцию f. Другими словами, существует множество А,
дополнение к которому по мере \i имеет нулевую меру, такое, что для
каждого *е Л последовательность fn(x) сходится к f(x) при п,
стремящемся к -j- oo.
Доказательство. Предположим прежде всего, что
последовательность fn просто сходится всюду к f. Пусть В —
произвольное подмножество F. Обозначим через Ап прообраз fn1 (В),
а затем через s4-m пересечение (")* Ап. Множество зФт пред-
ставляет собой множество таких точек х, для которых все fn(x)
при п ^ т лежат в В. Множества s&m образуют некоторую
возрастающую последовательность множеств, объединение
которых мы обозначим через зФ.

512
Гл. IV. Интегральное исчисление
Поскольку каждое из множеств fn{x) измеримо, то для
открытого или замкнутого подмножества В каждое из Ап
измеримо и, следовательно, множества s£m и s& измеримы.
Предположим, что В открыто, и покажем,^что в этом случае
множество s& заключено между f~l(B) и f~l(B):
Г1 {В) с si с Г1 (В). , (IV, 3; 13)
Прежде всего очевидно включение s& cz f~' (В). В самом
деле, HEi означает, что х принадлежит одному из s£m с
подходящим т. Значит, fn(x)^B для п ^ т, а, следовательно, f(x)e
ее i? (теорема 15 гл. II). В рассуждении не требуется, чтобы
множество В было открыто.
Пусть теперь В открыто; покажем, что f-l(B)czs£. Если
xef"'(B), то это говорит о том, что f(x), равный пределу f„(x),
является элементом у из В. Поскольку В открыто, существует
некоторая окрестность элемента у, лежащая в В. Из
определения предела вытекает, что существует т^кое целое число
т, что для любого п ^ т элемент fn(x) принадлежит В. Но
тогда х принадлежит Ап для всех п^т и, следовательно,
принадлежит $Фт и тем более si-. Таким образом, мы не знаем,
измеримы ли прообразы f_1(S) или f~l(B), но мы знаем, что если
В открыто, то существует измеримое подмножество s&,
заключенное между ними.
Пусть теперь В — произвольное замкнутое подмножество F.
Обозначим через Вк объединение всех шаров1) радиуса l/k
с центрами в В. Это множество как объединение открытых
шаров открыто. Последовательность Bh, k=l, 2, 3, ..., является
убывающей последовательностью, а пересечение Bh равно В,
В самом деле, очевидно, что это пересечение содержит В. С
другой стороны, если х принадлежит этому пересечению, то
расстояние от х до замкнутого множества В не больше l/k при
любом k, т. е. равно нулю, а это означает, что хеВ, В свою
очередь пересечение замыканий Bh совпадает с В. В самом
деле, с одной стороны, оно_содержит В, но с другой, если точка
принадлежит замыканию Bh, она является пределом точек из
Bh и, в силу непрерывности функции расстояния (см. гл. II,
стр. 83), расстояние от_ х до В ^ l/k. Таким образом, если х
лежит в пересечении Bh, то его расстояние до В равно нулю,
т. е. х лежит в В. Мы образовали две убывающие
последовательности множеств: открытые множества Bh и множества Bh,
пересечение которых равно В. Поскольку Bh открыто, то из
сказанного выше вытекает, что между множествами f-l(Bh) и
f-1(.B/i) можно вставить измеримое множество s&W. Пересечение
измеримых множеств s&(h\ являющееся измеримым, должно
') Надо сначала выбрать в F какую-нибудь метрику.

§ 3. Продолжение положительной меры
513
содержать пересечение множеств f_1 (Bk) и содержаться в
пересечении множеств f-l(Bh). Тем самым обязательно измеримо
множество f_1(S), чем и доказывается теорема для этого случая.
Перейдем теперь к общему случаю, при котором
последовательность fn только почти всюду сходится к f. Обозначим через
А множество тех х, для которых последовательность fn(x)
сходится к f(х). Изменим все функции f„, полагая fn(x) = с прих,
принадлежащем С Л, где с — произвольный фиксированный
элемент F. Измененные функции fn почти всюду равны исходным
функциям fn и, следовательно, каждая из них измерима
(теорема 21). Однако теперь последовательность измененных функций
fn. сходится всюду к функции, равной f во всех точках
множества А и равной постоянной с во всех точках множества СЛ.
Эта функция, согласно изложенному выше, измерима, и
поскольку она почти всюду равна f, то f также измерима. Эта
теорема допускает следующее очень важное обращение.
|д-этажные функции
Этажные функции по отношению к мере Радона ц^О на
локально компактном пространстве X обобщают ступенчатые
функции, введенные для определения интеграла Римана.
Пусть F— произвольное множество. Отображение f прост-,
ранства X в множестве F называется \к,-этажньт или просто
этажным (когда это не приводит к недоразумению), если
существует разбиение X на конечное число непересекающихся
подмножеств Xi, X&, . .„ , Хп, таких, что каждое из них ц-измеримо
и на каждом из них отображение f постоянно. Такое разбиение
называется допустимым разбиением для отображения f.
Естественно, что для данного отображения f может существовать
бесчисленное множество таких разбиений точно так же, как это
было для ступенчатых функций. Среди них существует
наилучшее в том смысле, что оно содержит наименьшее возможное чис-
■> ->•
ло частей,'но оно нас не интересует. Если f и g — две этажные
->•
функции со значениями в векторном пространстве F, то сумма
f + g и произведение f на постоянный скаляр являются
этажными функциями.
Последнее утверждение очевидно. Первое же вытекает из
того, что если (ЛГ/)/бЕ/ является допустимым разбиением X для
-> ' -> .
f и (Xj)t^j является допустимым разбиением для g, то
каждое из множеств Xi П Xj измеримо и на каждом из них функция
f и функция g постоянны, а вместе с ними постоянна функция
f-f-g. Другими словами, этажные функции на X со значениями
17 Зак, 1339

514
Гл. IV. Интегральное исчисление
в векторном пространстве F образуют векторное подпростран-
■> ■>
ство Fx всех функций, заданных на X со значениями в F.
Теорема 23г. Для того чтобы отображение локально
компактного счетного в бесконечности пространства X в метризуе-
мое пространство F было ^.-измеримым, необходимо и
достаточно, чтобы оно было пределом [i-почти всюду некоторой
последовательности pi-этажных функций.
Доказательство. Каждая этажная функция измерима,
поскольку прообраз каждой части при отображении,
определяемом этой функцией, есть объединение измеримых частей X, на
которых функция постоянна. Согласно теореме 23, этим
свойством будет обладать функция, являющаяся пределом почти
всюду последовательности этажных функций.
Обратно, пусть f—измеримое отображение X в метрическое
сепарабельное пространство F. Пусть а0, аи а2, ... — некоторая
последовательность, плотная в F4 Зададим произвольное е>0.
Объединение всех шаров В(ап, е) равно F. Но эти шары не
являются непересекающимися. Образуем последовательность
множеств Сп,Е=В(ап, е)ПСВ(а0)е)П С5(аье)П • • • П CB(a„_i,e),
Множества С„,е не пересекаются, а их объединение равно F.
Множества D„, е = !~х(Сп, e) не пересекаются, и их объединение
равно X. Кроме того, Сп, г являются борелевскими множествами,
а, следовательно, Dn, e измеримы. Пусть К — некоторый компакт
X. Множества Dnt e [} К не пересекаются, измеримы, а их объ-
оо
единение равно К. Следовательно, ряд 2н.фп, г Л Л) сходится,
л=0
а его сумма равна ii(K). Для каждого б >0 можно определить
целое число N(e,K,8), зависящее от е, К, б и такое, чтобы
объединение Dhi е Л К для всех k > N имело меру <^б. Пусть
Е(г,К,б) является объединением множеств Dh 8 при k >
> N(e, К, б). Тогда ц(£(е, К, б) П К) ^ б.
Определим теперь следующим образом функции fn. Пусть
Кп — такая возрастающая последовательность компактов,* что
о
X является объединением внутренностей К„ (см. в лемме 3 к
теореме 11 последовательность Вп).
Известно, что для любого компакта К множества X
существует такое целое число ш, что КаКп Для п^. т. Положим
I ак, если xe=Dk,un, k^N(\/n, Кп> Шп+1),
[ а в других случаях.
Множества Dh, i/n для k = 0, 1, 2, ... не пересекаются,
измеримы и в объединении дают все множество X. Значит, fn
является по построению этажной функцией. Если ' х е Dhl i/n,

§ 3. Продолжение положительной меры 515
k < N(l/n, Kn, 1/2"+»), то fn{x)=ak, и так как f(Dkilln)<=
с Cfe, i/„ c= B(ak, 1/л), то имеем f (л:) <= B(aft, 1/я). Но тогда
d(f(x), fn(x)) ^ 1/я. Следовательно, /„(я) не сходится к /(*)
при л, стремящемся к бесконечности, только в том случае, когда
для бесконечного числа значений п точка х находится в
объединении множеств Dk, i/n, k>N(l/n, Кп, 1/2п+|), т.е. в
Е(1/п, Кп, l/2n+1). Множество Е точек X, в которых f„(x) не
сходится к f(x) при п, стремящемся к бесконечности,
удовлетворяет для бесконечного множества п соотношению Е с
с=£(1/л, Кп, 1/2»+'), а, значит, Е с (J £(1/л, /(„, 1/2"+') для
любого т. ге>т
Пусть К— произвольный компакт из X и m — такое целое
число, что Кт =з К. Тогда Е П /( с (J (£ (1/л, /(„, l/2re+I) П /Q.
ге>т
а, следовательно, ц(£ПЮ< 2 l/2re+I = 1/2"\
Так как в качестве m можно взять ско'ль угодно большое
целое число, то \i(E f) К) = 0. Поскольку это справедливо для
каждого компакта К из X, то \i(E) = 0, и, значит, /„ сходится
к f почти всюду при п, стремящемся к бесконечности.
Следствие 1. Пусть Fu F2, ..., Fm— некоторые
метрические пространства. Для того чтобы отображение f пространства
X в произведение F4 X ^2 X • • • X Fm, определенное
отображениями fi из X в Fit было измеримым, необходимо и достаточно,
чтобы каждое из составляющих отображений ft было
измеримым. В частности, для того чтобы отображение X в аффинное
конечномерное пространство, снабженное системой координат,
было измеримым, необходимо и достаточно, чтобы каждая из
его составляющих была измеримой.
Доказательство. Совершенно ясно, что если
отображение / измеримо, то каждое из его составляющих отображений fi
измеримо. В самом деле, каждая составляющая получается как
композиция/ и проекции F на Fit являющейся непрерывным
отображением. Остается лишь применить теорему 22.
Обратное утверждение носит более глубокий характер. Оно
опирается на теорему 23г. По предположению, ft является
измеримым отображением. Следовательно, существует
последовательность этажных отображений (Д)п множества X в Ft,
сходящаяся к ft, при п, стремящемся к бесконечности, всюду, кроме
точек множеств BidX меры нуль. Объединение В множеств Bi
также имеет нулевую меру. По определению топологического
произведения, в каждой точке ^еСВ последовательность
fn(x) = ((f\)n(x), {f2)n(x), ..., (fm)n(x)) СХОДИТСЯ К f(х). Сле-
довательно, f, являясь пределом почти всюду
последовательности этажных функций, измерима.
17*

516
Гл. IV. Интегральное исчисление
->
Следствие 2. Если F является векторным нормированным.
-> -> .■-*■.'
пространством, fug — измеримыми отображениями X в F и k —
скалярной измеримой функцией, то отображения f -\- g и kf
измеримы, т. е. ^-измеримые на X функции со значениями в F
образуют некоторое векторное пространство.
Доказательство. Отображение х—*■ f(x) + g(x)

является композицией отображения x->(f (x), g(x)) множества X в из-
-> ->
меримое, по следствию 1, множество F X F и непрерывного ото-
сражения (f, g)->f-\-g пространства F X F в пространство F.
Согласно теореме 22, это отображение измеримо. Точно так же
->
отображение x-+k(x)f(x) является композицией измеримого
-> ->
отображения х-*- (k(x),f(x)) множества X в К X F и непрерыв-
-> -> -> ->
ного отображения (k, f)->kf множества К X F в F.
Следствие 3. Пусть F, G, Н — векторные нормирован-
ные пространства, f и g — измеримые отображения X в F и G
соответственно, и пусть В — билинейное непрерывное отображе-
■*->-> -> -> ■> ->
ние F X G в Н. Тогда отображение B(f, g): x-+B(f(x), g(x))
->
из X в Н измеримо.
Доказательство. Рассматриваемое отображение яв-
ляется композицией измеримого отображения х-*- (f (x), g(x))
множества X в пространство F X G (следствие 1) и непрерыв-
> ■* ■*-
ного отображения В пространства F y^ G в пространство Н,
а, значит, согласно теореме 22, является измеримым
отображением1).
Из предыдущих теорем можно сделать вывод, что все
функции, встречающиеся на практике, измеримы. Для случая, когда
X — прямая и (л = dx, никто не может привести явный пример
неизмеримой вещественной функции. Конечно, пользуясь
аксиомой выбора, можно доказать существование вещественной
неизмеримой функции, например, характеристической функции
множества А, построенного на стр. 504.
') Предположение о том, что В билинейно, излишне. Мы приводим это
следствие потому, что оно полезно на практике.

§ 3. Продолжение положительной меры 517
Борелевские функции
Отображение f топологического пространства X в
топологическое пространство F называется борелевским, если прообраз
при отображении / каждой открытой части F является
борелевским множеством. Так как части F, прообразы которых при
отображении f является борелевскими, образуют, очевидно, а-ал-
гебру частей из F, то эта а-алгебра может содержать открытые
множества (или замкнутые множества) лишь тогда, когда она
содержит борелевские. Поэтому в определении можно заменить
открытые части на замкнутые или борелевские части из F. Это
понятие зависит только от топологии X и F. Например, часть из
X будет борелевской тогда и только тогда, когда ее
характеристическая функция является борелевской. Мы видим, что еслиХ
локально компактно и счетно в бесконечности, а метризуемое
пространство F сепарабельно, то борелевская функция на X со
значениями в F универсально измерима, т. е. ц-измерима по
любой мере Радона ц ^ 0 на X.
Борелевские функции обладают следующими свойствами.
1°) Композиция двух борелевских отображений является
борелевским отображением: если f является борелевским
отображением X в Y, a g— борелевским отображением Y в Z, то g ° f
является борелевским отображением X в Z, поскольку прообраз
борелевского множества является борелевским множеством.
2°)' Предел последовательности борелевских отображений X
в метризуемое пространство F является борелевским
отображением. Доказательство то же самоед что и доказательство
теоремы 23; следует лишь заменить в нем везде слово «измеримый»
на «борелевский»,
3°) Не ясно, является ли каждая борелевская функция
пределом последовательности этажных борелевских функций (под
этим понимается функция, принимающая лишь конечное число
значений на некоторых борелевских множествах; все это без
какой-либо связи с мерой Радона). Воспользуемся
обозначениями, введенными при доказательстве теоремы 232. Пусть ип —
функция, равная ап в множестве Dn,\in- Так как B(ak, l/n), а,
значит, Ck, l/n и, следовательно, Dk, \\n являются борелевскими
множествами и d(f, un) ^ 1/п, то функция ип является
борелевской. Однако она имеет счетное множество этажей Dk, i/n,
следовательно, не является этажно-борелевской. Функция ип
является простым пределом при пг, стремящемся к
бесконечности, этажно-'борелевских функций у„, т, где у„, m=ah в Dk, yn
для k sg m и уП| m=a e F вне этих множеств. Таким образом,

518
Гл. IV. Интегральное исчисление
каждая борелевская функция f со значениями в метризуемом
сепарабельном пространстве F является равномерным пределом
последовательности борелевских функций ип, каждая из
которых является простым пределом последовательности этажно-бо-
релевских функций и„, т.
4°) Для того чтобы отображение f пространства X в произ^
ведение F\ X ^2 X • • • X Pm было борелевским, необходимо и
достаточно в случае метрических сепарабельных пространств /•",-, .
чтобы каждая из составляющих ft отображения f была
борелевским отображением X в Ft. В самом деле, каждое
отображение ft является композицией / и непрерывной проекции F на Ft.
Так как / является борелевским отображением, то ft- также
будут борелевскими отображениями. Обратно, предположим, что
/,- — борелевские отображения и Fj — метризуемые сепарабель-
ные пространства. Теперь можно воспроизвести доказательство
следствия 1 теоремы 23г, но с двумя последовательными
переходами к пределу. Пользуясь свойством 3°), получаем, что
отображение / борелевское.
Замечание. Теперь можно существенно улучшить
результат теоремы 232.
1°) Пусть сначала Л — измеримое множество конечной меры.
Тогда существует убывающая последовательность открытых
множеств Сп =э Л, таких, что (д,(Сп) =£= 1*(А) + 1/га-
Пересечение Л* множеств Оп является борелевским множеством,
содержащим А, и ц(А* — Л)=0. Заменяя открытые множества
Оп =э А на компакты /(„с<4, можно построить борелевское
множество Л* сг А так, что |д,(Л—Л») = 0. Если мера
множества А не конечна, то его можно представить в виде
объединения множеств А Г) Кп, где Кп — возрастающая
последовательность компактов, объединение которых дает X, и, значит, во всех
случаях можно найти два борелевских множества Л* и Л„
такие, что Л» с: Л с Л* и ц-(А* — Л,)= 0.
Можно сказать, что с точностью до множества нулевой
(i-меры всякое ц-измеримое множество является борелевским.
Это обстоятельство весьма интересно, поскольку борелевские
множества универсально измеримы и зависят только от
топологий X. Можно еще сказать, что а-алгебра (д,-измеримых
подмножеств X (зависящая от \у) является наименьшей а-алгеброй,
содержащей все борелевские множества (зависящие лишь От
топологии X) и подмножества нулевой (а,-меры.
2°). Пусть теперь f является ц-измеримой функцией со
значениями в метрическом сепарабельном пространстве F- При
построении этажных функций fn в теореме 232 вместо того, чтобы
брать ./п = ah на Dk,\in, мы положим fn = Ьь, где Ьн-^ произ-

§ 3. Продолжение положительной меры 519
вольная точка множества B(ah, 1/я). Теперь можно bh выбирать
в образе f(X) cz F (ибо, если Dk, i/n не пусто, то f(X) Л В (ah, \/n)
не пусто). Таким образом, можно считать, что все функции fn
принимают значения в образе f(X).
3°) Пусть А — этажи функции /„. Каждый этаж является
объединением некоторого борелевского множества В,-_ п и
некоторого множества нуяевой меры. Функция gn, равная /п
на множествах Bit n и любой фиксированной точке
множества f(X) вне Bitn, является борелевской и почти всюду
равна /„. Поэтому функции gn могут полностью заменить
функции /п. Эти функции gn сходятся к / только почти всюду. Пусть
N—множество точек, в которых они не сходятся. Пусть N*—
борелевское множество нулевой меры, содержащее N. Пусть
hn— функция, равная gn на С N* и фиксированному элементу
множества f(X) на N*. Тогда hn будут борелевскими функциями
со значениями в f(X). Однако теперь они сходятся всюду к
некоторому пределу h, почти всюду равному / и принимающему
значения в f(X). Предел h последовательности борелевских
функций является борелевской функцией. Поэтому
окончательно получаем следующее:
Каждая измеримая функция /, определенная на X, со
значениями в F почти всюду равна некоторой борелевской функции,
принимающей значения в f(X), которая сама является почти
всюду пределом'последовательности этажно-борелевских
функций, значения которых лежат в f(X).
4°) Приведем улучшение другого рода. Предположим, что F
компактно, или просто, что f(X) содержится в компакте
множества F. Тогда для .каждого п найдется конечное число шаров
B(ah, l/n)t покрывающих это множество. Для построения
функции /„ вместо числа N(l/n, Kn, l/2n+1) в общем случае можно
взять конечное число этих шаров. Так как при этом d(fn,f) ^
^ 1/п, то этажные функции /„ сходятся всюду и равномерно
к функции /. Можно даже в этом случае выбрать их так, чтобы
fn(X)czf(X). Однако их невозможно взять борелевскими (за
исключением того случая, когда сама функция / является
борелевской; тогда по самому построению они будут
борелевскими).
Предположим, например, что F = С и что / является огра:
ничейной борелевской функцией с компактным носителем /С
Свои значения она принимает в некотором компакте
пространства С, а, следовательно, является равномерным пределом неко:
торой последовательности этажных борелевских функций, огра;
ничейных в их совокупности и имеющих носители в
фиксированном компакте (поскольку всегда можно умножить их на
характеристическую функцию компакта К).

520 Гл. IV. Интегральное исчисление
Интеграл от векторной этажной функции
->•
Пусть / есть (х-этажная функция с компактным носителем.
Тогда интегралом от этажной функции f no мере |х называют
величину
jTdii = ^lf,ii(Xl) (IV, 3; 14>
для допустимого разложения функции /. Здесь /г- — постоянные
значения функции / на Х{. Непосредственно видно, как мы в этом*
убедились в случае интеграла Римана, что такая величина не
->•
зависит от выбранного разложения функции /. Интеграл от
характеристической функции измеримого множества с компактным
замыканием является его мерой. Таким образом определенный,
интеграл является линейным отображением пространства этаж-
ных функции с компактным носителем и значениями в г в век-
-*■ -*■ '
торное пространство F. С другой стороны, если / является этаж-,
ной функцией, равной нулю в дополнении к измеримому
множеству А, то мы сразу же получаем оценку
</||/№<11?1ЫЛ). (IV.3; 15)
Если fug являются этажными почти всюду равными
функциями, то они имеют один и тот же интеграл.
Верхний интеграл от вещественной неотрицательной функции
Определение. Пусть X — локально компактное
пространство, счетное в бесконечности, снабженное мерой Радона
ц^О. Пусть /—вещественная функция ^0, определенная
на X, с конечными или бесконечными значениями1). Если /
ограничена и имеет компактный носитель, то верхним
интегралом от функции f относительно меры |х называется точная
нижняя грань интегралов относительно jx от этажных функций g
с компактным носителем ~^\. Пусть теперь / — произвольная
функция. Тогда верхним интегралом от / относительно jx
называется точная верхняя грань, конечная или равная +оо,
верхних интегралов от ограниченных функций ^0 с компактным
носителем, не превосходящих /.
') В этом случае выражение «вещественная функция» не верно, так как
функция принимает значения не в R, а в R.
jfdil

§ 3. Продолжение положительной меры
521
Верхний интеграл от / относительно ц обозначается через
Г fdn1), или J f(x)dn(x), или Г /, если это не приводит
к недоразумению.
Замечание. Пусть М — некоторое число ^0 и К —
некоторый компакт множества X. Обозначим через /м, к функцию,
равную f(x) в точках х компакта К, в которых f(x)^. M,
равную М в точках компакта К, в которых /(*)> М, и равную О
вне К. Тогда fM, к является ограниченной функцией с
компактным носителем, а ее верхний интеграл описывается согласно
первой части определения. Вторая часть эквивалентна
следующему утверждению: верхний интеграл от / является точной
верхней гранью верхних интегралов от функций fM, к- Можно также
сказать, что если Мо, Ми М2, . . . является числовой
последовательностью, стремящейся к -f-oo при п, стремящемся к -f-oo, и
если Ко, К\, Ki, . ■■ является возрастающей последовательностью
компактов, дающих в объединении X (такая последовательность
всегда существует, поскольку X предполагается счетным в
бесконечности), то верхний интеграл от / является пределом при п,
стремящемся к -f- со, верхних интегралов от функций }м , к •.
Теорема 24. Если функции fug почти всюду равны, то их
верхние интегралы равны.
Доказательство. Предположим сначала, что обе почти
всюду равные функции / и g ограничены числом Л(>0 и имеют
носители, лежащие в компакте К. Пусть В — множество нулевой
меры точек х, в которых f(x) Ф g(x).
Пусть теперь /i — этажная функция ^/. Если через g\
обозначить верхнюю огибающую функции /i и произведения М на
характеристическую функцию В, то gi будет этажной, gi^g,
и поскольку U и gi почти всюду равны, то J g < J gt = Г /|.
Если взять теперь точную нижнюю грань интегралов от /ь то
') Существенная разница между верхним интегралом Римана
(относительно dx) и верхним интегралом Лебега (относительно произвольной меры
ц^О) состоит в том, что первый получается одним переходом к пределу, в то
время как второй требует двух предельных переходов при вычислении точной
верхней грани и точной нижней грани. Здесь мы произвели четыре перехода
к пределу: два для того, чтобы определить измеримые множества, и два теперь.
Однако это всего лишь видимость, вызванная методом изложения, не
являющимся, как мы об этом уже говорили, наилучшим (см. примечание на стр. 490).
В действительности определение верхнего интеграла можно свести к двум
предельным, переходам, но не к одному.
Позже мы получим следующее соотношение между верхним интегралом
Римана и верхним интегралом Лебега: для ограниченной с компактным
носителем функции / Зг 0 на R при у, = dx верхний интеграл Римана ^
верхнего интеграла Лебега^

522'
Гл. IV. Интегральное исчисление
мы увидим, что ) g ^ ) /. Такое же рассуждение показывает,
что ) / ^ I g- Предположим теперь, что / и g —
произвольные функции. Пусть теперь /г—некоторая ограниченная функт
ция ^/ с компактным носителем. Если через g2 мы обозначим
нижнюю огибающую функций g и /г, то получим g2 ^ g- Кроме
того, так как /г и g2 почти всюду равны, ограничены и имеют
компактный носитель, то g^ \ ё2~ \ fz- Переходя к
точной верхней грани в верхних интегралах от /2, получаем:
I ё^ I /• Аналогичное рассуждение с перестановкой fug
окончательно приводит к равенству g= f.
Следствие. Если функция / ^ 0 почти всюду равна нулю,
то ее верхний интеграл равен нулю.
Теорема 25. Пусть fug-*- две функции ^ 0 на X и k —
скалярная постоянная. Тогда если f ^ g, то ) / ^ g.
Кроме того,
я * я * я * я * « *
/(/ + £)<//+/ ё и j kf = kj f. (IV, 3; 16)
Первая формула является неравенством выпуклости. В
противоположность тому, что имело место для интеграла Римана,
эта формула распространяется на счетное неравенство
выпуклости •), в чем проявляется существенное преимущество интеграла
Лебега над интегралом Римана.
Доказательство. Свойства эти очевидны. Докажем,
например, первую из формул (IV, 3; 16).
Предположим сначала, что fug ограничены и имеют
компактный носитель. Тогда, с точностью до очевидных изменений,
доказательство совпадет с доказательством, приведенным для
интеграла Римана в теореме 2. Рассмотрим теперь общий
случай, когда fug произвольны. Если ввести определенные выше
функции /м, к, то мы получим неравенство
V + g)M.K<fM.K + gM.K, (IV.3; 17)
откуда
f(f + e)M,K<f + J" g«.K<l'f+fg'
') Следствие 3 теоремы Щ,

§ 3. Продолжение положительной меры 523
Переходя в интеграле (/ + g)Mi K к точной верхней грани по
всем значениям М и всем компактам К cz X, получаем
требуемый результат.
Легко видеть, что если А является некоторой частью X и
фд — ее характеристическаяфункция, то
$\А = ц'(А)1). (IV, 3; 18)
В частности, | 1 является мерой X, т. е. нормой \х.
• Т е о р е м а 26. Если верхний интеграл от f ^ 0 конечен, то
функция f почти всюду конечна. Если верхний интеграл от f
равен нулю, то и функция / почти всюду равна нулю.
Доказательство. Пусть сначала / < +°°-
Обозначим через Ап множество точек х, в которых f(x)^n. Если фп
является его характеристической функцией, то / ^ Яфп, откуда
вытекает неравенство
1*!>п\х'{Ап). (IV, 3; 19)
Если через А обозначить множество точек х, в которых
f(x)= +°°. то ПРИ любом п будет справедливым неравенство
р>.лцШ ■ (IV, 3; 20)
из которого следует, что ц,*(А)= 0, т. е. / почти всюду
принимает конечные значения.
Предположим теперь, что J"/ = 0. Обозн ачим на этот раз
через Bh множество точек х, в которых f(x)^ l/k, а через ф& —
его характеристическую функцию. Так как /^-г-фй, то имеет
место неравенство
° = f/>THW. (IV,3;21)
из которого следует, что \x,*(Bk)—0. Множество В точек х,
в которых /(х)>0, являясь объединением счетной совокупности
множеств Bh с нулевой мерой, само имеет нулевую меру, а,
следовательно, функция / почти всюду равна нулю.
') Это очевидно, если А компактно. Если же А произвольно, то, согласно
замечанию 1°) к теореме 19, результат можно получить с помощью формулы
ц*(А)= sup р.* (А П ft) (ft — компакты).
К<=А

524
Гл. IV. Интегральное исчисление
Интегрируемость функций с векторными значениями
Определение. Пусть X— локально компактное
пространство, снабженное мерой Радона ц ^ 0 и F — векторное
нормированное пространство над полем вещественных или
комплексных чисел. Говорят, что функция /, определенная на X,
со значениями в F ^-интегрируема, или интегрируема
относительно ц, или просто интегрируема, когда это не приводит к
недоразумению, если, каково бы ни было е > 0, существует такая
функция g, определенная на X, со значениями в F, ц-этажная
и с компактным носителем, для которой имеет место
неравенство:
f\\7-g\\d\x<e. (IV,3;22)
Сказанное эквивалентно следующему определению:
существует такая последовательность /,, /2, h, ... этажных
функций с компактными носителями, определенных на X, со
значениями в F, что величина ) \\f— f„\\ стремится к нулю при п,
стремящемся к бесконечности. Такая последовательность назы-
вается аппроксимирующей последовательностью функции f для
интеграла Лебега относительно ц. Вместо интегрируемая
функция говорят также суммируемая.
Если две функции, определенные на X, со значениями в F
почти всюду равны и если одна из них интегрируема, то
интегрируема и другая функция, которая будет иметь ту же
аппроксимирующую последовательность (теорема 24).
'Замечания. Замечания Г)—3°) на стр. 424—425 могут
быть здесь повторены с заменой слов «интегрируема по Риману
относительно dx на R» словами «имеет компактный носитель и
интегрируема по Лебегу относительно ц на X» (ограничение
«с компактным носителем» не нужно для замечания 1°)) и
слова «ступенчатая» на слово «ц-этажная». Если нам надо будет
сделать ссылку на это замечание, то мы будем говорить: см.
замечания Г), 2°) или 3°) на стр. 524.
Интеграл Лебега от функции с векторными значениями
Теорема 27. Пусть f — отображение X в банахово про-
странство F. Если f интегрируема и если fn образуют
аппроксимирующую последовательность этажных функций с ком-

§ 3. Продолжение положительной меры
525
пактными носителями для f, то интегралы fn имеют предел,
не зависящий от выбора аппроксимирующей
последовательности.
Доказательство аналогично доказательству теоремы 3.
Определение. В условиях предыдущей теоремы общий
предел интегралов (п по всем аппроксимирующим
последовательностям называется интегралом от функции f
относительно ц. Интеграл этот обозначается различными способами:
Jfdli, {?ц, jl(x)dlx(x), j?1). (IV,3;23)
Если две интегрируемые функции почти всюду равны, то они
имеют один и тот же интеграл, поскольку у них одни и те же
аппроксимирующие последовательности.
Если f является отображением некоторой части У множе-
->■ ->
ства X в F, то говорят, что f интегрируема на У, если интегри-
-> • -> ->
руемой будет функция f, определенная на X, равная f на У и О
вне У. При этих условиях полагают
|T=jf2)- (IV,3;24)
у
Замечание. Естественно, каждая этажная функция с
компактным носителем интегрируема и ее интеграл определяется
по формуле {IV, 3; 14).
-> ->
Теорема 28. Если fug— две интегрируемые на X функ-
-> -> ■>
ции со значениями в F и k — скалярная постоянная, то f + g
■*■
и kf также интегрируемы; кроме того, имеют место следующие
равенства:
jkj=kjj и J(T+g)==Jt+JJ. (IV,3;25)
Доказательство аналогично доказательству теоремы 4.
Эта теорема говорит о том, что ц-интегрируемые на X
функции со значениями в F образуют векторное пространство по
') Имеется такое множество различных обозначений для интеграла от
f относительно (i, что остается лишь сказать: всякая формула, в которой
присутствует векторная функция / и мера р.^0, означает интеграл от f
относительно р..
■> ■ f -*■
2) Если f уже определена всюду на X, то / является произведением f(fy
функции f на характеристическую функцию ф.у множества Y.

526
Гл. IV. Интегральное исчисление
отношению к полю скаляров К и что интеграл является
линейным отображением этого векторного пространства в F.
Следствие 1. Если Y и Z — два подмножества X, то функ-
ция I будет интегрируемой на их объединении тогда и только
тогда, когда она интегрируема на каждом из этих подмножеств;
при этом
J f^l'F+l?- (IV,3;26)
Y[)Z Y Z
Доказательство аналогично доказательству следствия
теоремы 4.
Следствие 2. Если f является этажной функцией, J=
= 2/гфу> где ft — постоянные, a q> — характеристические
i i I
функции измеримых множеств Xi конечной меры (не обязатель-
но имеющих компактное замыкание), то f интегрируема и имеет
место соотношение (IV, 3; 14). В частности, если А является
измеримым множеством конечной меры, то \ <рА = \i (A).
Доказательство. В силу теоремы 28, достаточно
доказать только последнее утверждение. Пусть Кп — возрастающая
последовательность компактов, объединение которых равно X.
По теореме 19, ц(Л) = lim ц(А [\Кп) и lim ц(Л — Л ПКп) = 0.
П->- оо П->- оо
Характеристические функции <РАпк являются этажнЫми с
компактным носителем. Поэтому Ф^пк =(* (Л [\Кп)_ и (согласно
(IV, 3; 18)) f (Фд - Флп^) = ц* (А - А П Кп) =_ I* (Л - А П Кп)
стремится к нулю. Таким образом, (рАГ1К образуют
аппроксимирующую последовательность для q>A, которая поэтому
оказывается интегрируемой и Г ф .= lim Г ф-п„ = lim ц(Л Г\Кп)=^{А).
J П+<х>-> 11Л« Я->-оо
Т е о р е м а 29. Если функция /, определенная на X, со значе-
->• -> ->
ниями в F интегрируема, то функция ||/||: х—* ||/(х)|| также
интегрируема и имеет место неравенство
llfflkfllfll. (IV,3;27)
Доказательство аналогично доказательству теоремы 5.

§, 3: Продолжение положительной меры
527
Следствия. Здесь можно повторить следствия теоремы 5.
В следствиях 3 и Зг надо заменить [а, Ь] на произвольную
измеримую часть Y множества X и (Ь — а) на ц(У). Ссылаясь на эти
результаты, мы будем говорить: следствия 1, 2, 3, 32, 4, 5
теоремы 29.
Теорема 30. Если ф является функцией с комплексными
значениями, принадлежащей множеству W(X), то она
интегрируема относительно ц и ее интеграл ф совпадает с ц(ф).
Эта теорема весьма существенна. Она говорит о том, что
довольно сложное построение, выполненное нами для
интегрирования, дает некоторое продолжение исходной линейной
формы ср->-ц(ф), определенной на W{X).
Доказательство. Докажем прежде' всего, что каждая
функция (ре?(1) интегрируема и, более общо, что каждая
непрерывная с компактным носителем К функция / на X со
значениями в F интегрируема. Пусть Т — некоторая компактная
окрестность К, и пусть задано произвольное число е > 0. Для
каждой точки сеК выберем такую ее окрестность Та а Т,
чтобы для х*=Уа выполнялось неравенство || / (х) — / (а)||^
^e/jx(F). Конечное число таких окрестностей покрывает все
множество К. Пусть это будут окрестности Та^, Уа2, ■ ■ ■ > Уап-
Положим d = rat, С2 = Га2 П CTai, ..., Сп = Гап[\С (П, U
U У a U • • • U "У а _ )• Каждое из множеств С< является бореле-
вским, а значит, измеримым. Обозначим через /е функцию, рав-
ную /(а,) в С; и равную 0 в дополнении к объединению Та,.
Функция /е — этажная, имеет компактный носитель и ||7—Те 11^
^—Т¥\ • поэтому ||/ — /81| ^е. Поскольку е произвольно,
f интегрируема.
Остается теперь доказать, что для любой функции (ре?(1)
|х(ф)= фйц. Для доказательства нам понадобятся две
леммы.
Лемма 1. Пусть А — измеримая часть X, ф — непрерывная
функция с компактным носителем, мажорируемая
характеристической функцией %А множества А. Тогда ц(ф) ^ц(Л).
Доказательство леммы 1. Очевидно, ф^ I %д =
= |х(Л). Однако нас интересует не ф, а ц (ф), и мы еще не
знаем, равны ли они между собой.

528
Гл. IV. Интегральное исчисление
Пусть О — некоторое открытое множество zd А. Если мы
покажем, что (j,(ф) ^ ц(С), то, переходя к точной нижней грани
по всем О, мы получим нужный нам результат. Все сводится
к тому, чтобы исключить А и заменить его на открытое
множество О. Затем можно предположить, что О компактно.
Действительно, если У является компактной окрестностью носителя (по
предположению компактного) функции ф, то можно будет за-
о
менить множество О на множество О Л У, имеющее компактное
замыкание. Наконец, можно считать функцию ф ^ 0 или в
противном случае заменить ее на ф+. Пусть теперь Кп — компакт
{х ^ X; ф(х)^ \/п}, п ^ 1. Пусть ап — непрерывная функция,
О ^ а„ <; 1, с носителем в О, равная 1 на Кп (следствие 1
теоремы 11). ' .
Положим ф„ = апф- Функция фп непрерывна, имеет носитель
в О, 0 ^ ф„ ^ 1, а, значит, ц(фп) ^ и(С) (см. определение на
стр. 490). Однако |ф — ф„| = (1 — а„)ф^1/п и носитель этой
функции лежит в О. Следовательно, ц(ф — Ф„) ^—1| ц ||j и> зна"
чит,
ц(ф)<(*(ф») + ||||г1^<1*(С0 + 711|*1Ь-.
Так как п произвольно, то лемма доказана.
Лемма 2. Пусть g — векторная этажная функция с
компактным носителем, мажорируемая по норме числом М, причем
число множеств, на которые разбито пространство X, равно N.
Тогда, каково бы ни было число 6 > 0, существует такая раз-
ложимаях) непрерывная функция у с компактным носителем,
что:
1°) й~ч\\<Ш;
2°) у = g всюду, кроме множества с мерой <:6;
3°) если функция g является скалярной, а, следовательно,
уе=9{Х), то Jy-|i(y)|<6;
4°) если g ^ 0, то у ^ 0.
Доказательство леммы 2. Пусть g—2igt%A' гДе
»=1 '
%Д—характеристическая функция этажа л\- функции g, на
' -> -> -> ■
котором g принимает постоянное значение gi ф 0. Пусть К —
компакт и Oi — открытое множество, такие, что /С,- с: Л, сг О и
n{Oi) — ii(Ki)s^8lNM', где М' = тах(М,1). Пусть уг — не-
') Это понятие било введено в следствии 8 теоремы Ut

§ 3. Продолжение положительной меры 529
прерывная функция, 0 ^ уг ^ 1> с носителем в О и равная 1 на
некоторой окрестности компакта Ki. Положим у = 2j gi\i- Тогда:
1°) 0<5С^< 1, 0<у,<1, а, следовательно | у,-— X^l5^1
H||J-Yll<2ll?<ll|x,!,-Y*|<tfAf.
2°) На Ki у1=%А.= \,ъаС01 у/ = Хлг = 0. а, следовательно,
всюду, кроме множества 0{ — К{ меры ^.6/NM' ^.6/N. Поэтому
-> •>
g = Y всюду, кроме некоторого множества, содержащегося
ЛГ
в U^'-*')' меРы <N(6/N) = 6.
»=i
Замечание. Из 1°) и 2°) вытекает, что \\g— у II ^ bNM.
3°) Пусть F = C, a J Yi и ц(уг) оба заключены между ц(К{)
и ц (<?<), а, следовательно, J Yi — Hy*) < ЦГ(<Л) — Ц (^i) <
б
N'M'
h
4°)
^ NM
— и- (y) J
Если g
Тогда
ЛГ
i ^ 0, то у
0.
Доказательство теоремы. Пусть фе??(Х).
Зададим е > 0. Тогда найдутся такие этажные функции g и А^О
с компактным носителем, что |ф — g]^h и I Л^е/2 (см.
замечание 2°) на стр. 524). Пусть М — максимум модулей
величин 1, ф, g, fi и N— максимальное число этажей функций g и h.
Применим последовательно к g и h ^ 0 лемму 2 при б =
= е/[2(1 -\-5MN)]. Согласно этой лемме, найдутся две
непрерывные функции аире компактными носителями,
обладающие свойствами 1°)—4°). Прежде всего,
|/ф-|*(ф)|<|/ф-/а| + |/а-|*(а)| + 1|*(а)-ц(ф)|. (IV,3;29)
Далее,
1°) |ф_а|<|ф-£| + |£-а|<Л + |Я-а|.
где Г h <!е/2. Функция g — а равна нулю всюду, кроме
множества меры ^ б, на котором она мажорируется по модулю

530
Гл. IV. Интегральное исчисление
числом NM, а, значит, \\g — а|=£^6ЛШ. Окончательно получаем
|| Ф- |а|<|- + 6ЛШ. (IV,3;30)
2°) I J а — |* (а) <б. (IV, 3;31)
3°) | |л (а) — |х (ф) | = | |х (а — Ф)'К|х (| а — ф |).
Из 1°) следует, что |а — ф|<й+|£ — а|<р'+|Л— р| +
~\-\g — а|. Далее, функция \g — а\ равна нулю всюду, кроме
множества меры б, где она мажорируется числом MN; функция
\h — р| также равна нулю всюду, кроме множества меры б, где
она мажорируется числом NM. Поэтому |а — ф|—Р является
непрерывной функцией с компактным носителем, равной нулю
• всюду, кроме некоторого измеримого множества меры ^26, на
котором она мажорируется числом 2NM.
Применяя к (|ф — а\ — $)/2MN лемму 1, получаем:
I |i (а) - ц (ф) К 26 • 2NM = AN Мб. (IV, 3; 32)
Из (IV,3;30) — (IV,3;32), в силу соответствующего выбора б,
получаем:
J Ф — |х (ф) < у + 6ЛГМ + 6 + 46NM < е. (IV, 3; 33}
Так как е произвольно, то I ф = |х (ф).
Замечание. Смешно проводить доказательство для такого
очевидного утверждения, но это пришлось сделать в качестве
неизбежного наказания за избранное изложение теории Лебега
(см. примечание на стр. 490).
Следствие 1. Мера Радона ц ^ 0 на X будет известной,
если будут известны меры открытых множеств (или компактных
множеств) ').
Прежде всего, формулы ц (/С) = inf ц{0) и ц {О) = sup ц (К)
0=>К К<=0
говорят о том, что если известны меры открытых множеств, то
известны меры компактов, и наоборот. Но тогда будут известны
меры всех множеств, а, значит, интегралы всех функций. Из
равенства ц (ф) = фф, вытекает, что ц(ф) известна для
Ф е^(Х) и потому известна мера ц.
') Мы не утверждаем, что можно произвольно выбирать меры открытых
множеств. Мы говорим лишь, что две меры Радона ^0, дающие для
открытых множеств однц ц те же меры, совпадают.

§ 3.' Продолжение положительной меры
531
Следствие 2. Мера Радона ц ^ 0 на вещественной
прямой R будет известной, если будут известны меры открытых
интервалов (или замкнутых интервалов).
Прежде всего из формул ii{[a, b]) = Птц(]а — е, b + e[)
е-»0
и ц(]а, 6[) = П'тц([а + е, b — e]) вытекает, что один из этих
е-И)
случаев следует из другого.
Затем легко показать, что каждое открытое множество из R
является объединением счетного множества непересекающихся
интервалов. Тогда меры открытых множеств известны, и
остается лишь применить следствие 1.
Например, теория интеграла Римана (§ 1) позволила
построить меру Радона dx на R, которая для каждого интервала
\а,Ь\ дает меру b-г-а. Настоящее следствие говорит о том, что
в этом случае достаточно, знать только это свойство.
Замечание. Пусть теперь ф — скалярная непрерывная
функция с некомпактным носителем,' но такая, что носитель ц
и носитель ф имеют компактное пересечение К. Мы определили
ранее ц(ф) (теорема 16) даже в том случае, когда ц является
векторной мерой. Легко видеть, что если ц ^ О, то функция ф
является ^-измеримой и ц(ф) совпадает с | у dp.
В самом деле, если aef(I) равна 1 на некоторой
окрестности К, то ц(ф) нами определялась как ц(аф)- Функция аф
лежит в Ч?(Х), а, следовательно, интегрируема и, согласно
теореме 30, ц(аф)= Г (аф)^ц. Функции аф и ф равны на носителе
ц1), поэтому они ц-почти всюду равны между собой;
следовательно, ф интегрируема и J фф,= Г (аф) d[i = ц (аф) = ц (ф).
Т е о р ем а 31. 1°) Если f является ограниченной
вещественной функцией Z^O с компактным носителем на R, то ее верхний
интеграл Римана по dx не меньше ее верхнего интеграла
Лебега.
2°) Если f является функцией, определенной на
вещественной прямой, со значениями в F, интегрируемой по Риману
относительно меры dx, то дна тем более интегрируема по Лебегу и
ее интеграл в смысле Лебега равен интегралу в смысле Римана.
Доказательство. Докажем сначала 1°). Обозначим че-
рез f (соответственно J f) верхний интеграл в смысле
') В каждой точке носителя ц либо а = 1 (если эта точка лежит в К),
либо ф = 0; поэтому всюду аф = ф. С другой стороны, мы видели на стр. 492 '
в замечании 3°), что дополнение к носителю имеет нулевую меру.

532
Гл. IV. Интегральное исчисление
Римана (соответственно в смысле Лебега). Поскольку каждая
ступенчатая функция является этажной функцией, то,
вспоминая определение этих двух верхних интегралов, получаем:
Неравенство не обязательно может перейти в равенство.
Может иметь место знак <;. Рассмотрим, например, функцию /,
равную 1 во всех рациональных точках отрезка [0, 1]и0восталь-
ных точках. На стр. 492 мы видели, что I /=1. Однако
так как множество рациональных чисел имеет меру, равную
нулю, то Г / = 0.
->
Пусть теперь /—некоторая интегрируемая по Риману
функция н /„ — аппроксимирующая последовательность,
образованная из ступенчатых функций с компактными носителями, а, зна-
чит, тем более и из этажных функций. Тогда ||/ — /п||^
^ II/ — /nil стремится к 0. Это значит, что /„ образуют
аппроксимирующую последовательность для интеграла Лебега, а,
следовательно, / интегрируема по Лебегу, и ее интеграл J,
являющийся пределом интегралов Г /„= fn, равен /.
Напротив, указанная выше функция / ^ 0 интегрируема по
Лебегу, имеет интеграл, равный нулю (поскольку она почти
всюду равна нулю), однако не интегрируема по Риману.
Теорема 32. Каждая непрерывная на X функция со зна-
■ ■*■ ' ->
чениями в F и компактным носителем интегрируема. Пусть f —
функция, определенная на X, со значениями в F. Для того что-
->
бы f была интегрируемой, необходимо и достаточно, чтобы, ка-
->
ково бы ни было е > 0, существовала такая функция g, опреде-
ленная на X, со значениями в F, непрерывная и с компактным
носителем, что \\J—gll^e, или необходимо и достаточно,
чтобы, существовала аппроксимирующая последовательность
функции /, образованная из непрерывных функций с
компактным носителем. Эти функции могут даже быть выбраны
разложимыми1).
') См. определение в следствии 8 теоремы И.

§ 3. Продолжение положительной меры
533
Доказательство. Интегрируемость непрерывных
функций с компактным носителем была установлена в начале
доказательства теоремы 30. Следовательно, всякая функция, имеющая
аппроксимирующую последовательность, образованную из
непрерывных функций с компактным носителем, интегрируема.
Пусть теперь / — произвольная интегрируемая функция.
Тогда существует такая этажная функция g с компактным носи-
телем, что ||/ — g||<Ie/2. Затем, согласно лемме 2, из
доказательства теоремы 30 следует существование такой
разложимой непрерывной функции \ с компактным носителем, что
fill"— YlKSMW. Выбирая б = e/2NM, получим Jill" — YlKe/2,
откуда || J—Yll^e, что и требовалось доказать.
■>
Замечание. Эта теорема в особенности удобна, когда F
является полем комплексных чисел, так как тогда она
представляет , / как предел величин \i(g), получающихся
непосредственно из определения ц как линейной формы, заданной на
пространстве Ф(Х).
Интегрируемость и интегралы от функций,
определенных почти всюду
Пусть сначала / является вещественной функцией ^0,
определенной почти всюду на X. Продолжим ее произвольным
образом до некоторой функции f ^ 0, определенной всюду на X.
Г* ^
Интеграл / не зависит от выбранного продолжения,
поскольку любые два таких продолжения почти всюду равны
между собой. Общее их значение называется верхним
интегралом от / и обозначается через /. Точно так же, если /
является функцией, определенной почти всюду на X, со
значениями в F и f— произвольное продолжение этой функции до
функции, определенной на всем X, со значениями в F, то ин-
тегрируемость f и величина ее интеграла не зависят от
выбранного продолжения.
Если f интегрируема, то говорят, что / интегрируема и об-
/• ~% -*■
щее значение интегралов / называется интегралом от / и
обозначается через /.

534
Гл. IV. Интегральное исчисление
§ 4. ТЕОРЕМА ЛЕБЕГА О СХОДИМОСТИ. ПРОСТРАНСТВО I'
Теорема о сходимости, которую мы сейчас докажем,
значительно сильнее всего того, что излагалось в связи с интегралом
Римана, и именно благодаря этой теореме интеграл Лебега
обладает существенным преимуществом по сравнению с
интегралом Римана. Условия, лишь немногим более ограничительные,
чем обычная сходимость функций, оказываются достаточными
для обеспечения сходимости интегралов.
Вначале мы приведем теорему, показывающую, как можно
перейти от простой сходимости к тому, что напоминает
равномерную сходимость.
Теорема 33 (Егоров). Пусть /„—последовательность
измеримых отображений X в метрическое пространство F.
Предположим еще, что эта последовательность просто сходится
^-почти всюду к функции /. Тогда, каким бы ни был компакт К из X
и каково бы ни было число б > 0, найдется такая компактная
часть К6 компакта К, что ц(К — К&) =SS б, при этом на К&
отображения fn равномерно сходятся к отображению /.
Доказательство. Заранее ограничимся компактом К-
Зададим фиксированное число е' и обозначим через Ап, г-
множество точек х из К, в которых d(/„(x),/(х)) > г'.
Докажем сначала, что это множество Ап,г- ^.-измеримо.
Поскольку каждая из функций /„ и / измерима (теорема 23), то
отображение х->-(/„(х),/(х)) является измеримым
отображением К в произведение F X F (следствие 1 теоремы 23г). Так
как (х, у)-*- d(x, у) является непрерывным отображением F X F
в JR (теорема 17г гл. II), то из теоремы 22 следует, что
вещественная функция x->-d(/„(x),/(х)) измерима. Множество
А„, е' является пересечением /Си прообраза открытого
множества ]&', +оо[ из R при этом отображении. По определению, это
множество измеримо. Обозначим теперь через £tm,e'
объединение (J Ап,в'. Множество эФт<&> измеримо. Точка х е К
принят
надлежит этому объединению тогда и только тогда, когда
существует такое целое п ^ т, что d(fn(x), /(х))>- &'.
Последовательность st-m.e' является убывающей последовательностью
измеримых множеств. Если точка х принадлежит пересечению
-оо
Р) $Фт,г множеств эФт,г', то последовательность fn(x) не мо-
т=0
жет сходиться к /(х), а поскольку /„ сходятся почти всюду к /,
то это пересечение имеет меру, равную нулю. Так как
убывающая последовательность множеств s4-m.e' пересекается по
множеству меры нуль, то из п. 5°) теоремы 19 следует, что для задан-

§ 4. Теорема Лебега о сходимости*
535
ного б' > О существует такое целое пг, что \i {s£m, г) =5^6'').
Обозначим через s&v,w это множество зФт>г'-
Таким образом, мы доказали следующий результат:
Каковы бы ни были числа б' н е' > 0, существуют такое
целое число пг' = т'(б', е') и такое множество s£&',е-с/С меры
^б', что для всех п ^ пг'(8', е') и любого х е К — stv.s' имеет
место неравенство d (/„ (х), / (х)) ^ е'.
Будем теперь брать последовательно 6' = 6/2v+l, e'=l/2v,
v=l, 2, .... Рассмотрим последовательность целых чисел
mv = m'(6/2v+1, 1/2V) и множеств s&y = ^e/2v+', 1/2*- Обозначим
через ,s$6 объединение множеств .s^v. Множество s&& является
измеримым множеством меры ^6/2, содержащимся в К. Каково
бы ни было v, для п ^ mv, теперь имеет место неравенство
d{fn(x), /(x))^l/2v, лишь бы только х не принадлежал
множеству s&&. Это означает, что на дополнении Ко этой части зФь
по отношению в К последовательность /п равномерно сходится
к/. Имеем: \i (Кб) = ц (К — ^б)^ МЮ — 6/2. Теперь, по
определению меры множеств, найдется такой компакт /Св,
содержащийся в Кб, что (i(/Ce) ^ (i(/C)—б или \i(K — /Сй)^б и
на /Св функции /п равномерно сходятся к /, чем и заканчивается
доказательство теоремы.
Замечания. 1°) Может показаться, что возможно найти
такую часть К& компакта К, чтобы ц(К—К&)= 0 и чтобы на
К6 функции. /п сходились равномерно к /, но это не так.
Рассмотрим, например, последовательность вещественных функций,
определенных на R по формуле
f 1 для 0<х< 1/га,
/,W= n (IV, 4; 1)
[ 0 в остальных точках.
Очевидно, при п, стремящемся к +оо, fn сходятся просто к 0.
На компакте [0, 1] при любом е, 0 < е <' 1, и любом п
множество точек х, в которых |/п(*)|>е, имеет меру 1/га > 0, что
противоречит предположению.
2°) Если X не компактно, то заменить К на X невозможно.
В самом деле, рассмотрим вещественные функции вещественной
переменной и возьмем в качестве /п функцию, определенную по
формуле
f 0 при х<п,
МО ={l при Х>п. <IV'4;2>
') Только здесь мы воспользовались тем фактом, что рассмотрение
ведется на компакте К; множества зФт е, имеют конечную меру, и теорема мо-
?кет быть применена.

536 Гл. IV. Интегральное исчисление
Очевидно, что последовательность функций /„ просто сходится
к функции 0. Однако, каково бы ни было е, 0 < е < 1, и каково
бы ни было п, множество точек х, в которых справедливо
неравенство |/п(*)|>е, измеримо и имеет бесконечную меру.
Следствие (свойство Лузина). Пусть f — отображение X
в метризуемое сепарабельное пространство F. Если f
^-измеримо, то, каким бы ни был компакт К из X и каково бы ни было
б > 0, найдется такой компакт K&czX, что ц(К—К(,)^б, a
сужение f на К6 является непрерывным отображением, и
обратно.
Доказательство. 1°) Предположим сначала, что /
является этажной функцией. Эта функция принимает постоянные
значения U на конечном числе непересекающихся множеств At,
i = 1, 2, . .., N, объединение которых равно X. Пусть К—
некоторый компакт. Для каждого i обозначим через Кг такой
компакт czAi П К, что \i(Ki) ^ \i(Aif] К)—б/Xf. Тогда в
качестве Кь достаточно взять объединение Кг- Множество Кь яв-
N
ляется компактом, ц {К — К&) ^ \ -тг = jt N = б и, кроме
того, К6 является объединением непересекающихся и
замкнутых множеств Кг- Поскольку прообраз каждого замкнутого
множества (и даже всего множества) из F при отображении /6
является объединением Кг, а, следовательно, замкнут, то
сужение /в функции / на К(, непрерывно на К&-
Пусть теперь / — произвольное измеримое отображение.
Согласно теореме 23г, существует последовательность этажных
функций /„, сходящихся почти всюду к / при п, стремящемся
к бесконечности. Согласно теореме Егорова, если мы выберем
некоторую метрику на F, то найдется такой компакт К&,
ц (К — Кб) <^ 6/2, на котором функции /„ сходятся равномерно
к /. Поскольку /„ является этажной функцией, то из только что
доказанного вытекает, что можно найти такой компакт Кп с
с: Кб, ц(Кп — К&) ^б/2"+2, чтобы функции fn были непрерывными
оо
на Кп- Положим теперь Кь= f] Кп- Это множество является
некоторым компактом из к и к-Кь^к-кди U(k«-*«)Ь
ОО
а, следовательно,у.{К — К6) <и(К— 'Кб) + ^^{Кб — Кп) <у +

§ 4. Теорема Лебега о сходимости
537
-f-—=6. Кроме того, на К& все функции /„ непрерывны и
равномерно сходятся к /, а, значит, функция / непрерывна на К&-
Мы использовали теорему Егорова, в которой пространство F
предполагается метрическим (для того чтобы иметь
возможность говорить о равномерной сходимости). Однако
окончательный результат (непрерывность / на К6), очевидно, не зависит от
этой метрики.
2°) Обратно, предположим, что свойство Лузина для
функции / выполнено. Пусть О — некоторое открытое множество F
и B = f~](0). Поскольку / непрерывна на /С6, то В П Кй
является открытым множеством компакта Къ. Таким образом, это
множество является пересечением некоторого открытого
множества из X и компакта /С6,а, значит, [х-измеримо. Далее,
I* (В Л Кь) <ц. (В Л К) <И* (В Л Ю<И (В Л К6) + ц* (В Л {К - Кь))<
<ц(ЯЛ*в) + |1(*-*в)<ИЯЛ*в) + в,
а, следовательно, ц*(В [} К) — ц*{В [] К) ^ б. Поскольку б
произвольно, то \i*(B Л /С)= ц*(В П К), что означает
измеримость множества ВПК. Так как полученное справедливо для
любого компакта К и X является счетным объединением
компактов, то В = f~v(0) измеримо, а / является измеримым
отображением.
Замечание. Обратное утверждение 2°) справедливо для
произвольного топологического пространства F (лишь бы, как
всегда, X было счетным в бесконечности). Напротив,
утверждение 1°) использовало теорему Егорова, из-за которой F
предполагалось метризуемым, и теорему 232, в которой требуется, как
это видно из ее доказательства, чтобы F было метризуемым и
сепарабельным. Таким образом, свойство Лузина, вообще
говоря, является^ более сильным, чем измеримость, однако оно
ему эквивалентно, если метризуемое пространство F сепара-
бельно. Напомним, что на стр. 510 мы дали предварительное
определение измеримости, предполагая метризуемое F сепарабель-.
ным. Теперь мы можем дать окончательное определение: каково
бы ни было топологическое пространство F, отображение f
называется измеримым, если оно обладает свойством Лузина.
Теперь можно показать, что теоремы 21, 22 и следствия 1, 2, 3
теоремы ,232 верны без каких-либо условий, налагаемых на F;
теоремы 23, 232 верны тблько для метризуемого пространства F;
георема Егорова 33 предполагает F метрическим (для того
чтобы можно было говорить о равномерной сходимости). Послед*
нее следствие (Лузина) можно перефразировать, говоря, что
если / измерима, то прообраз каждого борелевского множества

538
Гл. IV. Интегральное исчисление
из F измерим, в то время как обратное утверждение справедливо
лишь в том случае, когда метризуемое F сепарабельно.
Учитывая сказанное в примечании на стр. 510, мы проявили
осторожность, рассмотрев только предварительное определение,
предполагающее F метризуемым и сепарабельным, для того
чтобы высказать утверждение с предположениями,
соответствующими окончательному определению.
Теорема 34 (частная теорема Лебега). Пусть X —
локально компактное пространство, снабженное мерой Радона а ^ 0,
и F — пространство Банаха. Пусть fn — последовательность
функций, определенных на X, со значениями в F, имеющих
носители в одном и том же компакте К и мажорируемых по норме
->■
одним и тем же числом М ^ 0. Если функции /„ интегрируемы,
->
измеримы ') и просто сходятся почти всюду к f при п, стремя-
щемся к -f-oo, то f интегрируема и измерима, fn сходятся к
J J и даже J || / — [п \\ сходится к 0.
Доказательство. Зададим е > 0. Из предыдущей
теоремы вытекает, что для числа б = е/4М можно найти такую
измеримую часть К6 компакта К, что"|х(К — К6) <; б, и такую,
что на К6 последовательность /„ равномерно сходится к /•
Теперь можно выбрать такое целое число р, что для всех п ^ р
и любого х е К6 имеет место неравенство
-> ->
е
11/W-ZnWIK^^. (IV, 4; 3)
-> ■>
Отсюда следует, что для я ^ р функция ||/ — /„|| не превос-
ходит функции, принимающей значение е/2|х(К) на
множестве Кб, равной 2М на множестве 'К — К6 и равной 0 на
дополнении к компакту К- Поэтому для п ^ р имеет место оценка
J * II?- ?» II < 2JIW •* {К) + ШЬ = 8> (IV' 4; 4)
Это неравенство показывает, что последовательность ин-
■>
тегрируемых функций /„ является аппроксимирующей последова-
тельностью для функции /. Отсюда следует, что / интегрируема,
/ является пределом /„и ||/ — /„II сходится к нулю.
') Предположения излишни. В теореме 39, п. 1°) будет показано, что
ограниченная функция с компактным носителем интегрируема тогда и только
тогда, когда она измерима. Но мы пока еще этого не знаем.

§ 4. Теорема Лебега о сходимости
539
Теорема 35 (общая теорема Лебега). Пусть X — локально
компактное пространство, снабженное мерой Радона [i Гз= 0, и
->•
пусть F — банахово пространство. Предположим, с одной сто-
->•
роны, что последовательность fn, состоящая из интегрируемых
->
и измеримых функций '), просто сходится почти всюду к f при п,
стремящемся к +оо,и, с другой стороны, что существует такая
вещественная интегрируемая определенная на X функция g ^ О,
при которой имеет место неравенство ||fnll^ S- Тогда функция f
интегрируема и измерима, | /„ сходится к J и \\J — fn\\
сходится к нулю.
Естественно, общая теорема Лебега содержит частную
теорему Лебега. Достаточно положить функцию g равной
произведению М на характеристическую функцию компакта К- Кроме
того, поскольку теорема 35 будет доказана независимо от
теоремы 34, можно было бы привести теорему 34 как простое
следствие теоремы 35. В целях простоты мы предпочли сначала
доказать теорему 34.
Доказательство. Зададим е > 0. Поскольку
функция g интегрируема, то существует такая ограниченная по
модулю числом М > 0 с компактным носителем К функция у ^ 0,
что имеет место неравенство
Г'.
К т- (IV, 4; 5)
По теореме 33, для б = г/8М можно найти такое подмноже-
ство К6 компакта К, что ц(К — К&)^ б. на котором fn
равномерно сходится к /. Найдем теперь такое целое число р, чтобы
при п ^ р на К(, имело место неравенство
Очевидно, справедливо неравенство
J,|lT-f»ll<J'llT-f„ll+ J* IIГ-fall- (IV, 4;7)
Первый интеграл справа является интегралом от функции,
не превосходящей е/2ц(К), и, следовательно, этот интеграл <[е/2
для всех п ^ р. Поскольку ||/„ II мажорируется функцией g и
-') Здесь также требование измеримости чрезмерно. В теореме 39, п. 2°)
будет показано, что интегрируемая функция измерима.

540
Гл. IV. Интегральное исчисление
fn(x) стремится к f{x) почти для всех х, то \\f\\ почти всюду
мажорируема функцией g, а, значит, второй интеграл не
превосходит
j* 2g< j* 2Y+ f 2|g-Yl =
= j* 2Y+J*2|g-Yl<2m + ^ = |. (IV,4;8)
В итоге мы получаем неравенство
fllf-fnll<e для п>р. . (IV,4;9)
Это неравенство говорит о том, что последовательность fn
является аппроксимирующей последовательностью для
функции {, составленной из интегрируемых функций. Отсюда следует,
что функция /интегрируема, \Jn сходится к Г f и \\\J—fn\\
сходится к нулю.
Примеры применений теоремы Лебега
1°) Рассмотрим интеграл
J *"**■= 7ГТТ* (IV, 4; 10)
10.11
При п, стремящемся к бесконечности, он сходится к нулю. Это
можно было предвидеть с помощью теоремы Лебега.
Действительно, хп сходится к 0 при п, стремящемся к бесконечности, во
всех точках полуоткрытого интервала ]0, 1], т. е. почти всюду
на интервале интегрирования. Функции \хп\, кроме того,
мажорируемы постоянной 1. Здесь мы можем воспользоваться
частной теоремой Лебега. (Легко видеть, что хп не сходятся
равномерно к своему пределу.)
2°) Рассмотрим последовательность вещественных функций,
определенных для п ^ 1 по формуле
1па для 0 < х С —,
^"' (IV, 4; 11)
0 вне этого интервала.
Эти функции просто сходятся к 0. Интеграл от /„, очевидно,
равен па~1 и потому стремится к 0 при а <. 1*

§ 4. Теорема Лебега о сходимости
541
Наименьшая мажоранта, общая для всех функций f„,
определяется формулой
g.w=J [тГ «ля о<*<1'). (IV4;12)
( 0 вне этого интервала.
При а < 1 функция g мажорируется на [0, 1] интегрируемой
функцией 1/ха2), а, следовательно, интегрируема. Это значит,
что при а < 1 применима теорема Лебега. Напротив, при а ^ 1
теорему Лебега применить невозможно, поскольку мы имеем
последовательность функций, просто сходящихся к 0, интеграл от
которых к нулю не сходится. В самом деле, поскольку функция
Г 1 1а 1
— ;> —— 1 не интегрируема на [0, 1], то функции fn не ма-
L х j х
жорируемы одной и той же интегрируемой функцией g. Этот
пример показывает, что ограничения, фигурирующие в
формулировке теоремы Лебега, неизбежны. Однако имеется случай,
для которого такие ограничения не нужны. Так будет тогда,
когда функции fn образуют возрастающую последовательность
вещественных функций (см. теорему 36).
Замечание. Теорема Лебега сформулирована только для
последовательности fn. Пусть теперь Т — некоторое
топологическое пространство, А — часть Т и а — точка пространства Т,
принадлежащая замыканию А.
->
Предположим, что ft является интегрируемой на X функцией
со значениями в F, зависящей от параметра t^A.
Предположим еще, что при /б/4, стремящемся к а, функция ft просто
сходится почти всюду к f и что имеет место неравенство
llfill^g', где g — фиксированная интегрируемая функция ^ 0.
Возникает вопрос: можно ли при этих условиях утверждать, что
f интегрируема и что | Jt e F сходится к Г J, когда t
стремится к а, оставаясь в множестве Л? Это будет именно так, если
Т метризуемо. В самом деле, выберем в Т некоторую метрику.
Прежде всего, а, находясь в замыкании А, является пределом
не менее одной последовательности точек из А (теорема 15 гл.
II). При этом fan сходятся просто почти всюду к f при п,
стремящемся к бесконечности, и удовлетворяют неравенству
') М — целая часть п.
2) Мы еще не доказали, что Мха интегрируема на [0, 1] тогда и только
тогда, когда а<С1. Однако здесь речь идет только о примере, обоснование
которого можно найти в обычных учебниках по математическому анализу.

542
Гл. IV. Интегральное исчисление
\\Та \^ё- Из теоремы Лебега следует, что f интегрируема.
Кроме того, для любой последовательности этого вида Г Jan
сходится к \ f. Предположим, что \ Jt для значений /е/1,
сходящихся к а, не сходится к Г f. Тогда найдется такое е > О,
что при любом г\ > 0 можно будет найти такую точку /е/1,
для которой d(t, а) <; г\ и Г Jt — \ F > е.
Задавая значения г\ = 1, 1/2, 1/3, ..,, \/п, ..., мы можем
определить такую последовательность а\, а2, аз. •••, а„, ... эле-
II г -> г ■> II
fa — / >е- Но это не-
[ J я J у
возможно, так как Г [ап должен сходиться к I f, чем и
доказывается наше утверждение.
Теорема 36 (теорема Фату). Пусть fo, fu fz, ... —
возрастающая последовательность функций ^0 на X (с конечными
или бесконечными значениями), т. е. f0 ^ fi <1 /г ^ ■ •. . Если
при этих условиях f является пределом функций fn, то
справедливо соотношение
lim Г f„= f f<+°o. (IV,4; 13)
Доказательство. Очевидно, левая часть не
превосходит правой; поэтому нам достаточно доказать
противоположное неравенство. С этой целью мы сначала докажем лемму.
Лемма. Пусть fo, ft, fz,. ... — возрастающая
последовательность неотрицательных функций, определенных на X. Пусть
go, gi, g2, • • • — такая последовательность интегрируемых
функций {не обязательно возрастающая), мажорирующих fQ, fu
h, ■ • •, что
$gn<ffn+^r. -(IV. 4-14)
Тогда, если через \п обозначить верхнюю огибающую
функций go, g[, g2, ■ ■■, gn, мы получим неравенство
J><f 7л + е(1-^). (IV, 4; 15)
Это неравенство, очевидно, справедливо при п — 0.
Докажем его справедливость при любых п по индукции, предполагая,
что оно верно для п— 1.

§ 4. Теорема Лебега о сходимости. 543
Для любых вещественных чисел справедливо равенство
и + и = sup (и, v) + inf (и, v). (IV, 4; 16)
Отсюда следует, что можно написать следующее равенство:
\уп = \ sup.(Yn-i, gn) =
= J4-.+J"g«-J"inf(Y«-i, gn). (IV, 4; 17)
Рассмотрим члены правой части. В силу предположения
индукции, первый интеграл не превосходит f„_] + e(l — 1/2").
Второй член, в силу неравенства (IV,4; 14), не превосходит
ff„ + e/2"+1.
С другой стороны, поскольку gn-i мажорирует f„_i, то Yn-i
мажорирует fn-i- To же самое будет иметь место и для
функции gn, мажорирующей f„ и тем более fn-\- Поэтому
справедливо неравенство inf (\п-ь gn) IS* /n-ь откуда
Jinf(Y„i„g„)>J*f»-i- (IV, 4; 18)
Окончательно получаем, что выражение уп допускает
такую оценку:
Jy,<J"*/,.-, + «(i-£) +
+ ffn + ^-ffn-l=ffn + z{l--^T), (IV, 4; 19)
что позволяет закончить доказательство неравенства (IV,4; 15)
по индукции.
Перейдем теперь к доказательству теоремы Фату.
1°) Предположим сначала, что / ограничена сверху числом
М ;> 0 и имеет компактный носитель К. Зададим е > 0. Для
каждой функции /„ можно найти такую этажную ограниченную
функцию gn^fn с компактным носителем, для которой
справедливо неравенство (IV, 4; 14). Вполне можно предполагать,
что сама функция gn ограничена числом М и имеет компактный
носитель К- В противном случае ее можно заменить на 0 во всех
точках х, не принадлежащих К, и на М во всех точках х, в
которых gn(x)>- М. Образованная таким образом новая
последовательность этажных функций будет удовлетворять
неравенству (IV, 4; 14).
Обозначим через уп верхнюю огибающую функций go, gu ■ •<
...., gn- Тогда последовательность уп будет возрастающей
последовательностью этажных функций'2^0. Они имеют предел у,

544
Гл. IV. Интегральное исчисление
который не превосходит М и имеет носитель в К- Согласно
частной теоремы Лебега (теорема 34), y интегрируема и уп
сходятся к [ Y-C другой стороны, согласно лемме, справедливо
неравенство (IV, 4; 15).
Поскольку теперь, как это мы видели ранее, \п сходится
к Г Y> то имеет место неравенство
f v.< Ит Пп + г, (IV, 4; 20)
Где предел существует, так как речь идет о некоторой
возрастающей последовательности неотрицательных чисел. Однако
поскольку для любого п справедливы неравенства y s> уп s> fn,
то v ^ / и мы получаем соотношение
f/<Hm f*/„+e. (IV,4;2I)
Это соотношение верно при любом е > 0; поэтому
справедливо требуемое неравенство
П<Пт Г/„. (IV, 4; 22)
2°) Предположим теперь, что / ^ 0 произвольна.
Обозначим, как всегда, через }м,к функцию, равную / во всех точках х,
принадлежащих К, в которых f(x)^.M, равную нулю вне К и
равную М в точках хе/С, в которых /(*)> М.
Построим такие же функции для /„. Тогда
последовательность функций (/п)м, к является возрастающей
последовательностью функций ^0, сходящейся к Jm, к. В силу только что
доказанного,
Г/я,-*=Нт f(/nUtf<Hm Г/,. (IV,4;23)
Переходя теперь к точной верхней грани по всем
значениям Ми К, снова получаем (IV, 4; 22), чем и заканчивается
доказательство теоремы Фату.
Следствие 0. Пусть А0, Аи Аг, ... — некоторая
возрастающая последовательность частей X, объединение которых
дает А. Тогда
ц*(Л)= Итц'(Ап). (IV,4;232)
П->оо
Это соотношение вытекает непосредственно из теоремы Фату
и соотношения (IV, 3; 18),

§ 4. Теорема Лебега о сходимости
545
Следствие 1. Пусть /„ — последовательность
интегрируемых 'функций произвольного знака, заданных на X, со
значениями в R. Предположим, что эта последовательность
монотонна (т. е. для всех п либо /n ^ /n_i, либо /„ ^ /n_i) и
сходится к /. Тогда
1 °) если j |/ |< + оо, то / интегрируема и | /„ сходится
к [f;
2°) если | |/|=+ оо, то j'не интегрируема и | /„ стремится
к ±о°.
Доказательство. Докажем утверждение 1°).
Предположим, для определенности, что последовательность /„ является
возрастающей. Тогда имеет место неравенство /0 ^ /п ^ /.
Отсюда следует, что |/„|< |/о| + |/|, а, значит,
|{/«|<Г Ifl + Jlfol- (IV,4;24)
Последовательность вещественных чисел /„ оказалась
возрастающей и ограниченной. Значит, она имеет предел. Поэтому
для любого е > 0 можно найти такое целое число р, при
котором для всех m ^ n ^ p имеет место неравенство
{/т-{/„<е или |(/m-f„)<e'). (IV, 4; 24,)
Последовательность функций fm—/„ при фиксированном п
и пг, стремящемся к бесконечности, является возрастающей
последовательностью неотрицательных функций. Поэтому мы
можем применить теорему Фату и записать
/*(/-/„) <е для п>р. (IV, 4; 25)
Поскольку речь идет о неотрицательной функции, то
[ (f —fn) —J \f-fn\- Отсюда получается, что
последовательность fn является аппроксимирующей последовательностью
для /, состоящей из интегрируемых функций, чем и
заканчивается доказательство нашего утверждения.
Для доказательства утверждения 2°) предположим, что
Г |/|=-{-оо. Если / интегрируема, то интегрируемой будет
функция |/|, что противоречит равенству Г |/|= + оо.
Поэтому / не интегрируема.
') Функция fm—/„ не определена в тех точках, где обе функции fm и {п
равны бесконечности. Однако эти точки образуют множество нулевой меры,
и на него можно не обращать внимания.
18 Зак. 1339

546 Гл. IV. Интегральное исчисление
С другой стороны, если предположить, как ранее, что
последовательность /п возрастает, то мы получим, что /п—/о
образуют возрастающую последовательность неотрицательных
функций, сходящихся к / — /о. По теореме Фату в этом случае
можно написать
f(/-/o)=Hm f./„- f/o. (IV, 4; 26)
Так как имеет место неравенство
1/1<1/о1 + 1/-/о1, то +oo = J*|/|<J|/0|+J,|/-/0|,
(IV, 4; 27)
откуда J I/ —/ol = + оо, так что соотношение (IV, 4; 26)
полностью доказывает наше утверждение.
Предыдущие результаты получены при некоторых
предположениях относительно Г |/|. Можно наложить условия на
величины Г /„, и тогда мы получим следующие эквивалентные
результаты.
Следствие 2. В условиях следствия 1:
1с I
/„ ограничены, то f интегрируема и
J /„ сходится к | /;
2°) если величины Г /„. не ограничены, то f не интегрируема
и fn сходится к ±оо.
Из теоремы Фату как следствие, вытекает теорема о счетной
выпуклости, значение которой мы уже подчеркивали.
Следствие 3 (неравенство счетной выпуклоети). Пусть
"о, "ь "2, •••, "п, ••• — последовательность вещественных
неотрицательных функций (с конечными или бесконечными
значениями), определенных на X. Тогда имеет место неравенство
счетной выпуклости:
(оо \ оо
S«»<Sf «»<+«>• (IV, 4; 28)
п==0 / п=0
m
Доказательство. Для конечной суммы 2 неравен-
ство выпуклости справедливо (теорема 25). Правая часть
при от, стремящемся к бесконечности, стремится к правой части

§ 4. Теорема Лебега о сходимости
547
соотношения (IV, 4; 28) независимо от того, конечна она или
нет.
С другой стороны, поскольку сумма ы0 + «i + •.. + "ш
возрастает вместе с /и и сходится при /и, стремящемся к бесконеч-
оо
ности, к сумме 2 ип, то по теореме Фату левая часть будет
ге=0
сходиться к левой части соотношения (IV, 4; 28), откуда и
вытекает требуемый результат.
Замечание. Из теоремы следует, что если \ Г ы„ < + оо,
то Г I 2j un I < + °°> а, следовательно, согласно теореме 26,
оо
ряд 2 ип почти всюду сходится.
№=0
Следствие 4 (о перестановочности знаков 2 и [ Для
рядов с положительными членами). Если ип обрадуют
последовательность неотрицательных и интегрируемых функций (с
конечными или бесконечными значениями) на X, то имеет место
равенство
/ оо \ оо
f 2"» =S/""<+00' (IV,4;29)
\«=0 / n=0
Если же одна из частей этого равенства принимает конечное
оо
значение, то функция S=2«„ интегрируема и
л=0
оо оо
/S""==S/""- (IV, 4; 30)
Л=0 №=0
m / m \
В самом деле, равенство j Sm = ^ j н„ I где Sm=^M„j
л*=0 V ft=0 /
справедливо для любой конечной суммы. Остается лишь,
учитывая теорему и следствия 1 и 2, перейти к пределу при /и,
стремящемся к бесконечности.
Мы видим, насколько полезна теорема. Фату при
интегрировании рядов, составленных из положительных функций.
Напротив, теорема Лебега 35 в ее прямой форме мало приспособлена
для операций над рядами, поскольку для того чтобы иметь
->
возможность написать равенство (IV, 4; 30) для функции и„
с векторными значениями, необходимо знать, будет ли разность
18»

548
Гл. IV. Интегральное исчисление
S — Sn, т. е. остаток /?„, мажорироваться по норме при произ«
вольном п некоторой интегрируемой функцией g ^ 0, а это,
вообще говоря, установить трудно. Тем не менее, имеет место
весьма важная теорема.
>
Теорема 37. Пусть ип — последовательность функций,
определенных р-почти всюду на X, со значениями в банаховом
пространстве F. Тогда, если ряд V Г \\ип II сходится, то ряд
2 ип (х) \у-почти всюду сходится абсолютно. Следовательно,
этот ряд определяет ц-почти всюду некоторый вектор S (х). Если
функции ип интегрируемы, то определенная таким путем ц-почти
всюду на X функция S со значениями в F ц-интегрируема и
имеет место равенство
J*-
Кроме того,
где Rm — остаток
= 2| "л. или { 2"n==S I ""•
га=0 п=0 п=0
||JS||<|||S||<2JII"»»'
п=0
lim f||#m|| = 0,
oo
2 Mi,-
(IV, 4; 31)
(IV, 4; 32)
(IV, 4; 33)
n=m+l
Доказательство. Сначала можно продолжить «„туда,
где они не определены, и считать их определенными всюду,
оо
Если мы предположим, что ряд \. Г \\ип || сходящийся, и
п=0
обозначим через f неотрицательную функцию, определенную
равенством
оо
'f(*)=2llM*)||<+oo, (IV,4;332)
то, согласно (IV,4; 29), получим | /<-f°°.
Теперь из теоремы 26 получаем, что функция f почти всюду
конечна Так как в точках х, в которых f(x) конечна, ряд

§ 4. Теорема Лебега о сходимости
549
2j un(x) абсолютно сходится в F, то, согласно теореме 55 гл. II,
■>
он тем более просто сходится. Обозначим через S(x) его сумму.
Очевидно, S является функцией, определенной почти всюду на X,
* ^ * £i* ■*
со значениями в F. Если теперь мы положим Sm= 2jUn и Rm =
■> -»■ ■>
— S — Sm, то для Rm получим оценку
(oo \ oo
n»=m+l ' n=m+l
Поскольку ряд У f II "»t II с неотрицательными членами схо-
дится, то из последнего неравенства следует, что \\ Rm\\ cxo~
дится к 0 при т, стремящемся к бесконечности. Следовательно,
■> ->
если ип интегрируемы, то последовательность Sm является ац-
■>
проксимирующей последовательностью для функции S, состав-?
->
ленной из интегрируемых функций, а, значит, S интегрируема
и \ Sm стремится к \ S, откуда и вытекают соотношения
(IV, 4; 31). Нами даже доказано большее, поскольку мы знаем,
что ||5 — Sm|| = J \\Rm\\ стремится к 0 при пг, стремящемся
к бесконечности, т. е. справедливо равенство (IV, 4; 33).
Соотношение (IV, 4; 32) является результатом применения соотно-
-> ■>
шения (IV, 4; 34) к S вместо Rm.
■>
Теорема 38. Пусть / — функция, определенная почти всю-
ду на X, со значениями в F, и пусть fn — аппроксимирующая
■>
последовательность функции f, т. е. такая последовательность
функций, что Г ||/—/nil сходится к 0 при п, стремящемся
■>
к бесконечности. Тогда из последовательности /„ можно извлечь
такую подпоследовательность, которая будет почти всюду схо-
-*■
диться к f l).
В самом деле, шаг за шагом можно определить строго
возрастающую последовательность целых чисел ро, Ри Рг ...,
->■ ■>
') Функции fn и f не предполагались интегрируемыми, но именно этот
случай будет наиболее интересным. Эта теорема (которую можно было бы
доказать значительно раньше) дает интересное освещение поведения
аппроксимирующей последовательности, ' -

550 Гл. IV. Интегральное исчисление
таких, что
J"|f-fPJ<^r. (IV, 4; 35)
При этом имеет место оценка
J
|fp,+1-fBJ<^r. <IV,4;36)
и, следовательно, если мы положим un = fp — fp , то получим
неравенство JKJ ||ы„||< + оо.
п=0
Из теоремы 37 теперь следует, что ряд 2 ип является почти
всюду сходящимся, другими словами, что гюдпоследователь-
->
ность fp сходится почти всюду к некоторой предельной функ-
-*■
ции g. Кроме того, из доказанного в теореме 37 следует, что
1 fpn — g I сходится к 0, а поскольку |/Рп — /| также схо-
»••>•> -> ->
дится к 0, то интеграл II/ — g II равен нулю. Значит, fug
->
почти всюду равны, а это означает, что последовательность fPn
. ->
почти всюду сходится к /.
Замечание. Этот результат весьма важен. Он
показывает, что из последовательности fn или из любой ее
подпоследовательности можно извлечь частичную подпоследовательность,
->
сходящуюся почти всюду к f. Однако будет неверным считать,
->
что сама последовательность fn необходимо сходится почти
->
всюду к f.
В самом деле, рассмотрим следующий пример. Возьмем в
качестве X тригонометрическую окружность, а в качестве меры \i
выберем меру dQ. Рассмотрим последовательность точек ап,
определенных по формуле ап = 1 + 1/2 + 1/3 + .. /+ 1/л, п~^.\,
и обозначим через /„ функцию, равную 1 в интервале [ап, ап+\\
и равную 0 вне его. Так как Г /„= 1/(п+ 1). то Г |/п|
сходится к 0 при п, стремящемся к бесконечности. Функции /„
образуют аппроксимирующую последовательность для
функции 0. Однако, как легко видеть, последовательность /„ не
сходится ни при каком значении jckO. В самом деле, поскольку ряд
оо
2 1/« расходится, то точки ап проходят бесконечное число
раздав

§ 4. Теорема Лебега о сходимости
551
по окружности и, следовательно, каждая точка х для
бесконечного числа значений п содержится в интервале [ап, ап+\], а
значит, для бесконечного числа значений п fn(x) = 1. Теорема же,
напротив, утверждает, что из последовательности fn можно
выделить подпоследовательность, почти всюду сходящуюся к 0.
В самом деле, определим последовательность целых чисел рп
таким образом, чтобы интервал [ар ,аРп+\] содержал
фиксированную точку с. Поскольку длина этого интервала стремится
к 0, последовательность fPn сходится к нулю в каждой точке
ф с, т. е. всюду, кроме одной точки, а, значит, почти всюду.
Характеристика интегрируемых функций.
Интегрируемость и измеримость
->
Теорема 39. Пусть f — отображение локально
компактного пространства X, снабженного мерой Радона ц ^ 0, в ба-
->
нахово пространство F.
■>
1°) Если функция f ограничена и имеет компактный
носитель, то, для того чтобы она была интегрируемой, необходимо и
достаточно, чтобы она была измеримой.
->
2°) Если f произвольна, то, для того чтобы была
интегрируемой, необходимо и достаточно, чтобы она была измеримой
и чтобы верхний интеграл Г ||fl| был конечен.
Доказательство. Заметим, прежде всего, что первая
часть теоремы является частным случаем ее второй части.
Предположим сначала, что / интегрируема. Тогда, в силу
теоремы 29, || / || также интегрируема и, следовательно, согласно
следствию 4 из теоремы 29, интеграл Г ||7ll= Г II f II необхо-
->
димо конечен. С другой стороны, если fn является аппроксими-
->
рующей последовательностью для функции /, составленной из
этажных функций, то из теоремы 38 следует, что из
последовательности /„ можно извлечь подпоследовательность, сходящуюся
-> -> -
почти всюду к f. Таким образом, функция f является почти
всюду пределом некоторой последовательности измеримых
функций и, следовательно, по теореме 23 измерима.
Докажем теперь обратное утверждение. Предположим, что /
измерима и что интеграл Г ||7ll конечен.
Г) Предположим сначала, что f ограничена по норме чис^
лом М>0 и имеет компактный носитель /С,

552
Гл. IV.- Интегральное исчисление
Мы зйаем, что тогда / будет почти всюду пределом
некоторой последовательности этажных функций /„ (теорема 23г). За-
меняя [п на /„—^— на тех этажах, где норма >М (это не
И Ml
->
нарушает почти всюду сходимости к /), можно предполагать,
->
что все [| /„ || ограничены числом М. Кроме того, их носители
можно считать лежащими в К, ибо в противном случае их
можно умножить на характеристическую функцию компакта К. Из
частной теоремы Лебега 34 теперь вытекает, что / интегрируе-
ма, а /„ образуют ее аппроксимирующую последовательность.
2°) Перейдем теперь к общему случаю произвольной
функции /. Пусть Ко, К\, Кг, ... — возрастающая последовательность
компактов, объединение которых составляет X.
-> ->
Обозначим через /„ функцию, равную / на множестве #„
точек х е Кп, в которых ||/(д:)|| ^ п, и равную 0 вне его.
Множество Нп является пересечением компакта Кп и прообраза ин«
->
тервала [0, -\-п\, определяемого измеримой функцией || / || (ком-
->
позиция функции / и нормы; см. теорему 22). Следовательно,
->
#„ как пересечение измеримых множеств измеримо. Функция /„
является произведением f<pH и, следовательно, также
измерима (следствие 3 теоремы 23г). Поскольку она ограничена и
имеет компактный носитель, она интегрируема. Мы знаем так-
же, что функции ||/„ || измеримы. Эти функции образуют
возрастающую последовательность неотрицательных функций и их
предел равен || /1|. В силу предположения Г ||/||< + °о, из
->
следствия 1 теоремы Фату получаем, что || /1| интегрируема. Но
тогда функции /„ сходятся к / при п, стремящемся к
бесконечности, и мажорируемы по норме интегрируемой функцией
•-> ->
11/11^0- По теореме Лебега 35 функция / интегрируема.
->
Следствие 1. Всякая ограниченная измеримая функция/,
равная нулю вне некоторого множества Y конечной внешней
меры, интегрируема.
В самом деле,
J"iiTn< in fin ц*(У)<+оо.
Следствие 2. Если || ц || < -f-°°> то всякая ^-измеримая и

§ 4. Теорема Лебега о сходимости
553
ограниченная функция f, и в частности всякая непрерывная и
ограниченная функция, интегрируема.
В самом деле,
fllflKIII/lllllnll.
-*■
Следствие 3. Для того чтобы / была интегрируемой,
необходимо и достаточно, чтобы она была измеримой и верхние
интегралы от функций \\J\\M,K, определенные на стр. 521, были
ограниченными независимоот выбора М и К. Достаточно даже,
чтобы ограниченность имела место для последовательности Мп,
стремящейся к бесконечности, и для возрастающей
подпоследовательности компактов Кп, объединение которых равно X.
Это утверждение вытекает из того, что при этих условиях
Г llfll является пределом величин Г \\J\\M „.
Следствие 4 (выпуклость и среднее значение). Пусть
С — выпуклое замкнутое множество из F. Если / интегрируема
на измеримом множестве А конечной меры ФО и если f(A)cz С,
то ее среднее значение на А: —т-тг- Jd\t. принадлежит С.
А
Доказательство. Предположим раз и навсегда, что
ОеС. Будем-продолжать функцию / нулем вСЛ так, чтобы
имело место соотношение f(X)czC.
Предположим сначала, что 7—этажная функция. Ее можно
N
записать в виде f—2i gi%A,> гДе gi <= С и %А — характери-
стические функции множеств А{. В противоположность тому,
как это делается в других случаях, мы будем включать слагае-
мое 0 • %Ао там, где / принимает значение 0, с тем расчетом,
л
чтобы можно было считать Л4 непересекающимися и (J At = X.
i=\
Тогда, согласно барицентрическому свойству выпуклости,
вектор
1
J,fa*=irw2^,i(i4'fM)
А /=1
+ N
лежит в С, поскольку 2 И (At Л А)== М> (Л).
*=1

554
Гл. IV. Интегральное исчисление
Предположим теперь, что / ограничена и имеет компактный
носитель. Часть 1°) доказательства теоремы 39 дает нам
возможность с помощью теоремы 23г и ее замечания 2°) построить
аппроксимирующую последовательность для /, образованную из
этажных функций /„ со значениями в f(X) с С. Согласно пре-
дыдущему,* —тдт fndp будет лежать в С, а, значит, в силу
А
замкнутости С, там же будет находиться и —rjr [ / dp.
А
Пусть, наконец, / — произвольная функция. Часть 2°)
доказательства теоремы 39 дает нам аппроксимирующую
последовательность для функции /, образованную из ограниченных с
компактным носителем функций /„, принимающих свои значения
в С и {0} = С. Новый переход к пределу дает необходимый ре-
-> •>•
зультат. Доказательство закончено, если ОеС.
Пусть, в общем случае, с— некоторая точка С. Тогда множе-
-> -> > -> •>
ство С— с замкнуто, выпукло и содержит 0. Функция f— с
принимает значения в этом выпуклом множесте. Поэтому
А
что и требовалось доказать.
Замечание. Ограничение ц(А)=Ф0 можно убрать, если
написать
J
А
fdpt е \i (А) С.
Замечания. 1°) Как мы уже говорили на стр. 516,
функции, встречающиеся на практике, обычно измеримы. В этих
случаях интегрируемость f эквивалентна неравенству Ц/IK °°-
2°) Пусть f — измеримая неотрицательная функция,
определенная на X. Если J. / конечен, то эта функция интегрируема
и (согласно следствию 4 теоремы 29) имеет место равенство
f = J /. Если J /=-foo, то J f смысла не имеет. Однако
если J измерима ^0 и J /=-|-oo, то теперь будет разумным

§ 4. Теорема Лебега о сходимости
555
писать /= /= + °° (однако это не означает, что /
интегрируема!). Таким образом, если f измерима и ^0, то во всех
случаях I / = ] /. Впрочем, для измеримого подмножества А
множества X в случае ц*(Л) =+оо мы уже писали ц(Л)=+оо.
Теория интегрирования, основанная на свойствах
непрерывных и полунепрерывных снизу функций
В предыдущем изложении теории продолжения Лебега мы
отвели существенную роль ^viepe множеств и этажным функциям*
Этого можно было бы полностью избежать, воспользовавшись
полунепрерывными снизу функциями со значениями в R (см,
определение на стр. 85).
Прежде всего, непосредственно видно, что верхняя или
нижняя огибающего конечного числа полунепрерывных снизу функ-
ций также является полунепрерывной снизу функцией и что
верхняя огибающая (но не нижняя огибающая) произвольного
конечного или бесконечного семейства полунепрерывных снизу
функций является полунепрерывной снизу функцией. В
частности, верхняя огибающая семейства непрерывных функций
является полунепрерывной снизу функцией. [Полунепрерывные
сверху функции обладают аналогичными свойствами. Однако на
этот раз полунепрерывной сверху является нижняя огибающая
произвольного семейства полунепрерывных сверху функций
(в частности, непрерывных функций). Впрочем, / полунепре-
рывна сверху тогда и только тогда, когда —/ полунепрерывана
снизу.] Характеристическая функция некоторой части А
множества X полунепрерывна снизу (соответственно сверху) тогда и
только тогда, когда эта часть открыта (соответственно
замкнута). Свойства открытых и замкнутых множеств, относящиеся
к.объединению или пересечению конечного или произвольного
числа множеств, являются выражением свойств
полунепрерывных снизу или сверху функций относительно верхних или
нижних огибающих конечного или произвольного семейства-
функций. Сумма конечного числа полунепрерывных сверху или снизу
неотрицательных функций со значениями в R (но не в R,
поскольку тогда сумма может оказаться неопределенной или
равной +оо, —оо) обладает тем же самым свойством. Сумма
бесконечного семейства полунепрерывных снизу (в частности,
непрерывных) неотрицательных функций полунепрерывна снизу,
поскольку она является верхней огибающей конечных частных
сумм.
Полунепрерывная снизу (или сверху) функция / является
борелевской, а, значит, измеримой по любой мере Радона ^0,

556
/"л. IV. Интегральное исчисление
В самом деле, при любом а множество /_1(]а> +°°]) открыто.
Поэтому, составляя разность, находим, что при любых а и b
множество /-1(К ЭД) будет борелевоким, а вместе с ним будет боре-
левским и множество f_1 (]a, b[)= (J f~l{]a, b — l/n]).
n=l,2....
Однако каждое открытое множество О из R является
объединением счетного множества открытых непересекающихся
интервалов. Поэтому /-1(С0 будет борелевским множеством, а вместе
с этим функция / будет борелевской.
Теорема 39г. Верхний интеграл от полунепрерывной снизу
неотрицательной функции / ^ 0 (с конечными значениями или
нет) является точной верхней гранью интегралов от
неотрицательных функций (ре?(X), которые минорируют f.
Доказательство. Пусть /■—полунепрерывная снизу
функция, принимающая значения в R+. Для каждой функции
(pe'iP(X), О^ф^Д имеет место неравенство |д,(ф)= Г ф^ Г /.
Мы должны показать, что для любого А < ) / можно найти
такую функцию ф <= 'ё'(Х), что 0 ^ ф ^ / и ц(ф) ^ А.
Прежде всего, из определения верхнего интеграла следует,
что если А<В< Г /, то найдутся такое число М ^ 0 и такой
компакт КсХ, что 1м,к^В1)- Введем открытую
окрестность У компакта К, ее характеристическую функцию %г и
функцию g = M(f,My>y,). Так как fM,K^g ^/, то J" g^B.
Функция g, кроме того, полунепрерывна снизу как нижняя
огибающая двух таких функций. Теперь функция g ограничена и
имеет компактный носитель. Пусть хл, п — характеристическая
функция множества Он, п — g^OkM/n, M[). Это множество
открыто, поскольку g полунепрерывна снизу. Положим теперь
gn= V — %k,n- Функция gn является этажной функцией, при-
нимающей значения kM/n на множествахg'l(]kM/n, (k-\-l)Mn/n[)
и равной 0 вне этих множеств. Таким образом, gn^g и g — gn^
^ М/п. При п, стремящемся к бесконечности, функции gn,
имеющие носители в фиксированном компакте У, сходятся
равномерно Kg, а, значит, J gn сходятся к J g. Следовательно,
существует такое целое число п, что \ gn> А. Зафиксировав
') Смотри определение {м % на стр. 521.

§ 4. Теорема Лебега о сходимости
557
такое п, положим б= gn — A>0. Для каждого k найдем
такие непрерывные функции щ ^ 0 с компактными носителями
в Ok,n, что ц(фй) ^ ц{Oh, n) — б/Ж. Функция Ф = 2^ГФ*
k=l
неотрицательна, имеет компактный носитель, мажорируема
функцией gn (а значит, мажорируема функцией g и,
следовательно, функцией /) и такова, что
M*)»%^MO>,,)-"i*i-fe,-^>A-
ft=l ft=l
Замечание. Этот результат для полунепрерывных снизу
неотрицательных функций является весьма частным. Если,
например, взять характеристическую функцию / множества
иррациональных чисел в R, то ее верхний интеграл равен +00- Однако
для любой функции ф е ^{Х), такой, что 0 ^ ф ^ /, имеет
место равенство ц(ф)= 0.
Для произвольной неотрицательной функции имеет место
Теорема 39з. Верхний интеграл неотрицательной функции
является точной нижней гранью верхних интегралов от
полунепрерывных снизу функций, мажорирующих данную функцию.
Доказательство. Зададим е > 0. Пусть вначале
функция / ограничена и имеет компактный носитель. Пусть g —
такая этажная 'функция с компактным носителем, что g ^ / и
Г Г* «■
J.g'^J / + e/2. Функция g- имеет вид 2j gi%A{> где
^—постоянные >0 и Ai — измеримые множества конечной меры.
Пусть теперь М = max | gt |. Найдем для каждого i такое
открытое множество Oi =э Aiy чтобы \ь{ОА ^ цИО + e/{2NM),
N
и положим h = 2 gt%~ . Тогда, так как Oi — открытое множе-
ство, каждая функция ха полунепрерывна снизу, а,
следовательно, h также полунепрерывна снизу и имеют место
неравенства
лг
что и доказывает теорему для этого случая.
Пусть теперь функция / произвольна. Рассмотрим функцию
fn к (Дл — возрастающая последовательность компактов,

558
Гл. IV. Интегральное исчисление
объединение которых равно X; определение fM, к см. на стр. 521).
Эта функция ограничена и имеет компактный носитель.
Следовательно, существует полунепрерывная снизу функция gn,
такая, что
fn,Kn<gn И J£„<f/„,*„ +-^ТГ-
Если теперь мы положим уп = sup (go, gu ..., gn), то из
леммы, использованной при доказательстве теоремы Фату 36,
вытекает неравенство
K<fU„ + e(l-^)-
Последовательность уп является возрастающей, каждая из
функций уп полунепрерывна снизу, а их предел у при п,
стремящемся к бесконечности, являющийся также их верхней
огибающей, полунепрерывен снизу. Для любого п имеет место
неравенство- fn к ^ уп ^ Y> а> значит, / ^ у- С другой стороны, по
теореме Фату
J y= lim f Y„<limj / +e=J / + е,
чем и заканчивается доказательство теоремы в общем случае.
Замечания. 1°) Заменить полунепрерывные снизу
функции на непрерывные функции, очевидно, невозможно. Например,
если / является характеристической функцией рациональных
чисел на R, то ее верхний интеграл равен нулю, однако любая
мажорирующая ее функция ^1 и имеет бесконечный интеграл.
2°) Как мы это видели в примечании на стр. 521, здесь мы
получаем верхний интеграл от некоторой неотрицательной
функции с помощью двух предельных переходов, исходя из
функции ц(ф):
Г/= inf ( sup ц(Ф)). (IV, 4; 40)
(g>f. e полунепр. снизу) 0<q)<g
<Pe=g-(X)
По-видимому, введение верхнего интеграла по этой формуле,
взятой за определение, было бы наилучшим и наиболее
коротким. Однако такой метод будет более абстрактным. Затем
можно было бы определить непосредственно скалярные
интегрируемые функции по теореме 32, т. е. с применением
аппроксимирующей последовательности, составленной функциями из 'S'(X).
Тогда интеграл [q> был бы, по определению, равен ц(ф) (что
позволило бы избавиться от «идиотской» теоремы 30). Меру
множеств можно определить, после определения интеграла от
функций, как интеграл от их характеристической функции. Ко-

§ 4. Теорема Лебега о сходимости 559
нечно, фундаментальные теоремы останутся теми же самыми,
а некоторые доказательства окажутся более сложными, чем
в принятом нами изложении.
Для того чтобы определить интеграл от векторных функций,
->
введем пространство <^{X)^F непрерывных разложимых
функций с компактным носителем, т. е. функций вида g —
— 2л ё№ь где gt — постоянные из F и % g f (X). Положим, по
N
определению, Г g = Vgj|A(<Pi) (что полностью совпадает с соот-
ветствующим интегралом в принятой нами теории). Можно
убедиться в том, что результат совершенно не зависит от частного
представления непрерывной и разложимой функции g (как мы
уже это делали при введении интеграла от этажных функций).
Так снова определяются те же самые интегрируемые функции,
что и ранее, и тот же самый интеграл. В самом деле, каждая
интегрируемая функция в этой новой теории имеет
аппроксимирующую последовательность, образованную из интегрируемых
-> ■
функций в прежнем смысле (функции из <e'(X)®F), и тот же
самый интеграл. Обратное утверждение справедливо в силу
теоремы 32.
Для полунепрерывных снизу неотрицательных функций
имеется обобщение теоремы Фату, справедливое для несчетных
семейств:
Т е о р е м а 394. Пусть (fi)isI — произвольное семейство по-
полунепрерывных снизу неотрицательных функций, и пусть f —
их верхняя огибающая. Предположим, кроме того, что
семейство является «возрастающим» в следующем смысле: какими
бы ни были индексы i, j ее /, существует такое йё/, что fk ^
> sup (fufj). Тогда f / = sup f /,-.
Доказательство. Совершенно очевидно, что Г /^
^ sup | f{. Пусть теперь А — произвольное число < | /. Со-
гласно теореме 39г, можно найти такую функцию qjE^fX),
О ^ Ф =SJ /, что ф>Л. Пусть К—носитель функции ф и
б = ( Г ф — А\/\л(К)- Для каждого а ее К можно выбрать такой
индекс ia ее /, при котором ft (a) ^f(a) — 6/2 ^ ф (а) — 6/2. При
этом, поскольку ф непрерывна и /г полунепрерывна снизу,

560
Гл. IV. Интегральное исчисление
найдется такая открытая окрестность Уа точки а в X, что для всех
х^Уа справедливо неравенство /г (х)^<р(х) — б.
Множество К может быть покрыто конечным числом множеств Та.
Пусть это будут множества Та , Уа2, ..., Уап- Обозначим
теперь через k индекс, при котором /fe^sup (fia , fla fta \
(условие «возрастания»). Тогда на всем К имеем fh ^ <р — б,
и, следовательно, всюду fn ^ (ф— б)%к, поскольку вне К
вторая функция равна нулю, а первая ^0. При этом \ fk^
^ Г ф — бц(/С)^ А, что и доказывает наше утверждение.
Это почти единственное свойство теории интегрирования,
справедливое для предела несчетных семейств функций. Этот
результат не верен для произвольных /* ^ 0. Пусть, например,
/ = 1 на R и ц = dx. Возьмем в качестве /,- характеристические
функции конечных множеств. Тогда Г /г = 0 и f = -\-oo.
Замечание. Существенно, что мы всегда предполагали X
счетным в бесконечности. Вот пример того, что может случиться,
если не делать этого предположения. Пусть пространство X
является суммой несчетного числа прямых R. Точнее, пусть /
является несчетным множеством индексов и для каждого ie/
множество R* изоморфно R. Множества R* предполагаются
непересекающимися в X, а их объединение считается равным X.
Введем в X следующую топологию: подмножество X считается
открытым, если открыто его пересечение с каждым множе-
ством R,-, г'е/. Множество X не является счетным в
бесконечности. В самом деле, множества R4 образуют открытое
покрытие любого компакта К, из которого можно выбрать конечное
подпокрытие. Другими словами, К содержится в объединении
конечного числа множеств R,-. Следовательно, счетное
объединение компактов из X содержится в счетном объединении
множеств R,- и не может совпадать со всем X. Введем на каждом R*
меру dx. Тогда будет определена мера Радона ц ^ 0 на X. В
самом деле, если ipef(I), то ее компактный носитель
содержится в конечном объединении R;: (J R{, и можно будет
пологе/
жить ц (ф) = V Г фг dx, где ф,- — сужение ф на R*. Рассмотрим
*е=/
теперь множество А, образованное из точек 0 всех множеств R*.
Оно замкнуто, однако не является измеримым в смысле
определения, данного на стр. 501. В самом деле, всякое открытое
множество, содержащее А, должно содержать открытые непустые
множества на всех R,-, а, значит, его мера равна +°°- Каждый
компакт, содержащийся в А, содержит только нули конечного

§ 4. Теорема Лебега о сходимости
561
числа множеств R*. Следовательно, его мера равна нулю.
Таким образом, ц*(Л)= +°° и ц»(Л)= 0. Поэтому, например,
равенство ц*(Л)= sup \i*{A П К) для каждого компакта К из X
неверно. Пусть %А — характеристическая функция множества А.
Она не измерима в смысле, указанном на стр. 510. Тем не менее
она обладает свойством Лузина, которое в случае счетности
в бесконечности влечет за собой измеримость. Ее верхний
интеграл, определенный так, как это указано на стр. 520, является
точной верхней гранью верхних интегралов от ограниченных
функций с компактным носителем, минорирующих эту функцию.
Далее, каждая неотрицательная функция с компактным
носителем, ограничивающая снизу функцию %А, имеет интеграл,
равный нулю, поэтому хл = 0 =т^= ц* (Л). Напротив, каждая
полунепрерывная снизу функция ^ха имеет бесконечный интеграл.
В теории интегрирования, где верхний интеграл определяется
полунепрерывными снизу функциями, I %А = ц* (А) = + оо.
Значит, различные теории интегрирования не эквивалентны. Если
попытаться в одну теорию включить случай множества X, не
счетного в бесконечности, то интеграл нужно определять с
помощью полунепрерывных снизу функций. Мера множеств
определяется интегралом от их характеристических функций.
Измеримые функции определяются по Лузину. Множество называется
измеримым, если измерима его характеристическая функция,
т. е. обладает свойством Лузина. В этом случае большая часть
прежних теорем сохраняется, но не все. Предположение о том,
что X счетно в бесконечности, мы повторяли в условиях теорем
только тогда, когда это было необходимым, и даже в теории
интегрирования, построение которой исходило из
полунепрерывных снизу функций. Однако каждый человек, обладающий
элементарной осторожностью, будет остерегаться даже думать
о локально компактных пространствах X, не являющихся
счетными в бесконечности, так как при этом возможны самые
грубые ошибки
Пространства J£P(X, ц; F)
Пусть / — вещественная неотрицательная функция с
конечными или бесконечными значениями, определенная ц-почти
всюду на X. Назовем нормой порядка р функции f, где р —
вещественное конечное число ^ 1, число, определяемое по
формуле
Np(f) = Np(X, ц; f) = (fy>yp. (IV, 4; 41)

562
Гл. IV. Интегральное исчисление
Теорема 40. Если f ^ g, то Np (f) ^ Np (g). Имеют место
соотношения
NPif + g)<Np(f) + Np(g), Np(kf) = \k\Np(f) (IV, 4; 42)
(неравенство выпуклости или неравенство Минковского). Более
общо, имеет место неравенство счетной выпуклости:
/ оо \ оо
#Р 2Un <2#Р(и,), (IV, 4; 43)
\п=0 ] п=о
где ип ■— неотрицательные функции, определенные на
множестве X.
Доказательство. Соотношение для kf очевидно.
Рассмотрим функции fug. Предположим сначала, что они
являются этажными функциями с компактным носителем и что
имеют место разложения
f='kfi<?xl, g=2ig&Xl, (IV, 4; 44)
где U и gi — постоянные и Х{ — измеримые подмножества X.
■> ■>
Интеграл Np(f) является нормой порядка р: || Z \\р, где Z—
вектор пространства .С" с составляющими Zu Z2, . .. , Z„ (где
Zj = U) относительно весов с\, с% . . ., сп, ct = ц{Х^.
Рассматривая точно так же функцию g, можно убедиться в том,, что
неравенство выпуклости является неравенством Минковского,
доказанным в теореме 35 гл. III.
Предположим теперь, что / и g — произвольные, но
ограниченные функции с компактным носителем. Обозначим через f\
и gi этажные функции с компактным носителем, мажорирующие
функции fug. Тогда имеет место неравенство
JVp if + g) < Np (f1 + gi)<Np (/,) + Np (gl). (IV, 4; 45)
Переходя справа к точной нижней грани, получаем искомое
неравенство выпуклости для функций fug.
Перейдем теперь к случаю произвольных неотрицательных
функций fug. Если мы построим определенные ранее функции
/м, к, gu.K, (f + g) м,к, то получим неравенство
(f + g)M.K<fM.K + gM,K> (IV, 4; 46)
откуда вытекает неравенство
JVp ((/ + g)M. к) <КР (fM, к) + Np (gMt K) <JVP (f) + Np (g). (IV, 4; 47)
Чтобы получить нужную формулу, достаточно слева перейти
к точной верхней грани по всем М и К<

§ 4. Теорема Лебега о сходимости 563
Докажем, наконец, неравенство счетной выпуклости. Для
конечного числа m первых членов имеет место неравенство
#p(«o + «i+ ••• + um)^Np(u0) + Np(ui) + ... -\-Np{um).
(IV, 4) 48)
Для получения нужного результата надо, пользуясь
теоремой Фату 36, перейти к пределу при т, стремящемся к
бесконечности.
Определение. Пусть X — локально компактное
пространство, счетное в бесконечности, снабженное мерой Радона
\у ^ 0, и пусть F — некоторое банахово пространство. Пусть
р — конечное вещественное число j^l.
->
Говорят, что функция /, определенная на X, со значениями
-> -> ->
в F, принадлежит пространству 2'р(Х,ц; F), или просто S'p(F),
если это не может привести к недоразумению1), или что она
имеет интегрируемую р-ю степень, если, каково бы ни было
число е > 0, существует такая этажная функция g с
компактным носителем, определенная на X, и со значениями в F, при
которой имеет место неравенство N„ (|| / — g ||) ^е, или иначе:
если существует последовательности /о> /i>/г> ••• этажных
-> ->
функций с компактным носителем, для которых Np(\\ f — fn\\)
сходится к 0 при п, стремящемся к бесконечности. В этом
случае говорят, что последовательность fn является
аппроксимирующей последовательностью для функции / в простран-
стве 3?р {X, ц; F), составленной из этажных функций2).
Иногда, допуская вольность речи, говорят, что функция / при-
->
надлежит пространству 3?p(F), если она определена только
почти всюду и если любое ее продолжение туда, где она не оп-
-> ->
ределена, принадлежит Sp (F). Пространство &1 {X, ц; F)
является пространством интегрируемых функций со значениями
в' F. Таким образом, мы обобщаем понятие пространства инте-
>) Напротив, не следует в обозначении опускать /. Обозначение 3?Р(Х, |i)
->■
или 2?р применяется в том случае, когда F является скалярным полем.
2) Если провести рассуждение, аналогичное доказательству теоремы 32,
опираясь при этом на лемму 2 к теореме 30 с б = (е/2АШ) , то можно
увидеть, что этажные функции можно заменить на непрерывные разложимые
функции с компактным носителем.

564
Гл. IV. Интегральное исчисление
грируемых функций. Однако для р Ф 1 интегрируемость
функции, принадлежащей пространству 2?Р(Х, ц; F),
гарантирована.
->•
Теорема 41. Если f принадлежит пространству 2,p(F), то
неотрицательная функция ||/||: х-* \\f(x)\\ принадлежит
пространству 3?р.
Доказательство проводится точно так же, как
доказательство теоремы 29 для случая р = 1.
Теорема 42. Пространство £р (F) является векторным
пространством, и в этом пространстве функция Np,
определенная формулой
ЛГр(В = Л^р(||Г||) = ({*||Т|Г)1/Р, (IV, 4; 49)
является полунормой.
Доказательство. Пусть Jn и gn — две аппроксимирую-
и g в 3?р (F). Тогда из
неравенства Минковского следует, что сумма /„+ gn является
аппроксимирующей последовательностью для f-\- g,
принадлежащей поэтому к &р (F). Аналогичное рассуждение можно
провести относительно функции Щ, где k — скалярная
постоянная. Полунормой в векторном пространстве называется
неотрицательная скалярная функция N, удовлетворяющая
соотношениям:
N(kX) = \k\N(X), ,iv,«m
+ + + + (IV, 4; 50)
N (X+Y)t£N (X) + N (Y).
■> ■> ->•
Если, кроме того, из N(X) =0 следует ^=0, то мы
получаем обычную норму. Тот факт, что Np является полунормой,
тривиальным образом вытекает из теоремы Минковского 40.
Однако, как легко видеть, эта функция не является нормой.
В самом деле, если Np(f)=0, т. е. если Н/11р = 0, то это
■>
означает лишь, что функция f почти всюду равна нулю
(теорема 26), и, значит, она не обязательно должна быть нулевым
элементом векторного пространства 3?р {F).
Теорема 43. Пусть ип является последовательностью
функций, определенных почти всюду на X, со значениями в F,

§ 4. Теорема Лебега о сходимости
565
принадлежащих 2'P(F) и таких, что ряд 2 AL (ип) является
°° ->
сходящимся. Тогда ряд 2 ип (х) почти всюду абсолютно схо-
га=0
дится, и если через S (х) обозначить его сумму S (х) = 2j "«(х),
га=0
->
то S будет функцией, определенной почти всюду и
принадлежащей пространству 3?р(F). Кроме того, имеет место
соотношение
2 «„< 2 #„(«„)• (IV, 4; 51)
и=0 / га=0
(неравенство счетной выпуклости). Величина NP(S — Sm) =
= Afp (Rm) стремится к 0 при пг, Хтремящемся к бесконечности,
-> ->
a Np(Sm) стремится к NP(S).
Доказательство аналогично доказательству,
проведенному для р = 1 (теорема 37). Хотя Nv является полунормой,
а не нормой, и, следовательно, &р' (F) является лишь
полунормированным векторным пространством, часто применяется язык
теории нормированных пространств. Например, если fn являет-
ся последовательностью функций из 9?р'(F) и если Np(f — fn)
стремится к 0, то говорят, что «/„ стремится к / в 3?р (F)». Од-
нако здесь предел не единствен. Если /„ «стремится к» /, то эта
функция также стремится и к g, лишь бы только эта функция
была почти всюду равной /. В теореме 43 утверждается, что Sm
-> -> -> ->
стремится к S в 9?р- (F), поскольку Np (S — Sm) стремится
к нулю при пг, стремящемся к бесконечности. В ней говорится
также, что ряд Zj ы„ является сходящимся в 9?р (F) и даже
абсолютно сходящимся. (Мы снова допускаем вольности речи,
поскольку S определена лишь почти всюду. Аналогичная воль-
-> ->
ность заключается уже в самой записи Se^fF).)
->
Следствие. Если последовательность функций fn сходит-
-> ->
ся к функции f в 9?р (F) при п, стремящемся к бесконечности,
то из рассматриваемой последовательности можно извлечь та-
>
кую подпоследовательность, которая сходится почти всюду к f.

566 Гл. IV. Интегральное исчисление
Доказательство аналогично доказательству теоремы 38.
Теорема 44. Для того чтобы функция f, определенная на
X со значениями в банаховом пространстве F, принадлежала
пространству 3?P(F), необходимо и достаточно, чтобы она
была измеримой и чтобы интеграл ||/||р был конечным.
Доказательство остается тем же самым, что и в случае
р = 1 (теорема 39).
Следствие. Если f принадлежит пространству 3?P(F),
то функция \\f\\p: х -> \\f (х) \\р интегрируема на X. Более общо,
если q ^ р, то функция \\f\\p принадлежит пространству
gfpiqixtv) = 2plq.
Доказательство. Из сформулированного условия и
теоремы вытекает, что функция f измерима. В силу непрерывности'
нормы, то же самое имеет место для функции \\f\\4 (теорема 9
гл. II и теорема 22). Теперь нужный результат вытекает, в
силу теоремы 44, из неравенства < + оо.
Теорема 45 (о применении линейного непрерывного
отображения). Пусть L — линейное непрерывное отображение ба-
-> > >
нахова пространства F в банахово пространство G. Если f
является функцией, определенной на X со значениями в F, принад-
лежащей пространству 2'P(F), то функция Lof принадлежит
пространству 3?р (G) и, кроме того, имеет место неравенство
Np(LoJ)^\\L\\Np(f). (IV, 4; 52)
->
Если, в частности, р = 1, то Lof интегрируема и
JLof=L(jfj. (IV, 4; 53)
-»• >
Так как \\(L°f)x\\ <: ||L|| \\f(x) \\, то неравенство очевидно.
Рассматривая аппроксимирующую последовательность, легко
убедиться в справедливости заключительной части теоремы.
Мы видим, чю непрерывное линейное отображение L
пространства F в пространство .G определяет линейное непрерывное

§ 4. Теорема Лебега о сходимости 567
отображение пространства &р (F) в пространство SSP (G)
с нормой ^ ||L|| *).
Теорема 46 (о применении билинейного непрерывного
отображения; неравенство Гёльдера). Пусть f принадлежит
-> -> ->
9?р {F) и g принадлежит <£ (G), а В является непрерывным
> -> ->
билинейным отображением Fy^G в Н. Если теперь г ^ 1
определено из равенства 1/г = \/р -\- \/q, то функция B(f;g):x-+
-*■ ■» ->
—► B(f(x),g(x)) принадлежит пространству 3?Г{Щ и, кроме
того, имеет место неравенство Гёльдера:
Nr (В (Т, J)) < || В || Np (T) Nq (g). (IV, 4; 54)
Доказательство. Предположим сначала, что fug
являются вещественными неотрицательными функциями. Тогда
неравенство Гёльдера относительно произведения fg доказывается
точно так же, как доказывалось неравенство Минковского
(теорема 40). Только на этот раз надо свести его к теореме 36
гл. III. Затем неравенство (IV, 4; 54) можно получить и во всех
остальных случаях, так как, в силу неравенства || В (f (x), g (x)) ||<!
<|| В||||7(л:) |||| g(x) ||, задача сведется непосредственно к случаю
произведения двух вещественных неотрицательных функций.
Заметим теперь, что в силу предположений, наложенных на
функции fug, оли измеримы, и поэтому из следствия 3
теоремы- 232 вытекает, что B(f,g) является измеримым
отображением X в Я. Для того чтобы убедиться, что эта функция
принадлежит пространству 3?r (H), теперь достаточно применить
теорему 44.
Замечания. 1°) Если г < 1 (например, если р = 1,
q = 1, а значит, г= 1/2), то никакого определенного
заключения сделать невозможно.
2°) Содержание теоремы можно передать, сказав, что
(ь я) -* В ui g) является билинейным непрерывным отображе-
нием пространства 9!р (F) X 21 (G) в пространство 2"'(H) (в
упрощенном изложении, принятом на стр. 565).
Следствие 1. Пусть pup' — два сопряженных
показателя^, е.показателя, удовлетворяющих соотношению \/p-\-\jp'=l,
') Здесь опять допущена некоторая неточность языка, о которой мы
говорили на стр. 565, ибо 2Р (F) является всего лишь полунормированным.

568
Гл. IV. Интегральное исчисление
или р'=1/(1— р). Если fug принадлежат соответственно
пространствам 3?P(F) и Sp'{G)t то функция В (л g)
интегрируема и имеет место неравенство:
|| J В (f, g) | < || В || Np (f) AV (I). (IV, 4; 55)
Для доказательства достаточно пременить теорему, учитывая
тот факт, что I Г В (f, g)| < f ||. В (?, g) || = Nl (В f , J)).
I! v If •*
Это следствие играет особо важную роль в том случае,
когда рассматриваются функции с вещественными или
комплексными значениями и когда билинейное отображение является
обычным произведением. В этом случае имеет место неравенство
\)fg\<Np(f)Nf(g)- (IV, 4; 56)
Следствие 2. Если fug принадлежат соответственно про-
странствам 3r{F) и 2r {G), то функция B(f,g) интегрируема
и имеет место неравенство
|| J В (Т, g) || <|| В ||N2 $ N2 (|). (IV, 4; 57)
Эта теорема особенно важна в случае функций с
комплексными значениями,для которых имеет место неравенство Коши—
Шварца:
1йИЯ'>П1И,/2- <IV'4;58>
Общеизвестно прямое доказательство этого неравенства.
С этой целью записывают очевидное неравенство
Jtf + W + *g)=J|/ + a,g|2>0 (IV, 4; 59)
и, разлагая левую часть по Я, получают, что трехчлен
Jl/l2 + Ajgf + VjV+|ApJ"|g|2 (IV, 4; 60)
при любом Я должен быть неотрицательным. Это означает, что
его дискриминант должен быть неположительным, откуда
следует неравенство (IV, 4; 58).
Совсем просто это получается из неравенства Коши —
Шварца (теорема 23 гл. III), примененного к полуторалинейной
форме (f, g)-> \ fg, определенной в векторном пространстве 9?г.

§ 4. Теорема Лебега о сходимости
569
Однако для того, чтобы иметь право говорить о векторном
пространстве 3?z, определять указанную полуторалинейную форму
и иметь возможность писать (IV, 4;. 59) и (IV, 4; 60), надо
показать, что если f е &г и g е 3?г, rofg интегрируема и f-{-g e 3?г.
Это можно сделать непосредственно следующим образом.
Функции / + g и fg измеримы. Так как
l/ + gl2<2(|/|2 + |g|2) и |/#|<|/|2 + Ы2, (IV,4;61)
то N2(f-{-g) и Ni(fg) конечны и результат вытекает из
теоремы 44. Полезно знать, в кавдм случае в (IV, 4; 58) имеет место
обобщенное неравенство ^ и в каком случае — строгое нера-
->
венство <. Если, с одной стороны, Л^(#) >0и если, с другой,
для каждого значения X норма Nz(f + Xg) > 0, то трехчлен
(IV, 4; 59) в нуль никогда не обратится, а его дискриминант
будет отрицателен, а, следовательно, неравенство будет строгим.
Мы видим, что всегда имеет место строгое неравенство, за
исключением того случая, когда существуют две комплексные
постоянные а и В, не обращающиеся одновременно в нуль и такие,
-> ->
что функция а/ + 6g равна почти всюду нулю.
Следствие 3 (критерий принадлежности различным
пространствам 2?р(F)). Если ||fi|| < + оо, то каждая функция,
принадлежащая 3?р'(F), принадлежит всем пространствам
3? (F) для г ^ р -и, кроме того, имеет место неравенство
Nr(T)<\\nfr-llpNp(1j. (IV,4;612)
Доказательство. В самом деле, для доказательства до-
->
статочно к функции / и к постоянной скалярной функции g = 1
применить теорему 46. Функция В.в этом случае является
билинейным отображением (/, k) —*■ kf пространства F X К в F.
Число q определяется из равенства l/q = i/r— l//?1).
Эта теорема особенно важна в различных приложениях.
Если, например, X является ограниченным интервалом
вещественной прямой и (i = dx, то при г ^ р принадлежность к &?
влечет за собой принадлежность к 3?т. В частности, функция,
') Доказательство одной принадлежности }^2?r{F) без неравенства
(IV, 4; 61) очевидно. В самом деле, f измерима. Далее, \\f{x)\\r^\\f(x)\\p,
если НГ(*)11>1. и s£l, если Щ*)11< 1. Значит, 111 (*) II' < 1 + If/(*) Ир
и верхний интеграл от ||/||г конечен (так как 11цII < + о°, то J 1 конечен).

570
Гл. IV. Интегральное исчисление
принадлежащая к какому-либо пространству 9?v, принадлежит
к 3?у и, значит, интегрируема. Напротив, как легко видеть:
1°) Между пространствами SBP не существует отношений
обратного порядка. Функция, принадлежащая 3?р, вовсе не
обязана принздлежать SB* при s > р. Пусть, например, на
компактном интервале [0,1] прямой- R в качестве меры взято
йц — dx и рассматривается функция f(x) = l/xa. Тогда для
.а = 1/2 она принадлежит SB1, но не принадлежит 3?г.
2°) Если норма меры ц бесконечна, то между различными
пространствами SBP не существует никаких отношений
включения. Возьмем, например, X = R и da = dx. Тогда пример,
приведенный в п. 1°), показывает, что принадлежность функции
к 3?р не влечет за собой ее принадлежности к 9?a, s>p.
Обратно, функция f(x) = 1/]/ 1 + х2 в этом случае принадлежит
iz?2, но не принадлежит iz?1.
3°) В пространстве (Ct0> l])cb комплексных непрерывных
функций, определенных на интервале [0, 1] вещественной
прямой R, нормы Np относительно меры dx при различных р не
эквивалентны. Этот факт дает нам простой пример
неэквивалентных норм в векторном бесконечномерном пространстве (см. на
стр. 58 теорему 13 гл. II). В этом пространстве Np является
нормой, а не только полунормой. В самом деле, если Np(f) = 0,
то функция / должна быть почти всюду равной нулю. Эта
функция непрерывна. Пусть с — произвольная точка [0,1]. Для
любого е > 0 должно существовать такое число ц > 0, что из
неравенства \х — с\ ^ г) следует неравенство \f (х) —/(с) | ^ е.
Множество таких точек х заполняет интервал длины ^ г),
а функция / почти всюду равна нулю. Следовательно, должна
существовать хотя бы одна точка х, такая, что f(x) = 0, а,
значит, \f(c) | sg; е. Так как е произвольно, то f(c) = 0. Поскольку
с произвольно, функция / тождественно равна нулю, а число Np
является нормой,
Рассмотрим Для каждого п функцию fn(x) (см. рис. 16),
определенную по формуле
ш =
п{\ — пх)- для 0<х< —,
0 для х> —.
(IV, 4; 61а)
Эта функция непрерывна, и имеет место равенство
Np(fn) = nl-^(j^r)UP. (IV,4;613)
Устремим п к бесконечности. Тогда для q > p невозможно
найти такое фиксированное число k > 0, при котором

§ 4. Теорема Лебега о сходимости
571
Nq(fn) ^kNp(fn), и из теоремы 12 гл. II вытекает
неэквивалентность Ng и Np.
л
0
\
1
ъ
1 ■•■■■ ' -т
Рис. 16.
Следствие 4. Если функция f одновременно принадле-
жит пространствам 2Р (F) и 2Ч (F), то она принадлежит всем
■>
3?r{F), р <; г t£^.q, и имеет место неравенство
где
Nr(f)<{Np{f))a{Nj)?,
а =
1 1
г q
1 1 '
р я
1 1
6= '" г
н 1 1
Р Q
(IV,4;614)
Доказательство. Поскольку функция f измерима, то
достаточно (теорема 44) проверить соотношение (IV, 4; 614) для
•>
||f|| или же для произвольной измеримой вещественной функции
8>0*).
Поскольку р sg; r <; q, то \\q ^ l/r ^ \\р. Число \\г
определяет барицентр точек \)р и \\q с весами а и р>0, а + р= 1.
Поэтому \\r = alp + р/<?. Числа аир равны числам,
указанным в условии теоремы. Поскольку а + р= 1, то g = ga gp и,
кроме того, ga e= S£p,\ £ е= <?«/р и Л^а (/) = (tf, (g))a, Nm (/)=
= (^(g))P.
') Если проверяется лишь .принадлежность / пространству 9Sf (F), а не
соотношение (IV, 4; 6I4), то этот факт очевиден. В самом деле,
поскольку / измерима, то достаточно доказать, что Nг (/) конечна. Далее,
1/(*)1Г<11 /МП'. если
Ч*)И<1. и <|| f(x)\\i, если ||/(лс)||>1.-
Поэтому ||/ (х) \\r ^|| f (х)\\р -J- || f (x)\\q и ее верхний интеграл, очевидно,
конечен.

572 Гл. IV. Интегральное исчисление
Если теперь к произведению gag$ == g применить
неравенство Гёльдера (IV, 4; 54) с показателями р/а, q/$, —.—| «г —
= — , то мы получим соотношение (IV, 4;6Ц).
В качестве следствия получаем: множество конечных чисел
р~^\, для которых заданная функция f принадлежит 9?P(F),
является интервалом из [1, + оо[ (открытым, полуоткрытым или
замкнутым). Кроме того, неравенство (IV,4; 6Ц) показывает,
что на этом интервале функция | —► In N\i\ (f) выпукла (см,
стр. 204).
■>
Пространства Lp(X,fi; F). Теорема Фишера—Рисса
При изучении пространств 3£р'(F) постоянно приходится
испытывать существенные затруднения, связанные с наличием
полунорм вместо норм, не позволяющих пользоваться теоремами,
относящимися к нормированным векторным пространствам.
Для того чтобы обойти эти затруднения, мы введем новое
нормированное пространство. В пространстве SBP (F) множество
функций /, для которых Np(f) = 0, является некоторым
векторным подпространством, а именно подпространством функций,
почти всюду равных нулю. Мы можем теперь рассматривать
факторпространство пространства &р (F) по этому векторному
подпространству. Это факторпространство называют
пространством Lp (X, \л; F) или просто LP(F), когда это не приводит к
недоразумениям. Элементом Lp (F) является не. функция,
определенная на X со значениями в F, а класс попарно почти
всюду равных между собой функций. Две функции,
определенные на X, называются ^-эквивалентными в смысле Лебега, или
просто эквивалентными, когда это не приводит к
недоразумениям, если они ц-почти' всюду равны. Тогда Lp(F) является
«пространством функций, принадлежащих SBP (F) и
определенных с точностью до эквивалентности».
-> ■
Конечно, LP(F), будучи факторпространством некоторого
векторного пространства по векторному подпространству, само
является векторным пространством (гл. I, стр. 20). Кроме того,
это векторное пространство нормировано. В самом деле, каж-
дый элемент /" пространства LP(F) является множеством
функций J из 3?р (F), имеющих одну и ту же полунорму Np(f). Эту
общую полунорму называют нормой рассматриваемого эле-

§ 4. Теорема Лебега о сходимости
573
мента f пространства LP(F). To, что это норма, очевидно.
Действительно, она тривиальным образом удовлетворяет неравен-
ствам (IV, 4; 50). Кроме того, если Np(f') = 0, то f* является
классом, составленным из функций, почти всюду равных нулю,
т. е. нулевым элементом пространства LP(F).
Теорема 47 (Фишера — Рисса). Векторное нормированное
-> ->
пространство LP(X, ц; F), где F — некоторое банахово
пространство, само является банаховым пространством, т. е. это
пространство полно.
Доказательство. Для доказательства мы можем опе-
реться на теорему 56 гл. II. Пусть и),—такая последовательность
-> °° -»■
элементов из LP(F), при которой ряд 2 ^ (и.Л сходится. Вы-
■>
берем в каждом классе н„ некоторый представитель, т. е. эле-
мент ип из класса и'п. Тогда будет иметь место соотношение
°° ■+ °° ->
2 Np(un)< + оо. Из теоремы 43 следует, что ряд 2 «п сх°-
й=0 ге=0
дится почти всюду к некоторому элементу S из 3! (F) и что,
■> ■>
кроме того, NP(S — Sm) сходится к 0 при ш, стремящемся
-»• -»•
к бесконечности. Если через S" обозначить класс S, то он бу-
оо
дет некоторым элементом пространства LP(F), а ряд 2 и'п бу-
дет сходиться к S* в LP(F). Этим рассуждением заканчивается
доказательство полноты рассматриваемого пространства.
Теорема 48. Пусть f — некоторый элемент пространства
LX(F). Будем рассматривать \f как значение Г f на произ-
вольном элементе f из класса f. Тогда этот интеграл является
линейным непрерывным отображением пространства V<(X, ц; F)
в пространство F с нормой, равной 1. При этом имеет место
T\<N,<?-). (IV, 4; 62)
I
Доказательство тривиально, по крайней мере в той его
части, которая утверждает, что норма <:1. То, что норма в
точности равна 1, доказывается сложнее, и мы это утверждение
примем без доказательства. Впрочем, оно очевидно в том
случае, когда £ является скалярным полем, ибо тогда для неотри*

574
Гл. IV. Интегральное исчисление
цательной функции / имеет место точное равенство /' =N1(f)t
Теорема 49. В пространстве У(F) множество классов
этажных функций с компактным носителем или множество
классов непрерывных разложимых функций с компактным
носителем плотны.
Утверждение, относящееся к этажным функциям, очевидно,
поскольку, если f е LP (F) и / е 3?р (F) является представи-
телем класса f, то для функции / найдется аппроксимирующая.
последовательность, образованная из этажных функций L. При
этом элементы f'n сходятся к элементу /• в LP(F). Что
касается непрерывных функций, то для доказательства следует
обратиться к примечанию2) на стр. 563.
Замечание. Мы говорили (теорема 41 гл. II), что
каждое нормированное конечномерное векторное пространство
полно. Однако это неверно для бесконечномерных векторных
нормированных пространств. Пространство Lp([0, 1], dx) полно, но.
его векторное подпространство, составленное из классов
непрерывных функций, плотно и, значит, не замкнуто, а
следовательно, не полно (следствие I теоремы 42 гл. II). Отсюда легко
получить, что пространство (С10, ЩсЬ, снабженное нормой NP
'(см. стр. 570), также не полно.
Пространства J£°°(F) и L°°(F)
Определение. Говорят, что [г-измеримая вещественная
неотрицательная функция /, определенная на X, ^-существенно
ограничена или просто существенно ограничена, когда это не
приводит к путанице, если существует такое число М, что почти
всюду функция / не превосходит М. Точная нижняя грань М0
чисел М, обладающих этим свойством, называется
существенной верхней гранью f и обозначается через N^ (/). Это число
характеризуется следующими двумя свойствами:
1°) Каково бы ни было число е > 0, найдется такое
множество значений х с мерой > 0, что имеет место неравенство
f(x) >М-г.
2°) Неравенство f(x) > М может иметь место только на
множестве значений х нулевой меры.
Если функция / не является существенно ограниченной, то
полагают N<*>(}) = + °о. . .
Нетрудно видеть, что Nx (f -f- g) ^ Nx (/) -f Nx (g) и что
NK-(kf) =kNx{f) для k^O,

§ 4. Теорема Лебега о сходимости
575
Через 2°° (X, ц; F) или просто 2°° (F), когда это не
приводит к недоразумению, .обозначается множество функций,
определенных на X со значениями в F, измеримых и существен*
но ограниченных, т. е. таких, что функция ||/|| является ц-суще-
ственно ограниченной. На этом пространстве с помощью равен-
f -*■ . ■>
ства Nooif) =^«,(11/11) определяется полунорма М»(/).
-У ->
Через L°°(X, ц; F) или просто L°°(F), когда это не приводит
к недоразумению, обозначается векторное факторпространство
пространства 2°° (X, ц; F) по векторному подпространству
функций, [л-почти всюду равных нулю. Это пространство является
некоторым векторным нормированным пространством с нормой
Л^оо(Д') = Мзо(/), где / — произвольный элемент из класса /.
Без труда проверяется, что теоремы 40—47 остаются в силе,
если некоторые из показателей будут равны -f- °°-
Теорема 44 исчезает, так как она включается в определение
2°° (F). Следствие теоремы 43 может быть значительно
улучшено: если /п является такой последовательностью функций из
2°° (F), что при га, стремящемся к бесконечности, #'(/ — /„)
стремится к 0, то функции /п почти всюду сходятся к / (нет
необходимости извлекать сходящуюся подпоследовательность).
В самом деле, пусть Вп — множество таких значений х, что
II/W— /„(*) II>Л^(Я (/ —/„). Это множество имеет нулевую меру.
Объединение В множеств Вп также имеет нулевую меру. Пусть
-> > -> -> ■
А=СВ. Так как sup||/(*) — /„ {х) \\ = Np(f — /„) стремится
к 0 при га, стремящемся к бесконечности, то функции / п СХОДЯТСЯ
просто, и даже равномерно, к функции /. Сходимость в 2?°° (F)
является «с точностью до множества меры нуль» равномерной
сходимостью функций.
Отсюда вытекает, что в рассматриваемом пространстве
теорема 49 места не имеет! В самом деле, пусть X — R и ц = dx.
Если g— непрерывная функция, то Nx (g) совпадает с \\\g\\\.
Действительно, множество точек х, в которых ||g(*)|| > Nx (g),
является открытым множеством и имеет меру, равную нулю,
->
т. е. пусто, и, следовательно, Nx (g) действительно является точ-
ной верхней гранью для ||g[|, т. е. равна |||g|||. Если f e 2°° (F)
является пределом непрерывных функций /„, то Л^0о(/т —/„),

576 Гл. IV. Интегральное исчисление
■>
а вместе с ним и |||/т — /„|||, стремится к 0 при тип,
стремящихся к бесконечности. Функции fn образуют последовательность
Коши в {FR)cb, и, поскольку это пространство полно (следствие 2
теоремы 65 гл. II), они равномерно сходятся к непрерывной и
ограниченной функции g. При этом |||/„ — g\\\, а вместе с ней и
Л^оо (/„ — g), сходится к 0. Мы получаем, что N„ (/ — g) = 0, т. е.
f и g почти всюду равны. Таким образом, единственными
пределами непрерывных функций могут быть функции из 2?°° (F),
почти всюду равные непрерывным функциям.
Характеристическая функция интервала [а, Ь] этим свойством не обладает.
Теорема 50. Пусть f — измеримая функция, определенная
на X, со значениями в F. Множество точек р интервала [1, + оо],
-> ->
для которых f e &p (F), образует открытый, полуоткрытый или
замкнутый интервал \ р\, Рг \ ■ Функция р —* Np (/) является
непрерывной функцией, определенной на \р\, Рг]. со значениями
>0 в R. Если, кроме того, ||ц|| = 1, то эта функция является
всегда возрастающей и даже строго возрастающей, кроме того
случая, когда \\ f || почти всюду равна одной и той же
постоянной с, а тогда она постоянна и равна с. Функция |—* \nNi/i(f)
всегда выпукла на 11/рг. l/pi|-
Доказательство. Тот факт, что множество точек р, для
которых j е. 3!р (F), образует некоторый интервал, вытекает из
следствия 4 теоремы 46, распространенного на бесконечные
показатели.
Докажем непрерывность функции Np. При этом достаточно,
очевидно, ограничиться случаем, когда / вещественна и
неотрицательна. Пусть сначала ро — внутренняя точка интервала.
Пусть р\ и р'2 таковы, что р1<р'1<р0<р'2<р2. При р,
стремящемся к ро, функция fP сходится просто к /р\ В силу
примечания на стр. 571, для .р^^р^р^ имеет место неравенство
f'p ^/р' + f"\ правая часть которого не зависит от р и
интегрируема. Из теоремы Лебега 35 следует, что f сходится
к [ f°. Следовательно, N р Q) = [\ fpy" сходится к NPa(f) —
= I ) f°'\ °, и непрерывность функции Np в точке ро доказана.
Можно было бы также воспользоваться теоремой 7г»

§ 4. Теорема Лебега о сходимости
577
Пусть теперь р0 = Р\. Если Р\ ^\р\,рг\, то надо будет взять
такое р'2, чтобы р1<р'2<р2. Затем достаточно заменить [р(, р'2]
на [р,, р£] и провести то же самое рассуждение, что и в
предыдущем случае, чтобы доказать требуемую непрерывность.
Единственным новым случаем будет тот, когда р\ fS=|pi,p2|, т. е.
когда NPl(f) = + oo. В этом случае надо показать, что Np(f)
стремится к +оо при р, стремящемся к р\ по значениям >рь
Зададим А > 0; поскольку NPl(f) = + <х>, то существует такое
число М>1 и такой компакт К из X, что J {fMiK)Pl'^2A.
Для р, стремящегося крх так,-что р,<р<р^ функция (/м, к)р
сходится к (fM, K)"\ сохраняя свой носитель в К и оставаясь
ограниченной числом М"2. Следовательно, по частной теореме
Лебега 34, при р, стремящемся к ри Г (fMl K)p стремится
к | (fMt K)Pi. Значит, существует такое ц > 0, что из р ^ р\ -\- г\
вытекает неравенство (fM, к)р ^ А и тем более неравенство
Г fp ^ А, чем полностью доказывается непрерывность в
точке ри Непрерывность в точке рч. доказывается точно так же,
если только р2 < +оо.
Предположим теперь, что р2=-)-°°, и положим М = N*>(f) ^
^ +оо. Надо показать, что при р, стремящемся к +оо, Np(f)
стремится к М. Зададим М' < М и выберем М[ так, чтобы
М'<М[<М. Тогда существует множество У меры >0, на ко*
тором f(x)^M', и Np(f)^M{(\x{Y))llp. При р, стремящемся
к +°°> последняя величина стремится к М[. Следовательно,
существует такое число q', что при р ^ q' имеет место
неравенство Np {f) $г М\
Этого достаточно для доказательства непрерывности в точ*
ке рч = -boo, если Nm(f)= -\-<x>. Если же М.= No,if) < +°°,
то надо еще установить неравенство противоположного
смысла. Пусть теперь М" > М. В неравенстве (IV, 4; 6Ц), в ко*
тором вместо р, q, г взяты ри оо, р, имеем: а = (l/p)/(l/Pi), Р =
= (1/pi—l/p)/(l/pi). Очевидно, при р, стремящемся к
бесконечности, а стремится к 0 и р стремится к 1. При этом правая
часть неравенства (IV, 4; 614) стремится к (NPl(f))0(Noo(f))l = M.
Таким образом, существует такое целое число q", что при
p~&zq" имеет место неравенство Np(f)^. M". При этом, если
q = sup {q\ q"), то из неравенства р ^ q следует неравенство
М' <^ Np (f) <^ M", и непрерывность рассматриваемой функции
в точке рч. полностью доказана^
19 Зак, 1339

578
Гл. IV. Интегральное исчисление
При || (i|| = 1 неравенство (IV, 4; 61) означает, что функция
p-+Np(f) является возрастающей. Можно показать, что если /
не равна почти всюду некоторой постоянной, то эта функция
является строго возрастающей. Мы это примем без
доказательства.
Продолжение мер, не обладающих свойством неотрицательности
Мы только что видели, что для вещественной меры Радона
(1^0 функцию ф->-!1(ф), первоначально определенную на
^{Х), можно продолжить до функции /-> f d[i, определенной
в значительно более широком векторном пространстве З?1 (X, ji).
Мы даже определили этот интеграл для векторных функций
f e 2" (X, ц; Р).
Можно ли сделать что-либо подобное, когда мера ji
вещественна, но не является ^0 или когда она является комплекс*
ной или векторной?
Такая теория продолжения существует, но мы о ней в
настоящий момент говорить не можем. Тем не менее мы сейчас
изучим частное продолжение хотя бы для того случая, когда
■>
мера ji принимает значения в конечномерном векторном
пространстве.
Обозначим через Г(Х) векторное пространство комплексно-
значных борелевских ограниченных функций с компактным
носителем на X. Пространство ^(Х) является векторным
подпространством пространства Т(Х). Мы не будем вводить
топологию на Т(Х), но введем некоторое понятие сходимости, которое
мы назовем L-сходимостью (L — начальная буква фамилии
Лебег). (Можно показать, что эта сходимость не соответствует
сходимости в топологическом пространстве.)
Последовательность /0, /ь /2, ... из Г(Х) называется L-сходя-
щейся к /, если при п, стремящемся к бесконечности, функции /„
сходятся к /, оставаясь' в совокупности ограниченными по
модулю и сохраняя свой носитель в некотором компакте К
множества X.
Пусть ji — мера Радона ^0. Ее лебеговское продолжение
позволяет определить некоторую функцию /-*- f dp,
определенную на Т(Х), принимающую комплексные значения и
обладающую следующими свойствами:
1°) Эта функция линейна.
2°) Если последовательность /„ является L-сходящейся к /,
то Г /„ dji сходится к / dji.

§ 4. Теорема Лебега о сходимости
579
3е) Пусть О — открытое множество X с компактным
замыканием и %д — его характеристическая функция. Тогда, каково
бы ни было е > 0, существует такой компакт К cr О, что для
каждой функции ф из 'ё'(Х), О ^С ф ^С 1, равной 1 в некоторой
окрестности компакта К и имеющей носитель в С, имеет место
неравенство
J %д dp — j Ф d\i
<8.
4°) Эта функция положительна в том смысле, что если / ^ О,
то J f dy. > 0.
->
Если Е является банаховым пространством, то всякое ото-
->
бражение пространства Т(Х) в Е, удовлетворяющее трем
предыдущим условиям, будет называться линейным L-непрерывным
-> ->
отображением Т(Х) в Е. Если Е = С и выполняется четвертое
условие, то отображение будет называться положительным
(^0). Таким образом, продолжение Лебега некоторой меры
Радона [х ^ 0 определяет линейную L-непрерывную'форму ^0
наГ(Х).
Условие 3е) эквивалентно аналогичному условию 3°2): каковы
бы ни были компакт К из X и е >0, существует такое открытое
множество О m /С, что для любой функции фе? (X), 0 ^ ф ^
^С 1, равной 1 на некоторой окрестности К и имеющей носитель
в О, имеет место неравенство J %к а"ц — ц (ф) ^е. В самом
деле, пусть заданы компакт К, число е и выполняется
условие 3 ). Выберем открытую окрестность °Ы компактного
замыкания К и найдем компакт Я открытого множества °U — К,
существование которого утверждается в 3е). Тогда открытое
множество °U — Н — 0 удовлетворяет относительно компакта К
условию 3°2). Аналогично проводится доказательство обратного
утверждения.
Если X метризуемо, то каждое отображение Т(Х) в Е,
удовлетворяющее условию 2°), автоматически удовлетворяет
условию 3е); В самом деле, рассмотрим последовательность
компактов Кп = {х е О; d(x, СО) > \/п}. Для заданного е > 0 при
достаточно большом п компакты Кп удовлетворяют условию 3°).
Если бы это было не так, то для каждого п можно было бы
найти функцию ф„е?(1), 0^ф„^1, равную 1 на
окрестности компакта Кп, с носителем в О и такую, что
\tgdii— ф«йц >8. Последовательность ф„ сходится к % ,
а это противоречит условию L-непрерывности. Однако если X
не метризуемо, то условие 3°), в котором используется своего
19*

580 Гл. IV. Интегральное исчисление
рода предел несчетного семейства, не будет получаться из
свойства 2°), имеющего место только для последовательностей.
Условие 3°) вводилось не ради удовольствия усложнять себе жизнь:
оно будет нужно в теореме единственности 502.
Для каждого L-непрерывного линейного отображения а про-
странства Т(Х) в Е будет удобным через \х(А) обозначать зна-
чение \х на характеристической функции некоторой борелевской
части А пространства X с компактным замыканием.
'-> . "
Теорема 502. Пусть Е — банахово пространство. Каждое
линейное и L-непрерывное отображение пространства Т(Х) в
Е, равное нулю на векторном подпространстве W (X),
тождественно равно нулю.
Доказательство. Из условия непрерывности 3°)
вытекает, что эта функция заведомо равна нулю на
характеристических функциях открытых множеств с компактным замыканием.
Поэтому нам потребуется следующая лемма.
Лемма 1. Пусть Щ—топологическое пространство и ЗГ ^
множество частей Ш, обладающее следующими свойствами:
1°) Устойчивость относительно разности:
если /l£f, BgJ и В а А, то А — В^ЗГ.
2°) Устойчивость относительно возрастающего предела:
если Ап образуют возрастающую последовательность частей,
принадлежащих ЗГ, то их объединение принадлежит ЗГ.
3°) Устойчивость относительно убывающего предела:
если Ап образуют убывающую последовательность частей из
ЗГ, то их пересечение принадлежит ЗГ; если ЗГ — наименьшее
множество, обладающее ■ свойствами Г)—3°), содержащее все
открытые части °U, то ЗГ является о-алгеброй борелевских
частей Щ.
Докажем эту лемму. Заметим, что предыдущие свойства не
позволяют сразу утверждать, что ЗГ представляет собой ог-ал-
гебру. Мы не знаем, принадлежит ли пересечение Л П В двух
частей из ЗГ множеству ЗГ. Если мы это докажем, то тогда сможем
утверждать, что ЗГ есть ог-алгебра. В самом деле, устойчивость
относительно пересечения двух частей влечет за собой
устойчивость относительно пересечения конечного числа частей, а затем,
в силу условия, наложенного на убывающие
последовательности, устойчивость относительно счетных пересечений. С другой
стороны, из устойчивости относительно разности следует, что
дополнение некоторой части из ЗГ принадлежит ЗГ, поскольку
Щу как открытое множество, принадлежит &". Устойчивость

§ 4. Теорема Лебега о сходимости 581
теперь будет иметь место для любых счетных объединений, и,
следовательно, ЗГ в действительности представляет собой
©-алгебру.
Рассмотрим теперь для открытой части О пространства Щ
множество ЗГд всех таких частей А из Щ, что А Л О
принадлежит ЯГ. Очевидно, это множество частей устойчиво относительно
разности, объединения возрастающих последовательностей и
пересечения убывающих последовательностей. С другой стороны,
это множество содержит все открытые множества, поскольку
пересечение двух открытых множеств является открытым
множеством, а &~ содержит все открытые множества. Поскольку, по
предположению, ЯГ является наименьшим множеством частей Ш,
обладающим указанными тремя свойствами, то множество ff'g
содержит ЯГ. Другими словами, для каждой части А множества
ЯГ и каждого открытого множества О из Щ множество А П О
принадлежит ЯГ. Пусть теперь А — некоторая часть ЯГ.
Рассмотрим множество ЯГА частей В из 41, таких, что А {] В
принадлежит ЯГ. Это множество является семейством частей, устойчивым
относительно разности, объединения возрастающих
последовательностей и пересечения убывающих последовательностей.
Согласно только что установленному, оно содержит все открытые
части Ш. Кроме того, оно необходимо содержит все семейство ЯГ.
Отсюда следует, что если А и В принадлежат ЯГ, то А (") В
также лежит в ЯГ. Это означает, что ЯГ является о-алгеброй.
Поскольку ЯГ содержит все открытые множества, то ЗГ
содержит борелевскую. о-алгебру. Однако борелевская о-алгебра
обладает всеми тремя условиями устойчивости, и ЯГ — наименьшее
множество частей, обладающих этим свойством. Значит, ЯГ
совпадает с борелевской о-алгеброй, и лемма 1 доказана.
Вернемся теперь к доказательству теоремы. Множество Ш
борелевских частей А, содержащихся в открытом множестве Щ
пространства X с компактным замыканием, для которых
■> ■>■
\i(A)—0, очевидно, в силу линейности ц, устойчиво относи-
->■
тельно разности, а в силу L-непрерывности \i, устойчиво
относительно объединения возрастающих последовательностей и
пересечения убывающих последовательностей. С другой стороны,
согласно только что доказанному перед леммой 1, Ш содержит
все открытые части 11. Лемма 1 тогда показывает, что Ш
содержит все борелевские части Ш. Обратим внимание на одно
небольшое затруднение: у нас нет уверенности в том, что часть А
множеству %1, борелевская относительно Ш, будет борелевской
относительно X. По этому поводу мы докажем вторую лемму,
распространяющую теоремы 5 и 6 гл. И на борелевские части.

582
Гл. IV. Интегральное исчисление
Лемма 2. Пусть <2/ — некоторая часть X. Всякая часть А
множества °11, борелевская, в X, является борелевской в °U, и
обратно, если только множество Щ само борелевское в X.
В самом деле, рассмотрим все части В множества X,
пересечения которых с °U и Q,°U являются борелевскими множествами
в топологических пространствах °U и 0,°И. Очевидно, они
образуют некоторую а-алгебру частей X. Так как эта а-алгебра
содержит все открытые множества X (поскольку они пересекаются
с Ш по открытым множествам в 41), то она содержит все боре-
левские части X. Отсюда вытекает, что каждая часть В
множества X, борелевская в X и содержащаяся в CU, борелевская в еИ.
Рассмотрим теперь множество частей С множества Ш,
являющихся борелевскими, если их рассматривать в X.
Непосредственно видно, что если °11 является борелевским в X, то это
множество является а-алгеброй частей еИ. (Все свойства,
необходимые для образования а-алгебры, выполняются очевидным
образом, кроме, быть может, свойства, относящегося к
дополнению. Однако если часть А с <2/ борелевская в X, то часть
ОацА = °11 — Л = Х — CU — А будет борелевской в X, если
только часть С<2/ борелевская в X, т. е. если часть <2/
борелевская в X.) Поскольку оно содержит все открытые части из
°11 (ибо открытая часть °U, будучи пересечением °U с некоторой
открытой частью X, является борелевским множеством в X,
поскольку °U и открытая часть борелевские в X), то оно
содержит все борелевские части °U. Следовательно, если С является
частью °U, борелевской в %L, то она будет борелевской в X, что
И утверждается в лемме 2.
В силу этой второй леммы мы теперь знаем, что функция ц
равна нулю на всех борелевских частях X с компактным
замыканием (т. е. на всех их характеристических функциях). Дока*
зательство будет закончено с помощью последней леммы.
->
Лемма 3. Линейное L-непрерывное отображение ц прост-
-*•
ранства Т(Х) в Е, равное нулю на характеристических функциях
множеств, является нулевым. Линейная L-непрерывная форма
(Е = £,) на Т(Х), неотрицательная на характеристических
функциях множеств, неотрицательна.
-*•
Функция ц равна нулю (соответственно ^ 0) на всех боре-
левских этажных функциях (соответственно этажных ^ 0)
с компактным носителем из Т{Х).
Согласно замечанию, следующему за теоремой 232, каждая
борелевская функция на X с компактным носителем является
равномерным пределом некоторой последовательности
ограниченных в совокупности борелевских этажных функций с
носителем в фиксированном компакте и ^0, если она ^0. Приме-

§ 4. Теорема Лебега о сходимости
5§3
нение L-непрерывности показывает, что ц равна нулю на всем
Т(Х) (соответственно ^0 на Г+(Х)).
Следствие 1. Если два линейных L-непрерывных отобра-
-> -> ->
жения щ и ji2 пространства Г(Х) в Е совпадают на 'S'(X) или
на характеристических функциях множеств, то они совпадают
всюду.
Следствие 2. Если ц является линейной L-непрерывной
формой на Т{Х) и если,кроме того,она положительна на <&+{Х)
или на характеристических функциях множеств, то эта функция
положительна на Г+(Х) и является продолжением Лебега в Г(Х)
некоторой меры Радона ^ 0.
Положительность на характеристических функциях, в силу
леммы 3, влечет за собой положительность на Г+(^), а, значит,
на <&+(Х). Поэтому при обоих предположениях имеет место
положительность на <S'+(X).
Если рассматривать ц как линейную форму на №(Х), то из
L-непрерывности вытекает, что она непрерывна на каждом
'ё'к(Х), т. е. что она является некоторой мерой Радона, и,
следовательно, мера Радона ^ 0. Эта линейная форма и
продолжение Лебега этой положительной меры являются линейными
/.-непрерывными формами на Г(Х), совпадающими на 'ё'(Х), а,
следовательно, на Г(Х).
->
Пусть теперь ц — некоторая мера Радона на X со значения-
•» ->
ми в банаховом пространстве Е. Говорят, что ц допускает боре-
левское продолжение, если существует линейное L-непрерывное
отображение пространства Г(Х) в Е, совпадающее с nHa'iP(X).
Из теоремы 50г вытекает, что если такое продолжение суще'
ствует, то оно единственно.
Легко видеть, что такое продолжение существует не всегда,
В самом деле, имеется по крайней мере одно необходимое
условие продолжения: если последовательность функций из &(Х)
L-сходится к 0, то последовательность ц(фп) должна сходиться
к 0 в Е. Возьмем, к примеру, «тождественную меру»,
определенную на стр. 489, не допускающую абсолютной мажоранты: X —
компакт, Й=9(Х), ц(<р) = <р [<р eV{X), J(q>) е=£ = 9(Х)].
Здесь L-сходимость последовательности ф„ к 0 не влечет за со*
■> ->
бой, очевидно, сходимости ц(ф„) в Е, т. е. равномерной
сходимости фп. (Пример: X = [0, 1], ф„(л:) = 0 для j; = 0 и«> 1/п,
Чп(х) = 1 для х = 1/(2/г) и ф„ аффинна в каждом из интервалов
I0, 2ra~J' 12п> ~п\')

584 Гл. IV. Интегральное исчисление
Теорема 503. Множество Ж (X; Ё) мер Радона,
определенных на X со значениями в банаховом пространстве Е,
допускающих борелевское продолжение, является векторным про-
странством, а отображение (ц, /)-> /ац является билиней-
-> ' -> ->
ным отображением множества Ж (X; С) X Г (X) в Е. Если Е
конечномерно, то каждая мера со значениями в Е допускает
борелевское продолжение.
-> ■»■
Доказательство. Если ц и v являются двумя мерами,
допускающими борелевское продолжение, то ц + v, а также
k\i при скалярном k допускают борелевское продолжение. В
самом деле, достаточно определить это продолжение по форму*
лам
J/d(J + v)= J-/rfjt+ J/dv и |/d(M = fe J/rfJ,
как тем самым будут определены линейные L-непрерывные ото-
бражения Г(Х) в Е, совпадающие соответственно с ц-f-v и k\i
на 'ё'(Х). Одновременно доказывается, что Ж{Х\ Е) является
некоторым векторным пространством и что рассматриваемое
отображение билинейно. По теории Лебега Ж (X; С) содержит
меры Радона ^ 0, а, следовательно, вещественные меры как
разности неотрицательных мер (теорема 18), а значит, и
комплексные меры (ц = hi -f- i\i2, где hi и цг вещественны). Если
теперь ц является скалярной мерой и е — элемент из Е, то мера
це, заданная формулой (це) (ф) =ец(ф), допускает
продолжение, определенное по формуле fd (це) — e\f d\i. Если прост-
ранство Е конечномерно и ех, е2 е„ — некоторый его базис,
то каждая мера ц со значениями в Е запишется в виде ц =
2 Ше< а,
следовательно, она продолжима.
Теорема 504. Пусть ц — вещественная мера на X.
Формулы, доказанные в теореме 18 для ц+, ц" и [ц[, сохраняются для
борелевских продолжений:
f/rfji+= sup fffrf|* (Зля fe=r(X), />0,
, °<g<f f (IV, 4; 63)
f/rf|nl= sup |#ф для /еГ(1), />0.
J ger(X) J
|g|<f

§ 4. Теорема Лебега о сходимости 585
Для каждой борелевскои части А множества X с компактным
замыканием имеют место равенства
H+G4) = supn(B), |х- (Л) = sup (— |a (S)). (IV, 4; 64)
Вс=Л Вс=Л
Доказательство. Во всех случаях ясно, что левая часть
не меньше правой. Поэтому достаточно установить неравенства
обратного смысла. Прежде всего, если О является открытым
множеством с компактным замыканием, то существует такая
функция фе?(1), 0 ^ ф ^ 1, с носителем в О, что ц+(ф) ^
^ ц+((У) —е/2. Согласно формуле (IV, 2; 41), существует такая
функция -ф е'й'(Х), 0 < г|з гСф < ха, что ц(г|з) ^ ц+(ф) — е/2.
Мы имеем, таким образом, неравенство ц(г|з) ^ ц+(С)—е,
которое доказывает первую формулу в случае, когда / является
характеристической функцией некоторого открытого множества
(и тогда, очевидно, можно даже ограничиться функцией g из
Пусть теперь А является произвольным борелевским
множеством с компактным замыканием и характеристической
функцией %А. Пусть О — такое открытое множество, что | \х \ (О—А) ^
^ е/2. Пусть г|з — функция, определенная предыдущим способом
относительно открытого множества О и такая, что ц('ф) ^
~^\л+(0)—е/2, а, значит, ^ ц+(Л)—е/2. Рассмотрим теперь
функцию (разрывную) g = ty%A, 0 ^ g ^ %а- Из неравенства
| i|4GA4i=-|i № - J too-Adp>v№ ~ I H I <0 - A) > |x (i|>) - e/2>
^ц+(Л)— e вытекает первая формула для случая, когда /
представляет собой характеристическую функцию множества А.
Используя соответствующие линейные комбинации, легко
убедиться, что эта формула верна для любой этажной борелевскои
функции /^0 с компактным носителем.
Пусть, наконец, / ^ 0 — произвольная функция из Г(^),
М — ее точная верхняя грань и К — ее носитель. Эта функция
является равномерным пределом последовательности этажных
борелевских неотрицательных функций с носителем в К,
ограниченных числом М. Каково бы ни было е > 0, можно
определить такую этажную борелевскую неотрицательную функцию h
с носителем в К и ограниченную числом М, что |/ — /г|^б =
= е/ (4ц+ (К)). Если мы положим k = (h — б)+, то получим
0 < k < / и / — k < 26- Отсюда | k d\i+ > J" / d\i+ — 26ц+ (К) =
= J" / dv+ - е/2.
') Если / полунепрерывна снизу, то можно ограничиться непрерывной
функцией g, но только не тогда, когда / произвольна, даже если уже ц ^ 0
(см. замечание после теоремы 39г).

586
Гл. IV. Интегральное исчисление
Только что мы видели, что существует такая функция
g е Т(Х), 0 ^ g ^ k, а, значит, ^ /, удовлетворяющая
соотношению Г g dn !> Г k d\i+ — е/2 и, следовательно, ^ J / ^ц+ — е.
Первая формула (IV, 4; 63) полностью доказана. Вторая
формула (IV, 4; 63) доказывается точно так же. Остается
доказать соотношения (IV, 4; 64).
Пусть Л — борелевская часть множества X с компактным
замыканием. Пусть задано е > 0. Возьмем произвольные числа
б, г) > 0. Позже мы установим, что они зависят от е. Согласно
(IV, 4; 63), можно найти такую функцию g е Т(Х), 0 ^ g ^ %А,
что ц+(Л)^ Г £б?ц^ц+(Л) — 6. Отсюда вытекает, что ц+(Л)^
^ Г g б?ц+ ^ ц+ (Л) — б, а, следовательно, Г g d\i~ = J g б?ц+ —
— Jgd|i<6-
Обозначим через В борелевское множество точек х, в
которых g(x) ^ т). Так как функция ч\%в заключена между 0 и g, то
тр~(В) = Г т)хв б?ц~ ^ Г gd\i~ ^6,а, значит ц_(В) ^ б/г). Если
теперь рассмотреть функцию k, равную 1 на В, г) на Л — В
и 0 на СЛ, то она будет заключена между g и /А; поэтому будут
иметь место соотношения ц+(В)-f-тр+(Л — В) = | kd\i+^
^ J gdix,+ ^[i+(A) — б и, следовательно, ц+(В) ^ ц+(Л) — б —
— т)ц+(Л —В) > ц+И) — S — ЛИ+ИЬ
Окончательно получаем:
ц (В) = ц+ (В) - ц- (В) > 0*+ (Л) - б - щ+(А)) -А.
Множество В зависит от выбора б и г\. Однако если мы
выберем 6 ,г) так, чтобы б + ЛИ* И) + б/т) ^ е, то получим такое
борелевское множество ВсгЛ, что ц(В) ^ ц+(Л)—е, и формула
(IV, 4; 64) будет доказанной. Такой выбор б, ц возможен. Надо
сначала взять г) = е/(2ц+(Л)), т. е. г)ц+(Л) = е/2, а затем
взять б так, чтобы б (1 + 1/г|) = е/2, или 6 = e/[2(-l-J-1/т))].
Таким образом, теорема 504 полностью доказана.
В дальнейшем окажется полезным следующее понятие.
Пусть ц — некоторая вещественная мера. Говорят, что она
вполне положительна (соответственно вполне отрицательна,
вполне нулевая) на некоторой части Л множества X, если для
каждой борелевской. части В множества Л с компактным
замыканием имеет место неравенство ц(В)^0 (соответственно
<0, =0);
Тот факт, что ц вполне положительна (соответственно отри-

§ 4. Теорема Лебега о сходимости
687
цательна) на А, записывается в виде: \i(A) 2> 0 (соответственно
ц(А) <0). Если ц вполне положительна на А, то она заведомо
вполне положительна на любой части А. Если д вполне
положительна на счетном множестве борелевских частей, то она вполне
положительна на их объединении А. (В самом деле, если В c:(J An,
то B=(jB„, где Вп— непересекающиеся борелевские МНО-
жества и BnczAn: B0 = B f] A0, S, = S П Л, П СА0, .-,,, Вп =
со
= Bf]Anf] СЛ„_,П... ПСЛ0. Теперь ц (В) = 2 ц (5„) > 0.)
Для того чтобы \i(A) было >> 0, необходимо и достаточно,
чтобы А имело для ц~ нижнюю меру, равную нулю.
R самом деле, пусть А имеет для ц~ нулевую нижнюю
меру. Для- каждого борелевского множества В czA с
компактным замыканием будет справедливо равенство ц~(В) = 0,
а, следовательно \i(B) = \i+(B) ^ 0, и значит, ц вполне
положительна на А. Обратно, предположим, что ц(А) ^> 0. Тогда
(i(/C)^>0 для каждого компактного подмножества К с Л. Из
формулы (IV, 4; 64), примененной к /С и д-, получаем
д~ {К) = sup (— д (В)) = 0, а, следовательно, ц~(А).
в<=.к
Теорема 50s. Если ц является вещественной мерой на
локально компактном счетном в бесконечности пространстве X, то
это пространство можно представить в виде объединения двух
борелевских дополнительных множеств Х+ и Х~, таких, что мера
д будет вполне положительной на Х+ и вполне отрицательной
на Х~.
Доказательство. Пусть К — некоторый компакт
X. В предыдущей теореме мы видели, что р,+ (/С) = sup ^ (Л).
AczK
Значит, можно определить последовательность таких борелевских
частей пространства X, содержащихся в К: Л о, Аи А% ..., что
ц(Лп) >(i+(*)-l/2n.
Положим теперь Вп= (J Ар. Имеют место соотношения:
№+ {Ап) ^ И+ (К) — -к/т > а следовательно,
(1+(В„) = ц+(/0;
ц~(Ап) = ц+{Ап)-ц(Ап)^-^;, поэтому
^(Вп)<^=т.

588
Гл. IV. Интегральное исчисление
Если мы через К+ обозначим пересечение Г | Вп и через
К~—множество К— К+, то сразу получим равенства
ц+ (К+) = ц+ (К), ц- (К+) = О,
ц+(К-) = 0, ц-(^С-) = ц-(Ю. ^iV'4'№>
Тем самым мы определили две искомые части для компакта
К. Пусть теперь Ко, Kt, /(2,.--—возрастающая
последовательность компактов, объединение которых равно X. Для каждого
из Кп по предыдущему способу можно определить части К% и
Кп- Положим теперь X+=[jKn и X'~=[jKn. Поскольку
мера ц вполне положительна на Кп, то она вполне
положительна на их объединении Х+,а поскольку она вполне отрицательна
на Кп, то она вполне отрицательна на Х'~.
Нельзя быть уверенным, что пересечение Х+ и Х'~ равно нулю.
Однако если это пересечение обозначить через Y, то мера \х на
Y будет одновременно вполне положительной и вполне
отрицательной, т. е. будет вполне нулевой. Заменяя затем Х+ иХ'~ на
Х+ иХ~ — Х'~ — Y,получим множества, удовлетворяющие усло«
виям теоремы.
Замечание. Интересно выяснить степень
неопределенности только что найденной системы множеств Х+, Х~. Пусть У+,
Y~ — другое решение этой же задачи. Множество Х + (] Y~ точек,
принадлежащих Х+ и не принадлежащих У+, или множество
Х~ П Y+ элементов, принадлежащих Y+ и не принадлежащих Х+,
являются частями X, на которых \х одновременно вполне поло*
жительна и вполне отрицательна, т. е. вполне нулевая. Можно
сказать, в некотором смысле, что Х+ и Y+ отличаются на
некоторое множество вполне нулевой меры по ц, т. е. нулевой меры
для |ц|. То же самое имеет место для Х~ и Y~.Обратно,
совершенно очевидно, что если изменить Х+ и Х~ на множества, на
которых ц вполне нулевая, то их свойства не изменятся.
Следствие. Для того ■ чтобы две меры ц, v ^ 0 были
дизъюнктными (т. е. такими, что inl(\x, v)'= 0), необходимо и
достаточно, чтобы можно было представить X в виде
объединения таких двух множеств Х^ и Xv, что у(Х^) = 0 и \i(Xv) = 0,
и тогда их можно выбрать борелевскими и дополнительными
друг к другу.
Доказательство. Предположим, что указанное
представление возможно. Тогда для'каждой меры Я ^ 0,
.мажорируемой одновременно мерами ц и v, справедливы неравенства
ЦХ») ^ v(AV) =0и ЦХЧ) ^ |*(XV) = 0, т4 е. ЦХ)=0, а, зна-

# 4. Теорема Лебега о сходимости
589
чит, К — 0. Так как inf (ц, v) ^ 0, то этот inf = 0, и меры \jl и
v — дизъюнктны. Обратно, пусть \х и v — дизъюнктные
меры. Положим к = \л — v. Из inf (ц, v) = 0 следует, что
sup (\а, v) = \a + v (см. стр. 481). Но тогда К+ = sup (\а — v, 0) =
= sup (n,v) — v = [x + v — v = [x и точно так же Аг ±= v.
Нужный результат получается, если положить Х^ = Х+ и Xv = X~,
где оба множества борелевские и дополнительные друг другу.
^Замечание. Говорят, что некоторая мера ц ^ 0
сосредоточена на части А пространства X, если СЛ имеет jx-меру,
равную нулю. Это определение не имеет прямой связи с носителем.
Носитель является наименьшим замкнутым множеством, на
котором сосредоточена мера [х. Однако часть А не обязательно
замкнута. Например, если av являются рациональными числами
из R и если ряд Zi сч, cv>0, сходится, то мера 2 c^(av) co"
V V
средоточена на Q, но ее носителем является R. Впрочем, не
существует наименьшего множества, на котором сосредоточена
мера [i, кроме случая атомических мер (стр. 468), ибо из А
всегда можно удалить произвольное множество нулевой [х-меры.
Например, меру dx на R можно считать сосредоточенной на
множестве иррациональных чисел. Теперь предыдущее следствие
может быть записано в следующем виде:
Для того чтобы меры ц и v (-^ 0) были дизъюнктными,
необходимо и достаточно, чтобы существовало два
непересекающихся множества из X, на которых сосредоточены
соответственно меры [х и v. на дополнении СХ^ сосредоточена мера v, а на
дополнении CXV сосредоточена мера р, (т. е. если Х^, и Xv —
дополнительные множества, то на Х^ сосредоточена мера [х, а на
Xv сосредоточена мера v).
Например, если jx является некоторой атомической мерой ^ 0
на X (т. е. имеет вид 2 сф(а \, где 2 cv < + °° Для каждого
компакта К; здесь av образуют бесконечное счетное множество-
на К, а, значит, и на объединении X счетного множества
компактов) и если v является некоторой рассеянной мерой (т. е.
такой, для которой каждая точка, а, значит, и всякое счетное
множество, имеет нулевую меру), то меры ц и v являются
дизъюнктными, поскольку они сосредоточены соответственно
на множестве точек av и его дополнении.
Можно также дать следующее эквивалентное условие,
которое выглядит асимметричным.
Для того чтобы меры \jl и v (^=0) были дизъюнктными,
необходимо и достаточно, чтобы мера v была ^.-сингулярной, т. е.
сосредоточенной на множестве, \х,-мера которого равна нулю.

590
Гл. IV. Интегральное исчисление
В самом деле, сказать, что на множестве А нулевой ц-меры
сосредоточена мера v, означает сказать, что \i{A) = 0 и
\{СА) =0.
§ 5. УМНОЖЕНИЕ МЕРЫ НА ФУНКЦИЮ
Произведение векторной меры на непрерывную
скалярную функцию
->•
Пусть ц — Мера на локально компактном пространстве X со
значениями в векторном нормированном пространстве Е. Пусть,
Кроме того, р — непрерывная скалярная функция на X. Произ-
ведением меры ц на функцию р, обозначаемым через p\i, или
d(p\i), или pd[i, называется мера v на X со значениями в Е,
определяемая по формуле
v(q>) = /?(q>) = iT(/xp), фе?(Х). (IV, 5; 1)
Эта формула действительно определяет некоторую меру.
В самом деле, пусть qp принадлежит множеству 'S'(X).
Поскольку' функция р непрерывна, то функция />qp также непрерывна,
а ее носитель, содержащийся в носителе функции ср, компактен.
Поэтому р!ф также лежит в 'ё'(Х), так что правая часть в
(IV, 5; 1) имеет смысл. Эта часть линейно зависит от qp, и
поэтому v является линейным отображением W(X) в Е. ■■
Остается доказать непрерывность этого отображения.
Предположим, что носитель qp лежит в компакте К. множества X.
Тогда справедливо неравенство
Hv(f)|| = ||'J(/xp)||<||J||Jfsup|p(*)||||?|||> (IV, 5; 2)
хе=/С
•>
доказывающее непрерывность функции v и дающее
одновременно оценку
1М1к<||ц||к8ир|/,(х)|. (IV, 5; 3)
Это определение показывает также, почему нельзя умножать
меру на функцию, не являющуюся непрерывной скалярной
функцией. В самом деле, правая часть в (IV, 5; 1) имеет смысл только
в том случае, когда pqp является непрерывной скалярной;
функцией с компактным носителем, а это верно лишь тогда, когда р
является непрерывной скалярной функцией.

§ 5. Умножение меры на функцию
591
Пример 1. Если ц является мерой Zi cvfyav), то имеет
место формула
pf2cv6(av)\ = 2cvp(av)6(av). (IV, 5; 4)
В чаСТНОСТИ, р6(а) = р(й) б(а).
>
Пример 2. Пусть ц — мера, обозначавшаяся нами ранее
через р dx, и q — непрерывная скалярная функция. Тогда мера
q(pdx) является уже известной мерой (qp)dx. В частности, если
р является непрерывной скалярной функцией, то pdx является
мерой-произведением непрерывной скалярной функции р на
скалярную меру dx.
Элементарные свойства
Носитель меры рц, очевидно, содержится в пересечении
носителя р и носителя ц. Он может быть строго меньше, чем это
пересечение. Возьмем, например, в качестве ц вещественную
меру Дирака б на R, а в качестве р функцию х. Тогда, согласно
(IV, 5; 4), лсб = 0.
Здесь носителями являются соответственно нуль и вся
прямая, и они пересекаются в нуле, в то время как их
произведение, будучи равным нулю, имеет пустой носитель.
Отображение (р, \i)->~ p\i, ставящее в соответствие каждой
паре, состоящей из непрерывной скалярной функции и меры со
->■ -»-.
значениями в Е, некоторую меру со значением в Е, является,
очевидно, билинейным.
Наконец, имеет место следующее правило ассоциативности:
если р и q являются двумя непрерывными скалярными
функциями, то
р fan) = (pq) ц. (IV, 5; 5)
Случай, когда (i—вещественная мера^ 0
В том частном случае, когда ц является вещественной мерой
Радона ^ 0, известно значение ц на функциях, не являющихся
обязательно непрерывными с компактным носителем. Поэтому
в даннрм случае произведение можно определить в более широ*
ком смысле и даже умножать jx на функции с векторными
значениями.

592
Гл. IV. Интегральное исчисление
Определение. Пусть ц — вещественная мера Радона ^0
на локально компактном, счетном в бесконечности пространстве
X. Пусть р— функция, определенная ц-пбчти всюду на X, со
значениями в банаховом пространстве Е и локально
^-интегрируемая, т. е. ц-интегрируемая на каждом компакте из X1). Тогда
-> -> • ■ ■>
произведением рц называется мера v на X со значениями в Е,
определенная по формуле
рц(ф) = J/*pdne=£. (IV, 5; 6)
Покажем, что эта формула определяет некоторую меру на
X со значениями в Е. Если ф принадлежит (ё'(Х),то она, в
частности, (х-измерима и ограничена, а ее носитель содержится в
компакте К пространства X. Так как функция р, по
предположению, интегрируема на К, то функция рф (следствие 2 теоремы
232) ц-измерима, а верхний интеграл J ||рф||*/ц^|||ф ||| ||р||ф
/с
->
конечен. Отсюда следует, что функция рф интегрируема и,
следовательно, правая часть соотношения (IV, 5; 6) имеет смысл.
Естественно, что эта правая часть линейно зависит от ф и
тем самым определяет некоторое линейное отображение %? {X)
в Е. Что же касается непрерывности, то она очевидным образом
следует из последнего неравенства, которое, кроме того,
означает, что норма меры рц на компакте К допускает- оценку
ll№ll*<j"llp№. (IV,5; 7)
к
Переходя к точной верхней грани по всевозможным
компактам К, отсюда получаем:
|| 5* || < /«?№■ (IV, 5; 7j)
Можно показать, что неравенство переходит в равенство в
том случае, когда р принимает скалярные значения или лежит
в одномерном векторном пространстве. Однако это, вообще го-
') Функция р локально (i-интегрируема тогда и только тогда, когда она
(i-измерима и когда для каждого компакта К из X имеет место неравен-
ство || р || dx < + оо,
К

§ 5. Умножение меры на функцию
593
-=► ->
воря, не так, если р принимает значения в пространстве Е
размерности ^2.
Если р является функцией с комплексными значениями
(соответственно вещественными, соответственно вещественными
^0), то же самое будет иметь место и для произведения р\х,.
Здесь носитель рц содержится в пересечении носителей р и ц.
Кроме того, мы полностью обосновали теперь применявшееся
ранее обозначение pdx для некоторых мер на прямой.
Теорема 51. Пусть \х, является вещественной мерой ^0
на локально компактном, счетном в бесконечности пространстве
X, р — вещественная функция ^ 0, локально [^-интегрируемая
•>
на X, и f — функция, определенная на X, со значениями в бана-
-> ->
ховом пространстве Е. Функция f рц-интегрируема' тогда и
только тогда, когда \х-интегрируема функция pf. Кроме того,
Jfd(№)=j*(pf)<V) или J?Wn) = J"(fp)dn. (IV, 5; 8)
Мы примем эту теорему без доказательства. Ее
доказательство основывается на следующем равенстве, относящемся к
верхним интегралам: если / — произвольная функция ^ 0, то
j*f(pdli)=j'(fp)dlx. (IV, 5; 9)
Эта теорема,"очевидно, особенно полезна, и ею постоянно
пользуются на практике, зачастую этого и не замечая.
В частности, если для функций с вещественными значениями
^0 рассматривается выражение fgdyi, то безразлично,
будем ли мы рассматривать его как интеграл от fg no d\x,, или как
интеграл от / по мере-произведению gd\i, или как интеграл от g
по мере fd\i. Все это, конечно, при условии, что все эти меры-
произведения имеют смысл, т. е. что функции / и g локально
^-интегрируемы.
->
Следствие. Если р является функцией на X со значения-
->
ми в Е, q — вещественной локально ц-интегрируемой функцией
^ 0, то функция р локально q^-интегрируема тогда и только
->
тогда, когда pq локально ^-интегрируема и меры-произведения
-> ->
p(qn) и {pq)\i совпадают.
') Легко видеть, почему рекомендуется применять обозначение pdp. В
соотношении (IV, 5; 8) d(pii) совпадает с pd\i. Мы уже писали pdx.

594. Гл. IV. Интегральное исчисление
В самом деле, они имеют одно и то же значение на каждой
-> •>
функции фе^(1). Говорят, что мера p\i имеет плотность р по,
отношению к вещественной мере ц ^ 0.
Меры с базой ]i. Меры с базой ^0
Говорят, что мера v, определенная на X, со значениями;
•>
в банаховом пространстве Е является мерой с базой ц, где ц —
вещественная мера ^ 0, если она может быть записана в виде
■*• ■*•
p\i, где р — некоторая локально ^-интегрируемая функция на X
•> ->■
со значениями в Е. Говорят, что v является мерой с базой ^ 0,
если существует такая мера ц ^ 0, что v есть мера с базой ц.
Теперь можно рассмотреть следующие вопросы:
1°) Сколькими способами может быть выражена одна и
•> •> •
та же мера v в виде рц, где мера ц задана?
2°) Каков характер мер, которые могут выражаться в этом
виде, т. е. мер с базой ц?
Теоремы 52—53—54 (Лебега — Никодима и Данфорда —
Петтиса) *). Пусть X — локально компактное счетное в
бесконечности пространство и ц — некоторая мера Радона ^0 на X,
1°) Пусть v — некоторая другая мера >0 «а I Если v
имеет базу ц, то каждая ^-измеримая функция и ^-измеримое
множество v-измеримы. Кроме того, каждое множество нулевой
]х-меры также имеет нулевую v-меру. Обратно, если каждая бо-
релевская часть с компактным замыканием и нулевой ц-мерой
имеет также нулевую v-меру, то v является мерой с базой \х,
v = рц, где р — единственная с точностью до значений на
множестве нулевой ц-меры функция. (Если Р\ц = Рг\ь, то р\ и рг
ц-почти всюду равны.)
Для того чтобы мера v ^ 0 была мажорируема мерой ц,
необходимо и достаточно, чтобы v ==» рц, где р ^ 1 • ]х-почти
всюду.
•>
2°) Каждая мера v со значениями в банаховом пространстве
Е с базой ^ 0 допускает борелевское продолжение, абсолютно
мажорируема и имеет наименьшую абсолютную мажоранту.
Если предполагается, что v имеет базу ^ 0, то для того, чтобы
она имела базу ц, необходимо и достаточно, чтобы каждое бо-,
') Мы собрали несколько теорем в одну. Часть 1°) принадлежит Лебегу и
Никодиму, часть 2°) является частным случаем более общей теоремы
Данфорда и Петтиса,

§ 5. Умножение меры на функцию
595
релевское подмножество с компактным замыканием и нулевой
->
\х-мерой имело также нулевую v-меру. При этих условиях
v = р\к, где р определяется с точностью до изменений на
множестве нулевой \х-меры. Для того чтобы она была абсолютно
мажорируема мерой ц, необходимо и достаточно, чтобы v = р\х
и || р || ^ 1 \х-почти всюду. При этом для каждой ограниченной
борелевской функции f с компактным носителем имеет место
неравенство
HJfUv|<Jind|i. ' (IV,5;9s)
Для того чтобы эта функция имела ц в качестве наименьшей
-> ->
абсолютной мажоранты, необходимо и достаточно, чтобы v=p\i,
->
где || р || = 1 \1-почти всюду.
->
3°) Если Е конечномерно, то каждая мера v со значениями
->
в Е является мерой с базой ^ 0. В частности, каждая
скалярная мера имеет базу ^ 0.
4°) Если р и q являются вещественными, локально
^-интегрируемыми функциями на X, то р\х, ^ q\x, тогда и только тогда,
когда р ^ q \х-почти всюду. Мера (sup(p, <?))ц является точной
верхней гранью мер р\к и q\x,. Если v является мерой с базой
^ 0 и со значениями в Е, то для того, чтобы она была
абсолютно мажорируема мерой q\i, необходимо и достаточно, чтобы
-> -> ->
v = рц и || р || г^ Я \х-почти всюду.
Доказательство. А) Предположим сначала, что v ^ 0,
v = р\х,, р ^ 0 локально ц-интегрируема. Пусть Л есть ц-изме-
римая часть с компактным замыканием. Пусть Оп —
последовательность таких открытых множеств, содержащих множество Л,
что \х((Уп) ^ ц(Л) + 1/",' и пусть Кп— последовательность
таких компактов, содержащихся в А, что ц-(/С„) ^ ц(Л) — \/п.
Пусть A* = f]0n и Af—-[jKn- Множества Л* и Л* являются
п п
борелевскими, а, значит, измеримыми множествами при любой
мере Радона, Л»с=Л с Л* и ц(Л* — Л*) = 0. Тогда v (Л*— Л„)=
■= J" pd\x=0. Так как v(A,) ^ v*(A) < v*(A) < v (Л*), то
А*-А*
часть Л также v-измерима. Если часть Л не имеет
компактного замыкания, то такое заключение сохраняется в силу того, что
измеримость А эквивалентна измеримости ее пересечений с
компактами, при этом если й(Л) = 0, то v^) = J pd\x — 0.
А

596
Гл. IV. Интегральное исчисление
Измеримость функций сводится к измеримости множеств.
Каждая ц-измеримая функция является v-измеримой.
Обратно, предположим, что каждое борелевское множество
с компактным замыканием и нулевой ц-мерой имеет также ну*
левую v-меру. Тогда мы сможем построить некоторую функцию
р ^ 0, локально ц-интегрируемую и такую, что v = рц. При
этом v будет мерой с базой ц. Если v sgC ц, то из построения
будет видно, что р ^С 1. Первая часть теоремы, однако, еще не
будет доказана, поскольку нужно показать, что р определяется с
точностью до произвольных изменений на множестве нулевой
ц-меры.
Построим искомую функцию р. Пусть k и п — целые числа
k
^ 0. Если мы введем меру v —-^гц, то, согласно теореме 505,
множество X можно представить в виде объединения двух таких
непересекающихся борелевских множеств Xt, n и Xk, n, что на
первом мера v — тргц будет вполне положительной, а на
втором— вполне отрицательной. Для k = 0 мы положим Хо, п — Х
и Хо,п=®.
Пусть теперь Лб,„=Л'£ „ (] Xk+i, n, и пусть h < k. Нельзя быть
уверенным в том, что ДдС^л' Однако если через Nh,h,n
обозначить борелевское множество Хй, nf\Xk, n точек,
принадлежащих первому множеству, но не принадлежащих второму, то
это множество будет иметь нулевую ц-меру. В самом деле, для
каждой борелевской части В с компактным замыканием
данного множества имеют место неравенства
v(S)<-|ni(S) и v(B)>^rli(B),
что возможно только в том случае, когда ц(В)=0, а значит,
ц* {Nh, ft, n) = 0. Так как это множество борелевское, а
значит, ц-измеримо, то ц(Л^ и, п) =■ 0. Если мы обозначим через Nn
объединение всех Nht ki n, соответствующих всем значениям h, k,
h <C k, то получим некоторое множество нулевой ц-меры. Если х
не принадлежит этому исключительному множеству Nn и если
х^Х^п, то x^Xk, n для всех k~^h. Отсюда вытекает, что
пересечение Ah,n и Аи, п, h ^= k, содержится в Л/~п, а
следовательно, имеет нулевую ц-меру. (В самом деле, предположим,
например, что h < k. Тогда (Ah, п П Ак, п) <= (ХЙ+\, п П Xt, п) <= М„.)
Объединение всех Аи, п при фиксированном а и k = 0, 1, 2,...
содержит почти все X. В самом деле, пусть х е X. Предположим
сначала, что существует хотя бы одно такое целое число h, что
ie^„ Тогда найдется первое целое h, обладающее этим
свойством (поскольку X^n = Q, то h ^ 1). При этом хфХ^-1>п

§ 5. Умножение меры на функцию
597
и, следовательно, хеЙ-и. а потому хеЛл-i, п- Однако
если мы рассмотрим множество Мп точек х, не принадлежащих
-ни одному из Х^п, k = 0, 1, 2 то это будет множество
точек, принадлежащих всем Xt,n- Следовательно, для каждой бо-
релевской части В с компактным носителем множества Мп при
k
любом k имеет место неравенство v{B)~^-^i\i{B), из которого
следует; что \х(В) = О, так что нижняя ц-мера множества Мп
равна нулю. Поскольку это множество борелевское, то его
ц-мера также равна нулк\ Все это можно подытожить
следующим образом: для фиксированного п и й=0, 1, 2, ... множества
Ah, п, с точностью до множеств нулевой ц-меры, попарно не
пересекаются и в объединении дают множество X. Обозначим
теперь через рп функцию, равную й/2" на множестве Akt n. Ее
невозможно будет определить по этому правилу в точках
пересечения двух множеств Ak, „ или в точках, не принадлежащих
объединению этих множеств, т. е. на борелевском множестве
Nn U Мп нулевой ц-меры. Положим на этом множестве,
например, рп = 0. Тогда функция рп будет борелевской. Кроме того,
она будет и локально ц-интегрируемой, поскольку для каждого
компакта К
J*p„4i=2 { |r4i<2v(tfn^,„)<v(/0< + °°.
Таким образом, мы можем полностью определить меру рпц- На
каждом из множеств Аи,п имеют место неравенства рп\а <v<
•С (p„ + l/2n)u. Эти же неравенства сохраняются на U Ah n.
Множества Мп имеют нулевую ц-меру, а, следовательно, в силу
сделанного предположения относительно v и ц, они имеют
нулевую v-меру (это используется только здесь). Значит,
неравенства справедливы на Мп и, следовательно, справедливы на
всем X.
Будем теперь изменять п. Выполнив построение для п, мы
его можем использовать для п + 1, полагая X2k, п+\ = Xk, «• Это
возможно, поскольку на этих множествах должны выполняться
одинаковые неравенства
Множества Azh, n+i и A2k+i, п+и с точностью до множеств ц-меры
нуль, попарно не пересекаются и в объединении дают множество
Ah, п- Поэтому ц-почти всюду имеем рп ^ pn+i ^ рп + 1/2".
Если мы изменим функции рп, полагая их равными нулю на
борелевском множестве нулевой ц-меры M\J N, М = U Мп,
л>0

598
Гл. IV. Интегральное исчислений
N—[)Nn, то они будут по-прежнему обладать теми же
свойство
вами, однако всюду будут иметь место неравенства рп ^
^ Pn+i =£^ Рп + 1/2™. Последовательность функций рп
оказывается возрастающей и имеющей некоторый предел р, где рп ^
^ р ^ рп -f- 1/2™. Функция р является борелевской и локально
ц-интегрируемой, а, значит, определяющей меру p\i. Для
каждого ф из Ф(Х), ф Г> 0, имеем
р„Ф ф + -дг | ф d(i,
J Р«Ф Ф < j W ф < J р„ф ф + -gn j ф Ф.
откуда
| j pydfl— j\dv|<-^- |фф-
Поскольку и произвольно, левая часть равна нулю. Значит, рц
и v совпадают на 9+(Х) и, следовательно, на ^{Х), т. е. равны.
Это как раз то, что мы хотели доказать. Если, кроме того, v ^
^ ц, то можно взять Х~п п~Х и Х*п „ = 0> а, значит, рп ^ 1
И/)^1.
•> ->
В) Пусть v — мера со значениями в пространстве Банаха Е
-> -> ->
и с базой Я, ^ 0, так что v = qk, где q локально ^-интегрируема.
Эта мера тривиальным образом абсолютно мажорируется мерой
11?11Я^0. Согласно теореме 18, она должна иметь наименьшую
абсолютную мажоранту. Она также допускает борелевское
продолжение, определяемое формулой
J/rfv= \fqdX. (IV,5;93)
->
Мы определили некоторое линейное отображение Г(Х) в Е,
продолжающее отображение, определенное мерой v на ^{Х),
поскольку если функция / борелевская, а значит, ^-измерима,
то и функция fg ^-измерима. Функция |/| ограничена числом
М^О и имеет компактный носитель К, а функция q локально
^-интегрируема, поэтому %Kq ^-интегрируема. Значит, II/g II ^
^М% \\q\\ имеет конечный верхний А,-интеграл, а,
следовательно, fq ^-интегрируема. Остается доказать L-непрерывность
этого отображения. Предположим, что функции /„ сходятся к /,
оставаясь ограниченными по модулю числом М и сохраняя свои
-> ->
носители в компакте К. Функции fnq сходятся к fq, оставаясь
мажорируемыми по норме ^-интегрируемой фиксированной функ-

§ 5. Умножение меры на функцию
599
цией %^M||gi|. Из теоремы 35 о сходимости Лебега следует, что
тогда | fngdX сходится к Г fq dX. Однако надо еще проверить
условие непрерывности 3°) (см. стр. 579). Итак, пусть О —
открытое множество с компактным замыканием. Функция ||^||
интегрируема на множестве О. Поэтому существует такое число
М^О, что (|| q || —1| q ||л) dX ^е/2, и существует такой ком-
о
пакт KczO, что %{0 — К)^г/2М. Компакт К удовлетворяет
-> .
относительно v условию 3°). В самом деле, если фе?(Х),
О ^ ф ^ 1, равна 1 в некоторой окрестности компакта К и
имеет носитель в О, то
l|v(q>)-v«?)||< \ || J||<ft< J IUIU^ +
в-к в-к
в-к
Замечание. На стр. 489, 583 мы привели пример не
абсолютно мажорируемой и не имеющей борелевского продолжения
меры. Вышеизложенное показывает, что она не является мерой
с базой ^ 0. Можно также привести пример абсолютно
мажорируемой меры (а, следовательно, имеющей наименьшую
абсолютную мажоранту), но не имеющей базы ;>0. Оба понятия не
эквивалентны, 'одно из них сильнее, чем другое.
-> ■>
С) Мера вида рц, где ц-почти всюду ||р|| ^ 1, очевидно,
абсолютно мажорируема мерой ц. Поэтому нам следует лишь
доказать обратное утверждение. При доказательстве мы
ограничимся случаем сепарабельного пространства Е. Сначала мы до-
кажем лишь частичное обратное утверждение: если v имеет вид
р\х, и если эта мера абсолютно мажорируема мерой \х,, то ||р||^ 1
ц-почти всюду. Предположим, что множество \х е X; \\р(х) || >
> 1} имеет ц-меру > 0. Так как оно является объединением
множеств Ле = {х el; \\р(х) II ^ 1 + 2е} для е= 1, 1/2, 1/3,
то существует такое е > 0, при котором это множество Ае имеет
ц-меру > 0. Мы будем выбирать е < 1/2 по причинам, которые
выяснятся позже.
Пусть а —некоторая точка единичной сферы 5 пространства
Е, и пусть В (а, в)—шар с центром в точке а радиуса е. Этот
шар — замкнутое выпуклое множество. Обозначим через К(а, е)
объединение шаров, полученных из шара В (а, е) путем
гомотетии с центром в нуле пространства и с вещественным

600
Гл. IV. Интегральное исчисление
коэффициентом подобия ^ 1. Непосредственно видно, что
К(а, ё) также является выпуклым замкнутым множеством.
В самом деле, пусть ах и $у — две точки этого множества,
где а^1, 8^1, х и у лежат в шаре В (а, х). Тогда точку
tax + (1 — t)$y можно записать в виде y(sx + (1 — s)y),
где y = ta+(l — t)$>l, s = tal[ta + (1 — /)P], 1 —s =
= [(1— 0'P№a+ (1 — 0PL Так как s* + (1 — s)y"e B(a, e),
то рассматриваемая точка лежит в К(а, е), а это означает, что
множество К (а, е) выпукло.
Предположим теперь, что некоторая последовательность то-
чек knxn этого выпуклого множества сходится к пределу у из Е.
Поскольку нормы векторов хп не меньше 1—е, то числа kn
ограничены сверху. Однако они также ограничены снизу
числом 1, поэтому из последовательности kn можно извлечь
подпоследовательность (для которой мы сохраним прежнее
обозначение kn), сходящуюся к некоторому пределу k~^\. Но тогда
-*■ ->■->■
точки хп будут сходиться к пределу х = ylk, принадлежащему
■+ ->- -*•
замкнутому множеству В(а, е). Здесь у = kx, k ^ 1, х е В{а,г),
->
а поэтому у принадлежит множеству К{а, е), которое тем самым
оказывается замкнутым. В силу сепарабельности Е, найдется
счетное множество точек а (пусть это будут а\, аг, а3,. ..), таких,
что шары В(ап, е) покрывают сферу S1). Выпуклые замкнутые
множества К{ап, е) покрывают множество всех точек с нормой
-*•
^ 1 из Е, а множества (1 -\-2г)К{ап, е) покрывают, множество
->■
всех точек из £ с нормой ^ 1 +2е.
Множество Ае является объединением ц-измеримых под-
-*•
множеств Ап = Ае (] р~1((1 + 2г)К{ап, е)). По крайней мере
одно из них имеет ц-меру > 0. Пусть это будет, например, А\.
Пусть К\ а А} есть некоторый компакт ц-меры > 0. Поскольку
p(Ki) с: (1 -{- 2г)К{а\, е), то из неравенства выпуклости
(следствие 4 теоремы 39) следует, что р йцец (/([) (1 + 2e)/C(ai,e),
кг
рйц 1^ц(К\) (1 + 2е) (1 — е)>ц(/(1), поскольку
|i(/Ci)^=0 и е'< 1/2.
') Всякое подмножество 5 метрического сепарабельного пространства Е
само сепарабельно. В самом деле, пусть последовательность точек Ьп плотна
в Е. Выберем а„ в S так, чтобы d(an, bn) ^ d(bn,s)-\-\jti. Тогда последоэа-
тельность точек ап будет плотной в $.

§ 5. Умножение меры на функцию
601
Однако это невозможно, так как мера p\i предполагалась
.абсолютно мажорируемой мерой ц. Таким образом, для каждой
II г "^ II
<$рйц Ь^ц(ф). Условие Зр
■^-непрерывности (см. стр. 579) означает, что I х^рф,!^.
^.\i(Ki) для каждого компакта Ki- Таким образом, если мерарц
абсолютно мажорируема мерой ц, то \\р\\ ^ 1 почти всюду.
D) Из предыдущего, в частности, вытекает, что если мера рц
равна нулю, то, каково бы ни было вещественное число k > О,
•мера kp\i абсолютно мажорируется мерой ц, а, следовательно,
величина k\\p\\ ц-почти всюду мажорируема числом 1, т. е.
норма ||р|| ц-почти всюду мажорируема числом l/k. Устремляя те-,
перь k к бесконечности, можно убедиться в том, что норма \\р\\
ц-почти всюду равна нулю. Следовательно, если pi\i и p2\i
представляют одну и ту же меру, то функции р\ и рг ц-почти всюду
равны. Это доказывает единственность, фигурирующую в
утверждениях 1°) и 2°) теоремы. Таким образом, п. 1°) теоремы
полностью доказан.
* ->
E) Предположим теперь, что v = p\i имеет меру ц в качестве
наименьшей абсолютной мажоранты. Тогда \]р\\ ^ 1 ц-почти
всюду. Однако мера p\i всегда абсолютно мажорируема
величиной ИрНцг^ц. Поэтому, если мера ц является наименьшей
абсолютной мажорантой, то ||/>||ц —ц, а> значит, норма \\р\\
ц-почти всюду равна 1. Обратно, предположим, что \\р\\ ц-почти
всюду равна 1. Тогда мера p\i абсолютно мажорируема мерой ц.
Покажем, что мера ц является наименьшей абсолютной
мажорантой.
В самом деле, пусть наименьшей абсолютной мажорантой
является мера К. Тогда К ^ ц. Предположим, что К < ц. Тогда
найдутся такое число е, 0 <С е ^ 1/2, и такое борелевское
множество А с компактным замыканием, что \i(A) > (1 -f- 2е)К(А).
(В самом деле, если для каждого е > 0 имеет место
неравенство ц(А) ^ (1 +2е) К (Л),то, согласно следствию 2 теоремы 50г,
ц <g; (1 -f- 2e) L Из последнего неравенства следует, что ц ^ К,
что противоречит предположению.) Однако \\р\\ = 1 и единич-
ная сфера из Е, которая по предположению сепарабельна,
покрыта счетным, множеством (замкнутых и выпуклых) шаров

602 Гл. IV. Интегральное исчисление-
В(ап, е). Поэтому хотя бы для одного из множеств
АА= А [\р-х{В(аА, е)), например для п=1, ц (Лй)>(1 + 2е)Я (Лй).
Теперь можно найти такой компакт KiCzAu что n(Ki) >
> (1 -\-2e)k(Ki). Так как на К\ функция р принимает значения
в выпуклом замкнутом множестве В(а\, е), то имеет место
соотношение выпуклости I pd\i e [i (K\) B(alt е), или
к,
1J UA> (1 - в)ц (/(,)>(1 - е) (1 + 2в) Я (/С,) >Л Ю,
II Ki II
т. е. I pd\i\>\{К\)> что противоречит, как мы уже видели,
IU, 1
предположению, согласно которому рц абсолютно мажорируема
мерой к. Следовательно, рц имеет меру ц в качестве
наименьшей абсолютной мажоранты тогда и только тогда, когда \\р\\
ц-почти всюду равна 1.
-*■ -*■
Пусть теперь рц (где р локально ц-интегрируема) есть
некоторая мера. Ее можно записать в виде
-VOIPIM. где -Ы=1>).
Ир II II. II pill
Ее наименьшей абсолютной мажорантой является мера \\p\\\i.
F) Пусть v — мера с базой ^ 0, абсолютно мажорируемая
мерой и. Если мы знаем, что v = рц, то из С) следует , что
-> ->
\\р\\ ^ 1 ц-почти всюду. Покажем, что.v является мерой с ба-
-*■ -*■ ■
зой ц. Она имеет базу ^ 0, а, следовательно, v = qk. Мы только
что видели, что ее наименьшей абсолютной мажорантой являет-
-*■
ся мера WqWk. Поскольку она абсолютно мажорируема мерой ц,
-*■
то WqWk ^ ц. Согласно А), мы можем теперь утверждать, что
\\q\\k = gp, 0 s£ g ==£ 1. Отсюда
-> ->
v = <7A=-4-(||?||X) = -|-gli=pli,
II 7 II II 7 II
') p/l!pll не определена в точках, где р = 0. Однако такие точки образуют
множество точек, ||р||ц-мера которых равна нулю. Мы можем значения р/||р||
На этом множестве выбирать произвольно, но норма при этом должна быть
равной 1, для того, чтобы эта норма была всюду равной 1»

§ 5. Умножение меры на функцию
603
что полностью доказывает наше утверждение. Точно так же,
если мера v имеет базу ^0 и имеет меру jx в качестве
наименьшей абсолютной мажоранты, то для нее мера jx, в частности, яв-
ляется абсолютной мажорантой, а, значит, она имеет вид p\i и
тогда, согласно Е), получаем, что \\р\\ == 1 ц-почти всюду. Мы
нашли следующее необходимое и достаточное условие того, что-
бы мера v с базой ^ 0 была абсолютно мажорируема мерой \х
(соответственно того, чтобы мера v имела ц в качестве наимень-
->->■->■
шей абсолютной мажоранты): v = р\х,, где \\р\\ гс; 1
(соответственно = 1) (х-почти всюду.
Неравенство (IV, 5;92), справедливое по предположению,
когда функция f взята из *$? {X) (и уже использованное в два
приема при доказательстве в случае, когда f являлась
характеристической функцией некоторого компакта), теперь
очевидным образом верно для любой функции f из Т(Х), поскольку
-> > ■>
v = р[л, где \\р\\ =gC 1 (х-почти всюду, и имеет место равенство
(IV,'5;93).
G) Если мера v имеет базой меру jx, то каждое борелевское
множество с компактным замыканием нулевой jx-меры также
имеет нулевую v-меру. Докажем обратное, предполагая, что у
имеет базу ^ 0. Положим v = qX, где ||^|| = 1, что возможно,
если в качестве К взята наименьшая абсолютная мажоранта.
Пусть А— борелевское множество с компактным замыканием
и нулевой ц-мерой. Тогда это множество, как и все его борелев-
ские подмножества, имеет нулевую v = qX-меру, а, следователь-
но, мера %AqX, равная нулю на всех борелевских множествах
с компактным замыканием, является нулевой мерой. Отсюда
вытекает, что функция %Aq, а, значит, и ее норма % Я-почти
всюду равны нулю. Иначе говоря, множество А имеет Я-меру,
равную нулю. Согласно А), мера К имеет базу jx, а, значит,
такую же базу имеет v = qX.
Нами полностью теперь доказаны п. 1°) и 2°) теоремы.
Н) Множество мер на X со значениями в £ и базой ^ 0
является некоторым векторным пространством. В самом деле, если
-> -> ■>■>■>■>
меры vi и v2 имеют базы Xi и Х2, vi = qtXi, v2 == q2X2, то меры Xi
и Х2 обе мажорируемы мерой X = Xi + Х2, а, следовательно,
Xi = gih Х2 = g2X, где функции gi и g2 заключены между 0 и 1.
->->■>.->
Отсюда следует, что мера vi^v2= (qigi:^q2g2)X имеет базу

604
Гл. IV. Интегральное исчисление
^ 0. Точно так же, если мера v имеет базу ^0и k — скаляр, то
мера kv имеет базу ^ 0. Всякая вещественная мера, являясь
разностью двух мер ^ 0, будет мерой с базой 15* 0 (точнее,
мера v имеет базой меру |v|, являющуюся ее наименьшей
абсолютной мажорантой). Каждая комплексная мера v = vi -+- tV2
имеет базу ^ 0. Если теперь пространство Е конечномерно и
->■->• ->• ->.->.">
если ei, е2, .. •, еп — базис в Е, то v= 2j et\h где v, — скаляр-
•>
ные меры с базой ~^ 0. Но тогда меры е%\и а вместе с ними и
->■
мера v будут иметь базы ^0. Итак, доказан п. 3°) теоремы.
I) Утверждение 4°) теоремы теперь тривиально. Пусть р—
вещественная локально ц-интегрируемая функция. Известно, что
\p\a\ является наименьшей абсолютной мажорантой функции рц
(см. сказанное после теоремы 18). Кроме того, из окончания
п. Е) следует, что \р\ц является этой наименьшей абсолютной
мажорантой. Поэтому |рц | = |р | ц. Но тогда
, .+ |рц | + p\i \p\ + p +
(PV) =2 = 2 I*= Р *
и аналогично ,(рц)~ = Р~Р»
Если теперь функции ри ? вещественны и локально ц-инте-
грируемы, то
sup (рц, q\i) — рц + ((q — Р) ц)+ = (p + (q — р)+) Ц = (sup (p, q)) ц
и аналогично inf (рц, qn) = (inf (p, q))n. В частности,
неравенство p\i ^ q\i означает, что точной верхней гранью мер p\i и q\i
является мера q\i, а, следовательно, sup(p,q) = q ц-почти
всюду или р г£С q ц-почти всюду (рц ^ 0 эквивалентно: р ^ 0
ц-почти всюду).
Наконец, пусть значения р лежат в Е, а значения q
вещественны и ^ 0, и пусть мера рц абсолютно мажорируема мерой
flu. Тогда, так как, согласно Е), ее наименьшей абсолютной
мажорантой является || р II и, то II р II u ^ q\i, а, следовательно,
||р|| ^ q u-почти всюду. Однако если мера v со значениями в Е
и базой ^0 абсолютно мажорируема мерой flu, то, согласно
->■
F), мера v имеет базой меру flu, а, следовательно, и меру и.
' ->■■->■ •>
Это означает, что v = pu и тогда ||р|| ^ q u-почти всюду. Этим
заканчивается доказательство утверждения 4°) и, значит, всей
теоремы.
Замечание 1. Во всех условиях, относящихся к мере v со
значениями в Е, предполагалось, что v имеет базу ^ 0 (напри-

§ 5. Умножение меры на функцию
605
мер, если мера v с базой ^ 0 абсолютно мажорируема мерой |л,
то v = p\i, \\р\\ ^ 1 |л-почти всюду). Контрпримеры показывают,
что это условие неизбежно, за исключением, конечно, случая,
когда пространство Е конечномерно, так как тогда любая мера
со значениями в Е имеет базу ^ 0. Общая теорема Данфорда —
Петтиса дает широкий класс пространств Е, для которых нет
необходимости предполагать v имеющей базу ^ 0.
Замечание 2. Физики часто интерпретируют меру Дирака
б на прямой так, чтобы ее можно было записать в виде Ь(х) dx,
т. е. в виде произведения dx на некоторую функцию. Мы теперь
видим, что такая запись невозможна. В самом деле, начало
координат является множеством меры нуль для dx, а не для б.
Поэтому б не будет мерой с базой dx.
Следствие 1. Пусть ц и v— две меры ^ 0 на X. Тогда
существуют наибольшая мера vi с базой ц, мажорируемая
мерой v и определяемая по формуле
v, = sup (inf (v, пи)), (IV, 5; 94)
и ц-сингулярная l) наибольшая мера vz, мажорируемая мерой v.
Мера v может быть записана в виде v = vi + \г, и это
единственное представление v в виде суммы двух мер ^ 0, таких, что
первая мера имеет базой меру ц, а вторая ц-сингулярна. Кроме
того, vi и V2 — дизъюнктные меры.
Доказательство. Прежде всего, inf (v, n\\) мажорируем
мерой n\i и поэтому, согласно п. 1°) теоремы, имеет вид рпц,
Рп ^ п |л-почти всюду. При возрастании п так определенные
меры возрастают; поэтому pn\i ^ pn+i№ или рп ^ pn+i |л-почти
всюду. Последовательность функций Рп с точностью до множеств
ц-меры нуль оказывается возрастающей. Пусть р — ее предел,
определенный ц-почти всюду. Так как рп ц-измеримы, то
функция р также |л-измерима. С другой стороны, для каждого боре-
левского множества А с компактным замыканием Г pnd\i ^.
А
<v(/4) и, следовательно, по теореме 36 Фату, Г р ф < v (Л),
А
а, значит, функция р локально |л-интегрируема и определяет
некоторую меру рц = vi ^ 0 с базой |л, мажорируемую мерой v.
') См. стр. 589. Это означает, что \2 сосредоточена на некотором
множестве Ц-МерЫ НУЛЬ ИЛИ ЧТО V2 И JA ДИЗЪЮНКТНЫ

606 Гл. IV. Интегральное исчисление
Для каждой функции ф ^ 0 из 'S'(X) имеет место
соотношение (Фату или Лебега) q>pd\i~ lim <$рпй\л, а, значит,
= sup \ урп d\i. В силу формулы (IV, 2;41в), отсюда вытекает,
что мера vi является точной верхней гранью для мер р„ц, а,
значит, удовлетворяет формуле (IV, 5; 94). Если произвольная
мера X ^ 0 мажорируема мерой v и имеет базой меру ц, то она
имеет вид q[a. Если </„ = inf (q, n), то из п. 4°) теоремы следует,
что inf (X, гщ) = inf (q\i, пц) = qn\i,. Однако из неравенства ?i, ^
^ v следует, что q„n = inf (X, гщ) ^ inf (v, пц) ^ vt. Кроме того,
из неравенства дпц^\и или ф<7„ ф ^ v, (ф), имеющего место
при любой функции ф ^ 0, фе?(Х), согласно теоремам Фату
и Лебега, получаем неравенство щ dn^v^qi), или Я'= q\i ^
^ vi. Значит, vi является наибольшей мерой ^0,
мажорируемой мерой v и имеющей базой меру ц.
Мера v2 = v — vi теперь >0 и мажорируема мерой v. Эта
мера ^-сингулярная. В самом деле, если положить 8 =
= inf (v2, ц) ^ 0, то мы увидим, что vi + 8 мажорируема мерой
vi + V2 = v и имеет базой мер-у ц, поскольку 8 ^ ц. Таким
образом, vi + 8 = vi и 8 = 0, а, значит, v2 и ц дизъюнктны.
Согласно следствию теоремы 50s, существует некоторое множество
нулевой л'2-меры, на котором сосредоточена мера ц. Однако на
этом же множестве также сосредоточена мера рц, а, значит, меры
v2 и рц = vi также дизъюнктны (более общо, это рассуждение
показывает, что если две неотрицательные меры Xi и Я2
дизъюнктны, то две меры с базами соответственно Xi и Х2 также
дизъюнктны). Пусть теперь X—некоторая мера ^0,
мажорируемая мерой v и дизъюнктная с мерой ц. Как мы только что
видели, она является дизъюнктной с мерой vi. Из inf (X, vi) = 0
вытекает, что sup (X, vi) = X + vi. Однако меры X и vi
мажорируемы мерой v, а, значит, это также можно сказать о мере
sup (Я, vi), или, что равносильно, мере X-\-vi. Поэтому Л ^ v —
— vi = V2 и, значит, v2 является наибольшей мерой ^ 0,
мажорируемой мерой v и дизъюнктной с мерой ц.
Теперь легко видеть, что v = vi+ v2 является единственным
представлением меры v в виде суммы двух мер ^0
соответственно с базой ц и ^-сингулярной. В самом деле, если v = 81+
+ 82 является таким разложением, то, согласно максимальному
свойству мер vi и v2, имеем 82 ^ v2, а, следовательно, 81 ^ vi.
Так как одновременно 81 ^ vb то 81 = vi и 82 = v2.
->■
Пусть теперь v — векторная мера с базой ^0. Мы будем
->■
говорить, что v сосредоточена на части А множества X, если QA

§ 5. Умножение меры на функцию 607
имеет нулевую меру для наименьшей абсолютной мажоранты
|v|. Тогда v будет называться ц-сингулярной или дизъюнктной
с мерой ц, если она сосредоточена на некотором множестве
нулевой ц-меры.
->
Следствие 2. Пусть |д — некоторая мера ^ 0 на X, a v —
векторная мера с базой ^ 0. Эта мера допускает единственное
■>.->-> -> ->
разложение v = vi + V2, где vi имеет базой меру ц, a V2 ц-син-
гулярна. Кроме того, разложение, соответствующее наименьшей
абсолютной мажоранте \v\, имеет вид |v| = |vi| + ]V21.
■ -> '
Доказательство. Так как мера v имеет базу !> 0, то
-> ->
можно записать v = qX. Пусть Я=Я1 + Яг— такое разложение
Я относительно |д, что Я4 имеет базой меру ц, а Яг ц-сингулярна
(следствие 1). Поскольку Xi и Я2 не превосходят А, и функция q
локально Я-интегрируема, то она заведомо локально Ягинтегри-
руема и локально Яг-интегрируема, при этом qX ~ qXi + qXi.
Однако мера Xit а, значит, и мера qX\ имеют базой меру ц. Мера
-> ->
Яг дизъюнктна с мерой ц, а, значит, такой же будет и мера qX*,
как это мы видели при доказательстве предыдущего следствия-.
Тем самым мы получили разложение требуемого вида.
Поскольку |v| = Н^НЯ, |vi| = ||<7l^i и |v2| = 1М1Я2,тоочевидным образом
-^ -^ -^
получаем, что [v| = | Vi| + |V2j- Что же касается единственности,
то она сводится к следующему: если vi + v2 = 0, где vi имеет
■*■ "*■■*■
базой меру |д, a V2 ц-сингулярна, то vi и V2 суть нули. Но это
действительно так. Если А является множеством нулевой (д-ме-
ры, на котором сосредоточена мера Vz, то, поскольку |vi| имеет
базой меру (д, множество А имеет нулевую |vi| -меру. Так как
мера V2 сосредоточена на множестве А, то множество СЛ также
имеет нулевую |vi| = Кг|-меру. Значит, X является множеством
нулевой vi -меры, а, следовательно, vi = 0 и v2 = 0.
Следствие 3. Пусть v — мера с базой ^ 0 и (д — мера
^ 0. Для того чтобы мера v имела базой меру ц, необходимо и
достаточно, чтобы для каждого компакта К и любого числа е>0
существовало такое число 8(К,е) = б > 0, что для любого бо-
релевского множества А а К, такого, что (д(Л) ^ 8, имело ме~
сто неравенство \\\(А)\\ sg е.

608
Гл. IV. Интегральное исчисление
Доказательство. Пусть сначала мера v = рц.
Поскольку функция р интегрируема на К, то существует такое число
М^О, что /(||?||-11?11д|)Ф<7. где ||?IU = inf(||p||. M)
к
(теорема 35 Лебега, примененная к разности ||р||— \\р\\м при М,
стремящемся к +оо). Теперь достаточно положить б = г/2М.
В самом деле, если \i(A) ^ б, то
II v (А) || =
Jpef|i||< J"||p||"ef|i =
А || А
= JllplU^+|(llpll-||pU^<M6 + | = e.
А А
Обратно, предположим, что имеет место указанное свойство.
Тогда каждое борелевское множество с компактным замыка-
нием нулевой (i-меры имеет также нулевую v-меру и, согласно
теореме Лебега — Никодима, v имеет базой меру ц.
Следствие 4. Пусть заданы мера v с базой ^0 и мера
(i ^ 0. Для того чтобы мера v имела базой меру ц, необходимо
и достаточно, чтобы для каждого открытого множества О с
компактным замыканием и любого е > 0 нашлось такое число
х\ {О, е) = т) > 0, что для функции фЕ?(Х) с носителем в О,
0 sg: <р ^ 1, из ц(ф) ^ т) вытекает неравенство Ц-v (<р) II ^е1).
Смысл следствия заключается в том, что оно дает возмож-
ность выяснить, имеет ли мера v базой меру ц, не используя
продолжение Лебега. Обе меры рассматриваются только как
функции, определенные на <ё'+(Х).
Доказательство. Предположим, что v = рц. Пусть б и
М — числа, определенные так же, как и в предыдущем следст-
вии, относительно множества О и числа е: (|| р|| — || р \\м) d\x ^
W
^ е/2 и б = г/2М. Если теперь функция qief^) имеет
носитель в О, 0 ^ ф ^ 1, и если ц(ф) ^ б, то
l|v(q>)||< /ф||р№ =
=/||?||л,ф^+ /(Нр11-11р1Уф^<М6 + | = 8.
') Внимание! Это неравенство не имеет места, если не предполагать,
что ф < 1.

§ 5. Умножение меры на функцию 609
Число т] = б обладает требуемыми свойствами относительно
С и е.
Обратно, предположим, что мера v с базой ^ 0 обладает
свойством, сформулированным в условии следствия. Пусть
сначала v ^ 0. Выберем такое множество А с компактным
замыканием, что |а(Л)=0, и пусть О — некоторое открытое
множество с компактным замыканием, содержащее А. Каждому е > 0,
согласно предположению, соответствует некоторое число ц —
— ц((У, е), обладающее указанными свойствами. Выберем такое
открытое множество зФ, что Лс^сС и ц(^) ^ т). Для
каждой функции фЕ?1 (X), 0 ^ ф ^ 1, с носителем в $$■ имеют
место неравенства ц(ф) <С ц(^) ^ ц, а, значит, у(ф)^е.
Переходя к точной верхней грани по всем ф, получаем \(s&) ^ e и,
следовательно, у*(Л)^е. Так как е произвольно, отсюда
следует, что v*(A)=0. Значит, каждое борелевское множество
с компактным замыканием нулевой ц-меры имеет также
нулевую v-меру. Теорема Лебега — Никодима говорит, что в этом
случае мера v имеет базой меру ц.
Пусть теперь мера v вещественна. Пусть ц = ц (О, е)— число,
соответствующее, согласно предположению, множеству О и
числу е. Если функция фе^(Х), 0 ^ ф ^ 1, имеет носитель в О и
Ц (ф) ^ Л> то Для каждой функции ife? (X), 0 ^ \р ^ ф, имеет.
место неравенство ц (\р) ^ ц, a, 3Ha4Ht |v(\f)| ^ е. Переходя к
точной верхней грани по всем \р (формула (IV, 2; 41)), получим
\+(ф) ^ е. Точно так же проверяется справедливость
неравенства v-^) ^ е. Таким образом v+ и v обладают свойствами,
указанными в условии следствия, и ^ 0. Значит, они, а вместе
с ними и мера v, имеют базой меру ц.
->
Пусть теперь v —мера со значениями в конечномерном про-
странстве Е. Пусть (в,-), t = 1, 2, ..., N,— некоторый базис Е
-». N .».
над полем R. Тогда v= 2j \tet.
Отображение «i-я координата» является R-линейным, непре*
->
рЫвным отображением £ в R, Значит, существует такое е', что
из ||v(q>)||^e' следует |v,-(ф) | ^ е. Если теперь ц — ц((У, е')~-
число, соответствующее по лемме v, О и е', то из неравенства
ц(ф)^Л будет следовать неравенство 1к(ф)|| ^ е', а, значит,
I v» (ф) j «^ е. Поэтому каждая мера v* имеет базой меру ц, и,
следовательно, такую же базу имеет мера v.
Мы здесь не приводим доказательства для случая произволь-
<■
ного банахового пространства Е.
20 Зак. 1339

610
Гл. IV. Интегральное исчисление
Применение к продолжению меры с векторными значениями
До настоящего времени мы определяли интегралы f d\y, где
/ не является функцией из *<? (X) только тогда, когда
ц—вещественная мера ^ 0 или когда / — борелевская ограниченная
функция с компактным носителем (стр. 578). Теперь можно дать
определение для более общих случаев. Пусть ц — некоторая
мера на X со значениями в банаховом пространстве Е.
Предположим, что она имеет базу ^ 0, т. е. что ее можно представить
-*■ -»■
в виде р\хо, где цо—вещественная мера >0 и р — локально
цо-интегрируемая функция со значениями в Е. Попытаемся дать
следующее определение.
Скалярная функция /, определенная на X, ^-интегрируема
тогда и только тогда, когда щ-интегрируема функция pf, и
тогда, по определению,
J/dJ=J(pf)-dm). (IV, 5; 10)
Точно так же, если ц является скалярной мерой, то она
может быть записана хотя бы одним способом в виде рц0, где цо—
мера ^ 0, р — определенная на X вещественнозначная локально
цо-интегрируемая функция. Теперь можно сказать, что функция
>
/, бпределенная на X со значениями в банаховом пространстве
->
F, ^-интегрируема тогда и только тогда, когда ^-интегрируема
функция pf, и положить
Jfd|i = |(рТ)Фо- (IV, 5; 11)
Точно так же можно определить операцию, обобщающую две
предыдущие. Пусть ц — некоторая мера на X со значениями
в Е, выражаемая в виде р\х,й, где [ю—мера >0и р — локально
^о-интегрируемая функция, определенная на X, со значениями
в Е. Пусть f — некоторая функция, определенная на X, со
значениями в F, и пусть В — билинейное непрерывное отображение
Е X F в банахово пространство G. Посмотрим, какой смысл сле-
дует придать выражению B(d\y,,f),
->■ •>
Если / есть ц-этажная функция, т. е. функция, представимая
в виде / = 27i<Pxj! где fi — некоторые постоянные, а <рх.— ха-

<5 5. Умножение меры на функцию 611
рактеристические функции ц-измеримых множеств X, конечной
ц-меры (т. е. таких, что ц(Х{) = Фх;^ имеет смысл, согласно
(IV, 5; 10)), то можно будет положить
J В (dj, f) = J В fe), S). (IV, 5; 12)
i
Теперь для произвольной функции f можно утверждать, что
j В (d\i, J) имеет смысл тогда и только тогда, когда функция
B(p,f) :х-*В(р(х), f{x)) щ-интегрируема, и положить
J В (tfj, Т) = J В (?, Ь dii0. (IV, 5; 13)
Эти определения оправданы в силу следующих двух
соображений. Во-первых, если мера ц сама ^ 0, то из теоремы 51
следует, что новое определение (IV, 5; 11) совпадает со старым; во-
вторых, имеет место
> •>
Теорема 54г. Если меру ц можно представить в виде pi\it
-> •> ■
и в виде p2\i2, где обе меры щ, цг ^ 0 и где pi (соответственно
■>
Р2) локально щ-интегрируема (соответственно ^-интегрируема);
то оба интеграла вида Г В (d\i, J), определенные по формуле
(IV, 5; 13), совпадают. Другими словами, Г В (р2, J) d\ax имеет
смысл тогда и только тогда, когда имеет смысл Г В (р2, J) d\i2,
и значения этих интегралов совпадают.
В самом деле, обозначим через 0 меру-сумму щ + ц2-
Тогда Ц( < 0 и, согласно теореме 53, найдется такая
вещественная функция gi ^s 0, что мера hi будет равна g$. Теперь, со-
•> •>
гласно следствию теоремы 51, мера pmi = pi(giQ) равна мере
(?i«i)8.
Затем, согласно (IV, 5; 13), интеграл I В (d\i, ( ) имеет смысл
•> •>
относительно представления \i в виде pini тогда и только тогда,
когда имеет смысл B(plt f) ф,,, а, согласно теореме 51,
последнее выражение имеет смысл тогда и только тогда, когда
имеет смысл Г (B(plt J) gi)dQ = I В (p[ glt f) dQ и выполняется
равенство
J В (dj, f)=JB (p, gir ft dQ. (IV, 5; 14)
20*

612 Гл. IV. Интегральное исчисление
Если теперь левую часть определить исходя из представле-
-> -*•
ния (х в виде ргу.2, Щ = #20, то мы получим:
J В (djt, Т) = J В (}2g2, T) db. (IV, 5; 15)
-> ■>
Однако, поскольку (pigi)Q и (p2gz)Q представляют одну и ту
же меру (х, то из теоремы 52 вытекает, что pigi и p2g2 равны
8-почти всюду, так что два значения, полученные для
В (d\i, f), существуют одновременно и одинаковы.
Таким, образом мы можем продолжать векторную меру [х
каждый раз, когда она имеет базу ^ 0.
-»•
Следствие. Пусть Е — векторное конечномерное простран-
-> ■*
ство, \i — некоторая мера на X со значениями в Е конечной
-»-
нормы и f — непрерывная и ограниченная функция, определен-
->■
ная на X, со значениями в банаховом пространстве F. Тогда для
' ■> ■>
билинейного непрерывного отображения В из Ey^F в банахово
пространство G интеграл I В (d\i, f) имеет смысл.
Доказательство. Согласно теореме 54, \i = q\i0, где
(хо = |(х| имеет конечную норму и 11^11=1. Тогда отображение
B(q,f) (хо-измеримо (следствие 3 теоремы 232) и ограничено, а,
значит, (хо-интегрируемо, ибо \ю имеет конечную норму
(следствие 2 теоремы 39).
Применение к интегрируемости функции по нескольким мерам
Теорема 543. Пусть (х и v — две меры ^ 0 на X. Если
функция f, определенная на X, со значениями в банаховом
пространстве F одновременно интегрируема по ц и v, то она
интегрируема по (х + v, и при этом
J7d0x + v) = j74i+ J7dv. (IV, 5; 16)
В самом деле, по теореме 53, (х = р(ц + v) и v = q(\i + v),
где р и q ((x + v)-измеримы и мажорируются числом 1. Кроме
того, (х-|- v = (р + q) ((х-f- v) и поэтому, согласно теореме 52,
p-\-q (ц-\-v)-почти всюду равна 1. Поскольку функция / [х-ин-
тегрируема, то, в силу теоремы 51, функция fp (\i -f у)-интегри-

§ 5. Умножение меры на функцию
613
руема и, кроме того,
J?d|i=j7/w/(|i + v). (IV, 5; 17)
■>
Точно так же проверяется, что функция fq (ц +
v)-интегрируема и
jfdv=jfqd(vL + v). (IV, 5; 18)
->
Следовательно, (ц + v)-интегрируема функция f(p + <7), a
поскольку р + q = 1 (n + v)-no4TH всюду, то (ц +
v)-интегрируемой будет сама функция f\ складывая равенства (IV, 5; 17)
и (IV, 5; 18), мы получим (IV, 5; 16).
->
Пример. Пусть Е — евклидово конечномерное простран-
-> -> ->
ство над R и (^|К) —скалярное произведение в £, являющееся
билинейной непрерывной формой. Если ц — некоторая мера на
X со значениями в £ и f — функция на X со значениями в Е,
то можно придать определенный смысл выражению Г (йц| 7) и
считать его равным вещественному числу. В самом деле, по от-
-> -> ->
ношению к ортонормированному базису £i, e2, • • • . еп
-> п -> -> п ■
и = 2 м-i^i и / = 2 U
п
2J U dvi
tiei.
Если при этом
имеет смысл, то можно говорить, что интеграл Г (d\i\J) также
имеет смысл и равен той же величине. Можно также утверж-
<•->->■ ->
дать, что I (d\i\f) имеет смысл, если ц имеет конечную норму,
-*•
а борелевская функция f ограничена.
Замечание. Мы предполагали, что В является билиней-
-> ■>
ным отображением, определенным на £ X F, и обозначали его
->->-> -> -> ->
через В(Х, F),Ig£, KgF. Соответствующим образом обозна-
чается интеграл. I B(d(i, /) Для М- со значениями в Е и f со зна-
-*•
чениями в /\ Если В обозначается другими символами, то
аналогично надо обозначать и интеграл. Мы учли это в случае ска-
лярного произведения, которое мы обозначили через (^[К), и

614
Гл. IV. Интегральное исчисление
соответствующим образом обозначили интеграл (d\i\f).
Можно было бы то же самое скалярное произведение обозна-
->■ •>
чить через (п1), и тогда тот же интеграл записать в виде
(/ | dy). Предположим теперь, что Е = F = R3, и пусть В
является векторным произведением, т. е. билинейным непрерывным
отображением (X, Y)-*-X Л У пространства R3 X R3 B R3- Тогда
(X, У)-»-У ЛХ является противоположным билинейным
отображением. В этом случае мы получим два противоположных
вектора: Г dp. Al и J/\ d\i. В физике постоянно приходится
встречаться с интегралами такого типа.
Сопряженность пространств V и Lp
Пусть X — локально компактное пространство, снабженное
мерой Радона ц ^ 0. В дальнейшем пространство Lp (X, ц) мы
будем кратко обозначать через V. Точно так же, как в
следствии 1 теоремы 46, для 1 ^ р ^ +оо положим р' = р/(р— 1),
так что 1/р + 1/р' = 1. Пусть h ef' (через И. мы обозначаем
класс эквивалентности, т. е. множество функций h^Lp',
попарно почти всюду равных между собой). Этот элемент определяет
по формуле
(ut, f)=l h(x)f(x)dli(x), /е=/, (IV,5; 19)
х
некоторую линейную непрерывную форму на Lp. В самом деле,
согласно следствию 1 теоремы 46, правая часть имеет смысл, так
что ый является линейной формой на Lp. Непрерывность этой
формы вытекает из неравенства Гёльдера, причем
sup I(и , I)I
М- Np(f) <Np'{h)- (IV'5;20)
Отображение h-*~u^ является теперь линейным
отображением пространства Lp' в пространство (Z/)', сопряженное к
пространству Lp.
Теорема 544. Определенное выше отображение h->ufi
является при 1 ^ р <С + сю изометрической биекцией V на (Lpy.
Если же р = -f-°°, то оно является изометрической инъекцией
V в (Lp)', которое не может быть сюръекцией, если носитель
ц содержит бесконечное множество точек.
Перед доказательством теоремы уточним ее смысл: изомет-
рия означает, что ||ий| = АГ, (Л), или также, чтой-»-ай являет-

§ S. Умножение меры на функцию 615
ся инъекцией, поскольку ый = 0 тогда и только тогда, когда
ft = 0. С другой стороны, когда мы говорим, что при р <С -f-oo
имеет место сюръекция, то мы этим хотим сказать, что каждая
линейная непрерывная форма на W может быть выражена
(единственным образом) в виде ый, где fteLp'. Поэтому при
р <С -f-oo можно отождествить пространство (Lp)', сопряженное
к пространству У, с пространством W. Однако L1 ,является,
вообще говоря, только некоторым подпространством
пространства, сопряженного к пространству L°°. (Следует иметь в виду,
что сопряженным к L1 является пространство L°°, однако
пространство, сопряженное k4L°°, не совпадает с пространством ZA)
Доказательство. Докажем, что при р = -f-°°
отображение ft->ый изометрично (а, следовательно, инъективно).
Обозначим через / функцию ft/|ft| (давая ей, например, значение 1
там, где ft = 0). Очевидно, jfeS"10 и |/|==1. Из неравенств
Г А
вытекает, что IIый||^yVt (ft), а, следовательно, ||"J| — N\ (h), чем
и доказывается изометричность в случае р = -f-oo. Можно было
бы провести то же самое рассуждение для р <С -f-°°, но мы
в этом случае будем одновременно доказывать и изометричность,
и сюръективность. Пусть 1^р<С+оо, и пусть и —
непрерывная линейная форма на Lp. Тогда
|(М> |<||«ИЗД. (1У,5;21)
Продолжим линейную форму и на пространство 3?р,
полагая ее равной нулю на всех ц-почти всюду равных нулю
функциях. Тогда она будет определять линейную форму на 'ё'(Х),
очевидно, непрерывную на каждом Wk (X), где К — компакт из
X. Действительно, если <р сходится к нулю в Ч?к (X), то она тем
более сходится к нулю в 3?v. Значит, форма и определяет
некоторую меру Радона v на X.
Если р = 1, р' = +оо, то
|у(ф)| = |(и,фЖ||и||^1(ф) = ||ы|||1(|ф|). (IV, 5; 22)
Отсюда следует, что мера v абсолютно мажорируема мерой
\\и\\ц. Согласно теореме 52—53—54, существует ц-измеримая
функция ft, |ft|<||u||, а, следовательно, Mx>(ft) sg: ||ы||, такая, что
v = h[i. Если 1 <С р <С -f- оо, то для того, чтобы показать, что
мера v имеет базой меру ц, можно применить теорему 52
Лебега— Никодима. Мера v допускает, как мы это отмечали на
стр. 584, борелевское продолжение в Г(Х). В свою очередь

616
Гл. IV. Интегральное исчисление
форма ипродолжима на &v и Т(Х) czS'p. Естественно выяснить,
является ли продолжение v на Т(Х) сужением и на Т{Х). Для
этого достаточно доказать, что сужение и на Г(^), являющееся
непрерывным в топологии, определяемой пространством S'p,
будет также L-непрерывным. Прежде всего, очевидно, что если
некоторая последовательность функций /пеГ(1) сходится
просто к 0, оставаясь ограниченной и сохраняя сбой носитель
в фиксированном компакте, то она сходится к 0 в S'p (частная
теорема Лебега 34). Так как форма и непрерывна в S'p, то
{и, fn) сходится к 0. Пусть О — открытое множество из X с
компактным замыканием, и пусть задано е > 0. Тогда можно найти
такой компакт К, что ц((3■— К)^(г/\\и\\)Р. (Здесь существенно
то, что р < + се.) При этих условиях для каждой функции ф из
'ё'(Х), 0 ^ ф ^ 1, равной 1 на некоторой окрестности компакта
К и имеющей носитель в О, имеют место неравенства
| (и, %а) - (и, Ф> | < II и || Ыр (хо - Ф) < II и II #р (%а-к) =
= 1|и||(М<?-Ю)1/Р<е.
из которых следует L-непрерывность и на Т(Х) и,
следовательно, совпадение и и борелевского продолжения v на Г (Х).Но
тогда, если А является борелевским множеством с компактным
замыканием и ц-мерой, "равной нулю, то его характеристическая
функция [i-почти всюду равна нулю и значение и на этой
характеристической функции равно нулю. Но тогда также \(А) =
= 0. Согласно теореме Лебега — Никодима (теорема 52), v
является мерой с базой ц. Значит, существует такая локально
ц-интегрируемая функция ft, что v = h\i.
Пусть М — некоторое число ^0 и К— компакт пространства
X. Обозначим через hM, к функцию, определенную так, как на
стр. 521: при ft ^ 0 она равна ft в каждой точке К, в которой
|ft(*) | ^ М, и равна 0 во всех остальных точках.
Пусть теперь / — функция| hM, K |0'-2 %м,к, равная нулю там,
где Лм, к — 0. Ее модуль равен |ftM, к|р'-1 и ft/= [ftM k|p'.
Мы видели, что каждая измеримая функция ц-почти всюду
равна некоторой борелевской функции. Поэтому можно, изменяя при
необходимости функцию / на множестве нулевой ц-меры,
предполагать ее борелевской и, поскольку |/|^MP_1,
принадлежащей Г (X). Теперь имеем неравенства
|иИ>
(и,П\
jfhd»\ j\hM.Kf&
tfp(f) tfpU) ~ ,. VJ
J_
= (J* I hM,K f rfji) "' = Np, (hM, K). (IV, 5; 23)

§ 6. Образ меры при отображении 617
Так как эти неравенства справедливы при любых М и К, то,
переходя к точной верхней грани, можно получить неравенство
NP< (Л) < II " II и, следовательно, Ле^'". (IV, 5; 24)
Теперь линейная форма и и форма «й, определенная, исходя
из Ае^, совпадают на множестве 'ё'(Х). Так как множество
'S'(X) плотно в &р (еще раз в силу того, чтор < + °°; см.
теорему 49), то эти формы совпадают на 2Р. Этим доказывается
сюръективность, а из неравенств (IV, 5; 20) и (IV, 5; 24)
одновременно следует изометричность ЦыйЦ — ^ Лh), чем и
заканчивается доказательство позитивных частей теоремы. Что же
касается ее негативной части, а именно того, что каждый раз,
когда носитель ц содержит бесконечное множество точек,
отображение h—ytifr не сюръективно и, следовательно,'сопряженное
к пространству L°° не может быть отождествлено с L1, то эту
часть мы примем без доказательства.
->
Замечание. Пусть теперь Е — произвольное банахово
1- <-
пространство. Тогда каждый элемент h из Lp (E') определяет на
U (Е) некоторую линейную непрерывную форму ий по формуле
(и*,Т)= \(h,f)dix, (IV, 5; 25)
и, кроме того, .с помощью того же неравенства Гёльдера мы
получаем неравенство |ий|^Л/р, (Л). Тем самым определено еще
*■ , <-
одно отображение h -+и<- пространства L (Е') в пространство
h
->■ ->•
(LP(E))', сопряженное к пространству LP(E).
Можно показать, что если Е конечномерно и р < 4- со, то
это отображение является изометрической биекцией, а это
позволяет еще раз отождествить пространство, сопряженное к про-
странству Lp (Е), с пространством V (£'). Этот факт мы
примем без доказательства. Однако без дополнительных условий
->
это утверждение не верно, если Е окажется бесконечномерным
банаховым пространством.
§ 6. ОБРАЗ МЕРЫ ПРИ ОТОБРАЖЕНИИ
Если ц — мера, определенная на локально компактном
пространстве X и принимающая значения в векторном норми-
рованном пространстве £, и ?сли £— линейное непрерывное

618
Гл. IV. Интегральное исчисление
отображение Ё в векторное нормированное пространство F, то,
очевидно, можно определить новую меру L ° ц по фор"муле
(L = it)(<p) = L(it(<p)). (IV, 6; 1)
->
В самом деле, L°\i является линейным отображением 9!?{Х)
->
в F, и если функция <р имеет носитель в компакте Л", то имеет
место оценка
11(£°й(ф)||<||£|||1Ни1|ф|||, 0ТКУДа HWII*<ll*<IIIIHbr-
(IV, 6; 2)
->
Эта мера называется образом меры ц при линейном
непрерывном отображении L.
Однако мы хотим рассмотреть образ другого характера,
играющий весьма важную роль в практике. Пусть ц — мера со
значениями в Е, определенная на локально компактном
пространстве X, и пусть Н — отображение X в локально
компактное пространство Y. Покажем, что если Н обладает
необходимыми свойствами, то существует образ меры, обозначаемый че-
->
рез Нц, являющийся мерой на локально компактном
пространстве Y со значениями в Е.
Известно, что если функция ф принадлежит 'S'(K), то она
имеет прообраз Я*ф, являющийся функцией на X, определенной
по формуле
Я*ф = фсЯ, или (/Г<р)(;с) = ф (//(*)). (IV, 6; 3)
Тем самым мы естественным путем пришли к тому, чтобы
определить образ Нц, по формуле
(ЯЙ (ф) = jt (Я*ф) = J Ф (Я (х)) с& (х). (IV, 6; 4)
Однако это определение может иметь смысл только в том
случае, когда имеет смысл правая часть равенства (IV, 6; 4) и
когда, кроме того, она в самом деле определяет некоторую меру
на Y со значениями в Е. Разберем два возможных случая.
1-й случай. Н — непрерывное собственное отображение.
Определение. Непрерывное отображение Н локально
компактного пространства X в локально компактное
пространство Y называется собственным, или непрерывным в
бесконечности, если прообраз каждого компакта из Y при отображении И
является некоторым компактом пространства X,

§ 6. Образ меры при отображении 619
Если X компактно, то каждое непрерывное отображение Н
пространства X в У является собственным. Действительно,
каждый компакт из Y замкнут, а, следовательно, его прообраз при
отображении Н замкнут в X, и поскольку X компактно, то он
компактен (теоремы 21 и 22 гл. II).
Если X не компактно, то постоянное отображение X в У не
может быть собственным. Ортогональная проекция на одну из
координатных осей плоскости R2 не является собственным
отображением.
Т е о р е м а 55. Если X и У — метрические пространства, в
которых все замкнутые шары компактны, то непрерывное
отображение Н будет собственным тогда и только тогда, когда
прообраз каждого ограниченного подмножества У при отображении Н
является ограниченным подмножеством пространства X.
В самом деле, так как отображение Н непрерывно, то
прообраз замкнутого множества замкнут, и поскольку замкнутые
шары компактны, то компакты совпадают с замкнутыми
ограниченными множествами1).
Следствие. Если X и У — такие метрические
пространства, в которых замкнутые шары компактны, то непрерывное
отображение Н пространства X в У будет собственным тогда и
только тогда, когда образ при отображении Н каждой
неограниченно удаляющейся последовательности точек в X является
неограниченно удаляющейся последовательностью точек в У.
Говорят, что последовательность точек хп метрического
пространства неограниченно удаляется при п, стремящемся к
бесконечности, если расстояние от точек хп до некоторой
фиксированной точки а стремится к +оо. Так как d(b,xn) ^d(a,xn) —
— d(a,b), то в этом случае расстояние хп до любой другой
фиксированной точки b также стремится к +оо.
Доказательство. 1°) Предположим сначала, что
отображение Н собственное. Тогда, если последовательность точек хп
неограниченно удаляется на X, то Н{хп) неограниченно
удаляется на У. В противном случае можно было бы найти
подпоследовательность, содержащуюся в некотором шаре, т. е. в
некоторой ограниченной части У, и тогда, в силу того что
отображение Н собственное, соответствующая подпоследовательность
хп должна, в силу теоремы, остаться ограниченной, что
противоречит предположению о том, что хп неограниченно удаляется.
') Компактная часть произвольного метрического пространства замкнута
и ограничена. Обратно, в метрическом пространстве, в котором замкнутые
шары компактны, замкнутая ограниченная часть содержится в некотором
замкнутом шаре, т. е. в некотором компакте, и так как она замкнута, то она
компактна. Это — доказательство п. 1°) и 2°а) теоремы 23 гл. II.

620
Рл. IV. Интегральнее исчисление
2°) Обратно, пусть рассматриваемое свойство выполнено, т. е.
пусть отображение Н каждую неограниченно удаляющуюся
последовательность в X преобразуете неограниченно удаляющуюся
последовательность в У. Тогда отображение Н собственное. В
самом деле, если В — некоторая ограниченная часть У, то ее
прообраз должен быть ограниченным. В противном случае в нем
можно найти неограниченно удаляющуюся последовательность
точек, образы которых будут также неограниченно
удаляющимися, что противоречит тому, что эти образы лежат в
ограниченной части В. Согласно теореме, отображение Н
собственное.
Пример. Отображения х-+хп при произвольном целом
п ^ 1 являются собственными отображениями вещественной
прямой R на себя.
Название «непрерывное в бесконечности» для собственного
отображения оправдывается доказанным следствием. Если
к множеству X добавить «бесконечно удаленную точку» и то же
самое сделать для множества У, а затем отображение Н
продолжить, полагая, что образом бесконечно удаленной точки в X
при отображении Н является бесконечно удаленная точка У, то
отображение Н будет собственным тогда и только тогда, когда
таким способом продолженное отображение будет непрерывным
в бесконечно удаленной точке.
Теорема 56. Если Н — собственное отображение локально
компактного пространства X в локально компактное
пространство У, то образ каждой замкнутой части пространства X при
отображении Н является замкнутой частью пространства У1).
Доказательство. Пусть А — замкнутая часть
пространства X. Положим В = Н(А) и докажем, что В замкнуто. Надо
показать, что каждая точка прикосновения 6еУ множества В
принадлежит В. Обозначим через р компактный шар с центром
в точке Ь. Поскольку b является точкой прикосновения
множества В, то этот шар пересекается с В и, кроме того, b является
точкой прикосновения пересечения рПВ2). Так как отображение
Н, по предположению, собственное, то прообраз #_1(Р) является
компактной частью X. Он пересекается с Л по некоторой
компактной его части К. Если теперь точка х принадлежит К, то ее
образ принадлежит одновременно р и В, а, следовательно, и их
пересечению р (1 В. Обратно, если некоторая точка у принадле-
') Если Н непрерывно, то прообраз замкнутого множества замкнут и
образ компакта компактен. Если, кроме того, Н собственное, то прообраз
компакта компактен и образ замкнутого множества есть замкнутое множество.
2) Напомним, что b является точкой прикосновения множества, если
каждый шар с центром в точке b пересекается с этим множеством.

§ 6. Образ меры при отображении
621
жит пересечению р П В, то она принадлежит В и, следовательно,
является образом по крайней мере одной точки Хо^А, а
поскольку она принадлежит р, то ^0eW"'(P) т. е. х0^К. Таким
образом, образ Н(К) совпадает с пересечением р П В. Так как
отображение Н непрерывно, а К компактно, то отсюда следует,
что множество р П В компактно, а, следовательно, замкнуто.
Значит, точка Ь, являющаяся его точкой прикосновения,
принадлежит этому множеству и тем самым принадлежит множеству
В, что и требовалось доказать.
Собственные непрерывные отображения дадут нам пример
отображений, при которых4образ Н\х имеет смысл.
Теорема 57. Если X и Y — локально компактные простран-
.-> ->
ства, Е — нормированное векторное пространство, ц — некоторая
■*■
мера на X со значениями в Е и носителем А и если Н является
непрерывным отображением X в У, сужение которого на А есть
собственное отображение А в У, то формула (IV, 6; 4)
определяет Н\х как некоторую меру на У, называемую образом ц при
отображении Н.
Эти условия, естественно, будут выполнены, если
отображение Н является непрерывным и собственным отображением X
в Y или если отображение Н непрерывно и \х имеет компактный
носитель.
Доказательство. Пусть ф — некоторая функция из <&{Y)
с компактным носителем К. Ее прообраз Я*ф = ф °'#
непрерывен как композиция двух непрерывных отображений. Выясним,
каким будет носитель этого отображения. Пусть Q — множество
таких точек у, что <р(у)_Ф 0. Согласно определению носителя
функции ф, замыкание Q = К. Множество точек х, в которых
.функция Я*ф отлична от нуля, является прообразом #_1(Q).
Поскольку прообраз Н'ЧК) замкнут и содержит #_1(Q), носитель
Я*ф, очевидно, содержится в Н~*(К). Естественно, этот прообраз
Я-1 (К) не обязательно компактен. Он был бы компактным, если
бы отображение Н пространства X в пространство Y было бы
собственным, но это предположение несколько ограничительно.
Мы будем предполагать, что только сужение Я на Л является
собственным. Это означает, что пересечение Н~{(К) и А является
компактной частью А. Но тогда, как мы видели в теореме 16,
->
можно придать смысл выражению ц(#*ф), поскольку Я*ф —
непрерывная скалярная функция и поскольку пересечение носителя
\х и носителя Я*ф компактно. Теперь видно, что выражение,
стоящее - справа в (IV, 6; 4), имеет определенный смысл и

522
Гл. IV. Интегральное исчисление
линейно зависит от ф. Если ф сохраняет свой носитель в
фиксированном компакте К пространства У и равномерно
сходится к 0, то Я*ф сохраняет свой носитель в замкнутом
фиксированном множестве Н~1(К), пересечение которого с А
компактно, и сходится равномерно к 0. Из теоремы 16 следует, что
(х(Я*ф) также сходится к 0. Этим доказывается, что правая
часть соотношения (IV, 6; 4) определяет некоторую меру на Y
со значениями на Е и, следовательно, Н\х существует1).
Теорема 58. 1°) В условиях теоремы 57 относительно норм
имеет место неравенство:
№11<||ц1К+°о. (IV, 6; 5)
2°) Если мера \х комплексна (соответственно вещественна,
соответственно вещественна ^0), то такой же будет и мера Н\х.
-*■ ■*■
3°) Носитель Н\х содержится в образе носителя \х при
отображении Н.
■> •>
4°) Если носители мер (л и (д,2 лежат в таком замкнутом
множестве А, что сужение Н на А является собственным, то
И (На + Н^) = #Нч + #Ц2.
Н (JfeJ) = k (Яц),
(IV, 6; 6)
иначе говоря, отображение ц-*~Нц линейно2).
Доказательство. 1°) Предположим, что функция
фе'^'(У) такова, что |ф| ^ 1. Тогда также |Я*ф|^ 1. В силу
(IV, 2; ЗЗг), отсюда получаем неравенство
№(ф)1М1ИЯ>)1К1Й> (IV, 6; 7)
из которого следует неравенство (IV, 6; 5).
2°) Очевидно.
->•
3°) Пусть А — носитель ц в X, и пусть В — его образ Н(А),
' По теореме 56 множество В замкнуто. Пусть теперь ф —
некоторая функция из 'ё'(У), носитель которой К не имеет общих
точек с В. Тогда носитель функции Я*ф, который содержится
в прообразе Н~1 (К) носителя К функции ф при отображении Н,
не может пересечься с А. Следовательно, ц(//*ф) =0, а, зна-
') Примеры мы приведем позже на стр. 628. Однако полезно посмотреть
их сейчас.
2) Заметим, что отображение Н непрерывно и собственно, но не обладает
свойством линейности, а локально компактные пространства X и У не являются
векторными. Однако, несмотря на это, отображение ц->-#)г линейно!

§ 6. Образ меры при отображении
623
чит, и (#ц.)ф = 0. Другими словами, мера Яц равна нулю в
дополнении к В, а ее носитель лежит в В. Этот носитель может
оказаться строго меньше В. Тем не менее легко показать, что
если мера ц вещественна и ^ 0, то носитель меры Яц в
точности равен В1).
4°) Очевидно.
2-й случай. Мера ц вещественна и Г^О.
Теорема 59. Пусть X и Y — локально компактные
пространства, счетные в бесконечности, ц — вещественная мера
^0 на X и Я — такое ^-измеримое отображение X в Y, что
прообраз при этом отображении каждого компакта из Y имеет
конечную меру относительно ц. Тогда формула (IV, 6; 4)
определяет Н[ц как некоторую меру ^ 0 на Y. Кроме того, если К
является некоторым компактом из Y, то имеет место оценка
№1|*< J rfn, откуда ||Я|1|К||ц||. (IV, 6; 8)
и-1 (Ю
Мы будем говорить, что отображение Я ц-собственное, если
оно удовлетворяет предыдущим условиям. Эти условия всегда
выполняются, если Я измеримо, а ц имеет конечную норму.
Доказательство. Последнее утверждение очевидно: если
отображение Я измеримо и мера ц имеет конечную норму, т. е.
ц(%) < +°°. то Для каждого компакта К множество Я-1 (К)
измеримо и имеет конечную меру.
Пусть теперь задана некоторая функция фе?(У). Согласно
теореме 22, ее прообраз Я*ф = ф о Я является комплексной
|л-измеримой функцией на X. Эта функция ограничена
величиной ||]ф|||. Поскольку множество точек, в которых эта
функция =й=0, очевидно, содержится в прообразе носителя К
функции ф при отображении Я и, значит, в измеримом множестве
конечной меры относительно ц, то |(Я*ф)|ф, конечен. Из
теоремы 39 теперь вытекает, что Я*ф ц-интегрируема. Поэтому
можно придать смысл правой части равенства (IV, 6; 4). Эта
правая часть линейно зависит от ф и ^0, если ф ^ 0.
С другой стороны, если ф имеет носитель в К, то |||Я*ф|||
равна |||ф|||, и имеет место оценка
|(Яц)(ф)|<|||ф||| J dp, (IV, 6; 9)
//-'«)
') Это вытекает из следствия 1 теоремы 60. В самом деле, пусть Si с В
является носителем меры Яц. Если В\ Ф В, то CSi является открытым
множеством Яц-меры нуль, пересекающимся с В.'Следовательно, Я-1 (СSi)
будет открытым множеством нулевой ц-меры, пересекающимся с носителем А
меры ц, что невозможно.

624 Гл. IV. Интегральное исчисление
из которой следует, что Нц непрерывна на 'S'k(Y) и, значит,
является некоторой мерой, и что имеет место неравенство (IV, 6; 8).
Теорема 60. Пусть в условиях теоремы 59./ — некоторое
отображение пространства Y в банахово пространство F. Для
того чтобы отображение f было Н\у.-интегрируемым
(соответственно Неизмеримым), необходимо и достаточно, чтобы про-
-> ■*■
образ H*f = f о Н был ^-интегрируемой функцией на X со значе-
■>
ниями в F (соответственно ^-измеримой), и тогда имеет место
следующее равенство:
| Jd (Hii) = J (H*J) dii=j 1{H (х)) d» (x). (IV, 6; 10)
Эту теорему мы примем без доказательства, в котором
следовало бы воспользоваться равенством
J *fd(//|i) = J" (//•/) d|i<+«>, (IV, 6; 1П
справедливым для вещественных функций ^ 0.
Легко получается
Следствие I. Пусть выполнены условия теоремы 59 и В —
некоторая часть Y. Часть В Неизмерима тогда и только тогда,
когда \у.-измерим ее прообраз Я-1 (В), и в этом случае имеет
место равенство
Нц (В) = ц (Н~\В)) < + оо. (IV, 6; 12)
Следствие 2. Справедливо равенство
№И = Ы1<+°°. (IV, 6; 13)
Для доказательства достаточно применить следствие I к
множеству В = У.
Теорема 61 (о транзитивности образов мер). Пусть X, Y,
Z — три локально компактных пространства, Н — отображение X
-> ->
в Y, К — отображение Y в Z и ц — мера на X со значением в Е.
1°) Если Н и К непрерывны и если сужение сложного
отображения К°Н пространства X в Z на носитель и, является соб-
-> ->
ственным, то К(Нц) и (К°Н)ц, согласно теореме 57, имеют
смысл и равны между собой.
2°) Если мера ц вещественна и ^ О, X, Y, Z счетны в
бесконечности и, в условиях теоремы 59, существует /С(Яц), то, в силу
этой теоремы, существует (К°Н) (и) и имеет место тождеству

§ 6.- Образ меры при отображении 625
Доказательство. 1-й случай. Пусть А— носитель меры
\х и В = Н(А). Пусть С — компактная часть множества Z.
Тогда образ пересечения H-i(K~i(C'))f\A при отображении Я
равен пересечению /С-1 (С) (IS. Так как /С°Я по условию
является собственным на А, то первое из этих множеств
компактно. Тогда второе множество также компактно, поскольку
оно является образом компакта при непрерывном отображении,
а это означает, что сужение К на В является собственным.
Пусть теперь В'—компактная часть пространства Y и С—ее
образ при отображении К. Тогда пересечение Я_1(В')П А
содержится в пересечении Я-1 (/С-1 (С)) П Л, которое по
предположению компактно. Таким образом, прообраз каждого компакта из;
У при сужении Я на Л является замкнутым множеством,
содержащимся в некотором компакте X и, значит, является
компактом. Это говорит о том, что Я является собственным отображе-
нием на носителе А меры \х. Теперь мера Нц имеет смысл, а ее
носитель лежит в В (теорема 58,3°). Следовательно, К, будучи
собственным на В, является собственным на этом носителе. Со-
гласно теореме 57, К(Н\х) имеет смысл. Пусть теперь ф —
некоторая функция из 'e'(Z). Тогда справедливы равенства
((/С ° Я) (Г) (Ф) = J ф (К (Я {х))) dl (x),
, , * (IV, 6; 14)
(к (Вд (ф)= J ф(Ш)<*МФ))=/<р (* (//(*)))#(*),
откуда (К °H)\i = K(H\i) .
2-й случай: ц ^ 0. Пусть теперь отображение Я ц-собствен-
ное, а отображение К (Яц) -собственное. Пусть С — замкнутое
подмножество Z. Так как отображение К Яц-измеримо, то
прообраз /С-1 (С) является //^-измеримым. Но тогда, согласно
следствию 1 теоремы 60, в силу того, что Я является ц-собствен-
ным, его прообраз Я"-1 (/С-1 (С)) необходимо ц-измерим, а это
означает, что К' Я есть ц-измеримое отображение.
Кроме того, если С компактно и отображение К Яц-соб-
ственное, то К~1 (С) имеет конечную Яц-меру. Отсюда в силу
того, что Я ц-собственное, вытекает, что Н'1(К'1(С')) имеет
конечную ц-меру. Это доказывает, что К°Н является
^-собственным. Пусть теперь ф — некоторый элемент C(Z).
По определению (К°Н) ц, имеем
((Я°ЯЫ(ф)=/ф(/((Я(л:)))4Ф). (IV, 6; 15)
Согласно теореме 60, это выражение можно записать в виде
/ф(/Ш)<*(Яц(*/)) или (/С(Яц))(ф), (IV, 6; 16)
нем и доказывается равенство (К°Н) ц = К(Нц).

626
Гл. IV. Интегральное исчисление
Замечание. Условия применимости обоих случаев
являются крайне различными. В первом случае указанное условие
предполагалось выполненным для К°Н, а не последовательно
для Я и для К, тогда как во втором случае условия
предполагались выполненными последовательно для Я и для К, но не
для К°Н. Легко доказать, что условия такого рода не могут
быть переставлены. Например, в первом случае может случиться,
что Я непрерывно и является собственным на носителе ц, К не-
->
прерывно и является собственным на носителе Я ц, и тем не
менее К°Н не является собственным на носителе ц1). Во вто-
->
ром случае вполне может оказаться, что К ° Я ц-измеримо, хотя
Я не является ц-измеримым2).
Случай, когда Н является гомеоморфизмом А на У
Если отображение Я— гомеоморфизм, то оно, очевидно,
удовлетворяет всем условиям, позволяющим определить Яц для
меры \i, определенной на X. В этом случае существует обратное
отображение Н~ , которое также является некоторым гомеомор-
-1 "*■ -1 "*"
физмом. При этом, согласно теореме 61, Я (Нц) = (Н °Я)ц =
-*■ -*• _i>
= ц. Впрочем, в этом случае, полагая H*v =H v, можно
->-
также определить прообраз при отображении Я меры v,
определенной на Y, и образ функции фе?" (I) при этом
отображении, если положить Ягр = (Я_1)*ф = ф о Я-1. Для каждой меры
->
\i на X и для каждой функции (fGf(I) имеют место
соотношения
(ЯФ)(у) = ф(Я-'(г/)); ЯФ(Я(д)) = Ф(*); х^Х, y^Y; g
//JOtf^/r'fo)); Я|Г(Яф) = |Г(ф); Ф е=?(Л), Ф e=f (Г). '
-> ->
Интеграл от Я/ по H\i равен интегралу от f по \х, а мера
множества Я (Л) (если ЛсХ) по отношению к H\i равна мере
множества А по отношению к ц.
') Пусть, например, X = Y = Z = R. В качестве собственного
отображения Я возьмем х-*-х2. Мера ц равна xdx. Тогда Яц(<р) = <p(x2)xdx = О,
а, следовательно, Яц = 0. Если отображение К постоянно, то оно
собственное на носителе меры Яц (который пуст). Однако К"Н постоянно на R и,
следовательно, не собственное.
2) Если в качестве Я взять не ц-измеримое отображение, а в
качестве К — постоянное отображение, то К°И будет постоянным отображением,
а, значит, (х-измеримым!

$ 6. Образ меры при отображении
62?
Так как ф(//-1 («/)) является функцией Яф, то первая из
формул (IV,6; 17) побуждает использовать обозначение (1ц(Н^(у))
для образа Н\а. При этом формула (IV, 6; 10) запишется в очень
удобной форме:
J" f(y)dlx(H-\y)) = J* /(//(*)) 4Ф), (IV; 6; 172)
как бы полученной «заменой переменной у = Н(х)».
Кроме того, если d\i имеет вид р dX, d^(x) = p{x)dX{x), то
d(i (Н~\у)) = p(H-\yj) dk (Н-\у)). (IV, 6; 173)
В самом деле, для фе'й'(К) имеем:
J" Ф (у) dp (Я"1 (у)) = J Ф (Я (х)) dp (*) = J" Ф (Я (*)) р (х) dX (x) =
= J" Ф(Я (х))р(Н-\Н (x)))dX(x) = j 4,(y)[p{H-\y))dk {1Г\у))\.
(IV, 6; 174)
Обобщение теоремы 59 на случай, когда р. не ^0
Методы, рассмотренные в предыдущем пункте, позволяют
с помощью теоремы 59 определить H\i даже в том случае, когда
-мера (i векторная, лишь бы только она имела базу ^0. В
самом деле, перед теоремой 542 мы выяснили, что следует
понимать под (i-интегрируемой скалярной функцией /, не
принадлежащей <8 (X). Говорят, что Нц существует, если, какова бы ни
была функция фе?(1), функция Я*ф (i-интегрируема, а если
Ф равномерно сходится к 0 и сохраняет при этом носитель в
фиксированном компакте, то интеграл (H*(f)d\i сходится к 0.
В этом случае полагают по определению
//Ц (ф) = J" (Я>) djt = J Ф (Я (*)) dj (x). (IV, 6; 18)
Это произойдет, в частности, тогда, когда ц имеет конечную
норму, Е конечномерно и Я непрерывно, так как, в силу
непрерывности и ограниченности Я*ф, можно воспользоваться
следствием теоремы 54г. Согласно теореме 54, ц = q\io, где мера
цо ^ 0, имеет конечную норму и ||<7|| = I. При этом имеет место
неравенство
I J (//»"? dm, | ^ II Ш) IIII! Ф III. (IV,6;182)

628
Гл. IV. ИнтегральнЬе исчисление
показывающее, что || Нц II <: II ц0 II = II Ы II- В действитель-
ности можно даже доказать, что || Нц || ^ || ц ||.
Различные примеры образов мер
Г) Предположим, что Н — постоянное отображение X в Y.
Образ X при этом отображении — это некоторая точка Ь е Y.
Здесь
/Гф(*) = ф(//(*)) = Ф(&), (IV, 6; 19)
и, следовательно,
(//Й(ф) = (/«Й)ф(*0, или //JI = (JdJ)e(W. (IV, 6; 20)
->
Образ меры ц является точечной массой в точке Ь, равной
полной массе меры ц, d\i.Такой же результат ожидается и
интуитивно:' Я переносит X целиком в точку Ь; следовательно, это
отображение переносит в точку b всю массу.
Этот результат предполагает, что рассмотрение ведется
в сформулированных выше условиях, т. е. X компактно,
например, или мера ц вещественна, ^0 и имеет конечную норму.
Здесь очень хорошо видно, почему надо рассматривать
ограничения на Я. Если, например, Я — постоянное отображение
вещественной прямой X = R в Y и если d\i = dx есть мера Лебега
пространства R, то отображение Я не является ^-собственным.
Если бы существовала мера Нц, то она должна была бы иметь
массу +оо в точке b = Я(К), что невозможно, ибо точка,
будучи компактным подмножеством, не может иметь бесконечную
меру.
2°) Предположим, что ц— это линейная комбинация мер
Дирака, а именно ц = 2 cv&(av\- В этом случае мера Нц, если
V
она определена, задается равенством
Яц = 2л cvSh(ov) и, в частности, Яб(а) = б(Н(а))- (IV, 6; 21)
Этот пример показывает конкретный физический смысл об-
раза меры. Если мера ц составлена из некоторого числа масс,
расположенных в некоторых точках, то ее образ получается
«переносом» этих масс в соответствующие точки с помощью
преобразования Я. Априори ясно, что операция (IV, 6; 21) существует
для меры, образованной из суммы конечного числа точечных
масс. Смысл изложенного в этом пункте заключается в том,

§ 6. Образ меры при отображении 623
чтобы показать, что перенос меры при отображении Я является
операцией, возможной в значительно более общих случаях1).
3°) Предположим теперь, что X — аффинное конечномерное
пространство, и пусть Л—некоторый вектор из присоединенного
векторного пространства X. Возьмем в качестве преобразования
Н параллельный перенос т-*, определяемый вектором h с по-
h
мощью формулы л:—► л: + Л. Это преобразование является
гомеоморфизмом (и, следовательно, к нему можно применить
различные формулы (IV, 6; 17)). Образ функции <р, определенной на
А', задается по формуле
т->ф (х) = Ф (*_*А = Ф (х — Л)2). (IV, 6; 22)
-> ■*
Образ меры ц на А" при переносе h является мерой,
определяемой по формуле
(fjii) (Ф) = И (iff) = И (*_£Ф) = J Ф (х + Л) djt (дс). (IV, 6; 23)
Согласно теореме 60, в случае, когда мера ц вещественна и
-> >
^0, функция f со значениями в банаховом пространстве F
является т^-ц-интегрируемой тогда и только тогда, когда функция!
h
-> -> >
т-*. f: х -> f (л: + h) является ц-интегрируемой, и тогда имеет ме-
h
сто равенство
•j7d(Ttti)= jf(x+h)dii(x). (IV, 6; 24)),
') Отождествим каждую точку oeJfc мерой б(а). Отождествим также X
с некоторой частью множества 1?'(Х), а У отождествим с некоторой частью'
множества ^'(У). Тогда отображение Н: х^-Н(х) станет отображением!
б(х) -»■ бн(х), и отображение ц-»-Яц есть линейное продолжение
отображения И в некоторое отображение %?'(Х) (или некоторой его части) в ^'(У).
2) К этим формулам надо привыкнуть: параллельный перенос ф,
определяемый вектором А, задается формулой х-»-ф(л:— А). Предположим, что
X — вещественная прямая R, и построим график функции у = ф(х).
Перенести функцию ф означает перенести график ф параллельно оси х. Значе-
->
ние 1->ф в точке х является значением ф в точке t -*■ х = х — А.
h —h
»*?(*) U'lhfW'Wx-V
fWV
Рис. 17.

630 Гл. IV. Интегральное исчисление
В обозначениях (IV, 6; 172) можно написать, что
->
x->\ii — d\i{x — А), (IV, 6;242)
и тогда (IV, 6; 24) запишется в виде
J 7(x) d\i{x-h)=j f(x + A) dii (x), (IV, 6; 243)
■>
Возьмем X = R. Если d\x, имеет вид p(x)dx, то с помощью
замены переменной ' * + А = | (IV, 6; 243) запишется в виде
J / (£) Р (Е -■ Л) d£, так что
d\L(x — h) —р(х — h) dx и d(x — h) = dx для /?=1. (IV, 6; 244)
4°) Возьмем теперь в качестве Н отображение R на R,
определяемое гомотетией с центром в начале координат и
отношением k. Если k = 0, то отображение Н постоянно. Этот случай
уже был рассмотрен в (IV, 6; 20).
Предположим теперь, что k ф 0. В этом случае Н является
гомеоморфизмом. По определению, имеет место формула
(Яф)(*) = Ф(£). (IV, 6; 25)
Здесь формула (IV, 6; 17г) дает
J J(x) dii (-£■) = J* 7(kx) dii (x). (IV, 6; 26)
Если, в частности, мера ц является мерой р(х) dx, где
функция р локально интегрируема по dx, то, используя общую
формулу замены переменной (IV, 9;72) (которая будет доказана
позже), получаем формулу
Яц (ф) = _[ Ф (Я (*)) d|i (х) = J ф (kx) р(х) dx = J" ф (г/) р (-J) ^-,
(IV, 6; 27)
откуда
<4tH(t)w и "(т)=7ГГ- (iv'6;28)
§ 7. ШИРОКАЯ СХОДИМОСТЬ МЕР РАДОНА
Сходимость по норме. Локальная сходимость по норме
Выясним более тщательно, в каком случае следует говорить,
->
что последовательность мер Радона \in на X со значениями в
векторном пространстве Е сходится к предельной мере ц. Можно
было бы считать, что сходимость имеет место, если || ц„ — ц ||

§ 7. Широкая сходимость мер Радона
631
сходится к нулю, когда п стремится к бесконечности.
Это — сходимость по норме. Но такое определение сходимости
не отражает сходимости мер, поскольку норма меры может
оказаться бесконечной, и, значит, несмотря на свое название, она
не будет настоящей нормой1). Естественно дать следующее
определение.
->•
Говорят, что последовательность мер \in на X со значениями
->• ->
в Е сходится к предельной мере ц при п, стремящемся к
бесконечности, если, каким бы ни был компакт К множества X, после-
-> ->•
довательность норм ||ц„ — |х||к сходится к 0 при п, стремящемся
к бесконечности.
Согласно тому, что мы отметили на стр. 149 относительно
сходимости, определенной с помощью нормы на пространствах
линейных непрерывных отображений одного векторного
пространства в другое, это просто означает, что, каким бы ни был
компакт К из X, функции \in на пространстве <&{Х) сходятся
к функции \i равномерно относительно единичного шара из
^'к(Х) ■ Такая сходимость является локальной сходимостью по
->•
норме. Говорят, что меры \in локально сходятся по норме
->
к мере \i.
Пример. Пусть \i — вещественная фиксированная ^0 мера
Радона, и пусть рп — последовательность функций со
значениями в банаховом пространстве Е, локально ц-интегрируемых,
просто ц-почти всюду сходящихся к предельной функции р при
п, стремящемся к бесконечности, и таких, что имеет место
неравенство ||pn(*)H^ g(x), где g — фиксированная
неотрицательная локально ii-интегрируемая функция.
->•
Теперь меры-произведения pn\i будут локально сходиться по
->
норме к мере p\i при п, стремящемся к бесконечности.
В самом деле, пусть К — некоторый компакт X. Тогда имеет,
место неравенство
Ili^-Ill* <_[||?Я-?П41- (IV, 7; 1)
к
Нормы \\рп — pll сходятся просто ц-почти всюду к 0 и
мажорируемы функцией 2g ^ 0, ii-интегрируемой на К. Согласно
') Это обстоятельство уже было отмечено на стр. 154 относительно
сходимости последовательности отображений множества Е в метрическое
пространство F. Однако предыдущее определение можно взять за определение
сходимости на подмножествах, образованных мерами с конечной нормой.

632 • Гл. IV. Интегральное исчисление
теореме Лебега (теорема 35), правая часть сходится к 0 при п,
стремящемся к бесконечности.
Несмотря на естественность этого определения, оно, вообще
говоря, слишком жестко.
Рассмотрим, например, последовательность точек а„ из X,
стремящихся к а при п, стремящемся к бесконечности. Было бы
естественным надеяться, что меры Дирака б(ап\ сходятся к мере
Дирака б(0) при п, стремящемся к бесконечности. Однако при
предыдущем определении сходимости этого не будет. В самом
деле, если, например, X компактно и если ап отличны от а, то,
согласно (IV, 2; 7), |б(а„) — о<0)| = 2 и, следовательно, эта
величина не стремится к 0 при п, стремящемся к бесконечности.
Отсюда вытекает необходимость введения нового определения.
Широкая сходимость
->
Говорят, что последовательность мер Радона ц„ на X со
значениями в Е широко сходится к предельной мере ц при п,
стремящемся к бесконечности, если, какова бы ни была функция q>
из 'ё'(Х), последовательность векторов Ц"(ф) сходится в Е
•> ->
к вектору ц(ф) при п, стремящемся к бесконечности. Если Е
является полем скаляров, то речь идет о сходимости чисел цп(ф)
к числу ц(ф)- Если ц„ вещественны (соответственно ^0), то
то же самое будет и для меры ц. Если меры рассматривать как
функции на 'S'(X), то широкая сходимость является простой
сходимостью этих функций и потому ее часто называют простой
сходимостью. Естественно, что локальная сходимость по норме
влечет за собой широкую сходимость1).
Примеры. 1°) Если ап является последовательностью
точек из. X, сходящейся к а при п, стремящемся к бесконечности,
то меры Дирака Ь^^широко сходятся к мере Дирака 6(0).
В самом деле, какова бы ни была функция фе1'(Х),
функции ф(ап) сходятся к ф(а), ибо каждая из функций ф
непрерывна.
2°) Предположим, что X — конечномерное аффинное про-
странство. Тогда для каждого вектора /геХ можно определить
параллельный перенос меры Радона т-> ц (формула (IV, 6; 23)).
h
') Возникла довольно любопытная ситуация. В § 15 гл. II мы видели, что
понятие простой сходимости является слишком слабым, .и, потому нам
пришлось определить равномерную сходимость. Здесь же. мы замечаем, что понятие
равномерной сходимости является слишком сильным, и мы вынуждены
возвратиться к простой сходимости!

§ 1. Широкий сходимость мер Радонй 633
■noli ■ •- ■ - . •
-*■ ■*
Если теперь hn является последовательностью векторов из X,
■> ■*
сходящейся к h, то перенесенные меры t-> ц широко сходятся
hn
к перенесенной мере т*ц. В самом деле, согласно определению,
Л
(** S-**"*)^** J (Ф(^ + Лп)-Ф(х + Л))^(л0. (IV,7;2)
Наше утверждение будет доказано, если мы покажем, что
функции х -*- ф(х -\- hn) сходятся равномерно к функции
х~*(р(х-\- h). В самом деле, эти функции сохраняют-свои
носители в фиксированном компакте К. (Пусть Ко — носитель ф.
Он компактен и, следовательно, если на X ввести некоторую'
норму, Ко будет содержаться в некотором замкнутом шаре
с центром а0 радиуса /?о- Пусть теперь р — точная верхняя грань
■>
всех ||ЛП||. Тогда носитель т -». ф будет содержаться в
компактном шаре с.центром а0 радиуса /?о+р.) Следовательно, они
сходятся в 9!?к\Х). Наше утверждение будет вытекать из того, что
■>
\х является непрерывной функцией на пространстве Фц {X).
Докажем поэтому, что имеет место равномерная сходимость.
Так как функция ф непрерывна и имеет компактный носитель,
то она равномерно непрерывна. В самом деле, пусть, как было*
сказано выше, B0(ao,Ro)—некоторый шар, содержащий
носитель Ко функции ф. Функция ф на компакте В(а0, /?о + 1)
равномерно непрерывна (теорема 31 гл. II). Следовательно, при
заданном е > 0 найдется такое г\, 0 <; r\ ^ 1, что из неравенства
IIлс' — х"|| ^ Л вытекает неравенство |ф(х') — у(х") |^ е для;
любых х' и х" из В(а0, R0 -f- 1). Если х' и х" одновременно не'
лежат, в предыдущем шаре и удовлетворяют неравенству
||х' — х"|| ^ г\, то они лежат вне шара В(а0, Ro) и тем более вне'
носителя Ко функции ф. Поэтому ф (х') = ф (а-") = 0, так чтс
окончательно во всех случаях имеет место неравенство
|ф(;с')—ф(х")|^е, означающее, что функция ф равномерно'
непрерывна на X.
Если теперь \\hn— h\\ ^ц, то для любой точки ie£ спра-
ведливо неравенство |ф(х-г-/1п)—ф (x-f-Л) | ^ е, из которого
вытекает равномерная сходимость т ■* ф к т -»ф при hn, стремя-
■> -*■
щемся к h; мы тем самым доказали, что т* ц широко сходится
-*■ >
к т* и, когда hn стремится к h.
h *

634
Гл. IV. Интегральное исчисление
3е) Если в предыдущем примере ц является мерой ^0 (или,
более общо, с базой ^ 0), то доказательство становится еще
проще. В самом деле, равномерная сходимость функции
-> ->
(p(x-\-hn) к q>(x-\-h) не является необходимой. Имеет место
->
простая сходимость; функции q>(x-\-hn) ограничены по модулю
числом |||ф||| и сохраняют свой носитель в фиксированном
компакте. Поэтому результат вытекает из теоремы 34 Лебега.
Полученный результат можно обобщить следующим образом:
Пусть Нп — последовательность непрерывных отображений
X в У, просто сходящихся при п, стремящемся к бесконечности,
к некоторому непрерывному отображению Н. Пусть ц —
некоторая мера ^0 на X с конечной нормой1). Тогда образы мер Нпр.
широко сходятся к образу меры Н^.
В самом деле, для Hn\i, Н\у, и фе?(У) имеет место
формула (IV,6; 4). При п, стремящемся к бесконечности, ц>(Нп(х))
сходится просто к (р(Н(х)) и при этом по-прежнему остается
ограниченной постоянной |||ф|||. Эта постоянная интегрируема,
поскольку ц имеет конечную норму. Результат вытекает из
теоремы 35 Лебега.
4°) Если X = [а, Ь] — ограниченный интервал R, то мера
И» = 7ГТТ (6<а> + 6(а+<?=±) + ■■■ + \a+k izfL) + • • • + б<»)
(IV, 7; 3)
при п, стремящемся к бесконечности, широко сходится к мере
dx/(b — а). В самом деле, если ф принадлежит *<Р([а, Ь]), то
имеет место формула о среднем (IV, 1; 40), доказывающая наше
утверждение.
Функции, ц-интегрируемые по Риману
Рассмотрим следующую задачу. Пусть цп — последователь-
>
ность мер Радона, широко сходящихся к предельной мере ц при
п, стремящемся к бесконечности. Можно ли тогда утверждать,
что ф d\in сходится к ф d\i при п, стремящемся к
бесконечности, для таких функций <р, которые не принадлежат ^(Х)}
Ясно, что это неверно при произвольной функции ф. Рассмотрим,
'например, снова последовательность точек ап из X, сходящихся
к а, при п, стремящемся к бесконечности. Мы видели, что bia \
широко сходится к 6(д). Если теперь ф — некоторая функция,
') Для простоты мы предположим, что ц имеет конечную норму. Можно
было бы исходить из других предположений типа «собственных отображений».

§ 7. Широкая сходимость мер Радона
635
разрывная в точке а, то, очевидно, ф(ап) не будет, вообще го-
воря, сходиться к ф(а), что и является контрпримером для
предыдущего предположения.
Следовательно, нужно рассматривать особые функции ф. Мы
ограничимся случаем вещественных мер ^0.
Определение. Пусть ц, — вещественная мера Радона ;^0
на X и f — вещественная функция ^0 на X, ограниченная и
имеющая компактный носитель. Верхним интегралом Римана
функции f относительно меры ц, f d\i, называется точная-
нижняя грань мер |д,(ф) по всевозможным функциям фе?(Х),
мажорирующим функцию f.
На первый взгляд это определение кажется странным, так как
оно не соответствует определению верхнего интеграла Римана
относительно dx, которое было дано в § 1. Однако легко
показать, что когда мера ц, является мерой dx на R, то оба определе-
ния совпадают. Обозначим через и верхние интегралы
Римана в смысле § 1 и в смысле введенного определения при
\i = dx. Пусть ф — некоторая функция из 'ё'(Х), мажорирующая
функцию f. Так как любая функция из^(Х) интегрируема поРи-
ману в смысле § 1, то J f dx <! J (fdx — ц (ф), откуда,
переходя к точной нижней грани по всевозможным функциям ф, полу-
чаем неравенство J f dx ^ J f dx. С другой стороны, можно
найти такую ступенчатую функцию с компактным носителем g>0,
что | ' fdx^z | gdx — ~. Функция g имеет вид j$ g{%\a.,b.\>
где gi постоянны и \аи bi\ суть N интервалов из R. Положим
N
M = maxgit а' = а — &/4MN, Ь' = Ь + г/AMN и обозначим че-
рез фг функцию, равную 1 на [а{,ЬЦ, 0 на ]— оо, а^] и [b't, -f ооГ
и аффинную в каждом из интервалов [а'г аД, [6Г 6^]. Обозначим
N
через ф функцию 2 ё^Фг-Гогда, с одной стороны, f ^ ф, а, с
другой стороны, справедливо неравенство
| gdx> | <pdx — -~-M-2N= jydx — j,
из которого вытекает неравенство
J f dx^ I (fdx — е> fdx — e.

636 Гл. IV. Интегральное исчисление
Так как е произвольно, то полученные соотношения показывают,
что оба понятия верхнего интеграла Римана совпадают. В
соответствии с тем, что мы видели в примере для dx (стр.532),
верхний интеграл Римана, который всегда не меньше верхнего
интеграла Лебега, вообще говоря, строго больше его. Если ц — мера
Радона на вещественной прямой R, отличная от dx то имеется
две возможности для определения верхнего интеграла
Римана: одна — с помощью функций из 'ё'(Х) и другая — с
помощью ступенчатых функций с компактным носителем. В § 1 у нас
не было другого выбора, ибо мы знали лишь интегралы от
ступенчатых функций и не были знакомы с интегралами от
непрерывной функции с компактным носителем. Только после
введения в §' 1 понятия интеграла Римана dx стала мерой Радона на
R. Напротив, для произвольной меры Радона ц на R мы можем
выбирать одну из двух возможностей. Эти два определения,
вообще говоря, не совпадают. Если, например, мы будем
рассматривать меру ц на R как сумму меры dx и меры б и если в
качестве функции / возьмем характеристическую функцию
интервала ]0, 1], являющуюся ступенчатой функцией, то получим ра-
венство fdn=\fdn=\. Если же взять произвольную
функцию фЕ^Д, мажорирующую функцию /, то получим:
ф(0) ^ 1 и J cpdns3s2, а, следовательно, J f d\i !>2 или
на самом деле — 2.
- Однако совершенно ясно, что наиболее интересным
определением в общем случае будет определение, использующее
функции из 'ё'(Х). Это объясняется не столько тем, что лишь это
определение позволяет иметь дело с произвольным локально
компактным пространством X, а не только с прямой R, сколько
наличием ряда важных свойств этого интеграла, о которых речь
будет идти позже.
.Если / — ограниченная функция с компактным носителем со
значениями в банаховом пространстве F, то говорят, что эта
функция ц-интегрируема по Риману, если она обладает
аппроксимирующей последовательностью относительно верхнего
интеграла Римана, образованной из непрерывных разложимых
-> ->
функций с компактным носителем: fn^'S'(X)'SiF (см.
рассуждения перед следствием 8 теоремы 11), и Г \\J—Tn\\d[i сходится
к 0 при п, стремящемся к бесконечности. Теперь можно
определить интеграл Римана от функции /. Функции fn образуют
аппроксимирующую последовательность для / в смысле ин-

§ 7. Широкая сходимость мер Радона 637
тегрирования по Лебегу. Поэтому / интегрируема по Лебегу и ее
интеграл Римана совпадает с ее интегралом Лебега.
^аждая непрерывная функция с компактным носителем
интегрируема по Риману, поскольку (см. следствие 8 теоремы 11)
она является равномерным пределом разложимых функций
с носителем в фиксированном компакте. На вещественной
прямой R правильная функция не обязательно интегрируема по
Риману в противоположность тому, что утверждалось в следствии
2 теоремы 8 для ц = dx: при it, — dx-\-& характеристическая
функция интервала ]0, 1] не может быть интегрируема по
Риману, так как в противном случае ее верхний интеграл Римана,
равный 2, совпал бы с интегралом Римана, или, чго то же
самое, с интегралом Лебега, равным 1.
Теоремы 1 и 6 остаются справедливыми вместе с
сопровождающими их замечаниями, а следствия (кроме того, что
относится к интегралам от характеристических функций интервалов)
справедливы при замене ступенчатых функций непрерывными
разложимыми функциями. Заметим, что так же, как и в § 1,
в смысле Римана интегрируются только ограниченные функции
с компактным носителем.
Теорема 62. Пусть ц„ — последовательность вещественных
мер Радона ^ 0 на X, широко сходящаяся к пределу ц при п,
стремящемся к бесконечности. Пусть f — ограниченная с
компактным носителем функция, определенная на X, со значениями
в F, измеримая -по каждой из мер цп и интегрируемая по
Риману относительно меры ц. Тогда \ f d[in сходится к \ f d\i.
Доказательство. Прежде всего, f интегрируема по
Лебегу по всем цп и ц. Согласно замечанию 2°) на стр. 424 (где
ступенчатые' функции заменены непрерывными разложимыми
функциями), можно найти непрерывную с компактным
носителем разложимую функцию g со значениями в F и вещественную
^0- непрерывную функцию h с компактным носителем, такие,
что -||f — glls^A и n(h) s^ е/8. Поскольку ц„ широко сходятся
к ц, можно найти такое целое число р, что для п ^ р имеет
место неравенство |цп(Л)—ц (ft) | sg: s/8, а, следовательно,
ц„(А) ^ е/4.
N N
С другой стороны, из равенства J g dv~2j J ЯгФг dv= Vg^v (<p)
£=1 j=l
следует, что сходимость ц„ к ц при любой непрерывной
разложимой функции .g с компактным носителем влечет за собой

638
Гл. IV. Интегральное исчисление
сходимость gd\in к g d\i, и потому существует такое целое
q, что для всех n ^ q имеет место неравенство
| jgdn„— jgdv\<j-
Отсюда для п^ max(p, q) непосредственно следует
неравенство
I J" Jd\in — J" ifd(i|< J"||f— g№„-f| jgdnn— J|dn|| +
+ J II5 - hdv < »n (h) + | + fi (A) <e,
из которого следует утверждение теоремы.
Замечание. Эта теорема очень интересна: относительно
->
функции / требуется всего лишь ее ^-интегрируемость по Ри-
ману по предельной мере ц и не делается никаких аналогичных
предположений относительно интегрируемости по цп (конечно,
->
предполагается, что / ц„-измерима, а, следовательно, цп-инте-
г'рируема по Лебегу).
Теорема 63. Для того чтобы ограниченная с компактным
-> ->
носителем функция f, определенная на X, со значениями в F
была ^-интегрируемой по Риману, необходимо и достаточно,
чтобы множество ее точек разрыва имело ц-меру Лебега,
равную нулю.
->
Доказательство. 1°) Предположим, что / ц-интегрируе-
ма но Риману, и пусть g и h — функции, определенные так же, как1
-> ->
в теореме. 62: ||/ — gll^A. ц(А)^е. Назовем колебанием функ-
-> ->
ции / на окрестности Т точки а величину со (/; Т) =
-> -> ->
= sup || / (х) — / (у) ||. Колебанием функции / в точке а назовем
число со(/; a) = inf со(/; T), где inf берется по всевозможным
окрестностям Т точки а1). Функция f непрерывна в точке а
тогда и только тогда, когда ее колебание в этой точке равно
->
нулю. Так как функция g непрерывна, то имеет место
неравенство со(/; a)<co(g; а) + со(/ — g; a) = a(j — g; а). В каждой
') Это определение совпадает с частным определением колебания, данным
на стр. 196 для правильных функций.

§ 1. Широкая сходимос-tb мер Радона 639
окрестности Т точки а имеет место неравенство
II (Г(*) - ?(*)) - (Ну) - g (у)) II < л (*) + а (у).
Поскольку функция Л непрерывна, то мы получаем отсюда,
-> ->
что со(/ — g; a)< 2Л(а).
Обозначим теперь через Аа множество (хе^; со (/, л:) ^ а},
а > 0. Это множество содержится в множестве {xel; к{х)^
^ а/2}. Так как ц(И)^. е, то его внешняя [i-мера мажорируется
числом 2е/а. Поскольку это справедливо для любого е > 0, то
[i-мера равна нулю. Так как этот результат имеет место при
любом а* то множество тех точек, в которых колебание функ-
-> ->
ции f больше 0, т.е. множество точек разрыва функции /, имеет
нулевую [i-меру.
2°) Обратно, предположим, что множество точек разрыва
->
функции / имеет [i-меру, равную нулю. Покажем сначала, что
->
отсюда будет следовать [i-измеримость функции / (и,
следовательно, поскольку она ограничена и имеет компактный
носитель, [i-интегрируемость в смысле Лебега). Действительно, она
очевидным образом удовлетворяет критерию Лузина (следствие
из теоремы 33): если К — произвольный компакт и если
множество А точек разрыва функции / имеет [i-меру, равную нулю",
то можно найти такое открытое множество О, содержащее А,
ц.-меры ^ б, что для К6 = КО СО имеет место неравенство
ц(К— К6) ^ б.. В каждой точке К6 функция / непрерывна на
X и, следовательно, тем более непрерывно ее сужение на К6.
Поскольку функция / [i-интегрируема по Лебегу, то,
согласно теореме 32, существует такая разложимая непрерывная
■> ■* ■> г
функция g с компактным носителем, что \\[—g||=A, где /jrffi^
^е/2. Обозначим через А* «верхнюю функцию»,
присоединенную к h, т. е. функцию, определенную следующим образом: для
каждой окрестности Т точки а в X полагают А* (Т) = sup A (*),
а затем полагают h* (а) = inf A* (T). Легко видеть, что А* полу-
т
непрерывна сверху. В самом деле, каждая точка а имеет такую
открытую окрестность Т, что h*(T)^. A*(a) + е, и поэтому для
каждой точки х е Т имеют место неравенства А* (х) <g; h* (T) ^
^A*(a)-f-e. Впрочем, А* совпадает с А в каждой точке, где h
непрерывна, т.е. [i-почти всюду. Поэтому hd\i= h*d\i.
Пусть k — произвольная непрерывная интегрируемая
функция, мажорирующая функцию А* (например, fee?(I)). Тогда
k — А* полунепрерывна снизу, ^0 и, значит, борелевская. Она

640 Гл. IV. Интегральное исчисление
мажорируется функцией k и поэтому интегрируема. Согласно
теореме 392, J (k — ft*) йц является точной верхней гранью для
мер \i(ty), tp^^W» О ^ if ^ й — ft*, а, значит, J h* d\i
является точной нижней гранью мер \i(k—г|э) = ц(ф) для всех
непрерывных интегрируемых функций ф ^ 0, мажорирующих
ft* (в пространстве функций фе?(1), если функция k взята
также в ^(Х)), Таким образом, можно найти такую функцию
?е?(Х), ф> А»> А", чтоц(ф)< J Л*^ + е/2= Jft^ + e/2<
->■ ■>
^е. Но тогда || / — g || ^ ф, где (х(ф)^е. Поскольку это
справедливо для любого е > 0, то функция / ц-интегрируема
по Риману.
Следствие 1. Для того чтобы часть А множества X с
компактным замыканием имела ^-интегрируемую по Риману
характеристическую функцию, необходимо и достаточно, чтобы ее
граница имела ц-меру (Лебега), равную нулю.
Доказательство. Так как в окрестности каждой
внутренней точки части А характеристическая функция постоянна
и равна 1, а в окрестности каждой внешней точки этой части
она постоянна и равна 0, то множество точек разрыва
характеристической функции множества А является совокупностью
граничных точек этого множества.
Следствие 2. Если меры цп ^ 0 на X и широко сходятся
к \i при п, стремящемся к бесконечности, и если А есть часть X
с компактным замыканием, измеримая для всех ц„, граница
которой А имеет нулевую меру для предельной меры \i, то
Ип(А) сходятся к |д,(Л).
С л е д с т в и е 3. Если меры Радона цп на R при п,
стремящемся к бесконечности, широко сходятся к мере dx и если
ограниченная с компактным носителем функция ф измерима при
всех \in и интегрируема по Риману относительно dx, то \ q>d\in
сходится к J ydx.
На прямой R имеет место теорема, обратная к предыдущим
теоремам, которая представляет и самостоятельный интерес:
Теорема 64. Пусть цп — меры Радона 5^0 на прямой R.
Если для каждого ограниченного интервала [а, Ь], такого, что
м((а}) = n(W) = 0. пРи п> стремящемся к бесконечности,
\*п([а,Ь]) сходятся к \i([a,b]), то меры ц„ широко сходятся
к мере у,.

§ 7, Широкая сходимость мер Радона 641
Читателю предлагается доказать эту теорему в качестве
упражнения.
Широкая сходимость и равномерная сходимость
Рассмотрим теперь задачи другого характера. Предположим,
что меры ц„ широко сходятся к некоторому пределу ц.
Выясним, можно ли для функций ф найти такие множества s4- функ-
'■ ' -> ->
ций ф, чтобы н-п(ф) сходились к |л(ф) равномерно на s4-.
Как мы видели ранее, такая равномерная сходимость не
может, иметь места, если бФ является единичным шаром из ^(Х).
Значит, нужны множества меньшие, чем единичный шар.
Здесь мы воспользуемся следующей общей теоремой
функционального анализа:
Теорема 65 (Банаха — Штейнгауза). Пусть ип
—линейные непрерывные отображения банахова пространства Е.
в векторное нормированное пространство F. Если функции иПу
определенные на Е, со значениями в F при п, стремящемся,
к бесконечности, просто сходятся к некоторой предельной
функции и, то нормы \\ип\\ ограничены некоторым фиксированным
числом М, функция и линейна и непрерывна, а
последовательность ип сходится к и равномерно на каждой компактной части
бФ пространства Е.
Д о к а зател-ьст во. Здесь существенным является тот
факт, что Е банахово, т. е. полно. Без этого предположения все
результаты становятся неверными. Рассматриваемая теорема —
одна из редких теорем, в которых исходное пространство надо
считать полным. Теорема Банаха — Штейнгауза является одной
из наиболее глубоких и плодотворных теорем современного
анализа.
Докажем сначала, что нормы функций ип ограничены одним
и тем же числом М ^ 0, но для этого нам понадобится
следующая лемма.
Лемма (теорема Бэра)1). Пусть Е — полное метрическое
пространство, и пусть 0q, О и Оъ, ...— последовательность
открытых множеств, плотных в Е. Тогда их пересечение А = [*"|с?„
(которое теперь не должно быть открытым) также плотно в Е.
') Мы ее назвали леммой, хотя это одна из наиболее важных теорем
анализа, значение которой далеко выходит за те границы, которыми мы
ограничили здесь ее применение.
21 Зак. 1339

642
Гл. IV. Интегральное исчисление
Доказательство леммы. Пусть Q — произвольное
открытое множество из Е. Нам надо доказать, что Q П А не пусто.
Поскольку множество Оо плотно, то существует по крайней мере
одна точка пересечения Q П С?о- Поскольку последнее множество
открыто, существует даже некоторый замкнутый шар Во =
= В(ао, бо), полностью содержащийся в Q П 0q. Повторим те-
О
перь эту операцию, заменив О'0 на 0\ и Q на открытый шар В0.
Тогда найдется некоторый замкнутый шар В\ — В(а\, 61), пол-
о
ностью лежащий в В0 (I 0\. При этом мы выберем 6i <: 1.
Продолжая так далее, мы сможем построить последовательность
точек ап и последовательность чисел б ^ 1/и, такие, чтобы
каждый замкнутый шар Вп = В(ап, б„) содержался в откры-
том шэре B„_i = Bn_i(an_i, бп-i) и в Оп. Все эти замкнутые
шары лежат в Q.
Последовательность центров шаров ап является
последовательностью Коши. В самом деле, все точки ап+р при р ^ О
содержатся в замкнутом шаре Вп и поэтому d(an+p, ап)^. 1/"-
Поскольку пространство Е предполагалось полным,
последовательность точек ап сходится к некоторой предельной точке а.
Так как все точки ап+Р при р ^ О содержатся в шаре Вп, то
точка а заведомо лежит в Вп, а, следовательно, и в Q П Оп.
Поскольку это верно для любого и, то а е Q П А, чем и
заканчивается доказательство леммы.
Часто оказывается удобным пользоваться этой леммой,
применяя переход к дополнениям. Дополнение к открытому
множеству замкнуто,, а дополнение к плотному множеству,
внешность которого пуста, является множеством с пустой
внутренностью. Поэтому имеет место такое утверждение:
Пусть. Е — полное метрическое пространство и Fn —
последовательность замкнутых множеств с пустой внутренностью.
Тогда объединение F = [jFn (которое не обязано быть замк-
л>0
нутым) имеет пустую внутренность (в частности, F Ф Е).
Совершенно ясно, что неполное метрическое пространство
этим свойством не обладает. Например, поле Q рациональных
чисел с обычной метрикой является объединением счетного
числа множеств, сводящихся к одной точке; каждая точка
замкнута в Q и имеет пустую внутренность.
Докажем теперь первую часть теоремы, а именно
ограниченность норм || ып II. Обозначим через F& множество точек х е Е,
>
в которых все ||и„(х)|| не превосходят k. Так как функция ип
■>
непрерывна, то множество Fn, ft = {х <= Е; \\ип(х)\\^.Щ за-

§ 7. Широкая сходимость мер Радона 643
мкнуто, а, следовательно, Fh=f]Fnt k также замкнуто. Объеди-
п
нение множеств Fu при k = О, 1, 2, ... дает все пространство Е.
В самом деле, для каждой точки х е Е по предположению
функции ип(х) имеют предел, а, значит, их значения
ограничены, т. е. существует такое целое число k (зависящее от х), что
>
все \\un(x)\\^.k и, значит,, х е Fh. Поскольку Е — полное
метрическое пространство (банахово), то согласно лемме Бэра
внутренность всех Fu не может быть пустой. Значит, существует
такое k, при котором Fu имеет непустую внутренность, а,
следовательно, имеется некоторый шар В (а, р), содержащийся в Fh-
>
Теперь для ||х|| <; р и для любого п имеем ||ил(*)11 =£^
-> ——>
< ||ип(* + а)|| + ||ы„(а)|| <2fe, a, следовательно, ||и„|| < 2ft/p,
чем и завершается доказательство нашего утверждения.
(Заметим, что в этом результате вовсе не требуется, чтобы
функции и„ сходились. Надо лишь, чтобы для каждого х е Е
>
нормы ||ып(*)11 были ограниченными некоторой константой,
которая, вообще говоря, произвольно зависит от х. Однако из
предыдущего доказательства следует, что ||и„|| ограничены, т.е.
si-
существует такое число М, что эта константа для || ип (х) \\
будет ^М || * ||.)
Очевидно, функция и линейна. В самом деле, так как
-> -> -> ->
ип (х + у) = ип \х) + ип (у), то переходом к пределу получаем,
что и(х + у)= «(*) + и (у). Точно так же проверяется, что
и(kx) = ku(x). Из неравенства ||и„(*)|| <: М || х || переходом
к пределу можно получить неравенство ||ы(#)|| ^ М \\ х ||, из
которого следует, что функция и непрерывна и ее норма ^.М.
Пусть теперь S4- — некоторый компакт пространства Е.
Зададим е > 0. Тогда найдется конечное число открытых шаров
с центрами в множестве S4- радиуса е/ЗМ, покрывающих $$■
(в силу определения компактного множества). Пусть (a^[sl —
центры этих шаров. Согласно предположению о простой
сходимости, для каждого из этих центров аг- можно найти такое
целое число р{, что при п ^ pi имеет место неравенство
||ыя(Й -uCai) II <|. (IV,7; 16)
Если теперь через р обозначить наибольшее из чисел piy то
можно убедиться, что для п ^ р и X, находящихся от аг- на
21*

644
Гл. IV. Интегральное исчисление
расстоянии < е/ЗМ, имеет место неравенство
|| н„ (х) — и (л;) || < || ы„ (л;) — ы„ (аг) || + || ы„ (аг) — « (аг) || +
+ ||U(ai)-«W||<Al^|r + 4 + Al^r = e. (IV, 7; 17)
Однако так как каждая точка зФ находится на расстоянии
->
'< е/З-М от одной из точек ait то окончательно для любой точки
-> -> ->
jtei и п^р получаем неравенство ||ы„(л;) — и(*)-|| <: е.
Значит, ип сходится к и равномерно на множестве s£, и этим
заканчивается доказательство теоремы.
->
Следствие 1. Пусть меры ц„ на X со значениями в век-

шторном нормированном пространстве Е при п, стремящемся
->
к бесконечности, широко сходятся к некоторой мере ц. Тогда
->
для каждого компакта К нормы \\цп\\к равномерно ограничены.
->
Если s£ — некоторый компакт пространства 'ё'к(Х), то ^п(ф)
->
сходятся к ц((р) равномерно по ф в s4-1).
Так как 'ё'к(Х)—банахово пространство (см. стр. 447), то
это следствие непосредственно вытекает из сформулированной
теоремы.
->
Следствие 2, Пусть цп — меры, широко сходящиеся
.->
к мере ц, и срп — функции из 'S'(X), равномерно сходящиеся
к некоторой функции ср и сохраняющие свои носители в одном
и том же компакте К. Тогда ц„(фп) сходятся к ц(ср).
Доказательство. По следствию 1 нормы ||ц,„||к
ограничены одним и тем же числом М ^ 0. С другой стороны, срп
Сходятся в Ч?к{Х) к ср. Далее,
Vn (фп) — И (ф) = Vn (ф„ — ф) + (Ип (ф) — V- (ф))- (IV, 7; 172)
В силу условия широкой сходимости второй член правой ча-
->
сти сходится к 0. Так как норма первого члена мажорируется
величиной М ||| ф„ — ф |||, то он также стремится к нулю, чем
и заканчивается доказательство следствия.
') Вообще говоря, 'S'k(X)—бесконечномерное пространство. Его
единичный шар не компактен, и поэтому в качестве S& нельзя брать единичный шар,
как мы это уже отмечали ранее.

§ 7. Широкая сходимость мер Радона 645
Компактные подмножества пространства VK(X)
Для того чтобы иметь возможность применить следствие 1,
нам надо уметь определять компактные множества в
пространствах 'ё'к(Х). В дальнейшем мы займемся общим изучением
компактов, а сейчас ограничимся частными случаями этих
множеств.
Теорема 66. Пусть А, В, С — три топологических
пространства, А — компактное, а С — метрическое. Пусть f —
непрерывное отображение А X В в С. Тогда для каждого у^ В
можно определить частное отображение fy: x-*-f(x,y)
множества А в C,fy(= (СА)сь-
Если у сходится к b в пространстве В, то частная функция
fv сходится к частной функции fb равномерно на А. Кроме того,
отображение y~*fv,' которое каждому элементу у^В ставит
в соответствие частную функцию fy, является непрерывным
отображением В в (СА)сь.
Доказательство. Зафиксируем точку ft в В и зададим
произвольное е > 0. Какова бы ни была точка а, функция /
непрерывна в точке (а, Ь). Следовательно, существует такая
открытая окрестность <Ua точки а и такая окрестность Та
точки ft в множествах А и В соответственно, что для х^Ща и
у еУ„ имеет место неравенство
d<f\x,y),Ha,b))<,\. (IV, 7; 18)
Тем более, выполняется неравенство
d(f(x, b), f(a, &))<-|. (IV, 7; 19)
Отсюда можно вывести неравенство, имеющее место для
х<=Ша,у<= Та-
d(f(x, у), f(x, b))^d(f(x, у), f(a, b)) + d(f(a, b), f(x, ft))<e.
(IV, 7; 20)
Когда точка а меняется, окрестности Ща образуют открытое
покрытие компакта А. Следовательно, можно выбрать конечное
покрытие (llai) множества А. Этим окрестностям aUai
соответствуют окрестности Та . Обозначим через У пересечение
всех Та. Множество Т является некоторой окрестностью
точки Ь в В. Тогда для х из <Uai и у из Т имеет место
неравенство (IV, 7; 20). Поскольку окрестности °Uai образуют
Покрытие А, предыдущее неравенство имеет место для каждого
х^А и каждого у^Т, что можно записать так: d(fy, /ь)=^е
для у е Т, а это соотношение доказывает теорему.

646 Гл. IV. Интегральное исчисление
Замечание. Если оба пространства А и В метрические
и компактные, то доказательство становится значительно проще.
В самом деле, в этом случае, согласно теореме 31 гл. II,
функция f равномерно непрерывна. Значит, для любого е > 0
можно найти такое ц > 0, что из неравенств d(x', x")^.y], d(y',y")^
^ti следует d(f(x',y'), f(x",y"))^e. В частности, из d(y,b)z^.
^ г) при любом х следует неравенство d(f(x, у), f(x, b))^ e и„
следовательно, d(fy,fb)^ e, что и доказывает теорему.
Следствие 1. Пусть А и В— компактные пространства^
С — метрическое пространство и f — непрерывное отображение
А\ В в С. Тогда множество частных отображений fy из А в С„
когда у пробегает пространство В, является компактным
подмножеством пространства (СА)сь.
В самом деле, мы имеем здесь образ компакта. В при
непрерывном отображении y-+fy.
Следствие 2. Пусть X — локально компактное
пространство, Т — компактное пространство. Пусть <р — функция с
вещественными ■ или комплексными значениями, непрерывная на
X X Т. Тогда, каким бы ни был элемент t еГ, существует
частное отображение <рг, являющееся вещественной или
комплексной функцией,' непрерывной на X. Предположим, что, когда t
пробегает Т, функция ф( имеет носитель в одном и том же
компакте К пространства X. Тогда, если t пробегает Т, множество'
функций ф( образует компактную часть пространства ^К(Х)^
Для доказательства достаточно применить следствие t
к f = Ф, А = К, В = Т, С = R или С.
Следствие 3. Предположим, что выполнены условия след-
ствця 2. Пусть \in — меры Радона на X со значениями в
векторном нормированном пространстве Е, широко сходящиеся
->-
к предельной мере \i при п, стремящемся к бесконечности. То-
гда интегралы ф(х, t) d\in(x) при п, стремящемся к
бесконечности, сходятся к ф (х, t) du (x) равномерно по t в
пространстве Т.
Широкая сходимость последовательности мер к мере Дирака
Теорема 67. Пусть ц„ — последовательность мер ^0 на
локально компактном пространстве X. Предположим, что в
каждой компактной окрестности У точки йе!
последовательность интегралов Г d\in сходится к 1 при п, стремящемся

§ 7. Широкая сходимость мер Радона
647
к бесконечности. Тогда меры \хп широко сходятся к мере
Дирака б(а).
Перед началом доказательства заметим, что в нашем
предположении подразумевается, что, каким бы ни был компакт К
пространства X, не содержащий a, d\an сходится к 0 при п,
к
■стремящемся к бесконечности.
В самом деле, дополнение к К является некоторым
открытым множеством X, т. е. некоторым локально компактным
пространством1). Пусть теперь У— компактная окрестность точки
■а в этом пространстве, т.е. компактная окрестность точки а в X,
не имеющая общих точек с Л'.
Тогда, с одной стороны, J d\in сходится к 1, а с другой —
■ v
| d\xn сходится к 1 и, значит, | d\xn сходится к 0.
Условия теоремы означают, что общая масса на конечном
расстоянии стремится к 1 и стремится сконцентрироваться
в точке а.
Доказательство. Пусть <р — некоторая функция из
*&(X) с компактным носителем К. В силу непрерывности <р, при.
заданном е > 0 существует такое открытое множество,
содержащее а, что для любой точки х из этого множества имеет
место неравенство | ф(лг)—<р(а) | ^ е/4. Если У— компактная
окрестность точки а в этом открытом множестве, то это
неравенство тем более сохраняется на У. Разложим теперь разность
фф.„ — ф(а) в сумму трех членов, а именно:
1
j Ф dy.n — ф (а) = J ф d(x„ + J (ф (х) — ф (а))-йцп (х) +
Су V
+ Ф(а)
J ф„ — 1
(IV, 7; 21)
Последовательно оценим сверху модули этих трех членов.
1°) Первое слагаемое правой части стремится к 0 при п,
•стремящемся к бесконечности. В самом деле, поскольку ф имеет
носитель в К, интеграл на СУ в действительности является
интегралом на пересечении К 0 СУ. Поэтому он мажорируется
числом HI ф ||| J йцп, где А — замыкание К(]СУ. Так как
А •
это множество замкнуто и содержится в компакте К, то
множество^ компактно. С другой стороны, поскольку множество
') Смотри примечания на стр. 453 и на стр. 475.

648 Гл. IV. Интегральное исчисление
Л содержится в СУ и а не является точкой прикосновения
множества А, то множество А не содержит точки а.
Согласно замечанию, предшествовавшему доказательству,
| d[in сходится к 0.
А
2°) Рассмотрим теперь третье слагаемое. По условию,
величина, заключенная в квадратные скобки, стремится к 0, и,
следовательно, третье слагаемое также сходится к 0 при я,
стремящемся к бесконечности. Значит, существует такое целое
число р', что при я ^ р' сумма абсолютных величин первого и
третьего слагаемых не превосходит е/2.
3°) Рассмотрим, наконец, второе слагаемое. Согласно
выбору Т, оно мажорируется величиной -т d\nn. Последний ин-
т
теграл стремится к 1 при я, стремящемся к бесконечности.
Следовательно, существует такое целое число р", что этот интеграл
для п ^ р" не больше 2. Но тогда для я ^ р" второе слагаемое
не превосходит по модулю е/2. Если теперь через р обозначить
наибольшее из целых чисел р' и р", то мы увидим, что для
п^р будет иметь место неравенство <fd\in— <р(а) ^е, и
теорема доказана.
Пример 1. Пусть (д,„ — последовательность мер ^0,
полная масса которых [ d\in сходится к 1 и носитель которых
равномерно сходится к точке а. Под этим мы понимаем
следующее: какова бы ни была окрестность У точки а, носитель
меры (д,п для достаточно больших я содержится в Т. Тогда
меры (д,„ широко сходятся к 6<Q) при я, стремящемся к
бесконечности. Это очевидно, так как условия теоремы выполняются.
Пример Ь. Как частный случай рассмотрим
последовательность функций рп ^ 0 на вещественной прямой R,
интегрируемых относительно меры dx и таких, что J pn(x)dx сходится
к 1 при я, стремящемся к бесконечности, причем носитель
функции рп равномерно сходится к точке а. Тогда меры pndx
широко сходятся к мере б(а).
Этот пример дает новую интерпретацию некоторых случаев,
для которых не применима теорема о сходимости Лебега.
Рассмотрим, например, следующую последовательность
функций рп на R:
[ п для 0 < х ^ 1/я,
Рп{х) = { п (IV, 7; 22)
г ч 10 в остальных точках.

§ 7 Широкая сходимость мер Радона
649
Эти функции всюду сходятся к 0 при га, стремящемся к
бесконечности. Однако они не мажорируются никакой функцией
;з=0, локально интегрируемой по мере dx (см. формулу
(IV, 4; 11)). Следовательно, теорема Лебега здесь не
применима, и лучшим доказательством этого факта служит то, что все
интегралы \ рпНравны 1 и, следовательно, не стремятся к 0.
Если теперь ф принадлежит 'iP(R), то j q>pndx не сходится
к 0. Мы отмечали этот результат в связи с теоремой Лебега.
Теперь дадим ему другое истолкование: из сказанного в
примере Ь вытекает, что меры рп dx широко сходятся не к мере 0,
,а к мере б.
Интеграл pn4>dx сходится к ф(0). Такое явление
встречается довольно часто. Когда функции рп просто сходятся
почти всюду к предельной функции р, но таким образом, что
нет сходимости интегралов, то это часто означает1), что меры
pndx сходятся к сумме меры pdx и меры, представляющей
некоторые точечные массы.
Пример 2. Пусть / — некоторая функция >0 в
пространстве R", интегрируемая по мере dx = dxx dx2 . .. dxn с j f dx=\.
Если для вещественного k Ф 0 положить
Hk = \k\nf(kx)dx, (IV, 7; 23)
то цй будет образом fdx при гомотетии x-*x/k (см. формулу
(IV, 6; 28) для га = 1, а затем теорему 102 для произвольного
п). Меры ци' широко сходятся к мере Дирака б при k,
стремящемся к бесконечности. Это можно увидеть, применив
теорему 67, или непосредственно, используя замену переменных. Для
(pe?(Rn) имеем:
\ik(<P)=j<P(x)f(kx)\k\ndx. (IV, 7;24)
Производя замену переменных kx = £, получаем (см. далее
теорему 102):
Мф)=/ф(-|-)Ш^. (IV, 7;25)
При k, стремящемся к бесконечности, %jk стремится к 0.
Так как функция ф непрерывна, то при этом ф(£/й) сходится
просто к ф(0), а, следовательно, функция Ь,—»ф (£/&)/(£)
сходится просто к ф(0)/(£). Поскольку она остается ограниченной
') Конечно, не всегда! Если вместо п, как в (IV, 7; 22), мы возьмем па>
как в (IV, 4; 11), при а > 1, то ничего подобного не получится.

650
Гл. IV. Интегральное исчисление
неотрицательной функцией |||ф|||/Ш> интегрируемой по cfij„
то из теоремы 35 Лебега следует, что цл(ф) при й, стремящемся
к бесконечности, стремится к Ф (0) Г / (|) с?| == qp (0), откуда
следует требуемое заключение.
Имеется и более прямое доказательство. Мы видим, что
\ f dx есть мера ^0, имеющая полную массу, равную 1.
Гомотетия с центром в 0 и отношением \/k при k, стремящемся
к бесконечности, стягивает все массы к началу координат.
Пример 3°) на стр. 634 теперь дает самое короткое доказательство:
гомотетия Hh с отношением l/k при k, стремящемся к
бесконечности, сходится к гомотетии Я с нулевым отношением, т. е.
к постоянному отображению лг —*-0, а, следовательно, Нкц
сходится к Нц. Поскольку масса ц равна +1, то, согласно
примеру Г) на стр. 628, Яц = 6.
Вот два часто используемых примера,
а) Функция f на R определена формулой
f(x) = rp=re-*fl. (IV, 7; 26)
Она полностью удовлетворяет требуемым условиям,
поскольку, как мы увидим позже, интеграл от f равен 1.
Последовательность мер \/~п f (Уп х) dx:
И«
/2л
пх' _
' 2 Vn dx
(IV, 7; 27)
широко сходится к б при п, стремящемся к бесконечности.
На рис. 18 изображены графики двух из этих колоколооб-
разных кривых, представляющих плотности мер цп по
отношению к мере Лебега, т. е. функции VnfiVnx).
Можно также взять
f (х) = е~пх\ V~nf(Vnx)= Vn e~n™\ (IV, 7; 28)
Рис. 18.

§ 7. Широкая сходимость мер Радона
651
Ь) Функция f задана формулой
fW = TTh?' (IV, 7; 29)
Ее интеграл, очевидно, равен 1, и потому меры
Р"~ я (*+«»*») (IV, 7; 30)
при п, стремящемся к бесконечности, широко сходятся к мере б.
Замечание. Эти свойства были бы невозможными без
введения понятия широкой сходимости: если К — компактный
интервал [—А, А], то, согласно сказанному относительно
формулы-(IV, 2; 16),
\Vk
-6\\K = \\f(kx)\k\ndx-6\\K равно j f{kx)\k\ndx+l
и стремится к 2 при k, стремящемся к бесконечности.
Локальная сходимость по норме отсутствует!
Теорема 68. Существует такая последовательность
полиномов Рп ^ 0 вещественной переменной, что меры Pndx широ.-
ко сходятся к б при п, стремящемся к бесконечности.
Эта теорема имеет большое значение. Из нее в дальнейшем
будет получена теорема 80г Вейерштрасса (о приближении
непрерывных функций полиномами).
Доказательство. Пусть еп — последовательность
положительных чисел, стремящихся к -)-оо при п, стремящемся
" к бесконечности. Положим
2 2\™
"■«-Tsrl'—irJ- (IV-7i3,)
Для четного п эта величина, очевидно, ^0.
Покажем, что Рпйх широко сходятся к б при п, стремящемся
■к бесконечности, если только числа е„/\Лг стремятся к нулю.
Для этого можно было бы использовать теорему 67, но
доказательство также просто можно провести и непосредственно.
Пусть фе??(Р). Тогда
/ 2 2\"
(Л,dx) (Ф) = J у1= [l --^-J ф (jc) dx. (IV, 7; 32)
Пусть [—A, A] — интервал, содержащий носитель функции ф.
Последний интеграл фактически вычисляется на [—А, А].

652
Гл. IV. Интегральное исчисление
Выполним замену переменных епх = |. Тогда
(Рп dx) (Ф) = yL, J (1 - £)" Ф (J-) rfj, (iv, 7; 33)
где интеграл в действительности вычисляется на [—епА, ~{-епА].
Для фиксированного | при /г, стремящемся к бесконечности,
функция ф(£/е„), в силу ее непрерывности в начале координат,
стремится к ф(0). Переменная (1—12/2п)п стремится при этом
к e-W. Поэтому интегрируемая функция сходится просто
к функции ф(0)е-£2/2. Если применима теорема 35 Лебега, то
правая часть равенства (IV, 7; 33) сходится к -у= Г е-&,/2й| = ф(0),
и тогда теорема будет доказана.
Найдем оценку сверху для подинтегральной функции. Для
0<н< 1 из разложения логарифма в ряд следует, что
In (1 — и) ^ —и, откуда 1-а<г»и, значит, (1—£2/2/гг<е~^/2
при 12/2п<1.
Подинтегральная функция равна ф(|/еп)(1—12/2п)п, а,
значит, для |||^e„i4 мажорируема величиной |||ф|||,(1—12/2п)п
и равна нулю для |£|>е„Л. Для |||^епЛ имеем: l2/2n ^
<|(Л2/2) • (е^/п). Поскольку е„/]/« стремится к 0 при п,
стремящемся к бесконечности, существует такое целое число р, что
(А2/2)-(еЦп)<1 при п^р.
Теперь для л ^ р имеет место неравенство
К1 -■£)" 4>(i)|<l^*-w. (IV, 7; 34)
правая часть которого интегрируема. Значит, применима
теорема Лебега и потому Pndx действительно сходятся к б.
Узкая сходимость последовательности мер конечной нормы
■>
Пусть ц — мера Радона на X со значениями в векторном
нормированном конечномерном пространстве Е, имеющая
конечную норму.
Согласно следствию из теоремы 54г в этом случае для
каждой скалярной непрерывной и ограниченной функции ф на X
можно определить Г yd\i. Тем самым мы пришли к
следующему определению, играющему фундаментальную роль в
теории вероятностей:
Определение. Говорят, что последовательность мер \in
на X со значениями в конечномерном векторном нормирован-

§ 7. Широкая сходимость мер Радона
653
ном пространстве Е, имеющих конечную норму'), узко сходится
к мере ц с конечной нормой, если, какова бы ни была
скалярная непрерывная и ограниченная функция ф на X при п,
стремящемся к бесконечности, интеграл фй|хп сходится к Г фйц.
Естественно, что узкая сходимость влечет за собой широкую
сходимость. Однако узкая сходимость слабее сходимости по
норме, которая означает, что ||ц„ — ц\\ сходится к нулю и,
следовательно, I фй|хп сходится к фйц равномерно, если
функция ф остается ограниченной по норме на X.
Если меры цп узко сходятся к мере ц, то, полагая ф s= 1,
получаем, что d\y,n сходится к d\y,. В частности, если меры
\хп и ц неотрицательны, то \\цп\\ сходится к ||ц||.
Теорема 69. Если меры цп на X со значениями в
конечномерном векторном нормированном пространстве Е сходятся
узко к мере ц при п, стремящемся к бесконечности, то нормы
[|ц„|| ограничены в совокупности.
->
Доказательство. Каждая мера \хп определяет
некоторое линейное непрерывное отображение ип пространства (Кх)сь
скалярных непрерывных ограниченных функций на X в про-
■> г ->•
странство Е, а именно: ф—> I yd\xn-
-*■
Из определения ||цп||, как точной верхней грани норм
||ц.п(ф)Н при фе?(Х) и ||| Ф |||.< 1, следует, что ||«„|| >
SsHIHnll2)- Так как (Кх)сь является банаховым пространством
(следствие 3 теоремы 65 гл. II), то из теоремы Банаха — Штейн-
гауза следует, что ип ограничены и тем более ограничены \\цп\\-
Теорема доказана.
Пусть ц — некоторая неотрицательная мера с конечной
нормой. Будем называть верхним интегралом Римана по мере ц,
от ограниченной функции f ^ 0 (с произвольным носителем)
точную нижнюю грань интегралов от непрерывных функций
^ 0, мажорирующих эту функцию. Если функция f имеет
компактный носитель, то мы возвращаемся к определению,
') Мы говорим, что нормы «конечны», а не ограничены. В теореме 69 мы
увидим, что это условие влечет за собой ограниченность НцЛ в их
совокупности.
2) Можно даже доказать, что Н«п11 = 11Цп11.

654
Гл. IV. Интегральное исчисление
данному на стр. 635. В самом деле, если непрерывная
ограниченная функция g мажорирует функцию /и если а^О является
непрерывной функцией с компактным носителем, равной 1 в
некоторой окрестности носителя f, то ag по-прежнему мажорирует
функцию fa j f d\i ^ J ag d\i ^ I g d\i.
Непрерывную ограниченную функцию, определенную на X,
со значениями в F будем называть разложимой, если ее можно
представить в виде конечной суммы 2л g№i> где g{ — векторы
из F, а ф,- — скалярные непрерывные ограниченные функции.
Говорят, что функция f на X со значениями в F ^-интегрируема
по Риману, если она имеет аппроксимирующую (в смысле
верхнего интеграла. Римана) последовательность непрерывных
ограниченных разложимых функций.
Теорема 69г. Если цп образуют последовательность мер
^0 с конечными нормами, узко сходящихся к некоторой мере
р, с конечной нормой при п, стремящемся к бесконечности, и
если ф является вещественной или комплексной функцией,
определенной на X, ограниченной, измеримой относительно всех
jx„ и ^-интегрируемой по Риману, то ф й\кп сходится к \ ф d\i.
Доказательство аналогично доказательству теоремы 62.
Теорема 70. Ограниченная функция f, определенная на X
и принимающая значения в F, ^-интегрируема по Риману тогда
и только тогда, когда множество ее точек разрыва имеет ц-меру
(Лебега), равную нулю.
Доказательство аналогично доказательству теоремы 63.
Следствие 1. Для того чтобы часть А множества X
имела .характеристическую функцию, ^-интегрируемую по Риману,
необходимо и достаточно, чтобы ее граница А имела ц-меру
(Лебега), равную нулю.
Следствие 2. Если меры цп^0 с конечными нормами
узко сходятся к некоторой мере ц с конечной нормой и если
А — часть X, измеримая по всем цп, граница которой имеет
ц-меру, равную нулю, то цп(А) сходятся к ц(А) при п,
стремящемся к бесконечности.
Сходимость широкая и сходимость узкая
Теорема 71. Для того чтобы последовательность мер
цп ^ 0 на X с конечными нормами сходилась узко к некоторой
мере (г ^ 0 с конечной нормой, необходимо и достаточно, чтобы

§ 7. Широкая сходимость мер Радона
655
эти нормы сходились к ц широко и чтобы ||ц„|| = \ dn„
сходились к ||ц|| = Г d\a.
Доказательство. Условие это, очевидно, необходимо,
поэтому остается доказать лишь его достаточность.
Пусть ф — непрерывная ограниченная функция на I и
М = I ф II. Зададим е > 0. Согласно определению нормы
меры ц, существует такая непрерывная функция а с
компактным носителем, 0 ^ а =£С 1, что
J<x4i>J'4i—j^. (IV, 7; 36)
Поскольку меры ц„ сходятся широко к ц при п,
стремящемся к бесконечности, Г аф,„ сходится к Г ad\x. Так как,
по предположению, Г d\in сходится к Г ф., найдется такое
целое число р', что для п"^ р'
jadixn>jdixn--^-, (IV, 7; 37)
или
/(1-а)41»<-д5г и |(1_а)ф<1^.. (IV, 7; 38)
Теперь для функции (ре^(X) имеем следующее разложение:
И* (ф) — И (ф) .= (цЛ (аф) — И (аф)) + М(1 — а) <р) — ц ((1 — а) ф).
(IV, 7; 39)
В силу предположения о широкой сходимости, первый член
правой части сходится к 0. Значит, найдется такое целое число
р", что для всех п ^ р" будет иметь место неравенство
1Маф)-ц(аф)|<|. (IV, 7; 40)
В силу неравенства (IV,7; 38) для двух других членов при
и :> р = sup {р', р") имеет место неравенство:
1МФ)-ИФ)1<!+ М^й- + М1^-<е, (IV, 7; 41)
чем и заканчивается доказательство теоремы.
Замечание. Если мы вернемся к примерам I, Ь и 2
широкой сходимости к б (стр. 648—649), то увидим, что в этом
случае имеет место и узкая сходимость. То же самое можно
сказать относительно примеров 1°), 3°), 4°) на стр. 632-^
634.

656
Гл. IV. Интегральное исчисление
Если теперь мы снова вернемся к теореме 68, то
уверенности в узкой сходимости у нас уже не будет, поскольку, если
Рп — полиномы >0, то J Pn{x) dx = +00, откуда не следует,
что нормы мер конечны.
Если ап составляют последовательность неограниченно
удаляющихся точек из X (когда X— метрическое пространство;
см. определение в следствии из теоремы 55), то &(ап) широко
сходятся к 0, ибо при фЕ1"(Х) для достаточно больших
значений п точки ап находятся вне носителя функции ф
(компактного, а потому ограниченного), и, следовательно, ф(а„) = 0.
Однако, так как ||в(ап)||—Ь т0 &(а„) не сходится узко к 0.
Этот факт дает нам физическое истолкование узкой
сходимости. Широкая сходимость учитывает лишь происходящее на
конечном расстоянии. Последовательность мер ц„ ^ 0 может
сходиться широко к некоторой мере ц, и, однако, это не мешает
значительной части масс ц„ «потеряться» в бесконечности. Узкая
сходимость, напротив, мешает этому, поскольку || цп II стремится
к ||ц||.
Теорема 72. Пусть X — локально компактное
пространство и Т — некоторое компактное пространство. Пусть ф —
скалярная непрерывная и ограниченная функция на X X Т. Пусть,
кроме того, задана последовательность цп мер Радона Г3=0 на X
с конечными нормами, узко сходящаяся при п, стремящемся
к бесконечности, к некоторой предельной мере ц,.
Тогда интегралы <р(х, t)d\in сходятся к интегралу
Г (р(х, t)d\x равномерно, когда t пробегает компакт Т.
Доказательство. Теорема естественным образом
обобщает следствие 3 теоремы 66 на случай узкой сходимости.
Положим М = sup \q>(x, t) |. Если вернуться к обозначениям,
принятым в доказательстве теоремы 71, то можно найти
функцию а, зависящую от числа М и удовлетворяющую
соотношению (IV, 7; 36), а следовательно, и (IV, 7; 38) для п ^ р'.
Произведем теперь разложение (IV, 7; 39) относительно частной
функции ф<: х -*(p(x,t). Первый член ц,п(аф<) стремится
к n(cwpi) равномерно относительно t из Т. В" самом деле,
поскольку мы имеем непрерывную скалярную функцию (x,t)—*
-+a(x)q>(x, i) и для любого / функция х —► а(х)ф(х, t),
определенная на X, имеет носитель в фиксированном компакте,
а именно в носителе а, то мы находимся на этот раз в
условиях следствия 3 теоремы 66. Следовательно, можно
независимо от t определить р" так, чтобы при п ^ р" относительно ф{
имело место неравенство (IV, 7; 40). Что же касается вто-

§ 8. Тензорное произведение мер
657
рого и третьего членов, то они могут быть оценены независимо
от t, исходя из соотношений (IV, 7; 38). Поэтому для п^р=^
= sup (/?', р") и любого <еГ имеет место неравенство
(IV, 7; 41), чем и заканчивается доказательство теоремы.
§ 8. ТЕНЗОРНОЕ ПРОИЗВЕДЕНИЕ МЕР. КРАТНЫЕ ИНТЕГРАЛЫ
Постановка задачи
Пусть А и Y — локально компактные пространства. Из
определения окрестностей непосредственно вытекает, что А X У
также компактно. Кроме того, если А и У счетны в
бесконечности, то таким же будет пространство X X У- В самом деле, если
Нп составляют некоторую последовательность компактов,
дающих в объединении пространство X, а Кп— последовательность
компактов, объединение которых равно У, то Нп X Кп является
последовательностью компактов, объединение которых
совпадает с пространством X X У-
Пусть теперь ц — некоторая мера Радона на А и v —
некоторая мера Радона на Y. Рассмотрим, можно ли, исходя из этих
мер, построить новую меру Радона на А X У- При этом мы
ограничимся скалярными мерами Радона1). В пространстве
Rn мера dx\dx2... dxn, обычно служащая для определения
кратных интегралов, является «произведением» мер dxit
определенных на множителях R произведения R X R X • • • X R-
Покажем, что если (д, и v — скалярные меры, то существует
мера-произведение или тензорное произведение, которое мы
обозначим через ц ® v, или цх <8> v„, или dp(x) <8> dv (у), или
dn(x)dv(y)-. Интеграл от функции f, определенной на А X У,
-*■
со значениями в банаховом пространстве F по отношению
к этой мере-произведению называется двойным интегралом и
обозначается в обычных символах двойных интегралов:
J fd (ц (8) v) = J J f(x, у) dn (x) dv (у)2). (IV, 8; 1)
') Для мер со значениями в конечномерных векторных пространствах
имеют место аналогичные результаты. Но они не верны для мер со
значениями в нормированных бесконечномерных векторных пространствах.
2) Обозначение d\>.(x)d\(y) для меры-произведения некорректно,
поскольку х и у не являются переменными! Напротив, в формуле (IV, 8; 1)
это же обозначение вполне корректно, так как х и у фигурируют в ней дважды
и могут быть заменены любыми другими символами. Точно так же будет
вполне корректным для Л = ц ® v писать dX(x, у) = й\к{х) ®dv(y) или
dyi(x)dv(y).

658
Гл. IV. Интегральное исчисление
Пусть и и v — функции, принадлежащие соответственно
пространствам W(X) и W(Y). Рассмотрим теперь функцию ф,
определенную на X X У по формуле
Ф (jc, y) = u(x)-v (у). (IV, 8; 2)
Эту функцию обозначают также через и ® и. Функция
(х,у)-*х-*и(х) как композиция двух непрерывных функций
непрерывна. Точно так же непрерывна функция (x,y)-*-v(y).
Поэтому наша функция, являющаяся произведением двух
непрерывных функций, также непрерывна. Кроме того, она имеет
компактный носитель. Если Н и Д'—-носители функций и и v
в X и У соответственно, то ее носитель равен произведению-
Н X К. В самом деле, обозначим через А и В множества
точек, в которых и и v отличны от нуля. Тогда ф=^0 в том и
только том случае, когда и и v Ф О, т. е. на А X В. Носитель
Ф есть, следовательно, замыкание А X В, которое равно
произведению Ау(В замыканий, т. е. произведению Я X К.
В этом случае хотелось бы, очевидно, чтобы двойной
интеграл выражался в виде
J J и (х) v (у) d\a (л) d\ (у) = у и (х) d\n
(IV, 8; 3>
т.«. чтобы имело место соотношение
(ц <8> v) (и ® и) = ц (и) v (и). (IV, 8; 4>
Мы сейчас увидим, что этого достаточно для того, чтобы
единственным образом определить меру — тензорное
произведение ц ® v.
Существование и единственность тензорного произведения
Теорема 73. Пусть X и У — два локально компактных
пространства, а ц и v — меры Радона, вещественные или
комплексные, на X и У соответственно. Тогда существует, и притом
единственная, мера Радона X на Xy^Y, удовлетворяющая
равенству
Mu®o)=»Mu)v(o). (IV, 8; 5)
5га мера называется тензорным произведением мер ц и v
и обозначается через ц ® v.
Доказательство этой теоремы мы проведем в несколько
этапов.
Первый этап: единственность тензорного произведения.
Пусть Н и К — компактные множества из X и
У-соответственно. Рассмотрим сначала все «разложимые» функции ф вида

§ 8. Тензорное произведение мер 659
и <8> v, где и принадлежит пространству <ё'н{Х), a v —
пространству Wk(Y). Рассмотрим теперь все функции <р,
являющиеся конечной суммой (но заранее не ограниченной)
разложимых функций. Такие функции <р могут быть записаны
в виде
Ф(х, у) = S Щ(*) vt(y), Ui<=<&H{X), vtf=VK(Y). (IV,8; 6)
Множество таких функций образует некоторое векторное
подпространство ГЯХЛ пространства ^ {XXY). Имеет место
следующая теорема:
Теорема 74 (теорема о плотности). Пусть Н0 и Ко—
некоторые компакты пространств X и Y соответственно, а Н и
К — компактные окрестности множеств Н0 и Ко1). Тогда
замыкание векторного подпространства ^нхк в пространстве
^нхк(Х X У) содержит подпространство 1>?н*х кЛ% X У)-
Эта теорема означает, что функция <р, непрерывная на
X X У, с носителем в #0ХЛо является равномерным
пределом некоторой последовательности функций, каждая из
которых может быть записана в виде (IV, 8; 6), где носители
функций щ лежат в Я, а носители функций иг- лежат в К-
Доказательство. Ограничимся случаем метрических
пространств X и У. В произведении X X У мы введем одну из
естественных метрик произведения.
Пусть ф — некоторый элемент пространства ФнихкЛХ X У)-
Эта функция равномерно непрерывна (см. стр. 633), т. е.
каково бы ни было е > О, существует такое г\ > 0, что из
неравенств d(x',x")^j\, d(y',y")^j\ вытекает неравенство
|ф(*', У')—4>(х"> У") I ^ е. Каждая точка Н0 будет являться
центром открытого шара, содержащегося в Н, радиус
которого можно считать ^ т]/2. Множество этих открытых шаров
образует покрытие Н0, и, следовательно, из него можно извлечь
конечное подпокрытие, образованное из шаров Uit ie/,
радиуса ^ т]/2, содержащихся в Н. Точно так же можно
образовать конечное покрытие Ко шарами Vj, j'e/, с радиусами
^ т]/2, целиком лежащими в К- Точка V\ X Vj образуют
некоторое конечное покрытие множества Н0 X Ко, целиком лежащее
в НХК.
Если x'^Ut, fet/|, (/'еУ;, у" &.V j, то d{x', л/'Хл и
d {у', у") ^Л- Отсюда следует неравенство | ф (х', у')—<р (х", у") | ^е.
Положим /' == / U {0} и /' = /U{0} и рассмотрим открытые
) Такие окрестности существуют. Смотри примечание на стр. 457.

660
Гл. IV. Интегральное исчисление
покрытия (Ui)le/, множества X и (Fy).e/, множества У, где
U0=CH0 и V0 = CKo- Пусть теперь (ал)/е/, и (Р/)/(=г —
разложения единицы, соответствующие этим покрытиям (это
означает, что X и Y счетны в бесконечности; можно избавиться
от этого условия, но мы этого делать не будем). Выберем в
каждом из множеств Ut некоторую точку xt, а в каждом
Vj — точку yt и определим функцию Ф на X У, Y по формуле:
Ф(х, у)= 2 «t(x)h(y)v(xt,yi). (IV, 8; 7)
ПОСКОЛЬКУ При раВНЫХ НуЛЮ i ИЛИ / фуНКЦИЯ ф(ЛГг, t/j) = 0,
то вместо 2 можно писать сумму 2 • Функция
Ф имеет вид (IV,8;6) относительно множества индексов /ХЛ
где, например, можно считать иц(х) = оц{х), Vij(y) =
= ф(*ь #j)p\i(#)- Тогда для i и /, отличных от 0, функции иц
имеют носитель в Я, а функции i>,-j— в К. Заметим, что
произведения а* ® Pj, (i,/)e/'X^', образуют некоторое
разложение единицы для X\Y, подчиненное покрытию его
множествами UiXVj, (j,/)e/'X/'. Поэтому имеет место равенство
Ф (л;, у) — 2 а» (*) Р/ (у) ф (х, у), где суммирование может
относиться как / X Л так и к /' X /'• Поэтому
I Ф (х, у) - Ф (х, у) | < 2 а, (*) Р/(у) | ф (*„ ^) - ф (х, у) |. (IV, 8; 8)
Члены правой части отличны от нуля только тогда, когда
i Ф0^ф 0, (х, y)e=UiX V}. Но тогда \<p(xt, ^) — <р(х, у)|<е
и, следовательно, правая часть не превосходит 2 аДлс) Р/(у) 8=
= е; доказательство теоремы закончено.
Следствие. Если меры ц ы v заданы на X и Y, то
существует только одна мера А,, удовлетворяющая условиям
теоремы 73.
В самом деле, для функции ф е^яихКо(X X Y) существует
последовательность функций фп ^Фнхк (X X У) вида (IV,8;6),
сходящаяся равномерно к ф при п, стремящемся к
бесконечности. Поэтому, если мера Я, существует, А, (ф) = lim А, (ф„). Од-
нако в этом случае, в силу равенства (IV, 8; 5), известно ее
значение на разложимых функциях и ® v, а, следовательно,
после суммирования — на всех функциях \рп; предыдущий
переход к пределу говорит о том, что А,(ф) определена для любой

§ 8. Тензорное произведение мер
661!
функции фе^^Х^! чем полностью доказывается
единственность тензорного произведения1).
Создавшаяся ситуация подобна, очевидно, ситуации,
имевшей место в теореме 49 гл. II (о продолжении линейных
непрерывных функций, определенных на плотных
подмножествах). Однако в данном случае имеется небольшая трудность,,
заключающаяся в том, что мы не рассматривали Ф(Ху(У)
как топологическое пространство. Это обстоятельство
вынуждает нас провести прямое доказательство следствия.
Второй этап: существование тензорного произведения.
Теорема 75. Пусть ф — некоторая функция из W (X X Y)..
Тогда для каждого фиксированного х^Х можно вычислить-
интеграл
${x)=j<t(x,y)dv{y). (IV, 8; 9)
Функция г|з: х -*■ ф (х) непрерывна и имеет компактный
носитель в X. Следовательно, можно вычислить
Я- (ф) = J * (*) dn (x) = J [ J Ф (х, у) dv (г/)] dp (x). (IV, 8; 10>
Линейная форма ф—»Л,(ф) является мерой Радона на
X X У, удовлетворяющей соотношению (IV, 8; 5).
Доказательство. Обозначим через Н и К проекции
носителя ф на пространства X и Y соответственно. Эти
множества, как непрерывные образы некоторого компакта, сами
компактны. Тогда .носитель частной функции фж: х/-»-ф (*,*/) при
любом х лежит в К. Впрочем, фж == 0, если х ф. Н. В теореме 66
мы видели, что при х, стремящемся к а, частная функция фх
стремится к частной функции фа равномерно на компакте К
(а, значит, равномерно на Y, поскольку ее носитель всегда
лежит в К) и, следовательно, фж стремится к фа в
нормированном векторном пространстве WK(Y). Из определения меры у
как линейной формы на 'S'(Y), сужение которой на ^к(^)
непрерывно, следует, что г|з(дс)= |фжс?у сходится к г|з(а) =
= Г q>adv, т. е. что функция г|з непрерывна на X. Так как при
хфН, фж = 0, а, значит гр(я) = 0, носитель этой функции
лежит в Н. Следовательно, она принадлежит пространству ^Р(Я),.
и мы можем вычислить м-('Ф)> а потому имеет смысл
выражение (IV, 8; 10). Очевидно, эта функция линейно зависит от ф..
') Независимо от нахождения тензорного произведения мы доказали
большее: две меры %\ и Я2 на X X Y, принимающие одно и то же значение на
каждой функции ф из "&{Х X Y) вида и ® v, ue?(Jf), se?(F),
принимают одно и то же значение для любой функции фе^(^,У), т. е. равны
между собой.

662
Гл. IV. Интегральное исчисление
Если ф сохраняет носитель в фиксированном компакте Н X К,
то ty сохраняет носитель в Я и удовлетворяет неравенству
Ж*)1<|||ф1|ПМ1*. (IV, 8; 11)
Отсюда вытекает оценка
1Мф)1<ЫЫ1Ы11'<ЫЫМИ11ф111- (IV, 8; 12)
Мы видели, что Я является мерой на X X У и, кроме того,
имеет место неравенство
11Я|1яхк<11и11л1М1к. (IV, 8; 13)
Остается лишь убедиться в том, что Я удовлетворяет
соотношению (IV,8;5). Если мы положим ф(х,у) = и(х)v(у), то
получим, что ^(л:) = и(х) j v(y)d\(y) = u(x)\(v), а,
следовательно, Я(ф) = v(t>) j u(x)d\i(x)= \x(u)\(v), чем и
заканчивается доказательство теоремы.
Следствие. Если заданы ц и v, то найдется хотя бы
одна мера Я, удовлетворяющая условиям теоремы 73.
Таким образом, теорема 73 установлена путем
доказательства двух не зависящих друг от друга утверждений —
существования и единственности.
Замечание. Можно было бы начать с того, чтобы
зафиксировать у и вычислить интеграл
Э (у) = { Ф (х, у) <*ц (*). (IV, 8; 14)
Полученная функция Э была бы непрерывной функцией
с компактным носителем в У, и можно было бы вычислить
Я (Ф) = { 9 (у) dv{y) = { [ j Ф (*, у) dp (x)] dv (у). (IV, 8; 15)
Таким путем можно определить другую меру Радсна Я,
удовлетворяющую соотношению (IV, 8; 5). Из единственности,
доказанной в следствии теоремы 74, следует, что мы получим
тот же результат. Поэтому имеет место соотношение
j[ { Ф (х, у) dv (у)] dp (х) = { [{ Ф (*, У) d\i (*)] dv (у). (IV, 8; 16)
Последнее равенство составляет содержание теоремы о
перестановке знаков интегрирования.
Примеры тензорных произведений
Если а является точкой X, а Ь — некоторой точкой У, то
между соответствующими мерами Дирака имеет место
следующее очевидное соотношение:
6(a) ® 6(6) = 6(в, 6) или d6(a) (x) d6(b) (у) = cf6(a, 6) {х, у), (IV, 8; 17)

§ 8. Тензорное произведение мер
663
вытекающее из того, что его правая часть удовлетворяет
равенству (IV, 8; 5).
Пусть теперь ц является мерой 2c(fya.\. a v — мерой
i ч "
2^/6(6.). Тогда имеет место формула
2 С(б(Я;) ® 2 d/6(6/) = 2 Cidjb^., bty (IV, 8; 18)
Элементарные свойства
Легко видеть, что отображение (ц, v)—>• ц <8> v пространства
<ё"(Х)Х'ё"(У) в пространство ^"(^Х у) является билинейным
отображением '), т. е. имеют место равенства:
О-Ч + Иг) ® (vi + v2) = Ц! ® V! + ц, ® v2 + Ц2 <8> V! + ц2 ® v2,
(IV,8;19>
/гц <8> kv = /г6(ц ® v), где h и 6 — скаляры.
Очевидно также, что если ц и v вещественны, то функция
ц <8> v также вещественна и что, если ц и v ^ 0, то и ц ® v ^
> 0. В самом деле, для того чтобы проверить неравенство,
(ц <8> v) (ф) ^ 0, достаточно при ф ^ 0 провести вычисления
теоремы 75.-
Наконец, соотношение (IV, 8; 13) показывает, что если ц и
v имеют конечные нормы, то конечную норму будет иметь
произведение ц <8> v, и при этом
lln®v||<|||i||||v||. (IV,8;192).
Носитель меры ц ® v
Теорема 76. Если А — носитель меры ц, а В — носитель
меры v, то носитель меры ц <8> v есть множество А\ В.
Доказательство. Iе) Так как мера ц равна нулю
в С Л, то в открытом множестве С Л X Y произведение ц®у
равно нулю. Точно так же мера n<8>v равна нулю в X X СВ,
ибо v .обращается в нуль в СВ. Значит, мера ц <8> v равна
нулю в объединении этих двух открытых множеств (теорема
13). Это объединение равно дополнению множества Л X В,
Значит, носитель меры ц <8> v лежит в А У, В.
2°) Пусть теперь (а, Ь)—произвольная точка множества
А X В, и пусть $Ф (соответственно Ж) является некоторой
открытой окрестностью точки а в X (соответственно точки b
') Этим и объясняется название — тензорное произведение.

•«64
Гл. IV. Интегральное исчисление
в Y). Согласно свойству носителя (теорема 14), найдется
такая функция ие?(Х) с носителем в s&, что ц(и)Ф0. Точно
так же найдется такая функция v е'^'(У) с носителем в 38, что
■v(v) ФО. Если теперь мы положим <р(я, у) = u(x)v(y), то
получим (ц <2> v) (ф) = ц(ы)у(и) ф 0. Этим доказано, что не
существует такой окрестности точки (а, Ь), в которой мера ц <2> v
была бы равна нулю, и что, следовательно, точка (а, Ь)
принадлежит носителю меры ц ® v. Значит, этот носитель
совпадает с А X В.
Вычисление двойного интеграла путем двух последовательных
простых интегрирований
В теореме 75 предлагается способ вычисления двойного
интеграла с помощью двух последовательных простых
интегрирований. Однако эта теорема применима лишь в том случае,
когда рассматривается интеграл от функции ф, принадлежащей
пространству ?(ХХ^)- Для Ц и v ^ 0 имеет место
значительно более общая теорема.
Теорема 77. (Фубини — Лебега). Предположим, что X и
У—локально компактные пространства, счетные в бесконечности.
->
Пусть ц и v — меры >0 на X « Y соответственно. Пусть F—■
->
.некоторое пространство Банаха, a f — функция, определенная
->
на X'XY со значениями в F и интегрируемая (соответственно
измеримая) относительно ц <2> v. Тогда для фиксированного
-> ->
хеХ частная функция fx: y~+f(x,y) не всегда интегрируема
(соответственно измерима) относительно v, однако она
интегрируема (соответственно измерима) относительно v no край-
лей мере для \х-почти всех значений х из X. Можно также для
ц-почти всех значений х определить ')
J (х) = J T(x, у) dv (у) е F. (IV, 8; 20)
Функция g:x-+g(x), определенная \1-почти всюду на X,
хо значениями в F будет ^-интегрируемой, и имеет место
формула
J -J f(x, у) dp (x) dv (у) = J" g (x) йц (x) = J" [ J" f(x, y) dv (y)] dvi (x).
(IV, 8; 2 1
') Мы предполагаем теперь, что функция / интегрируема. Дальнейшие,
^рассуждения больше не связаны со случаем «соответственно измерима».

§ 8. Тензорное произведение мер
665
Эту формулу обычно пишут в виде
j" j" f(x, у) d» (x) dv (у) = j" d» (x) j" f(x, y) dv (у). (IV, 8; 22)
Это обозначение несколько необычно. Чтобы не писать
скобок, мы записываем g (x) d\i (x) в виде d\i (x) g (x). К этим
часто применяемым обозначениям следует привыкнуть.
Доказательство. Докажем сначала такое
утверждение:
Лемма 1. Пусть f — функция ^0 (с конечными или
бесконечными значениями), полунепрерывная снизу на XX У-
Тогда имеет место формула
fdix(x)ff(x, y)d4(y)=jff(x, y)d»{x)dv(y). (IV,8;222)
,' Рассмотрим множество ^+(XytY;f) всех функций Z^sO из;
'ё'(Х'ХУ), ограничивающих снизу функцию f. Функции этого-
множества обладают свойством возрастания в смысле
теоремы 394. Кроме того, верхняя огибающая этих функций равна
f. [В самом деле, эта огибающая, очевидно, ^/. Однако если
ael, то найдется такая открытая окрестность У точки а,-
что f(T)^(f(a)—е)+ = max (/(а)—е, 0). Значит, существует
некоторая компактная окрестность W точки а в У, а потому,,
согласно следствию 1 из теоремы 11, существует непрерывная
функция \|з, 0 ^.\|з ^ 1, с носителем в У, равная 1 в W. Имеем:
0 ^(f(a) — е)+\|з ^ f (это справедливо в Т, а вне Т обе
функции равны нулю). Эта функция в точке а принимает значение
(f(a)—е)+. Следовательно, точная верхняя грань величии
ф(а) по всевозможным функциям <р из Ф+^Xy^Y),
мажорируемым функцией f, равна f(a).] К множеству <&+{Ху^ У;/) можно
применить теорему 394. Это снова, впрочем, дает теорему ЗЭг,^
а. именно:
\{ f(x, у) dy. (x)d\ (у) = sup (ц ® v) (ф).
Рассмотрим, кроме того, множество соответствующих
частных функций фж: у—* ф (х, у). Это множество является
множеством непрерывных функций ^0, удовлетворяющих условию
возрастания теоремы 504, а его верхней огибающей является
функция !х'-Ут+1(х,у). Из тееремы следует, что
Г f {х, у) dv (у) = sup f ф (х, у) dv (у).
J <t.^V+(XXY;f)->

666 Гл. IV. Интегральное исчисление
Однако для каждой функции ф функция J<$:x —►
—*■■ | ф(*.y)dv(y) непрерывна, ^0 и имеет компактный
носитель на X (теорема 75). Значит, верхняя огибающая таких
функций /<р, т. е. функция F: х —*■ J f{x, y)d\(y), является
полунепрерывкой снизу функцией ^0. Так как /ф и Уф
мажорируемы функцией /ф+ф, а, значит, sup(/<p,/^) ^/ф+ф, то
множество /ф удовлетворяет условию возрастания теоремы 394. Зна-
■ чит, можно снова применить эту теорему и тогда
f d\i {x) f f (x, у) (y)d\ = sup f d\x, (x) f ф (х, у) d\ (у) =
= sup (ц ® v) (ф)Л) = [ [ f (x, y) d\i {x) d\ (y),
<e^V+(XXY;f) •> •>
чем и доказывается лемма 1.
Лемма 2. Пусть / ^ 0 — произвольная функция на ^ X У.
Тогда
f dn(x) ff(x, у) dv{y) < \ ff(x, у) d» (x) dv (у)2). (IV,8;23)
В самом деле, пусть g~^f и полунепрерывна снизу. В силу
леммы 1,
j" d\i (х) j" / (х, у) dv (у) < j" d\i{x) j g (x, у) d\ (у) =
= J" J" 8 (х, у) d\i (x) dv {у).
Переходя, согласно теореме 50з, в последнем члене к
точной нижней грани при переменной функции g, получим
| | / (*> У) d\i (x) dv {у), откуда и вытекает (IV, 8; 23).
-»-
Перейдем теперь к доказательству теоремы. Пусть / —
некоторая (ц <8> v)-интегрируемая функция на Л" X У со значе-
ниями в F. Эта функция имеет аппроксимирующую
последовательность, образованную непрерывными разложимыми
функциями /п с компактными носителями вида 2 ё'глФ/л» Ф*л е
i
')' В силу теоремы 75.
2) Результат леммы 1 может навести на мысль, что полунепрерывные
снизу функции занимают весьма привилегированное положение среди
неотрицательных функций в том смысле, что для них имеет место равенство вместо
неравенства. Теорема 78 покажет, что равенство имеет место и для всех
(fi ® v) -измеримых функций ^ 0 на X X У, в частности, для всех борелевских
функций, а всякая полунепрерывная функция борелевская.

§ 8. Тензорное произведение мер
667
ef^X^). Для такой функции теорема Фубини — Лебега
очевидна. Она сводится к случаю функции из ^(Xy^Y), а это
в силу теоремы 75 является следствием определения тензорного
произведения.
Величины J *ф(*) f\\f-fn\\dy{yXJjYf-7n\)d\i(x)d\(y)
(лемма 2) сходятся к 0. Но тогда в силу теоремы 38 можно
выбрать такую подпоследовательность, которую мы будем по-
прежнему обозначать через /„, для которой \\f — fn\\d\ (у)
сходится к 0 для d|x-no4TH всех х из X. Значит, существует
такое множество А из X нулевой ц-меры, что для х ф. А эта
сходимость имеет место. Функция (fn)x: y-*fn(x, у)
непрерывна, разложима, имеет компактный носитель и v-интегри-
->
руема. Поэтому, для каждого х^А, fx v-интегрируема и (fn)x
образуют аппроксимирующую последовательность:
IМ = \ Т(х, у) d\ (у) = lim f /„ (х, y)d\ (у) — Игл gn (х).
->
Каждая из функций gn непрерывна, разложима и имеет
компактный носитель (теорема 75), а, следовательно, ц-инте-
грируема и J gn d\i = J J /„ d (ц ® v). Функция g определена
[х-почти всюду и
f\\g-L\\dli<fdliM$'\\j*-Tn\\dv(y)^$f\\f-Ud(\x®v)
-> -*•
стремится к нулю. Следовательно, g ц-интегрируема, a gn
образуют аппроксимирующую последовательность:
f d\i (x) \ f(x, у) d\ (y)= \ g d\i = lim f gnd\i =
= lim f f /„ d (ц ® v) = f f f d (ц ® v).
tt-Ьоо J J . J J
Теорема доказана.
Замечания. 1°) Естественно, что можно было бы идти
в обратном порядке и получить формулу
J J" Т(х, у) ф (*) dv (у) = j" dv (*/) J f(jc, г/) <*|х (*). (IV, 8; 24)
Отсюда, в частности, вытекает следующее: если заранее из*
->
вестно, что функция f интегрируема по ц ® v, то можно написать

668
Гл. IV. Интегральное исчисление
формулу изменения порядка интегрирования
J dix (x) J" f(x, у) dv (у) = J" dv (у) J" f(x, у) ф (х). (IV, 8; 25)
2°) Если f не интегрируема по ц ® v, то может случиться,
что одна часть в равенстве (IV, 8; 25) имеет смысл, а другая —
нет. Может даже случиться, что обе части имеют смысл, но
значения их не совпадают.
Рассмотрим, например, на квадрате [0,1]Х[0,1]
пространства R2 меру-произведение dx ® dy и вещественную функцию
/, определенную по формуле
f {х, у) = \*!+£? для (х, у) Ф (0, 0). (IV, 8; 26)
Мы не затрудняем себя .определением /(0,0), поскольку
при любом фиксированном х эта функция может быть не
определена лишь при одном значении у и, наоборот, при любом
фиксированном у — лишь при одном значении х. Однако мно-.
жество, состоящее из одной точки, имеет меру нуль
относительно dx или dy.
Покажем, что выражение
[ dx Г х2~У2
J J (х* + у2?
[0. II [0, 1]
dy (IV, 8; 27)
имеет смысл и что оно равно л/4.
В самом деле, для фиксированного х Ф 0 первообразной по
у для непрерывной функции у —> , 2 , 2.2 является функция
у -*• Л 2 . Поэтому для х Ф 0 имеем:
[0, 1]
J
Для того чтобы применить формулу (IV, 8; 27), нет
необходимости вычислять интеграл при х = 0, ибо множество {0}
имеет нулевую меру относительно dx. Окончательно получаем
\dx l (Й^=/тТ^ = Т- '(IV.8;29)
[0, I] [0, 1] 0
Если теперь мы попытаемся вычислить этот интеграл в
обратном порядке
I dy j * "ff, dx, (IV, 8; 30)
[0, 1] [0, 1]

§ 8. Тензорное произведение мер 669
то, переобозначая переменные интегрирования х и у через у и х,
придем к интегралу
j dx J (g ~;22)2 dy, (IV, 8; 31)
[О, 1] [0, 1]
противоположному интегралу (IV, 8; 27) и, следовательно,
равному —л/4. Таким образом, хотя оба интеграла (IV, 8; 27) и
(IV, 8; 30) имеют смысл, их значения не совпадают. Это
означает, что теорема Фубини в этом случае не применима, а,
следовательно, функция / не интегрируема относительно меры-
произведения dx <8> dy. С помощью методов, которые будут
подробно изложены позже, в этом можно убедиться
непосредственно, выполнив предварительно замену переменных
перехода к полярным координатам х = г cos <р, у = г sin <p
(формула (IV, 9; 92)), а затем применив следствие 4 из теоремы 108
при а = 2. '
->
3°) Нельзя надеяться на то, что fx будет интегрируемой
по у для всех значений х.
В самом деле, если мы вернемся к примеру с мерами dx
и dy на R, то увидим, что / можно изменить на прямой х = а,
параллельной оси у, не изменяя ее интегрируемости по
отношению к мере dx <Э dy, поскольку прямая х = а является
множеством меры нуль в R2.
Это позволяет нам в качестве функции г/ —> / (а, /у) брать
произвольную функцию от у, которая не обязана быть
интегрируемой по у 'относительно dy. Однако это обстоятельство не
играет никакой роли в том вопросе, который нас интересует.
->
Как только мы узнали, что функция g определена для ц-почти
всех значений х и интегрируема относительно ц, нам этого
достаточно для того, чтобы вычислить двойной интеграл путем
двух последовательных простых интегрирований. В этом даже
состоит некоторое удобство, которым надо еще уметь
пользоваться: если для некоторых исключительных значений х,
образующих множество ц-меры нуль, интеграл | / (х, у) dv (у) или
не существует, или сложен для вычисления, нет никакой
необходимости заниматься им в этих точках.
4°) Теорему Фубини можно сравнить с теоремой
суммирования по блокам в безусловно сходящихся рядах (теорема 59
гл. II). В этой теореме точно так же мы должны сначала
предположить, что ряд безусловно сходится для того, чтобы иметь
затем возможность суммировать его блоками. Мы видели, что
существует, однако, случай, когда не нужно знать заранее,
сходится ли ряд безусловно, а именно случай,- когда члены ряда

670 Гл. IV. Интегральное исчисление
вещественны и ^0. То же самое имеет место и здесь, как это
видно из следующей теоремы и ее следствия 1,
Теорема 78 (Фубини — Фату). Пусть X, Y — локально
компактные пространства, счетные в бесконечности. Пусть f —
некоторая функция -^0 (с конечными или бесконечными
значениями), определенная на X У( Y и (ц, ® v) -измеримая на нем.
Тогда имеет место такое равенство:
0 < J * dii (х) J" * f (х, у) dv (у) = J" J" * f (x, у) dp (x) dv (y) < + oo.
(IV, 8; 32)
Док аз ател ьство. Поскольку функция f (ц, <8> v)
-измерима, она является пределом некоторой возрастающей
последовательности измеримых ограниченных функций f„ ^ 0 с
компактным носителем (например, функций !м,к, указанных на
стр. 521). Для каждой функции fn, согласно теореме Фубини —
Лебега (теорема 77),
J dp (x) J" fn {х, у) dv (у) = J" J" fn (x, у) d(i (x) dv (y),
где второй интеграл левой части равенства, fn{x,y)dv{y),
имеет смысл для ц,-почти всех значений х. То же самое
равенство будет иметь место, если везде вместо интегралов I
взять имеющие смысл интегралы (с конечными
значениями или нет). Теперь остается устремить п к бесконечности
и применить два раза слева и один раз справа теорему 36
Фату.
Замечание/Можно утверждать несколько больше. Пусть
Ап — множество нулевой ц,-меры точек х, для которых
функция {fn)x не является v-интегрируемой. Пусть А = U Ап; А так-
п
же имеет ц-меру, равную нулю. Для хфА все функции (/„)*
v-измеримы, а, следовательно, измерим их предел fx- Таким
образом, частная функция fx v-измерима для ц,-почти всех
значений х (см. обобщение следствия 4).
Кроме того, gn (х) = J' fn (х, у) dv (у) и g(x)= j f (x, у) dv (у)
определены на СЛ„ и ц-измеримы. Следовательно, g
определена на СЛ и ц-измерима.
Однако мы видели, что для измеримой функции ^0 вместо
Г можно писать , если даже она принимает бесконечные
значения (замечание 2 после следствия 3 теоремы 39). В
наших условиях для (|i <8>.v)-измеримой функции f^O можно

§ 8. Тензорное произведение мер
671
написать такие соотношения:
0< j dii(x) j* f(x,y)dv(y)=jjf(x, y)dn{x)dv(y)^+oo.
(IV, 8; 33)
Здесь второй интеграл в левой части равенства имеет
смысл для ц-почти всех значений х как интеграл (конечный
или бесконечный) от v-измеримой функции fx ^ 0. Первый
интеграл левой части (конечный или бесконечный) является
интеграло^ от функции g ^ 0, определенной ц-почти всюду
и ц-измеримой. Двойной интеграл в правой части является
интегралом от (ц ®v)-измеримой функции f ^ 0.
Следствие 1. Пусть X и Y — локально компактные
пространства, счетные в бесконечности, ц и v — меры Радона ^0
на X и Y соответственно, f—вещественная функция 2^0,
измеримая относительно меры ц <8> v. Пусть для [i-почти всех
значений х частная функция fx: y-*f(x,y) интегрируема по v,
а функция g, определенная для ц-почти всех значений х по
формуле
g{x)=jf(x,y)dv(y), (IV, 8; 33а)
интегрируема по ц. Тогда функция f интегрируема по ц <8> v.
и имеет место равенство (IV, 8; 22).
Доказательство очевидно. Условия теоремы означают, что
левая часть равенства (IV, 8;ЗЗг) конечна, а, следовательно,
будет конечной- и его правая часть. Поскольку функция f
[л <8> v-измерима и ее верхний интеграл конечен, то, согласно
теореме 39, она интегрируема.
->
Следствие 2. Если функция f со значениями в банахо-
вом пространстве F определена на пространстве X X У "
(ц <8> v)-измерима на нем, а хотя бы один из трех интегралов
JJ'llTu. y)№(x)dv(y), fdn(x)f\\7(x,y)\\dv(y),
(IV, 8; 34)
fdv(y)f\\f(x,y)\\dli(x)
конечен, то функция f интегрируема относительно \i <8> v и
имеют место формулы (IV, 8; 22) и (IV, 8; 24).
->-
В самом деле, поскольку функция ||/|| измерима, то можно
применить теорему Фубини — Фату в предыдущем виде, и
тогда тот факт, что один из трех рассматриваемых интегралов
конечен, будет означать, что конечны все три рассматривав-

G72
Гл. IV. Интегральное исчисление
мых интеграла, а, следовательно, в частности, конечен интеграл
\\l{x, y)\\d(\x, ® v). Из теоремы 39 вытекает, что если функ-
и
ция / (ц ® v)-измерима, то она и (ц® v)-интегрируема. Мы
попадаем тем самым в условия применимости теоремы Фу-
бини — Лебега.
Замечание. Естественно, что теорему Фубини можно
применить к интегралам вида J J f(x, у) d\x (x) dv (у), где А
А
является (ц ® v)-измеримым подмножеством пространства
->
X X У> лишь бы только функция / была интегрируемой на
множестве А или была на нем (ц ® v)-измерима и ^0.
Поскольку это утверждение сводится к вычислению интеграла
И? ■ •>' ->
f (x, у) d\x (x) dv (у), где f — функция, равная функции / на
Л и 0 вне А, то новой теоремы мы не получаем. Пусть А (а)
при иеХ — это сечение множества А вертикалью с
абсциссой а, т. е. множество точек j/ёУ, таких, что (а, г/)еЛ.
Тогда
J J Т(х, у) dix (x) dv (у) = J ф (х) j" Т(х, у) dv (у). (IV, 8; 35)
А X А{Х)
В частности, если / = 1 на Л, то
(ц ® v) (Л) = J v (Л (х)) dp (x), (IV, 8; 35^
где у(Л(х)) является v-мерой сечения А(х), определенной для
ц-почти всех х (конечной или бесконечной).
Следствие 3. Пусть А есть (ц ® v) -измеримая часть
пространства X X У- Для того чтобы она имела нулевую (ц ® v)-
меру, необходимо и достаточно, чтобы для \х,-почти каждого
значения х ее сечение А (х) имело v-меру, равную нулю.
В самом деле, J v (Л (х)) d\x (x), согласно теореме 26,
равен нулю тогда и только тогда, когда подинтегральная функция
ц-почти всюду равна нулю.
Замечание. В этой формулировке существенно
предположение, что Л (ц <8> v)-измеримо. Можно (с помощью аксиомы
Цермело) доказать существование такого подмножества Л из
R2=RXR. которое с каждой из прямых х = const
пересекается в единственной точке, но (dx ® dy)-мера которого не
равна нулю (потому что оно не (dx ® dy)-измеримо).

§ 8. Тензорное произведение мер
673
Следствие 4. Пусть f — функция со значениями в мет-
ризуемом сепарабельном пространстве F. Если f (ц ® v)
-измерима, то для \1-почти всех значений х^Х частная функция
fx '■ У ~* f (*> У) является v-измеримой.
Доказательство. Пусть А — борелевская часть
пространства X X У- Тогда для каждой точки iel сечение А (х)
борелевское. В самом деле, части X X У, сечения которых для
данного х борелевские, очевидно, образуют а-алгебру,
содержащую все открытые множества из X X У, и, следовательно,,
все борелевские множества.
Если теперь / — борелевская функция на X X У, то все ее
частные функции fx борелевские. В самом деле, если О —
некоторое открытое множество из F, то f~x{0) = (f~l((J)) (x)
является борелевским множеством как сечение, проходящее
через точку х борелевского множества }~1((У).
Если теперь / (fi ® v)-измерима, то существует
борелевская функция g, равная всюду функции /, кроме точек
некоторого множества А (^ <8> v)-Mepbi нуль (см. замечание после
теоремы 232). Сечение А{х) для (а-почти всех значений х имеет
v-меру, равную нулю (следствие 3), и fx совпадает с борелев-
ской функцией gx всюду, кроме множества А(х), а, значит,
эта функция v-измерима.
Случай, когда интегрируемая функция является произведением
функции от * и функции от у
Теорема 79. Пусть ц. и v — меры ^0 на локально ком-
->■
пактных пространствах, счетных в бесконечности. Пусть f —
функция, определенная на X, со значениями в банаховом
пространстве F, a g — функция, определенная на У, со значениями
в банаховом пространстве G, и пусть В — непрерывное били-
■*■■*■ -У
нейное отображение F X G в банахово пространство Н.
■ ■*■ ' •>'
Если J ^-интегрируема {соответственно \х,-измерима) и g
v-интегрируема (соответственно v-измерима), то функция
B{f, g)' {x, у)-* B{f{x), g{y)) является (fi <8> v)-интегрируемой
(соответственно (ja ® v) -измеримой) *) и имеет место формула
j j B(f,g)d fa.® v) = В (J fdii, jgdv). (IV, 8; 36)
') В противоположность тому, что было сделано в теоремах Фубини, для
получения измеримости по отношению к ^ ® v здесь исходят из измеримости
относительно ц и v.
22 Зак. 1339

674
Гл. IV. Интегральное исчисление
Обратно, если F, G и Н — скалярные поля, В — обычное
произведение, а функция fg (ц ® v) -интегрируема и ни одна из
двух функций f и g не равна почти всюду нулю, то функция f
^-интегрируема, а функция g ^-интегрируема.
Прежде чем проводить доказательство, заметим, что если
F — G = Н является скалярным полем и В есть обычное
произведение, то (IV, 8; 36) записывается в виде
jjfWg(У)^(х) dv(//)=(J f (х)йц(х)) (J g (у)dv (у)). (IV,8;37)
Этот результат непосредственно из определения (IV, 8; 4)
меры (д, ® v не вытекает, ибо f и g не являются непрерывными
функциями с компактным носителем.
Доказательство. Докажем сначала обратное
утверждение. Предположим, что fg интегрируема относительно ц ® v.
Тогда из теоремы Ф.убини — Лебега следует, что для ц-почти
всех значений х функция y-+f(x)g(y) является v-интегрируе-
мой. Поскольку мы предположили, что / не является почти
всюду равной нулю, найдется хотя бы одно значение х, для
которого функция y-J>-f(x)g(y) будет v-интегрируемой и f(x) ФО.
Отсюда следует, что функция g v-интегрируема. Точно так же
можно показать, что функция / ц-интегрируема *).
Для доказательства прямого утверждения нам понадобится
Лемма. Если часть А множества X имеет нулевую меру
относительно ц, то множество А X У имеет меру, равную нулю,
относительно ц, ® v.
Эта лемма важна потому, что при ц(Л) = 0 мера v(Y)
может, вообще говоря, быть бесконечной. Мы уже видели, что
в плоскости R2 прямая, параллельная одной из координатных
осей, имеет нулевую меру по мере dxdy.
Доказательство. Зададим е > 0. Пусть К —
некоторый компакт пространства У. Он имеет конечную меру и
существует такое открытое множество О' zd К из У, что v(0")=sC
^v(^)+l. Тогда найдется такое открытое множество OidA
из X, что [х,(0)^ e/(v(/()+ 1). Так как множество 0^0'
открыто в X X У, то он° (ц ® v)-измеримо, и мы можем к его
характеристической функции применить формулу (IV, 8; 33),
которая даст равенство
(n®v)(tfX<?') = n(<?)v(0")<e. (IV, 8; 38)
') За исключением рассмотренного частного случая этот результат, вообще
говоря, не верен. Он, например, очевидным образом не верен для В ез 0.
Точно так же, если f = 0, то функция f(x)g(y)=0 и, следовательно,
(Ц ® v) -интегрируема, хотя отсюда вывести v-интегрируемость функции g
невозможно.

§ 8. Тензорное произведение мер 675
Значит, (ji®v)*(^X/(Xe. Так как е произвольно, то
(ц <8> v) (А X К) = 0. Однако Y является объединением
возрастающей последовательности компактов Кп\ поэтому А X У,
как объединение последовательности множеств А X Кп
(\i <8> у)-меры, равной нулю, имеет (ц <8> v)-Mepy, равную нулю.
Окончание доказательства прямого утверждения теоремы
.*■>->
Сначала докажем, что функция B(f,g) является (}a<8>v)-
измерим&й.
-> ■ ->
Поскольку f (соответственно g) измерима, то, согласно тео-
->■ ->■
реме 32, для f (соответственно g) найдется аппроксимирующая
последовательность, образованная непрерывными функциями, и*
которой, в силу теоремы 38, можно извлечь подпоследователь-
ность fn (соответственно gn), ц (соответственно v)-почти всюду
сходящуюся к f, т. е. сходящуюся к f (соответственно g) на
множестве А (соответственно В), дополнение которого имеет ц-меру
(соответственно v-меру), равную нулю. Функция В (f„, gn) непре-
рывна и сходится к B(f,g) на множестве АХ В, дополнение
которого С (Л ХЯ) = (СМ X ^)U(*XC В), согласно лемме, имеет
■>■->••
меру нуль. Значит, по теореме 23, функция B(f,g) измерима.
Для того чтобы доказать ее интегрируемость, достаточно
показать, что верхний интеграл от ее нормы конечен. Этот
интеграл допускает, оценку
jj'\\B(tg) \\d(ii® v) <|| В || J" J*|| f\x) \\\\ g(y) \\dix(x) dv (y).
(IV, 8; 39)
-> -»•
Аналогично, функция (х, y)-*\\f(x)\\ \\g(y)\\ (ц ®
v)-измерима, и, поскольку она ^0, к ней можно применить теорему
Фубини — Фату. Эта теорема (при = ) дает
J" j lift*) IHI g (у) || d» (x) dv (у) = J" ф (x) j lift*) IHI g (y) || dv (y).
(IV, 8; 40)
■>
Поскольку g по условию v-интегрируема, последний инте-
■f г ■*■
грал конечен и равен II f WIIJ \\g(y)Wdv(y). Следовательно,
искомый верхний интеграл равен (J |1Л1ф) (Jllglldv) <+оо
и, значит, функция B(f, g) является (ц <8> v) -интегрируемой.
22*

676
Гл. IV. Интегральное исчисление
К ней можно теперь применить теорему Фубини — Лебега
и записать, что
Ц В(Т, g)d(ii®v)=j dii(x) J В(Т(х), g(у)) dv (у). (IV,8; 41)
->■
Функция g v-интегрируема и для фиксированного х отобра-
жение g-*B(f(x),g) из G в Н линейно и непрерывно.
Теорема 45 (о перестановочности интеграла и линейно
непрерывного отображения) дает равенство
j B(f{x),g'(y))dv(y) = B(Hx), jgdv), (VI, 8; 42)
откуда
j J" В (t g) d (ц ® v) = J В (f(x), J | dv) dn (x). (IV, 8; 43)
Так как f [г-интегрируема, a f-> В if, \ g dv] является
линейным непрерывным отображением F в Я, то та же
теорема 45 дает
J В (f(х), J | dv) dii(x) = B(j fdii," J ? dv). (IV, 8; 44)
чем и заканчивается доказательство теоремы.
Замечание. Если F=Q = H — скалярные поля и В
представляет собой обычное произведение, то конец
доказательства упрощается. Достаточно доказать, что функция
(х, y)-*f(x)g(y) интегрируема, и тогда сразу можно будет
написать равенства
J" J f (*) g (у) dii (x) dv (у) = J dn (x) J f (x) g («/) dv (</) =
= J f(x) dn (x) J g (y) dv (</). (IV, 8; 442)
Следствие 1. Пусть А и В — части множеств X и Y
соответственно. Если они соответственно ^-измеримы и \-изме-
римы и имеют конечные или бесконечные меры, то множество
Ау^В является (ц. <8> v) -измеримым, а его мера равна
произведению мер
(ц <8> v) (А X В) = ц (A) v (В)< + оо, (IV, 8; 45)
где произведение считается равным нулю, если один из
множителей равен нулю, даже если другой равен -\-<х>.
В частности, (ц ® v) (X X v) = vl{X)v{Y).

§ 8. Тензорное произведение мер
677
Обратно, если множество А X В измеримо относительно
(\i ® v) и ни одно из этих двух множеств не имеет нулевой
меры, то А ^.-измеримо, а В v-измеримо.
Следствие 2. Пусть \i и v — меры ^0 на X и Y, и пусть
р и q — комплексные функции, определенные соответственно
на X и Y и такие, что функция р локально \х-интегрируема,
а функция q локально v-интегрируема. Тогда функция р ® q:
(х, y)-*p(x)q(y) локально (\х ® v)-интегрируема и мера
(р ® q) (у. ® v) совпадает с мерой рц ® qv.
Локальная (ц ® v)-интегрируемость вытекает из теоремы.
Равенство произведения тензорных произведений (р®<7)(ц®у)
и тензорного произведения двух произведений p\i ® qv
вытекает из того, что эти две меры принимают одно и то же
значение на каждой функции ф из ^(X^Y) вида и ® и, где
u^W(X) и »е?(У), а именно значение ( Г pud\i) ( Г qvdv\
(см. примечание на стр. 661).
Обобщение на произвольные кратные интегралы
Пусть X, Y, Z — три локально компактных пространства,
снабженных скалярными мерами Я, ц, v. Тогда с помощью
теоремы, аналогичной теореме 73, можно сразу определить меру
на Xy^Yy^Z как тензорное произведение мер Я ® \i ® v. На
этот раз для ме?(Х), v^W(Y), w^W(Z) следует
положить
(Я ® \i ® v) (и ® v ® w) = Я (и) \i (о) v (да). (IV, 8; 46)
Интегралы относительно A®(i®v тройные. Точно так же
определяются интегралы произвольной конечной кратности.
Можно также определить сначала меру Я ® \i на X X Y,
затем меру (Я ® ц) ® v на множестве (Jf X У) X £»
совпадающем с множеством X у YyZ. С помощью формул (IV, 8; 46)
и (IV, 8; 4) легко убедиться, что обе меры Я ® ц ® v и
(Я®ц)®у совпадают на ^Х^Х^. Тем самым доказана
ассоциативность тензорного произведения. Естественно, что метод
вычислений, изложенный в теореме 75, сохраняет свою силу
и при Я, ц, v ^ 0 имеет место теорема Фубини, обобщающая
теоремы 77 и 78. Пусть, например, надо вычислить интеграл
J" J" J" f(x, y, z) dk (x) d\i (y) dv (г), (IV, 8; 47)
■>
если заранее известно, что функция f интегрируема
относительно Я ® [i ® v или что она измерима и ^0.

678
Гл. IV. Интегральное исчисление
Можю было бы, например, сначала вычислить двойной
интеграл, а затем простой интеграл по формуле
J dp (у) j j f(x, у, z) dk (x) dv (z), (IV, 8; 48)
где двойной интеграл имеет смысл для ц-почти всех
значений у.
Можно было бы сначала вычислить простой интеграл, а
затем двойной по формуле
J J" dv (у) dv (z) J f(x, y, z) dk (x), (IV, 8; 49)
где простой интеграл имеет смысл для (ц®у)-почти всех
значений (y,z).
Можно было бы вычислить последовательно три простых
интеграла по формуле
J dn {у) J dk (x) j f(x, у, z) dv (z), (IV, 8; 50)
где интеграл по dv(z) имеет смысл для (к ® ц)-почти всех
значений (х,у), следующий интеграл по dk(x) имеет смысл для
ц-почти всех значений у.
Все три полученных интеграла совпадают.
Этот метод часто применяется для вычисления объемов.
Предположим, например, что все три пространства X, Y,
Z представляют собой вещественную прямую R и что dk =
= d\i = dv являются мерами Лебега. Тогда мера-произведение
dxdydz является мерой объемов в пространстве R3.
Пусть теперь А— измеримая часть пространства R3;
предположим, что нам надо вычислить ее объем, т. е. интеграл
| dx <8> dy ® dz. Согласно формуле (IV, 8; 35), в рамках тео-
А
ремы Фубини — Фату этот интеграл может быть вычислен, на
пример, по формуле
J S (z) rfz <•+оо, (IV, 8; 51)
где через S(z) обозначена площадь сечения A{z) множества
А плоскостью, перпендикулярной оси z, т. е. двойной интеграл
jjdxdy^+oo. (IV, 8; 52)
А (г)
Эта площадь может быть также вычислена с помощью
формулы
I j 1(х, у) dxdy^+ оо, (IV,8;53)

§ 8. Тензорное произведение мер
679
где через 1(х,у) обозначена «длина» сечения множества Л
прямой, параллельной оси z с координатами х, у, т. е. интеграл
J dz< + oo. (IV, 8; 54)
А (х, у)
Пусть рассматривается пространство R", являющееся
произведением п экземпляров пространств R. Если через dx\,
dx2 dxn обозначены канонические меры [. '•» меры Лебега)
на пространствах-сомножителях1), то dxx ® йх2 ® ... <8>dxn
будет мерой, определенной на R". Эту меру называют
канонической, или мерой Лебега, на R" и обозначают через dx или
dX]dx2 ... dx„.
Широкая сходимость тензорных произведений
Теорема 80. Если при п, стремящемся к бесконечности,
последовательность мер цп на X широко сходится к мере ц,
а последовательность мер vn на Y широко сходится к мере v,
то последовательность мер ц.п ® vn при п, стремящемся к
бесконечности, широко сходится к мере p,®v.
Доказательство. Пусть <р — некоторый элемент
пространства ^(Xy^Y). Воспользуемся методом вычислений,
изложенным в теореме 75. Величины Г y(x,y)dvn(y) сходятся
к y(x,y)dv(y) для всех х, в силу предположения о широкой
сходимости.
Кроме того, согласно следствию 3 теоремы 66, эта
сходимость равномерна относительно точек х, принадлежащих
некоторому компакту. Если через #ХХ обозначить
произведение компактов, содержащее носитель функции <р, то все эти
интегралы будут равны нулю для хф.Н. Иначе говоря,
функции \рп, определенные в доказательстве теоремы 75, при п,
стремящемся к бесконечности, сходятся к функции 1|з
равномерно на Н с сохранением носителей в Н. Теперь, учитывая
следствие 2 теоремы 65, мы получаем, что \in{tyn) сходятся
к р,(1р), чем и заканчивается доказательство теоремы.
Следствие. Существует такая последовательность Pi
полиномов Г^О на пространстве Rn, что меры Pidx (где dx =
= dx\ ® dx2 ® ... ® dxn) широко сходятся к б при I,
стремящемся к + оо.
1) Обозначение не корректно (см. примечание на стр. 443). Все
пространства-сомножители одни и те же. Следовательно, это всюду одна и та Же мера!
Нужно было написать \(х{]йхи l(x2)d*2 \(xn)dx п» ЧТО И В СЗМОМ ДбЛб
дает одну и ту же меру.

680
Гл. IV. Интегральное исчисление
Доказательство. В теореме 68 мы -видели, что
существует такая последовательность полиномов Q; ^ 0 на R, для
которой меры Qi(x)dx при /, стремящемся к бесконечности,,
широко сходятся к мере 8 = d8(x). Теперь полиномы
Pi(xit х2 *п)= Qi(Xi)Qi(х2) ... Qi(xn) неотрицательны и,.
по теореме 80, мера Qt(Xi)dxi <8> Ql\x2)dx2 ® ... ® Qi(xn)dxn
при /, стремящемся к бесконечности, стремится к мере d6(*i)®;
<8>d8(x2)<8> ... <8>d8(xn) = d8(xi,x2 хп).
Теорема 80г (теорема Вейерштрасса о полиномиальной'
аппроксимации). Пусть К — компакт пространства R" и / —
непрерывная функция на К со значениями в банаховом простран-
->
стве F. Тогда, каким бы ни было число е>0, можно найти
такой полином Q, определенный на R", со значениями в F, что
maxllf (х) — Q (х)\\^.г. Или иначе: существует такая последо-
-> ->
вательность полиномов Qh, которая сходится к функции f
равномерно на К при k, стремящемся к бесконечности.
Доказательство. Формула g = 2j f N (at) at = Zi gm»
ajeC(R"), использованная в следствии 8 из теоремы 11
(о разложении единицы), дает сначала некоторую непрерывную»
разложимую функцию g на R" с компактным носителем и та-
-> ->
кую, что \\f — g\\ ^ е/2 на К').
Пусть теперь Р; — последовательность таких полиномов, что-
их меры, согласно предыдущему следствию, широко сходятся
к б. Положим
Qi(x)=jj}(x-t)Pl(t)dt= J" Pl(x-t)g(t)dt =
= j j ■■■ j g {X\ — tu X2 — h Xn — tn)X
X Pi {tu h tn) dt, dt2... dtn. (IV, 8; 55>
Все рассматриваемые величины имеют смысл, поскольку они
представляют собой интегралы от непрерывных функций с
компактным носителем.
->
') В условии следствия 8 функция / предполагалась определенной на
всем X (здесь Rn) и имела компактный носитель. Но это не имело смысла*
так как рассматриваются лишь значения / на К.

§ 8. Тензорное произведение мер
681
-г
Докажем, что последовательность величин Qt равномерно
->■
сходится Kg на К и что они представляют собой некоторые
полиномы. Тогда среди них можно будет найти один такой по-
.лином Qi, что || Q/ — g\\ <: е/2 на К, и теорема будет доказанной.
Прежде всего, имеем: P; = 2cp*p (B обозначениях, приня-
р
тых на стр. 266, P = (pv Р2> ••■•• P„)eN" и . дс" = «f1^ ... х"пп,
для простоты мы убрали стрелки). Отсюда
Ч<Р
Pt(x-t)=^cp(pq)x" (-ty-q, (IV, 8; 56)
р. я
<7<P,
p. <7
<7<p
а, следовательно, Q/ является полиномом.
Докажем теперь равномерную сходимость. Так как g разло-
жима: g = ^j gtat, то вопрос непосредственно сводится к до-
.=1 .
казательству того, что каждый интеграл |а<(дс—t)Pt{t)dt cxo-
дится к а,- (я) = Г at (x — t) dd (t) равномерно относительно х в К.
Rn
Но (x,t)-*at(x — t) является непрерывной функцией на
KXR". Когда х пробегает компакт К, частная функция
t-+ai(x — t) сохраняет носитель в некотором фиксированном
компакте R", а именно в векторной сумме К — Ти где 7\
является носителем at. Мы оказываемся в условиях
применимости следствия 3 теоремы 66 с изменением ролей переменных х
и t, чем и заканчивается доказательство теоремы.
Замечание. Существуют другие методы доказательства
теоремы Вейерштрасса, но это доказательство позволяет
получить некоторые гораздо более сильные результаты.
->■
Предположим, что f определена и непрерывна не только на
->■
К, но и на всем R". Тогда для построения функции g с компакт-
->■
ным носителем, близкой к f на К, имеется значительно более
->■ ->■
простой способ: возьмем g = af, где а — непрерывная функция,
или даже класса С°°, с компактным носителем, равная 1 в не-
лоторой окрестности компакта К (следствие 1 теоремы 11).

682
Гл. IV. Интегральное исчисление
Тогда мы получим, что g равна f в некоторой окрестности К.
-> -> ->■
Полиномы Qi сходятся к g, а, следовательно, к f равномерно
>
на К. Правда, функция g не разложима и непосредственно
применить следствие 3 теоремы 66 невозможно. Легко убедиться,
что доказательство этой теоремы проводилось лишь для
скалярных функций в связи с наличием векторных мер. Однако она
остается справедливой и для векторных функций в случае
скалярных мер.
При этих условиях полиномы Qi обладают гораздо более
сильными свойствами сходимости. Предположим, что на скрест-
->■
ности компакта К функция f принадлежит классу Ст. Тогда,
если а принадлежит классу Ст и имеет носитель в этой окрест-
->
ности, то g принадлежит классу Ст во всем К . Тогда для
-»• -»•
каждого р ^ т производные DpQi сходятся к Dpf равномерно
на К. Другими словами, можно осуществить полиномиальную
аппроксимацию одновременно и для f, и для ее производных.
В самом деле, мы имеем простейший случай, когда допустимо
дифференцирование под знаком интеграла (см. далее следствие
теоремы 115), так что
D'Qi (х) = J* D'g (x - t) P, (t) dt, (IVj 8. 57)
и мы пришли к исходной задаче, где вместо g стоит DPg.
§ 9. ЧАСТНЫЕ СВОЙСТВА МЕР РАДОНА
НА ВЕЩЕСТВЕННОЙ ПРЯМОЙ R
Свойства, которые мы будем рассматривать в этом
параграфе, используют тот факт, что вещественная прямая R не
только является локально компактным пространством, но и
образует вполне упорядоченное множество. Если а и b—две
точки пространства R, то через [а, Ь[ мы будем обозначать
интервал a sg: х < Ь при а < Ь и интервал b < х <; а при b <.а.
Точно такой же смысл будут иметь обозначения ]а, b], [a,b],
]а, Ь[. Следовательно, это будут скорее интервалы в смысле
определения, данного на стр. 26, чем интервалы в смысле
определения, данного на стр. 183.
Введение символа Г dp
Определение. Пусть ц—мера Радона на интервале Rt
(открытом, полуоткрытом или замкнутом) вещественной пря-

§ 9. Частные свойства мер Радона
683
мой R со значениями в банаховом пространстве Ё.
Предположим, что эта мера имеет в качестве базы \хо вещественную меру
1^0. Тогда ее можно, в частности, продолжить на
характеристические функции компактных интервалов.
ь
->■
Обозначим, если а и Ь принадлежат Rb через J d\x вели-
а
чину, определенную по формуле
Г dp, если а< Ь,
ь
->■
/ф =
1а,Ы
О, если а = Ь, (IV, 9; 1)
— j d\x, если Ъ < а').
lb, а[
В частности, если мера d\i записана в виде p(x)dx, где р —
локально интегрируема относительно меры dx, то по
определению имеем
I Г р (х) dx, если а ^ Ь,
& I j
fdj= "Y1-* (IV, 9; 2)
a ' I — \ p(x)dx, если a^b.
I lb, a]
Теорема 81. Имеет место соотношение Шаля:
Ь с а
j dj + j dp+ j" 4 = 0. (IV,9;3)
a b с
Доказательство очевидно. Достаточно рассмотреть все
возможные случаи.
Неопределенные интегралы
Определение. Говорят, что функция М, определенная
на Ri, со значениями в аффинном нормированном полном
пространстве Е, является неопределенным интегралом от меры. Ра-
дона ц, заданной на Ri со значениями в £ и имеющей
вещественную базу ^ 0, если, каковы бы ни были а и & из Ri, имеет
■) Будьте внимательны: мера ц, возможно, имеет точечные массы, и тогда
небезразлично, что брать — полуинтервалы, включающие левый конец, или
полуинтервалы, включающие правый конец.

684
Гл. IV. Интегральное исчисление
место равенство
М(Ь)-М (а) = J ф. (IV, 9; 4>
Если |х имеет вид dn = pd\i0, где цо — некоторая
вещественная мера ^0 и р — локально цо-интегрируемая функция, то
говорят, что М есть неопределенный интеграл от функции р
по мере ц0.
Теорема 82. Пусть Е — полное аффинное нормированное-
пространство, |х — некоторая мера Радона на R\ со значениями
->- •>
в Е и базой ^0. Тогда мера ц имеет бесчисленное множество
-=*■
неопределенных интегралов со значениями в Е. Если с — точка
X
Hi, то функция М: х-> d\x является неопределенным интегра-
с
->-
лом со значениями в Е, а, добавляя к ней произвольные
постоянные элементы из Е, можно получить все неопределенные
интегралы со значениями в Е.
Доказательство. То, что функция М обладает
указанным свойством, вытекает из соотношения Шаля. Кроме того,,
->-
если две функции со значениями соответственно в Е и Е яв-
■*■
ляются неопределенными интегралами от меры ц, то из
формулы (IV, 9; 4) следует, что их разность принимает одно и то>
же значение в произвольных точках а и Ь пространства Ru т.е.
является постоянной на R]. Обратно, сумма какого-либо не-
определенного интеграла со значениями в £ и некоторой
постоянной из Е является неопределенным интегралом со
значениями в Е.
Пример. Рассмотрим функцию Хевисайда —
вещественную функцию Y на R, определенную по формуле
f 0 для х<0,
^Hl Для *>0. (IV'9;5>
Эта функция является неопределенным интегралом от меры
X X
б: Y(x)= Г db или Г db, где а^.0 — произвольное число.
—оо а
Замечание. Можно также показать, что разность двух
неопределенных интегралов со значениями в Е является неко-

£ 9. Частные свойства мер Радона
685
торой постоянной в Е и что сумма неопределенного интеграла
со значениями в Е и постоянной из Е является неопределенным
интегралом в Е.
Теорема 83. Каждая функция М со значениями в Е, яв-
->•
ляющаяся неопределенным интегралом от меры Радона ц на R,
->
со значениями в Е, непрерывна слева в любой точке Rlm Эта
функция ^непрерывна справа в точке с прямой Rt тогда и только
■*■ "*"
тогда, когда ц({с}) = 0. Во всяком случае у нее существует
->•
предел справа и ее скачек равен ц(с).
>
Доказательство. При Л^О разность М(с) — М(с — Л)
является мерой ц([с — h,c[) или интегралом относительно р
характеристической функции ф/, этого интервала. Пусть d\i =
= pdno, цо ^ 0. Тогда ц ([с — /г, с[) = I (php с!ц0. Если Л > О
стремится к 0, то характеристическая функция cpft сходится
просто к функции 0, т. е. к характеристической функции пустого
множества. Отсюда следует, что функция щр просто сходится
к 0. При h t^L п0 она ограничена по норме функцией ||р||фл,. Так
как р локально цо-интегрируема, то эта функция ^0 и цо-инте-
грируема. Согласно теореме Лебега, распространенной на
обобщенные пределы (см. замечание на стр. 541), предыдущие
разности сходятся к 0 при h, стремящемся к 0, что
доказывает непрерывность функции слева. Если мы теперь будем
проводить рассуждения для разностей М(с-\-Н) — М(с) =
= 1 tyhpd\io, где гр/, — характеристическая функция интервала
[с, с -\- h [, то увидим, что функции гр/, сходятся к
характеристической функции гро множества {с}, состоящего из одной точки с.
->
Функции ptyh будут мажорироваться некоторой интегрируемой
фиксированной функцией ^0. Из теоремы Лебега следует, что
эти разности при h, стремящемся к 0, сходятся к f %pd^i0 =
= ц({с}). Отсюда вытекает, что непрерывность справа имеет
место тогда и только тогда, когда множество {с} имеет нулевую
меру относительно ц. Кроме того, функция М всегда имеет пре*
дел справа и М (с + 0) = М (с) + ц ({с}).
Замечание. Пусть а и с — точки Rb а <С с. Предыдущие
рассуждения означают, что р([а, с'[) стремится к ц([а, с[) при

686
Гл. IV. Интегральное исчисление
с, стремящемся к с по значениям <; с, и ц([а, с[) стремится
■> ■> •>
к ц([а, с]) = ц,([а, с[) + ц({с}), когда с' стремится к с по
значениям >с. Конечно, ц([а, с']) имеет пределами соответственно
•> •>
ii([a,c[) и ц([а,с]).
■>
Следствие 1. Если функция р определена на Ri со
значениями в банаховом пространстве Е и локально интегрируема
относительно меры Лебега dx, то каждь1й неопределенный ин-
X
геграл х-> [ р (t) dt является непрерывной функцией х.
с
•>
В самом деле, относительно меры pdx любая точка имеет
нулевую меру.
Следствие 2. Неопределенный интеграл от меры на Ri
является правильной функцией, а, значит, борелевской и,
следовательно, измеримой по отношению к любой мере Радона на Ri.
Тот факт, что эта функция правильная, вытекает
непосредственно из теоремы. Поскольку характеристическая функция
интервала борелевская, то борелевской будет ступенчатая
функция, а, значит, правильная функция, в чем можно убедиться
переходом к пределу (теоремы 8 и 23).
Функции с ограниченной вариацией на прямой
Пусть М — отображение некоторой части Rj вещественной
прямой R в метрическое пространство Е. Полной вариацией
функции М называется точная верхняя грань V(M)= V(Ri,M)
сумм
S = S d (М (с,), М (с<+1)) (IV, 9; 6)
д »=о
по всевозможным разбиениям А множества Ri, т. е. по
всевозможным конечным возрастающим последовательностям точек
Со, с\, ..., сп из Ri. Полная вариация — это некоторое
неотрицательное число, конечное или равное +оо. Если R2c:Ri, то
V(R2, M)^. V(Ri, M). Если V(Ri, M) конечна, то говорят, что
функция М имеет ограниченную вариацию на Ri (надо было бы
говорить: имеет ограниченную полную вариацию). Чаще всего
рассматриваются случаи, когда Ri — или интервал
(ограниченный или нет, открытый, полуоткрытый или замкнутый), или
множество N целых чисел ^0 (см. стр. 142), или множество Z
всех целых чисел. С этого момента мы будем предполагать, что
R! — интервал.

§ 9. Частные свойства мер Радона 687
Функция, удовлетворяющая условию Липшица на ограниченном
интервале R\ прямой R, имеет ограниченную вариацию
В самом деле, из неравенства d(M(x"), М(х')) ^ k\х"— х'\
следует, что полная вариация функции М мажорируется числом
к, умноженным на длину интервала R;. В частности, функция
М на Ri со значениями в аффинном нормированном
пространстве Е, дифференцируемая и имеющая ограниченную
производную, на интервале Ri конечной длины имеет ограниченную
вариацию^ Эта функция, в силу следствия 2 из теоремы 13
гл. III, удовлетворяет условию Липшица.
Конечно, если N принимает значения в аффинном
нормированном пространстве Е, а М принимает значения в
присоединенном векторном пространстве Е и k — некоторый скаляр, то
V(N + M)^V(N) + V(M)t
■> -> (IV, 9; 62)
V (Ш) = | k | V (М).
Это говорит о том, что функции с ограниченной вариацией
на Ri со значениями в Е образуют некоторое векторное про-
странство. Однако функция M-*V(M) не является нормой
в этом пространстве. В самом деле, равенство V(M)=0 экви-
валентно тому, что М = const, но не обязательно М =.0.
Заметим, что при замене последовательности ct конечной
последовательностью, содержащей данную, сумма (IV, 9; 6) не
убывает. Следовательно, при вычислении точной верхней грани
можно ограничиться рассмотрением таких разбиений А, у
которых среди Ci фигурирует конечное число заранее заданных
точек.
Теорема 83г. Если а, Ь, с — три заданные точки Ri, a'<j
< b < с, то полная вариация функции М в [а, с] является сум*
мой полных вариаций этой функции в [а, Ь] и [Ь, с]:
V([a, с]; M) = V([a, b];M) + V([b, с]; М)').
В самом деле, левая часть может быть вычислена как
точная верхняя грань сумм 2, соответствующих конечным после-
д
') Можно было бы ожидать, что справедливы соотношения вида
V{[a, c[; M) = V([a, Ь[; M) + V([b, c\, M).
Однако, это, вообще говоря, не верно. Указанное соотношение справедливо,
если М непрерывна слева в точке Ь, ибо тогда (лемма 2, стр. 689);
V([a,b];M)= V({a,b[;M).

688
Гл. IV. Интегральное исчисление
довательностям точек с0 = а, си сг с„ = с, среди которых
находится точка Ь.
Теорема 84. Каждая функция ограниченной вариации на
интервале R; прямой R со значениями в метрическом
пространстве Е ограничена. Если Е полно, то эта функция правильная,
а следовательно, борелевская и, значит, она измерима
относительно любой меры Радона на R\.
Если полная вариация функции М конечна, то для х и у из
Ri она мажорирует число d(M(x), M(у)). Следовательно,
функция М ограничена. Докажем теперь, что если пространство Е
полно, то эта функция правильная.
Пусть Хо, Х\, х2, ... — некоторая последовательность точек
>с, стремящаяся к с при п, стремящемся к бесконечности. Для
упрощения доказательства сходимости последовательности
М(х0), М(х\), М(х2), ... к некоторому пределу при
неограниченном возрастании п, переставим так члены этой
последовательности, чтобы можно было считать последовательность хп
п-\
убывающей. Тогда независимо от п сумма 2 d(M(xi), M(xl+X))
<=о
оо
ограничена полной вариацией М. Значит, 2 d(M (xt),M-(xl+l))<.
1=0
< -f оо. Таким образом, для пг ^ п + 1 при m и п, стремя-
т—1
щихся к +°°. сумма 2 стремится к 0, и тем более Стремится
i—n
к нулю расстояние d(M(xn), M(xm)). Это означает, что
последовательность М(хп) является последовательностью Коши.
Поскольку Е полно, эта последовательность сходится. Ее предел
не зависит от выбора последовательности хп. В самом деле, из
двух последовательностей (x'n)nesN, (К)п^м можно образовать
смешанную последовательность х'0, х%, х\, х", х'2, х" на
которой последовательность значений М должна иметь
некоторый предел, а потому последовательности М(х'п) и М(х'{\
также будут иметь тот же предел. Пусть М(с-\-0) — общий предел
этих последовательностей. Тогда М(х) стремится к M(c-fO)
при х, стремящемся к с по значениям >с. В противном случае
существовало бы такое число е > 0, что для каждого п ^ 1
можно было бы найти число х„, с ■< хп <; с + 1/«. для которого
выполняется неравенство d(M(xn), M(c + 0))>e. Но тогда
последовательность хп стремилась бы к точке с при п,
стремящемся к бесконечности по значениям >с, а последовательность
М(хп) не стремилась бы к /W(c-fO), что противоречит ранее
полученным результатам.

§ 9. Частные свойства мер Радона
689
Точно так же можно показать, что М(х) имеет предел
М(с — 0), когда х стремится к с по значениям <с Значит, М
в точках Ri правильная.
Замечание. Обратное утверждение не верно. Правильная
и даже непрерывная на интервале [а, Ь] прямой R функция
с вещественными значениями не обязательно имеет
ограниченную вариацию.
Рассмотрим, например, следующую вещественную функцию
М на [0, [}-. в точках с абсциссой l/п, п ^ 1, М(1/п) = (—\)п/п,
в интервалах [\/(п + 1), \/п] она линейна, а в точке х = 0 она
равна 0. Функция М, очевидно, непрерывна, а ее полная
вариация равна (1 + 1/2)+ (1/2 + 1/3)+ (1/3+ 1/4)+... = +оо.
Теорема 842. Пусть М — отображение [а, Ь] (а <. Ь) в Е
ограниченной вариации. Обозначим через V([a, x]\ M) полную
вариацию сужения функции М на интервал [а,х]. Функция
x-*~V([a, x]\ M) возрастает и непрерывна слева (соответственно
справа) в точке с тогда и только тогда, когда М непрерывна
слева (соответственно справа) в точке с
Мы докажем две леммы, из которых вытекает эта теорема.
Лемма 1. Если М — отображение [а, с[ в метрическое
пространство Е, то при х\ стремящемся к с по значениям <с,
V([a, х]; М)^ + оо стремится к V([a, с[; М)^ + оо.
Доказательство леммы 1. Рассматриваемая функция
возрастающая, "а, следовательно, при х, стремящемся к с по
значениям <с, она имеет предел ^.V([a, c[; M). Однако если
V является произвольным числом <V([a, c[; M), то по
определению существует такое разбиение А интервала [а, с [: со =
= а <: с\ ^ с2 ^ ... ^ сп <С с, что
%>V. (IV, 9; 7)
Тогда тем более для сп ^ х < с
V ([а, х]; M)>V ([а, сп]; М)> 2> V, (iV, 9;8)
что и требовалось доказать.
Лемма 2. Если М является отображением [а, с] (а < с)
в метрическое пространство Е с ограниченной вариацией, то
V([a, с]; М) = V([a, с[; М) тогда и только тогда, когда М
непрерывна слева в точке с1).
') Если М не является функцией с ограниченной вариацией на [а, с], то
она не имеет _ ограниченной вариации на [а, с[ и выполняется равенство
V([a, с]; М) — V([a, с[; М) — + оо независимо от того, является ли
функция М непрерывной слева в точке с или нет.

690
Гл. IV. Интегральное исчисление
Доказательство леммы 2. Легко видеть, чта
V([a,c[;M)^.V([a,c];M). Предположим сначала, что М
непрерывна слева в точке с. Тогда при заданном е > О
существует такое т] > 0, что из с — х ^ ц, х <С с, следует
неравенство d(M(c), M(x))^.el2. С другой стороны, существует такое
разбиение Д: с0 = а, с\, Сг, ..., сп = с отрезка [а, с], что
%>V([a,c];M)-±. (IV;9;9),
д
Можно предполагать, кроме того, что сп-\ ^ с — г\ (в про*
тивном случае можно пополнить Д точкой с — г\, отчего сумма
2 может лишь возрасти). Тогда
д
V([a, с[; М) > V ([а,'ся_,]; М)> J) - d (M (с), М(сп^))^
д
> (V ([а, с]; М) - |) - -| = V ([а, с]; М) - е. (IV, 9; 10>
Так как в произвольно, то V([a, с]; М) = V([a, c[; M).
Обратно, предположим, что последнее равенство имеет
место. Тогда существует такое разбиение Д интервала [а, с[, при
котором имеет место соотношение (IV, 9; 7), где V —
= V([a, c],M) — e. Поэтому для сп^х < с будем иметь
V ([а, с]; M)-e<2<2+d (м (*). м (C)XV ([fl> СЬ М), (IV, 9; 11}
д д
откуда
d(M(x), M(c))<e для сп^х<с, (IV,9; 12>
а, значит, функция М непрерывна слева в точке с.
Доказательство теоремы. Мы только что доказали,
что функция х—* V([a,х]\ М) непрерывна слева в точке с тогда
и только тогда, когда функция М непрерывна слева в этой
точке. Мы даже нашли в обоих случаях предел V([a, x]; M),
когда х стремится к с по значениям <с.
Если теперь х стремится к с по значениям >с, то V([x, b];M)r
как показывает рассуждение, подобное рассуждению,
использованному в лемме 1, стремится к V(]c, b]\ M). Рассуждая так же,,
как в лемме 2, можно убедиться, что последнее выражение
равно V([c,b];M) тогда и только тогда, когда функция М
непрерывна справа в точке с. Далее, V([a, х]; М) = V([a, b]\ M) —
— V([x, b]\ М) стремится к V([a, с]; М) = V([a, b\; M) —
— V([c, b]\ М) тогда и только тогда, когда М непрерывна справа
в точке с.
Если Ri — замкнутый интервал [а, Ь] и если М непрерывна
слева1), то, вместо того чтобы выражать полную вариацию. М
') Или, естественно, непрерывна справа.

§ 9. Частные свойства мер Радона 69 I
как точную верхнюю грань, ее можно выразить как предел сумм
(IV, 9; 6), соответствующих произвольной последовательности
До, Ль Лг, ... разбиений [а, Ь] с наибольшей длиной
интервалов разбиения, стремящейся к нулю, при п, стремящемся к
бесконечности:
Теорема 85. Пусть М — отображение замкнутого
интервала [а, Ь] (а < Ь) прямой R в метрическое пространство Е,
всюду непрерывное слева. Тогда, каким бы ни было число Vit
строго меньшее полной вариации V(M) функции М в [а,Ь],
найдется число ц > О, обладающее следующим свойством:
какова бы ни была конечная возрастающая последовательность
с0 = a sg; C\ ^ c2 sg; ... ^ сп = Ь точек [а, Ь], такая, что длины
всех интервалов [с,-, ci+i] не превосходят % имеет место
неравенство:
2d (Af Ы, М (сш)) > К,. (IV, 9; 13)
(=0
Доказательство. Пусть V2— такое число, что V\ <
< V2 < V(M). В силу определения полной вариации как
точной верхней грани, существует такое разбиение До: d0 — а,
du d2, ..., dN = b, что
JV—I
S = 2 d (Af (d,), M (d/+1)) > V2. (IV, 9; 14)
До /=0
Выберем теперь ц настолько малым, чтобы:
1) т] <dj+l — dj для всех /. Тогда, если сш — с{ ^ r\, to
интервал [си ci+{\ содержит не более одной точки dj.
2) Из d(x, dj)^t], x<dj, следует, что d (Af (х), Af (d3)) <
<(V2—Vi)/2(iV—1) для всех / = 1, 2 JV— 1.
Такой выбор ц возможен, так как М непрерывна слева
в каждой точке dj.
Покажем, что такое число ц решает поставленную задачу.
Пусть Л: с0 = а, си ..., сп = b — разбиение [а, Ь] на части,
длины которых не превосходят т). Если к с{ добавить точки dj,
то мы получим новое разбиение Д', дающее сумму 2> не мень-
д'
шую, чем 2 > т. е. V2. Но тогда
д
2 = 2-2(d(Af(C/), M(d,)) +
+ d (Af (d,), Af (C|+I)) - d (Af (c,),_ Af (C|+I))), (IV, 9; 15)
при этом последняя сумма распространяется на все системы
(d, dj, сш), такие, что ct < d3 < ci+l.
Имеет место оценка (неравенство треугольника):
d(M{dj), M(ci+l))-d(M(c{), Af (cl+I))<d(Af (с,), M(d,)), (IV, 9; 16)

692 Гл. IV. Интегральное исчисление
откуда
d(M(ct), M(d,)) + d(M(d,), M{ci+i))-d(M{ct), M(ci+l))K
< 2d (M (ct), M (d,)) < 2 2(V-i} • (IV- 9; 17)
Поэтому
^i>^i-2(N-l)^^J=^-(V2-Vl), (IV)9;18)
и поскольку 2 S> ^2, то 2 S& Kj.
Д/ Д
Следующая теорема позволяет охарактеризовать функции
ограниченной вариации со значениями в нормированном
конечномерном аффинном пространстве:
Теорема 86. Пусть Е — аффинное нормированное
пространство размерности п над полем вещественных чисел с си-
стемой координат О, еи е2, . . ., еп. Для того чтобы функция М
на интервале Rj прямой R со значениями в Е имела
ограниченную вариацию, необходимо и достаточно, чтобы каждая из
ее составляющих имела ограниченную вариацию. Для того
чтобы вещественная функция на Ri имела ограниченную вариацию,
необходимо и достаточно, чтобы она была представима в виде
разности двух возрастающих и ограниченных функций.
Доказательство. В силу теоремы 12 гл. II, при замене
нормы в Е эквивалентной нормой функция ограниченной
вариации остается функцией ограниченной вариации1). Введение
системы координат в Е позволяет отождествить это пространство
с пространством R", и мы можем заменить норму в Е эквива-
п
лентной нормой (теорема 13 гл. II): \\(хх, х2, .. ., х„)||= 2 I */1
на R". Если теперь функция М на Ri представима в виде
М {х) = 0-{-2j Xj(x)ej, то для любого разбиения Д отрезка
1—1
R] имеем:
\\M(ci+1)-M(^)\\= 2 I X,(ct+X)-X,(ci)\. (IV, 9; 19)
Следовательно, полная вариация функции М не меньше
полной вариации каждой функции X, и не больше суммы полных
') Значение полной вариации, естественно, изменяется вместе с
изменением нормы. Однако если она конечна в одной норме, то она остается
конечной и в любой другой эквивалентной норме.

§ 9. Частные свойства мер Радона
693
вариаций этих функций1). Это означает, что М имеет
ограниченную вариацию в том и только в том случае, когда
ограничены вариации функций Xj.
Пусть теперь М — вещественная функция на Ri. Если она
монотонна, то все разности M(ci+\) — M(Ci), соответствующие
некоторому разбиению А, имеют один и тот же знак и сумма
(IV, 9; 6) при любом разбиении А равна \М(сп)—Л1(с0)|.
Следовательно, если функция М монотонна и ограничена, то она
имеет ограниченную вариацию. Поэтому разность двух
возрастающих неограниченных функций является функцией
ограниченной вариации. Обратно, пусть М — вещественная функция
ограниченной вариации на Ri. Выберем точку с е R}. Для
каждой точки х из Ri обозначим через V(x) величину
V{x) =
вариация М на [с, х], если х > с,
О, если х = с, (IV, 9; 20)
—(вариация М на [х, с]), если х < с.
Очевидно, V(x) является возрастающей и ограниченной
функцией JteR]. Если у > х, то разность V(y)—V(x) будет
полной вариацией функции М на интервале [х, у], а,
следовательно, она не меньше чем М(у) — М(х). Поэтому
V(y)-V(x)>M(y)-M(x),
V(y)-M(y)>V{x)-M(x), (IV'9;21)
т.е. разность V — М является возрастающей и ограниченной
функцией W, а, следовательно, М = V—W будет разностью
двух возрастающих и ограниченных функций.
Следствие. Пусть \а,Ь\ — некоторый интервал прямой R.
Если функция М на \а,Ь\ вещественна, ограничена и кусочно
монотонна, то она имеет на \а,Ь\ ограниченную вариацию.
Говорят, что М кусочно монотонна, если интервал \а, Ь\
является объединением конечного числа таких интервалов
|«о, «i]> [«1.02], •.••, [ап-\,ап\, а0 = а, ап — Ь, что в каждом из
интервалов ]at, a,+i [ эта функция монотонна (все обычно
используемые функции кусочно монотонны для ограниченного
интервала \а, Ь\). Предполагая теперь, например, что \а, Ь\ =
') Если снова воспользоваться тем фактом, что сумма (IV, 9; 6) при
замене последовательности с% на содержащую ее последовательность может
лишь возрасти, то легко убедиться в том, что вариация функции М в
точности равна сумме вариаций функций Xj.

€94 Гл. IV. Интегральное исчисление
— ]а, Ь[, можем записать:
У (| а, Ь |; M)=V (| а0, а,]; Ж)+У ([а„ а2]; М)+... +К([а„-„ а„ |; М)=
= 2 I М (аж - 0) - Af (а, + 0) | +
»=о
п-1
+ 2 (I Af (а,) — Af (а, — 0) | +1 Af (af + 0) — Л* (a,) D- (IV, 9; 22)
Функции ограниченной вариации и неопределенные интегралы
Функции ограниченной вариации были введены по той
причине, что для них имеются простые соотношения, связанные
с неопределенными интегралами от мер Радона. Будем
говорить, что некоторая функция на Rj со значениями в Е имеет
локально ограниченную вариацию, если ее сужение на каждый
компактный интервал [а, Ь] из Rj имеет ограниченную вариацию.
->■
Теорема 87. Пусть ц — мера Радона на интервале R i пря-
->■
мой R со значениями в банаховом пространстве Е и базой
•>->■-
Я ^ 0: \к = рХ. Тогда каждый неопределенный интеграл М от
меры (.1 является функцией с локально ограниченной вариацией
и эта функция имеет ограниченную вариацию на каждом таком
интервале (открытом, полуоткрытом или замкнутом) \а,Ь\ из
R ь на котором р Х-интегрируема. Для каждого интервала \а,Ь\
.из Rb a <.b, имеет место равенство
V(\a, Ь\; М)= J \\p\\dX^ + oo. (IV, 9; 23)
\а,Ы
Все утверждения теоремы вытекают из (IV, 9; 23). Если
■Со, Си с2, ..., с„ — некоторое разбиение А интервала \а, Ь\, то
п-1
п-1
4+1
<
J || р || Л.
S=5JiiAf(C,+1)^Af(4n=5; j pdx
«'=0 «=0 cl |a, b[
(IV, 9; 24)
Переходя в суммах 2 к точной верхней грани, получаем не-
д
равенство
V(\a, Ь\; М)< J \\p\\dX. (IV, 9; 24^
|о, ы

§ 9. Частные свойства мер Радона
695
Мы доказали соотношение (IV, 9; 23) со знаком <g вместо
знака =. Докажем сначала, что знак равенства имеет место,
если р непрерывна на Ri и если [а, Ь] является замкнутым,.
а, следовательно, компактным интервалом в Ri. В самом деле,.
ъ
положим Л = Г dK. Функция р равномерно непрерывна на [а, Ь].
а
Следовательно, для любого е > 0 найдется такое ц > О, что
из | *' — хСГ К ц следует \\р{х') — р(х") || < е/2Л.
Пусть теперь Д — некоторое разбиение интервала [а, Ь\.
Со = а, сп — Ь, максимальная из длин интервалов в котором
^т]. Тогда для с,- ^ х ^ ci+l имеем
-»• >• >
IIIpWII-IIp(ci)III<IIp(jc)-p(c()|K-^-. (IV,9;25>
Теперь можно установить следующие соотношения:
M(ci+1)-M(Ci)= J }(x)dK(x) = p(Ci) j dX +
ч+i
+ J (Jw-Jfo))<&(*), (IV,9;26>
ci+\ ci+\
\M(cl-+l)-M(ci)\\>\\p(ci)\\ J" dK-^l dk.
Однако
ci+l cl+l cl+l
\\p{Ci)\\ \ dX> \ \\p(x)\\dk(x)- \ \\p(x)-p(ci)\\dk(x)^
ci+l 4+1
> J" HP 11^-Ж J" dk. (IV,9;27>
Окончательно,
с
i+l 4+1
||M{cl+l)-M{c)) ||> J ||p||dX - -f J" d\. (IV,9; 28)
Отсюда получаем
б 6 6
V ([a, ft]; M)>Yi>[ II ?U<tt - X J dA > J" И ?U a_e- (IV' 9:29>

696
Гл. IV. Интегральное исчисление
ь
Так как е произвольно, то V ([а, Ь\, М)~^ f ||p||dA,, что
а
вместе с (IV, 9; 24г) дает (IV, 9; 23). Если теперь р—
произвольная функция и [а, Ь], как всегда, компактен, то функция
р А,-интегрируема на [а, Ь]. Следовательно, согласно теореме 32,
при заданном е > 0 существует такая непрерывная на [а, Ь]
->
функция <7, что
J II р-? II <**<-§. (IV, 9; 30)
а
Пусть N— неопределенный интеграл от меры qX с базой А,.
Тогда
V([a, b]; M)^V([a, Ь]; N)-~V([q, Ь]; M-N). (IV, 9; 31)
Так как функция q непрерывна на [а, Ь], то
ь
V([a, Ь]\ N)=^\\q\\dk. (IV, 9; 32)
а
Согласно (IV, 9;24г), можно написать неравенство
V([a, Ь]; М-лГ)< J II?-JII<&<-£■. (IV, 9; 33)
а
Следовательно,
ь
V([a,b];M)^j\\q\\dX.-±>
а
Ь Ь Ь
> j\\p\\dl- J II ?-?||<&--§■> j\\p\\dX-e. (IV, 9; 34)
а а а
Отсюда, поскольку е произвольно, вытекает (IV, 9; 23).
Если же функция р произвольна, а отрезок \а, Ь\ не
обязательно замкнут, то формула сохранится после перехода к
пределу. Например, если ]а,Ь[ является открытым интервалом, то
согласно лемме 1 к теореме 842, V(]a,b[;M) является преде'
лом V([a', b']\ M), когда а' стремится к а по значениям >а,
а Ь' стремится к b по значениям <Ь, и, согласно теореме 36
Фату, flip II <& является пределом интеграла |[р||сй.
\а, Ь[ [а', Ь'{

§ 9. Частные свойства мер Радона
697
Следствие. Если р — некоторая функция на R\ со зна-
чениями в банаховом пространстве Е, локально dx-интегрируе-
X
мая, то неопределенный интеграл М: х—*■ \ p(t)dt есть непре-
с
рывная функция ограниченной вариации на каждом замкнутом
интервале [а,Ь] из Ri. Ее полная вариация на интервале \а,Ь\
(а < Ь) {открытом, полуоткрытом или замкнутом) из Ri onpe-
деляется~по формуле
V(\a,b\;M)= J" \\p(t)\\dt. (IV,9;35)
->■
Если Е конечномерно, то имеет место ■ обратное утверждение.
Теорема 88. Пусть М — функция, непрерывная слева и
имеющая локально ограниченную вариацию на интервале Ri
прямой R, со значениями в конечномерном аффинном
нормированном пространстве Е. Тогда М является неопределенным
->■ ■>
интегралом от некоторой меры ц на R\ со значениями в Е и с
базой ^0. Эта мера определяется единственным образом, если
-*■
Ri не имеет наибольшей точки или если предполагается, что ц
не содержит массу в этой точке. Кроме того, для каждого
интервала \а,Ь\ из Ri, a < Ь, имеем:
ъ
j d\p\ = \u\([a,b[) = V([a,b[;M) = V([a,b);M), (IV,9; 36)
а
где \\i\ — наименьшая абсолютная мажоранта меры \i. Мера ц
имеет конечную норму на Rj тогда и только тогда, когда М
имеет ограниченную вариацию на R\.
Если L является вещественной возрастающей непрерывной
слева функцией на Ri, то она будет неопределенным интегралом
от некоторой меры X ^ 0. Если для каждой пары точек х', х"
из Ri, x' ^ х", имеет место неравенство
|| М (х") - М (х') || < L (х") - L (*'), (IV, 9; 37)
->■
то, когда Ri не имеет наибольшей точки или когда \i не имеет
массы в наибольшей точке, мера \i абсолютно мажорируется
мерой л ^ 0.
Легко видеть, почему следует предполагать функцию М не*
прерывной слева—этого требует теорема 83. Лемма 2 к
теореме 84г обеспечивает равенство двух последних членов в
соотношении (IV, 9; 36).

€98
Гл. IV. Интегральное исчисление
Обычно меру, для которой функция М является
неопределенным интегралом, обозначают не через ц или d\x, а через dM
и говорят при этом, что эта мера является производной мерой
для функции М.
Мы увидим, что в силу следствия 1 теоремы 89 для функции
М, принадлежащей классу С1, эта мера равна M'(x)dx.
Доказательство. Покажем прежде всего, что если М
есть неопределенный интеграл от некоторой меры (л на Ri со
значениями в £ и интервал Rj не имеет наибольшей точки, то
->•
мера ц единственна.
->
В самом деле, мы знаем выражение ц([а, Ь[) для
полуоткрытых интервалов [а, Ь[ интервала R\. Если [а, Ь]— замкнутый
интервал из Rj и Ь не является наибольшей точкой Rj, то
ц([а, Ь]) есть предел значений ц([а, Ь'[) при Ь', стремящемся
к b по значениям >Ь (замечание, следующее за теоремой 83),
■*■
а, значит, меру ц([а,Ь]) также можно считать известной. Точно
->
так же мера ц(]а, Ь[) может быть определена как предел чи-
->
сел ц([а',Ь[), когда а! стремится к а по значениям >а. Нако-
-> ->
нец, ц(]а, Ь]) является пределом ц([а', Ь]) при а', стремящемся
к а по значениям >а. Если Rj не имеет наибольшей точки, то
•>•
мера (л(ф) будет известна для каждой ступенчатой функции ф
с компактным носителем. Поскольку любая функция ф из
^(Ri) является равномерным пределом таких функций,
имеющих носители в некотором фиксированном компакте из Rj, то
->
|л(ф) известна для каждой функции ф из ^(Ri), а,
следовательно, (л определяется в рассматриваемом случае
единственным образом. Проведенное рассуждение, очевидно, не годится
для случая, когда Rj имеет наибольшую точку bo. В этом слу-
чае к (л можно добавить произвольную массу, расположенную
в точке Ь0- Это не изменит неопределенные интегралы, в
определение которых входят только открытые справа интервалы
вида [a, b [ из Ri. Напротив, если (л определяет в точке bo неко-
-> ■ ->
торую массу (л ({bo}) Ф 0, то ее можно удалить, т.е. из ц вы-
•>
честь меру ц ({Ь0}) 6ф„) и получить новую меру без массы в Ь0,
для которой функция М является неопределенным интегралом.
Такая мера без точки bo уже будет единственной.
Покажем теперь, что каждая функция М со значениями
в конечномерном пространстве Е, имеющая локально ограни-

§ 9. Частные свойства мер Радона 699
ченную вариацию, есть неопределенный интеграл от некоторой
меры.
-*■
В самом деле, пусть 0, (e*)2e/—некоторая система
координат пространства Е относительно поля R. Тогда М =
= 0+ 2 М{е{, где каждая из функций М{ вещественна, не-
прерывна слева и имеет локально ограниченную вариацию.
Если мы докажем, что она является неопределенным
интегралом от некоторой вещественной меры ц„ то М будет неопреде-
■+"-»■
ленным интегралом от меры ц = 2 V^fii- Поэтому нам доста-
точно ограничиться вещественными функциями.
Вещественная функция М, непрерывная слева и имеющая
локально ограниченную вариацию, способом, изложенным в
теореме 86, может быть выражена в виде разности двух
возрастающих функций: М = V — (V — М). Функции V и V — М
непрерывны слева (теорема 84г). Если каждая из функций V и
V — М является неопределенным интегралом от некоторой меры
^=0, то М будет неопределенным интегралом от некоторой
вещественной меры. Таким образом, задача свелась к
доказательству того, что всякая вещественная возрастающая
непрерывная слева функция на Ri есть неопределенный интеграл от
некоторой меры ^0.
Пусть М — такая функция. Если М непрерывна и строго
возрастает, то утверждение очевидно, ибо тогда М является
гомеоморфизмом- х —*■ у = М(х) интервала Ri на некоторый
интервал R2 из R (теорема 37 гл. II). Пусть М-1 — обратный
гомеоморфизм. Обозначим через ц образ при отображении М-1
меры Лебега dy из Кг- Пусть теперь [а,Ь[— некоторый
интервал из Ri и [а, р[ =[М(а), М(Ь)[ — его образ в R2 при
отображении М. Тогда, согласно следствию 1 из теоремы 60,
получим, что ii([a,b[) = (M-4dy))([a,b[) = dy([M(a), M{b)[) =
= M(b)—M(a), а, следовательно, М действительно является
неопределенным интегралом для меры ц.
Пусть теперь М — возрастающая функция (не обязательно
строго), не обязательно непрерывная. Пусть at — ее точки
разрыва (их счетное множество), и пусть d — ее скачки. Для
каждого интервала [а,Ь] из Ri имеем: 2 ct^M(b) — М(а).
о; е [а, Ь[
Рассмотрим меру Радона X = 2 с{д(а.у Эта мера имеет
неопределенный интеграл L (теорема 82). Интеграл L имеет
точки разрыва а, и скачки с* в этих точках (теорема 83). Из
предыдущего следует, что М (Ь)—М(а)^ 2 ct—L{p) — L(a),

700
Гл. IV. Интегральное исчисление
поэтому Ж — L также возрастающая функция, но теперь уже
непрерывная. Далее, функция М — L -\- гх строго возрастает
и непрерывна. Значит, она является неопределенным
интегралом or некоторой меры Радона цс, а тогда М является
неопределенным интегралом от меры ц = цс + К — гйх. Сразу не
видно, что мера \х 5= 0, но мера \х + гйх ^ 0. Поскольку ц не
зависит от способа ее вычисления (единственность была
доказана выше), т. е. от выбора е, то ц ^ 0.
Предположим теперь, что существует такая возрастающая
вещественная функция L на Ri, для которой имеет место ра-
венство (IV, 9; 37). Пусть ц и К — меры, имеющие функции М
и L своими неопределенными интегралами. На каждом полу-
открытом интервале [а,Ь[ выполняется неравенство||ц([а,Ь[)\\^
^.К([а,Ь[). Если R| не имеет наибольшей точки или если ц
не имеет массы в наибольшей точке, то переходом к пределу,
как это делалось ранее, можно убедиться, что последнее
неравенство остается верным для интервалов других типов. Если
Ф^0 — ступенчатая функция с компактным носителем на Ri,
то ||ц(ф) II ^ Мф)- Переходом к пределу можно установить то
же неравенство для любой функции ф 5= 0 из ^(Ri), а это
->
означает, что ц абсолютно мажорируется мерой К. Заметим,
->• -> ■>
наконец, что если К ^ 0 есть база для ц, \х = рК, то, согласно
теореме 54, |ц| является мерой \\p\\dX и тогда соотношение
(IV, 9; 36) эквивалентно соотношению (IV, 9; 23).
Мера \х имеет конечную норму на Ri тогда и только тогда,
->■ ->■
когда \\х\ имеет конечную норму. [В любом случае ■ ||ц|| ^
«£С || | |i| II. Мы видели, что в случае, когда размерность Е не
меньше 2, равенство, вообще говоря, места не имеет (см. тео-
рему 15). Поэтому из неравенства ||ц||< + 00 неравенство
|||ц|||< + оо непосредственно не вытекает. Однако в случае,
когда пространство Е конечномерно, это будет именно так.
■> > ->
Пусть (e^t е; — некоторый базис в Е над полем R, ц==
= 2 £iV4- Тогда 2 II £t III Ц/1 является абсолютной
мажоранте/ *е=/
->■
той меры \х (стр. 488). Если \х имеет конечную норму, то
такими же будут меры ц,-, а, значит, и \[ii\, имеющие ту же
норму (теорема 18). Если некоторая абсолютная мажоранта
меры ц имеет конечную норму, то такой же будет наименьшая
абсолютная мажоранта. То есть она имеет конечную норму тогда

§ 9. Частные свойства- мер Радона
701
и только тогда, когда J d|fi|< + °°> или тогда и только тогда,
когда М имеет ограниченную вариацию на всем R].
Следствие. Для того чтобы функция М на интервале R\
прямой R со значениями в аффинном нормированном
конечномерном пространстве Е удовлетворяла условию Липшица с
коэффициентом Липшица, равным k, необходимо и достаточно,
чтобы она была неопределенным интегралом по отношению
к мере Лебега от некоторой функции р на Ri со значениями
->
о Е с нормой, всюду мажорируемой числом k.
Доказательство. Если, для х' ^ х", М{х") — М{х') =
X"
= | ~p{x)dx, \\p(x)\\^k, то \\М{х") — М(хг) [| <-: k(хи-х').
х'
Обратно, если имеет место последнее неравенство, то имеет
место неравенство (IV, 9; 37) при L(x)—kx. Следовательно, М
■>
является неопределенным интегралом некоторой меры ц.,
которую можно считать не имеющей массы в наибольшей точке
интервала Ri (если такая точка существует). Очевидно, ц.
абсолютно мажорируется мерой kdx. Поэтому из теоремы 53 Дан-
-> > ->
форда — Петтиса следует, что d\i=pdx, где \\р\\ ^ k на Ri.
Длина пути в метрическом пространстве
Согласно определению, данному на стр. 90, путем в
метрическом пространстве Е называется непрерывное отображение
М отрезка [а, Ь] прямой R в метрическое пространство Е.
Длиной этого пути называется полная вариация V(M)
функции М, 0 ^ V(M) ^ +°°- Путь имеет конечную длину
тогда и только тогда, когда функция М имеет ограниченную
вариацию. Если Е является конечномерным аффинным
пространством, снабженным некоторой системой координат, то
путь будет иметь конечную длину тогда и только тогда, когда
составляющие функции М имеют ограниченную вариацию.
Предположим, в частности, что Е является аффинным нор-
>
мированным пространством. Пусть t~*A-{-t(B — А)1) есть
«прямолинейный» путь, концы которого А и В соответствуют
значениям ^ = 0 и t— 1 соответственно. Для каждого разбие-
') При изучении путей и их длин мы будем чаще пользоваться
обозначением переменной через t или и вместо х. Именно так обычно поступают
в аналитической геометрии при параметрическом задании кривых.

702
Гл. I V'. Интегральное исчисление
ния А интервала [0,1] имеем равенство \\M(a+i)—М(сг)|| =
> _>.
= (сг+1 — Ci)\]B — Л||, откуда 2j = l|fi—Л|| и, значит, длина
д
прямолинейного пути, как это и следовало ожидать, равна
>
\\В— Л||. Если теперь рассмотреть произвольный путь М а
разбиение Д: с0 = а, си сг, ..., сп = Ь интервала [а,Ь], то
величина 2, определенная по формуле ^IV, 9; 6), соответствую-
д
щая этому пути, является длиной ломаной, вписанной в этот
путь, с вершинами М(с0), М{сх), ..., М(сп). Полная вариация
или длина пути определяется как точная верхняя грань длин
ломаных, вписанных в этот путь.
(Если Е — произвольное метрическое пространство, то мы
будем иногда пользоваться понятием точной верхней грани
длин вписанных ломаных, когда, строго говоря, нельзя
использовать понятие ломаной, а расстояние й{М(СЛ), M(Ci+\)) можно
определить, не проводя отрезка прямой, соединяющей эти
точки.)
Рассмотрим два эквивалентных*) пути в Е. Это означает,
что мы имеем два отображения М и N двух отрезков [а, Ь]
и [а, р] прямой R в Е, и предполагаем, что существует такой
гомеоморфизм | отрезка [а, р] на отрезок [а, Ь], что N = М о |,-
В этом случае, очевидно, оба пути имеют одну и ту же длину.
Функция, которая каждому пути ставит в соответствие его
длину, является функцией, определенной на всевозможных пу«
тях в £ со значениями в [0, -f-oo] и обладающей двумя
следующими очевидными свойствами:
1°) Каким бы ни был путь с началом в точке А и концом
в точке В пространства Е, его длина не меньше, чем
расстояние d(A,B), соответствующее простейшему разбиению сп — а,
С\ — Ь. В случае аффинного нормированного пространства это
означает, что прямая является кратчайшим путем,
соединяющим две точки 2).
2°) Если путь составлен последовательно из двух путей, то
его длина равна сумме их длин3).
') В том же смысле, в каком эквивалентны параметрические многообра'
зия; см. стр. 352.
2) Однако она не обязательно будет единственной, обеспечивающей
кратчайший путь. В некоторых нормированных аффинных пространствах можно
взять систему из трех точек А, В, С, не расположенных на одной прямой и
таких, что II С — А\\ = || Ъ~^А || + II С^В\\.
3) Следует обратить внимание на особый характер этой аддитивности.
Если, например, при t, изменяющемся в [a, b], M(t) описывает сначала
отрезок [Л, С], а затем отрезок 1С, А] так что М(а) = М(Ь) = А, то длина будет
равна, конечно, 2||С — А\\, а не 0.

§ 9. Частные свойства мер Радона
703
Уточним, о чем же здесь идет речь.
Пусть Mi — некоторый путь, т. е. непрерывное отображение
отрезка [а, Ь], а < Ь, в Е. Пусть М2— другой путь, т. е.
отображение отрезка [Ь, с], Ъ < с, в Е. Предположим еще, что
М\{Ь) =М2(Ь) =В. Тогда Mi и М2, очевидно, определят
непрерывное отображение М отрезка [а, с] в Е:
\ М, (t) для a^.t *СЬ,
M(t) = { .... uZ>*^ (IV,9;372)
w [ M2 (t) для b < t < с, "
которое задает путь, называемый путем, составленным из
первых двух путей. Утверждение 2°) тогда вытекает из (IV, 9;6з).
Функция длины является наименьшей функцией,
определенной на путях из Е, принимающей неотрицательные
значения и обладающей двумя указанными свойствами.
В самом деле, если некоторая функция обладает двумя
этими свойствами, то длина пути будет, очевидно, >0 длины
любой из вписанных ломаных, а, значит, и их точной верхней
грани, т. е. той длины пути, которую мы только что
определили.
Из теоремы 85 следует, что длина пути может быть
определена как предел длин последовательности вписанных
ломаных, а не обязательно как их точная верхняя грань.
Пусть Ri—некоторый не обязательно замкнутый интервал
прямой R, а М — непрерывная функция на Ri со значениями
б метрическом пространстве Е. Говорят, что эта функция
определяет некоторый несобственный путь. Говорят, что этот
несобственный Путь спрямляем, если для каждого компактного
интервала [а, Ь] из Rt сужение М[а, щ функции М на [а, Ь]')
определяет путь конечной длины (сам несобственный путь
может иметь бесконечную длину, это только означает, что
функция М имеет локально ограниченную вариацию).
Пусть теперь с — некоторая точка Ri. Каждой точке t из
Ri можно поставить в соответствие вещественное число s(t),
определенное следующим образом: если t ^ с, то s(t) равно
длине дуги M[Ci t]', если t <C с, то s(t) равно числу,
противоположному длине дуги M[t, с]. Таким образом на Ri задается
функция s: t-*s(t) с вещественными значениями (уже
определявшаяся в формуле (IV, 9; 20)), непрерывная (теорема 842),
!) На стр. 16 сужение функции /, заданной на Е, на часть А этого
множества мы обозначали через fA- Иногда в этом случае используется также
обозначение f\A. Тогда рассмотренная выше дуга является путем, определен»
ным суженным отображением Л^а_ bj, или М\[а, Ь\.

704
Гл. IV. Интегральное исчисление
возрастающая и в общем случае строго возрастающая
Функция s(t) называется криволинейной абсциссой относительно
/eRi, когда точка с берется за начало отсчета оси абсцисс1).
Если функция s строго возрастает, то она определяет
гомеоморфизм интервала R] на некоторый интервал R2
вещественной прямой (теорема 37 гл. II). Так как при этом функция
s-^t(s) обратима, то можно взять s в качестве параметра и
таким образом определить новую параметризацию
несобственного пути, эквивалентную исходной параметризации.
Различные параметризации, полученные при изменении с или при
изменении знаков + и — в определении s, эквивалентны. Их
называют натуральными параметризациями (они зависят,
очевидно, не только от топологии, но и от метрики пространства
Е). Если функция s не является строго возрастающей, она не
определяет эквивалентной параметризации пути. Однако если
число So задано и существует бесконечное множество значений
t, для которых s(t) — s0, то эти значения образуют некоторый
интервал из Ri, на котором М постоянна, так что
соответствующие значения M(t) совпадают с одной и той же точкой
Яо из Е. Следовательно, если положить Р0 = Mo(so), то можно
убедиться в том, что на некотором интервале R2 прямой R
существует такая функция Мо, что M(t) = M0(s(t)). Функция
М0 непрерывна и даже обладает свойством Липшица, ибо
образ, интервала [s\ s"] при отображении Мо имеет длину,
равную \s" — s'\, а, следовательно,
|| М0 (s") - М0 (sf) || < | s" - s' |. (IV, 9; 373)
Эта функция не определяет эквивалентного пути, поскольку
s не является инъекцией и потому не будет гомеоморфизмом
Ri на R2. Мы видим, что параметризация М0 сохраняет
«интересные» свойства параметризации М (и даже практически
представляет больший интерес, чем параметризация М), и
потому мы продолжаем называть ее натуральной
параметризацией несобственного пути. (Допуская вольность речи,
отмеченную на стр. 16 и состоящую в том, что даже после замены
переменных для функции сохраняется прежнее обозначение,
вместо Mo(s) часто пишут M(s), говоря, что это та же
функция, выраженная через переменную s вместо переменной /.)
Возрастающая функция s на Ri является неопределенным
интегралом от некоторой меры Радона ^0 на R'i (теорема 88),
по отношению к которой весь интервал [?, t"\ из [а, Ь] имеет
в качестве меры длину \s" — s'\ пути M[t',t"]- Обычно эту
') Криволинейную абсциссу точки Р нельзя, вообще говоря, обозначать
через Р = M(t), поскольку одна и та же точка Р из Е может быть образом
при отображении М нескольких точек t отрезка [а, Ь] («кратные точки» пути).

§ 9. Частные свойства мер Радона 705
меру на Ri обозначают через ds (когда переходят к
натуральному параметрическому представлению, она становится
настоящей мерой Лебега ds). Заметим, что ds является мерой
на IRi, а не на образе пути. Эту меру называют мерой длин на
пути.
Из самого определения s (формула (IV, 9; 20)) и
теоремы 88 (формула (IV, 9; 36)) вытекает, что если Е является
аффинным нормированным конечномерным пространством, то
ds есть наименьшая абсолютная мажоранта меры dM. Из
теоремы 54 Данфорда — Петтиса следует, что можно написать
-> -> ->
dM=pds, \\р\\ = \ ds-почти всюду.
Если Е является локально компактным пространством,
счетным в бесконечности, и если отображение М является
ds-собственным, то существует образ предыдущей меры — мера
Радона ^0 на Е, носитель которой содержится в замыкании
образа пути. Зачастую, несмотря на путаницу, к которой
могут привести неточные обозначения, вместо M(ds) пишут ds.
->
Если / является функцией, определенной на Е, со значе-
->
ниями в банаховом пространстве F, то можно говорить о
криволинейном интеграле f ds, полагая его по определению
равным / (М (t)) d(s(t)). Согласно теореме 60, этот интеграл
R
->
является интегралом от функции / по отношению к образу
меры M(ds), если он существует1).
Теорема 882. Образ спрямляемого несобственного пути
в пространстве R" имеет нулевую меру по отношению к мере
dx=dxi ® dx2® . .. ®dxn.
Доказательство. Поскольку путь спрямляем, то для
доказательства этой теоремы можно заменить его путем
М0: s—*M0(s), соответствующим натуральной параметризации,
ибо образы путей М и М0 совпадают.
Пусть [а, Ь] — некоторый интервал из R2. Пусть А —такое
разбиение [а, Ь]: с0=а, сь с2, . . ., Ci=b, что длина
наибольшего из отрезков ^т). Пусть c't — середина [ci; ci+i]. Поскольку
длина любой дуги не меньше длины хорды, соединяющей ее
') Обозначение f ds неполно, так как в него не входит М. Лучше
будет писать f ds — интеграл относительно пути, определяемого отображе-
(М)
нием М.
23 Зак. 1339

706
Гл. IV. Интегральное исчисление
концы, то расстояния от точек M(t), t ^[cit ci+i], до Af(c£)
мажорируются длинами дуг Afrc/ л, т.е. числами (сш— с*)/2.
Тогда образ пути М^,с+1] содержится в кубе с центром М(с'Л
со сторонами длины ct+i — с*, параллельными осям. Объемная
мера этого образа мажорируется, как нетрудно видеть, числом
(ci+i — Ci)n ^ Tin_1(c,-+i — Ci). Объемная же мера отрезка [а, Ь]
мажорируется величиной х]п~1(Ь — а). Так как ц произвольно,
то объем этого образа равен нулю. Поскольку множество Кг
является счетным объединением интервалов вида [а, Ь], то его
образ также имеет объем, равный нулю.
Замечание. Не надо думать, что этот результат будет
верен в случае неспрямляемого пути. См. по этому поводу
замечание к следствию 1 теоремы 102г.
Неопределенный интеграл и первообразная
->
Теорема 89. Пусть f — функция, определенная на
интервале R] вещественной прямой R, со значениями в банаховом
->
пространстве Е, локально интегрируемая по мере Лебега. Тогда
->
неопределенный интеграл F от функции f no dx со значениями
в аффинном нормированном пространстве Е с присоединенным
векторным пространством Е имеет f{c) в качестве
производной (соответственно производной слева или производной спра-
->
ва) в каждой точке с, в которой функция f непрерывна
(соответственно непрерывна слева или непрерывна справа).
Доказательство. Докажем, например, дифференциру-
емость F в случае, когда функция / непрерывна.
Имеем
c+h
F(c + h)-F(c) f,„v_ 1 f *
f(c) = {J (f(x)-f(c))dx, (IV, 9; 38)
откуда вытекает оценка
lFic + hl~F(c) -?(c)\< sup \\f(x)-f(c)\\. (IV,9;382)
И ■ я II |x-c|<ft
В силу предположения о непрерывности, правая часть
стремится к нулю при /г, стремящемся к нулю, что и доказывает
теорему.
Следствие 1. Пусть J— непрерывная функция на Ri со
•> ->
значениями в Е. Тогда неопределенные интегралы от f до dx со

§ 9. Частные свойства мер Радона
707
значениями в Е и первообразные функции f со значениями в
Е, т. е. функции, имеющие f в качестве производной, совпадают.
Каждая функция на Ri со значениями в Е класса С1 является
неопределенным интегралом от своей производной функции по
отношению к мере Лебега dx.
Доказательство. Теорема говорит о том, что любой
неопределенный интеграл является некоторой первообразной.
Так как разность между двумя первообразными есть некоторая
->
постоянная из Е (теорема 22 гл. III), то каждая
первообразная отличается от неопределенного интеграла на постоянную,
а, значит, также является неопределенным интегралом
(теорема 82).
Замечания. 1°) Известно, что в основе интегрального
исчисления лежит вычисление первообразных. Если F — неко-
торая первообразная функции /, то
->• ъ
F(b)-F(a) = \J(x)dx. (IV,9;383)
а
У
2°) Пусть F — функция двух переменных: (х, у) —* \ f (t) dt,
х
а функция / всюду непрерывна. Тогда F имеет, очевидно,
полную производную, определяемую в дифференциальных
обозначениях по формуле
dF = {Ff (х, у)) • d (х, у) =| (у) dy - 7(х) dx. (IV, 9; 39)
В самом деле, согласно соотношению Шаля,
Р{х, У)=\ ?(9 dt - J J(t) dt, (IV, 9; 40)
a a
причем эти интегралы (один, являющийся лишь функцией х,
другой — лишь функцией у) имеют в качестве производных
функции f{x) и f{y).
3°) Дифференцируемая функция, производная которой не
является всюду непрерывной функцией, не обязательно будет
неопределенным интегралом от своей производной, которая,
впрочем, не обязательно локально интегрируема по мере
Лебега.
23*

708
Гл. IV. Интегральное исчисление
4°) Следствие связывает два довольно разных понятия.
Первообразная связана с производной. Отыскание
первообразной обобщается следующим образом. Пусть Е и F—
аффинные нормированные пространства и Q— открытое множество
->
из Е. Пусть / — некоторая непрерывная функция на Q со зна-
-> ->
чениями в S'(Е; F). Отыскивается функция на Q со значениями
->
в F, допускающая / в качестве производной. Неопределенный
интеграл связан с понятием меры Радона. Можно говорить о
->
неопределенных интегралах от некоторой меры \х, или от неко-
•>
торой функции / по отношению к мере % ^ 0. Здесь
сравниваются первообразные от / и неопределенные интегралы от /
по отношению к мере их.
Следствие 2. Пусть М — отображение класса С1
интервала R[ прямой R в аффинное нормированное пространство
Е. Это отображение определяет некоторый спрямляемый путь,
и на каждом интервале \а, Ь\ из Rb а ^ Ь, длина дуги М\а.ь\
вычисляется по формуле
s(b)-s (а) = J || ЛГ (9 || dt. (IV, 9; 402)
\а.Ь\
В самом деле, согласно следствию 1, функция М является
неопределенным интегралом от M'(t)dt. Следовательно, эта
функция имеет локально ограниченную вариацию (теорема 87),
а, значит, определяет некоторый спрямляемый путь. Согласно
(IV, 9; 23) или (IV, 9; 35), длина пути М\а,ъ\, или полная
вариация М на |а,Ь|, равна (IV, 9;402).
Теорема 892. Если функция М, определенная на Кь со
значениями в аффинном нормированном пространстве Е
принадлежит классу С1, то функция криволинейная абсцисса s
также принадлежит классу С1. В каждой точке t0, где №(1й)Ф
Ф 0, путь имеет касательную и единичный вектор этой
касательной задается формулой M'(to)/\\M'(t0) ||. В окрестности
точки t0 функция М0 является функцией класса С1
криволинейной абсциссы s, и имеет место равенство
4Щ-=(#) • (IV,9;403)
||ЛГ(*о)И V US У*=*о
определяющее единичный вектор касательной.
Кроме того, если две точки V и t" стремятся к точке t0, то
дуга, соединяющая точки M{t') и M(t"), имеет длину,
эквивалентную длине стягивающей ее хорды.

§ 9. Частные свойства мер Радона
709
Доказательство. Так как, согласно следствию 2
теоремы 89, s представляет собой неопределенный интеграл от не-
>
прерывной функции /-* \\М'(t) ||, то s является функцией /
класса С1. Если теперь эта производная в точке t0 отлична от
нуля, то из теоремы о неявных функциях (теорема 29 гл. III)
следует, что в некоторой окрестности точки t0 можно
выразить / как функцию s класса С1. Производную этой функции
б точке t0 можно вычислить по формуле
Й9 =7^ = —-> • (IV,9;404)
\ dt h=u
Отсюда вытекает, что функция M0(s), которая может быть
вычислена без каких либо предположений о ее
дифференцируемое™, дифференцируема по s в точках s, близких к s(t0),
и ее производная задается-формулой
(dMo) . _dM_ dt _ W(tt) П\7й.л<\\
\ as ;s=So at as \\M'(t0)\\
В условии теоремы говорилось о касательной к пути в точке.
Это вовсе не касательная, к множеству образа пути в смысле
определения, данного на стр. 218, ибо одна и та же точка,
например M(t0), может быть такжеч образом при отображении
М бесконечного множества других точек / ф t0,
соответствующих различным «ветвям кривой», проходящим через ту же
точку, и рассмотрение только лишь производной М в точке t0
не может дать никаких сведений относительно касательной
в этой точке. Касательной к пути в точке t0 мы называем
предел, если он существует, прямой, соединяющей точки M(t0) и
M(t0-{-At) при At Ф 0, стремящемся к 0. Если существует про-
-*■
изводная Ф0, то можно утверждать, что каждая касательная
>
существует и что M'(t0) является вектором этой касательной^).
Поскольку здесь dMo/ds есть вектор с нормой I, то он
определяет единичный вектор касательной. Говорят также, что
этот вектор является единичным вектором полукасательной,
соответствующей «возрастающему направлению /», поскольку
эта полукасательная является пределом полупрямой с началом
в точке M(t), проходящей через M(t-\-At) при At,
стремящемся к 0 по значениям >>0.
') Точно так же можно определить контингенцию в точке некоторого
параметрического многообразия класса С, не имеющую ничего общего с кон-
тингенцией образа параметрического многообразия.

710
Гл. IV. Интегральное исчисление
Пусть теперь V и t" — два числа, стремящихся к t0.
Соответствующие значения s' и s" криволинейной абсциссы
стремятся к s0. По формуле о конечных приращениях (следствие 1
теоремы 13 гл. III) можно записать:
М0 (s") - М0 (s') = М'0 (s0) (s" - s') + со | s" - s' |, (IV, 9; 406)
где
■>
со ||< sup ||M0(e)-Mo>o)ll-
6 e [s', s"]
Так как || M' (s0) || = 1, то мы получаем отсюда
11| Mo (s") - M0 (s') || -1 s" - s' 11 < || M0 (s") - M0 (s') ■
-Maso)(s"-s')IKIIcu|||s"-s'|. (IV,9;407)
Непрерывность производной dMo/ds обеспечивает
стремление к нулю нормы ||со|| при s' и s", стремящихся к s0; тем
самым полностью доказана эквивалентность длины дуги \s" — s'|
->
и длины хорды ||M0(s") — Mo(s')ll.
Естественно, что теорема 89 дает достаточное условие для
того, чтобы неопределенный интеграл F функции f был
дифференцируемым. Он может иметь производные даже в тех точ-
ках, где. f разрывна. Впрочем, иногда случается, что функция /,
локально интегрируемая по мере dx, является разрывной во
всех точках прямой, как в примере, построенном на стр. 532.
Тем не менее, функция F для некоторых значений х
необходимо имеет ](х) в качестве производной, как это видно из
следующей теоремы, доказанной Лебегом (мы примем ее без
доказательства в силу его сложности).
->
Теорема 90. Если f является функцией, определенной на
интервале R\ прямой R, со значениями в банаховом простран-.
■*■
стве Е и локально интегрируемой по мере Лебега dx, то каж-
■*■
дый неопределенный интеграл F от функции f относительно dx
->
имеет f{x) в качестве производной для dx-почти всех
значений х.
Конечно большего, чем dx-почти всюду, ожидать не
приходится, поскольку F не изменяется, если менять f на
множестве меры нуль.

§ 9. Частные свойства мер Радона
711
Следствие 1. Каждая функция F на Rt со значениями
в аффинном нормированном пространстве Е, имеющая всюду
производную, ограниченную по норме числом k, удовлетворяет
условию Липшица с коэффициентом Липшица k. Каждая
функция F на Ri со значениями в конечномерном пространстве Е,
удовлетворяющая условию Липшица с коэффициентом k, имеет
dx-почти всюду производную с нормой sg;&.
Первая часть является следствием 2 теоремы 13 гл. III,
а вторая Еытекает из теоремы 90 и следствия теоремы 88.
Замечание. Обе части следствия не будут в точности
обратными друг к другу. Если известно, что некоторая
функция F удовлетворяет условию Липшица, то отсюда еще не
следует, что она имеет всюду производную (пример: х —*\х\
удовлетворяет условию Липшица с коэффициентом 1, но не имеет
производной в начале координат). Если известно лишь, что
некоторая функция F имеет dx-почти всюду производную с
нормой ^Zk, то она не обязательно будет удовлетворять условию
Липшица и даже не обязательно будет непрерывной (функция
Хевисайда (формула (IV, 9; 5)) имеет dx-почти всюду
производную, равную нулю).
Следствие 2. Пусть t-*~M(t) — спрямляемый путь
некоторого конечномерного аффинного нормированного
пространства Е, ds — мера Радона и криволинейная абсцисса s
является неопределенным интегралом от ds. Тогда этот путь
ds-почти всюду имеет касательную.
Здесь снова мы говорим «касательная к пути» вместо
«касательная к образу пути».
Доказательство. Рассмотрим натуральное
параметрическое представление'кривой s-*M0(s). На стр. 705 мы ви-
—->■ -> ■>
дели, что dMo=pds, \\р\\ — I ds-почти всюду. Согласно тео-
>
реме Лебега 90, М0 имеет ds-почти всюду функцию р в
качестве производной. На стр. 709 мы видели, что в каждой точке,
где существует производная =#=0, имеется касательная к пути.
Следовательно, путь ds-почти всюду имеет касательную с
единичным вектором р.
Последовательные первообразные непрерывной
функции на прямой
Пусть, как и прежде, Ri— некоторый интервал прямой
R, Пусть / — непрерывная функция на R со значениями в

712
Гл. IV. Интегральное исчисление
банаховом пространстве Е. Мы видели уже, как интегрирование
позволяет находить первообразную функции /.
Покажем теперь, как последовательные первообоазные
•>
функции /, требующие a priori нескольких последовательных
интегрирований, могут быть вычислены с помощью одного
интегрирования.
->■
Теорема 91. Если f является непрерывным отображением
некоторого интервала R] прямой R в банахово пространство
-> ' •■>
Е, то существует, и притом единственная, гп-я первообразная Fm
->■
отображения f, обращающаяся в нуль вместе со своими
последовательными производными до (т—\)-го порядка
включительно в некоторой точке х = с из Rb и эта производная
задается интегралом
X
£"(*) = / V-")» ft^'>- (IV,9;41>
с
Доказательство. Единственность первообразной
порядка пг, удовлетворяющей заданным условиям, очевидна.
В самом деле, согласно теореме 22 гл. III, разность между
двумя первообразными порядка m является некоторым полит
номом степени ^т—1. Однако, если требовать, чтобы
первообразные вместе с их производными до (т — 1)-го порядка
обращались в нуль в точке с, то эти полиномы вместе с
производными до (т— 1)-го порядка должны равняться нулю
в точке с и, следовательно, в силу формулы Тейлора для
полиномов, должны быть тождественно равны нулю. Нам
остается лишь доказать, что формула (IV, 9; 41) действительно
определяет некоторую первообразную порядка т,
удовлетворяющую условиям теоремы.
Теорема очевидна для т— 1. Предположим, что она верна
относительно первообразной порядка т— 1, и докажем ее
справедливость относительно первообразных порядка т ^ 2. Иначе
говоря, предположим, что функция
х —2
^- W = 1 {X(m-l)\ - f® ^ (*V' 9; 42>
о
есть первообразная (т—1)-го порядка функции /,
обращающаяся в нуль вместе со своими производными порядков
') Эта формула требует большого внимания; | является переменной
интегрирования, а х, не являющаяся переменной интегрирования, фигурирует
х
одновременно в и под знаком интеграла!

§ 9. Частные свойства мер Радона
713
<Im —2 в точке с. Тогда существует первообразная Fm по-
->
рядка m от f, обращающаяся в нуль вместе с производными
порядков до m—1 в точке с, и эта первообразная вычисляется
по формуле
L (x) = J Fm-i (0 dt=\dt\ ((~1У Г(1) rfl- (IV, 9; 43)
с ее
Предположим сначала, что х >» с. Тогда два
последовательных интегрирования можно заменить одним интегралом:
Hl\m^l)'^)dtdl' (IV'9;44)
л
где через А обозначено множество точек плоскости R2,
определяемое неравенствами c^l^^^x1), xeRi. В самом
деле, последний интеграл имеет смысл, поскольку речь идет
-о некоторой непрерывной функции, определенной на компакте,
а тогда теорема Фубини показывает, что выражение (IV, 9; 43)
равно (IV, 9; 44).
Полученный двойной интеграл можно вычислить, начиная
интегрирование по t, а затем интегрируя по \, другими
словами, изменяя порядок интегрирования. С помощью формулы
(IV, 8; 35) получаем:
Fm(x)=*\*f(l)dl\ {\Z-V dU <IV>9;45)
где последний интеграл равен (х — |)m_1/(m — 1)'-
Утверждение доказано, так как аналогичные рассуждения для х < с
приводят к той же формуле.
Следствие 1. Пусть f — функция, удовлетворяющая
условиям теоремы. Тогда на R{ существует, и притом единствен-
пая, первообразная Fm порядка m для функции f со
значениями в аффинном пространстве Е с присоединенным вектор-
ным пространством Е, последовательные производные которой
до (гп—\)-го порядка включительно принимают заданные
значения Fm (с), Fm (с), ..., Fm {с) в точке с. Эта первообразная
') Можно было бы вместо ^ писать <, так как это изменяет подинте-
.гральную функцию только на множестве меры нуль.

714
Гл. IV. Интегральное исчисление
вычисляется по формуле
Fm(x) = Fm(c) + ^F'(c)+ ... + l\~S)il'&~liW +
X
+ |п[~-Г)! ^hs- (IV'9;46>
с
Доказательство. Единственность очевидна. Если мы
заметим, что функция Fm,"определенная по формуле (IV,9;46),
является суммой некоторой первообразной порядка т,
производные которой до (m+1)-го порядка в точке с обращаются
в нуль, и некоторого полинома, задаваемого своим
разложением Тейлора, производные которого до (m+1)-го порядка
в точке с принимают заданные значения, то результат
становится очевидным.
Следствие 2 (новая формула Тейлора для функции
одной вещественной переменной). Пусть f — некоторая функция,
определенная на интервале Ri прямой R, со значениями в
аффинном нормированном пространстве F, имеющая
непрерывные производные порядков ^m-j-1. Тогда имеет место
формула
f(x) = f(c) + ^f(c) + ..• +^r-fm(c) +
(x~J)mf(m + l)(t)d$, (IV, 9; 47)
с
а также формула
f(x + h) = f(x)+±T'(x)+ ... +%rVm)(*) +
i
{-^=j¥-J(m+l)(x + th)dtl). (IV, 9; 48)
о
+ J
+г*ч
Доказательство. Первая формула является на самом
деле формулой (IV, 9; 46), в которой f, Fm и m заменены
на f(m<-i)( f и m+1. Формула применима, так как /является
первообразной порядка m+1 непрерывной функции f<m+1> и ее
') Надо было бы предполагать пространство a priori полным, как это
делалось в теореме с тем, чтобы быть уверенным в существовании интеграла.
Однако здесь это не является необходимым, так как при заданной функции f
этот интеррал существует.

§ 9. Частные свойства мер Радона
715
производные порядка 0, 1, 2, ,.., m принимают значения f(c),
f(c),f'(c), ...,Jw(c) в точке с.
Вторая формула получается заменой переменной или же
применением первой формулы к интервалу [0,1] для функции
t—.f(x + th).
Следствие 3 (новое общее выражение формулы
Тейлора). Пусть f — отображение класса £>+• открытого множества
Q аффинного нормированного пространства Е в аффинное
нормированное пространство F. Если весь отрезок [х, х + И]
содержится в Q, то имеет место формула:
+ J ^f- (fm+i) (x + th) hm+l) dt. (IV, 9; 49)
Доказательство. Для доказательства достаточно
применить формулу Тейлора (IV, 9; 47) к интервалу [0,1] и функ-
->
ции t—>f(x-\-th). Согласно теореме о сложной функции, про-
-> ->
изводная порядка k в точке t этой функции равна fW(* + th)hk.
Полученная формула Тейлора значительно важнее формулы,
приведенной в гл. III. В самом деле, она дает явное выражение
для остаточного члена. Однако она требует несколько больше,
а именно — функция / должна иметь производную (т+1)-го
порядка, непрерывную в области Q. При этом дополнительном
предположении можно снова получить различные виды
формулы Тейлора, приведенные в гл: III.
Если, например, / принимает вещественные значения, то
можно воспользоваться теоремой о среднем в виде (IV, 1;31).
Тогда найдется такое число 6, 0 <С 6 <С 1, при котором
j^^(fim+l)(x+th)hm+l)dt =
о
=r+V+e£)^oi^^=^^^
(IV, 9; 50)
что снова приводит нас к формуле Тейлора (III, 7; Ь). Если
не делать никаких предположений относительно F, то согласно
формуле (IV, 1; 24) имеет место следующая оценка остаточного

716
Гл. IV. Интегральное исчисление
члена:
1
<
j±^(j{m+1\x+th)hm+l)dt
о
<„J|r.|jr+.)|||Jil^d/e|||^+.»|,,.^L.i (IV,9;51>
о
и мы снова возвращаемся к формуле Тейлора (III, 7; 2).
Если L является (т + 1) -линейным непрерывным отобра-
жением Е в F, то, учитывая равенство J ^— dt
(м+1)! *
о
можно записать:
\^^{r+X){x+th)hm^)dt^
ьт+1 +1 -^^((Г+,)^+^)-1)лт+1)^
(IV, 9; 52)
где последний интеграл мажорируется величиной
' V-t)m dt =
sup \\r+l)(x+th)-L\\\\hm+i[
m!
= sup Hr+V+^-Ll 7^nt; (IV,9;53>
мы вернулись к формуле Тейлора в виде (III, 7; 9).
Окончательно, все найденные ранее выражения для
формулы Тейлора являются следствиями нового выражения.
Однако, напомним еще раз, что они были' доказаны при. менее
ограничительных условиях и, как мы видели в главе о
дифференциальном исчислении, эти менее ограничительные условия
очень полезны в некоторых теоремах (см., например,
доказательство теоремы 14 гл. III).
Формула интегрирования по частям
Теорема 92. 1°) Элементарный случай. Пусть и и v —
функции класса С1, определенные на замкнутом интервале
[а,ЬУ) прямой R, со значениями в банаховых пространствах
') В этой формуле а и b — произвольные точки R: а < b, a = b ила
а > Ь.

§ 9. Частные свойства мер Радона
717
Е и F соответственно. Пусть В — непрерывное билинейное ото*
-> -> ->
бражение пространства E\F в банахово пространство G.
Тогда имеет место формула интегрирования по частям:
ъ
J В(и(х), v'(x))dx =
а
Ь
= В (и (Ь), о (Ь)) - В {и {а), о (а)) - J В (и' (х), о (*)) rfx. (IV, 9; 54)
а
-> ->
2°) Общий ■ случай. Пусть ц и v — две меры Радона,
определенные на замкнутом интервале [а,Ь] прямой R, со значе-
ниями в банаховых пространствах Е и F соответственно,
имеющие базы ^0. Пусть В — непрерывное билинейное отображе-
-> . -> -> -> >
ние Ey^F в банахово пространство G. Пусть М и N — неопре-
деленные интегралы мер ц и v со значениями в Е и F. Если
li и \ не имеют общих точечных масс, то интегралы В (М, dv)
а
Ь
и В (rf[i, N) имеют смысл и справедлива общая формула ин-
а
тегрирования по частям:
ь ь
J В (М, dv) = В(М (Ь), N (Ь)) -В{М (a), N (а)) - J В (djT, NT).
(IV, 9; 55)
Доказательство. Если учесть формулу
дифференцирования билинейного непрерывного отображения (теорема 12
гл. III)
Р'=7=В (и', v) + B (и, о'), (IV, 9; 56)
то первая формула вытекает из формулы (IV, 9;383), приме-
ненной к F — В (и, v).
Легко видеть, почему формула общего случая является
обобщением частной формулы интегрирования по частям. В са-
-> -> -> -> -»• ->
мом деле, если положить d\y = u' dx и dv = v' dx, то М = и и
N — v будут неопределенными интегралами от р, и v. Меры [х
и v имеют в качестве базы меру dx ^ 0. Поскольку меры
(г и v не имеют точечных масс, то они не имеют общей

718
Гл. IV. Интегральное исчисление
точечной массы, а, следовательно, формула (IV, 9; 55) (с
учетом определения (IV, 5; 13)) сведется к формуле (IV, 9; 54).
ь
Докажем теперь общий случай. В силу соотношения =
= — всегда можно считать a <Z.b.
ь
Пусть цо и vo — такие вещественные меры ^0, для которых
\i имеет в качестве базы меру ,u0, a v имеет в качестве базы
меру vo- Если положить Ко = цо + vo, то мы увидим, что обе
меры (Ло и vo мажорируются мерой Ко, а, следовательно
(теорема 53 Данфорда — Петтиса), имеют в качестве базы меру Ко.
Поэтому й[ай=ройКо и d\o=qodKo, где р0 и <7о локально Хо-инте-
-> -> -*• ■»
грируемы. Поскольку одновременно djx—pdjxo, dv=qdvo, то
окончательно получим (следствие теоремы 51):
■> ■ ■>. ■> ■> ■> ■>
d\i = (pp0)dKQ = fdK0, dv = (qqu)dh(i — gdK0. (IV, 9; 57)
Рассмотрим теперь двойной интеграл
\\ B(f{x),g(x))dK0(x)dK0(y). (IV, 9; 58)
[а, Ы X [а, Ь[
Поскольку / и g являются ййо-интегрируемыми на компакте
\а, Ь], этот интеграл, согласно теореме 79, существует. Та же
самая теорема говорит, что этот интеграл равен
В J fA» jgdK0\ = B(M(b)-M (a), N(b)-N (a)). (IV, 9; 59)
\а а ■
Представим теперь квадрат [а, Ь[ X [а, Ь[ в виде
объединения трех непересекающихся множеств (и, конечно, Хо-измери-
мых как пересечение открытых и замкнутых множеств):
1°) множество a =sC у < х < Ь, отмеченное на рис. 19
цифрой 1;
2°) множество а ^ х < у < Ь, отмеченное на рис. 19
цифрой 2;
3°) диагональ квадрата, т. е. множество а ^ х = у < Ь,
отмеченное на рис. 19 цифрой 3.
Рассмотрим интеграл, аналогичный (IV, 9; 59), на первом
множестве. Согласно теореме Фубини — Лебега (теорема 77),
X
j" j" = J dK0 (x) J В (f{x), g (у)) dK0 {у). (IV, 9; 60)
(I) ]а, Ь\ а
Функция g является А.о-интегрируемой на интервале [а, х[,
и, поскольку отображение g-*B(f(x),g) является непрерыв-

§ 9. Частные свойства мер Радона
719
■да» -да-
ным отображением F в G, можно записать
J В (f{x), g (у)) dX0 (у>= В (?(*), jgdtJ. (IV, 9; 61)
а
->
Здесь интеграл J gdX0 равен УУ(л;)—N(a). Кроме того,
а
х
\ g dX0=Q при х = а. Поэтому второй интеграл Г можно
1а. Я
о
заменить на [ = I . Отсюда мы получаем значение первого
[а, Ь[ а
интеграла. С учетом (IV,5; 13) получаем интеграл
ь ь
\\ = \ В {f{x), N{x)-N (a)) dX0 (x) = J" В (dj(*), N (х) - N (а)),
(1) а а (IV, 9; 62)
обязательно имеющий смысл.
Совершенно такие же рассуждения относительно интеграла
по множеству 2 дадут следующий результат:
ь
j* j* = j" в (М (х) - М (a), dv (*)). (IV, 9; 63)
(2) а
Покажем теперь, что интеграл, рассматриваемый на
множестве 3, т. е. на диагонали, равен нулю. Его можно
вычислить по теореме Фубини. Если зафиксировать х, то надо будет
У
, i
Ь
2 /
3
0\ а %
Рис. 19.
сначала на множестве {*} вычислить J В (f(x), g (у)) dX0 (у). Этот

720
Гл. IV. Интегральное исчисление
интеграл всегда равен нулю, кроме того случая, когда его
мера Яо имеет точечную массу в точке х. Обозначим через
Яо({*}) эту точечную массу. Тогда предыдущий интеграл равен
->■ ->
B(f(x),g(x))Ko{{x}), и, следовательно, интеграл по диагонали
будет определяться формулой
ь
J J = \ В(Т(х), g(x))X0({x})dX0(x). (IV, 9; 64)
(3) а
Заметим, что масса меры ц в точке х, т. е. интеграл отно-_
сителыю fdKo от характеристической функции множества {х},
->
сводящегося к точке х, равен f(x)ko({x}). Точно так же масса
меры v в точке х равна g{x)Xo({x}). Предположение, что ц и v
не имеют общих точечных масс, равносильно утверждению, что
для каждой точки х, в которой ко имеет точечную массу, по
крайней мере одна из функций f или g равна нулю. Но тогда
функция х—*B(f(x), g(x) )Яо({х}) тождественно равна нулю,
а, следовательно, интеграл (IV,9;64) равен нулю.
Сравнивая (IV, 9; 59), (IV, 9; 62) и (IV, 9; 63), получаем:
В (М (Ь) - М (a), N(b)-N (a)) =
ь - ь
= J В (dp (ж), N(x)-N (a)) + J" В (М (х) - М (a), dv (*)).
(IV, 9; 65)
Раскрывая и производя, как в (IV, 9; 61), перестановку
интеграла и линейного непрерывного отображения, получаем
B(M(b), N(b)) -B(M(a), N{b))-B(M(b), N (а)) + В (М (а), N(a)) =
= J" В {dpi, N) - В N djt, N{a) I + f fi(Af, dv) - S I M(a), j dv I.
а ^а 'а \ а '
(IV, 9; 66)
Поскольку dn = M(fr) — M(a) и dv = N (b) — N (а), то
а а
после взаимного уничтожения равных членов в обеих частях
равенства мы получим искомую формулу (IV, 9; 55).
Замена переменных при вычислении простых интегралов
Теорема 93. Пусть t—>x = g(/)— некоторая функция
класса С1, определенная на интервале [а, р] прямой R, такая

§ 9. Частные свойства мер Радона
721
что |(а) = а и |(р) = Ь1). Пусть f — непрерывная функция,
определенная на интервале [а,Ь], со значениями в банаховом
пространстве F. Тогда справедлива формула «.замены
переменной»:
ь в
\ J(x) dx=\ 7(1 (/)) V (t) dt. (IV, 9; 67)
а . a
Доказательство. Рассмотрим функцию Ф,
определенную равенством
и
Ф(ы) = j f{x)dx. (IV, 9; 68)
a
-> ■>
Так как / предполагалась непрерывной, то функция Ф
принадлежит классу С и является первообразной функции /.
■> > ■>
Кроме того, Ф(а) = 0, а Ф{Ь) совпадает с левой частью ра-
-> ■>
венства (IV,9;67). Функция s—►4r(s) = Ф(|($)), согласно
теореме о сложных функциях, принадлежит классу С1. Она удов-
■>->->
летворяет условию W(a) = Ф(а) = 0, а ее производная
вычисляется по формуле
W(s) = &($(s))$'(s)=f(i(s))t(s). (IV, 9; 69)
Отсюда следует, что для любого значения s можно
записать
4(s) = j7(l{№'(f)dt. (IV, 9; 70)
a
При s = p получаем ^(Р) — Ф(Ь), левую часть равенства
(IV,9;67), а так как правая часть равенства (IV, 9; 70)
совпадает с правой частью (IV, 9; 67), то теорема доказана.
Применяемая здесь формула не обобщается на кратные
ь
интегралы, поскольку ее вывод опирается на интеграл ,
а
относящийся исключительно к прямой. Нам будет полезно
воспользоваться другой формой интеграла, использующей
символ
[а, Щ
') Здесь а, |3, а, Ь — произвольные числа на R, a §§ р, о Щ Ь.

722
Гл. IV. Интегральное исчисление
Пусть / — интервал [а, Ь] или [Ь,а] в зависимости от того,
какая из величин а или b больше, и пусть / — интервал [а, р]
или [р, а].
Если к предположениям теоремы 93 мы добавим новое
условие: g является монотонной функцией на J, то формулу
(IV, 9; 67) можно будет записать в виде
jf{x)dx=JHUt))\r(t)\dt. (IV, 9; 71)
В самом деле, если | возрастает, то ||'(01 совпадает
с i'(f)S*0. С другой стороны, интегралы Г и | являются
ь р
интегралами вида е и е , где е=±1. Так как функция
а а
| предполагается возрастающей, то значение е будет одним и
тем же в обоих случаях. Если же функция | будет убывающей,
то функция ||'(0| равна —|'(0- Значения, которые принимает
е в обоих предыдущих интегралах, противоположны друг
другу. '
Формулу (IV, 9; 71) мы докажем для несколько иного
случая.
Теорема 94. Пусть О и Q — два открытых множества
вещественной прямой R. Пусть | — гомеоморфизм Q на О,
принадлежащий вместе со своим обратным гомеоморфизмом клас-
>
су СК Пусть f — непрерывная функция на О с компактным
носителем, принимающая значения в банаховом пространстве
F. При этих условиях имеет место формула
jf{x)dx=jj(l{t))\l'(t)\dt. (IV, 9; 72)
о а
Доказательство. Рассмотрим произвольную точку но-
-У
сителя f. Поскольку О является окрестностью этой точки,
существует не менее одного открытого интервала с центром
в этой точке, замыкание которого целиком лежит в О.
Множество всевозможных таких открытых интервалов, образованных
->
для всех точек носителя f, является покрытием этого носителя.
Поскольку носитель компактен, то достаточно конечного
числа интервалов, например ]ait fe,[, ie/, для покрытия этого
носителя.

§ 9. Частные свойства мер Радона
723
Пусть теперь у* — некоторое разбиение единицы,
относящееся к покрытию интервалами ]а:,Ь{[. Тогда
J f(x) dx=^ J Y< M T{x) dx. (IV, 9; 73)
Функция l~l должна быть гомеоморфизмом интервала
]аи bt[ на его образ. Значит, функция |-1 вместе со сбоей
обратной функцией £ строго монотонна в ]ai,bi[1) (теорема 37
гл. II). Если мы положим а, —£(ос,), Ьг = £(Рг)> то в силу
монотонности I можно применить формулу (IV, 9; 67) и записать
равенство
J yt(x)T{x)dx= J Vi(t(t))f(t(t))\t'(t)\dt, (IV, 9; 74)
из которого вытекает, что
jf(x)dx = yi j Vi&(t))f(t(t))\l'(t)\dt =
О is I | a., P; |
= Ц J Yi(i (0) f(i (0) I Г (0 I <W = J f(S (0) I Г (t) IЛ- (IV, 9; 75)
i <= / 2 2
Теорема доказана.
Следствие 1. В условиях теоремы образ меры \l'(t)\dt
на множестве Q при отображении I множества Q в множество
О является мерой Лебега dx на множестве О.
Для доказательства в качестве / следует взять какую-либо
скалярную непрерывную функцию с компактным носителем на
О. При этсм мы придем к определению образа некоторой
меры.
Следствие 2. Если \ удовлетворяет условиям теоремы
и если f является произвольной функцией на О со значениями
> >
в банаховом пространстве F, то f будет -интегрируемой
относительно dx на и тогда и только тогда, когда интегрируема на Q
') В противном случае существовали бы такие три точки и, v, w этого
интервала, что и < v < w и g_1 (и) ^ |_1 (v), |-1(ю) ^ £~'(и) или
|-1 (и) ^ |_1(ц), |-1 (w) ^|_1(ц). Рассмотрим, например, первое условие со
знаком ^. В действительности, в силу биективности £-1, можно было бы
взять даже знак <. Однако тогда в силу следствия теоремы 33 гл. 11
функция |-1 принимала бы не менее двух раз каждое значение, заключенное
строго между §~1(и) и sup(|-1(u), £_l(ai)): один раз в интервале [и, v[ и
один раз в интервале ]v, w], что невозможно, так как эта функция
биективна.

724
Гл. IV. Интегральное исчисление
относительно dt функция t —*f (%(t)) \l'(t) |, и при этом
справедливо равенство (IV, 9; 72).
В самом деле, по следствию 1, dx является образом
|£'(^)|Л при отображении £. При этом, в силу теоремы 60,
функция / интегрируема относительно dx тогда и только тогда,
когда будет интегрируемой относительно |g'(/)|df функция
f(%(t))- В силу теоремы 51, последнее имеет место тогда и
только тогда, когда функция /(£(/)) |£'(0 I интегрируема
относительно dt. Соотношение (IV, 9; 72) следует из теорем 60
и 51.
Несобственные интегралы на прямой
Пусть \а,Ь[, а -< Ь, — некоторый интервал прямой R, не
содержащий своего правого конца Ь. Пусть \i — мера Радона на
\а,Ь[ со значениями в банаховом пространстве £ и с базой
^0. Несобственный интеграл \ d\i называется сходя-
\а, + Н
щимся, если интеграл d\i при каждом Ь' из \а,Ь[ имеет
| а, Н
смысл и при Ь', стремящемся к b по значениям из \а,Ь[,
существует предел в Е. Вместо мы пишем (где —*Ь
\а,Ь[ | а, -> 6[
означает, что в \а, Ь[ берутся значения Ь'', стремящиеся к Ь),
поскольку это выражение в первом обозначении не имеет
смысла как интеграл от некоторой интегрируемой функции.
Выражение « "сходится» означает, что для каждого неопре-
деленного интеграла М от \i, со значениями в аффинном
нормированном пространстве Е с присоединенным векторным
пространством Е, М(Ь') имеет предел при Ь', стремящемся к b
по значениям из \а,Ь[.
->
Пусть X — некоторая мера ^0, а / — локально Л-интегри-
->
руемая функция со значениями в банаховом пространстве F.
Говорят, что несобственный интеграл /Л от f
по
сходится, если сходится d\i, \i = fX. Говорят, что
J
|а,->6|
f dX абсолютно или нормально сходится, если сходится
|а, -*Я

§ 9. Частные свойства мер Радона
725
интеграл ) ||7ll^- Аналогичные определения даются для
\а, ->И
интегралов вида
]а<г,Ь\
Можно рассматривать интегралы вида . Говорят,
что такой интеграл сходится, если существует предел
интеграла ) , когда а' и Ь', оставаясь в ]а, Ь[, стремятся неза-
] а', Ъ>\
висимо друг от друга соответственно к а и Ъ. Если, например,
а < Ь, то это означает, что, каково бы ни было число е > О,
найдутся такие a'Q> а и b'0<b, что для всех а<а'^.а'0 и
1С Г II
— I I <е.
] а ■<-,-> Ъ[ ] а', Ь'\ fl
Это также означает, что для произвольного с из ]а, Ь[ оба
интеграла и имеют смысл.
I с, -> Ы ] а <-, с\
Нередко а и b равны ± оо. В частности, можно
рассматривать . Вводят иногда также и обозначения вида
] —ОО <г, -> + 00[
-*Ь ' Ь -*Ь
■/• М-
а а<- а<-
->
Теорема 97. Пусть к — мера Радона >0 на \а,Ь[ и f —
функция, определенная на [а, Ь[, со значениями в банаховом
пространстве F, Х-интегрируемая на каждом интервале \а, Ь'[,
где b'e=\a,b[. Для того чтобы интеграл fdk был абсо-
| а, -> Ь{
лютно сходящимся, необходимо и достаточно, чтобы при Ь',
с ■*■
изменяющемся в | а, Ь[, интеграл \\f\\ dk был ограничен.
I а, Ъ'[
Необходимо и достаточно также, чтобы функция f была
интегрируемой относительно меры X на интервале \а, Ь[, и тогда
интеграл fdX сходится и равен | fdX.
\а, ->Ь[ \а,Н
Как мы уже видели, эта теорема говорит о том, что
понятие интегрируемости в смысле Лебега соответствует
обобщенному понятию абсолютно сходящегося несобственного
интеграла Римана, рассматриваемому в курсе математического
анализа. Напротив, условно сходящиеся несобственные интегралы

726
Гл. IV. Интегральное исчисление
Римана не являются интегралами от функций, интегрируемых
в смысле Лебега. В этом случае запись / dК не имеет
смысла, и с точки зрения излагаемой теории абсолютно
необходимо писать J Jdk '). Эта теорема, с другой стороны,
|а,-*6[
показывает, что на этой стадии понятие абсолютно
сходящегося несобственного интеграла никакого интереса для нас не
представляет, ибо оно не дает ничего нового по отношению
к интегралу Лебега. Новыми являются лишь условносходящиеся
несобственные интегралы, т. е. сходящиеся, но не абсолютно
сходящиеся.
Доказательство. Обозначим через щ
характеристическую функцию интервала [а, Ь[.
1°) Поскольку Ь'-> J ||/||fito, является возрастающей
I а, Ь'[
функцией, эта функция имеет предел при Ь', стремящемся к Ь,
тогда и только тогда, когда она ограничена. Следовательно,
J \\f\\dk сходится тогдч и только тогда, когда при пере-
|а,->6[
менном Ь' ограничен интеграл | ||/||сМ,.
\а,Ь'[
2°) Локально интегрируемая функция f измерима (см.
примечание на стр. 592). Следовательно, эта функция
интегрируема тогда и только тогда, когда | \\J\\dl= | ||/||фб^А,< -f-oo.
\a,b[
Однако, по теореме 36 Фату, это выражение является
пределом от J || / || qty dA, — Г \\J\\dk= J||/||dA.. Следовательно,
\а,Ь'[ \а,Ь'[
f интегрируема тогда и только тогда, когда имеет смысл
интеграл J ||/||dA..
') Мы говорим «с точки зрения излагаемой теории необходимо», так
как в большинстве случаев стрелка не ставится! Например, всегда пишут
+ 00
Г sin* . я sin х , , „ .
dx = -jj-, в то время как не интегрируема по ах на | 0, + оо[.
о
->+оо
Надо было бы писать dx или dx.
J х J x
| о, ■*+ «>[ о

§ 9. Частные свойства мер Радона
727
3°) Если эти условия выполнены для фиксированной инте-
грируемой функции ^ 0, то при Ь', стремящемся к Ь, /фь-
будет просто сходится к /ф& и имеет место неравенство
11/Фь'И ^11/11- Из теоремы 35 Лебега следует, что при Ь',
стремящемся к ft, интеграл fdX = J /фЬ' dX сходится к fdX —
I а, Ъ'\ \а,Ь\
= Г f<fbdX, а, следовательно, J fdX сходится и равен
|я.-»6[
J JdX.
\а,Ы
Следствие 1. На каждом ограниченном интервале [а, Ь],
a <Lb, содержащем начало координат, функция \1\х\а
интегрируема по мере Лебега тогда и только тогда, когда а< 1.
На интервале [а, + оо[ или ]—оо, а], не содержащем начала, это
функция интегрируема тогда и только тогда, когда а> 1.
Функция 1/|х|а непрерывна в С 0, а, следовательно, локально
интегрируема в ]—оо, 0[ и ]0, +оо[. Пусть, например, a^O^fe,
8 1
а <Ь. Функция ■; ;—~т, где е = +1 для х > О и е = —1
1-а \х
для х < 0, является первообразной функции 1/|х|а в СО при
аф1, а функция eln|x является ее первообразной при а=1.
Для 0 < с < d < -f-oo имеем:
1
i,H
аЫ^-^) ПРИ аФ1>
l-aUa_1 с""'/ (IV, 9; 76)
\с,"сЦ]Л] [ Ind — \пс для а=1.
Так как функция l/х"- ^ 0, то она интегрируема в ]0, Ь\
тогда и только тогда, когда сходится несобственный интеграл
, т. е. тогда и только тогда, когда его первообразные
10 ч-,ы
имеют конечный предел, если х > 0 стремится к 0. Для этого
необходимо и достаточно, чтобы a < 1, и тогда
Г dx___ Г dx _ 1 1_
J xu ~ J ха 1 — a ' ba~l '
Тот же самый результат имеет место для интервала \а, 0].
Однако 1/|х|а интегрируема в интервале \а,Ь\ тогда и только
тогда, когда она интегрируема в [а,0] и [0, &], т. е. тогда и
только тогда, когда а<1.
Пусть теперь а >■ 0. Функция 1/ха будет интегрируемой
в \а, +оо[ тогда и только тогда, когда сходится несобственный

728
Гл. IV. Интегральное исчисление
интеграл I dx/xa, т. е. тогда и только тогда, когда ос> 1.
I а, ->•+<»[
При этом
С dx_ С dx_ 1 1
, J ,/ ~ J , ха ~~ а-1 ' а""1 '
I а, +°°[ | а, -» + <»[
Точно такое же рассуждение можно провести для интервала
]—оо,а|, а < 0.
Следствие 2. Обозначим через 1/ха при комплексном
а и вещественном х > 0 число е~а1ах. Функция х-+1/ха
интегрируема по мере Лебега в ]0, а |, а > 0, гог<За и только
тогда, когда Rea<l. Эта функция интегрируема в \а, +оо[
тогда и только тогда, когда Rea>l. Кроме того, интегралы
dx/xa и dx/xa сходятся лишь тогда, когда они схо-
30<-, а\ |а, -» + <х>[
дятся абсолютно.
В самом деле, функция 1/ха непрерывна, а, значит,
измерима. Она интегрируема тогда и только тогда, когда ее
абсолютная величина \/хЯеа интегрируема, и мы вернулись к
следствию 1.
Для доказательства сходимости интегралов мы используем
ту же самую первообразную ■ или \пх. Опираясь
на формулу (IV, 9; 76), можно заключить, что сходимость имеет
место для только при а < 1 и для • только при
]0<-,а\ I a, + <х>[
ос > 1, т. е. тогда, когда имеет место абсолютная сходимость
или интегрируемость.
Распространим теперь на несобственные интегралы
относительно меры dx методы интегрирования по частям и замены
переменной.
Теорема 98 (интегрирование по частям).
1°) Элементарный случай.
■> >
Пусть и и v — функции класса С1, определенные на
интервале [а,Ь[ прямой R, со значениями в банаховых пространствах
-> >
Е и F соответственно. Пусть В — непрерывное билинейное
-» -» • > '
отображение Е X F в банахово пространство G. Если выраже-
> >
ние B(u(x),v(x)) при х<.Ь, стремящемся к Ъ, имеет предел,
то В (и, v') dx существует тогда и только тогда, когда су-

§ 9. Частные свойства мер Радона
729
ществует В (и', v) dx, и при этом имеет место формула
а
-*Ь
f В (и, o')d* = lim В (и (Ь'), % {Ь')) — В (и (а), о (а)) —
J Ь'-*Ь
а
-*Ъ
- J В (и', о) dx. (IV, 9; 77)
а
-2°) Общий случай1).
-> >
Пусть (л ы v — лерьг Радона на [а,Ь[ со значениями соот-
> •>
еетственно в банаховых пространствах Е и F, имеющие базу
^О.и не имеющие общей точечной массы. Пусть В — непре-
-> >
рывное билинейное отображение пространства Е X Р в бана-
->
лгово пространство G.
' -> -> > ->
Пусть М и N — неопределенные интегралы от ц и v со зна-
> ->- •> >
чениями в Е и F. Если при этом B(M(x),N(x)) имеет предел
-*ь
п/?ы х, стремящемся к Ь, то \ В (М, dv) существует тогда
а
-*Ь
« только тогда, когда существует интеграл В (d\i, N), при
а
этом
-*ь
j В (М, dv) =
-*ь-
= lim В (М (Ь')г N (Ь')) ~В(М (а), N (а)) - f В (djt, N). (IV, 9; 78)
Ь'-*Ь J
а
Доказательство получается сразу, если написать формулу
для пары а, Ь' и устремить Ь' к Ь.
Следствие (критерий Абеля для полу сходи мости несоб-
-> -> ■
ственных интегралов). Пусть и и v — функции, определенные
на интервале [а, Ь[ прямой R, —схз<а<6^ + оо, со значения-
ми в банаховых пространствах Е и F. Пусть В — билинейное
') В приложениях часто пользуются так называемой «второй формулой
О среднем», которая является частным случаем рассматриваемой здесь
формулы.

730
Гл. IV. Интегральное исчисление'
непрерывное отображение Е X F в банахово пространство G.
-*■-*■
Предположим, что функции и и v обладают следующими
свойствами:
1°) функция и имеет ограниченную вариацию на [а, Ь[ и
и(х) сходится к нулю, когда х < Ь стремится к Ь;
-*■
2°) функция v локально dx-интегрируема и имеет ограни-
-*■
ценные неопределенные интегралы, т. е. величины orCid =
= v{x) dx независимо от выбора cud ограничены по норме.
\c.di
Тогда, если пространство Е конечномерно1), имеет смысл
интеграл I В (и (х), v (x)) dx. Кроме того, если через U(c)
\а.-*Ы
-*■ >
обозначить полную вариацию функции и на ]с, Ь[ и через
V(c) — точную верхнюю грань величин \\ac,d\\ для de[c,6[, то
имеет место оценка
1 J B{u{x), 1>{x))dxl^\\B\\U{c)V{c), a^c<b. (IV,9;79)
lie-»M 0
Для простоты мы проведем доказательство в случае, когда
Е, F, G совпадают с полем .С, а отображение В является
умножением чисел. В этом случае рассматривается интеграл
uv dx. По условию функция и имеет ограниченную ва-
|с.-»М
риацию, через U(c) обозначается ее полная вариация в ]с, Ь[
и считается, что и(х) стремится к 0 при х < Ь, стремящемся
к Ь. Предполагается, кроме того, что функция v локально
dx-интегрируема, а неопределенные интегралы
V(c)= sup
c<d<b
J v(x)
dx
\cd[
ограничены. Тогда интеграл J uv dx должен иметь смысл
|с, -*ы
') Это ограничение необходимо, если с помощью теоремы 88 хотят
получить, что и является неопределенным интегралом от некоторой меры ц с
базой 3*0. Однако, если этот факт известен заранее (например, если и
принадлежит классу С1, —следствие 1 теоремы 89), то в таком ограничении
необходимости нет.

§ 9. Частные свойства мер Радона
73 Г
и должна иметь место следующая оценка:
J uvdx <C/(c)V(c). (IV, 9; 80)
I с -*Ы
Как мы сейчас увидим, все утверждения опираются на
интегрирование по частям. В самом деле, поскольку функция и,
которую мы будем обозначать через М, имеет ограниченную
вариацию, то dM = ц, есть мера Радона на [а, Ь[ конечной
нормы (теорема 88). Точнее: U(c)= d\n\. Рассмотрим
загс Ь[
тем меру vdx = v и через Л' обозначим какой-нибудь неопре-
х
деленный интеграл от v. Положим, например, N(x)= v{t)dt
с
так, чтобы N(c) — 0. Функция Л' непрерывна, ограничена и
и V (с) = sup | N (л:) |. Нам надо вычислить интеграл
с^х < Ь
Г М (х) dN (x). Меры ц, и v не имеют общей точечной массы,
1с-»*[
поскольку ее нет у меры v. Поэтому можно применить
теорему 98: рассматриваемый интеграл имеет смысл тогда и только
тогда, когда имеет смысл интеграл N (л:) dM {x) и первый
\а.-*Ь[
интеграл равен
(UmW(x)N(x))-M(a)N(a)- f N(x)dM(x). (IV, 9; 81)
х-*Ъ , J .,
Далее, при х, стремящемся к Ь, функция М(х) стремите»
к 0. Так как функция Л^(л:) по предположению ограничена, то
функция М (х) N (х) также стремится к нулю. Кроме того,
интеграл в правой части абсолютно сходится, так как \i=dM
имеет конечную норму и N ограничена. Это означает, что
рассматриваемый интеграл также сходится (но не обязательно
абсолютно). Поэтому, заменяя а на с и учитывая, что N(c) =
= 0, получаем:
| uv dx = — I N (х) dy. (л:),
|с->*[ [с,М
а, следовательно,
J uvdx < J" \N(x)\d\ii(x)\^V(c)U(c), (IV,9;812)
|с-»ь[ tc.*[
чем и доказывается неравенство (IV, 9; 80).

732
Гл. IV. Интегральное исчисление
В частном случае, когда и = М принадлежит классу С,
формула (IV, 9; 81) записывается в виде:
\а,-*И
\ uvdx= \ М (х) v (x) dx —
I, -*Ь[
= (\imM(x)'N(x)) — M(a)N(a)— f M'(x)v(x)dx
J uvdx = — f M'vx,
la, 61
I c, -»•&[
\c.b[
а, следовательно,
J ну dx
i с, -»M
: V (c) J | yW' (x) | dx = f/ (c) V (c). (IV, 9; 813)
\c'b\
Замечание. Теперь становится ясным то, что не было
столь очевидным в случае теоремы Абеля для рядов: суть
теоремы Абеля составляет формула интегрирования по частям.
Теорема Абеля о рядах является частным случаем теоремы
Абеля относительно интегралов. В самом деле, пусть в усло-
-> ->
виях теоремы 63 гл. II заданы последовательности ип и vn.
-> ->
Обозначим через и и v функции, определенные на полупрямой
[О, +оо[ по формулам:
и (х) ■■
>
v(x)-
->
--и„
vn
для п <^.х < п + 1,'
для п ^.х < п + 1.
(IV, 9; 82)
Мы видим, что последовательность ип имеет ограниченную
вариацию тогда и только тогда, когда имеет ограниченную ва-
риацию на R функция и. Мы видим также, что частные суммы
> >
<Ут,п Для последовательности vn ограничены тогда и только
тогда, когда ограничены интегралы v (x) dx. Но тогда из
\с, d\-. •
только что доказанной теоремы вытекает теорема 63 гл. II
и оценка (II, 14; 31) при с=т + 1.
Примеры применения критерия Абеля
Пусть и — некоторая функция, определенная на полупрямой
[а, +оо[, с комплексными значениями, имеющая ограниченную
вариацию и стремящаяся к нулю на бесконечности.

§ 9. Частные свойства мер Радона
733
Тогда для вещественного Я ф 0 сходится интеграл
J eil*u(x)dx, (IV, 9; 83)
\а, -»+°°[
и имеет место неравенство
I J ea*u(x)dxi^U(c)jtj. (IV, 9; 84)
I I C, -»+°oI II
В самом деле, если мы положим у(л;) = eilx, то увидим,
что интеграл
a,,d = J v(x)dx = j^—
\c,d\
допускает оценку: I crc, d I ^ т^т •
Естественно, результат не верен при л = 0.
Точно так же можно рассмотреть аналогичные интегралы
cosXx u(x)dx, sin Кх и {х) dx, (IV, 9; 85)
}а, -*оо[- \а, ->+оо[
для которых проводится то же самое рассуждение. Последний
интеграл, кроме того, имеет смысл при Я, = 0, так как он тогда-
равен нулю2).
') Проведем в этом примере интегрирование по частям, лежащее в
основе доказательства теоремы Абеля. Имеем:
\с, d{ c [с, й\
Предел существует при d, стремящемся к бесконечности.
2) Если функция и вещественна, ^ 0, убывает и стремится на
бесконечности к 0, то теорема о знакопеременных рядах снова обеспечивает
сходимость. В самом деле, интеграл
и (х) sin Xx dx
Inn (га+1)я ]
X ' X \
имеет знак (—1)п, при возрастании п убывает по абсолютной величине
(поскольку и(х + п!Х) ^.и(х)) и стремится к 0 при п, стремящемся к бесконеч-
иости (этот интеграл мажорируется по модулю величиной Т" и I~зГ"))'
Значит, он является общим членом сходящегося ряда. Этим доказывается, что
последовательность.интегралов ' при п-»-оо имеет некоторый предел.

734
Гл. IV. Интегральное исчисление
Во всех трех рассматриваемых случаях, если функция и не
интегрируема на [а, +оо[, мы будем иметь дело с
несобственными полусходящимися интегралами.
Особый интерес представляют интегралы
J ^-dx, j ^-dx, J -O^-dx. (IV, 9; 86)
10. ->+»[ * |0. ->+oo[ * |0, -* + oof *
Функция и, поскольку она имеет особенность в начале
х=0, не имеет ограниченной вариации. Поэтому эти интегралы
условиям теоремы Абеля не удовлетворяют. Однако для
обоснования сходимости достаточно их разбить на сумму двух ин-
1 -»+оо
тегралов | и .
о 1
Если считать для первых двух интегралов а<1, а для
1
третьего а < 2, то интегралы J будут иметь смысл, поскольку
о
в этом случае мы имеем дело с функциями, интегрируемыми
-»"+оо
по Лебегу. Остается, следовательно, изучить интеграл [ . Что
1
касается этого интеграла, то мы находимся в условиях
применимости теоремы Абеля, поскольку функция 1/ха, будучи
убывающей и ограниченной, имеет ограниченную вариацию и при
а > 0 стремится к нулю на бесконечности.
Таким образом, рассматриваемые интегралы сходятся: два
первых при 0 < а < 1, а третий при 0 < а < 2. Заметим, что
здесь функция и на интервале ]0,+оо[ принадлежит классу
С°° и что мы рассматриваем «наиболее» классический случай
интегрирования по частям! Эти интегралы играют очень
важную роль в анализе и физике. Позже мы научимся их
вычислять, основываясь на новой функции, так называемой Г-функ-
ции. Приведем для примера два из этих интегралов:
J ^Ldx==?L для-АХ), (IV, 9; 87)
Ю, -»+оо[
cos Ял
£- dx= J ^^- dx = -j/-^ при I > 0. (IV, 9; 872)
J V x J Yx
IP.-*+»[ r |o, -*+»[
_ tin ., ,,^, (n + 1) я f
Однако при -^г— ^6 <J-—-т-1— интеграл заключен между интегра-
I а, ь' |
Г и . Значит, интеграл сходится.
I пя I | (п+1) л

§ 9. Частные свойства мер Радона
735
Теорема 99 (о замене переменной). Пусть [а, р[ и [а,Ь[ —
два ограниченных или нет интервала прямой R. Пусть | —
такое отображение класса С1 интервала [а, р[ на интервал [а, Ь[,
что |(а) = а и lim 1(р") = b '). При этих условиях интеграл
Р'-*Р
I f{x)dx, где f — локально dx-интегрируемая функция, опре-
а >
деленная на [а, Ь[, со значениями в банаховом пространстве F,
сходится тогда и только тогда, когда сходится интеграл
->Р
I / (I (0) I' (0 ^> пРи этом имеет место равенство
а
J f (jc) d* = J T(l (0) V (*) dt. (IV, 9; 88)
a a
Для доказательства достаточно записать формулу для
интервала [а, р'[ (следствие 2 теоремы 94) и устремить р' к р2).
Пример. Интегралы Френеля. Так называются интегралы
J cosXx2dx и J sinAjt2dJt. (IV, 9; 89)
| 0, -»+oo[ 10, -»+ооГ
Так как подинтегральные функции при х, стремящемся
к бесконечности, не сходятся даже к 0, то сходимость этих
интегралов вовсе не очевидна. Однако изучение кривых,
изображающих эти функции3), показывает, что они сильно
колеблются и что было бы естественным ожидать сходимости этих
интегралов. В самом деле, достаточно здесь произвести замену
переменной л; = Уt для того, чтобы прийти к рассмотренным
ранее интегралам (IV, 9;87г). Исходя из этих формул,
справедливость, которых будет доказана позже, приходим к
следующим результатам:
J cosXx2dx = J" sinXx2 dx^^y^^ . (IV, 9; 90)
| 0, -»+°o[ 10, -»+°o[
') Относительное расположение a и (5, так же как а и b, произвольно.
2) При монотонной функции £ отсюда легко получаются формулы,
соответствующие (IV, 9; 71).
а) Нулями функции sin Яд:2 являются точки Кх2 = пл, или х—~\/ —— ,
0, 1, 2 Расстояние между двумя последовательными нулями
/?<""
чг ,„+ 1 — у~п) ~ Л/ т^ при п, стремящемся к бесконечно-
X У X lYn
сти, стремится к нулю. Сходимость этих интегралов (см. примечание на
стр. 733) вытекает сразу же из теоремы о знакопеременных рядах.

736
Гл. IV. Интегральное исчисление
Главное значение в смысле Коши
Пусть задан некоторый интервал \а, Ь\ прямой R и точка с
из )а,Ь[. Пусть / — функция, определенная на \а, Ъ\ — {с}, со
значениями в банаховом пространстве F, интегрируемая по
мере Лебега на \а, с — б| и на \c-\-6', Ь\ при любых б и
б'> 0, но не обязательно интегрируемая на \а,Ь\. Когда
говорят, что / dx сходится как несобственный интеграл, то
\а,Ь\
этим хотят сказать, что оба интеграла f dx n f dx
I a, ->c[ ]c <r,b\
сходятся. Это означает, что интеграл + сходится
| а, с—б | \с+6',Ь\
к некоторому пределу при б и б', стремящихся независимо друг
от друга к нулю.
Может случиться, что этот предел не существует, однако,
существует предел при б, стремящемся к нулю, когда б' = б.
->
В этом случае говорят, что интеграл от / сходится в смысле
главного значения Коши, и пишут
v. p. J f{x)dx — lim [ j + J
\a,b\ &~>° \ \а,с-Ь\ |с+6, i
Теорема 100. Для того чтобы существовал предел
v. р- f{x)dx, необходимо и достаточно, чтобы в окрестно'
\а.Ь\
сти точки х=с функция / являлась суммой антисимметричной
-»■->*
функции /] (/!(с + ы) = —/](с — и)) и такой симметричной
функции /2 (/2(с + ") =Ыс—")), для которой сходится
интеграл /2 (х) dx.
}Ctr,b\
При с = 0 симметрия и антисимметрия называются
четностью и нечетностью. Заменяя переменную х = с -\- и, можно
всегда перейти к последнему случаю, когда с = 0. Каждая
функция / единственным образом может, быть представлена
ь окрестности точки х = 0 в виде суммы четной и нечетной
функции:

§ 9. Частные свойства мер Радона
737
Поскольку ft нечетна, то ее интеграл в симметричном
интервале равен нулю. Следовательно, если а выбрать так, чтобы
а ^ —а < 0 < а ^ Ь, то мы получим:
j Jfl{x)dx+ | Ti(x)dx = 0. (IV, 9; 92)
I—а, б | |+6, +а|
Сходимость в смысле v. р. в \а, Ь\, или, что то же самое,
в интервале [—а, а], одна и та же как для f, так и для f2.
Так как функция f2 четна, то
J f*2(x)dx + j %(x)dx = 2 jj2(x)dx, (IV, 9; 93)
1-а. -б| |+б, +a | | 6, a |
так что интеграл от f существует в смысле v. p. тогда и только
тогда, когда сходится интеграл I J2 {x) dx, чем и заканчи-
]0ч-, a|
вается доказательство теоремы.
Пример. Предположим, что в окрестности точки х = с
* £_
функция f может быть представлена в виде f {х) = —^—^-
-*• ■>
+ с0 + с1(х — с) + ....Так как функция 1/(х —с)
антисимметрична, то интеграл в смысле v. p. существует.
Впрочем, если мы будем вычислять I J(x) dx, то его
к+6, ь\
можно будет записать в виде
C_,0n(6-C)-lne)- J (f(x)_-^L.)rfjc.
|с+6,6|
Второе выражение при б, стремящемся к нулю, имеет предел
(и даже /W —]~7 интегрируема в \а,Ь\). Первое же
выражение из-за члена —In б предела не имеет. Если теперь
вычислить f (x) dx, то мы получим
|а, с—б |
с-,(1пв-1п(с-й))+ J (f(x)_-£ri_)dx.
I a, c-6 |
При этом второе слагаемое имеет предел при б, стремящемся
к нулю, а первое слагаемое предела не имеет из-за наличия
24 Зак, 1339

738
Гл. IV. Интегральное исчисление
члена In б. Если образовать сумму ~Ь .то члены
_>. \а. с—д| |с+в, Ь\
± с_1 In б взаимно уничтожаются и сумма при б, стремящемся
к 0, будет иметь предел. Поэтому мы получим:
v.p. j f(x)dx^--c.1\n(^) + J" (fW__£=L.)dx. (IV,9;94)
I a, b\ la, 6|
Точно так же для функции f, интегрируемой на каждом
конечном интервале, существует понятие главного значения
интеграла в смысле Коши для интервала ]—оо, +оо[:
v. р. ( J(x) dx = lim |
1-со. +со| °^ |-В, +B)
Для того чтобы существовало такое главное значение, необ-
■>
ходимо и достаточно, чтобы f можно было представить в виде
> > ■> ->
/ = fi + /2, где fi — четная, а f2 — нечетная функции, и чтобы
интеграл U(x)dx был сходящимся.
(при а Ф О, Ь Ф 0), (IV, 9; 95)
(функция нечетна). (IV, 9; 96)
]—оо, +оо[
Замечание. Аналогично вводится понятие главного
значения в смысле Коши для рядов, множеством индексов которых яв-
+ оо >
ляется множество Z целых чисел любого знака. Если 2 "« —
П=—оо
такой ряд, то, поскольку Z=^N, понятие сходимости для него
не определено. Существует лишь понятие безусловной сходи-
мости (эквивалентное абсолютной сходимости, если ип
принимают значения в конечномерном пространстве (см. замечание
+0° '■*
2°) на стр. 133). Однако обычно говорят, что ряд 2 ип схо~
П==—оо
дится, если сходится каждый из двух рядов 2 ип и 2 ы_„.
Это утверждение означает, что сумма 2 ип имеет предел,
(7 = —ЛГ,
когда Л/| и N_z независимо друг от друга стремятся к +оо.
Легко
|0-»+оо [
подсчитать,
v. р.
v.p.
Г dx
J X
а,Ь\
\
ЧТО
._.„
■dx
X
i
0

§ 9. Частные свойства мер Радона
739
+°° *
Однако можно было бы считать, что 2 ип сходится
П=—оо
в смысле главного значения Коши, если сходится сумма
2 "« при N, стремящемся к бесконечности. Если, напри-
n=-N
мер, ип =—«_„, то такая сходимость всегда будет иметь место,
а сумма будет равна нулю.
Главное значение в смысле Коши можно определить для
кратных интегралов. Если f является некоторой функцией на
R", суммируемой на каждом множестве \х\ ^ б > 0, то гово-,
рят, что интеграл от этой функции сходится в смысле главного
значения Коши, если имеет предел при б, стремящемся к О,
интеграл ) ... \ f{x)dx. При п=\ мы снова возвращаемся
1*1>в
к главному значению на R.
Приведем пример, который играет особо важную роль в
квантовой механике и в котором используется понятие главного
значения Коши.
Теорема 101. Пусть \а,Ь\ — такой интервал прямой R,
что а <С 0 << Ь. Пусть f — интегрируемая функция, определен-
->
пая на \а,Ь\, со значениями в банаховом пространстве F.
Если I дифференцируема в начале координат или, более
общо, если величина [f(x) — /(0)]/|л:|а, a > 0, х Ф 0, остается
ограниченной, когда х стремится к нулю, то интеграл
(f(x)/x)dx существует в смысле главного значения Коши в
\а,Ь\
начале координат. Кроме того, интеграл
->
f -У^-d* (IV, 9; 97)
J х + ty \ . /
\а,Ь\
сходится при у, стремящемся к 0, по значениям знака е (е =
= ±1) к
->
v. p. j -Ц^-Лк-еш)(0). (IV, 9; 98)
la. 61
Естественно было ожидать появления члена v. р. , а не
->■
второго члена —einf(0), хотя существенным здесь является
именно наличие 2-го члена.
24*

740
Гл. IV. Интегральное исчисление
Доказательство. Функция f(x)/(x + iy) на ]а, — А | и
| + Л, -\~Ъ[, А > 0, измерима и мажорируема по норме
величиной ||f(*)||/i4, а, значит, интегрируема. В силу теоремы 35
Лебега, при у, стремящемся к 0, интеграл —ЦГ^Г^х схо-
\А,+Ы
-> ->
дится к -*-^-dx. Остается показать, что v. p. dx
\А,+Ь\ \-А. +А\
-> ->
Г f (х) Г / (х)
существует и что _i_ -, dx сходится к v. p. v dx —
J X \ I у J X
l-A,+A\ \-A, + A\
— ешТ(О).
Запишем очевидное разложение:
Г Ji^Ldx^h) Г —JV+ Г Г(х)7Г(0) dx.
J х + гг/ ,w J x + iy J х + и/
1-А+Л1 1-Д+Л1 \-A,+A\ ■
(IV, 9; 99)
Изучим сначала его первый член. Для определенности
положим 8 = +1. Рассмотрим в открытом дополнении к
полупрямой {z=x + iy; г/=0, х ^ 0} комплексной плоскости
функцию In z, определенную на стр. 164. Положим z=rei(P, где
—л<ф<л, и In z=ln r -f- г'ф. Таким образом определенная
логарифмическая функция принадлежит классу С1, а ее
производная равна 1/z. Следовательно, функция х -» In (л: + iy)
дифференцируема на прямой при у фЬ и ее производной
является функция х —* 1 /(х -f- iy) ■ Отсюда следует, что первый
интеграл в (IV,9; 99) равен
J{0№(x + iy)]xxZ+AA. (IV, 9; 100)
Так как \х-\- iA\ = \x — iA\, то логарифм модуля исчезает,
и выражение (IV,9; 100) будет равно f(0)г(ф2 — фО, где через
Фг обозначен аргумент точки А -f- iy, a ■ через ф1 ■— аргумент
точки —A -f iy. Если устремить у к 0, то. эти аргументы будут
стремиться соответственно к 0 и л и, следовательно, первый
->
интеграл будет сходиться к — iitf(O).
Рассмотрим теперь второй интеграл. При у, стремящемся
-> ->
к 0, функция х -> ~ просто сходится к функции
7(х)-Т(о)
jt_>j_i_j—i-i—i- всюду, кроме начала координат, где, впрочем,
последняя функция не определена. Поэтому можно сказать, что

§ 9. Частные свойства мер Радона
741
рассматриваемая функция просто сходится почти всюду к этой
функции. Кроме того, она мажорируема по норме функцией
х-» " || ' которая является неотрицательной и
интегрируемой. Последнее вытекает из того, что функция х —>
^ jlllj—ll_!± мажорируема функцией JL[-L-!—' v ;" - =—-,
|*| | ж Г 1*1
а последняя не превосходит постоянной, умноженной на 1/| х \ ~а
при 1—а<1. Из теоремы Лебега следует, что переход
к пределу для второго интеграла оправдан и что при у,
стремящемся к 0, он сходится к интегралу
J fM-fto)^ (IV, 9; 101)
\-А,+А{
Поскольку подинтегральная функция интегрируема, ее
интеграл совпадает с ее интегралом в смысле главного значения
Ко"ши, а это в силу нечетности l/х дает
v.p. J %^*-f(0)v.p. J ~ = v.p. { ttfdx.
1-Д+Л1 I-Л, +A\ \-A,+A\
(IV, 9; 102)
Складывая теперь оба предела, найденные для двух
интегралов в (IV, 9; 99), получаем требуемый результат.
Если у стремится к 0 по значениям <<0, то фг также
стремится к 0, ф1 стремится к —л, а величина (IV, 9; 100) стре-
мится к -\-inf(0).
Замечание. Если изложенные результаты применить
к скалярной непрерывной функции / с компактным носителем
на вещественной прямой, то в этом случае хотелось бы
сказать, что мера dxj(x + iy), зависящая от параметра у, при у;
стремящемся к 0 со знаком е, широко сходится к мере
v. p.(dx/x)+ е/яб. Однако этого делать нельзя, поскольку
функция l/х не является локально интегрируемой относительно их,
а следовательно, v.p.{dx/x) не является мерой Радона.
Впрочем, предыдущая сходимость имеет место не для всех
непрерывных функций f с компактным носителем, а лишь для
дифференцируемых функций или функций, удовлетворяющих
некоторым дополнительным условиям в начале координат.
В теории распределений можно увидеть, как
интерпретируется предыдущий переход к пределу.

742
Гл. IV. Интегральное исчисление
§ 10. КРАТНЫЕ ИНТЕГРАЛЫ НА R" . ДЛИНЫ, ПЛОЩАДИ И ОБЪЕМЫ
В КОНЕЧНОМЕРНОМ АФФИННОМ ЕВКЛИДОВОМ ПРОСТРАНСТВЕ.
ЗАМЕНА ПЕРЕМЕННЫХ В КРАТНЫХ ИНТЕГРАЛАХ НА R"
Формула (IV, 9; 72) может быть обобщена на кратные
интегралы на R" относительно меры dx = dx\dxi ... dxn.
Теорема 102. Пусть О и Q — два открытых множества
из R" и £— гомеоморфизм Q на О, принадлежащий вместе со
своим обратным гомеоморфизмом классу С1. Пусть f —
непрерывная на О функция с компактным носителем и значениями
в банаховом пространстве F. Тогда имеет место формула
JJ ... J / (х) dx = J" J" ... J" f (I (/)) I det (Г (0) I dt, (IV, 10; 1>
о ^
в которой через dx обозначено dx\dxi. . . dxn, а через dt
обозначено dt\d.t2 ... dtn; что же касается det£'(/), то это —
якобиан отображения £ в точке /.
Доказательство. При п — 1 якобиан есть не что иное,
как производная, а рассматриваемая теорема переходит в уже
доказанную теорему 94. Поэтому дальнейшее доказательство
можно будет провести по индукции.
Предположим, что теорема верна для кратного интеграла
порядка п— 1; докажем ее справедливость для кратного
интеграла порядка п ^ 2.
Доказательство в одном частном случае.
Функция £ определена системой п функций |ь £г, •••, in от "
переменных t\, t2, ..., tn. В рассматриваемом частном случае
мы будем проводить доказательство, предполагая, что
функция g,- равна'|i(0 = tj. По теореме Фубини можно записать
J J ... J" f(x)dx= J" da J" ... J" f(xu ..., хг_,, a, xi+u ..., xn)X.
О 0(a)
Xdx{ ... dxt-t dxt+l ... dxn, (IV, 10; 2)
где (У(а) является множеством точек (х\,... ,Xi_\,xi+i,... ,хп)
из R""1, таких, что (Х\,... ,x,_i, a, xi+u ... ,х„)е О. Множество
О {а) является некоторым открытым множеством пространства
R"-1 (сечение множества О гиперплоскостью Xi = а,
совпадающей с R""1). Интегрируемая функция имеет компактный
носитель на О (а), поскольку этот носитель лежит в компакте,
являющемся пересечением гиперплоскости с компактным носи-
телем f в О.

§ 10. Кратные интегралы на Rn
743
По предположению индукции, мы можем с помощью
замены переменных преобразовать {п—1)-кратный интеграл на
О (а). Отображение
Vl> ...» tj-\> tj + i, ..., tn)—>\X\, ..., ЛГ^_1, Xi + i, ...> Xn),
где xk—lk(ti,...,ti-u a, tj+u. . .,/„),£= 1,... ,t — 1, t'-f 1,...,«,
является, вместе со своим обратным отображением,
гомеоморфизмом, принадлежащим классу С1, множества Q(a) на,
О (а), где Q(a) — открытое множество точек (tu ..., ^_ь
ti+u...,tn) из R"-1, таких, что (/ь •••, *j-i, Mj+i, ...,/„)<= Q.
При этом
j ... j f{x)dx1 ... с?лгг_! dxi+l ... cfx„ =
-J... JfttW)
0(a)
D{xv..., x,_v *,,,..., xn)
2(a)
X
°('i.--</-r'/+i <»)
Xdt, ... dtHldtl+1 ... dtn. (IV, 10; 3)
Остается подставить это выражение в (IV, 10; 2). Однако,
так как xt = tj, то
D(x, х,_,, х,..,..., х„) , .,i4-i D (x., x0, ..., х„)
\i ,_L i+A ^.=а(_1)«+/ U 2 ^__ (IV,10;4)
/>(<,,.-<,_,, </+1,...,<в) ^ ' />(*,, <2 tn)
а, значит, модули обоих определителей одни и те же.
Окончательно по формуле Фубини получаем
JJ ... J7(x)dx =
= J da J ... J T(E (/l ..., //_„ a, t,+u ..., /„)) X
Q<a)
XI detfc' (/„..., //-j, a, //+j, ...,/„) | d/, ... dtHi dtl+i ... dtn =
= //•■• \l{l{t))\te4'{t)\dt, (IV, 10; 5)
Q
чем и заканчивается доказательство формулы (IV, 10; 1) в этом
частном случае.
Доказательство общего случая. Пусть т —
некоторая точка Q. Поскольку % и £-1 принадлежат классу С1, то
в этой точке detl'(t) отличен от нуля, а значит, существуют
хотя бы один индекс i и один индекс /, такие, что частная' про-
изводная -jjj— (т) ф 0.

744
Гл. IV. Интегральное исчисление
Рассмотрим теперь отображение 6г, определенное по
формулам
Ui = ti, 1ф /,
и -lit t M (IV. Ю; 6)
Якобианом этого преобразования в точке % является не
равная нулю частная производная dlJdtj. Согласно теореме о
неявных функциях, существует такое открытое множество Qt,
содержащее т, что отображение 8Т является гомеоморфизмом
(принадлежащим вместе с обратным гомеоморфизмом классу
С1) этого множества Qx на открытое множество °UX из Rn.
Уравнения (IV, 10; 6) при заданном у — (уи у2,..., уп) из °UX
могут быть разрешены: ti=yu l¥=j, и tj=r\j(yi, y2, ■ ■ ■, Уп),
где rij принадлежит классу С1. Пусть Ох — образ Qx при
отображении |. При переменном х открытые множества Ох
образуют покрытие С? и, в частности, покрытие компактного носи-
->
теля К функции f. Но тогда обязательно среди них найдется
конечное число множеств, покрывающих К. Обозначим эти
множества через 0Xi, i'g/.
Рассмотрим теперь разложение единицы yt относительно
этого конечного покрытия К- Можно написать:
jj* ... lHx)dx= J Jj* ... lyt(x)f(x)dx. (IV, 10; 7)
О isl 0X
Теперь отображение | множества йт. в 0Х{ может быть
разложено на два С'-диффеоморфизма, а именно: | = (|°
обТЛ'^бг^ Первый диффеоморфизм QX[ определен формулой
(IV, 10; 6), а второй £,==go07. может быть записан в виде
(УиУ2, ■ ■ ■, Уп)-*(хи х2,..., хп), где
Хъ = 1АУи •••> У 1-й 41 (Уи Уъ •••> Уп)' Уi+i Уп), k=£i,
(IV, 10; 8)
xt = yt.
Теперь можно воспользоваться уже изученным случаем, ибо
гомеоморфизм £°8т~. имеет такой же вид, как и в первом
случае. Поэтому можно записать формулу
/ J • ■ • J Yi (*) Т(*) dx =
= J" J" ' • • J" Y< в И ? & (i/)) I det ^ <*) 1rf^ <IV' 10« 9>
<4,

§ 10. Кратные интегралы на R™
745
Гомеоморфизм 8Т множества QX{ на cUxt имеет такой же,
и даже более простой, вид, поскольку здесь имеется лишь
замена относительно одной из переменных. Поэтому
J J ... J yt{x)T{x)dx =
= J J ... J yt (I (0) fa {t)) | det l\ (0T. Щ11 det 0^ (t) | dt.
(IV, 10; 10)
Из формулы умножения якобианов (следствие 3 теоремы 11
гл. II) теперь следует, что
| det % (0t| Щ | • | det Q>X{ (t)\=\ det Г (0 I-
Поэтому
1 J ••• J" \i(x)f{x)dx =
oXs
■= J J ... J yt(l (0) 7(1 (0) I det E' (0 | df. (IV, 10; 11)
Суммируя по различным значениям i, получаем (IV, 10; 1),
и теорема полностью доказана.
Замечание. Предположение биективности |, очевидно,
необходимо. Так как отображение t-*~x = t2 не является
гомеоморфизмом ]—1, +1[ на [0, 1[, то в случае одной переменной
J 2\t\dt = 2фl= j dx. (IV, 10; 12)
1-1,+1[ (0,1[
См. по этому поводу формулу (IV, 10; 23г). Напротив, в весьма
частном случае одной переменной, рассмотренном в теореме 93,
не было необходимости предполагать, что | является
гомеоморфизмом, и, положив х = t2, мы получим формулу
+ 1 +i
J 2tdt= J dx = 0. (IV, 10; 13)
-i +i
Следствие 1. В условиях теоремы образ меры
\tet\'(t)\dt при отображении \ на Q является мерой dx =
= \{x)dxuaOl).
') Может показаться странным применение различных букв х и t, тем
более что О и Q лежат в одном и том же пространстве Rn. Однако из-за
формулы (IV, 10; 1) такая запись удобна, поскольку | входит в формулу
t-*-x = g(?). Позже, в следствии 4 и после следствия 5, мы будем
применять одну и ту же букву. См. примечание на стр. 443.

746
Гл. IV. Интегральное исчисление
Доказательство. В самом деле, если формулу
(IV, 10; 1) применить к скалярной непрерывной функции /
с компактным носителем, то мы придем к определению образа
меры.
Замечание. Поскольку £ является гомеоморфизмом, то,
естественно, образ dx при отображении £-> равен |det|'(0|^-
Образ dt при отображении £ равен |det(i—')'(л:) \dx.
В соответствии с обозначениями, введенными на стр. 627,
можно будет писать dx = d(£,(t)) = |det £,'(t) \dt.
>
Следствие 2. Пусть f — некоторая функция, определен-
->
ная на О, со значениями в банаховом пространстве F. Для того
->
чтобы f была интегрируемой по мере dx, необходимо и
достаточно, чтобы функция t-*7(£(0) I det £'(/) | была
интегрируемой относительно меры dt, и тогда будет иметь место
формула (IV, 10; l)^1).
Это утверждение является значительным обобщением тео-
ремы', в которой функция / предполагалась непрерывной я
имеющей компактный носитель.
Доказательство. Следствие 1 позволяет применить
теорему 60: j(х) является dx-интегрируемой тогда и только
тогда, когда f(£(0) будет (| det £'(/) | dt) -интегрируемой. Согласно
теореме 51, это будет тогда и только тогда, когда df-интегрй-
руема функция f(l(t)) |det£'(0 I-
Следствие 3. Пусть А — часть Q, измеримая по мере
Лебега в R". Тогда ее образ \(A)czO измерим по мере
Лебега и имеет меру, равную | rfjc = Г | det (£' (/)) | dt.
НА) А
Для доказательства достаточно применить формулу
(IV, 10; 1) к характеристической функции множества 1(A).
Следствие 4. Мера Лебега dx = dx\dx2 ... dxn на
векторном пространстве R" инвариантна относительно любого
сдвига R". Мера подмножества А из Rn равна мере его
сдвигов. Другими словами, какими бы ни были элемент а из R№
и сдвиг х>: х^>х-\-а, имеем %->(dx) = dx.
') На этот раз мы берем меры dx и dt, т. е. одну и ту же меру в R",

§ 10. Кратные интегралы на R™
747
Доказательство. Якобиан сдвига £ = т->, где £(Л =
а
— t-{-а, равен 1 в любой точке пространства R".
Позже мы увидим, что мера dx, с точностью до множителя
пропорциональности, является единственной мерой,
инвариантной относительно сдвигов: любая комплексная мера Радона на
JR", инвариантная относительно сдвигов, имеет вид cdx, где
с — некоторая комплексная постоянная. Более общо, любая
мера Радона на R" со значениями в нормированном векторном
->
пространстве Е, инвариантная относительно всех сдвигов, имеет
-> ->• *■
вид с dx, где с — фиксированный вектор из Е.
Следствие 5. Пусть | — линейное отображение
пространства R" в себя. Если А—множество из R", измеримое по мере
Лебега в R", то его образ |(Л) также измерим по мере Лебега
и, кроме того, (мера |(Л)) —|Д| [мера А), где А—
определитель линейного отображения £.
Доказательство. Так как якобиан линейного
отображения является постоянной величиной, равной А, то достаточно
применить следствие 3; в нем предполагается, что £ является
гомеоморфизмом, а, значит, А Ф 0. Однако результат остается
верным, если А = 0, поскольку здесь мера 1(A) равна нулю,
ибо £(Л) содержится в векторном подпространстве
пространства R" размерности <л (см., например, следствие 1 теоремы
]022).
Здесь мы получаем новое важное истолкование модуля
определителя линейного отображения: [ А [ = мера для
каждого измеримого по мере Лебега множества А. Пользуясь
языком следствия 1, мы можем сказать, что образ меры |A|dx
при отображении | является мерой dx или образ меры dx при
линейном отображении | с отличным от нуля определителем
|Д| является мерой уд-г dx. (Если А является измеримым по
мере Лебега множеством R", то его мера относительно dx
должна разняться мере его образа 1(A) по мере образа Z,(dx).
Это действительно так, поскольку | (dx) = угт dx и поскольку
мера 1(A) по dx равна определителю |А|,. умноженному на
меру А.)
Если | является гомотетией с отношением k, то мера |(Л)
по мере Лебега равна |Д| = |&|", умноженному на меру А:
мера kA = | k Г X мера А.

748 Гл. IV. Интегральное исчисление
Следствие 52. Мера Лебега п-параллелепипеда1) в Rn
-> ■*■ >
с вершиной а, определенного векторами Хи Хг, ..., Хп, равна
модулю определителя этих векторов.
Пусть Xjj, j= 1, 2, ..., п, — координаты векторов Xi.
Определителем этих векторов является, по определению,
определитель, составленный из чисел Хц.
Рассмотрим теперь линейное отображение £, преобразую-
•> -*■
щее г'-й вектор et канонического базиса R" в вектор Х{. Так
>
как векторы et определяют /г-параллелепипед объема 1 (этот
параллелепипед является произведением [О, 1]Х[0, 1]Х ■ ■ ■ Х[0. 1]>
а, следовательно, его мера равна /г-й степени меры Лебега
отрезка [0, 1] прямой R, т.е. равна 1), то из следствия 5
вытекает, что искомый объем равен |det£| —модулю определителя
п векторов Х^
Следствие 6. Пусть а — некоторая точка Q, А — часть
Q, измеримая по мере Лебега. Тогда отношение мер Лебега
множеств £(Л) и А сходится к |det£'(a)|, когда множество А
равномерно стягивается к точке а.
Переменное множество А мы называем равномерно
стягивающимся к а, если точная верхняя грань расстояния от а до
точек множества А стремится к 0.
Доказательство. Запишем разность е = "мера л
— | det l'(a) | в виде
JJ ... J" det [ (Г (0) I dt
e =
dt
-|det-|'(a)l =
A
J J .... J (| det (Г (0) I — I det (Г (a)) j ) rf^
Я ".-J
dt
(IV, 10; 14)
- ') В аффинном пространстве E над полем вещественных чисел р-парал-
лелепипедом с вершиной а, определенным векторами Xit Х2 Хр, назы-
W-. -> -> ->
вается множество элементов из Е вида а + t}Xj + t2X2 + • • ■ + tpXp, где
tt e [0, 1}, i = l, 2, ..., р. Векторы эти не обязательно должны быть
независимыми. Число р может быть больше размерности Е. В настоящем следствии
задано п векторов в R™. Если они зависимы, то следствие применимо, и мера
«-параллелепипеда будет равной нулю.

§ 10. Кратные интегралы на R" 749
отсюда следует, что эта разность допускает оценку:
| е | < sup 11 det (Г (0) | -1 det (£' (а)) 11. (IV, 10; 15)
Из полученного неравенства вытекает утверждение леммы,
если учесть, что по условию | принадлежит классу С1 и что,
следовательно, функция /->|det£'(/) | непрерывна.
Замечание. Доказанное следствие дает важную
интерпретацию для |det(|'(a)) I. Интуитивно это можно представлять
следующим образом. Пусть еи е2, ..., еп — канонический базис
R". Его образ при производном отображении £'(а) образован
векторами _£|_/„\ dg , , dg / ■, Если в качестве мно-
3/, к h dt2 к >' ••" 3/„ к h
жества А взять малый /г-параллелепнпед с вершиной в а,
->
определенной векторами kex при малом k, то его образ будет
«приближенно» представлять собой /г-параллелепипед с верши-
->
ной |(а), определяемый векторами k-~-{a). Отношение
объемов этих /г-параллелепипедов равно модулю определителя
векторов -щ-(а), т. е. | det (£'(«)) |.
Однако здесь мы очень далеки от строгого доказательства
следствия 6.
Пример замены переменных. Вычисление интеграла в полярных
координатах. Займемся сначала полярными координатами на
плоскости. Здесь мы имеем дело с отображением Р: (г, ф) —►
—> (х, у) плоскости R2 в R2, изученным в гл. III на стр. 242,
х —г cosy, у = г sin ср. (IV, 10; 16)
Якобиан отображения Р равен г. Если мы перейдем к
сужению отображения на открытое множество Q, определяемое
неравенствами г > 0 и 0 < ф <С 2я, то Р будет гомеоморфизмом,
принадлежащим вместе со своим обратным гомеоморфизмом
классу С1 и отображающим Q на свой образ О, являющийся
в R2 дополнением к множеству у = 0, х ^ 0. Пусть теперь f —
некоторая функция (x,y)-*f(x,y), определенная на R2, со зна-
->
чениями в банаховом пространстве F. Она будет интегрируемой
на R2 тогда и только тогда, когда она интегрируема на О; при
этом ее интегралы на R2 и О будут одними и теми же,
поскольку дополнение к О имеет нулевую меру Лебега в R2.

750
Гл. IV. Интегральное исчисление
Согласно следствию 2, эта функция интегрируема на О
тогда и только тогда, когда будет интегрируемой на Q
функция (г, ф)-»/(г cos ф, г sin ф)г, причем справедлива формула
■ J" J" f(x, y)dxdy = J" J" f"(rco$<p, r sin <p)rdr flf9. (IV, 10; 17)
В этой формуле интеграл по Q можно заменить на
интеграл по области Q, т. е. по множеству, определенному
расширенными неравенствами г ^ 0, 0 ^ ф ^ 2л, ибо по мере dr dq>
мера множества Q — Q = Q, определяемого соотношениями
{г = 0, 0 sg: ф ^ 2л или г > 0, ф = 0, или г > 0, ф = 2л}, равна
нулю.
Часто бывает выгодно для вычисления якобиана применить
геометрический метод. Выполним эти вычисления на примера
полярных координат в трехмерном пространстве R3. У нас
имеется" отображение Р пространства R3 в R3, определяемое
по формулам m(r, 6, ф)—>М(х, у, z), где
х = г sin 6 cos ф,
у = г sin 6 sin ф, (IV, 10; 13)
'2 ==Г COS 6.
Если ограничиться открытым множеством
Q = {г, 9, ф; г > 0, 0 < 0 < л, 0 < <р < 2л},
то Р будет представлять собой С'-диффеоморфизм множества
Q на его образ — открытое множество О из R3, являющееся
дополнением к полуплоскости {x,y,z;y — 0,х^ 0}.
Как и в предыдущем случае, СО и Q = Q — Q имеют
нулевую меру.
Частная производная дР/дг в точке m = (r, 9, ф) является
единичным вектором i, направленным по радиус-вектору точки
>
М = (х,у,z) = P{m). Частная производная дР/dQ является век-
-> ->
тором г/, где / — единичный вектор касательной к меридиану
в точке М в направлении возрастания значений угла 9. Част-
ная производная дР/ду является вектором г sin 9 k, где k —
единичный вектор, направленный по параллели, проходящей
через М, в направлении возрастания значений ф. Поэтому
в дифференциальных обозначениях можно написать формулу
dM = P' (m)dm =7 dr + rfdQ-\- r sin 6 kd<p. (IV, 10; 19)

§ 10. Кратные интегралы на R"
751
Якобианом отображения Р в точке m = (r, 0, ф) является
дР дР дР
определитель системы трех векторов -=j—. -gjf, -gr- по
отношению к векторам базиса R3. Этот определитель равен произ-
ведению г2 sin Э на определитель системы векторов i, /, k.
Последний же, как определитель системы трех единичных
взаимно перпендикулярных векторов, равен ±1 ')• Поэтому имеем
det Р' (г, 6, <р) = ± г2 sin Э Ф 0.
Формула замены переменных в полярных координатах
в трехмерном пространстве имеет, таким образом, следующий
вид:
->
/ [х, у, z) dx dy dz =
/(гзтЭсоБф, r sin Э sin ф, r cos Э) г2 sin Э dr d% dy.
(IV, 10; 20)
ш
-ш
Обобщение теоремы 102 и следствий 1, 2, 3, 6. Теорема 102
и следствия 1, 2, 3 остаются справедливыми, если | является
гомеоморфизмом, принадлежащим классу С. Обратный
гомеоморфизм I"1 при этом не обязан принадлежать классу С1, т. е.
det|'(/) для некоторых значений (ей может обращаться
в нуль. Следствие 6 остается справедливым, если | является
некоторым отображением класса С1 и не обязательно
представляет собой гомеоморфизм. Эти факты мы примем без
доказательства. Из них теперь можно получить следующую теорему:
Теорема 102г. Пусть | — некоторое отображение класса
О открытого множества Q из Rn в R". Обозначим через А
множество точек Q, в которых якобиан отображения | равен
нулю. Тогда его образ \(А) относительно меры Лебега имеет
меру нуль eR".
Доказательство. Ограничимся для простоты случаем,
когда Q = Rra. Меру Лебега некоторого множества будем
обозначать через mes. Пусть aei Согласно следствию 6,
распространенному, как только что было сказано, на
произвольное отображение £ класса С, существует при заданном е >"0
-> > >
') Это означает, что параллелепипед, определяемый векторами i, /, k,
имеет объем, равный 1. Конечно, этот факт «известен», но не забывайте, что
до построения теории интегрирования теория мер объемов не была строго
обоснована! Это будет сделано в этом параграфе.

752
Гл. IV. Интегральное исчисление
такой открытый шар Ва с центром в а, что для любой части
В шара Ва, измеримой по мере Лебега в R", имеет место
неравенство
mes£(B)<emesB. (IV, Ю;21)
Пусть Л' — компакт множества А. Тогда Ва, а е К,
образуют открытое покрытие К. Для него существует некоторое
конечное подпокрытие, например В\, В2 BN. Положим
В\=К[\ВХ, В'2 = КПВ2ПСВ'и В^КПВзПСВ'^СВ^ и т. д.
Тогда множества В\, В2 B'N, являющиеся пересечениями
измеримых множеств, будут измеримыми. Кроме того, они не
пересекаются и образуют покрытие К. Но тогда \{В\), \{В2), ...
..., i,(B'N) образуют покрытие £(/().
Поэтому имеем
N N
mes|(/C)<S mes|(fl{)<e2mes(fif) = emes/C. (IV, 10; 22)
Так как е произвольно, то это означает, что mes|(/C) = 0.
Заметим теперь, что множество А замкнуто, поскольку оно
является прообразом множества {0} при непрерывном
отображении t—► detg'(/) пространства R" в R. Если через Кт обо-
->
значить пересечение А с шаром ||х|| ^ т из Rn, то Кт будет
компактом А, а само А — объединением Кт1)- Каждое
множество |(/Ст) имеет, как мы только что видели, нулевую меру.
Множество i(A), представляющее собой объединение
счетного числа множеств \{Кт) нулевой меры, имеет меру,
равную нулю.
Следствие 1. Пусть V — многообразие класса С1,
счетное в бесконечности. Пусть Н — отображение класса С1 Мно-
жества V в R". Если размерность V ^ п—1, то его образ
H(V) имеет нулевую меру Лебега в R".B частности, если
множество V является многообразием класса С1 в R " размерности
s^.n — 1, то оно имеет меру, равную нулю.
Доказательство. Пусть / — размерность многообразия
V, I ^ п—1. Пусть Ф: (У-+Ф((У) — карта многообразия V.
Тогда сложное отображение #°ф является отображением О
в R", принадлежащим классу С1.
Если положить '
I (t, и) = {Но Ф) (*) для te=0, «e R"-',' (IV, 10; 23)
') В этом месте использовано упрощенное предположение Q = R". Оно
позволяет непосредственно показать, что А является счетным объединением
компактов. Однако утверждение справедливо и в общем случае.

§ 10. Кратные интегралы на R"
753
то рассматриваемое отображение продолжается до
отображения класса С1 открытого множества б?ХКп_г из R™ в
пространство R™.
Так как дуди ^ 0, то якобиан этого отображения будет
равен нулю и, следовательно, согласно теореме, образ Я»
оф(С) = 1-((У X Rn~l) имеет меру Лебега, равную нулю. Это
означает, что образ при отображении Я образа Ф((У) карты
Ф имеет нулевую меру. Пусть теперь К является некоторым
компактом V. Так как он может быть покрыт конечным
числом образов карт, то его образ при отображении Я заведомо
имеет нулевую меру. Поскольку V, по предположению,
является объединением счетного множества компактов, то теперь
ясно, что образ V при отображении Я также имеет меру,
равную нулю.
Замечание. Не следует думать, что этот результат
останется верным для многообразия класса С0, т. е. топологических
не дифференцируемых многообразий. Если, например, в
плоскости мы рассмотрим кривую Жордана, т. е. множество, гомео-
морфное отрезку прямой [а, Ь], и если гомеоморфизм Я отрезка
[а, Ь] на эту дугу только непрерывен, но не дифференцируем,
то мера этой кривой Жордана по мере dx<8>dy не обязательно
равна нулю. Непрерывное отображение Я отрезка R в R"
является путем в R" в смысле определения, данного на стр. 90.
Путь же, если он только непрерывен; т. е. не дифференцируем,
может иметь образ, целиком заполняющий куб в R", с
мерой >0.
Следствие 2. Пусть g — отображение класса С
открытого множества Q из R" в открытое множество О из R".
Обозначим для каждой точки х<=(? через v(x) число точек
прообраза £"'({*})■ Отображение g является собственным
относительно меры \&e.t%(t)\dt множества Q тогда и только тогда,
когда v локально dx-интегрируема в О; в этом случае образ
меры |detg'(0|<# множества О. при отображении \ является
мерой v(x)dx множества 0. При этом, если f — функция,
определенная на О, со значениями в банаховом пространстве F,
то функция v(x)f(x) является dx-интегрируемой тогда и только
тогда, когда dt-интегрируема функция f (£(/)) ]detl'(t) \,
причем имеет место равенство
, JJ ... J7(*)v(*)d*=jj ••• J" Hi (0)1 det Г (01 dt.
в Q
(IV, 10; 23a)
Полагая здесь v=l, мы снова получим следствия 1 и 2
теоремы 102.

754
Гл. IV. Интегральное исчисление
Измерение объемов в аффинных евклидовых
конечномерных пространствах
Пусть Е— аффинное евклидово пространство размерности
N. Возможность измерения объемов в таком пространстве
кажется интуитивно очевидной; остается обосновать ее со всей
строгостью.
-> -> -»
Пусть 0, еь е2, ..., eN — ортонормированная система
координат в Е. С ее помощью можно отождествить Е с RN и таким
образом определить меру как тензорное произведение dx =
= dxl<8)dx2<S> ... <S>dxN.
Более строго, следует говорить, что выбор системы
координат определяет линейную биекцию Р: (х\,х2,... ,xN)-*a -\-
-> >
-\-Xiei-\- .. . + Xb-eN пространства .RN на £ и что при этих
условиях можно определить образ меры P(dx) при отображения
Р меры Лебега dx = dxxdx2 ... dxn пространства RN.
Допускаемая нами вольность речи заключается в том, что вместо
P(dx) мы пишем просто dx.
Теорема 103 (основная теорема измерения объемов).
Пусть Е — аффинное евклидово пространство размерности N.
Мера, определенная в ортонормированной системе координат
по формуле dx = dxxdx2 ... dxN, не зависит от выбранной
системы координат.
-> > >
Доказательство. Пусть а, в\, е2, ..., eN — некоторая
> -> . -*■
ортонормированная система координат, a b, fh /2, ■■■» /л- —
другая ортонормированная система. Координаты х и у одной
и той же точки в этих системах координат связаны формулой
замены переменных:
N
yi=ai + 1t m„xh
''=' (IV, 10, 24)
а{ = {а — Ь\Т{), mi,={el\f{).
Согласно следствию 1 теоремы 102 о замене переменных
в кратных интегралах имеем: dy — \A\dx1), где А —
определитель матрицы JC, составленной из чисел т^. Однако
определитель ортогональной матрицы равен ±1, так как она
удовлетворяет условию М %Jl = /, где" lJC — транспонированная,
') Здесь допускается отмеченная вольность речи. На самом деле две
системы координат определяют две биекции Р и Q пространства RN на£иР =
— Q°J(, где Л является отображением RN на RN, определенным по
формуле (IV, 10; 24). Теперь P(dx) = Q(Jl(dx)) = Q(\&-l\dy), или \b\P{dx) =
= Q(dy), что мы записали в виде |A|d* = dy.

§ 10. Кратные интегралы, на R"
755
а / — единичная матрицы, и поэтому А2— 1 '). Абсолютная
величина этого определителя равна I. Отсюда следует, что dx =
= dy, и теорема доказана.
Итак, в аффинном евклидовом пространстве существует
вполне определенная мера Радона ^0, которую мы будем
обозначать через dx. Эта мера инвариантна относительно сдвигов
и, более общо, относительно движений пространства, т. е.
относительно аффинных обратимых преобразований, сохраняющих
скалярные произведения. Так как эта мера в ортонормирован-
ной системе координат равна dxxdx2.. .dxN, то к ней
применимы следствия 5 и 5г теоремы 102.
Пусть теперь А — некоторое измеримое множество из Е. Его
объемом в евклидовом пространстве называется его мера
относительно dx. Если А является прямоугольным
параллелепипедом со сторонами аь а2, ..., aN, то его объем, очевидно, равен
произведению ах а2 ... aN, если выбрать ортонормирозанную
систему координат, базисные векторы которой параллельны его
сторонам.
-> ■> ■>
Теорема 103г. Если Х\, Х2, ..., XN являются системой N
векторов с общим началом, то объем N-параллелепипеда,
образованного этими векторами, вычисляется по формуле:
К2 =
№Ui) (*,1*2)
(*il*w)
(Х2|Х.) (Х2\Х2) ... (X2\XN)
(XN\X,) (XN\X2)... (XN\XN)
(IV, 10; 25)
Доказательство. Выберем ортонормированную систему
координат. Мы знаем, что К2 является квадратом определителя
системы N векторов (следствие 52 теоремы 102). Поэтому, для
того чтобы получить предыдущую формулу, достаточно
вычислить по правилам умножения определителей произведение
определителя этой системы на себя.
Эта формула, очевидно, удобнее, чем формула,
использующая определитель п векторов относительно некоторой системы
координат, поскольку она включает лишь скалярные
произведения и потому не зависит от какой-либо системы
координат.
') Невольно чувствуешь большой соблазн доказать это свойство
определителя ортогональных матриц, опираясь на геометрическое понятие объема!
Однако понятие объема не дано свыше и должно быть введено со всей
строгостью с помощью той же теории интегрирования! Поэтому надо иметь
алгебраическое доказательство свойства Д = ±1.

756
Гл. IV. Интегральное исчисление
Измерение длин в аффинном евклидовом пространстве
Аффинное евклидово пространство нормировано, а, значит,
в нем можно измерять длины кривых (см. стр. 701). Если
t-r*-M(t) при t, пробегающем некоторый интервал Rt прямой R,
является параметрически заданной кривой, принадлежащей
классу С1, то длина этой кривой равна интегралу [ || М '(t) \\dt
(формула (IV, 9;402)), равному j {AV^t) \ wXt))''2 dt. Если
Xi — составляющие М в ортонормированной системе координат,
то это дает | 1/ ^ х'2 (?) dt.
R, i=\
Измерение n-мерных площадей в линейном многообразии
размерности п аффинного евклидова
конечномерного пространства
В аффинном евклидовом конечномерном пространстве мы
смогли определить, с одной стороны, длины дуг кривых,
а с другой,-—меры объемов. Однако нам бы хотелось
определить все промежуточные величины — площади поверхностей и,
более общо, «-мерные площади «-мерных многообразий при
0 < « s£ N.
Займемся для начала случаем, когда F является линейным
«-мерным многообразием аффинного пространства Е. В этом
случае само F является некоторым аффинным евклидовым
пространством, и, следовательно, в F существуют меры объемов.
Если в F выбрать ортонормированную систему координат и
отождествить его с R", то эта мера равна dx\ dx2... dxn. Однако,
поскольку F является пространством п измерений, то вместо
слова «объем» мы будем употреблять слово «n-мерная
площадь», или «п-площадь-». Если F\ и F2— два линейных
многообразия одной и той же размерности «, то каждое аффинное
отображение F\ на F2, сохраняющее скалярные произведения,
переводит ортонормированную систему координат пространства
F[ в ортонормированную систему координат пространства F2,
а, следовательно, сохраняет «-площади. Каждое аффинное
отображение, являющееся подобием с отношением k, т. е.
отображением, умножающим длины на k и скалярные произведения
на k2, имеет якобиан относительно ортонормированных систем
координат Fi и F2, равный ±kn, а, следовательно, умножает
«-площади на \k\n. Если Хи Х2, ..., Хп — векторы из F с
общим началом, то n-мерная площадь определяемого ими «-парал-

§ 10. Кратные интегралы на R"
75Г
лелепипеда задается формулой:
№11.) №1*2) ... (f,if„)
&|Х,) (Х2\Х2) ...' (f2lf„)
s2 =
= det (A-, 1 A-,). (IV, 10;26>.
«, ;
(XnW (Xn\X2) ... (Xn\Xn)
Упражнение. Иногда полезно предыдущую формулу
записать в иной форме. Предположим, например, что речь идет
о двух векторах X и У. Тогда она запишется в виде
S2 = (/| /) (У | У) - (1 i У)2. (IV, 10; 27)■
В силу тождества Лагранжа ее можно переписать так:
2№К;-ед2, (IV, 10; 28)-
i. i
>
где Х{ (соответственно Уг) — координаты векторов X (соответ-
->
ственно У) относительно некоторой ортонормированной системы
координат. Таким образом, S9- является суммой квадратов
площадей параллелограммов — ортогональных проекций исходного
параллелограмма на плоскости, порожденные всевозможными
парами векторов базиса. Эта формула обобщается на п-мер-
ные площади при произвольном п.
Теорема 104. n-мерная площадь п-параллелепипгда
равна произведению (п—\)-мерной площади какого-либо из его
оснований на длину соответствующей высоты.
Доказательство, n-параллелепипед определяется своей
-> -> ' ->
вершиной и п векторами Х1г Х2, ..., Хп. Предположим
сначала, что эти п векторов линейно зависимы. Тогда п-мерная
площадь параллелепипеда равна нулю. Однако в этом случае
или же п — 1 векторов Х1г Х2, ..., Хп-\ зависимы, и тогда
(п—1)-мерная площадь основания равна нулю, или же они не-
-*•
зависимы, и тогда вектор Хп лежит в векторном подпростран-
стве Fn, порожденном векторами Хи Х2, ..., Хп-{, а, значит,.,
в нуль обращается высота. В обоих случаях утверждение
теоремы справедливо.
Предположим теперь, что исходные п векторов линейно
независимы. Рассмотрим основание параллелепипеда, определен-
-> -> ->
иое его вершиной и векторами Х\, Х<>, ..., Х„_,. Выберем та-
-*•
кой ортонормированный базис в F, в котором первые п — I:

758
Гл. IV. Итегральще исчисление
элементов лежат в векторном подпространстве Fn-\, порожден-
-> -> ->
ном векторами Х1г Х2, ■ ■■, Хп_и а n-й вектор базиса является
-> ->
единичным вектором еп, ортогональным к пространству Fn-i-
Далее, n-мерная площадь tt-параллелепипеда является модулем
определителя, составленного из п векторов относительно этого
базиса. Можно написать, что Xn — ln-\-Yn, где ортогональная
->• ■> ->
проекция |„ вектора Хп на Fn_t является линейной комбина-
■*->-> ■*->->->
цией векторов X], Х2, ..., Хп-Х, а длина вектора Yn = {Xn\en)en
-> ->• ■>
равна \{Хп\еп)\. Вектор Yn является г высотой параллелепипеда,
относящейся к выбранному основанию. В этом случае опреде-
-> -> ■>
Литель векторов Х\, Х2, ..., Хп является также определителем
-»• -> -> >
векторов Хи Х2, ..., Xn-i, Yп. Однако его последняя строка
-> ->•
состоит из элементов 0, 0, ..., О, (Хп\еп). Поэтому
определитель равен произведению определителя, составленного из век-
->• -> ->•
торов Х\, Х2, ..., Хп-Х, модуль которого является (п—1)-
-> ->
мерной площадью основания, на число (Хп\еп), модуль кото-
рого дает длину высоты Yn, чем и заканчивается
доказательство теоремы.
Следствие 1. n-мерная площадь п-параллелепипед'а, оп-
ределяемого п векторами Хи Х2, ..., Хп, не превосходит
произведения длин этих векторов. Она всегда строго меньше этого
произведения, кроме того случая, когда все векторы попарно
ортогональны.
Доказательство. Утверждение очевидно для п = 1.
Предполагая, что оно верно для п—1 векторов, докажем его
справедливость для п векторов.
tt-мерная площадь tt-параллелепипеда равна произведению
(п — 1)-мерной площади основания, порожденного векторами
-> -> -> -> ->
Хи Х2, ..., Хп^и на длину || У„ || высоты Y'„. По
предположению индукции, первый сомножитель не превосходит произведе-
■*->->
ния || XiHIl Х2||. .. || Хп-! || и строго меньше его, если векторы
Х1г Х2, ..., X„_i не являются попарно ортогональными. Второй
-> ->
сомножитель не превосходит \\Хп\\ и строго меньше его, если Хп
■ -*■ -*■ -*■
не ортогонален векторам Х1г Х2, ..., Xn-V чем и
заканчивается доказательство следствия.
Следствие 2. Пусть №/)1</<п l<j<n — квадратная
матрица, составленная из вещественных чисел и состоящая из

§ 10. Кратные интегралы на R"
75»
п строк и п столбцов. Тогда определитель Л этой матрицы
допускает следующую оценку:
| Д |< Vx2n +...+*?„ Vx221 + ... 4 -Xln • • • Vxlx + ...+ X\n.
(IV,10;282)
Для доказательства достаточно аналитически записать
предыдущий результат.
Замечание. В случае комплексных чисел Хц это
неравенство сохранится, если заменить Хц на | Хц \ , однако era
доказательство будет значительно сложнее. Неравенство
(IV, 10; 28г) было доказано Адамаром и нашло значительное
приложение в теории интегральных уравнений Фредгольма.
Теорема 105 (об ортогональной проекции площадей
гиперплоскостей). Ясли F и G — гиперплоскости евклидова
аффинного пространства Е размерности Л/, то (Л/ — 1) -мерная
площадь ортогональной проекции на G измеримого множества
А гиперплоскости F равна произведению площади А на косинус
острого угла, образованного гиперплоскостями F и G.
Доказательство. Можно считать, что F и G не
параллельны друг другу, так как в противном случае теорема
очевидна. Пусть Н — пересечение F и G. Размерность этого пере-
-> ->
сечения равна N — 2. Пусть / и g— единичные векторы про-
-> -> ■>
странств F и G, перпендикулярные Н и выбранные так, что они
составляют острый угол 0, равный по определению углу между
гиперплоскостями F и G (этот угол является также углом ме-
жду нормалями к F и G). Таким образом, (f\g) = cos 0 ^ 0.
Выберем в Н ортонормированную систему координат 0, hiy
-> -> ->->"-> ->
h2, ..., hN-2- Тогда 0, hx, h2, ..., hN_2, /образуют ортонорми-
-> -> -> ->
рованную систему координат в F, а 0, ht, h2, ..., hN^2, g—
ортонормированную систему координат в G. Введение
указанных систем координат отождествляет эти пространства с
Проекция F на G является аффинным отображением,
оставляющим неизменной точку 0, а, следовательно, определяется
некоторой матрицей относительно этих систем координат. Про-
■> -> ■>
екции векторов hb h2, ...,hN_2 совпадают с самими век-
-> ■>
торами, а проекция вектора / равна gcosQ. Следовательло,
матрица этого отображения является диагональной с элементами
1,1,..., cos 0. Определитель Д этой матрицы равен cos 0, и
потому результат вытекает из следствия 5 теоремы 102.

760
Гл. IV. Интегральное исчисление
и-мерная площадь л-мерного параметрического многообразия
Попытаемся теперь определить л-мерную площадь
л-мерного многообразия класса С1 аффинного евклидова
пространства Е. Мы не будем здесь строить общую теорию, как это мы
делали для длин и для объемов. Мы рассмотрим только случай
многообразия класса С.
1°) Пусть *¥: О—*х¥{0) — отображение класса С1
некоторого открытого множества О из R" в пространство Е.
Производное отображение W(u) в точке и из R" переводит
систему л векторов базиса R" в систему л векторов -т—• (и)
из Е, i= 1, 2 л. Она определяет некоторый
параллелепипед, л-мерная площадь которого D(u) определяется по формуле
^(M)=l/det(|i(M)|-^(«)). (IV, 10; 29)
По определению, n-мерная площасЬ_ n-мерного
параметрического многообразия класса С, определяемого отображением
W, задается интегралом
5=1 ... I D (и) йи = I ... j D (ы1( и2, ..., ип) dux du2 ... dun.
в в
(IV, 10; 30)
Причины, по которым мы дали такое определение, ясны.
Разобьем множество О на малые параллелепипеды со
сторонами, параллельными осям. Образ при отображении 4х
параллелепипеда с вершиной и и сторонами, параллельными осям,
длины du\, du2 dun является «приближенно» параллелепипе-
->
aw
дом с вершиной ^(и), определяемым векторами -г—(u)dult
-> ->
■■-д—(u)du2 -5—(u)dun, площадь которого равна D(u) X
У( du\ du2 <.. dun. Искомая площадь является «суммой этих
элементарных площадей», откуда и получается интеграл
(IV,10;30).
Теорема 106. n-мерная площадь параметрического
многообразия XV, определяемого по формуле (IV, 10; 30), не
изменится, если данное многообразие заменить эквивалентным
многообразием. Другими словами, если 4х i и W2 — отображения
класса С1 двух открытых множеств 0\ и 02 из R" в Е и если
..существует С1-диффеоморфизм Н множества 0\ на 02, такой,

§ 10. Кратные интегралы на R"
76 Г
что *Pi = 4*2 ° Н, то имеет место равенство
J ... J Я, (и) d« = J ... J Я2(и) rf«- (IV, 10; 31)
О, Oi
Доказательство. Пусть ai e d, а2 = Н(а\)<^02 и
jc = 4ri(ai) = ^(аг). Подпространство, порожденное л векто-
рами -у-1-(а^, имеет размерность ^л и равную л, если эта
векторы независимы. Обозначим через F л-мерное
подпространство, содержащее рассматриваемое подпространство.
Поскольку линейное отображение W[ (a,) является композицией ^2(^2)°
о Я'(а,), в которой H'(ai) есть биекция, то это
подпространство совпадает с подпространством, порожденным векторами
~д-^-(а2) (следствие 4 теоремы 11 гл. III). Выбирая в этом
векторном пространстве F произвольный ортонормированный •
базис, мы можем отождествить его с пространством к".
Если теперь мы положим Al=Dl(ai) и A2 = D2(a2), то-
множитель А\, определяющий площадь параллелепипеда, поро-
жденного векторами -г-1 (ctj), равен модулю определителя ли-
Otlj
нейного отображения ^{(ctj) пространства R" в R", а
множитель А2 равен модулю определителя линейного отображения
Ч"2(а2) из R" в R".
Соотношение *Р\ (ctj) = W2 (а2) ° Я' (ctj) означает, что между
определителями имеет место равенство
Dl(ai) = \detHf(a1)\Da(aa)'=\detH/(al)\Da(H(al)). (IV, 10; 32)
Так как это равенство справедливо для любого ai из (У\, то
из формулы (IV, 10; 1) замены переменных для кратных
интегралов следует, что имеет место равенство
а,
. J D2 (a2) da2 = j ... j" D2 (Я (a,) | det H' (a,) I йщ =
о,
= J ... J A (a,) da, (IV, 10; 33)
и, следовательно, оба интеграла, определяющие л-мерные пло*
щади для 4*1 и W2, равны между собой.
Пример. Поверхности в аффинном евклидовом
трехмерном пространстве. В этом случае обычно через и, v принято»

762 Гл. IV. Интегральное исчисление
обозначать координаты множества параметров OczR2, через
х, у, г— составляющие отображения -W по осям ортонормиро-
ванной системы координат в Е = R3, через А, В, С — якобианы:
ду_
ди
dz
ди
dz
dv
дх
dv
dz
. du
dx
du
dy
dv
dz
dv
A:
B==
,> dx dy dy dx
du dv du dv
(IV, 10; 34)
через E, F, G — величины:
->
E =
ffv
du
'-(#
G =
dv
=m+m+{ti
ffV_
dv
U# + 4£-* + -£-£. (IV. 10; 36)
du dv du dv
2 . Ldz\*
°=m+m+m
и через Я — то, что мы ранее обозначали через D. Согласно
(IV, 10; 27), имеем
(IV, 10; 36)
h = Veg.— f*,
а согласно (IV, 10; 28),
Я = У А2 + В2 + С2.
(IV, 10; 37)
,2°) Вернемся теперь к параметрическому многообразию V,
определенному отображением Ч*-.
Выражение D(u)du определяет некоторую меру Радона dS
на О. Если А является множеством из О, то меру этого
множества относительно меры Радона можно рассматривать как
«-мерную площадь сужения W на это множество. Если 4я
является собственным относительно этой меры dS, то образ при
отображении 4я этой меры Радона есть некоторая мера W(dS) ^
^0 в аффинном пространстве Е. Обычно через dS мы будем
обозначать меру на О или ее образ. Эта мера служит для
определения поверхностных интегралов. Если / является функцией,
определенной на Е, со значениями в банаховом пространстве F,

§ 10. Кратные интегралы на R™
763
то интегралом ... fdS1), по определению, называют
J ... lfdS=l ... J(f»V)dS= J ... [f(V(u))D(u)du.
о о
(IV, 10; 38)
Это — интеграл от f относительно образа меры 4?(dS), если
последний существует. Впрочем, если мы вернемся к ситуации
теоремы 106, то увидим, что если через dSi и dS2 обозначить
меры, определенные на ^0\ и 02 с помощью предыдущего
процесса относительно эквивалентных многообразий 4^1 и Ч'г, то
dS2 является образом H(dSi) меры dS^ при гомеоморфизме Я.
Об этом, действительно, говорит следствие 1 теоремы 102. Так
как
W, (dSt) = (W2 о Я) (dS,) = W2 (Я (dSt)) = V2 (dS2),
то ^(dSi) и y¥2(dS2) представляют собой одну и ту же меру
на Е (если они существуют).
3°) Теперь мы можем дать корректное определение
n-мерной площади произвольного параметрического многообразия
размерности п класса С1 в аффинном пространстве Е
размерности N.
Пусть V — многообразие (абстрактное или погруженное
в аффинное пространство) размерности п класса С. Пусть Я—
некоторое отображение V в Е класса С1, определяющее тем
самым некоторое n-мерное многообразие, параметрическое или
особое, класса С.
Пусть Ф. 0-*Ф(0)— некоторая карта многообразия V.
Тогда *F = Я ° Ф является отображением 0 в Е класса С1 и,
значит, можно определить n-мерную площадь dS<$, меры ^0 в (?.
Ее образ при гомеоморфизме Ф является мерой Ф(й5ф) на
открытом множестве Ф(0) многообразия V. Если теперь
рассмотреть две Карты этого вида, например Ф1 и Ф2, и если открытые
множества Oi(Ci) и Ф2{02) имеют непустое пересечение Q, то
можно через Qi и Q2 обозначить прообразы Q при
отображениях Ф1 и Ф2. Сужения Ф] и Ф2 на &! и Q2 определяют теперь
эквивалентные параметрические многообразия, поскольку
>) Как и для криволинейного интеграла (см. примечание на стр. 705),
надо было написать ... / dS — интеграл относительно параметрического
многообразия (Ч?). С другой стороны, символ кратного интеграла •••
совершенно не обоснован, поскольку нет и речи об интегралах относительно
тензорного произведения мер. Это, к сожалению, всего лишь некоторый прием,
позволяющий указать, что речь идет об интеграле на многообразии
размерности > 1.

764
Гл. IV. Интегральное исчисление
Я1,2==ФГ1 °Ф1 является гомеоморфизмом класса С1 (следствие 1
теоремы 33 гл. III) и поскольку Oi = Фг ° #i, 2. Сделанное выше
замечание показывает теперь, что мера dS<t>2 на 02 является
образом меры dSo, на 0\ при отображении #ii2 и что
образы этих мер, т.е. меры Oi (dS®,) и Ф2(й5ф,), в Q совпадают.
Рассмотрим теперь систему всех открытых множеств Ф(<У),
являющихся образами всех карт Ф на V. В каждом из этих
открытых множеств мы имеем некоторую вещественную меру
^0 <D(dS<& ), а в пересечении Q двух из этих открытых
множеств Oi (<?i) и Фг^г) меры Ф1 (dSo,) и Ф2(й5ф2),
определенные соответствующими картами Ф1 и Фг, совпадают. Значит,
мы находимся в условиях теоремы о кусочной склейке мер
(теорема 17) и можно утверждать, что на V существует
некоторая вполне определенная мера Радона, которая на каждом
образе карты Ф((У) совпадает с «-мерной площадью 0(dS<j>),
•определенной этой картой. Имение эту меру Радона на V
называют мерой «-мерных плошадеи на особом многообразии и
обозначают через dS. Если /1 — часть V, то ее называют
«-мерной площадью А (или сужения Н в А), т.е., по определению,
это мера А относительно dS. Если норма dS конечна, то она,
т.е. интеграл ... dS, является «-мерной площадью пара-
v
метрического многообразия. Эта площадь не изменяется, если
параметрическое многообразие будет заменено эквивалентным
.параметрическим многообразием. Если отображение Н является
dS-собственным, то существует на Е образ меры H(dS), часто
обозначаемый через dS, носитель которого лежит в замыкании
B(V) образа H(V). Если f является некоторой функцией
на Е со значениями в банаховом пространстве F, то можно
говорить об интеграле Г ... Г fdS1), равном по определению
... (foH)dS. Это — интеграл от функции f относительно
v
В (dS); если только образ меры существует.
Предыдущие результаты можно подытожить и
сформулировать в виде следующей теоремы:
Теорема 107. Пусть Н: V-* Е — отображение класса С1
многообразия V класса С1 размерности п в аффинное евклидово
') Или лучше интеграл ... \ f dS относительно параметрического мно-
(Я)
гообразия, определенного отображением Н многообразия V в Е. Заметим, что
мы ввели три рода мер ^ 0: меру ds0 на О, меру Ф(с(5ф)на Ф((7), склейку
мер Ф(с(5ф), дающую меру dS на V, и, наконец, меру ff(dS) на Е.

§ 10. Кратные интегралы на R™
765
пространство Е размерности N, определяющее параметрическое
многообразие в Е. Для каждой карты Ф: О—*■<&(&)
многообразия V через dS<j> обозначим меру D(u)du^O на О,
определенную по формуле (IV, 10; 29). Тогда на V существует, и
притом единственная, мера dS ^ 0, совпадающая с <J)(dS<i,) на ка-
"ждом множестве Ф{0). Эту меру называют п-мернэй площадью
на параметрическом многообразии. Если А является (dS-изме-
римой) частью многообразия V, то интеграл Г... dS дает
А
площадь А. В частности, \ ... \ dS = \\dS\\ является пло-
v
щадью параметрического многообразия.
Эти результаты, естественно, применимы, если V —
многообразие, лежащее в Е, а Н — тождественное отображение.
Замечания. 1°) Если V является открытым множеством
О из R™, то в качестве карты Ф можно взять тождественное
отображение, и тогда сразу же получаем dS = dS$> —D(u)du:
Впрочем, этот случай был уже нами разобран перед
теоремой 106 (тогда V и Н обозначались через (У и W).
2°) Пусть при п = 1 многообразие V является открытым
интервалом Ri вещественной прямой R и Н представляет
собой отображение, обозначаемое через М, интервала R: в Е.
Тогда мы приходим к случаю, рассмотренному выше в
замечании Г). Здесь D(t) (для переменной из R\ мы пишем / вме-
> ->
сто и) является длиной M'(t) и ds = D(t)dt = \\M'{t)\\dt. Мы
снова возвращаемся к длине (формула (IV, 9; 402)). Однако
длина кривой может быть определена в произвольном
нормированном аффинном пространстве и даже в произвольном
метрическом пространстве (стр. 701), в то время как n-мерные
площади при п > 1 могут быть определены только в аффинных
евклидовых пространствах.
3°) Если V при п = N является открытым множеством Q из
Е, а Н — тождественным преобразованием, то мера /V-мерных
площадей будет просто мерой объемов dx. В самом деле, теперь
мы находимся в условиях замечания 1°), и, положив ф = # =
= тождественное преобразование, мы получим D(u)—l.
4°) Если Q — некоторое открытое множество из RN, a | —
отображение Q в £ класса С1, то оно определяет некоторое
параметрическое многообразие в Е класса С1. Точно так же,
как в п. 3°), /V-мерную площадь некоторой части А множества Q
можно называть ее объемом. Однако, поскольку отображение |
не обязательно инъективно, эта величина не обязательно будет
объемом образа 1(A). Если в Е выбрать ортонормированную
систему координат и отождествить это пространство с R^, тоу

766 Гл. IV. Интегральное исчисление
согласно (IV, 10; 30), этот объем всегда будет равен
J Г ... Г | det g'(0 \dt. В следствии 3 теоремы 102 мы видели,
А
что это выражение равно объему ^(Л), если только Ъ, является
некоторым гомеоморфизмом. В общем случае, если для каждой
точки х е £ через v(x) обозначить число тех точек Й, образ
которых при отображении g равен х, 0 ^.v(x)^. -\-оо, то,
согласно (IV, 10; 232), будет иметь место равенство
11 ... 11 det I' (t) | dt = J" J" ... J" v (x) dx. (IV, 10; 382)
A HA) '
Мы получили «объем ?;(Л), в котором каждая точка
учитывается столько раз, сколько она покрывается при
рассматриваемом отображении».
5°) Предположим теперь, что п = 0. Многообразие нулевой
размерности в'Е является множеством изолированных точек Е.
В этом случае 0-мерная площадь такого многообразия
определяется как число (конечное или бесконечное) этих точек;
0-мерная площадь точки равна 1.
Следствие 1. При преобразовании подобия с отношением
k n-мерные площади умножаются на \k\n.
Пусть V — некоторое многообразие, класса С1 размерности
п и Н: V —*Е — параметрическое многообразие, пространства В
класса С. Если отображение g пространства Ё является
подобием с отношением к, то Ь, = Н будет новым параметрическим
многообразием, имеющим V в качестве многообразия
параметров. Поскольку g изменяет «-мерные площади
«-параллелепипедов в \k\n раз, то непосредственно видно, что мера D(u)du
относительно |.°# равна мере относительно Н, умноженной на
\k\n, а, следовательно, мера dS на V относительно g ° H равна
мере относительно Н, умноженной на \k\n, откуда и следует
сформулированное утверждение.
Следствие 2. Пусть V — истинное многообразие
размерности п аффинного евклидова пространства Е класса С1. Если
V замкнуто, то n-мерная площадь любой ограниченной dS-из-
меримой части А многообразия V конечна. Если многообразие
V замкнуто и. ограничено, то его площадь конечна.
В самом деле, замыкание А подмножества Л относительно
V замкнуто в многообразии V. Так как V замкнуто в Е, то Л
замкнуто в £ и, поскольку это множество по условию еще и
ограничено, то оно компактно (теорема 23 гл. II).
Следовательно, мера действительно конечна.

§ 10. Кратные интегралы на R" 767
Следствие 3. Пусть Н: V-+E— параметрическое
многообразие размерности п аффинного евклидова пространства Е
класса С1. Если V счетно в бесконечности и W является
некоторым подмногообразием V размерности <Ln класса С1, то его
n-мерная площадь равна нулю.
Это следствие является обобщением следствия 1
теоремы 1022.
Доказательство. В самом деле, пусть Ф :0 -*Ф{0) —
некоторая карта многообразия V. Поскольку Ф является
О-диффеоморфизмом, то прообраз при отображении Ф
многообразия-пересечения W и Ф{0) является многообразием из О
размерности <Ln класса С1 (следствие 2 теоремы 32 гл. III).
Тогда этот прообраз имеет нулевую меру относительно du
{следствие теоремы 1022), а, значит, и относительно D(u)du =
= dS<s>. Поскольку Ф является некоторым гомеоморфизмом, то
№Г\Ф((У) имеет нулевую и-мерную площадь в V. Так как
каждый компакт К из V покрывается конечным числом образов
таких карт, как Ф^), то WC\K также имеет нулевую площадь.
Наконец, поскольку V является счетным множеством
компактов, то W является счетным объединением множеств нулевой
n-мерной площади, а, значит, также имеет и-мерную площадь,
равную нулю.
Пример 1. Площадь сфер радиуса R в аффинном
евклидовом трехмерном пространстве. Выбор некоторой ортонорми-
рованной системы координат отождествляет Е с R3. Если в R2
взять открытое множество 0 < 8 < л, 0 < qp < 2я и положить
>: = /?sin8cos(p,
у = R sin 8 sin qp, (IV, 10; 39)
z = R cos 8,
то полярные координаты (IV, 10; 18) определят некоторую
карту Ф; Ф(0) является открытой частью сферы, дополнительной
к полумеридиану у = 0, х ^ 0. Поскольку этот полумеридиан
является объединением некоторой полуокружности без концов,
являющейся многообразием размерности 1 класса С1, и двух
полюсов — многообразий размерности 0 класса С1, то он имеет
нулевую площадь. Следовательно, площадь сферы равна
площади Ф(0). Если А является каким-либо подмножеством
сферы, то его площадь равна площади его пересечения с Ф^).
Следовательно, знание только лишь карты Ф совершенно
достаточно для изучения сферических площадей; Ф((У) dS-почти
всюду совпадает с многообразием. Именно так чаще всего
бывает на практике. Согласно вычислениям, проведенным на
стр. 750, мы знаем векторы дФ/дВ и дФ/dcp. Эти векторы

768 Гл. IV. Интегральное исчисление
взаимно ортогональны и имеют длину R и R sin 0, а,
следовательно, площадь образованного ими параллелограмма равна
D (0, ф) = R2 sin 0. Значит, площадь части А сферы будет
вычисляться по формуле
S{A)= {{ R2sinQdQdq>. (IV, 10; 40)
Ф-'(Л)
В частности, площадь сферы равна
S= IJ R2 sin в dQdq> = R2( j sin Q dQ\f J d<p\ = 4nR2.
0<8<я \|0, я | /\|0,2я| /
0 < <p < 2Я
(IV, 10; 41)
Позже мы вычислим площадь сферы в евклидовом
пространстве произвольной размерности.
Пример 2. Вычисление телесных углов в аффинном
евклидовом пространстве. Пусть H-.V-+E— некоторая
параметрическая гиперповерхность, т. е. (N—1)-мерное
параметрическое многообразие класса С1 в аффинном пространстве Е
размерности N. Пусть О — некоторая точка пространства Е.
Поставим задачу определения «телесного угла, под которым
заданная гиперповерхность видна из точки О»1). Мы определим
абсолютный телесный угол, а не алгебраический угол, так что
он всегда будет неотрицательным числом. Мы должны будем
всегда предполагать, что точка О не принадлежит образу
многообразия V. (В противном случае через V0 можно обозначать
дополнение в У к прообразу Я-1 ({О}). Так как прообраз
Я-1 ({О}) замкнут, то множество V0 открыто и, следовательно,
является некоторым многообразием, а сужение Н на V0
является некоторым параметрическим многообразием, образ
которого не содержит точки О. Телесный угол относительно V, по
определению, будет телесным углом относительно V0.) Пусть
М — произвольная точка множества Е — О. Полупрямая ОМ
пересекает единичную сферу с центром О в некоторой точке
т. Тем самым определяется некоторое отображение |: М—>
—>-т = |(Л1) множества Е—О в Е, принадлежащее, очевидно,
классу С1, образ которого является единичной сферой с
центром О. Отображение |о# определяет новое параметрическое
многообразие класса С1, где V есть, как всегда, многообразие
параметров. Образ этого параметрического многообразия
содержится в единичной сфере с центром О. Тогда, по определе-
') Понятие определено весьма интуитивно. При этом результат (IV, 10; 48)
просматривается почти сразу же. Мы его установим со всей строгостью в
качестве типичного примера. На практике обычно знают, что хотят получить,
и к цели идут быстрее1

§ 10. Кратные интегралы на R"
769
нию, телесный угол, под которым из точки О видно
параметрическое многообразие, определяемое отображением Н, является
(N—I)-мерной площадью параметрического многообразия,
определяемого композицией \ ° Я: V -> Е.
Мера площадей, связанная с параметрическим
многообразием | о Я, является некоторой мерой dco ^ 0 на V, которую
называют мерой телесных углов. Можно говорить также
о мере относительно со части А множества V. Полный
телесный угол параметрического многообразия равен j[ rfсо || =====
= ... da ^ -f~ оо. Очевидно, что если V является просто
v
некоторым открытым множеством единичной сферы и Я
является тождественным отображением, то этот телесный угол
будет площадью самого множества V. В частности, если V
представляет собой всю единичную сферу или какую-либо
сферу с центром О, то в качестве телесного угла получают
площадь единичной сферы в Е. Телесный угол инвариантен
относительно гомотетии с центром в точке О.
Найдем производное отображение отображения | в точке
М0 ^ Е. В пространстве Е мы можем произвольно выбрать
ортонормированную систему координат. Выберем ее так, чтобы
N — 1 первых координат точки М0 были равны нулю, а N-я
координата равнялась расстоянию г0 от точки М0 до точки О.
Формулы, определяющие преобразование |: х—*у, тогда будут
иметь вид:
g'==T-=ss^7=== 2Х' /=1> 2'-"> N- (IV, Ю; 42)
V х\ + х\+ ... +х%
Отсюда дифференцированием получаем
dyi^^-^-dr, где dr = 2 "Г"djc/' (IV'10:43)
Ввиду особого расположения точки М0 относительно
выбранной системы координат это дает dr = dx^, откуда
dyi = ^r- Для / = 1, 2, ..., N-l, dyN = 0. (IV, 10;44)
'о
Отсюда вытекает, что искомое производное отображение
|'(М0) сводится к ортогональному проектированию каждого
вектора X на гиперплоскость, перпендикулярную
радиус-вектору ОМ0 в точке М0 и последующей гомотетии с
отношением 1/г0.
Пусть теперь Ф: 0-+Ф{0) — некоторая карта V, ы0еС? и
М0 = Я(Ф(и0)). Тогда множитель D{u0), относящийся
25 Зак. 1339

770
Гл. IV. Интегральное исчисление
к (N—1)-мерным площадям на V, является (N — 1)-мерной
площадью в Е параллелепипеда, построенного на системе век-
->
торов Х{ = Н' (Ф(и0))-^~(и0). С другой стороны, для телесного
угла мы имеем множитель А («о), который должен быть
(N—1)-мерной площадью параллелепипеда, построенного на
->
системе векторов У,, полученных из предыдущих векторов при
отображении %'{М0). Согласно теореме 105 о проекциях
площадей и следствию 1 теоремы 107, А(и0) = D(«0)cos в0//"о'-1,
где 9о = 0(«о) —острый угол, образованный ОМо с нормалью
к многообразию V в точке М0.
Окончательно, на открытом множестве О из R" имеет
место формула
cos 8 (и)
(г (и))"
d(oФ = ^(u)du = -^^vD(u)du. (IV, 10; 45)
Образ этой меры при отображении Ф дает меру углов в
открытом множестве Ф(С) многообразия V. Это можно
записать так:
ф №ф) = Т^Т ф (<Юф). (IV, Ю; 46)
где для точки-у е V величины 9 и г относятся к точке H(v)^
е Е. Легко находится та же самая мера для любого
открытого множества Ф(0) из V:
dco = ^-dS=-^jgrdS(y). (IV, 10; 47)
г (г (v)y
Телесный угол dS-измеримого подмножества А из V или
всего множества V находится, следовательно, по формуле
Q = j ... J dco или J ... J -^J- dS, (IV, 10; 48)
■A V Г
как этого и следовало ожидать из геометрических
соображений.
Вычисление объемов с помощью поверхностных интегралов
Пусть Ф есть С-диффеоморфизм открытого множества
£?сКя на открытое множество Q аффинного евклидоза
пространства Е.
->
Если / — функция, определенная на Q, со значениями в
банаховом пространстве F, то интеграл J j...J f(x) dx, где

§ 10. Кратные интегралы на R" 771
dx— мера, связанная с аффинным евклидовым пространством,
может быть, согласно следствию 2 теоремы 102 о.замене
переменных в кратных интегралах, вычислен по формуле (IV, 9; 76):
J J ... J f(x) dx = j j ... j f(Ф («)) | det Ф'(«) | rfu, (IV, 10; 49)
Q 0
в которой выписанный определитель является якобианом
преобразования относительно произвольно выбранной в Е орто-
нормированной системы координат. Этот определитель дает
объем параллелепипеда, определяемого векторами Л^=-т— (и),
/ = 1, 2 N.
Положим u = (v,w), где v = (uit..., uN-t) и w = uN.
Зафиксируем ш>. Тогда сужение отображения Ф на множество
значений и, соответствующее этому значению тю, является ги-
->■
перповерхностью 2W в Q класса С. Рассмотрим векторы Х(.
Первые N — I из них будут векторами, касательными к
гиперповерхности в рассматриваемой точке, а N-и вектор XN будет
расположен вне касательной гиперплоскости.
Обозначим через v единичный вектор нормали к
гиперповерхности 2Ю в рассматриваемой точке Ф(«). Объем
параллелепипеда, определяемого векторами Xt, является
произведением (Л/—I)-мерной площади параллелепипеда,
порождаемого первыми N — 1 векторами, на длину ортогональной
проекции последнего вектора на нормаль: |(,Yw|v)|. Однако
указанная (Л/—1)-мерная площадь определяется множителем
D(v,w)1), позволяющим вычислить площади на поверхности
2.Ю. Поэтому мы имеем право записать:
$ $ ... $T(x)dx= $ \ ... $Tmu))\D(v,w)(4£(u)\Vl
du.
(IV, 10; 50)
->
Если известно, что функция / интегрируема, или если
известно, что она вещественна, ^ 0 и измерима, то можно
') Эта функция обязательно зависит от v и ш. Для фиксированного w
она зависит лишь от v. Следовательно, D(v, w)dv = dSw является мерой
площадей относительно параметрического многообразия 2Ш: я-»-Ф(г), w).
Ее образ при гомеоморфизме Ф является мерой площадей на самом
многообразии 2„. Хотя эта мера на 2Ю изменяется вместе с w, она всегда
допускает представление через dS. (Обиходная математика была бы слишком
сложной, если бы мы не пользовались упрощенным языком!)
25*

i72
Гл. IV. Интегральное исчисление
применить теорему Фубини и результат записать в виде
\dw\...\ 7(Ф(и)) | D (v, w)[^ (и) | v) | dv, (IV, 10; 51)
или
\dwj...jT(x) (■
dw
dS. (IV, 10; 52)
Таким образом этот Л/-кратный интеграл может быть
вычислен последовательно как некоторый поверхностный
интеграл по гиперповерхности 2ц,, зависящей от параметра w, а
затем как простой интеграл относительно w.
Рассмотрим теперь частный случай, представляющий
самостоятельный интерес. Пусть h — некоторая вещественная
функция класса С1, определенная на открытом множестве Q
аффинного пространства Е, производное отображение которой
к'(а) отлично от нуля в каждой точке aefl. Зафиксируем
некоторую точку а. Поскольку производное отображение h'(a)
отлично от нуля, существует по крайней мере одна частная
производная h относительно некоторой ортонормированной
системы координат в Е, не равная нулю. Пусть, для
определенности, это -г—'-(а). Тогда, согласно теореме о неявных функ-
oxN
циях (теорема 28 гл. III), существует такая окрестность Qa
точки а в Q, в которой уравнение w~h(xuX2,... ,xN) может
быть разрешено относительно xN в виде xN = g(xu .. .,xN_hw),
где g — функция класса С1. Кроме того, согласно правилу
(Ш,8;23), та же самая теорема дает 7) ~7j/j7d—* Если
теперь перейти к сужению на открытое множество Qa и
воспользоваться формулами
Xt=sUi = vh ■ . г = 1, 2, ...,N-1, (IV, Ю; 53)
XN — g(uU ...,«jv_i, UN) = g(vu ..., VN-U W),
то мы окажемся в описанных выше условиях. Мы определили
С'-диффеоморфизм Ф открытого множества Оа с: RN на Qa
так, что подпространства w = const стали
гиперповерхностями 2и> с уравнением h(x) = w. Поскольку хи i^.N—1,
не зависят от w, то вектор -г—(и) является вектором,
параллельным оси xN, с составляющей
дв (и){-
dw (U)l -
_ ' >
dh .
**s (X) >
по этой
оси. Если учесть, что, согласно следствию 5 теоремы 334 гл. III,

§ 10. Кратные интегралы на R"
773
единичный вектор нормали v = ±grad/2/||grad/z||, то проекция
вектора v на ось xN равна ± -j^— (x)/\\ grad h (x) ||.
Отсюда следует формула
дш
dh
dx.
dh
дх>
llgrad /
llgrad/
(IV, 10; 54)
Если / является некоторой интегрируемой на fiQ функцией
со значениями в банаховом пространстве F, то можно
вычислить ее объемный интеграл с помощью поверхностного по
следующей формуле:
jj ... jf(x)dx=jdwj ...j
Т(х)
llgrad h (x)
dS. (IV, 10; 55)
могут быть выполнены
fiQ, являющегося окрест-
Эти вычисления, естественно,
только для открытого множества
ностью точки а. Однако окончательный результат не зависит
от специального выбора координат относительно тонки а.
Формула (IV, 10; 55) представляет самостоятельный интерес и не
связана с выбором системы координат. Если теперь покрыть
компакт К из & конечным числом таких открытых множеств
fia, то мы получим, что этот результат верен для каждой
функции с компактным носителем в Й и со значениями в F.
Пользуясь переходом к пределу, для произвольной интегрируемой
на Q функции со значениями в F можно получить формулу
И- lfWx=jdw J ... J
7(х)
llgrad h{x)
dS. (IV, 10; 56)
Таким образом, справедлива
Теорема 108. Пусть Q — открытое множество аффинного
евклидова пространства Е, и пусть h — вещественная
функция класса С1, определенная на Q, производная которой в
каждой точке =7^=0. Если через 2и> обозначить гиперповерхность,
определенную уравнением h(x) — w, и если f является
функцией, определенной на Q, со значениями в банаховом прост-
ранстве F, интегрируемой по мере объемов dx в Е, то для
почти всех значений w функция л/llgrad А|| интегрируема на Ею от-
носительно поверхностной меры dS, интеграл \ ... [ 1»—dS,
J s llgrad A||

774
Гл. IV. Интегральное исчисление
определенный для почти всех значений w, является функцией
w со значениями в F, интегрируемой по мере dw, и имеет место
формула (IV, 10; 56). Если f есть dx-измеримая, вещественная,
не обязательно интегрируемая функция ^ 0, то обе части
равенства (IV, 10; 56) равны и одновременно являются конечными
или бесконечными.
Замечание. Геометрически предыдущий результат
довольно ясен. Элемент объема dx может быть представлен как
произведение поверхностного элемента dS поверхности 2ц, на
расстояние вдоль нормали dv, разделяющее поверхность 2W
>•
от поверхности IiW+dw- Вектор grad h является вектором
нормали к поверхности 2ц, длины —т— . Отсюда следует, что
, dw , ■ dS dw ^
dv = -r=> и, следовательно, dx = ^=> . Это рассуж-
!lgradA|| llgradAH
дение лишено строгости; четкие рассуждения были проведены
ранее.
Следствие 1. Пусть Е — евклидово аффинное
пространство, и пусть г — функция «расстояние от точки О в Е», т. е.
■> ->■
г(х)= \\х — 0\\. Пусть f-+ функция, определенная на Е, со зна-
->
чениями в банаховом пространстве F, интегрируемая по
объемной мере dx. Тогда почти для всех значений г функция f
интегрируема относительно поверхностной меры на сфере 2Г
с центром О радиуса г.
Интеграл \ ... \ f (x) dS от этой функции, определенный
для почти всех значений г, интегрируем по мере dr, и имеет
место равенство
j j ... J" f{x) dx= j dr f ... jf(x) dS. (IV, 10; 57)
|0, +oo[ " 2r
Если f есть dx-измеримая, вещественная, не обязательно
интегрируемая функция ^0, то обе части равенства (IV, 10; 57)
равны и одновременно принимают конечное или бесконечное
значение.
Для доказательства достаточно применить теорему к
дополнению Q к точке О в Е относительно функции h = г.
Градиент этой функции в каждой точке М является единичным
вектором, лежащим на ОМ, и, следовательно, длина градиента
тождественно равна 1, откуда следует требуемый результат.

§ 10. Кратные интегралы на R"
775
Следствие 2. Пусть f — некоторая функция,
определенная на полупрямой R+, т. е. на множестве чисел ^0 прямой
R. Пусть г— скалярная функция, определенная на аффинном
евклидовом пространстве Е размерности N соотношением х—*
> >
—*г(х)— \\х — 0\\, где \\х — 0\\—расстояние от х до точки
Ое£. Тогда функция for: x^>-f(r(x)), определенная на Е со
значениями в F, зависит только от расстояния переменной х
->
до точки О (что коротко записывается в виде f(r)). Функция
->
for измерима на Е по мере объемов тогда и только тогда,
когда функция f измерима на R+ по мере Лебега. Функция
for интегрируема на Е по мере объемов тогда и только тогда,
когда функция t-+tN-lf(t) интегрируема на R+ по мере
Лебега, и имеет место равенство
J" J" ... J" f(x) dx = SN J" f(t) t»-1 dt, (IV, 10; 58)
E R+
где SN — площадь сферы радиуса 1 в Е. Наконец, образ меры
объемов dx при отображении г: х-*г(х) из Е в R+ является
мерой Sjv^-'d/ на R+.
Вообще говоря, г используется как переменная
интегрирования в правой части (IV, 10; 58): SN J f (r)rN~l dr.
I o, + °o|
->
Доказательство. Если f — непрерывная скалярная
функция с компактным носителем на R+, то к ней можно
применить следствие 1. Поскольку на сфере Sr радиуса г функция
f постоянна и равна f(r), то величина [ ... j f(r)dS равна
произведению f(r) на площадь сферы радиуса г. С помощью
гомотетии (следствие 1 теоремы 107) получаем, что эта
площадь равна произведению rN~l на площадь SN сферы
радиуса 1, откуда и следует равенство (IV, 10; 58).
Эта формула означает, что образ меры dx при
отображении х—*г(х) является мерой SNtN~ldt на R+. Но тогда из тео-
->
ремы 60 следует, что если f является некоторой функцией на
R+, то функция f(r) dx-интегрируема тогда и только тогда,
когда / (SNtN~ldt) -интегрируема на R+, а из теоремы 51
следует, что f интегрируема относительно (S^^dt) тогда и
только тогда, когда d^-интегрируема функция S^f^t1*-1.

776
Гл. IV. Интегральное исчисление
Это следствие означает также, что вычисление объемного
интеграла от функции, зависящей лишь от одной переменной
г, можно свести к вычислению обычного интеграла. Достаточно
лишь знать площадь SN единичной сферы в RN, а она хорошо
известна для N = 1, 2, 3:
S1=21), S2 = 2n, S3 = 4n.
->
Обратно, если на R+ существует функция f, для которой
известны значения Г Г... | J{r)dr и | J{t) tN~ldt, то они дают
В R+
значение SN (если интегралы не равны нулю). Это как раз то,
что мы сделаем позже, положив f{t) = e~p. Так можно найти
(сделайте это в качестве упражнения), что
SA = 2я2, S5 = -g- я2, S6 = я3, ... .
Площадь сферы радиуса R равна SNRN~l, что дает
2, 2яЯ, 4яЯ2, 2я2Я3, -|я2Я4, я3Я5, ... .
Следствие 3. В аффинном евклидовом пространстве
размерности N объем шара радиуса R равен sN ^
(первообразная площади сферы SNRN~X, обращающаяся в нуль при
R = 0).
В самом деле, этот объем вычисляется по формуле
(IV, 10; 58), ибо он является интегралом от
характеристической функции шара — функции, зависящей только от г. Здесь
f(r) = 0 для г > R и =1 для г ^ R. Мы приходим к
значению SN j* rN-4r = SN-^r.
Таким путем для N = 1, 2, 3, 4, 5, 6 получаем:
2R, nR2, jnR\ \n2R\ j^n2R5, |я3Я6.
') Si является 0-мерной площадью. Сфера в R с центром в 0 радиуса 1
сводится к множеству {—1, +1}, состоящему из двух элементов, площадь
которого равна 2 (замечание 5°) после теоремы 107). Впрочем, если
некоторая функция на прямой R зависит только от расстояния до начала
координат, то это означает, что она четна, и в этом случае формула (IV, 10; 58)
примет вид f (x) dx = Si f (x) dx, откуда Si = 2.
1 — о°, +°°[ |0, +оо|

§ П. Функции, представимте рядами или интегралами 777
Следствие 4. Пусть г — расстояние от точки О в
N-мерном аффинном евклидовом пространстве. Интеграл \\ ... Г—£.
г<1
(соответственно . | [ ... Г -£-\ конечен тогда и только тогда,
\ r>i Г I
когда а <. N (соответственно а> N).
Это следствие является обобщением следствия 1 теоремы 97,
соответствующим N=1.
Доказательство. По следствию 2, предыдущие
интегралы конечны тогда и только тогда, когда конечны соответ-
Г rN~l Г 1
ствующие простые интегралы I —~dr= а-ы+\ ^г- Это
так в том случае, когда ос —W-|-1<1 (соответственно >1)
или ос < N (соответственно >N).
§ 11. ФУНКЦИИ, ПРЕДСТАВИМЫЕ РЯДАМИ ИЛИ ИНТЕГРАЛАМИ
Функции, представимые рядами
Пусть /0, fy, f2, ...— последовательность отображений
множества Е в множество F. Предположим, что эта
последовательность просто сходится при п, стремящемся к
бесконечности, к некоторому отображению / из Е в F. Функция /
называется пределом последовательности функций.
Поставим задачу изучения различных свойств функции /
в зависимости от выбора Е и F и свойств функций /„:
непрерывность / для топологических пространств Е и F;
интегрируемость /, если Е — X представляет собой локально компактное
■>
пространство с мерой Радона ц ^ 0, a F — некоторое банахово
пространство; дифференцируемость / в случае аффинных
нормированных пространств Е п F. Вообще говоря, вместо того
чтобы иметь дело с последовательностями, в анализе чаще
всего рассматривают ряды. В этом случае Е является некото-
■> ■>
рым множеством, F — пространством Банаха, а функцию 5
определяют по формуле
£(*) = 2 "„(*). хе=Е. (IV, 11; 1)
Предположим, что с помощью некоторых критериев можно
доказать простую сходимость этого ряда; рассмотрим задачу
изучения непрерывности, интегрируемости и дифференцируемо-
■> •>
сти суммы 5, исходя из аналогичных свойств функций и„.
'/,25 Зак, 1339

778 Гл. IV. Интегральное исчисление
Совершенно очевидно, что в этом случае подход, использующий
ряды, не отличается от подхода, использующего последова-
тельности, ибо S является пределом последовательности функ-
ций $п= 2* иь и, обратно, если функция / есть предел
некого
->
торой последовательности функций /„, то она будет суммой
ряда /о + Ч\ — То) + (/г— м) + • • • -С теоретической точки зре-
->
ния, в том случае, когда F— банахово пространство, оба
подхода равносильны. Представление функций в виде пределов
последовательностей является более общим подходом,
поскольку оно возможно в произвольных топологических
пространствах. На практике для представления функций чаще
всего используют ряды.
Если F — поле комплексных чисел, то может случиться, что
нам придется иметь дело с функциями, представленными
оо
в виде бесконечного произведения, а именно И{х) = Ц ип {х).
В этом случае предполагается, что можно доказать простую
сходимость этого произведения, и ставится задача изучения
непрерывности, интегрируемости или дифференцируемое™
функции П, исходя из аналогичных свойств членов
произведения.
Большая часть критериев уже рассматривалась в
предыдущих главах. В таких случаях мы будем довольствоваться
лишь их напоминанием, а здесь приведем только новые
критерии.
Непрерывность суммы ряда
В нашем распоряжении имеется теорема 65 гл. II, которую
мы сейчас лишь напомним:
Пусть /п — последовательность отображений
топологического пространства Е в метрическое пространство F, сходящаяся
к некоторому пределу f локально равномерно на Е. Дели при
этом функции /„ непрерывны, то непрерывной будет и
функция f.
Естественно, эта теорема, сформулированная для предела
некоторой последовательности, также верна для суммы ряда
или для предела бесконечного произведения.
Интегрируемость суммы ряда относительно некоторой меры ^ О
Здесь мы располагаем теоремами 34—36, их следствиями
и теоремой 37 предыдущей главы. Приведем только следующее
их уточнение:

§ 11. Функции, представимые рядами или интегралами 779
Теорема ПО. Пусть ]„ — последовательность
^-интегрируемых на X функций со значениями в некотором банаховом
пространстве F. Предположим, что f„ просто сходятся ц-почти
->
всюду к некоторому пределу f и по норме мажорируются
одной и той же фиксированной ^-интегрируемой функцией g ^ 0.
Тогда, какова бы ни была ^.-измеримая часть Y множества X,
интегралы \ f„ сходятся к \ f . равномерно относительно ча-
У У
сти У, пробегающей множество ^.-измеримых частей
множества X.
Доказательство. В теореме 35 Лебега мы видели, что
J IIТ— Тп\\d\x сходятся к 0, т. е. при заданном е>0
существует такое целое число р, что для всех « ^ р имеет место
неравенство Г ||7—- 7„||йц<е.
Для каждой измеримой части У множества X мы имеем
одно и то же неравенство Г ||7— /лН^Ц^е, откуда заведомо
у
следует неравенство Г /^ rfjx— Г fd\x ^е, полностью доказьь
1у у I
вающее теорему.
Следствие. Пусть f„ — последовательность функций,
определенных на замкнутом интервале [а,Ь] прямой R, со
значениями в банаховом пространстве F, dx-интегрируемых и
равномерно сходящихся при п, стремящемся к бесконечности, к не-
р
которой предельной функции f. Тогда Г f„ (x) dx сходятся к
а.
{x)dx равномерно относительно а и р из [а, Ь].
J*
Дифференцируемость суммы ряда
Что касается дифференцируемое™, то у нас до сих пор не
было никаких теорем.
Пусть fn — последовательность отображений аффинного
нормированного пространства Е в аффинное нормированное
пространство F.
Предположим, что все эти отображения дифференцируемы.
Выясним, можно ли из достаточно сильной сходимости f„ к /,
например равномерной, получить дифференцируемость пре-

780
Гл. IV. Интегральное исчисление
дельной функции и сходимость f'n к /'? Легко видеть, что такое
утверждение не верно, поскольку из оценок, налагаемых на
функции, получить оценки на производные невозможно.
Рассмотрим, например, последовательность комплексных функций
одной вещественной переменной, определенных по формулам
М*)=-^, л>1. (IV, 11; 2)
Эта последовательность равномерно сходится к 0 на всей
вещественной прямой R при п, стремящемся к бесконечности.
Однако, ее производные определяются по формуле
&{х) = 1пе1*\ (IV, 11; 3)
и модуль производной f'n стремится к бесконечности при и,
стремящемся к бесконечности, для всех значений х.
Точно так же можно рассмотреть ряд Вейерштрасса:
со
S(x) = ^^^. (IV, 11; 4)
л=0
Этот ряд, составленный из вещественных функций
вещественной переменной, равномерно сходится на прямой R,
поскольку его общий член мажорируется по модулю числом 1/2".
Значит, этот ряд .представляет собой некоторую непрерывную
функцию.
Ряд же, составленный из производных
об
2 (4)" cos 3"*, (IV, 11; 5)
не сходится. Более того, Вейерштрасс показал, что функция S
не имеет производной ни при каком значении х — это был
первый пример функций такого рода
Таким образом, налагаемые условия должны быть связаны
не только со сходимостью функций, но также и со
сходимостью их производных. Мы сейчас убедимся, что если сделать
предположение о равномерной сходимости производных и
сходимости функций всего лишь в одной точке, то из него будет
следовать равномерная сходимость самих функций и будет
обоснован переход к пределу для производной.
Теорема 111. Пусть fn — дифференцируемые
(соответственно принадлежащие классу С1) отображения открытого
множества Q аффинного нормированного пространства Е в аф-

§ 11. Функции, представимте рядами или интегралами
финнов нормированное пространство F. Пусть производные V
(функции на Q со значениями в 9?(E;F)) сходятся локально
равномерно к некоторому пределу g, a fn(a) сходятся к
пределу 1(a) хотя бы в одной точке а множества Q. Если
множество О. связно, а пространство F полно, то f„ сходятся
локально равномерно в Q к некоторому пределу f. Функция f
дифференцируема (соответственно принадлежит классу С1), и
ее производная равна g.
Если же множество Q не связно, а пространство F не полно,
но f'n сходятся локально равномерно к некоторому пределу g и f^
сходятся просто к некоторому пределу f, то сходимость fn к f
будет локально равномерной, a f будет дифференцируемой
(соответственно принадлежащей классу С), при этом f = g.
Доказательство. Поскольку сходимость f' локально,
равномерна, то существует такая окрестность точки а, в котр-
рой f'n равномерно сходятся к функции g. Обозначим через
В = В(а;р) шар с центром а радиуса р > 0, содержащийся
в этой окрестности. Если х принадлежит этому шару, то мы
можем применить формулу конечных приращений (теорема 13
гл. ПГ) к функции Jmn = lm~fn и написать:
| /,*.(*)-/«>) I < Р ,, ^Р || Vmn (6) |. (IV, 11; 6)
Функции f'mn — f'm — f'n сходятся равномерно к 0 в шаре В
при man, стремящихся к бесконечности. Следовательно,
левая часть Сходится равномерно к 0 в этом шаре. Поскольку,
по предположению, fmn(a) = fm(a)~fn(a) сходятся к 0, то
отсюда следует, что fmn = fm — fn сходятся равномерно к О
в этом шаре при пят, стремящихся к бесконечности.
Функции /„ не обязательно являются ограниченными в В.
Но если мы выберем целое число п0 так, чтобы при п ^ «о
->■
имело место неравенство sup |/„,(£) — /„ (Ш ^ 1, то все
llf^lKP*
>
fn — /п» будут ограниченными по норме числом 1 в шаре В
-> •>
и функции (fm — fnt) — (fn — /J, m > «о, и > n0, будут
равномерно сходиться к 0 в шаре В при т и «.стремящихся к беско-
нечности. Это говорит о том, что функции fn — fntl, n^n0, об-
разуют в метрическом пространстве (FB)Cb последовательность
Коши. Если F полно, то это метрическое пространство также

782
Тл. IV. Интегральное исчисление
полно (следствие 2 теоремы 65 гл. II), и тогда разность
f —f , а вместе с ней и fn сходятся равномерно к
некоторому пределу в В при п, стремящемся к бесконечности. Если
F не полно, но если заранее известно, что функции fn сходятся
просто к некоторому пределу f, то отсюда следует, что
сходимость равномерна в В. В самом деле, каково бы ни было
8 > 0, существует такое целое число р, что из неравенств
->
m^z p, n^z р для всех х из В следует: \\fm(x) — fn(x) || < в.
Переходя к пределу, при ш, стремящемся к бесконечности
(при фиксированном х), получаем отсюда, что при п~^.р для
->
каждого !сбВ имеет место неравенство \\f(x) — fn(x)\\ ^ е,
доказывающее наше утверждение.
Если заранее известно, что fn сходятся просто к
некоторому пределу f, то только что проведенное рассуждение
сохранится для произвольной точки Q, а это означает, что
сходимость fn к f локально равномерна. Если же известно лишь,
что fn(a) сходятся к f(a), F полно, a Q связно, то необходимо
провести новые рассуждения.
Обозначим через 8 множество таких точек х из Q, для
которых последовательность fn(x) сходится к некоторому
пределу при п, стремящемся к бесконечности. Это множество
открыто. В самом деле, если точка Ъ принадлежит 8, то,
проведя для точки Ь то же самое рассуждение, что и для точки а,
мы увидим, что существует содержащийся в Q шар с центром
в точке Ь, в каждой точке которого функции fn сходятся к
некоторому пределу. Следовательно, множество & открыто.
Покажем теперь, что оно замкнуто в Q. Для этого предположим,
что bo, bu . ■ ■, bj, ... является последовательностью точек из Q,
сходящейся при /, стремящемся к бесконечности, к некоторой
предельной точке b e Q, и докажем, что если все bj принадле-.
жат 8, то и b принадлежит 8.
По предположению, существует некоторая окрестность
точки Ь, в которой последовательность f сходится равномерно
к g. Следовательно, существует некоторый шар В(Ь;р') с
центром в точке Ь, полностью лежащий в этой окрестности.
Поскольку при /, стремящемся к бесконечности, bj сходятся к Ь,
существует такое целое /о, что при / ^/V выполняется
неравенство ||6j — b\\ ^ р'/З. Но тогда шар с центром в bj радиуса
2
-д-р' содержится в В(Ь;р'), и, следовательно, в этом шаре f''
равномерно сходятся к g, a fn(bj) сходятся к f(bj). К точке Ь}
можно теперь применить то же рассуждение, которое было
только что проведено относительно точки а. Мы увидим, что

§ 11. Функции, представимые рядами или интегралами 783
в каждой точке х шара В(6;;2р/3) функции fn(x) сходятся
к некоторому пределу. Точка Ъ составляет часть этого шара,
а, следовательно, она также принадлежит множеству <8,
которое тем самым оказывается замкнутым. Так как множество Q
предполагалось связным, то непустое множество &
(содержащее точку а) может быть одновременно и открытым, и
замкнутым только в том случае, когда оно совпадает с самим
множеством Q. Мы доказали, что fn сходятся к некоторому
пределу f всюду в Q, а в этом случае, как мы видели выше,
сходимость заведомо локально равномерна.
Нам надо теперь доказать, что f дифференцируема и ее
производная равна g. Поскольку а уже не играет особой, роли, то
достаточно показать, что производная функции f в точке а
равна g(а). Обозначим через kn функции, определенные на
В(а;р), со значениями bF по формуле:
**(*) =
fn(x)-fn(a),-f'n(a)(x-a)
=> Для хфа,
II*-а|| (IV, 11; 7)
О для х = а.
Эти функции просто сходятся в В к функции k,
определенной формулой:
£(*)=
f(x)-f(a)-g(a)(x-a)
) для х =f= a,
||дг-а|1 (IV, 11; 8)
О для х = а.
Из формулы конечных приращений, взятой в виде,
указанном в следствии 1 теоремы 13, следует неравенство:
l*.w-*.w|< дир КЯ.ю-ш-СЯ»-/;(«))!•
ii5-aii<p (IV, П;9)
-> ->
Отсюда вытекает, что разность km — kn сходится равномер-
->
но к 0 в В при тип, стремящихся к бесконечности. Но тогда
проведенные ранее рассуждения относительно /„ показывают,
что kn сходится равномерно к k в В при п, стремящемся к
бесконечности. Согласно определению производной f'n{a), каждая
функция kn непрерывна в точке х = а. По теореме 65 гл. II
равномерный предел k также непрерывен в точке х = а. Это
означает, что функция f дифференцируема в точке а и f'(a) =
= g(a).
Наконец, если функции f„ принадлежат классу С1, то f'n
непрерывны, и, поскольку они сходятся локально, равномерно

784
Гл. IV: Интегральное исчисление
к g, то, согласно теореме 109, функция g непрерывна, а, значит,
функция / принадлежит классу С1, и теорема полностью доказана.
Замечания. 1°) Поскольку в теореме речь идет лишь
о дифференциальном исчислении, то ее можно было привести
в гл. III. Однако мы решили собрать в этом параграфе ряд
результатов одного характера.
2°) Конечно, первая часть теоремы будет неверной, если
не считать пространство F полным, а множество Q — связным.
Приведем контрпример для случая, когда множество Q не
связно. Пусть Q — дополнение к началу координат на
вещественной прямой R, а /„ — функция, равная нулю для х < 0
и равная постоянной п для х > 0. Тогда производные f
тождественно равны нулю, и, следовательно, последовательность
равномерно сходится к нулю при п, стремящемся к
бесконечности. Функции f„ сходятся к некоторому пределу в любой
точке х < 0. Однако они не сходятся ни к какому пределу на
всей вещественной оси R.
3°) Существенным во всех этих вопросах является
равномерная локальная сходимость. Если даже предполагать, что
сходимость f'n к g равномерна в Q, то можно утверждать лишь,
что fn сходится к f локально равномерно.
Рассмотрим, к примеру, на вещественной прямой функции
fn(x) = x/n. Они просто сходятся к 0 при п, стремящемся
к бесконечности. Их производные f'n(x) = \/n сходятся к 0
равномерно на R. Отсюда следует (и это было ясно a priori),
что функции fn сходятся к 0 равномерно на любом компакте
(или локально равномерно). Однако они не сходятся к 0
равномерно на R, поскольку |||/„|||= +оо.
Следствие 1. Пусть /„ — отображение открытого
множества Q аффинного нормированного пространства Е в
аффинное нормированное пространство F, принадлежащее классу Ст.
Если для каждого k ^ т функции /<,*>, определенные на Й,
со значениями в &ъ. (Ek; F) локально равномерно сходятся
к некоторому пределу fh и /0 = f, то f принадлежит классу С'™
и fh = f<ft> для k^m.
Доказательство очевидно.
Следствие 2. Если Q является открытым множеством
аффинного нормированного пространства Е, a F — аффинным
банаховым пространством, то пространство (FQ)Cb;m полно.
Напомним, что /е(/га)сь;т, если f является непрерывным
ограниченным отображением fief и если для каждого k ^ m
производная этого отображения порядка k является непрерыв-

§ 11. Функции, представимые рядами или интегралами 785
ным ограниченным отображением Q в 9?h{Eh;F). В этом
случае |||f||L= 2 ШРЧНо (см. стр. 267).
0<fe<m
Доказательство. Пусть fn — последовательность Коши,
принадлежащая (Fa)cb.m- Согласно определению норм,
производные функции f<£\ O^fe^m, образуют последовательность
■* ■*■ ">
Коши в Sk{Ek\ F))®b. 0. Так как пространство F полно, то полно
"*'■*•
пространство 3?k(Ek; F) (теорема 53 гл. II), а вместе с ним
•» •>
полно и пространство (3?k(Ek; F))°b.0 (следствие 2 теоремы 65
гл. II). Следовательно, функции fW сходятся равномерно на Q
к непрерывному ограниченному пределу fk на Q.
Согласно следствию 1, функция f принадлежит классу Ст
и fm = fk> т.е. f лежит в {Fa)cb.m- Поскольку каждая
последовательность fw равномерно сходится к fk—fw, то fn сходится
к f в пространстве (FQ)cb.m, которое тем самым оказывается
полным.
Примеры. Предыдущая теорема была сформулирована
для последовательностей, но на практике она чаще
применяется к рядам. ^
Пусть задан ряд (IV, 11; 1), где функции ип определены
на открытом множестве Q аффинного нормированного прост-
->
ранства Е и имеют значения в банаховом пространстве F.
Вообще говоря, заранее известно, что этот ряд просто сходится
■>
(и даже локально равномерно) в Q. Функции ип непрерывны,
■> » ->
а это значит, что сумма ряда S также непрерывна. Если ип
дифференцируемы, то возникает вопрос, дифференцируема ли
функция S. Для его решения применяется следующий метод:
почленно дифференцируют предыдущий ряд и полагают a priori
оо
S' (х) = 2 и'п(х). (IV, 11; 13)
ОО
Если ряд из производных 2 и'п М локально равномерно схо-
дится в Q, то S дифференцируема и формула (IV, 11; 13)
справедлива.
■> "•>
В самом деле, в этом случае функции Sm— 2j un сходятся
•> m
к S, и в то же самое время функции S'm= 2 «» локально
п=0

786 Гл. IV. Интегральное исчисление
равномерно сходятся к 2л и'п.Из теоремы следует, что 5 диффе-
п=а
ренцируемаг и ее производная равна предыдущему пределу.
> -*■
Рассмотрим для примера ряд Фурье, в котором ап и S(x)
являются векторами некоторого банахового пространства F:
-> +? ->
' S{x) — 2j ane,nx, где х вещественно; (IV, 11; 14)
/J= —ОО
предположим, что ап удовлетворяют неравенству
IIа»II<т-£+г. (IV, И; 15)
где р— целое число ^0 и А —постоянная >0.
->
Функция S, представимая этим рядом, принадлежит по
крайней мере классу С. В самом деле, если мы
продифференцируем ряд почленно k раз, k^Lp, то получим следующие
формулы:
-> +°° .>
S<*>(*)= 2 {in)kaneinx. (IV, 11; 16)
И=—оо
Так как || (m)fta„|| ^ Л/|я|2, то каждый из этих рядов
равномерно и даже нормально сходится, и, следовательно,
необходимый результат вытекает непосредственно из теоремы.
Если же лучшей оценки, чем (IV, 11; 15), нет, то, вообще
говоря, мы не можем произвести еще одно дифференцирование.
Замечания. 1°) Тот факт, что теорема не применима, еще
не означает, что предел f функций fn или сумма S ряда 2j un
не может иметь производной. Все, что можно сказать о про-
изводной 5' функции 5 в случае, когда ряд из производных
расходится, — это то, что производную S', если она существует,
оо
нельзя представить в виде ряда 2 и'.
Рассмотрим, например, тригонометрический ряд
оо
Vi sin 2™, (IV, 11; 17)
AU пп
л=1
Согласно теореме Абеля (теорема 63 гл. II), он сходится
всюду и сходится равномерно в каждом интервале [б, 1 — б],-
б > 0. В самом деле, сумма
| sin {2пх) + sin (2я2я) + ... + sin {2лпх) \

§ 11. Функции, представимые рядами или интегралами 787
мажорируется величиной 2/\e2iDX—1| и, следовательно,
числом 2/ e2inb — 11 при б < х ^ 1 — б, а последовательность
1/пл убывает и стремится к 0 при п, стремящемся к
бесконечности. Согласно (II,14; 31), остаток при этом допускает
оценку:
2
,Лл1<"Я(„.+ 1)|в2'«в_1|'
доказывающую наше утверждение. Однако сходимость,
очевидно, не будет равномерной на [0,1]. Следовательно, имеет
место локально равномерная сходимость на ]0,1[, а ряд
представляет собой непрерывную функцию на этом открытом
интервале. Почленное дифференцирование дает всюду
расходящийся ряд
оо
2 2соз2япх. (IV, 11;172)
Отсюда вовсе не следует, что функция S не
дифференцируема. Позже мы увидим, что S определяется по формуле:
( 0 для х = 0 и х = 1,
S(x) = \ 1 .^ ^ . (IV, II; 18)
у —л: для 0 < л: < 1. '
Эта функция разрывна при х = 0 и х = I. Из-за этого
разрыва, несмотря на сходимость на [0,1], равномерная
сходимость ряда имеет место только в интервале [б, 1 — б], б > 0.
Во всем интервале ]0,1[ эта функция дифференцируема и
даже принадлежит классу С°°. Ее производную, равную —1,
в виде ряда (IV, 11; 17) представить нельзя, поскольку он
расходится. Из этого примера видно, что метод, с помощью
которого Вейерштрасс доказал, что ряд (IV, 11; 4) представляет
функцию, не имеющую ни в одной точке производной, не"
является очевидным. Из того факта, что почленное
дифференцирование ряда приводит к расходящемуся ряду, вовсе не
следует, что рассматриваемая функция не дифференцируема. Всего
навсего он говорит лишь о том, что такая возможность не
исключена!
Дифференцируемость бесконечного произведения
Предположим, что некоторая функция определена в виде
бесконечного произведения функций с вещественными или
комплексными значениями:
п(х) = П М*). (IV, И; 19)
п=0

788
Гл. IV. Интегральное исчисление
В этом случае можно, опираясь на сходимость этого
произведения и сходимость ряда логарифмических производных
выяснить, будет ли функция П дифференцируема и будет ли
ее логарифмическая производная определяться по формуле
тт' °° '
Следует заметить, что доказательство этого утверждения
нельзя свести непосредственно к рассмотрению функций 1пып,
ибо речь здесь идет о функциях с комплексными значениями,
не обязательно Лежащими в области {z = re{f, r > 0, — л <
< Ф < п} комплексной плоскости, а, значит, нет уверенности
в том, что вычисление логарифмов законно. Однако, если /
является дифференцируемой функцией, определенной в открытом
множестве аффинного нормированного пространства Е и
принимающей всюду комплексные значения =^0, то
логарифмическую производную f'/f можно вычислять без предварительного
перехода к логарифмам').
Теперь можно сделать следующие замечания.
1°) Если / и g — функции с комплексными значениями,
дифференцируемые и фО на Q, то логарифмическая производная
произведения (соответственно дроби) является суммой
(соответственно разностью) логарифмических производных:
MSL—L + IL il!ML — L_gL /TV м-9«и
fg ~~ f "*" g ' fig ~ f g * ^'и'гг>
В самом деле, речь идет об уже известных формулах
(fg)' = fg + fg', (-£-)'= ^^. (IV, 11; 23).
2°) Если / — дифференцируемая на Q функция с
комплексными значениями, то по теореме о сложной функции
логарифмическая производная функции ef равна (eff')/ef = /'.
3°) Если множество Q связно, а логарифмическая
производная функции / равна нулю в Q, то эта функция постоянна,
В самом деле, производная /' этой функции равна нулю.
') f(x) является элементом поля К (== R или С), a f'(x) является
линейным непрерывным отображением £ в К. Поэтому f'(x)/f(x) также
является линейным непрерывным отображением £ в К (элементом
пространства, сопряженного к пространству £).

§ 11. Функции, представимые рядами или интегралами 789
Отсюда следует, что если f и g— две функции, имеющие
одну и ту же логарифмическую производную, то их отношение
постоянно, ибо логарифмическая производная отношения f/g
равна нулю.
4°) Для комплексных функций f„ на топологическом
пространстве Q (см. стр. 168) мы отмечали, что равномерная
сходимость In к I и равномерная сходимость fn/f к 1 (если f всюду
=5^=0) не эквивалентны. Однако, если функции fn непрерывны,
то соответствующие локально равномерные сходимости
эквивалентны (см. стр. 168 гл. II).
Точно так же, если функции fn (соответственно gn)
сходятся равномерно к f (соответственно к g) при п, стремящемся
к бесконечности, то отсюда еще не следует, что fngn сходятся
равномерно к fgl). Однако это утверждение справедливо для
равномерной сходимости, если fn и gn непрерывны.
В самом деле, пусть йёй. Тогда найдется такая
окрестность У" точки а, в которой fn (соответственно gn) равномерно
сходятся к f (соответственно к g). Обозначим через Т" такую
окрестность точки а, в которой функции fug, непрерывные
как локально равномерные пределы непрерывных функций,
ограничены по модулю. Тогда имеем:
\fngn-fg\<\fn\\gn-g\ + \fn-f\\gl (IV, И; 23j)'
Покажем, что на множестве У = У П У" правая часть
равномерно сходится к 0. Второе слагаемое, очевидно, обладает
этим свойством. Что же касается первого слагаемого, то
заметим, что существует такое целое число п0, что для п^ п0
выполняется неравенство |fn —/|^1. Так как функция |f|
ограничена в У", то при п ^ п0 функция |fn| также будет
ограниченной в У", а, значит, первое слагаемое также стремится
равномерно к 0 в У.
5°) Если Q является интервалом R, a f — комплексной
функцией =7^=0 на Q, принадлежащей классу С1, то имеет место
формула:
X
J(f'(U/f(l))dl
f(x) = f(a)e« . (IV, 11-, 24)
В самом деле, левая и правая части, согласно п. 2°), имеют
©дну и ту же логарифмическую производную f'/f;
следовательно, они, согласно п. 3°), пропорциональны, а так как обе части
совпадают при х = а, то они равны между собой.
') Произведение, как отображение С X С в С, не является равномерно
непрерывным.

790
Гл. IV. Интегральное исчисление
В случае, когда |^'/Л^=М, можно указать следующие
оценки:
fix)
fix)
f(a)
fifi)
- 1
<e*l*-«l (IV, 11; 25)
<eAfi*-a|__i, (IV, 11; 26)
Если теперь f является комплексной функцией класса С1,
заданной на открытом множестве Q аффинного пространства
Е, всюду =7^0, и если ее логарифмическая производная по норме
мажорируется числом М, то, применяя неравенства (IV, 11; 25) и
->
(IV, 11; 26) к функции t-*f(a-\-t(x —а)), определенной на
[0,1], получим такие же неравенства, где вместо \х— а\ будет
>
стоять \\х — а\\.
Имеет место следующий результат:
Теорема 112. Пусть fn — последовательность
комплексных функций класса С1, определенных на открытом множестве
Q аффинного нормированного пространства Е и всюду =^0.
Если их логарифмические производные f'n/fn локально
равномерно сходятся к пределу g и если значения функций fn{a)
сходятся к некоторому пределу {(а)Ф01) хотя бы в одной
точке aeQ,a множество Q связно, то fn сходятся к некоторой
предельной функции f локально равномерно в Q. Функция f
нигде не обращается в нуль, она принадлежит классу С1 и
имеет функцию g в качестве логарифмической производной.
Если Q не связно, но заранее известно, что fn просто сходятся
всюду в О. к некоторой не равной нулю функции, то
сформулированные выводы полностью сохраняются.
Доказательство. Положим fmn = frjfn- Пусть В =
= В(а;р) — некоторый шар с центром в а, в котором функция
f'njfn равномерно сходится к g. Тогда при тип, стремящихся
к бесконечности, f'mnlfmn равномерно сходится к 0 в В. Из
(IV, 11;26) вытекает, что fmn(x)/fm.n(a) равномерно сходится
К 1. ПОСКОЛЬКУ fmn(a) СХОДИТСЯ К 1, ТО fmn = fm/fn При ГП И П,
стремящихся к бесконечности, равномерно сходятся к 1.
В частности, существует такое п0, что для всех п^п0 имеем
fn 1
'tin
^Y> а> значит, для п^п0 и ieB выполняется нё-
') Если f(a) = 0 и £2 связно, то без труда доказывается, что функции fn
сходятся локально равномерно к нулю.

§ П. Функции, представимте рядами или интегралами 791
равенство у|/„,| <|/„| <y|/„J- Теперь для всех ieB, m>n0,
п^п0 будет иметь место неравенство
|/mM-/nM|<IU*)|
!m(x)
fn(x)
<4lU*)l
fm(x)
ТйхТ
-1
а, следовательно, \fm(x) — fn(x)\ сходится к нулю при man,
стремящихся к бесконечности. Поскольку поле комплексных
чисел С полно, отсюда следует, что /„(х) для всех xeS имеют
предел f(x). Кроме того, из |/п (*) | > |/„„ (*) |/2 следует, что
i/(*)lj> !/„„(*) |/2 > 0, т.е. что / не обращается в нуль в В.
Наконец, если по заданному s > 0 выбрать р так, чтобы при
пг^р и п^р для всех хеВ имело место неравенство
\fm(x)/fn(x)— 1\^.г, то при п^р для всех лей будет
справедливым неравенство | / (*)//„ (*) — 1 | <! s, а это означает, что
///„ равномерно сходится к 1 в В.
Теперь, используя метод теоремы 111, можно убедиться, что
если Q связно (или если известно заранее, что /„ сходятся
просто к некоторой функции /, которая всюду =7^0), то /„
сходятся просто к некоторому пределу / всюду =^0 и ///„
сходятся локально равномерно к 1, или /„ сходятся локально
равномерно к / согласно результатам п. 4°) на стр. 789.
Отношение f'Jfn тогда локально равномерно сходится к g, a /„ к /
и поэтому /„ = (/„//„)/„ сходятся к gf, поскольку речь идет
о непрерывных функциях (см. замечание 4°) на стр. 789).
Теорема 111 теперь утверждает, что функция / дифференцируема
и ее производная равна gf, т. е. логарифмическая производная
равна g, чем и заканчивается доказательство теоремы.
Следствие. Если комплексные функции ип на Q при-
со
подлежат классу С1 и всюду =^0 и если ряд 2 "„/«„ локально
равномерно в Q сходится к некоторой предельной функции g
оо
и, кроме того, произведение JJ ип сходится хотя бы в одной
л=0
точке а из £1, то когда Q связно, это произведение сходится на
всем Q локально равномерно, а определяемая им функция П
принадлежит классу С1 и имеет логарифмическую
производную, равную g. Если множество Q не связно, но заранее из-
оо
вестно, что произведение Ц ип(х) сходится для любого xeQ,
л=0
то указанные выводы полностью сохраняются.

792
Гл. IV. Интегральное исчисление
Функции, представимые интегралами
Рассмотрим интеграл
f{x)=\t{x,t)d»{t), (IV,11;262)
т
где (х — мера Радона ^0 на локально компактном простран-
->
стве Т, счетном в бесконечности, и h — функция на ХУ(Т со
■>
значениями в банаховом пространстве F.
Предположим, что для каждого х^Х частная функция
-> ->
hx: t-+h(x,t) является ^.-интегрируемой. В дальнейшем это
условие будет считаться выполненным, и мы не будем больше
об этом напоминать. Предыдущий интеграл в этом случае
определяет некоторый вектор f(x) из F и, следовательно, опре-
-> >
деляет некоторую функцию f:x-+f(x). Рассмотрим задачу
изучения непрерывности, интегрируемости и дифференцируемости
->
этой функции, исходя из аналогичных свойств функции h.
Непрерывность функции, представимой интегралом
Наиболее важный критерий дает теорема 35 Лебега,
которую мы сформулируем следующим образом.
Теорема 114. Пусть пространство X метризуемо. Если
->
для [i-почти всех значений t функция h раздельно непрерывна
по х в точке а и существует такая окрестность Y точки а, для ко-
->
торой наТХТ имеет место оценка \\h(x, t) ||«s: k(t), где k есть
->
^-интегрируемая функция ^0 на Т, то f непрерывна в точке а
пространства X.
В самом деле, если "л; устремить к а, то, начиная с
некоторого момента, х будет находится в Т, и тогда, в силу
теоремы 35 Лебега и следующего за ней замечания, f(x) будет
стремится к f(a).
Надо быть внимательнее и не смешивать различные
предположения.
■>
Для (х-почти всех значений t мы считаем, что функция h
непрерывна по я в точке а. Это естественно, поскольку изу.-
->
чается непрерывность функции / по х в точке а. С другой' сто-
>
роны, предполагается, что ||А|| мажорируется (х-интегрируемой
функцией k переменной /, что также естественно, поскольку

§ 11. Функции, представимте рядами или интегралами 793
производится интегрирование по ц в пространстве Т
переменной t.
->
Следствие. Пусть ft — непрерывная функция на X У^Т со
->■
-значениями в F и для каждой точки ае! существует такая
ее окрестность Т и такой компакт К из Т, что для «еУ но-
-> -» ->
ситель частной функции hx: t—*h(x,t) лежит в К. Тогда f яв-
->
ляется непрерывной функцией из X в F.
Доказательство. При х, стремящемся к a, hx сходится
-> ->
к ha в (FK)cb (теорема 66). Следовательно, существует такая
->
окрестность Tq с T точки а, что для х^У0 норма ||ftx||
ограничена. Обозначим через М ее границу. Тогда можно
применить предыдущую теорему с k(t) — M%K(t), где ^ —
характеристическая функция компакта К.
Непосредственно можно получить соотношение:
\\7(x)-J(a)\\^n(K)snp\\h(x, t)-h(a, 011 =
= lx(K)\\hx-ha\\, aV,ll;263)
где норма берется в (FK)cb и результат получается из теоремы
66 без ссылки на теорему Лебега (это позволяет не
предполагать пространство X метризуемым).
Интегрируемость функции, представимой интегралом
Речь идет о следующей задаче. Предполагается, что
пространство X локально компактно и снабжено мерой Радона Х^О.
Надо выяснить, будет ли функция / Я-интегрируемой и можно
ли будет вычислять интеграл от этой функции, интегрируя сна-
->
чала ft по X при фиксированном /, а затем интегрируя
результат по / и по мере ц, т. е. имеем ли мы право писать:
J dX (x) J ft (x, t) dn (t) = J d\x (0 J ft (x, t) dX (*)? (IV, 11; 27)
XT T X
Основные критерии справедливости последнего равенства
дают теоремы 77 и 78 Фубини и следствие теоремы 78.
Формула (IV,11; 27) справедлива в том случае, когда функция ft
интегрируема на Ху(Т по мере тензорного произведения Х®и,
или если она измерима и ^0, или если она измерима и одни
->
из величин, аналогичных (IV, 11; 27), относящихся к ||ft||,
конечна.
26 Зак. 1339

794
Гл. IV. Интегральное исчисление
Дифференцируемость функции, представимой интегралом
Будем считать, что X — Q является открытым множеством
аффинного нормированного пространства Е.
То, что нам приходилось видеть в рядах, наводит на мысль,
->
что f может быть дифференцируемой только тогда, когда
интеграл, относящийся к частной производной h по х, сам обладает
подходящими свойствами.
В противоположность тому, что было сделано в теореме 111,
мы не будем стараться свести дело к общему случаю, в
котором / предполагается существующей только в точке а
области Q.
Теорема 115. Предположим, что для ц-почти каждого
->
значения t частная функция x-+h{x, t) дифференцируема
{соответственно принадлежит классу С1) на Q. Пусть ее
производил "*■ *"
нал функция х-*-т~{х, t) является отображением Q в 3?{Е; F).
-*•
Предположим, что в каждой точке а функция t->-^-{a, t)
•*• -*•
{определенная \ь-почти всюду на Т со значениями в 3!{Е, F))
^.-измерима ') и что существует в Q такая окрестность Т точки а,
-*•
что на Т)К.Т имеет место неравенство Ur- {x, t)\^.k{t), где
k — неотрицательная и ^-интегрируемая функция на Т.
При этих условиях функция /, отображающая Q в F,
дифференцируема {соответственно принадлежит классу С1), и для
каждой точки а е Q ее производная вычисляется по формуле
-§£■ {a, t) dii (t) 6= & {E; F). (IV, 11; 28)
f(a) = i
') Эта измеримость будет автоматически выполняться, если
пространство Е конечномерно. Предположим для простоты, что Е = К есть поле
скаляров. Тогда для ц-почти всех значений t имеет место равенство
^.О-цщ^ + ^-^^З?,
дх 5-*о 1
-> -*•
Функции t -+h(x -)- |, /) и t^-h(x,t) ц-измеримы (и даже ц-интегрируе-
мы). Следовательно, для фиксированного х функция t->-^—(x,t) является
ц-почти всюду пределом некоторой последоьательности ц-измеримых
функций, а, следовательно, ц-измерима.
Напомним, кроме того, что все встречающиеся на практике функции
измеримы!

§ 11. Функции, представимте рядами или интегралами 795
Прежде чем проводить доказательство этой теоремы,
сделаем несколько замечаний по поводу ее условий.
Подинтегральная функция при заданной точке а
определена [х-почти всюду на Т, измерима и мажорируема некоторой
интегрируемой функцией &~">0, а, значит, интегрируема (со-
-> ->
гласно теореме 50 гл. II, пространство 3?(Е; F) полно). Таким
образом, условия теоремы обеспечивают существование
правой части равенства (IV,11;28).
Добавим, что если для jx-почти всех значений t частная
->•
функция hi не только дифференцируема по х, но и
принадлежит классу С1 в Q, то условие мажорируемости производной
->•
функцией k влечет за собой непрерывность производной /', т. е.
->
принадлежность f классу С1 на Q. Однако это условие необ-
->
ходимо даже для доказательства дифференцируемости /.
Доказательство. Надо доказать только тот факт, что
функция / имеет производную, определяемую формулой
->
(IV, 11; 28). Все сводится к тому, чтобы доказать, что при X,
->
стремящемся к 0, величина
->•
-±- J [h{a + X, t)-h{a, t)-^(a, t)X)dp(f)
стремится к 0. Эта величина не превосходит
Д1 II ■*■ ■*" ■*" rth -> \
-L-\h{a + X,t)-h{a,t)-%{a,t)X )d»{t). (IV, И; 30)
II -ЛЕГ || 1 вх J
В силу частной дифференцируемости h, подинтегральная
-> ->
функция / сходится просто |д-почти всюду к 0, когда X
стремится к 0. Если мы сможем промажорировать ее некоторой
неотрицательной [х-интегрируемой функцией /, то результат
будет получен в силу теоремы 35 Лебега. Далее, если через р
обозначить такое число >0, при котором шар В(а;р) будет
содержаться в У, то для [х-почти всех значений t можно
применить формулу конечных приращений в виде следствия 1
->
теоремы 13 гл. III, лишь бы только \\Х\\ ^ р, а это даст
-L-\h(a + X, t)-h{a, t)-^(a, t)x\\^
(IV, 11; 29)
дх
||ЛГ ах
-> ->
< sup \\^(l,t)-^(a,t)\<2k(t) (IV, 11; 31)
(где k по условию ~^0 и [х-интегрируема), откуда следует
доказательство теоремы.
26*

796
Гл. IV. Интегральное исчисление
Практически поступают следующим-образом. Если функция
/ определена интегралом (IV, 11;262), то для того, чтобы
убедиться в ее дифференцируемости, формально дифференцируют
под знаком интеграла и пишут равенство (IV, 11; 28). Формула
будет обоснованной, если выполнены условия теоремы
(которые в случае, когда ht ц,-почти всюду на Q принадлежит классу
С1, позволяют утверждать, что функция, определяемая правой
частью равенства (IV, 11; 28), непрерывна).
Укажем простое, но весьма важное следствие.
->
Следствие. Пусть f — функция, определенная по
формуле (IV, 11; 262) при следующих условиях:
■> ■>
a) h является непрерывным отображением Q X Т в F;
-> ->
b) h имеет всюду частную производную по х и dhjdx яв-
■> ■>
ляется непрерывным отображением Q X Т в 2'(Е; F);
c) для каждой точки аей существует в Q такая
окрестность Y этой точки и такой компакт К. из Т, что для всех х из
■> ->
У непрерывная на Т частная функция hx со значениями в F
имеет носитель в К-
->
Тогда функция f принадлежит классу С1 в Q и ее
производная задается формулой (IV, 11; 28).
Доказательство аналогично доказательству следствия
теоремы 114. Следует только убедиться, что из этих условий
вытекают условия теоремы 115.
Замечание относительно исследования последовательных
первообразных функции, непрерывной на интервале прямой R.
Вернемся к ситуации, которая рассматривалась в теореме 91.
->
Функция Fm, определенная по формуле (IV, 9; 41), является
■>
первообразной функции f порядка пг, обращающейся в нуль
в точке с вместе во всеми своими производными до порядка
m — 1 включительно. Это было доказано с помощью
преобразования двух последовательных интегралов к одному
интегралу. Теперь мы можем дать другое доказательство этого
утверждения путем непосредственной его проверки.
->
Дифференцируема ли функция Fm? Непосредственно этого
не видно. Эта функция зависит от х, с одной стороны, потому,
что х является верхним пределом интегрирования, ас другой,—
потому, что х находится под знаком интеграла.

§ П. Функции, представимые рядами или интегралами 797
Функцию Fm(x) можно рассматривать как значение при
у == х функции двух переменных
у ,
Gm(x,y)=jl(i) (X{~TX)[ dl- (IV, 11;32)
Покажем, что эта функция имеет полную производную. Для
этого достаточно доказать, что она имеет непрерывные частные
производные по х и у, а затем применить теорему 15 гл. III
(см. далее формулу (IV, 11; 36)). Прежде всего, согласно
теореме 89,
dGm (х, у) =7 iy) ^ifu! . (IV, И; 33)
(х - t)m~x
ду v-> У)— I \У> (от_ П1
и полученная функция непрерывна по {х,у).
■Для фиксированного у к функции (*,£)->/(£) (т_1)!
применима теорема 115 (здесь вместо х и t у нас написаны
х и I, вместо d\\,{t) написано й\, а отрезок [с,у] взят в каче-
•>
стве компакта К=Т), Поэтому функция Gm имеет частную
производную по х, определяемую по формуле
^gf (*. y)=j7il) ('~-2)Г ^ Для m>2- (IV, И; 34)
с
Покажем, что dGm/dx также непрерывна по (х,у)1).
Зафиксируем (х0, г/о) и предположим, например, что Уо^с. Тогда
можно написать:
^г(*. У)=\^1)Ь1)^~^-^1, (IV, 11; 35)
R,
где щ является характеристической функцией интервала [с, у].
Для фиксированного | при (х,у), стремящемся к (х0, у0),
-> /v t\m—2 ■> ^v t\m—2
%(^)"тД)Г схо*ится к ФУ.«)/<6) U;ot1)2)! всюду,
кроме, быть может, | = г/0 (поскольку тогда фьг{^) не сходится
к ф (g), если г/ стремится к г/о по значениям <г/о)-
Следовательно, для с?|-почти всех значений | (всех, кроме одного: г/о)
частная функция (х, у) -> фу (£) / (£) (от_2), непрерывна
в точке (хо, г/о) - Если л; и г/ будут пробегать компактные окре-
') В действительности, если учесть замечание 1°), следующее за
теоремой 15 гл. III, проводить доказательство этого факта не нужно.

798
Гл. IV. Интегральное исчисление
стности точек х0, уо в Ri, то подинтегральная функция будет
ограниченной, иметь носитель в фиксированном компакте, а,
следовательно, из теоремы 114 будет следовать, что dGm/dx
непрерывна в точке {х0,Уо)-
->
Таким образом, Gm принадлежит классу С1 на RiX^i- Но
тогда по теореме о сложной функции (следствие 5 теоремы 11)
->
функция Fm принадлежит классу С1 и ее производная
вычисляется по формуле
4гМ = 4г(х'х'>+%■(*'*)• (IV. П; 36)
Если учесть, что (х — у)т~2 при т^2 обращается в нуль при
у = х, то для т ^ 2 получаем:
# W = % <*• *> = J Т(Б) iT=¥^ dl. (IV, 11; 37)
с
Таким же образом можно поступать и далее,
последовательно дойти до производной (т—1)-го порядка включительно
и получить формулу
х
(х - 1)т-"~1
jji К (*) = j f(£) %}\ 1 ц, «*£ -£»-» («), *<m-l,
(IV, 11; 38)
->
из которой следует, что производные в точке с функции Fm до
(т— 1)-го порядка обращаются в нуль.
Вычислим теперь производную порядка т от функции Fm.
К функции F] можно применить ту же формулу, но на этот
раз мы получим:
х
Fl{x) = \l{l)dl,
(IV, 11; 39)
Таким образом, нами доказано, что производная m-го по-
рядка функции Fm равна /, и, следовательно, функция Fm,
определенная по формуле (IV, 9; 41), является первообразной по-
->
рядка т для функции /, обращающейся вместе со своими
производными до (т—1)-го порядка включительно в нуль в точке
с, что является новым доказательством теоремы 91,

§ 11. Функции, представимые рядами или интегралами 799
Случай несобственных сходящихся интегралов
->
Пусть h — функция, определенная на произведении ZX^i.
со значениями в банаховом пространстве F. Здесь Rj —
некоторый интервал \а, Ь[ прямой R. Рассмотрим интеграл
f{x) = j h{x, t) d\i (t). (IV, 11; 40)
\a,-*H
Будем предполагать, что |j. является некоторой мерой
Радона на Ri и что для каждого хеХ несобственный интеграл,
определяющий функцию f(x) (см. определение на стр. 724),
является сходящимся. Говорят, что несобственный интеграл
равномерно сходится при х, пробегающем некоторую часть А
множества X, если собственный интеграл J сходится
I а, Ь'[
к несобственному интегралу Г (при Ь', стремящемся к b
I a, ->&[
так, что Ь' <.Ь) равномерно относительно ^еА Это еще
означает, что «остаток» сходится к 0 при Ь', стремя-
16'.->Я
щемся к Ь равномерно относительно хеЛ. Можно сказать
также, что при любом е > 0 можно найти такое число b0 < b
(не зависящее от х), что для любого хеЛ из b0^.b'<ib
следует неравенство | | N=£-
I |&'Л»»[|
Необходимые свойства функции / могут быть получены
в два приема. Сначала доказывают, что собственный
интеграл I обладает требуемыми свойствами, а затем устрем-
1а, Ь'{
ляют Ъ' к Ъ.
Не ставя целью рассмотреть возможно более общие
случаи, мы приведем следующие теоремы:
Теорема 116. Пусть f — функция, определенная на X по
формуле (IV, 11; 40), в которой несобственный интеграл
предполагается сходящимся для каждого хе! Предположим, что
1°) Л является метризуемым пространством и для каждого
b' <c b собственный интеграл
М*)= J" h{x, t)dp{f) (IV, И;41)
I a, VI
определяет на X некоторую функцию f., со значениями в F,

800
Гл. IV. Интегральное исчисление
непрерывную в точке х = Xq пространства X (например, по
теореме 114).
2°) Существует такая окрестность У точки х0, что несоб~
ственный интеграл равномерно сходится относительно х из Т,
В этом случае функция f непрерывна в точке х0
пространства X.
■>
Теорема очевидна. По предположению, функция fb, непре-
■» •» ■»
рывна на Тв точке х0 и функция fb, сходится к /ь = /
равномерно на Т. "Остается лишь применить теорему 65 гл. II.
Теорема 117. Пусть задан несобственный интеграл
(IV, 11; 40), в котором X = Q есть открытое множество
аффинного нормированного пространства Е. Будем предполагать, что
Iе) Для каждого b' < b собственный интеграл (IV, 11; 41)
представляет собой некоторую функцию fb, на Q, удовлетво-
ряющую условиям теоремы 115, из которой следует, что fb,
дифференцируема (соответственно принадлежит классу С1) на
Q, а ее производная определяется по формуле
&(*)=' J -fH*. 04*С). (IV, 11; 42)
I а, Ь'\
2°) Несобственный интеграл
g(*)= J Ц-(*. t)dix(t) (IV, 11; 43)
1 a, -»fl
сходится для каждого «ЕЙ локально равномерно на Q.
3°) Множество Q связно, F полно, а несобственный инте-
грал (IV, 11; 40) сходится хотя бы в одной точке х = а
области Q или же Q и F произвольны, а этот несобственный
интеграл сходится для каждого «ей.
Тогда несобственный интеграл (IV, 11; 40) сходится для
каждого х из й; эта сходимость локально равномерна на Q,
■>
функция f, определенная по формуле (IV, 11; 40),
дифференцируема (соответственно принадлежит классу С1) на Q, а ее
производной является функция g.
->
В самом деле, когда Ь' стремится к Ь, функции fb,
удовлетворяют условиям теоремы 111 ').
') Здесь речь идет не о последовательности /„, а о семействе fb,,
зависящем от вещественного параметра Ь' и некотором пределе при Ь',
стремящемся к Ь. Легко проверяется, что для этих функций все сказанное Остается •
в силе.

§ П. Функции, представимые рядами или интегралами 801
Пример 1. Рассмотрим интеграл (в котором neR):
г eltx
(IV, 11; 44)
Функция /-> 1/(1 + ^2) интегрируема на R. Поэтому,
применяя теорему 114 с Т= R и k{t) — 1/(1 -f- t2), получаем, что
функция / непрерывна на R.
Дифференцируя по х под знаком интеграла, получаем
интеграл
Г lteitx
1 + t2
dt,
(IV, 11; 45)
не имеющий смысла, поскольку функция t/(\-\-t2) не
интегрируема. Поэтому доказать дифференцируемость /, рассматривая
лишь собственные интегралы (теорема 115), невозможно.
Рассмотрим теперь несобственный интеграл
g(x)--
ite1
tx
1 + t2
dt.
(IV, 11; 46)
1 — oo<- , -> +oo(
Применяя теорему Абеля, можно убедиться, что для х ф 0
он является условно сходящимся. В самом деле, функция t -*-
-+t/(\-\-t2) (производная которой равна (1 — t2)/[(\ + t2)2})
монотонна в каждом из интервалов ]— оо,—1], [— 1,-f-l] и
[+1,+оо[. Так как эта функция непрерывна и при t,
стремящемся к бесконечности, стремится к 0, то она ограничена и,
согласно следствию теоремы 86, имеет ограниченную вариацию.
Функция t-+eiix имеет при х Ф 0 «ограниченные
неопределенные интегралы» (оценка (IV, 9; 107)):
->с, <г\
[^
dt
_2
1*1
ттг- (IV, 11; 47)
Поэтому из критерия Абеля (следствие теоремы 98) следует
условная сходимость (IV, 11; 46) для х Ф 0. Эта условная
сходимость локально равномерна на открытом множестве Q = СО
прямой R. В самом деле, для каждого заданного числа б > 0
при с ^ 1 и \х\ ^ б имеет место оценка (в обозначениях
теоремы Абеля)
I
] — те*-, -с]
1+С, -»+°°[
< U (с) V (с) =
1 + с2
V)
б
(IV, 11;472)
') Для с^г 1 функция t/(l + t2) монотонна в [с, +«>[, и ее полная
вариация в точности равна с/(1 + с2).

802 Гл. IV. Интегральное исчисление
— величина, стремящаяся к 0 при с, стремящемся к
бесконечности, и фиксированном б.
При фиксированном с собственный интеграл
Ы*) = J* -TFfidt' (IV, 11; 48)
1-е, +с]
в силу теоремы 115 или даже ее следствия, принадлежит на
Я (или даже на R) классу С1. Поэтому мы можем устремить
с к +оо и применить теорему 117. Функция / оказывается
дифференцируемой в Я = С0, а ее производная определяется
несобственным интегралом g из (IV, 11;46).
Если теперь мы формально вычислим вторую производную
Г —t2ettx
J-ГП^' (IV, 11; 49)
то получим выражение, не имеющее смысла ни при каком
способе рассуждений.
Позже мы увидим, что функция / задается формулой
f(*)*=jte-l*i. (IV, 11; 50)
Эта функция непрерывна на R, принадлежит классу С1 на
дополнении к началу координат и не имеет производной в на^
чале координат. Однако эта функция принадлежит классу С°°,
т. е. имеет последовательные производные всех порядков на
дополнении к началу координат. Здесь, как и в замечании 1°)
на стр. 787, предыдущие теоремы позволяют предвидеть, когда
функция, представимая интегралом, дифференцируема;
невыполнение условий теорем еще не означает, что она не будет
дифференцируемой.
В качестве второго примера мы докажем очень важную
в теории рядов и интегралов Фурье формулу.
Пример 2.
Теорема 118. Имеет место формула
■J ^y±dt = j, X>0. (IV, 11; 51)
[0, -> + °°1
Эта формула уже была приведена в (IV, 9; 87). Полагая
Xt = f, перейдем к случаю %=\. Для доказательства
рассмотрим функцию /, определенную следующим образом:
/(*)=» J e-xt^Y~dt. (IV, 11; 52)
[0. -> + °°[
При х > 0 под интегралом в правой части стоит
интегрируемая функция. Поэтому этот интеграл собственный (теорема97),

§ 11. Функции, представимые рядами или интегралами 803
При х = 0 это не так. Интеграл будет несобственным
сходящимся по теореме Абеля.
Докажем, прежде всего, что интеграл правой части
является несобственным интегралом, равномерно сходящимся при
х ^ 0. В самом деле, если к с > 0 применить теорему
[с, -»+°°[
Абеля, где
u(t) = -~-, o(/) = sinf, (IV, 11; 53)
то и будет убывающей функцией, стремящейся к 0 при t,
стремящемся к бесконечности, т. е. функцией ограниченной
вариации, a v будет функцией с ограниченными неопределенными ин-
.2. Поэтому непосредственно при-
тегралами:
Ic. d]
менима оценка (IV, 9; 79):
| sin t dt
J
e-*«±Ldt
с с
(IV, 11; 54)
— величина, стремящаяся к 0 равномерно относительно х ^ 0
при с, стремящемся к бесконечности. Поскольку при конечном
фиксированном с, согласно следствию теоремы 114, J (х, с) =
= Г является непрерывной функцией х, то функция /, по
|0, с)
теореме 116, непрерывна на полупрямой R+, т.е. на множестве
вещественных чисел ^0. Выясним теперь, будет ли эта
функция дифференцируемой? Продифференцируем ее формально под
знаком интеграла:
/'(*) = _ J е-* sin* Л. (IV, 11; 55)
[0, -* + <»[
Интеграл, стоящий в правой части, является интегралом от
некоторой интегрируемой при х > 0 функции, тогда как при
х = 0 он является несобственным расходящимся интегралом.
Поэтому нет более необходимости пользоваться здесь теоремой
Абеля, поскольку нет возможности каким-либо образом
получить информацию о производной в начале координат. Однако
можно просто воспользоваться теоремой 115. Функция
v+ sin / „ , /->i
x—>-e~xt—т— для всех значении г принадлежит классу С на
Q = ]0, +оо[, имеет производную, равную —e-^sin*, и при
х ^ б > 0 выполняется неравенство
\e-xtsint\^e-&t, (IV, 11;56)
где справа стоит интегрируемая функция ^0.

804
Гл. IV. Интегральное исчисление
Из теоремы 115 следует, что функция / на Q = ]0, -(-оо [
принадлежит классу С1 и ее производная определяется формулой
(IV, 11; 55). Но тогда интеграл, стоящий в правой части, может
быть вычислен элементарно. В самом деле, производя дважды
интегрирование по частям (теорема 98), его можно записать
в виде
с р~х*
У (х) = — cos t dt =
|0, -»+oo|
= [-4^cos^°0+ j J^L sin tdt = --^-J-^t (IV, И; 57)
откуда
J'W = -TT*-' x>0- (IV, 11; 58)
Заметим, что J'(x) имеет предел, когда х стремится к 0.
Из теоремы 14 гл. III следует, что функция / имеет при х = О
производную и эта производная равна —1. Однако мы видели,
что это невозможно было ни предвидеть, ни представить /'(0) =
= —1 с помощью не имеющего никакого смысла интеграла
— sintdt.
[0, ->+<*>(
Из предыдущего следует, что функцию / можно получить,
отыскивая первообразную правой части равенства (IV, 11; 58),
что дает
/(*) = -arctg* + c. (IV, И; 59)
Постоянная с легко вычисляется. Действительно, при ху
стремящемся к +оо, функция t-*(e~xt sin t)/t просто сходится
к 0, и, поскольку она при х ^-. 1 мажорируется неотрицательной
интегрируемой функцией t—»(e-(|sin /| )/t, то из теоремы Лебега
следует, что J(x) стремится к 0 при х, стремящемся к -j-co.
Постоянная правой части равенства (IV, 11;59) тогда
равна л/2. Следовательно, в силу непрерывности функции /
в начале координат, 7(0) = л/2, чем и заканчивается
доказательство теоремы. В теории эйлеровых функций мы
познакомимся с одним обобщением этой формулы.
Применение к делимости дифференцируемых функций
Теорема 119. Пусть U — функция, определенная на
открытом множестве Q пространства R^1), со значениями в ба~
паховом пространстве F. Предположим, что пересечение Q с ги-
') Можно было бы всюду заменить R на С,

§11. Функции, представимые рядами или интегралами 805
перплоскостью xN = 0 состоит из нулей функции U порядка, не
меньшего k, т. е. функция U на нем равна нулю вместе со
своими частными производными до порядка k — 1 включительно.
->
Если функция U принадлежит классу С™ с m\^k, то най-
->
дется единственная функция V, определенная на Q, со значения-
ми в F класса Ст~ , такая, что будет, иметь место тождество
U{x) = xkNV(x). (IV, 11; 60)
В некотором смысле можно сказать, что тот факт, что функ-
ция U имеет на гиперплоскости xN = 0 нуль порядка k, влечет
>
за собой «делимость U на xkN». Следует заметить, что
отношение не принадлежит тому же классу дифференцируемое™, что
и функция U.
Доказательство. Г) Если такая функция V существует,
то она определяется единственным образом, ибо в каждой
точке, где xN Ф 0, она задается отношением VQ (х) = U (x)lxkN .
Так как по условию m ^ k, т. е. m — k ^ 0, то эта функция
непрерывна и с помощью предельного перехода может быть
определена в точке, где xN = 0 ').
•>
2°) Докажем существование функции V. Для простоты
предположим, что область Q выпукла и можно применить
формулу Тейлора2). Для каждой точки xeQ с координатами Х\,
х2, ..., xN к функции одной переменной и—U(x_,...txN-._,u)-
можно применить формулу Тейлора до порядка k — 1
относительно точки 0 и приращения xN. Поскольку производные до
порядка k—1 включительно на Н равны нулю, то эта формула
сводится к остаточному члену, и мы можем написать (формула
(IV, 9; 49)), что
Тк \— k f- dkV { t \ 0-0*-' jt
U [Xv ..., XN) XN J щ(Х1 XN-V lXN) (k— 1)! " *
0 N
_____ (IV, 11; 61)
') Это пункт 1°) доказательства теоремы 45 гл. II.
2) Существование V будет очевидным, если V0(x) = U
(x)lxN,определенная для xN Ф 0, имеет предел при х, стремящемся к такой точке а,
■>
что aiv = 0, и если функция, равная V0(x) для xN Ф 0 и равная
предыдущему пределу при xN = 0, принадлежит классу Cm~k. Таким образом, для
каждой точки а, такой, что aN = 0, можно ограничиться рассмотрением того,
что происходит в некоторой окрестности точки а. Это позволяет ограничиться
открытой выпуклой окрестностью.

806
Гл. IV. Интегральное исчисление
Мы видим, что в качестве V можно взять функцию,
определяемую интегралом
->
V \Х\, х%, ..., Хм) ■
-J
Х7Г(*1 *"-., *хы) {\kS)\ dt (IV, П;62)
о "xn v '
Эта функция принадлежит классу Cm_ft в Q. В самом деле,
поскольку функция U, по предположению, принадлежит классу
С™, то ее производная dkV\dxkN принадлежит классу Cm~h, и
тогда для вычисления производной порядка ^ m—k функции
->
V мы можем воспользоваться дифференцированием под знаком
интеграла. Теперь мы находимся в условиях применимости
следствия теоремы 115, что и доказывает теорему.
->
Замечания. 1°) Тот факт, что F является пространством
-> ->
Банаха, т. е. полно, существен. Так как V {х) = U {x)jxkN, то для
->
точек х, не лежащих в гиперплоскости xN = 0, V(x) является
элементом F. Для точек х, находящихся в этой гиперплоскости,
интеграл (IV, 11; 62) в неполном пространстве может не иметь
->
смысла. Поэтому предел V(x) при х, стремящемся к некоторой
точке гиперплоскости xN = 0, существовать не обязан.
■*■
2°) Можно было бы надеяться, что функция У принадлежит
классу С"1', где m' > m — k. Однако это не верно, и наилучшим
является число m — k.
->
Рассмотрим частный случай Л/ = 1 (RAr=R), F = R и
функцию U, определенную формулой
С/ (jc) == | jc (IV, 11; 63)
Она, очевидно, принадлежит классу Ст, но не принадлежит
классу Ст+Х. В начале координат она имеет нуль порядка т + 1
и, следовательно, в частности, любого порядка k ^ т.
Отношение V здесь запишется в виде
y(JC) = |JC|m-ft+4 (IV, И;64),
Это отношение принадлежит классу Cm~h и не принадлежит
классу Cm-ft+I.
->
Следствие. Пусть U — некоторая функция класса Ст на
открытом множестве Q аффинного конечномерного пространства

§ 11. Функции, представимые рядами или интегралами 807
Е со значениями в банаховом пространстве F. Пусть Б —
гиперповерхность класса Ст, содержащаяся в Q, a f(x) = 0 —
нормальное уравнение этой гиперповерхности1). Если эта гипер-
->
поверхность состоит из нулей функции U порядка, не меньшего
■>
k, то существует функция V класса Cm~h, определенная един-
■>
ственным образом на Q со значениями в F и такая, что
U(x) = (f(x))kV(x). (IV, И; 65)
Доказательство. Здесь, как и при доказательстве
теоремы (см. замечание 2°) на стр. 805), достаточно для каждой
точки а гиперповерхности дать доказательство, относящееся
к некоторой окрестности этой точки. Выберем некоторую
систему координат в Е. Поскольку /(*) = 0 является нормальным
уравнением поверхности 2, то в точке йе2! хотя бы одна из
частных производных f относительно хи х2, ..., xN отлична
от 0. Предположим, например, что это -^— (а).
Рассмотрим теперь функции, определенные равенствами
U\ =ЛТ|, Uo^^ Хо, . . ., Мдг^1 == ЛГдг — 1,
_fl ч (IV, 11; 66)
Эти функции определяют некоторое отображение Ф
множества В в Rw класса О. Якобиан этого отображения =^=0 в
точке а, поскольку он равен , (а). Согласно теореме о неявных
"XN
функциях (следствие 2 теоремы 31 гл. III), существует такая
открытая окрестность со точки а ъ Q,, что сужение Ф на со
является Ст-диффеоморфизмом со на некоторое открытое
множество coi из R". Обозначим через Ф-1 его обратный
диффеоморфизм. С помощью Ф можно перенести каждую фигуру из со
на coi.
Пересечение 2 с со перейдет на гиперповерхность 2i = Ф(2),
являющуюся пересечением гиперплоскости uN = 0 с множе*
ством соь
Диффеоморфизм ф преобразует функцию U на со со значе-
■> ■> ■>
ниями в F в функцию (7[ на coi со значениями в F, равную
(У, = (7оф-'-.
Легко проверить, что гиперплоскость uN = 0 состоит из ну-
■>
лей порядка k функции Ui2).
') Смотри следствие теоремы ЗЗг гл. III.
■> ■> j*
2) Так как Ux = U« Ф"1, то производные U\ определяются по теореме
о сложных функциях. Вычисление их громоздко, но индукцией по k легко
доказать, что все они равны нулю до порядка k — 1 включительно.

808
Гл. IV. Интегральное исчисление
Из теоремы следует, что в <»i существует такая функция V\
класса Cm~h, определяемая единственным образом, для которой
-> •> ->
имеет место тождество U} = u^Vv В этом случае Vi является
->■
результатом преобразования Ф-1 функции V на ю, определенной
-> •> *
соотношением V= У\оФ. Функция V на оэ принадлежит
классу Cm~h, и на ю имеет место тождество U = fhV, чем и
заканчивается доказательство теоремы.
Следствие 2. Пусть Б — гиперповерхность класса С°°
открытого множества й конечномерного аффинного пространства
Е с нормальным уравнением f(x) = 0. Все другие ее
нормальные уравнения g(x) = 0 можно получить, полагая g = fV, где
V — некоторая скалярная функция класса С°° на Q всюду ф 0.
Доказательство. Прежде всего, если g=fV, а
функция V не имеет нулей и принадлежит классу С°°, то функция
g также принадлежит классу С°° и g(x) = 0 определяет
гиперповерхность Б. Кроме того, для точки aeS
tffr) = ПЙ V (а) + f{a) \Г(а) =Ш V (а) Ф 0,
а, следовательно, g(x) = 0 есть нормальное уравнение
гиперповерхности Б.
Обратно, пусть g(x) = 0 — нормальное уравнение
гиперповерхности Б. Тогда g принадлежит классу С°° и обращается
в нуль на Б, т. е., согласно следствию 1, g =fV, где V
принадлежит классу С00. Можно также сказать, что g{x) = 0 является
нормальным уравнением Б, а / принадлежит классу С°° и
обращается в нуль на Б, т. е. / — gW, где W принадлежит классу
С00. Поэтому g = fV = gWV, откуда следует, что VW = 1 там,
где g не обращается в нуль, т. е. вне Б. Поскольку W и V
непрерывны, то функция WV также непрерывна, а, следовательно,
WV == 1 всюду. Это означает, что V ф 0 всюду, и следствие
доказано.
Замечания. 1°) Интересно отметить, что интегральное
исчисление оказывается полезным для изучения таких чисто
дифференциальных свойств.
2°) Исходя из следствия 2, можно доказать (но это очень
сложно), что каждая замкнутая гиперповерхность Б класса С0?
аффинного конечномерного пространства может быть полностью
определена одним нормальным уравнением f{x) = 0.
Для простоты следующую теорему мы приведем лишь в слу*
чае k = 1.

§ 11. Функции, представимые рядами или интегралами 809
Теорема 120. Пусть Q — открытое множество простран-
->
ства R^ и U — некоторая функция на Q класса Ст со значения-
->• •»•
ми в банаховом пространстве F. Предположим, что функция U
обращается в нуль на пересечении Q с векторным п-мерным
подпространством, определяемым уравнением xn+i = ...
... = xN = 0. Тогда можно найти {вообще говоря, бесконечным
числом способов) такие функции Vn+U Vn+2, ..., VN класса
->
С™-1 на Q со значениями в F, что
U(x) = xn+1Vn+i(x)+ ... +xnVN(x). (IV, П; 67)
Доказательство аналогично доказательству
теоремы 119. Формула конечных приращений (формула Тейлора для
k—1=0) применяется здесь' к функции N— п переменных:
\ип + \> ип+2> •••> UN)—> (J (X{, Х2 Хп, Un + i, ..., UN). ПрИ
этом получается, что
U \Х\, х%, • ■ ., Хц) =
= {и (jf|, х2, .. ., хп, txn+], ..., tXft)•([), ..., 0, xn+i, ..., xN)) dt =
о
N 1 >
= ]У] xt J -q^(xx, x2, ..., хп, txn+l, ..., txN)dt. (IV, 11; 68)
i=«+l 0 (
Поэтому для i = n-j- 1, n + 2, ..., N можно положить
i >
■* С дО
Vi(x)=j -j^{Xi, х2, ..., хп, txn+l, ..., txN)dt, (IV, 11; 69)
о 1
чем и заканчивается доказательство теоремы.
Замечание. Здесь при n^.N — 2 единственного решения
не будет. К функции VN-i можно добавить функцию xN,
а к функции VN функцию Jfy-i, и это приведет лишь к
добавлению и вычитанию xN-ixN из U.
Следствие. Пусть V — многообразие класса Ст
открытого множества Q конечномерного аффинного пространства Е,
определенное системой нормальных уравнений fi(x) = 0,f2(x) =
>
-—0, •■_•! fi(x) — 0. Пусть U — функция класса Ст на Q со

810
Гл. IV. Интегральное исчисление
значениями в банаховом пространстве F, равная нулю на V. То-
гда существует система функций Уь V2, ..., Vt (вообще говоря,
->■
их бесконечно много) класса Cm~l на Q со значениями в F,
такая, что
U = f ,V, + f2V2 + ... + UVt. (IV, 11; 70)
Доказательство аналогично доказательству следствия 1
теоремы 119 с некоторыми усложнениями, требующими
применения разложения единицы. На нем мы останавливаться не
будем.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютно мажорируемая векторная
мера 488
-— сходящееся бесконечное
произведение 165
— сходящийся несобственный
интеграл Римана 725
ряд 129, 160
Абстрактное многообразие
размерности п класса Ст 334
Аксиома отделимости Хаусдорфа
44
Алгебра 127
<т-алгебра частей множества 505
Антисимметричность 21
Аппроксимирующая
последовательность 424, 524, 563
Ассоциативность тензорного
произведения 677
Атлас многообразия 326
Атомическая мера 441
Аффинная контингенция 219
— система координат 176
Аффинное многообразие 176
— нормированное пространство 179
— отображение 178
— пространство 174
— — касательное в точке к
многообразию 338
Аффинно линейная функция 151
Банахова алгебра 127
Банахово пространство 117
Барицентр 184
Безусловно сходящийся ряд 131
Бесконечно дифференцируемое
многообразие 319
Бесконечное произведение 162
Биективное отображение 13
Биекция 13
Билинейное отображение 121
Борелевская а-алгебра 505
Борелевское отображение 517
— подмножество 505
Брахистохрона 369, 384
Вектор касательный в точке к
множеству 218
Векторная контингенция 219
— мера 450
Векторное подпространство,
касательное к многообразию в точке 220
— поле 222
— пространство, касательное к
абстрактному многообразию в точке
338
многообразию в точке
338
Верхний интеграл 520
Римана 421, 635, 653
— предел последовательности 79
Верхняя огибающая 25
Вещественная мера Радона 476
Вещественное многообразие 333
Взвешенное геометрическое среднее
360
Внешность множества 48
Внешняя мера 490, 494
Внутренность множества 47
Внутренняя мера 492
Возрастающее отображение 25
Вполне нулевая мера 586
— отрицательная мера 586
— положительная мера 586
— упорядоченное множество 23
Выпуклая функция 204
Выпуклое множество (часть) 43
в аффинном пространстве 184
Галилеева система координат 195
Гармоническая функция 415
Геодезическая кривая 389, 398
Гиперплоскость 177
Гиперповерхность 327
Главное значение в смысле Коши
736
Гомеоморфизм 54
Гомеоморфные пространства 55
Градиент функции 221
Граница 48

812
Предметный указатель
Двойная последовательность 61
Двойной интеграл 657
Делимость дифференцируемых
функций 804
Дизъюнктные меры 588
Ст-диффеоморфизм 336
Дифференциал 213, 217
Дифференцируемая гиперповерхность
292
— функция 227
Дифференцируемое многообразие 218,
319
Дифференцируемость бесконечного
произведения 787
— неявной функции 298
— суммы ряда 779
— функции, представимой
интегралом 794
Длина пути 701
Достаточные .условия экстремума 287
Дуга 90
Евклидово аффинное пространство
185
— векторное пространство 185
— скалярное произведение 184
Единичный шар 42
Единственность тензорного
произведения мер 658
Естественная топология 64
Зависимые функции 350
Задача Дирихле 415
— Плато 414
Заключение 36
Закон инерции 194
Замена переменных 16, 394, 720, 742
Замкнутая кривая 353
— часть 45
Замкнутый интервал 26, 46
— параллелепипед 46
— шар 41, 46
Замыкание 49
Измельчение разбиения 418
Измеримое множество 500, 501
— отображение 510, 537
Изолированная точка 47
Изотропные векторы 192
Изотропный конус 192
Индуцированная метрика 50
— топология 59
Интеграл Лебега от функции с
векторными значениями 524
— от векторной этажной функции по
мере ц 520
функции, определенной почти
всюду 533
по мере ц 443
— Римана 426
на прямой 416
ступенчатой функции с
компактным носителем 419
— сходящийся в смысле главного
значения Коши 736
— Френеля 735
Интегрируемая функция с
векторными значениями 524
ц-интегрируемая функция с
векторными значениями 524
Интегрируемая функция со
значениями в пространстве Банаха 423
Интегрируемость в смысле Лебега
725
— суммы ряда 778
— уравнений Эйлера 383
— функции по нескольким мерам 612
представимой интегралом 793
Инъективное отображение 13
Инъекция 13
Истинное параметрическое
представление 321
Исходное множество отображения 11
Каноническая инъекция 12
•— мера прямой R 448
— сюръекция 19
Кардинальное число 28
Карта 326
— множества 326
— покрывающая точку 326
Касательная к пути 709
Касательный вектор к многообразию
в точке 344
Квантор 37
Класс эквивалентности 18
Колебание функции в точке 196, 638
— — на окрестности точки 638
Компактная часть 68
Компактное топологическое
пространство 69
Комплексная мера Радона 476
Комплексное многообразие 333
Комплексно сопряженная мера
Радона 477
Композиция отображений 15
Конечное множество отображения 11
Континуум-гипотеза 35
Кратный интеграл 677
на R" 742
Кривая 327
— Жордана 753
— класса С™ 353

Предметный указатель
8!3:
Криволинейная абсцисса 704
Криволинейный интеграл 705
Критерий Абеля 732
— равномерной сходимости 161
— условной сходимости 142
Круг 41
Лемма Хаара 379
Линейное многообразие, касательное
к многообразию в точке 220
— L-непрерывное отображение 579
— отображение ПО
Линейно связное пространство 92
Локальная карта класса Ст 326
■— равномерная сходимость
бесконечного произведения 168
— сходимость последовательности
мер Радона по норме 631
Локально компактное пространство
74
— линейно связное пространство 95
— равномерно сходящаяся
последовательность функций 153
— связное пространство 94
Локальный гомеоморфизм 312
Мажоранта 23
Мажорируемая часть 23
Максимум 23, 25
Матрица Якоби 211
Мера Дирака 441
— — в точке 440
— допускающая борелевское
продолжение 583
— Лебега 448
— множества 501
— плотности р по отношению к
вещественной мере 594
— Радона 440
— — на вещественной прямой 682
— — — локально компактном
пространстве 447
равная нулю 465
— с базой 594
—. ц-сингулярная 589
— сосредоточения на ^я.-~-
пространства 589
л-мерная площадь л-мерного
параметрического многообразия 760, 763
Метризуемое топологическое
пространство 59
Метрическое пространство 40
— свойство 58
Минимум 24
Миноранта 23
Минорируемая часть 23
Многообразие, дифференцируемое m
раз 319
— принадлежащее классу Ст 320
— размерности л, принадлежащее
классу Ст 320
— т раз непрерывно
дифференцируемое 319
Множество 9
— линейных отображений 15
— непрерывных отображений 15
— нулевой меры 506
— отображений 15
Множитель Лагранжа 353
Монотонная функция 202
Мощность 27
— континуума 33
Натуральная параметризация 704
Независимые функции 350
Необходимые условия экстремума
285, 287
Неограниченно удаляющаяся
последовательность точек 619
Неопределенный интеграл, 694, 706
от меры Радона 683
функции по мере 684
Неподвижная точка отображения 107
Непрерывная функция многих
переменных 65
с компактным носителем 463
Непрерывно дифференцируемая
функция 227
— дифференцируемое многообразие
319
Непрерывное в бесконечности
отображение 618
— отображение 52
— слева отображение 195
— справа отображение 195
Непрерывность суммы ряда 778
— функции, представимой
интегралом 792
Неравенство выпуклости 562
— Гёльдера 364, 567
— Коши — Буняковского — Шварца
43
— Коши — Шварца 366
— Минковского 361, 562
— счетной выпуклости 546, 562, 565
Несобственный интеграл 724
— путь 703
Нечетность 736
Неявная функция 293
Нижний предел последовательности'
79
Нижняя огибающая 25
Норма 41

814
Предметный указатель
— билинейного отображения 124
— линейного отображения 113
Нормальная система уравнений 331
Нормальное пространство 462
Нормально сходящийся ряд 129, 160
Норма меры 449
— порядка р 359, 561
Нормированная алгебра 127
Нормированное векторное
пространство 42
Носитель 417
— меры 663
Радона 466
Обобщенное евклидово пространство
192
— эрмитово пространство 192
Образ карты 326
— меры при отображении 617, 618,
621
— множества при отображении 13
— отображения 113
— параметрического многообразия
352
Обратное отображение 139
Общая, или аффинная, система
координат 176
— теорема Лебега 539
Объединение 10
Ограниченная часть 23
Окрестность точки 46
Окружность 41
Ортонормированный базис 190
Основная теорема измерения объемов
754
Особое многообразие размерности п
класса Ст 352
Отделимое пространство 58
Открытое множество 44
— отображение 311
Открытый интервал 26
— параллелепипед 45
— прямоугольник 64
— шар 41, 45
Относительно компактная ч-асть 68
Относительный максимум 285
— минимум 285
— экстремум 393
Отношение порядка 21
— эквивалентности 17
Отображение 11
— ц-измеримое 510
— класса С* 336
— непрерывное в точке 52
— ц-собственное 623
Отрезок 43
Отрицательная мера Радона 478
i— часть элемента 481
Паракомпактное пространство 453
Параллельный перенос меры Радона
632
Параметрическое многообразие
размерности п класса Ст 352
Параметрические многообразия,
Ст -эквивалентные 353
Первообразная 706
Пересечение множества частей 10
Перестановка 13
— членов ряда 130
—2 и J для рядов с
положительными членами 547
Плотная часть 50
Плотность по отношению к мере
Лебега 449
Площадь «-мерная 756
Поверхность 327
Подмножество (или часть) 9
Подпокрытие 67
Покрытие 67
Полная вариация последовательности
142
функции 686
— дифференцируемость 253, 266
— масса 474
— производная 213
— решетка 482
Полное метрическое пространство 101
Полный дифференциал 213
Положительная мера Радона 478
— часть элемента 481
Полулинейная форма 187
Полулинейное отображение 187
Полунорма 564
Полуоткрытый интервал 26
Полусходящийся несобственный
интеграл Римана 725
Полуторалинейная форма 187
Полуупорядоченное векторное
пространство 480
Пополненная прямая 26
Последовательность 15
— имеющая ограниченную вариацию
142
— Коши 101
— мер Радона, широко сходящаяся
к предельной мере 632
— ^.-сходящаяся 578
Постоянное отображение 13
Правило нахождения относительного
максимума или минимума 289
Правильная функция 197
Предел последовательности 60
функций 777
Преобразование 13
Принцип кусочной склейки мер 475

Предметный указатель
815
Продолжение меры 473
с векторными значениями 610
— положительной меры 489
— равномерно непрерывных
отображений 104
Проекция 12
Произведение меры на функцию 590,
592
— множеств 11
— нормированных векторных
пространств 118
— топологий 64
— числовых рядов 137
Производная 199
— билинейного непрерывного
отображения 225
— матрица 211
— мера 698
— отношения 238
— отображения 198
слева 198
справа 198
— порядка m 199
— произведения 236, 268
Производное отображение 213
Производный вектор 215
Прообраз множества при
отображении 13
— функции при замене переменных
16
Простая сходимость
последовательности функций 149
Пространство я раз
дифференцируемых функций 267
Псевдоизмеримое множество 500, 501
— подмножество 496
Пустой носитель меры Радона 466
Путь 90
Равномерно дифференцируемая
функция 253
— непрерывное отображение 86
— стягивающееся множество 748
— сходящаяся последовательность
150, 152
— сходящийся ряд 160
Разбиение 418
Раздельно непрерывная функция 67
Разложение единицы 452
подчиненное покрытию 452
Разложимая функция 463, 654
Рассеянная мера 443
Расстояние 40, 82
Расходящееся бесконечное
произведение 163
Регулярное пространство 59
Решетка 481
Рефлексивность 17, 21
Свойство Больцано — Вейерштрасса
76
— выполняющееся почти всюду 508
ц-почти всюду 508
— Гейне — Бореля 68
— Лузина 536
Связанные точки 93
Связная компонента 93
Связное пространство 88
Сдвиг 150
Сепарабельное пространство, 50, 510
Сжатие 107
Симметричное билинейное
отображение 259
— я-линейное отображение 262
Симметричность 17
Скачок функции в точке 196
Собственное отображение 618
Совершенное множество 507
Соотношение Шаля 175, 683
Сопряженное пространство 115
Спрямляемый несобственный путь 703
Среднее значение функции, на
интервале 438
— порядка р 359
Стационарная точка 287
Строгий относительный максимум 285
минимум 285
Строго возрастающее отображение 25
— убывающее отображение 25
Ступенчатая функция 418
Сумма безусловно сходящегося ряда
131
— Коши — Римана 436
— ряда 128
Суммирование по блокам безусловно
сходящегося ряда 134
Существенная верхняя грань 574
Существенно ограниченная функция
574
Существование тензорного
произведения мер 661
Сфера 41
Сходимость мер Радона по норме 631
Сходящаяся двойная
последовательность 61
—• последовательность 60
мер Радона 631
Сходящееся бесконечное
произведение 162
Сходящийся несобственный интеграл
724
— ряд 128
Счетное множество 27, 31

816
Предметный указатель
Сюръективное отображение 13
Сюръекция 13
Трансфинитное число 28
Трансцендентное число 33
Тензорное произведение мер 658
Теорема Абеля 143, 732
— Банаха — Штейнгауза 641
— Бернштейна 27
— Бэра 641
— Вейерштрасса о полиномиальной
аппроксимации 680
— Даламбера 84
— Данфорда — Петтиса 594
— Егорова 534
— Лебега — Никодима 594
— — о сходимости 534
— об интегрировании по частям 728
ортогональной проекции
площадей гиперплоскостей 759
— о замене переменной 735
неподвижной точке 108
— — неявной функции 305
— — перестановке интеграла и
линейного непрерывного отображения
430
— — переходе через таможню 92
— — плотности 659
— — постоянном ранге 345
— — применении билинейного
непрерывного отображения 567
•— линейного непрерывного
отображения 566
— — сложной функции 230
среднем 433
•— Рисса 106
— Ролля 200
— Фату 542
— Фишера — Рисса 573
— Фубини — Лебега 664
Фату 670
Тождественное отображение 12
Топологическая группа 66
Топологическое векторное
пространство 66
— множество 320
— подпространство 59
— произведение 63
— пространство 58
— свойство 58
Топология пополненной прямой 60
Точка прикосновения 49
— разрыва первого рода 196
— сгущения 75
Точная.верхняя грань 24
— нижняя грань 24
Транзитивность 17. 21
— образов мер 624
Убывающее отображение 25
Узкая сходимость
последовательности мер конечной нормы 652
Радона 654
Узко сходящаяся последовательность
мер 653
Универсальный атлас 326
Уравнение колебания струны 239
— Эйлера 378
Уравнения Гамильтона 408
Условие 36
— Гёльдера 87
— Липшица 87
Условия трансверсальности 400
Условно сходящееся бесконечное
произведение 165
— сходящийся ряд 129
Условный максимум 353
— минимум 353
Факторгруппа 19
Фактормножество 19
Факторпространство 20
Формула интегрирования по частям
716
— конечных приращений 200, 247
— Лейбница 268
— Тейлора 201, 272, 276, 279, 292,
714, 715
Фундаментальная последовательность
100
— система окрестностей 47
Функции, ц-эквивалентные в смысле
Лебега 572
Функциональное пространство 146
Функция 11
— Гамильтона 407
— длины 702
— имеющая интегрируемую р-ю
степень 563
локально ограниченную
вариацию 694
— интегрируемая по Риману 423
— ц-интегрируемая 610
— — по Риману 634
— Лагранжа 407
— полунепрерывная сверху 85
— — снизу 85
— представимая интегралом 777, 792
рядом 777
— принадлежащая классу Ст 199
— т раз непрерывно
дифференцируемая 199, 266

Предметный указатель
817
— Римана 168
— с ограниченной вариацией 686
— ^-существенно ограниченная 574
— удовлетворяющая условию Гёль-
дера 87
— — — Липшица 87
— характеристическая 30
— Хевисайда 684
Частная дифференцируемость 253,
266
— производная вдоль вектора 209
— ■=— отображения 224
— сумма с индексом п 128
— теорема Лебега 538
Часть (подмножество) множества 9
Четность 736
Шар 41
Широкая сходимость
последовательности мер к мере Дирака 646
Радона 630, 632, 654
тензорных произведений 679
Эквивалентные метрики 56
— нормы 56
— пути 702
— функции 572
Экстремаль-378
Экстремум 285
Эрмитова положительно
определенная матрица 192
Эрмитово аффинное пространство 187
— векторное пространство 187
— скалярное произведение 187
Этажная функция 513
ц-этажная функция 513
Ядро отображения 113
Якобиан 212

ОГЛАВЛЕНИЕ
Предисловие редактора перевода 5
Предисловие 7
Глава I. Теория множеств 9
§ 1. Множества. Элементарные операции 9
Части множества 9
Отношение включения. Дополнение 10
Объединение. Пересечение 10
Произведение множеств 11
§ 2. Отображения. Функции 11
Примеры отображений 12
Инъекции. Сюръекции. Биекции 13
Образ и прообраз подмножества 13
Множество отображении. Семейства. Последовательности ... 15
Композиция отображений 15
Замена переменных и замена функций 16
§ 3. Отношения эквивалентности. Фактормножество 17
Классы эквивалентности. Разбиения 18
Фактормножество 19
Факторгруппа по инвариантной подгруппе 19
Факторпространство векторного пространства по векторному
подпространству 20
§ 4. Отношения порядка . 21
Примеры отношений порядка 22
Мажорируемые части. Мажоранты. Максимум. Точная верхняя
грань 23
Возрастающие функции 25
Пополненная прямая 26
§ 5. Мощности. Счетные множества 27
Мощности. Кардинальные числа 27
Счетные множества 31
Мощность континуума 33
Трансцендентные числа 33
Континуум-гипотеза 35
§ 6. Некоторые основные понятия логики 36
Глава II. Топология 40
§ 1. Метрические пространства. Элементарные примеры 40
Сферы. Шары 41
Нормированные векторные пространства 41
§ 2. Открытые и замкнутые части. Окрестности. Внутренность.
Граница. Замыкание. Плотные подмножества 44
Открытые части 44
Замкнутые части 45
Окрестности 46

Оглавление
819
Внутренность . 47
Внешность 48
Граница 48
Замыкание 49
Плотные подмножества . 50
Подпространства. Индуцированная метрика 50
§ 3. Непрерывные функции. Гомеоморфизмы 52
Гомеоморфизмы 54
§ 4. Метрические пространства и топологические пространства ... 55
Топология пополненной прямой R . 60
§ 5. Последовательности. Пределы. Сходимости 60
§ 6. Топологическое произведение 63
Сходящиеся последовательности в произведении ...... 64
Непрерывные функции многих переменных 65
Топологические группы. Топологические векторные пространства 66
Раздельная непрерывность функции двух переменных .... 67
§ 7. Компактные пространства. Элементарные свойства 67
Локально компактные пространства . 74
Точка сгущения последовательности 75
Верхний и нижний пределы вещественной последовательности . 79
§ 8. Свойства непрерывных функций на компактных пространствах 79
Равномерная непрерывность .86
§ 9. Связные пространства 88
Линейно связные пространства 90
§ 10. Дополнение по общей топологии связных пространств .... 92
Некоторые применения понятия связности. Критерии
негомеоморфности 97
Существование и непрерывность обратной функции для строго
монотонной непрерывной функции 98
Применение: метрики, определяющие топологию в R 99
§ 11. Полные метрические пространства 100
Продолжение равномерно непрерывных отображений 104
Частные свойства конечномерных топологических векторных
пространств 106
§ 12. Теорема о неподвижной точке . 107
§ 13. Элементарная теория нормированных векторных пространств и
пространств Банаха ПО
Ядро и образ непрерывного линейного отображения 113
Произведения нормированных векторных пространств . . . .118
Билинейные непрерывные отображения произведения
нормированных векторных пространств в нормированное векторное
пространство 121
Мультилинейные непрерывные отображения 126
Алгебры. Нормированные алгебры 127
§ 14. Ряды в нормированных векторных пространствах 128
Перестановка членов ряда 130
Суммирование по блокам безусловно сходящегося ряда .... 134
Действие линейного непрерывного отображения на ряд .... 136
Произведение двух числовых рядов. Применение билинейного
непрерывного отображения к двум рядам 137
Обратимые отображения в банаховых пространствах .... 139
Критерий условной сходимости 142
§ 15. Наиболее употребительные примеры функциональных пространств.
Сходимость простая и равномерная 146
Функциональные пространства • 146
Простая сходимость последовательности функций 149
Равномерная сходимость последовательности функций .... 150

«20
Оглавление
Другие применения выражения «равномерная сходимость» .152
Пространства, порожденные структурами пространств Е и F . . 154
Непрерывность локально равномерного предела
последовательности непрерывных функций 155
Некоторые контрпримеры ...... 157
Ряды функций со значениями в нормированном векторном
пространстве 159
§ 16. Бесконечные произведения вещественных или комплексных чисел
и функций 162
Бесконечные произведения и логарифмические ряды 164
Бесконечные произведения вещественных или комплексных
функций 167
Применение к функции £ Римана 168
Глава III. Дифференциальное исчисление 174
§ 1. Аффинные пространства 174
Аффинные многообразия 176
Линейные отображения. Аффинные отображения 178
Аффинные нормированные пространства 179
Выпуклые множества в аффинных пространствах 183
Евклидовы векторные и евклидовы аффинные пространства . . 184
Эрмитовы векторные и эрмитовы аффинные пространства . ■ 187
Изоморфизм (или полуизоморфизм) конечномерного евклидова
(или эрмитова) пространства и его сопряженного пространства 189
Ортонормированные базисы 190
Обобщенные евклидовы или эрмитовы пространства 192
§ 2. Вещественные функции вещественной переменной. Непрерывность
справа и слева 195
Разрывы первого рода. Правильные функции 196
Производная вещественной функции вещественной переменной . 198
Монотонные функции 202
Дифференцируемые функции и теоремы о промежуточных
значениях ......■■ 204
Выпуклые функции 204
§ 3. Производная отображения одного аффинного пространства в
другое. Производный вектор функции скалярной переменной . . . 208
Общий случай. Частная производная вдоль вектора 209
Матрица Якоби. Якобиан 211
Недостатки понятия производной вдоль вектора 212
Полная производная, или производное отображение ..... 213
Понятие дифференциала . 217
Геометрическая интерпретация производного отображения:
дифференцируемое многообразие и линейное касательное многообразие 218
Градиент вещественной функции в евклидовом пространстве . . 221
Случай, когда F является произведением аффинных пространств 223
Случай, когда Е является произведением аффинных пространств.
Частные производные отображения ........... 224
Производная билинейного непрерывного отображения ... 225
Дифференцируемые функции. Непрерывно дифференцируемые
функции 227
Примеры непрерывно дифференцируемых функций 228
Пространства дифференцируемых функций 229
■§ 4. Теорема о сложной функции 230
Примеры вычисления обычных производных 235
§ 5. Формула конечных приращений 247
Полная дифференцируемость и частная дифференцируемость . . 253

Оглавление
821
§ 6. Производные высших порядков 257
Последовательные производные 261
Случай произведения пространств. Полная и частная
дифференцируемое™ 266
Пространства п раз дифференцируемых функций 267
Производная произведения (формула Лейбница) ...... 268
§ 7. Формула Тейлора. Максимум и минимум 272
Применение формулы Тейлора для вычисления производных . . 276
Формула Тейлора относительно некоторой системы координат . . 279
Применение к изучению максимумов и минимумов. Определения 285
Необходимые условия экстремума 285
Нахождение необходимых и достаточных условий экстремума
функции ... . ........ 287
Частный случай вещественной функции / двух вещественных
переменных х, у . . 290
Применение формулы Тейлора к изучению расположения
гиперповерхности по отношению к касательной гиперплоскости . . . 292
§ 8. Теорема о неявной функции. Постановка задачи 293
Существование неявной функции 294
Дифференцируемость неявной функции 298
Дифференцируемость функции и-»-и-1 на 9?{F\G) 300
Частный случай, когда Е = F = G = К— скалярное поле . . 306
Случай, когда Е, F, G конечномерны . 308
Обратная функция как неявная функция 309
Вычисление производных высших порядков неявной функции . . 314
Техника замены переменных и замены функций 318
§ 9. Дифференцируемые многообразия 319
Определение многообразия при помощи его параметрического
представления .......... 321
Определение многообразия с помощью неявных уравнений , . 331
Вещественные и комплексные многообразия ........ 333
Абстрактные многообразия 334
Векторное пространство, касательное в точке к многообразию
аффинного пространства Е размерности N 338
Векторное пространство, касательное к абстрактному
многообразию в точке 343
Теорема о постоянном ранге 345
Зависимые и независимые функции 350
Особые, или параметрические, многообразия 352
§ 10. Условные максимумы и минимумы 353
Практический способ вычисления условного максимума или
минимума 356
Применение теории условных максимумов. Неравенства Гёльдера
и Минковского . 358
§ 11. Вариационное исчисление 369
Постановка задачи . 369
Дифференцируемость / 372
Необходимые условия экстремума 378
Лемма Хаара 379
Простые случаи интегрируемости уравнений Эйлера 383
Уравнение геодезических на поверхности 389
Относительный экстремум 393
Замена переменных 394
Приложение к задаче о геодезических 396
Переменные концы. Условие трансверсальности 400
Применение к геодезическим кривым 405

822
Оглавление
Канонические уравнения Гамильтона ... 406
Применения к механике 409
Вариационное исчисление для кратных интегралов 410
Глава IV. Интегральное исчисление 416
§ 1. Интеграл Римана на прямой 416
Ступенчатые функции 418
Верхний интеграл Римана от ограниченной функции / > 0 с
компактным носителем 421
Интегрируемые функции со значениями в пространстве Банаха 423
Интеграл от интегрируемой функции 425
Примеры интегрируемых по Риману функций ....... 433
Вычисление интеграла функции с помощью сумм Коши — Римана 435
Среднее значение функции на интервале 438
§ 2. Меры Радона на локально компактном пространстве 439
Мера Радона на компактном пространстве 439
Примеры мер Радона 440
Меры на локально компактном пространстве 446
Примеры мер Радона 448
Применения к механике и физике 450
Векторные меры 450
Разложение единицы 452
Носитель меры Радона 465
Продолжение меры на непрерывные функции ф с некомпактным
носителем 473
Принцип кусочной склейки мер 475
Комплексные и вещественные меры 476
Вещественные положительные меры 478
Решетки 481
§ 3. Продолжение положительной меры. Теория Лебега 489
Внешние меры открытых множеств 490
Внутренняя мера компакта 492
Измеримые множества. Мера множеств 494
Множества нулевой меры . 506
Свойства, выполняющиеся почти всюду 508
ц-измеримые функции со значениями в метризуемом сепарабель-
ном пространстве 510
ц-этажные функции 513
Борелевские функции 517
Интеграл от векторной этажной функции 520
Верхний интеграл от вещественной неотрицательной функции . . 520
Интегрируемость функций с векторными значениями .... 524
Интеграл Лебега от функции с векторными значениями . . 524
Интегрируемость и интегралы от функций, определенных почти
всюду 533
§ 4. Теорема Лебега о сходимости. Пространство L1 534
Примеры применений теоремы Лебега 540
Характеристика интегрируемых функций. Интегрируемость и
измеримость 551
Теория интегрирования, основанная на свойствах непрерывных и
полунепрерывных снизу функций 555
Пространства 9?Р(Х, ц; F) 561
Пространства 3?Р(Х, ц; F). Теорема Фишера — Рисса .... 572
Пространства З?™ (F) и L"(F) 574
Продолжение мер, не обладающих свойством неотрицательности 578

Оглавление 823
§ 5. Умножение меры на функцию 590
Произведение векторной меры на непрерывную скалярную
функцию 590
Элементарные свойства .... 591
Случай когда ц — вещественная мера ^ 0 591
Мера с базой (i. Мера с базой j> 0 594
Применение к продолжению меры с векторными значениями . . 610
Применение к интегрируемости функции по нескольким мерам . 612
Сопряженность пространств Lp и Lp 614
§ 6. Образ меры при отображении . 617
Случай, когда Я является гомеоморфизмом X на Y 626
Обобщение теоремы 59 на случай, когда ц не ^ 0 627
Различные примеры образов мер 628
■§ 7. Широкая сходимость мер Радона 630
Сходимость по норме. Локальная сходимость по норме . . . 630
Широкая сходимость 632
Функции, ц-интегрируемые по Риману 634
Широкая сходимость и равномерная сходимость 641
Компактные подмножества пространства 'ё'к(Х) 645
Широкая сходимость последовательности мер к мере Дирака . 646
Узкая сходимость последовательности мер конечной нормы . . 652
Сходимость широкая и сходимость узкая 654
§ 8. Тензорное произведение мер. Кратные интегралы 657
Постановка задачи 657
Существование и единственность тензорного произведения . . 658
Примеры тензорных произведений 662
Элементарные свойства 663
Носитель меры H®v 663
Вычисление двойного интеграла путем двух последовательных
простых интегрирований 664
Случай, когда интегрируемая функция является произведением
функции от х и функции от у ...... 673
Окончание доказательства прямого утверждения теоремы . . . 675
Обобщение на произвольные кратные интегралы 677
Широкая сходимость тензорных произведений 679
<§ 9. Частные свойства мер Радона на вещественной прямой R . . 682
ь
Введение символа d(i 682
а
Неопределенные интегралы 683
Функции с ограниченной вариацией на прямой ... ... 686
Функция, удовлетворяющая условию Липшица на ограниченном
интервале Ri прямой R, имеет ограниченную вариацию . 687
Функции ограниченной вариации и неопределенные интегралы 694
Длина пути в метрическом пространстве 701
Неопределенный интеграл и первообразная 706
Последовательные первообразные непрерывной функции на прямой 711
Формула интегрирования по частям 716
Замена переменных при вычислении простых интегралов . . . 720
Несобственные интегралы на прямой 724
Примеры применения критерия Абеля 732
Главное значение в смысле Коши . 736
•§ 10. Кратные интегралы на R™. Длины, площади и объемы в
конечномерном аффинном евклидовом пространстве. Замена
переменных в кратных интегралах на R" 742

824
Оглавление
Измерение объемов в аффинных евклидовых конечномерных
пространствах 754
Измерение длин в аффинном евклидовом пространстве .... 756
Измерение га-мерных площадей в линейном многообразии
размерности п аффинного евклидова конечномерного пространства 756
га-мерная площадь re-мерного параметрического многообразия . 760
Вычисление объемов с помощью поверхностных интегралов . . 770
§ 11. Функции, представимые рядами или интегралами 777
Функции, представимые рядами 777
Непрерывность суммы ряда 778
Интегрируемость суммы ряда относительно некоторой меры ^ 0 778
Дифференцируемость суммы ряда 779
Дифференцируемость бесконечного произведения 787
Функции, представимые интегралами 792
Непрерывность функции, представимой интегралом 792
Интегрируемость функции, представимой интегралом 793
Дифференцируемость функции, представимой интегралом . . . 794
Случай несобственных сходящихся интегралов 799
Применение к делимости дифференцируемых функций .... 804
Предметный указатель . , . , 811