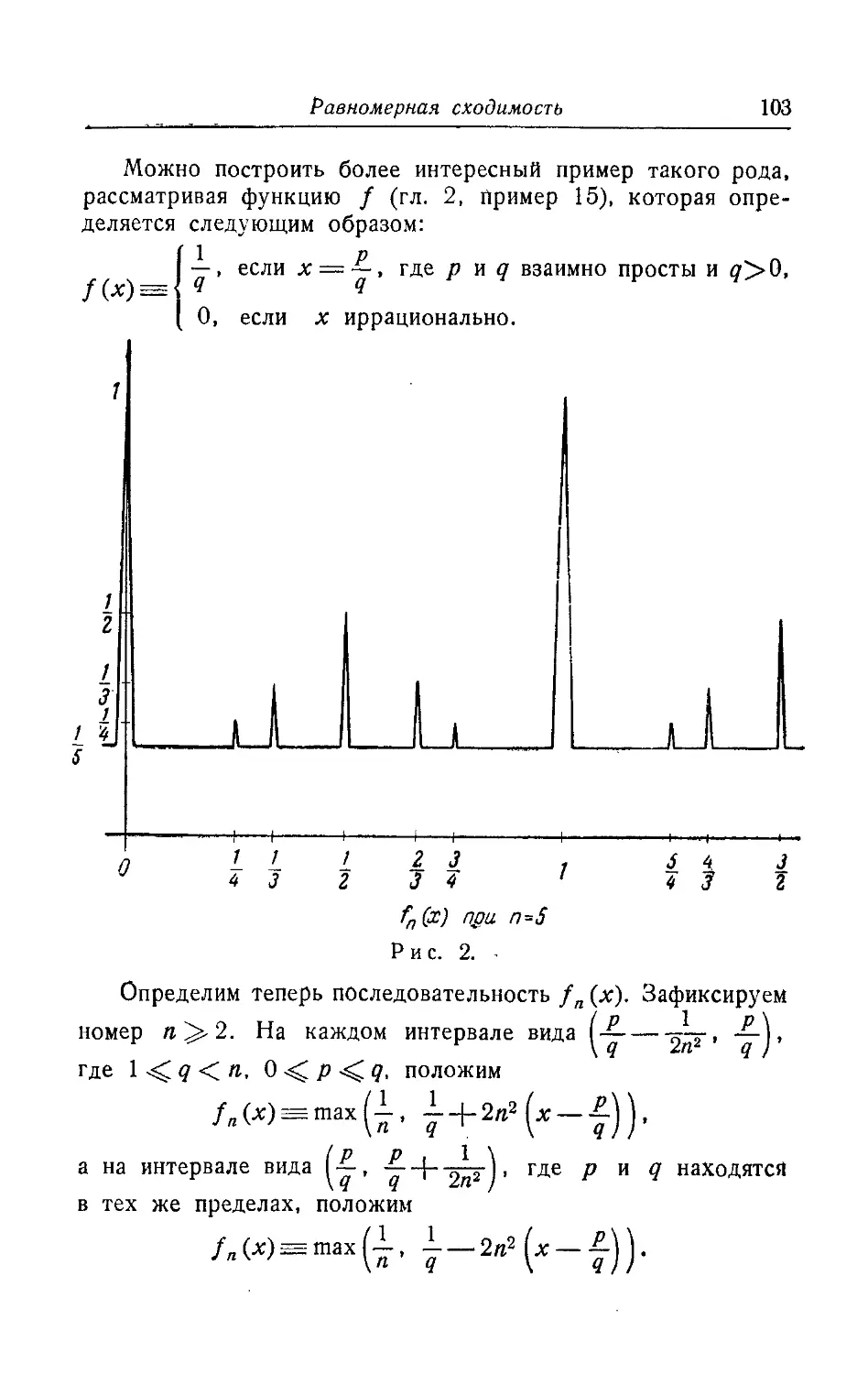
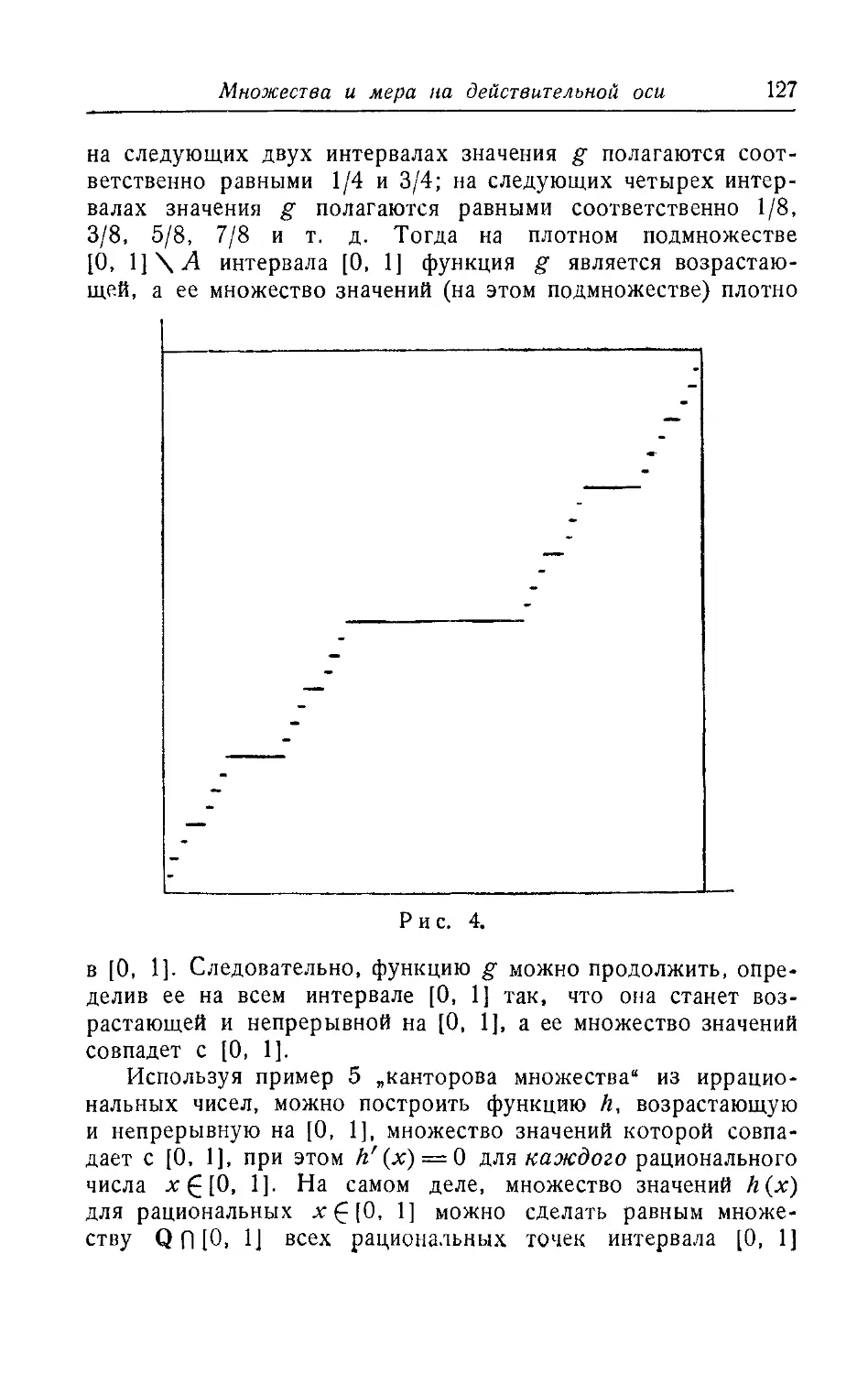
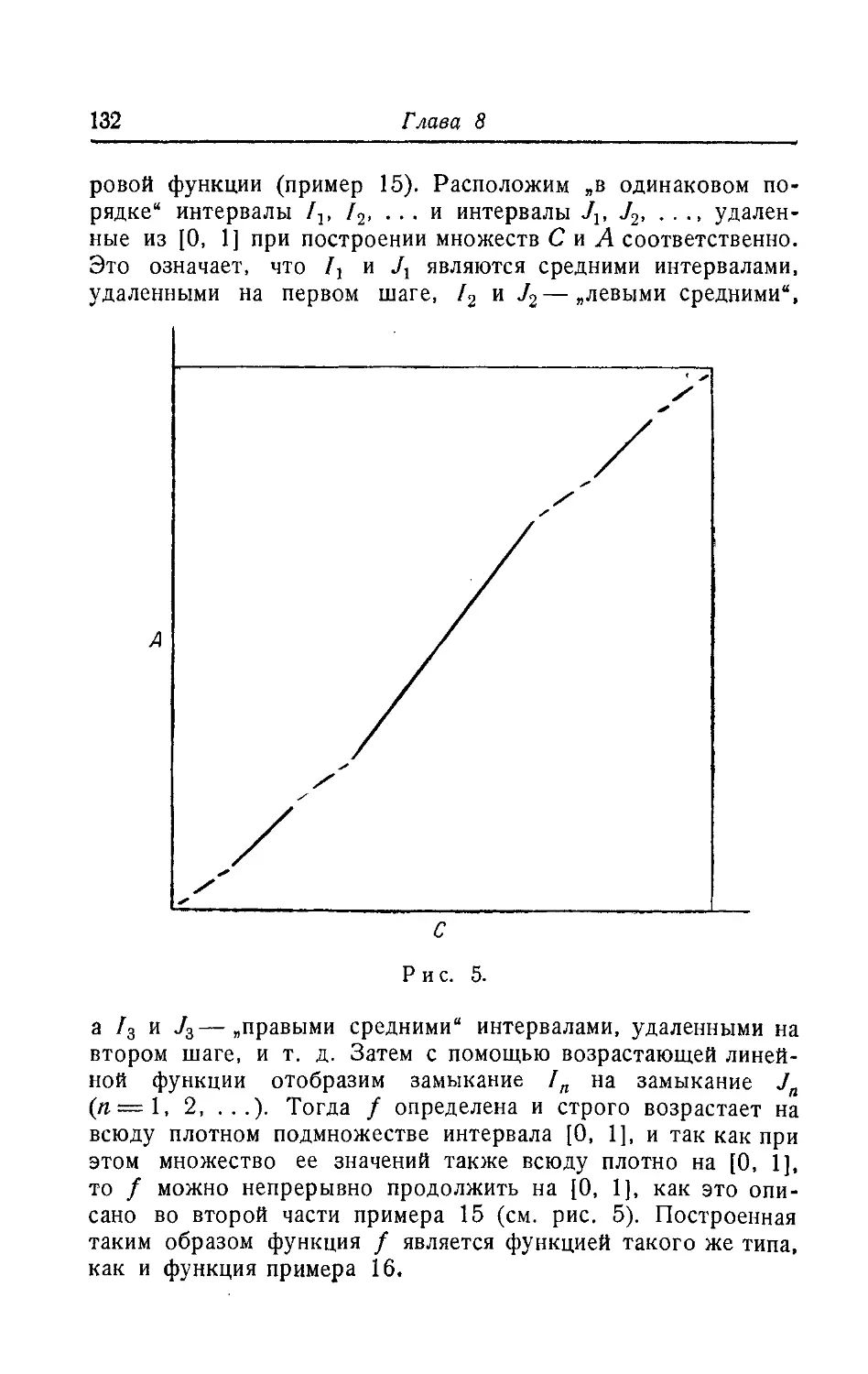
Текст
Б. ГЕЛБАУМ, ДЖ. ОЛМСТЕД
КОНТРПРИМЕРЫ В АНАЛИЗЕ
Перевод с английского
Б. И. ГОЛУБОВА
Под редакцией
П. Л. УЛЬЯНОВА
ИЗДАТЕЛЬСТВО • МИР • МОСКВА 1967
BERNARD R. OELBAUM
University of California, Irvine
JOHN M. H. OLMSTED
Southern Illinois University
COUNTEREXAMPLES IN ANALYSIS
HOLDEN-DAV, SAN FRANCISCO, LONDON, AMSTERDAM, 1964
УДК 517.1
В книге рассматриваются многочисленные примеры
из математического анализа и теории функций действи-
тельного переменного, цель которых — обратить внима-
ние на ряд „опасных" вопросов, на которые неопытный
читатель может дать неправильные ответы. Такие контр-
примеры систематически подобраны авторами, и по-
этому книга может служить очень хорошим дополне-
нием к обычным учебным курсам. Часто авторы не
дают подробных доказательств, ограничиваясь лишь
основными идеями построения соответствующих при-
меров. Это позволит читателю активно включиться
в изучение материала.
Книга будет полезна студентам университетов,
пединститутов и втузов, изучающим математический
анализ и теорию функций.
Редакция литературы по математическим наукам
Инд. 2-2-3
ОТ РЕДАКТОРА
Предлагаемая вниманию читателя книга „Контрпримеры
в анализе" написана американскими математиками Б. Р. Гел-
баумом и Дж. М. Олмстедом. В ней приведены многочислен-
ные примеры из математического анализа и теории функций
действительного переменного, а также — в небольшом коли-
честве—примеры из топологии и функционального анализа.
Многие из них хорошо известны и могут быть найдены
в тех или иных источниках. Однако главным достоинством
книги является именно то, что в ней собрано вместе большое
количество полезных и интересных примеров.
Авторы называют примеры, помещенные в книге, контр-
примерами, поясняя в предисловии различие между этими
понятиями. Однако эти пояснения довольно неопределенны,
и если их придерживаться, то многие результаты по желанию
можно отнести как к примерам, так и к контрпримерам. По
нашему мнению, основная цель большинства разбираемых при-
меров (по терминологии авторов — контрпримеров) состоит
в том, чтобы обратить внимание студентов (и вообще чита-
телей), изучающих математический анализ и теорию функций,
на ряд „опасных" вопросов и моментов, при встрече с ко-
торыми, не имея достаточного опыта, легко можно дать не-
правильные ответы или же неправильно представлять себе
истинную суть дела. Этим, в частности, объясняется и за-
главие книги — „Контрпримеры в анализе".
В книге наряду с совсем простыми примерами имеется
довольно много и сложных. Изложение зачастую ведется так,
что подробных доказательств авторы не дают, а указывают
лишь основные моменты в построении соответствующих при-
меров, оставляя читателю подробные выкладки и доказа-
тельства. Следует также сказать, что авторы весьма часто
используют те или иные определения без напоминания и ука-
6
Предисловие к русскому изданию
зания их даже в том случае, когда они приведены в книге,
но совсем в другой главе и значительно раньше. Поэтому
от читателя книги требуется определенное знакомство с осно-
вами математического анализа и теории функций. Для пони-
мания многих разделов книги достаточно знания втузовского
курса математики, но некоторые другие разделы требуют
математической подготовки в объеме первых трех курсов
математических факультетов университетов. В силу сказан-
ного предлагаемая книга не является учебником, по которому
следует начинать изучение анализа.
Заметим еще, что в книге не всегда отмечаются авторы
примеров, и это частично оправдывается тем, что иногда их
вообще трудно установить. Тем не менее нам представляется,
что автсроз некоторых широко известных примеров следо-
вало бы указать (например, назвать именами их авторов
функции Дирихле и Римана, о которых часто говорится
в книге). В связи с этим в некоторых местах мы сделали
соответствующие примечания. Кроме того, часть наших при-
мечаний относится также к замеченным неточностям, если их
исправление не было внесено нами в текст. О содержании
книги можно судить по оглавлению, в которое вынесены
полные формулировки приводимых примеров.
Мы думаем, что предлагаемая книга будет полезна широ-
кому кругу лиц, изучающих математический анализ и тео-
рию функций, особенно студентам-математикам университетов
и педагогических вузов. Она будет, вероятно, небезынте-
ресна и специалистам-математикам, в той или иной степени
интересующимся анализом.
П. Л. Ульянов
ПРЕДИСЛОВИЕ
„Истинно ли утверждение S?“—это, пожалуй, наиболее
типичный для математики вопрос, когда утверждение имеет
вид: „Каждый элемент класса А принадлежит также классу
В: Ас В“. Доказать, что подобное утверждение истинно, —
значит доказать включение Ас В. Доказать, что оно лож-
но,—значит найти элемент класса А, не принадлежащий
классу В, иными словами, привести контрпример. Напри-
мер, если утверждение S таково: „Каждая непрерывная функ-
ция дифференцируема в некоторой точке", то множества А
и В состоят соответственно из всех непрерывных функций
и всех функций, дифференцируемых в некоторых точках.
Известный же пример Вейерштрасса непрерывной, но нигде
не дифференцируемой функции / (см. пример 8 гл. 3) является
контрпримером для включения А с В, поскольку / является
элементом А, не принадлежащим В. Рискуя впасть в чрез-
мерное упрощение, можно сказать, что математика (за исклю-
чением определений, утверждений и выкладок) состоит из
двух частей — доказательств и контрпримеров, а мате-
матические открытия состоят в нахождении доказательств и
построении контрпримеров. Большая часть математических
книг посвящена доказательству верных утверждений. В на-
стоящей книге мы обращаемся к контрпримерам для ложных
утверждений.
Вообще говоря, примеры в математике бывают двух
типов — иллюстративные примеры и контрпримеры. Первые
показывают, почему то или иное утверждение имеет смысл,
а вторые — почему то или иное утверждение лишено смысла.
Можно утверждать, что любой пример является в то же
время контрпримером для некоторого утверждения, а именно
для утверждения, что такой пример невозможен. Мы не же-
лаем придавать термину контрпример столь универсальный
8
Предисловие
смысл, но допускаем', что его значение достаточно широко,
чтобы включить в себя все примеры, роль которых не огра-
ничивается иллюстрацией верных теорем. Так, например, по-
лином как пример непрерывной функции не есть контрпри-
мер, но полином как пример неограниченной или непериоди-
ческой функции является контрпримером. Подобным же
образом класс всех монотонных функций на ограниченном
замкнутом интервале как класс интегрируемых функций не
есть контрпример, однако этот же самый класс как пример
функционального, но не векторного пространства является
контрпримером.
Круг лиц, для которых предназначается эта книга, до-
вольно широк и разнообразен. Большая часть материала
доступна студентам, которые еще не закончили изучение
начального курса анализа, а также может быть полезной
преподавателям для иллюстрации ошибок, возможных при
изучении анализа. Студенты старших курсов найдут в ней
тонкости, которые обычно не рассматриваются в учебниках.
Студенты-дипломники, готовящиеся к выпускным экзаменам,
могут пополнить свой запас важных примеров, ограничиваю-
щих область справедливости изученных ранее теорем. Мы
надеемся, что и специалисты-математики найдут некоторые
места книги достойными внимания.
Собранные в этой книге контрпримеры почти целиком
ограничиваются областью анализа, известной под названием
теории функций действительного переменного. Однако среди
них есть несколько примеров из области метрических и то-
пологических пространств. В некоторых примерах исполь-
зуются также комплексные числа. Мы отнюдь не претендуем
на полноту. Несомненно, многие читатели не встретят своих
любимых примеров в этой книге, которая, нужно признаться,
составлена по нашему собственному вкусу. Некоторые про-
пуски сделаны нами умышленно и объясняются либо недо-
статком места, либо нашими вкусами, другие вызывают и
у нас искренние сожаления.
Эту книгу нельзя считать учебником, хотя она может
служить полезным дополнением к некоторым учебным курсам.
Если какое-либо место книги покажется читателю слишком
трудным, мы советуем пропустить его и поискать что-либо
более интересное дальше. Нами была предпринята попытка
расположить материал по степени трудности при помощи
Предисловие
9
расположения глав, выделения подборок внутри глав и по-
рядка примеров. Предполагается, что читатель знаком с за-
тронутыми в книге вопросами, ввиду чего материал изла-
гается с минимумом пояснений. Каждая глава начинается
с введения, где приводятся обозначения, терминология и
определения, а также даются формулировки важнейших тео-
рем. В конце книги помещена обширная библиография, на
которую делаются частые ссылки в тексте. Эти ссылки
предназначаются как для того, чтобы помочь читателю
в отыскании дальнейшей информации, так и для того, чтобы
воздать дань уважения авторам упомянутых сочинений. Если
указания на авторство того или иного контрпримера отсут-
ствуют, мы искренне сожалеем об этом. Все эти пропуски
носят непреднамеренный характер.
В заключение мы выражаем надежду, что читатели этой
книги получат столько же удовольствия и пользы, как и ее
авторы. Наш собственный опыт дает нам основание утвер-
ждать, что математическая задача, решенная при помощи
контрпримера, столь же увлекательна, как острая захваты-
вающая пьеса. По нашему мнению, многие-из самых глубоких
и изящных математических открытий относятся к этому
жанру.
Эрвин, Калифорния
Карбондейл, Иллинойс
Б. Р. Г.
Дж. М. X. О.
ГЛАВА I
СИСТЕМА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
Введение
Мы начинаем с введения некоторых основных определе-
ний и обозначений анализа, которые являются существенными
для данной главы. Эти определения и обозначения даются
в сокращенной форме с минимумом пояснений. Для более
подробного ознакомления с ними следует обратиться к кни-
гам [16], [1.7], [19] и [31] (см. библиографию).
Если А — произвольное множество элементов, то утвер-
ждение „элемент а принадлежит множеству А* симво-
лически записывается так: а £ А. Запись а(^А означает, что
элемент а не принадлежит множеству А. Если А и В — мно-
жества, то утверждение „А является подмножеством мно-
жества В* (символически Ас В) означает, что каждый эле-
мент х множества А принадлежит и множеству В; последнее
равносильно импликации х £ А=^х £В!). Выражение тогда
и только тогда мы часто будем заменять символом О-
Для удобства элементы множеств часто будут называться
точками. Запись [а, Ь, с, ...} обозначает множество, со-
стоящее из элементов а, Ь, с, ... . Символ '{... | ...} исполь-
зуется для обозначения множества, общий элемент которого
записывается между первой фигурной скобкой и вертикаль-
ной чертой, а определяющие это множество свойства запи-
сываются между вертикальной чертой и второй фигурной
скобкой. Объединение и пересечение двух мно-
жеств А и В определяются следующим образом:
A (J В = {х | х £ А или х£В},
Д П В = | * Е А х£В},
*) Знак следует понимать как „влечет*. — Прим, перев.
12
Глава 1
при этом запятая в последней формуле заменяет союз
Разностью множеств А и В называется множество
-4 \ £?= {х| х £ .4, х(£В].
Если рассматриваются множества, которые все являются
подмножествами некоторого основного, универсального мно-
жества 5, то разность S \ А называется дополнением
множества А и обозначается символом А'. Вообще же раз-
ность Л \ Z3 называется дополнением множества В
относительно А.
Для обозначения пустого множества, т. е. множества,
не содержащего ни одного элемента, используется символ 0.
Если А и В — два непустых множества, то их декарто-
вым произведением Ау^В называется множество всех
упорядоченных пар {а, Ь), где а£А, а Ь£В, так что
А^В = {(а, Ь)\а£А, Ь£В}.
Если (й, й)(ЛХВ, то й называется первой коорди-
натой элемента (a, b), a b — его второй координатой;
первая и вторая координаты также называются проек-
циями. Любое подмножество р произведения А X В назы-
вается отношением из А в В. Такое отношение f назы-
вается функцией из А в В, если никакие два различных
элемента из f не имеют одинаковых первых координат.
Условимся обозначать выражения „существует* или „суще-
ствуют* квантором существования Э, а слова „такие, что* —
символом Э- Тогда область (или множество) опре-
деления D = Df и область (или множество) зна-
чений R — Rj, функции f определяются так:
D — Df={x\3y3(x> у)Е/},
R = Rf= }у|ЭхЭ(х, у) ef}-
Будем говорить, что функция f (или отображение)
определена на А, если ее множество определения сов-
падает с А; в общем же случае будем говорить, что / опре-
делена в А. Будем называть / функцией со значениями
н а В, если ее множество значений совпадает с В; в общем же
случае будем говорить о функции / со значениями в В.
Говорят, что функция / из А в В осуществляет взаимно
однозначное соответствие между-Л и В, если она
Система действительных чисел
13
является функцией, определенной на А со значениями на В
и притом такой, что никакие два различных элемента из f
не имеют одинаковых вторых координат. Значениями
функции f называются элементы множества R?. Если функ-
ция f осуществляет взаимно однозначное отображение мно-
жества А на множество В, то функция
Г1 = {(х> у)|(у, *)£/},
которая получается, если поменять местами область опреде-
ления и область значений функции /, называется обратной к /.
Рис. 1.
а — отношение из А со значениями в В; б—отношение на А со значениями в В;
в—отношение на А со значениями на В; г —функция из А со значениями в В;
д—функция иа А со значениями в В; е — функция на А со значениями на В;
—взаимно однозначное соответствие; з —постоянная функция.
Постоянной функцией называется функция, множество
значений которой состоит из одной точки.
Различные типы отношений и функций указаны на рис. 1.
Во всех случаях в качестве множеств А и В взят замкнутый
единичный интервал [0, 1], состоящий из всех действитель-
ных чисел х, таких, что
Пусть f — функция, определенная на А и принимающая
значения в В. Мы будем записывать ее двумя следующими
14
Глава 1
способами:
/: А->В,
А-^В.
Если х — произвольный элемент множества А, то существует
в точности один элемент у множества В, такой, что (х, у) £ /.
Этот элемент у множества В мы будем обозначать симво-
лом f (х) и записывать
У = /(*)•
Другие способы обозначения функции:
/: у==/(х), х£А, у£В
f- х£А, f(x)^B;
y = f{x)-. х£А, у£В.
Если же из контекста ясно, что обозначение /(х) предста-
вляет функцию, а не просто одно из ее значений, то мы
будем пользоваться такой записью:
/(х): х£А.
Если f — функция с областью определения D, a S является
подмножеством D, то сужением функции / на S назы-
вается функция g, область определения которой есть S и
такая, что
Множество значений сужения f на S мы будем обозначать
символом f(S). Таким образом,
/(5) = {у|ЗхС5Э/(х) = у).
Если g является сужением /, то f мы будем называть про-
должением g.
Пусть f и g — такие функции, что множество значений g
является подмножеством области определения f. Тогда ком-
позицией / о g функций / и g называется функция, значе-
ние которой во всякой точке х области определения функции g
есть f(g(x)\, короче, композицией функции f(u) и функ-
ции u — g(x) называется функция У = f (g(x')')v). (Следует
i) В советской математической литературе вместо термина „ком-
позиция' часто используется термин „суперпозиция".—Прим. ред.
Система действительных чисел
15
заметить, что композиция / и g, вообще говоря, не совпа-
дает с композицией g и /; контрпример: (х-ф- I)2 Ф х2 + 1.)
Если А — непустое множество, то всякая функция, опре-
деленная в (на) А X А со значениями в А, называется би-
нарной операцией в (на) Л. В классической арифметике
существуют две основные бинарные операции: сложение и
умножение. Многими свойствами этих арифметических опе-
раций обладают и операции в более абстрактных множествах,
поэтому последние сохраняют те же названия. Если бинарная
операция называется сложением и если z = F{(x, у)),
то используется и обычная запись г = хАгУ- Если бинарная
операция G называется умножением и если z = G ((х, у)),
то z, как обычно, записывают в виде z = xy или z — x-y.
Определение I. Непустое множество F называется
полем, если на F определены две бинарные операции,
называемые сложением и умножением, причем
А. длясложения:
(i) справедлив закон ассоциативности
х, у, г£Р=>х + (у-ф-.г)==(х-ф-у)-ф-.г,
(ii) 3 элемент 0 множества F, такой, что
x£F=>x-|-0 = x,
(iii) х £ F => 3 (— х) £ F Э х -ф- (— х) = О,
(iv) справедлив закон коммутативности
х, y€F=>x + y = y-|--x;
В. для умножения:
(i) справедлив закон ассоциативности
х, у, z £ F => х (yz) — (ху) z,
(») Э элемент 1 множества F, такой, что 1 0 в
х £ F =>х • 1 — х,
(iii) х £ F, х Ф 0 =^> З-^-1 £ F Э х • х-1 = 1,
(iv) справедлив закон коммутативности
х, y£F=>xy = yx;
С. для сложения и умножения:
справедлив закон дистрибутивности {точнее
умножение дистрибутивно относительно сложения)
х, у, z£F =>х(уф- z) = xy-^-xz.
16
Глава 1
Элемент 0 поля F из п. A (ii) называется нулем (или адди-
тивной единицей) поля F. Элемент (—х) поля F из п. A (iii)
называется противоположным (или аддитивным обрат-
ным) для х. Бинарная операция х — у, определенная фор-
мулой х — у^х4-(—у), называется вычитанием. Эле-
мент 1 из п. В(ii) называется единицей (или мультипли-
кативной единицей) поля F. Элемент х-1 поля F из п. В (iii)
называется обратным (или мультипликативным обратным)
для х. Бинарная операция х/у, определенная формулой
х/у = ху-1, где у Ф 0, называется делением. Деление
является бинарной операцией в F и не является бинарной
операцией на F, так как „деление на нуль" исключается.
Непустое множество G называется группой, если на G
определена бинарная операция, которую мы обозначим зна-
ком -ф- и назовем сложением, причем эта операция обладает
свойствами A(i), (ii) и (iii) (в этом случае группа называется
аддитивной). Если же, кроме того, справедлив закон ком-
мутативности A(iv), то G называется абелевой или ком-
мутативной группой. Таким образом, всякое поле отно-
сительно сложения образует абелеву аддитивную группу.
А множество ненулевых элементов поля образует абелеву
мультипликативную группу относительно умножения.
Определение II. Упорядоченным полем на-
зывается поле F, содержащее подмножество Р, такое, что
(i) Р замкнуто относительно сложения, т. е.
х£Р, у€Р=>х + у£Р;
(ii) Р замкнуто относительно умножения, т. е.
хер. у Ер^^у €Р;
(iii) х Е F => справедливость и притом только одного
из следующих трех утверждений'.
хЕР; х = 0; —хЕР-
Элемент х поля F называется положительным,
если хЕР. и отрицательным, если —хЕР-
Неравенства в упорядоченном поле определяются в тер-
минах принадлежности к Р. Например,
х < у^у — х^Р;
Х>у£фх —уЕР или X —у.
Система действительных чисел
17
Если F — упорядоченное поле, то функция /, определен-
ная ври принимающая значения в F, называется возра-
стающей (или неубывающей) на некотором подмно-
жестве А своей области определения, если
х.уСА х < у=>/(х)</(у).
Функция f называется строго возрастающей на Л,
если
х.уЕД х<у=ф/(х)</(у).
Термины убывающая (или невозрастающая) и
строго убывающая функция определяются аналогично.
Функция называется монотонной на некотором множестве,
если она является возрастающей или убывающей на этом
множестве. Нетрудно дать и определение строго моно-
тонной функции.
Если F—упорядоченное поле, то абсолютная вели-
чина | х | элемента х £ F полагается равной х в случае х ^> 0
и —х в случае х < 0.
Ниже приводится несколько стандартных свойств абсо-
лютной величины (где х, у, е — элементы упорядоченного
поля F):
(i) | х | > 0; = — 0;
(п) | ху | = | х | • | у |;
(Ш) если е > 0, то | х | < еф^ — е < х < е;
(iv) неравенство треугольника:
_ |* + У |<|х| + |у|;
(v) | х | = Ух2, т. е. | х | есть единственный элемент мно-
жества PU {0}, квадрат которого равен х2;
(vi) ||х| —|у||<|х —У|.
Если F — упорядоченное поле и a, b£F, а<Ь, то сле-
дующие множества называются конечными или ограни-
ченными интервалами:
открытый:
замкнутый:
полуоткрытый
(или полузамкнутый):
полуоткрытый
(или полузамкнутый):
(а, Ь)= (х | х £ F, а < х < Ь},
[a, Ь] = [х | х £ F,
[a, 6)={x|x£F,
(й, == (х | х £ F, а < х <; 6).
2 Зак. 587
18
Глава 1
Бесконечные или неограниченные интервалы
определяются подобным же образом:
открытый:
открытый:
замкнутый:
замкнутый:
(а, -|-оо)=={х|х > а],
(—оо, а) = {х | х < a j,
[а, -]-оо) = {х|х;>а},
(—оо, а] = {х|х<^а),
открытый и замкнутый: (—оо, -]-oo) = F.
Окрестностью точки а упорядоченного поля F назы-
вается открытый интервал вида (а—е, а-]-е), где е — поло-
жительный элемент поля F. Эту окрестность можно записать
также в терминах абсолютных величин:
N (а, е)==(а — е, а —е) == {х 11 х — а | < е}.
Проколотой окрестностью точки а называется
окрестность точки а, из которой исключена сама точка а.
Таким образом, проколотая окрестность D(a, е) точки а для
некоторого е > 0 определяется так:
D(a, е)== {х |0 < ' | х — а 1 < е1-
Бинарные операции шах и min на F определяются сле-
дующим образом:
[ X, если х>у,
тах(х,
1 у. если х < у;
Г У. если X i>y,
minfx,
( X, если х<у.
Если F—упорядоченное поле, «£F их<^« для всякого
элемента х непустого множества А точек поля F, то и на-
зывается верхней гранью А. Непустое множество в F
называется ограниченным сверху в F, если в F суще-
ствует элемент, который является верхней гранью этого
множества. Если $ является верхней гранью А и если 5 меньше
всякой другой верхней грани А, то $ называется точной
верхней гранью А и обозначается так: 5 = sup (Л) =
=sup А. Аналогично определяются н и ж н я я грань, огра-
ниченность снизу и точная нижняя грань, обо-
значаемая через I = inf (Л) = inf Л, непустого множества Л.
Система действительных чисел
19
Определение III. Полным упорядоченным
полем называется упорядоченное поле F, в котором
для каждого непустого подмножества, ограниченного
сверху в F, существует точная верхняя грань.
Любые два полных упорядоченных поля F и Fz изоморфны
в том смысле, что существует взаимно однозначное соответ-
ствие х -«-> х', где х £ F и х' Q F', сохраняющее бинарные
операции и порядок, т. е.
(х + у)' = х'+/, (ху)' = х'у', х <у^х' <у'.
(Доказательство см. в [37], стр. 128—131.) С точки зрения
структуры система действительных чисел однозначно описы-
вается следующим определением:
Определение IV. Системой, действитель-
ных чисел R называется полное упорядоченное поле.
Функция, отображающая множество А на В, называется
действительнозначной, если В с R; если же А с R,
то эта функция называется функцией действитель-
ного переменного.
Функция sgnx является действительнозначной функцией
действительного переменного и определяется следующим об-
разом: sgnx=l, если х > 0; sgn№—1, если х < 0;
sgn0 = 0.
Если S — произвольное непустое множество, а А — любое
его подмножество, то характеристическая функ-
ция /л множества А является действительнозначной функ-
цией и определяется следующим образом: ул(х)=1, если
х£А, и хл(х)н^0, если х£Д' = 5\А
Определение V. Индуктивным множе-
ством в упорядоченном поле F называется множе-
ство А, обладающее следующими двумя свойствами-.
(9 16Л
(ii) х£Д=фх+1€А
Определение VI. Элемент п упорядоченного поля F
называется натуральным числом, если п является
элементом каждого индуктивного множества поля F.
Множество всех натуральных чисел поля F обозначается
символом N.
2*
20
Глава 1
Из этого определения вытекают известные свойства нату-
ральных чисел (см. [37], стр. 17—18), в том числе
Основная теорема индукции. Если S является
индуктивным множеством, состоящим из натуральных чисел,
то S = N.
Если N и N* — множества всех натуральных чисел двух
упорядоченных полей F и F* соответственно, то N и N* изо-
морфны (см. [37], стр. 34—35).
Определение VII. Элемент х упорядоченного по-
ля F называется целым числом, если х £ N, х = 0
или —x£N. Элемент х упорядоченного поля называется
рациональным числом, если существуют целые
числа т и п, п #= 0, такие, что х — т/п.
Множество всех рациональных чисел упорядоченного поля F
вместе с операциями сложения и умножения и порядком поля F
также является упорядоченным полем. Оно обозначается сим-
волом Q. (Любые два упорядоченных поля рациональных
чисел изоморфны; см. [37], стр. 67.)
Определение VIII. Кольцом называется непу-
стое множество В вместе с двумя бинарными операциями
на В, называемыми сложением и умножением, такими,
что выполнены требования пунктов A(i), (ii), (ill), (iv),
В (i), С из определения I, а также второй закон дистри-
бутивности
С'. х, у, ,г£В=ф(х-[-у).г — xz-j-yz.
Определение IX. Областью целостности
называется кольцо D, в котором выполнены требования
В (ii) и (iv) из определения I, а также требование
D. x£D, y£D, х #= 0, у =/= о=фху #= 0.
Иными словами, выполнены все аксиомы определения I,
за исключением В (iii), которая заменена ослабленным
требованием D.
Тот факт, что требование D является ослабленной фор-
мой (т. е. следствием) требования В (iii), можно доказать
следующим образом. Предположим, что существуют х #= 0
и у =/= 0, такие, что ху — 0. Тогда х-1 (ху) = (х-1х)у =
= 1у = у=^0, в то время как х-10=0. (Противоречие.)
Система действительных чисел
21
В любом кольце требование D равносильно следующему
утверждению:
D'. Закон сокращения. xy = xz,x=pQ^-y=z.
(В самом деле, D=^D', так как xy = xz^=?x(y— z) =
— 0; обратно, D'=^D, ибо равенство ху = 0 можно запи-
сать в виде ху = х0.)
Множество всех целых чисел упорядоченного поля F
вместе с операциями сложения и умножения этого поля
является областью целостности и обозначается символом I.
Всякие две области целостности, состоящие из целых чисел,
изоморфны (см. [37], стр. 64).
Пусть f — функция, определенная в упорядоченном поле F
и принимающая значения в нем же, и пусть а £ F. Тогда f
называется непрерывной в точке а, если а принадлежит
области определения D функции / и для всякого положи-
тельного элемента е поля F 3 положительный элемент б этого
поля, такой, что неравенство |/(х)—/(а) | < е справедливо
для каждого х из области D, удовлетворяющего неравенству
|х—а | < б. С помощью символа V, называемого кван-
тором общности и заменяющего слова „для всех, для
произвольного, для любого или для каждого11, определение
непрерывности функции f в точке а области D в терминах
окрестностей можно записать следующим образом:
Ve > 03б> 09/(ЛПб)) cz N(J(д), е).
Точка р упорядоченного поля F называется предель-
ной точкой его непустого подмножества А, если всякая
проколотая окрестность точки р содержит по крайней мере
одну точку множества А, т. е.
Ve>0 3af=D(p, е)ПА
Пусть /— функция, области определения и значений ко-
торой содержатся в F, а — предельная точка ее области
определения D и b£F. Тогда говорят, что предел /(х),
когда х стремится к а, существует и равен b и пишут
lim f(x) — b,
х-> а
если
Ve>0 36>03/(Dn£>(a. б))сЛф, е).
22
Глава 1
Односторонние пределы определяются подобным же образом
и обозначаются соответственно lim /(х) и lim У(х).
х •> а + 0 х -> а — О
Функция / с областью определения и областью значений,
содержащимися в упорядоченном поле F, называется равно-
мерно непрерывной на некотором подмножестве Д ее
области определения D, если
Ve>03d>09
Хр х2£Д I*! —х2|<д=>|/(Х1) —У(х2)|<е.
Если / — функция с областью определения и областью
значений в упорядоченном поле F, а—точка области опре-
деления D функции у, то символ f (а) обозначает элемент
поля F, определяемый равенством
У'(а)^ Нт Пт /(а + Л)-/(а)
х -> а х~а Л->0 h
при условии, что последний предел существует. Функция
У'(х), если она имеет смысл для всех х из области опреде-
ления D, называется производной функции f.
Говорят, что функция у из упорядоченного поля F в F
обладает свойством Коши на некотором интервале /,
содержащемся в ее области определения, если
Va, b£l, d£F3a<b
и либо у (а) < d < У (Ь), либо У(а)>й?> у (Ь), то
3 с Э а < с < b, f(c) = d.
Последовательностью называется функция, опре-
деленная на множестве натуральных чисел N. Ее значение,
или член последовательности для данного натурального п,
обычно обозначается через ап, а сама последовательность —
символом [ап}. Последовательность [ап], члены которой
принадлежат некоторому упорядоченному полю F, называется
сходящейся к элементу b поля F, если
УееРЗЛ^МЭя>М=Ж —&|<е,
где Р — множество всех положительных элементов поля F.
В этом случае говорят также, что последовательность {ап}
имеет предел Ь. Последовательность называется расходя-
щейся, если она не является сходящейся, т. е. если у нее
Система действительных чисел
23
нет предела. Последовательность [а„], члены которой являются
элементами некоторого упорядоченного поля F, называется
фундаментальной или последовательностью
Коши, если
Ve£P3NCN9 — ап | < е.
Каждая сходящаяся последовательность является фундамен-
тальной, а если F=R, то всякая фундаментальная последо-
вательность сходится (см. [36], стр. 57, а также [52]*, т. 1,
стр. 84) ’).
Комплексным числом называется упорядоченная
пара (х, у) действительных чисел х и у. Сложение и
умножение комплексных чисел определяются следующим
образом:
(х, у)+(и, ©) = (х + «, ®).
(х, у) (и, и) = (хи — yv, XV — уи).
Комплексные числа образуют поле С (см. [36], стр. 497)
с нулем (0, 0) и единицей (1, 0). В дальнейшем для записи
комплексного числа (х, у) будет употребляться обычное
обозначение х-\-1у.
1. Бесконечное поле, которое нельзя упорядочить
Если поле F не содержит подмножества Р, обладающего
тремя свойствами определения II, данного во введении, то
говорят, что поле F нельзя упорядочить. Предварительно от-
метим, что, поскольку всякое упорядоченное поле бесконечно,
никакое конечное поле не может быть упорядочено ([37],
стр. 38).
Примером бесконечного поля, которое нельзя упорядо-
чить, является поле С комплексных чисел. В самом деле,
предположим, что существует подмножество Р поля С, удо-
влетворяющее определению II. Рассмотрим число z ^=(0, 1).
Так как i ф (0, 0), то существуют две взаимно исключаю-
щие друг друга возможности. Первая из них состоит в том,
что Z£P. В этом случае Z2 = (—1, 0)£Р и, следовательно,
Z4 —(1, 0)£Р. Но элементы Z2 и Z4 являются противополож-
ными и, поскольку такие элементы не могут одновременно
') Звездочкой отмечены работы, включенные в библиографию
переводчиком. — Прим, перев.
24
Глава 1
принадлежать Р (см. определение II, (iii)), то мы получаем
противоречие, что и требовалось. Вторая возможность со-
стоит в том, что —Z = (0, — 1)£Р. В этом случае (—i)2 =
— (—1, 0)£Р и, следовательно, (—£)4 = (1, 0)£Р, и мы
получаем такое же противоречие, как и выше.
2. Поле, которое можно упорядочить двумя различными
способами
Рассмотрим множество F всех чисел вида г -s У2, где
г и s — рациональные числа, и пусть операции сложения и
умножения в F те же, что и в системе действительных чи-
сел R, для которой F является подмножеством. Тогда F
будет упорядоченным полем, если в качестве подмножества Р
определения II взять множество всех элементов из F, кото-
рые являются положительными элементами в R, т. е. поло-
жительными действительными числами. Рассмотрим теперь
другой способ упорядочения поля F. Для этого определим
множество В следующим образом:
г + s /2 е Вфг -s У2 Р.
Легко проверить, что множество В удовлетворяет всем
требованиям определения II.
Поле Q рациональных чисел и поле R действительных
чисел являются упорядоченными полями, причем ни одно
из них нельзя упорядочить двумя различными способами
([37], стр. 146).
3. Неполное упорядоченное поле
Упорядоченное поле Q рациональных чисел не является
полным. В этом можно убедиться следующим образом: мно-
жество А всех положительных рациональных чисел, квад-
раты которых меньше 2,
А={г |r £Q, г > 0, г2 < 2},
не пусто (1 £А) и ограничено сверху рациональным числом 2.
Предположим, что Q полно. Тогда должно существовать
положительное рациональное число с, которое должно быть
точной верхней гранью множества А. Но так как не суще-
ствует рационального числа, квадрат которого равен 2 (см.
Система действительных чисел
25
[37], стр. 126, а также [52]*, т. I, стр. 18), то либо с1 2 < 2,
либо с2 > 2. Предположим сначала, что с2 < 2 и определим
положительное число d следующим образом *):
min • *)•
Тогда c-\-d будет положительным рациональным числом,
которое больше с и квадрат которого меньше 2:
(c4-rf)2 < с24-й?(с+ I)2 < 2.
Но это означает, что с 4- d £ А, в то время как с является
верхней гранью множества А. (Противоречие.) Теперь пред-
положим, что с2 > 2 и определим положительное число d
следующей формулой:
д— с2“2
2 (с+ 1)2'
Тогда с — d будет положительным рациональным числом,
которое меньше с и квадрат которого больше 2:
(с — й?)2 > с2 — d (с 4- 1 )2 > 2.
Следовательно, с — d будет верхней гранью множества А,
которая меньше точной верхней грани с, и мы снова полу-
чили противоречие.
4. Упорядоченное неархимедово поле
Упорядоченное поле F называется архимедовым,
если множество N натуральных чисел поля F не ограничено
сверху в F (т. е. если a, а > О, > О, то существует
натуральное число п, такое, что па > Ь). Пусть / — поли-
ном, отображающий R в R:
п
f(x)= ^акхк, <zft£R, k = 0, 1......................п,
/г=о
и пусть g— ненулевой полином (это значит, что g(x) не
равняется тождественно нулю). Далее, пусть f'g — рацио-
’) Так как
ред.
1 Q А, то с 1 и потому d =
1 2 — с2
"2 (с 4-1)2 ’ ~ПРим-
26
Глава 1
нальная функция h, определенная формулой й (x)=/(x)/g (х);
ее область определения состоит из всех действительных чи-
сел х, для которых g(x)^0. Пусть Н — множество, со-
стоящее из всех несократимых рациональных функций (/ и
g могут иметь в качестве общих множителей лишь кон-
станты). Сложение и умножение в Н определяются равен-
ствами
/ [ г _ fs-}-gr
g's gs ’ g ' s gs ’
правые части которых приводятся к несократимым рацио-
нальным функциям. Тогда множество Н будет полем ([37],
стр. 104). Если определить подмножество Р поля Н как
множество, состоящее из всех ненулевых функций f[g, таких,
что старшие коэффициенты (т. е. коэффициенты при членах
наивысшей степени) полиномов f и g имеют одинаковый
знак, то Р будет удовлетворять всем требованиям определе-
ния II и Н превратится в упорядоченное поле. Но любая
рациональная функция //1, где f—полином с положительным
старшим коэффициентом, является верхней гранью множе-
ства N натуральных чисел поля Н (натуральными числами
поля Н являются постоянные рациональные функции вида п/1,
где п—полином, тождественно равный натуральному числу п).
Более детальное изложение читатель сможет найти в [37]
(см. стр. 99—108).
5. Упорядоченное поле, которое нельзя пополнить
Говорят, что упорядоченное поле F нельзя пополнить,
если не существует полного упорядоченного поля R, содер-
жащего F и такого, что операции сложения и умножения
и отношение порядка поля F совпадают с соответствующими
операциями и отношением порядка поля R. Поле Н рацио-
нальных функций предыдущего примера нельзя пополнить
в этом смысле, другими словами, его нельзя вложить в си-
стему действительных чисел (см. определение IV). Причина,
вкратце, состоит в том, что если бы Н можно было вло-
жить в R, то натуральные числа поля Н должны были бы,
очевидно, совпадать с натуральными числами поля R. А так
как N ограничено сверху в Н и не ограничено в R ([37],
стр. 122), то мы получили бы противоречие.
Система действительных чисел
27
6. Упорядоченное поле, в котором множество
рациональных чисел не плотно
Множество „рациональных чисел" упорядоченного поля Н
примера 4 не плотно в Н. Это означает, что существуют
два различных элемента поля Н, между которыми нет ни
одного рационального числа. В самом деле, всякое упорядо-
ченное поле F, в котором множество рациональных чисел
плотно, является архимедовым. Чтобы убедиться в этом,
предположим, что а—произвольный положительный элемент
поля F, a mln—рациональное число, расположенное между О
и 1/а. Мы можем предположить, не теряя общности, что
тип оба положительны. Тогда
п п а
откуда п > а. Следовательно, а не является верхней
гранью N, и так как а произвольно, то N не ограничено
сверху. Но в поле Н аксиома Архимеда не выполнена, по-
этому множество рациональных чисел поля Н не может
быть плотным в Н. Примером двух различных элементов
поля Н, между которыми нет ни одного рационального числа,
могут служить любые два (различных) полинома, не являю-
щиеся тождественно постоянными, с положительными стар-
шими коэффициентами.
7. Неполное упорядоченное поле, полное в смысле Коши
Если упорядоченное поле Н рациональных функций (при-
мер 4) расширить при помощи классов эквивалентности фун-
даментальных последовательностей, то в результате получится
упорядоченное поле, в котором каждая фундаментальная по-
следовательность сходится. Однако, согласно примеру 5, это
пополнение в смысле Коши не может быть полным в смысле
определения в терминах точных верхних граней, которое
было дано во введении. (О пополнении в смысле Коши см.
[54], стр. 152, и [16].)
8. Область целостности, допускающая различные
факторизации
Единицей области целостности D называется такой ее
элемент и, для которого в D существует обратный элемент v,
т. е. uv=l. (Единицами области целостности I целых чисел
28
Глава 1
являются 1 и —1.) Каждый элемент из D, являющийся произ-
ведением двух ненулевых элементов из D, ни один из кото-
рых не совпадает с единицей, называется составным. Не-
нулевой элемент из D, не являющийся ни единицей, ни со-
ставным числом, называется простым. Будем говорить, что
область целостности D допускает единственную фак-
торизацию, если каждый элемент из D, не совпадающий
с нулем или единицей, можно представить как произведение
конечного числа простых элементов из D, причем такое пред-
ставление единственно с точностью до порядка сомножите-
лей и умножения их на единицы.
В системе действительных чисел R определим множество Ф
всех чисел вида а-\-ЬУ§, где а, Ь£Л. Тогда Ф будет
областью целостности. Далее нетрудно доказать следующие
два факта (см. [37], стр. 144):
(1) Единицами Ф являются все числа вида a-j-by^, такие,
что | а2 — 5Ь2 |=1.
(ii) Если а-\-Ь~^5 не совпадает ни с нулем, ни с еди-
ницей, то | а2—5Ь2|)>4. Следовательно, если 1 < | а2 — Г>Ь2 | <
<16, то число а-\-Ь~^5 является простым. В частности,
2, 1 + /5, -1+/5 являются простыми числами в Ф,
так как для каждого из них | а2 — 5Z>21 = 4. Более того, сле-
дующие два разложения числа 4 на множители
2.2 = (1 + /5)(-1 +/5)
являются различными в указанном выше смысле: ни один из
сомножителей левой части не совпадает (с точностью до умно-
жения на единицу) ни с каким сомножителем правой части.
(См. также [37], стр. 145.)
9. Два числа без наибольшего общего делителя
Элемент т называется делителем элемента п в области
целостности D (символически т | я), если существует эле-
мент р из D, такой, что тр = п. Элемент d из D назы-
вается наибольшим общим делителем двух элемен-
тов а и b из D, если
(i) d | а и d | b\
(ii) c | a, c\b=^c\d.
Система действительных чисел
29
В области целостности Ф предыдущего примера числа 4
и 2(1 +^5) не имеют наибольшего общего делителя. (Под-
робное изложение см. в [37], стр. 145—146.)
10. Дробь, не допускающая единственного представления
в виде несократимой дроби
Рассмотрим дроби, состоящие из пар элементов области
целостности Ф примера 8. Тогда дробь 2(1 можно
представить в виде несократимой дроби двумя следующими
способами:
2(1+У~5) ,_1+К5 2
4 2 — 1+V 5 ‘
Эти представления различны в указанном выше смысле.
11. Функции, непрерывные на замкнутом интервале и
не обладающие известными свойствами, если система
чисел не полна
Мы закончим эту главу примерами функций, определен-
ных на замкнутом интервале [a, 6]cQ и принимающих зна-
чения, принадлежащие множеству Q. Эти примеры станут
невозможными, если неполную систему рациональных чисел Q
(см. пример 3) заменить полной системой действительных
чисел R. Упорядоченное поле Q мы будем считать вложен-
ным в R, чтобы иметь возможность пользоваться такими
символами, как У 2. Буквой х мы будем обозначать рацио-
нальные числа.
(а) Функция, непрерывная на замкнутом интервале
и не ограниченная на нем (поскольку интервал огра-
ничен, эта функция не является на нем равномерно
непрерывной)'.
f(x~)= Х2~С_2 ’ 0<х<2.
(Ь) Функция, непрерывная и ограниченная на замкну-
том интервале, но не являющаяся равномерно непре-
рывной на нем'.
0,
/(*) = { j
0<х< У 2,
/2 < х < 2.
30
Глава 1
(с) Функция, равномерно непрерывная (и, следова-
тельно, ограниченная) на замкнутом интервале, но не
имеющая на нем максимума-.
/ (х) = х — х3, 0 х 1.
(d) Функция, непрерывная на замкнутом интервале,
но не обладающая свойством Коши.
Пример b или f(x) = x2 на [1, 2]. Последняя функция
не принимает значения 2, которое расположено между 1 и 4.
(е) Дифференцируемая функция, не являющаяся по-
стоянной, производная которой обращается в нуль всюду
на замкнутом интервале.
Пример Ь.
(f) Дифференцируемая функция, для которой не спра-
ведлива теорема Ролля (и, следовательно, теорема
о среднем).
Пример с.
.(g) Монотонная равномерно непрерывная функция,
которая не является постоянной и обладает свойством
Коши, а ее производная обращается в нуль всюду на
интервале.
Этот пример более трудный, чем предыдущие. Его можно
построить с помощью канторова множества, определенного
в гл. 8. Подробности см. в примере 15 гл. 8.
ГЛАВА 2
ФУНКЦИИ И ПРЕДЕЛЫ
Введение
В этой главе необходимо расширить некоторые опреде-
ления гл. 1 и ввести новые. Если не оговорено противное,
то все рассматриваемые множества будут являться подмно-
жествами системы действительных чисел R, а все функции
будут предполагаться действительнозначными функциями дей-
ствительного переменного.
Сначала распространим понятия объединения и пересече-
ния на бесконечные совокупности множеств Alt А2,
+<х>
(J Ап = Д; U А2 U ... ~{х\х £ Ап по крайней мере
для одного п=1, 2, ...},
+оо
f") Ап — Д п А2 п . . .~{х\х£Ап для каждого
л=1
п= 1, 2, ..
Множество А называется замкнутым, если оно со-
держит все свои предельные точки; другими словами, ни
одна точка множества А' не является предельной точкой
множества А. Множество А называется открытым, если
всякая точка этого множества имеет окрестность, целиком
содержащуюся в множестве А. Точка р называется гра-
ничной точкой множества А, если каждая окрест-
ность точки р содержит по крайней мере одну 'точку мно-
жества А и по крайней мере одну точку множества А'.
Множество всех граничных точек множества А называется
границей А и обозначается символом F(Д). Точка р на-
зывается внутренней точкой множества А, если суще-
ствует окрестность точки р, целиком лежащая в А. Мно-
жество всех внутренних точек множества А называется
ядром А и обозначается через /(Д). Любое замкнутое мно-
жество А является объединением своего ядра и границы:
32
Глава 2
А — I (Д) U ^(Д). Замыканием А множества А назы-
вается объединение множества А и множества всех предель-
ных точек А. Открытым покрытием множества А
называется любое семейство {Ua} открытых множеств Ua,
объединение которых содержит А; в этом случае говорят,
что семейство [Ua] покрывает А. Множество А назы-
вается компактным, если каждое его открытое покрытие
содержит конечное подсемейство, которое покрывает Д1).
В пространстве R множество компактно тогда и только
тогда, когда оно замкнуто и ограничено. (Первая часть этого
утверждения есть теорема Гейне — Бореля; см. [36], стр. 202,
а также [33]*, стр. 43.)
Множество А называется счетным, если оно либо
конечно, либо существует взаимно однозначное соответствие
между множеством всех натуральных чисел N и множе-
ством Д.
Важное свойство системы действительных чисел состоит
в том, что для любого действительного числа х существует
единственное целое число п, такое, что
я<Сх<«~Г1 или х—1<я<х.
Поскольку п определяется однозначно как наибольшее целое
число, не превосходящее х, мы получаем тем самым функ-
цию, которая обозначается символом [х]2). Функция / (х)=[х]
определяется, таким образом, одним из неравенств
[х] х < [х] Д- 1 или х—1 < [х]<х,
где [х] — целое число. В дальнейшем квадратные скобки
будут обозначать целую часть числа лишь в том случае, если
будет сделано соответствующее пояснение.
Функция /, являющаяся отображением множества R в R,
называется периодической с периодом р, если
f (х + Р) = f (х) для всех х £ R. Функцию называют перио-
дической, если она является периодической с некоторым
отличным от нуля периодом р.
Пусть а является предельной точкой области определе-
ния D некоторой функции /, и пусть /(х) ограничена в не-
которой окрестности точки а для x£D. Верхний пре-
') Такие множества часто называют компактами. — Прим. ред.
г) [х] называется целой частью числа х. — Прим, перев.
Функции и пределы
33
дел и нижний предел функции / в точке а, которые
обозначаются соответственно lim /(х) и Пт /(х), опреде-
х-+а х-*а
ляются следующим образом. Для б > 0 положим
<p(6)==sup {/(х)|х£Г>П D(a, б)},
ф(б)==ПД {/(х)|х££>П D{a, б)}.
Тогда
lim f(x)= lim <р(б) = inf (<р(б) |б > 0},
х-»а й->+0
lim f(x)= lim ф(б) = sup {ф(б) |б > 0}.
х~^л +0
Функция f называется полунепрерывной сверху
в точке a£D, если lim /(x)<C/(fl): если же lim /(^)>/(л),
х->о х-+а
то f называется полунепрерывной снизу в точке а;
наконец, / называется полунепрерывной в точке а,
если она либо полунепрерывна сверху, либо полунепрерывна
снизу в точке а.
Функцию / назовем локально ограниченной
в точке а (которая либо принадлежит, либо является пре-
дельной точкой области определения функции /), если суще-
ствует окрестность точки а, в которой / ограничена. Функ-
ция / называется локально ограниченной на неко-
тором подмножестве А ее области определения, если /
локально ограничена в каждой точке множества А.
Бесконечные пределы ± оо и пределы f(x) при х-> ±оо
определяются, как и в случае lim f(x) — b, только в каче-
стве окрестностей бесконечности используются
£>(-|-оо, N) = (N, -J-oo),
О(—оо, 7V) = (—оо, N).
Например,
lim /(х) — -|- оо, если V/C Вб > 0 3f(D П D(a, б))с
х->а
сО(+оо, К),
lim f(x) = b, если Ve > 0 3 N 3 f (Р П D(—oo,
X->-oo
c: N (b, e).
3 Зак. 687
34
Глава 2
Основные определения сходимости и равномерной сходи-
мости, а также признак Вейерштрасса для равномерной схо-
димости бесконечных рядов предполагаются известными (см.
[36], стр. 381, 444, 445, а также [52]*, т. II, стр. 423—425
и 430).
1. Всюду разрывная функция, абсолютное значение
которой есть всюду непрерывная функция
( 1, если, х рационально,
У(х) = .
[ —1, если х иррационально.
2. Функция, непрерывная лишь
мер 22)
( х, если х
[ —х, если х
в одной точке (см. при-
рационально,
иррационально.
Единственной точкой непрерывности этой функции является 0.
3. Непрерывная и неограниченная функция, определенная
на произвольном некомпактном множестве
(а) Если А — неограниченное множество действительных
чисел, то положим
f(x) = x, х£А.
(Ь) Если А — ограниченное, но не замкнутое множество
действительных чисел, то положим
/(*) = Т=7’ Х^А'
где с — предельная точка множества А, не принадлежащая А.
Если же f непрерывна на компактном множестве А,
то / ограничена на нем (см. [38], стр. 80).
4. Неограниченная функция, определенная на Произволь-
ном некомпактном множестве и локально ограниченная
на нем
Пример 3.
Если же / локально ограничена на компактном множе-
стве А, то она ограничена на нем.
Функции и пределы
35
5. Функция, всюду конечная и всюду локально
неограниченная
Пусть х — рациональное число, равное т/п, где т и п—
целые числа, такие, что дробь т/п несократима и п > 0.
Тогда яг и я определяются однозначно (см. [37], стр. 53), и
потому следующая функция определена корректно:
я, если х рационально, х = т!п — несократимая
/(х) =
дробь, я > 0,
0, если х иррационально.
Если бы / была ограничена в N(a, е), то для всех
дробей т/п в N (а, е) знаменатели я были бы ограничены,
а, следовательно, были бы ограничены и числители т. Но
отсюда следовало бы, что в интервале N (а, е) существует
лишь конечное число рациональных чисел. (Противоречие.)
(См. пример 27 гл. 8, где определена функция, обладающая
еще более сильными патологическими свойствами. См. также
пример 29 гл. 8.)
6. Непрерывная ограниченная функция, определенная на
произвольном некомпактном множестве и не имеющая
экстремальных значений
(а) Если А — неограниченное множество действительных
чисел, то положим
Функция f (х) не имеет наибольшего значения на множестве А.
Если же f (х) определить формулой
/W^(_i)"-ti xLTi хеЛ
где [ | х | ] — целая часть числа | х |, то /(х) не будет иметь
ни наибольшего, ни наименьшего значения на множестве А!).
‘) Пример, приведенный в пункте 6 (а), не корректен. Именно,
если Л={2я], где я=1, 2, ..., то функция /(х) имеет наи-
меньшее значение при х — 2. Если же взять А = (—со, -(-оо).
то функция fix) будет разрывной, например, в точке х = 1.—
Прим. ред.
3*
36
Глава 2
(Ь) Если А — ограниченное, но не замкнутое множество
действительных чисел, то положим
/(х) =— |х — с|, х£А,
где с — предельная точка множества А, не принадлежащая этому
множеству. Функция / (х) не имеет наибольшего значения
на А. Если же /(х) определить формулой
/(х) = (—1)|1/|Л"г И{А —|х —с|},
где L — длина некоторого интервала, содержащего множе-
ство А, а квадратные скобки обозначают целую часть за-
ключенного между ними числа, то /(х) не будет иметь ни
наибольшего, ни наименьшего значения на А').
7. Ограниченная функция, не имеющая относительных
экстремумов на компактном множестве
Возьмем в качестве компактного множества замкнутый
интервал [0, 1] и для х £ [0, 1] положим
/(х) =
(—1)Л п
п 1 ’
если х рационально, x-mfri, где т/п—
несократимая дробь и п > О,
О, если х иррационально.
Тогда в каждой окрестности любой точки из [0, 1] най-
дутся значения функции /, как угодно близкие к числам
1 и —1, однако все значения функции f лежат строго между
этими числами (см. [22], стр. 127).
) Пример, приведенный в пункте 6(b), не корректен даже
для множества А = (0, 1), так как в этом случае можно взять
L = 1, с = 0, для которых функция /(х) разрывна в точке х = -^-.
Если же А — |-2~ | (п = Е 2, ...), то при L — 1, с = 0 функция
f (х) достигает своего наименьшего значения при х=-^-. —Прим,
ред.
Функции и пределы
37
8. Ограниченная функция, не являющаяся полунепре-
рывной ни в одной точке
Функция примера 7 не является полунепрерывной сверху
ни в одной точке отрезка [0, 1], так как lim/(х) всюду
х-*а
равен 1, и, следовательно, ни в одной точке а не может быть
выполнено неравенство lim /(х)^/(о). Подобным же образом
устанавливается, что эта функция не является полунепре-
рывной снизу ни в одной точке. (Заметим, что функция
примера 1 полунепрерывна сверху в каждой рациональной
точке и полунепрерывна снизу в каждой иррациональной
точке.)
9. Периодическая функция, отличная от постоянной
и не имеющая наименьшего периода
Периодами функции примера 1 являются все рациональные
числа.
Периоды любой действительнозначной функции с областью
определения R образуют аддитивную группу (т. е. множество
периодов замкнуто относительно вычитания). Эта группа или
плотна (как в настоящем примере), или дискретна, и тогда она
сострит из всех целых кратных наименьшего положительного
элемента. Последний случай имеет место для всякой перио-
дической функции с областью определения R, если она
отлична от постоянной и имеет по крайней мере одну точку
непрерывности. (См. [38], стр. 549.)
10. Иррациональные функции
Функция Ух не является рациональной (см. пример 4
гл. 1), так как она не определена для х < 0.
Функция [х] также не является рациональной, поскольку
она имеет разрывы в некоторых точках ее области опреде-
ления.
Функция | х | является иррациональной по той причине,
что она не имеет производной в некоторой точке ее области
определения.
Функция У х21 также иррациональна. В этом можно
убедиться следующим образом. Если У х21 — f (х)/g (х)
38
Глава 2
для всех х, то j/'x2-^- \/х = f (x)/xg (х) для х =/= 0 и, следо-
вательно, lim /(x)lxg(х) = 1. Отсюда вытекает, что /(х)
-Г~> +оо
и xg(x') являются полиномами одинаковой степени и потому
lim /(x)/xg(х) — 1, в то время как lim угх2-]-1/х = —1.
л->-оо х->-со
(Противоречие.)
11. Трансцендентные функции
Функция / называется алгебраической, если В поли-
п
ном р(и) = 2) ак (х) коэффициентами которого служат
ЬО
действительные полиномы а0(х), ^(х)....ая(х) (т. е. все
их коэффициенты действительны), одновременно не обращаю-
щиеся тождественно в нуль, такой, что композиция р(/(х))
обращается тождественно в нуль в области определения
функции /. Функция называется трансцендентной, если
она не является алгебраической.
Примером трансцендентной функции может служить функ-
ция ех, ибо если предположить, что
а0(х) + <г1(х)ел+ ... + <гя(х)е"л = 0,
где ао(х)^О, то, переходя к пределу в обеих частях этого
тождества при х—> —оо и пользуясь правилом Лопиталя,
мы получим равенство
lim ао(х) = О,
которое невозможно в силу предположения ао(х)^О.
Другим примером может служить функция sin х, ибо если
(х)(х) sin х + ... -|-#я (х) sin" х = 0,
где полином #о(х)^О, то 6о(6л) = О для всех целых k.
(Противоречие.)
Дальнейшими примерами трансцендентных функций (по
тем же причинам) являются In х (функция, обратная к ех)
и остальные тригонометрические функции.
Примерами алгебраических функций могут служить сле-
дующие иррациональные функции примера 10: |х|
(|х| = /х2) и уЛх2-)-!.
Функции и пределы
39
12. Функции у =/(«), a£R, и u = g(x), x£R, компо-
зиция которых y=f(g(x)) всюду непрерывна и
такова, что lim f(u)=c, lim g(x)=b, lim f(g(x))
u->b x-^a x->a
Если
f o
/(M)=| J
при a #= 0, и £R,
при и = 0,
то lim/(и) = 0. Если же ^(х)==0 для всех x£R, то
и->о
/(g-(x))=l для всех х и, следовательно, lim /(g(x))=l.
х->0
Этот контрпример будет невозможным, если добавить
следующее условие: х Ф a =^g(x) =£ b.
13. Две равномерно непрерывные функции, произведение
которых не является равномерно непрерывной функ-
цией
Функции хи sinx равномерно непрерывны на R, так как
их производные ограничены, но их произведение xsinx не
является равномерно непрерывной функцией на R.
Если же обе функции / и g ограничены на общей об-
ласти определения D и равномерно непрерывны на ней, то
их произведение fg также равномерно непрерывно на D.
Так как функция, равномерно непрерывная на ограниченном
множестве, ограничена на нем, то пример, подобный настоя-
щему, возможен лишь в том случае, если общая область
определения не ограничена и по крайней мере одна из функ-
ций не ограничена.
14. Непрерывное на некотором интервале, взаимно одно-
значное отображение, обратное к которому разрывно
Для этого примера необходимо, чтобы интервал не был
замкнутым и ограниченным (см. [36], стр. 192) и чтобы
функция принимала не только действительные значения (см.
[36], стр. 50 и 52, упр. 25). В качестве примера мы исполь-
зуем комплекснозначную функцию z = f(x) действительного
переменного х. При этом непрерывность определяется точно
так же, как и в случае действительной функции действитель-
40
Глава 2
ного переменного, только под абсолютной величиной ком-
плексного числа z = (а, Ь) следует понимать его модуль
| z | = | (а. Ь)\ = (а?+
Определим функцию z=f(x) следующим образом:
z = /(x) = (cosx, sinx), 0<^х<2л.
Тогда / отобразит полуоткрытый интервал [0, 2л) непрерывно
и взаимно однозначно на единичную окружность | z | = 1.
Но так как единичная окружность является компактом, то
обратное отображение не может быть непрерывным (см. [36],
стр. 192), а именно оно разрывно в точке (1, 0).
15. Функция, непрерывная в иррациональных и разрыв-
ная в рациональных точках
Если х — рациональное число вида т\п, где тип — целые
числа, дробь т/п несократима и п>0, то положим / (х) = 1/п.
Если же х иррационально, положим /(х) = 0. (См. [36],
стр. 124.)1)
В примере 10 гл. 8 будет показано, что не существует
функции, непрерывной во всех рациональных точках и раз-
рывной во всех иррациональных точках.
16. Полунепрерывная функция с плотным множеством
точек разрыва
Функция примера 15 полунепрерывна сверху в каждой
точке а, поскольку
lim f (х) = 0</(с).
лг-»а
17. Функция с плотным множеством точек разрыва,
каждая из которых устранима
Пусть а — рациональное число. Переопределим функцию
примера 15, положив /(о) = 0. Тогда
lim / (х) = 0 = / (а),
х-ьа
т. е. функция f становится непрерывной в точке а.
‘) Построенная функция /(х) известна под названием функции
Римана. — Прим, ред.
Функции и пределы
41
18. Монотонная функция, точки разрыва которой обра-
зуют произвольное счетное (возможно, плотное)
множество
Пусть А — произвольное непустое счетное множество
действительных чисел аг, а2, а3....и пусть 2 Рп — К0‘
нечный или сходящийся бесконечный ряд положительных
чисел с суммой р (ряд конечен тогда и только тогда, когда
конечно множество А, и имеет столько же членов, сколько
элементов в множестве А). Если А ограничено снизу и х
меньше любого элемента множества А, положим /(х) = 0.
В противном случае положим f(x) = 2 Рл> т- е- /(*)
равна сумме всех членов рт ряда 2 Рп> таких, что ат-^,х.
Тогда f возрастает на R, непрерывна в каждой точке, не
принадлежащей А, и разрывна со скачком, равным рп,
во всякой точке ап /т. е. lim f(x)— lim f(x) — pn\.
\ x-»a„+o -^-*«„-0 )
Следует отметить, что для монотонных функций этот при-
мер не допускает дальнейших усилений, ибо для всякой моно-
тонной функции множество точек разрыва счетно (см. [38],
стр. 59, упр. 29, а также [33]*, стр. 223). Пример 1 пока-
зывает, что если не требовать монотонности, то множество
точек разрыва может совпадать с R.
19. Функция с плотным множеством точек непрерывности
и плотным множеством точек разрыва, ни одна из ко-
торых не является устранимой
Для этого достаточно в примере 18 в качестве множе-
ства А взять множество Q всех рациональных чисел.
20. Нигде не монотонное взаимно однозначное соответ-
ствие между двумя интервалами
Определим f(x) для 0<;х^1 следующим образом:
[ х, если х рационально,
f(x) = \ .
[1 — х, если х иррационально.
Тогда на [0, 1] не существует подинтервала, на котором /
монотонна. Множество значений / есть снова интервал [0, 1],
причем отображение f взаимно однозначно,
42
Глава 2
Следующая функция обладает тем же свойством и отобра-
жает интервал [a, t>] на интервал [с, d}-.
c-{-(d — c)xh_a ’ если -у_а рационально,
g- (х) =г х — а х — а
d-\-(c — d) ’ если 6 иррационально.
21. Непрерывная нигде не монотонная функция
Положим f1 (х) =-1 X | для |х|<1/2 и продолжим эту
функцию периодически с периодом 1, т. е. положим (хф-га)=
— /1 (х) Для всякого действительного числа х и всякого
целого п. Далее для я> 1 положим fn (х) = 4~л'1 (4л-1х).
Таким образом, для всякого натурального п функция /„—
периодическая с периодом 4~л+1 и максимальным значением
__.4-л+1. Наконец, определим на R функцию / так1):
П=1 Л = 1
Так как | fn (х) | • 4~л+1, то по признаку Вейерштрасса
этот ряд равномерно сходится на R и функция f всюду не-
прерывна. Если точка а имеет вид а — k • 4~т, где k — целое,
а т — натуральное, то /п(а) = 0 для п > т. Следовательно,
/(а) = /1(«)+ + /«(«)• Пусть = 4”2т“л, где от —
произвольное натуральное число. Тогда fn (а -ф- йт) = 0 при
я>2т-ф1 и, следовательно,
/ (« + йга) - / («) = 1/1 (« + М - /1 («)] + • • •
• •• +[/m(« + ^m)-/m(a)] +
+ fm + l(a + + ••• +/2zn + l(a + ^zn)^-
> — «1/г,„ф(тф \)hm = hm > 0.
Аналогично
/(«—*m) —/(«)> —/пйтф(/пф 1)йга = йт > 0.
‘) Пример функции /(x) был фактически рассмотрен Ван дер
Варденом в связи с другим вопросом (см. гл. III, пример 8). —
Прим. ред.
Функции и пределы
43
Но так как точки вида а — k • 4-m всюду плотны в R,
то отсюда следует, что не существует открытого интервала,
на котором f монотонна.
Конструкции, подобные описанной выше, приводят к сгу-
щению особенностей.
22. Функция, точки разрыва которой образуют произ-
вольно заданное замкнутое множество
Пусть А—-замкнутое множество. Определим множество В
следующим образом:
х£В, если x£F(A) или x£/(X)f|Q-
Далее положим
1, если х £ В,
0, если х(^В.
Если с£А, то f разрывна в этой точке. В самом деле, если
с£Л(Л), то /(с)=1, в то время как с является предель-
ной точкой множества R \ А, на котором f тождественно
равна 0; если же c£/(X)f|Q, то /(с)=1, причем с
является предельной точкой множества /(X)\Q, на кото-
ром f равна 0; наконец, если c£/(X)\Q, то /(с) = 0,
в то время как с является предельной точкой множества
/(Л)ПО. на котором f тождественно равна 1. Отметим, что
на множестве R \ А функция f непрерывна, поскольку это
множество открыто и функция f постоянна на нем.
23. Функция, точки разрыва которой образуют произ-
вольно заданное множество типа Fo. (См. пример 8
гл. 4 и примеры 8, 10 и 22 гл. 8.)
Множество А называется множеством типа Fo, если оно
является объединением счетного множества замкнутых мно-
жеств (см. пример 8 гл. 8). Пусть А = Аг (J Л2 U ... есть
заданное множество типа Fa, причем Др Л2, .. . замкнуты
и Д„сЛ я+1 для п— 1, 2, .... Обозначив через Ло пустое
множество 0, определим последовательность непересекаю-
щихся множеств Ва (п= 1, 2, .. .) следующим образом:
х£Вп, если <
I или х£/(Ап \An_1)[}Q.
44
Глава 2
И наконец, определим искомую функцию /, положив
2-л, если xGB„,
I 0, если ....
Покажем, что если с£А, то f разрывна в точке с.
В самом деле, если сС(4\4-1)\/(Л\Л-1). то
f(c') = 2~", причем с является предельной точкой некото-
рого множества, на котором / принимает значения, отли-
чающиеся от 2-л по крайней мере на 2-л~1; если же
то /(с) = 2 ”, причем с является
предельной точкой множества / (А„ \ А/г_1) \ Q, на котором /
тождественно равна 0; наконец, если с £ I (Л„ \ Xn_j) \ Q,
то /(с) = 0, в то время как с является предельной точкой
множества / (Ап \ Ап_г) f] Q, на котором / тождественно
равна 2-л. Остается показать, что если с(£Д, то / непре-
рывна в с. Пусть задано е > 0. Возьмем W, такюе, что
2~N < е, а затем выберем окрестность точки с, не имеющую
общих точек с множествами А2, .... AN. Тогда в этой
окрестности / (х) < 2-7V < е, и непрерывность функции /
в точке с доказана.
Следует отметить, что для любой функции /, отображаю-
щей R в R, множество точек разрыва является множеством
типа Ра (см. [38], стр. 84, упр. 30—33; стр. 332, упр. 41,
а также [1]*, стр. 152).
24. Функция, не являющаяся пределом последователь-
ности непрерывных функций. (См. пример 10 гл. 4.)
Функция / примера 1 обладает тем свойством, что не
существует последовательности {/„] непрерывных функций,
такой, что lim /л(х) —/(х) для всех действительных х.
л->+со
Однако доказательство этого факта не является элементар-
ным, подробности и дальнейшие ссылки см. в [9], стр. 99—103.
Идея доказательства состоит в том, что / всюду разрывна,
в то время как функция, являющаяся пределом последова-
тельности непрерывных функций, должна иметь плотное мно-
жество точек непрерывности.
Функции и пределы
45
Покажем, однако, что характеристическая функция мно-
жества Q всех рациональных чисел является пределом после-
довательности {£„} функций, каждая из которых есть предел
последовательности [hn] непрерывных функций. Действи-
тельно, пусть {гл} — последовательность всех рациональных
чисел. Положим
1,
О
если х — гр г2, .... или гп,
в противном случае.
Всякая функция gn является пределом последовательности не-
прерывных функций, каждую из которых можно выбрать
в виде ломаной. Эти ломаные строятся следующим образом.
Каждая из них равна 1 в тех точках, где gn(x) = 1, равна О
на замкнутых подинтервалах, являющихся внутренними для
интервалов, образованных двумя соседними точками, в кото-
рых gn(x) = l, и линейна на оставшихся интервалах. По-
строение ведется таким образом, чтобы основания пиков стя-
гивались к точкам, в которых ^л(х)=1.
Заметим, что для каждого х последовательность {^п (х)}
возрастает, в то время как последовательность, которая схо-
дится к gn(x), может быть выбрана убывающей.
25. Функция, определенная на [О, I], множество значений
которой на каждом невырожденном подинтервале со-
впадает с [0, 1]. (См. пример 27 гл. 8.)
Функция, обладающая этим свойством, впервые была по-
строена А. Лебегом (см. [28], стр. 85). Описание этого по-
строения можно найти в [9] (см. стр. 71, а также [22], стр. 228).
Пусть х — произвольное число из [0, 1], и пусть
х — 0,аха2а3 . . .
— его десятичное разложение. В случае, если х допускает
два различных разложения, одно из которых является конеч-
ной десятичной дробью, другое же имеет цифру 9 в периоде,
то можно взять любое из этих разложений. Для определен-
ности условимся брать лишь конечные разложения. Значения
функции /(х) будут зависеть от того, является ли дробь
. периодической или нет, т. е. является ли число
46
Глава 2
f(x)=
О, «1«з«5 • . рациональным или нет (см. [37], стр. 178):
О, если 0,aia3a5 .. . иррационально,
0,a2na2n+2a2n+4 • • • > если • • • рационально
и периодическое повторение совокупности цифр
начинается с а2л-1-
Пусть I—произвольный подинтервал из [0, 1]. Выберем
цифры ар а2......а2„_2 так, чтобы числа 0,а4а2 . . а2п-2®
и 0,... принадлежали /, а цифра а2п_3 была
отлична от 0 и 1. Далее положим a2n_j = а2п+1 = ...
... = а4п_5 — 0, а a4n_3= 1. Затем эти п цифр будем перио-
дически повторять, располагая их на местах с нечетными
индексами. Таким образом, мы определим все а2/г-г Если
теперь у = O,b4b2b3 ... —произвольная точка из [О, 1], то
положим
х = 0 а}а2а3 . . . о-2п_1Ь1а2п+-[Ь2а2п+3 ....
Число х принадлежит интервалу / и таково, что разложение
0,«i«3«5 • • • а2п_3а2п_4а2п+1 .. .
является периодической десятичной дробью, первый период
которой начинается с Следовательно,
/(х) = 0Д^3 ....
Точки графика функции f расположены всюду плотно
в единичном квадрате [0, 1] X [0. 1]» хотя каждый вертикаль-
ный отрезок {х} X [О, 1] пересекает график лишь в одной
точке.
В примере 27 гл. 8 определяется функция, множество
значений которой на каждом непустом открытом интервале
совпадает с R и которая равна нулю почти всюду (а следо-
вательно, измерима). (См. также следующий пример 26.)
Так как единичный интервал [О, 1] содержит бесконечное
множество непересекающихся открытых интервалов (напри-
мер । п—1, 2, ...), то функция /настоящего
примера принимает каждое свое значение бесконечное мно-
жество раз. Еще одна функция, которая каждое свое значе-
ние принимает бесконечное множество раз, определена в при-
мере 9 гл. 10.
Функции и пределы
47
26. Разрывная линейная функция
Функция /, отображающая R в R, называется линейной,
если f (х -ф- у) = f (х)—f (У) для всех х, y£R. Линейная
функция, которая не является непрерывной, должна быть
„очень сильно0 разрывной. В самом деле, ее график должен
быть всюду плотным на плоскости R X R- Эти вопросы рас-
сматриваются в [9] (стр. 108—ИЗ), где приведены дальней-
шие ссылки. В случае же, если f непрерывна и линейна,
она должна иметь вид /(х) = сх. В этом можно убедиться,
рассматривая последовательно классы чисел N, I, Q, R.
Построение разрывной линейной функции можно осуще-
ствить, используя базис Хамеля в линейном пространстве
R вещественных чисел над полем Q рациональных чисел (см.
ссылки [29], [30] и [32] из [9]). Идея состоит в том, что
этот процесс приводит к множеству S = (га| действительных
чисел га, таких, что всякое действительное число х является
единственной линейной комбинацией конечного числа эле-
ментов из S с рациональными коэффициентами ра: х =
= р г -ф- . . . -ф- р г . Функцию f можно определить так:
“1 “1 ak ak
+ +рак>
поскольку представление числа х в виде линейной комбина-
ции единственно. Линейность функции f следует непосред-
ственно из ее определения, а тот факт, что f не является
непрерывной, вытекает из того, что все ее значения рацио-
нальны, но не все одинаковы (/ не обладает свойством Коши,
т. е. не принимает некоторые промежуточные значения).
27. Теорема Колмогорова: для каждого ra£N существуют
я(2га-[-1) функций (J = ^2......
7=1, 2,..., 2га+1), таких, что
(а) все функции ср/у(ху) непрерывны на [0, 1];
(Ь) для любой функции /(хъ х2, ..., х„), непрерывной
на 0<хъ х2, ..., х„<1, существуют 2га -ф-1 функ-
ций фр /==1, 2,..., 2га—[— 1, каждая из которых не-
прерывна на R, причем
48
Глава 2
Эта теорема принадлежит А. Н. Колмогорову [25]. Она
разрешает знаменитую седьмую1) проблему Д. Гильберта и
формулируется в этом случае следующим образом: каждую
непрерывную функцию f{xlt х2....хп) п действитель-
ных переменных, 0 хг, х2........можно предста-
вить в виде суммы {внешняя сумма приведенной выше
формулы) 2/г —1 суперпозиций непрерывных функций
одного переменного и суммы {внутренняя сумма указан-
ной формулы) п непрерывных функций одного переменного.
Доказательство этой теоремы в высшей степени остро-
умно, но доступно каждому читателю, который готов терпе-
ливо проследить за довольно длинной цепью индуктивных
рассуждений.
Отметим лишь, что функции ф/;- являются универсальными,
т. е. они не зависят от /. Функции фг, напротив, однозначно
определяются функцией /. Подробное доказательство можно
найти в цитированной работе.
*) Здесь речь должна идти, вероятно, о тринадцатой проблеме
Гильберта, а не о седьмой.—Прим. ред.
ГЛАВА 3
ДИФФЕРЕНЦИРОВАНИЕ
Введение
В некоторых примерах этой главы термин производная
будет применяться и к бесконечным пределам
.. /(х-фЛ)— f (х) . .. /(х4-Л) — /(х)
Л->0 h h-+0 h
Однако термин дифференцируемая функция используется
лишь в том случае, если функция имеет конечную производ-
ную в каждой точке своей области определения. Функция
называется бесконечно дифференцируемой, если
она имеет (конечную) производную любого порядка в каждой
точке области определения.
Показательная функция с основанием е будет обозна-
чаться символом ех или ехр(х).
Как и в предыдущей главе, предполагается, что все мно-
жества, включая области определения и множества значений
функций, являются подмножествами R. В противном случае
будет сделано соответствующее уточнение. Это предполо-
жение будет оставаться в силе вплоть до гл. 8.
1. Функция, не являющаяся производной
Функция sgnx (см. введение, гл. 1) и вообще всякая
функция с разрывом в виде скачка не имеет примитивной,
т. е. не является производной никакой функции, поскольку
она не обладает свойством Коши принимать все промежуточ-
ные значения, а это свойство присуще не только непрерыв-
ным функциям, но и производным (см. [36], стр. 84, упр. 40,
а также [52]*, т. I, стр. 224). Ниже приводится пример раз-
рывной производной.
4 Зак. 587
50
Глава 3
2. Дифференцируемая функция с разрывной производной
Рассмотрим функцию
/(*) =
2 • 1
х2 sin — ,
X
0,
если
0,
если х = 0.
Ее производная
/'(*) =
0-1 1
2х sin--cos —,
х х
О,
если х =# О,
если х = О,
разрывна в точке х = 0.
3. Разрывная функция, всюду имеющая производную
(не обязательно конечную)
Для того чтобы такой пример стал возможен, надо рас-
ширить определение производной так, чтобы оно включало
значения ± оо. Тогда разрывная функция sgn х (пример 1)
имеет производную
( 0, если х #= О,
о- ;
( -|- оо, если х = 0.
4. Дифференцируемая функция, производная которой
не сохраняет знака ни в какой односторонней окрест-
ности экстремальной точки
Функция
[ х4 l^-l-sin— 'l, если х + О,
= | х'
( 0, если х —О,
имеет абсолютный минимум в точке х = 0. А ее производная
[ х2 [4х (2 -4-sin — — cos— 1, если х =£ О,
/'(х) = -| L \ х>
[ 0, если х = 0,
в любой односторонней окрестности нуля принимает как
положительные, так и отрицательные значения. Функция f
не является монотонной ни в какой односторонней окрест-
ности точки х = 0.
Дифференцирование
51
5. Дифференцируемая функция, производная которой
положительна в некоторой точке, но сама функция
не монотонна ни в какой окрестности этой точки
Функция
| х 4~2х2 sin Д-, если х #= О,
/(•*) = х
[ 0, если х = 0,
имеет производную, равную
l+4xsin —-------------------2cos — , если х =£ О,
= { х х
1, если х — 0.
/'(*) =
В любой окрестности нуля производная /'(х) имеет как
положительные, так и отрицательные значения.
6. Функция, производная которой конечна, но не огра-
ничена на замкнутом интервале
Рассмотрим функцию
/(х)==
2 • 1
x2sin—
х2
0,
если
х 0,
если
х — 0.
Ее производная
/'(*) =
если х =# 0,
если х = 0,
не ограничена на [—1, 1].
7. Функция, производная которой существует и ограни-
чена, но не имеет (абсолютного) экстремума на зам-
кнутом интервале
Функция
f (х) =
х4е 4 sin -Д, если х 0,
х3
0, если х — 0,
4*
52
Глава 3
имеет производную
/'(*) =
е-хг/4 Г(4хз— *\sjn 8— 24 cos -У ,
L\ 2) х3 х3 J
О,
если х =£ О,
если х = 0.
В любой окрестности нуля эта производная имеет значе-
ния, как угодно близкие к 24 и —24. С другой стороны,
для 0 < h = | х | < 1 (см. [36], стр. 83, упр. 29) имеем
0 < <1—| &e-h^ < 1 — А Л2,
4 ^16
и
\ . , х5\ . 8 „. 8 . о. , 9 ,,
4х3 — -о- Isin—— 24 cos -= < 24 -4--н- Л3.
\ 2) х3 _г3 ~ 1 2
Поэтому из неравенства 0 < h < 1 следует, что
(Q \ / Q \ О
1 —ЙЛ2) (24 + тЛЗ) < 24—уЛ2(1 —А)<24.
Следовательно, множество значений функции f на [—1, 1]
имеет точную верхнюю грань, равную 24, и точную нижнюю
грань, равную —24, и ни одна из этих граней не достигается.
8. Всюду непрерывная, но нигде не дифференцируемая
функция
Функция | х | всюду непрерывна, но не дифференцируема
в точке х — 0. С помощью сдвига этой функции можно
определить всюду непрерывную функцию, которая не диф-
ференцируема в каждой точке произвольно заданного конеч-
ного множества. В этом параграфе мы приведем пример,
использующий бесконечное множество сдвигов функции | х |.
Покажем, что функция примера 21 гл. 2 нигде не диф-
ференцируема. Пусть а — произвольное действительное число,
и пусть для всякого натурального п число hn, равное 4~п
или — 4~", выбрано так, что |/я(а-|-Ля)— fn (а)| — ] hn |.
Тогда величина |/т(а-|-йя)— fm (а) | имеет одинаковое зна-
чение | hn | для всех и равна нулю для т > п. Тогда
разностное отношение (/(а-|~ hn) — f (a))lhn является целым
числом, которое четно при четном п и нечетно при нечет-
Дифференцирование
53
ном п. Отсюда следует, что предел
lim / (Д + hn) — f (а)
П->+оо
не существует, а поэтому не существует и f'(а).
Приведенный примерт) является модификацией примера,
построенного Б. Л. Ван дер Варденом в 1930 г. (см. [51],
стр. 394). Первый же пример непрерывной нигде не диф-
ференцируемой функции был построен К. В. Т. Вейерштрас-
сом (немецкий математик, 1815—1897 г.):
+ оо
/ (х) = 2 cos (я"лх),
ч-0
где а — целое нечетное число, а число Ь таково, что
з
0<6<1 и аб > 1-g-л* 2). В настоящее время известны
примеры непрерывных функций, которые ни в одной точке
не имеют даже односторонней конечной или бесконечной
производной. Эти примеры и дальнейшие ссылки можно
найти в ]51] (стр. 392—394), [9] (стр. 61 — 62, 115, 126),
а также в [16] (т. II, стр. 401—412).
Как было показано ранее (см. пример 21 гл. 2), функция
настоящего примера не является монотонной ни на каком
интервале. Более того, существует пример функции всюду
дифференцируемой и нигде не монотонной (см. [16], т. II,
стр. 412—421). Конструкция этого примера очень сложна и
приводит к функции, которая всюду дифференцируема и
имеет плотное множество относительных максимумов и плот-
ное множество относительных минимумов.
9. Дифференцируемая функция, для которой теорема
о среднем не имеет места
В этом примере мы снова вынуждены обратиться
к комплекснозначной функции. Функция
/ (х) = cos х +1 sin х
') Точно в таком же виде пример функции /(х) изложен
в книге П. С. Александрова „Введение в общую теорию множеств
и функций», 1948, стр. 223—225.—Прим. ред.
2) На самом деле, как показал Г. Харди (Hardy О. Н.,
Weierstrass’s nondifferentiable function, Trans. Amer. Math. Soc.,
17 (1916), 301—325), эта функция нигде не дифференцируема лишь
в предположении, что 0 < Z» < 1 и ab^> I. — Прим, перев.
54
Глава 3
действительного переменного х всюду непрерывна и диффе-
ренцируема (см. [36], стр. 509—513). Однако не существует
такого интервала [а, 6], а < Ь, для которого при некотором
Ь) справедливо равенство
(cos b-\-1 sin Ь) — (cos а -ф-1 sin а) = (— sin g, —]— £ cos £) (b — а).
Если предположить, что это равенство возможно, то,
приравнивая квадраты модулей (абсолютных значений) обеих
его частей, мы получим равенство
(cos b — cos а)2 -ф- (sin b — sin «)2 = (Ь — ар,
которое после элементарных преобразований примет вид
Но так как не существует положительного числа h, такого,
что sin Л = Л (см. [36], стр. 78), то мы получили противо-
речие.
10. Бесконечно дифференцируемая функция f(x), поло-
жительная при положительных х и равная нулю при
отрицательных х
Функция
( е-1'* , если х > О,
/(х) | о, еСли
бесконечно дифференцируема, а все ее производные в точке
х = 0 равны 0 (см. [36], стр. 108, упр. 52).
И. Бесконечно дифференцируемая функция, положи-
тельная в единичном интервале и равная нулю
вне его
( e~Vx2{l-x)1t если О < X < 1,
f (х) — <
J ( 0 в противном случае.
12. Бесконечно дифференцируемая функция, равная I
на [1, -фоо), равная 0 на (—оо, 0] и строго моно-
тонная на [0, 1]
/(x)s
exp
1
(1-х)2
0,
1,
если 0 < х < 1,
если х<0,
если х 1.
Дифференцирование
55
13. Бесконечно дифференцируемая монотонная функ-
ция f, такая, что’) lim f(x) — 0, lim /'(*)=£ О
Если не требовать монотонности, то тривиальным при-
мером такой функции будет, например, (sinx* 2)/x. Построим
пример монотонной функции, обладающей указанным свой-
ством. Положим f (х) равной 1 для и равной 1/л на
замкнутых интервалах [2п—1, 2п] для п=1, 2,
На оставшихся промежуточных интервалах вида (2п, 2п-^-1)
определим f (х) с помощью функции примера 12, применяя
горизонтальные и вертикальные сдвиги и умножение на соот-
ветствующие отрицательные множители2).
') В примерах такого типа предел lim f (х) не существует
X + оо
(ни конечный, ни бесконечный), так как если бы он существовал,
то из равенства f (х) — f (0) + J вытекало бы, что
о
lim f (х) = 0. — Прим, перев.
х->+оо
2) Приведенные рассуждения не убедительны. В самом деле,
если через (х) обозначим функцию из примера 12, то f (х) =
= — fi (х —2п)-|- — ПРИ х^(2п, 2п -|-1) и потому
sup I f (х) I = Sup I /1 (t) I, что влечет
lim f' (х) = 0. Для построения корректного примера достаточно
Х-> +со
положить f (х) = 1 при X < 2, f (х) = — при xg^n-|-jy, п + 1 j =а
= [«„, Ьа\ (я>2) и /(х) = -^4й)/1<п3(х-*«-!))+“1
при xg ап) с п>2. — Прим. ред.
ГЛАВА 4
ИНТЕГРАЛ РИМАНА
Введение
Определение интеграла Римана функции /, заданной на
замкнутом интервале [а, Ь\, а также элементарные свойства
этого интеграла предполагаются известными. То же самое
предполагается относительно основных несобственных инте-
гралов, а в примере 14 — относительно интеграла Римана —
Стильтьеса.
В некоторых примерах настоящей главы важное значение
имеет понятие множества меры нуль. Множество А с: R на-
зывается множеством меры нуль, если для всякого е>0
существует открытое покрытие множества А счетной сово-
купностью открытых интервалов, длины которых образуют
бесконечный сходящийся ряд с суммой, меньшей е. Ядро
всякого множества меры нуль пусто. Говорят, что некоторое
утверждение справедливо для почти всех точек или
почти всюду, если множество всех точек, для которых
это утверждение не имеет места, является множеством меры
нуль. Для того чтобы функция /, заданная на замкнутом
конечном интервале [a, ft], была интегрируема по Риману
на этом интервале, необходимо и достаточно, чтобы она была
ограничена и почти всюду непрерывна (см. [38], стр. 153,
упр. 54, а также [33]*, стр. 145).
1. Ограниченная функция, не интегрируемая по Риману
на конечном замкнутом интервале
Характеристическая функция множества Q всех рациональ-
ных чисел, рассматриваемая на замкнутом интервале [0,1],
не интегрируема по Риману на нем (см. [36], стр. П2)1).
‘) Эта функция известна под названием „функции Дирихле”.—
Прим. ред.
Интеграл Римана
57
2. Функция, интегрируемая по Риману и не имеющая
примитивной
Функция sgn х (пример 1 гл. 3), рассматриваемая на ин-
тервале [—1, 1], интегрируема на нем, но не имеет прими-
тивной.
3. Функция, интегрируемая по Риману и не имеющая
примитивной нН" на каком интервале
Если в примере 18 гл. 2 положить A = Qn[0, 1].
то функция f будет интегрируема на (0, 1], так как она
монотонна на этом интервале. Однако эта функция не имеет
примитивной ни на каком подинтервале из [0, 1], поскольку
множество точек ее скачков всюду плотно в интервале [0, 1]1).
4. Функция, имеющая примитивную на замкнутом
интервале, но не интегрируемая на нем по Риману.
(См. пример 35 гл. 8.)
Функция / примера 6 гл. 3 имеет (конечную) производ-
ную g(x) в каждой точке х некоторого замкнутого интер-
вала /. Следовательно, функция g имеет примитивную. Однако
функция g не ограничена, а поэтому не интегрируема по
Риману.
Два предыдущих примера (примеры 3 и 4) представляют
особый интерес в связи с основной теоремой интегрального
исчисления. Первый вариант этой теоремы таков: если функ-
ция f (х) (1) интегрируема на интервале [а, Ь] и (ii) имеет
примитивную F (х) на этом интервале (F'(x) = /(х) для
а х <^£), то интеграл Римана функции f (х) можно вы-
ft
числить по формуле J f(x)dx = F(b) — F (а). Второй ва-
а
риант гласит: если функция /(х) непрерывна на интервале
[а, £], то справедливы утверждения (i) и (ii) с G(x) =
X
= J в качестве некоторой примитивной, причем для.
а
’) Если lim /(х)— lim /(х) =£ 0, то а называется точкой
ж->в+о х->а-0
скачка функции / (х). — Прим, перев.
58
Глава 4
ь
всякой примитивной F (х) имеет место формула J f(x)dx =
а
— F (р) — F (а). Наконец, третий вариант этой теоремы можно
сформулировать так: если f(x) интегрируема на [а, t>], а функ-
ция Л (х) непрерывна на [а, 6] и имеет производную F'(х),
равную f(x) во всех точках интервала [а, Ь], за исключе-
нием, быть может, конечного числа точек, то интеграл Римана
ь
функции f (х) можно вычислить по формуле J f(x)dx =
= Р(р)-Р(а)').
5. Интегрируемая по
множеством точек
Риману функция со всюду плотным
разрыва
Этим свойством обладает функция примера 3, которая
к тому же является монотонной.
Функция примера 15 гл. 2 также обладает этим свой-
ством, однако она нигде не монотонна. Для этой функции
ь
J /(x)dx = 0 при всех а и Ь.
а
х
6. Функция f, для которой g(x) = | f(t) dt всюду диф-
0
ференцируема, однако g' (х) =£/(х) на всюду плотном
множестве
Если /— функция примера 15 гл. 2 (см. также преды-
дущий пример), то g(x)s= J f(t)dt является тождествен-
о
ным нулем и, следовательно, g' (х) = 0 для всех х. Поэтому
равенство g'(х) = f (х) справедливо лишь для иррацио-
нальных х.
‘) Нетрудно видеть, что эти три варианта основной теоремы
интегрального исчисления не эквивалентны. — Прим, перев.
Интеграл Римана
59
7. Две различные полунепрерывные функции, „расстояние"
между которыми равно нулю
В этом случае расстояние d между двумя функ-
циями f и g, интегрируемыми на [a, ft], определяется как
интеграл от абсолютной величины их разности:
ь
rf = j | f (х) — g (х) | dx.
а
Если /—полунепрерывная функция предыдущего примера
(см. пример 16 гл. 2), а функция g — тождественный нуль,
то / (х) и g(x) не равны во всех рациональных точках х
(и, следовательно, / и g, несомненно, являются различными
функциями), в то время как определенное выше расстояние d
между этими функциями равно нулю.
8. Интегрируемая по Риману функция, множество точек
разрыва которой совпадает с произвольно заданным
множеством типа Fo и меры нуль. (См. пример 22 гд, 8.)
Этот пример несколько напоминает пример 23 гл. 2.
Пусть А — заданное множество типа Fa и меры нуль:
А = Aj L) А2 U • • •, где Ар Д2, ... — замкнутые подмноже-
ства некоторого интервала [«, ft], причем Ап с. А„ + 1 для
п—1, 2.......Далее, пусть Ао обозначает пустое множе-
ство 0. Определим функцию f следующим образом:
2 ", если х^А„\Ал_1,
О, если х А.
Если с £ А, то f разрывна в этой точке. Действительно,
пусть с САЛЛ-i- Поскольку A„\A„_J является множе-
ством меры нуль, то у него нет внутренних точек, и, сле-
довательно, с является предельной точкой множества, на
котором / принимает значения, отличающиеся от 2~" по край-
ней мере на 2-"-1. Если же с(£А, то f непрерывна в этой
точке. В самом деле, пусть задано е > 0. Выберем такое 2V,
что 2-ЛГ < е. После этого возьмем такую окрестность точки с,
которая не содержит ни одной точки множеств Ар Д2.....AN.
Тогда в этой окрестности /(х) < 2~N < е.
60
Глава 4
9. Две функции, интегрируемые
которых не интегрируема по
гл. 8.)
по Риману, композиция
Риману. (См. пример 34
Пусть для 0 < х 1 и /(0)==0. Далее, пусть
g— сужение функции f примера 15 гл. 2 на замкнутый ин-
тервал [0, 1]. Тогда /(g(x)) является сужением на [0, 1]
характеристической функции множества Q всех рациональных
чисел. Эта функция равна 1, если х рационально, и равна О,
если х иррационально. (См. пример 1 этой главы.)
10. Не интегрируемая по Риману ограниченная функция,
являющаяся пределом возрастающей последователь-
ности интегрируемых по Риману функций. (См. при-
мер 33 гл. 8.)
Рассмотрим последовательность {£„} функций, опреде-
ленных в примере 24 гл. 2. Если ограничиться замкнутым
интервалом [0, 1], то эта последовательность является воз-
растающей последовательностью интегрируемых по Риману
функций, т. е. для каждого х£[0, 1], gn(x)-^gn+x (х) при
п — 1, 2......Положим g(x) = lim gn(x) для х£[0, 1].
+СО
Тогда g является сужением на замкнутый интервал [0, 1]
характеристической функции множества Q всех рациональных
чисел, и, следовательно, (см. пример 1) g не интегрируема
по Риману на [0, 1].
11. Расходящийся несобственный интеграл, имеющий
конечное главное значение в смысле Коши
+ со
Несобственный интеграл J х dx расходится, но его
— СО
главное значение в смысле Коши равно нулю:
а
Нт х dx = Нт 0 = 0.
а~>+оэ J d->+co
-а
(См. [36], стр. 145, упр. 30.)
Интеграл Римана
61
+ со
12. Сходящийся несобственный интеграл J f(x)dx, под-
1
интегральная функция которого положительна, непре-
рывна и не стремится к нулю при х->4-оо
Положим g(n)= 1 для всякого целого п > 1, а на замк-
нутых интервалах [п — п~2, п] и [га, га-фга-2] функцию g
определим как линейную и равную нулю в концевых неце-
лых точках. Наконец, в тех точках где g(x) еще
не определена, положим g{x)=Q. Тогда функция
/(x) = g(x) + ^-
положительна и непрерывна для х 1, равенство lim /(х)=0
Х-> -фоо
не имеет места, а несобственный интеграл
+ оо
J / (х) dx
1
сходится.
Если опустить требование положительности функции,
то простым примером, который удовлетворяет оставшимся
требованиям (см. [36], стр. 146, упр. 43), является интеграл
+со
J cosx2dx.
1
13. Сходящийся на интервале [0, -ф-оо) несобственный
интеграл, подинтегральная функция которого не
ограничена на любом интервале вида [а, 4-оо), где
а > О
Этим условиям удовлетворяет несобственный интеграл
4-со
J xcosx4rfx. (См. [36], стр. 146, упр, 43.)
о
Можно построить такой же пример с положительной и
всюду непрерывной подинтегральной функцией. При этом
можно воспользоваться методом, подобным тому, который
был применен в предыдущем примере, полагая g(ra)esra и
рассматривая замкнутые интервалы [га — га-3, га] и [га, га-ф-га-3].
62
Глава 4
14. Функции f и g, такие, что интеграл Римана —
Стильтьеса от / относительно g существует на [a, &]
и [Ь, с], но не существует на [а, с]
Положим
( о.
/(*)^| j
если 0 х < 1,
если 1 х 2,
0,
1,
если 0 х 1,
если
1 < х<2,
и пусть а = 0, Ь—\ и с = 2. Тогда
1 2
J/(x)dg(x)==0, J f(x)dg(x)= 1.
0 J
Но поскольку / и g имеют общую точку разрыва х— 1,
то интеграл
2
J f(x)dg(x)
о
не существует (см. [36], стр. 151, упр. 10, а также [33]*,
стр. 249).
ГЛАВА 5
ПОСЛЕДОВАТЕЛЬНОСТИ
Введение
Понятия последовательности, последовательности Ко-
ши, сходимости и расходимости были определены во вве-
дении к гл. 1, а понятия верхнего и нижнего предела в (ко-
нечной) точке для функций даны во введении к гл. 2.
Соответствующие определения для последовательностей дей-
ствительных чисел предполагаются известными. Первые шесть
примеров настоящей главы касаются только последователь-
ностей действительных чисел. Следует подчеркнуть, что для
этих последовательностей термин предел иногда употреб-
ляется и для обозначения бесконечных пределов. Однако под
сходящейся последовательностью всегда понимается после-
довательность, имеющая конечный предел. В примере 7
предполагается, что читатель знаком с определением и эле-
ментарными свойствами равномерной сходимости последо-
вательностей функций. В примере 8 сформулированы опре-
деления сходимости и расходимости последовательностей
множеств, которые затем используются в примерах 8 и 9.
Всюду в этой книге под словом последовательность пони-
мается бесконечная последовательность, если не оговорено
противное.
1. Ограниченные расходящиеся последовательности
Простейшим примером ограниченной расходящейся после-
довательности, по-видимому, является последовательность
О, 1, 0, 1....
которую можно записать в виде {«„}, где ап = 0, если п
нечетно, и ап=\, если п четно, т. е. a„=-g-[l-f-(—1)"].
64
Глава 5
Более сложным примером является последовательность {гя}
всех рациональных чисел интервала [0, 1], т. е. (гя) есть
взаимно однозначное соответствие между множеством N и
Q Л [0, 1].
2. Последовательность с произвольно заданным замкну-
тым множеством предельных точек
Всякая точка, которая является пределом некоторой под-
последовательности последовательности {ая}, называется пре-
дельной точкой или частичным пределом по-
следовательности {«„}. Всякая предельная точка множества
значений последовательности есть предельная точка самой
последовательности, однако обратное утверждение, вообще
говоря, неверно. Контрпример: последовательность 0, 1.0»
1, ... имеет две предельные точки 0 и 1, однако ее мно-
жество значений не имеет ни одной предельной точки.
Множество всех предельных точек любой последователь-
ности {ая} всегда замкнуто, ибо оно является замыканием
множества значений последовательности {ая}'). Нижеследую-
щий пример показывает, что таким путем можно получить
любое замкнутое множество А, т. е. в действительности А
является множеством предельных точек некоторой последо-
вательности {ая), состоящей из различных точек. Отсюда
будет следовать, что А является не только множеством пре-
дельных точек последовательности {«„}, но и множеством
предельных точек ее множества значений.
Если А — пустое множество, то положим ап = п для
га= 1, 2.....Пусть теперь А — произвольное непустое замк-
нутое множество (действительных чисел), и пусть {гя} — по-
следовательность всех рациональных чисел, среди членов
которой нет равных ({/•„} — взаимно однозначное отображение
множества N на Q). Последовательность {а„}, для которой А
будет множеством предельных точек, мы определим рекур-
рентным способом. Сначала разобьем множество R на четыре
') Это утверждение не точно. Множество предельных точек
любой последовательности {а„} замкнуто, но оно не обязано со-
впадать с замыканием множества значений последовательности {ая}.
Так будет, например, если ая = — 1). — Прим ред.
Последовательности
65
непересекающихся интервала: (— оо, -1), [-1, 0), [0, 1)
и [1, Н~оо). Если Af)(—оо, —1)4=0, то в качестве
возьмем первый член последовательности {/•„} (т. е. член с наи-
меньшим номером п), принадлежащий интервалу (—оо, —1);
если А П (— оо, —1) = 0, а А П [—1, 0) ф 0, то в качестве аг
возьмем первый член последовательности, принадлежащий ин-
тервалу [—1, 0); если же А П (— оо, 0) = 0, но А П 10,1) =f=
=40-то в качестве возьмем первый член последовательности,
принадлежащий [0, 1); наконец, если А П (—оо, 1)=0, то в
качестве ах возьмем первый член последовательности, принад-
лежащий [1, 4~оо). Пусть элемент <4 выбран. В случае если
Af)[—1. +°°) ¥= 0. подобным же образом выбираем a2^alt
рассматривая последовательно интервалы [—1, 0), [0, 1) и
[1.4- оо). Если же А П [— 1, 4- °0) — 0 > то на этой стадии
другие члены не выбираются. Таким образом, на первой ста-
дии определяется по крайней мере один член но не более
четырех членов аг, а2, а3, а4 последовательности {ая}. На
второй стадии R разбивается на 2 - 22 4- 2— 10 интервалов
(—оо, —2), [—2, —3/2)........[3/2, 2), [2, 4-сю). На каждом
шаге, после того как av а2......ап выбраны, элемент ая+1
выбирается из некоторого интервала /, а именно если А П / 4=0.
то ая+1 есть первый член {/•„), отличный от уже выбран-
ных и принадлежащий I. На k-Vi стадии R разбивается на
k -2*4-2 интервалов: (—оо, —k), [—k, —й4~2-*+1), ...
.. ., [* —2"*+1, k), [Лг, 4~оо). Нетрудно показать, что по-
следовательность {гг„}, определенная, таким образом, рекур-
рентно, обладает требуемыми свойствами. Заметим, что если
A = R, то {ая} является взаимно однозначным соответствием
между N и Q, которое, возможно, отлично от {rj1).
!) Построение последовательности можно осуществить
проще. Именно, так как множества 1(A) и В==(—оо, оо) — А от-
крыты, то они суть суммы не более чем счетного числа непересе-
кающихся интервалов: / (Л) = ck), В = [J (dm, ет). Пусть
k т
{г' W) = (^- С*)ПО. а {/•" (m)} a (dm, ет)П Q — такая последова-
тельность различных точек, предельными точками которой являются
лишь dm и ет. Занумеровав в одну последовательность множества
последовательностей (*)] и Jr" (m)} (* = 1,2,...; т = 1, 2, ...),
мы и получим искомую последовательность {«„}.— Прим. ред.
5 Зак. 587
66
Глава 5
3. Расходящаяся последовательность (а„), для которой
lim («я+р — ап) — 0 при любом натуральном р
л-> +со
Пусть ап обозначает га-ю частичную сумму гармонического
ряда
Тогда последовательность {ая} расходится, однако для р > О
имеем
1 . , 1 ~ р п
ап.п— ап=—гт4- ••• Ч--------i——тт->0-
п+р л «4-1 «4-/’ ^«4-1
Заметим, что предельное соотношение lim («я+р—а„)=0
л->+оо
выполняется неравномерно относительно р. В самом деле,
утверждение, что это .предельное соотношение выполняет-
ся равномерно относительно р, эквивалентно критерию Ко-
ши для сходимости последовательности ([36], стр. 447,
упр. 43).
Основную идею предыдущего абзаца можно высказать
и в следующей форме: если {ая} расходится, то существует
строго возрастающая последовательность {ря} натуральных
чисел, таких, что ап+рп — Для последовательности
частичных сумм гармонического ряда в качестве {/?„} можно
взять последовательность {«}, поскольку в этом случае
1 , , 1 п 1
ал+рп ап — л+1 . • 4“ п^п > п_^п — 2 •
Следующий пример связан с другим аспектом этого вопроса
(при <р(«) = «4-/?я).
4. Расходящаяся последовательность {а„}, такая, что
для заданной строго возрастающей последовательности
{Фл1 = [ф (я)} натуральных чисел lim (а<р(Я)—ап) = 0.
Пользуясь индукцией, легко установить, что ф(«)^-«
для всех л=1, 2, ...; более того, ф (« -j~ k) п 4- ф (k)
для всех п и k— 1, 2, .... Следовательно, lim ф(«) = Ч-оо.
«-> + СО
Рассмотрим два случая.
Если последовательность ф(«)— п ограничена, например
ф(«) — п^К для всех /г=1, 2, .... то в качестве после-
Последовательности
67
довательности {ап} можно взять последовательность частичных
сумм гармонического ряда, так как
1 । , 1 - К п
а<Р(л) ап — л_|_1 + • • • + ф(Л) < л_|_1 ~*0-
Если же последовательность ф(п)— п не ограничена, то
поступим следующим образом. Пусть k — наименьшее нату-
ральное число, такое, что <р(&)> k. Положим ап — 1, если
n = k, ф(&), ф(ф(&)), ... , и ап — 0 в противном случае. По-
скольку {ф(га)} строго возрастает, то существует подпосле-
довательность последовательности [а„], состоящая из единиц,
а поскольку ф(и)— п не ограничена, то существует подпо-
следовательность последовательности [ап), состоящая из нулей.
Следовательно, {а„} расходится. С другой стороны, ач^)=ап
для каждого га=1, 2, .... и потому w — ап —> 0.
Этот пример можно обобщить в различных направлениях.
Например, достаточно лишь предположить, что ф (л)со
при и—>—|—оо, при этом можно потребовать, чтобы после-
довательность {ая} была неограниченной. Однако мы не будем
вдаваться в подробности.
5. Последовательности (а„} и {&„}, такие, что lim an~h
-j-lim&n < lim(a„+&«)<liman4-Hm&„<lim(a„+&«)<
< lima« + lim bn
Пусть {ая} и —последовательности с периодами, со-
стоящими из четырех цифр:
{ап} : 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1,2, 1, .. .,
Р„) : 2, 1, 1, 0, 2, 1, 1, 0, 2, 1, 1, 0, 2, 1, 1,0...
Тогда требуемые неравенства примут следующий вид:
0<1<2<3<4.
6. Последовательности (ащ), (аги}, ..., такие, что
lim (am + а2п + ...) > lim am + Пт а2п + ...
п-»+со п->+со и->+оо
Положим amn—l, если т = п, и атп = 0, если m=f=n,
т, п—1, 2, .... При этом оба ряда, .входящие в форму-
лировку утверждения, сходятся, и требуемое неравенство при-
нимает следующий вид: 1 > 0.
5*
68
Глава 5
Следует отметить, что неравенство, установленное в этом
примере, невозможно в случае, если имеется лишь конечное
число последовательностей. Например, всегда справедливо
неравенство
lim (а„4-6я)< lim ая+ lim Ьп.
Л->+СО Л~>4-ОО /1->4-СО
(См. [36], стр. 59, упр. 19.)
7. Две равномерно сходящиеся последовательности функ-
ций, последовательность произведений которых не схо-
дится равномерно
Пусть функция f определена и не ограничена на множе-
стве Z)1), которое мы примем за область определения всех
функций настоящего примера. Определим последовательности
{/„} и {g„} следующим образом:
fn(x) = f(x). gn(x) = ^.
Тогда fn-+f и >0 равномерно на D, однако fngn-+Q
неравномерно на D. В частности, в этом примере можно по-
ложить Z) = R, f(x) = x.
Следует заметить, Ито если обе последовательности огра-
ничены и равномерно сходятся на D, то их произведение
также равномерно сходится на D.
8. Расходящаяся последовательность множеств
Верхний предел lim Ап и нижний предел
п -> 4*00
lim Ап последовательности множеств ]ЛЯ] определяются
л->+оо
следующими формулами:
4*оо Г +оо
lim Л-U П Ат
/г~>4-оо /г—1 \-т=п
-т-оо Г 4-оо
А»= П I U
4*00 «-.I
Последовательность }ДЯ] называется сходящейся, если
lim Ап = lim Ап. В таком случае говорят, что она схо-
Л->+со п^+оэ
') Отсюда следует, что множество D бесконечно. — Прим, персе.
Последовательности
69
дится к этому общему значению верхнего и нижнего пределов.
Если же последовательность множеств не сходится, то она
называется р а с х од я ще й с я. Поскольку lim Дя = {х|х£
£ бесконечно многим А„], a lim Ап — {х|х £ всем Ап, за
л->+оо
исключением, быть может, конечного их числа), то верхний
предел осциллирующей последовательности А, В, А, В, А,
В, ... равен объединению Лий, а ее нижний предел равен
пересечению А П й. Следовательно, последовательность такого
типа сходится тогда и только тогда, когда А — В.
Следует обратить внимание на тесную аналогию между
этим примером и примером последовательности чисел [а, Ь,
а, Ь, . ..} (см. пример 1).
9. Последовательность {4„) множеств, которая сходится
к пустому множеству, но кардинальные числа этих
множеств ->4-оо
Пусть Ап — множество п натуральных чисел, каждое из
которых больше или равно п, но меньше 2га:
{rai|/ra£N, га<^гаг<2га), га—1, 2, ....
Тогда, поскольку никакое натуральное число не принадлежит
бесконечному множеству членов последовательности {Ля},
то ее верхний и нижний пределы пусты.
Предыдущий пример можно наглядно пояснить следующим
образом. Пусть у нас имеются биллиардные шары, которые
занумерованы числами О, 1, 2......Будем помещать в ящик
по два шара и одновременно вынимать из него один. Напри-
мер, за минуту до полудня поместим в ящик шары с номе-
рами 0 и 1 и удалим из него шар с номером 0. За 1/2 ми-
нуты до полудня поместим в ящик шары с номерами 2 и 3,
а шар с номером 1 удалим. За 1/3 минуты до полудня до-
бавим шары с номерами 4 и 5 и вытащим шар с номером 2.
Продолжая этот процесс, естественно задать вопрос: „Сколько
шаров будет в ящике в полдень?" Ответ: „Ни одного".
Поскольку натуральные числа можно привести во взаимно
однозначное соответствие с обратными им, а все конечные
множества, как подмножества R, компактны (замкнуты и огра-
ничены), то все множества Ап этого примера компактны
70
Глава 5
и даже можно предположить, что они равномерно ограничены
(все они заключены в одном ограниченном интервале). Если
предположить, что последовательность {Ая} является убываю-
щей (Ая+1сАя для п = 1, 2, ...), то предел lim Ап будет
Л->+ОО
+оо
равен пересечению |")АЯ и может быть пустым множеством,
Л = 1
в то время как кардинальное число каждого множества Ап
бесконечно. В то же время каждое множество Ап может
быть ограничено (пример: {1/га, 1/(«+ 1), ...}) или замкнуто
(пример: [п, /г—1, ...}). Однако оба эти условия (огра-
ниченность и замкнутость) не могут быть выполнены одно-
временно (см. [36], стр. 201).
ГЛАВА 6
БЕСКОНЕЧНЫЕ РЯДЫ
Введение
Если на оговорено противное, то все рассматриваемые
в настоящей главе ряды предполагаются действительными,
т. е. их члены являются действительными числами. Пусть
—последовательность частичных сумм бесконечного ряда
2ап = а-i 4“ «2+ • • • 4“ • • • > т- е- = ап
для я=1, 2, .... Если lim s„ существует и конечен, то
П->4- со
говорят, что ряд 2 сходится. Этот предел s называют
суммой ряда 2 ап и пишут
4-со
2 ап = 2 an = s.
Л = 1
Если же ряд 2 не сходится, т. е. предел lim sn беско-
л -> + со
нечен или не существует, то говорят, что ряд расходится.
Утверждение 2ал —4*°° означает, что lim s„ = 4~co-
л-> +со
Ряд 2ап называется неотрицательным (соответственно
положительным), если ап 0 (соответственно ап > 0)
для всякого п. Аналогичные определения даются для после-
довательности {«„). Для неотрицательного ряда 2ал утвер-
ждение 2 ап < + 00 означает, что ряд сходится, а утвер-
ждение 2 ап — + 00 означает, что этот ряд расходится.
Иногда удобно, чтобы ряд начинался с члена ай. В этом
+ СО
случае запись 2 ап обозначает ряд 2 ап или сумму этого
4-со
ряда. Для степенного ряда 2 апх-п член aoxQ считается рав-
л = 0
ным а0, даже если х = 0, т. е. мы здесь полагаем 0°=1.
72
Глава 6
Для ряда Маклорена
24^*
л-0
член, соответствующий п — 0, считается равным /(0); другими
словами, /(0) (х) = / (х).
1. Расходящийся ряд, общий член которого стремится
к нулю
Гармонический ряд 2 11п-
2. Сходящийся ряд У, ап и расходящийся ряд 2 Ъп,
такие, что ап>&п, л=1, 2, ...
Положим ал = 0 и Ьп~— Ijn, п = 1, 2, ... ,
3. Сходящийся ряд 2 ап и расходящийся ряд 2 Ьп,
такие, что | ап | > | bn |, п — 1, 2, ...
В качестве 2ал можно взять условно сходящийся знако-
чередующийся гармонический ряд2(—а в качестве
2^л — расходящийся гармонический ряд 2 Vй-
4. Для произвольно заданного положительного ряда су-
ществует либо мажорируемый им расходящийся, либо
мажорирующий его сходящийся ряд
Говорят, что неотрицательный ряд 2ал мажорирует
ряд 2^п' если ал>1М для »= Ь 2...........Пусть задан
положительный ряд 2 Ъа. Положим ап =s bn. для п = 1, 2.
Тогда, если ряд 2 расходится, то он мажорирует рас-
ходящийся ряд 2ал! если же Ряд 2^л сходится, то он
мажорируется сходящимся рядом 2 ап- При этом с помощью
множителей 1/2 и 2 можно добиться, чтобы все неравенства
в определении мажорирующего ряда стали строгими.
Бесконечные ряды
73
Этот простой результат можно высказать в следующей
форме: не существует положительного ряда, который
одновременно мог бы служить для установления схо-
димости и расходимости рядов при помощи сравнения
их с данным рядом. (См. ниже пример 19.)
5. Об условно сходящихся рядах
У всякого условно сходящегося ряда 2ап> например
у знакочередующегося гармонического ряда 2(—1)п+1/ге-
члены можно переставить таким образом, чтобы новый ряд
сходился к любой наперед заданной сумме или стал расхо-
дящимся. Среди расходящихся рядов, полученных этим спо-
собом, существуют такие, что последовательность {$„} их
частичных сумм имеет предел 4-00’ —00 или вообще не
имеет предела. Более того, последовательность {$„} можно
определить таким образом, что множество ее предельных
точек будет совпадать с произвольно заданным замкнутым
интервалом, ограниченным или нет (см. пример 2 гл. 5). Это
объясняется тем, что ряд из положительных и ряд из отри-
цательных членов ряда 2 ап расходятся.
В качестве примераукажем перестановку ряда 2(—1)л+1 /п,
такую, что последовательность ($я) частичных сумм имеет
своим множеством предельных точек замкнутый интервал
[а, Ь]. Начнем с первого члена 1 и будем добавлять к нему
отрицательные члены
2 4 6 8 •- • 2/
до тех пор, пока не получим первую сумму < а. Затем будем
добавлять к этой сумме неиспользованные положительные
члены до тех пор, пока не получим первую сумму
_1_ 1— _1 । ± । 1 - j_L_
2 4 2/^ 3 -г 5 2£-Н ’
которая превосходит Ь. Продолжая этот процесс, мы будем
добавлять к полученной сумме неиспользованные отрицатель-
ные члены до тех пор, пока не получим первую сумму
74
Глава 6
< о, а затем будем добавлять к ней неиспользованные по-
ложительные члены до тех пор, пока не получим первую
сумму > Ь. Продолжая этот процесс неограниченно, мы
получим некоторый ряд с частичными суммами sn. Поскольку
абсолютная величина 1/л общего члена (—1)лН/л стремится
к нулю, то каждое число замкнутого интервала [а, Ь] при
некоторых достаточно больших п приближается частичными
суммами sn с как угодно большой точностью. Более того,
этим свойством не обладает никакое число вне интервала
[а, Ь\.
Если изменить только что описанное построение так,
чтобы суммы сначала стали больше 1, затем меньше —2,
на следующем шаге стали больше 3, а затем меньше — 4
и т. д., то последовательность частичных сумм так полу-
ченного ряда будет иметь своим множеством предельных
точек всю систему действительных чисел.
В. Серпинский (см. [46]) показал, что если —
условно сходящийся ряд с суммой $ и s' < s, то при помощи
некоторой перестановки, использующей лишь положительные
члены (отрицательные члены остаются на их первоначальных
местах), можно получить ряд, сходящийся к сумме s'. Такое
же замечание справедливо для чисел s" > $ и перестановок,
использующих только отрицательные члены. Ясно, что это
есть обобщение замечательной „теоремы Римана о переста-
новках" (см. [38], стр. 232, теорема III), все . существенные
детали которой иллюстрируются построением, описанным
в настоящем примере.
Существует обобщение этой теоремы и в другом напра-
влении. Пусть — условно сходящийся ряд комплексных
чисел. Тогда множество сумм всех сходящихся (или расхо-
дящихся к оо) рядов, полученных из ряда 2 ап с помощью
всевозможных перестановок его членов, является либо пря-
мой на комплексной плоскости (включающей бесконечно
удаленную точку), либо всей комплексной плоскостью (также
включающей бесконечно удаленную точку). Более того, если
— условно сходящийся ряд векторов в конечномер-
ном пространстве, то суммы, которые можно получить
всевозможными перестановками, составляют множество,
являющееся линейным многообразием в этом пространстве
(см. [57]).
Бесконечные ряды
75
6. Для произвольного условно сходящегося ряда 2 ап
и произвольного действительного числа х существует
последовательность {е„}, где |е„| = 1 (п=1, 2,....),
такая, что —х1)
Используемое здесь построение аналогично тому, которое
применялось в примере 5. Поскольку У, | ап | = -|- оо, мно-
жители еп, по абсолютной величине равные 1, можно выбрать
таким образом, чтобы -|- ... &пап = | аг | . .
. . . 1 ап | > х. Пусть л, — наименьший из номеров п, для
которых выполняется это неравенство. Затем мы выбираем
множители еп, по абсолютной величине равные 1, так, чтобы
выполнялось условие
61^1 -|- • • • Н- Snfliii — I а1 I . -|-1 ^Л, |-
| ant + l I • • • I Ял2 I С X
(где /г2 — наименьшее из возможных п). Продолжая этот
процесс неограниченно, мы получим ряд У еяал, частичные
суммы которого попеременно то больше, то меньше х.
Поскольку ал—>0 при д->-(-оо, то этот ряд сходится к х.
7. Об условиях теоремы Лейбница для знакочередую-
щихся рядов
Теорема Лейбница о знакочередующихся рядах утверждает,
что ряд 2елсл" где |е„|=1 и сп > 0, д=1, 2.............схо-
дится, если
(i) ея = (—l)n+1, n = 1, 2, ....
(ii)c„ + i<c„. п=1. 2........
(iii) lim сл = 0.
л -> + СО
Никакие два из этих трех условий сами по себе не обеспе-
чивают сходимости, т. е. ни одно из этих трех условий
нельзя опустить. Этот факт подтверждается следующими
тремя примерами.
*) В этом примере члены ряда можно считать комплексными
числами. Разумеется, множители сп тогда также должны быть ком-
плексными. — Прим, перев.
76
Глава 6
(i) Положим ея = 1, ся=1/л, п=1, 2.........С другой
стороны, существенно именно чередование знаков у членов
ряда. В этом можно убедиться на том же примере, если
в качестве {ея] взять следующую последовательность из
троек чисел: 1, 1, — 1, 1, 1, — 1, 1, 1,— 1...
(ii) Положим сп=1/п, если п нечетно, и ся=1/п2, если
п четно.
(iii) Положим ся = (л-|- 1)/л (или, что еще проще, cn = 1),
n = 1, 2.....
8. Расходящийся ряд с общим членом, стремящимся
к нулю, который при подходящей расстановке скобок
становится сходящимся к наперед заданной сумме
Расставить скобки у бесконечного ряда — это значит
сгруппировать его последовательные члены в конечные группы
(каждая такая конечная группа состоит по крайней мере из
одного члена) и получить новый ряд, последовательность ча-
стичных сумм которого будет, таким образом, подпоследо-
вательностью частичных сумм исходного ряда. Например,
у знакочередующегося гармонического ряда можно расставить
скобки следующим образом:
V 2/^\3 4/‘ ‘ 1-2 3-4 ' ' ‘'
—I_____1_____|_
' (2п — 1) 2п ~ • • • •
Любой ряд, полученный из сходящегося ряда расстановкой
скобок, сходится и имеет сумму, равную сумме исходного ряда.
Требуемым свойством обладает последний из рядов, ко-
торые описаны в примере 5, поскольку подходящая рас-
становка скобок в нем дает ряд, сходящийся к наперед
заданному действительному числу.
9. Для произвольно заданной положительной последо-
вательности {&„} с нижним пределом, равным нулю,
существует расходящийся ряд У, а„, общий член
которого стремится к нулю, причем lim ая/&„ = 0
П -> + со
Возьмем подпоследовательность \bn ), такую, что lim bn =
= 0, причем дЯ[, .......ЪПк< ... не являются последова-
тельными членами последовательности {£„}> и положим
Бесконечные ряды
77
аП)г~Ь2Пк для k=l, 2, .... Для остальных значений tv.
п — т1, т2, т3< .... mj........ положим amj=\)j. Тогда
ал->0 при п—>-\-оо, ряд расходится и an [bntt =
= ЬПк~>-0 при k->-\-oo.
Этот пример показывает, в частности, что как бы быстро
ни стремилась к нулю положительная последовательность {#„},
всегда существует положительная последовательность {ал},
которая стремится к нулю столь медленно, что ряд 2 ап
расходится, и все же последовательность {ал} имеет подпо-
следовательность, стремящуюся к нулю быстрее, чем соот-
ветствующая подпоследовательность последовательности {#„}.
10. Для всякой положительной последовательности {&„}
с нижним пределом, равным нулю, существует по-
ложительный сходящийся ряд У а„, такой, что
lim anlbn — -f- оо
п -> + оо
Выберем из последовательности {£>„} подпоследователь-
ность Ьп^ Ьп^ , . Ъпь, .... такую, что bn^ < /г-3 для вся-
кого натурального k, и положим = для k= 1, 2, . . ..
Для остальных значений п положим ал = /г-2. Тогда У ап <
в то время как anklbnk = k —> -|- оо.
Этот пример показывает, в частности, что как бы мед-
ленно ни стремилась к нулю положительная последователь-
ность [Ьп], всегда существует положительная последователь-
ность {«„}, которая стремится к нулю столь быстро, что
ряд У ап сходится, и все же последовательность [ап] имеет
подпоследовательность, стремящуюся к нулю медленнее, чем со-
ответствующая подпоследовательность последовательности рл}.
И. Для всякой положительной последовательности {с„}
с нижним пределом, равным нулю, существуют
положительный сходящийся ряд 2 ап и положитель-
ный расходящийся ряд У Ьп, такие, что ап!Ьп = сп,
п= 1, 2, . ..
Выберем из последовательности {сл} подпоследователь-
ность сп , сп . •. сп..такую, что с„ < /г"2 для всякого
12 k К
78
Глава 6
натурального k и положим аПк = сПк< Ь„к = 1 для k = 1, 2..
Для остальных значений п положим <z„ = n~2, bn = (ге2сл)-1.
Тогда ряд2ал сходится, ряд расходится, поскольку
длт*0 при п->-|-сю, и ап1Ьп — сп для п=1, 2..........
Этот пример показывает, в частности, что как бы мед-
ленно ни стремилась к нулю положительная последователь-
ность {cj, всегда существуют два положительных ряда, один
из которых сходящийся, а другой расходящийся, такие, что
отношение их п-х членов равно сп.
12. Положительная непрерывная при х>-1 функция,
+ °° +ОО
такая, что интеграл | f(x)dx сходится, а ряд 2/(я)
J п-1
расходится
См. пример 12 гл. 4.
13. Положительная непрерывная при х>1 функция,
+со
такая, что интеграл J f(x)dx расходится, а ряд
1
4-со
2/(») сходится
л—1
Для каждого п > 1 положим g(n) = 0, а на замкнутых
интервалах [п — п~г, п] и \п, п + п-1] определим функцию g
как линейную и равную единице в нецелых концевых
точках. Наконец, в тех точках в которых функция
g(x) еще не определена, положим ее равной 1. Тогда
функция
/(х) = ^(х)4--Ь
+ 00
положительна и непрерывна при х^>1, J f(x)dx — -J- оо,
1
4-со +оо
а 2 f W = 2 п~2 < -|- оо.
/1=1 /1«1
Бесконечные ряды
79
14. Ряды, к которым не применим признак Даламбера
Если существует конечный или бесконечный предел
Пш ^д+L^p,
л->+00 ап
то положительный ряд S «л, согласно признаку Даламбера
(см. [36], стр. 390, а также [52]*, т. II, стр. 273),
(I) сходится, если 0 р < 1,
и
(ii) расходится, если 1 < р + со.
При р= 1 этот признак не решает вопроса о сходимости
или расходимости ряда. Точнее, существуют как сходящиеся,
так и расходящиеся положительные ряды, для каждого из
которых р= 1. Соответствующими примерами являются
+ оо 4-со
л=»1 л=1
Признак Даламбера не решает вопроса о сходимости и
в том случае, когда предел р не существует. В этом случае
положительный ряд также может быть как сходящимся, так
и расходящимся. Например, ряд
V g( —1)”-л _ 1 , I , 1 , 1 , 1 । 1 ।
z 22 "т" 21 ' 24 ' 23 "т” 26 25 ' ' ' ”
где
lim £zl±L = 2, lim -2д+1 = 1,
«->+“ ап а-п °
сходится, а ряд
2 2я-(-1)'‘ = 22 + 21 + 24 4- 23Ч-264-25 4 . . .,
л«=1
где
ШЙ £л+1_ = 8< Ijm >
л-»+°о „iT® а" 1
расходится.
80
Глава 6
Признак Даламбера можно усилить следующим образом:
(iii) если lim —"t1 < 1, то ряд У, ап сходится;
п->+оо ап
(iv) если lim — > 1, то ряд расходится’).
--- ^п.
Л->+со п
Признак Даламбера в такой форме не решает вопроса о схо-
димости, если выполнены неравенства
Иш Дд+L^i Пт
л-> + оо й/! л->+оо ап
Соответствующие примеры, когда оба эти неравенства вы-
полнены и даже в строгой форме, были приведены выше.
15. Ряды, к которым не применим признак Коши
Если существует конечный или бесконечный предел
п
lim Уап = <5 (0 о <[ + оо),
л->+оо
то неотрицательный ряд У ап, согласно простейшей форме
признака Коши (см. [36], стр. 392, а также [52]*, т. И,
стр. 272),
(i) сходится при 0 < о < 1
и
(ii) расходится при 1 < о 4" со.
Признак Даламбера и признак Коши связаны между
собой: если существует конечный или бесконечный предел
п
lim (а„+1/а„), то существует и равен ему предел lim У аа
(см. [36], стр. 394, упр. 31, а также [52]*, т. II, стр. 274).
Следовательно, если можно применить признак Даламбера
в форме (i) или (ii) (пример 14), то можно воспользоваться
и признаком Коши. Более того, первые два -примера, для
которых не применим признак Даламбера (пример 14), могут
служить примерами, к которым по той же причине не приме-
') Предполагается, что члены ряда либо все положительны,
либо все отрицательны. —Прим, перев.
Бесконечные ряды
81
ним и признак Коши. Напротив, последние два примера по-
казывают, что иногда можно применить признак Коши (см.
пример 16) и в том случае, когда признак Даламбера не при-
меним.
Признак Коши в сформулированной выше форме не при-
меним к сходящемуся ряду
+ 00
у/5 + (-1)"\-\__ 1 .11.1,1,1
\ 2 ] 2 ' З2 ' 23 ~Г" З4 "г 25 "г" З6 ' " ' ' ’
П=1
___ п ____ п
так как lim у ап — 1/2, a lim 1/У = 1/3. Его также
Л-> +СО п_у
нельзя применять и к расходящемуся ряду
4-со
(5 + (-1)«у» >
л-1
________ п г___ п __
ибо lim ya„ = 3, a lim а = 2.
л->+со л->+оо
Признак Коши может быть усилен следующим образом:
п
(iii) если lim У ап < 1, то ряд 2ал сходится,
П -> +СО
__ П
(iv) если же lim уга„> 1, то ряд расходится.
Л->оо
В этой форме признак Коши не слабее (на самом же
деле он сильнее: см. пример 16), чем признак Даламбера
в его усиленной форме (пример 14), поскольку (см. [36],
стр. 394, упр. 31)
Пш Дд+L^ Пт /Г < firn VaZ < lim
_____ П _ ___ Г п Г п /7
л-»+оо л п->+оо л->+оо л->+со п
Признак Коши в усиленной форме позволяет установить
сходимость и соответственно расходимость двух предыдущих
рядов, поскольку для первого из этих рядов верхний предел
____ л
lim ]/ал равен 1/2, а для второго он равен 3.
Л~>00
6 Зак. 587
82
Глава 6
Признак Коши в усиленной форме не решает вопроса
о сходимости или расходимости лишь в том случае, если
п
lim У ап=\. Примеры такого типа уже отмечались ранее.
72-> +со
16. Ряды, для которых эффективен признак Коши, но не
эффективен признак Даламбера
+ о° п
Для сходящегося ряда 2 2(-1) ~п признак Даламбера не
Л = 1
эффективен (пример 14), однако для него эффективен при-
знак Коши. В самом деле,
л _ (-1)”-» .
+ 00
Подобным же образом для расходящегося ряда 2 2
примера 14 имеем
п __
Уап = 2 п —»21 = 2>1.
17. Два сходящихся ряда, произведение которых
расходится
4-оо
Произведением (по Коши) двух рядов 2ал и
л=0
Ч-оо +оо
2 Ьп называется ряд 2 СП' где
п
сп—’^1 ak^n-n = а<Рп 4" а1^л-1 + • • • 4" апРй‘
к-0
Согласно теореме Мертенса (см. [38], стр. 239, упр. 20),
если ряд 2«« сходится к А, а ряд 2^л сходится к В,
причем по крайней мере один из этих рядов сходится абсо-
лютно, то их произведение 2 сп сходится к АВ.
Пусть ряды 2 ««« 2 Ьп совпадают, причем
«л = ьп=(-!)"(«4-1)“1/2. « = 0, I............
Бесконечные ряды
83
Тогда, согласно признаку Лейбница, ряды ^ап и ^Ьп схо-
дятся (пример 7), однако ряд У, сп расходится. Действительно,
пользуясь тем, что функция рг( 1 х) (п 4 1—х.) на замк-
нутом интервале [0, п] достигает максимума при x = nJ2,
имеем
^УзУп— 1 ’ ’’
4~ 11^ 1 «4-2 га 4 2 « 4~ 2 п-\-2
= 2("^Д>1, п — 0, 1, .
18. Два расходящихся ряда, произведение которых схо-
дится абсолютно
Произведением (по Коши) следующих двух рядов:
24-24-22 4-234- ... +2"4- .... «=1, 2.....
—1 -I- 1 1 -j_ 1 -I- ... 4- 1Я-+ ..., «=1,2......
является ряд
— 24-0 + 04-04-... 4-ол4-.... « = 1,2............
В более общей форме, если ап = ап и bn = bn для «4 К
причем а^Ь, то член сп ряда, являющегося произведением
рядов и ^ьп, равен (при «4-1)
сп = aQbn + boan 4 4 ап~2Ь2 4 ап~3Ь3 4 ... 4 «д”"!=
= а0Ьп 4 Ьоа" — ап — Ьп + («я+1 — Ьп+1)1(а —Ь) =
= {«” [а +(Ь0~1)(а~Ь)]-Ьл lb-j-(l-a0)(a-b)]}/(a-b).
Следовательно, с„ = 0, если а—(1—Ь0)(а — Ь) и b =
= («0—1)(а—^)- Если при этом а и b связаны равенством
а—Ь=\, то «0 и Ьа вычисляются по формулам а0 =
= ^41=«, д0=1 — « = — Ь.
6*
84
Глава 6
{+со 'I
2 атп ( .
m=l J
я—1, 2, положительных сходящихся рядов су-
4-со
ществует положительный сходящийся ряд У, ат .
т=1
{4-со "к
У атп}
т=1 )
4-со
Утверждение, что ряд У ат можно сравнить с рядом
т = 1
+оо
2 атп ПРИ некотором фиксированном натуральном п, озна-
т-1
чает, что
М=$ат^атп,
и потому утверждение, что такое сравнение невозможно,
записывается следующим образом:
VM 6N Вт > МЭ ат > атп.
Для всевозможных натуральных М и п положим
4-оо М 4-оо
2 S &тп' ^Мп== ^пиг
т-l т = 1 т—М+1
Тогда числа Sn, SMnn RMn положительны. Далее для каждого
n£N выберем М(п) так, чтобы 1 М (1) < М (2) < ... и
^(1), 1 < 2 ,
шах (/?Л'2), !• 2,
max(RMMtV .... /?Л(П),П)<2 п.
Теперь для всякого натурального т положим
а
т
2ат1, если 1 т •< М (2),
(А4-1)тах(ат1, ат2.....amk),
если М (k) < т М (k 4- 1)
для k > 1.
Бесконечные ряды
85
Чтобы доказать сходимость ряда 2 ат< установим сначала
следующее неравенство для (конечных) сумм членов этого
ряда при М (k) < т + М (k + 1), где k > 1:
2 am^ 2 [(£ + 1) 2 amnl —
m=M(6)+l m=M(k)+l n~l
k jM(* + 1) k
= (* + 1)21 2 2 Ямм.п<
n = l m=M(k)+l n = l
k
+1)2 < (k + I)2 2"*.
Л-1
Следовательно,
+OO jM(2) Jf(3)
2 am~ 2 am~\~ 2 am+ • • +
m=l m—\ m—Л1(2)+1
M(2) +oo M(fe + D
+ CO
< 25^(2) i + 2 4“ О 2 < + oo.
k = 2
С другой стороны, для всякого фиксированного п при
k п и т > М (А) имеем ат/атп k + 1, откуда
+оо
lim flm/flm„= + co. Таким образом, ряд 2 ат нельзя
m->+oo
+оо . +оо
сравнить с рядом 2 атп- На самом же деле ряд 2 ат
т=1 т=1
+ СО
нельзя сравнить с рядом 2 атп Даже в том случае, если
т=1
сравнение определить следующим образом:
ЭМ и К N Э tn > М + ат Катп.
В этом случае отрицание возможности сравнения выглядит так:
VH4 и К 6 N 3 m > Л4 9 > Катп.
Последовательность положительных сходящихся рядов
назовем универсальной последовательностью
сравнения, если произвольный положительный ряд схо-
дится тогда и только тогда, когда его можно сравнить
по крайней мере с одним из рядов этой последовательности.
86
Глава 6
Другими словами, последовательность положительных сходя-
щихся рядов является универсальной последовательностью
сравнения тогда и только тогда, когда сходимость или рас-
ходимость любого положительного ряда можно установить
сравнением его с каким-либо рядом этой последовательности.
Пример 19 показывает, что таких универсальных последо-
вательностей сравнения не существует.
20. Матрица Теплица Т и расходящаяся последователь-
ность, преобразуемая матрицей Т в сходящуюся
последовательность
Бесконечной матрицей называется функция, при-
нимающая действительные или комплексные значения с обла-
стью определения N X N, обозначаемая через Т = где
+ оо ?
г и j£N. Если бесконечный ряд 2 hjaj> где —задан-
ная последовательность чисел, сходится для каждого z£N,
то последовательность определяемая равенствами
+ оо
7-1
называется преобразованием последовательности {а-}
посредством матрицы Т. Бесконечная матрица Т = (1ц) назы-
вается матрицей Теплица1), если для всякой сходящейся
последовательности последовательность {#(-} имеет смысл,
причем предел lim Z>z существует и равен пределу lim aj.
»->+оо у->+со
Важнейшая теорема теории матриц Теплица состоит в сле-
дующем: для того чтобы бесконечная матрица Т = была
матрицей Теплица, необходимо и достаточно, чтобы были
выполнены следующие три условия (доказательство см. в [50]
или в [26]*, стр. 79):
+со
(1) BAicR^vieN,
7=1
(2) lim
i -> + co j = 1
(3) V7 6N, lim M = 0.
/-> 4-co
*) В честь немецкого математика Отто Теплица (1881—1940 г.).
Бесконечные ряды
87
Пусть Т — матрица Теплица
1 <С J i> и tij = О' если i < J’
1 0 0
1 1 0
2 2
т = 1 2 1
3 3 3
1 1 1
4 4 4
(tij), где ^=1/1, если
О .. .
О ...
О ...
4 • ’ •
Последовательность {а?-} = 1, —1, 1, —1, ..., (—1)я+1, ...
не сходится, но ее преобразование посредством матрицы Т
дает последовательность
№} = 1, О,
± о 1 о -1 + (-1)г+1
3 ’ и’ 5 ’ ............. 2г-
которая сходится к нулю.
Вообще, если [ап\—произвольная расходящаяся после-
довательность, каждый член которой есть либо 1, либо —1,
то существует матрица Теплица Т, которая преобразует {ая}
в сходящуюся последовательность!). В самом деле, матрицу Т
в этом случае можно определить так, что (ггя) преобразуется
в последовательность, состоящую лишь из нулей. Такую
матрицу Т можно-построить следующим образом: пусть
{пг}—строго возрастающая последовательность целых поло-
жительных чисел, такая, что аЯ/ и ап. +1 имеют противопо-
ложные знаки для I— 1, 2.........Положим
( 1/2, если j — nt или j = nz-]- 1,
[ 0 в противном случае.
Тогда Т будет матрицей Теплица, преобразующей последо-
вательность [ап] в последовательность 0, 0......
*) Этот результат справедлив и в том случае, если {ггя}—про-
извольная расходящаяся ограниченная последовательность. — Прим,
перев.
88
Глава 6
21. Для всякой матрицы Теплица существует
последовательность {»>), каждый член которой есть
либо 1, либо —1, такая, что преобразование {&/}
последовательности {«/} посредством матрицы Т рас-
ходится ’)
Используя условия (1)—(3) примера 20, выберем две
последовательности 1Х < z2 < /3 < .... jx < у2 < /3 < ...
следующим образом. Пусть номер 1Х таков, что при 1Х
имеем
+ 00
2 ttj = 1 +
j-i
Rizl < 0.05.
Это возможно в силу условия (2). Затем, на основе усло-
вий (1) и (2), выберем номер j\ так, чтобы
/1
2 = 1 и
7-1
+ оо
2 1^/1 <0.05.
/-/1+1
причем | dx | < 0,1.
После этого, используя условия (2) и (3), выберем /2 >
так, чтобы для I /2
2 1^1 <0.05
/=1
и 2fy=el + e2z> | е21 I < (0,05)2.
Затем снова воспользуемся условиями (1) и (2) и выберем
Л > 71 так> чтобы
Л +ОО
ii2j и I ^2/I < (0.05)2,
/ = 1 /"Л+1
где | d21 < 2 • (0,05)2. <
Если z'i < /2 < ... < /* и y’j < j2 < ... < jk уже вы-
браны, то, опираясь на условия (2) и (3), выберем 1к+1 > /А
так, чтобы для Z^-zA+1
4
2 I ti} I < (0.05)ft
’) Это утверждение и следующий ниже метод его доказатель-
ства фактически принадлежат Штейнгаузу (см. [26]*, стр. 93). —
Прим. ред.
Бесконечные ряды.
89
и
2^^' +eA+i, i’ I ek+i, 11 < (0,05)*+1.
/-1
Затем, используя (1) и (2), выберем Д+1 > jk так, чтобы
4 + 1 +О=
2,Ч+17=И-^+1 и 2 |Ч+1/|<(0.05/+1,
7-1 1-'k+l+l
где | dk+x | < 2 (0,05)*+1.
Теперь определим последовательность (aj:
( 1 для Л<7<Л..........
(—1 для Л<;<Л> /з<7<Л.................
Если k нечетно и k > 1, то
If ^к
Все суммы 24 j, за исключением 2^А/=1+<4. по
/-1 * /=1 й
абсолютной величине меньше, чем (0,05)“~ \ Таким образом,
учитывая, что
+ со
2 tikJaj
j-ik+x
4* со
«ода*.
получаем
bi > 1 — 2(0,05)*-1 — 2 (£ — 1) (0,05)*-1 — (0,05)* =
= 1 — [2 (ft — 1) 4- 2,05] (0,05)*-1,
90
Глава 6
Из последнего неравенства вытекает, что lim bt^> lim bt 1.
i -> co k -> co
Рассматривая четные значения k, мы получим, что lim bt
i->co
lim btk^.— 1 и потому последовательность {dz} рас-
k ~>СО
ХОДИТСЯ.
Примеры 20 и 21 показывают, что, хотя некоторые
матрицы Теплица преобразуют некоторые последовательности,
члены которых равны ±1, в сходящиеся последовательности,
однако не существует матрицы Теплица, которая преобразует
все такие последовательности в сходящиеся последователь-
ности.
Усложняя технику, которой мы пользовались выше, можно
прийти к следующему заключению: если {Ут)—последовав
тельность матриц Теплица, то существует такая после-
довательность {«„), что | ап | = 1 при п = \, 2, .... при-
чем для каждого т преобразование последователь-
ности {«„} посредством матрицы Тт расходится. В самом
деле, при выборе строго возрастающих последовательностей
натуральных чисел {zft} и {Д} будем в отличие от выше-
изложенного поступать следующим образом. Выберем сна-
чала i\ и j\ так, чтобы выполнялись соответствующие условия
для матрицы Тр затем выберем z2 и /2 так, чтобы соответ-
ствующие условия выполнялись как для матрицы Тх, так и
для матрицы Т2 и т. д. Последовательность {«„} определим
так же, как это сделано выше. Для всякого фиксирован-
ного m последовательность {а„} преобразуется в некоторую
подпоследовательность [Ьт/г]. Но поскольку числа и jk
при k > т образуют последовательность, для которой спра-
ведливы все условия предыдущего контрпримера в приме-
нении к матрице Тт, то отсюда следует, что предел lim bmn
не существует ни при каком т. «->+»
22. Степенной ряд, сходящийся лишь в одной точке.
(См. пример 24.)
4 со
Ряд ^п\хп сходится при х = 0 и расходится при х^=0.
Бесконечные ряды
91
23. Функция, ряд Маклорена которой сходится всюду,
однако представляет функцию лишь в одной точке
Функция
е-1/х2, если / * О,
О, если х = 0,
бесконечно дифференцируема, а все ее производные при
х — 0 равны 0 (см. пример 10 гл. 3). Следовательно, ее ряд
Маклорена
сходится при всех х к функции, тождественно равной нулю,
а потому он представляет данную функцию / (т. е. сходится
к ней) лишь в одной точке х = 0.
24. Функция, ряд Маклорена которой сходится лишь
в одной точке
Функция с таким свойством описана в [9] (стр. 153).
Функция
/ (х) — 2 е~п cos »2х
всюду бесконечно дифференцируема, поскольку множители е~п,
которые присутствуют во всех рядах, получаемых последо-
вательным почленным дифференцированием исходного ряда,
обеспечивают равномерную сходимость всех этих рядов. Ряд
Маклорена этой функции содержит лишь члены четной сте-
пени. Для абсолютной величины члена порядка 2k этого ряда
справедливо неравенство
при любом » = 0, 1, 2, ... и, в частности, при п = 2k.
Для этого значения п, и любого х =£ 0 имеем
92
Глава 6
если только k > ] е/2х |. Отсюда следует, что ряд Маклорена
функции / расходится при всяком х 4= О,
+ со
Как было указано в примере 22, ряд "^п\хп сходится
л = 0
лишь в точке х — 0. Естественно задать вопрос, является ли
этот ряд рядом Маклорена какой-либо функции /(х). Утвер-
дительный ответ на этот вопрос привел бы к другому при-
меру функции такого же типа, как и функция, уже рассмо-
тренная в настоящем примере. Мы покажем, что, действи-
тельно, можно построить бесконечно дифференцируемую
функцию /(х), для которой данный ряд будет рядом Мак-
лорена. Для этой цели определим функцию <рл0 (х) следующим
образом. Для п=1, 2, ... положим
((» - 1)!)2, если 0 < | х |<2-"/(га!)2,
0, если | х | 2-n+1/(/i!)2.
Затем функцию <р„0(х) доопределим на оставшихся интерва-
лах так, чтобы она стала бесконечно дифференцируемой
всюду. Это можно сделать при помощи функции из примера 12
гл. 3. Далее пусть /1(х) = <р10(х); положим для п — 2,
3, ...
<P«iO)= J фл0(О^.
о
Ф«2 (*) = / ф«1 (0 dt,
о
ФлоО)^
/«(х)==<р„1„_1(х)ЕЕ5 | <р„, n^(t)dt.
о
Таким образом, /'(х) = ФЛ> л_2(х), f" (х) = <рл> л_3 (х), .. .
.... /<«-1>(х) = фл0(х), /W(’x)=<p;0(x). Принимая во вни-
мание неравенства
|<рл1(х)|<2-п+7/г2,
lT«2Wi<[2-n+7ft2] • И-
I Ф„, п-г О) I < (2“"+1/n2) • I * Гкп - 2) !,
Бесконечные ряды
93
получаем оценку
| /„*> (х) | < (2-"+1/n2) | х \п-к~21(п - k — 2)!,
справедливую для любого х при 0 — 2. Ряд
+оо
У; fW (х) сходится равномерно на любом замкнутом конеч-
л=1
ном интервале при k = 0, 1, 2........ В самом деле, если
| х |< К, то
t/n-k-2
| Л J W | < „22л-1(/г_й_2)1
при п = k-\- 2, k 4- 3, ...
и равномерная сходимость вытекает из признака Вейер-
штрасса (см. [36], стр. 445, а также [521*, т. II, стр. 430).
Следовательно, функция
ОО
/(х)=2/„(х)
/г = 1
бесконечно дифференцируема, и для k — 0, 1, 2, ... спра-
ведливы равенства
4-со
/W(x)=S/W(x).
Но для имеют место равенства /(*)(0) =
= <р(*)_'г+О(0) = 0, а для и k = n—1 справедливы
равенства (0) = <рл0 (0) = ((п—I)!)2- Наконец, для 0 k <
< п,— 1 имеем /W(0) = 0. Таким образом, ряд Маклорена
+ оо
функции /(х) совпадает с рядом У п!х".
72== О
25. Сходящийся тригонометрический ряд, не являющийся
рядом Фурье
Мы приведем два примера, в первом из которых инте-
грирование производится по Риману, во втором —по Лебегу.
+оо
V! sin пх г\ а т
Рад 7j ——, где 0 < 1/2 сходится при любом дей-
п
ствительном х. В этом можно убедиться (см. [36], стр. 533,
94
Глава 6
а также [52]*, т. 11, стр. 432), применяя признак сходимости,
принадлежащий Н. X. Абелю (норвежский математик,
1802—1829 г.). Однако этот ряд не может быть рядом Фурье
никакой интегрируемой по Риману функции f (х~). В самом
деле, если бы это было не так, то, согласно неравенству
Бесселя (см. [36], стр. 532, а также [52]*, т. Ill, стр. 586),
мы бы имели
Л
it +
-л
где п— 1, 2....Но так как f (х) интегрируема по Риману,
то [/(х)]2 также интегрируема по Риману. Отсюда следует,
что правая часть предыдущего неравенства конечна, в то
время как при 1/2 левая часть этого неравенства не огра-
ничена при п—(Противоречие.)
+ оо
г» 1ч V Slnnx Л
Ряд1) 2j ' in „ также сходится при любом действитель-
// = 2
ном х. Положим
Если предположить, что этот ряд является рядом Фурье —
Лебега функции /(х), то функция
f(x)= J f (f)dt
о
должна быть периодической и абсолютно непрерывной. Но
так как / (х) — нечетная функция (/ (х) = — / (— х)), то
функция F(х) является четной (F(x)—А(—х)). Поэтому
ряд Фурье функции F(x) имеет вид
2 а
п-0
cos пх,
п
') В связи с исследуемым вопросом этот ряд впервые был рас-
смотрен Фату. — Прим. ред.
Бесконечные ряды
95
л
где а0 = — J F(x)dx, а для п^>2 коэффициенты
о
л
2 С
ап = — F (х) cos пх dx =
б
sin их Iя
п 1о
л
2 f cz / ч sinnx ,
-----г (х)----------dx =
я J 4 ' п
о
о
sin пх J
-------ах
п
п In п
(Производная Ff (х) почти всюду существует и почти всюду
равна /(х).) Поскольку функция F (х) имеет ограниченную
вариацию, ее ряд Фурье сходится в каждой точке, в част-
+QO
ности в точке х = 0. Отсюда следует, что ряд 2 ап схо“
п«=2
+со
дится. А так как ап — —1/nlnn и ряд 2(—1/n In/г)
п-1
расходится, то мы приходим к противоречию с предположе-
нием, что f (х) интегрируема по Лебегу.
Наконец, нам остается показать, что тригонометрический
+ оо
Ssin пх
—не является рядом Фурье никакой интегрируе-
п-1
мой по Лебегу функции. Это вытекает из следующей тео-
ремы (доказательство ее см. в [20]): если тригонометри-
ческий ряд является рядом Фурье некоторой функции g,
интегрируемой по Лебегу, и если он сходится почти
всюду к некоторой функции f, то f(x) — g(x') почти
всюду, и, следовательно, функция f интегрируема по
Лебегу, а данный тригонометрический ряд является ее
рядом Фурье,
96
Глава 6
26. Бесконечно дифференцируемая функция f(x), не
являющаяся преобразованием Фурье никакой функ-
ции, интегрируемой по Лебегу, и такая, что
lim f(x) = 0
I X |-> +оо
Пусть {cj, /г=0, ±1, ±2, .... есть последователь-
ность, бесконечная в обе стороны и такая, что ряд
4-оо
2 спе1пх
П=- —оо
сходится для всех х, но не является рядом Фурье никакой
функции, интегрируемой по Лебегу на [—л, л] (см. при-
мер 25). Мы покажем, что если h(x)— произвольная беско-
нечно дифференцируемая функция, обращающаяся в нуль вне
интервала —и такая, что й(0) = 2л, то в качестве
искомой функции можно взять функцию
/(х)= 2 с„й(х —п).
П = —ОО
Так как функция й(х) обращается в нуль вне интервала
[—Т’ т] ’ то Рад’ пРеДставляюЩий функцию /(х), при
любом фиксированном х имеет лишь конечное число отлич-
ных от нуля членов. Следовательно, этот ряд сходится при
всех х и представляет некоторую функцию /(х). По той же
причине на любом конечном интервале этот ряд и все ряды,
которые получаются из него почленным дифференцированием
конечное число раз, сходятся равномерно. Более того,
4-со
/(fc,(x)= 2 c„ftw(x — /г), k = 0, 1, 2, . . . .
Л— —00
Пусть функция F(t) интегрируема по Лебегу и удовле-
творяет условию
+оо
J F (t) e~ltx dt = f (х).
— СО
Положим
+оо
g(t) = 2 F(t -^2ят).
Бесконечные ряды
97
Так как F (t) интегрируема по Лебегу, то g(f) определена
для почти всех t и для этих значений t справедливо равен-
ство g (t -f- 2л) = g (Z), причем
Л 4-со Л
j | g (Z) I dt < J} J I /=• (Z 4- 2nm) I dt =
—Л m=— оо —л
+co
= J | F (Z) | dt < 4~ oo.
— CO
(Обоснование этих фактов, а также равенства, которое исполь-
зуется ниже, см. в [29], стр. 179 и 192—193.) Далее имеем
j g(t)e~int dt = -^ J F(Z4-2nm)e-^dZ =
—Л m=—co —л
S / /:'(Z4-2n/7i)e_z'!(z+2rtm)dZ —
m— — co —л
-boo
=4 j =
—co
+OO
Таким образом, cn являются коэффициентами Фурье инте-
грируемой по Лебегу функции g(t). Это противоречие и
доказывает тот факт, что /(х) не является преобразованием
Фурье никакой функции, интегрируемой по Лебегу.
27. Для произвольного счетного множества £с[—л, л)
существует непрерывная функция, ряд Фурье которой
расходится в каждой точке х £ Е и сходится в ка-
ждой точке х £ [— л, л) \ Е
Идея этого примера принадлежит Фейеру и Лебегу. Под-
робности можно найти в книге [20], т. I, стр. 474, где
даются также ссылки на первоначальные работы.
7 Зак. 587
98
Глава 6
28. Функция, интегрируемая (по Лебегу) на [—л, л],
ряд Фурье которой расходится всюду
Этот пример принадлежит А. Н. Колмогорову. Подроб-
ности и нужные ссылки см. в [20], т. I, стр. 488—494.
29. Последовательность {а„} рациональных чисел, обла-
дающая тем свойством, что для всякой функции f,
непрерывной на [0, 1] и равной 0 при х = 0
(/(0) = 0), существует строго возрастающая после-
довательность натуральных чисел {»„} (»j^0),
такая, что
+ ОО / л„+1
/(•*) = 2 2 апхп
v-o + l
причем сходимость является равномерной на [0, 1]
Предварительно сделаем следующее замечание:
Для всякого натурального т множество всех полиномов
с рациональными коэффициентами, которые содержат лишь
степени х" с п^т, плотно в пространстве Со([О, 1]) всех
функций, непрерывных на [0, 1] и обращающихся в нуль
в точке х — 0. При этом плотность понимается в смысле
„равномерной топологии", которая задается формулой
Р(/. £) = ||/ — £|| = тах { |/(х) — g (х)|. 0<х<1].
Это следует из теоремы Стоуна — Вейерштрасса (см. [44],
стр. 182, и [29], стр. 19).
Пусть теперь {/„}—счетное множество функций, всюду
плотное в Со( [0, 1]). Например, в качестве {/„} можно
взять последовательность, состоящую из всех полиномов
с рациональными коэффициентами, которые обращаются
в нуль при х = 0. Пусть Ру— один из таких полиномов, и
пусть для него р(/р А>1)=||/] — PJ^l. Далее, пусть
Р2—полином такого же типа, у которого все его члены
с ненулевыми коэффициентами имеют степень, превышающую
порядок полинома Ру, и для которого, кроме того, выпол-
нено неравенство р(/2 — Р\> P^ — Wfz—(^*i + P-i) II < 1/2.
Пусть полиномы Ру, Р2, .... Рп, принадлежащие С0([0, 1])
Бесконечные ряды
99
и имеющие рациональные коэффициенты, определены так,
что
(а) степень любого ненулевого члена полинома /3й+1
больше порядка полинома Pk, k=\, 2, .... п, — 1,
к
1
k ’
(b) fk-^Pi
k = 1, 2............n.
Тогда в качестве Pn+i в Co([O, 1]) возьмем полином с рацио-
нальными коэффициентами, такой, что
(а7) степень любого ненулевого члена полинома Pn+i
больше порядка полинома Рп,
(Ь')
1
п +1
Пусть m,j — наименьшая из степеней ненулевых членов
полинома Pj, a Mj — порядок полинома Pj. Тогда
nij < mj+1 для всякого /£N. Определим теперь
последовательность {ап} следующим образом: ах=а2 — ...
.. . — ami^i = 0, ami равен коэффициенту при хт> в поли-
номе Pi, amt + \ равен коэффициенту при хт' + 1 в Р\.....
равен коэффициенту при хм< в Pv Вообще, если
Aly < п < то полагаем an=Q\ если же wiy+1
п то ап равен коэффициенту при хп в поли-
номе Р]+\- Пусть /£Со([О, 1]), а последовательность
О < kx < k2 < ... такова, что |)/ — - fk < 1/ц для каждого
p£N. Тогда
<И--Л„1+
Следовательно, если положить по = О и nv~Mk^ для
V £ N, то
+ оо / ”v+l \
/(х)=2 2 апх'1
V—0 \п^п +1 /
причем ряд в правой части сходится равномерно (членами
ряда считаются суммы, заключенные в скобки).
7*
100
Глава б
Этот поразительный результат принадлежит В. Серпин-
скому. Следует отметить его большое сходство с примером 5
настоящей главы. В последнем случае в результате некото-
рой перестановки был получен ряд, обладающий тем свой-
ством, что для произвольно заданного действительного числа х
существует подпоследовательность частичных сумм (т. е. спо-
соб расстановки скобок у этого ряда), которая сходится
к х. В настоящем же случае мы имеем степенной ряд,
обладающий тем свойством, что для произвольной функции f
из пространства Со ([0, 1]) существует подпоследователь-
ность частичных сумм (т. е. способ расстановки скобок
у этого ряда), равномерно сходящаяся к /.
ГЛАВА 7
РАВНОМЕРНАЯ СХОДИМОСТЬ
Введение
В примерах настоящей главы рассматривается равномерная
и неравномерная сходимость последовательностей функций,
заданных на некоторых множествах. Предполагается, что
читатель знаком с основными определениями и теоремами
(см. [36], стр. 441—462; [38], стр. 270—292, а также [52]*,
т. II, стр. 422—453).
1. Последовательность всюду разрывных функций, схо-
дящаяся равномерно к всюду непрерывной функции
( 1/п, если х рационально,
| о, если х ИррацИОНальНо.
Ясно, что lim /я(х) = 0 при —оо < х < -|-оо, причем
Л-> +оо
сходимость является равномерной.
Этот простой пример может служить иллюстрацией сле-
дующего общего принципа: равномерная сходимость со-
храняет „хорошие* свойства и не сохраняет „плохие*.
Этот принцип будет неоднократно подтвержден последую-
щими примерами.
2. Последовательность бесконечно дифференцируемых
функций, которая равномерно сходится к нулю, а
последовательность производных этих функций всюду
расходится
Положим fn(x) = (sinnx^lYп. Поскольку | fn(х)|
•С l/j/^ra, то эта последовательность равномерно сходится
к нулю. Чтобы убедиться в том, что последовательность
(/я(х)} расходится всюду, рассмотрим последовательность
Ьп = /' (х) = У п cos rax,
102
Глава 7
где х фиксировано. Если х = 0, то Ьп — п —> оо при
л-> + оо. Докажем теперь, что для всякого х -=Г 0 после-
довательность рл} не ограничена и, следовательно, рас-
ходится. Для этого покажем, что существуют как угодно
большие значения п,такие, что | cos пх | 1/2. В самом деле,
для всякого натурального т, такого, что | cos тх | < 1/2,
имеем
| cos 2тх | = | 2 cos2 тх — 11 = 1 — 2 cos2 тх > .
Таким образом, существует номер п > т, для которого
| cos пх | > 1/2.
3. Неограниченная функция, являющаяся пределом не-
равномерно сходящейся последовательности ограни-
ченных функций
Положим
. ( 1 \ А / / 1
mm га,— , если 0<х<_1,
если х — 0.
Тогда каждая функция fn(x) ограничена на замкнутом
интервале [0, 1], однако предельная функция f (х), равная 1/х,
если 0<х</1, и равная 0, если х = 0, не ограничена на
этом интервале.
Следует отметить, что в подобном примере сходимость
не может быть равномерной.
4. Разрывная функция, являющаяся пределом последо-
вательности непрерывных функций
Тривиальный пример такого типа доставляет последова-
тельность,
tnin(l, rax), если х^-0,
щах(—1, гах), если х < 0.
Ее пределом является функция sgn х (см. гл. 3, пример 3),
которая разрывна в точке х = 0.
Равномерная сходимость
103
Можно построить более интересный пример такого рода,
рассматривая функцию f (гл. 2, Пример 15), которая опре-
деляется следующим образом:
fn(x) при. п=5
Рис. 2. •
Определим теперь последовательность /я (х). Зафиксируем
номер га 2. На каждом интервале вида ------
где 1<^9<га, 0 р 7, положим
/л(х) = шах(|, 1-|-2га2(х —-И V
{р р < 1 \
а на интервале вида где р и q находятся
в тех же пределах, положим
Л(х)^тах(1,
104
Глава 7
В тех точках интервала [0, 1], в которых fn(x) еще не
определена, положим fn(x')=\jn. Наконец, продолжим
функцию fn(x) за пределы отрезка [0, 1] периодически
с периодом, равным единице. График функции fn(x) пред-
ставляет собой бесконечную ломаную линию, звенья которой
либо расположены на горизонтали у=1/га, либо подни-
маются к изолированным точкам графика функции /, причем
угловой коэффициент наклона равен + 2га2 (см. рис. 2).
При возрастании п пики становятся все более узкими и
крутыми, а горизонтальные звенья ломаной приближаются
к оси х. Легко видеть, что для всякого га — 1, 2, ...
и
lim /я(х) = /(*).
л-> +со
При этом каждая функция fn всюду непрерывна, а предель-
ная функция / разрывна на всюду плотном множестве Q
рациональных чисел (см. пример 24 гл. 2).
5. Не интегрируемая по Риману функция, являющаяся
пределом последовательности функций, интегрируемых
по Риману. (См. пример 33 гл. 8.)
Каждая из функций gn, определенных в примере 24 гл. 2,
интегрируема по Риману на замкнутом интервале [0, 1],
поскольку каждая из этих функций ограничена на этом
интервале и имеет конечное число точек разрыва. Последо-
вательность {£„} является возрастающей последовательностью
для каждого х и п—1, 2, ...), сходя-
щейся к функции f примера 1 гл. 4, которая равна 1 на
множестве Q П [0, 1] и равна 0 на множестве [0, 1] \ Q.
6. Последовательность функций, для которой предел инте-
гралов не равен интегралу от предельной функции
Положим
2га2х,
га — 2га2 (х — ,
\ 2га)
0,
если
если
если
Равномерная сходимость
105
Тогда
1
f 11
lim \fn(x)dx— lim =
л->+оо^ л->+со z
однако
1
1
f lim fn(x)dx— f Qdx = <d.
0 "->+“ 0
Другим примером подобного типа является последова-
тельность {/„ (х)}, где /„ (х) — п2хе~пх при 0 <; х <; 1.
Еще более замечательным свойством обладает последо-
вательность функций
2га3х, если
0, если
В этом случае
ь
lim f fn(x)dx= lim у = -|-оо
л-> +оо * л->+со &
для всякого ££(0, 1], в то время как
ъ ь
f lim fn (х) dx = f 0 dx = 0.
о "->+о° о
7. Последовательность функций, для которой предел
производных не равен производной от предельной
функции
Положим fn (х) = х/( 1 4“ И2Х2) ДЛЯ ---1 х 1 и
п—1, 2, .... Тогда предельная функция /(х)= lim / л(х)
л-> 4-со
существует и равна 0 для всех х£[—1, 1] (при этом схо-
димость является равномерной, поскольку наибольшее и наи-
меньшее значения функции fn(x) на интервале [—1, 1] равны
106
Глава 7
соответственно 1/2га и —1/2га). Производная предельной
функции тождественно равна 0. Однако предел последова-
тельности производных
1 ti^x^
lim f'(x)= lim *77—i—
1, если x = 0,
0, если 0 < | x I 1.
8. Последовательность функций, равномерно сходящаяся
на каждом замкнутом подинтервале, но не сходя-
щаяся равномерно на всем интервале
Положим fn(x)~xn на открытом интервале (0, 1).
9. Последовательность {/„}» равномерно сходящаяся
к нулю на интервале [0, -|-оо) и такая, что
+оо
J f„(x)dx-A0
О
Положим
— , если 0<^х<^га,
0, если х > п.
Тогда /я равномерно сходится к нулю на [0, 4-оо), однако
4-со
j fn(x)dx = i-»i.
о
Еще более замечательный пример доставляет последова-
тельность функций
2_
п ’
0,
если
если
0 х га2,
х > га2.
+ со
В этом случае J fn (х) dx = га —> -|- оо.
о
Равномерная сходимость
107
10. Неравномерно сходящийся ряд, общий член которого
стремится к нулю равномерно
Этим свойством на полуинтервале [0, 1) обладает ряд
+со
2 хп1п. Так как общий член этого ряда мажорируется на
Л = 1
[0, 1) числом 1/п, он стремится к нулю равномерно на [0, 1).
СО
Сходимость ряда 2 вытекает из того, что он мажори-
Л = 1
руется рядом 2 х”- сходящимся на [0, 1). Однако исходный
ряд сходится неравномерно. Это следует из того факта, что
его частичные суммы не являются равномерно ограничен-
ными (гармонический ряд расходится; см. [36], стр. 447,
упр. 31, 32).
11. Неравномерно сходящаяся последовательность, обла-
дающая равномерно сходящейся подпоследователь-
ностью
Положим
[ х
—, если п нечетно,
п
—, если п четно,
I «
причем все функции определены на множестве действитель-
ных чисел R. Эта последовательность сходится к нулю не-
равномерно, но подпоследовательность {/2„ (х)] =
сходится равномерно.
12. Неравномерно сходящиеся последовательности, удо-
влетворяющие любым трем из четырех условий
теоремы Дини
Теорема Дини утверждает, что если {/„} — последова-
тельность определенных на множестве А функций, сходящаяся
на А к функции /, и если
(i) fn непрерывна на А, п = 1, 2, .. . ,
(ii) / непрерывна на А,
(iii) последовательность [fn (х)} монотонна,
(iv) А компактно,
108
Глава 7
то данная последовательность сходится к функции / равно-
мерно.
Никакие три из этих условий не обеспечивают равно-
мерной сходимости. Другими словами, ни одно из этих четырех
условий не может быть опущено. Этот факт подтверждается
следующими четырьмя примерами:
! 0, если х = 0 или —
0) i
1, если 0 < х < —.
Тогда {/„(•*)} —убывающая при кЗждом фиксированном х
последовательность, которая на компактном множестве [0, 1]
неравномерно сходится к непрерывной функции f (х) = 0.
(ii) Убывающая последовательность {%") на компактном
множестве[0, 1]неравномерно сходится к разрывной функции
0, если 0 < 1,
1, если х = 1.
/(*) = {
(iii) См. пример 6.
(iv) Последовательность {х"\ на [0, 1).
ГЛАВА 8
МНОЖЕСТВА И МЕРА НА ДЕЙСТВИТЕЛЬНОЙ
ОСИ
Введен не
Если не оговорено противное, то все рассматриваемые
в настоящей главе множества предполагаются подмножествами
системы действительных чисел R. Непустой класс 91 множеств
называется о-кольцо м, или сигма-кольцом, если он
замкнут относительно операции объединения, примененной
счетное множество раз, и относительно операции разности
+со
множеств (А-А........ ea^UAesi и а\АЕ^).
Л = 1
Если 91 — какой-либо непустой класс множеств, тоо-кольцом,
порожденным классом 91, называется пересечение всех
о-колец, содержащих 91 (о-кольцо, порожденное классом 91,
всегда существует, так как всегда существует по крайней
мере одно о-кольцо, содержащее 91, а именно класс всех
подмножеств R). Естественно представлять себе о-кольцо,
порожденное классом 91, как наименьшее о-кольцо, содер-
жащее 91. Сигма-кольцо, порожденное классом б всех ком-
пактных подмножеств R, называется классом 93 борелев-
ских множеств (таким образом, множество является
борелевским, если оно есть элемент о-кольца, порожденного
классом б).
Если А—произвольное подмножество R, ах—какое-
либо действительное число, то сдвигом множества А на
число х называется множество, обозначаемое символом х-\-А,
которое определяется следующим образом:
х-|-Л={у|у = х + й, а £ Л] = {х-|-а | а £ Л}.
Класс 91 множеств называется замкнутым относи-
тельно сдвигов, если
ЛЕ91,
Если <5 есть о-кольцо подмножеств пространства X, то
функция множества р с областью определения <5 называется
по
Глава 8
неотрицательной функцией в широком смысле,
если ее значения для множеств S £ 3 удовлетворяют нера-
венству 0 p(S) со. Неотрицательная функция в широ-
ком смысле, заданная на о-кольце 3, называется мерой
на 3, если р(0) = О и р счетно аддитивна на <3:
S2, . .,£3, SmQSn = 0 для
/+от \ +ОО
Р U5« =2р(5">-
\/г-1 / л-1
Если р есть мера на о-кольце 3 подмножеств пространства X
и если Л"£3, то упорядоченная пара (X, 3) называется
пространством с мерой, а р—мерой на простран-
стве с мерой (X, 3). Если из контекста ясно, о каком
классе множеств <5 идет речь, то пространство с мерой
будет обозначаться одной буквой X. Пусть р и о — две
меры на одном и том же пространстве с мерой (X, 3).
Мера р называется абсолютно непрерывной относи-
тельно о (это обозначается так: р<С^о), если
Л£3, о(Л) = 0^р(Л) = 0.
Если р—какая-либо мера на пространстве с мерой (X, 3),
то н у л ь-м н о ж е с т в о м для р называется любое подмно-
жество элемента А из 3, имеющего нулевую меру, т. е.
р(Л) = 0. Мера р на (X, 3) называется полной, если
всякое нуль-множество для р является элементом класса 3.
Мерой Бореля называется мера р. на пространстве
с мерой (R, 23), которая каждому ограниченному замкнутому
интервалу сопоставляет его длину:
Ц ([а, b]) = b — а, если а Ь.
Этим условием мера Бореля определяется вполне одно-
значно. Классом 23 измеримых по Лебегу множеств называется
о-кольцо, порожденное объединением класса 23 и класса
всех нуль-множеств для меры Бореля на 23. Мера Лебега
есть полная мера на 23, которая однозначно определяется
тем, что ее сужение на 23 является мерой Бореля; другими
словами, мера Лебега является пополнением или полным
продолж ением на 23 меры Бореля, заданной на 23.
Так как длина компактного интервала [а, 6] инвариантна
относительно сдвигов, то о-кольца 23 и 23 замкнуты отно-
Множества и мера на действительной оси
111
сительно сдвигов, а меры Бореля и Лебега инвариантны
относительно сдвигов:
Д С 23, x£R=>x-}-X£23, ц (х Д- Д) == ц (Л),
Л^ЗЗ, х6И=>х + Л£®, ц(х +Л) = ц(Л).
Для всякого множества Е с R определим внутреннюю
меру Лебега 1Ц (£) и внешнюю меру Лебега ц* (Д)
следующим образом:
p/B^sup (р(Л)| АсЕ, А £23},
p*(£)==inf {ц(Л)| А =>Е, Л^й}.
Эти определения эквивалентны следующим:
р.(Д) = 8ир{р(Л)|Л сЕ, Л £23} =
= sup [р(Л)| А с Е, А компактно},
p*(£) = inf {|Д(Л)| А => Е, Л £ 23} =
= inf {р (Л) | А о Е, А открыто}.
Доказательства этих фактов и дальнейшие подробности
можно найти в [17], [31], [32] и [53].
Иногда мы будем ссылаться на аксиому выбора или на
такие ее варианты, как теорема о полном упорядочении или
лемма Цорна. Их иногда объединяют под общим названием
принципа максимального элемента. По поводу этого круга
вопросов отсылаем читателя к [17], [31] и [49].
Мы предполагаем также, что читатель знаком с понятиями
отношения эквивалентности и класса эквивалентности.
Эти понятия и связанные с ними вопросы рассматриваются
в [17] и [19].
1. Совершенное нигде не плотное множество
Совершенным множеством называется замкнутое
множество, каждая точка которого является предельной точкой
этого множества. Фундаментальный результат, относящийся
к совершенным множествам, состоит в том, что всякое не-
пустое совершенное множество А действительных чисел
(или, более общо, всякое непустое совершенное множество
в полном сепарабельном метрическом пространстве) несчетно;
на самом же деле мощность множества А равна с — мощности
112
Глава 8
множества R, т. е. между R и А существует взаимно одно-
значное соответствие. (Доказательство и подробности см.
в [54], стр. 153—162.)
Нигде не плотным множеством называется мно-
жество А, замыкание которого А не имеет внутренних точек,
т. е. /(Л)=0. Ясно, что множество нигде не плотно тогда
и только тогда, когда его замыкание нигде не плотно, и что
любое подмножество нигде не плотного множества нигде
не плотно. Менее очевидным является тот факт, что объеди-
нение любой конечной совокупности нигде hq плотных
множеств нигде не плотно. Доказательство этого факта можно
провести по индукции, рассмотрев сначала следующий част-
ный случай: если А и В замкнуты и нигде не плотны,
то MU В нигде не плотно. (Если U—непустое открытое
подмножество множества A U В, то U \ В — непустое откры-
тое подмножество множества Д.)
Знаменитый пример совершенного нигде не плотного мно-
жества был построен Г. Кантором (немецкий математик,
1845—1918 г.) и известен под названием канторова мно-
жества. Это множество С получается из замкнутого еди-
ничного интервала [0, 1] последовательным удалением откры-
тых интервалов, называемых „средними третями11, следующим
образом. Сначала удалим все точки х, лежащие между 1/3
и 2/3. Затем удалим средние трети (1/9, 2/9) и (7/9, 8/9)
(двух оставшихся замкнутых интервалов [0, 1/3] и [2/3, 1]
соответственно. После этого удалим средние части (1/27,2/27),
(7/27, 8/27), (19/27, 20/27) и (25/27, 26/27) четырех остав-
шихся замкнутых интервалов [0, 1/9], [2/9, 1/3], [2/3, 7/9]
и [8/9, 1] соответственно. Продолжая этот процесс до бес-
конечности, мы удалим в результате из интервала [0, 1]
множество, являющееся объединением последовательности
открытых интервалов, т. е. открытое множество. Оставшееся
замкнутое множество и есть множество С. Поскольку каждую
точку множества С можно сколь угодно точно приблизить
концевыми точками удаленных интервалов (все эти концевые
точки принадлежат С), то множество С совершенно. А так
как внутри [0, 1] не существует открытого интервала, кото-
рый не имел бы общих точек по крайней мере с одним
из интервалов, точки которого были удалены на некоторой
стадии, то (замкнутое) множество С нигде не плотно.
Множества и мера на действительной оси
113
Канторово множество С можно определить при помощи
троичной (с основанием 3) системы счисления. Точка х £ С
тогда и только тогда, когда х можно представить троичной
дробью, используя лишь цифры 0 и 2. Например, 0,022222 . ..
и 0,200000 .. . являются концевыми точками первого удален-
ного интервала, т. е. соответственно точками 1/3 и 2/3
в десятичной системе. По поводу этого описания множества С
см. [32], [53] и [33]*, стр. 57, а также следующий пример 2.
2. Несчетное множество меры нуль
Канторово множество С примера 1 несчетно, ибо оно
является непустым совершенным множеством, а его мера
равна нулю, поскольку множество точек, удаленных из замк
нутого интервала [0, 1], имеет меру
1
_£ I 1 2.1 2 2 । _ 3
3 + 3,з + з’з'з+---~ 2~ Е
1 3
Можно воспользоваться троичными разложениями для точек
канторова множества и показать, что мощность множества С
равна с, т. е. мощности множества R всех действительных
чисел. (Этот метод доказательства не зависит от указанного
выше метода, основанного на свойствах совершенных
множеств.) С одной стороны, точки множества С находятся
во взаимно однозначном соответствии с троичными разложе-
ниями, использующими лишь цифры 0 и 2, и, следовательно,
с двоичными разложениями, использующими цифры 0 и 1.
С другой стороны, бесконечные двоичные разложения на-
ходятся во взаимно однозначном соответствии с точками
полуоткрытого интервала (0, 1] и, следовательно, с множе-
ством всех действительных чисел. Это показывает, что мно-
жество всех двоичных разложений (а потому и множество С)
несчетно и его мощность не меньше с. Чтобы доказать,
что эта мощность в точности равна с, нам остается лишь
заметить, что множество конечных двоичных разложений
счетно (или еще проще, что С с R). Дальнейшие приложения
только что описанного отображения можно найти в примере 14
этой главы.
3 Зак. 587
114
Глава 8
3. Множество меры нуль, разностное множество кото-
рого содержит некоторую окрестность нуля
Если А — произвольное непустое множество, то его
разностным множеством D (А) называется множество
всех разностей между его элементами:
D(A)={x—у\х£А, у £ Л).
Важным фактом в теории меры является то, что если
А — измеримое множество положительной меры, то точка
х — 0 является внутренней для разностного множества D(A)
(см. [53], стр. 72). Канторово множество С примера 1 является
множеством нулевой меры, которое обладает таким же свой-
ством. В самом деле, его разностное множество О (С) есть замк-
нутый интервал [—1, 1]. Простейший способ убедиться в этом
состоит в следующем. Рассмотрим множество С X С и пока-
жем, что для всякого числа а, такого, что —1</а</1,
прямая у—х-фа пересекает множество С X С по крайней
мере в одной точке (см. [9], стр. 110; там же указаны
дальнейшие ссылки). Так как множество С получено после-
довательным удалением „средних третей", то множество
С X С можно представить в виде пересечения счетного
семейства замкнутых множеств Ср С2....... где каждое
из множеств Сп есть объединение „угловых квадратов"
(см. рис. 3). Множество С} состоит из четырех замкнутых
квадратов со сторонами, равными 1/3, расположенных по
углам полного квадрата [0, 1] XfO, 1]: [0, 1/3] X [0. 1/3],
[0, 1/3] X 12/3, 1], [2/3, 1]Х [0, 1/3] и [2/3, 1] X [2/3, 1];
множество С2 состоит из шестнадцати замкнутых квадратов
со сторонами, равными 1/9, расположенных по углам
четырех квадратов множества (по четыре в каждом
квадрате); множество С3 состоит из шестидесяти четырех
замкнутых квадратов со сторонами, равными 1/27, располо-
женных по углам шестнадцати квадратов множества С2
(по четыре в каждом квадрате) и т. д. Для всякого данного
а£[—1, 1] прямая у = х-]-а пересекает по крайней мере
один из четырех квадратов множества Выберем один
такой квадрат и обозначим его через Эта прямая должна
пересечь по крайней мере один из четырех квадратов мно-
жества С2, лежащих внутри Выберем один такой квадрат
и обозначим его через S2. Продолжая этот процесс, мы
Множества и мера на действительной оси
115
получим последовательность замкнутых квадратов {S„}, такую,
что 5л+1 с Sn для п=1, 2, .... Так как длина стороны
квадрата Sn равна 3-л, то существует в точности одна точка
(х, у), которая принадлежит каждому квадрату последова-
тельности {£„} (см. [36], стр. 201, упр. 30). Следовательно,
точка (х, у) должна принадлежать множеству С X С, а так как
эта точка должна принадлежать и прямой у —х-[-а, то мы
получили элементы х и у множества С, разность между
которыми равна данному числу а.
4. Совершенное нигде не
тельной меры
Метод, использованный в
торова множества С, можно
плотное множество положи-
примере 1 для построения кан-
в измененном виде применить
8*
116
Глава 8
для построения полезного семейства совершенных нигде не
плотных множеств. Каждое из этих множеств, которые мы
также назовем канторов ы ми, есть множество точек,
остающихся на интервале [0, 1] после удаления из него по-
следовательности интервалов следующим образом. Пусть а —
произвольное положительное число < 1. Сначала удалим из
го 11 ( 1 1 1 , 1 \
[О, 1] все точки открытого интервала l-^-— jd, у + ^а!
1 1
длины -у а с центром в точке Из двух оставшихся
г„ 1 1 ] Г1 । 1 J
замкнутых интервалов 0, а и Ч> каж'
„ 1/, ‘I \
дый из которых имеет длину II—al, удалим сред-
ние открытые интервалы, длина каждого из которых равна
I о
g-a. Затем из оставшихся четырех замкнутых интервалов,
I I. I I \
длина каждого из которых равна -^-il —-g-a — a), Уда'
лим средние открытые интервалы, каждый из которых имеет
длину gg-а. Из восьми оставшихся замкнутых интервалов,
I I, I I I \
длина каждого из которых равна -3- I —-^-а------га---a ,
о \ 2 4 о /
удалим средние открытые интервалы, каждый из которых
имеет длину -^Ч- а. После п шагов мера удаленных откры-
тых интервалов будет равна а (у+ 4’“^’''' и- сле-
довательно, мера совокупности удаленных открытых интер-
валов после бесконечной последовательности удалений будет
равна а. Мера оставшегося канторова множества будет равна
I —а. По этой причине построенные таким способом кан-
торовы множества часто называют канторов ы ми мно-
жествами положительной меры. Все они являются
совершенными нигде не плотными множествами. Ниже, в при-
мере 23, будет показано, что все канторовы множества по-
ложительной или нулевой меры гомеоморфны (см. введение
к гл. 12). Тогда из второй части примера 2 будет следо-
вать, что любое канторово множество имеет мощность с,
равную мощности множества R.
Третий способ построения канторовых множеств таков:
пусть 0<р<1, и пусть ((}„}—последовательность поло-
Множества и мера на действительной оси
117
жительных чисел, такая, что 2 2”рл = р. Удалим из [0,1]
л=0
открытый интервал /0 длины р0 с центром в точке 1/2. За-
тем из [0, 1]\70 удалим два открытых интервала /J, /?•
каждый из которых имеет длину и расположен в центре
одного из двух непересекающихся замкнутых интервалов,
объединение которых совпадает с множеством [0, 1 ] \ /0.
Продолжим этот процесс, как и в предыдущих построениях:
на га-м шаге будут удалены 2" открытых интервалов /„• Лг, • •
2"
.... 1п , каждый из которых имеет длину рп и расположен
должным образом на замкнутых интервалах, составляющих
остаточное множество после (п— 1)-го шага, га — 1, 2, ... .
5. Совершенное нигде не плотное множество иррацио-
нальных чисел
Можно построить пример совершенного нигде не плот-
ного множества, используя последовательность {гл}, члены
которой составляют множество всех рациональных чисел ин-
тервала (0, 1). Поступим как и при построении канторова
множества С, однако расширим открытый интервал так,
чтобы его центр находился в точке 1/2, концы были ирра-
циональными и чтобы он содержал точку На следующем
шаге удалим из каждого из двух оставшихся замкнутых
интервалов открытый интервал таким образом, чтобы его
центр находился в центре соответствующего замкнутого ин-
тервала, концевые точки были иррациональными и чтобы
было удалено второе рациональное число fj1). Продолжая
этот процесс неограниченно, мы получим в результате со-
вершенное нигде не плотное множество D. А так как все
рациональные числа, заключенные между 0 и 1, были
удалены, то это „канторово" множество D содержит, за
исключением двух точек 0 и 1, только иррациональные числа.
Если концевые точки первоначального интервала выбрать
иррациональными, то подобным же образом можно построить
совершенное нигде не плотное множество, состоящее только
из иррациональных чисел.
.*) Если оно не было удалено на предыдущем шаге. — Прим,
перев.
118
Глава 8
6. Всюду плотное открытое множество, дополнение
которого имеет положительную меру
Пусть А—канторово множество положительной меры
на [0, 1]. Положим В = Л' = К\Л. Тогда В будет всюду
плотным открытым множеством, а его дополнение А имеет
положительную меру.
7. Множество второй категории
Говорят, что множество А есть множество первой ка-
тегории, если оно является объединением счетного числа
нигде не плотных множеств. Любое подмножество множества
первой категории есть множество первой катесории, и вся-
кое объединение счетного множества множеств первой
категории является снова множеством первой категории. На-
пример, множество Q рациональных чисел является мно-
жеством первой категории. Если множество не является мно-
жеством первой категории, то говорят, что это множество
второй категории. Примером множества второй кате-
гории является множество R всех действительных чисел. Бо-
лее общо, любое полное метрическое пространство есть мно-
жество второй категории (см. [38], стр. 338, упр. 33 и [45]*,
стр. 87). Этот общий результат принадлежит Р. Бэру (см. [2],
стр. 108; [54], стр. 162 — 165 и [27], стр. 425). Из него
следует, что множество R \ Q иррациональных чисел является
множеством второй категории. Сейчас независимо от только
что упомянутой общей теоремы мы приведем краткое дока-
зательство того факта, что любое множество А действи-
тельных чисел с непустым ядром 1(A) есть множество вто-
рой категории. Предположим противное. Тогда найдется не-
пустой замкнутый интервал С=[а, 6], содержащийся в ядре А,
который можно представить в виде С = Fx J F2 [J . . ., где
множества Fn (п — 1, 2, . . .) замкнуты и нигде не плотны.
Пусть Cj — замкнутый интервал [04, Z>1]gz(«, й)\^р далее
пусть С2 — замкнутый интервал [а2, d2]c(a]t &Y) \ F2; вообще
для «>1 пусть Сп = [а„, bn} c(an_v bn_x) \ Рп. Тогда
существует точка р, принадлежащая каждому Сп, п=1, 2,. ..
(см. [36], стр. 201, упр. 30 и [33]*, стр. 44 — 45), и, сле-
довательно, р£С. Но это невозможно, так как р не при-
надлежит ни одному множеству Fn, п= 1, 2......(Проти-
воречие.)
Множества и мера на действительной оси
119
8. Множество, не являющееся множеством типа Fa
Напомним (гл. 2, пример 23), что множеством типа Р
называется множество, являющееся объединением счетного
множества замкнутых множеств. Можно привести много при-
меров множеств типа Fg. конечные множества, замкнутые
интервалы, открытые интервалы (например, интервал (0, 1)
является объединением множеств [1/га, (га — 1)/га]), полуот-
крытые интервалы, множество всех рациональных чисел (если
рациональные числа расположить в последовательность
/•р г2, то Q есть объединение одноточечных замкнутых
множеств {/•]), (г2), ..., {/•„), ...). Примером множества,
которое не является множеством типа Рп, может служить
множество R \ Q всех иррациональных чисел. Чтобы дока-
зать это, предположим противное. Тогда R \ Q = Q |J С2 U ....
где каждое Сп замкнуто (га =1,2, . . .). Но так как ника-
кое подмножество множества R \ Q всех иррациональных
чисел не имеет внутренних точек, то каждое замкнутое под-
множество этого множества нигде не плотно. Отсюда сле-
дует, что множество R \ Q первой категории. (Противоре-
чие; см. пример 7.)
9. Множество, не являющееся множеством типа (75
Множество Л называется множеством типа G6, если
оно является пересечением счетного множества открытых
множеств. Для дополнений множеств справедлив закон двой-
ственности (закон де Моргана):
'+оо V +со / +оо V 4-оо
ил = рх, рл =(jx.
71-1 ' /2 = 1 = 1 / л=1
Из этого закона следует, что множество А является мно-
жеством типа 06 тогда и только тогда, когда его дополне-
ние А' = R \ А является множеством типа Ро. Поэтому,
учитывая, что множество R \ Q всех иррациональных чисел
не является множеством типа Fg, заключаем, что множе-
ство Q всех рациональных чисел не является множеством
типа Gfi.
Если рассмотреть объединение счетного множества мно-
жеств типа Gfi и пересечение счетного множества множеств
120
Глава 8
типа Fa, то мы получим два новых класса множеств, назы-
ваемых множествами типа G6g и Fo6 соответственно. По-
добным же образом можно составить две бесконечные по-
следовательности классов множеств, которые обозначают
соответственно через Fg, F^, Fg&g, ... и Ge, Ова, G6g6..
Дальнейшие подробности об этих множествах см. в [54].
10. Множество А, не являющееся множеством точек
разрыва никакой функции
Пусть А — множество R\Q всех иррациональных чисел.
Так как А не является множеством типа Fg, то не сущест-
вует действительнозначной функции действительного пере-
менного, множество точек разрыва которой совпадает с А
(см. последнее замечание к примеру 23 гл. 2). Другими сло-
вами, не существует функции, отображающей R в R, кото-
рая непрерывна в каждой рациональной точке и разрывна
в каждой иррациональной точке. (См. пример 15 гл. 2.)
11. Неизмеримое множество
Используя аксиому выбора, можно построить множество,
не измеримое по Лебегу. В действительности же множество,
построенное этим способом, не может быть измеримым от-
носительно любой нетривиальной счетно аддитивной меры,
которая инвариантна относительно сдвигов. Точнее, если ц—
мера, определенная для всех множеств А действительных
чисел, принимающая конечные значения на ограниченных мно-
жествах и такая, что
ц (х Д- А) = р (Д)
для каждого x£R и .AcR, то ц(Д) = 0 для всякого ДсР.
Сейчас мы докажем этот результат.
Определим на (0, 1] X (0> 1] отношение эквивалентности ~
следующим образом: х—у, если х — y£Q. Этим отноше-
нием эквивалентности полуоткрытый интервал (0, 1] раз-
бивается на непересекающиеся классы эквивалентности С.
Если применить аксиому выбора к этому семейству классов
эквивалентности, то мы получим множество А, обладающее
следующими двумя свойствами: (1) никакие две различные
точки из А не принадлежат одному и тому же классу
Множества и мера на действительной оси
121
эквивалентности С; (2) каждый класс эквивалентности С со-
держит некоторую точку А. В терминах отношения экви-
валентности эти два свойства принимают такую форму:
(1) никакие два различных элемента из А не эквивалентны
друг другу; (2) каждая точка х интервала (0, 1] эквивалентна
некоторому элементу множества А. Далее для всякого
г £(0, 1] определим на множестве А операцию, называемую
сдвигом по модулю 1:
(r + A)(modl) = [(r + A)U((r- 1) + А)]П(0, 1] =
= ((г + Л)П(0, 1]}и{((г-1) + >1)П(О, 1]}.
Для сдвига по модулю 1 из установленных выше свойств мно-
жества А следует, что (1) любые два множества (г-ф-Д) (mod 1)
и (s-ф- A) (mod 1) при различных рациональных числах
г и s из (0, 1] не пересекаются; (2) каждое действи-
тельное число х интервала (0, 1] является элементом неко-
торого множества (г-ф-А) (mod 1) для некоторого рациональ-
ного числа г из (0, 1]. Другими словами, полуоткрытый
интервал (0, 1] является объединением счетной совокупности
попарно непересекающихся множеств {(r-ф-A)(mod 1)}, где
r€Qn(0> 1].'Важное свойство множеств, полученных из А
сдвигами по модулю 1, состоит в том, что (на основании
предположений, сделанных относительно ц) все они имеют
ту же меру, что и А:
ц ((гф- A)(mod 1)) =
= р((г + А)П(0, 1] ) + и(((г - 1) +А) П(0, 1]) =
= Ц((г-}-А)П(0, 1] ) + ц((г +А)П(1, 2]) =
= Ц((гфЛ)(|(0, 2]) = р(г4-А) = р(А).
Если предположить, что А имеет положительную меру, то
из счетной аддитивности Ц мы получим, что
Н((0, 1])« 2 p((r + A)(modl)) =
г€ОП(0,1]
— 2 Н (А) — -ф- оо,
г CQ Г1(0,1]
122
Глава 8
но это невозможно, так как множество (0, 1] ограничено.
Следовательно, ц(А) = 0 и
И((0, 1])= 2 ц ((г + A)(mod 1))= 2 р(А) = 0,
г€ОП(0,1| '•€ОП(0,1J
и потому
+оо 4-оо
= 2 ц((«. «+1])= 2 н((о. 1]) = о.
й = - со п — — со
Отсюда вытекает, что Ц — тривиальная мера, для которой
любое множество имеет меру нуль.
Наконец, если принять во внимание, что мера Лебега —
нетривиальная инвариантная относительно сдвигов мера, для
которой ограниченные интервалы имеют положительную ко-
нечную меру, то предыдущие рассуждения показывают, что
множество А не измеримо по Лебегу.
Так как все множества типа Fo и все множества типа
являются борелевскими множествами и потому измеримы, то
построенное неизмеримое множество дает пример множества,
которое не является ни множеством типа Fg, ни множеством
типа Gj.
Описанную выше конструкцию можно применить и к мно-
жествам на окружности. Рассмотрим единичную окружность
1^{г|г^С, | z | = 1} на комплексной плоскости С как
группу относительно умножения. Для каждого z £1 сущест-
вует единственное 0, 0 0 < 1, такое, что г = е2я<9. По-
ложим 10== [z | z — е2я‘в, 0£Q, 0 0 < 1}. Тогда 10 будет
нормальной подгруппой, и существует факторгруппа S = 1/10.
Пусть S — полное множество представителей всех классов
смежности группы S в I (при этом из каждого класса
смежности в I входит лишь один элемент), полученное при-
менением аксиомы выбора, и пусть мера Лебега ц на [О, 1)
преобразуется в меру ц на I по следующему правилу:
Ecl измеримо тогда и только тогда,
когда F ~ {01 е2лг0 £ Е, 0 0 < 1}
измеримо по Лебегу и ц (£) = 2 лц (Д).
Множества и мера на действительной оси
123
Тогда S не измеримо. В самом деле, e2lu0S есть
0€РЛ[О, 1)
объединение счетного множества непересекающихся множеств,
каждое из которых измеримо и имеет ту же меру, что и S.
Более того, это объединение совпадает с I, так как S — полное
множество представителей, откуда следует, что если S изме-
римо, то I является объединением счетного множества непе-
ресекающихся измеримых множеств одинаковой меры. Так
как Ц (I) = 2л, то мера ц (S) не может быть положительной.
Но если ц(§) —О, то ц(1) = 0.
Описанный выше процесс можно распространить на более
общие топологические группы, например на компактные
группы, имеющие счетное множество нормальных подгрупп.
(Определения и подробности относительно групп, нормаль-
ных подгрупп и т. д. см. в [19], относительно топологиче-
ских групп см. [29].)
12. Множество D, такое, что для всякого измеримого
множества А справедливы равенства (D П Л) = О,
ц*(/>ПЛ) = ц(Л)
Множество D, обладающее такими свойствами, является,
так сказать, крайне неизмеримым — оно настолько неизмеримо,
насколько может быть неизмеримо множество вообще! Мно-
жество D, как и неизмеримое множество А примера И,
строится при помощи аксиомы выбора, однако в этом случае
построение несколько сложнее. Его можно найти в книге [53],
стр. 74. Этот пример показывает, что всякое измеримое мно-
жество А содержит подмножество, внутренняя мера которого
равна нулю, а внешняя мера равна мере А. Он также пока-
зывает, что всякое множество положительной меры со-
держит неизмеримое подмножество.
Ф. Гельвин построил семейство {EJ, 0t1, попарно
непересекающихся подмножеств интервала [0, 1], каждое
из которых имеет внешнюю меру, равную 1.
13. Множество А меры нуль, для которого любое дей-
ствительное число является его точкой конденсации
Точка р называется точкой конденсации множе-
ства А, если всякая окрестность р содержит несчетное мно-
жество точек из А. Пусть С—канторово множество при-*
124
Глава 8
мера 1. Для любого замкнутого интервала [а, 0], где а < 0,
определим множество С (а, 0) следующим образом:
С (а, 0)={а + (0 — а)х|х£С].
Тогда С (а, 0) — совершенное нигде не плотное множество
меры нуль. Далее, пусть множество В является объедине-
нием всех множеств С (а, 0) для всех рациональных а и 0,
таких, что а < 0. Так как В есть объединение счетного
семейства множеств меры нуль, то оно также является мно-
жеством меры нуль. С другой стороны, так как всякий.
открытый интервал / содержит некоторое множество С (а, 0)
и так как каждое множество С (а, 0) несчетно, то любое
действительное число должно быть точкой конденсации мно-
жества В. (См. [22], стр. 287.)
14. Нигде не плотное множество А действительных чисел
и его непрерывное отображение на замкнутый еди-
ничный интервал [0, 1]
В качестве множества А можно взять любое канторово
множество (примеры 1 и 4), поскольку все канторовы мно-
жества гомеоморфны (пример 23). Мы опишем специальное
отображение <р, используя в качестве А канторово множество
примера 1. Рассмотрим отображение, описанное во второй
части примера 2. Пусть 0, CjC2c3 ...—троичное разложение
произвольного числа х£С, где сл = 0 или 2(и = 1, 2, ...).
Положим
<p(x) = 0,f-^ ...
и будем рассматривать правую часть как двоичное разло-
жение некоторого числа, использующее лишь цифры 0 и 1.
Очевидно, что образом С при отображении <р является
некоторое подмножество интервала [0, 1]. Покажем теперь,
что [0, 1]с<р(С). Для этого возьмем произвольное у £ [0, 1]
и рассмотрим его двоичное разложение
у = 0, bxbj}3 ... 1).
Положим
х=0,(2^)(2^)(2(>з) ....
!) Если число у допускает два разложения в двоичную дробь,
то можно рассматривать оба разложения. — Прим, пере в.
Множества и мера на действительной оси
125
где правая часть рассматривается как разложение числа х
в троичную дробь. Тогда х£С, причем ф(х) = у. Следова-
тельно, [О, 1]<=ф(С). Таким образом, <р(С)—[0, 1]. Нетрудно
доказать и непрерывность отображения ф. Однако это удобнее
установить из геометрических соображений так, как это
сделано в следующем примере, где рассматривается непре-
рывное продолжение отображения ф на весь единичный
интервал [0, 1].
Следует заметить, что отображение ф не является взаимно
однозначным. В самом деле, в этом случае взаимно одно-
значное непрерывное отображение вообще невозможно, ибо С
и [0, 1] не гомеоморфны, а любое взаимно однозначное не-
прерывное отображение одного компактного множества на
другое есть гомеоморфизм. (См. [36], стр. 192.) (Множе-
ство С вполне несвязна, так как связными являются лишь
его одноточечные подмножества, в то время как его полный
образ [0, 1] есть связное множество.) Примером двух точек
множества С, имеющих один и тот же образ, могут служить
точки 0,022000000 ... и 0,020222222 .... ибо их образами
являются соответственно 0,011000000... и 0,010111111 —
= 0,011000000 .... Вообще две точки х} и х2 множества С
имеют один и тот же образ при отображении ф тогда и
только тогда, когда они имеют вид
хг = 0, с^с2 . .. сл2000 ..., а х2 = 0, С]С2 ... сл0222 ....
Другими словами, ф(х1) = <р(х2) тогда и только тогда, когда
Xj и х2 являются концевыми точками одного из интервалов,
которые были удалены при построении множества С. Таким
образом, ф-—возрастающая функция на С и притом строго
возрастающая, если исключить указанные пары концевых
точек. (Ср. пример 30.)
Усилением предыдущей „теоремы существования” является
следующая общая теорема, указывающая на возможные в
метрических пространствах непрерывные и гомеоморфные (то-
пологические) образы канторова множества (а на самом деле
любого канторова множества, см. пр. 23) и его подмножеств
(определение см. во введении к гл. 12): каждое сепара-
бельное метрическое пространство есть непрерывный
образ некоторого подмножества канторова множества.
Каждое компактное метрическое пространство есть не-
прерывный образ канторова множества. Каждое ком-
126
Глава 8
пактное вполне несвязное метрическое пространство есть
гомеоморфный образ некоторого замкнутого подмноже-
ства канторова множества. Каждое компактное вполне
несвязное совершенное метрическое пространство есть
гомеоморфный образ канторова множества. (См. [2],
стр. 119—122.)
15. Непрерывная монотонная функция, производная
которой равна нулю почти всюду
Продолжим функцию предыдущего примера на весь еди-
ничный интервал [0, 1] следующим образом. Если х £ [0, 1] \ С,
то х принадлежит одному из открытых интервалов (а, д'),
удаленных из [0, 1] при построении множества С, и потому
гр (а) = <р (#); положим <р(х) = <р(а) = <р (Z>). Другими словами,
гр постоянна на замыкании каждого интервала, удаленного
при построении множества С. Точнее <р (х) = 1 /2 на интер-
вале [1/3, 2/3]. На интервалах [1/9, 2/9] и [7/9, 8/9] зна-
чения гр равны соответственно 1/4 и 3/4. На интервалах
[1/27, 2/27], [7/27, 8/27], [19/27, 20/27] и [25/27, 26/27] зна-
чения гр равны соответственно 1/8, 3/8, 5/8 и 7/8. Продолжая
этот процесс до бесконечности, мы получим возрастающую
функцию, определенную на [0, 1] и (локально) постоянную
в некоторой окрестности каждой точки множества [0, 1] \ С
(см. рис. 4). Поскольку гр возрастает на [0, 1] и множество
ее значений составляет полный интервал [0, 1], то <р не имеет
скачков. А так как монотонная функция не может иметь
других разрывов, кроме скачков (см. [36], стр. 52, упр. 24.
а также [33], стр. 238), то гр непрерывна. Наконец, по-
скольку гр локально постоянна на открытом множестве
[0, 1] \ С, мера которого равна 1, заключаем, что <р'(х) = 0
почти всюду на [0, 1]. Определенная выше функция назы-
вается канторовой функцией.
Аналогично тому как канторова функция была определена
с помощью канторова множества, можно определить подоб-
ные „канторовы функции", исходя из других канторовых
множеств (положительной меры). Вероятно, простейший способ
определения канторовой функции g, соответствующей задан-
ному на [0, 1] канторову множеству Л, состоит в том, что
сначала g определяют на замыканиях последовательно уда-
ляемых интервалов: на центральном интервале ^(х)=1/2;
Множества и мера на действительной оси
127
на следующих двух интервалах значения g полагаются соот-
ветственно равными 1/4 и 3/4; на следующих четырех интер-
валах значения g полагаются равными соответственно 1/8,
3/8, 5/8, 7/8 и т. д. Тогда на плотном подмножестве
[О, 1 ] \ А интервала [0, 1] функция g является возрастаю-
щей, а ее множество значений (на этом подмножестве) плотно
Рис. 4.
в [0, 1]. Следовательно, функцию g можно продолжить, опре-
делив ее на всем интервале [0, 1] так, что она станет воз-
растающей и непрерывной на [0, 1], а ее множество значений
совпадет с [0, 1].
Используя пример 5 „канторова множества0 из иррацио-
нальных чисел, можно построить функцию А, возрастающую
и непрерывную на [0, 1], множество значений которой совпа-
дает с [0, 1], при этом й'(х) = 0 для каждого рационального
числа х £ [0, 1]. На самом деле, множество значений h(x)
для рациональных х£[0, 1] можно сделать равным множе-
ству Q П [О, 1J всех рациональных точек интервала [0, 1]
128
Глава 8
вместо множества точек вида ш/2", как в предыдущих слу-
чаях. Таким образом, мы получим функцию, удовлетворяю-
щую требованиям примера 11(g) гл. 1.
Непрерывная строго монотонная функция с производной,
равной нулю почти всюду, рассматривается в примере 30.
16. Топологическое отображение замкнутого интервала,
не сохраняющее измеримость н нулевую меру
Пусть <р — канторова функция примера 15. Определим
на [0, 1] функцию ф следующим образом:
ф (х) = x-j-(p (х), о<;х<;1.
Множество значений этой функции есть интервал [0, 2]. Так
как <р возрастает и непрерывна на [0, 1], то отображение ф
строго возрастает и является топологическим на [0, 1] (т. е.
непрерывно, взаимно однозначно и имеет непрерывное обрат-
ное отображение, определенное на множестве значений ф).
Далее, поскольку всякий открытый интервал, удаленный
из [0, 1] при построении канторова множества С, отобра-
жается функцией ф на некоторый интервал такой же длины
из [0, 2], то Ц(ф(/ \ С))=ц(/ \ С)= 1 ’), откуда ц(ф(С))= 1.
Но мера множества С равна нулю, и мы получили, таким
образом, пример топологического отображения ф, которое
отображает множество меры нуль на некоторое множество
положительной меры. Пусть теперь D — неизмеримое под-
множество множества ф.(С) (см. пример 12). Тогда ф-1(Д) —
подмножество множества С меры нуль, и потому оно также
имеет меру нуль. Следовательно, ф является примером топо-
логического отображения, которое отображает измеримое мно-
жество на неизмеримое.
Ниже будет рассмотрен еще один подобный пример
(см. пример 23).
17. Измеримое неборелевское множество
Множество ф-1(£)) примера 16 измеримо, но поскольку
оно является образом неборелевского множества D при топо-
логическом отображении, то ф-1(Д) не является борелевским
множеством (см. [54]),
J) Здесь / = [0, 1]. — Прим, перед.
Множества и мера на действительной оси
129
18. Две непрерывные функции, разность которых не
является постоянной, но их производные (конечные
или бесконечные) совпадают всюду
Этот пример построил Рей Пастор [40] (см. также [9],
стр. 133). Пусть <р — канторова функция примера 15. На еди-
ничном интервале [0, 1] определим функцию /z(x) следующим
образом. На канторовом множестве С положим ее равной
нулю, а на каждом открытом интервале (а, Ь), удаленном
при построении множества С, определим h (х) так, чтобы ее
график состоял из двух конгруэнтных полуокружностей
с диаметром на оси х, причем одна полуокружность распо-
ложена над осью х на левой половине (a, Z>), а другая—под
осью х на правой половине (а, Ь):
h (х)=
За + b \2i>/2
4 ) J
Г/й — а\2 / д4-Зй\2-|>/2
если
если
, ,а4-Ь
Функция h непрерывна всюду на интервале [0, 1]. Далее
положим / (х) == 2<р (х) 4- h (х) и g (х) ss гр (х)-|- й(х). Тогда
//(x) = g'(x) для 0<^хД1. В самом деле, если х при-
надлежит кантОрову множеству С, то f' (х) = g' (x) = -j-°°-
Если же х — средняя точка некоторого интервала, удален-
ного при построении множества С, то f'(x) = g'(х) =— оо.
Наконец, для остальных точек х£[0, 1 ] \ С имеем //(х) =
= g'(х) = h'(х). С другой стороны, /(х) — g(x) = (p(x),
а функция q>(x) не является постоянной.
19. Множество полной меры1) и первой категории на [О, I]
Первый пример', пусть А„ — канторовы множества на
[О, 1] меры (и—1)/я, п = 1, 2, .... и пусть А = Д U А2 U ... .
Так как множества Д(/г=1, 2, .. .) нигде не плотны, то
множество А первой категории. С другой стороны, поскольку
р(Д) = -^=1<р(Д<1
для «=1, 2....то ц(Д=1.
’) Если мера множества Е с. [а, Ъ] равна Ь — а, то говорят,
что это множество полной меры на [а, й]. — Прим, перев.
9 Зак. 587
130
Глава 8
Второй пример-, множеством такого же типа является
дополнение до единичного интервала множества из второго
примера п. 20.
20. Множество меры нуль и второй категории на [0, 1]
Первый пример-, пусть А — множество первого примера
из п. 19. Тогда его дополнение А' — [0, 1] \ А есть мно-
жество второй категории (если бы оно было множеством
первой категории, то интервал [0, 1] являлся бы объедине-
нием двух множеств первой категории и потому также был бы
множеством первой категории) и меры нуль (ц([0, 1]\Л)-|-
+ ц(А)=1).
Второй пример-, пусть Q П [0, 1] есть множество значе-
ний последовательности {гл), и пусть через Ikn, где k и п—
произвольная пара натуральных чисел, обозначен открытый
интервал длины < 2—содержащий точку гп. Положим
4-со
Дб = (J 1кп и Bk = [Q, 1]\Aft. Тогда Ak—открытое мно-
Л=1
жество, содержащее Q ПЮ, 1] и имеющее меру p(Aft)<2
и потому Bk—компактное нигде не плотное множество меры
1—2“*. (Мера Ак не превосходит суммы длин ин-
тервалов Ikn, л=1, 2, .. ., а Вк не имеет внутренних точек,
ибо оно состоит лишь из иррациональных точек.) Следова-
+ со
тельно, множество В= (J Bk есть подмножество [0, 1] пол-
ной меры и первой категории, и потому множество А =
4-00
= Р|ДЙ = [О, 1]\В есть подмножество [0, 1] меры нуль
ы
и второй категории.
21. Множество меры нуль, не являющееся множеством
типа F„
Первый пример-, рассмотрим множество первого примера
из п. 20. Оно не может быть объединением счетного мно-
жества замкнутых множеств Рь F2, .... В самом деле,
в противном случае каждое множество Fn было бы замкнутым
множеством меры нуль и, следовательно, нигде не плотным.
Множества и мера на действительной оси
131
Но это означало бы, что рассматриваемое множество было бы
множеством первой категории. (Противоречие.)
Второй пример-, множество второго примера из п. 20
(по тем же причинам) также обладает требуемыми свойствами.
Третий пример: неборелевское множество примера 17
имеет меру нуль, однако оно не может быть множеством
типа Fa, ибо всякое множество типа Fa является борелевским.
22. Множество меры нуль, такое, что не существует
функции (интегрируемой по Риману или нет), для
которой это множество является множеством точек
разрыва
Любое множество примера 21 обладает требуемым свой-
ством, поскольку для всякой функции, отображающей R в R,
множество точек разрыва является множеством типа Fa
(см. гл. 2, пример 23, а также гл. 4, пример 8).
Настоящий пример представляет особый интерес в связи
со следующей теоремой: действительная функция, опре-
деленная и ограниченная на компактном интервале,
интегрируема на нем по Риману тогда и только тогда,
когда множество ее точек разрыва имеет меру нуль
(см. [38], стр. 153, а также [33]*, стр. 145). Невнимательное
чтение этой теоремы может привести к неправильному пред-
ставлению, будто каждое множество меры нуль может быть
множеством точек разрыва некоторой интегрируемой по Ри-
ману функции, поскольку это условие и необходимо, и до-
статочно.
23. Два совершенных нигде не плотных гомеоморфных
множества на [0, 1], лишь одно из которых имеет
меру нуль
Мы докажем несколько больше, а именно если С — кан-
торово множество меры нуль на [0, 1] и А—любое канто-
рово множество положительной меры на [0, 1], то сущест-
вует гомеоморфизм / интервала [0, 1] на [0, 1], такой, что
/ (С) = А. Непосредственным следствием этого результата
является утверждение, что все канторовы множества гомео-
морфны.
Идея, лежащая в основе, построения этого отображения,
подобна той, которая использовалась при построении канто-
0*
132
Глава 8
ровой функции (пример 15). Расположим „в одинаковом по-
рядке" интервалы /]( /2, . . . и интервалы J2....удален-
ные из [0, 1] при построении множеств С и А соответственно.
Это означает, что Zj и Jj являются средними интервалами,
удаленными на первом шаге, /2 и Л—„левыми средними".
Рис. 5.
а /3 и J3—„правыми средними" интервалами, удаленными на
втором шаге, и т. д. Затем с помощью возрастающей линей-
ной функции отобразим замыкание 1п на замыкание Jn
(/г=1, 2, ...). Тогда / определена и строго возрастает на
всюду плотном подмножестве интервала [0, 1], и так как при
этом множество ее значений также всюду плотно на [0, 1],
то f можно непрерывно продолжить на [0, 1], как это опи-
сано во второй части примера 15 (см. рис. 5). Построенная
таким образом функция f является функцией такого же типа,
как и функция примера 16.
Множества и мера на действительной оси
133
24. Два непересекающихся непустых нигде не плотных
множества действительных чисел, таких, что каждая
точка любого из них является предельной точкой
другого
Пусть А — произвольное канторово множество на [0, 1],
а В — подмножество А, состоящее из всех концевых точек
открытых интервалов, которые были удалены из [0, 1] при
построении А. Тогда множества В и Е = А\ В удовлетво-
ряют требуемым условиям.
Если рассматривать не только подмножества системы R,
то подобные примеры строятся очень просто. Например,
требуемым условиям удовлетворяют следующие два множе-
ства на евклидовой плоскости: множество на оси х с рацио-
нальными первыми координатами и множество на оси х
с иррациональными первыми координатами.
25. Два гомеоморфных множества действительных чисел,
являющихся множествами разных категорий
Определим на [0, 1] возрастающую непрерывную функ-
цию, подобную канторовой функции, построенной во второй
части примера 15. Пусть {/„}—описанная в примере 23
последовательность открытых интервалов, удаленных из [0, 1]
при построении канторова множества А, а {хл}—взаимно
однозначное отображение N на Q Л (0, 1). Определим после-
довательность {гл} следующим образом: положим rj^slt
r2 = s„, где п — наименьшее натуральное число, такое, что
sn < /-j; rz~sn, где п — наименьшее натуральное число, такое,
что sn > Гр Далее положим r4 = sn, где наименьшее натураль-
ное число, такое, что sn < r2; r5 = sn, где п — наименьшее на-
туральное число, такое, что r2 < sn < Гр г6е=хл, где /г —наи-
меньшее натуральное число, такое, что r4 < sn < r3; r7~sn,
где п—наименьшее натуральное число, такое, что sn > г3. Если
продолжить этот процесс, то рациональные числа, заключен-
ные между 0 и 1, будут занумерованы в последовательность
{гл} таким образом, что их отношение порядка будет соот-
ветствовать отношению порядка последовательности интерва-
лов Jn, как это указано на рис. 6. Другими словами, гт<гп
тогда и только тогда, когда Jm лежит левее Jn. Определим
теперь функцию /, положив / (х)=г„, если х принадлежит
замыканию Jn интервала Jn, /г = 1, 2.....Тогда, как и
в примере 15, функция / определена и возрастает на плотном
134
Глава 8
подмножестве интервала [0, 1], а множество ее значений
плотно в [0, 1]. Следовательно, ее можно продолжить до
непрерывной возрастающей функции, отображающей [0, 1]
на [0, 1]. Если теперь определить множества В и Ё так,
как в примере 24, то функция f отобразит В на множество
Q Г1 (0, 1), а Е — на множество (О, 1)\Q всех иррациональ-
ных чисел, заключенных между 0 и 1. Отображение Е на
(О, 1)\Q является строго возрастающим и бинепрерывным.
(Непрерывность обратного отображения следует из того,
что при отображении ,Е на (0, 1) \ Q сохраняется отношение
в 9 ЮН 12 13 74 15
I—----1--------1—;—।---1--1-1----1--1
Z7 Г4 гг Г; Г, Гв Г3 Г, 1
J2 ^5 J* ^3 Ji
М-М-----М-М—--------:--------МЧН------М-Н
О '
Рис. 6.
порядка.) Следовательно, Е и (О, 1)\Q гомеоморфны. Таким
образом, всякое канторово множество с удаленными
„концевыми точками" гомеоморфно множеству иррацио-
нальных чисел интервала (0, 1). Но Е нигде не плотно и
потому является множеством первой категории, в то время
как (0, 1) \ Q — множество второй категории (см. пример 7).
Следует заметить, что в отличие от примера 23 гомео-
морфизм, описанный в настоящем примере, не порождается
гомеоморфизмом интервалов, содержащих эти множества. Если
два пространства гомеоморфны и если два множества соот“
ветствуют друг другу при этом гомеоморфизме, то можно
утверждать следующее: если одно из множеств нигде не
плотно, то нигде не плотно и другое; если одно из множеств
является множеством первой категории, то и другое также
является множеством первой категории.
26. Два гомеоморфных множества действительных чисел,
таких, что одно из них всюду плотно, а другое нигде
не плотно
Если в примере 25 под последовательностью {/„} понимать
не последовательность рациональных чисел интервала (0, 1),
Множества и мера на действительной оси
135
а последовательность, исчерпывающую все множество Q,
то мы получим гомеоморфизм между Е и множеством Q'—R \ Q
всех иррациональных чисел. Множество Е нигде не плотно,
а множество Q' всюду плотно. (См. последний абзац при-
мера 25.)
27. Функция, определенная на R, равная нулю почти
всюду и такая, что множество ее значений на каж-
дом непустом открытом интервале совпадает с R
Построение функции /, обладающей указанными свой-
ствами, мы разобьем на несколько этапов. Сначала построим
на открытом интервале (0, 1) функцию g, отображающую
множество С О (0, 1) на R, где С — канторово множество
меры нуль. Если <р — канторова функция (пример 15), то
функцию g можно определить так:
g(x)sstg[n^p(x) — -1)], 0<х<1.
Второй шаг состоит в том, чтобы для произвольно задан-
ного открытого интервала I = (а, Ь) определить подмно-
жество Zj меры нуль и функцию gj с областью определения
Z, и областью значений R. Это можно сделать следующим
образом:
Zj={a--\-(b— a)xjx£Cn(0, 1)},
, ч lx — а\ ,
^(х) = ^^у-—J, x^Z,.
Приступая к построению искомой функции /, положим
ее ..равной нулю на множестве I всех целых чисел. Далее
определим последовательность {£/„} открытых множеств сле-
дующим образом: Ux = R \ 1, т. е. Ux есть объединение
всех открытых интервалов вида (л, п-1- 1), где п — целое
число. Внутри каждого из этих интервалов I определим
множество Z] меры нуль и на нем функцию g, так, как это
сделано выше. На множестве Z, функцию / полагаем рав-
ной gj. Пусть U2 — подмножество Uv на котором / еще
не определена. Тогда U2 — открытое множество/и потому
оно является объединением непересекающихся открытых ин-
тервалов. Внутри каждого из этих интервалов I определим
множество Z; меры нуль и на нем функцию' gt так, как это
136
Глава 8
сделано выше. На множестве Z7 функцию f полагаем рав-
ной gr Пусть [73—подмножество U2, на котором f еще
не определена. Тогда (73 также является открытым мно-
жеством и потому является объединением непересекающихся
открытых интервалов. Если снова определить множества Z,
так, как это сделано выше, то функцию f можно продолжить
и на эти множества меры нуль. Продолжая этот процесс,
получаем последовательность {(7„) открытых множеств, до-
полнение каждого из которых имеет меру нуль. Таким образом,
функция / будет определена на некотором множестве меры
нуль, а именно на дополнении пересечения множеств Uv
U2, .... или, что то же самое, на объединении их дополне-
ний Ui, U2, . При этом каждый непустой открытый
интервал содержит по крайней мере один из открытых ин-
тервалов I, составляющих открытые множества Uп, и потому
некоторое множество Z,, на котором множество значений /
совпадает с R. Наконец, положим функцию f равной нулю
в тех точках, в которых она еще не определена.
28. Функция, определенная на R, график которой всюду
плотен на плоскости
Этим свойством обладает функция примера 27.
29. Неотрицательная всюду конечная функция f, такая,
ь
ЧТО J /(Х) rfx=4-oo для любого непустого открытого
а
интервала (а, Ь)
Функцию, обладающую этими свойствами, можно по-
строить, используя метод примера 27. Однако в этот метод
нужно внести следующие изменения: (i) множество С следует
заменить канторовым множеством меры 1/2 на [0, 1] и (ii)
функцию gj положить равной
£/(*) = руХ(2/)-
где |/ I обозначает длину интервала /, а х(А)—характери-
стическую функцию множества А (см. введение к гл. 1).
Каждое множество Z7 имеет меру у | /1, и поэтому интеграл
Множества и мера на действительной оси
137
от g, по I равен 1/(21/|). Так как каждый непустой интер-
вал (с, d) содержит подинтервалы I произвольно малой длины,
d
то интеграл J f(x)dx равен -ф-оо.
с
30. Непрерывная строго монотонная функция с производ-
ной, равной нулю почти всюду
Функцию /, обладающую этими свойствами, впервые по-
строили А. К. Цаанен и В. А. Дж. Люксембург [59]. Пусть <р—
канторова функция примера 15. Положим ф(х)^<р(х), если
х£[0, 1], и ф(х)^0, если x£R\[0, 1]. Далее, пусть
[а„, £>„]}—последовательность замкнутых интервалов [0, 1],
о, yj, |д, 1J, [0, j], [j, .....[о, g-], .... Иско-
мой функцией будет ')
/(х)= V 2~M^M 0<х<1.
\ ип ап /
л=1
31. Ограниченная полунепрерывная функция, не интегри-
руемая по Риману и не эквивалентная никакой функ-
ции, интегрируемой по Риману
Характеристическая функция / любого канторова множе-
ства А положительной меры на [0, 1] ограничена и всюду
полунепрерывна сверху. Но так как множество ее точек
разрыва есть А и мера множества А положительна, то f
*) Приведенный пример функции f (х) некорректен, так как f (х)
разрывна и не монотонна. Это вытекает из того, что указанный
ряд сходится равномерно и потому
тогда как
ЙЙ /(х)>1фЩ + ±ф(1)=1, /(0)=0,/(1)>|.
Корректный пример см. в [45]*, стр. 155. — Прим, ред.
138
Глава 8
не интегрируема по Риману на [О, I]1). Две функции назы-
ваются эквивалентными, если их значения совпадают
почти всюду. Если значения функции f изменить на некотором
множестве меры нуль, то множество точек разрыва вновь
полученной функции также будет иметь положительную меру.
32. Ограниченная измеримая функция, не эквивалентная
никакой функции, интегрируемой по Риману
Этим свойством обладает функция примера 31.
33. Ограниченная функция, являющаяся пределом моно-
тонной последовательности непрерывных функций,
не интегрируемая по Риману и не эквивалентная
никакой функции, интегрируемой по Риману. (См.
пример 10 гл. 4.)
Представим функцию / примера 31 как предел убываю-
щей последовательности {/„} непрерывных функций следую-
щим образом. Для любого открытого интервала [ =(а, Ь),
где 0 а < b 1, и для любого натурального п определим
функцию
1, если
1, если
0, если
линейна, если
линейна, если
Если теперь {/„}—последовательность открытых интервалов,
удаленных из [0, 1] при построении канторова множества А
положительной меры (см. пример 23), то искомая после-
довательность {/„) определяется так:
Л — &1, J,'
' S 2, j2.
') См. введение к гл. 4. — Прим, перев.
Множества и мера на действительной оси
139
34. Интегрируемая по Риману функция f и непрерывная
функция g, определенные на [0, 1] и такие, что их
композиция /(g’(x)) не интегрируема по Риману на
[О, 1] и не эквивалентна никакой функции, интегри-
руемой по Риману на этом замкнутом интервале.
(См. пример 9 гл. 4.)
Представим функцию примера 31 в виде f(g(x)). Для
этого положим f(x) = 0 для 0<^х<1 и /(х)—1 для
х=1. Далее положим g(x)—1, если х^А, и g(x) =
= 1 —~(b — а)-|-|х— у (а -|- Ь) |, если х принадлежит
какому-либо интервалу I — (а, Ь), удаленному из [0, 1] при
построении А. Функция g(x) непрерывна, ибо для любых
Xj и х2 из [О, 1] имеет место неравенство | g (xj— g'(x2)|<f"
<|Х1— х2|.
Заметим, что функции f п примера 33 и функцию g при-
мера 34 можно заменить бесконечно дифференцируемыми
функциями. Этого можно добиться, если функции g^ при-
мера 33 и функции, составляющие функцию g примера 34,
заменить бесконечно дифференцируемыми. Для этой цели
можно использовать функции такого же типа, как и в при-
мере 12 гл. 3.
Наконец, следует отметить, что функции f и g в настоя-
щем примере нельзя поменять местами. Другими словами,
всякая непрерывная функция (заданная на компактном интер-
вале) от функции, интегрируемой по Риману, также инте-
грируема по Риману. (См. [38], стр. 153, упр. 55.)
35. Ограниченная функция, имеющая примитивную на
замкнутом интервале, но не интегрируемая на нем
по Риману
Определим функцию g для положительных х формулой
g(x) = х2 sin (1/х). (См. пример 2 гл. 3.) Далее для всякого
положительного числа с обозначим через хс наибольшее по-
ложительное число х, не превосходящее с и такое, что
gz(x)=0. Наконец, для 0<х<^с Определим функцию'
g (х), если 0 < х хс,
g(xc), если х^^Сх^с.
140
tлава 8
Пусть А — какое-либо канторово множество положитель-
ной меры на [0, 1]. Определим функцию / следующим обра-
зом: если х£А, то положим / (х)^0; если же х принад-
лежит какому-либо интервалу I = (а, Ь), удаленному из [0, 1]
при построении А, то положим
gc (х — а), если
[ х + Ь), если
а < х (а Z>),
у (а + ^)< х < Ь,
1 /А
где с = -^(Ь — а).
Если х—какая-либо точка множества А, а у—какая-
либо другая точка из [0, 1], то либо /(у) = 0, либо у при-
надлежит некоторому удаленному интервалу I = (а, Ь).
В первом случае | (/ (у) — f (х) )/(у—х) | = 0 < | у — х|.
Во втором же случае, обозначив через d тот конец интер-
вала (а, Ь), который ближе к у, имеем при с=-^-(Ь — а):
god У —d
y — d
=|y-rf|
у — d | * 1
Следовательно, в обоих случаях | (/ (у) — /(х))/(у — х)|<^
| У — х\, и потому f'(x) = 0 для каждого х£А.
С другой стороны, если х принадлежит какому-либо уда-
ленному интервалу (а, Ь), то
I f' (х) К | 2г sin (у) — cos (1) J < 3,
где z — некоторое число между 0 и 1. Таким образом, f диф-
ференцируема всюду на [a, 6] и ее производная f' ограни-
чена на этом интервале.
Наконец, учитывая, что lira g/(y)=l (см. введение
у->+ о
к гл. 2), заключаем, что для всякой точки х множества А
справедливо равенство lim /'(у)=1. Следовательно, функ-
у->х
Множества и мера на действительной оси
141
ция f разрывна в каждой точке множества А, т. е. на мно-
жестве положительной меры. Таким образом, функция f' удо-
влетворяет всем требуемым условиям.
Построение, подобное описанному выше, было (по-види-
мому, впервые) проведено итальянским математиком В. Воль-
терра (1860—1940 г.); см. Oiorn. di Battaglinl, 19 (1881),
353—372.
36. Функция, для которой существует несобственный
интеграл Римана и не существует интеграл Лебега
Положим f(x)^sinx/x, если х=М и /(0)=1. Тогда
4-со
несобственный интеграл J f(x)dx сходится (см. [36], стр. 465,
о
+ оо
а также [52]*, т. II, стр. 569), однако J | / (х) | dx = 4- сю.
о
Это означает, что функция | f (х) | не интегрируема по Лебегу
на [0, -|-оо), а поэтому не интегрируема и функция /(х).
37. Функция, измеримая по Лебегу и не измеримая по
Борелю
Этим условиям удовлетворяет характеристическая функ-
ция измеримого по Лебегу неборелевского множества. (См.
пример 17.)
38. Измеримая функция/(х) и непрерывная функция g-(x),
такие, что композиция f(g(x)) неизмерима
Применяя обозначения примера 16, положим Е = ф-1(£>).
Тогда характеристическая функция f = -^E множества Е изме-
рима, а функция непрерывна. Однако композиция
этих функций f (g (х)) неизмерима, поскольку она является
характеристической функцией неизмеримого множества D.
Следует заметить, что в этом примере функции f и g
нельзя поменять местами. Другими словами, любая непре-
рывная функция от измеримой функции измерима.
142
Глава 8
39. Непрерывная монотонная функция g'(x) и непрерыв-
ная функция f(x), такие, что
1 1
J f(x) dg (х) J f(x) g' (х) dx
о о
Пусть /(х)=1 на [0, 1], и пусть g — канторова функ-
ция примера 15. Тогда интеграл Римана — Стильтьеса (см.
[38], стр. 179, а также [33]*, стр. 249) или интеграл Ле-
бега— Стильтьеса (см. [30], [31] и [53]), стоящий в левой
части, равен <р(1) — <р(0) = 1, в то время как интеграл Ле-
бега, стоящий в правой части, равен 0, ибо подинтеграль-
ная функция почти всюду равна 0.
40. Различные виды сходимости функциональных после-
довательностей
Пусть функции /р /2’ /з- • • • заданы и интегрируемы
по Лебегу либо на единичном интервале [0, 1], либо на мно-
жестве всех действительных чисел R (в более общем случае
эти функции могут быть заданы и интегрируемы по Лебегу
на измеримом множестве конечной или бесконечной меры).
Тогда существует много способов интерпретации равенства
lim fn — f-
Мы рассмотрим здесь четыре специальных вида сходимости
и укажем включения, которыми они связаны. В тех случаях,
когда включения отсутствуют, мы приведем соответствующие
контрпримеры.
Пусть одна и та же буква S обозначает либо [0, 1], либо R
в зависимости от того, где заданы рассматриваемые функ-
ции. Мы рассмотрим четыре интерпретации упомянутого
выше предельного равенства.
(1) Сходимость почти всюду1):
lim /л(х) = /(х) для почти всех x£S.
п -> 4- со
’) С этим видом сходимости тесно связана сходимость всюду
которая является частным случаем сходимости типа (1).
Множества и мера на действительной оси
143
(ii) Сходимость по мере:
Ve > 0, lim р, {х 11 fn (х)— /(х)|>е}=0.
л->4-со
(iii) Сходимость в среднем1):
Hm f |/«(х)~ 7(*)|dx = 0.
(iv) Сходимость с интегрируемой мажоран-
той2):
Последовательность {/„ (x)} сходится почти всюду и суще-
ствует интегрируемая по Лебегу функция g, такая, что
|/n(x)|<(|g'(x)| Для « = 1. 2, .. . и почти всех xgS.
Сформулируем сначала два утверждения относительно
включений, связывающих сходимости видов (i) — (iv). Если
мера S конечна, то
(lv) {(Ш) }=»<|1)-
Если же мера 5 бесконечна, то
f (О
<i',)=»l (Ш)^(В).
(См. [30], [32] и [53].)
Приведем теперь примеры, которые показывают, что дру-
гих включений, кроме указанных выше, не существует. Все
эти примеры, кроме последнего, будут справедливы как для
случая конечной, так и для случая бесконечной меры, поскольку
все участвующие в них функции равны нулю для x£R\ [0,1].
>) Это есть сходимость в банаховом пространстве L' всех инте-
грируемых функций, среди которых отождествлены те, которые
совпадают почти всюду. Этот вид сходимости можно обобщить,
рассмотрев сходимость в банаховом пространстве Lp измеримых
функций, которые интегрируемы вместе с р-й степенью их модуля.
(В этом случае также отождествляются функции, совпадающие
почти всюду.) Дальнейшие подробности см. в [17], [29], [32] и [53].
2) Можно определить еще один вид сходимости, а именно схо-
димость с интегрируемой мажорантой в Lp; для этого (Ш) заме-
няется сходимостью в Lp и требуется выполнение неравенства
I fn (х) | < | g (х) |, где g£Lp.
144
Глава 8
(i) (iii). Достаточно положить /(х) = 0 для всех
а
( п, если 0 < х < 1/п,
| о, если (о, 1/п),
для п = 1, 2, ....
(i)^(iv). В самом деле, так как (iv)=^(iii), то требуе-
мое утверждение вытекает из предыдущего.
(iii) ЙИО- Пусть /(х) = 0 для всех x£R. Представим
каждое п £ N в виде п — 2ъ^гт, где 0 т < 2k, k — 0, 1........
Тогда k и т однозначно определяются числом п. Положим
, т . , т 4- 1
1, если — X < --------!,
2* 2*
О для остальных х £ R.
Тогда j |/л(х) — f(x)\dx — 2 >0 при я->-|-оо, однако
s
lim fn(x) не существует ни для какого х £ [0, 1].
д->+оо
(iii) 7т> (iv). Так как (iv)^(i), то требуемое утвержде-
ние вытекает из предыдущего.
(ii)^(i). Воспользуемся примером, опровергающим вклю-
чение (iii)=^(i). Для функций fn этого примера и для
любого положительного е имеем
ц{х||/„(х) — /(%)|>е)<(2 *—>0 при п—
(ii) (iii). Пусть f (х) = 0 для всех x£R, и пусть
для всякого п £ N числа k и т определены так, как в примере
для утверждения (iii) (i). Положим
ck т ' ' т -4-1
2В, если — < х <4---------!— ,
2к 2к
О для остальных х £ R.
Тогда для любого положительного е
ц(х||/л(х)— /(х)| > е) С2 *—>0 при л->4-оо,
однако
/nW — f(x)\dx = 1 -/*0 при 71->-|-оо.
s
Множества и мера на действительной оси
145
(ii)^(iv). Так как (iv)=^(i) и (1у)=ф(ш), то требуе-
мое утверждение вытекает из доказанных ранее, а именно
из того, что (ii)^(i), или того, что (ii)^(iii).
Наконец, приведем пример, в котором множество 5 = R
имеет бесконечную меру.
(От^(Н). Положим для всех и
( 1, если /г < х <</г-I-1,
J ' [0 для остальных x£R.
41. Две меры ц и v на пространстве с мерой (X, S),
такие, что ц абсолютно непрерывна относительно v,
однако не существует функции f, удовлетворяющей
равенству ц (Е) = J/(х) dv (х) для всех Е£(5
Е
Пусть X = R, а <$ —класс всех подмножеств простран-
ства X. Для всякого множества Е £ <5 положим
{О, если Е счетно,
-|-оо, если Е несчетно,
{п, если Е состоит из п точек, п О,
4-оо, если Е бесконечно.
Тогда v(E) = O=^E=0 и, следовательно, ц(Е) = О. Таким
образом, ц абсолютно непрерывна относительно v. С другой
стороны, если / такова, что
Н(£)= J /(x)dv(x)
Е
для всех множеств Е, то это равенство справедливо, в част-
ности, когда Е — {у} — произвольное одноточечное множество.
В этом случае
ц (Е) = 0 = J f (х) dv (х) = / (у).
Е
Но это означает, что функция f тождественно равна нулю
и, следовательно, ц(Е) = О для любого Е£®. (Противо-
речие.)
10 Зак. 587
146
Глава 8
Если принять, что ± оо • 0 равно 0, то справедливо
следующее утверждение: если f — неотрицательная дей-
ствительнозначная функция в широком смысле, измери-
мая относительно меры, v на пространстве с мерой
{X, <S), и если
Н (£) = / f W dv (х)
Е
для всех измеримых множеств Е, то ц является мерой
на (X, (©), абсолютно непрерывной относительно v. Пре-
дыдущий контрпример показывает, что без ограничений об-
ратная теорема не верна. Теорема Радона — Никодима (см. [53])
указывает ограничения, при которых обратная теорема имеет
место.
ГЛАВА 9
ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Введение
В этой главе предполагаются известными понятия непре-
рывности и дифференцируемости функций двух переменных,
а в двух последних примерах, кроме того, предполагается,
что читатель знаком с криволинейными интегралами, одно-
связностью областей и векторным анализом. Если / (х, у) —
дифференцируемая функция двух переменных х и у, то ее
частные производные мы будем обозначать следующими сим-
волами:
j5 = /x(*’ У) = /1(х- У). = y) = f2(x, у),
5г = fxx (х, У) = /11 у). ~^=fxy У)=/12 (X, у)....
Областью называется любое непустое открытое мно-
жество R, любые две точки которого можно соединить ло-
маной линией, целиком лежащей в R.
1. Разрывная функция двух переменных, непрерывная
по каждой переменной в отдельности
Пусть функция /(х, у) с областью определения RXR
определена следующим образом:
/(х, у)=
—> если х2 + у2¥=0,
О, если х = у = 0.
Тогда f разрывна в начале координат, поскольку в произ-
вольно малой окрестности точки (0, 0) существуют точки
вида (а, а), в которых значение функции равно 1/2. С дру-
гой стороны, для всякого фиксированного значения у (рав-
ного нулю или отличного от нуля) функция g(x) = /(x, у)
10*
148
Глава 9
является всюду непрерывной функцией переменной х. По
той же причине f(x, у) является непрерывной функцией
от у для всякого фиксированного значения х.
2. Функция двух переменных, не имеющая предела в на-
чале координат, но имеющая равный нулю предел
при приближении к началу координат по любой прямой
Пусть функция f(x, у) с областью определения RXR
определена следующим образом:
/(х, у) =
если х2 + у2 =£ О,
О, если х = у = О,
и пусть L — произвольная прямая, проходящая через начало
координат. Если L — какая-либо координатная ось, то функ-
ция f(x, у) на L тождественно равна нулю и, следовательно,
имеет предел, равный 0, когда (х, у) ->(0, 0) вдоль L. Если
же L — прямая вида у = тх, то на L при х 0 имеем
,. ч тх3 тх
f (х, тх) — xi т2х2 —
Следовательно, lim/(x, mx) = 0. Однако, несмотря на это,
х->0
функция f (х, у) разрывна в точке (0, 0), ибо в произвольно
малой окрестности точки (0, 0) существуют точки вида (а, а2),
в которых функция f принимает значение, равное 1/2.
3. Обобщение предыдущего примера
Пусть функция f (х, у) с областью определения R X R
задана формулой
—. - , если х =^= 0,
/(х, у)= e~w + y2
0, если х = 0.
Далее пусть С — проходящая через начало координат кри-
вая вида хт — (у/с)л, т. е. у = схт1п, где тип — взаимно
простые натуральные числа, а с — постоянная, отличная
от нуля (в случае четного п предполагается, что х 0).
Функции двух переменных
149
Тогда, если точка (х, у) приближается к началу координат
вдоль С, то
гр-1!х\-т/п
(См. пример 10 гл. 3.) Но несмотря на то что предел функ-
ции /(х, у), когда точка (х, у) стремится к началу ко-
ординат вдоль любой алгебраической кривой вида у — схт'п,
равен нулю, функция /(х, у) разрывна в начале координат.
В самом деле, в произвольно малой окрестности начала ко-
ординат существуют точки вида (а, е~1/а2), в которых функ-
ция f принимает значение, равное 1/2,
4. Разрывная (и, следовательно, недифференцируемая)
функция двух переменных, имеющая всюду частные
производные первого порядка
Этим свойством обладает каждая из функций, рассмотрен-
ных в трех предыдущих примерах.
б. Функции /, для которых существуют и равны лишь
два из следующих пределов:
lim f(x, у), lim lim/(x, у), lim lim/(x, у)
(X, Ь) х->а у+Ь у->Ь х->а
Обозначим вышеуказанные пределы через (i), (ii) и (iii)
соответственно. Каждая из следующих ниже функций такова,
что для нее указанный предел не существует, но два других
предела существуют и равны между собой.
(i) Пример 1, где (а, Л) = (0, 0).
( у-|-х sin (1/у), если у =£ 0,
(ii) /(х, у)==Ц „ „
v ( 0, если у = 0,
при этом (а, Ь) = (0, 0).
( х 4-У sin(l/x), если х 0,
(iii) /(X, у)= . .
v ( 0, если х==0.
при этом (а, &) = (0, 0).
150
Глава 9
В примерах (ii) и (iii) имеем
1/(*. у) I < | X | + I у I < 2 (х* + /)1/2
и, следовательно, lim f(x, у) = 0. Тот из повторных пре-
(х, у)->(0, 0)
делов, который существует в примерах (ii) или (iii), равен 0.
Следует заметить, что если оба предела (i) и (ii) суще-
ствуют, то они должны быть равны. То же самое справе-
дливо и для пределов (i) и (iii). (См. [36], стр. 184,
а также [52]*, т. I, стр. 361.)
6. Функции /, для которых существует лишь один из
следующих пределов:
lim f(x, у), lim lim f(x, у), lim lim/(x, у)
(x,.y)->(a, ft) A:->a
Как и в примере 5, обозначим три вышеуказанных предела
через (i), (ii) и (iii) соответственно. Каждая из следующих
ниже функций такова, что указанный предел существует,
а два других нет:
[ xsin(l/y) + y sin (1/х), если ху =# 0,
(1)/(х. 0, ес„„х, = 0.
при этом (а, Л) = (0, 0).
(ii) fix, у)==
+ ysin(l/x), если х =£ 0,
0, если х = 0,
при этом (а, 'Ь) = (0, 0).
(iii) f(x, У) =
sin(l/y), если у 0,
0, если у —0,
при этом (а, Ь) — (0, 0).
Функции двух переменных
151
7. Функция для которой пределы lim lim/(x, у)
х->а у+Ь
и lim lim/(x, у) существуют, но не равны между
х+а
собой
Положим 1*2 ____ v2 о , „2 . если x2-f-y2=#0,
/(х, у)== -*2 + У 0, если х = у = 0.
Тогда
/ 1*2 \
lim lim/(x, y) = lim(—1 = 1,
х->0 у>0 х->0 \ х '
limlim/(x, y) = lim(-----—Л ——1.
у->0 х->0 у->0 ' У '
8. Функция f(x, у), для которой предел lim/(x, у) =
Х->0
—g(x) существует равномерно относительно х, предел
lim/(x, y) — h(y) существует равномерно относительно у,
х->0
lim g(x) = lim h (у), однако предел lim f(x, у) не суще-
х->0 _у->0 (х, у)->(0,0)
ствует
Положим
{ 1, если ху =# 0,
/(X, у)^
[ 0, если ху = 0.
Тогда
sslirn/(х, у) = < 1, если х '=# 0,
g(x)
у->о 1 . о> если х — 0,
А (у) = lim/(х, Г 1, если У ¥=0,
х->0 j если у = 0,
причем оба предельных соотношения выполняются равномерно
относительно всей системы действительных чисел. Но так
как в произвольно малой окрестности начала координат су-
ществуют точки, в которых f равна 0, и точки, в кото-
рых f равна 1, то функция /(х, у) не имеет предела при
(х, у)->(0, 0).
152
Глава 9
Следует заметить, что, согласно теореме Мура — Осгуда
(см. [38], стр. 313), контрпример указанного вида невозмо-
жен, если из области определения функции f исключить точки
вида (0, у) и точки вида (х, 0).
9. Дифференцируемая, но не непрерывно дифференци-
руемая функция двух переменных
Положим
х2 sin (1 /ат) у2 sin (1/у), если ху #= 0,
x2sin(l/x), если х =А 0, а у = 0,
f(x> у) y2sin(l/y), если х = 0, а у =£ 0,
0, если х = у = 0.
Тогда обе частные производные
[ 2xsin(l/x)— cos (1/х), если х =# 0,
/Х(х, у) =
[ 0, если х = 0,
( 2у sin (1/у)— cos(1/у), если у =# 0,
/y(^> У) | д, если y==oj
разрывны в начале координат, и, следовательно, функция f
не является непрерывно дифференцируемой в этой точке.
Однако f дифференцируема всюду. Например, f дифферен-
цируема в точке (0, 0), поскольку при А2-|-А2=#0 прира-
щение f(h, k) — /(0, 0) можно представить в виде
/ДО, 0)А + /у(0, 0)А-|-е1(А, А)А + е2(А, k)k,
где
lim £j(A, k) = lim e2(A, A) = 0.
(Л, *)->(0, 0) (Л, *)->(0, 0)
В самом деле, это представление имеет такой вид:
/(А, А)-/(0, 0) =
^Asin А -|-ДА sin-^J если =/= 0,
^А sin у) А + 0 • А, если А =# 0, а А = 0,
0 • А f A sin у) А, если А = 0, а А #= 0,
Функции двух переменных
153
10. Дифференцируемая функция, имеющая неравные сме-
шанные частные производные второго порядка
Положим
f(x, У) = ХУ %2 4-y2' еСЛИ 0, если х = у = 0.
Тогда х, если х =# 0,
fy(X. 0) = 1- Z(0>k) А lim - - , = 0, если х — 0, k->0 k — у, если у #= 0,
Л(0,У) = lim /°-* — о, если у = 0.
Следовательно, в начале координат имеем
/ (°, 0) = lim ------т-------= hm T = 1,
Л->0 n Л->0 n
, AX I- /х(0. ^) —/x(0, 0) — k
fyx(°- °) = ,Iim—------------=lim—£—=-
1.
k
Функция f непрерывно дифференцируема, так как обе част-
ные производные df/dx и df/dy непрерывны всюду. В част-
ности, df/dx непрерывна в начале координат, поскольку для
л;2 —у2 =£ 0 имеем
1-^-1
I дх |
|х4у + 4х2у3 — №1 +
(*2 + У2)2 (х2 + У2)2
6 (х2 -|- №)’/2.
Настоящий пример станет невозможным, если предполо-
жить непрерывность смешанных частных производных fxy
и fyx в некоторой окрестности начала координат. В самом
деле, имеет место теорема (см. [36], стр. 263, а также [52]*,
т. I, стр. 405): если функция f имеет частные производ-
ные fx и fy в некоторой области R и если смешанная
производная fху (соответственно fyx) существует и не-
прерывна в некоторой точке (а, Ь) области R, то сме-
шанная производная fyx (соответственно fxy) также
существует в точке (а, Ь), причем в этой точке fxy — fyx-
154
Глава 9
li. Непрерывно дифференцируемая функция f двух пере-
менных х и у и область R на плоскости, такие, что
dffdy = 0 в области R, но функция / зависит от у
в этой области
Пусть /, — луч (т. е. замкнутая полупрямая). в плоскости
R X R, т. е.
L={(x, у)| х^> 0, у=0],
a R — область (R X R) \ L. Тогда функция
( х3, если х > 0 и у > О,
/(х, у) = {
[ 0 в остальных точках (х, у) £ R
непрерывно дифференцируема в области R; более того, она
имеет непрерывные частные производные второго порядка.
(Если же х3 заменить на е~1/х\ то f будет иметь непрерыв-
ные частные производные всех порядков.) И хотя частная
производная первого порядка f2(x, у) функции f тождест-
венно равна нулю в области R, функция f зависит от у;
например, /(1, 1)= 1, а /(1, —1) = 0. Можно показать,
что функция, имеющая частные производные первого порядка,
которые тождественно равны нулю в некоторой области R,
постоянна в этой области. (См. [36], стр. 280, а также [52]*,
т, III, стр. 50—55.) Настоящий пример показывает, что следую-
щее рассуждение при доказательстве этого факта было бы
ошибочным: „так как dfjdx = §, то f не зависит от х; так
как dffdy — Q, то f не зависит от у; следовательно, /не
зависит ни от х, ни от у и поэтому должна быть постоян-
ной". Отметим, что в случае когда каждая прямая, параллель-
ная оси у, образует в пересечении с областью R интервал,
утверждение настоящего контрпримера становится невозмож-
ным. (См. [36], стр. 228, упр. 32.)
12. Локально однородная непрерывно дифференцируемая
функция двух переменных, не являющаяся однород-
ной
Функция /(х, у) называется однородной степени п в об-
ласти R, если для всех х, у и положительных X, таких, что
точки (х, у) и (2.x, 2.у) принадлежат R, имеет место равен-
ство /(2.x. 2,у) = 2,"/ (х, у). Функция /(х, у) называется
Функции двух переменных
155
локально однородной степени п в области R, если она
является однородной степени п в некоторой окрестности ка-
ждой точки области R.
Пусть L — луч (т. е. замкнутая полупрямая) в плоскости
R X R:
Zss((x, у)|х = 2, у>0],
a R — область (R X R) \ L- Функция
( И/х, если х > 2 и у > О,
/(х, у)^ Л / У^'
( уЛ в остальных точках (х,
y)£R
непрерывно дифференцируема в R (на самом деле f имеет
непрерывные частные производные второго порядка). Так
как для всякой точки (х, y)£R при Л, достаточно близких
к 1, справедливо равенство /(Хх, Zy) = Z3/ (х, у), то f ло-
кально однородна степени 3 в области R. Однако f не яв-
ляется однородной степени 3 в области R, поскольку для то-
чки (х, у) = (1, 2) и X — 4 имеем /(х, у) — 8, а /(4х, 4у) —
— /(4, 8) = 1024 #= 43 • 8. Вместе с тем функция f не яв-
ляется однородной степени п ни при каком п =# 3, так как
в противном случае она была бы локально однородной сте-
пени п, что, очевидно, невозможно.
13. Дифференцируемая функция двух переменных, не
имеющая экстремума в начале координат и такая,
что ее сужение на любую прямую, проходящую через
начало координат, имеет строгий локальный минимум
в этой точке
Функция
/(х, у)=н(у — х2) (у — Зх2)
нс имеет локального экстремума в начале координат, так как
в произвольно малой окрестности начала координат сущест-
вуют точки вида (0, Ь), в которых f положительна, и точки
вида (а, 2а2), в которых / отрицательна: Рассмотрим суже-
ние функции f на ось х. Мы получим функцию Зх4, кото-
рая имеет строгий абсолютный минимум в точке х = 0. Рас-
смотрим, далее, сужение f на ось у. Получим функцию у2,
которая имеет строгий абсолютный минимум в точке у == 0.
156
Глава 9
Наконец, рассмотрим сужение f на прямую у = тх, прохо-
дящую через начало координат, где 0 < | /и | < 4~оо . Полу-
чим следующую функцию параметра х:
g(x)~f(x, тх) = (тх— х2)(тх— Зл:2) —
— т2х2 — 4 тх3 -ф- 3 х4.
Эта функция имеет строгий локальный минимум в точке
х = О, так как g/(0) = 0, a g" (0) = 2т2 > 0.
14. Обобщение предыдущего примера
Функция
f(.X,
( (у — с-1/х2)(у— Зе-1/*2),
( у2, если х — 0,
если х =# 0,
не имеет локального экстремума в начале координат. (См.
пример 13.) Рассмотрим сужение f на алгебраическую кри-
вую у = схт/п, где т и п — взаимно простые натуральные
числа, ас — постоянная, отличная от нуля (в случае четного
п предполагается, что х 0). Мы получим следующую функ-
цию параметра х:
g(x) = f (х, схт-'л) = (cxm-'« — e-V^2)(cxm/« — Зе-1/*2) —
_ х2т/п [С2 — 4се-1/хгд.-т/л _|_ зе-2/х2д.-2т/л].
Эта функция имеет строгий локальный минимум в точке х = 0,
поскольку множитель х2т/п положителен при х #= 0, а функ-
ция, заключенная в квадратные скобки, имеет положительный
предел с2 при х -> 0.
ь ь
15. Функция/, для которой f(x, y)tfy=# J [^/(х, у)] dy,
а а
хотя оба интеграла существуют в смысле Римана
Функция
/(х, у) =
Д- е~х2/У, если у > 0,
0, если у = 0,
определена в замкнутой верхней полуплоскости у0. Для
любого фиксированного значения у эта функция является не-
прерывной функцией переменного х, а для любого фиксиро*
Функции двух переменных
157
ванного значения х— непрерывной функцией переменного у.
Однако как функция двух переменных она разрывна в точке
(О, 0) (в этом можно убедиться, полагая у — х2). Интегрируя,
получаем
1
g(x~)= J /(х, y)dy — xe~x2
о
для всякого действительного х (включая х = 0), и, следова-
тельно, g' (х) — е-х2(1 —2х2) для всякого действительного х
(включая х = 0). Если х #= 0, то
J /1(х, y)dy=J e-x2/y(^-^dy = e-x\l-2x2).
о о
Если же х = 0, то, принимая во внимание, что ^(0, у) = 0
для всех у (включая у — 0), имеем
1 1
/ /1(0. У)<*У = J = 0.
о о
Следовательно,
1
g'(0)=l #= J А(0. y)dy = Q.
о
Отметим, что все интегралы, которые встречались в данном
примере, — собственные, так как подинтегральные функ-
ции являются непрерывными функциями переменной интег-
рирования.
1 1
16. Функция f, для которой J J f(x, у) dy dx Ф
с с 00
4= f(x, y)dxdy, хотя оба интеграла сущест-
0 о
вуют в смысле Римана
Положим
у-2, если 0<х<у<1,
— х-2, если 0<у<х<1,
/(х, у)=={
0 в остальных точках
( квадрата 0<^х^1, 0<^у~^1.
158
Глава 9
Для 0 .< у < 1 имеем
О Оу
и, следовательно,
1 1 1
J ]"/(*> y)dxdy— J \dy — 1.
0 0 о
Аналогично для 0 < х < 1 имеем
= *- = -1
О Од:
и, следовательно,
1 1 1
J / (х< y)dydx = J (— 1) dx — — 1.
оо о
17. Двойной ряд 5 атп, для которого 2 2 ®тл=#2 2 «тл
т, п т п п т
Пусть (й/м)* где т обозначает номер строки, а п — но-
мер столбца, — следующая бесконечная матрица (см. при-
мер 20 гл. 6):
л 1 1 1 1 1
о 2 4 8 16 32 • • •
1 Л 1 1 1 1
2 и 2 4 8 16 ‘ ’
__± 1 1 1 1
4 “У 0 2 4 8 ’ • •
1 1_ 1 о 1 1
8 4 2 и 2 4 ’ • •
. . . .
Тогда
+оо
2«тя = 2-'"-+ ••• = 2~m+I, /и = 1, 2.......
л-1
Функции двух переменных
159
и, следовательно,
-f-oo -f-оо
2 2 = 1 4“ 2 1-{~2 2 4- =2.
т—1 л = 1
Аналогично
4-оо 4-оо 4-оо
2 2«тя = 2(-2'л+1)--2.
«=1 т=1 я=1
(См. [22], стр. 109.)
18. Дифференциал Рdx-^ Qdy и плоская область R,
в которой Pdx-\~Qdy является локально полным,
но не полным дифференциалом
Выражение
Р dx-\-Q dy,
где Р и Q — функции, непрерывные в некоторой области R
плоскости R X R, называется полным дифференциа-
лом в R, если существует дифференцируемая функция ср,
определенная в R и такая, что
,^Ф==(3
дх ду
всюду в области R. Выражение Рdx-\-Qdy называется ло-
кально полным дифференциалом в области R,
если оно является полным дифференциалом в некоторой ок-
рестности каждой точки области R. Выражение Р dx-\-Q dy
является полным дифференциалом в. некоторой области R
тогда и только тогда, когда для всякой кусочно гладкой
замкнутой кривой С, лежащей в этой области, справедливо
равенство
J Рdx-\-Qdy — Q.
с
(См. [36], стр. 587, а также [52]*, т. III, стр. 50.) Выра-
жение Pdx-]-Qdy, где Р и Q — непрерывно дифференци-
руемые функции, является локально полным дифференциалом
160
Рлава 9
в некоторой области R в том и только в том случае, если
в каждой точке области R справедливо равенство
дР __ dQ
ду дх '
Выражение
Р dx Q dy = х2 у2 dx -j- _|_у2
является локально полным дифференциалом всюду в „про-
колотой плоскости'
у)|х2 + у2 > 0},
так как
дР. = dQ_ у2 —х2
ду дх (х2 + у2)2 ’
если х2-|-у2>0. С другой стороны, Pdx-\-Qdy не яв-
ляется полным дифференциалом в R. В самом деле, если С —
единичная окружность x = cos0, у = sin0, 0-^0 <^2л, то
2л
J Р dx -|- Q dy = J [(— sin0)(— sin 0) —cos2 0] б/0 = 2л =# 0.
с о
Следует заметить, что если область R односвязная
(см. [36], стр. 598), то Р dx-\-Q dy будет полным диффе-
ренциалом в R тогда и только тогда, когда оно будет ло-
кально полным дифференциалом в R. (См. [36], стр. 601.)
19. Соленоидальное векторное поле, заданное в односвяз-
ной области и не имеющее векторного потенциала
Пусть Р, Q и R — непрерывно дифференцируемые функ-
ции в некоторой области W трехмерного евклидова прост-
ранства. Векторное поле (см. [36], стр. 568, а также [52] *,
т. III, стр. 367) Pi Rk называется с о л е н о и д а л ь -
н ы м в области W, если его дивергенция тождественно равна
нулю в этой области:
дР dQ _1_ dR — о
дх “г ду "т" dz ~
Функции двух переменных
161
Если векторное поле F является ротором (см. [36], стр. 572)
некоторого векторного поля G в области W, то векторное
поле О называется векторным потенциалом для F.
Так как дивергенция ротора тождественно равна нулю
(см. [36], стр. 572, а также [52] *, т. III, стр. 375), то лю-
бое векторное поле, имеющее векторный потенциал, является
соленоидальным. Однако обратное утверждение, как показы-
вает следующий пример, неверно. Положим
F ~ (х2 у2 4)"3/2 (xi у/ + zk)
в области
1^={(х, у, z)| х2-]-№ + z1 > 0].
Тот факт, что F является соленоидальным полем, прове-
ряется непосредственным дифференцированием:
{(Х2 + + Z2)-3/2 + _д_ ((%2 + у2 + z2)-3/2 у} + . . . =
= (х2 4- у2 -4- 4)~5/2 [(—2х2 4- У2 4- Z2) 4-
4-(х2 —2у244)4-...] = о.
Наконец, чтобы показать, что поле F не имеет никакого
векторного потенциала О, рассмотрим сферу х2у2z2 = 1.
Если п обозначает единичный вектор внешней нормали
к этой сфере S, то поверхностный интеграл J j F • ndS
s
равен
J J [42 4- № 4- *T3/2 4 + x
s
X (x24-y24- 22)-1/2(xz4- yj 4 zk)dS = j j 1 dS = 4 л.
s
Но, если бы поле F было ротором некоторого векторного
потенциала, то по теореме Стокса (см. [36], стр. 636, 637,
а также [52] *, т. III, стр, 298) поверхностный интеграл
И Зак. 587
162
Глава 9
J J Fn dS по замкнутой поверхности S должен был бы
$
обратиться в нуль. Отметим, что область W односвязна.
(См. [36], стр. 639, 640.)
Односвязность области можно понимать следующим обра-
зом: всякую простую замкнутую кривую, лежащую в этой
области, можно стянуть в точку, не выходя при этом за
пределы области. В случае „проколотой пространственной
области" W данного примера всякую простую замкнутую
кривую, не проходящую через начало координат, можно стя-
нуть в точку в этой области. Для области W причина того
патологического свойства, которое наблюдается в настоящем
контрпримере, состоит в том, что не все сферические по-
верхности— поверхности „типа сферы"—можно стянуть
в точку, не выходя за пределы области W.
ГЛАВА 10
МНОЖЕСТВА НА ПЛОСКОСТИ
Введение
В этой главе предполагается, что читатель знаком с эле-
ментами топологии евклидовой плоскости, включая понятия
ограниченных, открытых, замкнутых, компактных, всюду
плотных и нигде не плотных множеств. Некоторые другие
понятия определяются ниже. Во всех случаях в качестве
пространства рассматривается евклидова плоскость Е2.
Расстояние d(A, В) между двумя непустыми множе-
ствами А и В определяется формулой
d(A, B) = int[d(p, q)\p£A, q£B},
где d(p, q) = [(x2 — *1)2 + (У2~ У1)2]’/2— расстояние между
точками p = (xlt yj) и q = (x2, у2). Таким образом, расстоя-
ние между двумя множествами всегда неотрицательно. Если
множества имеют общую точку, то оно равно нулю. Однако
расстояние между непересекающимися множествами также
может быть равно нулю. Если же множества не пересекаются
и компактны, то расстояние между ними положительно.
(См. [36], стр. 200, упр. 17.) Диаметр б (Л) непустого
множества А определяется формулой
d(X)=sup [d(p, q)\p£A, q^A}.
Диаметр множества всегда неотрицателен и является конеч-
ным тогда и только тогда, когда Л ограничено. Если Л
компактно, то существуют две точки множества А, расстоя-
ние между которыми равно диаметру Л. (См. [36], стр. 200,
упр. 18.)
Замкнутым кругом называется множество вида
{(х, У)|(х — Л)2+(у — А)2<г2}.
где (й, й)— некоторая точка, а г — положительное число.
Если в этом определении неравенство заменить строгим
П*
164
Глава 10
неравенством < , то мы получим определение открытого
круга.
Два непустых множества А и В отделимы, если они
не пересекаются и ни одно из них не содержит предельных
точек другого: Af]B = AflB—0. Непустое множество Е
называется связным, если его нельзя представить в виде
объединения двух непустых отделимых множеств А и В.
Говорят, что множество, содержащее более одной точки,
вполне несвязно, если у него нет других связных под-
множеств, кроме одноточечных множеств. Множество А
называется локально связным, если для любой точки
р £ Л и любой окрестности N этой точки существует такая
окрестность М точки р, что всякая пара точек М принад-
лежит некоторому связному подмножеству из N ’).
Любое непрерывное отображение замкнутого интервала
в Е2 или множество значений этого отображения называется
дугой (в качестве интервала можно взять единичный интер-
вал [0, 1]). В последнем случае, когда дуга рассматривается
как точечное множество, соответствующее отображение назы-
вается параметризацией дуги. Если отображение имеет
вид f (t) = (x(f), У (/)), то функции х(Г) и у(/) называют
параметризующими функциями отображения. Пусть
f (/), a b, — некоторая дуга и а = а0 < < ... < ап —
— Ь; тогда ломаная, составленная из отрезков /(а0)/(а1),
f(ai)f(a2)..../(an-i)f(ап)’ называется ломаной, впи-
санной в данную дугу, а точная верхняя грань длин
rf(/(«o). + /(«2)) + • • • /(«„))
по всем вписанным ломаным называется длиной данной
дуги. Дуга называется спрямляемой, если ее длина ко-
нечна. Для того чтобы дуга была спрямляемой, необходимо
и достаточно, чтобы обе ее параметризующие функции были
функциями ограниченной вариации. (См. [38], стр. 353,
упр. 27.) Дуга /(/), называется замкнутой
кривой, если =
Простая дуга f (t) определяется взаимно однозначным
отображением. В этом случае обратное отображение также
непрерывно, а исходное отображение есть гомеоморфизм.
’) Здесь должна идти речь об окрестностях и связности на мно-
жестве А (см. [54], стр. 171). — Прим. ред.
Множества на плоскости
165
(См. [36], стр. 240.) Если функция y = g(x) непрерывна на
[а, 6], то ее график является простой дугой (с параметриза-
цией х = Л у — g(t), t£[a, 6]). Простой замкнутой
кривой называется дуга f (t), такая, что если область опре-
деления f есть замкнутый интервал [а, Ь], то —
лишь в том случае, когда tx—t2 или {/р t2] = {а, Ь}.
Иными словами, простой замкнутой кривой называется вся-
кий гомеоморфный образ окружности.
Областью называется связное открытое множество.
Согласно теореме Жордана, дополнение всякой простой
замкнутой кривой С состоит из двух непересекающихся обла-
стей, для каждой из которых С служит границей (см. [34]).
Жордановой областью называется всякая область,
границей которой служит некоторая простая замкнутая кри-
вая С. В противном случае говорят, что область является
нежордановой.
Если {Ся} —убывающая последовательность непустых ком-
пактных множеств (СяоСя+1 для п = 1, 2, .. .), то суще-
ствует по крайней мере одна точка, принадлежащая каждому
С„, п—1, 2, ...; иными словами, пересечение множеств СП
+ ОО
непусто, т. е. Q Ся —0. (См. [38], стр. 201, упр. 30.)
л — 1
Множество А называется выпуклым, если отрезок,
соединяющий любые две точки А, целиком лежит в А.
(Одноточечные множества следует рассматривать как частный
случай отрезка.) Так как всякое пересечение выпуклых мно-
жеств выпукло и так как вся плоскость также является вы-
пуклым множеством, то всякое выпуклое множество на пло-
скости содержится в некотором „наименьшем выпуклом мно-
жестве", а именно в пересечении всех выпуклых множеств,
содержащих данное множество. Это наименьшее выпуклое
множество называют выпуклой оболочкой данного мно-
жества. Замыкание выпуклой оболочки множества является
наименьшим замкнутым выпуклым множеством, содержащим
данное множество. (См. [38], стр. 332, упр. 39.)
Говорят, что отображение открыто, если образ всякого
открытого множества из его области определения является
открытым множеством. Отображение называется замкну-
т ы м, если образ всякого замкнутого множества из его
области определения является замкнутым множеством.
166
Глава 10
В некоторых примерах данной главы предполагается, что
читатель знаком с мерой и интегралом Лебега на плоскости.
По теории интеграла Лебега в библиографии указана лите-
ратура, которую мы цитировали в гл. 8.
I. Два непересекающихся замкнутых множества, рас-
стояние между которыми равно нулю
Положим F1-={(x, у)|ху = 1}, у)|у = 0}(т. е.
F2 есть ось х). Тогда Fx и F2 замкнуты и не пересекаются.
Однако для любого е > 0 существуют две точки (2/е, е/2)
и (2/е, 0), принадлежащие Fx и F2 соответственно, расстоя-
ние между которыми -2-е<е.
2. Ограниченное множество на плоскости, для которого
не существует минимального замкнутого круга, со-
держащего это множество
Минимальным замкнутым кругом, содержащим
данное ограниченное плоское множество А, называется замк-
нутый круг, содержащий А и содержащийся в любом замк-
нутом круге, который содержит А. Любое двухточечное
множество не имеет минимального круга. Однако в противо-
положность этому всякое непустое ограниченное плоское мно-
жество содержится в некотором замкнутом круге минималь-
ного радиуса. Кроме того, любое непустое множество А
на плоскости содержится в некотором минимальном замкну-
том выпуклом множестве, а именно в замыкании своей вы-
пуклой оболочки, которая содержится во всяком выпуклом
замкнутом множестве, содержащем А. В одномерном про-
странстве R каждое непустое ограниченное множество содер-
жится в некотором минимальном замкнутом интервале.
3. „Тонкие" связные множества, не являющиеся про-
стыми дугами
В данном случае слово „тонкие" означает „нигде не
плотные на плоскости".
Первый пример. Множество
Sj=E{(x, y)|y = sin (1/х), 0 < х< 1} (J {(0, 0)}
Множества на плоскости
167
не является простой дугой, потому что оно не компактно
({0}Х1—1. IJcSj).
Второй пример. Пусть Sj — множество из первого
примера. Положим
= {(х, у)|у = sin(I/x), 0 < х< 1} U({0} X [—1, 1]).
Тогда, хотя S2 и компактно, но удаление произвольного
множества точек из отрезка {0) X [—1, 1] не нарушает
связности S2. В примере 11 будет показано, что множество S2
настоящего примера не является дугой. Далее, в примере
24, мы рассмотрим связное множество на плоскости, которое
становится вполне несвязным при удалении из него всего
лишь одной точки.
4. Два непересекающихся плоских контура, содержа*
щихся в квадрате и соединяющих его противополож-
ные вершины
. В этом примере под „контуром" понимается нигде не
плотное связное множество. В качестве квадрата возьмем
[—1, 1] X I—1- И- а искотлые „контуры" определим следую-
щим образом (см. рис. 7):
Cj = {(x, y)|y=±y.v —-i-. —1<х<о|и
U {(-*, У) | У = у sin (л/2х) + , 0 <х < 1 |и
1||(Х, у)|х = 1, 1 }•
С2=|(х, у)|у = — 2-х + у, —1<х<0|и
U {(х, У)|у — у sin (л/2х) — j, 0<х< 1|и
и|(х, у)|х = 1, — 1<у<-^|.
168
Глава 10
Тогда С} соединяет точки (—1, —1) и (1, 1), а С2—точки
(—1, 1) и (1, — 1), причем С1[)С2= 0.
5. Отображение интервала [0, 1] на квадрат [О, 1JXIO, 1]
Пусть / £ [О, 1), и пусть 0, •••—двоичное разло-
жение t. Для того чтобы разложение было однозначным,
мы будем рассматривать лишь разложения, содержащие
бесконечное множество нулей. Отображение / определим
так: если £ С [0, 1), то ее образом является точка (х, у)
единичного квадрата Ss[0, 1] X [0, 1], где
х 0, .... у = 0, t2t^t^ ... .
Если же t— 1, положим / (О=(1, 1)- Нетрудно видеть,
что f отображает [0, 1] на S однозначно, но не взаимно
однозначно. Например, точка (0,1; 0,1) является образом трех
Множества на плоскости
169
различных точек: 0,11, 0,100101010101... и 0,011010101...
(и только этих точек).
Отображение / не является непрерывным. Например, если
{/„} — последовательность точек
0,0011, 0,001111, 0,00111111, 0,0011111111, ...
и если (хп, уп) = f (tn), то последовательности {%„} и {уя}
совпадут с последовательностью
0,01, 0,011, 0,0111, 0,01111.........
Тогда tn—>0,01, (хп, Ул)—>(0,1; 0,1), в то время как
/(0,01) — (0,0; 0,1) /=(0,1; 0,1). Таким образом,
lim f(ta)=k
+со
f( lim /Л
\л->+оо J
В качестве упражнения читателю предлагается доказать,
что отображение / не является ни открытым (образ откры-
того интервала (0,101; 0,111) содержит точку (0,1; 0,1),
которая, однако, не будет внутренней точкой образа), ни
замкнутым (точка (0,1; 0,1) не принадлежит образу замкну-
того интервала [0,001; 0,01], но будет предельной для этого
образа).
6. Кривая Пеано на плоскости
Кривой Пеано мы называем дугу, лежащую в евкли-
довом пространстве, размерность которого больше единицы,
и имеющую непустое ядро в этом пространстве (эта кривая
не является нигде не плотной). В 1890 г. итальянский мате-
матик Дж. Пеано (1858—1932 г.) поразил математический мир
первым примером подобной кривой. Ниже мы приводим опи-
сание (данное в 1891 г. немецким математиком Д. Гильбер-
том (1862—1943 г.)) кривой, которая заполняет единичный
квадрат S = [0, 1] X [0, 1]. Подобным же образом можно
описать и многомерный аналог этого примера.
Как видно из рис. 8, идея построения состоит в том,
чтобы разбить S и единичный интервал I = [0, 1] на 4я рав-
ных замкнутых квадратов и подинтервалов соответственно
и установить соответствие между этими квадратами и под-
интервалами так, чтобы сохранялось отношение включения
(т. е. на каждой стадии разбиения, если некоторый квадрат
170
Глава 10
соответствует некоторому интервалу, то его подквадраты
соответствуют подинтервалам указанного интервала).
Определим теперь непрерывное отображение f интер-
вала I на S: если х£1, то на каждой стадии разбиения х
принадлежит по крайней мере одному замкнутому подинтер-
валу. Если этих подинтервалов два, то выберем один из них.
Ему соответствует некоторый квадрат. Таким образом, мы
получим убывающую последовательность замкнутых квадратов,
соответствующих некоторой убывающей последовательности
1 Г -~ 1 1 3 *— 1 1
1 1 ] 1
л
/ г з “
► -«--—।—
/
/
Рис. 8.
замкнутых интервалов. Эта последовательность замкнутых
квадратов обладает тем свойством, что существует и притом
только одна !) точка, принадлежащая всем этим квадратам.
Эту точку мы и возьмем в качестве /(х). Остается пока-
зать, что (i) точка f (х) определена корректно, т. е. она не
зависит от выбора интервалов, содержащих х; (ii) множество
значений f есть S и (iii) / непрерывно. Доказательство мы
предоставляем читателю.
Следует заметить, что отображение /, определенное выше,
не является взаимно однозначным (например, каждая из трех
точек 1/6, 1/2 и 5/6 отображается в точку (1/2, 1/2)). Это
не случайно, так как если бы отображение f было взаимно
однозначным, то оно было бы гомеоморфизмом, в то время
') Следует принять во внимание, что длины сторон квадратов
стремятся к нулю. — Прим, перев.
Множества на плоскости
171
как I и S не гомеоморфны (удаление любых трех точек
нарушает связность I, но не нарушает связности S). Тот
факт, что отображение f однозначно, но не взаимно одно-
значно, в какой-то мере парадоксален, поскольку кажется,
что будто бы в I больше точек, чем в S!
7. Кривая Пеано, стационарная почти всюду
Пусть <р — канторова функция примера 15 гл. 8, а / —
отображение, определенное в предыдущем примере. Тогда
g (х) = f (<р (х)) отображает канторово множество С на еди-
ничный квадрат [0, 1] X [0, 1]. При этом дополнительное
множество [0, 1] \С отображается на образ при отображе-
нии f множества точек вида m 2~п, где m и п— натураль-
ные числа, связанные неравенством m < 2”.
Таким образом, полученная кривая Пеано является стацио-
нарной почти всюду.
8. Кривая Пеано, дифференцируемая почти всюду
Термин „почти всюду дифференцируемая“ означает, что
кривая определяется параметризующими функциями, которые
дифференцируемы почти всюду. Требуемым свойством обла-
дает отображение, определенное в примере 7.
9. Непрерывное отображение интервала [0, 1] на себя,
принимающее каждое значение несчетное множество
раз
Этим свойством обладает каждая из параметризующих
функций кривых Пеано примеров 6 и 7 и вообще каждая
параметризующая функция любого непрерывного отображения
интервала [0, 1] на [0, 1] X [О- Ч- Кроме того, каждая из
параметризующих функций отображения примера 7 обладает
дополнительным свойством: она дифференцируема почти
всюду, причем производная почти всюду равна нулю
(см. [58]).
10. Простая дуга, расположенная в единичном квадрате
и имеющая плоскую меру, сколь угодно близкую
к единице
Как было показано в примере 6, никакая простая дуга
не может заполнить весь единичный квадрат .5 = [0, 1] X !]•
172
Глава 10
По тем же причинам всякая простая дуга на плоскости
нигде не плотна. Из этого следует, что простая дуга не
может заполнить „слишком большую" часть S. В частности,
она не может заполнить почти весь квадрат S, так как
если бы простая дуга А, расположенная в S, имела меру,
равную 1, то она была бы плотна в S, а так как она замк-
нута, то она совпала бы с S. Однако простая дуга А может
щиеть положительную плоскую меру. Более того, если
е — произвольное число, заключенное между 0 и 1, то суще-
ствует простая дуга А, плоская мера которой больше, чем
1 — е. Сейчас мы наметим схему доказательства этого заме-
чательного факта.
Модифицируем построение, которое проведено в при-
мере 6, вырезая открытые „каналы" между смежными под-
квадратами из S, которые не соответствуют смежным под-
интервалам из I. После первого шага вместо подквадратов
получаем четырехугольники, которые в свою очередь разде-
лены прямыми, проходящими через середины противополож-
ных сторон. Затем вырезаются открытые каналы, и каждый
замкнутый четырехугольник заменяется последовательностью
из восьми меньших четырехугольников. Первое подразделе-
ние и общая схема, в которой для простоты вместо четы-
рехугольников используются квадраты, показаны на рис. 9.
Второй шаг отражен на рис. 10. В обоих случаях удален-
ные каналы выделены штрихами. После п шагов получим 8я
замкнутых четырехугольников, которые нумеруются сле-
дующим образом: если четырехугольник после п—1 шагов
имел номер k (k— 1, 2, .., 8я-1), то четырехугольники,
Множества на плоскости.
173
получившиеся из него после n-го шага, получают номера
от 8ft — 7 до 8ft. Кроме того, нумерация такова, что на
каждом шаге два четырехугольника являются смежными тогда
и только тогда, когда они имеют последовательные номера
Рис. 10.
и, следовательно, соответствуют смежным подинтервалам из
I — [0, 1]. Нетрудно показать, что диаметр каждого четырех-
угольника составляет не более 3/4 от диаметра содержащего
его четырехугольника, который был построен на предыду-
щем шаге. Следовательно, любая убывающая бесконечная
последовательность вложенных четырехугольников опреде-
ляет единственную точку, а именно точку их пересечения.
2 4 е 8 10 12 К 16 18 20 22 24 26 28 30 32 3
Рис. 11.
Множества на плоскости
175
Поэтому отображение можно определить точно так же, как
и в примере 6. Это отображение непрерывно по тем же при-
чинам, что и в примере 6. Более того, оно является взаимно
однозначным, так как мы удалили соответствующие каналы.
Наконец, поскольку можно удалять каналы сколь угодно
малой площади, то их общая плоская мера также может быть
сделана сколь угодно малой, а поэтому остающаяся после их
удаления простая дуга имеет плоскую меру, сколь угодно
близкую к 1.
Другой метод построения простой дуги с положительной
плоской мерой указан на рис. 11. Этот метод несколько
проще по замыслу, чем описанное выше построение, но имеет
тот недостаток, что некоторые подинтервалы из [0, 1] отоб-
ражаются на множества нулевой плоской меры. Построение,
указанное на рисунке 11, приводит к простой дуге, содер-
жащей множество А \ А, где А — канторово множество.
Так как для 0 < е 1 мы можем выбрать А с (линейной)
мерой, не меньшей чем 1 — е , то дуга, о которой идет
речь, будет иметь плоскую меру, не меньшую чем 1 — е.
Американский математик У. Ф. Осгуд (1864 — 1943 г.)
в 1903 г. построил (см. [39]) простую дугу с плоской мерой,
превосходящей 1 — е, используя канторово множество А ли-
нейной меры, большей, чем 1 —е . При этом простая дуга
была построена таким образом, что она содержала множе-
ство
11. Связное компактное множество, не являющееся дугой
Пусть S2 — второе множество примера 3. Это множество
не является дугой, ибо оно локально несвязно: если
N = {(х, у) | (х, у) £ S2, х2 -f- у2 < 1/2], то не существует
окрестности начала координат, которая принадлежит N и
любые две точки которой можно соединить связным множе-
ством, лежащим в N. (См. [56], стр. 204.)
12. Плоская область, не совпадающая с ядром своего
замыкания
Пусть {(х, у) | х^А-У2 < 1} \ ([0, 1] X {0} ). т. е.
S — открытый круг с радиальным разрезом. Тогда
•$ = {(х, у)|х2-|-у2< 1],
а ядром 5 является I (5) = {(х, у) | х2-1- у2 < 1].
176
Глава 10
Так как каждая жорданова область совпадает с ядром
своего замыкания (см. [38], стр. 477), то мы тем самым
получили простой пример области, не являющейся жордано-
вой. Однако пример 14 показывает, что не каждая область,
совпадающая с ядром своего замыкания, является жордановой
областью.
13. Три непересекающиеся плоские области с общей
границей
Этот пример проще всего описать в форме рассказа.
Представим себе, что на острове в океане живет человек.
На острове имеются два водоема с пресной водой, причем
в одном из них вода холодная, а в другом — теплая. Чело-
век хочет, чтобы все три источника воды находились на
подходящем расстоянии от любой точки острова. Для этого
он начинает рыть каналы, но таким образом, что остров
все время остается гомеоморфным своей первоначальной
форме. Сначала он проводит канал от океана в глубь острова
так, чтобы его воды находились от любой точки суши
на расстоянии не более одного фута и чтобы канал не вхо-
дил в соприкосновение с источниками пресной воды. Затем
он подобным же образом проводит канал от источника хо-
лодной пресной воды и канал от источника теплой пресной
воды, чтобы в результате каждая точка оставшейся суши
находилась от этих трех каналов не далее одного фута.
Неудовлетворенный этим результатом обитатель острова по-
вторяет описанный тройной процесс так, чтобы каждая точка
оставшейся суши отстояла от каждого канала не далее
чем на полфута. Но и это не удовлетворяет его, и он до-
водит приближение к каждой точке суши до одной четверти
фута. Так он продолжает этот процесс до бесконечности,
всякий раз уменьшая вдвое критическое расстояние и время,
затрачиваемое на каждый шаг, стремясь закончить работу
в конечный отрезок времени. Предположим теперь, что
„остров"—это компактный круг, из внутренности которого
удалены два непересекающихся открытых круга, а „океан" —
его открытое плоское дополнение, лежащее вне этого круга.
Предположим далее, что расширения каждой из трех перво-
начальных областей остаются на каждом шаге гомеоморфными
их первоначальной форме. Тогда в результате мы получим три
Множества на плоскости
177
взаимно непересекающиеся области /?р R2 и ^з> каждая из
которых является объединением бесконечной последователь-
ности областей, а часть суши F, которая останется от острова,
будет общей границей областей R2 и А?3. Так как дополне-
ние F состоит из трех непересекающихся областей вместо двух,
то ни одна из областей Rx, R2 и R3 не является жордановой.
(Подробности и доказательство теоремы Жордана см. в [34].)
С другой стороны, как мы увидим в примере 14, каждая из
этих трех областей совпадает с ядром своего замыкания.
Предыдущее построение можно провести с любым ко-
нечным (на самом деле со счетным) множеством непересе-
кающихся областей. Если взять более четырех областей,
то мы сможем построить таким путем „карту", на которой
все „страны" имеют общую границу. Это показывает, что
знаменитая проблема четырех красок требует точной форму-
лировки, в противном случае она имеет тривиальное отри-
цательное решение (см. [10]).
14. Нежорданова область, совпадающая с ядром своего
замыкания
Пусть R — любая из областей Rlt R2 и R3, определенных
в примере 13. Как было отмечено, R не является жордано-
вой областью. С другой стороны, как мы покажем сейчас,
R совпадает с ядром своего замыкания. В самом деле, так
как R cz R и R открыто, то R=I(R) cz I (R). Теперь нам
остается доказать обратное включение I (R) = I (R (J F) a: R.
Но если бы это включение не имело места, то нашлась бы
точка р £F, которая была бы внутренней для множества
R U F. А это означало бы, что существует окрестность N
точки р, которая лежит в R U F и, следовательно, не со-
держит ни одной точки из двух оставшихся областей. Тем
самым мы получили бы противоречие с тем фактом, что
каждая точка F является предельной для любой из трех об-
ластей Rv R2 и R3.
15. Ограниченная плоская область, граница которой
имеет положительную меру
Пусть А—канторово множество положительной меры
на [0, 1], и пусть
/?=((о, i)x(-i. 1))\И х [о. 1)).
12 Зак. 587
178
Глава 10
Множество R есть область с границей
= х[—1. 1])U({1} X [-1. 11)11
имхю. i))u((o. 1)х{i])u((o. i)х{—i}).
Следовательно, у. (F (/?)) = у, (Л) > 0. Ясно, что R не яв-
ляется жордановой областью (/ (/?) =/= R). (См. [22], стр. 292.
Относительно жордановой области, имеющей границу поло-
жительной плоской меры, см. пример 4 гл. 11.)
16. Простая дуга бесконечной длины
Первый пример. Положим
( 0,
/(хН у».
если х=1/п, n£N, п нечетно,
если x=l/n, n£N, п четно.
Далее положим /(0) = 0, и пусть /(х) линейна на каждом
интервале [l/(n-1~ 1), 1/n], n£N. Тогда вследствие расходи-
мости гармонического ряда график /(х) для х£[0, 1] будет
простой дугой бесконечной длины.
Второй пример. Положим f(x) = x sin(l/x) для х£(0, 1]
и /(0) = 0. Тогда график f (х) для х£[0, 1] снова будет
простой дугой бесконечной длины по той же причине, что
и в первом -примере. Длины вписанных ломаных превосходят
сумму высот отдельных волн графика /(х), а эта сумма
имеет вид 2 21(%п—1)л-
В противоположность двум предыдущим примерам график
функции /(x) = x2sin(l/x) для х£(0, 1] и /(0) = 0 имеет
конечную длину, так как эта функция дифференцируема
и ее производная ограничена на [0, 1]. (См. [38], стр. 353
(упр. 24 и 27), стр. 176 (теорема II).)
17. Простая дуга бесконечной длины, имеющая каса-
тельную в каждой точке
Если /(х) —x2sin(l/x2) для х£(0, 1] и /(0) = 0, то
график /(х) для х£[0, 1] будет простой дугой бесконечной
длины по тем же причинам, что и во втором примере пре-
дыдущего пункта. Однако график /(х) имеет касательную
в каждой точке, поскольку / (х) всюду дифференцируема.
Множества на плоскости
179
18. Простая дуга, такая, что ее длина между любой
парой точек бесконечна
Первый пример. Пусть f (t) = (x(t), — любая кри-
вая Пеано, отображающая [0, 1] на [О, 1 ] X [0, 1] и обла-
дающая следующим дополнительным свойством: f отображает
всякий невырождающийся в точку интервал из [О, 1] на мно-
жество, имеющее непустое (двумерное) ядро. (Этим свойст-
вом обладает, например, отображение примера 6.) Тогда
график каждой из функций x(t) и y(Z) для /£[0, 1] обла-
дает требуемыми свойствами. Например, чтобы установить,
что график х (t) для а t b имеет бесконечную длину,
мы можем воспользоваться тем фактом (см. пример 9), что
существуют по крайней мере два значения, каждое из ко-
торых принимается функцией x(t) несчетное множество раз.
Второй пример. Пусть / — отображение такого же типа,
как и в примере 10, и пусть, кроме того, оно отображает
всякий невырождающийся в точку подинтервал из [0, 1] на
множество положительной плоской меры. Тогда / обладает
требуемыми свойствами, так как всякая спрямляемая простая
дуга имеет плоскую меру, равную нулю. (См. [38], стр. 436.)
Третий пример. График любой функции, которая всюду
непрерывна, но нигде не дифференцируема на замкнутом
интервале (см. пример 8 гл. 3), также обладает нужными
свойствами. В самом деле, если бы этот график был спрям-
ляемым, то функция имела бы ограниченную вариацию, а лю-
бая функция ограниченной вариации дифференцируема почти
всюду. (См. [17], а также [33]*, стр. 238.)
Четвертый пример. См. [22], стр. 190.
19. Гладкая кривая С, содержащая точку Р, которая
не является ближайшей точкой этой кривой ни для
какой точки выпуклой области, ограниченной этой
кривой
Пусть кривая С есть график функции у3==х4. Эта кри-
вая всюду вогнута вверх. Положим P = (Q, 0). Если (а, Ь) —
точка, лежащая выше С, и а =£ 0, то ясно, что точка
(а, а4/3) ближе к {а, Ь), чем (0, 0). Если же b — произволь-
ное число, не меньшее единицы, то точка (1/8, 1/16) ближе
к (0. Ь), чем (0, 0). Наконец, если b — произвольное поло-
12»
180
Глава 10
жительное число, меньшее единицы, то точка (Z>3, Z>4) ближе
к (О, Ь), чем (0, 0). Идея этого примера заключается в том,
что начало координат является точкой бесконечной кри-
визны (нулевого радиуса кривизны) кривой С. (См. [36],
стр. 258, а также [52]*, т. I, стр. 568.)
20. Подмножество А единичного квадрата S=[0, 1]Х[0, 1],
плотное в S и такое, что всякая вертикальная или
горизонтальная прямая, пересекающая 5, имеет
с А лишь одну общую точку
Очевидно, достаточно построить взаимно однозначное
отображение / интервала [0, 1] на себя с графиком, всюду
плотным в S. Начнем с последовательного определения f(x)
для х£(0, 1] П Q- Пусть точки множества В = ((0, 1]PIQ)X
X ((0> И П Q) расположены в виде последовательности (хр yj,
(х2, у2)...На нулевом шаге положим /(х1)=у1. На пер-
вом шаге мы разделим В на четыре непересекающиеся части
вертикальными и горизонтальными прямыми:
((0, 1/2] HQ)X((0, 1/2] PQ),
((0, 1/2] р Q) Х((1/2. 1] PQ). ...
и занумеруем эти множества в каком-либо порядке: Вп, Bv2,
Bi3, В14. Пусть (хп, уп) — первая из точек последователь-
ности {(хп, у„)}, принадлежащая и такая, что хп #= х4
и уп Ур Положим /(хп) = уп. Далее пусть (х12, у12) —
первая из точек последовательности {(х„, у„)}, принадле-
жащая В12 и такая, что х12 #= хр х12 =/= хп и у12 =/= Ур Уп^Уп*
Положим/(x12)Esy12. Затем, аналогичным образом определив
f (х13) = у13, обозначим через (х14, у14) первую точку после-
довательности [(хп, уя)}, принадлежащую В14 и такую, что
х14 отлично от Хр хп, х12 и х13, а у14 отлично от ур уп,
У12 и У13’ и положим /(х14)=у14. На этом заканчивается
первый шаг построения. На втором шаге подобным же об-
разом множество В разбивается на 16 частей В21, В22.В216
вертикальными и горизонтальными прямыми. Затем снова,
как и выше, расширяется область определения и множество
значений функции /. Продолжая этот процесс до бесконеч-
ности и деля множество В на /г-м шаге на 4я конгруэнтных
Множества на плоскости
181
частей, мы получим функцию /, обладающую требуемым
свойством относительно множества (0, 1] П Q- Наконец, чтобы
получить искомую функцию, достаточно продолжить функ-
цию f на [0, 1] следующим образом: /(х) = х для
х£[0, 1]\((0, 1JPQ).
21. Неизмеримое плоское множество, имеющее с каждой
прямой не более двух общих точек
Этот пример принадлежит В. Серпинскому [47]. Его по-
строение опирается на принцип максимального элемента
в форме теоремы о полном упорядочении, а также в форме
леммы Цорна. (См. [17], [31] и [49].) Сначала мы приведем
четыре утверждения относительно кардинальных и порядко-
вых чисел.
(i) Если а — бесконечное кардинальное число, то а2 = а.
(См. [17] и [49].)
(ii) Мощность f множества всех замкнутых множеств по-
ложительной плоской меры равна мощности с множества R.
(В самом деле, поскольку замкнутые множества и их допол-
нения находятся во взаимно однозначном соответствии, то f
не превосходит мощности множества всех открытых мно-
жеств. А так как каждое открытое множество является
объединением счетного множества открытых кругов с рацио-
нальными радиусами, центры которых имеют рациональные
координаты, то f<Ic. С другой стороны, так как замкнутые
круги с центрами в начале координат образуют множество
мощности с, то f>c.)
(ill) Пусть W обозначает первое порядковое число, соот-
ветствующее мощности с. (См. пример 10 гл. 12.) Тогда
множество {а|а<Чг} имеет мощность с.
(iv) Если Е— линейное множество положительной линей-
ной меры, то мощность Е равна с. (Е содержит некоторое
замкнутое линейное множество Е положительной линейной
меры, a F является объединением некоторого счетного мно-
жества (быть может, пустого) и некоторого (обязательно
непустого) совершенного множества. См. [33]*, [48] и [54].)
Пусть а -> Fa есть взаимно однозначное отображение
множества {а|а<Чг} на множество всех замкнутых мно-
жеств положительной плоской меры. Далее, пусть F — сово-
182
Глава 10
купность всех функций р (а), таких, что их области опре-
деления имеют вид [1, р) для некоторого их множе-
ства значений являются подмножествами плоскости и, кроме
того,
(а) р (а) £ Fa для каждого а из области определения р (а),
(Ь) никакие три точки из множества значений р (а) не
коллинеарны ’).
Пусть G — множество всех множеств значений функций
из F, и пусть G частично упорядочено по отношению вклю-
чения. Тогда по лемме Цорна (см. [17], [31] и [49]) суще-
ствует максимальное множество Е £ G, которое является
множеством значений некоторой функции q(a) из F. Пусть
область определения q есть [1, р). Покажем, что р = Т.
Предположим противное, т. е. пусть р < Т. Тогда, если
обозначить через b кардинальное число, соответствующее
порядковому числу р, то Ь Ь2 < с (строгое неравенство
Ь < Ь2 имеет место, если 1 < Ь и Ь конечно). Это означает, что
мощность множества всех направлений, определяемых парами
точек, принадлежащих множеству значений Е функции q(a),
меньше с и, следовательно, существует направление 9, отличное
от всех направлений, определяемых парами точек из Е. Но тогда
некоторая прямая L, имеющая направление 0, должна пересе-
каться с множеством Е^ по множеству положительной линей-
ной меры (согласно теореме Фубини). А так как это последнее
множество имеет мощность с, то существует точка р$ £ F&,
такая, что р$ не коллинеарна никакой паре точек из области
значений q(a). Продолжим теперь функцию q(a) так, чтобы
она была задана на [1, р] = [1, р-р-1) и чтобы ^(Р) = Рр.
Но тогда эта продолженная функция q(a) будет обладать
свойствами (а) и (Ь) и ее множество значений будет больше
максимального члена Е из G. Мы получили противоречие.
Следовательно, р = Т, т. е. область определения функции q(a)
состоит из всех а, меньших 47, а множество значений Е функ-
ции ^(а) содержит некоторую точку ра из каждого замк-
нутого плоского множества Ра положительной плоской меры.
Покажем теперь, что множество Е неизмеримо. В самом
деле, если бы Е было измеримо, то было бы измеримо и
его дополнение Е'. А так как Е' не содержит ни одного
’) То есть не лежат на одной прямой. —Прим, перев.
Множества на плоскости
183
замкнутого плоского множества положительной плоской меры,
то оно должно иметь меру нуль. Но с другой стороны, так
как каждая прямая на плоскости пересекает Е не более чем
в двух точках, то (согласно теореме Фубини) Е также должно
иметь меру нуль. Следовательно, и вся плоскость, являясь
объединением двух множеств Е и Е' меры нуль, должна
иметь меру нуль. Таким образом, мы получили противоречие,
и неизмеримость множества Е доказана.
Отметим также, что если 5 — произвольное множество
положительной плоской меры, то пересечение •$(]£ неизме-
римо. Если предположить противное, то, применяя теорему
Фубини, получим, что ц (S ПЕ)=0, в то время как р (S \ £)>0.
Таким образом, S \ Е содержит некоторое замкнутое мно-
жество F положительной плоской меры. Но так как F П Е = 0,
то мы получаем противоречие с основным свойством множе-
ства Е: пересечение множества Е с каждым замкнутым мно-
жеством положительной плоской меры непусто.
С. Мазуркевич [30] построил плоское множество Е, пере-
секающееся с каждой прямой на плоскости в точности в двух
точках. Однако такое множество Е может быть измеримым
и в этом случае оно обязано иметь меру нуль. Это объяс-
няется тем, что этот метод построения зависит лишь от су-
ществования на плоскости множества Ех, пересекающегося
с каждой прямой по множеству мощности с. Само же мно-
жество Е строится затем как подмножество Ех.
Однако множества, обладающие тем же свойством, что и
fp могут иметь нулевую плоскую меру. Например, пусть
С — канторово множество на [0, 1]. Положим
^(RXQUCCXR).
Тогда ясно, что каждая прямая пересекает Ех по множеству
мощности с, однако Ех является (замкнутым) множеством
нулевой плоской меры.
В статье [59] приведено построение „множества Мазурке-
вича“ как ответ на одну проблему, поставленную в этом
журнале.
Ф. Гельвин доказал следующее: если где
Ко — мощность множества N, то существует неизмеримое
множество 5 на плоскости, такое, что пересечение S с каждой
прямой состоит в точности из п точек.
184
Глава 10
22. Неотрицательная функция f(x, у), такая, что
ii ii
J j f(x, y)dxdy = j j f(x, у) dy dx, = 0,
0 0 0 0
а интеграл
j j f(x, y) dx dy,
s
где S=[0, 1]ХЮ, I]
не существует
Мы приведем два примера. В первом из них интеграл
понимается в смысле Римана, во втором — в смысле Лебега.
Первый пример. Пусть f — характеристическая функция
1
множества из примера 20. Тогда | f (х, y)dx = 0 для каждого
о
1
у £ [0, 1] и J/(х, y)dy = 0 для каждого х£[0, 1], причем
о
оба интеграла являются интегралами Римана. Однако двойной
интеграл Римана по 5 не существует, так как для функции f
верхний и нижний интегралы Римана равны 1 и 0 соответ-
ственно.
Второй пример. Пусть f—характеристическая функция
множества из примера 21. Тогда оба повторных интеграла
снова равны нулю, причем их можно рассматривать как в смысле
Римана, так и в смысле Лебега. Однако функция / неизме-
рима на 5, и поэтому двойной интеграл Лебега не существует.
23. Действительнозначная функция одного действитель-
ного переменного, график которой является неизме-
римым плоским множеством
Определим функцию f (х) для x£R следующим образом:
шах{у|(х, у)£Е], если {у | (х, у)£Е]Ф0,
0, если {у |(х, у)£Е} = 0,
где Е — множество из примера 21. Положим
Е! = {(х,/(x))|xCR} E2=E\EV
Множества на плоскости
185
Тогда либо fj, либо Е2 (либо оба эти множества) должно
быть неизмеримым, так как их объединение есть Е. Если
неизмеримо Е1г то множество
F={(x, /(x))|x6R}
— график функции f — является объединением Е} и неко-
торого подмножества оси х. Но так как последнее имеет
нулевую плоскую меру, то F неизмеримо. Если же неизме-
римо Е2, то определим функцию g (х) для х £ R следующим
образом:
Imin {у|(х, у)£Е], если {у|(х, У)£Е} состоит из
двух различных точек,
О в противном случае.
Тогда множество Gs={(x, g(x) )|х £R} — график функции
g— является объединением Е2 и некоторого подмножества
оси х и потому неизмеримо. Итак, в любом случае суще-
ствует функция, график которой есть неизмеримое плоское
множество.
24. Связное множество, которое становится вполне не-
связным при удалении одной точки
Пусть С — канторово множество примера 1 гл. 8, и пусть
В — подмножество С, состоящее из всех концевых точек
открытых интервалов, удаленных из [0, 1] при построении С.
Положим Е = С \ В (см. пример 24 гл. 8). Далее для каждого
х£С через L(x) обозначим замкнутый отрезок, соединяющий
две точки (х, 0) и (1, 1) на плоскости. Наконец, для х£В
через S(x) обозначим множество всех тех точек из L(x),
ординаты которых иррациональны, а для х^Е тем же сим-
волом S(x) обозначим множество всех тех точек из L(x),
ординаты которых рациональны. Тогда множество 5(х)
?ес
обладает требуемыми свойствами.
Мы приведем доказательство лишь в общих чертах: под-
робности можно найти в [24].
Связность множества 5 доказывается с привлечением по-
нятий множеств первой и второй категории, и мы его опускаем.
186
Глава 10
Покажем лишь, что множество 50 = 5\{(1, 1)] вполне
несвязно. В самом деле, если EaS0 содержит более
одной точки и является подмножеством какого-либо множества
S(x), х£С, то Е, очевидно, несвязно. С другой стороны,
если р и q—две точки множества So, расположенные на
двух различных интервалах L(x) и Z(y), где х и у при-
надлежат С и х < у, то в дополнении множества So суще-
ствует прямая линия, проходящая через точку (1, 1) и такая,
что точки р и q лежат по разные стороны от нее. Такой
прямой является всякая прямая, проходящая через точку (1, 1)
и любую точку вида (а, 0), где х<а<у и а(£С.
ГЛАВА 11
П Л О ЩА ДЬ
Введение
В основе понятия площади лежит понятие двойного инте-
грала Римана. Говорят, что ограниченное плоское множе-
ство S имеет площадь, если его характеристическая
функция интегрируема (по Риману) на замкнутом прямо-
угольнике R, который содержит S и стороны которого па-
раллельны координатным осям. В этом случае площадь
A (S) множества S по определению полагается равной двой-
ному интегралу от по R:
A (S)^ / / XsdA-
а
Эти определения, очевидно, корректны, поскольку понятия
„имеет площадь" и „площадь" не зависят от прямоугольника R,
содержащего множество 5.
Пусть прямоугольник R разделен на меньшие прямо-
угольники при помощи сетки с#’ прямых, параллельных его
сторонам. Тогда некоторые из этих прямоугольников могут
быть подмножествами S, а некоторые из них могут быть под-
множествами дополнения S' множества S. Для каждой такой
сетки е/У через а обозначим сумму площадей всех прямо-
угольников, являющихся подмножествами S (если таких прямо-
угольников нет, то положим а (е^°)=0), а через А (а/К)—сумму
площадей всех прямоугольников, не являющихся подмноже-
ствами S' (т. е. таких прямоугольников, пересечение которых
с множеством S непусто). Внутренняя площадь Л(5)
и внешняя площадь A (S) множества S определяются
соответственно как sup а (&/^) и infzl(e/f/=) для всех сеток
прямых, параллельных сторонам прямоугольника R, т. е.
Л(5)= sup а (е/К), A (S) = inf A (e/f°).
188
Глава 11
Очевидно, эти определения не зависят от R. Ограниченное
множество S имеет площадь тогда и только тогда, когда
A (S) = A (S). В этом случае A (S) — A (S) = A (S).
Для того чтобы ограниченное множество 5 имело пло-
щадь, необходимо и достаточно, чтобы его граница Л(5)
имела площадь, равную нулю, или, что эквивалентно, чтобы
F (S') имела внешнюю площадь, равную нулю. Но так как для вся-
кого ограниченного множества 5 его граница F (S) является
компактным множеством (и, следовательно, она измерима как
плоское множество) и так как для компактных множеств
внешняя площадь и внешняя плоская мера (Лебега) совпа-
дают, то ограниченное множество имеет площадь тогда
и только тогда, когда его граница имеет нулевую плоскую
меру.
Все предыдущие утверждения относительно площади можно
распространить подобным образом и на объемы множеств,
расположенных в трехмерном евклидовом пространстве. Су-
ществует обобщение понятия площади и объема, так назы-
ваемая мера Жордана, которое применимо к евклидовым про-
странствам любого числа измерений и даже к более общим
пространствам. (См. [38], стр. 431.) Мера Лебега является
обобщением меры Жордана в том смысле, что любое мно-
жество, имеющее меру Жордана, измеримо по Лебегу и его
мера Жордана совпадает с мерой Лебега. Принципиальным
преимуществом меры Лебега над мерой Жордана объясняется
широкое применение меры Лебега к предельным процессам.
Элементарные сведения о площади и объеме, а также дока-
зательства многих сформулированных выше утверждений
можно найти в [38], стр. 431—465.
В примерах 7 и 8 настоящей главы речь идет о площади
поверхности-, определение этого понятия см. в литературе,
указанной там же.
1. Ограниченное плоское множество, не имеющее
площади
Рассмотрим множество S = (Q П [О, 1])X(QH [0. 1])всех
точек единичного квадрата, обе координаты которых рацио-
нальны. Это множество не имеет площади, так как его гра-
ница F(S) не имеет нулевой площади. (Множество F (S)
Площадь
189
совпадает с самим единичным квадратом и, следовательно,
имеет площадь, равную 1.) Внешняя площадь множества S
равна единице, а внутренняя — нулю.
2. Компактное плоское множество, не имеющее площади
Пусть А — канторово множество положительной меры е
(см. пример 4 гл. 8). Положим S = 4 X [О, П- Тогда F (S) = S
и плоская мера множества F (S) равна линейной мере е мно-
жества А. Но так как множество F(S) = S компактно, то
его внешняя площадь равна его мере и потому положительна.
Следовательно, 5 не имеет площади. Внешняя площадь S
равна е, а внутренняя-—нулю.
3. Ограниченная плоская область, не имеющая площади
Этим свойством обладает область примера 15 гл. 10.
4. Ограниченная плоская жорданова область, не имею-
щая площади
Пусть е —положительное число, меньшее единицы, и пусть
А — простая дуга с параметризующей функцией /(/), 0<//<;1,
лежащая в единичном квадрате [0, 1] X [0- 1] и имеющая
плоскую меру, большую чем 1—е/2. (См. пример 10 гл. 10.)
Далее, пусть С — замкнутая простая кривая, образованная
объединением множества А и трех сегментов {0] X I—е/2, 0],
{1} X {—е/2, 0} и [0, 1]X {—е/2). Наконец, пусть — огра-
ниченная область, границей которой служит С. Тогда F будет
жордановой областью, а внешняя площадь ее границы больше
1 — е/2 > 1 — е> 0.
5. Простая замкнутая кривая, плоская мера которой
больше плоской меры области, ограниченной этой
кривой
Пусть С — кривая, а А*— область, определенные в при-
мере 4. Тогда если ц — плоская мера Лебега, то
p(/?UQ = p(/?)+ir(C)<l+ye.
190
ГЛава It
Но так как у,(С)> 1---^е, то отсюда следует, что
ц(/?)<е.
Поэтому если е < 2/3, то мера R. меньше меры С. Заметим,
что при этом мера R. может быть сделана сколь угодно близ-
кой к нулю, а мера С —сколь угодно близкой к единице.
6. Две функции ф и ф, заданные на [0, 1] и такие, что
(а) ф(х)<ф(х) для х£[0, 1],
1
(Ь) | [ф(х)—ф(х)]с?х существует и равен 1,
о
(с) 5= {(х, у) 10 X х X 1, Ф (х) < у < ф (х)} не
имеет площади
Пусть ф(х) — характеристическая функция множества
Q П [0, 1], и пусть ф (х) = ф(х)-|-1 • Тогда условия (а) и (Ь),
очевидно, выполнены. В то же время граница F(S) есть
замкнутый прямоугольник [0, 1] X [0. 2] положительной пло-
щади, и потому S не имеет площади. При этом внешняя пло-
щадь 5 равна 2, а внутренняя — нулю.
Этот пример представляет интерес в связи с принципом
Кавальер и, который состоит в следующем: если каждая
плоскость П, параллельная заданной плоскости По, пересекает
два трехмерных множества VT1 и VT2 так, что площади сече-
ний равны, то и имеют равные объемы (см. [53]).
Двумерный аналог этого принципа формулируется так: если
всякая прямая L, параллельная заданной прямой £0, пересе-
кает два плоских множества Sj и S2 по отрезкам равной
длины, то Sj и S2 имеют одинаковые площади. Приведенный
выше пример показывает, что если не предполагать, что
и S2 имеют площадь, то это утверждение теряет силу. (В ка-
честве множеств 5] и S2 можно взять соответственно мно-
жество S пункта (с) и замкнутый квадрат [0, 1] X [3, 4],
а в качестве семейства параллельных прямых — семейство
всех вертикалей.) В качестве упражнения читателю предла-
гается построить аналогичный контрпример в трехмерном
пространстве.
Площадь
191
7. Пример Шварца, в котором боковой поверхности пря-
мого кругового цилиндра сопоставляется сколь угодно
большая конечная или даже бесконечная площадь
Пусть S — прямой круговой цилиндр
s == {(%, у, z) | %2 + у2 = 1. о z < 1}
с радиусом основания 1 и с высотой 1. Для каждого нату-
рального т определим 2/и 1 окружностей Скт следующим
образом:
= У, z)\z = Лг = О. 1....................2т.
На каждой из этих 2т Д- 1 окружностей возьмем п равно-
мерно распределенных точек Pkmj (J = 0, 1.........п—1):
/ 2 /л . ’ 2 /л k \ ,
cos----, sin —-, 77— , если k четно,
\ п п 2т I
Р — I
— / (2/-4-1) Л . (2/4-1) Л k \ ,
cos-1--1, sin 1——, 7:— , если k нечетно.
\ п п 2тj
На каждой окружности Скт точки Pkmj, j = 0, 1.........п,
являются вершинами правильного многоугольника, имеющего п
сторон. Если 0 < k 2т, то каждая сторона многоугольника
с вершинами на окружности Скт расположена над некоторой
вершиной многоугольника, вписанного в и образует
с этой вершиной некоторый (плоский) треугольник в про-
странстве. Аналогично, если 0 k < 2т, то каждая сторона
многоугольника с вершинами на Скт расположена под неко-
торой вершиной многоугольника, вписанного в Cft+li т, и об-
разует с этой вершиной треугольник. Нетрудно видеть, что
существуют всего 4тп конгруэнтных треугольников, построен-
ных таким способом и расположенных в пространстве так, что
их вершины лежат на данном цилиндре. Площадь каждого
из этих треугольников равна
Эти треугольники образуют многогранник Птя, вписанный в 5.
Площадь Л(ПШП) его боковой поверхности равна
^(nw„) = 2Jt 1/1 4 4/я?(1 — cos-)2 .
4 тп' (л/n) Y \ п /
192
Глава 11
Если т и п— >—|—оо, то длины сторон упомянутых треуголь-
ников стремятся к нулю и поэтому естественно было бы ожи-
дать, что площади боковых поверхностей вписанных много-
гранников стремятся к некоторому пределу, а именно к пло-
щади боковой поверхности цилиндра, равной (2л- 1)- 1 = 2л
(площадь боковой поверхности прямого кругового цилиндра
вычисляется по известной формуле 2лгй, где г — радиус
основания, a h — высота цилиндра). Однако мы увидим, что
результат зависит от относительных скоростей возраста-
ния т и п.
Заметим сначала, что при предел множителя,
стоящего перед радикалом в формуле для А(Птя), равен 2л,
а подкоренное выражение не меньше 1. Поэтому, если А(Птя)
имеет предел, то он должен быть не меньше 2л. Теперь
обратим внимание на выражение под радикалом, точнее на
функцию
,, . „ I. л\ я2т 2я4т , 2л6от
f (т, п) == 2т 1 — cos — = —=---гт—г- 4- -g-r-»—- . . . .
J v ' \ п) п2 4! п4 1 6 п®
Рассмотрим три случая:
(i) Если т = п, то
f (п, п) = 2п f 1 — cos С
л2 2л4 .
п 4! п3 '
Следовательно, lim f(n, п) = 0, a lim А(Пяя) = 2л.
П->+<Х> Л->+со
(ii) Если же т — [ап2], где квадратные скобки обозначают
целую часть числа (функция [х] определена во второй главе)
и если 0<а<-|-оо, то
91 ч аг 91(1 л\ л2 Гал2] 2л4 Гап2] .
f ([ап2], п) = 2 [ап2] 1 - cos -) = ------.
Таким образом, lim f ([ап2], п) = ал2, a lim А (П|ал21, а)—
Л->4-СО Л->-рСО
= 2 л У1 -4- а2л4.
(iii) Наконец, если т — п3, то
/(п3, п) = 2п3 (1 — соз^ = л2п —•...
lim f(n3t ri) — Ц-00 и Пт Л (Плз| л) = + со.
п->4-GO rt->+OO
Площадь
193
В заключение отметим, что в зависимости от способа
стремления т и п к бесконечности в качестве предела А (Птап)
может получиться любое конечное или бесконечное число,
не меньшее 2л. Хотя предел lim Л(Птп) не существует,
т, л~> + со
но можно утверждать, что
lim А (Птя) = 2л.
т, +со
Приведенный выше пример принадлежит Г. А. Шварцу
(Gesammelte Mathematische Abhandlungen, vol. 2, p. 309,
Berlin, Julius Springer, 1890). Он показывает, что понятие
площади поверхности гораздо сложнее понятия длины дуги.
Подробное рассмотрение этих понятий и дальнейшие ссылки
можно найти в [42]. Элементарные сведения о площади по-
верхности см. в [36], стр. 610—635 (а также [52]*, т. III,
стр. 248—257).
8. Для любых двух положительных чисел е и М в трех-
мерном пространстве существует поверхность S,
такая, что
(a ) S гомеоморфна поверхности сферы;
(Ь ) площадь поверхности S существует и меньше е;
(с ) мера Лебега в трехмерном пространстве поверх-
ности S существует и больше М
Этот пример принадлежит А. С. Безиковичу (см. [6]).
При его построении используются идеи, подобные тем, на
которые опиралось построение простой дуги положительной
плоской меры (пример 10 гл. 10), однако само построение
в данном случае гораздо сложнее. Для его полного описания
потребовалось бы ввести определение площади поверхности,
и потому мы не будем вдаваться в подробности.
Обсудим некоторые интересные аспекты примера 8.
а. Существует некоторая аналогия между примером 8 и
призером 5. В обоих случаях граница тел „массивнее" их
внутренности. Однако линейная мера (длина) кривой в при-
мере 5 бесконечна, в то время как плоская мера (площадь)
поверхности в примере 8 конечна и мала.
Ь. Вспомним известные соотношения между объемом куба
и его боковой поверхностью, а также между объемом шара
13 Зак. 587
194
Глава 11
и его боковой поверхностью. Объем куба = X длина реб-
ра X площадь поверхности, а объем шара = -§• X длина ради-
уса X площадь поверхности. Эти соотношения могут навести
на мысль, что если мала площадь замкнутой поверхности одно-
временно с объемом трехмерной области, которую она огра-
ничивает, то должна быть мала и мера этой поверхности,
рассматриваемая в трехмерном пространстве. Пример 8 пока-
зывает, что это не так.
с. Можно построить прямую цилиндрическую „банку“ ко-
нечной высоты, в основании которой лежит неспрямляемая
жорданова кривая, имеющую конечный объем (меру в трех-
мерном пространстве), но бесконечную площадь поверхности.
(Таким образом, эту „банку“ можно наполнить краской, но
всю ее поверхность закрасить не удастся!) Этот пример
в некотором смысле двойствен примеру 8.
9. Плоское множество сколь угодно малой плоской меры,
внутри которого направление отрезка единичной длины
можно поменять на обратное непрерывным движением
Этот пример был построен в 1928 г. А. С. Безиковичем
как решение проблемы, поставленной в 1917 г. С. Какея.
(См. [4], [5] и [21], а также [7], где приводятся наиболее
полные сведения.)
ГЛАВА 12
МЕТРИЧЕСКИЕ И ТОПОЛОГИЧЕСКИЕ
ПРОСТРАНСТВА
Введение
Метрическим пространством называется упоря-
доченная пара (X, d), где X — непустое множество, a d—дей-
ствительнозначная функция, определенная на X X X, причем
(i) d строго положительна'.
х£Х =^d(x, х) = О,
х и у£Х, х^=у =>d(x, у) > 0;
(ii) справедливо неравенство треугольника'.
х, у и z£X=^d(x, z)^d(y, x)-Jt-d(y, z).
Из (i) и (ii) сразу следует, что
(iii) d симметрична:
х и у £ X ==> d (х, у) = с? (у, х).
Функция d называется метрикой метрического про-
странства (X, d), а число d(x, у) — расстоянием между
точками х и у. Когда из контекста ясно, о какой метрике
идет речь, можно использовать одну букву X для обозначе-
ния как метрического пространства, так и множества его
точек.
Топологическим пространством называется
упорядоченная пара (X, ©), где X — непустое множество,
а © — семейство подмножеств из X, такое, что
(9 0С® и Х£@,
(ii) © замкнуто относительно операции пересечения конеч-
ного числа подмножеств:
Ор ... [\Оп£6,
где п—произвольное натуральное число;
13*
196
Глава 12
(iii) © замкнуто относительно операции объединения:
(%ел и охе®.
лел
где Л—произвольное непустое множество индексов.
Семейство © называется топологией топологического
пространства (X, ©), а элементы этого семейства—откры-
тыми множествами. Семейство © называют также топо-
логией множества X. Если же из контекста ясно, какое
семейство открытых множеств имеется в виду, то одна и
та же буква может быть использована как для обозначения
топологического пространства, так и множества его точек.
Очевидно, условие (ii) эквивалентно такому же условию при
п = 2. Топологическое пространство (Y, 0) называется под-
пространством топологического пространства (X, ©),
если YczX и 0 = {Y П О | О £ ©}; в этом случае говорят,
что топология $ индуцируется топологией ©.
Множество называется замкнутым, если его дополне-
ние открыто. Открытым покрытием множества А назы-
вается класс открытых множеств, объединение которых со-
держит А. Множество С называется компактным, если
каждое открытое покрытие С содержит конечное подпокры-
тие. Топологическое пространство называется хаусдорфо-
в ы м, если для любых двух его различных точек х и у
существуют два непересекающихся открытых множества, одно
из которых содержит х, а другое — у. В любом хаусдор-
фовом пространстве каждое компактное множество замкнуто.
Говорят, что точка р является предельной точкой мно-
жества Л, если каждое открытое множество, содержащее р,
содержит по крайней мере одну точку из Л\{р). Замы-
канием А множества А называется пересечение всех замк-
нутых множеств, содержащих А Оно состоит из всех точек,
которые являются либо элементами А, либо предельными
точками А. Замыкание любого множества А замкнуто. Мно-
жество А замкнуто тогда и только тогда, когда оно совпа-
дает со своим замыканием, т. е. А = А. Локально ком-
пактным пространством называется топологическое
пространство, каждая точка которого содержится в некото-
ром открытом множестве, замыкание которого компактно.
Базисом топологии топологического пространства (X, ©)
называется подсемейство & семейства ©, обладающее тем
Метрические и топологические пространства
197
свойством, что всякий непустой элемент из & является объе-
динением некоторой совокупности элементов из $. Систе-
мой окрестностей топологического пространства (X, ©)
называется совокупность о# упорядоченных пар (х, N), такая,
что x£N для всякой пары (х, причем совокупность
всех N, таких, что (х, является базисом топологии ©.
Примером системы окрестностей является множество всех пар
(х, Л), таких, что х£А и А £ <£?, где «^ — некоторый базис
топологии пространства (АГ, ©). Если <£?— произвольное не-
пустое семейство подмножеств множества X, то <£? будет
базисом некоторой топологии © в X, если выполнены два
следующих условия: (i) X является объединением элементов
из $, и (ii) если Qx и G2— элементы семейства <£?, пере-
сечение которых не пусто, и х £ Gj ("] G2, то существует
элемент G£<£?, такой, что x^GczG1nG2. Если выполнены
условия (i) и (ii), то топология 6, порожденная семей-
ством определяется множествами, которые являются объеди-
нениями элементов семейства <£?. Последовательность
точек топологического пространства называется сходя-
щейся к точке х, а х называется пределом последо-
вательности {%„}, если
V открытого множества О, содержащего х,
3/w£N9ra(;N, я >«=>%„£ О.
Во всяком хаусдорфовом пространстве сходящаяся последова-
тельность имеет единственный предел.
Если ©j и ©2 — две топологии в одном и том же мно-
жестве X и если ©!с:©2, то говорят, что ©х слабее ©2,
а ©2 сильнее ©1. Самой слабой из всех топологий в X
является тривиальная топология ©=[0, X], а самой
сильной — дискретная топология © = 2Х, состоящая из
всех подмножеств множества X.
Если (X, d) — метрическое пространство и х£Х, то
окрестностью (или сферической окрестностью)
точки х называется множество вида
(у|у6Х, d(x, у)<е),
где е>0 (х называется центром, а е—радиусом этой
сферической окрестности). Сферическую окрестность иногда
называют открытым шаром. Множество всех сферических
окрестностей любого метрического пространства удовлетворяет
14 Зак. 587
198
Глава 12
двум упомянутым выше условиям и порождает топологию
метрического пространства. Множество всех упорядоченных
пар (х, N), где N — сферическая окрестность точки х, яв-
ляется системой окрестностей этой топологии. Топологическое
пространство (X, ©) называется метризуемым, если в X
существует такая метрика d, что 6 является топологией
метрического пространства (X, d). Замкнутым шарол метри-
ческого пространства (X, d) называют множество вида
{у|уЕХ, d(x, у)<е},
где х £ X, а е>0 (х называется центром, а е — радиусом
шара). Всякий замкнутый шар есть замкнутое множество.
Часто вместо „замкнутый шар“ говорят просто „шар“. Множе-
ство в метрическом пространстве называется ограничен-
н ы м, если оно является подмножеством некоторого шара. Если
пространство (X, сГ) ограничено, то d называется ограни-
ченной метрикой. Если метрические пространства (X, d)
и (X, d*') имеют одну и ту же топологию, то говорят, что
метрики d и d* эквивалентны. Пусть (X, d) — произ-
вольное метрическое пространство. Метрика d*, определен-
ная формулой
d*(x у)—
а (х, у) _ j d ,
является ограниченной метрикой, эквивалентной d. Таким
образом, всякое метризуемое пространство можно мет-
ризовать с помощью ограниченной метрики. В любом
конечномерном евклидовом пространстве с обычной евкли-
довой метрикой множество является компактным тогда и
только тогда, когда оно замкнуто и ограничено. По-
следовательность {хп} точек в метрическом пространстве
(X, d) называется фундаментальной последова-
тельностью (или последовательностью Коши), если
Ve>03tfeN}
т и п £ N 1
,, . f -“X & (.Xfn, XГ)
в п>К;
е.
Метрическое пространство называется полным, если каждая
фундаментальная последовательность точек этого пространства
сходится (к некоторой точке пространства). В противном слу-
чае пространство называется неполным. Такие понятия, как
Метрические и топологические пространства
199
связное множество, вполне несвязное множество и совер-
шенное множество, определяются точно так же, как и в евкли-
довых пространствах (см. введение к гл. 10).
Говорят, что топологическое пространство удовлетворяет
второй аксиоме счетности, если существует счетный
базис его топологии. Множество в топологическом простран-
стве называется всюду плотным, если его замыкание
совпадает со всем пространством. Топологическое простран-
ство называется сепарабельным, если оно содержит
счетное всюду плотное множество. Метризуемое пространство
удовлетворяет второй аксиоме счетности тогда и только
тогда, когда оно сепарабельно.
Если (Л", ©) и (Y, 3) — топологические пространства,
a f — отображение X ъ Y, то f называется непрерывным,
если В £ (В) £©, — открытым, если
£7,— замкнутым, если А' £ © =^>(/(Д))' £ д.
Если f — отображение топологического пространства X на
топологическое пространство Y, то f называется гомео-
морфизмом (или топологическим отображением), если f
взаимно однозначно, a f и /-1 непрерывны.
Пусть V — аддитивная группа с элементами х, у, z, ...,
a F— поле с элементами А, р, v, ... . Тогда V называется
векторным пространством (или линейным про-
странством) над полем Р, если существует функция (X, х) -> Ах,
отображающая Р X V в V и такая, что для всех А и р из F
и х и у из V выполнены следующие условия:
(i) А (х “I- у) = Ах —|— Ау,
(11) (А —|— р) х === У.х —|— рх,
(iii) А(рх) = (Ар)х,
(iv) 1 • х = х.
Точки векторного пространства называют также векторами.
Пусть Р обозначает либо поле R действительных чисел, либо
поле С комплексных чисел. Векторное пространство V над
полем Р называется нормированным, если существует
действительнозначная норма || ||, удовлетворяющая для всех
хиуизКиАизГ следующим условиям:
(v) ||х|| = 0<4х = 0,
(vi) ||х + у||<1|х||+||у1|.
(vii) ||Ах|[ = | А | • ||х||.
14*
200
Глава 12
Каждое нормированное векторное пространство является метри-
ческим пространством с метрикой d(x, у) = ||х— у||. Бана-
ховым пространством называется полное нормирован-
ное векторное пространство.
Дальнейшие сведения о топологических пространствах и
отображениях см. в [11], [12], [13], [14], [23], [27], [48], [54]
и [56], о векторных пространствах — в [19], о банаховых
пространствах—в [3] и [29].
1. Убывающая последовательность непустых замкнутых
ограниченных множеств с пустым пересечением
Введем в пространстве R ограниченную метрику d(x, у) =
= -J*—г и положим F„ = [n, Ч-оо), п=1, 2, ....
1 + | X — у| л 1’1 />
Тогда каждое множество Fn замкнуто и ограничено,
4-оо
а П Fn = <z>-
п = 1
Настоящий пример невозможен в конечномерном евклидо-
вом пространстве с обычной евклидовой метрикой, поскольку
всякая убывающая последовательность непустых компактных
множеств имеет непустое пересечение.
2. Неполное метрическое пространство с дискретной топо-
логией
Пространство. (N, d) натуральных чисел с метрикой
d (т, п) — \т — п \/тп имеет дискретную топологию, по-
скольку в нем всякое одноточечное множество открыто.
Однако оно неполно, так как расходящаяся последователь-
ность {«} фундаментальна.
Этот пример показывает, что полнота не является
топологическим свойством, поскольку пространство N
с обычной метрикой и полно, и дискретно. Иными словами,
два метрических пространства могут быть гомеоморфными
даже в том случае, если одно из них полно, а другое нет.
Другим примером таких пространств являются два гомео-
морфных интервала (—оо, -j-оо) и (О, 1), из которых полным
в обычной метрике R является лишь первый.
Метрические и топологические пространства
201
3. Убывающая последовательность непустых замкнутых
шаров с пустым пересечением в полном метрическом
пространстве
Рассмотрим пространство (N, d) натуральных чисел
с метрикой
( 1 , 1
1 -ч---;—, если m #= п,
d(m, п)={ т + п
0, если т. = п,
и положим
Вп = [пг | d(m, п')<^ 1 + 1/2«) = [п, «+1, ...}
для п—1, 2.......... Тогда |ВЛ} удовлетворяет требуемым
условиям, а пространство полно, поскольку каждая фунда-
ментальная последовательность является „почти постоянной".
Если не требовать полноты пространства, то можно при-
вести совсем тривиальные примеры — например, последова-
тельность {у| | 1/л — у|<^ 1/га) в пространстве Р положитель-
ных чисел с обычной метрикой пространства R. С другой
стороны, такой пример становится невозможным, если полное
пространство является банаховым (см. [18]).
Настоящий пример (см. [48]) представляет интерес в связи
с теоремой Бэра (см. пример 7 гл. 8, а также [2], [3], [27]
и [54]), утверждающей, что каждое полное метрическое
пространство является множеством второй категории
или эквивалентно, что пересечение счетного множества откры-
тых всюду плотных множеств в полном метрическом простран-
стве всюду плотно. При доказательстве этой теоремы строится
убывающая последовательность замкнутых шаров, радиусы ко-
торых стремятся к нулю, а потому она имеет непустое пере-
сечение. Таким образом, мы видим, что если шары умень-
шаются, они должны иметь общую точку, в противном же
случае такая точка может и не существовать.
4, Открытый шар О и замкнутый шар В с общим центром
и равными радиусами, такие, что В =# О
Пусть X — произвольное множество, содержащее более
одной точки, и пусть (X, rf) — метрическое пространство
с метрикой
1 1, если х у,
d(x, у) — ] п
(0, если х = у.
15 Зак. 587
202
Глава 12
Далее пусть х — произвольная точка множества X, а О и
В — соответственно открытый и замкнутый шары с центром
в точке х и радиусом 1. Тогда
О = [х}, В = Х,
и так как топология дискретна, то О = О ф В.
Подобный пример невозможен в любом нормированном
векторном пространстве. (Доказательство этого факта предо-
ставляется читателю в качестве упражнения.)
5. Замкнутые шары В\ и Вч с радиусами г\ и п соот-
ветственно, такие, что Bi <=. Вг, а Г\ > Гг
Пусть (X, d) — метрическое пространство, состоящее из
всех точек (х, у) замкнутого круга в евклидовой плоскости
Х=\(х, у)| х2 + у2< 9}
с обычной евклидовой метрикой. Положим В2 = Х, а
у)|(х-2)2 + у2< 16}.
Тогда jBj cz jB2, a r1 = 4>r2 — 3.
Подобный пример нельзя построить ни в каком нормиро-
ванном векторном пространстве, поскольку в этом простран-
стве радиус любого шара равен половине его диаметра.
(Доказательство предоставляется читателю в качестве упраж-
нения.)
6. Топологическое пространство X и его подмножество Y,
такие, что множество предельных точек Y не замкнуто
Пусть X — произвольное множество, содержащее более
одной точки. Наделим его тривиальной топологией © =
= {0, X}. Если у — произвольный элемент из X, то положим
Y = {у}. Тогда предельными точками множества Y будут все
точки X, за исключением самой точки у. Таким образом,
множество предельных точек совпадает с X \ Y, а так как Y
не является открытым, то X \ Y не замкнуто.
7. Топологическое пространство, в котором предел после-
довательности не единствен
Первый пример. Этим свойством обладает всякое про-
странство, наделенное тривиальной топологией, если оно со-
держит более одной точки. В самом деле, в этом простран-
стве каждая последовательность сходится к любой его точке.
Метрические и топологические пространства
203
Второй пример. Пусть X — бесконечное множество.
Наделим его топологией ©, состоящей из 0 и всех допол-
нений конечных подмножеств из X. Тогда каждая после-
довательность различных точек X сходится к любому эле-
менту X.
8. Сепарабельное пространство, обладающее несепара-
бельным подпространством
Первый пример. Пусть (R, 6) — пространство действи-
тельных чисел с топологией 6, порожденной базисом, со-
стоящим из множеств вида
{x}U(QnO — е, х -1- е), e£R, е > 0,
и пусть (Y, fj)— его подпространство иррациональных чисел
с дискретной топологией (оно действительно является под-
пространством, ибо всякое одноточечное множество в Y
является пересечением Y и некоторого элемента из 6). Тогда Q
будет счетным всюду плотным подмножеством (R, ©), однако
в (У, И) не существует счетного всюду плотного подмно-
жества.
Второй пример. Пусть (X, @) — пространство всех
точек (х, у) евклидовой плоскости, таких, что у 0, и пусть
& — топология, порожденная базисом, состоящим из мно-
жеств следующих двух типов:
{(х, у)| [(х —а)2Ч~(у —-6)2]1/2 < min(6, е)}.
a£R, b>0, е > 0,
{(а, 0)} U {(-V. У) | (х — а? Ч~ (У — #)2<е2}, a£R, е > 0.
Тогда множество ((х, у) | х £ Q, у £ Q П Р} есть счетное всюду
плотное подмножество в (X, <д), однако пространство
{(х, у) | х £ R, у = 0), наделенное дискретной топологией,
является подпространством пространства (X, 6), не имею-
щим счетного всюду плотного подмножества. (См. [2],
стр. 29, 5°.)
9. Сепарабельное пространство, не удовлетворяющее вто-
рой аксиоме счетности
Любой из двух примеров предыдущего пункта удовле-
творяет требуемым условиям, поскольку (1) каждое простран-
ство, удовлетворяющее второй аксиоме счетности, сепара-
бельно и (2) любое его подпространство также удовлетворяет
15*
204
Глава 12
второй аксиоме счетности. Если бы какое-либо из пространств
предыдущего пункта удовлетворяло второй аксиоме счет-
ности, то рассматриваемые подпространства были бы сепара-
бельными.
10. Множество с различными топологиями, имеющими
одни и те же сходящиеся последовательности
Первый пример. Пусть (X, ©) — произвольное несчетное
пространство, топология 6 которого определяется пустым мно-
жеством 0 и дополнениями всех счетных (возможно, пустых
или конечных) множеств. Тогда последовательность {схо-
дится к х тогда и только тогда, когда х„ — х для п, пре-
восходящего некоторое wi£N. Иными словами, сходящимися
последовательностями являются те и только те последователь-
ности, которые сходятся в пространстве (X, 0), где д —ди-
скретная топология; при этом очевидно, что © 4= 3 •
Второй пример. Пусть X — множество всех порядковых
чисел, не превосходящих й, где й — первое порядковое
число, соответствующее несчетному множеству. (См. [49]
и [54].) Далее пусть 6 — топология, порожденная интервалами
[1, р), (а, Р) (а, Й],
где а и р£ X. Так как каждое счетное множество из X \ {й}
имеет верхнюю грань, принадлежащую Л'\(й), то никакая
последовательность точек из X \ {й} не может сходиться
к й. Следовательно, последовательность точек в X сходится
к й тогда и только тогда, когда все ее члены, за исключе-
нием конечного числа, равны й. Другими словами, сходя-
щиеся в X последовательности совпадают с теми, которые
сходятся в топологии, полученной присоединением к под-
пространству X \ {й} пространства X точки й как изо-
лированной точки (это означает, что {й} есть одноточечное
открытое множество нового пространства X).
Третий пример. (Определения и дальнейшие подроб-
ности см. в [3] и [29].) Пусть X — банахово пространство 1Х
действительных (или комплексных) последовательностей х —
ОО
= {хп}, таких, что У11 хп | < -1- оо с нормой ||.v||=s
П=1
+оо
s 2 I хп I • Сильной топологией пространства X назы-
п = \
Метрические и топологические пространства
205
вается топология метрического пространства (Л", d) с метри-
кой d(x, у) = ||х— у||.
Определим теперь в X другую топологию, называемую
слабой, при помощи следующей системы окрестностей:
+оо
(Уп Хп)
е, m — 1, 2, . . ., р
где х £ X, е > 0, а (атп) — ограниченная матрица с р стро-
ками и бесконечным числом столбцов. Можно показать,
что [Nx] удовлетворяет сформулированным в введении усло-
виям и порождает топологическое пространство (X, 0).
Чтобы доказать, что сильная топология X действительно
сильнее слабой топологии, мы покажем, что любая окрест-
ность произвольной точки х в слабой топологии содержит
некоторую сферическую окрестность этой точки. Это сразу же
следует из неравенства треугольника для действительных рядов:
+ оо
2 ^тп (Уп Хп)
П = 1
Ф-со
2 |у„—= *11-
П»1
где К — верхняя грань множества абсолютных значений эле-
ментов матрицы (атп). Чтобы доказать, что сильная тополо-
гия строго сильнее слабой, покажем, что каждая окрест-
ность в слабой топологии не ограничена в метрике
сильной топологии (и, следовательно, никакая окрестность
в слабой топологии не может быть подмножеством какой-
либо окрестности в сильной топологии). Пусть (атл)—матрица
с р строками и бесконечным числом столбцов для некоторой
окрестности Nx в слабой топологии, (Zp z2, .... zp+i)—
нетривиальный (р -ф- 1)-мерный вектор, такой, что
р+1
2 = ° ДЛЯ 2, .... р.
П = 1
Далее положим zp+2— zp+3 — ... =0. Тогда вектор
у (а) = х -ф az = {у„ (а)) = [х„ Д- az,,} принадлежит 2VX для
любого действительного а:
ф-СО ф-СО /74-1
2 атп (Уп (а) — хп) = 5 amnazn = а 2 amnzn = 0,
п — 1 л=1 л=1
т = 1, 2.......р.
С другой стороны, || у (а) — х || = Цаг || = | а | • ||z||, a [|z||=£0.
206
Глава 12
Теперь обратимся к последовательностям точек в X. Мы
уже знаем, что всякая последовательность точек в X, кото-
рая сходится к х в сильной топологии, должна сходиться к х и
в слабой топологии. Докажем обратное: если lim х(т)=-х
т-^+со
в слабой топологии, то lim х^ = х в сильной mono-
m-> +со
логии. Отсюда будет следовать, что слабая и сильная топо-
логии в X определяют одни и те же сходящиеся последова-
тельности.
Предположим, что существует последовательность, сходя-
щаяся к х в слабой топологии, но не сходящаяся к х в силь-
ной топологии. В силу линейного характера операции предель-
ного перехода мы можем предположить, не теряя в общности,
что х есть нулевой вектор. Более того, если рассматриваемая
последовательность не сходится к нулю в сильной топологии,
то из нее можно выделить подпоследовательность, нормы
элементов которой отделены от 0. Если обозначить эту под-
последовательность через {х(т)}, то найдется положительное
число е, такое, что
|| х<т> || > 5е
для т=\, 2........Так как {х(т)|—подпоследовательность
некоторой последовательности, сходящейся к 0 в слабой
топологии, то {х(т)} также должна сходиться к 0 в слабой
топологии. Если мы запишем в виде
x(m) = (4m), 4m).....4m). ...),
то последовательность {х(т)) может быть представлена бес-
конечной матрицей М, каждая строка которой соответствует
одному из векторов последовательности Следующий
шаг состоит в том, чтобы показать, опираясь на сходимость
{х(т)| к нулю в слабой топологии, что каждый столбец
матрицы М есть действительная последовательность, сходя-
щаяся к 0, т. е. что при лг->-|-оо предел n-R коорди-
наты для всякого фиксированного n= 1, 2, ... равен 0,
т. е.
lim х(Пт) — 0.
т->+оо
Но это непосредственно следует из рассмотрения окрестности
нуля, задаваемой матрицей (атп), состоящей из одной строки,
на п-м месте которой стоит 1, а на остальных 0.
Метрические и топологические пространства
207
Теперь мы можем по индукции построить две строго
возрастающие последовательности натуральных чисел
тх < т2 < ... и < п2 < .... такие, что для J £ N
Л s
J +со
л-1 л“лу+1 + 1
и, следовательно,
(Ь) 2 |<7)|>3е-
Л-Лу + 1
Наконец, определим последовательность {ап} следующим
образом:
1, если 1 п <
йп sgn x^i\ если ny4-1 <n<ny+1
для 7=1. 2......Если No — окрестность нулевого вектора,
определяемая числом е и матрицей (атп), состоящей из одной
строки, составленной из членов {ил},
{+оо 1
у = {ул} 112 апуп I <6 •
1 л-1 1 J
то никакая точка x^mf> подпоследовательности {после-
довательности {х(т)} не является элементом 2V0:
Л J I I /Is
+оо 7+1 j
Л —I Л-Лу+1 Л-1
+оо
— I 2 апх^1>'> I > 3е — 6 — е — е.
'л-л/+1+1
Но это означает, что {х(т)} не может сходиться к 0. (Про-
тиворечие.)
11. Пример топологического пространства X, множества
АсХ и предельной точки этого множества, не
являющейся пределом никакой последовательности
точек из А
Первый пример. Пусть X — пространство из первого
примера п. 10, и пусть А — какое-либо несчетное правиль-
ное (или собственное) подмножество из X. Тогда любая точка
208
Глава 12
множества X \ А будет предельной точкой А, но поскольку х
не может быть пределом последовательности точек йз А
в дискретной топологии, то это же справедливо и для топо-
логии, описанной в этом примере.
Второй пример. Пусть X—пространство из второго
примера п. 10 с топологией, которая была введена в начале
примера. Положим Л = Х\ {Q}. Тогда Q будет предельной
точкой Л, но никакая последовательность из А не может
сходиться к й.
Третий пример. (См. [35], где построен аналогичный
пример, а также [3], [18], [29] и [31], где даны определения
и излагаются дальнейшие сведения.) Пусть X — гильбер-
тово пространство /2 всех действительных (или ком-
плексных) последовательностей чисел х={х„|, таких, что
4-оо / 4-оо \
2 х2п < 4- °° I или 2 I хп I2 < 4“ 00 в комплексном случае I.
Л=1 \ Л=1 /
В этом пространстве для любых двух точек х = [хл] и
у =; {ул) определено скалярное произведение (или
4-со / 4-со
внутреннее произведение) (х, у)=н 2 хпУп или хпУп
Л=1 \ Л=1
в комплексном случае).
Это скалярное произведение обладает следующими свой-
ствами для любых х, у, z£l2 и X£R (с этого момента в на-
стоящем примере рассматривается лишь пространство дей-
ствительных последовательностей):
0) (х 4- У< z) = (x, z) 4- (у, z),
(ii) (kx, у) = X (х, у),'
(iii) (у, х) = (х, у),
(iv) (х, х) О,
(v) если || х|| = (х, х)1/2, то || || является нормой, отно-
сительно которой /2 является банаховым пространством.
Превратим теперь пространство X —12 в топологическое
пространство (X, ©), введя в нем систему окрестностей,
определенную аналогично тому, как это сделано в третьем
примере п. 10:
Nx=[y\b£B=^\(y — x, *)|<е}.
где х£Х, е > 0, а В — любое непустое конечное множество
точек из X.
Метрические и топологические пространства
209
Пусть А — множество точек {х(т)}, где х(т)—точка,
m-я координата которой равна Ут, а все остальные коорди-
наты равны нулю, т. е.
х(т) = (0, 0..0, Ут, 0, . . .).
Покажем сначала, что нулевой вектор будет предельной точ-
кой Л. Предположим, что окрестность нуля
N0=[y\b£B=^\(y, Z>)|<e}
(где е > 0, а В состоит из точек Z>(1) == (Z^1’}.b<!’} — {z^f1})
не содержит ни одной точки х(т). Это означает, что
Vm€NBA€{l, 2......р}У\УтЬ%У^
и, следовательно,
р 4-оо 4-оо р 4-оо
s W=SW)2>S4=+-
/? = 1 т=1 т=1 ft —1 т~1
4-оо
что противоречит предположению о сходимости ряда 2
m-l
для k = 1, 2, . . ., р.
Наконец, покажем, что никакая последовательность точек
из А не может сходиться к нулевому вектору. Легко пока-
зать, что если
%(т4, х(^), ..., х(тУ ...->0,
то последовательность пгр т2, ... не ограничена. Следова-
тельно, не ограничивая общности, можно предположить, что
тг < т2 < ... и
V 1 / ।
7. --<4-оо-
Я;
7-1
Чтобы закончить доказательство, определим окрестность 1У0
точки 0 при помощи е=1 и множества В, состоящего из
единственного вектора Z>, пг?-я координата которого равна
1/Уm.j для /=1, 2, ..., а все остальные координаты
равны нулю. Тогда никакая точка последовательности
не может принадлежать No, ибо Z»)—1 для J = 1, 2.
Четвертый пример. См. пример 12 этой главы.
210
Глава 12
Отметим, что явление, описанное в настоящих примерах,
не может иметь места в метрическом пространстве и, следо-
вательно, ни одно из описанных выше пространств не является
метрическим и даже не метризуемо.
12. Неметризуемое топологическое пространство X
с функциями в качестве точек и топологией, соот-
ветствующей поточечной сходимости
Пусть (X, ©) — пространство всех действительнозначных
непрерывных функций, заданных на [0,1], и пусть топология©
порождается системой окрестностей
Nf=[g\x£F=$\g(x) — f(x)\ < е},
где f£X, е > 0, a F—конечное непустое подмножество
замкнутого интервала [0,1]. Ясно, что если в этой топологии
gn->g при и—то gn(x)-+ g(x) при /г —> —оо для
каждого х£[0,1], поскольку в качестве F можно брать одно-
точечные множества (х). С другой стороны, если gn(х)->g (х)
при л->-|-оо для каждого х £ [0,1], то gn -> g при я-> -]-оо.
В самом деле, для каждого е > 0 и конечного подмножества F
интервала [0,1] можно выбрать п настолько большим, что-
бы выполнялось неравенство | gn (х) — g (х) | < е для каж-
дого х£ F.
Пусть А — множество всех функций / из X, таких, что
(а) х С [0,1] =#>0 </(х)< 1,
(Ь) р({х|/(х)=1})>1/2.
Тогда 0 является предельной точкой А. Однако если
некоторая последовательность {/„} элементов из А сходится
к 0 в топологии 6, то {/„ (х)) сходится к 0 в каждой точке
х £ [0,1]. Следовательно, по теореме Лебега о возможности
предельного перехода под знаком интеграла в случае равно-
мерно ограниченной последовательности функций получим
1
J fn(x)dx —>0 при я->-|-оо. Но это противоречит нера-
0
1
венству J fn (х) dx 1/2. Наконец, принимая во внимание
о
последнее замечание к примеру 11, заключаем, что X не
метризуемо.
Метрические и топологические пространства
211
13. Непрерывное отображение одного топологического
пространства на другое, не являющееся ни открытым,
ни замкнутым
Первый пример. Пусть функция f(x) = excosx задана
на R, где определена обычная топология. Легко видеть, что f
отображает R на R непрерывно, однако множество /((—оо, 0))
не является открытым, а множество ./({—nn|n£N}) не
является замкнутым.
Второй пример. Возьмем в качестве X пространство R
с дискретной топологией, в качестве К — пространство R
с обычной топологией и рассмотрим тождественное отображе-
ние первого пространства на второе.
14. Отображение одного топологического пространства
на другое, являющееся одновременно открытым и
замкнутым, но не являющееся непрерывным
Первый пример. Пусть X — единичная окружность
{(х, у)| х2—j-y2= 1} с топологией, индуцированной обычной
топологией на плоскости. Далее, пусть Y — полуоткрытый
интервал [0, 2л) с топологией, индуцированной обычной
топологией в R. Наконец, пусть / — отображение (х, у)->9,
где x = cos9, у = sin 9 и 0^9 < 2л. Тогда f одновременно
и открыто, и замкнуто, поскольку обратное отображение
непрерывно. Однако f разрывно в точке (1,0).
Второй пример. Отображение, обратное к отображению
из второго примера п. 13.
15. Замкнутое отображение одного топологического про-
странства на другое, не являющееся ни непрерывным,
ни открытым
Пусть X — единичная окружность {(х, у) | х2 -|- у2 = 1}
с топологией, индуцированной обычной топологией на пло-
скости. Далее, пусть Y — полуоткрытый интервал [0, л) с то-
пологией, индуцированной обычной топологией в R. Наконец,
пусть f — отображение
( 0, если 0 9 л,
(cos 9, sin9)-><
(9 — л, если л < 9 < 2л.
212
Глава 12
Тогда f не является открытым, так как открытая верхняя
полуокружность из X отображается в точку. Кроме того, f
не является непрерывным в точке (1,0) (см. первый пример
п. 14). Однако, как мы сейчас убедимся, f замкнуто. Пред-
положим противное, т. е. что f не замкнуто. Тогда в X
существует замкнутое множество А, такое, что B = f(A)
не замкнуто в Y. Следовательно, существует последователь-
ность {£>л} точек из В, такая, что а Ь(^В. Пусть
ftPnl^-bn- гДе Ддя «=1, 2........ Поскольку А
компактно, то без ограничения общности можно предполо-
жить, что сходится, p„->p(zA. Но так как f{p^)->
то f разрывно в точке р и, следовательно,
р = (1, 0). Это означает, что существует подпоследователь-
ность последовательности стремящаяся к точке (1,0)
либо по верхней, либо по нижней полуокружности. В первом
случае Ьп->0£В, а во втором случае рл} не может схо-
диться в К. Итак, в обоих случаях получено противоречие;
следовательно, f замкнуто.
16. Отображение одного топологического пространства
на другое, являющееся непрерывным и открытым,
но не являющееся замкнутым
Пусть (X, ©)—евклидова плоскость с обычной топологией,
(У, £7)—пространство R с обычной топологией, и, наконец,
пусть отображение / есть проектирование Р: (х, у)->х. Тогда
Р, очевидно, непрерывно и открыто, однако /’({(х, у) | у —
= 1/х > 0}) не замкнуто в (Y,
17. Открытое отображение одного топологического про-
странства на другое, не являющееся ни непрерыв-
ным, ни замкнутым
Первый пример. Пусть A’ = E = R с обычной тополо-
гией, и пусть f — функция, определенная в примере 27 гл. 8,
множество значений которой на всяком непустом открытом
интервале совпадает с R. Эта функция, очевидно, является
открытым отображением, поскольку образ всякого непустого
открытого множества есть R. Кроме того, f всюду разрывна.
Покажем, что отображение f не замкнуто. Пусть точка
Метрические и топологические пространства
213
хп£(п, п-|-1) такова, что </W<| Для «=1> 2..............
Тогда {хл} замкнуто, а {/(%„))—нет.
Второй пример. Пусть (X, ©) — плоскость с тополо-
гией 6, состоящей из пустого множества 0 и дополнений
счетных множеств, а (К, </) — пространство R с топологией 0,
состоящей из пустого множества 0 и дополнений конечных
множеств. Наконец, в качестве отображения рассмотрим
проектирование Р- (х, у)->х. Тогда Р открыто, поскольку
любое непустое открытое множество в (X, 6) должно содер-
жать некоторую горизонтальную прямую, образ которой
есть R. С другой стороны, Р не замкнуто, так как множе-
ство точек (и, 0), где n£N, замкнуто в (X, ©), а его образ
не замкнут в (Y, 0). Наконец, Р не является непрерывным,
так как прообраз любого открытого в (К, 0) множества, кото-
рое является правильным подмножеством в Y, не может быть
открытым в (X, ©).
18. Непрерывное замкнутое отображение одного тополо-
гического пространства на другое, не являющееся
открытым
В качестве пространств X u Y возьмем замкнутый интер-
вал [0, 2] с обычной топологией. Положим
( 0, если 0< х< 1,
J [х—1, если 1<х<С2.
Тогда отображение /, очевидно, непрерывно и, следовательно,
замкнуто, так как X и У — компактные метрические про-
странства. С другой стороны, множество /((0, 1)) не является
открытым в Y.
19. Топологическое пространство X и его подпростран-
ство Y, содержащее два непересекающихся откры-
тых множества, которые не являются пересечением
подпространства Y с непересекающимися открытыми
множествами пространства X
Пусть /^N, а открытыми множествами являются 0 и
дополнения конечных множеств. Пусть далее У = {1, 2].
Тогда {1} = У П(2^ \ {2}) и {2} — У fl (X \ {1)), так что
топология подпространства У дискретна. Однако непересе-
кающиеся открытые множества {1} и {2} подпространства У
214
Глава 12
не являются пересечениями подпространства Y с непересекаю-
щимися открытыми множествами пространства X, поскольку
любые два непустых открытых множества пространства X
пересекаются.
20. Два негомеоморфных топологических пространства,
каждое из которых является непрерывным взаимно
однозначным образом другого
Первый пример. Пусть X и Y — следующие подпростран-
ства пространства R, наделенного обычной топологией:
-(-оо
X== ((Зга, Зга 4- 1) и {Зга4~ 2) ),
л=0
К==(Х\{2})и{1}.
Определим отображение •$ пространства X на Y и отобра-
жение Т пространства Y на X формулами:
fl
-% у, если у 1,
[ х, если х 4= 2, I .
S(X)^{1, если х = 2, если 3<у<4,
у— 3, если у > 5.
Тогда S и Т непрерывны, взаимно однозначны и
являются отображениями на. Однако Л’ и К не гомеоморфны,
так как при любом гомеоморфизме Y на X точка 1 про-
странства Y не может иметь образа.
Второй пример. Пусть X и Y — множества на плоскости
с обычной топологией, указанные на рис. 12. Вертикальные
отрезки имеют длины, равные 2, и являются открытыми на
верхних концах, а окружности имеют единичные радиусы. Ото-
бражение S пространства Л" на У определяется следующим об-
разом: верхняя часть рис. 12 при помощи параллельного пере-
носа накладывается на нижнюю так, что горизонтальная прямая
множества X отображается на горизонтальную прямую мно-
жества Y, окружности Dn — на Cn+V отрезок — на Clt
отрезки Лл+2— на Вл+1, ra£N. Отображение же отрезка Л2
на окружность Вг определяется отдельно формулами
x=sinn£, у=1 —cosn£, где 0<^<2. Отображение Т
множества Y на X определим так: нижнюю часть рис. 12
сместим влево и наложим ее на верхнюю так, чтобы, окруж-
Метрические и топологические пространства
215
ность jBj совпала с Dv горизонтальная прямая множества
Y — с горизонтальной прямой множества X, окружности
Сл+1— с £>л+2, отрезки Вл+1 — с Лл, n£N. Наконец, сег-
мент Cj отобразим на окружность £>2 при помощи формул
такого же типа, как и выше. Отображения S и Т обладают
нужными свойствами. Предлагаем читателю в качестве упраж-
нения доказать, что пространства X и Y не гомеоморфны.
0} В2 В] Л А? А3 At
-OOOI I I I-
С4 Cj Сг Cj 6, Вг Bj
-ООО I О I 1 -
У
Рис. 12.
21. Разбиение трехмерного евклидова шара В на пять
непересекающихся подмножеств Si, S2, S3, S«, S5 (при
этом So состоит из единственной точки), таких, что
при жестких движениях Rt, R2, R3,Ra, Rs справед-
ливы следующие соотношения:
5 = Я1 (Si) U Ri (S2) R3 (S3) U Rt (Si) U Rs (Ss)
(Здесь символ ~ означает „конгруэнтен". См. ссылку,
которая следует ниже.)
22. Для любых двух евклидовых шаров Вг и Вм, радиусы
которых суть произвольно заданные числа е > 0 и
М > 0, всегда существует разбиение шара Вг на
конечное число непересекающихся подмножеств
Si, S2, ..., S„, таких, что при жестких движениях
Rt, R2, , Rn справедливо» равенство
Вм = Ri (Si) U R2 (S2) U ... U Rn(Sn)
Два последних примера впервые были построены в рабо-
тах Хаусдорфа, Банаха, Тарского, фон Неймана и Робинсона.
Однако мы ограничимся лишь одной ссылкой, где они изла-
гаются наиболее подробно (см. [43]).
ГЛАВА 13
ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА
Введение
Функциональным пространством, или простран-
ством функций, называется совокупность функций, имеющих
общую область определения D. Обычно предполагается, что
функциональное пространство обладает какой-либо алгебраи-
ческой или топологической структурой. В настоящей главе
мы сосредоточим внимание на алгебраических структурах
некоторых пространств действительнозначных функций дей-
ствительного переменного, общая область определения кото-
рых есть некоторый фиксированный интервал I.
Функциональное пространство •$ действительнозначных
функций, заданных на интервале I, называется векторн ым
пространством (или линейным пространством) над R
(системой действительных чисел), если <5 замкнуто относительно
линейных комбинаций с действительными коэффициентами,
т. е. если
/, g'es, К V^=^f+pg£S,
где функция X/ определяется следующим образом:
(Х/)(х)=1(/М).
Легко показать, что пространство действительнозначных
функций, заданных на некотором интервале, является вектор-
ным пространством тогда и только тогда, когда оно замкнуто
относительно двух операций, а именно относительно сложе-
ния f g и умножения на скаляр kf. Абстрактное поня-
тие векторного пространства определено аксиоматически
в введении к гл. 12. (Дальнейшие сведения см. в [19] и [15]*.)
Многие наиболее важные классы функций, встречающиеся
в анализе, являются линейными пространствами над R (или
над полем комплексных чисел С; в этом случае коэффи-
циенты X и ц— произвольные комплексные числа). Приме-
рами пространств действительнозначных функций, которые
являются линейными пространствами над R, могут служить:
Функциональные пространства
217
1. Совокупность всех (действительнозначных) функций на
интервале I. 2. Совокупность всех ограниченных функций
на интервале I. 3. Совокупность всех функций, интегри-
руемых по Риману на замкнутом интервале [а, й]. 4. Сово-
купность всех функций, измеримых по Лебегу на интер-
вале 1. 5. Совокупность всех функций, интегрируемых по
Лебегу на интервале I. 6. Совокупность всех функций, изме-
римых на интервале I, p-я степень абсолютных значений кото-
рых интегрируема по Лебегу на I (р 1). 7. Совокупность всех
функций, непрерывных на интервале I. 8. Совокупность всех
функций, кусочно непрерывных на замкнутом интервале [а, &].
(См. [36], стр. 131.) 9. Совокупность всех функций, кусочно
гладких на замкнутом интервале [а, б]. (См. [36], стр. 131.)
10. Совокупность всех функций, имеющих производные и-го по-
рядка на интервале /, где п — некоторое фиксированное нату-
ральное число. 11. Совокупность всех функций, имеющих
непрерывные производные n-го порядка на интервале I, где
п — некоторое фиксированное натуральное число. 12. Сово-
купность всех бесконечно дифференцируемых функций на
интервале I. 13. Совокупность всех {алгебраических) поли-
номов на интервале I. 14. Совокупность всех (алгебраиче-
ских) полиномов на интервале I, степень которых не прево-
сходит некоторого натурального п. 15. Совокупность всех
тригонометрических полиномов на интервале I, имеющих
вид
п
2 cos ix + Pzsin lx, (1)
z=o
где n — любое неотрицательное целое число. 16. Совокуп-
ность всех тригонометрических полиномов вида (1), где п
фиксировано. 17. Совокупность всех ступенчатых функ-
ций на замкнутом интервале [а, б]. 18. Совокупность всех
постоянных функций на интервале I. 19. Совокупность
всех функций, удовлетворяющих данному линейному одно-
родному дифференциальному уравнению на интервале I, на-
пример уравнению
rf3y , . rf2y । х dy n
-p-^- + sin x -4- e --------xy — 0,
dx3 1 dx2 ' dx
на интервале I. Если в предыдущих примерах рассматривать
комплекснозначные функции, то получим еще девятнадцать
примеров линейных пространств над R.
218
Глава 13
Линейные пространства играют существенную роль в ана-
лизе. Однако существует несколько важных классов дей-
ствительнозначных функций, которые не являются линейными
пространствами. Некоторые из них указаны в следующих
пяти примерах: (1) класс всех монотонных функций на интер-
вале [а, й], (ii) класс всех периодических функций на
(—оо, —оо), (iii) класс всех полунепрерывных функций на
интервале [a, Z>], (iv) класс всех функций, квадраты которых
интегрируемы по Риману на [a, Z>], (v) класс всех функций,
квадраты которых интегрируемы по Лебегу на [а, й]. Можно
сказать, что эти пространства являются нелинейными на
интервале [а, &].
Пространство S действительных функций, заданных на
интервале /, называется алгеброй над R, если оно замк-
нуто относительно линейных комбинаций с действительными
коэффициентами и относительно операции произведения функ-
ций, т. е. если S есть линейное пространство над R и
/€$, gсS =>fgсS.
(Точно так же, как и понятие линейного пространства,
абстрактное понятие алгебры определяется аксиоматически.
См. [19], т. II, стр. 36, 225.) Из тождества
/g = |(/ + g)2-^(/-g)2 (2)
следует, что линейное функциональное пространство является
алгеброй тогда и только тогда, когда оно замкнуто относи-
тельно операции возведения в квадрат.
Пространство S действительнозначных функций, заданных
на интервале I, называется структурой, если оно зам-
кнуто относительно двух бинарных операций V и А- кото-
рые определяются следующим образом:
(/ V g) (*) = max (/ (х), g (х)),
(/Л g)(x)==min(/(x), g(x)).
(Абстрактное понятие структуры определяется аксиоматически.
См. [8].) Вместе с данной действительнозначной функцией /
часто рассматриваются неотрицательные функции /+ и
определяемые следующими равенствами:
/+ = /V0. /- = (-/) V0. (3)
Функциональные пространства
219
Эти функции связаны такими соотношениями:
/ = \f\=f+ + T> (4)
г (5)
Отметим также, что для операций максимума и минимума
справедливы следующие равенства:
f V ^ = -[(-/) Л (-£% (6)
f Л £ = -[(-/) V (-5% (7)
f + + (8)
f = (9)
Из равенств (3) — (9) следует, что линейное функциональное
пространство является структурой тогда и только тогда,
когда оно замкнуто относительно какой-нибудь одной из
следующих операций:
/V^./Л^. (Ю)
Л Г. 1/1- (И)
Среди приведенных выше примеров линейных пространств
как алгебрами, так и структурами являются пространства
примеров 1—4, 7, 8, 17 и 18. Ни алгебры, ни струк-
туры не образуют пространства примеров 14 (см. ниже при-
мер 6), 16 и 19. Пространства примеров 9, 10, 11 (см. ниже
пример 7), 12, 13 и 15 являются алгебрами, но не являются
структурами. Пространства примеров 5 (см. ниже пример 8)
и 6 являются структурами, но не являются алгебрами.
1. Две монотонные функции, сумма которых не моно-
тонна
sinx-|-2x и sinx— 2х на [—л, л].
2. Две периодические функции, сумма которых не имеет
периода
sinx и sin ах (а иррационально) на (—оо, -|-оо).
Если бы функция sin х-]-sin ах имела отличный от нуля
период р, то для любого действительного х были бы
220
Глава 13
справедливы следующие тождества:
sin (х -1- p)-[-sin(ax-)-ap) = sinx-]- sin ax,
sin (x + p) — sin x — — [sin (ax ap) — sin ax],
/ . I \ . (1 \ / ,1 \ . I 1 \
cos I x-J-y p I sin Iу p I = — cos lax-)—2" ap I sin I у ap 1,
. /1 \ , , . /1 \
cos x sin I у pl = — cos (ax) sin I у ap I. ,
„ 1
Если положить x = у л, то левая часть последнего тожде-
ства обратится в нуль. Следовательно, sin-g-ap = 0, а по-
этому ар кратно 2л. Если же положить ах = уЛ, то обра-
тится в нуль правая часть этого тождества. Следовательно,
sin у р = 0, а поэтому р кратно 2л. Но это противоречит
предыдущему, так как а иррационально. (См. [38], стр. 550,
замечание.)
3. Две полунепрерывные функции, сумма которых не
является полунепрерывной
Положим
1, если X > о, 1, если X >0,
/GO= 2, если X = 0, g(x)= —2, если X = 0,
. —1, если X < о, • —1, если X < о.
Тогда f (х) всюду полунепрерывна сверху, g(x) всюду полу-
непрерывна снизу, однако /(х)-|-g(x) не является полу-
непрерывной в точке х = 0.
Возможны и более интересные примеры, когда каждая
из функций f и g полунепрерывна всюду, однако в одних
точках эти функции полунепрерывны сверху, а в других —
снизу. Для построения таких примеров условимся, что обо-
значение p!q, где р и q — целые числа, представляет собой
Функциональные пространства
221
несократимую дробь, причем <?>0. Число нуль будем пред-
ставлять в виде отношения 0/1. Положим
{1, если x — p!q, q нечетно,
0 в противном случае,
— 1, если x — plq, q четно,
п
0 в
противном случае.
Тогда
f(x) + g(x) =
1,
—1,
0,
если х = plq, q нечетно,
если х — pfq, q четно,
если х иррационально.
Следовательно, / (х) -|- g (х) полунепрерывна тогда и только
тогда, когда х рационально, т. е. fg почти всюду не яв-
ляется полунепрерывной.
Теперь рассмотрим следующие три функции:
. G (х) =
/7(х) =
4/7, если х = р/q, q нечетно,
F(x) = —2— 4/7, если х = р/q, q четно,
—2, если х иррационально,
— 1 — 1/q, если х — plq, q нечетно,
1 -ф- \fq, если х — pfq, q четно,
— 1, если х иррационально,
— 1 — 1/q, если х = р/q, q нечетно,
3 -|- 1/7, если х = plq, q четно,
3, если х иррационально.
Каждая из функций F, О и И полунепрерывна всюду,
однако их сумма
fW + O(x)f//(x) =
—2 -ф 2/7, если х = plq, q нечетно,
2 — 2/q, если х — р/д, q четно.
0, если х иррационально,
не является полунепрерывной ни в одной точке.
16 Зак. 587
222
Глава 13
4. Две функции, квадраты которых интегрируемы по
Риману, но квадрат их суммы не интегрируем по Риману
Положим
/(х) = {
если х иррационально,
если х рационально,
( 1, если х — алгебраическое число,
g О) = < ,
[ —1, если х — трансцендентное число.
Тогда
/(*)+£ (х) =
2, если х — алгебраическое иррациональ-
ное число,
О в остальных случаях.
Очевидно, функции /2 и g2 являются постоянными, и, следо-
вательно, они интегрируемы на любом замкнутом интервале,
в частности на [0,1]. В то же время функция (/ g)2 раз-
рывна всюду и поэтому не интегрируема по Риману ни на
каком интервале, в частности она не интегрируема на [0,1].
5. Две функции, квадраты которых интегрируемы по
Лебегу, но квадрат их суммы не интегрируем по Лебегу
Пусть £] —неизмеримое подмножество интервала [0,1],
а В2— неизмеримое подмножество интервала [2,3]. (См. при-
мер 11 гл. 8.) Положим
/(*) =
g(X) =
1, если х£ [0,1] U Е2,
— 1, если х£ [2,3] \Е2,
0 в остальных случаях,
1, если х £ [2,3] U Ev
— 1, если х£ [0,1] \£\,
0 в остальных случаях.
Следовательно,
[2,
если х е U Е2,
в остальных случаях.
Функциональные пространства
223
Но так как
/2(х) = ^2(х) =
а
(/(лг) + g (х) )2 =
1, если х£ [0,1] U [2,3],
О в остальных случаях,
4, если х е U Е2,
О в остальных случаях,
то отсюда следует требуемый результат, поскольку множе-
ство Ех (J Е2 неизмеримо.
6. Линейное функциональное пространство, не являю-
щееся ни алгеброй, ни структурой
Совокупность полиномов сх -]-• d степени не выше 1 на
замкнутом интервале [0,1] образует линейное пространство.
Это пространство не является алгеброй, поскольку ему не
принадлежит квадрат элемента х. Это пространство не об-
разует и структуры, так как элемент 2х — 1 принадлежит
пространству, а элемент | 2х — 1 | ему не принадлежит.
7. Линейное функциональное пространство, являющееся
алгеброй, но не являющееся структурой
Рассмотрим пространство всех функций, непрерывно диф-
ференцируемых на [0,1]. Как следует из формулы (fg)' =
= fg' 4- f'g, оно образует алгебру. Однако оно не является
структурой. В самом деле, функция
I 0, если х — 0,
.... _
[xJsinl/x, если 0<х<^1,
непрерывно дифференцируема на [0,1], но ее абсолютное
значение уже не будет дифференцируемо на бесконечном
множестве точек, где /(х) = 0. В действительности же
функция | / (х) | даже не является кусочно гладкой.
8. Линейное функциональное пространство, являющееся
структурой, но не являющееся алгеброй
Множество всех функций, интегрируемых по Лебегу на
[0,1], является линейным пространством и структурой.
16*
224
Глава 13
Однако это пространство не образует алгебры, поскольку
функция
О, если х = 0,
х“1/2, если 0<х<^1,
принадлежит пространству, а ее квадрат ему не принадле-
жит.
9. Две метрики в пространстве С( [0,1]) функций, не-
прерывных на [0,1], такие, что дополнения единичного
шара в одной из метрик всюду плотно в единичном
шаре другой метрики
Метрики р и о определим следующим образом: для
/, g-£C([0,l]) положим
Р(/. g) = |/" j |/(х) —g(x)|2 dx = ||/ —g||2,
<*(/. £) = sup |/(х) — g(x)\=\\f —
0< 1
Пусть Р= { /| р(/, 0)<1 ), 2= ( /| о(/, 0)< 1 } —еди-
ничные шары в этих метриках. Очевидно, 2сР. Покажем,
что дополнение S всюду плотно в Р. В самом деле, пусть
f £Р и 0 < е < 1. Если ||/Ни > 1, то f 2 и / принад-
лежит любому шару в метрике р с центром в точке /.
Если же Ц/Ноо^Е то положим
0, если 0 х
е2
— или
g(x)~
„ 1
о, если х = —,
2
линейна на оставшихся интервалах.
Тогда /(x)4-g(x) ^2 и
II / — (/ + g) ll2 = II g II2 < V9 • (е2/9) = е.
Этот последний пример выявляет существенное различие
между конечномерными и бесконечномерными нормированными
Функциональные пространства 225
линейными пространствами. В обоих случаях замкнутый еди-
ничный шар обладает тем свойством, что всякая прямая,
проходящая через его центр (т. е. совокупность элементов,
которые получаются умножением фиксированного ненулевого
элемента на всевозможные скаляры), пересекает шар по
замкнутому отрезку, средняя точка которого совпадает с
центром шара. Тем самым в конечномерном пространстве
топология определяется единственным образом. Настоящий
пример показывает, что в бесконечномерном пространстве
этот факт не имеет места.
БИБЛ ИОГРАФИЯ
Александров П. С., КолмогоровА. Н.
[I]*1) Введение в теорию функций действительного переменного
М.—Л., 1938.
Александров, Хопф (Alexandrov Р., Hopf Н.)
[2] Topologie, Springer, Berlin, 1935.
Банах (BanachS.)
[3] Theorie des operations lineaires, Warsaw, 1932. (На украин-
ском языке: Курс фуикщонального анал!зу, Ки!в, 1948.)
Безикович (BesicovitchA. S.)
[4] Snr deux questions de I’integrabilite, Journ. Soc, Math, et
Phys, a 1’Un.iv. a Perm, 2 (1920).
[5] On Kakeya’s problem and a similar one, Math. Z., 27 (1928),
312—320.
[6] On the definition and value of the area of a surface. Quart.
J. Math., 16 (1945), 86—102.
[7] The Kakeya problem, Math. Association of America Film,
Modern Learning Aids, New York; Amer. Math. Monthly, 70,
№ 7 (1963), 697—706.
Биркгоф Г.
[8] Теория структур, М., ИЛ, 1952.
Боас (Boas Р.. Р.)
[9] A primer of real functions, Carus Math. Monographs, № 13,
John Wiley and Sons, Inc., New York, 1960.
Б p а у e p (В г о u w e r L. E. J.)
[10] Zur Analysis Situs, Math. Ann., 68 (1909), 422—434.
Бурбаки H.
[11] Теория множеств, M., изд-во «Мир», 1965.
[12] Общая топология. Основные структуры, М., Физматгиз
1958.
[13] Общая топология. Числа и связанные с ними группы и
пространства, М., Физматгиз, 1959.
Вайдьянатхасвами (Vaidyanathaswamy R.)
[14] Treatise on set topology, Part 1, Indian Math. Soc., Madras,
1947.
•) Звездочкой отмечены работы, добавленные при переводе.
Библиография
227
Гельфанд И. М.
[15]* Лекции по линейной алгебре, М., изд-во «Наука», 1966.
Гобсон (Н о b s о n Е. W.)
[16] The theory of functions, Harren Press, Washington, 1950,
Грейвз (Graves L. M.)
[17] Theory of functions of real variables, 2d ed., McGraw-Hill
Book Company, Inc., New York, 1956.
Данфорд H., Шварц Дж. T.
[18] Линейные операторы, Общая теория, М„ ИЛ, 1962.
Джекобсон (Jacobson N.)
[19] Lectures in abstract algebra, vols. 1 and 2, D. Van Nostrand
Company, Inc., New York, 1951.
Зигмунд A.
[20] Тригонометрические ряды, т. I и II, M., изд-во «Мир»,
1965.
Каке я (KakeyaS.)
[21] Some problems on maximum and minimum regarding ovals,
Tdhoku Sci. Reports, 6 (1917), 71—88.
Каратеодори (C a r a theo d о г у C.)
[22] Vorlesungen tiber reelle Funktionen, 2d ed., G. B. Teubner,
Leipzig, 1927.
Келли (К e 11 e у J. L.)
[23] General topology, D. Van Nostrand Company, Inc., Prince-
ton, New York, 1955.
Кнастер, Куратовский (Knaster В., Kuratowski C.)
[24] Sur les ensembles convexes, Fund. Math., 2 (1921),
201—255.
КолмогоровА. H.
[25] О представлении непрерывных функций нескольких пере-
менных суперпозицией непрерывных функций меньшего
числа переменных, ДАН СССР, 108 (1956), 179—182.
К у к Р.
[26]* Бесконечные матрицы и пространства последовательностей,
М., Физматгиз, 1960.
Куратовский К.
[27] Топология, т. I, М., изд-во «Мир», 1966.
Л е б е г А.
[28] Интегрирование и отыскание примитивных функций,
М.—Л., 1934.
Л ю м и с Л.
[29] Введение в абстрактный гармонический анализ, М., ИЛ,
1956.
228
Библиография
Ma3ypKeBH4(MazurkiewiczS.)
[30] Compt. Rend. Soc. Sci. et Lettres de Varsovie, 7 (1914),
322—383, especially 382—383.
Мак-Шейн, Боте (McShane E. J., Botts T. A.)
[31] Real analysis, D. Van Nostrand Company, Inc., Princeton,
N. Y„ 1959.
Манро (M u n г о e M. E.)
[32] Introduction to measure and integration, Addison-Wesley
Publishing Company, Inc., Reading, Mass., 1953.
Натансон И. П.
[33] * Теория функций вещественной переменной, М., Физматгиз,
1957.
фон Нейман Дж (von Neumann J.)
[34] Zur Algebra der Funktionaloperationen und Theorie der
normalen Operatoren, Math. Ann., 102 (1930), 370—427.
Ньюмен (Newman M. H. A.)
[35] Elements of the topology ol plane sets of points, Cam-
bridge Univ. Press, Cambridge, 1939.
Олмстед (Olmsted J. M. H.)
[36] Advanced calculus, AppletonCentury-Crofts, Inc., New
York, 1961.
[37] The real number system, Appleton-Century-Crofts, Inc., New
York, 1962.
[38] Real variables, Appleton-Century-Crofts, Inc., New York,
1956.
Осгуд (О s g о о d W. F.)
[39] A Jordan curve of positive area, Trans. Amer. Math. Soc.,
4 (1903), 107—112.
Пастор (P a s t о r J. R.)
[40] Elementos de la teoria de functiones, 3d ed., Ibero-Ameri-
cana, Madrid — Buenos Aires, 1953.
Поллард (Pollard H.)
[41] The theory of algebraic numbers, Carus Math. Monographs,
№ 9, John Wiley and Sons, Inc., New York, 1950.
Радо (R a d 6 T.)
[42] Length and area, Amer. Math. Soc. Colloquium Publications,
30, New York, 1958.
Робинсон (Robinson R. M.)
[43] On the decomposition of spheres, Fund. Math., 34 (1947),
246—266.
Рудин У.
[44] Основы математического анализа, М., изд-во «Мир», 1966.
Сакс С.
[45]* Теория интеграла, М., ИЛ, 1949,
Библиография
229
Серпинский (Sierpinski W.)
[46] Bull. Intern. Ac. Sciences Cracovie (1911), 149.
[47] Sur tin probleme concernant les ensembles mesurables su-
perficiellement, Fund. Math., 1 (1920), 112—115.
[48] General topology, University of Toronto Press, Toronto,
1952.
[49] Cardinal and ordinal numbers, Warsaw, 1958.
Теплиц (Toeplitz O.)
[50] Uber allgemeine lineare Mittelbildungen, Prace Mate-
matyczne-Fizyczne, 22 (1911), 113—119.
Титчмарш E.
[51] Теория функций, M., Гостехиздат, 1951.
Фихтенгольц Г. М.
[52]* Курс дифференциального и интегрального исчисления,
тт. I—III, М„ 1960.
X а л м о ш П.
[53] Теория меры, М„ ИЛ, 1953.
ХаусдорфФ.
[54] Теория множеств, М., Гостехиздат, 1937.
Хенкок (Н а п с о с k Н.)
[55] Foundations of the theory of algebraic numbers, Macmillan,
New York, 1931.
Холл, Спенсер (Hall D., Spencer G.)
[56] Elementary topology, John Wiley and Sons, Inc., New York,
1955.
Штейниц (Steinitz E.)
[57] Bedingte konvergente Reihen und konvexe Systeme, Journ.
fur Math., 143 (1913), 128—175.
[58] Amer. Math. Monthly, 68, № 1 (1961), 28, Problem 3.
[59] Amer. Math. Monthly, 70, № 6 (1963), 674.
Указатель обозначений
((<£) принадлежит (не принадлежит) 11
с является подмножеством и
ф влечет 11
тогда и только тогда 11
{а, Ь, с, ...} множество, состоящее из элементов а, Ь, с, ... 11
{••• 1 ..•} множество всех ... таких, что 11
= равно по определению и
лиа объединение множеств А и В 11
лпа пересечение множеств А и В 11
А\в разность множеств А и В 12
А' дополнение А 12
0 пустое множество 12
(а, Ь) упорядоченная пара 12
АХВ декартово произведение 12
3 существует (существуют) 12
Э такой, что 12
Df область определения f 12
Rf множество значений f 12
Гг функция, обратная к f 13
f-.A^-B, А ~->В функция f^Df = А, Р[<^В 14
f°g композиция (суперпозиция) f и g ((f°g)(x) = f(g(x))) 14
F поле 15
G группа 16
Р множество положительных элемен-
тов поля 16
<, символы упорядочения 17
1 х\ абсолютное значение х 17
Указатель обозначений
231
(а, Ь), [а, Ь)
(а, 6], [л, 6]
(а, -f~oo), (—со" а)
[л, +°°)' (—а]
(— °0. + °0)
W (л, е)
D (а, е)
max(x, у)
min (х, у)
inf (Л), inf Л
sup (Л), sup Л
х ч-> х'
R
sgn X
N
Q
В
D
I
lim f (x)
x->a
V
f (a)
{««}
(x, y)
C
x + «y
H
Ф
m | n
-|-CO i +oo >
U An [ ГК
Л = 1 \n = l
F (A), 1(A), A
{^a}
[x]
интервалы упорядоченной
системы
17
18
окрестность 18
проколотая окрестность 18
наибольший из элементов хну 18
наименьший из элементов х и у 18
точная нижняя грань Л 18
точная верхняя грань Л 18
взаимно однозначное соответствие
(отображение) 19
система действительных чисел 19
специальная функция 19
характеристическая функция множе-
ства Л 19
множество натуральных чисел 19
поле рациональных чисел 20
кольцо 20
область целостности 20
кольцо целых чисел 21
предел функции в точке 21
для всех, для произвольного, для
каждого 21
производная функции f (х) в точке
х = а 22
последовательность 22
комплексное число 23
поле комплексных чисел 23
комплексное число 23
поле рациональных функций 26
{а + &/5| а, 60} 28
m делит п 28
объединение (пересечение) счетного
множества множеств А2, ... 31
граница, ядро, замыкание множе-
ства А 31
открытое покрытие 32
sup {п |n£N, л<х} 32
232
Указатель обозначений
lim f (х) I lim / (x)\ верхний (нижний) предел функции
) f (x) в точке x = a 33
D (± оо, Af) проколотая окрестность ± co 33
lim f (x) предел функции f (x) при x -> co 33
+oo
lim f (x) = ± co бесконечные пределы 33
x->a
Fa множество типа F „ 43
lim A„ f lim верхний (нижний) предел последова-
П->+со yn_>_|_oo тельности множеств Ait А2, ... 68
e ii e Q /1 бесконечный ряд 71
n—l
(ilj> матрица 86
(x) л-я производная функции / (х) 91
о-кольцо КОЛЬЦО 109
VI класс множеств 109
G класс компактных множеств 109
x 4- a сдвиг множества А на число х 109
SB класс борелевских множеств 109
©. о-кольцо 109
pO мера р абсолютно непрерывна отно-
сительно о 110
A, (A, @) пространство с мерой ПО
S класс функций, измеримых по Лебегу ПО
0 мера по
и, (Ю внутренняя (внешняя) мера 111
c канторово множество 112
c мощность множества 111
DG4) разностное множество (множества А) 114
^6» ^a6’ • • • множества типа Gj, Fafj, ... 120
(r + Л) (mod 1) сдвиг (множества А на число г) по модулю 1 121
I {г | г£С, |z| = l} 122
Io {г| г = г2я/е, 0gQ, О<0 < 1} 122
S факторгруппа 1/10 122
H мера на I 122
4> канторова функция 126
71 длина интервала I 136
df d2f дх ' dxdy ’ J x' fxy>
fi> fzi> частные производные функции 147
Указатель обозначений 233
P dx Q dy дифференциал 159
F векторное поле 161
e2 евклидова плоскость 163
d (А B) расстояние между множествами А и В 163
d (p. q) расстояние между точками р и q 163
б(Л) диаметр множества А 163
a бесконечное кардинальное число 181
f мощность множества всех замкну-
тых множеств на плоскости 181
¥ первое порядковое число мощности с 181
A (S), A (S), A (S) площадь, внутренняя площадь, внеш-
няя площадь плоского множества S 187
dr сетка прямых 187
(X, d) метрическое пространство 195
d метрика 195
d (x, y) расстояние между точками х и у 195
(X, 6) топологическое пространство 195
6 совокупность открытых множеств,
топология 196
3 индуцированная топология 196
» базис топологии 196
<Л система окрестностей 197
(0. X), 2* тривиальная, дискретная топология 197
d* (x, y) эквивалентная ограниченная метрика 198
II-II норма 199
£2 первое порядковое число, соответ-
ствующее несчетному множеству 204
(*. У) скалярное произведение элементов
X И у 208
(fV g) (x) max(f(x), g(x)) 218
(/ A g) (x) min (/ (х). g (х)) 218
f+.f~ /VO, (-/) АО 218
УКАЗАТЕЛЬ
Абель Н. X. 94
Абсолютное значение 17
Аксиома выбора 120
— счетности вторая 199
Алгебра 218
Александров П. С. 53
Архимеда аксиома 25, 27
Базис Гамеля 47
— топологии 196
Банах С. 215
Безикович А. С. 193, 194
Бесселя неравенство 94
Борелевское множество 109
Бореля мера 110
Бэр Р. 118
Бэра теорема о категориях 118
Ван дер Варден Б. Л. 42, 53
Вейерштрасс К. В. I. 53
Векторный потенциал 161
Вольтерра В. 141
Вычитание 16
Гельвин Ф. 123, 183
Гильберт Д. 48, 169
Главное значение в смысле Ко-
ши 60
Граница множества 31
Грань верхняя 18
— нижняя 18
— точная верхняя 18
---нижняя 18
Группа абелева 16
— коммутативная 16
— мультипликативная 16
— топологическая 123
Движение жесткое 215
Двоичная дробь 124
Декартово произведение 12
Деление 16
Делитель 28
— наибольший общий 28
Диаметр множества 163
Дивергенция векторного поля
161
Дифференциал 159
— локально полный 159
— полный 159
Дополнение множества 12
Евклидова плоскость 163
Единица 27
Закон ассоциативности 15
— двойственности де Моргана
119
— дистрибутивности 15
— коммутативности 15
• — сокращения 21
Замыкание 32
Значение функции 13
Изоморфизм 19
Интеграл Лебега 96
— Лебега — Стильтьеса 142
— Римана 56
Интервал бесконечный 18
— замкнутый 17
— конечный 17
— открытый 17
— — и замкнутый 18
— полузамкнутый 17
— полуоткрытый 17
Какея С. 194
Кантор Г. 112
Квантор общности 21
— существования 12
Указатель
235
Класс, замкнутый относительно
сдвигов 109
— эквивалентности 111
Колмогоров А. Н. 48, 98
Кольцо 20
Композиция функций 14
Контур плоский 167
Координата пары вторая 12
--- первая 12
Кривая замкнутая 164
— Пеано 169
— спрямляемая 164
Круг замкнутый 163
— минимальный 166
— открытый 164
Лебег А. 45, 97
Ломаная, вписанная в дугу 164
Люксембург В. А. Дж. 137
Мазуркевич С. 183
Матрица бесконечная 86
— Теплица 86
Мера 110
— абсолютно непрерывная 110
— Бореля НО
— внешняя 111
— внутренняя 111
— Лебега 110
— полная 110
Метрика 195
— ограниченная 198
Множество борелевское 109
— вполне несвязное 164
— всюду плотное 27
— второй категории 118
— выпуклое 165
— замкнутое 31
— значений функции 12
— измеримое по Лебегу ПО
— индуктивное 19
— канторово 112
— — положительной меры 116
— компактное 32
— локально связное 164
— меры нуль 56
— неизмеримое 120
— непустое 12
— нигде не плотное 112
— открытое 31
— первой категории 118
Множество плоское 163
— полной меры 129
— положительной меры 115
— пустое 12
— связное 164
— совершенное 111
— счетное 32
— типа Fa 43
— типа G в 119
Неравенство Бесселя 94
— треугольника 195
Норма 199
Нуль 16
Нуль-множество НО
Область 147
— жорданова 165
— значений функции 12
— нежорданова 165
— односвязная 162
— определения функции 12
— целостности поля 20
Оболочка выпуклая 165
Объединение множеств 11
Окрестность точки 18
--- проколотая 18
------ сферическая 197
Операция бинарная 15
Осгуд У. Ф. 175
Основная теорема индукции 20
--- интегрального исчисления
57
Отображение 12
— взаимно однозначное 12
— замкнутое 165, 199
— непрерывное 16, 199
— открытое 165, 199
— топологическое 128, 199
Параметризация 164
Параметризующие функции 164
Пастор Р. 129
Пеано Дж. 169
Пересечение множеств 11
Площадь 187
— внешняя 187
— внутренняя 187
— поверхности 193
Покрытие открытое 32
236
Указатель
Поле архимедово 25
— векторное 160
--- соленоидальное 160
— полное 16
---в смысле Коши 27
--- упорядоченное 19
Полином 25
Полное продолжение меры Бо-
реля 110
Последовательность Коши 23,
198
— расходящаяся 22
— сходящаяся 22
— фундаментальная 23
Предел бесконечный 33
— верхний 33
— нижний 33
— функции 21
---множеств 68
— последовательности 22
---частичный 64
Преобразование Фурье 96
Признак Даламбера 79
— Вейерштрасса 34, 93
— Коши 80
Примитивная 57
Принцип Кавальери 190
— максимального элемента 111
Продолжение функции 14
Проекция пары 12
— вторая 12
— первая 12
Произведение декартово 12
— рядов по Коши 82
— скалярное 208
Производная 22
Пространство банахово 200
— гильбертово 208
— линейное 199
— локально компактное 196
— метризуемое 198
— метрическое 195
— неполное 198
— нормированное векторное
199
— полное 198
— сепарабельное 199
— с мерой НО
— топологическое 195
— функциональное 215
— хаусдорфово 196
Радиус 197
Разностное множество 114
Разность множеств 12
Расстояние между двумя мно-
жествами 163
-------функциями 59
Робинсон Р. 215
Ротор векторного поля 161
Ряд гармонический 72
— мажорирующий 72
— Маклорена 72
— неотрицательный 71
— положительный 71
— расходящийся 71
— степенной 71
— сходящийся 71
— тригонометрический 93
— условно сходящийся 73
Свойство Коши 22
Сдвиг множества 109
---по модулю 1, 121
Серпинский В. 74, 100, 181
Сигма-кольцо 109
Система действительных чисел
19
— окрестностей 197
Сложение 15
Соответствие взаимно одно-
значное 12
Структура 218
Сужение функции 14
Сумма ряда 71
Сходимость в среднем 143
— по мере 143
— почти всюду 142
— с интегрируемой мажоран-
той 143
Сходящаяся последователь-
ность 22
---множеств 68
— — функций 101
Тарский А. 215
Теорема Гейне — Бореля 32
— Дини 107
— Жордана 165
— Колмогорова 47
— Лейбница 75
— Мертенса 82
— Мура — Осгуда 152
Указатель
237
Теорема о полном упорядоче-
нии 111
— о среднем значении 53
— Радона — Никодима 146
— Римана 74
— Ролля 30
— Стокса 161
— Стоуна — Вейерштрасса 98
Теплиц О. 86
Топология дискретная 197
— индуцированная 196
— порожденная 197
— сильная 204
— слабая 205
— тривиальная 197
Точка внутренняя 31
— граничная 31
— конденсации 123
— предельная 21
Троичная дробь 113
Фату 94
Фейер 97
Фон Нейман Дж. 215
Функция алгебраическая 38
— бесконечно дифференцируе-
мая 49
— возрастающая 17
— действительного переменно-
го 19
— действительнозначная 19
— дифференцируемая 49
— измеримая 141
— интегрируемая по Лебегу 96
---по Риману 56
— канторова 126
— линейная 47
— локально ограниченная 33
--- однородная 155
— множества счетно аддитив-
ная 110
— монотонная 17
— неизмеримая 141
— неотрицательная ПО
— непрерывная 21
— ограниченная 33
— однородная 154
Функция периодическая 32
--- с периодом р 32
— полунепрерывная в точке 33
--- сверху 33
— — снизу 33
— постоянная 13
— равномерно непрерывная 22
— рациональная 26
— строго возрастающая 17
--- монотонная 17
— трансцендентная 38
— убывающая 17
— характеристическая 19
Харди Г. X. 53
Хаусдорф Ф. 215
Цаанен А. К. 137
Центр сферической окрестности
197
Цорна лемма 111
Частные производные 147
Число действительное 19
— кардинальное 181
— комплексное 23
— натуральное 19
— порядковое 181
— простое 28
— рациональное 20
— целое 20
Член последовательности 22
Шар замкнутый 198
— открытый 197
Шварц Г. А. 191, 193
Штейнгауз 88
Эквивалентные метрики 198
— функции 31
Элемент множества 11
— отрицательный 16
— положительный 16
— противоположный 16
— составной 28
Ядро множества 31
17 Зак. 587
ОГЛАВЛЕНИЕ
От редактора...............................................5
Предисловие............................................. 7
Глава 1. Система действительных чисел......................И
Введение . ................................................П
1. Бесконечное поле, которое нельзя упорядочить . 23
2. Поле, которое можно упорядочить двумя различными спо-
собами ...................................................24
3. Неполное упорядоченное поле............................24
4. Упорядоченное неархимедово поле........................25
5. Упорядоченное поле, которое нельзя пополнить...........26
6. Упорядоченное поле, в котором множество рациональных
чисел не плотно......................................... .27
7. Неполное упорядоченное поле, полное в смысле Коши ... 27
8. Область целостности, допускающая различные факторизации 27
9. Два числа без наибольшего общего делителя ...... 28
10. Дробь, не допускающая единственного представления в ви-
де несократимой дроби.................................... 29
11. Функции, непрерывные на замкнутом интервале и не обла-
дающие известными свойствами, если система чисел не полна 29
Глава 2. Функции и пределы................................31
Введение ................................................ 31
1. Всюду разрывная функция, абсолютное значение которой
есть всюду непрерывная функция........................... 34
2. Функция, непрерывная лишь в одной точке (см. пример 22) 34
3. Непрерывная и неограниченная функция, определенная на
произвольном некомпактном множестве ......................34
4. Неограниченная функция, определенная на произвольном
некомпактном множестве и локально ограниченная на нем 34
5. Функция, всюду конечная и всюду локально неограниченная 35
6. Непрерывная ограниченная функция, определенная на про-
извольном некомпактном множестве и не имеющая экстре-
мальных значений..........................................35
7. Ограниченная функция, не имеющая относительных экстре-
мумов на компактном множестве.............................36
Оглавление
239
8. Ограниченная функция, не являющаяся полунепрерывной ни
в одной точке......................................... . 37
9. Периодическая функция, отличная от постоянной и не имею-
щая наименьшего периода....................................37
10. Иррациональные функции.................................37
11. Трансцендентные функции............................... 38
12. Функции y=f(u), u £R, и u=g(x), х £R, композиция кото-
рых y=f(g(x)) всюду непрерывна и такова, что
lim I (и) = с, lim g (х) = b, lim / (g (х)) #= с. . . . 39
и-^b х->а х-^а
13. Две равномерно непрерывные функции, произведение кото-
рых не является равномерно непрерывной функцией .39
14. Непрерывное на некотором интервале взаимно однозначное
отображение, обратное к которому разрывно..................39
15. Функция, непрерывная в иррациональных и разрывная в
рациональных точках ............... ..... ................ 40
16. Полунепрерывная функция с плотным множеством точек
разрыва ................................................. 40
17. Функция с плотным множеством точек разрыва, каждая из
которых устранима........................................ 40
18. Монотонная функция, точки разрыва которой образуют про-
извольное счетное (возможно, плотное) множество .... 41
19. Функция с плотным множеством точек непрерывности и
плотным множеством точек разрыва, ни одна из которых
не является устранимой.....................................41
20. Нигде не монотонное взаимно однозначное соответствие
между двумя интервалами....................................41
21. Непрерывная нигде ие монотонная функция...............42
22. Функция, точки разрыва которой образуют произвольно за-
данное замкнутое множество 43
23. Функция, точки разрыва которой образуют произвольно за-
данное множество типа Fa (см. пример 8 гл. 4 и примеры
8, 10 и 22 гл. 8) ... .....................................43
24. Функция, не являющаяся пределом последовательности не-
прерывных функций (см. пример 10 гл. 4) ...... 44
25. Функция, определенная на [0,1], множество значений кото-
рой на каждом невырожденном подинтервале совпадает
с [0,1] (см. пример 27 гл. 8)..............................45
26. Разрывная линейная функция ............................47
27. Теорема Колмогорова: для каждого п £N существуют п(2п+1)
функций <pij(j%) (/= 1, 2, ..., п, i=l,2, ..., 2/i+l), таких, что
(а) все функции <ро(*0 непрерывны на [0,1];
(Ь) для любой функции f(xi, х2, ... , хп), непрерывной на
0<Х|, х2, ... , хп<1, существуют 2п + 1 функций ф,,
1 = 1, 2, ... , 2/г+1, каждая из которых непрерывна на
R, причем
2и+1 / п \
Н-И. ......хп) = S Ф/ 2Ф'7(х/)................47
\j-i /
\Т
240
Оглавление
Глава 3. Дифференцирование................................49
Введение ................................................ 49
1. Функция, не являющаяся производной.....................49
2. Дифференцируемая функция с разрывной производной . 50
3. Разрывная функция, имеющая всюду производную (не обя-
зательно конечную) .................................... 50
4. Дифференцируемая функция, производная которой не со-
храняет знака ни в какой односторонней окрестности экстре-
мальной точки .... ............................50
5. Дифференцируемая функция, производная которой положи-
тельна в некоторой точке, но сама функция не монотонна
нн в какой окрестности этой точки.........................51
6. Функция, производная которой конечна, но не ограничена
на замкнутом интервале.................................. 51.
7. Функция, производная которой существует и ограничена, но
не имеет (абсолютного) экстремума на замкнутом интервале 51
8. Всюду непрерывная, но нигде не дифференцируемая функция 52
9. Дифференцируемая функция, для которой теорема о сред-
нем не имеет места................................... . 53
10. Бесконечно дифференцируемая функция f(x), положитель-
ная при положительных х и равная нулю при отрицатель-
ных х ...... .............................................54
11. Бесконечно дифференцируемая функция, положительная в
единичном интервале и равная нулю вне его.................54
12. Бесконечно дифференцируемая функция, равная 1 на
[1,4-сю), равная 0 на (— со,0] и строго монотонная на
[0, 1]....................................................54
13. Бесконечно дифференцируемая монотонная функция f, та-
кая, что lim / (х) = 0, lim f' (х) 0................55
х-> + оо Х-> +ОО
Глава 4. Интеграл Римана..................................56
Введение............................................... 56
1. Ограниченная функция, не интегрируемая по Риману на ко-
нечном замкнутом интервале.............................. 56
2. Функция, интегрируемая по Риману и не имеющая при-
митивной ............................................... . 57
3. Функция, интегрируемая по Риману и не имеющая прими-
тивной ни на каком интервале........................ .57
4. Функция, имеющая примитивную на замкнутом интервале,
но не интегрируемая на нем по Риману (см. пример 35
гл. 8)....................................................57
5. Интегрируемая по Риману функция со всюду плотным мно-
жеством точек разрыва................................ . 58
х
6. Функция f, для которой g (-*) = J f (0 di всюду дифферен-
о
цируема, однако g'(x) на всюду плотном множестве 58
Оглавление
241
7. Две различные полунепрерывные функции, „расстояние”
между которыми равно нулю....................................59
8. Интегрируемая по Риману функция, множество точек раз-
рыва которой совпадает с произвольно заданным множеством
типа Fa и меры нуль (см. пример 22 гл. 8)....................59
9. Две функции, интегрируемые по Риману, композиция ко-
торых не интегрируема по Риману (см. пример 34 гл. 8) 60
10. Не интегрируемая по Риману ограниченная функция, яв-
ляющаяся пределом возрастающей последовательности инте-
грируемых по Риману функций (см. пример 33 гл. 8) . . 60
11. Расходящийся несобственный интеграл, имеющий конечное
главное значение в смысле Коши ..............................60
+со
12. Сходящийся несобственный интеграл f (х) dx, подин-
i
тегральная функция которого положительна, непрерывна и
не стремится к нулю при х -> 4- оо........................61
13. Сходящийся на интервале [0,4-со) несобственный интеграл,
подинтегральная функция которого не ограничена на любом
интервале вида [а, 4-со), где я>0............................61
14. Функции fug, такие, чго интеграл Римана—Стильтьеса
от f относительно g существует на [а, 5] и [5, с], но не су-
ществует на [а, с] .........................................62
Глава 5. Последовательности..................................63
Введение ............................. . , , 63
1. Ограниченные расходящиеся последовательности .... 63
2. Последовательность с произвольно заданным замкнутым
множеством предельных точек .................................64
3. Расходящаяся последовательность {яп}, для которой
lim (вп+р — ап) = 0 при любом натуральном р. ... 66
д-> -f-оо
4. Расходящаяся последовательность {ап}, такая, что для за-
данной строго возрастающей последовательности {<р„}=
={<₽(«)} натуральных чисел lim (аф („>—«„) = 0 ... 66
Л->4-со
5. Последовательности {о„} и {&„}, такие, что lim ап -Ц—lim b„ <
< lim (an-\-bn) < Итяд -|- нт < Пт (дл _|_ < Пт а„-|-Ит Ьп 67
6. Последовательности {йщ}, {°2п}, .... такие, что
lim («1Л-|-«2л+ ...)< Нт lim агл+ 67
Л->+СО п-^+со п-^+'оо
7. Две равномерно сходящиеся последовательности функций,
последовательность произведений которых не сходится
равномерно ..................................................68
242
Оглавление
8. Расходящаяся последовательность множеств..................68
9. Последовательность {Л„} множеств, которая сходится к
пустому множеству, но кардинальные числа этих мно-
жеств -> + со............................................... 69
Глава 6. Бесконечные ряды.................................71
Введение ................................................ 71
1. Расходящийся ряд, общий член которого стремится к нулю 72
2. Сходящийся ряд ап и расходящийся ряд У, Ьп, такие,
что а-n^-bn, п=1, 2,......................................72
3. Сходящийся ряд и расходящийся ряд такие, что
I ап I >1 bn |, п= 1, 2,..................................72
4. Для произвольно заданного положительного ряда существу-
ет либо мажорируемый им расходящийся, либо мажорирую-
щий его сходящийся ряд.................................. 72
5. Об условно сходящихся рядах.......................... 73
6. Для произвольного условно сходящегося ряда 2 ап и
произвольного действительного числа х существует последо-
вательность {е„}, где |е„|=1 (п=1, 2, ...), такая, что
+со
У = х .............. .... 75
П = 1
7. Об условиях теоремы Лейбница для знакочередующихся ря-
дов ......................................75
8. Расходящийся ряд с общим членом, стремящимся к нулю,
который при подходящей расстановке скобок становится
сходящимся к наперед заданной сумме.......76
9. Для произвольно заданной положительной последователь-
ности {&„} с нижним пределом, равным нулю, существует
расходящийся ряд У, ап, общий член которого стремится
к нулю, причем lim a„Jbn = 0.............................. 76
«-> +со
10. Для всякой положительной последовательности {&„} с ниж-
ним пределом, равным нулю, существует положительный
сходящийся ряд V ап, такой, что lim an/bn — -\-ео. ... 77
" л->+со
11. Для всякой положительной последовательности {с„} с ниж-
ним пределом, равным нулю, существуют положительный
сходящийся ряд ап и положительный расходящийся ряд
2 Ьп, такие, что ап1Ьп—сп, п=1, 2,.......................77
12. Положительная непрерывная при х>1 функция, такая,
+ °° + оо
что интеграл f (х) dx сходится, а ряд 2 f (”) рас-
1
ходится .................................................78
Оглавление
243
13. Положительная непрерывная при х^ 1 функция, такая, что
+°° +со
интеграл f (х) dx расходится, а ряд 2 f (п) сходится 78
’ л-1
14. Ряды, к которым не применим признак Даламбера .... 79
15. Ряды, к которым не применим признак Коши................80
16. Ряды, для которых эффективен признак Коши и не эф-
фективен признак Даламбера................................ 82
17. Два сходящихся ряда, произведение которых расходится 82
18. Два расходящихся ряда, произведение которых сходится
абсолютно ................................................. 83
19. Для произвольной последовательности < У1, атп >, п — 1, 2.
( т = 1 J
положительных сходящихся рядов существует положитель-
со
НЫЙ СХОДЯЩИЙСЯ ряд 2 а^' не сравнимый ни с одним из
ш=1
{+со 1
У, атп ? .......................................84
m = l J
20. Матрица Теплица Т и расходящаяся последовательность,
преобразуемая матрицей Т в сходящуюся последовательность 86
21. Для всякой матрицы Теплнца T=(/ij) существует после-
довательность {«Д, каждый член которой есть либо 1, ли-
бо— 1, такая, что преобразование {&,} последовательности
{а,} посредством матрицы Т расходится...................88
22. Степенной ряд, сходящийся лишь в одной точке (см. при-
мер 24).................................................... 90
23. Функция, ряд Маклорена которой сходится всюду, однако
представляет функцию лишь в одной точке.....................91
24. Функция, ряд Маклорена которой сходится лишь в одной
точке .... ........................... 91
25. Сходящийся тригонометрический ряд, не являющийся ря-
дом Фурье ..... .............................93
26. Бесконечно дифференцируемая функция f(x), не являющая-
ся преобразованием Фурье никакой функции, интегрируемой
по Лебегу, и такая, что lim f (х) = 0.......................96
27. Для произвольного счетного множества Е сд [—л, л) суще-
ствует непрерывная функция, ряд Фурье которой расхо-
дится в каждой точке х £ Е и сходится в каждой точке
х С [—л) \Д..................................................97
28. Функция, интегрируемая (по Лебегу) на [—л, л], ряд Фурье
которой расходится всюду.....................................98
29. Последовательность {а„} рациональных чисел, обладающая
тем свойством, что для всякой функции (, непрерывной на
[0,1] и равной 0 при х = 0 (f(0)=0), существует строго воз-
растающая последовательность натуральных чисел {nv}
244
Оглавление
(по = О), такая, что
причем сходимость является равномерной на [0,1] .... 98
Глава 7. Равномерная сходимость ......................101
Введение ................................................. 101
1. Последовательность всюду разрывных функций, сходящаяся
равномерно к всюду непрерывной функции................101
2. Последовательность бесконечно дифференцируемых функций,
которая равномерно сходится к нулю, а последовательность
производных этих функций всюду расходится...................101
3. Неограниченная функция, являющаяся пределом неравномер-
но сходящейся последовательности ограниченных функций 102
4. Разрывная функция, являющаяся пределом последователь-
ности непрерывных функций ..................................102
5. Не интегрируемая по Риману функция, являющаяся преде-
лом последовательности функций, интегрируемых по Ри-
ману (см. пример 33 гл. 8) . . ......................104
6. Последовательность функций, Для которой предел интегра-
лов не равен интегралу от предельной функции . •. . . 104
7. Последовательность функций, для которой предел производ-
ных не равен производной от предельной функции .... 105
8. Последовательность функций, равномерно сходящаяся на
каждом замкнутом подинтервале, но не сходящаяся равно-
мерно на всем интервале ....................................106
9. Последовательность {/„}, равномерно сходящаяся к нулю
+ со
на интервале [0, + со) и такая, что J fn(x) dx-f*Q . . . 106
о
10. Неравномерно сходящийся ряд, общий член которого стре-
мится к нулю равномерно.................................... 107
11. Неравномерно сходящаяся последовательность, обладающая
равномерно сходящейся подпоследовательностью .... 107
12. Неравномерно сходящиеся последовательности, удовлетво-
ряющие любым трем из четырех условий теоремы Динн . . 107
Глава 8. Множества и мера на действительной оси............109
Введение ....................................... . . . . 109
1. Совершенное нигде не плотное множество..................111
2. Несчетное множество меры нуль...........................113
3. Множество меры нуль, разностное множество которого со-
держит некоторую окрестность нуля . ... ‘...............114
4. Совершенное нигде не плотное множество положительной
меры ................................................... 115
5. Совершенное нигде не плотное множество иррациональных
чисел ......................................................117
Оглавление
245
6. Всюду плотное открытое множество, дополнение которого
имеет положительную меру.............................118-
-7, Множество второй категории........................118
8. Множество, не являющееся множеством типа Fa .... 119
9. Множество, не являющееся множеством типа Gft . . . . 119
10. Множество А, не являющееся множеством точек разрыва
никакой функции ......................................... 120
11. Неизмеримое множество ............................... 120
12. Множество D, такое, что для всякого измеримого множе-
ства А справедливы равенства и* (D ("] Л) =0, р.*(£>П/1) =
= р.(Л) ..............................................123
13. Множество А меры нуль, для которого любое действитель-
ное число является его точкой конденсации ............... 123
14. Нигде не плотное множество А действительных чисел и его
непрерывное отображение на замкнутый единичный интер-
вал [0, 1] . . ............... ...... 124
15. Непрерывная монотонная функция, производная которой
равна нулю почти всюду................................... 126
16. Топологическое отображение замкнутого интервала, не со-
храняющее измеримость и нулевую меру ....... 128
17. Измеримое неборелевское множество......................128
18. Две непрерывные функции, разность которых не является
постоянной, но их производные (конечные или бесконечные)
совпадают всюду ........................................ 129
19. Множество полной меры и первой категории на [0, 1] . . 129
20. Множество меры нуль и второй категории на [0, 1] ... . 130
21. Множество меры нуль, не являющееся множеством типа Fa 130
22. Множество меры нуль, такое, что не существует функции
(интегрируемой по Риману или нет), для которой это мно-
жество является множеством точек разрыва.............. 131
23. Два совершенных нигде не плотных гомеоморфных множе-
ства на [0,1], лишь одно из которых имеет меру нуль ... 131
24. Два непересекающихся непустых нигде не плотных множе-
ства действительных чисел, таких, что каждая точка любо-
го из них является предельной точкой другого ............. 133
25. Два гомеоморфных множества действительных чисел, являю-
щихся множествами разных категорий......................133
26. Два гомеоморфных множества действительных чисел, та-
ких, что одно из них всюду плотно, а другое нигде не плотно 134
27. Функция, определенная на R, равная нулю почти всюду
и такая, что множество ее значений на каждом непустом
открытом интервале совпадает с R...........................135
28. Функция, определенная на R, график которой всюду пло-
тен на плоскости ..... .............................. . 136
29. Неотрицательная всюду конечная функция f, такая, что
ь
f (х) dx — + со для любого непустого открытого интер-
а
вала (а, Ь)............................................. 136
30. Непрерывная строго монотонная функция с производной,
равной нулю почти всюду.......................................137
246
Оглавление
31. Ограниченная полунепрерывная функция, не интегрируемая
по Риману и не эквивалентная никакой функции, интегри-
руемой по Риману....................................... . 137
32. Ограниченная измеримая функция, не эквивалентная ника-
кой функции, интегрируемой по Риману .....................138
33. Ограниченная функция, являющаяся пределом монотонной
последовательности непрерывных функций, не интегрируе-
мая по Риману и не эквивалентная никакой функции, ин-
тегрируемой по Риману (см. пример 10 гл. 4)...............138
34. Интегрируемая по Риману функция f и непрерывная функ-
ция g, определенные на [0, 1] и такие, что их композиция
f(g(x)) не интегрируема по Риману на [0, 1] и не эквива-
лентна никакой функции, интегрируемой по Риману на этом
замкнутом интервале (см. пример 9 гл. 4)..................139
35. Ограниченная функция, имеющая примитивную на замкну-
том интервале, но не интегрируемая на нем по Риману . . 139
36. Функция, для которой существует несобственный интеграл
Римана и не существует интеграл Лебега....................141
37. Функция, измеримая по Лебегу и не измеримая по Борелю 141
38. Измеримая функция f(x) и непрерывная функция g(x), та-
кие, что их композиция f(g(x)) неизмерима.................141
39. Непрерывная монотонная функция g(x) и непрерывная функ-
ция f (х), такие, что
1 1
J- f (х) dg (х) #= j f (х) g'(x)dx..........142
о о
40. Различные виды сходимости функциональных последователь-
ностей ...................................................142
41. Две меры ц и v на пространстве с мерой (X, ©), такие,
что ц абсолютно непрерывна относительно v, однако не су-
ществует функции f, удовлетворяющей равенству ц (Е) =
= J f (х) dv (х) Для всех £ С ®...........................145
Е
Глава 9. Функции двух переменных..........................147
Введение ................................................ 147
1. Разрывная функция двух переменных, непрерывная по каж-
дой переменной в отдельности ........................... 147
2. Функция двух переменных, не имеющая предела в начале
координат, но имеющая равный нулю предел при прибли-
жении к началу координат по любой прямой..................148
3. Обобщение предыдущего примера..................... . . 148
4. Разрывная (и, следовательно, недифференцируемая) функ-
ция двух переменных, имеющая всюду частные производ-
ные первого порядка ..................................... 149
Оглавление
247
5. Функции f, для которых существуют и равны лишь два из
следующих пределов:
lim f (х, у), lim lim f (х, у), lim lim f (х, у). . . 149
(х, у)->(а, b) х-*а у-^b у-*Ь х->а
6. Функции f, для которых существует лишь один из следую-
щих пределов:
lim f(x, у), lim lim f (х, у), lim lim f (x, у) . .150
(x, y)^(a, b) x->a y->b y-tb x^a
7. Функция f, для которой пределы lim lim f(x, у) и
x->a y->b
lim lim f (x, у) существуют, но не равны между собой 151
у->ь х->а
8. Функция f(x, у), для которой предел lim i (х, у) = g (х)
у^-о
существует равномерно относительно х, предел lim f (х, у) =
х->0
— h (у) существует равномерно относительно у, lim g (х) =
— lim h (у), однако предел lim [ (х, у) не существует 151
»->0 (х, У)-»(О, 0)
9. Дифференцируемая, но не непрерывно дифференцируемая
функция двух переменных............................... 152
10. Дифференцируемая функция, имеющая неравные смешанные
частные производные второго порядка ................... 153
11. Непрерывно дифференцируемая функция f двух переменных
х и у и область /? на плоскости, такие, чго df/dy—O в об-
ласти R, но функция f зависит от у в этой области 154
12. Локально однородная непрерывно дифференцируемая функ-
ция двух переменных, не являющаяся однородной .... 154
13. Дифференцируемая функция двух переменных, не имеющая
экстремума в начале координат и такая, что ее сужение
на любую прямую, проходящую через начало координат,
имеет строгий локальный минимум в этой точке.............155
14. Обобщение предыдущего примера........................156
ь ь
15. Функция f, для которой j f (х, у) dy =f= f f (х, dy,
а а
хотя оба интеграла существуют в смысле Римана .... 156
16. Функция f, для которой
11 11
J J f (х, у) dy dx -ф J J / (х, у) dx dy,
о о оо
хотя оба интеграла существуют в смысле Римана .... 157
17. Двойной ряд У, атп, для которого 2 У атп =#22 158
т, п т п пт
18. Дифференциал Pdx+Qdy и плоская область R, в которой
Pdx+Qdy является локально полным, но не полным диф-
ференциалом .................... 159
19. Соленоидальное векторное поле, заданное в односвязной
области и не имеющее векторного потенциала...............160
248
Оглавление
Глава 10. Множества на плоскости...........................163
Введение ................................................. 163
1. Два непересекающихся замкнутых множества, расстояние
между которыми равно нулю.................................166
2. Ограниченное множество на плоскости, для которого не
существует минимального замкнутого круга, содержащего
это множество........................................... 166
3. „Тонкие” связные множества, не являющиеся простыми
дугами ...................................................166
4. Два непересекающихся плоских контура, содержащихся в
квадрате и соединяющих его противоположные вершины 167
5. Отображение интервала [0, 1] на квадрат [0, 1]Х[0, 1] . . . 168
6. Кривая Пеано на плоскости...............................169
7. Кривая Пеано, стационарная почти всюду..................171
8. Кривая Пеано, дифференцируемая почти всюду ..... 171
9. Непрерывное отображение интервала [0, 1] на себя, прини-
мающее каждое значение несчетное множество раз . . . 171
10. Простая дуга, расположенная в единичном квадрате и
имеющая плоскую меру, сколь угодно близкую к единице 171
11. Связное компактное множество, не являющееся дугой . . 175
12. Плоская область, не совпадающая с ядром своего замы-
кания .................................................. 175
13. Три непересекающиеся плоские области с общей границей 176
14. Нежорданова область, совпадающая с ядром своего за-
мыкания 177
15. Ограниченная плоская область, граница которой имеет по-
ложительную меру........................... 177
16. Простая дуга бесконечной длины........................ 178
17. Простая дуга бесконечной длины, имеющая касательную в
каждой точке . ..........................................178
18. Простая дуга, такая, что ее длина между любой парой то-
чек бесконечна .......................................... 179
19. Гладкая кривая С, содержащая точку Р, которая не яв-
ляется ближайшей точкой этой кривой ни для какой точки
выпуклой области, ограниченной этой кривой .............. 179
20. Подмножество А единичного квадрата S—[0, 1]Х[(), 1], плот-
ное в S н такое, что всякая вертикальная или горизонталь-
ная прямая, пересекающая S, имеет с А лишь одну об-
щую точку............................................... 180
21. Неизмеримое плоское множество, имеющее с каждой пря-
мой не более двух общих точек ............................181
22. Неотрицательная функция f(x, у), такая, что
11 11
J J f (•*. У) dx dy = J J f (x, y) dy dx — 0,
0 0 0 0
а интеграл j j f (x, y) dx rfy, где S = [0,l]X[0,l], не существует 184
s
Оглавление
249
23. Действительнозначная функция одного действительного пе-
ременного, график которой является неизмеримым плоским
множеством ............................................. . 184
24. Связное множество, которое становится вполне несвязным
при удалении одной точки .................................. 185
Глава 11. Площадь........................................187
Введение ............................................. 187
1. Ограниченное плоское множество, не имеющее площади . . 188
2. Компактное плоское множество, не имеющее площади . . 189
3. Ограниченная плоская область, не имеющая площади . . 189
4. Ограниченная плоская жорданова область, не имеющая пло-
щади .....................................................189
5. Простая замкнутая кривая, плоская мера которой больше
плоской меры области, ограниченной этой кривой . . . .189
6. Две функции (риф, заданные на [0, 1] и такие, что
(b) J [ф(х) — <p(x)]rfx существует и равен 1,
О
(с) 5={(л, у) 10 < х < 1, <р(х) <г/<ф(х)} не имеет площади190
7. Пример Шварца, в котором боковой поверхности прямого
кругового цилиндра сопоставляется сколь угодно большая
конечная или даже бесконечная площадь . ...................191
8. Для любых двух положительных чисел е и М в трехмерном
пространстве существует поверхность S, такая, что
(a) S гомеоморфна поверхности сферы;
(Ь) площадь поверхности S существует и меньше е;
(с) мера Лебега в трехмерном пространстве поверхности S
существует и больше М .................................193
9. Плоское множество сколь угодно малой плоской меры, внут-
ри которого направление отрезка единичной длины можно
поменять на обратное непрерывным движением.................194
Глава 12. Метрические и топологические пространства .... 195
Введение .................................................. 195
1. Убывающая последовательность непустых замкнутых огра-
ниченных множеств с пустым пересечением.....................200
2. Неполное метрическое пространство с дискретной топологией 200
3. Убывающая последовательность непустых замкнутых шаров
с пустым пересечением в полном метрическом пространстве 201
4. Открытый шар О и замкнутый шар Вс общим центром
и равными радиусами, такие, что В ФО .... . 201
5. Замкнутые шары Si и В2 с радиусами rt и г2 соответствен-
но, такие, что а ...................... 202
6. Топологическое пространство X и его подмножество Y, та-
кие, что множество предельных точек Y не замкнуто . • 20_
250
Оглавление
7. Топологическое пространство, в котором предел последо-
вательности не единствен ............................ ..... 202
8. Сепарабельное пространство, обладающее несепарабельным
подпространством ...........................................203
9. Сепарабельное пространство, не удовлетворяющее второй
аксиоме счетности........................................ 203
10. Множество с различными топологиями, имеющими одни и
те же сходящиеся последовательности.........................204
11. Пример топологического пространства X, множества A <Z X
и предельной точки этого множества, не являющейся пре-
делом никакой последовательности точек из Л ............... 207
12. Неметрнзуемое топологическое пространство X с функция-
ми в качестве точек и топологией, соответствующей пото-
чечной сходимости...........................................210
13. Непрерывное отображение одного топологического простран-
ства на другое, не являющееся ни открытым, ни замкнутым 211
14. Отображение одного топологического пространства на дру-
гое, являющееся одновременно открытым и замкнутым, но
не являющееся непрерывным................ 211
15. Замкнутое отображение одного топологического простран-
ства на другое, не являющееся ни непрерывным, ни от-
крытым .................................. ..... 211
16. Отображение одного топологического пространства на дру-
гое, являющееся непрерывным и открытым, но не являю-
щееся замкнутым ................. 212
17. Открытое отображение одного топологического пространства
на другое, не являющееся ни непрерывным, ни замкнутым 212
18. Непрерывное замкнутое отображение одного топологическо-
го пространства на другое, не являющееся открытым . . . 213
19. Топологическое пространство X и его подпространство Y,
содержащее два непересекающихся открытых множества,
которые не являются пересечением подпространства Y с не-
пересекающимися открытыми множествами пространства X 213
20. Два негомеоморфных топологических пространства, каждое
из которых является непрерывным взаимно однозначным об-
разом другого..........................................214
21. Разбиение трехмерного евклидова шара В на пять непере-
секающихся подмножеств Si, S2, S3, S4, S5 (при этом S5 со-
стоит из единственной точки), таких, что при жестких дви-
жениях /?1, /?2, /?3, /?4, R$ справедливы следующие соотно-
шения:
... 215
22. Для любых двух евклидовых шаров Ве и Ви, радиусы
которых суть произвольно заданные числа е>0 и Af>0,
всегда существует разбиение шара Ве на конечное число
непересекающихся подмножеств Si, S2, ..., Sn, таких, что
при жестких движениях Bi, Rz.......Rn справедливо равен-
ство
Вм- ^(^)U/?2(S2)U ••• U/?n(S„)...............215
Оглавление
251
Глава 13. Функциональные пространства.....................216
Введение .... ...................................... ..... 216
1. Две монотонные функции, сумма которых не монотонна'219
2. Две периодические функции, сумма которых не имеет пе-
риода .................................................. 219
3. Две полунепрерывные функции, сумма которых не является
полунепрерывной ..........................................220
4. Две функции, квадраты которых интегрируемы по Риману,
но квадрат их суммы не интегрируем по Риману .... 222
5. Две функции, квадраты которых интегрируемы по Лебегу,
но квадрат их суммы не интегрируем по Лебегу .... 222
6. Линейное функциональное пространство, не являющееся ни
алгеброй, ни структурой ........ ........................ 223
7. Линейное функциональное пространство, являющееся алгеб-
рой, но не являющееся структурой..........................223
8. Линейное функциональное пространство, являющееся струк-
турой, но не являющееся алгеброй .......... 223
9. Две метрики в пространстве С([0, 1]) функций, непрерывных
на [0, 1], такие, что дополнение единичного шара в одной
из метрик всюду плотно в единичном шаре другой метрики 224
Библиография ........................................... 226
Указатель обозначений ................................... 230
Указатель ............................................... 234