Текст
62 к.
fin*.
'б-ДВАЙТ
АБЛИЦЫ
ИНТЕГРАЛОВ
И ДРУГИЕ
^МАГИЧЕСКИЕ
формулы
TABLES OF INTEGRALS
AND OTHER
MATHEMATICAL DATA
HERBERT BRISTOL DWIGHT
FOURTH EDITION
NEW YORK
THE MACMILLAN COMPANY
19 6 1
Г. Б. ДВАЙТ
ТАБЛИЦЫ ИНТЕГРАЛОВ
И ДРУГИЕ
МАТЕМАТИЧЕСКИЕ ФОРМУЛЫ
Перевод с английского
Н. В. ЛЕВИ
Под редакцией
К. А. СЕМЕНДЯЕВА
ИЗДАНИЕ ЧЕТВЕРТОЕ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1973
517.2(03)
Д22
УДК 517.3(083.3)
Таблицы интегралов и другие математические формулы Г, Б. Двайт
Книга содержит весьма подробные таблицы
неопределенных и определенных интегралов,
а также большое число .других математических
формул: разложения в ряды, тригонометрические
и другие тождества, справочный материал по
специальным функциям.
В книге учтены все дополнения и исправления,
внесенные в четвертое американское издание,
н исправлены замеченные опечатки.
Г. Б. Двайт
Таблицы интегралов и другие математические формулы.
М., 1973 г., 228 стр, с илл.
Редактор Г. Я. Пирогова
Техн, редактор С. Я. Шкляр. Корректор А. Д. Халанская.
Печать с матриц. Подписано к печати 18/VI 1973 г. Бумага 60х90'/>«. тип. № 2. Физ. печ,
л, 14,25. Условн, печ. л, 14,25, Уч.-изд. л. 10.48. Тираж 75 000 экз. Цена книги 52 коп.
Заказ № 881,
Издательство «Наука».
Главная редакция физико-математической литературы.
117071, Москва. В-71, Ленинский проспект, 15.
Союзполиграфиром при Государственном комитете Совета Министров СССР по делам
издательств, полиграфии и книжной торговли. Отпечатано в ордена Трудового Красного
Знамени Ленинградской типографии № 1 «Печатный Двор» имени А. М. Горького. Ленин-
град, Гатчинская ул., 25. с матриц ордена Трудового Красного Знамени Первой Образцо-
вой типографии имени А. А. Жданова, Москва, Ж-54, Валовая, 28
0225—1713
Д 042(02)-73
74-73
СОДЕРЖАНИЕ
№№
пунктов
Предисловие редактора .......................................... 6
I 1. Алгебраические функции.................................. 7
60. Алгебраические функции—Производные....................21
80. Рациональные алгебраические функции—Интегралы.........22
180. Иррациональные алгебраические функции — Интегралы ... 40
II 400. Тригонометрические функции ............................70
427. Тригонометрические функции—Производные.............. 82
429. Тригонометрические функции — Интегралы................83
III 500. Обратные' тригонометрические функции..................ЮЗ
512. Обратные тригонометрические функции — Производные . . . 105
515. Обратные тригонометрические функции —Интегралы.......106
IV 550. Показательные функции ................................Н5
563. Показательные функции — Производные ..................Н6
565. Показательные функции — Интегралы....................116
V 585. Интегралы вероятности...............................119
VI 600. Логарифмические функции .............................120
610. Логарифмические функции — Интегралы .................123
VII 650. Гиперболические функции..............................130
667. Гиперболические функции — Производные................133
670. Гиперболические функции — Интегралы................ . 131
VIII 700. Обратные гиперболические функции....................141
728. Обратные гиперболические функции—Производные.........143
730. Обратные гиперболические функции — Интегралы.........144
IX 750. Эллиптические функции................................151
768. Эллиптические функции — Производные..................153
770. Эллиптические функции—Интегралы......................153
X 800. Бесселевы функции...................................161
835. Бесселевы функции—Интегралы..........................177
XI 840. Сферические многочлены (многочлены Лежандра).........173
XII 850. Определенные интегралы..............................180
XlII 890. Дифференциальные уравнения..........................223
Литература....................................................227
ПРЕДИСЛОВИЕ РЕДАКТОРА
Таблицы Двайта представляют собой довольно обширные таблицы
неопределенных интегралов, к которым добавлено еще много разно-
образных формул (разложения в ряды, тождественные соотношения,
определенные интегралы и т. п.).
В Советском Союзе таблицы Двайта были выпущены Издательством
иностранной литературы в 1948 г. на английском языке фотомеха-
ническим способом. В настоящем издании текст переведен на русский
язык, американские обозначения заменены принятыми в СССР. Перевод
сделан с четвертого американского издания (1961 г.), причем вос-
становлена глава, посвященная дифференциальным уравнениям, опу-
щенная в издании 1948 г.
Список литературы составлен заново, в основном из книг на
русском языке. В ссылках в тексте число в квадратных скобках
означает номер в списке литературы на стр. 227 — 228. Однако
ссылки на литературу, преимущественно учебную, относящуюся
к отдельным формулам, в настоящем издании опущены, так же как
в издании 1948 г. Кроме того, исключены числовые таблицы, состав-
ленные не очень логично, помещение которых в настоящем справоч-
нике недостаточно оправдано.
К. Семендяев
I
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
L (1+х)”=1 + лх+2^г-^х2 +
Ч-------3j * + +(л_г)| rl х Ч- ' »•
Здесь и далее всюду полагаем 01 = 1.Еслн п—целое положительное число,то
выражение состоит из конечного числа членов. В противном случае ряд
сходится при х2<1; причем, если л>0, то ряд сходится также при х2==1.
2. Коэффициент при хг в 1 обозначается или Сгп.
Величины этих коэффициентов даются в следующей таблице.
Таблица биномиальных коэффициентов С^.
3. (1—х)"=1— х2 —
я(я-1)(я-2) . л!
31 ХЧ-...ЧЛ Ч („_ Г)( г1 х Ч- ...
(См. примечание к 1.)
8
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
14
4.
4.2.
4,3.
4.4.
6.1.
5.2,
6.3.
5.4.
5.5.
6.
7.
8.
9.01.
(а ± х)п = д»( 1 ± -7)П.
(1 ± х)2 = 1 ± 2x4-Xs.
(1 ± х)’ = 1 ± Зх 4- Зх2 ± х’.
(1 ± х)* — 1 ± 4х + 6х2 ± 4х’ 4- х*,
и так далее, используя коэффициенты из таблицы 2.
(1±Х)*/^1±|х-^х2±1^х’-
1.3.7.11 ,л ,
4.8.12.16х ±---’
(1 ± хУГ = 1 ± |х-^|х* ± |^|х2-
(х2 < 1].
[х’^1].
(1±х),/2 — 1 ± 2 х 2 4х ±2.4,6х’
|х2<1].
(1 ± х)’,2= 1 ± vх4-s-jх* 4- 2~4~6Х’ 4-
л • *х Z • *т • U
, 3-1.1-3 л 3.1.1.3.5 6 ,
+ 2-4-6.8Х 2-4.6.8-10X + • • ”
(1±хГ._1±|л: + Мх.±Ц>х._
5-3-1-1 . 5.3.Ы.З 5 _
2.4-6-8 ^г^-б-в-Ю •••’
[X2 1].
[х2^Г].
л । .д-п__1 „„ । п (п 4-1) ..2 П (п 4-1) («4-2) ,
(1 4- X) — 1 — пх 4-~2j-х--------3!----х +
+ ••• + (- .... к2<1].
(l-x)-»=l + «x4- l^x24-n-^ + 13;(”-+--2)x24-
+ ••• +7п-^н'х'+ 1х2<’].
(а ± хТп = а-"( 1 ±
(1 ± х)-’/4 = 1 т Тх + г1х* х’ +
"* 4-8.12-16х4 •••’ 1Х <'11-
10]
ряды
9
9.02. (1 ±x)-’/‘ = t т|х + ^х*Т^х’ +
9.03. (1 ±х)"'/2 = 1 Т1х + ^х’т|^|х’ +
+2Laz8-^---’
9.04. (1±х)'' = 1Тх+?ТхЧх‘Т ..., [х2 < 1].
9.05. (1 ±х)-/‘ = 1 Т-|х + |^х2т|4г6*’ +
+KS*‘*-- ^<ч-
9.00. (1 ± х)"2 = 1 Т 2х+3х2 Т 4х3 +5х* ..., [х2<1].
9.07. (1 ± х)~‘/г — 1 у х4- ^4Х* 2 4 6х'
9.08. (1 ±х)“’ = 1 Ту72{2:3хТ 3-4х2 + 4-5х’
Т5-6х4+ ...}, [х2<1].
9.09. (1±х)-‘ = 1 Tpl^^2,3*4-1'^3,4,5^^4,5,6^
Т5-6-7х4+ ... }, [х’<1].
9.10. (1 ± х)-‘ = 1 {2-3-4.5хТ 3-4-5.6х2 +
+ 4-5-6.7х’ Т 5.6-7-8Х4 + ...},
10.
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 3 62880
Ю! = 36 28800
11! = 39916800
12! = 4790 01600
1/2! =0,5
1/3! =0,16666 66667
1/4! =0,04166 66667
1/5! =0,00833 33333
1/6! =0,00138 88889
1/71 =0,1984126984.10"’
1/8! =0,24801 58730-10"4
1/9! =0,27557 31922-10"’
1/10! =0,2755731922-10"’
1/11! =0,25052 10839-10"’
1/121=0,20876 75699-10"8
Более подробную таблицу см. [18].
10
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
U1
И. lim ^77=/2л-
Эта формула позволяет .получать приближенные значения п! при боль-
ших п. Результат получается с избытком в 0,7% для п = 12 н 0,4% для
п = 20 (см. также 851.4 и 850.4).
12. п 2" п 2" п 2-«
2 4 15 32 768 2 0,25
3 8 16 65 536 3 0,125
4 16 17 131072 4 0,0625
5 32 18 262 144 5 0,03125
6 64 19 524 288 6 0,015625
7 128 20 1 048 576 7 0,78125 • ю-2
8 256 21 2 097 152 8 0,39062 5 •10“2
9 512 22 4 194 304 9 0,19531 25 •Ю"2
10 1 024 23 8 388 608 10 0,97656 25 • 10"3
И 2 048 24 16777216 И 0,48828 125 • Ю”
12 4 096 25 33 554 432 12 0,244140625 • 10”
13 8 192 26 67 108 864 13 0,12207 03125 •10”
14 16 384 27 134 217 728 14 0,61035 15625 •10'*
15.1 . (а + b + с)2 == аг % Ьг + сг % 2ab + 2Ьс + 2са.
15.2 . (а-\-Ь—с)г ~ аг-j-Ьг-f- c3~l~2al)—2Ьс — 2са.
15.3 . (а — b—с)2 — а3-\-Ьг с* — 2ab-\-2bc—2са.
16. (а 4- Z?-f- c-f- of)2 = а* + Ьг 4- с* -|- d3 + 2ab + 2ас -|-
+ 2ad 4- 2bc 4- 2М 4- 2cd.
17. (а4~ Ь-\- с)’ = а3 4~й’ 4- с3 4-6яйс%
4- 3 (а2Ь 4- ай2 % 62с 4- be* 4- сга 4- ся3).
20.1 . а%х = (я3—хг) /(а — х).
20.11. l-f-xs=(l —х3)/(1 —х).
20.2 . аг 4- ах4- хг = (я3—х3) Ца—х}.
20.3 . а3 4- я3х + ахг 4- х3 (я4— х4) / (я — х)
= (я24- х2)(я-|-х).
20.4 . я4 4- я’х 4- я2х2 4- ах3 + х%(я! — х5) / (а — х).
20.5 . я5 4-я4х 4-я’х2 4-я2х’4-«х4 4-х'
= (я6— х*) / (я— х) ss (я3 4- х3) (я2 4- ях 4- х2).
21.1. я—х—(я3 — х2)/(я4-х).
21.2. я2 — ях4-х2 = (я3 4-х3) / (я 4-х).
28.3)
ФОРМУЛЫ
11
21.3.
21.4.
21.5.
22.
22.1.
23.
25.
26.
26.1.
27.
28.1.
28.2.
28.3.
e’-a!x4- ахг — хг = (а*~х*) / (а х) S3
= (аг -ф- хг) (а — х).
а*— агх-\- агхг— ахг 4- х* = (а5 4- х5) / (а 4- х).
а5— а4х-(- агхг— агх* 4- ах*—х* —
= (а* — х*) I (а 4- х) = (а2 — х*) (аг — ах-\- х2).
а1 + Й2Х2 + X4 55 («’— х’) / (я2 — х2)==
= (а*4- ax-j-x2) {а* — ах 4 х2).
а4— а2х2 4- х* = (а8 4~ х’) / (а2 4- х2).
а* 4- х4 = (а2 -|- х2)2 — 2а2х2 s=
= (а2 4- ах|/"2 4~ х2) (а2— ах)/"2 4- х2).
Арифметическая прогрессия первого порядка (с посто-
янными первыми разностями) из п членов
а (а 4- d) 4~ 4~ 2^Z) 4- {а 4- 3zZ) 4- • • • 4~ { а 4- (я — 1) d )
= ла4-ул(л—1)б/ =
= (1-й член4-д-й член).
Геометрическая прогрессия из п членов
а4- аг-)- аг2, аг* 4- ... 4- arn~' = а (1 — rn) / (1 — И 53
= а(гп-1)/(г-1).
Если г2<1, предел суммы бесконечного числа членов
будет а / (1 —г).
Обратные величины членов арифметической прогрессии
первого порядка образуют (по определению) гармоническую
прогрессию. Так,
_1_ 1 1 1
a' а А-d' a-'r‘2d' а-\-(п—1)4
есть гармоническая прогрессия.
Средняя арифметическая п величин:
— (а, 4- аг 4- а3 4- . .. 4- й„).
Средняя геометрическая п величин:
(а,а2а3. .а„)'^.
Н— средняя гармоническая п величин определяется сле-
дующим образом:
+£)•
12 АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ (28.4
28.4. Средняя арифметическая некоторого числа положительных
величин больше или равна их средней геометрической,
которая в свою очередь больше или равна их средней гар-
монической.
29. Арифметическая прогрессия k-го порядка (й-е разности
постоянны).
Последовательность: а„ д2, иг,..-., ип.
Первые разности: du d2, d,,...,
где dj = «2—и,, d2 = «2— и2 и т. д.
Вторые разности: dt, d2, dt........
где й(, == +—d, и т. д.
Сумма п членов последовательности равна
п 1 , п ! у । п ! ,
(га— 1) I 1 I U»+ (га —2) 12/ + (га —3) 13 1 “1 +
29.01 . Если таблица функции ип дана для равноотстоящих зна-
чений аргумента с интервалом h, а именно /(а) = ар
f(a+ h) = u2, f(a-\-2h) = ut и т. д., то
/(я + р/г)=и1 + рй(!+^=-^ d,+P(p~g)(P—~ Ф +...,
где р<Д, a dit d, и т. д. даны в 29. Коэффициенты при
dt, d\, di и т. д. называются интерполяционными коэффи-
циентами Грегори — Ньютона.
Численные значения этих коэффициентов см. [25].
29.1. 1+2 + 3+... + л=|(л-)-1).
29.2. 1г Н- 2г З2 Н- ... + л2 = |(л+ 1)(2л+ 1) =
= -^ (2л’ + 3л + 1).
29.3. 1’ + 2г + 3’+ ... + гГ = £ (л+ I)2 =
= 2-(Л« + 2«+1).
29.4. 1‘ + 2‘+3‘+... + /г‘ =
= ^(л+1)(2л+ 1) (Зя’ + Зя- 1) =
= (6л‘+ 15л’+ Юл’ —1).
35.4]
РЯДЫ
13
отбрасывая члены с л0 и последующие. Величины 8„
Bv... см. 45.
Приведенные формулы можно использовать для нахож-
дения суммы рядов, л-й член которых выражается через
п, п\ пг и т, д,
30.1. 1 4-34-54-74-9+ ... 4-(2л —1)=л2.
30.2. I4-84- 164-244-324- ... 4-8(л —1) = (2л —I)2.
33.1. 14-3x4-5x24-7x’4-...=it^.
33.2. 14-ax4-(a4-Z>)x24-(a + 2Z>)x24-... =
. ах4-(&—а) ха
-Ч- (1—х)’ *
33.3. 14-2,х4-3,х24-4‘х,4-...
33.4. 1 4- З’х4- 52х2 4- 72х’ 4- ... = .
35* а а + Ь^а + 2Ь а4-3б + ‘ ~ J1 4-x»rfx
[a, 6>0].
35.1 . 1_14-1—±4-^-_ ... = £.е [См. 120 и 48.31.]
35.2 . l_| + 2._iL + ^_...._|^+ln2j.
[См. 165.01.]
35.3 . +
[См. 165.11.]
35.4 . 1—^-4-§—П + ]7-...=
==“^ + 21” (/2 4-1)}. [См. 170.]
14
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[38
38 . Степенной ряд для / (Л) имеет вид:
/ (Л) =/(0)4- hf (0) + (0) + h^f" (0) + .. .
{Ряд Маклорена.)
38.1г /(/г) = /(О) + Л/'(О) + ^/"(О) +
+ у/" (0) + ... + /(П' ” (0) + Rn,
где при некотором значении 6, заключенном между 0 и 1,
R„ = 5/<"’ (6Л), или (1 - б)”' ’/<”> (6Л).
39 .' /(х + М=/(х) + ЛГМ + 7”М + 7"' (*)+...
{Ряд Тейлора.)
39.1. /(х+Л)=/(х) + Л/(х) +
/? 2 А”-1
где при некотором значении 0, заключенном между 0 и 1,
или (^Л!(1-6)"'7<П)(х+6Л).
ill \(ъ I f I
40. f(x+h, y+k) = f(x, y)+{hd-l^ + kdl^} +
, 1 I h2 (x, y) , 9,. d*f (x, y) 2 d2f{x, y)|
+ 2 Г dx2 + zflR dxdy ~rR dy2 / +
1 31 I dx2 1 dx2dy 1 dx dy2 ’
+ a’ !+...+/?„,
ди2 I 1 1
где при некоторых значениях 6, и 62, заключенных между
0 и 1,
/?-’ = пт{ЙЯА?’+иЛП
+4г1’ +••+*" £.}/(*+ ОЛ .V+0,4.
42.1. Число делится на 3, если сумма его цифр делится на 3.
42.2. Число делится на 9, если сумма его цифр делится на 9.
42.3. Число делится на 2", если число, состазленное из п его
последних цифр, делится на 2”.
47.3]
ФОРМУЛЫ И РЯДЫ
15
Числа Бернулли и числа Эйлера
45. Числа Бернулли Числа Эйлера 1g Ея
s. -1 1,221 8487 1 0
= 30 2,522 8787 £г= 5 0,698 9700
B° =42 2,376 7507 £,= 61 1,785 3298
= 30 2,522 8787 £4 = 1385 3,141 4498
Bs =Д 5 00 2,879 4261 Е5= 50 521 4,703 4719
r -L2L • 2730 1,4033154 £„= 2 702 765 6,431 8083
a.-4 0,066 9468 Е7 = 199 360 981 8,299 6402
3617 ~ 510 0,850 7783
_ 43 867 °2 798 1,7401350
174611 °i° 330 2,723 5577
R _ 854513 138 3,791 8396
Существуют различные обозначения для чисел Бернулли и
Эйлера. Принятые здесь обозначения определяются формулами
47.1 и 47.4.
£ --_____^2п)1 £____________Е 4- -М I)"-1
« (2я —2)12! (2и —4)! 4 ! '1-2 ~ ‘‘ ’
принимая 0! = 1 и Et — \,
R - 2п Г (2п—1)! F _
Dn 22,‘(22" —1) [_(2л — 2) 1 1! ’ 4
_ (2л—1)1 , — 1)"-11
(2л —4)! 3> ”-г ‘ 1 J"
(2п)1 Г, , 1 , » , 1 , ]
Dn — л2/,22п“1 1 * 22П ’ 32П ' 42/г ’ * ’ ' •
р (2«)! Pi_______________L_|_J______Li 1
Dn — л2я ^2zn~1___1) I 1 22П ' 32rI 42” ’ * ’ j '
p . 2(2»)' [~i , , ‘ । , I
« “ л2П (2art— 1) [1 32» 1* 52« "1* 72« t” • • • ] •
16
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[47.4
47 4 Е 2а”~|'а(2п)! [._______________1_ , _1________-4-
-Ж«.1. 1^п ^ги + l I1 £2П + 1 Г £2П+1 ?2П + 1 »
48*001• 14_7_Ч*-у"|*“Т‘4“ • . . == ОО.
Z о 4
48.002. 1 +52 + ^2+42+ ... я2 = Л /?, = _ = = £ (2) = 1,64493 40668. (См. 45.)
48.003. 1 +<р+ Js+ Js+ • • • = с (3) = 1,20205 69032.
48.004. 1+т*+т*+^+ ••• л* _ л* ~ J ^“90“ = £ (4) =1,08232 32337. (См. 45.)
48.005. 1 +^s+ §7+45+ • • • = С (5) =1,03692 77551.
48.006. 1 + 2« + зв + р+ • • • 2лв „ л’ — V ~ 945 ~ = (6) = 1,01734 30620. (См. 45.)
48.007. 1 + ? + р + ^+--- = £ (7) =1,00834 92774.
48.008. 1 +^>+55 н-4* н— _ Л8 О Л8 — 315 й* “9450“ (См. 45.)
= £ (8) =1,00407 73562.
1 1 ) 2аи_1па"
48.08. =
\п—целое, положительное]. (См. 45, 47.1.)
48.09. 14-^ + ^+^+ . ..=£(р), дзета-функпия Римана.
Таблицу численных значений этой функции см. [16].
48.11. 1+4 + 4 + 4+ ...=ео.
48.12. 1+^ + 1г + 254-... = ^В, = у. (См. 45.)
48.13. ' l + + + ... = уЦ3) = 1,0517997903.
(См. 48.09.)
48.39]
РЯДЫ
17
48.14. l + l + l+7l+..._^B, = g = !5!;(4)= (См. 45.)
= 1,01467 80316.
48.18. 1+^ + б4и + 74+...=&1^вп. (См. 45, 47.3.)
48.19. l+^ + ^ + ^+...=(i_^S(p). (См. 48.09.)
48.21. 1 — 1+-L—14.... =1п2. (См. 601.01.)
48.22. 1 — да + 32 — 42 + ... =2’si = l2• (См. 45.)
48.23. 1—1 + 1—1+... = (1-1)^(3) = 0,90154 26774.
v (См. 48.09.)
48.24. 1-|4+|-1+ ... = <1=212ва = 12 = <См‘ 45->
= (1 — 1) С (4) = 0,94703 28295.
48.28. 1-^ + зк-^+... (См. 45, 47.2.)
48.29. 1-^ + ^-^+-.. ==(1-2^)С(Р). (См. 48.09.)
(Для р = 1 см. 48.21.)
48.31. 1 — у + 4~Т‘+ • • • =Т^ = Т- (Согласно 46.1 £0 = 1.)
48.32. 1 — 1 + 1—12 + ... = 0=0,9159655942.
48.33. l-l, + J,_^+..._gE, = «'. (См. 45.)
48.34. 1—1 4-1 — 1 4-... =0,98894 455.
48.36. 1— I4-I —-L4- ... =0,99868 522.
О □ /
48.38. 1-1 +1-1+...=0,999850.
48.39. 1 32/1+1 + 52/1+1 72/1+1 + ... = 2-2п+2 (2п) [См. 45, 47.4.]
18
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[50
Обращение рядов
50, Пусть известен ряд
у = ах-(- Ьх2 сх2 4- dx2 А- ех3 4- /х’ 4- gx2 4- ..[а=/=0],
тогда коэффициентами ряда
х = Ау 4- By2 + Су2 + Dy2 4- Еу2 4- Ру* 4- Gy2 -
будут
Л=-, С=Д(262 —ас),
а а3 а5
D = X; (5abc — a2d—5b2),
E = ^{5a2bd + За2 с2 4- 146* — а2е — 21 ab2c),
Р=-^(7а2ЬеА- 7а2с</4- 84а6’с — a*f— 28а2 b2d—
— 28а26с2 —426s),
G=-^,{8aibf+3aice + 4aid2+\2Qa2b2d+ \8Qa2b2c2 +
4-1326е — asg— 36а’ b2e — 72a2 bed— 12а2 c2 — 330a6‘c).
Степени 5 = a 4- bx 4- ex2 4- dx2 4- ex* 4-/-xs4- ...
51.1. S2 = a2 4- 2abx-p (b‘-(-2ac) x24- 2 (ad 4- be) x2 4-
4-(c24-2ae4-2M)x*4- 2 (af be-\- cd) xs 4- ...
51.2. S'2=a'/2 [1 4-4- -*4-(4~— +
L 2 a 1 \ 2 a 8 a2 / 1
,/'ll___v2_l
Ц.2 a 4 a2 ' 16a’/X
. f 1 e 1 bd 1 c2 . 3 Ьгс_5 b*\ 4
' \ 2 a 4 a2 8 a2(6 a3 128 a2) X '
51.3. S-^ = a-’/2 L < 1x4-(44--)x!4
L 2a \ 8 а2 2а/
[ 3 be Id 5 b’\ .
”** \ 4 a2 2 a 16 a3/
, <з_м 2 ид.
+ 4 a2 + 8 a2 2 a 16 а3 ф 128 a2) X 1 ’ '
58.3]
формулы и ряды
19
Б1.5. S-2 = a-2 [1 — 2~х+(^-г—2-'\хг-\-
L а \ аг а /
+ (б-,—2- — 4-Лх’ +
' \ аг а а*) 1
। Zz? bd . „ с2 „ е tc,b2c , , b*\ . , 1
+ ( 6 -8+3-2—2-------12—.4-5-. х‘4- ... .
' \ аг аг a a3 a4/ J
Корни квадратного уравнения
55.1. Корни ахг + Ьхс = 0:
— &+V&2—4ас —2с
а =---—В------- =----г -~ ,
2о 6-|- Уьг—4ас
о —Ь— У Ъг—4 ас —2с
2a b—УЬ2—4 ас'
Чтобы избежать потери точности при вычитании, следует
пользоваться той из двух формул, которая требует арифметиче-
ского сложения.
55.2. Если один из корней а вычислен точно, то
о Ь а с
р =—a----или р = —.
1 а г аа
Квадратные корни из комплексных чисел
58.1. ]/^+7} = ± [ |/’ф+ i .
58.2. ]/Т^=±
Здесь х может быть положительным или отрицательным,
у— положительно,
г— + K^s+js> 1 = У~ 1.
Квадратные корни из (г + х)/2 и (г — х)/2 следует считать
положительными.
58.3. Другой метод—представить x-\~iy в форме
/+ + (см. 604.05),
где г = Vх2 4- уг, cosf) = y, sin 6 = у , а k—целое число
или 0. Тогда
У х-\-1у = Уге‘в = ± У гет,1= ± У г (cos у-|-/ sin у) .
20
алгебраические функции
I&9.1
59.1.
59.2.
59.3.
Определитель
%
агр а2д
Определитель
а а. а
1Г
а9п 2р а*я а2Г
а а а*.
»р »q ir
— аи>(а2д atr
% а2Г
а»<7 а2Г
= arp a29-a2„
ач
а*я
а2г>~ а29(а2ра2Г— %«„) +
“Ь ®ir (^гр ®гд ®гр агр
Если дана система трех линейных уравнений
а1рх + а1дУ + а,гг=и
^2pX+a24y+a2^=.V>
a,Px + a,qy+airz = w,
то
иача,г Va2g^2r
V Wa,ga,r
и» — a a a м м » "to ’3 "to a a a M W Q <5 » » » M M —
o' sT a P 2" N*
5) —— a,p'Wa2r
у — «" <s" to" to" fe" r> N •» « e « N M* « « « »
9 —- a a a M № to 43 -to a a a M N H. О "to "Q. g c g
Л/ a a a M *to a a » S « « a a s> M N “ -1 -I 41 «
Корни системы линейных уравнений с ббльшим числом
неизвестных, если число уравнений равно числу неизвест-
ных, выражаются аналогичными формулами, если знамена-
тель отличен от нуля.
72)
ПРОИЗВОДНЫЕ
21
Алгебраические функции — Производные
60.
61.
63.
64. 1
64.3
65.
66.
68.
69. 1
69.2
69. 3
72.
d(au) du
—^sa— Где a—постоянная
dx dx'
d(u+v)du .dv
dx dx‘ dx'
d(uvw) dw , du , dv
-Ч—- = uv -r-4- vw т-4-Ш t
dx dx * dx 1 dx
62.
64.
d(uv) dv . du
dx “dx' dx
d(xn)
—j—-—nx" .
dx
. = 64.2.
dx 2 fa dx xz
.. d(x~n) лх-(«+1)
dx
du d~
d (u)v) I du и dv_______ dx dx
dx v dx v2 dx d*
df (t<)_df (u) , du R- d2f(u) _df(u) d2u . d2f(u) / dnV
dx du ’ dx’ , ’ dx2 du dx2 ' du2 \dx) ’
dn (uv) dnu , ~dv dn~lu , n (n—l)d2vdn~2u ,
dx'1 ~V dxn‘n~dxdx"-~,~' 2! d?dxn-a +
, . n I dkv dn~ku . udnv
"г • • • "r (n~k)! «! dxk dxn~& ”** ’ ’ * **" dxn
ч
^y(x)dx=f(q) {p — постоянно),
p
D
^-\/(Х)ах = -/(р)
(q— постоянно).
” + c>)Tc~^P' C}Tc’
p t>
Если <p(a)=0 и 'ф(а) = 0, или если (р(а) = оо и 1|)(а) = оо,
то
lim Tlf) __ Ф' (а>
,:“>(*)" Ф' (а>‘
Если также <р'(а) = 0 и ф' (а) = 0, или если ф'(а) = оо и
ф' (а) = оо, то
lim
х-^а
Ф (X) _ Ф" (а)
ф(х) - ф’(а)
и т. д. *).
) Более точную формулировку см., например, [1]. (Прим, ред.)
22
алгебраические ФУНКЦИИ
172.1
72. 1. Если функция имеет вид 0-оо или оо—оо, то ее нужно алгебраическим или каким-либо другим преобразованием 0 оо привести к виду или —.
72. 2. Если функция имеет вид О’, оо’ или 1®, то ее надо сна- чала логарифмированием привести к виду 0-оо, а затем 0 оо к виду w или —. J 0 оо
79. Общая формула интегрирования по частям J и dv = uv— v du, или f , f du , . 1 u dv — uv— 1 dv. Рациональные алгебраические функции — Интегралы *) Интегралы, содержащие хп
80. ^dx — x. 81.2. ^xidx = 1^.
81. 1. pdx = y. 81.9. 1].
82. 1. C dx 1 — = 1п|х|. (См. примечание перед 600.) В этом случае нельзя интегрировать от отрицательного зна- чения х до положительного. При отрицательном х надо взять In | х |, поскольку 1п (—1) ss (2й + 1) iti войдет в постоянную ин- тегрирования (см. 409.03). (См. рисунок на стр. 23).
82.2. С^=-1. 82.3. -L J х2 х J х3 2х2
82.4. С dx 1 on С dx i J F “ Зх5’ ’°* J ? ~ 4F’
82.9. fx"'- (n-Dx"-1
) Здесь и далее произвольная постоянная интегрирования опущена.
89J интегралы, содержащие X—a-\-bx 23
Интегралы, содержащие .ЛГ==а-|-&е
83. J(a + Mndx = lJx’’dX=^r) [«¥=-!].
84.1. J xm(a-\-bx)n dx можно интегрировать почленно после раз-
ложения (а + ^х)” по формуле бинома Ньютона, если п.
целое положительное.
84.2. Когда т целое положительное и если т<С.п или п дроб^
ное, может быть, лучше использовать формулу
j хтХп dx = j (Л— а)тХпdX
Рис. 82.1. Графики функций у—1/х (пунктир-
ная линия) и у=1п |х | (сплошная линия).
85. Интегрирование рациональных дробей—см. соответствую-
щий раздел в учебниках интегрального исчисления.
89. Общая формула для 90—95:
f хт dx 1 C(X—a)mdX 1 т!(— ayxm-n-s+x ]
J Хп~Ьт+') Хп ~bra+t —s)!s! (m-n-s + 1)] ’
за исключением т—п — s-|-l=0. В этом случае соответствую-
24
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[90
щий член суммы в квадратных скобках должен быть заменен на ml(-a)n,-n+1 (w—n + l)!(n—1)' 1Л|’ Все буквы означают действительные величины. При наличии 1п|Х| нельзя интегрировать на интервале, содержащем точку Х = 0. Если X—отрицательная величина, то надо брать In I X |, так как In (—1) = (2й-J-1) лг войдет в постоянную интегрирования.
90. J Хп~(п — l)bXtt~l
90. 1. J у- In | X\. |См. примечание к 89|.
90.2. f L 00 3 f — ' J X2 ЬХ ‘ J Xs ~ 2ЪХг'
90.4. f dx 1 an с f I JX4 = 3&X>’ Jx‘“ 4bXv
91. Cxdx_ 1 [ —1 a 1 J Xn ~Ьг [(n-2)Xr1-2 1 (n — l)Xn-lJ (кроме случая, когда какой-либо из показателей степени X равен нулю, см. 89).
91.1.
91.2. ['"W+fl.
91.3. С xdx 1 Г 1 . а 1 J 'X3' ~ 1? [ X + 2X2 J *
91.4. C xdx 1 Г 1 , a 1 J X1 ~ Ьг [ 2X2 ’ 3XSJ’
91.5. P xdx I T 1 a [ J 6! [ 3XS 4X1] •
92. Cx2dx 1 Г —1 , 2a аг I J Xn b3 L(n —3)Xn-s 1 (n —2)X”~2 (n- (кроме случая, когда какой-либо из показателей степени X равен нулю, см. 89).
92.1. (* X2dx 1 ГХ2 О v , t 1 I V |1 J ”2Г = й5 1 2аЛ+ а 1п 1 Х1J • Другое выражение, отличающееся на постоянную: х2 ах , а‘ . . , , л? “~та + "Тя In 1 л *4- Ьх » 2Ь Ь2 1 bs * ' 1
04)
ИНТЕГРАЛЫ, содержащие Х = а-\- Ьх
25
92.2.
92.3.
92. 4.
92.5.
92. 6.
92.7.
93.
93. I.
93. 2.
93. 3.
93. 4.
93. 5.
93.6.
93.7.
94.
х2 dx 1
~Х^ ~ Ь3
х2 dx 1
~ХГ~'Ь3
х! dx ! Г v „ > , .л, а2!
-^- = р Л— 2а in | X| — yj.
^dx 1 ftni у I _1_2а °21
X2 ~ b' [1п1л l + x 2X2J •
x2 dx I Г 1 2a a2 j
X4 = &’ [ X + 2X2 Зх’] ’
1 . 2a a2
2Хг+ЗХ2 4X4]'
1 ( 2a a8
3X»+4X1-5X5]*
0 x2dx I Г 1 2a a3 1
J ~ХГ~ P [ 4X4 ' 5Х* — 6Х' Г
f* x’ dx 1 Г — I 3a
J Xn ~ P |(n — 4)Xn-<+ (n —3)ХЯ-2
3a2 a3 ]
~(п-2)Хп-г + (п-1)Хп-Ч
(кроме случая, когда какой-либо из показателей степени X равен
нулю, см. 89).
= S-S + V-Flnia + ^l + const-
С x3dx 1 ГХ2 „ v , п г, । Vi । a’l
j ~Х*~~ [2---ЗаХН- За In | Х\ Ц- yj.
J Xs ~ b3 Р За п I Х\ х +2Х2]’
0 x3dx I Г. । yr I 3“ За2 а3 1
J 'Х3--Р [1П1 Л1 + X—2Х2 + ЗХ8р
f* х3 dx_ I Г I За За2 а3 1
J "X2" ~ b5 [ X + 2Х2 зх^+тх5]’
Cx3dx_ 1 Г 1 За За2 as I
J X’ — Ь3 [ 2Х2 + ЗХ2 4Х1 + 5XS J '
Cx3dx_ 1 Г 1 За За2 а3 1
J ТхГ ~ Р [ ЗХ2 "''4Х1-_5Х2 6Х2]-
С х3 dx I [ — I , 4а
J'X5“~P [(л—5)Xn-s + (n-4)Xn-<,—
6а2 4а’ а4 1
— (п—3)ХИ-2 + (а—2) Xй-2 ~ (n—DX”-1 ]
(кроме случая, когда какой-либо из показателей степени при X
равен нулю, см. 89).
26
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[94.1
94. 1. (* x' dx J x t>5 ГХ4 -4aX3 6a2X2 4 3 2 4a’AT+ a4 In | Af|
x4 ax3 , a2x! ' a’x .a4. . + ^ln|a
4b 3b2 + 2b3 fe4
94. 2. (* x4 dx 1 ГХ3 4aX2 , „ 2V [З 2 +&aX 4a’ln| X\— £|.
J X2 bs
94. 3. С x1 dx J 'x3-== J_ bs Г Y2 ‘ pL_4ax+6a2ln| АГ| + 4a3 a4 1 X 2X2J *
94. 4. Cxidx 1 pT— 4aln| АГ| 6a2 . 4as a4l
J X4 “ bs X ' 2X2 3X3J-
94. 5. C x*dx J xs “ 1 bs [in| АГ| +^- 6a2 2X2 4a3 3XS 1 4X4 ]"
94.6. Г x*dx 1 Г 1 4a 6a2 ( 4a3 a4 1
J X3 “ bs [ X 1 2X2 3X3 । 4X4 5X5] *
94. 7. (* x*dx 1 Г 1 । 4a 6a2 , 4a3 a4 1
J x’ “ bs [ 2X2 + 3X3 4X4 ** 5XS bX’j’
95. C x5 dx I Г 4- 5c I
J xn [(n—6)Xn-e 1 10a2 (n — 5)Xn~s , 10a3
(n — 4)X”~4 1 (n- -3)Xn- 3 5a4
1 (n—2)X”-2
+ 14-const.
95. 1.
а5 “1
(п —1)ХП-*]
(кроме случая, когда какой-либо из показателей степени при X
равен нулю, см. 89).
x5 dx 1 ГХ5 5aX4 , 10a2X3 10a3X2 , 5^4^. a’lnlATl] —
X ft® [б 4 4 3
_ x_s — 5b' ax4 462 , a2x3 + 36s a3x2 264 1 fe5 fce In 1 a+tecj 4- const.
95.2. = | ^-^Ч-^-10а\¥+5а41п|.¥|+£|.
95. 3. J ± {J~5-~ + 1Оа'АГ- 10as In | X| - ~ ,
п. . С х5 dx 1 ГХ2 с v , si । vt 1 |Оа’ 5а4 । “М
9о. 4. J X4 — 6® 2 + 10« ' ।n I -^ | + % 2Х2 ЗХ® J '
__ Cx5dx I Г iz к i I izi । Ю<23 5a1 , «s 1
95.5. j %5 — й„ 5a In | X| x + 2X2 ex’^X4]'
_ 0 x5 dx l Г, | 5a 10a2 10a3 5a4 as 1
”• j xe ~ &» Ln л + x 2X2 + 3X2 4X4+5X’J ‘
102.2]
интегралы, содержащие X=a-±bx
27
95. 7. С xs dx 1 Г 1 5а 10а2 . 10а’ 5а4 а’ 1 J X' &• L X + 2Х2 ЗХ2 + 4Х4 5Х’ -г 6Хв] '
95. 8. С Xs dx 1 Г 1 5а 10а2 10а2 5а4 а’ 1 J X8 ba [ 2Х2 ЗХ2 4Х4 ' 5Х’ 6Х» т- 7%’J • .
100. Общая формула для 101—105 / % хт + п-ъ с dx _ —1 — J хтХп \ х ) т + п-г =. Г У (т + п — 2) ! Xm-s-l( — b)s 1 am+n-i (т + п — s — 2)! s 1 (т — s — 1)хт~s~1 ]' кроме т—s—1 = 0, когда соответствующий член в квадратных скобках заменяется на (m-l)l(n —1)Г ' |х Г
101. 1. f^ = -1 in ш J хХ а 1 х 1
101.2. г j£2==_Uinix|+^i J хХ a2 L 1 х | 1 X j
101.3. (* dx _ 1 Г] IХ I . 2bx bVl J хХ3 а3 [1П | х X 2X2J '
101.4. С dx _ _ J_ р. |Х| 3bx 3bV , &3х3~| J хХ4 а4[П|х + X 2Х2 + 3X’J *
101.5. C_dx___ __L Ft Iх 1 4&x 6bV 4b3x3 b4x4~l J xX5 a3 L n 1 x 1 + X 2X2 1 ЗХ’ 4X4] ‘ Другие выражения, отличающиеся на постоянную:
101.92. Г dx _ _1 J_ . IX I J хХ2 аХ а2 П 1 х |‘
101.93. С_Ё£_ 1 । 1 _ 1 1 Iх I J хХ’ 2аХ2'а2Х а3 П | х Г
101.94. С —- —J- 1 . 1 _ 1 1 Iх I J хХ4 ЗаХ2 + 2а2Х2 + а’Х а41П | х
101. 95. , _1_ , _L_, 1 _1| |х| J хХ’ '4аХ4 + За2Х2 2а2Х2 + а4Х а3 П | х
102. 1. С4* _цгх_,1п^П. J х2Х а2 [ х 1 х IJ
102.2. С dx 1 Гх nl. । 1х 1 b2x 1 J xzX* а3 1 х х X J
28
АЛГЕВРАИЧЕСКИЕ ФУНКЦИИ
(102.3
На этой странице Х~а+Ьх.
102. 3. e dx _ J x2X3~ I ! a1 ГХ 1x — 361n| X j X 1 36®x , X 4 6’x2] 2X2J *
102. 4. r dx 1 ГХ — 46 In IX 1 6&2x , 4b3x2 ft**3")
J x2X4 a3 X 1 x 1 X ' 2X2 ЗХ’Г
Другие выражения, отличающиеся на постоянную:
dx b_ IX I
x2X~ ax'a2 jx|'
102.91.
102. 92. Г dx _ J x2X2“ Ь [a2X + 1 1 4l* c <Х|Ъ 1 _|5
102.93. P dx i^X3~ _ . Г i P [2a2X2 , 2 1 3. H|1 ‘ asX ' a3bx a4 n ( x |j
102.94. (* dx J x2X4 _. Г [3a2X3 , 1 2a3X2 a’X a4bx as i IX Г In — 1 x 1 •
103. 1. Г dx _ J x3X~ 1_ rx^_ a3 l2x2 __L+± 2ax2 a2x ^ + 64n|*f| = * 1 x IJ fc21 1X I . ~,n|T| + const-
103.2. P dx _ J x3X2 “ 1 Г X2 3bX , „. 2 . I X I , bsxl 1 ят-' ^36 n — 4- -y- . a4 [2x2 x ' 1 x | ' X J
103.3. (* dx 1 Г X2 4ftX , „,2. 1 X I 4ft3x 6“x2'|
J x3X3 ~~ «s 2x2 x ~t'00 " x 1 + X 2X2J 1
104. 1.
dx _____1_ Г X3 36X2 , 3b2X , i |X|]_
x4X a4 [3x3 2x2 ’ x ° I x (J
1 , b & b3 , IX I ,
== —T---j+s-FT-----5— 4--J In — 4- const.
3ax3 ' 2a2x2 a3x ’ a4 I x | ‘
104.2.
105. 1.
dx 1 [ X3 4bX2 , f«2X ла»1~1лг1 *‘xl
cfi [3x3 2x2 + x W n| x I XJ-
dx ___ 1 b b2 b3 __________________fr1 . I X I
x5X 4ax* ' 3a3x3 2a3xs~4 a4x a3 n| x |‘
Интегралы, содержащие линейные множители
ПО. Г^г^- = х + (а—с)1п| с4-х].
J WT*)
ПО.!. Г£±^=^ + ^1П1С +
J t^+gx) g' g2 1 1
120.91
ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ X = а2 + X3
29
111. С dx 1 . 1 с+х 1 . . 5 (а + х) (с-Н) — а-с П |a+J Если а —с, см. 90.2.
111.1. С dx 1 , Ic+gxl . ,д .) (a+fx) (fi+gx) = ag—cf П 1 a+fx | C^’ Если ag = cf, cm. 90.2.
111.2. J (fl+x)(c+x)e(a-c)lelnle+xl Hnk + x!}.
112. C dx 1 . 1 | a + x I ' (a+x) (c-|-x)2 (c—a) (c+x) ‘ (c —a)2 n|c-J-xr
112.1. C x dx c a 1 a 4- x 1 ' (a+x) (c-f-x)2 (a—c)(c4-x) (a — c)2 n |c-j-x
112.2. Г x3 dx c3 . ctl . , _. , j (a+x) (c-f-x)2 (c—a) (c+x) (c — a)3 nia ‘ x . c3— 2ac ... . 1 \c—a)2 1
113. C dx —1/1 , । 1 \ । 2 . 1 ct -|- x I j (a+x)2 (c + x)2 (a —c)2 \a-f-x • <•+«/ * (a — с)3 n|c-|-x|"
113.1. C x dx | / a , c \ . a +c . 1 a+x 1 J (a + x)2 (c+x)2 (a—-c)2\a + x * с-}-х) ‘ (а—с)3 П|с+х|' ?
113.2. C x2 dx —1 f d2 ' . c3 \ 2ac . 1 a-}-x 1 J (a+x)2 (c+x)2 (a—c)2\a4-x * c-f-x/ • (a —c)3 n|c-|-x[’ Интегралы, содержащие X = a3 -j-x*
120. C dx \ j x2 = arctg x (см. рисунок на стр. 30).
120.01. C dx 1 , bx J a3+bW ~-ab arCtg a '
120.1. f dx £ dx 1 , x 3 Л “ J a2+x2 = a arctg a '
120.2. C dx x . 1 , x J Л2 = 2a3X "t* 2a? arCtg o’’
120.3. C dx x . 3x . 3 , x J X3 ~ 4a2№ 8a3X 8a<* arctg a~ ’
120.4. ? — * 1 5x . 5x , 5 x J X4 6a2X3 24a4X2 1 16aeX •" 16a’ arCtg a ‘
120.9. C dx x 2n — 1 Г dx J (a24-62x2)«+i 2na3 (a3+b3x3)n 1 2na3 J (a3+b3x3)"'
30
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
Ц21
121. Интегралы вида
С
J (а2 ± х2)«
подстановкой x2 = z приводятся к
1 С гт dz
2 J (а2 ± г)” ’
о которых см. 89—105 (для т положительного, отрица-
тельного или равного 0).
тирная линия) и z/ = arctg х (сплошная линия).
< п. , С х dx С х dx 1 , z 9 । 9\
12LL J — = Т1п(й +х)-
1919 V Xdx ______ 1 1913 С Х ^Х _________—
12I.Z. J Л2 — 2Х ' J X3 “ 4Х2'
191 4 f х ^х —_______!—
J X* “ 6Х3‘
12'-9. ( J-Й - - I” * «I-
inn . С х2 dx , х
122.1. \ = х — a arctg—.
J A Q,
Cx2dx х.1 , х
122.2. — + -arctg-.
, х2 dx х . х ,1 , х
122.3. 4%2 4- 8а2Х 4- arctg у.
128.1] ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ Х—С^ + х2 31
122.4. Г x2dx — X -1- x 4- x 4- 1 arete x
J X4 6X3 1 24a2X2 1 16a4X 1 16as ё a '
122.9. f* x2dx J Xя+l —x . 1 Г dx 2nXn ' 2n J Xn ‘
123.1. C = („Л’.
J X 2 2
123.2. C xsdx J ~X^ =4+4'"*-
123.3. P Xsdx 1 . a2
J X2 2X + 4X2"
123.4. (• x’dx ] a2
J X1 4X2 1 6X2"
123.9. p x*dx __ — 1 , a2 [«>!].
J Xn+' 2(n — l)X“-> 1 2nX"
124.1. C xldx J X = y— a2x+a3 arctg •£.
124.2. C xtdx J , a2x 3a . x = X+2X—2 аГС^Т-
124.3. C x'dx a2x 5x , 3 .x
J X3 4X2 8X + 8a аГС g a '
124.4. P xldx a2x lx , x , 1 , x
J %4 6X3 24X2 ' 16a2X ' 16as e ° a ’
125.1. C xidx J X x4 a2x2 . a4 . v -4 2+2ln*.
125.2. C x*dx J X2 *2 a4 ,, v - 2 2X a In X.
125.3. p x'dx J X3 Jljlinx X 4X2-1 2 •
125.4. C x*dx l a2 a4 .
J X1 2X + 2X2 6X3 •
125.9. P x'dx — 1 ( a2 a4 l«>2].
J xn+1 “ 2(n—2)X”-2 + (n — 1)X"-' 2nX"
126.1. P x*dx x' a2xa , , 5 , x
J X 5 3 g a 4
127.1. p x'dx x® a2x4 , a4x2 a’ ] v
J X 6 4 + 2 2 1ПЛ-
128.1. C x’dx J x x’ azx5 , a“x’ , . , , x -7 5 + 3 ax + a arctg a.
/\ cJ /у U (о »
82
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
(131.1
На этой странице Х = а2+х2.
131.1. С dx (’ dx 1 . х2
J хХ j х(а24-х2) 2а2 а2-|-х2*
131.2. С dx 1 . 1 . х2 3 ТХ2 ~ 2а2X 2<? 1П X ‘
131.3. V ' * । 1 . 1 । X2 J хХ3 “ 4а2 X2 1 2а4Х 2а° 1П X •
131.4. С dx 1 . 1 1 1 х2 } хХ1 6а2Х3 ’г’ 4а4Х2 + 2а°Х 1 2а8 1П X '
132.1. С dx 1 1 , х J х2Х а2х а3 ® а
132.2. С dx 1 х 3 , х J х2Х2 “ а4х 2а4Х 2а6 arCtgXz ‘
132.3. С dx 1 х 7х 15 , х J х2Х3 — asx 4а4Х2 8а“Х 8а’ arCtg а '
133.1. С dx 1 1 . х3 3 XX — “ 2а2х2 2а4 П X •
133.2. С dx 1 1 1 , х2 ) х3Х2 “ 2а4х2 2а4 X а8 1П X ’
133.3. С _ 1 1 1 3.x2 3 х3Х3 “ 2а6х2 а6Х 4а4Х2 2а8 1П X ’
134.1. С dx _ 1 .1.1 I х j х4Х За2х3 ~~ а4х ‘ а8 аГС g а ’
134.2. Г dx 1.2.x, 5 , х J х«Х2 ~ — За4х3 + а8х + 2а3Х + 2а’ arCtg а ‘
135.1. С dx 1.1.1.x2 J х^Х ~ “ 4ХХ + SaV + 2F 11 X *
135.2. С dx _ 1 , 1 . 1 , 3 . х2 ,1 х^Х2 ~ 4?F + + 2а8Х 2а8 П X ”
136. С 1 Г 1 । х 1 <
J (f + g*)(a2 + x2) (f2+a2g2) |_ь 17 1 1
- 1п (а4 + х2) + L arctg 5
140.3|
. ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ X = О* — X3
Интегралы, содержащие Х=а? — х*
33
140. 1 "-^8 = Уln 1[ • (Си. примечание к 140.1.)
Функция 1/(1—х2) и интеграл от нее могут быть определены
и для отрицательных значений х. См. рис. 140.
140.01
dx (* dx
х2—1 \ 1—х2
[См. 140.]
140.02.
С dx ________ 1 . I a-j-bx I
j a2—62x2 2ab n|a — bx | ’
Заметим, что
1 ina±6x= 1 Arth — [£2x2<a2[,
2ab a—bx ab a L 1
> 1П = 1 Arcth - [&2x2 > a2].
2ab bx—a ab a L 4
линия) и у = -i- In | 1 (сплошная линия).
140.1. -^-2 = In I I. [См. замечание к 140.02.]
1 /ь -J t* Л ЛЛЛ j W At I
140.2.
140.3.
dx x . 1 I a-f-x I
X2 — ^AX 4a4 1H | a—x I’
dx __ x . 3x 3 . I a-f-x I
X» — 4a2X2 8a4X + 16<? ln |?=х’Г
2 Г. Б. Двайт
34
Алгебраические функции
[140.4
140.4. (* dx X t 5x , 5x t 5
J х4 6a2X3 1 24a4 X2 1 16a3X 1 32a’
140.9. [* dx x ( 2n — 1 P dx
J (а2 — b2x2)'‘+1~ 2na2 (a2 — b2x2)n 1 2na2 J (a2—b2x2)'l\
141.1. С х dx C. xdx _ 1 , । . . .
J X J a2— -x2 2 1 ।'
141.2. Р х dx J X2 1 2X‘ . .. n P x dx 1 141.3.
141.4. Р х dx J X* 1 6X3‘ 141 9 C 2Ldx — l4!! 1 vn + i t 1 2nX”
142.1. Р x2dx J X “ _x+4ini^i 1 2 la—x|
142.2. Р i^dx J X2 X 2X 4a |a—x|
142.3. Р x2dx J X’ X 4X2 Л L in H+^l 8a2 X 16a’1 |a—x|*
142.4. Р x2dx J X1 X 6№ X x 1 . 24a2X2 16a4X 32 a5 11 | a—x|
142.9. Р x'ldx X 1 Cdx
J хи+* 2nXn 2n J Xя •
143.1. Р x’dx J х x2 2 -y In H|.
143.2. Р x’dx J X2 2Xn у!п|Л|.
143.3. (• x’dx 1 /7.2 P x*dx 1 (
t- 14Q 4 I
J X’ - 2X ' 4X2 ' 1 j X4 4X2^
143.9. Р x’dx -1 , a2
J xn+* 2 (n — DX»-1,1 2nXn
144.1. P x’dx J x 1 x’ 3 2 , a’ , | a + x I — a‘x+-^ In —— . 1 2 a — x
144.2. P x’dx _ J X2 ~ , a2x 3a. | a + x | * + 2X-4 ‘"И-
144.3. x’dx a2x .|£. 3 j |a + xl
J Xs 4X2 8X~16a |a—x|
144.4. P x’dx J X1 a2x 6X’ 7x x . 1 . 24X2 16a2X 32a3 ln |й|.
145.1. P x’dx J X X4 4 -"-^ln|X|.
[я =# 0].
а2
6 Xs*
154.2|
ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ X = О.2 — X2
35
145.2. + +
145.3. +
145.4. Р х2 dx 1 а2 . а4 \ "Х4 2Х — 2Х2 ‘~6Х2’
145.9. f х5 dx 1 а2 а4 [я >2].
J X«+1 2(п—2)Х«-2 (п— 1)Х«-! 1 2пХп
146.1. ?x»dx_ & а2х» . , а» . [ а+х | J ~Х 5 3 Л 2 1П|а—х|'
147.1. Р xldx х2 а2х4 а4х2 а® . . v. 3 X ~~ 6 4 2 2 ।
148.1. Р х8 dx х2 а2х2 а1х3 e , а . 1 а+х| }-)Г= ~Т~~5 г “ а х+т1п|^|-
151.1. С dx _ С dx _ 1 1„ I *2 .1
j хХ J х(а2—х2) 2а2 П|а2—х2(*
151.2. 151.3. 151.4. С dx 1 . 1 . 1 х2 1 J хХ2 ~ 2а2Х + 2а4 1П | X | * С ^х _ 1 , 1 | 1 1пР2| J хХ3 ~ 4а2Х2 -Г" 2а4X 2а® | X | ‘ Р dx 1 , 1 . 1 । 1 Ixi 1
J хХ4 ’ 6а2Х8 1 4а4X2 Г 2а® X 1 2а® | X Г Р dx 1 . 1.1 а+* I J х2Х а2х "t" 2а3 | а—х |' Р dx 1 , х 3 |а+«1
152.1. 152.2.
J х2Х2 а4х 1 2а4X 1 4«й* |а-х|’
152.3. Р dx _ 1 . х . 7х 15 1 a-j-x 1 5 х2Х3 ~~ аах + 4а4Х2 1 8а»Х 1 16а* 1П|а—х|’
153.1. С ^х 1 _1_ 1 lu Ixi I
3 хРХ — 2а2х2 1 2а4 | X | ‘
153.2. 153.3. f dx- = — —!—и —-—и — in I — 1 J хЫ2 2а4х2 2а4X Т а® | X J ’ f 1 -4- 1 4- 1 4- 3 in I *2 |
3 хЗХ3 “ 2а4х2 1 а»Х 1 4а4Х2 1 2а8 JX ]’
154.1. С ! L + _L in 1 I 3 х®Х За2х? а4х “ 2а6- | а-х |'
154.2. 1 х®Х2 За4хЗ а®х т 2а®Х “ 4а* |а-хГ
2*
36
алгебраические функции
|155.1
155.1. C dx 1 1 1 | x21 J № 4а2х* 2а*х2 2a’ ln | X | •
155.2. ( dx 1 1_ _1 3 I x2 1 J x4X2 4 a4 x4 - a¥ *" 2a’X 2a’ 1П | X |' В 155.1 и 155.2 X = a2—x2.
156. 5 (f+gx) (a2-*2) “ a2g2-/2[^1п!/+^| — -f lnja2-x2! -/-ln|?-±^|l. 1 ' 2a |a — x |J Интегралы, содержащие A = ax2 ^-bx-^c
160.01. f - = ?.=. arctg f 4ac > b2l,
Jx faac—b2 &^4ac-b2 1
160.02. 1 , 2ax+&— ^б2— 4ac , ~ -.-y-= In ! ^=== f£2>4ac], Кб2—4ac 2ax4-6+K 62 — 4ac 1 = ~r^—t In | 1 [Z>2 > 4ac], a(p — q) ]x — q | I*' “ J, где p и q — корни уравнения ax2 bx + c = 0, = — =.... Arth 2.g£+L ^62 — 4ac К b2 — 4ac [ft2 > 4ac, (2ax 4- b)2 <z b2 — 4ac], = _ Z^Arcth-^L К б2—4ac У b2—4ae [Z>2 > 4ac, (2ax + b)2 >b2 — 4ac], = 2м+б \ [^-4ac|. (Положить 2ax -j-b = г.) f dx 2ax-j-b , 2a C dx , J X2 ~ (4ac-b2)X * 4ac-b2 J X ' 1Cm’ 160-01-]
160.03. C dx 2ax-\-b 3a (2ax + b) . J X« “ 2 (4ac—b2} X2 1 (4ac— b2}2 X 1 + (4ac — b2)2 J X * ^M- 160.01.]
160.09. f dx 2ax-\-b (2л — 3) 2a C dx J Xя ~ (n— 1) (4ac —б2) Xя"! 1 (n— 1) (4ac — b2) J Xn~^‘
160.11. P x dx 1 , । •» 1 b C dx r _ In ] 160.01.]
160.12. (’ x dx bx-4-2c b C dx J X» “ (4ac-b2)X 4uc-b2 J X * ^См' 1SO-O1-1
165.21] ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ -\-Ьх-\-С 37
160.19./ Р х dx bx-\-2c b (2п—3) Р dx J Хп (п — 1)(4ас— Ь3)Хп~1 (п— 1) (4ас —б2) J Хп~1'
160.21. Р X^dx X Ь » । vz I 1 •“*“2йС Р dx г л i лзгч л< 1 J X ~а 2а21пИН—Г^х- [См. 160.01.]
160.22. f2g£= (&8-2ac> * + + 2с Р dx [См. 160.01.] J № а (4ас—b3} X 4ас—Ь3 J X 1 J
160.27. С xmdx хт~‘ с Р xm~3dx b Р xm~ldx J X (т— 1)а a J X a J X
160.28. С xmdx хт~1 J Х:‘ “ (2п — т — \.}аХп~1' . (т — 1)с Cxm~3dx (п — т) b Р хт~М.1а * (2/г— т—1) a J Хп (2л— т— l)aj Хп [т =# 2п— 1].
160.29. При т = 2п—1 С x3n~'dx 1 Р x3n~3dx с Р x3n~3dx b Р x?n~3dx J Хп a J Xй-1 a J X" a J Хп ’
161.11. [См. 160.01.]
161.19. Р dx 1 b Р dx . 1 Р dx J хХп ~2с(п-\)Хп-' 2cJXnl с}хХп-'-
161.21. ?-4г = 6Д-1и|-4|— “ + Т- [См- 160.01.] J х*Х 2с* \ г \ сх ' 2cz j л 1 1
161.29. Р dx 1 J хтХп“" (т—1)схт-‘Хп-‘ (2п + т—3) а Р dx (п + т—2) b Р dx . . (т— 1)с J хт-3Хп (т—\}а J хт~'Ха Интегралы, содержащие a’±x’
165.01. Р dx 1 , (а + х)2 1 , 2х —а J а3 + х3 ~ 6аз1Па3-ах + х3 1 1ГС ь а/Т’
165.02. Р dx х . 2 (* J (а‘-f-x‘)8 — За‘(а‘Н-х*) * 3a,Ja‘ + *’'
165.11. Р xdx 1 . а‘ — ах + х? . 1 , 2х—а ]□’ + ? 6а П (a+i? 1 аГТаГС1га|<з’-
165.12. Р х dx х3 1 Р х dx J (а’ + лс’)’~3а’(а’ + л:’) ‘ За’ j а’ -|- х3 ‘
165.21. Р x‘dx I.,., 3, j з 1п1а 1-
38
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[165.22
165.22. р x3dx 1
J (as+xsj2 3 (a3 + x3) •
165.31. р __ J а3 + х3 Х s C dx a Ja3-|-x3’ [Cm. 165.01.]
165.32. Р x3dx —x , 1 (* dx [Cm. 165.01.]
J (а’ + х3)2 3(a3 + x3) 1 3 J a3 + x3‘
165.41. Р x'dx X2 5 P x dx [Cm. 165.11.]
J а3 + *5 2 a J a3 + xs'
165.42. x'dx x2 2 P x dx [Cm. 165.11.]
J (а3+х3)2 3(a’ + x3) 1 3 J a’ + x3 •
165.51. Р x3dx х3 J а3 + х3 3 «’ln|a’ + x’|. О
165.52. f xsdx a’ 4- — In 1 a3 4- xs 1
J (а3 + х3)2 3(a3 + xs) 1 3 '•
166.11. (* dx _ - 1 Ini—— !
J x (a3 + x’j ’ 3a3 |a3 + x31 '
166.12. P dx 1 4- — In 1 - s [
J x(a3 + x3)3 -3a3(a3 + x3) 1 3a6 ] a3-f-x* | *
166.21. P dx 1 1 x dx [Cm. 165.11.]
J x2 (a3 + xs) a3x a3 J a’ + x’'
166.22. f dx 1 X2
J x2(a3 + x’)2 — a6x 3ae (a3 + x3j
4 f x dx [Cm. 165.11.]
3a° J a3 + x’ *
166.31. P dx 1 1 P dx [Cm. 165.01.]
J x3 {a3 + x3) ~ га’х2 a3 J a3 + xs '
166.32. P dx 1 x
J x3 {a? + x3)2 2ae x2 3«s(a’ + xs)
5 P dx ~~ 3a3 J a’4- x3 • [Cm. 165.01.]
166.41. P dx = > + > ln|^3|. 3a’xs 1 3ae 1 x3 |
J x4(a3 + x3)
166.42. p dx 1 1 i 2 1n|flS + X’l
J x3 (d“ + №)’ 3a°x3 3ae (a3 + x3) 'г 3a9 1 x3 г
168.01. P dx J a3 — x3 f 1 1ra2 + Q-t + x2 1 .»• xx2111 (a—x)2 1 0«/3arCtg 2x + a a K”3 *
168.02. (* dx x 2 P dx [Cm. 168.01.]
J (a3—x3)2- ”3a3(a3—x3) 1 3a3 J a3—x3’
169.42]
ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ а*+Х*
39
168.11.
Р xdx 1 . a’-f-ax-f-x2 1 2х-\-а
Jyrp-Si1" —ГГТ3'"3 J7T-
168.12. р xdx X? 1 1 Р xrfx [См. 168.11.]
J (а8 — х’)2 ~ За’(а8—х8) ' 3a8Ja’ —х8*
168.21. С x2dx J аг—х! -у In) а*—х’|.
168.22. р x*dx _ 1
J (а’-х8)2 3(а3—х3) •
168.31. Р x’dx -Х4-аг f dx [См. 168.01.]
J а’ — х3 Х 1 ° J а8—х8*
168.32. Р x3dx х 1 р dx [См. 168.01.]
J (а3 —х’)2 3(а8 —х8) 3 J а8 —х8'
168.41. Р x'dx х2 , s р xdx [См. 168.11.]
) #3 ~ 2 ’1-а J аа-ха'
168.42. р x’dx х* 2 р xdx [См. 168.11.]
J (а3—х8)2 '3(а8—х8) 3 J а8— х8-
168.51. р x3dx J а3 —х8 “ 4-|31п|а’-х’|.
168.52. р x3dx 3{a>-х3) + 3ln 1
J (а8 —х8)2 “
169.11. р dx 1 ,„| х8 |
J х(а3—х8) ' "За31П|а8—х8) •
169.12. р dx • . 1 । 1 1
J х(а8—х8)2 “За3 (а3—х8) 1 За’“‘|а8—х8!
169.21. р dx 1 , 1 Р хdx_ [См. 168.11.)
J х2(а8— х’) а’х • a3 J а*—х!'
169.22. р dx 1 , 1 ± Р xdx
J х*(аг — х’)! а’хЗа’(а3—х8) * За®, J а3—х8" [См. 168.11.)
169.31. р dx 1 1 р dx [См. 168.01.)
J х3(а8— х’) ““ 2а3х2 ' a8 J а8 — х8 *
169.32. j хцаг _xty = 2а‘х* За’ (а8 —х8)
+з?]г£?- р“- 168Л1-1
169.41. § х»(я>_= ЭаЧ’^'Зл* |п| д’—-п *
. ЛЛ 4П С dx 1 | I________l__?_ln! ** I
169.42. J (as За’х3 г Здб •" За* 1П| а3—х3| ’
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[17Q
Интегралы, содержащие а*±х*
40
170.
170.1.
170.2.
170.3.
171.
171.1.
171.2.
171.3.
173.
С dx = 1 In ** + ах 2 + а* 1 1 ах У~~2
j а4+х‘ 4а*. У^2 х1 — ах У~2 + а3 2аа V"2~ ЗГС g а* — х2
С xdx 1 . х3
J оЯ7*"1 ~ 2а5 alCtg а’ •
|* x2dx 1 |пх*+ахУ~2 4-д* 1 дХ ]/~2~
J а‘4-х‘ ' 4а У"2 хг—ах У^+а3^ 2а у~~2аТС % аг—хг ’
J W = 7,n(a +х >-
С dx 1 , I а + х I . 1 , х
J а4 —х4 — 4а* " |ЯЯ;| + 2a*arctg а ‘
С xdx 1 । I а24- x‘ I
J а4—х4 4а’ П|а2— х21 ‘
С x3dx 1 . |а + х| 1 . х
Jfl—?=45ln|^|-25arCtga-
С -^4j= —1 In I a* —x4|.
J a*—x* 4 1 1
C dx________1 , I xm I .
J x(a + bxm) am n|a + frxmr
Иррациональные алгебраические функции—Интегралы
Интегралы, содержащие хч*
180. \ xPi‘dx = —т-9 +>Ч
180.1. 180.3. 181. J x'^dx = J V х dx = х*!*. jX‘4\
§ x3/*dx = р dx J V" ’ сл| Ю 4 M № 180.5. J xi!idx =
(p-2)?p-’^
181.1. f _ Г dx о vi/> 181.3. Г dx _ 2
J x1'2 J К x J X>I2 xiJi *
181.6. f dx 2 181.7. p dx 2
J7'1 J x'1*- ЬхЧ*'
188.21)
ИНТЕГРАЛЫ, содержащие №»
41
* x'l2dx
, a2 + b2x
185.11.
185.13.
185.21.
185.23.
186.11.
***'’_?“ arct? bx'l*
~b*~ b2 afCtS ~
x?,2dx _ 2 x2'2 2a2xll> 2a’ , bx'1*
Ja’ + b’x-T b2 — b* + *’arctg-a-*
x'l2dx x'l> , 1 bx112
(a2+b2x)2~~ b2 (a2-t-b2x)~’~ ab’arCtg a ‘
x2,2dx 2x2/a , 3a2x,/2 За nr bx3!2
{a2 + b2*)2 — b2(a2 + b2x) + bl (а2 + b2x} — b5 arC g a '
dx _ 2 bx1/2
(а24-Ь2х) x1/2 ~ ab аГС g a ’
186.13.
186.21
dx ________
(аг + Ьгх)х3^~
dx ________
(a2 + 62x)2x*/2
____2 26
a2x3>2 a, arctg
х>>г , 1 bx1'2
«а (a2 + b2x) + Эб arct& — .
186.23.
3b’x'/2
i’x’/’ а’(а’ + 62х)х*^ а’(а24-62Х)
36 . bx,/2
“Farctg ~
x'12 dx 2x’^’
F
a . b2 ln a + Ьх'1*
a—bx'1*
187.11
a2—b2x
1R7 IQ f x^dx 2 x2'2 2a2xvs , a3, a + bx1'2
1О/ •IO* J a2—b’x 3 b2 b1 1 bs n a—bx'12
2
187.21.
62x)’
XV2
6’(a’—6!x)
2ab> ln
a + bx1'2
a-bxil3
187.23.
x3l,dx 3a2x’/2-26’x5'2
(a2—6’x)’— 6‘(a2—6’x)
3a
26s ln
а + бх1'2
a—6xl/2
1 OQ 1 1 C dx _1 ln a + bxi/2
100*1 1* J (a2—b’x) x1^2 ab a—bx1!2
188.13. f--------—------=------1- 4- - In
J (a’-6’x) x2'2 a2x,/2 a2
a + bx'l2
a-bx112
f dx_________________________x1/2 i
J (a2 — b’xj’x1''2 «а (a2 —b2X) ~^2а3Ь П
а + Ьх,1г
a — bx12
42
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
{188.23
188.23.
dx _________ —2
(а2 — й2х)2х3'2 а2 (а2 — Ь2х) х’^2
ЗЬ2х'’г
а* (а2— Ь2х)
. ЗЬ . а + Ьх'^
+ 2Vln
189.1.
189.2.
189.3.
189.4.
x'^dx
а14-х2
__ — 1 । х + a ~\f 2х + а2
~ 2aV~2 х — аУтх + а2
1
—т= arctg
а У 2 ь
а фл2х
а2—х
f dx____________1 х + а |^2х 4- а2
J (а*4-х2) х'/2 “2аг /7 1п х-о/&+ а2 +
, 1
/?7тагс‘г
а 1^2х
а2—х
Г x':2dx
J а^Т?
1 ,
=- п
2а
dx
(а*—х2) х'12
а 4-х’/2
а-х*'2
2а21п
1 , х’/2
------arctg--------.
а to а
а + х'12
а-х1'2
, 1 t х'1г .
+ ^аг^“-
Интегралы, содержащие А1'2 — (а-{-Ьх)Ч2
190. f x?dx J Х™ L f (x- -а)Ч dX XP:2 [9>o].
При целом положительном q йинома Ньютона. разложить числитель . по формуле
191. Г dx — 2 191.01. f-^- J X1'2 = 4'Y*/2- b
J ХР/2 (p — 2)bX^-2}l2‘
191.03. Г dx — 2 191 05 C dx _ — 2
J х2<2 ЬХЧ2' ' ’ J Xs/2 3t>X’/2'
191.1. С х dx 2 Г -1 a "|
J XPI2 6* [(p—4)X<P-4»2 ' (p-2)X<₽-2,/2J ’
191.11. Г X dx J XV2 2 /X’12 — b2 \ 3 -aX'!2^ .
191.13. С х dx J X’/2 2 / __ -± / - b2 ( 1 X'!2) ’
191.15. f х dx 2 /-1 4- a
J x^2 d2 x*/2 1 3X2I2J *
191.17. f x dx 2 / — t 4- a
J x’/2 “ ьг\зх2/2 ' 5XS/2/ •
192.23]
ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ АГ'/г =(a-f-^x)7a
43
С x‘dx___2 Г______— 1_______।______2а_________
J Х^ ” [(р_б) Х,₽-6)''2 + (р-4)Х(₽~4>/2
(р—2) Х'₽~2)/2
191.21. Г x2dx J Х^ = 2 /Х5'2 ~ bs\ 5 0 /
191.23. С x2dx _ J X3'2 _ 2 М2,г d’\ 3 — 2аХ'!2 — а2 \ X1'2/ '
191.25. Г x2dx J л5'2 2а а2 \ X1'2 ЗХ3'2/ '
191.27. Г x2dx 2 / —1 1 2а а2 \
J х’/2 * ~ bs \_x'l2 ‘ ЗХ3''2 Е х5'2)
192.1. Г dx 2 1 Г dx
J xXpl2 (р—2)аХ<р~2}!г 1 а J хХ1р~ 2)/2 1Г^'1Ь
192.11. С dx J 'xXX2 а'!2 1П X'l’-a'l* Х'12 + а'1г [а>0. ^>0],
2 — а'<2 V1 /2 Arth ~ аЧ2 [а>Х’>0],
2 ~ а1'2 X'12 АгсШ — а 1 [Х>а>0],
2 . х1/2 [а<0, Х>0].
(-а)1'2 “*”ь (—а) У2
(Положить X'l2 — z. См. 120.1 и 140.1.)
192.13. Г dx 2 4- 2. f dJt а J xx'i2 • [См. 192.11.]
J хХ3'2 аХ'!з '
192.15. Г dx 2 X 2 , 1 Г dx [Cm. 192.11.]
J хХ5'2 ЗаХ312 ' a2X'l2 1 a2 J хХЧ2-
192.17. Г dx 4 2 2 4 1 ( • dx [Cm. 192.11.]
J хХ212 5аХ5/2 За2Х312 ' а3Х'1‘ ГГ a3j хХ'/2 ’
192.2. Г dx — 1 pb С dx
J х2ХР'2 алХ<₽_ 2)/2 2а J лх₽/2 •
192.21. С dx _ _ -Х1/2 b С dx [Cm. 192.11.]
J х2хЧ2 ах 2а J хХЧ2'
192.23. С dx — 1 ЗЬ ЗЬ Г dx [Cm. 192.11.]
J х2Х3'2 ахХ'12 а2Х1/г 2а2 J xX'l2'
44
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[192.25
192.25. f dx —1 bb 5b. 5b f dx fc 192 111 J x2X5' 2 axX2'2 За2Хг'2 asXli2 2а’J xX‘'2 ’ 1 ’
192.9. f dx _ -X1'2 _ (2p —3)b f dx J x^X1'2 (p-l)axP-' (2p —2)aJ x^-'X1'2’
193. f^x = 2Z2^. J (p + 2)b
193.01. f A'12dx = . 193.03. f A’/’rfx = . J 3b J 5b
193.1. C vn!J 2 /X(p+”'2 aXtp + 2>/2\ J b2V p + 4 P4-2 /
193.11. f 2 fxSI‘ aXV‘\ J xX dx — &2 5 3 J .
193.13. f vsi. 2 /X7'2 aX’/2\ J xX dx ~ b2 \. 7 5 ) *
193.2. f 2 /х(р + в>/2 2aX(0+4>/2 , a2X(p + 2)/2\ 1 X Xi> !dx = -г,- — -я— ) . J b’ \ p + 6 p + 4 p + 2 J
193.21. [ x’X> 2dx = | .
194.1. fXp'2dx 2Хр,г , Г X(p-2l'’dx I = a J * P J X
194.11. [X^==2X‘/2 + a f ~. [Cm. 192.11.] J * J xX1'2 1 J
194.13. f^£=2^2 + 2 ^1/2 + a. f _dx [Cm. 192.11.] J x 3 T J xX1/2 1 1
194.15. 2агХчг + аа f-^д. [См. 192.11.]
J х о J j xX‘i
С Xp/2dx W2*2 pbCX^dx
*94.2. ]-П?~---------НГ"+й]~Г“-
ю/| <11 f Xr!*dx X1/2 b С dx г- __ .
194.21. -------[См. 192.11.]
1О. fX’Mx (2a + bx)X*/2 b2 f dx ._
194.51. J -------------—j [См. 192.11.]
1971 ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ Л1/» = (a4-Z>x)’h И U'h = (f+gx)'11 45
Интегралы, содержащие №<* =,(a-f-Z>x)V’ и U4* = (/4-gx)'i*
Здесь всюду k — ag—bf.
195.01. ( = arctg 1/ j хчги^* V-bg s V ьи Lg<01’ V—bg bf—ag U<oJ ’ = [^>0]. V bg
195.02. (* dx 2 , g%1/2 ,, ^-L-in gx1/2~ |^>0| /*g gX'^+fkg ° S
195.03. Г dx = 2X‘^a J X^lf1* kU'l*‘
195.04. {U^dx X'W* k (* dx tr ,aent1 J b 26Jx>^- [Cm. 195.01.]
195.09. Г Undx 2 /хцгцп Г Un~'dx\ J x*/’. '(2л + 1)ДЛ U x’/* /'
196.01.
196.02. Г xdx _XiliUil* ag+bf Г dx _ J XV’U1'* bg 2bg J Х4ги'>*' 195,01*J
196.03. f dx 1 J X1/a f _3\ C 1 Jx1'V,“‘ (n—1)* 1 \Л 2 ) b J X'^U"-1) •
196.04. f X,i*Undx = ,n ’ , (2XV‘Un+i+k f — \ . J (2n +3)g T J x*/» ) [Cm. 195.09.]
196.05. (*X'l^dx 1 / X'l* , b C dx \ ,r ,,o , J Un ”(«-l)g( Un-' 1 2 J x'/’U»-1/ ’ 1СМ‘
197. f F _ f f ( шг \ au J Va + bx? У V— 6uaJ(l-bu2)’ где u = - r—=. И a 4 bx2
46
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[200.01
Интегралы, содержащие г = (хг4-а*)1!1
200-01'
Заметим, что
ln|*_±r|==Arshi = ilnl^|.
| а | а 2 |г—х|
Надо брать положительные значения г и а.
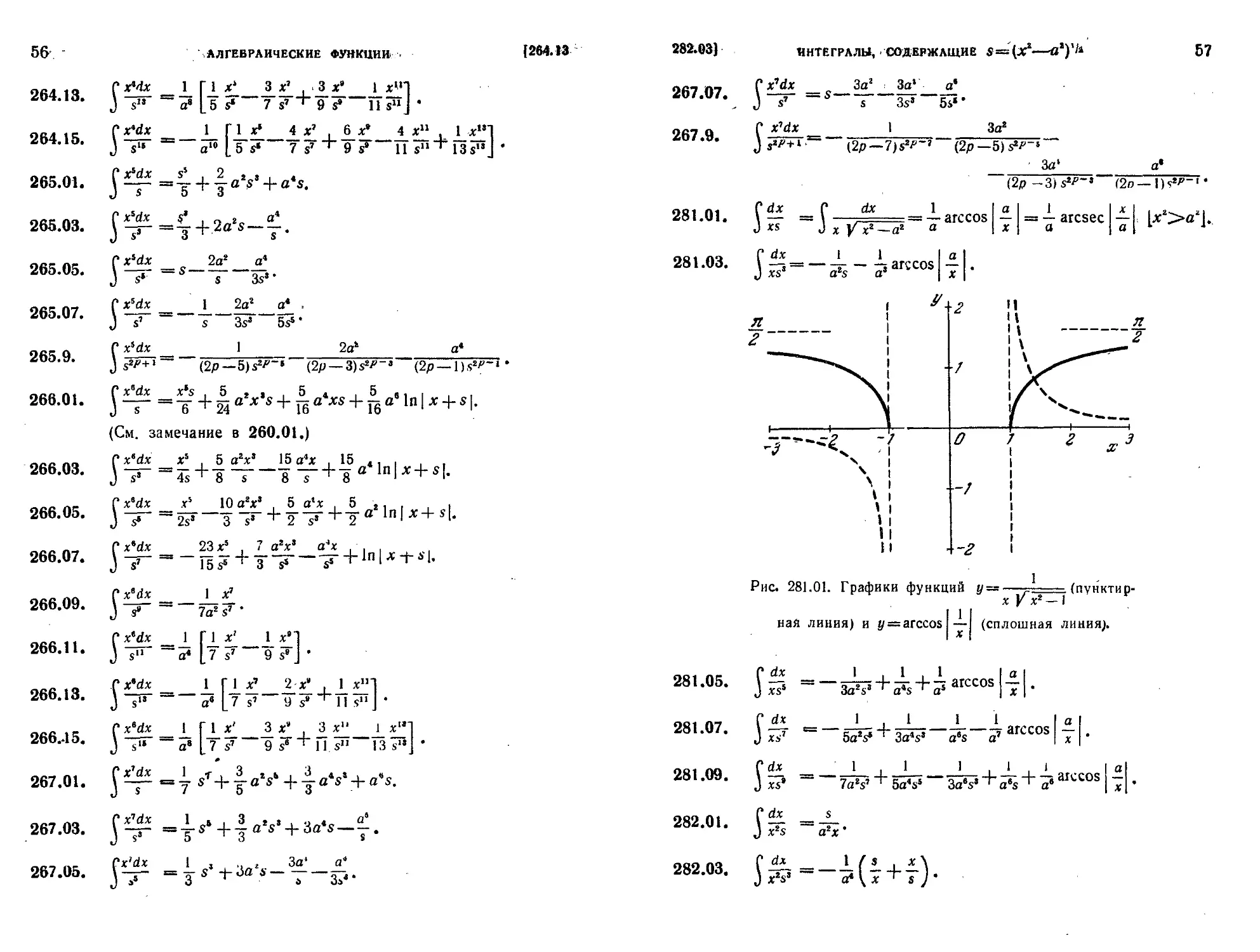
200.03. Рис. 200.01. Графики функций у — . * — у х'2 +1 (пунктирная линия) и i/ = ln [х+ 1]
(сплошная линия).
С dx 1 х
J 7®" ” аг г *
200.05. 0 dx 1 Гх 1 х’1 . J г® а* [ г 3 г’] * С dx 1 Г х 2 х3 i х®1
200.07. J г’ ~ а* [ г 3 г® + 5 г® J ’ р dx 1 Г х 3 х® 3 х® 1 х7Т
200.09. J 7» = а* [Г-' Т г3 *" "5 г“— 7 7> ] •
200.11. Р dx _ 1 Г х 4 ха 6 Xs 4 х’ . 1 х’1 Jr"~a,0L/- 3 г3 + 5 г® 7 г7 9 г’] ' Р dx 1 Г х 5 х’ , 10 х® 10 х7 , 5 х’ 1 хп1
200.13. J 7Ti~^i L~— TT’-1- Т7®~7 9 “iiT^J • Pdx 1 Гх 6 Xs 15х® 20х7 15х‘ 6 х11 1 х”1
200.15. J ris~ali [г 3 г’+ 5 г® 7 г7’’" 9 г’ 11 г" 13 г1’] ’
Интегралы 200.03—200.15 находят посредством подстановки;
„ х2 . adz
г =-г~,—г’ ТОГДа “* =--------
х +аг (1— z2)3/
204.01]
ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ Г= (х* + а*)'^
47
201.01. р х dx ~r. 201.03. =
J Г J f8 r
201.05. С xdx J г* 201.07. C^ = . Jr* J r7 1_ 5rs‘
201.9. f х dx 1
J r2/?+I (2p —1)^~‘ *
202.01. C x*dx J r xr —2 ln|x+r|. (См. замечание в 200.01.)
202.03. P xtdx J ~ =3 — ~ + In I x + r|.
202.05. С x2dx J ” 1 x’ ~з?н •
202.07. p x2dx 1 Г1 x’ 1 xs]
J ~ “ 7‘ L3 r’'~“‘5r8 J ’
202.09. J x2dx _ 1 ~ a’ Г 1 2 ? , U71 [3 r2 5 r5 *' 7 r’J •
202.11. p x2dx 1 Г 1 x’ 3 xs 3 x’ 1 x’1
J 7fl~ a8 [ 3 r’ 5 rs + 7 r7 9 r’ J •
202.13. p x2dx 1 Г 1 x’ 4 xs . 6 x7 4 x9 . 1 *”1
J ~a‘<> [3 г8”-K r8"‘~7T7 ~9‘r2 *11 r" J •
202.15. P x2dx 1 Г 1 x’ 5 xs 10 x7 ' 10 x8
~a>2 |з r2 . 5 rs 1 7 r7 9 r> +
5, «2 _1
"г 11 . 13 г'2] ’
203.01. f *3-x J r г» а — J — ar.
203.03. p x2dx J r3 a2 = r + -. r
203.05. p x2dx J ” \ , a2 7^3^2‘
203.07. C x^dx 1 — 1 i a‘ ~ Зг2 ^5г2’
203.9. f x’dx 1 , a2
j rilx + l (2p—3)r2f-2 1 (2p — Dr277-’*
204.01. p xldx x’r 3 2 . 3 . , , = -&axr+-ga ln|x-|-/|.
(См. замечание в 2011.01,)
48
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[204.03
204.03. С x*dx 1 xr . a’x 3 a, . , . « j + ~ j a’ln|x + r|.
204.05. (* x“dx J “ X 1 x^ = —7-jf? + ‘nl*+d.
204.07. р x*dx J ~ __ 1 xi ~ 5a2's ‘
204.09. С xadx J ~ — 1Г1_ 1 i! 1 ~ a* L 5 Xs 7 r7 J *
204.11. f x*dx J “ 1 Г1— --4- 1 **] = a’ [ 5 rs 7 Ti "+ 9 r> ] *
204.13. (* x*dx J — 1 Г1- —J.J/ 1 x”’l ~ а3 [б rs 7f’ + 9r' 11 r”J *
204.15. p x“ax J = а,0[5г 7г’+9г® 11 г11 + 13 rlsJ •
205.01. Г x5dx J r г* 2 j. j 4 « -5- a ‘r ’ + a *r. 0 О
205.03. у ^r‘2a3r-^. О V
205.05. p xsdx J ~ 2a3 a' = r+ x 3r’’
205.07. p xsdx J “ 1 2az a* . — — -±3f.s— ^s-
205.9. (* xsdx 1 2aa
J r2/, + 1 (2p — 5)r2P~s 1 (2p —3)^-’ a4
(2p— l)rV~>*
206.01. Г x*dx J r “T-24a X r + r&a xr~l6a +
- (См. замечание в 200.01.)
206.03. f x’dx Xs 5 a2x’ 15 a’x . 15 4. , .
J '• 4r 8 г 8f+8a n'X + fl'
206.05. (* x’dx x5 10a2xs 5a‘x 5 x] । , 1
J ' 1 2r5 3 r8 2 r8 2 a n**
206.07. p x’dx J r’ ' 23 x5 7 a’x3 a’x . . l5f5 3 fi _ fi +b|* + '|.
206.09. Г x’dx _ ' x‘ 7a3 r’ ‘
222.03] интегралы, содержащие г=(хг4-аг)'1г 49
206.11. г x’dx _1 Г1 — L _1 J г" а* [7 г’ 9 г’] •
206.13. С x’dx 1_ П £ _2£ 1 х11"! J г1’ а’ [7 г’ 9 г9 + 11 г'1] *
206.15. С x’dx 1 Г 1 х’ 3 х’ . 3 х’1 1 х1’] J ~г1Г~'а* р г-Тг» +П'7П— 1з7г’]-
207.01. х dx I7 3 * $ । 3 л * r 1 = а rs + -5-a‘r — а г. Jr 7 5 1 3
207.03. f x’dx 1 ,1 3 . , . „ . . а* \ —— = —г а’г 4-За‘г 4~ — . J г3 5 3 'г
207.05. f x’dx 1 5 „ г За* . a6 J d 3 г 1 Зг3
207.07. С x’dx За2 За’ а’ J ~~Г +~г Зг’ "'"бг5’
207.9. С x’dx 1 За2 J^+i^ (2р—7)^-’ । (2р—5)^“’ За’ . а’ (2р—3)г2Р-3 1 (2р — l)rV-*’
, 221.01. С dx Г dx 1 , 1 а + rl 1Г, _л, J хг “J х = ° 1 х (См.рисунок иастр. 50). Заметим, что —- In I 1 — L Arcsch I — I = — — Arsh 1 — 1 = а 1 x | а |а| а | х1 = -1 ln(L±f\ 2а \г—а) Надо брать положительные значения а и г.
221.03. fl* J хг ач а3 | х 1
221.05. f dx 1_ , J 1 in|a + 'l J хга За’г3 ' а’г а’1 | х |'
221.07. С dx 1 1 1 1 . I а 4- г | J хг’ 5а2г’+ За’г’+ а’г а’1П | х 1 ‘
221.09. 0 dx 1 1 , 1 , 1 1 । |а + г| J хг’ 7aV 1 5а‘г’ г За’г’+а’г а’1п | х Г
222.01. С dx г J х’г а2х ’
222.03. С dx 1_ / г х \ J х’г’ а’ 1 х ' г J *
50
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[222.05
222.05.
222.07.
222.09.
223.01.
223.03.
dx _____ 1 f г . 2х Xs \
х2г5 а’ \ х ’ г Зг’у '
dx _____ 1 f г . Зх Зх8 х5 \
х2г7 а8 \ х ’ г Зг’ ' 5г5 / *
(сплошная линия).
Jdx г 1 1 |° + г|
2агхг+2а,П1 х |*
Как и в 221.01 имеем
In) I = Arcschl — I = Arshl — I = ~ In I
I x I J a I I x I 2 |r — a|
C dx________1_____3____। 3 . I a-j-r I
J х’г’ 2агхгг 2a*r ' 2<f- | x |’
232.01]
ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ Г=(х* + аг)Ч*
51
223.05. р dx 1 5 5 5 I а + г 1 J xsrs ~ 2агхгг2 6о4г’ 2а8г"г 2о’ | х | '
224.01. р dx I /г г2 \ J Х'г а1 \ х Зх’ ) ‘
224.03. р dx 1 / х , 2г г’ \ J х4г’ а8 \ г х Зх’ ) ‘
224.05. р dx 1 / х8 3x.3г —А J хМ ~ а5 \ Зг*‘ ~'х Зх2)' В 222 и 224 положим а *2 2< — —2 2 г2 ’ тогда , a dz dx = rz. (1—г2)5'2
225.01. Р dx г . 3 г 3 . 1а4-г| . J х’г ~ 4а’х4 + 8 а4х’ 8а’ П | х |'
225.03. Р dx 1 . 5 ,15 15 . 1 a + r 1 J х5г’ 4а2х4г ' 8а4х2г 1 8а8г 8а’ П | х | *
220.01. р dx 1 / г 2г’ г8 \ J х*г а8 \ х ' Зх’ 5xs) '
226.03. р dx 1 f х Зг Зг’ J х’г’ а8 \ г х ‘ Зх’ 5xs) ‘
230.01. Jrdx = y+yln|x + r|. Как и в 200.01, имеем In 1 I = Arcsch — = Arsh — = 4- In 1 1 1 I а 1 a x 2 |r—x|
230.03. J r’ dx = -i- xr’ 4- агхг + a* In | x + r
230.05. C rs dx = yrxr* -j-Jj a2xr’ 4--Д a‘xr 4-a’ In | x 4~r I. J 0 Z4 'lb 'lb iii
231.01. Jxrdx = ^-.
231.03. J xr’ dx = y.
231.9. C J 2p4-3"
232.01. P . . xr’ a2xr a4 । , , \xrdx- 4 8 8 In | X 4-r |.
52
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[232.03
232.03. Г . . . хг5 о’хг’ а*хг а*. . , . Jxr dx 6 24 16 16 П ।Х + Г 1’
233.01. 3 .
233.03.
233.9. rtP+S а2г‘Р+г J ax 2p + 5 2P+3 •
234.01. P 4 , x’r’ a’xr’ , a“xr , a’ . , , , jXrfifx~6 8 + 16 +i6,nl* + H. Как и в 200.01, имеем In 1 I = Arsh — — Arcsch — = -i- In 1 1. 1 a | a x 2 |r—x|
234.03. Г j a2xr* , a4xr’ , 3 , , J X Г dX 8 16 + 64 +128aXf + + il8a’lnlx + /'l
235.01. P । , r’ 2a2r5 , a‘r’ Jxr^_7 5 + з •
235.03. P 5 , . r* 2a2r’ , a4r* . 7 + 5 .
235.9. C л*+* z/r - ^+T 2ayp+'. J ax 2p + 7 2p-f-5 2p'+3 •
241.01. J — r—aln^^-^|. (См. замечание в 221.01.)
241.03. Pr’dx r* . > ,. |a+r| J—=3- + ar-a ln|-H
241.05. P r’ dx r3 , aV 14 Sl la+r| J x =б+ 3 +ar a 1П| x I’
241.07. J x =7+ 5 + 3 +ar a ln| x I*
242.01. =—у 4- In | x + r |. (См. замечание в 200.01.)
242.03. j x2 x+2xr + 2a ln|x + r|.
242.05. C r-^-~ — — + + У^агхг + a* In | x -[-r|. J x» jc 1 4 1 8 '8 111
260.03] ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ г— (х2 4-а2)'/» 53
243.01. '—1 inlfL+l| (См замечание в 221.01.) J х’ 2х* 2а 1 х 1 • ' • '
243.03. (• г’ dx г3 3 3 ,1 а 4-г 1 \ —j- =— тп + тг'"— Train —— . J х2 2х2 * 2 2 1 х 1
243.05. С г5 dx г5 , 5 j . 5 2 5 5, la-4-rl \ —3- = — 5-2 + тгГ’ + va2r—5 a In —— . Jr 2x2 6 2 2 j r 1
244.01. C r dx r3 J x4 3aV
244.03. p r® dx Г& F \-p—= —gp — —+ ln|x + r|. (См. замечание в 200.01.)
244.05. C r‘ dx a2r3 2a2r . xr 5 г, . ) ? " 3x’ x + 2 + 2 « ln(x+r|.
245.01. C r dx r r , 1 . I a + r | J x5 4X* 8a2x2-r8a3 П| x |‘
245.03. C r3 dx r‘ 3 r3 3 r 3 . Ia4-rl J x’ 4x4 8 aV 1 8 a! 8a " | x |‘
246.01. C rdx r3 /2 1\ J x“ 5a2x’ \ 3a2 Xs J ’
246.03. C r3 dx rs J x“ SaV'
247.01. C r dx r r , r 1 . 1 a +r 1 J x’ ”a бх" 24a2x* * 16a4x2 16a5 П | x | ’
248.01. Г* r dx r3 ( L . J xs 7a2x* \ X* * 5a2x2 15a4) ’ Интегралы, содержащие s = (x’—a2)’/*
260.01. f dx C dx ii.i J S J Ух2—a2 1 [x2>a2](CM. рисунок на стр. 54). Заметим, что ln| 1 «-у In — Arch I — 1 1 a 1 2 \x—sj lai* Для положительных значений x надо брать положительное значение Archj-^-|, для отрицательных — отрицательное, s надо всегда считать положительным.
260.03. И | н •
54
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[260.05
260.05.
260.07.
260.09.
260.11.
С dx_ 1 Г х 1 хП
J s5 а* [ s 3 s’ ]
С dx____ 1 Гх 2 х* . 1 х*1
(пунктирная линия) и у = In | х + х1—1|
(сплошная линия).
260.13.
dx 1 Гх 5 х’ 10 х5 10 х7 . 5 х9 1 х”1
V’- а“ [s 3 7,+ б" Т9-77’ т“9 Т9“П71] *
dx_______1_ Г_х_ 6_£’ , 15 «*_20^ , £5х8__
sis — а11 [ s 3 s’ ' 5 s’ 7 s'+ 9 s'
_ J6 х^1 2_ х”1
11 s" + 13 s,sJ *
Интегралы 260.03—260.15 находят посредством подстановки:
261.01.
xdx
----= s.
s
, х2 . —adz
гг —------; тогда dx=---------
х2—а2 (г8—1)’/г
261.03.
261.05. = — 1
J s’ 3s’
261.07.
J s
£
S •
С xdx 1
(2р—Ds2/'-1'
262.01. У —у- = у + у In Iх+ s | • (См* замечание в 260.01.)
264.11] ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ s — (x2—а‘)‘ь
55
262.03. С х2 dx J s* In I x + «| .
262.05. C x2 dx J s’ = — _1_ X* За2s’ *
262.07. J x2 dx _ 1 a* Г 1 x’ lx5! [is5-!s~J ‘
262.09. C x2 dx J s8 = — 1 Г 1 x3 2 x* 1 x’l a3 [ 3 s’ 5 s5 ' 7 s’J *
262.11. (* x’ dx _ 1 Г1 ? 3 x3 3 x’ 1 x9J 1/3 s’-Ts~ + 7si’_ If s^J •
J s11 a8
262.13. C x2 dx 1 Г 1 x3 4 x3 . 6 x1 4 x9 11 SnJ ‘
J s” a10 L 3 s’ 5 s’ + 7 s’ 9 s’
262.15. С x2 dx _ 1 П x3 5 x8 । 10^_10£9 ! [ 3 s’ 5 s5 * 7 s’ 9 s9'
J s15 a11
5 x'1 1 x”l
+ 11 s11 13 s1’] *
263.01. J x’ dx _s^ 3 + cfs.
263.03. § x’ dx = s- a2 s
263.05. f x3 dx 1 a2
J s5 s 3s’*
263.9. f x3dx 1 a2
J sv+‘ (2p~3)s2P~3 (2p- DsV-1’
264.01. J x“dx x’s ~~~4 ' + a2xs + -|- a* In | x+ s|.
(См. замечание в 260.01.)
264.03. J x*dx xs “2* —v + ye21nlx + 'sl.
264.05. Г x“dx J ~ = — x lx®,.. , „, 7— y^-+lnl* + s|.
264.07. (• x1dx J” = — 5a’ s’ ’
264.09. (* xidx J “ “a* Г-L — 1 x’i . [5 s* 7 s’ J *
264.11. Г x*dx J = — 2. Г1 — 1—л.1 —1 a3 L5 s’ 7 s’ + 9 s’J •
56 -
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
(264.13
264.13. J _ 1 Г 1 £ 3 f .3 f 1 x"'l a8 [5 s’ 7 s’ + 9 s’ 11 s”J '
264.15. Г x’dx 1 [lx* 4 f 6 x' 4 x11 1
J s“ = a10 [ 5 s’ 7 s’ "f" 9 s’ 11 s11 13 s”J *
265.01. С xi^x J S «5 9 = -E- + ya^’ + a‘S* и О
265.03. Р x5dx J s’ =4+2Л-т-
265.05. р xsdx J s’ 2a2 a* S s 3s’'
265.07. p x*dx 1 2a2 a* .
J s’ — s 3s’ 5s* ’
265.9. P x*dx 1 2a’ a*
J sv+1 (2p—(2p — 3)s2?~3 (2p — l)sv~1'
266.01. P x"dx x^s . 5 * i । 5 д . 5 «« । t = ‘6 +24a X S+16a xs + l6a lnl* + S|.
(См. замечание в 260.01.)
266.03. P x‘dx J "s’” Xs 5 a2x’ 15 a*x . 15 t. = 4s + 8 s 8 s +8 a lnl*+4
266.05. P x‘dx J s’ xs 10 a2x’ 5 a’x 5 г. . , ~ 2s’ 3 s’ + 2 s’ *" 2 a ln । sl*
266.07. P x*dx 23X5 7 a’x’ a^x ,
J s’ ~ 15s5 ' 3 s’ s’ Tlnlx + 4l’
266.09. P xedx J s’ lx? ~ 7a2 s’ *
266.11. P xfdx J s" ~ a* [ 7 s’ 9 s’ J "
266.13. P x'dx J s” “ a8 [ 7 s’ 9 s’ 1 11 s11 J *
266.-15. P x‘dx J s“ _i г1*! 2 «' 2 £1___L X"1 “a8 [7 s’ 9 s8' Il s” 13 s1’] ’
267.01. Jx’dx = -t sT+ 4- aV + 4- Л14- a's. / □ □
267.03. P x^dx J V = 4-s* 4-4 a’s’4- 3a*s — —. □ u s
267.05. Ркгйх ] 34 ~ 1 , -г За1 ал = _s ±3a4____.
ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ $=7(Х*----
57
282.03]
267.07.
267.9.
281.01.
281.03.
x7dx
s’
_ _3a£_3ay______
~S s 3s’ 5s*
x7dx
s’/'t ‘
dx
xs
1______________3a2
(2p—7)s2p~7 (2p—Sjs2/'-5
3a*
a*
(2p -3) sV’“(2o —DsV
dx
х У хг—а2
1
— arc cos
a
arcsec | у
281.05.
281.07.
281.09.
282.01.
282.03.
dx
xs‘
dx
77
dx
xs‘
dx
x2s
dx
X2S:
• , 1 , 1
гп + -г +1 arccos
3a2s’ 1 a*s 1 a*
J- + J_
5a’s* 3a’s’
1 1
-5----, arccos
a‘s a7
7a2s7 'r 5a4ss 3a’s’ "r a‘s + a‘ al€C0S
__ s
~ a2x'
58
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[282.05
282.05. II °.|- X 1 + и1х t«|
282.07. С dx l_/_s_. Зх Зх3 . х5\ ‘ J xss7 а3 \ х ' s 3s3 ' 5s5) "
282.09. f* dx 1 / s 4x 6x3 . 4x5 x’ J x2s“ a” \ x ' s 3s3 '5s5 7s’) '
283.01. C dx s , 1 lai т = + o~j arc cos — . J x3s 2a*x2 1 2a3 1 * 1 (См. замечание к 281.01.)
283.03. c dx 1 3 3 lai J x3s! 2a!x2s 2a4s 2a5 aTCC0S | x | ’
283.05. C dx 1 5 5 . 5 lai J x’s5 2a2x2s3 6a4s3 ' 2a’s + 2a’ artC0S| x ] •
284.01. C dx 1 / s s3 \ J A a4 \ x 3x3J "
284.03. 0 dx 1 / x . 2s s3 \ J x4s3 a’ V s ' x 3x‘) ’
284.05. C dx £ f x3 3x . 3s . J x4ss a8 \ 3s3 ' s ' x 3xs J * Интегралы 282 и 284 находят посредством подстановки: , х2 , — adz г‘ = -г; тогда dx = s‘ (z ~ 1)3/2
290.01. ^sdx = ^~—у In | х -|- s |. (См. замечание к 260.01.)
290.03. р 1 з з \ s,dx — -^xsi—-g-a2xs + g-a*ln|x + s|.
290.05. С sf‘dx = ^- xs* — ^a2xs* —^a* In 1 x + s|. J 0 IO 10 1
291.01. [xsdx — ^ё. 291.03. Jo JO
291.9.
292.01. j x*s dx = ^ + ^~ — jln|x-H|. (См. замечание к 260.01.)
292.03. С 2 xs5 . a2xs3 a4xs . a’ . . . J x S dx.~ b 24 16 16 n‘
304.01]
ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ S=(№—й2)'/а
59
293.01. 293.9. Г* с® Р е’ \x’ssdx=^ + ^-. 293.03. = .
§x3s2p+'dx _ i aSs2p+3 2p 4~ 5 2p -f- 3
294.01. § xls dx = - c’s3 , a2xs3 , a4xs a’ , . , , 6 + 8 + 16 161П l* + Sl‘
(См. замечание к 260.01.)
294.03. J xis3dx — xV_, a2xss a4xs3 3 « i 3 „> In 1 r I ?] 8 r 16 "1 64 128 XS ’’"128 ln|-v + sl-
295.01. § x3s dx = s’ 2a2s5 . a4s3 7 + 5'3’
s9 2a2s7 , a4s5
295.03. У x3s3dx = 9+7 L 5 ’
S‘P+7 . 2a2s2^+3 a4sV+3
295.9. § x3s2p+‘dx 2p + 7 1 2p + 5 1 2p + 3’
P s dx 1 a 1
301.01. l — s — J * - a arccos — . 1 x 1
301.03. P s’dx s3 J x 3 2 , 3 I д I — a s-}-a arccos — .
301.05. P s*dx s’ J x 5 ass3 .4 s „ I a 1 —g--]-a 5—a arccos у .
301.07. C s’ dx s1 J x 7 4_л3_a«s _|_arccos I— 1. 5'3 1 1 x 1
302.01. P s dx J x2 у -|- In ] x 4- s |. (См. замечание к 260.01.)
302.03. P s’dx J x2 y+y xs—у a2ln|x + s|.
302.05. P s’ dx J x2 y-|_.|-xs’—ya2xs + y a4ln|x-|-s|.
C s dx s , 1 I a |
303.01. J Xs ~ 5-14- s- arccos — . 2x2 1 2a | x |
P ssdx s3 , 3s 3 lai
303.03. J Xs 2x24- 2 2 « arccos | J.
303.05. P s5 dx J Xs s5 , 5 з 5 2 , 5 3 lai 2x2+6s 2as + -2a arccos| x ].
P .s dx s3
304.01. J x4 3a2x3'
60 АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ [304.03
304.03. = —7Г3—“+In I * + (См. замечание к 260.01.)
304.05. Р ss dx aV ( 2a‘s xs 5 2. , ' , • J ~3x3^7+2 2a lnl* + sl-
305.01. P sdx s s 1 lai J x5 4x4 + &a*x‘ + 8a3 rtC0S | x | ’
305.03. Cs’dx s’ , 3 s3 3 s , 3 lai J x* 4x4 + 8 aW 8 a! 4 artC0S | x | *
306.01. P sdx s3 / 1 2 \ J xe 5a2x3 \ xs ‘ 3a2 J '
306.03. P s3dx s3 J x3 5a2xs •
307.01. P sdx s s , s , 1 lai J x’ 6x8 + 24a2x3 + 16a*Y2 + 16a5 3rCC0S ) x [ •
$08.01. P sdx s’ / 1 4 8 \ J x’ 7агх3\х^ 5a2x2 + 15a1 J' Интегралы, содержащие t — (a*— хг)11*
320.01. fyfe arcsln a lx2<a2l- Надо брать положительные значения t и а.
320.03. №-7Т-
320.07. Р dx 1 Гх . 2 х3 . 1 х5] j7? = ar |Г + 3 F + 5 ’
320.09. Р dx 1 Г х . 3 х3 . 3 xs . 1 х’ 1 J Т7- а5 [7 +з-+ 5 ts "i"7 /’] •
320.11. Р dx _ 1 «*1 J Й7-а13 [/ + ЗР+5Р + ?Р "1" 9 /’] ’
320.13. Р dx 1 rx.5x^ l0xs.10x^,5.x^ J_ х»»1 , J П* ~ а12 + + 5 78’1' 7 t7 "* 9 t* +11 И1] "
320.15. Р dx 1 Гх 6 х^ 15^ 20 £ 15£ 6^ £ х”1 J «13==а“ [/ 3 /’ 5 f8 ** 7 Р + 9 /’ "'"И tu И H’J * Интегралы 320.03—320.15 находят посредством подстановки; , х2 . adz г — -г г; тогда d х = —. а2—х2 (1 4-г2)3'2
61
322.13| ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ t = (а2 — х*)’&
321.01. - - t. 321.03. J у.
лл 4 /чм С X dX 1 Ось! Л*7 t _______ I
321.05. -р- = 3^5. 321.07. ^-fj~ = 574-
991 a t xdx = 1
ол i.v ;ар+1 (2р — 1) /2Р-1 •
(пунктирная линия) и y = arcsinx (сплошная
линия).
___ _, С х2 dx xt . а2 . х
322.01. \ -у- = — у + у arcsln у-
Sx2 dx х . х
—0- = у — arcsin
322.05.
С х2 dx_ 1 х3
3 ~Р~ ~ 3? Р •
322.07.
х2 dx ।
a = [ 3 W + T £ J
ooo 09 4.1^4. LfL]
dzz.u». tv — вв[з ^+5 ftT 7 <г].
422 11 x*dx 1 Г» ** 1 3 1 3 ** 1 1 x8]
ллл.11. /u — ae[3flT5<s-1-7<J-T-9 <»]•
322.13.
x2 dx l Г I . 4 x° . 6 x'i , t x2 , 1 x11!
[j + s’ в + 7 a + 9 a + П ]•
62
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[322.15
322.15.
323.01.
323.05.
323.9.
324.01.
324.03.
324.05.
324.07.
324.11.
324.13.
324.15.
325.01.
325.03.
325.05.
325.9.
326.01.
326.03.
326.05.
х2 dx 1 Г 1 x'J , 5 x° . 10 x‘ . 10 x« 5 x11
IS- — a12 L з t3 5 fl fl + 9 (• + 11 /ч ’
х3 dx t ~ fl 3 ' — a.4. 323.03. ‘ x3 dx . . aa J ~A r + 7
х3 dx 1 _i a2
fl ~ t + зА'
x3 dx 1 , a2
flP+i (2р —3) t2?~3 + (2р— 1) flP~>
х4 dx__ x3t
~г ~ ~ т
3 2 , , 3 . . х
-s- a3xt 4- — a* arcsm —
О о CL
x4 dx ~fl~ ~ xt . a2x 3 , . x 2~ + ~Г-Та arcsin7f
x4 dx X . 1 X3 . . X
~т + Т7з+агС81ПТ-
x4 dx ~fl 1 X3- апл лл С X4 dx 1 Г 1 X8 . 1 5^ fl- 324-09* + т
x4 dx 1 Г 1 x6 2 x’- 1 x’1
~flf — a6 L 5 fi 1 7 fl 1 9 flj*
x4 dx 1 Г 1 x3 3 x’- , 3 x’ 1 x11]
~fl3~ ~ a8 L 5 fl + 7 fl + 9 fl + 11 fl1]’
x4 dx 1 Г 1 x3 , 4 x’- 6 x° . 4 x11 , 1 x13l
"Ils уь L + 7B + T 7? + '9 fl + И 7П + Тз И •
x6 dx fl 2a2t3 ..
~—h — a t*
t 5 ~ 3
xB dx “fl- — -^ + 2a3t+^.
x5 dx , 2a2 . a4 ___ C x5 dx 1 2a2
~fl -^-'г+зУ 325-07- = T“3fl
x6 dx 1 2a2 , a4
flp+l — (2p - 5) flP-§ (2p - 3) АР' а 1 (2p — 1) flP-i •
x* dx ~t x^t 5 n л, 5 a 1 । 5 e x —ъ пт a2x3t — тё crxt 4- rx a? arcsin —» 6 24 16 1 16 a
xe dx X3 5 a2x3 . 15 a4x 15 . . x
fl ~ *1 1 °°i 00 00i ; c c G »J
xe dx x5 . 10 a2x3 5 a4x 5 2 x
~fl 2fl + 3 fl 2 fl + 2 a arc?in a •
+ 5fl
341.05]
ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ t = (a*—Хг)'^
63
326.07.
x’dx___23 х5
“ — Тб 7®
7 а2х’
ТТ3"
, а‘х . к
+ —— arc sin — .
326.09.
326.13.
326.15.
327.01.
327.03.
327.05.
327.07.
327.9.
341.01.
J = 1 е —| «7’ — а’/.
С х’dx_ 1 ,5 о 2х । а
J ~i*~~ з’г ~йа t + з/’‘
С x’dx , За2 За4 . а8
J ~f~ ~ f + t 3Z’ г 5ZS ’
С x’dx _ 1 ,
J Z2^ = —(2р—7)Z2^-’ +
, За2 За1
+ (2р—5)Z^~S (2р — 3)Z^~3 +
।
' (2р —
. dx
х У а2—хг
Заметим, что
(пунктирная линия) и
- 1п|
а I х
—1- Arch
а
------^-Arsch — =
а а
а 1 . (a 4-Z \
- = — о~1п —).
х 2а \а—Z /
(сплошная линия).
Надо брать положительные значения Arsch, Arch, а и г.
341.03. f-^г=-к—Л1п — •
J xts аЧ а? х
341.05.
dx __ * । * 1 1 а+^
xZ5 За2!3 ‘ аЧ а5 Л х *
64
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[341.07
341.07. Г dx J ~хР ~ ба2/3 ~ ЗаЧ3 ~ (fit а’ | х Г
341.09. С dx 1 + 1 4- 1 + 1 1 1п|а + Ч
J х!3 ~ 7а2/’ г- 5а«/5 1 ЗаЧ3 1 cfit а» | х |’
342.01. С dx j х¥ ~ /_ а2х ”
342.03. С dx }x2i3~ 1 1 t , х \ а» \ 7 + 7 )'
342.05. С dx J X2/6 1 / t , 2х х3 т дЦ х + t + 37 )’ -
342.07. С dx }xW~ 1 / t . Зх . Зх3 . х6 \ <7 \ 7 + 7 + 3t3 + 57") •
342.09. С dx J х2Р~ 1 / t . 4х , 6х3 . 4х5 , х7 \ 5w 7 + 7 + ЗР + + 7/’ )•
343.01. С dx J х3/ ~' -т~Л1п| —I- 1См- 341.01.] 2а2х2 2а3 | х I L
343.03. С dx J х3?3 — !___ . _3 3 ._|а + /| 2aVt “ 2aU 2а3 | х Г
343.05. f dx 1 . 5 + 5 5
J X3/6 ~ 2a2x2t3 ' 6а4/3 ' 2a3t 2а1 | х Г
344.01. С dx J ~x*t ~ _ L[L 4. J3 \ а1 \ х Зх3 / ’
344.03. С dx Jx*P~ _ _1_ / _ £ 2£ ае \ t ' х ' Зх3 J ‘
344.05. С dx 1 f х3 Зх , 3/ . /3 \ ~а3\37 Т ~х г Зх3)'
Интегралы 342 и 344 находят посредством подстановки:
о х2 . a dz г2 = . тогда dx= гг. д (1+г2)3/-
345.01. С dx _ ' xbi “ Г 7 । 3 < । 2 inl^l] [4а2х4 ~ 8 а4х2 т 8а6 I х |]‘
345.03. С dx . Г 1 , 5 15 15'1п|а + И1
1 X6/3 ~~’ ” |4а2х4/ 1 8а4х2Г 8аЧ 1 8а’ | х |_Г
361.03]
ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ t = (а* — Х*)'<3
65
846.01. Г dx J j?t = i 2’ V « ~ Зхг ' 5x5
846.03. f dx _ J?? ~ 1 f x ,3t a3 \ ~i'~x • + - + + 3x» + 5x‘ J *
850.01. f . . xt у dx = , a2 , x + -5- arcsin — 1 2 a
850.03. Q fl +4at^+i '4 , * . ra arcsin—. i a
850.05. 4*24 a*x^ ”1"' ^alxt + 5 • , x rz a arcsin — . 16 a
851.01. J xt dx — — ta 351.03. ’ fxt> dx— — 0
851.9. 'F+3.
852.01. J x'tdx = — xt3 , a3xt , < 4 1 8 1 J* o-arcsin 0 X a *
852.03. J xtt3dx — — xfi , a’x/’ , 6 1 24 1 a*xt a3 16 + 16 arcsin —. । a
853.01. J x't dx —Ц-. 353.03. | 0 J ’ f a3ts X t dX — -~ E-. ( 0
353.9. рР+ь a‘ttp+t 2p4-5 2p4-3'
854.01. J xlt dx — - x3t3 a3xt3 6 8 , c^xt , , + 16 a3 , x 7^ arcsin —. 16 a
354.03. J x‘z’rfx = - x’<5 a3xt3 8 16 a<x/’ 1 64 1 3 3 128 a‘^+128a’ arCSln
355.01. J x3tdx = — f , 2a2<5 7 ! 5 a3t3 3 *
355.03. t' , 2a2f a3t3
9 + 7 5 ’
355.9. jx5i^+,dx = г‘Р+’ , 2a2/2/,+‘ 2p+7 * 2p+5 a3t3p+3 2p+3 *
361.01. Cz / 1 J —— , J * “'m- (См. замечание к 341.01.)
361.03. f t3dx t3 , 2. Sil J—=-3+«<-« In ^1-
3 Г, Б. Двайт
66
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
[361.05
На этой странице t = (a2— х2)'/,
361.05. С fdx f a2t2 t ,. Ia+t1 J x “5+ 3 +at a lnl x I'
361.07. C fdx f a2f a4f , ,, .. |a-H| J x 7+5 + 3 +at a 1П| x I'
362.01. f tdx t . x I —5- = arcsin —. j № x a
362.03. f fdx t2 3 , 3S . x J x2 ~ x 2Xt 2a arCSln a •
862.05. CL^== — 1 A xi2 — a*xt — ~al arcsin—. Jr x 4 8 8 a
863.01. = — * -j. 2. ]n | £+? 1 (См. замечание к 341.01.) J x2 2xs ' 2a 1 x | 1 '
863.03. P fdx f 3t 3a । 1 a-j~t I J x2 2x2 2 + 2 ° | x |'
363.05. 1 « d 1 №| — a>| сл Г ЬО[ СЛ & + to| СЛ а № 1 °
364.01. P tdx t2 J x4 3a2x’’
364.03. P fdx f , t . . x J x4 ~ 3x’+x+arCS,na*
364.05. P fdx cff , 2a2t . xt . 5 г . x 1—г- — rrH Н-з- + тг« arcsin—. J x4 3№ 1 x 1 2 1 2 a
365.01. f* t dx t t 1 . |a + H J xs 4x4 + 8a2x2 + 8as П | x
365.03. r fdx 3 1 1I J xs 4x4 + 8 a2x2 + 8 a2 8a П | x
366.01. Г tdx f 7 1 2 \ J x2 5a2x2 + 3a2/
366.03. P fdx f J x" 5a2xs’
367.01. P tdx t_ t t , 1 . |o + H J x’ 6хе + 24а2х4+16а4хг+16а2 П| x
368.01. c^= M-+—+—'I J xe 7a2x’ \ x4 5a2x2 15a4 j '
380.005} ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ Х'^ = <.ахг + Ьх 4- С}4* 67
Интегралы от биномиальных дифференциалов.
Формулы приведения
370. хт (ахп-[ b)p dx =
= ———г Гх'л+1д/'+ npb С xmuF~1dx].
m-j-np +1 L J J
371. j xm (axn + bY dx =
= MpTb [—л-т + ’а‘о+1 + (/и +л +i) jx'"up+’rfx]
372. J x“ (ax" 4- b}p dx =
= [x»V— a (m 4- n 4-np 4-1) Jx'”+nzA/xj .
373. xm (axn + ЬУ dx =
= , r-1 , „ |x'"-"+,ap+' — [m — n + \)b ^xm~nuFdx\ .
a (m-f-np 4-1) [ J I
Здесь u=axn-{-b и a,b,p,m,n могут быть любыми,
лишь бы не обращались в нуль знаменатели при после-
довательном применении формулы.
Интегралы, содержащие Х"*— (ахг-\-Ьх-\-с)'<*
380.001. С^-
J X1'2
== -4т- In I 2 (аХУ2 4- 2ax4- fa>0],
a 12
1 . . 2ax 4 b
= -T- Arsh-----------——
a (4ac — Й2) ,2'
= 4— In I 2ax4~
a 12
[а>0, Ьг = 4ас, 2ах4-^>0],
=------гт—1 пI 2ах 4-&I [а>0, Ьг = 4ас, 2ах4*6<01,
а ,2
— arrrin <2а*+в> Г а<0, 62>4ас,
(— a) 2 {b2~4ac) 12 [ |2ax4- b\ <(6 — 4ac)42_
4ax +2fe
“О”8-
380.005. 4а*-±^т;-
J X5''2 3(4ас—62)Х’/>
8а \
4ас—&2у '
68
АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
(380.009
880.009.
880.011.
880.013.
880.019.
880.021.
dx_______________4ах + 2b________,
A(an+i)/2 — (2n—1) (4ас— Ьг)Х<гп " М+
8а (п—1) С dx
+ (2n—1)(4ас—b2) J х<2П-,)/2*
xdx
X'l*
ь С dx
а 2а J х11*'
___ 2Ьх + 4с
(4ас—Ьг)Х,'г’
[См. 380.001.]
X - Л/Х? + с
г
[* х dx ____ 1 _b С dx .
J^(2n+i)/2~ (2n_1)аХ(2"-1)^ 2а J х<гп+'}1г"
С x3dx [ х 36 \ । ЗЬ2—4ас С dx lr.
Jl^=^-4?r/’ + —1См-
880.111.
dx
xX'l*
-Л.[а\&+^ + Ь
c'l* X X
---’ Arsh--
с'1г |х |(4ас—Ь2)’/2
4ас > b* J ’
880.119.
в=-----L.ln|^i2E| [с > 0, Ь* — 4ас, Ьх4-2с>0],
= -4у- 1п | j [о О, b* — 4ас, Z>x4~2c<0],
1 , Ьх4-2с
е=-----— arcsin ---------
(—с)’/2 |х|(Ь2—4ас)
dx _____ 1 ।
хХ<2П+1>/2 ~ (2n— 1) сХ(2П ~,)/2 +
Ьг
dx
dx
^X(in-T)ii 2с J х(2П+
Ь
880.121. С_^ = —^2—2 f [См. 380.111.]
J х:Х'№ ex 2cJxx',s 1 1
880.201. f X'/‘dx = ^±^ f-^. - [См. 380.001.]
J 4а 8а J х'№ 1 J
880.209. С X(»»+')/»rfx= (2а**?)*(л+1> >~|~
J 4а (n +1)
_(^-р(2п + 1)
8а (n-1-1) J
380.211. j xXWx = x1^—
_bHflc-b2) C_dx ^Cm 380 001 j
16а2 J x'/‘ 1 J
387] ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ Х*Ъ = (йХ* 4" ЬХ 4~ С)Ч* 69
380.219. р v(2n + a>/2 ь (, 1 хЛ'(гя+1>'г</х = ^— ~\X<*n+Wdx. J (2а+3)а 2а J
880.311. QX^dx b р dx J * Х + 2 J X'11 +CJ х*,/8 ’ [См. 380.001 и 380.111.]
380.319. eX^+Wdx^"^ b_ Г С J х 2п +1 1 2 J 1 J »
380.321. СХЧЧх^ Х'г С dx b С dx J х8 * * а J х1 ,г 2 J хХ1 № ’ [См. 380.001 и 380.111.]
383.1. С ——- = -Д (ах* 4- bxyi*. J-х^ах1 -(-bx)ll* Ьх
383.2. С dx \ — = arcsin . J (2ах—х*)‘/г а
383.3. С Х ,,, = — (2ах—х2)1-'2 4- a arcsin (. J (2ax—x*)'i‘ \ а )
383.4. § (2ах—х*)1Ъ1х — (2ах — х‘У^ 4- у arcsin —
384.1. С dx = — — In I в + ^+Д8)1'21 х(хп 4-а2)1/8 па 1 xnl* 1
384.2. f dx 2 1 а 1 \ гт. = — arccos —- . J х(хп—аг),1г па | дЛ/г |
384.3. р xll2dx 2 . ( x\W \ те = т arcsin — ) . J (а’—х*)1'2 3 \а J
387. Р dx J (ах* 4-6) V fx* +g = ——* ; arctg [а^г 2> bf\ Кб Kag—bf f^b yrfxt+g 1 = —— *- —In Кб t^fx‘+g + x ^bf — ag thf^nlA 2]^b fbf—ag у~ь V ^+g—xybf—ag
400.01.
400.02.
400.03.
400.04.
400.05.
400.06.
400.07.
400.08.
400.09.
400.10.
400.11.
400.12.
400.13.
400.14.
400.15.
400.16.
401.01.
401.02.
401.03.
401.04.
II.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
sin® А + cos2 А = 1.
sin А — ]/1 — cos2 А
cos А = ]/1 — sin2 А.
tg А = sin Л/cos А.
ctg А = cos Л/sin А = 1 /tg Л.1
sec Л = 1 /cos Л.
esc Л = 1 /sin Л.
sin (—Л) — — sin Л.
cos (— Л) = cos Л.
tg ( — Л) = — IgA.
sec2/— tg2 л = 1.
sec Л = ]/l + tg2 A .
tg A == sec2 A — 1 .
esc2/—ctg2 A = 1.
esc A = ]/l + ctg2 A.
ctg A = ]/csc2 A — 1.
Заметим, что для действительных значений А знак вышеука-
занных радикалов зависит от того, в какой четверти находится
угол А.
sin (Л Л- В) = sin Л cos В + cos A sin В.
sin (Л—В) = sin Л cos В—cos Л sin В.
cos (Л + В) = cos A cos В — sin A sin В.
cos (Л— В) — cos Л cos В-\- sin Л sin В.
402.06] формулы 71
401.05. 2 sin A cos B = sin (4 4- B) 4- sin (4— B).
401.06. 2 cos A cos В = cos (4 4- B)4- cos (4— B).
401.07. 2 sin A sin B= cos (4— B) — cos (4 4-3).
401.08. sin 4 4-sin 3 = 2 sin ~ cos .
401.09. sin 4— sin 3 = 2 sin - cos 1~—.
2 2
ЛА1 in XI Г> n Д 4“ В A—В
401,10. cos Д +cos 3 = 2 cos——cos——•
401.11. cos4—cos3 = 2 sin — y— sin 6 2 .
401.12. sin2 A— sin2 3 = sin (4 4- #) sin(4— 3).
401.13. cos2 A— cos2 B=sin (A 4- B) sin (B—A).
401.14. cos2 A—sin2 3 = cos (4 4- 3) cos (4— 3) = cos2 3—sin2 At
401.15. sec2 A4- esc2 A =sec2 A esc2 A= . f-4—j-j.
1 sin8 A cos2 A
401.2. p cos 4 4- q sin A = r sin (4 4-0),
где _____
r = ]/p24-<72, sinO=p/r, cos0=<7/r
или
p cos 4 4~ Q sin A = r cos (4 — <p),
где _____________
r =]/p2 + ?\ cosq) = p/r, sincp=g;'r.
Заметим, что p и q могут быть положительными и отрица-
тельными
402.01. sin (4 4- З4-С) = sin 4 cos 3 cos С4- cos 4 sin 3cos34-
4- cos A cos 3 sin C— sin 4 sin 3 sin C.
402.02. cos (4 4- З4- Q = cos 4 cos 3 cos C— sin A sin 3 cos C—
— sin 4 cos 3 sin C— cos 4 sin В sin C.
402.03. 4 sin 4 sin В sin C = sin (4 4- 3— 3) 4~ sin (34* C— 4) -f-
4-sin (C4-4—3)— sin (4 4- З4- C).
402.04. 4 sin 4 cos 3 cos 3= sin (4 4-3—C)—sin(3-|-3—4)4-
4-sin (34-4—3) 4-sin (4 4-3 4-C).
402.05 . 4 sin 4 sin 3 cos C = — cos (4 4- 3— 3) 4- cos (34- 3— 4) 4-
4~ cos (34“ 4 — 3) — cos (4 4- 3-f- 3).
402.06. 4 cos4cos 3cos3 = cos(44-3—3)4~cos(34~3—4)4-
4-cos (34-4 — 3)4-cos (4 4-3-j- 3).
72
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
(403.02
403.02, sin 2А = 2sln A cos А = .
l+tgM
403.03. sin 34 = 3 sin Z—4 sin’/.
403.04. sin 4A = cos A (4 sin/—8 sin’/).
403.05. sin5/= 5 sin/—20 sin’/4-16 sin’/.
403.06. sin 6/ = cos / (6 sin A — 32 sin’ A 4- 32 sin’ /).
403.07. sin TA — 7 sin /— 56 sin’ /4-112 sin’ A — 64 sin’ Z.
403.10. Для целого положительного четного п
sin л/=(—1 р+’ cos A |2n“1 sin""1 A — 11=^2"-’ sin"'’ A 4-
4- 2n-’ sin"-’ A —
_(n 4)(n 5) (n-6) 2B-,sin»-, д + .. 1
Ol J
ряд обрывается, когда коэффициент обращается в нуль.
403.11. Другой ряд:
sin nA = п cos A sin А
(п2—22) . , (п2—22)(п2—42) . , л
:—gj—- sin’ А 4-------sm’ А —
(п2—22) (п2—42) (п2—62) _[п> л [ . j
[л четное и >0].
71
403.12.
Для нечетного целого л > 1
sinn/ = (—1) 2 [г""* sin"/ — 2я-’sin""2/4-
4-2^5Г^) 2“"‘ sin"“ /—”*п~4^-~5) 2”"’ sin""’ А +
। п(п—5)(п—6) (п—7) 2„_, sInn-« А_ j
ряд обрывается, когда коэффициент обращается в нуль.
403.13. Другой ряд:
sin nA = л sin/ — --t” sin* А 4-
п(п2-12)(н2-32) ,
| gj Э1Х1 zl • • •
[л нечетное и > 0].
404.24J
ФОРМУЛЫ
73
403.22 cos 2/4 = cos* A— sin’,Л = 2 cos’ A— 1 = 1—2 sin’ A = 1—tg2 A cig A—tg Д 1 +tg2 A = ctg A 4-tg Д *
403.23. cos 3/4 = 4 cos’ A — 3 cos A.
403.24. cos 4A = 8 cos4 A— 8 cos’ A 4- 1.
403.25. cos 5Д = 16 cos’ A—20 cos* /4 4- 5 cos A.
403.26. cos 6/4 = 32 cos' /4—48 cos4 A 4- 18 cos’ A — 1 ‘
403.27. cos 7/4 =64 cos’ A— 112 cos’ A 56 cos’ A— 7 cos A.
403.3. cos nA = 2“"‘ cos" A—2"“’ cos""’ A 4- + cos""4 A—n (n~4) (n~^ 2"-’ cos A + «51 + 2"“’ cos""8 A-... Формула обрывается, когда коэффициент обращается в нуль (п целое и > 2).
403.4. sin у = у (1 — cos /4). 403.5. cos-^ = |/ — (1 cos А).
404.12. sin’ А = ( — cos 2/4+ 1).
404.13. sin’ А = -|- (— sin 3/4 4- 3 sin А).
404.14. sin4 А = ( cos 4Д — 4 cos 2/4 4- 4 ). 0 \ 2 /
404.15. sfn’ А = (sin 5/4 — 5 sin 3/4 4-10 sin Д).
404.16. 1 / 90 \ sin' A = 575 ( — cos 6Д 4- 6 cos 4A —15 cos 2Д 4- -5- ). oZ 2 f
404.17. sin’ A = — sin 7A 4- 7 sin 5/4 — 21 sin 3/44- 35 sin/).
404.22. cos’ A = (cos 2/ 4- 1).
404.23. cos’ A = у (cos 3/ 4- 3 cos /4).
404.24. cos4 A = i cos 4/4 4- 4 cos 2A 4- \
74 ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ {404.25
404.25. cos’ А — Y (cos 5А 4- 5 cos ЗА 4-10 cos А).
404.26. cos3 А — Y ( cos 6А4- 6 cos 44 4- 15 cos 2А 4- <3.4 \ £ j
404.27. cos’ A — Y (cos 1A 4- 7 cos 5A 4- 21 cos SA 4- 35 cos A). (Очевидно, 404 можно продолжить, используя биномиальные коэф- фициенты.)
405.01. ta (А 4- В} = = ctg А + ctg В- 1-tgAtgB ctgActgB —Г
405.02. fст/A — R} — lg Л~tg 5 — ctg B —ctg A °) i+tgAtgB ctg4ctgB4-l’
405.03. ct„ (A 4- В) = *е Л tgB ' »' ' ctg A 4-ctg fl tg/1 4-tg в ’
405.04. rfCT /4 — R\ — Ctg Лс^б+1 _ 1 -F-tg Л tg g ctg B—ctg A tgA—tgB *
405.05. tgA4-tgfl=sin (л + ц- 405.06. tgA-tgB = g-(^~fiJ. s ' ° cos A cos В ° cos A cos В
405.07. . ... о sin (A 4-B) cig A 4- ctg B= ~ '. to ’ to sin A sin В
405.08. . . . D sin(B — A) Ctg A Ctg В — t—; 5" . & & sin A sm В
405.09. , л 1 . D cos (A —B) tg A 4- Ctg В — : 77' . 6 & cos A sin В
405.10. . . . D cos (A + B) Ct%A tg e sin A cos В •
406.02. tCT 2A - 2tg^-- = 2-£lgA = 2 — 1 — tg2 A ctg2 A — 1 ctgA —tgA*
406.03. fg 3^ 3 tg A — tg A tg 1- 3 tg2 A •
406.04. t2 4tgA —4tg3A 1 — 6 tg2 A4-tg‘A ’
406.12. ria 9 Л - _ 1 - ‘g2 Л _ ctg л~1ёЛ- g 2 ctg A 2 tgA 2
406.13. - 0 . ctg5 A —3 ctg A %е.Ем-1 •
406.14. . .. ctg4 A — 6 ctg2 A 4-1 . Ct£ 4Л 4 .tg3 A — 4 ctg A "
408.02]
ФОРМУЛЫ
75
406.2. X А tgy = 1 —cos 4 sin A sin A 14- cos A -» f 1 — cos A r 1 + cos 4 ’
406.3. Ctg-2 = sin A _ J 4- cos A _ , /1 + cos 4 V 1 — cos 4 *
1 — cos A sin A
407. sin 0° = 0 = cos 90°.
sin 15° = S,nT2 = /3—1 _ 2 /2 ~ cos 75°.
sin 18° . Jt = slnio = К 5 — 1 _ 4 “ cos 72°.
sin 30° = sin — «= 0 "2 ~ cos 60°.
sin 36° - sin —• — b. I/5— /f __
2 /7
sin 45° . Jt = sin — = 4 1 __ /2 cos 45°.
sin 54° . 3л sin 10 K5 + I = 4 : COS 36°.
sin 60° . Jt — Sin -5- = 0 /З 2 = cos 30°.
sin 72° . 2л — sin -=- = 0 /54-/5 _ 2 /2 = cos 18°,
sin 75° . 5n -sin12- . Гз+J 2/2 = cos 15°.
sin 90° . Jt = sin^ = = 1 = cosO°.
sin 120° . 2л = sin— = /з~ 2 ’ sin 240° — sin 4л 1 V 3 2 ’
cos 120' > 2л = COS -S- = 0 J_ 2 * cos 240° — cos 4л 'T ’ 2 *
sin 180° = sin.n = = 0. sin 270° = sin Зл ~2~ ~~ 1.
cos 180’ ’ = COS Л = 1. cos 270° = cos Зтс л Т = и'
408.01. sinx=^r(e,x — е~,х), где/ — 4- ]/ — 1.
Заметим, что в электротехнической литературе вместо i часто
употребляется j.
408.02. cosx=y(e!X4-e~'x).
76
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
[408.03
(fix_f-ix\ f рЧх_
408.04. e'* = cos x 4-z sin x. (Формула Эйлера.)
408.05. e*+!* = e*(cosx4- isinx).
408.06. az+‘* = a* [cos (x In a) 4- zsin (x In a)].
408.07. (cos x -|- i sin x)B = e,nx = cos nx 4- i sin nx.
(Формула Myaepa.)
408.08. (cos x 4- isin x)"B = cos nx— isin nx.
408.09. (cos x4- i sin x)~ * — cos x— i sin x.
408.10. sin (zx) = i sh x.
408.11. cos (zx) = ch x.
408.12. tg (zx) = i th x.
408.13. ctg (zx) = — i cth x'
408.14. sec (zx) == sech x.
408.15. csc(zx) =— zcschx.
408.16. sin (x ± iy) — sin x ch у ± /cos xsh y.
408.17. cos (x ± iy) — cos x ch у FF i sin x sh y.
408.18.
tg
(x ± iy) =
sin 2x £ < sh 2y
cos 2x + ch 2z/
. л ..... sin 2x T f sh 2«
408.19. ctg(x±^) = -3r2FZ^-
409.01. ce‘x — ce‘ ,x + iltr\ rjie k—целое число или нуль.
= с (cos х4- i sin х).
409.0^. 1 = g<>+ikT\— cos о 4- / sin 0.
Заметим, что
cos 2fen = cos 2л — cos 0 = 1.
409.03. — 1 =e0+<8*+,,'4 = cos л 4- zsinn.
Заметим, что
ln(— 1) = (2*4-1)л/.
409.04. ]/T = . Эта величина может принять два различных
значения в зависимости от того, четно или нечётно k.
Этими значениями будут соответственно
gzrra — cos 0 4- i sin 0 = 1, e,2r+,> п‘= cos л 4-z sin л — — 1,
где г — целое число или нуль.
40в.10]
ФОРМУЛЫ
7Т
409.05. V—1 — e<ir + ” п‘1*. Этот квадратный корень ""имеет два
значения в зависимости от того, четно или нечетно г;
эти значения соответственно
cos л/2 i sin л/2 — i, cos Зл/2 4-* sin Зл/2 =— I.
409.06. =etkltll>. Этот корень имеет три различных значения:
е2Л1' е= cos 0 4- i sin 0 = 1,
t я cos — 4- i sin i = ®>
— cos / Sjn = _ 1_ / О = о)2,
о о Z Z
409.07.
409.08.
y/\=etklti^*. Этот корень имеет четыре различных значе-
ния:
e2r*‘ = cos 0 4- isin 0 = 1,
е<ггл+1л/4) i я- cos п[2 4- i sin л/2 = i,
е(ггл+4я/4) i — cos л 4~ / sin л = — 1,
е(ггл+вя/4) i— cos 3j^2 4- i sin Зл/2 = — I.
(Cm. 409.04 и 05.)
]/T= e(4s+i)ni/« (получается из 409.05 при r = 2s). Этот
корень имеет два значения
ел</4 _ cos " 4. i sin А — -1— _J_
4 4 /2 /2
5л . . . 5л / 1 .
einlt _ cos -г 4- * sin -7- = — ( -7= 4
4 4 \ К2
(а четно),
i \ , .
р== \ (а нечетно).
409.09. у/1 = eiknlin = cos — 4- i sin —~
принимает л различных значений, соответствующих различ-
ным значениям k. Уравнение йп = 1 имеет л различных
корней:
п , , п 1 2л , . . 2л
и. = cos 0 4-1 sin 0 — 1, о, = cos-i sin — ,
0 1 ’ ’ п 1 п
_ /2л\ . . . о/2л\ . .2л ... .2л
о) = cos 2 — I 4-1 sin 2 — , ..., со* = cos k-И t sm k — ,
8 \ П j \ П J IK n ' n
, ,, 2л . . . . ,, 2л
®n-i = cos («—!)—4-«Sin (л—1) — .
Заметим, что согласно 408.07
G)2 == й)8 = О)^ (оА = й^ (t)0==(Bj>.
409.10. Все л корней л-й степени из какого-либо числа могут
быть получены из любого корня умножением этого корня
на л корней из единицы, которые указаны в 409.09.
78 ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ (410
410, Формулы для плоского треугольника. Пусть
а, b и с—стороны, противолежащие углам А, В и С.
410.01. аг==ЬгА-с2 — 2bc cos А.
410.02. = J—=
sin A sin В sin С
410.03. а = b cos С 4 с cos В.
410.04. Лф£-|-С = л радианов = 180®.
410.05. sin~ = j/~гДе Р — (а + Ь 4 с).
410.06. cos ф== 1/^(Р,~а).
2 г Ъо
410.07. tg 4-
410.08.
410.09. Чтобы найти с no а, b и С при помощи таблиц логариф-
мов тригонометрических функций, положим
. д п 4" b, С . ,, С д
tgO = tg у ; тогда с —(а—b) cos у sec и.
410.10. Площадь треугольника
1 . . _ , /—----—-----гт~.---г a2 sin В sin С
-^absmC = V p(p—a)(p—b)(p—c)=j—inA .
410.11. Если С =90’, то сг = аа + £2. Чтобы найти с = 4- b2
при помощи таблиц логарифмов, положим tgO = -^-, тогда
c = asec9.
Это оказывается полезным в разных случаях.
410.12 В плоском треугольнике
(Q _.
-г cos А 4- cos 24 4-...
Ь 1 2Ь 1
сп \
••• +^-пСОЗПА+ . .. j [с<6],
1 / b . , Ь2 _ .
= 1п с— — cos А 4- cos 2А 4 ...
\ с ' 2с2 1
С05яЛ+ •• ) [&<cb
[См. 418.]
416.02]
РЯДЫ
79
Ряды
415.01. ллЗ м.7 • л Л л , • г 9 ' sin х = х— 37 + 57 — п+--. [№<оо].
415.02. cosx=l — 27 + 47 — б| + .-. [х<оо].
415.03. tg X — 3 +]5^ +з15х । 2835 Х +•’• , 2яп (2^-1) Вп г„_, , Ь2 -Н ’ (2п) 1 Х L 4 J * [См. 45].
415.04. _ 1 X Xя 2х5 Xя CtgX~ х~3 45 945 4725 [См. 45.]
415.05. secх— 1 4- 2 +24* 4 12Qx | g064x + ... * * • + (2п) 1 + 1" * L 4 J ' [См. 45].
415.06. 1 , х , 7 , 31 5 , 127 7 CSC Х х 6 360 Х + 15 120 Х । 604 800 Х 1 ' ‘ ..+^SrF21^—+... [x’c+i. [См. 45].
415.07. sin (0 -|-х) = sin 9 + х cos 0——77-— хя cos 0 . Xя sin 9 . -
31 + 4!
415.08. СПЧ 0 cos (0 + х) = cos 6 — х sin 6 27 1- , xs sin в Xя cos 9 + 31 1 41
416.01. л . , sin Зх , sin 5х , sin 7х . 4-s.nx + ^—| g-+ 7 - 1 ... [0<х<л].
416.02. ' 4с f . . sin Зх . sin 5х . Постоянная с = — sinxH 5 1 = Н * 5Т \ о с)
419.1] ряды 81
80 ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ [416.03
416.03. „ 4с f . лх , 1 Злх , 1 . 5лх , С =й(8,пт+з8!п a +sSin а + 4-у sin^y 4-...) [0<х<а].
416.04. л cos Зх . cos 5х cos 7х , - Г л . л 1 4 C0SX з + 5 7 +••• [ 2<X<2J ‘
416.06. Постоянная с = (cosx-^4-^-^4- ...) л \ 3’5 7 / Г 5Т 5Т 1 [—2<Х<-2]’
416.06. е-1г(с05К-±С05^ + 1со5^-±С05^+...) 5Т О и О D Cl i Cl j
416.07. nf . sin2x , sin Зя sin4x , \ г . x=2^sinx § 1 g 5 |-...j [—Л<Х<л].
416.08. п ( , . sin 2х , sin Зх . sin 4х , \ х=л— 2 ^sinxH —1-— h— 1- ... j [0<х<2л].
416.09. 4 f . sin3x , sin5x sin7x , \ х- Дшпх 3t + 5, r +..J Г * л 1 1 2 -=х^ 2] •
416.10. *=7-Hcosx+^+^+CV+•••) [ОгСХгСл].
416.11. х = -3 — 4^cosx у—ь—у р-+ ... j [—n^xsSn],
416.12. , л* 8 f cos Зх , cos 5х х = COS X 55 « 4 л \ З3 ' 5’ cos 7х , \ Г л л 1 -уз-4-..J |~2<*<2].
416.13. X*—л2х = , о ! . sin 2х . sin Зх sin 4х . \ 12 SIH X 53—4 53 73— Ч- ... 1 \ 2s ’ З8 4s /
I— Л О Jg Л]
416.14. . 4/1 cos 2х cos 4я cos 6я \ s,ax~ л\ 2 1-3 3-5 5-7 ••J Г Л _ Л 1 [—-у < X < -у] .
416.15. 8 (sin 2х . 2 . . . 3 . „ , COSX = — <-7-5—Ч~5~Е Sln 4x4-F-Ч Sin 6x4- ... Л ( 1 • 3 3-0 О'/, •••+ (2n-l)(2„4-l) sin2nx+---} [0 < х<л].
416.16. 2 sin ал f sin х 2 sin 2х . 3 sin Зх - 1 sin ах- я (1г_а, v-а' 1 3‘-У •••(’ где а — не целое число [—л < х<л].
416.17. 2а sin ал / 1 , cos х cos 2х cos Зх I cosax- п 4- ...f. где а — не целое число. [—л^х^л].
417.1. г1 "—Д' д~~г—j®3 1 Ч—;—т Sin 26 -4- Sin 36 1—2acos94-a sin 9 ' 4-a‘sin 464- ...) [а*< 1].
417.2. 1-2^~й+;? = 1 + 2 (a cos 6 4- a* cos 264- a* cos 304- ...) [а!<1].
417.3. l-2acos0+a‘ 1 + flCOs64-a cos204-a cos304-... [а‘<1].
417.4. ,—_ sin 8„ 3 = sin 6 4- a sin 26 4- a‘ sin 36 4~ ••• [a‘ < 11. 1— 2a cos 61 J
418. In (1 — 2a cos 6-|-0f) = — —2 ^acosO + y cos 26 4- у cos 364- ... ) [a2 < 1], n . . . o / cos 9 cos 29 cos 39 X . , -21n|a| 2( a 4- 2аг 4- 3aS 4-..J [a‘> 1].
419.1.’ __ , . rx sin 9 ггхг sin 29 r’x’ sin 39 e sin bx=—yy-4 у 1 g-j 1- ... , где r = Vas-{-b‘, a = r cos 6 и b — r sin 6.
82
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
J419.2
419.2.
cos bx = 1 +
где л и 9 те же, что и в 419.1.
r’xs cos 30
31
. п + 1 , пп
sin a sin -у
420.1. sin а 4- sin 2а 4- sin За 4- ... 4- sin па = ------------------
sin |
420.2. cos а + cos 2а 4- cos За 4- ... + cos па =-------------
sin|
420.3. sin а 4- sin (а 4- 6)4- sin (а 4- 26) 4- • • •
Sin ( а 4-— Olsin-x-
... 4 sin {7.4- (п— 1)6} = —--------------------
sin у
420.4. cos а 4- cos (а 4- 6) + cos (а + 26) 4- ...
/ . п— 1 е\ , nb
cos ( а 4--— о I sin —
... 4- cos {а4- (п— 1) 6} = —4----—-----.
sin —
421. Если sin 9 = х sin (94-а), то
9 4-лп = х sin а 4-4-sin 2а 4- 4- х* sin За 4- ... [х2 < 11,
2. о i j
где г — целое число.
422.1. sin9 = 9^1 — 244 ) (1 ~ з44“) '" *
422.2. cos9=(1-^)(1-^-2) (1-Д-,)... [92 < оо].
См. также 818.1—818.4.
Тригонометрические функции — Производные
427.1. _ = cos х. 427.4.
ах
427.2. = — sin х. 427.5.
dx
427.3. Hi±=sec2x. 427.6.
dx
d ctg x
dx
d sec x
-^- = secxtgx.
d esc x
dx
esc2 X,
esc x ctg x.
429]
интегралы
83
Тригонометрические функции — Интегралы
При вычислении определенных интегралов часто бывает полезно-строить
график подынтегральной функции. Некоторые кривые, такие как график
тангенса, имеют точки разрыва. Вообще, интегрирование не должно произ-
водиться в пределах, между которыми имеется точка разрыва.
429. Подстановки:
и du sin X COS X tg-r X dx
(1) sin х cos x dx U К1— и2 и К1 -и2 arcsin и du К1 — и2
(2) COS* — sin x dx Kl-u2 и V l-u2 и arccosи du К 1— и2
(3) tgx sec2 x dx и V 1+u2 1 К 1+u2 и arctg и du 1 +и2
(4) sec x sec x tg x dx К u2—1 и 1 u V и2— 1 arcsec и du и Ки2-1
(5) , x tg 2 1 2 X J у ser у dx 2u 1 + u2 1—ц2 1 +u2 2п 1 - иг 2 arctg и 2du 1 +и2
ctgx, sec х, esc х можно заменить
Примечание, а)
Ь)
с)
1 1
соответственно на 7,
tg х ’ cos х ’
F (sin х) cos х dx, — использовать
F (cos x) sin x dx, — использовать
J ^(tgx) sec2 x dx, — использовать
1
sin х
(1);
(2);
(3).
Из таблицы следует выбрать подходящую подстановку для
замены тригонометрических функций алгебраическими и обратно.
Так, например, если встречаются только tgx, sin2x, cos2x, сле-
дует применять (3).
84 ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 1430.IG
Интегралы, содержащие sinx
430.10. ysinxdx = — cosx.
430.101. J s\n(a-\-bx)dx =--g-cos {a 4- bx).
430.102. C sin— dx = — a cos —.
J a a
430.11. J x sin xdx — sin x—xcosx.
430.12. J x* sin x dx — lx sin x—(x*—2) cosx.
430.13. J x’ sinxdx = (3x‘—6)sinx—(x*—6x)cosx.
430.14. J x4 sin x dx — (4x* — 24x) sin x— (x4 — 12x! 4- 24) cos x.
430.15. J x’ sin x dx «= (5x4—60x‘ 4-120) sin x—
— (x* — 20x’ 4- 120x) cos x.
430.16. J x’ sin x dx — (6x’—120x’4-720x)sinx—
—(x’ — 30x4 + 360xs—720) cos x.
430.19. J Xя* sin x dx — — xm cos x 4- m xOT"1 cos x dx.
[Cm. 440.]
P , . . x sin2x x sin x cos x
430.20. \ sin8XrfX==-2--4~ = "2------2----’
n. P . . . x* x sin 2x cos 2x
430.21. 1 x sin* x dx — ----------g—.
P , . . . x’ f X1 ’ 1 \ . n X cos 2x
430.22. 1 x sin x dx — -----g- sin 2x-----—..
J О \ 4 о / 4
p , . , . я4 f x* 3z\ , n /Зле’ 3\ n
430.23. \ x’sin xdx = -g—( sin 2x—(-5-----= cos2x.
J 0 \ 4 о / \ о 10/
430.30. f sin* xdx — —cos x.
V *3
P , . . xcos3* ,sin3x 3 . 3
430.31. 1 xsin’xdx = —гх— -—хд----— xcos x + -j smx.
(Выражая sin’x согласно 404.13.)
S. 4 , 3x sin2x . sin4x
sin4xdx=-z------т-4—575-.
0.4 oZ
432.11] ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ Sin X 85
430.50. Р . j , 5 cosx , 5 cos Зя cos5x jsm’xdx- 8 + 48 80 •
430.60. f . « , 5x 15sin2x , 3sin4x sin 6x JSin X dX ~16 64 64 192" •
430.70. f , , . 35 cos x , 7 cos 3x 7 cos 5x , cos 7x pm xdx- 64 4- 64 320 4- 448 . (Интегрируя выражения из 404.)
431.11. P sin x dx c, , . x* , x5 x’ . J X -si(x)-x 3.3I4-5.5i 7.7,+ -.- Таблицу численных значений этой функции см. [22].
431.12. С sin х dx sin х . С cos х dx г^м 111 J. х* “ х ' J х 1 ’
431.13. С sin х dx sin х cosx 1 С sin я dx ^gj ц i J я’ 31 2я* 2x 2 J x I ’ 'J
431.14. C sin x dx _ sinx cos я . sin я 1 C cos x dx гр ц i J x* Зя’ ,6x* ' 6я 6 J x ' * ’
431.19. C sin я dx sin я 1 C cos x dx J xm (m—l)xm~' ' m— 1J x1”-’ *
431.21. J sin! я dx = in , x | _ | у £21^/ £*). [См. 441.11.]
431.31. Csin’xdx 3 f* sin xdx 1 C sin3x d (3x) rp ^gj ц , Jx 4 J x 4 J 3x i
431.9. J S"”• Выразить sin”x согласно 404 и интегрировать почленно согласно 431.1 и 441.1.
432.10. J^4cscxdx==inMI== 1 , 14-cosx ‘ । = Т- In -j-1 — In CSC X — ctgx = 2 1—cosx 1 & 1 = (лямбда-функция). [См. 641 и 603.6.] См. рисунок на стр. 86.
432.11. Сxdx । *’ । 7x5 I 31x7 _| 127х* । J sinx * + 3-31 + 3-5-51 + 3-7-7I +з-5-91 + ’ ” • + 2<22. + 1»l’V*'+-- [См. 4S.1
86
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
[432.12
432.12.
хЧх_хг . х* 7х* 31 хе 127/° ,
sinх 2 ’4.31 3-6-51 + 3-8-71 + 5-5-6-8!
2(2»--])
(2п4-21(2/1)! п
[См. 45.]
432.19. J lin^ • Разложить согласно 415.06, умножить на хт
и интегрировать [т>01.
432.20.
432.21. ^7^= — х ctg *4-In 1 sin X [.
432.30. Р dx cos x .1 . 1 x I ‘J sin3 x 2sin2x । 2 n 2 1*
432.31. f 4^ = —4^—7ГГ- + 1 f [Cm. 432.11.] J sin3x 2sin2x 2sinx 1 2 J smx 1 J
432.40. P dx cos x 2 . ctg’ x ) sin4 x 3 sin’ x 3 X C ,= X 3 (J S11 ’ X и □ 111 л О О
432.41. P x dx x cos x 1 2 . . 2 , . . , \ -r-j- = — 5—r-; — X Ctgx+ —- In SIH X . J sin4 x 3sin3x 6sin2x 3 & 3 1 1
432.50. P dx cos x 3 cos x , 3 . 1, x 1 J sin5 x 4 sin4 x 8 sin2 x ' 8 П 2 1'
434.05] ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ 81П X 87
432.60. С dx cos х 4 cos х 8 J sinex 5sin5x 15siri3x 15 Cg'*'1
432.90. C dx C n j cosx , n — 2 f dx J SHI * X J (tl — 1) sin” 4 ' n—1 J sin” 4 [n>l].
432.91. C xdx x cos x 1 , J sin"x (n—1) sin"-1 x (n— 1) (n — 2) sin" 2x ' , n — 2 P xdx r ol + n-li sin"“2x 1л>21-
433.01. P dx /it x \ J 1 + sin x ® \ 4 2 / *
433.02. Г dx , / it x \ J 1 — sin x g \ 4 + 2 ) *
433.03. \ ГГ-— = ~ x tg H тг I + 2 In cos -x- . J 1 + sin x b\4 2 / ' | \ 4 2/|
433.04. P x dx . ( it x \ , n . < it x \ | jl-sinx=XCt4 4 2)+21TinU-2j|-
433.05. P sin x dx , . f it x \ j l+sinx~X + t44 2/'
433.06. jl-sinx" X + tgl4+J-
433.07. P dx . ( it x \ , | , x 1 , J sinx(l+sfnxj tg 4 2j+ n|tg 2 Г
433.08. P dx . f л , x \ , , I x I . J sin x (1 —sin x) tg 4 + 2 ) + n 1tg 2 | ’
434.01. P dx 1/it x'X 1 j / it ,-x \ J (1 + sin x)2 2 tg \ 4 2 ) 6 tg 4 2 ) •
434.02. C —^—== 1 Ct2 f — — - W - eta’f J (1— sinx)2 2 CCg \ 4 2j + 6 Ctg \ 4 2 J*
434.03. P sinxdx 1 /it x \ 1 s / it x_\ J(l+sinx)2 2 tg \ 4 2/+GtgV4 2/
434.04. P sin x dx 1 . / it x \ , 1 . , / it x\ Jd-Siux)2 2 ctg I 4 2 ;+6 CtS V 4 _ 2 ;•
434.05. C . ^X. 2 = —^-arcsin f—'2 *j~|4 [Cm. 436.6.] J 1 + sin2 x 2 у 2 \ sin x + 1 / 1 J
88
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
|434.0в
434.06. Г г = Г = tg х. [См. 442.20.1 J 1 — sin2 X J COS2 X ь 1 J
435. . Г . . , sin (т — п) х ' sin (m + n) х \ sin тх sin nx dx — \ 4- J 2 (т — п) 2 (ffi + n) Если то см. 430.20.]
436.00. С dx J а + b sin х „ atg-^+6 = —~== arctg —7==- \аг > ft’l, Уа*—Ь* Уа‘-Ьг 1 . atg 4 + fc— K&2—a* = 1 n ' fo* > a‘l, a a tg 4-b + Kt»2—a* _<) atg-^ + й Кб’-о* V b2 —a2 > a2, |atg-^4-Z>|< Vb*—a’j, _2 atg4+ft — ; Arc th —7==- V bs—a2 V b2-—a2 p8>a8, jatg ± + >]/&’_ Подынтегральная функция обращается в бесконечность (если Ь2 > а2) при х = пл + (— 1)" arcsin .
436.01. Р sin х dx х а Р dx Ja4-6sinx b & J a 4-6 sin х ‘
436.02. P dx 1 । 1 x I b_ P dx , J sin x (a + b sin x) a | ® 2 | a J a + b sin x *
436.03. P dx b cos x a P dx j (a 4- b sin x)* (a2—Ьг) (a -pb sin x) ' a2—62J a 4-t> sin x'
436.04. P sin x dx a cos x b P dx J(a4~&sinx)2 (&2—a2) (a +b sin x) ‘ t>2—a2 Ja4-t> sin x * [K 436.01—436.04 cm. 436.00.]
436.5.
С______arctg
Ja2 + 6asin2x ауал + Ь*
а
ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ COS X
89
440.141
436.6.
436.7.
437.1.
437.2.
437.3.
437.4.
Когда а — b = 1,
f ——— « arctg (]/ 2 tg х).
J 1 Ч-sin® х У 2
Другое выражение, отличающееся иа константу, дано
в 434.05.
dx
аг—b2 sin8 х
__ 1 in У й2—аг tg х + а
2а УЬг—а2 УЬг—a’tgx—а
Если Ьг — аг, см. 434.06.
sin х dx 1 . т cos х
У1 + тг sin8 х т У1 + тг
sin х dx lii , iZT---—-~s—I
-----—-----In \m cos x 4- у 1 — tn sin x .
У 1 —m’sin’x m '
(sin x) УI + sin2 x dx —
cos x , r~.—;——г— 1 4- m2 , m cos x
=------у 1 4- m sin x------4— arcsin -7=.
2 r. 2m 1 4- тг
(sin x) УI — mi sin* x dx = — yj — тг sin8 x—
— - ~~m- In I m cos x 4-1 — m‘ sin* x I.
9/M 1 * r 1
Интегралы, содержащие cosx
440.10. J cos x dx = sin x.
440.101. J cos (a 4- bx) dx — у sin (a + bx).
440.102. C cos — dx = a sin —.
J a a
440.11. J x cos x dx — cos x + x sin x.
440.12. J x* cos x dx = 2x cos x-f- (x2— 2) sin x.
440.13. J x’ cos xdx — (3x2 — 6) cosx + (Xs — 6x) sin x.
440.14. f x* cos x dx= (4x“— 24x) cos x 4- (x4— 12x2 4-24) sinx.
90
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
|440.15
440.15. ^x5cosxdx =
= (5х4— 60x’4- 120) cos х + (х5— 20х’ 4- 120х) sin х.
440.16. J х’ cos х dx = (6х5 — 120xs + 720х) cos х +
+ (№ — ЗОх4 + 360х’ — 720) sin х.
440.19. хт cos xdx = хт sin х—т1^ х"!-‘ sinxdx. [См. 430.]
ллп пл С 2 j х , sin 2х х , sinx cosx
440.20. j cos8 x dx = g- 4—= - 4-----------.
ллп 01 C 2 j x2 . xsin2x . cos 2x
440.21. 1 xcos xdx = — 4--—------1---g—.
..Л nn C 2 2 . X3 .! X2 1 \ . _ , xcos2x,
440.22. 1 x cos xdx = —4-i-^—gJsin2xH---------—.
ллл no C s г j x4 . ( x3 3x\ . п , /Зх2 3 \ n
440.23. 1 x cos x dx = -^ sin 2x 4- -5-cos 2x.
J о \ 4 о J \ о 10 /
440.30. у cos’x dx = sin x— .
. .n о, C , . x sin 3x . cos3x . 3 . ,3
440.31. \xcos xdx — —-------1—gg—\-~^x sin*+ 4-cosx-
(cos’x выражается согласно 404.23.)
440.40. У cos4x dx _ 3x sin 2x sin 4x 8 + 4 + 32 •
440.50. У cos5xdx = _ 5 sin x 8 , 5 sin 3x । sin 5x . 1 48 1 80 ‘
440.60. У cos’ x dx: 5x , 15sin2x , 3sin4x , sin 6x ,
16^ 64 64 192 '
440.70. У cos’ x dx 35 sin x 64 7 sin 3x 7 sin 5x sin7x 1 64 1 320 + 448 *
(Интегрируется выражение из 404.)
441.11. p cos x dx 1 n 1 V 1 x2 ( x4 x’ t
J x 1П 1 Az j 2-2! +4-4l 6-6! + • • ’
Таблицу численных значений см. [22].
441.12. (* cos xdx cos-x (* sin x dx [Cm. 431.11.]
J x2 X J X
441.13. f cos x dx COS X , sin x 1 f cos x dx [Cm. 441.11.]
J x’ 2X2 2x 2 J x
442.31] ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ cos X 91
441.14. С cos х dx cos x . sin x , cos x , 1 C sin x dx J x4 3x’ 1 fix2 1 6x "* 6 J x ’ [Cm. 431.11.]
441.19. f cos x dx cos x 1 P sin x dx J xm (m—1) xm-1 tn—1J Xй"1
441.21. C £OS^x_dx_ 1 ln|x|+ < C cos_2x rf (2x) , |-Cm 441>llei
441.31. P cos’ xdx 3 P cos xdx 1 P cos 3x d (3x) • j । i J x 4 J x 4 J 3x ’ ‘ ’ ’’J
441.9. P cos" x dx J x“ ‘ Выразить cos" x согласно 404 и интегрировать почленно согласно 441.1.
442.10. Р dx С . j 1. { л , х \ I \ = \ secxflx = In tg (т + лт I , Jcosx J | & \ 4 2) 1 ’ . , , . , 1 , 1+sinx = In sec tg X = -к In ;—, 1 ' » i 2 1—sinx = Z,(x) (лямбда-функция). [См. 640.]
442.11. C x dx _ x2 x4 5x° 61x8 , 1385x10 Jcosx 2 +4-21 + 6-4! ' 8-61 + 10-8! 1 """ 'I ДМ1 । lC“-45-l
442.12. P x2dx _ , x5 5x7 61x9 I385x" . J cosx 3 r 5-21 + 7-41 + 9-61 + 11-81 + * P r2« + l 1 еДт/р.-а! 1 Iе"- 45-l
442.19. P XmdX r, 1 . , _ n- ,a 1 . Разложить согласно 415.05, умножить на х J cosx cosx и интегрировать [т ф 0].
442.20. С dx Га. \ \ sec х dx = tg х. J COS2 X J &
442.21. P x dx . . , । । J W-x = XtgX+ ln iC0SXl-
442.30. P dx __ sin x , 1 , 11 / л , x \ 1 J cos3 x 2 cos2 x 2 n|g\.4~’-2/|‘
442.31. P x dx _ x sin x 1 1 P x dx , J cos’x 2 cos2 x 2 cosx 2 J cosx" I M’ ’ *"J
92
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
(442.40
442.40.
442.41.
442.50.
442.60.
442.90.
442.91.
dx ____ sin х
cos1 x 3 cos’ x
x dx
cos*x
dx
cos’ X
xsin x
_2
3
3 cos’ x 6 cos’ x
sin x , 3 sinx
4 cos1 x 8 cos’ x
2 2
у xtgx-|--g-ln|cosx|.
3
8
P dx ___ sin x , 4 sin x 8
J cos’ x~ 5 cos’x+ 15 cos’x-*- 15 ° ’
C dx P n j
v —=-= v sec xdx =
J COSnX J
’(n—l)cos"-,x~n—1 J cos”-’»
x dx______x sin x ___________1__________.
cos"x (n— 1) cos"-1 x (n— 1) (n—-2) cos"-’ x '
, n—2 P x dx
n —1 J cos"-’»
[n>2].
tg x — tg x-f~
I
443.01. С—Д—= tg4.
J 1 +cos x » 2
443.02. f , dx == — ctg 4 .
J 1—cosx 6 2
443 03-
143-°4- Jr^--’a2l+21"|slni|-
443.05. f ~^-xdx. = x—tg 4 .
J 1 +cosx & 2
лв P cos x dx . x
443.06. 11----= — x—ctg —.
J. 1—cosx ° 2
«’•O’- Ь|1%ъг|,МтЧ)|-1»г
443-»8-
.ЛЛЛ1 C dx 1 . x , 1 ,X
444.01. J (] +cosx)a — 2 т + 'б tg 2 •
444.02. J(1_cosx)2= — уctg-Fj—g-ctS 2".
444’03* j(T+^=2 tg2~6tg 2’
446.04] ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ COS Л! 93
444.04. Р cos х dx 1 , х 1 , i х Jr—c-osxj^ i?^ 2 6Ct8 2-
444.05. [ —— = —arcsin (—. (См. 446.6.] J 14-cos2 x 2F2 \ l+cosax/ 1 '
444.06. f « f = — ctg x. [Cm. 432.20.1 J 1 —cos’x J sin’x 1 •*
445. P . sin(m—-n)x . sin (m + n)x \ cos mx cos nx dx = — (— + -777—-J / • J 2(m —n) 2(m + n) [тг n\ Если m2 = n2, to cm. 440.20.)
446.00. P dx _ J a + b cos x (a-6)tg4 7i._ -arctg— [a* >&*], ba Va3—b* 1 1 . (b—a) tg~+ Kfea—a2 = ^=L=ln ? [b2>a2], К*2-«a (6_Q) tg f Ьг-аг (b—O)tgy = -7-_. . _ Arth - V ьг-аг У b-—a- р2> аг, |(b—a)tg-£ |<]/b2—a2j , (b-a)tg4 = - Arcth —r -— И 6a-aa V Ь3—аг p>2>a2, |(b— a)tg-£ |>/b2— a2j . Подынтегральная функция обращается в бесконечность (если ba> а2) при х=2пл ± arccos j .
446.01. С cos х dx х °C 4х J а + b cos х b Ь J а 4- b cos х'
446.02. С dx __ 1 |n 11 t x । _л \ [ Ь_ P dx J (a-f-bcosx)cosx a1 |®\2 4J1 a J a-f-bcos x*
446.03. P dx bsinx a P dx J (a-f-bcosx)2 (b2—a2)(a + bcosx) b2—aaJa4-bcosx*
446.04. P cos x dx a sin x b P dx J (a-j-bcosx)2 (a2—b2) (a 4* b cos x) a2 — b2 J a-f-bcosx’ [K 446.01 — 446.04 cm. 446.00.)
94
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
{446.2
446.2.
446.5.
446.6.
446.7.
f dx 2 Па + Ч i *1 г„ м
J a24-ft2 —2a&cosx —|а2—й2| aICtg Ila—tg 2 J I
[Cm. 446.00.]
fdx 1 , a tg x i„^ m
a2 4* b2 cos2 x a a2 4* b2 V a2 4~ b2
При a = b— 1
C dx 1 , / tg x \
I -------- = __ arctg 1 _2_ .
J 1 4- cos2 x у 2 \ у 2 /
Другое выражение, отличающееся на константу, дается
в 444.05.
Г dx 1 , a tg х
|/ --------------------arctg -7==
J а2 — b2 cos2 х а ]^аг — Ь2 у а2 — Ь2
[а2 > Ь2, а>»0],
1 in а U х— УЬ2—а2
' 2а Ь2— a2 a tg х 4- У~ Ь2— а2
\Ь2~>аг, а>0].
Если £2 = а2, см. 444.06.
Интегралы, содержащие sin хи cos х
С . . sin2 х cos2 х ,
450.11. \ sin х cos х ах = —— =----—{-const.,
cos 2х ,
=----------4 const.
4 '
„ f* , . , cos’ x
450.12. I sin x cos x dx =--—.
, П C . 8 j cos’ X
450.13. \ sin x cos x dx =--—.
rri .Л C • n J cos" + ’ X
450.19. \ sin x cos x dx =------r-r-.
J «4-1
450.21. у sin2 x cos x dx = .
450.22. у sin2x cos2x dx =y ( x—-” ~.
450.23. У sin’x cos’x dx =sin X^QS-- 4- sin2 x.
450.31.
C . a . sin* x
\ sin x cos x dx = —-—.
451.41] интегралы, содержащие sin X И COS X 95
450.81. С • • sin х , г » \ sin xcosxdx = п— \тФ—1]. J т +1 11 (При т = — 1 см. 453.11.)
450.9. У sin"1 х cos”x dx — Sinra + ' X COS"”1 X . П—1 С . m , _ i sin x cos x dx, m-\-n /72 + Л J ’ sin1”-1 x cos'’4’1 x , m—1 P . w_a n , i i— \ sin xcos xdx m + n m+n j \m +=— tv, см. 480.9]. [См. также 461.]
451.11. C = In | tg x |. J sm X COS X ° 1
451.12. C dx 1 . , 1, x ] \ = Hn t° — 1 J sin x cos2 x cos x | ® 2 1 *
451.13. C dx 1 । i 1, i \ — 5— = о 2 Ь 1П tg X . J Sin X COS® X 2 COS2 X 1 ° ‘
451.14. P dx 1 1 . j 1 x ] J sin x cos1 x 3 cos’ x 1 cos x | ® 2 | *
451.15. C dx 1 . i , . ।. , \ —: 5— = Д 1- + 7i Г- + In tg X . J sin x cos5 x 4 cos4 x 2 cos2 x * 1 & 1
451.19. f dx 1 .C dx [—л.,! J sin x cos" x (n — l)cos"-Ix J sin X cos"-2 X L * г
451.21. P dx 1 . i 1. ( я , x \ 1 \ —r~2 = Ь In tg -Г + -O • J sin2 x cos x sin x I \ 4 1 2 у 1
451.22. p dx i -г-; j- = — 2 ctg 2x = tg x— ctg x. J sin2 X cos2 x » & b
451.23. C dx sin x 1 , 3 , 1 . 1 я . x \ I 1 3~ = -K 5 : k 7Г In tg — 4- -S’ 1 . jj J sin2 x cos3 x 2 cos2 x sm x ' 2 |&\4 ’ 2 J |
451.24. C dx _ 1 _8 9 J sin2 x cos1 x 3 sin x cos’ x 3 C X'
451.31. C _ dx _ — )- In 1 tg x 1. J sm3 X cos X 2 sin2 X 1 b 1
451.32. C dx 1 cos x 3 . 1 x 1 J sin3 x cos2 x cos x 2 sin2 x ' 2 | 2 | ”
451.33. P dx 2 cos 2x . _ , .. , J sin3 x cos3 x sin2 2x ’ n [ S I-
451.41. f dX = 3 cos2 x~4 _L 1 If ( n 1 x \ 1 j sin1 x cos x 3 sin’ x '|^\4~’_2/*
96 ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 1451.91
451.91. У sinm х cos х (m— 1) sin'"-1 x ' У sinra-a x cos x Iя* П*
451.92. Lnwx-r’LX»- iCm- 432-i
451.93. P dx J sinra x cos" X 1 । m + »-*-2 P dx (n—1) sinra-1 x cos"-1 x * n — 1 J sinm xcos"-’x [«>!], 1 । m + n — 2 P dx (m— 1) sinra-1 xcos"-1 x * m— 1 J sinra-a x cos" x
452.11. 452.12. f sin X dx J COS X f sin x dx _ J tg x dx = — In | cos x | = In | sec x | 1 . [Cm. 480.1.}
J COSa X COS x.
452.13. (* sin x dx J cos’ X = 4 tg! x + const. 2 cos’ x 2 &
452.14. f sinxdx_ 1
J COS* X 3 cos’ x ’
452.19. (* sin x dx 1 [«¥•!].
J cos" x (n—l)cos"-1x
452.21. P sina x dx J COS X . i L f л . x \ | — Sinx + ln| tg^Y+2 ) •
452.22. (* sina x dx J cos’ x §tg3xdx = tgx—x. [Cm. 480.2.]
452.23. P sin’ x dx J cos’ x sin X 1 ] I . ( л x \ I 2 cos’ x 2ln|tg\4+2j|'
452.24. P sin’ x dx J cos’ X у tg’ X.
452.29. (*sin’ xdx sin x 1 p dx [л^1].
J cos"X (n—l)cos"_,x n — ljcos"_’x
452.31. (* sin8 x dx J COS X sin’ x , , . —‘—2 In | cos x|.
452.32. P sin8 x dx _ J cos2 x cos x-|-.sec x.
452.33. P sin8 x dx J cos8 x J tg8 x dx = у tg’ x + In | cos x [. [См. 480.3.]
453.24]
ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ Sit! X И COSX
97
452.34,
sin8 х dx 1 1
cos4 x 3 cos8 x cos x
psin8xdx 1 , . 1 1 , .
452.35. \-----s— = т tg x = ---j----5—5— + const,
j cos’ x 4 ® 4 cos4 x 2 cos’ x
пл C sin8 xdx 1 1 r , . o-l
452.39. \---------------и—=-1----------xt—„-г- [я ¥= 1 или 31.
J cos"x (n—l)cos" lx (n—3) cos" 8 x 1 1
f sin4 xdx . sin8x , . I , f л , x \ I
452-41- ----------3----s1nx+ln|tg(T + -)|.
452.7. [ȴ*!].
J cos" X П—1 I * J’
452.8.
452.9.
P sin" x dx P. n j tg 1 x p, .
\ -r-й— = \ tg" x dx =——;---------\ tg" 1 x dx
J cos" x j ® n — 1 J ®
[n* I; cm. 480.9].
P sin"1 xdx_
J cos"x
sinra+1 x
m—n 4-2 f* sin"1 x dx
(n—l)cos"-,x n — i J cos"-2x
sin'”-,r m—1 C sin"1-2xdx
(m — n) cos"-1 x m — nJ cos"x
sin"1-1 x m —I p sin111-2 xdx
(n — l)cos"_,x n—1
cos"-2 X
1],
[m 4=- я],
[« 1].
453.11.
453.12.
453.13.
453.14.
453.19.
453.21.
453.22.
453.23.
cos x dx
sin x
cos x dx
sin2 x
cos x dx
sin8 x
cos x dx
sin4 X
cos x dx
sin" x
J ctg x dx — In | sin x |.
1
7----= — CSC X,
sin X
1
2 sin2 x
1
3 sin8 x
[Cm. 490.1.]
ctg2x . .
—------H const,
(n— 1) sin"-1 x
. = COSX + In tg 4-
sin x 1 I 2 I
cos’ x dx
cos2 x dx
sin2 x
— Ctg X — X.
[Cm. 490.2.]
cos8 x dx
sin8 x
cos x 1 . . x
к—2------TT In tg 77
2 sin2 x 2 “2
Iя + П-
P cos2x dx 1 . з
453-24- 1 "^77" = “тctg x-
bill Л о
98
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
[453.29
453.29. С cos** dx cos x 1 P dx , .. J sin"x (n— 1) sin"-1 x n— ljsin"-2x 1л J*
453.31. P cos’ x dx cos2 x . . , . . j"sinx’ "2 -Hnls-nxl.
453.32. P cos’ x dx J 'sin2* “ SinX CSCX-
453.33. ~s7;i’x* = In Isin-d- [Cm. 490.3.]
453.34. P cos’xdx 1 1 J sin4 x sinx 3sin’x"
453.35. P cos’xdx 1 . 4 1 1 J sin’x - 4 ct§ X-2^2 x-4sin4r-’- const
453.39. P cos’ X dx 1 1 . J sin" x (n—3)sin"-’x (n—1) sin"-1 x Iя 1 или dj.
453.41. Pcos4xdx cos’x , , , I . x I J sinx = 3 +cosx+ln|tg2|.
453.7. P cos"- 2 xdx ctg"-1 x , ., J sin"x - n-1 Iя
453.8. J sin"x W XdX n-l J ctg" ‘xdx [л 1; см. 490.9].
453.9. P cos"x dx j sin®1 x _ cos”+1 x n— m-f-2 P cos" xdx . . (tn — 1) sin®1-1 x tn— 1 J sin1"-2x FT11]. cos"-1 x n— 1 P cos”-2 x dx . . (n — tn) sin"1-1 x+ n—tn J sinm x 4“ я]. cos"-1 x n — 1 P cos"-2 xdx . , .1 (m—1) sin1"-1 x m— 1J sin®-2x
454.01. P sin xdx , . \ -f; — In (1 4- COS x). J 1 -bcos x ' 1 1
454.02. P sin x dx ... . \ -j = In (1 — cos x). JI — COS X ' 1
454.03. P cosxdx 1 , x 1 T-7^— = In (1 + sin x). J 1 + sin x ' '
454.04. P cos x dx ... . . \ : — = — 1П (1 — SIU X). J 1 —sinx ' '
454 05 С 4
J sinx(i 4-cosx) и 2(1-j-cosx) '
455.07] ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ Sit! X И COSX 99
454.06. Р dx 1 , 1 . 1 _Х | • J sfn х (1—cosx) 2(1—cosx) ' 2 1П| & 2 | *
454.07. f* dx 1 1 . 1 f л , x\| J cos x (1 + sin x) 2 (1 -J- sin x) ' 2 | ® \ 4 ' 2 J [ *
454.08. f* dx 1 . _1_. 1 J cosx(1 —sin x) 2(1 —sin x) ' 2 n | ® \ 4 2 ) | ’
454.09. C sin x dx । 11 4-cos x 1 J cosx (1 + cosx) I cosx ]’
454.10. P sinxdx Inf *—cosrl J COS X (1 —COS X) | COS X | *
454. И. P cos x dx । 11 4-sin x 1 J sin x (1 4- sin xj 1 sin x 1 *
454.12. P cos xdx jn 1 1—sinxl Jsinx(l—sinx) 1 sinx |*
454.13. P sin x dx 1 1 . 1 f re . x \ 1 J cos x (1 4- sin x) 2 (1 4- sin x) ' 2 ” | \ 4 ‘ 2 j | ’
454.14. (* sin x dx 1 J. I f я .*\l J cos x (1 — sin x) 2(1 — sin x) 2 П 1 \ 4 ' 2 J [ *
454.15. P cosxdx 1 i 1 i I* i| j sin x (1 4- cos x) 2 (1 4- cos x) ‘ 2 П | ® 2 | *
454.16. P cosxdx 1 1.1 x | 1 J sinx(1—cosx) 2(1—cosx) 2 ^П| ® 2[*
455.01. P dx 1 i L f x . re \ I J sinx4-cosx /"2 Itgk 2 "T 8 Jl •
455.02. f -———=4=in| tgf4—411 • J sinx—cosx у % 1 & \ 2 8/|
455.03. Г11,1 + [Cm. 482.2 « 492.1.]
455.04. [Cm. 482.2 я 492.1.]
455.05. fs-iS^n = 7 + rln> sinx + cos*l- [Cm. 482.1 и 492.2.1
455.06. P cosxdx x . 1 , . . . \ = — -K' + ’S’in sinx — cosx . J sinx—cosx 2 1 2 1 * [Cm. 482.1 и 492,2.]
455.07. (* dx j_. / J (sinx4-cosx)2 2 ™ \ 4 J ’
TOO
тригонометрические функции
[455.08
455.08. С --—------a = -L tg f x + 4 V
J (sin x—cos*)2 2 1 4 /
455.09. f . L dx , , = ± In 11 ± tg i I .
J 1 4-cos x ± sinx I 6 2 |
лса < C dx 1 i I. * + ® I
456. I . 1 T----;---;- = — In tg —X— ,
J b cos x + c sin x r | & 2 I
где r = ]/^2 c‘, sin0 = i>/r, cos 6 = clr.
[Cm. 401.2 и 432.10.]
456.2.
460.1.
460.2.
461.
465.
470.1,
470.2.
(*_______dx______________ C d (x + 0)
J a + 6cos x+c sin x J a-j-rsin (x + 6) ’
где гиб даны в 456.1. [См. 436.00.]
С ~—а - г = 4 arctS ( — tg х^ . [См. 436.5.]
J аг cos2 х 4-fe2 sin2 х ab ® \ a b j 1 J
f-2---——.i- Л ln Iffi ~° I • [См. 436.7.1
J a2 cos2 x—62sin2x 2ab |Z>tgx—a| 1 >
sin”xcos"xdx. Если одно из чисел т или п нечетное
целое положительное, то следует сделать подстановку
sin2x=l — cos2x и sinxrfx = — dcosx
или
cos2x=l — sin’x и cos x dx = d sin x.
Если оба числа тип четные целые положительные, то
следует сделать подстановки
sinsx = 4-0 — cos 2х), cos2x = 4(1 + cos 2х)
Л Л
и
Sin X COS X = у sin 2х.
Получив аналогичные выражения, но с аргументом 2х
вместо х, преобразовать их далее подобным же образом.
См. также 450.9.
Р , , cos(m—п)х cos (m + n)x
1 s п тх cos nx dx ------[----------:—?-
J 2 (m — n) 2(m4-n)
[«’=?ь л2]. [При тг = пг см. 450.11.]
f - j--cos x dx— «= — In (m sin x 4- У 1 4- «2 sin2 x),
J V 1 + m2 sin2 x m
f cos x dx 1 ,
| . ....-— = — arcsin (m sinx).
JK1-m2sin2x m
482. IJ ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ tg X 101
470.3. J (cos x) V 1 4- m? sin2 x dx = = V 1 + sin2 x 4- ~ In {m sin x 4- V 1 4- тг sin2 x).
470.4. J (cos x) V 1 —m* sin2 x dx = _ Sinx у | —тг sin2 x arcsin (да sin x).
475.1. §f(x, sinx)dx =— —У> cosjjdy, Л где У=~2"~х-
475.2. ^/(x, cosx)dx =——У> sinj^dj, л где y=-^~ x. Интегралы, содержащие tgx
480.1. Jtgxdx =— In | cosx| =ln|secx|. - [Cm. 452.11 и 603.4.]
480.2. J tg2 xdx = tgx —x. [Cm. 452.22.]
480.3. У tg’ x dx =y tg2 x 4- In | cosx[. [Cm. 452.33.]
480.4. У tg4 x dx = у tg’ x — tg x 4- x.
480.9. У tg"x dx = ^—у — ytg"~2xdx [n^=l; cm. 452.8].
481.1. (* , . x’ , x5 , 2 17 , J x tg x dx - 3 4- 15 4- 105 x | 2835 x 4- ' t. 62 x-“ 1 I , 1 11-2835 1 1 (2n +1)! x +••• [x’C^-; cm. 415.03 и 45].
481.2. Ctgxdx , r2 , 2 5 . 17 , j x ~*+ 9 +75% Ъ205Х + -4- 62 x’ 4- 4- 1 1 9-2835x 1 1 (2n—1)(2п)! X + ‘ [x2 < cm. 415.03 и 4б].
482.1. f tgxVI= ± + t ln isin x ±cosx i- J g [Cm. 456.05 и 455.06.]
102
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
1482.2
482.2.
483.
490.1.
490.2.
490.3.
490.4.
490.9.
491.1.
491.2.
492.1.
492.2.
493.
Г 1gXdx С dx х _ 1 , , . , ,
\ 7-=—ГТ = \ Т1---1— = Т -F Т In Sin X 4- COS X .
J tgx ±1 J 1 ± ctgx 2 2 1 1
[Cm. 455.03, 455.04
f dx ____P cos x dx ______
J a b tg x J a cos x b sin x
= (ax 4- b In | a cos x 4- b sin x |).
и
492.1.]
Интегралы, содержащие ctg x
J ctgxdx = In |sinx|. [Cm. 453.11
ctg’x dx =— ctgx —x.
j* ctg’ x dx -ctg2 x — In [ sin x f.
Г ctg’x dx =—г ctg’ x 4- ctgx +x.
V
—У ctg”-2xdx [n^ 1; CM. 453.8].
x’ x5 2x’
'“9 225 — 66l5-
^aBn „tn+i__
(2n4-l)l
1 x x! 2xs
~T—T35—4725“
— —[См. 415.04 в 45.]
[• tgxdx
J tgx ± 1 ’
C dx
J tgx ± 1 *
Ssin x dx
a sin x 4* b cos x
(ax—b In | a sin x4- b cos x |).
У х ctgxdx = x
х*
9-4725 "
х’
7-4725
х
f* dx _____________
Ja+bctQX~
и
603.1.]
[См. 453.22.]
[См. 453.33.]
[См. 415.04 и 45.]
[См. 482.2.]
[См. 482.1.]
III.
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
500. Приведенные ниже формулы относятся к главным значениям
обратных тригонометрических функций: для arcsinx н arctgx в пре-
делах от----до , для arccosx и arcctgx от 0 до л. Инте-
грируя эти функции, следует выбирать пределы таким образом,
чтобы между ними не было точек разрыва. Полезно предвари-
тельно построить график подынтегральной функции, так как он
может состоять из нескольких ветвей.
501.
502.
503.
504.
505.1.
, х> , l-Зх1 , 1-3-бх7
arcsinx — х + 2 34-2.4,5 + 2.4.6-7
^Получается разложением в ряд
интегрированием его.^
х’ 1-Зх5 1-з-5х7
2-3 + 2-4-5 + 2-4-6-7
= и последующим
arccos х =
1 . 1 . 1-3 . 1-3-5 .
arccscx — х 4- 2>3х,+ 2.4-5х’*^ 2-4-6-7х7^
л /I , I , 1-3 , 1-3-5 , \
arcsecx —2 4- 2.3х’*^2-4-5х’ + 2-4-6-7х7 +
К>1]*
arctg х = х—-у 4--^---у-4-..«
(Получается разложением в ряд . и последующим
интегрированием его.)
505.2. arctgx = i-|4-i-i + ^-... [х>1].
505.3. arctg х = - -14- •
104 ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ [505.4
SOM. arctgx-TT7,[1+7(Ti7,)+^(TA_,) +
. 2-4-6/ х2 \’ , 1 г 2 1
+ 3^7кТ+р) +’••] [*<«>]•
506.1. arcctg х =-5-— х +--4~ + 4---[х2< 1].
506.2. arcctgx=l-i + A__l,+ ... [Х>1].
506.3. arcctgx = n + -|—..Г [х < — 1].
Оу
507.10. Arcsin (х ±/у) = лл+ (—1)" arcsin ?
±/(_1)"АгсьЦ^.
Значения р и q см. 507.11 и 507.12.
Величина г = К—1, а п—целое число или 0. Вели-
чина х может быть положительна или отрицательна,
а у—положительна.
507.11. Здесь обозначено р — КО + х)г + у2.
507.12. Здесь обозначено q = К(1—х)2-|-у2.
Заметим, что при у = 0 и х > 1, q — х— 1 и р -|- q = 2х.
- При у = 0 и х<1 7=1 — х и р + <7 = 2.
Иначе:
507.13а . Arcsin А = — /1п(± К1 — А2-Н'А) + 2£л
или
507.136. Arcsin А == i In (± /1 — А2— /А) +2Ал,
где А может быть комплексной величиной, a k—целое
число или 0.
О квадратном корне из комплексной величины см. 58, а
о логарифме см. 604. Выражения 507.13а и 507.136 тождественны.
Из них следует выбрать то, в котором не происходит потери
точности при вычитании.
507.20. Arccos (х + iy) = ± (arccos jq^ + 2fcrc— i Arch^pQ .
507.21. Arccos(x—/у) = ± (arccos 4*/Arch ,
где у положительно. Здесь берется положительное зна-
чение Arch^i^. Значения р и q см. 507.11 и 507.12.
512.5]
ПРОИЗВОДНЫЕ
105
Иначе:
507.22а. Arccos А = T i In (А + V А*— 1) +2&Л или
507.226. Arccos А = ±/1п(А — V А2—1) 4- 2/гл, где А может быть комплексной величиной. См. примечание к 507.13.
507.30. Arctg (х -Ну) = р2А + 1) л — arctg — arctg —j -j- , i .„О+^ + х2 -f 4 ul(l-i/)2-i-x2 • Иначе:
507.31. . , , , . . 1 . 2x , i . (1+^ + x* Arctg (x + ry) — 2 arctg 1 br+ 4 In , где k—целое число или нугь; arctg 1_х2_^2 берется в квадранте, определяемом знаками числителя и знамена- теля (а не в смысле главного значения).
507.32. Arctg(x+zy)— 2 In j + yy + ix+ Ъкя. [См. 604.]
508. Для малых значений arccos х, arccos х= (1 — х) + -|- (1 —х)2 + + ^(1-х)2 + ^0—х)4 + •••] . Последним членом можно практически пренебречь. Числен- ное значение квадратного корня можно брать из подробных таблиц квадратных корней (см., например, [18]).
Обратные тригонометрические функции — Производные
512.1. d arcsin dx X a 1 К a2 — x2
512.2. d x — 1
— arccos
dx a V аг— хг
512.3. d arctff - x a
dxarLtg , a аг + ^ '
512.4. d dxaICCtg X — a
a аг +x2 *
512.5. d -г- arcsec dx X a
a x V хг—аг
I п . х . п 1
0 < arcsec — < -н- .
L а 2 J
106
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
[512.6
612.6. d х —а Г л х _ 1 ~г- arcsec — = —-jt < arcsec — < л . ах а х/?- с? I2 а J
512.7. а х а Г л _ х „1 ~г- arccsc — = —т== гг < arccsc — < 0 . ах а х И х2 — а2 L 2 а J
512.8. d х —а Гл х _ п 1 ах а х у х2—а2 L “ 2 J (а> 0 всюду, кроме 512.3 и 512.4.)
Обратные тригонометрические функции — Интегралы (а>0)
515. \ arcsin — = х arcsin — + V а2 — J а а * г
516. J ( arcsin dx = х^ arcsin —2х+2Уа2 —х3 arcsin-^- .
517.1. Г х . ( х2 а2 \ . х , х —j г- \ хarcsin — dx= f -5 — ) arcsin—f-~y а—x .
517.2. Г x’ arcsin — dx = 4" arcsin — + 4- (x* 4- 2а3) У а2 — x3. J GO GV
517.3. C » . x . f x4 3a4\ . x . 1 X arcsin — dx — I —: ) arcsin h J a \ 4 32 / а 1 + 55 (2x* 4- Зха2} У а2 — х\ ал
517.4. С 4 . х , Xs . х , 1 х*arcsin— dx — ~ arcsin —[• J а 5 а 4-k (Зх4 + 4х’а* 4- 8а4) У а2 — х2.
517.5. С . , х . /Xе 5а’\ . X . \ х arcsin — dx — -г -„с-) arcsin —к J а \ 6 96 / а ' + 2^8 (8Х’ + 1 °Х’а2 + 15ха4) У — х"-
517.6. С х’ arcsin — dx == 4- arcsin — 4- ok + 6х4а2 4- J Q, ! Cl ZrtO 4-8x3a44- 16a’)Va3— x3.
517.9. On , x . xn+l , x if x”+1dx r . tl 1 x" arcsin —ax== —— arcsin гт \ > [«=5^— 1L J a n4-1 a n 4-1J ya2_x2 ' 1 [Cm. 321 — 327.]
518.1. C 1 „ x , x , 1 x2, 1-3 x5, J x arcsln a dx a +2-3-3 a2 +2-4-6-5 a2 + , 1-3-5 x2 ( 2 21 1 2-4-6-7-7 a’ + • •• Iх <a ]•
522.9]
ИНТЕГРАЛЫ
107
518.2. 1 arcsin — dx = — arcsin - In 1 if 1. J x* a x a a | x I
518.3. Cl . x . 1 . x Ka3—хг I -у arcsin — dx — —тгт arcsin —. J x9 a 2x2 a 2a2x
518.4. Г 1 . x . 1 . x V a2—x2 J x* arcsin adx= 3x, arcsin a бл2 ‘ ln|.a+/Q2-^l 6a3 1 x | *
518.9. fl . x . 1 . x , \ —jf arcsin — dx = — -j ri_~. arcsin — 4- J xn a (n—l)xn 1 a ‘ + _L. f $= 1л 7^1] [См. 341 — 346.1 1 /1-1J x""1 Iх a2—x2 1 J 1 J
520. i arccos — dx = x arccos——1/a2—№. J a a r
521. ff arccos—^ dx — x (arccos ——2x — 21/a!—x3 arccos-. J к a) \ a) a
522.1. Г x j / x2 a2 \ x x -5 s- \ x arccos — dx == -r? r | arccos -V a — x . J a \ 2 4 J a 4 '
522.2. f x2 arccos — rfx = 4“ arccos — —4- (*2 + 2а2)У a2 —x*. J a о a 9 ' 1 ,r
522.3. \ № arccos — dx — J a (x‘ 3a* \ x 1 т — (-4 32*) arccos-—gg (2x* 4-3xa ) ]/ a3 —x ,
522.4. § x* arccos dx = = arccos ——(3x* 4- 4x‘a‘ 4- 8a4) У a**—x*.
522.5. C s x , f x* 5a’\ x i x arccos — dx = ) arccos J a \ о 96 / a —~(8х1+\0х,а1+\5ха*)Уаг-х\
522.6. C e X , X7 X i x arccos — dx — -= arccos J a 7 a —(5x“ 4-6x*a* 4-8№a4 4-16a") 1/a*—x3.
522.9. C n x . xn+1 x . 1 •(* xn+,dx I x arccos — dx = —r-г arccos — l -7== J “ «4-1 a ' nH-l J j/^aa—x2 [лу=-1]. [См. 321 — 327.]
108 ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ [523.1
523.1. Г 1 х j л . . . х 1 х3 1-3 х5 J х - а 2 1 1 а 2-3*3 а3 2-4-5-5 а5 1-3*5 X » в 21 2-4-6-7.7 а1 •” Iх <а ]•
523.2. f -4 arccos — dx = arccos - + - In / a^~ — ° ~x 1. J xz a x a ' a 1 x |
523.3. fl X , J X l/’n2 j-2 \ — arccos — dx = — arccos —к “ a x J x’ a 2x2 a 2a2x ‘
523.4. fl x , 1 x a1 — x’ 1 — arccos — dx = — -5-3 arccos —к e .—h Jr a 3xe а ' 6a2x2 K , 1 . I a 4- V as — x! I 4- 7—2 In —' . 6fl2 1 x [
523.9. fl x , 1 x \ -7Г arccos — dx = arccos J xn a (n— 1) xn 1 a 1^1]. k". 341 346.1
525. J arctg dx = x arctg — — In (a2 4- x2).
525.1. J x arctg dx = (x* 4- a2) arctg — 7 .
525.2. C x2 arctg— dx = -^- arctg— — ~e~ in (a2 + x2), J a a 3 & a 6 ‘ b
525.3. C » . x , l,4 4ч . X axs a3x j Xsarctg- dx=T(x‘— a)arctg-—12+ — .
525.4. j X arctg a dx- 5 arctg q 20 4- 10 10ln(a+x2).
525.5. C s . X , 1 . . , .X ах5 , a’x2 o5x j Xsarctg a dx-6 (x’ + o )arctg a 30 + j8 6.
525.6. (* . , x , x’ , x ax’ . a’x4 a’x2 J x arctg-dx- 7 arctg q 42 + 28 14 .+ + 4Ма’ + *‘).
525.9. Cx"arctg — dx — -^-375 arctg — ^-7 f x2 [nф— 1 ]. J ° a ra-J-1 ° a n 4-1 J a 4- x2 1 ' J [Cm. 121-128.]
528.9]
ИНТЕГРАЛЫ
109
526.1. С — arctg— dx= ———йгт+... [**<<**]»
J x to a a 3aas 52a5 72a7 ’ 1 1
я i . . . a a3 , a5 a7 Гx 11
— 2 ln I x I + x 32X3 + 52xs 72X7 + • • • [ a > 1 J ’
л , I . , , a а’ а’ а1 Гх il
— 2 nlxl+ x 32x’ + 5!x’ 72x’ + -’-[a < *J ’
глл n ci . X , 1 . x I , a2+ x2
526.2. \ arctg — dx —-------arctg--------x- In —r—.
J x2 b a x a 2a > x2
хлл О Cl I X J 1 ( 1 1 \ L X 1
526.3. j -t arctg - dx = - T 4- -t) arctg .
. С 1 . x , 1 . x 1,1. a2 4-x2
526J. j p arctg - dx = - др arctg - - — + —, In .
_o/, _ fl . x . 1/1 1 \ . x 1,1
526,5, J x’arCtg a'dX“ 4 (a4 x4) arctg a 12ax’+4a2x‘
526.9. jp,arctg- dx = — {n_l}xn-, arctg — 4- —, j x„_t (аг + х^‘
[л=#1]. [См. 131 — 135.]
528. У arcctg-^ dx » x arcctg 4- In (a2 4- x2).
528.1. j* x arcctg dx = 1 (x* + o2) arcctg p- .
528.2. C x2 arcctg — dx = ^- arcctg — 4-~ In (o2 4- x2).'
do d о о
„ C 2 l x , I,. 4. x x , ax2 a’x
528.3. \ x’arcctg - dx = j (x—o*) arcctg — 4--jj—j-.
528.4. j x1 arcctg - dx = -^ arcctg - 4- -io- + To n + x
528.5. j x’arcctg-dx = -g-(x’4-o’) arcctg-4--3Q-iy + '-g-.
528.6. yx’arcctg^-dx=yarcctg^-4--^-—^|-4-
+тг-Г41п^2+х*)-
f* Y У /1 P fly
528.9. j xn arcctg - dx = arcctg- + — J —г [Л^=-1].
[См. 121 — 128.]
110
529.1.
529.2.
529.3.
529.4.
529.5.
529.9.
531.
531.1.
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ (529.1
у ТГ У У* I у® у’
ircctg— dx = —In |х|—— 4-^5—5^54-^7 — • • •
=_ ___________________
X + 32х* Vx^Fx’ ••• L«^ J’
= Л ln[x| 4-^-j — ^-.4-^-;—...
11 x ~ 32x8 52x8 7*x7
fl . X , 1 ! 1 I fl2+rl
j 7 arcctg T dx = - T arcctg т + sln •
(* 1 . x , 1 . X . 1 I 1 . x
} 7* arcctg 7 dX = - 7? arCCtg a + 2S + 2^ arctg 7
Cl . x j 1 . x , 1 1,
i -3 arcctg — dx — — ^-5 arcctg—— т-jln
J x4 b a 3xa b a1 6ax2 6a*
Cl , -x , 1 . x . 1
J -s arcctg - dx--arcctg - 4- -
____1
4a’x
*2
1 , x
4^arCtSa
C 1 . x j 1 , x
j -n arcctg - dx = - (n_t)Vr-- arcctg - -
----Ц f » {n Ф 1]. [Cm- 131 —135«]
n — 1J x"~’(a2-J-x*) 1 ' 4 1 J
\ arcsec — dx — x arcsec —— a ln|x-|- x2 — o2l
J a a ’
[л x л 1
0 < arcsec 7 < у »
e=xarcsec у + a ln|x4-]/x2 — a2[
[Л x 1
у < arcsec — < л .
P JC X2 X Q. 1 / 'Г"" 2
\ x arcsec — dx «arcsec---------77 у x — a
J a 2 a 2 9
ГЛ x л 1
0< arcsec — <-n .
I a 2 J ’
= -arcsec-4-2 Vx2-a
[Л X 1
у < arcsec у < л
532 3j
ИНТЕГРАЛЫ
111
531.2. С x2 arcsec — dx = arcsec — —
J a 3 a
—у /x2 —о2 — у In I x+/х2- a2 I
[0 < arcsec <Z -y j,
= у arcsec у 4- у ]/x2 — a2 4- у In | x4- ]/x2 — a21
[n x _ 1
-- < arcsec — < л.
2 Q J
_ (* n x , xn+i x a P xndx
531.9. \ x arcsec — dx = —гт arcsec------гт \ ,
J a «4-1 a «4-1J yx2—a2
[0 < arcsec у <;-yj > ln¥=—11»
xn+’ x , а Г xndx Г я x 1
= —гт arcsec —------гт I r .....- -r- < arcsec—< л ,
«4-1 a 1 «4-1 J у Хг — аг L 2 « J
[,/Z =7^- 1 ].
532.1.
532.3.
fl x j л , , . . , a , a’ . 1 • 3a‘
J T arcsec 7 — IF ln I * I + T + 2.3.3xa + 2-4-5.5xs +
. l-3-5a’ , x я 1
+ 2-4-6-7.7x’+’ ’ ’ [° < arcsec a < 2 ]•
532.2.
arcsec — dx =-------- arcsec — 4-
a x a '
1 x
—--------arcsec —
x a
x
arcsec —
a
л x
-x- < arcsec — <; л
2i G>
1 x ,
arcsec — dx —
xa a
1 x . Vхг—аг 1 lai
= — T arcsec —-----------—=—h -r-, arccos —
2x2 a 4ax2 '4a2 | x |
[ 0 < arcsec — <
I a 2
1 x У'х2 — a2 1 lai
= arcsec у----------------------г arccos | -1
[Л X '
-x- < arcsec — <л
2 a
112 ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ [532.4
632.4.
х , 1
arcsec — dx — — %—. arcsec
а Зх’
X
а
(2х8 + аг)
9а’х’
1
= — др arcsec
[0<
х • (2х2 4- а2)
а 9aaxa
х -
arcsec — <
а
л х _
-тг <arcsec — <л
2 а
532.9.
534.
534.1.
534.2.
1 х .
-= arcsec — dx =
х" а
1 х . а Г dx
== — т-----<т-тп arcsec —-------------; i ----------—
(n— 1)хп ’ a n—I J x" Kx2 —a2
[o < arcsec у < -yj 1 ],
1 x a f dx
“ (n—1) xn~l arcsec a га—1 J xn |/'Xs_a2
£-y < arcsec <nj, [n#= 1 ].
В формулах 531—532.9, х2>а2.
arccsc — dx = x arccsc — a In lx4- l^x2 — a* I,
a a 1 1 1 ’ 1 ’
Гл x n
[0<arccsc-<-y
= x arccsc у—a In | x-|-j/x2—a2|
Г n x
I—< arccsc — <0
xarccsc — dx — ^-arccsc -4- [Zx2—a2
a 2 a ‘ 2
Гл x _ я'
0 < arccsc — < -x-
a 2
X* X а ,Г~г-------2
= у arccsc ——-g- у x — a
Г Л _ X
---у < arccsc — <0
i Xе arccsc — dx =
I s a _______ s ___________________
= у arccsc у + -y Vx2 — a2 4-у In |х4-}/Л*2—a2[
ГО < arccsc — < -J
L a 2
x“ x ax tr~i--------2 aa , , , ./-»----2i
= v arccsc--------— У x—a—In x4- V xr—а
3 a о ’ 6 1 1 1
arccsc
635.4] ИНТЕГРАЛЫ 113
„ С п х . хп+‘ х . a f хп dx
534.9. j х” arccsc ~dx = ~{ arccsc - + —, J
(- X 71 ~I r • « *
0 < arccsc— < у , [л#=— 1],
xn+1 x a C xn dx
= ——r arccsc-------г \ - r ......
n+1 a n + 1 J у x2—a‘
Г—< arccsc<oj, [л#= — 1].
. Cl x J
535.1. arccsc— dx —
J x a
__ (a । 1 a> л. a* । 1'3‘5 «’ \
— — ^Y + 2^3 x* + 2-4-5-5 x“ + 2-4-6-7-7 x’ + ' " )
[-y < arccsc x< A
535.2.
1 x , 1 x
s arccsc — dx —---------arccsc —
x2 a x a
Kx<=T2
ax
535.3.
535.4.
0 < arccsc
1 x .
—--------arccsc —k
x a 1
arccsc — dx =
a
1 i
= — 2p- arccsc
n-г arccsc
2x8
ax
arccsc
X
a
a
хг—a2
4ax‘
V x2 — a2
4ax2
x , 1 x
arccsc — dx = — m arccsc —
a 3x’ a
1 x
= -3-s arccsc -
(2хг + аг)
9a’x’
x
arccsc —
a
(2x2 + a2)
9a’x’
114
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
(535.9
arccsc — dx —
a
1
(га —1)х"-*!
X
arccsc —
а
dx
xn Кx2—a2
< arccsc <o] , [«¥=1].
x а Г dx
n—\ J xn V xl—a2
Го < arccsc-£< Я > [л#=1].
L I» * J
В формулах 534—535.9 x*> as.
= —-------—— arccsc —
(n — l)xnl a
Я
1-0
tc
i f -^йлЫ^\»^}№У!1^-<МЬм
^UJt-----------------------
0
IV.
ПОКАЗАТЕЛЬНЫЕ ФУНКЦИИ
550. е’ = 1+^ + г + |-| + ... + ^+... [х’Соо].
550.1. ах = е*1па =
х Ina (х In а)г (х In а)" rr’L-nol
= 1+ — +~27— +••• +~П—+’•• 1*<°о].
550.2. + [х‘<оо].
__ х . х SjX2 Вгх* ,В,х* В4х8
Ойь ех—\~~ 1— 2 + 2! 4! + 6! 81 *
[х*<4л’; см. 45J.
een . -tn,, 1 . . 3«* 8“* 3u’ । 56и’ | t,,t ^
552.1. ^« = 1+и + -_—-— + -^-4-... [и <ooj.
552.2. = + 1«’<оо].
___ „ tou . . a’ . За’ . 9и4 37и3 Г « -я*1
552.3. е‘Е» = 1 + и + 5у + зг + —+ тг + ...
552.4. е^« = \+и'+^ + ^+~+... [и‘<1].
552.5. e^« = l+a + g+ («*<!].
Общий член этого ряда — где
552.6. е-*' 4- е-™ + е~^ 4---
Второй рид может сходиться быстрее первого.
553. limxne“* = 0 для любого п.
л->в
116
ПОКАЗАТЕЛЬНЫЕ ФУНКЦИИ
(563
Показательные функции — Производные
563. = 663.1. ^- = аеах. 563.2. ^- = а:
ах ах dx
563.3. = саех1па. 563.4. ~ = ау (In а)
dx dx ' ' dx
где а— константа.
563.5. ^- = уиУ-'^+иУ (1п«)^.
dx dx ' dx
563.6. %^уХУ-' + хУ(\пх)¥-.
dx •' 1 4 ’ dx
563.7. ^ = x*(l+lnx).
Ina.
Показательные функции — Интегралы
565. {exdx=ex. 565.1. С eaxdx = - еах.
J J a
565.2. {e~xdx =— e~x. 565.3. {axdx — ^—.
J J Ina
566. {f(eax}dx = —
J о J 2
где z = eax. Заметим, что
ax = ex ,n ° н acx = ecx ,n a.
567.1. J, xeax dx = eax —y2j.
567.2. §x*eaxdx — eax +
567.3. = +
J [ a a2 1 a9 a4]
A уПлвХ л» A
567.8. \xneaxdx = —-----— I x^'e^dx.
J a a J
567.9. J x?eax dx = eax [y—..
... + (_1Г-п2А+(_1)»Д]
U U J
_„o , Ceaxdx
568.1. — =
. . . , ax , aV , a‘x‘ , . anxn ,
= lnlxl + ц +2-21 +3-31 + ’•
[a^O].
. [x2<oo ].
j.0гяг
576.2]
ИНТЕГРАЛЫ
117
668.11. Для 1 _._ следует заметить, что c*=e*ln6?.
668.2. Р ettx dx еах Р еах dx rn . x+aJ х • [См. 668.1.]
668.3. С еах dx еах аеах , аг С еах dx rr _яо . . Г*’"- 2V~ 2x+2J х • [См. 668.1.]
668.8. Р еах dx еах . а Р еах dx , '>11 J х" (п—1)х"”’ 1 п — 1J х"-’ * '*
668.9. Р еах dx еах аеах J х" (п—-1)х"-1 (п — 1) (п — 2) хп~2 ап-‘еах ап~’ Р eaxdx (п—1) I х ' (П—1)1 J X [л>1]. [См. 568.1.]
669. С , d.X--x = X—1п(1 + «>*) = In J 1 + ех ' 1 + е
669.1. J a+bePx а ар 1 1
670. C xex dx e* J (1 + x)2 “ 1+x-
670.1. P xeax dx eax J (1 + ax)2 ' <?(1 4-ax) p eax
675.1'. \ eax sin x dx — g~r~'; (a sin x— cos x). •) a 4“ 1
675.2. P eax fz 2 \ \ eax sin2xe/x = -o—r asin x—2sinxcosx-|— ) t J a2 4- 4 \ a J
675.3. ^eaxs\n*xdx — eax f . , п , г , 6 (a sin x—cosx)l = -ГТ5 a sln x~ 3 sin x cos-^H TTZT • аг + 9 [ a‘ +1 J
675.9. I eax sinnxdx——гП—r~-(asinx—«cosx) + J a2 4- n2 ' + P sin’-’xflfx. a24-n2 J - p eax
676.1. \ eax cos xdx — tt-t (a cosx + sin x)' J <r +1
576.2. P eax (9 2 \ \ ea* cos2xcZx= * , ; ( a cos2x4- 2 sinxcosxj— |. J Gr 4“ 4 \ a /
ПОКАЗАТЕЛЬНЫЕ ФУНКЦИИ
[576*3
118
576.3.
576.9.
577.1.
677.2.
Je х cos’x dx — cos’х-ЬЗ sinxcos’x+
। 6 (a cos x+sin x) 1
+ a2 4-1 ]•
roc4v«“"cos"-1*,
J cos x dx----- (a cos x+ n sin x) -f-
-| n (n 1) P ax n_x
* a? j- ' J * cos x dx,
sin nx dx = (a sin nx— n cos nx).
Je cos nx dx — (a cos nx 4~ n sin nx).
> Jg tn.nxdx -
0
X ---------------
JJ^ в /'A^o
° Mr ~ а1~^г • aS' , k'f _ it. * , ,.
- 4% t . >•( я* м aZ « z (»
“ A/f"'
/ о
d. / Jrt “ x £
jjje kwizdz - eimnz - er + A
кл'" , .уч 3a'ft .
> MiSA(a^ '
iff
^5
лдлл^. / Hit й*- i(((
JJjj# ~ hnitz. ~в '
6 iM 9 "" JUf ,1,1 и,
. /• /А z + /%* i- Me , M =-7T—r,
I * 6fa ffiy
1A,M . Jt/f n , -
Z
585. Интеграл вероятности J е~р1г dt = erf =
[см. 590]
../'2 \ '/а Г. х2 , х* ' х’ , ] г _________,
~Х\я) L 2-113 *22-215 2’-3l 7‘ ‘ ‘ ‘ J Iх <°°Ь
586. Для больших значений х можно пользоваться следующим
асимптотическим рядом:
К2л J
. / 2 !*'• е"11'1 Г. 1 1-3 1-3-5 , 1-3-5-7 1
R=1 \ л / х I1 хг+ х* х8 + х8
Ошибка окажется меньше последнего взятого члена.
590. Иногда интегралом вероятности называют функцию
___ 2х Г1 ** I । 1 (х2 <<
[ 1! 3 -Г 215 317
гп. . . е-хг Г. 1 , ЬЗ 1-3-5 . 1
591 л erf L 2х2 22х4 28х® • • • J•
592. Другой вид того же ряда:
. . е-х* Г. 21 41 61 , 1
епхяа! xpGtl1 11(2х)2 + 21(2х)4 3! (2х)’+ ‘ * ’J•
Ошибка оказывается меньше последнего взятого члена.
Таблицы значений интеграла вероятности см. [196J.
VI
ЛОГАРИФМИЧЕСКИЕ ФУНКЦИИ
В этих алгебраических выражениях In обозначает натураль-
ный, или Неперов, логарифм, a 1g — десятичный логарифм.
600. 1п а = 2,3026 1g а. 600.1. 1g а = 0,43429 1п а.
у2 у8
601. |п(1 + х) = х--2+у-^ + 5-... [—1<х<1].
При х=1 отсюда получается известный ряд:
601.01. I„2_l_± + l_±+j._...
[у2 yS у4 ^5 П
[— 1 *Сх< 1].
601.2. ln(l^)=s[x+£+£_|4+...],
= 2Arthx [х’< 1]. [См. 708.]
= 2Arcthx [х2>1]. [См. 709.]
601.4. 1п(Ц-!-) =
= 2 [ I I _ *____j_____!____|_ 1
[_2x-f-1 + 3(2х+1)’ + 5(2х+1)’^ ’ ‘ ’]
[(2х+1)’>1].
601.41. In(х+а) = 1пх-4-2 [2x + fl.+ 3(2х-|-а)’ + 5(2х + а)? + •"]
[а2 < (2х-|- а)2].
601.5. 1пх=(х-1)—
[0<х<2].
602.6]
РЯДЫ
121
ent с 1 х~^ I (*~О* I (*—1)’ I
601.6. 1пх = — + L_± + —- + ...
6017 1пх = 2 Г*~1 I I*-"1)3- I . UL । 1
’ * in х 2[ж+1+з(х4-1)’ + б (х + 1)5+’,ф-1
во2.1. |„(£+/^т;)_
__ х ) ха , 1.3 х5 1.3-5 х’ .
“ аТЗ a’ + 2^T5ai 2-4.6-7ог + •”
1 2х_,_ 1 а2 1-3 а4 1-3-5 а’
' а ’ 2-2х2 2-4-4х4 '+'2.4.6-6хв
- . 12х I 1 а2 ( 1 -3 а* 1 -3.5 а6
П|’а | —‘Г2х2' + 2^Г4х4 2-4-б.бх4 +
= Arsh — = Arcsch —.
а х
[х>0].
[См. 706.]
602.2. In(/J + 1- -0----------------1о(Д+ /£+ 1).
Ряд из 602.1 умножить на —1.
602.3.
1-3-5 а4 ' 'Гх
2-4.6-бх4 ”• [а
1 а2 ___ 1-3 а4
2-2 х2 27^4?
[См. 260.01 и 707.]
602.4.
602.5.
_ а 1 а' ЬЗ а’ 1-3-5 а’ . г 2 ат
“Т-гТзлУ+гТТЗх4"-2-4-6-7Р’4' ••• Iх >а
_. 2а 1 х2 1 • 3 х4 1 • 3 5 х4 Га.
— П7 + 2^2аг — ^Ма^^г^-б-б а4 ’
. |2а| 1 Xs 1-3 х4 ЬЗ-5 х4 Г а :
= 1П| х I 2-2а2 ' 2-4-4 а4 2-4-6-6 а4 + ' " [ х < ’
= Arcsch— = Arsh — . [См. 602.1 и 711.].
ах 1 J
002.0. —1п(у+ /? + ')•
Ряд из 602.5 умножить иа —1.
122
ЛОГАРИФМИЧЕСКИЕ ФУНКЦИИ
(602.7
602.7. |"(т+ /?-')- . 2а 1 х2 1-3 хг 1-3-5 х' .. Га 11 = П х Ч-Чаг Ч-Ь-Ьа* 2-4-6-ба’ ”• [х >] ’
602.8. '"(г-/?-1)- . 2а 1 х2 1 -3 х^ , 1 -3-5 х’, Г — 11 П х ~'г2-'2аг 1 2-4-4 а* 1 2-4-б-ба4''" ' ” [х 1 ] » = -1п(^-4- [См- 710,1
603.1. 1 1 I ** ** X4 22П-,В„Х2П ln|sinx| In | х 1 -J 18(j 2835 ... n(2n)( [x2<«2J. (Интегрируя 415.04. См. 490.1 и 45.)
603.2. ... , . n „ cos 4x cos 6x In Sin X 1 = — In 2 — COS2X 5 5 . . . Z о [0<х2<л2].
603.3. . x* x4 x9 17x9 2гп-,(2га — 1)^пхгп 1 n cns X == ———— — — ' _f* _ uiiuw 2 12 45 2520 ... n(2n)! [x2<-|-] . (Интегрируя 415.03. См. 480.1 и 45.)
603.4. ln|cosx|=-ln2+cos2x-^ + ^-... [0<xx<n2/J.
603.5. In COS X = l[sin’x + s-!^+S£ + ^i+...] [*<£]-
603.6. ln|tgx|-ln|x| + 3+go^4- 2835xe + ... , 22П (22n~' —1) Bnx2" , • • ’ 1 n (2n)l “Г ' ’ * L 4 J ’ [Cm. 415.06, 432.10 и 45.]
604. In {x 4- iy) = In r + i (0 4- Ink), где r = ]/ x2 4-уг, cos 0 = x/r, sin0=y/r, k—целое число или 0, г—положительно, /=К=Т.
604.05. х4- iy — re1 <|)+гл*;| [0 в радианах]. [См. 604.]
604.1. 1п(— 1) = 1п 1 4-(2й4-1)ш = (2й4-1)^. [См. 409.03.]
605. limxlnx=0, [См. 72.] X -*о
613.3]
ИНТЕГРАЛЫ
123
Логарифмические функции — Интегралы Здесь всюду х и а положительны (если нет особой оговорки).
610. In xdx — X In X—X.
610.01. In (ах) dx — х In (ах) — x.
610.1. Р X2 X2 Ixlnx fifx = -g-lnx j.
610.2. Cx2 In x dx — v In x—. t) . J у
610.3. C № Inx Jx — Inx—77 .' J 4 16
610.9. Jx/’ln(ax)rfx-p + 1 ln(ax) (p + 1)« ' № И.
611.1. C’-^dx- M!. J x 2
611.11. у!нвл=1.{|п („)}.
611.2. 611.3. ClVrfx = _^_’ . J x2 XX J Vs 2x2 4x2
611.9. C 'n (°*) dx_ _ ln ! г п=ы j
612. ^(ln x)2 dx — x (In X)2 — 2x In хЦ-2х.
612.1. j x (In x)2 dx = (Inx)2—у In x + j .
612.2. У x2 (In x)2 fifx= у (In x)2 — y- In x + yr
612.9. П 9VF+1 9x^+1 Jxp(lnx)2dx-p + 1(lnx)2 (p + i), !nx4-(p+i), [P* Ч-
613.1. C (I*1 dx (In x)‘ J x 3 ’
613.2. P(lnx)8dx_ (In x)2 21nx 2 J хг X XX* P (In x)2 dx (Inx)2 Inx 1
613.3. J x’ 2хг 2x’ 4x2 ‘
124
ЛОГАРИФМИЧЕСКИЕ ФУНКЦИИ
[613.9
2
613.9.
614.
615.
616.1.
616.2.
616.3.
617.
617.1.
617.2.
617.9.
618.1.
618.2.
618.3.
618.9.
619.1.
619.2.
P(lnx)2dx_ (Inx)2 2 Inx
J xp ~ (p — l)xP~l (p —I)2 xP-‘ (p —l)V-‘
1P#= !]•
(In x)‘ dx — x (In x)‘ — 3x (In x)2 6x In x—Gx.
(In x)9dx = x (In x)9—q (In x)9~' dx {q^=— 1].
C(lnx)9 dx (lnx)9+I , ,,
J—x—=='7+T“ (9#=-П.
У xp (In x)9 dx = ~~j *? j xp (In x)9-1 dx
3-3!
(3 In х)8
(P, 9=# — И.
f(lnx)9dx — (Inx)9 . q [* (In x)9~* dx _л=ьц
J xP — (p—1) xP-1^ P—Ij xP {p'
j^_1n|l,x| + l„x + ^ + ^+...
f 1^7 “ln 11 ” x I + 21" *+T# =-
aj 111 A. 4 1 Zl
j">_iniinx|+3inx+^
j^# = !n|lnx[ + (p+l)lnx +
I (P 4-l)a (In x)a (p+l)2(ln x)2
"r 2-2f 'r 331 'г*-..
[ == ?—7^-, где y = (p 4- 1) In x; cm. 568.11.
3-3F
dx
Ж=1П|1П*|-
^ = ln(lnx|-lnx + <^-M
dx
x! In X
dx
x/'lnx
2-21 3-3!
In | In x | —2 In X 4- (~£-. .
= In ] In x 1 — (p—1) In x2^.2^ln —
(p— 1 )3 (inx)*
C dx____________— 1_____
J x (In x)9 (q— I) (In x)^~l
CxPdx ___ — xP+' .
J (In x)« ~~ (p-1) (In x)9~l
3-31
19#= И-
xPdx
(inx)?"1
623.5]
ИНТЕГРАЛЫ
125
619.3. f* dx — 1 p—1 f* dx J X'f'On x)9 x?~' (q— 1) (Inx)9-1 q — 1 J xP(lnx)9-' 19=/= 1 J.
620. J In (a -|- bx) dx — ° bx In (a 4- bx)— x.
620.1. 1 x\n(a-j-bx)dx=—^—In (а4-6х) + л7~т .
621.1. C In (a + bx) dx J X . f \f О I bx b*X2 . b2X9 b*X* . ГД2.Л s> = (In a) In x-f- a 22fl2-f- Зго« 42a«+ ••• x <a 1» _(ln&x)8 a , a8 1Л8х8^а81 ~ 2 bx PbV 3W 4W * • • x a i.
621.2. f = 1 1 п X - ( i + *-) 1 n (a + bx). J x® a \ x ' a J 1
621.9. f* In (a + bx) dx In (д 4- bx) . (* b dx J xP ™ (p — \)xP~l ' J (p~ 1) (a-)-bx)xP~l |р=£1]. [См. 101—105.]
622. C Inxdx (In x) In (a + bx) Cln(a + bx) dx ir „„ J a 4- bx b J bx 1
623. У In (x8 4- a8) dx = x In (x8 4-a’)—2x4-2a arctg ,
623.1. yxln(x84-a8)dx=-| |jx84-a8)ln(x84-as)—x8^ .
623.2. У x8 In (x8 4- o8) dx = = 4- [x* ln(x84-a8)—4x84-2xa8 —2a’ arctg-M . <? | 0 и J
623.3. У x‘ In (x8 4- a*)dx — = | px*—a*)ln(x84-a’) —j + x8a8j .
623.4. У x* In (x8 4- a8) dx — -g- [xs In (x8 4- a8) —| x’ 4- 4-^ x’a8—2xa*4-2a’arctg—1. a. J
623.5. J x’ In (x8 4- a8)rfx = = А [(Xе 4- «’) I" (хг + a2) “4 + ^-*’«‘1 •
126
ЛОГАРИФМИЧЕСКИЕ ФУНКЦИИ
[623.8
623. 6. j* х' In (х24- a2) dx — y p’ln(x’H-a’)—|х’4-
4--|-х'а’— -|- х*а2 4- 2ха2— 2а2 arctg у] .
623. 7. j* х1 In (х2 -|- a2) dx — у j\x’ — a2) In (х2 4- а') —
хв х*аг х*а* . 2 el
“4 +—--------------------------------------------Т+Ха J*
624. j* 1п | х2—а21 dx = xln| х2— а'| — 2х + a In
624.1. j* xln | х2 — а21 dx — ~ [(х'—а2) In | Xs—а21 — х2].
624.2. jx2ln|x2 — a2|dx = | [х* In | х2— а21 — | Xе —
— 2ха2 a2 In I 11.
I < ~а I J
624.3. Jx’ 1п|х2 — a2\dx=>
= j |\х*—а*)1п|х2 — а‘\ — —x'a’j.
624.4. Ух‘1п|х2 — a2|dx —у р’1п|х2—а2|—Xs —
— -1 х>а‘-2ха14- a2 In I х-±^ 11 •
3 I х—а | J
624.5.
х‘ 1п | х2 — а21 dx — -i- [(х«—а1) In [ х2 — а2| —
х* х*а2 2 ,
~3-------~Ха
624.6. j* х’ 1п| х2— а2\ dx — у £х71п| х2— а2| — у х’—
— — х*а2 —х’а*— 2ха* 4- а’ In I 11.
.. 5 3 I х—a IJ
624.7. j* х’ In | х2 — а21 dx = -g- ^(х* — а’)1п|х’ — а2/ —
4 3 2 * J.
Эти же выражения могут применяться к интегралам типа
Г хР In (а2 х2) dx.
626.9]
ИНТЕГРАЛЫ
127
Интегралы, содержащие г = (х’ + а’р’
Здесь всюду г > 0.
625. J]n(x4-r)dx = xln(x4-r)—г. [См. 730.]
625.1. Jxln(x + r)dx==^ + j)ln(x + r) —[См. 730.1.]
625.2. Jx’ln(x+r)dx = ^ln(x4-r)—J + [См. 730.2.]
625.3. Сх’ln(x-|-r) dx= f j—1п(х4-г)—^-f-^a’xr.
[См. 730.3.]
625.4. С х* 1п (х-)-г) dx = ^-In (х Ч-r) — +Д а*гг — .
J О лО I о , о
[См. 730.4.
625.9. Jx^ln(x4-r) dx ln(x + r)--^j
[₽¥=—!]. |См. 201.01—207.01 и 730.9.]
626.1. fXlnf-^4- )/§+l)dx =
X 1 х’ , 1-3 Xs 1-3-5 х’ , ,
*“ a 2-З-За’2-4-5-S а’ 2-4-6-7-7 а1 + * * * 1л:<а1-
1 /, 2xV 1а2. 1-3 а1 ЬЗ-5 а" , , . _ ,,
= 2 \П a J 2’х2^~2-4’х4 2-4-6’х4'^ * *' lXjaZ>l].
1 Л 12х | \2 , 1 а2 1-3 а4 , 1-3-5 а2
= 2 \‘П I а I ) + 2‘ х2 2-4’х4 i^2•4•6,x,
[х/а<—1]. [См. 731.1.]
626.2. f dx — — ?п (Х+-Л)— In I I >где Л = (** + а’)‘/2.
[См. 731.2.]
626.3. = 1См. 731.3.]
Л Л/Л Л
R9RQ [>|П(Х + Г)(УГ- ln<x + r) , 1 Г dx гп=А11
626.9. j—р— dx-------+
[См. 221.01 — 226.01 и 731.9.]
128
ЛОГАРИФМИЧЕСКИЕ ФУНКЦИИ
(627
Интегралы, содержащие s = (x!—а')72 Здесь всюду s > 0.
627. lci(x-b$)dx = x Iti(x-bs)—s. [См. 732.]
627.1. + [См. 732.1.]
627.2. Cx4n(x+s)dx = vln(*+$)—[См. 732.2.]
627.3. J Хг In (Х4-s) dx=^—1п(х4-у)— —т?—i^xs. [См. 732.3.] 10 «32
627.4. J x4ln(xH-y)rfx=y ln(x4-s)— [См. 732.4.]
627.9. p'ln(x + $)dx-p+1ln(x4-$) ₽+1j s [p#= 1]. [Cm. 261.01—267.01 и 732.9.]
628.1. C 1 . f * . ,/ x2 , \ . 1 fi 2xV , 1 a2 , 1-3 a* . 1 •— 1П ( — “p 1/ — 1 j dx = “5" ( 1П — ] Ч- ля *“3 4- а ,<з *4“ J x \ a 1 r a2 / 2 \ a J ' 2s x2 ‘ 2*4® x4 1 + ^5^+... lx/a>l]. [Cm. 733.1.]
628.2. C ln <* + s> dx = — ln(*+ij) 4- -L arcsec 1 - 1 J x2 x 1 a 1 a | [0< arcsec |x/a|< л/2]. [См. 733.2.]
628.3. = s [Cm. 733.3.] J x® 2x2 1 2a2x J
628.9. C In(x-H) In (x + s) , 1 C dx г J xP ax (p—l)xP-' 1 p-lj xP-'s LP^1!- [Cm. 281.01—284.01 и 733.9.]
630.1. P X® X® \ In sin xdx = x In x—Х—-ГГ—— J 1 о yUu 22'1-1 В„хга+1 - rn _ . 19845 n(2n-M)! [О<Х<Л]. [См. 45.] [Интегрируя 603.1.] , n sin 2x sin 4x sin 6x - x!n2 2 2<22 2<3, ... [0<х<л]. [Интегрируя 603.2.]
642.5J
ЛЯМБДА ФУНКЦИЯ И ГУДЕРМАНИАН
129
630.2. (*. . ? Is г’ |7г’ J ,П cos xdx 6 60 315 22680 [см. «.j [Интегрируя 603.3.| . n , sin 2х sin 4х . sin 6х “ xln2-|- 2 -..2^+2>3,. ... [х2<л2/4]. [Интегрируя 603.4.]
630.3. J Intg xdx = xlnx—Х + 7j- + ^o + 2»"(28'—^1)В . 1 19845 1 • • • 1 п (2П + 1У [0<х<л/2]. [См. 45.] [Интегрируя 603.6.]
631.1. р 1 1 1 sin In X dx = у X sin In X— у X cos In X.
631.2. J COS lnXfi?X=y XSin lnx + yX cos Inx.
632. C eax \nxdx = — eax In x— 1 C — dx. [Cm. 568.1.] J a ci J x 1 1 Лямбда-функция и гудермаииаи
640. Если х— Intg + у = In (sec 6 4* tg0), то 0 называют гудерманианом х: 0 = gdх = 2arctgех—у.
641.*) х = gd-1 0 = X (0)— лямбда-функция.
642.1. sli х = tg 0. 642.2. ch х = sec 0.
642.3. thx = sln0. 642.4. th^y^=tg^y^.
642.5. 542.6. = [-f<»<4]. Если имеется таблица 8 в зависимости от х, то можно нахо- дить гиперболические функции по таблице тригонометрических.
*) означает функцию, обратную гудерманиану.
VII.
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
650.01. ch1 х— sh2 х = 1.
650.02. shx = p/ch2x—1 [x 0], — — |/ch2x — 1 (x<0].
650.03. 650.04. 650.07. 650.08. 650.09. 650.10. 650.11. ch x = V 1 sh2 x. 650.05. sech x — 1 /ch r. thx=shx/chx. 650.06. csch x = 1 /shx. th2x-f- sech2x = 1. cth2x—csch2x = 1. sh (— x) — — sh x. ch( — x) = chx. th (— x) = — th x.
651.01. sh (x ± y) = sh x ch у ± ch x sh y.
651.02. ch (x ± y) = ch x ch у ± sh x sh j.
651.03. 2 sh x ch у = sh (x + y) + sh (x— y).
651.04. 2 ch x ch у = ch (x -f- _y) H~ ch(x—y).
651.05. 2shxsh j = ch (x-4- _y)—ch(x—y).
651.06. sh x -|- sh у = 2 sh ch x—^.
651.07. sh x— sh у = 2 sh ch .
651.08. chx-|- ch_y = 2 ch ch x-^.
651.09. ch x — ch у = 2 sh sh .
653.7J
ФОРМУЛЫ
131
651.10. sh2 x— sh2y = sh (x-bj) sh (x—y) = ch2 x— ch2 y.
651.11. sh2 x 4- ch2 у = ch (x -|- y) ch (x—y) = ch2 x 4- sh2 y.
651.12. csch2 x— sech2 x = csch2 x sech2 x = sha •
651.13. (sh x 4- ch x)" = sh nx 4- ch nx.
651.14. :— = ch x— sh x. sh x-bch x
652.12. sh 2x = 2shxchx.
652.13. sh 3x = 3 sh x 4- 4 sh’ x.
652.22. ch 2x = ch2 x 4- sh2 x = 2 sh2 x 4-1 = 2 ch2 x— 1.
652.23. ch 3x = 4 ch’ x— 3 ch x.
652.3. sh2 x = (ch 2x — 1).
652.4. ch2 x = y (ch 2x4- !)•
652.5. sh-| = (chx —1) [x>0], = — У 4 (chx— 1) [x<0].
652.6. ch| = ]/ y(chx4-l).
653.1. .. , , . th x ± th и th (x±у) = т , -7, . \ 1 £ th x th у
653.2. th (x ± — sh X ± sh \ 2 ) ch x 4- ch у
653.3. th 2x=,2/^r-. 1 4-th2 x
653.4. thx±thj,=^v>. * ch x ch у
653.5. , x chx — 1 shx 2 shx ch x4-1 ’
653.6. ,. , , . cth x cth и ± 1 cth (x ± y) — cth y ± cth x .
653.7. cth2x= Ctr^--. 2 cth x
5*
132
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
[653.8
653,8.
х___ sh х _____ch х +1
2 ch х— 1 sh x
654.1. shx = -i(e* — e"*) = y ^ln"’x—» где 1n”’x = e*..
Такое обозначение напоминает, что значения этой вели-
чины могут быть получены обратной интерполяцией из таб-
лицы натуральных логарифмов, чтобы не пользоваться ря-
дом 550, медленно сходящимся при больших х. Обратную
интерполяцию можно производить и по таблице десятичных
логарифмов, если воспользоваться тождеством 1п"’х =
= 1g"’(0,4343 х).
654.2.
654.3.
ch№|(eJ‘ + e-J')=-i(ln-,x + 1^^).
(См. примечание к 654.1.)
th — еХ~ е~* — е**~ I
Х~ ех+е~х~ еы+\
654,4. chx-|-shx = e*. 654.5, chx—shx = e"*.
654.6. sh((x) =(sinx. 654.7. ch((x) —cosx.
654.8. th (ix) = I tg x.
655.1. sh (x ± iy)= sh x cos у ± i ch x sin y.
655,2. ch (x ± iy) = ch x cos у ± i sh x sin y.
655.3.
th (x ± iy) =
sh 2x ± i sin 2y
ch 2x -j- cos 2y ’
e__ . .« , , . , sh2x^isin2u
655.4. cth x ± iy) = -гт— .
chzx —cos2r/
656.1. sh0 = 0. 656.2. chO = l.
657.1. shx = x + gj4--^-+-^-+...
уЛ y4 у®
657.2. chx = l+g + J+g7+...
656,3. th 0 = 0.
[x* < oo],
[x! < oo].
657.3.
„ A’ , 2 17 , , 62 ,
thx—X 3 +15* 315х + 2835 х
(2n)l °«x
[x« < j-: cm. 45^.
667.6|
ПРОИЗВОДНЫЕ
133
657.4.
657.5.
657.6.
658.1.
cth х — х -j- з 45 4- 945 4725 + • • •
+ [х'<п2; см. 45].
. ' , хг , 5 4 61 , . 1385 „
sechx=l — + ¥ х — -^х +-8T--V8- ...
к!<т:см-451'
. 1 x . 7x‘ 31 x5
CSChx — — — 6 4-ggg 1512o+---
.2(-l)n(22"-1-l) fv’^n2- см 451
... Hr -----(24)1--- + • • • (X < Л , CM. 4oj.
При x больших положительных
th x = 1 — 2 (е~гх — е-4*4-е-в*— ...).
При х отрицательных, воспользоваться формулой
th (— х) — — th х.
658.2. При х больших положительных
cthx = l 4-2(е-2ж + е-4х4-е-вж + ...).
При х отрицательных воспользоваться формулой
cth( — х) = —cthx.
658.3. При х больших положительных
schx = 2(e-x — е~,х 4~е~5х— ...).
При х отрицательных, воспользоваться формулой
sch( — x) = schx.
658.4. При х больших положительных
csch х — 2 (е~х-±- е~,х-±- e~ix 4- ...).
При х отрицательных воспользоваться формулой
csch (— х) — — csch х.
Гиперболические функции — Производные
667.1. '~ = chx. 667.3. = sech2х.
ах ах
667.2. shx. 667.4. = — csch’x.
dx ax
667.5. - s^ch-x = — sech x th x.
ax
667.6. = — csch x cth x.
134 ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ [670 Гиперболические функции — Интегралы
670. Интегралы, содержащие тригонометрические функции, часто можно преобразовать в соответствующие интегралы, содер- жащие гиперболические функции, заменяя х на ix и пользу- ясь формулами: sin(ix) — /shх, cos(/x)=chx, tg(/x) = zthx и т. д. [См. 408.10—15.] Эта замена бывает полезна и в других видах формул. Интегралы, содержащие shx
671.10. sh х dx = ch х.
671.101. Г sh — dx = a ch — . J a a
671.11. J x sh x dx = x ch x— sh x.
671.12. x‘ sh x dx = (x2 + 2) ch x— 2x sh x.
671.13. x’ sh x dx = (x’ + 6x) ch x— (3x2 + 6) sh x.
671.19. xpsh x dx— xpch x—p xp~' ch x dx. [Cm. 677.1.]
671.20. C < » j sh 2x x, \ sh x ax ~ — — . J 4 2
671.21. C . 2 , x sh 2x ch 2x xt \ xsh2xdx==—3 з -. J 4 8 4 *
671.30. f , s ch*x 1 sh x dx — ch x.
671.40. Г t,4 j sh 4x sh 2x , 3x jshxdx- 32 4 + 8 .
671.90. У shpxdx = shp-Ix ch x— shp-2xdx.
672.11. f sh x , , x3 . x5 , x1 . J x dx 3-31 + 5-5! + 7-71+•• •
672.12. iifc. [Cm. 678.11.1
672.21. J^dx=-lln|x| + 4fC4rrf(2*)- LCm. 678.11.]
677.20] ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ ch X 135
673.10. Jshx Jcschxdx-ln|th | Ini I — 2ln +
673.11. C xdx x’ 7xs 31 x’ 127x“ J shx X 3-3» ' 3-5-5! 3-7-71 ' 3-5-9! •••+<-1)0 ^£wLfinX2n+’+ ix‘<n’-См- 45i-
673.19. P x^dx 1 )"shT‘ Разложить согласно 657.6, умножить на xp и интегрировать
673.20. J£4csch2xdx==-cthx-
673.21. У ГР7 = “xcthx + 1п 1 sh x I.
673.30. У^-УС8СЬ’Х</Х- 2sh2x 2 lnlth2 I*
673.40. p dx cth’x 1 -T4- = cthx 5-- - J sh4x 3
673.90. C dx ch x p—-2 P dx <- J sh₽x (p—lish/’-’x p—1 J shP-2x У "'> '*
675. p , , , sh(m-f-n)x_ sh(m — n)x \ sh mx sh nx dx = —:—т 7- J 2(m + n) 2(m — n} \тг=£пг-, при mt = ni см. 671.20]. Интегралы, содержащие chx
677.10. ch х dx — sh x.
677.101. f , X . , X \ ch — dx = a sh — . J a a
677.11. J x ch x dx — x sh x— ch x.
677.12. xi ch x dx = (x2 + 2) sh x— 2 x ch x.
677.13. x’ ch x dx — (x’ + 6x) sh x— (3x2 + 6) ch x.
677.19. J xf ch x dx = xp sh x—p Jxp_,shxdx. [Cm. 671.1.]
677.20. f , , , sh 2x , x 1 ch2 x dx = + у .
136
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
1677.21
677.21. Р , , , х sh 2л ch 2х , х* j xch2xdx = — g- + j •
677.30. C ch’ x dx = sh x. V О
677.40. P t.4 j sh 4л , sh 2л , 3л j ch 32 + 4 4- 8 .
677.90. C ch' x dx = — sb x ch'"1 x -1- — — fch'-2 xdx.
J P p J
678.11. C ch x . ,ii, x2 , x4
J x X 1П Iх 1 1 2-21 * 4-41 6-6M • •
678.12. P ch x , ch x , P sh x , \ —j- ax = 4- \ — dx. J X2 x ' J x [См. 672.11.]
678.21. Cch2x dx I,, । , 1 C ch 2л J л “ 2 1П । X 1+ 2 J 2x d (2x). [Cm. 678.11.)
679.10. p C J = 4 sech x dx = arctg (sh x) — 2 arctg ex 4- const.
679.11. C xdx хг л* , 5x‘ 6lx’ , 1335x’°
J ch xe 2 4-2! "t* 6-41 8-61 * 10-8! • • •
| 1 D"^ „2Л-И , [x 2<^-\ Cm. 45].
••• 1 <2n-b 2) (2n)J 1 •••
679.19. px?dx 1 iTh-** Разложить согласно 657.5» умножить на xf и
интегрировать [p^o].
679.20. V -^2- ” \ sech’ xd х = th г. J ch2* J
679.21. C == x th x— In ch x. J ch2x
679.30. P dx sh x , -1 . , , > \ -тг = + тг arctg (sh x). j ch’x 2ch2x 1 2 °
679.40. P dx th’x \ 5“ • j ch4* 3
679.90. (* dx sh x , p—2 {* dx [Р>Ц-
J chPx (p — l)chP-Ix ' p—1 J chP-2x
681. P . . . sh (m-|- n)x . I ch mx ch nx dx = ~ 4- sh (m—n) x
J 2(m + ,ij r 2 (m—n)
682.01. [m‘^=n C dx — th * J chx+1 2 ’ 2; при тг - = я2 см. 677.20.)
ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ Sh X И Ch X 137
685.22]
682.02.
682.03.
682.04.
682.05.
682.06.
682.07.
682.08.
682.09.
682.10.
682.11.
682.12.
685.11.
685.12.
685.13.
685.19.
685.21.
685.22.
С dx ,, х
J chx—1 = —cthV-
С -xtb4 —21ncb 4-
J ch x +1 2 2
C x dx ,, x , „, . , x .
\ ; == — X cth -jr 4- 2 In sh -s- .
J cu x— I 2 1 1 2 1
C ch x dx ,. x
\ -Г—гт = x— th-тг .
J ch x + 1 2
P ch x dx .. x
\ т---г — x~ cth.
J ch x— 1 2
f т—A* in = arctg (sh *) — th 4 .
J ch x (ch 1) a ' 2
Jdx . , . . .. x
-r—y-r---j- = — arctg (sh x) — cth —.
ch x (ch x- 1) ° ' ’ 2
(* . dx__— A_ th —__- th’ —
J (chx+ 1)2 2 2 6 2 *
P dx 1 .. x 1 ,.sx
\ /-Т-r-. = TCth —— T-Clh 7Г .'
J (ch x— I)2 2 2 6 2
P dx _ 1 . . /3ch2x— IX
J ch2x + l 2K2" ГС \ch2x + l/’
для x>0 берется положительное значение Arch, а для
x<0—отрицательное.
f h?—= f --------------cth x. [Cm. 673.20.]
J ch’x—1 J sh2x 1 J
Интегралы, содержащие shx и chx
J. . , sh2 x ch2 x . . ch 2x , .
sb x ch x dx — —g— — ~2—b const = —-—[-const.
Ct. j ch’x
\ sb x ch x dx = —g— .
V
Cu t.3 j ch’»
\ sh x ch x dx = —r- .
J
Ct. t.c j chP+* x r ,
1 sh x ch” jf dx = ~ — 1].
P ., . j sh’-*
\ sh x ch x dx — —3— .
C t.i .2 j sh4x x
\ sh x ch xdx = —55---3- •
J ол о
138
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
[685.31
685.31. C sh8 x ch x dx = -7-^ . J 4
685.91. P sh?* ’ x \ shp x ch x dx = •
686.11. C dx = J sh x ch x In | thx|.
686.12. f* dx In] th 4 1. ch x 1 2 1
J sh x ch2x
686.13. C dx „ -U- + In |thx |. 2ch2x 1 ‘ 1
J sh x ch’x
686.19. f* dx 1 C dx
J sh x chPx “ (p—l)chP“’x * JshxchP-’x)
686.21. C dx shx arctg(shx).
J sh2 x ch x
686.22. f* dx — 2cth 2x.
J sh2 x ch2 x
686.31. Г dx _ — 'n 1 thx[.' 2sh2 x 1 1
J sh’ x chx
686.91. f* dx 1 C dx 1].
J sh*1 x ch x (p—l)sh^-1x Jsh/'-2xchx
687.11. (• sh x dx f J ch x J th x dx — In chx. [Cm. 691.01.]
687.12. (• s'l X dx 1 .
J ch2 x ch x
687.13. C sh x dx J ch’ x 1 th2x " 2ch2 x “ 2 +COnSt
687.19. f sh x dx 1 H П-
J ch? x (p—1) chP-* x
687.21. C sh2x . \ —r— dx = J ch x sh x — arctg (sh x).
687.22. C sh2 x , \ -Г5- dx = j ch2 x У th’x dx — x — th x. [Cm. 691.02.]
687.29. f sh2 x . \ dx = J ch” x sh x , 1 f dx IP^ И-
(p — 1) chP-* x ' p— ljctd'-’x
С sh’ х , sh2 х . .
\ -т— dx = —~------In ch х.
J ch x 2
f sh’x , , ,
) ch2"* dx ~ x sec“ x’
687.31.
687.32.
689.02] интегралы, содержащие sh х и ch X 139
687.33. J^dx = Jth’xdx== — ^-flnctix. [См. 691.03./
687.34. fcSrfx = 3S4-cT7-
«J Lil Л OLII X СП л
687.39. C^#-dx = .---гД^=1----;---бАР [p =# 1 или 3].
Jch^x (p —l)ch^ lx (p —3)ch^~’x u *
aa_ - CshP-*x. W>~'x ,
687.7. \ —To— ax =--7- p =/= 1 .
J chP x p — l 1
688.11. J^-~dx == Jcthxdx = In] shx|. [Cm. 692.01.]
688.12. C^^dx =------= — cschx.
J sh2 x sh x
aoa .о C ch x . 1 cth2 x ,
688J3« J^rfx==-2iP7 =----------— +const.
688J9- (p-bsV^I- 1^4-
688.21. J^yo!x = chx + lnjthy| .
688.22. J^7rfx = Jcth2xdx = x — cth x. [Cm. 692.02.]
688.29. \^p^dx— (p— i) sh^"1 x'+ p-И J sh/’"2x Ь ll-
688.31. f^dx«^4-ln|shx|.
Sil X X
P ch x
688.32. 1 dx = sh x — csch x.
688.33. fca’x , С . 1 -гт- dx = \ cth x dx = — J shs x J Cch’x , 1 1 + In | sh x [. [Cm. 692.03.]
J sh1 x “ 3sh3 x sh x '
688.39. Г ch’ x _ 1 Jsh/'xflX~ -(p-l)sh/’-,x (p^sh/'-’x l^1 или 31-
688.7. Pch'f'-’x . cth^_1* J sh^ dX^ p-Г [p Ч-
689.01. Jchx + l~ln(ChX+l)-
689.02. f^£ = ln(chx_l}. J ch x — 1 '
140
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
[689.03
689.03. f dx 1 , 1 , |.u х 1 1 —~ _L_ n th
J sh х (ch х 4- 1) 2 (ch х-|- 1) 1 2 1 2 | ’
689.04. C dx _ 1 1 In 1 th x 1
Jshx(clix—1) 2 (ch x— 1) 2
689.05. P sh x dx f ch x \ J ch x (ch x 4- 1) ° \ ch x 4- 1 / '
689.06. f sh x dx , /ch x— 1 \
J ch x (ch x — 1) \ ch x j ‘
689.07. C sh mx ch nx dx — - + J 2(m + «) 1 ch (m — n) x 2 (m — n} !2; при тг = = n* CM. 685.11].
Интегралы, содержащие thx и cthx
691.01. У thxdx = Inchx. (Cm. 687.11.]
691.02. J ih’xdx = x — thx. (Cm. 687.22.]
691.03. J th’ x dx — — + In ch x. [Cm. 687.33.,]
691.09. f th7’xdx = — Cth'’"2 J P— 1 J xdx [P ¥= !]•
692.01. j cth x dx — In | sh x |. [Cm. 688.11.]
692.02. cth2xdx = x— cthx. (Cm. 688.22.]
692.03. С j cth2x . . . , 1 cth xdx = 1- In | shx (Cm. 688.33.]
692.09. j" cth7 x dx = — j - + j* cth7' x dx Ip =i= i j.
VIII.
ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
700. Arsh х == Arch )/х2 -f- 1.
При положительном х берется положительное значение Arch,
при отрицательном х —его отрицательное значение.
700.1. Arsh х = Arth -% х—. = Arcsch — =
*
= — Arsh(—х) = In [хЧ- ]/x2 + I}.
[См. 602.1 и 706.]
701. Arch х = ± Arsh ]/ х2— 1 = Arth ^-—х—- =
в Arsech у = ± In [х + ]/х2 — 1}
(х > 1J. [См. 602.3 и 707.]
702. Arthx= Arcth 1 =1 In [л:2<11. [См. 708.1
703. Arcthx = Arth~=y 1п^ [х2 > 1 ]. [См. 709.)
704. Arsech х ~ ± In [0 <х < 1]. [См. 710.]
705. Arcschх = In + [См. 711.]
706. Arshx_x-5!3x- + J^x-_5Lg?,-+...
_ 1-/0^ , 1 1-3 , 1-3-5
- 1П(^ХЛ-2>2<8 2-4-4x1+2-4-6-бх’
[х>1],
= In I 2x1 — 1 I 1 ‘3________1-3-5
11 2-2х» '2-4-4x* 2-4-6-6x’ ' ' ’'
[x<—1]. [Cm. 602.1.)
142
ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
[707
707. . , , [ . 1 1-3 1-3-5 I Archx—± рп (2х) 22л,2 2-4-4Х1 2-4-6-6х“ "’J [х> 1]. [См. 602.3 и 602.4.]
708. Arth x=x+4 + 4+v+••• (См- 601.2.J
709. Arcthx = l + ^ + ^ + ^+... [х2>1]. [См. 601.3.]
710. . 1. , Г| 2 1 2 1-3 4 1-3-5 . ] Arsech х = 4- In z-zx — s-n х — _ .-x-g х — ... -1- [ х 2«2 2-4*4 2’4«6‘6 J [0<х<1]. [См. 602.7 и 602.8.]
711. ли 1 1.1-3 1-3-5 , г..2^1] х 2-Зх3 1 2«4-5х5 2*4*6’7х7 1 1 ' . 2 , J 2 ЬЗ 4 , 1-3-5 в — 1 П к — X — K-j—: X 4- „ . с—„ X — . . . х 2’2 2’4«4 2’4’6*6 [0<х<1], _._1п12| Lx»+ 1-3-5-х» + - n 1 х. I 2-2* 1 2-4-4Х 2-4-6-6ХН^" [— 1<х<0]. [См. 602.5.]
720. Arsh (-£ х + iy) = ± (— 1)" Arch 4- 2w 4- i (— I)" arcsin 4- inn, . u s 4* i здесь берутся положительные значения Arch——, п—це- лое число или 0, х положительно, у положительно или отрицательно. Значения s и t см. 720.1 и 720.2.
720.1. s = 1^(1 4-_у)2 + *2 (положительное значение корня).
720.2. / = р^(1—_у)24*х2 (положительное значение корня). Заметим, что при х = 0 и у>1, t — y—1 и s4-/ = 2_y. Если х = 0 и _у<1, t — \y—y и $4-^ = 2. Иначе:
720.3а. Arsh А = In (± V 1 + А2 + А) 4- ЙАл или
720.36. ArshA = — ln(±V 1 + ^2 — Л) 4- i2kn, где А может быть комплексной величиной, a k—целое число или 0. 0 квадратном корне из комплексной величины см. 58, а о логарифме см. 604. Формулы 720.3а и 720.36 тождественны.
728.4]
ПРОИЗВОДНЫЕ
143
721.1. Arch (х 4- iy} — ± ( Arch + i arccos + i2kn'\ .
721.2. Arch (x — iy) = 4- ( Arch — z arccos 4- I2kn ) ,
Z J_\ 2 p + <7 /
, « lP+</
здесь надо брать положительное значение Arch —у ;
х положительно или отрицательно, у положительно.
721.3. р — К(1 + ХУ +У* (положительное значение корня).
721.4. q = |/(1— х)2 4- у2 (положительное значение корня).
Иначе:
721.5а . Arch А= ± In (А + /А2 - 1) + Z2fen
или
721.56. Arch А = Т In (А - + i2kn.
(См. примечание к 720.3.)
722.1. А г th (х + iy) = | In j-'+g+^ +
+ 7 {(2ft+ 1) л-arctg-y^ —arctg-^} .
Иначе:
722.2. Arth (x 4- iy) — у In \ j~-8 + 4- arctg :——5 + ink,
' ' 4 (1—x)2+y2 1 2 1—x2 — ys 1
где k есть нуль или целое число, а арктангенс берется
в квадранте, определяемом знаками числителя и знамена-
теля (а не в смысле главного значения).
722.3. Arth (х + iy) =* 1 In + . [См. 604.]
£ IX I у
Обратные гиперболические функции — Производные
728.1. т- Arsh dx X _ 1
a V~ хг +d2
728.2. d » u 3- Arch X _ 1
dx a V" x2 — a2
728.3. 4- Arch dx X -1
a V" x2—a2
728.4. 4 . .. — Arth dx X a a a2—x2
Arch - >0, -> 1 | .
a a ]
Arch —< 0, - > 1| .
a a J
[х2<а2].
144
ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
(728.5
728.5. Arcth—
dx о
728.6. — Arsech dx X о —a X у^—X*
728.7. d * — Arspcn X (J
dx a x у а^ — х*
728.8. и — Arcsch x —a
dx а X Vx2+a2
(Всюду, кроме 728.4 и 728.5,
[х2>а2].
[A.sech|>0, 0<i< >] .
[Arsech — < О, О< — < 1] .
I в о J
в должно быть положительным.)
Обратные гиперболические функции — Интегралы
Здесь всюду а > О
730.
730.1.
730.2.
730.3.
730.4.
730.9.
731.1.
\ Arsh — dx = х Arsh —— ]/х2 + оЛ
J a a
f x Arsh — dx = ( Arsh -— r2 + a2?
J a \ 2 ' 4 / a 4
C x’ Arsh — dx = X Arsh — + -Q ~x- ]/x2 + a2.
J a 3 a 1 9 r
x’ Arsh — dx —
a
( x* 3a'\ , . x . 3a2x—2x’./-—~:—г
= [~—32) Arsh7 + —32— Vx +fl*
x4 Arsh — dx —
a
x’ . , x 8 a4—4a2x2 + 3x4j—---g-
» Arsh------------_g- T— V x2 + a2.
5 a 75 r
[Cm. 625 — 625.4.]
f p к i. x j xP+' л . x 1 Г xP+’dx , , ..
\ xp Arsh — dx = —г-r Arsh----—: \ r p 4= — I .
J a p+1 a P+lJ(G* + o2 1 1
(Cm. 201.01 —207.01 и 625.9.]
Г— Arsh — dx =
J x о
— _l/l 12* I A ’ 4. 1 1-3 a4 1.3-5a“
2 \ln I a I ) 2* x2 2-4’++2-4-e+e
_X 1 x’ 1.3 X5 1-3-5 x’ . 21
a 2-3-3 а’ + 2-4-5-5 a5 2-4-6-7 - la1 + --a 1-
12.2, 1-3 a4 1-3-5 a6
2s *2 + 2-4’x4 2-4-6’ ” *
732.31
ИНТЕГРАЛЫ
145
731.2. Cl. и х . 1 . . х 1 . 1 а + Кт4- чг \ s Arsh — dx — Arsh In — !— • Jr о x a a \ x \
731.3. f 1 . . x . 1 л . x Ухг + а‘ i \ -sArsh — dx — —Arsh —« . J x’ a 2x2 a 2trx « [Cm. 626.1—626.3.]
731.9. С Л Arsh — dx — —. , Arsh — + J xP a (.p — DxP-1 о 1 p dx + p—]J xp~'Vx2 + a2 [Cm. 221.01—226.01 и 626.9.[
732. C Arch — tfx—x Arch —— Vx2 — a2 Arch—>0 , J a a a ==x Arch £ + j/x2 — a* Arch£<0 .
732.1. C x Arch — dx — Arch — — 4- V x2— a2 J a \ 2 4 / a 4 r [Arch— >oL I a 1 / x3 a2 \ x , x . / - f— j = (2—4jArch7+4 ~a [Arch— <oj. 1 a J
732.2. f x2 Arch —dx = ^ Arch ——-° — ]/x2— a2 J a 3 a 4 ^Arch-i->(/j, ^Arch £ + 2^j/x2-a2 [ Arch — <Z ol. [ a J
732.3. C » л i. * j Iх* ^а*\ . . x За2* 4- 2x’,/ 2 г \ x Arch — dx = 1 -г—-so ) Arch xj— у x — a2 J a \ 4 32 J a 32 |^Arch £ > oj, f xl 3a*\ . . x . 3a2x 4-2x’.5 , -U 32jArch^ ZT-V* a ГArch £ <ol.
146
ОБРЭТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
(732.4
732.4. Jx4Arch^-dx =
= £ Arch ±-8аа+-4^.+^ /РСТр
5 а 75
^Arch^. >0],
Arch /3?=^
5 а 1 75
[Arch-^ <о1. [См. 027—027.4.]
732.9. jx^Arch^x =
___x^+1 . х 'Г xP+’dx
~~ р + 1 АГС" ~а ~ Р+Л J Vл;2—а2
Г Arch — > 0, р4=—Л,
L a J
__хр+’ . х 1 Р xP+'dx
~ ЯП Агс" и + ЯП J
ГагсЬ-^ <0, р+— 1). [См. 261.01—267.01 и 627.9.]
733.1.
С — Arch — dx =
J х а
1 fi 2xY л.1 a‘j_1,3 °4 1>3'5 a’_i_
2 V0 а ) + 28№ + 2-4‘ х1 + 2-4-6’х“+ •* ‘
[Arch- >0
L а
Г 1 2л V , 1а2, 1-3 а1 , 1-3-5 а" , ]
[2 \ а ) *t'23x2’t2.4’x1 + 2-4. 6’л" + ’ ’ 'J
[ Arch— <0
L а
733.2. f ^5 Arch — dx = —- Arch — 4- — arcsec I — I
Jr a x a ' a | a |
[Arch—>0, 0 < arcsec I — I <^-
l О. ' I a | 2
1 . . x 1 I x I
=------Arch--------arcsec —
x a a | a |
|_Arch-|-<0, 0 < arcsec ||
735.4]
ИНТЕГРАЛЫ
147
733.3.
dx — — m Arch —- 2-
2x2 a 1 2a2x
== —Arch —
2x2 a
2a2x
)]. [Cm. 628.1—628.3.]
733.9.
dx =
,---n p-i Arch
(p—\)xP 1
dx
l/~ ^_n2
734.
734.1.
734.2.
734.3.
734.9.
735.1.
735.2.
735.3.
735.4.
— 1 Д h _ 1 C -
(p—\)xP~l ГС a p — 1 J xP~' Ух2—a2.
[Arch-^-<0, p=£lj. [Cm. 281.01—284.01 и 628.9.]
От 732 до 733.9 всюду -^ > 1.
J Arth dx = х Arth +• In (аг— хг).
j х Arth - tfx==—2-Arth - + у .
f x2 Arth - dx = Arth - + ^ + ^ In (a2 -x2).
J a 3 a 6 6
\ x‘ Arth — dx— ——
J a 4
Г x-’’Arth — dx = Arth x
J a p + 1
С — Arth — dx
J x a
. ,, x . ax3 , a3x
Arth 7+1Т + -Г-
xp+1 dx
a p + 1 J a2—x2
[p^ — 1]. [Cm. 141.1—148.1.]
r 32a* 52a5 72a’ ‘
dx — —- Arth ~In (- .
x a 2a \ x2 J
x x
a **
2ax '
С Д Arth — dx=
Jr a
1 . ,, x . 1 1 , (a2—x2
3x’ a €ax2 6a’ \ x2
148 ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ 1735.5
735.5. f 1 . .. X , 1/1 1 \ « .1, X 1 1 \ — Arth —dx = — ) Arth ттг—»—T~r~ • j x5 a 4 \a* x4/ a ISax9 4a*x
735.9. ^xPArihadX- (p_i)x/,_1Artha-|- + p-lj xp-’(a‘-x*) tp¥dl- [Cm. 151.1—155.1.] В 734—735.9 всюду x2 <аг.
736. C Arcth —rfx = x Arcth — + In (x*—a2). J a a 1 2 ' '
736.1. C * x . хг—a3 . .. x . ax I x Arcth — dx==—-—Arcth }-лг . J a 2 a 1 2
736.2. f Xs Arcth - dx = £ Arcth ± + + f In (x2 — a2). J a 3 a 1 6 ‘ 6 '
736.3. f . , .. x , x*—a* . .. x . ax* , a“x I x Arcth — dx — —— Arcth h -nr + J a 4 a 1 12 ’ 4
736.9. C „ , ..x , xP+' . .. x a PxP+'dx \ xp Arcth — dx = —г-; Arcth „ , , \ =• J a P-f-l ap + lj о —x2 [p=/=—1]. [Cm. 141.1—148.1.]
737.1. P 1 , .. x . a a3 a3 a1 J x a x З^х9 &xs 7*х7
737.2. Cl.tt.Xj l»it* 1 । (—a‘\ I -r Arcth — dx= Arcth — In —5— . Jr a x a 2a \ x2 J
737.3. pl» it X , l/ll 1 \ » LtX 1 \ -r Arcth— rfx = — 5) Arcth —- . J x1 a 2 \a2 x*) а Чах
737.4. C 4 Arcth — dx = J x4 a 1 . ,. x 1 L /x2—a2> “ 3x’AfCth a ~6ax‘ 6a2 П у x2 J*
737.5. f 1 » .t- x j 1/1 1 \ » »t- x 1 1 \ -1 Arcth— dx— т -j ! Arcth 7-—j—-r-y . J xs a 4 \a4 x4J a \2ax* 4a*x
737.9. ^xPA^hadx- (p.j^p-.Arcth^ + p — 1 \хР~'(аг—x2)
[См. 151.1—155.1.1
В 736—737.9 всюду х3 > а*.
739.1J
ИНТЕГРАЛЫ
149
738. J Arsech dx = x Arsech ~ 4- a arcsin -j
[Arsech —>o],
л L a J
= x Arsech — — a arcsin —
a a
^Arsech <oj.
738.1. C xArsech — dx=^ Arsech— — 4 Va2—x2
J a 2 a 2
Arsech у
= Arsech — + 4 V — x2
2 a 1 2 "
[Arsech — <01.
L a J
738.2. J x2 Arsech ^-dx — Arsech —— К— x* +^- arcsin
^Arsech ~ > 0],
x3 , . x , ax-,/—5-2 a3' x
= -5-Arsech —h-r V a —x —arcsin —
3 a 1 6 6 a
[Arsech — < ol.
738.9.
739.1
Уп . i* j xP+ л t. x . a f XP dx
xp Arsech — dx~ —r-т Arsech ———r I -^=
a p+1 a 1 p + 1 J уQ2_X2
[^Arsech-^->0 p=+ — 1
a C xp dx
P+ 1 J Ka2—x2
Л I*
=----г Arsech —
p + 1 a
[Cm. 320.01—327.01.]
Pl. . x , If. a \ . 4a lx2 1-3 x
I — Arsech — dx= —-r-1 In — in
J x a 2 \ x J
1-3-5 x“
2-4-6’a* ’’ ’
1 (1 a \ , 4a f 1 x2 f 1 -3 x4 , . ,
2 Vn x J П x + 2’ a2+ 2-4’a‘+ 2-4-6’a’‘+‘ '
Arsech —
1 a
x 2’a2 2-4* a*
Arsech — > 0 ,
L a J
1-3-5 xe ,
150
ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
1739.2
п С 1 » u х _ х , V а2 — х2
739.2. 1 -з Arsech — dx -------Arsech —-------------
J x2 a x a ax
[ Arsech — > o],
L a ]’
1 . u x V'az—x2 f x nl
=----Arsech---------------— Arsech —<0.
x a ax L a j
pi x
739.9. 1 Arsech — dx =
j x'
— —1------n Г'-’i Arsech ------~T f---
(fj-l)xf' a p—i J xf Ya2—X*
[Arsech >0,
1 , . x , a f dx
(p — IjxP-1 a p — 1 J xp /a2_x2
[Arsech ^-<0, p=#ll. [Cm. 342.01—346.01.]
В 738—739.9 всюду 0<x<a.
740. 1 Arcsch — dx = x Arcsch — + a Arsh — .
J a a ‘ a
740.1. C x Arcsch — dx = ^- Arcsch — + хг 4- a2.
J a 2 a 1 2
740.9. [‘^Arcsch-rZx=—Arcsch-+-4т
J a P + 1 a p+1 J V\2 +a2
[f¥= — 1]. [Cm. 200.01—207.01.]
741.1.
741.9.
0 1. ,x j a , la’ 1-3 a‘
\ — Arcsch — dx = — —J- а’'о—о ~з ““ n . - c —г -4-
J x a x 1 2‘3«3x3 2‘4.5‘5x5 1
ЬЗ.5 a1
+ 2.4.6-7.7x7
[№ > a2],
! /. a \ . 4a 1 x2 1-3 У* 1-3-5 x“
= 2 ‘n x J ‘n x +2» a2 2-4’ a4 + 2-4-6* a* "
[0<x<a],
1 . I a I . 14a| 1 x2 , 1 -3 z4 1-3-5 x° ,
— 7 ln| 7 | П| 7| — ¥аг + 2-4’ a4 2-4.b’ ae + ’ ’ '
[—a<x<0].
0 1. , x ,
J ^Arcsch- dx =
_________* Arcsch —______C
(р-1)^-‘ЛГС5СП a p-i)xpK^+^
[p=/=l] [Cm. 222.01—226.01.1
В 740—741.9 всюду a > 0, z>0 (кроме 741.1J.
IX.
ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
ф
750. Обозначим и = f —d(p [А2<1],
J Kl-A2sin2<p 1
о
л
« f г dxr [х = Sin ф],
J К1 — X2 К1— kV 1 TJ
О
= Л(ф, k) (эллиптический интеграл первого рода, см. 770).
751.1. <р называется амплитудой, k—модулем.
751.2. ф = ати.
751.3. sin ф = sn и = х. 751.4. cos ф = cn u = j/1 — х2.
751.5. Дф или Д(ф, А) =1^1 — A2 sin2 ф = dn и = |/ 1 — А2х2.
751.6. tg ф = tn п = -.
V 1 — хг
751.7. Дополнительный модуль Д'= j/l — А2.
752.*) и = ат“’(ф, A) = sn“’ (х, k) = сп“’ {КI —хг, А) =
= dn"4prl — kV, A} = tn“’ r X , A
753.1. am । (— и) = — ат и. 754.1. ат 0 = 0.
753.2. sn ( — и) = — sn и. 754.2. sn 0=0.
753.3. СП ( — и) = СП и. 754.3. сп 0 = 1.
753.4. dn ( — и) = dn и. 754.4, dnO = 1.
753.5. tn( — и) = — tn и. 755.1. sn2« + сп2 и = 1.
*) Здесь показатель степени — 1 применяется в смысле обратной функ-
ции. (Прим, ред.)
152
ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
1755.2.
755.2. dn* «4 A‘sn*a = 1. 755.3. dn2u — A2cn*« = k'\
756.1. „ , . ... sn и cn v dn и ± сп и sn v dn и SO(U±V)-
756.2. . , ... сп и cn v Т sn и sn v dn и dn v СП U ± » = j ; ; . , 1 — k2 sn2 и sn2 V
756.3. . . , . dn и dn v + k2 sn и sn v сп и cn v dn(U±v)- . {_k2sn>u^v
756.4. 1 tn и fn v dn и dn v
757.1. _ 2sn и cn и dn и sn 2u = —: г;—j . 1 — k2 sn4 U
757.2. cn2u—sn2u dn2u 2cn!u , 1 — kz sn4 и 1—Z?2sn4w
757.3. . _ dn2u — &2sn2ucn4 2dn’u d n 2u = :—rs 3 = 3—~—3 1. 1—k2 sn4 и 1—ft2sn4u
757.4. , _ 2tn и dn и tn 2b = i—r~i—3-5- • 1 —tn2 и dn2 и
758.1. U -,f\ —СП U sn -Л- = 1/ 3-3—3 . 2 V 1 +dn и
758.2. и -. /"сп и 4 dn и СП 2 V 1+dnu *
758.3. dn4=-i/S2±+d^. 2 r 1 +cn и
759.1. sn (iu, k) = i tn (u, k').
759.2. Л)-сп(п, k'} •
759.3. dn({W) = . ' ’ ’ cn{u, k )
760.1. snu = u — (I +A2)£ + (1 +14A«4Jfe«)“‘_ O' O’ — (1 + 135Aa-b 135fe‘+ A") +..
760.2. cnu = 1 — 21+0 + 4A2) — (1 4 44A* 4 16A‘) gj’4 4(1 4408A14912A‘464A’)^—.
772J
ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
153
760.3,
760.4.
dn и = 1 - А2£ + (4 + k‘) А2£-(16 + 44А2 + А*)А2 gj +
+ (64 + 912А2 + 408А* + А’)А2 £ -
О!
amu = u—А2£ + (4 + А2)А2£-(16 + 44А2 + А1) А2^-
о! О! /I
+ (64 4-912А2 + 408А‘ + А’) А2£-
768.1.
768.2.
768.3.
Эллиптические функции — Производные
d .
— snu = cnudn«.
du
а л
— cn и = — sn и an u.
du
dn и = — k* sn и cn u.
du
Эллиптические функции—Интегралы
770.
Эллиптический интеграл первого рода
ч>
f dV
(ф| A) j у sin2 ф
о
771
Г______dx_____
= J К1-W
о
Эллиптический интеграл второго рода
*
Е (ф, А) = J Y1 — A2 sin2 ф </ф =
о
[х== sin<p].
[См. 750.]
772.
f V1 — А2х® ,
= I х._ = dx
' Kl —Xs
[х = sin ф].
Эллиптический интеграл третьего рода
ч>
f___________
J (1 -|- п sin2 <p> V~ 1—fe2 sin2 <p
О
X
П (ф, п
ах
— J (1 +пхг) fl-x* f 1—kW
о
n называется параметром.
Таблицы значений эллиптических интегралов см. [27], [28].
[х = sin ф]
154
ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
[773.1
Полные эллиптические интегралы
Я/2
773.1. К = f . 2 =
J V 1 — £-sin2<p
2 \ + 22 2M2 22-42-62 + ’')
773.2. tf = ^(l + /«) + .
. l2-3’-52 » , 1
22-42-62 ’ I ’
где m = (l — k')[(} + k').
Этот ряд сходится быстрее, чем 773.1, поскольку m2<z k*.
773.3.
12-32 Л 4 2 2 \ ,4
+ 2*-42\ 1-2 3-4/ ‘Ь
12 - 32 - 52 /. 4 2 2 2
*" 22-42-62 \ П k' 1-2 ЗД 5-(
где k' — [/1 — fe2.
774.1. £= J V1 — k2 sin2<ptftp =
= 1 k* *2‘3 l2-32-5 e
2 V 22 22-42 22-42-62 K
1].
тг Г /М2 I2 . 12.42 1
774.2. E = 2(1 +m) [ 1 + 2^ + 2M2 m *" 22-42-62 m + • • • j >
где m — (\ — 4-k').
Этот ряд сходится быстрее, чем 774.1, поскольку тг < k‘.
774.3.
£-,+Н|л?-^)4'’+
. 12,3 6 4 2 1 V'4 ,
^22-4\'Пй' 1-2 3-4)fe *"
, 12-32-5 /. 4 2 2 1
т iMMV «' b2 3‘4 5-6
781.01]
ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
155
С ач
775. F((p, k) = J у x_k2shi2(f =
= К— Sin Ф созф (± A2k* 4-Atk* 4-
Л у л Z • л
I 1-3-5 Д А» I \
+ 2-4-6 + • • • J »
где
з 1 л 3 , 1 . г
А2=.-2> + = 21 + 4- Sin2ф,
л 3-5 . 5 . 2 ,1.4
А — oVF + л-? sln ф + г-sinф,
6 2’4-6 1 4-6 т 6 т
А = +StsiI? ч’+is,si"4 ф+4sin’ (р-
а Д' находится по формуле 773 или из таблиц.
776. Аф, k)=(f + ^viki + ~viki + ~^vikli+ ...,
где
<р
u2n = J 5!п2пфЛр. [См. 430.]
О
ф
777. Е(ф, —/г2 sin2 ф <Уф =
о
= ~ Е 4- sin ф cos ф (j Агкг 4- Ajt* 4-
4-^4Jfes4-...V
1 2-4-6 ’ 1 ) ’
где Д2, Л4,... те же, что и в формуле 775, а Е может
быть получено из формулы 774 или из таблиц.
Г dx
’S’-1- j гт+? rr+f-g °1п (*' *> "> ° f (atclg x'
[x>0].
f dx 1 _. f x b\ *\ 1 с-,
781.01. 1 r - sn 1 -r, — | > = — р(ф, k)
J }fаг—хг ]^b2—x2 a \b’ a) a '
0
[ф=агс5!п+, & = ^-| , [0 <. x<Z b <Z a].
*) Здесь через sn-1 (x), tn 1 (x) обозначены функции, обратные sn x и tnx
(область изменения от 0 до К)- (Прим, ред.)
156
ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
(781.02
781.02. 1^=^==- = ! {K(k} — F(a>, &)}
Кх*-&2 v ’’
b
( . (Va2—x*\ , a2—6*1 tn l i
Ф « arcsin ( . ), k =------ , [0 < b < x < a],
L \/aa—&»/ a J> I .1
K(k)=F^~, — полный эллиптический интеграл. Как
обычно, интеграл от х, до х2 получается как разность
интегралов от b до х2 и от b до хг
781.03. f = 1 {A-W- F(у, k)}
J У —а2 ух2 — Ь2 а
а
[ф —arcsin (а/х), k=bja], [0 <Zb <Z а<х].
dx
t.-,)» f^-b2^*) 1
I f~ —r .. . = — tn < -T , -----> = — Г (ф. RA
J f & + x2 vь2 + х2 a \b' a ) a
0
, [0 < b <. a-, 0 < x].
Ф = arctg , k
X
Р-ГХ-1^ьГ^Т = (<₽• }
J у a2 4- x2 у b2 — x2 у a2 + b2 .
0
X Ь 1 гл . i
q>^ arccos — , k
T b
У a2 + 6* _
781.06 . r____rt—.— = -^=L=F(m, k)
J Уа2+х? Vx2 — Ъг /а* + 62 H
b
Ф = arccos—, k = , [0<6<x; 0<а].
/ Ka*+&*J 1
[* d x
781.11. -2 .^=r=aF(<p, fe)—а£(ф, k)
J у a2 — x* у b2— X2
0
[ф = arcsin (x/6), k=b^d\, [D<%<6<a],
X
781.12. f r___—-dXr -- k\ — aB{^,k}
J ]Fa2—x2 fx2—b2 \2’ } '
b
Г Va2—x2 , Ya2—b21 |A _
Ф = arcsin r-- =, k =--- , 0<6<x<a
LH a2—b2 a J 1
) См. подстр. прим, на стр. 155.
781.22] ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ 157
781.13. X С х8 dx У х8—а8 Ух8—Ь8 , J х2—а’ Их2—^2 х а ±aK(k)—aF(q>,k) — aE^, fe) + aE(<p. k} ^Ф = arcsin—, = <Zb <a<Zx\.
781.14. C *zdx хУаг + хг J Уа2 + х2 У^+х2 Уь2+хг <P’ 0 Г x l^a3 b3 1 Ф = arctg у , k = -— , [0 < x; 0 < b < а].
781.15. ‘W ‘’1- _ * A)] У 0* M <p = arccos 4, k = , 10 <.x<_b\. L b Уа2 + Ь2 J 1 1
781.16. f x8 dx ' J Ка’ + х2 Уtf -b2 Уа2 + хг Ух^—И2 b« < 2-~т2' „. x" “+ ./--ir-rs F(<₽' 1/а+Л8Е(<р, k) * V аг + Ьг Гф = агссоз-£, k = ], (0<0<x; 0<aJ. L x V аг + b8 ]
781.21. Г Va3 — ^ J p===- dx — aE (<p, k} [0 < x < b < a], 0 Г x к и Ф = arcsin — , « = — . LT aJ
781.22. f ^,b - dx — aE (<p, k) — F(<p, k> J У a2—x2 о 0 f x b 1 1 <p = arcsin —, A =—1 , [0 <х<£<а].
158
ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
[78123
781.23. -у-У: dx =
J У Ь2 + х2
О
-^= + ^(4», k)-aE(tp, k}
<jp = arctg у, k =
[0<х; 0</><л].
781.24.
У a2 +x2 Ух2 — b2
+- ]/ a2 + 62 {F (<p, k) — E(fp. k)}
ф = arccos —, k = —r— 1 [0<6<Cx; 0<a].
x Уаг + Ьг J 1
_____xl dx____хУаг — хгУьг—x2 ।
У a2—x2 У b2— x2 3
+е±^(ф, *>
Г . х bl
]<P = arcsiny , k = - .
781.61. ^уаг—хгУьг—х2ах=^х^аг x‘+
+ (ж+2зГ—‘>+(«’+«»-?-») Е(Т. *’
[. х , Ь1
Ф= arcsin -г-, k = — .
т b ’ а
ф их
С sin2.® dtp Га. Г х2 dx
782.01. I , —т — =1 sn и du = I г- г.
J У1—k2 sin 2ф J J У1—х2 У1—k2X?
о т о о
= ^{/7(ф' *)—£((₽, k)\
ф их
С cos2 ф dtp С г J f
\ -тг— г т-— = I сп и da = I -
J у 1— fe2 sin2 ф J J 1
= £М._Ц^Г(ф, k}
[х = sin<p].
[x==sinrp].
У1—X2 .
77- ....dx =
/ 1—fe2X2
787.4J ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
<Р и
782.03. f - = С tn2 и du = ’/l-^2sin2q)
J К1 — fe2 sin® <p J 1 —fe2 T
о о
782.04.
v
C Jj/ф
J cos2 ф 1 — fe® sin® <p
0
К1 — 1,2 Sill2 ф . , c . , .
----f.feT- tg ф + £ (Ф, k)
782.05. f — CQ^aфШ — = tgФ 1 -fe* sin2<p + £(tp, k)
WO ф
<p
782.06. § tg2 <p К1 sin2(p rfcp = tg<p —/г2 sin2<p +
H- E (Ф, k}
159
E (<P. fe)
1—fe2 ’
E (ф. fe)
1—fe2 *
-£(rp, k),
2£(<p, k).
785.1.
785.2.
785.3.
786.1.
786.2.
786.3.
787.1.
787.2.
C sn и du = — 1 Arch ('j.
J сп и du = у arccos (dn u).
J dn и du = arcsin (sn u) = am и.
c_^=inf_
J sn и \cn и 4- dn и j
f* du___L |n f fe' sn и + dn u\
J cn и k' \ cn и J ‘
C arctg fp?-u7cn“\
Jdnu k \fesnu-f-cnu/
u
Jsn2urfa = -p{a — £(amu, k)}.
0
J. cn2 и du = -p {E (am u, k) — k'‘u}.
787.3.
787.4.
V
J dr? и du = E (am u, k).
0
и
C tn2 и du = {dn и tn и — E(am u, k)}.
160
ЭЛЛИПТИЧЕСКИ!! ФУНКЦИИ
(788.1
788.1.*)
788.2.
788.3.
789.1.
789.2.
С . -1,1 «. [ V 1 -*гхг 1
I sn 'xdx=xsn х-Ь-rch -------- .
J ’ I fr I
J cn-1 x dx = x cn-1 x—arccos Кfe'2 -|- fe’x2,
f . . I
I dn xdx = xdn x—arcsin --z.
J L k J
- = _(£- fO.
дЛ- 1 (_£_аЛ
dk ~~ Т\к'г *)'
*) См. подстр. прим, на стр. 151.
X.
БЕССЕЛЕВЫ ФУНКЦИИ
800. Дифференциальное уравнение Бесселя имеет вид:
+ + -4к = 0.
dx2 ' х dx ' \ х2 /
Бесселева функция первого рода Jn(х)
Обозначим ~Jn(x) через J'n и т. д.
801.1. xJ'n = nJn - xJ„+1. 801.3. 2nJn = xJn_1 + xJnJtl.
801.2. xJ'n — —nJn + xJ„_i. 801.4. =
801.5. 4J’n = J„_2 - 2Jn + J„+2.
801.6. ~{x^Jn)^xnJn_1.
801.7. (x~nJn) == - x'4+1.
801.82.
801.83. =
801.84. = -#Vo + 4(4- ’Vi.
801.85. Л=т(1 + +
801.90. —jj.
801.91.
lft5 Г. Б. Двайт
162
БЕССЕЛЕВЫ ФУНКЦИИ
[801.92
801.92. /3 = -^ + (1
801.93. Л = (-§-“ 1) Л+ (5-^)4-
ол, ПЛ 8 ( 12 i\ > / 192 40 ,
801.94. Jj— I 2 И Л ( J.4 у2 4" 1 / Л-
801.95. Л_(»_« + 1)Л-(>“-«+1з)Л
Таблицы Jo (х) и (х) см. [10, 15; 17, 19з, 20].
<ь»2 у4 уб у8
802.22. J2(x) = 2221 2413! 2в2!41 ~ 28315! 4"‘''
802.3. При л целом положительном
802.4. При л целом
•Ъ.(*) = (-1)пЛ(х)-
802.5. Если п — не целое положительное число, то в формуле 802.3
заменить л! через П (л). (См. 853.1.)
Я 09 О1 Г ( 1 — 1 Зх2 . 5х*__________7х» .
BUZ.O1. J1W— 2 2ЗЦ2| т 262|3| 2’3141*^’“
802.62. Л (-*) — х 4Х3 । 4 2‘113! 1 бх5 8x1 . 262141 243151 1
802.69. Л(х) = хл-1 (л+2)х»+>
2« (л— 1)1 2«+21l (л+1)1 1 (я4) Xя'1'3 "Г 2я+421 (л 4-2)1 (л + 6)хя+б .
2Я+631 (л 4-3)1 1 • • •
(л целое положительное).
803.41}
БЕССЕЛЕВА ФУНКЦИЯ ПЕРВОГО РОДА
163
Асимптотические ряды для больших
значений х
803.1. Л (*) = (-^)1/2 [po (*)cos (х - j) - Qo (Оsln (•* - j)]. где
803.11. p . IM2 I2 • 32 • 52 • 7a _ l2.3a-6a-7a-9a. lla । F° (X) 1 2| | 4| (8x)4 6| (8^e 1 • • •
803.12. la la. 3a • 52 I2 • 32 • 52 72 92 , ц8д. 1 3|(8x)3 51 (8x)5 1 •”
Знак «а означает асимптотическое равенство.
803.2. , , . /2 . ( Зл \ „ . . . / Зя \] Л = \ / Г1 W COS “ ТГ Q1 Sln Г ~ t)] ’ где
803.21. p, P.3.5 la-3a-5a-7-9 la . 32 • 52 • 72-9a • 11 • 13 F1W~1 1 21 (8x)2 41 (8x)« 1 6!(8x)» Начиная co второго члена знаки чередуются.
803.22. П ( \ 1 -3 12-32-5-7 1а. З2 • 5а • 72 9 • 11 WiW«=»ll8x 3|(8x)3 1 51 (8х)6
803.3. Л Iх) = ( nj)1/2 [Л, (х) cos (х - ™ - -Q„(x)sln(x —™ где
803.31. D , . « (4na—1а) (4па—За) . pn(.x)^i 2|;8\)2 ' + , (4n2—I2) (4п2—За) (4па—5а) (4па—7а) + 41 (8х)4
803.32. п . 4n2 — I2 (4па— la)(4n2— З2) (4па—б2) , ц8ж - 31 (8х)3 1 •••
803.4. . /2 \1/2 Г П(1, , . . / пп п\ . Jn (X) = — J (X) Sin ^Х — + Q'„1’(x)cos(x- - £У|, где согласно 801.4
803.41. 1 ~ 1 - (4па-1а)(4па + 3х5) (XJ ~ 2| (8ж)2 (4na—1а) (4па—За) (4л2—б2) (4п2 + 7 X 9) + 41 (8х)4
1б4
БЕССЕЛЕВЫ ФУНКЦИИ
[803.42
803.42.
П'1>ГИ~4/г2+1 х3 (4л2—I2) (4л2—З2) (4n2-f-5 X 7)
% 1!8х 3! (8х)з
Закон образования следующих членов очевиден. Сле-
дует помнить, что приведенные здесь ряды для больших
значений х являются асимптотическими, и существует пре-
дел точности, которую они могут дать.
804.01. / 2 \1/2 л (х) = — sin х. 2 ' '
804.03. , , ч /2 \1 /2 / sin X \ 'з(х)= 1 \ х COSX1. 2 ' 7 ' 7
804.05. , , . /2 \ 1/2 1/3 . \ . 3 1 = ^-1 Sinx--cos^. 2 \ / \ /
804.21. . < ч / 2 \!/2 у_2(х)= — 1 COS X. 2 ' 7
804.23. <_з (Х) = (— — sinx 2 \ ! \ COS X \ X Г
804.25. l 4 w=(гх Г {4sin *+(1 -1) c°s 4-
Бесселева функция второго рода Y„(x)
Некоторые авторы употребляют вместо Yn (х) обозначение Nn (х).
805.1. xYn^=nY„ — xY„^. 805.2. x Y'n = — n Yn x Y^.
805.3. 2nYn^xYn^+xYn+1. 805.4. 2Yn^Yn_l-Yn^l.
805.5. 4r;=rn_2-2Fn+Fn+2.
805.6. ^(x-Yn)^xnYn_1.
805.7.
805.82. у 2^i у 805.83. r8 = (A_ 1WX_ IT».
806.3|
БЕССЕЛЕВА ФУНКЦИЯ ВТОРОГО РОДА
165
805.84. У4 = (1 -g) Го + |(|- 1)
805.85. Ув = L2 Л В уо + ^4 _ 72^ Л
805.90. И = — Fv 805.91. У[ = Го - £.
805.92. Га == 4- (1 - -V) У1
805.93. г; = (^-1)г0 + (5-^)^.
805.94. Г; = 4 (g - 1) Го - (Ь? - + 1) Гр
805.95. Г8 = (9^-^+1)г0-ет-448+13р.
’ • \ X* X2 ' J U \ X* X2 ' / X
Таблицы Г0(х) и Гг(х) см. [10, 15, 17J.
М ?
806.1. t-0(x)-|(c + ln|)j.W+|lil-
/_1_ \* „ /J_ \«
где С —эйлерова постоянная 0,5772157. (См. 851.1.)
806.2. Г1(х) = ^(с + 1п|Ъ1(х)-А_
л у X» / лх
оо
р=0
80в.з. - r.w _ |(с+ш ') у. и -1J И=г=1М -
р=0
_ 1 У (~1)р (х\2р+п(] 4-1-1-14-
л Zj pl (»+р)1 \ 2 / \ ”1" 2 3 "I" ‘ ‘
₽=о •••
••• + 7+1 + т + --- + гЬ)'
где п целое положительное. При р — 0 последнюю скобку
следует положить равной II +... ф —
166
БЕССЕЛЕВЫ ФУНКЦИИ
[807.1
Асимптотические ряды для больших значений х
807.1. Н/2 I Ра (х) sin (х— т) 4- Q„ (х) cos (х~т)]-
807.2. Л(х) = | < jr < ПХ t \t/2 1 Рг (х) sin [х~ Зл\ ~ ) 4- (х) cos Ь?)] •
807.3. ВД = ( f 2- nxt у/2 1 Рп (х) sin пл ’~2~ -1-)+
4- Qn (х) cos ( X — пл Я \1 Т T/J • [Ряды для Р и Q см. 803.]
807.4. Yn (х) — (— \ 71Х \ 1/2 ГРд 1 (X) cos fx- П31 “У С Л \ ~4 )
2 4 )
— Qn}{x} sin (х— ™------
[/#>(*) И Qn}{x) см. в 803.41 и 803.42.]
Бесселевы функции от мнимого аргумента
v первого р о д а /„ (х)
808.1. xJn = nln 4- х/я+808.3. 2и?п- х/п-1 х/п+1.
808.2. х1п = — nln+xln_v 808.4. 27д = 1п-Л+
808.5. 4/п — + 2/п4- [п+г.
808.6. 808.7. 3^(Х ^п)~х ^п+1'
808.82.
808.83.
808.84.
808.85. . f 384 . 72 X , 12 /16 Z« — х1 + х2 + 1 J '* X \ X2
808.90. 4 = Л.
808.91.
808.92.
808.93. ?-“(р + ,)/"-(?+5)т
811-3]
БЕССЕЛЕВЫ ФУНКЦИИ ОТ МНИМОГО АРГУМЕНТА
167.
Таблицы /0 (х) и /, (х) см. [10, 15, 21J.
,, v (Н‘ (!')'
809.1. + +1£^. + |^£+....
где i — V — 1.
/IV /IV
, 1 (у*) (o'*)
809.2. 7, (х) = Г1 J. (ix) ~ I, (х) = -L x+^f + + ...
809.3. При п целом положительном
809.4. При я целом
7_п(х) = 2„(х).
809.5. Если п не целое положительное, то надо в 809.3 заменить я!
на П(я).
[См. 853.1]
А симптотические
ряды для больших значений х
Г р 1’.32 , 1
811.1. /4(х) «а [* + ТГвх"^ 2! (8х)2 + •••]•
f (£t4 Ь Л U -Л
рх г
811.2. / (х)«а—Д= 1
" /2лх L
4яг — Р , (4п2 — Р) (4 пг—З2)
11 8х + 21 (8х)а
Я11 Ч f IИ ~ -1L— Г1 — 4”г+1 х 34- (4Я2 —Р)(4п2 + 3 х 5)
811.3. ln (X) . [ 1 1[8д, -f- 2!(8х)2
(4n2—Р) (4я2—З2) (4п2 + 5 х 7)
31 (8х)2
Члены ряда 811.3 те же, что и в рядах 803.41 и 803.42.
168
БЕССЕЛЕВЫ ФУНКЦИИ
|814.1
Бесселевы функции от мнимого аргумента
второго рода Кп(х)
814.1. хК’п — пК',— xKn+v
814.2. ' хКп~—пКп—хКп_у.
814.3. ' 2nKn = xKnlr — xKn_t.
814.4. 2К'п = Я„+1.
814.5. 4/d = ^_s + 2/<n + /<n+2.
814.6. й(^я)=-Л„.г
814.7. ^(х~яКя) =—х~а K„+t.
814.82. Кг = Кл + ^.
814.83. К,^^+ (А + 1) ЛГ,.
814.84. ^ = (р + 1)^ + 4(7 + 1)АГ,.
814.85. К, = 72(р + 1) Ко+(? + 5 + !Х
814.90. /< = — /<,.
814.91.
814.92. ^ = — (р + 1)*,.
814.93. К.----(§ + 1) *_(“+s)^. ~
814.94. ^ = -4(? + 0*o-(v + P + ’X
о,л пе 1/ /ЭбО . 84 , „ /1920 . 408 Kt
814.95. + -4-1 ^/<о—+ -^-4-13J —.
Таблицы К, (х) и Кг (х) см. (10, 15, 17, 21].
818.3. БЕССЕЛЕВЫ ФУНКЦИИ ОТ МНИМОГО АРГУМЕНТА 169
815.1. К„(х) = -(с+1п *)/,(х) +
(Я (Я/ ix (Яг 1 П
+ (II)* + (21)г (1',’2)+ (3!)г (' + 2 + з) ’
где (7 = 0,5772157 — эйлерова постоянная. (См. 851.1)
815.2. К„(х) = (- 1)п+’ (с+ 1п |)/„(х) +
, 1 (_1)Р(п-р-1)1 ( к \*Р~” ,
+ 2 Z- pi \ 2 J г
, (-1)” V 1 f х\гР+п
-t- —2~ Z- р| (п + р)| \ 2 )
р=0
у О+4+1+ •••+7+1+4+ •••+Я)’
где п—целое положительное. При р = 0 последнюю скобку
следует положить равной ( 1 +у + • • • + •
Следует заметить, что иногда, особенно в более ранней
литературе по бесселевым функциям, буквой /(обозначается
совсем другое выражение.
815.3. При п целом К_п(х) = Кп(х}.
815.4. При п нецелом Кп (х) = 2-^-пл (х)— 1п (х)}.1
Л/ Э111 llJi
Асимптотические ряды для больших значений х
&16.1.
„ . . ! л \v« _ХГ Р Р.З* Р-З’-б2 1 ,
Л»(Л’^\2х/ й II 8х + 21 (8х)2 3! (8х)’ ' * ’'] *
Ш.2. + +
, (4n«-l«)(4n2-38) , 1,
*" 2! (8x)s ’’••••j*
816.3. ^(х) е-*[1 Н--П*1^- +
, (4п’—Р)(4пг4-3 X 5) , (4л‘~1‘)(4л‘—3‘)(4л‘4-5x7) , 1
+ 2! (8х)г • + 31 (8хр + • • • | .
[Из 814.4.J
Нетрудно видеть, как продолжить этот ряд.
170
БЕССЕЛЕВЫ ФУНКЦИИ
[817.1
Функции Ганкеля
817.1. 77(’)(г)-70(г) + /У0(г). 817.2. К0(г) = ^Я<')(й).
817.3. №’(г) = 7п(г)4-гУя(г). 817.4. Н1*' (г) = Jn (г) - iYn (г).
817.5. Кп (г) = ein^H'2 \iz).
Для любых значений х и <р:
818.1. cos (х sin <р) = J0 (х)2.72 (х) cos 2<р 4-2.74 (х) cos 4<р4-...
818.2. sin (х sin ф) = 2J4(x)sin <р 4-2.73(х) sin Зф + 2.76 (x)sin 5<р + - • •
818.3. cos (х cos <р) = Jo (х) — 2.72 (х) cos 2ф ф- 2.74 (х) cos 4ф —...
818.4. sin(xcosф) = 2Jj(x)cosф — 278(х)со5 3ф 4-2J5(x)cos 5ф —...
Бесселевы функции от аргумента xz]A
первого рода
820.1. Ьег х ф-zbei х = Jq(xz ]/z) = /0 (х pQ) = ber0 х 4-zbei0 х.
820.2. Ьег' х = ~ Ьег х, и т. д.
820.3.
820.4.
820.5.
/ 1 \4 / 1 \8
, \ 2 Х) Д 2 Х)
Ьегх— (2|)2 4- (4|)2
/1 \з /IV / 1 \и
\~2Х) \2/ \~2Х)
Ьег х — — ------к ------— --------к
х 1121 314! 5161
820.6.
nei х 2 х 2|3| -t- 4|5|
821.1. Для больших значений х
Ьег х е Г£0 (х) cos Д= — -Д — Mo (х) sin " YI,
K2iwL \/2 8/ ’ \/2 8/J’
822.3| бесселевы функции от xl ]/"I 1-го рода 171
821.2. bei х = [Л4О (х) cos +
+ L0(x)sin^-^,
где
„п, „ , , ' , , Р я , Р-32 2я , 12 - 32 - 52 Зя.
821.3. L0(x)^ 1 +-pgjcos 4 + 2| (8x)acos 4 + 31 (8x)3 cos 4 + • • •>
, .. . . Р.п Р-32 . 2я Р-32 - 52 . Зя
821.4. Л40(х)^ H8xsn 4 2l(8x)2Sn4 31(8)3 sln 4
821.5. Ьег х — cos 8 )
-T'oWsln^ + l)]-
821.6. bei' x = ^[r0(x) cos^ + +
+ 5o (x) sin ^2 4" ~8")J’
где
on. ч ozs . 1-3 я P-3-5 2я
821.7. So (x) 1 —-j-j-g- cos 4- — 2| cos -j-
P-32-5-7 Зя P-32 - 52 - 7 - 9 4л
31 (8x)3 C0S 4 41 (8x)« C0S 4
on. о -n Z \ 1 • 3 . я . P • 3 • 5 . 2я ,
821.8. ГО(Х)~ n ^Sin 4 +2| (8x)2 Sin 4 4-
. P-32-5-7 . Зя . P-32 - 52 - 7 - 9 . 4я .
31 (8x)3 Sin 4 + 41 (8x)4 Sin 4
822.1. При n целом положительном
bern x 4- i bei„ x = Jn (xi У1) = inln (x p7).,
ber. x- 2 -7’7(У— -£Т--
p = 0
/1 \д4-2р
co П^+P+l —x
822.3. bel.x- £ -------------------Slnl2±^.
p = 0
172
БЕССЕЛЕВЫ ФУНКЦИИ
[822.4
822.4.
822.5.
„ (п 4-2р) л
cos-—-~-4—
4
ber„x
(п+2р)л
4
823.1. Для больших значений х, при целом положительном я:
Г г , \ ( х я , пя\
ь“-х " Fss I1•w с“ (7Т ~S’+-
где
сои о г z.a^_>« 4па—Is__ я , (4n2—I2) (4л2—32) 2л
823.3. £„(*)« 1--— cosT+----------------cosT-...
BQQ л ял I \ 4п*—I2 1 Л И”2—12)(4л2—З2) . 2л
823.4. ------------------------------!sln7+...
823.5. beI;Je_^{s.Wcos(^? + i + "^-
823.8. tel;,_^g[7,Wcos^ + | + ^) +
. с /..ч / х Iя! плХ!
+ S„Wsin^ ^-+ 8 + 2 JJ*
где
823.7.
Sn(x)« I
4л2+1хЗ_______л , (4n2—I2) (4n2-f-3x5)
1! 8х °S 4 21 (8х)2
cos
2л
Т
(4n2—I2) (4n2—З2) (4п2+ 5x7) Зл ,
3! (8х)« C0S 4 <
Т (ji-)~4"‘ + lx3-in Я 0п2-12)(4л2 + 3х5) 2л ,
823.8. /В(Х)----H8^SlnT-------------2Н8^Л sinT +
, (4n2— l2)(4n2—З2) (4п2 + 5х7) Зл
+ 31 <8х)« S1" 4
824.6]
бесселевы функции от xi]fi 2-ГО РОДА
из
Бесселевы функции от аргумента xl УТ
второго рода
>•
824.1. ker х 4- i kei х = (хi).
824.2. ker' х = 4- ker х, и т. д.
dx
824.3. ker х = Г1пу—ber х 4- bel х—
где С= 0,5772157. (См. 851.1.)
824.4. keix=^lny—C^belx—у bet х4-
10
4-fl+ — 4- — + — + — 1—— --------...
(5I)2
174
БЕССЕЛЕВЫ ФУНКЦИИ
(825.1
825.1. Для больших значений х
keiх = е~Х,УТ [Lo (-*)cos (т2= + ?) +
825.2. kelx = ( " У Гмо(-х) cos f-^=+-
x)sin s') '
Cm. 821.3 и 821.4 с подстановкой—x вместо x.
825.3. ker' x----cos (yy—?) +
+’'.I-*)
825.4. Wx —
Cm. 821.7 и 821.8 с подстановкой —x вместо x.
826.1. При целом положительном n
kern x 4- i kein x = i~n Kn (x V/).
826.2. kernx= ^Iny—bernx4--^ bei„x +
±1 V (— l)n+f(n —P —1)1 fx\ip-n ,
+ 2 p' V 2 J ° 4 +
p=o
+1 jb(i+4+3’+••
p=o 4
+?+1+t+4+-"-+
/ I \n-W
X pl (л +Р)!
(n +2p) it
4
827.21
БЕССЕЛЕВЫ ФУНКЦИИ ОТ Х/]/Г2-ГО рОДА
175
826.3.
ке!„х = (In ——beLx— ber_x-f-
+ ± у (-1)я^(п-Р-1)1 Гх_у~п sin (n+2p)rt
2 р_о pl \ 2 / 4 j
—4£(1+4+|+-- - +4+,+4+4+•••+rU)x
4 0 = 0
/ 1 \»+s/>
\2Х . (п+2р)л
х—р1(;+-р/—s,nL-^— •
826.4. ker'х= (in-?- —с) ber„x— + bei'„x+
_|_1 V (— В n+/,(2p—n) (n-p— 1)! Л£у^»-’ cos (n+2p)jt
p = o 2
co
826.5. ket'nx = (ln|— c) bei'„x— 7 ber^x+
4-1 (-1)"+Р(2р-п)(п-р-1)! у/'-'1-1 sjn (п+2р)л
4 p=o p! ' 2 '
S1(l+4+4,•••+7+1+4+4+•••
p=o '
f 1 V+2/7-1
(^l)n+P(„ + 2p)
x pi (» + р)Г
Sin(2 + 2P)^;
4
827.1. Для больших значений x при целом положительном /г:
, /л\'/г _Х/УТ Г г , . f х , л , пя\ .
кег»х=(&?) е [/:„(-x)c°s(y=+ 8-+Tj +
827.2. kel.x- [л,(-x)cos-
• . . • f X 1 Л . M Л \ ”1
-L„(-x)sin + t +
[Cm. 823.3 и 823.4.]
176
БЕССЕЛЕВЫ ФУНКЦИИ
|827.3
8273. ker. « - - (а)''е’"кГ [s. f+ ¥) +
+ 7п(-а,)8|п^-Л + ^].
on- t 7 / /ft XV* _*/ГГГт . . „ / X л . лл\
827.4. keinx—"“’(jjx) e | n X C0S \ V~2 8”^~ 2 )
— S„(— x) sin (y=—| + y)]- [Cm. 823.7 и 823.8.]
Нужно заметить, что ряды для больших значений х—это
асимптотические разложении, и степень точности, которую они
дают, ограничена.
Рекуррентные формулы
828.1. Ьег, х = (Ьег' х— bei' х).
828.2. bei, х = р= (ber'х-(-bei'x).
828.3. ber. x — ber x. 828.4. bei, x bei x. 2 X X
828.5. . ' . , 2ber.x bers x — — ber x —.
828.6. beijX = — bei' x— —x.
829.1. . n 1^2 .. . , . , bern+ix— x (berBx— bel„x)— ber„_, x.
829.2. n y/~ 2 bei„+Ix — (bern x-f- bei„ x)— beiB_, x.
829.3. bernx- ^-(ber^.x+bei^.x) x"x.
829.4. bei„x= (ber„_, x belB_, x) / .
830. Формулы 828—829 годятся и для бесселевых функций вто- рого рода, если заменить Ьег на ker и bei на kei. Таблицы значений функций от аргумента xtсм. [8J, (11], (16].
837.2|
ИНТЕГРАЛЫ
177
Бесселевы функции — Интегралы
836.1. J xnJh _ i (х) dx = xnJn (х).
835.2. $х~"7„+1 (х) dx — — x~nJn (x).
835.3. 5 *n4-i U) dx = xnln (x).
835.4. $ x~nIn+1 (x) dx = x~nln (x).
835.5. xnKn _ i (x) dx = — xnKn (x).
835.6. J x-^„+1 (x) dx — — x~n Kn (x).
836.1. X x ber xdx =xbei'x. 0
836.2. X x bei x dx — — x ber' x.
836.3. X i xkerxdx = x kei'x. 0 »
836.4. X x kei x dx — — x ker' x.
837.1. $ x (ber„ x + bein x) dx = x (bern x beinX — bei„ x ber,J x).
837.2. \ x (ber^2 x + bein2 x) dx — x (ber„ x ber„ x bein x beiA x).
XL
СФЕРИЧЕСКИЕ МНОГОЧЛЕНЫ (МНОГОЧЛЕНЫ ЛЕЖАНДРА)
840. Р0(ц)=1.
, Р1(Р) = Р-
Л(н) = |(Зц2-1).
^>з(р) = 4’(5Р3-3Р)-
^(ц) = 214(5-7|х4-2-3.5^4-1-3).
7W) = ^4 (7 • - 2 • 5 • 7И3 + 3 • 5И).
7’6(н)=27Гб(7-9-”?х6-3-5-7-9^ +
4- 3 • 3 • 5 • 7 р.2 - 1 • 3 • 5).
W = 2ТТТ/9 •11 ‘13^? “ 3 ‘ 7 ’ 9 •11 +
4-3-5 7.9^3-3-5-7ц).
Коэффициенты в скобках составлены из биномиальных коэф-
фициентов, а затем других множителей.
841 Р Сitl — (2от~') (-т~3) ••• 1 Гт т(т—1) т-2 <
ОЧ1. /"mW- т! [И 2(2т-1)^ '
м(т-1)(т —2) (т —3) т-4 _ ]
-Т" 2-4 (2т—1) (2т —3) и "Т
При нечетном т ряд кончается членом, содержащим р., а при
четном т —членом, не .зависящим от р.
842. («4- 1)7эт+1(ц) = (2/«4- !)ц7’т(ц)-отРт.Пц)-
843. (ц2- 1)Рт(ц)=мцРт(}1)- тРт_г(ц).
844. Для больших значений т
Pm(cos0)«а С—7У/2sin +
т v 7 \тл sin 6/ (\ ' 2 у '41
8451 МНОГОЧЛЕНЫ ЛЕЖАНДРА 179
844.1. 1 лт dxm (Х •
844.2. Ря(1) = 1.
844.3. ргт{— x)=pim(x):
844.4. Ргт + Л Х)~ P^m + jM-
845. Первые производные Р'т (.р) ~j^Pm (I*)- Р„ (р) = 0. Х(Р) = П Рг (р) = Зр. Л(р) = |(3-5рг-1-3). А(р) = у(5-7р!-3-5р).’ Рв(р) = ^(5-7-9р4—2-3-5-7}? + 1-3-5). р;(ц)=Л(7.9.11ц5 —2-5.7.9p3 + 3-5-7p). р;(р) = _1_(7.9.Ц -13ра — 3-5-7-9-Иц4+ + 3-3-5-7-9.и,2 — 1-3-57). Коэффициенты в скобках составлены из биномиальных коэф- фициентов, а затем других множителей. Таблицу значений многочленов Лежандра см. [16].
XII
J( !i4y_’dx=m
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
850.1. Jx”“’e“^x =
О
Г (и)— гамма-функция. Интеграл имеет конечную величину
при я > 0.
850.2. Г(п4-1) = пГ (я).
850.3. Г (я) Г (1 — я) == — [я не целое].
SIH flit 1
850.4. Г (я) = (я— 1)!, когда я целое положительное.
850.5. Г(1) = Г(2)=1.
850.6. 850.7. Г(4)=тг.
850.8. Г(я+ -J-) = 1-3-5- ••• (2л—3)(2л—1) ]ЛГ/2В
(л целое положительное).
851.1 1пГ(1 + х) = — Сх+^-—+ ---- [хг<1],
где С— эйлерова постоянная:
С= lim [—1пр+1 + 4- + -5-+...+-1 = 0,5772157
р-»оо I Z о PJ
Sp=1+r₽ + i+--- (См. 480.]
851.2. in Г (1 + х) = 1 In Cx— . [x! < 1].
854il2l ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ 181
8ИА 10Г(1+х)=|1па=;-11п}±-- +
+(i-Q*-<s.-i>7—(S.-D?---------------
Для значений к больше чем -i использовать 850.2 и 850.3 и
эти ряды.
851.4. Г(х-|- \)^ххе~хУ 2лх [1 +^ + 28^'“
139 571 , 1
51 840х» 2 488 ЗгОх4"1" ’ ' * J *
Эта формула дает асимптотическое выражение для xt,
когда х—большое целое число. [См. 11.]
851.5. 1пГ(х+ 1п(2л)—х-|- (-* + 4) 1пх +
• 81 8» I 8; ___
~*“].2х 3.4х’"г5-6*5
[ВрВ2,... — числа Бернулли]. [См. 45 и 47.1.]
Это—асимптотический ряд Стирлинга. Абсолютная
величина ошибки меньше, чем абсолютная величина первого
отброшенного члена.
852.1. j e~x\nxdx =— С,
где С= 0,5772157, как в 851.1.
853.11. П(я) = Г(я-]-1). [См. 850.]
П(я) иногда называют гауссовой функцией.
853.12. При п целом положительном Щя) = п!.
853.13. П(0) = 1.
853.21. fjcm-’(l — х)п-'ах = ^Ц^- = В(т, п) (бета-функция)
1 \tn ’ф’ fl)
[т, л>0].
864-"-
h-1. 2, ...j.
сел «О CxP-'dX 1 1.1 1 , г
’ J 1-]-х? р Р + <7 р + 2<7 р + 3<? ’ 1^’ ^'> 1’
[См. 35.]
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
|854.21
182
854.21.
854.22.
855.11.
855.12.
855.13.
855.14.
855.15.
855.21.
855.31.
f dx Л
J 1 +* + х2 0 з Кз ’
f dx 2л
J 1— x+x2 0 3 /з ’
P xp~'dx_ Л
0 sin рл
\ 1 +*2 0 dx = —5— 2cos
1
Pxp + x~pdx___ л
I x9 + x~f х ~ / р л \
1
f dx л
in^
0. 9
1
f dx __ л
.прл
о Я
Pxm-'+xn-i V(m) Г(п)
J (1+х)т+« аХ~ Г (т+п)
[—q<P<q\.
[?>!]•
[О <p<q\.
[т, п>0].
f *т dx 2-4~с ••• И—1)
J VfZTp ~ 3-5-7 ... т
о
1-3-5 ... (т— 1) л
~ 2-4-6 ... т 2
\т—нечетное целое >• 1],
[т—четное положительное
целое],
[т— произвольное >• — 1 ].
[Положить sinx=j^ в 858.44 или 858.45.]
856.04]
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
183
1 1
856.32. \ xm]/l-x2dx = —hr \
J r т+2 J /ТЗ^а
о о
[т — произвольное> — 1]. [См. 855.31.]
855.34.
855.33.
[л>0].
хт dx
/1—
[от + 1, я > 0].
г . г(р+1)г(^±1')
855.41. i xm(l-x2)pdx =---[р+1, от4-1 >0].
] 2Г +=±2)
Г Г(р + 1)Гр±1)
855.42. I xm{\-xn'fdx =---
J пГ P + 1+^
о \ п 1
[Р +1, от+1, я>0].
а '
855.51. х”1-1 (а - х)”'1 dx = ат+п~1 ГгУ У(”? [а, т, п > 0].
J • z * х.^ “г
0
оо
856.01. —I- [0<<7<1].
J (1 -|-*) sin qn i i а
о
Положить <7=1—р. Тогда
856.02.
ОО
С хР-1 dx________л _______ л
j 1 + х sin (л—рл) sin рл
о
[0<р<1].
856.03.
С dx
J (14-х)V+
л.
865.04.
ОО
С хР~* dx лдР-1
J а 4- х sin рл
и
[а> 0, 0 <р <; 1].
184
.ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
1856.05
856.05.
856.06.
856.07.
856.08.
856.11.
856.12.
856.21.
856.31.
856.32.
856.33.
857.01.
857.02.
f dx
I Т+яР
о
л
р sin—
р
оо
f х? dx рте
J (1 +ох)а “ o*+1 sin рл
о
оо
!хР dx ____ я
14-Х2 ~~ о рл
2cos^-
00
f хР"* 1 dx_ л
I 14-х® . рл
I 1 о sin —
о <7
оо
С х1”"1 dx _ Г (т) Г (л)
J (1 +х)'я+п ~ Г (m-j-л)
xm~idx _ Г (m) Г (л)
(а+Ьх)т+п апЬтГ(т+п)
00
С dx . 1 • 3 • 5 ... (2 л — 3) л
А (а24-х2)" ~ 2-4.6 ... (2л —2) 2л2»'1
V ^0,
dx я
(а2 4-х2) (624-х2) ~ 2аЦа+Ь)
dx л
(а2 4-х2) (а" 4-х») ~ 4а«+1
1_______1 \ dx q
14- х2 14-* / *
-------------= ...' - arcctg -/•'
ах2 4-26x4-с-V ас—b2 Vас—Ь2
[а>
dx 1 [
------------ГГ = ----------7=- I d.
(ах24-Ьх+с) '• Ьрс-рсуа
lp>lj.
[а>0, 0<р< 1].
[О ср < ?].
[т, л>0].
[а, Ь, т,
[а>-0; п = 2, 3, ...].
[а, b > 0].
[а>0].
ас — Ь2 > 0; см. 500.]
с, b V сс |/а>»0].-
о
Bit-
d^ ' 32 a 3
Л?й‘7
PScU' ^7%^
о L " ts*
? /;' >>£.
Jjffyz = I _ з 'J
о L 3 /
f №>dzL - 3r/~ f -^- - X .
У ^Zl3 a^a^y
858.44)
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
185
857.03.
857.11.
858.1.
858.3.
xdx ______________J_____
(a№ + b* + ,3 о V с + b V~<*
CD
f dx ______________ л
J ax* +2bx‘-j-g~ 2 Ксй ’
0 _____
где ft = 2(ft + Kac)
[а, с, а с + & у4 a > 0].
[a. c, ft >0]
л/з J sin’ х dx = . 0 858.2. tr/i \ cos xdx=-^ 0
я п
У sin’ х dx = § cos’ , я xdx = ~2-.
0 0
Среднее значение sin’x или cos* x на любом интер-
я 1
вале, концы которого кратны , равно .
858.41. 7Г/2 J sin’mxdx = я/г = J cos’ mx dx — ~ (pi= I, 2, ...
0 0
858.42. Л J sin’ mx dx = Л • j JT = \ cos mx ax — -^- [ffi = l, 2, ...
0 0
858.43. 2Л 8Л 1 sin’ mx dx — i cos* mx dx = n p»=l, 2, ...
0 0
858.44. n/1 § sin₽xd№ Л/» J cos p x dx =
0 0
2-4-6 ... (р—1) г
= —о с" - IP—нечетное целое число
.1 • 5 • 7 . . . D L
1-3-5 ... (р—1) я г
= —п~л~ё— -----о IP—четное целое положи-
2-4-0 ... р 2 1
тельное число],
*5 Г(Чг)
= ^5---т-----\ [р—произвольное >—1].
Полагая т = 0 в 858.502, получим тот же результат,
что и в 858.44, несколько в другой форме.
186
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
[858.45
858.45. вТ/2 ггт/2 С . о , С d j лГ(р4-1) 1 sinp х dx — \ cos р х dx — —7- —r-rj J J {r [p>-1]. fft Г
858.46. 1 sinpxdx = 7-A _Z [p>— 1], J r f+> 0 ' Л/2 = 2 У sinpxrfx.‘ 0 [Cm. 858.44. Можно использовать также и 858.45.] С г Р+Ч
858.47. 1 xsin?xdx=^-’— . 2 [р>— 1], J г(т+>) 0 JT/2 = л J sin р х dx. 0 [См. 858.44. Можно использовать также и 858.45.] ГГ/2 П12
858.48. С tgpxdx=f ctgpxdx = — [₽’<!]• J J 2cosv 00 z ГГ/2
858.491. f M^==2G = 2-0,915 9656. [См. 48.32.] J sin X ’ 1 J 0 Л/2
858.492. f ^ = 41n2. J tg x 2 0 Л/2
858.493. C xs dx , „ \ -т-2- = л1п2. J sin2 X 0 П/2
858.501. § cos'" x cos mxdx= -^+1 [w»+l>0]. 0
858.5151
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
187
858.502. jr/s Гр я Г(р+1) 1 cosp х cos тх dx = —: £—г j 2^> г(£±^+1)г(е^+1) [р+1, p + ffi + 2, р—от + 2>0].
858.503. f sinmxsinz»xdx = ^isin [от+1>>0]. 0 Л (* . тл Г- / . 1. 1 я sinГ (р+-1)
858.504. | sinp х sin тх dx = -iy!> ——j г г J 2'г(+=+1) г(£++1) [р+1, р + ®+2, р—т + 2>0].
858.505. J sin” х cos тх dx = cos ~ [т + 1 > 0]. 0 л | я cos-g-rip + l)
858.506. 1 sinp х cos тх dx = —-г—г г г J 2'r(+=+i)r(+^+i) [p4“lj p-p/w-j-S) р—tn -j- 2 0]. Я/1
858.511. J sin!3+,xcos!4+,xdx-(a+6 + 1)!2. 0 Jt/l
858.512. C sin,a+Ixcos'"xdx = 2'-6 (2а)'1-3-5 •..Г2й_~_У J Sln xcos xax 1-3-5 ... (2a + 2& + l) 0 Л/1
858.513. (* • ta «4+1 1-3-5 ... (2a—1).2-4.6 ... (26) J sln xcos xdx** i g 5 _ (2a+2&+D 0 n/l
858.514. f . ta tb . n 1-3-5 ... (2a^l).1.3.5 ... (2&-1) j sin x cos xdx— 2 2-4.6 ... (2a+ 24) 0 В 858.511—.514 a и b—целые положительные числа. л/t
858.515. [ , „ а . \ 2 \ 2 | sinp X COS’ X dx = 1 7 Ь г-2- J 2г(Мр+1) 0 [р и q произвольные числа >—1].
188
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
[858.516
$58.516.
sin тх sin nxdx = О
[т^п],
л
2
[т = п]
[т и л—целые числа].
[т^=п],
858.517.
cos тх cos nxdx
= 0
л = 2 [т — п] [т и п—целые числа].
858.518. J sin тх cos nx dx = 0 [т = п],
0 '=0 2m т*—пг [т=^п; (т+ л) четно], [т=£п; (т + п) нечетно] [т и п—целые числа].
Tffit п/г Л S -тг—arcsin a
яса коп 1 с 2 _ arccos а
858.5^0. J 1+oslnx 0 J 1+acosx 0 К1 — аг V1 - аг
В формулах 858.520—858.535 0<а<1 и, сле-
довательно, углы arcsine и arccosа лежат в первом
квадранте.
858.521.,
858.522.
858.523.
л,г л/2 л .
г г . -х-Ч-arcsine
I dx_________1 dx ________ 2__________
J 1—asinx J 1—acosx у \___________at
0 0
[См. примечание к 858.520.]
л
[* dx________л —2 arcsin a _ 2 arccos a
Jl+asinx- у f_L a3 ~ у ] _aa •
0 '
[См. примечание к 858.520.]
я
Г dx ________л + 2arcsln а
J 1 —asinx уj _a2 *
о
[См. примечание к 858.520.]
858.524.
dx___________л
1 ±a cos х у j_____ог
189
858.541]
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
«Л 851 Г dx , Г dx _ 2л
858«525« 1 l±asinx J 1 i a cos х К1 -<?'
О 0
858.530. tn /2 i dx n/t I dx -y-arcsina д
J (1+asinx)2 _J (l+^osx)2 (1—a2)’/a 1~‘ z2
0 0 [См. примечание к 858.520.]
858.531. C dx _ nil 4- arcsin a
J (1— asinx)2 J (1—acosx)2 (1 — a2) 1 ~ cr
- 0 0 [См. примечание к 858.520.]
858.532. , л p dx __ л —2 arcsin a 2a
J (1+asinx)' (l-a2)’'’ 1 —a2 ’ -
0 [См. примечание к 858.520.]
858.533. ST p dx л+ 2 arcsin a 2 2a
J (1—asinx)2 (l-a2)*'2 1 —a2’
0 [См. примечание к 858.520.]
858.534. я p dx Л
J (1 ± a cos x)2 0 (l-a2)8'2’
858.535. 2Л p dx 2Л f dx 2л
J d±asinx)2 0 J (l±acosx)! 0 (1 —a2)”^’'
858.536. л p cosmxdx n(/i-a2-l)‘ - [0 < a < 1; m = 0 , 1,2, ...].
J 1 4- a cos x 0 am /1—a2
858.537. Я/2 p dx _ 1 [a, />>0].
J (a sinx + ^cosx)2 at) 0
858.540. Л/1 ' p dx n/e p dx я
J l-|-a2sin2x 0 J 14- a2 cos® > 0 2/1+a2
n/i p dx л/s p dx Л
858.541. ] 1— a2 sin® x • J 1 — ascoss 0 « 2 Kl —a2
190
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
[858.542
858.542. л/2 л/2 С d* f dx л 2 + a2
(l+a2sin2x)2 J (1-{-a2 cos2 х)2 4 (l+a2)’^’
858.543. Л/2 Л/2 ( dx f dx л 2 — a2 [a®< :ij.
J (1—a2sin2x)2 e J (1 — a2 cos2 x)2 — 0 0 2 (l-a2)’A
Л
858.544. C x sin mx dx л2 j 1 + cos2 mx 4m2 [/7Z> > 0].
858.545. Л f x dx лф
J 1 + cos <p sin x sin <p*
858.546. Л f sin2 x dx л [a, a2 - b2 >0].
Ja + 6cosx
Л/2
858.550. f dx _ л [ab >» 0].
j a2 sin2 x + i2 cos2 x — lab
858.551. Л f dx л >0].
J a2 sin2 x + Z?2 cos2 x ab 0
858.552. Л/2 Л/2 f sin2 x dx f dx Л [a, b >0].
J a2 sin2 x-f-62 cos2 x ” \ a24-62ctg2x 2a (a + b)
858.553. Л/2 Л/2 f cos2 x dx f dx Л [a, bZ: >0].
J a2 sin2x + Z?2cos2x e J Z?2 + a2tg2x" 0 0 _ 26(a+&)
858.554. Л/2 C dx я л a2 + &2 >0].
j (a2 sin2 x + &2 cos2 x)2 — 4 a3№ 0
858.555. Л/2 f sin2 x dx л [aA >0].
J (a2 sin2 x + i2 cos2 x)2 ™ 4a3b
858.556. Л/2 f cos2 x dx л [ab X >0].
j (a2 sin2 x + Ьг cos2 x)2 ~ 4a№
о
858.631] ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ 191 со со
858.560. sin (а2х2) dx = ( cos (а2х2) dx = 1а > 0]. о о а со оо
858.561. С . лхг , С лхг j 1 \ sin -g- dx = \ cos g- dx = у. 0 0 [Интегралы, Френеля.] 00
858.562. sin (хр) rfx = Г [ 1 + Д sin 9Яп [р>1]- Л \ р / ^р со
858.563. cos (хр) rfx = Г (S 4- y)cos^ [/’>!]• 0
00
858.564. С-»» < Кл./я m2 \ \ sin алхг cos mx dx = sin Н— 1 а > и]. ,) 2а \ 4 4аг / 1
О
858.565. СО ' cos а2х2 cosmx dx = cos [а>0]. 0 со
858.601. ( smmx _ я q или _ я в зависимости от того, будет J х 2 * 2 0 ли т положительным, нулем или отрицательным, со
858.611. С cos тх—COS ПХ J i п г m \ dx = In — [т, п > 01. J х т 1 J 0 co
858.621. \ ^-^dx = ^r. 0 или — — в зависимости от того, будет J х 2 ’ 2 0 ли т положительным, нулем или отрицательным, со со
858.630. С sin2mx , С cos’mx , \ dx = \ dx — оо. J X 0 х 0 0 СО
858.631. С sin2mx — sin2 пх , 1 . т г . \ dx = -я- 1п — [т, п 01. 1 х 2 п i > -г- t
О
192
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
1858.632
858.632. п¥=0].
О
858.641. [л»>0].
J x 4 1 '
О
oco Ало fsin8p+’ffix . 1-3-5 ... (2p—1) л
858.649. J-------------dxB-2>4i6 J?2p)
[p= 1, 2, 3, ...; m> 0].
«> to
oeo cen f sin mx . C cos mx ,
858.650. \ —j— dx = \ dx = oo.
J хг J X*
858.651. CO 0 cos mx—cos nx . , : dx=(n x1 ' -w)-2 [p > m >0].
858.652. co sin8 mx . —3— dx = 1 Iя’ |ш|-2 . [Cm. 858.711.]
0
858.653. 00 0 sin’ mx . —5— ax== X* --- m In 3. 4
858.654. co 0 sin’mx . —s— dx = X*
858.659.. co 0 sin’P mx . ;— ax = Xs 1-3.5 ... 2-4-6 ... (2p-3) (2p—2) | m | n 2 [p = 2, 3. 4, ...].
858.661. co 0 sin’ mx . 5— rfx = x’ ТтЯ И >0].
858.701. co • sin mx cos nx JS . n dx = -^ JI ~ 4 [от> n \m = n >0]. >0],
= 0 [л> m >0].
858,802]
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
858.702.
J x 2 m—n
\m > n > 0]
ceo C cos mx cos nx .
858.703. \------------dx — oo
J *
858.704. js-^.?£8i"^dx==A
0
__ Я
~ 8
= 0
00
OEO -,«< f sin mX Sin nX J mn
858.711. I---------dx — -y-
0
ПЛ
= T
co
opo-rm f sin2 ax sin mx . m+2a , , , n . .
858.712. i---------dx = ——In ] m + 2a | +
0
. 4-m~^2a In | m—2a |— ~lnm
358.713. J.si.n8fl^os^dx = ^-(a-f)
0
= 0
858.721. J.;-gs^.rfx==^r
0
00
oeo io, f sin8 ax sin mx . лат яп'
858.731. J----p----dx = —-------
0
_______________ла2
~T
858.801. f^dx=f^dx = -^-
J K7 J K2m
0 0
858.802. C~dx = Vtoim
[2a>ffi>0],
[2a = m > 0]
[m > 2a > 0]
[rt Ss m > 0}
[ffi n> 0]
[w>0]
194
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
1858.811
858.811. . [0<р<2,- »>0].
. 2sln^r(P)
К тому же численному результату приводит другая
формула:
858.812. f х4"1 sin mx dx — -Г sin^
J mfl 2
[0<<7! <1; zn>0].
Для q, близкого к нулю и равного нулю, пользоваться
формулами 858.601 или 858.811.
858.813. |0<р<1; |»>01.
J *' 2c»s!2rW
К тому же численному результату приводит другая
формула:
858.814. С хч~' cos mx dx = cos
J nv 2
0
858.821. \^Lmx^snx dx =
J Ух
0
J__? . +__L. I XX
l У m + n, Vm—n. J2/2
858.822. C -sin2X* dx = Утл
J x Ух
0 «
co
858.823. C sin8 ™x dx'= (iKlzzll i/Il
J уx 4 ' ^m
___ or.. f sin’ mx j (3— V 3) -,/-x
858.824. \----7= dx = ----/—- у 2тл
J хУх 4
О
858.83!. f arctgxdx_ = nL
J (1+x) Ух 4
|P<? < 1; л»>0].
pn>n>0],
[m>0].
[m >0].
[«> 0].
859.008]
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
195
858.832. J arctg sin mx dx = (1 — e~am) [a, m > 0] 0
858.841. f —,sin*d- = tf(/e) [0 < k < 1]. J X V 1 — k2 sin2 X 0
858.842. f i«i<n. J X У 1 — k2 CQS2 X 0
858.843. C sinxcosxdx__ = > J x У 1 —k2 sin2 x k Для 858.841—.843 см. 773.1, 774.1.
859.001 Л <J3 s 4 0 cos mx . я ma a2+x2 2a [a^ >0; m 0].
859.002. 00 = e~2^) a2 + x2 4a' [a>0; 0].
0 00
859.003. c™^dx==£-(4 + e-ima) a2+x2 4a ' ' >0; 0].
- 0 00
859.004. 0 xsinmx j я -ma a2 + x2 2 [a 0; m >0].
859.005. co sin mx л ,< _mcr. x(a2+*2) 2a2 { ' [a>0; m 0].
0 co
859.006. 0 00 sin mx sin ПХ f Л _ ma i- a2+x2 dx^2ae Shna [a>0; m s г n ds- 0].
859.007. 0 00 COS mx COS ПХ dx==±_ e-ma ch a2+x2 2a [a> 0; m s 2/1^0],
859.008. J x sin mx cos nx t л _ma « —X dx = -7- e ch na - a2 + x2 2 [<z>0; > n > 0],
= — Ae-na shma [a>0; m >0].
196
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
(859.011
СО
859.011. ( = тхО + та) е~та [а, т> 0J. J (а2 4-х2)2 4дй' 1 ' i j 00
859.012. С xsinmx , ят г ^01 } (яа4-яа)а Х 4а 0 оо -
859.013. С x2cosmx , я г \ TS-,—dx = -г- (1 — та) е та [а, т > 01. J (а2 4-я2)2 4а4 7 1 ’ j 0 00
859.014. t ..^.^-dx^ — fl _Цтае-та\ [а, т>0]. /1 х (а2-(-х2)2 2а4 \ 2 / 1 J ОО
859.021. С cos тх dx (ё~тЬ ч е~та\ я J (а2 + х2)(62+х2) — ( b a /2(а2—Ь2) 0 [а, Ь, /и >> 0; а=£ &].
859.022. 0° . С х sin тх dx (е т°—е~та\ л J (а2 + х2)(*24-х2) ~ \ а2—*2 /2 0 [а, Ъ, т > 0; а =^= &]. too
859.031. С cos mx , л^-та . . \ , л-i dx = ~-о - (sin та 4-cos та). J х4 + 4а4 8а3 v 1 7 00
859.032. С sin тх 1 л /л ч \ --/-д-д-и ас dx — к-z (1 — е та cos та). Jx(x44-4a4) 8а4 4 7 0 оэ
859.033. С х sin тх , я . \ .7-.^;-dx = у-j е masrnrna. Л я44’4а4 4а2 со
859.034. С х2 cos тх , я . \ . , . . ах = -г- е та (cos та — sin та). J х4+4а4 4а v 1 ОО
859.035. С ж3 sin тх , л \ х4+4а4 dx= 2 е та cos та.
Для 859.031—.035 а, т^>0.
859.1131
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛЫ
197
859.041. f ~^^=<1х = Кй(,та}. [См. 815.1.] [та>0].
J Уа24-х2
859.042. ( -^^=-dx = £j0 (т).
g У 1-х2 2
Л ________
859.043. . dx = 1/ -^-h) [0 < b < а].
/а ± * cos x Va + b \Г <*+*/ 1 J
I= A2 = sin2 9. Cm. 773.1.]
[a+* J
Л/2 М2
ocq i ло C _______\ ________________d*__________=
j 14-2asinx+a2 J 14-2acosx + a2
я . ' 2a 2a
tj- — arcsin f-j—r arccos ——5-
__ 2 1 + a2 ___ 1 + a2
— |1— a2 | ~ |1— a2 | •
[См. примечание к 859.112.]
859.101.
859.111.
859.112.
Л/2 М2
С ______dx________ С ______dx_______
J 1—2asin«4-a2 J 1—2acosx4-a2
о 0
я . .2a
2~+arcsmT+^-
| 1 — a2 |
[См. примечание к 859.112.]
_ 2g л, 2a
% ,, я—2 arcsin -ri—г 2 arccos -r—:—-
C_______ax____________________1 +g2______________1 4-g2
5 1 + 2a sin x + a2 |1—a2 | |1 — a2 |
[См. примечание к 859.112.]
Л
I о , 2a
, я+2 arcsin ——Т
_______dx____________ ____________1 + °2
1 — 2a sin x + a2 | 1 — a2 |
В 859.100—.112 a >0; a^=l; arcsin и arccos везде в первом
квадранте.
859.113.
Л
С ______dx_____________я
J а2 ± 2ab cos х + Ь2 ] а2—Ь2 |
[а2 £>2].
7 Г, Б. Даайт
198 ОПРЁДЕЛЕННЫЕ ИНТЕГРАЛЫ [859.121
859.121. Л sin х dx — Arth a = a a 1 —a [a2 <U,
1—2а cosx+a2
= 2 « .и — Arcth a = a a a—1 [a2 > 1].
859.122. л cos mx dx nam {a2 < 1; m = 0, 1, 2, 1
о 1—2acosx4-a2’'~ 1 —a2 • • • ]»
л [a2 > 1; ffi = 0, 1, 2, 1
am (a2 —1) . . . J.
859.123. л x sin x dx yln(l + 6 A [a2 < 1],
о 1—2a cos x + a2
== Tto(' + _1_\ a J [a2 ^1].
л
859.124. (a—bcos x) dx ЛГ \a > b > 0],
a2—2ab cosx + 62 a
= 0 lb> a > 0].
859.131. л sin2 x dx Л [a > b > 0],
о a2—2ab cosx + &2 2a2
Л ^2^ {b> a >0].
859.132. л cos2x dx я p + a*A [a2 < 1],
1—2acosx+a2 ' 2 U— a2)
0 я f a2 + 1 >
~2a2\a2— 1; [a
859.141. л sin x sin mx dx яа”-’ m = 1, 2, 3,'
0 1 —2a cos x + a2 2
Л = 2am+I [a’> 1; 2, 3, ...I.
859.142. Г cosxcosmxdx яа22р+а;\ fa* < 1; = ], 2, 3, ...], J 1—2acosx + a2 2 \1—a2)
860.05]
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
199
859.151.
859.161.
859.162.
859.163.
859.164.
859.165.
859.166.
860.01.
860.03.
860.04.
860.05.
л Г sinxdx 2 г . h " >0],
J V аг—ЯаЬсоьх-^-Ь1 а
>0].
С dx == ф [—л< C<p< С я].
J 14-2xcos<p+ х2 2siti<p 1 0
При ф = 0:
I С dx 1 1 rpM qn о 1
}l + 2x+^~2• [См. ШМ.] 0
00 с dx <р г Сф< "л].
J 1+2ХСОЗФ+Х2 з[пф 1 0
При <р = 0:
00 С dx t rpM qn п j
J 1 + 2х+?-1* [СМ. Уи.^,1 0
00 С dx л
11—Зх’созф+х4 . . ф J т ' 4sin 0 Сф< Сл].
С xPdx == Л31ПРФ rO^DCl- 0< «*/ п л].
J l+Sxcosqp+x2 sinprtsintp 1 > 0 «1ф <
О0 00 §e-axdx=~ [а>0]. 860.02. J xe~axdx = о 0 >0].
00 Г* 9 j x'e-^dx^ [а: >0].
C x'^e~axdx~ J 2а у a 0 [«; >0].
00 /• — C x~l^e~axdx = -yi J ya >01.
ft
200 ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ (860.06
860.06. f ./~4—. 1-3-5...(2р—1) у е ах™ 2р о а а |а>0; р=1, 2, (См. 860.07, второй вид ответа.)
860.07. ^e'axdx = ~ [а> 0; л=1, 2, ...], 0 = 4^ (а>0; л-Н >0). 00 «
860.11. = (г >01. 0
860.12. § xe-'^dx = ^. 0 . 00
860.13. §x2e-™dx = ^ [г > 0]. 0
860.15. (г>0: а=1, 2, ...)', 0 00
860.16. jxi8e-^dx= 1 [г > 0; а = 1,2, ...]. 0
860.17. с 1 х"е-г^ах= УД./. (Л+ 1, г > 01 0 (положив т — 2 в 860.19).
860.18. f e~™mdx== Л Г ( — [г, т > 0] J пи? \ т J 0 (положив л —0 в 860.19).
860.19. jxBe-<«)“dx = -Lnr(^±l) lfl+1, г, т>0]. О Все предыдущие формулы 860 могут быть получены из этой при соответствующих значениях п, г и т.
866.38]
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
201
860.21. оо Р *-ах 1 -—dx J * 0 = co.
860.22. J А* (1 -b* b — dx — \n—- a {а, b > 0],
860.23. 00 P e-ax<_~e ~bx° ... 1 1_ b (а, Ь, с > 0],
J X 0 dx in g a
860.24. 00 P 1 —e ~ OX2 J X2 0 dx —У ал [а > 0].
860.25. J 2a 0 ]а, b > 0].
860.30. 00 f dx
0 [а > 0].
860.31. OD C x dx J 0 л8 ба* [а > 0].
860.32. f x2dx J 2£(3) 2-1,202057 а* - ' а* la > 0J.
860.33. 00 P x’dx J eax—[ ~ 0 л4 15а4 [См. 48.003.1 1а > 0].
860.37. Cx^-’dx
J 1 0 а2п t ' пагп Вя
860.38. P x2r‘dx J eax—l • ]а >0; л = 1, 2, ...]. ]См. 45.] [См. 860.39.]
о
202
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
1860.39
860.39. = + ± + ...] = L^S(p)
о
[а>0, р>1; р не обязательно целое число]. [См. 48.09.]
Таблицу ^-функции Римана, содержащую и дробные
значения аргумента р, см. [16].
860.40. ? dx _In2 ra ->oi [См. 601.01.]
3 е^+1 а 0
со
860.41. С xdx — л2 г Qi [См. 48.22.]
12а2 1 0
860.42. F х2 dx 2! 3 3-1,202057 [а>0]. [См. 48.003 и 48.23.]
J еах+1 а3 4 2а3 0
860.43. ©О С х3 dx 7 л4 J еах+\ “ 120 а4 0 [а>0].
860.47. ©о С х2л-1 dx __ 22л’1— 1 я2л о J е°*+1 2п а2л 0 [а>0; я=1, 2, ...]. [См. 45 и 48.28.]
©о
860.48. С х2л dx J ’ 0 [См. 860.49.]
860.49. f xP-i dx _ Г(р)Л _ 2\f J ~ ap 2Р/^УИ) 0 [a, p>0; p не обязательно целое [См. 48.29.] число]. [Для р = 1 см. 860.40.]
860.500. ОО со С dx Г 2 dx
j sh ах ” j е0" — ё~ах ”” 0 0
860.501. ©О С xdx jrt2" J sh ax 4а2 [а>0].
860.518] ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ 203 СО
860.502. $re=2(2!)(1+i + ^ + i + '--)/a’ ==2^^3)’ = 4,1’05180^3- [См. 48.13.] ОО
860.503. С х3 dx л4 , п. \ih^ = 8? 1а>°1- 0 оо
860.504. С dx 93 । AQcnoi к = У 1’03693^5- 0
00
860.507. f x2«-i dx _ л2" (22«-1) г 1 о \ sh ах "" 2па2п В" [а>0, Л—I, 2, ...].
О
[См. 45 и 48.18.] ОО
860.508. х^п Их —. [См. 860.609.] ОО
860.509. J shox аР \ [а > 0; р > 1; р не обязательно целое число]. [См. 48Л9.] СО
860.511. С х dx \ Т5— = ОО. J sh2ax и оо
860.512. е x*dx _ л2 , \ sh2 ах ~ 6а« 1а > ОО
860.513. S К = 4 • Ь202057М [См. 48.003.] 0 оо
860.514. С х4 dx л4 j sha ах 30а5 оо
860.518. (* vZH fl у зт2^ \й>«-а«чв- [*>0]. [См. 45.]
U
204 ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ 1860.519
860.519. exPdx Г(р + 1) /. . 1 . 1 , 1 , ' А J sh’ax 2Р-'аР+' \ 1 "Г2Г,'Г3^'Г 4Р *"••• } [а>0; р>1; р не обязательно целое число]. ]См. 48.09.] СВ оо
860.530. Jsfe-J I-»»)- |Си. 679.10.) 0 0
860.531. J^ = 2G/aa = 2.°,9159656/a’. ]См. 48.32.] О
860.532. 03 СхМх я’ . . J ch ах 8а’ > 0]. О
860.533. j^^12*0,98894455^4- [См. 48-34-) 0 со
860.534. f x*dx 5 я* Jchax-32а* [в>°Ь О Cx*ndx л л п -
860.538. "-О’ ’• 2- •••! Iе"- 45-» 0
860.539. QxP-'dx 2Г(р)/ 1,1 1 , \ J ch ах аР V 3? + б^ 7P'^,"J ]а, р>0]. 0 Для целых значений р см. 48.31—.39. Для р нецелых сумму ряда приходится находить численно.
860.541. со С х dx In 2 J ch2 a* a’ * 0 co
860.542. (* x*dx __ я2 J сЬ’ах“12а‘ la > UJ. 0
860.543. C dx 2.. 1 202057ta* 9 ~ (3) J ch’ax “8 1>2O^Oj7/a - 8 a* • 0
860.99]
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
205
860.544. С * dx — 7 я* Г а "> 01 J ch8 ах 240 ай 1 О
860.548. f (У""1 —1) „,Яр Гп^Л. и —1 9 1 J ch2 ах ~ з^'а2”-*-’ Я В* [«>0. « 1. 2> •••]• <о / 2 \ |См. ^®»1
860.549. f хР Ях V 2р) г (р +1) - г„^л. — И 1 ch2ах 2Р"1 ар+‘ в(р) [а>0, р>1]. 0 При р = 1 см. 860.541. [См. 48.29.|
860.80. 00 1 е~ах sin mx dx = 1а > 01.’ J aa + m8 1 1 О 'г »
860.81. С — ах • j 2d/и । к л1 j х* * sin mx dx = ^-^ [а>0]. О
860.82. со С з ^лх 1 j 2ffi (За8 —mh » \ х е sin mx dx = У,—[а > 0]. J (a24-m2)3 0
860.89. CD f х?~'е~ах sin mx dx = -Г-ffiL?1" n, а m>01, J (a! + ma)*’/2 0 где sin0 = m/r, cos 0 = a/r, r = (a2 + m')1/3.
860.90. ^e-ax cosrnxdx^a2 + m, [a>0], 0
860.91. CD (* д8 j xe~aX cos mx dx = (аЗД» [« > 01. 0
860.92. P^-°*cosmxdx [a>0], 0
860.99. CD C xP-’e-^ cos mx dx = J (a2 + m2)p/2 0 [a, p > 0], определение 0 см. в 860.89.
206
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
[861.01
861.01. СЮ С е~ах т \ —-— sin тх dx = arctg — |а> 0]. 0 сю
861.02. \ cos тх dx = оо. J х 0
861.03. сю J ~—(1 — cos тх) dx = -у In Q +-^г) [а>0]. 0 сю
861.04. f е“в* / \ j 1 , о24-п* ( j —j— (создал— cos nx)dx = -7i In [а>0]. 0
861.05. Pe-eJt — е~ь* . 1 , b’+'n’ . _ , J cos mx dx - 2 In a, +m, [a, b> 0]. 0
861.06. J e~ax cos’ mx dx - fl (Д W) [a > 0]. 0
861.10. СЮ C e~ax sin’ mx dx = - . 2.- [a > 0]. J a (a2 + 4/zr) 1 J 0
861.11. (* e~ax , s . 1 i f. , 4m! X r n1 \ —— sin mx dx = у In ( 1 4—у J [a Z> 0]. 0
861.12. CD Г e~‘ax ,2 . . 2m a . /, , 4m* X r м \—-j— sin mx dx = да arctg -r- In 1 1 4—-r-) [a>Oj. j/ Jp Cl 4 \ Cl j 0
861.13. co C -ax , > J 2amn \e sin mx sin nx dx = —— J •|a2 + (m—п)’Ца +(m -j-n)2} [a>0].
861.14. C -ax , J т(аг+т* — n’) \ e sin mx cos nx dx = 1—7———' — J {a’4-(m—n)2} {a’-f-(m-l-n)’} [a>0],
861.15, C -ax J в la* + mz 4-Пг) 1 e x cos mx cos nx dx = Z / J {«’+('»—orHa’+tm+n)2} [л>0],
861.62] ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ 207
861.16. Ь'“ • л 11 a’ + (m + rt)’ j —j— sin/их sin/zx dx— 4 + [a->OJ. 0
861.20. ( е~агхг cos mx dx = -?£- e 4a2 [a>0].
861.21. \ хе~агх2 sin mx dx = ——e 4a2 [a>0]. 0
861.22. f e~°2*2 . , n f m\ r m \ —-— sin mx dx = erf (J [a > 0 j. [Cm. 590.] Таблицы см. [196].
861.31. (* e~ax , (a + Vаг + m2)’12 \ -4=- cos mx dx = ———T,,,--S==r— [a > 0]. J J<x (a2+^2),/2/2 1 J 0 “ yp m
861.32. \ e~ax sin У~тх dx = —^=e 40 [a, m>0]. J 2a V a 1 J 0
861.33. p e-ax —HL \ - r" cos у mx dx = ~=^ e ia [a, m > 0]. J У x У a 0
£e--sin(px + g)^^Qsi^+y0S-
861.41.
861.42.
861.51.
861.61.
861.62.
C -ex / । \ j a cos a—p sin fl
j e cos (px + q)dx =-----a'+p'
0
[a>0].
[a>0].
sin mx . f 2 sin mx , л .. nm
—— ax=\ -ax—dx =-5- tn -75—
sh ax J eax—e ax 2a 2a
00
icos mx j л
—------dx —------—
ch ax „ , am
2a ch -K-
2a
[a>0].
la>0].
268
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
[861.63
0D
861.63.
861.64.
861.65.
861.66.
861.71.
861.72.
861.78.
861.81.
861.82.
861.83.
0
0
0
sh qx ax 2q 8 2q
ch.px _ л
ch qx яр
2qcOs-^.
th qx sin mx dx = —-—
n u nm
2flsh^-
sinmx .
-тг— ax =
th qx
я
n *U ПГП
2<7<h 2?
I sin mx cos nx ,
1-----г------ax==
J sh ax
о
I cos mx cos nx
J ch ax
о
cos mx .
0
[~q<p<q; ?>0],
. tnn
я sh —
_____a
mn / , nn
----к ch —
a a
. mn < пл
ясЬ_сЬ—.
«№—7---------
a ch--к ch —
Я7П
2a* sh^
2a
, nm
, . sh -77—
x sin mx . я’ 2a
—г----dx=-w----------7-г
ch ax 4a* ,, (пт \
ch1 ()
\ 2a )
r x cos mx . n‘
I —г-----dx --------7---r
I shflX 4a* ch1!— \
J \2a J
0 '
C th ax . . ,. nm
\-----cos mx dx— In cth ~
J X 4a
[a>0].
[a>0].
[a> 0].
[a, m>0].
0
862.4Ц
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
209
862.01. СО \e~axshbxdx = [<z>Z?S&0]. J qa— qa ь 0 оо
862.02. ? е~ахchbxdx = [a>b^0]. л QA qA 0
862.03. \ xe~aV sh bx dx = <?<“’ [a > 0]. j 4as 0 6a
862.04. \ e~ax sh (b J^x) dx = —~ eia [a >» 0]. J 2a V a 0
862.П. co J eax_|_i ' 2m 2ash(wn/a) oo
862.12. f sin mx , „ n 1 t nI j eax—1 2ath(nm/a) 2m
862.21. OO e«x+1 dx 2a sin (пр/a) 2p [«>/»> 0].
862.22. OO 2p 2aig(np/a) [a >P > °]- 0
862.31. oo C - = —£a + (sh m) In (1 + e-m) {m > 0]. J (14-x2) sh ях 2em 1 v / 1 " 1 Г th -Д-
862.32. J -j-j-^sinmxdx= — (sh tn) In (1 — e~2'n) [m > 0]. 0 co
862.33. f Sin^_ = _(sh/W)lnth^ [OT>01. J (l+x2) th и z
г к sin —
862.41. Г cos тх dx = ---------------------------
J sh 9х 2(7 cos ря 4-ch
о Я Ч
[—q^P^q-, ?>0].
210
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
(862.42
862.42.
от , тл
с , sh —
1 ch рх . ,. л q
I —+~— sin тх dx = л-----------------
I sh qx 2q рл , , тл
J 4 4 cos— 4-ch—-
о <7 <7
[—<7 «g р «g <7; <7>0J.
862.43.
sh рх
ch qx
J я
sin/их ax = —
<7
. рл , тл
sm + sh -д—
2<7 2?
рл . . тл
cos — + ch —
<7 <7
[—<7«gp=g<7; ?>°]-
862.44.
рл . тл
cos +- ch -д—
л 2р 2р
со
!ch рх ,
г--- cos тх ах
ch ох о рл , , тл
cos — 4-ch —
<7 <7
I— q^p^<r,
?>0].
863.01.
i
S (1п+)? <** = Г(? + 1)
о
[? +1 > 0]. [См. 850.1.]
863.02. xp In - dx = . J-,..-
J x (p+1)2
(* / 1 \2 9
863.03. \ xp ln-Wx==r-+7^
J \ xj (p-M)3
863.04. £ xp (in IV dx =
J \ x] (p4-1)?+*
[p-H>0].
[p+l>0].
[p-f-1, ?+ 1 >0].
863.05. C fin -Y/2 dx =
J \ x / 2
0
p / i \ —1/2 _ ___
863.06. \ (in—) =
J \ x j f
0
863.10. (
j !_x ax - 6 .
863.35]
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
211
863.11. ----------------------F-
f* xs In — t . .
863.12. p-—i-
f In — i
863.20. Jrrx^=^.
o 1 "T" X 12
Cxln — ,
8«3-21- ^-Г+7^=1-ТТ-
n X x пг 3
863.22.
0
863.30. f — dx — ~ — 1.
J 1 —x x о
о
863.31.
0
863.32.
0
863.33. j '•
0
i ln-b
863.34. \ -,-7^-^= 0=0,9159656. [Cm. 48.32.]
V 1 "P л
0
’ ln~
863.35. \ .-г—^?dx = ln2.
U v "г •* ’
о
864.01]
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
213
212 ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ (863.36
863.36. f 1— х . 1 . 2л’ « , ”’7Г in— dx = -iyj- . J 1 4-аг х 27 0
863.37. (* 1+х . 1 , 4л’ 1 •. a- In — = J 1—х* х 27 0 i In —
863.41. f -^=dx = vln2. J V 1-x2 2 0 i X In 4
863.42. I — --rfx = 1 — In 2. J V 1-x2 0
863.43. j (lnl)/l-x,dx = -j(ln2 + 4). 0
863.51. C xP dx J In x ~~ 0
863.52. C^=fSdx==ln£±4 [p + l,<7+1>0]. J In x q +1 ir ’ J 0
863.53. P xP-x* t J p+^ + 1 J Inx X ax lnq+r + l - [p+r+l,4'+r+1 >0].
863.54. f (1-^) (»-«*) _ 1 n (P-H-M) J Inx ax ln (p4-l)«7-|-l) [p+ M+ l.P+«+ l>0].
863.55. f f\—x\ dx 2_ J VT*/ Inx -ln rt ’ 0
863.61. С (1ПХ)* Лу-Я>’ J14-x’aX 16* 0
863.71. * Л 3 1 In (1 — x) rfx— —- 1. 863.72. xln(l — x)dx = — -j. • ®
p i P+1 ।
863.73. j xnn(l-x)dx = -^1j;- [p = 0, 1,2, ...]. 0 n =1
863.74. C bd-x) . л’ J x ax~^ 6 • 0
863.81. 1 У In (1 4- x) dx = 2 In 2—1. 0
863.82. 1 У x In (14- x) dx — -j. 0
863.83. j x‘Hn(14-xHx = ^j21n2-£<-4U 0 ' n =1 ' [p = 0, 1,2,
863.84. Д 1 ’P ( 1АП-1 У x’P-4n(14-x)rfx = ^£L_^- [p=l,2, ...j. o rt=l
863.85. Cln(l±x)rfx = ^ J x 12 0
863.91. 1 У lnxln(l — x)dx = 2— 0
863.92. 1 Г In x In (1 4-x) dx =2—2 In2—£5. t) 0
863.93. 1 У xlnxln(l — x)dx=t — 0
863.94. 1 C xlnx In(1 4-x)dx = ^— t) A 0
864.01. 1 У In 2-0=iln2-0,9159656. [Cm. 48.32.]
214
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
[864.02
864.02 . f ЦЩг-* dx = In 2.
J A T"* °
о
864.03 . C r-j-i; In dx = v In 2 + G.
J 1 + x‘ x 8 1
0
864.04 . ( УУ7У dx = у In 2 — G.
J I "T" *
о
864.11. f In z/x = 21n2.
J V"**/
о
864.12. ( —In </% = ?.
J x \1— x) 4
0
864.21. ( lfl(1~xj?) dx = — У
J x Qp
0
864.22. ( ML+^D dx =
J x 12p
0
864.31. f = — 2O~£ln2.
J /1—x2 2
0
864.32. f -A±5 dx = 2(7—i In 2.
J Kl-x3 2
0
864.33. f dx = (g + (In 2)’ I.
J V 1 —x‘ - (I
0
I
864.41. § (1 — x) e~x ln~ dx = 1 —
0
CD
[Cm. 48.32.]
[Cm. 48.32.]
[p>0].
[P>0].
[Cm. 48.32.]
[Cm. 48.32.]
[0 <р<1].
864.51. (• xP~l . 1 \ -j In — dx = ns
J l-*-X X 0 sin2 pn
865.01]
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
215
СО
864.52. ? In 1 dx =
J 14- х х st
о
оо
864.53. £_£Ц~ <** = ?•
J х2 —• 1 4
о
864.54. 0 In x , n , —5- dx = =- ln a x2 + a2 2a
864.55. co 0 (In x? dy. _ Л? x2 + 1 X~ 8 *
864.61. co 0 !n <V±£). 'qTx = " in 2 + 0. 14-x2 4 1
864.62. oo 0 л 1„ (!+«»)
864.63. co 0 = i !„(<, + »)
864.71. 00 0 In (1+x) . я x2-p ' (1—p) sm pit
864.72. 00 ln(l+x)//y._ Я
0 x1 + 4 ' q sin nq
864.73. co ln(l+xP) , л x« X ' M . я(</-1)'
864.74. 00 0 In |xP —1 | , л
865.01.
т:/4
( In sin х dx = — -v In 2 —
3 4 2
[0<p< 1].
[a>0].
[Cm. 48.32.]
[a, b > 0].
[a, b>0].
[0 </><!].
[0<9<l].
[0<9-1<р].
[0< <7-!</>].
[Cm. 48.32.]
216
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
1865.02
Л/4
865.02. (lncosxdx =— -^-In 2[См. 48.32J4- J 4 & 0 П/4
865.03. In tg x dx = — Q. [Cm. 48.32.] П/4
865.04. ( In (1 + tg x) dx = £ In 2. V ° rr/4
865.05. In (1 — tg x)dx =-?-In 2 — G. [Cm. 48.32.] Л/2 Л/2
865.11. \lnsinxdx = \ In cos х dx =— у In 2.
865.12. 0 0 rr/2 In tg x dx = 0.
865.21. Л/2 (sin x) In sin x dx *= In 2 — 1.
865.22. Л/2 (cos x) In cos x dx = In 2 — 1. 0
865.23. п/2 л/2 (cos x) In sin x dx — (sin x) In cos x dx = — 1. 0 0
865.24. rr/2 С \ (tg x) in sin x dx = — H7. •) *“ **
865.25. я/2 (sin2 x)lnsinxdx = (1 — 2 In 2). 0
865.26. Л/2 \ (cos 2ях) In sin x dx = — ~ [n > 0].
865.42]
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
217
865.27. П./1 С In cos х . п* \ —: ах тг • J sinx 8 о Л/2
865.31. J In (1 + cos х) dx = 20— 2^-: [См. 48.32.] 0
865.32. Л/2 J In (1 — cos х) dx = — 20— - 2° -. [См. 48.32.] 0 Л/2
865.33. J ln(l+tgx)dx=G+^y^. [См. 48.32.] 0 Л/2
865.34. J 1п(1 + psin* x)dx = 0 = J in (1 4- р cos* х) dx = л In 1 - [(14- p) 0]. 0
865.35. Я/2 J In (a* sin’x-Ь 6*cos’x) dx — л In - [a,ft>0]. 0 Л/2 Л/2
865.36. j In (a’+ ft’tg’x) dx = J ln(a*4-ft2ctg*x)dx«nln(a + &) 0 0 [a,Z>> 0]. Л/2
865.37. P . /'a + &sinx\ dx \ In ( Г—: ) =S J \ a—b sin x J sin x 0 Л/2 C . fa + bcosx\ dx , (b\ J \a~-bcosx/cosx \ a} [l>2 a2]. Л
865.41. У In slnxdx= —л!п2. 0
865.42. f , . n2 ln2 \ x In sinxdx — .
О
218
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
[865.43
865.82]
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
219
л
865.43. J In (lj2cosx)dx = — л In 2. 0
865.44. Р, , , , . . , /а+Ка2—/>2) \ In (а ± b cos х) ах = л In < % ( [aSs b ; >0].
Л
865.45. Р In (1 4-acosx) . „ . \ —1—! l dx — л arcsin a J COS X 0 [0< a< ^1].
865.51. 1 P , . , . Si (m) I (cos mx) In x dx — — • [Cm. 431 .11.]
Таблицы см. [22].
865.52. 1 J xp-1 sin (q In x)dx = pi +’ 2 0 [p: >0].
865.53. 1 JxP-’cos(?lnx)dx= pip+q2 0 [p~ >0].
865.54. C^sin(?_lnx) . J Inx 6 p + 1 [p + i: >0].
0 CD
865.61. j hl(l+J)cosmxdx==^-(1— e~am> [a, m' >0].
0 CD
865.62. [a, b, m' >0].
0 co
865.63. j^lnldx = -f(lnm + Q [m I >0].
0 [Cm. 851.1.]
865.64. Pln(gmx) «! Zshma\ J a24-x2 a \ ema )
я , /1 — е~гта\ -а’Ч 2 ) [m, a: >0].
865.65. CD 0 DO In (cos’mx) . л . /ch ma\ —-гт-т- dX — — In —ma J a’+x® a \ e ° J [m, a. >0].
865.66. j In (tg2 mx) , л . ,. \ 2— dx = — n th ma a’-f-x2 a [m, a >0].
0 Л
865.71. In (1 ±2a cos x -f a’) dx = 2л In a [« >1].
0 = 0 [a’ ^1).
865.72. Л In(a’±2akcos x+ b2) dx = 2л Ina [a>ft >0],
0 = 2л1пй [b^= a >0].
271 I
865.73. In (a’±2a/> cosx + b*) dx — 4л In a [а5г b >0].
— 4 л Infi [ft> a >0].
865.74. § In (1 —2а cos х + a’) cos тх dx = —ат
[О < а < 1; т = \, 2,...].
865.75. j ±2а«СДГХ~1'p2) dx = £ In (1 ± ре~та)
[0<jpsg 1; т, а>0],
= 7 1n(p±e-me)
[р> 1; т, а> 0].
865.81. jln(1 + e-*)dx = ^.
со
865.82. j*ln(l — e~x)dx= —
О
220
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
[865.83
865.83. о о •
865.901. J е_ох In у rfx (In а+Q [а >0]. [См. 852.1.]
Относительно постоянной С см. 851.1. C = 0,5772157.
865.902. J хе~ах In у dx =-~j (In а— 1 + С) [а>0].
0 00
865.903. ^х*е-ах]п^ах ==р (1п а—4 + с) 0 [а>0].
«е-ах1п{ у~-
865.904. j "/х </*= ^(lna+21n2+Q [а>0].
0 00
865.905. (-(г4 e-ex>)dx = ln- + C J X \ 1 +рх J р ' [а, р>0].
0 00
865.906. С - ( г-г-п— е~ах} dx = in - н- С J х \ 1 4- р2х2 J р ’ [а, р>0].
0 ее
865.907. С (-у1 . iAdx — с. J \е* — 1 хе31 J 0
865.908. ^ln ^ln -i-) dx — — С. 0
865.909. С [ ’—h-j-i-A dx~C. J Vnx1 1— x) 0
865.911.
00
J е~ах sin mxdx =
о
= (a2-f-m2) {У 'n(a +да2) aarctg —+тс|
[т, а>0]. [См. 851.1.]
886]
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
221
865.912. § (in у) е~ах cos тх dx =
О
= {j ln (fl2 + '»’) + '» arctg“ + ас|
[от, а>0]. [См. 851.1.]
n / i \
Г ( In — ) е~ах sin тх .
865.913. 1 --------dx = jу In (а* + тг) + С | arctg -
[т, а>0]. [См. 851.1.]
Значительная доля интегралов в 850—865 может быть
найдена в [6]. См. также [3]—[7].
Л л
866.01. У cos (х sin ф) cos (х cos ф) йф — aJe (х).
о о
л
866.02. j cos (лф— х sin ф) dq> = nJn (х),
О
где п—нуль или целое положительное число.
(Интегралы Бесселя.)
866.03. $e*,c<”*dx=n/0(p), как в 809.1.
Таблицы к 866 см. [20] и [21].
880. Правило Симпсона. Если известны значения y=f(x)
для равноотстоящих значений х с шагом h, то численное
значение интеграла приближенно выражается формулой:
ь
j/ (х) dx^ [Л+43'1+2Л+4Л+2Л+... +4yi„_1 + yin],
где А = хг—х0—постоянная разность между соседними
значениями х, т. е. 2лЛ —А—а. Коэффициенты равны
поочередно 4 или 2, как указано. Приближение обычно тем
точнее, чем больше п. Таким методом можно получить чис-
ленный результат, когда аналитическое выражение для ин-
теграла не может быть найдено. Используя таблицу /(х)
и арифмометр, можно провести это вычисление без проме-
жуточных записей.
222 ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ [881
881. Погрешность приведенной выше приближенной формулы
равна
nhrfv (х) _ (b — a)h*flv (х)
90 180 ’
где для оценки величины tff™ (х) может быть взята наи-
большая четвертая разность в интервале (а, Ь).
882. Другая формула, которая во многих случаях более точна,
чем формула 880. По ней тоже можно производить вычис-
ление на арифмометре без промежуточных записей:
ь
§ '/(х) dx А [ 1,4у„ + 6,4Л + 2,4_у2 + 6,4у3 + 2,8_у4 +
+ 6,4_v8 + 2,4_ув + 6,4_у7 4- 2,8_у8 4-...
• • • + 6,4у4п_3 -f- 2,4_у4п_2 4- 6,4yin_i 4* 1,4Лп]>
где 4nh = b — а.
XIII
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
890.1. Разделение переменных. Если уравнение может быть
представлено в виде (х) dx = /2 GO dy, то и левая и пра-
вая его части могут быть проинтегрированы.
890.2. Разделение переменных при помощи подста-
новки. Однородные уравнения. Если уравнение
имеет вид
Л (х, j) dx +/2 (х, j) dy = 0,
где функции однородны по х и у и притом одинаковой
степени, то надо положить у = их. Тогда
• dx_ f2 О, и) du
х ~ ME u)+uf2 (1, и) ’
Если удобнее, то можно положить х = иу.
890.3. Разделение переменных при помощи подста-
новки в уравнениях вида
А {ху) у dx +/2 (ху) xdy = 0,
где Л и /2 — произвольные функции. Пусть и = ху. Тогда
dx___________________ f2 (и) du
X ~ u{fz(u)~fi (u)} •
890.4. Уравнение вида
(ах + by + с) dx + (fx+gy + h) dy = 0
может быть сделано однородным, если положить х — х'-\-т
и у—у'-^п. Величины т и п могут быть найдены из си-
стемы двух совместных уравнений, которые получаются из
требования однородности. Этот метод непригоден, если
но в таком случае можно сделать подстановку ах-\-Ьу — и
и исключить х или у.
224 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [890.5.
890.5. Уравнение в полных дифференциалах. Если
для уравнения Mdx-\-Ndy — Q удовлетворено условие
дМ _ dN
ду дх ’
то это—уравнение в полных дифференциалах. Оно ин-
тегрируется так: находят интеграл j Mdx, считая у по-
стоянным, и, добавляя неизвестную функцию f(y), диффе-
ренцируют результат по у. Полученное выражение прирав-
нивают N; из полученного уравнения определяют неизве-
стную функцию fly). Таким образом, решение будет иметь
вид:
Мdx+f(y)+ С = 0.
Если удобнее, то можно поменять ролями М и N и соот-
ветственно X и у.
891.1. Линейные уравнения первого порядка. Диффе-
ренциальное уравнение называется линейным, если оно со-
держит только первую степень функции и ее производг
ных. Линейное уравнение первого порядка имеет вид:
= Q или dy + Руdx = Qdx,
где Р и Q не зависят от у, но могут содержать х. Реше-
ние такого уравнения:
' 0^+с].
891.2 Уравнение Бернулли. Если уравнение имеет вид
d£+Py~Qyn,
где Р и Q не содержат у, то его можно сделать линейным
при помощи подстановки и = у'~П. Прежде чем делать эту
подстановку, надо разделить уравнение на уп.
892. Нелинейные уравнения первого порядка. По-
лагаем
Если удается разрешить заданное уравнение относительно
Р и проинтегрировать каждое из полученных уравнений
в отдельности, то тем самым будет получено решение
исходного уравнения.
895J
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
225
893. 1. Уравнения второго порядка, явно не содер-
жащие у. Полагаем
Уравнение превратится в уравнение первого порядка, содер-
жащее р и х. Его можно решить каким-либо из рассмот-
ренных выше методов.
893. 2. Уравнения второго порядка, явно не содер-
жащие х. Полагаем
dy
Тх=Р-
Тогда
d2^ dp dy dp '
dx2 dy dx P dy’
Получается уравнение первого порядка, содержащее р и у,
и его можно решить каким-либо из рассмотренных выше
методов.
894. Чтобы решить уравнение
dx* 1 dx 1 J
где А и В постоянные, надо найтв корни вспомогательного
уравнения р2 4- Др 4- В = 0. Если его корни а и b дейст-
вительны и не равны между собой, то решение заданного
уравнения будет y — heax + kebx, где h и k—произвольные
постоянные. Если его корни — комплексные величины: т-]-1п
и т—in, то
у = emx (h cos nx 4- k sin nx).
Если оно имеет два равных корня а, а, то
у = еах (hx + k).
895. Линейное однородное дифференциальное
уравнение п-го порядка с постоянными коэф-
фициентами
dny-L.Adn~'y-i-Rdn~iy-L. -UA'v—О
dT” + A d^ ... + Ky-Q.
Решением его будет сумма членов вида heax, где каждое
а есть один из различных действительных корней вспомо-
гательного уравнения
р" + Арп~* -|- Врп~* -J- ,.. К — 0.
Если а—двукратный корень вспомогательного уравне-
ния, то соответствующий член будет eax(hx-\-k).
226
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
(896.
Если а — трехкратный корень, то соответствующий член
будет еах (hx* + kx +1) и т. д.
Когда имеется пара комплексных корней m-\-in и
т—in, то в решении появится член
етх (h cos nx + k sin nx).
Если это—пара двукратных корней, то соответствую-
щий член в решении будет
етх {(hx Ч- k) cos nx + (sx + t) sin nx}
и т. д.
896. Линейное дифференциальное уравнение с по-
стоянными коэффициентами с правой частью
dn У । д dn 'У . р dn гу . , ty _ у
dxn' А dxn-' + Вdxn-2+ ••• + лу — Л,
где X содержит х.
Сначала полагаем Х = 0 и решаем полученное уравнение
894 или 895. Затем нужно прибавить к этому решению
частный интеграл, который удовлетворяет заданному урав-
нению и который не должен содержать постоянных интегри-
рования, так как такие постоянные уже вошли в решение.
897. Уравнение Эйлера второго порядка
преобразуется в линейное уравнение с постоянными коэф-
фициентами
при помощи подстановки х — е°.
898. Линейное дифференциальное J уравнение
в частных производных первого порядка
дх ду
Чтобы его решить, нужно сначала решить уравнения
dx___________________dy dz
P'~Q'=:R
и представить решения в виде a — Clt v = Cv Тогда иско-
мым решением будет
<р(«, •») —О,
где ф—произвольная функция.
ЛИТЕРАТУРА
А. Общие руководства и справочники
1. Фихтенгольц Г. М., Курс дифференциального и интегрального
исчисления, т. 1—3, Физматгиз, 1958—1960.
2. Араманович И. Г., Гутер Р. С. и др., Математический анализ
(дифференцирование и интегрирование), Серия «Справочная математическая
библиотека» под общей редакцией Л. А. Люстерника и А. Р. Янпольского,
Физматгиз, 1961.
3. Рыжик И. М. и Г р а д ш т е й н И. С., Таблицы интегралов, сумм,
рядов и произведений, нзд. 4-е, перераб. при участии Ю. В. Геронимуса и
М. Ю. Цейтлина, Физматгиз, 1962.
4. Смолянский М. Л., Таблицы неопределенных интегралов, изд.
2-е, Физматгиз, 1963.
5. Гарди Г., 'Интегрирование элементарных функций, перев. с англ.,
ОНТИ, 1935.
6. Bierens ое Haan D., Nouvelles tables d’integrales definies, Edition
1867, corrected, N. Y. Hafner, 1957.
7. Li nd man C. F., Examen des Nouvelles tables d’integrales definies,
de Bierens de Haan, N. Y. Hafner, 1957.
8. Уиттекер E. T. н Ватсон Г. H., Курс современного анализа,
ч. I и II, Физматгиз, 1963.
9. Лебедев Н. Н., Специальные функции и их приложения, нзд. 2-е,
перераб. и дополи., Физматгиз, 1963
10. Ватсон Г. Н., Теория бесселевых функций, ч. 1 и 2, ИЛ, 1949.
11. Грей Э. и Мэтьюс Г. Б., Функции Бесселя и их приложения к
физике и механике, ИЛ, 1953.
12. Гобсон Е. В., Теория сферических и эллипсоидальных функций,
ИЛ, 1952.
13. Ахиезер Н. И., Элементы теории эллиптических функций, Гос-
техиздат, 1948.
14. Журавский А. М., Справочник по эллиптическим функциям,
изд-во АН СССР, 1941.
Б. Таблицы
15. Сегал Б. И. н Семендяев К. А., Пятизначные математические
таблицы, изд. 3-е, Физматгиз, 1962.
16. Янке Е., Эмде Ф., Лёш Ф., Специальные функции (формулы, гра-
фики, таблицы), перев. с 6-го нем. изд. под ред. Л. И. Седова, Физматгиз,
1964.
17. Ха яши К., Многозначные таблицы круговых, гиперболических и
других функций, изд-во ВЦ АН СССР, 1963 (намечено к выпуску).
228
ЛИТЕРАТУРА
18. Комри Л., Шестизначные таблицы Чемберса, Физматгиз, 1964.
19. Библиотека математических таблиц, изд-во ВЦ АН
СССР.
а) Таблицы круговых и гиперболических синусов и косинусов в радиан-
ной мере угла.
б) Таблицы вероятностных функций, т. 1 и 2.
в) Таблицы функций Бесселя дробного индекса и /v для v=±-|-|
2.
г) Таблицы круговых и гиперболических тангенсов и котангенсов в ра-
дианной мере.
д) Таблицы натуральных логарифмов, т. 1 и 2.
е) Многозначные таблицы элементарных функций (sin х, cosx, е*, е~х).
ж) Таблицы обратных тригонометрических функций.
з) Таблицы функций Бесселя целого положительного индекса.
и) Таблицы антилогарифмов 10х.
20. Фаддеева В. Н. н ГавуринМ. К., Таблицы функций Бесселя
Jn (х) целых номеров от 0 до 120, Гостехиздат, 1950.
21. Таблицы значений функций Бесселя от мнимого аргумента, изд-во
АН СССР, 1950.
22. Таблицы интегрального синуса и косинуса, изд-во АН СССР, 1954.
23. Таблицы интегральной показательной функции, изд-во АН СССР, 1954.
24. Таблицы ех и е~х, изд-во АН СССР, 1955.
25. Кармазина Л. Н., Курочкина Л. В., Таблицы интерполяци-
онных коэффициентов, изд-во АН СССР, 1956.
26. Table of binomial coefficients, Royal Society, Mathematical tables,
Cambridge University Press, 1954.
27. Самойлова-Яхонтова H. С., Таблицы эллиптических интегра-
лов, ОНТИ, 1935.
28. Беляков В. Л., Кравцова Р. И., Раппопорт М. Г., Таблицы
эллиптических интегралов, т. 1, изд-во АН СССР, 1962.
29. Шулер М., Гебелей и X., Таблицы эллиптических функций,
изд-во ВЦ АН СССР, 1960.