А. П. КИСЕЛJ!В, н. А. РЫБКИН


rЕОМЕТРИЯ


ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ


для 8, 9 классов


ИЗДАНИЕ 7-е


и з д д. т Е Л Ь С Т В О «П Р О С В Е Щ Е Н И Е,
Моек вз 1971




513 (075)
r 35
ОТ ИЗДАТЕЛЬСТВА
Предлаrаемое пособие содержит материал, соответству.
IОЩИЙ n porpa мме, для УI 1 1 класса п о тема м: «Свойства биссек-
трисы BHYTpeHHero уrла треуrолъника» и «Пропорциональные
отрезки в прямоуrольном треуrольнике и Kpyre», а для 1 Х
класса по теме «Последователь ности». Этот матер иал взят
из учебника А. п. Киселёвз «rеометрия», ч. 1, Учп едrиз,
1962 r., а упражнения  из задачника Н. А. Рыбкина «Сбор-
ник sадач по rеометрии», ч. 1, «Просвещение», 1964 r.
Содержание параrрафов взято из указанных выше I{ниr
без именений, за ИСI<лючением следующих: ССЫЛI{И на пред-
ложения предыдущих параrрафов учебника эаменены фор-
мулировкой соответствующих преДЛО)l{ений,  237 эаменён
новым (Э 21), в  33 (269) внесено уточнение.
В целях возможноrо использования полных изданий
учебника А. П. Киселёва и задачника 11. А. Рыбкина в на-
стоящем пособии введена двойная нумерация параrрафов
учебника и номеров задач из  8 задачника. В скобках ука-
зана ста ра я нумерация.
Данное пособие подrОТОВJlено к изданию К. П. С и l{ О р.
С К И м.
6-6

ВОСЬМОЙ КЛАСС
свойство БИССЕКТРИСbl BHYTPEHHErO уrЛА
JРЕуrОЛЬ'НИI(А
1. (186.) Т ео рем а 1 . Биссектриса (BD, черт. 1) любоzо
уzла т.реуzольн,и1(,а (АВС) делит п.РОIIIU80положную сто-
рону на части (AD и CD), проnорциональн,ые nрилежа-
щu.м сторонам треуzол.ьнuиа.
Требуется доказать, что если / ABD == L DBC, то AD : DC ==
== АВ : 8С. .
Проведём СЕ 11 BD До пересечения в точке Е с продолжением
стороны АВ. Тоrда, corпaCHO теореме о пропорциональности отрез-
ков, образующихся на прямых, пересечённых неСКОJIЬКИМИ парап-
лельными прямыми, будем иметь пропорцию:
AD :DC == АВ: ВЕ.
Чтобы ОТ этой пропорции пеРt:йти к той, которую требуетс.я дока-
зать, достаточно обнаружить, что ВЕ == ве, т. е. что  ВСЕ равна
бедренный. В этом треуrоль-
нике L Е == L ABD (как уrлы
соответственные при параллель..
ных п.рямых) и / ВСЕ ==
== L D ВС (как yrJIbI накрест ле..
жащие при тех же параллель
ных прямых).
Но' L ABD == L DBC по
условию; значит, L Е  L ВСЕ, Д
а потому равны и стороны
ВЕ и 8е, лежащие против paB
ных уrлов. Теперь, заменив_
в написанной выше пропорции ВЕ на 8е, получим ТУ. пропор..
цию, которую требуется доказать.
Ч и с л е н н ы й при м е р. Пусть АВ == 10; ВС == 7 и АС::::
== 6. Тоrда, обозначив AD буквой х, можем написать пропорцию:
х : (6  х) == 10 : 7,
е
D
с
ч ерт. 1
1 В скобках з-деСh и дальше указаны номера параrрафов по КНИl"е
А. п. 'К'иселёва ({rеомтриЯt. Учебник для 69 клаССОD семилетней и средней
ШКОЛЫ, ((асть 1, Учпедr-из, 1962.
"

отсюда найдём:
7х == 60  IOx; 7х + 10х == 60; 17х == 60;
60 9
X== 17 ==3 17 '
Следовательно,
DC == 6x ==63 ! =::: 2.
17 17
Задачи из i 81.
J. (17.) BD. биссеI{трИ'са уrла в треуrольнике
Свойство бис- АВС. Требуется определить:
т;:ие. 1) отрезки AD и DC, если АВ ::::: ]0 м, ВС ==
:= 15 м и АС == 20 м;
2) сторону 8С, если AD : DC == 8 :.5 и АВ == 16 м;
3) сторону АС, если АВ : ве ,== 2 : 7 и DC  AD === 1 М.
2. (18.) Уrол треуrольника, заключённый между сторонами в
9 см и 6 см, разделён пополам. Один из отрезков третьей стороны ока-
sался равным ОДНОЙ из даIiНЫХ сторон. Определить третью сторону.
3. (20.) В треуrольник АВС вписан ромб ADEF так, что верши-
ны D, Е и F лежат соответственно на сторонахАВ, ВС и АС. Оп..
ределить отрезки ВЕ и ЕС, если АВ === 14 см, ВС  12 СМ и АС ==
== 1 О см.
4. (21.) Стороны треуrольника равны 51 см, 85 см и 104 сМ. Про-
ведена окружность, которая касается обеих меньших сторон, а
центр имеет на большей стороне. На какие части б6льшая сторона
делится центром?
5. (22.) В равнобедренном треуrОJlьнике высота равна 20 СМ,
а основание относится к боковой стороне, как 4 : 3. Определить
радиус вписанноrо Kpyra.
6. (23.) В равнобедренном треуrольнике центр вписанноrо Kpyra
делит высоту в отношении 12 : 5, а боковая сторона равна 60 СМ.
Определить основание.
7. (24.) В раВQобедренном треуrольнике радиус вписнноrо
2
]{pyra составляет 7" высоты, а периметр этоrо треуrОJ1ьника равен
56 см. Определить ero стороны.
8. (25.) Хорда АВ == 15 м, хорда АС == 21 м и хорда Ве ==
== 24 м. Точка D  середина дуrи СВ. На какие части ВЕ и ЕС
делится хорда Ве прямой AED?
J В скобках в этом парrрафе указаны номера задач из книrи Н. Рыбки..
1J8 «Сборник задач по rеометрии для 69 классов средней школы», часть ] f
Планиметрия, Просвещение», 1964. В ()TBeTa к задачам указаны номера
'l'олько по задзt1НИНУ.
-4

9. (26.) В треуrольнике АВС даны стороны й, Ь и с. B.D 
биссектриса уrла В; О  TOKa пересечения BD и биссеКТрИСLJ
уrла С. Требуется определить' отношение OD : ОВ.
о 10. (27.) В треуrольнике АВС сторона АВ == 15 см и АС ==
== ]0 С.м; AD ------ бffссектриса уrла А; из точки D проведена прямая,
параллельная АВ, дО пересечения с АС в точке Е. Определить
АЕ, ЕС и DE.
11. (28.) В равнобедренном rреуrольнике АВС сторона АС ===
== Ь, сторона ВА == 8е == а; AN и СМ  биссектрисы уrлов А
и С. Определить длину. MN.
ftr1ЕТРИЧЕСКИЕ СООТНОШЕНИЯ МЕЖДУ Э.ПЕМЕНТ ДМИ
прямоvrольноrо ТРЕуrОJ1ЬНИJ\А.
2. (188.) Теорема. В пРR.моуzолноя mреуzольнlt"е
перnендикуляр, опущенны,й из вершины пряжоz,о уz,ла
на zиnотенузу, есть средняя nропорцuональная вели-
чина между отрезк.а.l"U' на «оторые основание перпен..
ди1(,уляра делит z,Q,поmенуз)', а юаждый 1(,атет есть
средняя пропорцltональная .между 2uпотенузоii IJ, nри-
лежащи'м' 1(, втолу "атету отрезком z,ипотенузы.
Пусть AD (черт. 2) есть перпендикуляр, опущенный из вершины
прямоrо уrла А на rипотенузу ВС. t Требуется доказать следующие
три пропорции:
1) BD == AD . 2) 8е == B . 3) дС == АС .
AD DC' АВ BD' АС ОС
Первую пропорццю мы докажем из подобия треуrольников ABD
и ADC. Эти треуrольники подобны, потрму что
L-l ==L4 и L2==L3
как острые уrлы с соответственно' перпе"ндикулярными сторонам1".
Возьмём в Ь ABD те стороны BD и Ай, которые составляют пер-
u
вое отношение доказываемои пропорции; сходсtвенными сторонами
в Д ADC будут AD и DC 1 , 'поэтому -
BD : AD == AD : DC.
Вторую пропорцию дока.щем ИЗ подобия треуrольников АВС
и ABD. Эти треуrольники подобн.ы, потому что ОНИ прямоуrольные
] Чтобы безошибочно опредеЛИТЬ 1 какие стороны взятых треуrольников
сходственны между собой, полезно держаться TaKoro пути:
1). указать yr лы, против которых .пеЖ,ат взятые стороны одноrо треуrоль-
ника;
2) найти равные им yr.iIbI в друrом tpeyroJ]bJ-JЕке;
3) взять противолежащие им стороны.
Напримt:р, для треуrольников ABD и ADC рассуждаем TK: в треуrоль
нике ABD стороны BD и AD J1ежат против уrлов 1 и 3; в треуrольннке ADC
этим уrлам равны 4 и 2; против них лежат стороны AD и DC. Значит, СТО-
роны Ап Я DC сходственны со сторонами BD и AD.
5

п острый уrол В у них общий. В д АВС возьмём те стороны ве и
АВ, которые составляют первое отношение доказываемой пропор-
ции; сходственными сторонами в  ABD будут АВ и BD; поэтому
Ве : АВ == АВ : BD.
Третью пропорцию докажем из подобия треуrольни'ков АВС
и ADC. Эти треуrольники подобны, потому что они оба прямоуrоль-
А А
D
с
в
в
D
с
Черт. 2 Черт. 3
ные и имеют общий острый уrол е. :а  АВС возьмём стороны ВС
и АС; сходственными сторонами в  ADC будут АС и DC,; поэтому
ВС : АС == АС : DC.
3.., (18.) С л е Д с т в и е. Пусть А (черт. 3) есть произвольная
точка окружности, описанной на диаметре ВС. Соединив концы
диаметра с этой точкой, МЫ получим прямоуrольный  АВС, у ко-
Toporo rипотенуза есть диаrvlетр, а катеты суть хорды (по свойству
вписанноrо уrла, опирающеrося на диаметр). Применяя доказаННУIО
вше теорему к этому треуrольнику, ПрИХОДИ1 к следующему зак-
лючению:
Перnенд и куляр , опущенный из какой-либо точки OKPYJICHOCmU
на диаметр, есть средняя nроnорцuональная величина между оmрез-
К(1,М,и, на KOmOpbte основание nерnендикуляра делит диаметр, а хор-
да, соединяющая эту точку с концом диаметра, еСlnЬ средняя про-
порциональная между диаметром и прилежащим к хорде опlрез-
КОМ диаметра.
4. (190.) 3 а д а ч з. Построить отрезок, средний nроnорцио..
нальный между двумя отрезками а u Ь.
Задачу эту можно решить двояким путём:
1) На произвольной прямой (черт. 4) откладываем отрезки АВ ==
:.== а и ВС == Ь; на АС, как на диаметре, описываем: полуокруж-
ность; из В восставляем до пересечения с окружностью нерпенди с
куляр BD. Этот перпендикуляр и есть искомая средняя пропорцио-
нальная между АВ и ВС.
2) На произвольноЙ прямой (черт.. 5) откладываем от точки А
отрезки а и Ь. На большем из этих отрезков описываем полуокруж-
ность. Проведя из конца меньшеrо отрезка перпендикуляр к АВ ДО
пересечения ero с окружностью в точке D, соединяем А с D. Хорда
AD есть средняя пропорциональная между а и Ь.
6

5. (1,91.) Теорема Пифаrора. ДОI<зззнные выше теоремы поз-
воляют Qgнару}кить замечательное соотношение ме)кду сторонами
люб0rQ пр,ямоуrол'ьноrо треуrольника. Это соотношение было впер-
вые замечено rречеСI{ИМ reoMeTpoM Пифаrором (vI в. дО Н. э.) И но-
сит поэтому ero имя 'T е о р е м а П и Ф з r о р а.
.0
I h
,
\.
А 1.,;
а
Черт. 4
Черт. 5
Если cnlopOHbI, пРJlel1f,О20ЛЬНОZО тре20льни"а изме-
рены одной и /liou же единицей, то к.вадрап;, длины 2а--
nОlnенузы равен сумме 1(,вадратов длин катетов.
Пусть АВС (черт. 6) есть прямоуrольный треуrольник, AD ......
перпендикуляр, оп,ущенны
й на rипоrrенузу из вершины прямоrо
УI'ла. Поло}!{им, что стороны и отрезки rипотенузы измере'НЫ'оДной
и той }!{е единицей, причём rtолучи'л.ись числа а, Ь, с, с' и Ь' (при-
нято длины сторон треуrольника обоз- А
начать малыми буквами, соответству-
ющими бол.ьшим буквам, котор,ыми
обоаиачены противолеll<ащие уrлы).
Применяя теорему  2 (188), fviожем
наnи€вть пропорции:
а : с == с : с' и а: Ь == Ь : Ь' t
h
откуда
в
 1 :
с'
а
I
Ь' 4
: J
ас' == с 2 и аЬ' == Ь 2 . Черт. 6
СЛО}l{ИВ почленно эти два равенства, найдём:
ас' + аЬ' == с 2 + Ь 2 , или а (с' + Ь') == с 2 + Ь 2 .
Io с' + Ь' == а, следовательно,
а 2 == с 2 + Ь 2 .
Эту теорему обыкновенно выра}кают СОI<ращённо так: квадрат
zип.оте-,,,узы, равен су-м-ме квадратов к.атет(!в 1 .
I Теорема Пифаrора имеет еще друrУIО формулировку: площадь KBaд
рата, nOCTpoeHHoro В(] rипотеllузе прямоуrольноrо треуrольника J равна сум-
ме площадеЙ I<вздратов, построенных на катетах. . "
7

При м е р. ПОЛО}I{ИМ. - что катеты; измереп.ные какой-нибудь
линейной единицей, выражаются числами 3 и 4; тоrда rипотеНУ38
в той же единице выразится числом х, удовлетворяющим уравнению:
х 2 ;::::; 32 + 42 == 9 + 16 == 25, откуда х == V 25 == 5.
3 а м е ч а н и е. Пр ямоуrольный треуrольник со сторонами 3...
4 и 5 называется часто еrипетски" треуrольником, так как он был
известен ещё древним еrиптянам. Так, их землемеры для построе
ния прямоrо уrла на земной поверхности ПОЛЬ30вались таким приё..
мом: бечёвку посредством узлов они разделяли на 12 равных частей;
затем, связав концы, натяrивали' её на земле (посредством кольев)
в виде треуrольника со сторонами в 3,4 и 5 делений; тоrда уrол l\Ilеж..
ду сторонами, равными 3 и 4, оказывался прямым!.
6. (192.) С л е Д с т в и е. Квадраты катетов относятся между
соБС)u, как nрuлежащuе оmрезки еunоmенузы. Действительно, из ypaB
нений предыдущеrо параrрафа находим:
с 2 : Ь 2 == ас' : аЬ' == с' : Ь'
7. (193.) 3 а м е ч а н и е_о К трёl\f равенствам, которые мы BЫ
вели выше:
1) ас' == с 2 ; 2) аЬ' === Ь 2 и 3) а 2 == Ь 2 + с 2 ,
можно присоединить ещё следующие два:
4) Ь' + с' == а и 5) h 2 === Ь' с'
(если буквой h обозначим ДЛI;IНУ высоты AD). Из этих равенств
третье, как мы видели, составляет следствие первых двух и четвёр..
тoro, так что из пяти равенств только четыре независимы; вслед..
ствие этоrо можно по данным двум из шести чисел находить осталь..
иые четыре.
Для примера положим, что нам даны отрезки rипотенузы Ь' ==
:z:::: 5 м и с' == 7 м:; тоrда
а::;: Ь' + с' == 12; с == Vac' == V 12. 7 == V 84  9,165 ...
Ь == V 00' == У 12 · 5 == V60 == 7,745 ...
h == V c'b' == V 5. 7 == V35 == 5,916 ...
1 Прямоуrльные треуrольники, у которых СТОрОНЫ измеряются
Ц е л ы м и ч и с л а м И, носят название пифаrоровых треуrОЛЬНИКО8,
Можно доказать, что катеты х и у и rипотенуза z таких треуrОЛЬНИI(ОВ
выражаются следующими формулами: ..
х  2аЬ, у =:3 а 2  Ь 9 , Z  а ! + Ь 2 ,
rJ.le а и 11  производьные целые числа при условии, что а > 11..
8

Задачи из  10.
в ПрЯ\IОУrоЛЬНО\.1 треуrольнике обозначаюl': а и lJ ...... катеты; а.... rиrtоте.
пуза; ас и Ь С ..... проекции катетов а и Ь на rипотенуэу; h...... 9ысота из вер-
шины прямоro уrла. Предполаrается, что отрезки измерены ОДНОЙ и той же
единицей..
t. Вычислить rипотенузу, если даны оба Karer81
1) 12 см и 35 см; 2) 56 см и 33 CM
3) 4 АС И 9 дм; 4) 60 см и 91 СМ-;
5 ) 21 и 3 l 6 ) ! И .
4 ' 2 1'6 '
7) 16,8 И 2,6; 8) 5 и 6.
2. ВЫЧИСЛИТЬ ВТОр'ОЙ катет, если даны rипотенуза и. первый ка-
тет 1 : ,
1) 289 и 240: '2) 269 И 69; 3) 145 и 143;
, 2
4) 42,5 и 6,5: 5) 17 и 155* 6) 10 и 7.
3. По двум данным элементам прямоуrольноrо треуrольника
вычислить остальные четыре:
1)' а == 15, Ь == 20; 2) а == 24, Ь == 7; 3) а == 4, Ь == 5;
'4) а == 100, с == 125; 5) Ь == 65, с == 169; 6) а == 600, с == 625J
7) а == 6, ас == 3,6; 8) Ь == 7. Ь с == 1, 96;
6
9) с == 29, ас == 15; 10) с ==: 3, Ь а == 2;
29
1 2
1 1 ) а == 1....... Ь == 2. 12 ) а == 2 Ь == 18.
с 2' с 3' с ? r. ,
13) а == 136, h == 120; 14) Ь == 9, h == 8 32 .
41
4. По данной сумме двух отрезков и среднему пропорциональ-
ному этих отрезков построить отрезки.
5. По данной разности двух отрезков и среднему пропорциональ-
НОМУ этих отрезков построить отрезки.
.6. Доказать, что в ПрЯМОУI:'ольном треуrольнике аЬ == ch.
7. Катеты относятся, как 5 : 6, rипотенуза .равна 122 см. Най-
u
ти отрезки rипотенузы, отсекаемые высотои.
8. Катеты относятся, как 3 : 2, а высота делит rипотенузу на
отрезки, из которых один на 2 м больше друrоrо. Определить rH-
. потенузу.
9. Катеты относятся, как 3: 7, а высота, проведённая на rипо."
тенузу, равна 42 см. Определить отрезки rипотен)'зы.
ПРОПОрЦИ3-
нальиые ОТ-
резки Ii ПРЯМО-
уrольном тре-
уrольиике.
1 В задаче 2 и во мноrих друrих случаях выrодно при вычислении
раЭНQСТЬ квадратов заменять произведением суммы на разность.
2 Заказ 62С>
9

10. Доказать, что диаметр окру}кности, вписанной в равнобедрен-
ную трапецию, есть средняя пропорциональная ежду параллель-
ными сторонами трапеции.
11. Доказать, что отношение квадратов l<aTeToB равно отноше-
нию их проекций на rипотенузу.
12. 1) Построить два отрезка, квадраты которых относятся, KaI{
т : n. .
2) Построить два" отрезка, которые относились бы, !{ак квадраты
двух данных отрезков.
13. Узнать, какими тремя последов а тел ьны-
Теорема ми целl}IМИ ч;ислами MorYT выражаться стороны пря-
. Пиф аrора моуrольноrо треуrольника.
14. Между двумя. фабричными зданиями
устроен покатый жёлоб для. передачи материалов. Расстояние
между ;зданиями равно 10 м, а концы жёлоба расположены на вы-
соте 8 м и 4' м над землёй. Определить длину жёлоба.
15. 1) Точка внутри прямоrо уrла удалена от ero сторон на .рас-
стояния а и Ь. Найти её расстояние от вершины.
2) Стороны прямоуrольника равны 60 см и 91 см. Чему равна
ero диаrональ?
16. Требуется выфрезовать квадратную rоловку со стороной.
32 мм. Чему ДОЛ}l{ен быть равен наименьший диаметр круrлоrо
железа, rодноrо для этой цели?
17. 1) Сторона квадрата равна а. Чему равна ero диаrональ?
2) Определить сторону квадрата, если она меньше диаrонали
на 2 см.
18. Диаметр бревна 12 см. Можно ли из этоrо бревна вытесать
квадратный брус со стороной 10 см?
19. l)'Стороны ПРЯf\t10уrольника равны а и Ь. Определить ради-
ус описанноrо Kpyra.
2) В Kpyr вписан прямоуrольник, стороны KOToporo относятся,
как 8: 15. Определить эти стороны, если радиус Kpyra равен
34 СМ.
20. 1) Катеты прямоуrольноrо треуrольника равны 8 дм и 18 СМ.
Определить радиус описанноrо Kpyra.
2) Катеты прямоуrольноrо треуrольника равны 16 см и 12 СМ.
Определить медиану rипотенузы.
21'. 1) В равнобедренном треуrольнике боковая сторона равна
17 см, а основание 16 см. Определить высоту.
2) Определить стороны раВН,обедренноrо треуrольника, если ero
высота равна 35 см, а основание относится к боковой стороне" как
48 : 25.
3) В равнобедренном треуrольнике основание равно 4 см, а уrол
при нём равен 450. Определить боковую сторону.
22. Стропильная ферма (черт. 7) имеет ноrи АВ и СВ по 9 .м
и пролёт АС в 15 At. Определить высоту фермы BD.
10

23. 1) Биссектриса пр ямоrо уrла делиr rипоrенузу пр я моуrоль..
1 6
Horo треуrольника на части, равные 27М и 27 м. Определ'ить ка-
теты.
2) Катеты прямоуrольноrо треуrольника равны 15 см и 20 СА!
ИЗ вершины прямоrо уrла проведены высота и биссектриса. На
какие отрезки разделилась rипотенуэа?
24. 1) В 'равностороннем треуrольнике определить высоту по
данной стороне а.
2) В равностороннем треуrольнике определить сторону по дан"
ной высоте h.
8
с
д
1)
4 ерт. 7
3) В равностороннем треуroльнике высота меньше стороны на .т.
Определить сторону.
4) В прямоуrольном треуrольнике один из уrлов равен 300, а
больший катет равен 6 СМ. Определить две друrие стороны этоro
треуrольника.
25. 1) Боковые стороны треуrольника равны: а == 25 см и Ь 
== 30 см, а высота hc == 24 сМ. Определить основание с. ,
2) В треуrольнике больший уrол при основании равен 450, а
высота делит основание на части в 20 СМ и 21 см. Определить боль-
шую боковую сторону.
3) Из одной точки проведены к данной прямой перпендикуляр
и две наклонные. Определить длину' перпендикуляра, если наклон.
вые РаВНЫ 41 см и 50 см, а их проекции нз. данную прямую отно"
сятся, как 3: 10. .
26. 1) Диаrонали ромба равны 24 см и 70 см. Определить сторо-
ну.
2) Определить диаrонали ромба, если они относятся, как 3 : 4,
а периметр равен 1 М.
27. 1) В равнобедренной трапеции основания равны 10 см и
24 С-М, боковая сторона 2,5 см. Определить высоту трапеции.
2) В равнобедренной трапеции боковая сторона равна 41 СМ,
высота равна 4 дм и средняя линия 45 см. Определить основание..
28. Параллельно прямой дороrе, на. расстоянии 500 м от неё,
.,
раСПОЛО}l{ена цепь стрелков: расстояние между краиними стрелка-
ми равно 120 м, дальность полёта пули равна 2,8 км. Ка'КОЙ уча-
сток дороrи находится под обстрелом этой цепи?
:t
11

29. На чертеже 8 изобра}кена заклёпка ОСТ 302 (ОСТ  обще-
союзный стандарт) с потайной rоловкой. Уrол а == 600. Вычислить:
1) D, если d == 16,5 мм и h == 7 ,5 MM
2) d, есл D == 30 мм и h == 9,5 мм;
3) h, если D == 35 мм и d == 22 мм.
Написать формулу, связывающую между соб9Й D, d и h.
30. 1) В треуrольнике АВС проведена
D высота AD. Доказать, что АВ2  АС 2 ==
== BD2  CD2.
2) Если М........ некоторая точка BbICOTbI
AD треуrольника ABC t то АВ2  АС 2 ==
== ВМ2  СМ2. Доказать.
31. 1) Доказать, что в _ прямоуrольной
трапеции разность квадратов диаrоналей
равна разности квадратов оснований.
2) В прямоуrольной трапеции меньшая
диаrональ равна' наклонной боковой сторо-
не. Определить большую диаrональ, если
наклонная боковая сторона равна а, а мень-
шее основание равно Ь.
32. Из листа iкелеза требуется выштам-
повать круrлые шайбы диаметром в 28 ММ.
Найти расстояние между прямыми, на ко-
торых следует раСПОЛОiКИТЬ центры шаЙб
(черт. 9).
33. 1) Радиус Kpyra равен 89 aJrt, хорда 16 М. Определить её рас-
стояние от центра. ,
2) О  центр; Аса  хорда; OCD  радиус, перпеНДИI<УЛЯР-
вый к ней, ОС == 9 см и CD == 32 Ct. Определить хорду.
3) Радиусы двух пересекающихся окружн/остей рав'ны 13 с-м
и 15 см, а общая хорда равна 24 см. Определить
расстояние между центрами.
4) АВ и CD........ две параллельные хорды,
расположенные по разные CTO}J'OHbI от центра О
ОКРУil{НОСТИ радиуса R == 15 см. Хорда
АВ == 18 см, хорда CD == 24 СМ. Определить
расстояние ме}кду хордами.
5) Две параллельные хорды АВ и CD распо-
ложены по одну сторону от центра О ОI{РУЖНО-
сти радиуса R == 30 см. Хорда АВ == 48 см,
хорда CD == 36 см. Определить расстояние
между хордами.
34. Чтобы измерить диаметр большоrо ПJКИ"
ва, установили штанrеНIlИРКУЛЬ таи, }{ак пока-
вано на чертеже 10. Длина НО)Еек штан-
..с:
\t/
d
4 ерт. 8
J2
Черт. 9

rенциркуля s == 25 мм, расстояние между конuами HO}I{eK 1 ==
== 200 МJИ.
1) Определить длину диаметра;
2) вывести формулу, выраiкающую зависимость диаметра от
s и [.
35. В cerleHTe хорда равна а, а высота h. Определить радиус
Kpyra.
36. Радиус Kpyra равен 25 см; Две параллельные хорды равны
14 см и 40 см. Определить рассТояние между ними.
37. Расстояния от одноrо конца
диаметра до концов параллель-
ной ему хорды равны 13 с-м и 84 СМ.'
Определить радиус Kpyra.
38. 1) К окружности радиуса,
paBHoro 36 СМ, проведена касатель-
ная из точки, удалённои от цент-
ра на 85 см. Определить длину
касательной.
2) Из общей точки проведены
к окружности две касательные.
Радиус окружности равен 11 С,м, а
сумма касательных равна 120 СМ.
Определить расстояние от центра
до исходной 'точки касательных.
3) К окружности радиуса, paBHoro 7 СМ, проведены две каса..
тельные из одной точки, удалённой от центра на 25 СА!. Определить
расстояние между точками касания.
,39. Два Kpyra радиусов R и r внешне касаются. Из центра одно..
ro Kpyra проведена касательная к ДPYMY Kpyry, а из полученной
точки касания проведена касательная к перВОl\IУ Kpyry. Опредепить
длину последнеft касательной.
40. 1) Два Kpyra касаются извне. Определить длину их общей
внешней касательной (между точками касания), если радиусы рав-
HqY 16 CA-t и 25 СМ.
2) Радиусы двух KpyroB равны 27 с,м и 13 см, а расстояние .l\fежду
центрами равно 50 см. Определить длину общих касательныI..
41. Касательная и секущая, проведённые из общей точки к одной
окружности, взаимно перпендикулярны. Касательная равна 12 м,
а внутренняя часть секущей равна 10 м. Определить радиус ОКРУ}К-
ности.
42. АВ и CD  параллельные прямые. АС  секущая, Е и F .......
точки пересечения прямых АВ и CD с биссектрисами уrлов С и А.
Дано: АР == 96 СМ и СЕ == 110 см. Требуется определить АС.
43. В тупоуrольном равнобедренном треуrольнике АВС ОСНО"
вание АС == 32 м, а боковая сторона 20 м. Из вершины В проведён
перпендикуляр к боковой стороне до пересечения с основанием.
На какие части он делит основание?
Черт.
, 13

44. I(aTeT АС == 15 см; катет СВ == 8 см. Из центра С радиусом
СВ описана дуrа, отсекаЮЩая от rипотенузы часть BD, которую
и требуется определить.
45. Дуrа, описанная из вершины прямоrо уrла прямоуrольноrо
треуrОЛЬНИI{а радиусом, равным меньшему катету, делит rипотенузу
на отрезки в 98 см и 527 см (начиная от меньшеrо катета). Опреде-
лить катеты. ,
46, АВ....... диаметр Kpyra; Ве  касательная; D  точка пере-
сечения прямой АС с окружностью. Дано: AD == 32 см и DC ==
=== 18 см. Требуется определить радиус.
47. АВ....... диаметр; ВС и CDA  касательная и секущая. Опре-
делить отношение CD : DA, если ВС равна радиусу.
48. В прямоуrольном треуrольнике биссек-
, Биссектриса в триса прямоrо уrла делит rипотенузу в отноше
прямуrоль", нии 7: 9. В каком отношении (считая части
110М Tpeyrob В том же по р ядке ) делит ее высота?
нИ ке.
49. Определить катеты,. если биссектриса
прямоrо уrла' дит rипотенузу на части в 15 см и 20 см. .
50'. В равнобедренном прямоуrольном треуrольнике катет ра-
вен а. На какие части делит ero биссектриса противолеЖ8щеrо уrла?
51. В прямоуrОЛЫ-IОl\f треуrОЛЬНИI<е биссеI{триса OCTporo уrла
делит катет на отрезки т и п (т > п). Определить друrой катет
и rипотенузу.'
52. В прямоуrольном треуrольнике) катеты I{OTOpOro равны
15 дм и 2 М, проведены: высота из вершины прямоrо уrла и биссект-
рисы обоих уrлов, образуемых высотой с катетами. Определить от-
резок rипотенузы, заКЛlочённый мел{ду биссектрисами.
53. В прямоуrольном треуrольнике АВС катет ВС =::: 6 СМ И
rипотенуза АВ ::::: 10 СМ. Проведены биссектрисыI уrла АВС и уrла,
с ним смежноrо) пересекаlощие катет АС и ero продол}кение в точ-
ках D и Е. Определить длину f)E.
54. В равнобедренном треуrольнике АВС боковая TopOHa АВ==
== 10 .м и основание АС == 12 м. Биссектрисы уrлов А и С пере-
секаются в точке D. Требуется определить BD.
55,. 1) В равнобедренном треуrольнике основание равно 30 см,
а боковая сторона равна 39 см. Определить радиус вписанноrо
Kpyra.. 
2) В равнобедренном треуrольнике центр вписанноrо Kpyra
делит' высоту в отношении 17 : 15. Основание равно 60 см. Найти
радиус этоrо Kpyra.
56. Из точки В проведены к данной прямой
перпендикуляр ВС и наклонная БА. На АС взя-
тв точка D) и прямая BD продол}кена до пере-
сечения в точке Е с прямой АЕ, перпендикуляр-
ной к АС. Определить АЕ, если БА == 53 д-м,
AD == 8 дм и DC == 20 дм.
57. 1) В ранобедренном треуrольнике оспо-
Высота и сто-
роны . прямо-
уrоль"ом тре-
уrоль ни ке,
ромбе и тра..
пеци и.
.34

вание равно 30 дм, а высота 20 дм. Определить высоту, опущенную
на боковую сторону.
2) В равнобедренном треуrольнике высота, опущенная на осно-
вание, равна 3 дм, а высота, опущенная на боковую сторону,
равна 4 дм. Определить стороны этоrо треуrольника.
3) Диаrонали ромба равны 14 дм и 48 дм. Определить ero высоту.
58. 1) rипотенуза АВ == 34 см; катет ВС == 16 СМ. Определить
длину перпендикуляра, восставленноrо к rипотенузе из её середины
до пересечения с катетом АС.
2) Радиус Kpyra равен (. Определить длину хорды, проведённой
из конца данноrо диаметра через сереину перпендикулярноrо
к нему радиуса.
59. В прямоуrольном треуrОЛЬНИI<е АВС катет АС ::-= 16 дм
и катет ЕС == 12 дм. Из центра В радиусом ВС описана окружность
и к ней проведена касательная, параллельная rипотенузе (причём
касательная и треуrольник лежат по разные стороны rипотенузыl..
Катет ВС продол}}<ен до пересечения с нроведённой касательной.
Определить, на сколько продолжен катет.
60. Из одной точки проведены к Kpyry две касательные. Длина
касательной равна 156 д, а расстояние между точками касания
равно 120 дм. Опр'еделить радиус Kpyra.
61. В прямоуrольной трапеции основания равны 17 aAl и 25 дм,
а большая боковая сторона равна 10 дм. Из середины этой стороны
проведён перпендикуляр к ней до встречи с ПРОДОЛ)I{ением друrой
боковой стороны. Определить длину этоrо перпендикуляра.
. 62. АС и СВ....... катеты; CD ........ высота;
.;' Смешанные DE" ВС. Определитьотношение АЕ: ЕС, если
задачи на пря- А С : СВ == 4 : 5.
моуrольный 63. АС и СВ ........ катеты; CD ........ BЫCOTa
треуrольник. DE J.... АС и DF  СВ. Определить DE и DF,
если АС == 75 дм и ве == 100 дм.
64. В двух равнобедренных треуrольниках боковые стороны
имеют одинаковую длину, а сумма уrлов ПРI1 вершинах равна 180°.
Основания относятся, KaI{ 9 : 40, а длина боковой стороны равна
41 дм. Определить основания.
65. 1) В треуrольнике основание равно 60 М, высота 12 м и ме-
диана основания 13 м. Определить боковые стороны. .
2) В прямоуrольном треУIольнике найти отношение aTeTOB,
если высота и медиана, выходящие из вершины прямоrо уrла,
относятся, как 40 : 41.
66. Определить радиус Kpyra,' описанноrо около равнобедрен-
Horo треуrольника, если основание и боковая сторона треуrОЛЬНИI\а
соответственно равны: 1} 6 дм и 5 дм; 2) 24 м и 13 м.
67. В прямоуrольном треуrольнике катеты равны 13 дht и 84 дм.
Определить радиус вписанноrо Kpyra.
68. Расстояние между центрами двух окру}кностеЙ, ле}[(ащих
одна вне друrой, равно 65 дА!; длина их общей внешнеЙ касательной
15

(между точками I<асания) равна 63 a,,t, длина ихобщей внутренней
касательной равна 25 дм. Определить радиус окружностей.
69. Длины двух параллельных хорд равны 40 дм и 48 дж, рас-
стояние между ними равно 22 дм. Определить радиус Kpyra.
70. В равнобедренной трапеции, описанной около Kpyra, осно-
вания равны 36 СМ и 1 М. Определить радиус Kpyra.
71. ОI{ОЛО Kpyra, радиус KOToporo равен 12 СМ, описана равно..
бедренная трапеция с боковой стороной в 25 см. Определить осно-
вания этой трапеции.
72. Около Kpyra радиуса' описана равнобедренная трапеция,
у ноторой параJlлельные стороны относятся, как т : n. Определить
стороны этой трапеции.
73. АВ и АС'  касательные к одному Kpyry с центром о; М 
точка пересечения прямой Ай с окружностью; DME....... отрезок
касательн<;>й, проведённой через М между АВ и АС. Определить
длину DE, если радиус Kpyra равен 15 дм, а расстояние АО ==
=== 39 дм.
74. Катеты прямоуrольноrо треуrо.пЬНИI{а равны 15 дм и 20 дм.
Определить расстояние от центра вписанноrо Kpyra до высоты,
проведённой на rипотенузу.. 
75. В ПРЯflлоуrольном треуrольнике АВС из вершины С пря-
Moro уrла опущен перпендикуляр на rипотенузу, и на нём, как на
диаметре, описана окружность, которая на катетах СА и СВ даёт
внутренние отрезки т и n. 0пределитъ катеты (т == 12; п == 18).
76. В прямоуrольном треуrольнике катеты равны 75 д,м и 100 дм.
На отрезках rипотенузы, образуемых высотой, построены полу..
круrи по одну сторону с данным треуrольником. Определить от-
резки катетов, заключённые внутри этих полукруrов.
77. Если два Kpyra имеют внешнее касание, то их общая внеш-
няя I<асательная есть средняя пропорциональная между их диамет-
рами. Доказать.
78. В трапеции ABCD меньшая диаrональ BD перпендикулярна
к основаниям AD и ВС; сумма острых уrлов А и С равна 900.
Основание AD == а и ВС == Ь. Определить боковые стороны АВ
и CD
ПРОПОРЦИОНАЛЬНЫЕ линии в I(PYrE.
8. (199.) Некоторые пропорциональные линии в I{pyre мы ука-
зали ранее в Э 3 (189); теперь укажем ещё друrие.
Теорема. .Если через mоч1(, (М, черт. 11), взяmю
внутри 1(,pza, pOBeдeн,ы 1(,а1(,ая..н,ибдь хорда (АВ) и
диаметр (CD), то произведен,ие отрезков хорды (АМ · МВ)
равно произведенuю отрезков диаметра (MQ.MC).
Проведя две вспомоrательные хорды АС и BD, мы получим два
треуrольника АМС и Л1ВD (покрытые на чертеже штрихами), ко-
16

торые подобны) ТЗJ{ как у них уrлы А II D равны, как вписанные,
опираlощиеся на одну и ту же дуrу ВС, и уrлы С и В равны, как
вписанные, опирающиеся на одну и ту же дуrу AD. Из подобия тре..
."
уrольников выводим:
АМ : MD == МС : МВ,
откуда
АМ · МВ == MD · МС.
9. (200.) С л е Д с т в и е. Е ели Ч:е-
рез точку (М, черт'. 11), взятую
внутри Kpyza, nроведено сколько уеод-
но хорд (АВ, ЕР, KL, ...), то nроизве-
дение отрезков каждой хорды есть чи-
сло постоянное для всех хорд, так как
для ка}I{ДОЙ хорды это произведение К L
равно произведению отрезков диамет-
ра CD, проходящеrо через взя'fУЮ точ-'
ИУ М.
10. (201.) Теорема. Если из
rnочки (М, черт. 12), взятой вне
Kpza, nроведены 1(, нему какая..
нибудь секущая (МА) и каса- Черт. 11
пtельная (МС), то произведение
сеущей на её внешнюю часть'" равно кюрату Kaca
тельной (предполаrается, что секущая оrраниченз второй точкой
переечения, з касательная  точкой касания).
Проведём вспомоrательные ХОРДЫ АС и ЕС; тоrда получим два
треуrольника МАС и .МВС (покрытые на черте)ке штрихами), ко-
торые подобны, потому что у них .уrол М общий и уrлы МСВ и
САВ равны, так КЗI{ каждый ИЗ них измеряется половиной дуrи ВС.
Возьмём В L. МАС стороны МА и МС; сходственными сторонами
в д МВС будут МС и
1\1В; поэтому С
М
МА : МС == МС : МВ,
откуда
1\1А · МВ == lVIC2.
11. (202.) С л е Д с Т-
в и е. Если из точки
(М, черт. 12), взяп10Й
вне КрУ2а, проведены к не-
му сколько yzoaHO секу-
щих (МА, MD, МБ, ..),
lnО nроuзведенuе каJJсдой
А
Черт. 12
17

секущеЙ на ее внешнюю чаСlпь есть число 1l0Сl1l0янное для всех
секущих, так как для каждой секущей это произведение равно ква-
драту' !<асательной (МС 2 ), проведённой из точки М.
Задачи из % 11.
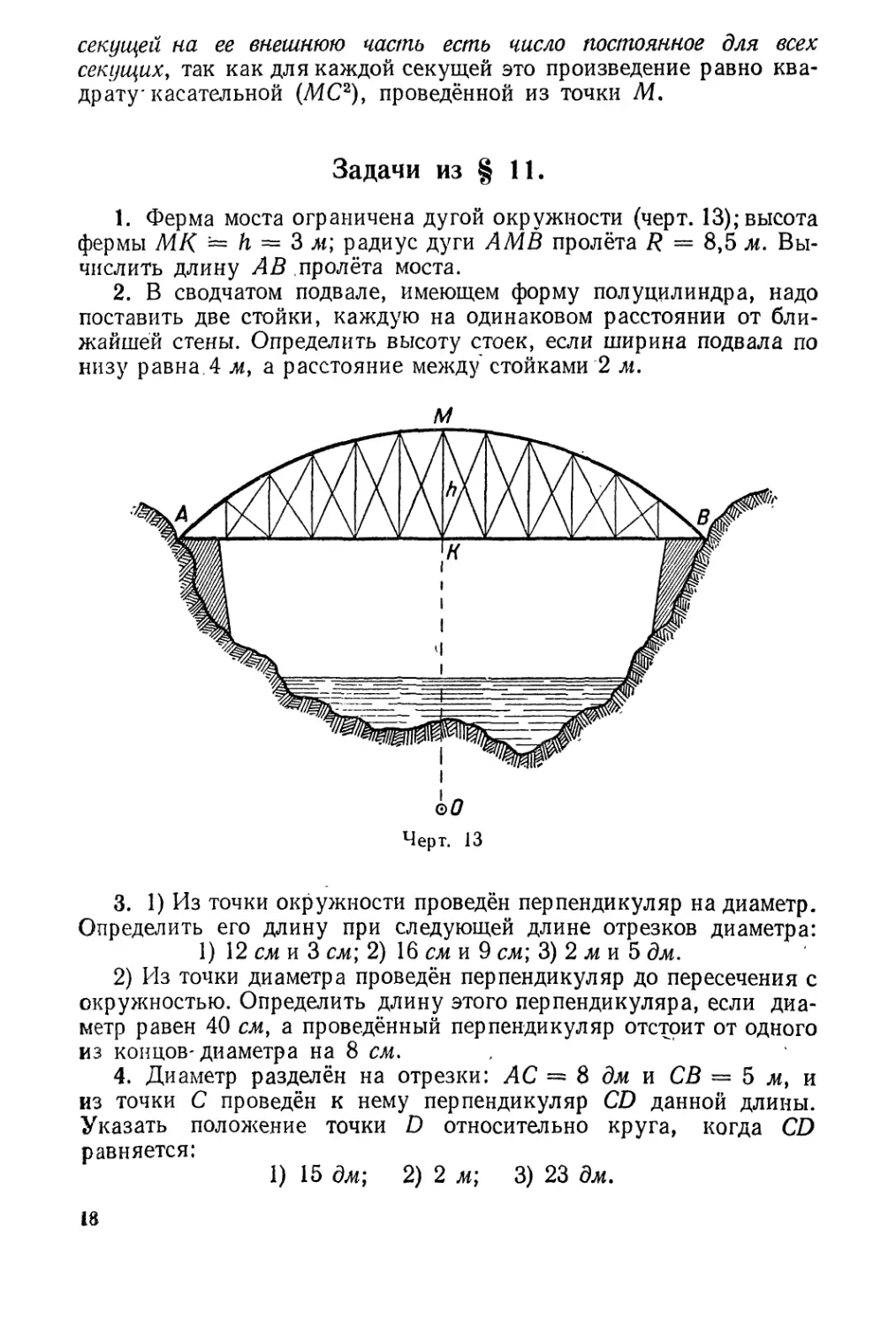
1. Ферма моста оrраничена дуrой окружности (черт. 13); высота
фермы МК :....... h == 3 At; радиус дуrи АМВ пролёта R == 8,5 м. Вы-
ЧИСЛИТЬ длину АВ .пролёта Моста.
2. В сводчатом подвале, имеющем форму ПОЛУЦЛИНДра, надо
поставить две стойки, каждую на одинаковом расстоянии от бли-
жайшеЙ сТены. Определить высоту стоек, если ширина подвала по
низу равна,4 м, а расстояние ме}кд)' стойками '2 A-t.
м
I
I
,
00
Черт. 13
3. 1) Из точки ОКРУ}КНОСТИ проведён перпендикуляр на диаметр.
Определить ero длину при следующей длине отрезков диаметра:
1) 12 см и 3 см; 2) 16 см и 9 см; 3) 2 ..м и 5 дм. '
2) Уlз точки диаметра проведён перпендикуляр до пересечения с
окру}т{ностью. Определить длину этоrо перпендикуляра, если Диа-
tvfeTp равен 40 см, а проведённый перпендикуляр ОТС'(9ИТ от одноrо
из концов' диаметра на 8 см. ,
4. Диа1\1етр разделён на отреЗI{И: АС == 8 дм и СВ == 5 м, и
ИЗ точки С проведён к нему перпендикуляр CD данной длины.
Указать ПОЛО)l{ение точки D относительно Kpyra, !{оrда CD
равняется:
1) 15 дм;
2) 2 м;
3) 23 д-м.
18

5. АСВ  ПОЛУОКРУЯПIОСТЬ; CD.......... перпендикуляр на диаметр
АВ. Требуется:
1) определить DB, если AD == 25 и CD ==: 10;
2) определить АВ, если AD : DB == 4 : 9 и CD == 30;
3) определить AD, если CD == 3AD, а радиус равен '; .
4) определить AD, если АВ == 50 и CD == 15.
6. 1) Перпендикуляр, опущенный из точки окружности на ра..
Дl;lУС, равный 34 СМ, делит ero в отношении 8 : 9 (начиная от центра).
ОпреДeJ1ИТЬ длину перпендикуляра.
2) Хорда BDC перпеНДИКУJJярна к радиусу .ODA. Определить
ВС, если ОА == 25 СМ и AD === 10 СМ.
3) Ширина кольца, образqванноrо двумя концентричеСКI1МИ ОК"
ружностями, равна 8 дм; хорда большей окружности, касательная
к меньшей, равна 4 М. Определить радиусы окру}кностей.
7. С ПОlvIОЩЬЮ сравнения отрезков доказать, ,что 'среднее ариф-
метическое двух неравных чисел больше их среднеrо rеометри-
ческоrо.
8. Построить отрезок, средний пропорциональный между отрез-
ками 3 СМ и 5 СМ.-
9. Построить отрезок, равный: V 15 ; V IO ; V 6; V З.
10. ADB  диаметр; АС  хорда; CD  перпендикуляр к
диаметру. Определить хорду АС: 1) если АВ == 2 м и AD == 0,5 м;
2) если AD == 4 СМ и DB == 5 см; 3) еСlIИ АВ == 20 М и DB ==
== 15 м.
11. АВ  диаметр; АС  хорда; AD  её проекция на диаметр
АВ. Требуется: 
1) определить AD, если АВ == 18 СМ и АС == 12 СМ;
2) определить радиус, если АС == 12 М и AD == 4 м;
7
3) определить DB, если АС == 24 СМ и DB == ..... AD.
9
,. 12. АВ  диаметр; АС  хорда; AD ....... её проекция на диаметр
АВ. Требуется:
1) определить АС, если АВ == 35 СМ и АС == 5AD;
2) определить АС, если рдиус равен, и АС == DB.
13. Две хорды пересекаются внутри Kpyra. Отрезки одной хор-
ды равны 24 СМ и 14 СМ; один из отрезков друrой хорды равен 28 СМ.
Определить второй её отрезок.
14. Мостовая ферма оrраничена дуrой окружности (черт. 13):
длина моста АВ == 6 М, высота h == 1,2 м. Определить радиус дуrи
(ОМ , R).
15. Два отрезка АВ и CD пересекаются в точке М так, что NIA==
== 7 см, МВ == 21 СМ, МС == 3 СМ и MD == 16 см. Лежат ли точки
А, В, С и D на одной окружности?
16. Длина маятника МА == 1 == 1 м (черт. 14), высота подъёма
ero, при отклонении на уrол а, СА == h == 10 см, Найти расстоя-
ние ВС точки В от МА (ВС == х).
19

17. Для переВQда }{<елезнодорожноrо
пути шириной Ь =:: 1,524 Jt в месте АВ
(черт. 15) сделано закруrление; при
этом' оказалось, что ве == а == 42,4 м.
Определ,ИТЬ радиус закруrления ОА == R.
18. Хорда АМВ повёрнута около
точки М так., что отрезок МА увеличил-
ся в 2 раза. Как изменился отрезок
2
МВ?
19. 1) Из двух пересекающихся хорд
одна разделиласъ на части в 48 см и 3 С,м"
а друrая ...... пополам. Опрдел.ить длину
второй хорды.
2) Из двух пер есекающи хся хорд
одна РЗЗДeJIил.ась на части в 12 А! и
18 м, а друrая....... в отношении 3: 8.
Определить длину второй хорды.
20. И:з двух пересекающихся хорд первая равна 32 с-м, а отрезки
друrой хорды равны 12 см и 16 CJd. Определить отрезки первой
Х<?РДЫ.
21. Секущая АВС ,повёрнута около внешней точки А так, что
внешний её отрезок АВ уменьшился в три раза. Как измени-
пась длина секущей?
22. IlycTb ADB И АЕС  Д
две прямые, пересекающие
окружность': первая....... в точ- В
ках D и В, вторая........ в точ"
ках Е и С.
Требуется:
1) определить АВ, если
AD ==, 5 см, DB == 15 см и
АС == 25 см;
2) определить BD, если
А В == 24 М, А С == 16 м и
ЕС == 10 м;
3) определить АВ и АС,
если АВ + АС == 50 м, а
AD : АЕ == 3 : 7.
23" Радиус окружности ра-
вен 7 см. Из точки, удалённой
от центра На 9 см, проведена
секущая так, что она делится
окружностью пополам. Опре-
делить длину этой сеI<ущей.
/
/
/
/
/1
/
/
/
I
'   C 
. ..... ___ ...; h
-... .... .
Черт. 14
20
а
I
I /D
t I
I I
;'
I ;
I
) I
I I
I I
I "
, I
J I
I I
, {i
t "
I I
I I
11
)J
О
Черт. 15

24. МАВ и MCD  две секущие к одной ОКРУЖНОСТИ. Тре-
буется:
1) определить св, если МВ == 1 м, MD == 15 д-м и CD == МА;
2) определить MD, если л-tА == 18 см, АВ == 12 см и
М С : CD == 5 : 7;
3) опреДeJIИТЬ АВ, если АВ == МС, МА == 20 и CD == 11.
25. Две ХОрДЫ продолжены до взаимноrо пересечения. Опреде-
лить длину полученных продолжений, если хорды равны а и Ь,
а их продолжения относятся, как т : n.
26. Из одной точки проведены к окружности секущая и каса-
'тельная. Определить длину касательной, если внешний и внутрен-
u . u
нии отрезки секущеи соответственно выражаются следующими чис-
лами: 1) 4 и 5; 2) 2,25 и 1,75,3) 1 и 2.
27. Касательная равна 20 см, а наибольшая секущая, проведён-
ная из той же точки, равна 50 см. О'пределить радиус pyra.
1 '
28. Секущая "больше CBoero внешнеrо отрезка в 2 раза. ВО
4
сколько раз она больше касательной, проведённой из той же
точки?
29. Общая хорда двух пересекающихся окружностей продол-
жена, и из точки, взятой на продолжении, проведены к ним каса-
тельные. Доказать, что они равны. .
30. На одной стороне уrла А отложены один за друrим ОТрезки%
АВ == 6 см и Ее == 8 см; а на друrой стороне отло}кен отрезок AD ==
== 10 см. Через ТОЧI{И В, С И D проведена окружность. Узнать, ка-
сается ли этой окружности прямая AD, а если нет, то будет ли точ-
ка D первой (считая от А) или второй точкой пересечения.
31. Пусть будет: АВ  касательная и, ACD  секущая той
же ОI<РУЖНОСТИ. Требуется:
1) определить CD, есЛИ АВ == 2 см и AD  4 СА!;
2) определить AD, если АС : CD == 4 : 5 и АВ  12 см;
3) определить АВ, если АВ == CD и АС == а.
32. 1) Как далеко видно с воздушноrо шара (черт. 16), подняв-
шеrося на высоту 4 к.м над землей (радиус земли равен  6370 км)?
2) ropa Эльбрус (на КаВI<азе) поднимается над уровнем моря
на 5600 М. Как далеко можно видеть с верIlIИНЫ этой ropbI?
3) Л1  наблюдательный пункт высотой h метров над землёй
(черт. 17); радиус земли R, М Т == d ест ь наибольшее видимое рас-
стояние. Лоназать, что d == Y2Rh + h 2 .
3 а м е ч а н и е. Так как h 2 вследствие своей малОСТи сравнитеЛЬRО
с 2Rh на результат почти не влияет, то можно пользоваться приближённой
формулой d  Y 2Rh
33. 1) Касательная и секущая, выходящие из ОДНОЙ точки, соот-
ветственно равны 20 см и 40 см; сеКУIlая удалена от центра на 8 CJl.
Определить радиус Kpyra.
21

.2) Определить расстояние от Цlpa до той ТОЧКИ, ИЗ кото-
рой ВЫХОДЯТ каоательная и сеКУI.цая, если они соответственно
равны 4 см и 8 с'м, а секущая удалена от центра на 12 СМ.
34. 1) Из общей точки проведены к окружности касательная и
сеКУlцая. Определить длину касательной, если она на 5 см больше
внешнеrо отрезка секущей и на столько же меньше BHYTpeHHero
отрезка"
2) Из ОДНОЙ точки проведены к окружности секущая и касатель-
ная. Секущая равна а, а её внутренний отрезок больше внешнеrо
отрезка на длину касательной.. Определить касательную.
fv1
/
I
I
I

/
I
/
I
I
I
Чер1'. 17
35. Из одной точки проведены к одной окружности касательная
и секущая. Касательная больше BHYTpeHHero и 8нешнеrо отрезков
сеКУUlей соответственно на 2 см и 4 с'м. Определить длину секущей.
36.' vlз одной точки проведены к окружности касательная и се..
кущая. Определить их длину, если касательная на 20 см меньше
впутрениеrо отрезка секущей и на 8 см больше внешнеrо отрезка.
37. 1) Из ОДНОЙ точки проведены к QКРУЖНОСТИ секущая и ка-
сательная. Сумма их равна 30 СМ, а внутренний отрезок секущей на
2 С.М меньше касательной.. Определить секущую и касательную.
.2) Из одной точки проведены к окружности секущая и касатель-
ная. Сумма их равна 15 см, а внешний отрезок секущей на 2 сМ
меньше касательной. Определить секущую и касательную.
38. Отрезок АВ продолжен на расстояние ВС. На АВ и АС,
K31< на диаметрах. построен'ы окружности. К отрезку АС в точке
В проведён перпендикуляр BD до пересечения с большей окру>к-
"остью. Из точки С проведена касательная СК к меньшей окруж
пости. Доказать, что CD == СК.
39. К данной окр у}кности проведены две пар аллельные касатель.
ные и третья касательная, пересекаlощая ИХ. . Радиус есть средняя
пропорциональная ме)I<ДУ отрезками третьей касательной. Доказать.
22

40. Даны две параллельные прямые на расстоянии 15 allt одна
от друrой; ме)JIДУ ними дана ТОЧI{а М на расстоянии 3 aJ11 от одноЙ
ИЗ них. Через точку М проведена о!{ружность, касательная к
обеим параллелям. Определить расстояние rvlежду проекцияrvfИ
центра и точки М на одну из данных параллелей. '
41. В Kpyr радиуса r вписан равнобедренный треуrольник, у ко-
Toporo сумма высоты и основания равна диаметру KpYIa. Опреде-
лить высоту.
42. Определить радиус Kpyra, описанноrо около равнобедрен-
Horo треуrольника:
1) если основание равно 16 см, а высота 4 с"и;
2) если боковая сторона равна 12 дм, а высота 9 д.м;
 3) если боковая сторона равна 15 м, а основание 18 м.
43. В равнобедренном треуольнике основание равно 48 д/l"
а боковая сторона равна 30 дм. Определить радиусы KpyroB, опи-
caHHoro и вписанноrо, и расстояние между их центраrvrи.
44. Радиус равен " хорда данной дуrи равна а. Определить
хорду удвоенной дуrи.
45. Радиус окружности равен 8 дм; хорда АВ равна 12 дм.
Через точку А проведена касательная, а из точки В  хорда ВС,
параллельная касательной. Определить расстояни f\1ежду каса-
тельной и хордой ВС. ,
46. Точка А удалена от прямой MN на расстояние а. Данным
радиусом r описана окру}кность так, что она проходит через ТОЧI{У
А и касается линии MN. Определить расстояние между полученной
точкой касания и данной точкой А.

ДЕВЯТЫЙ К ЛАсе
ВЫЧИСЛЕНИЕ ДЛИНЫ О КРУЖНОСТИ И ЕЕ. ЧАСТЕЙ.
12 (226).: Предварительное разъяснениеf) Отрезок прямой можно
u
сравнить с друrИ1 отрезком прямои, принятым за единицу, так как
прямые линии при наложении совмещаются. Действительно, только
по этой причине мы можем установить, какие отрезки ПРЯfЫХ счи-
тать равными и неравными; что такое сумма отрезков прямой; ка-
кой отрезок больше друrоrо в 2, 3 4, ... раза и т. п. Точно так же
дуrи окружностей одинаковоrо радиуса можно сравнить между собой
вс.ледстие Toro, что такие дуrи при наложении совмещаются. Но
так как никакая часть окружнос.ти (или друrой кривой) не может
совместиться с прямой, то нельзя путём наложения установить,
какой криволинейный отрезок должно считать равным данному
прямолинейному отрезку, а следовательно, и то, какой криволи
нейныЙ отрезок больше данноrо прямолинейноrо в 2, 3, 4, ... раза.
Такиrvl образом, является необходимость особо определить, что мы"
будем подразумевать п о Д Д л и н о й о к р у ж н о с т и (или
части её), коrда сравниваеrvl её с прямолинейным отрезком.
Для этой цели мы дол)кны ввести новое понятие, имеющее исклю
чительно большое значение во всей математике, именно п о н я
т и е о п р е Д е л е.
Предел числовой последовательности.
13. (227.) Во lvlноrих вопросах алrебры и rеометрии приходится
встречаться с последоватьностями чисел, написанных одно за
друrим по определённоrvlузакону. Например, натуральный ряд
чисел:
1, 2, 3, 4, 5, ...,
арифметическая и rеОl'vlетрическая проrрессии, продолженные He
оrраниченно:
а, а + d, а + 2d, а + 3d, ...,
2 3
а, aq, aq , aq , ...,
представляют собой бесконечные последовательности чисм, или
бесконечные числовые послеДQвательности.
Для ка}кдой такой последовательности можно указать правило,
по которому составляются её члены. Так, в арифметическоЙ про-
rрессии ка}кдый член разнится от предыдущеrо на одно и то же
24

u u
число, в rеометрическои проrрессии каждыи член равен предше-
ствующему, умноженному на некоторое определённое число (зна-
менатель проrрессии).
Мноrие последовательности составляются по более сложным пра-
вилам. Так, например, . вычи-сляя 112 с недостаТКОl\;1 сначала с точ-
ностью до 0,1, затel\tI с точностью до 0,01, затем с точностью до 0,001
и продолжая, это вычисление неоrраниченно, мы получим беско-
нечную числовую последовательность:
1,4; 1,41; 1,414; 1,4142, ...,
дающую приближённое значение 112 с возрастающей степенью
точности.
Для этой последовательности нельзя указать npOCToro правила,
по которому можно было бы получить новые её члены, зная преды-
дущие, но всё же мо}кно определить любой член этой последов а-
тель-ности. Так, чтобы получить 4..й её член, нужно вычислить V2
с точностыQ до O,OqOl, для пО'лучения 5-ro члена нужно вычислить
112 с точностью до 0,00001 и т. д.
Допустим, что члены данной бесконечн,ой последовательности
а 1 , а 2 , аз, ..., а n , ... по мере повышения их номера неоrрани"
ченно приближаются к некоторому числу А. Это значит следующее:
существует некоторое число А такое, что,' какое бы. малое поло}{(и-
тельное число q мы ни взяли, в данной последовательности ожно
отыскать член, начиная с KOToporo все члены последовательности
по абсолютноЙ величине отличаются от А меньше, чем на q. Мы
будеl'll это свойство коротко выражать так: абсолютная величина
разности а п  А неоrраниченно убывает с возрастанием номера n.
В этоrvI случае число А называется пределом данной бесконечной
числовой последовательности. Приведём пример такой последова..
тельности. .Составим послдовательность десятичных дробей:
0,9; 0,99; 0,999;
Здесь ка}кдый член получается из предыдущеrо приписыва-
ниеl'Л HOBoro десятичноrо знака 9.
Леrко заметить, что члены этой последовательности неоrрани"
ченно приближаются к единице.
Именно, первыЙ член отличается от единицы на 0,1, второЙ на
0,01, третий на 0,001, и если достаточно продолжить эту последова-
тельность, то можно найти '.В ней член, начиная с KOToporo все по-
следующие члены будут отличаться от единицы на сколь уrодно
малую, заранее указанную величину. Следовательно, мы MOiI{eM
сказаТЬ, что взятая нами бесконечная числовая последовательность
имеет пределом единицу. Друrим ПрИl\fером числовой последов а..
тельности, Иl\rеющей предел, служит последвательность прибли-
жённых значений длины отрезка, несоизмеримоrо с единицей дли-
НЫ, вычисленных с недостатком, сначала с точностью до 0,1, затем
до 0,01, затем ----- до 0,001 и т. д.
25

ПределО1\1 этой последовательности слу}кит бесконечная десятич-
ная дробь, преДстаВЛЯIощая точную меру ДЛИНЫ данноrо отрезка. В
самом деле, величина бесконечной десятичной дроб,И заключена
ыежду двумя её приближён'ными значениями, вычисленными с оди-
наковой Точностью........ одно с недостатком, .друrое с избытком.
KaI{ было показано выше, эта разность неоrраниченно убывает
по мере повышения степени точности приблия{ённых значений.
Следовательно,' должна неоrраниченно убывать и разность между
самой бесконечной десятичной дробью и её приближёнными значе-
НИЯМIJ по мере повышения степени точности этих значений. Зна-
чит, бесконечная десятичная дробь слу}кит пределом последова-
тельности всех её приближённых значений, взятых с недостатком
(или всех прибли}кённых значений, взятых с избытком).
Леrко заметить, что не всякая бесконечная последовательность
имеет прдел; например, натуральный ряд чисел:
1, 2, 3, 4, 5, ...,
..
очевидно, никакоrо предела не имеет, так как ero члены неоrрани-
ченно возрастают и ни !{ какому числу не прибли}каются.
14. (228.) Теорема. Всякая бесконечная числовая
последовательность может иметь только один предел.
В справедливости этой теоремы леrко убедиться доказательством
от f!ротивноrо. В Cal\IfOM деле, предположим, что А?на последователь-
ность
а 1 , а 2 , аз, ..., а п , ...,
которая имеет два раз л и ч н ы х предела А и В. В таком случае,
в силу Toro, что А есть предел данной последовательности, абсолют-
ная величина разности а п  А ДОЛ}J{на неоrраниченно убывать с
возрастанием n. В силу Toro, что В есть то}ке предел данной после-
довательности, абсолютная величина разности а п  В также-должна
неоrраниченно убывать с возрастанием n.
Но' в таком случ.ае абсолютная величина разности.
(а п . ------ А)  (а п  В)
должна такя{е или неrраниченно убывать, или быть равной НУЛIО.
Но эта последняя разность .равна разности чисел В .......... А и, следо-
..
вательно, есть некоторое вполне определенное, отличное от нуля'
число'. Это число не зависит от номера n и при возрастании пвовсе
не изменяется. Таким образом, предположение, что существуют два
предела числовой последовательности, привело нас к противоречию.
15. (229.) Предел возрастающей бесконечной числовой по-
следовательности.. Рассмотрим такую последовательность a t , OZt
аз, ..., а п , 40" в которой каждый следующий член больше
предыдущеrо, т. е. а п + 1 > а п , 11 в то }ке время все члены последо-
вательности меньше HeKoтoporo определённоrо числа М, т. е. для
любоrо номера n а п < М.
26

в эnwм случае nоследоваtпельн OCтh UAteeпl оnределёНflЫЙ предел.
(Теорема Вейерштрасса.)
16. (231.) Предел перемеН:IОЙ величины. Если дана последова..
тельность
й 1 ' й 2 , аз. ..., а п , ....,
то n-й член её а п можно назвать переменной велиц,иной, числовое ЗНа-
чение которой зависит от её номера n. Этим выражением «перемен..
иая величина» часто пользуются для упрощения речи. Так, вместо
выражения «дана бесконечная числовая последовательность Й{.
й2' а З1 ..., а п , ...» принято roворить «дана переменная величина й п .
ПРИJIимающая последовательно р5!Д значений а 1 , й2, аз, ...». Если
пользоваться этим способом выражения, то можно rоворить не о
u
пределе последовательности, а о пределе переменнои величины.
В таком случае, предложение, доказанное в  14 (228), можно
высказать в форме: «.Всякая переменная величина может стремить-
ся пишь к одному ,пределу». 8то предложение 9асто высказьmают
так: «Если даны две переменные величины а п и Ь n ,' причём все зна-
чения первой равны соответствующим значениям второй:  == b 1 ,
й 2 == Ь 2 , ..., й п == Ь п , ..., то предел первой величины, конечно, если
он существует, равен пределу второй», или короче: «Если две пере..
менные величины равны, то равны и их пределы».
Предложение ( 15) о пределе возрастающей числовой последова-
тельности можно высказать так: если neременная величина а п воз..
растает с возрастанием номера n и в то же время остается меньИle
нeKoтopoZo noсmоянноео числа, то эта neременная величина Uhteem
предел.
Длина окружности.
17. (232: j Понятие о пределе даст возможность точно опреде-
лить, что мы подразумеваем под длиной окружности. Предвари-
тельно докажем следующие леммы.
Л е м м а 1. Выnу"лая ЛО.l,f,аная (ABCD, черт. 18) .меньше
вся"ой друzой ломаноii (AEFGD), объемлющей первую.
Выражения «объемлющая ломаная}), «объемлемая ломаная» име..
ют следующий смысл. Пусть две ломаные (KaI< те, которые изобра-
}кены у нас на чертеж) имеют од-
ни и те }ке концы А и D и распо.. С,
ложены таким образом, что одна
ломаная (А BCD) вся лежит внут"
ри мноrоуrольника, образованноrо
друrо.й ломаной и отрезком AD, со-
единяющим концы А и D: тоrда
внешняя ломаная называется А О
объемлющей, а внутренняя лола-
ная ........ объемлемой. Черт, 18
21

Предстоит доказать, что объемлемая ломаная ABCD (если она
выпуклая) короче всякой объемлющей линии AEFGD (всё равно .......
выпуклой или невыпуклой), т. е. что 
АВ + 8С + .GD < АЕ + ЕР + РО f. GD.
ПРОДОЛ)l{ИМ стороны выпуклой ломаной так, как указано на чер-
те}ке. Тоrдз, приняв во внимание, что отрезок прямой меньше вся-
кой ломаной, соединяющей концы отрезка, мы можем написать
следующие HepaBeHtTBa:
АВ + ВН < АЕ + ЕН;
ве + ек < вн + HP + Ра + GK
CD < СК + KD.
Сложим почленно все эти неравенства и затем от обеих частей по-
лученноrо неравенства отнимем вспомоrательные отрезки ВН
и CK далее, заменив сумму ЕН + HP отрезком ЕР и сумму
ок + KD  отрезком GD, {IОЛУЧИМ то неравенство, которое треба-
валось доказать.
3 а м .е ч а н и е. Если бы объемлемая линия не была выпуклой
(черт. 19),10 изложенное доказательство нельзя было бы применить.
В этом случае объемлемая ломаная может оказаться и больше объем
лющей.
18. (233.) JI е м м а 2. ПеРll.метр 8ыпук.лоzо .мНОZОУZОЛЬ-
ника (ABCD) ,,{еньше пери-м,етра 6СЯКОZО дрzоzо M,."ozo-
уzольнuк,а (MN PQRL), объемлющеzо перВЫЙ (черт. 20).
Требуется доказать, что
АВ + ве + CD + DA < LM + MN + NP + PQ +QR + RL.
Продолжив в обоих направле.. N
ниях одну какуюнибудь сторону О
AD выпуклоrо мноrоуrольника, 11 В
применим к ломаным линиям ABCD
т
s
4 ерт. 20
А
8'
Черт. 19
и А TMN PQRSD, СО,единяющим точки А и D, лем'му предыдущеrо
параrрафа; получим неравенство:
АВ + ВС + CD < А Т + т м + MN + N Р +
+ Р Q + QR + RS + SD.
С друrой стороны, так как отрезок ST меньше ломаной SLT,
то MO)l{eM написать:
ТА + AD + DS < TL + LS.
28

СлОЖИf\,f почленно эти два неравенства и отнимем от обеих частей
вспомоrательные отрезки А Т и DS; далее, заrvfенив сумму TL + тм
отрезком [М и сумму LS + RS отрезком LR, получим то, что
требовалось доказать. .
1.9. (234.) Определение длины окружности, Впишем в данную
окружность (черт. 21) правильный мноrоуrольник, например шести-
уrольник, и на какой-нибудь прямой MN (черт. 22) отложим отрезок
ОР., равный периметру этоо шестиуrольника (на нашем чертеже
периметр изображён по недостатку свободноrо .
места в уменьшенном виде). Удвоим теперь чис..
ло CTopdH вписанноrо шестиуrольника, т. е.
" d
вместо шестиуrольника возьмем правильныи
вписанный 12"уrольник. Найдём также ero
периметр и отложим ero на той же ПрЯlVlОЙ MN
от той же точки о; пусть тоrда получится от-
резок ОР 2 , который должен быть больше OP j ,
так как вместо каждой стороны шестиуrольни"
ка мы теперь берём ломаНУIО (из двух сторон
12-уrольника), которая длиннее прямой. Черт. 21
Удвоим снова число сторон вписанноrо
12-уrольника, т. е. возьмём теперь правильный 24-уrольник
(на чертеже он не указан), найдём ero периметр. и отложим ero на
MN от той }ке точки о; мы получим тоrда отрезок ОРз, который
будет больше ОР 2 по той же ПРИЧl1не, по какой ОР 2 больше OP t .
Вообразим, что такой процесс удвоения и откладьmания пери-
метров продолжается всё далее и далее. Тоrда мы получим бесконеч-
ную последовательность периметров ор!, ОР2' ОРз, ..., которая
является возрастаlощей последовательностью. Однако возрастание
х
I J-o- N
Pz Р З
t1 
О
I
Р,
Черт. 22
это не может быть неоrраниченным, так как периметр Всякоrо
вписанноrо мноrоуrольника (выпуклоrо), каково бы ни было число
е['о сторон, всеI'да остаётся меньше периметра любоrо описанноrо
мноrоуrольника (как ero объемлющеrо). Вследствие этоrо получен-
ная последовательность периметров правильных вписанных MHoro-
уrольников имеет определённый предел (9 15). Этот предел и при-
нимают за длину окру)кности. Таким обраЗОl\f, fbI принимаем следу..
ющее о п р е Д е л е н и е: за дUHY ОКРУЖНОСfпu nрuнuмается тот
предел, к которо_иу стремится (приближается) nеременный пери-
меп1Р nравUЛЬflоео мносоусольнuка, вписанноео 8 эту окружность,
Koдa число cnzopoH е20 flеораничеНflО удваивается.
3 а м е ч а н и е. i\'\ожно доказать (МЫ опускаем это доказательство» что
преll.ел этот не зависит от Toro, с KaKoro Мноrоуrольника мы начинаем
29

удnоеnие. Более Toro, можно доказать, что если да>}{е вписанные мноrоуrоль..
НИКИ и не будут правильные, все же периметры их стремятся к тому же
самому пределу, Kal< и периметры правильных мноrоуrольников, лишь бы
ТОЛЬКО стороны их неоrрзниченно уменьшались (и, следовательно, число CTO
рон их неоrраниченно у'величивалось) путём ли удвоения, как МЫ это пред
полаrали для правильных мноrоуrольников, или по какомунибудь иному за-
кону (мы опускаем это доказательство).
Таким образом, для каждой окружности существует свой единственный
предел, к которому стремится лериметр вписанноrо выпуклоrо мноrоуrольни.
ка, коrда стороны ero неоrраниченно уменьшаlОТСЯ; предел этот и принима.
ется за длину ОI{РУ}I<:НОСТИ.
Равным образом за длину какойнибудь дуrи окружности АВ
(черт. 23) принимается предел,.!{ которому стремится переменный
D
с
в
в А
А
Черт. 23.
Черт. 24
пеРИl\1етр ломаной линии, вписанной в эту дуrу и имеющей с ней
ОДНИ И те же КОНЦЫ, коrда число сторон ломаной неоrраниченно
удваивается.
208; (235) Допущения.. Для простоты изложения мы примем
без доказательства следующие, почти очевидные, предложения:
Длина дуси окружности: 1) больше сtnяеивающей ее хорды,' но
2) меньше nеримеmра вся1Wй ЛОАiаной линии, описанной около этой
дуеи u имеющей с ней одни u те же концы (черт. 24).
21. Нахождение длины окружности.; Для этой цели можно вос"
пользоваться формулой, выражающей сторону (а п ) правильноrо
n-уrольника чеР,еэ радиус (R) описанноrо Kpyra:
. 1800
а п == 2R · Sln  .
n
Тоrда периметр п-уrольника (Р п) MO)l{HO выразить в виде формулы:
1800
Р п == апn == 2R п · sin ................
п
Польэуясь семизначными таблицами синусов уrлов, lIаЙдём
Ре == 2R · 6 sin 30° == 2R · З.
Р12 == 2R · 12 sin 15° == 2R · 3,10582...
Р 2А. == 2R · 24 sin 7°30' == 2R · 3,13262...
Р 48 == 2R · 48 sin 3°45' == 2R · 3,13935...
Р96 == 2R · 96 sin 1°52'30" == 2R · 3,14103...
P192==.2R · 192 sin 56'15" == 2R · 3,14145...
P84== 2R · 384 sin 28'7",5 .. 2R · 3'14156....
30

При Ka}KДO1 последующем удвоении числа сторон праВИЛЬНОI'Q
вписанноrо мноrоуrольпика мы получаем последовательность зна-
u 2 R . 1800 К u u
чении произведения п · Sln. а}кдыи последующии член
n
этой последовательности больше предыдущеrо и в то же время
каждый её член меньше HeKoToporo определённоrо числа. Эта пQс-
л€довательность, как' показано в  19 (234), имеет предеЛ, который
и принимают за длину окружности. Таким образом пер и метр пр а-
вильноrо вписанноrо мноrоуrольника даёт приближённое зна-
чение ДЛИНЫ окружности" причём по мере продол}кения процесса
удвоения числа сторон этоrо мноrоуrольника точность значения B03
раста'ет.
22.. (238.) Отношение. ДЛИНЫ окружности к диаметру. Pac
сматривая процесс нахоя{дения длины окру}кности, можно заме
тить, что число, на которое нужно умножить диаметр, чтобы полу
чить ДЛИНУ окружности, не зависит от величины caMoro диаметра,
. так что если мы нашли, что длина какой-нибудь окружности равна
её диаметру, умно}кенному на некоторое число, то и длина всякой
друrой окружности будет равна её диаметру, YMHO}KeHH01rIY на ТО
же самое число.
В самом деле, возьмём две окру}кности: одну раДиуса R, др у-
rую радиуса '. Длину первой окружности обозначим через С, дли-
ну В"fОрОЙ  через с. Впишем в каждую из них правильный мно-
rоуrольник с одним и тем же.. числом сторон и будем удваивать
число сторон каждоrо из этих мноrоуrольников.
Обозначим через Р п переменный пер и метр правильноrо МНО"
rоуrольника, вписанноrо в пеРВУIО окружность, и через Рп перемен..
ный периметр правильноrо мноrоуrольника с тем же ЧИСЛОIVI сторон,
вписанноrо во вторую окружность.
, Н Ф Р 2R . 1800, u f;. 21
\ а основании ормулы п == n · SlП n ' даннои в  , МЫ
Р п Рп
можем напи'сать: 2R == 2,
Переменный периметр Р п имеет пределом длину С первой ОКРУЖ-
ности. Переf\.fенный периметр Рп имеет пределом длину с второй ак-
р Р . с с
РУЯ{НОСТИ. 1:- потому из равенства 2R === 2; вытекает . 2R == 2f
( 14 и 16). Таким' образом, мы MO)l{ervI сказать, что отношение дли-
ны 'окружности к ее aUQhtempy есть число постоянное для всех OKPYJ/C-
настей.
Это постоянное число принято обозначать rреческой буквой n 1 .
Мы можем, таким образом, для длины С окружности написать
такую формулу:
с == 2R · л, ИЛИ С == 231R.
1 Обозначение это введено, по всей вероятности, в XVII столетии. Буква
n (ли) есть начальная буква rреческоrо слова nepL<pepea (окружность).
31

Доказано', что число 1& является числом иррациональным, и, зна-
ЧИ!, оно не может быть выражено точно никаким рациональным
числом. Но ero прибли)кённые значения можно находить различ-
ными способами с какой уrодно точностью. Приняв периметр впи-
caHHoro 96уrольника за приближённую длину окружности, МЫ
получим для зt приближённое значение 3,14 с недостатком  с точ-
ностью до 0,01. Эта точность для практических целей часто бываеТ
достаточна. Для более точных вычислений можно брать л  3,14159.
Пользуясь современными вычислительными машинами, нашли
более 3000 знаков числа п.
Полезно заметить, что ещё в 111 веке до начала нашей эры знаме-
нитый сиракузский reoMeTp Архимед нашёл для 3t очень простое
число 22/7' Т. е. 31/7' это число несколько более n и разнится от Hero
"1енее чем на 2 тысячных.
При решении rеометрических задач часто встречается число, об-
1
ратное чИсЛ.у п, т. е. равное дроби n . Полезно запомнить несколь-
ко цифр этоrо числа:
1
 == 0,3183098...
'П
23. (239..) Длина дуrи, содержащей п rрадусов.: Длина окруж
. о 21tR nR
насти есть 2лR, значит, длина дуrи в 1 равна. 360 == 180 ; следо-
u о
вательно, длина s дуrи, содеР)I{ащеи п , выразится так:
xRn
s == 180 .
Если дуrа выражена в минутах (п') или в секундах (n"), то дли-
на её определяется соответственно формулами:
nRn лRn
s == 180 . 60' или s == 180. 60 . 60
rде n  число минут или секунд.
24. (240.) 3 а д а ч а. Вычислить с точностью до 1 .мм радиус
такой окружности, дУ2а которой, содержащая 81°2] '36", равна
0,452 М.
Обратив 81°21'36" в секунды, получим число 292 896.
Из уравнения
0,452 == nR · 292 896
1 ВО · 60 . 60
находим:
R == 0,452 · 180 · 60 · 60 ===  == 0,3]8 (м).
292 896 n n
25. (241.) 3 а д а ч а. Определить число срадусов дуси,
длина к.оmорой равна радиусу.
32

Заменив в формуле, определяющей длину дуrи в пО, величину s
на R, получим уравнение:.
R === nRn или l..... пn
1800'  1800:'
откуда
пО == 1800 == 1800 . .!=: 1800 . 0',3183098 == 57'\295764 == 57017' 44", 8.
3t n
Заметим, что дуrа, р а в н а я радиусу, называется р а Д и а.
н о М.
ПЛОЩАДЬ KPyr А и Ero ЧАСТЕЙ.
26. (262.) Л е м м а. При неоzран,иченном удвоении числа
сторон правuльноz'о 81t1l:CaHHO'zo .мноzоуzольни"а сmоро..
на ezo может сделаться как yzoiJHo .малой.
Пусть n есть число сторон правильноrо вписанноrо мноrоуrоль.
ника и \р ....... ero пери метр; тоrда длина ОДНОЙ стороны этоrо MHoro.
уrольника выразится дробью  . При. неоrpанИ'ченн"Ом удвоении
числа сторон мноrоуrольника знаменатель
этой дроби будет, очевидно, BopaCTaTЬ Heorp&-
ниченно, а числитель, т. е. р, хотя и будет воз..
растать, но не беспредельно (так как пери..
метр всякоrо вписанноrо выпуклоrо MHoro-
уrольника всеrда остается меньшим перимет..
ра любоrо описанноrо мноrоуrольника)'. Если
же в какой-нибудь дроби знаменатель ней]'..
раниченно возрастает, а числитель остаётся
меньше некоторой постоянной величины, то
дробь эта может сделаться как уrодно ма..
лой. Значит, то }!{е caMoe можно сказать о
стороне правильноrо вписанноrо мноrоуrоль..
ника: при неоrраниченном удвоении числа сторон она мо}кет
сделаться как уrодно малой.
27. (263.) С л е Д с т в и е. Пусть АВ (черт. 25) есть сторона
правильноrо вписанноrо мноrоуrольника, ОА  радиус и ОС.......
апофема. Из  ОАС наХОДИJlvf:
АО  ОС< АС,
т. е.
D
Черт. 25
1
АО  ОС<  АВ.
2
Но при неоrраниченном удвоении числа сторон правильноrо
u
вписанноrо мноrоуrольника сторона ero, как мы сеичас доказали,
может сделаться aK уrодно малой, значит, то же самое можно ска-
зать и о разности АО  ОС. Таким образом, при неоrраниченном
33

удвоении числа сторон правильноrо вписанноrо мноrоуrольника
разность между радиусом u апофемой может сделаться как уеодно
.малой. Это же можно высказать друrими словами так: при He9rpa"
ниченном удвоении числа сторон правильноrо вписанноrо MHoro..
уrольника предел, к. которому стремится апофема, есть радиус.
28. (264.) Площадь KPyra. Впишем в Kpyr, радиус KOToporo обо..
значим R, какой-нибудь правильный мноrоуrольник. Пусть
площадь этоrо мноrоуrольника будет q,
периметр »»» р,
апофема »»» а.
По формуле вычисления площади правильноrо мноrоуrольника
имеем:
1
q == 2" ра.
ВообраЗf11\f теперь, что число сторон' этоrо мноr6уrольника иеоrра..
ниченно удваивается. Тоrда пери метр р и апофеl\Iа а (следовательно,
и площадь q) будут увеличиваться, причём периметр будет стре..
миться { пределу, ПРИНИfаемому за длину С окружности, апофема
будет стремиться l{ пределу, равному радиусу R Kpyra. Из этоrо
следует, что площадь мноrоуrольника, увеличиваясь при удвоении
1
числа сторон, будет стремиться к пределу, равному 2 С. R. Пре-
дел этот принимается за численную величину площади KpYI'a.
Таким образом, обозначив площадь Kpyra буквой К, можем на..
писать:
1
К == ..... с · R,
2
т. е. площадь КРУ2а равна половине nроизведеflИЯ длины окружности
на радиус.
Так как С == 2-лR, то
1
К. == ..... · 2л;R · R == л:R2,
2 ,
т. е. площадь к,РУ2а равна MaJpalnY радиуса, умноженному на отно..
UleHue длины окружности к диалt(,етру.
29. (265.) С л е Д с т в и е. П лощадu КРУ208 относятся, ка/\,
квадраты радиусов или диаметров.
Действительно, если К и К 1 будут площади двух KpyroB, а R
и R 1  их радиусы, то
К == :лR 2 и К 1 === лR 1 2 ,
откуда
к лR2 R2 4R2 (2R)
 ===  == 2 == -----т == ·
К 1 лR' l R 1 4R 1 (2R 1 )2
34

30. (266.) 3 а д а ч а 1. Вычислить площадь круеа, длина
окружности котОРО20 равна 2 М.
ДЛЯ этоrо предварительно находим радиус R из равенства;
'1
2:rr.R == 2, откуда R ==..... == 0,3183 ... .
n
Затем определим площадь Kpyra:
, К == лR2 == Л (  )2 ==  == 0,3183 .'0 м 2 .
31.. (267.) 3 а д а ч а 2. Построить квадрат, равновеликий
aaHH01ftY КРУ2У.
Эта задача, известная под названием к в а Д р а т у рык р у..
r а, не может быть решена при помощи циркуля и линейки. Дейст"
вительно, если обозначим буквой х сторону искомоrо квадрата, а
буквой R радиус Kpyra, то получим уравнение:
х 2 == 1tR 2 ,
откуда
лR : х == х : Я,
т. е. Х есть средняя пропорциональная ме}кду по.пуокру}кностью и
радиусом. Следовательно, если известен отрезок, длина KOToporo
равна длине полуокружности, то леrко построить квадрат, равнове-
ликий данному Kpyry, и, обратно, если известна сторона квадрата;
равновеликоrо Kpyry, ТО можно построить отрезок, равный по длине
полуокружности. Но с помощью циркуля ИJIИf:lейки нельзя. постро-
ить отрезок, длина KOToporo равнял ась бы длине полуокружности;
следовательно, нельзя в точности решить задачу о построении квад..
рата, равновеликоrо Kpyry. Приближённое решение можно выпол-
нить, если предварительно наЙти приближённуюдлину ПОЛУОКРУ)К-
ности И затем построить среднюю пропорциональную ме)кду отрез-
ком этой длины и радиусом.
32. (268.) Т е о р е м 8. Площадь сектора равна пРОllзве..
дению длины ezo дуzu на половину радиуса.
Пусть дуrа АВ (черт. 26) сектора АйВ содержит пО. Очевидно,
что площадь сектора, дуrа KOToporo содерх{ит 10, составляет 
360
7tR2
часть площади Kpyra, Т. е. она равна .' Следовательно, пло-
. 180
щадь S сектора, дуrа KOToporo содержит пО; равна:
лR2 n лRп R
S-----==.
 360 180 2 ·
Tal{ как дробь xRn выражает длину дуrи АВ ( 23), ТО, обозна-
180
чив её буквой 5, получим:
R
S == s · .
2
з3

33.. (269.) Площадь cerMeHT8.. Для нахождения площади cerMeH"
та, оrраниченноrо дуrой s и хордой АВ, надо отдельно вычислить
площадь сектора АОВвА и площадь треуrольника АйВ. Затем из
ПЛJщади сектора AOBsA вычесть площадь треуrольника АОВ,
если дуrа cerMeHra меньше 180°. Если же дуrа cerMeHTa больше
1800, то к площа,nи сектора AOBsA надо прибавить площадь тре..
уrольника АйВ (черт. 26 и 27).
s
s
д
Черт. 26 Черт. 27
Задачи из  15.
t. Вычислить длину окружности, если радиус
Длина окруж- равен:)) 10.м; 2) 15 м; 3) 35 СМ.
ности И дуrи. 2.. Вычислить радиус, если длина окружности
.равна: 1) 1 м; 2) 25 см; 3) 4,75 дм.
3. Расстояние ме.жду серединами двух зубцов зубчатоrо колеса,
имеющеrо 0,66 .м в диаметре, равно 34,5 ММ, считая по дуrе. Сколь..
ко зубцов имеет колесо?
4. Шкив имеет в диаметре 1,4 .м и делает 80 оборотов в минуту.
Определить скорость точки, лежащей иа окружности шкива.
5. ПО данному радиусу R определить длину дуrи, содержащей:
1) 450; 2) 24030'; .3) 50 14' 15' , .
6. Определить радиус дуrи, если её длина равна 1, а rрадусная
мера: 1) 1350; 2) 10040'.
7. Окружность шкива (черт. 28) иrvlеет длину 540 .м-м, ремень
касается шкива по дуrе длиной 200 .мм. Определить уrол обхвата
шкива ремнёlVI (а).
8. Радиус железнодорожноrо закруrления равен 1200 .м; длина
дуrи равна 450 .м. Сколько rрадусов содер>кит дуrа? .
9. 1) Окружность радиуса 2 С-М разоrиута в дуrу радиуса 5 см.
Найти получившийся центральный уrол.
2) Дуrа радиуса 4 см, измеряющая
центральный уrол в .1200, равна длине
некоторой окружности. Найти радиус
этой окружности.
3) Окру>кность радиуса 6 см разоr"
нута в дуrу, измеряющую центральный
Черт 28 уrол в 3000. Найти радиус дуrи.
86

10. Определить число rрадусов дуrи, если дан её радиус R
и длина 1: 1) R == 1 О, 1 == 45; 2) R === 15, 1::::: 6.
11. Сколько rрадусов и минут в дуrе, длина которой равна радиу-
су (..!..== O,31831)?
11:
12. По данной хорде а определить длину её дуrи, если она содер-
жит: 1) 60°; 2) 900; 3) 120°.
13. По данноЙ длине дуrи 1 определить её хорду, если дуrа со-
держит: 1) 600; 2) 90°; 3) 1200.
14. Определить радиус окружности, если она длиннее cBoero диа-
метра на 107 см.
15. 1) На сколько увеличится длина ОКРУJI{НОСТИ, если радиус
увеличится на т?
2) Вообразим, что земной шар обтянут по экватору обручем и
что подобным же обраЭОl\1 обтянут и футбольный мяч по ero большо-
му Kpyry. Далее, вообразим, что окружность кждоrо обруча удли-
нилась на 1 М. Тоrда обручи отстанут от поверхности тел, которые
они Р3fIьше стяrивали, и останется некоторый прозор (промежу'J'ОК).
В каком слуае этот прозор БЬfЛ бы больше: у земноrо шара или
мяча?
16. 1) Железная труба со стенками толщиноЙ в 6.ММ имеет внеш-
нюю .0КРУ}l{НОСТЬ В 22 сМ. Найти длину внутренней окружности.
. 2) Из двух концентрических окружностей одна равна 167 см,
а друrая 117 см. Определить ширину кольца.
17. Определить длину ОКРУ)I{НОСТИ, если она более пери метр а
правильноrо вписанноrо шестиуrольника на 7 см.
18. Дуrа cerMeHTa содержит 1200и имеет длину 1. Определить
длину окружности, вписанной в этот сеrмеит.-
19. Из концов дуrи АВС, содержащей 120°, прqведены кас?тель-
ные до взаимноrо пересечения в точке D) и в ПOJIученную фиrуру
ABCD вписана окружность. Доказать,
ЧТО длина этой окружности равна длине
дуrи АВС.
20. На чертеже 29 даны вид и размеры
в сантиметрах коленчатой трубы паровой
машины. Найти её длину. (Её длина 20
измеряется по средней ПУНеКТИРНОЙ ли-
нии.). .
21. Найти радиус' такой ОКРУЖНОСТИ t
длина и площадь Kpyra которой выра-
жаются одним и тем же числом.
22. Определить относительную по-
rрешность при замене длины полуокруж-
. 1
ности "2 С через а з + а 4 (для прибли-
жённоrо спрямления <?кружности).
23. Одно из приближённЪ1Х спрямле- Черт. 29
37

ний окружности состоит В том, что .её заменяют. периметром пря-
5
моуrольноrо треуrольника. у Koтoporo один катет равен  диамет-
. . 6
3 .
ра, друrой -катет составляет....... диаметра. Определить абсолютную
5
поrрешность.
.
24. Определить площадь Kpyra при следующей
длине радиуса: 1) 10 м: 2) 4 aMI 3) 2,6 с'м
(взять n == 3, 14).
25. Определить радиус Kpyra, если ero пло-
щадь равна: 1) 2 с,М2; 2) 50 M 2 j 3) 17 д,М2.
26. Лошадь ;привязана к колу верёвкой, длина которой равна
10,5 м. Найти площадь участка, на котором она может пастись.
(С точностью до 0,01 КIJ.. м..)
27. Найти площадь Kpyra поршня воздушноrо насоса, диаметр
I\OToporo ра,вен 10 см.
28. Поршень насоса имеет площадь сечения в 12,56 с.м 2 . Найти
диаметр поршня.
29. .Дерево имеет 1,884.м в обхвате. Чему равна площадь
ero поперечноrо сечения, и меющеrо (приблизительно) форму
Kpyra? .
30. Какой rруз выдерживает пеньковый канат, имеющий 18 ом
в окр у>!<ности , если допускаемая HarpY3Ka равна 100 К2/СМ,2?
31. 1) Определить площадь Kpyra, если длина окружности равна
8, еЛl.
2) Определить длину ОКРУЖНОСТИ, если площадь Kpyra равна
18 см 2 .
32. 1) Пропускная способность трубы 111 (черт. 30) та )ке, что
и у труб 1 и 11 вместе. Определить
Ш построением величину х по данным на
чертеже размерам.
2) Две трубы с диаметром в 6 см и
в 8 см требуется заменить одной тру..
бой той же пропускной способности
Найти диаметр этой трубы.
33. Определить площадь Kpyra,
Черт. 30 I если площадь вписанноrо квадраТа
равна Р..
34. Вычислить площадь I<pyra, если она менее площади описан..
Horo квадрата на 4,3 м 2 .
35. НаЙти отношение ме,кду площадями вписанноrо и описан-
Horo I<pyroB: 1) для правильноrо треуrольника: 2) для квадрата;
3) для правильноrо шестиуrольника.
3.6. Вертикальный цилиндрический котм
78.см в диаметре и весящий 752 ке имеет в дни-
ще круrлое отверстие, наружный диаметр кота..
poro равен 36 см. Всей площадью cBoero днища
Площадь
Kpyra.

п
12 .
Площап.ь
кольца.
38

!{отёл опирается на фундаl\1ент. Определить давление, ОI<азываемое
котлом вследствие ero тяжести, на 1 см;2 поверхности .фундамента.
37. В кольце, образованном двумя концентрическими ОКРУ)К-
ностями, хорда большей окружности, каающаяся меньшей, равна
а. Определить площадь кольца. ,
38. Kpyra касаются шесть равных ему KpyroB, касающихся так-
же ме.II<ДУ собой, и полученное соединение семи равных KpyroB
охвачено таким концентрическим кольцом, которое равновелико
их cYMI\-fе. Доказать, что ширина кольца равна радиусу KpyrOB.
3"9. Определить . площадь
сектора, если радиус равен
" а дуrа содержит: 1) 67030';
2) 15045'.
40. Определить раДИУС сектора, если ero пло-
щадь равна q, а центральный уrол равен: 1) 720;
2) 36'.
41. Радиус сектора равен " а площадь рав-
на q. Определить величину центральноrо уrла
(или дуrи). .
42. Определить площадь cerMeHTa, если ра-
диус равен R, а дуrа содержит: 1) 900; 2) 600;
3) 450; 4) 300. .
_ 43. Определить площадь cerMeHTa t если хор-
да равна а, а дуrа содержит: 1) 1200; 2) 900; 3) 600.
44. Определить площадь окна (черт. 31),
Площадь фи-
ryp, оrрани- имеющеrо форму прямоуrольника, эаl{онченноrо
ченных оря- вверху дуrой Kpyra в 6Cf; высота окна, считая
МЫМИ И дуrами от середины дуrи до основания, равна 2,4 М,
окружностей. ширина ero 1,6 м.
45. 1) ПОЛУОКРУ}l{НОСТЬ радиуса, разделена на три равные час-
ти, и точки деления соединены с концом диаметра. Определить пло-
щадь средней части полукруrа.
2) Концы дуrи CD одинаково удалены соответственно от концов
диаметра АВ. Определить площадь, эаключённую между дуrой
CD и хордами АС и AD, если площадь Kpyra равна Q и дуrа CD со..
держит пО.
46. В Kpyre радиуса R проведены по одну сторону центра дe
параллельные хорды, из которых одна стяrивает дуrу в 120°, а дру"
rая  в 600. Определить часть площади Kpyra, заключённую между
хордами.
47. Общая хорда двух пересекающихся окру>кностей равна а
и стяrивает в одном Kpyre дуrу в 600, а в друrом ...... дуrу в 900.
Определить площадь общей части KpyroB (два случая).
48., Площадь Kpyra Q. Определить площадь вписанноrо в Hero
прямоуrольника, стороны KOToporo относятся, как т: n.
49. В Kpyr радиуса R вписан прямоуrольник, площадь Koтoporo
Сектор
и cerMeHT.
\
\
\
\
, I
\ 60 о I
\'
, I
V
I
I
I
I
Черт. 31
з9

составляеr половину площади Kpyra. Определить стороны эrоrо
прямоуrольника.
50. Около Kpyra, площадь KOToporo равна Q, описан ромб с
уrлом в 300. Определить площадь 9Toro ромба. .
510 Около правильноrо треуrольника с площадью Q описана
OKpJКHOCTЬ) и В тот же треуrOJIЬНИК вписана окружность. Опреде
лить площадь кольца, заключённоrо между 9ТИМИ окружно-
стями.
52. АМВ ...... дуrа, содержащая 120°: ОА и 08  радиусы;
АС и 8С  касательные; DME  дуrа, описанная из центра С.
м,ежду С и АСВ и касающаяся дуrи АМВ.
Найти отношение между площадями сек-
торов CDME и ОАМВ.
53. ИЗ КОНЦОВ дуrи АСВ проведены
касательные до пересечения в точке D.
Определить площадь DACB, заключён-
u
ную между двумя касательными и дуrои,
если' радиус равен R, а дуrа содержит:
1) 900; 2) 120°; 3) 600. .
54. Из центра paBHocTopOHHero тре-
уrольника описана окружность, пере-
секающая ero стороны так, что внешние дуrи содержат по 900.
Обозначая сторону 9TOro треуrольнкка через а, определить
площадь, оrраниченную внутренними дуrами и средними отрезка-
ми сторон.
55. 1) ВО СКОЛЬКО раз увеличится площадь Kpyra, если диаметр
ero увеличить в 3 раза? Во сколько раз площадь уменьшится, если,
радиус У1\,fеньшить в 5 раз?
2) Во сколько раз надо уменьшить радиус Kpyra, чтобы площадь
уменьшил ась в 4 раза? Во сколько раз надо увеличить диаметр кру-
ra, чтобы площадь увеличилась в 5 раз? '
56. \10ЖНО ли водопроводную трубу диаметром в 50 мм заменить
ДВУl\fЯ трубами диаметром в 25 мм каждая? Одинакова ли площадь
сечения ОДНОЙ большой тру-
бы и двух малых?
./ 57. Вычислить площадь
заштрихованной части пря-
мо)'rолЬ'ника, данноrо на
чертеже 32.
58. Qпределить пло-
lli,'здь фиrур, заштрихован-
ных на чертежах 33........36,
по данным размерам.
59. Два равных полукруrа нало}кены так, что диаметры их па-
ралдельпы, а полуокружность одноrо проходит через центр друrо-
то. Определить площадь общей части полукруrов по данному их ра-
диусу R.
й
Черт. 32
O
 / / 
/;,-  /


  ,
\

а
'
.1
Черт, 33
Черт. 34

60. На каждой стороне квадрата, принятой за диаметр, описана
поуокружность, лежащая внутри квадрата.. Определить площадь
полученной розетки, если стороны квадрата равны а.
61. На сторонах ромба описаны, как на диаметрах, полуокруж-
ности, обращённые внутрь. Диаrонали ромба равны а и Ь. Опреде-
лить площадь полученной розетки. .
Черт. 35 Черт. 36
62. Диаметр разделён на равные части, из обоих ero концов про..
ведены полуокружности во все точки де;rzения, причём из одноrо
конца все полуокружности сверху, а из друrоrо все снизу. Доказать,
что полученными изоrнутыми линиями Kpyr разделился на части
равной величины, а периметр аждой части равен ДЛИне окруж-
ности.
63. В равностороннем треуrольнике проведены дуrи Iежду
каждыми двуrvIЯ вершинами через центр треуrольника (черт. 37)..
м
А
Черт. 37
Черт. 38
Сторона треуrольника равна а. Определить площадь полученной
розетки.
64. Между точками А и В проведены две дуrИ t обращённые вы-
пуклостью в одну сторону: дуrа АМВ содержит 2400, а дуrа ANB
120°. Расстояние между серединами этих дуr равно а. Определить
площадь луночки (черт. 38). .
41

65. АВ и CD ........ два взаимно перпендикулярн,ых ДИ8метра. 11з
ТОЧl<И' D, как иа центра, радиусом DA описана дуrа АМВ. Доказать.
что луночка АМВС равновелика треуrол.ьнику ABD.
66. Из точки С данной полуокружности опущен перпеНДИКУJIЯР
CD надиаметр АВ., и на отрезках AD и DB построены HOBblf полу"
окру-жности ПО одну сторону с
данной. Доказать, что площадь,
.. заключённая между тремя полуок-
ружностями, равна площади Kpyra
с диаметром CD.
67. Вычислить площадь фиrу.
ры, заштрихованной на чертеже 39.
Размеры даны в миллиметрах. .
68. Вычислить площадь сечения, изобра>кённоvо н'а чертеже 40.
Размеры даны в мил.пиметрах.
69. Определить площадь поперечноrо сечения детали, показан.
Horo на чертеже 41.
..
Черт. 39
'......
.r .
11
Q
111
80
со
t::)
t'\I
70
IV
......,
100
а
Черт. 40
Чер", 4]
70. Две параллельные хорды равны 15 ht и 40 м, а расстояние
ме}J{ДУ ними 39 М. Определить площадь Kpyra.
71. Определить радиус Kpyra, вписанноrо в данный сектор, если
радиус сектора равен R, а дуrа содер>!{ита rрадуаов[tx равно: 1) 6О О ;
2) 900; 3) 1200].

ОТВЕТЫ
к задачам из 5 8.
17., 1) AD ==,8 м и DC == 12 м; 2) 10 м; 3) 1,8 М. 18. 10 см.
23-: ВЕ == 7 СМ; ЕС == 5 см. 21.: 39 СМ И 65 СМ. 22.; 8 СМ. 23.; 50 СМ.
Ь
24.- 16 СМ, 20 см, 20 СМ. 25.. ВЕ  10 М, ЕС=; 14 М. 26..  . 27 J. 6 см,
а+с
аЬ
4 СМ И 6 см 28  .
а+Ь
К задачам из  10.
16 1) 37 СМ; 2) 65 СМ; 3) 41 дм; 4) 109 СМ; 5) 21 ; 6) 1 .;
4 16
7) 17; 8) V 61 7,81. 2.. 1) 161; 2) 260; 3) 24; 4) 42; 5) 7;
5
6) V5I  7,14.
3
а I ь I с ас Ь С I h
1) (15) (20) 25 9 16 12
(7) 25 1 24 18
2) (24) 23 ..... 1 6
25 25 25
(5) У 41 16y 25y 20y
3) (4) ..... 41  41 41 41
41 41
4) ( 1 00) 75 (125) 80 45 60
5) 156 (65J ( 169) 144 25 60
6) (600) 17 (625) 576 49 168
7) (6) 8 10 (3,6) 6,4 4,8
8) 24 (7) 25 23,04 (1 ,96) 6,72
- ( 15 2 ) 23 14
9) 21 20 (29) 13 ----- 14
у6 29 29
10) уз (3) 1 (2) У2
1 3 1 (1  ) (2 : )
11) 2..... 4..... 2
2 3 6
12) 2 У I0 6 У I0 20 (2) (1 6
13) ( 136) 255 289 64 22 (120)
41 1 40 ( 32'
14) 40 (9) 39 l 8)
41 41 41
43

4.. Указание. Восполэоваться  4. (190). 5 УказаflU. Если раз-
ность отрезков х  у == r, а среднее пропорциональное V ху == р,
. u
то сумму отрезков можно наити как rипотенузу прямоуrольноrо
треуrольника с катетами r и 2р. 7ftЗ 50 С-М и 72 см. 8 5,2 .A. 9.. 18 см,
98 СМ. 12. Воспользова ться за дачей лr2 11. 13. 3, 4, 5. 14, VТf6
 10,8 (М). 15. 1) У а 2 + Ь 2 ; 2) 109 см. 16. 32 У 2  45 (ММ).
17, 1) aY2; 2) 2 (v2 + 1) сМ. 18. Нет. 19. I).! Уа 2 +Ь 2 ;
2
2) 32 СМ и 60 СМ. 20., 1) 41 СМ; 2) 10 СМ. 21. 1) 15 СМ; 2) 125 C,М
125 СМ, 240 см; 3) 2 У 2 СМ. 22. BD  5,0 м. 23 1) 3 м и 4 М;
2) 9 СМ, 1  СМ) 14! СМ. 24. 1)  V з; 2) 2h УЗ ; 3) 2т (2 +
: 7 7 2 3
+ V з) ; 4) 2'V З см и 4 Vз СМ. 25. 1) 25 СМ или 1] см; 2) 29 СМ.
3) 40 СМ. 26. 1) 37 СМ; 2) 3 дм и 4 дм. 27. 1) 24 см; 2) 36 С'м
и 54 СМ.' 28. Около 563() м. 29. 1) D  25 .И,И; 2) d, 19 мм;
3) h11 ММ; Dd+!hV3 31.2) Уа 2 +3Ь 2 . 32. 24 мм.
3  '
33. 1) 39 дм; 2) 80 сМ; 3) 14 см или 4 см; 4) 21 см; 5) 6 см.
12+4s2 а 2 + 4h 2
34. 1) D == 425 мм; 2) D == . 35. . 36. 9 СМ или 39 СМ.
48 8h
37 42,5 см. 38. 1) 77 СМ; 2) 61 'СМ; 3) 13,44 см. 39. У == V 2Rr.
40. 1) 40 СМ; 2) внешняя касательная равна 48 СМ; внутренняя
касательная равна 30 см. 41. 13 м. 42. 73 СМ. 43. 7 м и 25 М.
9
44& 7....... С.М. 45. 175 см и 600 СМ. 46. 20 СМ. 47. 1: 4. 48. 49 :'81.
17
49. 21 с-м и 28 СМ. 50 с а <У 2 ........ 1) и а (2 ........ 1/ 2) . 51.. n V m + n
тn
И т V m + п . 52€ I М. 53. 15 СМ. 54. 5 м. 55. 1) 1 О СМ; 2) 7,5с'м.
тп ,
56. 18 дм. 57. 1) 24 дм; 2) 2,4 v5 дм; 1,8 У 5 дм; 3) 13',44 дм.
1  .
58. 1) 9  СМ; 2) 0,8 r У5. 59. 15 дм. 60. 65 дм. 61. 35 дм.'
15
Указание. Провести среДНЮIО линию и высоту из вершины тупоrо
уrла. 62. АЕ: ЕС== 16:25. 63. 36 at, 48 дм. 64. 18 дм и 80 дм.
65. 1) 37 м и 1/ 769  27,7 (М); 2) 4: 5. 66.. 1) 3,125 дм; 2) 16,9 м.
67. 6 дм. Указание. Отрезки rипотенузы, образуемые точкой каса-
J-IИЯ, равны nРИJ]ежащим к НИМ отрезкам катетов. 68.. 38 дм и 22 дм.
69. 25 дм. Указание. Ввести вспомоrательное неи3вестное......... рас-
стояние от центра До одной из хорд. 70. 30 см. 71" 32 см и 18 см.
44

2т, 2n, (пl + n)!
72.) Основания:  и   боI{овая сторона ........ . 73. 20 дм.-
утп Утп Утп
т 2 +, п 2 т 2 + п 2 .
74 ез 1 дм. 7Б СА == 39; СВ== ==26. Указание.
т 11
Соединить КОНЦЫ отрезков т и п с основанием перпендикуляра.
76-з 27 дм и 64 дм. 77. ) Указание. Вырази ть дли ну общей в нешне й
касательной через радиусы. 78., АВ == Va(a+b); CD== Vb(a+b).
к задачам из * 11.
1., А В  13 м. 2. V 3  1, 7 (м). 3. 1) 6 см, . 12 СМ, 1 М;' 2) 16 СМ.
4. 1) Внутри Kpyra; 2) на ОКРУЖНJСТИ; 3) вне Kpyra. 5., 1) 4; 2) 65;
3) !... ; 4) 5 или 45. 6. 1) 30 СМ: 2) 40 см; 3) 21 дм и 29 дм. 10. 1) 1 м;
5 _
2) 6 см; ,3) 1 О M 11. 1) 8 СМ; 2) 18 М; 3) 14 СМ. 128; 1) 7 СМ;
2) , <Vs........ 1)  1,24r. 13.: 12 СМ. 14. R==4,35 М. 15. Нет. 16.,43,6 СМ.
J 1
1'7. R:::::: 591 М. 18. Уменьшился в 2  раза. 19. 1) 24 СМ; 2) 33 М.
: 2
20.. 24 см и 8 см. 21.) Увеличилась в 3 раза. 22., 1) 4 СМ; 2) 20 м;
3) АВ == 35 м и АС == 15 м. 23.) 8 СМ. 24. 1) 9 дм; 2) 36 см; 3) 25.
ат ..... Ьп 1 V  .
25. тх и пх, rде Х == . 26. ) 6; 2) 3; 3) 3. 27. 21 см.
. п 2 ---- т 2
 1 :
28. B..J. раза. 30. Вторая точка пересечения. 31. 1) 3 сМ; 2) ]8 см;
. ..,.
3) ; < У5 1 + 1). 32. 1) 226 км; 2) 270 КМ. 33., 1) 17 см; 2) 13 см.
34 1) '10 см; 2)  . 35.; 18 e-. З68j 12 см и 36 см. 37 1) ]8 СМ и 12 c.4t.
2
. 1 1 2
2 ) 9 см и 6 см или 12  см и 2 ..... см. 40. 6 дм. 41. r. 42 J ) 10 см' ,
. . 2 2. 5
2) 8 дм; 3) 9,375 м. 43. 25 дм, 8 дм, 15 дм.' 44.} !!.. V 4r 2  а 2 .
,
45. 9 дм. 46. -v 2й"--:
к задачм из  15.
1.: 1) 62, м; 2) 94,2 м; 3)  220 см. 2. 1) 16 см; 2)  4,0 см;
м :лR 49лR 419nR
3)  0,76 дм. .3. 60. 4.;  5,9 се" . 5.: 1) 4 ; 2) З60 ; 3) 14400 '
6. 1) 41 ; 2) 1351 . 7. 133020' . 8.  21 0,5. 9. 1) 1440; 2) 1  см;
.Зл 831 3
'.' 180°1 810° 720 о I па
3) 7,2 см. 104: Х == ............... R ; 1) ; 2) . 11. 5 7 18 · 121 ])  3 .
ппп
...j ..j..... 31
 1,05 а; 2) na r 2  1,11 а; .3) 2nа; 3  1,21 а. 13. 1)  ::::::: 0,951;
4 п
45

2l у.... 3l уз
2) " {  0,901; 3) .  0,831. 14. 25 СМ. 1,5_- 1) 2пт; 2) прозар
n 2п
1
и для земноrо шара и для мяча один и тот же и равен .....  О, 16 (м).
2л:
3
16. 1)182MM;2) 8,OcM.17€50п157(cM).18.l.20 119CM.
4
21. 2. 22. O, 15 О/О' 23«  0,00005 D. 24.. 1)  314 м 2 ;
2) 50,2 д.м 2 ; 3) 21,2 см 2 . 25. 1') 0,8 см; 2) 4 м; 3) 2,3 дм.
26  346,28 м 2 . 27  78,5 см2, 28.:  4 см. 29..  0,2826 .м 2 .
30.  2,6 т. 31. 1)  5,1 см2; 2)'  15 см. 32. 10 см. 33. .
2
К2 а 2
34.:  15,7 м 2 . 35., 1) 1 :4; 2) 1 :2; 3) 3:4. 36.  0,2  . 37. .
. см 2 4
39. 1)  1,(r 2 ; 2) 2. лr 2 . 4Q-: 1) V 5Q ; 2) V 600Q . 418) 3600. 3.... .
16 160 n n 1tr 2
42.. 1) R2 (л  2)  O,275R2; 2) R2 (2л  3 V з)  0,09R2;
. 4 12 .
R2 ..... R2 а 2
3) ..... (л  2 }.i2)  O,04R2; 4)  (п ....... 3)  0,01 R2. 43. 1)..... ( 4л .........
8 12 36
   
....... 3 V 3)  0,20а 2 ; 2)..... (п2)O, 14а 2 ; 3)  (2л:  3 VЗ) О,О9а 2 .
. 8 12
1 Qn :лR2 а 2
44. 3,7 м2. 45. 1)  л:r2О,5r2; 2)  . 46.  . 47.  (7п.......6........
6 360 6 24
6 Y 3)  О,23а 2 или а 2 (1331+ 66'V З)  1,52а 2 . 48. 4Qтn .
24 11: ( т 2 + п 2 )
49. R <V 4 + n + 1/4 ....... п)  1,8R и R (V 4 + п  у 4 ....... л) 
2 2
 O,87R. 50. BQ  2,55Q. 51. 1tQ уз  1,82Q. 52. 1 : 2.
11: 3
53. 1) R2 (4....... л)  0,215R2; 2) R2 (3 уз  л)  0,68R;
. 4 3
R2 V ..... а2
3)  (2 3  п)  0,05R2. 54...... (л + 6)  О,38а 2 . 55. 1) В 9 раз,
6 24
в 25 раз; 2) в 2 раза, в уБ-  2,236 раза. 56. Нет, надо 4 такие
малые трубы. 57.. а 2 . 58. 1) 0,215r2; 2) abO,215b; 3) O,393R2;
R2 ..... а 2
4) O,858r2. 59. ..... (4п 3 V3)  1,23R2. 60.  (л  2)  О,57а 2 .
6 2
n аЬ a..... а 2
61. ..... (a+ Ь 2 )  ...... 63.  (2л  3 V3)  О, 18a 2 . 64.  (2л: +
в 2 6 6
+ 3 V З)  1 ,9а 2 . 67.. 988 см 2 . 68.. 25 см'. 69. (1,57 R + 2а) t ........
R V 
....... t,215t s . 70. 625л м а . 71. 1) -----; 2) R ( 2....... 1)  O,4R;
3
3) R (2 уз  3)  O,46R.
46.

СОДЕРЖАНИЕ
8 класс
Свойство биссеКТРИСbl BHYTpeHHero уrла треуrОJIьника . . I , . з
Зада чи из  8 . . . . . . . . . . . . . . . . . ... 4
МетричеСI{ие соотношения между элементами прямо-
уrольноrо треуrольника . . . . . . . . .. 5
Задачи из  10 . . . . . . . . . . . . . . 6 Ir  . 9
Пропорциональные линии в Kpyre . . . . . . . . . . . . 16
Зада чи из  11 . . . . . . . . I . . . . . . ': t 18
9 класс
Вычисление длины ОI<РУЖНОСТИ и ее частей . . . . . . . . 24
Предел числовой последовательности . . .. ...
Длина окружности ... ......... 27
Площадь Kpyra и ero частей . . .. ........ 33
Задачи из  15 . . . . . . . . . . .. . 36
Ответы .... .. ... о..... ;' . 43

Андреи Петрович к.uселёв
НUfCOлай Александрович Рыбкuи,


rЕОМЕТРИЯ


Редактор Н. и. Нuкитuн.а
Художественный редактор В, C
 Эрденко
Технический редактор В. В. НовосёЛО8а
Корректор М. В. rолубева
Подписано к печати
 матриц 10NIII970 r.
БОХ90 l /tв. Тип. N9 3. Печ. л. 3,0. УЧ.-изд.
л. 2,55. Тираж 1400 тыс. ЭКЭ. Заказ 620.
Издательство
«Просвещение» Комитета
по печати при Совете Министров РСФСР.
Москва, 3.й проезд Марьяной рощи, 4,r:
Саратовский полиrрафический комбинат
Росrлавполиrрафпрома Комитета по печати
при Совете Министров РСФСР. Саратов,
ул. Чернышевскоrо, 59.
Цена 3 КоП.