А.Я.Дороговцев
ЭЛЕМЕНТЫ
ОБЩЕЙ ТЕОРИИ
МЕРЫ
и ИНТЕГРАЛА
Допущено
Министерством высшего и среднего
специального образования УССР
в качестве учебного пособия
для студентов
математических специальностей
университетов и технических вузов
Киев
Головное издательство
издательского объединения
«Выща школа»
1989

ББК 22.161я73
Д 69
УДК 517.51@7)
Рецензенты:
чл.-кор. АН УССР, д-р физ,-мат. наук, проф. Пшенич-
Пшеничный Б. Н. (Институт кибернетики АН УССР), д-р физ.-мат.
наук, проф. Паулаускас В. Й. (кафедра математического
анализа Вильнюсского университета)
Редакция литературы по информатике и автоматике
Редактор О. А. Диптан
Дороговцев А. Я.
Д69 Элементы общей теории меры и интеграла.—
К. :Выща шк. Головное изд-во, 1989.— 152 с,
2 ил.— Библиогр.: 16 назв.
ISBN 5-11-001190-7.
Пособие содержит изложение основ общей теории меры
и интеграла, а также классических частных случаев — мер
и интегралов Лебега и Лебега — Стилтьеса. Книга включа-
включает: описание основных классов множеств и свойств мер, тео-
теорию продолжения, свойства зарядов, теорию измеримых ото-
отображений и функций, теорию интеграла Лебега, в частности
свойства интегралов Лебега, зависящих от параметров, об-
общую формулу замены переменной, теорему Радона — Ни-
кодима и теорему Фубнни. Приведены основные свойства
функциональных пространств. Теоретический материал со-
сопровождается упражнениями для самостоятельной работы.
Для студентов математических специальностей вузов и
университетов.
1602070000-002
Д М211@4)-89 123-89 ББК 21Л61я73
ISBN 5-11-001190-7
© Издательское объединение
«Выща школа», 1989

ОГЛАВЛЕНИЕ
Предисловие 5
1. Основные классы множеств
1.1. Полукольцо и полуалгебра 6
1.2. Кольцо и алгебра 7
1.3. а-кольцо и а-алгебра 7
1.4. Монотонный класс 8
2. Порожденные классы множеств
2.1. Минимальные кольцо, алгебра, а-колыю, а-алгебра, мо-
монотонный класс, содержащие заданный класс множеств 10
2.2. Борелевские множества 12
2.3. Монотонный класс и а-кольцо, порожденные кольцом 13
3. Функции множеств. Меры
3.1. Основные классы функций множеств 14
3.2. Меры. Элементарные свойства мер 16
3.3. Непрерывность меры 19
3.4. Примеры мер 21
4. Продолжение меры
4.1. Продолжение меры с полукольца на порожденное по-
полукольцом кольцо 26
4.2. Внешняя мера 28
4.3. Х*-измеримые множества. Теорема Каратеодори ... 30
4.4. Полные меры 32
4.5. Измеримость множеств исходного кольца 33
4.6. Единственность продолжения 34
4.7. Теорема о приближении 35
4.8. Мера Лебега на прямой 36
4.9. Мера Лебега на Rm 39
4.10. Мера Лебега — Стилтьеса на прямой 40
4.11. Измеримое пространство, пространство с мерой, веро-
вероятностное пространство 41
5. Заряды
5.1. Разложение Хана 41
5.2. Разложение Жордана 44
6. Измеримые отображения и функции
6.1. Измеримые отображения, примеры 45
6.2. Одно условие измеримости 47
6.3. Борелевские функции. Функции, измеримые по Лебегу 49
6.4. Суперпозиция измеримых отображений 50
6.5. Свойства измеримых функций 51
6.6. Критерий измеримости в терминах простых функций 53
6.7. Эквивалентные функции 55
6.8. Сходимость почти всюду 57
6.9. Сходимость по мере 60
6.10. Вероятностная терминология 67
а

7. Абстрактный интеграл Лебега
7.1. Определение интеграла ............. 68
7.2. Элементарные свойства интеграла Лебега 73
7.3. Счетная аддитивность интеграла Лебега 77
7.4. Другие свойства интеграла Лебега 79
7.5. Теорема об интегрировании монотонной последователь-
последовательности и аддитивность интеграла 84
7.6. Основные предельные теоремы 88
7.7. Сравнение интегралов Римана и Лебега на отрезке пря-
прямой 94
7.8. Критерий интегрируемости функции по Риману ... 96
7.9. Несобственные интегралы и интеграл Лебега .... °>7
7.10. Интеграл Лебега — Стилтьеса на прямой ..... 100
7.11. Историческая справка 101
8. Интегралы Лебега, зависящие от параметра. Формула за-
замены переменной
8.1. Непрерывная зависимость от параметра 102
8.2. Дифференцирование по параметру 102
8.3. Формула замены переменной 104
9. Абсолютная непрерывность
9.1. Абсолютная непрерывность и сингулярность .... 106
9.2. Теорема Радона — Никодима 108
9.3. Замечание к формуле замены переменных 112
10. Интегрирование иа произведении пространств
10.1. Измеримые множества в произведении пространств 113
10.2. Измеримые функции на произведении пространств 114
10.3. Произведение мер 115
10.4. Теорема Фубини 119
11. Пространство Lp(X, ?Д)
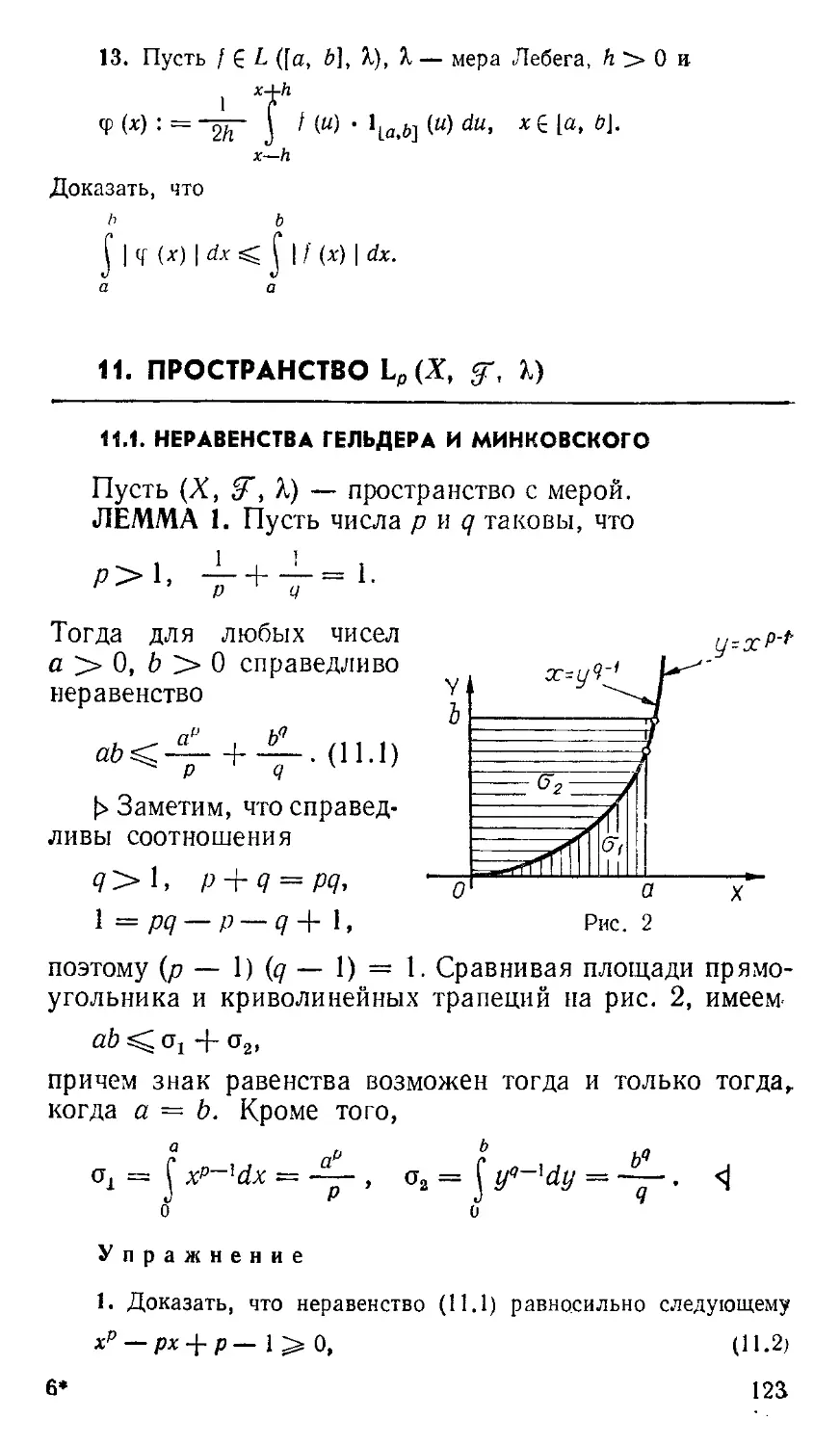
11.1. Неравенства Гельдера и Минковского ....... 123
11.2. Пространство Lp (X, &, к), р ? [1, + °о) 126
11.3. Полнота пространства Lp (X, &, X), рёСЫ-00) 127
11.4. Плотные подмножества LP(X, &, %), рё[1, 4-°°) 13i
Решения и указания 134
Приложение 144
Список рекомендуемой литературы 148
Указатель обозначений 149
Предметный указатель 150

ПРЕДИСЛОВИЕ
Теория меры и интеграла Лебега была разработана
в начале XX в. в связи с нуждами анализа и теории функ-
функций. К настоящему времени абстрактный вариант этой
теории является математической основой ряда теоретиче-
теоретических и прикладных разделов современной математики:
дисциплин теоретико-вероятностного цикла, отдельных
глав функционального анализа, теории оптимизации,
математических методов экономики, некоторых моделей
квантовой теории поля, теории образов. Интенсивное
развитие математической теории меры и интеграла,
появление новых интересных проблем этой теории в по-
последние десятилетия целиком обязаны приложениям
в упомянутых выше разделах математики и других при-
прикладных дисциплин.
Настоящее пособие посвящено абстрактному варианту.
По содержанию оно соответствует программе норматив-
нормативного курса теории меры и интеграла для специальностей
«математика» и «прикладная математика» и охватывает
только фундаментальную часть теории. Представлены
основные понятия и факты, которые являются рабочим
аппаратом современной математики и ее приложений.
Пособие предназначено для первоначального изучение
курса. Изложение материала полное и сопровождается
упражнениями для контроля усвоения материала и са-
самостоятельной работы. Упражнения и содержащиеся
в них утверждения и факты составляют неотъемлемую
часть настоящей книги. Все они, за исключением отме-
отмеченных звездочкой, как более трудных, предназначены
для самостоятельного решения и включают материал,
используемый в дальнейшем. Типичные и наиболее важ-
важные рассуждения, которые используются при решении
упражнений, приведены в указаниях или ответах. В ряде
случаев даются ссылки на литературу. Всего помещено
270 упражнений. Включены также краткие историче-
исторические сведения. Учебное пособие написано на основе лек-
лекций, читаемых автором на механико-математическом фа-
факультете Киевского университета.

1. ОСНОВНЫЕ КЛАССЫ МНОЖЕСТВ
1.1. ПОЛУКОЛЬЦО И ПОЛУ АЛГЕБРА
Пусть X — некоторое фиксированное множество.
Предполагается, что X Ф 0. Далее рассматриваются
различные классы подмножеств множества X. Мно-
Множество X называется основным множеством.
Обозначение: 2х есть множество всех подмножеств
множества X, включая 0 а X.
Определение 1. Непустой класс множеств Н с 2х
называется полукольцом, если
(i) {A, ?}cfl => (А (]В)?Н и
(и) V{.4, В}с=Я 3«€N 3{Ct Cn)<=Hf
С, {]С,= 0, 1ф\ : Л\Б= U Q.
Класс Н называется полуалгеброй, если Н — полукольцо
и X ?Н.
Упражнения
1. Пусть Н — полукольцо. Доказать, что 0 € Я.
2. Доказать, что класс Н есть полуалгебра: а) Н = 2х, б) Н =>
= {0, X).
3. Пусть X = R и
Я={[а,6) | —оо<а<й< + оо} U {0}.
Доказать, что Н — полукольцо.
4. Пусть ах < *!, а2 < Ь2 — фиксированные числа,
X = [ait b±) X [а2, 62) и
Я = {[%, pj X [а2> р.) | <n<ai<p<<ft/,f=l, 2} U {0}.
Доказать, что Я—полуалгебра.
5. Пусть Hi с: 2 ', t= 1, 2 — полукольца. Доказать, что
класс множеств
H1xH2: = {Ai XA2 | /ЦЬ Hi, 1 = 1.2)
есть полукольцо подмножеств Х1 X Х2.
6. Проверить, что объединение двух множеств из полукольца Я
не обязательно принадлежит Я,

1.2. КОЛЬЦО И АЛГЕБРА
Определение 2. Непустой класс множеств Н с 2х на»
зывается кольцом, если
(i) {A, B)czH => (A U В)?Н и
(И) [А, В}с=Я => (А\В)?Н.
Класс Н называется алгеброй, если Н — кольцо
и X ? Н.
Упражнения
7. Пусть Н — кольцо. Доказать, что: а) 0?Я;б) (Л, В} с
с: Я => (А П В)?Н; в) {Лх Ап] с Н => U Ак 6 Я и
П Л* g Я.
ft=i
8. Проверить, что кольцо является полукольцом.
9. Доказать следующие утверждения. Класс всех подмножеств
R2, измеримых по Жордану, есть колыю. Класс всех подмножеств
[0, I]2, измеримых по Жордану, есть алгебра. Указание: об измери-
измеримых в смысле Жордана множествах см. 4].
10. Доказать, что класс множеств Н с: 2х есть кольцо тогда и
только тогда, когда Н полукольцо и
\А, В) <=Я => (A U S)g H.
11. Пусть Н — алгебра. Проверить, что А : = (X \ А) ? Н.
12. Доказать, что непустой класс множеств Н cz 2 есть алгеб-
алгебра тогда и только тогда, когда
{А,В}<=Н г> (А{) В)?Н и А?Н г> А ? Н.
13. Пусть s — класс подмножеств X такой, что для любых раз-
различных множеств ЛиВизеЛ A 6=0,и
H:= U ЛН/teN, (Л, Л„} се U f0}.
Доказать, что Н — кольцо.
1.3. о-КОЛЬЦО И о-АЛГЕБРА
Определение 3. Непустой класс множеств Яс2" на-
называется а-кольцом, если
(i) \Alt A.2, ..., Ап, ...)czH ф. U Ап?Н и
(и) {А, В}с=Я =>

Класс Н называется о-алгеброй, если Н — ст-кольцо и
Замечание. В условии (i) определения 3 требуется,
чтобы объединение любого счетного набора множеств
из Я принадлежало Н.
Упражнения
14. Проверить, что классы 2х и {0, X] есть а-алгебры.
15. Проверить, что а-кольцо есть кольцо.
16. Пусть Н — а-кольцо. Доказать, что
{Ait Аг Ап, ...}(= Н => р Ап? Н.
Указание. Рассмотреть множество
/ с
/со \
l\ U (А^Ап) .
\л=2 /
17. Множество A cz R2 называется симметричным, если (xlt x.z) Q
g A => (—xlt —х.г) g A. Пустое множество симметрично. Дока-
Доказать, что класс всех симметричных подмножеств R2 есть а-алгебра.
18*. Доказать, что не существует а-алгебры, состоящей из бес-
бесконечного счетного набора элементов.
у
19. Пусть Hi cz 2 ', i — 1, 2, а-кольца и
Н1 X #2: = {Аг X А2 | At ? Ни (=1,2}. Доказать, что класс Н1 X
X #2 есть полукольцо подмножеств Хх X Х^. Привести пример, по-
показывающий, что класс Я1 X Н2 не всегда является кольцом.
1.4. МОНОТОННЫЙ КЛАСС
Определение 4. Последовательность множеств {Ап :
: /г]>1} называется монотонно возрастающей, если
Ап cz An+i, n ;> 1. При этом
lim Л„: = U К-
Последовательность множеств \Ап : п~^\\ назы-
называется монотонно убывающей, если Ап гэ Ап+\, п~^\.
При этом
НтЛп:= П Лп.
Я-юо П—1
Последовательности, монотонно возрастающие или
монотонно убывающие, называются монотонными.

Упражнение
20. Проверить, что
lim [0, n) = [0, + оо); lim [n, + оо) = 0.
Определение 5. Непустой класс множеств Н с 2х
называется монотонным классом, если для любой моно-
монотонной последовательности {Ап : п ^ 1} с Н множество
lim Ап ? Н.
П-юо
Упражнения
21. а-кольцо есть монотонный класс.
22. Пусть X = R и
Н : = {[т, п] | {т, n|cZ,m<n) U
U {(-оо, я] |п€ ZJ U ([я, +oo)|neZ} U {R}.
Проверить, что Н — монотонный класс.
ТЕОРЕМА 1. Монотонное кольцо есть а-кольцо.
\> Пусть Н — кольцо и Н — монотонный класс. Тогда
условие (и) из определения 3 выполнено. Пусть [Ап :
: п ]> 1} с: Н. Поскольку Н — кольцо, то
V т > 1 :
Кроме того,
Vm>l :
т
т
U А,
><= и
Ак.
m
Поскольку Н — монотонный класс, то lim U A-k?H',
т. е.
оо / т \ оо
U U Ак = U Ат?Н.
m=l \ft=l / m—\
Следовательно, условие (i) определения 3 также выпол-
выполнено. <1

2. ПОРОЖДЕННЫЕ КЛАССЫ МНОЖЕСТВ
2.1. МИНИМАЛЬНЫЕ КОЛЬЦО, АЛГЕБРА, о-КОЛЬЦО,
о-АЛГЕБРА, МОНОТОННЫЙ КЛАСС, СОДЕРЖАЩИЕ
ЗАДАННЫЙ КЛАСС МНОЖЕСТВ
Пусть X — основное множество и Я — некоторый
класс подмножеств X.
Определение 1. Кольцом, порожденным классом Н,
или минимальным кольцом, содержащим класс Я, на-
называется следующий класс множеств:
= П К.
К—кольцо,
KZ3H
Замечание. Кольца, содержащие класс Н, существуют. Напри-
Например, 2 — кольцо и 2 гэ Н. Кроме того, справедливо следующее
утверждение.
ЛЕММА 1. Пересечение произвольного семейства
колец есть кольцо.
\> Пусть {Ко. | а ? Щ — семейство колец. Тогда
{A,B)cz П Ка => Va?9f : {А, В} с /(о =>
€21
=> Va?9l : {Л (J
Ф{А[) В, Л\В}с
Таким образом, |~) Ка есть кольцо. <j
Из леммы 1 следует, что класс k (H) из определе-
определения 1 есть кольцо.
Упражнение
1. Доказать, что утверждение леммы 1 справедливо для: а) ал-
алгебр, б) а-колец, в) а-алгебр, г) монотонных классов.
Определение 2. Алгеброй а (Я) (о-кольцом а/г (Я),
а-алгеброй аа (Я), монотонным классом т. (Я)), по-
порожденной классом Я, называется
а{Н):= П A{ok{H):= П А,
Л—алгебра, Jh—о-кольцо,
10
аа(Н): = П А, т{Н):= [\ Л).
Ла-алгебра, $—монотонный
ДН класс, JlH

Классы а (Я), ok (Я), оа (Я), т (Я) называются также
соответственно минимальной алгеброй, минимальным а-
кольцом, минимальной а-алгеброй, минимальным моно-
монотонным классом, содержащим класс Я.
Упражнения
2. Доказать, что: а) Н1 сг Н2 <= a (HJ => а (Ях) = а (Я2),
6) Hi а Н2 а оа (HJ => оа (HJ = оа (Я2).
3. Пусть В с X фиксировано. Доказать, что
ok (Н Л В) = ok (Я) Л В.
Здесь для класса множеств ММ Л В : = {А Л Е \ А ? М).
Указание. Проверить, что: ok (Я) Л В zd H Л В, ok (Я) Л
Л В — а-кольцо.
4. Проверить, что оа (оа (Я)) = оа (Я).
ГЕОРЕМА 1. Пусть Н — полукольцо. Тогда
*(/0 = {(U1^l/ieN, {Л, 4,}c
?> Пусть
Имеем Н cz M cz k (Н). Проверим, что М — кольцо.
Действительно для {А, В) с М (А {] В) ? М согласно
определению класса М. Если {А, В] cz M, то
А = U At, В = у Ву, {Лх, .... Лп; В3) ... , Bm) a
с: Я,
и
п / т \ п т
А \ В = U A,\ U В/1 = U П (А,\ В,).
<=i \/=i / с=1 /=i
Поскольку Я — полукольцо, то можно предполагать,
что
А1{]А,= 0, Bt(\B,= 0, 1ф].
Кроме того,
At \ В,- = U Clfk, {C,,k} с: Я, I = / (г, /),
причем C,/v П Сг/ц = 0, v Ф ]х. Поэтому
п т I
А \В = U П U Cr,k. <t
i=\ /=1 A=l
11

Упражнения
.5. Пусть Н = \Alt А2, ..., Ап) cz X. Доказать, что: а^ а (НУ
содержит не более 22" множеств; б) а (Н) = аа (Н).
Указание, а) Рассмотреть все множества вида
Л, П К Л • • • Л Ап,
где прн каждом 1 < i ^ n At равно At или X \ Л,-.
6. Доказать, что минимальное полукольцо, содержащее класс
Я={(-оо, я] | aSR),
есть
{(а, Ь] | — оо<а<й< + оо} U {0}.
Указание. Определение минимального полукольца аналогично
определению 1.
2.2. БОРЕЛЕВСКИЕ МНОЖЕСТВА
Пусть (X, р) — метрическое пространство, # — класс
всех открытых в (X, р) подмножеств X.
Определение 3. a-алгебра
В(Х)\ = оа(&)
называется о-алгеброй борелевских множеств.
Упражнения
7. Пусть Н = {В (х, г) | х S X, г > 0}, здесь В (*, г) : =
= {У 6 X | р (у, аг)< г}. Доказать, что $ (X) = aa (H).
Указание. Проверить, что Н с & cz аа (Н).
8*. Пусть (X, р) — сепарабельное метрическое пространство.
Доказать, что существует счетный класс множеств Я с 2х такой,
что аа (Я) = % (X).
9. Пусть & — класс всех замкнутых в (X, р) подмножеств X.
Доказать, что
%(Х) = оаEГ) = оа({В(х, г) | х?Х,г>0}),
здесь S"(*, г) : = {у 6 X | р (у, х) < л).
10. Доказать, что:
а) одноточечное множество является борелевским;
б) любое счетное множество является борелевским.
11. Пусть gg : = 33 (R) — a-алгебра борелевских множеств
на R с расстоянием р (дс, ^) : = | аг — у \, {х, у] cz R. Доказать, что
следующие множества являются борелевскими:
а) Q — множество всех рациональных чисел;
б) R \ Q — множество всех иррациональных чисел;
в) (а, Ь]\ {а, Ь) с R, а<Ь.
г) множество всех действительных чисел, в десятичной записи кото-
которых цифра 4 встречается бесконечно много раз.
12

12. Доказать, что
<% = оа({(— со, а] | aGR}) = cra({(— со, а] |
= аа({(а, Ь\\—со<5а<6< + со}).
13**. Пусть (X, р) — сепарабельное метрическое пространство.
Доказать, что gg (X) имеет мощность, не большую континуума.
2.3. МОНОТОННЫЙ КЛАСС И о-КОЛЬЦО,
ПОРОЖДЕННЫЕ КОЛЬЦОМ
ТЕОРЕМА 2. Пусть Я ¦,— кольцо подмножеств X.
Тогда ok (Я) = т (Я).'
\> Поскольку ok (Я) есть монотонный класс, то, со-
согласно определению т (Я), имеем включение т (Н) с:
с= ok (Я).
Докажем, что т (Н) — кольцо. Для любого В ?
? т (Н) рассмотрим следующий класс множеств:
L(S): = {Cc:X | {В [) С, В\С, С\В}<=
czm(H)}.
Справедливы следующие утверждения:
(i) поскольку Н — кольцо и Я с: яг (Я), то V Л €
: ЯсЬ(Л);
(И) V В ? т (Я) : L (В) — монотонный класс. Дока-
Докажем утверждение (п).
Пусть {Сп : п > 1} с: L (В), Сп czCn+un > 1. Тогда
для п ~^>- 1
(С„ UB)c(Cn+i U В), {Сп \В)а(Cn+1 \В),
(В \ Сп) =>(В\Сп+1); {В U Сп, В \ Сп, Сп\В}с:
<= m (Я).
Поскольку т (Я) — монотонный класс, то
т(Н)Ъ U (Сп {) В) = U Сп [) В,
т (Я);
m(H)
поэтому
и сп
Э
э
е
„и-1( п
оо
n (fi4
n=i
L(S).
\
\
В) =
С„) =
сп\
оо
\ и
п=1
в,
Сп,
и
11=1
Случай убывающей последовательности {С„ : п^Ц
рассматривается аналогично, утверждение (п) доказано.
13

Так как, согласно (ii), L (Л) — монотонный класс
для любого А ? И и, согласно (i), H czL (А), го
УЛ?Я : m(H)c:L(A) =>
=> VA?H УС^пЦН) : [А[}С1,А\С1,
Cl\A}czm(H) Ф ff
^> V{CU C2}czm(H) :
{С, U Q, QXC,, Сг\С!}с:
Таким образом, /л (Я) — кольцо.
По теореме 1 п. 1.4 т (Я) — а-кольцо, а потому
а& (Я) czm(H).
Следовательно, m (Я) = ok (Я). <)
Упражнение
13. Пусть Я — алгебра множеств. Доказать, что аа (Н) =
= т (Н).
3. ФУНКЦИИ МНОЖЕСТВ. МЕРЫ
3.1. ОСНОВНЫЕ КЛАССЫ ФУНКЦИЙ МНОЖЕСТВ
Пусть X — основное множество и Н cz 2х — неко-
некоторый класс множеств. Объектом изучения теории меры
являются функции вида
\а : Я->(— оо, -f °°)i
удовлетворяющие некоторым специальным требованиям.
Реальными примерами таких функций являются длина,
площадь, объем, определенные для некоторых классов
множеств соответственно на прямой, плоскости, в про-
пространстве. Другого типа пример представляет заряд
частей пространства в электрическом поле. Эти реаль-
реальные примеры приводят к узкому, но важному для мате-
математики, классу функций. Например, площадь неотри-
неотрицательна; площадь фигуры, состоящей из объединения
двух непересекающихся частей, равна сумме площадей
частей и т. п. Упомянутые выше специальные требования
на функции множеств частично состоят в переносе в аб-
абстрактную ситуацию свойств реальных функций мно-
множеств, а частично связаны с математическими потребно-
потребностями.
14

Далее рассматриваются функции, принимающие
значение 4-°°- Например, естественно считать, что
длина прямой есть +оо. При этом предполагается,
что +оо +оо : = +оо и
VaGR : a<z+°°; a -f- oo : = -f- оо -f- а: = -f- оо.
Определение 1. Функция ц: Н -> (—оо, +оо] назы-
называется на Н
(i) неотрицательной, если
(ii) конечно-полуаддитивноч (полуаддитивной), если
У{ЛХ Л„}с:Я, U
n
!=1
(iii) конечно-аддитивной (аддитивной), если
= 0, t
(iv) счетно-полуаддитивной (о-полуаддитивной), если
У {Ап :
(v) счетно-аддитивной (а-аддитивной), если
{ >} U
= 0, 1Ф1 •¦
(vi) монотонной, если
У {А, В}с:Н, Ас:В :
IB

(vii) конечной, если
VA?H : МЛХ +
(viii) о-конечной, если
3{Ап :
n—\
Упражнения
1. Предположим, что 0 б Я, \i — аддитивна на Я и
3 А ? Н : ц (А) < + со. Доказать, что ц @) = 0.
2. Предположим, что 0 ? Я, (i @) = 0 и ц — а-аддитивна на
Н. Доказать, что ц — аддитивна на Н.
Указание. Воспользоваться равенством
A U B = A l)flU0U ••• U0U ¦•••
Замечание I. Функции \i, принимающие значение + оо на каж-
каждом множестве из Я, далее не рассматриваются.
3.2. МЕРЫ. ЭЛЕМЕНТАРНЫЕ СВОЙСТВА МЕР
Определение 2. Мерой называется неотрицательная
и а-аддитивная функция, заданная на полукольце.
Упражнения
3. Пусть (J, — мера. Тогда ц @) = 0.
Указание. См. замечание 1.
4. Мера ц — аддитивная функция.
5*. Пусть Х={аг1, аг2 *„,...}, Н=2Х; Pi>0, г>1,
S Р1=\ и
Доказать, что ц мера на Я.
6. Пусть X = [0, I]2, Я— алгебра всех измеримых по Жор-
дану подмножеств X и ц — «мера Жордана» на Я. Проверить, что
(г — неотрицательная и аддитивная функция на Я.
ТЕОРЕМА 1. Пусть К — кольцо и (i- мера на К.
Тогда
A) ц — монотонна на К',
B) V {А, В) <= К, А <= В, fi (Л) < +оо:
16

C) если IА, В} с: К и, по крайней мере, одно из значе-
значений [I (А), [I (В) конечно, то
U В) =
D) если {A, Blt .... Вл) <=. К и А с: U Bk, то
E) ц — а-полуаддитивна на К-
\> A) Пусть {А, В\ cz К и А с: В. Тогда
В = Л U (В\Л),
причем Л П {В \ А) = 0. Используя аддитивность
и неотрицательность ц, имеем
H(B) = (i(i4) + fi(B\i4»(iD). C.1)
B) Если ц (А) < -f оо, то из C.1) имеем
C) Если \i (А) < + оо или \i (В) < + оо, то, соглас-
согласно A), ц (А П В)< + оо. Кроме того,
А и В = (Л\(Л П В)) U В,(Л\(ЛП В"))П S = 0,
откуда с помощью аддитивности р. и свойства B) получим
U В)=|
D) С помощью свойства A) и аддитивности ц имеем
It (Л)< р (\U ( Bt j = |х f Si U (В, \ В,) U
U (В,\(Вх U В2)) U • • • \)(вп\ V B
<S i* (в*).
E) Аналогично доказательству свойства D) с исполь-
использованием а-аддитивности имеем
17

здесь
U Ak:= 0. <J
Замечание 2. Свойства A) — D) теоремы 1 имеют место для не-
неотрицательной и аддитивной функции ц.
Упражнения
7. Доказать, что неотрицательная, аддитивная и а-полуадди-
Тивная функцня ц на кольце К есть мера иа К.
оо
Указание. Пусть {Ап : я > 1} с: К, V Ап? К и Ат П Ап =
= 0, т ф п. Из монотонности и аддитивности имеем
/ - \ I п \ п
( U Дь >Ц MJ Л* =? ИАО. л>1.
а=1 / \fc=l / ft=l
8. Пусть [I — мера на а-кольце Я и лля {Ап : п > 1} с: Я
Vn>l : }1 (Л„) = 0. Доказать, что
Указание. Воспользоваться свойством а-полуаддитивности.
9. Пусть ц— мера на а-алгебре Н, причем ц (X) = 1, и для
{Ап : «>1}с:Я V«>1 : ц(Лп)=1. Доказать, что
И П Ап =1-
\я=1 /
Указание. Воспользоваться правилом двойственности и упраж-
упражнением 8.
10. Пусть ц — аддитивная конечная функция на кольце К.
Тогда для любых Alt A2, А3 из К справедливо равенство
ц (А1 U4U4) = H (^i) + И (Л2) + Ц (А3) - ц (At Л Лг) —
- (i (Л Л Л3) — \х(А2(] Ая) + ц (А1 Л Л2 Л Л)-
Доказать это утверждение.
11. Пусть ц — мера на алгебре Я с 2*, причем ц (X) = 1.
Доказать утверждение: если для {А1у ..., Лп} с Я
то
/
12*. Пусть ц — мера на а-алгебре Я с 2Л, причем ц (X) = 1,
и последовательность {Ап : п ^ 1} сг Я такая, что
18

Рассмотрим множество
В : = 1* ? А | х принадлежит конечному числу множеств Ап,
1 или х ? U А„\.
]
Доказать, что ц (В) = 1.
Указание. Заметить, что
оо оо
_
8= П U Л"
и воспользоваться монотонностью и а-полуаддитивностью меры ц.
В есть множество всех тех х, которые принадлежат бесконечному
числу множеств из Ап, п !> 1.
3.3. НЕПРЕРЫВНОСТЬ МЕРЫ
ТЕОРЕМА 2 (о непрерывности меры снизу). Пусть
К — кольцо и (I — мера на К- Тогда для любой моно-
монотонно возрастающей последовательности \Ап : п >
> 1} с: К такой, что (J Ап? К,
п=\
\> I. Если 3 п0 : \а (Л„„) = +оо, то в силу монотон-
монотонности и, на К
следовательно, утверждение теоремы выполнено.
II Пусть V п ^ 1 : \i (Л„) < +с«. В силу а-ад-
дитивности имеем с учетом свойства B) теоремы 1
) U
[](Лп \Л„_,) U
k=2
п
к-\)) = Нт

Упражнение
13. Доказать, что неотрицательная, аддитивная и непрерывная
снизу на кольце К функция ц есть мера.
ТЕОРЕМА 3 (о непрерывности меры сверху). Пусть
ц — мера на кольце К- Тогда для любой монотонно убы-
убывающей последовательности {Ап : п^1}аК та-
оо
кой, что ц (Ах) < +оо и П А-п 6 К,
Ап)= Птц(Ап).
п
\> Согласно теореме 2 имеем
ц (л, \ П Ап) = р(и (А, \ Л„)) = lim p. (At \ Ап),
откуда, с учетом условия \л (At) < +00 и свойства B
теоремы 1, получим
П ^») = Нт (|* (Л^ - (i D))- <
\Л=1 / Л-voo
Упражнения
14. Пусть X=N, /C=2NH(J, — мера на К, определяемая ра-
равенствами: (г @) = 0; ц ({&}) =1, ? 6 N. Положим Ап : = {я>
п+ 1, ...}, «> 1. Тогда
Ап-=>Ап+х, я>1; fl 4 = 0.
Проверить, что
Таким образом, условие ц (Л^ < +°° в теореме 3 является су-
существенным.
15. Доказать, что неотрицательная, аддитивная, конечная и
непрерывная сверху иа 0 функция на кольце К есть мера.
16. Построить пример меры ц и кольца К таких, для которых
существуют монотонно убывающие последовательности [Ап : п~^
> 1} с ц (Ап) = + м, я > 1 такие, что
а) ц(
в)
20

17*. Пусть ц — мера на кольце К и последовательность
{An '¦ п ^ 1} с К удовлетворяет условиям:
Л Ап?К; цСУЦХ + оо;
V К, я,} с N 3 п3 е N : Л„з С ЛП] П А^.
Доказать, что
Л Л1 — inf J* (Л^-
л=1 / 1»
18. Для произвольной последовательности [Ап : п ^2> 1} под-
подмножеств X множества
От Ап ¦ = U Л ль '^ л": = Л U л*
называются соответственно нижними верхним пределами последова-
последовательности множеств [Ап : «> 1). Если
lim Ап — lim Ап = : lim An,
/Г^*оо fl-юо а-* оо
то последовательность множеств {Ап : п > 1} называется сходя-
сходящейся или имеющей предел.
Пусть ц — мера иа а-алгебре & подмножеств X и [Ап : п. J>
^1} — произвольная последовательность множеств из f. Дока-
Доказать, что
(х (lim Л„) ^ lim ц (Л„).
При дополнительном условии
оо
U '
.1=1
доказать также, что
rt->oo п-*оо
Отсюда следует, что если последовательность {Ап : я> 1} схо-
/ оо \
дится иц U<4n)<+ooiT°
[i (lim Л„) = lim ц (Л^).
п-*оо п-*оо
3.4. ПРИМЕРЫ МЕР
Важным для различных разделов математики, напри-
например для теории вероятностей, является пример меры,
определенной на а-алгебре всех подмножеств счетного

множества X, из упражнения 5. Наиболее существенными
примерами мер являются следующие. Далее число т ?
? N — фиксировано.
ТЕОРЕМА 4. Пусть К — кольцо всех измеримых по
Жордану подмножеств R и ц — m-мерная «мера Жорда-
на» на К. Функция ц — а-аддитивна на К-
\> Пусть {Ап : п > 1} сг К, А : = (J Л;1 € /<",
4 0 4 = 0. /я ==?п.
Л/
I. Поскольку У N ^ I : U ЛП с: А, то, в силу
монотонности ц на К, имеем
поскольку ц аддитивна на /(, то
п=1
Отсюда
X !4)j C.2)
II. Пусть произвольное е > 0 фиксировано. Рассмот-
Рассмотрим Rm как метрическое пространство с евклидовым
расстоянием. Согласно конструкции «меры Жордана»
[4], для множества А ? К существуют замкнутое множе-
множество F б К и открытое множество G ? К такие, что
FczAczG, n(G) —n(F)<e.
При этом
|iD)<|i(F) + e. C.3)
Аналогично для каждого и ^ 1 для множества Ап ? /(
существует открытое множество G,, ? /( такое, что
An cr Gn, №(Gn) — ц(Л„)< ~— • C.4)
Имеем
00 00
P ,— A II A ,— || /-,
22

Таким образом, замкнутое и ограниченное, то есть
00
компактное, множество Fc [| Gn. Поэтому существует
п=1
N 6 N такое, что
Из этого включения, монотонности и полуаддитивности
ц на К сначала получим
n=l I n=\
затем с учетом C.4)
S (|(Л0?)!
n=l \ 2. I n=\
Из этого неравенства и неравенства C.3) следует, что
S
Поскольку е >¦ 0 произвольно, то, устремив е ->- О,
приходим к неравенству
1*И)<ЕИ4). C.5)
Из C.2) и C.5) получим
ц(Л) = ? Ц(Л„). <J
СЛЕДСТВИЕ 1. Пусть X = R, полукольцо
iV = {(a. 6]| —oo<a<6< + oo} U {0}
и и @) : = 0; ц ((а, Ь\) : = 6 — a, (a, b] ? $>v Тогда у,
есть мера на 5Y
t> ^ есть сужение на ^ одномерной меры Жор дана. <J
СЛЕДСТВИЕ 2. Пусть X = R2, полукольцо
92: = f(alt М X (а2, Ь.г\ | — оо < Oj < 6, <
< + оо, /=1, 2} и {0};
23

И @): = 0; ц (fai, 6i] X @4, &,]): = FX — at) x
XF2 — «2). (ai> bj X K. &21 € ^V Тогда ц есть мера
на 2>2.
(> ц есть сужение на Ф2 двумерной меры Жордана. <J
ТЕОРЕМА 5. Для X = R и полукольца (iP1 пусть
М0): = О; М(а. 6|)т = F(b) — F(a), (a, b\?9>lt
где F : R -> R — монотонно неубывающая и непре-
непрерывная справа на R функция. Функция ^F есть мера на
(> Функция kF неотрицательна и аддитивна на Vul. До-
Докажем, что Хр — а-аддитивна на ty^ Пусть
{(а,,, bn] : n > 1} с ^lf (am, 6m] fj (а„, Ьа] = 0,
m ф п и
U (а„, 6„] = (а, 6] е ^.
I. С учетом определения полукольца имеем
N т
Vtf>l : (a,b]\ U (а„, 6„] = U С*,
п=1 4=1
{Cv ...,Cm)a ^, d fl Q = 0, t =?fc/.
Следовательно,
(а, Ь\ = }}=х (an, bn] U U=i Ск,
откуда с учетом аддитивности "Кр на ЧР1 получим равенство
N т
М(я, b]) = S ^(@», Ьп\) + S Я,,(С„).
Поэтому
V Л^ > 1 : Хр ((a, b]) > S ^ ((«,- Ьп]),
п=1
откуда
00
^((а, 6])>S ^((о„, ftj). C.6)
II. Поскольку F — непрерывна справа, то
Ve>0 За16(а, 6) : F(a1) — F(a)<г ^>
24

Ф XF ((a, b)) — \F ((a', b\) = F(b) — F (a) -
- (F (b) - F (a')) = F (a') -F(a)< e; C.7)
=> %F {{an, b'n\) - If ((an, bn\) - F (b'n) - F (an) -
- (F (bn) - F (an)) = F (bn) - F {bn) < JL.. C.8)
Заметим теперь, что
\a',b\cz (a, b\= U (an, bn] с U (an, b'n),
откуда, поскольку [a1, b] — компакт на прямой, то
: [a1, b] cz [} (ап, bn) с (j (an, b'n].
\ 1
( ) (j
п=\ л=1
Теперь из полуаддитивности Кр имеем
м ])<s ык ixs
откуда с учетом неравенств C.7) и C.8) получаем
Устремив е -> 0+, приходим к неравенству
00
К ((а, Ь))^%ХР((ап, bn\),
которое возможно вместе с неравенством C.6), если
Упражнение
19. Пусть G : R -*¦ R, G € С (R) П BV (R) и для X = R и
полукольца ^,
vG@): = O; va((a,b]): = G{b)—G(a), (a, ft]
Доказать, что vfi есть а-аддитивная функция иа &1ш
25

4. ПРОДОЛЖЕНИЕ МЕРЫ
4.1. ПРОДОЛЖЕНИЕ МЕРЫ С ПОЛУКОЛЬЦА
НА ПОРОЖДЕННОЕ ПОЛУКОЛЬЦОМ КОЛЬЦО
Пусть X — основное множество.
Определение 1. Пусть %t а 2х, ц;: %t ->- (—оо,
+°°], i = 1, 2. Функция ц2 называется продолжением
функции Ц! (ц! называется сужением функции ц2), если
\ с S2 и V Л € §i : Hi (Л) = ц2 (Л).
ТЕОРЕМА 1. Пусть Ц — мера на полукольце 5s.
Мера Ц единственным образом продолжается до меры на
k (\Р), при этом продолжение конечно (а-конечно), если
ц конечна (а-конечна).
(>1. Определение продолжения. Для
А б k (У) имеем
Л = Д С„ {Q С„} с р, С, Л С, = 0, »=,«=/,
положим
Это определение корректно. Действительно, рассмотрим
еще какое-нибудь представление
А = О D/, {А. ... , Z)m} c^>, D( Л D,= 0, i
Тогда для любых 1 < i < п, 1 < / < m имеем
С, = С, Л Л = U i (С, Л О/), D, = А Л D, =
1М, ПД
причем множества {С/ Л Я/ | 1 <! t ^ п, 1 ^ / ^
^ т) с ty и попарно не пересекаются. Используя ад-
26

дитивность ц на ф, получим
2 мед = 2 ii(и (С, л о,)) = S 2 |i(c( n О/) =
= S i*( и (Ct n ?>,)) =
Продолжение ц аддитивно на /г (#>).
II. Единственность продолжения.
Пусть X — аддитивное продолжение и, на k (xP). Тогда
V A?k(V):
А = .U С{, {С, Сп] а 9, Сс (]С,= 0, 1Ф и
1=\ 1=1
III. ст-ад д и т и в н о с т ь п р о д о л ж е н и я (i.
Пусть
\Ап : п>1|сА(П Ап[\Ат=0, пфт;
Л:= U An?k{&).
/i=i
Тогда
т
А= []¦ В,, {В,, ..., Вп}с9>, Вс{] В, = 0, »#/;
/=|
и для каждого п ^ 1
г{п)
Ап = U Cni, [Сщ СпПп)) с ^, Cni fl Cni = 0,
i
Используя сначала а-аддитивность ц на 5s, а затем адди-
аддитивность ц на й Es), получаем
= 2 MB/ n и и сп/ = 2 I* и и (в, п с*) =
т оо r(fi) oo
= 2 2 2 ii(B/ficn,)=2 iiH»). <l
/=1 n=l ?=1 П=1
27

Замечание. Задача о продолжении меры состоит в следующем.
Каким образом, зная меру на узком классе множеств, например, на
полукольце ^ в плоскости из следствия 2 п. 3, продожнть ее на более
широкий класс множеств J"" с сохранением свойств меры. Для плос-
плоскости желательно, чтобы в класс & входили такие фигуры, как круг,
ограниченные эллипсом, и т. п. Исторически процесс продолжения
для конкретных мер — площади из следствия 2 и объема на все более
и более широкие классы множеств длился около 2000 лет. При этом
первоначально предполагалось, что, например, в случае плоскости
все фигуры имеют площадь, а главная задача состояла в построении
метода ее вычисления. Нужная для дальнейшего теорема 1 как ре-
решение в какой-либо мере задачи о продолжении интереса ие пред-
представляет. Например, в плоскости k (&.2) не содержит даже треуголь-
треугольников. Дифференциальное и интегральное исчисление позволило
просто и эффективно вычислять, например, площади и объемы прак-
практически всех множеств, встречающихся в приложениях. Задача вы-
вычисления площади и объема отошла на второй план, а развитие ма-
математического анализа, в частности теории интеграла Римана, при-
привело к необходимости рассмотрения длины или площади — меры
весьма общих множеств. Дж. Пеано A858—1932) и К. Жордан
A838—1922) продолжили длину (аналогично площадь, объем) на
кольцо множеств, измеримых по Жордану. При этом свойство а-ад-
дитивности не рассматривалось. Однако и это продолжение оказалось
недостаточным. Например, множество Q П 10, 1] не измеримо .по
Жордану, хотя в ряде задач ему желательно приписать длину 0.
Важность понятия а-аддитивности была замечена Э. Борелем A871—
1956). Продолжение длины (объема, площади) как а-аддитивной
функции на а-алгебру J2" подмножеств прямой осуществлено А. Ле-
Лебегом A875—1941). Это продолжение оказалось в некотором смысле
окончательным — было установлено, что длину с сохранением ее
свойств нельзя продолжить на класс всех подмножеств прямой (по-
(подробнее см. в [15]). Общее определение меры было введено И. Радо-
Радоном A887—1956) и М. Фреше A878—1973). Детальные исторические
сведения можно найти в [6, 7].
4.2. ВНЕШНЯЯ МЕРА
Определение 2. Функция "к*: 2х -> (—оо, + °°] на-
называется внешней мерой, если:
(i) X*@) = 0, "к* — неотрицательная функция;
(и) \/{А; Ап : п^\}^2х, А с (J К •
п—1
Упражнение
1. Доказать, что внешняя мера монотонна и полуаддитивна
на 2х.
Указание. Для {Л, В) с2х, Л сВ имеем
ACZBU 0 U ••• U 0 U ••••
28

Определение 3. Пусть ц — мера на кольце К подмно-
подмножеств X. Пусть для Л ? 2х
О
[Ап х
ОО
U Ап
=зЛ
Л = 0
К, при условии,
хотя бы одна
что
такая
последовательность
существует
в остальных
чаях
слу-
+ оо
ТЕОРЕМА 2. Функция ц* из определения 3 есть внеш-
внешняя мера.
\> Условие (i) определения 2 выполнено. Проверим ус-
условие (И). Пусть
{А; Ап ! л>1}с2\ Лег U Л„.
I
Достаточно рассмотреть только случай, когда ц* (Л„) <
< -f оо, п ^ 1. Согласно определению 2 и определению
точной верхней грани имеем
Ve>0 Vn>l 3{Bnf i />1)с:/С,
и i fi«/ => к »
/=i z
Отсюда с учетом включений
ОО ОО ОО
U U Bn,iD Ц АпиА
n=l /=I n=l
получим с помощью определения 2
1=1 /=1 f!=l
Устремим е -»- 0+, имеем
29

Замечание. Функция ц * из определения 3 называется внешией
мерой, порожденной (индуцированной) мерой ц.
Упражнение
2. Пусть Х= R, <?= {(*, k+ 1] | k?Z] U {0}; M0): =
= 0; Я ((&,: А + 1]) : = 1, ft ? Z. Проверить, что Я — мера на &.
Пусть Я— продолжение Я на k C>). Построить внешнюю меру Я*,
индуцированную мерой "Я. Найти Я* (|~2"|). Я* (("о"» ¦
4.3. ^'-ИЗМЕРИМЫЕ МНОЖЕСТВА.
ТЕОРЕМА КАРАТЕОДОРИ
Определение 4. Пусть Я* — внешняя мера на 2х.
Множество А с: X называется Я*-измеримым, если
V В с= X : Я* (В) = Я* (В П А) + Я* (В \ А).
Замечания. 1. Обратим внимание на то, что
В\А = В[)А, А:=Х\А.
2. Для любых A с X, В с X
й=E Л A) U (В\Л),
а потому в силу полуаддитивпости внешней меры Я* имеем
Упражнения
3. Доказать, что множество А Я*-измеримо тогда и только
тогда, когда
Vt/C-4 WcI : k*(U \J V) = к* (U) + X* (V).
4. Определить класс всех Я*-измеримых множеств для внешней
меры Я* из упражнения 2.
Ответ. Класс всех не более чем счетных объединений множеств
из
Множество (-я-, 1 не является Я*-измеримым.
ТЕОРЕМА 3 (Каратеодори). Пусть \* — внешняя
мера на 2х и 5 — класс всех ЯЛизмеримых множеств.
Класс 5 есть а-алгебра, а сужение Я* на 5 есть мера.
\> 1. S — алгебра. Заметим, что 0 ? 5, поскольку
VBczX 1 У(ВО0) +
и что из А ? S следует, что Л ? 5, так как
30

Пусть {G, F] cz 5, тогда для любого В сг X имеем
X* (В) = | ^-измеримость G | = Я* {В Л G) -f
+ Я,* (В П 5) = | ^-измеримость F | = Я* (В П G) -f
+ Я*(ВП G 0/0 + ^E П Gn Л, D.2)
X* (В П (G U /0) = | ^-измеримость G | =
= Я*(В Л (G U Л П G) + Я*(В Л (G U F) П G) =
= X*(B(]G) + l*(B [] F (]G). D.3)
С учетом D.3) из D.2) получим равенство
Я* (В) = Я* (В П (G U F)) + Я.* (В П ("GlJTj).
Таким образом, (G \J F) ? S, откуда
11. S — а-алгебра и сужение X* на 5 есть мера. Пусть
со
{Ап : п > 1} cz S. Нужно доказать, что [}Ап ? 5. По-
п—\
скольку 5 — алгебра, то можно предполагать, что Ат П
П Ап = 0, т Ф п. Для любого В с X из Я,*-измери-
мости Ах имеем
Я.* (В П {Ах U 4)) = Я.*(В П (Аг U А2) П Лх) +
+ Я*(В П(Лх U Л) П Дх) = ^*(В П 4) + Я* (В П Л2),
с учетом этого равенства и Я,*-измеримости Л3 получим
Я*(В П (A, U 4 U А,)) = ^(ВП Л3) + Я^*(В П
i=l
Аналогично для любого п !> 1 имеем равенство
ЯП U A =S Я,*(ВП А). D-4)
\ г=1 / г = 1
п
Используем теперь последовательно Я,*-измеримость (J Л,,
i=i
равенство D.4) и монотонность внешней меры
я* (В) = х*[в о Л i л,| + 1*(вп ? л,] >
>? Ъ*(В П Л,)+Я.*(в П U Л,).
1=1 \ 1=1 /
31

Таким образом,
*•(?)> f Ъ*(В П At) + k*[B П U
П .U( л) + Х*|ВП Ji Л,j, D.5)
последнее неравенство основано на свойстве (ii) определе-
определения 2. С учетом D.1) заключаем, что
X* (В) = ^ВП {U i A,J + ^ВП Д( А,).
Поэтому
U A,?S,
а соотношение D.5) выполняется со знаками равенства.
сю
Положив в D.5) В = U Л;, получим
i
Упра жнение
4. Привести пример внешней меры X* на 2х такой, что S =>
= {0, X).
4.4. ПОЛНЫЕ МЕРЫ
Определение 5. Пусть ц, — мера на а-алгебре5.Мера
|д, называется полной, если
Замечание. Если А ? S, ц. (Л) = О, В а А и В ? 5, то в силу
монотонности меры ja (В) = 0.
СЛЕДСТВИЕ 1. При условиях теоремы 3 мера X* на
5 является полной.
|> Пусть А ? 5, X* (А) = 0 и С с= Л. Для любого
В сХ с учетом монотонности внешней меры X* и ^-из-
^-измеримости Л имеем
X*(В)> Я*(В П 5) > Я,*(В Г) Л) = А*(В П ^4) +
32

поскольку 0 < X* (В П А) < X* (Л) = 0. Аналогично
X* (В 0 С) = 0. Поэтому С ? 5. <|
Упражнение
5*. Пусть |х — мера на о-алгебре S и
S°: = {yiU© I A?S; Фс В, ц (б) = 0),
ц°(Л иФ): = М4 И 1)Ф)е5°.
Доказать, что S° — о-алгебра и что |х° — полная мера на S°.
4.5. ИЗМЕРИМОСТЬ МНОЖЕСТВ ИСХОДНОГО КОЛЬЦА
Если X* — внешняя мера, то, согласно теореме 3,
класс 5 всех Х*-измеримых множеств есть а-алгебра.
Однако эта а-алгебра может быть весьма бедной, возмож-
возможно, что S = {0, X).
Сейчас мы рассмотрим случай, когда внешняя мера
\х* индуцирована мерой jx, заданной на кольце К- Как
и выше, 5 — класс всех |х*-измеримых подмножеств
X, обозначим также
Мера \i есть продолжение меры ц с кольца К на а-алгеб-
ру S, если К с S.
ТЕОРЕМА 4. К cz S.
|>1. Докажем сначала, что
Действительно, [i* (Л) ^ \х (А), поскольку
Л<= А и 0 U 0 U ••• •
Кроме того, для любой последовательности {Лп : п !>
со оо
>l)c/(,/lc UЛ„ имеем Л = U (Л П ^«)- о-адди-
/1=1 Л=1
тивность и монотонность меры \i на К приводят к соотно-
соотношению
f f
/1=1 П=1
Поэтому, согласно определению 3, jx (Л) ^ ц* (Л).
II. /С с S. Пусть Л ? /( и е > 0 заданы. Рассмотрим
произвольное множество В cz X, |х* (В) < + оо. Соглас-
2 8-1569 33

но определению 3
3{Л„ . n>l}cr/e i |1(В) + >?цD).
п=\
Отсюда с учетом аддитивности меры ц, на К и определе-
определения 3 получим
со
ц*(В) + е> ? (ц(Л„ П Л) + ц(Д, П Л))>
>ц*(В П Л) + ц*(В П А).
Пусть теперь е -v 0 +, тогда
\х*(В)>1х*(В(] А) + ^{В[\ А).
Из этого неравенства и полуаддитивности внешней меры
D.1) следует ц,*-измеримость множества Л. <\
Упражнение
в. Проверить, что ok (К) с аа (К) a S.
7. Пусть р. — а-конечная мера на кольце К. Тогда внешняя ме-
мера |х* на 2х и мера |х на S о-конечны.
8*. Для А ? 2Л положим
(°° _ °° )
V ц(Ап)\{Ап : O>I)CS, U AnZ>A\.
n-i «=' J
Доказать, что (i** = |х*.
4.6. ЕДИНСТВЕННОСТЬ ПРОДОЛЖЕНИЯ
Пусть \i — продолжение из теоремы 3 меры ц, с кольца
К на а-алгебру 5 всех |х*-измеримых множеств, при этом
S ZDOk (/<).
ТЕОРЕМА 5. Продолжение а-конечной меры \х с коль-
кольца К ка о/с (/() единственно и а-конечно.
$> I. Пусть мера ?и — некоторое продолжение на ok (/Q
меры [I. Предположим сначала, что одна из мер К, \х конеч-
конечна на ok (К). Положим
при этом К cz О с: ok (/Q. Q — монотонный класс. Дей-
Действительно, для последовательности
{Ап i n>l)c:Q; An<=Aa+i, «>1
34

с помощью теоремы о непрерывности меры снизу имеем
@ «) („)йп) = ц( 0 Ап),
со
а потому [}Ап ? Q. Аналогично с помощью теоремы о не-
п=1
прерывности меры сверху и предположения конечности
одной из мер А., \х доказывается, что классу Q принадле-
принадлежит предел убывающей последовательности множеств
из Q.
Поэтому т. (К) cz Q cz ok (К), кроме того, согласно
теореме 2 п. 2.3 т (К) = ok (К). Следовательно, Q =
= ok (К).
II. Пусть А ? К — множество, для которого одна из
мер "к, (.1 конечна. Тогда по I меры Я, и jx совпадают на
А П ok (К) = ok (А П Ю- Кроме того, любое множество
из ok (К) содержится в объединении счетного набора
множеств из К с конечным значением меры ц, каждое. <j
Упражнение
9*. Доказать, что мера |х на S есть пополнение меры ц на
ck (К).
Замечание. Условие о-конечности меры |х на К в теореме 5 су-
существенно. Пример см. в [1], гл. 111, § 13.
4.7. ТЕОРЕМА О ПРИБЛИЖЕНИИ
ТЕОРЕМА 6. Пусть ц, — а-конечная мера на кольце
К и \i ее продолжение на ok (К). Тогда
V А б ok (К), й(Л)< + оо Ve>0 ЭС^/С I
Й(Л \Ои(С\Л))<е.
|> Пусть |х* — внешняя мера, индуцированная мерой ц,
при этом \i = (.1* на ok (К). Пусть е > 0 фиксировано.
Согласно определению внешней меры для р. (А) — \х* (А)
и числа -j- имеем
k=l *=1
35

Отсюда с помощью а-аддитивности и монотонности меры
р получим для каждого п ;> 1
Кроме того, в силу непрерывности меры \i снизу
\fc=l У п-кх> \*=| /
Следовательно,
Зпо>1 : jlfff ^J + -J->ilf U ЛЛ). D.7)
Пусть
По
Тогда из неравенств D.6) и D.7) получим
Упражнение
10. Пусть |х* — внешняя мера, индуцированная заданной на
кольце К мерой \i, причем ц* (X) < +оо. Доказать, что
A?S <Ф Ve>0 3C€/C : ц* ((Л \ С) (J (С \ А))< е.
4.8. МЕРА ЛЕБЕГА НА ПРЯМОЙ
Пусть X = R,
^i = {(a. 6] I —°°<а<Ь< + оо} U {0} — полу-
полукольцо подмножеств R
О; >.((а,6]):=6 —a, (a,6l€^i.
Значение функции Я. на множестве из "J5! есть длина этого
множества. Согласно следствию 1 п. 3.4 функция К есть
мера на 5^. По теореме 1 п. 4.1 функция к единственным
образом продолжается до меры на k (t^i), это продолже-
продолжение также обозначим "к. Пусть к* — внешняя мера, ин-
36

дуцированная мерой Я. и определенная на всех подмно-
подмножествах R, а 5 — класс всех ЯЛизмеримых множеств.
По теореме 3 класс 5 — а-алгебра и 1* — мера на 5.
Определение 6. Множества из а-алгебры S называются
множествами, измеримыми по Лебегу, а мера Я,* на 5
(обозначаемая далее также Я.) — мерой ЛеЗега (или од-
одномерной мерой Лебега).
Справедливы включения
Таким образом, все борелевские множества измеримы
по Лебегу. Рассмотрим некоторые примеры борелевских
множеств на R и определим их меру Лебега.
1. Для любого х ? R одноточечное множество {х\ ?
? Ш (R), так как
По теореме о непрерывности меры сверху с учетом ра-
равенства
Я, ((х — 1, х]) = 1 имеем
*,({*}) = lim х((х — — , x\)=s Iim — = 0.
Следовательно, любое счетное множество A cz R
является борелевским и его мера Лебега в силу а-адди-
тивности Я, равна 0. В частности, Я. (Q) = 0. Кроме того,
ХAа,Ь]) = Ща)) + Х((а,Ь])=Ь-а,
X ((a, b)) = b — a.
2. Пусть G Ф 0 — открытое подмножество R, G —
борелевское множество. Тогда [4]
G = U («*, Р*);
(„ Р,)П(/ Р/) 0 Ф1; t
В силу а-аддитивности меры Лебега
Замечания. Взяв последнее равенство в качестве определения,
Э. Борель A898 г.) построил продолжение длины на % (R).
На рис. 1. схематически представлены различные продолжения
длины; Ж — класс всех подмножеств R, измеримых в смысле Жор-
дана. Обоснование к схеме приведено в упражнениях 11—14.
37

L.
г—; 1
с
[ 9,,А-длина )
[ на полуинтервалах )
Х,Л-мера
.Жордана A892 г.)
%(R), Л-мера |
Бореля A898 г.)
5, А -мера
Лебега ('1902г.)
2* Л* внешняя мера, индуцированная Л
Рис. I.
Упражнения
11. Проверить, что борелевское множество (Q П [0. Ч) ? •
12*. Канторово множество. Пусть Уо : =• [0, 1], далее
Множество ?п для п ^ 1 есть объединение 2" отрезков, длины 3 "
каждый. Пусть
со
и-.= п а п.
Доказать, что замкнутое множество U имеет мощность континуум и
измеримо по Жордану. Доказать также, что все подмножества U так-
также измеримы по Жордану. Доказать, что совокупность множеств
^ (R) имеет мощность континуум. Следовательно, существуют не-
борелевские множества в Ж.
13*. Представим полуинтервал [0, 1) в виде объединения по-
попарно непересекающихся множеств следующим образом: два числа
х и у из [0, 1) принадлежат одному множеству тогда и только тогда,
когда их разность (х — у) ? Q. В каждом множестве возьмем дейст-
действительное число г, множество всех таких г обозначим через А. Мно-
Множество А не измеримо по Лзбегу.
Указание. Для г ? [О, I) П Q, пусть
Аг: = {х + г | х?А, x+r<\} (J {x+r— I | х?А,х +
Доказать, что АГПАГ,= <Z,r Фг'Л* (Аг) =* \* (А), А = U А,
г€[0,1)Л<}
(см. п. 4.8,/, Подробное обсуждение этого примера см, в [I], гл. 111,
§ 16.
38

14*. Доказать, что icS.
15. Пусть A ?S, a?RnB: = а+А: ={а+х | х ? А].
Доказать, что В ? S и равенство к (А) = к (В).
16. Проверить, что для ограниченного множества А ? ffi (R)
МДХ +
МХ +
17*. Пусть Ло (Л&) — множество всех чисел отрезка [0, 1], не
содержащих в десятичной записи цифры 3 (содержащих в десятичной
записи цифру 3 конечное число раз). Доказать, что
\А0, Ak) С 5 и что к (А„) = X (Ак) = 0.
18. Пусть Л € S, к (А) < + со и
Кх):=к(АГ\ (—со, дс)), х 6 R.
Доказать, что /? С (R).
19. Пусть А ? S — ограниченное множество с X {А) > 0. До-
Доказать, что
Va?@, к (A))
20*. Доказать, что существует множество А ? S, X (А) > 0,
не содержащее никакого интервала вида (а, Р), а < Р.
'
4.9. МЕРА ЛЕБЕГА НА R
Пусть X = Rm, m б N,
U {0}— полукольцо подмножеств Rm и
^@):= 0; Хт( U (а„ bA = fl (bc-at).
Случай т. = 1 рассмотрен в п. 4.8. При т = 2 функция
Я,2 есть площадь на прямоугольниках вида (аи Ьг] X
х (а2, 62] из "Т'а. При т — 3 функция Я,3 есть объем на
брусах вида (alt bj X (а2, b2] х (о3, 63] из ^3-
По теореме 4 п. 3.4 кт есть мера на полукольце ^>т.
Эта мера, согласно теореме 1 п. 4.1, единственным обра-
образом продолжается до меры, также обозначаемой Хт, на
k ('?,„). Пусть Х'т — индуцированная мерой Хт внешняя
мера и Sm — класс всех А^-измеримых подмножеств Rm.
По теореме 3 класс Sm — а-алгебра, а Хт на Sm — мера.
Определение 7. Множества из а-алгебры Sm называ-
называются множествами, измеримыми по Лебегу, а мера Хт
на Sm (обозначаемая далее Хт) — мерой Лебега (или т-
мерной мерой Лебега).
Справедливы включения
39

Упражнения
21. Доказать следующие утверждения:
(а) для любой точки (дг, у) ? R2 одноточечное множество {(дг, у)} G S2
иЯ,2({(дг, у))) = 0; б) отрезок/= {(х,у) \ а < х < Ь, у = с} 6 52
н Я,2 (/) = 0; (в) пусть / — прямая в R2, тогда / ? S2 и А,2 (/) = 0;
(г) множество Г= {(дг, / (дг)) | дг ? R) с: S2 и к2 (Г) = 0, где
/еС (R); (д) множество Г = {(дг, у) | a s? дг < Ь, 0 < у < / (дг)] б
€52и
ft
Л2 (Г) = j / (х) dx,
а
где /g С ([а, Ь]) и неотрицательна иа [а, Ь\.
22. Пусть X = R2,
& : = {(а, Ь] X R | — со<а<6< +оа] [J {0},
|х @) : = 0; ц ((а, 6] X R) : = Ь — а.
Доказать, что & — полукольцо и что (i — мера на &. Пусть ц* —
внешняя мера, индуцированная мерой (i. Найти |х* (А) для множе-
множества
(а) А={(х,у) | 0<дг<1, у = х);
(б) Л={(л:, г/) | дг2 + ^<1}>
Описать класс всех |х*-измеримых множеств.
23. Пусть X = R2, S = S2 и Я,2 — мера Лебега на S2. Для мно-
множества А ? S2 положим
/ @ : = *, И П {(*!.*,) I *? + а4<'2}). ^>0.
Доказать, что / ? С ([0, + сю)).
24. При условиях упражнения 23 пусть Я,2 (А) < + оо и
g @ = = Ь2 М Л {(Xi. *2) I txx - 4 < 0}), / > 0.
Доказать, что g ? С (@, + сю)).
25*. Доказать, что множество Л с: Rm измеримо по Лебегу тог-
тогда и только тогда, когда
V е > 0 3 G — открытое, G zd A : X*m (G \ А) < е.
4.10. МЕРА ЛЕБЕГА — СТИЛТЬЕСА НА ПРЯМОЙ
Пусть X = R,
9V={(a,&] | -oo<a<6<+oo} у {0}
и F : R -> R — монотонно неубывающая и непрерыв-
непрерывная справа на R функция. Положим
U @): = 0; >., ((a, b]): = F (b) - F (a), (a, b] ? ^.
Согласно теореме 5 п. 3.4 функция Kf есть мера на ^1ш
Обозначим также кр единственное по теореме 1 п. 4.1
40

продолжение этой функции на k (^i), а через А,/? — внеш-
внешнюю меру, индуцированную мерой Xf- Пусть Sf — класс
всех ^-измеримых подмножеств R. По теореме 3 Sf —
с-алгебра, a Х*Р — мера на Sf-
Определение 8. Множества из а-алгебры Sf называют-
называются измеримыми, а мера XF на SF (обозначаемая далее
Хр) называется мерой Лебега — Стилтьеса.
Справедливы включения
Упражнения
26. Доказать, что
V*<ER : [x)^SfhKf([x)) = F(x)-F(x-).
27. Существует не более чем счетное множество Э' cr R такое, что
Vxtg : XF({x})>0.
28. Доказать, что для F (х) = х, х ? R мера KF совпадает с ме-
мерой Лебега X.
Замечание. Аналогично определению 8 определяется мера Лебе-
Лебега — Стилтьеса в Rm, см. [31, гл. 2, п. 2.5.
4.11. ИЗМЕРИМОЕ ПРОСТРАНСТВО, ПРОСТРАНСТВО
С МЕРОЙ, ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
Определение 9. Пусть X — основное множество, С1 —
а-алгебра подмножеств X. Пара (X, &) называется изме-
измеримым пространством, а множества из <F называются
измеримыми. Пусть |j, — мера на 3'. Набор (X, 3', ц)
называется пространством с мерой. Если ц (X) — 1,
то мера |j, называется вероятностной, а (X, 3', ц) — веро-
вероятностным пространством.
5. ЗАРЯДЫ
5.1. РАЗЛОЖЕНИЕ ХАНА
Определение 1. Пусть (X, 3) — измеримое простран-
пространство. Функция v : #*„-»-(—с», + сю] называется за-
зарядом, если
(ii) функция v ст-аддитивна на W.
41

Замечания. 1. Заряд v аддитивен на 5Г.
2. Заряд v обладает следующим свойством. Пусть А ?
v (А) < + оо. Тогда
V
Действительно, поскольку в силу аддитивности
v(A) = v(B)+v(A\B),
то из предположения v (В) = + оо и неравенства v (А \ В) > — со
следует, что v (А) = + оо.
Упражнения
1. Доказать, что для заряда справедливы теоремы о непрерыв-
непрерывности снизу и сверху, см. п. 3.3.
2. Пусть Я, |х — меры на !?, причем к {X) < + оо. Доказать,
что функция v : = |х — Я есть заряд на &.
ТЕОРЕМА 1. Пусть (X, 9~) — измеримое простран-
пространство и v — заряд на 3~. Тогда
где Х_:=Х\Х+.
Представление пространства X — Х_ U Х+ называ-
называется разложением Хана пространства X относительно за-
заряда V.
\> I. Множество Р ? & назовем положительным, если
\/АаР, А^Я : у(Л)>0.
Множество N ? & назовем отрицательным, если
У AdN, A?&' : v(il)<0.
Сначала докажем, что
siA(z3', у(Л)<+оо ЗЛ^— отрицательное, Ncz
czA : E.1)
Для этого установим, что
Ve>0 3 Лс=Л, Ае?& : E.2)
vD)<v(i) и VBc Л8, BG^" : v(fi)<e.
Действительно, если для числа е > 0 такого Ае не
существует, то множество А не годится в качестве Ag
и потому
42

Далее, множество А \ Bt с v (A \ Bt) = v (Л) —
— v (Bj) < v (Л) также не годится в качестве Лв, а по-
потому
3B2czA\B1, B^W : v(B2)>e
и т. д. Получим последовательность {Вп : п 1> 1} cz
cz &~, удовлетворяющую условиям Bt (] Bt = 0, i Ф j.
оо
Тогда для множества В : = [} В„ cz A
v(B)=f v(Bn) = + oo,
что невозможно, поскольку v (А) < + оо. Таким оора-
зом, утверждение E.2) выполнено.
При каждом п~^\ пусть Ап: = A i — множество
п
из E.2), соответствующее е = —, причем Ап =э Ап+\-
Тогда для множества
в силу непрерывности заряда v сверху и по построению
множеств Ап, п ^ 1, имеем
v (N) = lim v (Л„) < v (Л);
= v( П (В П Л„))= lim v(fl П i4B)<lim-j- = 0.
\n=l / n-юо п-юо '
Тем самым утверждение E.1) доказано.
II. Пусть
a:=ini{v(A) | А?&}^0.
Согласно определению величины а
l{Nn : п>1|<=^ : v(Nn)-+a, п-+оо.
В силу утверждения E.1) можно предполагать, что при
каждом п ]> 1 множество М„ отрицательное. Множество
А'_: ¦-= U Nn
43

также отрицательное в силу счетной аддитивности v.
Кроме того, для каждого п ^ 1 имеем
v (Л_) = v (Х_ П Nn) + v (Х- П #„) <
Поскольку v (Nn) -v а, п -> оо, то v (X_) s^ а. Таким
образом,
() , —оо.
Множество
Х+ : = X \ Х_ положительно. Действительно, если
ЭВб2~, 8сХ+ : v(fi)<0,
то
v(Л_ U В) = v(X_) + v(В)<а,
последнее невозможно согласно определению числа a. <j
Упражнение
3. Разложение Хана не является единственным. Пусть
X = Х_ U X,, X = Х_ (J X , — два разложения Хана про'
странства X относительно заряда v. Доказать, что
VA?F : v(X'_ П A) =v(Xln A),
v (Х^_ П А) = v (Х^ П Л).
5.2. РАЗЛОЖЕНИЕ ЖОРДАНА
Следующее утверждение представляет собой далеко
идущее обобщение теоремы Жордана о представлении
функции ограниченной вариации в виде разности моно-
монотонно неубывающих функций.
ТЕОРЕМА 2. Пусть (X, %) — измеримое пространство
и v —заряд на 3'. Тогда существуют конечная мера v_ и
мера v+ на 5" такие, что
УЛб?" : v(A) = v+(A) — v_D). E.3)
При этом v+ конечна (а-конечна), если заряд v конечен
(а-конечен).
Замечание. Представление E,3) называется разложением Жор-
Жордана заряда v.
44

\> Пусть X = X_ U X+ — разложение Хана про-
пространства X относительно заряда v. Функции
v_(i4): = -v(X_n A), v+(,4):=v(X+n A); A^W
являются мерами на $" и
Определение 2. Пусть для заряда умеры v_> v_j_ — из
доказательства теоремы 2. Мера
I v |: = v_ + v+
называется полной вариацией заряда v.
Упражнение
4. Пусть v_, v+ — меры из доказательства теоремы 2. Доказать,
что
v_(A) = — im (v(B) | В^ЗГ, В а А);
v+ (A) = sup {v (B) |
6. ИЗМЕРИМЫЕ ОТОБРАЖЕНИЯ И ФУНКЦИИ
6.1. ИЗМЕРИМЫЕ ОТОБРАЖЕНИЯ, ПРИМЕРЫ
Сначала напомним некоторые факты, связанные с поня-
понятием отображения
Т : Х^Х',
где X, X' — некоторые множества.
Образом множества А а X при отображении Т назы-
называется множество
ТА:^{Тх | х^А), Т0: = 0.
Прообразом множества А' а X' при отображении
Т называется множество
Т-1А': = {х | Тх?А'), Г-'0: = 0.
Нужные в дальнейшем элементарные свойства обра-
образов и прообразов приводятся в упражнениях. Далее ш —
произвольное множество индексов.
Упражнения
1. Пусть для любого а ? со Аа с X. Доказать, что
U Aa)= U ТАа.
ае<в
45

2. Пусть для любого а ? со Аа а X'. Доказать, что
r~lULAa)~il»T~lAa'
Л АЛ- Л т-'4.
3. Пусть &' — о-алгебра подмножеств А". Доказать, что класс
Т-1Р': = {Т-1А' | А'?&'\
есть а-алгебра подмножеств X.
4. Пусть X = X' = » и ?' = f (R). Найти Т~1^' в следую-
следующих случаях:
(i) 7x = -cJ, -t€ R; (ii) Tx = \x\, x?R,
fiii) Tx*=\ : (iv) Tx = cosx, x?R.
Определение 1. Пусть (X, $"), (X', .9"') — измеримые
пространства и / : X -> X'. Отображение / называ-
называется & — ^"'-измеримым, если f~l (<f) c= <F, то есть если
В том случае, когда X' = R, .Т' = ЭЬ (R), J— ^"'-измери-
^"'-измеримое отображение / называется ^-измеримой функцией.
Упражнения
5. Пусть & = 2 . Доказать, что любое отображение / : X -*¦ X'
& — ^"'-измеримо.
6. Пусть & = {0, X). Какие функции ^"-измеримы?
7. Пусть \АХ Ап) ^Sr, At 0 Aj= 0, i Ф j;
n
U Ai = X; t(x):=x't, x ? A(, l<i<n,
1=1
где x\, ..., xn—фиксированные элементы из X'. Проверить, что
отображение / f — ^'-измеримо.
8. Описать класс ^-измеримых функций:
(j) $r = {0, А, А, А'), Лс X, А фиксировано;
(ii) Л = R, Г = {A U (- А) | Лс R);
(ш) & — аа(Н), где
(iv) A = R, & = аа (^>), где
46

^={(n, n+ 1] I n?Z} U {0};
(v) X=R, ^"= {AcR I Л± 1 = /!}; A±\ :={
(vi) X = R, ^" = aa (&>), где
^¦={(—oo,—5); [n, n+l), -5<n<4;
[5, +oo)} и {0};
(vii)X=R2, ,T = (AcR3 ! (xltx2)?A => (x2, л^) 6-4};
(viii) X = R2, ,T = (^cR! | (Jtp ^G-4 =>
=> V {m, /iKZ2 : (xl + m,xi + ri)?A);
(ix)X = R2, F=(AcR2 | («!, a:2) 6 A =>
=> V(« «)?R2 и+« =
(x)X = R2, ^" = аа(^), где
&>= {[m, m+\) X [n, n+l) | (m, n) e Z2} (J {0}.
Замечание. Аналогичным понятию измеримости из определения
1 способом описываются непрерывные отображения. Именно, пусть
(-К> W)> Wt W) — топологические пространства. Тогда
/еС(Х, X') о Г1 (Т')аТ.
9. Пусть (X, 9~) — измеримое пространство такое, для которо-
которого любая ^-измеримая функция принимает конечное число различ-
различных значений. Доказать, что о-алгебра У состоит из конечного чис-
числа множеств.
6.2. ОДНО УСЛОВИЕ ИЗМЕРИМОСТИ
ТЕОРЕМА 1. Пусть (X, &"), (X', &') — измеримые
пространства, причем
&' = оа(Н), На 2х'.
Отображение/ : X -> X' является *3- —^"'-измеримым
тогда и только тогда, когда /"' (Я) с= W, то есть
VA'?H : /-'(Л')е^.
^Необходимость условия теоремы 1 очевидна.
Достаточность. Пусть /"' (Я) с: 5". Рас-
Рассмотрим класс
Тогда Я с= Q a <F' = аа (Я). Докажем, что класс Q
есть а-алгебра. Действительно, 3 — а-алгебра и потому
0GQ, так как /-'@) = 0 € 5";
X'GQ, так как /-• (X') = Х^$\
47

\A', B-\d Q^> (A'\B')?Q, так как
/-¦ (A'\ в') = /-< (Л') \ /-• (В') es\
Аналогично, если {Л„ : n>l}c:Q, то U Лп ? Q,
так как
Г' U Л„)= U
\п=1 л=1
Следовательно, аа (Я) с Q а оа (Я) и Q = $*'. <j
СЛЕДСТВИЕ 1. Пусть (X, #") — измеримое простран-
пространство и / : X ->- R. Следующие утверждения эквива-
эквивалентны:
A) функция / является #"-измеримой;
B)VaGR : /-'((- oo, a)) = {х?Х | /(д:)<а}^;
C)Va€R : /-'((-°°. «1) = U€ X
D)VaGR : /-' ((а, + оо)) = {х?Х
E)Va?R : /-' ([а, + с»)) = {д^Х
|> Доказательство следует из теоремы 1 для X' = R,
Sr' = 33 (R) и соотношений
#(R) = aa({(—oo, a) | a€R}) =
= аа ({(—oo, a] | a?R}) = oa{{(a, + <х>) \ a?R)) =
= аа ({[а,+ оо) | a^R})- <|
Упражнения
10. Функция / ^"-измерима. Доказать, что
При помощи утверждения упражнения 12 п. 4 доказать, что обратное
утверждение неверно.
11. Доказать, что функция f= \A ^-измерима тогда и только
тогда, когда А 6 ^.
12. Для функции / : X -*¦ R положим
О, /(*)>0; f+{X):'~ { 0,
Доказать, что для ^"-измеримой функции / функции Д_ и /+ ^-изме-
^-измеримы.
13. Доказать, что для ^"-измеримой функции / функция
Ь, х : f(x)>b:
а, х : f (x)<a, a <b,
также ^-измерима,
48

14. Пусть X = X' = Z, Ж = Т' = аа (Н), где
Я= {{?}, {2ш, 2ш+ 1} | <seZ
Проверить, что функция / (га) = га + 2, n ? Z имеет обратную /~',
причем f является У—^'-измеримой, a f~l не является 5*"'—^-из-
5*"'—^-измеримой.
Замечание. В ряде случаев удобно рассматривать функции /,
определенные на X и принимающие кроме значений из R значения
+со или —оо, то есть функции
/ : X-*-R, R: = R U { —°°. +°°)-
В этом случае класс
_ nalt by), (а2, Ь2\, I —оо<а,-<^< + с
"~t[fls, Ь3], [fl4, bt) | 1= 1, 2, 3, 4
есть полуалгебра, а
_ (Л, /1 П {— оо), А И {+со}, )
&<*>=/,,, . , Резеда •
Ы U { — схз, -boo} J
Функция /: X -*¦ R является ^"—^ (Й)-измеримой тогда и только
тогда, когда одно из четырех включений B) — E) из следствия 1 вы-
выполняется для каждого a g R.
6.3. БОРЕЛЕВСКИЕ ФУНКЦИИ. ФУНКЦИИ,
ИЗМЕРИМЫЕ ПО ЛЕБЕГУ
Определение 2. Пусть Y — метрическое пространство,
& = j3 (У) — а-алгебра борелевских множеств, м (Y) —
измеримая функция /: Y ->- R называется борелев-
ской.
Упражнения
15. Пусть X = R. Доказать, что функции из класса С (R) яв-
являются борелевскими. Аналогично для X = Rm, т € N функции из
С (Rm) — борелевские.
16. Пусть X = [а, Ь]. Доказать, что функции из класса С ([а,
Ь]) — борелевские. Аналогично, если X ? j§ (R) и / ? С (X), то / —
борелевская.
17. Пусть X = R или X = (а, Ь]. Доказать, что монотонная
на X функция является борелевской.
Определение 3. Пусть Sm — а-алгебра измеримых по
Лебегу подмножеств Rm, т ? N; X ? Sm. 5т-измеримая
функция /: X -*¦ R называется измеримой по Лебегу.
49

Упражнения
18. Пусть X ? 58 СО- Проверить, что борелевская функция /:
X -*¦ R измерима по Лебегу.
19. Множество всех точек разрыва функции /: [а, Ь] -*¦ R имеет
меру Лебега 0. Доказать, что / измерима по Лебегу.
6.4. СУПЕРПОЗИЦИЯ ИЗМЕРИМЫХ ОТОБРАЖЕНИЙ
ТЕОРЕМА 2. Пусть (X, W), (X', &'), (X", Г") — из-
измеримые пространства, отображение/: Х-*-Х' W—<F'-
измеримо и отображение g: X' -*• X" cF'—cF"'-измери-
cF'—cF"'-измеримо. Тогда отображение g (/): X -> X" &—?Г^'-изме-
&—?Г^'-измеримо.
|> Пусть А" ? <F", согласно условию теоремы 2, имеем
А': = g-1 (Л") ? &'• Поэтому с учетом 5"—^"'-измери-
5"—^"'-измеримости /
(A"): = {x?
СЛЕДСТВИЕ 2. Пусть (X, <Г) — измеримое простран-
пространство, для каждого i ? {A, 2, ..., /п} функция fc: X -*¦
-у R ^"-измерима, множество А ? 3$ (Rm) такое, что
и F: Л -*¦ R — борелевская функция. Тогда функция
r. /„): X^R
^"-измерима.
\> Применим теорему 2 к измеримым пространствам
и отображениям
Докажем, что отображение ф ^* — В (Rm) — изме-
измеримо. Поскольку
т
П(-оо,ак) | ak?R, l<
U=i
50

то, согласно теореме 1, достаточно доказать, что
=i
Однако последнее включение имеет место, так как
Ф-' (Д (_ оо, ak) J = {* ? X \ (П(х), ..., 1п (х)) ?
m
}
€П(_оо,а,) = Л {
Согласно теореме 2 отображение
F(q>) = F{ft L)
3" — ИВ (Й)-измеримо. <)
Упражнения
20. Пусть /, g; R -*¦ R — борелевские функции. Доказать,
что функция g (/) — борелевская.
21. Функции /, g: N -*¦ R таковы, что
Г1 (SSffDcr1 (®(R)).
Доказать, что существует борелевская функция F: R -*¦ R такая,
что I (x)= F (g (х)), x?N.
Замечание к следствию 2. Известно, что для функции F, изме-
измеримой по Лебегу, и даже непрерывных flt ..., fm для X = R, ^" = S
суперпозиция F (ft, ..., /m) не обязательно измерима по Лебегу |1],
гл. IV, § 19.
6.5. СВОЙСТВА ИЗМЕРИМЫХ ФУНКЦИЙ
ТЕОРЕМА 3. Пусть (X, &) — измеримое простран-
пространство и f(: X -*¦ R, i = 1, 2, ^"-измеримые функции.
Тогда .^"-измеримы следующие функции:
c/i(ceR). /i +/2. h — h, fi ¦ /2. min(/1; /2),
max(/lf/,), -^-
^Доказательство получается с помощью следствия 2,
которое нужно применить к следующим значениям т
и борелевским функциям F на R'n
т=\, F(Mj) = cui, m = 2, F(uv u2) = их + и2,
F(«!, и2) = ых — «2, Z7 («х, г/2) = «1 ' «2.
51

F («p иг) = min («!, и2), F (иг, иг) = max (uv u2);
m=l, F(ul) = -^-, F(u1) = \ul\. <j
Упражнения
22. Доказать, что любая ^-измеримая функция может быть
представлена в виде разности двух неотрицательных ^"-измеримых
функций.
23. Пусть / ? BV ([а, Ь\). Доказать, что / борелевская функция.
24. Пусть fug — ^"-измеримые функции. Доказать, что мно-
множества
{х?Х | J{li) > g (x)}, (х?Х | [/ (х) -j-g (x)] = 1}
принадлежат ^",
TEOPEIWA 4. Пусть (X, <?) — измеримое простран-
пространство и fn: X -*¦ R, п ^ 1 — последовательность Я- -
измеримых функций. Тогда ^-измеримы следующие
функции:
gx (х): = sup fn (x), g2 (x): = inf /„ (х),
g3(x):= \hnfn(x), gt{x):= \imfn(x); x^X.
В частности, функция
/W:= lim/„(*), x^X,
если предел существует наХ, ^"-измерима, а множество
г- =1Х с у
у р
последовательность {/„ {х) : п > 1 )\г<г
сходится к некоторому числу из RJ^ '
1
Воспользуемся следствием 1.
a}= П {д: | /,W<
II. Va?R i {л; | g2(x)<a} =
= {x | inf/nW<fl}= U {x | /nW<}
III. g3(x) = inf sup/*(•«). g-4W = supinf fk(x),
IV. С={л: | ftW = g4W, \g,(x) K + o
52

Упражнения
25. Доказать, что
С= П U Г) U I 1Ы*)-//МК— }•
и=| т=1 *,/=т ( П )
26. Доказать, что сумма сходящегося поточечно иа X ряда нз
^"-измеримых конечных функций есть ^"-измеримая конечная
функция.
27. Доказать, что сумма ряда из неотрицательных ^"-измери-
^"-измеримых функций есть ^-измеримая функция со значениями в R.
28. Пусть fn : R -»• R, п ^ 1 — последовательность борелев-
ских функций, а / — поточечный на R предел этой последовательно-
последовательности. Доказать, что / — борелевская функция.
29. Для функции /: R ->¦ R на R существует производная /'.
Доказать, что /' — борелевская функция. Аналогично, если функ-
функция /: (а, Ь) -*¦ R имеет в точках (а, Ь) производную /', то /' — бо-
борелевская функция.
30. Пусть (X, &~) — измеримое пространство, {Ап : п 23= 1} с
с &, причем Аг U A2 U ••• = X. Предположим, что для функции
/: X -* R при каждом п ^ 1 функция / • 1А 5^-измерима. Дока-
п
зать, что / ^"-измерима.
31. Пусть (X, &) — измеримое пространство и Е — всюду плот-
плотное на R подмножество R. Доказать, что /: X -*¦ R ^"-измерима
о V а 6 ? : {х I / (х) < а] 6 &.
6.6. КРИТЕРИЙ ИЗМЕРИМОСТИ
В ТЕРМИНАХ ПРОСТЫХ ФУНКЦИЙ
Пусть (X, 9") — измеримое пространство.
Определение 4. Функция /: X -*¦ R называется про-
простой, если множество / (X) состоит из конечного числа
чисел, то есть если
3«€N 3{A4} с 2* АПА 0 1Фи
t: = X Э [<h, ... , о»} cz Ri
Замечание. Если \А1 ..., Ап] с ^", то простая функция / ^"»
измерима.
Упражнение
32. Доказать, что сумма и произведение простых функций так-
также простые функции.
ТЕОРЕМА 5. Пусть (X, &) — измеримое пространство
и /: X -*¦ [0, +о°] — неотрицательная функция. Функ-
53

ция f ^"-измерима тогда и только тогда, когда существует
монотонно неубывающая последовательность простых
неотрицательных ^"-измеримых функций, поточечно на
X сходящаяся к /.
|> Достаточ ность следует из теоремы 4.
Необходимость. Предположим, что функция
/ ^"-измерима. Рассмотрим множества
, 1,2 п2"-1}:
При каждом п ^ 1 множества
An, 0<*<n2n—1; Вп
попарно не пересекаются и
U А*п[)Вп = Х.
Введем функцию
п2п—1
которая неотрицательна, ^-измерима и простая.
Покажем, что последовательность {gn : п ^ 1}
удовлетворяет требованию теоремы 5. Сначала проверим,
что
Пусть п ^ 1 фиксировано. Если х ? Л* для некоторого
k, то
и, следовательно, согласно определению gn и Jfn+i, имеем
Ik
х ? Alk4.i
2n+l , х
откуда gn (x) ^ gn+l (х). Если же х ? Вп, то
(n+lJ"+'-I k
54

и потому
( k
гс+1, х?Вп+и
откуда gn (x) ^ gn+\ (x).
Докажем теперь, что последовательность {gn : п^
> 1} сходится к / поточечно на X. Если для значения
х f (х) = +оо, то
п=\
Рассмотрим теперь значение х с / (х) <С +°о. Тогда
СЛЕДСТВИЕ 3. Функция /: X -> R" ^"-измерима
тогда и только тогда, когда существует последователь-
последовательность простых ^-измеримых функций, поточечно на X
сходящаяся к /.
Упражнение
33. Предположим, что для функции / из теоремы 5
sup / < + оо.
X
Доказать, что
sup \f(x) — gn(x)\-*-0, п -еоо.
6.7. ЭКВИВАЛЕНТНЫЕ ФУНКЦИИ
Пусть (X, $, к) — пространство с мерой.
Определение 5. Пусть Р — некоторое свойство такое,
что каждый элемент х ? X либо обладает свойством Р,
либо не обладает свойством Р. Свойство Р выполнено
55

почти всюду относительно меры К на X, если
{х?Х | Р(х) не выполняется} ?#" и
к({х?Х | Р(х) не выполняется}) = 0.
Обозначение: Р (х) (mod к) или Р (х) п. в. X на X.
Примеры
1. X = R, &" = S,k — мера Лебега. Свойство Р выполнено для
х ? R о х е (R \ Q). Тогда
xg (R\Q) (mocU),
так как
X({*€R | *e(R\Q)})=MQ)=0.
2. X = R, 9~ = S, к — мера Лебега, / = 1Q.
Тогда
lQ(x) =0 (mod к).
3. В ситуации примера 2 пусть
+оо, х? {пп | «6ZJ.
Тогда
/ (х) конечна п. в. к на R.
Определение 6. Пусть А ?<Г и f,g: Л-vR. Функции
f и g называются эквивалентными относительно меры X
на А (эквивалентными, если ясно, о каких множестве
А и мере к идет речь), если
Обозначение: f (x) — g (х) п. в. X на А, или / =
= g (mod X), или / ~ g.
Упражнения
34. Рассмотрим пространство (R, S, к) из примера 1. Какое из
следующих утверждений верно: (a) 1q п. в. к на R непрерывна, (б)
lq равна п. в. к на R непрерывной на R функции?
35. Доказать, что для любой измеримой по Лебегу функции /
существует борелевская функция g такая, что / ~ g.
36. Пусть при каждом п 2з= 1 функция jn = 0 п. в. к на X. Рас-
Рассмотрим функции
оо
gl (х) : = sup /„ (х), е2 (*) : = inf fn (x), g3 (x) = У n2fn (x).
п>\ i>i „=1
Доказать, что g, = 0 (mod A), i = 1, 2, 3.
56

ТЕОРЕМА 6. Пусть (X, 3', X) — пространство с пол-
полной мерой, А 6 #". Предположим, что функция f: A -»-
-¦*¦ R ^"-измерима, а функция g: A -> R такова, что
/ = g (mod к). Тогда g ^"-измерима.
^ Для любого а ? R имеем
U
. А
Упражнение
37. Пусть {/, j(cC(R)h/ (х) = g (х) п. в. Я на R, I — мера
Лебега на R. Доказать, что / (х) = g (x), x ? R. Доказать также, что
функция h п. в. X, непрерывная на R, измерима по Лебегу.
6.8. СХОДИМОСТЬ ПОЧТИ ВСЮДУ
Пусть (X, &, X) — пространство с мерой.
Определение 7. Пусть/, fn: X -*¦ R, п > 1 — некото-
некоторые функции. Последовательность функций {/„ : п ^
]> 1} сходится почти всюду относительно меры X на X
к функции /, если
\ А,(Ф) = 0 1 Ух?Х\Ф l\mfa(x) =
п-*оо
Обозначение: /„->-/ п. в. Я, на X или /„ -*¦ f (mod Я,).
Упражнение
38. Доказать, что
fn-+f (mod к) и fn->-g (modX) => /=g(mo<U).
ТЕОРЕМА 7. Пусть (X, S-", X) — пространство с пол-
полной мерой, /, /„: X -> R, п > 1 — последовательность
#"-измеримых функций и /„ -> / (mod Я,). Тогда функция
/ — ^"-измерима.
\> Пусть Ф g F", X (Ф) = 0 и
57

Тогда функция /: X \ Ф -*- R-измерима согласно тео-
теореме 4. Функция /: Ф -v R ^"-измерима в силу пол-
полноты меры X. <)
Упражнение
39. Доказать, что fn -*¦ f (mod к), причем /: X-*R, тогда и
только тогда, когда {/„ : п > 1} — фундаментальна почти всюду
относительно меры К иа X, то есть
Э Ф е :Г, X (Ф) = О У*6*\Ф Ve>0,
: | fm (x) — fn (x) | < e.
ТЕОРЕМА 8 (Д. Ф. Егорова). Пусть (X, 3, к) — про-
пространство с мерой, причем К (X) < + оо;/,/„: X ->- R,
л ^ 1 — ^"-измеримые функции и /„->-/ п. в. Я, на X.
Тогда
Ve>0 3As?ST, Х(АЕ)<в i
(*) —/(*)!-»-О,
sup
6^л
оо.
(> Пусть Ф б
\/х?Х\Ф
Для каждых /
", Я, (Ф) = 0 и
fn{x)-+f(x), «-voo
1, fe^ 1 рассмотрим множество
H
При каждом & ^ 1 имеем
•Следовательно,
Л Е,к с Ф.
Отсюда с учетом условия теоремы 8 и согласно теореме
о непрерывности меры сверху
/=1
Пусть теперь е >» 0 задано. Из последнего равенства
имеем
к
V k > 1 3 / (к, е) 1 \ (Ецц,в),и) < ~Т •
58

Рассмотрим множество
для которого согласно а-полуаддитивности
Если д; ? X \ Ае, то
*€ Л ?/(*.е).* =>
sup iLw-zwK sup i/nw-/wi<4-.
/»>/(*, e). <j
Упражнения
40. Доказать, что теорема 8 верна для функций /, /„, п > 1, каж-
каждая из которых п. в. X на X конечна.
41. Проверить, что условие X (X) <С +оо в теореме 8 сущест-
существенно. Пример: X = R, & = S, X — мера Лебега и / (х) = 0;
/и (*)=¦>;„.+»,(*), *6R. «>1.
42. Пусть X = R, & — S, X — мера Лебега. Доказать, что по-
последовательности
a) fn (х) = ехр (—n sin2 пх), х ? R; п > 1; б) fn (х) = sin" (х3 —
— пх), х 6 R; « > 1
сходятся почти всюду на R, и найти предельные функции.
43. Пусть / — ^"-измеримая функция такая, что
Va>0 : ХЦхеХ \ |/(*)|>а}) =0.
Доказать, что / = 0 п. в. X на X.
Указание.
| ц)} и
44. Пусть X (X) < -{- оо и /, /n, n ^ 1 — конечные и ^"-измери-
^"-измеримые функции. Доказать утверждение
/„ -> / (mod X) о
oVe>0 : x(\J {х \ |/t W-/W |>е})-*0, в-*оо.
Указание. Рассмотреть множество
U Л U I* I I//W-/WI>4*
A=l n=\ i*=n \ К )
59

45. При условиях упражнения 44 доказать, что
оо
п=\
-*¦ f (mod X).
46*. Пусть X (X) < -I-00 и fn, п 2з= 1 — конечные ^"-измери-
^"-измеримые функции, удовлетворяющие условию: существует последова-
последовательность {е„ > 0 : «> 1}, для которой
+
4=1 П=1
Доказать, что /„ -»¦ / (mod X), где / — некоторая ^-измеримая ко-
конечная функция.
47**. Пусть X=R, &~=SuX— мера Лебега. Доказать, что
любая измеримая по Лебегу функция на R является пределом почти
всюду на R последовательности непрерывных на R функций.
6.9. СХОДИМОСТЬ ПО МЕРЕ
Пусть (X, #", X) — пространство с мерой.
Определение 8. Пусть функции /, /„: X -> R, п. !>
]> 1 — #"-измеримы. Последовательность функций
г{/„ : п ^ 1} сходится по мере А, к функции /, если
Ve>0 j X({x?X | |/
П—>• оо.
Обозначение: /„—->/ или Я lim /„ = /.
ТЕОРЕМА 9. Если /„ -- / и /„ --» g, то / = g (mod л).
|> I. Сначала имеем для любого п ^ 1
Ve>0 ! 1({х | |/(*)
При этом использована полуаддитивность X и включение
)-Ш\>-±-\ U

II. Поскольку
то с учетом части 1 доказательства и а-полуаддитивности X
4U I f(x)?=g(x)}) = 0. <\
Примеры
1. Из сходимости по мере не обязательно следует сходимость
почти всюду (и даже сходимость в какой-нибудь одной фиксирован-
фиксированной точке). Пусть X = [О, 1], !F = S — а-алгебра подмножеств
[О, 1], измеримых по Лебегу, и Я — мера Лебега. Рассмотрим функ-
функции
fl = '[O.I], h = *L0,2—4* ^3 = ![2-1,1]' ¦ • ' ' h '
'2*+1 [2—*,2.2—*]' ' ' ' ' '2*+'—1 [B
/М=0, ^610, 1].
Тогда для 0 < 8 < 1
где й определяется из неравенств
2*<и<2*+', F.1)
причем k -*¦ оо при и -»• со. Следовательно, /п > /.
Пусть х g [0, 1] фиксировано и число п > 1 задано. Для k, оп-
определяемого неравенствами F.1), определим натуральное т так,
чтобы
™<X<-?L^±-, F.2)
при этом 0 ^ т < 2* — 1 (при m = 2* — 1 второе неравенство в
F.2) нужно заменить на <). Тогда
Следовательно, последовательность {/„ (л;) : п > 1} предела
имеет
имеет.
имеет.
2. Из сходимости почти всюду относительно меры Я не следует
сходимость по мере к. Пусть X = R, ^ = S пХ — мера Лебега иа
S. Рассмотрим функции
fn (х) = \n,+oo) (x),n>\; f (х) = 0, хе R.
Тогда
У«>л; : /„ (х) = 0 => fn (х) ->- 0, я -* оо,
61

Однако для любого е > 0 и любого я > t
I \fn(x)—f(x)\>s))=+oo.
Упражнение
48. Пусть fn —> f и gn —> g. Доказать, что:
a) I /„ I --> I /1; 6) fn±gn--+f± g; в) (fn)+ L- (/+); г) | f\
< h (mod А.), если | /n | < h (mod X), n > 1.
ТЕОРЕМА 10 (А. Лебега). Пусть функции /, /„: X
R, n > 1 — ^"-измеримы и ?i (X) < +oo. Тогда
заданного е > 0 при каждом п > 1 рассмотрим
множества
n:= U
5:= П Bn.
n=l
По условию Я, (Б) = 0, а по теореме о непрерывности
меры сверху
Я,E)= НтК(Вп).
П-*ео
Счедовательно,
Нш^(Л„Х lim Я, (В„) = 0. <j
rt-*oo fl-юо
Упражнения
49. Пусть X = R, F = 5, Я — мера Лебега и /„ -»• / (mod A,).
Доказать, что
Ve>0 Va>0 : Я ({л:6[— а, а\ | | /„ (х) —
—/WI>8})>0, п->оо.
50. Проверить, что теорема 10 остается верной и для функций /,
/„: X -*¦ R, и > 1, каждая из которых почти всюду относительно Я,
на X конечна.
Определение 9. Пусть /„: X ->R, п ^ I, ^"-измери-
^"-измеримые функции. Последовательность функций {/„ : п. ^
^г 1} называется фундаментальной по мере Я,, если
Ve>0 V6>0 3N Vtn^N Vn^N i
ЬЦх?Х I |/n(*)--/„(*) I>е})<в.

Замечание. Если fn —> /, то последовательность {fn : п ^ 1}
фундаментальна по мере Я. Действительно, для любых е > 0, т ^ 1,
п 5* 1 справедливо включение
* I I /m W — /n \X) | ^ Sf —• jx | | /m (¦«) — / \X) -f
и
U {* I \f(x)-fn (x) \>-Y\>
откуда с помощью полуаддитивности X имеем
М{* I \fm(x) — fn Wl>8}) <
l/n(*)_f(x)l>_L
ТЕОРЕМА П. Пусть \fn : «> 1} — фундамен-
фундаментальная по мере К последовательность функций. Тогда
существуют подпоследовательность \fnW : k^l) и
^"-измеримая функция /: X -*- R такие, что
Согласно определению 9
Пусть
«A):
я C): = max (я B)+ 1, ^C)), ...
При каждом k ? N рассмотрим множества
для которых имеем с учетом а-полуаддитивности А,
63

Поэтому для множества
Ф: = П Вк
k=i
в силу теоремы о непрерывности меры сверху получим
Я,(Ф)= 1и
fc-t-o
Пусть элемент х ? Ф. Тогда существует v ? N такое,
что
x?Bv => х$Ъу => х? П А/ 5>
=^> V/>V
Следовательно, последовательность {/ч(*> (х) : k ^ 1}
фундаментальна и, согласно критерию Коши,
Положим также для лг^Ф / (я) : = 0. Получим
^-измеримую функцию /: X -*¦ R, для которой
-/(mod Я,).
Пусть е > 0 задано. Зафиксируем m?N такое, что
2~m+l < е. При этом в силу монотонности меры
Докажем, что
i {* | |/п(*,(*)-/(*)|>-^Ь-}с:В„.
F.1)
Действительно, если х ^ Б„„ то
, ^> V,>m i |
Д- ^» V/>/n
П А,
/тл WKS.
64

Поэтому
I/(*)-/*/>(*) I <-^=Г.
следовательно, х не входит в левую часть F.1) Тем самым
включение F.1) доказано. Теперь имеем
Таким образом, для подпоследовательности
{U(k) • Л > 1} утверждения A) и B) теоремы 11 вы-
выполнены. <j
СЛЕДСТВИЕ 4 (Ф. Рисса). Пусть /„ -- /. Тогда су-
существует подпоследовательность \fn(k) '. k ^> 1} та-
такая, что
l,nk) -> / (mod I).
Упражнения
51. Пусть fn —> / и /„ -*¦ g (mod Я). Доказать, что f—g (mod X).
52. Пусть (X, &, к) — пространство с мерой, Я (X) < +со. До-
Доказать, что сходимость fn —> / равносильна условию: каждая под-
подпоследовательность последовательности {fn : п > 1} содержит в
себе подпоследовательность, которая сходится к / почти всюду отно-
относительно меры %.
53. Пусть при условиях упражнения 52 /„ —> / и g: К -*¦ R
^"-измеримая функция. Доказать, что
Stn^ gf-
54. Пусть при условиях упражнения 52 /„ —> /, gn —> g. До-
Доказать, что
(a) f2n Л^ 1\ (б) fngn -^ fg.
55. Пусть ]п -*• / (mod к). Доказать, что
sin/n->-sin/ (mod X).
Если /„ —> /, то сходимость
sin fn -L» sin /
не обязательна. Последняя сходимость имеет место, если предполо-
предположить, что к (X) < +со. Доказать эти утверждения,
3 8-1569 65

СЛЕДСТВИЕ 5 (критерий сходимости по мере).
Пусть /„: X -v R, п ^ 1, #"-измеримые функции. По-
Последовательность (/„ : п~^\\ сходится по мере X
тогда и только тогда, когда она фундаментальна по мере X.
^Необходимость была установлена в замеча-
замечании к определению 9.
Достаточность. Пусть {/„ : п > 1} — фун-
фундаментальная по мере последовательность. По теореме 11
существуют подпоследовательность \fnk) : k^l) и
.^-измеримая функция /: X ->- R такие, что /„<?> --> /.
Поэтому для заданных е > 0, б > О
В силу фундаментальности последовательности
: п> 1}
BN Vj>N Vk^zN ! к([х |
Тогда
V п > max (N, n (m)) i X({x | \fn{x) —
-§-})< 6,
где /г — какое-нибудь число, большее т. <|
Замечания. 1. Важное свойство измеримых функций было уста-
установлено Н. Лузиным. Пусть X = R, > = 5 и К — мера Лебега.
Для Л ? S пусть f: A -*¦ R, измеримая по Лебегу функция. Тогда
Ve>0 3S?S, kF)<e : /?С(^\В)-
Подробности см. в [8].
2. Определение 9 и последующие утверждения справедливы
для функций вида /: X -»• R ^"-измеримых и почти всюду относи-
относительно меры X конечных.
Упражнения
56. Функция /: [а, Ь] -*• R измерима по Лебегу и принимает
два значения. Доказать, что
Ve<0 ЗЛес[а, Ь\, X(Aj<n : / ? С ([а, Ь\ \ Ле)
(Я, — мера Лебега).
66

57. Пусть f, g, fn- X
чем fn-+ f (mod k): ' r, |
Ve>0 : > {* X
¦ R, n > I, ^"-измеримые функции, при-
приg (mod 1), л > I и
| g (x) > e
Доказать, что /„ — -» /.
6.10. ВЕРОЯТНОСТНАЯ ТЕРМИНОЛОГИЯ
Теория меры и интеграла есть математическая основа
современной теории вероятностей. При этом ряд введен-
введенных выше понятий называются отличными от приведен-
приведенных терминами. Приведем краткий указатель к основ-
основным терминам, подробности см. в 19].
1. Основное множество X
Пространство эле-
элементарных собы-
событий А'
— Элементарное со-
событие х ? X
— 1} — а-алгебра
случайных со-
быти й
— А ? & — случай-
случайное событие
— 0 — невозможное
событие
— X — вероятность
на 3
— Случайная вели-
величина I
— Последователь-
Последовательность случайных
величин {?„ : /г>
;> 1} сходится с
вероятностью 1
к случайной ве-
величине ?
— Последователь-
Последовательность случайных
величин{?„ : п >
^ 1) сходится по
вероятности
к случайной ве-
величине |
Большие циклы задач, посвященных понятиям схо-
сходимости с вероятностью 1 и по мере, а также обсуждению
их связи, содержит III раздел книги [10]. -
3* 67
2. Точка х ? X
3. 9" — о-алгебра подмно-
подмножеств X
4. А ? ^"-измеримое множество
5. 0 — пустое множество
6. К — мера на 3, к (X) = 1
7. ^-измеримая функция
Б: X ->R
8. Последовательность функ-
функций )?„ : л ^ 1; сходится
почти всюду к функции |
Последовательность функ-
функций {|„ : п. ;> 1} сходится
по мере к функции |

У п ра ж не н и я
58. Пусть а, Ь: X -*¦ R ^"-измеримые функции. Существу-
Существует ли .^"-измеримая функция /: X -*• R, удовлетворяющая соотно-
соотношению
1г (х) — 2а (х) f (х) — Ьг (х) = О, х ? X?
Описать все такие функции.
59. Пусть а: X -*¦ R ^"-измеримая функция. Доказать, что
существует ^-измеримая функция /: X -»¦ R, удовлетворяющая со-
соотношению
max (t exp (_ A + а2 (*)) <•)) = / (х) ехр (- (I + а* (х)) f (x)),
л: ex.
60. Пусть а: X -»• R ^-измеримая функция. Доказать, что
существует ^"-измеримая функция /: X -*¦ R, удовлетворяющая со-
соотношению
mm
<GR
61. Пусть (X, p) — метрическое пространство, G с: С (X),
йф 0 и
g (*) : = inf {/(х) | /€G}, ft(A:):=sup{^(A:)|/eGJ.
Доказать, что функции g к h борелевские.
7. АБСТРАКТНЫЙ ИНТЕГРАЛ ЛЕБЕГА
7.1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА
Пусть (X, &", X) — пространство с мерой. Далее ^"-из-
^"-измеримые функции называются измеримыми.
Определение 1. Функция р: X -v R называется прос-
простой, если множество значений р (X) — конечно.
Замечание. Пусть р — простая функция, для которой р (X) со-
состоит из различных чисел a1,ai, ..., ат. Рассмотрим множества
Aj: = {x?X | />(*)= а/}, 1</"</п.
Тогда
AiC]Aj=Z, 1ф]\ U Л< = Х. G.1)
(=1
Обратим также внимание на то, что сумма и произведение про-
простых функций есть простые функции.
68

Упражнения
1. Функция р из замечания к определению 1 ^"-измерима тогда
и только тогда, когда Л/ 6 &, 1 ^ / ^ т. Проверить это утвержде-
утверждение. Обратить внимание на то, что представление G.1) единственно.
2. Пусть X = R, &= S. Являются ли следующие функции
простыми (измеримыми по Лебегу):
а) />(*) = »q (*), *е R;
л=1
3. Пусть для
|г»Г_*_ .*+! v х^°> »•
"=0 [ 2п' 2"
Найти
lim р„(х), хе\О, 1).
Определение 2 (часть первая). Пусть р — не-
неотрицательная измеримая простая функция с представ-
представлением G.1) и А ? 3~. Интегралом Лебега от функции р
по множеству Л называется величина
с с т
pd\:= p(x)dl(x):= ? а/Х(А Л А,), G.2)
А А /=1
причем произведение aft (A [\ Aj) : — 0, если а,- — 0 и
X (А П Aj) = +оо и а;-А. (Л П ^у) : = +°°, если at > О
и Я (Л П Лу) = +оо.
Замечание. Величина G.2) удовлетворяет неравенствам
-оо.
[ pdk
4
Если X = R, ^ = S, X — мера Лебега, то
оо Г | 1
для В = U 2и, 2и + —- . Таким образом, значение + оо также
ч=1 L д J
возможно.
69

Упражнения
4. Пусть {А, В} с &. Доказать равенства
(a) С dX = Я (Л), (б) f I ,dX = Я (А),
X х
= Я(Л П В).
5. Пусть pt и р% — неотрицательные измеримые простые функ-
функции такие, что рг (х) < р2 (х), х ? X, Доказать, что
Указание. Для функций р± и р2 использовать представление G.1),
определение G.2) и аддитивность меры Я.
Определение 2 (часть вторая). Пусть А ? <F
и /: Л ->- R измеримая и неотрицательная на Л функ-
функция. Интегралом Лебега от функции / по множеству Л
называется величина
J fdX : = J / (х) dk (х): = sup J pdX, G.3)
где К (/) — класс всех неотрицательных простых измери-
измеримых функций р, удовлетворяющих неравенствам
О</>(*)</(*). х?А.
Замечание. Отметим, что
О< [ /ЙЯ< + со,
а также то, что для простой функции / величина G.3) совпадает с ве-
величиной G.2).
Пример. Пусть X = [О, I], ?" — а — алгебра измеримых по
Лебегу подмножеств [О, I] и Я—мера Лебега. Неотрицательная
функция / (х) = х, х? [О, I] непрерывна на [0, 1], следовательно,
является борелевской. Найдем интеграл
xdk (x).
[ОЛ]
При каждом п > 1 функция
п— i
Рп М := У —
70

является неотрицательной на [0, 1] измеримой по Лебегу простой
функцией, причем
*)<*, *6[0, 1], «>1;
1 п (л — 1) 1
X = Цг-5 "-ГГ ' Я-»-ОО.
л 2я2 2
Поэтому
1 xd"k (x) :— sup
Пусть р — произвольная функция из К (f), при этом
= S а/
т
А, П ^. = 0, 1Ф\, U Лу = [0, 1].
/=i
Поскольку при каждом /, 1^|Хти каждом п
то
причем а, < , если А/ П —, — ] Ф 0.
Поэтому
т
[0.1
<
71

Таким образом,
V р 6 К (/) : J рЛ < — .
[0.1]
Следовательно,
J лЛ (л:) = -у .
to.i]
Для множества А ? 3" и функции / : Л -> R введем
функции
/+ (л;) : = max (/(*), 0), f- (x): = - min (/ (*), 0), * 6 A.
Функции /+, /_ неотрицательны и
Кроме того, для измеримой функции / функции /_ и f+
также измеримы.
Определение 2 (часть третья). Пусть А ? Я" и
/: Л -> R — измеримая функция. Если хотя бы один
из интегралов
\ f+d%, I f-d% G.4)
А А
конечен, то величина
J fdk : = J / (х) dk (x): = J /+Л — J /_^ G.5)
называется интегралом Лебега от функции / по множе-
множеству А.
Если оба интеграла G.4) конечны, то функция / на-
называется интегрируемой по Лебегу по множеству А.
Обозначение:
f?L(A, X) о / — интегрируемая по Лебегу по
множеству А относительно меры X.
Замечание. Интегрируемые по Лебегу функции называются так-
также суммируемыми. Условимся также считать, что
[ fdk := 0.
0
Упражнение
6. Пусть X = N, & = 2N и Я, @) : = 0,
72

Проверить следующие утверждения:
(а) К — мера на &;
(б) любая функция /: N ->- R, то есть любая последовательность
{/(ft) : «> 1} действительных чисел, измерима;
<b)/6L(JV,X) о ? 1Ш1<+<Х>;
(г) для / 6 L (JV, X)
N "=1
<д) если для функции / ряд
_ п
сходится условно, то / ? L (N, Я.).
7.2. ЭЛЕМЕНТАРНЫЕ СВОЙСТВА ИНТЕГРАЛА ЛЕБЕГА
Г. Если Л ? #", А, (Л) = 0 и функция / измерима,
то
J fdX = 0,
поскольку
2°. Пусть Л ? #*, Я (Л) < + со и функция / постоянна
на Л, то есть для некоторого числа C?R / (х) = С.
х?А. Тогда /6 L (А, X) и
J Cdl = О, (Л).
3°. Пусть Л ? ^* и измеримые функции /, g: Л ->- R
удовлетворяют условию 0 ^ / (х) ^ g (х)> х ? А. Если
(ЛД/^(ЛД
А
|> Оба утверждения есть следствия определения 2 (часть
вторая) и включения /( (/) с: К (g)- <1
73

4°. Пусть А g W, А ф 0, к (А) < + оо, функция
: А -*¦ R — измерима и ограничена на Л. Тогда / ?
МЛ, Я) и
inf/- Я(Л)< ( M<sup/- Я (Л). G.6)
4 4
|> I. Сначала рассмотрим случай, когда f (х) ^* 0, х
? Л. Тогда m ^ / (х) <1 УИ, х ? Л, где
/и := inf/, М := sup/,
и согласно свойствам 2° и 3° имеем f ? L (А, к) и
fdk < j
4
откуда следует G.6).
II. Случай, когда функция принимает положитель-
положительные и отрицательные значения. Поскольку
V х?А : /_(х)<С, /+(*)< С,
где С : = sup | / |, то, согласно свойствам 2° и 3°, {/_,
А
f+) c= L (А, к), следовательно, интегралы из G.4) конеч-
конечны и / ? L (А, X). Кроме того, поскольку
то
О < j f+dX < MX (A), 0 < j f-dX < (— т) X (Л),
А А
— j f_dk < J /+Л — J /_dA, < J f+dX
III. В том случае, когда / (х) ^ 0, х ? A f = —/_ и
J fdk = - j /_rfA,.
4 4
Нужное неравенство теперь получается из Г. <i
5°. Пусть / ? L (Л, А,) и с 6 R. Тогда
(cf)?L(A,k) и
74

|> I. Утверждение очевидно при с — 0. Пусть с> 0
и f (х) >0, х? А. Тогда
p^Kicf) о -f € /С (/),
а потому для функции р ? К (с/) имеем
pdX = с j -^
А А
Следовательно,
Аналогично, если q ? К (J), то
Таким образом, равенство G.7) доказано.
II. Пусть с> 0. Тогда (с/)+ = cf+, (с/)_ = с/_ и,
согласно уже рассмотренному случаю 1,
J (с/) <R = J (с/)+ Л - J (c/)_ d^ = J (c/+) dl -
4 -4 /1 А
- f (с/_) Л = с f /+dX — с j /_dA, = с f /dA.
^1 4 4^
III. Пусть с<0. Тогда (с/)+ = (—с) /_, (с/)_ =
= (-с) /+ и
J (с/) Л = J (c/)+ dl - J (c/)_ rfX = (- с) f /_ dl -
Л Л d 4
J
А
6°. Пусть {/, g)cL (Л, Я) и / (х) < g (х), * 6 Л.
Тогда
3 А
75

J> Поскольку
О </+(*)<?+(*) <g
то, согласно свойству (З), имеем
у
j f+dl - J
А А
J JJ
откуда после сложения неравенств находим
А л
7°. Пусть Л?^, В cz А и В^^ги / — измеримая
и неотрицательная на Л функция. Тогда
j fdl < J
8°. Пусть f?L(A, к), В cz A. B?3~. Тогда
€ ? (Я, ^).
?> Действительно,
_,/+} czL(ЛД) ^>
Упражнения
7. Пусть (X, Т) — измеримое пространство, Х1 и Х2 — меры на
&, X = X.J + Я.2. Доказать, что
L (X, Я,) = L (X, Я-i) П /- (X, А2)
н для / g L (X, Я.) равенство
XXX
8. Пусть (X, &, X) — пространство с мерой, причем X (X) <
< +со и /2 ? L (X, X). Доказать, что {/, | / |} с: L (X, X) и неравен-
неравенство
Указание. Для функции р ? К (| / |) с представлением G.1) с
помощью иеравенства Коши доказать, что
Замечание. Аналогично доказывается, что из включения | / |
L (X, Я,) с р > 1 следует, что | / I € L (X, Я,) и
1 |р ей • X (Х)р~]
х \л I
76

7.3. СЧЕТНАЯ АДДИТИВНОСТЬ ИНТЕГРАЛА ЛЕБЕГА
Следующий факт играет фундаментальную роль в те-
теории интеграла Лебега. Он основан на счетной аддитив-
аддитивности меры, фигурирующей в определении интеграла,
и является источником эффективных общих предельных
теорем теории, которые, например, для интеграла Римана
не справедливы.
ТЕОРЕМА 1. Пусть / ?L(X, к). Тогда функция
А$дг
счетно аддитивна на F', то есть является зарядом.
\> Функция ц определена и конечна на <f в силу свой-
свойства 8° п. 7.2. Поскольку
то утверждение теоремы достаточно доказать для неотри-
неотрицательной функции /.
Пусть функция / измерима и неотрицательна на X,
+ оо, В?$г. G.8)
в
Рассмотрим произвольную последовательность (Л,
: п > 1} с= W,
At П А,= 0, 1Ф], А:= U Ап.
Если при некотором k ;> 1 ц {Ак) = + оо, то, со-
согласно определению 2 (часть вторая) интеграла, ц (А) =
= + оо и равенство
Е И(.) G.9)
п—1
выполнено.
Далее предполагаем, что ц (Ап) < + оо, п ^ 1. За-
Заметим теперь, что для простой измеримой и неотрицатель-
неотрицательной на X функции р с представлением G.1) функция
ЫА:=? а,к(В П
счетно аддитивна в силу счетной аддитивности меры Я,.
Поэтому с учетом определения 2 (части второй) для функ-
77

ции р ? К (Л имеем
Г v Г \" Г
a потому и
\ fdk^ V j /dX. G.10)
Пусть е > 0 задано. Согласно определению 2 (части
второй) существует функция р ? К (Л на Ах (J Л2 такая,
что
^, »=1, 2,
следовательно,
2к + j pdX + J pdk = 2e + J pdA, > j fdk + j
-4, A, 4,\JA, ¦ A.
2г + J fdk > J /dX + j /dX.
Поскольку e > 0 произвольно, то
j /dX > J /dX + j fdk.
Поэтому для любого п ^ 1 имеем
( /dX>? \fdk,
b— 1
а с учетом свойства 7°
A *=•
следовательно,
G.11)
Из неравенств G.10) и G.11) следует равенство G.9). ^
78

Замечание. При доказательстве теоремы 1 установлено, что для
измеримой и неотрицательной на X функции / функция (i есть мера,
эта мера кбнечна, если / ? L (X, X). При условиях теоремы 1 ц —
конечный заряд.
Упражнения
9. Определить меры ц+ и [i_ из разложения Жордана заряда ц
из теоремы 1.
10*. При условиях теоремы 1 доказать, что
V е > 0 Э S > 0 V А е Т, "к (А) < б : | ц (Л) | < в.
7.4. ДРУГИЕ СВОЙСТВА ИНТЕГРАЛА ЛЕБЕГА
Г. Пусть/ ? L (X, к) или /-измерима и неотрицательна
на X. Тогда
j /dX = J fdX + J fdk.
A\JB А В
\> Следствие теоремы 1. <\
2°. Пусть f?L(X, I), {An : п>1)сгГ — мо-
монотонная последовательность и Л ее предел. Тогда
J fdk = lim J fdk.
A "--°° An
\> Следствие теоремы 1 и теорем о непрерывности
меры. <^
3°. Интеграл Лебега не зависит от значений подын-
подынтегральной функции на множестве меры 0. Точнее, пусть
А ?&,
f : A-+R, f?L(A,k); Ф6ГД(Ф) = 0. Тогда
\fdk= J
1 4\Ф
?> Следствие аддитивности A) и свойства 1° п. 7.2. <)
4°. Пусть f ?L (А, к) и g = / (mod Я) на Л. Тогда
^(л, л) и
= J gdk.
A
5°. Пусть А?3" и /: Л-vR —измеримая функция.
Тогда
) о \f\?L(A,k).
79

Необходимость. Сначала заметим, что
J
А
Рассмотрим множества
| f(x)<0), A+:={x^A \ f(x)>0),
Согласно 1° и свойству 7° п. 7.2
4_
00.
Достаточность. Пусть \f\?L(A, Я,). По-
Поскольку на А
то, с учетом свойства C) п. 7.2,
-Л< + оо, U
А
следовательно, / ? L (А, Я.). <^
6°. Пусть / ? L {А, К), а функция g: A -> R измери-
измерима и удовлетворяет условию
Тогда g6LH, Я).
[> Следствие свойств 5° и 3° п. 7.2. •<
7°. Если / ? L (А,Х), то / конечна почти всюду относи-
относительно меры X на А.
\> Пусть для « :> 1
Согласно свойствам 7° и 2° п. 7.2 имеем
поэтому
80

Кроме того, множество
откуда
Таким образом, к (В) = 0. <J
8°. Пусть функция / ? L (Л, X) неотрицательна на А
и
J /ЯА, = 0.
Тогда / = 0 почти всюду относительно меры Я, на Л.
\> Для множества
имеем
0= J/dX> f fdk^z — X(An), n>l.
^ Л, "
Поэтому Я, (Л^ = 0, n ^ 1. Множество
0}cr U Л„,
для него в силу счетной полуаддитивности меры Я. полу-
получим
п=1
Упражнения
И. Пусть }?L(X, X) и
Доказать, что / = 0 почти всюду относительно меры Я. на X.
Указание. Проверить, что
С f_dk = \ f+dk = О,
х х
а затем использовать свойство 8°.
12*. Пусть 3е = аа (Я), причем множество X содержится в объе-
объединении счетного набора некоторых множеств из Н, f ? L (X, Я.) и
V А 6 Н : [ fd% = 0.
А
Доказать, что / = 0 (mod к).
81

Указание. Рассмотреть класс множеств
I
Используя теорему 1, доказать, что Q есть а-алгебра.
13. Пусть X = R, & = Sj, Я, — мера Лебега и / € L (R, Я) та-
такова, что
V {а, 6} с R, а < 6 : ( fdk = 0.
Доказать, что /= 0 (mod Я).
14. Пусть X = R2, & — 52 и Я, — двухмерная мера Лебега,
Я — множество всех треугольников в плоскости, а функция / ? L X
X (R2, Я,.г) такова, что
V А ? Я : \ /dA,, = 0.
Доказать, что / = 0 (mod Я2).
15. Пусть / б L (X, Я). Доказать, что множество
содержится в счетном объединении множеств из & конечной меры Я,.
16. Пусть / ? L (X, Я). Доказать, что
ап:=пк({х | |/(х) |>п})-»-0, п->-оо.
Указание. Заметить, что
\f\dX, Ап:={х | |/W|>n|; «>1.
кроме того, Л„ => Л/1+ , п^ 1. Использовать теорему 1 и свой-
свойство 7°.
17. Пусть X = R, & = Si, Я, — мера Лебега и / ? L (R, Я). До-
Доказать, что для любого ограниченного множества А ? Sx
lim
im f |/|Л = 0,
где Л + п:={д: + п | xg Л}.
Указание. Заметить, что
J
где Д„ = (—oo, —n) U (n, +oo). С учетом теоремы 1
82

18. Пусть функции /¦„, п > 1,— измеримы и неотрицательны и
X, причем
I fndk -*¦ 0, п -*¦ оо.
х
Доказать,что /„ —> 0.
Указание. Рассмотреть неравенство
гк({х | /„(Jt)>8))<j/A е>0.
х
19*. Пусть {/„ : п > 1) — последовательность измеримых
функций, fn -*¦ } (mod Я,) и для некоторой функции g ? L (X, Я.)
\f n I ^ g (mod Я.), и 2? 1. Доказать, что
Ve>0 ЭЛ?^, Я.(Л)<е : sup |/„(*)—/(*) I-•¦
->0, я->-оо.
20. Пусть (X, 5Г, Я.) — пространство с мерой, причем Я. (X) <
< +со и для измеримых функций / и g
d (f, g) := j min A, | / (x) —g(x) |) dk (x).
x
Доказать, что
/„--/ О d(fn, f)-+0, n-+oo.
21. Пусть (X, 5Г, Я.) — пространство с мерой, причем Я. (X) <
< +оо, и для измеримых функций / и g
1Ш^Г
Л
Доказать, что
/„--/ о d(/rt, /)-0, п->оо.
22. Пусть X = R, У = 5^ Я. — мера Лебега и / g L (R, Я.).
Рассмотрим функцию
f(t)dk(t), x?R.
Доказать, что гр 6 С (R).
23. Пусть (X, &, Я.) — пространстио с мерой, причем Я, (X) <
< + оо. Для измеримой неотрицательной функции /: X -*¦ R пусть
Ап:={х | и-1</(
Доказать, что
/6L(X, Я.) о S и
Указаиие> Рассмотреть неравенства
? (п - 1) X (Л„) < f ^А = V f ^ < V
f!=2 Y /1=1 Л 1=1
83

24. Пусть выполнены условия упражнения 21 н
Доказать, что
Указание. Заметить, что Sn_, => Вп и
а потому
7.5. ТЕОРЕМА ОБ ИНТЕГРИРОВАНИИ МОНОТОННОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ И АДДИТИВНОСТЬ ИНТЕГРАЛА
ТЕОРЕМА 2. Пусть А С ?" функции /„ : X -»¦ R,
п~^ \, измеримы и
Vn>l VxGV : 0
Положим
Тогда
lim ]"/„<& = j/dA. G.12)
га-*°° А А
$> I. Если для некоторого т ? N J /mdA = + оо, то,
А
согласно свойству 3° п. 7.2,
V п~^& т '. \ fndX ^э \ fmdh — -f- oo;
i
аналогично
¦ = "Ь °°.
следовательно, равенство G.12) выполняется.
II. Предположим теперь, что J /„dA < + оо, п ^ 1.
А
Последовательность неотрицательных чисел
/ndA : п>
А
84

монотонно не убывает. Пусть
а:= lim ("/„<&< + оо.
Если а = -f- оо, то равенство G.12) выполнено, по-
поскольку
> [fndl, л>1. G.13)
Остается рассмотреть случай, когда а < + оо. Для
функции р ? К (f), чисел с ? @, 1) и п :> 1 рассмотрим
множества
При этом
,4„с: А,+), я>1; U Л„ = Л,
4=1
откуда с помощью свойств 7° и 3° п. 7.2 имеем
> \ fnd%^c\ pdX, л>1.
поэтому
^ fJX^c j" pdA,, n> 1.
С учетом теоремы 1 и определения а получим
а ^э с J pdX,
А
J
А
следовательно,
ос ;> с \ /dX.
Устремим теперь с -v 1 — и учтем неравенство G.13),
получим
а = j
А
ТЕОРЕМА 3. {/, g] с L (Л,
(Л X)
G.14)
85

\> 1. Рассмотрим сначала случай, когда / (л:) ^ О, g (х) ^
^э 0, х ? А. Заметим, что для простых измеримых и не-
неотрицательных функций р и q справедливо, согласно
определению 2 (части первой), равенство
Согласно теореме 5 п. 6.6 существуют монотонно неубы-
неубывающие последовательности \рп : п > 1) и \qn :
: п ^э 1} простых неотрицательных измеримых функ-
функций поточечно на А, сходящихся к / и g соответственно.
Поскольку при каждом п ^ 1
J (А,+ ?„)<&= \pndX+\qndK
то, применив трижды теорему 2, получим равенство G.14).
II. Пусть теперь / (х) > 0, g (х) < 0, х ? А. Вве-
Введем множества из &
g(x)<0), А+: =
Поскольку на множестве Л_ />0и - (/ + g) > 0, то
с помощью доказанного в части 1 имеем
G.15)
и аналогично
J \ (-g)dk.
G.16)
A+ A+ A+
По свойству 8° п. 7.2 f/, — g) cz L (Л_, Я,) П И+,
X), из G.15) и G.16) следует, что <f + g) ? ЦА, X) и
равенство G.14).
III. В общем случае использовать представление
0} U [х?
U {АгбЛ | f(x)<0,
86

Упражнения
25. Пусть {/, g] с L (X, X) и
hx (х) := max (/ (x), g (x)), h.2 (x) := min (/ (x), g (х)), х ? X,
Доказать, что {hlt Нг\ a L (X, X).
26. Пусть {/, g] ci (X, X) и
УЛе^" : f/<u= fgdX..
А А
Доказать, что f = g (mod X).
27. Пусть А, (Х)< + оо, /61 (X, X) и
Доказать, что / = 1 (mod A.).
28. Пусть Л € ^ и при каждом п > 1 функция /„ ё L (Л, Я.) и
неотрицательна на Л. Доказать, что
A W1=1
Если ряд
сходится, то ряд
сходится почти всюду на А.
29. Пусть f ? I. (А, X). Доказать, что
I J fdl < J | / | Л.
I A A
Указание. / = /_|_ — /_, | / I = /+ + /_. Это неравенство по-
постоянно используется.
30. Пусть {/„ : п > 1} cz L (X, X) и
п=1
Доказать, что fn -*¦ 0 (mod Я).
31* Пусть {/п : п > 1} измеримы и
/ (д;) : = lim /n (х), х ? А. Проверить, что равенство G.12) не обяза-
п-юо
тельио выполняется. В чем состоит причина отличия от теоремы 2 ?
Доказать также, ч о равенство G.12) выполнено при дополнительном
условии /„ (х) < g (х), х ? Л с функцией g ? L (А, X).
87

7.6. ОСНОВНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
ТЕОРЕМА 4. Пусть Л ? <F и функции /„, п :> 1 удов-
удовлетворяют условиям:
1) fneL(A,k), л>1;
2) Vn>l Улг?Л :
3) sup (/„?&< + <».
Положим / (jc) : = lim /„ (х), х ? Л. Тогда / ? L (Л, Я,) и
lim J /„йЯ, = J /dA,.
^ Функции
удовлетворяют условиям теоремы 2. Поэтому
Hm J (/„ - А) Л = J (/ - Л) dX, G.17)
"»"Л А
А
причем левая часть этого равенства конечна. Следова-
Следовательно, (f — fx) ? L (A, X), а потому с учетом теоремы 3
Добавив к обеим частям равенства G.17) j fjdk, no-
А
лучим второе утверждение теоремы. <j
ТЕОРЕМА 5 (П. Фату). Пусть А ? g* и {/„ : п >
^ 1} — последовательность измеримых и неотрицатель-
неотрицательных на множестве Л функций. Тогда
lim \ !„<&•> J (lim /n)dA,.
/l-юо Д А п-юо
<j Функции
§„(*):= inf fk(x), х?А; п~^\
удовлетворяют условиям теоремы 2. Кроме того,
lim gn(x)= \\mfn(x), x?A;
88

Из последнего неравенства имеем
А А
а в силу теоремы 2
J,d* = J (lim
п-°° А А п-юо
Следовательно,
lim j fndl> j (lim /„) dl. <j
n-*-oo A A n-*oo
СЛЕДСТВИЕ 1. Пусть А ? ? и функции /„, л > 1,
удовлетворяют условиям:
1) /п. п ^ 1 — измеримы и неотрицательны на Л;
2) /„-»¦/ почти всюду относительно меры Я на Л;
3) sup f /„dA. < + оо.
Тогда /GL (Л, X).
> Непосредственное следствие теоремы 5. <J
Упражнения
32. Проверить, что утверждение следствия 1 остается верным и
при замене условия 2) условием /„ —> /.
33. Пусть X = [О, 1], & — а-алгебра измеримых по Лебегу
подмножеств [О, 1] и Л, — мера Лебега. Для п ^ 1
(x), n — нечетное;
fn (x) :=
1 г , I
L°'T"J
^ „ — четное, х?[0, 1].
Найти
lim fndk, lim I fndX,
[0,1] "-00 "-°°[0,ll
— С С —
lim i fndfb, i lim fndK.
n— oKn tfir—
34. Пусть An <= An+l, n > 1; ([An= X, {An ! n\
для функции f: X -*¦ R
sup f | /|dX<+oo,
89

Доказать, что / ? L (X, X) и равенство
("/<&= lim f fdX.
Указание. Применить теорему 4 к функциям
/n(*):=l/ WI 1л W. *€*! «Ж
Затем использовать теорему 2.
35. Функция /: X -*¦ R измерима и
sup f л
sin (X)
dk (х) < + оо.
Доказать, что / € L (X, X).
Указание. Применить теорему 5.
36. Пусть числа рь ^ 0, к > 1, и
Ssin2 (sk)
^2 Pk < + °°-
Доказать, что
Указание. Пусть X = N, Я ({&}) = р/,, А > 1. Применить тео-
теорему 5.
ТЕОРЕМА 6 (А. _Лебега). Пусть А ? & и измеримые
функции /„: X -> R, n ^? 1, удовлетворяют условиям:
1) fn-*- f, п -*• оо, почти всюду относительно меры Я, на Л;
2) 3g?L(A, К) V л > 1 V х е Л : | /„ (*) К
< g (х). Тогда {/;/„, п > 1) с= L (А, К) и
\> Функция / измерима как предел последовательности
измеримых функций. Первое утверждение теоремы сле-
следует из условия 2) и свойства 6° п. 7.4.
К последовательностям
{g + fn ¦ П>\), {g-fn •¦ «>П
измеримых неотрицательных функций применим тео-
теорему 5:
Jim J (g+ /„) dX > У (g
П-ю° А
п-юо А
90

Отсюда с учетом интегрируемости имеем
j gdk +jim J fndk > J gdk + J fdK
П-+00 A
J gdk - lim J /„d* > J gdk - J /dA.
Следовательно,
d*. < Hm_ j fndk < fim J
4 /г~°° 4
Замечание. Теорема 6 часто называется теоремой о мажорируе-
мажорируемой сходимости.
Упражнения
37. Проверить, что утверждение теоремы 6 останется верным,
если каждое неравенство в условии 2) выполняется почти всюду
иа А.
38. Доказать, что утверждение теоремы 6 останется верным, ес-
если условие 1) заменить на условие: fn —* /.
Указание. Сначала доказать, что / g L (А, К). Затем рассмотреть
произвольную подпоследовательность \fn^ '¦ k~^\).Wo теоре-
теореме 11 п. 6 существует /„(^(Л) -*• / (mod К). Применить теорему 6.
39. Пусть {/„ : п ^ 11 — последовательность измеримых
функций, равномерно на X сходящаяся к функции /, причем
Доказать, что
lim Г lndk = f fdX.
x
Утверждение остается верным, если условие / € L (X, к) заменить
на {/„ : Ol)cL(X, X).
40. Функции /, fn : X -*¦ R, п > 1 измеримы и Я (X) <+ оо,
fn -»• / (mod X). Доказать, что
lim \ sin /„ (*) d% (x) = С sin / (х) d% (x).
41. Функция /: X -»• R измерима и % (X) < + оо. Вычислить
lim Г ехр (— п (/ (х) — IJ) dX (x).
П-*оо J
Указание. Рассмотреть отдельно предел интегралов по множе-
множе{ | /() 1} и { | /() 1|
/(
р
ствам {х | /(*)= 1} и {х | /(
Ответ. % {{х | /(лг)= 1}).
91

42. При условиях упражнения 41 вычислить предел
lira f sin2"/ (лс) dk (х).
"~°°х
Ответ, Я П* | / (х) =у + «п, me
43. Пусть X = R2 и X — двумерная мера Лебега. Вычислить
предел
lira f sin2" (*j — *2)
dl
для множества A— {(*,, x2) | x'\ + лг| < 9я2}.
44. Последовательность измеримых функций {/„ : я>1}
удовлетворяет условиям: /„ -> / (mod Я) н
3 С 6 R v * € X : | /„(*) |< С.
Доказать, что для любой функции g? L (X, К)
lira f /„gdA = f /gdX,.
45. Пусть {/„ : n > 1} — неубывающая последовательность
неотрицательных функций таких, что: //,-»•/ (mod Я); функция g
такова, что /g € L (X, Я). Доказать, что
lira
= f
46. Предположим, что функции /, fn, n > 1, неотрицательны
на X, принадлежат L (X, Я) и /„ -»¦ / (mod Я),
х
х
/ -oo.
х
Доказать, что
lira f|
Доказать также, что условие fa-*-1 (raod Я) можно заменить усло-
условием /„ —' /.
Указание. Заметить, что
(/ — /„)_<&+ е„, п>1; е„-*-0, «^оо,
х х
н к левой части применить теорему 6.
47. Предположим, что функции /, fn, n > 1, неотрицательны
на X, принадлежат L (X, Я), /„ -»- / (mod X.) и
92

Доказать, что
V А е & : Mm С fnd% = f fdX.
п~*оо 4 ^
А А
Указание. Заметить, что
2 И (/-/„) Л
J (f - fn) 0
A
<\\f-fn\dK n>l.
48*. Пусть Я (X) < + оо. Последовательность функций /„:
X -*¦ R, п > 1, называется равномерно интегрируемой, если
\fn\d\-*Q, а
sup
Пусть {/„ : га>1} — равномерно интегрируемая последователь-
последовательность функций такая, что />!->¦/ (mod Я). Доказать, что [f, fn :
n> 1} a L{X, %) и
lim ] fnd% = ) fdX, lim } | /„ — / | dX = 0.
Указание. Понятие равномерной интегрируемости подробно об-
обсуждается, например, в [3, 11].
49*. Пусть Я (X) < + оо и последовательность измеримых
функций {/„ : п > 1} такова, что
1) /л-W (mod Я); 2) sup Г f*dk < + °«.
Доказать, что для измеримой функции g, для которой g2 6 L (X, Я),
справедливо равенство
lim f /„ (лг) g (лг) rfX W = f / (лг) g (x) d% (x).
г,— J J
50*. Пусть Я (X) <+ оо и последовательность измеримых функ-
функций такова, что:
!)/„-*/ (mod Я); 2) sup f fnd% < + оо.
Доказать, что
lim (' fndk = \ fdX,
93

7.7. СРАВНЕНИЕ ИНТЕГРАЛОВ РИМАНА И ЛЕБЕГА
НА ОТРЕЗКЕ ПРЯМОЙ
Пусть [а, Ь] — фиксированный отрезок на R, R ([а,
Ь\) — класс всех ограниченных функций вида /: [а,
b] -> R, интегрируемых по Риману. Для / ? R ([а, 61)
Ь
\ f (х) dx — интеграл Римана от /. Используемые
а
ниже свойства интеграла Римана и обычные обозначения
содержатся в [4].
Рассмотрим в ситуации п. 7 X — [а, 61, Я- — а-ал-
гебру подмножеств [а, 6], измеримых по Лебегу, и к —
меру Лебега. Класс L (la, 6], к) — класс всех измеримых
функций вида /: [a, b] -> R. интегрируемых по Лебегу.
Для функции /? L ([а, 6], к) интеграл Лебега J fdk обо-
la. Щ
значается также и символами
й Ь
\ fdk или j f(x)dx,
а
в п. 7.7 этот интеграл будем обозначать символом
ТЕОРЕМА 7. Если / ? R ([а, 61), то / g L (\а, 6], к)
и
$> Пусть функция / ? R ([а, 6]), в частности / ограничена
на la, b]. Пусть {л (п) : п > 1} — последователь-
последовательность разбиений отрезка [а, 6] таких, что
а) при каждом п > 1 разбиение л (п -+- 1) есть подраз-
подразбиение л (п);
б) | л (п) | -> 0, п ->- оо.
При каждом п ;> 1 для разбиения
л(п) = {а = *0(л), /, (л) «*,„, (л) = 61
пусть для 0 ^ / ^ k (л) — 1
: = mi{f(x) | *€[*,(я),//
94

и L (f, л (n)), U (f, л (п)) — нижняя и верхняя суммы
Дарбу соответственно. С помощью разбиения л (п)
определим также функции ип, vn : [a, b] -> R следую-
следующим образом:
un(a) = vn(a): =
ип (х) : = т, (n), vn (х) : = М, (п), х ? (tj (n), ti+i (n)]
для 0 ^/ ^ k (п) — 1. Функции ип, vn, п ^ 1, измери-
измеримы по Лебегу. Кроме того, в силу предположения а)
справедливы неравенства
Vn>l \/xe[a,b\ : «„(*)< «»i+i (x)<^+i (x)<
inf /<«„(x)</(x) < vn(x) <sup /.
[a.b] [a,6]
Положим
«(x): = lim un (x), у (x): = lim у„ (x); xg [a, 6],
функции ы и и измеримы по Лебегу в силу теоремы 4
п. 6.5 и удовлетворяют соотношению
По определению интеграла Лебега
ь
\ G.18)
а
Согласно теореме Дарбу [4] при предположении б)
Ь b
L (/, я (л)) -> J f(x)dx, U(f, я(л))-* J / (х) dx; /г-> с».
В силу теоремы б
ь
а а
Ь Ь
95

Поэтому из равенств G.18) имеем
а а а
Огсюда с учетом свойства (8) п. 7.4 и = v — f почти всю-
всюду относительно меры Лебега Я, на [а, Ь] и / ? L ([а, Ь],
А). Поэтому
ь ь
(?)f/(*)d*=J/(*)d*. <\
а а
Замечание. Аналогичное теореме 7 утверждение верно н для
кратных интегралов.
Упражнения
51. Вычислить предел:
л ' / , \
1С I I |
ехр (—nsiax)dx, (б) lim V ехр I — «sin2—\dx,
" '" И-t-oo J \ ¦*¦ /
\f~~n \ ехр (— « sin x) dx) I .
о '
Указание. Для (а) и (б) использовать теорему 6.
52. Вычислить предел
lira [ sin2" (x\ + х22) dxxdxv
7.8. КРИТЕРИЙ ИНТЕГРИРУЕМОСТИ ФУНКЦИИ
ПО РИМАНУ
Воспользуемся обозначениями п. 7.7.
ТЕОРЕМА 8. Ограниченная на отрезке la, b] функция
/ ? R ([a, 6]) тогда и только тогда, когда / непрерывна
почти всюду относительно меры Лебега Я, на [а, Ь].
00
|> I. Пусть Ф = U л (п), множество Ф счетно и А, (Ф) =*
== 0. Сначала докажем следующее утверждение: для
х0 ? [а, Ь] \ Ф : и (х0) = v (х0) « / — непрерывна
в точке х0.
96

Если и {хп) — v (хп), то и (х0) = / (х0). Поэтому
V е > О -im V п^и m :
f (х„) — е < ип (х0) < / (х0) < vn (х0) < f (х0) + е.
Пусть
Имеем V х ? (/, (w), </+i (m)) i
(x0)
f-хли / непрерывна в точке х0, то
Ve>0 J6>() V л-, | x — x
а потому для номеров п, для которых | я (л) | < б,
имеем неравенство
vn (Хо) — ип (х0) < 2е.
II. Необходимость. Пусть / ? R ([а, Ы). Со-
Согласно доказательству георемы 7 и — v почти всюду,
следовательно, / непрерывна по I почти всюду относитель-
относительно меры Лебега на [а, Ь].
Достаточность. Пусть / ограничена на \а, Ь\
и непрерывна почти всюду относительно меры Лебега на
[а, Ь\. Тогда и = v (mod i) и
ь
lim L (/, я (л)) = lim f/ (/, л (л)) = 0?) f / (x) dx.
a
Согласно обычному критерию интегрируемости по Рима-
ну в терминах сумм Дарбу 14] / ? В ([а, Ь]). <\
7.9. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
И ИНТЕГРАЛ ЛЕБЕГА
Рассмотрим случай несобственного интеграла по полу^
прямой. Пусть а ? Н фиксировано. Если функция /: [а,
+ оо) -*- Н такова, что
то несобственный интеграл есть
\ / (х) dx ; = lim \ / ix) их. G.19)
4 8-1569 97

если предел существует и конечен. Несобственный ин-
интеграл G.19) сходится абсолютно, если сходится интеграл
\f(x)\dx; G.20)
а
интеграл G.19) сходится условно, если он сходится, но
интеграл G.20) расходится.
Пусть X = la, + оо), & — сг-алгебра подмножеств
[а, + оо), измеримых по Лебегу, Я, — мера Лебега. Для
функции / ? L (la, + оо), К) определен интеграл Лебега
J fdl,
который обозначается также символом
J f{x)dx,
а
в п. 7.9 будем использовать обозначение
ТЕОРЕМА 9. Пусть функция /: [а, + оо) -+ R тако-
такова, что 1) V А > а : / ? R ([а, А])\ 2) J |/ (*) | йк <
а
< + оо, т. е. интеграл G.19) сходится абсолютно. Тогда
/ 6 L (la, + оо), I) и
-f-00 -f-00
ф \ f(x)dx= j f(x)dx.
а а
Если же интеграл G.19) сходится условно, то / (j
6 L (ta, + оо), к).
|> При условии 1) функция/: [a, +oo)->R измери-
измерима, поскольку
f (х) = lim (f (x) - ltan] (ж)), д; б [a, + оо),
п-юо
и функция /1[a,ni измерима при каждом п > 1 в силу
теоремы 7. В силу теоремы 2 имеем
\f(x)\dx. G.21)
Кроме того, согласно теореме 7,
98

Поэтому из условия 2) теоремы следует, что | /1 ?
? L {[а, + со), Я,), откуда f ? L ([а, + со), К), и с учетом
теорем 6 и 7
(<?) J /(x)dx = lim
1-KJO J J
a a
Если интеграл G.19) сходится условно, то из равен-
равенства G.21) с помощью теоремы 7 получим, что | / | 6
5 L ([а, + оо), Я,). <\
Упражнения
53. Вычислить предел:
(a) lira С е~* sin2" xdx; (б) lim С e~* sin" кЧх;
<в) lira [ e~x sin2" — dx;
f(-+OO
(r) lim f exp (— I д:, I — | x% |) sin2" (at, + ^) i
54. Пусть / € С (R), / (a:) > 0, л; G R н
f I sin Sx I .... ^ ,
sup \ -1 я—- f (x) dx < + oo.
o<S<iJ л
R
Доказать, что
j1 | x | / (a:) dx < + oo.
55. Пусть / б С ([0, + со)), f(x)>0, x]
sup I g / (дг) dx < + oo.
о
Доказать, что
о
4* 99

56. Вычислить предел
л
•. I OX tux»
*§) *
57. Найти сумму ряда
dx
1=1
5.J-U-
Замечание. Утверждение, аналогичное теореме 9, справедливо'
и для несобственных интегралов от неограниченных функций.
7.10. ИНТЕГРАЛ ЛЕБЕГА — СТИЛТЬЕСА НА ПРЯМОЙ
Пусть X = R, F: 1\ ->- \\ — монотонно неубываю-
неубывающая и непрерывная справа на R функция, Sp — соот-
соответствующая а-алгебра и Кр — мера Лебега — Стилтьеса,
см. п. 4.10. В этом случае интеграл Лебега \ fdXh назы-
R
вается интегралом Лебега — Стилтьеса и часто обозна-
обозначается символом
\f{x)dF{x).
Упражнения
58. Пусть F (х) = llOfl) (х) + 2 • 1[1>+OOj (x), x?R. Какие
функции Sp-измеримы? Описать класс L (R, %F). Найти
lira
Г ^"
59. Пусть F (х) = [х], х 6 R. Описать классы S^-измеримых
функций и L (R, XF). Представить в виде суммы ряда значение
60. Пусть
F (х) = | х, 0 < * < 1
11, л:>1.
Описать классы S^-измеримых функций и L (R,
100

7.11. ИСТОРИЧЕСКАЯ СПРАВКА
Интеграл ЛеОег-а в случае А = R и меры Лебега X на прямо»
был введен А. Лебегом в 1902 г. А. Лебегу принадлежит также эф-
оективный критерий интегрируемости функции по Риману (теоре-
(теорема 8). Более общие интегралы были построены А. Данжуа A912 г.),
О. Перроном A914 г.), А. Данжуа и А. Я. Хинчиным A916 г.).Под-
г.).Подробное изложение см. в [12], [13]. Распространение теории интеграла
Лебега на случай функций в R" было выполнено А. Лебегом A910 г.)
для меры Лебега, для более общих мер В. Юнгом и Ф. Риссом »
Дж. Радоном A913 г.) для произвольной счетно аддитивной функции
множеств. Абстрактное определение принадлежитМ. Фреше A915 г.).
Обобщения понятия интеграла для функций со значениями в бана-
банаховом пространстве получены С. Бохнером A933 г.), И. М. Гель-
фандом A938 г.) и Б Петтисом A939 г.). Более детальные историче-
исторические сведения и ссылки на оригинальные статьи содержатся в кни-
книгах 16, 7], [141.
Следующие упражнения указывают отличные от приведенного
выше пути определения абстрактного интеграла Лебега.
Упражнения
61. Пусть (X, ^", А.) — пространство с мерой. Измеримое раз-
разбиение it — {Ах, ..., Ап\ cz !F пространства X есть набор множеств
такой, что
п е N; А. П Aj = 0, i Ф /; X = (j A{.
t—i
Пусть f—неотрицательная ^"-измеримая функция, положим
mk (it) : = inf {/ (х) | xeAk), 1<&<л,
для измеримого разбиения it, inf 0 : = 0. Доказать, что
sup
П п
Yi mk (я) A- (At) = J jdX, 0 • Н- со) : = 0.
* х
62. Пусть {X, &", Я.) — пространство с мерой и /: X -*¦ R
неотрицательная на X ^"-измеримая функция. Согласно теореме 5
п. 6.6 существует монотонно неубывающая последовательность
{рп '• п г> '} простых неотрицательных на X ^-измеримых функ-
функций поточечно на X сходящаиси к /. Положим
f fd% : = Mm f pnd\.
Доказать, что это определение корректно и приводит к постро-
построенному выше интегралу.
101

8. ИНТЕГРАЛЫ ЛЕБЕГА. ЗАВИСЯЩИЕ
ОТ ПАРАМЕТРА.
ФОРМУЛА ЗАМЕНЫ ПЕРЕМЕННОЙ
8.1. НЕПРЕРЫВНАЯ ЗАВИСИМОСТЬ ОТ ПАРАМЕТРА
ТЕОРЕМА 1. Пусть (X, 3, X) — пространство с ме-
мерой, А ? 5"; (Y, р) — метрическое пространство, G —
открытое подмножество Y и функция /: А X G ->- R,
удовлетворяющая условиям:
V(x, t)?(A\O2)x G
Тогда функция
A
непрерывна на G.
(> Без ограничения общности можно предполагать, что
условия 2) и 3) теоремы выполнены на А и А X G соот-
соответственно. Пусть t0 ? G фиксировано и
[tn :
Тогда
в силу теоремы 6 п. 7.6. <j
Упражнение
1. Пусть F(/)= f 3— -, /6(— 1, 1). Доказать, 4TOF6
6 С ((-1, 1)).
8.2. ДИФФЕРЕНЦИРОВАНИЕ ПО ПАРАМЕТРУ
ТЕОРЕМА 2. Пусть (X, Эг, Я.) — пространство с ме-
мерой, A G 5"; G — открытое множество на R и функция
/: А X G -*¦ R, удовлетворяющая условиям:
1) V/?G : f(-,t)cL(A, X);
2) ЗФ? &, ЦЩ = 0 V хб Л\Ф существует dj {хд' ° на G;
/ (АГ, 0
102

Тогда функция
l
дифференцируема на G и
A
|> Можно считать, что условия 2) и 3) выполнены на
всем А. Пусть значение i0 ? G фиксировано и
\tn ! я^1}сгС; 1пФ@, я^1; *п-*-'0> я -»- оо.
Поскольку при каждом х ? Л
hm tn_t = d< = /2 (x, /0),
то функция/? (•,/0) ^"-измерима. Кроме того, в силу тео-
теоремы Лагранжа
! / (х, tn) — I (х, tn)
П-»оо " tl П-t-QoJ
43
Поэтому, согласно теореме 6 п. 7.6,
lim — / 1,("' = I'm \ ' *' 7 Z/
Упражнение
2. Пусть Л =» R, ^" = S, Л, — мера Лебега, / ? /. (R, А,) н
функция
11 1 \
, *€(-!, 1).
О, лс?(—1. 1).
Для е > 0 положим а" : ¦» \ р (х) их,
^$^, I 6 R.
Доказать, что р ? С°° (R), FE 6 С°° (RJ. Пусть t0 точка непрерывнос-
непрерывности /, доказать, что
103

8.3. ФОРМУЛА ЗАМЕНЫ ПЕРЕМЕННОЙ
Пусть (X, if), (X', 3-') — измеримые пространства и
Т: X -*¦ X' 9~ — 9~' — измеримое отображение. Пусть
X — мера на W. Тогда равенство
определяет меру К' на &'. Мера К' обозначается также
•символом КТ~1.
Упражнения
3. Проверить, что К' — мера на &'.
4. Пусть X = X' = R, & = &" = S.X — мера Лебега и Тх =»
= I х |, х ? R. Проверить, что для А' ? S
V (А' П 10, +оо))=2Х(Л' П [0,+оо)).
5. В условиях упражнения 4 рассмотрим преобразование Тх =
= ах + Ь, х ? R; а 6 R, а ф 0, 6 6 R. Доказать, что
ТЕОРЕМА 3. Пусть (X, 3<\ X) — пространство с ме-
мерой, (X', %~') — измеримое пространство и Г: X -*¦
->- X' — <? — W — измеримое отображение. Пусть
/: X' -*¦ И ^"'-измеримая функция. Тогда справедливо
равенство
J( | (8
X'
если хотя бы один из интегралов формулы (8.1) конечен.
Здесь К' = КТ~1.
> Пусть Q — класс всех ^"'-измеримых функций, для
которых равенство (8.1) справедливо. Класс Q является
линейным.
В силу теоремы 2 п. 7.5 класс Q содержит поточечные
на X' пределы монотонно неубывающих последователь-
последовательностей неотрицательных функций из Q.
Согласно определению меры к' равенство (8.1) выпол-
выполняется для индикаторов множеств из W. Таким образом,
Q содержит неотрицательные <Г'-измеримые простые
функции.
В силу теоремы 5 п. 6.6 и теоремы 2 п. 7.5 класс Q
содержит все неотрицательные .^'-измеримые функции.
С учетом определении интеграла теперь можно ут-
104

верждать, что класс Q содержит все ^"'-измеримые функ-
функции такие, для которых хотя бы один (значит оба) из ин-
интегралов G.22) конечен. <)
Упражнения
6. Пусть X — R2, & — а-алгебра борелевских множеств в R2,
Х\= R, Sr' — а-алгебра борелевских подмножеств R и /: R -*¦ R —
борелевская ограниченная на R функция; X — мера на &, причем
X (R2) < +оо. Определим функцию F для фиксированных чисел а,
Ь, с, | а | + | Ь | ф 0 следующим образом:
F(t):=X ({(*!, х2) | одс,+6дс2 + с<<}), t e R.
Доказать, что функция F монотонно не убывает и непрерывна справа
на R. Пусть Хр — соответствующая F мера Лебега — Стилтьеса. До-
Доказать, что
[ I {ах, + Ьх2 + с) dX (*,, **) = [/ @ <&/=¦ (О-
RJ R
7. Пусть X = R, & = S, А, — мера Лебега, / ? Z. (R, ^ и чис-
число а > 0. Доказать, что
почти всюду относительно меры Лебега на R.
Указание. Доказать сходимость ряда
8. Пусть X = [0, 1],^"—а-алгебра измеримых по Лебегу под-
подмножеств [0, 1], X — мера Лебега; /: R -*¦ К — измеримая по Ле-
Лебегу периодическая с периодом 1 функция, причем / ? L ([0, 1], X).
Доказать, что
почти всюду относительно меры Лебега на R.
9. Пусть X = R, & = S,Х — мера Лебега, / ? L (R, к) и а > 0.
Доказать, что ряд
сходится абсолютно почти всюду относительно меры Лебега на R,
его сумма F периодична с периодом а и F ? L ([0, а], X).
10. Пусть (X, 5Г, А.) — пространство с мерой, причем X (X) <
< +оо; /: X -*¦ R — ^""-измеримая функция. Пусть
5 8-1569 105

Доказать, что F монотонно не убывает и непрерывна справа на R.
Доказать также, что
[ fd\= [ td%F{t), (8.2)
X R
если хотя бы один из интегралов в (8.2) конечен. Доказать, что для
неотрицательной ^-измеримой функции / справедливо равенство
fdk= (F (+00) — F {t)) dt, F(+oo):= lim F (t),
x i '-+-
с несобственным интегралом Римана в правой части.
11. Пусть выполнены предположения теоремы 3 и А' ? У, До-
Доказать справедливость равенства
J / (*') А' (х') = Г f(Tx)d\(x)
A' T-U-
7—1/4'
при условии конечности хотя бы одного из интегралов.
12. Пусть а — монотонно возрастающая непрерывная и неот-
неотрицательная на [0, +оо) функция, а / — неотрицательная на
[О, +оо) борелевская функция. Доказать равенство
+оо <Х(+оо)
J / (а (/)) da @ = J / @ <0
О <х@)
с интегралом Лебега — Стилтьеса в левой части и интегралом Лебега
в правой.
9. АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ
9.1. АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ
И СИНГУЛЯРНОСТЬ
Пусть {X, S", Д.) — пространство с мерой, ц, — заряд
Определение 1. Заряд (л называется абсолютно непре-
непрерывным относительно меры К, если
Обозначение: (д. <^ А, о заряд (мера) (д, абсолют-
абсолютно непрерывен относительно меры X.
Упражнения
1. Пусть (х, Я, — меры на ^", причем ц (X) < +°о. Доказать,
что
о ve>0 3б>3 v Л 6 ^", ^ (Л)< б : р(А)<&.
106

2. Пусть / б L (X, X) и
ц (Л) : =
Проверить, что ц<^.
3. Пусть \lt А.г — меры на 9" и v : = %г + Д,2. Проверить, что
А* < v, (=1,2.
Определение 2. Заряд (л называется сингулярным от-
относительно меры Я., если
ЗЛ?Г, ЦЛ) = 0 УБ?3",
Меры jii и Л, называются сингулярными, если
Обозначение:
(л _J_ Л. <=> меры (д, и Я, сингулярны.
Упражнения
4. Неотрицательные на X функции {/, g] с L (X, А.) таковы,
что
V х 6 X : } (х) g (х) = О,
Пусть
ц (Л) : = j /Л, v (Л) : =
Доказать, что (il v.
5. Для каких мер (г и А,
6. Пусть |i = |i+ — ц_ — разложение Жордана заряда ц. До-
Доказать, что |i^. J_ |i_.
ТЕОРЕМА 1. Пусть (д, — заряд на 3 с разложением
Жордана (л = |А+ — |л_, Я. — мера на ^". Следующие
утверждения эквивалентны
1° |*О;
2° ц+ < Л, ц_ < Я.;
3° | Ц I « Л.
> 1° ^ 2°. V Л ? F,X (А) = 0 : щ. (Л) : = ц (А (]
П А+) = 0, поскольку Я, (Л Л ^+) = 0- Аналогично
ц_ (Л) = 0.
5* 107

2° => 3°. V A ? &, I (A) = 0 : fx+ (Л) = ц_ (Л) =
= 0. Следовательно, | |д, | (А) = \i+ (A) + |A- (Л) = 0.
3°^1°. V Ai&, l(A) = 0 i \i+ (A) + ц_(Л) = 0.
Поэтому (д, (Л) = |д,+ (Л) — |д,_ (Л) = 0. <|
9.2. ТЕОРЕМА РАДОНА—НИКОДИМА
ТЕОРЕМА 2. Пусть (X, W, Ц — пространство с а-ко-
а-конечной мерой К, (д, — а-конечный заряд на eJ, \x <^
<^ Я. Тогда существует ^"-измеримая функция /: К ->- R
такая, что
УЛ6Г : n(i4)=J/dX. (9.1)
А
Если функции /и§ удовлетворяют соотношению (9.1), то
?> I. Рассмотрим сначала случай, когда (д, и X — конеч-
конечные меры на <F'. Положим
g>0 на X, geL(X,X), j
Множество Q Ф 0 и для функций {g^, g3} с: Q max
gg) ^ Q. Действительно, для любого Л ? «^ имеем
J max (gv gt) dk = J g,dA.
А А
j
Аг
где
Л3: = Л П {x?X | ft(
причем Л! П A2.= 0, Ax [) Л3 = Л.
Положим
а: = sup I gdh^.\i(X) < +оо.
Рассмотрим последовательность [gn : п ^ 1} с: Q та-
такую, что
X
108

и пусть
/„: = max(^i gn), n
При этом для п ^ 1
/4€Q, 0 </„</„+! на X.
Положим
В силу неравенства
X X
и теоремы 4 п. 7.6 имеем
lim J fndl = J fdX = a.
При этом
V Л 6 5" : J Л& < |a И),
A
поскольку
Пусть
По теореме 1 п. 7.3 функция ф есть конечная мера на S-',
причем ф <^ К. Докажем, что <р (Л> = 0 для любого
А ? S". Предположим, что- последнее утверждение невер-
неверно, то есть
ЗА*е& ¦ Ф(Л*)>0.
При этом к (А*) > 0, так как ф <^ X. Пусть Р >¦ 0 число
такое, для которого
Рассмотрим конечный заряд на
г|)(Л): = ф(Л)-
Для заряда -ф имеем
109

Пусть X = Х± U Х_ — разложение Хана пространства
X относительно заряда \|>. Тогда \р (Х+) > О, так как
0<Ч>(Л*) = ф(Х+ П Л*) + г|)(Х_ П А*).
Функция
входит в класс Q, поскольку она неотрицательна, принад-
принадлежит L (X, К) и для любого А ? &
Однако
J (/ + Р • U+) йЯ. = \ fdk + рЯ (Х+) > а,
что невозможно согласно определению числа а. Таким
образом, ф = 0 и представление (9.1) доказано с функци-
функцией /. Функция / почти всюду конечна на X относительно
меры X, так как / ? L (X, X). Изменив / на множестве ме-
меры 0, получим утверждение теоремы.
Если функции / и g удовлетворяют (9.1), то
J = О,
следовательно, / = g (mod К).
П. Пусть теперь (д, и X — а-конечиые меры. Тогда
3{Х„ : «>1}сГ; Хп(]Хп = 0, тфп; '
\jXn = X; ц(Х„)<+оо, К(Хп)<+оо, п>\.
Согласно доказанному в части 1 при каждом п ^ 1 \х <^
<СХ на 3~(]Хпи существует ^"-измеримая неотрицатель-
неотрицательная функция /„: Хп ->• R такая, что
V A<i3 : ц(Л Г) *„) f
ПО

Функция
n=\
неотрицательна, ^"-измерима и по теореме 2 п. 7.5 удовлет-
удовлетворяет для любого А ? W равенству
п=\ А
п=\
III. Если \i — а-конечный заряд, то в его разложении
Жордана [г = [д.+ — [л_ мера \i+ а-конечна, а мера
|г_ — конечна, причем в силу теоремы 1 ц+ <^ X и |г_ <^
<^ X. Соотношение (9.1) получается теперь из представ-
представлений для мер ц+ и [д._, полученных в части II доказа-
доказательства. <j
Замечание. Если \i — конечный заряд, то / ? L (X, X).
Определение 3. Пусть \i — заряд, X — мера на S-.
Если существует ^"-измеримая функция /: X -»- R такая,
что
то функция / называется плотностью или производной
Радона — Никодима заряда \i относительно меры X.
Обозначение:
f = —^- <=> / — плотность заряда ц относительно
меры X.
Замечание. Плотность определяется неоднозначно, однако, если
/ и g — плотности заряда \i относительно меры X, то / = g (mod X).
У пражнения
7. Пусть ц — заряд с разложением Жордана [i — \i, — (i_.
Найтн
d\i, d\i_ d Bц , — (i_)
dlHl ' « IM-I ' «ТИП '
8. Пусть (г, Я — меры, причем ц JL X. Доказать, что ji С ^ + ^'
d\i
н найти ——' .
111

9. Пусть цД — меры, причем и, — конечна и и < 1, f: = -?-
Пусть g: X -*- R — ^-измеримая функция, для которой gf
? L (X, X). Доказать, что
10. Пусть |л, v, X — конечные меры, причем ,u ¦< v, v <C X. До-
Доказать, что \i -С X и
ф ф rfv
—?- = —f— • —тг- (mod Я,).
dX. dv dX '
11. Пусть \i и X. — конечные меры, причем (г < Я и А, < р.. До-
Доказать, что
ф _ / dX
dX ~ \~фГ
12. Пусть {|л„ : п~^ \} — последовательность конечных мер
на 5Г. Доказать, что существует конечная мера X на & такая, что
ця < Я, для каждого « Зг 1.
Справедлива следующая теорема, приводимая без до-
доказательства, см. [3].
ТЕОРЕМА 3 (А. Лебега). Пусть заряд \i и мера А —
о-конечны. Тогда заряд \i можно единственным образом
представить в виде
с зарядами |д,х и \i2 такими, что
9.3. ЗАМЕЧАНИЕ К ФОРМУЛЕ ЗАМЕНЫ ПЕРЕМЕННЫХ
Рассмотрим при предположениях теоремы 3 п. 8.3
случай, когда X — X', ZF = &'. Предположим, что мера
к а-конечна и
a-
g . = ж
При условии fg ? L {X, А) формула (8.1) принимает вид
lfgdX=[f{Tx)dk{x).
X X
Доказательство этого равенства аналогично доказатель-
доказательству теоремы 3 п. 8.3.
112

10. ИНТЕГРИРОВАНИЕ НА ПРОИЗВЕДЕНИИ
ПРОСТРАНСТВ
10.1. ИЗМЕРИМЫЕ МНОЖЕСТВА
В ПРОИЗВЕДЕНИИ ПРОСТРАНСТВ
Пусть (Хъ ^i), (Х2, 3) — измеримые пространства.
Рассмотрим декартово произведение X : = Xt X Х2, мно-
множество
А : = Аг X Л2, Ai^&i, »=1, 2,
назовем измеримым прямоугольником в X, пусть
H; = S'lxS'2: = {A1xAt \ At?&t, i = 1, 2}.
Упражнение
1. Проверить, что класс Н есть полуалгебра.
Пусть &: = оа {$х X S~2), тогда (X, $)— измеримое
пространство.
Определение!. Пусть Е cz X = Хх X Х%. Для каждо-
каждого хх ? Хх множество
?*,: = {*2^а I {xvx2)^E}, EXlczX2
называется ^-сечением множества Е. Для каждого х2 ?
? Х2 множество *¦
?,2: = {др, е Хх | (Хх, дг8)'е ?}, Ех. с Xt
называется х2-сечением множества ?. Положим также
0л:,: = 0, 0*2: = 0.
Упражнение
2. Пусть А — АгХ А2, At <= Xj, j = 1, 2. Определить Л Л^. .
ТЕОРЕМА 1. Пусть ? б F" = оа (^ X g). Тогда
\> Доказательство приведем для случая хгсечений.
Пусть
G:={?€^ I V^e^i : ЕХх?&Л), Gcz?.
Класс G обладает следующими свойствами.
113

1° & x X if 2,CZ G, поскольку для множества А = Аг X Л2,
¦d; € #^i i = l,2 имеем
2е Если Е ? G, то Е ? G, так как для любого *г ? Хх
3° Если {Еп : п > 1} с G, то U En ?G, поскольку
л=1
= и {^2ex2 | (Xvx2)?En}= и ^,
Таким образом, G — а-алгебра, следовательно, G = ^*. <J
Упражнения
1. Доказать, что множество Е с X такое, что
не обязательно принадлежит 5Г.
2*. Доказать, что множество ? с X такое, что
V х,6 Х( : ЕХ[ 6*д0, I = 1, 2;^ / A) = 2, / B) = 1,
не обязательно принадлежит &.
10.2. ИЗМЕРИМЫЕ ФУНКЦИИ
НА ПРОИЗВЕДЕНИИ ПРОСТРАНСТВ
Пусть /: X, X Хг -> R — функция на произведении
пространств.
Определение 2. Для каждого хх ? Хг функция
М*г): = /(*!• *г). х'г € *2
называется д^-сечением функции /. Для каждого х% ^
^ Х2 функция
fxAxi) • = f (xlt х2), xi?X1
называется х2-сечением функции /.
ТЕОРЕМА 2. Предположим, что функция /: Х1 X
xXj^-R ^"-измерима. Тогда для любого хг ? Хх функ-
114

ция /v #-измерима, а для любого х2 ? Х2 функция
ht Fi-измерима.
t> Доказательство проведем для л^-сечений функции /.
Пусть хх ? Xt фиксировано. Имеем
. [х2?Х2 | /,,(*,)< а} =
^Х2 | f{xv x2)<a\ =
По условию теоремы
а по теореме 1
{(*i, *)€* I f(x1,x2)<a}x^^2. <\
10.3. ПРОИЗВЕДЕНИЕ МЕР
Пусть (Xh S't, ht), i = 1,2 — пространства с мерами.
В произведении пространств X = Хг X Х2 с сг-алгеброй
& = оа {&х X $) Для множеств вида А = Лх X Л2; At ?
Z 3ь Xt (Ас) < +оо, i = 1, 2, можно рассмотреть функ-
функцию
Функция X определяется аналогично определению пло-
площади в плоскости с помощью понятия длины. Является
ли функция X мерой?
ЛЕММА 1. Пусть (Х„ &"[, Xi), i= 1,2 — пространст-
пространства с о-конечными мерами. Тогда существует единствен-
единственная о-конечная мера X на & = ста (^"г X <?2) такая, что
X (Е) = J X2 (EXl) dX{ (Xl) = f X, (EX!) dX2 (x2).
x, x,
В частности, для Е = Ax x A2, At ? &t, Xt [At) < +oo,
i= 1, 2,
X(A1xA2)^X1(Al)X2(A2). A0.1)
Мера Я называется произведением мер XlwX2 и обо-
обозначается символом X = Хг х Х2.
115

\> I. Пусть сначала меры кги %2 — конечны. Рассмот
рим класс
функция Хг Э х1 н»- Я2 (.?*,)
$"г-измерима и принадлежит L(XX, А^);
Функция Х2Эх2^Х1(ЕХ2)
^-измерима и принадлежит L (Х2, К2);
G: =
„д.
[ X,
Класс G обладает свойствами:
1° Gcf
2° ^! х f 2 с G. Действительно, для множества Л =
= Лх х А2, At ?&"с, i = 1, 2, имеем
0, ЛГ]ё^1. ^/ЛЧ { О,
Следовательно, функция хх **¦ Х2 (AXt) ^"i-измерима и
X,
Аналогичное рассуждение справедливо относительно х2.
3° Пусть {Е, F\ cz G, E f] F = 0. Тогда (Е Ц F) ? G.
Действительно, поскольку для любого хх ? Хх
(Е U F)Xl = ЯД| U FXl, EXl П F,, = 0,
то
Л2 ((? U г)Л1) — Л2 (с^) + Л2 (г*,).
4° G — монотонный класс. Действительно, пусть
оо
Тогда для каждого хх ? Хг имеем
EXl
,, = U EnXl;
В силу непрерывности меры снизу
116

Поэтому функция хх и»- L> (?*,) ^-измерима и анало-
аналогично функция х2 >*¦ ^! (ЕХг) 5-измерима. Применив
дважды к соотношению
J К(Е2.)d\(Xl) = j I, (El)d%2(x2), n>\,
X, X2
теорему об интегрировании монотонной последователь-
последовательности, получим равенство
j К2 (EXl) dK (Xl) = j I, (?,,) dK (x2).
X, X.
Из свойств 1°—4е следует, что G — монотонный класс,
содержащий алгебру а C\ X 5). С учетом теоремы 2
п. 2.3 G = аа (^"г X ^2).
Для множества Е ? аа ($"г X 3~2) положим
% (Е): = j k2 (EXl) d%, (Xl) = j I, (EX!) dl2 (x2).
х, х.
Проверим, что функция Я есть мера на аа (<ti X
Согласно определению
Я@) = О; Х(Е)^0, Е^$\ к — конечна на
Пусть
{?¦" ! п>1}с=^"; Ет П Е" = 0,
?:= U Е".
Тогда для любого хх g Xx
Е„= U Е;,; Е?, П E2, = 0, т^»
а потому
По теореме об интегрировании монотонной последователь-
последовательности
х,
117

Построенная мера к удовлетворяет соотношению
A0.1). По теореме 5 п. 4.6 мера К, заданная на полуалгеб-
полуалгебре ?г X &2 соотношением A0.1), может быть единствен-
единственным образом продолжена до меры на аа (Зх X <Г 2).
II. Пусть теперь \ и Х2 — сг-конечные меры. Тогда
существуют {XI : п ;> 1} с: 3и i = 1, 2, такие, что
Х,= U XI; к(Хй<+оо, X? 0X1=0, гпфп,
для i=l,2. При этом
xlXx2= и (XT х xl),
причем
(Х\ X Х[) П (XT X X?) = 0, (i, j) ф (т, п).
Для множества Е ? #" пусть
?т'"! = ?П (Х™ XX?), /л, п>1.
Поскольку для любого хг € Хх
?*,= U ??Л ^¦/п^'" = 0, (»,/)^(/п,л),
m,n=l
^(^.)= S ^(?7;") A0.2)
m./i=l
и для каждой пары (т, n) ? N2 функция
х,»-^(?Г).
^"j-измерима согласно части 1 доказательства, то функция
х{ >*> Я2 (^,)
^"^измерима. Аналогично доказывается ^-измеримость
функции хг *>¦ Хг (EXi). С учетом равенства A0.2), теоре-
теоремы об интегрировании монотонной последовательности
и доказанного в части 1 утверждения леммы для X? X
X X", {т, п) с- N имеем
X, m."=' X,
«"=' x x
xa
118

Упражнения
3. Пусть Е ? &. При условиях леммы 1 доказать, что А. (Я) =0
О Xi (EXt) = 0 почти всюду по х1 относительно меры \ на Х1 <t»
Xt (ЕХг) — 0 почти всюду по х2 относительно меры Х2 на Х-г-
4. Прннцп Кавпьерл. Множества {?, F] с ^ таковы, что
А.2 (?^) = ?i2 (F ) почти всюду на X, относительно меры %L. При
условиях леммы 1 доказать, что X (Я) = Л (F).
5*. Пусть выполнены условия леммы 1 и меры Хг, Хг полны. До-
Доказать, что мера X не обязательно полна.
10.4. ТЕОРЕМА ФУБИНИ
Пусть (Хи #",, Кт) и (Х2, ^, Я2) — пространства с
о-конечными мерами. Рассмотрим также произведение
этих пространств
Х = Х1хХ2> Г = аа(Г1х^2), А. = ^ X V
В описанной ситуации при рассмотрении функций вида
/: Хг X Х2 -> R интегралы по Xt или Х2 относительно
меры %! или Я2 соответственно называются однократны-
однократными, а интегралы по Хх X Х2 относительно меры кг X
X Я2 — двойными. Интегралы вида
\x,
называются повторными. Равны ли эти повторные ин-
интегралы? Как они связаны с двойным интегралом ^ fdX>
х
Огвет на эти вопросы содержится в следующей теореме.
ТЕОРЕМА 3 (Г. Фубини). Пусть {Х1г $и Ъ), i= 1,
2,— пространства с а-конечными мерами и
их произведение с мерой к — произведением мер кг и к2.
Пусть функция /: X -*- R, / ? L (X, к) Тогда для почти
всех хх относительно меры кх на Хх функция fXl g L (X2,
к2), функция
х,
119

принадлежит классу L (Xl, kj и справедливо равенство
fdk = \ f (xt, х2) dk {x1, х2) =
Л j
= f f J /*, (*J ^. (**))<&i (*i)- (Ю.З)
\> I. Рассмотрим сначала случай неотрицательной на
t и ^"-измеримой функции f. Для множества Е cz X
поэтому равенство A0.3) верно и представляет собой
определение меры X из леммы 1 для функции
¦Следовательно, равенство A0.3) справедливо для простых
^-измеримых функций.
Согласно теореме 5 п. 6.6 для функции / существует
монотонно неубывающая последовательность неотрица-
неотрицательных простых ^-измеримых функций \рп : п;>1},
поточечно на X сходящаяся к /. Тогда для любого х1 ?
¦6 *г "
0<Й<С' на Х„
поточечно на Х2. При этом функции pnXi, n~^\, также
лростые. Для п ]> 1 имеем
рп{х1, x2)dk(xly х2) = И ] Рх,(ха)dk2(x2)\dXl(xl).
A0.4)
В силу теоремы 2 п. 7.5 и условия теоремы 3 левая часть
равенства A0.4) при п -*¦ с» сходится к
х
Последовательность функций
, (хг) dk2 (х2), п
есть неубывающая последовательность неотрицательных
#\-измеримых функций. Поточечный на Хх предел этой
лоследовательности, согласно теореме 2 п. 7.5, равен
pnx, (x2) dk.j (х2) = \ fXl (x2) dk2 {x2)
"-*00 х,
120

и является ^-измеримой функцией. Применив еще раз
теорему 2 п. 7.5, получим
1- Г / Г п, ...
lim \ \ Рх,(х2) «Л,
Л] \ Лг
^(xJdlzixMdliiXi).
Таким образом, равенство A0.3) доказано. Утвержде-
Утверждения об интегрируемости есть следствие свойства
G) п. 7.4.
II. В общем случае функцию / представим в виде
причем каждая из функций /+, /_ неотрицательна и при-
принадлежит L (X, К). С помощью формул A0.3) для функ-
функций /+1 /_ и линейности интеграла получаем- утвержде-
утверждение теоремы 3 для функции /. <\
Замечание. При условиях теоремы 3 имеем также
Г [I [
х х,\ х,
следовательно, повторные интегралы совпадают и равны двойному:.
Упражнения
6. Пусть (Xlt &~lt At) — пространство с а-конечной мерой At и
неотрицательная функция f: X, -»¦ R принадлежит L (X,, А,). Пусть
Х.2 = R, ^2 — а-алгебра измеримых по Лебегу подмножеств R а
А2 — мера Лебега, А = At X А2. Найти А (А) для множества
7. Пусть (X,-, 5^1, A,-), i = 1, 2,— пространства с а-коиечными
мерами и А = Aj X А2. Для конечных функций /, ? L (Х<, A;), i = 1,
2, положим
g (ж,; х2) : = /j (хг) /2 (х.2), (ж,, х.2) g Xj X A2.
Доказать, что:
(а) функция g — аа (Tt X ^)-измерима,
(б) g ? L (Хх X А2, А),
Г
\в) .) '1 (•'-i) '2 (*г) "^ (*l> xt) ==
8. Пусть (R, S, А) — прямая с ст-алгеброй измеримых по Лебегу
подмножеств R и мерой Лебега A; (R2, S.,, Х.г) — плоскость с «-ал-
«-алгеброй измеримых по Лебегу подмножеств!?2 и Х.2 — двумерная мера
Лебега. Для конечных функций {/, q) cz L (R, h положим
h (*!, x2): = / (*, — л2) g (х.г), (xlt л-,) 6 R2.
6 8-1569 121

Доказать, что:
(а) функция h — 52-измерима,
(б) для почти всех х1 ? R относительно меры Лебега К существует
интеграл
(/ * В) (xi): = J / (*i — 4) S D) dK (x2);
R
(в) функция f * g, называемая сверткой функций / и g, принадлежит
L (R, X).
9. Пусть А — измеримое по Лебегу подмножество [а, Ь]. Дока-
Доказать, что для и > О
ь
1 с
Л, (А П (х — и, х -f и)) dx ^ л (Л),
'X — одномерная мера Лебега.
10. Пусть (Xi, ^, Я-,), « = 1, 2,— пространства с а-конечпыми
•мерами и /: Х1 X Х2 -* R — неотрицательная аа (^ X 5г2)-из-
меримая функция такая, что:
(а) для почти всех х1 относительно меры %± fx ? L (Х2, Я2),
(б) функция
принадлежит L (Xlt Xj). Доказать, что / ? L {Xx X X2, IjX Я2)
•и справедливо равенство A0.3).
11. Пусть / (xlt x2) = *lF (*!, х2) ? [0, I]2, а функция g: [0,
Л]2 -> R — такова, что
g(x0 I) =sinnAr1, j?! € [0, 1];
.Вычислить интеграл Лебега
В (xi> 4) dxtdx2.
J
0
12. Пусть 52 — а-алгебра измеримых по Лебегу подмножеств
l0, I]2, & = {Л X [0, 1] | Л^51},где51 — сг-алгебра измеримых
подмножеств [0, 1], Я2 — двумерная мера Лебега на S2. Пусть
/ : [0, I]2 -*¦ R — 52-измеримая функция из L ([0, I]2, Х2). Доказать,
что
(а) & с 5,,
¦^б) существует ^"-измеримая функция/jr : [0, I]2-»- R такая, что
: \ UdX2 = \ fd%2;
в в
в в
¦^в) определить функцию f^ для функции
/ (*1. Х2) = Ч + ^2. / (*1> -^2) = V2i (*!> Ч) 6 [°. U2.
122

13. Пусть / ? L (\a, b], I), I — мера Лебега, h > О в
х-\
Ф W : =
1
du< x e
x—h
Доказать, что
/ (X) | rf*.
11. ПРОСТРАНСТВО Lp (X, gr,
11.1. НЕРАВЕНСТВА ГЕЛЬДЕРА И МИНКОВСКОГО
Пусть (X, ZF, Я) — пространство с мерой.
ЛЕММА 1. Пусть числа р и q таковы, что
Тогда для любых чисел
а > О, Ъ > 0 справедливо
неравенство
[> Заметим, что справед-
справедливы соотношения
q > 1, p + q = pq,
1 = pq — P — q+ 1,
a x
Рис. 2
поэтому (/7 — 1) (g — 1) = 1. Сравнивая площади прямо-
прямоугольника и криволинейных трапеций на рис. 2, имеем
причем знак равенства возможен тогда и только тогда,
когда а = Ь. Кроме того,
oi =
о " о
Упражнение
1. Доказать, что неравенство A1.1) равносильно следующему
хр — рх-\- р— 1 > 0, A1.2)
6* 123

где
I
х= ab
o-l
Рассмотреть левую часть A1.2) как функцию от х > 0. С помощью
производной доказать, что неравенство A1.2) выполняется со знаком
?> при х > 0, х ф 1.
ЛЕММА 2. Пусть р > 1 и {a, b) cz R. Тогда
[>Прир = 1 неравенство выполнено. При р> 1 функ-
функция у = хр, х ^ 0, выпукла вниз на [0, -|-°°), поскольку
у = р (р — 1) хр-2 > 0 для х ? @, +<х>). Поэтому
l
ЛЕММА 3 (О. Л. Гельдера). Пусть числа р и q тако-
таковы, что
'функции / и g ^"-измеримы и |/|pgL(X, X), \gf(z
? L (X, X). Тогда fg ? L (X, X) и справедливо неравен-
неравенство
lf\\f\)\g\ A1.3)
X
Достаточно рассмотреть случай, когда
x
Для каждого х ? X применим лемму 1 к числам
Получим следующее неравенство:
После интегрирования этого неравенства по множеству
X имеем
424

P\\ftp i
Замечание. Если р — 2, то q = 2 и неравенство Гельдера в этом
случае называется также неравенством Коши, неравенством Шварца
или неравенством Буняковского.
ЛЕММА 4 (Г. Минковского). Пусть р ^ 1, функции /
и g ^"-измеримы и { | / |р, | g \") cr L (X, X). Тогда
I / + & I" € ? C^i ty и справедливо неравенство
/ + g Г ^)'/Р < f JI / Г а)ш + (JI * Г
J \х I \х 1
(П.4)
J> Неравенство верно при р = 1 или
х
Далее /7 > 1 и
отметим, что | / + g \p G L {X, %) в силу леммы 2. Для
любого х ? X имеем
<\f(x)\-\f(x)+g(x)rl+\g(x)\-\f(x)
Проинтегрируем полученное неравенство по X и приме-
применим дважды неравенство Гельдера
J I / + 8 Г dX < (J | / Г dlT .([\f
X \X f \X
Г1
Отсюда с учетом равенств (р — 1) q — р, 1 = —
следует утверждение леммы 4. ^
125

Упражнения
2. Пусть {/х /„} d L (X, К), числа аг ап положитель-
положительи аг -+" ... + а-п — !• Доказать, что
1 П|/*|в*л<П (\\fk\di) .
X kl fcl \Х /
1
X k=l fc=l
3. Пусть (X, ^", Я) — пространство с конечной мерой и / —
ограниченная на X и ^"-измеримая функция. Доказать, что
lim ( [ |/|"<й) =inf [а>0 \ I ({х | | / (х) | > а}) = 0}.
+ /
4. Доказать, что знак равенства в неравенстве Гельдера A1.3)
возможен тогда и только тогда, когда существуют неотрицательные
числа аир, а+р>0 такие, что
<5. Доказать, что при р > 1 знак равенства в неравенстве Мин-
ковского A1.4) возможен тогда и только тогда, когда существуют не-
неотрицательные числа аиC, а+Р>0 такие, что
11.2. ПРОСТРАНСТВО Lp (X, &, V), р?\\, +°о)
Определение 1. Пусть (X, W, X) — пространство с ме-
мерой, р ? [1, +оо). Тогда множество
/ — ^"-измерима,)
\f\p?L{X,X) 1
называется множеством интегрируемых в р-й степени от-
относительно меры Xфункций. Для/ ? Lp (X, $,Х) положим
ТЕОРЕМА 1. Совокупность функций Lp (X, &, X)
является линейным пространством, то есть
A) fqLp(X,F,X), a?Rz>af?Lp{X,&,X)\
B) {f, g) cz Lp (X, W, X)>(f + g)(z Lp (X, f, X).
Функция ft*-1|/||p есть полунорма на LP(X, W, X),
то есть
C)J0x|p = 0, 0x(x):=0, x?X; ||/||p>0, f?Lp(X, &,\);
D)Hl = \a\-\\Hl> a?K. /€ЬР(Х,^Д);
5) ||/ + g|k<[|/l!P + llg|U [f,g}-<=Lp(X,8-,X).
126

1> Утверждение A) тривиально, утверждения B) и E)
следуют из леммы 4, утверждение C) следует из определе-
определения || • \\р, аналогично получается и утверждение D). <j
Замечание. Из равенства || [\]р= 0 следует лишь, что функция
f= О почти везде относительно меры X на X. Отметим также, что
Lt (X, sr, X) = L (X, X).
Упражнения
6. Пусть X (X) < +со и 1 ^ р < г < -f-co. Доказать, что
Lr (X, Т, X) с Lp (X, Г, X).
Указание. Заметить, что 1Х ? Lp (X, &, X), и применить нера»
венство Гельдера к функциям [/]'", \х и числам —, .
7. Пусть 1 < р < /• < -f-оо и s ? (р, /•). Доказать, что
Lp (X, JT, X) П Lr (X, 5f, X) с U (X, sr, X).
8. Пусть {/, g} с: Lp (X, ^, Я). Доказать, что
{min(/, g), max(/, g)} <=LP(X, &, X),
9. Совокупность L,^ (X, ^", А,) есть множество всех почти всюду
относительно меры X ограниченных на X функций и
i/|L: = inf{a>0 | |/| <a (mod X)}, f 6 Ц» (X, <?, X).
Доказать, что L^, (X, ^", X) есть линейное пространство и что функ-
функция / !-*¦ |] / !„, есть полунорма на L^ (X, &, X).
11.3. ПОЛНОТА ПРОСТРАНСТВА Lp(X, ^", А,), />6[1 +°°)
Определение 2. Последовательность функций {/„ :
.' п ^ 1) cz Lp (X, If', X) сходится в Lp (X, 3', Я) (сходит-
(сходится в среднем порядка р) к функции / ? Lp (X, 3', Ц, если
Упражнения
9. Проверить, что f := g (modX), если
10. Пусть f ? Lp (X, &, X) и а 6 @, -f-co). Доказать неравен-
неравенство Чебышева
Л плгt л | / (к) ^а & 1*1 "л.
11. Пусть lfn — / ||р ->• 0, п -*¦ со для функций {/,2 : /г ^ 1; /}
Л.
с: Lp (X, ^, X). Доказать, что /„ -* /.
12. Пусть {g; '„ : п > 1} с= Lp (X, ^, X) и fn-*f (mod X),
/л — S lip -*• 0i я -*¦ °°. Доказать, что / = g (mod Я).
127

13. Функции f; fn, n > 1 ^-измеримы, fn-*-f и
Доказать, что || /„ — / ||t -> 0, я -»- oo.
14. Пусть {/; /„ : /г ^ 1} с Lt (X, *", Я,), [| /„ - / I ¦* 0,
и -t- oo н g G I'm (X, &, Я). Доказать, что
Ufa — gf\\i-*O, П-+&Э.
15. Для X = [a, b], & — cr-алгебры измеримых по Лебегу под-
подмножеств [a, b] н меры Лебега Я /; /„, п 53 1, измеримые функции
такие, что
A) sup||f,1||00<+oo; B) /„-.-/(mod*,).
Доказать, что для р ? [1, -j-oo)
\fn — f lip -* 0. « -> оо.
16*. Пусть р>\, ) =1 и Я, (X)<-f-oo. Функции
Р Ч
{/„: /г > 1} с Lp (X, ^, k), fn -+ / (mod Я) и
sup
">' х
Доказать, что для любой функции g 6 Ц (X, 5Г, Я) справедливо ра-
равенство
lim \ fngdk = ] fgdX.
п-+оо х х
17*. Пусть ([a, b], &~, Я) — пространство, описанное в упраж-
упражнении 15, и /; /га, /г ^ 1,— измеримые функции такие, что
A) sup || /„ \\г < +°° для некоторого г ? A, -f-ooj;
B) /п -*¦ ^ (mod Я). Доказать, что для любого р ? [1, г)
ll/«-/Ip->0, n-*.«).
Указание. С помощью теоремы Фату сначала доказать, что f ?
i Lr ([a, 6],^, Я). Затем использовать теорему Егорова и неравен-
неравенство Гельдера.
18*. Пусть [f; fn, n > 1} с: Lp (X, ^, Я) н
Доказать, что каждое нз условий
A) /„-*- f (mod Я); B) /л -+ f
влечет сходимость
\fn-f\\p-+O, /i-э-оо.
Указание. Сначала с помощью теоремы Фату проверить, что для
любого А ? &
_нгД I/„I"л> J|/ip<a= \\t\Pd\- J i
п-»оо А АХ Х\А
128

_ f
X n-+oo X\A
- П5? f J |/„ |" л - j |/„|рд]= US
то есть
lim
"-°°Л Л
Затем для заданного 8 > 0 выбрать А ? 5е" с ?^ (А) <-[-оо та-
такое, что
Применить теорему Егорова к множеству Л и оцепить
lim [\fn—f\pdk.
п-*оо %
Определение 3. Последовательность {/„ : п ^ 1} cz
с Ц (X, <F, X) называется фундаментальной или после-
последовательностью 1?оши в среднем порядка р, если
Ve>0 3W Vm>-V Vn>/V i
1/™ —/»1<е-
Упражнения
19. Если || /л — / ||р -*¦ 0, /г -> со для функций (/; /Л1 я > 1} с
с Ц (X, ^, Я), то последовательность {/„ : я^1} фундамен-
фундаментальна в среднем порядке р.
20. Пусть {/„ : /г ^ 1} — фундаментальна в среднем поряд-
порядка 1 последовательность. Доказать, что для любого множества А ? ^
существует предел
lim \ fndX.
;i-.oo;,
ТЕОРЕМА 2. Пространство Lp (X, 9-, к), р?[1,+оо)
полно, то есть любая фундаментальная в среднем порядка
р последовательность {/„ : п ^ 1} cz Lp (X, W, X)
сходится в среднем порядка р к некоторой функции / ?
G lp (х, gr, i).
ь> Пусть {/„ : п ^ 1} — фундаментальная в среднем
порядка р последовательность. Тогда существует после-
129

довательность натуральных чисел
лA)<лB)< ••• <n{k)< ¦
такая, что
Для функций
Sk '• — I /n(l) I + I /«B) — fn(\) I + " • • +| /«(*+!> — fn(ft) |
имеем
Положим g: = lim gk. По теореме 4 п. 7.6 получим
g G Ц (X, ?", Л); lim J g?(U
Следовательно, ряд
oo
I /«(I) I + ? I fnU+i) — fn(D |>
/=1
а потому и ряд
с й-й частичной суммой /„(А) сходятся почти всюду отно-
относительно меры % на X. Таким образом,
lim !гцк) (x) = \f (x) ? R.
Положим / (х) : = 0, х ? X \ Л. Тогда / есть ^"-изме-
^"-измеримая функция.
По теореме Фату
JI f - L I"d* = J Ji_4 /„:/, - /m I
A-»oo X
130

следовательно, в силу фундаментальности в среднем по-
порядка р последовательности (/„ : п ^ 1} (f — /m) E
? Lp (X, S', Ц при больших т, а потому с учетом того,
что /ш б Ц (X, W, К), т > 1, и / ? Ц (X, Г, Я). Анало-
Аналогично | / — fm ||р -> 0, т->оо. <|
Упражнение
21. Доказать полноту пространства L^, (X, &', Я).
Замечание. Отношение / = g (mod Я) есть отношение эквива-
эквивалентности в пространстве Lp (X, &~, к). Пусть Lp (X, 5F, X) — со-
совокупность всех классов эквивалентных функций из Lv (X, &', %).
Для класса / € Lp (X, &', X) положим
i!/И*: =11/Ир. /€Л
Тогда функция / i-» | /||р есть норма на Lp (X, &, X) и пространство
(Lp (Л, 5Г, Я), || • ||р) есть банахово пространство. В частности,
Ц (X, ^", Я) со скалярным произведением
= j
x
есть гильбертово пространство.
Упражнение
22. Пусть /7 > 1, X == N, & = 2N; X (Л) : = | А | для конечного
множества Л (| А | — число элементов А), к (А) : = +оо для бес-
бесконечного множества А. Проверить, что Я — мера на &. Дока-
Доказать, что
1В : = Lp (N, У, Я) =
n=l
1/Р
Доказать также, что /D с: /г, если р < г.
11.4. ПЛОТНЫЕ ПОДМНОЖЕСТВА L0(X, &, К), р?[1-\-оо)
ТЕОРЕМА 3. Для любых функции / ? Lp (X, 5", Я)
и числа е > 0 существует простая ^-измеримая функция
h ? LD (X, <F, К) такая, что
131

t> I. Пусть сначала/6 LP(X, 3', X) и /!> Она X. Соглас-
Согласно теореме 5 п. 6.6 существует монотонно неубывающая
последовательность {hn : n^l] простых ^"-измери-
^"-измеримых неотрицательных функций, поточечно на X сходя-
сходящаяся к /. Поскольку
|/-й„Г<1/Г на X, п>\,
то по теореме Лебега о мажорируемой сходимости имеем
"¦+°°х х
Следовательно, существует т такое, что
j
х
при этом hm = (/—(/ — hm)) ? Lp (X, $~, К). Тогда
h: = hm.
П. Для / ? Lp (X, ^, Я) пусть / = /+ — /_. При этом
{/_, /+} с Lp (л, #", Я). Для заданного е > 0, согласно
части 1 доказательства, существуют простые ^"-измеримые
неотрицательные функции {/i_, /i+} с: Lp (X, <F, К) та-
такие, что
Тогда функция h: — h+ — Л_ является простой W -из-
-измеримой, принадлежит LD (X, 3, К) и | / — h \\р < е. <f
Замечание. Если утверждение теоремы 3 выполнено, то говорят
также, что семейство всех простых ^"-измеримых функций плотно в
Lp (X, ?, Я).
Упражнение
23. Проверить, что функция h из доказательства теоремы 3 удов-
удовлетворяет неравенству |h \ ^ | /\ на X.
ТЕОРЕИЛ 4. Пусть (X, 3', К) — пространство с
с-конечной мерой, #" = оа (Н), Н — полукольцо подмно-
подмножеств X. Тогда для любых функций / ? Lp (X, сГ, К)
¦я числа е > 0 существует функция вида
/»W=|c*4W« *?Х; A1-5>
{Ci с,,} с= R, {Л1( ..., Л„} с= Я,
для которой
132

\> В силу теоремы 2 утверждение теоремы 4 достаточно-
доказать только для простых ^-измеримых функций из
Lp (X, &", К). Далее, поскольку класс функций, для ко-
которых утверждение теоремы 4 верно, является линейным,
то утверждение теоремы достаточно доказать только для
функций вида
Mi A t У~ ] мс^р(^ч & > *Ч.
Однако по теореме 6 п. 4.7 для любого е >» 0 существуют
{Alt ..., Ап) с Н, At П А/ = 0, / =^ / такие, что
Следовательно,
п р
А -У, \Al
dl < e".
Замечание. В том случае, когда X = R или X = \а, Ь], функция-
вида A1.5), в котором каждое из множеств Дх, ..., Ап есть ограничен-
ограниченный отрезок, интервал или полуинтервал, называется ступенчатой.
Если при этом & есть а-алгебра измеримых по Лебегу подмножеств
R ([а> Ь\), а Я — мера Лебега, то теорема 4 утверждает, что множе-
множество всех ступенчатых функций плотно в Lp (R, 9', Я) (Lp ([а, Ь]г
Упражнения
24. Доказать, что множество всех непрерывных на R и равных О
вне некоторого отрезка (своего для каждой функции) функций плот-
плотно в U (R, jr, Я) (в Lp ([о, Ь], &, Я)).
25. Доказать, что семейство всех конечных линейных комбина-
комбинаций с действительными коэффициентами функций
[О, l]dxh+x2n, n = 0, 1, 2, ...
плотно в L2 ([0, 1], ЗГ, Я).
26. Доказать, что семейство всех конечных линейных комбина-
комбинаций с действительными коэффициентами функций
[0, я] 3*H»cos nx, п = 0, 1, 2, ...
плотно в L2 ([0, я], 5Г, Я).
27. Пусть fF — а-алгебра измеримых по Лебегу подмножеств
[0, I]2, Я — двумерная мера Лебега и G — совокупность всех конеч-
конечных линейных комбинаций с действительными коэффициентами функ-
функций из набора
[0, 1]2Э (*i. *2) >-»• *Г*"> т>®, «>0 : {m,n)
Доказать, что совокупность G плотна в La ([0, I]2, &, Я).

РЕШЕНИЯ И УКАЗАНИЯ
Глава 1
9. Класс измеримых по Жордану подмножеств R2 не есть а-коль-
¦цо, поскольку множество Q2 fl [О, I]2 счетно и не измеримо по Жор-
Жордану, а каждое одноточечное множество измеримо по Жордану.
18. Пусть X — основное множество и !F— а-алгебра, состоящая
из счетного набора подмножеств множества X, включая X. Для х 6
€ X, пусть
А(х):= П А< A(
Если {х, у) с X и х ф у, то либо А (х) — А (у), либо А (х) Л
Л А (у) — 0 согласно определению множеств А (х), А (у). Пусть
А1у Аг, ... все попарно различные множества из набора {А (х) |
* ? X]. В том случае, когда попарно непересекающихся множеств
-имеется только конечное число Аъ Л2, ..., Ап, то У конечна. Если
же имеется счетный набор Alt А2, ¦•¦ таких множеств, то мощность У
¦не меньше мощности множества всех подмножеств N.
Глава 2
8. Пусть [хп; п )> 1} —счетное всюду плотное подмножество X.
Тогда для числа г > О
X = у В (х, г)
я для любого шара В (х, г) существует элемент хп и рациональное
¦число р такие, что
х?В(хп, р) <=В(х, г).
13. Сначала с помощью рассуждений, аналогичных решению
упражнения 8, доказать, что 0-алгебра % (Х> является счегно порож-
порожденной, то есть такой, что
Э{Ап:п>\] <= 2х :% (X) = аа ({Ап: я > I!)
Пусть Q — множество всех множеств вида
еде каждое Вп есть одно из множеств Ап, Ап, п > 1, а каждое О,,
есть либо U , либо П . Проверить, что % (X) = Q. Зaтe^f определить
мощность Q.
Описание структуры порожденной а-алгебры опирается на транс-
трансфинитную индукцию. Подробное изложение и решение упражнения
13 содержатся в [5].
Д34

Г л а в а 3
5. Использовать свойства сходящихся рядов, в частности тео-
оо
рему Дирихле. Если условие сходимости ряда V рп не выполнено,
л=1
оо
то есть если ]?] рп = +оо, то функция |х, как и выше, мера, прини-
мающая на всем X и некоторых его подмножествах значение +оо.
11. Предположим, что |х I [) Аи ) = 0. Тогда
\/г=1
13. Пусть {An : n > 1} <= K, U <4,i ? К, Л,„ fl4= 0«.
тфп. Последовательность множеств
Л А ll/З A I I -4 11/1
возрастает и по теореме 2
(оо п \ / оо \ /г
U U Ак\ = ц I U Ап ) = Нт ? [i (ЛА).
15. Пусть {Л„ : л>1}<=/С, Л:= U Л„ЕК; Л„, ПЛ„ =
= 0, тфп. Последовательность множеств
\х U Л2), . . . , Д\1
убывает и имеет пустое пересечение. Поэтому согласно условию
/ п \
lira (.i Л\ у Лй 1 = 0.
Кроме того, в силу конечности (X (Л) и аддитивности (х
\ А=1 / fc=i
16. A' = N, K = 2N и (х({/г}) : = 1, ngN.
a) ^„ = N, п>1; б) Л„= {/г, /г + 1, . . .}, л
в) Л,= {1} U {", л+1, ...}, п>1.
17. Последовательность множеств
135

-убывает, причем fi (Aj) < +со. По теореме 3
Л Л« = Ига V Л
„=1 / "-*°° \fc=i /
Из условия упражнения следует также, что
Vn?N 3m(n)?N:Amin)a f) Л*,
а в силу монотонности (х для каждого п > 1
n
f) ЛА = inf [i (An).
Поэтому
Глава 4
9. См. [1|, гл. III, § 13.
12. О канторовом множестве см. [8], гл. IV, § 3. См. также ука-
)ание к упражнению 13 п. 2.
14. Пусть А — измеримое по Жордаиу подмножество R, дока-
докажем, что множество А — Х*-измеримо. Достаточно для множества
В с: R, X* (В) < +оо доказать неравенство
Я* (В П А) + Я* (В\А) < к* (В).
Пусть е > 0 задано. Согласно определению X*
3 С 6 S, С =э В i X (С) < %* (В) + е.
Тогда
л* (В П ^) + *¦* (S44) < Я* (С П А) + к* (С\А) =
= Я* (С) = X (С)< К* (В) + е.
17. См. указание к задаче 12.
19. Воспользоваться результатом упражнения 18.
20. См. [4], гл. 14, п. 2.3.
24. Воспользоваться теоремами о непрерывности меры.
25. Сначала рассмотрим случай \*т (А) < +оо. Пусть е > 0 за-
задано. По определению индуцированной внешней меры Кт существу-
существует последовательность {В„ : п ^ 1) с: &>т такая, чго
СО °° о
А <= U б«' Е X" (В«) > Хт <Л) + Т •
Далее, для каждого множества из ^"т
т
В = П (о*, &*]
136

существует для каждого fi > 0 открытое множество
т
В'=П(ам, b'$, bk>bk, l^
такое, что
Для л 2^ 1 и б = е2~"' пусть Вп — открытое множество, соответ-
оо
ствующее Вп. Положим G : = U Вп. Тогда G — открыто, А с G и
Если множество Л измеримо по Лебегу, то
е.
Для множества А измеримого и такого, что \т (А) — +оо, восполь-
воспользоваться а-конечностыо меры Лебега %т.
Предположим, что условие упражнения выполнимо. Пусть для
каждого л 2^ 1 Gn — открытое подмножество Rm такое, что
AczGn, X*m(Gn\A)<—.
Заметим теперь, что множество
П
п=1
измеримо по Лебегу и что для множества Ф : = Н \ А
поскольку
1
Поэтому множество А также измеримо по Лебегу.
Глава 6
4. (!) % (R);
(п) а-алгебра всех симметричных относительно точки х = О
подмножеств % (R);
(iii) аа ((—оо, 0], % (R) П @, +со)); (iv) а-алгебра всех перио-
периодических с периодом 2л подмножеств ^ (R).
8. @ с,\АЛ- сг\-А, {с,, с2) cR;
(ii) Совокупность всех четных на R функций;
(iii) Класс
со
V ,„1 , [cn:n> I} cR;
137
,";

(v) Класс всех периодических с периодом 1 на R функций;
(vii) Класс всех функций вида /: R2 -*¦ R, удовлетворяющих ус-
условию
, (viii) Класс всех периодических с периодом 1 по каждой из пе-
переменных функций;
(«). Класс всех функций вида
f (*i> Х2> = Ф (Х1 + *<>)• (*i> *г) ? R2>
где ф : [0, +оо) -»- R.
35. См. [1], гл. IV, § 21.
46. Доказать, что, за исключением множества меры 0, последо-
последовательность {/„ : п > 1} фундаментальна.
47. Сначала с помощью теоремы Лузина и результата упражне-
упражнения 44 доказать утверждение для конечного отрезка, Затем рассмот-
рассмотреть счетную систему отрезков типа [—п, п], п )> 1.
49. Провести рассуждение, аналогичное доказательству теоре-
теоремы 10.
57. Доказать, что для любого е > 0
затем использовать рассуждения, аналогичные доказательству тео-
теоремы 10.
58. Для любого А € ?
la (х) — У а? (х) + Ь2 (*), х ? Х\А.
60. Доказать, что при каждом а ? R уравнение ft + / — a = О
имеет единственное решение t (а), которое является непрерывкой по
о функцией.
Глава 7
10. Можно предполагать, что / конечна. При каждом n g N
функция
измерима, кроме того,
п+1,
U д(, = х.
Для любого Л ? & и п > 1 имеем
138

причем правая часть последнего неравенства стремится к 0 прЛ п -»¦ оо
согласно теореме 1. Для заданного числа е>0 пусть п взято та-
таким, что
Тогда для любого А ? & получим
\ I / I Л < \ I /n I dk + 4" < яЯ, (Л) + 4" •
2 4 2 2
13, 14. См. упражнение 12.
19. Сначала доказать, что для любого 8 > О
Я({*<ЕА: |g(*)>e})<+oo,
Затем использовать схему доказательства теоремы Егорова.
22. Можно воспользоваться результатом упражнения 10.
32. Рассмотреть сходящуюся почти всюду подпоследователь-
подпоследовательность, см. теорему 11 п. 6.9.
38. Рассмотрим произвольную подпоследовательность {}П(щ '.
k~^ 1). По теореме 11 п. 6.9 существует подпоследовательность
• / (mod к), j -*¦ со. По теореме 6 имеем f ? L (А, к) и
МЛ = С fdk.
А
Таким образом, последовательность
К fndk : л2>
имеет один частичный предел \fdk.
А
А
45. Для неотрицательной функции g применима теорема Р,
В общем случае использовать представление g = g+ — g_.
48. Пусть
0,
Имеем для /г ^
л х < х
+ 2 sup j | >п | dk.
Далее использовать георему 6.
139

49. При любом о>0 утверждение справедливо для функций
/J, п ;> 1, р. Кроме того,
(Л, - О
sup
<(X(X)sup f
60. Аналогично решению упражнения 49.
51. (в) Разбить отрезок интегрирования на три части: [0, п а],
[п~а, я — п~а], [л — п~а, л], -х- < а < 1. Использовать также
неравенство
2 л
smx> — х, 0<д;<-—.
л 2
Г л а в а 8
оо 1
I
—j \ /
гг=1 0
Глава 10
5. Мера Я, не является полной для Хг = Х2 = R, ^ = ^ = S,
Xj = Я2 — мера Лебега на 5. Предположить, что существует неизме-
неизмеримое подмножество R. См. [1], гл. VII, § 35.
9. Заметить, что
к (А Л (х - и, х + и)) = j 1(*_н>л;+н) (v) dX (v).
10. Доказательство аналогично доказательству теоремы Фу-
бини.
11. Заметить, что
r'{f(R)) = Mx[o,i] | леSB<[o, 1])}.
12. в) /^ = *! + -._ , f3r = -^ xv
Глава 11
2. Применим неравенство Гельдера к функциям
^ = i/iiai e= fl\ik\ak
140

1 1 „
и числам р = , q = -j . Получим
ai ' — °i
J П
Если n = 2, то получаем нужное неравенство, если л > 2, то нужно
применить иеравенство Гельдера к функциям
н числам
1 — а,-
р = L
— at — a2
и т. д.
3. Если число а > 0 таково, что
то
{дг|
Если же для числа 6 > О
то
(*,({* | |/М|>Ь})I/р, р>\.
Из полученных двух неравенств следует утверждение упражнения»
7. Применить неравенство Гельдера к функциям
/¦—5 S—р
| f \Г—р | S \Г—р
I' I > I' I
н числам
г — р ' — Р
r—S' ¦ — р '
заметить, что
9. Воспользоваться неравенством iMnHKOBCKoro.
12. Имеем также /„ --> g, а потому существует подпоследова-
подпоследовательность /П(А) -> g (mod X).
141

13. Применить теорему о мажорируемой сходимости.
16. Для а > О пусть
а. =
{Ф |ф(
10, I ф (х) | > я.
С учетом упражнения 6 и теоремы Лебега о мажорируемой сходимос-
сходимости для любого а > О имеем
lim Г langdX = \ fagdl.
tl->OO v v
X X
Кроме того, для любого п ^
{A \f'n(x)\>a}
SUP f If \P dl\— v
Имеем также
aP\({x |
SUp Г | fn \pdl
n>\ J
< + oo.
По теореме Фату f ? Lp (X, 3*", Я,). Следовательно, выбором числа а
обе разности
можно сделать сколь угодно малыми по абсолютной величине рав-
равномерно по п ^ 1.
17. По теореме Егорова для заданного е > 0 существует множе-
множество As ? &, As с [а, 6] такое, что
X ([a, b]\At) < е; sup | }п (к) — f (х) \ -* 0, п -> оо.
Согласно теореме Фату / ? L, (|а, Ь\, 5Г, Я.). Имеем для р ? [1, л)
. J.
f \ fnf
142

b]\A
( J
\[a.b]\AF
При этом были использованы неравенства
(а + 6I/*<а1/" + 61/", а>0, 6>0,
а также неравенство Минковского. Применим теперь неравенство-
Гельдера
j \fn\pdl<( j \fn\rdX\P/r(
r, п>\.
Аналогично оценивается интеграл \ \ f f dX.
[a.b] AE
22. Неравенства Гельдера и Минковского имеют для прост-
пространств /р, р ^ 1 следующий вид:
\1/р / оо \1/17
n=\ \n=l j \n=\
I 1
для {xn ! n > 1} ? lp, \un : n > 1} g / p > 1, 1
p p
\n=\
"^ 2j I *n I" 2j
для {{xn : n~^ \], {yn : n ^ \}} cz lp, p ^ \.
24. Достаточно доказать только, что функцию вида 1[а pj можно
сколь угодно точно приблизить непрерывными и равными нулю вне
некоторого отрезка в норме Lp.
25. В пространстве L2 (|—1, 1], S, X) множество всех многочле-
многочленов всюду плотно, поскольку, согласно теореме Вейерштрасса, лю-
любую непрерывную па отрезке [—1, 1] функцию можно сколь угодно
точно равномерно на [—1, 1] (а следовательно, и в норме L2) прибли-
приблизить многочленом. Поэтому любую четную на [—1, 1] и непрерыв-
непрерывную на [—1, 1] функцию можно сколь угодно точно приблизить
в норме L2 многочленами, включающими только четные степени пе-
переменной. Следовательно, любую непрерывную функцию на [0, 1}
можно сколь угодно точно приблизить в норме L2 многочленами,
включающими только четные степени переменной.
26. См. упражнение 25 и его решение.
27. См. упражнение 25. Использовать теорему Вейерштрасса
для функций двух переменных.

ПРИЛОЖЕНИЕ
Избранные задачи, предлагавшиеся
на математических студенческих олимпиадах
1. Вычислить предел
1 i
*1 + ... + *,, dxx ... dxn
¦•б б
¦(КГУ, 1977 г.).
2. Пусть Л с [0, 1] — измеримое по Лебегу множество а
•Я (Л) > О, X — мера Лебега. Доказать, что последовательность
{sin 2"ял:, х ? А : п > 1} неполна в L2 (A, X). (КГУ, 1977 г.).
3. Пусть X — мера Лебега на а-алгебре S измеримых по Лебегу
подмножеств [0, 1] и функция / ? Lt ([0, 1]) такова, что
V Л 6 S, X (Л) = -1- : J / (x) dx = -i- .
Что можно утверждать о функции f? (КГУ, 1982 г.).
4. Пусть (in v — конечные меры на ст-алгебре S борелевских
•множеств R2 и
D={{(x,y) | ax + by + c^O] | {a, b, cj с R}.
Предположим, что
УЛ??> : ц(Л) = у(Л).
'Совпадают ли меры ц и v на S? (КГУ, 1982 г.).
5. Случайная величина | имеет плотность распределения р (х)
= 2~'e~w, х ? R. Для функции
гесчц), м|^(?)|<+оо
доказать равенство
) = М (g (|) sign |)
(КГУ, 1982 г.).
6. Пусть (X, Э:, \х) — измеримое пространство с мерой; Ап ? Эг,
оо
п>1, ^] ц (Лп) < + оо. Пусть для m g N множество Вт есть
множество всех тех и только тех х ? X таких, что х ? Ап по крайней
мере для m значений индекса п. Доказать, что
1 °°
«=1
КГУ, 1983 г.).
444

7. Последовательность положительных случайных величи»
{in : п ^ 1} такова, что
М A + I?,)-* 0, п-+оо.
Вычислить предел
f
(КГУ, 1984 г.).
8. Пусть / g С (R); V* € R : / (*) > 0 и
f(x)dx=*l.
Для фиксированного г > 0 найти предел
lim С а Г nf(
tl—>ОО 1 1
J J k—\
(Всесоюзный тур 1981 г.).
9. Предположим, что для почти всех относительно меры Лебега
х из интервала @,1) существует
lim (sin a.nx-\- 3).
rt-юо
Доказать, что последовательность {ап : л 5s 1} сходящаяся (КГУ,
1987 г.).
10. Пусть S — ст-алгебра измеримых по Лебегу подмножеств
R2, X — двумерная мера Лебега на S и (i — конечная мера на S^
Предположим, что ц <С к. Доказать, что существует круг
К={(х,у) | *2 + (/2<г2}, г>0,
такой, что
|1 (К) = ц (R*\/0
(КГУ, 1988 г.).
11. Пусть (X, 5Г, ц) — пространство с конечной мерой. Описать
все ^"-измеримые функции такие, что
V*6R : |*(* I f(x)<t) = p(x -^-sin/(«)</)
(КГУ, 1988 г.).
12. Пусть кт — мера Лебега в Rm и F cz Rm, F — замкнутое-
множество. Доказать, что для произвольной последовательности
{/л (*)i х € F '¦ п ^ 1} непрерывных на F функций множество всех
ее точек сходимости измеримо по Лебегу. (Черновицкий универ-
университет).
Указания и ответы
1. Простое решение основано на зако не больших чисел и теореме-
Лебега о мажорируемой сходимости. Подробности см. в сб,: Мате-
Математика сегодня. 83. Киев : Вища шк., 1982, с. 141, 142.
Ответ, —— •
V3

2. Решение этой трудной задачи см. в рекомендованном к зада-
задаче 1 сборнике, с. 142, 143.
3. Интересное решение этой задачи приведено в книге:
В. А. Садовничий, А. А. Григорьян, С. В. Конягин. Задачи сту-
студенческих математических олимпиад. Изд-во Моск. ун-та, 1987,
с. 305, 306.
Ответ. / (ж) = 1 почти всюду на [0,1] относительно меры
Лебега.
4. См. решение в рекомендованном к задаче 1 сборнике, с. 165.
5. Полное решение этой задачи приведено в сб.: Математика се-
сегодня. 86. Киев : Вища шк., 1986, с. 171, 172.
6. Решение см. в рекомендованном к задаче 5 сборнике,
с. 181, 182.
7. Сначала проверить, что последовательность {;„ : п ^ 1} схо-
к + оо по вероятности. Затем, учитывая, что
1 \*
Н <е, х>0,
применить усиленный вариант (см. задачу 38, п. 7.6) теоремы о ма-
мажорируемой сходимости.
Ответ, е.
8. Первое решение. Пусть
L : = max / (х) < + оо.
*€L-/-./1
Тогда
п
А=1
,*Up — У |=<— .
1 \п k n J
при этом использована формула для объема га-мерного шара. См.
Г. М. Фихтенгольц. Курс дифференциального и интегрального исчис-
исчисления. В 3 т. Т. 3. М. : Наука, 1960, с. 392, 393. Легко проверить,
что правая часть соотношения (*) стремится к 0 при п -*¦ оо.
Второе решение. Пусть {l.k : k Э3 1} — последова-
последовательность независимых одинаково распределенных действительных
случайных величин с плотностью распределения / каждая. Тогда
величина, стоящая под знаком предела, равна
2
\ k n
В силу закона больших чисел
— I J
П k=\ R
с веро5гтностью 1. Поскол'ьку при данных условиях
146
х*1 (х) dx > 0,
R

то легко проверить, что
Ответ. 0.
9. Указание. Применить теорему Лебега о мажорируемой
сходимости.
10. Указание. Рассмотреть функцию
/ (г) : = |i (К (г)) - ц (R2\/C (г)), г > 0,
доказать непрерывность / и применить теорему Коши о промежуточ-
промежуточном значении.
11. Ответ. Функция /'почти всюду на X относительно меры ja.
л . п
принимает только значения — Y ' '  '
12. См, задачу 25, п. 6.5.

«ПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Я. Халмош П. Теория меры.— М. : Изд-во иностр. лит.,
1953.— 292 с.
2. Р у д и н У, Основы математического анализа.— М. : Мир,
1966.—320 с.
3. F и х м а н И. И. Введение в общую теорию меры и интеграла.—
К.; Донецк : Вища шк. Головное изд-во, 1971.— 172 с.
4. Дороговцев А. Я. Математический анализ.— К. : Вища
шк. Головное изд-во, 1985.— 528 с.
-б. Michel Н. Ма13 — und Integrationstheorie I.— Berlin: VEB
Deutsch. Verl. Wissen., 1978.—204 s.
5. Бурбаки Н. Интегрирование. Меры, интегрирование мер.—
М, : Наука, 1967.— 396 с.
7. Бурбаки Н. Очерки по истории математики.— М. : Изд-во
иностр. лит., 1963.— 292 с.
8. Б р у д и о А. Л. Теория функций действительного переменно-
переменного.— М. : Наука, 1971.— 120 с.
•9. КолмогоровА. Н. Основные понятия теории вероятно-
вероятностей.— М. : Наука, 1974.— 120 с.
10. Теория вероятностей: Сборник задач / А. Я. Дороговцев,
Д. С. Сильвестров, А. В. Скороход, М. И. Ядренко.— К. : Вища
шк. Головное изд-во, 1980.— 432 с.
П. Ширяев А. Н. Вероятность.— М. : Наука, 1980.— 576 с.
12. Сакс С. Теория интеграла.— М. : Изд-во иностр. лит., 1949.—
496 с.
•13. Натансон И. П. Теория функций вещественной перемен-
переменной.— М. : ГИТТЛ, 1957.— 552 с.
14. П е с и н И. Н. Развитие понятия интеграла.— М. : Наука,
1966.— 208 с.
15. X а д в и г е р Г. Лекции об объеме, площади поверхности и
изометрии.— М. : Наука, 1966.— 416 с.
J6. Ф е д е р е р Г. Геометрическая теория меры.— М. : Наука,
1987.— 760 с.

УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
2* б ь
k(H) 10 \f{x)dx 94
а (Я) 10 J
<за(Н) 10 ° ft
ЗДй <*>$/<*>* 94
й (X) 12
НЕ Л« 21 V /Л 98
[+1
21
„ Х1
\\т°А 8 21 B0 С / (х) dx 98
\ /Л,, \ / (*) dF (х) 100
fe R
\\т°Аа 8, 21
n-voo
^i, ^*2 23
<?т 39
XF 24 fe R
*.* 28 C°°(R) 103
К 39 ЯГ 104
(X, У, ц) 41 V* ,-L * 107
v", v, 44 "л
lvi 45 , Ex, Ex 113
7M, Г-'Л' 45 fx' f **..,
R 49 яГ'*х I" U5
f (R) 49 №XX2, aef^X
5m " Xi,) 119
C(X, Y),C(X) 49, 47 *' fj x € Л;
BV ([a, 6]) 52 1Л : = J .
f/ ли? (Л, fljcW е Л?й
¦ / (mod X) 57 и В е Я (возможно, Л = В)
-> f ер ц (X, ^, X), реп, +оо) 12в
tH. X) 72 ц (X, ^, Я.) 131
M.V,\O272 </' ^ 131
К (f) 70 L2 (X, f, X) 131
R ([a, b]) 94 lp 131

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютная непрерывность 106
алгебра 7
о-алгебра 8
алгебра (ст-алгебра), порожден-
порожденная классом множеств 10
а-алгебра, счетно порожденная
134, 12
Дифференцируемость по пара-
параметру интеграла Лебегу 102
Заряд 41
Интеграл двойной 119
— Лебега абстрактный 69, 70,
72
— •—, зависящий от параметра
102
по отрезку 94
— Лебега — Стилтьеса 100
— повторный 119
— Лебега — Стилтьеса 4!, 10S
— полная 32
Минимальное кольцо (алгебра,
а-алгебра, монотонный класс)
11
Множество борелевское 12
—, измеримое по Жордану 22, 38
—, измеримое по Лебегу 37, 38f
39
— канторово 38
— неизмеримое по Лебегу 38
— Д.*-измеримое 30
Монотонный класс 9
Мощность ст-алгебры борелев-
ских множеств 13
Непрерывность интеграла Лебе-
Лебега по параметру 102
— меры сверху 20
снизу 19
Неравенство Гельдера 124
— Минковского 125
— Чебышева 127
Кольцо 7
а-кольцо 7
кольцо (а-кольцо), порожденное
классом множеств 10
Критерий измеримости отобра-
отображения, функции 47, 48, 53,
55
— Лебега интегрируемости
функции по Риману 96
— сходимости по мере 66
Мера 16
— вероятностная 41
— внешняя 28
— индуцированная 30
— Лебега одномерная 37
в Rm 39
Образ 45
Отображение измеримое 46
Подмножества, плотные в
Lp (X, &, X) 132, 133
Полная вариация заряда 45
Полуалгебра 6
Полукольцо 6
Полунорма 126
Последовательность множеств
возрастающая 8
монотонная 8
— — сходящаяся 21
— — убывающая 8
— .фундаментальная в среднем
порядка р 129
—, — по мере 62
150

—, — почти всюду 58
— функций, равномерно ин-
интегрируемая 93
Предел последовательности мно-
множеств 21
— — верхний 21
— — нижний 21
Принцип Б. Кавальери 119
Продолжение меры 26
Произведение мер 115
Производная Радона — Нико-
дима 111
Прообраз 45
Пространство вероятностное 41
— измеримое 41
— LP(X, F, X), р € [1, +оо)
126
— L^ (X, &, к) 127
— с мерой 41
Разложение Жордана 44
— Хана 42
Свойство, выполняющееся поч-
почти всюду 55
Сечение множества 113
— функции 114
Сингулярность 107
Сужение меры 26
Сходимость в среднем порядка р
127
— по мере 60
¦— почти всюду 57
Теорема Егорова 58
— Каратеодори 30
— Лебега о мажорируемой схо-
сходимости 90
— — о разложении заряда 44
— Лузина 66
— Радона — Никодима 108
— Ф. Рисса 65
Теорема П. Фату 88
¦— Фубини 119
— о а-аддитивности меры Жор-
Жордана 22
— — дифференцировании по па-
параметру интеграла Лебега
102
— — единственности продол-
продолжения 34
¦— — непрерывности меры свер-
сверху 20
¦ снизу 19
— по параметру интегра-
интеграла Лебега 102
¦ полноте пространства
Lp (X, ST, к) 129
предельных операция»
над измеримыми функциями
52
— — продолжении меры с по-
полукольца на порожденное
кольцо 26 ;.
связи интегралов Лебега
и несобственного по полу-
полупрямой 98
Римапа и Лебега
по отрезку 94
— ¦ сходимости почти всю-
всюду и сходимости
по мере 62
счетной аддитивности" ин-
интеграла 77
— об интегрировании монотон-
монотонной последовательности 84
— ¦— измеримости сечений из-
измеримого множества 113
— — — — измеримой функции
114, 115
Формула замены переменной об-
общая 104, 112
Функция борелевская 49
¦— измеримая 46
по Лебегу 49
—, интегрируемая по Лебегу 72
— множеств неотрицательная 15
— — полуаддитивная 15
— — аддитивная 15
• счетно полуаддитивная 15
счетно аддитивная 15
¦ конечная 16
Функция множеств 0-конечная
16
— — монотонная 15
— простая 53, 68
— ступенчатая 133
Эквивалешность функций 56

Учебное пособие
Дороговцев Анатолий Яковлевич
ЭЛЕМЕНТЫ ОБЩЕЙ ТЕОРИИ МЕРЫ
И ИНТЕГРАЛА
Обложку оформил художник С. И. Райхлин
Художественный редактор Л. П. Духленко
Технический редактор Л. И, Швец
Корректор И, П, Берус
ИБ № 12804
Головное издательство издательского объединения
«Вьнда школа», 252054, Киев, ул. Гоголевская, 7.
Отпечатано с матриц головного предприятия республиканского
производственного объединения «ГЪлиграфкннга», 252057, Киев,
ул. Довженко, 3 в Харьковской типографии № 16, ул. Универ.
ситетская, 16. Зак. 1838.

ЭЛЕМЕНТЫ
ОБЩЕЙ ТЕОРИИ
МЕРЫ
И ИНТЕГРАЛА
А.Я.Дороговцев

25 к.