Текст
ИСТОРИЮ'
МАТЕМАТИЧЕСКИЕ
ИССЛЕДОВАНИЯ
/^KOBAB.S
ТРУДЫ СЕМИНАРА МГУ ПО ИСТОРИИ МАТЕМАТИКИ
ИСТОРИКО-
МАТЕМАТИЧЕСКИЕ
ИССЛЕДОВАНИЯ
ВЫПУСК I
ПОД РЕДАКЦИЕЙ
Г. Ф. РЫБКИНА и А. П. ЮШКЕВИЧА
О Г II 3
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1948 ЛЕНИНГРАД
11-5-4
Редактор А. П. Юшкевич»
Техн, редактор А. Я. Сипелёва.
А11425. Подписано к печати 25/XI 1948 г. 24 печ. л. 20,12 уч.-ивд. л.
33,525 тип. вн. в печ. л. Тираж 4000 эка. Цена книги 12 р.
Переплёт 2 р. Еаказ № 687.
1б-я тип. треста «Полиграфкнига» Oi Иса при Совете Министров СССР.
Москва, Трёхпрудный, 9.
СОДЕРЖАНИЕ
От редакции.......................................
РАЗВИТИЕ МАТЕМАТИКИ В МОСКОВСКОМ УНИВЕРСИТЕТЕ
С МОМЕНТА ЕГО ВОЗНИКНОВЕНИЯ
27. С. Александров, Б. В. Гнеденко и В. В. Степанов. Мате-
матика в Московском университете в XX в. (до 1940 г.). . 9
А. П, Юшкевич. Математика в Московском университете за
первые сто лет его существования..............z. . . . 43
М. Я. Выгодский. Математика и её деятели в Московском
университете во второй половине XIX в.................. 141
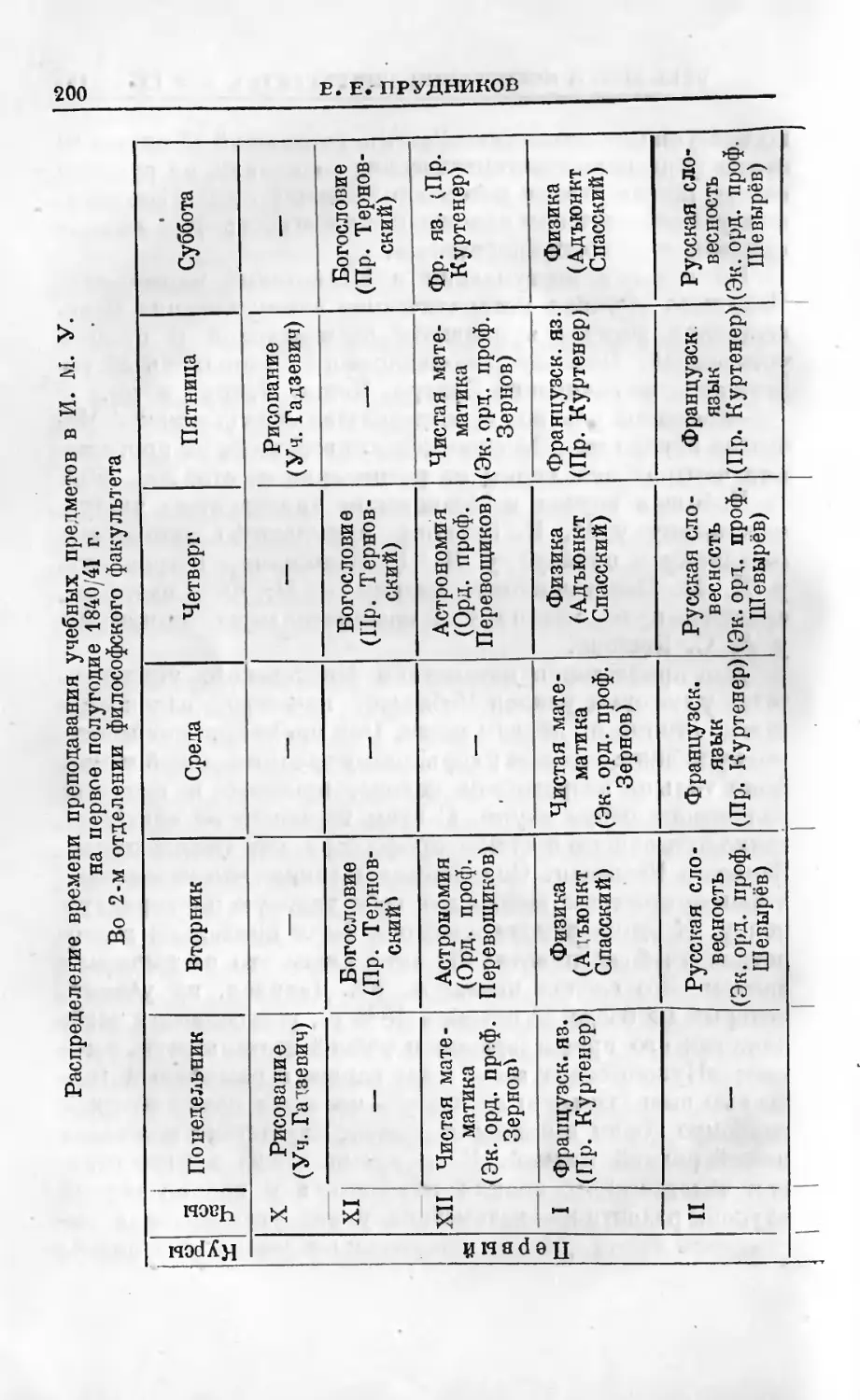
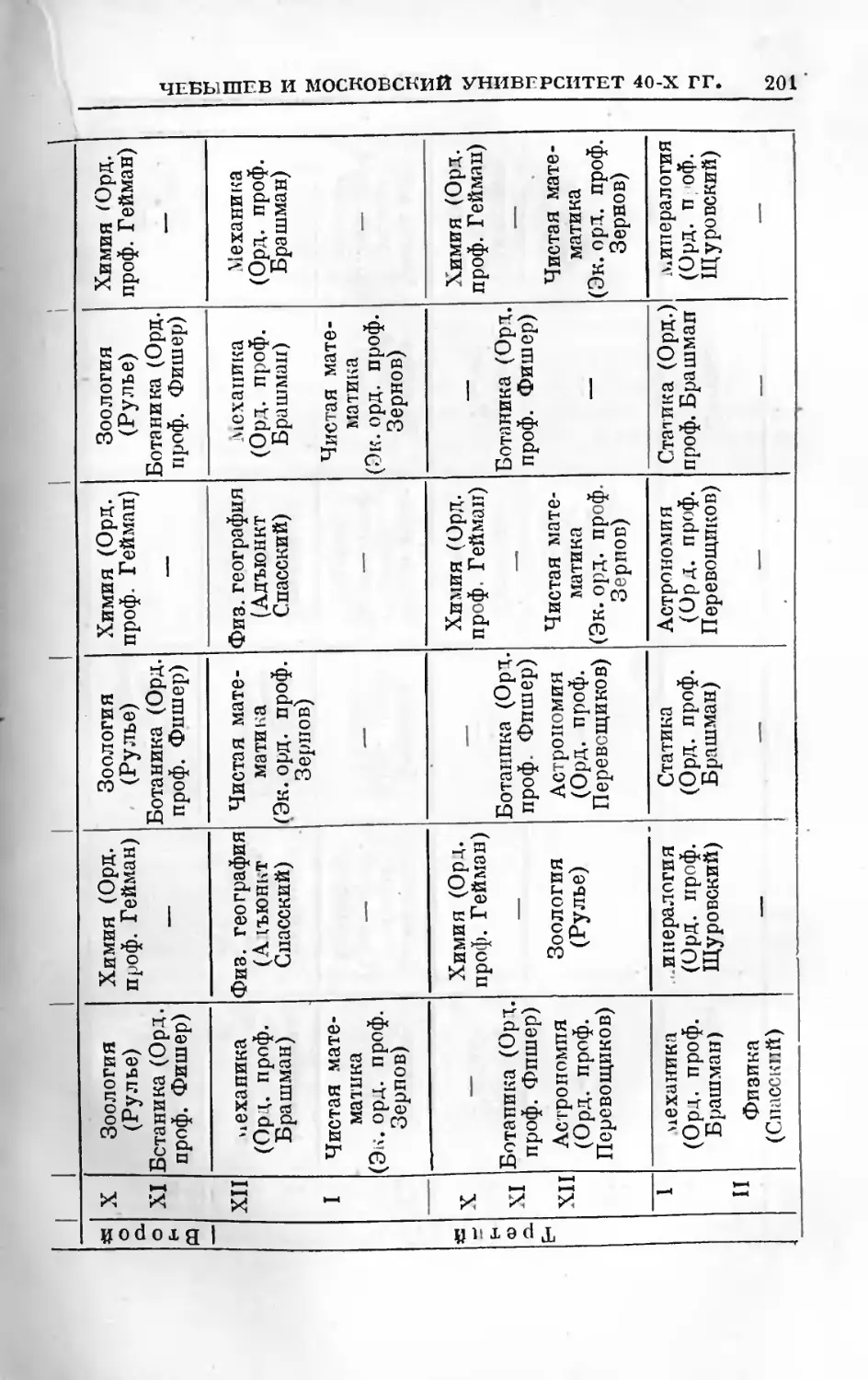
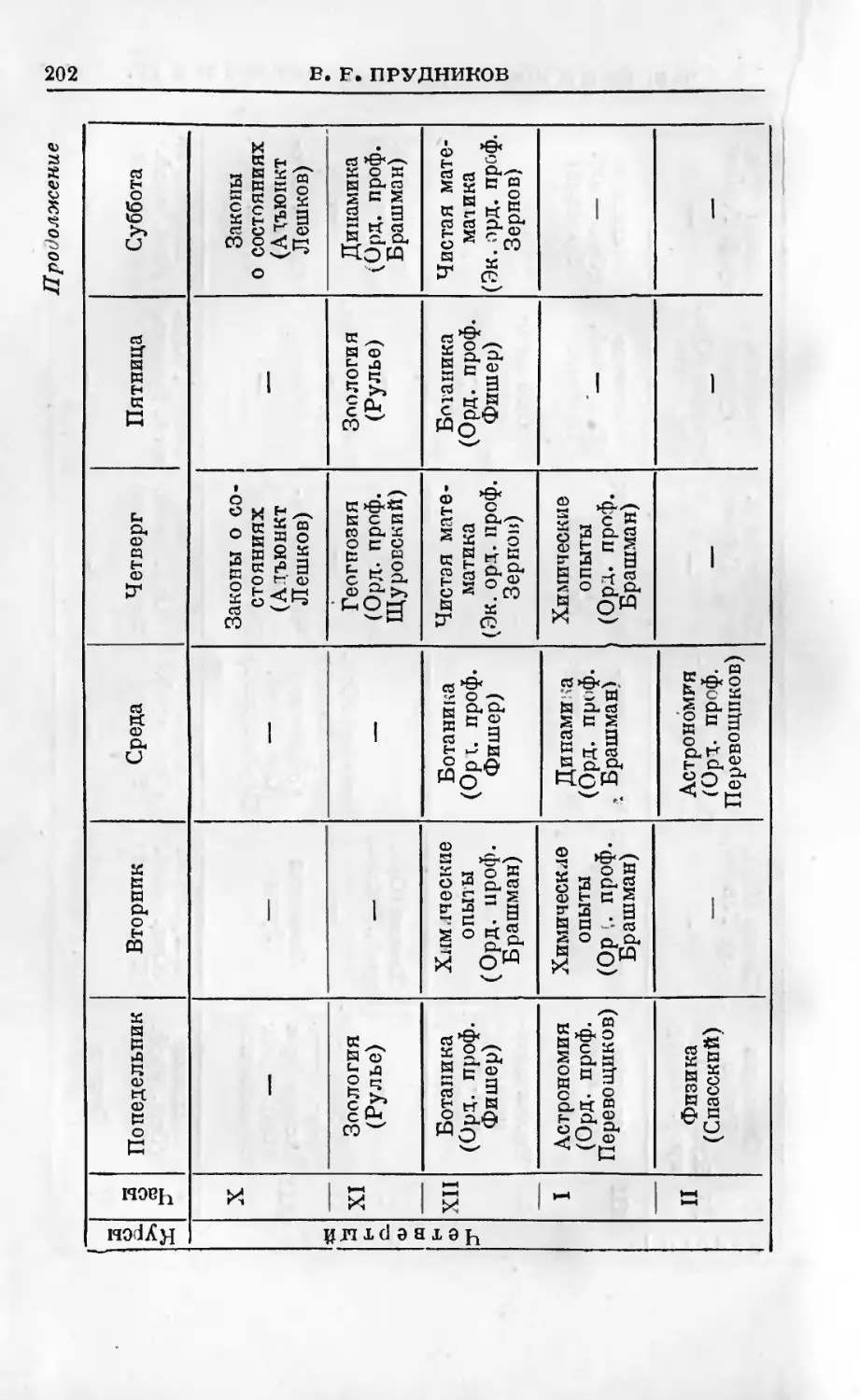
В, Е, Прудников. П. Л. Чебышев и Московский универси-
тет 40-х годов XIX века................................ 184
«НАЧАЛА» ЕВКЛИДА
М. Я. Выгодский. «Начала» Евклида..................... 217
И. Г, Башмакова. Арифметические книги «Начал» Ев-
клида..........................................5 . . . 296
А' И. Маркушевич. О классификации иррациональностей
в X книге «Начал» Евклида.............................. 329
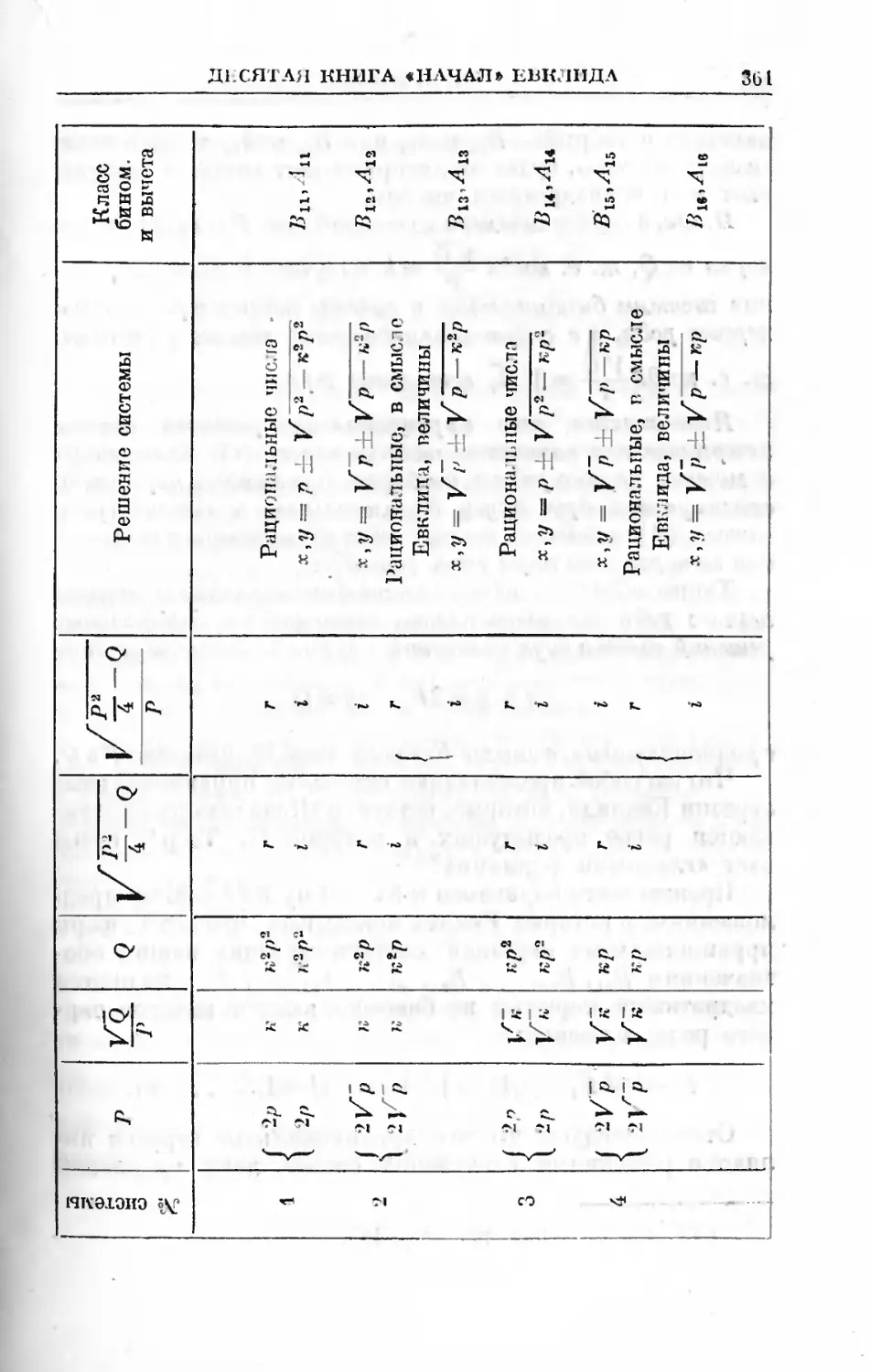
А. Е, Раик. Десятая книга «Начал» Евклида............. 343
ОТ РЕДАКЦИИ
Приступая к изданию «Историко-математических иссле-
дований», редакция стремится хотя бы отчасти удовлетво-
рить всё возрастающий спрос советских читателей на
литературу по истории науки. В самых широких кругах
интеллигенции нашей страны непрестанно повышается
интерес к научному прошлому человечества, особенно
к истории науки народов Советского Союза. Вклад, вне-
сённый в сокровищницу культуры нашей страной, поисти-
не огромен; исключительно велико, в частности, значение
математических открытий, сделанных лучшими предста-
вителями русской и советской математики: Лобачевским,
Чебышевым, Остроградским, Ляпуновым, Марковым
и другими учёными прошлых лет, а также их славными
преемниками нашего времени. До сих пор, однако, мы
недостаточно знаем и не в полной мере оцениваем всё ве-
личие достижений русской и советской математической
мысли, всю глубину её влияния на творчество многих
зарубежных деятелен и школ. Немало ещё замечательных
результатов и даже целых научных направлений, первен-
ство в открытии или создании которых всецело принад-
лежит нашему народу, носят имена иностранцев, «пере-
открывавших» их с опозданием, иной раз весьма значи-
тельным. Ещё менее изучена выдающаяся деятельность
учёных и педагогов, вроде Румовского, Гурьева, Браш-
мана, Зернова, Ващенко-Захарченко, Летникова, Млод-
зеевского и иных, чья плодотворная работа в науке
и в сфере просвещения не может и не должна быть нами
забыта. За последние годы советские учёные немало сде-
лали в исследовании исторического прошлого матема-
тики, вышел ряд книг о Лобачевском, Чебышеве и др.,
ОТ РЕДАКЦИИ
5
издаются сочинения классиков отечественной науки, но
большая часть работы ещё впереди.
Несколько иначе обстоит дело с историей математики
древности и в зарубежных странах. Иностранные учёные,
систематически пренебрегавшие историей математики в
России и СССР или искажавшие её, в прошлом немалое
сделали для описания развития математики в своих го-
сударствах. Однако их работы, содержащие большой
фактический материал, как правило, освещают его с не-
правильных, немарксистских позиций. Идеалистические
и шовинистические концепции господствуют в иностранной
литературе по истории математики от древнего Востока
и античной Греции до современности, и нашей задачей
является подлинно научный, марксистско-ленинский
анализ развития математики во всём мире. Впрочем, и в
чисто описательных разделах буржуазных сочинений по
истории математики имеется много пробелов и ошибок,
иногда связанных с небрежностью исследователя, чаще
же непосредственно вытекающих из неправильных общих
установок.
Редакция «Историко-математических исследований»
предполагает публиковать в сборниках оригинальные ра-
боты по истории математики как в нашей стране, так и в
зарубежных странах.
До публикации каждая работа докладывается и обсуж-
дается на семинаре по истории математики при Москов-
ском государственном университете, руководимом про-
фессорами С. А. Яновской, М. Я. Выгодскими А. П. Юшке-
вичем. Таким образом, «Историко-математические иссле-
дования» являются трудами этого семинара.
Материал, публикуемый в первом выпуске, разбивается
на две части. Один цикл статей посвящается истории мате-
матики в столице нашей Родины — Москве, начиная с мо-
мента организации Московского университета и до Великой
Отечественной войны. Назначение статей этого цикла —
показать и первые шаги московской университетской мате-
матики в XVIII в. и постепенный подъём её в тяжёлых для
развития научной мысли условиях царского режима, и,
наконец, невиданный размах и взлёт математического
творчества в советский период, связанный ©работой, уже
б
ОТ РЕДАКЦИИ
завоевавшей всеобщее признание Московской математи-
ческой школы.
Второй цикл работ отведён «Началам» Евклида, новый
русский перевод которых одноврехменно публикуется
Государственным издательством технико-теоретической
литературы1). Два с четвертью тысячелетия отделяют паше
время от времени выхода классического труда греческого
геометра, и всё же это сочинение до сих пор справедливо
продолжает привлекать внимание и учёных и педагогов.
Литература, посвящённая «Началам», почти необозрима.
Однако ряд вопросов, связанных с содержанием «Начал», до
сих пор вызывает споры, и анализ их с точки зрения совре-
менного состояния науки и методики преподавания яв-
ляется актуальной задачей историко-математической науки.
Статьи второго цикла не претендуют на всестороннее рас-
смотрение знаменитого труда. Часть из них содержит по-
пытку марксистского исследования системы «Начал»
в целом, их места и роли в античной науке, часть посвящена
наименее изученным арифметическим и десятой книгам
«Начал».
Выпуская в свет первый выпуск «Историко-математиче-
ских исследований», редакция приглашает читателей поде-
литься своими мнениями и пожеланиями, относящимися
к этому изданию, а тех из них, работы которых по исто-
рии математики могут быть обсуждены па семинаре, при-
нять участие в подготовке следующих выпусков.
*) «Начала Евклида», книги I—VI, М.—Л., 1948. Книги VII—X
будут выпущены в 1949 г., а XI—XIII— в 1950 г.
РАЗВИТИЕ МАТЕМАТИКИ
В МОСКОВСКОМ УНИВЕРСИТЕТЕ
С МОМЕНТА
ЕГО ВОЗНИКНОВЕНИЯ
МАТЕМАТИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ
В XX ВЕКЕ (до 1940 г.)
1Г, С. Александров, Б. В. Гнеденко
и В. В. Степанов
В XVIII и в первой половине XIX в. математическая
наука в Московском университете была представлена
только как предмет преподавания. Некоторое оживле-
ние научной мысли относится к 60-м годам прошлого
века, совпадая с эпохой буржуазных реформ в Рос-
сии. Эта свежая струя в московской математике связана
с именем Н. Д. Брашмана, с основанием Московского ма-
тематического общества и с началом издания «Математи-
ческого сборника» (1866).
Выдающимся учёным-геометром, положившим начало
образованию в Москве школы дифференциальной геометрии
и оставившим заметный след в мировой науке, является
К. М. Петерсон (1828—1881). Не состоя штатным профес-
сором Московского университета, он влиял па целое поко-
ление математиков как своими работами, печатавшимися
в «Математическом сборнике» и в заграничных журналах,
так и докладами в Математическом обществе. Им была
впервые поставлена задача об изгибании поверхностей
на главном основании и дано решение основных её
случаев.
Непосредственным продолжателем работ Петерсона
в этой области явился Б. К. Млодзеевский (1859—1923).
В своей деятельности Б. К. Млодзеевский внимательно
следил за прогрессом мировой науки и переносил её новин-
ки в Московский университет. Так, он прочёл в Москов-
ском университете первый курс по теории функций
10 П. С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО И В. В. СТЕПАНОВ
действительного переменного; отметим также его доктор-
скую диссертацию по многомерной геометрии—это пер-
вая в России работа по геометрии многомерных про-
странств.
Далее, примыкая к Петерсону, он разрешил ряд слу-
чаев изгибания на главном основании. Являясь крайне
разносторонним математиком, он дал, кроме того, ряд
исследований по проективной геометрии, алгебраической
геометрии, приложению геометрических методов к астро-
номии (орбиты двойных звёзд), к аэрофотосъёмке, по различ
ным вопросам анализа. Но главная заслуга Млодзеевского
перед Московским университетом состоит в систематической
работе над созданием московской геометрической школы.
С 1905 г. он возглавлял семинар по дифференциальной
геометрии, который объединял студентов старших курсов
и лиц, оставленных при Университете, сообщая им послед-
ние достижения современной науки и вовлекая в самостоя-
тельные исследования.
Десятилетием позже, в самом конце XIX в., начал
работу в области геометрии крупный математик
Д. Ф. Егоров (1869—1931). Ему принадлежит оригиналь-
ное по замыслу исследование о трижды ортогональ-
ных системах поверхностей, основные результаты кото-
рого вошли в известный трактат по теории поверхностей
Дарбу. Далее, он далеко продвинул решение задачи
Петерсона об изгибании на главном основании. Следует
от метить так же его оригинальный мемуар (1923) об образо-
вании поверхностей линиями, поставивший и разрешивший
новую проблему. В своей научно-педагогической работе
Д. Ф. Егоров занялся культивированием в Москве новых
направлений анализа, поэтому началом современной
московской школы дифференциальной геометрии явились
работы Петерсона и деятельность Млодзеевского.
В настоящее время это направление возглавляется в Мо-
сковском государственном университете С. П. Финиковым,
разносторонняя научная работа которого и началась
с исследования (в диссертации) той же задачи Петерсона.
Здесь им было дано общее формальное её решение. На ту
же тему одновременно была представлена диссертация
С. С. Бюшгенса. Дальнейшее развитие теория изгибания
МАТЕМАТИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ В XX В. Ц
на главном основании получила в работах А. Ф. Маслова.
Позднее С. П. Фиников и одновременно с ним С. С. Бюш-
гене занимались разработкой тесрии прямолинейных кон*
груенций; в эту работу были вовлечены и более молодые учё*
ные — С. Д. Россипскпй, С. В. Бахвалов и Л. С. Ермолаев.
Далее С. П. Финиковым начаты были изыскания в области
проективно-дифференциальной геометрии, первый толчок
к развитию которой в Москве дал тот же Млодзеевский
в своих специальных курсах.
Л. Н. Сретенский провёл дальнейшее исследование
введённых в докторской диссертации Егорова потенциаль-
ных поверхностей; им была дана исчерпывающая анали-
тическая и геометрическая характеристика класса этих
поверхностей с плоскими линиями кривизны.
Следует отметить также работы С. С. Бюшгенса по
теории плоских механизмов и по приложению дифферен-
циальной геометрии в технике.
Второе направление дифференциальной геометрии
в Московском университете—направление, использующее
методы тензорного анализа, начато было в Москве В. Ф. Ка-
ганом и продолжается под его руководством. Некоторые из
этих работ посвящены разработке аппарата тензорного
исчисления (работа Г. В. Гуревича о классификации три-
векторов).
Следующий круг идей относится к разработке теории
субпроективных пространств, в которой принимали участие
В. Ф. Каган, П. К. Рашевский, а также Г. М. Шапиро
и А. М. Лопшиц.
Цикл работ этой школы относится к идее метрической
двойственности, который в дальнейшем был углублён в
работах Рашевского (докторская диссертация). В основу
берутся пространства линейных элементов и из них
выделяются те, которые обладают двойственностью в изме-
рении расстояний и углов.
Одной из тем этой школы была разработка методами
тензорного анализа вопросов аффинной и проективной
дифференциальной геометрии. Отметим докторскую дис-
сертацию А. П. Нордена, которая касается вопроса о вве-
дении метрики на поверхности в проективно-дифферен-
циальной геометрии.
12 П. С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО II В. В. СТЕПАНОВ
Большое исследование принадлежит В. В. Вагнеру
о неголономных системах. Эта тема, связанная с вопроса-
ми механики, получила в работах Вагнера оформление
в виде законченной геометрической системы.
Школа В. Ф. Кагана занималась также применением
методов тензорного анализа к решению задач классиче-
ской дифференциальной геометрии поверхностей—че-
бышевские сети, одевание поверхностей (Я. С. Дубнов,
Н. В. Ефимов).
По инициативе В. Ф. Кагана Институтом матема-
тики в 1934 г. была созвана в Москве Международная
конференция по тензорному анализу, в которой приняли
участие, наряду с советскими учёными, также и крупней-
шие геометры Запада—Картан (Франция), Бляшке (Гер-
мания), Скаутен (Голландия) и др.
Второе течение геометрической мысли — проективная
и алгебраическая геометрия — ведёт своё развитие от пре-
подавательской деятельности блестящего профессора Мо-
сковского университета В. Я. Цингера (1836—1907). Его
влияние испытало на себе и старшее поколение диффе-
ренциальных геометров (Млодзеевский, Егоров).
Непосредственными учениками Цингера были К. Л. Анд-
реев и А. К. Власов. Андрееву принадлежит ряд интерес-
ных работ по проективной геометрии, развивающих идеи
о многозначных соответствиях и многоугольниках Пов-
селе. А. К. Власов (1869—1923) в своей научной дея-
тельности осуществлял программу построения проек-
тивной геометрии без всякой связи с метрическими эле-
ментами. Первая его большая работа относилась к проек-
тивному строению систем конических сечений; во второй
работе он чисто проективным методом построил поляр-
ные системы высших порядков в формах 1-й ступени.
К сожалению, вынужденный уход Власова из Москов-
ского университета в 1911 г. непосредственно после за-
щиты докторской диссертации, в связи с известными дей-
ствиями царского министра Кассо, не дал ему возмож-
ности привлечь широкие круги молодёжи к работе в этом
круге идей.
Математическая традиция А. К. Власова в последнее
время была представлена в Московском университете
МАТЕМАТИКА в МОСКОВСКОМ УНИВЕРСИТЕТЕ в XX В. 13
Н. А. Глаголевым (1888—1945). Его исследования в этой
области относятся к развитию теории вурфов (проектив-
ная теория гиперкомплексных чисел в n-мерном про-
странстве), к вопросам аксиоматики проективной и ев-
клидовой геометрии, к геометрии индефинитных форм и
задаче геодезического отображения для них. К области
исследования вурфов (мнимых линейных) относятся рабо-
ты И. Н. Бронштейна и В. Н. Депутатова. Н. А. Глаго-
лев работал также в области алгебраической геометрии.
Разработка прикладных вопросов проективной гео-
метрии привела Н. А. Глаголева к занятиям номографией.
Ввиду важности номографии для ряда технических дис-
циплин при Московском университете создан номографи-
ческий центр (научно-исследовательский семинар), объеди-
няющий номографическую работу. В этой области появил-
ся ряд работ московских математиков (О. В. Ермолова,
М. В. Пентковский, К. А. Андреев и др.).
Начиная с 1910 г., Д. Ф. Егоров стал систематически
вести^ математический^ семинар, посвящавшийся из года
в год" различным областям математики (задача Дирихле,
бесконечные последовательности и др.); многие матема-
тики впервые столкнулись с математической наукой
в этом семинаре. Кроме того, Егоров читал ряд специаль-
ных курсов, находившихся на высоком научном уровне.
Всё это привлекло к Егорову многих учеников и из его
школы вышли такие математики, как Н. Н. Лузин, В. В. Го-
лубев, И. И. Привалов, В. В. Степанов и др.
Егоров начал свою научную деятельность в области
геометрии, но его основная заслуга перед Университетом
заключается в том, что он создал семинар по анализу
и положил начало московскому направлению в теории
функций.
В 1911 г. Егоров доказал свою известную теорему
о последовательностях измеримых функций. Непосредст-
венно за этим Н. Н. Лузин опубликовал теорему о С-свой-
стве измеримых функций. Этими двумя результатами было
положено начало московской школе в области метри-
ческой теории функций действительного переменного.
В 1915 г. появилась фундаментальная монография (док-
торская диссертация) Лузина «Интеграл и тригономет-
14 П. С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО И В. В. СТЕПАНОВ
ричесиий ряд», подводившая итоги работ автора в области
метрической теории функций и послужившая отправным
пунктом для большого числа исследований московских
математиков.
Ряд математиков-студентов—А. Я. Хинчпн, Д.Е. Мень-
шов, М. Я. Суслин, П. С. Александров—участников семи-
нара Егорова, с осени 1914 г. стали работать под руковод-
ством Н. Н. Лузина и образовали первое поколение его
учеников.
В центре интересов этой группы молодых математи-
ков была теория функций действительного переменного,
причём Хинчин и Меньшов интересовались метрической
теорией, а Суслин и Александров—дескриптивной теорией.
В начале 1916 г., почти одновременно, вышли три
студенческие работы, опубликованные в докладах Париж-
ской академии. Это были: работа А. Я. Хинчипа об инте-
грале Данжуа, работа Д. Е. Меньшова по проблеме един-
ственности тригонометрических рядов и работа П. С.Алек-
сандрова о мощности борелевских многкеств. В 1917 г.
за ними последовала замечательная работа Суслина,
в которой были построены основы теории так называемых
A-множеств. После Суслина этому предмету были посвя-
щены исследования Лузина и ряда иностранных матема-
тиков, главным образом польских.
Перечисленными работами Лузина, Хинчина, Мень-
шова, Александрова и Суслина было положено начало
длинному и непрерывному ряду исследований московских
математиков в области теории функций действительного
переменного. Это был большой поток блестящих работ,
скоро завоевавших Москве мировое первенство в этой
области математики. Но это произошло уже после Вели-
кой Октябрьской социалистической революции.
Великая Октябрьская социалистическая революция,
открывшая Московский университет трудящимся, совер-
шенно преобразила весь облик замкнутого и малолюд-
ного математического факультета дореволюционного Мо-
сковского университета.
Этот огромный сдвиг сказался решительно во всём:
и в количестве студентов, и в их подлинном научном энту-
зиазме, п в отношениях, сложившихся после революции
Математика в московском университете в хх в. 15
между студентами и профессорами. Ранее имевшая место
официальность этих отношений, недоступность большин-
ства профессоров, сменилась простыми сердечными отно
шениями, основанными на всеобщем увлечении наукой.
Революционные сдвиги в стране существенно сказа-
лись и на формах организации творческой работы по мате-
матике в Университете. В 1923 г. был основан Институт
математики и механики Московского университета, объ-
единивший все научные работы по математике и механике
внутри Университета, а также подготовку многочислен-
ной аспирантуры. Эта новая форма научного объединения
резко повлияла на рост творческой продуктивности. Мате-
матики стали чувствовать, что их работа нс является
только их личной деятельностью, но представляет боль-
шое государственное дело, успехи которого живо интересу-
ют советскую общественность. Организация института при
несла с собой элементы планирования научной работы,
а это во многом помогло созданию крупных математиче-
ских направлений и исследований, касающихся основ
всей математики. Сочетание крупного организующего
центра творческой математической деятельности с под-
готовкой молодых математиков также целиком себя оп-
равдало.
Институт математики воспитал в своей аспирантуре
таких учёных, как академики Колмогоров и Петровский,
члены-корреспонденты АН СССР Гельфонд, Понтрягин,
Шнирельман и много других. Многие бывшие питомцы
института в настоящее время заведуют кафедрами на
периферии и продолжают научную деятельность, начатую
в Университете.
В подготовке учащейся молодёжи сыгрэло большую
роль создание ряда фундаментальных отечественных
руководств, постепенно охватившее все важнейшие
отрасли математики. Сюда относятся книги Привалова
«Введение в теорию функций комплексного перемен-
ного» и «Ряды Фурье», учебник по теории функций
действительного переменного Александрова и Колмо-
горова, курсы теории дифференциальных уравнений
Степанова и Петровского, курсы дифференциальной
геометрии Бюшгенса и Рашевского и т. д., а также
1(‘, П. С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО II В. В. СТЕПАНОВ
многочисленные оригинальные монографии по более
частным вопросам математической науки.
В начале 20-х годов нынешнего века большинство сту*
дентов-математиков, занимавшихся наукой, чувствовало
себя учениками Лузина и высоко ставило научный авто-
ритет Егорова, поддерживавшийся ого большим и широ-
ким пониманием разнообразнсцхпих отделов математики.
Лузин был переполнен свежими математическими идеями
в такой увлекательной для всех молодых математиков
области, как теория множеств и теория функций действи-
тельного переменного. Это сочеталось у него с большим
лекционным талантом и умением увлечь молодёжь и при-
вить ей веру в собственные силы. Немудрено, что всё это
поколение было чрезвычайно увлечено и лекциями и бесе-
дами Лузина. Это увлечение имело и свою отрицательную
сторону: в среде математической молодёжи подчас появля-
лось пренебрежительное отношение к так называемому
классическому анализу (так, уравнения с частными произ-
водными назывались в шутку уравнениями с «несчастными
производными», конечные разности—«разными конечно-
стями» и т. и.).
Период начала 20-х годов, период так называе-
мой «Лузитании» (так назывался коллектив учеников
Лузина) был довольно своеобразным явлением. Важ-
ным положительным фактором этой эпохи в истории мате-
матики Московского университета являлся безгранич-
ный научный энтузиазм молодёжи. Своей идейной почвой
этот энтузиазм имел великие патриотические идеи совет-
ской научной культуры, возбудившие в учащихся и учё-
ных то подлинное научное горение, которое с такой
силой никогда не проявлялось в стенах дореволюционно-
го математического факультета Московского университета.
К старшему поколению учеников Лузина, ещё до
1917 г., присоединился один из самых глубоких и блестя-
щих современных математиков 11. С. Урысон. После
Великой Октябрьской социалистической революции, от-
крывшей двери Университета и для женщин, школа Лузина
пополнилась девушками. Среди них на первом месте
надо назвать Н. К. Бари, с тех пор выросшую
в крупного советского математика.
МАТЕМАТИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ В XX В. 1?
В теории функций действительного переменного и при-
мыкающих к ней отделов теории функций комплексного
переменного необходимо отметить три направления ра-
боты Московской математической школы.
Первое—дескриптивная теория множеств, в которой
после первых работ Александрова, Суслина, Лузина
мы имели сначала ряд исследований Лузина, а затем
длинную цепь работ М. А. Лаврентьева, II. С. Новикова,
А. Н. Колмогорова, Л. В. Келдыш, А. А. Ляпунова и др.
Второе направление—метрическая теория функций—
слагается из ряда блестящих работ Д. Е. Меньшова,
И. II. Привалова, Н. К. Бари, А. Н. Колмогорова и др.
по теории тригонометрических рядов и рядов ортогональ-
ных функций, а также из фундаментальных исследований
А. Я. Хинчина по теории интегрирования и по общей
теории измеримых функций. Сюда же относится работа
В. В. Степанова но почти-периодическим функциям.
Степанов, не являясь непосредственным учеником Лузина,
испытал на себе его влияние, результатОхМ чего явилось
это исследование, которое ввело в классическую теорию
Бора идеи и методы теории функций действительного
переменного.
Особое место в московских работах по теории функций
действительного переменного занимают исследования
В. В. Степанова о полном дифференциале функций двух
переменных и примыкающие вопросы метрической теоре-
тико-множественной геометрии в работах Колмогорова
и его учеников И. Я. Верченко и Ф. И. Шмидова.
По особому руслу направились, с одной стороны, инте-
ресные исследования Н. К. Бари по теории непрерывных
функций, а с другой,—работа В. И. Гливенко о функциях
первого класса, работа Александрова об интеграле Пер-
рона, работа Бессонова по почти-эллиптическихм функ-
циям и др.
Замечательная работа М. А. Лаврентьева о распро-
странении непрерывных отображений, возникшая из его
занятий теорией функций действительного переменного
по существу принадлежит к топологии.
Наконец, к указанному второму направлению относят-
ся работы по метрической теории функций комплексного
2 Историко-математ. исследования
18 П. С, АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО И В. В. СТЕПАНОВ
переменного, в которых центральное место занимают
классические исследования И. II. Привалова и работы
Д. Е. Меньшова, о которых подробнее будет сказано
позднее.
Третье направление московской математической мысли,
ответвившееся от теории функций действительного пере-
менного, отражено работами по математической логике
и по основаниям математики. Эти работы, непосредственно
соприкасающиеся с проблемами философии математики,
принадлежат II. II. Жегалкину (1869—1947), В. II. Гли-
венко, 11. С. Новикову, А. II. Мальцеву, Д. А. Бочвару
и в особенности А. Н. Колмогорову. Вчастности, А. Н. Кол-
могорову принадлежит известная интерпретация интуи-
ционистской логики как исчисления проблем. В. II. Гли-
вепко (1897—1940) первый решил возникший за границей
спорный вопрос, показав, что интуиционистская логика
не есть исчисление, допускающее, кроме истины и лжи,
некоторое третье состояние. Используя в качестве аппарата
доказательства интуиционистскую математику, 11. С. Нови-
ков не только доказал непротиворечивость классической
арифметики, но и дал приём, позволяющий извлечь из
всякого доказательства существования числа, обладаю-
щего некоторым проверяемым для каждого индивидуаль-
но заданного числа свойством, эффективный способ его
вычисления. Д. А. Бочвару принадлежит простое и очень
остроумное решение проблемы парадоксов. А. И. Маль-
цев, используя методы математической логики, полу-
чил ряд теорем теории групп. В. II. Шестаков приме-
нил классическую и трёхзначную логику предложений
к электротехнике (релейно-контактные схемы). В об-
ласти философии математики необходимо отметить ра-
боту С. А. Яновской, в значительной степени связан-
ную с проблемами, возникшими вокруг теории мно-
жеств (философская критика интуиционизма и форма-
лизма).
Примерно в 1920 г. старшее поколение московской
математической молодёжи получило новое пополнение
в лице Л. А. Люстерника, М. А. Лаврентьева и А. Н. Кол-
могорова. По мере расширения коллектива московских
молодых математиков, по мере научного роста каждого
МАТЕМАТИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ В XX в. ц,
и» них, растут и разнообразятся научные интересы чле-
нов коллектива.
Теория функций действительного переменного ужо
не является единственным предметом интересов и работ
молодых московских математиков. Появляются суще-
ственно новые области исследования: А. Я. Хинчин начи-
нает интересоваться метрическими вопросами теории чисел
(диофантовы приближения) — с одной стороны, и теорией
вероятностей—с другой.
Работы Хинчина по теории вероятностей, сначала
по методам своим примыкавшие к теории функций дей-
ствительного переменного, скоро захватывают всё более
и более широкую проблематику и делают Хинчина не
только основателем московской школы теории вероят-
ностей, но и одним из признанных мировых авторитетов
в этой области.
П. С. Урысон в 1921 г. начинает заниматься тополо-
гией и быстро получает результаты первостепенного зна
чения.
В 1922 г. к его топологическим работам присоеди-
няются топологические работы Александрова и таким обра-
зом создаётся советская топологическая школа.
Здесь будет уместно сказать несколько более подробно
о двух исключительно одарённых советских математи-
ках, начавших свою работу уже при советской власти,
скончавшихся в совсем молодых годах и принадлежав-
ших к числу самых ярких и сильных математических даро-
ваний своей эпохи —М. Я. Суслине и II. С. Урысоне.
М. Я. Суслин (1894—1919), как уже упоминалось,
был основателем теории так называемых Л-множеств,
давшей дескриптивной теории множеств совершенно €но-
вое направление и положившей начало целому новому
периоду развития всей теории множеств.
Один из самых крупных представителей теории мно-
жеств во всём мире, М. Я. Суслин принадлежит к числу
самобытных русских талантов, вышедших из крестьян-
ской среды: он был родом из крестьянской семьи Сара-
товской губернии. Научная деятельность его продолжа-
лась едва два года. Опубликовав свои замечательные
открытия по дескриптивной теории множеств в 1917 г.,
2*
20 П. С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО II В. В. СГЕНАИоВ
он немного успел прибавить к ним за последние два года
своей жизни и умер в 1919 г. от сыпного тифа в возрасте
25 лет.
П. С. Урысон (1898 — 1924) является не только осново-
положником советской топологии, с тех пор занимающей
одно из первых мест в мире, но и сам принадлежит к
числу самых крупных топологов XX в. Созданная им
теория размерности является одной из центральных глав
топологии, совершенно преобразившей проблематику всех
частей топологии, развившейся на почве теории мно-
жеств и оказавшей огромное влияние на развитие топо-
логии в целом.
Его работы по так называемой общей или абстрактной
топологии (топологические пространства), в особенности
его метризационные теоремы, явились источником мно-
гих общих идей современной теоретико-множественной
математики.
Теория размерности является в полном смысле этого
слова созданием Урысона. Работы по абстрактной топо-
логии, главным образом по теории бикомпактных про-
странств, велись им совместно с Александровым. Эти работы
многим казались вначале чересчур абстрактными и общими,
пока дальнейшее развитие математики с полной убеди-
тельностью не доказало, что понятие бикомпактного про-
странства является одним из основных понятий современ-
ной математики вообще, значение которого выходит далеко
за пределы тех специально топологических проблем,
в которых это понятие зародилось.
Урысон был не только глубоким блестящим топологом,
он был одним из самых разносторонне одарённых матема-
тиков нашего времени, интересы которого захватывали
буквально всю математику, за исключением разве одной
теории чисел.
Несмотря на молодость Урысона, его работы сразу же
получили международное признание. Во время его поездки
за границу в 1923—1924 гг. его доклады в Геттингенском
математическом обществе, а затем и на Марбургском
общегерманском математическом съезде сразу же соста-
вили ему международную репутацию одного из самых
блестящих математических дарований. Несомненно, что в
МАТЕМАТИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ В XX В. 21
дальнейшей своей деятельности Урысон обогатил бы самые
различные отделы математики открытиями первостепен-
ного значения.
Но его работа и жизнь оборвались от нелепого случая:
17 августа 1924г., купаясь в бурную погоду в Атланти-
ческом океане у берегов Бретани, он был убит ударом
волны о скалу. Погребён Урысон в местечке Бате, в депар-
таменте Нижней Луары во Франции, близ места ката-
строфы. За свою короткую 26-летнюю жизнь Урысон опуб
ликовал свыше 30 работ, не считая нескольких первых
математических работ, выполненных в 1918—1919 гг.,
и работ по экспериментальной физике, сделанных под
руководством II. П. Лазарева ещё в 1915 г., когда автору
было всего 17 лет.
Вся научная деятельность Урысона в основном падает
на четырёхлетие с 1920 по 1924 г. Последнюю свою работу
он закончил буквально за четверть часа до смерти.
В 1925 г. школа топологов, созданная Урысоном и
Александровым, объединилась в топологический кружок.
Первые заседания кружка происходили в Коммунисти-
ческой академии, затем кружок перенёс свою деятельность
в Университет и вошёл как одна из организаций в состав
Института математики.
В начале своей деятельности кружок разрабатывал
проблемы абстрактной топологии, в частности метризации
(Н. Б. Веденисов, А. Н. Тихонов, В. В. Немыцкий),
теории размерности (Л. А. Тумаркин), теории кривых
(Л. М. Лихтенбаум, Ю. А. Рожанская, А. Н. Черкасов),
теории непрерывных отображений (Ю. А. Рожанская)
и гомотопических инвариантов (Л. А. Люстерник,
Л. Г. Шнирельман). П. С. Александров состоял предсе-
дателем кружка, секретарём был В. В. Немыцкий.
Работы Александрова относились главным образом к
построению новой комбинаторной геометрической тео-
рии топологических пространств, состоявшей в основном
из построения процессов аппроксимации топологических
пространств элементарно-геометрическими фигурами, по-
строения гомологической теории этих пространств (группы
Бетти и т. д.) и, наконец, из построения новой геометрико-
алгебраической теории размерности, охватывающей теорию
22 И. С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО II В. В. СТЕПАНОВ
размерности Урысона как некоторый определённый алге-
браический частный случай.
Из топологического семинара Александрова и тошь
логического кружка, начиная с 1924—1925 гг., выходит
ряд молодых топологов: Л. А. Тумаркин, В. В. Немыцкий,
Н. Б. Веденисов, А. Н. Тихонов, Ю. А. Рожанская,
А. Н. Черкасов и, наконец, один из самых блестящих
топологов и математиков вообще — Л. С. Понтрягин.
Этому молодому поколению топологов принадлежит
ряд замечательных работ, из которых надо отметить
работу Тумаркина по дальнейшему развитию урысонов-
ской теории размерности, работы Немыцкого по метриза-
ционным проблемам, специальные исследования Тихонова
по теории бикомпактных пространств, принадлежащие
к числу наиболее значительных достижений в теоретико-
множественной топологии.
Начав свою работу под руководством Александрова,
Л. С. Понтрягин скоро выдвинул свою собственную про-
блематику как в области самой топологии, так и в области
топологической алгебры, главным образом теории топо-
логических групп. Носящий имя Л.С. Понтрягина общий
закон двойственности принадлежит к числу крупнейших
топологических открытий нашего времени; огромные труд-
ности преодолены Л. С. Понтрягиным и в теории непре-
рывных отображений.
Теория топологических групп — интересная и важная
область математики, лежащая в самом центре современных
математических идей, получила в работах Понтрягина не
только ряд глубоких открытий, но и совершенно новую
проблематику. Влияние идей Понтрягина не только на
топологию наших дней, но и на всю математику нашей
эпохи чрезвычайно велико; дальнейшие перспективы его
работы представляются неограниченно широкими.
Очень тесно связан в своих математических интере-
сах с топологией Л. А. Люстернпк. Его исследования
относятся в основном к области так называемых тополо-
гических методов в анализе, главным образом в вариаци-
онном исчислении, где им получены, в значительной части
совместно с Л. Г. Шнпрельманом, математические ре-
зультаты основополагающего значения. В частности.
МАТЕМАТИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ В XX В. 23
Л. А. Люстерник и Л. Г. Шнирельман впервые полностью
решили знаменитую проблему Пуанкаре о замкнутых
геодезических линиях.
Л. А. Люстерник и Л. Г. Шнирельман не ограничились
решением этой задачи Пуанкаре; они построили полную
теорию всех связанных с нею явлений, принадлежащую
к прекраснейшим достижениям советской и мировой
математики. Позднее появляется ряд топологических
работ молодых топологов, выросших под руководством
II. С. Александрова и Л. С. Понтрягина (А. С. Пархо-
менко, И. В. Проскуряков, Гордон, Е. П. Сычёва, Чого-
швили, А. II. Полак, М. Ф. Бокштейн и др.).
Новых молодых работников привлекали топологи-
ческие методы в различных вопросах анализа. С одной
стороны, здесь работали С. В. Фролов, Л. Э. Эльсгольц,
отчасти Чогошвили, с другой—Хильми, Бебутов и др.
В 1934 г. появляются топологические работы A. H.JKon-
могорова, являющиеся одним из существенных новых
успехов советской топологии. В этих работах теория
топологической двойственности приобретает новое ос-
вещение и топология получает новый плодотворный
аппарат так называемых верхних циклов и верхних гомо-
логий, нашедший, властности, большое приложение в неко-
торых работах Л. С. Понтрягина и поставивший перед
топологией ряд совершенно новых проблем. Последние
работы П. С. Александрова в значительной степени йосвя-
щены этим новым понятиям.
Большие успехи советской топологической школы
нашли отражение на первой Международной топологи-
ческой конференции, созванной по инициативе Института
математики Московского университета в сентябре 1935 г.
Эта конференция нс только подвела итоги развитию топо-
логии за последние 15—20 лет, по и поставила перед миро-
вой наукой ряд новых проблем, в значительной степени
определивших проблематику мировой топологии в послед
ние годы.
Из московской топологической школы вышли две
Фундаментальные монографии: первый том «Топологии»,
написанный П. С. Александровым совместно с немец-
ким математиком Хопфом, и «Непрерывные группы»
24 П. С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО И В. В. СТЕПАНОВ
Понтрягина, фундаментальное сочинение, уже сделавшееся
классическим.
Топология была первым большим новым направлением
математических исследований, ответвившимся от мо-
сковской школы теории функций действительного перемен-
ного. В 1923 г., почти одновременно с топологией, от
той же школы теории функций действительного перемен-
ного ответвилось другое большое направление, в кото-
ром советская математика и Московский университет
по справедливости занимают первое место в мире. Это—
теория вероятностей.
Московская школа теории вероятностей начала свои
работы с исследований Хипчина, методы которого выросли
из его же работ по метрической теории функций дейст-
вительного переменного. Первая работа Хпнчина касалась
точной оценки роста сумм независимых слагаемых для
схемы Бернулли. Найденный Хинчиным результат полу-
чил впоследствии название закона повторного логарифма.
Затем А. Я. Хинчпн систематически проводил в своих
работах идею построения теории вероятностей на базе со-
временной теории функций. В течение 1925—1927 уч.
годов Хинчин читал специальный курс по теории вероят-
ностей, результатом которого явилась монография, вклю-
чающая в себя переработку доказательства знаменитой
ляпуновской теоремы, закон больших чисел и изложение
собственных тонких выводов автора в этой области и,
наконец, закон повторного логарифма.
В начале 20-х годов в Москве начал работать по теории
случайных функций Е. Е. Слуцкий (1880—1948), приме-
нивший методы, также очень близкие к теории функций
действительного переменного.
Приблизительно в это же время, в 1925 г., в работу
по теории вероятностей включился А. Н. Колмогоров.
Сначала он создал эскиз аксиоматики теории вероят-
ностей на базе теории меры. Затем последовали два его
исследования о законе больших чисел и законе повторного
логарифма. В обеих этих работах А. Н. Колмогорову
удалось получить фундаментальные результаты. Именно,
первой работой он завершил искания в области закона
больших чисел, указав необходимые и достаточные уело-
МАТЕМАТИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ В XX В. 25
ВИЯ, ВО второй же работе он дал обобщение результата
Хинчина на широкий класс случайных величин.
Существенный прогресс теория вероятностей полу-
чила в последующих исследованиях Колмогорова и Хин-
чина, в которых ими создавалась теория случайных про-
цессов.
В 1930 г. под влиянием исследований Колмогорова*
и Хинчина теорией вероятностей заинтересовался И.Г. Пет-
ровский. Он получил ряд блестящих результатов путём
привлечения метода верхних и нижних функций. Этот
метод послужил впоследствии А. Н. Колмогорову для
нового доказательства теоремы Ляпунова, а также для
решения ряда новых задач того типа, которые возникают
в теории диффузии.
В 1933 г. В. И. Гливенко и А. Н. Колмогоров кладут
начало новому кругу теоретико-вероятностных исследо-
ваний, доказав теоремы о сближении эмпирических кри-
вых распределения с соответствующими теоретическими.
Впоследствии это направление исследований продолжал
и продолжает систематически развивать воспитанник Мо-
сковского университета Н. В. Смирнов. Им получены
многочисленные общие результаты в этой области, имею-
щие первостепенное значение для математической ста-
тистики.
В том же году выходят в свет две известные моногра-
фии Колмогорова и Хинчина. Первая из них посвящена
аксиоматике теории вероятностей, вторая—подведению
итогов работы, главным образом московской школы, в об-
ласти случайных процессов диффузионного типа. Аксио-
матика, предложенная Колмогоровым, стала со времени
появления его монографии общепринятой.
В те же годы Хипчип публикует несколько работ,
посвящённых стационарным случайным процессам, и на-
ходит тесную связь этих процессов с общей тео-
рией динамических систем. Тогда же, приблизительно
одновременно с Биркгоффом, Хинчин доказал знаменитую
теорему, получившую названпе теоремы Биркгоффа-
Хинчина.
Очень близко к общей теории стационарных процессов,
разрабатываемой Хинчиным, подошел Е. Е. Слуцкий,
26 П. С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО И В. В. СТЕПАНОВ
исследовавший методы изучения периодических явлений
и сами эти явления. Е. Е. Слуцкий не только по-
строил математические теории и приёмы для обнару-
'/Кения периодичностей, но и провёл вычислительные
исследования в области метеорологии, физики Солн-
ца и пр.
Теория случайных функций также оставалась одной из
центральных проблем, интересовавших Е. Е. Слуцкого;
ряд исследований в этой области дал также А. Н. Колмо-
горов. Оба они получили в этой области далеко идущие,
основополагающие результаты.
В 1934 г. А. Н. Колмогоров, продолжая исследования
Бруно де Финетти, строит теорию безгранично делимых
законов, исходя из однородных случайных процессов
с независимыми приращениями, и высказывает гипотезу
о том, что класс предельных законов для сумм независи-
мых, пренебрегаемых в пределе слагаемых, совпадает
с классом безгранично делимых законов. Скоро, в 1935 г.,
ученику А. Н. Колмогорова Г. М. Бавли (ум. в 1941) уда-
лось доказать эту гипотезу для случая слагаемых, имею-
щих конечные дисперсии, а ещё год спустя А. Я. Хинчин
дал полное её доказательство.
В эти годы делают первые творческие успехи в теории
вероятностей молодые математики А. А. Бобров, Б. В. Гне-
денко, Д. А. Райков. В 1936 г. А. Я. Хинчин начал чте-
ние курса, посвящённого специальному вопросу предель-
ных теорем для сумм независимых случайных величин.
Широта постановки проблем и лекционный дар Хинчина
увлекли молодых математиков. Началась серьёзная и пло-
дотворная работа молодого поколения вероятностников
в направлении курса Хинчина. Одни за другими появ-
ляются результаты у Райкова, Гнеденко и др. В качестве
наиболее существенных успехов нужно отметить, во-пер-
вых, создание Гнеденко нового метода исследования пре-
дельных теорем, позволившего ему получить большое
количество новых и интересных результатов, а также
переполучить ряд старых, но уже почти без всяких вычи-
слений и, во-вторых, результат Райкова о связи закона
больших чисел с центральной предельной теоремой тео-
рии вероятностей.
МАТЕМАТИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ В XX В. 27
Начатое А. Я. Хинчиным новое направление исследо-
ваний по арифметике законов распределения также под*
хватывается молодёжью, и в короткое время Гнеденко
и Райков дают и в этой области свои результаты.
В это время А. Н. Колмогоров закончил построении
исчерпывающей теории цепей Маркова с конечным и счёт-
ным числом состояний и начал семинар по случайным про-
цессам. Отсюда возникла работа Миллионщикова (уче-
ника Колмогорова) по процессам в аэродинамических
трубах.
Возникшие на основе работы семинара по стационарным
последовательностям исследования Колмогорова внесли
в эту теорию существенный прогресс. Как непосред-
ственное продолжение этих исследований А. Н. Колмою
ров предпринял создание спектральной теории случай-
ных процессов со стационарными приращениями, а так-
же начал изучение турбулентного потока. Эта теория
развивается как раз в настоящее время. Исследова-
ния А. Н. Колмогорова притягивают к себе многочи-
сленную аспирантскую молодёжь, а также многих' ра-
ботников в области естествознания (метеорологов, физи
ков и др.).
Многие большие математические теории возникли в мо •
сковской школе теории вероятностей на почве изучения
и развития физики и естествознания. Таковы, например,
теория случайных процессов без последействия, разви-
тая А. Н. Колмогоровым, теория стационарных процес-
сов, развитая А. Я. Хинчиным и продолженная А. Н. Кол-
могоровым. По существу, в последние годы А. Я. Хин-
чиным заново создана математическая часть статистической
механики—отдела современной физики.
Помимо этого, методы московской школы теории ве-
роятностей позволили решить многочисленные задачи
теории производства. В первую очередь—это задачи ску-
ченности (телефонии, многостаночного обслуживания
и др.). Здесь работали А. Я.Хпнчин, А. Н. Колмогоров,
Н. В. Смирнов, Г. М. Бавли и Б. В. Гнеденко. Отдель-
ные задачи были решены также по заданиям текстильной
промышленности, железнодорожного транспорта, метал-
лургии, оборонной промышленности и пр.
28 П. С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО И В. В. СТЕПАНОВ
Возникшая на почве московской школы теории функ-
ций действительного переменного московская школа тео-
рии вероятностей завоевала признанный ^мировой автори-
тет и ведущее положение в современной науке.
Значительно слабее были представлены исследования
по математической статистике, но п здесь в одном на-
правлении результаты московской школы во много раз
перекрывают достижения всех остальных учёных мира,
работающих в той же области. Это направление—оценка
уклонения эмпирических кривых распределения от тео-
ретических. Начатая А. Н. Колмогоровым и В. И. Гливенко,
эта область исследований в руках Н. В. Смирнова разви-
лась в большую, прекрасно разработанную главу стати-
стики. В настоящее время в московской школе теории
вероятностей началос ь исследование принципиальных про-
блем статистики. Несомненно, что и в этОхМ направлении
советским математикам будет принадлежать почётное
место, и московская школа теории вероятностей займёт
здесь подобающее ей положение.
Московская школа теории вероятностей, несмотря
на специфику своей проблематики, не теряет связи с раз- *
витием других отделов математики и в первую очередь
с теорией функций, функциональным анализом и диф-
ференциальными уравнениями. Результаты, полученные
в теории вероятностей, нередко получают фундаменталь-
ное значение в других областях математики, а методы
других отделов находят живое применение в теории ве-
роятностей.
На той же почве теории функций действительно-
го переменного, как мы уже говорили об этом, возник
в Москве интерес к ряду вопросов теории чисел. Начиная
с 1922—1923 гг., А. Я. Хинчиным культивируется на-
правление метрической теории чисел. Полученные им здесь
результаты относятся к лучшим достижениям этой теории.
Достаточно напомнить две теоремы Хинчина: 1) среднее
геометрическое из последовательных элементов цепной
дроби при увеличении числа их для почти всех чисел стре-
мится к одному и тому же пределу; 2) корень n-й степени
из знаменателя n-й подходящей дробп для почти всех
чисел стремится при п —*оок определённому пределу.
МАТЕМАТИКА В МОСКОВСКОМ \ НИВЕРСИТЕТЕ В XX В. 29
В этом же направлении работали и работают некото
рые ученики Хинчина —А. В. Грошев, И. И. Жогин и др.
В 1925—1926 учебном году А. Я. Хинчин организо-
вал семинар по вопросам аналитическом теории чисел,
в работах которого принял участие ряд математиков
(А. О. Гельфонд, Л. Г. Шнирельман, Н. Г. Чудаков, Н. П. Ро-
манов, А. А. Бухштаб и др.). Многие из этих математиков
свои первые научные интересы в области теории чисел
получили именно в этОхМ семинаре и впоследствии обога-
тили эту область математического знания большим числом
первоклассных исследований.
Настойчиво и упорно двигавшийся своими собствен-
ными путями А. О. Гельфонд в 1929 г. получил блестя
щие результаты в теории трансцендентных чисел. В то
время ему удалось доказать трансцендентность целого ряда
чисел, в частности ете. Созданный им метод позволил
Р. О. Кузьмину (в Ленинграде) получить дальнейшие
результаты в том же направлении. Последовавшее раз-
витие метода А. О. Гельфонда привело его к полному
решению знаменитой проблемы Гильберта о том, что
всякое алгебраическое число в алгебраической иррацио-
нальной степени есть число трансцендентное. Этот резуль-
тат А. О. Гельфонда явился блестящим триумфом совет-
ской математики.
В 1929 г. начал занятия над вопросами, близкими
к теории чисел, Л. Г. Шнирельман. Его исследования
также имели своим источником теорию функций действи-
тельного переменного. Если А. Я. Хинчин в своих иссле-
дованиях исходил из понятия меры множества, то отправ-
ной точкой Л. Г. Шнирельмана было понятие плотности
множества. Л. Г. Шнирельман первым стал изучать
арифметические свойства плотностей произвольных число-
вых последовательностей. Это изучение в 1930 г. привело
его к ряду изумительных по глубине и силе результатов,
вызвавших впоследствии многочисленные исследования
как в СССР, так и за границей. Так, в 1930 г. Шнирельман
доказал одно замечательное предложение, которое ока-
залось первым шагом в решении знаменитой проблемы
Гольдбаха. Именно он показал, что всякое целое число
может быт ь представлено как сумма достаточно большого
3'> 11. С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО И В. В. СТЕ11АНОв
числа простых слагаемых. Впоследствии ряд математи
ков—Романов, Ландау и другие — путём развития ме-
тода Шнирельмана понизили число необходимых сла-
гаемых до 67. Псзднее академику И. М. Виноградову
иными методами удалось получить гораздо более силь-
ное предложение, давшее почти полное решение проблемы
Гольдбаха.
Идеи Шнирельмана получили дальнейшее развитие,
например, в исследованиях А. Я. Хинчина и многих
советских и иностранных математиков, относящихся
к области сложения плотностей последовательностей
чисел.
Л. Г. Шнирельман принадлежит к наиболее блестя-
щим и глубоким математическим дарованиям нашего вре-
мени. Его исследования отличаются богатством идей, про-
стотой и вместе с тем изумительной глубиной исходных то-
чек зрения.
Л. Г. Шнирельман родился в 1905 г. в семье учителя
в г. Гомеле. Уже мальчиком 12—15 лет он обнаружил не-
обыкновенные математические способности. В1921 г. он по-
ступил в Московский государственный университет и окон-
чил его через два с половиной года. В 1927—1928 гг.,
вместе с Люстерником, он развивал топологические методы
в анализе. В 1929 г. Шнирельман уехал в должности
профессора математики в Новочеркасск. Там он натол-
кнулся на изумительно простую и смелую идею рассматри-
вать общие свойства произвольных числовых последова-
тельностей. Этим, как мы говорили, был сделан шаг
в решении проблемы Гольдбаха, была обобщена проблема
Варинга и пр. Осенью 1930 г. он возвратился в Москву.
В 1933 г. был избран членом-корреспондентом Академии
наук СССР. Позднее он занимался разнообразными про-
блемами анализа и топологии.
В 1938 г. Шнирельман разрабатывал общую теорию
аналитических функций на дискретных алгебраических
телах. Эта теория, несомненно, найдёт себе многих про-
должателей. которые принесут ещё не один триумф её
создателю.
Работы Шнирельмана сравнительно немногочисленны,
так как он чрезвычайно строго относился к своим иссле-
МАТЕМАТИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ В XX В.
дованиям, однако каждая из них является произведением
блестящего таланта, глубокого ума.
Нелепая смерть в 1938 г. вырвала Л. Г. Шнирельмаыа
из рядов московских математиков: несомненно, он был
одним из весьма замечательных воспитанников Москов-
ского университета, немало способствовавших росту со-
ветской науки и культуры.
Теория функций комплексного переменного начала раз-
виваться в Москве только в эпоху, непосредственно пред-
шествовавшую Великой Октябрьской социалистической
революции, причём первоначальное её развитие было це-
ликом связано с кругом вопросов, близких к теории функ-
ций действительного переменного. Хронологически первой
работой в этом направлении была диссертация В. В. Голу-
бева об аналитических функциях с совершенным множе-
ством особых точек (1916 г. ). В обсуждении диссертации
самое живое участие приняло старшее поколение школы
теории функций действительного переменного (Лузин,
Привалов, Меньшов).
Вскоре затем последовали совместные работы Лузина
и Привалова, в которых была установлена инвариант-
ность множества меры нуль при конформном отображении
области, ограниченной спрямляемой кривой, а также
исследованы вопросы единственности аналитической функ-
ции, принимающей на окружности определённые значе-
ния. И. II. Привалову (1891—1941) принадлежат фунда-
ментальные результаты относительно интегралов типа
Коши и для них им впервые разрешены граничные
задачи (саратовская работа 1918 г.).
Далее московские математики занимались однолист-
ными функциями (Привалов, затем М. А. Лаврентьев
и II. А. Базилевич), условиями сходимости последова-
тельностей аналитических функций (Хинчин, Привалов).
В. С. Фёдоров в ряде работ детально исследовал
аналитические функции с совершенным всюду разрыв-
ным множеством особенностей. М. А. Лаврентьев всесто-
ронне исследовал всюду сходящиеся последовательности
полиномов комплексного переменного. Д. Е. Меньшов
посвятил ряд мемуаров условиям моногенности функций
комплексного переменного. М. А. Лаврентьев получил
32 11- С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО И В. В. СТЕПАНОВ
ряд интересных результатов, применяя прямые геометри-
ческие методы и используя экстремальные свойства ана-
литических функций.
Незадолго до Великой Отечественной войны М. А. Лав-
рентьев и М. В. Келдыш получили ряд важных резуль-
татов в смежной области—о представлении гармониче-
ских функций полиномами и в связи с этим об условиях
разрешимости задачи Дирихле. Рядами аналитических
функций занимался также А. И. Маркушевич, получив-
ший ряд результатов.
А. О. Гельфонд, работая в области теории чисел мето-
дами комплексного переменного, одновременно получил
существенные результаты в разнообразных отделах теории
аналитических функций. Первая его работа связана с тео-
рией целых функций, принимающих целочисленные зна-
чения. Работа о ньютоновской интерполяции послужила
базой для отмеченной выше фундаментальной работы
по теории чисел. К той же области комплексной интер-
поляции относятся работы В. Л. Гончарова, который,
приехав в Москву из Харькова, приобщил московскую
математику к кругу идей, разрабатываемых школой
С. Н. Бернштейна.
Начав своё развитие на пустом месте, теория функций
комплексного переменного в Московском университете
представлена в настоящее время рядом течений.
В предвоенные годы И. И. Привалов провёл большое
исследование по теории субгармонических функций—тео-
рии, созданной в 20-х годах этого столетия. Привалов
перестроил их общую теорию, углубил и систематизиро-
вал вопросы об их аналитическом представлении, поста-
вил и разрешил для них ряд граничных задач, подняв
в этОхМ направлении названную теорию в уровень с теми
глубокими результатами, которые ранее им же были
получены для аналитических функций. Необходимо также
отметить глубокие исследования М. А. Лаврентьева и его
школы в области расширения поля действия методов
теории аналитических функций (теория квазиконформных
отображений).
Математический анализ в узком смысле этого слова
не имел в Московском университете такой традиции,
МАТЕМАТИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ В XX В. 33
какая существовала в Петербурге со времён Остроград-
ского, а ещё раньше — Эйлера. Деятельность Имшенецкого
автора прекрасных исследований по уравнениям в частных
производных 2-го порядка, была лишь отчасти связана
с Москвой; работы П. А. Некрасова по аналитической
теории дифференциальных линейных уравнений являлись
лишь эпизодом в развитии математики в Московском
университете.
К началу XX в. относятся работы Д. Ф. Егорова по
уравнениям в частных производных 1-го и 2-го порядка,
где к теории этих уравнений широко применялся круг
идей Софуса Ли, в частности его учение об обобщённых
интегральных многообразиях. Эта работа тоже осталась
изолированной. К первым десятилетиям нашего века отно-
сится несколько работ по вариационному исчислению
в духе теории Вейерштрасса, а именно Д. Ф. Егорова
о проблеме Майера, а также работы рано скончави егося
(в 1929 г.) грузинского математика А. М. Размадзе, вос-
питанника Московского университета, об оборванных
экстремалях и о разрывных решениях вариационных
задач.
Новое развитие анализ получил в Московском универ-
ситете уже в послереволюционную эпоху в работах поко-
ления математиков, воспитанных на идеях теории функ-
ций действительного переменного. Сюда прежде всего
относится работа Люстерника (1926), где он прямым мето-
дом—предельным переходом от уравнений в конечных раз-
ностях к дифференциальным уравнениям—исследовал
классическую задачу вариационного исчисления, а также
решение задачи Дирихле для двухмерного уравнения Ла-
пласа. Позднее Люстерник дал ряд работ по разным отде-
лам вариационного исчисления (нелинейные уравнения
Штурма-Лиувилля, теория экстремумов в функциональном
пространстве).
Первая работа И. Г. Петровского по уравнениям
в частных производных непосредственно примыкала к пря-
мым методам Люстерника. В дальнейшем II. Г. Петровский
Дал необходимые и достаточные условия для гр.- нины
области, в которой разрешимо уравнение теплопровод-
ности. Наконец, И. Г. Петровский выдвинул широкую
3 Историно-математ. исследования
34 п. С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО И В. В. СТЕПАНОВ
программу___создать общую теорию систем уравнений в
частных производных. На этом пути Петровский успел
уже далеко продвинуться и получил результаты перво-
степенного принципиального значения. Им вполне охара-
ктеризован класс систем гиперболического типа и пока-
зана закономерность для них начальной задачи Коши
в том смысле, что эта задача имеет решение не только
для аналитических начальных данных, но и для диффе-
ренцируемых достаточное число раз; притом это решение
непрерывно зависит от начальных данных.
В следующих исследованиях Петровский определяет
системы эллиптического типа и доказывает аналитиче-
ский характер их решений — результат, далеко обобщаю-
щий аналогичный результат С. Н. Бернштейна. Работа
по указанной программе продолжается как самим Петров-
ским, так и его школой (С. А. Гальперн, Л. А. Мельцер,
А. Д. Мышкис, С. 3. Брук и др.). Наряду с этим работы
Петровского и его школы охватывают и отдельные частные
задачи уравнений в частных производных. Сюда относятся
исследования Н. С. Пискунова об уравнениях, являю-
щихся обобщениями гиперболических и параболических,
Н. И. Симонова и Фролова об эллиптических уравнениях.
А. Н. Тихонов проводил вместе со своими учениками
детальное исследование уравнения теплопроводности, осве-
тив ряд вопросов, остававшихся невыясненными — един-
ственность при начальных данных на бесконечной пря-
мой, условия разрешимости, периодические решения при
периодических граничных условиях, задача о прошлом
тепловом режиме, нелинейные задачи (излучение по закону
Стефана-Больцмана). Работы Тихонова тесно связывают
теорию уравнения теплопроводности с актуальными во-
просами физики и геофизики.
Следует упомянуть также ряд теорем существования
для нелинейных интегральных уравнений и различных
типов уравнений в частных производных, доказанных
с помощью топологического принципа неподвижной точки.
Сюда относятся работы В. В. Немыцкого, А. Н. Тихо-
нова и ряда их учеников.
Дисциплиной, в которой, быть может, в наибольшей
степени отразились синтетические тенденции современной
МАТЕМАТИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ В XX В. 3S
математики, опирающейся на теорию множеств, является
функциональный анализ. Фукциональный анализ, в рав-
ной мере опирающийся на алгебраические, топологические
и общеаналитические идеи, приобретает в последнее
время положение одной из наиболее ведущих матема-
тических дисциплин.
Идеями функционального анализа проникнуты многие
из работ Л. А. Люстерника; многие из крупнейших работ
А. Н. Колмогорова за последние годы в равной мере мо-
гут быть отнесены как к теории вероятностей, так и к
функциональному анализу. С переездом А. И. Плеснера
в Москву разработка вопросов функционального анализа
принимает в Московском университете более система-
тический характер. Занимаясь спектральной теорией ма-
ксимальных операторов, Плеснер своими курсами и семи-
нарами привлёк внимание математической молодёжи
к этому кругу идей. Под непосредственным влиянием
идей Колмогорова и Плеснера воспитался талантливый
молодой учёный И. М. Гельфанд, защитивший в 1940 г.
в качестве докторской диссертации блестящую работу
«О нормированных кольцах», устанавливающую глубокую
связь между фактами анализа и функционального ана-
лиза, с одной стороны, и топологии и алгебры,—с другой.
В настоящее время можно уже говорить о школе функ-
ционального анализа, возникшей в стенах Московского
университета и работающей под руководством И. М. Гель-
фанда, Л. А. Люстерника и А. И. Плеснера.
Методы функционального анализа начинают находить
широкое использование как в работах в области матема-
тического анализа, теории вероятностей, так и в других
областях математики.
В области обыкновенных дифференциальных уравнений
мы имели работы В. В. Голубева по теории дифференци-
альных уравнений 3-го порядка в комплексной области
с однозначными интегралами, работу М. А. Лаврентьева,
построившего пример уравнения 1-го порядка, у которого
через каждую точку проходит более одной интегральной
кривой, далее, произведённое И. Г. Петровским детальное
исследование особых точек систем дифференциальных урав-
нений в действительной области.
3*
36 п. С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО И В. В. СТЕПАНОВ
Но главным руслом, по которому течёт научная работа
в Москве в области обыкновенных дифференциальных
уравнений, является их качественная теория. Эта теория,
ведущая своё начало от А. Пуанкаре и А. М. Ляпунова,
вызвана в большой степени требованиями, предъявляе-
мыми к математике современной физикой и астрономией.
Работа в этом направлении ведётся в Москве и матема-
тиками, и астрономами, причём математики работают
отчасти в контакте с физиками (А. А. Андронов).
Математики рассматривают преимущественно системы
первого порядка в п-мерном «фазовом» пространстве. Путь
дальнейшей абстракции, созвучный в Москве общему
теоретико-множественному направлению, ведёт к рассмо-
трению динамических систем в абстрактном (метрическом)
пространстве.
Со времени Пуанкаре наметилось разделение этой
теории на две ветви — метрическую, в которой рассматри-
ваются системы, обладающие неизменяемой при движении
мерой множеств, и дескриптивную—исследующую общие
свойства динамических систем вне зависимости от меры.
Оба течения представлены работами московских мате-
матиков.
К метрической теории относится знаменитая эргоди-
ческая теорема, доказательство которой вслед за Бирк-
гоффом было дано в более общей форме А. Я. Хинчиным.
В этой постановке мера всего пространства предполагается
конечной. Обобщения эргодической теоремы на случай
бесконечной меры при различных предположениях сде-
ланы В. В. Степановым и Г. Ф. Хильми. К метрической
теории относится также работа В. В. Степанова и его уче-
ника М. В. Бебутова (погиб на фронте в 1942 г.) об
изменении меры при переходе к новой динамической
системе, в которой движения происходят по тем же
траекториям, что и в первоначальной. Сюда же отно-
сится работа Б. П. Демидовича о введении инвариантной
меры на множестве периодических движений.
В дескриптивном направлении отметим, прежде всего,
работу В. В. Немыцкого о вполне неустойчивых системах.
Все прежние исследователи предполагали ту или иную
форму устойчивости системы; Немыцкий первый поставил
МАТЕМАТИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ В XX В. 37
и решил задачу о системах, в которых все траектории
«уходят в бесконечность», показав, что такая система
топологически эквивалентна движениям по параллельным
прямым. Работа Немыцкого, проведённая для п-мерного
пространства, обобщена Бебутовым на абстрактные про-
странства.
Анализируя и детализируя введённые Биркгоффом
определения, Г. Ф. Хильми разработал теорию квазими-
нимальных множеств и минимальных центров притяжения.
Наконец, В. В. Немыцкий исследовал структуру семейств
кривых и выяснил условия, при которых эти кривые
являются траекториями динамической системы.
Направление качественного исследования динамиче-
ских систем возглавляется в Московском университете
В. В. Степановым и В. В. Немыцким. Особняком стоит
работа Л. С. Понтрягина о квазипериодических решениях
дифференциальных уравнений.
Работы по качественной теории дифференциальных
уравнений среди астрономов возглавляются Н. Д. Моисе-
евым. Моисеев, с одной стороны, углублял исследования
А. М. Ляпунова об устойчивости для фазового пространства
(введено понятие вероятности устойчивости, рассмотрены
новые типы устойчивости). Но основные вопросы для этого
направления связаны с уравнениями второго порядка,
типичным примером которых являются уравнения задачи
о трёх телах. Главное внимание Моисеева и его учеников
было обращено на изучение областных качественных
характеристик в задачах небесной механики, например,
построение областей однотипных контактов с кривыми
заданного семейства (области перигелиев и афелиев),
построение областей сплошной устойчивости и неустой-
чивости в смысле Ляпунова, а также в смысле Якоби
(последнее понятие введено В. В. Степановым в его работе
в 1936 г.). Наряду с этим была проведена работа по лока-
лизации периодических траекторий, т. е. по построению
полос, внутри которых заключены периодические или
непериодические решения. Г. Н. Дубошин с успехом
применял методы Ляпунова к актуальным проблемам
небесной механики как по линии устойчивости, так и по
нахождению периодических решений.
38 П. С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО И В. В. СТЕПАНОВ
В области приближённого решения дифференциальных
уравнений следует на первое место поставить широко
известный метод, предложенный С. А. Чаплыгиным
(1869—1942) и впервые доложенный им Московскому
математическому обществу. К этой работе, опубликован-
ной в 1919—1920 гг., примыкает ряд исследований мос-
ковских математиков, в частности очень интересная
статья Н. Н. Лузина; Д. Ю. Панов применил этот метод
к интегральным уравнениям.
Внимание московских математиков привлекли также
трудные вопросы приближённого решения уравнений
в частных производных. Д. Ю. Панов разработал метод
приближённого решения краевых задач уравнения Лап-
ласа, а Ф. И. Франкль (совместно с Алексеевой) дал
графический и численный метод решения уравнений
гиперболического типа, встречающихся в газовой ди-
намике.
Наряду с разработкой современных проблем матема-
тического анализа в Московском университете возобно-
вились прерванные со смертью В. В. Бобынина (1849—1919)
работы по истории анализа и других областей математики.
С. А. Яновская опубликовала комментированный ею же
перевод математических рукописей Маркса, содержавших
ценнейшие указания по истории идей обоснования анализа.
Были изданы снабжённые комментариями и историче-
скими очерками переводы произведений классиков мате-
матики: Кеплера, Декарта, Лопителй, Эйлера, Монжа,
Карно и др. С 1937 г. в Университете начал функцио-
нировать семинар по истории математики.
По истории математики в древнем мире работали
И. Н. Веселовский, М. Я. Выгодский, А. Е. Раик, по исто-
рии анализа в повое время Э. Я. Бахмутская, С. Е. Белозё-
ров, М. Я. Выгодский, А. И. Маркушевич, К. А. Рыбников,
А. II. Юшкевич, С. А. Яновская. Позднее начались работы
по истории русской математики, по изучению научного
творчества Лобачевского, Чебышева и других классиков
русской науки. В этой области ряд работ был выполнен
П. С. Александровым, М. Я. Выгодским, Б. В. Гнеденко,
В. В. Голубевым, В. Ф. Каганом, А. Н. Колмогоровым,
В. Е. Прудниковым, А. П. Юшкевичем, С. А. Яновской.
МАТЕМАТИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ В XX В. 39
А. Н. Колмогоров предложил схему периодизации исто-
рии математики (статья «Математика», БСЭ, т. 38).
В настоящее время в Московском университете рабо-
тает сильная научная школа в области алгебры, пользую-
щаяся заслуженным признанием как внутри Союза, так
и за его пределами. До Великой Октябрьской социали-
стической революции алгебра была в числе наиболее отста-
вавших учебных дисциплин математического факультета
Московского университета. Молодёжи, интересовавшейся
алгеброй как наукой, а не как «учебным предметом»,
подлежащим сдаче на экзаменах, в те времена в Москве
не было. Преподавание даже единственного обязательного
курса алгебры далеко не стояло на должной высоте и
никаких, даже элементарных навыков в алгебраических
конструкциях студенты не получали. На таком же невы-
соком уровне стояли и требования магистрантских экза-
менов. Правда, в программу этих экзаменов входили
как теория Галуа, так и элементы теории инвариантов,
но и то и другое изучалось вне всякой связи с большими
алгебраическими и общематематическими идеями совре-
менности и обыкновенно оставалось в научном бага-
же тогдашнего, даже хорошего аспиранта инертным
грузом.
Первыми научными начинаниями в области алгебры
явились специальный курс и специальный семинар
О. Ю. Шмидта по теории групп (1922 г.). В центре
научных интересов О. Ю. Шмидта лежали проблемы
теории групп, в особенности теории конечных групп,—
область, в которой О. Ю. Шмидт является одним из при-
знанных лучших специалистов. При этом надо отметить,
что лекции О. Ю. Шмидта отличались не только блестя-
щей формой, но и широким подходом к проблематике
теории конечных групп. Именно этот широкий научный
взгляд на вещи позволил ему ещё раньше написать
книгу по теории групп, значительно опередившую све-
жестью своих идей время (1914 г.), в которое она была
написана. В книге О. 10. Шмидта, впервые в математи-
ческой литературе, теория конечных групп излагается
в свете теории групп вообще; определения и доказатель-
ства, как правило, предполагают конечность данной
40 п. С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО II В. В. СТЕПАНОВ
группы лишь тогда, когда это предположение является
мотивированным существом вопроса. Это и другие досто-
инства книги О. Ю. Шмидта заставили одну из крупней-
ших алгебраистов современности Эмми Нётер отозваться
об этой работе как о наиболее передовой книге по тео-
рии групп из всех известных ей. Таким образом, книга
О. Ю. Шмидта явилась крупным вкладом в мировую
алгебраическую литературу.
Из лекций и семинара О. Ю. Шмидта, превратив-
шегося в постоянно функционирующий алгебраический
центр, вышла целая школа учеников О. Ю. Шмидта
в области теории конечных групп, плодотворно рабо-
тающих по этой дисциплине и получивших в ней ряд
серьёзных результатов. Среди учеников О. Ю. Шмидта
назовём, кроме А. Г. Куроша, специалистов в теории
конечных групп: А. А. Кулакова, В. К. Туркина и др.
Перу самого О. Ю. Шмидта принадлежит ряд работ по
теории групп, написанных в 20-х и 30-х годах. Среди
этих работ вполне классическим произведением алге-
браической литературы стала статья О. Ю. Шмидта о
единственности разложения групп в прямые произведе-
ния, где знаменитая теорема Ремака-Шмидта доказана
им с общностью и красотой, оказавшими большое впечат-
ление на алгебраистов всей Европы.
Дальнейшему усилению и обобщению теоремы
О. Ю. Шмидта посвящена была и первая алгебраическая
работа А. Г. Куроша. В известной мере примыкают к рабо-
те Шмидта и дальнейшие исследования Куроша о сво-
бодных произведениях групп, вошедшие в его доктор-
скую диссертацию. Работы Куроша знаменуют собой,
однако, существенное расширение проблематики москов-
ской алгебраической школы и поворот её в основном
в сторону теории бесконечных групп, а также и вооб-
ще в сторону так называемой общей или абстрактной
алгебры—теории колец и общей теории идеалов, теории
алгебраических тел, гиперкомплексных систем и т. д.
Будучи учеником П. С. Александрова и начав свою ма-
тематическую работу с абстрактной топологии, Курош
был, естественно, подготовлен к работе в этих наиболее
общих направлениях современно# алгебры.
МАТЕМАТИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ В XX В 41
д. Г. Курош является крупным представителем идей
общей алгебры в Советском Союзе. Не только ряд
его собственных исследований, главным образом в тео-
рии бесконечных групп, даёт ему право на эту квалифи-
кацию, но и его положение бесспорного руководителя
целой школы молодых алгебраистов, к которым принад-
лежат такие, уже вполне проявившие себя талантливые
молодые учёные, как А. II. Узков, Н. С. Черников и
др., а также в значительной степени А. II. Мальцев
(вообще являющийся учеником Колмогорова).
Работы Куроша, Мальцева, Узкова, Черникова и ряда
других молодых математиков позволяют говорить о пер-
воклассной московской школе в области алгебры, по су-
ществу своему выросшей на московской»почве теоре-
тико-множественной математики и являющейся большой
новой ветвью этого широкого математического напра-
вления, ветвью, которой несомненно принадлежит и боль-
шое будущее, и большое влияние на всё дальнейшее
развитие математических наук. Московская школа общей
алгебры тесно связана и с топологической алгеброй
(Понтрягин), и с функциональным анализом (в особен-
ности через работы Гельфанда), и с топологией в соб-
ственном смысле слова. Несомненно, что все эти связи
и научные взаимодействия будут дальше развиваться
и углубляться и содействовать развитию больших, объ-
единяющих всю математику, математических идей.
Московская математическая школа, выросшая в сте-
нах Московского университета, свои основные достиже-
ния последних двух-трёх десятилетий ведёт исторически
от работ в области теории множеств и теории функ-
ций действительного переменного. На почве этих ра-
бот возникло грандиозное научное сооружение, дале-
ко разветвляющееся и вширь и вглубь, которое может
быть охарактеризовано кратко: теоретико-множественный
анализ.
Это сооружение, охватывающее и топологию, и общую
алгебру, и функциональный анализ, и общую динамику,
и значительные разделы теории вероятностей, является
стержнем, объединяющим вокруг себя значительную часть
общих математических идей современности.
42 П. С. АЛЕКСАНДРОВ, Б. В. ГНЕДЕНКО И В. В. СТЕПАНОВ
Теоретико-множественная математика, характери-
зуясь общностью и часто неразрывно связанной с ней
отвлечённостыр своих методов, принадлежит как буд-
то к числу наиболее теоретических наук, казалось бы,
недостаточно связанных с практикой. Однако это не
так: в настоящее время идеи теоретико-множественной
математики являются доминирующими в ряде матема-
тических областей, непосредственно связанных с естест-
вознанием, и через функциональный анализ, теорию
вероятностей, теорию дифференциальных уравнений ока-
зывают существенное влияние на современную физику,
а через неё и на технику.
МАТЕМАТИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ
ЗА ПЕРВЫЕ СТО ЛЕТ ЕГО СУЩЕСТВОВАНИЯ
А. П, Юшкевич
История математики в Московском университете за
первые сто лет его существования разделяется на два
почти равных периода. Рубежом между ними явились на-
чальные годы XIX столетия, годы весьма серьёзной реор-
ганизации университета. Эти два полувека резко отлича-
лись один от другого. В первом полувеке математика
служила только вспомогательным предметом для изучения
других специальностей. Студентов-медиков, естествен-
ников, философов, юристов знакомили при этом с ариф-
метикой, алгеброй, геометрией, тригонометрией, отча-
сти с учением о перспективе. В начале второго полустоле-
тия было создано самостоятельное физико-математическое
отделение, начавшее выпускать математиков, физиков,
астрономов, механиков, химиков, а в программы были
немедленно включены аналитическая геометрия и начала
высшего анализа. На протяжении первого полувека пре-
подавание и руководство не претерпели почти никаких
изменений. Во втором—программы п учебники быстро
совершенствовались, отражая успехи математики и борь-
бу научных течений. В XVIII в. многие московские профес-
сора математики обладали ещё довольно ограниченным
кругозором. В первой половине XIX в. и особенно с 30-х
годов его в среде московских математиков начинают
преобладать квалифицированные специалисты, выдаю-
щиеся педагоги, люди с широкими интересами и с научно-
общественной инициативой. Первое пятидесятилетие
прошло почти целиком под заметным влиянием воль-
44
А. П. ЮШКЕВИЧ
фовской педагогической мысли, быстро отстававшей от
требований времени. В его математических! актив можно
записать главным образом подготовку первых москов-
ских преподавательских кадров. Второе пятидесятилетие
испытало на себе воздействие общественного и культур-
ного подъёма России. За короткий срок на физико-
математическом отделении выдвинулись такие крупные
деятели, как профессора Д. М. Перевощиков, Н. Е. Зер-
нов, Н. Д. Брашман, воспитавшие, в свою очередь, не-
скольких замечательных учёных и среди них акад.
II. II. Сомова и акад. П. Л. Чебышева, а также великого пу-
блициста и мыслителя А. И. Герцена. Всего через несколько,
лет после завершения рассматриваемого здесь периода,
по предложению Н. Д. Брашмана, при Университете было
создано Московское математическое общество и начато
было издание печатного органа общества—«Математиче-
ского сборника», т. е. был заложен краеугольный камень
фундамента Московской математической школы, которой
предстояло — уже в советское время—занять одно из
почётнейших мест в мире.
I. Преподавание математики в 1755—1803 гг.
Основание Петром I Навигационной школы в Москве
(1701г.) на некоторое время превратило Москву в рассад-
ник русского математического просвещения. В этой
школе начали работать выдающийся педагог Л. ф . Маг-
ницкий и приглашённый Петром абердинский математик
А. Фархварсон. Из московской типографии вышли пер-
вое русское печатное руководство по арифметике, алге-
бре, геометрическим и навигационным вычислениям—
«Арифметика» Магницкого (1703) и первый же на рус-
ском языке печатный курс геометрии — переводная «Гео-
метрия славснски измерение» (1708). Вскоре, однако,
центр математического просвещения переместился в Пе-
тербург. В 1715 г. там была открыта Морская академия,
куда переведён был проф. Фархварсон. Навигацкой
школе, в которой остался работать Магницкий, отведена
была роль второстепенного учебного заведения, и поне-
многу она захирела, а в 1752 г. была закрыта. С основа-
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 45
цием в 1725 г. Академии наук и при ней гимназии, уни-
верситета и типографии Петербург на долгие времена
превращается в основной центр русского естествознания
и математики. В Петербурге открываются новые воен-
ные и технические школы, а затем учительская семинария;
здесь воспитываются русские учёные-естественники и
математики; здесь издаётся обширная научная и учеб-
ная литература. Учреждение—по инициативе Ломоно-
сова—Московского университета вновь открыло перед
Москвой перспективу развития в ней естественно-науч-
ной и математической мысли.
Московский университет организован был в 1755 г.
в составе трёх факультетов: юридического, медицинского
и философского. Среди десяти созданных тогда кафедр
имелись естественно-научные: натуральной истории и ана-
томии, химии, теоретической п экспериментальной физики.
В студенты разрешено было принимать лиц, выдер-
жавших нетрудное испытание по курсу свободных наук
(собственно, по основам начальной математики и сло-
весности) и латинскому языку, имевших свидетельство о
благонравии и исключённых из подушного оклада.
Так как желающих и имеющих возможность вступить
в число студентов было крайне мало,—столь мало, что
вначале нельзя было даже разделить их по факультетам,—
то для подготовки будущих слушателей организовали,
по примеру Академии наук, гимназию. Она разделя-
лась на две «школы». В «русской школе» обучали русской
грамматике и началам латыни, в «латинской» — проходи-
ли, кроме языков, арифметику, геометрию, географию
и историю. Можно было вместо латинской школы прохо-
дить немецкую или французскую, в основном отличав-
шиеся изучением новых языков вместо древних. Но для
поступления в Университет знание латыни было обяза-
тельным. В 90-е годы добавлено было обучение началам
алгебры и тригонометрии. Высшей ступенью гимназии
являлся руководимый ректором «ректорский латин-
ский класс», где поступающие в Университет в течение
года восполняли пробелы в подготовке. В гимназии был
строго выдержан классово-сосливный принцип: разно-
чинцы и дворяне учились отдельно; но незначительные
46
А. П. ЮШКЕВИЧ
различия в программе, имевшиеся вначале, с 70-х гг.
исчезли. В1779 г., по предложению поэта М. М. Хераскова,
состоявшего ректором Университета, параллельно гимна-
зии был организован благородный пансион. В Универси-
тете, окончание которого давало преимущества при посту-
плении в гражданскую службу, разделение по сословиям
отсутствовало. В 1758 г. на тех же основаниях открыта
была тесно связанная с Московским Университетом
гимназия в Казани, из которой вышли впоследствии
Г. Р. Державин, С. Т. Аксаков и Н. И. Лобачевский.
При Университете, далее, создана была типография и
открыта библиотека. Обучались в гимназии лет по 7—8;
в Университете учились обыкновенно 4 года. При этом
строгого порядка прохождения курса в Университете дол-
гое время не было. По традиции, большинство студентов
сперва изучало философские предметы, логику, нраво-
учительную философию, а затем переходило к специаль-
ным. Некоторые слушатели начинали заниматься мате-
матикой с первого же года, другие—позднее. Переходных
экзаменов с курса на курс не существовало, но для окон-
чания Университета обязательно было сдать экзамены по
тому или иному кругу предметов.
Уже в конце 60-х гг. в Московском Университете
среди студентов имелись «гимназические информаторы»,
для которых читались особые курсы лекций и которых,
повидимому, готовили к педагогической работе. В конце
70-х гг. создана была педагогическая семинария, позд-
нее, в 90-х гг., называвшаяся учительской. В этой се-
минарии преподавались, наряду со специальными нау-
ками, и наставления педагогические и методические.
Математика при организации Университета не полу-
чила собственной кафедры. Для преподавания её
в 1755 г. был приглашён магистр Антон Барсов, вос-
питанник, а затем преподаватель университета Акаде-
мии наук. Подготовка специалистов-математиков в Уни-
верситете ещё не велась. Она была предоставлена Акаде-
мии, в Московском же университете сообщался ми-
нимум математических знаний, необходимых медику,
естественнику, философу, наконец, образованному чело-
веку, которому предстоит выйти в государственные чи-
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 47
новники или заняться своим поместьем. Самое большее,
что имелось в виду,— это подготовка в упоминавшейся
«семинарии» будущих педагогов для самого Университета
и его гимназий. Но и к их квалификации, в согласии
с программами этих заведений, больших требований не
предъявлялось. Арифметика, геометрия с плоской три-
гонометрией, элементы алгебры,—вот круг чисто матема-
тических наук, преподававшихся в течение почти полувека.
Московский университет не представлял в этом смыс-
сле исключения. В немецких и французских универси-
тетах положение математики было не лучше. Обучение
математике в немецких университетах носило в XVIII в.
в целом застойный характер. Чтобы не отпугнуть
слушателей, лекторы излагали предмет по возможно-
сти элементарно и углубляли свои знания лишь отдель-
ные лица. Показательно, что в Венском университете,
например, ещё в 1781 г. у Мецберга, читавшего элемен-
тарную математику по краткой обработке курса Хр. Воль-
фа, имелось 130 слушателей, а у Бауера, следовавшего
полному курсу Вольфа,—21; высшую математику Шер-
фер читал перед аудиторией в два человека, а лекции
по высшей астрономии, объявлявшиеся дважды, слуша-
телей не нашли1*).
Невысокий уровень преподавания математики в немец-
ких университетах XVIII в., отмечаемый немецкими же
историками, связан был с культурной отсталостью Герма-
нии XVIII в. В сфере математики после смерти Лейб-
ница и до появления Гаусса Германия переживала время
застоя. В конце XVIII в. в немецкой математике господ-
ствовала так называемая комбинаторная школа, «про-
странные сочинения представителей которой», как писал
в 1904 г. известный математик А. Прингсгейм, «часто
впадающие в самый пустой формализм, могли внушать
лишь величайшее отвращение» подлинным учёным2. Харак-
терно, что Фридриху II часто приходилось замещать
кафедры Берлинской академии и даже должность её
президента иностранцами. Впрочем, в XVIII столетии,
*) Примечания к этой статье помещены в конце статьи на
стр. 131—140.
48
A. 11. ЮШКЕВИЧ
да и ранее, европейские университеты вообще не играли
передовой роли в развитии науки. Рассадниками про-
гресса, как правило, являлись более молодые академии
и научные общества, а новые научно-педагогические
идеи развивались особенно успешно в технических и
особенно военно-технических школах. Лишь в XIX в.
университеты снова заняли достойное место в науке
и в просвещении. Так сложилось дело в России, и так
было повсюду в Европе.
Около 1760 г. в Московском университете произошло
выделение математики в особую кафедру. Магистр Барсов
читал сначала лишь чистую математику. Для слушания фи-
зики, обязательной на медицинском факультете, подготовка
студентов оказывалась недостаточной. Уже 4 июля 1758 г.8
проф. Керштепс докладывал профессорской конференции,
что мог бы приступить к чтению лекций по физике, но
слушатели абсолютно не знают механики и прикладной
математики. Конференция предложила курс прикладной
математики поручить Барсову, характеризуя его в про-
токоле, как «человека, весьма заслужившего рекомен-
дации по причине его знаний, его скромности, его трез-
вости, его ума и тысячи других хороших свойств»4. Бар-
сов, однако, отклонил предложение, выразив сомнение в
своих силах, и тогда решено было передать это дело
II. А. Росту, до того преподававшему английский язык
и ещё ранее изъявившему я елание обучать математике.
И. А. Рост, воспитанник Геттингенского университета,
получив созданную для него профессуру чистой и при-
кладной математики, принёс с собой приобретённые на
родине вкусы и навыки.
С начала шестидесятых годов велись, таким образом,
два математических курса. По чистой математике читались
перечисленные выше четыре дисциплины, по прикладной—
оптические науки, механика, астрономия, гидравлика,
аэрометрия, к которым нередко присоединялись воен-
ная и гражданская архитектура, геодезическая практика,
горное дело. Такие же курсы, входившие в прикладную
математику, читались и в университетах других стран.
В основу всего преподавания положен был одобренный
профессорской конференцией курс проф. И. ф. Вейдлера
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 49
(1691 или 1692—1755), написанный более чем за со-
рок лет до того. Книги Вейдлера, а затем близкие
к ним учебники Дм. Аничкова приобрели в Москве моно-
полию ещё на сорок лет б. Уже один факт такой «стабиль-
ности» учебника свидетельствует о рутинности тогдашне-
го преподавания. Но и в этом отношении Московский
университет вовсе не был исключением. Курс математики
Хр. Вольфа (1679—1754) в оригинале, сокращениях, пере-
делках лежал в основе университетского образования в
Германии без малого сто лет.
Учебные сочинения по математике, применявшиеся в
России и в других странах в XV—XVII вв., можно,
грубо говоря, разделить на две категории. В одну
входили издания и переводы античных классиков и книги,
им подражавшие. Эти сочинения не могли, однако, удовле-
творить запросам практической деятельности. Художники
и строители, военные инженеры и маркшейдеры, земле-
меры и артиллеристы, купцы и чиновники нуждались
не столько в Евклиде, Никомахе и даже Архимеде, труд-
ные книги которых почти не давали прямых указаний на
способы решения измерительных, арифметических и кон-
структивных задач, сколько в своего рода новом Г< ронг.
Начиная с середины XV в., а отчасти и ранее, в кругах
практических деятелей усиливается интерес к прикладной
математике. Результатом работы в этом направлении
явился ряд важных открытий, а с другой стороны, воз-
никновение иной категории математической литературы
со своим стилем и методом изложения. Эти книги, обыч-
но носивп ие названия «Практической арифметики» или
«Практической геометрии», ориентировались на широкие
читательские круги и ограничивались обычно рецептами
и примерами построений и вычислений. Всё излагалось
в форме подлежащих заучиванию наизусть (порой стихо-
творных) правил. Правилам предпосылались только опре-
деления терминов и иногда аксиомы, не находившие,
впрочем, употребления. За несколько столетий выросла
весьма обширная и влиятельная литература, нашедшая
применение и в университетах. Против ненаучного уклона
таких руководств и
Лейбница Хр. Вол
Историко-математ. исследования
выступили с большой энергией ученик
ьф и его последователи.
50
А. П. ЮШКЕВИЧ
Отличительной чертой курсов Вольфа было желание
пропитать обучение духом математического метода и
поставить во главу всего воспитание мышления. Вольф
и его последователи выступали против механического
вызубривания непонятных рецептов, требовали, чтобы
учащемуся был пояснён ход математического рассужде-
ния, и придавали далее чрезмерное воспитательное значение
математической вышколенности ума. Это прогрессивное
течение приняло, однако, в XVIII в. весьма своеобразную
форму. Стремление к детальному анализу понятий и тща-
тельному расчленению материала привело взявшихся за
математику логиков к чрезвычайным преувеличениям. Кро-
ме полезных разъяснений правил арифметики и алгебры,
иногда верных, иногда обречённых ещё на неудачу, эти
авторы внесли в изложение ошеломляющее количество
схоластических определений, терминов, подлежавших за-
тверживанию наизусть, длиннейшие списки некритиче-
ски подобранных и чаще всего ненужных аксиом и посту-
латов, бесконечные леммы и следствия. Отвлечённейший
подготовительный материал иногда занимал место немно-
гим меньшее, чем основанные на нём теоремы. Всё это мало
. считалось с возможностями восприятия новичка, осо-
бенно в детском возрасте. А наряду с этим, обилие тонких
дизъюнкций и неуловимо разнящихся аксиом сочеталось
с неменьшим обилием разнородных прикладных задач и
наставлений чисто ремесленного характера. Такие за-
дачи были полезны одни для геодезиста, другие для
архитектора, третьи для бочара, четвёртые для артилле-
риста и т. д., в своей же совокупности они, вместе с ввод-
ным материалом, оттесняли на задний план связи между
теоретическими предложениями и затемняли структуру
излагаемой пауки.
Впрочем, надо иметь в виду, что нас отделяет от Вольфа
двести лет. Мы теперь видим в его сочинениях, прежде
всего, смесь вредных па первой ступени образования и
часто схоластических тонкостей с грубым практицизмом,
педантическую сухость и догматическую веру в непо-
грешимость системы. Но в своё время они несли на смену
ненаучному преподаванию новые идеи и имели немалый
успех. Разнообразные практические задачи сообщали
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 51
больший интерес к математике, на которую широкие
круги ещё смотрели как на учёную ненужность. Но если
не виной Вольфа, то бедой для преподавания было рутин-
ное использование книг, написанных в начале XVIII в.,
пятьдесят и более лет спустя, когда в учебной литера-
туре был сделан огромный шаг вперёд и появились ори-
гинальные руководства Клеро, Эйлера, Безу и др.
Самое преподавание в Московском университете носило
лекционный характер, причём разделение по курсам отсут-
ствовало. Лекции были двухчасовые и первые годы чита-
лись часто на латинском языке; при этом лекция иногда тут
же переводилась каким-нибудь знающим латынь слуша-
телем. В 1767 г. было предложено читать лекции по
возможности на русском языке, что и начали постепенно
выполнять со следующего года. Как обычно было в те
времена, да и много позднее, лектор из года в год точно
придерживался раз избранного им руководства. Печат-
ные объявления о лекциях (называвшихся «публичными»,
ибо на них могли приходить и посторонние) позволяют
восстановить сроки прохождения математики. Д. С. Анич-
ков, преподававший с 1762 по 1780 г. по Вендлеру, а с
1780 г., когда вышла большая частьего курса, и до 1787 г.—
по собственным руководствам, читал чистую матема-
тику в два года по две двухчасовые лекции в неделю.
На первый год приходились арифметика с геометрией,
на второй—продолжение геометрии и тригонометрия;
алгебра, видимо, читалась не всегда. Эта система удер-
жалась надолго, как и дни и даже время лекций, именно
утренние часы вереду и субботу, выбранные ещё в 1757 г.
Барсовым. В те же дни недели читал после Аничкова до ре-
организации Университета трёхгодичиый курс (на третий
год—алгебру) В. К. Аршеневский. Изредка читал мате-
матику также и Рост, иногда даже параллельно с Анич-
ковым, по две лекции в педелю. Но главным предметом
И. А. Роста была прикладная математика, которую
он излагал трёхлетними циклами по понедельникам,
вторникам, четвергам и пятницам; эти дни унаследовал
и его преемник М. И. Панкевич. Первое изменение про-
граммы произошло только в 1800—1801 гг., когда Арше-
невский объявил, что в обычное время «по Вейдлерову
4*
SI
A. II. Ю1ЙКЕВИЧ
руководству преподавать будет тригонометрию плоскую,
алгебру и свойства кривых линий, в особенности кони-
ческих»6. Учебный год продолжался с 1 августа по 26
июня, а в хорошее летнее время преподаватели проходили
со слушателями геодезическую практику. Твёрдой обязан-
ности прочитать курс целиком не было. В 1791 — 1792 гг.
М. Панкевич, например, сообщал, что будет читать меха-
нику, гидростатику и, «если время позволит», аэрометрию.
И. А. Рост никогда не успевал изложить алгебру и неиз-
менно заканчивал свой курс словами: «однако, уже не
остаётся времени».
Сохранились отрывочные сведения о том, как читались
лекции. И. Рост, например, читал ясно, спокойно и с «прият-
ной живостью». Напротив, лекции его ученика М. И. Панке-
вич а были часто непонятны. Биограф сообщает: «А как
вообще он был упорен в мнениях и щекотлив, то весьма за-
труднялся, когда по причине ошибки в выкладке на лекции
получал ложный результат. Он этим сильно тревожился и
волновался внутренне и, желая поправиться и отыскать
свою ошибку, ещё более путался и сбивался. Это иногда
продолжалось три-четыре часа, потому и время лекций он
старался избирать последнее»7. Письменный слог Панкеви-
ча был тяжёл, устная речь его, невидимому, была не лучше.
В дополнение к лекциям по математике велись занятия
с отстающими, поручавшиеся лучшим окончившим студен-
там. Несмотря на такую помощь, успехи студентов были
невелики. Даже окончание Университета, на которое
полагалось вообще три года, ещё не свидетельствовало о
подлинных знаниях по математике. Экзаминаторы тогда
вообще нередко смотрели скеозь пальцы на пробелы в све-
дениях студентов; достаточно вспомнить известный рассказ
об университетском экзамене гениального автора «Недоро-
сля», обучавшегося в 1760—1762 гг. Одно происшествие
показывает, что при сколько-нибудь серьёзном опросе дело
часто оборачивалось плохо. Когда питомцы Университета
Третьяков и Десницкий вернулись из командировки в
Глазго, где получили докторскую степень по юридическим
наукам и где, согласно письменному свидетельству, за-
нимались также математикой, их подвергли общему прове-
рочному испытанию. Куратор Университета, математик
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ 8А ПЕРВЫЕ СТО ЛЕТ 58
и словесник Ададуров8 потребовал проэкзаменовать их
по математике, за обучение которой они заплатили в
Шотландии некоторую денежную сумму. Десницкии ре-
шительно не пожелал экзаменоваться. Третьякова, выра-
зившего согласие, экзаменовал И. А. Рост, отказавший
ему после беседы в знании даже начал чистой математики 9.
Это, впрочем, не помешало обоим получить профессуру
(по юриспруденции). Разумеется, не все были так слабы
по математике,.и многие выходили с порядочным запасом
знаний и уже одно это важно было для дальнейшего про-
гресса нашей науки. Но главным вкладом Московского
У ши ерситета того времени в развитие математики яви-
лось создание собственных педагогических кадров. Среди
воспитанников Университета мы встречаем профессоров
Аничкова, Панкевича, Перелогова, Аршеневского, Чума-
кова, Тростина, преподавателей Лобанова, Фёдорова
Любинского, Рогова, литератора магистра Ал. Дм. Барсова
и других 10. Эти люди, не оставив следа в пауке, в значи-
тельной мере содействовали распространению математи-
ческих знаний в Москве и за её пределами и не должны
быть нами забыты11.
II. Университетские математики второй половины
XVIII века.
Вот каков был типичный жизненный путь московского
профессора математики того времени1". Выходец из разно-
чинцев, оп, перейдя из духовной семинарии или из гим-
назии в Университет, обучался там с отличием, за успехи
получал золотые медали. Проявив способности и выразив
желание пойти в педагоги, он назначался в семинаристы
учительской семинарии при Университете для подготовки
к будущей своей деятельности. Выдержав экзамен, он
получал определение учителем в гимназию, где сначала
работал в арифметическом классе, затем в геометриче-
ском и тригонометрическом, наконец—в алгебраическом.
Одновременно или несколько позднее ему поручали
вести занятия в Университете. Для этого он сдавал маги-
стерский экзамен и защищал диссертацию, не обязательно
по чистой или прикладной математике, — она могла быть
54
А. П. ЮШКЕВИЧ
и философской. Излагая в меру умения знания, приобре-
тённые у своих наставников, он постепенно от адъюнкт-
ства переходил к экстраординарной, а затем ординарной
профессуре, получая своевременно повышения в чине,
денежные и иные награды.
Высшая математика лежала обычно за пределами гори-
зонта этого педагога. Позднее, когда ему необходимо оказа-
лось взять на себя чтение курса анализа на физико-мате-
матическом отделении, он должен был немало и нелегко
доучиваться. Мы знаем, например, каких трудов стоила
такая переподготовка ученику Роста Т. И. Перело-
гову, учительствовавшему в гимназии с 1784 г. Для по-
лучения университетской должности ему потребовалось
в короткий срок пройти аналитическую геометрию и ана-
лиз. Такой профессор часто не считал себя специально
математиком, но готов был читать, скажем, английский
язык, или философию, или физику и другие предметы, и
Наряду с преподаванием профессор нередко принимал
на себя административные функции, например, универ-
ситетского или гимназического инспектора, или работал
цензором, или давал частные уроки. Для собственного
употребления, иногда для издания, он переводил учебную
книгу, помогавшую ему в чтении лекций. Научная дея-
тельность его не захватывала. Петербургский академиче-
ский центр был далеко, культурный уровень и запросы
среды были невысокие, начальство исследовательской
работы не поощряло, а уважение сослуживцев и студен-
тов снискивалось без научных трудов. Но он всё же любил
и ценил знания и с охотой выступал с публичной речью
о пользе и значении науки.
Приведу краткие биографические данные о про-
фессорах математики Университета, работавших в XVIII в.
Первым лектором, как говорилось, был магистр Антон
Алексеевич Барсов (1730—1791), сын директора Москов-
ской синодальной типографии. Барсов сначала обучался
в Московской славяно-греко-латинской академии. В универ-
ситете при Академии наук, где он учился с 1748 по 1753г.,
он был на лучшем счету и у словесника Тредьяковского, и
у преподававшего математику физика Рихмана, и у фило-
софа Брауна. Академик Рихман писал о Барсове, что он
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 55
являет собой редкий пример математического даро-
вания и прилежания. В конце 1753 г. Барсов получил
степень магистра, но ещё тремя годами ранее начал пре-
подавание математики в академической гимназии. Управ-
ление академии уступило его Московскому университету
неохотно, считая, что теряет в нём большую силу. В Москве
Барсов преподавал математику ди 1761 г. По смерти
своего соученика проф. Поповского он перешёл на кафедру
словесности и в этой области оставил заметный след
в истории нашей культуры. Для университетской мате-
матики он воспитал Аничкова, который и заменил его
с 1762 г.13.
Дмитрий Сергеевич Аничков, сын мелкого служащего
Троице-Сергиевской лавры, также сперва попал в духо-
вное училище. В Университет он был принят в 1756 г.
За успехи он неоднократно получал золотые медали. Анич-
ков начал преподавать математику в 1762 г. одновременно
в гимназии и Университете, а с 1765 г. взял на себя также
чтение логики и метафизики. В качестве математического
руководства он выбрал, как мы знаем, книгу Вейдлера, а
затем написал собственный курс, о котором говорится
дальше. Философия была ему ближе, чем математика.
Для получения ординарной профессуры он написал дис-
сертацию «Рассуждение о начале и происшествии бого-
почитания у разных, а особливо невежественных наро-
дов». Здесь высказывалось мнение о земном происхо-
ждении религии, утверждалось, что «противно натуре
человеческой верить тому, чего в мыслях и воображении
представить не можно», что «бога в троице, без откро-
вения, натурально понимать не можно», что «древность
преданий много споспешествует к закоснению народов
в суеверии» и т. п. Цензура пропустила его сочинение,
но в профессорской конференции 24 августа 1769 г. ряд её
членов, среди них учителяАничкова Барсов и Рост, резко
протестовали против его явно деистических тезисов. Один
из присутствующих обвинил диссертанта в увлечении
Лукрецием—«porcum ex grege Epicuri» («свиньёй из стада
Эпикура»). Твёрдый характером, хладнокровный Аничков
вынужден был отступить, разъяснив, что, говоря о зем-
ном происхождении верований, он имел-де в виду лишь
56
А. П. ЮШКЕВИЧ
языческие религии и т. п. О его способностях биографы
говорили, что он отличался не столько блистательными
дарованиями, сколько основательностью знаний и неуто-
мимой деятельностью. Это подтверждают и труды его.
Аничков умер 1 мая 1788 г. и.
Иван Акимович Рост (1726—1791), преподававший
одновременно с Аничковым, был выходцем из ганновер-
ских дворян. Окончил он Геттингенский университет и
первоначально преподавал в Москве английский язык.
Он читал большей частью прикладную математику, изредка
чистую математику, но продолжал одно время обучать
и английскому языку. В публичных заседаниях Универси-
тета Рост прочитал несколько речей—о способах прек-
ратить массовые пожары, о вредном воздухе в жилищах
(1ерез год после чумы 1771 г.) и о других предметах обще-
житейского характера.
Василий Кондратьевич Аршеневский родился в Киеве
в 1758 г., с 1774 г. учился в московской гимназии, а с
1777 г. в Университете, где специально готовился к про-
фессуре. С 1779 г. он вёл в гимназии стари ий арифме-
тический класс, в 1785 г. получил степень магистра, а в
1795 г.—профессуру. После смерти своего учителя
Аничкова он занял его место. Большой заслугой Арше-
невского было введение в 1800—1801 гг. в курс матема-
тики учения о кривых. Арп еневский легко приспособился
к существенному расы прению программы обучения мате-
матики, наступившему в 1805 г., и уже в объявлении
о лекциях на 1805—1806 гг. сообщил, что «по руко-
водству Бюржа15 и других лучших новейп их писателей
преподаст Высшую Геометрию, в которой покажет пользу
и употребление Дифференциального исчисления». Про-
фессорам Иде и Аршеневскому мы обязаны первым чте-
нием курса высп-ей математики в Московском универ-
ситете. Аршеневскому принадлежат две речи: о пользе
математики и о связи между математикой и физикой.
И педагогическая деятельность Аршоневского, и его
литературные выступления рисуют его как культурного
и хорошо знавшего своё дело педагога. Он, между прочим,
был большим другом профессора физики Страхова16,
собравшего богатую библиотеку, и широко пользовался
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЬ Е СТО ЛЕТ 57
книгами своего приятеля и соседа. Долгое время Арше-
невский состоял инспектором университетской гимназии.
Отличительной чертой его были аккуратность и большая
требовательность к другим и к самому себе. Умер Арше-
невский 27 января 1808 г.
Учеником Аничкова и Роста был также нежинец Михаил
Иванович Панкевич. Выходец из духовного звания, он
учился в Киевской академии, азатем с 1780 г. в Универ-
ситете, готовясь к преподаванию. В 1788 г. он защитил
магистерскую диссертацию «О важнейших гидравлических
машинах»17, где, кажется, впервые у нас, описал печатно
паровую машину. Кафедру прикладной математики оп
получил после Роста в 1791 г. и сохранил её до смерти,
последовавшей 14июля 1812г.(дата рождения неизвестна).
В течение 15 лет Панкевич читал лекции по Вендлеру, но
в начале XIX в. и он начал совершенствовать свой курс.
В 1807—1808 гг., например, он объявил, что излагает ди-
намику и гидродинамику по Бюржа, «употребляя в пособие
и другие славнейшие по сим предметам сочинения». Ему
также принадлежит одна речь о пользе математических
наук. Это был старательный, но посредст енвый педагог,
много уступавший и Аничкову, и Аршеневскому.
III. Учебники и речи первых математиков
Московского университета
Мы получим более полное представление о том, чему
учились по математике московские студенты во второй
половине XVIII в., ближе познакохмившись с тогдашним
учебником.
В построении своего курса «Арифметики»18 Аничков
примкнул к Вейдлеру, в основном сохранив те же струк-
туру, метод, определения и порядок теорем. Однако
Аничков значительно дополнил учебники Вендлера,
а кое в чём с ним и разои ёлся. Несомненно, что
Аничков старался улучи ить руководство, освежить новым
материалом, облегчить усвоение теории путём увеличения
числа примеров и задач, более подробного изложения
выводов, а также исключения некоторых лип них деталей.
Он сравнивал свой прототип с другими авторами и на
58
А. П. ЮШКЕВИЧ
его книгах сказались влияния популярных в то врямя
учебников Румовского, Вольфа, Крафта, Такэ. В своей
работе Аничков не проявил настоящей оригинальности,
но курс его был лучше вейдлерова: доступнее, живее
и содержательнее.
«Арифметика» открывалась «Предуведомлением о мате-
матическом способе учения», знакомившим с терминами:
определение, основание (аксиома), постулат, теорема,
задача, короля арий (примечание), схолия (поучение).
Под аксиомами, вслед за Чирнгаузеном и Вольфом, разу-
мелись при этом истины, вытекающие прямо из опреде-
лений, «ясных и полных понятий» и не подлежащие дока-
зательству в силу своей ясности. Об отличии теорем от
задач говорилось так: «понеже знание математических
истин есть весьма полезное, того ради должно относить
оные к самой практике. Почему такое предложение,
которое учит нас сношению истины с самим делом, т. е.
что сделать должно, называется задачею» (стр. 5).
Количество, предмет математики, разделялось на
пребывающее, все части которого существуют одно-
временно и вместе, и последовательное, части которого
имеют бытие не вместе и не одновременно; кроме того,
количество расчленялось на непрерывное, части которого
соединены, и раздельное—число. Самое определение числа
формулировано было словами Румовского: «Число есть
множество частей одинакового роду, вместе взятых; и
всякая из оных частей называется единица» (стр. 10)19.
Легче всего представить себе количество раздельное,
и потому наука о числах, арифметика, есть первая среди
математических дисциплин. Определив числа равные,
большие, меньшие, подобные, «в которых всё одинаково,—
через что они между собой различны должны быть» (стр. 12),
«ровные», или чётные, и неровные и ещё некоторые
другие виды, познакомив с нумерацией и краткой её
историей, Аничков приводит 10 аксиом целого числа,
отдавая дань моде времени и не замечая аксиом лишних
и бессодержательных20. Отрицательные числа Аничков
вводил в точных терминах Румовского: «Когда случится
вычитать большее число из меньшего, то вычитается
меньшее из большего, а к остатку приписывается знак—»,
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 59
объясняя дело приходо-расходными образцами31 (стр. 27).
Для обучения операциям он приводил простейшие та-
блицы не только для сложения до 9-J-10, но и для вычита-
ния до 18—9. Деление он производил двумя способами,
именно обычным и тем, в котором делител ь помножается
на 1, 2, 3, 9, а затем из получившейся таблички бе-
рутся потребные последовательные вычитаемые и де-
сятичные знаки частного. Кроме взаимной проверки,
Аничков рекомендовал проверку девятью, не оговорив,
что она не даёт полной гарантии. Кое-где в изложении
Аничкова встречаются ляпсусы фактического пли мето-
дического характера. Например, чётное число опреде-
лялось как содержащее «два или несколько целых равных
чисел» (стр. 13). Отрицательные числа вводились в приме-
чании на стр. 27, после того как всего тремя страницами
ранее при разъяснении операции вычитания специально
указывалось, что «вычитаемое число должно быть меньше
того, из которого делается вычитание» (стр. 24).
Излагая приёмы действий, Аничков не входил в раз-
бор их свойств. Зато он доказывал теоремы вроде такой:
«числа слагаемые должны быть одного роду» (стр. 19).
Как достоинство изложения, с другой стороны, следует
отметить раннее введение знаков действий.
Довольно много места Аничков уделил действиям
над именованными числами, а затем свойствам пропор-
ций и арифметической и геометрической прогрессий.
Отношения или «содержания», по тогдашней терминоло-
гии, он расчленил на множество видов. Существуют,
именно, содержания большей неравности, когда предыду-
щие больше последующего, меньшей неравности, двойное,
тройное и т. д., полуторное, полутретное (5:2), половин-
ное, третное. Надо отдать должное умеренности Аничкова:
у Вейдлера список подлежащих заучиванию терминов,
перешедших от старой математики, был ещё длиннее;
У него мы найдём и ratio dupla sesquitertia (7:3), и
ratio subdupla sesquitertia (3 : 7), и т. д. В этом разделе
Аничков широко пользовался и буквенным обозначе-
нием количеств.
Правила действий над дробями автор старался обос-
новать. Например, умножить одно число на другое—
€0
А. П. ЮШКЕВИЧ
значит взять его столько раз, сколько во втором единиц,
а дробь есть часть целого; следовательно, умножая 3/4 на
2/3, нужно взять от 3/4 такую часть, какую выражает
второй множитель. «И понеже знаменатель есть одно
только имя, показующее, на сколько частей целое раз-
делено, то из одного токмо числителя 3 множимой дроби
должно взять такую часть, какую другая дробь 2/3 изо-
бражает, т. е. две трети», и т. д. (стр. 134—135). При деле-
нии дробей сначала рассматривался случай общих знаме-
нателей. Познакомив с теоремами о квадрате и кубе
двучлена, Аничков затем весьма детально объяснял спосо-
бы извлечения соответствующих корней. На 12-ти стра-
ницах он излагал, по Румовскому, учение о логарифмах,
вводимых с помощью сравнения арифметической и гео-
метрической прогрессий (у Еейдлера этот отдел занимал
5 стр.). Он ввёл также отсутствовавший у Вейдлера, но
ставший обязательным ко времени Аничкова отдел о
десятичных дробях. Записывал он по-старинному, в виде
I II III IV IV
3 4 6 3 или 3468
(наше 0,3468).
Теории периодических дробей Аничков не излагал,
а для дробей вроде 4/7 ограничивался указанием на необ-
ходимость пользоваться приближёнными значениями.
Весь этот материал находил себе применение во второй
части, которая называлась «О практической арифметике».
Основой её служит тройное правило, которое Аничков
подробно разъяснил на множестве примеров. Кроме
сложного тройного правила, давались ещё правила то-
варищества и смешения с одной задачей, взятой у Такэ,
и с обошедшей все учебники архимедовой короной.
Далее приводились без доказательства правила фальшивое,
с одним и двумя положениями, и слепое или девичье,
решавшее линейные задачи неопределённого анализа.
Аничков указывал, правда, что алгебра делает лишними
последние правила, и писал, что сообщает их лишь, дабы
показать, насколько легче решать те же вопросы алгеб-
раически (стр. 275). Скорее он следовал традиции и учи-
тывал, что алгебру осилят немногие. Как вто было
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ?А ПЕРВЫЕ СТО ЛЕТ 61
принято в учебной литературе того времени к книге
был приложен колоссальный список различных древних
и современных мер, более чем на 100 страницах: одни раз-
личные международные аршины занимали 12,5 страницы.
Для своего времени Аничков написал не оригинальный,
но и не уступавший многим другим учебник. «Руководство
к арифметике» Эйлера, к сожалению, не законченное
(ч. I, 1740 г; ч.II, 1760 г.), и «Арифметика» И. Курганова
(1771 г.) были, правда, доступнее и проще изложены.
Но сторонники вольфовского направления в преподавании
должны были приветствовать такую книгу. И в самом
деле, в издававшихся Академией наук «Ежемесячных
сочинениях и известиях об учёных делах» за декабрь
1764 г. рецензент писал: «Эта Арифметика кажется тем
прочих исправнее, что в ней наблюдён точно Математи-
ческий учения порядок, и последовало славному учителю
Вольфию, коего лучшего примера Господину Автору
избрать и не можно было» 22.
Лишь в 1780 г. появилось продолжение курса. Гео-
метрия23 делилась на лонгпметршо, планиметрию и
стереометрию. Наиболее любопытно для нас сочетание
теоретического материала с прикладными задачами, в
такой мере щедро рассыпанными по тексту, что неминуемо
утрачивалось представление о взаимной связи теорем.
Аничков и Еейдлер не объединяли теорем по группам, за
которыми следовали бы приложения, а преподносили всё
в трудно усвояемой смеси. Рассказав в главе первой об
определениях и своеобразно выбранных аксиомах и посту-
латах (конечно, планиметрических,—о пространственных
тогда не заботились), во второй главе Аничков детально
описывал устройство и употребление циркуля, рсйс(} едера,
зубчатого колеса для пунктира, линейки, наугольника,
землемерной цепи, отвеса, квадранта с диоптрой, астро-
лябии с нониусом, мензулы и т. д. Глава третья начиналась
с задачи о проведении прямой между двумя точками на
бумаге, дереве или камне (с помощью окрашенной верёвки),
на поле (с помощью кольев и цепи). Далее реи алась
задача об измерении прямого отрезка на бумаге циркулем
и в поле с помощью верёвки, вываренной в горячем м щле
и навощённой, чтобы от сырости длина её не менялась.
62
A. II. ЮШКЕВИЧ
За этим следовали теоремы о смежных и вертикальных
углах, а за ними—измерение углов астролябией, теоремы
о равенстве треугольников, приближённое проведение
паралелльной прямой на данном расстоянии как касатель-
ной к дугам данного радиуса, описанным их двух точек
данной прямой, построение перпендикуляра, вос-
становленного к прямой или опущенного на неё, табли-
ца хорд для измерения углов, теоремы об углах, обра-
зуемых прямой с двумя параллельными прямыми, и о
сумме углов треугольника (замечу, что параллельные пря-
мые определялись как равностоящие, возникающие при
движении вдоль прямой перпендикулярного к ней отрез-
ка, и что 9-я аксиома утверждала равенство отрезков,
образуемых на параллельных прямых двумя перпендику-
лярами к одной из параллелей). Теоремы о подобии
доказывались совершенно неубедительно, а затем реша-
лись задачи о делении прямой па равные части, о постро-
ении пропорциональных, об определении недоступных
расстояний и высот. Последняя глава лонгиметрической
части посвящена была теоремам о хордах и углах в
окружности и приближённому вычислению её длины.
Во второй, планиметрической, части мы находим ос-
новные предложения о четыреугольниках и многоуголь-
никах, приближённое построение правильных много-
угольников по способу Ренальдини24, правила измере-
ния площадей. Попутно Аничков подчёркивал, что равен-
ство периметров фигур не влечёт за собой равенства их
площадей. Теорема об отношении площадей двух кру-
гов основывалась на рассмотрении окружности как впи-
санного многоугольника со столь большим числом сто-
рон—хорд, что онп «от окружности ни мало не будут
разнствовать» (стр. 207). Затем доказывались теоремы
Пифагора и о квадрате стороны, лежащей против острого
угла, и без доказательства приводилось правило Герона
для определения площади треугольника по сторонам.
Большое место отводилось черчению планов, делению
площадей фигур па равные части и преобразованию од-
них плоских фигур в равновеликие другие. В третьей, сте-
реометрической, части применялся принцип Кавальери
и основанный на нём известный вывод для соотношения
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 63
объёмов шара и описанного цилиндра. Тут же мы нахо-
дим описание изготовления калибрированной линейки
для определения веса пушечных ядер, визира для измере-
ния бочек, совет, как измерять объём неправильного
тела, помещая его в сосуд с песком или водой, и т. п.,
причём за подробностями читатель отсылался к прак-
тическим геометриям—Клавия, Швентера и Такэ.
В общем, геометрия получилась хуже арифметики. Не
только студенты Университета—будущие юристы, врачи,
учителя, чиновники, но и практики-геодезисты знали
бы больше, если бы вместо хаотического нагромождения
аксиом и правил употребления навощённых верёвок и
астролябий им был бы дан систематический курс геометрии
и её приложений. Проблема изложения геометрического
курса в это время оживлённо обсуждалась на страни-
цах математической печати. Клеро, Даламбер и др. выска-
зали в этой области ряд новых идей, стали появляться
более однородные по содержанию и более лёгкие руко-
водства. В русской литературе эти проблемы были под-
вергнуты обсуждению уже после смерти Аничкова в
замечательном «Опыте о усовершении елементов геомет-
рии» акад. С. Е. Гурьева (Спб., 1798).
Тригонометрия Аничкова25 несколько ушла вперёд от
вейдлеровской, но в сравнении, например, с вышедшей
довольно вскоре книгой М. Головина2® представлялась
сильно отставшей. Во все определения и теоремы Анич-
ков вводил радиус г круга; знак тангенса брался ещё в пер-
вой и второй четвертях одинаковый; исследование три-
гонометрических линий (не функций!) различных допол-
нительных углов отсутствовало, зависимости между ними
почти не разбирались. Большое место отводилось описа-
нию способа вычисления тригонометрических таблиц.
Применялись теоремы синусов, тангенсов. Новыми у
Аничкова по сравнению с Вейдлером были теорема
о синусе суммы и разности, а также задачи на реше-
ние треугольника по углам и сумме сторон по прави-
лу Герона и некоторые другие. В конце учебника реша-
лись задачи на определение недоступных расстояний и
высот. Формул в учебнике не было, всё излагалось сло-
весно.
64
А. П. ЮШКЕВИЧ
Последняя часть курса Аничкова посвящена была ал-
гебре 27. В главе 1-й Аничков рассказывал о предмете ал-
гебры как науки, которая «из данных количеств, помощью
сравнений, находит другие неизвестные количества,
то го ж роду, о которых, в рассуждении данных, нечто
знать даётся» (стр. 3). Алгебру называют, говорит Анич-
ков, также всеобщей арифметикой, «потому, что чрез
оную вычисляется всё, что можно вычислить». Далее
Аничков знакомил с терминологией, обозначениями,
скобками, «положительными или подтвердительными» и
«отрицательными или недостаточными» или ещё «непри-
стойными» количествами, привлекая обычные матема-
тические иллюстрации. Во 2—4-й главах разъяснялись
действия над одночленными и многочленными выражени-
ями, алгебраическими дробями, степенями и радикалами.
Правило перемножения минуса на минус взято было приэтом
из курса Вольфа в переводе акад. С. К. Котельникова28.
В следующей главе рассказывалось о квадрате, кубе
и четвертой степени бинома и применении их к извлече-
нию корней. В 6-й решались простые примеры уравне-
ний первой степе чи с одним и двумя неизвестными и квад-
ратное уравнение вида х2+ах=Ь2, причём сообщался
лишь положительный корень; другие квадратные урав-
нения здесь но разбирались, хотя они и требовались
для решения последующих задач. К 6-й главе примыкали 7
и 8-я, где решались различные задачи на проценты, на
прогрессии, о ходоках, вышедших навстречу друг другу
из двух пунктов, и т. п. В главах 9 и 10-й алгебра прила-
галась к решению задач геометрии и тригонометрии, начи-
ная с простейших построений алгебраических выраже-
ний вроде у или корня квадратного уравнения. Здесь
имелись: деление отрезка в крайнем и среднем отноше-
нии, вычисление высоты треугольника по сторонам, ребра
тетраедра, вписанного в шар, и т. п. Неполнота изложе-
ния раздела о квадратных уравнениях была удивитель-
ной. Конечно, её нельзя отнести на счёт недостаточной
квалификации автора. Но Аничков плохо продумал содер-
жание этой главы. Между тем, на русском языке уже
давно к этому времени вышла знаменитая «Универ-
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 65
сальная арифметика» Эйлера (1769), да и в исполь-
зованном Аничковым руководстве Вольфа теория урав-
нений была изложена аккуратнее.
Книга заканчивалась главой 11-й, в которой рас-
сказывалось на 30 страницах о свойствах кривых.
Аничков вводил понятие «пошрешника» линии, делящего
параллельные хорды пополам, оси, сопряжённого диа-
метра, «семиординаты» (нашей ординаты) и абсциссы, па-
раметра и т. п. Конические сечения определялись уравнени-
ями, записанными словесно и буквенно, для параболы в
виде ах=у\ для эллипса и гиперболы отнесёнными к вер-
шине. Без доказательства сообщалось о фокальных свойст-
вах кривых и об асимптоте как прямой, проходящей через
центр и конец некоторого перпендикуляра к оси (её
основное свойство не отмечалось). В этом довольно кор-
ректно изложенном материале удивляет, что наряду
с верёвочным черчением эллипса предлагалось без ого-
ворок одно популярное построение, дающее некую оваль-
ную фигуру, но вовсе не эллипс. Кроме конических сече-
ний приводились ещё циклоида, конхоида с её асимпто-
той, квадратриса, логарифмическая кривая и спираль
Архимеда («геликса»). Для них давались определения,
позволяющие написать «уравнения», зависимости между
некоторыми специально подобранными отрезками, в про-
стой алгебраической форме, как было принято ещё в ли-
тературе XVII в. Циклоида, например, определялась
тем, что для любой её точки верхняя дуга я, отсекаемая
на образующем круге, находящемся в середине пути,
отрезком у, проведённым из этой точки параллельно
основанию, всегда равна длине этого отрезка, так что
уравнение её имеет вид х=у. В заключение Аничков ска-
зал несколько неясных слов о делении линий на геометри-
ческие или алгебраические и механические. Нужно заме-
тить, что и в «Алгебре» Вейдлера имелась глава «О натуре
' и свойствах кривых линий, и во-первых конических»,
занимавшая более 20 страниц. В Университете эта глава
на лекциях, видимо, не читалась, ибо много позднее
Аршеневский, впервые начиная излагать учение о кри-
вых, счёл нужным особо отметить это в объявлении о
своём курсе.
5 Историко-математ. исследования
66
А. П. ЮШКЕВИЧ
Мы не встречаем в рассматриваемое время почти ни-
каких математических трудов воспитанников Универси-
тета. Единственным исключением в этом отношении
явился Александр Дмитриевич Барсов, племянник
проф. Барсова и сам магистр философии и свободных наук,
скончавшийся около 1800 г. Ему принадлежат три пере-
водные работы. Одна из них представляла арифметику,
в центре которой было поставлено цепное правило, кото-
рое было тогда в зените славы. В предисловии особо
отмечалось, что здесь «все правила практической ариф-
метики подведены под одно всеобщее, называемое цеп-
ным... Оно изображается здесь наподобие алгебраического
уравнения между произведениями крайних и средних
членов, отлично от обыкновенного вида, которой при-
даётся сему правилу в других арифметиках»29. Барсов
несколько дополнил свой перевод, например главой о беско-
нечных десятичных дробях, составленный по Кестнеру.
Ещё ранее Барсов перевёл короткую, сухую и мало-
грамотную «Геометрию для детей от 8 до 12 лет» пастора
Якобия, как раз для детей вовсе не пригодную (1790).
Третьей и важнейшей работой Барсова был переработанный
перевод «Anfangsgrunde der Analysis endlicher Grossen»(1759)
и «Anfangsgrunde der Analysis des Unendlichen» (1761)
Кестнера30. Этот курс содержал обширнейший материал: вы-
вод бинома для целого показателя по методу полной индук-
ции, параллелограмм Ньютона, теорию алгебраических
уравнений, интерполяционные формулы, подробное из-
ложение теории бесконечных рядов, дифференциальное
и интегральное исчисления и интеграцию дифференциаль-
ных уравнений. Кестнер стремился сочетать полноту све-
дений со строгостью понятий и доказательств, не впа-
дая при этом в педантизм вольфианцев. Ему обязаны мы
практическим внедрением принципа полной индукции.
Анализ Кестнер строил, не достигая, впрочем, подлинной
ясности, на идее предела. Барсов выпустил свою обработ-
ку курсов Кестнера под новым названием и под собст-
венным именем. Основанием для этого явились, с одной
стороны, некоторые перестановки в изложении материала
и его сокращение а с другой—довольно многочисленные
дополнения, главным образом по интегральному исчис-
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 67
пению, интегрированию дифференциальных уравнений,
в том числе с частными производными, и по вариацион-
ному исчислению. Многие из этих дополнений заимство-
ваны были из классических «Instilutiones calculi inte-
gralis» Эйлера. Об употреблении труда Барсова в Москов-
ском университете сведений не сохранилось, и я думаю,
что при тогдашнем уровне знаний московского студента она
вряд ли могла найти много читателей. Тем не менее, выход
этой книги был весьма заметным событием в нашей учеб-
ной литературе того времени, ещё небогатой руководст-
вами по высшему анализу. До этого опубликованы были
только краткие изложения исчисления бесконечно малых
С. К. Котельникова в приложении к переводу «Сокра-
щения первых оснований математики» Хр. Вольфа
(Спб., 1771) и С. Е. Гурьева в приложении к переводу
«Навигационных или мореходных исследований» Э. Безу
(Спб., 1790—1791), а также «Сокращение высшей мате-
матики» П. Гиляровского (Спб., 1796), содержавшее
довольно много задач на геометрические и механические
приложения. Многие важные разделы анализа, таким
образом, Барсов изложил на русском языке впервые.
Влияние его труда — особенно пропагандировавшейся Бар-
совым теории пределов — отразилось на других наших
писателях, как, например, Л. Рахманове.
Литературная деятельность московских математиков
выразилась также#в торжественных речах на годичных
актах Университета. Подобные речи, обязательно публи-
ковавшиеся, в те времена имели большое значение.
Через их посредство шла пропаганда и популяризация
науки и рассчитаны они были на сравнительно широкие
круги общества. Такие же речи встречаем мы на публич-
ных заседаниях Академии наук. В обстановке ещё
неизжитого недоверия к науке и даже страха перед ней
разъяснение пользы просвещения вообще, той или иной
Дисциплины в частности, было особенно важным. Этой
теме посвящалось немало выступлений. Наряду с речами
о пользе прививки оспыг врачебными наставлениями
Для деревенских жителей, философскими и политическими
рассуждениями мы встречаем выступления «О происхож-
дении и пользе натуральной истории» (Политковский,
68
А. П. ЮШКЕВИЧ
1785), «О влиянии наук в общее и каждого человека
благоденствие» (произнесённое против руссоистов П. Стра-
ховым, 1788) и многие аналогичные. В начале XIX в.,
когда поставлен был вопрос о несколько более широком
распространении образования, профессорам пришлось
успокаивать перепуганных Французской революцией по-
мещиков, уверяя, что одни грамотность и знание начал
науки не повлекут ещё за собой безбожия непослу-
шания в народных массах. (См., например, «Слово о том,
полезно ли или же вредно, как вообще благонравию,
так в особенности благосостоянию целых государств,
вводить и распространять всеобщее просвещение» д-ра
медицины В. М. Рихтера, М., 1803.)
Математики не отставали от других. Первое «Слово о
подлинной цели математических наук и о сообразном ей
расположении упражнений в оных» написал М. Панке-
вич, речь которого зачитал 30 июня 1792 г. физик П. Стра-
хов. Велеречивая речь Панкевича, составленная из
длинных периодов, излагала тривиальные мысли. Вот
образец его стиля: «Итак, если справедливо то, что матема-
тические науки, вперяя познание полезных вещей, руко-
водствуют приятными, удобными и кратчайшими путями
к истине, то от вящщего распространения оных непременно
должно следовать ощутительнейшему их влиянию во
всеобщее просвещение и неразрывно ему сопутствующее
образование склонностей, во всеобщие выгоды жизни,
и следовательно от часу большему прйближению к отда-
лённейшей, общей сим наукам с прочими и самой глав-
нейшей цели, состоящей в споспешествовании умно-
жению и незыблемой подпоре общего благоденствия».
В преподавании математики Панкевич отдавал преимуще-
ство синтетическим доказательствам. Хотя, говорит он,
аналитические приёмы и очень хороши в нашей науке, но
менее подходят во всех других случаях, так что «не по
врему похвальны намерения тех,которые для сей удобности
и самую чистую математику стараются сколько можно
изъяснить алгебраическими доказательствами»31.
В противоположность речи Панкевича очень выгод-
ное впечатление производит содержательная речь В. Ар-
шеневского, написанная простым и свежим языком.
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ГА ПЕРВЫЕ СТО ЛЕТ 69
В этом выступлении Аршене вский держался принятого
тогда приёма: прежде всего показывал происхожде-
ние и естественный порядок математических наук, а затем
разъяснял их общественное назначение. «Слово о нача-
ле, связи и взаимном пособии математических наук
и пользе оных», произнесённое им 11 июля 1794 г.
в годовщину восшествия на престол Екатерины II,
начиналось, понятно, с панегирика императрице, впро-
чем, довольно короткого. Почти сразу Аршеневский пере-
ходил к делу. Свойства тел, наблюдаемые человеком при
изучении вселенной,—протяжение, непроницаемость, дви-
жимость и т. д.—не могут быть в действительности отделе-
ны от тел и друг от друга. Но человек, пользуясь отвле-
чением, умеет рассматривать каждое особо. Первым в по-
рядке свойств, без которого другие существовать не могут
и которое одинаково понимается и простолюдином,
и метафизиком, является протяжение, а с ним связаны
идеи точки, линии и поверхности, «предметы столь
неосновательных возражений, чрез которые люди, или не
понимая отвлечённых истин, или последуя вредному пир-
ронизму, хотели твёрдые математические начала сделать
сомнительными» (изд. 1794 г., стр. 6). Ясно, что первой
из математических наук является поэтому геометрия.
Так же просто и естественно, как протяжение, по-
нимает человек множество или число, ибо никуда не
может устремить чувств, не получая понятия о числе.
Если количеством непрерывным, протяжением, занимает-
ся геометрия, то арифметика есть учение о количестве
раздельном или числе. Геометрия, в соответствии со сте-
пенью сложности линий и поверхностей, делится на
простую и высшую, а возможность раздроблять фигуры на
бесконечно малые составляющие их начала или частицы
приводит к дифференциальному и интегральному исчис-
лениям. G другой стороны, раздельные количества
можно рассматривать двояко, пользуясь числами или
Же всеобщими знаками. Отсюда возникает алгебра, кото-
рая связывает также арифметику с геометрией через
посредство геометрических конструкций32. Далее, заме-
чаемые человеком из любопытства или из нужды движе-
ния и взаимодействия тел побуждают его применить
70
А. П. ЮШКЕВИЧ
к ним отвлечённую математику—и вот появляется меха*
ника с её подразделениями. Наконец, существование тел
жидких и «воздухообразных» и т. п. порождает физиче-
ские дисциплины и аналогично возникают оптика,' нави-
гация, астрономия и пр.
Все эти дисциплины служат человеку, как владыке
природы, ставящему её себе на службу, проникающему
в её тайны. Но человек слаб и должен охранять себя от
стихий, зверей и даже от себе подобных. И вот «разум
и нужда, которая,кажется, есть изобретательница многих
наук и искусств, побудили и научили человека строить
для себя твёрдые здания и надёжные противу неприятеля
защиты» (стр. 11), что породило архитектуру, артиллерию
и другие связанные с математикой науки.
Установив— как видно, с позиций философского мате-
риализма—генезис математических наук, Аршеневский
переходит к вопросу о пользе математики. Первая польза
её в том, что она развивает отчётливое мышление, облег-
чает память, приучает к системе; вторая есть «видимая
или ощутительная, которая разливается вне нас» (стр. 12).
Разумеется, в большинстве житейских дел достаточно са-
мых начальных знаний, а иногда и той доли, которой мы
одарены от природы. Но многие важнейшие вопросы, на-
пример мореходства, календаря, учения о машинах, тре-
буют гораздо более глубоких знаний из высшей математи-
ки. В частности, широко пользуются последней военные
науки, которым обязаны своей безопасностью государства.
Свою речь Аршеневский закончил защитой отвлечён-
ных геометрических исследований, казалось бы, лишён-
ных пользы, а на самом деле имеющих и общепозцава-
тельную и практическую важность. Его слова говорят о ши-
роте кругозора автора, и я приведу их почти полностью.
«Геометрия,—говорил Аршеневский,—содержит в себе
много таких предложений которые единственно служат
токмо к удовольству любопытства нашего и не обе-
щают, невидимому, никакой ощутительной пользы;
однакож, ежели их со вниманием рассмотреть, то должно
будет признаться, что они суть единые чистые и неопро-
вергаемые истины, на которых человеческий разум, ве-
домый собственным своим светом, может утверждаться;
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 71
а потому уже и нельзя почитать их суетными и бесполез-
ными: при том, есть ли исключить все те знания, которые
не приносят нам никакой ощутительной пользы, то
сколь бы тесны учинились пределы человеческого позна-
ния! ...». Но, кроме того, «в геометрии находятся некото-
рые совершенно теоретические истины, не представля-
ющие сами по себе никакой ощутительной пользы, кото-
рые однакож послужили действительно средством и
степенью к возвышению других полезных знаний... Мо-
жет быть многие из таковых имеют свои ещё более пре-
имущественные цели и употребления, но которых откры-
тием воспользуются будущие времена...» (стр. 15—16).
В 1802 г. Аршеневский произнёс также речь «О связи
чистой математики с физикой», относящуюся более к фи-
зике. Я упомяну здесь же более позднюю речь «О пользе
математических и физических наук для людей всех состо-
яний, особливо для военных», написанную в 1815 г. проф.
Ф. И. Чумаковым. Его слово читано было, когда Наполеон
вернулся с Эльбы. «На западе,—восклицал автор,—снова
восходит туча раздоров; снова чудовище, адом порождённое,
сорвав оковы, его связующие, изощряет смертоносное жало
своё на ^истребление рода человеческого, снова готовит нало-
жить цепи на освобождённую Европу». В этих политических
условиях Чумаков понятным образом более всего уделил
места вопросу о значении математического образования для
военных. «Не всякой ли военной человек,—заявлял он,—
должен иметь основательные сведения во всех отраслях
военного искусства, ибо кому не открыт путь в полко-
водцы?—а сие звание не требует ли глубоких сведений
во всех частях военного искусства: артиллерии, топо-
графии, геодезии, устройстве укреплений и т. д.»88.
IV. Реформа преподавания и организация
физико-математического факультета
В начале XIX в. система образования подверглась
в России глубокому преобразованию, которое отразилось
И на положении университетской математики. Ещё при
Екатерине II «Комиссии об учреждении училищ» поручено
было разработать план распространения и переустрой-
72
А. П. ЮШКЕВИЧ
ства гимназий и университетов. В феврале 1787 г. проект
был готов. В некоторых отношениях он был значительно
прогрессивнее действовавшего устава Московского универ-
ситета. Он предоставлял профессуре свободный выбор
руководств и изложения, открывал доступ в универси-
теты даже крепостным и ремесленникам. Единичные вы-
ходцы из «низших сословий»—а только об единицах могла,
разумеется, итти тогда речь,—не смущали авторов про-
екта. Но в структуру четырёх намечавшихся универси-
тетов (Москва, Пенза, Псков и Чернигов) изменений не
вносилось, мыслились они в составе тех же трёх факуль-
тетов. Революционная буря, пронесшаяся над Западной
Европой и ярко напомнившая про недавнее грандиозное
восстание пугачёвцев, заставила царское правительство
отложить в сторону планы широкого распространения
наук, от которых так пахло гильотиной, и заняться
борьбой с «тлетворным» духом демократического рацио-
нального знания. «Черни,—заявляла Екатерина II,—
не должно давать образования, покилику будет знать
столько же, сколько вы да я, то не станет повиноваться
нам в такой мере, как повинуется теперь».
Но та же Французская буржуазная революция, которая
в своём апогее сыграла для официальных руководителей
русского просвещения роль пугала, на склоне своём, уду-
шенная Наполеоном, отчасти побудила их сообщить этому
просвещению новый импульс. Неоценимые услуги, оказан-
ные армиям Французской республики химиками, физи-
ками и математиками, взявшими на себя руководство
изготовлением орудий, производством пороха, фортифи-
кационными и топографическими работами, деятельность
Политехнической школы, поставлявшей квалифицирован-
ных военных инженеров, лучше агитировали в пользу
точных наук, чем любые торжественные речи. Для.
офицеров оказывалось нужным серьёзное знание основ
высшей математики, механики, начертательной геометрии,
некоторые отделы которых представляли последнее слово
науки. Сами представители математики и естествознания,
как Монж,Карно и другие,зарекомендовали себя крупными
государственными деятелями, стратегами, организаторами.
Немаловажные успехи достигнуты были с помощью новых
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 73
научных методов и в промышленности. Наконец, юристы,
адвокаты и учёные, работавшие на высших и средних
бюрократических должностях административного аппа-
рата, создавшегося при Наполеоне, свидетельствовали о
реальном значении образования для исполнительного
и распорядительного чиновника, о котором так мечтали
у нас одно время Александр I и Сперанский.
Новое высшее образование оказалось серьёзной военной,
промышленной, административной силой. Правительство
молодого Александра придавало вопросахМ просвещения
большое значение. Оно поставило своей целью использо-
вать науку и образование для укрепления всё возра-
стающей военной и хозяйственной мощи государства,
для создания более работоспособного централизованного
аппарата управления, наконец, для пропаганды религии и
самодержавия в школе. Классовая сущность просвети-
тельной политики была предопределена заранее. Наиболь-
шую сумму знаний должно было приобретать дворянство.
Остальным группам населения полагалось знать то, что
требуется родом их деятельности,—не больше. Наиболее
способным одиночкам предоставлялась весьма про-
блематическая, хотя и декларированная в громких фразах,
возможность перехода в высшее сословие. Но ещё бо-
лее существенным для успехов русского просвещения в
начале XIX в. явился патриотический общественный
подъём в сравнительно широких кругах дворянской
и «третьесословной» интеллигенции, выразившийся, в
частности, в резком усилении тяги к знанию. Узкие цели
правительства, прикрытые пышными фразами о всесо-
словности образования, и прогрессивные устремления пе-
редовой части русского общества, таким образом, вре-
менно совпали. Довольно скоро, впрочем, им при-
шлось разойтись, ибо университеты и гимназии пре-
вратились в рассадники философско-научного и полити-
ческого свободомыслия, и правительство, после недол-
гих лет показного либерализма, перешло к суровым
репрессиям, к покровительству мистицизму и мрако-
бесию.
Для осуществления образовательной программы при
созданном в 1802 г. Министерстве народного просве-
74
А. П. ЮШКЕВИЧ
щения было организовано Главное правление училищ.
В него вошли, между прочим, математики-академики
С. Я.Румовскийи Н. И. Фус. Фус принял особо активное
участие в выработке плана университетов. С. Я. Румовский
назначен был попечителем Казанского округа. На пред-
варительных и окончательных проектах сильно отра-
зились идеи Кондорсе, изложенные в докладе, поданном
им в апреле 1792 г. Законодательному собранию84. Россия
разделялась на шесть учебных округов, в центрах кото-
рых учреждались университеты, а именно, кроме Москвы,
где он уже существовал, ещё в Петербурге (причём закры-
валась гимназия при Академии наук), Дерпте, Харькове,
Вильно и Казани. В губернских городах открывались
гимназии, в уездных—уездные училища.
План открытия университетов был реализован не
сразу. Прежде всего. были открыты университеты в
Дерпте*—Тарту (1802) и, на основе старой школы,
в Вильно (1803). В 1804 г. были утверждены уставы
Харьковского и Казанского университетов, а заодно
новый устав Московского (в Петербурге университет
был открыт 15 лет спустя). Московский университет,
по уставу от 5 ноября 1804 г., разделялся уже не
на три, а на четыре факультета. То были отделения
нравственных и политических наук, словесных наук, вра-
чебных или медицинских наук и, наконец, отделение
физических и математических наук. В последнем от-
крывались кафедры: 1) опытной и теоретической физи-
ки, 2) чистой математики, а) прикладной математики,
4) астрономии, 5) химии, 6) ботаники, 7) минералогии
и сельского домоводства, 8) технологии и наук, относя-
щихся к торговле и фабрикам. Нас не удивит, что чи-
стая математика получила только одну кафедру, на
которой, впрочем, работало 3—4 человека: курсы по специ-
альным математическим дисциплинам в то время ещё не
читались, да и специализация математики была не столь
велика. Юридическое и словесное отделения должны были
дать, прежде всего, чиновников, медицинское отделение
выпускало врачей, а физико-математическое готовило
в первую голову кадры гимназических учителей, в которых
ощущался исключительно острый недостаток, (^тсдода выхо«
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 75
дили преподаватели физики, математики и естественных
наук; для них не требовалось чёткой специализации, ибо
чаще всего -они совмещали преподавание этих наук. Ведь
даже в университетах имели ещё место подобные и даже
более широкие совместительства. Более определённая
специализация являлась уделом лишь тех немногих, кто
готовился в магистры, доктора, словом, к профессор-
ской кафедре. Что касается сельского хозяйства и тех-
нологии, к которой добавилось затем текстильное дело,
то включение их в программу факультета обусловлено
было различными соображениями. С одной стороны, всей
общеобразовательной системе сверху донизу сообщён
был прикладной уклон. И если в высшей технической
школе резко усилили в то время программу математики,
то в университетах ввели некоторые инженерно-экономи-
ческие предметы. Устав подчёркивал, что профессора
всегда должны иметь в виду связь теории с практикой.
С другой стороны, преподавание сельского хозяйства
должно было привлекать помещиков.
Согласно уставу, от профессоров требовалось не
только читать лекции наилучшим образом, сочетая теорию
с практикой и пополняя свои курсы новыми открытиями.
Преподаватели университетов были обязаны вести и науч-
ную работу и в особо для того назначаемых собраниях
совета рассуждать о новых открытиях, опытах, исследо-
ваниях. На них возлагалось и руководство окончившими
студентами, подготовлявшимися к дальнейшей научно-пе-
дагогической карьере, Для поощрения студенчества и
педагогов окончившим присваивался при поступлении на
службу 14-й класс, а лицам, поднимавшимся по учёной
лестнице, более высокие: кандидату—12-й класс, маги-
стру—9-й, доктору—8-й. Окончившие студенты приглаша-
лись, кроме того, на службу унтер-офицерами в Кадетский
сухопутный корпус, где после краткого курса военного
обучения их ожидало производство в офицеры.
Новые веяния отразились также на учебных планах.
Ещё до реформы, в 1800—1801 гг.,какмы видели, Ар шенев-
ский объявил о введении в свой курс конических сече-
ний, продолжая, впрочем, ещё несколько лет держаться
Вейдлера. После реформы в преподавание немедленно
76
А. П. ЮШКЕВИЧ
включены были дифференциальное и интегральное исчи-
сления и аналитическая геометрия, а изложение элементар-
ной математики было поставлено на новую основу. В 1805—
1806 гг., например, уже читалось три математических курса.
Магистр В. А. Загорский четыре раза в неделю читал «руко-
водствуясь сочинениями Эйлера и других новейших»
всеобщую арифметику, т. е. алгебру36. Незадолго до того
приглашённый молодой иностранец проф. И. А. Иде,
«окончивший уже в прошедшем году Аналитику опреде-
лённых величин и Теорию пределов», трижды в неделю
излагал дифференциальное и интегральное исчисления
с приложениями к высшей геометрии и смешанной матема-
тике36. Наконец, Ь. К. Аршеневский в начале года оповещал,
что будет три раза по часу «преподавать слушателям своим
вышнюю Геометрию, в которой покажет пользу и употре-
бление Дифференциальных и Интегральных исчислений».
Иде, лекции которого имели большой успех, умер осенью
1806 г. Вместо него в 1806—1807 уч. году взялся препо-
давать начала высшей математики наряду с оптикой
М. И. Панкевич. Вообще деятельность вновь учреждённого
факультета началась при благоприятных обстоятельствах.
Все кафедры были заполнены. Страхов читал теоретиче-
скую и опытную физику, Панкевич—механику, магистр
Г. И. Мягков—артиллерию и баллистику, Гольдбах—астро-
номические дисциплины и математическую географию,
Рейс—химию, Двигубский—технологию, Гофман—ботани-
ку, Фишер—естественную историю и сравнительную анато-
мию, ПроК( пович-Антоновский—зоологию и минералогию.
Изменения коснулись и учебной литературы. Курс
Вейдлера, конечно, исчез не сразу. В 1806—1807 гг.
Гольдбах читал астрономию по Вейдлеру, но уже с «нуж-
ными пополнениями и поправками», а через два года
сменил Вейдлера на Боде. И Панкевич, объявляя в
1811—1812 гг. курс прикладной математики, всё ещё
опирался на Вейдлера, но говорил об усовершенство-
ваниях. Из преподавания «чистой» математики Вейдлер
был изгнан ещё с 1804 г.: отныне преподавание ряд десяти-
летий проводилось под знаком новых и прогрессивных
идей, навеянных Французской революцией. Это естест-
венно объяснялось тем, что французская математика
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 77
заняла тогда в Европе господствующее положение бла-
годаря блестящим работам Лагранжа, Лапласа, Монжа,
Лежандра, позднее Фурье, Ампера, Пуассона, Коши и др.
Названные деятели, привлечённые к работе в созданных
революцией высших школах, произвели в обучении мате-
матике полный переворот. Они значительно повы-
сили научный и методический уровень преподавания.
Отбросив ложную строгость и вместе с тем примитивный
практицизм прежних, особенно немецких руководств, они
построили преподавание на началах сжатого, доступного и
последовательного изложения и несколько сухого изя-
щества, которые долгое время служили отличительным
признаком лучших французских курсов. Прогрессив-
ные русские учёные конца XVIII и начала XIX вв.
восприняли опыт французской научной школы—в Москве,
например, ещё с 1791 г. П. И. Страхов стал вести курс
физики по Бриссону. В 1803 г. широко образован-
ный попечитель Московского округа М. Н. Мура-
вьёв в своём отчёте писал: «С давнего времени Библи-
отека (университетская.—А, Ю.) оставалась в скудном
состоянии, и Университет лишён был единственного
способа соразмерять постепенные успехи свои с распро-
странением наук в Европе. Я не преминул препроводить
в Библиотеку новейших великих писателей, которые рас-
пространили в короткое время пределы человеческих
знаний в Химии, высокой Геометрии и Экономии Поли-
тической». Внизу приписаны были имена Лавуазье, Лалан-
да, Фуркруа, Монжа, Прони, затем Смита, Стюарта,
Бентама87.
Наибольший успех в первые 15 лет существования
физико-математического факультета выпал на долю курса
Безу, выпущенного в превосходном переводе В. А. Загор-
ского. Этьен Безу (Bezout, 1730 — 1783), член Парижской
академии, получил некоторые хорошие результаты в
алгебре, но особенно популярен был как автор математи-
ческих учебников для военных и морских учебных заве-
дений. Переводы его книг у нас появлялись и ранее,
начиная с 1784 г., полный же «Курс математики» в пяти
томах напечатан был в 1798—1803 гг., причём первые
четыре тома были переизданы в 1804—1806 гг. Это было
1S А. П. ЮШКЕВИЧ
очень доступное, хотя и далёкое по строгости, пособие
по всем отделам элементарной математики и началам
высшей. В арифметической части оно, правда, уделяло
много места разновидностям тройного правила, но зато
совсем чуждо было педантства и мелочности. Все части
книги были написаны ясно и живо и снабжены хорошими
примерами.
Я остановлюсь несколько на алгебре, её геометриче-
ских приложениях и исчислении бесконечно малых, ибо
в этих частях преподавание по Безу представляло
в Москве особые новшества. Алгебра начиналась с про-
стого и удачно построенного отдела о буквенном исчислении
и действиях с одночленами и многочленами. При рас-
смотрении линейных уравненш! (где, конечно, применя-
лось исключение неизвестных по «методу Безу») особо раз-
бирались системы неопределённые и несовместные. При-
нимались и отрицательные решения, которых Вейдлер
и Аничков избегали, причём Безу указывал, что они
«столько же существенные, как и положительные», что
они свидетельствуют о неправильной постановке вопроса
и о том, что «искомые количества должно принимать
в противном свойстве»38. При решении квадратных урав-
нений Безу не отвергал и «умственных», т. е. мнимых,
корней, которые, хотя и невозможны, но полезны, ибо ряд
задач можно решить лишь с помощью мнимостей, в ходе вы-
числений сокращающихся. Кроме квадратных и приво-
дящихся к ним трёхчленных уравнений, рассматривались
кубические и четвёртой степени. Излагался—без полного
вывода—бином Ньютона, применявшийся для приближён-
ного извлечения корней. Численные уравнения решались
приближённо по способу Ньютона.
«Применение алгебры к арифметике и геометрии»
прежде всего знакомило с прогрессиями и вычислением
степенных сумм членов арифметической прогрессии,
а затем с началами аналитической геометрии. Этот отдел
(стр. 277—495) изложен был довольно полно и по-своему
хорошо, но, разумеется, в духе XVIII в. Безу, после
определения основных понятий, прямо переходил к ко-
ническим сечениям; вводный отдел с уравнением пря-
мой и решением простейших задач отсутствовал. Преоб-
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 79
разование общего уравнения второй степени к нор-
мальным формам он проводил по Эйлеру-Декарту, т. е.
начиная с разрешения уравнения относительно одной
из координат. Учение о кривых второго порядка начина-
лось с вывода уравнений относительно вершины—сначала
эллипса, исходя из свойства г\ 4- r2 = const. Каждая
кривая подвергалась отдельному разбору, включая свой-
ства касательных, теоремы Аполлония и т. д. Давались
и центральные уравнения эллипса и гиперболы. Затем
доказывалось, что все три кривые совпадают с сечениями
конуса, проводилось упрощение общего уравнения и в
заключение кривые 2-го порядка прилагались к трисек-
ции угла и построению двух средних пропорциональных.
Исчисление бесконечно малых Безу излагал в духе
Лопиталя. Бесконечно Малые слагаемые подлежали от-
брасыванию в силу несравнимой малости; дифференциалы
определялись как разности значений переменной в данный
момент и в момент, непосредственно последующий. Содер-
жание курса было небогатое; высшие дифференциалы не
употреблялись, и, например, в учении об экстремумах
предлагалось выяснять их характер подстановкой значе-
ний аргумента в самую функцию. В интегральном исчисле-
нии рассматривались простейшие интегралы, применя-
лось приближённое интегрирование с помощью бинома
Ньютона и сообщались важнейшие геометрические при-
ложения.
Упрекать переводчика в выборе популярной книги
Безу не приходится; и во Франции Безу переиздавался
долго после 1800 г.39. Кроме Безу Загорский руководился
и «Универсальной арифметикой» Эйлера, вышедшей
в 1768—1769 гг. и затем в 1787 г., но об этой классической
книге, содержавшей слишком большой материал, осо-
бенно по неопределённому анализу, объявления о лекциях
говорят лишь раз. Мы, к сожалению, не знаем, каковы
были те «новейшие писатели», на которых ещё опирались
при чтении анализа. Один раз в объявлениях о лекциях
Загорского в 1808—1809 гг. упоминался Лакруа, однако
вообще курс этого знаменитого педагога (1796 и след, гг.),
позднее употреблявшийся в Петербургском университете,
в Москве применения не получил.
80
А. П. ЮШКЕВИЧ
Деятельность университета в первом десятилетии XIX в.
протекала в атмосфере общего сочувствия и большого
подъёма. «Вестник Европы», издававшийся с 1802 г.
Н. М. Карамзиным, горячо приветствовал новую политику
в области просвещения. Автор статьи «О новом образова-
нии народного просвещения в России» восторженно излагал
указ 24 января 1803 г., призывая дворян содействовать
намерениям правительства и не бояться введения сель-
ских школ. Августовский номер журнала за 1803 г.
содержал также перевод из книги «гражданина Биота»
«О благотворном действии наук во Франции во время
революционной войны», декабрьский—подробное описание
Геттингенского университета. Московский университет
откликнулся на повышение интереса к знаниям и орга-
низовал публичные лекции по различным вопросам.
Карамзин отмечал особенный успех лекций П. Страхова
по физике, сопровождавшихся демонстрацией опытов.
Эти и другие лекции собирали в университетском зале лиц
самого различного положения. «Любитель просвещения,—
писал Карамзин,—с душевным удовольствием видит там
знатных московских дам, благородных молодых людей,
духовных, купцов, студентов Заиконоспасской академии
и людей всякого звания». Другим начинанием Универ-
ситета, которое поддержал попечитель Муравьёв, было
издание в 1805—1807 гг. еженедельных «Московских учё-
ных ведомостей». Журнал этот помещал отчёты о деятель-
ности Университета, обзорные статьи и превосходную биб-
лиографию40. Мы находим в нём рецензии на новые кни-
ги по математике, появлявшиеся у нас и за грани-
цей,—на курсы Био, Лакруа, книгу Рахманова и др.
Наконец, при Университете был создан ряд научных
обществ.
Для нас особый интерес представляет попытка создать
первое в России математическое общество. Инициатором
его был подполковник Николай Николаевич Муравьёв
(1768—1840), человек высокообразованный, сын генерал-
инженера Н. Е. Муравьёва, автора первого русского
учебника алгебры («Начальное основание математики»,
Спб., 1752). В это общество вошли сын Муравьёва Михаил
Николаевич, студенты Терюхин, Щепкин (будущий про-
МАТЕМАТИКА. В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 81
фессор), Андреев, кандидат Афанасьев (также в будущем
преподаватель Университета) и др. 41. Устав «Общества
математиков в Москве» 1811 г. гласил, что целью его явля-
ется распространение математических наук. Математиче-
ские исследования не были,однако, основной целью в гла-
зах учредителей; главной задачей было обучение приклад-
ным дисциплинам военного характера и подготовка моло-
дёжи к военной службе43. В доме Н. Н. Муравьёва были
открыты курсы математики, механики и военных дисцип-
лин. Лекции имели большой успех. В 1816 г. из общества
выросло Московское учебное заведение для колонно-
вожатых, где математика проходилась в обширном
объёме. С 1816 по 1823 г. оно выпустило 138 офицеров, из
них большинство для Генерального штаба. В 1826 г.
это учебное заведение было переведено в Петербург. Судьба
первого математического общества характерна. Интерес
к самой математике в широких кругах интеллигенции лишь
пробуждался. Впрочем, серьёзная научная работа в пер-
вом Московском математическом обществе была невоз-
можна и потому, что слишком недостаточны были знания
его молодых сочленов.
Все эти начинания, казалось, обещавшие быстрый
прогресс математического и естественно-научного обра-
зования в Университете, не дали первоначально больших
результатов. «Общество математиков» превратилось в чисто
военные курсы, «Учёные ведомости» со смертью попечи-
теля закрылись в 1807 г., публичные лекции прекратились.
Успешная работа физико-математического отделения в
Университете в 1804—1810 гг. вскоре сменилась застоем.
Герцен, учившийся на факультете в сравнительно лучшие
годы, на двадцать лет позднее, вспоминал: «В те времена
начальство Университетом не занималось, профессора
читали и не читали, студенты ходили и не ходили.. ». Мно-
гие лекторы были мало пригодны для научного воспитания
юношества. Химик Рейс, например, попал на кафедру
случайно. Приглашён был в Россию его дядя, но старик
ехать не пожелал и отрекомендовал племянника, химию
знавшего плохо и читавшего её поэтому скверно.
I римером отсталого, или, по выражению Герцена,
«допожарного», профессора метема ики мог служить уже
Историко-математ. исследования
82
А* П. ЮШКЕВИЧ •
встретившийся нам Фёдор Иванович Чумаков (1782—1837).
Этот воспитанник Московского университета, сын ротми-
стра, пошёл сначала учителем матехматики в Благородный
пансион. В 1812 г. ему присвоили степень доктора мате-
матических наук' а с 1813 г. он почти два десятка лет
читал механику, «подгоняя формулы к тем, которые
были в курсе Пуансо, с совершеннейшей свободой поме-
щичьего нрава, прибавляя, убавляя буквы, принимая
квадраты за корни и х за известное» (Герцен). Только
чиновничьим равнодушием к преподаванию и студентам
можно объяснить такие лекции Чумакова. Ведь смог же
он, когда захотел, дать вполне приличный перевод курса
математики и механики Беллавеня с некоторыми собст-
венными дополнениями 43.
Преподавание математики в Московском университете,
резко поднявшееся в первые годы существования физико-
математического факультета, пошло на убыль. Иде скон-
чался в октябре 1806 г., через полтора года умер Арше-
певский, а в январе 1810 г. ушёл Загорский, продолжавший
после них читать анализ и теорию конических сечений.
На место Загорского приглашён был Прохор Игнатьевич
Суворов (1750—1815), вполне «допожарный» преподаватель
Морского кадетского корпуса, учившийся в Тверской семи-
нарии и окончивший со званием магистра Оксфордский
университет в 1775 г. Лет за тридцать до приглашения
в Москву П. И. Суворов мог считаться вполне знающим
своё дело человеком 44. Теперь он оказался совершенно не
на месте. Очень тяжело отразились на работе Универ-
ситета и военные 1812—1814 гг. В 1810—1814 гг. на
факультете преподавалась почти только элементарная
математика. Единственной уступкой требованиям вре-
мени со стороны Суворова было включение в курс начал
теории конических селений (читал он их по Безу).
В 1814 г. отделение, однако, спохватилось. В засе-
дании 18 августа, когда встал вопрос о замене ушед-
шего Суворова, отделение вынесло следующее решение:
«Между тем как отделением замечено, что в классе чи-
стой Математики с 1810 г. совсем не была объясняема
высшая Аналитика, как-то: функционное, дифференци-
альное, интегральное и вариационное исчисление, то и
МАТЕМАТИКА Б МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 83
считает обязанностью просить Совет, чтобы он благово-
лил подтвердить избранному на кафедру Чистой Мате-
матики, что он должен в своё время изъяснить своим
слушателям и высшую Аналитику» (см. протокол отде-
ления в Архиве Московского университета).
Преподавание высшей математики действительно возоб-
новилось и в 1814—1825 гг. вёл его Тимофей Иванович
Перелогов45. Первые годы он начинал свой курс с урав-
нений высших степеней, которые должны были, но не
успевали изучать в гимназии, переходил к коническим
сечениям, а затем к анализу. После он оставил за собой
один лишь анализ, передав чтение высшей алгебры й анали-
тической геометрии новым адъюнктам Щепкину и Перево-
щикову, пришедшим в Университет в 1817 г. и, соответ-
ственно, 1818 г. Чтение элементарной математики, т. е.
повторение полного гимназического курса, при этом не
прекращалось. Едва Перелогов начал излагать высшие
отделы, как выяснилось, что некоторые слушатели не
знают как следует геометрии и даже арифметики, о чём он
и сообщил отделению 20 октября 1814 г. Поэтому маги-
стру Афанасьеву4’ поручили дважды в неделю обучать
студентов арифметике и геометрии. В следующем году
вспомогательный курс включил также тригонометрию и
алгебру. Арифметику и геометрию читал недолго также
адъюнкт Тростин47.
В преподавании Перелогов долго следовал Безу, но
в 1821—1822 гг. сменил его на довольно известное руко-
водство Бушарла, по которому, между прочим, занимался
К. Маркс 48. Курс Бушарла содержал сравнительно
обширный материал, особенно во втором издании, допол-
ненном теорией особых точек кривых, экстремумами
функций двух переменных, кривыми в полярных коор-
динатах, двойными и тройными интегралами и простей-
шими уравнениями в частных дифференциалах. В прин-
ципиальных вопросах Бушарла стоял на эклектической
позиции. Метод пределов Даламбера, указывал он в
предисловии, дополняет метод бесконечно малых, а
метод Лагранжа восполняет метод пределов, связывая
дифференциалыше коэффициенты с чистой алгеброй. Соб-
ственно говоря, они образуют один метод. Принципы
6*
84
A. II. ЮП КЕВНЧ
дифференцирования покоятся на теореме о биноме, т. е.
на ряде Тэйлора. Самый ряд Тэйлора Бушарла выводил
двояко: и по способу неопределённых коэффициентов Мак-
лорена и по способу, изложенному в известном курсе
Лакруа, именно, исходя из выражения для наращённой
функции г/' = /(г-р/г) в виде у' = */+Ah +В№ ± Ch3-]-...,
du' du'
а также теоремы, что dx = позволяющей выразить
коэффициенты А,В,С,... через производные у по х. По
методу Лагранжа получались производные произведения,
степени, сложной функции и т. д. ,т. е. производные рас-
сматривались как дифференциальные коэффициенты ряда
Тэйлора. Вместе с тем Бушарла трактовал производную
как отношение пулей; скажем, для у=х* бралось равен-
ство У—^== Зя2+Зя/г-|-Л2 и полагалось /г = 0. «В уравне-
нии -J-® Зя2,— писал Бушарла, —нет ничего абсурд-
О
ного, ибо алгебра учит нас, что у может выражать лю-
бое количество... Так как символ этот не оставляет ника-
_ du
кого следа этих переменных, изооразим его через тогда
будет нам напоминать, что функцией было у, а перемен-
ной я. Но от этого dy п dx не перестанут быть количест-
венно нулями, и мы будем иметь = Зя2». На такой
основе излагалось дифференциальное исчисление в Москов-
ском университете в 1821—1825 гг. Мы не знаем, однако,
какой материал предлагал Перелогов в количественном
отношении.
Знания студентов по математике в первой четверти
XIX в. были очень невысоки. С ту «пате ли слегка приоб-
щались к анализу и высьей геометрии, лучье знакомясь
только с повторительным курсом элементарной матема-
тики. Об этом свидетельствуют кандидатские и маги-
стерские экзамены, о которых будет сказано ниже.Физико-
математическое отделение Московского университета того
времени уступало физико-математическим отделениям
Харьковского и Казанского университетов. II в Харь-
м XTFMATTKA В МОСК. УНИВТ PCIITFTE ГА DFPBKE СТО ЛГТ 85
кове, например, читалась начальная математика, но там
Тимофей Фёдорович Осиповскмй (1765—1832), выдаю-
щийся и квалифицированный педагог, работавший с осно-
вания факультета, хорошо поставил преподавание диф-
ференциального и интегрального исчислений. Кроме
того, москвичи лишены были русского учебника, мел ду
тем как в Харькове пользовались превосходным
«Курсом математики» Осиповского (3 тт., 1802—1823).
В Казани с 1808 по 1819 г. преподавал проф. М. Ф. Бар-
тельс, а с 1814 г. математические лекции начал читать
также Н. II. Лобачевский, сначала в звании адъюнкта,
ис 1816 г. в качестве профессора.
В некоторых технических учебных заведениях препо-
давание математики также стояло в то время выше, чем
в Московском университете. В этом убеждает самое беглсе
сопоставление вопросов «Программы для экзамена вос-
питанников Института инженеров путей сообщения» (Спб.,
1818), относившихся ко всем основным разделам анализа,
аналитической и начертательной геометрий, с простень-
кими задачами на кандидатских экзаменах в Москве.
И позднее в петербургских высших технических учебных
заведениях преподавание математики гелось на очень
высоком уровне.
V. Деятельность Д. М. Перевощикова и П. С. Щепкина
Т. И. Перелогов по воспитанию принадлежал к старому
поколению и вряд ли сам решил сменить Безу на Бушарла.
Скорее это следует приписать влиянию его молодых
помощников, именно Д. М. Перевощикова и П. С. Щеп-
кина. Щепкин и Перевощиков вообще сыграли крупную
роль в улучшении преподавания математики (и астро-
номии) в Московском университете, да и за его пределами.
В результате их деятельности уровень математического
образования на физико-математическом отделении прибли-
зился к уровню преподавания математических дисцип-
лин в Харьковском и Казанском университетах (о Петер-
бурге, где университет в 20-х годах лишь начинал
свою деятельность, говорить не приходится). Появились
и другие новаторы преподавания, вроде увлекательного
86
А. П. I0IDKELII4
натурфилософа М. Г. Павлова. В университетской работе
этих людей нашёл своеобразное отражение тот же обще-
ственно-национальный подъём, который мы наблюдаем
н в литературе и в других областях деятельности русской
интеллигенции этого времени. Перевощиков и Щепкин—
особенно первый—относились к науке с любовью и под-
линным интересом. Они следили за её успехами, пропа-
гандировали новые идеи и на свою деятельность смот-
рели, как на патриотическое служение.
Дмитрий Матвеевич Перевощиков, сын дворянина
Пензенской губернии, родился 17 апреля 1790 г: Он
получил образование в Казанской гимназии, затем в
университете. Преподавание математики там было пре-
восходно поставлено сперва адъюнктом Карташевским49,
затем Бартельсом. Когда Бартельс приехал в 1808 г.
в Казань, он был поражён знаниями и успехами слуша-
телей. С 1809 г. в течение семи лет Перевощиков учитель-
ствовал в Симбирской гимназии, а в декабре 1818 г. начал
читать высшую геометрию в Московском университете.
Общественные настроения молодого Перевощикова отчасти
отразились в математических сочинениях, в которых он
показал себя поклонником метрической системы. Это
весьма характерный показатель; достаточно вспомнить,
какие громы и молнии обрушены были в 1823 г. акад.
Фусом в рецензии на рукопись Лобачевского «Геометрия»
за предложение ввести в геометрию метрические меры
и десятичное деление углов. Перевощиков не только
подчёркивал достоинства метрической системы, но в своей
«Арифметике», изданной, когда при дворе и в Министер-
стве просвещения господствовала реакционная мистика,
прославлял революционных творцов этой системы. «Сия
счастливая мысль,—писал он,—родилась в головах фран-
цузского революционного Конвента, который предписал
составить особенный Комитет из славнейших учёных Фран-
ции: Лапласа, Лагранжа, Монжа, Борды, Лефевра,
Жино и проч.». Отмечая, что ещё имеются препятствия
к введению метрических мер в общее употребление,
Перевощиков призывал учёных особенно дорожить ими,
уважать и «навсегда оставаться признательными к тру-
дам мужей, желавших принести истинную пользу для всех
МАТЕМАТИКА в МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 87
народов и ДЛЯ всех времён»80. Выпуская другой учебник
арифметики в 1826 г., автор должен был отказаться от
упоминания о Конвенте, но сохранил восторженный отзыв
об учёных, проводивших метрическую систему в жизнь.
Д. М. Перевощиков был одарён и литературным и
лекторским талантом. По словам современников, он препо-
давал математику «вдохновенно, как поэт, как бы создавая
её во время изложения, со страстной любовью к ней,
которую сообщал и слушателям»81.
G 1818 по 1825 г. Перевощиков читал алгебру и анали-
тическую геометрию частью по Франкеру, частью по соб-
ственным руководствам. Затем он перешёл на препода-
вание астрономии, сферической тригонометрии и небес-
ной механики и с 1826 г. руководил кафедрой астрономии
в звании профессора.
Перевощиков написал и перевёл целый ряд руководств
по математическим наукам. Некоторые из них разобраны
далее. Здесь я ограничусь перечислением важнейших.
Вслед за упомянутой уже «Арифметикой» Перевощиков
выпустил «Главные основания аналитической геометрии
трёх измерений» (1822), а затем в течение ряда лет издавал
обширную и пользовавшуюся большой популярностью
«Ручную математическую энциклопедию» в 13 томах,
содержавшую курсы элементарной и высшей математики
(1—7 тт.), механики, физики и астрономии (1826—1837).
Далее вышли «Гимназический курс чистой математики»
(1838) и «Основания алгебры» (1854), рекомендованные
Министерством народного просвещения для гимназий.
Кроме того, Перевощиков перевёл отдельные части «Курса
чистой математики» Франкера (1819, 1824, 1825) и «Курса
чистой математики» Лакруа (1826, 1835). Перу его
принадлежало также много популярных и обзорных
статей по астрономии и по её истории. Научные труды
Перевощикова относились к небесной механике. Это
были «Гауссов способ вычислять элементы планет» (Спб.,
1853), «Вековые возмущения семи больших планет»
(Спб., 1859—1861) и «Теория планет» (Спб., 1863—1868).
Здесь нет необходимости входить в оценку этих астро-
номических работ Перевощикова. Плодовитый автор
успевал вести ещё административную работу, состоя то
88
A. . ЮШКЕ1ИЧ .
деканом, то ректором Университета. В 1852 г. Перевощиков
переехал в Петербург на работу в Академию наук, членом-
корреспондентом которой был с 1832 г. В 1855 г. он был
избран действительным членом Академии; Перевощиков
до глубоксй старости не прекращал своих трудов и скон-
чался 3 сентября 1880 г. девяноста лет отроду.
Жизнь Павла Степановича Щепкина не была в такой
мере пронизана идеей страстного служения науке и про-
свещению, но и ему физико-математическое отделение
обязано многим Щепкин, сын канцеляриста Московской
духовной консистории, учился сперва в гимназии,
а затем в Университете, который закончил кандидатом
в декабре 1811 г. Через четыре года он сдал магистерские
экзамены, защитил диссертацию «Об открытиях, сде-
ланных в Астрономии со времени изобретения телеско-
пов» (М., 1815) и поступил учителем математики в гим-
назию, где прослужил до 1822 г. С 1817 г. ему было
поручено ведение занятий по начальной математике
в Университете, в 1818 г. он получил звание адъюнкта.
Первые два года Щепкин читал по рукописи Чумакова,
составленной, вероятно, близко к курсу Беллавеня. Когда
к нему присоединился Перевощиков, оба они предпочли
учебники Франкера, которые сперва были положены в
основу элементарного курса, а с 1825 г. (когда Щепкин
занял место ушедшего Перелогова) и всего математического
преподавания в Университете. После 1820 г. Щепкин читал
лекции по высшей алгебре, а затем и аналитической
геометрии. Профессуру Щепкин получил в 1826 г.
Замена Безу и Бушарла на Франкера представляла
крупный шаг вперёд в научном и педагогическом отно-
шении. Но на Франкере Щепкин и остановился. Это
был человек знающий, 'добросовестный, но довольно
апатичный и не склонный к новшествам. Он не испыты-
вал ни малейшей потребности изменять курсу Франкера,
тем более, что за Франкером шли важнейшие помощники
Щепкина, читавшие при нём высшую алгебру и анали-
тическую геометрию, И. И. Давыдов и Н. В. Коцауров62.
П. С. Щепкина обвиняли в буквальной близости к выб-
ранному им руководствуй в том, что он не следил за успе-
хами математики. Его биограф и вместе с тем заместитель
MAU MATI KA I МОСК. У НИ Г PCHT-TF Г* Г1 PI J T СТО ЛГТ 89
по кафедре, проф. H. E. Зернов, отвергал последний
упрёк, указывая на цитаты в тетрадях Щепкина из Гарнье,
Лагранжа, Фурье, Коши. Не отрицая вместе с тем, что
Щепкин точно следовал за Фрэнкером, проф. Зернов
подчеркивал серьёзные достоинства курсов последнего.
«Франкер в своём курсе,— писал он в биографии
Щепкина, — есть один из лучших, можно сказать редких
учителей, по той связи, строгости и зависимости, в которой
поставлены у него истины, составляющие науку, начиная
от самых основных и до высших, по полноте содержания,
нисколько не обременяющей учащегося, по сжатости,
с совершенным сохранением понятности»63. Но книги
Фрэнкера, конечно, решительно уступали по своим пе-
дагогическим, а особенно по научным достоинствам кур-
сам Коши, которые появились в 20-е годы XIX в. и кото-
рые вскоре положил в основу преподавания сам Зернов.
Характер Щепкина отражался и на его лекциях: он
«проходил науку хладнокровно и медлительно, любя её вну-
треннею сосредоточенною любовью, но не торопясь к её
светлым и поразительным результатам, и заслужил от
своих современников прозвание Фабия-кунктатора»64. По
невыясненным причинам Щепкин покинул в 1833 г. Уни-
верситет, перейдя учителем в гимназию. Он скончался
15 июля 1836 г. примерно 43 лет. Как и другие профес-
сора, Щепкин занимался переводами, большинство ко-
торых, как «Астрономия» Био, «Основания геометрии»
Лежандра, осталось в рукописи. Свет увидела лишь 1-я
часть курса Фрэнкера, переведённая Щепкиным совместно
с Перевощиковым (XI., 1819).
Курс математики Фрэнкера, от арифметики доходив-
ший до вариационного исчисления, в первой половине
XIX в. принадлежал к числу популярнейших во Фран-
ции. Луи Бенжамен Франкер (Francoeur, 1773—1849),
репетитор Политехнической школы и профессор алгебры
в Парижском университете, был учеником Лежандра
и Лакруа. Под влиянием сочинений последнего, а также
пользуясь советами Пуассона, Ампера, Био, он и писал
свой курс, эпиграфом к которому выбрал слова Лапласа:
«Держитесь в преподавании общих методов, старайтесь
представить их в простейшей форме, и тогда вы увидите,
90
А. П. ЮШКЕВИЧ
что они почти всегда являются вместе с тем наиболее
лёгкими»65. В аналитической геометрии Франкер начи-
нал уже с простейших образов—прямой и плоскости.
Анализ он строил почти исключительно на исчислении
функций Лагранжа, несколько эклектически дополняя
его идеями бесконечно малых и предела, в чём он следо-
вал за Лакруа и приближался к Коши. В глазах тогдаш-
них математиков он нёс с собой освобождение от старой
рутины. «Было время,— писал в предисловии к переводу
«Высшей алгебры» И. Давыдов,— когда чистую математику
представляли ремеслом, нужным будто токмо для наук
военных, мореплавания, землемерия и тому подобного,
посему и курсы применяемы были к той или к другой
части в особенности». Франкер, продолжал И. Давыдов,
убедительно показал, что при изучении математики нужно
иметь в виду не столько затверживание истин, сколько
исследование их начал, их взаимных связей, чтобы изу-
чающие их «пришли сами в состояние изобретателей».
Высокую оценку книгам Франкера давали, как было ска-
зано, и профессора Н. Е. Зернов и Д. М. Перевощиков.
Содержание его курса ясно из дальнейшего.
При Щепкине, как видно из «Конспектов физико-
математического отделения» за 1826 г., курс математики
состоял из шести частей—арифметики, начальной ал-
гебры до уравнений 2-й степени, оснований геометрии,
аналитической геометрии (их читал тогда Н. В. Коцау-
ров), высшей алгебры, дифференциального и интеграль-
ного исчислений (их читал П. С. Щепкин). Аналитиче-
ская геометрия начиналась с приложения алгебры к ре-
шению геометрических задач на построение и вычисление
и с изложения «теории знаков +, —, извлечённой авто-
ром из обширного сочинения знаменитого Карно Geo-
metrie de Position» (стр. 150); далее следовала прямоли-
нейная тригонометрия. Потом переходили к самой анали-
тической геометрии—учению о прямой и круге, с простей-
шими задачами, к разбору отдельных конических сечений
и их свойств, включая теоремы Аполлония, к выводу урав-
нений касательных как предельных положений секущих
и полному исследованию уравнения кривой 2-го порядка
путём преобразования координат. В эту часть курса
МАТЕМАТИКА в МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 91
входили также ознакомление с полярными координатами,
а также исследование ряда кривых: конхоиды, циссоиды,
циклоиды, логарифмической кривой, спирали.
В геометрии трёх измерений разбирались последова-
тельно прямая, плоскость, шар, простейшие цилиндриче-
ские и конические поверхности. Довольно бегло изучалось
уравнение поверхности 2-го порядка без рассмотрения
прямолинейных образующих линейчатых поверхностей,
диаметров и т. д. Высшая алгебра включала: формулы сое-
динений, бином Ньютона с распространением (нестрогим)
на случай произвольного показателя и с приложением к из-
влечению корней, разложение алгебраического много-
члена на линейные множители, преобразование корней,
отыскание корней соизмеримых и кратных, приближён-
ные методы Ньютона, Лежандра, Лагранжа, правила
знаков Декарта, исключение неизвестных из двух урав-
нений, решение двухчленного уравнения, уравнений
3 и 4-й степеней, применение непрерывных дробей к опре-
делённым и неопределённым уравнениям первых двух
степеней, наконец, разложение рациональных дробей на
элементарные (здесь были опущены из курса Франкера
обширный отдел о симметрических функциях корней,
применение способа неопределённых коэффициентов к раз-
ложению в ряды многочисленных трансцендентных функ-
ций и к обращению рядов и общая теория логарифмов).
Дифференциальное исчисление состояло из двух отде-
лов. Первый, содержавший формальные приёмы, открывал-
ся выводом ряда Тэйлора и на его основе правил дифферен-
цирования основных функций, функции от функции и не-
явных функций. Затем разбирались по Лагранжу случаи,
когда разложение в ряд Тэйлора невозможно, «пределы
тэйлорова ряда», т. е. остаточный член, и вводился ряд
для функции двух переменных. Во втором отделе дава-
лись приложения: теория экстремумов, «способ каса-
тельных», т. е. вывод уравнений касательной и нормали,
формул подкасательной и т. п., теория соприкоснове-
ния кривых, кривизна, развёртки, асимптоты, учение об
особых точках. Всё это иллюстрировалось на кониче-
ских сечениях, циклоиде, спиралях и других кривых в
прямолинейных и полярных координатах. Интегральное
92
Л. П. ЮШКЕВИЧ
исчисление включало основные правила интегрирования,
дифференциальный бином, эйлеровы подстановки, рацио-
нальные дроби, интегрирование путём разложения в ряды,
задачи на квадратуры, спрямления, площади поверхностей
и объемы тел вращения. Теория интегрирования дифферен-
циальных уравнений затрагивалась мало, а исчисление
конечных разностей и вариационное совсем не входили
в программу.
В курсе математики за 1825—1831 гг. не произошло
почти никаких изменений, если не считать, что в 1830 г.
по приказу императора Николая во всех университетах
введено было для желающих счисление на счётах по спо-
собу генерал-майора Свободского66. Но в жизни Универ-
ситета произошло событие большой важности: в 1828 г.
произведено было, наконец, разделение студентов на три
«разряда» или курса и составлено покурсовое расписание
лекций. В этом году математика читалась только на пер-
вых двух курсах, но в 1833—1834 уч. году, последнем
году деятельности Щепкина, она распространилась на все
три курса. На первом читались: счисление на счётах,
прямолинейная тригонометрия, высшая алгебра, на втором
и третьем курсах—сферическая тригонометрия (её читал
Перевощиков), анализ и аналитическая геометрия. Само-
стоятельных упражнений в решении задач, повидимому,
не было.
VI. Новые веяния в преподавании математики
(Н. Е. Зернов и Н. Д. Брашман)
Середина 30-х годов XIX в. ознаменовалась для исто-
рии математики в Московском университете приходом
двух новых лиц, поднявших преподавание её на значи-
тельно более высокий уровень. Это были профессора
Н. Е. Зернов и Н. Д. Брашман.
Николай Ефимович Зернов (родился 7 ноября 1804 г.,
умер 23 ноября 1862 г.), отец которого происходил из ду-
ховного звания и служил на Московском почтамте, обу-
чался сначала в Ярославском уездном училище, а затем
в гимназии, которую окончил с отличием, особенно за
успехи в математике. В 1819 г. он принят был в студенты
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ УЗ
Демидовского лицея, но через год переехал в Москву,
где слушал ещё лекции Перелогова и Чумакова, а также
Перевощикова и Щепкина. В 1822 г. он окончил Универ-
ситет в звании кандидата. Несомненно влияние на заня-
тия и интересы начинающего учёного со стороны Пере-
вощикова. Так, тему магистерской диссертации «О суточ-
ном и годовом движении Земли» (л!., 1826), защищённой
Зерновым в 1827 г., предложил ему Д. М. Перевощиков.
Университетские штаты были заполнены, и Зернов посту-
пил в 1826 г. в Университетский благородный пансион
(с 1830 г. 1-я гимназия). С уходом Щепкина и освобож-
дением вакансии в Университете в 18^4 г. Зернов был
зачислен в адъюнкты, а в следующем году произведён
в экстраординарные профессоры. Полученное Зерновым
образование, влияние Перевощикова, а затем Н. Д. Браш-
мана, повысившиеся требования времени, личные инте-
ресы— всё содействовало успешной деятельности Зернова.
Он внимательно следил за текущей литературой, много
размышлял над своими лекциями и основательно изучил
математику.
Университетски!! устав 1835 г. безусловно требовал,
чтобы профессора имели докторскую степень, адъюнкты
же—магистерскую. Зернову пришлось защищать пер-
вую в России докторскую математическую-диссертацию57.
Она выгодно отличалась от прежних магистерских сочине-
ний, представлявших собой популярные обзоры какого-
либо вопроса, преимущественно из физики или астроно-
мии. «Рассуждение об интеграции уравнений с частными
дифференциалами» (М., 1837) содержало большой и серьёз-
ный материал, и если Зернов не произвёл оригинальных
открытий, то засвидетельствовал солидную эрудицию
в специальных вопросах. Это «Рассуждение» служило
впоследствии учебным пособием. Кроме* того, Зернов
написал «Начальные основания арифметики» для уча-
щихся пансиона (4., 1827), курс «Дифференциального
исчисления» (VI., 1842), заслуживший половину Деми-
довской премии (2500 руб.) Академии наук, и ряд
статей.
В преподавании Зернов сначала опирался па «Ручную
математическую энциклопедию» Перевощикова, излагав-
94
А. П. ЮШКЕВИЧ •
шего анализ отчасти по Карно, отчасти по Франкеру и
Лакруа; впрочем, он дополнял Перевощикова по Коши.
Затем он перешёл к чтению по собственному курсу,
а интегральное исчисление излагал по Курно и ученику
Коши—Муаньо. Благодаря Зернову преподавание ана-
лиза в Москве впервые стало на уровень современной
ему науки.
Аналитическую геометрию Зернов преподавал по пре-
восходному сочинению Брашмана, а также по Лефебюру
де Фурси. Курс анализа Зернов читал почти в течение
ЗОлет и сам охарактеризовал направление, которому следо-
вал, в таких выражениях: «В преподавании высших исчис-
лений он должен был сделать одно существенное измене-
ние.- Предшественник его П. С. Щепкин оставил употре-
бление бесконечно малых Лейбница и ввёл исключительно
систему производных функций Лагранжа. Но, несмотря
па то, что в Theorie des fonctions analytiques последний
знаменитый геометр даёт приложение своей системы и
к геометрии, и к механике, другое его творение Мёса-
nique analytique представляло обширное поприще упот-
реблению бесконечно малых, которые не устранены и при
новом издании книги, позднейшем, чем «Теория функций».
Все последующие геометры по примеру его и по тому
удобству, которое доставляет лейбницева система приклад-
ным частям математики, удержали его. Вследствие сего
па лекциях Зернова восстановлены бесконечно малые,
а употребление производной функции удержано только
в тех случаях, где опа сокращает или упрощает выраже-
ние, как это везде делается со времени Theorie des fonc-
tions. Но чтобы отклонить от себя всякое обвинение,
Зернов старался в приложении бесконечно малых соблю-
сти сколько возможно строгость; потому он везде отличает
приращения величин от дифференциалов их, принимая
только, что предел отношения первых равен отношению
вторых, а самые приращения и дифференциалы сближа-
ются по мере их уменьшения. Таким образом, учащийся,
руководимый строгостью, свойственной древним геомет-
рам, в чистом анализе и геометрии свыкается с мыслью
Лейбница о бесконечно малом, а потом уже смело поль-
зуется ею в прикладных частях математики. Эго состав-
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ 8А ПЕРВЫЕ СТО ЛЕТ 95
ляет главный характер изданного Зерновым «Дифферен-
циального исчисления»; тот же характер поддерживается
у него и в интегральном исчислении»58. Литературная
и педагогическая деятельность проф. Зернова свидетель-
ствует об его большом интересе к мето дологическим и мето-
дическим проблемам современного ему анализа. В конце
концов он занял точку зрения, очень близкую Коши.
Но мы не находим у Зернова интереса к быстро развивав-
шимся в ту эпоху теории функций комплексного пере-
менного, теории эллиптических функций и пр. Это ска-
залось и на программе обучения в физико-математическом
отделении.
Если Зернов впёс в преподавание современные
математические идеи, хотя и не поднял его на высоту более
специальных исследований в тех или иных разделах ана-
лиза, то Н. Д. Брашман вдохнул в него новую жизнь,
дух математического творчества. Николай Дмитриевич
Брашман родился 14 июня 1796 г. в еврейской семье,
проживавшей в местечке Росенове около г. Брюнна в Мо-
равии. По окончании Венского университета он в 1821 г.
стал репетитором по высшей математике. В Россию он
переехал в 1823 г. и после кратковременного пребывания
в Петербурге в 1825 г. был приглашён в Казанский уни-
верситет, где преподавал механику и математику. В 1834 г.
он получил место профессора на кафедре прикладной
математики в Московском университете. В Московском
университете он работал более тридцати лет, почти до
самой смерти, последовавшей 13 мая 1866 г.
Хотя основной специальностью Брашмана была при-
кладная математика и в этой области ему принадлежит
несколько работ и учебников, но и развитие математики
в России обязано ему весьма многим. В частности, для
университетского обучения он издал замечательный «Курс
аналитической геометрии» (М., 1836), о котором говорится
далее. Но главное — он горячо и деятельно заботился о
распространении математических знаний, о расширении
программы, о повышении квалификации студенчества и
старательно выпестовывал творческих научных работ-
ников, первый подавая пример своими реферативны-
ми и оригинальными статьями в «Учёных записках»
9$
A. II. ЮШКЕ БИЧ
Московского университета. Учениками его явились акаде-
мики II. Л. Чебышев и II. И. Сомов, проф. А. Ю. Дави-
дов и другие выдающиеся учёные и педагоги. Брашман,
наконец, на склоне жизни явился инициатором создания
Московского математического общества и «Математическо-
го сборника», первый том которого вышел вскоре после
его кончины.
Проследим теперь за изменениями в преподавании на
физико-математическом отделении, по уставу 1835 г.
переименованном во 2-е отделение философского факуль-
тета69, за последние двадцать лет разбираемого периода.
В 1834—1835 гг. математика читалась на всех трёх курсах
и попрежнему в неё входили вычисления на счётах и три-
гонометрия, но арифметика, начальная алгебра и геомет-
рия уже не преподавались. Факультет всё ещё давал широ-
кое естественно-научное образование с хозяйственным
уклоном, включавшее ботанику и зоологию, техноло-
гию и агрономию. Количество часов на математику
было невелико и к тому же значительная часть их
падала па счисление на счётах и элементарную триго-
нометрию.
По новому университетскому уставу 1835 г. число кур-
сов было увеличено до четырёх, а только что названные
отделы математики исключены. На I курсе читались анали-
тическая геометрия и высшая алгебра, на II—дифферен-
циальное и интегральное исчисления, а на III и IV—чита-
лось интегрирование дифференциальных уравнений, обык-
новенных и с частными производными, и вариационное
исчисление. С III курса начиналось, кроме того, разделе-
ние на математиков и естественников: для математиков
на III курсе не обязательны были ботаника и зоология,
а на IV курсе, кроме того, геогнозия. Но число лекцион-
ных часов по математике оставалось всё же незначитель-
ным, достигая в среднем за 4 года 23/4 недельных часа
из общего среднего недельного числа 19г/2 учебных часов.
Распределение часов в 1841—1842 гг., почти не изменив-
шееся и в 1854—1855 гг., когда математические дисци-
плины получили вместе с начертательной геометрией в сред-
нем Зх/2 недельных часа, на всех курсах было (в неделю)
следующее:
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ 8А ПЕРВЫЕ СТО ЛЕТ 97
I курс
II полугодие
I полугодие
Богословие...............
Русская словесность . . . .
Чистая математика........
Физика...................
Ботаника ................
Астрономия...............
Французский язык.........
Рисование и черчение....
3 Церковная история............3
3 Русская словесность - . . . 3
3 Чистая математика............3
3 Физика.......................з
3 Ботаника.....................3
3 Элементарная гео тез и я ... 2
3 Французский язык.............3
4 Рисование и черчение . . . . 4
II
I полугодие
Физическая география и ми-
нералогия ..............2
Дифференциальное и инте-
гральное исчисления ... 4
Механика..................3
Оптика....................3
Химия.....................3
Зоология ................ 3
Ботаника..................3
II полугодие
Физическая география и ми-
нералогия ..............2
Дифференциальное и инте-
гральное исчисления ... 4
Механика..................3
Оптика .................. 3
Химия..........'..........3
Зоология..................3
Ботаника ................ 3
III
курс
I полугодие
Чистая математика.........2
Статика и гидростатика ... 3
Математическая физика (ма-
гнетизм, электричество,
свет, теплота)...........2
Астрономия (и сферическая
тригонометрия)...........3
Химия.................... 6
Минералогия................4
II полугодие
Чистая математика..........2
Статика и гидростатика . . 3
Математическая физика (ма-
гнетизм, электричество,
свет, теплота)...........2
Высшая геодезия............3
Химия......................G
Минералогия................4
Теория и употребление астро-
номических приборов ... 2
IV курс
I полугодие
Чистая математика.........2
Динамика и гидродинамика . 2
Математическая физика ... 2
Астрономия.................2
Химия......................3
Законы о состояниях и госу-
дарственных учреждениях 2
1 Историкс-математ. исследования
II полугодие
Чистая математика........2
Динамика и гидродинамика . 2
Математическая физика ... 2
Астрономия................2
Химия.....................3
Законы о состояниях и госу-
дарственных учреждениях . 2
98
A. II. ЮШКЕВИЧ
В последующие годы программа понемногу продол-
жала обогащаться. В середине сороковых годов А. С. Ер-
шов60 начал на II курсе читать начертательную гео-
метрию и прикладную механику (в пятидесятые годы на-
чертательная геометрия была перенесена на I курс).
А. Ю. Давидов61 с 1850 г. по 2 часа в неделю читал
на III курсе теорию вероятностей, посвящая второе полу-
годие приложениям к страховому делу и обработке на-
блюдений. В 1852—1853 гг. Н. Е. Зернов излагал на III
и IV курсах некоторые главы теории поверхностей и исчис-
ление конечных разностей также по 2 часа. До середины
60-х годов дальнейшего увеличения числа математических
дисциплин не произошло. Преподавание в Казанском и
Харьковском университетах шло примерно на таком же
уровне, но Петербургский успел за это время опередить
своих собратьев. Начертательную геометрию, благодаря
близости технических высших учебных заведений, где
она была одним из важнейших предметов, в Петербург-
ском университете стали преподавать в конце 30-х годов,
и тогда уже появился там курс теории вероятностей.
Переход в Петербургский университет московских магист-
вов Сомова и Чебышева и деятельность в нём акад. Буня-
ковского подняли там преподавание на большую научную
высоту, и ещё до 1850 г. там читались, например, теория
эллиптических функций и теория чисел. В Москве даль-
нейшее движение вперёд началось с середины 60-х годов.
VII. Экзамены и диссертации в первой
половине XIX в. '
Проследим за теми изменениями, которые происходи-
ли в подготовке специалистов-математиков на протяже-
нии первой половины XIX в. Материалом послужат
здесь сведения об экзаменах на учёные степени и диссер-
тациях. .
Оканчивающие университет должны были подвер-
гаться выпускному экзамену по всем предметам и, в зави-
симости от успехов, получали звание действительного
студента или кандидата. Для получения звания адъюнкта
необходимо было сдать магистерский экзамен и защитить
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 99
публично диссертацию, для занятия профессуры—сдать
докторские экзамены и также защитить диссертацию.
Между сроками получения степени кандидата и магистра
полагался двухгодичный промежуток, между магистер-
ской и докторской защитами—трёхгодичный. От маги-
стерской диссертации требовалось, чтобы она свидетель-
ствовала о полноте сведений автора в системе наук в це-
лом и в частях; доктор должен был иметь основательные
и глубокие сведения о науках в их основании и развитии,
критически разбираться в принадлежащих его специаль-
ностям вопросах, в совершенстве знать связь и порядок
её частей, уметь производить самостоятельные открытия.
Практически эти требования выполнялись очень слабо,
многие получали профессуру без докторской степени,
и лишь в середине 30-х годов администрация начала реши-
тельно требовать выполнения устава. Но магистерская сте-
пень от преподавателя Университета требовалась неизмен-
но, а о кандидатской не приходится и говорить. Я нач-
ну с изложения кандидатского экзамена в начале XIX в.
30 октября 1813 г. в собрании физико-математического
отделения зачитано было прошение сына коллежского
советника, студента Александра Павловича Величко.
Гласило оно так:
«В отделение Господ Профессоров Физико-математи-
ческих наук.
Прошение
От своекоштного Студента Александра Величии.
1808 года произведён я студентом Императорского
Московского Университета. Обучаясь с тех пор на
своём иждивении у разных господ профессоров
разным наукам, занимался я болео в отделении
физико-математических наук Натуральною исто-
риею, Физикою, Алгеброю, Геометриею, Тригоно-
метрией) Плоской и Сферической, Дифференциаль-
ным и Интегральным исчислением и Механикою.
Подвергая себя испытанию, особенно в чистой мате-
матике, прошу Вас, Ученейшие Мужи! в силу Устава
Университета удостоить меня звания Кандидата
Физико-математического отделения и тем поощрить
7*
100
А. П. ЮШКЕВИЧ
мепя к дальнейшим успехам в науках. К сему про-
шению своекоштный студент Александр Величко
руку приложил. 1813 года Октября 25-го числа»62.
Заявление это—типичное; при этом никаких справок
о предыдущих студенческих испытаниях, как видно из
дела, не прилагалось. Тут же в собрании Величко пред-
ложены были по жребию четыре вопроса по математике—
два устных и два письменных. Письменные вопросы были:
«1) На чём основывается приискивание коэффициентов
при возвышении двухчленных количеств в какую-нибудь
степень? 2) На каких предложениях основывается реше-
ние прямоугольных треугольников, и как сии предложе-
ния доказываются?» Устно нужно было: «1) Показать
сходство и несходство эллипсиса с гиперболою и началь-
ные уравнения всех конических сечений. 2) Найти момент
составной силы нескольких параллельных сил, коих
направления находятся в разных плоскостях».
После удовлетворительного решения этих вопросов,
а также устных вопросов по другим предметам, на кото-
рые Величко отвечал «с похвалою», члены отделения
нашли его достойным «по долговременному пребыванию
в звании студента и по успехам им оказанным степени
Кандидата», в которой и просили утвердить его Совет
Университета.
Как видим, из трёх математических вопросов два при-
надлежали к элементарной математике, а один к простей-
шим аналитико-геометрическим. Это достаточно объяс-
няется ходом преподавания в 1810—1814 гг., когда в отде-
лении читались лишь элементарная математика и кони-
ческие сечения. Однако и позднее выпускникам нередко
задавались одни элементарные вопросы, как, например,
случилось 21 февраля 1825 г. с Цветковым, которому
предложили письменно изложить решение треугольника
по двум сторонам и углу между ними (ему в результате
присвоили звание действительного студента). В Харьков-
ском университете в 1816 г. вопросы были серьёзнее.
Там, например, спрашивалось, какие обыкновенные диффе-
ренциальные уравнения 2-го порядка сводятся к уравне-
ниям 1-го порядка, в чём состоит различие и сходство между
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ Ю1
дифференциалами и вариациями или же требовалось изло-
жить эйлеров метод интеграции уравнений с частными про-
изводными 2-го порядка, или вывести вариацию функции
многих переменных, стоящей под знаком интеграла63. Эле-
ментарная математика исчезает из выпускных экзамена-
ционных вопросов в Москве с середины 20-х годов. Когда
Н. Курляндцев, получивший в 1822 г. звание действитель-
ного студента, пересдавал экзамен на кандидата, ему
13 февраля 1826 г. дали письменную тему: «Найти поло-
жение такой точки в параболе, от которой расстояние
всех точек кривой выражалось бы функцией рациональ-
ной относительно абсциссы». К сожалению, в позднейших
протоколах не указывались вопросы на кандидатских
испытаниях.
Знакомый нам Величко через полтора года после кан-
дидатского испытания пожелал приобрести степень ма-
гистра и 22 января 1815 г. держал экзамен. Устно выпало
ему объяснить происхождение дифференциального и ин-
тегрального исчислений и объяснить теорию преломления
лучей, а письменно показать существенные различия всех
конических сечений и объяснить теорию рычага. Публич-
ный диспут па заданную ему тему «Рассуждение о силе
электрической и действии на неё воздуха» он успешно про-
вёл 28 апреля того же года. Уже в это время объём во-
просов на магистерском экзамене стал увеличиваться.
К Величко не применили требования экзаменоваться
по всем дисциплинам, но будущему профессору II. С. Щеп-
кину пришлось сдать полный магистерский экзамен.
Как сообщается в его биографии, 18 февраля 1815 г. он
отвечал на вопросы:
1. Предмет высших исчислений.
2. Метод исследования протяжённостей в аналити-
ческой геометрии; различие с элементарной геометрией.
3. Главные вопросы в высших исчислениях.
4. Какие статьи составляют механику твёрдых тел.
5. Что есть свет и преломление.
Экзамен продолжался 27 февраля. Щепкин должен
был рассказать:
1. Об общих свойствах металлов.
2. Сколько простых земель.
1()2
А. П. ЮШКЕВИЧ
3. Как находится склонение и прямое восхождение
звезды (письменно).
4. Объяснить теорию простого маятника (письменно).
5. О магнетизме.
6. Главные законы механики, диоптрики, катоптрики.
7. Разделение астрономии; куда относить гномонику
и хронологию.
15 июня Щепкин защищал диссертацию «Об открытиях,
сделанных в астрономии со времени изобретения теле-
скопов» (М., 1815), а незадолго до того 6 мая прочитал
в присутствии Совета отделения пробную лекцию о пре-
ломлении света.
Как видно, многие вопросы носили чрезвычайно общий
характер, и ответ мог сводиться к довольно расплывча-
тому рассуждению. Что касается диссертационной темы,
то исторические обзоры имели в то время особое распро-
странение; от магистранта не требовалось самостоятель-
ного исследования, но ему полагалось знать предмет
в историческом развитии. Такой же исторический обзор
представляла диссертация Величко, начинавшего с Фалеса
и кончавшего Лавуазье и Нолле и сделавшего некоторые
критические замечания о теориях электричества. Нередки
были также темы методологического характера. В Харь-
кове М. А. Байков защищал при трёх оппонентах 5 ноября
1821 г. магистерскую диссертацию «О различных спосо-
бах излагать дифференциальное исчисление и о достоин-
ствах каждого способа» (не опубликована). Этим вопро-
сом как, известно, тогда весьма интересовались64.
Диссертационные темы первоначально были мало свя-
заны с будущей специальностью магистранта. Это поло-
жение оставалось в силе лет пятнадцать. Будущему адъюн-
кту математики Н.Коцауровув1822 г.предложена была тема
«Рассуждение об измерении высот посредством барометра»,’
а Н. Е. Зернову, по совету Перевощикова, в 1825 г.—
«О суточном и годовом движении Земли» (М., 1826).
К 30-м годам и здесь наметилось изменение. В 1830 г.
Андрею Заблоцкому дали тему «О способе исследования
кривых линий второго порядка», Василию Рожалину—
«О способах нахождения несоизмеримых корней уравне-
ний». И вопросы становились постепенно сложнее. Зернов
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ ЮЗ
8 мая 1825 г. должен был письменно изложить теорию
простого маятника, составить и исследовать уравнение
линии, образуемой вершинами треугольников, имеющих
общее основание и такие углы при нём, что разность
их постоянна. Письменные вопросы по математике Заблоц-
кому (18 марта 1830 г.) и Рожалпну (22 апреля) были
таковы: первому—«1) объяснить способ находить вели-
чины переменного, при которых функции оного бывают
наибольшими и наименьшими, 2) изложить вычисления,
которыми открываются кратные точки в кривых линиях
по их уравнениям»; второму—«составить 1) формулы
для перемены координат в пространстве и 2) составить
дифференциальное уравнение поверхностей вращения».
Ответы обоих были довольно подробные; у Заблоцкого,
например, на 9 страницах. — Спустя шесть лет Николаю
Панову, специализировавшемуся по химии, пришлось
рассказывать письменно (4 сентября 1836 г.) об интегри-
ровании обыкновенных линейных уравнений и об устой-
чивом равновесии. По механике он изложил теорию устой-
чивого равновесия. Требования к магистрам нам теперь
представляются невысокими, но за двадцать лет после
тяжёлого времени Отечественной войны был сделан опре-
делённый шаг вперёд. Вместе с тем из ответов видно,
что готовились к экзаменам диссертанты по обычным
студенческим руководствам.
Разумеется, уровень требований на магистерских экза-
менах определялся уровнем преподавания и квалифика-
цией экзаменующих профессоров. Зернов и Брашман, рас-
ширяя и углубляя программы, требовали больше, чем
их предшественники. Вместе с тем магистерский экзамен
продолжал носить характер опроса по всем важнейшим
дисциплинам, читавшимся на отделении. Владимир Дра-
шусов сдавал в 1837 г. экзамены на степень магистра
астрономии и чистой математики в три срока. 12 мая
1837 г. его экзаменовали по зоологии (о классификации
животного царства, о насекомых и рыбах), минералогии
(° РУДах железных и серебряных) и химии (о селитрен-
ной и серной кислотах, об углекислом поташе и селитре).
25 мая состоялись экзамены по физике (о различных
способах возбуждать электричество, о составлении и
104
А. П. ЮШКЕВИЧ
действиях вольтова столба), механике (о приложении обще-
го уравнения равновесия системы к равновесию гибкой
системы, о равновесии плавающих тел, о правиле малей-
шего действия), ботанике (о началах естественной методы
растений, о классах методы Жюссье, подклассах Декан-
долля и главных признаках семейства крестоносных).
Наконец, 7 августа он сдавал письменное испытание по
прикладной математике (о правиле живых сил) и чистой
математике (о нахождении множителя дифференциаль-
ного уравнения, когда он зависит от одного переменного).
За письменные ответы он получил от обоих экзаминаторов,
Брашмана и Зернова, удовлетворительные оценки65.
Двадцать лет спустя усиление специализации студен-
тов сказалось и на изменении характера экзаменов. Мит-
рофан Фёдорович Хандриков (род. 1837), оставленный
по окончании курса при Московском университете, в
1859—1860 гг. сдавал магистерские экзамены. Распреде-
лены они были на пять сроков. 14 ноября 1859 г. сданы
были Хандриковым экзамены по астрономии и геодезии
(о виде и величине Земли, выводимых из градусных изме-
рений, общий способ Бесселя для вычисления затме-
ний и приложение его к покрытию звёзд Луной). 8 декабря
А. Ю. Давидов проводил экзамен по небесной механике
(определение измерения большой оси и эксцентрисите-
та, определение измерения произвольных постоянных
первых интегралов эллиптического движения, дифферен-
циальные уравнения возмущённого движения планет).
13 декабря проф. Н. А. Любимов экзаменовал магистранта
по физике (ахроматизм, сравнение инструментов диопт-
рических и катоптрических, скорость света). 25 января
следующего года Хандриков отвечал Зернову по чистой
математике (интеграл произведения целых и положитель-
ных степеней одной из элементарных трансцендентных
функций и аргумента, способ Фурье для решения алгеб-
раических уравнений). Наконец, 12 марта 1860 г. состоялся
экзамен по прикладной математике у Н. Д. Брашмана
(найти расстояние, с которого математическая точка
должна падать к кривой, чтобы, дошедши до неё, она
имела свою скорость по кривой; притяжение эллипсоида;
определение вида жидкого тела, вращающегося около
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ Щ5
осивв). Как видно, за эти годы в обучении на Физико-мате-
матическом факультете была пройдена дистанция немалого
размера!
Первую докторскую диссертацию по математике в Рос-
сии, как сказано, довелось защитить Н. Е. Зернову.
Для соискания степени Зернов написал «Рассуждение об
интеграции уравнений с частными дифференциалами»,
изданное и защищённое в 1837 г. Эта диссертация Зер-
нова, если сравнить её с упоминавшейся ранее его маги-
стерской диссертацией, свидетельствовала об его серьёзном
росте. Самостоятельным исследователем он ещё не был,
но эрудиция его достигла высокого уровня. Выбрал свою
тему Зернов потому, что она принадлежала к числу тех
отраслей математики, которые находят приложение в ис-
следовании природы, и как раз при современном ему
состоянии физики выдвигалась на первый план. Работа
разделялась на три главы—об интеграции уравнений с
частными производными в конечном виде или с помо-
щью бесконечных рядов, о различных видах интегралов
и, наконец, о геометрической картине решения и опреде-
лении произвольных функций.
Вот содержание первой главы. Автор начинал с линей-
ного уравнения Лагранжа Pp-\-Qq = R, решая его по
Лагранжу, по Лакруа и, наконец, по Арбогасту и иллю-
стрируя решение на классических примерах уравнения
рх + qy = Tvz, имеющего общий интеграл
и уравнения
(bz — су) р (сх — az)q — ay — bx
с интегралом
+ У2, + z2 = .$> (ах + Ьу 4- cz),
а также некоторых других. Далее он переходил к линей-
ным уравнениям с п переменными и к общим методам
.Решения уравнений первого порядка Лагранжа-Шарпи
106
А. П. ЮШКЕВИЧ
и Якоби. Вслед за ним излагался метод Монжа для урав-
нения Rr+ Ss^Tt = V, где среди примеров имелось
и уравнение колеблющейся струны (в виде r=c2t). Рас-
смотрев затем ещё некоторые случаи уравнений 2-го
порядка, интегрируемых в конечном виде, Зернов излагал
методы Фурье-Пуассона, применяющие показательно-три-
гонометрические ряды, беря для примера уравнение тепло-
dz d-z d2z Т)
проводности уравнение-^-^ = az и др. В гла-
ве второй он останавливался на теории полных, общих и
особых интегралов, следуя Лагранжу, Амперу и Пуассону.
Всюду автор указывал свои источники. Собственная работа
его сводилась, кроме переложения, к выбору более удачных
приёмов решения и небольшим изменениям в выводах.
Так, отдел об особых интегралах начинался словами:
«По Амперову способу интеграции, вместе с общими интег-
ралами видели возможность получать и особые решения,
но можно гораздо легче определять сии последние от-
дельно. Для сей статьи я имел источники в сочинении
Пуассона, помещённом в VI томе Journ. de ГЁс. Polyt.
и в Traite de Lacroix, который оттуда же заимствовал
оную. Но мне показалось более ясным следующее изложе-
ние, которое основываю на Лагранжевом объяснении сих
решений (см. Calcul des fonct., стр. 37) и предлагаю в виде
опыта» (стр. 95). В последней главе, где вводились поня-
тия характеристики, рёбра возврата и т. п., Зернов оста-
новился также на споре между Эйлером, Даламбером и др.
о природе произвольных функций, служащих общи-
ми интегралами уравнений с частными производными.
В прибавлении доказывалась нужная автору теорема
о дифференцировании интеграла с переменными пре-
делами.
Диссертация Зернова, не внося нового в науку, вполне
отвечала тем требованиям, которые ставил тогдашний
устав к докторанту. Как было сказано, ею пользовались
в качестве учебного руководства.
Все последующие магистерские и докторские диссерта-
ции писались в основном на уровне современной им науки
и относились к более или менее специальным вопросам.
Ближайшие несколько лет принесли ряд магистерских
МАТЕМАТИКА В МОСК, УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 107
защит. В 1838 г. В. Драшусов издал работу «О кривизне
поверхностей около каждой их точки», в 1839 г. Я. Лу-
кьянов— «Рассуждение о вариациях главнейших видов
функций», И. И. Сомов (1815—1876) в 1811 г. защищал
обширное (166 стр.) «Рассуждение об интегралах алгеб-
раических иррациональных дифференциалов с одной пере-
менной», излагавшее неизвестные тогда в русской учебной
литературе работы Абеля п Лиувилля и теорию эллипти-
ческих функций по Якоби. Будущий академик не получил
ещё в этой работе, весьма, впрочем, серьёзной и полезной,
собственных интересных результатов. Впрочем, он это
сам отмечал в предисловии: «Хотя я не был так счастлив,
чтобы раздвинуть пределы пауки, открытием чего-либо
нового значительной важности; по крайней мере, утешаю
себя тем, что моё сочинение, наравне с другими учебными
руководствами в нашей литературе, принесёт действи-
тельную пользу тем, которые изучают высший ана-
лиз» (стр. VIII)67.
П. Л. Чебышев в 1845г. написал для получения маги-
стерской степени «Опыт елементарного анализа теории
вероятностей», где излагал эту науку, включая теоремы
Бернулли, Байеса и учение о средних, без пользования
высшим анализом. Элементарное, по строгое построение
курса было специальной задачей Чебышева, полагавшего,
что это откроет доступ значительному числу читателей к
теории вероятностей. «До сих пор,—писал Чебышев,—
элементарные курсы теории вероятностей ограничивались
только изложением более или менее подробных результа-
тов, полученных посредством высшего анализа. Дать
возможность поверить все эти заключенияа анализом
строгим и простым, доступным до большей части уча-
щихся—есть большой шаг в способе элементарного изло-
жения теории вероятностей» (стр. И). Как указываем
акад. С. Н. Бернштейн, в этой работе важна была и об-
щая установка Чебышева, характерная для последую-
щих его открытий в теории вероятностей, именно: «точно
формулировать общие теоремы теории вероятностей и до-
казывать их, выдвигая на первый план неравенства
и оценку погрешности предельных формул»08. К большой
потере для Московского университета Сомов и Чебышев
108
А. П. ЮШКЕВИЧ
переехали в Петербург, свои докторские диссертации
защищали в Петербургском университете, и дальнейшая
их научная и педагогическая деятельность протекала
уже вне Москвы.
VIII. Литературные труды московских математиков
в первой половине XIX в.
Литературная продукция московских математиков во
второй половине XVIII в. была значительно меньшей,
чем петербургских. Кроме рассмотренных ранее учеб-
ников и переводов А. Барсова и речей Панкевича и Арше-
невского, здесь стоило бы упомянуть лишь о популярном
в ту эпоху «Теоретическом и практическом курсе чистой
математики» Ефима Войтяховского (М., 1787—1790, 5 тт.,
1-е изд.), бывшего учителя Петербургского артиллерий-
ского корпуса, а затем руководителя известной в Москве
частной «Математической школы».
G начала XIX в. литературная деятельность москов-
ских математиков оживилась. «Опыт об усовершении
елементов геометрии» акад. С. Е. Гурьева (Спб., 1798),
автор которого подвергал критическому анализу обычную
систему построения курса геометрии, с одной стороны,
и энергично пропагандировал теорию пределов, с другой,
встретил в Москве горячих поклонников. Так, учитель
математики Фёдор Кузьмин опубликовал в 1804 г. неболь-
шую книжку «Способ пределов и его употребление в гео-
метрии или предложения, касающиеся до заменения спо-
соба бесконечно малых, извлечённые из разных Сочинений
в пользу обучающегося юношества Ф. К.» Автор этой
книжечки, опираясь на «Опыт» Гурьева и воздавая ему
высокую хвалу, излагал основные определения и теоремы
б пределах, которые применял затем к вычислениям раз-
меров простейших фигур—круга, конуса, шара и его
сегмента. Труд Кузьмина имел успех и в несколько пере-
работанном виде был вскоре переиздан под названием
«Начала способа пределов и применение его к началам
геометрии» (М., 1806).
Московские любители математики, разумеется, сообща-
лис ь друг с другом и обсуждали интересовавшие их пробле-
МАТЕМАТИКА В МОСК, УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 109
мы. К этим любителям относились магистр А. Барсов, учи-
тель Ф. Кузьмин, проф. физики Страхов и некоторые дру-
гие. Наиболее яркой фигурой в этой среде был Пётр Але-
ксандрович Рахманов, родом из дворян, ученик пансиона
Войтяховского, по профессии военный, а по склонностям
математик и литератор, хорошо владевший своим остро
отточенным пером. Рахманов был знаком с Кузьминым,
который в конце своей книги частично использовал хра-
нившиеся у него записки Рахманова о началах дифферен-
циального исчисления. Рахманов, далее, дружил с П. Стра-
ховым, переписывался, а потом завёл и личное знаком-
ство с Гурьевым; возможно, что знал он и А. Барсова,
«Новую алгебру» которого упоминал в своих сочинениях69.
Рахманов был человек широкого математического обра-
зования, пополненного к тому же во время поездки в Па-
риж, где он слушал лекции в Коллеж де Франс и познако-
мился с Био, Лежандром, Лагранжем и другими учёными.
В литературной продукции Рахманова имелись и учёные
рефераты, и руководства, и яркие полемические статьи.
Я не могу входить здесь в подробный разбор творчества и
деятельности этого весьма замечательного человека, тем бо-
лее, что он лишь частично связан был с Московским уни-
верситетом и значительную часть своих работ опубликовал
в Петербурге. Первая книга Рахманова «Новая теория
содержания и пропорции геометрической соизмеримых
и несоизмеримых количеств, и в последнем случае ос-
нованная на способе пределов» (М. 1803), посвящённая
им П. Страхову, написана была под сильным влиянием
«Опыта» Гурьева (впоследствии Рахманов во многом разо-
шёлся со своим первым идейным учителем). Когда Рахма-
нов вернулся из-за границы, в Московском университете
начиналась новая жизнь. Он связался с университетски-
ми кругами и принял участие в составлении математиче-
ского отдела только что созданных «Учёных ведомостей».
В течение нескольких лет в «Московских учёных
ведомостях» существовал хорошо поставленный отдел
математических рецензий, в котором писали Рахманов,
Страхов и проф. Иде. В № 24 за 1805 г. была помещена
обстоятельная рецензия на «Traitё du calcul differentiel
et du calcul integral» (2 tt., 1797—1798) Лакруа, при-
110
А. П. ЮШКЕВИЧ
надлежавшая, невидимому, проф. Иде (она подписана
инициалом I). Автор высоко оценивал трактат Лакруа
но —с известным правом—иронизировал по поводу стре-
мления французских математиков вслед за Лагранжем
обойтись в анализе без понятия бесконечного. «Всяк
справедливо мыслящий,—писал рецензент,—пусть про-
стит, что они могут употребить к тому бесконечные ряды.
Если они (т. е. французы.—Л. 10.) способны во многих
других случаях, как в своих модах и системе правления,
чертить искусные круги, то для чего же иногда не делать
их и в логике». Рецензент отмечал, что и в разделе о квад-
ратурах Лакруа пришлось прибегнуть к бесконечно ма-
лым полоскам и высказывал убеждение, что «если бы он
положил за основание науку о пределах, то он бы освобо-
дился от всех сих трудностей». Напомню, что Иде читал
в Университете лекции по теории пределов (само собой
разумеется, теории пределов Даламбера!). Через пол-
тора года на сокращённое издание той же книги Лакруа
(2-е изд., 1806) дал отзыв в № 2 за 1807 г. Рахманов.
Рахманов упрекал Лакруа в том, что тот «приняв за осно-
вание способ пределов, нередко мешает его со способом
бесконечно малых». Он указывал на непоследователь-
ность Лакруа, который выводил дифференциалы алгеб-
раических функций непосредственно, а трансцендентных —
с помощью теоремы Тэйлора. Но «элементы интеграль-
ного вычисления и вычисление разностей конечных, — пи-
сал—он, предложены превосходно».
В № 25 за тот же год помещена была обстоятельная
и вдумчивая рецензия Рахманова на «Geometric analy-
tique» Био (2-е изд., 1805). Рахманов давал этому руковод-
ству высокую оценку: «Геометрия аналитическая г. Биота
гораздо более содержит в себе превосходного, нежели не-
удобного, и ничего в себе не заключает посредственного».
Он подчёркивал оригинальность книги. Био начинает с
определения положения точек прямых и плоскостей и пре-
образования координат (а не с кривых 2-го порядка).
Потом он выводит уравнение конической поверхности
2-го порядка и пересекает её одной из координатных
плоскостей, упрощает уравнение сечения и исследует
. свойства каждой из кривых 2-го порядка, а в заключение
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ Ш
проводит исследование поверхностей 2-го порядка. Вме-
сте с тем, рецензент высказывал некоторые критические
соображения. Био, например, не предпосылает выводу
уравнения поверхности конуса общего понятия об урав-
нении поверхности и каких-либо примеров. Это затруд-
нит учащегося. «Сие заключение,—писал Рахманов,—
вывел я из опыта, посещая разные французские школы,
в которых тогда учили аналитической геометрии по первому
изданию рассматриваемой книги». Рахманов возражал так-
же против вывода уравнений касательных путём прирав-
нивания координат двух точек пересечения в уравнениях
секущих. Если уж пе пользоваться дифференциальным
исчислением, основанным на теории пределов, то лучше
было бы употреблять известные синтетические приёмы.
Рахманов считал также более целесообразным предпослать
общую теорию касательных, диаметров и фокусов разбору
соответствующих свойств отдельных конических сечений,
а для угла между двумя прямыми на плоскости выводить
для единообразия с геометрией трёх измерений фор-
мулу косинуса, а не тангепса.
Я упомяну ещё про отзыв П. С. (Страхова) на «Опыт
о поверхностях вращения» самого Рахманова (1807, № 5)*
Рецензент по дружбе чрезмерно расхваливал оригиналь-
ные достоинства этой книги, служившей, как и рахманов-
ский «Опыт о цилиндрических и конических поверхно-
стях», только полезным изложением теорий Монжа (от
себя Рахманов добавил лишь вывод уравнений касатель-
ной плоскости по способу пределов).
После 1807 г. «Московские учёные ведомости» закры-
лись. Рахманов уехал в Петербург и был убит в битве
под Лейпцигом в октябре 1813 г. Ещё ранее умер Иде,
в 1813 г. скончался и Страхов. В течение последовавших
полутора десятилетий преподавание в Университете пере-
живало трудное время. На очереди, прежде всего, стояло
создание учебной литературы. Этим и занялись универси-
тетские преподаватели математики.
Выше говорилось, что вслед за руководствами Безу,
переведёнными В. Загорским, и курсом Бушарла, в основу
преподавания на физико-математическом отделении поло-
жен был курс Франкера. О содержании этого учебника
11^
А. П. ЮШКЕВИЧ
также рассказывалось, и здесь я остановлюсь лишь на
некоторых частностях и на переделках, внесённых на-
шими переводчиками. Своему переводу «Дифференциаль-
ного исчисления» Франкера (М., 1824) Перевощиков
предпослал предисловие, в котором указал на допущенные
им отступления от оригинала. «Перевод мой, — писал
он, —не есть буквальный, я хотел изложить сущность
пауки, как понимал её...». Он, например, дополнил
курс Франкера выводом теоремы о возрастании функ-
ций с положительной производной, сильно распро-
странил главу о поверхностях по Монжу и Лагранжу,
упростил, следуя тем же образцам, отдел замены пере-
менных и т. д. Франкер вообще следовал Лагранжу и для
единства изложения, Перевощиков исключил приложен-
ный Фрэнкером «способ бесконечно малых», с помощью
которого тот решал некоторые вопросы. Однако этот от-
каз от бесконечно малых был временным. В интегральном
исчислении пришлось восстановить исключённую методу
«по той причине,—как заявлял переводчик «Интеграль-
ного исчисления» И. Давыдов, — что в прикладных частях
математики она почти необходима и есть источник всех
новейших открытий в механике, физике и астрономии».
Включение Фрэнкером способа бесконечно мэлых—
явная уступка последователя Лагранжа нуждам матема-
тики и преподавания—довольно любопытно, ибо несёт на
себе следы влияний и Карно, и Даламбера, а отчасти
предваряет концепции Коши. Этот эклектизм был характе-
рен для лучших сочинений того времени до Коши. Для
представления о нём я приведу один отрывок: «Сей спо-
соб, принимающий дифференциалы за количества точные,
доводит до уравнений недостаточествующих70: несмотря
на это, конечный вывод всегда бывает справедлив, ког-
да имеем в виду исчисление последних отношений, ко-
торые суть одни и те же для дифференциалов и для
настоящих элементов. Таковое исчисление, допускающее
величины приближённые, вместо подлинных, кажется
сходным со способом приближения; но поелику он упо-
требляется для определения последних отношений, ко-
торые, как мы упомянули, суть одни и те же для коли-
честв сравниваемых, то сей способ получает алгебраи-
МАТЕМАТИКА В МОСК* УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ Ц.{
ческую точность. Подобная точность находится и в са-
мых выражениях бесконечно малые, дифференциалы, ибо
они напоминают, что сие исчисление употребляется при
нахождении последних отношений количеств. II так диф-
ференциал есть такая часть разности, которой отно-
шение с его разностью имеет пределом единицу»71. В недо-
статочно чёткой форме здесь речь шла о принципе замены
бесконечно малых приращений «эквивалентными» им диф-
ференциалами.
Не ограничившись переводом Франкера, Перевощиков
издал ряд собственных руководств. Вслед за «Ариф-
метикой» (1820) появились «Главные основания анали-
тической геометрии 3 измерений» (М., 1822, 82 стр.),
составленные по запискам, которые он излагал слуша-
телям. Перевощиков, согласно его предисловию, придер-
живался всё того же Франкера, но кое в чём его допол-
нял. Изложив простейшие задачи, Перевощиков пере-
ходил к прямой. После прямой, заданной уравнениями
z—a, у—b, рассматривалась прямая с уравнениями
^=az-|-p, которые, как показывалось, прина-
длежат плоскостям, перпендикулярным к двум коорди-
натным плоскостям. Затем решались некоторые задачи
на прямую и выводилось нужное для дальнейшего условие
пересечения двух прямых в пространстве. При выводе
уравнения плоскости Перевощиков жертвовал простотой
ради принципа. Он указывал, что Фурье предложил
выводить уравнение плоскости, как места точек, равно-
удалённых от двух данных (всё получается тогда очень
быстро). Но вслед за Монжем это свойство плоскости
он считал слишком сложным и заявлял: «не удивительно,
что здесь не принята в уважение удобность аналитиче-
ского вывода и при составлении уравнения для плоскости
строго соблюдены начала, изложенные Монжем о происхо-
ждении всех поверхностей вообще» (стр. 25). Плоскость
поэтому рассматривалась как поверхность, описываемая
прямой, движущейся параллельно самой себе вдоль другой
прямой. Перевощиков заставляет прямую с исходными
Уравнениями ?/=0, z=ax+b двигаться указанным образом
вдоль прямой я=0, z=ay+b. В новом положении урав-
нения движущейся прямой будут z=«.r4-6/; в силу
8 ПсториЕс-уг тег ат. исследорания
114 A. II. ЮШКЕВИЧ
пересечения co сторон прямой 6'=ар+6, так что y = $,
z^ax + afi+b, откуда получается уравнение искомой
плоскости z=ax +ay+b. Далее, излагались свойства «проло-
жении» (проекций), преобразование координат, эйлеровы
углы, беглое упрощение уравнения 2-й степени и разбор
основных поверхностей, понятие об уравнениях кривой
в пространстве, в том числе пример линии двоякой кру-
тизны, взятый из курса Лакруа. Чертежи поверхностей
не приводились.
Основным математическим трудом Перевощикова яви-
лась «Ручная математическая энциклопедия» в 13 томах
(М., 1826—1837). Первые семь томиков были отведены
математике, 8—10—механике, И—оптике, 12—физике,
13—астрономии; таким образом, писал Перевощиков
в предисловии к I тому, «кто соберёт все части, тот составит
небольшую библиотеку, содержащую физико-математиче-
ские науки в их нынешнем усовершенствованном состоя-
нии». Это сочинение свидетельствовало о большой начи-
танности составителя и чуткости к новым идеям, но вместе
с тем о недостаточно критическом отношении к источни-
кам, плодом чего явились отдельные методические про-
махи и, главное, эклектизм, против которого автор бо-
ролся, издавая Франкера.
В «Арифметике», развивая мысли более раннего своего
курса, Д. М. Перевощиков правильно выступал против
тройных правил, заявляя, что «числительная часть мате-
матики но имеет надобности в сем механическом пособии»
и что «особенно начинающие должны приучаться к сооб-
ражению услорий вопросов и разрешать их прямо с по-
мощью четырёх главных действии арифметики» (стр. 156).
Вместо тройных правил Перевощиков предлагал разбор
решения ряда типичных задач, обозначая при этом ис-
комую величину х. Интересно было, хотя вряд ли педа-
гогично, включение в учебник арифметики преобра-
зования периодических десятичных дробей в обыкновен-
ные (с указанием, что правило доказывается в алгебре).
Вряд ли уместным было употребление в приближённых
вычислениях непрерывных дробей и помещение в курсе
арифметики главы о логарифмах, вводившихся путём
сопоставления геометрической и арифметической прогрес-
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕГ ц5
сий. Чтобы не пользоваться при действиях с дробями
отрицательными логарифмами, Перевощиков при этом
учил умножать на нужные степени десяти (например,
jg.r=lg 5 — 1g 7, lg 10#= lg 50 — lg 7 и т. д.).
В «Основаниях геометрии» Перевощиков последовал за
акад. С. Гурьевым с его «Опытом об усовершении елемен-
тов геометрии» (1798). Как и Гурьев, он строил курс на
трёх началах—способе наложения,теории пропорциональ
ных величин и способе пределов, в котором применялись
теоремы о единственности предела монотонной переменной
и о том, что если — = А, то lim — = А. Как и Гурьев,
(в его учебнике геометрии) он доказывал постулат Евкли-
да о параллельных по Бертрану. Впрочем, в отличие от
Гурьева, написавшего, исходя из своих идей, чрезвычайно
громоздкое руководство, Перевощиков дал небольшой и
лёгкий курс. Существенно отступил он от Гурьева в том,
что применял в геометрии иррациональные числа. В курсе
алгебры, между прочим, выводились степенные ряды
для показательной и логарифмической функций. IV часть —
«Приложение алгебры к геометрии» — содержала не анали-
тическую геометрию, но алгебраическое решение гео-
метрических задач, теорию «противоположных количеств»
и плоскую и сферическую тригонометрию. Сюда вошли
также формула Моавра, ряды для различных тригоно-
метрических функций, получаемые по методу неопреде-
лённых коэффициентов72 или обращением ужо найден-
ных рядов (самое обращение изложено было в «Алгебре»),
ряды для Igsin х и Igcos х, формулы Эйлера, тригоно-
метрическое решение квадратных и кубических уравне-
ний и др.
Особенно эклектический характер в методологическом
части носили «Теории дифференциального и интегрального
исчислений» (М., 1827). Рассматривая отношение =
F (яЧ-Дя) — F (т) т-г
= —-----, Перевощиков говорит, что когда Д.г
бесконечно малое, т. ср делается меньше всякой величины,
не превращаясь в нуль, то и Аг/ бесконечно мало,—как он
пытался доказать ещё в «Алгебре». Бесконечно малые
3*
116
Л» IT. ЮШКЕВИЧ
приращения он называет дифференциалами. Беря для
примера функцию х* =г2 — у2, Перевощиков получает =
= — 4-дг п гов0Р,1Т’ чт0 пределом этой дроби будет — ,
«Но,— продолжает он, — если вместо &х, &у поставим дпф
ференциалы дх, ду и в дроби— |~^Д7СИП дифференциалы
мы уничтожим, то получим , дифференциальное
отношение неточное, поелику отношение достигает своего
предела только при Дя=0, Дг/=О», а тогда выражение
— теряет смысл. Чтобы получить правильный резуль-
тат из неточных уравнений, «надобно только исключать
отношение^ или ». Эту мысль автор поясняет, выводя
формулу подкасательной для окружности х2=Г2—у2 (с та-
кого же, по существу, примера начинал и Карно). Он
именно берёт формулу, выражавшую отрезок оси между
.. Дг
ординатой и секущей у и, заменяя приращения на
дифференциалы, получает «неточное» выражение для под-
дх хт дх
касательной у. Подставляя в него значение из опять-
таки «неточного» уравнения Перевощиков на-
ходит для подкасательной окружности точное значение
— (стр. 8—13). Перевощиков при этом прямо ссылался
па Карно. «Учение о дифференциальных отношениях,—
писал он, —изобрёл Лейбниц, развил Бернулли, привёл
в систему Лопиталь». Ньютон стремился заменить его
теорией флюксий и последних отношений, Даламбер —
способом пределов, Лагранж—исчислением функций, ко-
торое пытался усовершенствовать акад. Шуберт. «Но пре-
восходство навсегда останется на стороне способа Лейб-
ница, который можно назвать способом вознаграждения
погрешностей. См. соч. Карно Sur la Metaphysique du
calcul infinitesimal» (стр. 13). Это интересный пример
введения идей Карно в педагогическую практику, в чём
за Перевощиковым последовал отчасти и Зернов. Полвека
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ Ш
спустя «Reflexions» Карно горячо рекомендовал слуша-
телям для расширения кругозора проф. Л. К. Лахтин;
он ещё в 1924 г. советовал Ю. О. Гольдовскому, то-
гда студенту первого курса, перевести эту книгу на рус-
ский язык.
Фактическое построение анализа Перевощиков осуще-
ствлял, комбинируя разные приёмы. Простейшие произ-
водные он вычислял переходом к пределу, другие с по-
мощью бесконечных рядов. Вывод ряда Тэйлора давался
формальный, по Амперу, путём последовательного диф-
ференцирования по х выражения f(z)=f(x)~^P(z~х)™.
По содержанию отдел дифференциального исчисления был
обширен, включая функции многих переменных, формулы
Лапласа и Лагранжа, случаи . неприменимости ряда
Тэйлора для отдельных значений аргумента; разъясня-
лось и употребление остаточного члена для определения
границ погрешности.
В интегральном исчислении Перевощиков ввёл ряд
новинок. Например, он употреблял обозначение «частного
интеграла между пределами ит а до 6», предложенное
ь
Фурье, и выводил формулу dxf (х) =F (b)—F (а), если
а
\dzf(x)=F(x) +С-,
впрочем, этой формулой, сообщённой лишь в главе V,
он почти не пользовался. В эту часть курса входили ещё
дифференциальные уравнения 1-го порядка и в том числе
уравнение Риккати, понятие об особых решениях, про-
стейшие линейные уравнения с постоянными и перемен-
ными коэффициентами, приближённое интегрирование ря-
дами и некоторые уравнения с частными производными.
Приложения анализа к геометрии помещены были в
«Высшей геометрии» (М., 1828). Этот выпуск «Ручной
энциклопедии» открывался курсом аналитической гео-
метрии, причём прежде всего рассматривались прямая
и плоскость в пространстве, а затем кривые 2-го порядка
и некоторые специальные плоские линии. После решались
задачи па спрямление, квадратуры, находились особые
118
A. П. ЮШКЕВИЧ
точки, точки перегиба и экстремума, радиусы кри-
визны и т. п. в декартовых и полярных координатах.
В заключение разбирались поверхности, изучалась кри-
визна плоскостей, выводились дифференциальные урав-
нения простейших их классов и вычислялись объёмы
и площади поверхностей через двойные интегралы. По-
следний математический том «Ручной энциклопедии» был
отведён начертательной геометрии.
Если в воззрениях Щепкина преобладали идеи Ла-
гранжа, изложенные Франкером, а Перевощиков сочетал
воззрения Лагранжа, Гурьева и Карно, то Н. Е. Зернов
в основном вышел на путь современной ему научной
мысли. Это произошло не сразу; сначала взгляды Карно
занимали и у Зернова весьма видное место, хотя с самого
начала преподавания в Университете он пропагандиро-
вал также идеи Коши. В 1835 г. Зернов опубликовал
вступительную лекцию по анализу, а в 1842 г. учебник,
и по ним можно судить об этой эволюции. Лекцию он
начинал с понятия о функции и переменной, указывая,
что если переменные ж, у обладают как бы большей сте-
пенью изменяемости, чем параметры задач а, Ь, то в диф-
ференциальном исчислении вводится новый ряд перемен-
ных третьей степени изменяемости, которые могут стано-
виться, не изменяя всех прочих величин вопроса, менее
любой данной величины. Это—излюбленный мотив Карно.
Далее Зернов излагал очерк истории воззрений на при-
роду анализа. Лейбниц и его ученики ограничились тем,
что, отбрасывая бесконечно малые, получали точные
результаты, не доказывая их необходимости. Лагранж
попытался заменить исчисление бесконечно малых исчи-
слением функций, опирающемся на разложение функций
в ряды. Зернов не соглашался с критикой теории Ла-
гранжа, данной Коши, указывая, что Лагранж вывел
формулу остаточного члена (всего значения этой критики
Зернов, по крайней мере в то время, не понял). Но вместе
с тем, автор находил, что наука не выиграет от замены
бесконечно малых бесконечными рядами. Естественнее
выводить последние из дифференциального исчисления,
чем обратно. К тому же, все важнейшие открытия от
Лейбница до Пуассона опирались на пользование беско-
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ Ц9
нечно малыми, которых не избегал в своей аналитической
механике и сам Лагранж. Определение бесконечно малых,
данное Карно (оно почти совпадает с нынешним), устраняет
все трудности, связанные с принципом отбрасывания
бесконечно малых, и позволяет этот принцип оправдать.
Излагая основную теорему Карно, Зернов объяс-
нял, что если с помощью бесконечно малых найдено
соотношение конечного характера f(x, у)=0, то оно
не может быть далеко от истины, ибо отбрасывались лишь
бесконечно малые. Если бы погрешность в конечном соот-
ношении имелась, то её можно было бы ещё уменьшить,
приближая отбрасываемые величины к пулю ещё ближе
и не меняя прочих величии, а так как уравнение /(ж, у)=0
конечное, то понизить погрешность невозможно, и, зна-
чит, оно точное. Но полный свет па понятие бесконечно
малых (продолжал он) пролил Коши в своей теории раз-
личных порядков бесконечно малых. Тут Зернов приво-
дил ряд основных теорем из курса Коши, вводил понятие
предела, рассматривал пределы отношений бесконечно
малых. Лекция кончалась определением непрерывности,
производной, дифференциалов dy, dx как произвольных
чисел, отношение которых равно производной, и выяс-
нением геометрического смысла производной75.
«Дифференциальное нечисленно с приложением к гео-
метрии» Зернова (М., 1842) должно было заменить «Энци-
клопедию» Перевощикова, которой приходилось ему поль-
зоваться в первые годы преподавания. При писании
книги он опирался на труды Коши, Карно, Навье, Курно,
Муаньо и Дюгамеля. Влияние Коши, за которым шло
большинство названных авторов, разумеется, оказалось
наиболее сильным. Во введении говорилось, правда, ещё
о трёх степенях изменяемости переменных, но большая
часть его отведена была установлению понятия предела
и учения о порядках бесконечно малых. В первой главе
о дифференциалах и бесконечно малых, прежде всего, раз-
вивалось понятие непрерывности, и предметом дифферен-
циального исчисления объявлялись производные непре-
рывных функций как пределы отношений приращений.
Нет необходимости излагать содержание и методы этой
книги, достаточно близкие к знакомым всем руководствам,
120
II. ЮШКЕВИЧ
Я отмечу лишь чрезвычайное обилие геометрических при-
меров, простых и сложных, обязательно сопровождаемых
тщательно выполненными чертежами, а также приложе-
ния, помещённые в конце книги. В этих добавлениях мы
находим раздел о сходимости рядов и знаменитый пример
Коши функции е-1/х2, неразложимой в ряд Маклорена,
несмотря на существование производных любого порядка
при я=0. Зернов следил за новейшей литературой: он
включил в свой курс и признак Раабе, отсылал за под-
робностями к совсем недавним работам о сходимости
Лобачевского (1835) и Коши (1840); в последней главе,
посвящённой алгебре, доказывал теорему Штурма и т. д.
Книга его справедливо увенчана была Академией наук
половиной Демидовской премии.
За несколько лет до выхода руководства Зернова
проф. Брашман выпустил «Курс аналитической геомет-
рии» (М., 1836). Он отмечал в предисловии, что не только
учащиеся, но и преподаватели высших учебных заведе-
ний не располагают на русском язцке курсом, излагаю-
щим более новые достижения науки. Книга его должна
была восполнить этот пробел и дать не только обычный
материал, но и «элементарное руководство к новым иссле-
дованиям, изложенным в журналах Жергона, Кетле, Креля
и в сочинениях Понселе, Штейнера, Плюкера и пр.»
(стр. III). Превосходное руководство Брашмана было
весьма близко к употребляемым ныне. Он только начинал
с уравнений точки, прямой и плоскости в пространстве,
не выделяя особо прямую на плоскости; кроме того,
в исследовании кривых 2-го порядка не применялись
определители. Весь учебник был написан ясно и живо,
основные понятия подвергались подробному разбору;
он содержал занимательные детали, вроде известного
парадокса Крамера, примера кривой двоякой кривизны
и т. п. Между прочим, здесь выводились и особо
рекомендовались нормальные уравнения прямой в про-
странстве; уравнение плоскости прежде всего выводи-
лось из условия, что ее точки равноудалены от начала
и от симметричной с ним точки (х', у', z'\ Свежий мате-
риал представляли глава VIII «О подобии кривых» и осо-
бенно глава XIII «О взаимности фигур», в которой изла-
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 121
гались принцип двойственности, теория полюсов и поляр и
её приложения и, в частности, теоремы Паскаля и Бриан-
шона. В главе XIV сообщались краткие сведения о геомет-
рическом смысле неравенств. Учебник Брйшмана получил
полную Демидовскую премию Академии наук (5000 руб.).
Кроме педагогических трудов, мы встречаем во вто-
рой четверти XIX в. и другие литературные выступления
московских математиков, именно журнальные обзоры,
а иногда и самостоятельные статьи. Так, неустанный про-
пагандист точных наук Д. М. Перевощиков поместил
в «Соревнователе просвещения и благотворения» за 1825 г.
статью «О разложении рациональных дробей», в которой
критиковал способ определения коэффициентов, предла-
гаемый Коши. В «Новом магазине естественной истории,
физики и химии» за 18С0 г. он напечатал статью «О разре-
шении неопределённых уравнений I степени»; в этом же
журнале была опубликована статья И. Давыдова по
теории вероятностей. Но это были спорадические высту-
пления. Московский университет не имел ещё органа,
в котором могли бы регулярно помещать свои труды его
учёные и который стимулировал бы их литературную
деятельность. Первое начинание Московского универси-
тета—«Московские учёные ведомости» — оказалось, как
мы помним, очень недолговечным (1805—1807). После
большого перерыва с 1833 г. стали издаваться «Учёные
записки Московского университета», продолжающие выхо-
дить в ином виде до сих пор. Этот журнал содержал
разбитые по соответствующим рубрикам популярные и
научные статьи по различным вопросам, лекции про-
фессоров, рецензии, обзоры университетской жизни, учё-
ные известия из-за границы и т. п. В нём помещены были
ряд лекций Перевощикова по механике, его примечания
к «Аналитической механике» Лагранжа, имевшие целью
привлечь начинающих к чтению этого классического труда
(ч. IV, 1834, ч. XI, 1836), перевод работы Гаусса «Об
измерении земного магнетизма», сделанный А. Драшусо-
вым (ч. XI, 1836), лекции по механике Лобачевского
(присланные из Казани, ч. VII, 1838). Мы находим тут
ряд математических статей, многие из которых принад-
лежали Брашману, стремившемуся знакомить русского
122
Л. П. ЮШКЕВИЧ
читатели с новинками научной мысли. Так, он на-
печатал «Общие рассуждения о математическом ана-
лизисе и пример исследования дифференциальных уравне-
ний по способу Штурма» (ч. VI, 1834), «О трансцендентных
функциях Абеля» (там же), «Рассуждение Пуассона об
интегралах алгебраических функций» (ч. VII, 1835), «При-
мечание к общей теории наибольших и наименьших вели-
чин функций многих переменных» (ч. VIII, 1835)7в, «При-
ложение теории неравенств»77 и «Решение задачи из исчис-
ления вероятностей»78 (ч. X, 1835). Несколько статей дал
и Зернов: «О пространстве Российской империи» (ч. VI,
1833), где он, по предложению Перевощикова, заново
вычислил площади определённых частей государства,
затем известную уже нам лекцию по анализу (ч. VII, 1835)
и «Разбор рассуждения Коши о решении числовых уравне-
ний и теории исчисления» (ч. XI, 1836). Кроме москов-
ских авторов участвовали и иногородние. Н. Навроцкий,
член-корреспондент Академии наук и автор «Начертания
тригонометрии» (1821—1822), прислал статью «О спрямле-
нии окружности» (4.IV, 1834), содержавшую весьма про-
стое и довольно точное, до пятого знака, приближённое,
построение числа г. II. Лесн...ий поместил статьи «О
плоских кривых линиях, как о следах точек, взятых на
прямой» (ч. VI, 1834), где выводил уравнения конических
сечений, циссоиды и конхоиды79, и «О делении угла на
три части прямолинейно-геометрическим способом» для
частных случаев, приводящих к квадратным уравнениям
(и. IX, 1835). Профессор Одесского лицея Бруни напе-
чатал «Некоторые предложения из аналитической гео-
метрии» (ч. XII, 1836), в которых, опираясь на барицен-
трическое исчисление Мёбиуса, решал задачи об опреде-
лении вида конического сечения, проходящего через
данные пять точек или касающегося данных пяти пря-
мых. Мы находим также в «Записках» обстоятельный
и толковый обзор научного творчества Лежандра, причем
за оценкой «Оснований геометрии» Лежандра автор
обзора отсылал читателей к «Опыту» С. Е. Гурьева (ч. IV,
1834), и рецензию на «Алгебру» Лобачевского (ч. VI, 1834).
В последующие годы, однако, математические статьи исче-
зают со страниц «Учёных записок».
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 123
Следующие годы зато были отмечены публикацией ряда
математических диссертаций, перечисленных ранее,—Зер-
нова, Драшусова, Сомова, Лукьянова, Чебышева. В на-
чале 40-х годов были также опубликованы две заслуживаю-
щие внимания речи. Одна из них произнесена была Зер-
новым 19 июня 1843 г. Он говорил о «Теории вероятно-
стей с приложением преимущественно к смертности и стра-
хованию» (М., 1843). Тема эта (которую в те времена и
позднее неустанно пропагандировал у нас акад. В. Я. Буня-
ковский) носила тогда весьма актуальный характер:
правительство всячески содействовало развитию страхо-
вого дела. Зернов, прежде всего, излагал основные идеи
и теоремы теории вероятностей. Понятие математического
ожидания он иллюстрировал на примере лотереи. В поль-
зу страхования в речи Н. Е. Зернова приводились не
только математические, но и библейские и администра-
тивные доводы.
Другая речь «О влиянии математических наук на раз-
витие умственных способ остей» прочитана была 17 июня
1841 г. Н. Д. Брашманом (М., 1841). Он энергично поле-
мизировал в ней с известным шотландским философом
Гамильтоном, отвергавшим пользу математического вос-
питания для ума и, несомненно, имевшим в виду попытки
урезать преподавание математики в школе. Брашман
доказывал, что «надлежащее занятие математическими
науками увеличивает объём ума, изощряет его, и возвы-
шает нравственность» (стр. 4) и что хотя первопричины
явлений известны одному лишь богу, но «геометры не-
сравненно удачнее восходят от явлений к причинам,
нежели философы» (стр. 9). Конечно, говорил он, геометры
не лучше разбираются в практических делах, чем фило-
софы: тут просто нужен житейский опыт, но вообще
математические науки, а особенно теория вероятностей,
благотворно влияют и на суждения о житейских делах.
Очертив роль отдельных математических дисциплин
в познании мира, Брашман приходил к заключению:
«геометр не трудится просто для удовлетворения своего
любопытства: богатый запас форм геометрии, символов
анализа и его сложных действий не простая роскошная
уродливость умственной изобретательности, не собрание
124
A. II. ЮШКЕВИЧ
редкостей для любителей; напротив, это могущественный
арсенал, из которого исследование природы и техники
берут лучшие свои орудия» (стр. 25). Он подчёркивал нео-
жиданную подчас пользу на первый взгляд весьма отвле-
чённых исследований. Что могло казаться бесполезнее
размышлений древних о конических сечениях или Кеп-
лера о числовой гармонии, Бернулли—о форме свободно
подвешенной верёвки, — а ведь это привело к небесной ме-
ханике, к теории цепных мостов, к учению о распро-
странении звука и света и т. д.
Особо подчеркивал Брашман значение теории вероят-
ностей, столь важной для финансовой деятельности,
страхования и пр. Он высказывал сожаление, что её мало
преподают в университетах и что «до сих пор нет на рус-
ском языке ни одного сочинения, ни перевода не только
учёной, но даже элементарной теории. вероятностей...
Надеемся, что русские учёные постараются скоро воспол-
нить этот недостаток» (стр. 30—31). В. Я. Буняковский
вскоре после того издал обширные «Основания теории ве-
роятностей» (Спб., 1843), а лучший из учеников Н. Д. Браш-
мана Чебышев не только посвятил теории вероятно-
стей свою магистерскую диссертацию (1845), по и поло-
жил впоследствии начало замечательной русской школе
теории вероятностей.
В своей речи Н. Д. Брашман с огорчением отмечал
недостаток учёной литературы на русском языке. «Немно-
гие из открытий бессмертного Эйлера и других учёных
академиков перешли в национальную собственность»
(стр. 24). Вместе с тем Брашман справедливо указывал,
что «судя по деятельности русских университетов и дру-
гих учебных заведений, можем впредь надеяться, что
и наша очередь придёт, что полюбопытствуют читать не
только русских поэтов, но также геометров».
Эта деятельность, писал он, принесла уже первые
плоды. В Харьковском университете созданы Осиповским
хорошие руководства, в Казани известны своими учёными
трудами Лобачевский и Симонов. В Москве Перевощиков
написал курс астрономии и физику, изложенную на мате-
матической основе, Зернов—первое на русском языке
рассуждение об уравнении с частными дифференциалами,
Математика в mock, университете за першие сто лет 125
Сомов- теорию алгебраических уравнений. Стали выхо-
дить «Учёные записки» Университета. Имея в виду
акад. Остроградского, Брашман замечал: «Я не гово-
рил о первом нашем геометре... Нет сомнения, что если бы
он писал на русском языке, математическая наша лите-
ратура занимала бы уже почётное место между другими
в Европе; но все его сочинения написаны для учёного
мира на французском языке. Желательно, чтобы наш
знаменитый геометр оставил нам памятник русский, до-
стойный его редких дарований» (стр. 26).
В таких ярких выражениях Брашман подводил первые
итоги деятельности университетских математиков за сорок
лет и ставил новые важные для пауки и общества задачи.
IX, Итоги первого столетия
Я приведу некоторые количественные данные о вы-
пуске учащихся на физико-математическом факультете
Московского университета, к сожалению, во многом не-
полные, ибо статистический материал здесь ещё не раз-
работан. За 11 лет (с 1825 по 1836 г.) факультет окон-
чило 119 человек, т. е. выпускалось в среднем по 11 че-
ловек в год; за 18 лет (с 1836 по 1854 г.) его окончило
уже 453 человека, т. е. примерно по 25 человек в год.
Москва в это время оставляла далеко позади другие
университетские центры. В Харькове, например, число
выпущенных по физико-математическому отделению за
те же промежутки времени было 65 и 186, в Петербурге,
соответственно, 29 и 157. При этом в Харькове годич-
ный выпуск вырос за это время с 6 человек до 10, т. е. ме-
нее, чем в Москве, а в Петербурге приблизительно с 3 до
9. Интересно при этом заметить, что удельный вес окон-
чивших физико-математическое отделение постепенно уве-
личивался. В Москве доля их в общем числе кончающих
университет поднялась с 12 до 29%, чв Харькове—с 14,5
До 18,5%. В Петербурге, где юридическое отделение обла-
дало особенной притягательной силой, доля окончивших
физико-математическое отделение была значительно мень-
ше, составляя, например, в 1836 г. и многие годы спустя
около 8%. Она поднялась до 25% лишь к 60-м годам,
126
А* П, ЮШКЕВИЧ
т. е. в то время, когда тургеневские Базаровы стали изу-
чать «Материю и силу» Бюхнера и «резать лягушек»80.
Приведённые числовые данные свидетельствуют о по-
степенном росте в среднем (я не касаюсь отдельных пе-
риодов упадка), но вместе с тем и о малом коли-
честве естественников и математиков. Причиной медлен-
ного роста, срывов его и часто невысокого уровня под-
готовки учащихся была, прежде всего, политика прави-
тельства в области народного просвещения. Если в начало
XIX в. власти путём поощрительных мер стремились
привлечь в университеты молодёжь различных сословий,
хотя преимущественно и дворянскую, давали стипендии
и добивались, хотя бы формально, успешного окончания
курса, то уже в середине второго десятилетия положение
вещей изменилось. Освободительно-демократические дви-
жения в профессорской и студенческой среде вызывали ре-
шительные ответные меры правительства.
При Александре I дело ограничивалось главным образом
отдельными, хотя и жестокими, экзекуциями (особенно в Ка-
занском и Петербургском университетах). При Николае I,
после восстания декабристов, началось более планомерное
наступление на университеты. Главной целью было затруд-
нить доступ к образованию вообще, а «низшим» классам в
особенности. Министр просвещения в 1826 г. выступил с
планом, который должен был препятствовать людям полу-
чать образование выше того, какое им по сословному поло-
жению назначено правительством, и «расположитьучение в
каждом учебном заведении таким образом, чтобы оно могло
служить окончательным образованием того класса людей,
для которого таковые училища преимущественно учре-
ждаются». Приходская школа назначалась для крестьян
и мещан, уездная—для купцов, обер-офицерских детей
и дворян, гимназия и университет—для дворян, не го-
воря об отдельных исключениях. Эта программа прово-
дилась в жизнь с помощью целого ряда мероприятий.
Чтобы молодые люди, «рождённые в низших слоях об-
щества», не выходили «из круга их первобытного состоя-
ния без выгоды для них самих и для государства», при
приёмах в университет отдавалось преимущество дво-
рянам, сокращался самый приём и т. п.
MA'i EMA TH KA В МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 127
Тяга разночинской молодёжи к знанию особенно беспо-
коила правительство, и в высших сферах этого отнюдь
не скрывали. «При возрастающем повсюду стремлении
к образованию,—заявил министр просвещения Уваров
в 1840 г.,—наступило время пещисьо том, чтобы чрезмер-
ным этим стремлением к высшим предметам учения не
поколебать некоторым образом порядок гражданских
сословий, возбуждая в юных умах порыв к приобретению
роскошных знаний». Добиться преобладания в универси-
тетах дворянства было не так уж трудно, особенно при-
нимая во внимание, что это был тогда наиболее обеспе-
ченный и близкий к культуре слой населения. В Харь-
ковском университете, например, в 1832 г. из 276 студен-
тов дворян, чиновничьих и обер-офицерских детей было
195, разночинцев 61, т. е. соответственно 70 и 22%, в Пе-
тербургском в 1836 г. из 241 студента первых было 193
человека, т. е. почти 80%. Положение мало изменилось
за четверть века: в 1860—1861 гг. в Петербургском уни-
верситете на 1342 учащихся приходилось 1161 дворян
или чиновников, т. е. около 85%.
Закрывая двери в среднюю и высшую школу перед «тре-
тьим сословием», правительство старалось не слишком
распахивать их и перед дворянством. Беспоместный дво-
рянин часто был таким же носителем демократического
протеста, что и разночинец. Революция 1848 г. привела
к экстраординарным мерам. Число «своекоштных» сту-
дентов было ограничено в университетах небольшим ком-
плектом в 300 человек. Царь специально приглашал дво-
рянство на военную службу преимущественно перед
гражданской: «на сей же конец им открыта возможность
поступать в военно-учебные заведения или же прямо
в ряды войск, для чего университетское образование не
есть необходимость». Эти меры привели к тому, что число
студентов во всех университетах, достигшее было в 1847 г.
4000, в 1850 г. упало до 3000 и лишь по смерти Николая 1
вернулось к прежнему уровню (в гимназиях оно с 21 382
В 1847 г. упало в 1854 г. до 17 827). Всё это, конечно,
отражалось и на физико-математическом отделении.
Немалый ущерб наносили образованию и другие меро-
приятия правительства. Сильно потерпели науки о природе
128
А. П. ЮШКЕВИЧ
йо второй половине царствования Александра 1, когда на
университеты обрушилась волна полицейского мисти-
цизма, а «революционному безбожию», олицетворявше-
муся для правительства в современной пауке, объявлена
была варварская и бессмысленная война. Особенно отли-
чились в травле философии и науки попечители Казан-
ского и Петербургского округов—ренегат Магницкий
и Рунич. Вследствие их наветов уволено было много
наиболее культурных профессоров. Старались и другие.
Так, в Харькове уволен был математик Осиповский; для
тамошнего университета это была очень чувствительная
потеря.
Фальшивый и низкий карьерист Магницкий предлагал
вообще уничтожить Казанский университет, когда же эта
мера признана была скандальной и неподходящей, принял
все меры к унижению науки и разума и извращению истины.
Его инструкция требовала, чтобы профессор физики во всё
продолжение курса указывал на «премудрость божию»
и ограниченность наших чувств и орудий для познания
непрестанно окружающих нас чудес. Профессор есте-
ственной истории должен был толковать студентам, что
обширное царство природы, как ни представляется оно
премудро и непостижимо в своём целом, есть лишь слабый
отпечаток того высшего порядка, который ожидает нас
после кратковременной жизни. Астроному надлежало
указывать на тверди небесной начертанную пламенными
буквами «премудрость творца» и дивные законы тел небес-
ных, откровенные роду человеческому в отдалённой древ-
ности. Харьковский попечитель, невежда и мистик Кор-
неев, на лекции по электричеству «разъяснял» профессору
и слушателям, что молния падает, имея на конце обяза-
тельно треугольник, изображающий «святую троицу».
Так всё естествознание было взято под обстрел и подо-
зрение. Всему преподаванию естественных и математиче-
ских наук нанесён был на долгие годы тяжёлый удар.
Трудности прогресса высшего образования связаны
были и с плохой подготовкой гимназистов. Выше приходи-
лось рассказывать, что до середины 20-х годов даже на
выпускных студенческих экзаменах нередко задавались
вопросы из одной элементарной математики. Мы видели
Математика i; мо< к. \ ишя pein i те за hi гвьж < i о лег । j.
также, что до этого же времени па физико-математиче-
ском отделении приходилось вести занятия по алгебре,
геометрии и тригонометрии. В ЗО-е годы подготовка, сооб-
щаемая в гимназиях, начала несколько улучшаться, но
это был процесс весьма затяжной. Медленный рост сту-
денческих кадров в первой половине XIX в. объяснялся
и тем, что дворянство и нажившееся чиновничество, «про-
питанные дворянской и служебной спесью, отвращались
от университетов, где дети их должны были сесть в ауди
ториях рядом с детьми разночинцев и даже «черни»81.
Чего же искала па физико-математическом отделении
молодёжь? Для многих университет служил этапом на
пути, к материальной обеспеченности и общественному
но южепию. Физико-математическое отделение служило,
в частности, для подготовки учителей, и его питомцы, как
правило, выбирали именно этот род деятельности. О на-
учной карьере думали немногие. Перед молодым челове-
ком здесь стояло уже то препятствие, что число вакансий
в высшей школе было весьма невелико. Мы видели выше,
как мало математиков работало в Московском универси-
тете и сколько лет Зернову пришлось ждать освобождения
вакансии.
По были и другие ещё причины, отвлекавшие от ма-
тематики лучшую часть молодёжи. Герцен, учивший-
ся на физико-математическом отделении Московского
университета в 30-х гг., описывал свое поколение
в следующих выражениях: «Молодёжь была прекра-
сная в наш курс. Именно в это время пробу-
ждались у пас больше и больше теоретические стремления.
• Семинарская выучка и шляхетская лень равно исчезли,
не заменяясь ещё немецким утилитаризмом, удобряющим
умы наукой, 'как поля навозом, для усиленной жатвы.
Порядочный^ круг студентов^ не принимал больше науку
за необходимый, но скучный просёлок, которым скорее
объезжают в коллежские ассесоры. Возникавшие вопросы
вовсе не относились до табели о рангах». Но эти люди
почти не пошли в математику и вообще в точную нау-
ку. Вопросы, волновавшие их, касались политической зло-
бы дня. Лучшие представители тогдашнего студенчест-
ва вновь поднимали знамя борьбы с самодержавием и
Неторико-иатемат. исследовании
t;:o Л. II. ЮШКЕВИЧ
крепостничеством. «Наука,—писал тот же Герцен,—не
отвлекала от вмешательства в жизнь, страдавшую вокруг».
Но это «вмешательство» в тогдашних условиях неминуемо
отвлекало от теоретических проблем физики и математики.
Борьба предстояла серьёзная. Вести её приходилось сна
чала в сфере идеологии и в той части, которая ближе всего
соприкасалась с проблемами общественной жизни. Неда-
ром овладел тогда умами интерес к философии, так ярко
расцветали литература и критика. При отвлечённой науке
оставались немногие из этой молодёжи. Немало способ-
ных людей предпочло тогда математическим наукам об-
щественную борьбу и среди них сам автор «Былого и дум»,
па которого возлагал большие надежды энтузиаст астро-
номии Перевощиков82.
Всё же в этих трудных и сложных условиях в стенах
Московского университета вырастали и учёные матема-
тики. Разумеется, их не могло быть много. Ведь всё
физико-математическое отделение выпускало в конце
рассматриваемого периода около 25 человек в год.
Не могло их быть и среди учеников Суворова или Иерело-
гова. Но когда в Университете появились люди нового
склада, как Перевощиков, Зернов и особенно Брашман,
среди их учеников быстро нашлись и квалифицированные
преемники и замечательные творческие умы. И для того,
чтобы подвести общий итог деятельности физико-матема-
тического факультета в Москве за первую половину
XIX в., достаточно назвать славные имена некоторых его
воспитанников: акад. П. Л. Чебышева, акад. И. И. Со-
мова, акад. Ф. А. Бредихина, проф. В. Я. Цингера,
проф. А. Ю. Давидова, проф. М. Ф. Хандрикова, проф.
Н. А. Любимова, проф. А. Г. Столетова. А к этим именам
нужно добавить ещё наименования двух детищ физико-
математического факультета: Московского математиче-
ского общества и «Математического сборника».
ПРИМЕЧАНИЯ
1 Ср. П. Т i m е г d in g, Die Verbreitung der mathematischen Wissen
und math. Auffassung, B.—L.,1914, стр. 106 и след. Подробности
о ранних годах Московского университета и его гимназии см. у
С. Ш ев ы рёв а, «История ими. Московского университета», М,".
1855, и С. В. Р о ж-д е с т в е н с к о г о, «Очерки по истории систем
народного просвещения России в XVIII—XIX вв.», I, Спб., 1911
> «Ценность и мнимая не-ценность математики» (Новые идеи в ма-
тематике, сб. I, 2-е изд., Спб., 1917, стр. 113).
3 Все даты приведены в статье по старому стилю.
4 Протоколы профессорской конференции за XVIII в. хранятся
в архиве МГУ.
6 «Арифметика» Иоганна Фридерика Вейдлера. М., 1765, 2-е изд.,
1787, 3-е, 1795 (стр. 99). Его же«Аналитика специоза или алгебра»,
М., 2-е изд., 1795 (стр. 68). Его же «Геометрия теоретическая и
практическая», М., 1765, 2-о изд., 1778 (стр. 128). Его же«Плоская
тригонометрия», М., 1765; 2-е изд. 1778 (стр. 61). Об учебниках
Д. Аничкова см. прим. 18, 23, 25, 27.
* См. «Объявления о публичных учениях в императорском Москов-
ском Университете и обеих гимназиях оного преподаваемых»,
издававшиеся ежегодно на русском и латинском языках. Вот вы-
держки из объявления на 1777—1778 гг.: «Дмитрий Аничков,
Логики и Метафизики Профессор публичный ординарный, и обеих
гимназий Инспектор, в обыкновенные дни от 7 до 9 часов по утру,
Логику и Метафизику, по руководству М. Христиана Баумейстера;
по средам же и субботам, также от 7 до 9 часов по утру, Геометрию
и Тригонометрию по руководству Пог. Фридерика Вейдлера, сво-
им слушателям преподавать будет».
И. А. Рост «в обыкновенные дни чистую Математику, то-естт>
Арифметику, Геометрию и Тригонометрию изъяснять" будет по
руководству Йог. Фридерика Вейдлера и в приличное время года
присовокупит к тому геодезическую практику». (Рост в этом году
и в некоторые другие читал ещё физику по две лекции в неделю.)
7 См. «Биографический словарь профессоров и преподавателей
Московского Университета», ч. II, М., 1855.
8 Ададуров Василий Евдокимович (1709—1778), воспитанник уни-
верситета Академии наук, с 1733 г. адъюнкт математики, перевод-
чик I части «Арифметики» Эйлера, был куратором Московского
университета в 1762—1771 гг.
9*
134
A. 11. ЮШКЕВИЧ
мерин, фортификации и артиллерии из разных авторов собран-
ная... Дмитрием Аничковым». М., 1780 (123 стр.).
86 М. Г о л о в и н, «Плоская и сферическая тригонометрия,» Спб.,
1789, М. Е. Головин (1756—1790), ученик Эйлера, основывался на
важных открытиях и усовершенствованиях своего учителя.
37 «Начальные основания алгебры или арифметики литеральной,
служащие для удобнейшего и скорейшего вычисления как арифме-
тических, так и геометрических задач, в пользу и употребление рос-
сийского юношества, упражняющегося в математических науках,
собранные из разных авторов... Дмитрием Аничковым». М., 1781.
28 Чтобы перемножить 3—2 на —2, нужно —2 умножить на 1;
умножая —2 па 3, мы берём —2 два лишних раза, почему
нужно принять, что—2-—2=4-4 (стр. 19). Ср. Хр. В о л ь ф, «Со-
кращение первых основании математики». Спб., 1771, т. II,
стр. 338.
29 «Новейшая арифметика, заключающая в одном ценном правиле
большую часть тех правил, которые обыкновенно в Арифметиках
преподаются под особливыми именами, с показанием самых крат-
чайших средств к решению разных задач. Сочинённая II. Шмитом,
которую в пользу всех учащихся, а особливо купеческого юноше-
ства, с немецкого перевёл, удобнейшим порядком расположил и
нужными прибавлениями дополнил... Александр Барсов», М.,
1797.
30 «Новая алгебра, содержащая в себе не только простую аналитику,
но также дифференциальное, интегральное и вариационное исчис-
ление, которую в пользу начинающих упражняться в математике
издал... Александр Барсов». М., 1797. Барсов упоминает Кестнера
в тексте, но вместе с тем не указывает, что излагает, а местами про-
сто переводит его книгу. Не знал об этом, видимо, и В. Бобынин,
когда писал в своём обзоре истории русской математики, что почти
одновременно с акад. Гурьевым и независимо от пего занимался
усовершенствованием метода пределов Барсов (см. Энциклопеди-
ческий словарь Брокгауза и Ефрона, т. XXVIII, 1899, стр. 726).
Как раз в этом отделе Барсов не добавил к Кестнеру ничего нового.
31 См. «Речи, произнесённые в торжественных собраниях пмп. Мос-
ковского Университета русскими профессорами оного», ч. II, М.,
1820, стр. 326 и 337.—Не сказалось ли па предпочтении, ко-
торое Панкевич отдавал синтетическим методам, изучение «На-
чал» Ньютона, которые он, невидимому, переводил на русский
язык?
32 «Конструкцией Геометрическою называется такое искусство, по-
мощью которого члены алгебраических сравнений изображаются
линиями» (Д. Л н и ч к о в, «Начальные основания алгебры», стр.
144).
33 «Речи, произнесённые в торжественных собраниях ими. Москов-
ского Университета русскими профессорами оного», ч. П, стр. 10.
34 См., например. Г». Н Медине к и п. «История педагогики», ч. I,
гл Х1, 1938.
35 Об украинце Василии Андреевиче Загорском известно очень
немного. В 1798—J803 гг. вышел его перевод математического кур-
МАТЕМАТИКА 13 МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 135
са Безу, первые части которого назначались для университетского
пансиона, а последние две для самого Университета. Преподавал
он в Московском университете до января 1810 г., когда по состоя-
нию здоровья вышел в отставку. В 20-х годах он был ещё жив.
По отзывам современников, это был преподаватель «хороший,
твёрдый, отчётливый».
Загорский, как и многие его современники, весьма интересо-
вался вопросами обоснования исчисления бесконечно малых. Мс-
муар его на эту тему был рассмотрен акад. С. Гурьевым, кото-
рый, однако, не усмотрел в нём чего-либо заслуживающего впи
мания (см. Протокол конференции Академии наук от И апреля
1804 г., хранящийся в Архиве АН СССР).
34 Иван Пде, ученик Кестнера, прибыл в Москву в марте 1804 г.
Умер он 1 октября 1806 г., лет тридцати.
37 С. Шевырёв, «История Московского Университета», стр.
328.
38 «Курс математики г-на Безу, члена Французской академии, пере-
веден Василием Загорским в пользу и употребление благородного
юношества, воспитывающегося в университетском пансионе.
Ч. III, содержащая в себе алгебру, с приноровкой её к геометрии и
конические сечения», М., 1801, стр. 59—61.
3* «Cours de Mathematiques» Безу переиздан был специально для
Политехнической школы. Мне известно издание IV тома (в кото-
рый вошли исчисление бесконечно малых и механика) ещё от
1809 г.; Гарнье несколько дополнил его в мелком шрифте, но со-
хранил все основные установки автора.
40 Университет и ранее выпускал ряд журналов, по «Ведомости» бы-
ли его первым научным" органом.
41 М. II. Муравьёв (1796—1866) был близок затем к декабристам.
Впоследствии, оправдавшись перед Николаем I, он сделал круп-
ную военно-бюрократическую карьеру и вошёл в историю под име-
нем Муравьёва-вешателя.—О Терюхпне мне известно лишь, что он
издал под инициалами А. Т. не очень удачное, особенно в перечис-
лении аксиом, «Руководство к геометрии» (М., 1819).
4 ‘- «Но как из прикладных частей Математики вообще самые полезные
суть Механика и Военное искусство, то наипаче на них Общество
обратило своё внимание и устремило все труды к приуготовленпю
молодых людей в военную службу». См. «Периодическое сочинение
о успехах народного просвещения», XXX, 1811, стр. 56—57.
43 «Курс математики, изданный на французском языке Беллавенсм
для употребления в военных школах; с французского на русский
язык перевёл с некоторыми переменами и дополнениями...
Фёдор Чумаков», ч. 1—3 (последняя включала аналитическую гео-
метрию й механику). М., 1817—1821.
44 П. II. Суворову совместно с В. И. Никитиным (1739—1809) при-
надлежат перевод с греческого «Евклидовых стихий осьмь книг»
(Слб., 1784,2-е изд. 1789) и «Тригонометрий две книги.содержащие
плоскую п сферическую тригонометрию» (Спо., 1787)—курс до-
вольно полный, но написанный на устаревшей и в то время основе.
Суворов п Никитин, оба члены Российской Академии, известны
136
A. II. ЮШК1 1.II4
были своей борьбой против употребления г. математике иностран-
ных терминов и создали собственный лексикон на славяпо-гречс-
скОЙ основе (гипотенуза—подтягающап, теорема—мыслив, тео-
рия—мысльствпе и т. п.). Это предприятие успеха не имело, но
отдельные рекомендованные ими слова вошли в обиход (например,
чертёж).
15 Т II. Перелогов, сын священника Владимирской губернии, род.
в 1765 г. Учился в духовной семинарии, окончил Московский уни-
верситет. С 1784 г/преподавал математику и языки в пансионе.
В 1805 г. Перелогов быт произведен в адъюнкты, а профессо-
ром был назначен в 1814г. В 1825 г. он вышел в отставку и
умер 29 марта 1841 г.
48 Пафнутий Алексеич Афанасьев окончил Московский универси-
тет, с 1814 г. магистр. Был автором ряда учебных руководств:
«Арифметики» (М., 1814), «Алгебры по руководствам Франкера,
•Лакруа и других новейших математиков» (М., ч. 1—2, 1816),
«Таблиц логарифмов, простых чисел и тригонометрических линий»
(Спб., 1818). «Хронологического обозрения Российской империи»
(М., 1821). Афанасьев первый использовал в преподавании кур-
сы Франкера. Даты рождения и ранней смерти его неизвестны.
47 Димитрий Петроцлч Тростин, из духовного звания После Суз-
дальской семинарии обучался в Московской гимназии и Универси-
тете. С 1783 г. преподавал в гимназии латьшь, а с 1793 г. вёл
по несколько лет классы арифметики, геометрии, тригономет-
рии, алгебры. В Университете работал в 1816—1819 гг. Умер
в 30-х годах.
48 Жозеф-Лун Бушарла (Boucharlat, 1777—1848), репетитор Поли-
технической школы, профессор математики, написал два курса:
«Thdorie des courbes et des surfaces du second ordre ргёсёЯёе des
principes fondanientaux de la gdom£trie analytique» (1810) n «Ele-
ments de calc.nl бШёгепtiel et de calcul integral» (181.»). 9-е издание
которого в переработке Лорана выпью ещё в 1881 г. О Бушарла
см. статью С. А. Яновской «О математических рукописях К. Марк-
са» в сб. «Марксизм п естествознание». М., 1933.
49 Григорий Иванович Карташевский (1779—1840) сам был воспи-
танником Московского университета.
ьо «Арифметика для начинающих. Издана при Университетском
Благородном пансионе. Д. П.». М., 1820. стр. 73—77.
51 С. Шевырсв, «История Московского Университета», стр.
451.
52 Иван Иванович Давыдов (1794—1863). из дворян, студент Уни-
верситета с 1808 г., в 1815 г. доктор словесных паук, с 1831 г.
профессор словесности в Университете, с 1841 г. академик. Давы-
дов ряд лет читал математику в Благородном пансионе. Па физико-
математическом отделении с 1828 до 1831 г. преподавал высшую
алгебру. Докторская диссертация Давыдова была па тему: «О пре
образовании в науках, произведённом Баконом». Основные еги
труды относятся к философии и словесности. Он перевёл также
«Высшую алгебру» Франкера (М., 1824) и его же «Интегральное
исчисление и псчделение разностей» (М., 1825). В «Магазине естост-
MAT EM \TliKA В МОСК. УНИВЕРСИТЕТЕ ГЛ ПЕРВЫЕ СТО ЛЕТ 137
пенных наук», издававшемся Двигубским, Давыдов напечатал
статью «Об исчислении вероятностей».
Николай Васильевич Кацауров (род. в 1798 г.), сын офицера,
с 8 лет круглый сирота. Кончил Университет в 1816 г., в 1824 г
получил степень магистра. С 1820 г. преподавал математику в
пансионе, с 1823 г. аналитическую геометрию в Университете.
В 1834 г. покинул Университет.
53 См. «Биографический словарь профессоров Московского Уни-
верситета», т. II.
44 С. III е в ы р ё в «История Московского Университета», стр.
451.
55 «Cours complet des math6matiques pures» Франкера. Многократно
издавался во Франции. Русский перевод Христиана Крюкова и
Долотова вышел отдельно в Петербурге: «Полный курс чистой ма-
тематики» (1827); Франкер у принадлежал также ряд учебников
по механике, астрономии и т. д.
56 Свободской предложил способ производить на счётах все опера-
ции арифметики. В Московском университете этот предмет читал
Платон Николаевич Погорельский (1800—1852), магистр физико-
математических наук (1827). Погорельский вёл также курс анали-
тической геометрии, а одновременно преподавал в гимназии. С
1836 г. он перешёл полностью на работу в гимназию. Это был вы-
дающийся деятель средней школы; ему принадлежал распростра-
нённый гимтазическпй учебник алгебры. Между прочим, он был
домашним учителем П. Л. Чебышева.
57 Устав требовал также экзамена докторанта по двум предметам.
Зернов был освобождён от испытаний.
5* См. «Биографический словарь профессоров Московского Уни-
верситета». ч. II.
59 В 18.;0 г. оно вновь было названо физико-математическим отделе-
нием.
60 Александр Степанович Ершов (1818—1867), из дворян. По окон-
чании в 1839 г. Университета командирован был в Петербург, а
затем в Париж для усовершенствования в начертательной геомет-
рии и теории сопротивления материалов. Магистерскую степень
получил в 184< г., а в следующем стал читать названный курс на
физико-математическом отделении. Профессор с 1853 г. Организа-
тор Московского высшего технического училища.
81 Август Юльевич Давидов (1823—1885) происходил из еврейской
семьи, проживавшей в Курляндии По окончании Университета
в 1841 г. продолжал заниматься математикой под руководством
II. Д. Брашмана. В 1848 г. защитил магистерскую диссертацию
«Теория равновесия тел. погружённых в жидкость». Докторская
диссертация «Определение вида поверхности жидкости, заключён-
ной в сосуде» была Давидовым защищена в 1851 г. С 1853 г. Дави-
дов состоял профессором кафедры прикладной математики, а в
1862 г. перешёл на кафедру чистой математики. В I, II, IV, X тт
«Математического сборника» он опубликовал несколько статей по
математическому анализу. Широкой известностью пользовался
его учебник «Элементарной геометрии» (1-е изд. 1863 г.) и другие
13*
Л. И. ЮШКЕВИЧ
школьные руководства. Давидов был также одним из учредителей
Московского математического общества.
62 Обо всех экзаменах в Московском университете см. соответствую-
щие протоколы в «Журнале заседаний физико-математического
отделения», хранящемся в Архиве Университета.
03 См. «Физико-математический факультет Харьковского Универси-
тета за первые 100 лет его существования». Под ред. II. Осипова и
Д. Багалея, Харьков, 1908, стр. 162.
°4 Магистерский экзамен Байкова проходил на несколько более вы-
соком уровне, чем у Щепкина. 19 августа 1821 г. он отвечал устно
на вопросы: 1) как решаются разностные уравнения, 2) какие при-
ложения имеют особенные интегралы в высшей геометрии, 3) оп-
ределение кривизны поверхности (кроме того, были вопросы по
прикладной математике). 22 августа он вытянул следующие биле-
ты для письменной работы: 1)«*Ежели одна парабола будет дви-
гаться по другой так, чтобы плоскости обеих парабол оставались
всегда перпендикулярными между собой, и чтобы верх одной нахо-
дился на окружности другой; то произойдёт поверхность, для кото-
рой найти, первое, уравнение, второе, поверхность, заключён-
ную между двумя сечениями плоскостями, перпендикулярными к
осп неподвижной параболы, третье, толстоту отрезка оной поверх-
ности какой-нибудь плоскостью» и 2) «Изложить теорию зеркал
цилиндрических и конических» (см. «Физико-математический фа-
культет Харьковского Университета за первые 100 лет его суще-
ствования». стр. 165). М. А. Байков (1800—-Д840) одно время препо-
давал математику в Харьковском университете, а с 1826 г. состоял
там в течение шести лет профессором сельского хозяйства и домо-
водства.
65 На магистерском экзамене будущего профессора математики
II. А. Дьяченко (1809—1877) в Харькове в 1835 г., после опроса
по астрономии, механике, фортификации и артиллерии, естест-
венной истории, химии, физике и технологии, ему было предло-
жено вывести формулу для выражения показательных величин
и составления таблиц логарифмов, рассказать о вычислении корней
кубических уравнений в неприводимом случае, рассказать о при-
ближённом вычислении углов на поверхности большого шара, вы-
нести уравнения сечений конуса (4 марта) изложить методы реше-
ния уравнений с частными производными 2-го порядка и сущность
метода вариаций (5 марта) и, наконец, письменно ответить на во-
просы: «1) Как интегрирование дифференциальных функций спо
собствует к нахождению интегралов разностных уравнений?
2) Ежели бы земля притягивалась солнцем в обратной пропорцио-
нальности расстояний, то какую бы кривую линию она описывала?»
(7 марта). Диссертацию он защищал «Об успехах после Эйлера,
сделанных в нахождении интегралов определённых и об употреб-
лении их» (Харьков, 1835). См. «Физико-математический факуль
тет Харьковского Университета за первые 100 лет его существова-
ния», стр. 171—172.
ав В 1862 г. Хандрмков защитил диссертацию на степень магистра
астрономии («Сравнение способов, предложенных Гауссом, Бес-
МАТЕМАТИКА Б МОСК. УНИВЕРСИТЕТЕ ЗА ПЕРВЫЕ СТО ЛЕТ 139
селем и Гансеном для вычисления солнечных затмений») и в 1865 г.
—на степень доктора астрономии («Очерк теории определения пла-
нетных и кометных орбит по трём наблюдениям»). С 1870 г. он со-
стоял профессором Киевского университета. Из его руководств
особенно известна была «Элементарная теория эллиптических
интегралов. С приложением к решению основного вопроса геоде-
зии» (М., 1867).
67 Гремя годами ранее Сомов, окончившим Московский университет
в 1835 г., опубликовал «Теорию определённых алгебраических
уравнении высших степеней» (М., 1838), удостоенную Академией
наук Демидовской премии.
68 Сборник «Научное наследие II. Л. Чебышева», I, стр. 45 (М.— I.,
1945).
69 В издававшемся им «Военном журнале» Рахманов позднее поме-
стил отзыв на второе издание книги Кузьмина (XIX, 1812 ). Отме-
тив, что акад. Гурьев усовершенствовал вслед за Маклерском, Да-
ламбером и Барсовым способ пределов, Рахманов писал, что со-
чинения Гурьева могли бы прочесть лишь учителя. Кузьмин изло-
жил метод пределов в виде, пригодном для учащихся, и его книга
будет полезным дополнением к учебникам, употреблявшимся в
Москве.
70 Ср. у Л. Карно: «Я называю несовершенным уравнением всякое
уравнение, строгая точность которого не доказана, но относитель-
но которого, однако, известно, что если в нём существует ошибка,
то её можно предположить сколь угодно малой» («Размышления о
метафизике исчисления бесконечно малых», перев. II. Соловьёва,
М.,1933, стр. 94). «Несовершенные» уравнения приводят, по Кар-
но, к точным результатам в силу компенсации ошибок.
71 См. Фра и кер. «Интегральное и вариационное исчисление», М.,
1825, стр. 245—246. Вот ещё одна занятная деталь перевода Пере-
dy
вощикова. Он заменил символ Лагранжа /1 (я) на нигде,
впрочем, не рассматривая отдельно dyt dxt а производную функ-
цию назвал дифференциалом, «желая удержать сие слово к коему
привыкли от долговременного употребления».
72 Например, полагая
sin я==а,-|~С.г:3-Ь£^5-|-.. .иcosх=* 14-5л2-|-Рл4+... [noosinf—я) =
«—sin х, a cos (—я)= cos я],
он находит ряды для
2 sin я cos a =sin 2я, cos2 х—sin2 л ==cos 2х
п выводит искомые коэффициенты путём сравнения.
73 Первый перевод книги Карно (с 1-го издания 1797 г.) вышел в
Казани в 1823 г. по определению Совета Казанского университета
от 19 июля 1822 г.: «Рассуждение о метафизике начисления безко-
нечных: Сочинение Г-на Карнота. члена Парижского института.
Перевод профессора математики В. Шишацкого». В. Шишацкий в
140
A. II. ЮШКЕВИЧ
1801 г. был б заграничной поездке, в начале XIX в. преподавал
математику в Ярославском демидовском училище.
74 Этот вывод был изложен в статье ученика С. Е. Гурьева акад.
В. Л. Висковатова «О простейшем доказательстве Тэйлоровой
теоремы» (Умозрительные исследования Академии Наук, т. I,
1808, стр. 185—206), за которой последовала работа «Краткое
изложение способа знаменитого Лагранжа изъяснять исчисление
дифференциальное и приложение оного к геометрии кривых линий»
(Умозрительные исследования‘АН., т. II, 1810, стр. 183—314).
75 II. Е. 3 е р н о в, «Изложение предварительных понятий о диффе-
ренциальном исчислении», стр. 3—34; см. «Учёные записки Мос-
ковского Университета», год 2, ч. VII, 1835. Русские математики
рассматриваемой эпохи чрезвычайно интересовались вопросами
обоснования анализа. Я, однако, не могу входить здесь в разбор
сочинений С. Е. Гурьева. Ф. Шуберта, II. Рахманова и др. по
этому вопросу. Ср. мою статью об акад. Гурьеве в Трудах Инсти-
тута истории естествознания АН СССР, т. I, 1947.—«Краткое изло-
жение уроков о дифференциальном и интегральном исчислении»
Коши перевёл В. Я. Бунпковский (Спб., 1831).
76 Здесь Брашман исправлял одну неточность, допущенную Лаграп-
жем при разборе достаточных условий экстремума функций трёх
переменных, на которую внимание его обратил* акад. Остроград-
ский.
77 Речь шла о решении и геометрическом истолковании систем линей-
ных неравенств.
78 Разбирались условия карточной игры «бостон».
79 В статье отмеч*ается, что. как указали автору, для конических се-
лений его приём совпадает с ньютоновым «органическим» опи-
санием кривых.
80 Я но имею точных данных об отсеве студентов. Можно считать,
,что в конце 50-х годов доходило до конца обучения около трети
поступивших. В более раннее время, когда «казённокоштные» сту-
денты составляли большую долю учащихся, отсев был меньше.
Статистические сведения взяты мною из книги С. Шевырёва (цит.
соч.), В. В. Григорьева («Императорский С. Петербургский Уни-
верситет в течение первых 50 лет его существования», Спб., 1870)
и Журна'ла Министерства народного просвещения за разные годы.
81 В. Г р и г о р ь е в, цит. соч., стр. 29.
82 Беседа Герцена с Перевощиковым в 1844 г.столь характерна, что
я приведу из неё отрывок: «Жаль-с, у вас прекрасные-с были-с
способности-с»,—говорил ему профессор. Герцен возразил: «Да,
ведь, не всем же за вамп на небо лезть. Мы здесь займёмся, на зем-
ле, кой-чем».
МАТЕМАТИКА И ЕЁ ДЕЯТЕЛИ В МОСКОВСКОМ
УНИВЕРСИТЕТЕ ВО ВТОРОЙ ПОЛОВИНЕ XIX в.
М. /1. Выгодский
В течение первых 80 лет существования Москов-
ского университета развитие математики в нем отсе-
вало от того уровня, который в те времена был уже
достигнут в петербургской Академии наук. В первой по-
ловине XIX в., в силу ряда обстоятельств, математика
в Московского университете уступала также и казан-
ской. В то время как в Казани рождались блестящие
работы Лобачевского, в Москве еще не велась серьёзная
научная работа, а преподавание математики оставляло же-
лать лучшего. Нек оторые преподаватели Университета, по
справедливому замечанию А. И. Герцена, поступившего
на физико-математическое отделение Московского уни-
верситета в 1830 г., сами знали математику лишь р том
объеме, в котором они её преподавали: они точно следо-
вали курсу Франкера, не переходя в нём за пределы
известной страницы. На лекциях происходили «чудеса»,
подобные тем, которые творил профессор механики Чума-
ков, «подгонявший формулы к тем, которые были в курсе
Пуансо с совершеннейшей свободой помещичьего права,
прибавляя и убавляя буквы, принимая квадраты за корни
и х за известные».
Прошло десять лет, и в 1841 г. Московский универ-
ситет оканчивает двадцатплетний юноша Пафнутий Льво-
вич Чебышев; в Московском университете его блестящие
дарования получили первый толчок к развитию. Физи-
ко-математическое отделение Университета в это вре-
мя начинало становиться культурным высшим учебным
142
М. Я. ВЫГиДсКИН
заведением, а спустя ещё десятилетие в нём началась и на-
учно-исследовательская работа.
Этот важный для истории Университета и для русской
науки перелом связан с именем проф. Н. Д. Брашмана
(1796-1866)1).
Николай Дмитриевич Брашман приехал в Россию
молодым человеком (вероятно, в 1823 г.). Он получил
высшее образование в Вене (окончил Политехнический
институт и университет), где работал под руководством
известного астронома И. Литтрова (1781—1840)'2).
По окончании высшего образования он несколько лет
занимался обучением детей в домах богатых людей; в
поисках лучших условий работы он прибыл в далёкий
Петербург и здесь стал учителем Петропавловского
училища. Вскоре (1825) Брашман получил место адъюнк-
та в Казанском университете. В Казани он препода-
вал и чисто математические дисциплины и прикладные
(астрономию и механику) и усиленно работал над попол-
нением собственного образования.
В 1834 г. Брашман был назначен профессором при-
кладной математики в Московский университет. Естест-
венно, что вначале лекции Брашмана могли носить очень
элементарный характер, по из года в год они становились
всё более серьёзными, и выпущенный им в 1859 г. курс
теоретической механики стоит на высоком научном уровне.
Преподавал Брашман также и аналитическую гео-
метрию и другие предметы. Лекции его были содержа-
тельны и интересны, к аудитории своей Брашман относился
с исключительным вниманием; он был рад помочь каждому
студенту справиться с каким-либо затруднением. Прони-
цательным взором искал он среди своих слушателей
одарённых людей и побуждал их к самостоятельной работе.
Он сразу угадал талант Чебышева и с особенной любовью
руководил его занятиями в университетские годы, а также
О Одновременно с Н. Д. Брашманом в Московском универси-
тете было еще два серьёзных профессора математических наук:
И. Е. Зернов (математика) и Д. М. Перевощиков (астрономия).
*) Литтров в 1810—1816 гг. был профессором Казанского уни-
верситета. Вероятно, благодаря сохранённым им связям и Брашман
впоследствии получил назначение в Казань,
МАТЕМАТИКА U МОСК. УНИВЕРСИТЕТЕ ВО 2-й ПОЛ. XIX в. |4;{
цо окончании курса в течение трёх-четырёх 1ет, когда
Чебышев готовился к получению учёного звания. Чебы-
шев, как и другие ученики Брашмана, сохранил на всю
жизнь глубокое уважение к своему учителю, портрет
которого неизменно украшал рабочий стол великого
русского математика.
Литературная деятельность Брашмана начинается с
1834 г. и развёртывается преимущественно на страницах
«Учёных записок Московского Университета». 1хроизве-
дения Брашмана не отличаются оригинальностью идей,
но обнаруживают учёного, хорошо владеющего методами
современной ему науки. Брашман состоял в постоянном
научном общении с Остроградским, Чебышевым и другими
работниками Академии наук. В 1842 г. он предпринял
поездку за границу и вступил в личный контакт с круп-
нейшими учёными Германии, Франции и Англии. На
Манчестерском съезде Британской ассоциации от сделал
19 июня 1842 г. доклад «О молекулярных силах». Доклад
этот позднее был напечатан в его курсе статики.
Проф. Брашману на съезде был оказан самый
радушный прием; в день его доклада на повестке съез-
да стоял доклад Якоби, но первым был помещен доклад
Брашмана, которого президент Британской ассоциации
Ликок представил съезду как «знаменитого московского
профессора». Бессель и Пикок выступали с поздравитель-
ными речами после его доклада, а Гершель сказал: «Между
нами есть учёный из России, который написал мемуар
величайшей важности. Незадолго ещё мы считали бы
математический мемуар на русском языке явлением необык-
новенным, но науки двигаются вперёд, и успехи России
изумительны».
В этих словах была истина: в русских университетах,
в частности в Московском, через немногие годы после
организации физико-математических факультетов выра-
стало поколение замечательных математиков и механиков.
В Московском университете Брашман работал более
30 лет; в 1864 г., за два года до смерти, он оставил службу,
но связь его с учениками не прекратилась; па его квар-
тире регулярно происходили собрания кружка его уче-
ников.
144 м. н. выгодиши
Старый холостяк, Брашман все свои чувства перенёс
на выращенное им молодое поколение учёных, и, в свою
очередь, ученики его не могли не испытывать глубокой
признательности к наставнику. Конечно, торжественные
речи на торжественных собраниях редко бывают свободны
от риторических прикрас. Но в словах, которыми ученики
Брашмана проводили уходившего на отдых учителя,
звучат, .ноты глубокой искренности:
«Вьг? составили себе, Николай Дмитриевич, много-
численную семью, разбросанную по всей земле русском.
Сорок лет тому назад вступили вы на поприще профес-
сорской деятельности и с самого начала вложили в испол-
нение своих обязанностей то тёплое чувство, ту строгую
добросовестность, которые одни только служат ручатель-
ством верного успеха. Вы не довольствовались одним
чтением лекций; в своей аудитории вы постоянно искали
молодых людей, прилежных и способных, из которых
могли бы выйти достойные учёные. Вы лелеяли их, как
своих родных детей, ваш дом был их домом, ваш стол
их столом, ваши книги принадлежали им; в нужде и неу
даче они постоянно находили в вас совет и опору».
Кружок учеников Брашмана, к участию в котором
Брашман привлёк также и К. М. Петерсона 1), начал
свою работу 15 сентября 1864 г.
В первом заседании2) было решено организовать
правильно функционирующее научное общество, целью
которого было «взаимное содействие в занятиях матема-
тическими науками». Первоначально не имелось в виду
придавать обществу официальный характер; лишь через
год, в октябре 1865 г., было решено «просить об офици
алыюм учреждении общества и для этого пересмотреть
к следующему заседанию устав общества». Однако с первого
же дня были избраны президент и вице-президент
общества. Президентом, конечно, избрали Брашмана,
вице-президентом—старшего из находившихся в Москве
учеников Брашмана А. Ю. Давидова, тогда бывшего уже
МО К. М. Петерсоне и о других членах кружка будет расска-
зано ниже.
») Протокол его напечатан в «Математическом сборнике», т. XIV,
1888, стр. 471.
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ВО’П ПОЛ. XIX В. 145
проф. Московского университета, секретарём—В. Я. Цин-
гера. Было постановлено, что «действительными членами
общества могут быть магистры и доктора математических
наук, а также лица, заявившие себя трудами в этих нау-
ках*. Действительным членам предоставлялось право при-
глашать на заседания общества посетителей. Каждо-
му действительному члену устав вменял в обязанность
«следить за успехами избранного им отдела науки и сооб-
щать в заранее назначенные сроки письменные отчёты
и словесные объяснения о своих занятиях*. Этот пункт
сохранялся в уставе Московского общества долгое время
и после того, как оно получило официальное утверж-
дение. Таким образом, по своей структуре общество носило
характер научного семинара. Членов общества было
немного—всего 13 человек, и научные специальности они
поделили следующим образом:
I. Чистая математика
А. Ю. Давидов. Интегрирование уравнений с частными
дифференциалами.
А. В. 'Летников. Дифференциальные уравнения.
Н. Н. Алексеев. Интегрирование иррациональных
функций и эллиптические функций.
Ф. А. Слудский. Теория чисел1).
К. М. Петерсон. Аналитическая геометрия.
С. С. Урусов2). Теория конечных разностей.
Н. В. Бугаев. Теория чисел.
II. Механика
Н. Д. Брашман. Теория упругости.
В. Я. Цингер. Общая механика.
Потёмкин3). Гидростатика и гидродинамика.
*) После избрания в члены Общества Н. В. Бугаева (6 апреля
1865 г.), избравшего предметом занятий теорию чисел, ф. А. Слуд-
ский взял на себя занятия механикой.
2) Урусов был избран членом общества на втором его заседании
20 октября 1864 г.
3) В дальнейших протоколах имя Потёмкина не встречается.
Ю Историко-математ. исследсвания
146
М. Я. ВЫГОДСКИЙ
III. Астрономия
Ф. А. Бредихин. Физическая астрономия.
М. Ф. Хандриков. Теоретическая астрономия и гео-
дезия.
IV. Физика
Н. А. Любимов и К. А. Рачинский. Электричество
и механическая теория тепла.
О. О. Блажеевский. Теория света.
Заседания общества происходили раз в месяц; на пер-
вом же собрании были расписаны доклады членов обще-
ства на весь год вперёд. План выполнялся очень аккуратно.
Когда К. М. Петерсон по болезни не мог присутствовать
на заседании общества, на повестке которого стоял его
доклад, он прислал свою работу в письменном виде, и
работа была зачитана.
На заседаниях общества, помимо московских гостей,
бывали и иногородние. В частности, на одном из заседа-
ний присутствовал П. Л. Чебышев, сделавший сообщение
«О разложении функций при помощи непрерывных дро-
бей». Вообще Чебышев живо интересовался делами ново-
рождённого общества, во главе которого стоял его преж-
ний учитель. И после смерти Брашмана Чебышев присы-
лал своп доклады Московскому математическому обществу.
Уже в апреле 1865 г. общество решило начать издание
сборника статей, прочитанных на заседаниях. Сборник
предполагали издавать дважды в год.
Первый выпуск «Математического сборника» вышел
лишь в октябре 1866 г., следующие 4 тома выходили
через промежуток в одип год, а дальше дела пошли ещё
труднее, и между выходом двух последующих томов про-
ходило по два года. Причиной такого замедления темпов
был недостаток денежных средств: членские взносы по
5 руб. в год, доходы от продажи сборника (3 р. 50 к.
за том) и скудные субсидии, нерегулярно поступавшие
в кассу общества от Университета, не давали возможности
оборачиваться достаточно быстро, и первые пять лет
«Сборник» мог выходить лишь потому, что удалось найти
типографию, владелец которой (Мамонтов), бывший
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ВО II ПОЛ. XIX В. 147
воспитанник Московского университета, согласился ока-
зывать обществу долгосрочный кредит. Университетская
типография, в которой стал впоследствии печататься
«Сборник», видимо, не могла или не хотела меценатствовать.
Если со сроками выхода «Сборника» дело обстояло небла-
гополучно, то зато объём его был довольно внушителен:
в среднем страниц 650, а, например, XI том имел около
1 000 страниц.
«Математический сборник» был первым научным
русским журналом, посвящённым специально математиче-
ским наукам.
В настоящее время он имеет почтенный 80-летний
возраст и за свою многолетнюю жизнь испытал немало
различных изменений, начиная с внешнего вида и кончая
внутренней своей структурой.
Первоначальное направление «Математического сбор-
ника», сохранявшееся в течение первых 15 лет его суще-
ствования, значительно отличалось от установки после-
дующего двадцатилетия, и потому нам придётся особо
выделить первые 10 томов «Сборника» (1866—1882). Сопо-
ставляя их со вторым десятком томов, мы ясно видим соз-
нательное изменение характера журнала. И нельзя не
поставить этого в связь с изменением руководства Москов-
ского математического общества, к внешней истории ко-
торого мы и обратимся.
Первому президенту Московского математического об-
щества, Брашману, как герою библейской легенды удалось
увидеть обетованную землю, но не суждено было вступить
на неё. 13 мая 1866 г. Николай Дмитриевич Брашман умер
за месяц до достижения 70-летнего возраста.
На заседании 17 сентября 1866 г. общество избрало на
должность президента А. Ю. Давидова; вакансию вице-
президента занял бывший секретарь общества В. Я. Цин-
гер, а секретарём был избран М. Ф. Хандриков. Этот
обычай передвижки по ступеням должностей стал в обще-
стве нерушимой традицией, сохранявшейся до Великой
Октябрьской социалистической революции х). На том же
г) По старому уставу Общества должностные его лица иабира
лись пожизненно.
10*
148
М. Я. ВЫГОДСКИЙ
заседании обсуждался вопрос о том, из каких средств
оплачивать расходы по печатанию «Математического сбор-
ника», выпуск которого должен был вскоре состояться.
Было постановлено: «посвящая первый том памяти покой-
ного Н. Д. Брашмана, отказаться от сумм, обещанных Уни-
верситетом, и сделать уплату из собственных средств».
Разумеется, первый выпуск «Математического сборника»
открывался биографией Н. Д. Брашмана.
Фактическим редактором этого выпуска был, конечно,
Брашман, и содержащийся в нём материал, как мы знаем,
воспроизводит рефераты, прочитанные в Обществе за пер-
вые два года его существования. В этом первом выпуске
мы находим работы, которыми мог бы гордиться любой евро-
пейский журнал. Это—мемуар Чебышева «О разложении
в ряды при помощи непрерывных дробей» и мемуар К. М.
Петерсона «Об отношениях и средствах между кривыми
поверхностями».
Здесь уместно будет сказать несколько слов об авторах
упомянутых статей.
П. Л. Чебышев (1821—1894) в это время был уже про-
славленным математиком, членом Петербургской и Париж-
ской академий. Его участие в «А1атематическом сборнике»
нужно рассматривать не только как дань признательности
своему учителю, организатору этого журнала, но и как
рекомендацию новому изданию в научных кругах Западной
Европы. И впоследствии Чебышев не раз присылал свои
статьи в «Математический сборник»; нелишне отметить, что
в «Математическом сборнике» Чебышев помещал свои ра-
боты первостепенного значения. Так, во II томе «Матема-
тического сборника» был напечатан мемуар Чебышева «О
.средних величинах», в котором впервые была установ-
лена теорема, играющая важную роль в теории вероят-
ностей и по праву носящая сейчас имя Чебышева.
В рамках этого очерка невозможно сколько-нибудь пол-
но охарактеризовать многостороннюю деятельность этого
замечательного математика. К тому же и формально она
лишь небольшой своей частью связана с Москвой. Ограни-
чимся замечанием, что по оригинальности своих идей и
методов Чебышев может быть поставлен на одно из первых
мест во всей многовековой истории математики. Казалось
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ВО II ПОЛ. XIX В. 149
бы, по отношению к такому учёному влияния, оказанные
на него учителями, вообще не должны были бы иметь суще-
ственного значения. И всё же, как ни самобытен Чебышев,
влияние школы, пройденной им в Москве, влияние его
учителей, в первую очередь Брашмана, имело немаловаж-
ное значение для его научных интересов и направления
его деятельности.
Тема магистерской (по-нашему кандидатской) диссер-
тации Чебышева «Опыт элементарной теории вероятностей»
(1846 г.),несомненно, была выбрана им под влиянием Браш-
мана, который в эти годы много занимался теорией вероят-
ностей. Известно, какую значительную роль в научной дея-
тельности Чебышега имели проблемы теории вероятно-
стей; известно, что сам Чебышев явился основателем все-
мирно известной русской теоретико-вероятностной школы.
Известно, далее, какую роль в творчестве Чебышева
играли интересы прикладных наук, в особенности интере-
сы механики: водь, например, проблема о полиномах, наи-
менее уклоняющихся от нуля, была порождена пробле-
мой конструкции механизма, дающего движение, «наиме-
нее уклоняющееся» от прямолинейного. Эти вкусы были,
если не порождены, то во всяком случае воспитаны в
Чебышеве в стенах хМосковского университета тем же Браш-
маном. Знакомясь с научной деятельностью других учени-
ков Брашмана, мы найдём и у них проявления прикладных
тенденций.
Карл Михайлович Петерсон (1828—1881) стоит в
Московском математическом обществе особняком и по
своему общественному положению, и по своей научной
деятельности. Он был родом из рижской мещанской семьи,
в 1847 г. поступил в Дерптский университет, который
окончил в 1852 г. по физико-математическому отделе-
нию. В это время профессорами математики в Дерпте были:
ученик Бартельса Зенф (1810—1849) и ученик Гаусса
Миндинг (1806—1885). У Зенфа Петерсон слушал курс
теории пространственных кривых и поверхностей; нелиш-
не в связи с этим отметить, что в печатном курсе Зенфа
х) К. Е. S е n f f, Theoremata principalia ex theoria curvarum el
superficierum, Dorpat, 1831.
150
М. Я. ВЫГОДСКИЙ
мы находим часть результатов, впоследствии, лет 30
спустя, найденных Френе и Серре и известных под именем
формул Серре-Френе. Правда, Зенф получает эти резуль-
таты мимоходом и не кладёт их в основу теории простран-
ственных кривых.
Под руководством Миндинга, первого из математиков,
продолжившего исследования Гаусса об изгибании поверх-
ностей, Петерсон подготовлял и своё кандидатское сочине-
ние, на котором рукой Миндинга отмечено: ausgezeichnet
(превосходно). Эта работа не была напечатана: между тем в
ней, как это видно из краткого сообщения Кцезера, бывшего
вначале нашего столетия профессором Дерптского (Юрьев-
ского) университета1), были введены в рассмотрение три
величины, равносильные коэффициентам второй квадратич-
ной формы. Петерсон показал, что эти три величины вме-
сте с коэффициентами первой квадратичной формы одно-
значно (с точностью до движения) определяют поверхность.
(Эта теорема была позднее доказана Бонне (О. Bonnet) в
.1867 г.) Для доказательства Петерсоном были использо-
ваны соотношения, равносильные формулам Майнарди-
Ко дацци (Майнарди опубликовал эти формулы в 1856 г.;
работа Петерсона датирована 1853 г.).
Таким образом, уже из университета Петерсон вышел
зрелым самостоятельным учёным. Что делал Петерсон в
течение 12 лет после защиты диссертации, неизвестно. Во
всяком случае, с Дерптским университетом он связи не
сохранил. Когда он приехал в Москву, также неизвестно.
Известно только, что в 1865 г. Петерсон поступил приват-
ным учителем в Петропавловское немецкое училище в
Москве, где в это время работал также проф. А. Ю. Дави-
дов. Может быть, только этой случайной встрече мы обяза-
ны тем, что, снова найдя среду для научной работы, Петер-
сон получил импульс к дальнейшему творчеству. Он выпу-
стил ещё 6 работ по дифференциальной геометрии на рус-
ском языке (онипомещены в I, II, VIII, IX и X томах «Ма-
тематического сборника») и одну книгу «Uel erCurvenund
Flachen» на немецком языке (М. и Лейпциг, 1858).
х) Это сообщение приведено в статье S t А с k е 1, «Karl Peetr-
gon», Bibliotheca Mathematica, 3-е Folge, т. 2, 1902.
... МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ-ВО И ПОЛ. XIX В. 151
Невозможно в кратких словах сколько-нибудь исчер-
пать богатство идей, заключённых в этих мемуарах. Их за-
пас не исчерпан и поныне, хотя проблемами, которыми
занимался Петерсон, вот уже лет 50 занимаются крупней-
шие геометры мира. Упомянем, например, теорию изгиба-
ния поверхностей на главном основании, которой успешно
занимались и занимаются теперь московские математики
(Б. К. Млодзеевский, Д. Ф. Егоров, С. П. Фиников,
С. G. Бюшгенс, С. Д. Российский, А. Ф. Маслов). Между
тем в своё время работы Петерсона оставались совершенно
незамеченными. Их пе оцепили ни на «далёком» Западе,
ни в России. Правда, в 1879 г., за два года до смерти, Петер-
сон получил степень доктора honoris causa в Новороссий-
ском (Одесском) университете. Но эта степень была при-
суждена ему за его работы по дифференциальным уравне-
ниям, тогда как в этой последней области он, невидимому,
не получил особенно выдающихся результатов.
Работы Петерсона не нашли себе должной оценки даже
в среде Математического общества, членом которого он был.
При жизни Петерсона ни один автор не поместил в Сбор-
нике ни одной статьи, развивающей идеи Петерсона. Лишь
после того, как западноевропейские математики «переот-
крыли» ряд результатов Петерсона, вспомнили о работах
Карла Михайловича. Интересно, что первую ссылку на
Петерсона мы встречаем у Щварца в 1885 г., а первую ссыл-
ку в «Математическом сборнике» у Б. К. Млодзеевского
в 1887 г. Интересно также отметить, что после смерти члена-
учредителя Московского математического общества в орга-
не этого Общества не появилось, вопреки традиции,
никакого некролога о Петерсоне. Протокол заседания
от 21 апреля 1881 г. упоминает лишь: «сделано заявление
о смерти членов Общества К. М. Петерсона и Н. Н.
Алексеева».
Что работы Петерсона, вопреки мнению Млодзеевского1),
не были оценены в Московском математическом обществе,
свидетельствуется и тем, что учёную степень Петерсон по-
г) В «Математическом сборнике» (т. XXIV, стр. 1) Б. К. Млод-
веевский писал: «Что касается работ Петерсона по дифференциаль-
ной геометрии, то они высоко ценились ближайшими товарищами его
по Московскому Математическому Обществу».
152
М. Я. ВЬ.ГОДСКИЙ
лучил не в том университете, где руководящую роль играли
его коллеги. Здесь перед нами уже не только непонимание,
но и невнимание к учителю средней школы. Кстати, лишь
после получения докторской степени Петерсон получил
штатное место в училище, где он 14 лет должен был доволь-
ствоваться местом «учителя по найму».
С. П. Фиников1) говорит о Петерсоне: «Этот учитель сред-
ней школы, не претендовавший на университетскую ка-
федру, был одним из наиболее талантливых геометров с
живым и ярким воображением, намного опередившим своё
время». Петерсоном интересовались в Москве так мало, что
первый из русских математиков, продолживший исследова-
ние Петерсона, Б. К. Млодзеевский мог получить скудные
биографические сведения о своем предшественнике... лишь
в Киле у Штеккеля.
Следующие тома «Математического сборника» редакти-
ровал новый президент Математического общества А. Ю.
Давидов, и его научные взгляды и вкусы явственно отра-
жаются на направлении «Математического сборника» в
течение целого пятнадцатилетия.
Август Юльевич Давидов (1823—1885) родился в Либа-
ве в семье врача и получил среднее образование дома; в
1841 г. он подал заявление на медицинский факультет
Московского университета. Вступительный экзамен по
математике он сдавал Брашману, и тот со свойственной ему
прозорливостью угадал в юноше незаурядные математи-
ческие способности и вскоре склонил Давидова перейти на
физико-математическое отделение.
В 1845 г. А. Ю. Давидов окончил университет и в 1848 г.
защитил магистерскую диссертацию на тему «Теория равно-
весия тел, погружённых в жидкость». Выбор этой темы об-
наруживает влияние Брашмана. Это же влияние сказы-
вается и в том, что Давидов проявил большой интерес
к теории вероятностей и её приложениям.
Будучи назначен адъюнктом Московского университета
в 1850 г., Давидов начал свою преподавательскую деятель-
ность чтением курса теории вероятностей. Кроме того, за
) В предисловии к книге «Изгибание на главном основании».
М. 1937.
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ВО II ПОЛ. XIX В. 153
1854—1857 гг. он напечатал статьи о приложениях теории
вероятностей к стастистике. В дальнейшем Давидов зани-
мался интегрированием уравнений в частных производных
высших порядков, теорией эллиптических функций и дру-
гими вопросами анализа. По большей части эти вопросы
имеют близкое отношение к теоретической механике, кото-
рую особенно любил Давидов. И именно в этой области его
научные заслуги наиболее значительны. Число новых ре-
зультатов, полученных А. Ю. Давидовым в механике, пожа-
луй, и не очень велико: Давидовне слишком любил утруж-
дать себя чтением литературы. Благодаря этому он
не раз публиковал результаты, уже открытые за 20—30
лет до него. Но А. Ю. Давидова это мало смущало; он спра-
ведливо полагал, что научную значимость имеет не только
результат, но и метод. А методы А. Ю. Давидова, по автори-
тетному свидетельству знаменитого его ученика Н. Е. Жу-
ковского1), отличались своеобразием и богатством идей.
Впрочем, не всегда и результаты Давидова были уже из-
вестными. Так, его работа о плаваниитрёхгранпой призмы,
напечатанная в журнале Крелля за 1849 г., установила,
что число положений равновесия прямой трёхгранной
призмы, плавающей при горизонтальной образующей, не
может быть больше 12. По прежним исследованиям верхняя
граница была выше (15). Обнаружив, что равносторонняя
призма при плотности, заключённой между 7/,в и */<*> будет
иметь точно 12 положений равновесия, Давидов оконча-
тельно решил этот вопрос гидростатики.
Продолжая педагогическую традицию своего учителя
Брашмана, Давидов создавал в Московском университете
школу теоретической механики, и подобно тому, как Браш-
ман воспитал Чебышева, Давидов оказал большое влияние
на замечательного русского учёного Н. Е. Жуковского
(1847—1921), отца русской авиации и создателя ЦАГИ.
Педагогическая деятельность Давидова не ограничива-
лась рамками Университета; он посвятил много труда рабо-
те в средней школе.В течение 25 лет он был инспектором и
членом попечительского совета над частными уч бными
заведениями Москвы. В качестве такового он ежегодно
х) «Математический сборник», т. XIII, стр. 19—50.
154
м. я. выгодскии
тщательно прочитывал все письменные работы выпуск-
ников и на основании сделанных наблюдений рекомен-
довал различные мероприятия педагогического характера.
Давидов, начиная с 1863 г., выпускал и свои учебники
для школ по геометрии, алгебре, арифметике и тригоно-
метрии. Учебники эти, может быть, недостаточно учиты-
вают возраст учащихся и, особенно в начале своём, они
представляются учащимся трудными, но в других отноше-
ниях—это ценные пособия, по которым велось препода-
вание многие десятилетия и которые сейчас незаслу-
женно забыты. В своё время учебники Давидова были
свежи и новы тем, что они содержали не только теоре-
тический материал, но и хорошо подобранные задачи
и что в теоретическом изложении привлекали свежий
материал.
Так, в учебнике геометрии мы находим паскалеву
теорему о шестиугольнике, вписанном в круг; некоторые
сведения об инверсии, о полюсах и полярах; теорему Чевы,
теорему Менелая; понятие о полном четырёхугольнике и
гармоническом делении и т. д.
Технико-теоретические и педагогические интересы
А. Ю. Давидова не могли не отразиться на деятельности
Московского математического общества и характере его
печатного органа. На заседаниях общества часто заслу-
шивались доклады по механике не только теоретической,
но и прикладной, по физике не только вычислительной,
но и экспериментальной, по астрономии не только вычи-
слительной, но и описательной.
Откроем, например, протоколы 12 первых после офици-
ального оформления Общества заседаний (с 15/Ш 1869 г.
по 17/Х 1870 г.).
Из общего числа 24 прочитанных докладов прикладным
вопросам было посвящено 10; среди них, например, док-
лады об устойчивости плавающего тела (Преображенский),
о колебаниях в среде постоянной упругости (Умов), об
опыте Шведова, доказывающем существование интерфе-
ренции электрических волн (Любимов), об удельных тепло-
ёмкостях растворов (Булыжинский) и т. д.
Занималось Общество и вопросами философско-науч-
ного характера. Так, 16 декабря 1872 г. Ф. А. Слудский
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ВО П ПОЛ. XIX В. 155
сделал сообщение «Об одном доказательстве ограничен-
ности пространства». 17 ноября 1873 г. Столетов сделал
доклад «О дуалистическом и унитарном воззрении в элек-
тростатике».
Ещё большей широтой отличалась программа журнала,
издаваемого Обществом. Начиная со II тома и вплоть до
X тома, «Математический сборник» имел два отдела. Пер-
вый содержал научные исследования по всем упомянутым
выше разделам, второй носил популярно-научный характер
и был рассчитан на лиц, с высшей математикой не знакомых.
Впрочем, многие из статей этого раздела носили довольно
серьёзный характер. Здесь же во втором отделе читатель
мог найти задачи по элементарной математике, интересные
сообщения по истории математики, биографии, краткие
обзоры деятельности научных обществ за истекший год,
рецензии на элементарные школьные руководства и т. п.
Начиная с V по X том, в качестве особого приложения
к «Математическому сборнику» давалась по частям
«История геометрии» Шаля, переведённая вице-прези-
дентом Московского математического общества В. Я. Цин-
гером (на титульном листе переводчик не указан).
Этот второй отдел «Сборника» исчез из него, начиная
с XI тома (1882), с тем, чтобы больше уже не появляться.
Правда, с 1885 г. часть тематики второго раздела могла
найти себе место в журнале «Физико-математические науки
в их прошлом и настоящем». Здесь уместно сказать не-
сколько слов о редакторе этого журнала В. В. Бобынине,
который, хотя и принадлежал к числу научных работников
Московского университета и членов Московского мате-
матического общества, но всю свою жизнь работал в том на-
правлении, от которого интересы московского математи-
ческого коллектива в последней четверти XIX в. отстояли
довольно далеко.
Виктор Викторович Бобынин (1849—1919) происходил
из обедневшей дворянской семьи; в 1872 г. он окончил фи-
зико-математический факультет Московского университе-
та и стал преподавать математику в различных средних
учебных заведениях. Педагогическая деятельность пробу-
дила в нём страстный интерес к истории математики. При-
дя к убеждению, что история математических наук может
156
И. Я. ВЫГОДСКИЙ
дать драгоценнейшие указания для их преподавания, Бобы*
нин неустанно пропагандировал эту мысль в течение всей
своей жизни.
Литературная деятельность В. В. Бобынина начинается
с 1875 г. В 1882 г. Бобынин выпустил своё исследование
«Математика древних египтян», выполненное на основе
только что вышедшего (эйзенлоровского) издания Лондон-
ского математического папируса. Это исследование стоит
в одном ряду с работами западноевропейских историков
(Кантора, Роде и др.) на ту же тему. Оно дало Бобынину
степень магистра, и в том же 1882 г. Бобынин становится
приват-доцентом Московского университета. Но в е чле-
ны Московского математического общества он удостоил-
ся избрания лишь в 1886 г., когда выпустил свои «Очер-
ки развития физико-математических знаний в России» (ч.1).
Ни упомянутые, ни другие многочисленные работы
Бобынина не доставили ему докторской степени, а профес-
сором Московского университета он стал лишь после
Октябрьской революции. К сожалению, на Западе труды
Бобынина получили должную оценку гораздо раньше,
чем на его родные. Его работы печатались в иностран-
ных журналах (преимущественно в Bibliotheca Mathema-
tical и имя его пользовалось за границей заслуженным
авторитетом. В 1908 г. Бобынин, по предложению исто-
рика математики Кантора, написал для IV тома канторов-
ского «Курса истории математики» (этот том охватывает
вторую половину XVIII в.) статью «Элементарная гео-
метрия», которая была напечатана также и на русском
языке1).
Бобынин много работал по истории точных наук в Рос-
сии. Он составил библиографию русской физико-математи-
ческой литературы от начала книгопечатания до конца
XIX в.2). Он был первым русским историком математики
и первым историком русской математики. Однако в Мос-
ковском математическом обществе он был совершенно
одинок. «Математический сборник» не напечатал ни одной
его работы.
9 В журнале Министерства народного просвещения ва 1908 г.
2) Напечатанная часть этой библиографии доходит лишь до
начала XIX в.
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ВО II ПОЛ. XIX В. 157
Здесь сказывается перемена направления деятельности
самого Общества, связанная с болезнью и последовавшей
вскоре смертью Давидова, но имеющая и более глубокие
причины, о которых будет ещё речь ниже.
Чтобы убедиться в том, что упомянутая перемена дей-
ствительно имела место, достаточно сравнить содержание
’ первого отдела старого «Математического сборника» с
«Математическим сборником» последующих годов. Мы при-
ведём сейчас цифровые сведения о тематике статей «Сбор-
ника». Чтобы не вносить произвола при отнесении статьи
к той или иной дисциплине, мы воспользуемся той класси-
фикацией, которая дана в указателе1) содержания 15 пер-
вых томов «Математического сборника». Сообразно с этим
будут сравниваться 10 первых томов и 5 последующих или
по времени 15 первых лет и 10 последующих.
Мы получим тогда следующую картину:
Раздел В томах 1—10 В томах 11-15 Всего
Анализ2) 30 84 114
Теория прерывных функций . 4о И 51
Геометрия 13 7 20
Тесрия вероятностей .... — 2 2
Механика 45 8 53
Физика 18 4 22
Амрономия 18 4 22
164 12) 284
Как мы видим, в старом «Математическом сборнике» на
один том приходилось в среднем три работы по анализу; в
новом число это возросло до 16,8, т. е. более чем в пять раз:
если взять среднегодовое число статей, то в старом «Сбор-
нике» оно равно 2, в новом 8,4, т. е. имеем рост более чем
Указатель статей, содержащихся в первых 15 томах «Матема-
тического сборника», М., 1893.
2) К разделу анализа в указателе отнесг н также и ряд работ
по алгебре; в нарушение вышеупомянутого принципа я исключил
ид этого раздела работы по дифференциальной геометрии, отнеся их
в раздел геометрии.
158
м. я. выгодскии
в четыре раза. Удельный вес статей по анализу составля-
ет в старом «Сборнике* 18%, в новом—70%. Этот рост со-
провождается стремительным падением по всем остальным
отделам. Доля «Теории прерывных функций» (т. е. теории
чисел и связанных с ней вопросов алгебры, а также исчис-
ления конечных разностей и т. п.) резко падает, потому
что несколько иссяк поток работ Бугаева и его последова-
телей. Что касается остальных разделов, то сокращение их
вызвано не только сознательным ограничением тематики,
но, несомненно, также и уменьшением интереса к вопро-
сам конкретного характера.
Параллельно с этим можно заметить и сдвиг в философ-
ских позициях московских математиков. Конечно, нет
оснований полагать, что все математики, группировавшие-
ся около Московского университета и состоявшего при нём
математического общества, имели единую точку зрения
на все философско-научные вопросы. Однако, поскольку на
страницах «Математического сборника» мы не раз встре-
чаем полемику по философским вопросам, поскольку/
с другой стороны, эта полемика никогда не ведётся между
авторами, выступающими в «Сборнике», а всегда направ-
лена вовне, можно говорить о некоторых позициях, на
которых стояло официальное руководство Московского
математического общества. И вот эта позиция заметно
меняется при переходе через рубеж XI—XII томов. Лучше
всего это видно по статьям, относящимся к обоснованию
механики и геометрии.
В старом сборнике эти статьи стоят в общем на мате-
риалистических позициях. Пусть этот материализм непо-
следователен, пусть сами авторы чураются слова «матери-
ализм», который, выйдя из кабинета и аудиторий на рынок
и площадь, надеется победить весь мир1). И то и другое имеет
свои корни в том, что эти авторы не могут и не хотят быть
материалистами в вопросах социальных, что они боятся
широкой пропаганды материалистических взглядов. Но
в вопросах «кабинетной» науки они не только допускают
эту пропаганду, но и сами её ведут.
О Ф. А. Слудский, Механика будущего. «Математический
борник», т. IX, отд. 2, стр. 23.
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ВО II ПОЛ. XIX В. 159
Примером такой пропаганды являются две статьи Ф. А.
Слудского. Обе они относятся к вопросу о механических си-
лах. В первой Слудский берёт под обстрел только что вышед-
шую «Механику» Кирхгофа1).
Как известно, Кирхгоф излагает свой курс механики,
устраняя из рассмотрения понятие силы как причины, вы-
зывающей или стремящейся вызвать движение. Не отри-
цая пользы этого понятия при первоначальном обучении,
Кирхгоф находит, что оно страдает «неясностью, от которой
не могут быть освобождены понятия причины и стремле-
ния»2) и поэтому «желательно удалить эти темноты из
механики, хотя бы даже это было возможно лишь ценой
ограничения её задач». Термин «сила» употребляется
Кирхгофом лишь как синоним ускорения или произвольно
выделяемого слагаемого ускорения.
Слудский соглашается с Кирхгофом в том, что введение
в механику понятия силы вызывает некоторые неясности;
при начальном преподавании их приходится обходить, но
в дальнейшем по мере овладения фактическим материалом
эти неясности сами собой устраняются. Попытка же Кирх-
гофа во избежание этих неясностей вовсе устранить поня-
тие силы вызывает резкое возражение Слудского. Он не
может согласиться с тем, что механика сведена только к
математическому описанию движения: «понятие о силе, как
причине движения физических тел, есть душа механики;
оно оживотворяет сырой научный материал и создаёт из
него единое целое3). «Описать движение—значит, по его
(Кирхгофа) мнению, написать уравнение движения в про-
стейшей форме; он говорит, что происходящие в природе
движения, как показывают опыты (sic), описываются всего
проще при помощи дифференциальных уравнений второго
порядка. Вряд ли кто усомнится в том, что Кирхгоф не
делал попыток описывать происходящие в природе движе-
ния при помощи дифференциальных уравнений третьего и
Ф. А. Слудский, Несколько слов o’Kirchhof’s Vorlesun-
gen Cher math. Physik, «Математический сборник», т. VII, отд. 2,
стр. 1—14.
2) Kirchhof, Vorlesungenuber math. Physik, 1877, стр. III.
8) Цит. статья, стр. 9.
160
М. Я. ВЫГОДСКИЙ
высших порядков... Один из его примеров—движения пада-
ющих тел — прямо ведь показывает, что по крайней мере
некоторые движения описываются гораздо проще урав-
нениями третьего порядка...».
Даже Слудский указывает, что с точки зрения Кирх-
гофа в механике не должно быть места статике и что Кирх-
гоф непоследователен, когда вводит статику в свой курс.
Он приводит слова Кирхгофа: «Чтобы перейти от случая
движения к случаю покоя, мы должны принять действую-
щие силы такими,чтобы определяемые ими ускорения исчез-
ли: о таких силах говорят, что они находятся в равнове-
сии», и замечает, что в системе Кирхгофа эти положения не
имеют смысла. «Можно назначить, ничем не рискуя, милли-
онную премию за решение задачи: найти хоть малейший
смысл в кирхгофской псевдостатике».
Через четыре года Слудский вновь возвращается к во-
просу об основных понятиях механики. Полемизируя с
астрофизиком, иезуитом Секки, Слудский отмечает, что
механическое объяснение природы, развившееся с особой
силой в середине XIX в., принесло замечательные плоды,
благодаря чему естествознание не могло не признать меха-
нику основной естественной наукой. «Одновременно, и,
повидимому, не совсем случайно, вместе с усилившимся
стремлением к механическому объяснению природы возник-
ло стремление реформировать самую науку о движении и
силах. Основное механическое понятие—понятие о силе—
показалось не совсем пригодным и даже ненужным...».
Слудский вновь обрушивается на это течение и, в частно-
сти, на Секки, который для устранения общего понятия
силы как причины движения вводил в рассмотрение толчки,
имеющие место между частицами материи. Действие на рас-
стояние Секки отрицал. Слудский указывает, что дально-
действию механика не приписывает абсолютного значения;
подобно тому как прикосновение атомов, по Секки, яв-
ляется только «кажущимся», ибо абсолютное геометриче-
ское прикосновение в природе не имеет места, так же,
говорит Слудский, и дальнодейст ие является «кажущим-
ся» дальнодействием. Интересно, конечно, выяснить, как
передаётся действие через пустоту; не исключено, хотя
к мало вероятно, что дальнодействие можно объяснить
MATEM.Vj 1IKX В MOCK. N HilBAPGliTETl LOH Ho.i. XlX B. |(l|
ударами частиц; но этого рода объяснения могут иметь
значение ниш. тогда, когда уравнения динамики будут
выведены из теорем удара. Пока же, говорит Слудский.
останемся на позициях Ньютона ине будем отказываться
от дальнодействия и от общего понятия силы. Прежде в на-
уке господствовал идеализм, ci поэтому «многие серьёз-
ные физики стали отрицать самое вещество, признавая
одни силы». Воцарившийся теперь материализм, пола-
гает Слудский, ведёт к тому, чтобы признавать только
одно вещество, отрицая силы. II Слудский заканчивает
статью утверждением, что науку нельзя подчинить тому
или иному предвзятому философскому’ мнению, чти такого
рода гипотезы науке, по словам Ньютона, вовсе не нужны.
Из изложенного видно, что Слудский, не желая быть
материалистом, критикует современные ему воззрения
на основы механики по существу с материалистических
позиций: и его критика, хотя и менее глубокая, чем
критика Гельмгольца1), питается одним и тем же стрем-
лением подчеркнуть объективную роль причинности.
Вопросу об основаниях геометрии «Математический
сборник» также уделял место. В 111 томе сборника был
помещён перевод переписки Гаусса с Шумахером, тогда
ещё недавно опубликованной и мало известной в России2)
там же3) дан русский перевод «Геометрических исследова-
ний» Лобачевского. Этим переводам предпослано неболь-
шое введение А. В. Летникова (под инициалами А. Л-в),
который, по видимому, и был переводчиком упомянутых
статей.
Алексей Васильевич Летников (1837—1888), сын обед-
невшего дворянина, служившего бухгалтером в Москов-
ской казённой палате, учился в Московском межевом ин-
ституте; по окончании его (1856) был командирован для
пополнения математического образования в Московский
университет, где слушал лекции два года, а затем в Париж,
где он слушал лекции лучших математиков в Политехни-
ческой школе и в Сорбонне. По возвращения в Москву
Ч Н. Helmholz, Vorlesungen fiber math. Physik. т. I, стр. 11 Мф
Ч «Математический сборник», т. III. 1868, разд. 2 сгр. 82—88.
8) Стр. 88—120.
П Исторш.о--.!:;трипт. исследовании
162 М. Л. ВЫГоДСКНЙ ________________
был назначен преподавателем лМежевого института. После
получения учёной степени (1867 г.) занял кафедру высшей
математики в Московском высшем техническом училище,
только что основанном. Большая эрудиция и педагогиче-
ские способности Летппкова поставили ого в ряд луч-
ших московских преподавателей математики.
Летников политически бы. i весьма реакционным чело-
веком1). Но в вопросе о неевклидовой геометрии он занимал
позицию весьма передовую. Невзирая на традиции Остро-
градского и Бупяковского, недооценивших работы Лоба-
чевского. Летников говорит: «Лобачевский показывает,
что пр существует никакой причины утверждать а прпорп,
что сумма углов треугольника но может быть меньше
двух прямых углов и даже утверждает, что, кроме астроно-
мических наблюдений, мы не имеем другого средства удо-
стовериться в справедливости вычислений обыкновенной
геометрии. Такие смелые и оригинальные мысли, развива-
емые строго последовательно, очевидно имеют право на
внимание».
Конечно, это отзыв сдержанный, но во всяком случае
вполне доброжелательный. Летппкова нисколько не коро-
бит мыс л ь о том. что в справедливости геометрических истин
пас убеждает в конечном счёте опыт.
Совсем иной позиции держится но этому вопросу Мо-
сковское математическое общество через 25 лет. II января
1894 г. if резидент Московского математического общества
В. Я. Ципгер выступил на Съезде естествоиспытателей
и врачей с докладом «Недоразумения во взглядах на основа-
ния геометрии» 2).
«Некоторые из представителей нового учения,—говорит
Цингер,—пришли к заключению, что вопрос о том, какие
аксиомы лежат в основании геометрии, может быть решён
только посредством внешнего опыта. В этом мнении чувству-
ется влияние материалистических воззрений, которые в
пауке текущего столетия составляют самое слабое место
и самый тяжёлый грех. Я говорю об основном догмате
’) См., например, отрывок из речи Циигера в некрологе, посвя-
щённом сто памяти («Математический сборник», т. XIV, стр. XXI).
2) Речь эта была издана отдельной брошюрой.
МАТЕМАТИКА В Моск. УНИВЕРСИТЕТЕ во И ИОЛ. XIX В. 1G.J
эмпиризма, заключающемся в отрицании духовной сущ
кости сознания и духовного бытия вообще...».
В дальнейшем Цпнгор излагает своё мнение о характере
геометрических аксиом; оно состоит в апелляции к «воз-
зрению»: «способность воображать внешние предметы...
ни в малейшей степени не подчинена физическим законам».
Мы не будем следить за аргументами Цингера; ничего суще-
ственно нового после Канта он не сказал. Но, пожалуй,
любопытно привести ого критические замечания по адресу
Лобачевского, Гельмгольца и Римана. Цпнгор приводит
слова Римана: «теоремы геометрии не могут быть выведены
из общих понятий о величине; свойства, которыми отли
чается пространство от других мыслимых трёхкратно
протяжённых величин, могут быть выведены только из
опыта», и возражает: «один опыт может приводить к одним,
другой—к другим свойствам пространства: нынешний
опыт может завтра замениться другим. Таким образом
наука, древнейшая по происхождению и лежащая в осно-
ве всех других наук, наука Архимеда и Ньютона, ставится
в комическое положение неустойчивости... Геометриче-
ские представления п их законы имеют чисто умственное
происхождение».
Сдвиг в философско-научных воззрениях и научных инте-
ресах многих видных московских математиков нужно, как
мне кажется, поставить в связь с теми сдвигами, которые
произошли в умах части русской интеллигенции на почве
изменившихся исторических условий.
В 60-х годах, когда реформы Александра И открыли
широко двери для развития капитализма, среди русской
интеллигенции большое распространенно получили мате-
риалистические веяния; возрос интерес к точным наукам,
пробудилось критическое отношение к устоявшимся идеи
логическим нормам («нигилизм»), возникали радикальные
и революционные кружки. В 80-х годах русский капита-
лизм нашёл общин язык с помещичьей реакцией и повё i
жестокую борьбу с нарождавшимся рабочим движением:
буржуазная интеллигенция в своей массе стала на сторону
«порядка», т. е. оказалась оплотом полицейско-бюрократи-
ческого гнета; различные оттопки идеалистической фило-
софии стали находить для себя всё более благоприятную
И*
I (Л АГ. н. ВЫГОДСКИЙ
почву. В науке начал свивать себе ирочное гнездо пресло-
вутый «академизм».
Если «смена вех» в Московском математическом обще-
стве была обусловлена сдвигами, происшедшими на соци-
альной арене, то момент, когда произошла эта смена, не
случайно совпадает с переменой в составе президиума.
Пока был жив А. К). Давидов, сохранялось и научное на-
правление, которое он возглавлял с начала существования
Общества: человеку науки в конце жизненного пути не-
легко переходить на новые рельсы. В 1885 г. Давидов умер.
Общество постановило посвятить его памяти XIII том
«Сборника» и испросить из средств Министерства народного
просвещения 1 000 руб. па издание этого тома’). На следую-
щем заседании 18 февраля 1886 г. было доложено об ассиг-
новании испрашиваемой суммы, и общество произвело
очередную передвижку; президентом был избран В. Я. Цин-
гер, вице-президентом Н. В. Бугаев и секретарём 11. А.
Некрасов.
Василий Яковлевич Цингер (1836—1907) был сыном
преподавателя математики; в 1853 г. он поступил на физи-
ко-математический факультет Московского университета,
где в это время, кроме Брашмана и Зернова, преподавал
уже и Давидов. По окончании Университета (1857 г.) он
был оставлен при нём и в 1862 г. защитил диссертацию
на тему «Способ наименьших квадратов»; тема эта была да-
на ему Брашмапом. Впоследствии Цингер не возвращался
к занятиям аналитическими вопросами, а отдался геоме-
трическим и техническим работам; больше всего его при-
влекала проективная геометрия, в которой он сначала
ценил преимущественно методы Шаля, а затем методы
Штейнера. Курс проективной или, как он тогда назывался,
«высшей» геометрии Цингер читал многократно и блестяще.
Он внушал студентам любовь к синтетическим методам и
учил их, прежде всего, отчётливо воспринимать геометриче-
ский образ как таковой.
Как и Давидов, Цингер стремился к тому, чтобы как в
преподавании, так и в научных работах обходиться воз
можно более элементарными соображениями. Педагогп-
*) «Математический сборник», т. XIII стр. 23.
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ВО II ПОЛ. XIX В. 165
ческое значение деятельности Цингера, несомненно, очень
велико; он оказал влияние па направление научной дея-
тельности ряда математиков: Н. Е. Жуковского, К. А. Ан-
дреева. Б. К. Млодзеевского, Д. Ф. Егорова. Научная цен-
ность его математических работ не столь значительна;
впрочем, Н. Е. Жуковский и другие математики отмечали
изящество изложения и уподобляли математические про-
изведения Цингера картинам великих художников, кото-
рые навсегда врезываются в воображение зрителя. Цпнгер
был человеком с разносторонними вкусами и посвящал
много времени занятию предметами, далёкими от матема-
тики. В особенности много занимался он ботаникой, и в
этой области его работы, невидимому, более ценны, чем
работы математические. Цпнгер посвящал много времени и
занятию философией. Как мы видели, он примкнул к Канту.
За девять лет до смерти Цпнгер оставил работу в Уни-
верситете и поселился в деревне. На посту президента
Московского математического общества его сменил II. В.
Бугаев.
Николай Васильевич Бугаев (1837—1903) был сыном
военного врача, сосланного при Николае I па Кавказ.
Десятилетним мальчиком оп был отправлен отцом*в Мо-
скву для получения образования. Ещё в гимназические го-
ды Бугаев начал сам добывать средства, занимаясь репети-
торством. В Университет он поступил в 1855 г. Мы видели,
что в это время прикладная математика была в Московском
университете в большом почёте. Бугаев, видимо, был осо-
бенно увлечён техническими приложениями математики,
ибо по окончании Университета (1858) поступил в Военно-
инженерное училище в Петербурге. Там он избрал теоре-
тическое отделение, где среди профессоров выделялся акад.
Остроградский. Однако Бугаев но окончил училища: со
второго курса он ушёл вместе с группой слушателей
в виде протеста против увольнения одного из товарищей
(причина не известна; может быть, здесь была политиче-
ская подоплёка1)).Тогда Бугаев снова вернулся в Универсп-
’)* Андрей Белый (псевдоним Б. II- Бугаева, сына Н. В. Бугаева)
определённо это утверждает ( Па рубеже двух столетий», ивд. 2-е,
стр. 20.
166
м» я. вы год скип
тет. В 1863 г. он защитил магистерскую диссертацию ^Схо-
димость бесконечных рядов по их внешнему виду» и полу-
чил длительную заграничную командировку. В течение 21/2
лет Бугаев оставался за границей, слушал Куммера, Вейер-
штрасса, Лиу билля, Бертрана, Серре, Шаля, Ламе, Дюга-
меля и других математиков. В 1865 г., вернувшись в Мо-
скву, защитил докторскую диссертацию «О числовых тож-
дествах, находящихся в связи с символом Е». был назначен
профессором Московского университета и примкнул к
только что образовавшемуся Математическому обществу.
Он внервые читал в Москве курс теории функций ком-
плексного переменного; его .лекции но другим дисци-
плинам (вариационное исчисление, исчисление конечных
разностей, теория эллиптических функций) также изоби-
ловали свежим материалом.
Несмотря на сравнительно молодые годы, Бугаев, чело-
век в высшей степени темпераментный, приобрёл в Мате-
матическом обществе большое влияние. В частности, это
влияние сказалось при выборе языка «Математического
сборника».
Большинство членов Общества склонялось к тому,
чтобы - статьи в журнале печатались на иностранных
языках. Бугаев энергично протестовал против этого, за-
явив, что «кто не уважает родного языка, тот не заслужи-
вает уважения других. Когда на русском языке станут
печататься серьёзные математические работы, иностранцы
начнут заниматься нашим языком; если же они этого не
сделают, то будут в потере они, так как мы будем знать
больше их». В утверждённый устав Математического обще-
ства сообразно с этим был внесён следующий пункт: «Рефе-
раты действительных членов должны быть как сообщаемы,
так и печатаемы в изданиях общества не иначе как на рус-
ском языке; но от членов-корреспондентов и посторонних
лиц, не знающих русского языка, могут быть допу-
скаемы также статьи на общеупотребительных европейских
языках».
В течение первых 10—12 лет своего существования
«Математический сборник» был почти не известен в Запад-
ной Европе. С 1873 г. начинается регулярный обмен изда-
ниями между Московским и Французским математически-
ми обществами, ас 1881г. Математическое общество полу-
чает уже целый поток предложении об обмене от ряда
иностранных обществ и университетов. Благодаря
этому обмену Математическое общество могло составить
большую и ценную библиотеку; раньше же оно долж-
но бы.Го за скудостью своих средств прибегать к пользо-
ванию личными экземплярами книг отдельных своих
членов.
Наряду с активным участием в делах Математического
общества. Бугаев проявлял большую энергию в деле про-
паганды и популяризации технических приложении мате-
матики. В конце 60-х годов он становится одним из учре-
дителен «Общества распространения технических зна-
ний» и возглавляет учебный отдел этого общества.
В. 1875 г. некоторые руководители общества подверглись
репрессиям (каким именно и за что—мне не довелось уста-
новить). а остальные, репный было ликвидировать общест-
во. Бугаев убедил их продолжать работу. В 1894 г. учебный
отдел, приветствуя Математическое общество с его
25-летним юбилеем, it своём адресе глухо упомянул об
этом факте как о заслуге Бугаева.
Бугаев выступил также с проектом учреждения
технических отделений при физико-математических фа-
культетах университетов. Этот проект не был принят
в своё время, по для нас он небезынтересен потому,
что многие мысли Бугаева вполне созвучны нашему
времени.
«Обыкновенно говорят,- пишет Бугаев.—что университет
должен быть тем местом, где преподаётся только чистая
наука. В нём нет места наукам прикладным. Но разве раз-
деление наук на чистые и прикладные лишает последние
их содержания? Паука едина. Вопросы так называемых
прикладных наук суть те же вопросы чистой пауки. Они
отличаются только большей специальностью, а иногда и
большей трудностью. То обстоятельство, что они вызывают-
ся практическим и потребностями жизни, не тол ько не умен ь-
шает, а увеличивает их значение. Разве задача университе-
тов стоять тол ько в пределах вопросов, нс имеющих ника-
кого отношения к жизни?.. Многие теоретические вопросы
развилке ьп а почве чисто практических задач. Разве вопро-
к;; . м. я. выгодский
сы строительного искусства не вызвали появление начер-
тательной геометрии и математической теории упругости;
разве вопросы мореплавания не содействовали развитию
небесной механики?»
Исходя из этих соображений, Бугаев выставил следую-
щие пять пунктов:
«1. Полезно введение технических отделов прифизико-
математическом факультете.
2. Такие отделения составят существенное дополнение
к общей системе как университетского, так и технического
образования.
3. Для успешного прохождения курса этих отделений
следует прибавить лишний год.
4.. Высшие технические школы должны играть роль
высших технических институтов, в которых принимают
меры для того, чтобы задачи прикладных наук пред-
ставить в их современной практической обстановке.
Ф ] 5. В университетских технических отделениях можно
обращать более внимания на теоретическую разработку
вопросов прикладных наук».
Интересовался Бугаев и преподаванием в средней
школе. Он горячо восставал против того, чтобы средняя
школа с первых же годов обучения брала установку па опре-
деление профиля преподавания. В начальные годы школь-
ное обучение, по мысли Бугаева, должно было иметь еди-
ный характер и лишь в последние три года среднего обра-
зования начинается раздвоение на два отделения, в одном
из которых центр тяжести составляют точные, в другом—
гуманитарные науки. Школа должна, говорит Бугаев,
приучать учащегося к самостоятельной работе; для этого
он предлагает в старших классах вести как классные заня
тия, так и лекционное преподавание. Он предлагает выде-
лить один свободный день для самостоятельных занятий:
«В человеке дороже знаний должна цениться способность
самостоятельно, активно и энергично добывать эти знания,
а это достигается только тогда, когда школа оставляет
учащемуся свободное время для проявления самодеятель-
ности и личной энергии».
Ещё в 1869 г. в своей речи на торжественном собра-
нии Московского университета, посвящённом памяти
МАТЕМАТИКА в МОСК. УНИВЕРСИТЕТЕ LO II ПОЛ. XIX В. (69
Н. Е. Зернова1), Бугаев требовал, чтобы математическое
преподавание в средней школе захватывало Элементы
высшей математики до такого объёма, «который дал бы
почувствовать, что после Евклида жили Декарт, Лейбниц,
Ньютон, Монж. Необходимо, чтобы хотя бы в общих чер-
тах понятно было то глубокое значение, которое имеют
методы математики в сознании современного человече-
ства. Общему образованию принадлежит также задача сде-
лать нагляднее и очевиднее её солидарность с приклад-
ными науками».
Об общефилософских взглядах Бугаева в эту эпоху мож-
но судить лишь предположительно по его литературным
и общественным выступлениям. Во всяком случае в много-
численных высказываниях своих Бугаев не проявляет
никакой склонности к идеалистическим выводам и мисти-
ческим спекуляциям, которые характерны для послед-
них 20 лет его жизни.
Л. М. Лопатин, выступая после смерти Бугаева с речью
«Философское мировоззрение Бугаева»2), сказал: «Фило-
софские идеи Бугаева стали впервые слагаться в эпоху ши-
рокого господства позитивизма в нашем интеллигентном
обществе. И он долгое время был убеждённым позитиви-
стом... Я бы не мог с точностью сказать, когда именно
у Николая Васильевича произошёл поворот от позитивизма
к своеобразному метафизическому миросозерцанию, ко-
торое он потом ироноведывал всю жизнь. Мне представ-
ляется, что перемена должна относиться к 80-м годам».
Этому свидетельству черносотенного философа мы мо-
жем поверить; мы видели выше, что к середине 80-х годов
руководители Математического общества стали переходить
на идеалистические позиции. У Бугаева этот переход при-
нял, пожалуй, наиболее резкие формы. Свои мистические
настроения он начал ставить в прямую связь со своими мате-
матическими работами.
Дать оценку научной деятельности Бугаева для че-
ловека стоящего, подобно автору этих строк, вдалеке от
теории чисел, к которой относится большинство работ
1) «Математика как орудие научное и педагогическое» М., 1869.
-) «Математическии сборник», т. XV. стр. 272—292.
1'0
М. Я. ВЫГОДСКИЙ
Бугаева, чрезвычайно затруднительно. Ученики Бугаева —
А. П. Минин, Л. К. Лахтин и П. А. Некрасов—неодно-
кратно превозносили научные заслуги своего учители,
по на их оценки трудно положиться, как это можно видеть
из такого примера. Лекции Бугаева, которые, может быть,
и были интересными по форме (чего, однако, не видно по
изданиям этих лекций), во всяком случае в 90-х годах,
несомненно, страдали важными дефектами по существу.
Так, в литографированном курсе анализа, читанном
в 1898 г., мы находим такие курьёзы1):
Стр. 9. «Теорема 1. Разность двух бесконечно
малых есть величина бесконечно малая. Дано lim а—0;
lim 3 = 0; требуется доказать: lim (а — р) = 0. Дока-
з а т е л ь с т в о: а— 3<а. Отсюда очевидно, что
Lim (а —р) = 0».
Что это нс фантазия студента, составлявшего записки
(лекции вышли без просмотра профессора), видно из того,
что «на основании» теоремы 1 от противного доказывается
теорема 2: «алгебраическая - сумма бесконечно малых
величин есть величина бесконечно малая». Невозможно
допустить, чтобы студент додумался до такого выверта.
Стр. 114, § 10 («О разложении функций вообще»): «Вся-
кая конечная и непрерывная функция может быть разло-
жена в бесконечный рядно теореме Тэйлора или по теореме
Маклорена (ч. 1, § 31,32). Рядом Маклорена, дающим раз-
ложение функции независимо от приращения перемен-
ного, пользуются по преимуществу. Задача сводится к
тому, чтобы подметить закон составления высших провзвод-
иыхпри а=0 и вставить их значения в строку Маклорена»2).
Стр. 141, § 22 («Приложение теории неопределённых
выражений к учению о сходимости рядов по их внешнему
виду»): «Выражение lim —-J, входящее в основной при-
u,i
знак сходимости Д'Аламбера, есть, собственно, неопре-
делённое выражение, так как (п„)м_ м = 0; («п41)ll^oo = 0.
9 Они почти дословно сохранены в печатном курсе II. В. Бугае-
ва «Введение в анализ и дифференциальное исчисление». М., 1902.
2) В §§ 31—32 была выведена «строка Тэйлора» с остаточным чле-
ном Лагранжа; бтот остаточный член никак не учитывается при раз-
ложении в степенные ряды функций logx и т. д.
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ^ВО И ИОЛ. XIX В. 171
Продифференцировав числитель п знаменатель,
получим:
Г к»'и 1 = Г ‘Aj ] < |
L wn J ?1— о |_ ип J п—
Отсюда заключаем, что если ряд сходящийся. ти и ряд
его производных —тоже сходящийся».
Стр. 143.«lim ( — = lim (
оо \и п+1 у п=оо
Отсюда заключаем, что признаки Коши и Даламбера —
тождественны».
Л. К. Лахтин1) не мог не знать этих курсов Бугаева.
II вот он говорит: «Изложение самого Николая Василье-
вича как в изустном преподавании, так и в печатных рабо-
тах, всегда отличалось полной ясностью и простотой, хоте-
лось бы сказать—прозрачностью». «О мёртвых или хорошо
говорят или не говорят ничего»,—говорит латинская пос-
ловица; лучше было бы но говорить ничего.
Если отзывы Лахтина, серьёзного математика и добросо-
вестного человека, так далеки от действительности, когда
речь идёт о легко проверяемых вещах, то можно ли поло-
житься на отзывы не столь серьёзного Минина и не столь
добросовестного Некрасова, когда речь идёт о специаль-
ных вопросах? Думаю, пет.
С другой стороны, отрицательные суждения о работах
Бугаева, с которыми мне приходилось встречаться, исхо-
дят, несомненно, от людей, знакомых с работами Бугаева
лишь понаслышке.
1) Леонид Кузьмич Лахтин (1858—1927), ученик Бугаева, был
профессором сначала в Юрьеве (Тарту), а затем в Москве. Главные
его научные работы относятся к теории дифференциальных резоль
вент алгебраических уравнений; этому вопросу посвящены его
докторская диссертация и статья, отмеченная Феликсом Клейном.
В Московском университете Л. К. Лахтин в продолжение ряда лет
(после Н. В. Бугаева) читал основной курс анализа, а также курс
теории вероятностей. Начиная с первых ;ке лет советской власти
работал по применению методов математической статистики к вопро
сам народного хозяйства и стоял во главе группы статистиков в Ни
ституте. математики Московского университета
172
М. Я. ВЫГОДСКИЙ
Поэтому нам приходится ограничиться констатирова-
нием следующих фактов:
1. Работы Бугаева в настоящее время забыты. В свое
время Д. Ф. Егоров, Берви, И. И. Чистяков работали
в направлении идей Бугаева.
2. В них содержалось довольно много новых в своё
время результатов по теории чисел. В своём трёхтомном
справочнике Диксон упоминает о Бугаеве не менее 25 раз.
3. Как видно из упомянутой книги Диксона, резуль-
таты работ Бугаева часто «переоткрывались» на Западе
(Грам, Гегенбауер, Чезаро, Шелли) спустя 10—15 лет после
опубликования их на русском языке; невидимому, эти
переоткрытия были связаны и с некоторым их обобщением.
4. Из поверхностного обзора работ Бугаева представ-
ляется, что методы его элементарны и остроумны, может
быть, даже виртуозны. (В цитированной выше речи 18G9 г.
Бугаев сказал, между прочим: «Привыкнув темнотой и не-
ясностью изложения измерять глубину научного содержа-
ния, иные наклонны отказывать в глубокомыслии тому,
что ясно и просто».) Насколько они важны для других
исследований—об этом я, как сказано, судить не берусь.
Было бы, думаю, интересно пристальнее пересмотреть
наследство Бугаева.
Во всяком случае можно твёрдо сказах ь: достижения
Бугаева ни в какой мере не оправдывают широковещатель-
ной программы, которую он выставлял в своих речах
и философско-математических произведениях последнег)
15-летия своей жизни. Программа эта имела два ас-
пекта: философско-математический и математическо-фн
лософский.
В отношении философско-математическом Бугаев выд
винул тезис: вся чистая математика распадается на две рав-
ноправные области: анализ и «аритмологию». «Выдвинув-
шись под скромным названием теории чисел, аритмология
постепенно вступает в новую фазу своего развития. В на-
стоящее время всё приводит к мысли, что аритмология не
уступит анализу по обширности своего материала, по
общности своих приёмов, по замечательной красоте
результатов. Прерывность гораздо разнообразнее непре-
рывности. Можно даже сказать, что непрерывность есть
МЛ1Е1\1ЛТ11КА 1'. МОСК. УНИВЕРСИТЕТЕ ион НОЛ. Х1Х В. 17;»
прерывность, в которой изменение идёт через Гнтконеч
но малые п ранные промежутки» *).
А страницей дальше, не смущаясь формальным проти
воречием, Бугаев говорит: «Кроме анализа и аритмологии,
в область чистой математики входят геометрия и теория
вероятности».
Kai; прогноз блестящего будущего аритмологии, этот
прогноз не хуже всякого другого; ио работы самого Бу-
гаева. казалось бы, но выявили тех общих приёмов этой
пауки, о которых говорил Бугаев. Более того, до нашего
времени эти общие приёмы не существуют в «аритмологии».
Бугаев сам указывал на то трудности, с которыми связано
решение самой простой задачи, например, о вместимости
цилиндра, если, вместо непрерывной среды, заполняющей
цилиндр, взять, скажем, шарики. Но для преодоления этих
трудностей он но сделал ничего. В этом убедится всякий,
прочитав его статьи: «Геометрия произвольных величин»2)
и «Прерывная геометрия»3). Это—простые упражнения
в геометрической интерпретации элементарных дискрет-
ных функций, п кроме забавной терминологии («клип»,
«лоскут», «клинообразный .лоскут» и т. п.), они ничего
любопытного не содержат.
Если философско-математические* претензии Бугаева
были просто необоснованными, то философские ого притя-
зания носят совершенно комический характер. Впрочем,
они составляют продолжение его скоропалительных арпт-
мо л огичес к и х пр огноз о в.
Приведём некоторые выдержки из программной статьи
Бугаева4):
«Аналитические функции, определяющие законы при-
роды, бывают по преимуществу однозначными. Это соот-
ветствует нашему предположению, что данному закону
’) «Математика и научно-философское миросозерцание». Напе-
чатано в «Вопросах философии и психологии» ва 1889 г. Воспроиз-
ведено в «Математическом сборнике», т. XXV, стр. 352.
2) «Математический сборник», т. XIV, 1888, стр. 394—409.
3) «Математический сборник», т. XV, стр. 600—609.
4) «Математика и научно-философское миросозерцание». «Мате-
матический сборник-», т. XXV, стр. 352.
174
}R Я. ВЫГоДСКШ!
при данных обстоятельствах соответствует в природе
только одно определенное явление*.
«Под влиянием аналитического мировоззрения стало
ясно, что некоторые законы природы неизменны и постоян-
ны, и некоторые философы стали смело предполагать, что
аналитическая точка зрения приложима к объяснению
всех явлений..., что в мировых явлениях имеет значение
одна причинность и не играет никакой роли целесо-
образность*.
Но, говорит далее Бугаев, кроме анализа в математике
существует аритмология, а потому одной причинности недо-
статочно. Наши ощущения (приводится пример закона Ве-
бер а-Фехнер а)—прерывные функции впечатлений. Поэтому
в области наших чувств и поступков мы должны устранить
преобладающее господство таковой необходимости. «Та-
ким образом случайность выступает на сцену, как прису-
щее свойство некоторых мировых явлений*.
Вот беглый монтаж «математической философии*
Бугаева. Она приводит ого к туманной теории свободной
воли и ещё более туманной монадологии, которую он строит
по образцу лейбницевой. Сто восемьдесят четыре тезиса,
помещённые на 19 страницах егр статьи «Основы эволюцион-
ной монадологии*1), мне, признаюсь, полной ясности не
дали. По меня утешили заключительные слова длинной
речи Лопатина, в которой этот философ пространно изла-
гает учение Бугаева, а под конец признаёт, что «специаль-
ные занятия не позволили ему (Бугаеву) развить свои
философские взгляды в стройную и законченную систему.
Его теории... содержат много недосказанного и субъек
тнвного».
Если, тем нс менее, Лопатин помещал в своём журнале
статьи Бугаева, если он выступал с речью о философских
взглядах «Московского чудака*, то это нельзя объяснить
иначе, как тем, что мракобесам черносотенного лагеря
чрезвычайно выгодно было иметь в своих рядах представи-
теля точной науки, старческий лепет которого мог при-
дать наукообразным вид той поповщине, которую пропове
дывали лопатпны.
П «Ропросы философии и психологии», 1894.
M m МЛТПКЛ В МОСК*. УНИВЕРСИТЕТЕ ВО и ПО I. XIX В. 17л
Каково было отношение Бугаева к политическим иозн
цпям Московского психологического общества, сказать
трудно. Конечно, если бы он был человеком радикальных
взглядов, он не был бы завсегдатаем этого общества. Но
Бугаев нс только в эпоху реакции 90-х годов, но, поводи-
мому, и прежде никогда не был радикалом и его
любовь к родному языку и культуре уживалась с отста
лыми взглядами на развитие Poccnif1).
Но если Бугаев ие был в политике радикалом, то он,
с другой стороны никогда, насколько мне известно, но
выступа.। в ро in поборника и ш защитника тех притесне-
ний, которые правительство применяло во всех областях
политической и культурной жизни. Никогда не освящал
он авторитетом науки самодержавный строй, никогда по
вёл клерикалыюп пропаганды2).
Между тем распространено мнение, что Бугаев и вме-
сте с ним Московская математическая школа 90-х годов
были воинствующими обскурантами и клерикалами. Это
мнение имеет в своей основе клеветнические выступления
одного из членов Московского математического общества,
Н. А. Некрасова. Познакомимся с деятельностью этого в
своём роде «замечательного» человека.
Павел Алексеевич Некрасов (1853—1924) был сыном
священника и учился в духовной семинарии. В 1878 г.
он окончил Московский университет и был Бугаевым оста
плен при университете. В 1885 г. Некрасов был назна-
чен доцентом, а в 1886 г. профессором Московского уни-
верситета. Его диссертация «О трёхчленных уравнениях»
') См., например, его статью в «Математическом сборнике»,
т XXV.
2) Интересно заметить, что 21 марта 1900 г., когда в связи с выхо-
дом XX тома «Математического сборника» Московское математиче
свое общество чествовало своего президента, с приветствием от имени
физико-математического факультета Московского университета вы-
ступил К. А. Тимирязев. Прочитанный им адрес начинался словами:
«Глубокоуважаемый товарищ, Николай Васильевич! Более тридцати
лет продолжается ваше плодотворное служение Московском}' Уни-
верситету; ему посвятили вы все свои силы, работал в качестве про-
фессора, а за последнее время и в качестве декана факультета. Как
разрослось и усовершенствовалось преподавание математики на на-
шем факультете за это время!».
17ь
M. H. ВЫГОДСКИЙ
(1882) обратила на себя внимание в России (напечатана
в «Математическом сборнике», т. XI) и за границей (папе
ч стана B'«Mathematische Annalen»). В период 1883—1893 гг.
Некрасов занимался различными вопросами анализа и
теоретической механики и написал много работ (в «Матема-
тическом сборнике» их помещено 20), стоявших на уровне
современных ему научных исследований в этих областях.
В конце 1893 г. Некрасов получает назначение на долж-
ность ректора Московского университета. Назначение
это состоялось как раз в то время, когда наступающая
реакция повела атаку на университеты. В этих условиях
вновь назначенный ректор должен был играть роль поли-
цейского агента.
Царское правительство не ошиблось в своём выборе.
Некрасов оказался нужным человеком. Когда по истече-
нии своей ректорской работы он пожелал получить от-
ставку, министр народного просвещения счёл необходимым
передать его прошение на заключение царя. Александр III,
отметив заслуги Некрасова, приказал ему оставаться
на своём посту. Это царское повеление было сообщено
Некрасову через попечителя Московского учебного округа.
Оно сохранилось в личном деле II. Л. Некрасова, на-
ходящемся в архиве Московского университета.
Некрасов оставался ректором ещё четыре года, затем
был назначен полечите.тем Московского учебного округа
и, наконец, членом учёного совета Министерства народ-
ного просвещения. Вскоре Некрасов перестал заниматься
теми вопросами математики, которые прежде интересо-
вали его; с 1898 г. он начинает выпускать статьи и книги
по теории вероятностей. Уже в первой из статей1) мини-
стерского периода своей жизни П. А. Некрасов усваивает
чиновническую манеру письма, состоящую в том, что он
«вещает» результаты, не давая себе труда их как следует
обосновать. («Подробный вывод всех вышелзложенных
результатов будет мною представлен впоследствии, если
обстоятельства позволят заняться мне приведением моих
вычислений в порядок, удобный для их появления в пе-
*) «Общие свойства массовых независимых явлений», «Матема
тический сборник», т. XX, стр. 431—442.
МЛТЕМАШКЛ В МОСК. УНИВЕРСИТЕТЕ ВО II ИоЛ. XIX В. £77
чати».) Тотчас же после появления этой статьи на неё от
кликнулся акад. А. А. Марков, который указал («Известия
Казанского физико-математического общества», 1899) на
ошибки, допущенные Некрасовым. Некрасов не признал
своих ошибок, и между Некрасовым и Марковым возго
релась полемика, продолжавшаяся более 15 лет.
Острота, с котором велась эта полемика, зависела не
только и не столько от характера математических ошибок
Некрасова, сколько от того, что Некрасов теперь выступал
уже но как учёный, а как апологет самодержавия и право-
славия.
Читателю, который ноже.тал бы познакомиться с лже-
научными методами П. А. Некрасова, можно порекомендо-
вать перелистать второе издание его «Теории вероятно-
стей* (1913)1).
Нздание печаталось на средства Министерства народ-
ного просвещения, во главе которого стоял тогда реакцион-
ный министр Кассо. Этому жандарму от науки Некрасов
не стесняется выразить свою глубокую признательность.
Вряд ли мог Кассо найти лучшее употребление день-
гам, чем субсидирование книги Некрасова, в которой
вперемежку с математическими формулами даются «хими-
ческие формулы нормативного государства» вроде «кон-
ституционной формулы А Б В», о которой автор сообщает
следующее:
«Конституционная формула АБВ предполагает сосре-
доточение (представительство) в голове политического тела
разумных сил А, Б и В.
Средоточие стихии В есть государь с чинами
» » А » патриарх (синод) с собором
» » Б » Государственная дума с на-
уками и прессой.
Эти живые центральные символы для верящего хмышле-
ния суть суверенные священные залоги... устремления при-
близить к земному Отечеству царство божие»2).
х) Первое издание, вышедшее в 1896 г., представляло собой обыч
ный в то время университетский курс теории вероятностей, содер-
жавший чисто математическую сторону предмета.
2) П. А. Некрасов «Теория вероятностей». Над 2-е, 1913,
стр. 119.
12 Историко-математ. исследования
178
М. Я. ВЫГОДСКИЙ
А. А. Марков, который в 1902 г. подал в Синод заявле-
ние с просьбой отлучить его от церкви, обрушился против
попыток Некрасова со всей той силой, с какой это было
возможно в тех условиях. Наиболее острый характер дело
приняло в 1915 г., когда Некрасов в качестве члена совета
Министерства народного просвещения создал комиссию,
которая должна была разработать вопрос о введения
в программу средних школ элементов теории вероятно-
стей. На базе лженаучного использования теории вероят
костей предполагалось внушать учащимся некрасовский
бред о треугольнике, одной вершиной которого является
царь, другой—синод, а третьей—наука.
Тогда пи инициативе А. А. Маркова в Академии наук
была создана Комиссия, в состав которой, кроме Маркова,
вошли А. М. Ляпунов, В. *А. Стеклов, Д. К. Бобылёв
и А. Н. Крылов.
Комиссия эта вынесла решение, в котором говорилось:
«Взгляды Некрасова давно известны математикам,, но
пока они находили место в специальных математических
журналах, их можно было считать безвредными. Дело
меняется, когда распространителем их является официаль-
ный орган. Поэтому Академия Наук, как первенствующее
учёное сословие Российской империи (устав, § 1), могущее
входить во всё, касающееся просвещения (§ 8), и обязанное
иметь попечение о распространении просвещения и направ-
лении оного ко благу общему (§ 2, п. 6.), обязана высказать
своё суждение об основных ошибках и неправильных,
а потому вредных, идеях, распространяемых П. А. Некра-
совым с целью проведения их в обиход средней школы»...
Далее разбираются ошибки Некрасова: разбор этот
заканчивается словами:
«Комиссия полагает, что вышеупомянутые заблужде-
ния и... злоупотребление математикой с предвзятой целью
превратить науку в орудие религиозного и политиче-
ского воздействия... принесут неисправимый вред делу
просвещения».
Так квалифицировали деятельность Некрасова мате-
матики Академии наук, но в Москве, где Некрасов был
после смерти Бугаева президентом Математического обще-
ства, ректором Университета и попечителем учебного
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ВО II ПОЛ. XIX В. 179
округа, он буквально терроризировал математические
круги.
При жизни Бугаева Некрасов, насколько мне известно,
никогда не делал попыток связать свои реакционные идеи
с именем Московского математического общества. После
смерти Бугаева, сделавшись президентом Общества, Некра-
сов выступил с речью, посвящённой памяти Бугаева
(16 апреля 1904 г.). В этой речи он подвёл в качестве базы
под свою черносотенную пропаганду взгляды не только
Бугаева, но заодно и всех вообще основателен Общества.
Впрочем, в его речи в качестве его «единомышленников»
фигурируют Ферма. Декарт, Паскаль, Ньютон, Лейбниц
и другие учёные наряду с Победоносцевым. Хомяковым
и «преподобньш Антонием Храповицким»1).
По видимо му, сам Некрасов ощущал некоторую нелов-
кость, выступая в научном обществе со своим бредовым
докладом. Во всяком случае он счёл необходимым пред-
послать литературной обработке своей речи введение,
в котором, между прочим, сказано следующее:
«Считаем долгом упомянуть об особенностях изложе-
ния и стиля, которым написана настоящая статья. Для
выражения математического содержания принципов миро-
устройства общеупотребительный язык оказывается не
вполне подходящим. Перевод этого содержания на обще-
употребительный язык сопряжён с затруднениями почти
непреодолимыми, что и вынуждает математиков либо замы
каться в своей специальности, отказываясь навсегда от
общедоступного изложения важных жизненных метриче-
ских понятии, либо прибегать к сложнейшим оборотам
научной, философской, политической, общественной и
церковной речи, к повторениям и тяжёлым терминам, не
понятным для читателей, привыкших к бойкому стиль-
ному языку словесников-беллетристов и диалектиков-
эмпириков».
И, действительно, открыв наудачу страницу его статьи,
мы наталкиваемся на такие, например, «сложнейшие образ-
цы речи»: «Моральтриангуляция, данная в факте семьи
9 П. А.Некрасов, «Московскаяфизико-математическаяшко
ла», «Математический сборник» т. XXV, стр. 23, 70.
12*
18t>
М. Н. ВЫГиДСКиИ
(отец+мать+сын или отец+мать-[-дочь) и в пятой запо-
веди (чти отца и мать), естественно и искусственно (мо-
ральтехнически) развивается в свободосвязь общества*
(стр. 165).
Как было сказано, задача, которую поставил себе
Некрасов, состояла в том, чтобы представить Бугаева воин
ствующнм реакционером, каким последний вовсе не был.
Правда, сумбурные высказывания Бугаева в старческом
его возрасте облегчали Некрасову выполнение его плана.
Но Некрасов не удовольствовался этим и тем самым
разоблачил себя: «Полнота миросозерцания и автори-
тета,—заявляет Некрасов,—принадлежит всему союзу,
не дозволяя отделить Н. В. Бугаева от В. Я. Цингера и
Н. В. Бугаева от Ф. А. Бредихина, А. Ю. Давидова и
П. Л. Чебышева и всех этих от остальных»1).
Можно было бы принять выступления Некрасова за
бред сумасшедшего, если бы они не обладали чрезвычайно
целеустремлённым характером. Когда Некрасову было
нужно, он умел перевести свои мысли на «общеупотреби-
тельный язык». Так было, между прочим, и в полемике
с Марковым, о которой упоминалось выше и к которой
мы возврашаемся опять.
Акад. Буняковский в своём курсе теории вероятностей
счёл необходимым предостеречь от применения его формул
для вероятности свидетельских показаний к религиозным
верованиям: «формулы эти выведены в предположении, что
имеют место определённые физические законы», а так как
«в духовном мире есть факты, которые не подчинены физи-
ческим законам», то «все злонамеренные умствования лже-
философов рушатся» 2).
А. А. Марков в своём «Исчислении вероятностей» смело
выступил против Буняковского. Марков писал:
«Независимо от математических формул, ясно, что к рас-
сказам о невероятных событиях, будто бы происходивших
в давно прошедшее время, следует относиться с крайним
сомнением. И мы никак не можем согласиться с акад. Бу-
1) П. А. Некрасов, «Московская физико-математическая
школа», «Математический сборник», т. XXV, стр. 239.
2) В. Я. Буняковский «Основы математической теории
вероятностей», 1846, стр. 326.
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ВО II ПОЛ. XIX В. 181
ваковским, что необходимо выделить известный класс
рассказов, сомневаться в которых он считает предосуди-
тельным. Чтобы не иметь дела с ещё более строгими
судьями и избежать обвинений в потрясении основ, мы не
останавливаемся на этом предмете» х). Когда Некрасов
получил отпор в своих стремлениях использовать науку
для пропаганды религии, он решил возбудить против
своего обидчика обвинение в потрясении основ, т. е.,
попросту говоря, составил донос на Маркова. Он писал:
«Для суждения о том, что действительно непригодными для
подготовления учителей средней школы являются но
инкриминируемые мне идеи, а идеи А. А. Маркова, пред-
ложу вниманию читателя руководство А. А. Маркова,
«Исчисление вероятностей»* 2). Приведя затем известпую
нам цитату из Маркова, Некрасов заявляет3):
«Разрушая приведённые выше основоположения
акад. Буняковского, Марков тем самым облегчает наса-
ждение основоположений исторического материализма...
«Лучшего», чем книга Маркова, руководства не требует-
ся для систематической пропаганды крайнего беспочвен-
ного материализма... Ныне мне остаётся апеллировать
к миру учёных и педагогов, прося обсудить, кто из нас
превращает чистую пауку в орудие воздействия вредного
относительно здравости гражданского и религиозного
культа, коим подрастающие поколения воспитываются».
Таким образом, выступления Некрасова нельзя рас-
сматривать лишь как проявление расстройства психики.
Тем более печален тот факт, что Московское математи-
ческое общество терпело па посту президента человека,
позорившего имя научного учреждения. Справедливость
требует, однако, отметить, что терроризованное Некра-
совым Математическое общество лишь сносило его непри-
личное поведение, а не разделяло его.
В т. XXV «Математического сборника» мы находим,
протокол заседания Общества от 22 марта 1905 г., глася-
Ч А. А. Марков «Исчисление вероятностей», 1913, 3-е изд.
стр. 225.
2) П. А. Некрасов. ^Средняя школа, математика и научная
подготовка учителей», 1916, стр. 12.
3) Цпт соч., стр. 16.
182 М. Я ВЫГОДСКИЙ
щий: «Секретарь доложил письмо II. А. Некрасова1),
в котором он заявляет о своём желании напечатать в «Мате-
матическом сборнике» статью «Органические основы госу-
дарства. Морально-арифметический этюд об избирателях
и избираемых в их отношениях взаимных и к верховной
власти»... Вместе с тем П. А. просит занести в протокол
его заявление, а также ввиду особенностей темы, и мнение
общества по этому вопросу»*).
Ссылаясь на малочисленность собравшихся членов,
Общество отложило обсуждение заявления Некрасова и...
больше не возвращалось к нему. А 20 сентября Некрасов
сложил с себя звание президента Общества.
Общество постановило выразить Некрасову «призна-
тельность за его многолетнюю деятельность». Выполняя
это требование этикета, члены общества, вероятно, облег-
чённо вздохнули.
Преемником Некрасова на посту президента Москов
ского математического общества был избран крупнейший
учёный Н. Е. Жуковский. Кроме него в президиум обще-
ства в это время входили: Б. К. Млодзеевский, Л. К. Лах-
тин, II. II. Жегалкин. Деятельность этих учёных но только
но времени, но и по своему характеру, выходит за пределы
того периода, который мы рассматриваем в настоящей
статье.
Здесь мы ознакомились с некоторыми моментами из
полувекового периода развития математической мысли
в Московском университете. История этого периода ещё
не подверглась детальному изучению, и было бы интересно
проделать эту работу. Но уже из изложенного можно ви-
деть, что к началу нынешнего столетия физико-математи-
ческий факультет Московского университета представлял
собой совсем иное зрелище, чем за полвека до этого. Он
располагал довольно обширными квалифицированными
кадрами, он сам готовил кадры образованных педагогов для
средней и высшей школы. В стенах его существовало и ра-
ботало научное общество, имевшее многочисленные куль-
Ч Некрасов в это время переехал в Петербург и с февраля 1905 г
не принимал участия в заседаниях Общества.
2) Курсив мой.—М. В
МАТЕМАТИКА В МОСК. УНИВЕРСИТЕТЕ ВО II ПОЛ. XIX Б. 183
турные связи. Издаваемый Обществом журнал приобрёл
авторитет в России и за границей. Развернулась широкая
научная работа; в следующем поколении математиков, вос-
питанных в Московском университете, мы уже встречаем
людей, пошедших по большой дороге научного творчества
и в своей педагогической деятельности поднявших препо-
давание до уровня тогдашних научных требований. Из
этого выросшего па рубеже двух столетий поколения
математиков вышли научные руководители первых совет-
ских поколений математиков. Их знания и таланты нашли
себе небывало широкое поле применения. Посеянные ими
семена дали прекрасные молодые всходы, которыми Страна
социализма может гордиться наравне с замечательными
плодами творчества советского народа во всех других об-
ластях социалистического строительства.
И. Л. ЧЕБЫШЕВ И МОСКОВСКИЙ УНИВЕРСИТЕТ
40-х годов XIX века
В, Е. Прудников
Автором этой статьи найдены некоторые архивные
материалы, относящиеся ко времени пребывания Паф
путия Львовича Чебышева в Московском университете
и «публичного защищения» им магистерской диссертации.
Этот период в жизни Чебышева совершенно не освещён
в литературе. Между тем почти десятилетнее пребывание Че-
бышева в Московском университете (1837—1846) во многом
определило его дальнейшие научные устремления и, бес-
спорно, наложило отпечаток на его качества как профес-
сора и педагога.
Многое в этот период жизни Чебышева вызывает недо-
умение. Прежде всего:
а) почему за своё студенческое сочинение «О числовом
решении алгебраических уравнений высших степеней»
обнаружившее в Чебышеве но только математический та-
лант, но и педагогическое мастерство в распределении
и изложении материала и найденное 2-м отделением фило-
софского факультета1) «удовлетворительным во всех отно-
шениях», Чебышев получил в 1840—1841 уч. году только
серебряную медаль;
б) почему, блестяще защитив 8 июня 1846 г. при Мо-
сковском университете свою магистерскую диссертацию
«Опыт элементарного анализа теории вероятностей», Чебы-
шев не был оставлен там для дальнейшей научной деятель-
г) Так стало называться с 1835 г. физико-математическое отделе
ине Университета.
ЧЕБЫШЕВ И МОСКОВСКИЙ УНИВЕРСИТЕТ 40-Х ГГ.
185
кости; вообще, как случилось, что он не составил себе
преподавательской карьеры в Московском университете;
в) каков характер тех подробных замечаний ординар-
ного проф. Зернова, которые были сделаны к указанному
сочинению Чебышева и учесть которые при напечатании
2-е отделение вменило ему в обязанность.
Обычные ответы на первые два вопроса сводятся к то-
му, что во время пребывания Чебышева в Московском
университете к нему якобы тенденциозно относился все-
сильный тогда проф. Перевощиков. Это—вероятное
предположение, но оно нуждается в подтверждении доку-
ментальными данными, которых разыскать пока не уда-
лось. Действительно, Перевощиков в то время был дека-
ном 2-го отделения философского факультета и очень влия-
тельным членом профессорской корпорации. Бесспорно,
что судьба Чебышева во многом зависела от того, благо-
волил или не благоволил к нему Перевощиков. Но тща-
тельное изучение найденных архивных документов показы
вает, что последний относился к Чебышеву более чем
лойяльно. Надо учесть также при этом, что на стороне Чебы-
шева стояли такие, очень влиятельные в университетских
сферах люди, как попечитель Московского учебного окру-
га граф С. Г. Строганов и проф. Н. Д. Брашман. Строганов
любил знакомиться с успехами и способностями экзаме-
нующихся студентов и с особенным вниманием и участием
следил за теми из них, которые были у него уже па при-
мете по дарованию и прилежанию. Таких он прочил для
будущего их назначения на профессорские или учитель-
ские должности, как, например, было с Соловьёвым, Кат-
ковым, Кудрявцевым, Кавелиным, Ершовым, Давидовым,
Авиловым и др. К их числу принадлежал и Чебышев,
лично известный графу Строганову своим прилежанием
и выдающимися способностями.
Возможно, что Чебышев, на которого было возложено
устроение судьбы его родных братьев, сам не пожелал
остаться в Московском университете и по личному жела-
нию переехал для научной работы в С.-Петербург. Это
тоже вероятное предположение, но и оно опять-таки
нуждается в подтверждении документальными дан-
ными, которые найти не удалось. То, что найдено, отно-
В. Е. ПРУДНИКОВ
сптся к сдаче Чебышевым установленных письменных экза-
менов при соискании учёной степени магистра, защите им
1-й диссертации и избрании его в 1857 г. «почётным членом
Императорского Московского Университета».
К великому сожалению, найденный протокол защиты
настолько краток, что в нём не записаны ни возражения,
которые были сделаны Чебышеву по поводу его сочинения
официальными оппонентами (Зерновым и Брашманом),
ни возражения сторонних людей, ни ответы Пафнутия
Львовича.
Что касается документов с письменными ответами Чебы
шева на экзаменах, происходивших 29 октября и 5 ноября
1843 г. в присутствии депутатов от Совета Университета
ординарных профессоров Рихтера и Лешкова, то на них
выставлены две отметки: «весьма удовлетворительно»
и «удовлетворительно». Первая выставлена Н. Д. Брашма-
пом за письменный ответ Чебышева па вопрос: «Опреде-
ление закона о движении тела по циклоиде, когда кроме
тяжести действуют ещё какие-нибудь возмущающие силы».
Вторая выставлена Н. Е. Зерновым за письменный ответ
Чебышева на вопрос: «Множитель, вспомоществующий
нахождению интеграла ур. дифференциального; случаи, в
коих можем находить опыт, и главные его свойства».
Эти два ценных подлинных документа, написанных ру-
кою Чебышева, сохранились в весьма хорошем виде, и по
ним можно составить себе ясную картину о характере тех
требований, какие предъявлялись в 40-х годах прошлого
века к соискателю учёной степени, и об уровне математиче-
ской культуры этого соискателя (пусть даже необычного).
Также хорошо сохранились и все остальные документы,
составляющие три дела:
а) «Дело (№ 65 от 1843 г.) Совета Императорского Мос-
ковского университета о допущении к испытаниям на сте-
иень магистра математических наук кандидата Пафнутия
Чебышева».
б) «Дело (А° 137 от 1846 г.) Совета Императорского
Московского университета о защпщенпи кандидатом Паф-
нутием Чебышевым диссертации на степень магистра».
в) «Дело (№ 866 от 1857 г.) Совета Императорского
Московского университета об избрании в почётные члены
ЧЕБЫШЕВ И МОСКОВСКИЙ УНИВЕРСИТЕТ В 40-Х ГГ. 18"
Университета Академиков Буняковского, Чебышева и
Перевощикова».
Мы полагаем, что по отношению к такому выдающемуся
представителю русской математической науки, каким был
П. Л. Чебышев, интерес представляет даже всякая новая
деталь его частной жизни. II подавно должны представлять
интерес документы, проливающие известный свет на один
из самых неосвещённых периодов в жизни нашего знаме-
нитого соотечественника.
Прежде чем перейти к изложению фактов, связанных
с пребыванием Чебышева в Московском университете, мы
позволим собе кратко остановиться на личности первого
наставника Чебышева П. Н. Погорельского, а также бегло
охарактеризовать его первых руководителей по матема-
тике в Московском университете Н. Д. Брашмана и
Н. Е. Зернова.
Платой Николаевич Погорельский
II. Л. Чебышев получил первоначальное и среднее обра-
зование дома, хотя в начале 30-х годов жил вместе с роди-
телями в Москве1), где ужо четверть века существовала
1-я гимназия и намечалась к открытию вторая.
Учебно-воспитательная работа в московской гимназии
была поставлена вполне удовлетворительно, благодаря
хорошему составу учителей п тесной духовной связи её
с Московским университетом.
Несмотря на существование в Москве подобной гимназии
и на дешевизну обучения в ней, родители Чебышева, при
иадлежавшие к старинному и довольно состоятельному дво-
ряне кому роду, не послали своего сына учиться в неё.
Возможно, что здесь сказался сословный предрассудок,
свойственный русским дворянам того времени, которые
несколько презрительно относились к гимназиям как
общесословным школам. Они кичились своим происхожде
нием и не хотели видеть своих детей среди разночинцев.
Ч П. Л. Чебышев родился 26 мая 1821 г. в имении своих
родителей в с. Окатово. Боровского у Калужской губ. (умер
8 декабря 1894 г.).
188
F. E. ПРУДНИКОВ
Решив дать своему сыну домашнее образование, роди-
тели Чебышева пригласили к нему в качестве учителя мате-
матики Платона Николаевича Погорельского, одного из
лучших и наиболее известных педагогов Москвы того вре-
мени. Научные достоинства Погорельского были невы-
соки, и, сознавая это сам, оп избрал поприщем своей дея-
тельности не Московский университет, в котором приобрёл
степень магистра и одно время преподавал, а гимназию.
Это было правильно) так как учёный из Погорельского
вышел бы посредственный, а учителем и руководителем
гимназии он был первоклассным.
Как учитель математики П. Н. Погорельский пользо-
вался среди широкой московской публики того времени
известностью, необычайным уменьем держать весь класс
во время урока в неослабном напряжении и излагать свою
науку в ясной и общедоступной форме.
Сделавшись директором гимназии, Погорельский в ко-
роткий срок придал ей образцовое устройство, обратившее
внимание публики и начальства. Когда же в его ведение
как директора гимназии в 1841 г. были переданы народные
училища, Погорельский рядом удачно принятых мер сумел
быстро поднять начальное образование па такую высоту,
которая обратила па себя внимание министра народного
просвещения и заставила его потребовать, чтобы и все
остальные школы были устроены по образцу московских.
П. Н. Погорельский соединял в себе любовь к своим
воспитанникам со строгой взыскательностыо, но его суро-
вая строгость не мешала ученикам любить своего дирек-
тора.
Преподавание в гимназии Погорельский доверял только
опытным и знающим преподавателям, которых подбирал
с особой тщательностью и осторожностью. Несмотря па это,
он и сам много вносил в дело преподавания, особенно
в преподавание математики, уроки которой любил посе-
щать. Ему, конечно, было приятно следить за искусным
разъяснением этого предмета избранными им преподава-
телями. Не ограничиваясь наблюдением за преподаванием
учителей, Погорельский часто сам являлся руководителем
учеников в рекреационное время. Входя во время перемены
в класс, он слушал, как лучшие ученики объясняли своим
ЧЕБЫШЕВ II МОСКОВСКИЙ УНИВЕРСИТЕТ 40-Х ГГ. |t>V
товарищам непонятый ими урок. Он умел направлять на
верную дорогу неумелые объяснения. Слишком бойким
он говорил обычно: «спустись пониже, говори проще, если
хочешь, чтобы тебя поняли». Часто он сам брался за мел
и начинал объяснение.
Свою славу выдающегося педагога Погорельский умно
жил изданием руководств ио математике. Не найдя в со-
временной ему учебно-математической литературе, как пе-
реводной, так и оригинальной, учебника, соответствовав
шего его взглядам и педагогическим требованиям, он
перевёл (в начале 30-х годов) «Курс чистой математики»,
составленный по поручению ген. Беллавеня французскими
профессорами Аллезом, Пюиссаном и др. Этот перевод
переделка был так удачен и так хорошо приспособлен
к гимназической программе по математике, что в сравни
тельно короткое время выдержал многочисленные изда-
ния и был принят в качестве учебного руководства для
гимназий (особенно «Алгебра», вышедшая в 1863 г.
8-м изданием).
Мы видим, таким образом, что Погорельский стремился
совершенствовать методы преподавания элементарной мате-
матики и учебники по этой науке.
Все свои достижения в этом направлении он, прежде
всего, внедрял во вверенной ему гимназии. И не случайно
то обстоятельство, что ученики 3-й Московской реальной
гимназии, директором которой Погорельский был с момен
та её учреждения (1839) почти до конца XIX в., выказы-
вали какое-то особенное тяготение к математике; их успехи
по этому предмету были выше, чем по другим, и большая
часть окончивших курс избирала собе для дальнейшего
образования математический факультет. «Что посеешь,
то и пожнёшь». И мы полагаем, что первые семена любви
к математике, к сжатому, ясному и доступному изложению
её основ, строгость и высокую требовательность к своим
знаниям и к знаниям других — всё это было посеяно в со-
знании Чебышева ужо Погорельским.
о учебникам последнего он учился дома элементарной
математике, потому что в то время они были самые популяр
ные и переиздавались почти каждые два-три года. Эти учеб-
ники удачно соединяли полноту содержания с ясностью и
IVO
В. h. ПРУДНИКОВ
сжатостью изложения. Когда сейчас сравниваешь учебники
Погорельского с другими, им современными (например,
учебниками Перевощикова, Кушакевича и Киндерова и др.),
то бросаются в глаза мастерство изложения и точность
языка. В своих учебниках Погорельский стремился оту-
чить своего читателя от тяжёлого риторичного построения
речи и приучить его писать так, как говорят. Это, бесспор-
ро, и ценил в учебниках Погорельского Чебышев, когда,
будучи уже членом Учёного комитета Министерства на-
родного просвещения по математическим паукам, реко-
мендовал их, главным образом «Алгебру», в качестве учеб
ных руководств для гимназий.
Николай Дмитриевич Брашман
Когда Чебышев поступил на математическое отделение
Московского университета в 1837 г., Н. Д. Брашман (1796—
1866) преподавал там прикладную математику; иногда ему
поручалось преподавание аналитической геометрии и неко-
торых частей анализа.
Будучи инженером и математиком по образованию,
Брашман обратил особое внимание при преподавании
механики на практическую сторону этой науки, на её
приложения, что было важно для того времени. Тогда в
России насаждалось «реальное» образование: разрешалось
некоторым гимназиям открывать у себя «реальные» курсы
и оказывалось всяческое поощрение занятиям специаль-
ными предметами,' относящимися к торговле и промышлен-
ности. Такие же «реальные» курсы открывались и при
уездных училищах. Наша страна стала остро нуждаться
в преподавателях специальных наук. Это обстоятельство
не ускользнуло от внимания Брашмана. Он один из пер-
вых среди деятелей Московского университета понял, что
настоящее достоинство университетского образования
лежит в соединении «реального» направления с «гу-
манным».
На своих лекциях, а также в частных беседах он стре-
мился привить своим слушателям любовь к новому в то
время делу—«практической механике». Начиная с 40-х
годов, Брашман в курсе механики стал излагать теорию
ЧЕБЫШЕВ И МОСКОВСКИЙ УНИВЕРСИТЕТ 4и-Х ГГ. IV I
устройств водяных колёс, водосливов, водоподъёмных ма-
шин и т. д. Основная задача Брашмана при изложении
перечисленных вопросов заключалась г. том, чтобы пока-
зать своим слушателям теоретические начала для определе-
ния главных элементов машин и механизмов. При выпол-
нении этой задачи он пользовался всем, что было сделано
наилучшего в области гидравлики и машиноведения учё-
ными того времени.
По инициативе Брашмана в Московском университете
с начала 40-х годов стали предлагать для диссертации
темы по практической механике вроде: «Теория водяных
колёс», «Вода, как двигатель», и др. По его же инициативе
в Московском университете в 1846 г. была создана специ-
альная кафедра «практической механики», которую зани-
мал в течение почти двадцати лет Александр Степанович
Ершов—ученик Брашмана и основатель Московского выс-
шего технического училища.
В частных беседах со своими слушателями Брашман
нередко призывал их к работе в области практической ме-
ханики и советовал им нрп этом иметь в виду не одно пре-
подавание, но и ту пользу, какую они могли бы принести
отечественной промышленности. Сохранилось следующее
интересное в этом отношении свидетельство, принадлежа
щее А. С. Ершову и записанное им в своём дневнике.
«В этот день,—записывает А. С. Ершов 13 апреля
1843 г.,—я окончил последний из своих экзаменов для полу-
чения степени магистра—экзамен из прикладной матема-
тики... После экзамена я говорил с Брашмаиом о моём
будущем. Он с участием вызывал меня па новую работу
по практической механике, советовал иметь в виду не одну
учительскую должность, но и ту пользу, которую я могу
принести Москве и самому себе приложением своих зна-
ний»1).
Это свидетельство важно в двух отношениях: 1) оно
указывает на присущую Брашману черту—принимать оте-
ческое участие в судьбе своих учеников и 2) оно указывает,
что Брашман принадлежал к числу немногих профессоров
l) Н. А. Любимов, Воспоминания об А. С. Ершове. См. «От-
чёт императорского технического училища за 1869 год», стр. 4.
192
в. к. прудникоВ
Московского университета, которые стремились использо-
вать науку для развития народного хозяйства.
Последнее обстоятельство особенно важно. Оно, соб
ственно говоря, и определило то счастливое для Москов-
ского университета и для всей страны направление в раз
витии механики как предмете! преподавания и как науки,
которое оформилось окончательно в этом университете
к началу 80-х годов и благодаря которому этот университет
дал нам таких корифеев механической науки, как Н. Е. Жу-
ковский и С. А. Чаплыгин.
Застав преподавание механики в Московском универ-
ситете на первой ступени развития, Брашман приложил
много усилий к тому, чтобы поднять это преподавание на
ту высоту, какая была дана указанной науке трудами
Лагранжа. Этому же обстоятельству отчасти способствовали
и его собственные исследования, касающиеся теории рав-
новесия, расхода жидкости на водосливе, математического
обоснования «закона Бэра» и др.
Есть все основания утверждать, что Брашман заклады-
вал первые камни механики как науки и как учебного
предмета в Московском университете. Делал он это тогда,
когда многое ещё в самой этой пауке и в деле её преподава-
ния не выяснилось и не уложилось в определённые рамки.
Аналитические идеи Лагранжа давались студентам с тру-
дом, да и между учёными шли ещё споры о неко-
торых теоремах (например,о начале наименьшего действия).
Слушатели Брашмана с самых первых шагов убеждались,
что преподаваемый им предмет — нелёгкий, и серьёзно смот-
рели на занятия прикладной математикой. Небрежные и лег-
комысленные из них очень боялись экзаменов Брашмана.
Всем слушателям были памятны те многочисленные сцены
на экзаменах, когда после длинного испытания иной легко-
мысленный, но не лишённый самоуверенности юйоша, чув-
ствуя, что дело плохо, наклоняясь к Брашману, говорил:
«Я занимаюсь специально естественными науками». Или
•когда другой, более наивный, путаясь и краснея, твердил:
«Я—естественный, Николай Дмитриевич». —«А, вы есте-
ственный?»—говорил Брашман, обращаясь к такому,—ну,
я вам двойку поставлю». «Нельзя ли прибавить хоть за
то, что так долго спрашивали?»—«Ну, я вас ещё спро-
ЧЕБЫШЕВ И МОСКОВСКИЙ УНИВЕРСИТЕТ 40-Х ГГ.
193
шу»,—предлагал Брашман, и «сын природы» мгновенно
исчезал.
Брашман, как профессор, отличался особым уменьем
настойчиво искать между своими слушателями способного
молодого человека, а затем приглашать его к себе и зани-
маться с ним с необыкновенным упорством и терпением.
Особенно ценил он в своих слушателях способности и
охоту к математике.
По словам современников, Брашман, отыскав несколь-
ко таких слушателей, занимался с ними с такой неутоми-
мостью, что они «уходили от него обессиленными и выдер-
живали весьма немногие». Сохранились следующие пре-
красные слова о Брашмане, обращённые к нему одним из его
учеников, Н. А. Любимовым: «В древности философ днём на
улицах и торжищах с фонарём искал человека; не столь
эффектно, но не менее усердно вглядывались Вы в своих
слушателей и искали между ними математика. Как скоро
Вам казалось, что в каком-либо из Ваших учеников есть
зародыш математического таланта, зачаток той великой
силы, благодаря которой природа покорна человеку, Вы
с любовью сосредоточивали на нём своё внимание, руко-
водили, помогали, возбуждали к труду и ободряли» 1).
Поощряя в своих слушателях дух самостоятельной
деятельности, Брашман являлся верным служителем нау-
ки, примером отзывчивости на запросы и требования своего
времени. Основанием Московского математического обще-
ства он вписал одну из славных страниц в историю разви-
тия математики в России.
Влияние Брашмана на формирование научных взгля-
дов и интересов молодого Чебышева было очень значи-
тельно.
Поступив на математическое отделение Московского
университета, Чебышев сразу обратил на себя внимание
Брашмана, который быстро угадал в своём новом ученике
будущее математическое светило.
Заметив в Чебышеве серьёзное отношение к занятиям,
любовь и способность к науке, Брашман начал старатель-
1) «Московские ведомости», 1864, № 213, статья «Обед в честь
Брашмана».
13 Историко-математ. исследования
194
В. Е. ПРУДНИКОВ
но руководить его занятиями и постоянно убеждал его
посвятить себя исключительно математике, хотя матери-
альное положение многообещающего юноши одно время,
вследствие расстроенных дел отца, было крайне стесни-
тельно. Чебышев последовал совету своего учителя и,
окончив кандидатом курс в университете в 1841 г., отдался
всецело учёным трудам. В течение 5 лет, равно-
душно относясь к своему безденежью и не помышляя о карь-
ере, он твёрдо под руководством Брашмана продолжал из-
бранный путь. Не без содействия Брашмана Чебышев стал
известен Строганову, попечителю Московского учебного
округа, который поручил молодому учёному написать эле-
ментарный курс теории вероятностей, предназначавшийся
в качестве учебного руководства для камерального факуль-
тета Демидовского лицея в Ярославле. Отношения между
Брашманом и Чебышевым были всегда близкие. В библио-
теке А. Ю. Давидова, хранящейся в Московском универси-
тете, имеются некоторые из мемуаров Чебышева с автогра-
фами, содержание которых не вызывает никакого сомнения
о той светлой памяти о Брашмане, какую носил в себе Паф-
нутий Львович Чебышев. Кроме того, одну из своих статей:
«Разложение функций в ряды при помощи непрерывных
дробей», Чебышев написал в форме письма на имя Браш-
мана и закончил её так: «Сказанного мною достаточно,
чтобы видеть, как много интереса представляет предмет,
на который я был наведён Вашими лекциями и всегда
драгоценными для меня беседами с Вами»1).
Поездка Брашмана за границу в 1842 г. с научной
Целью, посещение им тех учреждений в Европе, где осо-
бенно интенсивно разрабатывались вопросы практической
механики (например, консерватории искусств и ремёсл
в Париже),беседы об этой поездке со своими слушателями—
всё это не могло также не оказать влияния на Чебышева.
Интерес Чебышева к теории механизмов и машин не
случаен, как не случайно и то обстоятельство, что он,
совершая в 1852 г. свою первую заграничную поездку,
интересовался в Европе теми же вопросами, что и его учи-
тель десятью годами ранее.
х) «Математический сборник», т. I, 1866.
ЧЕБЬ.ШЕВ И МОСКОВСКИЙ УНИВЕРСИТЕТ 40-х ГГ. 195
Николаи Ефимович Зернов
Чистую математику в Московском университете Чебы-
шев изучал под руководством проф. Н. Е. Зернова (1804—
1862). В начале 40-х годов курс чистой математики состав-
ля ли следующие дисциплины: аналитическая геометрия,
высшая алгебра, дифференциальное и интегральное исчис-
ления, интегрирование дифференциальных уравнений (обы-
кновенных и с частными производными), вариационное
исчисление и исчисление конечных разностей. Все эти
дисциплины Зернов излагал частью по своим собственным
сочинениям, частью по сочинениям Брашмана и Перево-
щикова, а в качестве пособий рекомендовал своим слушате-
лям сочинения Эйлера, Коши, Лакруа и др. Подобная
полнота в рекомендации математических руководств, из
которых многие являются классическими (Эйлер и Коши),
была для Московского университета эпохи Чебышева
большой новостью.
Блестящие достижения Коши во всех областях мате-
матики в то время только начинали распространяться во
всём мире.Влияние Коши шло на смену влиянию Лагранжа,
а вместе с этим возрастал интерес к теории пределов, кото-
рая постепенно вытесняла из математики лагранжеву
теорию функций. Эта смена влияний отразилась и на ха-
рактере преподавания математики в Московском универ-
ситете. Если в 20-х годах в нём безраздельно господство-
вала теория функций Лагранжа, то в середине 30-х годов
такое господство выпало на долю теории пределов Коши.
Большим поклонником и проводником последней явился
Зернов.
Крупным самостоятельным исследователем Зернов не
был. Это был больше труженик, чем творец, притом тру-
женик почтенный и весьма добросовестный. Его докторская
диссертация «Рассуждение об интеграции уравнений с
частными дефференциаламп» представляла собой первое об-
стоятельное сочинение на русском языке по этой важной
ветви анализа. Самостоятельных значительных результатов
в этой диссертации мы не найдём, но эрудиция автора оче-
видна. Особенно тщательно изучал Зернов труды Коши
и непрестанно следил за ними.
13ф
196
В. Е. ПРУДНИКОВ
Например, едва в 1829 г. Коши выпустил свои «Exerci-
ces des Mathematiques» (40 и 41 тетради), как Зернов в
начале 30-х годов отозвался на них статьёй «О рассужде-
нии Коши Sur la resolution des equations numeriques et
sur la theorie de I’elimination», помещённой в «Учёных
записках» Московского университета (1836, отдел критики).
В этой статье Зернов, относясь с большим уважением
к авторитету Коши, указывал на недостатки в некоторых
доказательствах «знаменитого геометра», но без претензии
на их исправление. Статья эта очень интересна для оценки
математической культуры того профессора, у которого
учился Чебышев чистой математике. Из неё видно, что
Зернов находился на том уровне логической строгости,
которая для его времени была передовой.
Зернов в своих лекциях строго ограничивался самым не-
обходимым и его курс бывал значительно короче, чем пре-
красный для своего времени его учебник по дифференциаль-
ному исчислению. Зернов как будто боялся сообщить сту-
дентам лишнее и, прочитав самое необходимое, обыкновенно
говорил: «Здесь кончается наука университетская и начи-
нается академическая». Лекции Зернова были содержатель-
ны, апо изложению очень доступны. Читал он «с самообла-
данием, спокойно, с единственным и неуклонным желанием
полностью разъяснить предмет перед внимательной ауди-
торией, с удивительным бережепием времени и умением
распорядиться им» х). Ясность и отчётливость изложения
у Зернова были таковы, что студент, мало-мальски зани-
мавшийся, всегда хорошо знал содержание прочитан-
ных лекций.
Зернов был учёный с жилкой конструктора и изобре-
тателя. Он любил заниматься расчётами и конструирова-
нием. Почти до конца XIX в. в Москве сохранялись неко-
торые из конструкций Зернова: солнечные часы в Нижнем
Кремлёвском саду над воротами, ведшими в Верхний; во-
дяной барометр в высоту трёх этажей в помещении мате-
матического факультета нового здания университета; пери-
скоп, сконструированный в связи с гибелью во время
О Н. А. Любимов, Воспоминания о Н. Е. Зернове, < Мо-
сковские ведомости», 1864, № 21.
ЧЕБЫШЕВ И МОСКОВСКИЙ УНИВЕРСИТЕТ 40-Х ГГ,
197
обороны Севастополя адмирала Нахимова, который был
ранен вражеской пулей в то время, когда он, высунувшись
из-за бруствера, рассматривал расположение противника.
Как профессор Зернов был учителем в лучшем и пол-
ном смысле этого слова. Кафедра для него была единствен-
ной сферой, где он чувствовал себя па своём месте, а жечь
«глаголом» сердца своих слушателей было его единственным
призванием.
К своему преподавательскому делу Зернов относился
с исключительной добросовестностью: лекций никогда не
пропускал и никогда на них не опаздывал. Если ему и случа-
лось по какой-либо причине опоздать, то это было целое про-
исшествие, о котором студенты толковали несколько дней.
Когда все профессора кончали чтение своих лекций,
Зернов ещё продолжал преподавать: читал до мая, читал
в мае и даже накануне экзаменов. Он идея обыкновение
в течение года делать две-три репетиции и требовал от
своих слушателей аккуратного их посещения. Он не терпел
студентов, не посещавших эти репетиции, однако такие
встречались, и Зернов на экзамене их не вызывал, а про-
сто ставил единицу. Так как это «портило кандидатство»,
то такой студент оправдывал свои пропуски репетиций
болезнью, доказывал, что «математику любит, серьезно
ею занимается», и требовал его экзаменовать. «Ну, ладно,—
отвечал обычно Зернов такому студенту,—всё равно полу-
чишь единицу. Бери билет из аналитики на плоскости».
Он всегда заставлял более слабых, по его убеждению, брать
билеты из аналитики на плоскости.
Большой популярностью Зернов не пользовался ни
в профессорской, пи в студенческой среде. Но слушатели
ценили его как наставника, «с увлечением преданного
своему делу, чувствовавшего себя среди учеников вполне
на своём месте; молодёжь и сознательно и инстинктивно
понимала, какие удобные пружины двигали тем, кто с та-
ким усердием и самоотверженностью был предан своему
делу, кто желал не только прочесть лекцию, но и действи-
тельно научить»1).
’) Н. А. Любимов, Воспоминания о Н. Е. Зернове. «Москов
ские ведомости», 1864, № 21.
198
В. Е. ПРУДНИКОВ
Прослушав в течение четырёх лет курс у Зернова,
посещая аккуратно его дополнительные лекции и репе-
тиции, Чебышев прошёл достаточно серьёзную первона-
чальную школу, познакомился с современным ему состо-
янием математической науки, что, бесспорно, облегчило
его дальнейшие самостоятельные исследования.
П. Л. Чебышев в Московском университете
На математическое отделение Чебышев поступил в
1837—1838 уч. году, т. е. спустя два года после получения
университетом 2-го устава и введения четырёх летнего срока
обучения. С переходом на четырёхлетний срок обучения
объём преподавания математики был значительно расши-
рен. В 1835—1836 уч. году математические дисциплины
по курсам распределялись так: 1 курс— аналитическая
геометрия и высшая алгебра (по 3 часа в неделю), II и
III курсы — дифференциальное и интегральное исчисления
(по 3 часа в неделю), IV курс—интегрирование уравнений
с частными производными, вариационное исчисление и
исчисление конечных разностей (по 1 часу в неделю).
Особый интерес представляет обзор тех руководств,
по которым студенты Московского университета изучали
математику в период пребывания в нём Чебышева. Здесь
мы находим: «Аналитическую геометрию» Н. Д. Брашмана,
изданную в 1836 г. и удостоенную С.-Петербургской ака-
демией наук полной демидовской награды; «Рассуждение
об интеграции уравнений с частными диференциалами»
Н. Е. Зернова, изданное в 1837 г. и представлявшее собой
первое обстоятельное сочинение на русском языке по этой
важной ветви анализа; педагогические качества этого сочи-
нения очень высоки, так как автор изложил теорию инте-
грирования различных видов уравнения с частными про-
изводными по первоисточникам; сочинение блещет эруди-
цией и показывает прекрасное знание его автором соот-
ветствующих трудов Лагранжа, Лапласа, Коши, Ампера,
Якоби, Монжа, Фурье и др.; «Ручную математическую
энциклопедию» Д. М. Перевощикова, тринадцать томиков
которой издавались на протяжении ряда лет, начиная
с 1827 г., и по которой в своё время училась вся Россия;
ЧЕБЫШЕВ И МОСКОВСКИЙ УНИВЕРСИТЕТ 40-Х ГГ. 193
по ней учился математике Гоголь, считавший её одним из
самых образцовых математических сочинений на русском
языке, по ней учился математике Лермонтов в «Благород-
ном университетском пансионе» и в бытность его в «школе
гвардейских подпрапорщиков».
Ко времени поступления в Московский университет
Чебышева «Ручная математическая энциклопедия» Пере-
вощикова считалась слишком элементарной и отчасти
устаревшей. Поэтому рекомендовалось дополнять её со-
держание из сочинений Эйлера, Коши, Лакруа и др.
«Предметы учения» и последовательность, в какой Че-
бышев изучал их в Московском университете на протяже-
нии четырёх лет, видны из расписания на стр. 200—202.
Чебышев изучал в Московском университете чистую
математику у Н. Е. Зернова, прикладную математику
(механику и оптику) у Н. Д. Брашмана, астрономию
у Д. М. Перевощикова, физику у М. Ф. Спасского,
практическую механику и начертательную геометрию
у А. С. Ершова.
Для профессоров математики Московского универси-
тета, у которых учился Чебышев, качество изложения
всегда стояло на первом месте. Они прекрасно понимали,
что приобщить юношей к серьёзному труду над собой можно
было только посредством ясного, простого и краткого
изложения основ науки. С этим не могли не считаться
такие отзывчивые и чуткие профессора, как Перевощиков,
Зернов и Брашман. Они понимали также, что математика
в нашем отечестве нашла для себя удобную плодородную
почву. К этому заключению они были приведены долго-
летней учебной практикой, хотя нигде это не выразили
словом. Это сделал позже А. Ю. Давидов, их ученик,
который на обеде 22 октября 1885 г., устроенном в честь
35-летия его профессорской и учёной деятельности, гово-
рил: «Нужно сознаться —и мы вправе с радостью и гор-
достью высказать это сознание—что наша наука пустила
глубокие корни в нашем отечестве, что математика стала
нашей родной наукой. В то время, когда другие отра-
сли человеческого знания находились у нас на первой
ступени развития, — математика у нас уже держала вы-
соко своё знамя. Достаточно указать в этом отношении на
Распределение времени преподавания учебных предметов в И. М. У.
на первое полугодие 1840/41 г.
Во 2-м отделении философского факультета
Курсы | Часы Понедельник Вторник Среда Четверг Пятница • Суббота
X Рисование (Уч. Гадзевич) — — — Рисование (Уч. Гадзевич) —
XI — Богословие (Пр. Тернов- скиЮ — Богословие (Пр. Тернов- ский) —- Богословие (Пр. Тернов- ский)
р в ы й XII Чистая мате- матика (Эк.орд. преф. Зернов^ Астрономия (Орд. проф. Перевощиков) — Астрономия (Орд. проф. Перевощиков) Чистая мате- матика (Эк.орд. проф. Зернов) Фр. яз. (Пр. Куртенер)
К I Фрапцузск. яз. (Пр. Куртенер) Физика (А 1ъюнкт Спасский) Чистая мате- матика (Эк. орд. проф. Зернов) Физика (Адъюнкт Спасский) Французск. яз. (Пр. Куртенер) Физика (Адъюнкт Спасский)
II — Русская сло- весность (Эк.орд. проф. Шевырёв) Французск. язык (Пр. Куртенер) Русская сло- весность (Эк. орд. проф. Шевырёв) Французск язык (Пр. Куртенер) Русская сло- весность (Эк. орд. проф. 1 Шевырёв)
1 1 1 1 1
200 Е. Е. ПРУДНИКОВ
| В т
Illi 1
X Зоология (Рулье) Химия (Орд. проф. Гейман) Зоология (Рулье) Химия (Орд. проф. Геймап) Зоология (Рулье) Химия Юрд. проф. Гейман)
XI Бетанина (Орд. проф. Фишер) — Ботаника (Орд. проф. Фпшер) — Ботаника (Орд. проф. Фишер) —
XII механика (Орд. проф. Брашман) Физ. география (А 1ъюнкт Спасский) Чистая мате- матика (Эк.орд. проф. Зернов) Физ. география (Адъюнкт Спасский) Механика (Орд. проф. Брашман) Механика (Орд. проф. Брашман)
I Чистая мате- Чистая мате-
матика (Эк. орд. проф. Зернов) — — — матика (Эк.орд. проф. Зернов) —
X — Химия (Орд. проф. Гейман) — Химия (Орд. проф. Гейман) — Химия (Орд. проф. Гейман)
XI Ботаника (Орд. проф. Фпшер) — Ботаппка (Орд. проф. Фпшер) — Ботаника (Орд. проф. Фишер) —
XII Астрономия (Орд. проф. Перевощиков) Зоология (Рулье) Астрономия (Орд. проф. Перевощиков) Чистая мате- матика (Эк.орд. проф. Зернов) — Чистая мате- матика (Эк.орд. проф. Зернов)
1 механика (Орд. проф. Брашман) ипералогия (Орд. проф. Щуровский) Статика (Орд. проф. Брашман) Астрономия (Орд. проф. Перевощиков) Статика (Орд.) проф. Брашмап Л1Ипералогия (Орд. п оф. Щуровский)
II Физика (Спасский) — — — — —
ЧЕБЫШЕВ И МОСКОВСКИЙ УНИВЕРСИТЕТ 40-Х ГГ. 201 ‘
Продолжение
Курсы I Часы Понедельник Вторник Среда Четверг Пятница Суббота
1 Четвертый 1 X XI — — — Законы о со- стояниях (Адъюнкт Лешков) — Законы о состояниях (Адъюнкт Лешков)
Зоология (Рулье) — — Геогнозия (Орд. проф. Щуровский) Зоология (Рулье) Динамика (Орд. проф. Брашман)
XII I Ботаника (Орд. проф. Фишер) Химические опыты (Орд. проф. Брашман) Ботаника (Ор [. проф. Фишер) Чистая мате- матика (Эк.орд. проф. Зернов) Ботаника (Орд. проф. Фишер) Чистая мате- матика (Эк. орд. проф. Зернов)
Астрономия (Орд. проф. Перевощиков) Химические опыты (Op f.. проф. Брашман) Динамика (Орд. проф. , Брашман) Химические опыты (Орд. проф. Брашман) —
II Физика (Спасский) — Астрономия (Орд. проф. Перевощиков) — — —
202 Е. F. ПРУДНИКОВ
ЧЕБЫШЕВ И МОСКОВСКИЙ УНИВЕРСИТЕТ 40-Х ГГ.
2)3
Лобачевского, учёного, стоявшего не только на уровне со-
временной ему пауки, по опередившего её во многом:
его идеи и исследования стали понятными только в наше
время. Когда другие науки делали только первые неуве-
ренные и неопределённые шаги, имена Остроградского и
Буняковского уже гремели в учёном мире и пользова-
лись заслуженным и всеми признанным авторитетом»1)’
Интересны в этом отношении цифры окончивших мате-
матический факультет Московского университета в 1847 —
1849 гг., приведённые профессором Брашманом в своём
неизданном сочинении -«Некоторые мысли о математиче-
ском факультете», которое удалось обнаружить в архиве
древних актов и книг при Историческом музее в Москве.
Вот эти цифры:
Годы В математиче- ском отделении Из нпх кандидатов В естественном отделении Из них • кап щдатов
1847 13 10 20 8
1848 13 5 33 7
1849 16 5 33 4
Анализируя эти цифры, Брашман подчёркивал, что
«в естественное отделение вступают с немногими исключе-
ниями не по склонности, но по сознанию невозможности
следовать за математическими курсами. Непосредственные
способности студентов естественного отделения вообще
видны из того, что число кандидатов не только в показан-
ных годах, но и во всех других почти со времени существо-
вания этого отделения постоянно меньше в сравнении
с числом математического отделения».
Считая русских юношей способными к математике,
Перевощиков, Зернов и Брашман принимали все меры
х) «Известия имп. общества любителей естествознания, антро-
пологии и этнографии», 1887, т. Ы, ч. III—«Воспоминания об
А. Ю. Давидове», под ред. Е. И Вейнберга.
204
В. Е. ПРУДНИКОВ
к тому, чтобы «открыть» среди них особые математические
таланты.
Говоря о профессорах, у которых Чебышев слушал
лекции в Университете, следует несколько слов сказать
ещё о А. С. Ершове, которому Чебышев обязан большим
интересом к вопросам практической механики. Ер-
шов-питомец Московского университета, по оконча-
нии которого был зачислен преподавателем механики и
математики в З-ю реальную гимназию, директором кото-
рой был Погорельский. Последний на средства гимназии
командировал Ершова изучать практическую механику
и начертательную геометрию сначала в С.-Петербург,
а затем в Париж, где А. С. Ершов слушал лекции извест-
ных профессоров, в том числе и знаменитого Понселе.
Будучи за границей, Ершов в свободное от учебных
занятий время осматривал фабрики, заводы, механические
заведения и мануфактуры. Вернувшись из-за границы,
он приступил к преподаванию практической механи-
ки в гимназии, придерживаясь руководств Понселе и
Ястржембского («Главные основания общей и прикладной
механики»).
В скором времени после возвращения из-за границы
Ершов защитил диссертацию, получил степень магистра
и приглашён был преподавать начертательную геометрию
и практическую механику в Московском университете.
У Ершова слушал лекции Чебышев, с молодых лет инте-
ресовавшийся проблемами практической механики. Лек-
ции Ершова оказали серьёзное влияние на молодого
Чебышева и определили у него на всю жизнь интерес
к вопросам теории механизмов и машин.
Для характеристики университетской жизни в 40-х
годах XIX в., когда учился Чебышев в МосковскохМ уни-
верситете, необходимо, прежде всего, отметить, что науки
в университетском преподавании разделялись на «факуль-
тетские» и «побочные». Первые составляли предмет глав-
ных специальных занятий студентов избранного факуль-
тета; баллы, полученные на экзаменах по этим наукам,
принимались в расчёт при определении степени окончив-
шего курс студента: 472 в среднем выводе давало сте-
пень кандидатам 3'/2—степень действительного студента;
ЧЕБЪ.ШЕВ И МОСКОВСКИЙ УНПВ1 РСИТЕТ 4 ЬХ ГГ. 205
«побочные» науки считались второстепенными и баллы,
полученные по ним, принимались во внимание только при
переходе с курса на курс, но для этого достаточно было
иметь Зх/2 в среднем; следовательно, можно было получить
по некоторым «побочным» наукам и двойку. Для математи-
ков такими «побочными» науками были науки есте-
ственные (ботаника, зоология, минералогия). Как правило,
математики на эти науки мало уделяли времени и труда,
занимаясь преимущественно «факультетскими»: чистой и
прикладной математикой, астрономией и физикой. По
приложенному выше расписанию учебных занятий на
1840—1841 гг. нетрудно установить, какие на каждом
курсе «факультетские» науки преподавались.
Студентам при поступлении их в Университет разда-
вались табели, т. е. краткие .правила поведения. Боль-
шинство студентов охотно и аккуратно посещали лекции.
На ординарных (общих) лекциях для двух факультетов
они стремились занять место на передней лавке, поближе
к профессору. В то время это считалось важным делом
для прилежного студента.
Московский университет в 40-е годы XIX в. поль-
зовался известной и большой славой, но не по причине от-
сутствия формализма и стеснений, а «по той оживлённой
научной деятельности, по той разумной трудовой жизни,
которая бесспорно преобладала тогда в Московском уни-
верситете»1). В нём читали известные профессора, имена
которых произносились с уважением: Крюков, Гранов-
ский, Редкин, Шевырёв, Брашман, Зернов, Перевощиков,
Кавелин и др.
Отличительной чертой хода учебного дела в Московском
университете было то, что профессора читали общие курсы,
а не специальные.
По свидетельству современников, литографированных
лекций тогда не было, студентам надеяться было не на
что, и они в большинстве аккуратно посещали университет,
слушали живое слово профессора, записывали читаемое
и составляли лекции. Все профессора заботились о том,
чтобы студентами усваивалось излагаемое ими с кафедры,
1) «Русская старина», 1887, т. 55, стр. 654.
206
Р» F. ПРУДНИКОВ
и вели дело так, что заставляли студентов работать само-
стоятельно. По каждому предмету производились полуго-
довые репетиции; каждый профессор рекомендовал и давал
желающим студентам книги по своему предмету и беседо-
вал со студентом о прочитанном.
Знакомство с обстановкой в Московском университете
в годы учения в нём Чебышева, а особенно с первыми учи-
телями Чебышева по математике позволяет судить о том
влиянии, какое они могли оказать на формирование науч-
ных интересов и стремлений Чебышева. От своих учителей
он, прежде всего, унаследовал любовь к педагогическому
делу и к профессии учителя. Для Чебышева, как и для
его наставников, аудитория «имела всегда неотразимую
притягательную силу и преподавательские обязанности
не были для пего отягощающим трудом, а напротив —
источником удовольствия».
По свидетельству одного из его учеников
(проф.К. А. Поссе), часы, проведённые на кафедре в аудито-
рии среди слушателей, принадлежали к лучшим моментам
жизни Чебышев а. Здесь именно создавалась та «нравствен-
ная связью, которая соединяла различные поколения слуша-
телей между собой и с обликом дорогого им учителя.
От своих наставников Чебышев в известной мере унаследо-
вал и привычку учить учеников по окончании университета.
Первые шаги на научном поприще тех из его слушателей,
которые посвятили себя занятиям математикой, были сде-
ланы под его непосредственным руководством и под влия-
нием его ценных указаний, которые он давал всем желаю-
щим и умеющим ими пользоваться.
Педантичная строгость, с которой Чебышев относился
к чтению своих лекций, никогда их не пропуская, никогда
на них не опаздывая и ни одной минуты лишней после
звонка не оставаясь в аудитории, хотя бы для этого лекцию
приходилось прерывать на полуслове; стремление Чебы-
шева читать своим студентам курсы небольшие по объёму,
по по содержанию и изложению очень доступные и удобо-
понятные; небольшие развлечения в антрактах между
объяснениями на лекциях, когда Чебышев рассказывал
о своих встречах с другими знаменитыми математиками
и о своих работах, —всё это в известной мере результат
41 БЬ П1ЕВ II МОСКОВСКИЙ УНИВЕ РСИТЕТ 40-Х ГГ. 207
влияния его университетских наставников по математике.
Интерес Чебышева к вопросам теории вероятностей тоже
был в значительной степени обусловлен влиянием руко-
водящих лиц Московского университета.
Следует, впрочем, заметить, что, как было уже указано,
работы Коши по теории функций комплексного переменного
в то время на лекциях в Московском университете не изла-
гались; внимание было сосредоточено на вопросах
обоснования классического анализа.
Быть может с этим отчасти связан слабый интерес
Чебышева к теории функций комплексного переменного.
Магистерские экзамены и диссертация П. Л. Чебышева
Московский университет Чебышев окончил в 1840—
1841 уч. году отличнейшихМ кандидатом, в чём ему был
выдан 17 июня 1841 г. диплом, подлинник которого
сохранился в деле Совета университета (№ 65 от
1843 г.).
В 1841 г. Россию постиг голод. Дела многих студентов,
в том числе и Чебышева, пошатнулись. Родители его
вынуждены были переехать на жительство в деревню и
перестали уделять своему сыну хоть малую часть своих
средств. Чтобы не терпеть нужды, молодому Чебышеву,
только что вышедшему из Университета, оставалось либо
поступить на службу и забросить любимые занятия, либо
итти на лишения. Чебышев выбрал последнее. Чтобы
как-нибудь существовать, он решил в доме своего
отца, предоставленном ему для житья, создать что-то
в роде пансиона и думал сам обучать математике
пансионеров, но оказался педагогом нетерпеливым, сер-
дитым, прекратил свою затею и решил, несмотря на
лишения, усиленно готовиться к магистерским эк-
заменам.
19 марта 1843 г. Чебышев подал в Совет университета
прошение о допущении его к установленным испытаниям
на степень магистра математических наук. 2-е отделение
философского факультета в заседании 29 апреля того же
года, под председательством декана Д. М. Перевощикова,
обсуждало отношение ректора Университета от 23 марта
208
Е. Б* ПРУДНИКОВ
о допущении к испытаниям на степень магистра кандидата
Чебышева.
Эти испытания по 101 статье университетского устава
1804 г., которая была почти в неизменённом виде сохра-
нена и в «Положении об испытании на учёные, степени»,
утверждённом 28 апреля 1837 г., рекомендовалось произ-
водить так: «Из определённого числа написанных и храни-
мых в тайне вопросов, относящихся особенно до каждой
науке, к отделению принадлежащей, выбираются по жре-
бию два вопроса для магистра и четыре для доктора, кои
они должны решить основательно и подробно. Засим сле-
дует производить словесное испытание в других предметах,
назначенных экзаминатором. Потом они должны решить
письменно такое же число и также по жребию выбранных
вопросов в присутствии члена отделения».
Статья 102 того же устава требовала, чтобы после
этих испытаний «ищущий магистерского достоинства
читал одну, а докторского три сряду публичных лекций
о предметах, от отделения назначенных». Но к 40-м« годам
эта статья свою силу утратила, выполнение её считалось
ужо необязательным. Наконец, университетский устав
требовал, чтобы от Совета университета были на испыта-
ния назначены депутаты.
«Положение об испытании па учёные степени» 28 апре-
ля 1837 г. было утверждено только в виде опыта на три го-
да. В 1844 г. 6 апреля этот опыт, проведённый на деле
и более развитый в подробностях, был утверждён под за-
главием «Положения о производстве в учёные степени». Для
магистерской степени один предмет был признан главным,
другой, тесно с ним связанный, второстепенным; для док-
торской степени оба предмета, тесно между собою связан-
ные, считались одинаково важными. От магистра требова-
лось «историческое» знание предмета, от доктора—«кри-
тическое».
Первое испытание Чебышева происходило 29 апреля
1843 г. по физике и физической географии в присутствии
депутатов, ординарных профессоров Рихтера и Лешкова.
Испытание производил адъюнкт М. Ф. Спасский, который
донёс 2-му отделению, что Чебышев на «предложенные
словесные вопросы отвечал удовлетворительно».
ЧЕБЫШЕВ И МОСКОВСКИЙ УНИВЕРСИТЕТ 40-Х ГГ. 299
В следующем заседании отделения 23 сентября 1843 г.
продолжалось испытание Чебышева по чистой и приклад-
ной математике ординарными профессорами Зерновым и
Брашманом. В протоколе этого заседания сказано, что
«кандидат Чебышев на предложенные словесные вопросы
отвечал удовлетворительно и определённо: в будущем за-
седании приступить к письменному испытанию кандидата
Чебышева».
Заседание отделения состоялось 29 октября 1843 г.
Согласно с правилами проф. Брашман предложил для
письменного решения вопрос: «Определение закона о
движении тела по циклоиде, когда, кроме тяжести, дей-
ствуют ещё какие-нибудь возмущающие силы». Ответ на
этот вопрос требовал от экзаменующегося умения приме-
нить общие законы принуждённого движения тела по
произвольной кривой к случаю, когда такой кривой явля-
ется циклоида.
За свой ответ Чебышев получил от проф. Брашмана
отметку «весьма удовлетворительно». И из этого ответа
ясно видно, что характерные вообще для Чебышева
методы классической ^тематики (а также механики)
были твёрдо усвоены им во время учёбы в Московском
университете.
Проф. Зернов предложил для письменного решения
вопрос: «Множитель, вспомоществующий нахождению ин-
теграла ур. дифференциального; случаи, в коих можем
находить оный и главные его свойства».
В своём ответе Чебышев показал, что 1) «всякое диф-
ференциальное уравнение первого порядка и первой сте-
пени, имеющее интеграл, приводится к полному дифферен-
циалу через умножение на некоторую функцию, которая
и известна под названием множителя вспомогательного»,
что 2) в таком случае существует бесчисленное множество
интегрирующих множителей, что 3) интегрирующий мно-
житель определяется в общем случае уравнением с част-
ными производными, интегрирование которого пред-
ставляет задачу более трудную, чем интегрирование
обыкновенных дифференциальных уравнений. Поэтому
он ограничился в своём ответе обычным рассмотрением
простейших случаев, когда существует интегрирующий
14 Историко-ыатемат. последования
210
В. Е. ПРУДНИКОВ
множитель z, являющийся функцией или одного только
х или одного только г/, а также случаем однородного
уравнения.
Предложенный Чебышеву вопрос не был интересен-не
только с современной точки зрения, но и для его времени,
так как не содержал упражнения для самостоятельного
применения какого-нибудь метода. Чего-либо выходящего
за пределы учебника по его поводу просто нельзя было
сказать. Чебышев в своём ответе и ограничился изложе-
нием материала учебников, но сделал это коротко, ясно
и просто.
Всё же проф. Зернов оценил его ответ только как удо-
влетворительный .
После успешного окончания 5 ноября 1843 г. письмен-
ных испытаний Чебышеву было предложено приступить
к сочинению рассуждения на тему «О бесконечно малых
качаниях». Однако Чебышев к работе над этой темой не
приступил1). В качестве диссертации он представил
в 1845 г. своё сочинение «Опыт элементарного анализа
теории вероятностей», написанное им по поручению по-
печителя Московского учебного округа графа С. Г. Стро-
ганова в качестве руководства для преподавания этой
отрасли математических наук в Ярославском демидов-
ском лицее.
В заседании 30 мая 1845 г. 2-е отделение занималось
обсуждением достоинств сочинения Чебышева и его одоб-
рило. Оно нашло, что Чебышев в представленном сочи-
нении, кроме внимательного изучения Лапласа и Пуас-
сона, показал «весьма похвальное и успешное усилие
дать собственное доказательство весьма важных теорем»,
приняло это сочинение взамен диссертации на предложен-
ную тему и «одобрило оное для напечатания, вменив однако
ж в обязанность Чебышеву сделать некоторые изменения
в изложении отдельных частей его сочинения согласно с
сообщёнными ему подробными замечаниями ординарного
профессора Зернова». В заключение 2-е отделение поста-
9 Сочинение «О бесконечно малых качаниях» немного позже
было предложено составить кандидату А. Ю. Давидову, который за
свою работу получил золотую медаль.
ЧЕБЫШЕВ И МОСКОВСКИЙ УНИВЕРСИТЕТ 40-Х ГГ.
in
новило донести об этом Совету университета и ходатайство-
вать «о допущении Чебышева к напечатанию и публичному
защищению написанного им сочинения».
Совет университета 6 июня 1845 г. постановил
написанное кандидатом Чебышевым сочинение напе-
чатать в желаемом количестве, экземпляров, из кото-
рых необходимо было в Совет представить 4 для
препровождения к попечителю и помощнику его для
оставления при делах Совета, а затем «по отпеча-
тании сочинения представить г. Ректору назначить
день для публичного защищения оного, о чём и пуб-
ликовать в «Московских Ведомостях» нащёт его Чебы-
шева».
Оппонентами были назначены профессора Зернов и
Брашман. Публичное заседание 2-го отделения философ-
ского факультета состоялось 8 июня 1846 г.
В «Московских Ведомостях» за этот день было напеча-
тано следующее извещение: «Сего июня 8-го дня, в 12 ч.
утра, ищущий степени магистра математических наук
кандидат Чебышев будет публично защищать написанную
им диссертацию: «Опыт элементарного анализа теории
вероятностей». Диспут будет происходить в новом универ-
ситетском доме».
Защите подлежали следующие положения:
«1) Теория вероятностей приносит надлежащую пользу
только при помощи анализа.
2) С началами алгебры может быть выведена вероятность
повториться нескольким событиям известное число
раз.
3) Определение вероятности, что числа повторений со-
бытий будут в данных пределах, требует составления осо-
бой таблицы.
4) Без посредства интегралов может быть дано
понятие об этой таблице и ряды для её вычислений.
5; С помощью этой таблицы мы можем составить
заключение о вероятности события по числу его по-
вторений.
6) Через посредство одной вспомогательной теоремы
относительно суммирований может быть также выведена
вероятность средних результатов.
14*
212
В. Е» ПРУДНИКОВ
7) С одними началами алгебры можно показать, что
величина произведения 1-2-3... (х—1)-я всегда заклю-
чается между величинами
Схх^2,в~х^1^12Х Сх а+1^2 t€~x^1/^x~1l^xZ
где С есть количество, не зависящее от ж».
Эти положения указывают на главную цель диссер-
тации Чебышева: «показать без посредства трансцендент-
ного анализа основные теоремы исчисления вероятностей
и главные приложения их, служащие опорою всем
знаниям, основанным на наблюдениях и свидетель-
ствах».
Достижение этой цели было важно во многих отноше-
ниях и, прежде всего, для пользы множества людей, кото-
рые в изучении математики ограничивались одной
алгеброй. Эту пользу и имел в виду попечитель - граф
Строганов, когда он предложил Чебышеву написать
сочинение по теории вероятностей, не прибегая при этом
к средствам высшего анализа, так как это сочинение долж-
но было служить руководством по указанной науке для
учащихся Ярославского демидовского лицея.
Предложение графа Строганова Чебышев выполнил
с присущей ему талантливостью. Он показал, что все во-
просы относительно повторения событий и определения
вероятности средних результатов можно решить с помощью
одной алгебры, привлекши дополнительно лишь простей-
шие сведения из теории рядов.
До сочинения Чебышева элементарные курсы теории
вероятностей ограничивались только более или менее
подробным изложением результатов, полученных посред-
ством высшего анализа. В своём же сочинении по этой
науке Чебышев показал, что возможно «поверить все
эти заключения анализом строгим и простым, доступным
до большей части учащихся». Это было большим шагом
в способе элементарного изложения теории вероятностей,
что, бесспорно, и ставилось в заслугу Чебышеву его
официал ьными оппонентами.
Согласно протоколу эти последние сделали свои возра-
жения диссертанту, но Чебышев их «разрешил весьма у до-
ЧГБЫШЕВ И МОСКОВСКИЙ УНИВЕРСИТЕТ 40-Х ГГ. 21 3
влетворительно» и математическое отделение признало
его достойным искомой степени магистра.
Чебышев справедливо считается одним из наиболее
ярких математиков, сознательно ставивших и решавших
чисто математические вопросы, исходя из вопросов практи-
ки. Он неоднократно подчёркивал это в своих речах и про-
явил это достаточно выпукло уже в своей первой диссерта-
ции. В ту пору в России страховое дело только-только
начало зарождаться. Население питало к нему мало дове-
рия, не понимало его пользы.
В. Я. Буняковский был в то время первым и весьма
энергичным пропагандистом страхового дела и теории
вероятностей в России. В своей статье «Мысли о неоснова-
тельности некоторых понятий, относящихся к общежитию,
преимущественно к играм и лотероям»(«Маяк», 1840, ч.Ш,
стр. 80—94) он писал о страховых обществах: «Теория ве-
дёт к заключению, что можно соразмерить премию, плати-
мую застрахователем, так, чтобы при верной прибыли для
общества нравственная выгода застрахователя увеличи-
лась. Эта истина обнаруживает несомненную пользу стра-
ховых учреждений». Эта статья Буняковского во многом
определила направление и ход мыслей речи Н. Е. Зернова
«Теория вероятностей с приложением преимущественно
к смертности и страхованию» (М., 184В), которая, в свою
очередь, оказала немалое влияние на сочинение проф.
Брауна «Руководство к политической арифметике» (Одесса,
1845).
Нет сомнения, что зарождение в России страхового
дела и упомянутые сочинения, пропагандировавшие
это дело, определили вкус у молодого Чебышева к вопро-
сам теории вероятностей.
Во время подготовки к защите своей магистерской
диссертации в 1845 г. Чебышев приезжал в Петербург,
чтобы поместить своего брата Николая Львовича в артилле-
рийское училище. В 1847 г. он определил туда же другого
брата Владимира Львовича и сам переехал в Петербург,
получив от Петербургского университета приглашение
занять в нём должность адъюнкта профессора.
Но и после отъезда Чебышева в Петербург не прерыва-
лась его тесная связь с Московским университетом. Он
214
В. Е. ПРУДНИКОВ
переписывался со своим учителем Н. Д. Брашманом, живо
интересовался успехами Московского математического
общества, сотрудничал в журнале «Математический сбор-
ник»1). Московский университет помнил своего знаменитого
воспитанника.
В 1857 г. Чебышев был избран физико-математическим
факультетом Московского университета в почётные члены.
Как почётный член Московского университета Чебышев
получил соответствующий диплом, подлинник которого
хранится в архиве Московского университета.
г) В «Математическом сборнике» Чебышев поместил следующие
работы: «Разложение функций в ряды при помощи непрерывных
дробей» (т. I, 1866); «О средних величинах» (т. II, 1867); «Об интегри-
ровании простейших дифференциалов, содержащих кубический ко-
рень» (т. II, 1867); «Об определении функций по значениям, которые
они имеют при некоторых величинах переменной» (т. IV, 1870); «О
простейших сочленениях» (т. IX, 1878).
НАЧАЛА» ЕВКЛИДА
«НАЧАЛА» ЕВКЛПДА1)
Л/. <Я. Выгодский
1. Значение «Начал»
Книги, как и люди, стареют. И старость для боль-
шинства книг наступает довольно быстро; лишь немногие
произведения живут веками.
Научная и учебная книга стареет быстрее всего. Как ни
замечательны труды Ньютона, никто сейчас, через
27а века, не будет изучать по ним интегральное исчис-
ление или оптику. Никто не будет сейчас изучать
астрономию по трудам Кеплера, химию—по произве-
дениям Ломоносова или Лавуазье.
Между тем геометрию люди изучали по Евклиду
в течение двух тысячелетий. И если в последнее столетие
«Начала» Евклида не играют уже роли стабильного школь-
ного руководства, то они всё же и теперь живут плодо-
творной жизнью.
Без преувеличения можно сказать, что все системати-
ческие школьные курсы геометрии, непосредственно или
через промежуточные звенья, испытывают на себе влия-
ние «Начал». Более того, даже теоретические работы по
элементарной математике вплоть до настоящего момента
имеют «Начала» Евклида своей исходной точкой, а в ряде
случаев и образцом.
г) Настоящая статья написана в связи с выходом в свет нового
перевода «Начал» Евклида на русском языке. Перевод этот сделан
проф. Д. Д. Мордухай-Болтовским при редакционном участии
И. Н. Веселовского и автора этой статьи. См. "Начала Евклида»,
книги I—VI. Гостехивдат, М.—Л., 1948. Последующие книги вый-
дут в 1949 и 1950 гг.
218
М. Я. ВЫГОДСКИЙ
И потому «Начала» Евклида изучали и изучают не толь-
ко историки науки, но и математики всего мира.
По числу изданий (на языке оригинала и в переводах)
«Начала» занимают, если не первое, то одно из первых
мест во всей мировой литературной продукции. При этом
огромное большинство переводов имело в виду узко учеб-
ные цели, и потому переводчики, стремясь сделать труд
Евклида возможно более доступным, подвергали его более
или менее значительным переделкам: опускали одни раз-
делы, добавляли другие, заменяли некоторые доказатель-
ства Евклида своими собственными, облегчали чтение
«Начал» стилистическими изменениями, к прибегали к
пересказам отдельных мест.
И в настоящее время имело - бы смысл предпри-
нять издание «облегчённого» перевода «Начал». При
соблюдении должного такта подобное издание, будучи
полезной математической книгой, дало бы в то же вре-
мя некоторое представление о бессмертном произведении
Евклида.
Но переработанный Евклид—это уже не Евклид. А
между тем, для того чтобы изучить подлинного Евклида,
стоит затратить некоторый труд, необходимый для преодо-
ления непривычных современному читателю особенностей
стиля, языка и мышления. Глубина и отточенность мысли
Евклида таковы, что даже самые осторожные изменения
в тексте могут исказить подлинную мысль автора и притом
с ущербом для цельности произведения. Вот почему нам
нужен также точный перевод Евклида.
Их всех прежних русских изданий Евклида лишь одно
ставило себе целью дать точный перевод «Начал». Это был
перевод, выпущенный Ф. Ф. Петрушевским в 1819 (книги
1—6, 11—13) и 1835 (книги 7—9) годах. Со своей задачей
переводчик справился блестяще. Но в настоящее время
переиздание этого перевода было бы нецелесообразным.
Даже для своего времени язык перевода был архаичным.
В наше же время он совершенно устарел. Кроме того, за
протекшие сто с лишним лет была проделана большая кри-
тическая работа, так что теперь мы можем лучше восста-
новить оригинальный текст Евклида? освободив его от
многих позднейших наслоений.
«НАЧАЛА» ЕВКЛИДА
219
Новый перевод «Начал» Евклида, сделанный Д. Д. Мор-
духай-Болтовским при редакционном участии И. Н. Весе-
ловского и автора этой статьи, сделан с греческого
текста, изданного И. Г. Гейбергом полвека назад и остаю-
щимся поныне лучшим критическим изданием Евклида.
Забота о литературной стороне перевода всё время стоя-
ла в центре внимания; но в тех случаях, когда сталкива-
лись друг с другом требования точности, с одной стороны,
и требования стиля, с другой,—предпочтение отдавалось
первым.
Совершенно естественно, что чтение произведения, на-
писанного двадцать два века назад, не может не вызвать
некоторых трудностей. Их устранению должен содейство-
вать комментарий, принадлежащий проф. Д. Д. Морду-
хай-Болтовскому. В этом комментарии освещается также
историческое развитие многих частных проблем, рассма-
триваемых в «Началах». Настоящая же статья ставит себе
целью облегчить понимание «Начал» в целом.
2. Биографические сведения
Об авторе «Начал» мы знаем очень мало. Уже первый
комментатор «Начал» неоплатоник Прокл (410—485 г.
н. э.) не мог указать ни места, где родился Евклид, ни даты
его рождения и смерти. Косвенные соображения (которым
нельзя отказать в основательности) привели Прокла
к заключению, что Евклид жил в Александрии при
Птолемее I. А так как последний правил Египтом
£,323 по 283 г. до н. э., то создание «Начал» можно дати-
ровать примерно 300 г. до н. э.
Об обстоятельствах жизни Евклида нам неизвестно
почти ничего. Тот же Прокл передаёт не лишённый инте-
реса эпизод из жизни Евклида, за достоверность которого
он, однако, сам не решается поручиться. Царь Птолемей
спросил будто бы Евклида, не существует ли более корот-
кого пути для познания геометрии, чем изучение «Начал».
Гордый ответ Евклида гласил, что в геометрии нет особой
царской дороги.
В достоверности этого анекдота можно сомневаться
хотя бы потому, что аналогичный рассказ мы находим
220
М. Я. ВЫГОДСКИЙ
у Стобея (IV в. н. э.) с той разницей, что действующими ли-
цами являются там Александр Македонский и математик
Менехм.
Однако если этот рассказ и выдуман, то он всё же весь-
ма характерен. Он показывает, что, по мнению современ-
ников, Евклид отвергал всякую мысль о популяризации
науки. И в самом деле, «Начала» написаны сухим и бес-
страстным тоном. Автор явно не ищет путей сближения'
с читателем, не стремится облегчить ему познание истины.
Он предназначает свой труд для тех, кто достаточно под-
готовлен или достаточно самоотвержен, чтобы отдаться
усвоению науки в её самой отвлечённой форме.
3. Философские взгляды Евклида
По своим философским воззрениям Евклид был, по-
видимому, последователем Платона. Так, по крайней
мере, говорит Прокл. Он добавляет, что именно поэтому
конечной целью «Начал» Евклид поставил построение пра-
вильных многогранников. Ив самом деле, последняя, 13-я,
книга «Начал» посвящена правильным многогранникам,
а последнее, 18-е, предложение этой книги даёт построение
рёбер всех пяти правильных многогранников, вписанных
в шар данного диаметра. С другой стороны, в космологи-
ческой теории Платона (изложенной в диалоге «Тимей»)
правильные многогранники играют особо важную роль.
Они служат формой четырёх «элементов»: элемент огня,
как наиболее лёгкий и подвижный, имеет форму тетраэд-
ра; воздуху приписывается форма октаэдра, земле—форма
куба и воде—форма икосаэдра. Пятый правильный
многогранник, додекаэдр, оставался неиспользованным,
и бог, если верить Платону, решил употребить его для
очертания вселенной.
Таким образом, для последователя Платона было бы
вполне .естественно увенчать свой труд теорией правиль-
ных многогранников. Не следует, однако, думать (не думал
этого, вероятно, и Прокл), что построение правильных
многогранников было единственной или хотя бы важней-
шей целью «Начал». Против такого предположения гово-
рит само творение Евклида. Было бы также неправильным
«НАЧАЛА» ЕВКЛИДА
221
считать, что помещение Евклидом теории правильных
многогранников в самом конце «Начал» является решаю-
щим доказательством его «платонизма». Такой порядок
мог диктоваться чисто логическими или эстетическими
соо бр аженпями.
И, в конце концов, вопрос о философских взглядах
Евклида мог бы нас мало интересовать, если бы он не имел
существенного значения для понимания «Начал». Между
тем, как мы увидим ниже, многие их особенности, могущие
показаться непонятными, легко объясняются, если мы
примем, что Евклид был платоником. Такое предположе-
ние, впрочем, и априори весьма вероятно ввиду того поло-
жения, которое философия Платона занимала в эпоху
Евклида.
4. Методологическая установка «Начал»
Влияние философии Платона сказывается в «Началах»
уже в основном вопросе о соотношении теории и практики,
II хотя Евклид и не подвергает этот вопрос специальному
рассмотрению, но позиции его обнаруживаются из самой
структуры «Начал».
Стобей рассказывает, что некий юноша стал изучать
геометрию под руководством Евклида. Когда юноша изу-
чил несколько первых теорем, у него возник естественный
вопрос о том, для чего нужно заниматься геометрией. II
он спросил Евклида: «А что даст мне изучение этого пред-
мета?». Евклид не удостоил ученика ответом. Обратившись
с своему рабу, он сказал: «дай ему три обола; он хочет
извлечь выгоду из учения».
Пусть это—только анекдот. Но легко представить себе,
что подобное происшествие могло случиться в действи-
тельности. В самом деле, в «Началах» не только нет ни
единого слова о практических приложениях геометрии, но
в них сознательно опущены некоторые чисто теоретические
вопросы, без которых не может обойтись измерительная
практика.
Так, Евклид находит отношение площадей двух кругов,
посоставляет без рассмотрения вопрос о сравнении площади
круга с площадью квадрата (или иной прямолинейной
222
М. Я. ВЫГОДСКИЙ
фигуры). Длина окружности не рассматривается вовсе,
в частности, остаётся без всякого внимания вопрос об отно-
шении окружности к диаметру.
В практической геометрии эти задачи играют очень
важную роль, и, как мы знаем, для их решения за много
столетий до Евклида были известны достаточно точные
правила. Вопросы эти и теоретически являлисьочень акту-
альными, и полвека спустя Архимед в своём сочинении
«Измерение круга» дал тот способ решения упомянутых
задач, идея которого сохраняется во всех нынешних школ ь:
ных учебниках.
В способе Архимеда нет ничего, что превосходило бы
уровен ь знаний или творческие возможности автора «На-
чал». Но Евклид не мирится с приближёнными методами.
Приближённые расчёты—дело практики, а по учению Пла-
тона наука не имеет с практикой ничего общего. «Под
именем науки,—говорит Платон в «Государстве» устами
Сократа,—я не могу разуметь ничего иного,кроме того, что
рассуждаете сущем и невидимом». Там же Сократ заявляет,
что геометрия есть наука лишь постол ьку, поскольку она
созерцает «сущее» (т. е. не материальное); поскольку же она
направляется на «битное»—она не наука.
Такими и только такими побуждениями мог руковод-
ствоваться Евклид, устранив из рассмотрения важнейшие
метрические задачи геометрии.
В «Началах» излагается не только геометрия, но и
«арифметика», т. е., по-нашему, теория чисел. Учению же
о счёте, которое сейчас мы называем арифметикой (в эпоху
Евклида оно называлось «логистикой»), Евклид не уделяет
ни строчки. И в этом нетрудно усмотреть влияние взглядов
Платона. Обсуждая вопрос о математической подготовке
ф^лоссфов, которым в идеальном своём государстве Пла-
тон отводит главенствующую роль, Платон устами Сокра-
та говорит, что они «должны заниматься арифметикой х)
не как простые люди, но до тех пор, пока не подымутся
мышлением до созерцания природы чисел, изучая её
не для купли и продажи, как купцы или торгаши, но для
х) Из последующего ясно, что ещё во время Платона «логистика»
и «арифметика» не были отделены друг от друга.
«ЙАЧАЛА» EEKЛИДА
223
войны и самой души с целью облегчить ей обращение от
бытных вещей к истине и сущему».
Этими соображениями мог руководствоваться Евклид,
устраняя из рассмотрения важнейшие задачи арифметики.
б. Предшественники Евклида
Итак, «Начала» Евклида—это сугубо абстрактное
произведение. Как показывает самое его название, оно
охватывает не все математические знания древних греков,
а лишь элементарные вещи. Они объединены в стройное
целое. Как из песни не выкинуть слова, так из «Начал»
нельзя устранить почти ни одного предложения без ущерба
для глубоко продуманного плана произведения. И если
по мнению многих историков Гомер как единоличный
автор «Одиссеи» никогда не существовал, то в существо-
вании единоличного автора «Начал» сомнений быть не
может.
Это, конечно, вовсе не означает, что Евклид создал свои
«Начала» на пустом месте. Напротив, Евклид широко
использовал и в научном и в педагогическом отношении
богатый материал, накопленный предшествующим раз-
витием греческой математики. Более того, «Начала»
Евклида не являются ’ первым сводным курсом мате-
матики.
В своём комментарии к 1-й книге «Начал» Прокл приво-
дит сообщение Евдема Родосского (конец IV в. до н. э.),
в котором говорится, что первые по времени «Начала»
были составлены Гиппократом Хиосским (последний жил
во второй половине V в. до н. э.). В том же сообщении ска-
зано, что некто Леон, который был поколением младше
Платона (т. е., значит, поколением старше Евклида),
«составил «Начала», обращая особое внимание как на
количество, так и на полезность доказываемых предложе-
ний». Вслед за Леоном у Евдема упоминается Фидий из
Магнезии, принадлежавший к афинской Академии, кото-
рый «составил прекрасные «Начала», сделав более общими
многие частные предложения». Эти труды до нас не дошли.
Очевидно, они были забыты после появления «Начал»
Евклида. Но хотя в этих последних, как мы увидим ниже,
224
М. Я. BI ГОДСКПЙ
и можно обнаружить следы влияния предшествующих
сводных работ, однако труд Евклида должен был сильно
от них отличаться. Это видно хотя бы из того, что на «полез-
ность доказываемых предложений» Евклид—мы в этом
убедились—не обращал ни малейшего внимания.
Гораздо больнее влияние должны были оказать на
Евклида теоретические исследования предшествующих
греческих авторов по отдельным вопросам математики.
Сам Евклид нигде не упоминает о своих первоисточниках,
а.упомянутые исследования до нас не дошли. И только
из дошедших до нас комментариев к «Началам», которые
составлены неизвестными лицами в неизвестное время,
мы узнаём, что, например, классификация несоизмери-
мых величин, проводимая Евклидом в 10-й книге «Начал»,
принадлежит Теэтету Афинскому. В другом, тоже безы-
мянном, комментарии сказано, что теория пропорций,
излагаемая Евклидом в 5-й книге «Начал», «открыта,
как говорят некоторые, Евдоксом, учителем Платона».
Эти отрывочные и не вполне достоверные сведения не
позволяют нам судить, в какой степени оригинальны
«Начала» Евклида. Но во всяком случае можно сказать,
что в основном «Начала» Евклида не содержали новых
для своего времени результатов.
6. Тексты «Начал»
Прежде чем перейти к обзору «Начал», нужно сказать
несколько слов об их тексте. До нас не дошла ни одна
античная рукопись «Начал» Евклида, если не считать
нескольких очень небольших обрывков, найденных при
раскопках в Египте и в Геркулануме. Древнейшая извест-
ная нам рукопись представляет собой копию, сделанную
6 888 г. монахом Стефаном для архиепископа Цезарейского.
Существует много рукописей, относящихся к X—XII вв.
Все они, невидимому, сделаны на территории Византий-
ской империи и в Западную Европу попали значительно
позднее. Неизвестно, сколько промежуточных копий лежит
между этими рукописями и их первоисточником. Но
существенно то, что они мало разнятся друг от друга,
а значит, и от оригинального текста.
НАЧАЛА» ЕВКЛИДА
Ранние арабские переводы (первый сделан в конце
IX в. Исхаком ибн Хупайном), имевшие оригиналом более
старые, недошедшие до нас, греческие копии, также в
общем сходятся с известными нам греческими рукописями.
Всё это даёт нам основание считать, что тот текст «На-
чал», которым мы располагаем, можно считать в основном
достоверным.
Однако в некоторых, иногда существенных, деталях
наши источники отличаются друг от друга. В таких слу-
чаях оказывается всё же возможным с большой достовер-
ностью восстановить подлинный текст Евклида, сличая
известные нам рукописи «Начал» с комментариями древ-
них авторов и с другими античными источниками, напри-
мер, с высказываниями Аристотеля по математическим
вопросам.
Так, например, исследования показали, что все извест-
ные нам рукописи, кроме одной (хранящейся в Ватикан-
ской библиотеке), копируют издание, относящееся к
1 \ в. н. э., сделанное Теоном Александрийским, последним
представителем языческой эллинской науки, автором
известного комментария к астрономическому труду Пто-
лемея. Теон, по его собственным словам, внёс в это издание
ряд дополнений. Поэтому в тех случаях, когда ватикан-
ская рукопись не содержит какой-либо фразы, имеющейся
во всех остальных рукописях, можно считать, что эта
фраза Евклиду не принадлежит.
Подобные соображения привели датс^рго лингвиста
Гейберга, посвятившего много лет тщательному изуче-
нию источников, к установлению того текста евклидовых
«Начал», с которого сделан новый русский перевод.
В ряде случаев предпочтение, оказанное Гейбергом
одному варианту против других, может быть оспариваемо.
Но рассмотрение такого рода вопросов имело бы интерес
лишь для немногих узких специалистов. Поэтому было
сочтено необходимым в новом переводе точно придержи-
ваться того текста евклидовых «Начал», который дан
Гейбергом во втором издании полного собрания сочинений
Евклида.
После этих замечаний мы можем перейти к существу
дела.
1° Историко-Уатсмат. псслсдоганпя
22G М. Я. ВЫГОДСКИЙ
7. Основоположения «Начал»
«Начала» Евклида разделены на 13 частей (книг).
Каждая книга начинается с определений вновь вводимых
понятий, и естественно, наибольшее число определений
(23) мы находим в 1-й книге. С определениями 1-й
книги тесно связаны следующие за ними «постулаты».
За постулатами идут аксиомы, которые, дополняя опре-
деления и постулаты, служат вместе с ними основой,
па которой Евклид строит здание геометрии.
Эту основную часть «Начал» нам придётся рассмотреть
с особым вниманием, так как в современной научной
педагогической литературе опа обычно недооценивается
и так как критика её носит односторонний характер.
Нот спора, что определения, постулаты и аксиомы
Евклида составляют наиболее уязвимое место «Начал».
Это и естественно, если принять во внимание трудности,
которые обусловлены существом дела. При современном
развитии математической логики нетрудно подвергнуть
фундамент Евклида суровой критике, и мы ниже отметим
наиболее существенные дефекты этого фундамента.
П всё же даже с точки зрения современной аксиомати-
ки основоположения Евклида, как мы ниже покажем,
не столь слабы, как обычно принято полагать.
Но помимо этого, всякая научная критика должна учи-
тывать точку зрения критикуемого автора. Мы можем но
разделять этой точки зрения, но мы должны понять её
и уяснить, насколько хорошо решена Евклидом та задача,
которую ставил себе он сам и современные ему логические
требования.
Постараемся сделать это и начнём—по порядку —
с определений.
8. Две группы определений 1-й книги
По своему характеру определения 1-й книги могут быть
разбиты (у Евклида этого деления нет) на две группы.
В первой (определения 1—9, 13, 14) вводятся первейшие
понятия геометрии (точка, линия, поверхность, прямая
линия, плоскость, угол, граница, фигура). С древнейших
«ВАЧАЛА » ЕВКЛИДА
227
времён и до-наших дней эти определения в наибольшей
степени были предметом критики. Мы оставим эту группу
пока в стороне и рассмотрим вторую группу, в которой
определяются основные геометрические фигуры (прямой,
тупой и острый углы, круг, треугольники и четырёхуголь-
ники различного вида, параллельные прямые). Эти опре-
деления очень близки к общепринятым в наше время;
однако в некоторых отношениях они носят своеобразные
черты, которые мы сейчас и рассмотрим.Возьмём для начала
определение 22, которое мы приведём в буквальном
переводе:
«Из четырёхсторонних же фигур четырёхугольная есть
та, которая является ]) и равносторонней и прямоугольной,
разносторонняя же та, которая (является)2) прямоугольной,
ио не равносторонней; бубен—та, которая (является) рав-
носторонней, но не прямоугольной; бубнообразная же
(фигура)—имеющая равные друг другу противополож-
ные стороны, а также углы, которая не является ни равно-
сторонней, ни прямоугольной. Все же четырёхсторонние
(фигуры) кроме этих пусть будут названы столиками».
Этот перевод значительно отличается от перевода
Д. Д. Мордухай-Болтовского. И в самом деле, современному
читателю было бы уж очень непривычно именовать ква-
драт «четырёхугольной фигурой» (хотя латинский термин
«квадрат» имеет именно этот смысл), прямоугольник —
«разносторонней фигурой», а ромб—«бубном» (по-гречески
бубен называется «ромбос»). Не менее странно^звучало бы
название «бубнообразная» (по-гречески «ромбоид») для
обозначения параллелограмма и «столик» («трапецион»)
для обозначения всех прочих четырёхугольников.
Мы полагаем, что многим читателям будет интересно
узнать, откуда произошли такие названия, как «ромб»,
«трапеция»; но не только с этой целью мы привели точный
перевод 22-го определения. Мы хотели, прежде всего,
отметить, что нигде в «Началах» Евклид не рассматривает
трапеций ни в смысле 22-го определения, ни в принятом
1) В оригинале «есть».
-) Слова, поставленные в скобки, в оригинале отсутствуют и под-
разумеваются по СМЫСЛV.
15*
М. Я. ВЫГОДСКИЙ
Ь$8
теперь (оно восходит, ц<> Проклу. к Посидонию—] в. н. э.);
точно так же нигде в «Началах») не рассматривается ромб.
Что же касается параллелограмма, то с ним Евклид имеет
дело очень часто. Однако он никогда не пользуется терми-
ном «бубнообразная фигура» и никогда не опирается
па приведённое выше определение. Впервые с параллело-
граммом мы встречаемся в 34-м предложении 1-й книги,
которое (в буквальном переводе) гласит: «В парал-
лельнолпнепных площадях противоположные стороны
и углы равны друг другу, а диаметр делит пополам
площади».
Слово «параллельнолинепное»1) (по-гречески «паралле-
лограммоп») и дало основу для термина «параллелограмм».
В дальнейшем Евклид часто пользуется этим словом как
существительным.
Казалось бы, в 34-м предложении^ Евклиду представ-
лялся случай отметить, что, по доказанному, параллело-
грамм тождественен с ромбоидом. Однако он не счёл
необходимым сделать это, так что термин «ромбоид» остал-
ся совершенно неиспользованным. Почему же этот термин
был введён?
В 1-й книге «Начал» с прямоугольником мы больше
не встречаемся вовсе. Он впервые появляется во 2-й книге,
которая начинается с определения: «про всякий прямо-
угольный параллелограмм говорят, что он «объемлется»
двумя прямыми, объемлющими (его) прямой угол». Ни
здесь, ни в дальнейшем Евклид не пользуется термином
«разносторонняя фигура», употреблённом в 22-м опреде-
лении 1-й книги. Почему же этот термин был введён?
На эти вопросы может быть только одий ответ: по тра-
диции. Она должна была иметь очень древние корни—об
этом свидетельствуют названия «бубен», «столик» и т. д.,
которые, очевидно, созданы непрофессионалом-учёным.
Об этом свидетельствует также естественная для нагляд-
ного восприятия, но неудобная для научных целей клас-
сификация четырёхугольников, согласно которой квадрат
не является прямоугольником, прямоугольник не являет-
Ч Подразумеваемые слова «площадь» или «фигура» по-гречески—
среднего рода.
'«НАЧАЛА» ЕВКЛИДА
229
> ся параллелограммом и т. д.1). Такую же классификацию мы
имеем в 19-м определении,согласно которому треугольники
и четырёхугольники (они названы здесь трёхсторонними
и четырёхсторонними фигурами) не являются многоуголь-
никами; лишь при числе сторон, большем четырёх, мы
имеем, по Евклиду, «многосторонний». Насколько не-
удобна такая классификация, можно видеть из такого
примера. В 20-м предложении 6-й книги Евклид доказы-
вает (мы переводим формулировку Евклида на совре-
менный язык), что отношение площадей подобных мно-
го угольников равно квадрату отношения сходствен-
ных сторон. Вслед за этим он должен сделать оговорку
(«поризм»), что тот же метод можно применить и к четы-
рёхугольникам и что для треугольников это предложение
было доказано раньше.
Итак, мы установили, что в своих определениях Евклид
связан исторической традицией. Этот вывод мы должны
будем учесть и при оценке определений первой группы, ибо,
как показывает история, во всякой пауке наиболее живу-
чими определениями являются определения основных
понятий.
9. Недостатки второй группы определений
Посмотрим теперь, каковы недостатки определений вто-
рой группы.
Бесспорно, введение неиспользуемых в дальнейшем тер-^
минов и понятий (ромб, ромбоид, трапеция) представляет
собой дефект системы. Вряд ли можно отнести к достоин-
ствам терминологии Евклида и то, что фигуры, которые
в 19-м определении названы «трёхсторонними», он в 20-м
определении подразделяет на равносторонние, равнобед-
ренные и косые треугольники.
Как видно из вышесказанного, эти дефекты имеют своим
источником влияние традиции. Впрочем, сами по себе
они носят, так сказать, технический характер и логической
стройности по существу не нарушают.
1) Ещё до настоящего времени во многих учебниках геометрии
мы находим остатки такой классификации: параллелограмм многие
авторы не считают трапецией.
230 Mr Я, ВЫГОДСКИЙ
Более серьёзным представляется другой упрёк, кото-
рый обычно делают Евклиду его критики. Они обращают
внимание на «перегруженность» многих определений вто-
рой группы. Действительно, для определения «бубнообраз-
ной фигуры» (параллелограмма) достаточно потребовать
равенства противоположных её углов (или сторон), а
Евклид требует равенства как сторон, так и углов. В ещё
большей мере режет глаз 17-е определение: «Диаметр же
круга естьнекоторая прямая, ограниченная с обеих сторон
окружностью круга; каковая также делит круг пополам».
Последняя фраза этого определения представляется совер-
шенно излишней, ибо в ней высказано предложение, под-
лежащее доказательству. В данном случае вряд ли можно
искатьпричину появления этой фразы в следовании тради-
ции,так как многие античные авторы приписывают Фалесу
Милетскому доказательство этого предложения.
В защиту Евклида можно, однако, сказать, что, во-
первых, упомянутая фраза ему здесь нужна по существу:
не будь её, не имело бы смысла следующее, 18-е, определе-
ние: «полукруг есть фигура, объемлемая диаметром и отсе-
каемой им дугой окружности». В самом деле, если бы
диаметр мог делитькруг на неравные части, наименование
«полукруг» не было бы оправдано.
Во-вторых, перегруженность определения отнюдь не
является его логическим недостатком. Евклид, если бы
это было ему нужно, имел бы право пойти в этом направле-
нии и дальше, включив в определение полукруга ещё
какие-либо его свойства, например, что вписанные в эту
фигуру углы—^прямые. Он только должен был бы впослед-
ствии доказать совместность всех поставленных требо-
ваний.
По отношению к 17-му определению Евклид этого тре-
бования не выполнил, и это его вина. Однако пробел этот
носит чисто технический характер, и его легко восполнить
средствами, которыми Евклид свободно владел. Что же
касается параллелограмма, то совместность требований,
устанавливаемых в его определении, строго установлена
Евклидом в 33-м и 34-м предложениях 1-й книги. То же
можно сказать и о всех других фигурах, упомянутых
в 22-м определении.
«НАЧАЛ V» ЕВКЛИДА
2*1
10. Аристотель о «первых началах»
Руководился ли сам Евклид теми соображениями, кото-
рые мы здесь высказали? На этот вопрос мы вправе отве-
тить утвердительно. Во времена Евклида, как и в те-
чение многих столетий после пего, господствующей логи-
ческой системой была система Аристотеля, развиваемая им
в ряде дошедших до нас произведений, в особенности
в «Аналитике» и «Топике».
Всякая дедуктивная наука, говорит Аристотель в «Ана-
литике», покоится на некоторых «первых началах»—опре-
делениях, постулатах и аксиомах. Постулаты и аксиомы
(в чём видит Аристотель различие между ними—мы скажем
дальше) представляют педоказываемые и в некотором
смысле (об этом тоже будет ниже сказано) недоказуемые
предложения,-устанавливающие истинность или ложность
чего-либо. Определения же ничего по говорят об истин-
ности или ложности, о существовании или несущество-
вании определяемых объектов. Они только должны быть
поняты.
Объекты науки, по Аристотелю, обладают различной
степенью логической простоты: одни объекты по самой
своей природе «первее» других. Основное требование,
которому должно удовлетворять научное определе-
ние, состоит, по Аристотелю, в том, чтобы определяе-
мый объект определялся с помощью объектов, кото-
рые логически «первее» его, логически «лучше из-
вестны».
Аристотель подчёркивает, что некоторые объекты, яв-
ляющиеся «лучше известными» или «более первыми»
в абсолютном отношении, могут быть «менее извест-
ными» в относительном смысле, т. е. для ученика,
опирающегося на житейский опыт. В качестве примеров
приводятся понятия точки и линии, единицы и числа.
Понятия точки и единицы логически «первее» понятий
линии и числа; точно так же понятие линии логически
«первее» понятия поверхности, а последнее «первое^, чем
понятие тела. Однако в преподавании позволительно,
считаясь с тем, что ученик не подготовлен к восприятию
научного определения, строить определения, исходя ИЗ
232
М, Я. ВЫГОДСКИЙ
понятии, которые «лучше известны» в относительном смыс-
ле, т. о. более привычны ученику. На этом, говорит Аристо-
тель, и построено определение точки как границы линии,
линии как границы поверхности и поверхности как грани-
цы тела.
Итак, с точки зрения Аристотеля, все понятия науки
должы быть определены, исходя из первейших.
Но и сами первейшие понятия, как можно видеть
из многочисленных примеров, разбросанных в раз-
личных произведениях Аристотеля, тоже подлежат опре-
делению.
Так, в «Метафизике» мы читаем: «Неделимое во
всех отношениях и не наделённое положением назы-
вается единицей; а неделимое во всех отношениях и
имеющее положение — точкой. Если что-нибудь дели-
мо в одном отношении (оно называется)—линией; в двух
отношениях—плоскостью1); (то, что делимо) по количе-
ству всячески, а именно в трёх направлениях — те-
лом»2).
Как было указано, определение по Аристотелю ничего
не утверждает о существовании или несуществовании опре-
деляемого объекта. Существование первейших объектов,
говорит Аристотель, принимается} существование же
остальных должно быть доказано} так, в арифметике су-
ществование единиц принимается, а существование чисел
разных видов (чётных, нечётных, квадратов, кубов и т. п.)
доказывается.
Точно так же в геометрии принимается существо-
вание точек и линий, а, например, существование несоиз-
меримых линий подлежит доказательству. Аристотель
отмечает при этом, что доказательство это должно осно-
вываться на аксиомах и постулатах.
Из изложенного ясно, что все определения «Начал»,
отнесённые нами ко второй группе, вполне удовлетворяют
требованиям Аристотеля. Обратимся теперь к определе-
ниям первой группы.
1) Здесь, как и в других случаях, Аристотель говорит «плос-
кость», понимая под этим термином поверхность вообще.
2) Аристотель, «Метафизика». Перев. Л, Кубицкого.ОГПЗ,
1934, стр. 86
« НЛЧА ЛА » ЕВКЛИДА
233
11. Определения первой группы
Первейшие понятия геометрии Евклид определяет сле-
дующим образом.
1. Точка есть то, что не имеет никакой части *).
2. Линия же есть бесширинная длина2).
3. Границы же линии—точки.
4. Прямая линия есть (та), которая равно лежит отно-
сительно точек на ней.
5. Поверхность же есть (то), что имеет только длину
и ширину.
6. Границы же поверхности — линии.
7. Плоская поверхность есть (та), которая равно лежит
относительно прямых на ней.
8. Плоский же угол есть наклонение друг к другу двух
линий, касающихся друг друга и не лежащих на (одной)
прямой.
9. Если же объемлющие угол линии суть прямые, то
угол называется прямолинейным.
13. Предел есть (то), что есть граница чего-либо.
14. Фигура есть (то), что объемлется каким-нибудь или
какими-нибудь пределами.
Эти-то определения и являются обычно объектом суро-
вой критики. Считается, что они туманны, что они опери-
руют такими понятиями, которые сами должны быть опре-
делены, как, например, понятия «длины», «границы».
Говорят, что определения, которые мы отнесли к первой
группе, совершенно не используются Евклидом при до-
казательстве теорем и, значит, они совершенно бесполезны;
их можно опустить, и от этого не будет никакого ущерба
для понимания последующих рассуждений. Полагают,
что определения первой группы играют у Евклида роль
описаний геометрических объектов и что даже как таковые
они выражены в весьма наивной форме. А раз так,
то основание, на котором построена система Евклида,
*) Дословный перевод был бы «точка есть (то), часть чего (есть)
ничто», но эта фраза на русском языке имеет не тот смысл, что в гре-
ческом. Приведённый в тексте перевод по смыслу точен.
„ Жертвуя литературными требованиями, мы даём здесь бук»
на льны и перевод.
234 М.. я. выгодскпп
оказывается совершенно непригодным для логического
построения геометрии J).
Для того чтобы судить о том, насколько заслужен
Евклидом этот суровый приговор, необходимо, прежде все-
го, уяснить, с каких позиций его критикуют, на каких
позициях стоял сам Евклид и если его позиции отличны от
позиций критиков, то являются ли они ошибочными или
первые столь же правомерны, как и последние.
На первый из поставленных нами вопросов ответить не-
трудно: современные авторы обычно критикуют Евклида
С точки зрения аксиоматической геометрии, нашедшей
своё завершение в известной работе Гильберта «Основания
геометрии». Если они этого не оговаривают, то, невидимо-
му, потому, что аксиоматическая точка зрения молчаливо
предполагается единственно возможной. Мы постараемся
показать, что это несправедливо.
12. Основные понятия геометрии по Гильберту
Сточки зрения Гильберта, основные понятия геометрии
«бессодержательны», т. е. они определяются исключитель-
но теми логическими связями, которые устанавливает меж-
ду ними некоторая система аксиом. Поэтому геометрия
может относиться к самым различным системам объектов;
она, как принято говорить, допускает различные «истолко-
вания». Скажем, под точкой и прямой линией можно
понимать те объекты, которые обычно называют этими
именами. Но можно назвать точкой, например, пару дей-
ствительных чисел X) у, а «прямой» — тройку чисел и, v, w,
имеющих данные отношения и : v : w. Можно, далее,
условиться говорить, что «точка» х, у лежит на «прямой»
и : v : w, если удовлетворяется уравнение
*) Высказанные здесь положения являются настолько общерас-
пространёнными, что перечислить авторов, высказывающихся в этом
смысле, нет никакой возможности. См., например, В. Ф. Каган,
«Основания геометрии. Исторический очерк развития учения об ос-
нованиях геометрии».Одесса, 1907, стр. 12; Н. В. Е ф и м о в,«Выс-
шая геометрия». Гостехиздат, 1945, стр. 9, 35; В. И. Костин,
«Основания геометрии», стр. 14.
«НАЧАЛА» ЕВКЛИДА
235
Тогда для этих «прямых» и «точек» справедливо утвержде-
ние, что через две точки (х1} ух) (яа, у2) можно провести одну
и только одну прямую. Оно обозначает фактически то, что
система уравнений:
!<Zll+ci/a + (V=0
имеет решение, причём все тройки чисел гг, и, w, удовлетво-
ряющих этой системе уравнений, имеют одни и те же отно-
шения
и : v : w.
Точно так же для вновь наречённых «точек» и «прямых»
справедливо утверждение, что две (различные) прямые
не могут иметь более чем одну общую точку—оно означает,
что два уравнения
и „«+^4-^=0
(где ult b'l, tt’i непропорциональны н2, и2, w2) могут иметь
не более одной пары корней.
Если обогащать наш условный язык новыми искус-
ственно созданными терминами, надлежащим образом
определёнными, то можно будет получить все те свойства,
которые выражают геометрические аксиомы, но они будут
относиться уже не к привычным объектам геометрии,
а к совершенно иным.
Итак, с аксиоматической точки зрения геометрия изу-
чает не только те объекты, которые в разговорном языке
именуются точками, прямыми и т. д., но также допускает
множество других объектов исследований.
Теоретико-познавательная ценность этой точки зрения
не подлежит никакому сомнению. Отвлекаясь от конкрет-
ных особенностей различных «изоморфных» систем объек-
тов, она позволяет в наиболее «чистом» виде установить
логические связи между ними. Она позволяет яснее видеть,
вытекает ли некоторое положение из системы других поло-
жений логически или при выводе его используется в
скрытом виде апелляция к опытному факту, к привычке
236
М. Я« ВЫГОДСКИЙ
связывать и рассматриваемым математическим объектом
некоторые физические закономерности. В самом деле,
придавая геометрическим понятиям некоторое необычное
истолкование, мы тем самым освобождаемся от привычных
физических представлений и, если не полностью, то во
всяком случае в большой степени становимся независимыми
от так называемой «интуиции».
Но именно вследствие того, что аксиоматическая гео-
метрия, допуская множественность истолкований, рас-
ширяет круг объектов, подлежащих изучению, именно
поэтому она вынуждена сузить цели исследования: она
оставляет вне поля зрения различие между многообразными
системами изоморфных объектов. Так, в рамках аксиома-
тической геометрии понятие о точке, которое имеет каждый
человек до изучения геометрии, неотделимо от понятия
о паре действительных чисел. Между тем, эти понятия
существенно отличны друг от друга, поскольку первое
представляет абстракцию от пространственных, а второе
от количественных соотношений действительного мира.
Можем ли мы игнорировать вопрос о различении одной
из этих интерпретаций от другой? Конечно, нет, хотя бы
потому, что тогда мы лишимся возможности применять
аксиоматическую геометрию к каким-либо объектам,
а тогда мы не нуждаемся и в самой аксиоматической
геометрии.
Гильберт устраняет этот вопрос из области математики.
Признаем за ним это право. Но на каком основании должны
мы отказать Евклиду, Ньютону или Лобачевскому в праве
включить этот вопрос в область геометрии?
Не является ли вполне закономерной точка зрения на
геометрию как на науку о пространственных формах
действительного мира?
Это означает, что из всех логически мыслимых систем
объектов мы избираем одну, вполне определённую, выбор
которой оправдывается многовековым опытом человечества.
Именно эту систему объектов и изучают Евклид, Ньютон,
Лобачевский и все математики до последней четверти
прошлого столетия. Одни из них, как Лобачевский, отчёт-
ливо сознавали зависимость этого выбора от соотношений,
имеющих место в действительном мире; другие, как Евклид,
«НАЧАЛА» ЕВКЛИДА
237
могли относить объекты! геометрии к миру идей. Но фак-
тически как те, так и другие изучали закономерности,
имеющие место в реальной действительности.
Итак, позиция Евклида существенно отлична от пози-
ции Гильберта, и этого не должен упускать из виду критик'
Евклида.
Нет спора, что аксиоматическая точка зрения может
быть с успехом применена к выявлению логических про-
белов в ряде рассуждении Евклида, что Евклиду, по отме-
ченным выше причинам, психологически было труднее
освободиться от вторжения интуитивного момента в .ло-
гическое доказательство. Но принципиально это ни-
сколько не опорачивает позицию Евклида, особенно,
если вспомнить, что и сам Гильберт в первых изданиях
«Оснований геометрии» допустил немало логических про-
белов.
Итак, позиция Евк.лида столь же правомерна, как и по-
зиция Гильберта; но они существенно отличаются друг от
друга в вопросе о предмете геометрии. Поэтому к критике
евклидовых определений точка зрения Гильберта совер-
шенно неприменима. Этого-то, по нашему мнению, и не
учитывают многие судьи Евклида.
13. Роль определений в системе Евклида
Определения Евклида, которые мы отнесли к первой
группе, имеют целью ответить на вопрос: что такое точка,
линия, поверхность? Иными словами: как интерпрети-
руются эти термины?
Как было выяснено, такой вопрос в геометрии Гильбер-
та не ставится вовсе.
Никак нельзя сказать,чтобы Евклид разрешил этот
вопрос вполне удовлетворительно; многое можно поставить
ему в упрёк. Об этом будет сказано ниже. Но обвинения,
которые обычно предъявляются Евклиду (мы привели
их в конце п. 11), совершенно несправедливы.
Евклиду ставится в вину то, что он не определил поня-
тий «граница», «длина» и т. д. Даже с аксиоматической точки
зрения это обвинение несостоятельно. С этой точки зрения
можно поставить Евклиду в вину лишь то, что он не
238
М. Я» ВЫГОДСКИЙ
сформулировал системы аксиом, которым подчинены упо-
мянутые понятия.
Следуя принципам аристотелевой логики, Евклид дол-
жен был определить точку, линию и поверхность с помощью
понятий, которые были бы логически и «более первыми»,
мы бы сказали — более общими. Удовлетворяют ли опре-
деления Евклида этому требованию? Относительно поня-
тия «граница» в этом, кажется, пет никаких сомнений.
Понятие же длины относится у ^вклпда не к мере геометри-
ческого объекта, а к его размерности, в чём легко убедить-
ся, если сравнить 2-е и 5-е определения 1-й книги «Начал»
с • определениями Аристотеля, приведёнными выше
(п. 10, стр. 232), Употребляемое в этом смысле понятие
длины «первее» понятия линии. Таким образом, Евклид
вовсе не должен был его определять.
Никак нельзя согласиться и с утверждением, что опре-
деления первой группы по существу бесполезны, не
связаны с остальным материалом «Начал» и могут
быть опущены без всякого ущерба для понимания
дальнейшего.
Это неверно даже с аксиоматической точки зрения, на
которую, как мы говорили, вообще не следует становиться
при критике евклидовых определений. В самом деле, если
Евклид во втором предложении первой книги ставит
задачу о построении отрезка данной длины при заданной
точке, то разве бесполезно определение 3-е, устанавливаю-
щее, что точка есть граница линии?
Разве ^полезно это же определение, когда Евклид,
скажем, в 5-м предложении 2-й книги берёт «по произ-
волу» точку на заданном отрезке? Можно поставить Евк-
лиду в упрёк лишь то, что он не оговорил, как это сделал
Аристотель, что точки суть «деления линий и кроме того
границы их». Мы знаем, что по отношению к первоначаль-
ным понятиям формулировка их определения предпола-
гает допущение их существования. Поэтому определение
3-е (в его расширенном понимании) даёт возможность Евк-
лиду брать «произвольную» точку на отрезке. Другими
словами, определение 3-е у Евклида играет ту же роль,
что первая часть гильбертовой аксиомы 13 (на каждой пря-
мой существует по крайней мере две точки).
«НАЧАЛА»1ВКЛИДД
2 ЗУ
Нам могут возразить, что Евклид вообще не видел
необходимости логически обеспечить существование по
крайней мере одной точки на прямолинейном отрезке.
Могут сказать (и говорят обычно), что Евклид просто
исходит из наглядных представлений. Но если бы это было
так, то зачем понадобилось бы Евклиду доказывать суще-
ствование середины отрезка, что он делает в 10-м предло-
жении 1-й книги? Нет, Евклид вовсе не так слепо идёт
на поводу у интуиции, как полагают нынешние его кри-
тики.
Таким образом, без ущерба для понимания дальней-
ших рассуждений евклидовы определения первой группы
опущены быть не могут. Но помимо этого они, как было
сказано, имеют целью ответитьна вопрос—что такое точка,
линия и т. д. И не будь их, Евклид не вправе был бы начер-
тить ни одной геометрической фигуры.
Во избежание всяких недоразумений оговоримся ещё
раз, что Евклид вовсе не считает себя вправе извлекать
из чертежа какие-либо выводы, не обеспеченные логиче-
ским рассуждением. Если иной раз это с ним случается,
то по по доброй воле. Даже самые очевидные предложения
Евклид стремится доказать логически; при этом иногда
он прибегает к помощи заведомо неверного чертежа. Так,
в 10-м предложении 3-й книги, утверждающем, что два
круга пересекаются не более чем в двух точках, Евклид
нарочно искажает фигуру одного из кругов.
Необходимость в строго логическом характере доказа-
тельства подчёркивал ещё Аристотель, который писал,
что геометр не основывает своих заключений на частных
особенностях проведённых им линий, но опирается на «то,
что проведённые им линии изображают». Так, он может
провести на чертеже кривую линию, но рассуждать о ней,
как о прямой.
На первый взгляд может показаться, что это сбли-
жает точку зрения Аристотеля с Гильбертом. Но это во-
все не так. По Аристотелю, можно вместо прямой начертить
кривую линию, но она от этого не станет прямой для гео-
метра. Поэтому геометр должен дать такое определение
прямой линии, которое позволило бы отличить её от
кривой.
м. я. ВЫГОДСКПЙ
21П
14. Материалистическая и идеалистическая точки зрения
на математические понятии
Нам предстоит теперь посмотреть, как справился Ев-
клид с задачей предметного определения геометрических
понятий. Попутно мы увидим, в какой мере справедливо
утверждение, что формулировки его определений туманны
и являются ли они описаниями, выраженными в наивной
форме.
Но, прежде чем ответить на эти вопросы, мы должны под-
черкнуть выступающие здесь во весь рост отличия между
материалистической и идеалистической точкой зрения на
математические представления вообще и геометрические
в частности.
С материалистической точки зрения эти представления
отражают пространственные формы действительного ми
ра: «Понятие фигуры, как и понятие числа, заимствовано
исключительно из внешнего мира, а не возникло вовсе
в голове из чистого мышления. Раньше, чем люди могли
прийти к понятию фигуры, должны были существовать
вещи, которые имели форму и формы которых сравни-
вали. Чистая математика имеет своим предметом простран-
ственные формы и количественные отношения действитель-
ного мира, т. о. весьма реальное содержание. Тот факт,
что это содержание проявляется в крайне абстрактной
форме, может лишь слабо затушевать его происхождение
из внешнего мира. Чтобы изучить эти формы и отношения
в их чистом виде, следует их оторвать совершенно от их
содержания, устранить его как нечто безразличное для
дела. Так получаются точки без протяжения, линии
без толщины и ширины...»4).
С этой точки зрения доброкачественность геометриче-
ских определений измеряется тем, насколько хорошо в них
отражены те отношения действительного мира, от которых
они отвлечены.
С идеалистической точки зрения геометрические пред-
ставления имеют значимость, не зависящую от реального
i) Энгельс, «Антидюринг», Соч. Маркса и Энгельса, т. XIV,
стр. 39.
«НАЧАЛА» ЕВКЛИДА
241
мира; они отражают соотношения в мире идей, они вро-
ждены человеческой душе. G этой точки зрения доброкаче-
ственность геометрических определений измеряется тем,
в какой мере они независимы от отношений действитель-
ного мира.
На этой точке зрения стоял Платон. В диалоге «Ме-
нон»1) Платон доказывает, что сущность всякого знания
состоит не в усвоении и систематизации опытных фактов,
а в припоминании тех сведений, которые врождены
душе и приобретены душой в мире идей. Это положе-
ние «доказывается», между прочим, следующим способом.
Сократ велит Менону позвать слугу-мальчика, никогда
не обучавшегося геометрии, и предлагает этому мальчику
решить задачу о построении квадрата, вдвое большего,
чем данный. После нескольких «наводящих» вопросов
Сократа мальчик даёт правильное решение: стороной
искомого квадрата будет диагональ данного. И Сократ
заключает отсюда, что «у человека есть верные понятия
о том, чего он не знает».
В противоположность Платону Аристотель стоял в этом
вопросе на материалистической точке зрения, хотя и не
выдерживал её последовательно. Во второй главе 11-й
книги «Метафизики» Аристотель отмечает трудности, свя-
занные с тем, что «линии и поверхности — это не отдельно
существующие сущности, но сечения и деления, в первом
случае поверхностей, а во втором — тел, а точки — деления
линий, и кроме того — пределы этих же самых величин;
все они находятся в другом и ничто не имеет отдельного
бытия»2).
Эти трудности Аристотель разрешает в следующей,
третьей, главе 11-й книги, и материалистическая позиция
его выступает здесь с полной отчётливостью: «В отноше-
нии сущего примером служит то рассмотрение, которому
математик подвергает объекты, полученные посредством
отвлечения. Он производит это рассмотрение, сплошь устра-
нивши все чувственные свойства, например тяжесть и лёг-
кость, жёсткость и противоположное ей, далее —тепло
J) Платон, «Менон», стр. 85.
2) Аристотель, «Метафизика», 1934, стр. 184.
В-Б Историко-математ. исследования
242
M. Я. ВЫГОДСКИЙ
и холод и все остальные чувственные противоположности,
а сохраняет только количественную определённость и не-
прерывность у одних —в одном направлении, у других—
в двух, у третьих —в трёх»1).
В. И. Ленин, изучая «Метафизику» Аристотеля, записал
в своих заметках: «книга 13, глава 3 разрешает эти труд-
ности превосходно, отчётливо, ясно, материалистически
(математика и другие науки абстрагируют одну из сторон
тела, явления, жизни). Но автор не выдерживает последо-
вательно этой точки зрения»2).
15. Евклид и Лобачевский
Мы говорили выше, что как Евклид, так и Лобачевский
видели в геометрии содержательную науку. Но содер-
жание геометрии они понимали по-разному. И мы пой-
мём, почему так различны системы их определений, если
учтём, что Лобачевский стоял на материалистических пози-
циях, а Евклид исходил из идеалистических взглядов
на предмет математики.
Принципиальная позиция Лобачевского выражена в
следующих его словах:
«Первые понятия, с которых начинается какая-нибудь
наука, должны быть ясны и приведены к самому мень-
шему числу. Только тогда они могут служить прочным
и достаточным основанием учения. Такие понятия при-
обретаются чувствами; врождённым не должно верить»3).
Именно поэтому Лобачевский отвергал евклидовы оп-
ределения. «Никакая математическая наука не должна
бы начинаться,—говорит он,— с таких тёмных понятий,
с каких, повторяя Евклида, начинаем мы геометрию»4).
Вместо определений Евклида Лобачевский устанавли-
вает совершенно иную систему определений. Она исходит
из рассмотрения тел и кладёт в основу понятие прикоснове-
*) Аристотель, «Метафизика», 1934, стр. 185—186.
8) В. И. Ленин, Заметки на «Метафизику» Аристотеля; напе-
чатано в цитируемом издании «Метафизики», стр. 15.
3) Н. И. Лобачевский, Сочинения, т. I, Гостехивдат,
1946, стр. 186.
4) Там же, стр. 185.
«НАЧАЛА» ЕВКЛИДА
243
ния тел. «Словами нельзя передать совершенно того, что
мы под этим разумеем; понятие приобретено чувствами,
преимущественно зрением, и сими-то чувствами мы его
постигаем. Отвлекая все прочие свойства, телу дают на-
звание геометрического». Далее, рассматривая различные
способы прикосновения тел, Лобачевский выделяет «при-
косновение в точке» и уже отсюда приходит к понятию
о точке.
Совершенно иначе поступает Евклид. Он начинает
с определения точки. В этом он следует Аристотелю. Но
Аристотель определяет точку как «неделимое во всех отно-
шениях и имеющее положение», Евклид же отбрасывает
вторую, положительную, часть этого определения. Это
делается, конечно, сознательно. Если точка, как и все
остальные образы геометрии, есть объект мира идей, то
она не может обладать положением, как не имеют поло-
жения бог и душа.
Возьмём ещё евклидово определение прямой линии
и аналогично построенное определение плоской поверхно-
сти. Они, действительно, туманны. Греческий текст здесь
допускает различные грамматические интерпретации, но
ни одна из них не позволяет с определённостью сказать,
ка#ое свойство прямой линии имеет в виду определение
4-е и какое свойство плоскости выражает определение 7-е.
Должны ли мы думать, что эта туманность есть плод кос-
ноязычия Евклида? Всякий, кто прочёл хоть несколько
предложений «Начал», должен будет признать, что язык
Евклида, пусть несколько тяжеловесный, обладает уди-
вительной ясностью и чёткостью и что этой чёткости
могли бы поучиться у Евклида многие авторы совре-
менных курсов геометрии. Как же могло случиться, что
в важнейшем пункте изложения Евклид допустил столь
туманную формулировку?
Удовлетворительный ответ может быть, мне кажется,
только один: Евклид исходит из какого-то традиционного
определения прямой, но стремится выразить его в такой
форме, чтобы устранить из него всё то, что апеллирует
к материальному миру.
Каково могло быть это традиционное определение?
оа ответом на этот вопрос естественно обратиться к
16*
244
М. Я. ВЫГОДСКИЙ
Аристотелю. В его «Топике» (книга 6, глава 11) мы находим
следующее определение: «прямая линия есть та, середина
которой служит препятствием для концов». Совершенно
такое же выражение мы встречаем в диалоге Платона «Пар-
менид» (137 Е). Смысл его может быть тол ько один: прямая
служит препятствием для того, чтобы с одного конца её
видеть другой. Если мы примем во внимание, что это свой-
ство прямой линии используется в землемерии и по настоя-
щее время для проведения прямых линий на местности
(провешивание), то мы будем иметь полное основание счи-
тать это определение традиционным. И если Евклид исхо-
дил именно из этого определения J), то он имел основание
перефразировать его так, чтобы в нём исчез всякий намёк
на процесс визирования. Для читателя, знакомого с тра-
диционным определением прямой, определение 4-е не
должно было казаться таким туманным, каким представ-
ляется оно нам.
Из изложенного ясно, что у Евклида определения пер-
вой группы имеют целью вызвать у читателя «воспомина-
ние» о понятиях, врождённых его душе, но отнюдь не пред-
ставление о реальных прообразах этих понятий. Поэтому
совершенно неправы те, которые считают эти определения
«описаниями геометрических образов». Наивными же их
можно считать лишь в той мере, в какой наивны идеалисти-
ческие установки Евклида.
16. Излишни ли евклидовы определения первых
понятий
С нашей, материалистической, точки зрения определе-
ния первой группы, как явствует из сказанного, решают
задачу содержательного определения геометрических по-
нятий совершенно неудовлетворительно, ибо Евклид со-
знательно уклоняется от выяснения тех пространствен-
ных форм действительного мира, отвлечениями которых
х) Таково мнение Гиса (L. Heath, The thirteen books of Euclid’s
Elements, Cambridge, 1926, т. I, стр. 168), которое мне представляется
весьма убедительным. Прокл и Симплиций истолковывают 4-е и 7-е
определения Евклида иначе. См. об этом комментарий Д. Д. Морду-
хай-Болтовского к 1-й книге «Начал».
«НАЧАЛА» ЕВКЛИДА
245
являются объекты геометрии. При всем том они не являют-
ся совершенно бесполезными, ибо устанавливают некоторые
существенные свойства геометрических образов.
Возьмём, например, определение 8-е. На первый взгляд
может показаться, что оно представляет чистую тавтоло-
гию, так как заменяет один неопределяемый термин (угол)
другим, который не в меньшей степени нуждается в опреде-
лении (наклонение). При ближайшем рассмотрении ока-
жется, что это не так.
В этом определении содержится два важных момента.
Во-первых, из него явствует, что две прямые, выходящие
из одной точки, не образуют угла, если они совпадают.
Таким образом, для Евклида не существует ни угла, рав-
ного нулю, ни угла, равного двум прямым углам, а, зна-
чит, и углов больших, чем два прямых. Может ли такое
определение «быть опущенным без ущерба для понимания
дальнейших рассуждений»?
Во-вторых, оно исключает понимание угла как «части
плоскости»; иными словами, мера угла ставится в зависи-
мость только от поведения его сторон в окрестности верши-
ны. Если мы вспомним, к каким парадоксам может приве-
сти измерение угла «частью плоскости», которую он «огра-
ничивает», если мы вспомним, в частности, известное осно-
ваннное на этих парадоксах «доказательство» постулата
параллельности, данное в XVIII в. Луи Бертраном, то мы
согласимся с тем, что и в этом отношении определение
8-е не излишне.
Не излишне и определение 3-е. Как-мы видели, оно
обеспечивает существование границ отрезка как на краях
его, так и в промежутке между краями.
Ту же роль играет и определение 6-е. Оно говорит о том,
что линия может служить границей поверхности, т. е. огра-
ничивать какую-либо область или разделять поверхность
на две области (сравни определение 14). Это свойство,
конечно, очень существенно, хотя, как мы ниже увидим,
сам Евклид не использовал его в должной мере.
Итак, каковы бы ни были недостатки определений Ев-
клида, излишними они не являются. Единственное опре-
деление, которое могло бы заслужить такой упрёк, это
определение 13-е, где термин «предел» объяснён с помощью
246
М. Я. ВЫГОДСКИЙ
термина «граница». Но даже и это определение, невиди-
мому, не было излишним для Евклида. В самом деле, сле-
дующее, 14-е, определение (фигура есть то, что объемлется
каким-нибудь или какими-нибудь пределами), вероятно,
было традиционным, и тогда Евклид должен был пояснить,
что термин «предел» равнозначен с термином «граница»,
который употреблялся в традиционных определениях
точки и линии.
17. Мнимые недостатки определений первой книги
Нам остаётся остановиться ещё на вопросах формаль-
ного характера, связанных с определениями первой
группы.
Многие критики Евклида считают недостатком этой
системы тот факт, что одно и то же понятие определяется
у Евклида двумя различными способами. Определения
1-е и 3-е различным образом определяют точку; опреде-
ления 2-е и 6-е различным способом определяют линию.
Во 2-м определении 11-й книги даётся определение поверх-
ности как границы тела, а в 5-м определении 1-й книги
поверхность определена как «то, что имеет только длину
и ширину».
Как мы видели, Аристотель отдавал предпочтение опре-
делениям 1-му, 2-му и 5-му с научной точки зрения, а 3-му
и 6-му определениям 1-й книги и 2-му определению 11-й
книги—с точки зрения педагогической. Быть может, Ев-
клид хотел соединить эти два преимущества, быть может,
исходил из каких-нибудь других соображений. Но при всех
обстоятельствах его поступок не заключает в себе ничего
предосудительного: как было показано, перегруженность
определения как с точки зрения Евклида, так и с совре-
менной точки зрения не может считаться логическим его не-
достатком, лишь бы было обеспечено существование опреде-
ляемого объекта. Но, по Аристотелю, существование точ-
ки, линии и поверхности не доказывается, а принимается.
Поэтому в данном случае Евклид не должен был дока-
зывать совместности определений 1-го и 3-го.
Но не только по Аристотелю, а и с современной точки
зрения поведение Евклида но стодь уж предосудительно.
«НАЧАЛА» ЕВКЛИДА
247
Действительно, наличие двоякого определения точки мо-
гло бы в худшем случае грозить несовместностью этих
свойств, их логической противоречивостью (в связи, ко-
нечно, с дальнейшими аксиомами и постулатами). Но от
этой опасности не избавлена никакая система основных
положений геометрии, в том числе и система Гильберта.
В самом деле, Гильберт доказал непротиворечивость гео-
метрии, сведя её к непротиворечивости арифметики. Не-
противоречивость же арифметики им не была доказана.
В неё он должен был верить. Но с равным правом Евклид
мог верить и, конечно, верил в непротиворечивость гео-
метрии.
Средневековые критики Евклида, а вслед за ними и не-
которые современные авторы упрекали Евклида в недо-
статочном выявлении объёма определяемых понятий. Так,
по мнению этих критиков, неудовлетворительным является
определение 1-е, так как под него подходит не только точка,
но и человеческая душа, которая также не имеет частей.
Этим критикам Евклид мог бы возразить, что душа не
может служить границей линии.
А тем критикам, которые считают первое определение
«Начал» плохим, потому что в нём отсутствует указание
того родового понятия, видом которого является понятие
точки, мы могли бы ответить следующее. Требование, чтобы
определение устанавливало содержание понятия с по-
мощью указания рода и видового отличия х), установлено
не кем иным, как Аристотелем. А сам Аристотель, как
мы видели, даёт такое определение точки, которое этому
треобванию не удовлетворяет.* Но Аристотель в дан-
ном случае не совершает никакой непоследователь^
ности.
В самом деле, требование, чтобы вид определялся
через род, имеет у Аристотеля не самодовлеющий характер.
Оно обусловлено тем, что родовое понятие j по Аристотелю
«первее», чем видовое, ибо, говорит он уничтожение рода
влечёт за собой уничтожение и вида. Таким образом, опре-
х) Например, в определении: треугольник есть многоугольник,
имеющий три вершины, родовым понятием является понятие много-
угольника, а видовым отличием — тот факт, что число вершин равно
трём. . . v
248
М. Я. ВЫГОДСКИЙ
деляя вид через род, мы определяем «менее известное»
через «более известное», что и является основным требо-
ванием, предъявляемым Аристотелем к научному опреде-
лению. И это требование соблюдено как в аристотелевом,
так и в евклидовом определении точки.
Мы надеемся, что из всего сказанного выше явствует,
что при всех своих недостатках определения Евклида
вовсе не заслуживают той уничтожающей оценки, кото-
рая им часто даётся.
18. Аксиомы и постулаты
За определениями 1-й книги следуют постулаты («тре-
бования» *) и аксиомы (именуемые у Евклида «общие
понятия»). Число тех и других, а также распределение
недоказываемых предложений на постулаты и аксиомы
в различных рукописях различны. Тот список постулатов
и аксиом, который принят Гейбергом, соответствует боль-
шинству лучших рукописей и, что не менее важно, совпа-
дает со списком, приводимым в комментариях Прокла.
Поэтому можно думать, что нижеприводимые постулаты
и аксиомы содержались в оригинале «Начал».
Вот их список:
Требования
1. Требуется, чтобы (можно было) через всякие две
точки провести прямую.
2. И ограниченную прямую непрерывно продолжать
по прямой.
3. И из всякого центра всяким расстоянием описать
круг.
4. И что все прямые углы равны.
6. И если прямая линия, падающая на две прямые,
делает меньшими двух прямых углы по одну сторону,
чтобы эти две прямее, будучи продолжены, совпали с той
стороны, с которой углы меньше двух прямых.
9 Латинское слово postulalym представляет буквальный пере-
вод термина —требование.
«НАЧАЛА» ЕВКЛИДА
249
Общие понятия
1. Равные одному и тому же равны друг другу.
2. И если к равным прибавить равные, то целые равны..
3. И если от равных отнять равные, то остатки равны.
4. И совпадающие друг с другом равны друг другу.
5. И целое больше, чем часть.
Прибавления к этому списку, которые можно найти
в различных изданиях «Начал», естественно объясняются
желанием издателей восполнить пробелы, которые, по,
их мнению, допустил Евклид. Что же касается отнесения
к числу аксиом некоторых постулатов (четвёртого и пя-
того, которые в ряде изданий фигурируют в качестве 10-й
и 11-й аксиом), то, несомненно, оно диктовалось жела-
нием провести классификацию с точки зрения некоторого
единого принципа.
Как понимал сам Евклид различие между постула-
тами и аксиомами, мы в точности не знаем. Не знал этого,
по видимому, и Прокл, ибо он приводит различные точки
зрения на этот вопрос, сам склоняясь, повидимому, ко
взгляду Аристотеля.
Во «Второй аналитике» (книга 1, глава 10) Аристотель
говорит, что предпосылки всякой дедуктивной науки раз-
деляются на две группы; одни имеют специальный харак-
тер, будучи присущи только данной науке; другие явля-
ются общими для всех наук, а в данной науке приме-
няются постольку, поскольку они приложимы к объектам
этой науки.
В качестве примера «общего начала» Аристотель при-
водит положение: «если от равных отнять равные, то
остатки равны». Оно, как мы видим, совпадает со вто-
рой аксиомой «Начал»х). Конкретных примеров «начал,
свойственных данной науке», Аристотель, к сожалению,
не приводит; он ограничивается замечанием, что к числу
1) Та же мысль содержится в «Метафизике»: «Положение «если от
равных отнять равные, остатки равны» является общим по отноше-
нию ко всем количествам, а математика, выделив, делает предметом
своего рассмотрения ту или иную часть относящегося к ней материа-
ла, например, линии или углы или числа». (Русский перев. А. В. Ку-
бицкого, Соцэкгив, 1934, стр. 186.)
250
М. Я. ВЫГОДСКИЙ
их принадлежит положение, что «такая-то линия имеет
такие-то характерные свойства, и подобным образом для
прямой линии». Очевидно, здесь речь идёт об определе-
нии различных линий. И из дальнейшего ясно, что к числу
«начал, свойственных данной науке», Аристотель отно-
сит, прежде всего, определения.
Аристотель говорит дальше и о постулатах, но с пол-
ной определённостью нельзя сказать, включает ли он их
в «первые начала» или нет. Дело в том, что под первыми
началами Аристотель понимает те, «истинность которых
невозможно доказать». А когда он говорит о постулатах,
он сопоставляет их с «гипотезами». О тех и других он
говорит, что учитель принимает их без доказательства,
хотя они подлежат доказательству. Разница между гипо-
тезой и постулатом, по Аристотелю, состоит в том, что
гипотезу учитель, а тем более ученик, принимает охотно,
тогда как относительно утверждения, содержащегося в
постулате, он либо не имеет никакого мнения, либо даже
держится противоположного мнения.
Как мы видим, у Евклида41 ^нет никаких «гипотез».
Между тем такое предложение, как «через две точки можно
провести прямую линию», вряд ли могло вызвать не только
возражение, но и какое-либо сомнение у античного мысли-
теля. Таким образом, полного согласия между Аристо-
телем и Евклидом нет. Всё же можно допустить, что Ев-
клид к числу постулатов отнёс предложения специально
геометрического характера, а к числу аксиомпредло-
жения общего характера. В пользу этого предположения
говорит и самое название «общие понятия», которым Ев-
клид обозначает аксиомы. По свидетельству Прокла этот
термин равнозначен термину «аксиома».
Против упомянутого предположения может говорить
лишь одно обстоятельство: наличие среди аксиом предло-
жения «совпадающие друг с другом равны друг другу»,
которое в списке Гейберга значится четвёртой, а по спи-
ску Прокла является пятой аксиомой. По своему харак-
теру это предложение, невидимому, носит не общий,
а специально геометрический характер. Поэтому неко-
торые авторы, считающие, что Евклид, следуя Аристо-
телю, относит к аксиомам недоказуемые предложения
«НАЧАЛА» ЕВКЛИДА
251
общего характера, склонны видеть в 4-й аксиоме поздней'
шую вставку х). Другие авторы, считающие 4-ю аксиому
подлинно евклидовой, ищут иных критериев различия
между аксиомами и постулатами 1 2). Как выше указыва-
лось, уже у Прокла приводятся по этому поводу много-
образные мнения древних авторов.
Мне кажется, что наличие 4-й аксиомы не исключает
возможности того, что Евклид относил к аксиомам ос-
новные положения общего характера. Ведь в этой аксиоме
не упомянут никакой геометрический объект. Не сказа-
но: «совпадающие фигуры» или «совпадающие линии», а
употреблено субстантивизированное причастие «совпа-
дающие» (£<pocpp.6<;ov~at), сопровождаемое определённым
членом (то), совершенно так же, как в других аксиомах
употреблено прилагательное «равные». Вполне допустимо,
что Евклид вкладывал в это понятие общелогический
смысл. Во всяком случае Прокл 3) прямо возражает про-
тив исключения Героном этого предложения из числа
аксиом. Правда, он мотивирует своё возражение только
тем, что геометры часто ссылаются на это положение.
Но он тут же возражает против включения в число аксиом
положения «две прямые не объемлют пространства»,
прямо ссылаясь на то, что оно не принадлежит к «роду
общих».
Для нас вопрос о подразделении «первых начал»
на аксиомы и постулаты представляется малосуществен-
ным. Но, с точки зрения Аристотеля, дело обстоит иначе.
В самом деле, аксиомы уже в силу того, что они носят
универсальный характер, не подлежат доказательству
ни в какой частной науке. Это, однако, не значит, что
Аристотель хочет принять их в качестве произвольного
соглашения или даже в качестве положений, не нуждаю-
щихся в исследовании в силу своей очевидности. Напротив,
аксиомы подлежат, исследованию, но не в какой-нибудь
частной науке, а в философии. «Ведь аксиомы обладают
1) Например, Гис, цит. соч., стр. 225.
2) Об этих критериях см. комментарий Д. Д. Мордухай-Болтов-
ского к 1-й книге «Начал».
8) Procli Diadochi in primum Elcnientorum librum commentarii
ed. Friedlein, 1873, стр. 196.
252
М. Я. ВЫГОДСКИЙ
наивысшей степенью общности и представляют начала
всего. И если не дело философа, то чьё же ещё —рас-
смотреть, что по отношению к ним правда и что
ложь?» х).
Нельзя не отметить, что и здесь Аристотель стоит
па точке зрения, близкой к материалистической. Аксиомы,
писал Энгельс, «выступают как недоказанные и, разу-
меется, также и недоказуемые математически... Они
доказуемы диалектически, поскольку они не чистые
тавтологии»2).
Иное дело постулаты. Они «принимаются и употребля-
ются, — говорит Аристотель, — без доказательства, хотя
и должны бы быть предметом доказательства».
Это различие, конечно, существенно. Никто не пытался
математически доказать, что «равные одному и тому же
равны друг другу». Но уже Прокл предлагал доказатель-
ство четвёртого постулата, а доказательства пятого посту-
лата представляют, как известно, интереснейшую и
важнейшую главу в истории математической мысли.
19. Первые предложения «Начал»
Чтобы лучше понять роль, которую играют «первые
начала» в системе Евклида, чтобы объективно оценить
выдающиеся достоинства и существенные недостатки ло-
гического построения «Начал», мы проанализируем не-
сколько первых предложений 1-й книги.
В предложении 1-м решается задача о построении
равностороннего треугольника на данной стороне. Такое
начало может удивить читателя, воспитанного па современ-
ной литературе и ожидающего в начале систематическо-
го курса геометрии найти доказательства каких-нибудь
свойств фигур, а затем уже решение задач, основанное
на этих свойствах.
Но не случайно Евклид начинает свой трактат с по-
строения. Вспомним, что, по Аристотелю, существование
Э Аристотель, «Метафизика», стр. 46.
2) Ф. Энгельс, «Диалектика природы», Госполитиздат, 1941,
стр. 207.
«НАЧАЛА» ЕВКЛИДА
253
всех объектов науки (кроме первейших, которые прини-
маются без доказательства) должно быть доказано. Евклид
так и поступает или, по крайней мере, стремится посту-
пать. И, прежде всего, он доказывает существование равно-
стороннего треугольника. Почему он начинает именно
с этого объекта? Это обусловливается всем планом пер-
вой книги, и, в конце концов, с чего начать—это дело
автора.
Что же такое «существование» для Евклида? Хотя
по этому, равно как и по другим философским вопросам
математики, Евклид прямо не высказывает никаких су-
ждений, по его тенденция совершенно ясна из чтения «На-
чал». Он хочет, чтобы во всяком доказательстве шла речь
только о таких объектах, которые можно «построить» на
основе введённых им постулатов. Насколько это желание
ему удаётся осуществить,— мы увидим ниже. Но в нали-
чии такого стремления не может быть никаких сомне-
ний. Евклид не придерживается привычной нам манеры
ссылаться на номера тех постулатов, аксиом и теорем,
которыми он пользуется. Он предпочитает цитировать
их полностью и делает это часто даже там, где читатель
без труда мог бы обойтись без подобных указаний. Так,
построив в 1-м предложении 1-й книги треугольник
АВС, в котором АС=АВ и ВС—В А, и желая заключить
отсюда, что АС=ВС=АВ, Евклид говорит:
«Каждая из прямых линий СА, СВ равна АВ, а рав-
ные одному и тому же равны друг другу; следовательно,
С А также равно СВ. Следовательно, три прямых линии
СА, АВ, ВС равны друг другу».
Это педантичное цитирование, невидимому, имеет
целью строгое соблюдение силлогистического принципа
Аристотеля1). Во всяком случае оно характеризует стре-
Э Стремлением к выполнению формальных требований доказа-
тельства можно объяснить и строгое расчленение доказательства на
части, что немало затрудняет чтение более сложных предложений
«Начал». Каждое предложение формулируется трижды: первый раз
в начале в общей форме, второй раз — непосредственно вслед за этим —
применительно к чертежу, третий раз снова полностью повторяется
в конце, для чего часто приходится тратить много слов, чтобы обосно-
вать переход от свойств, установленных на чертеже, к общим форму-
254
M. Я. ВЫГОДСКИЙ
мление Евклида к явному использованию всех логиче-
ских предпосылок доказательства.
Поэтому мы имеем полное основание строго критико-
вать Евклида за те или иные упущения в этом отноше-
нии, и можно не сомневаться в том, что Евклид, если
бы он мог услышать эту критику, был бы признателен
за неё.
Более того, мы вправе также высказать неодобрение,
если бы в числе постулатов или аксиом нашлись бы из-
лишние, т. е. такие, которые могли бы, будучи исклю-
чены из числа недоказанных предложений, быть дока-
занными на основе остальных.
Что Евклид сознательно стремится свести к минимуму
число недоказанных предложений, видно хотя бы из 2-го
предложения 1-й книги. Здесь решается задача о построе-
нии при данной точке А отрезка, равного данному отрезку
ВС. На первый взгляд может показаться, что с той же
степенью строгости эту задачу можно решить гораздо
проще: взяв где-либо точку X, провести прямую АХ
(первый постулат), затем, опираясь на третий постулат, из
центра А радиусом ВС описать окружность. В пересе-
чении прямой АХ или с её продолжением (второй посту-
лат) получим точку У, и отрезок AY будет искомым.
Существование точки У правда не обеспечено содержа-
щимися в «Началах» постулатами (об этом ниже), но
и в доказательстве предложения 2-го мы имеем тот же
пробел.
Евклидово построение много сложнее; но нетрудно
усмотреть, что это усложнение введено с определённой
целью сузить содержание постулатов. Именно, оказы-
вается, что в постулате третьем слова «при данной точке
данным расстоянием» нужно понимать в том смысле,
что отрезок, задающий расстояние, должен иметь одним
из своих концов данную точку. 2-е предложение, таким
образом, равносильно утверждению, что возможность
проведения окружности при любом центре А и где угодно
лировкам. В конце Евклид никогда не забывает поставить ставшую
теперь традиционной фразу: «что и требовалось доказать» (или «что
и требовалось сделать»).
«НАЧАЛА» ЕВКЛИДА
255
заданном отрезке ВС обеспечивается более слабым требо-
ванием, содержащимся в постулате третьем.
Выражаясь образно, можно сказать так. Пусть мы
располагаем хорошей линейкой и плохим циркулем, де-
фект которого состоит в том, что он не сохраняет своего
раствора, если оторвать его ножку от бумаги. Оказывается,
что с этими инструментами можно выполнять те же построе-
ния, что и с хорошими —только с большими хлопотами.
Заметим ещё, что уже во 2-м предложении «Начал» про-
является блестящее остроумие построения, характерное
для Евклида.
Столь же остроумно доказательство равенства углов
при основании равнобедренного треугольника, проводи-
мое в 5-м предложении 1-й книги. Оно совершенно безу-
пречно, если принять предыдущие четыре предложения.
Но оно гораздо сложнее привычных нам; и это потому,
что Евклид сознательно воздерживается от проведения
биссектрисы угла при вершине или иного аналогичного
построения, пока не показано, что биссектрису можно
провести. А это построение обеспечивается лишь в 9-м
предложении, которое существенно опирается (через про-
межуточные звенья) на 5-е.
Уже этих замечаний достаточно, чтобы судить о сте-
пени глубины и тонкости рассуждений Евклида. Этим
определяется и степень нашей требовательности к нему.
20. Критерий пересечения
Подойдём к оценке «первых начал» геометрии
Евклида критически. Однако будем помнить, что Евклид
стоит на позиции, существенно отличной от позиции Гиль-
берта (см. выше, п. 13).
Мы увидим, что в системе основных положений Евклида
имеются пробелы, и пробелы серьёзные. Но при всём том
нельзя, как мы полагаем, сказать, что «его постулаты
не дают почвы для логического обоснования геометрии».
Более того, можно сказать, что в наиболее тонком во-
просе обоснования геометрии—в вопросе о непрерыв-
ности — прогресс современной науки и логически и исто-
рически опирается на ту глубину мысли, которую проявил
2р6 М. я. ВЫГОДСКИЙ
Евклид в учениц о пропорциях и которая в течение двух
тысяч лет оставалась неоценённой даже такими корифеями
математической мысли, как Лежандр и Лобачевский.
Мы начнём с рассмотрения тех логических пробелов,
которые имеют принципиальный характер. Они обна-
руживаются уже при рассмотрении доказательств пер-
вых четырёх предложений. В предложении I, I1) при по-
строении равностороннего треугольника на данной сто-
роне АВ Евклид описывает две окружности радиуса
АВ — одну с центром в А, другую—с центром в В. «Из
точки С, в которой круги пересекают друг друга, про-
ведём, — говорит Евклид, —прямые линии СА, СВ к точ-
кам А, В». Но существования точки С Евклид не
доказывает.
Если скажут, что Евклид не мог усмотреть необхо-
димости в таком доказательстве вследствие очевидности
факта пересечения рассматриваемых линий, то на это
можно ответить, что в других совершенно аналогичных
случаях Евклид обнаруживает отчётливое понимание
этой необходимости. Так, в доказательстве предложения
II, 10 Евклид выполняет построение, в котором ему при-
ходится брать точку пересечения двух прямых ЕВ и FD.
При этом он строго доказывает, что такая точка суще-
ствует. А именно, сначала доказывается, что углы FEB
и EFD в сумме меньше двух прямых, а затем говорится:
«но прямые линии, продолженные от углов, меньших
двух прямых, встречаются». Эта фраза представляет
явную ссылку на пятый постулат.
Такого постулата, который обеспечивал бы пересече-
ние окружностей в I, 1, у Евклида нет. В современном
изложении оснований геометрии здесь пользуются аксио-
мами непрерывности. Но, как будет показано ниже, у
Евклида нет ни в явной ни в неявной форме никакого
эквивалента аксиомы Дедекинда,- хотя имеется (в 5-й
книге «Начал») эквивалент аксиомы Архимеда. Впрочем,
Евклид мог бы обойтись для своих целей более слабыми
средствами.
!) Здесь и в дальнейшем мы сокращённо обозначаем предложе-
ния «Начал» двумя числами: первое, записываемое римскими циф-
рами, обозначает книгу, второе — номер предложения.
«НАЧАЛА»ЕВКЛИДА
257
Киллинг предложил дополнить постулаты Евклида
следующим: «Если некоторая линия принадлежит неко-
торой плоскости, которую она делит на две части, и если
другая линия имеет по крайней мере по одной общей
точке с каждой из этих частей, то она должна также пере-
сечь границу между этими частями».
Мы полагаем, что в таком виде этот постулат не удо-
влетворяет ни требованиям аксиоматической геометрии,
ни установке Евклида. В самом деле, если говорят, что
«линия делит плоскость на две области» (внешнюю и вну-
треннюю), то эти слова не могут иметь никакого иного
смысла, как то, что непрерывная дуга, соединяющая
внутреннюю и внешнюю точки, имеет общую точку с рас-
сматриваемой линией. Таким образом, постулат Кил-
линга представляет не больше чем тавтологию.
С точки же зрения Евклида дело обстоит следующим
образом. В определении 15-м круг определён как плоская
фигура, объемлемая окружностью, в определении 14-м
фигура определена как то, что объемлется границей.
Таким образом, окружность есть граница некоторой об-
ласти, что, как сказано выше, по смыслу равносильно
утверждению, что другая линия (прямая или окружность—
иных линий Евклид не рассматривает) должна пересечь
окружность, если она имеет одну точку внутри, а другую
вне круга. И при доказательстве предложений I, 1 и I, 2
Евклид должен был доказать, что в рассматриваемых
случаях окружность (или прямая) действительно имеет
как внутреннюю, так и внешнюю точки. Этого он не сде-
лал, хотя это было совсем нетрудно.
Как бы таким образом ни подходить к оценке евклидо-
вых рассуждений в I, 1 и в других аналогичных случаях,
они содержат серьёзный логический пробел, нуждающийся
в восполнении внутри евклидовой системы.
21. Конгруентность и движение
Вторым слабым местом евклидовой системы является
обоснование учения о конгруентности фигур.
Как мы видели, аксиома 4-я устанавливает, что «совпа-
дающие друг с другом равны друг другу». Эту аксиому
U Историко-математ. исследования
258
М. Я. ВЫГОДСКИЙ
но следует понимать как отождествление равенства фигур
и их конгруептности (т. е. возможности привести их в со-
впадение). Понятие равенства фигур имеет у Евклида более
широкий смысл, чем понятие совпадения: оно равнозначно
нашему понятию равновеликости. Это явствует из много-
численных мест текста, например из формулировки
1, 35 («параллелограммы на одном и том же основании
и на одних п тех же параллельных равны друг другу»).
Таким образом, понятие равенства фигур носит у Евклида
чисто количественный характер и не тождественно с поня-
тием наложимости. То обстоятельство, что Евклид не
оговаривает этого, не следует ставить ему в строгую вину.
Действительно, вникнув, например, в доказательство
I, 35, мы увидим, что «равенство» рассматриваемых парал-
лелограммов (назовём их (А) и (В)) устанавливается на
основании аксиом 2-й, 3-й, 4-й. Именно, параллелограмм
(А) получается отнятием некоторого треугольника (С)
из фигуры, образованной треугольниками (D) и (Ё);
параллелограмм же (В) — отнятием (С) из (D) и (£"), где
Е' есть треугольник, конгруентный Е. В силу аксиомы
4-й (Е) и (Е') равны, а в силу аксиом 2-й и 3-й мы имеем
право сказать, что параллелограммы (А), (В) равны
ДРУГ другу.
Однако Евклид виновен в другом: он нигде не указы-
вает того, что для прямолинейных отрезков и прямолиней-
ных углов имеет место положение, обратное аксиоме 4-й,
т. е. что равные отрезки и углы могут быть приведены
в совпадение. Между тем это положение ему существенно
необходимо, скажем, при доказательстве I, 4. Уже Прокл
обратил внимание на этот пробел, а Генри Сэвиль (Savile)
в 1G21 г. наметил доказательство упомянутого положения
на основе постулатов первого, второго и аксиомы 5-й.
Но самый серьёзный пробел в доказательстве предло-
жения I. 4, устанавливающего, что если в треугольни-
ках АВС и А'В'С' соответственно равны: стороны АВ,
АС — сторонам А'В', А'С' и угол А—-углу А', то соответ-
ственно равны: углы В, С—углам В', С', третья сторона
ВС — стороне В'С и треугольник АВС треугольнику
А'В'С', остался, повидимому, незамеченным никем из
древних комментаторов Евклида.
«НАЧАЛА» ЕВКЛИДА
259
Пробел этот, как известно, состоит в том, что возмож-
ность наложения треугольников не обеспечена у Евкли-
да никаким постулатом, никакой аксиомой. Чтобы оце-
нить степень значительности этого пробела с точки зре-
ния античной математики, мы должны несколько под-
робнее подойти к вопросу.
Говоря в I, 4: «если треугольник АВС налагается на
треугольник DEI<\ Евклид пользуется для выражения
понятия «налагается» страдательным залогом того же гла-
гола, £(pa>}iQ^s’v, который был употреблён в аксиоме
4-й в смысле «совпадать». Таким образом, точнее можно
передать эту фразу словами: «если треугольник АВС при-
водится в совпадение с треугольником DEF». Ясно, что
понятие «совпадать» или «приводится в совпадение» рас-
сматривается Евклидом как понятие первоначальное. Пред-
полагается, что какие-то два различных геометрических
объекта допускают совмещение. Тем самым в геометрию
вводится движение.
Между тем не только Платон, но даже Аристотель
считали движение чуждым математике. Так, в седьмой
главе XI книги «Метафизика» Аристотель противопо-
ставляет физику, которая «занимается предметами, имею-
щими начало движения в самих себе», математике как
«теоретической науке, которая рассматривает предметы
пребывающие»г). Поэтому следовало бы ожидать, что
Евклид будет избегать движения, а значит, и применения
метода наложения.
Если, тем не менее, Евклид прибегнул к движению
то лишь потому, что без него он не может обойтись 1 2).
1) Аристотель, «Метафизика», стр. 191. В другом месте
«Метафизики» (стр. 33) читаем: «Математические предметы чужды
Движению, за исключением тех, которые относятся к астрономии».
2) Многие современные авторы считают, что Евклид стремится
избежать движения там, где это только представляется ему возмож-
ным. Основанием для этого мнения служит то, что метод наложения
употреблён в «Началах» лишь четыре раза (предложения I, 4; I, 8;
III, 14; Ш, 24). Как бы убедителен ни был этот довод, нужно при-
нять во внимание и те соображения, которые можно выставить про-
тив него. Прежде всего, эти предложения являются основными; на
них построено всё учение о прямолинейных фигурах (I, 4 и I, 8) и
об окружности (Ш, 14; III, 24). «Семь бед —один ответ». Евклид не
17*
260
М. Я. ВЫГОДСКИЙ
Ни один античный автор, невидимому, нс поставил в вину
Евклиду этого «грехопадения». Напротив, Архимед в
18-м предложении своего сочинения «О коноидах и сфе-
роидах» доказывает методом наложения равенство (по
объёму и по поверхности) двух частей, па которые «сфе-
роид» (т. е. эллипсоид вращения) рассекается плоско-
стью, проходящей через центр.
Лишь в середине XVI в. ревнитель геометрической
строгости и горячий поклонник Евклида Жак Пелетье
(Пелетарий) указал, что евклидово доказательство I, 4
неудовлетворительно вследствие применения наложения
и предложил принять I, 4 за аксиому; как известно, спустя
З-^-века это сделал Гильберт.
Но Евклид вряд ли поступил бы последовательно,
если бы сделал так. Ведь у него критерием равенства
прямолинейных отрезков, прямолинейных углов и дуг
равных окружностей по существу является их совмести-
мость. Отказаться же, как это делает Гильберт, от вся-
кого критерия равенства, введя это понятие аксиома-
тически, Евклид, как выше было показано, не мог бы
принципиально.
Поэтому Евклид скорее должен был бы ввести такую
аксиому, которая обеспечила бы возможность совмеще-
ния треугольников. Разумеется, ни о каком определении
понятия «совмещение» («совпадение» или «движение») не
могло быть и речи. Оно является у Евклида первона-
чальным.
мог не понимать, что принципиально не имеет значения, будет ли
предложение I, 8 (равенство треугольников по двум углам и стороне)
доказано при непосредственном использовании движения или без
такового, но со ссылкой на I, 4. Предположим, однако, что Евклид
желал свести к минимуму число предложений, использующих дви-
жение, чтобы впоследствии можно было доказать их, не прибегая к
наложению, или принять за аксиомы. Но тогда трудно понять, поче-
му наложение применено в предложении 1, 8 (равенство треугольни-
ков по двум углам и стороне), которое очень легко доказывается от
противного на основании I, 4 без непосредственного применения
наложения.
Все эти обстоятельства заставляют усомниться в справедливости
упомянутого выше мнения.
«НАЧАЛА » ЕВКЛИДА
261
Те, кто полагают х), что у Евклида совсем нет аксиом,
относящихся к движению, совершают, на мой взгляд,
ошибку. Постулат третий в соединении с постулатом
первым и определением 15-м представляют не что иное,
как утверждение о возможности вращательного движения
отрезка. Как показано в I, 2, отсюда вытекает (если при-
соединить аксиому, гарантирующую существование точки
пересечения), что отрезок можно не только вращать, но
и смещать. Таким образом, для отрезков свойства дви-
жения а) по существу указаны Евклидом.
Возможность движения угла доказана в I, 23 («при
данной прямой и при данной на ней точке построить прямо-
линейный угол, равный данному прямолинейному углу»).
Но это доказательство существенно опирается на пред-
ложение I, 8 (равенство треугольников по двум углам
и стороне), в котором Евклид пользуется движением тре-
угольника. А это последнее не обеспечено никакой
аксиомой.
На первый взгляд может показаться, что возможность
движения треугольника вытекает из возможности дви-
жения углов и отрезков. Во всяком случае евклидово
доказательство I, 4, и поныне приводимое в школьных
учебниках, представлялось убедительным не только школь-
никам, но и таким великим математикам, как Лобачев-
ский 8). Между тем, из возможности движения углов и от-
резков отнюдь не вытекает возможность движения тре-
угольника. Мы говорим, конечно, о таком движении,
которое сохраняет величины всех сторон и углов тре-
угольника.
х) «Понятие движения у Евклида не определено и свойства дви-
жения ни в каких аксиомах не перечислены». Н. В. Ефимов, «Выс-
шая геометрия», стр. 10.
2) Они по существу совпадают с теми, которые перечислены в
1-й, 2-й и 3-й аксиомах конгруентности Гильберта. Ясно, что Ев-
клиду не было нужды отмечать, что отрезок АВ наложим сам на себя,
ибо понятие наложимости у Евклида предметно.
•) Лобачевский в «Новых началах геометрии» доказывает нало-
жением единственность перпендикуляра, опущенного на прямую из
точки вне её (стр. 48), и равенство углов при основании равнобедрен-
ного треугольника (стр. 50). Н. И. Л о б а че в с к и й, «Новые начала
геометрии». Харьков, 1912, стр. 66, 67.
262
М. Я. ВЫГОДСКИЙ
Допустим, что материальный прямолинейный тре-
угольник АВС (слово «материальный» мы употребляем
в том же смысле, как в термине «материальная точка»,
т. е. отвлекаясь от всех свойств вещества, кроме его про-
тяжённости) находится в процессе движения. Пусть при
этом угол А и стороны АВ, АС сохраняют свою величину
(что предполагается при доказательстве I, 4). Всё, что
мы можем сказать при этом о стороне ВС,— это то, что
в каждом положении треугольника АВС она имеет вполне
определённую величину, так как точки В пС однозначно
определяют отрезок ВС1). Но ни откуда не следует, что
при этом отрезок ВС сохраняет свою длину, т. е. что
в новом своём положении ВС он может быть получен
перенесением отрезка ВС. Если это будет иметь место,—
движение треугольника возможно; если нет,— треуголь-
ник АВС обречён на «неподвижность».
В реальном пространстве движение треугольника, со-
храняющее длины его сторон и углов (по крайней мере
в пределах точности наблюдения), возможно, и эту воз-
можность Евклид (так же как и каждый из пас на первой
ступени изучения геометрии) склонен принять за логи-
ческую необходимость.
Чтобы лучше уяснить суть дела, вообразим, что наша
земля имела бы форму, сильно отличающуюся от сфери-
ческой, скажем, яйцеобразную. Тогда треугольник, начер-
ченный на поверхности земли, не мог бы, как мы сейчас
увидим, двигаться по этой поверхности.
Разумеется, на поверхности япца, как и на поверх-
ности шарообразного тела, нельзя проводить прямых
линий, но роль прямых играют кратчайшие линии (кото-
рые будут вместе с тем и «прямейшими»; на шарообразной
поверхности это — большие круги). Прямейшие линии
можно проводить так же, как проводятся прямые на пло-
скости—-натягивая нить между двумя фиксированными
точками. Эти «прямые» обладают всеми теми свойствами
обычных прямых, которые используются при доказатель-
*) У Евклида единственность прямой АВ не оговорена особо в
постулатах. Но, как увидим, она подразумевается в формулировке
ростулата первого.
«НАЧАЛА» ЕВКЛИДА
263
стве I, 4. Равенство «отрезков» таких «прямых» можно
проверять наложением. Следовательно, па пашей кривой
поверхности можно строить «окружности»; они не будут
окружностями в обычном смысле, но могут быть делимы
на равные части. Таким образом, возможно измерение
углов дугами. Хотя величина угла вообще будет зависеть
от радиуса окружности, однако при малых радиусах эта
зависимость практически будет незаметна. С помощью
предельного перехода можно совершенно устранить эту
зависимость, и тогда величина угла между «прямейшими»
будет в точности равна углу между «настоящими», пря-
мыми, касательными к «прямейшим».
На нашей яйцеобразной поверхности возможно выпол-
нить построения, произведённые Евклидом в I, 1; I, 2;
I, 3. Но рассуждения I, 4 неприменимы, и самая теорема
не верна. Действительно, если построить, скажем, равно-
бедренный прямоугольный треугольник с катетами а
у одной из вершин яйца и другой равнобедренный пря-
моугольный треугольник с катетами а у точки, равно-
удалённой от этих вершин (на «экваторе» яйца), то гипо-
тенуза первого будет значительно меньше гипотенузы
второго. Движение треугольника, таким образом, па
этой поверхности невозможно, хотя движение отрезков
и углов вполне осуществимо.
Итак, движение прямолинейного треугольника в пло-
скости возможно только в силу некоторого геометриче-
ского свойства плоскости. Точно так же движение фигуры
в пространстве возможно в силу некоторых геометриче-
ских свойств пространства. Евклид этих свойств в по-
стулатах не упомянул. Почему? Потому, что эти свой-
ства пространства он, повидимому, считал логически
необходимыми; он не видел их геометрического ха-
рактера.
В подтверждение этого объяснения можно привести
такой факт. Гений Лобачевского поднялся до понимания
того, что существование подобных фигур нс является необ-
ходимым свойством пространства и что оно зависит от
выполнимости евклидова постулата параллельности. Но
существование равных фигур даже Лобачевский считал
само собой разумеющимся и пользовался наложением
264
М. Я. ВЫГОДСКИЙ
так же, как делал это Евклид, не связывая его с каким-либо
постулатом.
Подведя итог, мы можем сказать: в системе посту-
латов и аксиом Евклида имеется два существенных про-
бела: 1) не дано критерия пересечения окружности с дру-
гой окружностью и с прямой линией, 2) не обеспечена
возможность наложения фигур. Первый дефект Евклид
был бы, безусловно, в состоянии заметить и устранить;
второй он вряд ли мог бы усмотреть, хотя устранить его,
сохранив весь строй «Начал» было бы и нетрудно.
22. Второстепенные недочёты логической
системы Евклида
Мы полагаем, что по существу этим и исчерпываются
дефекты логической системы «Начал». Остальные «про-
белы» либо носят характер редакционных недочётов, либо
вовсе не являются пробелами в системе Евклида.
Уже при первом взгляде на систему евклидовых посту-
латов бросается в глаза, что в постулате первом, кото-
рый утверждает существование прямой, проходящей через
две данные точки, нет явного указания на единственность
такой прямой. Это требование единственности необхо-
димо уже при доказательстве основного предложения I, 4,
и там Евклид мотивирует совпадение отрезков ВС и EF
с совпавшими концами В, Е и С, F следующим образом:
«если В совпадёт с Е и С с F, а основание ВС не совпадёт
с основанием EF, то прямые линии будут заключать про-
странство, что невозможно».
В соответствии с этим мы находим во многих рукописях
«Начал» (в одной в качестве шестого постулата, в осталь-
ных— в качестве 9-п аксиомы) предложение: «две прямые
не заключают пространства».
Гейберг с большим основанием считает 9-ю аксиому
позднейшим добавлением1). Тогда в «Началах» Евклида
i) Гейберг считает позднейшей вставкой также приведённую вы-
ше мотивировку в I, 4, хотя она имеется во всех без исключения гре-
ческих рукописях. Он основывается на том, что в одном арабском
переводе «Начал» эта мотивировка поставлена в конце предложения
4-го после слов «что и требовалось доказать».
«НАЧАЛА» ЕВКЛИДА
265
имеется пробел, но он носит чисто редакционный харак-
тер. Ужо во времена Прокла аксиома «две прямые не
заключают пространства» содержалась в списках «На-
чал», но сам Прокл считал её совершенно излишней,
полагая, что она является следствием единственности
прямой, соединяющей две точки *), и считая, что фор-
мулировка первого постулата с достаточной ясностью
говорит, что «две точки соединяются одной прямой, а не
двумя»* 2).
Мы можем присоединиться к этому мнению, выразив
только сожаление, что Евклид в формулировке посту-
лата первого поскупился на два-три лишних слова.
Более серьёзным был бы адресованный Евклиду упрёк
в том, что он поместил среди постулатов предложение
ос равенстве прямых углов; ведь он мог бы доказать это
предложение наложением, как это делал Лежандр и мно-
гие другие авторы 3).
х) Прокл, цит. соч., стр. 196.
2) Там же, стр. 239.
3) Должен, однако, заметить, что мне непонятен упрёк, который
делает Евклиду Гильберт, когда говорит: «На основании теорем 13
и 14 («Оснований геометрии» Гильберта.— М. В.) является возмож-
ным доказать следующую простую теорему, которую Евклид —по
моему мнению неправильно—поместил в числе аксиом: все прямые
углы равны между собой» (Гильберт, «Основания геометрии», Рус-
ское издание 1923 г., стр. 16). Бесспорно, что на основании аксиом
первых трёх групп Гильберта четвёртый постулат Евклида доказать
нетрудно. Но как мог бы это сделать Евклид, не прибегая к наложе-
нию? Ведь его аксиомы и постулаты, если исключить постулат чет-
вёртый, не содержат никакого эквивалента гильбертовой аксиомы
III, 4, обеспечивающей перенос угла. Возможность такого переноса
доказана у Евклида в предложении I, 23, но это доказательство само
опирается (черев промежуточные звенья) на четвёртый постулат. Та-
ким образом, постулат четвёртый следует рассматривать как экви-
валент 4-й аксиомы конгруентности Гильберта. Заметим, что для
остальных гильбертовых аксиом конгруентности, кроме 5-й, в «На
чалах» нетрудно найти (см. ниже п. 23) эквивалентную систему основ-
ных положений (для 5-й аксиомы Гильберта, обеспечивающей пере-
нос треугольника, у Евклида, как было покавано, эквивалента пет).
Таким образом, уже из изложенного ясно, что предложение о
равенстве прямых углов Евклид не мог бы доказать по плану Гиль-
г -Мы не говорим уже о том, что в евклидовом доказательство
I, 23 предполагается наличие пересечения окружности с прямой, ко-
торое не обеспечивается первыми тремя группами аксиом Гильберта.
266
М. Я. ВЫГОДСКИЙ
Однако в защиту Евклида можно было бы привести
следующие соображения. Без утверждения, содержа-
щегося в четвёртом постулате, нельзя было бы высказать
пятый постулат, потому что в пятом постулате говорится
об углах, которые в сумме меньше двух прямых углов.
До того, как установлено, что все прямые углы равны,
такое выражение было бы лишено всякого смысла. Ев-
клид, как мы видим, и здесь проявил большуюп^дусмот-
рительность. Конечно, он мог бы сформулировать пятый
постулат позднее —ведь впервые ои пользуется им в I, 29
(равенство накрест лежащих углов при параллельных).
Нечто подобное Евклид сделал в 10-й книге «Начал», где
определения вновь вводимых иррациональностей введены
не в начале книги, а перед предложениями X, 48 и X, 85.
Но там речь идёт о понятиях, имеющих специальную
область применения. В пятом же постулате речь идёт
об основном понятии всей геометрии, и переносить его
определение в середину первой книги значило бы нару-
шить принятый Евклидом порядок изложения. Если
к этому прибавить, что наличие излишнего постулата,
так же как и перегруженность определений, о которой
мы говорили в п. 9, не является логическим изъяном,
то упомянутый выше упрёк, так же как и первый, следует
отнести к числу несущественных.
23. Мнимые недостатки евклидовой системы аксиом
С аксиоматической точки зрения система Евклида
содержит целый ряд других недочётов. Так, у Евклида
совершенно отсутствуют так называемые аксиомы порядка.
Но в самой системе Евклида эти аксиомы не нужны.
Возьмём, скажем, 1-ю аксиому порядка Гильберта.
«Если А, В, С —точки одной прямой, и В лежит между А
и С, то В лежит также между С и Л». В системе Гильберта
эта аксиома совершенно необходима, потому что поня-
тие «между» является совершенно бессодержательным;
оно определяется единственно только аксиомами второй
группы.
Для Евклида же понятие «между» является таким же
первоначальным логическим понятием, как, скажем, союз
НАЧАЛА»ЕВКЛИДА
267
«и» и всякое другое слово человеческого языка. А без
пользования разговорным языком даже для Гильберта
было бы невозможно построение основ геометрии. Ко-
нечно, можно ввести язык символический, но ведь значе-
ние логических связей между символами нужно разъяс-
нить на разговорном языке. Значит, и принципиально
между позициями Гильберта и Евклида в этом вопросе
разница не столь уж велика: у Евклида число неопре-
деляемых логических соотношений больше, чем у Гиль-
берта.
Итак, понятие «между» для Евклида по своему смыслу
имеет порядковый характер; поэтому Евклиду не при-
ходится оговаривать, что фраза «В лежит между А и С»
равносильна фразе «В лежит между С и А», совершенно
так же, как Гильберту нет нужды оговаривать, что фраза
«точка А и прямая а» равносильна фразе «прямая а и
точка А». Равным образом Евклиду пот никакой надоб-
ности вводить аксиому II, 3 (из трёх точек прямой всегда
одна и только одна лежит между двумя другими). Ана-
логично обстоит дело с аксиомой II, 2 Гильберта. Что же
касается последней, 4-й, аксиомы («аксиома Паша»), то,
как известно, она логически равносильна предложению
о том, что прямая а, лежащая в плоскости а, разделяет
не лежащие на ней точки этой плоскости на две обла-
сти (полуплоскости); а это свойство указано в определе-
нии 6-м1).
Мы полагаем также, что неправы те критики Евклида,
которые полагают, что «необходимость аксиомы I, 3 (на
каждой прямой существует по меньшей мере две точки)
и большинства дальнейших аксиом этих групп Евклид
вряд ли мог заметить»2). Что Евклид во всяком случае
и мог, и даже должен был заметить такую необходимость,
если бы она действительно существовала, видно хотя бы
из того, что Евклид доказывает существование середины
Формулировка определения 6-го может дать повод думать, что
линия рассматривается Евклидом как кран куска поверхности. Но
Прокл справедливо указывает на то, что термин «граница» нужно
понимать в более широком смысле. Ср. высказывание Аристотеля,
приведённое на стр. 241 (п. 11).
2) Н. В. Ефимов, «Высшая геометрия», стр 35.
268
М. Я. ВЫГОДСКИЙ
отрезка (I, 10). Но существование двух каких-то (и даже
бесконечно большого числа) точек на прямой уже утвер-
ждалось в определении 3-м, которое как раз критики
и считают излишним наряду с другими определениями
первой группы. В самом деле, в определении 3-м содер-
жится утверждение, что точка может делить прямую
(или отрезок) на две области1); существование такой точки
должно быть, как мы видели в п. 10, «принято», т. е.,
выражаясь современным языком, принято за аксиому.
Итак, Евклиду не было никакой необходимости фор-
мулировать в качестве специальной аксиомы факт суще-
ствования точек па прямой, так как этот факт был уже
установлен в определении 3-м.
Можно было бы продолжить рассмотрение этих мни-
мых пробелов системы Евклида, но из сказанного, пожалуй,
достаточно ясно, что хотя в ней и есть существенные
недостатки, никак нельзя всё же сказать, что «основание,
на котором построена его система, чрезвычайно слабо».
Напротив, можно только удивляться тому, насколько
глубоко Евклид проник в тонкие вопросы обоснования
геометрии. Мы бы сказали далее больше: если учесть раз-
личие в принципиальных установках Евклида и Гиль-
берта, то внимательное рассмотрение гильбертовой системы
аксиом обнаруживает поразительную близость между их
системами основных положений2).
24. Отношение и число
Глубина и тонкость Евклида в вопросах обоснования
геометрии с наибольшей яркостью проявляются в заме-
чательной теории пропорций, изложенной в 5-й книге
«Начал». Она играет в системе Евклида ту же роль, кото-
рую в современной математике играет теория веществен-
ных чисел.
Недостаточность системы рациональных чисел была
впервые обнаружена в области геометрии. Мы не знаем
в точности, кем и когда была впервые установлена несоиз-
х) См. упомянутое высказывание Аристотеля и предыдущую
сноску.
2) См. п. 31 (стр. 294).
«НАЧАЛА»ЕВКЛИДА
2ft9
меримостьстороны квадрата и его диагонали—невидимому,
задолго до греков об этом знали вавилоняне, которым
ещё за 2000 лет до н. э. была известна так называемая
пифагорова теорема. Но нет сомнения в том, что когда
древние греки (вероятно, в V в. до н. э.) обнаружили
этот поразительный факт, это произвело настоящий пере-
ворот в математике. Недаром предание, сохранённое одним
безымянным комментатором Евклида, рассказывает, что
тот, кто впервые открыл тайну иррациональности, был
жестоко наказан судьбой: корабль его потерпел крушение,
и он был ввергнут в морскую пучину.
И если до открытия несоизмеримых величин число
представлялось надёжным инструментом геометрических
исследований, то теперь вся вычислительная геометрия
была поставлена под вопрос. Конечно, на практике, где
все измерения по природе своей имеют ограниченную
степень точности, продолжали находить площадь прямо -
угольника перемножением чисел, выражающих его осно-
вание и высоту в единицах определённого масштаба.
Но поступать так в строго логическом изложении гео-
метрии греческие математики не считали возможным.
Логически возможны были два варианта строгого построе-
ния геометрии.
Либо нужно было построить чисто арифметическую
теорию иррациональных чисел, тогда в геометрии можно
было бы на этой расширенной базе сохранить теорию
измерения площадей и объёмов с помощью масштабных
единиц. Либо нужно было отказаться от явного выражения
произвольных геометрических величин числами, создав
такой аппарат, который позволил бы иначе выразить коли-
чественные связи величин.
По первому пути, по пути «арифметизации геометрии»,
пошла современная математика. Греческая математика
пошла по второму пути. Почему? Многие полагают, что
Древние греки не любили или не были способны к вычи-
слениям. Мы не разделяем этого взглядах). Мы полагаем,
что второй путь был при всех обстоятельствах более
г) См. М. Я. Выгодский. «Арифметика и алгебра и древнем
мире». Гостехпздат, 1941, стр. 216—219.
270
М. Я. ВЬ ГОДСКПЙ
естественным: во-первых, с несоизмеримыми величинами
античная наука встретилась главным образом в области
геометрии, и, во всяком случае на первых порах, не ус-
матривалось никакой необходимости в построении чисто
арифметической теории; во-вторых, такая теория потребо-
вала бы большей степени абстрактности, ибо она связана
с диалектическим развитием понятия числа.
Евклид называет «числом» только целое число; теории
целых чисел он посвящает 7-ю, 8-ю и 9-ю книги «Начал».
В противоположность «логистике», где и дроби рассма-
тривались как числа, Евклид знает только отногиения
целых чисел1); понятие дробного числа ему чуждо.
Ту же тенденцию можно проследить и дальше. Нашему
понятию вещественного числа у Евклида отвечает понятие
«отношения величин». Но это понятие вводится не как
обобщение понятия «отношения чисел», а самостоятельно
и по существу опирается только на (целые) числа.
25. Евклидова теория пропорций
Пятая книга «Начал» открывается следующими опре-
делениями:
1. Величина есть часть величины, меньшая большей,
если она измеряет большую.
2. Большая же величина кратна меньшей, если она
измеряется меньшей.
3. Отношение есть некоторое количественное свойство
двух однородных величин.
4. Говорят, что величины имеют друг к другу отноше-
ние, если они могут, будучи взяты кратно, превзойти
одна другую.
г) Заметим, что и в современной теории арифметики рациональ-
ное число рассматривается как «пара целых чисел» и что целое число,
например 3, является рациональным числом лишь при том соглаше-
нии, что мы заменяем его «парой» целых чисел, скажем парой 3:1.
Равноправие целых и рациональных чисел создаётся, следовательно,
лишь после того, как само понятие целого числа изменяет своё содер-
жание. Евклид предпочитает сохранить исходное содержание поня-
тия числа. Эта классификация столь же неудобна, как его классифи-
кация фигур, в которой, как мы видели, прямоугольник — не парал-
лелограмм, а квадрат —не прямоугольник. Но формально Евклид
вправе проводить ту классификацию, которая ему нравится.
«НАЧАЛА» LI КЛНДА
271
Как мы видим из определений 1-го, 2-го,
понятие «величины» Евклид рассматривает как первона-
чальное. Если же посмотреть, какие свойства «величин»
Евклид в ходе доказательств предполагает выполняю-
щимися, то окажется, что молчаливо предполагается:
1) возможность их сравнения по признакам «больше»,
«меньше» или «равно», 2) возможность их сложения,
а следовательно, и возможность умножения на целое
число. В доказательстве предложения V, 5 существенно
предполагается ещё возможность деления величины на
любое число равных частей. Это предложение Евклид
легко мог бы, пользуясь обычными своими приёмами,
доказать и не прибегая к делению. Можно поэтому ду-
мать, что существенным свойством величины для него
являлась также делимость на любое число равных частей.
А поскольку в системе целых чисел это свойство не соблю-
дается, то можно думать, что число Евклид не рассматривал
как величину. Может быть, в этом и нужно видеть причину
того, что отношения чисел рассматриваются Евклидом
совершенно независимо от отношений величин, а не как
частный случай последних.
Таким образом, существенными признаком величины
для Евклида являлась, невидимому, её неограниченная
делимость.
3-е и 4-е определения дают некоторый ответ па вопрос,
что такое отношение величин. На первый взгляд может
показаться, что определение 3-е представляет простую
тавтологию. На самом же деле оно содержит важное
условие, необходимое для наличия отношения. Именно,
оно устанавливает, что сравниваемые величины должны
быть однородными. Таким образом, по Евклиду, площадь
и длина, вес и объём и т. д. не могут иметь друг к другу
отношения. Об отношении может итти речь, если мы имеем
два отрезка, два веса, два объёма и т. д.
Но при этом должно быть выполнено ещё одно усло-
вие, высказанное в следующем, 4-м, определении Это
условие, в несколько иной форме, было для линий, пло-
щадей и объёмов принято в качестве недоказываемого
положения Архимедом в его сочинении «О шаре и
цилиндре» и потому называется обычно «аксиомой
272
М. Я. ВЫГОДСКИЙ
Архимеда», хотя правильнее было бы назвать его аксио-
мой Евклида.
Не зря устанавливает Евклид это определение. Оно
исключает из рассмотрения трансфинитные величины; оно
исключает «неделимые линии», из которых составляли
«непрерывные» линии Демокрит и другие атомисты 1)
древности. Оно исключает возможность сравнения криво-
линейных углов с прямолинейными: в предложении
III, 16 «Начал» доказано, что «рогообразный» угол ме-
жду окружностью и касательной меньше всякого прямо-
линейного угла; между тем, если бы «рогообразный» угол
имел бы отношение к некоторому прямолинейному углу,
то последний можно было бы разделить на столь большое
число 2” частей, чтобы получился угол, меньший «рого-
образного».
Итак, на вопрос, что такое отношение, Евклид по суще-
ству отвечает следующим образом: отношение есть пара
однородных величин, удовлетворяющих требованию опре-
деления 4-го. Тому современному читателю, который
остался бы неудовлетворённым таким ответом, можно
было бы сказать, что совершенно так же в современной
арифметике определяется понятие рационального числа
как пары целых чисел. Это определение наполняется
большим содержанием после того как определяются кри-
терии равенства и неравенства, а также действия с рацио-
нальными числами.
Точно так же обстоит дело и с евклидовым понятием
отношения. Оно обрастает плотью и кровью после того,
цак в определениях 9—18-м 5-й книги объяснены
действия с отношениями, выполнение которых сущест-
венно опирается на установленные в определениях 5-м
и 7-м признаки равенства и неравенства отношений.
Термином «равенство» и «равные» и т. п. применитель-
но к отношениям Евклид не пользуется; он поступает так,
несомненно, умышленно. Ведь если бы он сказал, что каждое
1) См. в вып. IV «Хрестоматии по истории математики» Г. Вилей*
тпера отрывок IV (ГТТИ, 4932, стр. 23). Подробное изложение ан-
тичной теории неделимых —в книге С. Я. Лурье, «Теория беско-
нечно-малых у древних атомистов».. Изд. АН СССР, 1935,
«НАЧАЛА» ЕВКЛИДА
273
из отношений А : В и С : D равно отношению Е : F, то на
основании аксиомы 1-й можно было бы заключить, что
отношения А : В и С : D равны друг другу. Евклид же
доказывает это транзитивное свойство отношений (V, 11).
Весьма предусмотрительно поэтому он говорит: «Л
имеет к В то же отношение, что С к D», вместо того,
чтобы сказать: «отношение А : В равно отноше-
нию С : D».
Признак равенства отношений дан в 5-м определении,
на первый взгляд мало попятном.
«Говорят, что величины имеют одно и то же отношение,
первая ко второй и третья к четвёртой, если взятые по
какой угодно кратности равнократные первой и третьей
одновременно превосходят или одновременно равны
или одновременно меньше каждая каждой, равнократ-
ных второй и четвёртой, взятых в соответственном по-
рядке».
Это определение сначала может отпугнуть своей гро-
моздкостью. Но после того, как мы переведём его на со-
временный язык, каждый воздаст должное искусству Ев-
клида построить столь чёткое и краткое словесное опреде-
ление, содержащее очень глубокую идею.
Пусть мы имеем две пары величин А, В и А', В' и,
следовательно, два отношения А : В, А': В'. Отношение
А .В, по определению 5-му, таково же, что отношение
А' :В', если, каковы бы ни были целые числа т, п, всег-
да при mA > пВ имеет место также mA' > пВ'; при mA <пВ
всегда тА'<пВ', при mA = пВ (если такое равенство воз-
можно) всегда тА' = пВ'.
Чтобы облегчить читателю понимание этого опреде-
ления, допустим на минуту, что мы умеем выразить неко-
торым числом (рациональным или иррациональным) от-
ношение А : В и что к неравенствам вида тА>пВ можно
применять обычные алгебраические преобразования. Тог-
да определение 5-е высказывает следующее: если всякое
рациональное число п : т, большее вещественного числа
А: В, также больше числа А': В', а всякое рациональное
число ir.mt меньшее чем А: В, также меньше, чем
Л'• В' (и, значит, если п : т~А : В, то также п : т=^
==А' : В'), то числа А : В и А' : В' равны.
Псторико-матекат. исследовании
274
М. Я. ВЫГОДСКИЙ
Теперь легко видеть, что евклидово определение
5-е по существу совпадает с дедекиндовым определением
вещественного числа и вместе с тем даёт дедекиндов кри-
терий равенства вещественных чисел.
В самом деле, Евклид в определении 5-м различает
следующие три типа пар целых чисел ти, п (т. е. по суще-
ству рациональных чисел т : п): 1) такие, для которых
mA > пВ\ 2) такие, для которых mA < пВ, 3) такие, для
которых mA = пВ. Пары чисел третьего типа, если тако-
вые существуют, можно объединить с числами одного из
первых двух типов. Тогда окажется, что пары т : п раз-
биваются на два класса. К классу I относятся те пары,
для которых mA > пВ\ к классу II—те, для которых
mA < пВ. Нетрудно доказать, что если mXJ пх—пара I клас-
са, а т2, п2 — пара II класса, то *)
тхп.> > m2nlf
что, как известно, служит определением неравенства
двух рациональных чисел.
Итак, пара отрезков А, В вызывает разделение всех
целочисленных пар на два таких класса, что каждое
рациональное чи*сло, образованное парой I класса, больше
любого рационального числа, относимого ко II классу.
Тем самым всякая пара отрезков создаёт дедекиндово
сечение, т. е. вещественное число. А евклидов признак
равенства двух отношений обращается в признак равенства
двух вещественных чисел; именно эти числа равны, если
всякое рациональное число т : п, принадлежащее I клас-
су в одном сечении, принадлежит также I классу и в дру-
гом сечении, и обратно.
Точно так же можно показать, что 7-е определение 5-н
книги равносильно дедекиндову признаку неравенства
вещественных чисел.
Ч Для этого достаточно помножить неравенство тхА > пхВ
ла п.>, а неравенство т^А^п^В—на пх. Получим тхп2А > пхп2В
и т2пх 1^пхп2В, откуда тхпгА > т2?.и1, т, е. тхп2> т2пх.
«НАЧАЛА» ЕВКЛИДА
275
26. Постулат непрерывности
Сходство между евклидовой теорией пропорций и деде-
киндовой теорией вещественного числа столь велико, что
такой крупный математик, как Липшиц, считал, что
теория Дедекинда не содержит ничего нового по сравнению
с 5-й книгой «Начал». В этом, однако, он был неправ. Вся-
кое евклидово «отношение величин» создаёт некоторое
дедекиндово сечение, т. е. представляет некоторое веще-
ственное число — рациональное или иррациональное, смо-
тря по тому, соизмеримы или нет члены отношения. Но
всякое ли дедекиндово сечение создаёт евклидово «отно-
шение величин»? Иными словами, если в области целых
пар w, п произвести некоторое дедекиндово сечение (о^а.,)
и если взять некоторую величину, скажем отрезок А, то
найдётся ли такой отрезок В, чтобы отношение В : А
создало сечение (a^JVHa этот вопрос положительно отве-
чает аксиома непрерывности Дедекинда. Но у Евклида
такой аксиомы нет. Таким образом, вопрос о существо-
вании отрезка В, а значит и отношения В : А в евклидо-
вой системе остаётся совершенно открытым.
Но, как признавал и сам Дедекинд в своём ответе Лип-
шицу, в системе Евклида дедекиндов постулат непрерыв-
ности не нужен: «Евклид может применять своё опреде-
ление равных отношений ко всем тем величинам, которые
встречаются ему в его системе, и этого ему вполне доста-
точно»1).
В самом деле, как мы видели выше, Евклид хочет иметь
дело лишь с теми геометрпческимп объектами, которые
можно получить с помощью допущенных им построений,
т. е. построений, выполнимых линейкой и циркулем.
А эти построения никогда не выведут пас за очень «узкую»
область отношений 2 * * * *). В этой области нет, например, даже
ст ^„Dedekind’8 gesammelte Werke, В. Ill, Braunschweig, 1932,
2) Совокупность вещественных чисел, соответствующих этим от-
ношениям, состоит из 1) всех целых положительных чисел; 2) квад-
ратных корней из целых положительных чисел; 3) всех тех чи-
сел, которые получаются из чисел групп (1) и (2) «рационально»,
т- е. с помощью четырёх действий арифметики (таково, например,
18*
276
м. Я. вьгодскпп
такого отношения, которое отвечает числу 2. Иными
словами, в системе Евклида не существует куба, вдвое пре-
восходящего по объёму данный куб.
При таком самоограничении Евклид, естественно, не
нуждается в постулате непрерывности. Однако при этом
для пего становится невозможным рассмотрение некоторых
вопросов, естественно возникающих внутри его собствен-
ной системы.
Таков, прежде всего, вопрос о сравнении круга с прямо-
линейной фигурой. В предложении XII, 2 Евклид дока-
зывает, что круги (т. е. площади кругов) относятся как
квадраты их диаметров. Из хода рассуждения ясно, что он
не видит необходимости вводить определение площади кру-
га, считая само собой разумеющимся, что круг по площади
больше вписанного и меньше описанного многоугольника.
Но тогда, что препятствовало ему рассмотреть вопрос об
измерении площади круга квадратом его диаметра или
радиуса? В п. 4 мы отмечали, что Евклид не хочет
вводить приближённых соотношений. Однако почему
Евклид не рассмотрел несоизмеримое отношение круга 5
к квадрату радиуса? Этому помешало отсутствие постулата
непрерывности.
В самом деле, Евклид мог бы обратить любой вписанный
многоугольник / и любой описанный многоугольник F
в прямоугольник той же площади с основанием R. Тогда
отношения h: НиН: R высот этих прямоугольников к ра-
диусу круга равнялись бы отношениям / : R2 и F : R2. Но
об отношении S : Я2он мог бы говорить лишь в том слу-
чае, если бы существовал отрезок X, для которого X : R —
=S : R2. Этот отрезок X должен был бы превосходить все
отрезки h и быть меньше всех отрезков Я. Постулат непре-
рывности обеспечил бы существование отрезка X. Но так-
как у Евклида этого постулата нет, а циркулем и линеи-
(4 1 1/*9 __ V 1
—— --------I -J--------——- ; ») квадратных корней
2+ уз / (1 — КТб)3
из всех положительных чисел первых трёх групп; 5) всех чисел,
которые получаются из чисел групп (1)—(4) рационально; 6) всех
квадратных корней из положительных чисел предыдущих пяти
групп и т. д.
«НАЧАЛА» ЕВКЛИДА
277
кой построить У он не умеет (что это невозможно, он мог
и не знать), то он не может говорить об отношении
5 : R2 = X : R, которое мы обозначаем через тс. По той же
причине он не может говорить о длине окружности
(которая должна вдвое превосходить X).
27. Недостатки евклидовой теории пропорций
Если принять во внимание трудности, вытекающие из
самого существа вопроса, то евклидова теория пропорций
оказывается вовсе не столь громоздкой, какой она пред-
ставляется с первого взгляда. Напротив, нельзя не по-
ражаться изяществу построения 5-й книги «Начал».
Евклидова теория отношений по существу безупречно
строга и до 70-х годов прошлого века никем не была пре-
взойдена; многочисленные попытки замены её другими
теориями были столь же безуспешны, как попытки дока-
зательства пятого постулата.
Но, будучи безупречным по существу, построение Ев-
клида и здесь,’ как и в основоположениях геометрии, содер-
жит некоторые дефекты. Мы отметим здесь важнейшие
из них.
Прежде всего, определение 7-е без некоторых дополне-
ний, которых у Евклида нет, является недостаточным.
В этом определении даётся критерий неравенства двух отно-
шений, но из этого критерия не следует, что неравен-
ство А: В> А': В' исключает неравенство А’: В' > А: В.
Однако отмеченный недостаток легко устраним теми сред-
ствами, которыми пользуется (например в V, 4) сам
Евклид.
Действительно, согласно определению V, 7, неравен-
ство Л : В > А' : В' означает следующее: существуют два
таких целых числа т, п, что
mA > пВ
mA’ < пВ'.
(2)
Пусть одновременно с неравенством Л : В > Л' : В' имеет
место также неравенство А' : В' > А : Bt тогда суще
278
М. Н. БЫГОДСВ ПП
ствуют такие два целых числа р n v, что
р-4' > vl?' (3)
и
pA<vZJ. (/,)
Возьмём величины, соответственно v-кратные от щА
и пВ. Тогда в силу (1) имеем:
v/nA> 'тВ. (5)
Взяв теперь /г-кратные от р_4 и vB, получим в силу (4):
pnA<vnZ?. (6)
Сравнивая (5) и (6), имеем:
v/n.4 > рпА.
Значит,
v/?i > рп. (7)
Аналогично из неравенств (2) и (3) найдём, что
v/« < р/г. (8)
Неравенства (7) и (8) противоречат друг другу. По-
этому и неравенства Л : В > А' : В'\ А' : В' > А : В вза-
имно исключают друг друга.
Если бы кто-либо сказал, что Евклид «не мог» заметить
необходимости доказать соответствующее предложение
в силу «очевидности» последнего, то мы напомнили бы,
что Евклид заметил необходимость доказать ещё более
«очевидную» истину: два отношения, равные третьему,
равны друг другу. Мы имеем здесь, таким образом, столь
же непонятный, как и непростительный, недосмотр.
Ещё менее понятно и ещё менее извинительно то,
что Евклид не удосужился дать определения понятия
«составное отношение», которым он пользуется в дальней-
шем (VI, 23). Если сопоставить рассуждение, проведён-
ное в VI, 23, с определением V, 9, где речь идёт о частном
случае «составного отношения» —удвоенном отношении,
то недостающее у Евклида определение можно сформули-
ровать па современном языке так.
«Н ^ЧАЛА» ЕВКЛИДА
279
Пусть имеем два отношения
А : В и С : D
и пусть имеет место пропорция
С : D = B : X;
(9)
тогда отношение А : X называется «составленным» из
отношений А : В и С : D.
Легко видеть, что вещественное число, отвечающее
отношению А : X, есть не что иное, как произведение
чисел, отвечающих А : В и С : D, Действительно,
А А В А С
X В X В' 1)‘
«Удвоенное отношение», о котором говорится в опреде-
лении V, 9, есть отношение, составленное из двух равных
отношений. Иными словами, если имеет место пропорция
Л: В = В:Х,
(10)
то отношение А : X есть удвоенное отношение А : В.
Действительно, определение V, 9 гласит: «если три вели-
чины пропорциональны х), то говорят, что первая имеет
к третьей отношение вдвое большее, чем ко второй».
Аналогично определяются (определение V, 10) утроен-
ные, учетверённые и т. д. отношения. Так, если
А *. В = В : С = С : Y,
то отношение А : Y есть утроенное отношение А : В.
Обратим внимание на то, что определение У,9(и точно
так же более общее определение составного отношения,
опущенное Евклидом) отнюдь не обеспечивает возмож-
ности «удвоения» отношения (или составления двух отно-
шений). В самом деле, для «удвоения» нужно иметь про-
порцию (10); но существование величины X, удовлетво-
ряющей (10), пока еще ничем не обеспечено. Иными
словами, мы можем судить, является ли некоторое
l) Т. е. 4, В, X образуют непрерывную пропорцию (10).
280
М. Я. ВЫГОДСКИЙ
вещественное число а квадратом вещественного числа р,
по мы не имеем ещё уверенности в существовании ква-
драта данного числа.
Эта уверенность появляется лишь тогда, когда в пред-
ложении VI, 11 Евклид решает задачу «к двум данным
прямым найти третью пропорциональную». Следующее
предложение VI, 12 (к трём данным прямым найти чет-
вёртую пропорциональную), частным случаем которого
является VI, 11, позволяет находить отношение, соста-
вленное из двух данных.
Между тем — ив этом состоит третий недостаток постро-
ения Евклида —рассуждение 18-го предложения 5-й
книги, в котором Евклид применяет доказательство от про-
тивного, существенно требует существования 4-й пропорци-
ональной.
Трудно понять, как мог Евклид, который всегда про-
являет такую тщательность в обеспечении конструктив-
ного существования, не заметить упомянутого пробела.
Но что он его не заметил — это факт. И вина Евклида
лишь усугубляется тем, что он мог бы без труда устра-
нить этот недостаток. Уже Саккери (1733 г.) отметил,
что предложение VI, 12 (вместе с VI, 1 и VI, 2, на котором
основано VI, 12) Евклид мог бы доказать раньше, чем
V, 18, ничего не изменив в ходе рассуждений.
' Впрочем, такая перестановка могла бы не понравиться
Евклиду, который выделил в отдельную 6-ю книгу все
геометрические приложения теории пропорций. Но тогда
он мог бы доказать предложение V, 18 теми же средствами,
которыми доказано предыдущее V, 17, обратное для V, 18
предложение х).
Как мы видим, 5-я книга «Начал» Евклида, как и дру-
гие части этого произведения, не лишена важных дефек
тов. И всё же, читая эту книгу, нельзя не поражаться
замечательному её глубокомыслию.
х) Правда, точное подражание V, 18 для Евклида не было бы воз-
можным вследствие того, что сложению отрезков, выполняющемуся
в V, 17, отвечало бы вычитание, которое было бы не всегда выпол-
нимо (ив меньшего отрезка Евклид не может вычитать больший). Но
это затруднение преодолевается без труда, хотя, конечно, доказа-
тельство становится более громоздким.
«НАЧАЛА» ЕВКЛИД X
281
28. Планиметрические книги «Начал» (1 — 6)
Евклид, несомненно, понимал, что теория отношений
величин представляет собой высшую и труднейшую часть
«Начал». И, невидимому, это и определило основные
черты плана его произведения.
В первых четырёх книгах изложен тот геометрический
материал, который не требует применения теории пропор-
ций. Нельзя не отметить, что Евклид с замечательным
искусством сумел включить в первые четыре книги «Начал»
много таких предложений, которые на первый взгляд
требуют применения пропорций. Так, в I, 44, решается
задача о построении параллелограмма, имеющего дан-
ное основание, данный угол и площадь, равную площади
данного треугольника. В силу 1,42 задача сводится к
построению на данной прямой параллелограмма, имею-
щего тот же угол и ту же площадь, что другой заданный
параллелограмм. Таким образом, искомая вторая сторона
параллелограмма фактически является четвёртой пропор-
циональной к трём данным прямым. Между тем Евклид,
выполняя построение, совершенно не апеллирует к про-
порциональности. Точно так же Евклид обходится без
пропорциональности и при решении задачи II, 11, где
фактически выполняется деление отрезка в крайнем и сред-
нем отношениях.
Первая книга «Начал» содержит все основные гео-
метрические предложения и построения. Важнейшие её
результаты относятся к преобразованию площадей, а за-
ключительным аккордом является так называемая «тео-
рема Пифагора» (I, 47) и обратное ей предложение (1,48).
Вторая книга содержит так называемую «геометри-
ческую алгебру» древних греков. В ней рассматриваются
соотношения между площадями прямоугольников и ква-
дратов, построенных на отрезках, известным образом свя-
занных между собой. Так, в предложении 11,5 отрезок
АВ разделён пополам в точке С и по произволу в точке
В, и устанавливается следующее соотношение:
AD х DB + □<?/) = □ ВС, (1)
где через АВ X DBобозначена площадь прямоугольника,
282
м.я. выгодскии
построенного на отрезках AD и DB, а через □СТ),
□ ВС —площади квадратов со сторонами CD, ВС.
«Геометрической алгеброй» эта теория названа потому,
что при переводе её предложений на современный бу-
квенный язык мы получаем ряд алгебраических тождеств.
Так, если обозначить отрезок АВ через a, a AD через
6, то (1) примет вид •
6(б-6)+[|-(б-6)]!=(£)2. (2)
Весьма возможно, что предложения 2-й книги пред-
ставляют геометрический пересказ числовых тождеств,
употреблявшихся прежде греческими математиками, но
оказавшихся недостаточно обоснованными в применении
к несоизмеримым величинам. В пользу этого предполо-
жения говорит, помимо исторических соображений, кото-
рых мы за недостатком места не касаемся, также и тот
факт, что во 2-й книге речь идёт только о прямоугольни-
ках, тогда как вообще Евклид склонен рассматривать
параллелограммы произвольного вида.
Но если «геометрическая алгебра» и была порождена
алгеброй числовой (разумеется, словесной; символиче-
ская алгебра — создание позднейших эпох), то она
на много веков приобрела самостоятельное существо-
вание. Перед числовой алгеброй она имела преимуще-
ство не только в” логической строгости, но и в оператив-
ной гибкости. Так, если бы мы для алгебраического выра-
жения соотношения (1) ввели другие обозначения, ска-
жем, обозначили бы АС=СВ через т, a CD через п, то
вместо (2) получили бы
(т -р п) (т — п) 4- п2 = т2 (3)
или, что то же,
(иг 4- п) (т — п) == иг2 — п". (4)
Таким образом, соотношение (1) служит эквивалентом
не одного, а многих числовых тождеств.
Что Евклид отнюдь нс имел в виду построить геомет-
рический эквивалент арифметической теории, явствует
«НАЧАЛА» ЕВКЛИДА
283
и из того, что предложения II, 9 и II, 10 доказаны им
с помощью построения, требующего применения теоремы
Пифагора.
О содержании трет ь е й книги «Начал» достаточ-
но будет сказать, что в ней рассматриваются основные
свойства окружности, сё касательной, центральных и
вписанных углов. Третья книга завершается теоремами о
хордах, пересекающихся внутри круга (равенство прямо-
угольников, построенных на отрезках), и о секу-
щих, проходящих через внешнюю точку (прямоугольник
на секущей и внешней её части равен квадрату касатель-
ной, и обратная теорема). Эти теоремы доказаны, разу-
меется, без помощи теории подобия.
Четвёртая книга трактует о вписанных и описан-
ных многоугольниках и о построении правильных много-
угольников. Очень изящны в ней построения правильных
пятиугольников и пятнадцатиугольника (предложения
10-16).
О содержении п я т о й книги мы уже говорили выше.
О плодотворности её результатов позволяет судить сле-
дующая за ней книга.
Шестая книга начинается с доказательства тео-
ремы о том, что площади параллелограммов, имеющих
одну и ту же высоту, относятся как основания. Эта
теорема оказывается непосредственным следствием опре-
деления V, 5, и преодолённые в 5-й книге трудности с
лихвой окупаются теперь тем, что здесь, как и всюду в
дальнейшем, пет никакой необходимости отдельно рас-
сматривать случаи соизмеримости и несоизмеримости.
Тягостность этого подразделения хорошо известна всем
изучавшим геометрию и преподававшим её. Создавая
видимость строгости, оно не даёт пи логического, пи
эстетического удовлетворения. Его искусственность усу-
губляется тем, что соизмеримые и несоизмеримые отрезки
геометрически совершенно равноправны. В евклидовохМ
доказательстве VI, 1 это равноправие выступает с полной
ясностью.
С исключительной изящностью из VI, 1 Евклид полу-
чает в VI, 2 теорему о пропорциональности отрезков,
отсекаемых па сторонах угла парой параллельных при-
284
М. Я. ВЫГОДСКИЙ
мых. На этой теореме он строит учение о подобных фигу-
рах. На ней основано и построение четвёртой пропорци-
ональной для трёх данных отрезков (VI, 12); опираясь
на него, без труда можно решить аналогичную задачу
для площадей, преобразуя эти площади в прямоугольники
с данным основанием. Отметим ещё упоминавшееся выше
предложение VI, 23, в котором с исключительной про-
стотой доказана теорема об отношении площадей равно-
угольных параллелограммов. Идея доказательства состоит
в том, что к данным параллелограммам со сторонами
ах, и а2, Ь2 добавляется параллелограмм со сторонами
лх, 6Я. Если s2 и s суть площади этих параллело-
граммов, то в силу VI, 1
. s — bt : b2f
S • S2 — @1 • а2»
Значит (см. п. 27), отношение $х : $я составлено
из отношений : а2 и 6Х : Ь2.
Наконец, скажем несколько слов о предложениях
28—29-м 6-й книги. Их формулировки непривычны совре-
менному читателю и разъяснение их отняло бы слиш-
ком много места, поэтому мы отсылаем читателя к тексту
«Начал» и комментариям. Громоздкость этих формули-
ровок и тот факт, что в «Началах» они нигде не исполь-
зуются, были причиной того, что многие издатели «Начал»
опускали предложения 28—29-е. Однако они являются
едва ли не самыми важными предложениями 6-й книги,
ибо дают средства для геометрического решения тех
задач, которые приводятся к уравнениям второй степени
= $ (5)
и
ax\-^x~~sf (6)
где через а, д, с обозначены данные отрезки, через $-
данная площадь, а х есть неизвестный отрезок.
На первый взгляд может показаться, что для решения
этих задач было бы достаточно тех же средств «геомет-
рической алгебры», которыми Евклид в II, 14 решил
«НАЧАЛА» ЕВКЛИДА
2-s5
задачу о построении квадрата, равного данной площади,
что приводится к простейшему квадратному уравнению
x* 2 — s. (7)
И, действительно, на основании предложения II, 5 можно
было бы геометрически решить уравнение (5), а на осно-
вании 11,6—уравнение (6), но лишь при том условии,
что отрезки b и с соизмеримы. При несоизмеримости же
отрезков бисуравнения (5) п (6) можно привести к виду
а'х ± х2 — s', (8)
к которому применимы средства «геометрической алгебры»,
лишь с помощью теории пропорций.
Как было указано, в самих «Началах» предложения
VI, 28, 29 не находят применения. Но это служит лиш-
ним подтверждением того, что в задачу Евклида входило
не только самодовлеющее изложение некоторой суммы
фактов, но также и создание элементарной базы для
дальнейших геометрических занятий.
В этой связи интересно заметить, что вся теория кони-
ческих сечений Аполлония основывается на 28-м
и 29-м предложениях 6-й книги х).
О тщательности, с которой отнёсся Евклид к изложению
упомянутых предложений, можно судить по тому, что
в VI, 27 дано, разумеется в геометрической форме, усло-
вие, при котором задача, приводимая к уравнению (5).
имеет решение. Это условие равносильно неравенству 2)
г) См., например, аполлониеву формулировку определения эл-
липса: Г. В и л е й т н е р, «Хрестоматия по истории математики»,
вып. Ш, ГТТП, 1932, стр. И.
с / а X2
2) Как легко видеть, уравнение (5) при s пмеет
Два положительных корня. Евклид в VI, 28 даёт лишь одно (меньшее)
решение. Но так как другое решение получается совершенно анало-
гичным построением, то нельзя допустить, чтобы Евклид не видел его
существования. Тенденция же рассматривать все возможные случаи
вообще не свойственна Евклиду.
28G
М. Я. ВЬ.ГОДСКПЙ
В шести первых книгах «Начал» содержится по су-
ществу вся планиметрия, хотя полтора десятка плани-
метрических предложений изложены в 12-й и 13-й кни-
гах в тесной связи с рассматриваемыми там вопросами
стереометрии.
29. Арифметика (книги 7 —9) и классификация
иррациональностей (10 книга)
В соответствии с логическим порядком Евклид, каза-
лось бы, должен был теперь перейти к вопросам стерео-
метрии. Однако 7—9-я книги «Начал» посвящены ариф-
метике. II это вполне уместно. Евклид по хочет преры-
вать изложение стереометрии включением чуждого ей
материала. Между тем, ему нужно определить отношения
рёбер правильных многогранников к диаметру описан-
ного шара. А эти отношения имеют различную алге-
браическую природу. Для трёх многогранников (тетра-
эдра, октаэдра и гексаэдра) это —квадратичные иррацио-
нальности ^они соответственно равны |/^|, , 1^1) »
и Евклид легко может выразить их словами (он говорит,
например, в XIII, 13: «квадрат на диаметре сферы вдвое
больше квадрата стороны октаэдра»). Но для додекаэдра
отношение это равно
4 (/15-1/3),
а для икосаэдра
Эти отношения являются биквадратными иррационально-
стями, и хотя они фактически и выведены в предложениях
XIII, 17 и XIII, 16, однако для пх формулировки у Евклида
недостаёт словесных средств. Так, в формулировке XIII, 17
он вынужден ограничиться следующей фразой: «сторона
додекаэдра есть иррациональная прямая, называемая
апофемой». Здесь Евклид использует изложенную им в 10-п
«НАЧАЛА* ЕВКЛИДА
287
книге классификацию иррациональностей. Оту класси-
фикацию он, естественно, должен был предпослать сте-
реометрическим книгам «Начал». В свою очередь класси-
фикация отношений несоизмеримых величин основывается
на ряде предложений, относящихся к соизмеримым ве-
личинам; отношения последних выражаются целыми
числами, и потому между планиметрией и учением об
иррациональных линиях, естественно, вставляется учение
о целых числах и их отношениях.
Седьмая книга начинается с предложений, позво-
ляющих найти общий наибольший делитель или уста-
новить взаимную простоту целых чисел. Здесь впервые
изложен метод, ныне именуемый «алгоритмом Евклида».
Затем следует ряд основных предложений теории дели-
мости. В предложениях 10—20-м развивается теория
числовых пропорций.Она основана на определении VII, 20,
смысл которого состоит в том, что числа я, Ь имеют то же
отношение, что числа с, d, если а и с либо являются оди-
наковыми кратными чисел bud, либо содержат одно
и то же число одинаковых долей чисел bud.
Таким образом, теория числовых отношений построена
на иной основе, чем теория отношений величин, и нигде
Евклид не показывает, что пропорциональные числа удов-
летворяют определению V, 5. Поэтому хотя в Х,5 и Х,6
Евклид и доказывает, что «соизмеримые величины имеют
друг к другу отношение числа к числу» и обратно, но
доказательство его некорректно. Оно устанавливает лишь,
что пропорциональность величин Л, В числам а, Ь имеет
место в смысле определения V, 20 (если его распростра-
нить на любые соизмеримые величины). Здесь снова мы
имеем пример грубого недосмотра, тем более досадного,
что он легко устраним.
Восьмая книга посвящена теории непрерывных
числовых пропорций.
В девятой книге эта теория получает дальней-
шее развитие и содержит три очень интересных и важных
результата. Предложение IX, 20 доказывает существова-
ние бесчисленного множества простых чисел. Доказатель-
ство ведётся так же, как во всех современных курсах
теории чисел. Предложение I Х,35 содержит теорему о сумме
288
м. я. вь.годскпп
геометрической прогрессии. Хотя здесь рассматривается
прогрессия, составленная из (целых) чисел, но доказатель-
ство без изменений может быть перенесено на произ-
вольные величины. Наконец, в IX, 36 доказывается,
что если в произведении (1 + 2 + 22 + ... + 2”) 2" первый
множитель—простое число, то само произведение есть
«совершенное» число, т. е. оно равно сумме всех своих
делителей (включая 1,но исключая самого себя). Вопрос
о том, существуют ли совершенные числа, не принад-
лежащие к упомянутому классу, остаётся открытым и по
настоящее время.Этой замечательнойтеоремой завершается
9-я книга.
Десятая книга, как мы уже говорили, содержит
классификацию иррациональностей. Эта классификация
исчерпывает все биквадратные иррациональности. 10-я
книга, несомненно, является труднейшей книгой «Начал»;
по трудности порождаются не столько идейным её содер-
жанием, сколько громоздкостью аппарата: сложные соот-
ношения между величинами нелегко поддаются понима-
нию в словесном их выражении. Заметим, однако, что
общеупотребительная ныне алгебраическая символика
немногим облегчила бы изложение 10-й книги. Причина
состоит в том, что наш символ Уа ничего не говорит
о классе иррациональности соответствующего числа. Даже
если известно, что буква а представляет целое число, то
в зависимости от того, является ли оно полным квад-
ратом пли пет, число [/ а представляет отношение соиз-
меримых или несоизмеримых величин.
Необходимо особо отметить первые четыре основных
предложения 10-й книги. В X, 1 рассматриваются две
неравные величины. Из большей отнимается величина,
превосходящая её половину; от остатка отнимается вели-
чина, превосходящая его половину. Предложение утвер-
ждает, что если этот процесс продолжать, то получим
величину, меньшую, чем меньшая из двух взятых. Дока-
зательство основано на «аксиоме Архимеда», содержа-
щейся в определении V, 4.
Предложение X, 2 даёт критерий соизмеримости пли
несоизмеримости величин, основанный па применении
«алгоритма Евклида» и опирающийся на X, 1.
«НАЧАЛА» ЕВКЛИДА 289
В предложениях X, 3 и X, 4, опирающихся на X, 2,
разыскивается общая наибольшая мера двух и трёх соиз-
меримых величин.
Отметим, наконец, что в 10-й книге содержится ряд
предложений, используемых в качестве лемм, но име-
ющих большой самостоятельный интерес. Таковы, напри-
мер, предпосланные предложению X, 29 две леммы. В пер-
вой даётся способ разыскания двух целых чисел, сумма
квадратов которых есть полный квадрат. Иными словами,
лемма 1 даёт бесчисленное множество решений целочислен-
ного уравнения
x2 + y2==z2.
Способ, изложенный Евклидом, даёт все решения этого
уравнения, но Евклид этого не отмечает, ибо для него до-
статочно доказать существование таких чисел. В лем-
ме 2 даётся способ разыскания двух целых чисел, сумма
квадратов которых не является квадратом.
30. Стереометрические книги (11 — 13)
Одиннадцата я книга открывается длинным рядом
определений (телесной фигуры, наклонения прямой к пло-
скости, наклонения плоскости к плоскости, параллель-
ности плоскостей и т. д.). Среди них обращают па
себя внимание определения 9-е и 10-е. Последнее гла-
сит: «равные и подобные телесные фигуры суть те, кото-
рые объемлются подобными плоскостями, равными по
множеству и по величине». В определении 9-м аналогично
вводится понятие подобных телесных фигур. Так как
в доказательстве XI, 33 (подобные параллелепипеды нахо-
дятся друг к другу в тройном отношении соответственных
их сторон) существенно предполагается равенство объ-
ёмов двух параллелепипедов, «равных и подобных»
в смысле определения XI, 10, то теория объёмов тел ока-
зывается построенной на шатком основании. В самом деле,
Евклид нигде не доказывает конгруентностп фигур,
равных и подобных в смысле определения XI, 10. Необ-
ходимость такого доказательства видна уже из того факта
(который вряд ли мог быть неизвестен Евклиду), что
19 Историко-математ. исследования
290
М. Я. ВЫГОДСКИЙ
косоугольный параллелепипед нельзя совместить с его
зеркальным изображением. Сверх того, если не требо-
вать выпуклости тел, то два тела, имеющие соответ-
ственно конгруентные грани, могут иметь различные объ-
ёмы. Возьмём, например, внутри пирамиды SABC точку
Е и построим точку Е', симметричную ей относительно
основания АВС, Рассмотрим теперь два тела, из которых
одно получается изъятием пирамиды Е'АВС из SABC,
а другое—составлением пирамид S А ВС и Е'АВС. У этих
тел соответственные грани конгруентны, но объёмы их,
очевидно, не равны.
Но если Евклид допустил здесь серьёзную логическую
ошибку, то геометрическая интуиция не обманула его:
выпуклые тела, «подобные и равные» в смысле опреде-
ления XI, 10, всегда конгруентны или зеркально кон-
груентны х).
Вслед за определениями 11-я книга содержит ряд
основных предложений стереометрии, излагаемых при-
мерно так, как они и сейчас доказываются в школьных
учебниках. Так же, как и в планиметрических книгах,
Евклид обеспечивает построением существование рассма-
триваемых им тел и фигур. Но эти построения обоснованы
менее строго, чем плоскостные, так как Евклид не вводит
никаких стереометрических постулатов. Начиная с XI, 25,
Евклид излагает учение об объёмах параллелепипедов
и призм. Объёмы же остальных простейших тел рассмот-
рены в следующей книге «Начал», так как они требуют
выполнения предельного перехода.
Стержнем двенадцатой книги является, таким
образом, метод пределов в его своеобразной античной
форме. По существу он чрезвычайно близок к современ-
’) Этот замечательный факт был впервые доказан Коши в 1813 г.
Доказательство, данное Коши, хотя и элементарно, но идея его столь
своеобразна, что Евклид мог не найти его. Однако для случая много-
гранников с трехгранными углами, которые только и нужны Евкли-
ду, он мог бы без труда доказать теорему Коши, основываясь на кон-
груентности (прямой или зеркальной) трёхгранных углов с соот-
ветственно равными плоскими углами. Эта конгруентность факти-
чески доказана в предложении XI, 23, где выполняется построение
трёхгранного угла по трём плоским углам.
«НАЧАЛА» ЕВКЛИДА
291
ному, но внешняя форма столь разительно отличается от
привычной нам, что его следует рассмотреть подробнее.
В предложении XII, 1 Евклид доказал, что подобные
многоугольники, вписанные в круги, относятся как квад-
раты диаметров. Это предложение, на доказательстве
которого нет нужды останавливаться, служит базой для
предложения XII, 2: «круги относятся как квадраты на
диаметрах». Доказательство ведётся так.
Устанавливается, что квадрат, вписанный в круг, по
площади больше половины круга. Затем строится пра-
вильный вписанный восьмиугольник путём деления
пополам дуг, стягиваемых сторонами вписанного квад-
рата. Над квадратОлМ надстраивается, таким образом, че-
тыре треугольника; общая их площадь оказывается боль-
шей, чем половина общей площади соответствующих круго-
вых сегментов.
Это построение, выполняемое повторно, позволяет по-
лучить такой правильный многоугольник, который раз-
нится от круга меньше, чем на любую наперёд заданную
площадь F. Действительно, удаляя из круга сначала
вписанный квадрат, который по площади больше его поло-
вины, затем четыре треугольника, которые по площади
больше половины остатка и т. д., мыв силу X, 1 получим
площадь, меньшую F.
Обратив внимание на то, что установленный сейчас факт
на современном языке выражается словами «площадь
круга есть предел площади правильного 2"-угольника при
неограниченном увеличении числа п», мы проследим за
дальнейшим ходом мысли Евклида.
Евклид должен доказать, что площади и S2 двух
кругов относятся как квадраты, построенные на их диа-
метрах DI и D2. Он допускает противное и говорит, что
тогда отношение D* к Ь2 должно равняться отношению
Si к некоторой площади S, которая либо меньше, либо
больше, чем £*. Здесь, разумеется, предполагается суще-
ствование четвёртой пропорциональной; это предположе-
ние можно было бы оправдать лишь в том случае, если
принять существование прямолинейной фигуры, рав-
ной площади квадрата, чего Евклид (ср. п. 27) не вправе
сделать.
19*
292
м. я. выгод скип
Здесь мы имеем логический дефект; однако он не имеет
прямого отношения к методу пределов, так как обусло-
влен тем, что в XII, 2 рассматривается отношение
пределов. В других случаях, когда устанавливается
равенство пределов, прибегать к упомянутой гипотезе
не приходится.
Итак, допустим, что существует такая площадь S,
что
DiiD^S^S, (1)
и пусть сначала
5 < S2. (2)
Впишем в круг 53 такой правильный многоугольник Р2}
который по площади разнился бы от S2 меньше, чем S от
5а. Тогда
S<p2. (3)
А это тотчас же приводит к противоречию. В самом деле,
согласно XII, 1 имеем
DftD^P^.P, (4)
и, сопоставляя с (1), находим
51:5 = Р1:Р2 (5)
или
S^.P^S-.P,. (6)
Но круг больше вписанного в него многоугольника Plf
значит, должно быть также
S>P2t (7)
что противоречит неравенству (3), так что гипотеза 5<52
абсурдна.
Евклид мог бы воспользоваться описанными много-
угольниками и тем же способом доказать невозможность
«НАЧАЛА» ЕВКЛИДА
293
гипотезы S>S2. Он предпочитает пойти другим путём,
сведя этот второй случай к первому г).
Теперь теорема XII, 2 доказана.
В изложенной второй части доказательства Евклид
устанавливает для рассматриваемых величин тот факт,
что если переменные величины Рг, Р2 имеют постоянное
отношение D~t : D2,, то в том же отношении находятся и
их пределы 6\, S2. На первый взгляд может показаться,
что доказательство от противного, проводимое здесь Евкли-
дом, чуждо современному методу пределов. Однако это
не так. Теорема о единственности предела, на которую
опирается всякая теорема теории пределов, существенно
требует доказательства от противного.
Различие между евклидовым доказательством XII, 2
и современным её доказательством состоит, следова-
тельно, прежде всего в том, что у Евклида нет общих
теорем, на которые он мог бы ссылаться в отдельных
частных случаях; не введено у него явно и понятие
предела, хотя, как мы видели, фактически он нм
оперирует.
Аналогичный метод (он получил в XVII в. не очень
удачное наименование «метода исчерпывания») Евклид
применяет в ряде других предложений 12-й книги. С его
помощью доказаны теоремы об объёмах пирамиды (XII,
3—9), конуса и цилиндра (XII, 10) и теорема об отно-
шении объёмов двух шаров (XII, 18).
Метод исчерпывания в течение почти двух тысяче-
летий был единственным строго обоснованным приёмом
исследования предельных соотношений.
Его громоздкость побудила Архимеда, а затем и евро-
пейских математиков XVI—XVIII вв. искать более удоб-
ных в оперативном отношении приёмов. Когда эта цель
была достигнута, оказалось возможным на рубеже XVII
и XVIII вв. создать исчисление бесконечно-малых. Но
х) Именно, в предположении 5 > S2 площадь 51, удовлетво-
ряющая пропорции
DI: Dl = S2:Sl,
оказалась бы меньше, чем что, по доказанному (круги .Sj,
меняются ролями), невозможно.
294
М. Я. ВЫГОДСКИЙ
должно было пройти ещё столетие, пока обоснование
этого исчисления приобрело ту же степень строгости,
что античный метод исчерпывания. На этой базе Архимед
создал свои интеграционные методы, предвосхищавшие
методы интегрального исчисления, но по форме так же
мало походившие на них, как сам метод исчерпывания
мало походит на метод пределов.
12-я книга «Начал» вместе с 5-й, с которой она, как
мы видели, тесно связана, составляет самую замечатель-
ную, самую глубокую по идейному содержанию часть
творения Евклида.
Что касается тринадцатой, последней, книги
«Начал», то она, как мы видели, посвящена теории пра-
вильных многогранников и завершается доказательст-
вом того, что рассмотренные там пять тел являются един-
ственными правильными многогранниками.
31. Заключительные замечания
В нашем кратком обзоре мы далеко не исчерпали
всего богатства содержания «Начал». Мы должны были
оставить без внимания многие детали, выполненные с не-
сравненным изяществом и остроумием. Мы не имеем также
возможности проследить дальнейшие исторические судьбы
научных и педагогических идей, заложенных в «Нача-
лах». Скажем только, что эти идеи прямо или косвенно
живут и в наше время. Как ни различны, например,
позиции Евклида и Гильберта, — об этом мы достаточно
говорили,—но гильбертова система аксиом в общем чрез-
вычайно близка к структуре евклидовых «Начал».
В ней нашли себе отражение те основоположения, ко-
торые либо прямо сформулированы Евклидом, либо не-
явно содержатся в его рассуждениях. Гильбертово уче-
ние о пропорциях, изложенное в III главе «Оснований
геометрии», ставит себе задачей, по словам самого автора,
«обосновать учение Евклида о пропорциях в плоскости
и независимо от аксиомы Архимеда». И действительно,
в учении Гильберта основную роль играет то построение
четвёртой пропорциональной, с помощью которой, как
мы видели, Евклид по существу обеспечивает существова-
«НАЧАЛА» ЕВКЛИДА
295
ние составных отношений, т. е. умножение вещественных
чисел.
Евклидова теория пропорций послужила также стиму-
лом к новому построению теории вещественных чисел,
идея которого была указана акад. А. Н. Колмогоро-
вым в 1946 г. г) и детально проведена Н. И. Кавуном* 2) и
Н. Г. Алимовым 3).
Мы ограничимся этими замечаниями и надеемся, что
наша статья побудит читателей ознакомиться в подлин-
нике с бессмертным произведением Евклида.
г) Успехи математических наук, т. I, вып. 1 (И), 1946, стр. 217—
219.
2) Успехи математических наук, т. II, вып. 5, 1947, стр. 199—229.
8) Работа Н. Г. Алимова, которая ещё не напечатана, трактует
вопрос с точки зрения, особенно близкой к евклидовой, так как в
основу её положено понятие о величине и так как в ней, как и у Ев-
клида, может оставаться открытым вопрос о большем или меньшем
богатстве множества рассматриваемых величин.
АРИФМЕТИЧЕСКИЕ КНИГИ «НАЧАЛ» ЕВКЛИДА
17. Г. Башмакова
§ 1. Арифметические книги «Начал» Евклида
Числа-кратности и числа-отрезки х)
В противоположность геометрическим книгам «На-
чал» Евклида, которым посвящена обширная историко-
математическая и математическая литература, арифме-
тические книги «Начал» (VII—IX книги) были до сих пор
недостаточно исследованы.
Арифметические книги считались до некоторой степе-
ни чужеродным телом в стройном здании «Начал».
Ф. Ф. Петрушевский, который дал один из лучших
переводов «Начал» на русский язык, издал VII—IX
книги отдельно, не поместив их вместе с другими книга-
ми. М. Е. Ващенко-Захарченко вовсе не перевёл этих
книг, поместив X книгу сразу после VI, и этим почти
совершенно обесценил теоретическое значение X книги.
Прежде всего не было ясно, какое место занимают
арифметические книги в «Началах». Зачем нужно было
Евклиду излагать на новых основах ряд положений
из теории пропорций, доказанных им со всей общностью
в V книге? Знаток античной математики Г. Цейтен писал:
«... общая теория пропорций, изложенная в пятой книге,
была ещё слишком нова и недостаточно поэтому развита,
чтобы её можно было положить в основу всего, что она
охватывает в действительности». По его мнению, «сс-
2) Автор считает своим долгом принести глубокую благо-
дарность проф. С. А. Яновской за ряд ценных советов при под-
готовке этой статьи к печати.
АРИФМЕТИЧЕСКИЕ КНИГИ «НАЧАЛ» ЕРКЛИДА
297
хранившееся в седьмой книге учение о пропорциях пред-
ставляет образец более старого подхода к вопросу, когда
ещё не учитывали возможности того, что члены отноше-
ний могут быть несоизмеримыми»1).
Хотя дальше Цейтеп и оговаривается, что «в случае
целых чисел приходится иметь дело с рядом вопросов,
не интересующих общую теорию», но главной причиной
помещения VII—IX книг после V книги он считал всё-
таки новизну и недостаточную разработанность общей
теории.
Взгляд на VII —IX книги как на нечто более частное,
чем V книга, привёл к тому, что арифметические книги
«Начал» изучались невнимательно и поверхностно. Этим
отчасти объясняется следующее мнение Цейтена: «Евклид
не подвёл под теорию целых чисел столь глубокое осно-
вание, как под геометрию и теорию общих непрерыв-
ных величин» 2 3).
Более того, Цейтен считал, что доказательство основ-
ной теоремы теории делимости о том, что из дели-
мости произведения двух целых чисел на простое чис-
ло следует делимость па это число, по крайней мере, од-
ного из сомножителей, основано на порочном круге.
Этим он обесценивает построенную Евклидом теорию
делимости.
Другой историк математики, Мориц Кантор, остано-
вился на арифметических книгах «Начал» лишь очень
бегло, видимо, также не придавая им большого значе-
ния8).
В 1929 г. Дж. Лориа дал гораздо более высокую оцен-
ку арифметическим книгам Евклида, считая, что в них
«арифметика рациональных чисел изложена с общностью
и строгостью, не меньшими, чем ныне»4 *). К сожалению
Лориа не подкрепил своё утверждение никакими аргу-
*) Г. Г. Ц е й те н, «История математики в древности и в средние
века». Перев. И. С. Юшкевича, 2-е изд., М.—Л., 1938, стр. 108.
2) Там же, стр. 109.
3) М. Cantor, Vorlesungen iiber Geschichte dor Mathematik,
Leipzig, 1894 т I, стр. 252—253.
4) Gino Loria, Storia delle matematiche, Torino 1929, т. I,
стр. 92,
2°8
И- Г. БАШМАКОВА
ментами, поэтому трудно судить, как представлял он
себе, хотя бы в основных чертах, построение этих книг.
Однако именно в этих книгах «Начал» Евклид уста-
навливает свой знаменитый алгоритм для определения
общего наибольшего делителя двух целых чисел, доказы-
вает однозначность разложения целого числа на простые
множители, применяя при этом впервые так называемый
метод спуска, и устанавливает первую фундаменталь-
ную теорему о простых числах, а именно бесконечность
числа простых чисел в натуральном ряде. Казалось бы,
что этого достаточно, чтобы побудить историков мате-
матики к более внимательному изучению арифметиче-
ских книг.
Более внимательное изучение VII—IX книг покажет
нам ошибочность сложившегося о них мнения как о менее
строго обоснованных книгах, имеющих более частный
характер.
Чтобы не быть голословными, приступим к изложению
их содержания, причём будем обращать особенное внима-
ние на логическое построение этих книг. Мы попытаемся
выяснить, действительно ли эти книги менее строго
обоснованы, чем остальные книги, и после этого попы-
таемся установить их место Ь системе «Начал».
В начале VII книги Евклид помещает двадцать два
определения, важнейшие из которых следующие (цити-
рую в переводе Ф. Ф. Петрушевского).
Определение 1. «Единица есть то, в силу
чего каждая из существующих вещей называется одной».
Определение 2. «Число есть множество единиц».
Евклид выбирает произвольный отрезок Е, который
он принимает за единицу, и считает числом пЕ, где п= 1,
2, 3, ... Таким образом, под числом он понимает толь-
ко целое число, т. е. отрезок, в котором выбранная еди-
ница Е укладывается целое число (п) раз.
Определение 3. «Меньшее число называется
частным большего, когда оно содержится в большем».
О пределение 4. «А многочастным или частями,
когда не содержится».
Понятие «содержаться в» Евклидом не определяется.
Наиболее адэкратной этому понятию символической за-
АРИФМЕТИЧЕСКИЕ КНИГИ «НАЧАЛ» ЕЕКЛИДА
299
писью, как видно из дальнейшего, будет А—пВ, где
А и В — числа в смысле определения 2-го, т. е. А — аЕ,
B~bEt а, Ъ, и —отвлечённые числа, не являющиеся
числами в смысле Евклида, п показывает только, что
число В «содержится в» числе А.
В отличие от чисел в смысле Евклида, которые мы
будем обозначать большими буквами латинского алфа-
вита, числа, заменяющие понятие «содержаться в», мы
будем обозначать соответственными маленькими бук-
вами.
Мы останавливаемся на этом так подробно потому,
что смешение обоих этих понятий историками матема-
тики повело к «обнаружению» ими «порочных кругов»
у Евклида, к утверждению, что Евклид «не подвёл под
теорию целых чисел столь глубокое основание, как под
геометрию». Между тем, строгое разграничение обоих
этих понятий, во-первых, делает совершенно ясным всё
построение арифметических книг Евклида, а, во-вторых,
показывает, что обоснование этих книг во всяком случае
не менее строго и точно, чем обоснование геометрических
книг.
Что касается определения 4-го, то в нём говорится,
что если В не содержится в А, то В есть много-
частное J. Это значит, что существует такое чи-
сло X, которое содержится как в А, так и в В.
Если, например, A — nXt то В — тХ. Такой общей мерой
всегда является, например, единица Е: А — аЕ, В — ЬЕ.
Но у Л и В могут существовать и другие общие меры.
Пока общая мера определена неэффективно. Впослед-
ствии введением алгоритма Евклида будет доказано суще-
ствование общей наибольшей меры у любых двух чисел.
Определение 5. «Большее число называется
кратным меньшего, когда в нём содержится меньшее».
Определение 11. «Первое число есть то, в ко-
тором содержится только что единица».
Определение 12. «Взаимно первые суть те,
которые общею мерою или «общим делителем» имеют
только что единицу».
Определение 14. «Взаимно сложные те, кото-
рые общею мерою имеют какое-нибудь число».
300
II. Г. БАШМАКОВА
Из дальнейшего развития теории видно, что Евклид
пользуется некоторыми свойствами введённых пм целых
чисел, не говоря о них явно.
Так, он нс определяет операции сложения п вычита-
ния для своих чисел, по предполагает, что всякие два
числа можно сложить и что из большего числа всегда
можно вычесть меньшее.
Анализ теории Евклида показывает, что он пользуется
следующими свойствами операции сложения:
1) коммутативностью
А + В В + А,
2) ассоциативностью
А + (В + 0 = (А + В) + С.
Кроме того, предполагается, что любые из чисел мы
можем повторять произвольное число раз, причём в
результате снова получим число, т. е. определяется про-
изведение Ап (мы будем обозначать это произведение и
через п 4), причём для этой операции Евклид неявно
предполагает только следующие свойства:
1) п (mA) = (пт) А,
2) (т ± п) А — mA ± nA.
Далее, для чисел-отрезков используется отношение
неравенства. Хотя Евклид и не даёт соответствующего
определения, тем не менее ясно, что он считает А=кЕ
меньшим В = IE тогда и только тогда, когда /с</.
Дистрибутивность в другую сторону:
п (А + В) = пАА-пВ,
Евклид не предполагает, а доказывает.
Из приведённых определений ясно, что Евклид строит
линейно-векторное пространство с базисом, состоящим
из одного единичного элемента, над кольцом целых раци-
ональных чисел. Элементами этого пространства служат
целочисленные отрезки пЕ, которые Евклид называет
АРИФМЕТИЧЕСКИЕ КНИГИ «НАЧАЛ» ЕВКЛИДА 301
числами. Числа из основного кольца будем называть ска-
лярными множителями.
Следующий шаг Евклида состоит в том, что он опре-
деляет для чисел умножение (тогда как для скаляр-
ных множителей умножение уже предполагается опре-
делённым), после чего построенная им система становится
кольцом.
Определение 15. «Умножить одно число на дру-
гое значит сложить само с собою множимое столько раз,
сколько в другом единиц. Происшедшее через умножение
называется произведением», т. е. если В — ЬЕ, то
= ...Ц-Л=Лб.
Ь ] аз
Как мы видим, определение умножения, данное Евкли
дом, несимметрично. Отсюда ясна необходимость доказа-
тельства коммутативности умножения чисел
АВ — ВА,
что Евклид и делает в 16-м предложении VII книги.
Ещё раз оговариваюсь, что арифметика основного коль-
ца скалярных множителей предполагается. Операции
сложения, вычитания, умножения подчиняются в нём
законам ассоциативности, коммутативности и дпстри
бутивности.
Определение 20. «Числа называются пропор
циональными, когда первое второго, а третье четвёртого
суть равнократное, или равночастное, пли равномного-
частное».
Это и есть новое определение пропорции. Поль-
зуясь принятой нами символикой, его можно запи-
сать так.
Числа-отрезки А,В и С,D называются пропорцио-
нальными, если имеет место один из трёх случаев:
1) А=пС, или 2) тА^=С,
B = nD mB = D,
3U2
И. Г. БАШМАКОВА
3) или, если существует такое число X и существует
такое число У, что
А = тпХ, C = mY,
В = пХ, D = nY,
Очевидно, что это и нужно понимать под термином
Евклида «равномногочастные».
В подтверждение правильности нашей гипотезы о
различении Евклидом чисел-кратностей (или скаляр-
ных множителей) и чисел-отрезков приведём некото-
рые термины, которые Евклид употребляет в VII—IX
книгах.
У Евклида имеются два термина, означающие ум-
ножение: 1) — «брать кратное», т. е.
в наших терминах умножить число на скалярный множи-
тель, и 2) 6 игЛ... —«произведение из ...», т. е.
произведение двух или нескольких чисел.
Деление Евклид обозначает словом — «изме-
рить», тогда как уже Герои пишет pe^stv—т. е. «де-
лить».
Для сложения Евклид пользуется термином—
ftevat, т. е. «приставить».
Терминология Евклида показывает, таким образом,
что числа, для которых он строит арифметику, это— числа-
отрезки, т. е. некоторым образом формализованные числа.
Числа-кратности он предполагает известными и прини-
мает их содержательно. Ни разу на протяжении VII—IX
книг он не путает оба эти понятия.
§ 2. Алгоритм Евклида.
Коммутативное кольцо чисел-отрезков
VII книга посвящена развитию понятий, данных в опре-
делениях, построению для кольца чисел-отрезков поля
отношений, а также тому, чтобы все данные определения
сделать эффективными. Так, например, определения 3-е
и 4-е становятся эффективными только после установления
того, что любые два числа Ли В (А > В) имеют общую
АРИФМЕТИЧЕСКИЕ КНИГИ «НАЧ?Л» ЕВКЛИДА
303
меру, равную единице Е, некоторому числу X1) или В.
Особенно же нуждается в эффективизации определе-
ние пропорциональности четырёх отрезков.
Седьмую книгу Евклид начинает с установления алго-
ритма нахождения общего наибольшего делителя для
чисел-отрезке в2).
Заметим, что деление числа-отрезка на скаляр не упо-
требляется вовсе и что оно возможно только в том слу-
чае, если число единиц данного числа-отрезка нацело
делится на этот скаляр. Деление числа-кратности на число-
отрезок вообще невозможно. Алгоритм же Евклида опре-
деляется для чисел-отрезкев, которые, вообще говоря,
не делятся нацело друг на друга.
Первое предложение даёт алгоритм для случая, когда
общая наибольшая мера есть Е; второе предложе-
ние—когда она равна некоторому числу. Алгоритм нахо-
ждения общей наибольшей меры или, как более принято
говорить, общего наибольшего делителя двух целых
чисел А и В (А > В) заключается в следующем:
Из первого числа А вычитается второе число В до тех
пор, пока остаток не станет меньше В, затем то же самое
проделывается с числом В и полученным остатком ит. д.:
А — Bt<B
В—п^В^В^ B2<Bt
П, В, e-^k+l>
В к —
Тогда: 1) А и В делятся на 2) Bft+1 делится на любой
другой общий делитель чисел А и В.
х) Эти два случая Евклид рассматривает отдельно, так как со-
гласно его определениям, соответствующим общим воззрениям древ-
них, единица не есть число.
2) Операция деления чисел-отрезков у Евклида не определяется
явно. Один отрезок «делится» на другой, если первый получается из
второго путём умножения последнего на скаляр.
304
II. Г. БАШМАКОВА
Вк ! и будет общим наибольшим делителем чисел
А и В. Если В=-Е, то числа А и В называются взаимно
простыми.
Какие предположения использует Евклид в неявном
виде при построении общего наибольшего делителя?
а) Прежде всего, Евклид использует то обстоятельство,
что в множестве чисел-кратностей I, таких, что 1В^А,
есть наименьшее п, т. е. такое, что А, а (п — 1)5 < А.
Предложение это равносильно аксиоме полной матема-
тической индукции (если прибавить к нему требование,
чтобы каждое число, кроме единицы, имело предшест-
вующее).
Ь) Второе предположение, которое тут делает Евклид,
заключается в том, что после конечного числа шагов
процесс построения оборвётся, т. е. цепочка чисел
А > В > Bt > ... > Вк > ... всегда конечна. Это пред-
ложение можно предположить или обосновать (по-
следнее можно сделать, например, методом полной ин-
дукции).
Первое и второе предположения не независимы. До-
статочно предположить одно из них, и тогда другое
будет его следствием. Но Евклид не формулирует здесь
явно ни одного из них. На втором предположении
основан метод бесконечного спуска. Евклид сформули-
ровал его в этой же книге при доказательстве того,
что каждое целое число разлагается в произведение про-
стых чисел.
с) При обосновании алгоритма принимается, что из
делимости А на X нВ на X следует делимость А ± В на X,
т. е. если А = тХ, В = пХ,то тХ ±пХ = кХ. Это одна
из отмеченных нами неявных посылок Евклида.
После установления алгоритма нахождения общего
наибольшего делителя Евклид уже может доказать,
что если А > В, то либо А — кратное В, либо А и В
являются многочастными одно другого (предложе-
ние 4). Действительно, может иметь место один из трёх
случаев:
1) либо А и В взаимно просты, и тогда они являются
многочастными одно другого: А аЕ, В = ЬЕ;
2) либо А является кратным В: А—кВ\
АРИФМЕТИЧЕСКИЕ КНИГИ «НАЧАЛ» ЕВКЛИДА
305
3) либо не имеет места ни один из перечисленных
случаев, и тогда с помощью алгоритма деления находим
общий наибольший делитель чисел А и В.
Если общий наибольший делитель (4, B)~D, то
А и В являются мпогочастными
по отношению друг к другу.
4 = mD I
B = nD J
Следовательно, для доказательства того, что каждые
два числа соизмеримы, Евклид строит частный случай
общей меры, а именно, находит для них общий наиболь-
ший делитель. Но это вовсе но значит, что в дальнейшем
изложении, в местах, где Евклид говорит об общем дели-
теле двух чисел, он имеет в виду всегда общий наиболь-
ший их делитель.
Поэтому совершенно ошибочно следующее заключение
Цейтена:
«В теореме 4 устанавливается, что если а и b целые
числа, а / — их общая наибольшая мера, то можно всегда
написать a~mf, b = nf и, следовательно, а = т-~ ; если
а < 6, то 7П > 1, п > 1. Согласно этому т и и — числа первые
между собой; и если теперь, основываясь па этом, мы
попытаемся проверить согласно определению 20, что
а с
у = у , то мы вводим гипотезу, что в этом случае второй
d d
множитель с = т —, т. е. — есть целое число и, зна-
п п
чит, что раз произведение md делится на п, которое вза-
имно первое с /я, то на него должно делиться d.
Таким образом основное предложение теории чисел
содержится уже среди гипотез, и с теоретической точки
зрения не особенно большое значение представляет тот
факт, что Евклид получает в дальнейшем на основе этих
гипотез ряд теорем, содержащихся в названном предло-
жении: так, например, в 30 говорится, что если произ-
ведение делится на некоторое первое число, то па него
должен делиться один из сомножителей этого произведе-
ния. Упомянутые гипотезы используются особенно в пред-
ложении 20: если и если с и с? насколько можно
о d
Историке-математ. исследования
306
И. Г. БАШМАКОВА
малы, то а делится па с и Ь делится на d. Это последнее
предложение имеет важное значение для доказательства
теоремы 30»г).
Таким образом, Цейтен прямо обвиняет Евклида
в порочном круге. Однако утверждение Цейтена совер-
шенно по основательно. Дело в том, что для проверки
а с
того, что у=^-» вовсе не нужно пользоваться непре-
менно общим наибольшим делителем чисел а и Ь. Далее,
способом Евклида легко доказать, что если А, В п С, В
пропорциональны в смысле определения 20-го, то они
будут пропорциональными и в смысле определения через
общие наибольшие меры, т. е. при добавочном требовании
брать не просто некоторые общие меры X и Y пар чисел-
отрезков А, В и С, D, по их общие наибольшие ме}ы.
При этом также совсем не нужно пользоваться гипотезой
о том, что «раз произведение md делится на п, которое
взаимно первое с т, то па него должно делиться с?».
Доказательство проводится при помощи применения
алгоритма Евклида.
Из этого ясно, что гипотеза Цейтена, навязанная
им Евклиду, является совершенно излишней. Никакого
порочного круга здесь у Евклида нет.
При дальнейшем изложении основных предложений
VII книги мы будем внимательно следить, пользуется
ли Евклид навязанной ему Цейтеном гипотезой.
В предложении 5-м Евклид устанавливает дистрибу
тивность скалярного множителя по отношению к числам,
т. е.
An Вп = (А + В) п.
Доказательство Евклида опирается на свойства ком-
мутативности и ассоциативности сложения чисел. До
казательство это совершенно аналогично и базируется
на тех же основаниях, что и доказательство Ваи дер
Вардеьа* 2).
г) Цейтен, цпт. соч., стр. 108—109.
2) Б. Л. В а н дер Варден, «Современная алгебра» Перес
Д. А Райкова под род. А Г. Куроша, ч. 1, М.—-Л., 1947, гл. 3.
АРИФМЕТИЧЕСКИЕ КНИГИ «НАЧАЛ» ЕГКЛИДА
307
В наших обозначениях доказательство Евклида вы-
глядит так г):
Ап 4- Вп == (/1 -|- -4 4~ ... 4~ А) 4~ (j? 4- В {- ... 4- Z») =
п раз и раз
= (Л+В) + (Л + В) + ... +(Л + В) = (А + В) п.
гГраз
В предложении 6-м устанавливается, что
[ А = тХ, । C — mY, i A + C = mZ,
из < и ' следует < _
I B~nX | D==tiY J ’ В + D = nZ,
где Z = X + Y.
В следующих двух предложениях Евклид доказывает
аналогичные предложения для разности.
В 9-м и 10-м предложениях доказывается основное
свойство пропорций, равносильное доказательству того,
что средние члены в пропорциях можно менять местами
(теорема о «пременении»). В принятых нами обозначе-
ниях предложение это записывается так:
Если
f А = тХ, C — mY,
I B = nX, D = nY,
( A = pU, B = pV,
то найдутся такие U и V, что ~ тт _
C = qU, U — qV,
(Аналогичная теорема имеет место, если А п С являются
равночастными или равнократными, соответственно, В и D.)
В доказательстве этого предложения Евклид нигде не пред-
полагает, что т, п взаимно просты. Доказательство про-
водится следующим образом:
m
А = mX — X -|~ X 4~ ... -J~ X,
C^mY= Y J- Y 4- ...4- Y.
X-----------------------
m
9 Сам Евклид доказывает эту теорему для п=3, но формули-
рует её в самом общем виде.
23*
308
И. Г. БАШМАКОВА
X и У, как и всякие два числа, имеют общую меру (её
вовсе не обязательно предполагать наибольшей); пусть
X = pZ, Y = gZ;
тогда, по теореме 5,
А = X 4- X 4- ... + X = pZ 4- pZ 4- • • • 4* Р% ~
т раз
= Р (Z + z +..;+Z)T Р (mZ) = pU.
tn раз
Аналогично С — mY — qU.
Полученные предложения Евклид употребляет для
установления следующих свойств пропорций:
1. Если 4 = (А>С, B>D), то 4 = 77 (пРед'
ложепие 11).
2. Если -4- = t то ‘(предложение 12).
3. Если-~ = -^-, то (предложение 13).
4. Если имеется два ряда чисел А, В ,С nF ,G,H и
A F В G A F , ...
-J3~~G * ~С~ = ~Н ’ то С-3=7Г (пРеДложение W-
После этого Евклид приступает к доказательству
коммутативности умножения чисел (предложения 15 и 16).
Доказательство его основывается на теореме о «премепе-
нии» (предложения 9 и 10). Именно, пусть
| А = аЕ,
I С = аВ
(B = bE).
Согласно определению 20, это значит, что -^- = -у; тогда,
по теореме о «пременении», ; но так как B — bEf
то и С = b 4. Таким образом, получаем С = аВ — 6?1. Отсюда
уже следует, что АВ=^ВА. Действительно, по опреде-
лению, АВ — АЬ, где b—количество единиц в числе В.
Но, по доказанному, Ab= Ва = ВА, где А = аЕ, следо-
вательно, АВ = ВА. Если провести это доказательств
АРИФМЕТИЧЕСКИЕ КНИГИ «НАЧАЛ» ЕВКЛИДА
3)9
без ссылки на теорему о «премеиении», то получим:
АВ = АЬ= (аЕ) Ь — аЕ 4- аЕ 4- ... 4- аЕ =
Ь ] аз
= а (Е 4- Е 4- ... 4- Е) = а (ЬЕ) — аВ = В А.
Ь ] аз
Таким образом, теорема эта в конечном счёте опирается
на теорему о дистрибутивности скалярного множителя
по отношению к числам (предложение 5). Как мы видим,
доказательство проводится вполне строго и в нём нет
никакого порочного круга, который получился бы при
смешении понятий числа и скалярного множителя.
Кольцо, которое построил Евклид, является, таким
образом, коммутативным. После этого Евклид доказывает
. г, АВ В Ао В А В , .о
предложения 17: —- = — , 18: -777-= уг (предложение 18
есть простое следствие 17 и теоремы о коммутативности
Л с
умножения) и 19: если то AD = ВС, и обратно,
из AD = BC следует, что =~ .
Нам придётся подробно остановиться на доказатель-
стве предложения 19-го и предложения 14-го, так как при
доказательстве обоих этих предложений Евклид поль-
зуется усиленным1) свойством транзитивности определён-
ного им равенства двух отношений. В современных тер-
С Л. F А
минах это значит, что из — -77 и он заклю-
D л (j t>
С F гг
чает, что -& = . Предложение это, которое при таких
обозначениях кажется сводящимся к общей аксиоме
Евклида о том, что две величины, порознь равные третьей,
равны между собой, требует дополнительного обоснования,
если пользоваться определением пропорциональности,
данным Евклидом. Действительно, согласно первоначал ь-
Ъ Мы говорим об усиленном свойстве транзитивности потому
что Евклид пользуется одновременно и транзитивностью и симмет-
ричностью равенства двух отношений.
310
И. Г. БАШМАКОВА
ному определению> 77 = 77 означает, что существует такой
общий делитель X чисел А и В п такой общий делитель У
чисел С и D, что
А — тХ, C—mYt
В = пХ, D = nY.
77 — 77 означает, что существуют такие числа U и V,
что
A=kU, F=kV,
B = IU, G=IV.
При таком определении совсем не очевидно,что должны
найтись такие числа Т и 5, что
С=рТ, F~pS,
D = qTt G = qS.
Однако транзитивность становится очевидной, если пред-
положить, что Евклид пользуется таким определением
пропорциональности, которое предполагет, что X, У, V
являются общими наибольшими делителями пар чисел
Л, В- C,D и Ft G. Тогда
А = рХ, C = pYt
В — qX, D — qY,
а, с другой стороны,
A = pX, F = pVt
B = qX, G = qV-
C F
отсюда ясно, что —
Но против такого предположения говорит, во-первых,
то, что Евклид нигде не оговаривает, что он меняет пер-
воначальное определение, добавляя к нему требование,
чтобы при определении пропорциональности величин
брали всегда общую наибольшую меру. Во-вторых, при та-
АРИФМЕТИЧЕСКИЕ КНИГИ «НАЧАЛ» ЕВКЛИДА
311
ком изменённом определении многие теоремы становятся
менее сильными, так как часть того, что нужно доказать,
уже содержится в предпосылках, а некоторые из теорем
совсем теряют смысл. Особенно же страдает от этого теория
рациональных чисел, т. е. построение поля отношений
для введённых целых чисел-отрезке в А, В, С,.... которую
мы рассмотрим в следующем параграфе. Поэтому наиболее
вероятной кажется гипотеза о том, что Евклид при опре-
делении пропорциональности всё время пользуется не
общим наибольшим, а некоторым общим делителем.
Отсутствие доказательства транзитивности, разумеется,
является логическим пробелом, но пробел этот может
быть легко восполнен, если пользоваться методами самого
Евклида. Так, например, можно легко показать, что две
пары чисел, пропорциональные в смысле определения
20-го книги VII, будут пропорциональны также в смысле
определения 5-го книги V, а для любых величин, пропор-
циональных в этом последнем смысле, транзитивность
равенства двух отношений (или пропорций) Евклидом
доказана (предложение 11 книги V).
Действител ьно, если
А — пХ, С = nY,
В=тХ, D = mY,
то из кА > 1В омеру ет, что к (пХ) > I (тХ), или (kri) X >
> (Im) X, а значит кп > 1т. Но тогда и (кп) Y > (Im) Y,
или кС > ID. Аналогично доказывается, что из кА < 1В
следует kC<lD и из кА-=1В следует, что kC = lD,
т. е. пары А, В и С, D будут иметь «то же отношение»
в смысле определения 5-го книги V1).
При таком восполнении этого пробела никакого пороч-
ного круга не получается. В дальнейшем мы будем счи-
тать, что при доказательствах Евклид имеет в виду не
общий наибольший, а некоторый общий делитель. Не изме-
няя доказательства, будем следить, будет ли оно прохо-
дить или действительно* нужно где-нибудь специально
’) См. формулировку эгоги определения в § б
312
И. Г. БАШМАКОВА
предполагать, как это делает Цейтеп, что мера двух каких-
нибудь чисел-отрезков является наибольшей. При этом
мы увидим, что гипотеза Цейтена является совершенно
излишней.
§ 3. Построение Евклидом поля отношений
После того как Евклид построил в первых девятнад-
цати предложениях книги VII коммутативное кольцо
целых чисел, он приступет к построению поля отношений
для этого кольца, т. е. наименьшего поля, в котором
это кол ьцо содержится. Однако при этом он не даёт опре-
деления отношения. Две пары чисел А, В и С, D, пропор-
циональные в смысле определения 20-го, Евклид считает
имеющими «то же отношение», т. е. он понимает, что
отношение, устанавливаемое между двумя парами чисел-
отрезков этим определением, есть отношение типа равен-
ства. Далее, Евклид рассматривает множество всех пар,
имеющих «то же отношение», и однозначно сопоставляет
каждому такому множеству одну пару,—а именно, наи-
меньшую пару чисел-отрезков, имеющих «то ясе отноше-
ние».
С современной точки зрения свойство «иметь то же,
отношение» разбивает множество пар чисел на классы,
не имеющие общих элементов, так как отношение пропор-
циональности, через которое оно определяется, симмет-
рично, рефлексивно и транзитивно. То общее, что имеют
все пары чисел одного и того же класса, мы назвали бы
отношением или рациональным числом. Евклид этого
не делает. Он ограничивается тем, что выбирает в каждом
таком классе представителя—наименьшую пару этого
класса. Этим он как бы овеществляет неопределяемое им
понятие отношения (пли рационального числа). Евклид,
ка’к и вообще во всех своих построениях, не ограничи-
вается таким неэффективным определением наименьшей
пары, имеющей «то же отношение». Он даёт способ построе-
ния такой наименьшей пары и доказывает её единствен-
ность, т. е. доказывает, что из какой бы пары Л, В данного
класса мы бы ни исходили, мы всегда придём к одной
и той же наименьшей паре Ло, Вг
API ФМЕТЕЧ1 CKHE KHI ГИ «НАЧАЛ» ЕВКЛИДА 313
Сначала Евклид предполагает, что такая пара суще-
ствует, и выясняет, какими свойствами она должна обла-
дать. Он устанавливает:
1. Если Ло, Во—наименьшая пара, имеющая данное
отношение, а А, В—любая другая пара того же отношения,
то А тА0, В — тВй (предложение 21).
Доказательство проводится следующим образом: Ло
не может быть многочастным числа А. Действительно,
Ао А Ао Во
из = -g следует, что
т. е.
I Ло = кХ,
I Л = 1Х,
В0-АУ,
B = IY,
(к, I > 1),
а отсюда
д _ кХ _ Х + х-р... +х _ х
В. • kY - Y + Yp...+y - Y ’
и .40, BQ не была бы наименьшей парой, имеющей данное
отношение, что противоречиво. Из этого доказательства
и из предложения 35-го книги VII следует единственность
наименьшей пары чисел, имеющих <<то же отношение»,
в указанном выше смысле.
2. Наименьшие числа, имеющие данное отношение,
являются взаимно простыми и, наоборот, взаимно простые
числа являются наименьшими из имеющих то же отно-
шение (предложения 23, 24). Действительно, если бы
наименьшие числа, имеющие данное отношение Ао, Во,
не были бы взаимно просты, то они имели бы некоторую
общую меру X: Ло = кХ, Во = IX (X > £), но тогда Ай и Во
были бы представимы каждое как произведение двух
чисел 40 = ЛХ, B0 = LX, где К=кЕ, L = IE,
Д _ КХ _ К
Во LX L ’
т* Ло, Во не были бы наименьшими, что противоречит
предположению.
Обратно, пусть Ло, Во взаимно просты. Если бы они
не были наименьшими, то существовала бы другая пара
414 II. Г. БАШМАКОВА
А X
X, Y. имеющая то же отношение и наименьшая: ~ .
/>0 -*
Но тогда А0-тХ, B0—mY, т. е. А0 — МХ, B0 — MY>
и Ло, Во не взаимно просты, что опять таки противоре-
чит предположению.
После этого Евклид доказывает несколько предложе-
ний о делимости чисел, нужных ему для эффективного
построения наименьшей пары. Мы рассмотрим их отдельно,
так как они имеют большое и совершенно самостоятель-
ное значение для теории делимости целых чисел. Евк-
лид использует эти теоремы для построения наимень-
шей пары чисел, имеющих данное отношение (предложе
ние 35).
Пусть даны числа 4, В. Требуется найти наименьшую
пару чисел, имеющих то же отношение. Способ построения
такой пары следующий:
Если А, В взаимно просты, то они и составят наимень-
шую пару, имеющую то же отношение. Если А, В не вза-
имно просты, то находим их общий наибольший делитель D.
Пусть A — mD, B — nD. Тогда числа М = тЕ и N = nE
и составят наименьшую пару, имеющую то же отношение,
что и пара А, В. Действительно, если бы пара Л/, N была
бы не наименьшей, то нашлась бы наименьшая пара Н, К.
Тогда 4 = # « А=1Н, В = 1К. Ио A = MD = LH,
B = LK, следовательно, = п М>Н, но тогда и
М п
L>D что невозможно, так как D — общий наибольший
делитель чисел А и В.
Как видно, при доказательстве Евклид пользуется
одной не сформулированной явно гипотезой, а именно,
что в множестве пар целых чисел А, В имеется наименьшая
пара. (Если А, В и С, И—две пары, имеющие равное отно-
шение, то из А >С следует B>D, поэтому можно говорить
о наименьшей паре.) Гипотеза эта является следствием
предположения о том, что в каждом множестве целых
чисел имеется наименьшее число. А это предположение,
если принять ещё, что каждое число, кроме единицы,
имеет предшествующее, равносильно аксиоме полной мате
матической индукции. (Равносильно в том смысле, что
АРИФМЕТИЧЕСКИЕ КНИГИ «НАЧАЛ» ЕВКЛИДА 315
если прибавить к обоим предложениям, например, четыре
первые аксиомы Пеано, то они определят одну и ту же
систему объектов, а именно, натуральный ряд.)
§ 4. Основная теорема теории делимости
В нашем изложении мы выпустили предложения 25—
34, в которых Евклид доказывает основные положения
теории делимости целых рациональных чисел. А именно, он
доказывает следующие предложения:
1. Если (А,В)=Е и A ml, то (L, В)=Е.
2. Если (А, С) = Е и (В, С) = Е, то (АВ, С) = Е.
3. Если X — простое и X не содержится в А, то
(А,Х) — Е.
4. Если (А, В) ~ Е, то (An, Вп) — Е.
5. Если (А, В) = Е, то (А + В, В) = Е и (А + В, А) = Е.
6. Если АВ = пХ и Х = простое, то либо А — кХ,
либо В—IX.
ота последняя теорема выражает наиболее глубокое
свойство простых чисел. Невыполнение этого свойства для
целых чисел алгебраических полей К = R (6)г) ведет к неод-
нозначности разложения этих чисел на неразложимые
далее целые числа этих полей, которые вследствие их нераз-
ложимости математики склонны были считать простыми.
Именно невыполнение для этих неразложимых чисел основ-
ного свойства, характеризующего простые числа, побудило
Куммера к тому, чтобы перестать считать эти числа про-
стыми, а определить в поле К — R (G) другие, идеальные
объекты, которые уже удовлетворяют вышеуказанному
свойству.
Доказательство этого предложения Евклид проводит
следующим образом. Пусть в произведении АВ содержится
некоторое простое число X: АВ — пХ, и пусть X не содер-
жится в А; это значит, что (А, Х) = Е. По из АВ = пХ
следует, что существует такое число N — пЕ, что 4Z? - NX.
*) Здесь R—поле рациональных чисел, 6—корень алгебраиче-
ского уравнения с рациональными коэффициентами —поле, воз-
никающее в результате присоединения 0 к полю рациональных чисел
BIG
II. Г. БАШМАКОВА
Тогда ~ = 4г ; так как (-4, X) = Е, то пара А, X является
Л JD 1
наименьшей из всех пар, имеющих заданное отношение.
Следовательно, по предложению 24-му, N = кА, В~ кХ,
т. е. X содержится в В.
Таким образом, нет никакого основания утверждать,
как делает это Цейтен, что доказательство это имеет
«с теоретической точки зрения не особенно большое зна-
чение».
7. Во всяком сложном числе А содержится некоторое
простое число Р.
Доказательство этой теоремы (предложение 33)
Евклид проводит методом спуска, формулируя его
явно.
Если А—сложное, то это значит, что А=пВ. Если В —
простое, то всё доказано. Если В—сложное, то, в свою оче-
редь, В=п1В1. Но В содержится в А, следовательно, и Вх
содержится в Л: А — пВ == п(пг Bj) = (пп^) Вг. Продолжаем
процесс, пока пе дойдём до некоторого простого чис-
ла Р, которое содержится в А, А — кР. Действительно,
иначе мы получили бы бесконечную последовательност!,
целых чисел
В>В1>Вг> ...,
причём все они<А, что в числах невозможно. Евклид выра
жает это следующими словами: «в числе А будут содержать-
ся бесконечно многие числа, одно другого меньше, что
в числах невозможно».
Из этой и из предшествующей теоремы следует одно
значность разложения целого числа в произведение про
стых чисел.
Интересно, что следующее появление доказательстве
методом спуска встречается только в XIII в. у коммента-
тора Евклида Кампана из Наварры. Кампан сделал
13 добавлений к 16-му предложению IX книги. В последнем
из этих добавлений утверждается невозможность разде-
лить некоторое число па две части так, чтобы произведение
всего числа на его меньшую часть равнялось, квадрату
большей части.
АРИФМЕТИЧЕСКИЕ КН] ГИ «НАЧ?Л» Г1 КЛИЦА
317
Ход доказательства в алгебраических обозначениях
следующий: пусть мы разбили данное число а на такие ча
сти xt, xi} что
Хг > Хо.
(1)
Но тогда, вычитая из обеих частей равенства по единице,
получим:
а‘2 Ч - г2
а’з
xt л\,
ИЛИ = —------ .
Я 2 а’1 — -г2
(2)
Но xt > х2, следовательно, 0 < xt — х2 < х.,, т. е. получаем
соотношение (2) в целых числах такого же вида, как
и соотношение (1), но с меньшими числами. Проведённое
рассуждение можно повторить сколько угодно раз. Но
так как невозможно существование бесконечного множе-
ства всё уменьшающихся чисел, то сделанное допущение
ложно.1).
Однако только в работах Пьера Ферма бесконечный
спуск стал методом.
В конце VII книги (предложения 36 и 3S) Евклид поме-
щает построение общего наименьшего кратного двух или
нескольких чисел, т. е. числа G, содержащего А и В,
и такого, что любое другое число, содержащее А и В,
делится на G. Построение это проводится так: пусть нужно
найти общее наименьшее кратное двух чисел А и В. Если
А и В взаимно просты, то общим наименьшим кратным
будет произведение АВ.
Если А и В не взаимно просты, то находим наимень-
шую пару чисел С, D, имеющих то же отношение, что и 4, В,
= тогда число G = AD = ВС и будет общим наи-
меньшим кратным чисел А и В. Действительно, если бы это
было не так, то Л и В содержались бы в некотором числе
< G. Пусть F — mA и F = пВ, тогда F = М 4 = NB, где
1 /_ т-1 д т-1 А N А С
—mL, — , iio-g=jy, следовательно,
r l)M. Cantor, Vorlesun gen uber Gcschichte der Mathcmatik,
Leipzig, 1913, т. II стр. 105.
318
И. Г. БАШМАКОВА
7Й“= 77 • Но С, D — наименьшая пара из имеющих то же
отношение. Тогда N^pC, M = pD, F — МА~ pDA, т. е.
G содержится в Ff что противоречиво.
Таким образом, в VII книге Евклид построил обоснова-
ние теории делимости целых чисел и поле отношений для
этих чисел, т. е. рациональные числа.
В VIII и IX книгах Евклид строит теорию непрерывных
пропорций, отношение различных членов которых опре-
деляет степени чисел, доказывает некоторые теоремы
о корнях при помощи средних пропорциональных и даёт
формулу для суммы геометрической прогрессии (предло-
жение 35 книги IX).
В предложении 20-м книги IX Евклид доказывает
свою знаменитую теорему о бесконечности числа простых
чисел в натуральном ряде, а в предложении 36-м той же
книги дает способ построения совершенных чисел.
§ 5. Логическое построение и место в системе «Начал»
арифметических книг Евклида
Итак, теоретико-числовые книги Евклида не уступают
по глубине и строгости изложения остальным книгам
«Начал». При изучении их перед историком математики,
прежде всего, встают следующие проблемы:
1) объяснить место этих книг в системе «Начал» Ев-
клида,
2) объяснить форму построения этих книг, в частности,
объяснить, зачем Евклид строит систему целых чисел-от-
резков, изоморфную числам-кратностям, и доказывает для
них свойства, которые для чисел-кратностей принимает
без доказательства.
Прежде всего ясно, что VII—IX книги обосновываются
отдельно потому, что теория, излагаемая Евклидом в этих
книгах, не является простым частным случаем общей тео-
рии отношений, изложенной в V книге. Действительно,
в арифметических книгах Евклид строит теорию целых
чисел и фактически определяет рациональные числа,
а в V книге он обосновывает действительные числа, при-
чём его обоснование (свдоксова теория пропорций) в основ-
АРИФМЕТИЧЕСКИЕ КНИГИ «НАЧАЛ» ЕВКЛИДА
31У
ном эквивалентно дедекиндовой теории сечений. Ведь
и теперь никто не считает, что построение теории алгебра-
ических иррациональностей излишне, так как-де суще-
ствует общая теория всех вообще действительных чисел,
частным случаем которых являются и алгебраические ирра-
циональности.
Но именно на такую точку зрения встают некоторые
историки математики, когда считают, что теория пропор-
ций в седьмой книге является чем-то вроде рудимента
и что после V книги отдельное обоснование её является
излишним. Конечно, построив фактически в пятой книге
все действительные числа, Евклид тем самым построил и
рационалные числа, но для изучения свойств рациональных
чисел необходимо их отдельное построение. Итак, в VII—
IX книгах Евклида излагается теория целых чисел и стро-
ятся рациональные числа. Отдельное обоснование этих
книг было поэтому совершенно необходимо.
Обоснование это, как мы видели, так же строго, как и
обоснование остальных книг «Начал». Из этого можно
с большой вероятностью заключить, что если даже эти
книги и более древнего происхождения, то всё же Евклид
их переработал, и форма их изложения принадлежит ему.
За это говорит и тот факт, что язык этих книг нсархаичен,
тогда как язык, например, V книги отличается архаично-
стью, что как раз и позволяет предполагать, что она была
целиком заимствована у , Евдокса1)-
Однако было бы неправильно излагать теоретико-чис-
ловые книги отдельно от других книг «Начал». Особенно от
такого изложения страдала бы X книга. Но, прежде чем
устанавливать связь VII—IX книг с остальными книгами
«Начал», остановимся на форме их изложения.
Как уже говорилось, отвлечённые целые числа (мы их
называем скалярными множителями), означающие «число
раз» или кратности, принимаются Евклидом содержатель-
но. Относительно них не вводится никаких определений
и не доказывается теорем. Пользуясь этими числами-
кратностями, оп строит число-меру, т. е. отрезки, в кото-
Ъ Tropfke, Gcschichte der Elementar-Mathema^ik, Berlin
undLeipzig, 1937, т. HI, стр. 9.
320
И. Г. БАШМАКОВА
рых некоторый выбранный единичный отрезок укладывает-
ся целое число раз. Этим он достигает некоторой «форма-
лизации» понятия числа, выражает число символом (т. е.
отрезком). Конечно, построенная таким образом система
чисел-мер изоморфна системе чисел-кратностей, но, от-
правляясь от числа-меры, Евклид строит фактически рацио-
нальные числа как отношения пар чисел-отрезков, а
затем в X книге квадратичные иррациональности.
Однако отношение двух чисел-отрезков не является, с
точки зрения Евклида, числом; ещё менее является числом
длина отрезка,выражающаяся квадратичной иррациональ-
ностью по отношению к основной единице длины.
Числами, по воззрению древних, были только целые
числа: «Число есть множество, которое может быть изме-
рено единицей*1). Почти дословно Евклид повторяет это во
втором определении VII книги. Ясно, что при-таком опре-
делении числа ни рациональные, ни иррациональные вели-
чины не являлись числами. Поэтому для нужного ему
построения рациональных чисел и квадратичных иррацио-
нальностей Евклид должен сыл перейти к представлению
чисел отрезками. В этом первая причина своеобразной
формы теоретико-числовых книг Евклида.
С другой стороны, пользуясь числом-кратностью, он пе
мог построить теорию и самих этих чисел. Действительно,
у древних не было никаких символов для адекватного пред-
ставления общего логического понятия числа. Для по-
строения теории целых чисел нужны были объекты,
с которыми молено было бы удобно оперировать и которые
бы ли бы изоморфны числам-кратностям. Такими объек-
тами и являлись отрезки, соизмеримые с некоторым выб-
ранным раз и навсегда отрезком.
Насколько важным было такое представление чисел
отрезками,видно из того,что ещё во времена Аристотеля шли
споры о том, состоит ли число из одинаковых единиц или
единицы могут быть различными и являются ли единицы
в различных числах одинаковыми. К вопросу о значении
представления чисел отрезками мы ещё вернёмся в следую-
Ар пет отел ь, «Метафизика». Перев. А. В. Кубицкого,
М.—Л., 1934, стр. 174.
АРИФМЕТИЧЕСКИЕ КНИГИ «НАЧАЛ» I 1.КЛПДА
321
щем параграфе при разборе характерных особенностей
античной математики.
Перейдём к вопросу о выяснении места арифметических
книг в системе «Начал» Евклида. Прежде всего теория, по-
строенная Евклидом в VII—IX книгах «Начал», была ему
необходима для обоснования X книги, т. е. для постро-
ения теории квадратичных иррациональностей. Поэтому-то
отдельное издание этих книг и помещение X книги сра-
зу же после VI обесценивают теоретическое значение X кни-
ги. Кроме того, подобно тому как рациональные числа зада-
ются однозначным соотнесением им пары чисел-отрезков,
так и квадратичным иррациональностям в X книге ста-
вится в соответствие пара чисел-отрезков с указанием рода
и вида иррациональности. Таким образом, Евклид полу-
чает возможность индивидуализировать все отрезки, кото-
рые могут получиться в качестве решений квадратных и
биквадратных уравнений с рациональными в смысле Евкли-
да коэффициентами х).
§ 6. Некоторые особенности античной математики
На примере разобранных нами теоретико-числовых
книг Евклида можно заметить характерные особенности
построения «Начал», имеющие общее значение для всей
античной математики.
Первая особенность состоит в том, что целые числ а при-
нимаются сначала чисто содержательно (кратность, число
раз), а затем строятся их логические эквиваленты, числа-
отрезки, для которых и развивается вся теория. Числа-
кратности фигурируют как возможность повторять числа-
отрезки, точно так же, как при построении современных
формально-аксиоматических теории обычно содержатель-
но допускаются натуральный ряд и его свойства.
Свойствами чисел-кратностей Евклид пользуется как
Данными. Истинными объектами теории являются числа-
отрезки .
Вторая, уже отмеченная нами особенность состоит в
том, что при определении отношений двух целых чисел-мер,
т« е. фактически при определении рационального числа,
*) См . статью А. Е. Раи к в этом же сборнике.
Историко-математ. исследования
322
II. Г. БАШМАКОВА
Евклид останавливается на понятии равенства отношении
(пропорциональности) и не даёт определения отношения
как того общего, что имеют все пары чисел, находящиеся
в равном отношении, т. е. он не вводит отношения как
нового объекта. Обе эти особенности, как будет показано,
связаны друг с другом, и ими обусловливается до некото-
рой степени характер классической греческой математики.
Покажем, что выделенные нами особенности свойствен-
ны построению и других книг «Начал» и вообще постро-
ению сочинений древних, примыкавших к школе Евклида.
Разберём для примера теорию пропорций Евдокса,
изложенную в V книге Евклида. Теория эта строится па
двух принципах: 1) величины а, Ъ, для которых строится
теория, должны удовлетворять аксиоме Архимеда; 2) два
отношения а : b и а': 6' равны, если для любых пар целых
чисел т, п
из та>пЪ следует та >nb',
» т а=пЪ » та' == nb',
» та<пЪ » та' <nb',
т. е. два отношения равны, если они определяют одно и то
же сечение области рациональных чисел.
Далее, Евклид доказывает транзитивность так опреде-
лённого им равенства двух отношений. Вопроса о том, что
же общего имеют все равные между собой отношения, он
не ставит. Такая постановка вопроса привела бы его к
выводу, что это общее есть одно и то же сечение области
рациональных чисел, т. е. он пришёл бы к определению
через абстракцию, к определению вещественного числа (или
отношения), не зависящему от выбора представляющей его
пары величин. Но этого-то как раз он сделать не мог,
так как это предполагает более высокую ступень образо-
вания абстрактных понятий, чем та, которой располагал
античный грек. А именно, для этого он должен был мыслить
вещественное число отдельно от специальной, особенной
формы его выражения—протяжённости. Но для такой аб-
стракции нужно было обладать большим запасом величин
вообще. Запас же этот в силу структурных особенностей
античного общества был очень ограничен. «Так вообще наи-
более всеобщие абстракции возникают только в условиях
богатого конкретного развития, где одно и то же свойство
ХРПФМЕТПЧЕСКПЕ КНИГИ «НАЧАЛ» ЕВКЛИДА
323
обще многим или всем элементам. Тогда оно перестает
быть мыслимым только в особенной форме»1).
Аналогично этому Евклид нигде не определяет, что
значит «площадь круга», но определяет равенство или от-
ношение площадей двух кругов. Итак, общин приём Евкли-
да состоит в том, что новые объекты (например, отноше-
ния), которые он не может определить непосредственно,
он вводит через определение равенства этих объектов,
причём останавливается на стадии констатирования ра-
венства, не пытаясь притти при помощи равенства к оп-
ределению самих этих объектов. Иными словами, Евклид
нигде не доходит до определения через абстракцию2).
Чтобы лучше понять, каков был уровень образования
абстракций у греков, приведём несколько5тримеров образо-
вания общих понятий.
Вот, что пишет Аристотель о взглядах Евдокса на связь
между общим свойством (абстракцией) и вещью, о бла дающей
этим свойством: «они (т. е. общие идеи пли свойства.—
И. Б.) являются причинами таким же образом, как белое,
если его подмешивать, является причиной для белого
предмета»3). В одном из своих диалогов Платон писал:
«... стало быть, и самые виды делимы, Сократ,—ска-
зал Парменид,—и причастное нм должно быть при-
частно частей и в каждой вещи будет ужо не целый
вид, а всегда часть»4).
Эти примеры, конечно, нс означают, что Евклид не
представлял себе ясно отношения между объектом и его
свойством (или между элементом п множеством), но если
такие простые понятия были ему уже ясны, то гораздо
более трудное понятие вещественного числа так и не было
освоено греческой математикой.
На разобранном примере арифметических книг Евкли-
да видно, что отрезок при построении «Начал» играет
х) К. М а р к с, Введение к «Критике политической экономии».
К. М арке и Ф. Э и г е л ь с, Сочинении, т. XII, ч. 1, стр. 194.
2) Этот факт был впервые отмечен С. А. Яновской в статье «О так
называемых определениях через абстракцию». Сборник статей по
философии математики, М., 1936, стр. 108.
3) Аристотель «Метафизика», стр. 35.
4) Платон, «Парменид», Спб. 1891, стр. 254.
21*
324
И. Г. БАШМАКОВА
двойную роль. Во-первых, это геометрический образ, т. е.
собственно отрезок. Во-вторых, отрезок имеет ещё и функ-
циональное значение, а именно, отрезок является как бы
естественной формой существования числа, число ещё не
отделяется от отрезка. Рациональное число или квадратич-
ные иррациональности являются только свойствами отрез-
ка или пар отрезков. Абстрактно они ещё не мыслятся.
С другой стороны, отрезок, в некотором смысле, является
символом числа, его знаком. Для отрезков строится исчис-
ление, определяются правила действия над ними. В этом
смысле можно говорить о геометрическом символизме ан-
тичной математики. Таким образом, то, что у нас сущест-
вует раздельно—число и знак числа (буква)—в античной
математике былослито воедино в одном и том же отрезке.
В этом исчислении чисел-отрезков уже содержится воз-
можность замены отрезка буквой, т. е. создания буквенного
исчисления. Однако эта возможность не была и, как мне
кажется, не могла быть осуществлена в пределах греческой
математики и именно благодаря отсутствию абстрактного
понятия числа (рационального или вещественного), т. е.
благодаря первой функции отрезка.
Чтобы лучше уяснить себе эти особенности греческой ма-
тематики, проведём сопоставление с понятием стоимости у
древних. Воспользуемся анализом понятия стоимости у Ари-
стотеля, который дал Маркс: «Гений Аристотеля обнаружи-
вается именно в том,—писал Маркс,—что в выражении сто-
имости товаров он открывает отношение равенства. Лишь
исторические границы общества, в котором он жил, помеша-
ли ему раскрыть, в чем же именно состоит «в действитель-
ности» это отношение равенства»1).
«Обмен,—говорит он (т. е. Аристотель.—И. В,),—не
может иметь места без равенства, а равенство без соизмери-
мости»2). Таким образом, и здесь, как и в математике, грече-
ская мысль останавливается на констатировании равенства.
Дальнейшего обобщения не происходит. Для случая со стои-
мостью исчерпывающее объяснение этому факту дал Маркс.
*) К. М а р к с,« Капитал», К.Маркс иФ. Энгель с, Сочи*
нения, т. XVII, стр. 68.
2) Т а м же.
АРИФМЕТИЧЕСКИЕ КНИГИ «НАЧАЛ» ЕВКЛИДА
325
«Аристотель сам показывает нам, что именно сделало не-
возможным его дальнейший анализ: это—отсутствие поня-
тия стоимости. В чём заключается то одинаковое, т. е. та
общая субстанция, которую представляет дом для лож
в выражении стоимости лож? Ничего подобного «в дей-
ствительности не может существовать», —говорит Аристо-
тель. Почему? Дом противостоит ложу в качестве чего-то
равного и поскольку он представляет то, что действительно
одинаково в них обоих—и в ложе и в доме. А это челове-
ческий труд. Но того факта, что в форме товарных стои-
мостей все виды труда выражаются как одинаковый и,
следовательно, равнозначимый человеческий труд,— этого
факта Аристотель не мог вычитать из самой формы стои-
мости, так как греческое общество покоилось на рабском
труден, следовательно, имело своим естественным базисом
неравенство людей и их рабочих сил»1).
Стоимость в античном обществе ещё не отделялась от её
особенной формы. Такая неразвитая форма стоимости при-
водила ко взгляду на стоимость как на свойство благород-
ных металлов, сокровищ. Отсюда и стремление древних к
собиранию сокровищ, которое отмечает Маркс. Но деньги
в античном обществе являются не только воплощением,
материализацией стоимости, но и знаком стоимости2).
Конечно, нельзя установить таких непосредственных
связей между уровнем образования абстрактных понятий в
математике и структурой античного общества, как это было
сделано Марксом в случае с понятием стоимости. Однако
то обстоятельство, что при образовании абстрактных поня-
тий и в математике и в случае со стоимостью древние остано-
вились на одном и том ясе месте, далеко не случайно. Начи-
ная со времён античной Греции удаётся проследить парал-
лелизм основных моментов развития категории стоимости и
абстрактных понятий математики.Так, например, той ступе-
ни развития общества, когда всякий продукт труда рассма-
триваете я то л ько как товар, т.е. как сгусток безразличного
J) К. Маркс, «Капитал», К. М а р к с и Ф. 3 н ге л ь с’
Сочинения, т. XVII, стр. 68. См. также статью С. А. Яновской
«О так называемых «определениях через абстракцию» в Сборнике
статей по философии математики.
2) См. Архив К. Маркса и Ф. Энгельса, т. IV, стр. 221,
32G
II. Г. БЛШМАКОвд
человеческого труда, а политико-экономические теории
(Рикардо, Адам Смит) начинают рассматривать «форму
стоимости как нечто совершенно безразличное и даже
внешнее по отношению к природе товаров»1), соответ-
ствует такая ступень развития математической абстрак-
ции, когда математические объекты принимают фор-
му, безразличную к особому характеру предметов,
находящихся в рассматриваемых данной теорией отно-
шениях.
«Новостью, вполне понятой лишь к концу XIX века,
было то, что и геометрия, как математическая наука, нахо-
дится в таком же положении и ни в какой мере не связана
с тем, что мы обычно привыкли называть точками, прямы-
ми и т. д.»2).
На этой стадии развития может показаться, что форма-
лизованные математические объекты имеют значимость
сами по себе, что достаточно ввести известные символы
и определить действия над ними, чтобы создать математи-
ческую теорию. Этому явлению соответствует то, что
Маркс назвал товарным фетишизмом, т. е. замена отно-
шений между людьми отношениями между товарами, при-
чём эти последние кажутся первичными и существующими
сами по себе. Точно так же забывают, что формальные сим-
волы суть абстракции от реальных вещей или системы изо-
морфных вещей и что отношения немыслимы без реальных
вещей, находящихся в этих отношениях.
Объяснение этого параллелизма мы видим в том, что
содержание и форма науки определяются, в конечном
счёте, уровнем развития производства и структурными осо-
бенностями общества. Поэтому, говоря в самом общем смыс-
ле, каждому социальному строю соответствует своп харак-
тер мышления. В письме к Энгельсу от 25 марта 1868 г.
Маркс писал, что «логические категории... прямо вытекают
из наших отношений»3). «... Люди, производящие обще-
ственные отношения,... создают также и идеи и категории,
Э К. VI а р к с, «Капитал», цит. соч., стр. 91.
-) А. II. Колмогоров, «Современная математика». Сбор-
ник статей по философии математики, стр. 11.
8) К. Мар к с н Ф. Энгель с, Избранные письма, ОГПЗ
1917. стр. 201.
АРИФМЕТИЧЕСКИЕ КНИГИ «НАЧАЛ» ЕВКЛИДА
327
т. е. отвлеченные идеальные выражения этих самых обще-
ственных отношений»J).
Но наиболее общей и в то же время наиболее абстракт-
ной характеристикой общества, основанного на товарном
способе производства, является форма стоимости продук-
та труда, развитие которой более или менее отражается
в соответствующих теориях стоимости: «данный взгляд
экономиста... представляет более и/Лг менее адэкватное
теоретическое выражение экономических условий своего
времени» * 2).
Таким образом, ступени развития категории стоимости
примерно соответствуют развитию структурных особен-
ностей общества. А следовательно, и ступени развития
абстрактного математического мышления (способы образо-
вания понятий в математике, взгляд на природу матема-
тических объектов и т. п.), которые соответствуют, вообще
говоря, ступеням развития категории стоимости, опреде-
ляются, в конечном счёте, структурными особенностями
общества. «Религия, семья, государство, право, мораль,
наука, искусство и т. д.—это только особенные формы
производства, подчиняющиеся его всеобщему закону» 3).
Окидывая взглядом всю греческую математику, нельзя
не заметитьнесколько парадоксальную форму её развития:
с одной стороны, она достигла таких пределов строгости
(например, определение равенства вещественных чисел пу-
тём построения сечений или доказательство коммутатив-
ности умножения чисел), которые стали понятны для новой
математики лишь к концу XIX в., а с другой стороны, весь
характер её абстракций носил «натуральный» оттенок,
вещественное число не существовало само по себе, а только
как свойство пар величин; наряду со строгими доказатель-
ствами и чёткими определениями и аксиомами, мы нахо-
дим в «Началах» Евклида определение прямой как такой
линии, «которая лежит равно своими точками», или «линия
есть длина без ширины» и тому подобные описательные
предложения, которые потом но используются в тексте.
Ч К. М а р нс, Избранные произведения. 1935. т. I. стр. 2(88.
2) Ф. Э н г е л ь с. Предисловие к третьему изданию «Капитала»,
й. М а р к с и Ф. Энгель с, Сочинения, т. XV11, стр. 27.
3) К, М а р кс и Ф. Э н г е л ь с, Сочинения, т. 111, стр. 622.
328
II. Г. БАШМАКОВА
Аналогичное явление было отмечено Энгельсом в фило-
софии: с одной стороны, «в многообразных формах грече-
ской философии имеются в зародыше, в возникновении,
почти все позднейшие типы мировоззрения» ’), а с другой
стороны, Энгельс говорит о первобытной простоте мышле-
ния греков. Это соответствует всему характеру греческого
общества, в котором некоторые категории, свойственные
только высокоразвитому капитализму (например, капитал),
уживались с элементами натурального хозяйства, лежащи-
ми в основе рабовладельческого общества. Такая основа
хозяйства предопределяла оторванность науки от практи-
ки, делала производство античного общества в значитель-
ной мере независимым от науки. Это, разумеется, не могло
не сказаться и на характере самой науки. Ведь, как писал
И. Л. Чебышев, «сближение теории с практикой даёт
самые благоприятные результаты, и не только одна прак-
тика от этого выигрывает, сами науки развиваются под
влиянием её: она открывает или новые предметы для иссле-
дования, или новые стороны в предметах, давно извест-
ных..., она предлагает вопросы, существенно новые для
науки и, таким образом, вызывает на изыскания совершен-
но новых метод»* 2).
Всё это привело к такой форме античной математики,что
дальнейшее её развитие путём простого продолжения её
методов и традиций стало невозможным. Поэтому матема-
тика в XIV—XVI вв. не начала своё развитие с того места,
на котором остановилась античная наука. Она сразу же
начала с поисков новых путей, с выработки общих методов,
более отвечающих новым задачам, которые встали перед
наукой. В частности, вопросы теории делимости впервые
получили дальнейшее развитие только в работах Ферма.
х) К. М а р к с и Ф. Э н г е л ь с, Сочинения, т. XIV, стр. 340.
2) П. Л. Чебыше в,«Черчениегеографических карт» (1856).
См. Избранные математические труды. М.—Л., 1946, стр. 100.
О КЛАССИФИКАЦИИ ИРРАЦИОНАЛЬНОСТЕЙ
В X КНИГЕ «НАЧАЛ» ЕВКЛИДА
А. И. Маркушевич
1. X книга «Начал» Евклида—труднейшая для изуче-
ния часть этого произведения. «Несмотря на тщательное
изложение Евклидом материала, его трудно охватить,—
пишет Цейтен г),—ибо нелегко, не обладая никакой систе-
мой знаков, разобраться среди классифицированных в
этой книге иррациональных величин». К этому следует
добавить, что, даже используя алгебраическую символику
для перевода содержания X книги на привычный для нас
язык, мы всё же не избавляемся от трудностей, связанных
с тем, что от современного читателя ускользает, так ска-
зать, внутренняя связь между предложениями книги,
самая последовательность идей Евклида, принципы его
классификации. С точки зрения математической всё
содержание X книги можно охарактеризовать, напри-
мер, следующими словами А. де Моргана* 2): «Евклид иссле-
дует всё разнообразие линий, представляемых выражением
I/ У a±]fb, где а и b представляют две соизмеримые
линии. Он разделяет линии, которые могут быть предста-
влены этой формулой, на 25 видов и притом ему удаётся
открыть все возможные виды...». Формулировка, адэкват
*) Г. Г. Ц е й тен, «История .математики в древности и в средние
века». Перев. П. Юшкевича ГТТИ 1932, стр. 112.
2) Мы цитируем по статье II Ю Тимченко приложенной к рус-
скому изданию книги Ф К э д ж о р и, «История элементарной мате-
матики». Второе исправленное и дополненное издание, Mathesis.
330
И. МАРКУ1ИЕВИЧ
ная предыдущей по своему математическому смыслу, но
являющаяся результатом иного оригинального хода идей,
содержится в работе А. Е. Райк г): «... в X книге Евклид
построил полную классификацию решений квадратных
и биквадратных уравнений с рациональными в смысле
Евклида коэффициентами».
Соглашаясь с тем, что с точки зрения математической
каждый из цитированных тезисов полностью исчерпывает
содержание X книги, мы полагаем, однако, что и тот и
другой, прибегая к модернизации, почти неизбежной при
столь сжатых формулировках, оставляют открытым вопрос
о ходе идей, который мог бы фактически привести Евклида
именно к такому, а не к иному содержанию его труда.
Настоящая заметка представляет собой попытку дать
в самых общих чертах построение возможного хода идей
Евклида.
2. Прежде всего мы должны помнить,что даже в X книге,
которую исследователи считают наиболее оригинальной
частью «Начал», Евклид имел предшественников. Из них
нам известны Теодор (Феодор) из Кирены и его ученик
Тэетет. Платон в своём диалоге «Тэетет»-) от лица Тэетета
сообщает о том, что Теодор доказывал своим ученикам, что
стороны квадратов, имеющих площади 3,5,6,7,8,10,11,12,
13,14,15,17, несоизмеримы со стороной единичного квад-
рата.
Отправляясь от этого, Тэетет разделял все числа (нату-
ральные) на числа, являющиеся точными квадратами
(квадратные числа) и не являющиеся таковыми, продолго-
ватые (прямоугольные) числа и устанавливал, что стороны
квадратов, площади которых суть квадратные числа, не-
соизмеримы со сторонами квадратов, площади которых
суть продолговатые числа.
Если, таким образом, понятие о множестве Ег отрезков,
соизмеримых с данным отрезком, существовало в науке и
раньше, то заслугой Тэетета является выделение из всего
необозримого множества отрезков, несоизмеримых с Ег,
’) Статья Л. Е. Ран к печатается в настоящем сборнике.
а) Платон, «Тэетет».Персп. с греческого и примеч. В. Серёж-
пнкова М 1936, стр. 22 и след.
О КЛАССИФИКАЦИИ ИРРАЦИОНАЛЬНОСТЕЙ У ЕВКЛИДА 331
наиболее простого и близкого к Ег—множества ^отрезков,
соизмеримых «с первыми не в линейном измерении, а в пло-
щадях, для которых они суть корни». За это важное откры-
тие Тэетет удостаивается в диалоге Платона похвалы Сокра-
та, который в дальнейшем разговоре, побуждая Тэетета оха-
рактеризовать сущность знания, приглашает его поступать
при этом «подобно тому как корни, несмотря на всю много-
численность их, ты объединил в одном виде». Вот это-то
объединение многочисленного в одном виде или, примени-
тельно к интересующему нас вопросу, выделение подмно-
жеств (или классов) отрезков, несоизмеримых с Ех, по-
средством указания характеристического свойства элемен-
тов этого множества1) и являлось, по видимому, одной из
важнейших теоретических проблем математики того вре-
мени, интересу к которой впоследствии способствовал фило-
софский авторитет Платона. Из того же диалога видно, что
Тэетет пытался выделить ещё класс Е3 несоизмеримых
отрезков, обладающих тем свойством, что объёмы кубов,
построенных на них, не являются точными кубами («то же
проделаем мы и с кубическими телами»). Но здесь Тэетет
вступил в область, так сказать, «трансцендентную»с точки
зрения классической геометрии прямой и окружности,
линейки и циркуля. Известно, сколько усилий, в некото-
рых отношениях весьма плодотворных, потратили антич-
ные математики на решение так называемой «делосской
задачи», первой и основной задачи на путях изучения несо-
измеримых отрезков из Е^).
Диалог Платона не даёт указаний на другие открытия
Тэетета. К счастью, до нашего времени дошёл в арабской
рукописи Абу ибн Отмана из Дамаска отрывок из коммен-
тария к Евклиду Паппа Александрийского, опиравшегося
на более ранние источники, в частности, на утерянную
«Историю геометрии» перипатетика Эвдема Родосского.
В этом отрывке сведения, которыми располагал Тэетет,
х) В случае множества Е2 характеристическое свойство за-
ключается в соизмеримости площадей квадратов, построенных
на отрезках Е». г площадями квадратов, построенных на отрез-
ках Е1.
2) См. например, Цейтеи. цпт. иич., стр. 67 и след.
332
А. И. МАРКУШЕВИЧ
рисуются в значительно более полном виде. Вот относя*
щиеся сюда местах):
«Тэетет отличал величины соизмеримые по длине от
несоизмеримых и разделил хорошо известные роды ирра-
циональных линий по различным средним, относя среднюю
к геометрии, прямую с двумя именами к арифметике и
апотому к музыке, как об этом свидетельствует и расска-
зывает перипатетик Эвдем». Здесь мы встречаемся с клас-
сами несоизмеримых отрезков (средние прямые, пря-
мые с двумя именами или биномиальные, апотомы или
вычеты), о которых речь будет итти ниже, при разборе
книги Евклида.
Далее арабский источник говорит: «Что до. Евклида, то
он поставил целью дать строгие правила, которые он уста-
новил относительно соизмеримости и несоизмеримости во-
обще; он уточнил определения и различия величин рацио-
нальных и иррациональных и, наконец, он ясно показал
всё их многообразие».
Все эти свидетельства, указывающие на то, что должно
было быть известным Евклиду от его предшественников,
необходимо иметь в виду при анализе X книги.
3. В дальнейшем мы предполагаем, что читатель имеет
под руками какое-либо издание Евклида, например, един-
ственный русский перевод «Начал», содержащий целиком
всю X книгу—«Начала Евклида с пояснительным вве-
дением и толкованиями» М. Е. Ващенко-Захарченко, Киев,
1880 г.
Исходными у Евклида являются произвол ьный прямо-
линейный отрезок и построенный на нём квадрат, которые
он называет рациональными (ртдта), а мы будем называть
основными. Они играют роль, соответственно, произволь-
но выбранных единицы длины и площади. Имя рациональ-
ных присваивается также отрезкам и квадратам (вообще,
прямоугольникам, площадям), которые соизмеримы с выше-
названными. Но Евклид называет рациональными и те
отрезки, которые, будучи несоизмеримыми с основным,
’) Цитируем по статье Н. Vogt «Die Entdeokungsgeschichte des
Irrationalen nach Platou. s. w.», Bibliotheca Mathem., 3 F. 10 B, 1910.
стр. 134—135, где эти места приведены во французском переводе,
принадлежащем Вёпке (Woepke).
и КЛАССИФИКАЦИИ ИРРАЦИОНАЛЬНОСТЕЙ У ЕВКЛИДА 333
являются сторонами квадратов, соизмеримых с основ-
ным квадратом. Иными словами, он объединяет классы
Яхи Е2, рассмотренные Тэететом, в один класс рациональ-
ных отрезков.
Таким образом, рациональные прямые (отрезки) раз-
деляются на соизмеримые (аб^игтря) по длине с основной
прямой и соизмеримые с ней только в степени (fovapet
сэрьретро»). Ход идей, который ведёт от понятия отрезков
соизмеримых к более общему понятию отрезков рациональ-
ных, принадлежит, как мы видели, Тэетету. Мы назовём
этот ход идей, имеющий рекуррентный характер, прин-
ципом Тэетета и выразим его в следующей общей форме,
охватывающей различные его применения в X книге
Евклида.
Первый этап. Переход от прямых исходного клас-
са к классу построенных на них площадей (квадратов или
прямоугол ьников).
Второй этап. Выражение соотношений между по-
лучаемыми площадями и площадями ранее построенных
классов и затем, если понадобится, расширение нового
класса площадей до полного объёма множества, соответ-
ствующего найденному характеристическому свойству.
Третий этап. Получение класса (нового) прямых
при помощи некоторого ограничения, наложенного на
прямые (на стороны прямоугольника), производящие най-
денные площади.
Иллюстрируем в деталях эту схему на примере введения
понятия рациональных прямых.
Первый этап. От класса прямых, соизмеримых с
основной прямой, переходим к классу построенных на них
квадратов или прямоугольников.
Второй этап. Отмечаем, что все найденные
площади соизмеримы с площадью основного квадрата,
и, принимая это свойство за характеристическое, рассма-
триваем класс всех площадей, соизмеримых с основной.
Третий этап. Образуем класс прямых, являю-
щихся сторонами квадратов, принадлежащих построен-
ному классу.
В дальнейшем мы встретимся с неоднократным приме-
нением этого принципа в соединении с другим, восходящим
334
Л. II. МАРКУШЕВНЧ
также к Тэетету, который можно назвать принципом сло-
жения или вычитания несоизмеримых величин. О нём
речь будет идти ниже.
Сейчас отметим, что ограничение, о котором шла речь
в формулировке третьего этапа принципа, встречается
у Евклида в двух формах: либо из всех площадей опреде-
лённого класса выделяются одни лишьплощади квадратов
(как это было сделано в рассмотренном примере) и берутся
стороны квадратов, либо же выделяются прямоугольники
с основанием, равным основной прямой, и берутся высоты
этих прямоугольников.
4. Исходя из класса рациональных отрезков, Евклид
рассматривает всевозможные площади (прямоугольников)
с рациональными сторонами и замечает, что если эти сто-
роны соизмеримы между собой, то площадь будет рацио-
нальной (X, 20), а если стороны соизмеримы только в сте-
пени, то площадь будет иррациональной (адоуо».), т. о.
несоизмеримой с основной площадью (X, 22). Получаемые
таким образом площади он называет средними (peaiq); сред
ней называется также и сторона квадрата, равновеликого
средней площади. Очевидно, что название «средней» объяс-
няется тем, что сторона квадрата, равновеликого прямо-
угольнику, является средней геометрической между его
сторонами (рациональными). Мы сталкиваемся, таким
образом, в начальных предложениях X книги Евклида
с двукратным применением принципа Тэетета:
1) прямые, соизмеримые
между собой
2) прямые, соизмеримые
между собой только я
степени
построенные па
них площади
(рациональные
площади)
построенные на
них площади
(средние площа-
ди)
прямые, соизмери-
мые с исходны-
ми только я сте-
пени
средние прямые
Попутно Евклид устанавливает наличие важного соот-
ветствия между прямыми, соизмеримыми между собой
по длине или только в степени, с одной стороны, и рацио-
нальными и средними площадями, с другой стороны. Имен-
но,он доказывает, что высота прямоугольника с рациональ-
ным основанием будет также рациональной, соизмеримой
О КЛАССИФИКАЦИИ ИРРАЦИОНАЛЬНОСТЕЙ У ЕВКЛИДА 33;,
с основанием но длине или только в степени, в зависимо-
сти от того, будет ли площадь рациональной или средней
(X, 21 и X, 23).
Дальнейшее применение принципа Тэетета позволило
бы Евклиду получать всё новые и новые классы иррацио-
нальных прямых. Однако доказательство того, что новые
классы будут отличны от предыдущих, требует нредва-
рительного построения обширной теории.
Лишь в коЦце X книги (предложение 116) Евклид
устанавливает, что «из какой-нибудь средней прямой А
можно получить (путём неограниченного применения
принципаТэетета. —A. J/.) бесчисленное множество ирра
циональных прямых, отличных от всех предыдущих».
Мы полагаем, что это предложение и по его месту в книге1)
и по его принципиальному значению является венцом всей
книги. Цитированный нами выше арабский источник
в заключительных словах «et,en dernier lieu, il demon tr a
clairement toutc ]eur etendue» имеет в виду именно это
предложение.
То обстоятельство, что Евклид, так сказать, имеет
право приостановить пока дальнейшее действие принципа
Тэетета, выражается в двух предложениях (X, 25 и X,
26), которые утверждают, что площадь, построенная па
средних прямых, соизмеримых по длине или соизмеримых
только в степени, является сама рациональной или сред-
ней площадью. Эти предложения выражают собой своего
рода «замкнутость» классов рациональных и средних отрез-
ков и классов рациональных и средних площадей при до-
полнительном условии: не допускать (пока) к рассмотре-
нию площадей (прямоугольников) со сторонами, несоиз-
меримыми ни по длине, ни по площади.
5. Для дальнейшего развития классификации Евклид
привлекает второй принцип, который, как мы уже вскользь
говорили, отчасти был известен и Тэетету. Он заключается
в образовании сумм или разностей несоизмеримых пря
мых или площадей, принадлежащих к ранее построенным
Э За ним идёт лишь одно предложение 117-е, в котором устанав-
ливается несоизмеримость диагонали квадрата с его стороной. Поз-
волительно усомниться в том. что оно было поставлено на это место
самим Евклидом
336
A. lb МАРКУШЕВИЧ
классам, и обосновывается в предложениях X, 16 и X,
17, где Евклид отмечает, что сумма пли разность двух
величин соизмерима с каждой из них в случае, когда
эти величины соизмеримы между собой, и несоизмери-
ма в случае, когда эти величины между собой несоиз-
меримы.
Таким образом, выход за пределы ранее построенных
классов возможен только в результате сложения или
вычитания несоизмеримых между собой величин.
Проследим ход идей Евклида, ограничиваясь для
простоты формулировок сложением величин. Сначала
Евклид применяет принцип сложения только к от-
резкам и притом соизмеримым между собой только в
степени.
Таким образом, получаются следующие классы: а) сум-
ма двух рациональных прямых — б и и о м и а л ь н а я
или прямая с двумя именами (iq ix Suo Gvop-axiov); б) сум-
ма двух средних, дающих рациональную площадь по-
строенного на них прямоугольника —п ервая биме-
ди а л ь н а я (Т; ёх Buojxsacov теракт]); в) сумма двух сред-
них, дающих среднюю площадь построенного на них пря-
моугольника— в торая бимедиа л ьная (?) ёх оио-
p-eawv йеотера).
Очевидно, что этими тремя классами исчерпываются
все возможные здесь случаи.
После того как от классов рациональных и средних
прямых Евклид приходит к новым классам прямых:
а), б) и в), наступает очередь применения принципа
Тэетета, который, впрочем, используется здесь не в
столь явном виде, как на начальных степенях класси-
фикации.
Если прямую одного из классов а), б) и в) представить
в виде я+?/, то площадь квадрата, построенного на этой
прямой, по предложению 11,4 выразится следующим обра-
зом:
(« + у)а = х1! + ^ + 2ху,
т. е. составится из площади квадрата х2 + у2 (сложение вы-
полняется с помощью теоремы Пифагора) и прямоуголь-
ника 2ху.
О КЛАССИФИКАЦИИ ИРРАЦИОНАЛЬНОСТЕЙ У ЕВКЛИДА 337
Соответственно трём классам а), б) и в) будем иметь
три возможные структуры для площадей получаемых ква-
дратов:
2жг/
а) рациональная б) средняя в) средняя средняя рациональная средняя
Итак, отправляясь от классов прямых а), б) и в) и сле-
дуя первому этапу принципа Тэетета, мы приходим к клас-
сам а), б) и в) площадей, представляющихся в виде сумм
двух ранее построенных площадей (рациональных или
средних). Очевидно, что самое сложение может быть осу-
ществлено фактически с помощью теоремы Пифагора. Лля
этого каждую из двух площадей заменяем равновс’ли-
ким квадратом, а затем строим прямоугольный треуголь-
ник, катетами которого являются стороны квадратов.
Тогда квадрат, построенный на гипотенузе, и будет ис-
комым (X, 14).
Полученные площади: (х2 ) Чху , соответствовали
предположению, что х и у были соизмеримы между собой
в степени. Если от этого требования отказаться и (сообраз-
но с заключительной частью второго этапа принципа Тэо-
тета) допустить, что х и у, суммой которых является сто-
рона квадрата, могут быть несоизмеримы между собой не
только по длине, но ещё и в степени, то получаем ещё три
класса иррациональных прямых, имеющих вид х-\-у и
производящих такие площади:
а') в случае, когда площадь х2 4- у"' рациональная,
а 2 ту средняя, соответствующая прямая у называется
наибольшей иррациональной
б') в случае, когда х - у1 средняя, а Чху рациональная,
х у называется производящей рациональную и среднюю
площади s.sg • огъ гюп):
в') в случае, когда г' у и ху средние, х у называет
ся производящей две средние площади (х4 обо {.
22
Историцо-матеыат. исследования
338
A. II. МАРКУШЕВИЧ
G заменой суммы на разность получаем шесть клас-
сов иррациональностей, носящих соответственно наиме-
нования:
а) вычет — апотома '(атсотсрт^);
р) первый средний вычет (•/) pbiqi акоторт)
у) второй средний вычет (iq ргот]’. атготор) оеате^а);
а') малая иррациональная ekaaawv);
р') дополняющая рациональную площадь до средней
(•/) рета peoov тб 6Xov koiggx);
у') дополняющая среднюю площадь до средней пло-
щади (yjpsxa peaov то 6\ov тсо’.боа).
6. Описанные классы собственно и образуют евклидову
классификацию иррациональностей, состоящую таким
образом из 13 классов: средние,шесть классов,происходя-
щих от сложения и шесть классов, происходящих от вычи-
тания. Для того чтобы доказать, что одна и та же прямая
не может входить в два различных класса (X, 73, след-
ствие, X, 112 и следствие), Евклид предварительно деталь-
но изучает биномиальные и вычеты, расщепляя каждый
из этих классов на шесть других —п о р я д к и биномиаль-
ных или вычетов. Это расщепление основывается на соот-
ветствии между рациональными прямыми, с одной сто-
роны, и рациональными и средними площадями,с другой,—
соответствии, о котором мы уже говорили и которое за-
ключается в том, что площадь прямоугольника с рацио-
нальным основанием будет рациональной или средней в за-
висимости от того, будет ли высота прямоугольника рацио-
нальной соизмеримой с основанием по длине или только
в степени. Справедливо также и предложение, обратное
этому (X, 20, 21, 22, 23).
Таким образом, при наличии, например, общего рацио-
нального основания рациональные и средние площади
будут точно соответствовать рациональным—соизмеримым
или несоизмеримым с основанием высотам, и следова-
тельно, суммы (разности) рациональных и средних площа-
дей будут изображаться суммами (разностями) рациональ-
ных прямых. Поэтому все различия иррациональных пло
щадей, происходящих от сложения (вычитания) рацио
нальных и средних площадей, проявляющиеся в том, что
площади эти равновелики квадратам, построенным на пря-
О КЛАССИФИКАЦИИ ИРРАЦИОНАЛЬНОСТЕЙ У ЕВКЛИДА 339
мых шести различных классов, полученных сложением
(вычитанием), должны соответствовать некоторым разли-
чиям между суммами (разностями) рациональных прямых,
т. е. различиям внутри класса биномиальных (апотом).
В этом ходе мыслей мы можем видеть действие принципа,
родственного принципу Тэетета. Чтобы разобраться в ре-
зультатах, приведём здесь полную таблицу состава пло-
щадей квадратов, построенных на прямых х 4- у классов
а), б), в), а'), б'), в'):
я2 4- у2 2^2/
а) рациональная б) средняя в) средняя средняя ) рациональная > средняя J х2 и у2 соизмеримы
а") рациональная б') средняя в') средняя средняя ) рациональная [ средняя J х2 и у2 несоизмеримы
Переходя от площадей к соответствующим отрезкам,
мы заменяем столбцы ж2 + ?/2 и 2ху, изображающие пло-
щади (рациональные и средние), столбцами аир, изо-
бражающими рациональные прямые (соизмеримые или
несоизмеримые с основным отрезком, принятым за общее
основание площадей). Заметим, что соизмеримость или
несоизмеримость хъ и уг эквивалентна соизмеримости
или несоизмеримости ж2 + у2 и ж2—-у2, но последние вели-
чины относятся между собой, как а относится к а8 —р2;
поэтому в последнем столбце речь будет о соизмеримости
или несоизмеримости а и/а2-р2 (стороны квадрата,
а 1 ₽
А) соизмерима Б) несоизмерима В) несоизмерима А') соизмерима Б') несоизмерима В') несоизмерима несоизмерима ] соизмерима 1 несоизмерима J несоизмерима 1 соивмерима J несоизмерима J а И ]/" х2 — Р2 соизмеримы ХИ У о.2 — Р2 несоизмеримы
22*
340
A. 1J. МАРКУШЕВИЧ
представляющего избыток площади квадрата, построен-
ного на а, над площадью квадрата, построенного на §).
Сообразно шести имеющимся здесь возможностям мы
и получаем шесть порядков или категорий биномиальных
прямых а + ₽. Порядки А), Б), В), А'), Б'), В') представ-
ляют соответственно категории тех прямых, которые
являются высотами прямоугольников с рациональным
основанием и с площадями, равновеликими квадра-
там, построенным на прямых классов а), б), в), а'), б')
и в').
Прямые порядков А), Б), В), А'), Б') и В') называ-
ются первыми, вторыми, ..., шестыми биномиальными.
Аналогично, заменяя сложение вычитанием, получаются
шесть порядков вычетов: первые, вторые, третьи,
шестые вычеты. Мы подытожим всю евклидову классифи-
кацию в схеме, которая помещена на стр. 341—342 и
которой необходимо предпослать лишь следующие пояс-
нения.
Переход от классов первого столбца к классам второго
столбца и обратно совершается по принципу Тэетета. Пе-
реход этот показан стрелками. В первых трёх строках пло-
щади, производимые прямыми, суть прямоугольники, в
остальных—квадраты. Внутри второго столбца происхо-
дит расширение каждого из получаемых классов площадей
до максимального объёма, соответствующего обнаружен-
ному характеристическому свойству площадей (второй
этап принципа Тэетета). Обратный переход от площадей к
новым классам прямых соответствует переходу от площади
квадрата к его стороне (третий этап принципа Тэетета).
В третьем столбце показаны классы прямых, представляю-
щих высоты прямоугольников с площадями, принадле-
жащими классам второго столбца, и с рациональным
(основным) основанием. Очевидно, что эти классы дают
линейное выражение соответствующих площадей.
Всего получаем два класса рациональных и тринадцать
классов иррациональных прямых, из которых два разби-
ваются на двенадцать порядков. Если заменить эти два
класса указанными порядками, то всего получатся те 25
различных видов (неравноправных), о которых говорит
А. де Морган.
О КЛАССИФИКАЦИИ ИРРАЦИОНАЛЬНОСТЕЙ У ЕЕКЛИДА 341
Классификация Евклида
Прямые (I) Площади Прямые (II)
,1 Соизмеримые —> Рациональные —; _| ► Соизмеримые
равно; 1 Соизмеримые —> только в степени Средние —) • Соизмеримые только в степени
J 1 1 Средние —> Рациональные или—> средние (при ус- ловии, что основа- ние и высота соиз- меримы по длине или в степени) Рациональные
ы е (Сложение соизме- римых только в сте- пени прямых) (Сложение площа- дей)
ь н рациональная+ ра- циональная рациональная 4- 4- средняя первая биномп- ‘ алытая
а л средняя+ средняя_ с рациональным прямоугольником { средняя 4-средн яя—> со средним прямо- угольником (сложение несоиз- меримых в степени прямых) средняя 4- рацио- нальная | вторая биномп- ’ альная
н о средняя 4-средняя—) ► третья биноми- альная
я г ез
d d и 1 наиб, иррациональ—> ная рациональная 4- —> 4- средняя - четвёртая бино- миальная
4 рациональная и —-> средняя степенящая средняя 4- рацио - —> нальяая пятая биноми- альная
4 степенящая две сред- ние площади -> средняя + средняя— > шестая биноми- альная
-Г,-
342
A. II. МАРКУШЕВИЧ
Продолжение
Прямые (I) Площади Прямые (И)
(Вычитание соизме- римых только в степени прямых) рациональная—ра- - циональная 3 (Вычитание пло- щадей) -> рациональная — средняя -> первый вычет
а средняя—средняя —» с рациональным пря- л моугольпиком 1 средняя — раци опальная 1 > второй вычет
R средняя—средняя —> л со средним прямо- угольником д (Вычитание несонз- о меримых в степени прямых) S средняя—ср едняя- 1 -»третий вычет
3 малая иррациональ—* « ная рациональная — средняя средняя — раци- - ональная > четвёртый вычет
1 а дающая с рациональ - ной среднюю пло- щадь —> -» пятый вычет
S | дающая со средней- среднюю площадь > средняя — средняя- -» шестой вычет
ДЕСЯТАЯ КНИГА «НАЧАЛ» ЕВКЛИДА
А. Е. Раик
§ 1. Предварительные замечания1)
«Теоретическое естествознание, —говорит Энгельс2),—
если оно хочет проследить историю возникновения и раз-
вития своих теперешних общих положении, вынуждено
возвращаться к грекам».
К математическому наследию греков мы обращаемся
не только потому, что греки являются наиболее ранними
предшественниками современной науки, а главным образом
потому, что творения Евклида, Архимеда, Аполлония
изучались почти всеми великими математиками, творив-
шими её историю.
Особое внимание всегда привлекали «Начала» Евклида—
этот замечательный памятник классической древности.
Евклидова геометрия, законченная и завершённая в «На-
чалах», казалось бы, закрывала все возможности дальней-
шего развития геометрии. С другой стороны, идеологиче-
ская основа этого произведения, философия Платона, была
широко использована идеалистами. Кант, папример, дока-
зывал существование объективного, необходимого зна-
ния, ссылаясь на геометрию Евклида. Он аргументировал
против объективности пространства невозможностью
1) Автор считает своим приятным долгом поблагодарить своего
учителя, проф. Софью Александровну Яновскую, за ценные указания
и внимание, оказанное ему во время выполнения настоящей
работы.
2) Ф, Э н г е л ь с, «Диалектика природы», 1948, стр. 27
344
A. F. РАИК
мыслить геометрию, обладающей другими изначальными
свойствами, чем евклидовские.
И нужен был гений Лобачевского, чтобы вырвать гео-
метрию из двадцативекового застоя. Великий Лобачев-
ский открыл новые пути развития геометрии, которая
нашла своё широкое приложение в естествознании. Одно-
временно был нанесён удар и идеализму вообще, и Канту,
в частности.
Вполне естественно, что понять идеи Лобачевского
невозможно без овладения «Началами» Евклида. А между
тем, несмотря на огромную литературу, посвящённую
этому произведению, нельзя считать вопрос вполне исчер-
панным. Больше того, «Начала» чаще всего рассматри-
ваются по частям, разрозненно. Нет достаточно ясного
ответа на вопрос, каким же целям служили «Начала» в
целом, какая общая идея объединяет, казалось бы, не
связанные между собой все их 13 книг. Без решения этого
вопроса «Начала» Евклида продолжают оставаться непо-
нятыми, нераскрытыми.
С нашей точки зрения ответ на поставленный вопрос
даёт X книга «Начал».
X книга «Начал» Евклида является самой большой
наиболее трудной и наименее изученной.
Основная проблема, связанная с этой книгой,—опре-
делить её место в общей системе Евклида, выяснить её
содержание и роль. Если даже не сомневаться в правиль-
ности общепринятой квалификации содержания X книги
как некоторой классификации квадратичных иррациональ-
ностей, то всё же остаётся открытым вопрос, с чем связана
именно такая классификация, чему она служит, чем вы-
звана,—вопрос по поводу которого до сих пор не сущест-
вует единой достаточно убедительной точки зрения. Цей-
тен, например, утверждает, что «наиболеесамостоятельная
часть работы Евклида заключается несомненно в этом (речь
идёт о классификации иррациональностей. —А. Р.) и в при-
менении указанной классификации к определению рёбер
правильных многогранников»1). Эту же мысль высказы-
х) Г. Г. Ц е й т е н,« История математики в древности и в средние
пека», М.—-Л., 1932, стр. 83.
ДЕСЯТАЯ КНИГА «НАЧАЛ» ЕЕКЛИДЛ
345
вают и другие1). Действительно, рёбра правильных много-
гранников выражаются, как известно, квадратичными ирра-
циональностями через радиусы описанных и вписанных
сфер. В частности, ребро додекаэдра а = у R 15 —}/ Ь),
где R — радиус описанной сферы, а ребро икосаэдра
Иррациональности этих типов принадлежат как раз
к тем классам иррациональных отрезков, которые Евклид
рассматривает в X книге. Однако число рассматриваемых
Евклидом различных типов квадратичных иррациональ-
ностей гораздо больше, чем это нужно в применении
к сторонам и рёбрам правильных многоугольников и мно-
гогранников. Больше того, поскольку задачи у Евклида
решаются вообще не вычислением, а построением, само по
себе отнюдь не ясно, каким целям должно служить отне-
сение некоторого построенного отрезка к тому или дру-
гому типу иррациональностей в зависимости от выбора
единицы измерения. Более убедительными, на наш
взгляд, являются, утверждения, которые теснейшим обра-
зом связывают содержание X книги с теорией квадрат-
ных и биквадратных уравнений, достаточно общей, чтобы
включить все конкретные задачи (в том числе и о рёбрах
правильных многогранников), которыми занимался Ев-
клид, но не ограничивающейся всё же только последними.
Однако освещение конкретного содержания этой теории,
нам кажется, требует ещё ряда уточнений.
Что касается основного вопроса о значении и месте
X книги в системе «Начал», то довольно убедительной пред-
ставляется гипотеза Рейдемейстера2), согласно которой
цель X книги состоит не только в восстановлении роли
целого числа как основного понятия математики, но и в
возрождении его пифагорейского смысла, согласно кото-
рому «всё есть число».
См., например. Cl. Thaer, Euklid, Die Eleme te, 1936,
т. IV, стр. 103.
2) K. Reidemeis ter, Die Arithmetik der Grieche.., 1940K
стр. 27—29.
346
A. E. PAI1K
Что касается места X книги в системе «Начал», то
уже сейчас заметим, что обычно думают, будто VII, VIII
и IX книги «Начал» Евклида, посвящённые теории чисел,
являются инородным телом в его системе; между тем, они
необходимы для построения теории квадратичных ирра-
циональностей, которым посвящена следующая за ними
непосредственно X книга. Связь же квадратичных ирра-
циональностей с геометрическими объектами (отрезками
и площадями), изучаемыми Евклидом, никем, конечно,
не отрицается.
Если, таким образом, ясно, что положение X книги
в системе «Начал» отнюдь не случайно, то всё же конкрет-
ное выяснение вопроса о месте этой книги представляется
не только интересным, но и трудным. Для понимания
дальнейшего нам необходимо будет ввести некоторые тер-
мины, постоянно употребляемые Евклидом.
Евклид вводит следующие понятия: он выбирает отре-
зок, который называет рациональным (ртра) и который
во всём дальнейшем играет роль единицы измерения. Отре-
зок, соизмеримый с данным рациональным отрезком (т. е.
отношение их длин равно отношению целых чисел), назы-
вается также рациональным отрезком. Отрезок, для кото-
рого площадь построенного на нем квадрата соизмерима
с площадью квадрата рационального отрезка, называется
также рациональным. Таким образом, у а, где а выра-
жается через линейную единицу измерения рациональным
числом, есть, по Евклиду, тоже рациональная величина.
Отрезок, квадрат которого несоизмерим с единичным квад-
ратом, называется иррациональным1). Площадь, которую
Евклид называет рациональной, измеряется рациональ-
ным, в нашем смысле, числом. Площадь, которая изме-
ряется квадратным корнем из неквадратного рациональ-
ного числа, называется у Евклида средней площадью. Сто-
ронаквадрата, площадь которого есть средняя, называется
средним отрезком. Ясно, что средний отрезок измеряется
корнем четвёртой степени из неквадратного рационального
х) Таким образом, сумма двух рациональных, в смысле Евклида,
отрезков не есть обязательно рациональный, в смысле Евклида, отре-
зок.
ДЕСЯТАЯ КНИГА «НАЧАЛ» ЕВКЛИДА
347
числа, т. е. а или где а и b — рациональные
числа.
Само собой разумеется, что никаких формул у Евклида
нет. Они появляются при переводе его высказываний
на язык современной математики. Последним приёмом
мы будем существенно пользоваться и впредь. Перевод
определений и предложений Евклида на современный язык
формул даст нам возможность, с одной стороны, обозреть
весь материал X книги в целом и, с другой, лучше разо-
браться в деталях.
Прежде чем перейти к общему исследованию X
книги, остановимся сначала на некоторых отдельных её
предложениях и сделаем несколько предварительных
замечаний.
Раскрытие сущности X книги в значительной мере за-
трудняет форма её изложения. Синтетически построенные
доказательства предложений вызывают ряд недоумений.
К. Таер говорит: «X, 27—35 образуют труднейшую часть
сочинения, потому что Евклид не приводит никакого
анализа для своих построений»1).
Действительно, для того, например, чтобы найти два
средних отрезка, соизмеримых только в степени2), произ-
ведение которых образует рациональную площадь, Евклид
берёт два отрезка А и В, рациональных, но соизмеримых
только в степени, существование которых уже доказано
им, и с помощью этих отрезков строит, проводя окружности
и прямые линии, третий отрезок С, среднепропорциональ-
ный к ним, а затем, опять-таки с помощью геометрического
построения, находит отрезок D, четвёртый пропорцио-
нальный к трём А, В и С. Последние два отрезка С и D,
утверждает Евклид, и суть искомые средние отрезки.
Никаких объяснений происхождения такого построения
Евклид не даёт. Однако последнее просто и естественно
получается, если попытаемся решить задачу анали-
тически. В самом деле, задача сводится к решению
г) Cl. Thaer, цит. соч., стр. 111.
а) Отрезки, только квадраты которых соизмеримы, будем
впредь называть соизмеримыми в степени.
348
A. E. РАИК
системы двух уравнений с двумя неизвестными:
х — т
'v~~ /п ’
ху = кп
(т, п, к — рациональные числа, и отношение к \/ п,
а, следовательно, и произведение |/^ у'т не выра-
жаются рациональным числом).
Решим её:
о V п J
у х —— , ху = х2 -7^- = кп,
у т у т
следовательно,
х2 = к \^п • \/ т = кп ]/ кт.
Итак, необходимо, чтобы х, т. е. один из искомых отрез-
ков, был среднепропорциональным к двум, в смысле
Евклида, рациональным, но соизмеримым только в сте-
пени отрезкам. Другой же отрезок у должен быть четвёр-
тым пропорциональным к трём: х, р Лл и J/ кт, Евклид,
очевидно, так и находил условия, достаточность кото-
рых он доказывает; между тем, отсутствие доказатель-
ства необходимости придаёт решению характер искус-
ственности.
Особого внимания заслуживают 1-е, 3-е, 9-е, 17-е и
18-е предложения.
В 1-м предложении доказывается аксиома непрерывно-
сти Архимеда.
3-е предложение содержит известный алгоритм Ев-
клида, позволяющий отыскать общую меру двух соизмери-
мых отрезков.
9-е предложение утверждает следующее: два квадрат-
ных корня относятся между собой, как целые числа,
тогда и только тогда, когда подкоренные количества отно-
сятся между собой, как квадратные числа; в переводе на
современный язык это означает, что если квадратный
корень из целого числа не есть целое число» то он не есть
и рациональное число.
десятая книга «Начал» ееклнда
349
Вопрос об иррациональности квадратного корня из
числа занимал древних ещё задолго до Евклида. В V в.
до нашей эры учитель Платона, Феодор из Кировы, дока-
зал иррациональность квадратного корня из всех неквад-
ратных чисел от 3 до 17. Таким образом, 9-е предложе-
ние есть, по существу, обобщение этих положений.
17-е и 18-е предложения в переводе на современный
язык устанавливают необходимые и достаточные условия
существования рациональных корней системы
х-\-у~а, xy — bf
где а и Ь — рациональные, в нашем смысле, числа. Именно
система имеет рациональные корни тогда и только тогда,
когда j/fl2 —46 - г, где г —рациональное, в нашем смы-
сле, число.
§ 2. Номенклатура рассматриваемых Евглпдом
иррациональностей и посвящённая нм литература
Основным содержанием X книги является рассмотре-
ние 22 иррациональных отрезков, из которых 11 выража-
ются суммой двух отрезков «иг, удовлетворяющих опре-
делённым условиям, а 11—разностью. Отрезки первой
группы будем обозначать буквой В, а второй—А. Так как
все свойства и теоремы, относящиеся к каждой из этих
групп, совпадают с точностью до знака,то мы часто будем
объединять их попарно одной формулой со знаком ±:
В,А—и±и. Каждая группа, в свою очередь, разби-
вается на два рода.
Мы начнём с некоторой предварительной классифика-
ции, несколько отличающейся от классификаций Евклида
и, как мы увидим ниже, нуждающейся ещё в исправлениях.
Нам представляется не исключённой возможность, что
и сам Евклид шёл этим же путём, хотя, конечно, пользо-
вался другим языком. Обнаруженные при этом дефекты
классификации, легко, однако, устраняющиеся, должны
были привести его именно к той классификации, которую
мы и находим в X книге.
Следуя Евклиду, назовём иррациональный отрезок,
который представляет собой сумму двух рациональных,
350
Л. Е. PAIIK
но соизмеримых только в степени отрезков, биномиальным
отрезком (ex сио ovofxawv), а иррациональный отрезок,
который представляет разность такой пары отрезков,
будем называть вычетом (аготор;).
Аналитически биномиальный и вычет могут быть
представлены следующими формулами (а, Ь—рациональ-
ные, в нашем смысле, неквадратные числа, а > b, i — ирра-
циональное, в нашем смысле, число):
| Г»+/к£-.'.
в = - a + ]fb,y= = i,
]/ а + b, =1,
if a — bt =
v b
Рассмотрим сначала некоторые шесть классов биноми-
альных и шесть классов вычетов, которые различает и
Евклид, и объединим их в первый род каждой из
наших двух групп В и А. Так как остальные отрезки
из каждой группы являются, как будет показано ниже,
производными от этих, то мы их также объединим в один,
второй род и каждому в отдельности отрезку припишем
двойные индексы, первые из которых будут указывать род
в группе, а вторые—класс в данном роде.
Класс биномиального или вычета первого рода опреде-
ляется, по Евклиду, следующим образом: рассматривается
отношение квадратного корня из разности квадратов сла-
гаемых к первому слагаемому
Vw3 — У2
и
Существенно здесь и в дальнейшем, что и > и. Ясно,
что могут быть только два случая: либо это отношение
рационально в современном смысле, либо иррационально,
т. е.
. ум2-у2 , о у и2-у2
1. ------= г, либо 2. --------=G
и и
где г означает рациональное число, i — иррациональное.
ДЕСЯТАЯ КНИГА «НАЧАЛ» ЕВКЛИДА
351
В каждом из этих случаев могут быть три различных под-
случая:
a) w = r, г = /, Ь) u = Z, u = r, с) w = Z, v = i.
В зависимости от этого и получается шесть классов
биномиальных и вычетов:
. /и2 -
1. г -----— г-
и '
а) и = г, v = i, w±v = B11, Лц
(бином, и вычет первого класса),
Ь) u — i, v = r, u±voBlit Л12
(бином, и вычет второго класса),
с) u = i, u±v — Bl3t Л13
(бином, и вычет третьего класса).
2.
и ’
а) w = r, v~i, и ± v = Blit Al4
(бином, и вычет четвёртого класса),
b) u — i, v = r, и ± г = В15, Л15
(бином, и вычет пятого класса),
с) u = i, v — it u±u = Ble, Ли
(бином, и вычет шестого класса).
Иррациональные отрезки второго рода (по нашей клас-
сификации) определяются следующим образом. Прежде
всего, некоторые из В и Л, определённых нами выше, вхо-
дят также и во второй род; обозначим их через В21 и Л21,
отложив пока их более конкретное определение. В22
и Л22 (ex 8ио piacov и p.saij; апотор/у} тгрокт]) опреде-
ляются как сумма и разность двух средних отрезков,
соизмеримых только в степени и произведение кото-
рых образует рациональную площадь. Такими будут отрез-
ки, выражающиеся формулами
352
А. Г. РАИК
В23 и Л2Я (ix ?ио pEowv сеотЕ^а и pEOTj; Агстср^ сготЕ^а)
представляют собой сумму и разность двух средних отрез-
ков, соизмеримых только в степени, и произведение кото-
рых образует среднюю площадь. Таковы отрезки:
вгг, Лз --= аЬ ± J •
B2i и A2l (ue<iov и ёлаоасоу) получаются в результате
сложения и вычитания двух отрезков, несоизмеримых
в степени, произведение которых образует средний прямо-
угольник, а сумма квадратов, построенных на этих отрез-
ках, есть рациональная площадь,— т. е. они удовлетворяют
212 и3 .
системе ir + ir-=r, при условии, что ~2 -
В2п И А2. (pTpCV У7Л pEGO'J Ги^аиЕ^Т) и VJ psxa OTQTGU pfGGV
то oUv велось) представляют собой сумму и разность двух
отрезков, несоизмеримых в степени, произведение кото-
рых образует рациональный прямоугольник, а сумма
квадратов, построенных на этих отрезках, составляет
среднюю площадь. Эти слагаемые удовлетворяют системе
гг2 4-и2 = r1? uv = r, причём = Л
И, наконец, B2ti и А2Ъ (vj ;ug aEox Strop ev?) и 7) цеха
p-eggv -»eCqv tg 6agv толса ) определяются как сумма и раз-
ность двух несоизмеримых в степени отрезков, произведе-
ние которых образует средний прямоугольник, а сумма
квадратов, построенных на этих отрезках, есть тоже сред-
няя площадь, а именно, а и v удовлетворяют системе
и2 + и2 = ]/Г1> ао - j/’r., и
Естественно встают вопросы: какой смысл в такой клас-
сификации, какую цель опа преследует, каково её мате-
матическое содержание?
По существу, в литературе мы довольно редко встре-
чаем попытки ответить именно па эти вопросы.
У Евклида отсутствует такой мощный аппарат, как
язык формул современной математики. Поэтому естествен-
но, что комментарии и дополнения, которыми снабжены
переводы X книги, посвящены в основном именно переводу
ДЕСЯТАЯ КНИГА «НАЧАЛ» ЕВКЛИДА
важнейших её определений и предложений на современный
язык формул.
На русскОхМ языке имеется единственный перевод
X книги, сделанный М.Е. Ващенко-Захарченко (Киев, 1880).
Автор даёт в качестве приложения довольно подробное
изложение содержания. Однако дальше представления
иррациональных величин алгебраическими формулами он
не пошёл. Содержание всей книги в целом он определяет
как учение о несоизмеримых величинах и их приложениях
к геометрии.
Нетрудно было, конечно, обнаружить, что все класси-
фицируемые Евклидом иррациональные величины можно
рассматривать как корни квадратных и биквадратных
уравнений. Больше того, последние три формы иррацио-
нальных величин второго рода (по нашей классификации)
состоят из слагаемых, которые, в свою очередь, задаются
системой
u2 + v2 = Qlt uv = Q2.
Однако следует строго различать две вещи: системы
уравнений
®2+yS = 91> ^У=Чг, (О
решениями которых являются иррациональные величины
второго рода, от систем
и2 + v2 — Qi, uv = Q2 (2)
и
которыми определяются составные части и л г иррацио-
нальных величин х и у. Именно:
x = u + vt y-u — v.
Ибо, как мы увидим ниже, Евклид по-разному выражает
решения аналогичных систем (1) и (2) .
Связь евклидовой классификации квадратичных ирра-
циональностей с квадратными и биквадратными уравне-
ниями может быть исследована двояко: 1) можно исследо-
вать те квадратные и биквадратные уравнения, корнями
которых служат рассматриваемые Евклидом типы ирраци-
23 Псторпко-математ. исследования
354
A. F. УЛИК
ональностей, и 2) можно исследовать те квадратные и
биквадратные уравнения, которые приводит сам Евклид
и которые служат для определения составных частей
классифицируемых им иррациональностей.
С. А. Христензен1) рассматривает выражение
(3)
которое является иррациональным корнем квадратного
уравнения
х (а — х) = b
(для случая х (х ± а) — b он рассматривает соответственно
выражение
/?+* ± f )•
Если теперь обозначить выражение (3) через х ± у, то
условия, определяющие все шесть классов биномиальных
и вычетов первого рода, будут выражены равенствами
(»»., очевидно, неквадратное число. —А. Р.).
Выражая х и у формулами
х = тъ, У ~ т У а2 — р2,
mi
Х = j/xs-ps ’ У~т>
х = та У v, у = тУу'J/а7— р-,
х = /на, = | а2 —р,
пи
х — - > , у = т,
/а2-3 *
х = тх У Y, у = т ]/ у У а2 —р 2),
S. Л. Christensen, Ueber Gleichungen vierten Grades
im zehnten Buch der Elemente Euklid’s. (Zeitschrift fur M u P
XXXIV, 1889, стр., 201-ЧИ7).
2) m, а, 3 и у—рациональные числа.—A. P.
ДЕСЯТАЯ КНИГА «НлЧЛЛ» ЕГ.К.ЧПДЛ
355
он соответственно и получает все шесть классов биномиаль-
ных и вычетов первого рода. Так как х2 — у2 = Ь, он делает
естественный вывод, что все шесть классов биномиальных
и вычетов получаются в зависимости от характера коэф-
фициентов а и b квадратного уравнения.
В чём состоит, однако, специальный характер этих
коэффициентов, определяющий выбор рассматриваемых
Евклидом классов иррациональностей, так и остаётся не-
выясненным.
Что касается квадратичных иррациональностей второго
рода (в нашей классификации 2?21, В22,..., В2е, Л21,
А22... , Л2в), то Христензен ограничивается лишь указа-
нием, что они получаются, если сложить или вычесть
корни системы уравнений вида
и2 г2 = А, uv = В
при условии, что
т w2
L
1. А = г, В = i,
2. А = г, В = г,
3. Л = £, В = г;
Пи~“ •
1. .4 = ?, B = i,
2. Л = £, В = г,
3. Л = /, B = i.
Вопрос об уравнениях (соответственно,системах уравне-
ний), для которых рассматриваемые Евклидом иррацио-
нальности второго рода служат решениями, при этом совер-
шенно не рассматривается.
Более глубоко подходит к вопросу Г. Цейтен. Одно
из мест его книги «История математики в древности и в
средние века»х) даёт даже некоторое основание предпола-
гать, что Цейтен имел исчерпывающий ответ на поставлен-
ные нами вопросы. Действительно, место это гласит:
!) Издание 1932 г., стр. 50.
2.>*
356
А. Е. РАНК
«Так как всякий отрезок похож на любой другой отрезок,
то этим способом (геометрическим построением—А. Р)
нельзя было достигнуть прозрачности нашей алгебраиче-
ской символики и пришлось предпринятьклассификацию-
иррациопальных количеств, получаемых при последова-
тельных решениях уравнений второй степени. Попытку
такого рода классификации предпринял во времена Плато-
на Тэетет, работу которого продолжал Евклид, включив
её в десятую книгу «Начал». При разборе этой книги мы
вернёмся к этому вопросу».
Однако, возвращаясь к этому вопросу на стр. 112,
Цейтен пишет: «несмотря на тщательное изложение Ев-
клидом материала, его трудно охватить, ибо нелегко, не
обладая никакой системой знаков, разобраться среди
классифицированных в этой книге иррациональных ве-
личин».
Что мешает, однако, Цейтену ввести соответствующую
систему знаков? Повидимому, только убеждение в том, что
и выполнивши это, он пе получит достаточно простого, что-
бы его можно было поместить в учебнике по истории мате-
матики, результата. Иными словами, Цейтен убеждён
в том, что в основе классификации Евклида не лежат
какие-нибудь простые и легко обозримые принципы.
Действительно, Цейтен вовсе не избегает современной
символики при освещении содержания X книги. Непосред-
ственно вслед за приведённым местом он пишет: «Мы сами
ограничимся здесь тем, что попытаемся дать с помощью
современных символов некоторое представление о том, что
представляют собой классифицированные в этой книге
величины, не останавливаясь на вопросе о наименованиях,
служащих Евклиду для классификации их».
Таким образом, несмотря на обещание, Цейтен не дал
исчерпывающего ответа на интересующие пас вопросы.
По существу он ограничился указанием на то, что класси-
фицируемые Евклидом количества получаются «при по-
следовательных решениях уравнений второй степени».
Указание это, конечно, совершенно правильно, но, По-
скольку у Евклида и не могло быть никаких иррациональ-
ностей, кроме квадратичных, оно не только слишком обще,
но и совершенно тривиально.
ДЕСЯТАЯ КНИГА «НАЧАЛ» ЕВКЛИДА
357
Более полным является исследование X книги, принад-
лежащее Хису1). Он действительно показал, что положи-
тельные корни квадратного уравнения
х2± 2wp (4)
где р есть некоторый рациональный, в смысле Евклида, от-
резок, выражаются каждый одной из шести классов би-
номиальных и вычетов первого рода, т. е. одним из отрез-
ков Bllt Bl2,... , Bie, Ли, , Л1в в зависимости от
соотношения между коэффициентами аир и специального
их выражения. А именно:
1) если а есть рациональное, в нашем смысле, число и
то решениями будут Bllt Au и В12, Л12; если же р так
не выражается через а, то решениями будут 2?14, Л14, и
2) если а есть квадратный корень из неквадратного
рационального числа и
₽?п2 „ D т'г
= -v а*- или р =------; а-,
то решениями будут B1ZJ А13 при условии иррациональ-
ности ]/ а2 ± р; если же р так не выражается через а, то
притом же условии иррациональности )/а2±р решениями
будут В1в иА1в. Если/аЧГР рационален, ‘ то решени-
ями будут некоторые из отрезков случая 1).
Что касается отрезков, названных нами j?21, В22,..., В26,
A211A22,---, Л2в,то Хис отмечает, что они получаются,
если извлечь квадратные корни из произведений положи-
тельных решений квадратного уравнения (4) на р. Таким
образом, они являются решениями биквадратного уравне-
ния, сводящегося к квадратному,
х* ± 2ая2р2 ± рр4 = 0.
*) Т. L. Н е a th. The Thirteen Books of Euclid’s Elements. Vol.
III. 1926, стр. 5—7.
358
A. E. РАИК
Тут же он показывает вид тех биквадратных уравнений,
положительными решениями которых являются иррацио-
нальные отрезки второго рода, по нашей классификации,
а именно:
я4 - 2 (1 4- к)/х2 + (1 - Л)2/ = О = В31, х2 = Л21),
ж1-2|/'Л(1 + Л)1?ж2 + Л:(1-А:)2р4 = 0 (жх = В22, я2 = Л22),
+ (xt = Bi2, х,^Агг),
х* — 2,>2х2 Ч—*—12 р4 = 0 BZi) Х-2= Aztjt
х' ~ + (1+Л=)2 ?4 = 0 <**= х‘=л’5)’
х* — 2 |/"л р2#2 4- X j-_j_-£2 р4 = 0 (з/1 = В2в, я3 = Л2в),
(к и л—неквадратные рациональные числа.—А. А).
«X книга,—говорит Хис,—представляет склад резуль-
татов, к которым могут быть отнесены проблемы, завися-
щие от решения некоторых типов уравнений квадратных
и биквадратных, сводимых к квадратным».
Однако ни конкретного указания круга этих проблем,
ни вообще какого-нибудь объяснения, почему Евклид
ограничился своими 23 видами иррациональных коли-
честв, мы у Хиса не находим. Не освещён и вопрос о роли
и месте X книги в общей системе Ееклида.
Никто из указанных авторов даже не ставит вопроса
о полноте евклидовой классификации иррациональных
величин. Лишь А. де Морган1) отмечает, что рассматри-
ваемые Евклидом иррациональные величины представ-
ляют полную систему величин, выражаемых формулой
Уb, где а и Ь~соизмеримые величины, «без вся-
кого пропуска и без всякого излишка». Но и здесь мы не
находим ответа на вопрос о том, какие же цели преследо-
A.de Morgan^ Irrational Quantity (Penny Cyclopaedia,
1837, t. 13, стр. 35—38).
ДЕСЯТАЯ КНИГА «Н \ЧАЛ» ЕВКЛИДА
359
вал Евклид своей классификацией, чем объясняется вы-
бор иррациональностей именно такого вида. II. Тимчен-
ко1)—очень знающий историк математики, и безусловный
знаток всей существовавшей в его пору литературы ио
истории математики,—ссылаясь на Моргана, ограничи-
вается фразой: «Евклид исследует эти inediale, биномы
и отрезки и с ними всё разнообразие более сложных
иррациональных величин, заключённых в общей формуле
jZ а ± ]/" Ъ ». Это свидетельствует о том, что и после
Моргана остаётся неясным, какова цель X книги.
В арабском переводе греческого комментария к
X книге «Начал»2), открытом в середине прошлого столетия
Вёпке3), указывается, что целью этой книги являются
исследования соизмеримых и несоизмеримых, рациональ-
ных и иррациональных величин, причём эта теория, на-
чало которой восходит к пифагорейцам, была сильно раз-
вита Тэететом Афинским, который различал известные
виды иррациональностей, относя средние к геометрии
(среднегеометрические), биномиальные к арифметике
(среднеарифметические) и вычеты к гармонике (средне-
гармонические).
§ 3. Некоторые соображения о принципах
классификации
Вопрос о содержании X книги, её месте и значении в
системе Евклида, таким образом, и до сих пор нельзя
считать решённым. Мы попытаемся высказать ио этому
поводу некоторые соображения. В первую очередь нас
будет интересовать формулировка принципа, позвол я-
х) Ф. К эд ж о р и, «История элементарной математики». 2-е изд..
1917. Прибавления редактора II. 10. Тимченко, стр. 378—380.
2) II. Suter, Der Kommentar dos Pappus zum X Buch dos.
Euklidesausderarabischen Ubersetzung des Abu Othman al-Dimashki
ins deutscho iibertragen (Abhandlungcn zur Gcschichte der Natur-
wisseenschaften und der Medizin. Heft IV 1922, стр. 9—78).
8) F. W о e p c k e, Essai d’une restitution de travaux perdus
d*Apollonius sur les quantics irrationelles (M6moires present 6s
a 1’Academic dos Sciences. XIV, 1856, стр. 658—720).
360
A. E. РАИК
ющего легко и просто обозреть всю совокупность типов
классифицируемых Евклидом иррациональностей и, та-
ким образом, разобраться в них.
В качестве нашего отправного пункта мы возьмём си-
стему двух уравнений с двумя неизвестными
х + у=--2Р, xy — Q,
где Р есть отрезок, a (>—площадь. Пусть Р и Q—рациональ-
ные , в смысле Евклид а, величины, т.е. Р может выражать-
ся или рациональным (в нашем смысле) числом или
квадратным корнем из рационального числа, a Q только
рациональным ( в нашем смысле) числом. Так какР и Q
соизмеримые либо подлине, либо только в степени отрезки,
то отношение их равняется либо к, либо к, где к —
неквадратное рациональное число х). В зависимости от этих
условий относительно Р и к 2) различных систем может
быть только четыре:
1. х-\-у = 2р,
2. х+у = 2\Гр,
3. х + у = 2р,
4. х 4- у = 2 }/"р,
ху = №р~, '
ху = №р,
ху = к^, ।
ху=кр. J
(А)
Различных же иррациональных (в смысле Евклида)
решений этих систем будет точно шесть. В самом деле,
обратимся к таблице, помещенной на стр. 361.
Так как речь идёт о классификации квадратичных ирра-
циональностей, то случаи рациональных корней нас не
интересуют. Одновременно мы указали в этой таблице
и вид каждого решения по классификации Евклида, а
именно: иррациональным решением первой системы будут
Вц и Ли, второй — В12 и Л12 или В13 и Л18 в зависи-
мости от того, будет ли дискриминант системы квадрат-
ным числом или неквадратным, третьей — Ви и Л14 и,
*) Необходимость этого условия будет разъяснена ниже-
г) Ясно, что они независимы между собой.
№ системы р /<? р Q Решение системы Класс бином. и вычета
|/?-Q р
1 / к к2р2 г г Рациональные числа
1 2/' к *~Р" i 1 х, у = р р2 — к~р2 ^’и> hi
1 2/й к Kzp г i X , ?/ = /‘р Vp— и-р В12, Л1з
> 2//> к к2р i ( г Рациональные, в смысле
) I Евклипа, величины
' i х ,у = р 4 yf р — к2р
( 2 о кр2 г г Рациональные числа
1 )/ к кр- i i ^>2/ = />± уГрг-кр2 ^14>Х14
X / - /« кр г i Х>У = VР Vр -кр ^15>^15
1 /« кр 1 ( г Рациональные, в смысле
i Евклида, величины
’ i X ,у=Ур_ У р — пр ^1в>Ав
ДЕСЯТАЯ КНИГА «НАЧАЛ» ЕВКЛИДА
362
A. E. PA1IK
наконец, четвёртой— Z?15 и Л15 или В1в и Л16 тоже в зави-
симости от того, будет ли дискриминант системы квадрат-
ным или неквадратным числом.
Итак, в случае соизмеримости по длине Р и квадратного
корня из Q, т. е. когда = Л, получаем в качестве реше-
ния системы биномиальные и вычеты первых трёх классов
первого рода, а_в случае соизмеримости только в степени,
т. е, когда^О-=угк, остальные три.
Ясно также, что иррациональные решения систем
исчерпываются полностью шестью классами биномиальных
и вычетов первого рода и, наоборот, для каждой пары соот-
ветствующих друг другу биномиального и вычета среди
систем (А) найдётся только одна единственная система,
для которой эта пара есть решение.
Таким образом, шесть классов биномиальных и вычетов
первого рода являются полной системой иррациональных
решений систем двух уравнений с двумя неизвестными вида
х + у = 2Р, xy = Q
с рациональными, в смысле Евклида, коэффициентами Р и Q.
Что же собой представляют остальные иррациональные
отрезки Евклида, которые, кстати, в «Началах» рассматри-
ваются ранее предыдущих и которые К. Таер1) назы-
вает «главными формами»?
Прежде всего обратимся к 54—59-му и 91—96-му пред-
ложениям, в которых Евклид показывает, что все 12 форм
иррациональных отрезков, соответствующих нашим обо-
значениям В21, В22,... , В2в, Л21, А22,... , А2в, являются
квадратными корнями из биномиальных и вычетов пер-
вого рода, а именно:
В2/ = В1}’, A2j = ]/~Atf (j = 1, 2, ..., 6).
Отсюда следует, что эти иррациональные отрезки яв-
ляются решениями следующих систем двух уравнении
т) Cl. Т h а е г, нит. соч., стр. 105.
ДЕСЯТАЯ КНИГА «НАЧАЛ» ЕВКЛИДА
363
с двумя неизвестными, приводящихся к биквадратным
уравнениям:
V) x' +y^2q) xy~kq, _
2') »2 + y2 = 2/j, ay=k^q,
3') »2+?/2 = 2g, xy = ]^kq,
x--\-y" = 2y/'q, xy^y~k-}^q.
Коэффициентами этих систем служат рациональные
и средние площади. Заменой = У2 —У системы (В)
приводятся к системам (А) относительно неизвестных
х и у, коэффициенты которых рациональны, в смысле
Евклида, и удовлетворяют тем же соотношениям соизме-
римости и несоизмеримости, как и в системах (А).
Конечно, у самого Евклида мы такой замены не находим:
ведь, при этом ему пришлось бы рассматривать площади
ж2, у2, q как отрезки, так как возведение площади в квад-
рат для него лишено смысла. В качестве иллюстрации того,
как Евклид справляется с трудностями этого рода, при-
ведём доказательство 33-го предложения.
Тут требуется найти два отрезка, несоизмеримых в степе-
ни, которые были бы сторонами среднего прямоугольника,
а сумма квадратов, построенных на них, составляла бы
рациональную площадь. В переводе на современный язык
речь идёт об отыскании четырёх чисел и, г, а, 6,удовле-
творяющих условиям
где а и Ь должны быть рациональными, в нашем смысле,
числами, произведение которых—пеквадр атное число, а
и2
отношение ^- — иррациональное, в нашем смысле, число.
Так как и и v определяются выбором чисел а и Ь, то
фактически мы имеем дело с решением системы
364
Л. Е. РЛИК
Если внимательно проследить за ходом доказатель-
ства, то убедимся, что Евклид сводит систему
гг* 2 _|_ и2 = а, иу =
к системе
, , г- , . Ъ
и и = у (7, и г — —
заменой
и2 = и' |/а, г2 = и7 | а.
Действительно, он берёт два соизмеримых только
в степени отрезка = и BC = ]fb *), которые
удовлетворяют условию, что
АВ*—ВС2 несоизмерим по
/ длине с АВ2), затем делит
/ \\ АВ в точке Е на такие две
/ \Д части, произведение кото-
------------1—^ рых
Е АЕ-ЕВ^™-*
4 4
Так как [/ АВ* — ВС* несоизмерим по длине с АВ,
то, согласно 18-му предложению этой книги, отрезки
АЕ и ЕВ также несоизмеримы по длине между собой
и с АВ3 * *). Определив отрезки АЕ = и' и EB=v', полу-
чаем затем с помощью построения, указанного на ри-
сунке, отрезки и = AF и v = BF, которые удовлетворяют
условию поставленной задачи, а именно:
к2 4- е = AF* 4- BF* = АВ2 = а,
т. е. рациональной йлощади, а
uv — AB -EF = /a-l/
1 г 4 2
х) Произведение db есть поэтому неквадратное рациональное
число.
2) X, 30 содержит доказательство существования таких отрезков.
а—b
8) Если----неквадратное число, то и (а—Ь,а тоже неквад-
ратное число.
ДЕСЯТАЯ КНИГА «НАЧАЛ» ЕВКЛИДА
365
т. е. средней площади. Но AF есть средняя пропорциональ-
ная между АВ и АЕ, a BF— средняя пропорциональная
между АВ и ЕВ, таким образом, и2 = и J г а, V2 = и' j/a,
и3 и/
причем — = у = иррациональному, в нашем смысле, числу.
Итак, иррациональные отрезки второго рода В21,,
B*at Agl,... , А2в являются полной системой решений для
систем вида
x2 + y* = qlt xy = q2,
которые сводятся к системам
х+у=Р, xy = Q
с рациональными, в смысле Евклида, коэффициентами.
Само собой разумеется, что решения систем
х-у = Р, xy=Q,
xy=q„_
с рациональными, в смысле Евклида, коэффициентами
также принадлежат совокупности рассматриваемых Евкли-
дом квадратичных иррациональностей.
Таким образом, все классифицируемые Евклидом
иррациональные отрезки суть не что иное, как решения
следующих систем двух уравнений с двумя неизвестными
(Л, Р, Q—рациональные1) числа):
х ± у=2р,_
х ± у = 2|//>,
х ±у = 2р,^
х±у = 2\/'р,
.ж3 ± y* = 2q,
х3±/ = 2)/ q,
х" ±у' = 2q,
х- ± у2=2|/q,
xy = k"p\
xy=k"p,
xy=kp\
xy=kp,
xy=kq,
xy=k]/jp
xy=\^kq,
xy = ]^k- V q.
(C)
l) Если они встречаются под знаком корня, то ясно, что
речь идет о неквадратном рациональном числе.
3ft С Л. I . ПАНК
Отсюда мы вправе сделать вывод, что в X книге Евклид
фактически построил полную классификацию решений
квадратных и приводящихся к квадратным биквадрат-
ных уравнений с рациональными, в смысле Евклида,
коэффициентами. Понятно поэтому, почему среди рас-
сматриваемых нами систем пет, например, таких как
следующие:
х±у = 2р, ху=к\/р,
х±у = 2[/"р, ху=к]'р.
Здесь р—средняя площадьп не есть рациональная,
в смысле Евклида, величина. Других же систем с рацио-
нальными, в смысле Евклида, коэффициентами пет.
Евклид и здесь верен себе: он оперирует только од-
нородными величинами; в системах (А) Р есть отрезок, a Q—
площадь, поэтому Р может выражаться квадратным кор-
нем из рационального числа, a Q нет.
Однако следует здесь же сделать одно весьма существен-
ное замечание: на первый взгляд может показаться,что
речь идёт вовсе не о том, что содержится в X книге, так-
как Евклид классифицирует 22 иррациональные величины
(кроме средней), а у нас получается якобы 24. Но это не-
доразумение разъясняется довольно просто. Одновременно
мы получим ответы и на следующие вопросы. Во-первых,
почему Евклид, который, как уже было упомянуто, в
предложениях 54- 59-м и 91 —96-м доказывает, что
= и = выражают иррациональности
второго рода по через корни из иррациональностей
первого рода, а в виде суммы п разности двух величин?
И, во-вторых, почему Евклид классифицирует сначала
корни биквадратных уравнений, а затем лишь корни
квадратных уравнений?
Дело в том, что тут встаёт следующий вопрос, есте-
ственно связанный со всякой классификацией: рассматри-
ваемые в ней классы не должны иметь общих элементов,
одна и та же иррациональность не должна принадлежать
двум классам. Само собой разумеется, что рассмотренные
нами раньше 12 классов иррациональностей первого рода
ДЕСЯТАЯ КНИГА «НАЧАЛ» Е]КЛИДА
3G7
В16, А1в не имеют общих элементов. Поэтому
нс имеют общих элементов и рассмотренные нами классы
^21, Б22,..., Б2в, Л21, Л22,..., Л2в второго рода1). Однако
при сравнении между собой иррациональностей различных
родов Bkj и Ак}- (Л=1,2; /=1,2,...,6) немедленно обнару-
живается (Евклид доказывает это в предложениях 54 и 91,
утверждающих, что В1Г и Ап есть биномиальная и
вычет), что они могут иметь общие элементы. Именно
и Л21 = ]/ Лп могут принадлежать к любому
классу биномиальных и вычетов первого рода. Иными сло-
вами,
1 i 71 Г . / « + аЬ , , /а - ab
( а + а /1 — Ь2 = у + у , ,
где а 4- аУ 1 — Ь2 = Вц
(корни справа могут извлекаться, но не одновременно).
Таким образом, приведённая нами классификация по
классам Вк, и Akj по является удовлетворительной. Но
так как в пашем классе Вг1 и Л21 нет никаких иррациональ-
ностей нового по сравнению с остальными классами типа, то
Евклид выходит из затруднения очень просто: класса,
соответствующего нашему В21 и А21, в его классификации
пет. Поэтому мы находим в X книге не 24, а только 22
вида различных иррациональностей (кроме среднего отрез-
ка). Тут же мы получили и ответ на вопрос о том, почему
Евклид представляет иррациональности второго рода в
виде суммы и разности, т. е. аналогично биномиальным и
вычетам первого рода. Только такое представление и даёт
ему возможность обеспечить отсутствие общих элементов
в рассматриваемых им классах.
Теперь уже также совершенно ясно, почему Евклиду
следовало начать свою классификацию с корней биквадрат-
ных уравнений. Он, конечно, сразу должен был обна-
ружить, что корнями некоторых биквадратных уравнений
являются те же иррациональные величины, которые явля-
г) Евклид специально доказывает, что его классы иррациональ-
ностей ие имеют общих элементов в дополнении к 72-му предложе-
нию, в 111-м предложении и в дополнении к нему.
36 S
Л. F.РАИК
ютс.я корнями квадратных уравнений, т. е. что совокупность
корней биквадратных уравнений содержит как частный
случай и корни квадратных уравнений.
В связи с этим находит своё оправдание непонятное на
первый взгляд появление /(>( =/и2- и2) — величины,
отношение которой к Р(=и) собственно и производит раз-
биение биномиальных и вычетов первого рода, т. е. реше-
ний квадратных уравнений, на шесть классов. Ведь
можно независимо от этого отношения получить другую,
тоже полную систему взаимно непересецающихся классов
иррациональных решений квадратных уравнений. Одна-
ко необходимость этого условия вызывается классифика-
цией корней биквадратных уравнений. В самом деле,
решения биквадратных уравнений, сводящихся к квадрат-
ным вида x-Yy = P, xy = Q, выражаются формулами
II вполне естественно классифицировать эти величины в
зависимости от соотношений между Р и ]/ Q Отсюда сле-
дует, что основой евклидовой классификации квадратичных
1) Если класс иррациональности
олределлетел
рациональностью или иррациональностью величин
н пх отношения
, т. е. зависит от коэффициента Р и диск
римипанта системы
то класс иррациональности
х + у=Р,
xy^=Q,
представлен-
j/yi |/y-Q =/« + V
пой в виде
ДЕСЯТАЯ КНИГА «НАЧАЛ» ЕВКЛИДА
369
иррациональностей является классификация решений би-
квадратных уравнений.
Какой же смысл в этой классификации отрезков, кото-
рой посвящена большая часть X книги, если задачи ре-
шаются всё равно не вычислением, а построением?
Сточкизрения геометрии построенийпроводимая Евкли-
дом классификация смысла не имеет. Значит, объяснение
этого факта следует искать за пределами геометрии постро-
ений, невидимому, всё же в арифметике. И здесь уместно
вспомнить, что Евклид называет отрезок, соизмеримый
с единицей только в степени, тоже рациональной величиной.
Почему отрезок, который измеряется квадратным корнем
из рационального числа, Евклид включает в совокупность
рациональных величин?
Не хочет ли он тем самым показать, что такие отрезки
равноправны с рациональными отрезками, что они прин-
ципиально не отличаются от них? Прежде всего эти
отрезки однозначно выражаются с помощью рациональ-
ного числа (их подкоренного), причём сравнение их по
величине сводится к сравнению рациональных чисел (под-
коренных).
Но самое существенное состоит в следующем: для пас
геометрия начинается с линейных образов. В метрической
геометрии поэтому единицей измерения служит отрезок.
Сравнение площадей сводится к сравнению отрезков.
В известном смысле то же самое делает и Евклид. II у него
вводится в качестве единицы измерения рациональный
отрезок. Сравнение же площадей прямолинейных фигур
выполняется у Евклида следующим образом: уже в первой
книге он показывает, что всякую прямолинейную фигуру
определяется еще дискриминантом системы*
2и + 2и = Р,
2u. 2t> —Q,
4
равным О^Такпм образом, обе системы уравнений (1) и (2), о
которых у нас шла речь па стр. ЗоЗ которые лишь поочередно
привлекали внимание исследователей, должны играть роль при
определении класса иррациональности.
24 Историко-математ. исследования
370
A. E. РАИК
можно преобразовать построением в равновеликий ей
прямоугольник. Специальному изучению прямоугольни-
ков посвящена вторая книга, завершающаяся преобразо-
ванием прямоугольника в равновеликий ему квадрат (II,
14). Казалось бы, Евклид, таким образом, свёл сравнение
площадей прямоугольных фигур по величине к сравнению
отрезков. На самом деле для Евклида площадь в изве-
стной мере более общее понятие, чем отрезок. Дейст-
вительно, не только сравнение площадей может быть
приведено к сравнению отрезков, но и наоборот: сравне-
ние отрезков может быть сведено к сравнению площа-
дей квадратов, построенных на этих отрезках, при этом
несоизмеримым между собой отрезкам могут соответство-
вать иногда соизмеримые между собой площади. Так
обстоит дело в случае отрезков, рациональных в смысле
Евклида, т. е. выражающихся корнем квадратным из
рационального, в нашем смысле, числа.
Заметим, что это сведение несоизмеримых величин к
соизмеримым в системе Евклида проходит только для
отрезков, измеряющихся квадратными корнями из рацио-
нальных величин: 1) неквадратичные иррациональности
циркулем и линейкой не могут быть построены, 2) для
квадратичных иррациональностей более высоких степеней
площади их квадратов, вообще говоря, сами уже несоизме-
римы между собой. (Тут нужно иметь в виду, что произведе-
ние двух отрезков, равно как и квадрат, построен-
ный на отрезке, для Евклида есть всегда площадь, а
не отрезок.)
Однако и в новой области рациональности, содержащей
все те и только те числа,которые выражаются корнем квад-
ратным из рационального, в нашем смысле, числа, не
всякое квадратное и биквадратное уравнения с рациональ-
ными, в смысле Евклида, коэффициентами (и, конечно, с
положительными и действительными корнями) разрешимы,
так как а+]/Ь или j/a+j/H не всегда может быть выражено
в виде Ус, где с—рациональное число. То обстоятельство,
что Евклид не считает сумму двух рациональных, в его
смысле, величин также рациональной, говорит опять-
таки в пользу пашей гипотезы о сведении сравнения по
длине к сравнению по площади.
ДЕСЯТАЯ КНИГ\«НАЧАЛ» ЕЕКЛИДА
371
Нам кажется, что сами названия наиболее сложно пред-
ставимых квадратичных иррациональностей второго рода
также говорят в пользу нашей гипотезы. В самом деле,
например, греческое название В2Ь означает такой отрезок,
для которого площадь построенного на нём квадрата рав-
на сумме средней и рациональной площади, т. е. отрезок
измеряется площадью квадрата, построенного на нём. То
же самое относится и к отрезкам В2в, И2б и Л2в.
§ 4. Роль X книги в системе «Начал» Евклида
Теперь мы можем вернуться к вопросу, для чего нужна
Евклиду его классификация, если задачи всё равно ре-
шаются не вычислением, а построением. Для ответа на
этот вопрос заметим прежде всего, что Евклид отнюдь не
ограничивается своей классификацией. Он доказывает, и
это самое существенное, что в пределах каждого класса
иррациональностей всякая иррациональность единствен-
ным способом выражается в избранной им канонической
форме. В предложениях X, 42—47 и 79—84 Евклид дока-
зывает, что рассматриваемые им иррациональные отрезки
делятся только в одной точке на свои составные части.
А именно, если, например, 4- yfb — с -f- j/d, то
а —с и b = d.
В самом деле1), пусть
]/п + j/T = \/ с + j/d,
причём а > Ь, с > d и
Z;
последнее условие существенно, ибо в противном случае
у/’а = ку^Ь, где к—рациональное число, и ]/a-t-]/ b =
= (! + *)/6 есть рациональная, в смысле Евклида,
величина. Нужно доказать, что а = с и 6==d.
*) Мы приводим доказательство Евклида в несколько модерни-
зованной форме.
24*
372
A. F. P UIK
Для доказательства возведём равенство
в квадрат. Мы получим: a + 6-|-2]/a6 = c + d + 2)/cd
ИЛИ
2)/" cd — a-\-b — с — ab.
Обозначим a-\-b — c — d через R и допустим, что R =£0.
Тогда, так как
4cd = R* + 4afc + 42?j/ab ,
и
7 тт Vab У ь
где I —рациональное число. Но тогда и отношение = ^=-
егть тоже рациональное число, что противоречит усло-
вию (5). Следовательно, R = 0, и отсюда получаем:
a + b — c-\-d = A,
ab = cd = B.
Иными словами, обе пары чисел (а, Ь) и (с, d) суть корни
одной и топ же системы
х+у = А, ху~В,
которая имеет единственную пару решений:
Л + /Д2-4Д
х —---—-----= а --- с.
2
Л-/Л2-4Я . ,
-----2-----= b = d.
1
Таким образом, решения любого квадратного и биквад-
ратного уравнения, которые соответствуют системам (А),
можно выразить единственным образом в канонической,
по Евклиду, форме.
Итак, теперь каждое иррациональное решение квад-
ратного или биквадратного уравнения с рациональными,
ДЕСЯТАЯ КНИГА «НАЧАЛ» ЕВКЛИДА 373
в смысл© Евклида,коэффициентами может быть представ-
лено совершенно однозначным образом с помощью: а) ука-
зания её (т. е. иррациональности) класса в классифика-
ции Евклида; будем называть этот класс «фамилией»
иррациональности, Ь) отнесения ей собственного «имени»,
однозначно определяющего в пределах рассматриваемого
класса именно данную индивидуальную иррациональ-
ность. Заметим, что в качестве этого «имени» в рассмотрен-
ном, например, нами случае биномиальной третьего класса
первого рода, т. е. иррациональности вида слу-
жит пара чисел а. Ъ. Действительно, в данном случае
одного числа, одного «имени» недостаточно; с помощью од-
ного «имени» можно назвать только рациональные, в
смысле Евклида, величины.
Мы все с детства привыкли употреблять слово «бином»,
но мало кто из нас связывает с этим термином представле-
ние о двойном имени, которое является, однако, первона-
чальным его смыслом. «Бином»—это перевод на латинский
язык греческого термина: «ех био ovopawv» (означающего
буквально «из двух имён»).
Итак, проблему «невыразимости», которая встала в
связи с появлением иррациональности как результата
решения квадратных и биквадратных уравнений, можно
считать снятой для тех из них, коэффициенты которых суть
рациональные, в смысле Евклида, величины. Для этих
уравнений «всё» стало «выразимо» с помощью натуральных
чисел, и Евклиду может показаться, что девиз «всё есть
число» опять торжествует.
Можно думать, что именно в последнем и надо искать
ключ к основному вопросу о роли и месте X книги в си-
стеме Евклида.
Тут нужно предостеречь от впечатления, будто введение
квадратичных иррациональностей есть расширение
Евклидом понятия о числе. С нашей точки зрения, ничего
подобного у Евклида нет. Он не рассматривает полученные
им квадратичные иррациональности как новые числа. Это-
геометрические объекты, для индивидуализации которых
должны служить в качестве «имён» целые числа.
Теперь арифметические книги Евклида, в основном
X, для которой необходимы предшествующие книги, при-
374
A. E. РАИК
обретают вполне определённый смысл и законное положе-
ние в общей системе «Начал».
Появление иррациональности могло привести к попытке
отказаться вообще от применения арифметики к геомет-
рии. Однако из геометрии Евклидом исключаются не числа,
а приближённые вычисления. Приближённые вычисления
в древнем мире считались уделом рабов, а не свободных
людей, поэтому не удивительно, что Евклид исключает
их из своих «Начал». Так как в «Началах» нет никаких кри-
вых, кроме окружности и прямых, то построение с помощью
циркуля и линейки даёт теоретически точное решение всех
задач, рассматриваемых Евклидом в «Началах».
Вообще Евклид не допускает никаких неточных реше-
ний задач: ни приближённых вычислений, ни приближён-
ных построений. В его системе поэтому нет места для ло-
гистики1). Задачи решаются не вычислением, а построе-
нием. Для рассматриваемого Евклидом круга задач по-
следние являются теоретически точными. Из этого не сле-
дует, однако, будто не логистика, а арифметика занимает
подчинённое положение в системе «Начал». Наоборот,
можно думать, что именно арифметике принадлежит при-
мат над геометрией, так как только она даёт возможность
индивидуализировать решение задачи, выполненное с по-
мощью геометрического построения. Ведь Евклид не может
ограничиться тем, что продемонстрирует полученное реше-
ние непосредственно построенным отрезком, воспринимае-
мым в его отличии от других отрезков с помощью показаний
наших органов чувств. Он должен доказать возможность
выразить полученное им решение в абстрактных математи-
ческих понятиях, удовлетворяющих, однако, требованиям
индивидуализации выражаемого отрезка. Таким по-
нятием и служит для него арифметическое натуральное
число. Число для Евклида является тем промежуточным
звеном, которое связывает мир абстрактных идей с миром
чувственных вещей.
После X книги Евклид имеет возможность не только
указать общий алгоритм построений, решающий любую
2) Известно, что логистикой греки называли арифметику, вани
мавшуюся вычислениями в том числе и приближёнными.
ДЕСЯТАЯ КНИГА «НАЧАЛ» ЕВКЛИДА
375
из задач некоторого рода. Принципиально он доказал и
возможность индивидуально «поименовать» решение дан-
ной конкретной задачи, чтобы отличить его от решений
других задач того же самого типа в зависимости от коэф-
фициентов уравнения.
В VI книге «Начал» Евклид даёт метод построения кор-
ней квадратных уравнений. Но как отличить друг от друга
решения различных квадратных уравнений? Как сформу-
лировать ответ на предложенную задачу? Это можно, ко-
нечно, сделать, сказавши: чтобы получить ответ, выполни
такие-то и такие-то операции (проведи такие-то окружно-
сти и прямые в такой-то последовательности). Но как
назвать результат всех этих построений? Как индиви-
дуализировать решение данного индивидуального урав-
нения с данными коэффициентами? Тут Евклид огра-
ничивается случаем, когда коэффициенты рациональные,
в его смысле, отрезки и площади. Но для этого случая он
доказывает возможность однозначно поименовать полу-
чаемые в каждом отдельном случае решения.
По существу, Евклид тол ько теперь может сказать, что
он действительно умеет решить любое квадратное и при-
водящееся к квадратному биквадратное уравнение с ра-
циональными, в его смысле, ^коэффициентами.
Обычно говорят, что «Начала» Евклида посвящены
изучению таких объектов, которые могут быть построены
с помощью циркуля и линейки, т. е. общей теории квад-
ратных уравнений. В действительности, хотя Евклид
и оговаривает возможность построения квадратичных ир-
рациональностей произвольной степени, но действительно
полную теорию оп строит лишь для таких квадратичных
иррациональностей, которые являются решениями квадрат-
ных и приводящихся к квадратным биквадратных урав-
нений с рациональными, в его смысле, коэффициентами.
Но зато для этих иррациональностей он действительно
строит полную теорию, позволяющую ему (если выбрана
единица измерения) выразить с помощью одних только
целых чисел индивидуальные решения конкретных квад-
ратных и биквадратных уравнений.
Следует сделать одно добавление: у Евклида доказано
только существование, и притом однозначное, «двойного
376
A. E. РАИК
имени» для решений рассматриваемого им класса квадрат-
ных и биквадратных уравнений. Ни одного числового при-
мера такого «имени» Евклид не приводит. Но это находится
в полном соответствии с отсутствием вообще в «Началах»
каких-нибудь численных примеров. Последнее связано,
быть может, и с необходимостью определенного выбора
единицы измерения, т. е. с некоторым актом, имеющим
чувственный и практический характер, которого Евклид
явно избегает.
Таким образом, содержание X книги сводится в основ-
ном к следующему:
1. Евклид даёт полную классификацию иррациональ-
ных, в его смысле, решений всех квадратных и приво-
дящихся к квадратным биквадратных уравнений с рацио-
нальными, опять-таки в его же смысле, коэффициентами.
2. Так как каждое решение квадратного и биквадрат-
ного уравнений может быть представлено бесчисленным
множеством способов, Евклиду необходимо выбрать какое-
нибудь каноническое для них представление, удовлетво-
ряющее требованию однозначности. Это он и делает, опре-
деляя биномиальные и вычеты различных родов и классов
в каждом роде через два отрезка и и о, удовлетворяющие,
определённым приведённым*нами выше требованиям, т. е.,
мы бы сказали, определяет «фамилию» каждого рассматри-
ваемого им рационального отрезка.
Логическая строгость изложения Евклида проявляется
при этом как в том, что он доказывает каждый раз непу-
стоту класса иррациональностей, определяемого данной
системой условий, так и в том, что он действительно до-
казывает однозначность предлагаемого им канонического
представления.
Однако суть X книги заключается не только в проведён-
ной в ней полной классификации решений квадратных « не-
которых биквадратных уравнений с рациональными, в смыс-
ле Евклида, коэффициентами, а в «выразимости» классифи-
цируемых величин с помощью натуральных чисел.
При помощи этих идей разрешается Евклидом и проб-
лема построения правильных многогранников. Собственно,
для определения рёбер правильных многогранников нужно
уметь решать некоторые из уравнений тех именно типов,
ДЕСЯТАЯ КНИГА «НАЧАЛ» ЕВКЛИДА
377
решения которых рассматриваются в X книге. Таким обра-
зом, можно считать, что в X книге Евклид создал арифме-
тическую базу для построения стереометрии, вернее, для
её заключительного аккорда—построения правильных тел.
X книга—это венец всего творения Евклида. С помощью
арифметики она завершает логическое построение гео-
метрии.
Теперь «Начала» Евклида действительно представляют-
ся цельной и стройной системой. Всё оказывается на своём
месте и находит своё естественное оправдание. Наоборот,
отбросим эту роль арифметики, и «Начала» окажутся
конгломератом, состоящим из отдельных, не связанных
между собой частей.
Вместе с тем для пас становится ясной и идеологи-
ческая направленность этого произведения. Место, зани-
маемое его автором в борьбе партий, происходившей и в
специальных областях науки, достаточно характеризуется
стремлением спасти потерпевший крушение в связи с
открытием иррациональности старый пифагорейский прин-
цип «Всё есть число», не «запятнав» себя при этом «през-
ренными» вычислительными операциями с числами. Ре-
шение именно этой задачи потребовало от Евклида без-
дны труда и остроумия и удалось ему в конечном счете
только потому, что в угоду своим идеологическим уста-
новкам он мог беспрепятственно выбросить из геометрии
иррациональности, не укладывавшиеся в рамки его основ-
ной схемы. Но именно этим же объясняется и то обстоя-
тельство, что X книга «Начал» сыграла очень скромную
роль в дальнейшей истории математики. Передовым ма-
тематикам нового времени были чужды идеологические
установки автора «Начал», и они лишены были возмож-
ности сказать «тем хуже для фактов», если упрямые
факты не умещались на ложе идеалистической системы.
§ 5. Краткий обзор X книги
В заключение попытаемся сделать краткий обзор X
книги в целом.
X книга «Начал» содержит 115 предложений.
Первые 18 предложений этой книги посвящены вопросу
о соизмеримости величин. Это и попятно: Евклиду надо
378
A. E. РАИН
разобраться в некотором множестве величин, среди кото-
рых имеются и такие, отношения которых не выражаются
отношением целых чисел. Поэтому он, прежде всего, уста-
навливает общий критерий, с помощью которого можно
было бы, хотя бы принципиально, определить, выражается
ли отношение данных величин отношением целых чисел или
нет (алгоритм Евклида). С другой стороны, величины,кото-
рые рассматривает Евклид, являются квадратичными ирра-
циональностями, получающимися в результате решения оп-
ределённого типа квадратных и биквадратных уравнении.
Поэтому вполне естественно установить здесь же специаль-
ный критерий рациональности квадратного корня (9-е
предложение) и разрешимости квадратного уравнения в
рациональных числах (17-е и 18-е предложения).
Получив, таким образом, возможность отделить этот
класс уравнений от уравнений с иррациональными корня-
ми, Евклид действительно может перейти к исследованию
иррациональных корней квадратных уравнений. Но в
дальнейшем ему необходимо будет пользоваться не толь-
ко отношением величин, но и их произведением; поэтому
естественно определить характер произведения двух ве-
личин в зависимости от характера их отношения. Это
Евклид и устанавливает в следующих 19—26-м предложе-
ниях, играющих, таким образом, роль вспомогательных
лемм для дальнейшего. А именно: площадь прямоугольни-
ка, стороны которого рациональные, в смысле Евклида, и
притом соизмеримые по длине, будет рациональной.
Если стороны прямоугольника рациональные, в смысле
Евклида, но соизмеримые только в степени, то площадь
прямоугольника будет средней. Площадь прямоугольника,
у которого стороны средние, соизмеримые только в степени,
может быть как рациональной, так и средней.
Последующие 27—35-е предложения невольно вызыва-
ют, на первый взгляд, недоумение: прежде чем определить
рассматриваемые классы квадратичных иррационально-
стей, Евклид в этих предложениях фактически доказывает
построением, что каждый из его классов не пуст, что дей-
ствительно существуют отрезки кис, удовлетворяющие
данной системе условий, сумма и разность которых обра-
зуют все его классы квадратичных иррациональностей.
ДЕСЯТАЯ КНИГА «НАЧАЛ» ЕВКЛИДА
379
И лишь после этих доказательств существования он опре-
деляет соответствующие классы иррациональностей. Но
такое недоумение разъясняется, как только вспомним, что
Евклид так поступает всегда: он не определяет вещи до
тех пор, пока не покажет построением, что она действитель-
но существует, иначе определение не имело бы для него
смысла.
В следующих 36—41-м и 73—78-м предложениях Евк-
лид определяет те квадратичные иррациональности, кото-
рые являются корнями биквадратных уравнений. При
этом он даёт сначала только общее определение биномиаль-
ной и вычета без указания её класса, для остальных же
классов BS2,..., Z?2e> Л22,...,Л2з приводит затем полные
определения. Как уже было выяснено, Евклид начинает
свою классификацию не с решений квадратных, а с ре-
шений биквадратных уравнений.
Кроме доказательства непустоты каждого класса, ло-
гическая строгость классификации требует ещё, чтобы
каждому рассматриваемому иррациональному отрезку мож-
но было совершенно однозначно отнести соответствующий
ему класс, иными словами, предполагает доказатель-
ство того, что классы не имеют общих элементов. Та-
кое доказательство, и притом проведённое очень акку-
ратно, мы действительно находим в X книге. Однако так
как Евклид, поскольку это возможно, начинает, как нам
представляется, с более трудных и важных для него пред-
ложений, то доказательству того, что рассматриваемые
ИхМ классы иррациональностей не имеют общих элементов,
он предпосылает доказательство того, что каждой ирраци-
ональности определённой «фамилии» однозначно соот-
ветствует в пределах этой «фамилии» вполне определённое
«имя».
Соответствующие теоремы доказываются вслед за опре-
делением этих иррациональностей: для суммы в 42—47-м,
для разности в 79 —84-м предложениях.
До сих пор фактически шла речь о квадратичных ирра-
циональностях, которые являются корнями биквадратных
уравнений. Но среди этих иррациональностей В21 и Л21
могут выражать и корни квадратных уравнений. Только
теперь Евклид приступает к их классификации. Опреде-
380
Л. F. РАПК
ляя шесть классов биномиальных и вычетов, т. е. В1, hAjj
(/=1, 2,...,6), Евклид в предложениях 48—53-м и 85—90-м
доказывает построением теоремы существования для каж-
дого класса.
Евклид нигде, конечно, не говорит о цели классифика-
ции, не говорит о том, что рассматриваемые им квадратич-
ные иррациональности являются корнями определённого
класса квадратных и биквадратных уравнении. Однако в
предложениях 54—59-м, 91 —96-м и 60 —65-м, 96 -102-м
(для суммы п разности) он себя выдаёт: в них Евклид до-
казывает, что все квадратичные иррациональности второго
рода являются квадратными корнями из соответствующих
классов квадратичных иррациональностей первого рода,
т. е. что
Blj = ^2/ И = 4*/»
и, наоборот,квадраты иррациональностей второго рода суть
соответствующие классы иррациональностей первого рода
В предложениях 71—72-ми 108—110-м Евклид рассма-
тривает, какие классы иррациональностей могут быть
получены при извлечении квадратного корня из выраже-
ний видов
« ± j/6, j/ а ± j/&, a — b.
Именно, оказывается:
Биномиальная любого
класса первого рода
^24
Z?2-
К/гТ/Ц в\\
______ ( Вычет любого класса
V a — ]Sb = j первого рода
д2
Л5
-42з
^26
ДЕСЯТАЯ КНИГ \ «И Y4 VI» I1КЛНДЛ 381
. Теперь Евклид показывает ещё, что при замене еди-
ницы измерения соизмеримой с ней по длило класс ирра-
циональности не меняется (предложения 66—70 и 103—107).
Лишь после этого Евклид доказывает, что классы рас-
сматриваемых им иррациональностей не имеют общих
элементов. Это он делает в заключении в три приёма.
В конце раздела, в котором рассматриваются квадратич-
ные иррациональности, представляющие собой суммы двух
отрезков, Евклид показывает, что все В2, отличаются от
средних и различны между собой. Затем в конце раздела,
в котором рассматриваются квадратичные иррациональ-
ности, представляющие разности двух отрезков, доказы-
вается, что все Л2; также отличны от средних и различны
между собой. И, наконец, в 111-м предложении Евклид до-
казывает, что все биномиальные отличны от всех вычетов.
По существу, на этом X книга заканчивается, ибо в
предложениях 112-м, 113-ми 114-м доказываются равенства
= }Га - )/b, /а + J/6,
+ 1 ’ ’ /а-) Ь 1 '
(|/ а + (к а — к j/fe) = к (а - Ь),
которые непосредственного отношения к рассматриваемой
классификации квадратичных иррациональностей не
имеют, хотя их происхождение может быть более раннего
времени. Как указывают Хис1) и Таер2), утверждения
Гейберга о том, что эти предложения являются поздней-
шими вставками в X книгу, представляются вполне
у бе дител ьными.
В 115-м предложении утверждается, что пос ледова
тельным извлечением квадратного корня из средних можно
получить бесчисленное множество различных иррацио-
нальностей, отличающихся от всех предыдущих. Согласно
Гсйбергу, и это предложение есть тоже позднейшая
вставка.
В конце X книги «Начал» в некоторых изданиях дастся
ещё теорема о несоизмеримости диагонали квадрата с ого
стороной.
*) Т. L. Heath, цит. соч., стр. 246.
2) Cl. Thaer, цит. соч., стр. 119.
332
A. E. РАИК
Таким образом, нет сомнения, что X книга «Начал»
представляет собой стройное целое, позволяющее одно-
значно отнести каждому иррациональному решению квад-
ратного уравнения с рациональными, в смысле Евклида,
коэффициентами или биквадратного уравнения, сводяще-
гося к квадратным, его «имя» и «фамилию», и таким обра-
зом сделать выразимым то, что по самому названию akoyoi,
казалось, могло быть только невыразимым.
В связи с X книгой не только теперь, но и в древности
естественно возникал следующий вопрос: почему Евклид
ограничился решениями только квадратных и приводя-
щихся к квадратным биквадратных уравнений с рацио-
нальными, в его смысле, коэффициентами?
Идя дальше по пути обобщения, избранному Евклидом,
естественно было избрать следующие два направления:
1) в сторону повышения степени уравнения, но урав-
нения, очевидно, трёхчленного вида
ж3” + 2ажзМ-1 + b — О,
сводящегося к квадратным уравнениям рассмотренного
выше типа, и
2) в сторону образования величин, которые выражались
бы не двумя слагаемыми, а тремя, четырьмя, пятью и т. д.,
т. е. имели бы не двойное, а тройное и т. д. «имя», что
могло соответствовать решению квадратных и биквадрат-
ных уравнений, коэффициенты которых выражались бы
полученными ранее квадратичными иррациональностями.
В сторону второго направления мы действительно
находим дальнейшее развитие вработах Аполлония. Апол-
лоний строил отрезки, которые выражаются суммой трёх,
четырёх и более рациональных, в смысле Евклида, но
соизмеримых с единицей только в степени отрезков и
средних отрезков, каждая пара которых удовлетворяет
условиям, аналогичным тем, которым удовлетворяют сла-
гаемые евклидовых отрезков1).
А) См. F W о е р с к е, цит. соч.
ДЕСЯТАЯ КНИГА «НАЧАЛ» ЕВКЛИДА
333
В каком бы направлении Евклид ни пошёл, он должен
был убедиться в бесконечности процесса. Может быть, эта
«дурная бесконечность» и остановила его на первом этапе,
на первой ступени.
Оценивая роль X книги для современной математики,
М. Е. Ващенко-Захарченко1) говорит, что «эта книга в
настоящее время не имеет значения, но замечательна, как
образец самого глубокого синтеза древних геометров».
Это, конечно, верно. Правда, в свое время и X книга
сыграла некоторую роль в развитии математики. Именно
возможность представления квадратного корня из суммы
или разности а±)/ b в виде суммы или разности двух квад-
ратных корней привела Бомбелли к мысли о представлении
кубического корня из суммы или разности a±V Ъ в виде
суммы двух корней для объяснения того, каким образом
действительный корень неприводимого кубического урав-
нения может выражаться в виде суммы или разности
двух мнимых. Однако основная роль X книги состоит
в значении, которое она имеет для понимания «Начал»
Евклида. Только эта книга, по-нашему, даёт окончатель-
ный ответ на вопрос о том, какая задача стояла перед Евк-
лидом и как он её решал в своих «Началах».
Отметим в заключение, что на наш взгляд в
X книге «Начал» Евклида нетрудно обнаружить связь
классической греческой математики с вавилонской, зави-
симость первой от последней. Оставляя в стороне вопрос
о возникновении самой геохметрии греков, о путях её
развития до зрелого оформления в законченную дедуктив-
ную науку, не будет слишком смело утверждать, что гре-
ческая математика есть продолжение и развитие (через
борьбу противоположностей) вавилонской математики.
Это проявилось не только в численных методах реше-
ния квадратных уравнений, как думает Бортолотти2). В
самом деле, ведь основное содержание X книги Евклида
раскрывается с помощью именно тех канонических
форм квадратных и биквадратных уравнений, которые
х) М. Е. Banfeti ко-Захарченко, «История матема-
тики», 1883, т. I, стр. 68.
2) Е. Bortolotti, L’Algebra nella storia e nella Preistoria
della scienza. Osiris, том '1.
334
Л. Е. PAliK
характеризуют вавилонскую математику, как науку,
а именно:
х ± у — а, ху = Ь
х2 ± у2 = а, ху = Ь.
Нам представляется наиболее вероятным, что Евклид
решал задачи и исследовал непосредственно не квад-
ратные уравнения с одним неизвестным
х~ ± рх ± q = О,
а соответствующие системы двух уравнений с двумя неиз-
вестными
х ± у— а, ху—Ь,
причём в основу его классификации квадратичных
иррациональностей им было положено исследование си-
стемы
х у = а, ху = Ь.
Эта каноническая форма, как нам кажется, должна
была послужить для пего отправным пунктом, так как
она наиболее просто и сразу охватывает все классы бино-
миальных и вычетов. После того, как классификация про-
ведена относительно системы
х-{-у = а, ху = Ь,
было уже совсем просто показать, что все положительные
решения и для системы
х — у — а, ху = Ь
попадают в эти же классы величин.