Текст
Дж. САНСОНЕ
ОБЫКНОВЕННЫЕ
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
ТОМ I
Перевод с итальянского
н. я. виленкина
с предисловием
В. В. НЕМЫЦКОГО
и * л
ИЗДАТЕЛЬСТВО
ИНОСТРАННОЙ ЛИТЕРАТУРЫ
Москва—1953
G. SANSONE
EQUAZIONI DIFFERENZIALI
NEL CAMPO REALE
Parte Prima
Seconda Edizione
BOLOONA
1948
ПРЕДИСЛОВИЕ
Два тома книги Дж. Сансоне весьма богаты по своему содержа-
содержанию. В них нашли достаточно полнее освещение такие вопросы, как
краевые задачи для обыкновенных дифференциальных уравнений, асим-
асимптотическое поведение решений линейных уравнений, теоремы суще-
существования, единственности, непрерывности и дифференцируемости ре-
решений и многие другие. Пожалуй, главной темой книги являются
весьма важные для приложений математики краевые задачи и непо-
непосредственно связанные с ними задачи об асимптотическом поведении
решений на бескбнечности. В различных главах первого и второго
томов рассмотрены всевозможные постановки линейных и нелинейных
краевых задач и разобраны самые разнообразные методы их решения.
Автор книги всюду, где это возможно, иллюстрирует общие тео-
теоремы на примерах применений к специальным функциям, доводя
в этих вопросах выкладки до окончательных формул. Последние три
главы второго тома (около трехсот страниц) посвящены обстоятель-
обстоятельному изложению чисто прикладных вопросов — операционного исчи-
исчисления, графических и вычислительных методов решения дифферен-
дифференциальных уравнений, а также вопросов теории нелинейных колебаний.
Наличие этих глав делает книгу Сансоне полезной не только для
математиков, но и для инженеров и научных работников технических
институтов, которым приходится иметь дело с дифференциальными
уравнениями.
Вместе с тем читателю бросается в глаза следующий серьезный
недостаток книги Сансоне. Автор счел нужным подробно, вплоть до
маловажных деталей, разработать темы, развивавшиеся итальянскими
математиками, и почти совсем не рассмотрел вопросов, в решении
которых итальянцы не принимали участия. К таким забытым темам
относится, например, изучение структуры семейства интегральных
кривых около особой точки, которому уделено буквально несколько
страниц. Не упоминается даже такое важнейшее понятие, как хара-
характеристические числа А. М. Ляпунова, хотя асимптотическое поведе-
поведение решений линейных уравнений второго порядка на бесконечности
представлено довольно подробно. Можно указать и много других при-
примеров такого рода.
Вследствие этого недостатка сочинение Сансоне ни в какой мере
не может служить единственной книгой для желающих ознакомиться
1*
Предисловие
с современным состоянием теории обыкновенных дифференциальных
уравнений. Мы указываем ссновной список литературы, изучение
которой может заполнить этот важный пробел:
1. Биркгоф Дж. Д., Динамические системы, М.—Л., 1941;
2. Голубев В. В., Лекции по аналитической теории диффе-
дифференциальных уравнений, М.—Л., 1952;
3. Камке Эп Справочник по обыкновенным дифференциальным
уравнениям, М., 1950;
4. Малкин И. Г., Теория устойчивости движения, М.—Л., 1952;
5. Немыцкий В. В. и Степанов В. В., Качественная
теория дифференциальных уравнений, 2-е изд., М.—Л., 1949;
6. Айне Э. А., Обыкновенные дифференциальные уравнения,
Харьков, 1939.
Кроме того, при переводе ссылки автора на популярную учебную
и обзорную литературу всюду заменены соответствующими ссылками
на литературу, распространенную среди советского читателя.
В. Немыцкий
Глава I
НОРМАЛЬНЫЕ СИСТЕМЫ
ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
И ТЕОРЕМА СУЩЕСТВОВАНИЯ ДЛЯ НИХ
§ 1. Нормальные системы
1. Определения, а) Обыкновенным дифференциальным уравне-
уравнением называется любое соотношение, связывающее независимую пере-
переменную дг, функцию у (дг) этой переменной и производные функции у (х)
до некоторого порядка включительно. Обыкновенное дифференциальное
уравнение может быть приведено к виду
F(x. v аУ
V ' у' ~dx' •"
Число т, т. е. наивысший из порядков производных, входящих
в A), называется порядком уравнения.
Например, уравнение
у'+ху — е * =0 B)
является уравнением первого порядка, а уравнение
у+у"—х = 0 C)
'—второго порядка.
б) Пусть, вообще, даны т соотношений, связывающих независи-
независимую переменную дг, т функций ух (дг), у2 (лг), ..., ут (х) этой пере-
переменной и их производные до некоторого порядка включительно
(i = l, 2,..., от).
Тогда говорят, что эти уравнения образуют систему обыкновен-
обыкновенных дифференциальных уравнений, или проще, — систему диффе-
дифференциальных уравнений.
в) Любая система функций уг (дг), у2 (дг), ..., ут (дг), удовлетво-
удовлетворяющая уравнениям D), называется частным интегралом или реше-
решением этой системы уравнений; проинтегрировать систему уравнений
означает найти все ее решения.
Легко проверить, что, какое бы значение мы ни придали постоян-
_?!
ной cv функция у — е 2 (сх -f- x) будет решением уравнения B); точно
6 Гл. /. Нормальные системы дифференциальных уравнений
так же, какие бы значения мы ни придали постоянным сг и с2, функ-
функция у = с1 cos дг-f- с2 sin Jf -J-лг будет решением уравнения C); очевидно
также, что при любых значениях постоянных с1э ?2, ce Функции
E)
удовлетворяют системе уравнений
У —у^= О1). F)
(с2 + 2cs) х
в = К + 2 +
2. Порядок системы дифференциальных уравнений, а) Две си-
системы дифференциальных уравнений называются эквивалентными,
если они обладают одними и теми же решениями.
б) Всякая система дифференциальных уравнений эквивалентна
системе, в которую входят лишь первые производные искомых
функций.
В самом деле, система D) эквивалентна системе
г
(y
*
V v
(i=l, 2, .... m; fe = l, 2, .... /я),
состоящей из iB + fo —l) + (ra —1)+...+(rm—1) = /-! + ^ +
-4-...-J-rTO уравнений относительно неизвестных функций ^ft, j>^,
-Vfc' •••» У1к*~1} (числ0 которых также равно r1-\-ri-\-... +гш) и
их производных первого порядка.
*) Дифференциальные уравнения изучались впервые Лейбницем и Нью-
Ньютоном. Эти ученые заложили основы анализа бесконечно малых, открыв
взаимосвязь операций дифференцирования и интегрирования, и проинтегри-
проинтегрировали простейшее дифференциальное уравнение у' =/(jcI
Лейбниц в 1675 г. решил уравнение уу' = bly, сведя его к виду
bdx=y*dy (см. Лейбниц [1], стр. 161).
Решение уравнения _уя=/(л), определенное с точностью до многочлена
(п — 1)-й степепи, было дано Ньютоном в его работе Tractatus de quadratura
curvarum, написанной в 1676 г. и опубликованной в качестве приложения к
его .Оптике" в 1704 г.
/. Нормальные системы
Поэтому мы можем, не теряя общности, считать* что система диф-
дифференциальных уравнений имеет вид
ri(x, yv j2, ..., ут, dx, dx, .... dx
(t=l, 2, .... m).
Натуральное число т называется порядком системы G)J).
3. Нормальные системы, а) Предположим, что функции Ft, рас-
рассматриваемые как функции своих аргументов, непрерывны вместе
с частными производными первого порядка в „прямоугольном параллеле-
параллелепипеде" tf2m+i2) с центром в точке (*<>; у\, у\, ..., у°т; у[°, /2°,, ...,
• • ¦' У'т^' к00РДинаты которой удовлетворяют системе
Ъ(*ъ fv у%> ••¦• y°J у'Л /Л •••' Уж")=° (8)
(/=1, 2, ..., ш)
Р
и что в R$m+1 якобиан —^-?—* —^- отличен от нуля. Тогда
по теореме о системе неявных функций3) найдется прямоугольный
параллелепипед Rm+\ с центром в точке (хР; у\, у%, ..., у^), в кото-
котором система (8) может быть разрешена относительно всех т произ-
производных y'v у'2, ..., у'т и записана тем самым в виде
Ж=/<(*; Л. Л. • • •> JJ (/= 1, 2, ..., и), (9)
где функции ft непрерывны и дифференцируемы по всем аргументам
в любой точке Rm+1. Системы вида (9) называются нормальными си-
системами (см. гл. VIII, § 8, п. 2).
б) Заметим, что дифференциальное уравнение тя-го порядка,
имеющее вид
0=/(*-.^ У- •••>
эквивалентно нормальной системе (y=j/j),
dyi dym-t __ . аУт_*(х.
Поэтому уравнение A0) называют нормальной формой дифферен-
дифференциального уравнения m-го порядка.
!) Этот термин не общепринят. В советской литературе по дифферен-
дифференциальным уравнениям система, подобная G), называется системой т диффе-
дифференциальных уравнений первого порядка. — Прим. ред.
2) Здесь, как и в дальнейшем, символом /?то обозначается (если явно
не оговорено противное) прямоугольная область в евклидовом пространстве
/и измерений, состоящая из точек (jtj, х%...., хт), координаты которых
удовлетворяют неравенствам \xt — в*|<^ (г = 1,2,—, т) (Ь>0). Точка
(Oj, я2,.... ат) называется центром /?т, а постоянные 2 ftj, 2 fc2,..., 2 6ТО —
измерениями Rm.
3) См. Фихтенгольц [1], т. 1, стр. 518.—Прим. ред.
8 Гл. 1. Нормальные системы дифференциальных уравнений
§ 2. Получение систем
обыкновенных дифференциальных уравнений
путем исключения произвольных постоянных
1. Системы дифференциальных уравнений, полученные путем
исключения произвольных постоянных. Пусть даны т функций
?<(*; Ун Уз> • • •» Ут'> cv С2' • • •- ст) ('= !» 2, .... т) от 2т+ 1
независимых переменных, непрерывных вместе со своими частными
производными первого порядка, в прямоугольном параллелепипеде 7?2
с центром (дг°; у\, у%, ..., у°т; «J, с», .... ф, и пусть в
якобиан у1' *fa"" Чт отличен от нуля.
д(УьУ» ¦¦;Ут) 3
Предположим, что
Ъ(*Ъ y°v У» • • •• У°т> <%> <& • • •• С) = ° (* = !» 2' • • •' < О)
Тогда, в силу теоремы о системе неявных функций, найдутся т не-
непрерывных и дифференцируемых функций
yh(x; с1; с2, ..., ст) (k — 1, 2, ..., m), B)
тождественно удовлетворяющих системе уравнений
<Pi(*; Л, J2. • • •. Ут> CV С2> • • •» О = °. C)
когда дг изменяется в отрезке / с центром в дг0, a (cv с2, ..., ст)—
в прямоугольном параллелепипеде Rm с центром в (cj, с*, ..., с^).
Дифференцируя по правилу дифференцирования сложной функции
соотношение C) по переменной дг, получим систему равенств
которым также должны тождественно удовлетворять функции B),
когда дг изменяется в /, a (cv с2, , ст) в Rm.
Заметим, что левые части уравнений систем C), D) определены
для любой точки (х; yv ys, ..., ут; cv c2, ..., ст), принадлежащей
Rv и любых значений y'v у'2, ..., у'т. Положим
,о \dyh(x;c\, 4 е°т)
=1
dx
Может случиться, что среди Ъп уравнений систем C), D) найдутся т
уравнений, из которых возможно однозначно определить с1г с2,..., ст,
как функции от дг; уг, у2, .... ут; у[, у'2, ..., у'т в прямоуголь-
прямоугольнике Я^ с центром в точке (*<>; y°v у%,..., ,^У?> У?' ->
координаты которой удовлетворяют соотношениям
уЪ у1> •••. Я* у?' у?> •••> jO=c2 (k==sl> 2> ••¦•
5. Метод Пикаро — Пеано
Подставляя тогда полученные для cv с2, ..., ст выражения в осталь-
остальные т уравнений, мы получим систему дифференциальных уравнений
вида
Уг, у» .... Уш;&, &,..., &j*) = o (i=i,2, ...,т). E)
Можно найти такой отрезок / с центром х°, лежащий в /, и
такой прямоугольный параллелепипед Rm с центром в (cj, c\,..., с^,),
лежащий в Rm, что, когда х изменяется в /, a (cv с2, ..., ст) —
в Rm, точка с координатами
(v и (г г г \ и (г г г Л- аУ1(х''еъСу •••'ся»)
\х> У1\С1> С2> • • • > ст) i • • • > Ут (cv t2» • • •» cta)t ^ > • • •
dym(x; сь cit...,cm)\
'•¦' dx )
принадлежит прямоугольному параллелепипеду R2m+i, a m функ-
функций B) удовлетворяют системе E).
Когда мы выводили посредством дифференцирования систему D)
из системы C), величины cv с2, ..., ст рассматривались нами как
постоянные; поэтому говорят, что система дифференциальных урав-
уравнений E), полученная путем исключения cv сё, ..., ст из C) и D),
является результатом исключения т произвольных постоянных.
2. Обратная задача. Заметим, что т функций B) удовлетворяют
системе дифференциальных уравнений E), причем каждая из них
зависит от т постоянных величин cv с2> ..., ст, которые могут
быть выбраны произвольным образом, лишь бы точка (cv с2, ..., ст)
принадлежала Rm; естественно поэтому поставить вопрос: дана
система дифференциальных уравнений вида E), можно ли найти
решение этой системы уъ(х\ сг, с2, , ст), (k=l, 2, ..., т),
зависящее от т произвольных постоянных?
Например, система дифференциальных уравнений F), рассмотрен-
рассмотренная в § 1, п. 1 „в", имеет решение, зависящее от трех произволь-
произвольных постоянных. В § 5, п. 7, будет доказано, что при весьма общих
предположениях решения системы дифференциальных уравнений те-го
порядка зависят в точности от т произвольных постоянных.
§ 3. Доказательство основной теоремы
существования и единственности по методу
последовательных приближений Пикара — Пеано
1. Формулировка теоремы существования. Пусть дана нор-
нормальная система дифференциальных уравнений
y'i =fi (x; yv У& • • •. Ут) (' = !» 2, ..., т), A)
и пусть в определяемом неравенствами
'=•!. 2. •••» т) B)
10 Гл. 1. Нормальные системы дифференциальных уравнений
(о и ^ — некоторые постоянные величины) прямоугольном парал-
параллелепипеде R с центром в точке [а; $1У р2, ..., $т] функции
ft(x'> -Vi> У» •••' Ут) однозначны и непрерывны. Тогда функции ft
ограничены в R, иными словами существует такое число М1), что
для любой точки (х; yv у$, ..., ут) из R имеем
\ft(x; yv у* yJ\<M (/=1, 2, ..., m). C)
Предположим, далее, что функции ff(x; yv у2, ..., ут) удов-
удовлетворяют условию Липшица первого порядка относительно перемен-
переменных yit т. е. что существуют т постоянных Lv Ь%, ..., Lm, для
которых
|/«(*; j»lf ..., yr-v yr-\-h, yr+1 yj —
—ft (*; Л. • •.. ^r-i. Л» JV+i. • • •» Ут) К I ^ | Lr B)
(r, i=l, 2, ..., in). D)
Тогда, _каковы бы ни были точки (дг; yv yv ... , ут) и
(дг; yv у$, ..., _vm) из R для всех /= 1, 2, ..., от имеем
—Л (*; л. л. • • •. ут) I <
где через L обозначена наибольшая из величин Lv L2, ..., Lm
В самом деле,
\fi(x; Уи у» -L-,]>m)—fiix; yv у» ¦¦-,_ут)\<_
<\fi(xi уу у& ._.. yj—ft(x; ylt л, .... л»)| +
+ !/«(*; л» л» л • • • л.)—/«(*; л. л. ь. • • •> >Л + • • • +
-? \fi(*; л. л» • • •»j*»-!. j».) —Л (¦«; л» j'a» • • • t ym-i, yJ I <
<Lj!t\yk~ yk\.
ft=i
Мы хотим доказать, что если для функций ft выполняются ука-
указанные выше условия, то имеет место следующая теорема:
J) В качестве М в дальнейшем будем выбирать наибольшую из верхних
граней }fi(x; уъ у» ...,ут) \ в /?.
2) Соотношение D) выполняется, если абсолютные значения производных
чисел функций /4 (jt; _у1( _у2,..., ут) относительно переменных у%, yt ут
не превосходят соответственно величин Lb Lit ..., Lm. Постоянные
Lv Lz,.. .,Lm называются постоянными Липшица функции/,- (дг; уь у2,. -.,ут)
относительно переменных уъ у2,..., ут.
Заметим, что соотношение D) выполняется, в частности, если функции
fi (¦*? Уъ Уя • ¦ ¦ * Ут) обладают непрерывными в R частными производными
no.yi, у2,..., ут.
Условие D), необходимое при классическом доказательстве теоремы
существования н единственности, было дано Липшицем (см. Липшиц [1])
(ср. также § 6).
§ 3. Метод Пикаро — Пеано И
Пусть Ь — наименьшее из чисел а и-щ, л:0—точка, принад-
принадлежащая отрезку [а — 8, а-|-8], а у\, у\, ..., у°т — система на-
начальных значений, отличающихся по абсолютной величине от
соответствующих постоянных рг, р2, ..., рто не более, чем на -у,
иными словами, пусть справедливы неравенства
|*о—а|<8, ДО—р,|<? 0=1, 2, .... т). F)
Тогда существует одна и только одна система функций
У\ = У\ (*). У% = Ь (•*). • • • • Ут = Ут (х),
определенных в отрезке [а — 8, a-f-8],
|лт-«|<8 G)
и удовлетворяющих как системе дифференциальных уравнений A),
так и начальным условиям
уЛх°)=уЪ («"=!. 2 т). (8)
Эту теорему формулируют иначе, говоря, что задача Коши для
системы A) (и для начальных условий (8)) имеет одно и только одно
решение, называемое обычно решением Коши.
2. Доказательство теоремы существования по методу после-
последовательных приближений Пикара-Пеано'). Система A) эквива-
эквивалентна системе интегральных уравнений 2)
X
yt (х) =УЧ + //«(х; ух(х), у2(х), ..., yjx)) dx A=1,2, ..., т). (9)
т,
Если функции fi не зависят от аргументов yv у2, ..., у
то система A) может быть решена в квадратурах, так как соотно-
соотношения (9) приобретают в этом случае вид
(/=1, 2, .... т). (90
а!"
1) Метод последовательных приближений (подстановок) для систем ли-
линейных уравнений в действительной области впервые был указан Пеано
(см. Пеано [1] (ср. также гл. Ц § 2, п. 3).
Во всей общности этот метод был рассмотрен Пнкаром (см. Пикар [1]);
с помощью метода Пикара был выполнен ряд весьма важных исследований
в различных областях анализа.
2) Термин „интегральное уравнение" впервые встречается в работе
Дюбуа-Реймона (см. Дюбуа-Реймон [1], стр. 228).
12 Гл. I. Нормальные системы дифференциальных уравнений
В общем случае примем в качестве первой системы приближе-
приближений начальные значения у\, y%, ..., fm искомых функций и подставим
их в правые части соотношений (9) вместо у?х), у2(х) Ут(*).
Выполнив квадратуры, мы найдем вторую систему приближений
уЮ(х), у?Цх) -У??(*)» определяемых соотношениями
х
х;у»,у1, .... y°Jdx (i^l, 2, .... т).
J
Как будет видно из дальнейших рассуждений, вместо начальных
значений искомых функций можно было в качестве первых прибли-
приближений взять любую систему функций их {х), и2 (*) ит (х),
непрерывных в [а — а, a-f-а] и удовлетворяющих при а — 8<[
С^{^ неравенствам
Тогда в качестве вторых приближений мы взяли бы функции, опре-
определяемые соотношениями
х; их(х),щ(х) ит(дг))^лг(/=1, 2, ...,т).
*• (9,)
Докажем, что если х изменяется в отрезке [а — 8, а-|-8], то най-
найденные нами функции у^Цх) (/=1, 2, ..., т) отличаются от соот-
соответствующих р4 не более, чем на Ь. В самом деле, в силу соотно-
соотношений (9t), C), F), G) и того, что 8<4^> имеем
Я)
—р«|=1.у;—p«+J7i
Ji
Определим теперь третью систему вспомогательных функций
уф {х), у®> (лг), —, у® (х), подставив в правую часть соотношений (9)
вместо неизвестных функций ух (х), у#(х), ..., ут (х) найденные нами
ФУНКЦИИ уф(х), У$(Х) У^т(Х)- ^Ы полУчаем
(i=l, 2, ..., т). (%)
Повторяя проведенные выше рассуждения, выводим, что получаемые
путем выполнения квадратур функции yf*(x) непрерывны на отрезке
§ 3. Метод Пикаро — Пеано 13
[а — 8, а -|- 8] и отличаются на этом отрезке от р4 не более, чем
на Ь.
Вообще, если уже найдена {г-\-Х)~я система вспомогательных
функций, то мы определяем (г~\-2)-ю систему с помощью квадра-
квадратур по формулам
(i=l, 2, ..., m). (9r+l)
Каково бы ни было г, функции yW(x) конечны и непрерывны на
отрезке [а — 8, а -f- 8] и отличаются на этом отрезке от {34 не более,
чем на Ь.
Докажем теперь, что, когда г -> оо, функции уф (х) равномерно
сходятся на отрезке [а — 8, a -j- 8] к предельным функциям yt (x),
удовлетворяющим системе A) и начальным условиям (8); функ-
функции yt(x) и дают искомое решение системы (9).
Для того, чтобы доказать это утверждение, покажем сначала,
что ряд
Щ (х) + Df> (х) — и, (лг)] + \yf (лг) — yf (лг)] + ...
.. (I)
абсолютно и равномерно сходится на отрезке [а — 8, а —|— 8J. Так как
функции ^(лг) — и{(х) непрерывны на отрезке [а — 8, а-|-8], то
найдется такая постоянная С, что для всех лг в этом отрезке имеем
т
Из (92) и (9j) получаем, учитывая соотношения E) и A0а), что
—fi (х; их (х), и2 (х), ..., ит (лг)) | dx I <
т. е. что
\У?Чх) -yV(x)\<-§-[mL\x—x*\) A = 1,2 т). A02)
14 Гл., А Нормальные системы дифференциальных уравнений
Аналогично, из (98) и (9t) получаем, учитывая соотношения E) и
A00, что
\
Отсюда следует, что
и потому
IУ?>(х)-yf (х) |<? ^ !*-**№ . (ю8)
По индукции получаем, что
Принимая во внимание, что |л:—лО|<|д:—<x|-j-|jt°—а|<28, мы
получаем отсюда неравенство
Это неравенство показывает, что абсолютная величина членов ряда,
получающегося из ряда (I) отбрасыванием первых двух членов, не
превосходит величины соответствующих членов ряда
С \2mLb ¦ Bw/.8J , , BmLb)r-i , "I _ С шы Л1
4 II "г 2! "t~>I~f~ (г—1)! "•"• '•\~'m~ie ~1J>
а потому ряд (I) абсолютно и равномерно сходится на отрезке [а — 8,
а+ 8].
Положим теперь
yt (х) = Hm jpjr» (x) (/=1,2,..., т).
Из проведенных рассуждений следует, что функции yt (x) непрерывны
на отрезке [а — 8, а -J-8].
Докажем теперь, что последовательность функций
ft (х; их (х), щ (х), ...,ит (лг)); U (х\ У(? (х), у™ (х), ...,>« (*));...
также равномерно сходится на отрезке [а — 8, а -(- 8] к функции
U(х; уг(х), у2(х), ...,ут(*)),
$ 3. Метод Пакаро — Пеано 15
иными словами, покажем, что каково бы ни было положительное
число о, найдется такой номер г0, начиная с которого для всех х,
принадлежащих отрезку [а — 8, а -j-8], справедливо неравенство
I fi (*; Л (*)> ^W Уш (*)) —
-/< (*; УТ (х), У? (х), .... у$ (лг)) |< о. A2)
В самом деле, найдется такое /о, что при г > /q имеем
\Уи(х)— У%(х)\ <^ [г > r0; k= 1, 2, ..., т;
а— 8<лг<а-|-8].
Учитывая вытекающее из E) неравенство
мы убеждаемся в том, что при г>г0 справедливо соотношение A2).
Покажем, наконец, что полученные описанным выше образом
функции у{(х) удовлетворяют системе (9). Для этого положим
х
fi(х) = yt(х) —у°{х) — ff{(х; уг(х),у^х), ..., ут(х))dx
и покажем, что /^(j^ssO на отрезке [а — 8, а-)-8]. Из (9г+1) сле-
следует, что
—ft(х; Ул.(х), у2(х), ..., ут(х))]dx.
Поэтому если выбрать индекс г0 так, чтобы при г>г0 выполнялось
неравенство A2), то при r>r0 получим, что
I РЛ*)\< \У* (лг)-
В силу равномерной сходимссти _y(r+1) (х) к yt (лг) правая часть этого
неравенства может быть сделана сколь угодно малой при всех х,
принадлежащих отрезку [а — 8, а —}- 8]г), откуда и следует, что
Fi(x)==Q, когда а — 8^лг<[а-|-8.
Итак, мы доказали, что построенная нами система функций
удовлетворяет как системе дифференциальных уравнений A), так и
начальным условиям (8).
•) Рассуждения, проведенные в последнем абзаце, могли быть опущены,
так как достаточно было заметить, что, в силу равномерной сходимости по-
последовательности A1), в соотношении (9r+t) можно перейти справа к пре-
пределу при г -> со под знаком интеграла.
16 Гл. I. Нормальные системы дифференциальных уравнений
3. Доказательство Гурса теоремы единственности. Изложим те-
теперь доказательство теоремы единственности, принадлежащее Гурса (см.
Гурса [1], т. II, стр. 322).
Пусть гг(х), z2(x), ..., zm(x), |zk(х) — pft|<* (*=1, 2, ....
..., т), — система функций, удовлетворяющих уравнениям A) и на-
начальным условиям (8), т. е. таких, что
*«(¦*) "=.У« + [hi*; zi(x)> г2D • • •> zm(x))dx (i= 1, 2, ..., т).
J (Ю
Вычитая из них функции ySp (x), yW (х), ..., у№ (х), образующие
(r-j-l)-e приближение
as'1
получим
—У/> (*) «= / \fi (x; zv
и потому, в силу соотношения E),
ж
| Г SI^H-^-^WI^ . A3)
Неравенство A3) позволяет оценить разность \zt—у<р\. В самом
деле, из того, что (Зй — b ^ zk (x) -С Р^ -f- ^, вытекает неравенство
!**(*) — «»(*)|<2* (Л=1, 2....,т).
Поэтому, полагая в A3) г— 1, получаем неравенство
из которого выводим, полагая в A3) г =2, что
По индукции заключаем теперь, что при всех г имеем
1<Ю ^^-^Ч" (/=1, 2, .... тУ) A4)
и, так как при всех х, принадлежащих отрезку [а — 8, а -\- 8], пра-
правая часть A4) стремится к нулю, когда г->оо, то функции у!р(х)
1) Заметим, что эта формула дает величину наибольшей ошибки (г + 1)-го
приближения.
$ 3. Метод Пикаро — Пеано 17
равномерно на этом отрезке стремятся к функциям zt(x). Отсюда и
следует, что функции zt(x) совпадают с найденными ранее функ-
функциями yi(x).
4. Дополнения к формулировке теоремы существования, а) При
проведении изложенного выше доказательства существования мы пред-
предполагали, что х принадлежит отрезку [а — 8, а-|-8], где 8 не пре-
превосходит не только а, но также и -^. Последнее ограничение
было наложено для того, чтобы последовательные приближения у<р (х)
не выходили из области, в которой выполняются условия Липшица.
Это ограничение может быть снято, если соотношение E) выполняется
для всех значений х, принадлежащих отрезку [а — 8, а -J—S], незави-
независимо от значений у. В этом случае можно считать, что 8=за,
т. е. что решение нашей системы существует и единственно на всем
отрезке изменения х. Так будет, например, если найдется такое
число М, что для любых значений х, принадлежащих отрезку
[а — 8, a-J-8], и любых значений уь частные производные функ-
функций ft по переменным ух, у2, ..., ут существуют, причем
Щ<Ж (/=1, 2, .... т; ft=l, 2, ...,
К системам, обладающим описанными выше свойствами, принад-
принадлежат системы, для которых функции ft линейны по всем yh, т. е.
системы вида
т
i (*) (/=1,2,..., т),
где функции aiti(x) и щ(х) непрерывны при a—а\,
ибо в этом случае частные производные функций ft no yk зависят
лишь от х.
Полезно заметить, что если система имеет вид
i (*• *) (i = 1, 2, ..., /и),
где функции а^{х, X) и ut(x, X) непрерывны по х и X, когда a —
^JC^a-f-a, аХ пробегает область D, и голоморфны по параметру X
в области D, то все члены ряда (I) голоморфны по X в области D,
а сам этот ряд равномерно сходится в области D. Поэтому, в силу
теоремы Вейерштрасса, решения yt голоморфны по X в DJ).
б) Можно указать другие случаи, для которых имеют место от-
отмеченные в „а" обстоятельства; они имеют место, например, для
J) См. Привалов [1], стр. 175. — Прим. ред.
2 Зак. 627. Дж. Сансоне
18 Гл. А Нормальные системы дифференциальных уравнений
системы вида
т
=—• /i a^ j ("^y ^j Г" ^4 \^) \? *™ ^ ? "? • • • 1 f^J>
где aitl(x) и %(дг) — непрерывные на отрезке [а — а, а-\-а] функций,
в) Отметим еще, что если ограничиться нахождением решения
системы A), удовлетворяющего начальным условиям
Л(а) —Р< (*"=1» 2, ..<, /те),
trio в качестве 8 можно взять наименьшее из чисел а и -jt (причем,
если уИ = 0, то можно положить 8 = а). Для доказательства доста-
достаточно заметить, что при таком выборе 8 все рассуждения, проведен-
проведенные при доказательстве теорем существования и единственности, со-
сохраняют силу.
§ 4. Аналитическое продолжение решений.
Примеры
1. Аналитическое продолжение решений. Будем, сохраняя сде-
сделанные в § 3, п. 1, предположения, искать решение системы
У{ —ft (*l yv У* • • •» Ут) (i = 1, 2, ..., т), A)
удовлетворяющее начальным условиям
= Р<- B)
Согласно сделанному в § 3, п. 4 „в", замечанию, теорема суще-
существования и единственкссти обеспечивает существование этого решения
на отрезке [а — 8, а-|-8], где 8—наименьшее из чисел а и -vr-.
Этот отрезок составляет, вообще говоря, лишь часть первоначального
отрезка [а — я, a-J-а] изменения х. Однако отсюда не следует, что
это решение существует лишь на отрезке [а — 8, a-j-8], оно может
существовать и вне этого отрезка, но получается там с помощью
нового ряда последовательных приближений. В самом деле, пусть
8 < а и пусть построенное в § 3, п. 2, решение принимает при
л: = a-j-8 значения yt(a-j-b) = bt. Тогда если существует содержа-
содержащийся в R прямоугольный параллелепипед R с центром в точке
(a-J-8; bv *а, .... bm), в котором выполняются указанные в § 3,
п. 1, предположения, то можно построить новый ряд последователь-
последовательных приближений, который даст решение системы A), определенное
на отрезке [a-f-8 — Ь1г a-f-S+Sj] длины 28j и принимающее в точке
а-^-Ъ значения bv *s, ..., Ьт (фиг. 1). В силу теоремы единствен-
единственности это решение системы совпадает на отрезке [а-\-Ь—bv a-j-8]
со старым решением и, с другой стороны, определено на отрезке
[a-J-8, a-f-8-f-8j], на котором старое решение не было
^ 4. Аналитическое продолжение решении 19
определено; новое решение называется аналитическим продолже-
продолжением старого.
Повторяя последовательно процесс аналитического продолжения,
мы получим в качестве области существование решения системы,
удовлетворяющего начальным условиям B), либо весь отрезок [а—а,
Л-а а а+а
-¦-
vis, «.+<
tt-S - (t+8-8t cl+6 cc+S+S,
Фиг. 1.
a-\-a], либо его часть. Во всяком случае важно заметить, что это
решение системы дифференциальных уравнений A) однозначно
определяется дифференциальными уравнениями этой системы и
начальными данными.
2. Система дифференциальных уравнений, определяющая три-
тригонометрические функции. Рассмотрим систему
da dv ,„.
dt = v> 17 = ~и Р)
с начальными условиями
и@) = 0, о@) = 1. D)
Как известно, решение этой системы, удовлетворяющее начальным
условиям D), дают функции
и = sin х, v = cos x.
Покажем, как этот результат можно получить с помощью процессл
последовательных приближений.
Согласно сделанным ранее замечаниям, мы имеем
Д(дг; и, v) = v; /2(лг; и, v) = — u,
х изменяется от —оо до 4-°°» и условия Липшица выполнены.
Учитывая начальные условия D), получаем
at; 0, l]dx = x;
о
X
jAlx; х, l]dx = x;
о
as
|[г; х, \-Щйх = х—^;
2*
Гл. /.Нормальные системы дифференциальных уравнений
Я!
/2лг; О, l]dx=l;
о
/; х,
о
X
[; х, \-Щлх=\—?,
откуда, продолжая процесс последовательных приближений, выводим,
что функции и(лг) и v(x) разлагаются в ряды
«(*) = *—?+?-...; „(*) = |—*+-*_...,
сходящиеся при всех значениях х.
б) Докажем, независимо от сделанного выше замечания, что функ-
функции и(х) и v(x)— периодические, и выведем для них формулу сло-
сложения.
Из системы C) следует, что 2ии' -|- 2от' = 0, (и2 + 02)'= О,
и2-|-©2 = const, откуда, в силу D),
«¦(*) + *¦(*) = 1, E)
а потому функции и(х) и v(x) непрерывны и принимают значения,
лежащие на отрезке [—1, 1).
Так как и'@) = ©(())— 1, то функция и{х) возрастает, а потому
она положительна в некотором промежутке, расположенном справа
от точки * = 0; она остается возрастающей (и значит положитель-
положительной) до тех пор, пока не обратится в нуль ее первая производная <о (х),
т. е. в силу того, что «2(дг)=1 — иа(д:) до тех пор, пока и(лг) не
примет значение 1. Отсюда следует, что для всех х, принадлежащих
отрезку [0, К], где через К обозначено первое значение х, для кото-
которого и (/0=1, имеет место равенство и'{х) — У\ — к2 (в силу-ска-
силу-сказанного выше мы должны выбрать перед ксрнем знак -}-). Но тогда
_!
dx = {\ — i&) * da,
откуда, интегрируя от 0 до К, получаем
1
С da ( я\
" J ут=^ (= 27-
Положим
$ 4-. Аналитическое продолжение решений 21
Подставляя в C) вместо х значение х-\-К, найдем, что
a[{x) = vJ; «J(x) = —Bj,
и при дг = О
В силу теоремы единственности отсюда вытекает, что и^ (лг) = и (дг),
v1(x)s=sv(x), т. е. что
Подставляя в эти соотношения вместо л: значение х-\~К, мы видим,
что
и (Af+2/O <= — «(*)> w(*+2K)— ¦—«(¦*). Eа)
и, наконец,
и(х-{-4К) = и(х), v(x+4K) = v(x). E8)
Отсюда следует, что функции и (лг) и v(x) имеют период 4К{— 2и).
в) Для доказательства теоремы сложения положим
U (х) = и (х) •(«) + « (х) и (a), V(x)=~v (x) v(a) — u (лг) и (а),
где а—некоторая постоянная величина. Функции U(x) и V(x) удо-
удовлетворяют системе дифференциальных уравнений
U' (х) = У(лг), Vr(x) = — U (лг)
и начальным условиям
в(в), V@) = «(в),
т. е. той же системе уравнений и тем же начальным условиям, что
и функции и(х-^-а), v{x-\-a); в силу теоремы единственности от-
отсюда следует, что
и(лг-J-a) = u{x)v(a)-\-v{x)u(a); v{x-\-a) = v(x)v{a)—и(х)и{а).
Эти равенства можно записать в виде элементарных формул
sin (л: -J- а) = sin x cos a -J- cos л: sin а,
cos (л: -J- а) = cos x cos а — shut sin a.
3. Система дифференциальных уравнении, определяющая эллип-
эллиптические функции Якоби. а) Пусть k — положительное число, мень-
меньшее единицы, х изменяется от —оо до -J-oo и и, v, w — функции,
удовлетворяющие системе дифференциальных уравнений
du dv dw ,„ /-сч
с начальными условиями
«@)^0, г»@) = да@) = 1. G)
22 Гл. I. Нормальные системы дифференциальных уравнений
Пусть при изменении х от — 1 до 1 функции и, v, w отличаются
от своих начальных значений не более, чем на Ъ {Ь > 0), т. е.
Тогда функции 4 «w, —ига», —й2иг> не превосходят числа ()
а потому существует определенное на отрезке [—b(l-\-b)~2,
?A_|_#)-2] решение системы F), удовлетворяющее начальным
условиям G).
Но легко видеть, что функции и, v, w существуют при всех
значениях х; в самом деле, на любом отрезке, для которого доказано
их существование, абсолютные значения этих функций не превосходят
единицы (см. (8)). Поэтому их можно продолжить с этого отрезка
как вправо, так и влево на отрезок длины Ъ A -\- 6)~а.
б) Из F) получаем, что
y = 0 (#гаа _[_ WZ)' _ о,
откуда вытекают равенства
и2 -f- •Ф = const, А2и2 + та2 = const.
В силу G) эти равенства приводятся к равенствам
«2_|_гJ==1> #!И2-}-'К>2=1* (8)
Отсюда следует, что функции и и г» изменяются от — 1 до 1,
a w—от 1—ft2 до 1, а потому функции и(лг), v(x), w(x) опреде-
определены и непрерывны (в силу F) вместе со своими производными) на
всей оси, причем абсолютные значения этих функций не превосходят
единицы.
в) Положим
«i(*)—— «(— *)» wi (*) = «(— *). »!(*) = «(—*), (9)
тогда
Kl@) = 0, г»1@) = 'к>1@) = 1. G')
Отсюда заключаем, что функции их (лг), vx (лг), даг (л:) совпадают с функ-
функциями и(лт), v(x), w(x), т. е. что (см. (9))
и(—лт) = —и(лт), v{~ x) = v(x), w(—x)*=w(x). A0)
Таким образом, функция и(х) нечетна, а функции v(x) и w(x)
четны.
г) Из равенств F) и (8) следует, что и'2 = г»2®»2 = A —a2) (i —№и*),
а потому и'(х) обращается в нуль, когда и = г±:1; но при л: = 0
«'@) = !, откуда видно, что «(лг) возрастает в точке лт = О и, сле-
следовательно, остается возрастающей неположительной (но не^превос-
$ 4. Аналитическое продолжение решений 23
ходящей единицы), когда х изменяется от 0 до К, где через К обо-
обозначено первое положительное значение, для которого и(К) = 1.
Тогда для любого х между нулем и К имеем
«'(*)=УA-й>)A-*адо. <**=-==§===, (и)
у A и2) A я2а2)
где корни берутся в арифметическом смысле. Интегрируя это равен-
равенство по л: от 0 до 1, получаем
K=s С du _, A2)
откуда при х = К имеем
и{К) = \, v(K) = Q, w(K) = Vl — k?=kr, A3)
причем k' связано с k соотношением
s=l. A4)
Заметим, что в последнем из равенств A3) надо также рассматривать
положительное значение корня; это следует из непрерывности w (x)
и начального условия 10@) — 1.
Если положить в уравнении A1)
и = sin <j>,
то получим
i_
dx — A — ft2 sin2 у) 2 dtp
и потому
A6)
Дуга ^р называется амплитудой х и обозначается
«р = am х.
Поэтому
и = sin <j> = sin am лг, v = cos <j> = cos am x,
w = У1 — feasin2<j) = Vl —625}п2атлг = Д«р = Д am л:.
Функции sin am лг, cos am лг, Д am лг являются эллиптическими функ-
функциями Якоби и называются соответственно синусом амплитуды х, ко-
косинусом амплитуды х и дельтой амплитуды х; в настоящее время
они обозначаются введенными Гудерманном символами
и (лг) = sn (лг; k), v (лг) = сп (лг; k), w (лг) = dn (лг; к)
или более коротко
сил;, йах, .
^ Гл. /. Нормальные системы дифференциальных уравнений
Постоянная k • называется модулем эллиптических функций sn x,
СП л:, dnjc, а Ы'*— дополнительным модулем. Таблицы эллиптических
функций Якоби см. Милн—Томсон II]. На фиг. 2—4 приведены гра-
графики этих функций.
w=dnx
Фиг. 2.
д) Аналогично тому, как это было сделано в п. 2 „б", найдем
вещественные периоды эллиптических функций Якоби. В силу второго
v
1.0
0,5
0
-as
-1,0
•
k=0
v=cnx
я 2К
2n
Фиг. 3.
равенства (8) функция w(x) отлична от нуля, а потому можно ввести
функции
A6)
§ 4. Аналитическое продолжение решений
25
Тогда
и, в силу аналогичных рассуждений для V и W, функции U, V, W
удовлетворяют системе дифференциальных уравнений
U'^VW, V' = — UW, W'^ — kWW .A6i)
с начальными условиями
1/@)= 1, V@) = 0,
и
u=snx
*~x
Фиг. 4.
В силу F) и A3), тем же самым условиям A6j) и A62) удовлетво-
удовлетворяют функции
(
а потому
и, согласно A6),
откуда
en (лг -|- 2/C) = — en x,
sn (лг -\- AK) = sn x,
en (x -\- 4K) = en лг,
A72)
A78)
26 Гл. 1. Нормальные системы дифференциальных уравнений
Итак, функция dnje имеет (вещественный) период 2К, а функции
snx и сах — (вещественный) период 4К.
е) Функции бплг, enx и dn.*:, рассматриваемые как функции ком-
комплексного переменного, обладают вторым периодом. Положим
J УA—И2)A_й/2и2) Jyi_^
q = e~n^, x = ^v. A9)
Тогда
где b(v), Qt(v), %(v), в8(г») — так называемые тета-функции Якоби,
определяемые рядами
в (v) *= 1 + 2 2 (—1)"> ^ cos 2/иг»,
m=l
со 1
вх (г») = 2 2 (— l)?"*"BЯ>~4'sin Bm — 1)г»,
i
оо _1_
оо
2
m=l
(см. Якоби [1], т. I, стр. 497). Доказано, что
sn(x-\-2iK') = snx, cn(x-\-2K-\-2iK') =
dn (x -f- 4/АГО = dn x
и что эти функции имеют полюсы первого порядка в точках
x = 2mK+{2n-j-l)iKf
J B°)
и нули первого порядка в точках: 2mK-\-2niK' для snx,
в Bm-\-l)K~{-2niKf для сплг и в {2т-\-1)/С+ Bл-\-1)iK' для
d:, где т и п — целые числа1).
х) Более глубокое знакомство с эллиптическими функциями Якоби и
общей теорией эллиптических функций читатель может получить из книг
Гурвица_[1] и Ахиезера Н. И. [1]. — Прим. перев.
$ 5. Решения как функции начальных значений 27
§ 5. Решения дифференциальных уравнении
как функции начальных значений
1. Непрерывность, а) Пусть дана система дифференциальных
уравнений
y't^M*'' Уч Уъ •••» Ут'у *) ('=1. 2, .... т), A)
где функции ft непрерывны по их аргументам в прямоугольном
параллелепипеде i?m+a, определенном неравенствами
*=1, 2, ..., т), Bг)
B2)
причем х — независимая переменная, yv ya, ..., j/m — искомые
функции, X — параметр, и пусть в /?т+2 имеем
\fi(x;yv уъ, .... vm; Х)|<Ж (/=1, 2, .... т).
Предположим также, что функции ft удовлетворяют условиям
Липшица
т
1/«(*;л.л. • • •• j'»;х)—Л(*;л.j'e.-.j'»;^)!^ S 1л—л1 C)
и что 8 — наименьшее из чисел а и -ттг' Тогда, в силу результатов,
изложенных в § 3, каждой точке х° из [а—8, а-}-8], системе
начальных значений у\, у°, ..., у^, удовлетворяющей условию
и$-Р«1<т
и значению параметра К, принадлежащему (f — с, f-\-c), соот-
соответствует одно и только одно решение системы уравнений A), удов-
удовлетворяющее начальным условиям
yi(x°)=y°i («=1. 2. ••¦. да)- D)
Можно сказать, что это решение системы A) зависит от т~\-Ъ
аргументов лг, д;0; у\, у®, ..., у°т; к, изменяющихся в прямоугольном
параллелепипеде Rm+S, заданном неравенствами
|лг —а|<8, |^_«|<8; |>5_р<|<^., |Х—Т|<«. E)
Обозначив это решение символом уг (лг, х°; _yj, у°, ..., _)?,; X), мы
можем записать D) в виде
^°; УЬ У°р--'; УщО-) =Л (' = J, 2, ...,*). F)
28 Гл. I. Нормальные системы дифференциальных уравнений
Решение yt(x, л*; y°v У%,--',Ут1 *) непрерывно в прямо-
прямоугольном параллелепипеде /^д1). В самом деле, нетрудно пока-
показать, что при сформулированных выше условиях все вспомогатель-
вспомогательные функции,. получаемые путем последовательных приближений,
непрерывны в Rm+3, и что построенный в § 3, п. 2, ряд (I) равно-
равномерно сходится в Rm+B. Отсюда и следует непрерывность функций
yt(x, *°; .у», >»,...,.>?; X) в Яж+в.
б) В некоторых вопросах (см., например, гл. IV, § 6, п. 3) при-
приходится рассматривать начальные значения у\, у\, < •., у*т как непре-
непрерывные функции параметра X; проведенные только что рассуждения
показывают, что и в этом случае решения системы A) являются
непрерывными функциями параметра X.
2. Дифференцируемость. Сохраняя указанные выше предполо-
предположения о функциях ft, заменим условие Липшица C) более ограничи-
ограничительным условием, потребовав, чтобы функции ft(x; у^, у%, ...,ут; Ъ)
имели в Rm+% непрерывные частные производные первого порядка
по всем переменным yv у%, ..., ут, X; покажем, что тогда реше-
решения уг будут иметь непрерывные частные производные по аргу-
аргументам л*; у\, у°2, -.., /т; X.
Предположим, что мы доказали эту теорему и обозначим для
краткости
%&*=Zt(x, х*; у\, у*, ..., у>т; X) (*= 1. 2, ..., т), . G,)
Щс=У1шк(х,х*,у«,у*,...,у°я;к)A,к = 1, 2, ..., т), G2)
^ = Ut(x, xo; fv у*, ...,у°т;1) (/= 1, 2, ..., т), G3)
Ъ, ь(х; у[, л, ..,, ут; К) = ^ (/, k= 1, 2, ..., /и), (8г)
Ы*1 УЬ У*> ¦ • •> Ут> *) = %? ('=" 1. 2, ..., ж). (82)
Дифференцируя уравнения системы A) по аргументам лг°, у%, X
и предполагая, что в левых частях можно изменить порядок диффе-
дифференцирования, мы получаем для функций Zt, V(> к, Щ линейные
J) Зависимость решений от начальных значений и от параметров рас-
рассматривалась в работах Николетти [1], Линдедёфа [1], Лихтенштейна [11.
Блисса [1], Ритта [1], Гронуолла [1].
$ S. Решения как функции начальных значений 29
системы дифференциальных уравнений
%, i(x> Ун У» •¦¦> Ут\ *) Vi, ft 0". k = l, 2, .... т),
i=i
т
%,*(*;л. у» ¦> УтЛ)
(i=l, 2, ..., ж),
а дифференцируя равенства F) и учитывая систему A), получаем
для функций Zif Vfi k, U€ начальные условия
Zt(jfi) = -ft(pfi; у», У°2,-..,У°т;К) 0=1,2,..., ж), (92)
^«. ft (*°) = 4 ft С *¦ = 1. 2, • -.., ж; 84i ft = 0 при i * ft, \ H), A0b)
Ut(jfi)=*0 (/=1, 2,..., ж). (ll2)
Для доказательства этой теоремы и соотношений (9Х), (Юг), A1г)
докажем предварительно в п. 3 лемму Гронуолла, а в п. 4, 5, 6
покажем последовательно дифференцируемость по параметру X, по
начальным значениям у°, у%, ..., уйт и по начальному значению jfi
независимого переменного, а также покажем справедливость соотно-
соотношений A1Х), A0,) и (9Х).
3. Лемма Гронуолла.J) Пусть при х° ^.х^x°-\-h непрерыв-
непрерывная функция z(x) удовлетворяет неравенствам
X
0<*(*)< f(Mz+A)dx+B, A2)
где М, А, В — некоторые неотрицательные постоянные. Тогда
В самом деле, пусть z (х) = ем С37-*0) S (лг) и пусть хг — точка
(или одна из точек) отрезка [х°, лг°-}-Л], где ? (лг) принимает наи-
наибольшее значение. Тогда
ж,
0 < ем «»i-^ I (*г) < J [MeM <*-
J) См. примечание на стр. 28. Аналогичные леммы имеются в работах
Пеано [2} и Камке [1], стр. 92, а несколько более общая — в работе Джу-
лиано [1].
SO Рл. 1. Нормальные системы дифференциальных уравнений
и потому
О < еи <*-•* i (JCi) < 5 (лгг) J MeM ^-^ dx-\-A(x1—jfi)~\-B
а)"
— ^ (*j) [** ^'"^ — 1J + А (Х1 — -
Но отсюда следует, что
чем и доказана справедливость неравенства A2').
4. Дифференцируемость по параметру. Докажем теперь диф-
ференцируемость решений по параметру X, а также справедливость
равенств (llj) и (lls).
Обозначим через (ylt у$, ..., ут) и (у1г у& ..., у„^ два решения
системы A), отвечающих соответственно значениям X и к параметра
X, Кф\, и удовлетворяющих начальным условиям D); тогда
as
to л. л. • ¦ •» >«
a:0
откуда следует, что
Я!
3^« —л = J ift (*; л. л» • • '•. У»,; ^ —ft (*; л. >» • • •»^м;
и, в силу теоремы о среднем,
где для всех ipf j и Ф« через (_у*, _у*, ..., у^; к*) обозначена вну-
внутренняя точка_ отрезка, соединяющего точки (yv _у2, ..., ут; X) и
Пусть Жх и Л являются соответственно наибольшими значениями
в/?„,+2функций/и|%, й| (t, ft=l, 2, ...,т)и|^| (t = l,2, ...,/и).
Зафиксируем некоторые значения к и X, X ф к, и обозначим для всех лгJ),
принадлежащих отрезку [ж0, x°~\-h], через г(дс; X, X) наибольшее из т
*) Мы предполагаем здесь неявным образом, что х !> jk°, но при этом не
теряем общности, так как в противном случае мы заменили бы х на — х.
выражений
S. Решений кйк функции начальны.* значений 31
Уг —У г ~
¦А - (/=1| 2, ..., т). Функция z(x\ X, X) непре-
Л *-"~ А.
рывна по х на отрезке [д;0, x°-\-h], а потому, в силу леммы Гро-
нуолла на [х°, x°-\-h] справедлива оценка
* (/ = 1,2,..., т).
X —X
Как уже было отмечено в п. 1 этого параграфа, из доказанной
оценки следует, что решения yt (равномерно) непрерывны по X.
Так как теорема существования и единственности применима к си-
системе (llj) с начальными условиями A18) (см. §3, п. 4), дифферен-
щируемость решений по параметру X будет доказана, равно как и
соотношения A1г) и A18), если мы покажем, что -^ существует и
равно Ut.
Из (llj) и A12) следует, что
т &
Ui = 2 J Ъ, г (х; yv Уъ Ут, ^) иг dx+
и потому
Так как функции _у4 непрерывны по X, а функции <р», г и 'r't непре-
непрерывно зависят от своих аргументов, то для любого е найдется такое р,
что при | X — X | < р имеем J)
т
12 [<pit, (js; ^т» ^;, • • •, х»;х*)—?*, i с*; л» л» • • ¦»^«.' x)i ^i+
где i = l, 2, ..., т. Зафиксируем X и X и для всехх,-лежащих на
[х°, x°-\-h], обозначим через z(x; X, X) наибольшее из т выраже-
J) Отметим, что на отрезке [х0, xfi + h] функции ?/j ограничены в сово-
совокупности.
32 Гл. /. Нормальные системы дифференциальных уравнений
ний
X —X *
* Тогда, применяя снова лемму Гроиуолла, мы по-
лучим, что
1 А. — А.
равномерно при | к — X |< р, а потому Ut = lim у±~~у*. = -^, что и
требовалось доказать.
б. Дифференцируемое™ по начальным значениям решений.
Теперь легко показать, что функции yt дифференцируемы по началь-
начальным значениям решений, и доказать справедливость равенств A0j)
и A02). Подставим в систему A) вместо функций у1г у2, ..., ут
функции zv z2, ..., zm, связанные с ними равенствами
t tfi ('=1. 2, .... т). A3)
Функции zi удовлетворяют системе
eЪ (/=1,2, ...,«) A0
и начальным условиям zt = O при д: = дс°. Рассматривая _у^ как пара-
параметр, получаем в силу результатов предыдущего пункта 2), что
и что при д: = дс° -% = О. С помощью соотношений A3) мы убе-
ждаемся теперь в справедливости равенств (Юх) и
6. Дифференцируемость по начальному значению независимой
переменной. Для того, чтобы доказать, наконец, диффереицируемость
решений по х° и вывести соотношения (9j) и (92), обозначим через
У\> У'2» •••» Ут решение системы A), получающееся, если мы заме-
заменим Х° на х°, оставив неизменными у\, у°, ..., уйт. Используя оче-
х) Мы предполагаем при этом, что в системе A') г* изменяются иа
отрезке, лежащем внутри (рк—у°к—b, Pk—у%+Ь], центр которого лежит
в нуле.
$ 5. Решения как функции начальных значений 33
видные обозначения, мы получаем, что
он
( у2?
.у*=.5+
х __
г —yt __ г Л- (*; Уь ь-. .Уи»;х) —Л (*: Уь у» • - •. .у«г; >-)
г —yt __ г
f/ (^ yv y» • • •• д5».;
Ji\x > Ух > У г . • • • > ^„,
Из системы (9j) и начальных условий (92) получаем, что
i,i(x; yv y2, ..., ут;
откуда, с помощью рассуждений, аналогичных проведенным в п. 4 этого
параграфа, следует, что
7. Общее решение системы дифференциальных уравнений.
а) Пусть дана система дифференциальных уравнений
Х=Л(*; yv У* ¦¦¦> У,г) (' = 1,2,..., т), A)
причем функции fi удовлетворяют условиям, указанным в п. 2 этого
параграфа. Тогда для любой точки д:0 отрезка [а — 8, а-]-8] и любой
системы значений у\; у\, ..., у°т, удовлетворяющей указанным там
ограничениям, найдется одно и только одно решение системы A), удовле-
удовлетворяющее начальным условиям у^х°)=у\ (/ = 1, 2, ..., т). То
же самое решение получится, если взять в качестве начальных
значений в какой-либо другой точке отрезка [а—8, а-]-8] си-"
стему значений, принимаемых в этой точке рассматриваемыми реше-
решениями. Поэтому можно сказать, что решения системы A) являются
3 Зак. 527. Дж. Сансоне
54 Гл. I, Нормальные системы дифференциальных уравнений
функциями т~\-\ аргумента лг; у\, )%,..., у*т в прямоугольном
параллелепипеде, заданном неравенствами
Если обозначить функции у. через <р* (д:; у\, у\, ..., у^), то функ-
цииу^ъ (лг, у\, у\, . ..,y°J, У^ъ(х;у\, у°, ..., fj, ..., ут =
== ?»»(•*» -^i» -^2» * • •» ^) ^разуют общее решение или общий инте-
интеграл нашей системы.
б) Общее решение системы зависит от т произвольных постоян-
постоянных, причем зависит от них существенным образом.'
Последнее выражение означает, что невозможно найти меньшее
число постоянных cv с2, ..., сг (/<т) таким образом, чтобы тож-
тождественно выполнялось равенство
?<(*; y°v У°2> • • •> -О = ФД*; cv ся, - •., с,) (/ = 1, 2, ..., /и), A4)
где функции Фi имеют непрерывные производные по своим аргументам.
В самом деле, якобиан
d Oh. ?2. • • •» Тот)
имеет, в силу формулы G2), вид
-.у°т)
' «8,2 • " • ^
и поэтому, в силу A02), равен единице при х = хР. Но отсюда сле-
следует невозможность равенства A4) при /</я (см. Бианки [1],
стр. 30I).
§ 6. Доказательство теоремы существования
по методу Коши — Липшица
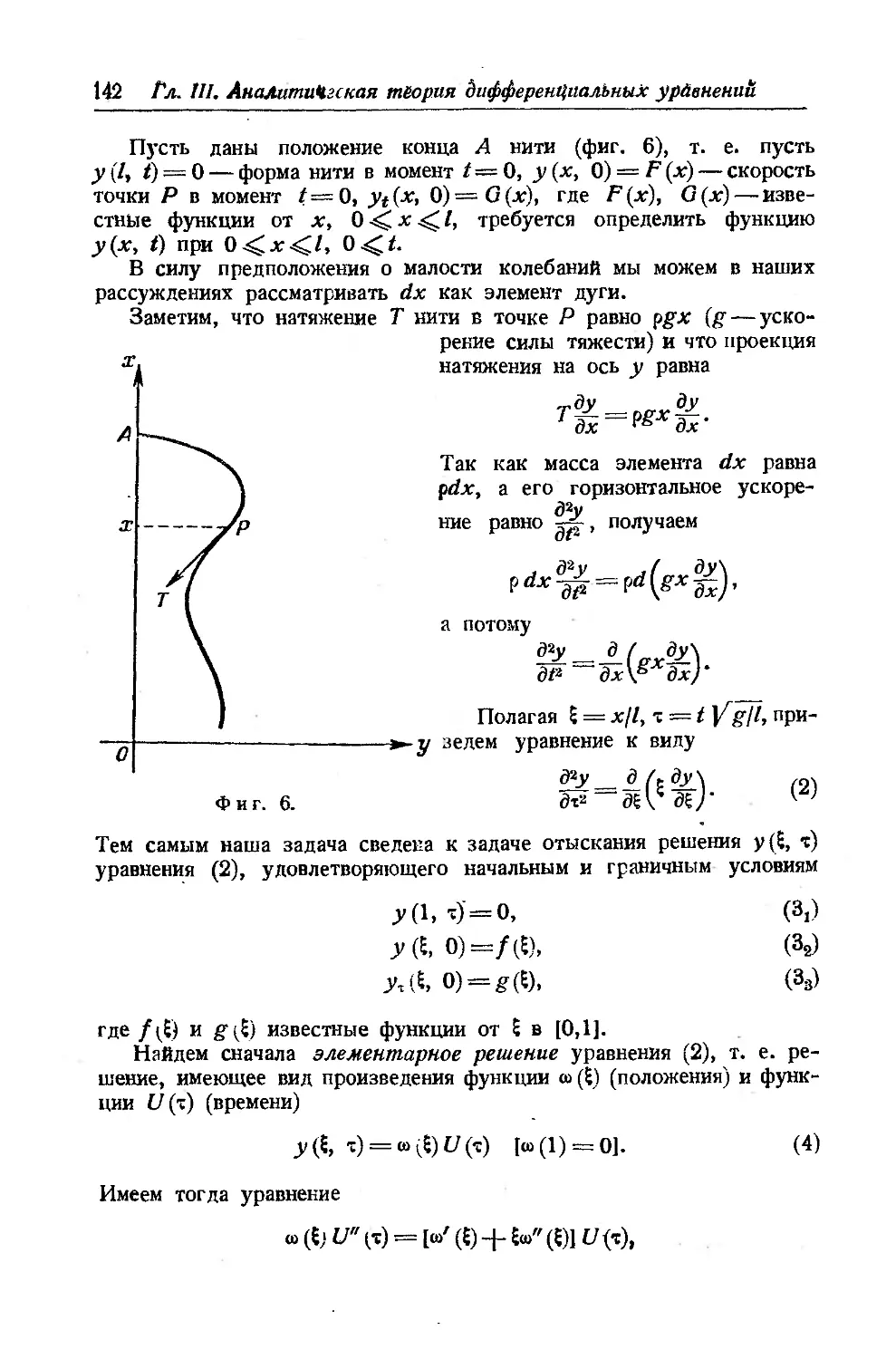
1. Геометрические рассмотрения, а) Рассмотрим сначала урав-
уравнение
dv
где функция /(лг, у) непрерывна в прямоугольнике /?2, определен-
определенном неравенствами
\х—а
и предположим, что каждой точке (д:0, у0) этого прямоугольника
соответствует одно и только одно решение у = у{х) уравнения A),
удовлетворяющее начальному условию у (д:0) = у0.
!) См. также Чеботарев Н. Г. [1], стр. 73.
6. Метод Roiutl—ЛипшиЦй
35
Рассматривая х и у как прямоугольные декартовы координаты на
плоскости, скажем, что у=у(х) является уравнением интегральной
кривой уравнения A), проходящей через точку Р0 = (х0, _у0). Наши
предположения означают, что через каждую точку Ро прямоугольника
/?2 проходит одна и только одна интегральная кривая уравнения A).
Вообще, уравнение A) фиксирует в каждой точке Р^(х, у)
из /?2 направление с угловым коэффициентом -r-—f(x,y). Назовем,
вместе с Ли (см. Ли [1], т. I, стр. 11) линейным элементом сово-
совокупность точки и некоторого направления. На прямоугольнике /?8
имеется оо8 линейных эле-
элементов, из совокупности
которых уравнение A) вы-
выделяет совокупность оо2
линейных элементов, рас-
распадающихся на оо1 инте-
интегральных кривых. Эти
рассуждения намечают
путь для установления
существования решения
уравнения A), который
был строго проведен Ко-
Коши в данном им первом
доказательстве теоремы
существования1).
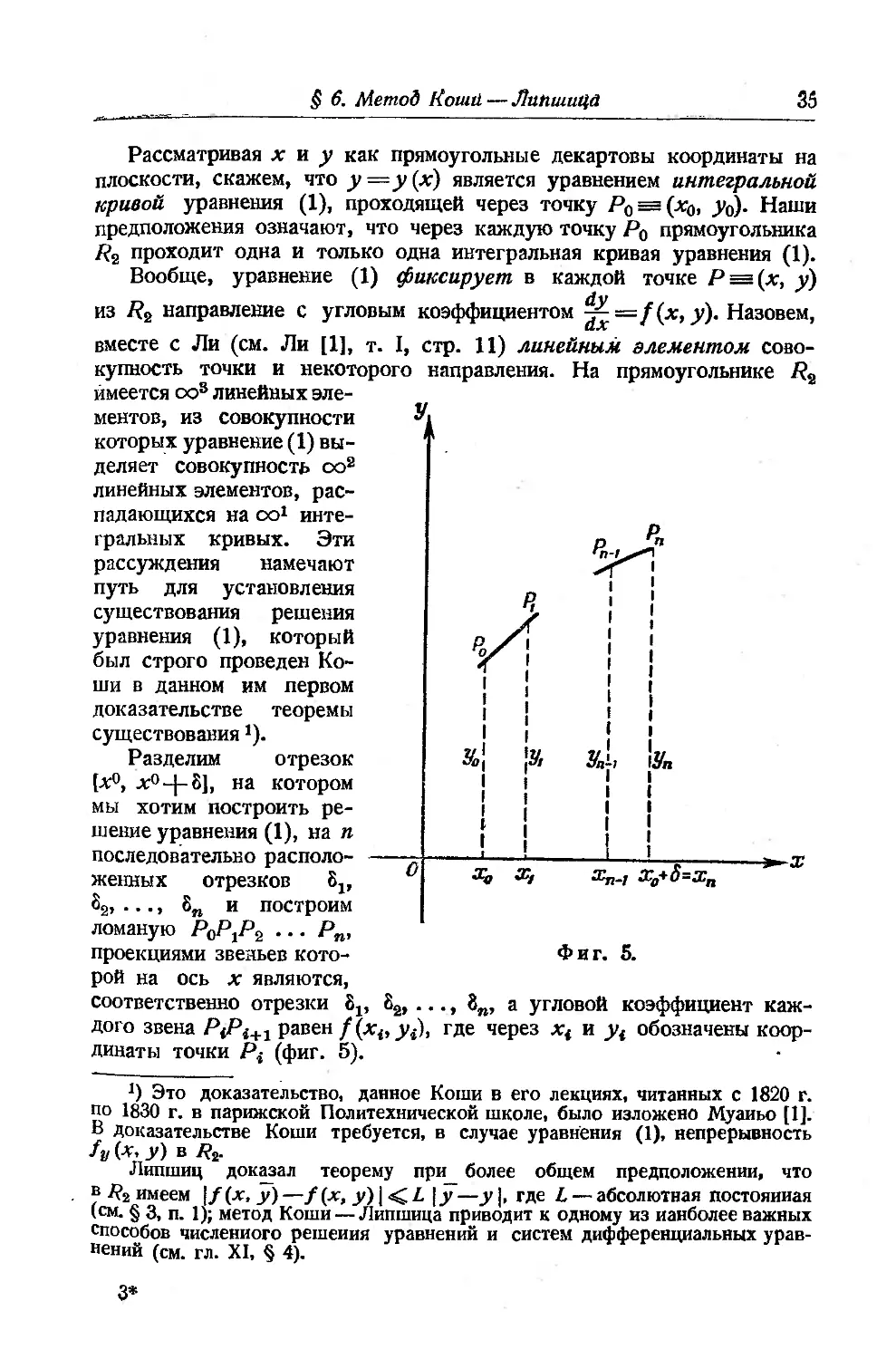
Разделим отрезок
[л:0, л:0-]-8], на котором
мы хотим построить ре-
решение уравнения A), на и
последовательно располо-
расположенных отрезков 8а,
82, • • • i 8И и построим
ломаную PqP^z ... Рп,
проекциями звеньев кото- Фиг. 5.
рой на ось х являются,
соответственно отрезки lv 82, ..., 8И, а угловой коэффициент каж-
каждого звена PiPi+1 равен f(xit yt), где через xt и yt обозначены коор-
координаты точки Р4 (фиг. 5).
J) Это доказательство, данное Коши в его лекциях, читанных с 1820 г.
по 1830 г. в парижской Политехнической школе, было изложено Муаиьо [1].
В Доказательстве Коши требуется, в случае уравнения A), непрерывность
Липшиц доказал теорему при более общем предположении, что
в #2 имеем \f(x, у) —f(x, у)|<L \у~—у |, где L — абсолютная постоянная
(см. § 3, п. 1); метод Коши — Липшица приводит к одному из ианболее важных
способов численного решения уравнений и систем дифференциальных урав-
уравнений (см. гл. XI, § 4).
0
У
Уо\
¦
а:
\у,
X,
х„., хо+8=ха
3*
36 Рл. 1. Нормальные системы дифференциальных уравнений
Пусть п стремится к бесконечности, а длины отрезков 8f равно-
равномерно стремятся к нулю; тогда, как мы увидим в п. 2, из ломаных
PoPJ3^ • • • Pn-i Рп можно выбрать последовательность, равномерно схо-
сходящуюся к искомой интегральной кривой.
б) Аналогично рассматривается случай двух дифференциальных
уравнений
g=/(*. У, *), ? = g(x,y,z) B)
с двумя искомыми функциями у и z. В этом случае каждой точке
Р = (д:, у, z) пространства соответствует направление с направляю-
направляющими косинусами
2 g[l+f2+ff2 C)
и, тем самым, точка Р определяет некоторый линейный элемент;
интегральными кривыми будут кривые, касательные к которым
в каждой точке имеют направление, определяемое формулами C).
Если функции fug удовлетворяют сделанным в § 3, п. 1 пред-
предположениям, то через каждую точку Р проходит только одна инте-
интегральная кривая, а потому интегральные кривые образуют двупара-
метрическое семейство кривых или, как говорят, конгруенцию.
в) Аналогичные рассмотрения можно провести и для систем
высшего порядка.
2. Теорема существования в формулировке Пеано. Доказа-
Доказательство Арцела. а) Докажем методом Коши — Липшица теорему
существования для системы
y'i =fi (x; yv у» ..., уJ (/=1,2,..., т). D)
Предположим, что функции /,(х; у1г у%, ..., ут) непрерывны
в прямоугольном параллелепипеде Rm+1 с центром [jfi-\-^; yl,
Уг. • • •. yinh определенном неравенствами
*°О<л:<>-|-й; — й<^— yi<b, (/=1,2 т),
и пусть в Rm+l
\fi(х; уи у» ..., уJ|<М. E)
Обозначим через 8 наименьшее из чисел а и -г..
М
Если ограничиться лишь теоремой существования, то, как
мы далее увидим, непрерывность функций ft (x; yv _у2, ..., ут)
достаточна для того, чтобы обеспечить существование хотя бы
одного решения уу {х), у2 (х), ..., ут(х) системы D), опреде-
определенного на [дг°, &-\-Ъ\ и удовлетворяющего начальным условиям
=у<> (/==1> 2>..., т). F)
§ 6. Метод Коша— Липшица 37
Этот важный результат теории дифференциальных уравнений при-
принадлежит Пеано (см. Пеано [3], [4]). Мы изложим доказательство,
аналогичное данному Арцела (см. Арцела [1], [2]I) для случая
уравнения у' =f(x, у).
Разделим отрезок [х°, jt°-f- 8] на 2й равных частей и положим
*П,* = *° + Ш-» (fc = O, 1, ..., 2»; л = 1,2,...). G)
Определим теперь на отрезке [х°, jc°-}-8] функции
по следующему закону: положим
*i, п (*», о) = У и • • •, &т, п (.Хп, о) = У°т (8о)
для точек х, принадлежащих отрезку (лгпО^д:^л:И
(/=1, 2,..., /га) для точек, принадлежащих [хп1, хп1-\-Ъ2~п],
—xn,i)filxn,v *i,n(*fm). • • •» *«t,n(^,i)l
и, вообще, для точек, принадлежащих [л:и fc; хи fc -j- 82-"] (k = О,
1 2» — 1),
Пусть
4*1,1»W=/it«e,ь Ф1,п(^,*).---» *«t,n(^n,k)b (9)
когда хп<к-^.х-^.хП1е-\-№~п _(ft = 0, 1, ..., 2n—1). Тогда для х,
принадлежащих [хп1, хпк-\-Ь2~п], имеем
Но
хп, к
Ф*, п (*«, к) = Фг,» (*«, к-1) + J <W, n (ж) <*¦*
..о
г, n («и, i) = J'? + / 4^ n (ж) ^ж.
*) Относительно уравнения y'=f(x, у) и нового метода доказатель-
доказательства, основанного на использовании аппроксимирующих многочленов, см. Се-
верини [1], [2] (ср. также гл. VIII, § 7, п. 1). Относительно приведенного
в тексте доказательства см. Камке [1], стр. 126—130,
38 Гл. I. Нормальные системы дифференциальных уравнений
Суммируя эти равенстна, получаем для любой точки х из [л*, х° -f- 8]
равенство
ж
f A0)
Легко доказать по индукции, что написанные формулы имеют смысл,
т. е. что
О'1)
Заметим, в самом деле, что в силу (80) |Ф/>и(лг°)—y°i\ = 0, а в силу
(9) |^*,nC*)|^Af на отрезке [д:п>о. xni]. Но тогда из соотношения
A0) вытекает, что
Тем самым показана законность формулы (82) и справедливость ра-
равенства A0) на [*„, 1, хп> г]. Переходя таким образом от каждого
отрезка к последующему, мы убеждаемся в справедливости не-
неравенств A1).
Если Ej, Е2—любые точки, принадлежащие [л*, JC°-j-8], то
в силу A0)
\]\^\, A2)
а потому функции
$1,1 (*), *1, 8 (*),..., Ф1, „(*),¦•• A3)
равностепенно непрерывны и равномерно ограничены в [х°, х°-\-Ь].
По теореме Асколи *) из последовательности A3) можно выделить
I) Для удобства читателя напомним интересующее нас предложение.
[См., например, Петровский И. Г. [1], стр. 36. — Прим. ред.]
а) Последовательность {fn{x)} непрерывных на отрезке [а, Ь] функций
называется равностепенно непрерывной, если для любого о > 0 можно найти
такое 8 > 0, что колебание каждой функции /„ (лг) на любом отрезке, длина
которого не превосходит 8, меньше или равна о.
б) Критерий Арцела: если разностные отношения функций fn (л:) огра-
ограничены в совокупности на [а, Ь], то функции fn (x) равностепенно не-
непрерывны на [а, Ь]. В самом деле, в этом случае найдется такая постоян-
постоянная М. что, каковы бы ни были точки х-у и х2 из [а, Ь\, имеет место не-
неравенство \fn(x\)—/n(jc2)|<Л11Х\ — х2\ и, следовательно, в качестве Ь
можно выбрать -jrr.
в) Докажем теперь теорему Асколи: пусть {fn(x)} — последователь-
последовательность равностепенно непрерывных и равномерно ограниченных на [а, Ь]
функций; тогда можно выбрать-из нее подпоследовательность, равно-
равномерно сходящуюся к непрерывной функции <р (х).
Рассмотрим всюду плотноеиа [а,Ь] счетное множествоjct,x2,..., хп, ...,
например множество рациональных чисел, заключенных между в и ft. Пусть
I/W|<M( 12<<>). Тогда последовательность {fn (x{)} огра-
§ 6. Метод Коши—Липшица 39
подпоследовательность
.., Ф*. х2 (х), ..., Ф1, Хр (х), ... [Хх < Xg <... < Хр <... ],
равномерно сходящуюся к непрерывной функции Ф^л:).
Но, в силу неравенства A2), функции последовательности
Ф2. \± (х), Ф2, х2 (х), -.., Ф2> Xj0 (*), ¦ ¦.
также равностепенно непрерывны и равномерно ограничены на
[Л*, jc°+8], а потому из нее можно извлечь подпоследовательность
равномерно сходящуюся на [л:0, дс°—{—8] к некоторой функции Ф2(л:).
Поэтому на [jc°, jc°-]-8] равномерно выполняются соотношения
Нт Фи р. (х) = Фх (*), Нт Ф2. - (*) = Ф2 (дг).
Продолжая таким же образом далее, мы получим т последователь-
последовательностей
Фг, v, (*), Фи. v, (х), .... Фц, Чр (х), ...
A=1, 2, .... т; Vj < v2 < ... < Vp <...),
таких, что на [jc°, jc°-J-8] равномерно выполняются соотношения
lim Фь, (х) = Фг (х) (/=1,2,..., т), A4)
ничена, так как —Ж <!/n (-^l) <!'Af и потому существует наибольший
предел <р (ati) этой последовательности. Из последовательности {fn (xi)}
можно выбрать такую подпоследовательность
/i,iD/ll2W /UW 0)
что
Hm /j „ (лп) = <p (д:1) [|Т (лп) | < M].
n->oo '
Повторяя это рассуждение для точки лг2, выделим из A) подпоследова-
подпоследовательность
Л, 1 (*)• Л, 2 (*) Л,« И. • • • B)
такую, что
I'm Л п(*i) = f (-fi). Mm Д„(дг2) = <р(х2), [ |<р(*2) |<М].
Продолжим этот процесс и рассмотрим подпоследовательность
/i, 1 (*)• Л, 2D- /„, „ W. • • • C)
Она сходится в точках xi, x2,..., хт, ... к значениям <р(xj), <p(лг2), ....
Ч (хт),... соответственно. Покажем, что оиа сходится в [а, Ь] и притом
равномерно.
Выберем, в самом деле, о>0 и найдем такое Ь, что колебание всех
функций /„ (л:) на любом отрезке, длина которого не превосходит 8, меньше
или равна о. Разделим [я, Ь] на р равных отрезков, выбрав р так,, что
< 8. Пусть это будут отрезки Si, Вг,..., 8^,. Так как множество {-*гп} всю-
40 Гл. I. Нормальные системы дифференциальных уравнений
и в силу (801 и второго неравенства из A1)
*i(*°)=*yM*,(*)— fi\<b, (*°<лг < л? + 8; 1= 1, 2,\.., т). A5)
Докажем теперь, что т функций
у1 = Ф1(х), у2 = %{х), ..., уш = Фт(х)
дают нам решение системы D). Для этого нам достаточно пока-
показать, что на [х°, jc°-}-8] равномерно выполняются соотношения
lim ф!. v (д) =/, \х\ Ф, (*), Ф2 (дг), ..., Фт (*)], A6)
1>->оо ^
ибо тогда, полагая в A0) n=-vp и переходя к пределу при р->оо,
мы получим равенства
из которых следует, что функции Фг(*) удовлетворяют системе ин-
интегральных уравнений, равносильных данной системе D).
Пусть jc° ^ х <[ д:° 4~ 8; Для данного д: и любого чр можно найти
такое k, что
"* ~V*\ A7)
и потому, в силу (8к+1), имеем
IФМр (*) ^Ф1. v^ (*v*) I < 82~V*Af. A8)
Аналогично доказывается, что
ду плотно на [в, ft], то в каждом из этих отрезков найдутся точки этого
множества. Обозначим через ^ первую из точек последовательности {хп},
лежащую внутри bv через ?2 — первую из точек этой последовательности,
лежащую внутри Bg, и т. д. Последовательность C) сходится в точках ?i,
?2 ?р, а потому наймется такое целое число те0, что при /к'>-/к0,
те">те° имеем
1Л»'.»,' (У —/•». «<г(У !<« (г = 1,2 р).
Пусть теперь л: принадлежит отрезку Sr; тогда
', т' W —fm", m'i W I = I Ifm'. m' ix) —f<m>, m' &¦)] —
откуда, в силу произвольности о, следует, что подпоследовательность C)
равномерно сходится к некоторой функции <р (лг), причем, в силу непрерыв-
непрерывности функций fn (х), функция <р (л:) непрерывна.
г) Из проведенного доказательства вытекает следствие: если функции
fn(x) последовательности {fn(x)} равностепенно непрерывны и равно-
равномерно ограничены на отрезке [а,Ь] и если эта последовательность схо-
сходится на некотором счетном всюду плотном в [а, Ь] множестве, то
последовательность ifn(x)} равномерно сходится на [а, Ь] к некото-
некоторой непрерывной функции у(х).
6. Метод Коши— Липшица 41
Отсюда, в силу A8) и равномерной сходимости в [лг°, л:0-}-8] по-
последовательности A4), вытекает, что в [х°, дг°-(-8] равномерно вы-
выполняется соотношение
Нт | Фг (х) — Фг, v (xv ь) | = О,
р-*<х> * "
а потому, в силу (9) и непрерывности функций ft (х; у1,у2, • • •, ут)
в Rm+V равномерно выполняется и соотношение A6).
б) Если функции fi{x\ у1г у2, ..., ут) определены в прямо-
прямоугольном параллелепипеде, заданном неравенствами
(i=l, 2, .... и),
то в отрезке [лг° — 8, л;0] система D) с начальными условиями F)
имеет хотя бы одну систему решений у1 = у1(х), у^= у%(х), ...,
ут=Ут(х) (относительно обозначений см. „а").
в) Из наших рассуждений не следует единственность системы
решений для D), F) и в гл. VIII будет показано, что непрерывности
функций fi(x; у у, у2, ..., ут) недостаточно для того, чтобы обе-
обеспечить эту единственность.
г) Отметим, наконец, что из проведенных в „а" рассуждений
вытекает следствие: если функции fi(x; у,, у2, , ут) определены
в полосе S
S: х°<х<х°-\~а, —оо<уиу2,...,ут<-\-со
и непрерывны и ограничены в этой полосе, то, какова бы ни
была совокупность т чисел у\, у\, • • -, у°т, найдется хотя бы
одно определенное во всем отрезке [х°, х°--\-а] решение системы
дифференциальных уравнений
/t=ft(*i yv У*, ¦ • ¦» Ут) (i= !. 2, ..., и),
удовлетворяющее начальным условиям
Точно так же, для любого дифференциального уравнения
такого, что функция f(x; у, у1, , у(п~хУ) непрерывна и огра-
ограничена в полосе S
g, —оо<^, /, у", ...,yl»-V<+co,
найдется хотя бы одно решение У~у(х), определенное
в [х°, х°~\-а] и удовлетворяющее начальным условиям
где у0, yQ, ..., у°п_х — любые постоянные величины.
42 Гл. 1. Нормальные системы дифференциальных уравнений
Для доказательства достаточно рассмотреть эквивалентную систему
у[ = Уа Уп-1 =Уп> У« =/(*» У* У* •¦¦> Уг)-
3. Доказательство Тонелли теоремы существования в форму-
формулировке Пеано. а) Мы хотим дать упрощенное доказательство тео-
теоремы Пеано, получающееся специализацией способа доказательства
теорем существования, разработанного Тонелли для функциональных
уравнений типа Вольтерра. Отметим, что способ Тонелли1), основан-
основанный в значительной степени на методе Коши — Липшица, не только
дает полезный метод эффективного вычисления решений, но позво-
позволяет также доказать теорему существования при значительно менее
ограничительных предположениях о функциях ft (х; yv у%, ..., ут)
(см. гл. VIII, § 8, п. 1).
б) Предположим, что система
.у* =*/*(¦*; yv у* • • •» у») ('=!»2» • • •» т)
удовлетворяет указанным в п. 2 „а" условиям. Покажем, что в этом
случае существует хотя бы одно определенное в [х°, х°-\~Ь] решение
У\ (¦*)> Уъ (*)• • • • i Ут (x)j удовлетворяющее начальным условиям
УЛ*?)=У1 ('=1, 2, ..., т). F)
Как и в § 3, п. 2, заменим систему D), F) эквивалентной ей
системой интегральных уравнений
. • • •. У» (х)) dx A9)
ж»
и покажем существование хотя бы одной системы непрерывных
функций уг(х), уъ(х), ..., ут(х), определенных в [х0, хо-{-8] и удо-
удовлетворяющих системе A9). Определим для любого натурального п
функции у&> (х)х yf> (х),..., у%Цх) на [лг°, jc°—J—S] по следующему
правилу:
t
X
ft
)) dx B02)
Я!'
') См. Тонелли [1]. Этот мемуар содержит теорему существования и не-
некоторые удобные условия теоремы единствевиости; относительно непрерыв-
непрерывной зависимости решений от начальных данных см. Чинквиии [1].
2) Для применения формулы B02) следует, учитывая формулу B00. найти
функции jffl (х) на отрезке -«Ч . х°-] , потом иайти те же фуик-
лЯ+-—, -ж°Ч—— I и так далее,
§ 6. Метод Коши—Липшица 43
Формулы B0j) и B02) показывают, что значения функции yf>(x)
не выходят из области, в которой существует /^(х; yv yv ..., _ym).
В самом деле,
!>$•>(*)—д$ К ил < а.
В силу формул B0х) и B0е) функции \у^>(х)}, {у&>(х)},...
•••> {3*йЧ*)} равномерно ограничены и равностепенно непрерывны.
Поэтому, как было указано в п. 2 „а", можно выделить т подпо-
подпоследовательностей
которые при п -> со равномерно сходятся к т непрерывным функ-
функциям
Начальные условия F) выполнены в силу построения. Легко до-
доказать также, что построенные функции удовлетворяют и системе A9)
В самом деле,
SB0
as
Во втором слагаемом в правой части можно перейти к пределу при
и —>• со под знаком интеграла, а третий член в правой части не пре-
превосходит по абсолютной величине значения -,— и потому стремится
к нулю при п -*¦ со. Поэтому, переходя в B1) к пределу при п -> оо,
получаем A9).
в) Пусть в системе
/i =fi (*>' yv У» • • •, yj (I = 1. 2, ..., m) D)
функции fi (x; yv y.2, • •., ym) определены в полосе Si
л?<*<*° + а; —оо<Л< + оо (i=l, 2, ..., m)»),
непрерывны там и удовлетворяют неравенству
\fi(x> yv З'а. •••• J'JK^W (' = 1» 2, ..., т),
где функция М(х) суммируема в смысле Лебега в [х°, х°-\-а].
J) Функции f{(х; уь у2,.... ут) могут обращаться в • точке х = л°
в бесцовечност-ь или же не быть определенными в этой точке.
44 Гл. I. Нормальные системы дифференциальных уравнений
Построим по формулам B0х) и B02) последовательности {
}» ¦••> (^(¦*)}! по Формуле B02) получаем, что
\yW(x')—yf){x")\ =
Л (*; д**(*). №(*). • • •. д№)*|
, в , в
п п
as
и, в силу абсолютной непрерывности Г Л! (л:) Ле, отсюда заключаем,
что функции последовательности {.^(-"ОЬ •••> {Д^Ч*)} равномерно
ограничены и равностепенно непрерывны. Повторяя рассуждение То-
нелли, мы убеждаемся, что при сделанных предположениях суще-
существует, по крайней мере, одна система определенных в [Xй, х° -\- а]
функций, которые абсолютно непрерывны в [дс°, х° -\- а] и являются
решениями системы
¦¦yt(*)=y°t-\
Эти функции удовлетворяют тогда при х° < х <[ л;0 -\- а си-
системе D) и начальным условиям yi№)=y% (t=l, 2, ..., т).
г) Если для системы D) при любом выборе начальных значений
УЬ У%> • * ¦ > Ут справедлива теорема единственности, то при выполне-
выполнении сделанных в „в" предположений описанный там процесс приводит
к соответствующему решению
Ух (*1 y°v Уг • • •. У1)' У2 (*•" У°1' У* ¦ • •» y°J> •••>ym(x'>yv У0»---, y°J-
Докажем, что если выполнены сделанные в „в" предположения
и если для системы D) имеет место теорема единственности
при любых начальных значениях у°, у%, ..., у° то все решения
yt (х; у\, у\,..., у^) непрерывно зависят от точки (х', у\, у\,..., у^)
из S1).
Положим, для упрощения записи, Р ^ {у\, у°, ..., у^), у. (х, Р) =
•=yt(x; yl, у\, ..., yl) (i=l, 2, ..., т) и докажем сначала, что
при любой точке Р == (у°, у°, ..., у^) для всех х справедливо ра-
равенство _
ШУ<(х; Р) =yt(x; P) (/=1,2,..., т). B2)
!) Относительно частного случая этой теоремы см. § 5, п. 1 „а". Отно-
Относительно теоремы, указанной в тексте, см, Каратеодори [1], стр. 673,
§ 6. Методы Коши — ЛипшЩй 45
Докажем это утверждение от противного. Предположим, что для
некоторого х можно найти хотя бы один индекс f(/ = l, 2, , т),
для которого равенство B2) не имеет места. Тогда можно было бы
найти такую последовательность точек {Рп}, Рп зз (у' °\ yf-0), ...
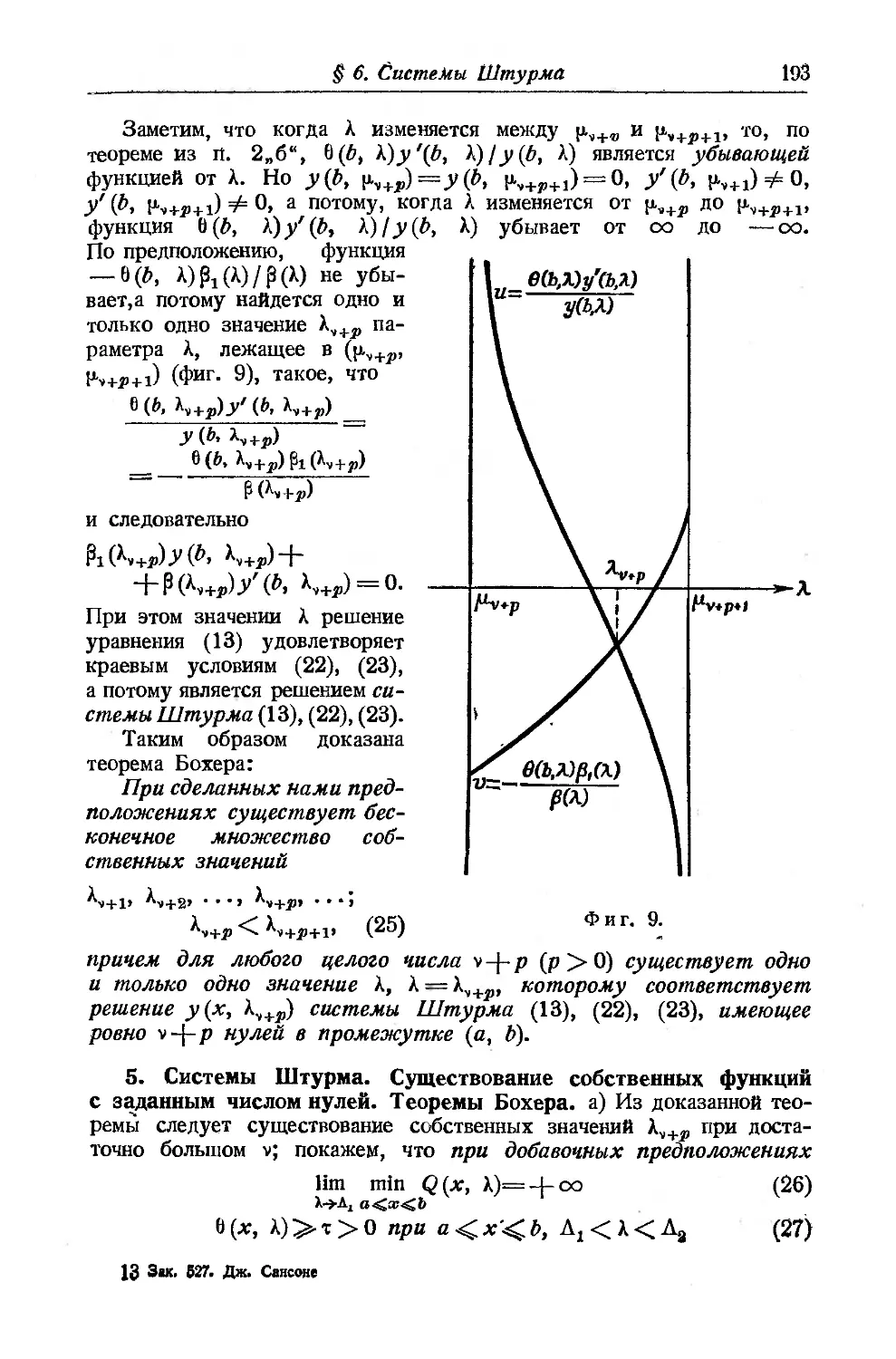
• • •. ^>0)). что lim Рп — Ръ
П->со
lim yt (x; Рп) = чФ yt (*; Р). B3)
• В самом деле, в силу неравенства
f M(x)dx,
функция yt (х; Р) остается ограниченной, когда Р изменяется в /я-мер-
ном шаре с центром в точке Р и радиусом р (р > 0). Обозначим
через Мп и тп соответственно верхнюю и нижнюю грани значений
функции Уг(х, Р) при условии, что Р пробегает m-мерный шар
(центр которого лежит в точке Ри радиус равен — J, не совпадая
при этом с точкой Р. Тогда оба предела lim Mn и lim mn конечны,
rt->oo те->со
причем хотя бы один из них, например lim Mn = -у, отличен от
__ П->оо
Уг(х; Р).
Отсюда следует, что для любого п найдется такая точка Рп,
Рп ф Р, что Рп лежит в сфере радиуса — с центром Р, причем
Переходя к пределу при п —> оо, получаем, что lim Pn = Р и
_ _ _ п-»оо
Пту<(х;Рп)=?тФу^х; Р).
я-» со
В силу того, что
ае+Н
; P)—yt(x; P)\<\f M(x)dx\ (i = l, 2, ..., m), B4)
ос
функции У{(х; Рп) (i= 1, 2, ..., тм; й= 1, 2, ...) равномерно огра-
ограничены и равностепенно непрерывны в [лг°, лг° -1- а] и по теореме
Асколи1) из последовательнсстей [yt(x; Рп)} A=1, 2, , т) можно
извлечь т подпоследовательнсстей, обозначаемых для простоты
х) См. примечание на стр. 38. Вместо функций /„ (л:) следует применить
указанные там рассуждения к функциям у (х; Рп), изменяющимся при изме-
изменении у точек Рп индекса и. [Нетрудно видеть, что для применимости тео-
теоремы Асколи безразлично, принадлежат ли ковцы отрезка [а, Ь\ к этому
отрезку. — Прим. ред.]
46 Гл. Л Нормальные системы дифференциальных уравнений
записи также через {у{(х; PJ}1), что для всех х, принадлежащих
[х°, x°-\-a], равномерно выполняется соотношение
Шп Л (х; Рп) = <?г (*) (/=1,2,..., и), B5)
П-*-со
где функции <?i(x) непрерывны в [лг°, jt°-j-a]. Так как
as
Уг{*> Рп) =У?'°> + /U(*;уг(х;Рп), у2(х;Рп\ ...,Ут(х; PJ)dx,
а /< непрерывны в S, то, переходя к пределу при п -»¦ со, получаем,
что
а;*1
Таким образом, функции 9<(*) образуют систему решений для D),
удовлетворяющую начальным условиям <Pi(x°)—y%, A=1, 2, ..., т),
а потому, в силу предположения «о единственности решения, имеет
место равенство
и, в частности, <р< (Jf) = ^< (лг; Р), вопреки B3) и B5).
Для того, чтобы доказать, наконец, непрерывность решений от-
относительно пары (л:; Р), заметим, что в силу B4)
I yt (x + h; P) —yt (x; P) | <л (л-+A; P) — yt (x; P) | +
+1Уг(x; P) —yt(x; P)|<| J M(x)dx\ + \yi(x; P) —yt(x; P)\,
X
as
откуда, ввиду абсолютной непрерывности интеграла Г M(x)dxvi ра-
равенства B2), и следует наше утверждение.
Относительно рассуждений см. п. 2 »а".
Глава II
НОРМАЛЬНЫЕ СИСТЕМЫ
ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
И НЕКОТОРЫЕ ПРЕОБРАЗОВАНИЯ
ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 1. Нормальные системы
линейных дифференциальных уравнений.
1. Нормальные системы однородных линейных дифференциаль-
дифференциальных уравиений и лииейные дифференциальные уравиеиия.
а) Нормальной системой однородных дифференциальных урав-
уравнений называется система вида1)
[ = «1,1^1 + «1,*Уъ + • • • + «1, тУт,
'2 = «2,1^1 + «2,2^2 +•••+ «2, тУтъ
т = аш, 1Уг + «Ч аУя + • • • + аш, тУт,
A)
где atik — непрерывные функции от х на отрезке [а — а, а-\-а],
a Уг> Уъ> •••» З7»»—искомые функции.
б) К системе типа. A) приводит решение однородного линейного
дифференциального уравнения порядка т
у(ш) ==. piy(m-l) + р^С-Ч +...+Рт.1У +РтУ, B)
коэффициенты которого pv p2, , рт„1У рт являются функциями
от х, непрерывными на отрезке [а — а, а -f- a].
В самом деле уравнение B) эквивалентно линейной системе
(см. гл. I, § 1, п. 2 ,а")
У»= л.
y'm-i — .у™
Обратно, система вида A) может быть при достаточно общих
предположениях приведена путем исключения т — 1 искомой функ-
•) Этот параграф посвящеи изучению нормальных линейных систем;
общая теория систем т лкиейиых дифференциальных уравнений, содержа-
содержащих т искомых функций и их производные, будет изложена в гл. X.
48 Гл. It. Нормальные системы линейных уравнений
ции к одному однородному линейному дифференциальному уравнению
относительно одной искомой функции, имеющему, вообще говоря, по-
порядок тJ). Например, если коэффициенты а^к системы A) имеют про-
производные т-—1-го порядка в [а — а, а-\-а], то мы можем последо-
последовательно дифференцировать первое уравнение системы A), учитывая
каждый раз остальные уравнения этой системы. Таким образом мы
получаем
у[ = ah Ly1 -j- alt,
+ • ¦ • + стУт-
Если определитель этой системы отличен от нуля на отрезке [а — а,
а + #]> то ее можно решить относительно yv y2, ..., ут, причем
для _yj получится требуемое уравнение.
в) В силу замечания, сделанного в гл. I, § 3, п. 4 „а", какова
бы ни была точка х° из отрезка [а — a, a -j- а] и какова бы ни
была система начальных значений cv с2, , с^, существует
одна и только одна система функций, удовлетворяющих системе
A) и принимающих в точке лг° значения cv c2, ..., ст соответ-
соответственно; эти функции, кроме того, непрерывно зависят от х° на
отрезке [а — а, а-|-я]2).
Отметим еще, что если выбрать в описанном в гл. I, § 3, п. 2
процессе последовательных приближений за первые приближения
И1 (¦*)> Й2(*) ит(х) начальные значения сх, с2, ..., ст, то при-
приведенный там ряд последовательных приближений (I) примет вид
yi(x) = ciyiil(x)-j-c2yii2(x)-j-... -\-cmyi>m{x) (« = 1,2, ..., т). C)
Отсюда следует, что содержащиеся в решении системы A) про-
произвольные постоянные входят в него линейно.
Функции
УиЛ*)' УъА*)' • • •• УтАх) (fe= 1, 2, ..., т)
образуют частное решение для A), так как оно может .быть полу-
получено из формулы C), если положить
сх = с8 = ... = ск_г = ск— 1 = сп+1 = ... — ст = 0.
Формула C) дает нам вид решения системы A). Мы рассмотрим
глубже этот важный результат в „г" и „в" п. 2ив п. 3.
*) Для линейных систем без предположения о нормальности этот вопрос
будет изучен в гл. X, § 4.
2) См. гл. I, § 5, п. 1. Отметим, что если с^ = с2 = ... = ст =± 0, то со-
соответствующие решения ^{х), у2(х},..., ут(х) тождественно равны нулю
или, как говорят, образуют нулевое решение.
§ /. Нормальные системы линейных уравнений 49
Применяя полученные результаты к уравнению B), мы видим,
что для любой точка х° из [а — а, а-^-а] и любых постоянных
величин ev с2, ..., ст существует одно и только одно решение
уравнения B), удовлетворяющее начальным условиям
= cv у' (*о) = с2, ..., дгО-
иными Словами, задача Коши для уравнения B) имеет одно и только
одно решение*).
г) Пусть вообще мы имеем р решений системы A)
Уии (*)> Уъ,к (.X), ..., ymtk (x) (ft r= 1, 2, ..., р), D)
иными словами, пусть
X, ь = 2яиЛ* ('== 1, 2, ..., m; ft = 1, 2, ..., р). E)
Умножая обе части этих равенств на постоянные cs и суммируя
по k от 1 до р, мы получим
р ю» р
2 )' = 2 амB
г1
а потому, каковы бы ни были постоянные clt с2, ..., ср, система т
функций
Л (¦*) = «Лл (*) + сгЛ,8 (*)+•••+ V*,/. (*)(<= 1, 2 j») F)
удовлетворяет данной системе уравнений.
Система F) называется линейной комбинацией р решений D)
с р произвольными постоянными,
2. Формулы Лиувилля и Якоби. а). Пусть даны р решений си-
системы A)
Л.*. У%ъ ¦ • •. Ут.* (Л = 1, 2, ..., р); G)
матрица
Л.1 Ям
G')
J'l.p З'э.р • • • Ут.р
называется матрицей этих р решений G).
б) Пусть даны т решений системы A)
•» .>4fc (ft = 1, 2, ..., /и).
J) Отметим, что если сх = с2 = ... = ст = 0, то соответствующее реше-
решение уравнения B) является нулевым решением у (х) = 0{
4 Зак. 527. Дж. Сансоне
Гл. it. Нормальные системы ланеаных уравнений
Рассмотрим определитель
Л.1 Л.1
Уг.ъ Уъ,ъ
Ут.1
У\,
т.т
(8)
их матрицы. Докажем, что если A(jt°) отличен от нуля в некоторой
точке х° из [а — а, а -J- а], то Д (х) отличен от нуля на веем отрезке
[а — а, а + а].
В самом деле, дифференцируя Д (л:) по столбцам, мы получаем
откуда, в силу E),
У\,
, т Л+1,я» • • • Ут,1
2
Интегрируя теперь от
Якоби [2J, стр. 222)
до х, мы получаем формулу Якоби (см.
,dx
из которой следует, что Д(лг)^О в [а — а, a-j-a].
в) Применим теперь полученные результаты к дифференциаль-
дифференциальному уравнению B). Пусть уи у2, ..., ут — система т решений
этого уравнения. Из замечаний, сделанных в п. 1 „б", вытекает,
что в этом случае определитель Д(лг) заменяется определителем
У1 У[ У" • • • УГ-1*
(8')
а формула (9) переходит в формулу Лиувилля
J Pi dx
W{x) = 1Г(лг°) е1
(90
(см. Лиувилль [1J, стр. 349).
Определитель W называется вронскианом т функций уг, _у2, ...,
..., ут; из наших рассуждений следует, что если вронскиан W
решений уравнения B) отличен от нуля в какой-либо точке
$ 1. ИорМйМнЫе дистеМы линейных уравнении 51
отрезка [а— а, а-)-а], то он отличен от нуля во всем этом
отрезке.
г) Полученные в „б" результаты могут быть обобщены следую-
следующим образом: если в некоторой точке х° отрезка [а — а, а-\-а]
ранг матрицы G') совокупности р решений G) равен р, то и
в любой другой точке этого отрезка ранг этой матрицы равен р.
Теорема верна, если р — т. Предположим, что р < т. Не теряя
общности, мы можем считать, что
Присоединим тогда к р решениям G) еще т—р решений
Уи и (*)> J4 * (<*)> • • • • Ут, и (х) (k =* Р +1, .... т), A0)
определяемых начальными условиями
Л. р+г (ХО)=... =Ур+г-1, р+г (Х°) =Ур+г, р+г (Х°) — 1 =
= 0, (г = 1, 2, .... т —р).
Определитель решений G) и A0) отличен от нуля в точке лг°, а по-
потому он отличен от нуля и на всем отрезке [а — а, а-f-а] и, сле-
следовательно, ранг составленной из его первых р строк матрицы G')
в любой точке отрезка [а — а, а-\-а\ равен р.
Из доказанной теоремы следует, что ранг матрицы, составлен-
составленной из любого числа решений системы A), постоянен на отрезке
[<х — а,
3. Независимые решения. Фундаментальные системы. Пони-
Понижение порядка системы линейных однородных уравнений, а) р ре-
решений системы A)
Лд. У*,*» -';Ут,ъ (Л = 1, 2, ..., р) G)
называются линейно зависимыми, если можно найти р постоян-
постоянных величин с1У с2, ..., ср, из которых хотя бы одна отлична
от нуля, так, что на отрезке [а — а, а-{-а] тождественно вы-
выполняются соотношения
сьУ«,1 + ^Л,5+---+^«,з> = ° (*= Ь 2, ...,«). A1)
В противном случае данные р решений называются линейно не
зависимыми.
Из этого определения следует, что если р решений линейно
зависимы, то хотя бы одно из них является линейной комбина-
комбинацией остальных решений.
б) Для того, чтобы р решений G) системы A) были линейно
независимыми, необходимо и достаточно, чтобы определитель
матрицы GГ) равнялся р в [а — а, a-f-а]-
4*
52 Гл. II. Нормальные системы Линейных уравнений ^
Условие достаточно: в самом деле, если ранг матрицы G') равен р,
то единственным решением системы A1) является нулевое решение.
Это условие также и необходимо, т. е. если р решений G) ли-
линейно независимы, то ранг матрицы G') равен р. Предположим, что
в некоторой точке дг° отрезка [а — а, а -\- а] ранг матрицы G') ра-
равен р' •< р; тогда из матрицы G') можно составить //-строчную
матрицу, состоящую, например, из первых р' строк, ранг которой
на всем отрезке [а — а, а-\-а] равен р'.
Выберем некоторое s, 1-^.s-^.p—р'. Тогда
+---+СрОЧР' ('" = 1. 2, ..., т),
где cv с2, ..., Ср-—некоторые функции от дг в [а — а, а-)-«].
которые рационально выражаются через yilt и, следовательно, диф-
дифференцируемы.
Из того, что функции Л1р'+8('==: 1, 2, ... т) удовлетворяют
системе A), получаем, что
B «ьл, *)' = 2 н i B съУ1, *)
к=1 1=1 Л=1
р' р' т
. к 4- 2 w'i, к=2 ск B н
к=1 Л=1 к=1 1=1
и следовательно
EL
Матрица этой системы линейных однородных уравнений относительно
неизвестных с^ имеет ранг //, а потому c't = с^ = ... = с', = 0.
Отсюда вытекает, что функций cv c2 ср< постоянны на отрезке
[a —a, a-j-a], а, следовательно, решение у^р'+8 является линейной
комбинацией первых р' решений, вопреки предположению. Полу-
Полученное противоречие доказывает наше утверждение *).
Из доказанной теоремы вытекает, что если ранг матрицы р ре-
решений системы A) равен г, то г из этих решений линейно неза-
независимы, а остальные решения являются их линейными комбина-
комбинациями.
в) Наибольшее число линейно независимых решений для A)
равно т, и мы покажем сейчас, что можно бесчисленным множе-
J) Независимо от проведенного только что доказательства, постоянство
Сх(х), с2(х), .... ст(х) в [а — а, о + й] можно доказать следующим обра-
образом: т функций
Л. P'+s(x) — C1(a)yi,1(x)—... —Cp- (<*)Уг,р'(х) A=1. 2, .... т)
образуют решение системы A), обращающееся в нуль в точке х=а; в
силу теоремы единственности это решение тождественно равно нулю в
[о — в, a-f-я], а потому cic(x)~ Cfc(a), Л==1, 2, ..., я, откуда и следует
что ei, Ср ... ср, постоянны в [а — а а + а).
/. Нормальные системы линейных уравнений
53
ством способов построить т линейно независимых решений си-
системы A).
Пусть, в самом деле,
до=[|^к[| (^ k = \, 2, ..., т)
— какая-либо матрица /я-го порядка с отличным от нуля определи-
определителем. Построим т решений системы A), принимающих в лежащей
на отрезке [а — а, а-\-а] точке дг° значения из первой, второй, ...,
/я-й строчки матрицы Д°; в силу полученных в п. 2 „б" результатов
определитель этих т решений отличен от нуля в [а — а, а~\-а],
а потому рассматриваемые т решений линейно независимы.
Назовем, следуя Фуксу (см. Фукс [1], стр. 126), совокупность т
линейно независимых решений для A)
Л.* Л.*. •••> Утл (* = 1. 2, .... т) A2)
фундаментальной системой. Из полученных в „б" результатов вы-
вытекает, что для того, чтобы система A2) была фундаментальной,
необходимо и достаточно, чтобы определитель (8) был отличен
от нуля в [а — а, а -\- а].
Если система A2) является фундаментальной системой ре-
решений для A), то общее решение системы A) имеет вид
2.
где ск — постоянные величины1).
Очевидно, что если система A2) является фундаментальной систе-
системой решений для системы A) и если [|cf(k|[—квадратная матрица
т-го порядка с постоянными элементами, определитель которой отлиг
чен от нуля, то, перемножая по столбцам две матрицы
ч. 1
Ь2.1
fcw, 1
с\, т с% т
ст,т
Ут,1
Л.»
Л.» Л.
it, т
J) Отметим, что если даны /и2 непрерывных вместе со своими первыми
производными на [а — а, а-\- а] функций
У1, к (¦*). J'a * (*) J'w.fc (*) (* = 1, 2. ..., /и), A2)
для которых определитель (8) отличен от нуля в [а — а, а-f-e], то суще-
существует одна и только одна система A), для которой эти функции образуют
фундаментальную систему решений; в самом деле, система
ik^=a(y1 + ay2lk+...+at>mymtk (I, ft=l, 2, ..., т)
определяет одним и только одним способом коэффициенты
54
Гл. II. Нормальные системы линейных уравнений
мы получим новую матрицу, элементы которой образуют новую фун-
фундаментальную систему решений для системы A): в самом деле, опре-
определитель получающейся матрицы отличен от нуля.
г) Применяя полученные результаты к уравнению B), мы видим,
что если yv у2, ... > ут являются т решениями уравнения B),
вронскиан которых W(yv j2, ..., ут) отличен от нуля в [а— а,
а-\-а], то любое другое решение имеет вид
у {х) = с1У1 (х) + с2у2 (*)+.-.+ стут {х),
где cv с2, ..., ст — постоянные *). Мы будем говорить в этом слу-
случае, что yv у2, ..., ут образуют фундаментальную систему ре-
решений уравнения B).
Если функции у1г у2, ... ут образуют фундаментальную систему
решений уравнения B), и если Цс<к[| —квадратная матрица т-го по-
порядка с постоянными элементами, определитель которой отличен от
нуля, то т решений yv у2, ..., ут,
yfc = ckily1~]rc1Ct2y2-{-...-\-cKmym (Л = 1, 2, ..., т),
образуют новую систему фундаментальных решений этого уравнения»
д) Докажем, в заключение, следующую теорему:
Пусть известны р линейно независимых решений системы A),
матрица которых содержит отличный от нуля во всех точках
отрезка [ос— а, а-\-а] минор порядка р. Тогда можно, с помо-
помощью невырождающегося линейного преобразования искомых функ-
функций, свести решение системы A) к решению другой линейной
нормальной системы, содержащей т—р искомых функций, и
к р квадратурам.
Пусть, в самом деле, известны р решений системы A)
и пусть во всех точках из [а—а, а-\-а]
Л» 8
Ур.1
У'р. 2
Уг,р У%р
Ур.р
фО.
A3)
J) Заметим еще, что еслиyi(x),у%(х), ...,ут(х) являются т функциями,
непрерывными в [а — а, а-\-а\ вместе со своими производными до /и-го
порядка включительно и если W (уь у%, .... ут) фО в [о — а, а + «]. то
существует одно и только одно уравнение B), для которого эти функции
образуют фундаментальную систему решений. Простейшей формой такого
уравнения будет
у у' у" ••
У\
Уг
= 0.
= j2,lK1+J2,2K24-...'
3*2+ • • • ~\-Ур,рУр>
$ /. Нормальные системы линейных уравнений 55
Положим
A4)
Ур+г =
(r=l, 2, .... т—р).
При этом обратимом в силу A3) преобразовании _ylf ^/2, ..., ут
в Yv F2, ..., FOT система A) переходит в систему
y'i = 2^Л (i = 1, 2, .... m), A5)
z=i
где функции Ait рационально выражаются через ajt1c и yjk
(j, k — \, 2, ...,'т).
В силу A4), система A5) имеет р решений
откуда следует, что первые р столбцов матрицы [|^ik|| (?, k =
1, 2, ..., т) тождественно равны нулю. Поэтому система A5) имеет
вид
^ «У« (*= I» 2, . . ., Р), A6!)
^m (r=l» 2,..., /Я р). A62)
Уравнения системы A62) образуют нормальную систему т—р
линейных уравнений cm—р неизвестными функциями, решив кото-
которую мы можем найти с помощью квадратур из уравнений A6Х)
функции Yv К2, ..., Yp, после чего из уравнений A4) находим
yv У» •••• У»-
Следует еще заметить, что при решении системы A62) мы полу-
получаем т—р произвольных постоянных, остальные р произвольных
постоянных возникают при квадратурах, необходимых для решения
системы A6Х), а потому из формул A4) следует, что решения
уг, у2, ..., ут содержат линейно и однородно т произвольных постоян-
постоянных; из того, что преобразование A4) обратимо, следует, что опи-
описанный нами способ дает общее решение системы A).
А. Сопряженная система дифференциальных уравнений.
а) Пусть (j,j, ji2, , jiTO будет т функций от х, дифференцируемых на
отрезке [а — a, ct-j-a]. Умножим выражение^—2а»,гЛ на (** И
56 Гл. /Л Нормальные системы линейных уравнений
просуммируем по индексу I. Мы получим тождественно
т / т \ т т mm
2 v-i [y'i—2
2 vi [y2 it tyij2 (i*y*J
откуда следует тождество
я» / от \ от / «\от
21ч(/» — 2 о*, iJViJ + 2 Л (^i + 2ai,#»J = 2(!ЧЛ)'- A7)
Из него вытекает, что если jx, j2, ..., jOT образуют решение
для системы A), a \>,v ji2, ..., jim — решение для системы
«>
l«i = -2fli,#i (ix=l, 2, .... я»), A8)
то функции _у€ и jif связаны соотношением
^Л + ^аУ2 + • • • + Y-тУт = const. A9)
Система A8) называется системой дифференциальных уравнений,
сопряженной с системой A) (см. Якоби [1], т. 4, стр. 404).
Очевидно, что данная система уравнений является сопряжен-
сопряженной для сопряженной системы дифференциальных уравнений.
Если d системе A)
aitl= — alti при 1ф1, ам = 0, B0)
т. е. матрица \\а^г\\ кососимметрична, то система A) совпадает
со своей сопряженной, или, как говорят, эта система дифферен-
дифференциальных уравнений самосопряжена.
Любые два решения (yv у2, .... ут) и (ц,, ji2, ..., рт)
самосопряженной системы дифференциальных уравнений удовлетво-
удовлетворяют соотношению A9) и, в частности, выбирая их совпадающими,
убеждаемся, что Ji-{-.уЦ~Ь • ¦ • H~JOT = const.
б) Мы хотим доказать, что если известна фундаментальная
система решений сопряженной системы дифференциальных урав-
уравнений, то можно, найти фундаментальную систему решений
данной системы уравнений с помощью рациональных операций.
В самом деле, если
* = 1. 2, .... т)
— фундаментальная система решений для A8), то определитель
A' = Det[|jj.fk|[ отличен от нуля в [а — а, а-[~а]. Поэтому система
линейных уравнений
'l ~Г ^2,1^2 ~Г • • • ~Т~ Рт.лУт == cv
I ¦ л л л I I ¦ л л ш ^*
'B1)
Л Нормальные системы линейных уравнений 57
разрешима относительно yv у2, ..., ут, причем
т
= 1, 2,..., л»), B2)
где Af,ti — алгебраическое дополнение элемента определителя Д',
стоящего в k-ш Столбце и г'-й строке.
При любых значениях постоянных clt с2, ..., ст формула B2)
дает нам решение системы A). В самом деле, учитывая A8), мы
получаем из тождества A7), что
in m
2 V-i. hiy't—2 ai, 1У1) = О (k *= 1, 2, ..., т).
i=l 1=1
Но Det||{i.i>ft[|#O, а потому
lb
Так как обратный к Д' определитель |ЛЛ4/Д'| отличен от нуля,
то функции
А * й Л
**1 i /In i •*>«« ?
образуют фундаментальную систему решений для A).
Из изложенного следует, что две проблемы — решение системы
однородных линейных дифференциальных уравнений и решение со-
сопряженной с ней однородной системы — могут рассматриваться как
эквивалентные.
5. Неоднородные линейные системы. Метод Лагранжа. Пусть
дана нормальная система неоднородных линейных дифференциальных
уравнений
2 i,iyi + i (/= 1, 2, ..., т), B3)
7=1
где aib ut—известные непрерывные функции от дг, определенные
в [а —я, а + я].
Покажем, что решение такой системы может быть сведено к ре-
решению однородной линейной системы и к квадратурам. Мы укажем
два различных пути такого сведения.
а) Рассмотрим вместе с однородной системой
«>
4= 2 «*. i*i>
58 Гл. II. Нормальные системы линейных уравнений
получающейся из данной системы B3), если положить и$ = 0, со-
сопряженную с ней систему
«>
П = — 2 «*,#*•
Пусть
V-i.w 1Ч*>---> Ы,к (ft —1, 2,..., т)
— фундаментальная система решений этой сопряженной системы. Из
тождества A7) следует, что
т in m
21Ч,кСУ< — 2 a-i, 1У1) = 2 fa», *ЛУ (* == 1, 2, .... ти),
ii ?i fi
откуда, в силу того, что Det Hft.kH^O» следует эквивалентность
системы B3) и системы
т т
2 (н *у<У—2 v-t, u"i = о-
Интегрируя последнюю систему, мы получаем систему уравнений
^НкУ€— Г2 V4.i^idx = ck (*=1, 2,..., ти),
о
решая которую, находим функции yt.
б) Изложим теперь принадлежащий Лагранжу метод решения си-
системы B3) при помощи вариации произвольных постоянных (см.
Лагранж [1], т. IV, стр. 159 и далее). Пусть
Л,к> J2,k» • • • > Ут, к Ф = 1, 2, . . ., т)
— фундаментальная система решений линейной однородной системы
2ч^» B4)
В силу доказанного в п. 3 „в" общее решение имеет вид
2 = 1, 2, ...,«), B5)
где ск — постоянные. Будем рассматривать теперь сп к"ак функции
от х. Тогда получаемые из B5) значения yt будут удовлетворять
данной системе B3), если
т т mm
2 съу\, к+2 с'к yt,k=2 а<. 1 B wi, к)+щ=
ft=l *=1 1=1 k=l
«> m
2*B
h=l 1=1
$ /. Нормальные системы линейных уравнений 59
В силу B4) для этого необходимо и достаточно, чтобы
т
S' /• 1 о \
Cjcyi Jc === U$ yl ^^ 1, &, • • • | /«J.
Определитель ||_v*. к П этои системы линейных зфавнений относи-
относительно fcj отличен от нуля в [а — а, а -\-а]. Поэтому при помощи
рациональных операций мы можем найти с'ъ как функции от дг
в [а — а, а-\-а], после чего т квадратурами находим, наконец, ск.
Чтобы получить выражение для ск в более явном виде, обозна-
обозначим через Yitk(x) приведенное алгебраическое дополнение элемента
yi1e в Det|[jf>k||, т. е. отношение алгебраического дополнения yilc
в bet|jj,k|] к'значению этого определителя. Тогда
42
и потому, в силу B5),
где
Ми{х, l) = %>i,i<{x)Yltk®, B52)
и cj, с°, ..., с^т — произвольные постоянные. (Относительно фор-
формул B5Х) и B52) см. Пиконе [1], стр. 26.)
В силу известных свойств определителей имеют место следую-
следующие соотношения для #*,»(*, 6):
, дг)==О при i=l, 2,..., т, 1ф1.
Почти излишне указывать, что первая сумма в правой части
равенства B5j) представляет общее решение однородной системы B4).
в) Рассмотрим теперь, в частности, неоднородное линейное диф-
дифференциальное уравнение
.Vм+Л W"-1' + ... +pm-i (*)/+Р« {*)У = Х(х) («>1), B0
где pt(x), р%(х), ..., рт(х), Х(х) — известные функции от х, непре-
непрерывные на отрезке [a —a, ct-f-a].
Предположим, что функции уг(х), у2(х), ..., ут{х) образуют
фундаментальную систему решений однородного уравнения
(i=l, 2,..., т\ B")
60 Гл. //. Нормальные системы линейных уравнений
а у0 (х) является частным решением данного уравнения B'). Тогда
общее решение уравнения B') имеет вид
у (х) = c{yt (лт) + см (*)+...+ стут (лг)+У о (*),
где clt с2, ..., ст — произвольные постоянные.
Метод вариации произвольных постоянных приводит к следую-
следующему выражению для уо(х):
ft=l
и
где через W=W(yvy2, ..., ут) обозначен вронскиан фундаменталь-
фундаментальной системы решений уи у2, ..., ут однородного уравнения B"), а
через W'n^ — алгебраическое дополнение элемента у^~х) в W.
Некоторые авторы называют функцию ciy1(x)-\-c2y2(x)-\-
+ ... -\-стут(х), представляющую общее решение однородного урав-
уравнения B ), дополнительной функцией.
6. Нормальные системы однородных линейных дифференци-
дифференциальных уравнений с постоянными коэффициентами, а) Предпо-
Предположим, что коэффициенты aiy г линейной однородной системы
постоянны.
Выясним, можно ли удовлетворить системе B6), положив
yt = ацГ, у2 = а2^, ..., ут = аш,Г, B7)
где сс1( ай, ..., ат и р постоянны, причем хотя бы одно ак отлично
от нуля1).
Подставляя эти значения в B6), мы получаем, что должны иметь
место равенства
2
т. е.
(«1.1 — P)al+fll,2«8+
.lal + a»M,2aS + --- + (a«n,«n P)a«n = °- .
B8)
») См. также Петровский И. Г. [11, стр. 143—167 и Степанов В. В, [11,
стр, 283—296. — Прим. перев, 1
/. Нормальные ЬМтеМЫ Линейных уравнений
61
Эти уравнения относительно а{ должны иметь ненулевое решение.
Для этого достаточно, чтобы р было корнем алгебраического уравне-
уравнения ти-й степени относительно р
?>(?) =
l.J Р а1.2
Й2,1 «2,2 —
i.i»
"то, 2
"т,т
—Р
= 0.
B9)
Обратно, если р является корнем уравнения B9), то система B8)
имеет ненулевые решения, а тогда формулы B7) дают решение пред-
предложенной системы B6).
Уравнение B9) называется характеристическим (или фундамен-
фундаментальным) уравнением системы B6).
б) Предположим, что уравнение B9) имеет т различных корней
pj, рз, ..., рто и обозначим через
of), af>, ..., aW (fc = l, 2, .... m)
ненулевое решение системы B8), соответствующее корню p = pft;
докажем тогда, что т решений
образуют фундаментальную систему решений для системы B6) *)•
В самом деле, если бы это было не так, то существовала бы, по
крайней мере, одна тождественно равная нулю линейная комбинация
ер1ж, е9'^, ..., е9*? с постоянными коэффициентами, не все из кото-
которых равны нулю, чего не может быть. Этот факт будет доказан
в более общем виде в „в"; в нашем простейшем случае достаточно
заметить, что
1 1 ... 1
Pi
Рг '
П«П— 1
?=0.
Отсюда следует, что при наших предположениях решения си-
системы B6) выражаются формулой
&№ (/= 1, 2, ..., /и),
где с„ с2,
- произвольные постоянные.
!) Проведенные нами рассуждения справедливы независимо от того,
являются постоянные а^ действительными или комплексными числами.
В случае, когда онн действительны, корпи рд могут тем не менее принимать
комплексные значения {попарно сопряженные); в этом случае, выражая
показательную функцию по формуле Эйлера, мы приводим ответ к действи-
действительной форме.
62 /Vi. If. Йормйльные системы линейных уравнений
в) Нам осталось рассмотреть случай, когда уравнение B9) имеет
кратные корни. Докажем следующую теорему:
Если р, — корень характеристического уравнения кратности р,
то ему соответствует р линейно независимых решений си-
системы B6), причем любое составленное из них решение имеет
вид
У г = *"Pt (*). У* = *"Р* (*). • • •. Л. = **Р* (*).
где Pi(-v), P2(jc), ..., Pm(jc) — многочлены от х, степень которых
не превосходит р — 1 (и которые линейно зависят от р произ*
вольных постоянных).
Доказательство проведем по индукции. Теорема верна, если р = 1.
Покажем теперь, что если она верна для корней характеристического
уравнения кратности р — 1, то ока верна и для корней кратности р.
Не теряя общности, мы можем считать, что рг = 0, так как в про-
противном случае с помощью преобразования
yl = e^Yl A=1, 2, .... и)
мы привели бы систему B6) к системе
^ = 4 Л+ • • • +К i-Pl) У<+ • • • +««. т*т,
характеристическое уравнение которой
ai,2 ••• a
i,m
fl2.1
«»,, 1 «.я. 2 . ««..«. — (Pl+P)
= 0
имеет, в силу сделанных предположений, корень р = 0 кратности р.
Итак, положим pj = O; в этом случае система B6) имеет частное
решение
У\ — aV У2 — а2« • • •» Ут = ат>
причем хоть одно из at отлично от нуля. Пусть, например, ох ф 0;
не теряя общности, мы можем считать, что ох = 1 (легко проверить,
что числа о^ определены с точностью до постоянного множителя).
Выполним тогда для системы B6) указанное в п. 3 „д" преобра-
преобразование, приводящееся в нашем случае к виду
Л = yv У* = «2^i + Y» ¦ ¦ •. Ут - *»Ух + У.- C0)
Мы получим новую систему (допускающую решение 1^=1,
Г2=...==Кт = 0)
Y[*=A1,2Y2-}-...-j-A1,mYm, C1X)
C12)
1. Нормйльные системы Линейных уравнении
63
где
К i = «1, г (/= 2, 3, ..., т), C2)
\ i = «*.»— «Л.1 (', / = 2, 3, ...,/«). C2')
Докажем, что если обозначить через Dx (p) лепую часть характе-
характеристического уравнения системы C1Х), C12),
— Р «1,2
О «2,2—
О «3,2—аЗ«1,2
«1,3
С2,3~°2#1,3
аз,з—аз«1,з — Р
«1, то
«2, ТО а2«Ъ ТО
«3, »п — аЗа1, т
О «й», 2 — аВ1«1, 2 «т, 8— ата1, 3
«то, то—ато«1,»»—Р
= 0, C3)
то Z)(p) тождественно равнр D1(p). В самом деле, прибавляя к эле-
элементам 1-й строчки умноженные на а{ элементы первой строчки
(i = 2, 3, ..., т), мы получим
2,2 — Р Й2.з
2, то
«з,з~ Р
- а»»Р
в, 2
t, 3
*т, то
— Р
Вычитая теперь из первого столбца умноженный на о2 второй
столбец, умноженный на о3 третий, ..., умноженный на ат т-й
столбец и учитывая, что
мы получим в точности определитель ?>(р); поэтому Dl(p)^(p)
Из C2), C2'), C3) следует, что р = 0 является корнем кратно-
кратности р — 1 для уравнения
—Р
d2,8
• • • «*«
•,3 Р • •' А.
8. m
*»», 2
b, 3
• • • "то.»» Р
C4)
а потому, в силу предположения индукции, система C12) имеет р — 1
линейно независимых решений, причем любое другое составленное из
них решение имеет вид
^2 = Q2 (*). ^з = Qb W. • • •, У» = Я» (x), C5)
где Q2 (x), Qs (x), ..., Qm (x) — многочлены от х, степень которых не
превосходит р — 2 (и которые линейно зависят от р — 1 произволь-
произвольных постоянных).
64
Гл. II. Нормальные системы линейных уравнений
Подставляя выражения C5) в C1Х), получаем
от as
C6)
1=2
где Сх — новая произвольная постоянная, а подставляя C5) и C6)
в C0), получаем, что ух, у2, ..., ут имеет указанный выше вид.
Остается показать, что с помощью описанного здесь процесса мы
получаем в точности р линейно независимых решений для B6). Заме-
Заметим для этого, что мы имели р — 1 линейно независимых решений
для C12)
(* —2, 3, ..., р 1)
*2, *> '8, ft»
и что ранг матрицы
1
т
2
1=2
. к
О О
v v
'3,2 ••• * т, 2
т
J=2 •>
1 т.р-1
составленной из р решений системы C1Х), C12), равен р. Этим же
рангом р обладает и матрица, составленная из соответствующих р
решений системы B6), построенных по формулам C0).
Итак, мы доказали, что любому корню рх характеристического
уравнения, имеющему кратность р, соответствуют р линейно незави-
независимых систем решений.
Если рх и р известны, то для того, чтобы построить эффек-
эффективно многочлены Рх (х), Р2 (jc), ..., Рт (х), достаточно подста-
подставить в данную систему вместо уи _у2, ..., ут, соответственно,
е?&р1(х), ef^Pz(х), ..., е?&Рт{х) и получить таким путем
для коэффициентов многочленов Рх (х), Р2 (лг), ..., Рт (х) линей-
линейную систему уравнений, решения которой содержат р произволь-
произвольных постоянных.
Заметим, наконец, что если поставить в соответствие каждому
корню характеристического уравнения столько линейно независимых
решений, какова его кратность, то совокупность решений, поставлен-
поставленных в соответствие всем различным корням характеристического урав-
уравнения, образует фундаментальную систему решений. Для доказатель-
доказательства этого покажем, что соотношение вида
Аг (х) е?& -{- Л2 (*) е№ -\-... -f Ав (х) е^ = 0, C7)
где pj, р2, ..., ps — попарно различные постоянные, а А1(х\
Л2(л:), ..., As(x) — многочлены, может тождественно выполняться
§ 2. Применение матричного исчисления 65
лишь в случае, когда все At (лс), As (дг), ..., Ав (х) тождественно
равны нулю *).
Этот факт очевиден, если s=l; докажем теперь справедливость
его в общем случае по индукции. Из C7) получаем
Продифференцировав это равенство «-{-1 раз, где я — степень мно-
многочлена А8{х), мы получаем тождество
в котором ^(а:), ?а(х), ..., Л8_1(лг) — многочлены той же степени,
что и Ах{х), А\(х), ..., Ав_1 (х) соответственно. Но это невозможно
по предположению индукции.
г) Применим теперь полученные результаты к частному случаю,
когда система получается из однородного линейного уравнения
= О, C8)
где а0, ау, ..., am_v ат — постоянные, аоФО. Тогда, если харак-
характеристическое уравнение
«оРт + «iP + • • • + «W_iP + ат = О
имеет корни рх, р2, ..., ря, кратность которых равна, соответственно,
plf pQ, ..., ps, (p1-\-ps4----+Ps = m)> T0 общее решение уравне-
уравнения C8) имеет вид
к=1
где cW, c<fc), .... №_1(k = l, 2, ..., 5) — произвольные постоянные.
§ 2. Применение матричного исчисления к определению
решений системы линейных дифференциальных уравнений
с переменными коэффициентами
1. Сведения по матричному исчислению. Приведем некоторые
сведения по „матричному исчислению" 2), необходимые для изложения
предложенного Пеано доказательства существования решения Коши
системы линейных дифференциальных уравнений. Это доказательство,
1) Решение задачи Кошн для случая, когда линейная система с постоял»
ными коэффициентами не является нормальной, будет рассмотрено в г*. X,
§ 7, п. 3 ,г\
2) См. Скорца [1], стр. 139—168. Шлезингер [1], стр. 132—143, Жюлиа [1],
стр. 109—110, Фрезер, Дункан, Коллар [!}. [См. также Гантмахер [1J.—
Прим. перев].
5 вас 827. Дж. Сансоне
66
Гл. //. Нормальные системы линейных уравнений
основанное на методе последовательных приближений, будет изло-
изложено нами в п. 3 1). Читатель увидит, что использование матриц по-
позволяет получить весьма короткое и изящное построение решений
Коши; оно представляет также интерес и с точки зрения прибли-
приближенных вычислений, так как приводит к процессу, позволяющему
находить одновременно все члены искомых функций, соответствую-
соответствующие одному и тому же шагу приближений,
а) Матрица с т строками и и столбцами
a\, 1
«2,1
а
1, 2
«2,2
am,l O,m, 2
обозначается символом A = || a4> ь [| и называется матрицей типа
(т, я).
Числа ait k, действительные или комплексные, называются эле-
элементами, или членами матрицы.
Две матрицы одного и того же типа называются подобными.
Две подобные матрицы A=\\aik§ и B=^bi§ ft|| называются
равными, если
«*,* = *<, ft C=li 2,..., ти; ft = l,2,.... я).
Матрица типа (/и, ти) называется квадратной матрицей по-
порядка т.
Если А=\\а^ ft|| (/, ft=l, 2, ..., /и) — квадратная матрица, то,
как известно из алгебры, ее определителем называется сумма
2 (— I)8 ai, j a2, j! • • • > ат, jm> распространенная на все перестановки
Л» Л» • • •» У» чисел 1» 2, . • •, т, где 5 обозначает число беспорядков
в перестановке jx, у2, ..., jm по отношению к основной перестановке
1, 2, ..., т. Мы будем писать
Det^ = 2(— l)s«ifi.a« * • • • 4
2, А
al, 1 °1, 2
a% 1 «8. 2
1, т
а
т.1
...a,
т,т
Квадратная матрица с отличным от нуля определителем называется
регулярной; если же ее определитель равен нулю, то она называется
нерегулярной (сингулярной, вырожденной).
l) См. примечание г) на стр. 11.
См. примечание ) на стр. 11.
) В дальнейшем мы будем обозначать матрицы знаком ||
делители квадратных матриц знаком | |.
||, а опре»
2. Применение матричного исчасления
67
Квадратные матрицы
а
1,1
О
2, 2
О...
О...
о
о
о
о
О... а
п,п
1
0
0
1
0 ...
0 ...
0
0
0
0
0
0
0
0
... 0
... 0
О О О ... 1
о о о ... о
называются соответственно диагональной матрицей, единичной
матрицей, нулевой матрицей. Единичная матрица обозначается
символом 1, нулевая — символом О.
б) Назовем суммой (разностью) двух подобных матриц А = \\aiik\\
и В = ||?iift|| и обозначим символом А-\-В (А — В) матрицу, эле-
элементы которой равны ait к -j- bit к (ait k — bit k); таким образом,
*И. А — В= ||ai>ft—bAtk\\.
Если о — действительное или комплексное число, то произведе-
произведением матрицы А = ||a1>ft|| на число а называется матрица ||ae<>fe||,
обозначаемая символами аА, Аа, т. е.
в)
Пусть
А =
«Л
даны
«i, i
«2.1
«и», 1
= Аа =
aal.
««2.
ааот
две матрицы
«1, 2 • • • «1,
flg Q • . • W«j
L am, 2 • •
• а»,
1
1
,i
п
»
га
««1,2
««2.2
«ЙТО,2
• ¦ •
1 2'
,га
. m
а«то, n
1
1
1V l
1, •
*2,2
Ьп, 2
... *i,r
• • • ^m, »•
типов (т, п) и («, г) соответственно, иными словами, пусть число
столбцов матрицы А равно числу строк матрицы В. Назовем про-
произведением матрицы А на матрицу В и обозначим символом АВ
матрицу АВ = С— ||cift|| типа (т, г), в которой каждый элемент
cifk является суммой произведений соответствующих элементов /-Й
строки матрицы А и й-ro столбца матрицы В; в символах
ci, k = Ч А, к + Я»,2*Й, к + • • • + ai,nK, k= 2 «i, A *•
Если
¦»=1
^2.1
-«2,2
1, я
2, я
. 2
, га
5*
68
Гл. П. Нормальные системы линейных уравнений
то произведение АХ= Y является матрицей типа (т, 1), причем,
если
Ут
то
t 2
Если Л и В являются матрицами типа (/», и) и (и, т), то можно
образовать два произведения АВ и ??А Вообще говоря, АВ ф ВА,
иными словами, произведение матриц не обладает свойством ком-
коммутативности.
Этот факт очевиден, если тф п, так как в этом случае мат-
матрицы АВ и ВА имеют различные порядки т и п. Но это же имеет,
вообще говоря, место и в случае, когда /и = «; например, если
О
2
I
то
АВ:
2 О
12 2
3 1
2 О
2 6
О 2
Если А и В — квадратные подобные матрицы, то по теореме
БинеJ)
Det A X Det В = Det AB.
Заметим, что
1.1
*1,2
«2,1 «2, 2
«2.»
*«,!
... а„
, и
X
a
0
0
0 ..
a ..
* ¦
. 0
. 0
. a
a
0
0
<
0 ...
a ...
0 ...
=
«l.i '
0
0
a
=
«1, la «1. 2* • • ¦ «1, na
«2. la «2. 2a • • • «2, na
71,2 ••• «1.»
«2, 1 «2, 2 • • • «2. w
"m, l «то, 2 • • • «jn, и
,.«ТО.И«
= aA,
См. Курош А. Г. [1], стр. 91.—Прим. перев.
2. Применение матричного исчисления
69
откуда следует, что умножение матрицы А на число о равносильно
умножению матрицы А на диагональную матрицу
а
0
0
0 ..
о ..
0 ..
. 0
. 0
. а
В дальнейшем, если A=laiihl {l=\, 2, ..., в)— квадратная
матрица, а а — число, то мы будем обозначать символом ct-j-Л
(о — Л) сумму (разность) диагональной матрицы
а
0
0
0 ...
а ...
0 ...
О
0
а
типа (и, я) и матрицы А, г. е. а±А= \\ab{ k±aik\\., где 84fft==O
при i ф к, i1t i = 1.
Если А, В, С, D, ... — матрицы, имеющие соответственно типы
(т, л), (я, р), (р, д), (q, г), ..., то, по определению, положим
ABC = {АВ)G, ABCD = {ABC)D, ...
Легко проверить, что {АВ)С=А{ВС), т. е. что произведение
матрац обладает свойством ассоциативности.
Имеет место также дистрибутивный закон
Произведение АВ может равняться нулю даже в том слу-
случае, когда ни одна из матриц А и В не равна нулю. Например,
если
1 О || _ J О ОII II О О
о
в=\
о
то АВ-
О О
Заметим, что если А и В—квадратные матрицы одного и
того же порядка, такие, что АВ = 0, и если определитель од-
одного из сомножителей, например DeM, отличен от нуля, то
второй сомножитель В является нулевой матрицей. В самом
деле, «ели Det^^O, то линейная однородная система уравнений
с неизвестными blilc, b%k, ..., ?nS
имеет лишь нулевые решения.
г) Если А — квадратная матрица, то полагаем, по определению,
Л°=1, Л1 = Л, An^An-iA (я = 2, 3, ...).
tti Гл. If. Нормальные системы линейных уравнений
Матрица А" называется п-й степенью матрицы А. В силу свой-
свойства ассоциативности имеем
А™Ап = Ат+п.
Если А — квадратная матрица, а р0, рг рп — некоторые
га
числа, то сумма 2 Р<АЧ также является матрицей, обозначаемой
кратко символом Р (Л); матрица Р(А) называется многочленом от А.
д) Пусть квадратная матрица Л = ||a<,ft||(i, k = l, 2, ..., я) ре-
регулярна, т. е. пусть Det A = D ф 0; тогда существует одна и только
одна матрица В, такая, что ЛЛ=1.
В самом деле, линейная система (84> к = 0 при i ф k, 8f< ^ = 1)
имеет одно и только одно решение, даваемое формулами
А — 4l j. Ак, 2 j. — -^fe, m /l 19 и"»
где через Лк> г обозначено алгебраическое дополнение элемента aftj г
в определителе А.
Если ЛЛ=1, то матрица В называется обратной для А и обо-
обозначается Л; по определению АА~1 = 1.
Непосредственно проверяется, что А~1А = 1.
Если А — регулярная матрица, а т — целое положительное число,
то полагаем по определению А~т = (А~1)т; легко проверить, что
равенство АтАп = Ат+п сохраняет силу для любых целых показа-
показателей от и и.
е) Если Л==|[а^ь|| является квадратной матрицей «-го порядка,
то я значений Л, удовлетворяющих равенству
Det(X — A) =
а2,1 ^
= 0,
т. е. п значений X, для которых матрица X — Л вырождена, назы-
называются характеристическими числами матрицы А; совокупность
характеристических чисел называется спектром этой матрицы.
ж) Назовем абсолютным значением матрицы Л = [|а4Ь|| (/=1,
2, ..., т; k = l, 2, ..., я) и обозначим символом [Л[ неотрица-
неотрицательное число
2]
(см. Фробениус [1], стр. 20—29 и 128—129). Очевидно, что для
любого элемента aih матрицы Л имеем | aik\ <^| Л |. -
§ 2. Применение матричного исчисления 71
Расстоянием между двумя подобными матрицами А к В на-
назовем число |В — А\. Будем обозначать его через Д(А, В).
Очевидно, что Д (А, В) = 0 тогда и только тогда, когда А = В.
Имеют место неравенства
(неравенство треугольника) A)
и
|АВ\^\А\-\В\ (неравенство произведения). B)
Последнее неравенство имеет смысл, если А к В являются матрицами
типов (т, п) и (и, р) соответственно.
Неравенство A) доказывается следующим образом. Имеем
но, в силу неравенства Лагранжа,
а потому |Л-|-5|2<!Лр-4-|Я|2 + 2И11#|| откуда и следует A).
Неравенство B) можно записать в виде
р п т п п р
2 212«,А*|2<B 2К*|2)B 21
i=lk=l ч=1 i=lfe=l i=lk=l
I«,*I2)B 2IM2)-
Чтобы доказать это. неравенство, заметим, что по неравенству
Лагранжа
Суммируя по i от 1 до т и по k от 1 до р, получаем
2 2B
2B
п р
2 2
B 2|^1)(
t=l v=l v=l fc=l
откуда следует нужное неравенство
т р п т р п
2 212Г2 2B
т р п р
2 212<чА*Г<|2 2BКА
i=lh=l v=l i=lfc=l v=l
72 Гл. N. Нормальные системы линейных уравнений
з) Пусть даиа последовательность А0, А*^\ .,., A(v), ... подоб-
подобных матриц, имеющих тип («t, л),
Aw«=|4?*| ('=1. 2, .... яч Jfc = l, 2, .... и).
Если тел последовательностей {«?У сходятся, когда v-»-oo, и
Urn а$?* = ««.* (/=1, 2, .... m; А = 1, 2, ... и),
v->oo
то мы будем называть матрицу A = \ait1tl пределом последова-
последовательности матриц {Ца^'йП и писать
Точно так же, если дана последовательность матриц {А^} типа
(от, и), такая, что тп рядов
+ ••• («-=1, 2,... m; ft = l, 2,..., и)
СХОДЯТСЯ, ТО ПОЛОЖИМ
v=0
со
будем называть матрицу A=||a4jftJ = f2 ^*j! суммой сходяще-
гося ряда матриц Л(о)-}-ЛA)-}- ... -}-Лм-}- ... и писать
Этот ряд называется абсолютно сходящимся, если сходятся /гаи ря-
дов S|«S?*|-
v=0
Покажем, что если ^4—квадратная матрица и |Л| — ее
лютное значение, то ряд
v=0
сходится абсолютно для всех значений X, таких, что [ X | > | А |.
Пусть -Av = 34?*||, тогда |4?»КИ*КИГ» * потому ряд
2 14?fcX~(v+1) | мажорируется геометрической прогрессией V ' * z,
v=0 *^ 1^1
которая сходится в силу того, что | X | > | А \.
Этот результат может быть уточнен; можно доказать, что если
спектр матрицы А состоит из чисел \1г Лз, ..., Лп, то ряды
со
2 e^feM* абсолютно сходятся при ] XI > р, где через р обозначено
v=0
§ 2. Применение матричного ижасления 7$
число pssmaxlAjl, |Л2|, ..., |Х„|), а тогда абсолютно сходится и
ряд C) (см. Жюлиа [1], стр. 101).
Пусть
v=0
— степенной ряд, радиус сходимости которого R > р, т. е. пусть.
круг сходимости ряда D) содержит внутри тонка спектра ква-
квадратной матрицы А; покажем тогда, что ряд матриц
«И E>
v=2
абсолютно сходится.
Пусть, в самом деле, е такое положительное число, что р -f- e < Rt
со
в силу сходимости ряда 2 \а<г}и\ |A[~(V+1) при |Aj>p найдется
••=0
такое постоянное число а, что | а,, * | < а (р + e)v+ и, следовательно^
kM<(pll
v=0 v=0
что и требовалось доказать.
В частности, «ели G(z)—целая функция, то ряд (б) абсолютно-
сходится, какова бы ни была квадратная иат,редд А. Это имеет место,,
например, для ряда матриц
v! '
v=0
который обозначается символом еА, иными словами, по определению»
полагается
оо
А*
v=0
Если А и В перестановочные квадратные матрицы одного ш
того же порядка, то ¦
В самом деле, так как матрицы А и В перестановочны, то при.-
любых целых положительных г я s имеем ArBs = BsAr. Поэтому,
оо со
перемножая ряды матриц ^Arlr\ и 2^7*' и|'группируя члены
0 fl
оо
с одинаковой суммой r-\~s, получим в результате 2
v=0
74 Гл. 11. Нормальные системы ланейных уравнений
и) Пусть элементы матрицы А{х) = \сц>и{х)\ типа (т, и) являются
функциями независимой переменной х, тогда
-|"
м потому для существования предела lim [A(x-\-h) — A(x)]lh необ-
Й->оо
ходимо и достаточно, чтобы все тп элементов ||a«,fc(je)|| матрицы А
были дифференцируемы в точке х. Матрица \daitk\x)ldx\ называется
производной от матрицы А и обозначается
f dA П dait д II
==«п==|| dx If
Легко проверить, что
~~dx^ dx"'
со
Пусть А (лг) = 2 ^ (•*)> гДе матрицы Л(у) (х) дифференцируемы
v=0
оо
в окрестности / точки х0, а ряд 2 <ММ (x)[dx равномерно схо-
v=0
•дится в I, т. е. для любого числа е > 0 можно найти такое v0, что
для всех х кз I имеет место неравенство
+~~^ h ••• <8 (р = о, 1, ...)•
Применяя тогда известные теоремы о дифференцировании рядов, по-
получаем, что при сделанных предположениях
dA _ у dyl(v)
v=0
Если элементы матрицы Л =||ai)fc(je)J являются голоморфными
•функциями от х в окрестности / точки а, то в любой точке ре, лежа-
лежащей внутри /, справедливо разложение в ряд Тейлора
к) Пусть3 A(x) = §aitk(x)l и пусть й»)Л(д:)—"действительные
¦функции действительной переменной х, непрерывные в [а — a, a -j- a],
¦а > 0. Матрица Г aif fc(т)rfiII, а — а^_х^.а-\-а называется инте-
2. Прамененае матричного исчисления 75
а!
гралом от а до х матрицы А (лг) и обозначается Г А (т) th или
d x
Из сделанного определения вытекает, что -т- QA (т) = А (х).
ох
ох а
Если aif ji (x) являются голоморфными функциями от х в открытой
области С и если а и д:—две точки из С, то полагаем аналогично
se so
f A(?)dx = QA (г) = | J д
а
а а а
где каждый из интегралов берется по любому регулярному пути в С,
соединяющему а и х.
Если функции ai1c(x) действительны в [а — а, а-|"й1 (голо-
(голоморфны в С) и удовлетворяют там неравенствам
1а*.*(*)|<? С = 1| 2, .... т\ k = l, 2, ..., и),
то
a
as
откуда получаем для абсолютной величины матрицы QA(x) неравен-
а
ство т
\QAWKVmnL\x—а\.
а
2. Матрицант квадратной матрицы, а) Пусть А = ||д$ к(лг)|]
(i, k = l, 2 ..., т) — квадратная матрица порядка т, элементы ко-
которой являются непрерывными в [а — а, а-\-а], действительными
функциями действительной переменной х. По определению имеем
X
SD I л П
и, вообще,
а!
QA (ij) QA (т) = I A (ij) [QA (?)] rf-Cj,
?0
тх) Зл (т) = Г Л (-g [QA (x,) QA (z)] d-cit
а а а ~ а а
QA (xj Q4 (*„_!) •.. • Q-A (г) = f Л (xj{QA (x,.,) ... QA (т)] А».
л л л »J я a
76 Гл. II. Нормальные системы линейных уравнений
Назовем матрицантом матрицы А и обозначим символом QA (т)
а
(см. Бекер [1], стр. 335) составленный из матриц ряд
QA (т) = 1 + QA (г) + QA (т,) QA (т) + QA (*2) QA (т,) QA (т) + ..., F)
а а а а а а а
где в правой части через 1 обозначена единичная матрица порядка т
(см. п. 1 „а").
Пусть для всех элементов матрицы А выполняется на отрезке
[а—а, a-j-а] неравенство
Тогда абсолютные величины элементов матрицы QA (т) не превосходят
в
тд
L | х—а |, матрицы A (ij QA (t) не превосходят ml? ] та — а J, матрицы
а
SB т, (В
QA (xj)QA(т) не превосходят ml?\x— а|2/2!, матрицы QA (т2) X
а а а
X Q^4 Aа)^Л (т) не превосходят от2!81 д: — а |8/3!, и по индукции полу-
а а
чаем, что элементы матрицы
а а а
не превосходят по абсолютной величине mn-lLn\x—а |»/и!. Поэтому
|QA(тп_а) О"Л(тп_2) ... QA(х)|<ж»1-1дг — а]«/«!,
а а а
и, следовательно, ряд F) мажорируется рядом
а потому ряд F) абсолютно и равномерно сходится в [а — а, а-}-а].
б) Рассмотрим теперь одно свойство ЙЛ (т), которое вскоре нам
а
понадобится.
Дифференцируя почленно ряд F), мы получим ряд
А (х) + А (х) QA (х)+А (х) QA (т,) QA (х)+
а а а
QA (JQ
о а а
который, в силу неравенства B) из п. 1 „ж", равномерно и абсо-
абсолютно сходится в [а — а, а-\-а\. Поэтому
\QA(i). G)
а
2. Применение матричного исчисления
77
3. Метод Пеано — Бекера. а) Мы можем теперь изложить так назы-
называемый метод интегрирования Пеано — Бекера системы линейных диф-
дифференциальных уравнений при помощи последовательных подстановок.
Метод был предложен в 1887 г. Пеано J), причем последний ис-
использовал для доказательства гиперкомплексную систему с т едини-
единицами или, что тоже самое, матричное исчисление. В 1903 г. Бекер 2),
независимо от Пеано, вновь нашел и развил способ Пеано, выведя
из него так называемый метод интегрирования Пеано—Бекера, к из-
изложению которого мы и переходим.
б) Пусть дана система линейных однородных уравнений
= 1, 2, .... ж),
где ait % (x) — непрерывные на отрезке [а — а, а -{- а] функции от л:,
и пусть надо найти решение системы, удовлетворяющее начальным
условиям
, г, ..., т).
(82)
Положим
У mix)
Тогда систему (8) можно записать в виде.
А
У0
J'm
и из G) вытекает сразу, что система A0) имеет решение
A0)
\ Го- (И)
а
Таким образом, существование решения Коши для системы A0) до-
доказано; единственность следует из изложенного в гл. I, § 3, п. 3.
в) Заметим, что если элементы матрицы А постоянные величины,
?. е. если система (8J имеет постоянные коэффициенты, то
(*-°)а | I л„ (*-«)» ,
!) См. Пеано [1]. Ср. также примечание на стр. 11.
Вскоре после этого Вольтерра опубликовал свое исследование (см. [1]),
где отметил (стр. 14), что дифференциальное и интегральное исчисления для
подстановок приводят к общей теории линейных диффереодиальных урав-
уравнений (см. также Вольтерра [2]).
2) См. упомянутые в п. 2 .а" работы, а также Бекер [2]. О дальнейших
приложениях теории матриц к системам линейных дифференциальных урав-
уравнений см. Лаппо-Данилевский И. А. [1], Цвирнер [1], Керубяио [1].
78 Гл. II. Нормальные системы линейных уравнений
а потому решение системы (вД (8g) получает весьма простой вид
который в точности совпадает с решением системы A0), получаемым,
при предположении о постоянстве А, путем формального решения
этого уравнения *).
§ 3. Частные преобразования линейных
однородных дифференциальных уравнений
1. Преобразование линейного однородного уравнения порядка
» в уравнение порядка п—1. Пусть дано линейное однородное
дифференциальное уравнение
«оУ"> + «13'('1-1) + ^<'1-2)+ ••• +«»-i/ + ««3' = 0, A)
где а0, ах, ай, ..., ап_х, ап—непрерывные на отрезке [а, Ь\ функ-
функции от х, причем а0ф0 в [а, Ь\; покажем, что если ввести новую
искомую функцию z, связанную с у соотношением
y = J**°, B)
то A) превратится в (нелинейное) уравнение порядка п—1.
В самом деле, имеем
и, подставляя в A) эти выражения, получаем после сокращения обеих
частей равенства на eitdx уравнение и— 1-го порядка относительно г.
2. Линейные дифференциальные уравнения второго порядка
и уравнение Риккати. В частности, уравнение второго порядка
«о/'-Ь «i/ + «У = 0
сводится преобразованием B) к уравнению Риккати 2)
а&? + а-о**+a\z + <h = 0-
Обратно, уравнение Риккати
+4 + ,
где L не обращается в нуль и дифференцируемо в [а, Ь\, сводится
преобразованием 8)
J
1) Отметим еще, что введенный в п. 2 матрицант получается при при-
применении к уравнению A0) метода последовательных подстановок, если со-
сократить все получающиеся при этом члены справа на общий множитель Уо.
2) Риккати [1]. Рассмотренное Риккати уравнение имело вид пхт+п~1=
= и' + и*х~п.
3) Относительно этого преобразования см. Дарбу [1], стр. 34.
$ 4. Относительная и каноническая нормализации 7&
к линейному уравнению второго порядка
= 0.
3. Линейные дифференциальные уравнения, у которых коэф-
коэффициент при у(п~1) равен производной коэффициента при yW.
а) Рассмотрим еще одно преобразование линейных дифференциаль-
дифференциальных уравнений, полезное иногда в приложениях.
Пусть X (х) — функция, необращающаяся в нуль на отрезке [а, Ь\1
умножая A) на Л(лс), получим эквивалентное уравнение
= 0.
Если мы хотим, чтобы в получившемся уравнении коэффициент
при j/C»»-1) равнялся производной коэффициента при yl"), то до-
достаточно выбрать множитель X (л:) так, чтобы \а^ = Х)'
\ = ±eJ~?d* (с = const). C>
б) Например, уравнение
при умножении на е °° 1а0 приобретает вид (самосопряженный»
см. § 5, п. 3 „б")
§ 4. Относительная нормализация
и каноническая нормализация линейных однородных
дифференциальных уравнений
1. Относительная нормализация и дифференциальные семиин-
семиинварианты, а) Если разделить уравнение A) из § 3 на а0, то оно
примет вид
Мы будем предполагать в этом и последующих пунктах, что коэф-
коэффициенты pv pv .... рп-х,Рп являются функциями от х, имею-
имеющими в [а, Ь\ все производные, которые нам придется рассма-
рассматривать.
„. (п\ Л (п\ п(п — 1) ... (я — k + l)._. 2 .
1) Здесь (^OJ = 1; {k) = — k\ (*-lf A •"' П)'
«О Гл. If. Нормальные системы линейных уравнений
Рассмотрим класс преобразований, определенный соотношением
где t—известная функция от х, имеющая в [а, Ь\ производные до
л-го порядка включительно, и рассмотрим соответствующее преоб-
преобразование уравнения A).
Имеем
=s (
г=к
k=Qr=k
r=0 k=0
откуда
где
k=0
и, в частности,
+(rr)prt],
Если выбрать множитель t так, чтобы i -\-p? равнялось нулю, или,
иными словами,
t=ce*Vl(Ue {с = const), E)
то в B) мы будем иметь ^==0. Полагая, в частности, с = 1, мы
получаем, что преобразование Т
~у = е JjPl и E')
переводит уравнение A) в уравнение
где
' " Vffk^j^ (r = 2 и). G)
$ 4. Относительная и каноническая нормализации 81
В частности, имеем
P*=Pv — P\—Pv Ръ=Ръ — *Р\Ръ + Щ—К- (8)
На языке проективной дифференциальной геометрии говорят, что
преобразование E') выполняет относительную нормализацию урав-
уравнения A), а F) называется полуканонической (семиканонической)
формой уравнения A).
б) Заметим, что, какова бы ни была постоянная с, уравнение A)
переходит при преобразовании y = ce~*Pidx в уравнение F), а также,
что две полуканонические формы, переводимые одна в другую пре-
преобразованием типа y = tu, совпадают.
Если мы применим к уравнению L (у) = 0 преобразование
7\ ~ у = hu и приведем преобразованное уравнение к полуканониче-
полуканонической форме с помощью преобразования 7^ — и = lv, то получим
уравнение
E) (?) (9)
которое должно совпадать с F); в самом деле, от полуканонической
формы F) можно перейти к полуканонической форме (9) с помощью
преобразования
Отсюда следует, что
Р* = П* (Л*=2, 3," .... я),
т. е. что определенные равенствами G) п — 1 величин Р2, Ps, ..., Рп,
являются инвариантами относительно класса преобразований
y = tu; они называются дифференциальными семиинвариантами.
2. Замена независимой переменной, а) Изучим, как влияет на
дифференциальное уравнение введение вместо независимой переменной
х независимой переменной %, связанной с х соотношением
5 = 5(*)»). A0)
1) Важность указанных в п. 1 и 2 преобразований вытекает из следую-
следующей теоремы Штекеля — Ли: наиболее общее точечное преобразование, пе-
переводящее линейное дифференциальное уравнение порядка я>3в уравне-
уравнение того же типа, имеет вид
(а)
(см. Вильчинский [1], стр. 14).
Заметим, что название „дифференциальные семиинварианты" в п. 1 свя-
связано с тем, что „абсолютные дифференциальные инварианты" уравнения A)
являются функциями коэффициентов рх, р2, ..., рп и их производных, кото-
которые остаются инвариантными как по форме, так и по значениям, при замене
независимой переменной и искомой функции, определенной в „а". По теории
Дифференциальных семиинвариантов и инвариантов читатель может посмо-
посмотреть гл. II цитированной книги Вильчинского; на стр. 39—40 он найдет там
ссылки на работы Кокля, Лагерра, Бриоски, Форсайта, Альфана, Бутона, Фано.
6 Зак. 627. Дж. Сансоне
Гл. П. Нормальные системы линейных уравнений
Если обозначить символами у, у", ..., у(п\ ...; ?', Е", ..., ?(п\ ...
производные функций у и ? по х, то будем иметь
.,,_dy_tiy<!i_trfbL
у ~ dx ~ d%dx ~~ 5 dk '
и с помощью последовательного дифференцирования найдем
A1)
и вообще
A2)
fc=l
где ЛТО) fe — целые рациональные функции от производных функции Е (х).
Легко проверить, что
а1Л—«; 2! —(*J» и —*»
Aa о
3,¦¦ — v*y. 2! "
Мы хотим показать, что вообще
(«-2,8,.,.),
A3)
A4)
A5)
Дифференцируя A2) и обозначая через Аттъ производную функ-
функции А^ъ по х, получаем
я»
k\
k\
ml
откуда
. 7c
_t (ft == 2,
A6)
A7)
$ 4. Относительная и каноническая нормализации 83
Из A3) следует, что Altl = V, а потому соотношение A4) непосред-
непосредственно следует из A6).'
Далее, имеем соотношения
я-1, *-2 ~~ ^*»_2, fc-2
Л —.
¦"«t-ft+2,1—
Умножая второе из них на (k — 1)$', третье на (ft—l)(ft—2)(?'J, ...
..., предпоследнее на (k—\){k — 2) ... 3 ($')fc~8, последнее на
(k — I)(к — 2) ... 3-2(E')ft~2 и складывая, получаем, что
—2) ... i
A8)
Полагая здесь k — m и учитывая, что А\, % = (/!) / (fc'/ ?", полу-
получаем соотношение
из которого и следует первое из равенств A5).
Полагая в A8) k = m—1, учитывая первое из равенств A5) и
известные свойства биноминальных коэффициентов, получаем
— А'т-1, т—2 + {т — 2) 1'А'т_2, т-Ь
— 2)(т— 3)(Е0
— 2)(т—3) ...
откуда и следует второе из равенств A5).
6*
§4 Рл. //. Нормальные системы линейных уравнении
б) Подставляя A2) в A), получаем
и-1 г
. . 1 (Я — г)\
Коэффициент при ^^ в правой части равен р0 ($')", [=E')nL и следо-
следовательно, Z-(^) преобразуется в
г)^ A9)
где
() А"п~7у (г=0> г> 2i ¦ • ••п)' B0)
В частности, имеем
или, полагая
^¦ = 4. B1)
^^] B2)
Далее, имеем
- Ап,п-2 . Аг-1,п-2 . п(п—1)А„-%п-2
) P2 = (^=2j!+" («-2)! Pl + ' 2 (^
_/г(/г— 1)(/г — 2)$C)^n_s _^_Зи(я—1)(я —2)(я —3)
откуда
Но, дифференцируя B1) по л:, получаем, что т/ -f- yj2 = У3)/?', и потому
^if\. B3)
$ 4. Относительная и каноническая нормализации 85
С помощью простого вычисления можно найти для семиинварианта Р2
уравнения A9)
выражение
где через tf обозначена производная t\ no х. Это выражение будет
использовано нами в п. 3.
3. Каноническая нормализация Лагерра — Форсайта. Покажем,
что если дано уравнение
то, применяя последовательно указанные в п. I и 2 преобразова-
преобразования, его можно привести к уравнению, не содержащему членов
с у»-У и у»-2).
С помощью преобразования
у = е J _у
получаем полуканоническую форму
) ^(и-2) + ( з ) ^з?й-3) + • ¦ • + С, 1,) ^-i/
где
Сделаем в получившемся уравнении преобразование у = Хк, где
А.—некоторая функция от х, которую мы определим несколько позже.
Получаем
и, в силу C),
B5)
86 Гл. //. Нормальные системы линейных уравнений
в то время как семиинвариант П2 равен, в силу сказанного в п. 1,
семиинварианту Р2.
Последнее уравнение преобразуется с помощью замены перемен-
переменной % = i(x) к виду
d»u , (п\- dn-iu , (п\- dn-
B6)
причем, в силу B2), B4), B1), имеем
14 = 576*1,
Предположим, что уравнение Риккати
2
имеет определенное на отрезке [а, Ь] решение. Найдем тогда (с по-
помощью квадратуры) \ таким образом, что"
Т + ^ = 0. B8)
Тогда Р2, pv а следовательно и рй, обращаются в нуль, и уравне-
уравнение B6) приводится к указанному выше виду.
Из B8) и B1) имеем
\ -ndx
dx-\-c,
а потому, применяя к уравнению A) последовательно преобразования
B9)
где i\ — решение уравнения Риккати B7) (мы предполагаем, что это
решение существует в [а, Ь\), получаем уравнение
Указанные преобразования называются канонической нормализа-
нормализацией Лагерра — Форсайта уравнения A), а B6') называется канони-
канонической формой уравнения A).
С помощью преобразования
-— I
— e 2 J
z — e
§ 4. Относительная и каноническая нормализации 87
(см. § 3, п. 2) уравнение B7) сводится к линейному уравнению вто-
второго порядка
/V=0' B7')
а потому можно сказать, что если уравнение B7'I) имеет положи-
положительное на отрезке [а, Ь] решение г, то, применяя к уравнению A)
последовательно два преобразования
мы приводим его к канонической форме B6^) 2).
4. Преобразования уравнений второго и третьего порядка.
а) Уравнение второго порядка {аоф0>)
приводится с помощью замены переменной ? = ?(л:) к виду
Поэтому, если выбрать I так, чтобы до?' = 1, т. е. сделать замену
переменной
k
то получится уравнение
б) Вообще, уравнение второго порядка (а0 ф 0)
можно записать в виде
й0
!) Мы увидим в гл. IV, § 2, п. 7 „в°, что для данного линейного диф-
дифференциального уравнения у"-\-ру'-\-qy = 0, в котором функция pug
непрерывны в [а, Ь], не всегда можно найти (действительное) решение, не
обращающееся в нуль на отрезке [а, Ь].
2) Относительно геометрического значения полуканонической и канони-
канонической формы линейного дифференциального уравнения см. Бомпнани [1].
3) Относительно рассматриваемых в этом пункте вопросов см., напри-
например, Курант и Гильберт [1], гл. IV.
В приводимых далее примерах мы, для удобства читателя, рассматриваем
неоднородные уравнения.
88 Гл. II. Нормальные системы линейных уравнений
(см. § 3, п. 3) и с помощью замены переменной
t= I e J °o dx-\-c,
свести к виду
Га, Го,
d?y _|_ й2 a I ^da; / 2 ) а
в) Рассмотрим уравнение третьего порядка (а0 Ф 0)
аоу'" -\- а-^у" -J- я2-у' -\- asy = f
или, что то же,
CLq CLq &Q &Q
По результатам предшествующих пунктов имеем
2 Зй0 9W 3W* 8~«b 3«^27e8 3W'
в то время, как уравнения B7) и B7') принимают вид
~/ L^2 3 р
1 ? ^ 2" 2'
1 4 |в0 3 ч«о/
Из результатов п. 3 вытекает, что если существует положитель-
положительное в [а, Ь] решение уравнения C2), то уравнение C1) приводится
подстановкой
у=е 8 J **>«, S = J^-
к виду
f ?>/5* C3)
Вид правой части определяется тем, что при первом из преобразо-
/« --- I — их
ваний и получается с коэффициентом е 3 J °° z2, а при замене
переменной умножается еще на z~6.
Вычислим явным образом р3.
В силу B8) имеем к' = — tqX, а потому
§ 5. Сопряженное уравнение Лагранжа 89
откуда, в силу B5) и B6), получаем
и, наконец,
+ 3 ao\ao) 2 \aj + 27UJ 3 ^ + ao
где все производные взяты относительно переменной х.
§ 5* Сопряженное уравнение Лагранжа
1. Сопряженные дифференциальные многочлены и уравнения.
а) Рассмотрим дифференциальный многочлен порядка п
L (У) = «оУИ) + «ijH"-4 + • - - + «„-а/ + впУ. A)
где йо, с1? ..., йгп — непрерывные функции от х, обладающие всеми
встречающимися в дальнейшем производными, а0 ФО в [а, д] и
у', у", ..., У") являются последовательными производными у. Рас-
Рассмотрим следующую проблему: существует ли такая функция z(x),
что для нее тождественно выполняется соотношение
zL(y)^?.my, г)}, B)
где функция ty(y, z) линейно зависит от у и ее производных до
п—1-го порядка включительно, или, как говорят, существует
ли множитель для дифференциального многочлена L(y)?
Ответ на этот вопрос положителен. В самом деле, последователь-
последовательным интегрированием по частям получаем
J {abz)/n-Vdx =.y<»-*-1>(afc2')—y(n-*-*\abz)'-\-y(n-1c-s>(akz)"-\-... -f-
+(- VT*-ly («a*)*-*+(- 1Г * J
откуда, дифференцируя по х, выводим, что
а потому тождественно выполняется соотношение
d
)' -j- ... + (-1)»-
90 Гл. //. Нормальные системы линейных уравнений
где положено
М(г)-(-1)»^g?> +(-1)»-
Из соотношения C) получаем тождество
*1 О) — УМ (г) в ^ [ф C/, *)], E)
где
и потому функция ty(y, z) является билинейной формой отно-
относительно у, z и их производных до п — 1-го порядка включи-
включительно.
Из E) и F) получаем, что если выбрать в качестве z решение
уравнения M(z) = 0, то, какова бы ни была функция у, произведе-
произведение zL(y) будет производной от ty(y, z) по лг, а потому z является
множителем для L(y); кроме того, если выбрать z указанным выше
образом, то линейное уравнение и—1-го порядка
*) = const G)
будет первым интегралом для уравнения
б) Уравнение М (z) = 0 называется сопряженным уравнением
Лагранжа для уравнения L(y) = 0, а многочлен М (z) — сопряжен-
сопряженным многочленом для L(yJ).
в) Покажем, что для М (z) сопряженным многочленом является
L(y), т. е. что отношение сопряженности двух дифференциальных
многочленов симметрично.
1) Если/(ж, у, у',..., Ум)) = 0—дифференциальное уравнение, то
любое соотношение вида F(x, у, у',..., уп~1) = const, которому удовлет-
удовлетворяют все решения этого уравнения, называется его первым интегралом.
2) См. Лагранж [1J, т, I, стр. 471. Подробное рассмотрение сопряженного
уравнения Лагранжа см. у Дарбу [1], т. II, стр. 112—149. Геометрическое
значение сопряженного уравнения и его главные свойства изложены в статье
Еореля [1]. Название „сопряженное уравнение* ввел Фукс [2], стр. 183.
$ S. Сопряженное уравнение Лагранжа 91
В самом деле, если Ьх(у)— сопряженный с М(г) многочлен, то
имеет место тождество
(z) — zLx (у) = ± [^ (^ *)]. E0
Складывая тождества E) и E'), получаем тождество
z [L (у) — L, (у)] =?х [ф СУ, *) + «К (У, г)\. (8)
Если бы дифференциальный многочлен ty(y, •гО + 'КО'» Z) содер-
содержал z или одну из производных г^\ то в правую часть равенства (8)
вошла бы, по крайней мере, одна производная от z, в то время как
в левую часть входит лишь z, чего не может быть в силу тожде-
тождественного характера соотношения (8). По той же причине этот диф-
дифференциальный многочлен не может быть отличной от постоянной
функцией у и производных yW, так как в противном случае правая
часть (8) зависела бы только от у и у№, в то время как левая
часть (8) зависит также и от z. Поэтому имеем z [L (у) — Lx (у)] =э О
и, в силу произвольности z,
г) Укажем еще на связь понятия сопряженной системы, введен-
введенного в § 1, п. 4 „а", с понятием сопряженного уравнения.
Пусть дано уравнение
у») + fli>,(»-i) + ... + йп1у + апу = 0.
Оно эквивалентно линейной однородной системе
dx ~~y*> dx~—yv-> dx ~~Уп>
2? = — апУх — "п-хУъ
сопряженной с которой является система
Из этой системы имеем
dzt__f ч (Pz.2_dzt d(an-xzn)
dx~{-nnh dx*~dx dx '
, ,-.n-idnzn , ^n-2d"-1z
92
Гл. //. Нормальные системы линейных уравнений
откуда, суммируя и приводя подобные члены, получаем
dnz un-id"-1 (chZn) ¦ ¦ <P(a
dx i ~"n
Таким образом, zn является решением уравнения, сопряженного
с данным.
2. Соотношения между фундаментальными системами решений
сопряженных дифференциальных уравнений. Пусть yvy$,—,yn—
фундаментальная система решений уравнения (!'). Тогда, полагая
Ух
Уг
У',
Уп
Уп
(см. § 1, п. 3), видим, что Д=/=Ов [а, Ь]. Так как dkjdyf> является
алгебраическим дополнением у№> в Д, то, полагая
(/==1, 2, ...,«),
получим, что
= 0, если
Поэтому, если с1г с%, ..., сп — произвольные постоянные, то
"* (рхУх ~\~ съУ2 ~Ь • • • "т~ спУп)== cii
следовательно, линейное дифференциальное уравнение порядка п
(9)
имеет те же решения, что и (I7); отсюда вытекает, что коэффициенты
этих двух уравнений пропорциональны, а потомуJ)
= ZiL{y) (/=1, 2, ..., я).
dx
Отметим, что если два дифференциальных уравнения
«оУп) + «1У"-1' + • ¦ • + а»-1У + апу = О,
Ья-,у + Ъпу = О,
где во Ф 0, bo Ф 0 в [а, Ь]; а0, аь ..., ап\ b0, blt..., bn непрерывны в [а, Ь],
имеют одни и те же решения, то их коэффициенты пропорциональны.
В самом деле, если функции у1г у2,..., уп образуют фундаменталь-
фундаментальную систему решений для обоих уравнений, то они удовлетворяют уравне-
§ 6. Сопряженное уравнение Лйгранд&а
93
Сравнивая коэффициенты при _у<п> в обеих частях, мы видим, что
Но, в силу равенства E) из п. 1 „а"
*«1 (у) —уМ(Zi)^?с
а потому
Повторяя проведенные в п. 1 „в" рассуждения, получаем, что
= 0 (i~l, 2, ..., пУ),
т. е. что функции гг, z2, ..., zn, полученные по формуле A0),
являются решениями сопряженного уравнения и, как мы сейчас по-
покажем, образуют фундаментальную систему решений.
В самом деле, по известным свойствам определителей
• • + гпУп =• 0,
Дифференцируя эти тождества, получаем
»—1),
Положим
... zn
... zU
нию я—1-го порядка
U bjy +Uo &oF +---+Uo йь Л
Но это уравнение, если оно не является тождеством, может иметь лишь я — 1
линейно независимых решений, откуда следует, что
«1 h _ «2 ?2 вп ?п
' -г J— ... = г— V.
Щ О0 UQ Oq UQ Oq
!) При этом мы имеем 6{ (у) = «J» (j', г<), а потому 4- (У{, г{) = 1, ^ (^, г^-) = 0,
если / =^= у.
Рл. It. Нормальные системы линейных уравнений
и умножим определитель Д на Да справа. Учитывая равенства A1),
получим
1
A2)
«о
а потому Д-! не равно нулю в (а, Ь) и, следовательно, z'v -г2, •.., zn
образуют фундаментальную систему решений сопряженного уравнения
0
0
о
0
0
(-1)»-»
. 0 —
«0
1
«0
3. Самосопряженные дифференциальные уравнения и много-
многочлены, а) Дифференциальное уравнение называется самосопряженным,
если оно обладает теми же решениями, что и сопряженное с ним
уравнение.
Для того чтобы уравнение L (у) = 0 было самосопряженным,
необходимо и достаточно, чтобы коэффициенты многочленов L(y)
и М (z) были пропорциональны *). Из того, что коэффициенты при yW
и zW> в A) и D) отличаются множителем (— 1)п, следует, что урав-
уравнение L (у) = 0 самосопряжено тогда и только тогда, когда тожде-
тождественно
^-О0=(—1)**Л1 Су)- A3)
Дифференциальный многочлен L (у) называется самосопряженным,
если для него и для сопряженного с ним многочлена выполняется
тождество A3).
Из A3) следует, что сумма (разность) двух самосопряженных
дифференциальных многочленов, порядки которых имеют одну и
ту же четность, является самосопряженным многочленом.
б) Из введенного определения вытекает, что для того, чтобы мно-
многочлен а^у'-^-а-^у был самосопряженным, должно выполняться тож-
тождество аоу1 -\- а^у = (аоу)' — а^у, 2й1 = йо, а потому самосопряжен-
самосопряженный многочлен первого порядка имеет вид
A4,)
Аналогично, если многочлен второго порядка аоу" -\- а^у'-\- а^у само-
самосопряжен, то имеет место тождество (аоу)" — (а^уУ -\- а2у = а^у" -f-
+ аху' -J- а%у, а потому 2 (со — at)yr -\- (а'о — а{) = 0, откуда а'о = ау
Поэтому самосопряженный многочлен второго порядка имеет вил
d
_____ Г Л \уЛ ... I,. И «I f Л _—— /у Л в__ ft Л 11 Л. Л
1^*0_У i I ^^1_У> L О — О) ^*1 ~' ' "'9j* \ -^-*9/
!) См. примечание иа стр. 92.
§ 5. Сопряженное уравнение Лагранжа
В частности, в силу результатов § 3, п. 3 „б", многочлен а^у" -|~
Л~ а\У' ~\~ а$У может быть приведен к самосопряженному виду
dx l dx] ' a0
путем умножения на
, Г*
*»
в) Докажем, что дифференциальные многочлены
самосопряжены.
В самом деле, имеем
J» —
а потому сопряженный с A5) дифференциальный многочлен имеет
вид
1 {А'у)
Но получившееся выражение равно ——^—- в силу тождества
A6)
!) Тождество A6) доказывается следующим образом. Составим для по-
последовательности
,-
96 Гл. //. Нормальние системы линейных уравнений
Аналогичным путем доказывается самосопряженность выражения
A52); достаточно, кроме тождества A6), учесть аналогичное тожде-
тождество для Aylp-1).
г) Покажем теперь, что самосопряженный многочлен четного
порядка 2т имеет вид
+ H
а нечетного порядка 2т — 1 — вид
В „б" мы показали справедливость этой теоремы для случая,
когда ш=1, и теперь можем провести доказательство по индукции.
Пусть L(y) — самосопряженный многочлен. Сравнивая в тожде-
тождестве A3) .коэффициенты при^Л"), получаем пагй — а1 = я1, 2й1 = ийо.
Рассмотрим в случае, когда и = 2т, разность L(y) — -r-m[
а в случае, когда п = 2т — 1, — выражение
Мы получим тогда самосопряженный многочлен порядка я — 2, чем
и доказывается наше утверждение.
л) Легко доказать, что если yv _y2, ..., уп^ образуют систему
независимых решений самосопряженного уравнения п-го порядка,
-1
то произведение с| ^(УиУцу • ¦ • • Уп-л) также является решением
этого уравнения.
таблицу последовательных разностей
?
?(АУ),
, A
Применяя известную формулу, выражающую р-ю разность через члены по-
последовательности, получим формулу A6). [См., например, Гельфонд А. О. [1],
стр. 40. — Прим. перев.]
$ 5. Сопряженное уравнение Лагранжа 97
В самом деле, положим в равенстве A0) из п. 2 i — n и заметим,
что, в силу самосопряженности уравнения, функция
" *» = Т0~К W(Jv У» •••> Уп-i)
также является решением нашего уравнения; но из формулы Лиу-
вилля (см. § 1, п. 2, „в") получаем
_Cqi
J а
2 J «» =
и потому
1 --1
2
(l/W(x0) является постоянным множителем).
4. Первый интеграл самосопряженного уравнения нечетного
порядка. Пусть L(y) — самосопряженный дифференциальный много-
многочлен нечетного порядка 2т — 1; подставляя в тождество E) вместо
M{z) многочлен —Ну), получим
^, г)]
и, полагая z=y, имеем
Таким образом, самосопряженный дифференциальный многочлен
L(y) имеет множитель у, а соответствующее дифференциальное
уравнение L(y) = 0 имеет первый интеграл (второй степени)
«l»СУ» у) = const.
5. Самосопряженные уравнения третьего порядка. В част-
частности, самосопряженное уравнение третьего порядка
+^[Д»Л] + [^[Л1>] + А1у] = 0 A7)
имеет первый интеграл
2А0уу" — А,/8 + АЬуу' + А ^ = const.
Если положить постоянную, стоящую в этом уравнении справа,
равной нулю и подставить г2 вместо у, то получится дифференци-
дифференциальное уравнение второго порядка
4A0z" + 2Л^' + Ахг = О.
7 Зак. 527. Дж. Сансоне
Щ Гл. II. Нормальные системы линейных уравнении
Если zx и z2 — два линейно независимых решения этого уравнения,
то z\ и г\ являются линейно независимыми решениями уравнения A7).
В силу полученных в п. 3 „д" результатов, уравнение A7) имеет
также решение
2z1zi 2z2z'2
z[ zi
= cztz2 (с = const =? 0) %
и потому уравнение A7) имеет фундаментальную систему решений
z\, ztz2 \%
§ 6. Преобразование линейного
дифференциального уравнения с начальными данными
в интегральное уравнение Вольтерра второго рода
Пусть дано дифференциальное уравнение
L{y)=f{x), A)
где
Pi(x), p2W' •••> Pn(x)i f(x) — непрерывные в [a, b] функции от х,
и пусть надо решить задачу Коши для этого уравнения, т. е. найти
решение уравнения A), которое в точке а удовлетворяет начальным
условиям
У (а) = с* уЦа) = cv ..., уЬ-Ъ (а) *= сп_х C)
(см. § 1, п. 1 „в" и п. 5 „в").
Примем _у<») (л:) за искомую функцию и положим
<?(*) D)
(»(дг) — искомая функция). Отсюда, учитывая условия C), получаем
По формуле Лиувилля (см. § 1, п. 2 „в") имеем
Ч
_i|4
йх
= W(xo)Ao2.
2) Относительно самосопряженных уравнений третьего порядка см.
Дарбу [1], т. II, стр. 129—130, а также Маммана [1] и Таллина [1].
$ 6. Преобразование в интегральное уравнение 99
откуда, дифференцируя г раз по х, находим
Подставляя полученные выражения в A), получаем для <р(х) инте-
интегральное уравнение Вольтерра второго рода
X
<р(х) — f K(x, t) ? (/)dt = F(x), G)
a
где ядро К(х, t) и функция F(x) определены, соответственно, выра-
выражениями
К(х, t) = -Pl(x)~?^.(x-t)
Ч~сп-2 (Я_г 2)! ~Ь ••* "bc*-+i~JI
я<*<*. (92)
Хорошо известно, что интегральное уравнение G) имеет одно и
только одно решениеJ).
Положим
Кх{х, fy=K(x, 0.
Кп (х, t) = J tf(*, г) /fn_, (г, 0 йг (« = 2, 3, ...)
t
[/Сп (лг, t) называется и-й итерацией ядра К(х, ?)]. Если обозначить
через М наибольшее значение \К(х, t)\ в квадрате Q, определенном
неравенствами (9j), то
1) В этой книге мы будем, когда найдем полезным, использовать теорию
линейных интегральных уравнений, считая, что она уже известна читателю.
[Относительно теории линейных интегральных уравнений см. Гурса [1],
т. III, стр. 3, Петровский И. Г. [2], Привалов И. И. [2], а также Курант
и Гильберт [1], т. I. — Прим. перев.)
7*
100 Гл. it. Нормальные системы линейных уравнений
а потому ряд
г(*. о =2 *"«(*, t)
равномерно сходится в Q и G) имеет единственное решение
[Г(х, t) называется резольвентой для G.)].
Подставляя полученное для у(х) выражение в E), получаем иско-
искомое решение у(х).
Таким образом, задача Коши для дифференциального уравнения A)
сводится к интегральному уравнению G), которое всегда имеет един-
единственное решение; отсюда следует, что если привлекать теорию
линейных интегральных уравнений, то указанное преобразование дает
новое доказательство теоремы существования и единственности
решения дифференциального уравнения A) с заданными начальными
данными.
Систематическое изучение линейных дифференциальных уравнений
посредством сведения их к интегральным уравнениям было впервые
проведено Дини (см. Дини [1], Коттон [1], стр. 16); хотя Дини не
употреблял в своих мемуарах слов „интегральное уравнение", но он
строил эти уравнения, когда это было нужно при изучении линейных
дифференциальных уравнений.
Глава III
АНАЛИТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
И НЕКОТОРЫЕ ЛИНЕЙНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
§ 1. Метод мажорант (Исчисление пределов Коши)
1. Метод Эйлера интегрирования дифференциальных уравне-
уравнений при помощи рядов. В предыдущих главах мы ограничивались
изучением дифференциальных уравнений в действительной области.
В этой главе мы изложим некоторые вопросы аналитической теории
дифференциальных уравнений, желая, во-первых, познакомить чита-
читателя с основанным на использовании мажорант в%ажным методом Коши,
а, во-вторых, исследовать некоторые важные для приложений к мате-
математической физике дифференциальные уравнения второго порядка').
Рассмотрим дифференциальное уравнение
/=П*,у), A)
где f(x, у) — функция комплексных переменных х и у, голоморфная
в некоторой области, содержащей внутри точку (я0, у0), и будем
искать решение этого уравнения, удовлетворяющее начальному усло-
условию y(jfl)—y°.
Без потери общности мы можем считать, что jc° = O, y = 0
(в противном случае мы заменили бы х и у па х— х° и у—у°),
а также, что функция / (дг, у) голоморфна в открытой области D,
определенной неравенствами | х | < R, \y\<C R'-
Предположим, что мы уже доказали существование решения
уравнения A), удовлетворяющего'начальному условию
B)
и разлагающегося в окрестности нуля в степенной ряд
.ш. . C)
Легко указать рекуррентный метод, позволяющий однозначным
образом определить коэффициенты сг, с2, ..., сп, ... .
*) Более полные сведения по аналитической теории дифференциальных
уравнений читатель может получить из книги Голубева В. В. [1J. — Прим.
пере в.
102 Гл. III. Аналитическая теория дифференциальных уравнений
Из A) получаем последовательным дифференцированием
Подставляя в A) и в получившиеся соотношения х — 0, у = 0, вы-
вычисляем последовательно у' @), у" @), у'" @), ... и, тем самым,
постоянные си с2, cSt ... [сп=_у<«)@)/я!}.
Этот метод введен в анализ Эйлером1) и широко используется
в тех случаях,, когда не удается решить дифференциальное уравнение
при помощи известных функций. Математиками XVIII века он счи-
считался достаточным для доказательства не только единственности, но
и существования голоморфного решения, в то время как на самом
деле следует еще показать, что
а) полученный рекуррентным процессом ряд C) имеет отличный
от нуля радиус сходимости,
б) изображаемая этим рядом функция у (х) удовлетворяет уравне-
уравнению A).
Второе утверждение является следствием первого; в самом деле,
функция у' (дг)—f(x, y(x)) голоморфна в достаточно малой окрест-
окрестности нуля и обращается в нуль вместе со всеми своими производ-
производными при х = 0, а потому тождественно равна нулю.
Осталось, таким образом, установить сходимость ряда C); для этой
цели Коши применил метод, названный им исчислением пределов,
а теперь называемый более часто „методом мажорант"; изложению
этого метода посвящены п. 2—42).
2. Основной принцип метода мажорант Коши. Пусть функция
f(x,y) голоморфна в области D, определенной неравенствами |дг|</?,
|.у|</?', и пусть существует функция F(x, у), также голоморфная
в D, которая имеет следующие свойства:
1. Она и все ее производные положительны в точке @, 0),
0)>0,
0)>0 (А,
= 0, 1, 2, ...)• I
*) Интегрирование с помощью рядов, использованное Эйлером для изу-
изучения движения Луны и для решения уравнения Риккати, изложено им в его
книге [1J, т. II, гл. VII и VIII.
2) Коши [1], т. 4—7, Ю. Вейерштрасс опубликовал в 1842 г. независимо
от Коши строгое доказательство теоремы существования, также основанное
на принципах метода Коши. Исследования по этому вопросу, проведенные
Брно и Буке, Мерэ, Кенигсбергером, Пикаром, Штекелем, Линделёфом, Пен-
леве, Гурса и Фейером, указаны в Enc. des Sc. Math* 3, fasc. 1 A910), 16—21.
/. Метод мажорант 103
2. Функция f(x, у) и ее производные удовлетворяют в точке
@, 0) неравенствам
|/(о, о) |</чо, о),. \
Назовем такую функцию F(x, у) мажорантой для f(x, у) и
будем, следуя Пуанкаре "(см. Пуанкаре [I], т. I, стр. 48), писать
(x,y). F)
Рассмотрим одновременно с уравнением A) уравнение
с начальным условием F@) = 0 и предположим, что радиус сходи-
сходимости построенного для этого уравнения ряда
равен р; тогда при | х | < р Y (х) является решением этого уравнения.
Из того, что
V" д2р _1_ 9 д2р V Л. д2р V2 _LdF V"
r — д&^~ 'дх~д?г ~т~Ш * ~г~дУ '
получаем, в силу E), что |.у(п)@)|< У(") @). Поэтому коэффициенты
ряда C) не превосходят по абсолютной величине коэффициентов
ряда G) и, следовательно, радиус сходимости ряда C) не меньше р.
Тем самым доказано, что ряд C) представляет в некоторой окрест-
окрестности нуля голоморфное решение уравнения A), удовлетворяющее
начальному условию B).
3. Доказательство теоремы существования методом мажорант.
а) Из проведенных выше рассуждений будет следовать теорема суще-
существования, если мы покажем, что для любой голоморфной в области D
функции f(x, у) можно построить такую мажоранту F(x, у), что
уравнение
обладает голоморфным в некоторой окрестности начала координат
решением.
Легко- видеть, что для заданной функции f{x, у) можно найти
сколько угодно мажорант F(x, у).
104 Гл. III. Аналитическая теория дифференциальных уравнений
В самом деле, функцию f(x, у) можно разложить внутри D
в абсолютно сходящийся двойной степенной ряд
со
fix, y)= 2 Акьх*у*. (8)
Если мы обозначим через Г и Г7 окружности на плоскостях ком-
комплексных переменных х н у с центрами в начале координат и радиу-
радиусами, соответственно, а и Ь, где
0<я<#, 0<6<#/,
то будем иметь1)
_4*у@.0)_ 1 f Г /<*--Г> dxdv (9)
Аьл— м Л, — Bя/J J J Л+1 к+1 ахау. (У)
Г' Г -^
Если обозначить через М наибольшее значение, принимаемое функ-
функцией \f(x, у)\, когда х к у описывают, соответственно, окружности Г
и V, то из (9) будет следовать, что
\АКЬ\<Ма-Ч-К (9')
Но в области D', определенной неравенствами |д;|<й, |j|<ft,
оо
двойная геометрическая прогрессия 2 Ma~bb~lixbyk сходится
ь, ft=o
к М{{\—а~1х)(\ — Ь~1у), а потому в области ГУ
Рассмотрим теперь уравнение
dx — / *-\ / Y\ ' У1У))
разделяя переменные и интегрируя, получаем, учитывая начальное
условие К@) = 0, что
а потому
[/"-(f)] (И)
где через In A — fl-1^) обозначена главная ветвь логарифма 1—а*
(голоморфная функция внутри круга радиуса а с центром в начале
координат), а под корнем понимается ветвь, принимающая в точке
д: = 0 значение -J-1.
1) См. Фукс Б. А. [1], стр. 75. — Прим. перев.
§ I. Метод мажорант 105
Корень обращается в нуль при лг = р, где
Поэтому при |д;|<р формула A1) изображает голоморфную функ-
функцию. Но тогда при | х | -^ р' < р имеем
Отсюда следует, что при сделанных предположениях при |*|<
< а{\ — е~ /<2 о)) существует голоморфное решение уравнения A);
радиус сходимости соответствующего степенного ряда не меньше,
чем р.
б) Другую мажоранту для f{x, у) можно получить при помощи
следующего метода, принадлежащего Штекелю [1].
сю
Из абсолютной сходимости ряда 2 Ан kahbk следует, что мно-
ь. й=о
жество чисел \Ahk\ahbk (А, ? = 0, 1, 2, ) ограничено сверху и
что если обозначить через G верхнюю грань этого множества, то
в неравенстве
И„.йК**<0, (h, ft = 0, 1, 2,...)
хотя бы для одной пары h, k имеет место знак равенства *).
В силу (9') G^.M, а потому ряд C) заведомо сходится в круге
радиуса
4. Теорема существования в общем случае, а) Проведенные
выше рассуждения применимы и к нормальной системе
У\ =/«(XI yv Уг>--> yJ (/=1,2,..., #я), A2)
где х; yv уг, ..., ут — изменяющиеся в области D
\х — а|<Я, |л_р4|<Я' (t=l, 2, .... и)
комплексные переменные.
Предположим, что функции /4 голоморфны в D и докажем (с по-
помощью метода мажорант), что внутри круга с центром в а суще-
существует одна и только одна система голоморфных функций yt(x),
у%(х), ..., ут(х), удовлетворяющих данной системе и начальным
условиям
Л(«) = Р« (*=1, 2, .... т).
Предположим для простоты, что ос = 0; Р4 = 0 (/=1, 2, ..., т).
!) В самом деле, если а—меньшее чем G положительное число, то при
h^h0 и k^ko имеем | А^ & |аьЬк<о, а потому G равно наибольшему из
(fto+l)•(*<,+ !) чисел \Аъ,'к\аЧ*A1 = 0, 1 Ло. * = 0, 1 *й).
106 Гл. III. Аналитическая теория дифференциальных уравнений
Такими же рассуждениями, какие были проведены в п. 1, убе-
убеждаемся, что если допустить существование голоморфных в некоторой
окрестности нуля искомых решений нашей системы
.. (i = l, 2,..., т), A3)
то коэффициенты этих рядов однозначно определяются уравнениями A2)
и уравнениями, получающимися из них путем дифференцирования;
таким образом, остается показать, что радиус сходимости для A3)
отличен от нуля.
Пусть 0 < а < R, 0 < Ь < R'. Обозначим через Mi наибольшее
значение модуля функции ft(дг; yv у2, ..., ут), когда х описывает
в плоскости х окружность с центром в начале координат и радиу-
радиусом а, а ух, у2, ..., ут — окружности в плоскостях уи yv •.., ут
с центром в начале координат и радиусом д, и пусть М является
наибольшим из чисел Мj, М^, . •., Мт. Тогда мы имеем
М
fcj... km\
J т @; 0. 0 0)
Если рассмотрим функцию
• \хг У\ > У%> • • •
М
то получим, что
= Ж
ft!
... kn\
SI S2 ••• J'm @; 0, 0 0)
и следовательно
fi(x'> yv Уъ> • • •» Ут) ^ F(x; yv Уъ • • •» Ут) (* = It 2, ..., т).
Наряду с системой A2) рассмотрим систему
dYi _ dY% _ dYm M
dx dx
dx
с теми же самыми начальными условиями
Из симметрии этих условий следует, что разложения функций
Yt (х), К2 (х), ..., Ym (x) в ряды совпадают, а потому, полагая
получим
/. Метод мажорант 107
Разделяя переменные и интегрируя при начальном условии К@)
получаем
где в правой части логарифм принимает главные значения, а корень
принадлежит ветви, принимающей в точке лг = О значение 1. (Найден-
(Найденное в п. 3 выражение A1) для Y является частным случаем выраже-
выражения A4), получаемым при т=1.)
Входящий в правую часть корень обращается в нуль при
х = а{\ — е~ьКт+1)Ма^ а ПОТОМу^ как и ранее> находим, что ряды A3)
сходятся в круге радиуса
-ь
р = аA — e("»+i)J"o) A5)
и представляют там искомую систему решений.
б) Итак, мы доказали, что при сделанных предположениях всегда
существует голоморфная система решений и что при предположении
о голоморфности решений такая система единственна. Однако мы еще
не можем утверждать, что при наших предположениях любая Система
решений для A2) обязательно голоморфна.
Это утверждение также можно доказать тем же самым методом
мажорант; мы докажем его в следующем параграфе с помощью про-
процесса последовательных приближений.
5. Метод суммирования Бореля и дифференциальные уравне-
уравнения. Метод решения дифференциальных уравнений с помощью рядов
применим также к уравнениям вида f(x\ у, у', у", ..., >><1П>) = 0,
где через / обозначен многочлен от переменных у, у', у", ..., д>(т>,
коэффициенты которого являются голоморфными функциями от х
в некоторой окрестности точки х°; зная значения в х° у (х°), / (х°),
v"(jc°), ..., yt™-1) (jc°), можно с помощью дифференцирования найти
y("*)(jfi), _y("|+1) (jc°), ; если радиус сходимости получающегося
таким образом ряда отличен от нуля, то этот ряд будет решением
нашего уравнения; если же радиус сходимости этого ряда равен нулю,
то, возможно, существующие (неголоморфные) решения следует искать
другим образом.
Рассмотрим, например, уравнение
л:я = 0 A6)
и попробуем найти голоморфное в окрестности точки л: = 0 решение
оо
= 2
0
2 *
И=0
получим
ср==с, =0;"ся—1, сп+, = — псп (и = 2, 3, ...)
108 Гл. Ш. Аналитическая теория дифференциальных уравнений
и потому придем к ряду
л;2—2Ьс8 + 3!лг4 — 4!*б+ .... A7)
который формально удовлетворяет предложенному уравнению, но
для которого радиус сходимости равен нулю; поэтому уравнение A6)
не обладает в окрестности начала координат голоморфным решением.
Просуммируем ряд A7) по методу Бореля; соответствующая этому
ряду функция имеет вид
- , ч дг2 х3 , х* хь , ,
и сумма В (Бореля) ряда A7) равна
+ОО +ОО
у (лг) = J е-*Ф (xt) dt= J e~* \tx — In A + tx)\ dt.
о о
Это выражение определяет аналитическую функцию, удовлетворяю-
удовлетворяющую уравнению A6). Затронутые здесь вопросы более глубоко из-
изложены в книге Бореля [2], стр. 148—151 *).
§ 2. Доказательство теоремы существования и единственности
с помощью метода последовательных приближений
1. Теорема существования и единственности, а) Пусть дана
нормальная система дифференциальных уравнений
У\ =f{(x'f yv У» • • •» Уп) (*'= l> 2> •••' m)' (!)
и пусть функции ft непрерывны в области D, определенной
неравенствами
\х—сс|О, |Л — fc|<ft (i=l, 2 т) B)
и голоморфны внутри этой области. Обозначим через М наи-
наибольшее значение модулей функций ft в Ь и через 8 меньшее из
чисел а а Ь\М, а через Г — открытую круговую область на пло-
плоскости х с центром в а и радиусом 8.
Покажем, что существует одно и только одно решение ух (х),
_у2(лг), ...,ут{х) для системы A), удовлетворяющее начальным
условиям
Л(«) = Р| (i=l, 2, ..., т). C)
Эти решения голоморфны внутри Г.
!) См. также Хардн [1], гл. VIII и Уиттекер и Ватсон [1], т. I, стр. 209.-
Прим. перев.
$ й. Метод последовйтельных приближении 109
Как и в гл. I, § 3, п. 2, рассмотрим последовательность при-
приближений
си
(x't Pl> P2» • • • >
а
D)
(/¦=1, 2,...),
где интегралы берутся по прямолинейному отрезку, соединяющему ос
и х, и соответствующий ряд
_у(!) -j- (_у<2) —уф) -|- ...-}- (yj+1 —уф) -}-... (/=1,2,..., т). E)
Пусть 8Х — положительное число, меньшее чем 8, а в остальном
произвольное. Покажем, что ряды E) равномерно сходятся в об-
области Г-р определенной неравенством | х — ос \ ^ bv и что их сумма
дает решение системы A), удовлетворяющее начальным условиям C).
Заметим сначала, что если х; yv у9, ..., ут изменяются в за-
замкнутой области /У, лежащей внутри D, то функции /4 удовлетво-
удовлетворяют условию Липшица.
В самом деле, вспомним, что если функция F{x) голоморфна
в замкнутой и выпуклой области Q и если L равно наибольшему
значению модуля F'(x) в Q, то
где интеграл взят вдоль прямолинейного отрезка, соединяющего
точки х и х, и, по теореме Дарбу1), |^(*) — F (х) [<[ Z, | л: — х\.
Отсюда следует, что если в D'
-Р- <L а, А; = 1, 2, ..., т),
дуъ I
то
_ _ _ m _
(см. гл. I, § 3, п. 1).
Из D) следует, что |^г+1'(-*) — P*|-^-M I-*— «l-^^ffij <| b,
а потому к модулю разности
можно применить неравенство F).
См. Маркушевич А. И. U J, стр. 152. -г- Прим. перее.
110 Гл. III. Аналитический теорий дифференциальных уравнений
Если f — регулярная кривая, дифференциал дуги которой равен ds,
длина равна S, а <р(лг)—непрерывная вдоль этой кривой функция
комплексного переменного х, то
S
т о
Учитывая это, нам достаточно повторить рассуждения, проведен-
проведенные в п. 2 и 3 из § 3 гл. I, чтобы доказать, что ряды E) равно-
равномерно сходятся к функциям yi(x), которые образуют решение для
системы A) и удовлетворяют начальным условиям, а также, что это
решение единственно.
Наконец, замечая, что, в силу D), члены ряда E) являются го-
голоморфными функциями от х в области Г-,, получаем, в силу тео-
теоремы Вейерштрасса2), что решения yt (х) голоморфны внутри Г.
б) Предположим, что в правые части уравнений A) входит пара-
параметр X и что функции" f{ непрерывны в области D, заданной нера-
неравенствами
|лг—«|<о; \yt — Р<|<* (/=1, 2, ...,w); |X —
и голоморфны внутри этой области, и обозначим снова через At
наибольшее значение модуля функций /( в D.
Выбирая в качестве начальной точки такую точку jc°, что,
|*о-а|<8, 8 = miii [в, ¦—],
а в качестве значений решений yf в х° такие числа у%, что
Lv?-P«I<T.
и заменяя в D) а на х° и р4 на у°, убеждаемся, что члены ряда E)
являются голоморфными функциями от х; х°; у®, у®, ..., у°т внутри
области, определенной неравенствами
|лг-а|<8, |*о-а|<8, ДО-р^*., |Х-Т
Поэтому, в силу теоремы Вейерштрасса, производные любого по-
порядка решений yt(x; x°; y°v y\, ..., у1^; X) по всем их аргументам
могут быть получены почленным дифференцированием ряда E).
Отметим, что из предположения о голоморфности функций /4
сразу следует дифференцируемость решений по начальным данным и
по параметрам, в то время как в гл. I, в действительной области,
доказательство этого свойства потребовало ряда дополнительных
рассуждений.
*) См, Маркушевич А. И. И], стр. 152. — Прим. перее.
2) См. Маркушевич А. И. [1], стр. 201. — Прим. перее.
$ 2. Метод последовательных приближений Ш
в) Заметим, что метод исчисления пределов обеспечивает суще-
существование решений в круге радиуса р = аA—е-Щт+1)Ша^ в то
время как метод последовательных приближений дает в качестве
значения радиуса 8 = min (a, b\M) (см. „а"); легко видеть, что
р -^ 8. Это неравенство очевидно, если а -^ Ь\М, если же Ь\М < а,
то, положив Ь\Ма = \, заметим, что 0 < ?< 1, а потому
2. Замечание Уинтиера относительно области существования
голоморфного решения. Пусть функция f{x, у) непрерывна в об-
области D, заданной неравенствами
|*|<«. \У\<»,
и голоморфна внутри D, и пусть у—у{х) является решением урав-
уравнения
обращающимся в нуль при х — 0. Если обозначить через М наи-
наибольшее значение \f{x, y)\ в ?>, то способ последовательных при-
приближений дает голоморфность у(х) внутри круга с центром в на-
начале координат и радиусом р(о, b, M) — min(a, bjM).
Встает Еопрос, можно ли при фиксированных a, b, M указать
такое число г (а, Ь, М) > min {a, b/М), что, независимо от выбора
f(x, у), решение уравнения G), обращающееся в нуль при х = 0,
голоморфно внутри круга с центром в начале координат и радиу-
радиусом л?
Покажем, что min (a, bjM) является наилучшей границей для
р(а, b, M) (см. Уинтнер [1]).
Если а <! Ь\М, то это очевидно, так как достаточно выбрать
f(x, у) независимой от у.
Предположим теперь, что а > bjM; тогда достаточно показать,
что можно указать пару b и М так, что для любого числа л>6/ЛГ
существует функция f{y) (независящая от х), которая обладает сле-
следующими свойствами:
1) функция f{y) непрерывна в круге I.yl-Cf' и голоморфна
внутри этого круга;
2) наибольшее значение |/(у)| в круге |.у|-С? равно М;
3) решение у{х) уравнения -н^-=/(_у), обращающееся в нуль
при х = 0, имеет особую точку в круге | х \ < г.
Рассмотрим функцию.
где в правой части для степени берется главное значение.
112 Гл. lit. Аналитическая теория дифференциальных уравнений
Решение уравнения
обращающееся в нуль при х = О, имеет вид
где
Точка л: = — сп является особой точкой для у (х), причем сп > Ь\М
и lim cn — bjM.
3. Применение матричного исчисления для определения фун-
фундаментальной системы решений системы линейных дифферен-
дифференциальных уравнений, а) Для того чтобы показать приложения мат-
матричного исчисления, краткое изложение которого было дано нами
в гл. II, § 2, укажем, как можно получить одновременное разложе-
разложение в ряд фундаментальной системы решений для системы линейных
дифференциальных уравнений, коэффициенты которых являются' го-
голоморфными функциями от х.
Пусть надо решить линейную систему
В (х) ^— = Л (х) Y, F(a) = Fft (8)
где
А (х) = К к {х)\\, В {х) = Ц*«, к (*)Ц (/, k = 1, 2, ..., т), (9)
функции ait к(х), bit к(х) голоморфны в круге С с центром в точке а,
Det B(x) ФО в С и
A0)
Уг{х)
Уъ (*)
У mix)
Л
л
"yi
Положим х—а=т, и пусть (см. гл. II, § 2, п. 1 „и")
(И)
Умножая эти ряды слева на В*1 (а), получаем
2. Метод последовательных приближений
113
где Uo, Ult ..., Un, ..., Vlt V2, ..., Vn, ... — матрицы порядка т
с постоянными элементами.
Пусть ylt к (х), у% к(х), ..., ут> к (х), (k = 1, 2, ..., т) ~ фун-
фундаментальная система решений для данной системы (8), удовлет-
удовлетворяющая начальным условиям
= 0, \
Полагая тогда
У\,
У и
Ут, I (*) Ут, в (*)••• ^я., »» (*)
A3)
A4)
получим, что 5(а) = 1, в то время как искомое решение должно
иметь вид
Y(x) = S(x) Ко= [1 +5^ + ^+ ... +5„г"+ ...] Yo, A6)
где 5j, 52, ..., Sn, ... — матрицы порядка т с постоянными эле-
элементами. Определим теперь эти матрицы.
Умножая равенство (8) слева на В~1(а) и учитывая A2) и A5),
получаем
.. 0 Го.
Сравнивая коэффициенты при одинаковых степенях ? в обеих частях
равенства, получаем, наконец, рекуррентные формулы
A6)
454 = (f/0 —
+ (f/2 — V^! + U3,
из которых находим Sv S2, Ss, , а тем самым и фундаменталь-
фундаментальную систему решений, удовлетворяющую начальным условиям A3).
В частности, если В(х)^=1, т. е. в случае, когда уравнение (8)
имеет вид
dYA(x\Y
8 Зах. 627. Дж. Сансоне
114 Гл. III. Аналитическая теория дифференциальиых уравнений
получаем из второго равенства A2), что V^^O* У2 = 0, ... и тогда
из рекуррентных формул A6) получаем
2! S^=
3! 5s =
4! SA=>
6?/3,
A7)
б) Проиллюстрируем изложенное на примере. Рассмотрим урав-
уравнение
z" = x*z A8)
и определим фундаментальную систему решений zv z2, удовлетво-
удовлетворяющих соответственно начальным условиям
Положим
Уравнение A8) эквивалентно линейной системе
dY «О, 1
Лх I лг2, 0
а потому, в наших обозначениях, имеем
О l|j
о о '
О 1 II [| 0 1
г2 ОI= || О О
0 0' 8
и получаем из A7), что
О 1 | | 0 01
С =|о о '
5»-"«o о!1
Y,
О О
О О
о о ||
1 0 '
1J00I
2 0'
2 О
О 6 f| •
Проводя далее вычисления, находим, что уравнение A8) имеет фун-
фундаментальную систему решений
z\ —
3-4-7.
§ 3. Линейные дифференциальные уравнений US
§ 3. Аналитическая теория линейных
дифференциальных уравнений второго порядка
1. Правильные и неправильные особые точки для дифферен-
дифференциального уравнения второго порядка. Пусть дано линейное диф-
дифференциальное уравнение второго порядка
коэффициенты р(х), q(x) которого являются голоморфными функ-
функциями от х в открытой круговой области С, определенной неравен-
неравенством |* — с|</?. Учитывая изложенное в § 1 гл. II и в преды-
предыдущем параграфе, получаем, что это уравнение имеет два линейно
независимых, голоморфных в С решения. Рассмотрим теперь случай,
когда р (х), q {x) голоморфны в С всюду, за исключением точки с,
в которой по крайней мере один из этих коэффициентов имеет полюс.
Согласно общей теории *), точка с является правильной точкой,
а уравнение является уравнением класса Фукса в окрестности точки
х = с, если р (х) имеет в этой точке полюс не выше, чем первого
порядка, a q(x)— полюс не выше, чем второго порядка, иными сло-
словами, если функции (х — с)р{х), {х — cfq{x) голоморфны в С.
Если же с является полюсом для р (х) или q (x), или для обеих
функций, причем указанные условия не выполнены, то с называется
неправильной точкой. Мы ограничимся изучением поведения решений
в окрестности правильной точки.
2. Правильные точки. Определяющее уравнение. Итак, пусть
с — правильная особая точка для A); умножая на (х — сJ, получаем
C)
где функции Р(х), Q(x) голоморфны в с, и потому
со
П=0
где р0, р„ р2, ...; q0, qv q%, ...—постоянные, а ряды сходятся
в замкнутом круге С' с центром в с и радиусом г, 0 <[ г <[ R.
Выясним, нельзя ли найти решение уравнения B) в виде
J ()+2
п=1
где at, a2, ...—постоянные.
!) См., например, Голубев В. В. [1], стр. 195, Уиттекер и Ватсои [1],
ч. I, стр. 272, Айне [1], стр. 491. — Прим. перев.
8*
116 Гл: III. Аналитическая теория дифференциальных уравнений
Предполагая, что радиус сходимости стоящего в квадратных
скобках ряда отличен от нуля, получаем
п=1
n=l
откуда, подставляя в B), выводим, что
со
(х— с)" [а (а — 1) + 2 йп 0х + п) (а + и — 1) (х — i
П = 1
со со
П=1 П=0
со со
П=1 П=0
Перемножая ряды и замечая, что левая часть должна тождественно
равняться нулю, получаем для а и для коэффициентов av а2, ...
следующие уравнения
(б)
= 0, F,)
+ 1+1 + l + p2 + % = 0, F2)
и вообще
—1
2 «„_„,[(a + я —я»)pm + ^J + «pn + ^„==0. FП)
т=1
=1
Уравнение E) называется определяющим уравнением для B)
в точке ^. Полагая
G)
его можно записать в виде
F(a) = 0. E')
Корни pj и р2 этого уравнения называются характеристическими
показателями уравнения B) относительно точки с.
Заметим, что в уравнениях F,), F2), , F„), ... коэффициенты
при в„ «а, ..., ап, ... равны соответственно F(a-J-I), F(a-|-2),...,
F(a-J-n), ... и что условие Z7 (a -j- и) Ф 0 при л = 1, 2, ... можно
$ 5. Линейные дифференциальные уравнения 117
выразить, сказав, что если а — pv то р2 ф pt -\-1, pt -j- 2, , а если
«=р2, то PiTfep2+l> Pa + 2, ... Отсюда следует, что если раз-
разность характеристических показателей не является целым числом, то
из уравнений F,), F2), ..., FП), ... можно рекуррентно найти две
последовательности коэффициентов ап, дающих два формальные
решения уравнения B).
8. Сходимость рядов в случае, когда разность характеристи-
характеристических показателей не является целым числом. Покажем, что
если pj — р2 не является целым числом, то указанный в преды-
предыдущем номере рекуррентный процесс приводит к двум линейно
независимым решениям уравнения B).
Пусть
(через Rx мы обозначаем действительную часть д:). Тогда, полагая
Pi— Pa^s. (8)
имеем /?s>-0. Заметим, далее, что F (р„ -j- и) = F (pt) + nF' (pt) -|-
+ n2F"(p,)/2 = n[2Pl + p0 — 1] + и2, и так как р0 —1= — р,—р2=
==¦ — 2Pl-|-s, 2p,+p0 — l = s, то
F(p1-\-n) = n(s+nj, [F(h +л) = «(« — *)].
Пусть N равно наибольшему значению модуля Р(х—с) и
Q(x—с) на окружности, ограничивающей круг С. Тогда
(я = 0, 1, 2, ...)•
Заменяя, если это необходимо, Л^ ббльшим числом М, получаем
\pn\<Mr-n, \qn\<Mr~n, \plPn+qn\<Mr~n A0,)
(и = 0, 1, 2, ,..),
М>1. (Ю2)
Из Fj) при a = pi получаем (|s-|-l |^. 1), что
| а, |< Mir. A1)
Пусть теперь неравенство
доказанное нами при и = 1, справедливо при и = 1, 2, , /те—1.
Докажем, что оно имеет место и при и = /те.
. 118 Гл. ///. Аналитическая теория дифференциальных уравнений
В самом деле
m-l
ат-ъ [(Pi + т — k)pk + gk] + Plpm + q
m-l
m-l
2 I u»»-k I I PiPk + 9* I +1 PU»m + 4m |+ 2 (OT — k) I я«"-к
m-l
m-l
2 (
k=l
m-l
m*\l+8ltn\
В силу того, что
(М/гГ_(т±1)
2ot|1+s/»t| '
0, имеем 11
1, а потому
A2)
Отсюда следует, что радиус сходимости ряда
не меньше, чем л/Ж.
Обозначим через а[, а'2, ..., «^ коэффициенты, соответствующие
корню р2, и покажем, что
\a'J< (М%1гУ (и = 1, 2, ...).
A2')
где через г обозначена верхняя грань числового множества
о -1
(это множество ограничено, так как s не является целым числом).
В самом деле, F (р2 + к) = п (и — s) = и2 A — s/и) и 11 —s/n| -1 < т,
а потому нам достаточно повторить проведенные выше рассуждения-
Заметим, наконец, что в случае, когда pt — р2 не является целым
числом, аналитические функции
п=1
оо
], (х-сГ [1 + 2 а'п{х-сГ\
п=1
§ 3. Линейные дифференциальные уравнения 119
линейно независимы. Поэтому аналитические функции
ап(х—сГ],
A3)
п=1
w2(x) = (x—с)Рг [l -J- 2 <*»»(¦*—с)"]
п=1
образуют фундаментальную систему решений уравнения B). Гово-
Говорят, что решения wt (x), w% (x) принадлежат соответственно пока-
показателям pj, p2.
4. Построение второго решения в случае, когда характери-
характеристические показатели совпадают или отличаются на целое число.
В разобранном выше случае (правильная) особенность точки с выра-
выразилась в присутствии множителей (х — с)р», (х — с)р* в формулах для
решений; естественно поэтому е случае, когда характеристические
показатели совпадают или отличаются на целое число, искать форму
решения, содержащую соответствующую (логарифмическую) особен-
особенность.
Заметим, что если pt — р2 = 0, то решение w% (x) совпадает с w1 (x),
а если s является натуральным числом, то /7(p2-}-s) = 0 и тогда
невозможно определить с помощью описанного в п. 2 алгорифма
коэффициент a's. Поэтому в обоих случаях проведенные в п. 3 рас-
рассуждения доказывают лишь существование одного решения w1 (x)
уравнения B).
Для того чтобы найти второе решение, сделаем в уравнении B)
подстановку (см. гл. II, § 4, п. 1 и гл. II, § 1, п. 3 „д")
Получаем
dx2/dx Wj x — с '
n=l
Полагая
п=1
=g{x),
видим, что g(c) = V, кроме того, функция g(x) голоморфна в круге
с центром в с, не содержащем особых точек Р(х), а также особых
120 Гл. III. Аналитическая теория дифференциальных уравнений
точек и нулей (х—с)-р> iol (x). Внутри такого круга имеем
со
п=1
а тогда при яфО из A4) следует (—2pt—Ро = — s—1), что
в-1
[-1 (л;_с)-в_2^-(л:-СГв+^1п
+ 2 Ae-tf1-]-
n=l
«=8+1
Поэтому, когда л: изменяется в достаточно малой окрестности точки с,
общее решение уравнения B) имеет вид
Aw, (x) + B[gsw1 (х)Щх — е) + да (*)], A5)
где А и .В — произвольные постоянные и
п=1 п=1
n9fra
Учитывая, что рх—s = p2> получаем
п=1
Формулы A5) и A6) дают выражение общего решения уравне-
уравнения B) для случая, когда s —¦ целое число, s > 0. Стоящий в A5)
в квадратных скобках множитель показывает на наличие в решении
логарифмической особенности.
В случае, когда s = 0, имеем
п-1
а потому общее решение нашего уравнения имеет вид
Aw1 (х) + В [W! {х) In (x—e) + w (x% A5')
где
§ 4. Линейные уравнения с тремя особыми точками 121
5. Правильные особые точки в бесконечности. Для того чтобы
изучить поведение решений дифференциального уравнения в беско-
бесконечности, сделаем подстановку
и рассмотрим поведение решений получающегося уравнения в окре-
окрестности точки jfx = 0. Ограничимся случаем, когда коэффициенты
уравнения регулярны или, в крайнем случае, имеют полюсы; тогда,
в зависимости от того, является ли точка хг — 0 обыкновенной точ-
точкой (коэффициенты уравнения голоморфны при ^ = 0), правильной
особой точкой, неправильной особой точкой, скажем, соответственно,
что бесконечность является обыкновенной точкой, правильной особой
точкой, неправильной особой точкой.
В силу того, что
dy_ a dy_ d?y _ 4 d*y ¦ 9 з dy
dx ~ Xl dxx' dx* ~ l dx\ ~1~ Axx'
получаем
] tk +
а потому преобразованное уравнение йлеет вид
Отсюда следует, что точка je = oo является обыкновенной, если
в окрестности х = оо имеют место разложения
со оо
2х—х*р (х) = 2 рпд^-», ** ? (д:) = S 9„^-и,
и правильной особой точкой, если
оо оо
хр (х) «= 2 р„лг-», ^ (*) = 2 ?п*"п.
п=о п=о
т. е. если р(дг) имеет в бесконечности нуль не ниже, чем первого
порядка, a q(x) — не ниже чем второго.
§ 4. Линейные дифференциальные уравнения
с тремя правильными особыми точками.
Гипергеометрическое уравнение
1. Уравнение Паперица и функция Р Римана. В опубликованном
посмертно мемуаре Римана намечено решение вопроса об определении
вида дифференциального уравнения по заданным особым точкам коэф-
коэффициентов и соответствующим характеристическим показателям.
122 Гл. III. Аналитическая теория дифференциальных уравнений
Ограничимся рассмотрением уравнений второго порядка, имеющих
лишь три правильные особые точки. Легко показать, что уравнение
gty {!-„-„' 1-р-р' ¦ 1—г—gdy
dx*~\ х — а *~ х—Ь *~ х — с \dx
Ь)(а-с) , pp'(fr-c)(fr — a)
1 x—с / (х — а)(х — b)(x — <
где
а —j- а' -|— р _j_ p' _J_ -(¦ _]_ -^' = 1 B)
имеет лишь правильные особые точки а, Ь, с, и что соответствующие
характеристические показатели равны а, а'; р, fJ'; -(, •{.
В самом деле, в точке х=а имеем ро=1—а — а', qo = aar
(см. обозначения п. 2 предыдущего параграфа), а потому корни опре-
определяющего уравнения равны а и а'.
Используя те же обозначения и учитывая равенство B), получаем,
что
2х—х*р (х) = 2х — A — « — «О хЦ1 — ajx) —
а потому функция 2х—х*р{х) регулярна в точке jc = oo. Аналогично
показывается, что xiq{x) также регулярна при jf = oo, откуда сле-
следует, согласно сказанному в п. 4 § 3, что точка jc = oo является
обыкновенной точкой для уравнения A).
Уравнение A) было найдено Паперицем [1].
Обратно, наиболее общее линейное дифференциальное уравнение
второго порядка с тремя правильными особыми точками имеет вид A),
причем постоянные а, а', C, C', ^, -f связаны соотношением B).
Для указания того, что функция у удовлетворяет уравнению A),
Риман применял обозначение (см. Риман [1], стр. 176—186 и 159—175)
Ь с "
р т *|. C)
' р' f J
где в первой строке стоят точки а, Ь, с, а в столбцах — соответ-
соответствующие им характеристические показатели.
Назовем у функцией Р Римана.
Например, гипергеометрическое уравнение (см. п. 3)
4. Линейные уравнения с тремя особыми точками
123
можно записать в виде
с t 1+а+Ь—с , 1— a — b~\ dy
a — b~\ dy , ab _
и потому
О оо 1
О а 0 х\
1 — с b с — а — b
2. Преобразования Римана для функции Р. а) Докажем следую-
следующую основную теорему.
Если при дробно линейном преобразовании (с постоянными
коэффициентами)
х = (Axt + В)((Сх1 + D), {AD — ВСфО)
точкам а, Ь, с соответствуют точки аг, blt cv то
\аЬс
Р{а р
f«i h с1 1
D)
Для доказательства нам достаточно показать, что равенство D)
имеет место при элементарных преобразованиях:
а) ;с = лг1-{-?, б) x — kxx, в) лг =—.
Для преобразования „а" наше утверждение очевидно; для „б" имеем
rfy__J_rfj^ d2y ___ 1 d2j>
а потому уравнение A) преобразуется в уравнение (а = kau b = kblt
)
Умножая это уравнение на ?а, убеждаемся в справедливости равен-
равенства D).
Наконец, рассмотрим преобразование „в". Положим а = \1ах,
b = llblt c = l/cv Тогда (см. § 3, п. 5)
а&У i 2хзау Р~°
X
A/X, - 1M) A/X, - I/ft,) A/X!—
¦=0.
124 Гл. III. Аналитическая теория дифференциальных уравнений
Складывая второй и третий член и деля на х\, убеждаемся в спра-
справедливости равенства D).
б) Если у является функцией Р, определенной выражением C),
то функция
также является функцией Р, причем
a b
я -j- k [3— k — /
a' + k ф — k — l
х
иными словами, показатели о, a'; f, f' увеличиваются, соответ-
соответственно, на k и I, а показатели C и C' уменьшаются на k-\-l.
Таким образом,
b с
,x-a\*(x-c\lp
\x-b) Хх-=ЬГ
Р Т
Р' ?
F)
Читатель может провести прямое доказательство этого утверждения;
впрочем, допуская, что уравнение A) однозначно определяется зада-
заданием точек а, Ь, с и соответствующих характеристических показате-
показателей, можно доказать это утверждение, заметив, что в силу E) функ-
функция ух имеет особые точки а, Ь, с, причем характеристические пока-
показатели по сравнению с функцией у увеличиваются в точке а на k,
в точке с на / и уменьшаются в точке b на k-\-l.
3. Гипергеометрическое уравнение Гаусса, Назовем гипергео-
гипергеометрическим уравнением уравнение
d?- aby
G)
Удовлетворяющую ему аналитическую функцию назовем гипергеоме-
гипергеометрической функцией 1).
В силу сказанного в п. 1, у является функцией Римана, причем
(8)
Это уравнение рассматривалось Эйлером в [1], т. II, п. 1035, 1039.
4. Линейные урйвненйя с тремя особыми точками
125
p
В силу соотношения F) имеем
a b с
а
«г X
а' |3'
к-« «+р'+т
Дробно линейная подстановка хг = (х—а) (с—b)j{x—b)(c— а) пре-
преобразует точки а, Ь, с, соответственно, в точки 0, оо, 1, а потому,
в силу полученных в п. 2 „а" результатов, имеет место следующая
замечательная формула
х
о
о
оо
1
0
(8')
4. Гипергеометрический ряд. а) Общая теория позволяет изучить
поведение решений гипергеометрического уравнения в окрестности
особых точек 0, 1, оо и продолжить их аналитически на комплекс-
комплексную плоскость с разрезами вдоль действительной оси от —оо до О
и от 1 до оо (в этой односвязной области все решения голоморфны).
Мы ради краткости ограничимся изучением поведения решений в ок-
окрестности точки дг = О.
Если с не является целым числом, то, согласно полученным
в § 3, п. 3 результатам 1), фундаментальная система решений имеет
вид
У\(х), У2(х) = х1-°и(х),
где функции ух {х) и и (дг) голоморфны в окрестности точки л: = 0.
Не теряя общности, можно считать, что
Положим
»=0
Подставляя это выражение в G), получаем
П=1
х) Для уравнения G) имеем ptp2 = ^о = 0. — pi
Pi = 0, р2 = 1 — с. — Прим. ред.
¦ ab 2j СпХ" == 0>
t—Po— l=c — 1,т.е.,
126 Рл. til. Аналитическая теория дифференциальных урйвнении
откуда
— и (я — l)cn+n(w
<Wl = (» + «) (» + *) ««/(» + 1) (Я + С). (9)
Так как с0 — 1, то
» л!с(с + 1)...(с + и — 1)
Соответствующий ряд
а-6 д(д+1)дF+1) о , ,
1Т~Ь7ЛГ"Т 2!с(е+1) * "•" ••¦ "+"
¦ д(Д+1)...(а + я—1NF+1)...(б + я — 1) ,
"• и!с(с+1)(с + я — 1) "* +"•
называется гипергеометрическим рядом и обозначается, согласно
Гауссу, символом
F{a, b, с; *)»),
указывающим его зависимость от jc и параметров а, Ь, с.
Таким образом, мы нашли для решения у1 выражение в виде
ряда
y1 = F(a, b, с; х)=_
радиус сходимости которого, в силу результатов § 1, равен единице.
Последнее обстоятельство следует, впрочем, непосредственно из того,
что, согласно (9), lim | cjcn+l | = 1.
П->оо
Для нахождения решения уй достаточно заметить, что
О оо 1
0 а — с + 1 0 лг|
с—1 Ь — с-f-l с — а — b
— c, b + l— с, 2 —с; х),
откуда
) »/7 с, ft+.1—с, 2-е; *). A1,)
х) См. Гаусс [1], т. III, стр. 125. Ряд A0) рассматривался Эйлером
в мемуаре [2]. Название гипергеометрический ряд было введено Куммером
(см. Куммер [1]).
Относительно литературы по гипергеометрической функции см. Кампе
де Ферье [1].
§ 4. Линейные урйвнекия с тремя особыми точками 157
Из (llj) и (П2) следует, что в круге с центром в начале коор-
координат и радиусом 1 любое решение гипергеометрического уравнения
имеет вид
y = ClF(a, b, с; x)-\-czxi-cF(a + l — с, Ь + \— с, 2-е; х),
где с1 и с2—произвольные постоянные,
б) Читатель легко проверит, что
F(—n, b, b; -*)^l+y*+"(w271)*a+ — =
, 1, 2; —лг)=1—f+-f— ....
а потому для главного значения логарифма 1 —J— лс имеем
) = xF(l, I, 2; — л:),
откуда
еж= limfl -\—~)~Ь== lim F(l, b, 1;
в) Установим, наконец, дифференциальное соотношение, которое
будет использовано в следующем параграфе.
Дифференцируя соотношение G) по лг, получаем
Таким образом, производная от гипергеометрической функции
также является гипергеометрической функцией, имеющей пара-
параметры e + 1, * + l, c-j— 1, и, в частности,
Вообще имеем
откуда, умножая на дг°+и-2A—х)а+ь~с+п~*, получаем
dxW '
128 Тл. ///. Аналитическая теория дифференциальных уравнений
Дифференцируя это равенство п — 1 раз, получаем рекуррентную
формулу
J^L. [xn+c-l (I ^
= (а + п — 1) (Ь + п — 1) ^i- [лг»+с-2 A —
Заменяя в этой формуле и на и—1, л — 2, ..., 2, 1 и перемножая
получающиеся равенства, имеем
JPL [хп+с-1 A — Х)а+Ъ-с+пу(п)] —
Ч1—*)о+ь""с.у- A3)
г) Пользуясь формулой A1Д легко доказать справедливость уста-
установленных Гауссом (см. Гаусс [2], стр. 130) соотношений для смеж-
смежных функций F
aF(a-\-\, b, с; x) — bF{a, b-\-l, с; x) = {a — b)F{a, b, с; х), A4)
= b ac ^Fia+l, b, c+l; x). A5)
Эти соотношения также будут использованы в следующем параграфе.
5. Гипергеометрический интеграл Эйлера. Рассмотрим введенный
Эйлером интеграл
1
о
предполагая, что и изменяется вдоль отрезка [0, 1] действительной
оси, с>?>0, |дг|<1, а A — их)~а принадлежит ветви, принимаю-
принимающей при и-»--|-0 (вдоль действительной оси) значение 1.
Тогда
В силу предположения |лг|< 1, стоящий справа ряд равномерно схо-
сходится, когда и изменяется от 0 до 1, а потому
1
J и* A — иH-1 A — их)-" du =
; / A6)
$ 5. ГитргеоМетриЧескйе Многочлены Якоби 129
В силу известных свойств гамма-функции')
__ (fr .f п — 1) (fr -f n — 2).,. ЬУ (b) Г (с — Ъ)
~ (с + я-1)(с + и—2)...-еГ(с)
Подставляя это выражение в формулу A6), получаем, что при | х | < 1,
с > b > 0 имеет место формула Эйлера
Ь-\1- иТЬ-Х A ~ «х)-da =
Можно доказать, что формула A7) справедлива, если R (с) > 7? (*) > 0.
§ 5. Гипергеометрические многочлены Якоби
1. Многочлены Якоби Рп . а) Если хотя бы один из параметров а
или b равен целому отрицательному числу —п, то гипергеометриче-
гипергеометрический ряд превращается в многочлен степени -\-п, называемый я-м
гипергеометрическим многочленом Якоби (см. Якоби [1], т. 6, стр. 191).
Этот многочлен обозначается одним из двух символов Р%' ® (х), Рп (х)
(л = 1,2,...). A)
По определению,
Р?-Р) = 1. B)
Коэффициент при хп в Рп имеет вид
(« + 1)(а + 2)...(« + «) (« + Р + и + 1)---(° + Р+2и)(-1)"и!( .» 1
и! и!(о + 1)(« + 2)...(а + и) 2я'
а потому
*) Мы предполагаем, что читатель знаком со свойствами гамма-функции
¦ +оо
(эйлерова интеграла второго рода) Г (й) = I xa~1e~x dx (Ra > 0) и бета-
о
функции (эйлерова интеграла первого рода)
1
В (а, Ь) == f д:0 A —х)ь~х dx =
См. примечание на стр. 144.
9 Зшс 627. Дж. Сансон*
1зО Гл. tit. Аналитических п:еЬрия дифференциальных уравнении
б) Для того чтобы получить дифференциальное уравнение для
многочленов Рп, достаточно заменить в гипергеометрическом уравне-
уравнении л: на A — ?)/2, заменив соответственно а, Ь, с на a-J-p-(-n-f-l,
— п, а-\-1', тогда получаем, что
я = 0. D)
в) Дифференцируя формулу A) по х и учитывая равенство A2)
из § 4, получаем
dPn
dx n\ a-fl
Х=^/?(а + р + н + 2, —«+1, a
т. е.
р/(«. Р) _ a
2. Формула Родрига. Производящая функция многочленов Р„'^.
а) Полагая в формуле A3) из § 4 Ь = — п и заменяя а и с на
<х-4-? + я+1 и а-\-1, соответственно, а х на A — ?)/2, получаем
так называемую формулу Родрига
Если в этой формуле заменить а и C на C и a, a jc на —х, то полу-
получаем, что
Pta\x) = {-\fPt-*\-x). G)
б) Формула F) позволяет найти так называемую производящую
функцию для многочленов Якоби.
Уравнение
У=х-^{\-у% (8)
где х является действительным или комплексным фиксированным
числом, а г — параметром, имеет корень
цГи_1—VI —Ягг + чГ 2лг-г
выбрать ветвь радикала, принимающую при г = 0 значение
-j- 1, то получим, что^@) = лг. Радикал обращается в нуль при
г = е, Г1; S =
и легко видеть, что 111 равно сумме полуосей проходящего через
точку х эллипса, фокусы которого находятся в точках -j- l и
5 A tanepzeoMempd4ecnue Многочлены Якоба 131
— 1 (см. Дарбу [2], стр. 21). В самом деле, полагая x==X-\~iY,
= peie (р>-1), имеем
i^p—l)s!ne],
и сумма полуосей соответствующего эллипса действительно равна
Р=|6|.
Поэтому при | г | < 111 1 функция у (г) является голоморфной,
и если f(y)— голоморфная функция от у, то при Irj-cClEl спра-
справедливо разложение в ряд Лагранжа (см. Лагранж [1], т. III, стр. 25,
а также Уиттекер и Ватсон [1J, т. I, стр. 178J
1-лгТ/(лг)]. (Ю)
п=1
Положим f(y) = (l'—yT A + yf и выберем для степеней A—:у)",
A -\~yf главные значения; f(y) будет тогда голоморфной функцией
от у всюду, за исключением точек у = ± 1; из (8) получаем
dy __ 1 _ 1
йл: 1 — гу V 1 — 2гл: + г2 "
Умножая A0) на A—дг;~"A-j-дг)"9 и учитывая равенство F), убе-
убеждаемся, наконец, что при | г | < 15 р1 имеет место разложение
в ряд Якоби (см. Якоби [1], т. VI, стр. 194)
3. Значения Я„(±1). Выполняя дифференцирование в правой
части формулы F) по теореме Лейбница и приводя подобные члены,
получаем
а потому
9*
Гл. Hi. Аналитический теория дифференциальных уравнении
откуда
И, в силу G),
(И)
Делая в формуле A2) подстановку x=={t-\-\)j{t—1), получаем
другую формулу, которую также полезно иметь в виду,
v=0
4. Рекуррентные формулы, а) Для многочленов Рп справедливы
соотношения
2) Р<,°+1> Р) (лг) =
в 2 (n +a
), A7)
вытекающие из формул A4) и A5) § 4, если учесть формулу A)
этого параграфа.
Переставляя а и [3 и принимая во внимание равенство G), полу-
получаем формулы
^ ^г), A8)
A + х) Bп + а + Р + 2) /#•р+1) (лг) =
= 2(« + p+l)/>^P)(AT) + 2(« + l)^;f^). A9)
б) Легко видеть, что для многочленов Рп справедливы сле-
следующие рекуррентные формулы (см. Дарбу [2J, стр. 378):
WUB (л-1,2,...). B0,)
где
2(а-Р)
г
B02)
(пв2, 3, ...), B4)
.<t 5. Гипергеометрические многочлены Якоба 133
где
Я _
2и
B1.)
В силу E), соотношение B0а) можно записать в виде
пК Р) __ е
Для доказательства этого равенства надо выразить, согласно фор-
формуле A6), Р?ш?) через Р{*-Ш) и P?li+1) и подставить вместо р?1р+1)
и Ри11+1) их выражения, получаемые из A8).
Аналогично для доказательства равенства B1Х) надо выразить
***-! по формуле A7) через Р^>Р) и Р^1'р.' и заменить последние
выражениями, получающимися из A8).
5. Ортогональность многочленов Р„ в (—1, 1J. а) Покажем,
что если а> — 1, р> — 1, то последовательность функций
{Рп'Р)(*)} ортогональна в [—1,1] относительно веса A—х)а A+дг/.
Умножая уравнение D) на A — лг)" A -j- •*/> приведем его к само-
самосопряженному виду
д:)'A -Ь^)РР„ = О B2)
(см. гл. II, § 4, п. 3 „б"). Умножая это равенство на Рт, интегрируя
от — 1 до 1 и полагая
1
ГЧР,Л<2л:, B3)
получаем
1
JO+1 P+1^^1^ B4)
Меняя местами п и т и вычитая получившееся равенство из B4),
получаем
134 Гл. III. Аналитическая теория дифференциальных уравнений
а потому при пфт имеет место следующее соотношение ортого-
ортогональности
f(l-xT(l+xfPnPmdx^O (пфт). B5)
-1
б) Умножая равенство B1,) на A—лт)"A -{-xfPn и интегрируя
от — 1 до 1, получаем, в силу B5), что
4, „ = Лп J * A - xf (I + xf РЛ-1 dx. B6)
Поступая аналогичным образом с соотношением
получаем (в множителе Рп заменено на {Рп^, что
1
J лгA — *)•(! +xfpJ>H_t dx-Cn+lIn_u n_v
Сравнивая это равенство с B6), видим, что
'п, п == ¦"«•"п+lC'n+l''n-J, n-V
Из этой рекуррентной формулы и из того, что
,о=/A ~*П1+*)?<**= 2O+P+1J ГA-
°
получаем
1
/ ? rf* = К («. Р), B7)
где
а о>_ Г(п + а
' Р^~2и + а + р + 1 Г(и + 1)Г(и + а + р + 1)
(л = 0, 1, ...). B7')
Итак, мы доказали, что система многочленов Якоби
является ортогональной нормированной (и, как можно показать,
замкнутой *) ) системой функций на отрезке [— 1,11 или, как иногда
J) См, Натзндон И. П. [1], стр. 41$. —Прим. перев.
? 5. Гипергеометрические многочлены Якоби 135
говорят, образует ортогональную декартову *) систему функций на
отрезке [—1, 1] относительно веса A — лг)"A +*)р.
в) Применим доказанную ортогональность многочленов Якоби для
вывода некоторых результатов, важных для приложений.
Пусть [ап]—некоторая последовательность действительных
со
чисел, и пусть ряд 2 апРп'й (*) равномерно сходится на отрезке
[—1, 11, причем сумма его равна f(x),
со
f ( у\ ^ ~ г№' Р) ( лЛ fO&\
] \Х) ^^ "и' П X™)' \"°)
п=0
Из сделанных предположений следует, что функция f(x) непре-
непрерывна. Если мы умножим обе части равенства B8) на A — х)а A-\- лг)р X
X Рп* (*) и проинтегрируем от — 1 до 1, то, пользуясь законностью
почленного интегрирования в правой части, получаем формулу
1
' A _ д)« A + Xff (ДГ) р'«- Ч {х) dx = ппК (а>
-^
1
* Г а 6 (в вЪ
л.
J'
выражающую коэффициенты разложения B8).
Известно, что коэффициенты ап называются коэффициентами
со
Фурье, а ряд 2an^n'fiW—рядом Фурье функции /(лг) относи-
п=о
тельно ортогональной системы [Рп'®(х)}>
Если функция /(лг) суммируема (в сйысле Лебега) на отрезке
[—1, 1], то для нее можно вычислить по формуле B9) коэффициенты
Фурье. Весьма важным вопросом анализа является изучение, поведе-
поведения соответствующего ряда Фурье на [—1, I]2). Читатель должен
иметь в виду, что сходимость ряда B8) в некоторой точке х проме-
промежутка (— 1, 1) является локальным фактом, т. е. зависит лишь от
значений f(x) в сколь угодно малой окрестности точки х. В п. 7 мы
докажем, что сходимость этого ряда в точке лг° комплексной пло-
плоскости, не лежащей на отрезке [—1, 1], влечет за собой его сходи-
сходимость во всех точках плоскости х, лежащих внутри проходящего
через точку лт° эллипса, фокусы которого лежат в точках — 1 и -f-1-
J) В русской литературе последний термин не применяется. — Прим.
перев.
2) См. Cere [1J, стр. 89. Более глубокое изложение теории многочленов
Якоби и теории ортогональных многочленов вообще содержится в книге
Джексона [1] н известной книге Сеге^[2],
136 Гл. III. Анал '.тическая теория дифференциальных уравнений
6. Теорема Пуанкаре и Нт Рп+\{х)}Рп{х). а) Для доказатель-
я-»оо
ства сформулированного только что утверждения нам понадобится
следующая теорема Пуанкаре. Пусть
^о = а«РН-..-, Я1 = #яр+..., ^а = слр+... C0)
— три многочлена от п, имеющих одну и ту же степень р, при-
причем Ro (и) фО ни при каком целом неотрицательном значении п,
а {Рп(х)} — определенная рекуррентным соотношением
последовательность многочленов от х. Тогда, если модули корней
уравнения
Ф + Ы+ = 0 C2)
различны, то Hm Pn+1(x)IPn(x) равен в общем случае большему
п->со
по модулю корню уравнения C2), а в исключительных случаях —
меньшему по модулю корню этого уравнения *).
1. Пусть корни уравнения C2) равны о и C и пусть | а | > | J31.
Положим
р id z—m C3.v\
'n+ll'n — vn> \OOJ
Тогда из равенства C1) вытекает, что
и, в силу C4), имеем
В силу C0) и C2), свободный член в числителе и коэффициент при Хп
в знаменателе являются многочленами степени пр~г. Кроме того,
a(aa$-\-b$-^-c)-\-$(acifl-\-ba-^-c) = O, а потому, деля числитель и
знаменатель в правой части на я*", получаем
где
е, е'
J) Пуанкаре [2], стр. 209. Относительно приводимого доказательства
см. Сансоне [1J.
А Гипергеометрические многочлены Якоби
137
2. Предположим, что существует такая бесконечная последователь-
последовательность индексов «j, л2, ..., ns, ...
«1 < «2 < ••• < Пв <
что
|Х„я|<Ж (в=1, 2, ...). C6)
Покажем, что в этом случае последовательность {|^п|} ограничена,
и, более того, существует такое целое число N, что при n^-Nимеем
\хп\<м.
В самом деле, при | z | ^ М, имеем
a
р
М\в —
Правая часть этого неравенства стремится к нулю, когда и->со,
а потому для числа М\\ — — найдется такое п0, что, каково бы
ни было п^-п0 и каково бы ни было z, \ z \ ^М, имеет место
неравенство
Выберем некоторый индекс ns > я0. Согласно C6), имеем \Хп \ -^ М,
а но C5)
Повторяя это рассуждение, получаем, что
(г=1, 2, ...; N=ns).
ограничена,
3. Из доказанного следует, что если последовательность {|„|}
неограничена, то lim | Хп \ = со и, по C4), lim vn = р. [Напомним,
п->оо п->со
что «и = (р — «^(l-^T1).]
4. Покажем, что если последовательность
\Хп\^М, то lim 1№ = 0 и потому lim ч)п = а.
п->со п->оо
Покажем предварительно, что каково бы ни было положительное
число о, не существует такого индекса п0, что при п^>п0 имеет
место неравенство
C7)
Если бы выполнялось неравенство C7), то мы имели бы
C8)
138 Гл. tit. Аналитическая теория дифференциальных уравнении
откуда, при достаточно большом п, я > N,
где через h обозначена такая большая единицы величина, что
А|р/«|<9/<1.
Но тогда из C8) при и > N мы имели бы
lim |Л"„| = 0,
n->co
вопреки C7).
Отсюда следует, что если последовательность {|Х„|} ограничена,
то для любого сколь угодно малого положительного числа о най-
найдется бесконечное множество индексов пи к2, ..., л8, , таких,
что \Хп |<о. Из сделанного здесь в разделе 1 „а" замечания сле-
следует, что в этом случае найдется такое Nc, что при и > Ns имеем
|.АГп|<с, а потому lim |Xn| = 0 н lim vn — a.
n->oo n->oa
б) Так как многочлены Якоби удовлетворяют рекуррентному соот-
соотношению B1j), то, по-доказанной теореме, имеем
lim |
где через I обозначен больший по модулю корень уравнения (р = 3,
а = 4, Ь=* — 8лг, с — 4) j
I2—2лг$+1=0.
Так как радиус сходимости ряда Якоби A1) равен S, то, по
известному свойству степенных рядов, получаем
lim |Ря+1 (*)//>„(*)| = |5|,
а потому исключительный случай теоремы не имеет места.
7. Ряды по многочленам Якоби в комплексной области. Дока-
Докажем теперь теорему, из которой следует сформулированное в конце п. 5
утверждение.
Если \ап\ — последовательность действительных ила комплекс-
комплексных чисел и есЛи ряд
„Л C9)
сходится в точке х° комплексной плоскости, лежащей вне от-
отрезка I—1, 1), то он сходится и притом равномерно в любом
эллипсе Е' с фокусами в точках —1 u —J— 1, лежащем внутри
эллипса Е, проходящего через точку х° и имеющего те же фокусы.
§ 5. Гапергеометрические многочлены Якоба
139
Так как ряд C9) сходится в точке х°, то существует положи-
положительная постоянная величина g, такая, что
а потому, если х некоторая точка из Е', то
n=0 n=0 n=0
Введем использованные ранее обозначения
и обозначим через | S' | сумму полуосей эллипса Е' [ | \ | ^ | V | < | S0 [ ];
из изложенного в п. 6 получаем
lim
П->оо
?'
> 1,
D0)
а потому ряд 2 i ^n (x)JPn (x0) I сходится. Поэтому сходится и ряд
0
i
п=0
п=о
«ra^n (-*)t причем, в силу D0), эта сходимость равномерна в Е'
8. Ультрасферические многочлены и их производящая функция.
а) Закончим этот параграф описанием специального класса много-
многочленов Якоби. Полагая в выражении A) [или F)] для многочленов
Якоби а = J3 = 0, получаем, как весьма частный случай последних,
(сферические) многочлены Лежандра (см., например, Джексон [2],
гл. II), для которых, как хорошо известно, производящей функцией
является A—2глг-{-г2)~1/2; вообще, получающиеся при а = {3 много-
многочлены называются ультрссферическими многочленами, и мы пока-
покажем, что производящей функцией для них является A—2r.*r-|-f2)~x
(см. Якоби [1], стр. 194).
Пусть X Ф 0. Полагая
J
получаем
_х = |A _гJ .
откуда, разлагая в биномиальный ряд, выводим, что
1)"
— г)-
ах-2п
п=0
0 В силу теоремы Вейерштрасса, сумма ряда C9) голоморфна при еде*
данных предположениях внутри ?,
140 Гл. III. Аналитическая теория дифференциальных уравнений
Разлагая далее в биномиальный ряд множители A—/-)~2Х-2" и соби-
собирая вместе члены, содержащие г", получаем, что
A — 2гх + г3)-* = 2 /*} (*) *". D1)
7» = 0
где
¦ и(и-1)(Х + 1)Х BХ + я)BХ + и + Р
~т" 2! 2ХBХ+1)BХ-Ь2)BХ + 3)
или
Поэтому, если ввести обозначение
+ а)= (я + «)(я+»-1)-(» + >) (я==0> lt...)t D2)
то, принимая во внимание A), получаем [Р^(лг)=1]
)
^гРЙ-*Х-П*)- D3)
Если, как обычно, положить jf-j-]A*ra—1 = 5, |1|!>-1, то функция
A — 2rx-j-rs)~x голоморфна при |г| < \Ц~1, так что разложение D1)
справедливо при \ г | < 111.
Из F) и D3) вытекает важная формула
" -1 (г-1У"п лЯ)-х+*Ь dn ц\ __ »
б) Найдем самое простое выражение для рЦ' (coscp). Имеем
A — 2rcos<?4-')~1 = A — re*?)-1 (I — re-*?) =
оо со
п==0 п=0
а потому
Р™ (cos 9) = е*я* + е* ("-а)? + ... + е~* (»-2)? -f- e~in<f =
= [?
И, наконец,
D5)
6. Уравнение Ёесселй 141
Из D2) и D3) имеем тогда
Полагая в формулах A6) и A8) а = — 72» Р = — Уа» получаем, со-
соответственно,
Sfn(<p/2) '
^n (cos<pj— 2й/г, cos (tp/2) >
а из A6) при о = — 8/2, р == — 2/2 получаем
р( 2 • 2 ) (cos ?) = ^5-Ш cos «9 >). D64)
§ 6. Уравнение Бесселя
1. Задача Д. Бернулли о малых колебаниях подвешенной
нити и уравнение Бесселя. Рассмотрим так называемое уравнение
Бесселя
-г=^-| :r--{-(l г)Д'==^ (п — действительное или комплексное
(XX X CtX \ X J
число). A)
Это уравнение при и = 0 встречается впервые в работе Даниила
Бернулли [1], посвященной изучению малых колебаний висящей нити
постоянной плотности с закрепленным концом, а для случая, когда
п — любое целое число,—в работе Бесселя об определении планетных
орбит (см. Бессель [1]).
Рассмотрим задачу Д. Бернулли. Пусть А — точка подвеса нити,
/—ее длина, р — масса единицы длины. Пусть ось х проходит
в вертикальном направлении через точку А, причем ее положитель-
положительное направление направлено вверх, и пусть ось у напраблена гори-
горизонтально. В качестве начала координат выберем такую точку О,
что ОА = /.
Пусть Р—точка нити, находящаяся на высоте х, ее коорди-
координата у в момент времени t является функцией у {х, f). Задача Д. Бер-
Бернулли формулируется следующим образом.
1) Многочлены P^'/s- ~1/г) (cos tp), pW* ад (cos tp) называются, соответст-
соответственно, многочленами Чебышева первого и второго рода (см. Чебышев П. Л.
[1], т. II, стр. 45 и 173).
142 Рл. III. АнаЛитиЧгская теория дифференциальных уравнений
П)хть даны положение конца А нити (фиг. 6), т. е. пусть
_у(/, t) = 0 — форма нити в момент /=0, у(х, O) = F(x) — скорость
точки Р в момент t = 0, yt (х, 0) == G (х), где F (x), G (х) — изве-
известные функции от х, 0 <[ х ^ I, требуется определить функцию
у{х, t) при 0<л:</, 0<<.
В силу предположения о малости колебаний мы можем в наших
рассуждениях рассматривать dx как элемент дуги.
Заметим, что натяжение Г нити в точке Р равно pgx (g — уско-
ускорение силы тяжести) и что проекция
натяжения на ось у равна
Так как масса элемента dx равна
fdx, а его горизонтальное ускоре-
ние равно ^, получаем
ду\
а потому
Полагая S = x/l, -z — t Vg/l, при-
зедем уравнение к виду
Фиг. 6. дт2 (
Тем самым наша задача сведена к задаче отыскания решения у(&, т)
уравнения B), удовлетворяющего начальным и граничным условиям
у(\, т)-=0,
У& 0)=/(Е),
Л F, 0) =
C,)
C2)
C.)
где /$ и g(ty известные функции от S в [0,1].
Найдем сначала элементарное решение уравнения B), т. е. ре-
решение, имеющее вид произведения функции ю (?) (положения) и функ-
функции (У(т) (времени)
[юA) = 0]. D)
(?)] [/(т
Имеем тогда уравнение
ш F; U" (х) = [«в'
§ 6. Уравнение ЁессеЛА 143
из которого, полагая
^ U(x).= О, E)
где Л — параметр, выводим, что ю (Е) должно удовлетворять уравнению
Общее решение уравнения E) имеет вид
U = acosyx-f Ьяп-^х, G)
где a a b — постоянные, и для того чтобы найти элементарное ре-
решение, достаточно решить уравнение F). Делая в нем подстанопку
4 (8)
получаем уравнение
$ + {^ + -=0 И*) = 0], (9)
совпадающее с уравнением A), в котором положено я = 0.
Откладывая до п. 8 формальное решение поставленной задачи,
перейдем к изучению решений уравнения A).
2. Функции Бесселя (цилиндрические функции) первого рода.
а) В уравнении A) точка * = 0 является правильной особой точкой
(полюсом); согласно обозначениям § 3, п. 2, имеем
а потому определяющее уравнение имеет вид cts — я2 = 0, а = и, —п.
Следовательно, если 2« не является целым числом, то существуют два
решения, принадлежащих показателям п, —я, т. е. имеющих вид
Jn(x) = xnP1{x), лг-"Р2(лг), где Рг{х) и Р2(х) — сходящиеся в окре-
окрестности нуля степенные ряды.
Мы будем считать, что из двух чисел я и —я через я обозна-
обозначено то, для которого
>
Положим тогда
сю
•v=0
Подставляя это выражение в A), получаем, что
а также, что имеет место рекуррентная формула
= 0 (v=l, 2,...)-
144 Гл. 111. Аналитическая теория дифференциальных уравнений
Так как 2п-\-\ фО, то g1 = gs— ... =0; из формулы A0) ре-
куррентно выводится, далее, что
а потому
Заменяя постоянную g0 ее значением
получаем, что
v=0
Если вынести в правой части за скобки множитель Xя, то в скоб-
скобках останется ряд, изображающий целую функцию; в самом деле,
lim
= lim | v (n -j- v) | = oo.
r) Напоминаем читателю, что гамма-функция (эйлеров интеграл вто-
второго рода) от действительного или комплексного аргумента х опреде-
определяется следующим образом.
Если /?лт>0, то полагаем
со
Г(л:)= Г е-*/* «И,
О
еслн.же •/?.*< О, но /?л;> — я, где я — целое положительное число, то по-
полагаем
со
Г(х) голоморфна во всей комплексной плоскости, за исключением точек
О, —1, —2,.... в которых она имеет полюсы первого порядка, характери-
характеризуемые соотношениями
lim l(x + п) Г (х)\ = ( —1)>! (я = 0, 1,...).
Имеем 1/Г(дг) = 0прн лт = О, —1, —2,...; 1/Г (х) является целой трансцен-
трансцендентной функцией и выражается формулой
6. Уравнение Бесселя 145
Определенная формулой A1) функция Jn{x) называется функцией
Бесселя или цилиндрической функцией первого рода порядка я1);
она может быть однозначным образом определена, как решение
уравнения Бесселя, превращающееся при умножении на х~п в
целую трансцендентную функцию, принимающую при х = О зна-
чение
()
Если разность 2я между корнями определяющего уравнения не
является целым числом, то уравнение A) имеет также решение,
принадлежащее показателю —я
-n+2v
Г( — n +
v=0
а потому общее решение уравнения Бесселя имеет вид
j_n(x), A3)
где Cj и с2 — произвольные постоянные.
Заметим, что если 2я — целое нечетное число, иными словами,
если я — половина нечетного числа, то формула A3) также дает
общее решение уравнения Бесселя.
б) Рассмотрим, наконец, случай, когда я — целое положительное
число. В этом случае, принимая во внимание, что 1/Г (х) = 0 при х = О,
— 1, —2,..., получаем
т)
где с — постоянная Эйлера
с= lira (i+I.-f.l-(- ... + -i-Inn\ = 0,57721
П->оо\ Z 6 П )
Функция Г(х) удовлетворяет соотношениям
Кроме того, если и — целое положительное число или нуль, то
Г (и + 1) = и!,
а прн л: = V2 имеем
[См., например, Уиттекер и Ватсон [1], т. II, стр. 5—43. — Прим. перев.]
J) Цилиндрические функции встретились Фурье при решении задачи об
охлаждении бесконечного однородного кругового цилиндра (см. Фурье [1],
стр. 341).
Ю Зак. 527. Дж. Сансоне
146 Гл. til. Аналитическая теория дифференциальных уравнении
следовательно, при целом положительном п имеем
•/_„(*) = (-1L, (*), A4)
а потому решение J_„(лг) линейно зависит от Jn{x).
Из полученных в § 3, п. 4 результатов следует, что в этом
случае показателю п принадлежит решение, имеющее логарифми-
логарифмическую особенность. Построение такого решения было указано там же.
Отсылая читателя за более полными сведениями к специально
посвященным теории бесселевых функций ккигам *), мы ограничимся
в последующих номерах изложением некоторых элементарных свойств
бесселевых функций.
3. Функции /i/2(jc), J-ih(x). При п = 1/% из (И) следует, что
но
а потому
и, аналогично,
4< Интегральные представления бесселевых функций первого
рода, а) Напишем снова выражение A1) для Jn(x), предполагая, что
п — целое число (положительное, отрицательное или нуль):
v=0
Заметим, что при целом неотрицательном р
x) См., например, Ватсон [1J, Грей н Метьюз [1], Кузьмин Р. О, [1].
Прим. перев.
6. Уравнение Бесселя 147
и потому s(p, я) = 0, если р < п или если р — п нечетно, а если
р — п ==¦ 2v, то
Отсюда
следует,
со
оо
2л 2и
р=0
оо
ЧТО
Р
'¦ fc=(
П
21
е Ш
^dt
р\ '
р=0 —к
оо
откуда, в силу равномерной сходимости ряда ^ ° '- = etoain<',
0
имеем
п
= i J [cos(л:sin/ — ni) + /sin(jcsini — яЭДЛ. A6)
Ho cos (л: sin t — nt) и sin(.vsintf — nt) являются, соответственно, чет-
четной и нечетной функцией от t, —K^.t-^'n, а потому
1С
Jn (д:) = -1 Jcos (д: sin t — ni) dt (и = 0, zt 1, ± 2, .. .)• A7)
о
б) Из A7) следует, что
\ Г 1 С
Jn (лг) = — J cos (x sin f) cos nt dt+— j sin (x sin <) sin nt dt.
о
Но при четном п
1С
^ J sin (лг sin t) sin ni dt = 0,
о
10*
148 Гл. It/. Аналитическая теория дифференциальных уравнений
а при нечетном п
п
— Г cos (x sin f) cos ntdt = O*),
и потому
1 г
я == 0 (mod 2), _/„(*) = — I cos (лг sin t) cos ntdt,
о
n == 1 (mod 2), Jn (x) = i- J sin (л: sin 0 sin n/ rf/.
A8,)
Заменяя в A8t) / на тг/2 — t, получаем
9 ? г"
я = О (mod 2), /„ W =-=-(— 1J J cos (л: cos *) cos nt dt,
о
2 -^ J
n=l (mod 2), /„(*) = —(—1) 2 I sin (л:cos t)cosniЛ.
• r
A8a)
5. Другие интегральные представления. Построим разложения
функций cos (x sin t), sin (x sin t) в ряды и получим с их помощью
новое интегральное представление для Jn(x).
Рассмотрим функцию cos(;esinf); она является голоморфной функ-
функцией от t с периодом я в комплексной плоскости t, а потому может
быть разложена в тригонометрический ряд по косинусам.
Имеем
ии
cos (х sin f) = у а0 -\- ^ «и cos "*
n=l
где
а„ = — I cos (x sin t) cos n/Л 2),
о
а потому ап = 0 при нечетном п и ап = 2Jn (x) при четном п. От-
Отсюда следует, что, каково бы ни было х,
cos (х sin t) = Jo (x) + 2Уа (дг) cos 2f + 2J4 (дг) cos 4/+ ..., A9,)
J) Если в этих двух интегралах сделать замену переменной /=п — т,
то при п четном меняет знак первый интеграл, а прн п нечетном — второй.—
Прим. ред.
2) См., например, Толстое Г. П. [1], стр. 39. — Прим. перев.
6. Уравнение Бесселя 149
и, аналогично,
sin {x sin t) = 2Jl (дг) sin f + 2/8 (jc) sin 3*+ 2/Б (дг) sin 5/ + A92)
Заменяя /на <-[--«-, получаем
cos (x cos 0 = Jo (x) — 2^2 (¦*) cos 2t + 2У4 (дг) cos U — .... A98)
sin (д:cost) = 2J,(дг)cos^ — 2J8(д:)cos3i + 2J6(x)cos5t— ..., A94)
откуда, умножая второе равенство на / и складывая, выводим, что
оо
eixooBt _. jQ (д.) _j_ 2 2 /»/„ (дт) cos Hi.
n=l
Умножим обе части этого равенства на cosnt и проинтегрируем от О
до я. Тогда мы получим, что
уп (д;) = i_fJ f e^cos * cos „^ Л- B0)
о
Предполагая, что п ф 0, и интегрируя по частям, получаем
а потому
J(x) — —^—
, (и = ±1, ±2, ...)• B1)
6. Рекуррентные соотношения между Jn(x). а) Легко устано-
установить две рекуррентные формулы, связывающие функции Jn(x).
Из B1) имеем
п-1
(я —1)/<Й-
ТЕ
-(~Г * Г
о
откуда, в силу B0),
Из A4) следует, что эта формула верна и при п==0.
150 Гл. III. Аналитическая теория дифференциальных уравнений
Дифференцируя формулу B0) по х, получаем
ах «
о
В силу B0) это означает, что
4-.W-4+iW = 2-^. B22)
Используя разложение A1), легко проверить, что формулы B2j)
и B22) верны не только при целых положительных- значениях п,
но и при любых действительных или комплексных значениях п1).
б) Складывая и вычитая формулы B2j) и B22), получаем
Откуда, умножая первое и второе из равенств B33) соответственно
на Xй и х~п, выводим
-^ (хЧп) = x»Jn_1(x), ^(x-nJn) = -x-4n+1(x). B24)
as
7. Интеграл Г xJn (ах) /„ (Ьх) их. а) Вычислим интеграл
о
X
J xJn(ax)Jn(bx)dx,
о
где а и Ь—постоянные величины, а2 — Ь*фО, п — действитель-
действительное число, п > — 1.
Предположим сначала, что постоянные а и Ь не равны нулю; из
уравнения A) имеем
) . dJn(ax) Ф . , .
<PJn(bx) . dJn(bx) и2
*) Н. Я. Соннн в своем мемуаре [1] назвал цилиндрическими функциями
и обозначил символом С, (х) аналитические функции двух переменных, удо-
удовлетворяющие рекуррентным соотношениям
= ^- С, (х); Cv_j (лг) - С,+1 (лг) = 2< (лг).
6. Уравнение Бесселя 151
Умножая первое равенство на Jn(bx), а второе на Jn(ax) и вычитая,
выводим, что
(ax) dJn(bx) Г (h^d
<ах) ^ J (bx>
dx\^\°n\"~J dx ->nK™J dx
= (a* — b*)xJn(ax)Jn{bx).
Так как и> — 1, можно интегрировать это равенство от 0 до х,
а потому
х
О
Нетрудно видеть, что это равенство справедливо и в случае, когда
одна из постоянных а или b равна нулю.
Переходя в формуле B3) к пределу при b -+ а и применяя к пра-
правой части правило Лопиталя, получаем
ев
J.2, ч .„ х Г dJn(ax) dJn(ax) . , ч d dJn(ax)~\
xJn(ax)dx = -^\ ? »* >-Jn(ax)-^ —sfc—J,
о
HO
<f dJn(ax) _ePJn(ax)ax . dJn(ax)
da dx d(axy* • d(«jr) '
и потому
ЫУа^лг^Я^^Т-У to)^(^-J"^)^"/flf\. B4)
J »v ¦* 2 \L d <йдг) J "v ' d (axy* ax d (ax) ) v
о
б) В гл. IV, § 3, п. 2, будет показано, что если п > — 1, то
Jn{x) имеет бесконечное множество нулей, причем все эти нули дей-
действительны и, за исключением д; = 0, простые. Принимая сейчас без
доказательства справедливость этого результата, обозначим через [кг]
последовательность положительных нулей Jn(x) *).
Полагая в формуле B3) верхний предел интегрирования равным 1,
a = \r, b = h8, rzfzs, получаем
1
xjn \лгх) Jn \*-gX) ах = и [г zp. s). [4°)
о
Таким образом, система функций {x'hJn(krx)} (г = 0, 1, 2,...;
п > — 1) ортогональна на отрезке [0, 1].
Полагая в формуле B4) х = 1, а = \г, получаем.
1
f xJl(lrx)dx = \-[Jn(
В силу A1), нулями Jn(x) являются X, и —Xr.
152 Гл. III. Аналитическая теория дифференциальных уравнений
В силу B2В), эту формулу можно также записать в виде
1
J xJl (Vc) dx = 14+1 (К) = jA-i (Ю- B6а)
8. Задача о разложении в ряды по бесселевым функциям.
Вернемся снова к рассматривавшейся в п. 1 задаче Д. Бернулли и
сведем ее к разложениям в ряды по бесселевым функциям.
Уравнение (9) имеет решение <о = Jo(•»]) = Jo(\У%), причем по-
постоянная X должна быть такой, что /0 (а) = 0, следовательно
А = Aj, A2, ....
Поэтому элементарное решение D) имеет вид
У F, 0 = /о (К /Г) [er cos ^ + *r sin ^].
В силу линейности уравнения в частных производных B) можно
предположить, что существуют такие две последовательности чисел
\ar}, \br), что функция
со
У (Е, *) = ? /о (*г/Ё) (вг cos'^- + ftr sin^) B7)
является решением уравнения B), удовлетворяющим условиям C,)
C2), C8).
Условие (Зх) выполняется в силу того, что Уо (К)== ^> условия же
C2) и C8) приводят к равенствам
со с»
= 2 "Jo (К VI), g$) = у 2 *^<> (^ ^
(второе получается при предположении, что ряд B7) можно почленно
дифференцировать).
Заменяя в B5) и B6а) х на У\, получаем соответственно
= O (гфз),
б. Уравнение Бесселя
153
Поэтому, умножая в равенствах B8) обе части на J0(XrYZ) и пред-
предполагая законность почленного интегрирования, получаем
B9)
Таким образом, вопрос сводится к нахождению достаточных условий
того, что для заданных дпух функций /(I), g(i) ряды
СО
вД> (Хг VI), 1 2 Wo (Ar /I),
r=l
r=l
коэффициенты которых вычисляются по формулам B9), сходятся
соответственно к /(?) и ?¦(?), или, как говорится, к задаче о разло-
разложимости функций /(?) и g(%) в ряды Бесселя *).
*) Относительно критерия сходимости в данной точке см. Ватсон [1],
стр. 591.
Глаза IV
КРАЕВЫЕ ЗАДАЧИ ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ВТОРОГО ПОРЯДКА
§ 1. Задача о нахождении решения
дифференциального уравнения «-го порядка,
проходящего через п заданных точек
1. Случай, когда уравнение линейно. Рассмотрим однородное
линейное дифференциальное уравнение порядка п
у(п) +Pl (*)j,fe-D + ... +Pn_j {x)y'-\-pn {х) у = 0, A)
коэффициенты которого pt{x), ..,, рп.1(х), рп(х) являются непре-
непрерывными функциями от х на отрезке [а, р].
Теорема существования и единственности (см. гл. II, § 1, п. 1 „в")
гласит, что для данной точки лс° из [а, |3] и данных значений у0,
У?> • • • > У°п-\ существует одно и только одно решение у (х) урав-
уравнения A), удовлетворяющее начальным условиям
В некоторых задачах математической физики и прикладной мате-
математики возникает необходимость отыскания решения уравнения A)
в случае, когда не все начальные условия заданы в одной и той же
точке х°. Например, часто требуется найти решение у (х) уравне-
уравнения A), проходящее через п заданных точек
Pj=3(ai, At), P2 = (a2, Л2), ..., Рп~(ап, Ап),
т. е. построить решение A), удовлетворяющее условиям
y(ak)=;Ak (ft = l, 2,..., п). B)
Если функцииу^{х), у2(х), ..., уп(х) образуют фундаментальную
систему решений для уравнения A), то общее решение этого уравне-
уравнения имеет вид схуг (х) + с2^2 (лг) -j- ... + с„У„ (х), где cvc2, ..., сп—
произвольные постоянные, и наша задача равносильна задаче о нахо-
нахождении Cj, с2, ..., сп из линейной системы
п
S = Ах (* = 1. 2, ..., я). C)
§ /. Решение, проходящее через п точек 155
Если при заданных av еа, ..., а„ определитель матрицы Д =
— ИЛ (ак) II отличен от нуля, то система C) имеет одно н только
одно решение, а потому задача однозначно определена, каковы бы
ни были постоянные А^. В этом случае два решения уравнения A),
имеющие и общих точек с абсциссами av а%, ..., д„, совпадают,
и, в частности, так как у (х) нз 0 также является решением уравне-
уравнения A), то любое решение, обращающееся в нуль в и точках д,, а2, ...
..., ап, тождественно равно нулю.
Обратно, если единственным решением уравнения A), обращаю-
обращающимся в нуль в точках а,, а2, , ап, является нулевое решение,
то DetA^rO, а потому исследуемая задача однозначно определена
для любых значений Ак. С другой стороны, если Det Д = 0 и одно-
одновременно А1 = Л2 = ... = Ап = 0, то система C) имеет ненулевое
решение си са, ..., сп, а потому существует не равное тождественно
нулю решение уравнения A), обращающееся в нуль в заданных п
точках а1, а2, ..., ап.
Если же DetA~=O, но не все постоянные А1г А%, ..., Ап равны
нулю, то система C) либо несовместна, либо имеет бесконечное мно-
множество решений, в зависимости от того, различны или совпадают
ранги матриц Д и Д', где Д' получается из Д присоединением столбца
Av Л2, ..., Ап. В случае, когда ранги матриц Д и Д' равны, суще-
существует бесконечное множество решений уравнения A), проходящих
через точки Pv Ps, ..., Рп\ общий вид этих решений получается,
если прибавить к одному из них общее решение уравнения A), обра-
обращающееся в нуль в п точках at, a%, ..., ап.
2. Теорема существования и единственности Валле-Пуссена
для линейного уравнения, а) Для приложений важно определение
положительного числа Ао, обладающего следующим свойством: ка-
каковы бы ни были и точек
Pi = (Gj, Л4), Р2 = (я2, As,), .... Ри = (аи, А„),
такие, что
существует одно и только одно решение' уравнения A), проходящее
через точки Р,, Р2, ..., Рп.
Это число будет определено в „в",
б) Для упрощения вопроса докажем. следующую лемму.-
Бели на отрезке [а, Ь] длины b — a = h функция <р(х)фО и
имеет по крайней мере п нулей, из которых хотя бы два раз-
различны, и если эта функция имеет в [а, Ь) непрерывную п-ю про-
производную, не превосходящую по абсолютной величине числа р., то
имеет место неравенство
Jg. D)
156 Гл. IV. Краевые задачи
Пусть
<p(afc) = O (ft = l, 2, ..., л),
а ап+1— любая точка из [а, Ь\. Рассмотрим функцию
9(х)- (*-Ъ)(х-Ъ> ¦¦¦(*-«„)
9(х)-
где
Функция Ф(дг) обращается в нуль в п-)-1 точке аи а2, —, ап,
ап+1, а потому существует точка 6 промежутка (й, Ь), такая, что
ф(«) (?) == о, иными словами, такая, что ю(и) (Е) — А = 0, следовательно,
<Р K+i) = (G«4-i — <*i) K+i — й2) • • • K+i — ап)
Так как ага+, — любая точка из [а, Ь], то отсюда вытекает, что
kWK-^y-K* — at)(x — g2) ... (л;*—an)|.
а потому {А > 0 и
^fx-aS(x-as)...(x-an)\dx. E)
а а
Если положить
ф (лг) = | (х— aa) ... (*—aJ |,
то имеем
ь
f F)
о,
Производная правой части по ах равна
о, Ь
Г tydx— I tydx
а в,
и потому возрастает от отрицательных значений до положительных,
когда «j изменяется от а до Ь. Поэтому наибольшее значение инте-
интеграла, стоящего слева, может достигаться либо когда а, совпадает
») Если .«! = а2, то вместо (х — Й1) (х — а2) и («n+i— «i)(«,,+i — й2)
берем, соответственно, (х — ejJ, (an+1 — а^. Аналогично поступаем в слу-
случае совпадения трех или более точек.
2) Это соотношение непосредственно получается, если применить к функ-
функции <j> (х) интерполяционную формулу Ньютона, учитывая, что <р (а,) =
= Ч («г) =...=<? (а„) =^ 0. [См., например, Гёльфонд А. О. [1], стр. 24—27. —
Прим. ред.]
ф /. Решение, проходящее через h точен 157
с а, либо когда at совпадает с Ь\ повторяя это рассуждение для
точек Ogt • • •» ап> убеждаемся, что наибольшее значение интеграла,
стоящего слева в формуле F), не превосходит наибольшего из чисел
ь
р = 0, 1, .... л).
С помощью подстановки х = a -j- ht получаем 1)
1
JP —n J * A—f/ « —« (я + 1)!
О
hn+t
*я + 1 •
Так как по условию среди точек av а^, ..., ап есть хотя бы две
не совпадающие точки, то рфО, рфп и потому
ь
J | (* - в1) (* — а2) ...(х — ап) | dx < *»+V(» +1),
а
а тогда из неравенства E) следует неравенство D).
в) Докажем теперь теорему Валле-Пуссена (см. Валле-Пуссен [2]).
Пусть дано дифференциальное уравнение
A)
коэффициенты которого р,(х), ..., рп_г(х), рп(х) являются не-
непрерывными функциями от х на отрезке [а, р], и пусть
Z-i, ..., Ln_v Ь„ — наибольшие значения модулей pt (x), ..., рп_х (х),
Рп(х) в ta» Pi; тогда, если обозначить через Ао положительный
корень -уравнения
то для любых п точек Р, = (а1} Aj), Р2 ^ (о^, Л8), ..., Рп=(ап, Ап),
таких, что
существует одно и только одно проходящее через них решение
уравнения (I)8).
J) См. примечания на стр. 129 и 144.
2) Левая часть в G) является возрастающей функцией от ft, отрицатель-
отрицательной при ft = 0 и положительной при достаточно большом положительном
значении ft.
3) Мы исключаем из рассмотрения случай Lt = L2 =...=/,„ = О, так
как тогда общее решение уравнения A) является многочленом и—1-й сте-
степени от х, и существует только один многочлен у (лг) и—1-й степени, удов-
удовлетворяющий условиям у (йд) = Aje (ft = 1, 2,..., и).
158 Гл. IV. Краевые задача
Проведем доказательство от противного. Предположим, что есть
два различных решения уравнения A), проходящих через точки
Pv Р2, ..., Рп, тогда существует решение у (х) этого уравнения, не
равное тождественно нулю и обращающееся в нуль в точках
аи «2, ..., Яд1); обозначим через р. наибольшее значение модуля
y.n-i)(x) в [а, р] и заметим, что у' (х) на [а,, ап] обращается в нуль
по меньшей мере п — 1 раз, у" (лг) — по меньшей мере п — 2 раза,...,
у-3>(л:) — по меньшей мере два раза. По предыдущей лемме имеем
тогда
^..••. (8)
Функция у*-"-1) (х) обращается в нуль, по крайней мере, в одной
точке отрезка [аи а„]. Обозначим через % одну из таких точек,
а через ^ — одну из точек, в которых у^"~^ (х) принимает значе-
значение ц. Тогда
-}>¦ = —fyMdx=f [Piy«-« + ... +pn_ly'+Pny\dx,
е ъ
откуда*
J lL1
и, так как |_у<" ^Kji, получаем, пользуясь неравенствами (.8),
+
+/
что невозможно, так как при 0 <
I h Л
г) Следует заметить, что сделанный выше вывод сохраняет силу
и в случае, когда ищется решение уравнения A), удовлетворяющее
в N заданных точках" av a2, ..., aN
!) В силу доказанного в п. 1, такое решение существует н в случае,
когда уравнение A) не имеет решения, проходящего через точки РьР2,„.,Рп.
I /; Решение, проходящее через п точек
условиям
У Ы = A*, i> У Ы = Л*, в. ..., У* Ы = Л*. „fc (9)
(ft = l, 2, ..., Л/), «j-|-a2-}-...-|-а^ = л,
иными словами, если а^—a^^-^h^, то решение у(х) уравнения A)
однозначно определяется условиями (9).
В самом деле, если существуют два различных решения yt (лг),
у2(х) уравнения A), удовлетворяющих условиям (9), то две кривые
УЛХ)> УЛх) имеют в точках (alt AU1), (я2, А% t), ..., (aN, AKi)
касание порядка at — 1, а2—1, ..., aN—1, соответственно, а по-
потому кривая yt —у2 имеет в точках av а2, ..., aN касание с осью х
порядка Oj — 1, а2—1, ..., aff—1, соответственно, и в проведен-
проведенных выше рассуждениях следует считать точки av as, ..., aN, соот-
соответственно, av a2, ..., aN раз J).
3. Теорема Валле-Пуссена для случая дифференциального
уравнения порядка п нормального вида. Докажем следующую тео-
теорему Валле-Пуссена (см. Валле-Пуссён [2], стр. 141 —143), частично
распространяющую доказанную в предыдущем пункге теорему на
дифференциальные уравнения порядка п нормального вида.
Рассмотрим дифференциальное уравнение порядка п
yW=f(x;y, /, ...,у(»-\>) A0)
и предположим, что функция f непрерывна в прямоугольном парал-
параллелепипеде R с центром з точке [a; |30, j3j, .,., Рп_1], который опре-
определен неравенствами
— a<*—а<а; — ?<у<*> — pf<*' (i = 0, 1, ..., п — 1).
Кроме того, предположим, что функция / удовлетворяет условию
Липшица по аргументам у, у', ..., дДга-0
<%ъ\У?ГУ?\
fescl
где через Llf L2, ..., ^.я_1, Ln обозначены постоянные Липшица
функции / относительно у(п~^, у(п~2\ ..,, у', у.
Мы уже знаем, что если обозначить через М наибольшее значе-
значение модуля f(x; у, у1, ..., yln-V) в R, а через 8 — наименьшее из
чисел а и bjM, то существует одно и только одно решение у (х)
*) Впервые этот вопрос изучался Николетти [2], см. также ГалликО [1].
Более глубокое изучение уравнения y"=f(x, у, у') см. у Пикара [2J,
стр. 1—14,
160 Гл. IV. Краевые задачи
уравнения A0), определенное на [а — 8, а-|-8] и удовлетворяющее
условиям
УЙ(«) = Р« (' = 0, 1, .... п— 1)
(см. гл. I, § 3, п. 4 „в").
Если мы зададим начальные условия з я точках из [а — а, а-{-я],
то нельзя будет гарантировать существование решения уравнения A0),
удовлетворяющего этим условиям. Однако мы докажем сейчас, что
существует число Ао, которому, как и в предыдущем пункте, соот-
соответствует некоторая теорема единственности. Точнее говоря, имеет
место следующая теорема Валле-Пуссена: обозначим через h0 поло-
положительный корень уравнения
ft" ft*1*'1 h
+ L + +L If —1==0>
где Ln, ?w_j, ..., Ly—постоянные Липшица функции f(x; у,
у', ..., ^(ra~J)) относительно у, у1, ..., у^п J), соответственно.
Тогда два различных решения уравнения A0) {принадлежащих
прямоугольному параллелепипеду R) могут иметь не более чем
п — 1 общих точек, абсциссы которых лежат между точками
а' и а" (а — а ^ а' < а" ^ а -|- а), если только разность h = а"—а'
не превосходит Aq1).
В самом деле, если yt и у2 — дна решения уравнения A0), то,
полагая Уо—Уъ—У и получаем
yf>=f(x; уг, у'2,..., yf-V)-f{x- yv y'v ..., у?-%
Поэтому, если ? и Ъх — две различные точки отрезка [а', а"], то,
принимая во внимание A1), имеем
J>W(x)dx= J [f(x; y2, /2, .. .,tf-V)—f(x; yv y[, ..., y<
a"
o'
Но если ух и _у2 имеют п общих точек в [а', а"], то их раз-
разность _у0 на этом отрезке п раз обращается в нуль, а потому для
доказательства нашей теоремы достаточно повторить проведенные
в предыдущем пункте рассуждения2).
J) В работе Чииквиии [2] при некоторых условиях иа f(x;y,yr, ...,у{п-Щ
доказан критерий существования уравнения A0), проходящего через п за-
заданных точек.
1) В случае Li = L2 = ••• =Ln = 0 достаточно заметить, что у о (х)
является многочленом и — 1-й степени (см. примечание3) иа стр. 157).
2. Уравнений второго порядка м теорема Штурма 161
§ 2. Дифференциальные уравнения второго порядка
и теорема сравнения Штурма
1. Исследования Штурма об уравнениях второго порядка.
В предыдущем параграфе мы рассмотрели одну частную краевую
задачу для дифференциальных уравнений порядка п; во всей общности
мы рассмотрим этот вопрос в гл. V, а в данной главе ограничимся
рассмотрением уравнений второго порядка.
Изучение этих вопросов начинается с классического исследования
Штурма [1]. Он заметил, что большая часть задач теории теплоты
приводит к уравнениям второго порядка, для которых трудно вычис-
вычислить значения решений в данной точке или выяснить для этих реше-
решений поведение нулей, полюсов, максимумов и минимумов даже в слу-
случае, когда решение получено в конечном виде или в виде ряда.
С помощью непосредственного изучения уравнений Штурм открыл,
что их решения имеют большое сходство с тригонометрическими и
показательными функциями, установил ряд чрезвычайно важных
свойств нулей решений и указал способ приближенного вычисления
решений с достаточной точностью.
Подробное изложение исследований Штурма и последовательное
развитие теории уравнений второго порядка можно найти в работе
Бохера [1], к которой мы и отсылаем читателя; здесь же, ради крат-
краткости, будут изложены лишь важнейшие моменты теории.
2. Общие замечания относительно уравнений второго порядка.
а) Пусть дано линейное дифференциальное уравнение второго порядка
y"-hP{x)y'+q{x)y = Q, A)
коэффициенты которого р(х), q(x) являются непрерывными функ-
функциями от х в [а, Ь\. Как уже напоминалось в предыдущем пара-
параграфе, теорема существования гласит, что какова бы ни была точка а
из [а, Ь] и каковы бы ни были значения у0, у'о, существует одно и
только одно решение у(х) уравнения A), которое определено в [а, Ь\
и удовлетворяет в а начальным условиям
У(а)=У0> /(«)== /0-
Отсюда следует, что если решение уравнения A) обращается
в нуль в точке а из [а, Ь\ вместе со своей первой производной,
то это решение тождественно равно нулю в [а, Ь]; в самом деле,
решение у (х) =э= 0 удовлетворяет этим условиям, других решений нет
в силу теоремы единственности1).
В дальнейшем под решением уравнения вида A) мы будем
понимать лишь решение, не обращающееся тождественно в нуль.
1) См. примечание J) на стр. 49.
И Зак. 527. Дж. Сансоне
162 Гл. IV. Краевые задача
Проведенные рассмотрения показывают, что если решение у(х)
уравнения A) обращается в нуль в точке о из [а, Ь], то его пер-
первая производная отлична от нуля в о, и потому у (х) меняет знак
при переходе через а.
Кроме того, ни одно решение уравнения A) не может иметь
в [а, Ь\ бесконечного множества нулей. В самом деле, если у(х)
обращается в нуль в бесконечном множестве точек отрезка [а, Ь] и
5—предельная точка этого множества, то .у(?)=./(Е) = О, а потому
у(х) = О в [а, Ь].
Отметим также, что если а является нулем для у(х), то
порядок этого нуля равен единице; в самом деле,
limy (х)/(х — а) =/ (о) ф 0.
б) Напомним еще (см. гл. И, § 1, п. 2 „в"), что если вронскиан
^—угу[ двух решений ух(х) и у2(х) уравнения A) обращается
в нуль в точке о из (а, Ь), то он обращается в нуль во всем отрезке
[a, b], a решения yt(x) и у$(х) линейно зависимы в [а, Ь] (см. гл. II,
§ 1, п. 3 „б").
В частности, два решения, обращающиеся в нуль в одной и
той же точке из [а, Ь], различаются лишь постоянным мно-
множителем; два решения, производные которых обращаются в нуль
в одной и той же точке из [а, Ь], отличаются друг от друга
также лишь на постоянный множитель.
в) Наконец, почти излишне отмечать, что для любой точки а из
[а, Ь] существует, в силу теоремы существования, по крайней мере
одно решение уравнения A), обращающееся в этой точке в нуль,
причем два таких решения отличаются друг от друга посто-
постоянным множителем.
3. Сопряженные точки, а) Частное решение уравнения A) может
быть выделено путем задания в начальной точке а значений .у (а),
^'(о), что геометрически эквивалентно заданию точки на интегральг
ной кривой и направления касательной в этой точке. Но, как уже
говорилось в § 1, п. 1, в приложениях используются и другие спо-
способы выделения решений; например, ставится следующая задача: даны
две точки (а, А), ф, В), а<!а < р<!й, требуется найти проходя-
проходящее через эти точки решение уравнения A). Для этой задачи особую
важность представляют пары различных точек о, |3, которым соот-
соответствуют решения, обращающиеся в нуль в о и [3; если для данных
двух точек а и Р из [a, b), a < р, существует не обращающееся
тождественно в нуль решение уравнения A), которое равно нулю
в этих точках, то точки « и р называются сопряженными точками,
причем р называется сопряженной справа для а, а а — сопряженной
слева для р.
$ 2. Уравнения второго Порядка и теорема ШтурМй Ш
Точки, сопряженные с данной точкой о (справа или слева), не
зависят от выбора решения, обращающегося в нуль в о, так как все
остальные решения, обращающиеся в о в нуль, отличаются от выбран-
выбранного лишь постоянным множителем.
Между точками, сопряженными с точкой о, различают первую,
вторую, ... сопряженную справа (слева) с а, определяя их условиями
« < «1 < «2 < • • • [<* > Я1 > Я2 > • • • 1«.
О =Л («) =Л Ы =Л (»а) = ¦ • •
и требованием, что ^(л:) не обращается в нуль ни в одной точке
промежутков (о, ot), (oj, o2), ,..
Заметим, что если точки a, av а2, ..., an_v an образуют после-
последовательность сопряженных точек, то обращающееся в нуль в точке о
SOL
а, следовательно, и в остальных точках) решение ух (л:) имеет изо-
изображенный на фигуре (фиг. 7) вид; график этого решения колеблется
около оси х и пересекает ее в точках о, av ..., an_v an.
Пусть, в самом деле, yfa) >0. Тогда у1 (х) возрастает в точке о
и потому положительно во всех точках промежутка (о, ох); а так как
в точке olf где решение ух (х) пересекает ось х, у[ (at) ф 0, то это
решение в точке av убывая [^ (ох) < 0] переходит от положитель-
положительных значений к отрицательным и остается отрицательным в точках
промежутка (alt <x2), пересекая снова ось х в точке о2.
б) Рассмотрим уравнение
Q, B)
где т — положительное число; общее решение этого уравнения имеет
вид
y = csinm(x — о),
где с и о — произвольные постоянные. Расстояние между двумя сосед-
соседними нулями этого решения всегда равно т://я.
Поэтому если длина отрезка [а, Ь] меньше, чем ir/те, то этот,от-
этот,отрезок не содержит пар сопряженных точек. Обозначим, вообще, для
данной точки о из [а, Ь] через kx и А2 такие целые числа, что
Тогда число точек отрезка [а, Ь), сопряженных с а, равно ftj
11*
164 Гл. IV. Краевые заЬача
Имеем
(ft, + К + 2)*\т >ь
^^ + 2>(*- a)ml1it>ft1
а потому наибольшее целое число, содержащееся в (ft — а) т/тх, равно
[(ft —в) «/«]=*!+ *8, Aj + ^+l1).
Отсюда следует, что число принадлежащих к [а, ft] сопряженных
г. а точек равно [(ft — а) те/т:] или [(ft — а)/я/тс] — 1.
4. Достаточное условие для несуществования сопряженных
точек, а) Рассмотрим уравнение
у"~ ту = О, C)
где т — положительное число. Его общее решение имеет вид
у^=с1ета:-\-с2е-тя>, где ct и с2—произвольные постоянные. Обра-
Обращающееся в нуль в точке о решение имеет вид
у = 2с sh т (х — о) = с [ет (*-а) — е~т <*-«)]
(с — постоянная). Это решение не обращается в нуль ни в одной
точке, кроме точки а. Таким образом, не существует ни одной
пары точек, сопряженных относительно уравнения C).
б) Свойства решения уравнения C) могут быть выведены из сле-
следующей теоремы. Если в уравнении
/'+p(x)/-]-q(x)y = O A)
функции р(х) и q (x) непрерывны в [a, ft], причем
q(x)<0 при a<jc<ft, D)
то, каковы бы ни были решение у этого уравнения и точка а
из [a, ft], произведение
возрастает в [a, ft].
В самом деле,
Так как у и у' не могут одновременно обращаться в нуль, то
• )
') Символом [аг] мы обозначаем наибольшее целое число, содержащееся
в х.
$ 2. Уравнения второго порядка и теорема Штурма 165
Из доказанной теоремы следует, что если решение у(х) уравне-
уравнения A) удовлетворяет в точке я соотношению у(а)У(а)~^>0, то для
любого значения х > я будет выполняться неравенство у (x)yf (x) > О,
а потому функции у (х) и у' (х), не обращающиеся справа от о в нуль,
имеют все время одинаковые знаки. Поэтому, если функция у(х)
положительна при л:>я, то она возрастает при дг>а, а если она
отрицательна при х > я, то она убывает при х^> я. Отсюда следует,
что если коэффициент q(x) уравнения A) удовлетворяет нера-
неравенству q (х) < 0 и если какое-либо решение этого уравнения
положительно {или равно нулю) и возрастает в точке о, то оно
положительно и возрастает в любой точке х > а; наоборот, если
решение у(х) отрицательно (или равно нулю) и убывает в точке я,
то оно отрицательно и убывает в любой точке х > я.
При выполнении условия D) на отрезке [а, Ь\ нет сопряжен-
сопряженных пар точек.
В самом деле, если в некоторой точке я изТ[й, Ь\ имеем у (я) = О,
а потому у (а)у' (я) = О, то для любого [3 > а выполняется неравенство
УФ)У$) > 0. а потому у$) Ф 0.
Из этого замечания следуют утверждения, указанные в „а".
в) Решение дифференциального уравнения A) называется неколе-
неколеблющимся на отрезке [а, 0], если оно не имеет нулей на [я, fi] или
имеет там лишь один нуль. Из доказанного выше следует, что при
выполнении предположения D) решения уравнения A) не колеблются
ни на каком отрезке [я, р].
Решение уравнения A), имеющее на отрезке [я, р] более одного
нуля, называется колеблющимся на этом отрезке. Например, решения
уравнения B) из п. 3 „б" колеблются на любом отрезке, длина кото-
которого не менее 2п/т.
5. Тождество Пиконе, а) Пусть дано уравнение
У+Р(х)/ + д(х)у = 0, A)
где р(х), q(x) — непрерывные функции от х в [а, Ь\. Если умножить
X
J p(x)dx
это уравнение на еа , то оно получит самосопряженную форму
(см. гл. II, § 5, п. 3„би)
Полагая х х
J Pdx J pdas
Ъ(х) = е° , Q(x) = — q(x)e° , E)
приводим это уравнение к виду
166 Гл. IV. Краевые задачи
где 6 (х) > 0 в [а, Ь]. Начиная отсюда, мы будем рассматривать
уравнения второго порядка в вине F).
б) Пусть даны два уравнения
такие, что 6 (х), 6' (х), Q (х), 6Х (х), b[ (x), Qt (x) являются непре-
непрерывными функциями от х в [а, Ь\, 6 (х) > О, 6Х (х) > 0, к пусть
у(х), z(x) — два решения этих уравнений; если в точке х из [а, Ь\
z (х) Ф 0, то справедлива формула
(I)
В самом деле, левую часть этой формулы можно записать в виде
откуда и следует равенство (I).
в) Пусть функции у(х) и z (дг) удовлетворяют на отрезке [о, |3],
соответственно, уравнениям F) и G), причем у(а)=у(ф) = О и
z (х) Ф 0 при а < х < р. Так как у5(х) имеет в точках а и Р нули вто-
второго порядка, а функция z (x) имеет в этих точках нули не более, чем
первого порядка (см. п. 2 „а"), то lim _y2/z = 0, lim y^/z = O,
aj->a+O ж->Р-0
а потому, интегрируя (I) от о до |3, получаем важное тождество
Пиконе
Р Р Р
0== J (Q~Qi)ySdx+J (e—ex)/2^+ J в^у—^р* (И)
се в а
(см. Пиконе [2], стр. 20).
6. Теорема сравнения Штурма, а) Тождество (II) позволяет
быстро вывести классическую теорему сравнения Штурма (см.
Штурм [1], стр. 125).
Пусть даны два дифференциальных уравнения
-о,
$ 2. Уравнения второго порярка а теорема Штурма 167
где Ь (х), 8' (х), Q (х), Ь1 (х), b[ (x), Qt (x) — непрерывные функции
от х в [а, Ь\, 6 (х) > О, 6Х (х) > 0; пусть, далее, ни на каком ле-
лежащем в [а, Ь] отрезке функции Q(x) и ^(я) не обращаются
одновременно тождественно в нуль и, кроме того, пусть
в(х)>81-(ж), Q (*)>$!(*). (8)
Докажем тогда, что если у(х) является решением уравне-
уравнения F), обращающимся в нуль в точках о к р, где р — первая
сопряженная справа точка для а, то любое решение уравнения G)
имеет по меньшей мере один корень, лежащий в (а, C), за исклю-
исключением случая, когда уравнения F) и G) совпадают в [о, J3],
а у(х) и z(x) отличаются постоянным множителем.
Предположим, что z (х) ф 0 при о < х < |3; тогда справедливо
тождество Пиконе (II), из которого, в силу (8), следует, что
(ад
(98)
Если на некоторой части отрезка [а, 0] 8 — Ь1ф0) то _)/ s= 0,
а потому ^ постоянно на этой части. Но тогда, в силу F) и (9Д
для этой части имеем тождественно 0 s= Q (х) = Qx (л:), вопреки пред-
предположению; таким образом, в [о, 0] Q (*) = Qx (л:), 6 (л:) == 6j (лг) и,
в силу (9з), у (х) — cz (х), где с — постоянная величина. Поэтому
если уравнения F) и G) не совпадают, или же, если они совпадают,
но отношение у(х) и z(x) не постоянно, то предположение, что
z (х) Ф 0 при а < х < Р, приводит к противоречию.
б) Из доказанной теоремы следует, что если решение уравне-
уравнения F) в [а, Ь] имеет п последовательно идущих нулей х1г лг2, ...
..., хп, а < хх < х2 < ... < хп < Ь, (и > 1), то любое решение
уравнения GI) имеет по меньшей мере п — 1 нулей, лежащих
в (х1г хп).
7. Теорема о разделении нулей, а) Если положить в тождестве
Пиконе 8j = 6, Q1 = Q и повторить проведенные в предыдущем но-
номере рассуждения, то получим следующую теорему.
Пусть дано уравнение
g\ = 0, F)
где функции Ъ(х), Ъ'(х), Q(x) непрерывны в [а, Ь], 8(дг)>0.
Тогда, если существует решение у (х) этого уравнения, обращаю-"
щееся в нуль в точках а и [3, где [3 — первая сопряженная с а
1) Если выполнены условия (8),
168 Гл. IV. Краевые задачи
точка, то любое другое решение z(x) уравнения F), линейно не-
независимое от у'(х), имеет по меньшей мере один нуль в (а, Р).
Легко видеть, что z (х) имеет в [а, Р] единственный нуль; в самом
деле, если бы z{x) обращалось в нуль в точках f и 8 из [а, C], то
у{х) должно было бы обращаться в нуль в (у, 8) и, тем самым,
Фнг. 8.
в (а, Р) (фиг. 8), вопреки предположению. Отсюда следует так назы-
называемая теорема о разделении корней. Пары (а, Р), (?, 8) последо-
последовательных сопряженных точек двух решений уравнения F) либо
совпадают, либо разделяют друг друга.
б) Если в [а, р], а < р нет точек, сопряженных концу а, то
в {а, Р] не может быть и точек, сопряженных (слева) с Р; в самом
деле, если бы точка рг была сопряжена с р, о < рг < р, то в [$v P]
должна была бы существовать хотя бы одна сопряженная с а точка,
вопреки предположению. Тем же путем доказывается, что никакая
внутренняя точка из [а, Р] не имеет сопряженных в [а, Р], а потому,
если один из двух концов [а, р] не имеет в [а, [3] сопряженных
точек, то на отрезке [а, Р] нет ни одной пары сопряженных
точек.
в) Если на отрезке [а, Р] из (а, Ь) нет сопряженных точек,
то существует решение уравнения F), положительное во всех
точках [а, р].
Пусть, в самом деле, уг (х) и у% (х) — решения уравнения F),
для которых ух (о) = 0, _у2 (Р) = 0; по предположению, тогда ух (Р) ф 0,
(
Каковы бы ни были положительные числа /йот, решение урав-
уравнения F)
принимает в концах аир отрезка [а, Р], соответственно, положи-
положительные значения / и т, а потому не может обращаться в нуль в (а, Р).
В- самом деле, если бы у (х) обратилось в нуль в некоторой точке
из (а, Р), то в этой точке у{х) пересекло бы ось х, а так как у(х)
имеет на концах отрезка [а, [3] одинаковые знаки, то у (х) должно
было бы обратиться в нуль по меньшей мере два раза, чего не может
быть; таким образом, у(х) не обращается в нуль в (о, |3] и, следо-.
§ 2. Уравнения второго порядка и теорема Штурма 169
вательно, сохраняет все время один и тот же знак (положительный —
в силу положительности / и т).
8. Теорема сравнения для полуоткрытых отрезков. В § 3 нам
понадобится теорема сравнения для полуоткрытых отрезков
в форме Сегё (см. Сегё [3]). Пусть даны два уравнения
ш- [8 W w]-Q (*)у (*)=о, (ю,)
<2,(*M*) = o, (io2)
где функции 6 (х), 6' (х), Q (x), Q1 (х) непрерывны при а < х <! Ь
и 6 (х) > 0, Q (х) >• Q± (x) при а<х<С&- Пусть Q (х) не равно
тождественно Q^x) на (а, Ь) и пусть, кроме того, существует
определенное при а<х^.Ь решение у{х) уравнения (loj, такое,
что
^(л:)>0 при a<x<b; y(b) = O. A1)
Тогда, если z(x) является решением уравнения A02) (не равным
тождественно нулю), для которого справедливо соотношение
lim 6(/*—_yz') = 0, A2)
то z(x) имеет по меньшей мере один нуль внутри (а, Ь).
Проведем доказательство от противного. Предположим, что z(x)
не обращается в нуль в промежутке (а, Ь), и пусть, например, z (х) > 0
при а < х < Ь.
Умножая зравнение (Юх) на z, а A02)—на у и вычитая, полу-
получаем
А [6 {гу -yZ')] _ (Q _ Ql)^ = 0.
Интегрируя от й-}-е(з>0) до Ь, выводим, что
b{b)z{b)/{b)~ в(в +
= J (Q—QO^d*. A3)
По предположению 6 (ft) > 0, z (b)~^- 0; с другой стброны, у1 (Ь) Ф 0,
а так как у (х) положительно слева от Ь, то у1 (Ь) < 0; отсюда
следует, что когда е->0, то предел левой части равенства A3)
отрицателен или равен нулю, в то время как предел правой части
положителен, что невозможно; полученное противоречие показывает,
что z{x) обращается в нуль в промежутке (а, Ь).
9. Выпуклость последовательности нулей решений одного диф-
дифференциального уравнения второго порядка частного вида.
170 Гл. IV. Краевые задача
Докажем для уравнения у"— Q(x)y = 0, где Q(x) — непрерывная
возрастающая функция, красивую теорему Штурма1), которая иногда
используется в приложениях.
Пусть дано уравнение
y"—Q(x)y = 0, A4)
где Q(x)—непрерывная возрастающая функция от х при
а пусть х1} л:2, ..., хп — последовательность нулей какого-либо
его решения у (х), расположенных в порядке возрастания
< *2 < ... < хп < ... < Ь.
Тогда последовательность {хп} выпукла, т. е.
0<л:2 —x1<xs—*2< ... . A5)
Положим jc8 — xt = d О 0); функция z (х) = у (х—d) обращается
в нуль последовательно в точках лг2, x%-\-d, x&-\-d, ... и удовле-
удовлетворяет уравнению
z"—Q{x—d)z = 0. A6)
Так как в (дг2, .%) имеем Q(x)>Q(x—d) и у (лг2) = у (дг8) = 0,
то, сравнивая уравнения A4) и A6), получаем по теореме Штурма,
что
или л:2 — л:1 = й<л:8—лга, откуда и следует A5).
§ 3. Применение теоремы сравнения
для отделения нулей ультрасферических многочленов
и бесселевых функций в главном случае
1. Нули ультрасферических многочленов. Ультрасферические
многочлены Р%? (х) (см. гл. III, § 5, п. 8 D3), и п. 1 „б", а = р==Х—»/г)
имеют по х степень и и удовлетворяют дифференциальному урав-
уравнению
Полагая
z = (sin yffty (cos <p), x =¦ cos <p,
находим для z уравнение
Предположим, нто 0<Х<1, или, как говорят, рассмотрим
главный случай.
. ^Относительно доказательства см. Сегё [3],
§ 3. Применение теоремы сравнения 171
Сравнивая уравнение A) с уравнением
решение которого имеет вид у — sin (n + X) (? — <Ро)> получаем по
теореме сравнения Штурма (см. § 2, п. 6), что в любом промежутке
длины тг/(в-{-Х) содержится по меньшей мере один нуль функции
Р$ (cos а>), а потому в каждом из п — 1 промежутков
((v — 1) «/(п + X), vit/(B + X)) (v = 2, 3, ..., в)
существует по меньшей мере один нуль функции г.
Так как lim {y'z—yzr} = 0, то по приведенной в п. 8 преды-
»0
дущего параграфа теореме Сегё Р^ (cos <р) имеет нуль в промежутке
(О, ir/(n-J-X); но Р%* (cose) имеет не более п нулей в @, я), а потому
из проведенных рассуждений следует, что Р« (cos») имеет п раз-
различных нулей <рц %• • • •» ?»> принадлежащих промежутку @, it),
причем выполняются неравенства
Так как Р%> ( — дг)= (— 1)пР^(х) [см. гл. III, § 5G), D3)], то
и потому
:4^) (v-1, 2,...,»). B)
При X = х/г (т. е. для случая сферических функций) эти не-
неравенства называются неравенствами Брунса (см. Брунс [1]).
2. Нули бесселевых функций. Изучим теперь нули бесселевых
функций действительного порядка,
а) Функция Jn(x) удовлетворяет дифференциальному уравнению
&г , 1 йг
а потому (см. § 2, п. 2 „а"), если /и(л;) = 0 и хФО, то дг является
простым корнем для /и(л:).
Легко проверить, что если в> — 1, то все корни уравнения
/„(*) = О
В самом деле, если бы это уравнение имело корень a = a-\-i$,
то, в силу формулы A1), из гл. III, § 6, п. 2, оно имело бы и
сопряженный с ним корень &=а—ip, a тогда для Действительных х
172 Гл. IV. Краевые задачи
мы имели бы равенство Jn(ax) — P-\-iQ, Jn{bx) = P— iQ, и по
формуле B5) из гл. III, § 6, п. 7,
а потому Рн==О, QssO. Но это невозможно, так как тогда целая
трансцендентная функция х~п Jn (ax) обращалась бы в нуль на целом
отрезке [0, 1].
б) Если п — действительное число, [ и [ <С х/а (или, как говорят,
в главном случае), то уравнение Jn (x) = 0 имеет бесконечное мно-
множество корней. Так как x~nJn(x) является целой трансцендентной
функцией, то эти корни не имеют предельных точек в конечной части
плоскости.
Если х — отличный от нуля корень Jn(x), то и —х также
является корнем, а потому достаточно рассмотреть положительные
корни х > 0.
Предполагая поэтому, что х > 0, введем новую функцию
Тогда уравнение C) преобразуется в уравнение
1
= 0. D)
Сравнивая по теореме Штурма (см. § 2, п. 6) это уравнение
с уравнением У+.у = 0, имеющим решение y — sin(x— >:0), убе-
убеждаемся, что Jn{x) имеет по меньшей мере один нуль в каждом
промежутке длины -к. Обозначая через jns (v = l, 2,...) положи-
положительные нули Jn{x), расположенные в возрастающем порядке, и
полагая /' п = 0
получаем, что
7»,v— ./«.v-iO. /M,v<vit (v = l, 2, ...)•
Отсюда следует, что jni4 — vtt убывает с возрастанием индекса v,
а потому
i»,v<y».i + (v— i)* (v=l, 2, ...). E)
Если заменить в уравнении A) из п. 1 к на т, а X на и + 72>
то получим уравнение
F)
§ 3. Применение теоремы сравнений 173
имеющее решение г = (sin <f>)n+u/* Рт+1>г) (cos<p); делая в D) замену
независимой переменной х = (т -f- n -j- 1j2) <(>, получаем уравнение
] 0. G)
Из того, что выполнено условие A2)
lim [z'u — zu']=0,
приведенное в § 2, п. 8, следует, что это уравнение можно сравнивать
с уравнением F) в промежутке, прилегающем справа к нулю.
Поэтому в каждом из т промежутков
+ «+I)) (v=l, 2,...,m)
содержится по меньшей мере один нуль P^+1-4\cos <в). Но jnitJ(m -\-
+ «+ 72) < 7t> а потому т нулей <pv <р2, ..., <?то функции
F^m+1'i;> (costp), содержащихся в @, тг), разделяются неравенствами
n'Vl<?*< n'v f (v=l, 2,...,i«). (8)
Пусть теперь v любое положительное целое число и т = 2v — 1,
Тогда (р, = ir/2 (Pi"—12) @) = 0), а потому, в силу только что доказан-
доказанного, -к- <Уи, V(KH~2v — '/й)- Принимая во внимание неравенство E),
получаем для чисел jKi ч неравенства
(v = l, 2, 3,...).
Так как по условию | к | < */2, то vir < (v -J- 1 -j- и/2 — J/4) ir, а потому
выведенные неравенства позволяют отделить нули-функции Jn{x).
Вспоминая, наконец, что _/_¦/, (х) = |/ — c°^jf, ^/,(*) = ]/ —X
X S^5 , получаем, что нули функции 7_и (л:) имеют вид (v~\-1/2)тг,
Ух
а нули функции />/,(¦*:)— вид vtt, где v — любое целое число.
в) Докажем, что если и — действительное число, то функция Jn (x)
имеет бесконечное множество действительных нулей, и что дей-
действительные нули функций Jn(x) и Jn+i(x) перемежаются.
В самом деле, в гл. III, § 6, п. 6 „б" было показано, что
? [x~njn (х)] = - х-Чп^ {х), А.
(х)] = xn^Jn (х), A0)
174 Гл. IV. Краевые задачи
а потому из теоремы Ролля следует, что между двумя соседними
нулями функции Jn(x) лежит по меньшей мере один нуль функции
Jn+i(x), а между двумя соседними нулями функции Jn+1(x) лежит
по меньшей мере один нуль функции Jn (x). Но так как при | и | -^ х/2
функция Jn(x) имеет бесконечное множество нулей, то и при любом
действительном п функция Jn (х) имеет бесконечное множество нулей.
Если заметить еще, что псе положительные нули функции Jn(x)
простые, из A0) следует отсутствие общих нулей у функций Jn(x)
и /и+1 (х). Поэтому нули этих функций взаимно разделяют друг
друга.
г) Пусть 0 < ]Пг j < уя> 2 < ... < уи> v < ...—последовательность
положительных нулей функций Jn(x).' Докажем, что при п> — 1
имеем
0<Уи.,<У„+1.1<Л.2<У»+1.2<... («> — !)• (И)
Для этого достаточно показать, что jn> j <уи+]> jj но это сле-
следует из того, что при п > — 1 функция xn*1Jn+1 (x) имеет два со-
соседних нуля, 0 и /'„+!, I, а потому, в силу второго из равенств A0),
первый положительный'нуль jnt х функции Jn(x) меньше, чем jn+ii ix).
§ 4. Осцилляционная теорема
1. Осцилляционная теорема, а) Рассмотрим уравнение
й
их
коэффициенты которого зависят от переменной х и от параметра X,
и предположим, что для любого значения X, принадлежащего дан-
ному промежутку (Ап А2) (возможно, простирающемуся в беско-
бесконечность в одну или обе стороны), функции 6 (х, X), -^-Ь(х, X), Q(x, X)
непрерывны по х в [а, Ь] и, кроме того, что 6 (х, X) > 0 при
а^х^Ь и X из (Aj, A2). Обозначим для любого X через max в
(maxQ) наибольшее значение Ъ{х, \)(Q(x, X)) в [а, Ь], и пусть
Докажем тогда, что для любого положительного целого числа v
найдется такое значение Xv числа X, что как для Х„, так и для
всех заключенных между Х„ и А2 значений X, любое решение
у(х, X) уравнения A) имеет в [а, Ь] не менее v нулей.
*) Читатель, желающий более глубоко ознакомиться с изложенными
вопросами, может изучить гл. XV книги Ватсона |1].
8) Не исключено, что A>A
§ 4. Осцилляционная тебрема 175
Из B) следует существование такого X', что для всех значений X,
заключенных между X' и А2 max Q(x, X) < 0; будем рассматривать
лишь такие значения X.
Положим max Q(x, Х) = Ж(Х), —max Q(x, Х) = ти(Х) и срав-
ним уравнение A) с уравнением
которое можно записать в виде
В § 2, п. 3, мы видели, что любое решение этого уравнения
имеет в [а, Ь] не менее чем
Ь-а
M(X)
нулей; но для данного v можно, в силу B), найти такое Х„ что для
всех значений X, заключенных между X, и А2, имеем
а тогда по теореме сравнения Штурма (см. § 2, п. 6 „б") для
рассматриваемых значений X любое решение уравнения A) имеет
в [а, Ь] не менее чем v нулей, т. е. не менее, чем v раз меняет
знак.
Отсюда следует, что когда X изменяется в (Alt A2), число коле-
колебаний решения у(х, X) в [а, Ь] стремится к бесконечности; поэтому
доказанная теорема называется осцилляционной теоремой.
б) Пусть для любого отрезка [av bt], лежащего в [а, Ь], имеем
— max Q (х, X)
Тогда существует такое Хв1, ь,, что для всех значений X, заключен-
заключенных между Xait bt, и А2, выполнено неравенство
J> '
где
max Qix> ^). ^fi(X)= max b(x, X).
Поэтому для таких значений X любое решение у(х, Л) уравнения A)
имеет по меньшей мере один нуль в \аъ bt], а потому, когда Х-»-А2,
не только число нулей решения у (х, X) стремится к бесконечности,
но эти нули равномерно распределены в [а, Ь].
176 Гл. ity. Краевые задача
2. Осцилляционная теорема для уравнения (ЬУ)'-\-[кА—В]у=0.
Предположим, что Ь(х, X) не зависит от X, a Q(x, X) зависит от X
линейно, т. е. рассмотрим уравнение
ж \ь Щ+[ХА (д:) - в <-х)]У = °'
где функции 6 (х), Ъ'(х), А(х), В(х) непрерывны в [а, Ь], 6 (х) > О
и А (х) не обращается тождественно в нуль.
Пусть на отрезке [а, |3], лежащем в [а, Ь], функция А(х) поло-
положительна (отрицательна), и пусть г и s—, соответственно, наимень-
наименьшие значения А(х) и —В{х) в [а; |3] (г— наибольшее значение А (х)
и s — наименьшее значение — В(х) в [а, ?!]).
Для положительных (отрицательных) значений X имеем в [а, |3]
ХА(х) — B(*)>Xr + s; — max[— \А(х)-\- В (л:)] > Xr-f-«,
и из осцилляционной теоремы получаем, что если среди значений
функции А (х) в [а, Ь] есть положительные (отрицательные) зна-
значения, то при стремлении параметра к к со [к — оо) число нулей
любого решения у(х, X) уравнения E), содержащихся в \axb], стре-
стремится к бесконечности, в то время как расстояние между двумя
соседними нулями у(х, X), содержащимися в интервале, на кото-
котором А (х) остается полоэюительным (отрицательным), стремится
к нулю.
§ 5. Решения, обращающиеся в нуль
в двух заданных точках. Собственные значения
и собственные функции
1. Постановка задачи. Пусть дано уравнение
о. A)
коэффициенты которого б (х, X), Q (х, X) удовлетворяют указанным
в предыдущем параграфе условиям. Из осцилляционной теоремы сле-
следует, что число нулей решения у(х, X) уравнения A), удовлетворяю-
удовлетворяющего условию у (а, X) = 0 (такие решения определены с точностью
до постоянного множителя), при стремлении X к Л2 становится больше
любого наперед заданного числа; поэтому встает вопрос о существо-
существовании таких значений X, для которых соответствующие решения обра-
обращаются в нуль в Ь, т. е. таких не обращающихся тождественно
в нуль решений уравнения A), что
у (а, \)=у(Ь, Х) = 0. B)
Если такие значения X существуют, то они называются особыми
значениями параметра, характеристическими значениями пара-
параметра, фундаментальными числами, чаще же всего их называют
собственными значениями. Соответствующие им решения называются
§ 5. Собственные значений и собственные функции 177
особыми функциями, характеристическими функциями, фундамен-
фундаментальными функциями и чаще всего — собственными функциями *).
В следующем параграфе мы изучим системы Штурма и докажем
существование собственных значений для уравнения A) при условиях
более общих, чем условия B). Тем не менее не лишено интереса
изучение системы A), B) способом, предложенным Маммана, так
как этот способ позволяет записать в явной форме решения уравне-
уравнения A) (см. Маммана [2], а также [3], стр. 190 и ел.).
2. Разложение оператора второго порядка в произведение
операторов первого порядка, а) Обозначим символом
где функции р{(х) непрерывны в [а, Ь], оператор, результатом при-
применения которого к и раз дифференцируемой функции f(x) является
функция
Иными словами, положим, по определению, СМ")/ = /.(/}.
Оператор СМ") называется дифференциальным оператором кр-
рядка п; оператор первого порядка имеет поэтому вид
Операторы первого порядка, как и все операторы, можно умно-
умножать друг на друга. Назовем произведением двух операторов Of\
O'ip и обозначим символом О^О^р оператор, получающийся, если при-
применить сначала оператор ОЧ\ а потом оператор Of1. Предположим,
^ Тогда
у = of
а потому
Отсюда следует, что два оператора перестановочны в случае, когда
х) Название собственные значения, собственные функции были приме-
применены впервые Буницким в [1], стр. 65—125, 84.
а) К свойствам дифференциальных операторов мы вернемся в гл. X.
12 Зак. 527. Дж. Сансоне
178 tji. iV.. Краевые задачи
б) Рассмотрим теперь следующую проблему (см., например,
Кели [1]): разложить данный дифференциальный оператор вто-
второго порядка
где р и q—непрерывные функции от х на отрезке [а, Ь], в про-
произведение двух операторов первого порядка, т. е. найти такие два
оператора первого порядка
что
0<2) ф ^ 0^i) [0(D ^ ^
Сравнение формул C) и E) показывает, что задача сводится
к разысканию, если это возможно, таких двух функций аир, что
Докажем, что для того, чтобы существовало искомое разло-
разложение с действительными символическими множителями, необ-
необходимо и достаточно, чтобы существовало решение уравнения
z" -{- pzr ~\- qz ==¦ 0, G)
не обращающееся в нуль ни в одной точке отрезка [а, Ь], или,
что то же самое, чтобы на отрезке [а, Ь] не было пар точек,
сопряженных относительно уравнения G) (см. § 2, п. 7„в").
Условие необходимо. В самом деле, если существуют две функ-
дии а и р, удовлетворяющие условиям F), то G) можно записать
в виде
а потому
й
и, следовательно,
X X
z — ce ° Г еа dx-\-cA,
а
где с и сх — произвольные постоянные; такое решение может обра-
обратиться в [а, Ь] в нуль не более одного раза, а потому на [а, Ь] нет
пар сопряженных точек.
§ 5. Собственные значения и собственные функций 179
Условие достаточно. Заметим сначала, что система F) эквива-
эквивалентна системе
' (8)
Пару функций, удовлетворяющих этой системе, можно построить
следующим образом. Так как на отрезке [а, Ь\ нет пар сопряженных
точек, то существует решение г уравнения G), не обращающееся
в нуль ни в одной точке отрезка [а, Ь\ (см. § 2, п. 7„вк). Функция
р = — г'\г (см. гл. II, § 3, п. 2) удовлетворяет второму из уравне-
уравнений (8) и потому а = р-[~г//г.
в) Докажем теперь следующую общую теорему: данный опе-
оператор
где функции pug непрерывны в [а, Ь], всегда можно разложить,
и притом бесконечным множеством способов, в произведение двух,
вообще говоря, комплексных, символических множителей первого
порядка.
В самом деле, для того, чтобы выполнялось равенство
где
О?) -[?+«], Of в [А + р],
необходимо и достаточно, чтобы функции аир удовлетворяли си-
системе (8).
Для определения C достаточно выбрать два линейно независимых
действительных решения гг и z2 уравнения G) и положить
(*1 + «») (8')
(/ — мнимая единица). Тогда функция р будет конечна во всем от-
отрезке [а, Ь], так как функции zx и г2 не могут на нем одновременно
обратиться в нуль (см. § 2, п. 2„б"), а в силу того, что г^ —
— г2гхф.О в [а, Ь], коэффициент при мнимой части в р отличен
в [а, Ь] от нуля.
3. Выражение для решения на отрезке, содержащем сопря-
сопряженные точки. Определим вид решения уравнения
f+P(x)/'+g(x)y = 0, (9)
где функции р(х) и q (х) непрерывны в [а, Ь], при условии, что
на отрезке [а, Ь] есть хотя бы одна пара точек, сопряженных
относительно этого уравнения.
Уравнение (9) эквивалентно уравнению
12*
180 Гл. IV. Краевые задачи
где, в силу показанного выше, функции а и C не принимают дей-
действительных значений и удовлетворяют соотношениям
« + Р = Р, Г + «Р = <7 (Ю)
(см. п. 2„б"). Пусть zx и z2 — линейно независимые решения урав-
уравнения (9) в [а, by, из (8') имеем
{u{x), h(x) действительны в [а, Ь]),
а потому
а=р — и — /A = v — ih [>=:P — и].
Второе из соотношений A0) принимает тогда вид
* Р' +«Р = «' + *¦*'4-
а потому h' ~\- h (у — и) = 0, откуда
Или, полагая
получаем, что
причем, в силу
А
Р(*)
а =
того,
= се
= е~
= v-
что
се
а
а;
¦J(, ц
1 /Io*
>о
), N
(с = const),
[* = cp(*)]f
=«+|ф(*),
(П)
A2)
в-А(а) = -1ш [<(я) + Ц(fl)]/[^(я) + i^2 (я)] * 0 »),
постоянная с отлична от нуля.
Решение уравнения (9), которое получается путем решения линей-
линейного уравнения
g+Pj-O,
имеет вид
а; я! ж
—J р йо! — J ийх —ie Jp (ж) йа;
где /—-произвольное действительное число, т. е., если мы положим
а; а:
— J"«te = 4(*), J"p«te = 5(jc), A3)
a a
то будем иметь
_y = fen И [cos cS (je) — i sin c5 (je)].
J) Символом Ima мы обозначаем „мнимую часть а", и если a = a-\-ib,
а п b действительны, то Im a = b.
$ 5. Собственные значения и собственные функции 181
Отсюда следует, что е1) И cos сЕ (л:) и e*i № sin c\ (х) являются двумя
линейно независимыми решениями уравнения (9), а потому общее ре-
решение этого уравнения имеет вид
у = ei И [Cl cos с? (л:) + с2 sin сб (л:)], A4)
где сх и св—произвольные постоянные.
Пользуясь тем, что сфО, обозначим через -у такой угол, что
cos ( — сТ) = c2lVc\ + 4 sin ( — сТ) = 4
и положим ft = (е^ _|_ C2)V». Тогда ft и -у можно рассматривать как
произвольные постоянные, вводимые вместо сх и с2, и равенство A4)
принимает вид
у = fte4 <*) sin с [Е (д:) — ^], A5)
в котором, изменяя, если это необходимо, знак k, мы можем считать,
что с > 0.
Формула A5) дает вид общего решения уравнения (9) при условии,
что в [а, Ь] есть хотя бы одна пара сопряженных точек. Этот вид
аналогичен виду общего решения
у s= ft sin с (х — у)
уравнения у" -j- с^у = 0.
Следует заметить еще, что в силу A3) и A1) V (лг) = р (л:) > 0,
а потому функция i(x) возрастает в [а, Ь] (и удовлетворяет усло-
условию Е(я) = О). Таким образом, аргумент c[l(x) — fl в формуле A5)
является возрастающей функцией от х в [а, Ь] !).
4. Теорема существования собственных значений. Доказа-
Доказательство Маммана. а) Формула A5) позволяет нам ответить на по-
поставленный в п. 1 вопрос.
Итак, пусть дано уравнение
коэффициенты 6 (х, X), Q {х, К) которого удовлетворяют следующим
требованиям:
1. Функции Ъ(х, X), -к~Ь(х, К), Q (х, К) являются непрерывными
функциями от х и \, когда х изменяется в [a, b], a \ — в про-
промежутке (Аа, Л2), причем 6 (л:, X) > 0, когда а -< х <[ b и X при-
принадлежит (Alt A2) 2).
— max Q (лг, X)
1) Относительно выражения решения уравнения (9) в виде A5) см. также
Боль [1]> стр. 302.
2) Как указывалось в § 4, п. 1, при этом не исключено, что Ai>A^ и
Что промежуток (Л1( Л?) бесконечен в одну или обе стороны.
182 Гл. IV. Краевые задача
Тогда существует бесконечное множество значений параметра X
(собственных значений), которым соответствуют решения у (х, X)
уравнения A6), удовлетворяющие условиям
у(а,Х) = 0, у(Ь, Х) = 0, A7)
причем число нулей решения у(х, X), соответствующего соб-
собственному значению X, стремится к бесконечности, когда Х->А2.
Из наших предположений следует, в силу осцилляционной тео-
теоремы (§ 4, п. 1), существование такого значения X параметра X, что
для всех значений X, содержащихся между X и Л2 на отрезке [а, Ь],
есть пара точек, сопряженных относительно уравнения A6). Но тогда,
как было выше показано, решение уравнения A6) имеет вид
у(х, \) = ke^-Vsinc(b)it(x, X) — 1],
причем, если оно обращается в нуль в точке а, то
у(х, \) = k^^-^Oac{^)%{xt X) [у (а, Х) = 0],
а потому в точке Ъ это решение принимает значение
y(b, X) = fte4(M)siric(X)E(ft, X).
Пусть яа(Х), я2(Х), й8(Х), й4(Х) — непрерывные в (А1? А^) функ-
функции от X, такие, что йг(Х)й4(Х)— а^(к)ав(К)ф0. Рассмотрим два
линейно независимых решения гг(х, X), z^{x, X) уравненияA6), опре-
определенных начальными условиями
гг(а, Х) = в1(Х),
z,(a, Х) = я8(Х),
По результатам, полученным в гл. I, § 5, п. 2, решения гг (х, X),
z%(x, X) и их первые производные по х являются непрерывными
функциями от X. Но u-\-ih = — (z^ -j- iz'^/(z1 -)- /г2), а потому и и А,
1 дВ л.
а вместе с ними и v = -g-4 и, являются непрерывными функ-
функциями от X. Так как
с (X) *= — Im {[й2 (X) + ш4 (Х)]./[йх (X) + ш8 (X)]},
то и с — непрерывная функция от X. Принимая, наконец, во внимание
формулы (И) и A3), убеждаемся, что в A8) -ц(х, X), Е(л:, X), с(Х)—
непрерывные функции от X в (Aj, A2).
Так как при стремлении X к А2 число нулей решения у (х, X)
стремится к бесконечности, то из того, что функция с(Х)?(лг, X) воз-
возрастает по х, когда х изменяется в [а, Ь], следует соотношение
lim с(КЩЬ, Х) = + оо, A9)
Х-* .А,
6. Системы Штурма 183
Из того, что с (К) % (д, X) является непрерывной функцией от X в (Лх, А2),
вытекает, что когда X —vAg, функция c(k)t(b, X) принимает беско-
бесконечное множество раз значения вида /it, где /—целое число. Но для
таких значений X имеем
у(Ь, X) = fte4<b-x>sin/ir = O.
Тем самым доказано, что существует бесконечное множество соб-
собственных значений параметра X, т. е. значений X, для которых соот-
соответствующие им решения уравнения A6) удовлетворяют условиям A7),
б) В § 6 мы докажем, при несколько более жестких требованиях,
что собственные значения образуют последовательность, для которой
А2 является единственной предельной точкой.
5. Собственные значения для уравнения (Ъу'У + Q*A — В)у = 0.
а) Рассмотрим теперь частный случай уравнения вида
= 0' B0)
где функции 6(лг), 6' (х), А(х), В(х) непрерывны в [я, Ь], 6(д:)>6
и А (х) не обращается тождественно в нуль. Учитывая доказанную
в § 4, п. 2 теорему, получаем, что если среди значений А (х)
в [а, Ь] есть положительные (отрицательные) значения, то, при
стремлении К к положительной (отрицательной) бесконечности,
Л бесконечное множество раз принимает собственные значения,
которым соответствуют решения уравнения B0), обращающиеся
в нуль в точках а и Ь, т. е. такие, что
у (а, Ц^ 6
б) В прежних доказательствах этой теоремы налагались более
ограничительные требования. Например, требовалось постоянство
знака А {х) в [а, Ь\% причем В (х) могла быть любой функцией, или же тре-
требовалась непрерывность А {х) и неотрицательность В(х) в [а, Ь]. Метод
Маммана позволяет доказать эту теорему во всей ее общности. Неко-
Некоторые уточнения этой теоремы читатель найдет в § 6, п. 6.
§ 6. Системы Штурма. Собственные значения.
Собственные функции
1. Задача о распространении тепла в тонкой проволоке и си-
системы Штурма, а) Пусть бесконечно тонкая прямолинейная проволока
постоянного сечения помещена в среду, температура которой равна
нулю. Обозначим через 6 (д:) коэффициент внутренней теплопровод-
теплопроводности, через ?f(.v) — удельную теплоемкость, через 1{х) — коэффи-
коэффициент внешней теплопроводности для точек сечения с абсциссой х,
а через о и е— соответственно, площадь и длину контура сечения
проволоки,
184 Гл. IV. Краевые задачи
Пусть температура проволоки в точках сечения с абсциссой х
равна V(x, t) в момент времени t. Мы хотим определить связь между
функциями 6(дг), gix), 1{х), V{x, f).
Рассмотрим два находящихся на расстоянии d друг от друга сече-
сечения проволоки Cj и с2, температура которых равна, соответственно,
Vx и V2, V2 > Vv причем d настолько мало, что можно считать
коэффициент внутренней теплопроводности постоянным на участке
между Cj и а2. Из экспериментальной физики известно, что количе-
количество тепла, проходящего за единицу времени через единицу площади
сечения от сечения с температурой Va к сечению с темпера-
температурой Vv равно 6 (л:) (V2—Vj)/rf; отсюда следует, что количе-
количество тепла, проходящего за единицу времени через сечение с абсцис-
абсциссой х, равно — 6 (х) ^— о, а потому количество тепла, проходящего
за единицу времени через сечения с абсциссами x-\-dxj2 и х — dx/2,
соответственно, равны
fi (x dx
дх
Поэтому, если пренебречь теплообменом с внешней средой, то коли-
количество тепла, приобретаемого за единицу времени элементом dx, равно
разности выражений B) и A), т. е. с точностью до бесконечно малых
высшего порядка
Принимая во внимание, что рассматриваемый элемент излучает
в единицу времени количество тепла, равное 1{х) Vedx, получаем,
что приобретенное за единицу времени элементом dx количество тепла
равно
Обозначим через р (д:) плотность элемента dx с центром в точке х.
Тогда масса этого элемента равна pad*, а так как удельная тепло-
теплоемкость этого элемента равна g(x), то в момент t он содержит коли-
количество тепла, рапное р(х) g(x) V(x, f)adx. Отсюда следует, что
скорость изменения количества тепла в этом элементе за единицу вре-
б. Системы Штурма 185
мени равна р (х) g (x) ^- о dx, откуда вытекает уравнение распро-
распространения тепла в проволоке (см. Пуассон [1], стр. 233 и след.)
~П*)У. C)
Обозначим через at и с2 крайние сечения проволоки, имеющие,
соответственно, абсциссы а и Ь, и рассмотрим наше явление в момент,
когда можно принять изменение температуры на концах равным нулю.
Тогда, если обозначить через 1г и /2 коэффициент внешней тепло-
теплопроводности в сечениях сх и с2, то
— 6 (a) Vx (a, t) о, + о,/, V{a, t) = 0,
b(b)Vx(b, Oc2 + o2/2V(ft, *) = 0
или
6 (a) Vx {а, () — /,V(a, t) = 0, б (b) Vx {Ъ, t) + l2V{b, f) = 0. D)
Предположим теперь, что нам известно начальное распределение
температуры в момент времени / = 0; тогда нам известно значение
функции V(x, t) при /=0, т. е. имеем
V{x, 0) =/(*), E)
где f(x) — известная функция, определенная в (а, Ь). Таким обра-
образом, задача об определении функции V (х, f) сводится к разысканию
решения уравнения C), удовлетворяющего условиям D) к E) в об-
области Д, определенной неравенствами
Следуя классическому методу математической физики, постараемся
построить элементарное решение уравнения C), т. е. решение вида
-х*
сЩ х) е
где с и К — постоянные, которое удовлетворяло бы граничным усло-
условиям D). Тогда должны выполняться равенства
b(a)W(a)~l1U(a) = 0, в(*)^ (ft)+^t/(*) = 0. D')
Предположим, что уже доказано существование последовательности
положительных значений \п параметра, X, которым соответствуют
функции Un{x), удовлетворяющие соотношениям C') и D')J); в силу
линейности уравнения C), какова бы ни была последовательность
чисел {сп}, функция 2jcAWe"X"' также является решением
J) См. относительно этого § 6, п, 6,
186 Гл. IV. Краевые задача
уравнения C). Таким образом, мы приходим к задаче: найти, если
это возможно, такую последовательность {с„}, что
V(x,f}=%cnUn(x)e'yn\ F)
n=l
Полагая в этом представлении ? = 0, получаем, в силу E), что
со
должно выполняться равенство f(x) = 2 сп^п(х)' В § 8, п. 4 „б"
п=-1
мы увидим, что если функция f(x) ограничена и интегрируема, то
числа сп однозначно определяются последним равенством, а потому
вопрос сводится к проверке, удовлетворяет ли определенная равен-
равенством F) функция V(x, t) всем условиям задачи.
б) Изучение системы C'), D') является частным случаем изучения
следующей задачи. Дано уравнение
^ [в (а:, Л) ^] _Q (Л:, Л)з; = 0. G)
Найти значения параметра X, которым соответствуют не обра-
обращающиеся тождественно в нуль решения этого уравнения, удо-
удовлетворяющие краевым условиям
0, G')
где а, а„ р, Pj не зависят отх, а^~\~а\фО, Р2 —|— Pf =?*= 0.
В случае, когда а = р = 0, мы получаем рассмотренный в § 5
случай. Здесь мы изучим общий случай систем, состоящих из ра-
равенств G) и G'), или, как говорят, дифференциальных систем
Штурма, или, проще, систем Штурма. Для этой цели полезно будет
указать некоторые дополнения к теореме сравнения и осцилляционной
теореме.
2. Дополнения к теореме сравнения, а) Пусть даны два ура-
уравнения
-Q(x)y = 0, (8)
dx
где функции Ь' (х), b[ (x), Q (x), Qj (лг) непрерывны, 6 (*) > 0, 6Х (*) > 0
при а-^.х-^.Ь,
х), (Ю)
причем ни в какой части отрезка [а, Ь] не выполняются одно-
одновременно равенства
б. Системы Штурма 187
а также не выполняется равенство
Пусть у (л:), г (л:) являются, соответственно, решениями ура-
уравнений (8) в (9), определенными при а <!*<!?. Предположим,
что если у(а)ФО, то
У {а) > *(«)" ' (П)
(а потому 2(й)=?0), если дасе _у(а) =0, то на г(а) не накладывается
никаких условий.
Докажем в этом случае, что если у{х) имеет в полуоткры-
полуоткрытом промежутке a<.x-^b m нулей, то г (х) имеет в этом
промежутке не меньше т нулей, из которых, по крайней мере,
один меньше первого нуля у {х) ').
Пусть хи л;2, .... хт суть т нулей решения у{х), расположен-
расположенных в порядке возрастания,
а < хх < х2 < ... < хт < Ь.
Из теоремы Штурма (§ 2, п. 6) вытекает, что в каждом из т — 1
промежутков (xv дг2), (д:2, л;3), ..., (лгот_,, хт), функция г(х) имеет
по меньшей мере один нуль. Поэтому достаточно показать, что г (х)
имеет еще один нуль в промежутке (a, aTj). Если у (а) = 0, то это
вытекает из теоремы Штурма. Если же у (а) Ф 0, то имеет место соот-
соотношение (ll)i Если бы z(x) не обращалось в нуль в промежутке
а < х < хи то, интегрируя от а до хг тождество (I) из § 2, п. 5,
мы получили бы, что
чего не может быть, так как левая часть отрицательна или равна
нулю, а правая положительна. Отсюда и следует, что z(x) имеет
в (a, jfj), по крайней мере, один нуль.
б) Пусть коэффициенты уравнений (8) и (9) и их решения у (х)
и z{x) удовлетворяют сделанным в „а" предположениям и пусть
в некоторой точке с промежутка (а, Ь) выполняются неравенства
у(с)Ф0, г(с)ф0. Из доказанной только что теоремы следует, что
в промежутке (а, с) не меньше нулей функции z (x), чем нулей функ-
функции .y(.v); докажем, что если функции у{х) и z(x) имеют одина-
одинаковое число нулей в (а, с), то
у (с) > z(c)
J) Говорят, что нуль функции г (х) меньше нуля функции у (х), если
абсцисса первого нуля меньше абсциссы второго.
188 Гл. IV. Краевые задачи
Если в (а, с) функции у(х) и z{x) не имеют нулей, то, инте-
интегрируя от а до с упомянутую выше формулу (I) из § 2, п. 5, полу-
получаем, что
откуда при сделанных предположениях и следует неравенство A2);
если же функция у{х) обращается в нуль в промежутке {а, с) и
xt — ближайший к с нуль, то, согласно „а", между xt и с нет нулей
функции z(x), а потому формулу (I) можно проинтегрировать от xt
до с, получив неравенство
из которого, в силу того, что стоящее в квадратных скобках выра-
выражение обращается в нуль при х = х^, следует неравенство A2).
3. Добавления к осцилляционной теореме, а) Рассмотрим
уравнение
где Ь{х, X) и Q(x, X) зависят от параметра X, изменяющегося
в промежутке (Aj, А2), А, < А2 1). Предположим, что функции
Ь(Х, Х)>0, ^'Ц, <?(*,*)
непрерывны как функции (х, X) когда а ^.х-^b и X лежит
в (Aj, A2). Предположим также, что при любом фиксированном х
из [а, Ь] функции Ь(х, X) и Q(x, К) являются непрерывными не-
возрастающими функциями от X когда X изменяется между At
и Ай, и что Q(x, X) яе обращается тождественно в нуль в одной
и той же части [а, Ь] для двух различных значений X.
Пусть, далее, ни в какой части отрезка [а, Ь\ не выпол-
выполняются для двух различных значений Хх и Хв параметра X оба
равенства
Ь(х, \J = b(x, X2), Q(x, Xx)^Q(a:, X2).
Наконец, пусть даны две постоянные а и аг или же две
функции а (Л), аг (X) параметра X, непрерывные в (Alf Л2) и не об-
обращающиеся одновременно в нуль, причем либо а (X) = 0 при всех
значениях X, либо а (К) Ф 0 при всех значениях X, а 6 {а, X) X
X «1 (Х)/а (X) является невозрастающей функцией от X.
Рассмотрим решение у(х, X) уравнения A3), удовлетворяющее
начальным условиям
у (а, X) = а (X), у (а, X) = а, (X) A4)
') Промежуток (Лх, Л?) может быть^бесконечным в одну или обе стороны,
$ 6. Системы Штурма 189
(или же решение, отличающееся от этого постоянным множи-
множителем).
В силу наших предположений применима теорема из п. 2 „а",
а потому, если для некоторого значения X из (Aj, A2) решение
у{х, X) имеет т нулей, больших чем а и не превосходящих Ь, то
при изменении X между X и А2 решения у{х, X) имеют по меньшей
мере т нулей, и до тех пор, пока число нулей остается рапным т,
они согласованно движутся от Ъ к а и потому остаются в проме-
промежутке (а, Ь).
б) Предположим, что при некотором значении X параметра X ре-
решение у (х, X) имеет ровно т нулей xv л:2, ..., хт, больших чем а
и не превосходящих Ь, а < х1 < дг2 < ... < хт eg b. Покажем, что
если хт = Ь, т. е. если у(Ь, Х) = 0, то можно найти такое по-
положительное число р, что для всех значений X, принадлежащих
промежутку X < X ^ X-j-p, решение уравнения A3), удовлетворяю-
удовлетворяющее условиям A4), имеет в (а, Ь) ровно т нулей, причем все эти
нули больше а, а потому, в силу „а", все лежат в (а, д).
В самом деле, имеем
dy(x.\)
dx
X) Ф 0 (i = 1, 2, ..., т). A5)
Рассмотрим сначала случай, когда у (а, X) = а (X) = 0 [а потому
а (X) = 0 в (Ах, А2)]. В этом случае
В силу непрерывности у'^х, X) по х и X (см. гл. I, §*5, п. 1пб"),
можно найти такие положительные числа р и е, что из неравенств
0<Х — Х<р, A7)
0<лг — я<е; |лг — д:4|<е (/= 1, 2, ...; т—1) A8)
00», — *<е
вытекает неравенство
у'х(х, \)Ф0. A9)
В т отрезках
[й-f-e, хг — е], to + is. Дг2 — е], ..., [*„,_!-f-е. д:т — е] B0)
решение у(х, X) не обращается в нуль. Обозначим через d наимень-
наименьшее значение \у(х, Х)| в этих отрезках.
Пусть о—-положительное число, меньшее d. Уменьшим, если это
необходимо, число р настолько, что при 0<Х—^Л<]рв отрезке [а, Ь\
190 Гл. IV. Краевые задача
выполнялось неравенство
\у(х, \)—у{х, Х)|<с.
Предположим, что функция у [х, X) положительна в [а -\- е, хг — е]
(рассуждения не изменились бы, если бы она была там отрица-
отрицательна). Тогда она отрицательна в (хг -\-е, х2 — в) и положительна в
[jc2 —}— е, лг3 — е], а потому, когда х принадлежит [я-f-e, хг — в], то
у(х, X)>j/(a:, X) —c^>d —с>0,
а когда х принадлежит [л^ + е, д:2 — е], то
Таким образом, функция у(х, X) при всех значениях X, принадле-
принадлежащих [X, X-j-p], не обращается в нуль ни в одном из т отрез-
отрезков B0) и принимает в них попеременно положительные и отрица-
отрицательные значения. Отсюда следует, что функция у {х, X) должна" обра-
обращаться в нуль по меньшей мере один раз в каждом из от — 1 проме-
промежутков (х1 — е, *! + «), (д:2 — е, *8 + .), .... (хт^— е, Хт_г-\-в),
причем из A9) следует, что она обращается в нуль в этих
промежутках только по одному разу. С другой стороны, так
как по предположению у (а, Х) = а(Х) = О, а по формуле A9)
У'ъ(*> *) Ф О ПРИ а<!лг-<а-}-е, то у(х, X) имеет в [а, й-j-e]
Только один нуль, находящийся в точке а. Таким образом, у{х, X)
имеет только т — 1 нулей, больших чем а и не превосходящих
хт — е. Но так как мы предположили, что существует т нулей,
больших чем а, то у(х, X) должно иметь по меньшей мере один
нуль в [хт — е, хт] и по A9) только один. Этот нуль, в силу до-
доказанного в „а", находится Тв промежутке {хт — е, хт); итак, мы
доказали, что при всех значениях X, X < X <^ X -}- р, у (х, X) имеет
в (а, Ь) ровно т нулей, причем все эти нули больше, чем а, и
меньше, чем Ь.
В случйе, когда а (X) Ф 0, то у (а, К)фО, и можно найти такие
положительные числа р и е, что из неравенств
0<Х — Х<р, а^.х^а-{-г
следует у (х, X) ф 0» после чего достаточно провести те же рассу-
рассуждения, что и выше.
в) Обозначим черев X* верхнюю грань значений X, для кото-
которых решения у(х, X) уравнения A3), удовлетворяющие начальным
условиям A4), имеют ровно т нулей, бблыиих чем а и не пре-
превосходящих Ь. покажем, что если Ах < X* < А2, то решение
у(х, X*) имеет т-\-\ нулей, больших а, из которых один на-
находится в Ь, а остальные т лежат внутри (а, Ь).
6. Системы Штурмй 191
Заметим сначала, что если р > О, то решение у (х, к*) (имеющее
по меньшей мере /га нулей, ббльших а), не может иметь т-\-р ну-
нулей в (а, Ь). В самом деле, если бы это было так, то, рассуждая
так же, как и в „б", мы могли бы найти таксе положительное
число р, что при всех значениях к, лежащих в (к*— р, А*), реше-
решение у(лг, А) имело бы по меньшей мере т-\-р нулей в (с, Ь), в то
время как мы предположили, что таких нулей не может быть
больше-/га. Отсюда следует, что у(х, А-*) имеет в (а, Ь) т — 1 или
т нулей. Если бы число этих нулей равнялссь /га—1, то Ъ должно
было бы быть также нулем, и, в силу доказанного в „б", можно
было бы найти такое положительное число р, что для всех значе-
кий А, заключенных между А* и А*-|-р, решение у(х, к) имеет
только /га нулей в [а, Ь], превосходящих а. Но тогда к* не имело бы
указанного экстремального свойства. Таким образом, у(х, к*) имеет
в (а, Ь) т нулей. Осталось доказать, чтоу(Ь, А*) = 0. Если бы
у(Ь, к*) было отлично от нуля, то, повторяя обычные рассуждения,
можно было бы найти такое положительное число р, что при
А* ^ А <^ А* -|- р решение у (х, к) имело бы в (с, Ь) только /га ну-
нулей, ббльших чем а.
Из доказанного следует, что если выполнены сделанные предпо-
предположения, то при изменении к от Ах до А2 увеличение числа ну-
нулей решения у{х, к) на единицу происходит тогда, когда один
из нулей совпадает с Ъ.
г) Наши выводы о решениях уравнения A3) сохраняют силу и
в случае, когда начальные условия A4) заменяются начальными
условиями
у (а, Х) = м(А), У (с, k) = ca1(k), A4')
где с—отличная от нуля произвольная постоянная; для доказатель-
доказательства достаточно заметить, что решением уравнения A3),. соответ-
соответствующим начальным условиям A4'), является функция су(х, к),
имеющая те же нули, что и у(х, к); поэтому полученные в „в" вы-
выводы сохраняют силу и для решений уравнения A3), удовлетво-
удовлетворяющих начальному условию
к) —а {к) у'(а, А) = 0. A4")
4. Системы Штурма. Существование собственных значений.
Теорема Бохера. Пусть дано уравнение
коэффициенты которого Ь(х, k), Q(x, к) удовлетворяют усло-
условиям, указанным в п. Зва". Пусть, далее, даны a, av p, $v ко-
которые являются либо такими числами, что | ас |. —|— | ах | =^= 0 и
| р | -j-1 рх | Ф р, либо такими непрерывными в (Av A2) функциями
параметра к [а (к), аг (к); $ (к), ^ (к) не обращаются одновременно
192 Гл. IV. Краевые задачи
в нуль], что или а (А) = 0 для всех значений к, или а (А) Ф О и
одновременно с этим Ь (а, A) at (А) / а (А) является невозрастающей
в (Alt Л2) функцией А} и, аналогично, или ф (а) = О, или ф (А) не об-
обращается в нуль ни для одного значения А из (Аг, Л2) и одно-
одновременно с этим b(b, A) j3, (A) / j3 (А) является невозрастающей
функцией от А в (Аг, Ла). Предположим, наконец, что
lim— max Q(x, A)/ max 6(лг, А) = + °°> B1)
и докажем, что тогда существует бесконечное множество значе-
значений параметра А (собственных значений), которым соответствуют
решения уравнения A3), удовлетворяющие краевым условиям
а, (к)у (а, А) - а (А) у' (а, А) = 0, B2)
Pi Р)У (Р, А) + р (А) / (Ь, А) = О B3)
(см. Бохер [2], стр. 63, Айне [1], стр. 313).
Из B1) следует существование такого числа А', что для всех зна-
значений А, заключенных между А' и А2, max Q(x, A)< 0. Мы будем
рассматривать лишь такие значения А. Когда А изменяется между А'
и Л2, то по теореме из § 4, п. 1, число нулей решений уравне-
уравнения A3), заключенных в (а, Ь), становится больше любого наперед
заданного числа *v. Пусть при некотором значении параметра А, ко-
которое мы обозначим через fiv, решение уравнения A3), удовлетво-
удовлетворяющее условию B2), имеет v нулей в промежутке {а, Ь). Обозначим
через [iv+1 верхнюю грань тех значений А, которым соответствуют
решения системы A3), B2), имеющие v нулей в промежутке (с, Ь).
Тогда, в силу теоремы, доказанной п. 3 „г", при A —[iv+1 система A3),
B2) имеет решение, у которого v нулей лежат в (а, Ь), а один
совпадает с Ъ. Рассуждая относительно jj-v+1 так же, как мы рас-
рассуждали относительно j*v, и повторяя это рассуждение далее, мы по-
получим монотонно возрастающую бесконечную последовательность чисел
имеющую единственной предельной точкой Л2 (см. п. 3„б"), причем
имеют место следующие свойства:
1. Решение у(х, fj.v+i)) уравнения A3), удовлетворяющее усло-
условию B2), имеет v-\-p—1 нулей в (с, Ь) и один нуль, совпадаю-
совпадающий с Ь.
2. Если А лежит между [i.v+i, и у-ч+р+1, то решение уравнения A3),
удовлетворяющее условию B2), имеет ровно v-j-p нулей, и все эти
нули лежат в (а, Ь).
Отсюда следует, что если j3 (А) =з 0 (^ (А) Ф 0), то наша теорема
доказана, и искомыми собственными значениями являются числа по-
последовательности B4). Рассмотрим теперь случай, когда в (Av Л2)
P(W
6. Системы Штурма
193
Заметим, что когда X изменяется между ^,+„ и f-»+#+i» т0> по
теореме из п. 2яб", Ь(Ь, Х)у'(р, Щу{Ь, X) является убывающей
функцией от X. Но у(Ь, \>.ч+р) = у (Ь, ^+г,+]) = 0, у'{Ь, \>.ч+1) Ф О,
У iPt l^v+^+i) т^ 0, а потому, когда X изменяется от [xv+i, до [>-ч+р+1,
функция Ь(Ь, Х)у'(Ь, ХIу{Ь, X) убывает от оо до —оо.
По предположению, функция
— 6(?, Х)рг(Х)/р(Х) не убы-
убывает, а потому найдется одно и
только одно значение Xv+p па-
раметра Л, лежащее в (+
(Фиг- 9)> такое, что
К+Р)у' {Ь, К+р) =
и следовательно
При этом значении X решение
уравнения A3) удовлетворяет
краевым условиям B2), B3),
а потому является решением си-
системы Штурма A3), B2), B3).
Таким образом доказана
теорема Бохера:
При сделанных нами пред-
предположениях существует бес-
бесконечное множество соб-
собственных значений
К+р
B5)
Фиг. 9.
причем для любого целого числа v-\~p (p > 0) существует одно
и только одно значение X, X = Xv+i>, которому соответствует
решение у(х, Xv+i>) системы Штурма A3), B2), B3), имеющее
ровно v-j-p нулей в промежутке (а, Ь).
5. Системы Штурма. Существование собственных функций
с заданным числом нулей. Теоремы Бохера. а) Из доказанной тео-
теоремы следует существование собственных значений Xv+2) при доста-
достаточно большом v; покажем, что при добавочных предположениях
lim min Q(x, X)=-]-oo B6)
6(лг, X)>t>0 при с<лг-<^, Л!<Х<Аа B7)
13 Зис. 627. Дж. Сансоне
164 Рл. IV. Краевые задачи
система Штурма A3), B2), B3) имеет бесконечное множество
собственных значений
^0> » • • •> Х„» • • •> Ху <^ \+р
таких, что соответствующие собственные функции у (лг, Х„) имеют
ровно v нулей, лежащих в (а, Ь) (см. Бохер [2], стр. 65—66).
Из B6) следует, что когда X близко к Alf min Q (x, X) > О,
<
а потому Q(x, X) > 0 в [а, Ь], и по результатам из § 2, п. 4„б"
для таких значений X любое решение уравнения A3) имеет в (а, Ь)
не более одного нуля; поэтому в последовательности B5) либо v = О,
либо v = 1.
Покажем теперь, что v = 0. В самом деле, рассмотрим уравнение
min 6(яг, Щ^\-{ min Q(x, А)]а = 0. B8)
?b axi g?b
Если положить
min Q(x, X)/ min 6(лг, Х) = /га2, т > 0,
6 <<Ь
то это уравнение можно записать в виде
Пусть jxv имеет то же значение, что и в п. 4, и пусть X — заклю-
заключенное между [iv и Л.) значение X. Тогда легко проверить, что функ-
функция1)
6 (л, I)] н Щ (ж_о) ,
и (Х) =
2т
[min 6 (*, X)] а (I) т - [min 6 (лг,1)] at (I)
e
удовлетворяет уравнению B8), а кроме того краевым условиям
[min 6 (*, Л)] а, (Г) я (с) —[mine (*, X)] а (I) и'(с) = 0. B9')
При а(Х) —0 функция и(лг) равна
min 6 (лг, X) aj (X) [ew <ж-°> — е-'й G»
й не обращается в нуль при с < л: <! й. Если же а (X) =^ 0 в [с, ?>],
то
,
[min 6 (ж, X)]
/п[штв(д:Д)]а(
«t (^ A _ 8и> (ж_о).-I
]а(л) l ;J
х) По типографским соображениям мы опускаем здесь и в дальнейшем
обозначение <?<*•<& под знаком ,min°.
6. Системы Штурма
Так как при X->Aj m стремится к -J-oo, то и в этом случае
и (лг) ф О при а<Сх4^.Ь', таким образом, в обоих случаях существуют
значения X, меньшие чем jav, для которых и(х) не имеет нулей при
а <*<?.
Так как
6(лг, л)>т1п6(лг, a), Q(x, X)>minQ(Ar, X)
и при а(К) ФО имеем
6 (я, \)у> (а, X) _ 6 (а, X) at (X) 6 (g, X) at (X)
) a(X) ^ а(Г) '
V [т1пв(д:Д)] а(Х) з/(йД)
то, сравнивая по теореме из п. 2„а" удовлетворяющее краевому усло-
условию B2) решение уравнения A3) с у_(х, X), заключаем, что при рас-
рассматриваемых значениях X функция у(х, X) не имеет нулей в (с, Ь\;
поэтому v = 0, и, следовательно, система Штурма A3), B2), B3) имеет
собственное значение Xlf которому соответствует собственная функция,
имеющая один и только один нуль внутри (с, Ь).
Нам осталось доказать существование Хо.
Так как у(х, X) и и{х) не имеют нулей в (с, 6], когда X доста-
достаточно близко к Aj, то по теореме из п. 2 „б" имеем
у(Ь,Х) ^ и{Ь)
Но из B9) следует, что
и потому \\ха.Ь{Ъ, \)y'(b, k)/y(b, Х) = -)-оо.
ХА
Пусть [i0—верхняя грань значений X, которым соответствуют реше-
решения у{х, X) уравнения A3), удовлетворяющие условию B2) и не имею-
имеющие нулей в (я, Ь)', повторяя проведенные в предыдущем номере рас-
рассуждения, получаем, что когда X изменяется от Aj до ji0 функция
Ь{Ь, к)у' (Ь, к)/у(Ь, X) убывает от -]-оо до _—оо, откуда легко сле-
следует существование собственного значения Х^.
б) Весьма интересна другая теорема существования собственных
функций с заданным числом нулей в (а, Ь), получающаяся при иных
дополнительных предположениях, чем предположения B6), B7).
Пусть коэффициенты 6(лг, X), Q(x, X) уравнения
13*
Ш Гл. IV. краевые задачи
удовлетворяют условиям, указанным в п. Зяа", и, кроме того,
условиям из п. 4, т. е.
lim — max Q (лг, A)/max 6 (лг, А) = -|- оо,
в 6 (с, X) <Xj (Х)/а (X), 6 ф, A) Pj (A)/j3 (А) являются невозрастающими
функциями, когда А изменяется в полуоткрытом промежутке
[Av Л2). Кроме того, предположим, что выполняются неравенства
min Q{x, А,)>0, а(А1)а](Л1)>0, р(А,)р, (А,)>0, |
<<ь } C1)
|« (А,) 1 + 1^(^I^0 IPCA^i + IP^AOI^O j
Докажем, что тогда существует бесконечное множество соб-
собственных значений
^0) лц • • • i Хч, . . .; Av <^ Av+1
системы Штурма A3), B2), B3) таких, что соответствующая
собственному значению Л, собственная функция у(х, X,) имеет
ровно v нулей в (а, Ь) (см. Бохер [2], чстр. 69).
Рассмотрим решение и(х) системы
min 6 (х, A,)} -gl - [ min Q (ж, Ах)] к = 0,1
<<6 "^J <Ь } C2)
Предположим сначала, что min Q(x, Ах)>0; полагая
mln Q (x,
е (дг, лх) ~ те '
о<ж<Ь
получаем
и (л:) = a (At) ch т (лг—с) + ?i^> sh /га (jc—a),
и так как без потери общности можно считать, что a (Aj) ^ 0,
aj(Aj)^O, то ы(лг)^>0 в [с, 6]; но a(Aj) и a1 (Aj) не равны одно-
одновременно нулю, а потому ц (лг) > 0 при с < х ^ ?
Обозначим через у(х, Ах) решение системы
(х,Ах)Щ-Я{х,А,)у = 0, \
«i'(Ai)^(«) —«(Ai)/(c) = 0. J
Так как и(х) не имеет в [с, ?>] нулей, больших чем а, то тем
более по теореме из п. 2„а" у(х, AJ не имеет нулей, больших а
и не превосходящих Ь\ с другой стороны, [min 6 (лг, AJ] и' {Ь)\и
<<6
и по теореме из п. 2„б" имеем, что
Ь{Ь>А1)у'ф,А1)/у(Ь,А1)>0.
§ 6. Системы Штурма 197
Рассуждая так же, как в п. 4, убеждаемся в существовании такой
последовательности чисел [х0, jij, ..., fiv, ..., At < [Xq, что решение
у{х, fO уравнения A3), удовлетворяющее условию B2), обращается
в нуль в точке Ь и имеет ровно v нулей в (с, Ь). Поэтому, если
j3(A)=O в [Л,, Л2), то теорема доказана; если же ф(к)фО, то при
возрастании А от А] до [Xq, функция — О (Ь, А) ^ (А)/р (А) возрастает
от отрицательного значения до нуля, в то время как функция
Ь(Ь, к)у (Ь, Х)/у(Ь, А) убывает от положительного значения до—сю,
а потому существует такое значение 1$ в (Aj, |i0), что
ЧЬЛп)у'{ЬЛп)_ 6 F,
и соответствующее решение у (лг, Ао) удовлетворяет системе Штурма
A3), B2), B3) и не имеет нулей в (а, Ь).
Предположим, наконец, что min Q(x, Aj) = O; тогда система C2)
имеет решение
и (лг) = «J (Аг) (х — а) + а (АД
а потому, предполагая, как и ранее, что a(Aj)^O,
получаем, что и (лг) > 0 при а < лг <^ Ъ и
[min 6 (л:, А,)] и' {Ь)\и (b) = [min 6 (лг, Aj)] ax (AJ/ц (^>) > 0.
Рассуждая относительно систем C3) и C2) так же, как и в п. 2пбв,
получаем, что
?, АО/(ft, А,)/у(*. А,) > [min в (ж, АО] iK
а потому 6 (?>, АО/ (*, АО/з' (^, А0=0 только тогда, когда Q (лг, АО^),
aj (А,) = 0, j3j (АО = 0. Отсюда следует существование собственного
значения Хо, которое больше, чем Aj и может совпасть c*Aj лишь
в случае, когда ф(лг, АО^О, aj(A0 = O, PA0
6. Системы Штурма — Лиувилля. Существование собственных
гначений. а) Мы видели в п. 1 этого параграфа, нто некоторые
дифференциальные системы, весьма важные для математической фи-
физики, имеют вид
а,у (а) — а/ (а) = 0, ^у ф) + р/ (Ь) = О, J
где функции Ь'(х), А(х), В(х) непрерывны в [а, Ь], 6(лг)>0,
А (лг) > 0 и a, a,, j3, $t являются постоянными, такими, что
I a I +1 ai I ^ 0, | Р | +1 Pi | Ф 0. Такие системы называются в анализе
системами Штурма—Лиувилля.
Согласно обозначениям, которые мы ранее употребляли, <?(лг, А)=«
;=?(лг) — \А(х), Aj== — оо, А? = -|-с>д. Нетрудно видеть, что
198 Гл. IV. Краевые задачи
соотношения B1), B6) и B7) выполнены, а потому в силу теоремы
из п. 5па" получаем:
Для данной системы Штурма — Лиувилля C4) существует
бесконечное множество действительных собственных значений
для которых единственной предельной точкой служит -J- оо,
причем собственная функция у (х, Xv), соответствующая собствен-
собственному значению Х„, обращается ровно v раз в нуль в промежутке
(а, ЬУ).
б) Предположим, что в системе C4) функции Ь' (х), А (лг), В (лг)
непрерывны в [а, Ь\; 6(лг)>0, Л(лг)>0, В(лг)>0, осос^О, PPi>0,
ll + llO IP| + |P|
ll + li | + |,
Тогда мы можем положить А1 = О, Л3 = -f- оо и, применяя тео-,
рему из п. 5„б", вывести, что все собственные значения системы C4)
положительны, за исключением случая, когда В (лг) г= 0, ctj = Pj = 0,
в котором Ao = O.
в) Предположим, что 6 (лг) > О, В (х) ;> 0, аа, ;> О, Р^ >> О,
fal + lail т^ 0; |P| + |Pi|?=O и что функция А(х) меняет знак
в [а, Ь\. Тогда существуют две последовательности действительных
собственных значений
принимающих соответственно положительные и отрицательные значе-
значения, имеющих единственными предельными точками -j-oo и —оо, и
таких, что соответствующие собственные функции
уо> УГ> •••' У7, ...
имеют в (с, Ь) столько нулей, каков их индекс.
Относительно доказательства этой теоремы мы отсылаем читателя
к цитированной выше работе Пиконе [2] и книгам Айнса [1] и
Бохера [2].
7. Ортогональность собственных функций системы Штурма —
Лиувилля. а) Докажем ортогональность собственных функций системы
Штурма — Лиувилля C4) (мы вернемся к этому вопросу в более общей
постановке в гл. V, § 2, п. 6, и § 3, п. 6).
Пусть Хг и К8 — два различных собственных значения системы C4),
и У г (х)' У в (х) — соответствующие собственные функции. Тогда
!) Заметим, что если А(х)<^0 в (а, Ь), то достаточно заменить
на—I, чтобы получить изучаемый случай,
6. Системы Штурма 199
Умножая первое равенство на ys, а второе — на уг и вычитая, получаем
Отсюда, интегрируя от а до Ъ, выводим, что
X==0. C5)
В силу того, что а^Да) — ау'г(а) = 0, ахув{а)— ay's(a) = Q, в то
время как | а | -|-1 ау | ф О, получаем, что yg (a)y'r (а) —yr (a)y'g (с) = О,
аналогично, у8(Ь)у'г(Ь)—yr(b)y'g(b) = 0, а потому из C5) следует,
что
(К — *8) / АугУа dx = 0, C6)
а
и так как Хг Ф Х8, то
&
Таким образом, собственные функции [уг(х)} системы Штурма —
Лиувилля C4) образуют ортогональную систему относительно веса
ИхI)-
б) Предположим теперь, что в {а, Ь) функция А(х) неотрица-
неотрицательна и не обращается тождественно в нуль. Если уг (х) — собствен-
собственная функция, то
Ъ _J_
Умножая собственные функции на постоянные ( Г Ay2r dx\ 2, можно
а
ь
добиться того, чтобы Г [Av*yr(x)f dx= 1, с гЛогда система
а
{Alf*(x)yr(x}} будет ортогональной и нормированной в [а, Ь].
8. Достаточные условия действительности всех собственных
значений системы Штурма — Лиувилля. а) Интересно отметить два
случая, в которых все собственные значения системы C4) действи-
действительны. Предположим, что А (х) ;> 0, причем А (х) не обращается
тождественно в нуль ни в какой части [а, Ь\; докажем, что тогда
все собственные значения системы C4) действительны.
См„ например, Джексон [!], стр. 170. — Прим. перее,
200 Гл. IV. Краевые задачи
В самом деле, если бы A = a-\-iz было собственным значением,
которому соответствует собственная функция s-^-it, то и о — h
было бы собственным значением с соответствующей собственной функ-
функцией s — it. В силу C6) мы имели бы тогда
ь
Так как функции s и t не могут одновременно тождественно равняться
нулю во всем отрезке [а, Ь\, то х = 0.
б) Предположим теперь, что А(х) меняет знак в [а, Ь] и что
и докажем, что и в этом случае все собственные значения си-
системы C4) действительны.
В самом деле, если Л = о -\~ h является собственным значением,
1=^=0, а s-^-it—соответствующей собственной функцией, то из
дифференциального уравнения системы C4) вытекает тождество
а потому
ъ
Отсюда следует, что Г (sS-^-tT^dx^^O, и, интегрируя по частям
а
это равенство, получаем, что
В силу того, что аах;^>0, PPt!>0, из краевых условий системы
C4) вытекают неравенства
а потому
J J
а а
Ь
— J#(s2-|- tf2) dx=0. C8)
6. Системы Штурма 201
Далее, — Г 6 (s/2 -\- f2) dx <^ 0, причем знак равенства может иметь
а
место лишь в случае, когда s' = O, /з=О. Но в этом случае, со-
согласно C40, (a~\-ix)A—.6 = 0, тА==0, и так как А меняет знак,
то г = 0, вопреки предположению. Итак,
ь
Так как собственные функции s-\-it и s — it соответствуют раз-
различным собственным значениям, то
б
J A(
а
Ь
Наконец, — Г В (s2 -J- tf2) dx <[ 0. Из доказанного следует, что равен-
а
ство C8) не может иметь места. Поэтому г = 0, вопреки предпо-
предположению.
Докажем, наконец, что если А (х) меняет знак в [а, Ь] и если
выполняются условия C7), причем В(х) не обращается тожде-
тождественно в нуль в [а, Ь], то для любого собственного значения X,.
и соответствующей ему собственной функции уг имеем
ь
XrfAy*rdx>0. C9)
а
В самом деле,
а потому
ь ь ь
К J Afr dx=j Bfrdx- [byry'rt + J Ь'г dx. D0)
a
Имеем
Так как предположение y'r ^ 0 влечет за собой тождество \fA == В,
которое не может иметь места, ибо А меняет знак в [а, Ь], то
ft
а тогда из D0) вытекает C9),
202 Гл. IV. Краевые задача
§ 7. Асимптотические разложения функций
Штурма — Лиувилля
1. Типичная форма систем Штурма — Лиувилля. Пусть дана
система Штурма—Лиувилля
V'(a) — h1V(a) = 0, V'iQ-t-H^W^O, B)
где b'(z), A(z), Bt(z)— непрерывные функции от z в [a, b],
6 [z] > 0, A (z) > 0, Aj и Hl — постоянные. Из теоремы § 6, п. 6„аи
следует существование бесконечной возрастающей последовательности
действительных собственных значений |хи, имеющих единственную пре-
предельную точку в -J- оо, которым соответствуют не обращающиеся
тождественно в нуль решения Vn системы A), B) (собственные функ-
функции), имеющие ровно п нулей на отрезке [а, Ь\. Мы хотим изучить
вопрос об асимптотике для (хи и Vn.
Предположим, что в [а, Ь] существуют и непрерывны функции 6"
и А"; если сделать замену независимой переменной, искомой функции
и параметра по формулам !)
Z —
2
где
-/(т)т*.
а
то легко проверить, что уравнение A) примет вид
где
в -
\dx)
причем новые краевые условия, соответствующие условиям B), за-
задаются в точках 0 и я. Это преобразование позволяет в достаточно
общем случае ограничиться рассмотрением следующей проблемы.
Дана система Штурма—Лиувилля
t/ = 0) C)
= O, D)
1) См. Кнезер [1], стр. 95 и Гобсон [1], стр. 375. Результаты этих работ
будут изложены в п. 1, ?, 3 этого параграфа,
§ 7. Асимптотические разложения 203
где функция В{х) непрерывна в [О, те], h, H—действительные
числа, не обязательно положительные', найти асимптотические
выражения для собственных значений Х„ и соответствующих соб-
собственных функций Un{x).
2. Уравнение для собственных значений. Уравнение C) можно
записать в виде
Применим к этому уравнению, считая правую часть известной функ-
функцией, метод вариации произвольных постоянных (гл. II, § 1, п. 5„б").
Так как соответствующее однородное уравнение имеет общее решение
вида cl cos kx -f- с2 sin \x, то мы получаем для U интегральное уравнение
х
?/ = <?!cos)ог+ с2sinХх +у § B(t)U(t)sink(x—t)dt, E)
о
а потому
ж
¦^ =—k^slnkxi-кс<ь cos kx+ f B(t)U(f)cosk(x — t)dt. F)
0
Первое из равенств D) показывает, что U @) ф 0, так как в про-
противном случае мы имели бы U' @) = U @) = 0, и функция U тожде-
тождественно равнялась бы нулю (§ 2, п. 2„а"). Пользуясь тем, что U{x)
определено лишь с точностью до постоянного множителя, мы можем
считать, что
1/@)= 1. G,)
Для этого достаточно положить в E) cl = l; учитывая первое из
равенств D) и G"i), получаем, что c2 = h/k, так что
а)
U (лг) = cos кх 4- y sin Хл:+-i- J В (i) U(t) sin к (х—t) dt, G2)
о
и задача сводится к определению параметра к таким образом, чтобы
соответствующее решение U(x, к) уравнения G2) удовлетворяло вто-
второму из равенств D).
.. Обозначим через U наибольшее значение | U (дг, к) \ в [0, я] при
заданном к; из G2) следует, что
1 .
204 Гл. IV. Краевые задача
и если рассматривать значения X, ббльшие чем Г | В (t) | dt, то
Отсюда следует, что для любого Хо > 0 можно найти такое число С,
что
|?/(х, Х)|<С @<х<*, Х>Х0>0). (8)
Для того, чтобы ?/(х) удовлетворяло второму из равенств D),
нужно выполнение равенства
-P2(X)], (9)
|де
p (X) = А + Я+ Г B{t) U(t) [cosXif — ^sin \i\dt,
J L I J
f СЮ)
P (X) = It" + f Б @ f/ @ fsin W + -^ cos хЛ rf<.
о
Увеличивая, если нужно, число С, мы можем в силу (8) считать,
что
Из изложенного следует, что собственные значения X и соответ-
соответствующие им собственные функции U(x, X) системы Штурма —
Лиувилля C), D) удовлетворяют интегральному уравнению G^
и уравнению (9).
Уравнение (9) было изучено Лиувиллем [2]; мы будем следовать
здесь методу Гобсона (см. Гобсон [1]), предпосланному им доказа-
доказательству теоремы о равносходимости рядов по функциям Штурма —
Лиувилля и тригонометрических рядов Фурье, которой мы будем
заниматься в § 8.
3. Асимптотические выражения для собственных значений и
собственных функций, а) Начиная с этого места, мы будем обозна-
обозначать на протяжении этого параграфа через а (х, X) ограниченную при
ОСС ХХ функцию от х и X
| а (х, X) | -^ L @ <[ л? ^ тс, X ^ Хо, L — абсолютная константа)
и через <х(Х)[а(х)] — функцию от \[х\, остающуюся ограниченной,
когда Х>Хо @<<)
$ f. Асимптотические разложения 205
Тогда, в силу (8), имеем
hsinХх+ J В(?) U(t)sin\{x—t)dt = a (X, х),
о
и равенство G2) можно записать в виде
a(\x) . A2)
Подставляя в правую часть формулы G2) это выражение, получаем,
что
1^ Ж
X
о
. A3)
Предположим, что функция B(f) непрерывна и имеет ограни-
ограниченное изменение в [0, it], пусть
и пусть полное изменение B(f) в @, it) равно V. Тогда из второй
теоремы о среднем (см., например, Зигмунд [1], стр. 23) легко сле-
следует, что
Г В (f) sin kt cos ktdt=±-(M + V) Г sin 2kt dt = Щ^Л,
о
ж
J Б @ cos2 ktdt=~ J Б @ [1 — cos 2Щ dt*=
Используя эти соотношения, получаем из формулы A3) следующее
асимптотическое выражение для собственных функций
Эту формулу мы используем в „в".
б) Теперь мы легко можем найти асимптотическое выражение для
собственных значений.
206 Гл. IV. Краевые задачи
Принимая во внимание равенство A4), получаем из формулы A0),
что
где
±f A5)
Но тогда из уравнения (9), дающего необходимое и достаточное усло-
условие для того, чтобы к было собственным значением, следует, что
Р , а(Х)
Когда к —> оо, то правая часть стремится к нулю, а потому
и, следовательно,
|де л — далое положительное число, и
с==(А4-А'4-Я)/я. A6)
Но тогда
следовательно п-е собственное значение, которое мы будем обозна-
обозначать А^, равно
К = п + ± + а-Р (и=1, 2, ...), A7)
где <х(л) — ограниченная функция от п. Формула A7) и дает асим-
асимптотическое выражение для Х„.
в) Подставляя A7) в A4), находим искомое асимптотическое выра-
выражение для Un(x). Имеем
cos \nx = cosfn + "J+П§гП х =
7. Асимптотическое разложений
207
а потому, обозначая через Un (x) собственную функцию, соответствую-
соответствующую собственному значению кп, выводим из A4), что
tc
я+ -J- { B(t)dt-cx
« (х, п) \
Но тогда
о
х
П*
i f B(t)dt-cx)cos2nxJ
о
и следовательно нормированная собственная функция <р„(х) равна
Отсюда получаем окончательную формулу для
г) Исходя из формулы F), получаем с помощью аналогичного рас-
dvn
суждения асимптотическое выражение для -—
4. Собственные функции, обращающиеся в нуль в двух задан-
заданных точках, и их асимптотические выражения. Пусть снова функ-
функция ^В(х) непрерывна и имеет ограниченное изменение в [0, я].
Рассмотрим задачу о разыскании значений параметра к, которым
соответствуют решения уравнения
0f C)
208 Гл. IV. Краевые задачи
удовлетворяющие краевым условиям
?/(О) = О, 1/(я) = О B0)
(см. Кнезер [2], стр. 136).
Первое из равенств B0) показывает, что в этом случае мы должны
положить в формуле E) с± = 0, следовательно
а)
?/=c2sinkx-\-у JB(f) U{f)sink(x—f)dt.
о
При этом с2 не может обращаться в нуль, так как иначе мы
имели бы U' @) = 0, а потому функция U тождественно равнялась бы
нулю. Пользуясь тем, что функция U определена с точностью до
постоянного множителя, мы можем положить с2 = V^2/it. Тогда U удо-
удовлетворяет интегральному уравнению
Рассуждая так же, как и в п. 2, получаем, что при
имеет место равенство
U(х) = -|/|-staU+ °(*' Х) • B1)
Но тогда второе из равенств B0) показывает, что
tg Xir х= Р1 (Щк + Р2 (к)], B2)
где
Г~~ * /— я
Р, (X) = у -J J 5 (О U @ smM<#, Р2 (X) = у I J Б (t) U(t) cos ^d^.
о о
Принимая во внимание формулу B1), получаем, что
о
Пользуясь этими формулами, получаем из уравнения B2) асимпто-
асимптотическое выражение для п-го собственного значения, которое мы
обозначим через кп,
п
* = ifB(f)dt (n = l,2,...), B3)
а из B1) получаем, что соответствующая нормированная собствен-
собственная функция <р„(х) имеет асимптотическое выражение
?1*п-*>. B4)
§ & Теорема Дина — Гобсона 209
§ 8. Теорема Дини — Гобсона о равносходимости
ряда Штурма — Лиувилля и тригонометрического ряда Фурье
1. Задача о разложении по функциям Штурма — Лиувилля.
Пусть на отрезке [0, it] дана ортогональная нормированная система
функций {<?„(#)}, имеющих суммируемый квадрат
<?m(x)dx = 0 (пфт), A)
и пусть функция f(x) непрерывна в [0, я]. Предположим, что функ-
функцию f(x) можно изобразить в [0, тс] равномерно сходящимся ря-
оо
дом 2 anv>n (х),
«=1 ОС
/(*) = 2 anvn(д), 0<х<«. B)
Тогда, умножая обе части равенства B) на &п(х) и почленно инте-
интегрируя, получаем, что
C)
о
а потому коэффициенты ап в формуле B) однозначно определены и
имеют вид (ЗI).
Пусть, вообще, дана суммируемая на отрезке [0, -к] функция / (х),
и пусть для любого п интеграл, стоящий в правой части формулы C),
имеет смысл. Тогда последовательность \ап) называется последо-
последовательностью коэффициентов Фурье функции f(x) относительно
ортогональной нормированной системы функций {?n(%)}> a ряд
со
2 «„«>„(#) — рядом Фурье функции f(x) относительно системы
п=1
{fn(x)}. Это записывается формулой
f(x)~2an9n(x). D)
n=l
Основная задача теории разложений в ряды заключается в указа-
указании достаточных условий, при которых в формуле D) можно заме-
заменить знак ~ знаком ==. Мы ограничимся рассмотрением этой задачи
для случая, когда последовательность [<рп(х)} является последователь-
последовательностью функций Штурма — Лиувилля.
I) Мы уже применяли этот способ в гл. Ш, § 5; п. 5„в" и § 6, п. 8,
при рассмотрении разложений в ряды по многочленам Якоби и функциям
Бесселя. Относительно выражения C) для коэффициентов ап для случая,
когда <Рп является последовательностью функций Штурма — Лиувилля, см.
упомянутую на стр. 220 текста теорему Хаара.
14 Зак. S27. Дж. Сансоне
210 Гл. IV. Краевые задачи
Эта задача изучалась Лиувиллем в связи с некоторыми вопросами
теории теплоты (см. Лиувилль [2]; см. также § 6, п. 1), причем пер-
первоначально изучение ограничивалось формальным рассмотрением
этих рядов. Теория получила более законченный вид в известной
работе Дини [2], в которой, наряду с разложениями в тригонометри-
тригонометрические ряды, для которых был известен классический признак схо-
сходимости Дирихле, рассматривались также разложения по функциям
Бесселя и по сферическим функциям.
Задача о разложимости в ряды рассматривалась В. А. Стекловым
[1], [2], Гильбертом [1] и Кнезером [2], [3]; при более общих пред-
предположениях эта задача была рассмотрена Дини в рукописи, состав-
составленной в 1904 г. для студентов пизанского университета и опубли-
опубликованной в рукописном курсе 1910 г.1) Дини установил критерий
равносходимости рядов Штурма—Лиувилля и тригонометрических рядов
Фурье (см. Дини [3], стр. 81—82). Почти одновременно с ним Гоб-
сон нашел критерий равносходимости в точке для функций с огра-
ограниченным изменением (см. Гобсон [1]). Позже Хааром были установ-
установлены другие весьма интересные результаты (см. Хаар [1]).
Мы укажем в гл. V, § 3, п. 6, результаты, вытекающие из теории
интегральных уравнений; здесь, следуя способу Уолша (см. Уолш [1]),
основанному на методах общей теории разложения в ряды, мы дока-
докажем теорему равкосходимости рядов по функциям Штурма — Лиувилля
системы, рассмотренной в § 7, п. 4, и тригонометрических рядов
Фурье (см. п. 4).
2. Предварительные леммы, а) Лемма 1. Если двойная после-
последовательность действительных чисел
{сп>к} (л, k = l, 2, ...)
такова, что
v=l
и ряд
НК*|}2 F)
сходится, то
*v,ncVifc = 0 (я, * = 1, 2, ...)• G)
11 = 1
Имеем2)
2Bкп,*1J(К„1)(к,1)= 2
п к пр. v п, ц, v
= 2 к,О-
J) См. Дини [3]. Курс был прочитан студентам в 1910 г., литографиро-
литографированное издание вышло в марте 1911 г.
2) Для упрощения записи мы будем в дальнейшем просто писать 2> если
суммирование по всем индексам ведется от 1 до оо.
§ 8. Теорема Дини — Гобсона 211
Так как стоящий слева ряд сходится, то сходится и тройной ряд
2 К,Ац,|. (8)
tup, v
равно как и содержащиеся в нем ряды
2 4* (9)
п,к
и 2 к,, „с,, ft | О-
v
Положим
<Ч* = с*.»+сп.*+2<ч» <4fc (я, ft= 1, 2, ...)
v
и докажем, что о„ ft = 0.
Имеем
. „J + 2 2 <?«. *«,. Л, fc + 2 2 <?*,»<\, «Су. л +
В силу того, что
2(^,fc+ft.w<>+2
л, к п,к п,к
ряд 2(cn fc + cfc nJ сходится; обозначим его сумму через s:
п, к '
*=2(ч*+<ж»J-
п, к
Из сходимости ряда (9) следует существование такого числа Ж,
что
K*l<^ (», ft=l, 2, ...),
а потому
2 K.*cv,ncv,*l<-M 2 k,,n^,fcl-
n к nk
v, n, к v.n.k
Следовательно, тройной ряд 2 сп,кс*.псч,к абсолютно сходится.
v, п, к
Принимая во внимание E), получаем, что
2^ Сп, к сч, псч, к ~ 2^ Сч, п 2j Сп, НС1, к— 2icv,n (cv, п ~\~ Сп, v)>
Л, л, ft v, л к v, n
х) Напомним, что над кратными абсолютно сходящимися рядами можно
выполнять те же действия, что и над обычными. [См. Фихтенгольц Г. М. [1],
т. II, стр. 384. — Прим. перев.]
14*
212 /л. IV. Краевые задача
и, аналогично,
*2 ск, «<Ч псъ к = 2 <\, *2с*. «<Ч „ = — 2<Ч fc (cv, fc + cfc, v) =
V, П, ft V, It и V, ft
= — 2 ?«, N (<4 V +- CV, n)'
V,JJ
Суммируя найденные только что два соотношения и принимая во
внимание A1), получаем, что
S <Ч fcCv. псо. к + S с*, „cV) ncv> fc = — s. A2)
v, п. к t,n,k
Из сходимости тройного ряда (8) следует существование такого
числа Мг, что
2|<>.»<V,*I<^1 (й) k = l, 2, ...),
и-
а потому
S, кс-,, «cv. л I < м\ К. „с,,
и
A, v, n, fc v, n, к
Таким образом, написанный четверной ряд абсолютно сходится, а по-
потому, принимая во внимание E), имеем
S (S <ч «<ч лJ=2 B <ч „cv, ь) (
п. ft v п, ft v A
= 2 ^4^»^»= 2 <
(i, v, я, ft ц. v, n
= — 2 <?mnCv.n(Cm» + Cv.|l) = -- 2ц. .и
Суммируя теперь соотношения A0) по индексам п и ft и прини-
принимая во внимание A1), A2), A3), получаем, что
24. fc = 5 —2s + 5 = О,
n, ft
откуда следует, что о„. fc = 0 при и, ft = 1, 2 ,...
б) Лемма 2. Пусть \ип{х)} и {«„(.*)} — две последователь-
последовательности ортогональных нормированных функций на отрезке [а, Ь\\
пусть функции \ ип{х) \ равномерно ограничены в [я, Ь], и пусть
п( n, и=1, 2, ...)•
V
Если ряд
F)
§ 8. Теорема Дина — Гобсона 213
сходится, то функции {\ип{х)\\ также равномерно ограничены
в [а, Ь], причем
М*) —«•(*) = 2 <Ч»М*) («<*<?) A5)
V
и
ь
q —. Г (ц~ /х\ и (х))и (x)dx (п k = 1 2 ) A6)
а
Кроме того, ряды, стоящие в правых частях формул A4) и A5),
равномерно и абсолютно сходятся в [а, Ь].,
Из сходимости ряда F) вытекает существование такого числа М,
что
2|cn,vl<-^ (я —1» 2,...).
v
Так как по предположению функции |и„(дг)| равномерно ограничены
в [а, Ь], то из формул A4) следует, что стоящие в их правой части
ряды абсолютно и равномерно сходятся в [а, Ь\, а потому функции
| и„ (х) | также равномерно ограничены в [а, Ь].
Умножая A4) на ик{х) и^интегрируя от а до Ь, получаем, при-
принимая во внимание законность почленного интегрирования в правой
части, что
ь
\ип\К) — ип\х))ик \Х)ах — сПшк [п, к— 1, z,....;,
а
т. е. формулу A6). Поэтому
ь
j ик {х)ип {х) dx = сп> к+8„, к,
а
где через Ьпк обозначен символ Кронекера (8ПП = 1; Ьп1е = 0,
при пФ k). '
Но тогда
ь ь
К, к = J и» (*) "к (*) dx=fun (х) [ик (х) + 2 си. Л (х)] rfx =
а о
= J и„ (*) иЛ (х) dx-j-2ckiSf ип {х) и, (*) dx =
8„.,) =
v
c»..fc+cfc.n+2cfc,v cn>v,
214 Гл. IV. Краевые задачи
значит выполняются соотношения E.), а следовательно, в силу леммы 1,
и соотношения
i | "V1 „ „ (\ (у\
V
Как было замечено в лемме 1, ряд2|^ ncv k\ сходится, а потому,
v, к
если мы умножим G) на ик(х) и просуммируем по индексу ft, то
получим
2 сК пик + 2 cn> fcHfc+2 cv> „2 c,ikuk = O,
к к v к
2 <>к. »«fc ¦+" (Й„ — И„) + 2 Сч. п (В, — «J = О,
ft v
что и требовалось доказать.
3. Теорема Уолша о равносходимости для рядов по орто-
ортогональным функциям, а) Теперь мы легко можем доказать теорему
Уолша о равносходимости для рядов по ортогональным функциям
(см. Уолш [1]).
Пусть {ип(х)}, {ап(х)} — две последовательности ортогональных
и нормированных в [а, Ь\ функций, и пусть функции \ип{х)\ —
равномерно ограничены в [а, Ь] и
««(*) — «»,,(*) = 2 ЧЛ(*) («=1,2,.:.). A4)
где 1)
ь
cn,*=f (un(x)-un(x))u]e(x)dx («, ft = l, 2, ...). A6)
а
Пусть, кроме тог/), ряд
2B|^,fc|J F)
сходится. Докажем тогда, что если функция f(x) суммируема
вместе со своим квадратом в [а, Ь], то оба ряда
= J
J) Читатель заметш. что, в силу доказанного в п. 2„б", формула A6)
следует из A4), F) и предположения о равномерной ограниченности |ип(д?I
в [а, Ь\.
§ 8. Теорема Дини — Гобсона 215
имеют одинаковый характер сходимости в том смысле, что ряд
абсолютно сходится, причем его сходимость равномерна в [a, b] a
со
0=2 («fcHfc (*) — bkuk {х)),
fci
Имеем
ь ь
bn-an^ J /(*)[«!,,(*) — ««(*)]<** = J /(*) B <w. Л (*))<**.
о о
Из равномерной сходимости ряда 2 сп, •, ип С*) (см- лемму 2) следует,
v
что в A9) возможно почленное интегрирование *), а потому
К — an = i>n,^v B0)
и, аналогично,
V
Из B0) и A4) получаем, что
= 2 Ка*—h) «fc (*)—К (и* — %I =
v.fc*v И4-2^М Kv]' B2)
[
ft V
Ряд 2 *« сходится в силу неравенства Бесселя2), а по известному
неравенству Лагранжа имеем
Полагая /?w =¦ 2 сп, чЩ (*) и применяя неравенство Буняковског01
получаем
ь N ь
Г . v«, (¦*)) ^- 2 сп,* Г /(*)и^ <*) dx
о
J
2) См. Фнхтенгольц Г. М. [1], т. III, стр. 705. — Прим. nepes.
в) Имеем
2
но трехчлен, стоящий справа, неотрицателен при любых действительных X,
поэтому
216 Гл. IV. Краевые задачи
в силу равномерной ограниченности функций | ип (х) |. Отсюда следует,
что ряд B2) абсолютно и равномерно сходится в [а, Ь], а также, что
2 (акик (х) — Ькик (х)) = 2 <Ч лМл — 2 *Л. Л =
, ft ft, v v, ft
= 2 c,,fc*vafc — 2 *A. fc»fc = 0.
tc. i . v, ft
б) Из доказанной теоремы следует, что если выполняются сделанные
предположения и если один из рядов A7) сходится (суммируем)
и имеет сумму S, то и. другой ряд сходится (суммируем) и
имеет \ту же сумму S; если расходится один из них, то рас-
расходится и другой; если один из них равномерно сходится
(суммируем) на некотором отрезке, то и другой равномерно
сходится (суммируем) на том же отрезке.
4. Теорема о равносходимости рядов Штурма — Лиувилля и три-
тригонометрических рядов Фурье, а) Мы располагаем теперь всем
необходимым для доказательства теоремы о равносходимости рядов
Штурма — Лиувилля и тригонометрических рядов.
Рассмотрим ортогональную и нормированную последовательность
функций Штурма — Лиувилля {ип(х)}, удовлетворяющих уравнению
^-В(* = 0 B3)
и краевым условиям
«й@) = ии(я) = 0, B4)
а также последовательность {и„ (х))
«„(¦*) = }/"|-sinn*. B5)
. Предположим, что функция В(х) непрерывна и имеет ограни-
ограниченное изменение в [0, тс]. Тогда, по формулам B4) и B3), из § 7, п. 4,
а(х, и)~1 , ¦ а (и)
Ь* ]' й==й~!—п'
причем существует такая абсолютная постоянная С, что
'|а(«)|<С (« = 1,2,..:),
\а(х, «)|'<С (дляО<^<тг; «=1,2,...).
,/*2
Так как функция и„(х) — и„(х) имеет в @, тг) вторую произ-
производную, то в [0, я] равномерно выполняется равенствох)
со
ип (х) — ип (х) =¦ 2 сп, кЧ (х),
-1) См., например, Толстое Г. П. [1], стр. 108 — Прим. перев.
§ 8. Теорема Дини — Гобсона 217
где
f ^_- I (it (уЛ_^_ /* (у^к\ tt (уi dx
п,к J \ n\ J п\ )> к\ ) »
О
или
/ О /• __
сЯ) fc = l/ — I и„ (дг) sin kxdx — 8n> fc (n, ft = 1, 2,...). B7)
о
Интегрируя по частям, получаем, что
~2 \ г —г
о
/2 1 Г —»
— тг I llftiX) Sltl кХ 4*Х. \~ )
О
В силу второй из формул B6), можно найти такое целое число N
что
|Х„ — п\<~ при n>N. B8)
Если рассмотреть все индексы п ^ TV, то из B3) и B6) следует
существование такого числа clt что
^ при«=1, 2.....М
Тогда
а потому ряд 21 сп, л I сходится, и, следовательно, существует
к
сумма 2 {2|с„ fc|J- Если бы нам удалось доказать сходимость
n<N ft ' '
ряда 2 {2 i сп к 112» т0 можно было бы применить теорему из п. 3.
п>N к ' '
Из B7) и B6) имеем
218 Гл. IV. Краевые задачи
а потому
К »!<-?• (« = 1,2,...), B9)
где с2 является абсолютной константой.
При Ифп имеем из B7')
'«. * = \\ -]?${>% —В (х)] а„ (х) sin kxdx =
О
а потому
те
о
В силу того, что я > N и k Ф п, а потому \п — ftj^-1, полу-
получаем, пользуясь B8), что
Поэтому, в силу C0),
и по неравенству Лагранжа
, C1)
к "О
ЧУ t
где штрих в символе 2л означает, что исключается значение k — n.
Имеем
1 1/1
A2— rP 2n\k — n n + kj' (ft2 — и2J ^ 2и2 \(А — и)'
П—1 со
' 1 vi I v^ 1 ,пг1 1
J
(А—иJ ^ (и-^АJ ' jU (А —иJ^
* к=1 к=п+1 к
S'
(ft +
§ 8. Теорема Дани — Гобсона 219
а потому
JU (*2 —Й2J ^ ~2tfi 2U A2 — „2 ' \°*>
к к
где с8 — абсолютная константа.
Раскладывая функцию В(х)ип(х) по ортогональной и нормиро-
нормированной в [0, тг] системе функций |l/ — sin ЛлгJ, получаем, в силу не-
неравенства Бесселя, что
2# Г f ?(*)«„(*)sinЬглЛ2<| f B»(*)^(*)<te,
ft о о
а потому, так как функции | ип (х) | равномерно "ограничены в [0, я],
то
2' [ /Я (*) и~ (*) sin kx dxf < ev
h о
где ci — абсолютная константа. Из C1), C2), C3) выводим, что
и, в силу B9),
где Сх — абсолютная константа. Отсюда следует, что ряд 2 B1 cn fc I J
M>ff ft
сходится. *
Принимая во внимание полученные в п. 3 результаты, получаем
следующую теорему.
Если {«„(¦*)} является ортогональной а нормированной систе-
системой функций Штурма—Лиувилля относительно уравнения
« краевых условий
и„@) = **„(*) = О,
(где ? (х) непрерывна и имеет ограниченное изменение в [0, к]) а
если"функция f{x) имеет в [0, тт] суммируемый квадрат, то ряд
Фурье функции f(x)
со и
аппп(х), an=ff(x)un(x)dx C4)
220 Гл. IV. Краевые задача
ведет себя так же, как и тригонометрический ряд функции f{x)
относительно ортогональной и нормированной в @, тг) системы
функций \у — яппх\
/ С*) —^bnsinnx, bn = —[f (x) sin nx dx C5)
n=i • о
в том смысле, что если один из рядов C4), C5) сходится {сум-
{суммируем) к сумме S, то и другой ряд сходится {суммируем)
к сумме S; если расходится один, то расходится и другой: если
один равномерно сходится {суммируем) на некотором отрезке
из [О, к], то и другой равномерно сходится {суммируем) на
том же отрезке.
"¦ б) В частности, если функция f{x} непрерывна и имеет огра-
ограниченное изменение в [О, тг], то ряд C4) сходится на [О, тг], при-
причем он равномерно сходится к функции f{x) на любом отрезке,
лежащем внутри [0,'и].
В самом деле, этим свойством обладают ряды C5I), откуда и
следует по теореме равносходимости наше утверждение.
Эта же теорема справедлива для всех разложений непрерывных
функций с ограниченным изменением в ряды Штурма — Лиувилля
(см. Гобсон [1J, стр. 386—387).
Сформулируем, наконец, следующую теорему единственности Хаара.
Если определенная в [0, л] функция f{x) ограничена и инте-
интегрируема, а {<?«(*)} — последовательность ортогональных и нор-
нормированных в [0, тг] функций Штурма—Лиувилля, и если ряд
со
2 ап9п1х) сходится в [0, тс] к f{x), то его коэффициенты ап
»=i
являются коэффициентами Фурье функции f{x) относительно
системы {ч„{х)\, т. е. ап выражаются по формулам C) (см.
Хаар'Ш, стр. 48J).
*) См. Фихтенгольц Г. М- [1). т. III, стр. 528. — Прим. перев.
2) В приложениях (например, в квантовой фнзнке) большую роль играет
также задача Штурма — Лнувилля на бесконечном промежутке. Отметим
основные факты, относящиеся к этой задаче. Пусть <р (лг; X) — решение диф-
дифференциального уравнения
y + {\-q(x)}y=G @<^<aD), (I)
удовлетворяющее начальному условию
<? @; X) cos a + <j/ @; X) sin a = 0, B)
и q (x) — действительная функция, непрерывная в каждом конечном проме-
промежутке. Существует монотонно возрастающая функция р (X), называемая
спектральной функцией и обладающая следующими свойствами. Любой
функции / (х) из Z.2 @; со) соответствует функция
п
F (X) = I. 1. m Г / (х) «у (х; X) dx, C)
п-»оо ¦'
$ 8. Теорема Дини — Гобсона 221
причем
с» с»
J P(x)dx= J>(X)dp(X)
О —со
A. 1. т. — предел в среднем по мере р (X)).
Обратно, каждой функции F(X) с интегрируемым относительно р(Х)
квадратом соответствует функция
Л.1
f (х) =l.i.m. (V (X) v (*; X) dp (X), D)
со oo
J ^(X)rfP(X)= f P(x)dx. E)
0
причем
Таким образом, получаются формулы обращения, аналогичные формулам об-
обращения Фурье.
Дополнение к множеству точек, н окрестности которых р (X) постоянна,
d%
называется спектром оператора -j-^—g(x). В зависимости от поведения
q (x) на бесконечности спектр может быть чисто точечным, непрерывным
или смешанным.
Функция р (X) определяется однозначно, если уравнение A) имеет при
всех недействительных значениях X единственное решение с интегрируемым
квадратом (случай предельной точки Вейля), и — неоднозначно, если при
любом недействительном X все решения имеют интегрируемый квадрат
(случай предельного круга Вейля).
Важное значение имеет также обратная задача Штурма — Лиувилля,
т. е. задача о восстановлении уравнения A) по функции р (\).
Задача Штурма — Лиувилля на бесконечном промежутке была впервые
рассмотрена с достаточной полнотой Г. Вейлем [W е у 1 Н., Uber gewOhnliche
Нпеаге Dffierenttalglelchungen mit slngularen Stellen und tore Elgenfunktionen,
Gottlnger Nachr. A909), S. 37—64; (iber gewohnliche DifferentlaiRleichungen
mit Singularitaten und die Zugehorigen Entwicklungen willkflrllcher Funktionen,
Math. Ann., 68, A910), 220—269].
Изложение результатов, полученных до 1946 г., содержится в книге
Е. Титчмарша [Tltchmarsh E. С, Elgenfuncttons expansions associated
with second-order differential equations, Oxford A946)].
Новое изложение теории и некоторые новые результаты содержатся
в книге Б. М. Левитана (Разложение по собственным функциям, М. — Л., 1950).
Решению обратной задачи Штурма — Лиувилля посвящен ряд работ, из ко-
которых особо отметим работы: Гельфанд И. М. и Левитаи Б. М.,
Об определении дифференциального уравнения по его спектральной функции,
Изв. АН СССР (серия матем.), 15 A951), 309—360. Марченко В. А.,
Некоторые вопросы теории однородных линейных дифференциальных опера-
операторов второго порядка, Труды Моск. Матем. Об-ва, I A952), 327—420 и 2
A953), 3—84. К р е й н М. Г., О некоторых новых задачах теории колебаний
Штурмовых систем, Прикл. матем. и мех., 16, вып. 5 A952), 555—568; Об
обратных задачах для неоднородной струны, ДАН СССР, 82, № 5 A952),
669—672. Карасева, Об обратной задаче Штурма — Лиувилля для неэр-
неэрмитова оператора, Матем. сб., 32 G4), № 2 A935), 477—484. Чудов Л. А.,
Обратная задача Штурма — Лиувилля, Матем. сб., 2S 'F7), № 3 A949),
451—456. — Прим. перев.
Глава V
КРАЕВЫЕ ЗАДАЧИ ДЛЯ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ л-го ПОРЯДКА (п>2)
§ 1. Билинейные формы. Канонический вид1)
а) Пусть [щ, ъ), i, 6 = 1, 2, , л— совокупность л2 чисел и
пусть даны 2л переменных xt, х2, ..., хп; yv _у2, ..., уп; выра-
выражение
F =
+
а2.
+
«
»,
п
i ft
A)
называется билинейной формой от 2л переменных
1» 2> ¦ * "' **w»
Определитель
А =
l, 1
2,1
2, 2
Оп,1
Яп, п
называется определителем формы F.
Мы будем предполагать, что АфО, или, как говорят, что форма F
невырождена.
б) Предположим, что над переменными xit yh выполнены линей-
линейные преобразования
5~^ = 2й.Л, B)
n
¦¦ 21
8 = 1
C)
!) Относительно вопросов, рассматриваемых в § 1, 2, 3 этой главы, см.
Бохер [2], гл. II и V, Айне [1], гл. IX и XI.
§ 1. билинейные формы. Канонический вид 223
определители которых
C = Det [|ci>r||, Z) = Det ||dfe8||
(i, r, k, s = l, 2, ..., n)
отличны от нуля (и, следовательно, эти преобразования обратимы).
Тогда
ЯП П
/?= 2 «i.fc 2 Ъ.гХу'Я dk- SYS,
i. 7c=l r=l 8=1
F= 2 в^ВД, D,)
Г, 8=1
где
n
«Г, « = 2 «i, kCi, rdic, s- Da)
i, k=l
Таким образом, мы получили новую билинейную форму относительно
переменных Xr, Ys, определитель которой
A' = ACD
также отличен от нуля, а потому, делая в невырожденной форме
преобразования B) и C), мы получаем новую невырожденную форму.
в) Назовем каноническим видом билинейной формы от 2я пере-
переменных хи лг2, ..., хп, yv y2, .... уп выражение
Докажем, что для данной невырожденной формы F и данного
линейного преобразования S над переменными х1г х2, ..., хп,
определитель которого отличен от нуля, существует одно и только
одно линейное преобразование Т над yv ya, ..., уп, такое, что при
одновременном выполнении преобразований S и Т форма F принимает
канонический вид
,. E)
Иными словами, должны выполняться равенства
п
о*, net, rd7c,8 = K, s (Г, s= 1, 2, ..., п)
(см. введенные выше обозначения), где 8Г> 8 — символ Кронекера:
8r> r = 1, 8Г, 8 = 0 при г ф s.
Т фиксированном s мы получаем для определения rfi, s, d2, s» • • •
, s систему линейных уравнений
п п
aiJe cit r)dk,s = 8r, „ (г = 1, 2, ..., и),
224 Гл. V. Краевые задачи для уравнений п-го порядка (п > 2)
определитель которой равен АС и, следовательно, отличен от нуля;
поэтому мы можем найти из этой системы величины d^ 8, *4, в» • • •
..., dn, 8 одним и только одним образом.
г) Сделаем в канонической форме, полученной описанным н „в"
методом, невырожденное линейное преобразование, оставляющее неиз-
неизменными переменные Хи Х%, —, Хт и переводящее переменные
Хт+1, ..., Хп в Хт+и ..., Х„. Тогда этому преобразованию соот-
соответствует преобразование переменных Yv K2, ..., Ym+1, ..., Yn
н Y[, Y2, ...» Y'm+i, ..., Yn, при котором билинейная форма остается
канонической. Укажем явные формулы, выражающие переменные Y[7
Y'2, ..., Y'm+1, ..., Y'n через переменные Yu K2, ..., Yn.
Имеет место тождество
ВД + Л^а+ ¦ • • +XmV»+Xm+1Yu+1+ ... +XnYn^ F)
Так как Jflt А, —, Хт, Xm+i, ..., Хп выражаются обратимым
образом через xv лг2, —, хп, то существует одна и только одна
система значений переменных xv х2, ..., хп, при которой
•^m+i = 0, ..., Xm+v-i — 0, Xm+V = 1, A"m+,+i = 0, ..., Хп = 0
[v = l, 2, ..., n —m],
^ = 0,..., Хт = 0.
Если при этой системе значений xt, х2, ..., хп переменные Хт+1, ...
..., Хп принимают, соответственно, значения Am+itV, ..., Ап> ¦», то
из тождества F) следует, что
[v = l, 2, ..:, n —m].
*Таким же образом можно получить выражения Y[, Y2, ..., Y'm
через Yv Ya, ..., Yn; в самом деле, если выбрать'значения xv x2, ...
..., хп так, чтобы выполнялись равенства
II* = 1, 2, ..., т],
т+1 = 0, . . ., Хп = 0,
и обозначить через Bm+liV., ..., Вп-У. [|* = 1, 2, ..., /и] значения,
принимаемые при этом переменными Хт+1, ..., Хп, то
|1Уи^=1, 2, ...,т]. G2)
Формулы GХ) и G2) и являются искомыми.
2. Сопряженные ii самосопряженные системы 225
§ 2. Сопряженные и самосопряженные
дифференциальные системы
1. Дифференциальные системы. Индекс совместности, а) Обоб-
Обобщим введенное н гл. IV, § 6, понятие системы Штурма — Лиувилля.
Для этого рассмотрим дифференциальное уравнение
коэффициенты р{ (х) которого определены па отрезке [а, Ь\, р0 (дг) Ф О
в \а, Ь], и будем искать решения этого уравнения, удовлетворяющие
на концах а и b m условиям:
U* (У) = ЪУ («О + 4V (а) + ... + of-V" («) + B)
(i=l, 2, .... /и),
где а,, а?> а^; pi( р?>, ..., pf-J> (/=1, 2, .... /и)-за-
данные действительные числа.
Система A), B) называется однородной дифференциальной систе-
системой 2). Если ей удовлетворяет только функция у (дг) == 0, то она назы-
называется несовместной 3). Если же она имеет k(k^.n) линейно незави-
независимых ненулевых решений ух(х), у2(х), ..., ук(х), то наиболее общее
решение системы A), B) имеет вид
где Cj, c2, ..., ск — произвольные постоянные. Число k называется,
индексом совместности дифференциальной системы A), B), а ух (дг),
у2(дг), ..., yie(x) — фундаментальной системой решений.
б) Следующие рассмотрения позволяют уточнить понятие индекса
совместности дифференциальной системы A), B).
Без потери общности мы можем считать, что т краевых усло-
условий B)
Ut{y) = 0 (/ = 1, 2, .... т)
линейно независимы, если рассматривать Ut(y) как линейную форму
от у {а), у'{а), ..., Г И*. У(Р)> /(*)• ¦••» У{п-1}(Ь)-
Пусть _Vi (*)t Уч, (•*)» • • •» JmW — фундаментальная система реше-
решений уравнения A) *). Тогда решения системы A), B) имеют вид
1) Начиная отсюда, мы рассматриваем лишь уравнения порядка _.__
2) Термин автора .дифференциальная система" не является общеприня-
общепринятым. — Прим. ред.
3) Этот термин также не общепринят..— Прим. ред.
4) Следует подчеркнуть, что здесь речь идет об и линейно независимых
решениях-уравнения A), а не системы A), {2). —Прим. ред.
15 Зак. 527. Дж. Сансове
226 tji. V. Краевые задачи для уравнении п-го порядка (п
где, в силу B), постоянные си с2, ..., с„ должны быть такими, что
(У») = 0.
Отсюда следует, что если ранг матрицы
равен п — k, то индекс совместности дифференциальной системы
A), B) равен k; справедливо и обратное,
2. Сопряженные дифференциальные системы. Пусть
* C)
— дифференциальное выражение порядка га, коэффициенты которого р{
являются непрерывными функциями от х в [а, Ь\\ пусть рг имеет
в [а, Ь] производные до п—1-го порядка включительно, а ро(х) не
обращается в нуль на отрезке [а, Ь].
Обозначим через M(z) сопряженное с L(y) дифференциальное
выражение (см. гл. II, § 5, п. 1)
D)
E)
F)
Тогда для L(y) и M{z) имеет место тождество Лагранжа
где ty(y, г) является билинейной формой от переменных
z z1 гС»-1) I
вида
G)
U. Сопряженные й СйМоСопря$кенные дидтеМы
22?
Определитель А(лг) формы ty(y, z) равен
• (-
1 \Я-2
1) Ро
О
О
О
О
О
О
О
Ро О .
и потому отличен от нуля в [а, Ь\\ таким образом, ty(y, z) является
невырожденной билинейной формой от переменных F).
Интегрируя равенство E) от а до Ь, получаем так называемую
формулу Грина *)
ь
J [zL (у) —ум (z)\ dx=ад су, *)]*:„. (9)
Правая часть этой формулы является билинейной формой относи-
относительно
у (а), / (а), ..., j,<»->> (а); ^ (*), / (Ь), ...,Г~1 (*), (ЮЛ
г (а), г* (в), ..., г(»-Ч (а); г (*), г' (*), ..., г(»-Ч (*). A0,,)
Определитель этой формы равен (— 1)" Д (а) А (Ь) = (—1 )** [р0 (с
и потому отличен от нуля; таким образом [ty(y, г)]* является невы-
невырожденной билинейной формой относительно переменных (ЮЛ, A02).
Пусть даИы 2п линейных выражений относительно переменных (ЮЛ
Uv f/2, ..., (/2п вида
+ ^у (»)+РРУ (
f - V-1» (*)
(i=l, 2, ..., 2и),
для которых определитель матрицы коэффициентов отличен от нуля;
тогда, в силу доказанного в п. 1, можно найти 2л линейных форм
относительно переменных A02)
так ,что
A2)
A3)
i) Формула (9) называется формулой Грина по аналогии с формулой
преобразования двойного интеграла в криволинейный интеграл.
15*
228 Гл. V. Краевые задачи для уравнении п-го порядка (п
и потому (9) принимает вид
ь
f [zL{y)~yM(z)]dx = U1V^+U^n-.1 + ... + U^V,. A4)
а
Система
I, 2, ..., 2и — т) J A5s)
называется линейной дифференциальной системой, сопряженной
с системой
L (у) = 0, 1
ЛСУ) = О (i=l, 2 m)»)J
Это определение оправдывается сделанным в п. 1„г" замечанием
о том, что если сделать линейное преобразование переменных (IOj),
при котором формы [/„ t/2, , t/m остаются инвариантными (в то
время как Um+U ..., U^ изменяются), то формы Vu V2, ..., V2n_m
преобразуются в формы Vi, V2, ..., V2n-m, каждая из которых
является линейной комбинацией V,, Vg, ..., V2n_m.
Заметим еще, что так как сопряженным для уравнения М (z) = О
является уравнение L(y) = 0 (ср. гл. II, § 5, п. 1„в"), то, в силу
симметрии равенства A3), дифференциальная система A5j) является
сопряженной с системой A52).
3. Индексы совместности для сопряженных систем, а) Для
того, чтобы установить связь индексов совместности двух сопряжен-
сопряженных систем, нам понадобится следующая лемма.
Лемма. Пусть индекс совместности системы
Ui{y) = ® («=1. 2, ..., /и)
равеи ft, и пусть д/j (л:), у2 (х), ..., _ук (л:) — фундаментальная си-
система решений этой системы. Докажем, что если линейные от-
относительно у (а), у'(а), ..., у(^п-1)(а); у(р), у'{Ь), ..., у(.п~1)(Ь)
формы Um+i, •.., ?/2п выбраны так, что формы Uv (/2, ..., Um,
J) Сопряженные системы в некоторых частных случаях рассматривались
Лиувиллем [3], стр. 604. Сопряженные дифференциальные системы второго
порядка рассматривались Мезоном [1]. Определение сопряженной линейной
системы для уравнения порядка п было дано при т = « Бнркгофом [1],
стр. 375. В общем случае определение сопряженной дифференциальной
системы дано Бохером [3]. Обращаем внимание читателя на то, что понятие
сопряженной линейной дифференциальной системы, Введенное здесь, отлично
от понятия сопряженной системы дифференциальных уравнений, введенного
в гл. II, § 1, п. 4,а".
2. Сопряженные и самосопряженные системы 229
Um линейно независимы, то ранг матрицы
равен k.
Предположим противное; тогда можно было бы найти такие
числа cv с2, ..., cfc, из которых хоть одно отлично от нуля, что
сiUi (Уд + cJUt Ы +•••¦+ СЛ (Л) = 0 (i = m +1, ..., 2n)
или
Таким образом, полагая у = с1у1-{-с2у2~\- ... ~{-скук, мы имеем
^*.СУ) = О (/=1, 2, ..., /и, /и + 1, .... 2я).
Но формы t/j, (/2, ..., ?/ю, (/,в+1, ..., t/2n линейно независимы,
поэтому
)У) i)-
и, следовательно, _у ^ 0, чего не может быть.
б) Теперь легко доказать следующую теорему.
Если формы их (у), ..., Un (у) линейно независимы, то индексы
совместности системы
L(y) = 0, 1
,00 = 0 (/ = 1, 2, ..., и) j A6)
A7)
и сопряженной с ней системы
М (z) = О,
у€(г) = О (i=l, 2, ..., и)
Пусть ft — индекс совместности системы A6), и пусть ylt y2, ...,
yh— ее фундаментальная система решений; пусть, кроме того,
zv z2, ..., zn — фундаментальная система решений уравнения
Полагая в формуле Грина A4) z = zx, z2, ..., zn, получаем
(У) К (*д +..-¦+ ^ ^) Ух (гх) = 0,
(У) У» (*») + • • • + Ц* (У) V7! (*«) = 0.
Эта система имеет k решений
(*=1. 2,..., Л),
230 Гл. V. Краевые задачи для уравнений п-го порядка (п">2)
которые линейно независимы в силу доказанной в „а" леммы. По-
Поэтому ранг матрицы
не превосходит п — k.
Но если индекс совместности сопряженной системы A7) равен ft',
то ранг указанной матрицы равен п — k' (п. 1„б"), следовательно,
и — k' ^ п — k\ аналогично доказывается, что п — k^n — k', откуда
в) Если тфл, то тем же самым способом можно доказать, что
k' = k~\-m~п (см. Айне [11, стр. 288).
4. Самосопряженные линейные системы. Дифференциальная
система называется самосопряженной, если она совпадает с сопря-
сопряженной ей системой (при йтом у (а), у' (а), ... ,_у(п-Ч (а); у (Ь), у' (Ь),...
..., У"-1) (Ь) рассматриваются как независимые переменные).
Отсюда следует, что если система
Ut(y) = 0 (i=l, 2,..., т)
самосопряжена, то уравнение L (у) = 0 самосопряжено (см. гл. II,
§ 5, п. 3), а системы иг(у) = 0 (i=l, 2,..., /и), V,(^) = 0
(*=1, 2, ..., 2л—т) эквивалентны и, в частности, т = п.
5. Самосопряженные системы второго порядка. Найдем теперь
в явной форме вид самосопряженных дифференциальных систем вто-
второго порядка.
Дифференциальная система второго порядка имеет вид
A8)
J
Ua (у) = РуУ (a) -j- Р2д> (b) -J- Pg_y' (a) -J- p^y' (b) ¦=¦ 0,
причем ранг матрицы
IK «2 «з«4
ft ft ft ft
II Pi Рй Рз Р4
равен двум.
Для упрощения записи положим
§ 2. Сопряженные и самосопряженные системы 231
и докажем, что для того, чтобы система A8) была самосопря-
самосопряженной, необходимо и достаточно выполнение равенства
КМа) = Ьиф{Ь). A9)
Предположим сначала, что 8ь2=И=0; положим тогда Ub-=yr{a),
иА=уг(Ь). Четыре линейные формы Uv ?/2, U3, С/4 от переменных
у (а), уф), у'(а), у' ф) линейно независимы, и, в силу (9) и A4), имеем
т. е.
6 ф) \z ф)у' ф) —у ф) z' ф)) — 6 (a) [z {а) у' (а) —у (a) z' (я)]
= 1«1У («) + «а У (*) + «з/ (в)
/ (в)
Так как это равенство должно выполняться тождественно относи-
относительно у (а), У (а), уф), у'ф), то имеют место четыре уравнения
решая которые, находим для Vj, V2, V3, V4 выражения
Vt = 6 ф) z ф)+± [8а, 46 (a) г' (в) + »,. 4
Г2 = — е (a) z (а) + ^ [82, з Ь (a) z' (а) + 8,.
J (а) г' (а) + «^ F) У (ft)],
Из самосопряженности системы A8) следует, что линейные формы
Vj, V2 должны быть линейными комбинациями Ut и t/8. Так как
в V"j не входит z(a), то эта форма может отличаться лишь постоян-
постоянным множителем от формы, получающейся исключением z (а) из ?/j (z)
и ?/2(г). Но это исключение приводит к форме
откуда видно, что ранг матрицы
кф) ^в(в) g|jj
равен единице, и, следовательно, выполняется равенство A9),
232 Гл. V. Краевые задача для уравнений п-го порядка (п > 2)
Равенство A9) можно получить также, выражая V2 в виде линей-
линейной комбинации Ux и Uv
Рассматривая оставшиеся пять возможных случаев
мы также приходим к равенству A9).
6. Самосопряженные системы Штурма — Лиувилля. Обобщая
введенное в гл. IV, § 6, п. 6, определение, назовем системой.
Штурма — Лиувилля систему
B0)
где функции 6' (л;), А(х), В(х) непрерывны в [а, Ь], 6(лг)=^0
в [а, Ь\.
Из доказанного в п. 6 следует, что такая система самосопряжена,
если
^) К
Например, задача о распространении тепла в тонкой проволоке
(см. гл. IV, § 6, п. 1) приводит к краевым условиям
а'у {а) — <х/(а) = 0, $'у(Ь) + Р/ (Ь) = 0. B2)
Так как в этом случае 81> 3 = 82 4 = 0, то получающаяся система
является самосопряженной системой второго порядка.
Заметим, что, исключая из B1) последовательно у'(а) и у (а),
получаем
8,, з/ (в) + К ъУ (*) + К «/ (*) = О,
и, следовательно, если 81>3 = 0, то система B0), B1) самосопряжена
тогда и только тогда, когда 824 = 0 и краевые условия имеют вид
B2); если же, наоборот, 81>3 =/= 0, то систему B0), B1) можно за-
записать в виде
У (а) = ьу ф) + ТУ (*). У И =
откуда видно, что эта система самосопряжена, если
В частности, если краевые условия B1) имеют вид
§ 3. Функция Грина
233
или, как говорят, если наложены периодические краевые условия,
то система самосопряжена, если
е (в) =
7. Самосопряженные системы четвертого порядка. Рассмотрим
уравнение
[в (*)/Т + [X А (х) + В (х)] у = О,
где функции 6"(лг), А (х), В(х) непрерывны в [а, Ь], 6 (х) > 0 в [а, #),
и будем искать решения, удовлетворяющие краевым условиям
Vi (У) = «i. 1 (W + «!, а (9/0 + «I, а/ + «ь ^I— = О»
^8 (У) = «2,1 («/')' + «2,2 (вУО + Ч. з/ + «8. «> U=a = О,
t/3 Cv) = *,. i (Ь'У + *,, 2 (S/0+*,. 3/+*,. <у Гь = о,
Можно доказать, что необходимым и достаточным условием само-
сопряженкости этой системы является выполнение равенств
?, 1
7
2 4
^2,2 «2,8
*1.1
/о о
У1,3
Do о 02j3
2)
§ 3. Функция Грина
и преобразование дифференциальных систем
в интегральные уравнения Фредгольма второго рода
1. Функция Грина для самосопряженной системы второго по-
порядка частного вида. Рассмотрим самосопряженную (§ 2, п. 6) си-
систему второго порядка
где функции Ь'(х), Q(x) непрерывны в [а, Ь\, а 6(лт)>0 в [а, Ь\.
Предположим, что эта система несовместна, а потому у = 0 является
единственным решением системы AJ, A2), или, что то же самое,
предположим, что точки а и b не сопряжены относительно уравне-
уравнения A,) (см. гл. IV, § 2, п. 3).
Если несколько ослабить условия, накладываемые на решение, то
можно найти функцию у(х), не равную тождественно нулю, которая
удовлетворяет системе (lj), (I2). Точнее говоря, мы покажем, что для
любой точки S промежутка (а, Ь) можно одним и только одним
!) Относительно самосопряженных систем второго порядка см. Камке [2],
[3]. Там же приведена библиография. Периодические краевые условия мы
рассмотрим в гл. VI, § 3.
2) См. Янчевский С. Я. [1]. стр. 522. Относительно общих свойств само-
самосопряженных систем см. Джексон [2], Летшоу [V.
234 Гл. V. Краевые задача для уравнений п-го порядка (п~>2)
способом построить непрерывную функцию x—G(x, Е), удовлетворяю-
удовлетворяющую в 1(а, Е) и (Е, Ь)\ данному уравнению, и такую, что ее произ-
производная имеет в точке % разрыв первого рода, причем скачок произ-
производной в точке Е равен 1/6 (ЕI).
Так как точки а и Ъ не сопряжены относительно уравнений A,),
то это уравнение имеет два линейно независимых решения у1 (л:) и
_у2 (л:), однозначно определенных краевыми условиями
ух (а) = 1, у, ф) = 0; j2 (а) = 0, ys (Ь) = 1. B)
Функция G(x, Е), которую мы хотим построить, должна иметь
в [а, 6) вид су1(х)-\-с^у2(х), где с и с2 — постоянные величины, но
так как мы хотим, чтобы G(a, E) равнялось нулю, то с = 0, а по-
потому при лг-<Е имеем
и, аналогично, при
где Cj — постоянная величина. Из условия непрерывности функции
G (л:, |) в точке л: = 6 следует, что с^уъ (Е) = с^ух F), откуда, если пред-
предположить yi (Е) =? 0, у2 (S) ^= 0, получается, что cjys F) = Cg/^ F) = А.
Поэтому при лг^Е имеем
O(jc, 5) =
а при Е-^л:
О(х, S) = h
Тогда
ОшF —0, ©«
а потому
= 1/в (Е),
С другой стороны, имеем
о=
Поэтому Ь(у2у[—УхУ'ъ) — с, где с — постоянная величина. Отсюда
следуют формулы
О(х, Q=-ytg)^W при
f2 при л:>Е. C.)
доказывающие существование и единственность G(jc, E).
1) При этом G(e, 5) = GF, ?) = 0. — Прим. перев.
2) Если Vi(S) = O, в то время >как j2(S)?=0i то принимаем с2 = 0. Тогда
при х^$, б\х, 5) = Qi » то время вдк прн 5^д; имеем G{x, 6) — ci^i (дг).
5. Функция Грина 235
Функция G{x, ?) называется функцией Грина1) для системы (lj),
A2) относительно полюса Е; из формул C) вытекает, что имеет место
весьма важное соотношение
С(лг, E) = G(E, x) D)
2. Функция Грина для дифференциальных систем. В п. 1
функция Грина определена для одного частного случая. Рассмотрим
теперь общий случай.
а) Пусть дана дифференциальная система
E)
Ut (у) = *0 (а) + сф/ (а) + ... + «<»-V»-4 (a) +
A«=1, 2, ..., я),
где функции р0, р„ ..., pn_lf pn непрерывны в [а, ft], ро(л0=?О
в [a, ft], a формы (Д, ?Л>, ..., f/n, рассматриваемые как линейные
формы от у (а), /(а), .... j>Cn-i)(a); ^(ft), /(ft),..., У») (ft),
линейно независимы. Предположим, что эта система несовместна,
т. е. что единственным решением системы E) является функ-
функция, тождественно равная нулю.
Докажем, что для любой точки Е, лежащей внутри (a, ft),
можно построить функцию y — G(x, E), имеющую следующие
свойства:
1. Функции G(x,l), Gx(x, ?), ..., G^n-g^, ?J) непрерывны
в [а, ft]i
2. Функция Gxn-i(x, Е) непрерывна в [a, ft] всюду, за исклю-
исключением точки I, где она имеет разрыв первого рода со скачком
3. з' == G (л:, Е) удовлетворяет всюду в {а, Ь\, за исключением
точки Е, системе E).
Кроме того, докажем, что функция G{x, E) однозначно опре-
определяется указанными свойствами.
!) Функция Грина для уравнения у" = 0 впервые рассматривалась Бурк-
хардтом [1]; для уравнения любого порядка функция Грина введена Бохе-
ром [4]. Относительно работ Биркгофа, Буницкого, а также относительно
библиографии см. Бохер [5], стр. 71.
Изящное свойство композиции функций Грнна для двух дифференциаль-
дифференциальных уравнений указано Трикоми [1].
?) обозначает ^Щ^^-. — Прим. ред
236 Гл. V. Краевые задачи для уравнений п-го порядка
Если _Vi (•*)» Уъ(х), ..., уп{х) — фундаментальная система реше-
решений уравнения L(y) = O, то функция G'(x, Е), -которую мы хотим
построить, должна иметь в [а, ?) и (Е, Ь], соответственно, выра-
выражения
G(х, Е) = а,у,(х) + а2у2(х) + ... + <*пуп(х); (а < * < I),
где at, с2, ..., с„; ^, 62, ..., ^„ — постоянные.
Непрерывность G и -ее первых и — 2 производных по л: в точке ?
и условие B) накладывают на п разностей сг — Ьг — at n условий
= О,
п E) = О,
О,
Определитель системы равен значению вронскиана W(yu у2, ... ,уп)
в точке ?, а потому отличен от нуля. Поэтому числа сг определяются
из этой системы одним и только одним способом.
Если положить Vi{y) = Ai{y)-\-Bi{y\ где
A- CV) = ЧУ (в) + «?У (в) + • • • + aJ-V"-4 (в).
и записать, что G(jc, ?) удовлетворяет п условиям t/<(y) = O (/ = 1,
2, ..., и), то получится, что
аЛ b>i) + М* Ов) + • • • + «i
0 («=1. 2, .... «).
Это можно записать также в следующем виде
Ой)
Определитель матрицы ||?/$Суй)||" (', fe = l, 2, ...,и) этой си-
системы отличен от нуля, так как функции yv _y2, ..., уп образуют
фундаментальную систему решений уравнения L (у) = 0, а система E)
несовместна (§ 2, п. 1„б"); следовательно, эта система однозначно
определяет значения величин bv Ьй, ..., Ьп, а так как ai^=bi — с{,
то и величины аг определены однозначно.
Тем самым сформулированная выше теорема доказана.
$ 3. Функция Гринй Ш
б) Полезно указать соотношение между функцией Грина неко-
некоторой системы и функцией Грина сопряженной системы.1)
Предположим снова, что система E) несовместна. Тогда и сопря-
сопряженная с ней система
ад = 0 (/-1, 2, ..., я)
также несовместна (§ 2, п. 3„б"). Обозначим через G(x, S) функ-
функцию Грина системы F).
Так как коэффициент при z^ в выражении M(z) равен (—1)про,
то __
?)—G^_x(e—о, еУ=(—iOPo(9e)-
Возьмем в промежутке (а, Ь) две точки, ?j и ?.2, предположив, для
определенности, что ?j ^ ?2. Тогда, интегрируя формулу E) из § 2,
п. 2, получаем, что
ь
где >> = G (л:, ^), z — G (х, $2).
Функция ${х, z) имеет разрывы лишь в точках ?j и Еа, а так как,
п силу E) и F) (см. A4), § 2, п. 2), имеет место равенство
то
Принимая во внимание, что по формуле G) из § 2, п. 2, все ела-.
гаемые в выражении <^{у, z) непрерывны, за исключением слагаемого
получаем, что
откуда и вытекает основное соотношение
О («1, У = О (*», «,)¦ G)
J5 Мы предполагаем здесь, что функциир^п~г) (л:) A = 0, 1,.... я) непре-
непрерывны в [а, Ь].
2) Заметим, что если система самосопряжена (см. § 2, ,п. 4) и имеет чет-
четный порядок, то U (x, J) = G (х, 5), если же система самосопряжена и имеет
нечетный порядок, то О (х, ?) = — О (лг, Е).
238 /Vi. V. краевые задачи Ьлкуравнений п'-го Порядка (п
I, i i -'
в) В частности, функция Грина самосопряженной системы четного
порядка симметрична
(в предыдущем пункте мы установили это свойство в одном частном
случае); а функция Грина самосопряженной системы нечетного порядка
кососимметрична
3. Запись в виде интеграла решения неоднородной дифферен-
дифференциальной системы, имеющей единственное решение, а) Рассмотрим
линейную неоднородную дифференциальную систему
, (8,)
(У) = W И + <4'У («)+••• + а?" V"
(/=1, 2, .... я).
Предположим, что функции р0, plt ..., pn-v Pw r(x) непрерывны
в [a, b], ро{х)ФО в [а, Ь], формы Uu t/2, ..., Un от переменных
У (а), У (а) У" И; у{Ь), у'{Ь), ..., уГ-Ъ{Ь) линейно неза-
независимы, а Oj, pi} ifj — постоянные величины.
, у%, ..., уп — фундаментальная система решений уравнения
а у0 — частное решение уравнения (8j); тогда общее решение уравне-
уравнения (8j) имеет вид
У — Wi + ^^2 + • • • -f- спУп +Уо,
где <?!, с2, ..., сп—произвольные постоянные. Это решение удовле-
удовлетворяет условиям (8^, если
«2^1 СУ2) + •; • + Cn^l CVn) = Tl — Vl
¦(9)
По теореме Кронекера — Капелли эта система, а, следовательно,
и система (8j), (82), имеет решение тогда и только тогда, когда
ранг матрацы
/i O2) - - •
равен рангу матрицы
i> 3, Функция tpuud 239
при этом, если ранги этих матриц равны п—k, то решение
системы (8\), (82) линейно зависит от k произвольных постоянных.
Рассмотрим наряду с системой (8j), (82) соответствующую ей
однородную систему у получающуюся, если положить г (л:) = О, f» = О
(i = l, 2, ..., я),
= 0 (i = l, 2,..., я). J
Заметим, что система (8j), (82) имеет одно и только одно решение
в том и только в том случае, когда ранги матриц (ЮД A02) равны п.
Но в этом случае система A1) несовместна, откуда следует, что для
того, чтобы система (8j), (8^) имела одно и только одно решение,
необходимо и достаточно, чтобы соответствующая ей однородная
система A1) была несовместна.
б) Предположим, что в (88) fi = 72 =•••!= \п — 0, т. е. рас-
рассмотрим систему
О = 0(/=1, 2, ...,«)• / К ]
Предположим, кроме того, что соответствующая ей однородная си-
система A1) несовместна.
Докажем, что если функция Грина системы A1) равна G(x, E),
то решение системы A2) дается формулой
A3)
В самом деле, в силу непрерывности в [а, Ь\ производных функ-
функции G(x, 6) по х до п — 2-го порядка включительно, имеет место
формула
ь
/^* = 1. 2,..., «-2). A4,)
а
Далее,
240 Гл. V. Краевые задачи для уравнениЬ. п-го порядка
откуда
a
Аналогичным образом получаем, что
ь
6
=f J д(*п 6> г F) Л + г (а:) [О^-, (х + 0, дг) — ОЛ„_, (а:—О,
и, следовательно,
Из формул A4^, A42), A43) следует, что
ъ
? 00 = J" Z, [О (-V, 6I г F) <# + л (а:) =
а
Наконец,
ь
= 0 (i=l, 2, ...,«),
чем и завершается доказательство того, что A3) является решением
системы A4).
в) Пусть вообще система (8^, (82) имеет единственное реше-
решение, а потому соответствующая ей однородная система A1) несо-
несовместна.
Если снова обозначить через G(x, l) функцию Грина соответ-
соответствующей однородной системы A1), а через Ot(x)—решение си-
системы
, (Gt) =..,== ?74_i (G,) = Ui+1 (Gt) = ... = Un (Gt) = 0,
= 1 (/=1, 2, ..., я)
(определенное и существующее в силу „а"), то таким же образом,
как и в „б", можно доказать, что решение системы (8j), (82)
имеет вид
ь
y(x) = $G (х, I) г (Е) d% + т&, [х) + T2G2 (*)+...+ Т„ОН (а:).
3. Функция Грина 241
4. Решения дифференциальных систем как решения инте-
интегральных уравнений Фредгольма второго рода. Рассмотрим диф-
дифференциальную систему
где L{y), Ui(y), r(x), at, pit ft удовлетворяют сделанным в п. 3„а"
предположениям, и предположим, кроме того, что функция g(x) не-
непрерывна в [а, Ь\.
Если предположить еще, что система
1
,..., и)/
несовместна, и обозначить через G(x, S) ее функцию Грина, то из
полученных в п. 3 „в" результатов следует, что решение у(х) си-
системы A5) удовлетворяет интегральному уравнению
и обратно.
Если положить
К(х,
то выражения /С(лг, 6), /(х) могут считаться известными, если
известно общее решение уравнения L(y) = Q. Мы получаем тогда
для у (х) интегральное уравнение Фредгольма второго рода
ь
f K(x,
A6)
Отсюда следует, что если система A1) несовместна, то си-
система A5) и интегральное уравнение A6) эквивалентны в том
смысле, что любое решение системы A5), при условии, что такое
решение существует, удовлетворяет уравнению A6), и обратно1).
5. Линейные системы, зависящие от параметра. Собственные
значения и собственные функции, а) По аналогии с гл. IV,
*) Относительно сведения дифференциальных систем к интегральным
уравнениям в более общих случаях см. Пиконе [3].
16 Зак, 527. Дж. Сансоне
242 Гл. V. Краевые задачи для уравнений л-го порядка (л > 2)
перейдем теперь к рассмотрению дифференциальных систем, содержа-
содержащих параметр, причем сначала мы остановимся на случае однородных
систем.
Пусть дана дифференциальная система
L{y) + \y sap0*?
(« = 1, 2 и),
A7)
где р0, pv ..., рй—непрерывные в [а, Ь] функции от х, независя-
независящие от параметра X, ро(х) ф 0 в [а, Ь], а и р — постоянные, а формы
(/j, i/2, ..., Un, рассматриваемые как формы от у (а), у'(а), ...
..., Уп~1)(а); у{Ь), У(Ь), ..., у(п~^{Ь), — линейно независимы.
Если система
^iO0 = O (* = 1. 2, ..., и)
несовместна, a G(x, E)— функция Грина этой системы (п. 2), то,
в силу результатов п. 4, система A7) эквивалентна однородному
интегральному уравнению второго рода
[g (х) = — X, г (х) == 0, fj = fa — • • • = In = 0J»
б
_у (лг) + X f G (дг, 5) j; (E) rf? = 0. A8)
а
Если положить
1, ^,) О(Ei, У... 0E,, у
у...
то из общей теории интегральных уравнений известно, что
о о
IP)
является целой трансцендентной функцией от X и что уравнение A8)
имеет решения тогда и только тогда, когда X является нулем
D(X) т. е. корнем уравнения
или, как говорят, если X является собственным значением (см., на-
например, Гурса [1], т. Ill, гл. XXXI, стр. 49).
§ 3. Функция tpuHu 243
Из так называемой второй теоремы Фредгольма следует, кроме
того, что если X является корнем порядка т уравнения D (А) = О,
то уравнение A8), а потому и система A7), имеет k линейно неза-
независимых решений, где 0 < k <^ т, или, как говорят, существует k
линейно независимых собственных функций, удовлетворяющих этой
системе (система A7) имеет поэтому индекс совместности k).
Следует заметить, что для заданной дифференциальной системы A7)
не ;всегда существуют соответствующие ей собственные значения и
собственные функции; в следующем пункте мы покажем, что для
самосопряженной системы четного порядка существует бесконечное
множество собственных значений, причем все они действительны.
б) Рассмотрим теперь неоднородную дифференциальную систему
, 2, .... и),
A9)
где коэффициенты р0, pv ..., рп и формы ?/« удовлетворяют сде-
сделанным в „а" предположениям; предположим, кроме того, что функ-
функции рг (»=1, 2, ..., и) имеют в [а, Ь\ производные до (и — i)-ro
порядка включительно, а функция г{х) непрерывна в [а, Ь].
Если система
= 0 (/=1,2,..., п) ) B0)
несовместна, a G(x, S) — соответствующая ей функция Грина, то
система A9) эквивалентна интегральному уравнению (п. 4)
ь
у(х)-\-\$О (х, 1)у F) <& =/ (*), B1,)
а
где
ь
г(9*. Bi2)
а
Сделаем еще предположение, что система
«/|О0 = О (* = 1, 2,..., и)
при заданном значении X несовместна, иными словами, что X не
является собственным значением; в силу результатов п. 3 „а" си-
система A9), а потому и уравнение B1,) имеют в этом случае одно и
только одно решение.
16*
244 Гл. V. Краевые задачи длА урйвнёнииЪ-го порядки (п
Из предположений, сделанных о системе B2), следует несовмест-
несовместность сопряженной с ней системы (§ 2, п. 3 „б")
,(z) = 0 (/=Ы, 2,..., в). J ^ }
Обозначим через Г(л:, ?; X) функцию Грина системы B3).
Если положить в формуле E) из § 2 у = G(x, ?,), г ==Г(х, 1%; к)
и повторить рассуждения из п. 2 „6м этого параграфа, то полу-
получится, что
и потому
ь
X J G (лг, 5,)Г (*, ?2; X) rfx = G ^, &,) — Г F,, 52; X). B4)
а
Из этого равенства легко следует, что при рассматриваемом зна-
значении X интегральное уравнение B1,) имеет решение
ь
%, x; k)f®<& B5)
а
В самом деле, уравнение B4) является уравнением резольвенты для
интегрального уравнения B1 х) (см. Гурса [Ц, т. Ill, гл. XXX,
стр. 23).
Иным образом это можно доказать следующим рассуждением:
заменим в B1 х) х на ?, умножим обе .части равенства на ХГ(?, х; X)
и проинтегрируем от а до р, тогда получим, что
ь ь ъ
Х/Г(?, х; k)y(l)dl-\-l* J $0A, у Г F, х;
х;
и, в силу B4),
ь
1 Г т> /с ~*
а
5. Функция Грана 245
а потому
ь ъ
1, лг;
в. а
откуда и следует, что B5) дает решение нашего уравнения.
6. Линейные самосопряженные системы четного порядка. Раз-
Разложения в ряды по собственным функциям и теорема Гиль-
Гильберта— Шмидта, а) Рассмотрим снова систему
(Л 00 = О A=1, 2, .... и), J
изучавшуюся нами в п. 5 „а", и предположим, что коэффициенты pt
в L(y) и формы Oj(y) удовлетворяют предположениям, сделанным
нами в п. 5„а",_яб". Предположим, кроме того, что п четно,
а система
?00 = 0, I
иЛУ) = 0 .(_/=!, 2, .... и) J
— самосопряжена и несовместна (т. е. что Х = 0 не является соб-
собственным значением).
Как мы уже видели, система A7) эквивалентна однородному инте-
интегральному уравнению второго рода
ь
?(*) + */О(х, ЕЬЧ6)<Й = 0 .A8)
а
с симметричным ядром G(x, l) (п. 2 „в").
Ядро G(x, l) замкнуто, то есть не существует' непрерывной
функции'г (лг), не обращающейся тождественно в нуль, и такой,- что
для любого х из [а, Ь\, выполняется равенство
, . ь
В самом деле, в противном случае функция у = ty (x) [ га 0] удовле-
удовлетворяла бы системе (п. 3 „б")
L(y)=r(x) \
и,(у) = 0 A=1,2,..., и):]
Но так как /,(У)=эО, то мы имели бы г(х)=гО, вопреки предпо-
предположению.
Из иззестных результатов .теории интегральных уравнений сле-
следует существование бесконечного ыщше$т$аК-собственных.зяаценцft.
246 Гл. V. Краевые задачи для уравнений п-го порядка (п > 2)
для которых уравнение A8) имеет решения, не обращающиеся
тождественно в нуль; все эти собственные значения действительны,
и их можно записать в виде последовательности, члены которой не
убывают по абсолютной величине, причем каждое Л выписывается
столько раз, сколько ему соответствует линейно независимых соб-
собственных функций.
Если обозначить через <pN собственную функцию, соответствую-
соответствующую собственному значению Я#, то
ь
= 0 (ЛГ=1, 2, ...). B6)
Кроме того, можно считать, что последовательность {<pN(x)} обра-
образует ортогональную и нормированную в [а, Ь] систему функций
6 ь
% B7)
J) См. Петровский И. Г. [2], стр. 77. — Прим. перев.
2) Второе из равенств B7) для случая, когда собственные функции <(>#
и 9дг соответствуют различным собственным значениям Х^ и Хм, легко дока*
зывастся следующим образом. Имеем
/ О (х, 5) <рж F) <К + ХуХя<рж (дг) J G (л:, 5) <tN E) <%
а а
Ь
а
Ь Ь Ь Ь
Тсс ее
¦¦ — Х^ХЖ I J G (x, I) <fjf (х) <рд E) djrdS— I I (
Заменяя в последнем интеграле х на ? и принимая во внимание свойство
симметрии G (*, 5), получаем, что
ь
- хж) J Чц (х) <РЖ (дг) йд; = О,
откуда, при Ху — Хж =jfe 0, и следует второе из равенств B7).
В п. 2 из § 4 мы дадим доказательство Тонелли существования соб-
собственных функций интегрального уравнения B6), основанное на прямых
методах вариационного исчисления.
§ 4. Краевые задача и вариационное исчисление 247
Возвращаясь к системе A7), получаем, что она имеет не обра-
обращающееся тождественно в нуль решение тогда и только тогда,
когда параметр К совпадает с одним из собственных значе-
значений \N, и что если в последовательности [KN) имеется k чле-
членов, равных \N, из которых \N имеет наименьший индекс, то все
решения системы A7) при k = kN имеют вид
У =
где cv ca, ..., ck — произвольные постоянные.
б) Относительно разложений в ряды по собственным функциям
справедлива следующая теорема Гильберта — Шмидта: любая функ-
функция F{x) вида
ъ
B8)
где функция h E) интегрируема вместе со своим квадратом
в [а, Ь], разложима в ряд Фурье вида
B9)
где
ь
Г=1, 2, ...), C0)
причем ряд B9) сходится абсолютно и равномерно на [а, Ь].
Относительно этого результата мы также отсылаем читателя
к учебникам по теории интегральных уравнений1).
§ 4. Краевые задачи для самосопряженных систем
четного порядка и вариационное исчисление
1. Экстремальное свойство собственных значений, вытекаю-
вытекающее из теории интегральных уравнений. Мы свели отыскание
собственных значений самосопряженной дифференциальной системы
A7) из'§ 3, п. 6 „а" к отысканию собственных значений интеграль-
интегрального уравнения A8) из § 3, п. 6 „а". Эти собственные значения
обладают найденным Гильбертом (см. Гильберт [1], стр. 78) класси-
классическим экстремальным свойством, выражающимся следующей теоремой.
Пусть симметрическое ядро К(х, у) [К(у, х) — К(х, у)] положи-
положительно (отрицательно) определено или положительно (отрицательно)
полуопределено в квадрате с противоположными вершинами (а, а),
См., например, Петровский И, Г. [1]. стр. 84,—Прим. перев.
248 Гл. V, Краевые задачи для уравнепий п-го порядка (п*>2)
id, b), иными словами, пусть для любой функции у(х) с интегри-
интегрируемым квадратом
ъ ь
/[?] = f $ К{х, у) <j> (*) <j> (у) dxdy > 0 {< 0} О-
а а
Пусть {1т} — последовательность собственных значений инте-
интегрального уравнения
' Ь
и {«ря» (¦*) } — соответствующая ортогональная и нормированная после-
последовательность собственных функций
ь
9т№ = *т / К{Х, у)<?
а
ь ь
При этих предположениях собственные значения \т образуют
последовательность с положительными (отрицательными) членами,
причем мы можем считать, что \т расположены в неубывающем (не-
возрастающем) порядке.
Тогда 1/Xj, т. е. обратная величина первого собственного значения,
равна наибольшему значению интеграла /[<р] на множестве всех
функций <?{х), интегрируемых вместе со своим квадратом в [а, Ь] и
таких, что
ь
*{x)dx=L
Это наибольшее значение достигается тогда и только тогда, когда
функция <р(х) является линейной комбинацией с постоянными коэфф-
коэффициентами собственных функций, соответствующих собственному
значению \v
Точно так же, если Хт_г < Х„,, то обратная величина l/lm m-rq
собственного значения равна наибольшему значению / [<р] на множег
J) Если имеет место знак > (О, то ядро называется определенным,
если же возможны как знак > (<)• так н знак = (для функций, не рав-
равных тождественно нулю), то полуопределенным. Эти определения сохра-
сохраняются и в случае, когда ядро К (х, у) несимметрично.
8) Очевидно, что от этого уравнения можно перейти к уравнению A8)
из § 3, если.доложить-К\х, у) = -r-G(Xi у).
$ 4. Краевые задачи и вариационное исчисление- 249
стве всех функций, интегрируемых вместе со своим квадратом в [а, Ь],
для которых выполняются условия
ь ь
JV(*)d*=l, J <P(x)<Pr(x)dx = 0 (r = l, 2, .... т — 1).
a a
Это наибольшее значение достигается тогда и только тогда, когда
функция <f{x) является линейной комбинацией с постоянными коэф-
коэффициентами собственных функций <рт, sWi» • • • > соответствующих
собственному значению Хт [Х„, = Хт+1 = ].
2. Доказательство Тонелли существования собственных зна-
значений с помощью прямых методов вариационного исчисления.
Сформулированное выше предложение Гильберта выражает характе-
характеристическое свойство собственных функций, а потому, оставляя
в стороне теорию интегральных уравнений, можно установить суще-
существование собственных функций для интегральных уравнений с сим-
симметрическими ядрами (и для соответствующих самосопряженных диф-
дифференциальных систем) при помощи вариационного исчисления. Мы
изложим здесь доказательство Тонелли существования собственных
функций, основанное на прямых методах'); для простоты поло-
положим а = 0, b = 1, а для большей общности будем понимать инте-
интегрируемость функций в смысле Лебега.
а) Пусть функция К{х, z) интегрируема вместе со-своим ква-
квадратом К2(х, z) в квадрате Q с противоположными вершинами (О, О)
и A, 1) и не эквивалентна функции, тождественна равной нулю в Q.
Обозначим через (L2) класс функций, интегрируемых вместе со своим
квадратом в [0, 1] и таких, что
О
и рассмотрим для таких функций интеграл
11
/[?] = // К(х, z) <j> (ж) <j> (z) dx dz,
о о
Для рассмотрения экстремумов 1[у\ в (Z2), рассмотрим класс (А)
абсолютно непрерывных в [0, 1] функций у(х), имеющих почти всюду
производную с интегрируемым квадратом, и удовлетворяющих усло-
условиям
J2rf*<l. A)
Относительно изложения этого вопроса jcm. Тонелли [2].
250 Гл. V. Краевые задача для уравнений п-го порядка (п
Рассмотрим в классе (А) интеграл
1 1
= / J *(*• *>? №У W dx dz-
0 О
Тогда по неравенству Буняковского имеем
11 11
/2 l/l <f f^(x,z)dxdz f f у'2 (х)/2 (z) dxdz4?
0 0 0 0
1 1
z)dxdz,
о о
откуда видно, что интеграл /[/] ограничен в (А), а, следовательно,
его экстремумы в этом классе конечны.
б) Докажем, что /[/] является непрерывным функционалом в (А),
в том смысле, что для любого е > 0 можно найти такое 8 > 0, что
для любых двух функций у (х) и у0 (х) из (А), всюду удовлетво-
удовлетворяющих условию \у(х)—Уо(*)\<Ъ> имеет место неравенство
И/] П1]\'<
Положим дли целого положительного п
Кп(х, г) = К(х, г), если —
Кп(х, z) = — и, если К(х,
Кп(х, z) — n, если К{х,
Тогда, каково бы ни было у(х) из (А),
1 1
| — f f Кп(х, г)у(х)у'(z)dxdz\ =
о о
11 11
п] уГ (х)уГ {z) dx dz
I{)
0 0 0 0
dx dz
)
Bn
где через Еп обозначено множество тех точек, в которых К(х, г) <
< — и или К(х, z) > и.
В силу интегрируемости К2(х, z) в Q, можно найти настолько
большое л, что
' § 4. Краевые задачи и вариационное исчисление 251
а потому для всех у {х) из (А)
1 1
|/[/]-//*-(*, z)y'(x)y'(z)dxdz\<^.
о о
Пусть теперь Pv (х, г), v = 1, 2, ... — такая последовательность
многочленов, что |Р,(#, г)|<и-}-1 и Рч(х, г) почти всюду схо-
сходятся при v->oo к К-(х, г) (см. Тонелли [3], стр. 19—20).
Тогда при любом v и любой функции у(х) из (А) имеем
11 11
| J J К- (х, г)у (*)/(*) dxdz- f J Pv (x, г)У (*), / (г) rfx^г | <
0 0 0 0
1 1
о о
Если v достаточно велико, то
о о
а потому для всед; ^ (д:) из (А)
11 11
| / j К-(х, г)У{х)У (z)dxdz-jj Р-(х, г)у (х)уг(г)dxdz
0 0 0 0
|
0 0 0 0
и, следовательно,
1 1
0 0
Пусть теперь у (х) и у0 (х) — какие-либо две функции из (А), для
которых в [0, 1] всюду имеет место неравенство \у(х)—Уо{х)\<.Ь.
Тогда
11 11
А = J J Р-{х, г)у (х)У (г)dxdz-$ Jp_ (дг, z)y'o(х)у'о(г)dxdz»
0 0 0 0
1 1
= fjP- (x, z) {у' {х)У (г)-^ (*)/ (г) +у'о {х)у' (г)-
1 1
= J fP-(x,
о о
1 1
v
в О
252 Гл. V. Краевые задачи для уравнений п-го порядка (п~>2)
1 1
?)—y'0(z)}dxdz =
о о
1 1
= $/(z)dz $Р-(х, z){/(x)-y'0(x)}dx
о о
1
о о
Интегрируя по частям, получаем х), что
1
p.(x, z){y'(x)-/0(x))dx =
\?РАХ, z)dx,
-(x, z){/(x)-y'0(x))dx
где нерез Z./2 обозначено положительное число, ббльшее, чем все
значения функций 1 Р_(х, у)|, j^Р_(х, у)|, |щР_{х, у)\ в Q.
Отсюда следует, что
¦\*\<bL{f\/(z)\dz+$\/0(x)\dx}.
о о
Но
. о о
а, следовательно,
| Д | < 28L.
х
Напомним, что если у(х) абсолютно непрерывна, то \y'(x)dx=s
о
См. Натансон И. П. [2J,CTpvЩ—Прам. ред.]'
о о
1 1
$ 4. Крйевыё задачи и вйрййционкоё исчисление 253
Поэтому, если 8 < e/6L, то
1 1
\П/]-П/0\\<
+1ПУ0)- J / Р-(х, г)у'о(х)У0(г)dxdz\ +
о о
1 1
-f | J J P- (х, г)У (х)У (z) dxdz —
-J fp.(x, z)yo(x)y'o(z)dxdz\<z.
о о
1 1
о о
в) Установив это, обозначим через М верхнюю грань значений
1[уг] в классе (Л). Пусть ^(д:), у2(х), ¦ —максимизирующая по-
последовательность для 1\У\ в (Л), т. е. такая последовательность
функций из (Л), что верхняя грань последовательности {/ [у'п]} равна М.
Если Е—совокупность непересекающихся отрезков \аи Ьу\, [а2, Ь2\,
••-, [ат Ь8] из [0, 1], то
\ \[/(*).\dxY<C Ux
4 J в
r=1 4 J в в
(mes? — мера множества Е). Так как уп@) = 0, то из доказанного
следует, что функции уп{х) равностепенно абсолютно непрерывны и
равномерно ограничены в 10; 1]. Поэтому из последовательности
функций {уп (х)} можно выбрать подпоследовательность (которую дла
простоты мы будем обозначать так же, как исходную последователь-
последовательность), равномерно сходящуюся к такой абсолютно непрерывной функ-
функции Уоа (X), ЧТО ^оо @) = 0 J).
1
Из полунепрерывности снизу2) интеграла Г у2 dx и из второго
о
соотношения формулы A) следует, что
J) См. примечание *) на стр. 38.
2) Функция /(дг) называется полунепрерывной сверху (снизу) в точке а,
если для любого е>0 существует 8>0, такое, что из \х—я|<С8 следует
неравенство f(x) —/(я) <. е (f(x) —/(я) > — е). — Прим. ред.
254 Тл. V. Краевые зйдачи ЬлА урйвнениЬ п-го поряЬкй in > 2)
а потому ут (х) принадлежит классу (Л), и, по непрерывности 1[У\
в (Л), получаем, что lim 1[у'п] = М,
Поэтому у^(х) дает абсолютный максимум для /[у*] в (Л).
1
Предположим, чтоМ > 0 '), и докажем, что тогда \y'lo(x)dx=l.
о
1
В самом деле, равенство j _y'L (x) dx = 0 не может иметь места, так
о
как тогда почти всюду в [0, 1] выполнялось бы равенство ут (х) = О,
из которого следует, что /[^оо1 = Л^ = 0; если же выполнялось не-
равенство Г у'%, (х) dx < 1, то, полагая
О
мы получили бы, что
сЧ [у'т] =
а это невозможно, так как функция су^, (х) принадлежит классу (Л).
Следовательно,
1
J /o
и функция .уоо(*) дает максимум для /[<»] в классе (Z.2), так как
максимум /[«] в (L2) не может превышать максимума / [у'\ в (Л).
В самом деле, каждому элементу у(х) из (L2) соответствует в (Л)
элемент
Итак, мы доказали существование абсолютного максимума
в (L2), при условии, что Му>0.
Поэтому, если верхняя грань значений /[<»] в B.2) положительна,
то существование указанного максимума доказано. В частности, это
х) Можно доказать, что верхняя грань / [<р] в (Z.2) не может быть отри-
отрицательной (см. Тонелли [3], стр. 7).
§ 4. Краевые задача и вариационна исчисление 255
существование имеет место, если ядро К(х, г) положительно опре-
определено, а также если оно лишь положительно полуопределено.
Аналогичные заключения можно сделать об абсолютном минимуме,
если нижняя грань значений /[<»] в (L2) отрицательна; поэтому если
/ [<»] принимает в B.2) как положительные, так и отрицательные значе-
значения, то /[«] имеет в B.2) как максимум, так и минимум.
г) Предположим теперь, что ядро К{х, г) симметрично, причем
оно интегрируемо вместе со своим квадратом К2(х, г) и не экви-
эквивалентно функции, равной почти всюду нулю.
Допустим, что максимальное (или минимальное) значение /[<»]
в (Lg) принимается, если а> = <р0, и что МФО. Покажем, что в этом
случае 90W является собственной функцией для К(х, г).
Пусть g(x)— любая функция, интегрируемая вместе со своим
квадратом в [0, 1]. Рассмотрим функцию ?о+'г1(Ро+е?г> гДе "Ч и
е—независимые от лг параметры. Эта функция интегрируема вместе
со своим квадратом. Определим ч\ как функцию от е, ri = ti(B),
таким образом, что
о
причем 7i@) = 0. Это возможно, так как
1
1 1
= 2 J <fotoo + rRo+*g)dx = 2 jl + TJ + S J <?ogdx},
о о
и, следовательно, производная равна 2(^0) при е = 0, 7i = 0. Таким
образом, функцию т|(е) можно единственным образом определить
в окрестности точки е = 0, причем она там непрерывна и дифферен-
дифференцируема. Кроме того,
V@>—— [2 f ^(?o + ^o + eg')^/2{l + 71 + ef vogdx\\
I J V J 'J,=o,4=
=o,4=o
l
= — j g<sodx.
о
Так как функция «po + 'rl(e)(Po+s5' принадлежит к классу (Z2),
когда е находится в некоторой окрестности нуля, то по максимальному
Щ Гл. V. Rpaeeui задача для уравнений п-го пдрядка (п>2)
свойству функции <р0 имеем
. о о
Но так как К(х, z) = K(z, х), то
о о
1 1
о о
1 11
}
о оо
или, полагая
А. X
0 = fJK(x,z) [<р0 (*) g (г) + <р0 (х) <р0 (г) ч' @)] <f* <fe =
К(х, z)uo(x)g{z)dxdz —
1 1
} {J J К(Х' г)9о ^ ^ ^ dxdzl,
о о
А= Г Г/С^» z)t9o{x)tD(j{z)dxdz ( = M),
J J
о о
11 1
Яр
К(х, z) а>0 (г) g(x)dxdz — А I «
0 0 О
1 1
0 = J IJ К(х, z)vo(z)dz — h<p0 (x) >
о о
В силу произвольности g(x), из последнего равенства следует, что
почти всюду в 10, 1] выполняется равенство
K(x, z)<po(z)dz — h<po(x) = O. B2)
В самом деле, если бы на множестве Е из [0, 1], имеющем поло-
положительную меру, левая часть в B2) была положительной, то, полагая
g(x) равным этой левой части в ? и равным нулю вне Е, мы полу-
получили бы, что интеграл в Bt) положителен, а не равен нулю; анало-
аналогичное рассуждение показывает, что левая часть в B2) не может
быть отрицательной на множестве положительной меры из 10, 1].
Если положить
1
$ 4. Краевые задачи и вариационное исчисление 257
то из Bg) следует, что почти всюду <в0 (х) = <р0 (х), а потому для
всех х из [0, 1] имеем
J К(х, г) % (г) dz — й<р0 (х) = 0.
о
В силу того, что А = М ф 0, функция а>о (дг) не может почти всюду
равняться нулю, а потому и <»о(-*0 не может почти всюду равняться
нулю. Отсюда следует, что функция »0(л;), доставляющая максимум
интегралу / [ад] в (L2), является собственной функцией. Соответствую-
Соответствующее собственное значение равно
л 1--!
0 h ~ M '
Но, если X является собственным значением, а ^(д;) — соответ-
соответствующей собственной функцией, причем
ТО
11
0 0 О
и, предполагая М > 0, получаем, что
1 1
Поэтому, если ЛТ > 0, то Хо является наименьшим из собственных
значений.
3. Экстремальное свойство собственных значений, выводимое
из теории дифференциальных систем. Доказательство Пиконе.
а) Как мы видели в предыдущем параграфе (п. 4 и 5), краевые за-
задачи для дифференциальных систем можно изучать при помощи
теории интегральных уравнений и, как было показано в п. 1 и 2
этого параграфа, эти задачи можно непосредственно связать с вариа-
вариационным исчислгнием.
Первые приложения вариационного исчисления к граничным за-
задачам для дифференциальных систем второго порядка были даны
Мезоном [1]. Указания на позднейшие работы читатель может найти
в недавней работе Рида [1], к которой приложена библиография по
17 Зме. S27. Дж. Сансоне
258 Л*. V. Краевые задачи для урйененйи п-го порядки (п |> й)
исследованиям о дифференциальных системах и вариационном исчис-
исчислении; мы ограничимся указанием на то, что при помощи методов
вариационного исчисления Блисс и Шенберг [1] распространили на
линейные самосопряженные дифференциальные системы второго по-
порядка теоремы отделения, сравнения и осцилляции.
Обратно, установлэно, что из теорем существования для диффе-
дифференциальных систем могут быть выведены теоремы вариационного
исчисления; здесь мы, основываясь на результатах гл. IV, § 5 и
следуя Пиконе *), непосредственно докажем экстремальное утверж-
утверждение гильбертовского типа (см. п. 1) для собствэнных функций
некоторой дифференциальной системы второго порядка.
б) Пусть функции 8 (х), Ь' (х), А (х) непрерывны в [а, Ь], 6 (х) > О,
А (х) > 0, и пусть Хо, Kv ..., А„, ... — последовательность соб-
собственных значений дифференциальной системы
= 0, C)
<?»(«) = ?n(b) = 0. D)
Так как элементы последовательности {А„} положительны, то мы
можем считать, что они расположены в порядке возрастания (см.
гл. IV, § 6, п. 6) и что собственная функция <?„(*), соответствую-
соответствующая собственному значению Хп, имеет в (a, b) n и только я нулей.
Рассмотрим теперь класс (С) функций и (х) следующего вида:
функции и (х) абсолютно непрерывны в [а, Ь\, обращаются в нуль
в тех же точках, что и уп(х), а производная этих функций
(существующая почти всюду) имеет интегрируемый квадрат и
существует в точках, где <?„(¦*:) обращается в нуль. Положим
для функций этого класса
ь
In W = J [в (gJ- M«2] dx. E)
а
а
Покажем, что 1п \и] ^> 0, причем знак равенства имеет место
тогда и только тогда, когда u{x) = k®n{x), где k — некоторое
число.
В самом деле, функции и/<»п, и2/<»п конечны и непрерывны в [а, Ь\,
причем Jiff = 2—— — —
dxfn 4ndx ^п
а, в силу C),
1) Пиконе [2], [4]. Здесь мы использовали § 1, 2, 3 второго мемуара.
Относительно минимального свойства собственных значений некоторых
уравнений четвертого порядка см. Чиммиио [1], стр. 52—58.
4. краевые- зйЬйЧи й edpaatfitottHbe йсЧасМНйб
Интегрируя справа по частям, получаем, что
и так как первый член в правой части равен нулю, то
ь ь ъ
а, следовательно,
G)
Из F) следует, что знак равенства в этой формуле может иметь
место тогда и только тогда, когда почти всюду
di <р„ dx —и*
Отсюда следует, что, каково бы ни было х,
а потому, в силу непрерывности — -j^, формула (8) справедлива
для всех точек из [а, Ь\. Но тогда в любом интервале, ограничен-
ограниченном двумя последовательными нулями функции «„, вронскиан функ-
функций и и <»п равен нулю, а потому эти функции отличаются лишь
постоянным множителем; так как в точках, где <»„ обращается в нуль,
tp'n Ф 0, то во всем отрезке [а, Ь\ должно иметь место равенство
и = k<pn, что и требовалось доказать.
в) Из доказанной в „б" теоремы мы выведем вариационную
характеристику собственных функций <»„; для этого мы докажем
предварительно следующую лемму.
Если ап1, оя>2, ..., оЛ> „ являются лежащими внутри (а, Ь) нулями
функции <?п{х), то определитель
<Ро («в, i) «Ро («п. а) • • • <Ро («», п)
D _ ?1 (ffln. l) ?1 («п. 2) • • • ?1 К,»)
отличен от нуля.
17*
2бО /л. V. краевые задачи для ураененпи п*го порядка (п >й)
Пусть, в самом деле, D = 0; тогда существует линейная комби-
комбинация
хоть один коэффициент которой отличен от нуля, обращающаяся
в нуль кроме точек а и Ь еще в и точках ап>1, а„B, ..., а„)П, a
потому, в силу „б",
Ь я-1 Ь »-1
а Л=0 а Л=0
Но при h Ф k имеем (гл. IV, § 6, п. 7)
ь
и потому из (9) получаем, что
= S 4(К — К)\ А4dx
Так как Xfc—Х„ < 0, то co = Cj= ... =сп_1 = 0, вопреки пред-
предположению.
Теперь мы можем доказать следующую теорему: если функция у (х)
абсолютно непрерывна в [а, Ь\, обращается в нуль в точках а и Ь,
имеет производную в точках, где «„ {х) обращается в нуль, причем
производная этой функции (существующая почти всюду) имеет
интегрируемый квадрат, то, при условии выполнения п равенств
ъ ь ь
fAvoydx=fA<Diydx=... = j4<pn_,jy<f.* = 0, A0)
а ' а О
справедливо неравенство
Знак равенства может иметь место в том и только в том
случае, когда y = k<on, где k — некоторое число.
§ 4. Краевые задачи а вариационное исчисление 261
В самом деле, по доказанной только что лемме можно найти
п чисел Со, Cj, ..., си_! так, чтобы функция
обращалась на отрезке \а, Ь\ в нуль в тех точках, где обращается
в нуль функция <рп. Но тогда, в силу „б",
4N>o. (П)
Согласно A0)
ь n-i . „ и-1
ft=0
a ft=o а к=о
Но
откуда, интегрируя от с до 6 и принимая во внимание A0), мы на-
находим, что
/
а потому
Ь и-1 ч Ь п~1
а к=о ' а к=о
П-Х
к=о
и, следовательно, из A2) получаем -.
Согласно „б", 1п[ч))>1пЫ и, таким образом, 1п[у]>/„[«рп].
Теорема доказана.
г) Для того, чтобы читателю стала ясна руководящая нить про-
проведенных выше рассуждений, заметим, что уравнение
262 Гл. V. Краевые задача для уравнений п-го порядка (п">2)
ь 2
является уравнением Эйлера экстремалей для интеграла Г в (-j—) dx
а
Ь
при условиях Г/4и2</лг==1, и (а) = и (Ь) — О. В самом деле, это
а
Ь
уравнение для интеграла Г F{x, и, u')dx, где F=b(-?-\ —Ы(х)и2,
имеет вид
4. Одно интегральное неравенство. Применим доказанные выше
утверждения для вывода одного важного интегрального неравенства,
часто применяемого в анализе.
Если функция у(х) абсолютно непрерывна в [а, Ь], обра-
обращается в нуль в точках а и b и имеет производную с интегри-
интегрируемым квадратом, то
причем равенство может иметь место лишь в случае, когда
j> = csin , , где с — некоторое число (см., например, Харди,
Литтлвуд, Полна [1], стр. 219).
В самом деле, если положить вCN = 1,Л = 1 и заметить, что наи-
наименьшее собственное значение дифференциальной системы, у"-\- ки=0,
у (а)=у (Ь) — 0, равно ^ ==: «8/(*—а)> а соответствующей собственной
функцией является <р0 = с sin [it (x — a)/(b — а)], то результаты из
п. 3„б" сразу приводят к неравенству A3).
§ 5. Существование бесконечного множества
собственных значений для однородных
линейных дифференциальных уравнений
с постоянными коэффициентами
Рассмотрим, наконец, один класс несамосопряженных дифферен-
дифференциальных систем, для которых при помощи изучения общего решения
можно непосредственно вывести существование бесконечного" множества
собственных значений. Докажем следующую теорему (см. Сансоне [2]).
х) Для вывода этого уравнения используется так называемое изопериме-
трическое правило Эйлера. [См., например, Лаврентьев М. А. н Люстер-
ИЯК Л- А. [1], стр. 133—146. — Прим. перев.)
$ 5. Существование бесконечного множества собственных значений 263
Пусть дано однородное линейное дифференциальное уравнение
порядка « > 2,
у(») -j-Ply(n-i) +ХРау<»-2> + ... + крп_у+1рпу = О, (I)
где pv р2,..., pn_vpn — действительные числа, р$фО, рпф0,
и пусть выбраны п различных действительных чисел аи я2,...,
таким образом, что единственным решением уравнения
) О, B)
обращающимся в нуль в п — 2 точках а2, аъ, ...,an_j, является
нулевое решение, а уравнение
= О C)
не имеет кратных корней. Тогда существует бесконечное мно-
множество значений параметра \ (собственных значений), для каждого
из которых уравнение A) имеет отличное от нулевого решение,
обращающееся в нуль в заданных точках av az, ..., an_v an,
т. е. такое, что
У (ai) =УЫ — • - • ==.У (e*-i) =У (ап) — °- D)
Рассмотрим характеристическое уравнение для A) (см. гл. II, § 1,
п. 6 „г")
и изучим поведение его корней а1 (К), а2 (X), ..., ап (X), когда X -> -j-°°
или Л-> — оо.
Уравнение E) можно записать в виде
X «" + Т" «"
а потому при Л -> оо два корня at (Л), а2 (Л) уравнения E) стремятся
к бесконечности, а «—2 корней а8(Х), ..., ап(Л) стремятся к «— 2
(различным по условию) корням уравнения C). Поэтому
lim [a8 (X) + ... + «n W1 = —
Х->±оо
и, в силу E),
lim [«i
Х-> ±оо
Но
Ит а!(Х)а2(Х)= lim (~1)ПХ;?"Л= Нт
264 Гл. V. Краевые задачи для уравнений п-го порядка (п > 2)
а потому, если /?2 > О, то при X ~> ~\- оо имеем
«1W = Ti (*) + *h W. «2 (*) = Ti W - «Та W»
где
«» TiW = [—Pi+Pe/Pj/ т
а при A-*> — оо корни at(A) и <%2(X) действительны, причем
lim ct1(A)= 4-°°> lim <x2(X) = — oo.
).->¦-со >.->-oo
Положение дел меняется на обратное, если р2 < О.
Мы будет считать, что р2 > 0; тогда, при достаточно большом
положительном X, уравнение E) имеет два корня fi M —'Те М» для
которых выполняется соотношение F), и п—2 попарно различных
корней, распадающихся на г действительных корней
PiW. Р.(*),.••. PrW G)
и 2s — 2 комплексных сопряженных корней
Тз (*) ± *fc W T*-i W ±' Т28 W, (г 4- 2* = «)«
а потому общее решение уравнения (I) имеет при достаточно большом
положительном X вид
у (х, К) = cteb W ж cos y2 (*¦) л:+^сь W ж sin
1=1
где С|, с2, ..., с8; rfj, rf2, ..., rf8; 6j, 62, ..., br—произвольные по-
постоянные.
Если потребовать, чтобы решение у (х, К) удовлетворяло усло-
условиям D), т. е. обращалось в нуль в точках x=alt a2. ..., ап,
то получится однородная линейная система уравнений относительно
постоянных с, d, b, допускающая ненулевое решение тогда и только
тогда, когда определитель Д(Х) этой системы
еъ W °i cos y2 Q) a t еъ W °»sin y2 (X) at ..
равен нулю.
Разлагая Д (К) по минорам второго порядка, содержащимся в первых
двух столбцах, получаем, что
п
Д (I) = Ц Pr> 8 (Л) sin (ar—ae) ъ (X),
Г, 8=1
где сумма распространена на все комбинации (г, s) чисел 1,2,..., п,
такие, что г > $,
§ S, Существование бесконечного множества собственных значений 265
По известному свойству алгебраических функций, функции Pr s (X)
непрерывны и стремятся к конечным пределам, когда X—»--}-оо,
функция же Ys Q) непрерывна и, в силу второго из соотношений F),
стремится к -j-oo, когда Х-»-}-оо.
Положим lim Р_ 8 (X.) = Рг 8; если заметить, что из равенства Pr s
Х-»-+оо
нулю следует существование решения дифференциального уравнения B),
обращающегося в нуль в и — 2 точках
ali •••> fls-l» as+.V •••» ar-U ar+V ••• an>
то из сделанного предположения о том, что уравнение B) не имеет
решения, обращающегося в нуль в точках а2, ..., an_v следует, что
Запишем теперь, что
и
А (X) = 2 Pr, s sin (ar — а„) Та (X) +
Г, о=1
п
+ 2 [Рг,. (>0 — -Рг, .1 sin {ar — as) Ts (X),
Г 1
и заметим, что вторая сумма в правой части стремится к нулю,
когда X -*-~\- оо. Поэтому для того чтобы доказать, что при
стремлении X к -f- оо А (X) обращается в нуль бесконечное множество
раз, достаточно показать, что, каковы бы ни были числа Рг>8, такие,
что стоящее при наибольшей разности ап — at число Рп> \ отлично
п
от нуля, наибольший из пределов функции от X, 2 Pr ssin(ar—яв)т2(Х),
Г, 8 = 1 '
>
положителен, а наименьший из ее пределов отрицателен.
Для этого заметим, что при Х-»--]-оо функция ^W стремится
к -|-оо, а потому нужное нам утверждение является следствием
известной теоремы: функция F (t) = А г sin dj ~\- Л2 sin d? -\- ... -\-
-j-^msinrfm/, где А1г А2, ..., Ат — отличные от нуля т чисел,
a dlt d2, ..., dm — положительные числа, d1 < rf2 <.. .< dm, имеет,
когда / изменяется в (О,-j-oo), положительный наибольший из пре-
делЪв и отрицательный наименьший из пределов (см. Сансоне [4],
стр. 36)!).
Ср. также Бор [1], стр. 40. — Прим. ред.
Глава VI
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
И СИСТЕМЫ УРАВНЕНИЙ С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ.
ПЕРИОДИЧЕСКИЕ И ПОЧТИ ПЕРИОДИЧЕСКИЕ
РЕШЕНИЯ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 1. Решения линейных дифференцнальных уравнений
с периодическими коэффициентами
1. Примеры. Первая часть этой главы посвящена изучению реше-
решений обыкновенных дифференциальных уравнений и систем уравнений
с периодическими коэффициентами; для первоначального выяснения
вопроса мы предпошлем изложению разбор некоторых примеров,
которые позволяют установить свойства решений таких уравнений и
систем.
а) Пусть дано уравнение
xr+p(f)x=O, A)
где функция p(t) определена в (— оо, -j-oo), непрерывна и имеет
период со > О,
Решая это уравнение, получаем
x(f) = ce °
(где с — постоянная), а потому
со
- f P(t)dt
*(*+«) = « * X(t).
Таким образом, при увеличении аргумента / на со, решение уравне-
ния A) умножается на е °
Положим
Тогда
х (f-j- ш)<!-« <*+¦»> = х {t) e~at.
$ /. Решения уравнений с периодическими коэффициентами 267
а потому функция v>(f), определяемая формулой «р (f) = х (f) e~at,
имеет период со. Решение уравнения A) имеет вид
а потому периодично тогда и только тогда, когда [а = 0]
со
fp(t)dt = O.
о
б) Рассмотрим уравнение второго порядка
х" + [2 + sin t]-1 (sin f) x = О,
коэффициенты которого имеют период 2и; функции ^(f), x2(t),
определяемые равенствами
о
t
B +sin О2 '
о
образуют фундаментальную систему решений; они удовлетворяют
соотношениям
Xl (t + йс) =- хг (t), хъ (t + 2it) = хг (t)+аг2 (/),
а потому первая из них имеет период 2-к, а вторая не обнару-
обнаруживает периодичности.
в) Рассмотрим, наконец, уравнение
где функция p(f) непрерывна в (— оо, -|-оо) и имеет период со;
если на отрезке [О, со] функция p(f) положительна, то (см. гл. IV,
§ 2, п. 4„б") это уравнение не имеет периодических решений.
2. Характеристическое уравнение, а) Рассмотрим з'равнение
')*=о, B)
где функции po(t), ргф, ..., pn(f) опрэделены в (—оо, +оо),
непрерывны и имеют период « [со > О],
(-оо</< + оо; Л = о, 1, .... «), C)
причем
Pq{Q>o,
268 Гл. VI. Уравнения и системы с периодическими коэффициентами
Пусть функции хЛ (t), лг8(/), ..., xn(t) образуют фундаменталь-
фундаментальную систему решений уравнения B); так как уравнение B) не ме-.
няется при замене переменной / на /-j-ю, то функции x1(t-^-a>),
лг2(/-|-со), ..., xn(t~\-<o) также образуют систему решений этого
уравнения. Поэтому существуют и2 чисел ai1t (i, k=\, 2, ..., «),
таких, что
*i = * (t + ш) = ait Л (t) -\- ait ^ (fi-\- ... + att nxn (t) D)
(i=l, 2, .... я).
Легко проверить, что вронскианы W(xv x^, ..., хп) и
W{XX, Х2, ..., Хп) связаны соотношением
W(XV Х2, ..., ЛП) = Н1Г(*1, *8, . .., хп),
где
«1.1
E)
Но (см. гл. II, § 1, п. 2bb")
-ff-e
о
а потому
(* 1Р\ С Pi
X X \ — се ° — ^° U7 (y r y \
Следовательно, функции x1(t-\-<a), xs(t-\-<a), ..., xn(t~\-w) образуют
фундаментальную систему решений уравнения B).
Из доказательства следует, что
со
Н^е ° Р° ФО, F)
причем, если pt (f) ^ 0, то имеет место формула Пуанкаре (см. Пуан-
Пуанкаре [3], стр. 202)
//=1. G)
б) На приведенных в п. 1 примерах мы уже видели, что диф-
дифференциальное уравнение с периодическими коэффициентами не
всегда имеет периодические решения. По аналогии с примером из
п. 1 „а" попытаемся найти (если они существуют) такие решения x(t)
уравнения B), что
*(' + «) = Р*(9, (— оо < * < +оо) 1), (8)
*) Изучение решений, удовлетворяющих условию (8), было проведено
фдоке в [1]. Теория, которую мы излагаем, называется теорией Флоке,
/. Решений уравнений с периодическими коэффициентами
где р—некоторая постоянная величина, или, что то жа самог, найти
(если они существуют) такиэ постоянные сх, с2, ..., сп, хотя бы
одна из которых отлична от нуля, что решение уравнения B)
х (/) = <гЛ (t) + c2x2 (t) 4- • • - + сиаг„ @ (9)
удовлетворяет соотношению
(О-
Принимая во внимание D), мы видим, что для этого должно вы-
выполняться равенство
п п
2 [2 с л, ft — pCft] xk (t) = О.
В силу линейной независимости функций хх (f), аг2 (tf), ..., х
равенство приводит к системе уравнений
это
*-i 4- (°fc, ft — р)
=l, 2,
«)• (Ю)
Эта система относительно неизвестных си с2, ...,
ненулевые решения тогда и только тогда, когда р равно корню уравне-
уравнения, получающегося путем приравнивания нулю определителя так
называемой характеристической (фундаментальной) матрицы
ai. I — P
.1
«2,2 —Р
*п, 1
ап, 2
2, и
т. е. корнем так называемого характеристического (фундаменталь-
(фундаментального) уравнения
21,2
fl2, 2 —Р
а»
Ч, п
= 0.
A1)
Так как О@) — Нф0, то все корни уравнения A) отличны от
нуля, и для каждого корня этого уравнения и для каждой системы
чисел cv c2, , сп, удовлетворяющей линейной системе A0), реше-
решение х {{), определяемое формулой (9), удовлетворяет соотношению (8).
Изучение решений, удовлетворяющих соотношению (8), связано,
таким образом, с изучением корней характеристического уравне-
уравнения A1), которым мы и займемся в п. 3, 4, 5.
270 Гл. VI. Уравнения и системы с периодическими козффиЦиёнЫйИй
3. Элементарные делители матрицы, а) Пусть р — независимое
переменное, и пусть {at>k} {bik} (I, k=l, 2, ..., n) — системы
из л2 элементов. Рассмотрим матрицу
?>(р) =
определитель которой будем обозначать тем же символом ?>(р).
Пусть р0 — корень уравнения D(p) = 0 кратности /о (/o^-l); на-
назовем разность р — р0 линейным делителем D (р). Рассмотрим ми-
миноры определителя ?>(р), имеющие порядок n — k, O^k^n — 1.
Среди этих миноров, рассматриваемых как функции от р, хотя бы
один не равен тождественно нулю, так как иначе мы имели бы
D (р) == 0, а потому А = 0, вопреки предположению.
Обозначим через 1к показатель, с которым множитель р — р0 вхо-
входит в наибольший общий делитель миноров (п — й)~го порядка опре-
определителя D (р), рассматриваемых как многочлены от р1). Покажем,
что числа /0, lv 4> • • • связаны неравенствами
В самом деле, хотя бы в один минор порядка п — k делитель
Р — Ро входит с показателем /ft. Но тогда производная этого минора
по р делится лишь на (р — роРс~1', так как эта производная выра-
выражается как сумма произведений элементов определителя ?>(р) на
миноры (и — k — 1)-го порядка определителя D (р), а в наибольший
общий делитель этих миноров р — р0 входит с показателем /fc+1, то
4 ^' !
1 »
Пусть /ч — последний отличный от нуля показатель. Тогда
и если положить
— eV '••> 'v-l—1'v==e*-l» 'v^
то
Легко проверить, что
В самом деле, если
L М
N Р
— минор определителя, взаимного
определителю /)(р), то имеет место тождество LP — MN=D(p)C*),
1) Условимся, что если какой-нибудь минор порядка л — k тожде-
тождественно равен нулю, то он делится на (р — Po)n~ft.
2) См. Сушкевич А. К. [1] стр. т. — Прам. перев.
§ t. Решений уравнений с периодическими тэффицйентЬми 2?1
где С — соответствующий минор п — 2-го порядка определителя D (р);
если выбрать в качестве С тот микор п — 2-го порядка определи-
определителя Z)(p), в который р—-ро входит с показателем /2, то в правую
часть нашего тождества множитель р — р0 входит с показателем
/0-{-/2, а в левую часть — по меньшей мере с показателем 2/2,
а потому 11Х <[ /0 + /2,1г — 4 ^ k — ^i и ео ^> ei-
Можно доказать, что, вообще,
(см., например, Бохер [6], гл. XX, стр. 239—254).
б) Пусть pj, р2, ..., рт — т различных корней уравнения D(p) = 0,
имеющих соответственно кратность /W, lf> Ь™); тогда, согласно
нашим обозначениям,
D (р) == А (р- рЛ - р/'\ .. (р - Pl)ev< X
X (Р — Р2)е° (Р Р2> 2 •¦•(? — ?2^г X
(tn) (m) (»»)
X(p-pJ° (p-pJ1 •••(p-pJv,
где
('=1. 2, .... я).
Множители (р — р<)^ (/=1, 2, ..., т; j — Q, 1, ..., v^) назы-
называются элементарными делителями матрицы D(p)\ между их
показателями и степенью п многочлена D(p) имеет место очевидное
соотношение
т Ч
Излишне отмечать, что элементарные делители матрицы D(p) не
изменяются при перестановке двух строк или двух столбцов, а также
при замене строк столбцами.
в) Пусть
Р\.\ Pi.z ••• Pvn
2,1 Р% 2 • • • Р% п
Рп.1 Рп.Ч
Рп.п
ФО.
х) Теория элементарных делителей была построена Вейерштрассом [1],
т. II, стр. 21. Относительно геометрической интерпретации теории элемен-
элементарных делителей см. Бертини [1], гл. IV, стр. 63—100.
й?й Гл VI. Уравнений и система, с периодическими коэффициентами
Выполним над переменными aik, bi>k линейное преобразование
которое равносильно умножению матриц Ця^Ц и ||#<,fcf на матрицу
\Pi,fc|| справа. Покажем, что тогда матрицы Dip) и ГУ(р), где
имеют одинаковые элементарные делители, или, иными словами, что
корни уравнения Z)(p) = 0 и элементарные делители остаются
инвариантными, если над aik и bik выполняется одно и то же
линейное преобразование с определителем, отличным от нуля.
Так как
п
К.* + *!.*= 2К,»Р+*(,.)Ра ('» k = l, 2, .... я),
то любой минор п — fe-ro порядка матрицы ГУ (р), например
равен произведению по строкам матриц
Pi, l P^. ]
Pn,l
Pi, h P% Jt
Pn.k
Pl,n~k P%n-k
Pn, n-k
я потому может быть выражен как линейная комбинация миноров
п—fe-ro порядка матрицы ?>(р). Поэтому множитель р — р0 входит
в каждый минор п — fe-ro порядка из D'(p) по меньшей мере с пока-
Л Решения уравнений с периодическими коэффициентами 273
зателем lk, а, следовательно, lk не превосходит показателя l'k, с кото-
которым р — р0 входит в наибольший общий делитель миноров (п — й)-го
порядка из Z)'(p). Выражая из A2) at g и b€ g через а'€ k и b\ k и
повторяя проведенные рассуждения, убеждаемся, что lk = l'k. Теорема
доказана.
Аналогичные выводы имеют место, если сделать над aik и bi>Je
линейное преобразование, соответствующее умножению на матрицу |]р< 'ft[|
слева.
г) Применим доказанную теорему к изучению решений дифферен-
дифференциального уравнения B)-. Назовем матрицу
Й1,1—р
й-, а
2.1
ft», в
. я
««,« —Р
характеристической матрицей дифференциального уравнения B)
и докажем, что корни и элементарные делители этой матрицы
не зависят от выбора фундаментальной системы решений, слу-
служащей для ее построения.
В самом деле, общим видом фундаментальных систем решений
этого уравнения x1(f), x2(t), ..., xn{t) является
я*я
(* = 1, 2, ..., я),
где c<>fc—произвольные п2 чисел, таких, что С = Det || cf> n || Ф 0.
Если обозначить через ii,k приведенное алгебраическое дополне-
дополнение элемента cik в определителе С (т. е. отношение алгебраического
дополнения Cik этого элемента в С к определителю С), то
Я@ ('= 1, 2, ..., я),
и, принимая во внимание D), получаем, что
я
2 <?«.r*r
r=l
г, 1=1
а потому
где
я _ п п
= 2 чл«т*.1**й= 2 [ 2 чл
J*f I> ft — 1 ft —I Y»l — 1
=i, 2,..., я),
я
<fc= 2
f, 1=1
18 Зак. 527. Дж. Сансоне
2?4 Гл. VI. Урйвнёний и системы с периодическими коэффициентймй
Так как характеристическая матрица
<i—JP <« —Op... <.„ —Op
<1—OP «2.2—1P-«- <n —OP
<.i—°P <2—op:.. «;,n-ip
относительно новой фундаментальной системы (мы сделали столбцы
строками, и наоборот) получается из матрицы
1. 1
1.2
— Ор...
!.„
Ор
— Ор а2>8 —1р... й2, „ — Ор
путем умножения матриц
*1.1 «1,2 •••
а
1. я
— 1 0
°
я,2
сначала справа на
Tl. 1 Tf2,
1
О 0
Тя. 1
О
—1
а потом
на
Tl, п >2, я • ¦ - Тя, я
С1, 1 С1, 2 • • • С1, п
Сп. 2
я, я
то наше утверждение следует из предыдущей теоремы.
д) Сумма корней характеристического уравнения равна aul-\-as 2-j-
-j- ...-}- on, „, а потому сумма alt г -j- о2,2 ~f~ • • • ~Ь йя, я we зависит
от выбора фундаментальной системы, служащей для построения
характеристического уравнения.
4. Решения в случае, когда показатели всех элементарных
делителей характеристической матрицы равны единице. Характе-
Характеристические показатели и числа, а) Как мы уже видели, характер
решений уравнения B) тесно связан с корнями характеристического
уравнения A1) и, как вскоре будет показано, с элементарными дели-
делителями характеристической матрицы Z)(p).
Предположим, что для любого корня р{ (i = 1, 2, ..., т) харак-
характеристического уравнения Z)(p) = O, имеющего кратность v1( ранг
$ Л Решений уравнений с периодическими коэффицйентйМи 275
матрицы Dfa) равен п — v<; тогда, применяя обозначения из п. 3,
мы видим, что
v< = 4fl > /i*} >... > /v^-i
а так как v< = 4fl > /i*} >... > /v^-i, то
e i, 4, .... e_i i,
т. е. показатели всех элементарных делителей характеристи-
характеристической матрицы равны единице.
Обратно, если показатели элементарных делителей, соответствую-
соответствующих корню р{, равны единице, а число этих элементарных делителей
равно vf, то при р = р< как сам характеристический определитель D (р),
так и все его миноры от п—1-го до п — v^-f-1-го порядка вклю-
включительно обращаются в нуль, в то время как хоть один минор
п—vi-ro порядка не равен нулю, а потому ранг матрицы D(p{) ра-
вен п — v4.
Итак, пусть рх, р2, ..., рт—различные корни характеристиче-
характеристического уравнения, имеющие, соответственно, кратности vlf v6, ..., vm,
и пусть для каждого корня р4 ранг матрицы D (р{) равен и — vt; если
положить в однородной системе A0) р = р<, то ранг матрицы коэф-
коэффициентов будет равен п — v<? а потому значения v< из неизвестных
cv c2, ..., сп можно выбрать произвольно, в то время как значения
остальных и — vf неизвестных определяются тем самым однозначным
образом; следовательно, корню р{ соответствуют vt линейно незави-
независимых решений, которые мы обозначим через
xi,o *2.«' •••» хн>* (I=1» 2> •••> т)>
для каждого из которых справедливо равенство
@ (^=1, 2, .... vf; i=l, 2, .... т).
Легко видеть, что полученные таким образом и решений линейно
независимы; в самом деле, в противном случае существовало бы
линейное соотношение с постоянными коэффициентами cXi$, из кото-
которых хоть один отличен от нуля, имеющее вид
Х1 Х1
v,
2<Xi*x,i@+ 2 <\,2*л,2@+ : •. +2
Х=1
Заменяя в нем t на t-\-k<a (fe = 0, 1, 2, ...» т—1), мы полу-
получили бы еще соотношения
[2
Х=1
18*
276 Гл. VI. Урйанёнйя а системы с периодическими коэффициентами
Но определитель этой линейной системы отличен от нуля, так как
является определителем Вандермонда для т различных чисел pj, р2,..., рт,
а потому должны иметь место тождества
2 см*м@ = 0 ('= *> 2" • " т)-
Х=1
В силу линейной независимости решений A3) отсюда следует, что
c\,t = Q (\=1, 2, ..., vf; i=l, 2, ..., /и),
вопреки предположению об отличии от нуля хотя бы одного сх €.
Таким образом мы доказали следующую теорему.
Если показатели всех элементарных делителей характери-
характеристической матрицы D(p) равны единице, то каждому корню pt
характеристического уравнения D(p)=O, имеющему кратность vit
соответствуют vf линейно независимых решений
таких, что
) (^-==1, 2, .... v<; i=l, 2, ..., т),
причем совокупность всех решений, соответствующих различным
корням характеристического уравнения, образует фундаменталь-
фундаментальную систему решений.
б) Обозначим через Ьк главное значение аргумента для корня pfc
и через лгй @ — соответствующее решение; тогда
(/ — мнимая единица). Положим
—главное значение логарифма от рк) и назовем ак характе-
характеристическим показателем, a eo-Mnlpj.! — характеристическим
числом.
Положим yjt(t) = xk(f)e~abf; тогда
а потому <j>fc имеет период о>. Следовательно, если для любого корня
Pi характеристического уравнения, имеющего кратность \, ранг
матрицы D (р) равен п —- vf при р = р^, то существует фунда-
фундаментальная система решений вида
1. Решения уравнений с периодическими коэффициентами 277
где функции <Pi(O» %@» •••» УпФ имеют период а, а показа-
показатели ак (характеристические показатели) равны а)-Чпрл.
в) Желая оставаться в действительной области, изучим отдельно
случаи pfc>0, pfc<0, pfc комплексно.
Если pft > 0, то соответствующие решения cv с2, ..., сп си-
системы A0) действительны, xk(f) действительно, равно как и afc =
=» ю-1 In pk, а потому % (t) тоже действительно.
-В случае, когда рк < 0, заметим, что
а потому
где <pk(t)— действительная функция, имеющая период 2о>.
Если же
Р* = |р*|А где
т. е. если корень рк комплексный, то характеристическое уравнение
имеет и сопряженный с ним корень | pfc | e~<9fc. Этим корням соответ-
соответствуют сопряженные решения xk(f), xk(t), причем соответствующие
характеристические показатели также сопряжены. Но тогда и функ-
функции <р*@» ?й@ сопряжены и имеют период ш, а потому
@ = **•""¦"*'[«в *?-/«te^
где функции ^1 (t), ф2 (t) действительны и имеют период <о. Складывая
и вычитая эти формулы, получаем, что данное уравнение имеет два
линейно независимых действительных решения
[cos%Ч (<)-*n^
г) Изучим теперь поведение решений уравнения B) при стремле-
стремлении t к -\- оо, или, как говорят, асимптотическое поведение реше-
решений уравнения B).
Из изложенного следует, что если показатели всех элементар-
элементарных делителей характеристической матрицы равны единице, то
для стремления к нулю при t-> -f- оо всех решений уравнения B)
необходимо и достаточно, чтобы выполнялись неравенства
In | p,j.| < 0 (k= I, 2, ...); т. е. чтобы все характеристические
числа были отрицательны (или, иными словами, чтобы модула
всех корней характеристического уравнения были меньше единицы).
278 Гл. VI. Уравнения и системы с периодическими коэффициентами
5. Решения в общем случае. Подгруппы Гамбургера. В случае,
когда не все показатели элементарных делителей равны единице,
имеет место следующая теорема, доказательство которой мы опускаем.
Если ро—корень характеристического уравнения D(p) = O
кратности /0 и если этому корню соответствуют элементарные
делители (р — ро)?°, (р—Ро)г', ..., (р — po)v» то Ро соответствуют
/0 линейно независимых решений, которые можно разбить на
v -f-1 подгрупп решений {подгруппы Гамбургера), причем решения
xf\ xW, ..., дг(в\ принадлежащие подгруппе, соответствующей
элементарному делителю (р — р0)« (s = о, 1, ..., v), характе-
характеризуются тем, что
6. Необходимое и достаточное условие существования перио-
периодического решения, а) Результаты предыдущего номера позволяют
сразу сформулировать необходимое и достаточное условие для суще-
существования периодического решения уравнения B); именно, имеет место
следующая теорема: для того чтобы уравнение B) имело решение
с периодом и, необходимо и достаточно, чтобы хотя бы один
из корней характеристического уравнения A1) равнялся единице.
Кроме того, число линейно независимых решений уравнения B),
имеющих период о>, равно числу элементарных делителей ма-
матрицы
«1, 1— Р а% 1
«1,2 «2, 2 —Р
а1,п а%п ¦•• ап, п — I
содержащих множитель р— 1.
б) Вообще, если один из корней характеристического уравне-
уравнения A1) является корнем k-й степени из единицы {k — целое поло-
положительное число), то ему соответствует решение, имеющее период k<a.
Справедливо и обратное утверждение. Пусть, в самом деле, реше-
решение x{f) уравнения B) имеет период йсо (k — целое положительное);
х) Впервые решения, соответствующие кратному корню характеристи-
характеристического уравнения, изучались Фуксом [1], стр. 136. Распределение решений
по подгруппам было установлено Гамбургером [1], стр. 121; связь подгрупп
Гамбургера и элементарных делителей матрицы D(p) указана Казорати [1].
Относительно доказательства сформулированной теоремы дм, Форсайт [1],
т, IV. стр. 60 и 416, и Соваж [1], стр. 326,
$ 1. Решения уравнений с периодическими коэффициентами 279
выразим тогда x{t) в виде линейной комбинации решений, принадле-
принадлежащих различным подгруппам Гамбургера; отождествляя x{t-\~k<a)
с х (/), мы получаем, что хотя бы один из корней уравнения D (р) — О
должен быть корнем &-й степени из единицы.
7. Периодические решения неоднородных линейных дифферен-
дифференциальных уравнений с периодическими коэффициентами.
а) Пусть дано уравнение
?^f A4)
где функции po(t), ргA), ..., pn(f), f(t) определены в (—оо, +со),
непрерывны и имеют период ш [ш > 0],
(Л = 0, 1, .... я);
Выясним, имеет ли это уравнение решения с периодом о>.
Пусть <ро@ — частное решение уравнения A4), а х1((), ^(),
..., xn(t) — фундаментальная система решений соответствующего
однородного уравнения B); общее решение уравнения A4) имеет
тогда вид
? @ = <?,*, (t) + сй*а @ + • • • + "Л @ + ?о @, A5)
где си с2, ..., си — произвольные постоянные.
Так как yo(t-\-<a) также является решением уравнения A4), то
существуют такие числа pj, Р2, ..., рп, что
и если все числа pfc равны нулю, то <oo(t) является периодическим
решением уравнения A4).
В общем случае, выражая по формуле D) xt (t -j- <о), лг2 (t -f- со), ...
..., лгп(^-]-а)) через лгх(<), л:2@> •••» xn(t), получаем, что
а потому решение <p(t) периодично тогда и только тогда, когда
можно выбрать числа cv c2, ..., сп таким образом, что
2
280 Гл. VI. Уравнения и системы с периодическими коэффициентами
т. е. числа с,, с2, ..., сп должны быть решениями системы
а1, 2 С1 + («2, 2 Ч С2 + • • • + «и, 2 Сп == Р2>
A6)
Определитель этой системы отличен от нуля, если ни один из корней
характеристического уравнения однородного уравнения
^^=0 B)
не равен единице, т. е. если однородное уравнение не имеет решений
с периодом о) (п. 6„а"). Итак, мы доказали, что если однородное
уравнение B) не имеет решений с периодом о>, то уравнение A4)
имеет одно и только одно решение с периодом со.
б) Наоборот, если уравнение B) имеет решение с периодом о>,
то либо уравнение A4) не имеет периодических решений, либо оно
имеет бесконечное множество таких решений, в зависимости от того,
является ли система A6) несовместной или же она имеет бесконечное
множество решений. Говорят, что как в том, так и в другом случае
имеет место так называемое явление резонанса г).
в) Проиллюстрируем изложенное следующим примером (см.
Иглиш [1]).
Пусть дано уравнение
A7)
где функция f{t) имеет период ш, а параметр Xs отличен от нуля.
Общее решение соответствующего однородного уравнения
A8)
имеет вид сг cos kt -j- c2 sin kt, где с1 и с2 — произвольные постоянные;
поэтому, если <ро(*) является частным решением уравнения A7), то
общее решение уравнения A7) имеет вид х (t) = c1 cos kt-\-cs sin it-\-
-|-90(<). Это решение имеет период ш, если х @) = х (ш), дг'(О) =
= д/(ш), а для этого необходимо и достаточно, чтобы ct и с2 удо-
удовлетворяли системе уравнений
Cj [1 COS Xffl] ~j- C2 Sin Ad) = <ро @) «О О
Хс,[ — sinXeo] — Ac2[l
Определитель этой системы равен 4Х sins (Хш/2), а потому уравне-
уравнение A7) имеет одно и только одно периодическое решение, когда
1) Относительно более глубокого изучения этого случая см. Файт ГЦ:
Ундервуд [1], [2], [3]. ¦ 1
1, Решения уравнений с периодическими коэффициентами 281
/Х (fe = =tl, ±2, ...), т. е. когда со не является целым
кратным периода решений однородного уравнения A8).
Если же со = 2-!:k/X, {k — =t 1, =t 2, ...), т. е. если имеет
место случай резонанса, то система A9) принимает вид
МО)—<?оН=о, <р?(о)—<?;»:= о,
а потому, если ®о(О имеет период со, то любое решение уравнения
A7) имеет период со и, следовательно, в случае резонанса либо все
решения уравнения A7) имеют период со, либо ни одно решение
не имеет такого периода.
Это свойство выводится также и из выражения общего решения
уравнения A7). По методу из гл. II, § 1, п. 5„ви, получаем для
общего решения уравнения A7) выражение
-j~ Cj cos It -\- cg sin te.
Если ia = 2%kjX (? = ±1, ±2, ), то это решение имеет период со
(каковы бы ни были сг и с2) тогда и только тогда, когда имеют место
равенства
oj m
Аг = ^ J/(н) cos Хи??к = О, А2 = ^ j f (и)sin kudu =0.
о о
Наоборот, если хотя бы одна из постоянных Av A2 отлична от
нуля, то, полагая
Д (t) =/(/) — Л] cos X/ — А2 sin It,
получаем, что
t
Г А (и) cos Хк du -j- ^! cos
sin >i]+^ [Ах sin X< — Л2 cos Ml.
Первый член в правой части имеет период со [ш = 2йтс/Х], в то время
как значения второго члена в точках t, rf-j-co, <-j-2co, ... образуют
арифметическую прогрессию.
282 Гл. VI. Уравнения и системы с периодическими коэффициентами
§ 2. Вычисление характеристических показателей
1. Исследование характеристических показателей. Из резуль-
результатов предыдущего параграфа следует, что для исследования пове-
поведения решений уравнения
^ о, О)
где функции р0, /?!, ..., рп определены в (— оо, -(- оо), непрерывны
и имеют период о> > О,
Pi(<+•) = Pi(*)(* = 0, 1, .... я; — оо< *<+<*>), po(f)>O,
необходимо знание характеристических показателей, что в свою оче-
очередь требует решения характеристического уравнения, для составле-
составления которого нужно предварительно вычислить входящие в D) из § 1
коэффициенты ait k.
Вычисление этих коэффициентов может быть проведено следующим
образом. Построим и частных решений xt (f), дг2 (t) хп (/), удо-
удовлетворяющих начальным условиям
*i {to) = К и К (t0) = 82> t 4"} (« = 8~, i B)
(/ = 1, 2, ... , и),
где 8fc) t — 0, если k Ф i, и 8^ h = 1.
Эти решения образуют фундаментальную систему, и, в обозна-
обозначениях из § 1, п. 2 [ср. D)], имеем
Xf (t-\- <o) = ait x
При t = t0, принимая во внимание B), получаем, что
(t=l, 2, ... , n),
а потому вычисление коэффициентов ait j, я^ 2, ... , c{> „ сводится
к вычислению значений дг4(<), дг^(/), ... ,' л^*** (V) при ^==io4-°>-
Вычисление этих значений проводится следующим образом. Рас-
Рассмотрим вместо A) другое уравнение
где X — параметр, и построим по методу последовательных прибли-
приближений решения этого уравнения, удовлетворяющие начальным уело»
§ 2. Вычисление характеристических показателей 283
виям B). В качестве первого приближения для xt (f) выберем многочлен
(га— 1)-й степени от /(/=1, 2, ... , га),
f (A—
g —ft
-^—
--Н—(и—1I *ч«- (б)
Тогда решение лг4(/) имеет вид (см. гл. I, § 3, п. 4 „а"),
• • • (''- 1. 2,...,«), F)
а потому функция xf(f) и ее производные до л-го порядка включи-
включительно являются целыми, трансцендентными функциями от X. Выра-
Выражение для д^г)(/) получается путем почленного дифференцирования г
раз ряда, стоящего справа1), а потому
(г=1, 2,..., га). F0
в=о
Следовательно, каково бы ни было X, при /=<о имеем
в=о
и потому
/8?i(« = «r+i,i; /?<(«= О G)
(г==0, 1, 2, ... , га; 5 = 1,2,...; /= 1, 2, ... , и).
Но
r=0
- 2 xVtt @+2 [S p«-r/?}i @] xe+1,
e=0 e=0 r=0
а потому при s = 0, 1, 2,...
я-1
Обозначая для большей ясности х^ (i) через хк (I, X), получаем, что
*? ft *)=»ь*<0+*?1.*@+..•+*•?**«>+...;
интегральной формуле Коши <р», * @ = к-: I g+1 dk, /e, k (t) =
г
= __ Г х*{ • '. dk, а потому, принимая во внимание теорему о дифферен-
г г
цированни под знаком интеграла, выродим, что /8< к (/) = <pt, r {().
но по
284 Гл. VI. Уравнения и системы с периодическими коэффициентами
откуда, принимая во внимание G), получаем рекуррентную формулу
^'«-r(«)/^(«)^. (8)
to Г=0
Если положить в формулах F), F') Х = 1 и t=t0-\-(o и при-
принять во внимание равенства C), то для коэффициентов ait r полу-
получаются выражения
со
= 1, 2, .... я; г = 0, 1, ..., я —1).
2. Исследования А. М. Ляпунова об уравнениях второго по-
порядка, а) Рассмотрим в качестве приложения изложенных выше ре-
результатов уравнение
§ = 0, (9)
где функция p{t) определена в (— оо, +оо), непрерывна и имеет
период «о >¦ 0, и напомним некоторые результаты А. М. Ляпуноваг).
Обозначим через f(t) и <p(t) решения уравнения (9), удовлетво-
удовлетворяющие начальным условиям
/@) = 1, /' @) = 0; ? @) = 0, ?' @) = 1 2). A0)
Тогда
24
и характеристическое уравнение (§ 1, п. 2„би) можно записать в виде
«1,1 Р «2.1 =р2_(Й1 л + а2>2)рН-(я ula2t2 — й1>2в2,1) = 0.
«1,2 02, 2—Р
Но по теореме Пуанкаре (§1, п. 2яа") eitlfl2 а — alt 2«2> i = 1, а по-
потому характеристическое уравнение приводится к виду
Согласно A0) и A1), имеем f (<*>) = allV 9/(<0) = «г, а> а потому
полагая
2Л=/(<о) + <р», A2)
получаем для характеристического уравнения следующее выражение
р2 —2Лр+1=0. A3)
1) См. Ляпунов А. М. [1], [2], [3], [4J.
Относительно изучения периодических решений приведенного в тексте
уравнения (9) см. Пикар [2], [3].
2) В обозначениях п. 1 имеем f=xi(i), ч —
§ 2. Вычисление харйктеристичееких нокйзйтелей 285
По результатам из п. 1 имеем1)
У„@ р@ро+2
п=1 п=1
где
/о = 1, Л+1V) = -•/ ('— в)р (a)/, (a) rfa,
а потому
или, полагая
(—1)
Л = 1 —
Из A4) и A5) имеем
2Al=f(<0 — u)p(u)f(
0
т. е.
2^
Если положить
t
n=l
А»=/«(°>)+<р«(Ч
Х^ + ^А,—\зАз+
>(u)du-j-fp(u)<?0(u)
0
со
4j = о) j p (и) г/и.
0
A5)
A6)
)du=a>f p(u)du,
о
о
то по индукции доказывается, что
где
в = [Q - Р («О + Р («2)] [РЫ — Р(и2)]... [Р(«„.О — Р(«„)],
б) Если предположить, что р (t) < 0, то /„ (со) > 0, <(/ (<о) > О,
постоянные Ап имеют знак (—1)п, а потому из A6) следует, что
при X > 0 постоянная А больше единицы. Следовательно, в этом
случае характеристическое уравнение имеет два действительных корйя
В обозначениях п. 1 имее»/„, i=/n, /№2 =
286 Рл. VI. Уравнения й сисЫМы с Периодическими козффщтнпАМй
Р! и р2, причем Р!>1 и 0<р2<1. Соответствующие характеристи-
характеристические показатели аг и а2 таковы, что
а1==Aпр1)/о)>0, о2 —Aпр2)/о)<0,
и общее решение уравнения A) имеет вид
где сг и с2 — произвольные постоянные, а aj(/) и а2(/)—функции,
имеющие период ш. Отсюда выводится асимптотическое поведение
решений этого уравнения при t-*oo (см. § 1, п. 4„г").
в) Если p(t)>0 (— oo<f<4-°°). то все А„ положительны.
В этом случае справедливы следующие результаты А. М. Ляпу-
Ляпунова, которые мы дадим без доказательства:
1- 0 < А»+« <
2. Для всех положительных значений X, таких, что
A7)
имеет место неравенство Л2<1. Поэтому, если р(^)>0 к выпол-
выполняется неравенство A7), то корни характеристического уравнения A3)
имеют вид p = A±iY^—Л2» р1 = е*е, р2 = е-*е, а потому общее
решение уравнения (9) имеет вид (§ 1, п. 4„в")
где <J»j(O, ^а@—функции, имеющие период ш, а с, и с8—про-
с8—произвольные постоянные.
При наших предположениях из найденного для x{t) выражения
легко вывести, что если дг(О является решением уравнения (9), удо-
удовлетворяющим начальным условиям х (t0) = дг0, xr(t^ = xo, то для
любого положительного числа е можно найти такое 8, что для всех
решений x(t) уравнения (9), удовлетворяющих начальным условиям
* (to) e *о + 81. * Со) = '
где |8j|<8, |8а|<8, и для всех t (— оо, +оо) имеет место нера-
неравенство
$ 2. Вычисление хйрйктёристиЧескпх показателей. 287
Иными словами, в этом случае решения уравнения (9) устой-
устойчивы, (см. гл. VII, § 1, п. 1).
Недавно ван Кампен и Уинтнер [1] показали, что условие A7) не
может быть улучшено, т. е. что из условий р (t) > 0 и
(е>0)
о
нельзя вывести устойчивость всех решений уравнения (9).
3. Метод Хилла вычисления характеристических показателей
при помощи бесконечных определителей, а) Мы хотим закончить
этот параграф изложением метода бесконечных определителей, при-
примененного астрономом Хиллом для нахождения характеристических
показателей ').
Пусть надо изучить решения уравнения
dj?+A(t)x = 0, A8)
где A(t)—непрерывная четная функция [А( — f) = A(i)], имеющая
период -к, [A(t-\-t:) = A(t)], и пусть разложение A(f) в тригономе-
тригонометрический ряд Фурье
/l@ = 604r261cos2f+262cos4*+...+26,lcos2n*+-.- A9)
таково, что ряд
21 <У B0)
п=о
сходится 2).
Предположим, что уравнение A8) имеет решение вида е^уф
(jj. — характеристический показатель), где функция <р(Ю периодична
с периодом iz (§ 1, п. 4„б"); разлагая о>(<) в ряд Фурье и выра-
выражая синусы и косинусы через показательную функцию, получаем,
что
я=—со
причем, из того, что функция <o(f) имеет непрерывную вторую про-
+со
изводную, следует, что 2 IКI < + °°'
П=-со
Положим
<и = е„ B2)
1) Хилл [1]. С этого классического мемуара начинается изучение диф-
дифференциальных уравнений с периодическими коэффициентами.
2) Это' имеет место, например, если функция А (I) имеет в [0, «] про-
производную, удовлетворяющую условию Липшица порядка о>0, \А' (ij) — i4'(^)K
<Z|^i—/2|« (см. Натансон И. П. [1J, стр. 188).
288 Гл. Vt. Уравнения и системы с периодическими коэффициентами
и подставим B1) в A8); допуская законность [почленного дифферен-
дифференцирования, получаем
4-со 4-со +со
2 (ц + 2шJ?иеA1+Ш)'+( 2 Ке*ш)( 2 V(ll+2in)') = 0.
П—~ со п=— со п=—со
Отсюда следует, что числа
должны удовлетворять бесконечной системе однородных линейных
уравнений с бесконечным множеством неизвестных, имеющих следую-
следующий вид
+оо
fbnJr 2 <W>n_w = 0. B3)
Предполагая, что 60=?Bя)а (я = 0, 1, 2, ...)i умножим уравне-
уравнение B3) на —1/[BгаJ— 60]. Мы получим тогда другую систему
»n=l
»n=l
(га—..., —2, —1, 0, 1, 2, ...),
определитель которой обозначим через Д(/р), иными словами,
42—е0 ' 42—ео> 42—е0' ф—е0* 4*—во'
^
2—е0' 22—е0 ¦ 22—v 22—v 22—%'••'
2_е0' 02—е0' 02—е0 ' №—v 02—V'1
22—60' 22 —в0' 2»—во' 22 —60 ' 22 — во'*"'
__ ?l_
2_e0' 42—e0' 42—v 42—%• 42—
Определитель Д (iji) называется определителем Хилла системы B4).
Предположим еще, что % — (ф. — 2гаJ^= 0 (га = 0, dtl, ±2,...);
если заменить уравнение B3) уравнением, получающимся из него
делением на 60—(ф. — 2гаJ, то получится новая система относительно
неизвестных Ьп, определитель Aj (i\>.) которой имеет вид ()
(«««*=..-, —2, — 1, 0, 1, 2, ...), где
^,«=1. «»,»» = — б„_т/[Bп —*»2-60] (n^m)
§ 2. Вычисление характеристических показателей 289
Непосредственно доказывается, что определитель Аг (/jj.) нормален
+ ОЭ
(см. Рисе Ф. [1], стр. 24); в самом деле, полагая ^.|в„| = /., имеем
Л=—со
+со со 4-со
+
A lBn-*»*-eo|-|^ +
я=—оо»»=—оо
Так как числа \Ьп\ ограничены в совокупности, то по известным
результатам теории бесконечных определителей из существования не-
ненулевого решения нашей системы вытекает равенство нулю опреде-
определителя Aj(ty.) (см. Рисе Ф. [1], стр. 29). Но
+оо
Д (»» = Д, (*» И [60- (if. — 2«)»]/[в0 - 4яЧ,
я=-оо
и так как по известной формуле Эйлера •) имеем
я=1
ТО
xf[(-^)(-
V 4 и^
sin -i-«(i> - Уад sin i-
и, следовательно, характеристический показатель \>. решения ё^1 «р (f)
удовлетворяет уравнению
б) Можно доказать, что
Д (»» = Д @) - sins (-1 «ц)/sin» (| ir /во),
а потому характеристический показатель у. удовлетворяет урав-
уравнению
Д @) sin* D- ir У^) = sin2 (^ «>)
(см. Уиттекер и Ватсон [1], ч. 2, стр. 241).
!) См. Привалбв И. И. [1], стр. 254. — Прим. перев.
19 Зах. 627. Дж. Саисов*
290- Гл. Vt. Уравнений ti система с периодическими коэффициентами
§ &. Самосопряженные системы второго порядка
с периодическими краевыми условиями
1. Существование собственных значений. Рассмотрим диффе-
дифференциальную систему
х(а, X) — х{Ь, Х) = 0, B)
х'(а, 1) — хгф, Х) = 0, C)
где функции 6 (t, X), Q (t, X) зависят от изменяющегося в промежутке
(Aj, A2), (Aj < А2) параметра X, и предположим, что:
а) Функции 6 (i, X), —d' > Q С> ^) являются непрерывными функ-
функциями от t и X при a^t-^b и Aj<X< Aa, причем, если придать
переменной t любое значение из [а, Ь], то функции b(t, X) и Q(t, X)
станут непрерывными невозрастающими функциями от X, Aj < Х<А2.
б) Ни в одной части отрезка [а, Ь] функция Q(t, X) не обра-
обращается тождественно в нуль при двух различных значениях X.
в) Ни в одной части отрезка [а, Ь] не выполняются одновременно
равенства 6(*, X1)=b(t, X^), Q(t, bt) = Q(t, Х2), если Xj Ф Х2.
Мы видели, что эта система самосопряжена, если выполняется
условие (гл. V, § 2, п. 6)
6 (а, Х)нв(*. X). D)
Изучим, существуют ли при сделанных нами предположениях значе-
значения параметра X (собственные значения), которым соответствуют не
равные тождественно нулю решения системы A), B), C).
Если кроме условия D) выполняются условия b't(a, X) = b't{b, X),
Q(a, X)=sQ(b, X), то уравнение A) можно рассматривать как урав-
уравнение с периодическими коэффициентами, определив функции 6 (t, X),
Q(t, X) при- —oo<rf<-j-oo соотношениями b[t-\-(b-~a), [XJ===
= 6(^, X), Q\t-\-(b — a), k\==Q(t, X), — oo<*<~j-oo. В этом слу-
случае коэффициенты имеют период b — а, а рассматриваемая задача
сводится к задаче о нахождении решений уравнения A), имеющих
период b — а; по этой причине система A), B), C) называется диф-
дифференциальной системой с периодическими краевыми условиями.
Допустим, что кроме предположений „а", „б", „в" и D)
коэффициенты Q(t, X), b(t, X) удовлетворяют одному из следующих
двух условий:
г,) litn — max Q(t, X)/max b(t, X) = 4-oo,
lim. min Q(t, X) = -4-oo, E.)
t, Х)>т>0, при a<f<* и A,
§ 3. Самосопряженные системы с hepuobmecti. краевыми усЛобийми 291
r2) [Aj, Аз) является полуоткрытым промежутком, причем
lim — max Q(t, A)/max 6(/, А) = + оо, E2)
Х>А <*<Ь <f<6
min Q(t, A,)>0.
Покажем, что при выполнении условий „а", „б", „в", „г," и D)
или „а", „б", „в", яг2" и D) существует бесконечное множество
собственных значений дифференциальной системы A), B), (ЗI).
Обозначим через х1 (t, X), x%{t, X) фундаментальную систему реше-
решений уравнения A), определяемую начальными условиями
, .ч . /, ., „ , .n /. ... 1
Тогда (гл. И, § 1, п. 2„в«)
xt (t, X) л:2 (t, X) 5 (д, X)
х[ (/, X) д4(«, А) ~в(/."Х)
и при /= ft
ж, (ft, X) 4 (ft, X) — л:2 (ft, X) х[ (ft, X) = 1. F)
Если Ci*:i(/, X)-|-с2дг2 (/, X) является решением, удовлетворяющим
периодическим краевым условиям B) и C), то должны выполняться
равенства
сг [1 — дг, (ft, X)] — с2лг2 (ft, X) = 0, — Clx[ (ft, X) + с2 [1 — х'2 (ft, X)] = О.
Эта система уравнений относительно сх и с2 имеет ненулевые решения
тогда и только тогда, когда X является корнем уравнения, получаю-
получающегося приравниванием нулю определителя матрицы
— *,(ft, X) — *2(ft, А) |
— x[{b, X) 1—x'2(b, i
В силу F), это уравнение можно записать в виде
' Ь, Х) = 0. (8)
Таким образом, собственные значения X совпадают с корнями урав-
уравнения (8).
Заметим, что если для собственного значения X ранг матрицы G)
равен единице, то ему соответствует только одна собственная функ-
функция, §сли же при этом значении X все члены матрицы G) обращаются
в нуль, то ему соответствуют две линейно независимые собственные
функции, удовлетворяющие системе A), B), C), и в этом случае X
называется двойным собственным значением.
]) См. Бохер [2], стр. 78 и 83, а также Хаупт [1], Эутлиигер [1], [2]
Камке [3]. *
19*
292 Гл. VI. Уравнений и системы с периодическими коэффициентами
Рассмотрим одновременно с системой A), B), C) систему
|[в(', *)§]-«('. *)* = <>, (9)
. *(в, Л) = 0, A0)
х(Ь, А) = 0, A1)
которая, в силу сделанных предположений, имеет так)"Ю последова-
последовательность собственных значений
что собственная функция x(t, \Lt), соответствующая собственному зна-
значению [Af, имеет в промежутке (а, Ь) ровно i нулей (см. гл. IV,
§ 6, п. 5).
Так как х2 (Ь, р.4) = 0 '), то, полагая А = p.f, выводим из F), что
Xl(b, щ)*?(А, ъ)^1, A2)
а потому хх (b, Pi) и х2 (Ь, ^) имеют одинаковые знаки. Но тогда
из (8) следует, что
-e V\x'2(b, ^)|'J»,
где б = -f-1, если х2 ф, \>+) > 0 и в = — 1, если х% {b, ^t) < 0.
Так как х'^а, Цо) = 1 и -^(^ Ы положительно в (я, 6), то
•*«(*! |*оХ'О; аналогично, из того, что хь(а, \lJ=1, a x^(t, pj
имеет ровно один нуль в промежутке (а, Ь), следует, что х'2 (b, (tj) > 0.
Продолжая это рассуждение, получаем, что
Ho F(k) является непрерывной функцией параметра Л, а потому урав-
уравнение F(X) = O имеет по крайней мере один корень в каждом из
отрезков [jx0, jij], [\lv jtg],
Легко проверить, что
< 0, F(pJ < 0, ..., F([x2i)) < 0, ....
В самом деле, собственная функция системы (9), A0), A1), соот-
соответствующая собственному значению \>^р, имеет в (а, Ь) ровно 2р
нулей, и, в силу тгоремы о разделении нулей (см. гл. IV, § 2, п. 7),
любое другог решение уравнения (9) (соответствующее значению
X = ji2i,), линейно независимоэ с этой собствгнной функцией, имеет
на отрезке [а, Ь] 2р -\-1 нулей {нечетное число). Поэтому таког
решение не может принимать одинаковые значения в концах отрезка
[а, Ь], что имело бы место, в силу B), если бы F{v-^ равнялось
нулю.
Очевидно, что х (b, pt) = х2 {b, fxt). — Прим. перев.
§ 3. Самосопряженные системы, с периодическ. краевыми условиями 293
Таким образом, уравнение /7(А) = 0 имеет $ каждом из про-
промежутков (jio, jig), (р.а, (t4), ... по крайней мере одну пару корней
(возможно совпадающих), чем и доказано существование бесконечного
множества собственных значений для дифференциальной системы A),
B), C).
2. Осцилляционная теорема, а) Пусть Л—г заключенное в проме-
промежутке (]А8р, jAjp+g) собственное значение для системы A), B), C); так
как собственная функция у(х, р?р) для системы (9), A0), (il) имеет
в промежутке (а, Ь) ровно 2р нулей, а предположения „а", „б", „в"
позволяют применить теорему сравнения (см. гл. IV, § 6, п. 3„а"),
то собственная функция x(t, К) системы A), B), C) имеет в (а, Ь)
по крайней мере 2р-\-1 нулей. Отсюда следует, что число нулей
собственных функций системы A), B), C) стремится к беско-
бесконечности при возрастании А. Естественно поэтому поставить вопрос
о существовании зависимости между индексами собственных значений,
расположенных в виде неубывающей последовательности, и числом
нулей соответствующих собственных функций.
б) Имеет место следующая теорема, приводимая нами баз доказа-
доказательства.
Если дифференциальная система A), B), C) удовлетворяет
условиям „а", „б", „вв, „rj" и D) или же условиям „а", „б",
»в"> 1,^" и D), то ее собственные значения можно так располо-
расположить в виде неубывающей последовательности
что собственная функция, соответствующая собственному знд-
чению ki, имеет в [a, b) i нулей, если i четно, и i-\-1 нулей, если i
нечетно (см. Бохер [2], стр. 89).
Например, если рассматривается уравнение х"-\-кх = 0 и ищутся
его решения, удовлетворяющие периодическим краевым условиям
то собственные значения в этом случае равны
у — о2 12 /2
причем все собственные значения, за исключениам X = 0,;— двойные,
и собственному значению А = Р соответствуют собственные функ-
функции sin It, cos it, первая из них имеет в 0 <! t < 2и 21 нулей, нахо-
находящихся в точках 0, 1у, 2-^-, .... Bi — 1) -?-, а вторая также
Имеет 2/ нулей, находящихся в точках
294 Гл. VI. Уравнения и системы с периодическими коэффициентами
§ 4. Дифференциальное уравнение Матье
и функции, связанные с эллиптическим цилиндром
1. Элементарные решения уравнения колебаний эллиптической
мембраны и уравнение Матье. а) Рассмотрим плоскую однородную
мембрану, имеющую эллиптическую форму, равномерно натянутую во
всех направлениях и закрепленную вдоль контура.
Выберем в качестве осей координат главные оси эллипса и рас-
рассмотрим задачу об определении смещения w(x, у, f) точки (*, у)
эллипса в момент времени t, когда мембрана выведена вначале из
положения равновесия.
Хорошо известно, что если обозначить через от2 отношение натя-
натяжения и плотности мембраны, то w(x, у, f) является решением урав-
уравнения
обращающимся в нуль на контуре мембраны *).
К уравнению A) приводят также и другие задачи математической
физики. Рассмотрим распространение электромагнитных волн; напря-
напряжение электрического поля Е будем считать параллельным оси z,
тогда компоненты напряжения магнитного поля Н будут (Нд., Ну, 0).
Уравнения Максвелла записываются в этом случае в виде
дЕ дН„ дН~ дН~. дЕ дН„ дЕ
dt~"~dx~~~''~W' ~di ~~С ду' dt ~~C дх'
где через с обозначена скорость света. [См. Тамм И. Е. [1], стр. 423. —
Прим. перев.]
Но тогда
1 д*Нх \_д*Е_дЧ[ , &Е_ п*.
dxdt с dydt' с* дР ~~дх*~1~ду* ( '
и если волны падают на проводник, имеющий форму эллиптического
цилиндра, главные оси сечения которого плоскостью г = 0 совпадают
с осями х и у, то вектор Е должен обращаться в нуль на поверх-,
ности этого цилиндра, а потому мы получаем для A*) ту же гранич-
граничную задачу, что и для A).
Будем искать решения, имеющие постоянную частоту р и вид
w = u(x, у) cos (pt-\-в). Тогда и(х, у) должно удовлетворять урав-
уравнению
х) См. Матье [1], стр. 197. [См. также Соболеэ С. Л. [1], стр. 13—16.—
Прам^перев.]
§ 4. Уравнение Матье 295
Пусть фокусы эллипса имеют координаты (±с, 0). Сделаем за-
замену независимых переменных по формулам
х = с ch ? cos 7j, у = с sh & sin ¦*) C)
(?, ¦») — эллиптические координаты); при этой замене координатными
линиями ? = const, 7) = const будут соответственно софокусные эллипсы
и гиперболы, имеющие фокусы в точках (—с, 0), (-\-с, 0).
Все точки мембраны получаются при ?]^-0 и — эт^7)^ет4 Про-
Простое вычисление показывает, что при замене переменных C) уравне-
уравнение B) принимает вид
д2и д2и , с2/?2. .„,. о \ п ,л\
+J(ch ч~ cos 2*))и = 0. D)
Найдем теперь элементарное решение получившегося уравнения,
имеющее вид
Подставляя это выражение в D), получаем уравнение
lr(z) ' m2 J L0^) «2 'J
Так как левая часть этого уравнения является функцией от Ч, а пра-
правая— от 7j, то обе эти части должны равняться постоянной величине А,
а потому
Укажем теперь в явном виде условия, которые надо наложить на
функции F и С для того, чтобы получилось ргшение, удовлетворяю-
удовлетворяющее граничным условиям нашей задачи.
Из непрерывности решения слгдует, что
а потому функция G должна иметь период 2эт, или, иными словами,
постоянная величина А в F) (собственное значение) должна быть
выбрана таким образом, чтобы это уравнениг имело решение с перио-
периодом 2и.
Если обозначить через а большую полуось эллипса и если %0
таково, что ссп|0 = а, то должно иметь место равенство /7(?0) = 0.
В силу E), это условие определяет функцию F(i) при заданном соб-
собственном значении А с точностью до постоянного множителя.
6) Если положить в F)
296 Гл. VI. Уравнения и системы с периодическими коэффициентами
то оно примет вид
= 0.
Это уравнение называется уравнением Матье. Уравнение Матье является
частным случаем уравнения Хилла (§ 2, п. 3) *).
2. Функции Матье и их классификация по типам, а) Рассмо-
Рассмотрим уравнение Матье
у" + [/— 2А2 cos 2х] у = 0 G)
и заметим, что в силу результатов из гл. III, § 2, п. 1 любое реше-
решение этого уравнения является целой функцией как относительно х,
так и относительно /.
Если у{х, I) является одним из решений уравнения G), то и
у(—х, I) будет его решением, а потому решениями уравнения G)
будут также функции [у(х, 1)-{-у(—х, /)]/2, [у(х, t)—у (— х, /)]/2,
из которых первая четна, а вторая нечетна. Поэтому нам достаточно
ограничиться рассмотрением четных и нечетных решений уравнения G).
При фиксированном значении / уравнение G) не может иметь двух
линейно независимых решений одинаковой четности; в самом деле,
производная целой четной функции обращается в нуль при х = 0
(нечетная целая функция обращается в нуль при * = 0), в то время
как уравнение G) имеет решение, удовлетворяющее условию у' @) = 1
(_у@)=1). Таким образом, фундаментальная система решений
уравнения G) может быть составлена из четного и нечетного
решения.
Заметим теперь, что, заменяя в уравнении A) из § 3, п. 1, /на х,
А на / и полагая 6=1, Q(x, f)= 2A2cos2a:—/, мы получаем уравне-
уравнение G). При этом, если положить Аа = — 2А2, [Q(x,— 2А2) =
=2ft2cos2;e-|-2A2^>0], А2 = -]-00» то в[—эт, эт] выполняются пред-
предположения „а", „б", „в", пг2" и D) из § 3, п. 1, а следовательно,
существует неубывающая последовательность собственных значе~
ний {1т), стремящаяся K-j-°°> которой соответствует последо~
вательность собственных функций \у(х, 1т)}, имеющих период 2тг,
Я— *. О=у («. L); У (- я, L)=У («, U,
причем у (х, 1т) характеризуется тем, что при четном т имеет
в \—я, я] т нулей, а при нечетном т имеет в [—я, эт] т-{-1
нулей.
б) Рассмотрим четное решение уравнения G), имеющее период 2и;
его можно разложить в равномерно сходящийся ряд косинусов2),
!) Относительно изучения уравнения Матье й полной библиографий
отсылаем читателя к следующим трудам: Уиттекер и Ватсон 111, ч. 2,
стр. 229-258, Гумберт [1], Стретт [1]. J
2) См., например, Толсто» Т, П. [1], стр. 39. J08, — Прим. персе.
4. Уравнение Матье 297
Если у{х) является решением уравнения G), то к у{х-\-п) также
является решением этого уравнения. Но уравнение не может иметь
линейно независимых четных решений, а потому у (х-\-п) должно
отличаться от у{х) лишь постоянным множителем, откуда следует,
что разложение у(х) в ряд косинусов может иметь один из следую-
следующих видов
со со
2 <V cos Bг +1) х, 2 cr cos 2гдг.
Аналогично нечетные решения должны иметь вид
со со
2<VsmBr-4-l)*, 2<V sin 2ГХ1).
r=o r=l
Назовем эти решения соответственно решениями типа Cv Co,
Sv So.
Принимая во внимание, что при й = 0 уравнение G) принимает
вид yn-\-fyz=Q, а это уравнение имеет собственные значения
/=/я2 (те=€, 1, 2, ...) и соответствующие им собственные функ-
функции cos mx, sin mx, условимся называть функциями Матье первого
вида периодические решения уравнения G), приводящиеся при А->0
(с точностью до постоянного множителя) к cos mx, sin mx. Они обо-
обозначаются соответственно символами
«1=0
оо
<*** (•*) = 2 Ап. 2т cos 2mx (и = 0, 1, ..., Ап> 2Я = 1),
в»=0 ]
оо
sezn+i (х) = 2 Вп. ЙЯ1+1 sin Bm +1) х (и = 0, 1, ..., В„, 2п+1 = 1),
оо
Se2n (*) = 2 вп. 2». sin 2тх (и = 1, 2, ..., Вп> 2П = 1).
»»о
e2n (
»»=о
в) Если известно собственное значение /, то с помощью рекуррент-
рекуррентного процесса можно найти соответствующую собственную функцию.
Пусть, например, требуется найти решение типа Сх; имеем
9-=0
(8)
и так как разложение Ct (х) в ряд получается двукратным лочленным
дифференцироваиием ряда (8), то
со
С" (*) = — 2 Bг + 1)й cr cos Br +1) -v.
Г=0
См. сноску г) на стр. 296.
298 Гл. VI. Уравнения и системы с периодическими коэффициентами
Подставляя в G), получаем, что
со оо
2Br+lJ<vcosBr+l)*—/2crcosBr+l)* +
r^O r=0
CO OO
-j- A2 2 <VcosBr + 3)*+ A22 <V cos Br— 1)*= 0,
9-=0 r=0
откуда вытекают рекуррентные соотношения
.11) = 0>(г=1, 2, ...).} (9l)
оо
Аналогично для решения типа Со, Со(#) = 21 crcos2rx, получаем
рекуррентные соотношения
— O, [22—fl<r1
= 0 (г = 2,3, ...), I ( *'
и таким же путем для решений
l ^i\ 0
9-=0 9-=1
имеют место рекуррентные соотношения
(г= 1, 2, ...),
[BгJ - /] < + Л2 (с^1 + <+1) = 0 (г = 2, 3, ...)•}
3. Отсутствие линейно независимых периодических решений,
соответствующих одному и тому же собственному значению.
Теорема Айнса. а) Формулы (9j), (9g), (93), (94) предыдущего но-
номера позволяют нам доказать следующую теорему Айнса.
Если А Ф 0, то любому собственному значению I уравнения G)
соответствует одна и только одна собственная функция (см.
Айне [2]).
Предположим, чзо собственному значению / соответствуют две
линейно независимые собственные функции уг и у2; в силу изложен-
изложенного в предыдущем номере мы можем считать, что одна из них
четна, а другая нечетна, и потому мы можем предположить, что ух
имеет тип Со или Сх, а у2 — тип 50 или Sv
Имеем
2A2 cos 2х] ух = 0, у1-\-\1— № cos 2x] ys = 0.
§4. Уравнение Матье
299
Умножая первое равенство на у2, а второе на ул и вычитая, полу-
получаем, что \у2у[—у1у'а]' = 0, а потому y2y't—yty'2= const. Отсюда
следует, что если ух имеет тип Cj(C0), то у2 имеет тип 5jE0);
в самом деле, если бы у1 имело тип Сг, а у%—тип SQ, то при
замене х на х-\~п выражение jyj—уху'2 должно было бы менять
знак, а потому оно равнялось бы нулю, и функции у1 и у2 были бы
линейно зависимы.
Пусть теперь функции у1 и у2 имеют, соответственно, типы С1
и Sj'); тогда в силу (9j), (98)
[Bг+1)а —
Vr]Zo}
Так как кфО, то, исключая / из (IOj) и A02), получаем, что
с0 ^
с' с'
сг сг+1
с' с'
Сг Сг+1
и, следовательно,
(И)
Но тригонометрические ряды
г=о г=о
являются рядами Фурье, а потому
и, следовательно, в силу A1) <гос^ = 0. Но h Ф 0, и из формул A0j),
A02) следует, что по крайней мере одна из последовательностей {сг},
\с'г} состоит из нулей, а потому либо уу ^ 0, либо у2 ^ 0, чего не
может быть.
б) Из доказанной теоремы следует, что любая собственная функ-
функция уравнения Матье должна быть либо четной, либо нечетной;
в самом деле, если у(х, I) является собственной функцией, имеющей
период 2эт, то у(—х, I) также является собственной функцией того
же периода, принадлежащей тому же собственному значению, и по
!) Аналогично проводится рассуждение в случае, когда у± и _у2 имеют,
соответственно, типы Со и So.
2) См., например, Фихтенгольц Г. М. [1]. т. Ш, стр. 519.-~ Прим. перев.
300 Гл. VI. Уравнения и системы с периодическими коэффициентами
доказанной теореме эти два решения могут различаться лишь посто-
постоянным множителем').
4. Интегральное уравнение Уиттекера для функций Матье.
Отметим, наконец, одно из весьма важных интегральных уравнений
Уиттекера, которым удовлетворяют функции Матье; с этими урав-
уравнениями связан ряд исследований английской школы, посвященных
этому важному классу функций (см. Уиттекер [1], а также Пуль [1]).
Докажем, что если у(х) является решением уравнения Матье,
имеющим период 2эт, типа Со или Sv то оно удовлетворяет инте-
интегральному уравнению Уиттекера с симметрическим ядром
1С
J
A2)
Заметим, что G) можно записать в виде
Предполагая, что 1У — собственное значение, а у (х) — соответствую-
соответствующая собственная функция, имеющая период 2эт, рассмотрим функцию
у (х) = J е
которая также имеет период
Легко установить, что
— 4АЙ ^ х) Y =
Г
/t — 4 A2 cos2 *)] у (Щ db,
но
4 A2 cos2 х sin2 0 — 4А2 cos2 x =
= 4Й2[A — sin2x)(l — cos28) — cos2*] =
= 4й2 [sin2 x cos2 6 — cos2 Щ,
я потому
Y"+{lx—4й2 cos2 x) Y=
¦ It
_ J e2b sin x sin e [4As sin2 x cosa a _ 2h sin x sin Й +
— 4A2 cos2 6)] у F) rf8.
?) Этот множитель >южет равняться иди 1, иди — 1, —¦ Прим, перев.
4. Уравнение Мйтьё 501
Интегрируя последовательно по частям и принимая во внимание
периодичность у F) и dy/dQ, получаем
С gshsinxsto» [4А2 sin2 х cos2 6 — 2й sin x sin b]y F) db =
_ _ J в2Й8та!в1пв2А sIn ЛГ COS 6 -^-rf6 =
— 1С
~" J db [e * йЪй ) e d№
и потому
у" + [/x — 4A2 cos2 x]Y =
1С
= J
= 0,
Таким образом, функция Y(x) удовлетворяет уравнению Матье.
Функция Y{x) не обращается тождественно в нуль, когда х из-
изменяется в [—я, it]. В самом деле,
со
O27isin:rsin6
v=0
Стоящий справа ряд равномерно сходится, когда 6 изменяется в
[—it, it], поэтому если бы К(лг) тождественно разнялось нулю в [—я, it],
то имело бы место равенстзо
v=0 -я
Но так как справа стоит ряд, расположенный по степеням sin*, то
из этого равенства следозало бы, что
, i, 2,
302 Гл. VI. Уравнений и системы с Периодичес/iuMu коэффициентами
и, по формулам Эйлера'),
— B/")cosBr — 2N +
f— 1)" 22r sln2r+16 = Br +') sin Br +1) 6 —
должны были бы выполняться равенства
К 1С
§ у F) cos 2rfl db = О, J у F) sin Br + 1) 6 db = 0
—it —it
(r —0, 1, 2, ...).
Так как .у(б) имеет, по предположению, тип Со или 5,, то все его
коэффициенты были бы равны нулю, а тогда и сама функция у(Ь)
тождественно равнялась бы нулю, вопреки предположению.
Но тогда, по теореме Айнса (п. 3), функция Y(x) может отли-
отличаться от у(х) лишь постоянным множителем А, а потому y(x) — KY(x)
и уравнение A2) следует из формулы A3).
§ 5. Системы линейных однородных уравнений
с периодическими коэффициентами
а) Укажем вкратце, как получить для систем однородных диффе-
дифференциальных уравнений с периодическими коэффициентами результаты,
аналогичные полученным в § 1 для линейных дифференциальных урав-
уравнений с периодическими коэффициентами.
Пусть дана система
п
^@ = 2я1!,г@-*г@ (' = 1. 2, ..., я), A)
коэффициенты которой а^ г (t) определены в (— оо, -j- оо), непре-
непрерывны и имеют один и тот же период ш (ш > 0),
ai, i ('+«>) = ai, г («О. (Л /= 1, 2, ..., я), — оо < t < +00. B)
!) Эти формулы легко вывести, возведя известную формулу Эйлера
х = ^ в с
Ньютона. — Прим. ред.
sin х = ^ в степени 2г-\-1 и 2г и раскрыв правую часть по биному
5. Система с периодическими коэффициентами
ЗоЗ
Пусть я решений системы A)
-W). •**.*(<). •••, xn>lt{t) (Л=1, 2, .... я) C)
образуют фундаментальную систему решений, и, следовательно,
'• *«.»(*)
• • • хп, п (*)
Как известно, общее решение системы A) имеет вид
xi (f) == *-lxt, 1 (О Н~ C2*», 2 (f) ~\~ ' ' • ~\~ ^nxi, та @ D)
(i=l, 2, .... я).
Определим теперь постоянные сг, с2, ..., сп так, чтобы существовала
такая соответствующая им постоянная р, что
Х{ (t-\- <o) = pxt (f) [i = 1, 2, ..., я; — оо <[ < < -|- оо]. E)
Из сделанных предположений следует, что я решений
также дают нам фундаментальную систему решений системы A);
в самом деле (гл. II, § 1, п. 2),
*1
F)
Поэтому существуют я2 чисел o,#k (/, fe=l, 2, ..., я), таких, что
*,-.к
«
та
)== 2Ч,гЧi(t) (i, h = 1, 2, ..., и). G)
2
Из D) следует, что
п та
,. , ч "V /"V ¦ \ /л
%i [}¦ 1~ ®) ^J \ ^J ^1с ]{ 1/ Xi I \r)i
1=1 fc=l
а потому для выполнения соотношений E) необходимо и достаточно,
чтобы постоянные cv с2, ..., сп были таковы, что
V4i —Pi)¦*<.!(*) == 0 (i=l, 2, .... я).
304 Гл. VL Уравнения а системы с периодическими коэффициентами
Ho Det||Ari(l|| = A(*)^O,
n
fc=i
или
а1, lCl *T" «2, JC2 ~T~ ' •
а потому должны иметь место равенства
-рег = О (/=
1, 2,..., я)
Таким образом, р должно быть корнем характеристического
D(p) =
«Li —P
«1.2
«1.»
а2.1
«2.2-Р ••
а2, w
• «».i
• «п.2
" Tit 91 Г
= 0.
0. (8)
уравнения
(9)
Итак, если р является корнем характеристического уравне-
уравнения (9), то, выбирая постоянные cv c2, ..., сп, удовлетворяющие
системе (8) при этом значении р, и строя по этим постоянным,
согласно формуле D), функции xt(t), x2(t), ..., хп(f), мы полу-
получаем решение, удовлетворяющее условию E).
б) Из доказанного следует, что для того, чтобы система A)
обладала решением, имеющим период ш, необходимо и достаточно,
чтобы соответствующее ей характеристическое уравнение (9)
имело корень р = 11).
§ 6. Системы дифференциальных уравнений,
зависящих от параметра. Периодические решения
Пусть дана система дифференциальных уравнений
^-^Xt{t; xv xz, ..., хп; k) (i=l, 2, .... я), A)
где t; xv x$, ..., xn; k изменяются в области Сп+2, определенной
неравенствами
— оо < t < + оо;
; /=1, 2, .... я); X» —
Предположим, что задание при t = fl> системы начальных значений
Xi~\~аи х2~\~«2, ..., хп-\-ап>
где lajl^a (/= I, 2, ..., я), и любого значения параметра X из
[к0—с, к°-\-с] однозначно определяет решение
*< = ?<('; «1. «2. •••» «#.; *) (*=1. 2, .... и, — оо<<<+оо), B)
!) Относительно распространения на линейные системы результатов из § 1,
касающихся дифференциальных уравнений, см. Гурса [1], т. II, стр. 409—412,
Моультон [1] стр. 317—348.
$ 6. Системы, зависящие от параметра. Периодические решений 305
удовлетворяющее начальным условиям
¦*°+«* = <Р»(*°; «1. «2 «„; *) (*=1, 2, ..., я). C)
Предположим также, что функции Хь рассматриваемые как
функции от t, имеют период ш > О,
; xv х2, ..., хп, k) = Xi(t; xv *2 хп; Л),
— аэ</<+аэ (/=1, 2, ..., я),
я также, что при Л = Л° выполняются равенства
9i(t°+<»; 0, 0, .... 0; Л°) = <р<(*°; 0, 0, ..., О; Х°) D)
(*=1, 2 я),
т. е. что функции ^(t; av ot2, •••» ап> ^) принимают одинаковые
значения при t = f> и при ^^^-(-ш, если
Л = Л°, at = a2 = ... = ап = 0.
Если переменная t означает время, то можно интерпретировать
уравнения A) как уравнения движения точки Ps(jelt jc2, ..., jcn)
в пространстве Sn. Тогда D) эквивалентно предположению, что при
движении, соответствующем значениям X = Л°, ax = a2... =an = 0,
точка Р принимает одинаковые положения в моменты Р и Р-^-ш.
Но из сделанных предположений следует, что, полагая в заданной
системе X = Х°, мы получаем систему, не изменяющуюся при замене
I на t-\-o>, а потому функции <р<(# 0, 0, ..., 0; Л°) (?= 1, 2, , п)
имеют период ш, или, иными словами, при Л = Л° решение
системы A)
*€ = *«(<; 0, 0, ..., 0; Л°),
удовлетворяющее начальным условиям
4=<р<(*°; о, о о;
периодично, равно как и движение точки Р.
Для приложений важен следующий вопрос: существует ли такая
окрестность (Х°—8, Л0-)-8) точки Л°, что любому X, принадле-
принадлежащему этой окрестности, можно поставить в соответствие
значения постоянных av a2, ..., an, которым соответствует
решение
«ц «2» •••! ап> Л) (f'==1» 2, .... и),
имеющее период ш?
Мы изучим этот вопрос в достаточно общем случае. Добавим
к сделанным выше предположениям требование существования у функ-
функций Xt(t; xv x?, ..., хп; Л) непрерывных в С„+2 частных произ-
производных первого порядка по xv дс2, .. -, хп; Л. Как указывалось
в гл. I, § 5, п. 2, из этого требования вытекает существование и
20 Зак. 627. Дж. Сансоые
Зоб tju VI. Уравнения и систёмп с Периодическими коэффициёнт&ми
непрерывность частных производных решений «р<(<; ац а2> • • •» ап> *)
по av а2, ..., ап; Л.
Предположив выполнение этого требования, заметим сначала, что
для периодичности решения B) необходимо и достаточно, чтобы
постоянные av а2, ..., ап удовлетворяли системе
ф<=<р<(<°+<»; «1. «2» •••>«»; *)—*«(<°;.о, о,.... о; к*)—а«=о
. (/=1,2 я). E)
При Х = Л° эта система имеет решение о1=-о2= = ап = 0, и
если ее якобиан
Й[«ь ап1
отличен от нуля в некоторой окрестности точки (*°, 0, 0, ,0; Ло), то,
в силу теоремы о неявных функциях, найдется настолько малое 8, что
при \\ — Х°|<<8 можно найти систему функцийа%(Л), а2(Л), ...,<хп(X),
удовлетворяющую системе E), а тогда соответствующее решение
<р,(/; в1(А), а2(Л), ..., аи(Л); Л) (i= 1, 2, .... и)
имеет период ш.
Если обозначить через (д-Ч частную производную функции Ф*
по afc, вычисленную в точке (t; 0, 0, ..., 0; К0), и положить
то функции V(k будут решениями линейной системы уравнений
в вариациях системы A) (см. гл. I, § 5, п. 2; гл. VII, § 1, п. 2)
*.iK <Pi(^ 0, 0,..., 0; Л«0, ..., <ри(г!, 0, 0,..., 0; Л<>)] vfc]k
F)
(/=1, 2, ..., и; ft=l, 2 я),
удовлетворяющими начальным 'условиям
V<,*(<°) = 8<.*[«<.<=1; 8i.fc = 0 при t>fe; i, fe=l, 2,..., R].
Имеем
/а(Фь Ф2,...,ФП)\ =
, а2, ..., ап) Уо
§ 7. О НериодиЧеЫих решениях уравнения Ьинймикй 307
В силу сказанного в § 5 обращение в нуль этого определителя
является необходимым и достаточным условием существования у си-
системы уравнений в вариациях F) решений, имеющих период ш; таким
образом, мы доказали, что при сделанных предположениях, если
система в вариациях F) системы A), соответствующая изве~
стному решению
Ъ(<; 0, 0,..., 0; А©),..., 9пу; о, 0,..., 0; Л»), G)
имеющему период ш, не имеет решений с периодом ш, то суще-
существует такое положительное число 8, что любому значению па-
параметра А, удовлетворяющему неравенству |А — А°|^8, соот-
соответствует периодическое решение системы A)
<Pi V, «t (А), -..,«« (А); А], ...., <ри [t; «! (А) ап (А); А] (8)
с периодом ш.
Более того, для любого положительного числа о можно указать
такое значение 8, что при |А — А°|^8и — оо < * < -|- оо выпол-
выполняются неравенства
|<р,(*; о,(А), о,(А),..., оя(А); А) —?«(<; 0, 0 0; А°)|<с
(i=l, 2, ..., и),
или, как говорится, периодическое решение G) системы A) устой-
устойчиво относительно совокупности периодических решений (8)
(см. гл. VII, § 1, п. II).
§ 7. О периодических решениях
дифференциального уравнения динамики точки,
движущейся по заданной траектории
1. Теорема Вейерштрасса. Пусть материальная точка Р посто-
постоянной массы т движется под действием силы F, зависящей от поло-
положения точки, по заданной траектории Г.
Выберем в качестве параметра длину дуги s кривой Г, а поло-
положительным направлением касательной будем считать направление,
совпадающее с направлением возрастания s. Если обозначить через
f(s) тангенциальную компоненту силы F, то уравнение движения
имеет вид
ms"=f(s) |> = g, где t— время]2). A)
*) Более глубокое изложение этих, вопросов, равно как и приложения
развитой теории к знаменитой проблеме трех тел изложено в книге Пуан-
Пуанкаре [1], т. I, гл. III и IV; см. также Пикар [4], т. III, стр. 167—186.
О некоторых случаях устойчивости, зависящей от параметра линейной
системы, см. Чезари [1].
*) См. Вейерштрасс [1], т. II, стр. 1—18; Леви-Чивита и Амальди [1J,
т. II, ч. I, стр. 19.
20*
908 /*л. Vi. Уравнения и системы с Периодическими коэффициентами
Мы будем считать, что функция f(s) непрерывно зависит от s. По-
Положим
Jf(s)ds=U(s). B)
Умножая A) на /, получаем, что
Интегрируя это равенство, получаем для кинетической энергии
Т(Т— /и5/2/2) равенство
T—U = E (E= const) C)
(интеграл энергии).
Положим
|-[!/(*)+ Е1 = Ф(*). D)
Тогда из C) следует, что
Мы воспользуемся уравнением E) для изучения поведения решений
уравнения A) в одном интересном частном случае.
Предположим, что функция Ф(я) имеет при в — в^ s = s2,
sx < s2 простые нули, т. е. пусть
lim Ф (s)/(s — sx) = Лх =?t О,
Нт Ф (s)/(s2 — s) == Л2 =jfe О,
F)
с яри st < s < s2 функция Ф E) сохраняет знак, например
Ф(я)>0 «рн ^<«<*2. G)
можем положить при st < s < s2
*)Ф!(*), (8,)
^)=Ля/(^,—*,). (8а)
Функция &t(x) непрерывна на отрезке [su s2].
Предположим, что в момент t = 0 движение начинается из поло-
положения s0, *i < *о < S2» например в направлении от sx к s2. В силу
E) начальная скорость v0 выражается по величине и значению ариф-
арифметическим значением корня
«о = V(s0 — *iK«e — SoXMsoI), (9)
!) Наоборот, если движение начинается в направлении от *2 к slt то
корень надо брать с отрицательным знаком.
§ 7. О периодических решениях уравнения динамики 309
и во время движения от sQ к s2 имеем
dt__ 1
ds*~ VfF- '
а потому при наших предположениях время tl = t(s0, s2), в которое
точка Р пробегает дугу (s0, s2), выражается сходящимся интегралом
ti = t(s0, s2) = Г , ds A0,)
В s2 скорость движения равна нулю, а так как тангенциальная
сила
ДШ\ m (d9\ т
отрицательна, то движение изменяет направление и точка начинает
двигаться от s2 к sv а тогда
^
ds Y(s — si)(s2
и потому за время <2 = < (s2, Sj), выражаемое сходящимся интегралом
* = t (S s) = — Г d5 , A02)
точка Р попадает в s,; здесь скорость обращается в нуль, а так как
тангенциальная сила
положительна, то движение изменяет свое направление и точка на-
начинает двигаться от st к s2 и за время tf3, выражаемое сходящимся
интегралом
«о
?, = *(*!, S0)= Г , ^ , A0„)
возвращается в первоначальное положение s0, имея скорость, равную
по величине и по знаку выражению (9), т. е. начальную скорость,
после чего движение-полностью повторяется.
х) Независимо от механических соображений, мы имеем s' (ti) = 0,
s" (ti)=f(s2)/m = — (s2 — st) Ф1 (*g)/2 < 0, а потому s(/) достигает в /t ма-
максимума, и при достаточно малом положительном ft >0 имеем s fa -|- h) <js (t{f.
Аналогичные рассуждения были проведены в гл. 1, § , п. 2, 3,
310 Гл. VI, Уравнения и системы с периодическими коэффициентами
Отсюда вытекает теорема Вейерштрасса:
Если при сделанных предположениях s = s(t) является реше-
решением уравнения A), определяемым начальными условиями
s @) = s0, v @) = v0,
где
si <С So ^ *2>
то s(t) имеет период 2z[s(t-\-2z) = s(t)], равный сумме ^-На^Нз»
т. е. в силу A0,), A02), A08) равный
2х = 2 Г , ds A1)
2. Формула Леви-Чивита для вычисления периода в первом
приближении, а) Пусть функция Ф($) имеет вид
= ^(s — si)(s2 — s) (ш = const, шфО). (Щ)
С помощью замены переменной
s = [(s2 + si) — E2 — *i) cos a]/2
мы получаем для соответствующего периода 2г0 значение
Рассмотрим теперь случай, когда
1E)=/7(е, 8),
где функция^ср^) непрерывна вместе с первой и второй произ-
производными в [su s2], st < s1 < s2 < s2, и предположим, что можно
пренебречь членами, содержащими е"/« или высшие степени е. Вы-
Выведем в этом случае красивую формулу Леви-Чивита (см. Леви-Чи-
Леви-Чивита [1], а также Картович [1]) для вычисления периода 2%,
Уравнение
F(s, *) = %(*)+ «&(*) = 0 A3)
удовлетворяется при значениях неизвестных е = 0, s = st, а так как
то уравнение A3) имеет при достаточно малом е корень
или
§ 7. О периодических решениях уравнения динамики 311
Аналогично показывается, что уравнение A3) имеет другой корень
st = sa-i~e „?l(Sa) .+е20A), A42)
причем из формул A4t) и A42) следует, что при достаточно малом е
Так как F(e, s*) = 0, F(e, s*) = 0, то по интерполящюнной фор-
формуле Ньютона, записанной с остаточным членом второго порядка,
получаем, что
F(e, ,) = F(s, s:) + {s-s*AF(°-sl)r:{e'S*) +
s2 — st
+ "(s-si)(s — s*2)/?(e, s),
где
/? (e, s) = <p0 (s) -\- e<pi (s) = — 2co2 -f- e«! (s), sx < s < s2,
а потому мы можем положить, что
F (г, s) == со2 (s — sj) (s* — s) [1 + ег (в, г)], A5)
где функция | г (е, s) \ равномерно ограничена при достаточно малом е
Подставляя A4J, A42) в A5) и принимая во внимание фор-
формулы A3) и A2j), получаем, что в (sv s2)
X
e, s)],
t —— •>-у) [Sq ~~^ Sj Г (J5j 2>j <pj ^J?J ——
где A(e, s) равномерно ограничено относительно г и s.
Положим
sv 52) =
A62)
312 Гл. VI. Уравнения и системы с периодическими коэффициентами
и при s ф siy s2 положим
Тогда
Но
Hm X(s) = —
1 6 (я, sb s2)
г(е, s)=X
0
/ !/ г-
(я — si)(s2 — s)
1 0
A7)
A8)
sf
<?№ 1 О
и, аналогично,
И»М«)=-ж=:
A92)
а потому функция X(s) конечна и непрерывна в [sx, s2], причем
легко проверить, что она имеет в [sv s2] непрерывную, а потому и
ограниченную, производную.
В силу (Hj), A42), A8) получаем теперь, что
(s — s\) (sl—s) [r (e, s) — X О?)] = (s—sj (st—s) [r (e, s) — X (s)] +
-f-eO(l)=eA(e, s)-f-eO(l) = efe(e, s),
где функция fe(e, s) равномерно ограничена относительно е и s,
а также, что
r(e, s) = X
(s—Sj)(s2—s)
Отсюда следует, что функция efe(e, s)/(s—s*)(*2 —s) равномерно
ограничена относительно е и s.
Из формул A1) и A5) получаем для периода 2т, соответствую-
соответствующего функции Ф($)> определенной A22), выражение
<0 J
ds
V(s-sl)(s*2-s)[l+tr(*, в)}
С помощью замены переменной
-cos a
B1)
§ 7. О периодических решениях уравнения динамики 313
это выражение приводится к
2-е = — f - * da,
BO
[l+er(e, 5)]-V.= l—ier(e,
а потому, учитывая B0), получаем, что
= 2т0 - -i- J X (я) rfa + e2 J __*^L_.de + .2О A), B2)
где s выражается формулой B1).
Заметим, что
но
It
Jek (e, s)
*w~*
J (s-4)D-S)
7i-e
*—^»—
1/, 1/ -i
и потому из формулы B2) следует, что
тс
2т = 2г0 — J X (s) da + е*/.О A),
314 Гл. VI. Уравнения и системы с периодическими коэффициентами
Принимая во внимание, что A(s) имеет ограниченную производ-
производную в [sv sa], получаем из B1), A4Д A42), что
= X
- *=%- cos a] + еО A),
откуда и вытекает формула Леви-Чивита для периода 2т1)
2i = 2*0 — -±- J Л (-^±А — -^=5L cos a] da + ea/.O A). B3)
]
о
б) Картович (см. Картович [1]) дал полезное преобразование фор-
формулы B3).
Положим
si + so s2—s,
— 9 2
Из A62) следует, что
а из A6^, что
а потому
lira Ш = lim ^. * cos^a = -U=l Hm |1 sin a = 0.
Аналогично доказывается, что
Но тогда, принимая во внимание формулу A7), получаем с по-
помощью очевидных преобразований
о
2 Г <f 6 2 Г
= —57 nT I -jrcosarfa = s-j г I <p'(s)dslna =
<»2(S2 — SjJ J dS o>2(s2 — *l) J TlV
о о
Уточнение члена ъ1г 0A) дано автором книги (см. Сансоне [3]).
5 & Задача о периодических орбитах 315
Замечая, наконец, что
(s2si) —siHs2 — s) ds = sifl2ada>
преобразуем формулу B3) к виду1)
«2
* ). B4)
§ 8. Задача о периодических орбитах
и вариационное исчисление
1. Задача о периодических орбитах, а) В некоторых вопросах
существование периодических решений получается с помощью при-
применения методов теории дифференциальных уравнений, причем при-
приходится накладывать слишком жесткие требования на уравнения.
Но иногда (например, в задачах динамики) исследуемые дифферен-
дифференциальные уравнения являются необходимыми условиями существова-
существования минимума некоторого заданного интеграла (интеграла действия).
Если в этом случае с помощью прямых методов можно установить
существование минимума, то тем самым одновременно доказывается
существование искомых периодических решений.
Мы уже имели случай применения прямого метода Тонелли (см.
гл. V, §4, п. 2). Другие приложения прямых методов будут изложены
в гл. XI, § 5, п. 3, в частности, для эффективного вычисления ре-
решений, соответствующих определенным краевым условиям. Здесь мы
остановимся вкратце на упомянутой выше задаче о периодических
орбитах и докажем, благодаря силе прямых методов, существование
таких орбит при весьма общих предположениях2).
*) Читатель может проверить формулу B4) на следующем примере.
Пусть 9i (s) = <Ро («); тогда
и второй член в правой части принимает вид
2е Г „ . rte
о
2) О приложениях вариационного исчисления к нахождению периодиче-
периодических решений нелинейных уравнений второго порядка см. Лихтенштейн [1],
стр. 24—51. Относительно же применения вариационного исчисления к изу-
изучению так называемого обобщенного уравнения Штурма — Лиувилля
— (р
2k V v
— (р -Ар
2k V v 4xtv
316 Гл. VI. Уравнения и системы с периодическими коэффициентами
б) Обозначим через / время, через л: и у—координаты точки Р,
движущейся под действием силы, обладающей потенциалом; пусть
связи зависят от времени, и пусть д/ и у' обозначают производные д:
и у по t. Уравнения движения в форме Лагранжа являются уравне-
уравнениями второго порядка
А^,-^ = 0, ^-Ly,-Ly = 0, A)
где через L обозначено выражение
±2 * B)
а Ь#, Ly, L^, Ly< обозначают частные производные от L по перемен-
переменным х, у, х1, У О-
Предположим, что коэффициенты а, Ь, с, а, [5, f являются непре-
непрерывными функциями от х и у, равно как и их частные производные
первого порядка, и что
с>0 (с>0), ас— ?2>0. C)
Рассмотрим, может ли точка Р описывать периодическую орбиту,
т. е. замкнутую кривую без точек самопересечения и самокасания,
иными словами, существует ли пара функций х (f), у (i), удовлетворяю-
удовлетворяющих в промежутках (to, tt) системе A), а на концах — периодическим
условиям
и таких, что x~=x(f), y = y(t) являются в B0, tt) уравнениями про-
простой кривой.
Если x(t), y(t) являются решениями системы A), то
а потому
'L+/L k* D)
выражающего обращение в нуль первой вариации интеграла
ь
F(x,y,y')dx
а
при условиях
ь
fy**dx=l,y(a)=:y(b) = Q (k=h 2,...)
а
[си. Люстерник Л. А. [1].
*) См. Бухгольц Н. Н. [1], т. II, стр. 53. — Прим. перев.
2) Говорят, что D) представляет собой первый интеграл системы A)
(см. примечание на стр. 90), называемый в нашем случае первым интегра-
интегралом энергии.
__ $ 8. Задачи о периодических орбитах 317
где k — постоянная величина, а так как уравнение A) остается не-
неизменным при увеличении L на постоянную величину, то можно счи-
считать, что й = 0,
x'La,.+/Lp. = L, E)
или, в силу B), что
~ [ах'2 + 2bx'/+с/2] = т. F)
Так как левая часть равенства F) является положительно определен-
определенной формой от переменных х1, у', то должно выполняться неравен-
неравенство f(x, у)^0, а потому, если x = x{t), y=y(t) является реше-
решением системы A), то оно должно принадлежать области, где
Т (*.>)> О-
Пусть даны две непрерывные замкнутые простые жордановы кри-
кривые 8j и ?2, первая из которых лежит целиком внутри второй, при-
причем вдоль этих кривых и в заключенной между ними кольцеобразной
области 91 плоскости л:, у выполняется неравенство
Ч(х, у)>0.
Покажем, что тогда области 91 принадлежит периодическая орбита,
окружающая кривую gt.
Уравнения A) траектории точки Р являются уравнениями Эйлера
для экстремали интеграла
, G)
to
причем, в силу B) и F), такой интеграл можно записать в виде
J* = J [V2f Vax? + 2д*У + су'2 + ад/ + р/] dt. (8)
Имеем тождественно
t
J - /* э 1 J \Vax* + 2bx'y' + су'2 - Vz^Y Л, (9)
to
a потому, если вдоль некоторой кривой выполняется равенство F),
то / — /* и 8(/ — /*) обращаются в нуль, т. е. для первых вариа-
вариаций J в J* выполняется равенство
8/ —8У*—О,
и 8/* должно обращаться в нуль при любых вариациях х и у, если
исходная кривая в плоскости х, у является орбитой системы A), F).
1) См. Лаврентьев М. А. и Люстерник Л. А. [1], стр. 15* 185. — Прим.
перев.
318 Гл. VI. Уравнения и системы с периодическими коэффициентами
Подинтегральная функция интеграла /* положительно однородна
порядка 1 относительно х' и у'; поэтому значение интеграла J* вдоль
некоторой дуги С зависит только от самой дуги, но не зависит от
ее параметрического представления x=x(f), y=y{f)' Но тогда
можно считать, что параметр вдоль орбиты выбран так, чтобы вы-
выполнялось равенство F) ]).
Если вдоль кривой 8/* = 0 и если параметр t выбран так, чтобы
выполнялось равенство F), то вдоль этой кривой 8/ = 8/* = О, а по-
потому x = x(t), y=y(t) представляет траекторию системы A), F).
Полагая
F = V*t V ах'2 + 2**У + су'2+ се
имеем
и по терминологии вариационного исчисления интеграл положи-
положительно регулярен (см. Тонелли [4]); поэтому задача о существовании
периодических орбит эквивалентна изучению замкнутых экстрема-
экстремалей положительно регулярного интеграла
fF(x,
/)dt,
принадлежащих заданной кольцеобразной области 91 и окружающих gj.
Существование таких замкнутых экстремалей следует из одной тео-
теоремы Тонелли, которую мы сформулируем в следующем номере,
2. Теорема Тонелли о существовании периодических экстре-
экстремалей, а) Впервые существование периодических орбит в так назы-
называемом обратимом случае (ау—$x==0) было указано Уиттекером
(см. Уиттекер [2]), но первое строгое доказательство было дано
независимо друг от друга Синьорини и Тонелли (см. Синьорини [1],
Тонелли [5]).
Позднее Биркгоф (см. Биркгоф [2]) рассмотрел необратимый слу-
случай (a, J3—любые) и доказал также существование замкнутых орбит.
В 1923 г. Тонелли (см. Тонелли [6]) дал простое доказательство
этого результата.
Критерий Биркгофа был обобщен Дамкёлером (см. Дамкёлер [1])
и упрощен и расширен Тонелли (см. Тонелли [7]). Изложим теперь
формулировки некоторых результатов Тонелли, о которых мы уже
упоминали в п. 1, отослав читателя за доказательствами к указанным
выше мемуарам.
!) См. Лаврентьев М. А. и Люстерник Л. А. [2], ч. II, стр. 190. — Прим.
перев.
^ § 8. Задача 6 периодически* орбитах 319
б) Обозначим через 91 кольцеобразную область плоскости д:, у,
ограниченную непрерывными жордановыми замкнутыми кривыми 8t
и й2, не имеющими кратных точек, из которых первая целиком лежит
внутри второй. Пусть функция F(x, у, х1, уг) определена и непре-
непрерывна вместе со своими частными производными первого порядка для
любой точки (л:, у) из 91 и любой пары чисел (aV, у'), не равных
одновременно нулю.
Пусть F(x, у, х1, у") является положительно однородной функ-
функцией первого порядка относительно х? и у', т. е. пусть для любого
k>0
F(x, у, kx', ky') = kF(x, у, х>, у').
Назовем комплексом 6 совокупность любого конечного числа
(которое может равняться единице и не обязательно одинаково для
всех комплексов) непрерывных замкнутых спрямляемых жордановых
кривых без кратных точек, на каждой из которых указано направле-
направление, Cv С2, ..., Ст, принадлежащих кольцеобразной области 91 и
удовлетворяющих следующим условиям:
1. Любая кривая Сг из 6 не может одновременно иметь как точек,
лежащих внутри другой кривой того же комплекса, так и точек,
лежащих вне этой кривой.
2. Две кривые Сг и С8 не могут состоять из одних и тех же
точек, даже в том случае, когда они ориентированы различным об-
образом.
3. Если кривая Сг из 6 не имеет точек, лежащих внутри какой-
либо другой кривой этого комплекса, то она ориентируется положи-
положительно (т. е. так, чтобы при обходе внутренняя область оставалась
слева); другие кривые С8 из (? ориентируются положительно или
отрицательно, в зависимости от того, четно или нечетно число кри-
кривых из d, содержащих внутри себя точки кривой С8.
4. Среди кривых Сг из 6 всегда есть нечетное число кривых,
окружающих полностью кривую 81; а потому всегда существует по
крайней мере одна кривая, полностью окружающая кривую 8j и по-
положительно ориентированная.
Положим
3® = 2 fF(x> У' *?> /) ds = 2
l J 1
2 f( У /) 2
где x=x(s), y=y(s), x1' = dx/ds, у' = dy\ds и ds обозначает диф-
дифференциал длины дуги кривой Сг.
Пусть в области 91*, для которой все точки кольцеобразной об-
области 91 являются внутренними точками, интеграл Зе регулярен
(т. е. либо всегда /^(д:, у, л/, _у')>0, либо всегда Ft (x,y, *',/)<О,
где Fi = FX'X'ly'2 s= — Fa,-у /а,- у = Fyylxf71) или нормально квази-
регулярен (т. е. всегда /^(л:, у, х', У)>0 или Fj(x, у, я?, /)<0,
520 Гл. Vt. Уравнения и системы с периодическими коэффициентами
причем значения 6, для которых F1(x, у, cos в, sin в) = 0, не запол-
заполняют никакого промежутка, лежащего в [0, 2тг]). Пусть, далее,
область % выпукла в малом в положительном направлении отно-
относительно функции F(x, у, xf, У) (т. е. пусть существует такое
число р > О, что все экстремали, соединяющие концы любой дуги
kj PtP% кривой ^ или й2 и лежащие вместе с этой дугой в круге
с центром в Pj и радиусом р, положительное направление которых
совпадает с положительным направлением дуги kj PjP2» целиком при-
принадлежат области 91); тогда существует, по крайней мере, одна
периодическая {замкнутая) экстремаль относительно F(x, у, а/, у'),
не имеющая кратных точек, окружающая 8г и имеющая поло-
положительное направление.
Если при тех же предположениях /^(л:, у, х', у')^-0, то
в множестве всех комплексов (?, на которых 3s достигает абсо-
абсолютного минимума, существует, по крайней мере, один комплекс,
составленный из конечного числа попарно непересекающихся зам-
замкнутых экстремалей.
§ 9. Почти периодические функции и почти периодические
решения дифференциальных уравнений
1. Почти периодические функции. Первые свойства, а) В по-
последние десятилетия Бор, Вейль, Валле-Пуссен, Бохнер, Фавар, Винер
с большим успехом изучали так называемые почти периодические
функции, а Биркгоф и Н. М. Крылов указали важные приложения
этих функций к динамике и математической физике. Здесь мы не мо-
можем изложить доказательства результатов этих ученых, а потому, чтобы
ориентировать читателя в этом круге вопросов, изложим здесь лишь
формулировки основных свойств этого класса функций и укажем
приложения этих функций к изучению одного частного вида неодно-
неоднородных линейных дифференциальных уравнений 1).
б) Действительная или комплексная функция f{x) действительной
переменной д:
f(x) = u(x)-\-w{x) (i — мнимая единица; и(х) и v(x) действительны),
конечная и непрерывная при — со < д: < -{- оо, называется почти
периодической, если для любого положительного числа е можно
найти такое число /
/ = /(/, в)> О,
что каково бы ни было действительное число а, в полуотрезке
[а, а-\-1) существует по крайней мере одно число •:
!) Относительно библиографии см. Бор [1], Безикович А. С. [1], Фавар [1].
[См. также Левитан Б. М. [1]; мы будем делать ссылки на эту работу.—
Прим. перев.]
§ 9. Почти периодические решения 321
называемое почти периодом функции /(дг) относительно е, для
которого при любом дг выполняется неравенство
Очевидно, что всякая непрерывная периодическая функция почти
периодична.
в) Почти периодические функции обладают следующими свой-
свойствами:
1. Если функция /(дг) поч'ти периодична, а а — некоторое число,
то функции /(дг-f-a) и f(ax) почти периодичны.
2. Почти периодические функции ограничены в (—оо, -f-oo).
3. Если функция/(ж) почти периодична, a k — некоторое действи-
действительное или комплексное число, то и функции f(x)-\~k и kf{x) почти
периодичны.
4. Если функция /(дг) = и (дг)-j-и> (дг) почти периодична, то и
функции /о (х) = и (дг)— iv(x) и |/(лг)| почти периодичны.
г) Почти периодические функции равномерно непрерывны в (— оо,
-f- оо), т. е. для любого положительного числа е можно найти такое
положительное число 8, что для любых двух действительных чисел xt
и дг2, удовлетворяющих неравенству | дг2 — xi | < 8, выполняется не-
неравенство |/{лг2) —/C^i) I <С е-
д) Если функции /,(дг), /2(*), ..., fn(x) почти периодичны, то
и функция Д (дг) -|-/3 (дг) -f-... -j- fn (x) почти периодична.
е) Если функции fn(x), (и= 1, 2, ...) почти периодичны и после-
последовательность {/„(дг)} равномерно сходится в (—оо, -f-oo) к функ-
функции /(дг), то и функция /(дг) почти периодична.
ж) Если {ап} — последовательность действительных или комп-
комплексных чисел, а К„ — последовательность действительных чисел и
оо
если ряд 2йис*ХиЯ! равномерно сходится в (—оо, -f-oo), то его
п=1
сумма является почти периодической функцией.
з) Если производная почти периодической функции /'(дг) равно-
равномерно непрерывна, то она также почти периодична.
и) Если функции /, (дг), /2 (дг), ..., /в (дг) почти периодичны, то
и их произведение ft (дг), /2 (дг) ... fn (дг) почти периодично.
2. Теорема о среднем. Для почти периодических функций спра-
справедлива так называемая теорема о среднем. -
Если функция /(дг) почти периодична, то существует конечный
предел
т
lim -L
Т-»оо у
21 Зак. 527. Дж. Сансоне
322 Гл. VI. Уравнения и системы с периодическими коэффициентами
Этот предел называется средним значением функции f(x) и обозна-
обозначается M{f(x)};
т
M{f(x)}= Urn ±ff(x)dx.
3. Ряды Фурье почти периодических функций, а) Справедлива
теорема:
Действительные числа Ап, для которых М {/(дс) е~ *»"} отлично
от нуля, образуют конечное или счетное множество.
Положим
Лп = М {f(x) е-"»"} (я = 1, 2, .. .);
тогда {Ля} называется последовательностью показателей Фурье
функции/(л:), {Ап} — последовательностью коэффициентов Фурье
этой функции, а ряд ^Апе*^па>—:ее рядом Фурье, обозначение:
П=1
f(x)~%AneiAn°. A)
n=l
б) Если функция /(#) периодическая, то определенный сейчас ряд
совпадает с обычным рядом Фурье функции f{x), т. е. если функ-
функция f{x) периодична и имеет период р, то ряд A) принимает вид
—со О
где 2iz/p=:k.
в) Имеет место равенство Парсеваля
П=1
и, вообще,
n=N+l n=l
со
Так как Нт 21 ^п Г== 0, то ряд Фурье почти периодической функ-
W-»oo N+1
ции f(x) сходится к ней в среднем в (—оо, -f-oo) в смысл* Бора.
г) Различным почти периодическим функциям соответствуют раз-
различные ряды Фурье.
д) Если функция f(x) почти периодическая, причем для нее имеет
х
место разложение A), и если интеграл J /E) Л ограничен при
§ 9. Почти периодические решения 323
— оо < х < -\- оо, то он почти периодичен, причем
^ e*V(c=const),
О И=1
ж
т. е. ряд Фурье для f/(?)<# получается почленным интегрированием
ряда A) (см. Бор [1], стр. 68—73).
е) Пусть почти периодическая функция имеет представление A),
тогда:
оо
1. Если все Ап положительны, то ряд 2^п сходится, и
п=1
2. Если все показатели Л5, А2, ..., Ап, ... линейно независимы,
т. е. ни для какой совокупности показателей Aj, А2, ..., Аи нельзя
найти таких рациональных чисел rv г2, ..., гв, не равных одновре-
со
менно нулю, что гхAj -j- г2Ай -(-...-(- г„Аи = 0, то ряд 21 А» I схо~
п=1
дится и ет
п=1
(см. Бор [11, стр. 104—116).
4. Теорема об аппроксимации. Многочлен вида
N
и=1
где ап—любые числа, а Хп — действительные числа, называется
показательным многочленом.
Показательные многочлены почти периодичны (см. п. 1 „д").
Имеет место следующая теорема об аппроксимации.
Если функция f(x) почти периодична, то можно построить
последовательность показательных многочленов
равномерно сходящуюся в (— оо, -(- оо) # / (#).
5. Неоднородные линейные дифференциальные уравнения. Тео-
Теорема Бора и Нейгебауера. Рассмотрим дифференциальное уравнение
21*
324 Гл. VI. Уравнения и системы с периодическими коэффициентами
где clt с2, ..., сп — действительные числа, а /(дг) — почти периоди-
периодическая функция, и докажем теорему Бора и Нейгебауера (см. Бор и
Нейгебауер [1]).
Любое ограниченное решение уравнения B) является почти
периодической функцией.
Пусть р—корень характеристического уравнения для уравнения B)
(см. гл. П, § 1, п. 6 „г")
Тогда тождественно
и потому уравнение B) можно заменить системой уравнений
Г+РГ=/(*). D)
Если функция у (х) является ограниченным в (— оо, -(- оо) реше-
решением уравнения B), то по теореме Эсклангона (см. Эсклангон [1],
стр. 192, а также Ландау [1]) функции уг, у", , v*") также огра-
ограничены в (—оо, -f-oo), а тогда тем же свойством обладает и функ-
функция Y [см. формулу C)]; таким образом, достаточно доказать, что
любое ограниченное решение уравнения D) почти периодично, чтобы
можно было вывести по индукции сформулированную выше теорему.
Пусть
p = r-\-i\ (г, А действительны, I — мнимая единица).
Рассмотрим отдельно случаи г > 0, г < 0, г = 0.
Если г>0, то общее решение уравнения D) имеет вид
as
K(*) = <rp3![ jV/(E)<#-r-c] (с = const),
—оо
и если |/(лг)|<В, то
as
I J I ^^ P I IP I '
1 —оо
а потому D) имеет единственное ограниченное в (— оо, -(- оо) решение
§ 9. Почти периодические решения
325
Зададим некоторое е>0. Пусть т — почти период функции /(дг)
относительно е; тогда
а>+т as
|
Y(х + т
= | <
t) J «*/ E) dS-<Tpx J *«V (Q D) | =
—со —оо
а потому функция К (#) почти периодична.
Аналогично рассматривается случай г<0.
Пусть г = 0, тогда решения уравнения D) имеют вид
E)
и потому функция Y(x) ограничена в (—оо, -f-oo) лишь в случае,
когда интеграл Г />E/($)d? ограничен при изменении х в (—оо, -|-оо)«
о
Но функция eihcf(x) почти периодична, и потому, если интеграл
ограничен при изменении х в (—оо, -|-оо), то он почти периодичен
(п. 3„д"), чем и доказана почти периодичность Y{x).
ЛИТЕРАТУРА
А й н с (I п с е Е. L.)
[1] Обыкновенные дифференциальные уравнения, Харьков, 1939.
[2] A proof of the impossibility of the coexistence of two Mathieu fonctions,
Proc. of the Cambr. Phil. Soc, 21 A922), 117—120.
Ариела (ArzelaC.)
[1] Sull' Integrality delle equazioni differenziali ordinarie, Mem. R. Ace. Sc.
dell' 1st. di Bologna E), V A895), 257—270.
[2] Sull' esistenza degli Integral! delle equazioni differenziaii ordinarie, Mem.
R. Ace. Sc. dell'Inst. di Bologna E), VI A896), 131—140.
АдиезерН. И.
[1] Элементы теории эллиптических функций, М. — Л., 1948.
Безнковнч (Besicovich A. S.)
[1] Almost periodic functions, Cambridge, 1932, p. 180.
Бекер (Baker H. F.)
[1] On the integration of linear differential equations, Proc. of the London
Math. Soc. A) 35 A903), 333—378.
[2] Note on the integration of linear differential equations, Proc. of the
London Math. Soc. B) A905), 293—296.
БернуллнД. (Bernoulli D.)
[1] Theoremata de oscillationibus corporum fllo flexili connexorum et cate-
catenae verticaler suspensae, Comm. Acad. Sc. Imp. Petrop., VI A732—1733).
Опубликовано в 1738 г.
Бертини (BertinlE.)
[1] Introduzione alia geometrla prolettiva degli iperspazi, Pisa, 1907.
Бессель (Bessel F. W.)
[1] Untersuchtmg des Theils der planetarischen Storungen, welcher aus der
Bewegung der Sonne entstehet, Berl. Abh. A824).
Бианкн (BianchiL.)
[1] Lezioni sulla teoria del gruppi continul di trasformationi, Pisa, 1918.
Биркгофф (Birkhoff G. D.)
[1] Boundary value and expansion problems of ordinary linear differential
equations, Trans, of the Am. Math. Soc, 9 A908), 373—395.
[2] Dynamical systems with two degrees of freedom, Trans, of the Am.
Math. Soc, 18 A917), 199—300.
Блисс (Bliss G. A.)
[1] Solutions of differential equations as functions of the constants of inte-
integrations, Bull, of the Am. Math. Soc, XXV A918—1919), 15—26.
Блисс и Шенберг (Bliss G. A., Schoenb erg I. J.)
[1] On separation, comparison and oscillation theorema for self-adjoint Sys-
Systems of linear second order differential equations, Am. Journ. of Math.,
53 A931), 781—800.
Боль (В о h 1 P.)
[1] Ueber eine DIfferentialgleichung der StOrungstheorie, Journ. fur die relne
und ang. Math., 131 A906), 268-321.
Бомпнани (Bomplanl E.)
[1] Forme normal! delie equazioni differenziali lineari e iora significato
Литература 327
geometrlco, Annales Scientiflqucs de 1'Universite de Jassy, XXIII A937),
Бор (Bohr H.)
[1] Почти периодические функции, М. — Л., 1934.
Бор и Нёйгеблуер (BohrH., Neugebauer О.)
[1] Ueber lineare Differentlalglelchungen mit konstanten Koefflzienten und
fastperiodischer rechter Selte. Nachr. Ges. Wiss. Gottlngen A926),
8—22.
Борель (В ore IE.)
[lJSur l'equation adjointe et sur certains systemes d'equatione dffierentielles,
Ann. Sc. de ГЁс. Norm. Sup. C), IX A892). 63—90.
[2] Lemons sur les series divergentes, Paris, 1928.
Бохер (BocherM.)
[1] Boundary problems in one dimension. Proceedings of the fifth. Int
Congress of Math. (Cambridge, 1913), I, 163—195.
[2] Lecpns stir les methodes de Sturm, Paris, 1917, p. 118.
[3] Applications and generalizations of the conception of adjoint systems,
Trans, of the Am. Math. Soc, 14 A913). 403—420.
[4] Green's functions in space of one dimension, Bull, of the Am..Math.
Soc. B), 7 A901), 297—299.
[5] Boundary problems and Green's functions for linear differential and
difference equations. Ann. of Math. B), 13 A911), 71—78.
[6] Введение в высшую алгебру, М. — Л., 1933.
Б р у н с (В г u n s H.)
[1J Zur Theorie der Kugelfunktionen, Journ. fur die reine und angew.
Math., 90 A881), 322—328.
Буницкий (BounitzkyE.)
[1] Sur la fonction de Green des equations differentlelies iineaires ordlnal-
res, Journ. de Math. par. et appl. F), 5 A909). 65—125.
Буркхардт (Btirkhardt H.)
[1] Sur ie fonctions de Green relatives a une domaine d'une dimension.
Bull. Soc. Math, de France, XXII A894), 71-75.
Б у хг'ольц Н. Н.
[1] Основной курс теоретической механики, ч. II, М. — Л. 1945.
Валле-Пуссен (de la Vail ее Poussin Ch. J.)
[1] Курс анализа бесконечных малых, М.— Л., 1933, т. 11,205—217.
[2] Sur reqttation dlfferentielle du second ordre. Determination d'une Inte-
Integrate par deux valeurs assignees. Extension aux equations d'ordren,
Journ, de Math. pur. et appl. (9), 8 A929), 125—144.
Ватсон
[1] Теория бесселевых функций, М„ 1949.
Вейерштрасс (Welerstrass К.)
[1] Zur Theorie der bilinearen und quadratischen Formen, Math. Werke II
(Berlin, 1895), 19—44.
[2] Ueber eine Gattung reel periodischer Funktlonen, Math. Werke II (Berlin,
1895), 1—18.
Вильчинский (Wilczynski E. J.)
[1] Projective Differential Geometry of Curves and Ruled Surfaces, Leipzig,
1906.
Винтнер (Wintner A.)
[1] On the exact value of the bound for the regularity of solutions of or-
ordinary differential equations, Am. Journ. of Math., 57 A935), 539—540.
Вольтерра(УоНеггаУ.)
[11 Sui fondamenti della teorla delle equazioni differenzlali lineari, Memorle
della Societa Hal. delle Sdenze C), VI B2/VI —37), 1—107.
[21 Sui fondamenti della teoria delle equazioni differenziali Hneari, Memorle
della Societa ItaL delle Scienze C), XII A902), 1-68.
328 Литература
Галлнко (GaiU с о V.)
[1] Sulle condizioni Iniziali che determinano gli integrali delle equazioni
differenziall ordinarie, Giorn. di Mat. di BattagHni, 55 A917), 165—230.
Таллина (GalUna G.)
[1] Sull'integrazione delle equazioni differenzlaU Hneari omogenee autoag-
giunte, Rendicontl. R. 1st. Lombardo Sc. e. Lett. B) 63 A930), 272—282.
Гамбургер (Hamburger M.)
[1] Bemerkung fiber die Form der Integrate der Unearen Differential-
gleichungen mit veranderlichen KoefHzienten, Journ. fur die reine und
angew. Math., 76 A873), 113—125.
Гантмахер Ф. P.
[1] Теория матриц, М. —JL, 1953.
Гаусс (Gauss С. F.)
fl] Disqulsitiones generates circa seriem infinitam
Comm. Soc R. Sc. Gottlngensis II A812). См также
[2] Gauss Werke, Bd. 3, Gottingen, 1866.
ГельфондА. O.
[1] Исчисление конечных разностей, M.— Л., 1952.
Гильберт (HUbert D.)
[1] Grundzuge efeier aligemeinen Theorie der Hnearen Integralgleichungen,
Nachr. Ges. Wiss. Gflttlngen, 1—6 Note, 1904.
Гобсон (Hobson E. W.)
[1] On a genera] convergence theorem and the theory of the representation
of a function by series of normal functions, Proc. of the London Math.
Soc. B). 6 A908), 349—395.
Голубев В. В.
[1] Лекции по аналитической теории дифференциальных уравнений, 2-е
изд., М.— Л., 1950.
Грей и Метьюз
[1] Функции Бесселя и их приложения к физике и механике, М„ 1953.
Гронуолл (Gronwall Т. Н.)
[1] Note on the derivatives with respect to a parameter of the solutions of
a system of differential equations, Ann. of Math. B), 20 A919), 292—296.
Гумберт (Humbert P.)
[1] Fonctions de Lame et fonctions de Mathieu, Paris, 1926, p. 1—55.
Гурвиц
[1] Теория аналитических н эллиптических функций, М.—Л., 1933.
Гурса (Goursat E.)
[1] Курс математического анализа, 3-е изд., М. — Л., 1936.
Дамкелер (Damk5hIer W.)
[11 Periodische Extremalen vom minimum Тур in Ringbereichen, Ann. della
R. Sc. Norm. Sup. di Pisa B), V A936), 127—140.
Дарбу (DarbouxG.)
[1J Lecons sur la Theorie Generalle des Surfaces, vol. I, II, 2-eme ed.,
Paris, 1914—1915.
[2] Memoire sur ^approximation des fonctions de ires grands nombres, et
яит une classe etendue de developpements en sferie, Journ. de Math,
pur. et appl. C), 4. A878), 5—56, 377—416.
Джексон (Jackson D.)
[11 Ряды Фурье и ортогональные полиномы, М., 1948.
[21 Algebraic properties of self-adjoint system, Trans, of the Am. Math.
Soc, 17 A916), 418—424.
Джулиано (Gullianp L.)
[I] Generalizzazlone di un lemma di Gronwall e di una diseguagUanza di
Peano, Rend. Ace. Naz. Lincei (8), 1 A946), 1264—1271.
Литература 329
Днии (Dini U.)
[1] Studi sulle equazloni differenziali Hneari, Ann. di Mat. pura
e appl. C), II A898), 297—324; III A899), 125—183.
[2] Serie di Fourier e altre rappresentazlonl analitiche delle funzioni di una
variabile reale, Pisa, 1880.
[3J SugH svfluppi fa serie per la rappresentazione anallttca delle funzioni
di una varlabile reale date arbltrarlamente in un certo Intervallo, Pisa,
1911, p. 377.
Дюбуа-Реймон (du Bois-Reymond P.)
[1] Bemerkungen fiber Дг = ^ + -^- = 0, Jonrn. ffir diereineundangew.
Math. v. Crelle, 103 A888), 204—229.
Жюлиа (Julia G.)
[1] Introduction malhematique aux theories quantique, t. I, Paris, 1936.
Зигмунд
[1] Тригонометрические рады, М. — Л., 1939.
Иглиш (Iglisch R.)
[1] Ueber den Resonanzbegriff bei nichtlinearen Schwlngungen, Zeitschr.
fur angew. Math, und Mech., 17 A937), 249—258,
Казорати (С a s о г a t i F»)
[1] Sur la distinction des integrates des equations differentielies lineares en
sous-groupes, С Rendus, Ac. Sci., XCII A881), 175—178, 238—241.
Камке (Kamke E,)
[1] Differentlalgleichungen Reeler Funktionen, Leipzig, 1930.
[2] Ueber die Existenz von Elgenwerten bei Randwertaufgaben zweiter
Ordnung, Math. Zeitschr., 44 A938), 619—634.
[3] Neue Herleitung der Osziilationssatze ffir die Unearen selbstadjungierten
Randwertaufgaben zweiter Ordnung, Math. Zeitschr., 44 A938), 635—658.
Камне де Ферье (Kampe de FtrietJ.)
[1] La fonction hypergeometrique, Memorial des Sciences Mathem., 85 A937),
Paris,
ван Кампея и Виятнер (van KampenE. R., WIntnerA.)
fl] On an absolute constant in the theory of variational stability, Am. Journ.
of Math., 59 A937), 270—274.
Каратеодори (Caratheodory C.)
[1] Vorlesungen fiber Reeler Funktionen, 2-е Aull., Leipzig.
Картович (CartovitshN.)
Ml Sul calcolo effettico del moto perturbato in un caso tlpico dl prlma
approssimazione, Rend. R. Ace. Naz. dei LIncei F), 27 A938), 65—70
Келн (Cayley A.)
[1] On linear differential equations (The Theory of Decomposition), Quar-
Quarterly Journ. of Math., 21 A886), 331—335.
К e p у б и я о (С h e r u b i n о S.)
[11 Applicazioni delle funzioni olomorfe di matrici ai sistemi di equazioni
differenziali Hneari, Rend. R. Ace. Naz. Lincei F), 25 A937), 541-547,
686—690.
Кяезер (КпеьегА.)
[1] Die Integralgleichungen und ihre Anwendungen in der mathematischen
Physik, Braunschweig, 1911, S. 243.
[21 Untereuchungen fiber die Darstellung willkfirlicher FunKtionen in der
mathematischen Phjsik, Math. Ann., 58 A904), 81—147.
[3] Beitrage zur Theorie der Sturm — Liouvillischen Darstellung willkurticher
Funktionen, Math. Ann., 60 A905), 402—423.
Коттон (Cotton E.)
[1] Approximation euccessives et equations dffiereaHelles, Memorial des
Sciences Math., 28 A928), Paris.
330 Литература
К о ш н (С а и с h у A. L.)
[1] Oeuvres Completes, 1897—1898.
К у з ь м и н Р. О.
[1] Бесселевы функции, М.— Л., 1935.
Куммер (KummerE.)
[1] Uebet die hypergeometrische Retae, Journ. for die relne urid angew.
Math., 15 A836), 39—83, 127—172.
Курант и Гильберт
[1] Методы математической физики, М.— Л., т. 1 и 2, 1951.
К у р о ш А. Г.
[1] Курс высшей алгебры, М.—Л., 1952.
Лаврентьев М. А. и ЛюстерннкЛ. А.
[1] Курс вариационного исчисления, М.— Л., 1950.
[2] Основы вариационного исчисления, т. I, ч. II, М. — Л., 1935.
Лагранж (Lagrange G.)
[1] Oeuvres, Paris, 1869.
Ландау (Landau E.)
[11 Ueber elnen Satz von Herrn Esclangon, Math. Ann., 102 A929),
177-188.
Лаппо-Даннлевский И. А.
[1] Теория функций от матриц и систем линейных дифференциальных.
уравнении, М. — Л., 1934.
[2] Mernolres sur la theorie des systemes des equations dlfferentielles lineares,
I, II, III, Труды Физнко-матем. ин-та им. В. А. Стеклова, VI—VIII,
1934—1936.
Левн-Чивита (LevI-CIvIta Т.)
[1] Sul calcolo effettivo del periode in un caso tlpico di pritna approssima-
zlone, Revista de Clencias (Lima, Peru), 38, № 421 A937), 71—78:
Левн-Чивнта и Амальди
[1] Курс теоретической механики, М., 1951.
Левитан Б. М.
[1] Некоторые вопросы теории почти периодических функций. I. Успехи
матем. наук, II, вып. 5 A947), 132—192. И. Успехи матем. наук, Н,
вып. 6 A947), 174—214.
Л е й б н и ц (L e I b п I г G. W.)
[1] Die Brlefwechsel von G. W. Leibniz mit Mathematikern, Berlin, 1899.
Л е т ш о у (Latshaw V. В.)
[11 The algebra of self-adjoint boundary-value problems, Bull, of the Am.
Math. Soc, 39 A933), 969—978.
Ли (Lie S.)
{1] Geometrie der Beriihrungstransformationen, Leipzig, 1896.
Линделёф (LindelofE.)
[1] Demonstration de quelques theoremes sur les equations dlfferentielles,
Journ. de Math. pur. et appl., E), 6 A900), 423 — 441.
Липшиц (LipschitzR.)
[1] Disamlna della possibillta di integrare completamente un dato sistema
di equazloni dffierenzlall ordlnarle, Ann. di Mat. pura et appL B), 2
A868 — 69), 288—302. Перепечатано в BulL des Sciences Mathem. et
Astronomiques, X A876), 149—159.
Л и у в и л л ь (LI о u v i 11 e J.)
[1] Note eur la Theorie de la Variation des constantes arbitrates, Journal
de math. pur. et appl. A), 3 A838), 342—349.
[2] Sur le developpement des fonctions ou partiee de fonctions en series
dont les divers termes sont assujetls a satisfalre a une meme equation
differentielle du second ordre, contenant tin parametre variable, Journal
de math. pur. et appL, I A836), 253—265; II A837), 16—35, 418—436.
Литература 331
Щ Sur la Theorie des Equations differenlielles'lineaires et sur le developp-
ment de Fonctlon9 en series, Jonrn. de Math. pur. et.appl., 3 A838),
561-T-614.
Лихтенштейн (LichtensteinL.)
[1] Zur Theorie der gewohnlichen Dlfferentialgleichungen und der partiellen
Differentlalglelchungen zweiter Ordnurig. Die Losungen als Funktionen
der Randwerte und der Parameter, Rend. Circ. Mat. Palermo, 28 A909),
267—306.
[2] Ueber einlge Existenzprobleme der Variationsrechnung, Journ. fur die
reine und angew. Math., 145 A914), 24—85.
Люстерник Л. А.
[II Обобщение уравнения типа Штурма — Лиувилля, ДАН СССР, XV
A937), 235—238.
Ляпунов А. М.
[1] Sur une serie relative a la theorie des equations dfflerentieUes lineaires
a coefficients periodiques, С Rend. Ac. Sci., 123 A896), 1248—1252.
[2] Sur une equation dffierentielle linealre du second ordre, С Rend. Ac.
Sci., 128 A899), 910—923.
[3] Sur une equation transcendente et les equations differentielies lineaires
du second ordre a coefficients periodiques, С Rend. Ac Sci., 128 A899),
1085—1088.
[4] Общая задача об устойчивости движения, М.—Л., 1935.
Манмана (Машшапа G.)
[1] L'equazione del terzo ordine lineare omogenea, Rend. R. 1st. Lombardo
Sc. et Lett. B), 63 A930), 272—289.
[2] Sopra un nuovo metodo di studio delle equazioni dlfferenziali lineari,
Math. Zeltschr., 23 A926), 734—748.
[3J Sistemi differenziali. Autovalori e Autofunzioni, Napoli, 1938, p. 1—207.
Маркушевич А. И.
[1] Теория аналитических функций, М.— Л., 1950.
Матье (Mathleu E.)
[1] Theorie de l'elasticite des corpe solides, pt. I, Paris, 1890.
Маультон (Moulton F. R.)
[1] Differential equations, New York, 1930.
Мезон (Mason M.)
[1] On the boundary value problems of linear ordinary differential equations
of second order, Trane. of the Am. Math. Soc 7 A906), 337—366.
Милн Томсон (Milne Thomson L. M.)
[1] Die elliptischen Funktionen von Jacobi, Berlin, 1931, S. 69.
Муаньо (Moigno F. N. M.)
[1] Lecons de calcul differential et de calcul integral, Pads, 1844.
Натансон И. П.
[1] Конструктивная теория функций, М. — Л., 1949.
[2] Теория функций вещественной переменной, М. — Л., 1950.
Николетти (Nicolettl О.)
[1] Sugli integral! delle equazioni differenziali ordlnarle considerati come
funzioni del loro valori inlzlali, Rend. R. Ace Naz. Llncel E), IV2 A895),
316—324.
[2] Sulle condizloni inlzlali che determlniano gll integral! delle equazioni diffe-
differenziali ordlnarie, Atti della R.AccScTorino, 33A897—1898), 746—759.
Паперитц (Papperitz E.)
[1] Ueber verwandte «-Funktionen, Math. Ann., 25 (I?85), 212—221.
П е а н о (Р e a n о G.)
[1] Integrazione per serie delle equazioni differenziali lineari, AM deiia
R. Ace. Sc. Torino, 22 A887). 293—302. Перепечатана с небольшими
изменениями в Math. Ann., 82 A888), 450—456.
12] Sur le theoreme general relatif a l'existence des Integrates des equations
differentielles ordinaires, Nouvelles AnnaUes de Math., XI A892), 79—82.
332 Литература
[31 Sull' integralita defle equazionl differenziali del primo ordine, Attl delta R.
Ace. Sc. Torino, XXI A885—1886), 437—445.
[4] Demonstration de l'integrabilite des equations differentiellee ordinaires,
Math. Ann., 37 A890), 182—228.
Петровский И. Г.
[1] Лекции по теории обыкновенных дифференциальных уравнений,
М. —Л., 1952.
[2] Лекции по теории интегральных уравнений, М.— Л., 1948.
Пикар (Picard E.)
[1] MemoJre sur la theorie des equations a«x derivees partielles et la гаё-
thode des approximations successives, Journ. de Math. pur. et appl., D),
6 A890), 145—210.
[21 Lecons sur quelques problemes aux limites de la Theoiie des jequations
differentielfes, Paris, 1930.
[3] Sur un theoreme general relatii aux equations Integrates de premiere
espece et sur quelques problemes de physique mathematique, Rend. Clrc.
Mat. Palermo, 29 A910), 79—97.
[4] Traite.d'Analyse, t. Ill, 3-eme ed., Paris, 1928.
Пиконе (Picone M.)
[11 Corso di Analisi Superiore. Equazioni differenziali, Catania, 1923.
[2] Sui valori eccezionail di un parametro da cui dipende un'equazione
differenzlale lineare del seconde ordine Annali della R. Sc. Norm. Sup»
di Pisa (I), XI, 1—141.
[3] Equaziotie integrate traducente 11 piu generale problema lineare per. le
equazioni differenziali linearl ordinatie dl qualsivoglia ordine, Rend. %,
Ace. Naz. dei Lincei, F), XV A932), 942—948.
[4] Sulle autosoluzioni e sulle formule di maggiprazione per gll integrali
delle equazioni dlfferenziaii ordinarle autoaggiuunte, Math. Zeltschr., 28
A928), 519—555.
Привалов И. И.
[11 Введение в теорию функций комплексного переменного, М. — Л., 1945.
[2] Интегральные уравнения, М. — Л., 1935.
Пуанкаре (Poincare H.)
[1] Les Methodes nouvelles de la Mecanique Celeste, Paris, 1892.
[2] Sur les Equations Lineaires aux Differentielles ordinaires et aux Diffe-
Differences finies, Am. Journ. of Math., VII A885), 203—258.
[3] Sur les groupes des equations lineaires, Acta Math., IV A884), 201—311.
Пуассон (Poisson S. D.)
[1] Theorie de la Chaleur, Paris 1835.
Пуль (P о о I e E. G. C.)
[1] On certain classes of Mathieu functions, Proc. of the London Math. Soc>,
B), 20 A921), 374-388.
Рид (Reid W. T.)
[1] Boundary value problems of the calculus of variations, Bull, of the Am.
Math. Soc, 43 A937), 633—666.
Риккати (Riccati J. F.)
|1] Acta Eruditorum, t. 8, fasc. 2, 1723.
Риман
[1] Сочинения, М. —Л., 1948.
Рисе (Riesz F.)
[1] Les systemes d'equations Hneaires a une infinite d'inconnues. Paris, 1913
Ритт (RItt J. F.)
[1] On the differentially of the solution of a differential equation with
respect to a parameter, Ann. of Math. B), 20 A919), 289—291.
Сансоне (Sansone G.)
[1] Sviluppo in serie e valutazione asintotica del rappoito tra due polinoml
consecutivi di Jacobi, Ann. di Mat. pura ed appl., D), 16 A937), 39—4a
Литература 333
[2] Esfetenza di Inflniti autovalori per le equazionl differenziali linear! omo-
genee a coefficient! costanti, Rend. Circ. Mat. Palermo, LV A931), 168—176.
[3] Vahitazione dell' erroie nel calcolo effettivo del periodo d*i raoto pertur-
bato in un caso tipico di prima approssimazlone, Bol). Un. Mat. It, B),
1 A939), 422-426.
[4] Sviluppi in serie di funzioni ortogonali, Bologna A935), 36.
Северини (Severfni G.)
[11 Suit' integrazione delle equazionl differenziali ordinarie del primo ordine,
Rend. R. 1st. Lombardo, Sc. e Lett., 31 A898), 657-667,
[2] Sull' integrazione approssimata delle equazioni differenziali ordinarie del
prima ordine, Rend. R. 1st. Lombardo Sc. et Lett, 31 A898), 950—959.
Cere (Szego O.)
[1] Asymptotische Entwicklungen der Jacobischen Polynomen, Schriften
der K6nigsberger Gelehiten Gesellschaft, 10 A933), 35—112.
[2] Orthogonal Polynomials, Am. Math. Soc Coll., 23, New York, 1939.
[3] Inequalities for (he zeros of Legendre polynomials and related functions,
Trans, of the Am. Math. Soc, 39 A936), 1—17.
Синьорнни (Slgnorini A.)
[1] Sul teorema di Wittaker, Rend, della R. Accad. Naz. del Lincel, E), 21
A912), 36—39.
[2] Esistenza di un eslremale chiusa dentro un controno dl Wittaker, Rend.
Circ. Mat. Palermo, XXXIII A912), 187—19a
С к о р ц a (S с о г z a G.)
[1] Corpi numeric! e algebre, Messina, 1921.
Соболев С. Л.
[1] Уравнения математической функции, М.— Л., 1950.
Соваж (Sauvage L.)
[1] Theorie des diviseurs elementaires et applications, Ann. Sci. de ГЕс.
Norm. Sup., C), VIII A891), 285—350.
С о н н н Н. Я.
[1] Recherches sur les fonctions cylindriques et le developpement des fonc-
tions continues en series, Math. Ann., 16 A880), 1—80.
Стеклов В. А.
[1] Задача об охлаждении неоднородного твердого стержня, Сообщ. Харьк.
Матем. Об-ва, A896), 136—181.
[2] Sur le developpement d'une fonction donnee en series procedant sul-
vant les polynomes Tshebycheff et, en particulier, suivant les polynomes
de Jacobi, Journ. fur reine und angew. Math., 125 A903), 207—236.
Степанов В. В.
[1] Курс дифференциальных уравнений, М. — Л., 1950.
Стретт
[1] Функции Ляме, Матье и родственные им в физике и технике, Харьков,
1935.
С ушке вич А. К.
[1] Основы высшей алгебры, М. — Л., 1937.
Т а м м И. Е.
[1] Основы теории электричества, М. — Л., 1949.
Толстое Г. П.
[1] Ряды Фурье, М. —Л., 1951.
Тонелли (Tone111 L.)
Ill Sulle equazioni funzionali del tino dl Volterra, Bull, of the Calcutta
Math. Soc, 20 A928), 31—48.
Su alcuni funzionali, Ann. di Mat. pura ed appl., D), 18 A939), 1—21.
Sulla rappresentazione analitica delle funzioni di piu variabiii real!, Rend.
Circ. Mat. dl Palermo, XXIX A910), 1—36.
Fondamenti di Calcolo delle Variationi, vol. 2, Bologna, 1923.
Sulle orbite periodiche, Rend. deJla R. Ace Naz. del Lincel, XXI A912),
251—258, 332—334.
Ill
it!
334 Литература
[61 Suite orbite periodiche irreversibill, Mem. R Ace. Sc. dell' Inst. di Bo-
Bologna (Classe di Sc. Fis.) (VIII), I A923—24), 21—25.
[7] Sulle eetremali complete, Ann. della R. Sc. Norm. Sup. dl Pisa B),
V A936), 159-168.
Три коми (Tricomi F.)
[11 Sulla funzione di Green dl un'equaztone dlfferenzlale decomposla In
fattorl simbolici, Atti Ace. delle Sc. di Torino, 80 A944—45), 159—183.
Уиттекер (Whlttaker E. T.)
[1] On the functions associated with the elliptic cylinder in harmonic ana-
analysis, Intern, Congr. of Math. (Cambridge, 1912), I A912), 366-371.
[2] On periodic orbits, Monthly Notices of the Royal Astronomic Soc. (Lon-
(London), LXII A902), 186—196.
Уиттекер и Ватсоя
[1] Курс современного анализа, т. I, И, М. — Л., 1933.
Ундервуд (Underwood F.)
[1] Note on the periodic solutions of linear differential equations, Ann. of
Math., B), 31 A930), 655—656.
[2] An Integral condition associated with linear differential equation»
having simply-periodic coefficients, Tdhoku Math. Journ., 86 A933),
269—274.
[3] A classification of certain ordinary linear differential equations having
simply periodic coefficients, Tdhoku Math. Journ., 86 A933), 275—302,
Уолш (Walsh J. L.)
[11 On the convergence of the Sturm — Liouvllle Series, Ann. of Math. B),
24 A923), 109—120.
Фавар (Favard J.)
[1] Lecons sur les fonctions presque-perlodiques, Paris, 1933, p. 181.
Файт (Fite W. B.)
[11 Periodic solutions of linear differential equations, Ann. of Math. B),
281 A927), 59-64.
Фихтенгольц Г. М.
[1] Курс дифференциального и интегрального исчислений, М— Л..
1948—1949.
Флоке (FloquetG.)
[1] Sur les equations dlfferentlelles Hneaires a coefficients periodiques, Ann.
Sc. de ГЕс. Norm. Sup. B), XII A883), 47—89.
Форсайт (Forsyth R.)
[1] Theory of differential equations, Cambridge, 1902.
Фрезер, Дункан, Келлар
[1] Теория матриц и ее приложения, М., 1950.
Фробениус (Frobenlus G.)
[1] Ueber der Rang einer Matrix, Sitzungber. der Kgl. Preuss. Ak. der
Wiss. zu Beriin A911), S. 20—29. 128—129.
Фукс Б. А.
[1] Теория аналитических функций многих комплексных переменных,
М.-Л., 1948.
Фукс (F u с h s L.)
[1] Zur Theorie der linearen Differetttialgleichungen mft veranderlichen
Koeffldenten, Journ. for die reineund angew. Math., 66 A866), 121—160.
[2] Ueber Relatlonen, welche for die zwiehen je zwei singularen Punkten
erstreckten Integrate der LOsungen Hnearer Dlfferentlalgleichungen
statffinden, Journ. for die reine und angew. Math., 76 A873), 177—213.
Фурье (Fourier J. B.)
[1] Theorie Analytique de la Chaleur, Paris, 1822.
Xaap (HaarA.)
[1] Zur Theorie der orthogonalen Funktionensysteme, Math. Ann., 69 A910),
331—371; 71 A912), 38-62.
Литература 335
Харди
[1] Расходящиеся ряды, М., 1951.
Харди, Литтльвуд, Полна
[1J Неравенства, М., 1948.
Хаупт (Haupt О.)
[1] Ueber eine Methode zum Bewelse von Oszillatlonstheoremen, Math.
Ann., 76 A915), 67—104.
Хил л (HI II G. H.)
[1J On the part of the motion of the lunar perigee which is a function of
the mean motions of the sun and moon, Cambridge. Ms. U. S. A., 1877.
Опубликовано с добавлениями в Acta Math., VIII A888), 1—ч$0.-
Цвирнер (Zwlrner G.)
[1] La teoria delle mafrlcl applicata ai slstemi di equazlonl differenziall
lineari, Rend. Sem. Padowa, 7 A936), 55—109.
Чеботарев Н. Г.
[1] Теория групп Ли, M.—Л., 1940.
Чебышев П. Л.
[1] Полное собрание сочинений, М., 1947.
Чезарн (Cesar! L.)
[1] Sulla stabilita delle soluzloni del sistemi di equazlont differenziall a
coefficient! periodici, Mem. della R. Ace. d'Ifalia F), 11 A940), 633—695.
Чиммино (CimmlnoO.)
[1] Autosoluzion! e autovalori nelle equazioni dffierenziali iineari ordinarie
autoaggiunte di ordine superiore, Math. Zeltschr, 32 A930), 1—58.
Чннквиии (CinquinlS.)
[1] Sulle equazioni funzionali del tipo di Volterra, Rend. R. Ace. Naz. Lin-
Lined F), XVII A933), 616—621.
[2] Problem! di valor! al contorno per equazioni differenziall di ordine n,
Annall della R. Sc. Norm. Sup. un di Pisa B), 9 A940), 61—77.
Шлезингер (Schleslnger L.)
[1] Einfuhrung in die Theorle der gewohnlichen Differenzialgleichufigen,
Berlin, 1922
111 т е к е л ь (S t а с k e4 P.)
[1] Sur la convergence des series representant les integrates des equations
dlfferentielles, С Rend. Ac Sci. Paris, 126 A898), 203—205.
Штурм (Sturm C.)
[1] Sur les equations differentilelles lineaires du second ordre, Journ. de
Math. pur. et appl.. 1 A836), 106—186.
Эйлер (Euler L.)
[11 Institutions Calculi Integralis, Petropoll, 1769.
[2] Specimen Transformationis Singularls Serlerum, Nova Acta Ac. Sc. Petr.,
12 A794), опубликовано в 1801, см. также Opera, Ser. I, XVI, 41—55.
Эльсгольц Л. Э.
[1] Вариационное исчисление, М.—Л., 1952.
Эсклангон (Esclangon E.)
[1] Nouveile recherches sur les fonctions quasi-periodiques, Ann. Obs. Bor-
Bordeaux, 16 A917), 51—236.
Эттлингер (Ettllnger H. J.)
[1] Existence theorems for the general real, self-adjoint linear system о
the second order, Trans, of the Am. Math. Soc, 19 A918), 79—96.
[2] Oscillation theorems for the real, self-adjoint linear system of the
second order, Trans, of the Am. Math. Soc., 22 A921), 136—143.
Якобн (Jacob! С G.)
[1J Gesammelte Werke, Berlin, 1886.
Янчевский С. А.
{11 Oscillation theorems for the differential boundary value problems of
the fourth order, Ann. of Math., 29 A927), 521—542.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аналитическое продолжение решений
нормальной системы обыкновенных
дифференциальных уравнений 18
Асколи теорема 38
Бекера и. Пеано метод интегрирова-
интегрирования системы линейных дифферен-
дифференциальных уравнений 77
Бесселя функции, см. функции Бес-
Бесселя
Бета-функция 129
Билинейная форма 222
канонический вид 223
Бора н Нейгебауера теорема о почти
периодичности 323
Бореля метод суммирования, приме-
применение к интегрированию дифферен-
дифференциальных уравнений 107
Бохера теорема о существовании соб-
собственных значений 191
о существовании собственных
функций с заданным числом нулей
193
Брунса неравенства для сферических
функций 171
Вейерштрасса теорема о периодиче-
периодическом решении дифференциального
уравнения движения точки по за-
заданной траектории 307
Вронскиан 50
Гамбургера подгруппы для линейных
однородных дифференциальных
уравнений с периодическими коэф-
коэффициентами 278
Гамма-функция 129, 144
Гаусса гипергеометрический ряд 125,
126
Гильберта—Шмидта теорема о раз-
разложении в ряды по собственным
функциям 247
Гнпергеометрические многочлены Яко-
би 129
Гнпергеометрический интеграл Эйле-
Эйлера 128
— ряд Гаусса 125
Гнпергеометрическое уравнение Гаус-
Гаусса 124
Грина функция, см. функция Грина
Гронуолла лемма 29
Гурса доказательство единственности
решений нормальной системы диф*
ференциальных уравнений 16
Дини—Гобсона теорема о равносхо»
димости рядов Штурма—Лиувилля
и тригонометрических рядов Фурье
209, 216, 219
Дифференциальное уравнение второго
порядка в действительной области
и теорема сравнения Штурма 161
• комплексной области
115
гипергеометрическое Гаусса 124
линейное неоднородное 59
дополнительная функция
60
решение методом вариа-
вариации произвольных постоянных 58
с периодическими коэф-
коэффициентами 279
линейное однородное 47
— вронскиан фундаменталь-
фундаментальной системы 50
с постоянными коэффи-
коэффициентами 65, 262
формула Лнувилля 50
" фундаментальная систе-
система 54
преобразование в инте-
интегральное уравнение 98
Матье 294
интегральное уравнение Унт-
текера для функций Матье 300
решения типа Ci, Co 297
теорема Айнса 298
фундаментальная система
296
Предметный указатель
337
Дифференциальное уравнение линей-
линейное, функции Матье первого вида
297
— —¦ с периодическими коэффициен-
коэффициентами 267
вычисление характе-
характеристических показателей 282
исследования Ляпуно-
Ляпунова А. М. 284
метод Хилла вычисле-
вычисления характеристических показате-
показателей 287
необходимое и доста-
достаточное условие существования пе-
периодического решения 278
— — подгруппы Гамбургера
278
формула Пуанкаре
268
характеристическая
матрица 269
— • характеристические
показатели и характеристические
числа 276
Дифференциальные системы, индекс
совместности 225
линейные, зависящие от пара-
параметра 241
несовместность 225
однородные 225
преобразование в интегральные
уравнения Фредгольма второго рода
233
— — самосопряженные 230, 233, 245
с периодическими краевыми
условиями 290
четного порядка 245
— — сопряженные 226
— уравнения, определяющие эллип-
эллиптические функции Якоби 21
Дифференцируемость по начальному
значению независимой переменной
32
начальным значениям решений
32
параметру 30
Задача Д. Бернулли о колебаниях
нити 141
— о разложении по функциям Штур-
Штурма—Лиувилля 209
—¦ — распространении тепла в тон-
тонкой проволоке 185
Интегральное уравнение Уиттекера
для функций Матье 300
Каноническая нормализация Лагер-
ра—Форсайта 85, 86
Каратеодори критерий непрерывности
решений от начальных значений 44
Колебания малые нити и уравнение
Бесселя 141
— эллиптической мембраны 294
Конгруенция интегральных кривых 36
Коши задача для системы дифферен-
дифференциальных уравнений 11
Кошн—Липшица доказательство тео-
теоремы существования 34
Коэффициенты Фурье 135, 209
Лагранжа метод вариации произволь-
произвольных постоянных 57
Леви-Чивита формула для вычисле-
вычисления периода в движении точки по
заданной траектории 310
Лемма Гронуолла 29
Линейное дифференциальное уравне-
уравнение второго порядка 161, 162
Линейные дифференциальные уравне-
уравнения второго порядка, аналитическая
теория 115
и уравнение Риккати
78
Линейный элемент 35
Ляпунов А. М., исследования об урав-
уравнениях второго порядка 284
Матрица вырожденная 66
— диагональная 67
—i единичная 67
— нерегулярная 66
— нулевая 67
— обратная 70
— расстояние между двумя подоб-
подобными матрицами 71
— регулярная 66
— сингулярная 66
Матрицант квадратной матрицы 75
Матричное нечисление 65
Матье дифференциальное уравнение,
см. дифференциальное уравнение
Матье
Метод вариации произвольных по-
постоянных 58
— интегрирования Пеано—Бекера си-
системы линейных дифференциальных
уравнений 77
— мажорант 101, 102
доказательство теоремы суще-
существования 103
— последовательных приближений,
доказательство теоремы существо-
существования и единственности 108
22 Зж. б?7. Дж.
338
Предметный указатель
Метод последовательных приближе-
приближений Пикара—Пеано для интегриро-
интегрирования системы дифференциальных
уравнений 9
— суммирования Бореля 107
— усиливающих (мажорантных)
функций Коши 117
— Эйлера интегрирования дифферен-
дифференциальных уравнений при помощи
рядов 101
Многочлены Чебышева 141
— сферические 139
— ультрасферические 139, 170
— Якоби 129, ортогональность 133
рекуррентные формулы 132
Модуль эллиптических функций Яко-
Якоби 24
Независимые решения 51
Непрерывность решений относительно
начальных значений 27, 44
параметров 28
Неравенства Брунса 171
Неравенство произведения 71
— треугольника 71
Нормализация относительная и кано-
каноническая линейных однородных
дифференциальных уравнений 79
Нормальные системы обыкновенных
дифференциальных уравнений 5, 7
линейных дифференциальных
уравнений 47
однородных линейных диффе-
дифференциальных уравнений с постоян-
постоянными коэффициентами 60
Общее решение системы дифферен-
дифференциальных уравнений 33
Определяющее уравнение 115
Особые точки линейных дифферен-
дифференциальных уравнении второго по-
порядка 1M, 121
Осцилляционная теорема 174, 188,293
Паперица уравнение 121, 122
Пеано и Бекер, метод интегрирования
системы линейных однородных диф-
дифференциальных уравнений 77
Пикар, метод последовательных
приближений для интегрирования
нормальной системы дифферен-
дифференциальных уравнений 9
— теорема существования для систе
мы дифференциальных уравнений 36
Периодические орбиты 315, 318
теорема Тонелли о существова-
существовании 318
Последовательные решения 278, 279
— — дифференциального уравненяв
движения точки по заданной траек-
траектории 307
системы дифференциальных
уравнений, зависящих от пара-
параметра 304
Периоды эллиптических функций
Якоби 24
Пиконе доказательство экстремаль-
экстремального свойства собственных значе-
значений 257
— тождество 165
Порядок системы дифференциальных
уравнений 6
Постоянные Липшица 10
Почти периодические функции 320
первые свойства 320
равенство Парсеваля 322
ряды Фурье 322
— теорема об аппроксимации
при помощи показательных много-
многочленов 323
о среднем 321
Произведение двух операторов 177
— первого порядка 178
— матриц 67
Производящая функция для много-
многочленов Якоби 130
Резольвента интегрального уравнения
Вольтерра второго рода 100
Резонанс 280, 281
Решение системы дифференциальных
уравнений 5
Решения дифференциальных систем
как решения интегральных уравне-
уравнений Фредгольма второго рода 241
уравнений как функции на-
начальных значений 27
Риккати уравнение 78
Ряд Фурье 209, 210
— Фурье относительно ортогональной
системы 135
Ряды по многочленам Якоби в ком-
комплексной области 138
Самосопряженные дифференциальные
многочлены 94
системы 230
уравнения Лагранжа 94
— системы второго лорядка с перио-
периодическими краевыми условиями 29С
— — Штурма—Лнувилля 232
Система дифференциальных уравне-
уравнений, зависящая от параметров 304
— дифференциальных уравнений, са-
самосопряженная 56
Предметный указатель
339
Системы линейных однородных урав-
уравнений 51
— Штурма 183, 186, 191, 193
— Штурма—Лиувилля, типичная фор-
форма 202
Собственные значения 176, 183
для однородных линейных диф-
дифференциальных уравнений с по-
постоянными коэффициентами 262
и собственные функции 176
асимптотические вы-
выражения 204
'- системы Штурма—Лиувилля
197, 204
действительные 199,
200
— ¦ — уравнение 203, 204
теорема существования 181,191
• экстремальное свойство 247,257
— функции 176, 183, 193
их асимптотические выражения
207
— — системы Штурма—Лиувилля,
ортогональность 198
Сопряженная система дифферен-
дифференциальных уравнений 55
Сопряженное уравнение Лагранжа
89, 90
Сопряженные дифференциальные си-
системы 226, 228
Сопряженный многочлен 90
Спектр матрицы 70
— оператора 221
Теорема Айнса 298
— Асколи 38
— Бора и Нейгебауэра 323
— Бохера о существовании собствен-
собственных значений 191
— функций 193
— Гильберта—Шмидта 247
— единственности, доказательство
Гурса 16
— единственности Хаара 220
— о разделении нулей 167
— сравнения Штурма 166, 186
— существования, доказательство
Коши—Липшица 34
Пнкаро—Пеаяо 9, II
и единственности Валле-Пус-
сена 155, 159
собственных значений 181
— Тонелли о существовании перио-
периодических экстремалей 318
— Уолша о равносходимости для ря-
рядов по ортогональным функциям
214
Теорема Шгекеля—Ли 81
Тождество Пиконе 165
Уравнение Бесселя 141
— Папернца 121, 122
Уравнения класса Фукса 115
— линейные с периодическими коэф-
коэффициентами 266
однородные с периодическими
коэффициентами 302
с тремя правильными особыми
точками 121
Условие существования периодиче-
периодического решения 278, 280
Формула Лиувилля 50
— Родрига 130
— Якоби 50
Формулы Лиувилля—Якоби 49
Фундаментальная система 53
решений уравнения 54
— — — системы линейных диффе-
дифференциальных уравнений 112
Функции Бесселя, нули 171
первого рода 145
— Матье 296'
интегральное уравнение Уитте-
кера 300
первого вида 297
— Штурма—Лиувилля, асимптотиче-
асимптотические разложения 202
Функция Грнна для дифференциаль-
дифференциальных систем 235
самосопряженной системы
второго порядка частного вида 233
— полунепрерывная 253
— Римана 121
Характеристические показатели ПС,
276
— — вычисление 282
— уравнения системы 61
— числа 276
матрицы 70
Характеристическое уравнение 267,
269
Хилла метод вычисления характери-
характеристических показателей 287
Частный интеграл 5
Эйлера гнпергеометрический инте-
интеграл 128
Элементарные делители 270
Якоби гипергеометрнческие многд-
чдены 129
22*
ОГЛАВЛЕНИЕ
Предисловие
Глава I
НОРМАЛЬНЫЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ И ТЕОРЕМА СУЩЕСТВОВАНИЯ ДЛЯ НИХ
§ 1. Нормальные системы 5
1. Определения 5
2. Порядок системы дифференциальных уравнений 6
3. Нормальные системы 7
§ 2. Получение систем обыкновенных дифференциальных уравнений
• путем исключения произвольных постоянных 8
1. Системы дифференциальных уравнений, полученные путем
исключения произвольных постоянных 8
2. Обратная задача 9
§ 3. Доказательство основной теоремы существования и единствен-
единственности по методу последовательных приближений Пикара — Пеано
1. Формулировка теоремы существования 9
2. Доказательство теоремы существования по методу последо-
последовательных приближений Пикара — Пеано 11
3. Доказательство Гурса теоремы единственности - 16
4. Дополнения к формулировке теоремы существования .... 17
§ 4. Аналитическое продолжение решений. Примеры 18
1. Аналитическое продолжение решений 18
2. Система дифференциальных уравнений, определяющая тригоно-
тригонометрические функции 19
3. Система дифференциальных уравнений, определяющая эллип-
эллиптические функции Якоби 21
§ 5. Решения дифференциальных уравнений как функции начальных
значений 27
1. Непрерывность • 27
2. Дифференцируемость 28
3. Лемма Гронуолла 29
4. Дифференцируемость по параметру 30
5. Дифференцируемость по начальным значениям решений . . 32
6. Дифференцируемость по начальному значению независимой
переменной 32
7. Общее решение системы дифференциальных уравнений ... 33
Оглавление 341
§ 6. Доказательство теоремы существования по методу Коши — Лип-
Липшица ' 34
1. Геометрические рассмотрения 34
2. Теорема существования в формулировке Пеаио. Доказатель-
Доказательство Арцела 36
3. Доказательство Тоиелли теоремы существования в формули-
формулировке Пеано 42
Глава II
НОРМАЛЬНЫЕ СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ И НЕКОТОРЫЕ ПРЕОБРАЗОВАНИЯ ЛИНЕЙНЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 1. Нормальные системы линейных дифференциальных уравнений . . 47
1. Нормальные системы однородных линейных дифференциаль-
дифференциальных уравнений н линейные дифференциальные уравнения . . 47
2. Формулы Лиувилля и Якоби 49
3. Независимые решения. Фундаментальные системы. Понижение
порядка системы линейных однородных уравнений 51
4. Сопряженная система дифференциальных уравнений .... 55
5. Неоднородные линейные системы. Метод Лаграижа 57
6. Нормальные системы однородных линейных дифференциаль-
дифференциальных уравнений с постоянными коэффициентами 60
§ 2. Применение матричного исчисления к определению решений си-
системы линейных дифференциальных уравнений с переменными
коэффициентами 65
1. Сведения по матричному исчислению 65
2. Матрицант квадратной матрицы 75
3. Метод Пеано — Бекера 77
§ 3. Частные преобразования линейных однородных дифференциаль-
дифференциальных уравнений 78
1. Преобразование линейного однородного уравнения порядка и
в уравнение порядка п — 1 • 78
2. Линейные дифференциальные уравнения второго порядка и
уравнение Риккати 78
3. Линейные дифференциальные уравнения, у которых коэффи-
коэффициент при у^п~1' равен производной коэффициента приу^ . 79
§ 4. Относительная нормализация и каноническая нормализация линей-
линейных однородных дифференциальных уравнений 79
1. Относительная нормализация и дифференциальные семиинва-
семиинварианты , 79
2. Замена независимой переменной 81
3. Каноническая нормализация Лагерра — Форсайта 85
4. Преобразования уравнений второго и третьего порядка ... 87
§ 5. Сопряженное уравнение Лаграижа 89
1. Сопряженные дифференциальные многочлены и уравнения . 89
2. Соотношения между фундаментальными системами решений
сопряженных дифференциальных уравнений 92
3. Самосопряженные дифференциальные уравнения и много-
многочлены 94
342 Оглавление
4. Первый интеграл самосопряженного уравнения нечетного
порядка 97
5. Самосопряженные уравнения третьего порядка 97
§ 6. Преобразование линейного дифференциального уравнения с на-
начальными данными в интегральное уравнение Вольтерра второго рода 98
Глава ///
АНАЛИТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
И НЕКОТОРЫЕ ЛИНЕЙНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
§ 1. Метод мажорант (исчисление пределов Коши) 101
1. Метод Эйлера интегрирования дифференциальных уравнений
при помощи рядов 101
2. Основной принцип метода мажорант Коши 102
3. Доказательство теоремы существования методом мажорант . 103
4. Теорема существования в общем случае 105
5. Метод суммирования Бореля и дифференциальные уравнения 107
§ 2. Доказательство теоремы существования и единственности с по-
помощью метода последовательных приближений 108
1. Теорема существования и единственности 108
2. Замечание Уиитнера относительно области существования
голоморфного решения 111
3. Применение матричного исчисления для определения фунда-
фундаментальной системы решений системы линейных дифферен-
дифференциальных уравнений 112
§ 3. Аналитическая теория линейных дифференциальных уравнений
второго порядка 115
1. Правильные и неправильные особые точки для дифферен-
дифференциального уравнения второго порядка 115
2. Правильные точки. Определяющее уравнение • . . 115
3. Сходимоств рядов в случае, когда разность характеристиче-
характеристических показателей ие является целым числом 117
4. Построение второго решения в случае, когда характеристи-
характеристические показатели совпадают или отличаются на целое число 119
5. Правильные особые точки в бесконечности 121
§ 4. Линейные дифференциальные уравнения с тремя правильными
особыми точками. Гипергеометрическое уравнение 121
1. Уравнение Паперица и функция Р Римана 121
2. Преобразования Римана для функции Р 12S
3. Гипергеометрическое уравнение Гаусса 124
4. Гипергеометрическнй ряд 128
5. Гипергеометрический интеграл Эйлера 128
§ 5. Гипергеометрические многочлены Якоби 129
1. Многочлены Якоби Р%р) . . . 129
2. Формула Родрига. Производящая функция многочленов Р^'" 13ft
3. Значения Р„(±1) Щ
4. Рекуррентные формулы • . . 1Я8
5. Ортогональность многочленов Рп в [— 1,1] 13*
6. Теорема Пуанкаре и Нт Ря+1(лг)/Ри(лг) . 1Ш
и">о°
7. Ряды по многочленам Якоби в комплексной области .... 138
$. Ультрасферические многочлены и их производящая функция 13S>
Оглавление 343
§ 6. Уравнение Бесселя 141
1. Задача Д. Бернулли о малых колебаниях подвешенной иити
и уравневие Бесселя 141
2. Функции Бесселя (цилиндрические функции) первого рода . 143
3. Функции/1/2(л:),/_1/г(л:) 146
4. Интегральные представления бесселевых функций первого рода 146
5. Другие интегральные представления 148
6. Рекуррентные соотношения между Jn (х) 149
so
7. Интеграл f xJn (ах) Jn(bx) их 150
6
8. Задача о разложении в ряды по бесселевым-функциям . . . 152
Глава IV
КРАЕВЫЕ ЗАДАЧИ ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ВТОРОГО ПОРЯДКА
§ 1. Задача о нахождении решения дифференциального уравнения
я-го порядка, проходящего через и заданных точек 154
1. Случай, когда уравнение линейно 154
2. Теорема существования и единственности Валле-Пуссеиа для
линейного уравнения 155
3. Теорема Валле-Пуссена для случая дифференциального урав-
уравнения порядка и нормального вида 159
§ 2. Дифференциальные уравнения второго порядка и теорема срав-
сравнения Штурма 161
1. Исследования Штурма об уравнениях второго порядка ... 161
2. Общие замечания относительно уравнений второго порядка 161
3. Сопряженные точки 162
4. Достаточное условие для несуществования сопряженных точек 164
5. Тождество Пиконе 165
6. Теорема сравнения Штурма 166
7. Теорема о разделении нулей 167
8. Теорема сравнения для полуоткрытых отрезков 169
9. Выпуклость последовательности нулей решений одного диф-
дифференциального уравнения второго порядка частного вида 169
§ 3. Применение теоремы сравнения для отделения нулей ультрасфери-
ультрасферических многочленов и бесселевых функций в главном случае . . . 170
1. Нули ультрасферических многочленов 170
2. Нули бесселевых функций 171
§ 4. Рсцнлляционная теорема 174
1. Осцилляционная теорема 174
2. Осцилляционная теорема для уравнения (Ъу'У + р-А — В] у = 0 176
§ 5. Решения, обращающиеся в нуль в двух заданных точках. Соб-
Собственные значения и собственные функции 176
1. Постановка задачи 176
2. Разложение оператора второго порядка в произведение опе-
операторов первого порядка 177
3. Выражение для решения на отрезке, содержащем сопряжен-
сопряженные точки .,.,,.,.,,., ч. ,,,,,,.,,.,. |79.
344 . Оглавление
4. Теорема существования собственных значений. Доказатель-
Доказательство Маммана . . 181
5. Собственные значения для уравнения (вуО' + (М — Щу = О 183
§ 6. Системы Штурма. Собственные значения. Собственные функции . . 183
1. Задача о распределении тепла в тонкой проволоке и системы
Штурма 183
2. Дополнения к теореме сравнения 186
3. Добавления к осцилляционной теореме 188
4. Системы Штурма. Существование собственных значений. Тео-
Теоремы Бохера 191
5. Системы Штурма. Существование собственных функций с за-
заданным числом нулей. Теоремы Бохера 193
6. Система Штурма — Лиувилля. Существование собственных
значений 197
7. Ортогональность собственных функций системы Штурма —
Лиувилля 198
8. Достаточные условия действительности всех собственных зна-
значений системы Штурма — Лиувилля 199
§ 7. Асимптотические разложения функций Штурма — Лиувилля . . . 202
1. Типичная форма систем Штурма — Лиувилля 202
2. Уравнение для собственных значений 205
3. Асимптотические выражения для собственных значений и
собственных функций ¦ ¦ ¦¦> 204
4. Собственные функции, обращающиеся в нуль в двух задан-
заданных точках, и нх асимптотические выражения 207
§ 8. Теорема Дини — Гобсона о равносходимости ряда Штурма —
Лиувилля и тригонометрического ряда Фурье 209
1. Задача о разложении по функциям Штурма — Лиувилля . . . 209
2. Предварительные леммы 210
3. Теорема Уолша о равносходимости для рядов по ортогональ-
ортогональным функциям 214
4. Теорема о равносходимости рядов Штурма — Лиувнлля и
тригонометрических рядов Фурье 216
Глава V
КРАЕВЫЕ ЗАДАЧИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ п-ГО ПОРЯДКА (п>2)
§ 1. Билинейные формы. Канонический вид 222
§ 2. Сопряженные и самосопряженные дифференциальные системы . . 225
1. Дифференциальные системы. Индекс совместности 225
2. Сопряженные дифференциальные системы 22§
3. Индексы совместности для сопряженных систем 228
4. Самосопряженные линейные системы 230
5. Самосопряженные системы второго порядка 230
6. Самосопряженные системы Штурма — Лиувилля 232
7. Самосопряженные системы четвертого порядка 233
§ 3. Функция Грнна н преобразование дифференциальных систем в инте-
интегральные уравнения Фредгольма второго рода 233
1. Функция Грина для самосопряженной системы второго по-
порядка частного вида 233
2, Функция Грина для дифференциальных систем , 235
ОглйвЛение 345
3. Запись в виде интеграла решения неоднородной дифферен-
дифференциальной системы, имеющей единственное решение 238
4. Решения дифференциальных систем как решения интеграль-
интегральных уравнении Фредгольма второго рода 241
5. Линейные системы, зависящие от параметра. Собственные
значения и собственные функции 241
6. Линейные самосопряженные системы четного порядка. Разло-
Разложения в ряды по собственным функциям н теорема Гиль-
Гильберта— Шмидта 245
§ 4. Краевые задачи для самосопряженных систем четного порядка н
вариационное исчисление 247
1. Экстремальное свойство собственных значений, вытекающее
из теории интегральных уравнений 249
2. Доказательство Тонелли существования собственных значений
с помощью прямых методов вариационного нечисления . . . 257
3. Экстремальное свойство собственных значений, выводимое
из теории дифференциальных систем. Доказательство Пиконе
4. Одно интегральное неравенство 262
§ 5. Существование бесконечного множества собственных значений
для однородных линейных дифференциальных уравнений с постоян-
постоянными коэффициентами 262
Глава VI
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ
С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ. ПЕРИОДИЧЕСКИЕ И ПОЧТИ
ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 1. Решения линейных дифференциальных уравнений с периодическими
коэффициентами 266
1. Примеры , . 266
2. Характеристическое уравнение 267
3. Элементарные делители матрицы 270
4. Решения в случае, когда показатели всех элементарных дели-
делителей характеристической матрицы равны единице. Характе-
Характеристические показатели и числа 274
5. Решения в общем случае. Подгруппы Гамбургера 278
6. Необходимое и достаточное условие существования периоди-
периодического решения 278
7. Периодические решения неоднородных линейных дифферен-
дифференциальных уравнений с периодическими коэффициентами . . . 279
§ 2. Вычисление характеристических показателей 282
1 Исследование характеристических показателей 282
2. Исследования А. М. Ляпунова об уравнениях второго порядка 284
3. Метод Хнлла вычисления характеристических показателей прн
помощи бесконечных определителей 287
§ 3. Самосопряженные системы второго порядка с периодическими
краевыми условиями 290
1. Существование собственных значений 290
2. Осцилляционная теорема 293
§ 4. Дифференциальное уравнение Матье и функции, связанные с эллип-
эллиптическим цилиндром 294
1. Элементарные решения уравнения колебаний эллиптической
мембраны и уравнение Матье , 294
346 Оглавление
2. Функции Матье и их классификация по типам 296
3. Отсутствие линейно независимых периодических решений,
соответствующих одному и тому же собственному значению.
Теорема Айнса 298
4. Интегральное уравнение Уиттекера для функций Матье . . . 300
§ 5. Системы линейных однородных уравнений с периодическими коэф-
коэффициентами 302
§ 6. Системы дифференциальных уравнений, зависящих от параметра.
Периодические решения ¦ 304
§ 7. О периодических решениях дифференциального уравнения дина-
динамики точки, движущейся по заданной траектории 307
1. Теорема Вейерштрасса 307
2. Формула Леви-Чивита для вычисления периода в первом при-
приближении . . 310
§ 8. Задача о периодических орбитах и вариационное исчисление . . 315
1. Задача о периодических орбитах 315
2. Теорема Тонелли о существовании периодических экстремалей 318
§ 9. Почти периодические функции и почти периодические решения
дифференциальных уравнений 320
1. Почти периодические функции. Первые свойства 320
2. Теорема о среднем 321
3. Ряды Фурье почти периодических функций 322
4. Теорема об аппроксимации 323
5. Неоднородные линейные дифференциальные уравнения. Тео?
рема Бора и Нейгебауера J. 323
Литература 326
Предметный указатель 336