Текст
Кибернетический
сборник
НОВАЯ СЕРИЯ
ВЫПУСК
6
Сборник переводов
Под редакцией
А. А. ЛЯПУНОВА и О. Б. ЛУПАНОВА
ИЗДАТЕЛЬСТВО «МИР*
Москва 1969
УДК 519.95
Научный совет по кибернетике
Академии наук СССР
Шестой выпуск новой серии кибернетических сборников состоит из двух
разделов: математические вопросы и математическая экономика.
В первом разделе представлены работы по теории кодирования,
теории автоматов, математической лингвистике и другим вопросам. Особый
интерес представляют две статьи С. Винограда по синтезу логических схем и
обзорная статья А. В. Ахоу и Дж. Д. Улмана по теории языков.
Второй раздел — математическая экономика — является новым для данной
серии кибернетических сборников. В нем помещены основополагающая
статья Э. Балаша об аддитивном алгоритме для решения задач линейного
программирования и замечания Ф. Гловера и С. Зайонца об этом алгоритме.
Сборник рассчитан на научных работников, инженеров, аспирантов и
студентов различных специальностей, занимающихся и интересующихся
кибернетикой в ее математическом аспекте.
Редакция литературы цо. математическим наукам
» 2-2-3
Инд. -щ-
Математические
вопросы
Один класс циклических кодов
с мажоритарным декодированием0
Ж.-Л1 Гёталс, Ф. Дейзарт
Изучается новый бесконечный класс циклических кодов2). К кодам этого
класса применима поэтапная процедура декодирования, использующая
мажоритарную логику. Некоторые из ранее известных кодов принадлежат к
рассматриваемому классу и, следовательно, допускают более простые
процедуры декодирования. Как исправляющие случайные ошибки, данные коды
по мощности близки к кодам Боуза — Чоудхури.
1. ВВЕДЕНИЕ
Изучается новый бесконечный класс циклических кодов,
обладающих тем интересным свойством, что к ним применима
мажоритарная логика декодирования в поэтапной процедуре,
используемой в общем декодере Меггита [10]. В качестве
собственного подкласса этот класс содержит предложенные Вил-
доном [3] циклические коды, задаваемые разностными
множествами. Коды Рида — Маллера с одной вычеркнутой
координатой [5, 6] также попадают в этот класс. Наконец, некоторые
коды Боуза — Чоудхури [11] принадлежат данному классу и,
следовательно, являются более просто декодируемыми.
Рассматриваемые коды определяются как ортогональные на
некоторых тактических конфигурациях, в проективных геометриях.
Для того чтобы сделать статью относительно
самостоятельной, вначале приводятся некоторые свойства конечных
проективных геометрий. Затем на основе результата Грэхема и
Маквильямс [4] исследуется размерность кодов. Обсуждаются
декодирование и реализация предлагаемых кодов.
l) Go et ha Is J.-M., Dels arte P., On a class of majority-logic deco-
dable cyclic codes, Trans. IEEE, IT-14, № 2 (1968), 182—188.
n П £ассматРиваемыи в этой статье класс кодов впервые был предложен
Ь. Д. Колесником и Е. Т. Мирончиковым (см. Колесник В. Д., Мирон-
ч и к о в Е. Т., Некоторые циклические коды и схема декодирования по
большинству проверок, Проблемы передачи информации, т. I, вып. 2, изд-во
«Наука», М., 1965, стр. 3—17; Колесник В. Д., Мирончиков Е. Т.,
Декодирование циклических кодов, изд-во «Связь», М., 1968), которые также
получили нижнюю оценку размерности этих кодов. В настоящей работе при-
одится алгоритм для нахождения числа информационных разрядов и в
одном частном случае найдена точная формула для этого числа. —Прим. ред,
a
Ж.-М. fercLAC, Ф. ДейзарТ
2. СВОЙСТВА КОНФИГУРАЦИЙ
В КОНЕЧНЫХ ПРОЕКТИВНЫХ ГЕОМЕТРИЯХ
Для полноты приведем сначала некоторые.свойства
конечных геометрий 1).
Пусть GF(q)—поле Галуа с q элементами, где q —
некоторая степень простого числа, скажем q = pn. Тогда GF(qm+])
может быть представлена как алгебра размерности (т+1)
над GF(q), и точки m-мерной конечной проективной геометрии
PG(m,q) могут быть представлены как (qm+%— \)j(q — 1)
различных подпространств размерности 1 над GF(q). Два
элемента а и р из GF((7m+1)» такие, что р=Яа для некоторого Я,
принадлежащего GF(q)y представляют, таким образом, одну
и ту же точку из PG(tn,q). Для s<m геометрия PG(s,q)9
содержащаяся в PG(m, q), определяется как множество точек
из PG(m,q), образующее (s+1)-мерное подпространство над
GF(q). Таким образом, проективная геометрия PG(syq) опре*
деляется (s+,1) линейно независимыми точками, и всего
существует
b{s,m,q) {qs+l_l){qs_lh^{q_l) W
различных PG(s,q), входящих в данную PG(m,q). Более того,
заданная PG{t,q) с t<s<m содержится точно в
Ш s т a) (^-1)(^-^-1)---(^-^-1) л»
%(t, s, т, q)- {qS-t_x){qS-t-y_lhAq_{). (2)
различных PG(s,q), содержащихся в данной PG(m,q). Легко
показать, что отношения инцидентности для b(symyq) различ*
ных PG(s,q) на точках заданной PG{myq) определяют уравно*
вешенную неполную блок-схему с параметрами
k = (qs+>- l)/(q- 1),
b = b(s, m, q\ (3)
г = Я(0, sy m, q\
А, = Я(1, s, m> q) для s>\ и Я=1 для s»l.
Нас интересует линейное подпространство над GF(p),
порождаемое Ь строками матрицы инцидентности такой
конфигурации. Дадим сначала конкретное представление этой
конфигурации.
1) Заинтересованный читатель может обратиться к [9] или [7].
Один класс циклических кодоб с мажоритарным декодированием 9
Пусть а будет примитивным корнем поля GF(qm+l). Тогда
р = а^-1) является примитивным v-м корнем из единицы и
(о =z<xv — примитивным корнем поля GF(q). Можно представить
(и мы представим) точки геометрии PG(m,q) через первые v
различных степеней а, так как равенство
невозможно, если d\ и d% оба меньше v. Пусть ad°, ad\ ..., ads
представляют (s+1) линейно независимых над GF(q) точек
из PG{m, q), и рассмотрим (q^1—l)l(q—1) ненулевых
линейных комбинаций этих точек
2^/-¾ -(4)
/-о
где Xij принадлежат GF(q\ и m такие, что любые два вектора
h=(Uo> iiu • ••* fas) независимы над GF(q). Так построенные
величины d являются элементами GF(qm+l) и могут быть
представлены в виде
£?,-©V', (5)
где di меньше, чем v\ более того, любые два dx различны, так
как в противном случае соответствующие векторы А,,- должны
быть зависимыми над GF(q). Таким образом, можно выбрать
(и мы выберем) k=(qs+l—l)/{q—1) точек adi в качестве
элементов геометрии PG(syq)> содержащейся в PG(myq).
Многочлен
и>(х)~х?* + х?*+ ... +/*-*, (6)
который мы берем как элемент алгебры по модулю многочлена
(xv — ,1) над GF(p), будет теперь представлять строку в
матрице инцидентности. Выбирая все возможные множества с
(s+1) линейно независимыми точками, получаем Ь различных
строк.
Заметим, что линейное подпространство, порождаемое этими
векторами, является циклическим. Действительно, если w(x) —
вектор из матрицы инцидентности, то xw(x) также обладает
этим свойством, так как из (4) и (5) следует, что
/-о
Таким образом [1], это циклическое подпространство является
идеалом в алгебре многочленов по модулю (^-1), и если
h — число v-x корней из единицы, являющихся корнями всех
10
Ж.-М. Гёталс, Ф. Дейэарт
многочленов w{x), то размерность этого идеала над GF(p)
равна (v — К). Следующий раздел посвящается определению
этого числа h.
3. РАЗМЕРНОСТЬ НАД GF(p) КОДОВ C(s,m,pn)
Обозначим через C(s,m,q) циклический код, порождаемый
над GF(p) множеством многочленов w{x) (6). Задача
определения размерности этого кода эквивалентна задаче
определения числа v-x корней из единицы, являющихся корнями всех
многочленов w(x).
Целью данного раздела является доказательство
следующего предложения, в котором и обозначает q—1=рп—1.
Теорема 1. Число v-x корней из единицы, являющихся
корнями всех многочленов w(x), равно числу целых чисел t,
отличных от нуля, не превосходящих v и таких, что
полиномиальные коэффициенты
(tu)\
(lou)l(liu)\...(lsu)l •
tt¥*0, /0 + /1 + ... +/, = /,
сравнимы с нулем по модулю р.
Для доказательства необходимы некоторые
предварительные результаты! Если а — примитивный корень поля GF(qm+l),
то р = ам является примитивным v-u корнем из единицы. Вместе
с w{x), задаваемым равенством (6), выпишем выражение
ИР') =2 Л (7)
которое с использованием (4), (5) и равенства (ом=1 может
быт|> переписано в виде
k — 1 / S \и*
»Ф')-2 2 м'/ , (8)
*-о\/-о /
где член, стоящий в правой части, является функцией от adi,
которую мы обозначим через
Fs, Пао, см, .. • , Obs),
принимая для adi обозначение ау Легко показать, что -эта
функция является симметричной относительно ccj, так как
сумма
w ($?) + w (<о§0 + .,, +оу((о?-2р'), (9)
Один класс циклических кодов с мажоритарным декодированием 11
равная (q—\)FS)t(ao, он, ..., а8), может быть представлена
в виде
2 (лл + цлн- ... +иа)м'> (Ю)
^0^1^2 ъ
где (ло, м-ь •. •, M-s независимо друг от друга пробегают все q
элементов поля GF(q).
Лемма 1.
FStt(ao, <*i> ...» <0=*
где /,=^0 и /0 + /i+ ... +/,»/.
Доказательство. В соответствии с (10) можно написать
(q- 1)/^,,(00, <*lf ..., <Ов
2 21w*o + Gai<Xi+ ... +|iA)le'.
»i,, и2..... и5 И0
Разлагая теперь в ряд член в квадратных скобках
(mao + ^-^ + lKf )^°^-1.
где л: обозначает (niai+ ... + [!«««) t и суммируя для |л0 по
всем элементам GF(q), получаем
И,, И2 Hj L f-i \n0 /J
Так как сумма
Но
равна (<7— 1) Для i, кратного w = q— 1, и равна нулю в
остальных случаях, то по модулю р соотношение (11) имеет вид
t
Но для /= £ сумма no |xi, p*, ..., и* равна 0 по модулю р, так
как она состоит из qs слагаемых a^; с другой стороны, можно
12
Ж.-М. Гёталс, Ф. Дейзарт
написать
2 (^i«i + ^2«2 + • • • + ИА)а~/)в - - Л-1, <-| (аь а2, ..., а,),
так что (12) приводится к следующему виду:
F*t = 2 ( ul ) а"^- F*-b <-'(ai» a2» • • •' a*)l- (13)
/-1
Используя индукцию, получаем требуемый результат.
Лемма 2. Если элементы ао, аь ..., ae nad'GF(q)
линейно зависимы, то FStt(ао, аь ..., as) равна нулю.
Доказательство. Как было показано выше, можно
написать
(q- l)Fe,*(<*o, «ь ..., (0 =
== 2 (^о«о + ^i«i + ... + |*а)"'э (14)
где jjij независимо друг от друга пробегают q элементов поля
GF(q). Предположим теперь, что ао является некоторой
линейной комбинацией остальных s элементов:
ao=^iai+X2a2+ ... +ksa8, (15)
и подставим в (14) вместо ао его выражение (15). Тогда все
члены станут линейными комбинациями s элементов аь •.., а8,
и те (q8—1) членов, которые не содержали ао, останутся
неизменными, а среди (q—\)qs остальных членов каждая из q*
различных линейных комбинаций появится точно (q— 1) раз.
Это очевидно, так как мы прибавляем фиксированные
элементы ао, соао, ..., а>*~2ао к qs различным линейным
комбинациям вида
fxiai + |Х2аг +...+ [isas,
где \xj независимо друг от друга пробегают q элементов поля
GF(q). Нуль, таким образом, появится (q—1) раз, а каждая
из (qs—1) ненулевых линейных комбинаций — точно q раз,
так что общая сумма по модулю р будет равна нулю.
Лемма 3. Функция FStt(ao, аь ..., а&) равна нулю цо
модулю р при всех возможных выборах (s+1) линейно
независимых элементов ао, аь ..., а« тогда и только тогда, когда
Один класс циклических кодов с мажоритарным декодированием 13
для U ф0 и lo+h+ ...+/s = / полиномиальные коэффициенты
^1 . (16)
(/<,!*)! i!iu)\ ...{lsu)\
равны нулю по модулю р.
Доказательство. Прежде всего, согласно лемме 2,
если FStt равна нулю для всех возможных выборов линейно
независимых элементов, то она равна нулю при любом выборе.
Далее, согласно лемме 1, FS)t является однородным полиномом
от переменных ао, аь •••, «s степени (/—1), меньшей, чем и,
который должен быть равен нулю при всех возможных выборах
переменных среди v элементов. Это возможно только тогда,
когда он тождественно равен нулю, т. е. только тогда, когда
полиномиальные коэффициенты (16) равны нулю по модулю р.
Отсюда легко выводится теорема 1.
4. ЦИКЛИЧЕСКИЕ КОДЫ С МАЖОРИТАРНЫМ ДЕКОДИРОВАНИЕМ
Предлагаемый класс циклических кодов получается из
определенных выше подпространств C(s%m,pn) переходом к
дуальным кодам С* (s, m, рп) над GF(p). Эти коды имеют блоковую
длину
y=(9m+l_l)/(9_l)
при q~pn и размерность h над GF(p), где Л —число целых
ненулевых чисел /, не превосходящих v и таких, что
полиномиальные коэффициенты (16) сравнимы с нулем по модулю р.
Метод расчета числа h приведен в приложении-1.
Будет показано, что эти коды могут быть правильно
декодированы с помощью мажоритарной логики, если произойдет
не более [//2] случайных ошибок, где, как обычно, [х] —
наибольшее целое число, не превосходящее х, и
/-fam-*+l_ 1)/(^-1). (17)
Л. Декодирование и реализация
В качестве порождающей матрицы кода C(s,m,q)
выбирается матрица инцидентности Ъ различных PG(s,q) на
точках заданной геометрии PG(m,q), определяющих
уравновешенную неполную блок-схему с параметрами (3). Эта матрица,
таким образом, может быть взята в качестве проверочной
матрицы для C*(s,m, q).
Заданная геометрия PG(s—1,?), входящая в PG(m,q)%
содержится точно в / геометриях PG(syq)t где / задается
14
Ж.-М Гёталс, Ф. Дейзарт
равенством (17). С другой стороны, каждая из точек геометрии
PG(m,q), не принадлежащая данной PG(s— l,q),
принадлежит точно одной PG(s,q), содержащей данную PG(s— l,q).
Это очевидно, так как s линейно независимых точек,
определяющих данную PG(s—I,?), совместно с дополнительной
(s-M)-fl точкой, не принадлежащей PG(s—1,<7)> определяют
одну и только одну PG(s,q). Следовательно, / проверочных
позиций, каждая из которых проверяет точки данной
PG(s—1,9), образуют на этих точках множество
ортогональных проверок порядка /. Согласно определению, данному
Месси [2], такое множество состоит из набора уравнений,
каждое из которых проверяет данное подмножество символов,
причем никакой другой символ не содержится в этом множестве
более одного раза. Пусть ег- будет ошибкой в i-й позиции, т. е.
где Ti есть i-и полученный символ, a tf есть 1-й переданный
символ. Тогда если предположить, что произошло не более [7/2]
ошибок, то, как показал Месси [2], сумма
а/= 2 eh (18)
/е=Гу
где Г;— множество индексов точек /-й геометрии PG(s—l,q),
задает правильное значение поля GF(p), если оно
соответствует большей доле из / проверок, ортогональных на Г-/. Суммы
Qj (18) могут быть построены для каждой из / геометрий
PG(s—1,9), содержащихся в заданной PG(m—l,q) и
содержащих данную PG(s — 2,9). Эти суммы в свою очередь
образуют множество проверок порядка /, ортогональных на
точках заданной геометрии PG(s — 2,9). Используя индукцию,
за s шагов приходим к множеству проверок порядка /,
ортогональных на геометрии PG(0, q), содержащей единственную точку;
следовательно, это множество правильно определяет ошибку eh
произошедшую в i-й позиции, если соответствующее значение
GF(p) соответствует большей доле среди / последних проверок.
Для декодирования этих кодов может быть использована
предложенная Месси мажоритарная схема общего декодера
Меггита [10]. Декодер этого типа иллюстрируется на рис. 1.
В буферной памяти запоминаются v символов и одновременно
вычисляется синдром. Если произошло меньше [7/2] ошибок,
то на выходе мажоритарного элемента образуется символ
ошибки, который был добавлен в канале к первому передаваемому
символу. Для получения цравильного значения первого символа
остается только прибавить к первому, полученному символу
символ, являющийся аддитивным обратным символа ошибки.
Один класс циклических кодов с мажоритарным декодированием 15
В силу циклической природы кода сдвиг регистра v раз
позволяет последовательно декодировать каждый из v символов.
Мажоритарный элемент имеет общую структуру s-уровневого
дерева с мажоритарными ячейками. Каждая мажоритарная
ячейка имеет / входов, и ее выход равен тому элементу поля,
который встречается наиболее часто среди ее / входов, если он
встречается по меньшей мере 1 +[//2] раз; в противном случае
выход равен нулю. Эта общая древовидная структура может
быть упрощена многими способами, поскольку согласно Мес-
си [2], для декодирования v символов необходимо не более v
мажоритарных решений.
6
ill err t
Рис. U Общий декодер Меггита.
■' — вход; 2 — буферная память; 5 —синдром; 4-мажоритарный элемент; 5-инвертор;
6- сумматор по модулю р; 7-выход.
В силу циклической природы кодов операции кодирования
и вычисления синдромов могут быть легко реализованы (см.,
например, Питерсон [1]).
В. Общие замечания; связь с некоторыми ранее известными
кодами
Прежде всего заметим, что так как код может действительно
исправлять любые ошибки вплоть до [7гЛ ошибок, то его
минимальное расстояние равно по меньшей мере (/+1).
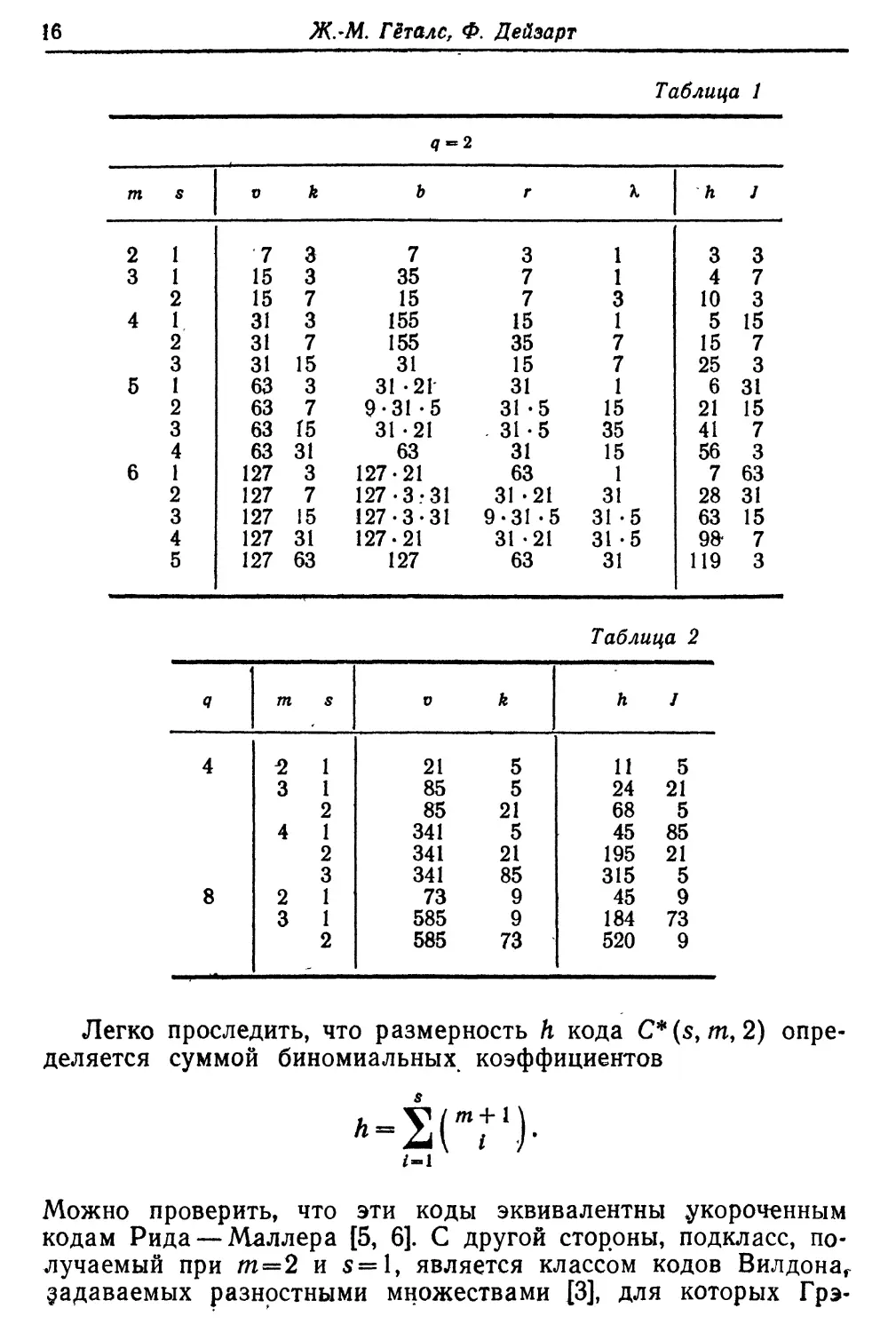
В табл. 1 и 2 приведены параметры нескольких первых
кодов над двоичным полем. Табл. 1 построена для проективных
геометрий над GF(2); табл. 2 дает параметры геометрий над
GF(22) и GF(23). Как было определено в (21), / равно числу
проверок, ортогональных на заданной геометрии PG(s—l,q);
h есть размерность кода C*(s, m, q), a v, k, b, г и К суть
параметры (3) уравновешенной неполной блок-схемы, матрица
инцидентности которой выбиралась в качестве проверочной
матрицы кода,
16
Ж.-М. Гёталс, Ф. Дейзарт
Таблица 1
<7-2
m
2
3
4
б
6
s
1
1
2
1
2
3
1
2
3
4
1
2
3
4
5
V
7
15
15
31
31
31
63
63
63
63
127
127
127
127
127
k
3
3
7
3
7
15
3
7
Г5
31
3
7
15
31
63
Ь
7
35
15
155
155
31
31 -21
9-31-5
31-21
63
127-21
127-3:31
127-3-31
127-21
127
г
3
7
7
15
35
15
31
31-5
31-5
31
63
31 -21
9-31-5
31 -21
63
Л
1
1
3
1
7
7
1
15
35
15
1
31
31 -5
31-5
31
h
3
4
10
5
15
25
6
21
41
56
7
28
63
98«
119
/
3
7
3
15
7
3
31
15
7
3
63
31
15
7
3
Таблица 2
я
4
8
m
2
3
4
2
3
5
1
1
2
1
2
3
1
1
2
-
V
21
85
85
341
341
341
73
585
585
к |
5
5
21
5
21
85
9
9
73
h
11
24
68
45
195
315
! 45
184
520
/
5
21
5
85
21
5
9
73
9
Легко проследить, что размерность h кода C*(s, m, 2)
определяется суммой биномиальных коэффициентов
Можно проверить, что эти коды эквивалентны укороченным
кодам Рида — Маллера [5, 6]. С другой стороны, подкласс,
получаемый при т=2 и s=l, является классом кодов Вилдонаг
Задаваемых разностными множествами {3], для которых Грэ-
Один класс циклических кодов с мажоритарным декодированием 17
хем и Маквильямс [4] доказали, что
Можно доказать, что для более общего класса кодов,
задаваемых разностными множествами, соответствующего s=m—1,
также справедливо равенство
Доказательство этого факта приводится в приложении 2. Кроме
того, в рассматриваемый класс попадают некоторые коды Боу-
за — Чоудхури, например такие, как первые шесть кодов из
табл. 1. Мимоходом заметим, что пятый код эквивалентен
(31, 15) коду Боуза — Чоудхури и не эквивалентен (31, 15)
квадратично-приведенному коду, который, как известно, имеет
такое же распределение весов. Действительно, дуальный для
обоих кодов (31, 16) код содержит уравновешенную неполную
блок-схему с параметрами t> = 31, &=7, #=155, г*=35 и Х~7;
но первый из них эквивалентен матрице инцидентности PG(2,2)
на точках геометрии PG(4,2), а второй — нет.
В качестве последнего замечания отметим, что f$v=l всегда
является корнем порождающего полинома для кодов C*(symyq)y
так что в двоичном случае все векторы имеют четный вес.
Можно показать, что двоичные коды размерности (ft+1),
получаемые выбрасыванием корня 1, также могут быть
декодированы с помощью мажоритарной логики, и их минимальное
расстояние равно по меньшей мере / (в двоичном случае /
всегда нечетно). Этот результат доказывается в приложении 3.
ПРИЛОЖЕНИЕ 1
Пусть (x)i обозначает j-ю «цифру» в разложении числа х
по основанию /?, т. е.
x=l>p4x)i> 0<(*),<р-1. (19)
Следующая лемма, доказательство которой будет опущено,
являете^ слабым обобщением леммы Грэхема и Маквильямс [4]
и может быть доказана аналогичным образом.
Лемма 4. Полиномиальный коэффициент
{а + Ь + с+ ... +м)1
а\Ъ\с\ ...п\
18
Ж.-М. Гёталс, Ф. Дейзарт
не сравним с нулем по модулю р тогда и только тогда, когда
<a)i-H(b)i+(c)i+... + (n)i =
= {а + Ь + с+...+п){<р—1, / = 0, 1, 2, ... .
Поставим числу х в соответствие число х
^=Mo+/?Mi+p2M2+ ... +рп-1[х]п-и
где [x]j означает сумму «цифр» числа х, номер позиции
которых сравним с / по модулю п, т. е.
оо
[х], - S (*)*„+/. (20)
Легко проверить, что при выборе основания q=pn число х
является суммой «цифр» числа х и
#==* mod(/?n—1). (21)
Мы покажем, что из существования (5+1)-номиального
коэффициента (16), не сравнимого с нулем по модулю /?, вытекает п
неравенств
(iH)>(s + l)(pn-l)9
(^)^(5+1)(/^-1),
(^)^(5+1)(/^-1), (22)
(pSZIte)>(s + 1)(рл-1).
Действительно, согласно лемме 4, такой полиномиальный
коэффициент существует тогда и только тогда, когда
(tu)i=(lou)i+{llu)i+{l2it)i+...+{lsu)h / = 0, 1, 2, ...,
где 1ииф0 и и = рп— 1. Из этого уравнения следует, что
(tu) = (ku) + (М + (¾) + ... + (й),
где (см. (21)) (to)>/?n—1 и, следовательно, имеет место
первое из неравенств (22). Остальные неравенства легко
получаются из соотношений
(pHu)i= (pU0u)i+ (p4iu)i+.... + (рН8и){
путем аналогичных рассуждений. Вводя неатрицательные числа
tfo> Яь 02» ...» #л-ь эти соотношения (22) можно переписать
Один класс циклических кодов с мажоритарным декодированием 19
в виде
[tu]0 + p[tu]l + p2[tu]2+ ... +pn-l[tu]n„l = (s + l+a0)(pn-l),
[tu]n_l + p[tu]0 + p2{tu]l+ ... +p*~l [^-2 = (5+1+^)(^-1),
[tu]{ + p[tu]2 + p*[tu]s + ... +Pn-][tu]0 = (s+l+an^)(pn-l),
что эквивалентно следующим соотношениям:
[tu]0 = (5 + 1) (р - 1) + ап^р - а0,
[tu]x = (s+l)(p-l) + an-2p-an-u (23)
[*4i-i - (в + 1)(р - 1) + а0р - ai.
В силу циклической переставляемости индексов всегда можно
полагать, что а0 является наименьшим среди aj. Тогда, вводя
обозначения
bj=dj — а0> 0, s'=s + a0,
соотношения (23) можно привести к виду
[tulo^is'+lHp-V + bn-xp,
[tu]{ = (s' + 1) (р - 1) + bn.2p - Ья-и
; (24)
[tu]n_2 = (s' + l)(p-l) + blP-b2t
['4.-1«(*'+1)(р-П -61.
Покажем теперь, что если удовлетворяются соотношения (24),
то (s'+l) чисел
mkH^k]o+p[mk]i+'p2[mk]2+ ... + pn-1[rafe]n_i,
где &=0, 1, 2, ..., $', могут быть подобраны таким образом,
что для / — О, 1, 2, ..., п—1 будем иметь
т*=Рл-1, (25)
[т0]/ + [/ni]/ + [mj/ + ... +[m^]/«[te]/.
Действительно, так как bj и [tu]j— неотрицательные числа,
то для каждого bj рекурсивным образом можно подобрать
такие (s'+l) неотрицательные числа
bj, о, bjt 1, bjt 2, .,., й;-, S',
40
Ж.-М. Гёталс, Ф. Дейэарт
что их сумма будет равна bj и
&о,а«0, bjth<p— l+pbj-\th, /=1, 2, ..., n—1,
ft-0, 1, ..., ^.
Тогда легко проверить, что при
[mh]n4=p— 1 +р Vi, h — bjtk>0 (26)
удовлетворяются соотношения (25). Теперь тривиально
находятся (s'4-l) чисел
mk - ]£{>"*)* р', 0 < (т*), < р - 1,
таких, что
2 (mk)in+n-ie [w*L-/>
где [m^ln-i определяются равенством (26) и
2(т*)/-(*и)/<р-1. (27)
fc~0
Так как т& es mft = (pn—1) mod(pn—1), то эти числа mk
являются ненулевыми кратными и~рп—1, скажем тк = 1ни, и,
согласно лемме 4 и равенству (27), полиномиальные
коэффициенты
- (tu)\ ( (tu)\
(l0u)l (/,«■)! ... (ls,u)\ • [(/0 +1{) u]\ (l2u)l ... (/,«)!
не сравнимы с нулем по модулю р, так что при s'>s всегда
может быть найден ($+1)-номиальный коэффициент (16), не
сравнимый с нулем по модулю р. Таким образом, мы доказали
следующее утверждение.
Теорема 2. Соотношения (22) являются необходимыми и
достаточными условиями существования {s+l) -номиального
коэффициента (16), не сравнимого с нулем по модулю р.
Проведя подсчет числа t, не превосходящего v и
удовлетворяющего условиям этой теоремы, получаем размерность кода
C(s,m,q) и, следовательно, число проверочных позиций кода
С* (s, m, q). Следующий пример иллюстрирует, как надо
производить такой подсчет.
Пусть ^ = 22 и т=*3. Тогда и=3 и 0=85. Числа /, 1 </<85,
подразделяются на классы: каждый класс содержит все
числа t, для которых [tu]o и [tu]t совпадают, т. е. t\ и t2 лежат в
одном классе тогда и только тогда, когда
[tiu]0=[t2u]o и [tiu]i=*[t2u]i.
Один класс циклических кодов с мажоритарным декодированием 2t
Пусть No, N\ — соответственно числа способов получения [tu]o
и [tu]\ как суммы (т+1) неотрицательных чисел, каждое из
которых меньше р=2. Тогда. N=N0Ni — число целых чисел t
в одном классе. С каждым классом свяжем число sm,
являющееся таким максимальным s, что существует
(s+1)-номинальный коэффициент (16), не сравнимый с нулем по модулю р.
Согласно теореме 2, число- sm является наименьшим из двух
чисел So и Si, для которых
(so+l)(p2-l) = [tu]0 + p[tu]u
(5l + l)(p2-l)«[to]1 + p[^]0.
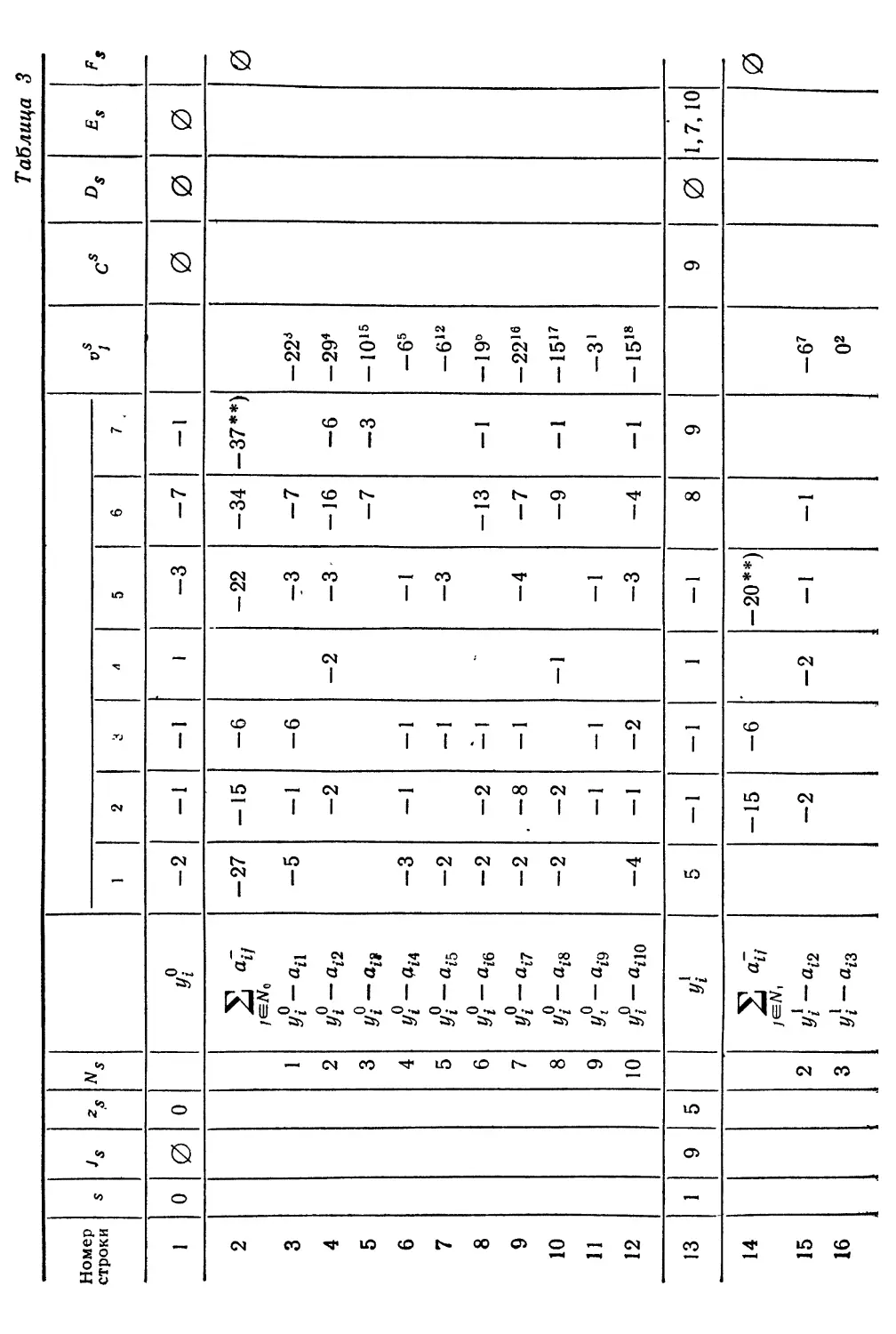
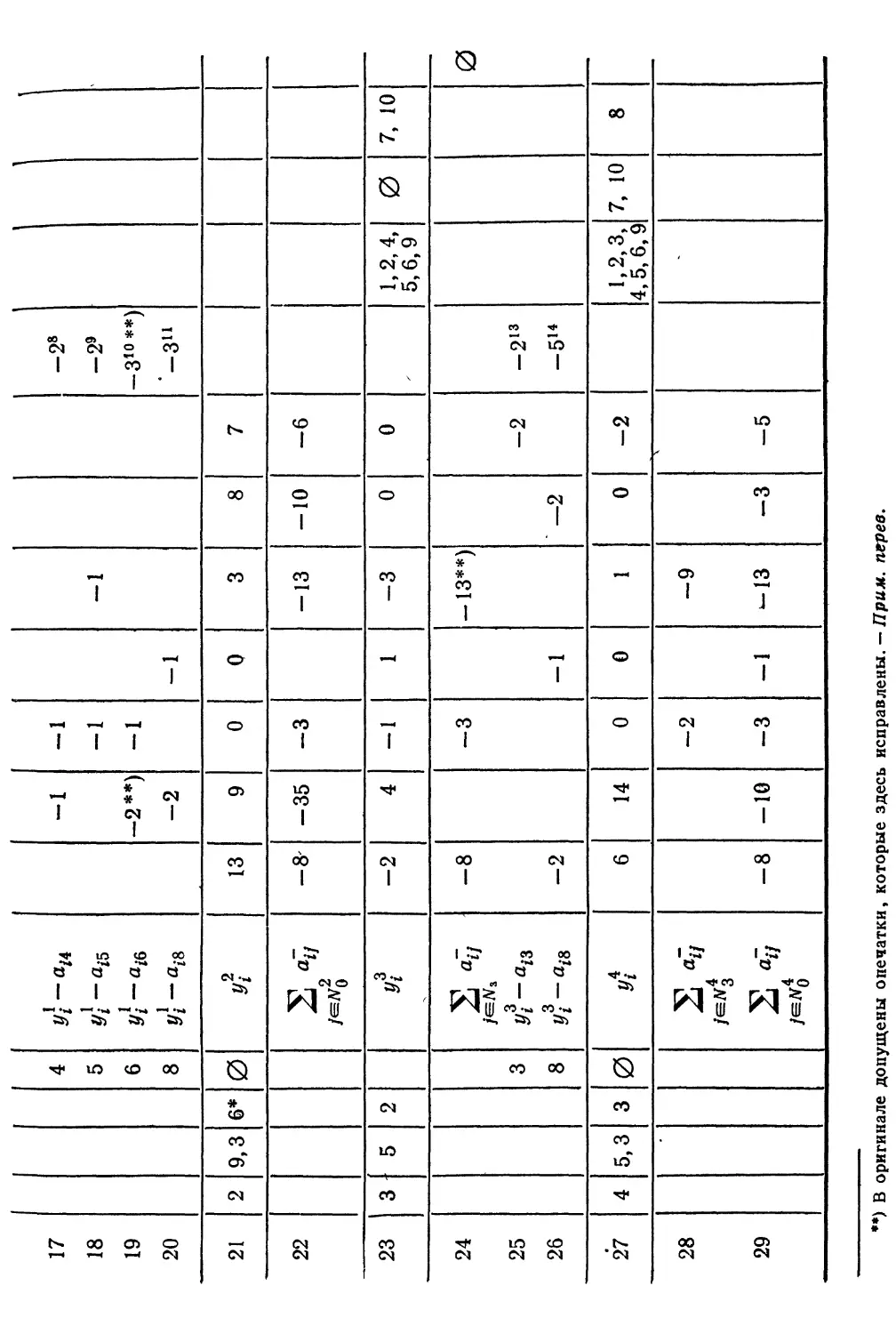
В табл. 3 для каждого класса приведены значения [tu]0i [tu]u
No, Nu N и sm. Легко проверить, что,коды С(2, 3, 4) и С(1,2,4)
соответственно имеют размерности 17 и 61. Дуальные коды,
приведенные в табл. 2, имеют, таким образом, размерности
соответственно 68 и 24.
Таблица 3
Huh
1
3
0
2
4
1
3
4
Huh
4
0
3
2
1
4
3
4
N9
4
4
1
6
1
4
4
1
Nt
4
i
4
6
4
1
4
1
N
16
4
4
36
4
4
16
1
*m
0
0
0
1
1
1
2
3
ПРИЛОЖЕНИЕ 2
Докажем, что число проверочных символов для общего
класса циклических кодов С*(m—l,m,pn), задаваемых
разностными множествами, в точности равно
°-Ч(Тг')Г+>-
Согласно теоремам 1 и 2г это число равно числу чисел t,
отличных от нуля, не превосходящих v и таких, что при s=m— 1
имеют место соотношения (22) или эквивалентно (23). Так как
очевидно, что [ta]j< (m+Д) (р— 1), то единственными
возможностями являются:
1) flo=ui-... =an_i= 1; отсюда [tu]0= [tu]\ = ... = [tu]n-\**
**(т+1)(р—1) и существует только одно соответствующее /,
а именно t=v.
22
Ж.-М. Гёталс, Ф. Дейзарт
2) a0=ai= ... =an-i = 0; отсюда [tu]0 = [tu]{ = ...= [to]n_! =
= m(p— 1). Так как [/н],- является суммой (m+1)
неотрицательных чисел, каждое из которых меньше /?, то число
способов получения [tu]j=em(p—1) равно числу способов получения
числа (т+1 — т) (р— 1) как суммы (т+1) неотрицательных
чисел, т. е. (см. [8], 6.6) имеет место равенство
/p-l + m\/m + p-i \
I m )-\ p-i ;•
Таким образом, в этом случае мы имеем
[(и,+-'г')Г
возможностей. Учитывая еще одну указанную выше
возможность, получаем сформулированный результат.
ПРИЛОЖЕНИЕ 3
Докажем теперь, что двоичный (и, h+ 1)-код, получаемый
из (и, ft)-кода C*(s, m, 2П) выбрасыванием корня f5v = 1
порождающего многочлена, является ортогонализуемым в (s+1)
шаг и имеет минимальное расстояние/= ((2n)m-8+1 — l)/(2n — l);
Действительно, пусть С* обозначает двоичный (о, А+Д)-код5
а Ci — дуальный ему код, содержащий все векторы четного
веса кода C = C(s, m, 2П) и, следовательно, двоичную сумму
любых двух векторов нечетного веса из С.
Пусть р0, Рь р2, • • •, Pj-i обозначает векторы
инцидентности / геометрий PG(s, 2П), содержащих данную геометрию
PG(s—1,2П), вектор инцидентности которой мы обозначим
через р'0. Так как ро, ри • •., Pj-\ образуют множество
проверок, ортогональных на р'0, то таким же является на р0 + р'0
множество векторов Ро + Ри Р0 + Р2, ..., Po+Pj-u
принадлежащих С\. Но p0 + pf0 является вектором инцидентности евклидовой
геометрии £G(s, 2П), так как точками покрытия .являются те
точки PG(s, 2П), которые не лежат в содержащейся в ней
геометрии PG(s—1,2П). Таким образом, С\ содержит множества
проверок порядка (/—1), ортогональных на точках любой
геометрии EG(s, 2П), содержащейся в данной PG(m,2n).
Далее так как имеется / геометрий EG(s, 2П), каждая из
которых содержится в данной EG(m,2n) и содержит данную
EG(s—1,2П), то для каждой EG(s—1,2П) всегда могут быть
построены множества ортогональных проверок. Проводя
индукцию, на (s+1)-m шаге приходим к множеству проверок
порядка (7—1), ортогональных на единственной точке, и,
следовательно, доказываем, что код С\ ортогонализуем в (s-fl)-ft
Один класс циклических кодов с мажоритарным декодированием 23
шаг; а так как каждое множество ортогональных проверок
имеет порядок, равный по меньшей мере (/—1), то
минимальное расстояние в С] равно по меньшей мере /.
ДОБАВЛЕНИЕ
После построения этих кодов авторам стала известна
неопубликованная ранняя работа Вилдона [12]. В ней предложен
класс двоичных кодов, мало отличающийся от описанных выше.
Результаты Вилдона так же, как и результаты авторов,
являются расширением и обобщением работ Рудольфа [13] и Ка-
зами, Лина и Питерсона [14].
Л ИТЕРАТУРА
1. Питерсон У., Коды, исправляющие ошибки, изд-во «Мир», М., 1964.
2. Мее си Дж., Пороговое декодирование, изд-во «Мир», М., 1965.
3. W е 1 d о n Е. J., Difference-set cyclic codes, Bell Sys. Tech. J., 45
(September, 1966), 1045—1055. (Русский перевод: В ил дон И., Циклические
коды, задаваемые разностными множествами, сб. «Некоторые вопросы
теории кодирования», изд-во «Мир», Мм 1970.)
4. G г a h a m R. L., Mac Willi a m^ J., On the number of information
symbols' in difference-set cyclic codes, Bell Sys. Tech. /., 45 (September,
1966), 1057—1070. (Русский перевод: Грэхем P. Л., Маквиль-
я м с Дж., О числе информационных символов циклических кодов,
задаваемых разностными множествами, сб. «Некоторые вопросы теории
кодирования», изд-во «Мир», М., 1970.)
5. Reed I. S., A class of mulfiple-error-correcting codes and the decoding
scheme, IRE Trans., Inf. Theory, IT-4 (September, 1954), 38—49. (Русский
перевод: Кибернетический сборник, вып. 1, ИЛ, М., 1960, стр. 189—205.)
6. Ми Пег D. Е., Application of Boolean algebra to switching circuit
design and to error detection, IRE Trans., Electr. Сотр., EC-3 (September,
1954), 6—12,
7. С a r m i с h a e 1 R. D., Introduction to the Theory of Groups of Finite
Order, New York, Dover, 1956.
8. Риордан Дж., Введение в комбинаторный анализ, ИЛ, М., 1963.
9. М a n n Н. В., Analysis and Design of Experiments, New York, Dover,
1949.
10. Meg git J. E., Error correcting codes and their implementation for data
transmission systems, IRE Trans., Inf. Theory, IT-7 (October, 1961), 234—
244.
11. Bose R. C, R ay-Chau dhuri D. K., On a class of error-correcting
binary group codes, Information and Control, 3 (March, 1960), 68—79.
(Русский перевод: Кибернетический сборник, вып. 2, ИЛ, М., 1961.)
12. Wei don Е. J., Non-primitive Reed-Muller codes. Dept. of Elec. Engrg.,
University of Hawaii, Honolulu, December, 1966.
13. Rudolph L. D., A class of majority logic decodable codes, IEEE Trans.,
IT-13 (April, 1967).
14. Kasami T, Lin S., Petersen W. W., Some results on cyclic codes
which are invariant under the affine groups, USAF Cambridge Research
Lab., Bedford, Mass., Tech. Rept. AFCRL-66-622, 1966.
Синтез циклически ортогональных
двоичных последовательностей
одного и того же наименьшего периода1
Д. Колабро, Дж. Паольело
Обсуждается построение циклически ортогональных двоичных
последовательностей одного и того же наименьшего периода. Показывается, что для
произвольного целого k и любого составного нечетного г могут быть
построены пары циклически ортогональных двоичных последовательностей с
длиной и наименьшим периодом N=2kr. Структура этих кодов очевидным
образом определяется правилом их синтеза; таким образом, коды любой
заданной длины указанного - вида являются легко конструируемыми.
Приводятся также границы для максимально возможного числа взаимно
циклически ортогональных двоичных последовательностей одного и того же
наименьшего периода.
1. ВВЕДЕНИЕ
Проблема построения циклически перестановочных кодов с
исправлением ошибок обсуждалась Гилбертом [1] и
Нейманом [2] в связи с асинхронными системами связи с уплотнением.
Эти коды обладают тем свойством, что расстояние по Хэм-
мингу от любого заданного кодового слова до всех
циклических перестановок всех других кодовых слов больше заданной
величины. Если все расстояния по Хэммингу равны N/2 (где
N — кодовая длина), то коды имеют нулевую взаимную
корреляцию и называются взаимно циклически ортогональными.
Для целей синхронизации желательно также, чтобы кодовые,
слова образовывали код без запятой. Для циклически
ортогональных кодовых слов необходимым и достаточным условием
того, что слова образуют код без запятой, является то, что их
наименьший период раве,н кодовой длине. Циклически
ортогональные N-ичные коды одного и того же наименьшего периода
были построены Вольфом и Левиттом [3, 4]. Двоичные
циклически ортогональные коды, конструируемые по предлагаемой
в этих работах методике, не обладают одним и тем же
наименьшим периодом. Недавно Маквильямс [5] доказала
существование и предложила метод построения пар циклически
*) С а 1 a b г о D., Р а о 1 i 11 о J., Synthesis of cyclically orthogonal
binary sequences of the same least period, Trans. IEEE, IT-14, № 5 (1968), 756—
759.
Синтез циклически ортогональных двоичных последовательностей 26
ортогональных двоичных кодов одного и того же наименьшего
периода. Наименьший период этих кодов равен удвоенному
квадрату простого числа.
В данной работе для любых целых k и любых составных
нечетных чисел г два множества двоичных кодов с наименьшим
периодом 2V, равным кодовой длине, строятся таким образом,
что любой представитель одного множества является
циклически ортогональным каждому коду другого множества.
Единственный класс длин, для которого не построены такие коды,
имеет вид 2hp\ где р' простое. Предлагаемый метод построения
пар циклически ортогональных двоичных кодов с длиной 2hpf
в этом случае приводит к кодам, период которых делит кодовую
длину.
В некоторых приложениях требуется построить множество,
содержащее максимальное число взаимно циклически
ортогональных последовательностей с периодом и длиной N.
Показано, что число последовательностей такого множества
ограничивается наименьшим из чисел (k + 1) и d, где 2k—
наибольшая степень двойки, делящая N, a d — число делителей числа
N/2h. Следовательно, если N=2r (где г — составное нечетное
число), то пары последовательностей, конструируемые по
предлагаемому здесь методу, будут исчерпывать такое множество.
Прежде чем переходить к основному предмету исследований
данной работы, дадим несколько предварительных
определений. Из этих определений следует, что утверждение о том, что
два двоичных (+1, —1) кода циклически ортогональны,
эквивалентно требованию о том, что периодическая взаимно
корреляционная функция кодов равна тождественно нулю.
2. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Периодическая взаимно корреляционная функция двух
двоичных (+J, —1) последовательностей длины N
Л = (ао, ...» Q>n^\)> m
B = (b0, ..., bN-X)
определяется как л(т) = 2 я^+г> где индексы берутся по мо-
дулю N.
Если две последовательности выражаются в форме поли*
номов
А(х)*=ао + а{х+ ... +aN-xxN~\
B(x) = b0 + bix+ ... +ьы„хх**-\ (2)
26
Д. Колабро, Дж. Паольело
где х — неопределенная неизвестная, то периодическая взаимно
корреляционная функция г(т) задается коэффициентом при
xn-\-x в многочлене
/?(*)== Л (х) В (~) х*-1 mod (xN - 1). (3)
Если R(x)=0 mod^—1), то коды А(х) и В(х) называются
циклически ортогональными. Ясно, что предыдущее условие
эквивалентно утверждению о том, что
г(т)=0, т=0, 1 iV— 1.
Предлагаемый здесь метод построения базируется на
понятии кронекеровского произведения последовательностей. Кро-
некеровским произведением С=Л®В двух
последовательностей
Л=(а0, ..., aA-_i),
В=* (Ь0, ..., 6M-i)
называется последовательность С = (с0, ..., cNM-\), задаваемая
равенством
СиМ-\-у == Q>uVyi
где 0*Cu4^N—1, О^Су^СМ—1, а индексы С выбираются по
модулю NM. Полиномиальное представление произведения
последовательностей имеет вид
С(х)=А(хм)В(х) mod(^M—1).
Период t последовательности Л = (ао, ..., aN-\)
определяется как наименьший положительный делитель N, такой, что
где индексы выбираются по модулю N. Эквивалентно период /
является наименьшим положительным делителем N, для
которого
х*А(х)=А(х) mod(**—1).
Таким образом, период последовательности определяется как
её наименьший период.
Для периода произведения последовательностей С = А ® В
Титсворс [6] доказал следующую лемму.
Лемма. Если периоды N и М соответственно
последовательностей А и В равны их длинам и N>2, то период
последовательности С—А ® В есть NM и он равен ее длине. Если
N = 2, то период t последовательности С определяется
структурой последовательности В: период t равен наименьшему поло-
Синтез циклически ортогональных двоичных последовательностей 27
тигельному числу, делящему 2М и такому, что
by^by+t для 0<г/<М-/,
by^ — by+t для M — t^y<M.
Синтез циклически ортогональных кодов одного и того же
периода основан на рассмотрении кронекеровского
произведения.
3. ПОСТРОЕНИЕ ЦИКЛИЧЕСКИ ОРТОГОНАЛЬНЫХ КОДОВ
Остановимся на синтезе двух множеств двоичных
последовательностей с длиной и периодом 2г, где г — составное
нечетное число, таких, что любой представитель одного множества
циклически ортогонален всем представителям другого. Затем
распространим этот метод синтеза на два множества двоичных
последовательностей длины 2V, просто построив кронекеров-
ское произведение синтезированных ранее последовательностей
и двоичных последовательностей с длиной и периодом 2k~l.
Действуя по этому плану, для построения множеств А' и В'
с требуемыми свойствами заметим прежде всего, что составное
нечетное число г может быть записано в виде произведения
двух нечетных чисел р и q, ни одно из которых не равно 1.
Множества Аг и В' строятся для любых конкретных р и q
следующим образом:
Л' = S <g> G ® #,
где
S-0, -1),
#-(Ао. ..., Vi)> (4)
A|-(-1)1.
Последовательность О пробегает все те последовательности
длины q, для которых S <& G имеет период 2q. Так как для
двойного произведения Кронекера справедлив ассоциативный
закон," то в силу ограничения, накладываемого на О, все члены
множества имеют период, равный 2pq*=*2r. В частности,
ограничению на G удовлетворяет последовательность из всех ( + 1);
следовательно, Л' не пусто. Для построения множества В' рас-
смотрим все последовательности вида
В = (£(ь • • • э Gpq-u Gpq-U •«•» #о) e (£» ^обращенное) э (5)
где fi-=F® Д F«(f0, .... f,-i),f«-(-l)<HD-(de dp-i)
есть произвольный код из элементов +1 и —1 с периодом р
28
Д. Колабро, Дж. Паольело
и такой, что D Ф Доращенное- Примером такого кода D является
dt — — dp»/-.i, %Ф—g—,
Так как период D равен р, то Т7® D имеет период р?;
следовательно, В не может иметь периода, меньшего, чем pq. Кроме
того, поскольку D Ф /Обращенное, то период В не может быть
равен pq. А так как период должен делить длину 2pq9 то все
члены множества В' имеют период 2pq=2r.
Для доказательства того, что каждый представитель из А'
циклически ортогонален любому представителю из В',
представим коды в полиномиальной форме и рассмотрим /?(х) =
=А(х) -В(1/х)х2м~1 mod(х2^ — 1). В полиномиальной форме
два произвольных представителя из А' и Вг запишутся
соответственно в виде
A(x)~(l-xpq)G(xp) хР+1
X + l ' (6)
B(x)^^r(D(x) + x^x^D(^)).
Далее В(\/х)х2^'1 является полиномиальной формой
обращенной последовательности В. Однако из (5) видно, что
последовательность Б и ей обратная совпадают. Следовательно,
многочлен R(x) может быть переписан в виде
R(x)=A(x)B(x) той(х2Ря— 1). (7)
Циклическая ортогональность последовательностей А(х) и
В(х) легко вытекает из рассмотрения выражения
*(*) = - {*"+~х1) (d{x) + xp«xp-*D {j))g(xp) mod (**м- 1). (8)
Так как r~pq является нечетным, а (р—1)—четным числом,
то х——1 является корнем многочлена
D{x)+xP<*xi>-lD{l/x).
Мы можем, таким образом, написать
D (х) + хмх*>-1 D (~) - (х + 1) L (х).
Подставляя это выражение в уравнение для R{x)y получаем
следующий результат:
R{x)^-^~{x+\)L{x)Q{xp) mod(**M-l)-
**-(x2m-\)L{x)G{xp) mod (**«*-l)-
«0 mod(x2w-l). (9)
Синтез циклически ортогональных двоичных последовательностей 29
Это доказывает существование и задает вид пар циклически
ортогональных двоичных последовательностей с периодом,
равным их длине 2г, где г — составное нечетное число.
Для обобщения доказательства на случай
последовательностей с длиной 2пг, где п — произвольное целое число,
рассмотрим последовательности
Ах = А®Ки
где К\ й /С2 — произвольные последовательности с длиной и
периодом п. Так как последовательности А и В имеют длину
и период 2pq, то длина и период последовательностей А\ и В\
равны 2npq. Для того чтобы показать, что последовательности
А\ и В\ циклически ортогональны, рассмотрим полином
#i (*) - Ах {х) В\ (~) ^w"!) tnod (*2w -1) =
^(А(хп)вЩ xn^^)[Ki(x)K2(^)xn'^ mod(j^w-l) ~
^R{^)(Ki(x)K2(j)^1) modO^-l). (11)
Ho R(x)*=0 mod (x2*« — 1) f следовательно, R(xn)—Q
mod{x2nn—l). Таким образом, Rx(x)—0 mod(х2пря — 1), что
и требовалось доказать.
Если п=2к~19 то длина последовательностей А\ и Bj
равна 2V. Таким образам, когда К\ и /Сг пробегают все
последовательности указанного вида, мы получаем два таких
множества двоичных последовательностей с длиной и периодом 2V,
что любая последовательность одного циклически ортогональна
ко всем последовательностям другого множества.
В качестве иллюстрации рассмотрим число Af=2-(3)2,
записанное в форме 2* (р')й, где р' простое. Выберем
последовательности
S«(+ -), (? = (+ + +),
#»(+-+), /7.(+-+),
£>-(- + +),
где О и D — приведенные выше примеры для иллюстрации
допустимых последовательностей G и D. Результирующие
последовательности А и В задаются равенствами
Л-(+ - + + - + + - + - + — + --+-),
В«(~ + + + + + + + + + +-).
30 Д. Колабро, Дж. Паольело
Эти две последовательности эквивалентны последовательностям
Маквильямс [5].
В случае последовательностей длины 2hp' (где р' простое)
получаем циклически ортогональные последовательности длины
2р'9 если взять 9=1, так что F = G = ( + ). В этом случае
последовательность В имеет период 2//, а последовательность А —
период 2. Перебирая кронекеровские произведения этих
последовательностей с произвольными последовательностями К\ и /(г
длины и периода n=2k~\ получаем два множества А' и В\
такие, что любой представитель одного циклически
ортогонален всем представителям другого. Все последовательности из В'
имеют период 2kp', а периоды последовательностей из А'
являются делителями числа 2ft, зависящими от структуры
последовательности К\ в соответствии с леммой.
4. ГРАНИЦЫ ДЛЯ ЧИСЛА ВЗАИМНО
ЦИКЛИЧЕСКИ ОРТОГОНАЛЬНЫХ кодов
В разд. 3 показано существование пары циклически
ортогональных двоичных последовательностей одного и того же
периода. Однако остается открытым вопрос, существует или нет
множество, содержащее более двух взаимно циклически
ортогональных последовательностей с периодом и длиной, равными
N=2kr. Ниже будет показано, что число последовательностей
в таком множестве ограничено меньшим из двух чисел (k+\)
и d, где 2k — наибольшая степень двойки, делящай Л/, a d —
число делителей нечетного числа г. Граница (k+l) была
получена Вольфом и Левиттом [3] для случая, когда на двоичные
последовательности не накладывалось требования о том, чтобы
их период совпадал с длиной N. Граница d соответствует
случаю, когда последовательности не обязательно должны быть
двоичными, но на них накладывается то ограничение, что
период равен длине М-
Для вывода границы d рассмотрим соответствующее
множество, взаимно циклически ортогональных последовательностей
длины 2V (£>1); произведение любых двух этих последбва-
тельностей в полиномиальной форме должно равняться нулю
по модулю (х2г—• l). Следовательно, неприводимые множители
многочлена (*2г— l) должны быть распределены между
любыми двумя многочленами множества. Эти неприводимые мно?
жители являются полиномами деления круга %, где i
пробегает все делители 2*г. Далее если Р\, Р2, ..., Pd — делители г,
то полиномы деления круга ф2*р, /=»1, 2, ..., d, должны быть
распределены между любыми двумя членами множества. За-
Синтез циклически ортогональных двоичных последовательностей 31
пишем полиномы (x2{k~x)r — l) и (*2r-^l) в виде произведений
их неприводимых множителей:
k d d d
^r-i = nvIIv...nt2v
/«I **/-1 ^/ /»=i ^ ^/
Отсюда с помощью деления находим, что
Теперь любая последовательность длины N = 2hry содержащая
в качестве множителя (x2{k~l)r + l), имеет период, не
превосходящий 2(fe_1V. Следовательно, представители множества
взаимно циклически ортогональных последовательностей с длиной
и периодом N=2hr не могут содержать в качестве множителей
все полиномы деления круга г|)2*р » i**h • ••> d. Так как
каждые два представителя такого множества должны вместе
содержать все эти полиномы, то множество может содержать
самое большее d последовательностей: для каждой из d
последовательностей множества вычеркивается один и только
один из d полиномов деления круга г|)2*р , /==1, ..., d.
Граница (k + 1), найденная Левиттом и Вольфом [3], также
может быть выведена из рассмотрения полиномов деления
круга я|у, / = 0, 1, ..., k. Эти многочлены также должны
быть распределены между любыми двумя членами множества.
Можно показать, что двоичные последовательности длины
N=2hr (где г — нечетное число) независимо от длины их
периода не могут содержать все (k+\) из этих полиномов в
качестве своих множителей. Следовательно, в силу аргументации,
аналогичной использованной выше, максимальное число
взаимно циклически ортогональных последовательностей с длиной
N = 2hr не может превосходить (k+l). Комбинируя обе
границы, получаем, что максимальное число взаимно циклически
ортогональных последовательностей с длиной и периодом Л7
равно меньшему из двух чисел (k+l) и d, где 2h —
наибольшая степень двойки, делящая N, a d — число делителей
числа да.
Необходимо отметить, что при исследовании чисел (k+l)
и d не использовался совместный анализ условий двоичности
кодов и равенства длины и периода. Это дает основание думать,
что существует граница, меньшая, чем приведенная выше.
32
Д. Колабро, Дж. Паольело
5. ЗАМЕЧАНИЯ
Остались нерешенными два вопроса, касающиеся двоичных
циклически ортогональных последовательностей:
1} Существуют ли последовательности* с длиной и периодом
N=-2hp' (// простое), имеющие требуемые свойства?
2) Могут ли существовать более чем две взаимно
циклически ортогональные двоичные последовательности с одной и той
же длиной и периодом?
Для случая N=2hp' (р'> простое) полученная выше граница
показывает, что могут существовать самое большее пары
последовательностей* с требуемыми свойствами. Как указывалось
в разд. 4, на самом деле граница может быть и меньше. Если
это так, то кодов с требуемыми свойствами и длиной 2*р'
(р' простое) не существует. Следующее обстоятельство
подтверждает это предположение: авторы умеют доказывать, что
для длин 2р' и Ар' (р' простое) не существует кодов с
требуемыми свойствами.
Благодарность. Авторам хотелось бы поблагодарить
д-ра Дж, К. Вольфа из Бруклинского политехнического
института за постановку задачи и тщательный просмотр рукописи.
ЛИТЕРАТУРА
1. Gilbert Е. N., Cyclically permutable error-correcting codes, Trans. lEgE,
IT-9 (July 1963), 175—182.
2. N e u m a n n P. G., On a class of cyclically permutable error-correcting
codes, Trans. IEEE, IT-10 (January 1964), 75—78.
3. Levitt K. W., Wolf J. K-, Correlation properties of multilevel cyclic
sequences, New York University, Tech. Rept. 400—125, November 1965.
4. W о 1 f J. K.f L e v й t K. W., Cyclically orthogonal sequences and an
application to asynchronous-multiplexing, Presented at the Symp. on
Information Theory, Los Angeles, Calif., 1966.
5. Mac Williams J., An example of .two cyclically orthogonal sequences
with maximum period, Trans. IEEE, IT-13 (April 1967), 338—339.
6. Tits worth R. С Correlation properties of cyclic sequences, Jet
Propulsion Lab., Tech. Rept. 32-388, July 1, 1963.
Одна комбинаторная задача1*
Я, Г. де Брёйн
1. Несколько лет назад И. К. Постумус сделал интересное
предположение относительно определенных циклов из знаков
О и 1, которые мы будем называть Рециклами2). Для
/1=1, 2, 3, ... определим Рп-цикл как упорядоченный цикл из
2П знаков 0 и Г, такой, что 2П возможных упорядоченных
множеств из п последовательных знаков этого цикла зсе различны.
Следовательно, любое упорядоченное множество из п
знаков 0 и 1 встречается в точности один раз в таком цикле.
Например, Р3-цикл 000101 И3) содержит тройки 000, 001,
010, 101, 011, 111, 110, 100, которые действительно есть все воз*
можные тройки из знаков 0 и 1.
Для п*1, 2, 3, 4 все Рециклы могут быть легко найдены.
Имеется только один Ргцикл, а именно 01, один Рг-цикл ООП,
два Рз-цикла 00010111 и^Н 1010001 и шестнадцать Рециклов,
восемь из которых следующие:
0000110100101 111, 1111001011010000,
0000100110101111, 1111011001010000,
0000101100111101, 111101О011000010,
0000110101111001, 1111001010000110,
а остальные восемь получаются изменением порядка каждого
из них на обратный.
Постумус нашел, что число Ps-Циклов равно 2048, и, таким
образом, для л=1, 2; 3, 4, 5 он имел следующее число
Рециклов:
1, 1, 2, 2\ 2»,
1) de Bruijn N. G.> A combinatorial problem, Proc. Коп. Ned. Akad.
v. Wet., 49, № 7 (1946), 758—764.
2) Задача возникла в теории связи.
3) В этих обозначениях 00010111; 00101110 и т. д. будем рассматривать
как*один и тот же цикл. (Точнее говоря, знаки следовало бы располагать по
кругу.) С другой стороны, мы не отождествляем циклы 00010111 и 11101000,
второй из которых получается изменением порядка в первом на обратный.
Впредь мы просто пишем Ф0О1О111 вместо 00010111.
34
H. Г. де Врёйн
ИЛИ
22°-i 221-"2. 222"*3 223~4 224~5.
Он сделал предположение, что число /^-циклов равно 22П~1~п
для любого п. В этой статье доказывается справедливость его
предположения. Доказательство получено в п. 3 как следствие
теоремы о специальном типе сетей, сформулированной и
доказанной в п. 2. Другое приложение этой теоремы дано в п. 4.
2. Рассмотрим специального типа сети, которые мы будем
называть Г-сетями. Назовем Т-сетью порядка m сеть с m
вершинами и 2т дугами, такую, что каждая вершина является
для двух дуг началом (из нее они исходят) и концом (в нее
они заходят). Сеть не обязательно плоская, или, другими
словами, допустимы пересечения дуг, которые не считаются
вершинами. Кроме того, не исключаются петли (дуга заходит в ту
же вершину, из которой исходит) и пары вершин, соединенные
двумя различными дугами как в одном, так и в
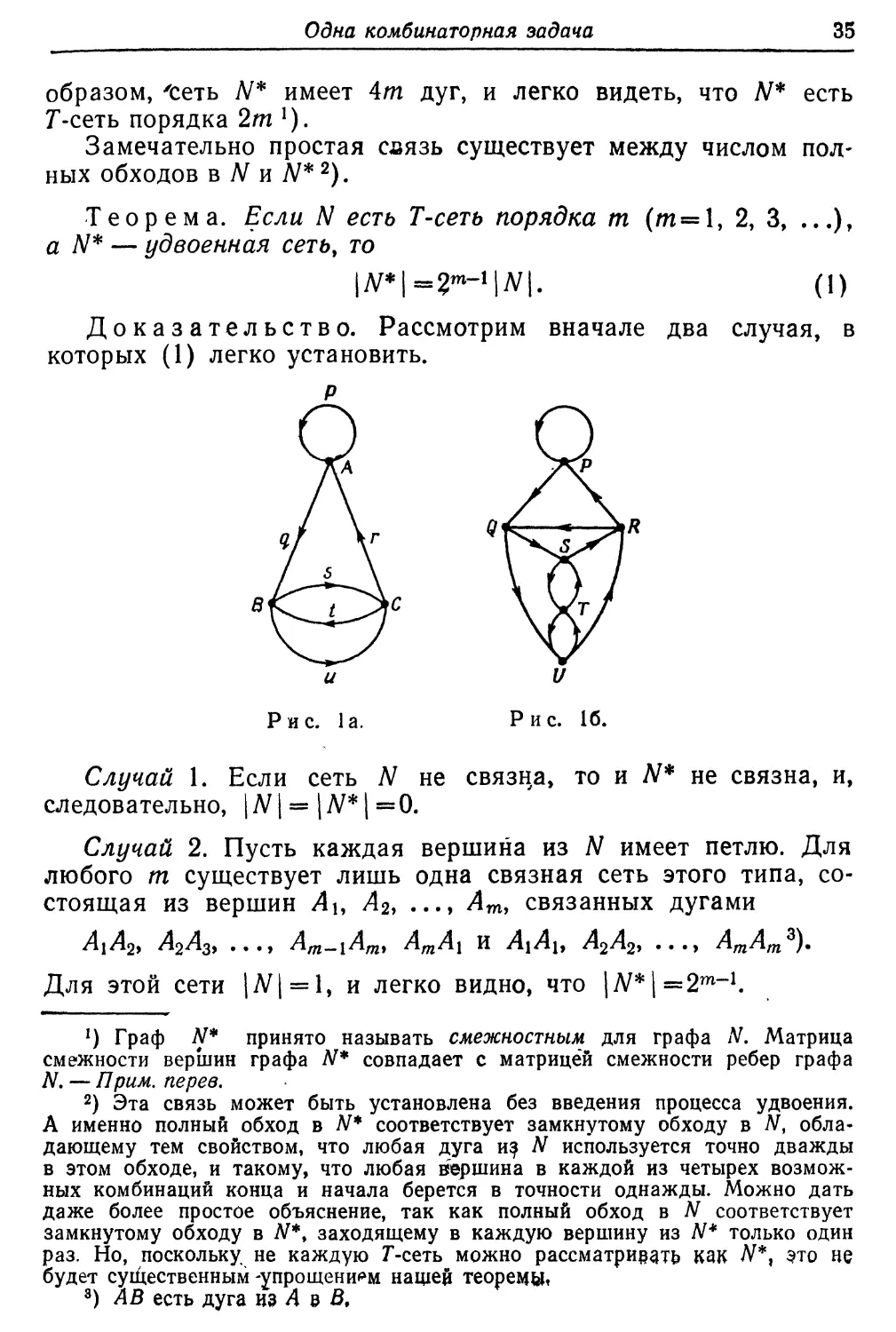
противоположных направлениях. Рисунки 1а и 16 дают примеры Г-сетей
порядков 3 и ,6 соответственно.
-Рассмотрим в Г-сети замкнутые обходы, обладающие тем
свойством, что любая дуга сети используется точно однажды
в предписанном направлении. Такие обходы будем называть
полными в этой Г-сети1). Два полных обхода будем считать
тождественными то**да и только тогда, когда
последовательность дуг2) в первом обходе есть циклическая перестановка
их во втором обходе. Сети на рис. 1а и 16 имеют 2 и 8 полных
обходов соответственно.
Число полных обходов Г-сети ./V будем обозначать через
\N\. Это число равно нулю, если сеть ./V не связна, т.е. если
сеть ./V может быть разделена на две отдельные Г-сети3).
Опишем процесс, который назовем удвоением Г-сети и
который проиллюстрируем связью между сетями, изображенными
на рис. 1а и 16. Пусть N есть Г-сеть порядка m с вершинами
А, В, С, ... и дугами р, q, г, ... . Построим «удвоенную» сеть
Л/*, взяв 2т вершин Р, Q, R, ..., соответствующих дугам из
сети N, и соединив дугой вершину Р с вершиной Q, если
соответствующие дуги р и q в N обладают тем свойством, что
конец р лежит в вершине из N, являющейся началом q. Таким
1) То есть речь идет об эйлеровых циклах в ориентированных графах
указанного типа. — Прим. перев.
2) Если мы заменим здесь слово «дуги» словом «вершины», то
предложение будет иметь другой смысл, так как две вершины могут быть
соединены двумя дугами одинакового направления.
3) Обратное также верно: для связной Г-сети мы имеем |ЛЧ>0. Тем не
менее мы не используем этого в нашей основной теореме.
Одна комбинаторная задача
35
образом, 'сеть W* имеет 4/л дуг, и легко видеть, что N* есть
Г-сеть порядка 2ml).
Замечательно простая связь существует между числом
полных обходов bJVh JV*2).
Теорема. Если N есть Т-сеть порядка m (m=l, 2, 3, ...),
а Л/* — удвоенная сеть, то
\N*\=2m~l\N\. (1)
Доказательство. Рассмотрим вначале два случая, в
которых (1) легко установить.
и и
Рис. 1а. Рис. 16.
Случай 1. Если сеть ./V не связка, то и N* не связна, и,
следовательно, |Л^| = |Л^*| =0.
Случай 2. Пусть каждая вершина из N имеет петлю. Для
любого m существует лишь одна связная сеть этого типа,
состоящая из вершин Аи А2, ..., Аш, связанных дугами
АгА2> А2А3> ..., Am-xAm% AmAx и AxAh А2А2, ..., AmAmz).
Для этой сети |N| = 1, и легко видно, что |Л^*|=2т-1.
1) Граф N* принято называть смежностным для графа jV. Матрица
смежности вершин графа N* совпадает с матрицей смежности ребер графа
N. — Прим. перев.
2) Эта связь может быть установлена без введения процесса удвоения.
А именно полный обход в N* соответствует замкнутому обходу в N,
обладающему тем свойством, что любая дуга щ N используется точно дважды
в этом обходе, и такому, что любая вершина в каждой из четырех
возможных комбинаций конца и начала берется в точности однажды. Можно дать
даже более простое объяснение, так как полный обход в N соответствует
замкнутому обходу в ЛГ*, заходящему в каждую вершину из N* только один
раз. Но, поскольку не каждую Г-сеть можно рассматривать как #*, это не
будет существенным -упрощением нашей теоремы»
3) АВ есть дуга из А в В,
36
Я. Г. де Брёйн
Докажем основной случай по индукции. Для т=1
возможна только одна Г-сеть, состоящая из одной вершины Л и
двух дуг из Л в Л. Эта сеть относится к случаю 2,
рассмотренному выше, и имеем \N\ = \N*\ ==1.
Предположим, что (1) верно Для всех Г-сетей порядка т—1
(где т> 1); пусть N есть* Г-сеть порядка т: Теперь
предположим, что можно выбрать вершину Л, не имеющую петли,
иначе N принадлежала бы случаю 2. Таким образом, у нас
есть четыре различные дуги /?, q, г, s; дуги р и-q заходят в Л,
дуги г и $ исходят из Л.
X ') f -Х-
N N, NZ
N* N{ /V2#
Рис. 2.
Получим сеть N\ из сети .N Путем выбрасывания Л, /?, q, г, s
и добавления двух новых дуг: одна идет из начала р в конец г,
а другая — из начала q в конец s.
Следующую сеть N2 получим аналогичным образом, .но
теперь комбинируем р с s, a q с г. Это показано на рис. 2; части
сетей, которые не изображены, совпадают для сетей N, N\ и Л/2.
Полный обход в N соответствует полному обходу либо в A/i,
либо в Л^2, и мы имеем
1^( = 1^1 + 1^1. (2)
Удвоением сетей Ni и JV2 получим сети N) и 'N*2. Докажем, что
|iV*| = 2|^I| + 2|iV;|. (3)
Одна комбинаторная задача 37
Сети N* и ЛУ получаются непосредственно из 'N* простыми
операциями. Если Я, Q, R> S — вершины в Л/*, соответствующие
дугам р, q, г, 5 в N, то сеть N\ получим опусканием дуг
PR, PS, QR, QS из jV* и отождествлением четырех вершин по
две: P—R и Q=S. Сеть Д^2 получим аналогично (P = S и Q — R).
На рис. 2 показаны соответствующие детали для N*9 N* и Л&
С этих пор мы имеем дело с N*t N\ и Nl, и более не
рассматриваем N, Nu N2.
Теперь введем новое понятие «пути». Путь есть
упорядоченная последовательность дуг, никакие две из которых не
одинаковы, и такая, что конец каждой дуги есть начало
следующей. Последняя дуга, однако, не обязательно ведет к
началу первоД
Всякий полный обход в N , N] или М\ содержит четыре
пути,- каждый из которых идет от одной из вершин R, S к
одной из вершин Я, Q так, что всякая дуга из А/*, кроме PR, PS,
QR, QS, принадлежит точно одному из этих путей. • Выбрав
определенную четверку таких путей, рассмотрим все полные
обходы в N*y N* и Nl> содержащие эти пути. Число таких
полных обходов обозначим через гс, П\, Щ соответственно.
Числа пу Пи ri2 допускают простое толкование. Пусть Л/**—
сеть, получающаяся из N* замещением каждого из четырех
путей одвой-единственной дугой с тем же началом и концом,
что и соответствующий путь. Таким же образом сети NT и N Г
получим из N*i и N*2. Очевидно, что я~|ЛГЧ fti=U/7|> «2 я
в1#2*|. Теперь убедимся, что
n = 2rti + 2n2, (4)
для чего рассмотрим два случая,
р s
GkoO
AT' <-V
Рис 3.
Случай А (рис. 3), Пути, начинающиеся из /?, ведут к
различным вершинам,
^8 Н. Г. де Брёйн
Четыре пути, таким образом, ведут соответственно из R
в Р, из R в Q, из S в Р, из S в Q. В этом случае N** состоит
из вершин Р, Q, /?, S с дугами Р#, PS, Q#, QS, #Р, RQ,
SP, SQ. Эта сеть допускает четыре различных полных обхода.
Сеть N*\* состоит только из двух вершин Р и Q с дугами РР,
PQ> QP> QQ. Эта сеть допускает только один полный обход.
Сеть N*2 эквивалентна JV*i\ Таким образом, мы получили л=4,
/71 = 1, п2 = 1, и (4) верно.
Случай В (рис. 4). Пути, начинающиеся из /?, ведут к одной
и той же вершине, скажем Р (аналогично для Q). Теперь
имеем четыре пути RP, RP, SQ, SQ.
ф<| ©-©о
Р Q
Рис. 4.
В этом случае N** состоит из вершин Р, Q, /?, S с дугами
Pi?, PS, Q#, QS, RP, RP, SQ, SQ. Эта сеть допускает четыре
полных обхода. Сеть N] состоит из двух вершин Р и Q с
дугами РР, РР, QQ, QQ и не связна. Сеть N*2 состоит из вершин Р,
Q с дугами PQ, PQ, QP, QP и допускает два полных обхода.
Теперь имеем д==4, fti=0, п2=2, и> следовательно, (4) верно
также и в этом случае.
Поскольку равенство (4) доказано для произвольной
допустимой системы из четырех путей, теперь становится очевидной
истинность равенства (3).
Наша теорема немедленно следует из (3). В самом деле*
так как N{ и N2 — сети порядка (т—1), то наше
предположение индукции дает
М|-2И-2|ЛМ, |Л^| = 2т-2|ЛЫ
а из (3) и (2) имеем
\N'\~2\N\\ + 2\Nl\-2m-l\Ni\ + 2m-l\N2\-2m~l\N\.
3. Доказанная теорема позволяет легко доказать
предположение Постумуса. Для м>2 построим сеть Nn порядка 2П
следующим образом: в качестве вершин возьмем упорядоченные
Одна комбинаторная задача
39
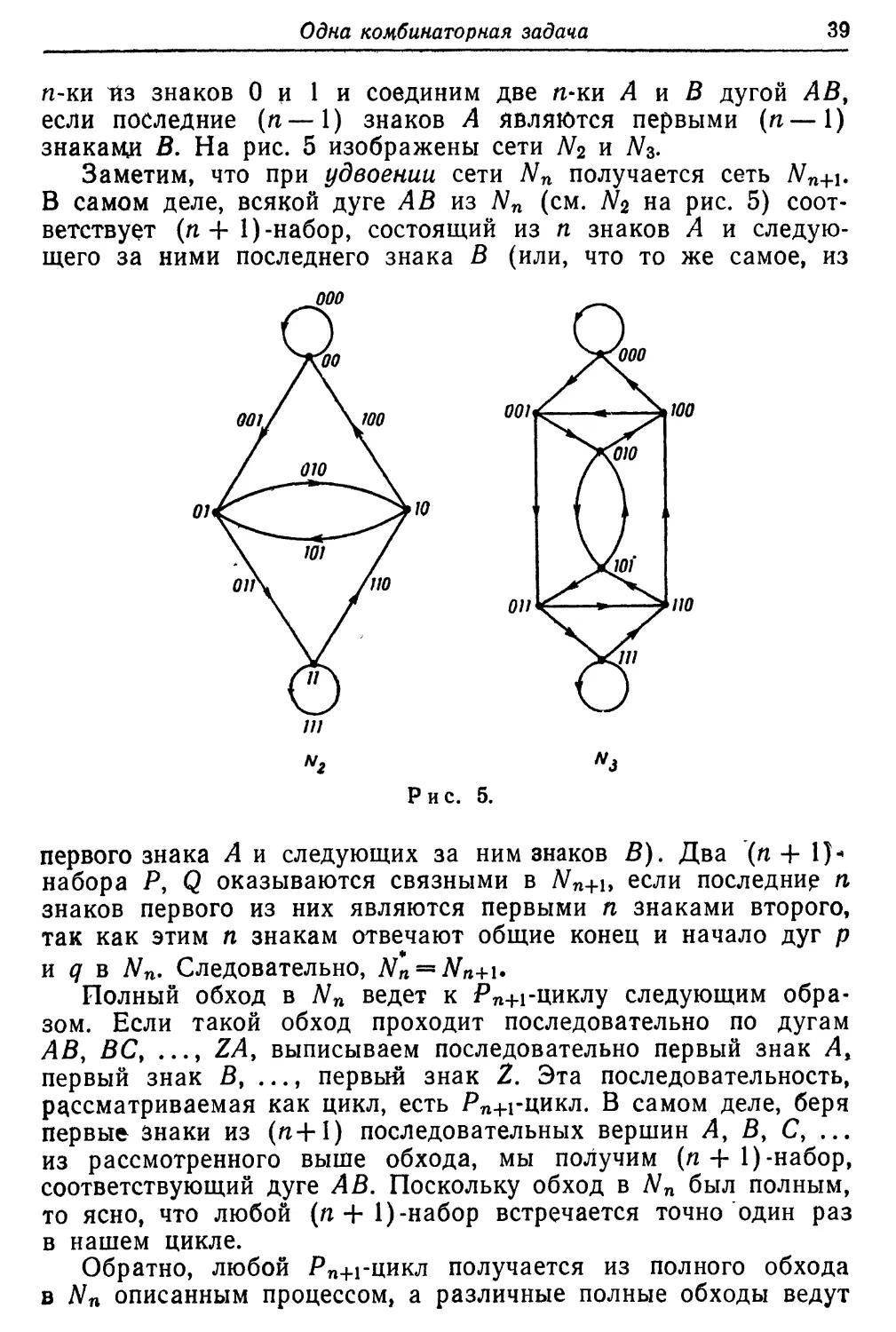
п-ки из знаков 0 и 1 и соединим две n-ки А и В дугой ЛВ,
если последние (п— 1) знаков Л являются первыми (гс— 1)
знакам^ В. На рис. 5 изображены сети N2 и N$.
Заметим, что при удвоении сети Nn получается сеть Nn+\.
В самом деле, всякой дуге АВ из Nn (см. Л^2 на рис. 5)
соответствует (п + 1) -набор, состоящий из п знаков А и
следующего за ними последнего знака В (или, что то же самое, из
первого знака А и следующих за ним знаков В). Два (п + 1)-
набора Р, Q оказываются связными в Nn+u если последние п
знаков первого из них являются первыми п знаками второго,
так как этим п знакам отвечают общие конец и начало дуг р
и q в Nn. Следовательно, Nn — Nn+i*
Полный обход в Nn ведет к Рп-н-циклу следующим
образом. Если такой обход проходит последовательно по дугам
АВ, ВС, ..., ZAy выписываем последовательно первый знак Ау
первый знак В, ..., первый знак 1. Эта последовательность,
рассматриваемая как цикл, есть Рп+Гцикл. В самом деле, беря
первые знаки из (п+1) последовательных вершин Л, В, С, ...
из рассмотренного выше обхода, мы получим (п + 1) -набор,
соответствующий дуге А В. Поскольку обход в Nn был полным,
то ясно, что любой (п+1)-набор встречается точно один раз
в нашем цикле.
Обратно, любой Рп+гцикл получается из полного обхода
в Nn описанным процессом, а различные полные обходы ведут
40
Я. Г. д<> Врёйн
к различным Pn+i циклам. Следовательно, число Рп+гциклов
равно |JVn|.
Теперь докажем предположение Постумуса по индукции,
Для и=1, 2, 3 справедливость предположения установлена в
п. 1. Возьмем /1>3и предположим, что число Рп-циклоз равно
22П~1~п, откуда J Nn„x \**2*lmml-n. Так как порядок Nn~\ равен
2Л-1, то по теоре'ме из п. 2 имеем
1^1-2^-4^-,1,
а, следовательно,
\Nn\=* 22П~х-х22П~1~п = 22"-»-1.
Поскольку число РЛ+1-циклов равно |iVn|, то предположение
Постумуса оказывается верным.
4. Другое приложение доказанной теоремы состоит в
следующем. Назовем n-ку из знаков 0, 1 и 2 допустимой, если
никакие два последовательных знака в ней не совпадают;
последний знак, однако, может быть тем же самым, что и
первый. Легко видеть, что число допустимых гс-ок равно 3-271-1.
Определим теперь фп-цикл как упорядоченный цикл из,3-211-^
знаков 0," i и 2 и такой, что любая допустимая гс-ка встречается
точно один раз среди п последовательных знаков этого цикла.
Например, существует двенадцать фз-Диклов. Два из них есть
012010202121 и 012020102121; а другие десять получаются
перестановками символов 0, I и 2.
Для произвольного п > 1 число Qn-циклов равна
3.23-2л-2-л-к# Доказать это можно аналогично тому, как это
сделано в п. 3.
О времени, требующемся
для выполнения сложения1
С. Виноград
Исследуется время, требующееся для выполнения групповой операции с
помощью логической схемы. Находится нижняя оценка этого времени, а в
случае абелевой группы показывается, что к этой нижней оценке
можно,приблизиться, если сложность используемых элементов растет. В частности, по*
казЫвается, что если групповая операция представляет собой сложение
целых, чисел по модулю и-, то нижняя оценка «едет себя как loglogtx(fx), где
a(jA) —наибольшая степень простого, которая делит ц.
1. ВВЕДЕНИЕ
Предметом исследования данной статьи яв-ляетея количество
времени, требующееся для "сложения двух целых .чисел с
помощью логической схемы. Каждое из слагаемых пробе!^ает
множество значений ZN*={0, 1, ..., N—1}, а сложение
производится по модулю, N. Эта задача рассматривалась Ю. П. Оф-
маном [1], который исследовал ее в случае N=2^ и в
предположении, что представление слагаемых входными сигналами, а
также представление суммы выходными сигналами
соответствуют представлению целых чисел в позиционной системе
счисления с основанием 2. Он показал, что в этих условиях для
выполнения сложения требуется количество времени, которое
растет как log2Jog2# = log2#, в то время как количество
требующегося оборудования растет как log2~N = л2). Другая схема
сложения, которая при упомянутых выше условиях также
требует времени, растущего как log2n, описана в [2]. Оценку
относительных достоинств различных схем сложения можно
найти в [6].
*) W i п о g г а d S., On the time required to perform addition, J. ACM,
12, №2 (1965), 277—285.
2) Оценка времени, полученная Ю. П. Офманожг, является точной лишь
по- порядку (с точностью до мультипликативной-константы). В тех же
условиях В. М. Храпченко установил асимптотику времени выполнения^ сложения
и показал, что существует схема сложения с асимптотически минимальным
временем работы и (одновременно) с минимальной, по порядку сложностью.
См. Храпченко В. М., Об асимптотической оценке времени сложения
параллельного сумматора, сб. «Проблемы кибернетики», вып. 19, М., «Наука»,
1967, стр. 107—122. — Прим. ред.
42
С. Виноград
В этой статье исследуется лишь время, требующееся для
выполнения сложения, невзирая на то, какое количество
оборудования требуется для реализации схем сложения. Находится
нижняя оценка этого времени и затем показывается, что для
конечных абелевых групп возможно приближение к этой
нижней оценке, если сложность используемых логических элементов
растет.
В разд. 2 дается более точная формулировка задачи;
нижняя оценка получается в разд. 3; в разд. 4 бГШсыйаются схемы
с временем работы, близким к нижней оценке.
2. ФОРМУЛИРОВКА ЗАДАЧИ 1)
В этом разделе дается более точное определение логической
схемы и ее способности вычислять фуйкцию за данное время.
Определение 1. Назовем d-значным логическим элементом
объект с г входными линиями и одной выходной линией.
Выходная линия так же, как каждая из входных линий, может
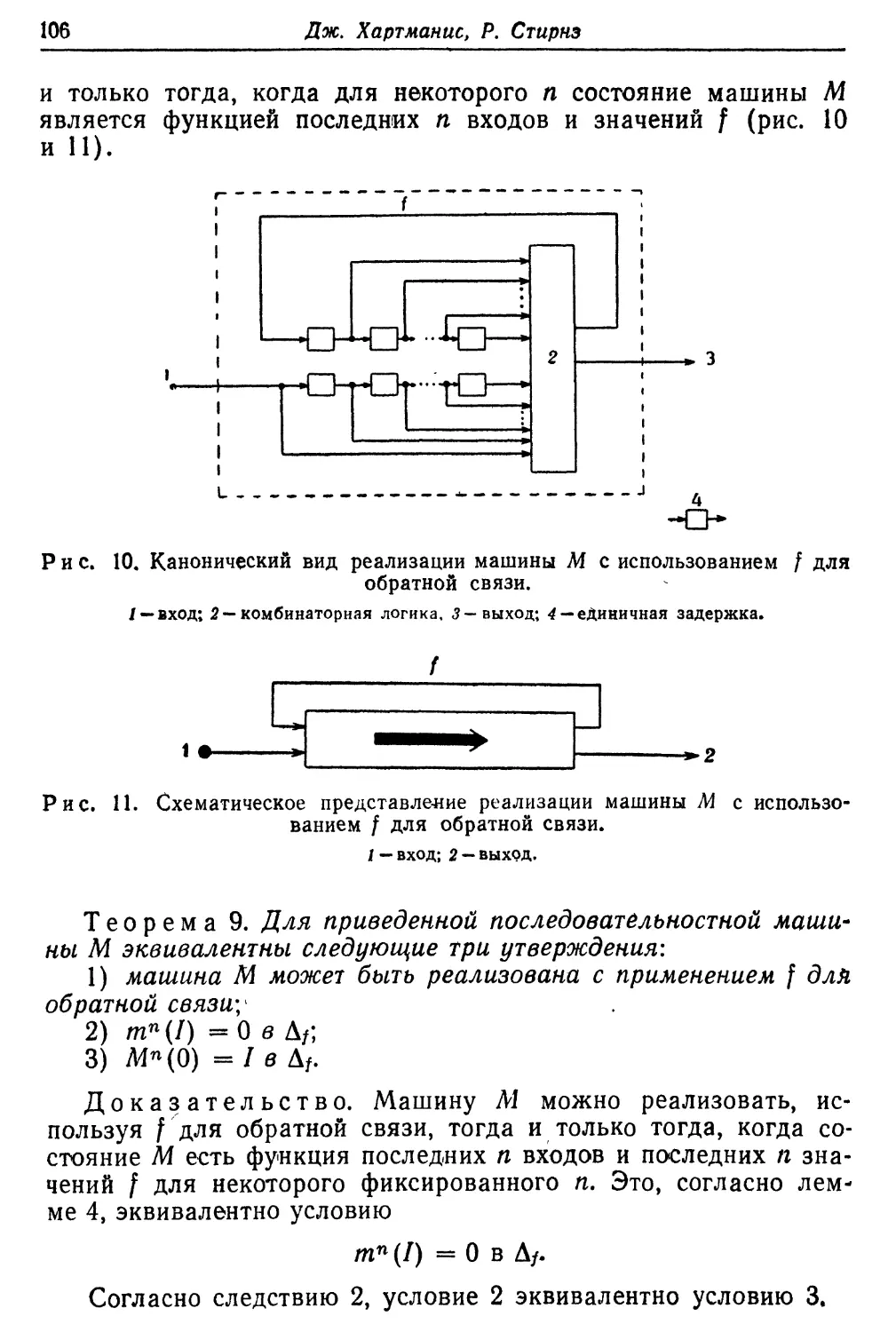
находиться в одном из d различимых состояний. Состояние
выходной линии в момент времени /+1 является функцией
состояний входных линий в момент времени t.
Определение 22). Назовем d-значной логической схемой
конечное множество rf-значных логических элементов и правило
соединений, которое разбивает множество линий логических
элементов на классы и отождествляет (соединяет) две линии
тогда и только тогда, когда они принадлежат одному классу.
Это правило соединений является причиной того ограничения,
что никакие две выходные линии не могут попасть в один
класс. Классы, не содержащие выходных линий, называются
входами схемы, некоторое выделенное множество классов
называется выходами схемы.
Пусть С — логическая схема. Обозначим через Sc
(конечное) множество всевозможных наборов состояний выходных
линий логических элементов схемы С, через /с— (конечное)
множество всевозможных наборов состояний входов схемы С
1) Здесь приводится перевод разд. 2 из другой статьи автора,
помещенной в настоящем сборнике вслед за данной статьей, в оригинале которой
соответствующие определения сформулированы более четко. — Прим. перев.
2) Данное определение отдичается от определения схемы из
функциональных элементов (см., например, статью О. Б. Лупанова «Об одном классе
схем из функциональных элементов», сб. «Проблемы кибернетики», вып. 7,
М., Физматгиз, 1962, стр. 61—114) только тем, что элементам схемы
приписываются функции d-значной, логики (а не двузначной), предполагается, что
каждый элемент имеет задержку, равную Ц и в схеме допускаются обратные
связи. — Прим. перев.
О времени, требующемся для выполнения сложения 43
и через Ос—(конечное) множество всевозможных наборов
состояний выходов схемы С. Поскольку выходы схемы С
образуют подмножество объединения множества входов схемы С и
множества выходных линий элементов из С, мы можем ввести
(проецирующую) операцию a: ScX/c-»Oc.
Поведение логической схемы может быть описано функцией
/: Sc X /с -*& X /с, где / (s, i) = {s\ i') (s, s' e= Sc, /, 1" e= /c),
причем if = t, a 57 находится путем установления входных линий
элементов из С в момент времени t в состояния,
соответствующие значениям s и i, и выбора в качестве s' набора состояний
выходных линий элементов из С, получившегося в момент
времени /+1. Функция f(s%t) может быть обобщена в виде
/*: ScX/cXiV-»ScX/c, где ./V—множество натуральных
чисел, если принять f*(s9i9l)*=f(s,t) и f*(sj,n+l)=f(f*(sj,n)).
Определим, наконец, с: ScX/cXJV->Oc посредством
равенства c(sfi,n)=*o(f*(s9i,n)).
Определение 3. Пусть ср: Х\Х X2-+Y— конечная функция,
Говорят, что схема С способна вычислить функцию у{хих2)
за время т, если существуют s0 е Sc, разбиение входов схемы С
на два класса, функции gy. Xj->/c,j (/= 1,2), где Ic,j —
множество наборов состояний входов схемы С из /Vro
класса, и взаимнооднозначная функция h: Y->Oc, такие, что для
каждой пары (х\, х2) е Х\ X Х2 имеет место равенство
с (so, (gi (х\), g2{x2)), т) = h (ф (хи х2)).
Понятие схемы, вычисляющей функцию, в том виде, как
это было описано в определении 3, в основном состоит в
следующем:
(i) в момент времени 0 внутреннее состояние схемы уста*
навливается в s0;
(и) каждый из аргументов вычисляемой функции кодируется
и подается на входы схемы;
(iii) входы схемы поддерживаются фиксированными до
момента времени т, в который проверяется, произвел ли выход
схемы результат вычисления (в кодированной форме).
В разд. 3 мы получим нижнюю оценку времени,
требующегося для вычисления функции ср: G X G —*G, где G — конечная
группа, а ср — групповая операция.
3, НИЖНЯЯ ОЦЕНКА
Пусть С —логическая схема. Будем использовать символ
Cj(s, i, т) для обозначения /-й компоненты набора c(s, /, т);
иными словами, если состояние выхода Oj есть /-я компонента
44
С Виноград
выходного состояния, то тогда Cj (s, 4 т) есть состояние Oj в
момент времени т при условии, что схема «стартовала» во
внутреннем состоянии s. и вход поддерживался фиксированным
и,равным L
Определение 4. Говорят, что выходная линия Oj s-незави-
сима (s&Sc) от входной линии 4 в момент времени т, ерли
для всех h&Ic и ^е/С1 отличающихся только^состоянием 4*
имеет место равенство Cj(s, i\,x) =Cj(s, н, т). Если выходная
линия не является s-независимой от линии 4 в момент
времени т, то" говорят, что она s-зависима от 4 в момент
времени т. Заметим, что если выход Oj s-зависим от входа 4, то
существует «путь» от 4 к о$, если рассматривать схему как
ориентированный граф.
Лемма 1., Пусть С — логическая схема, каждый из
элементов которой имеет не более г (г > 1) входных линий. Для
всех выходных линий Oj схемы С справедливо утверждение:
если Oj So-зависима от t входов схемы С в момент времени т,
то x^]logr ([{здесь ]х[ обозначает наименьшее целое, не
меньшее х).
Доказательство. Докажем лемму индукцией по /.
Если tfO, то неравенство очевидно.
Предположим, что о$ зависит от t>r входов схемы С и что
Oj — выходная линия элемента ej. Пусть О —множество
входных линий элемента е$\ хотя бы одна из эт#х линий является
выходом другого элемента из С, который зависит не менее чем
от — входов схемы С в момент времени т—1. Учитывая
предположение индукции, получаем
T-l>]logr }j[[» logrf[ = ]logr/[-l,
так что T>]logr£[.
Пусть С есть rf-значная логическая схема, вычисляющая
ф: GXG-^G, где G— конечная группа, а ф — групповая
операция. В оставшейся части раздела будем использовать запись
g\\g2 Для обозначения ф(#ьg*).' Поскольку С вычисляет^,
существует функция h: G—*Oc. Мы будем использовать
символ hj('g) для обозначения состояния /-й компоненты h(g).
Определение 5. Говорят, что элемент a^G обладает
свойством Ej по отношению к схеме С, вычисляющей ф, если для
всех b^gp(a) имеет место равенство hj(b)—hj(e)y где gp(a)
обозначает группу, порожденную а, а в обозначает единичный
О времени, требующемся для выполнения сложения 45
элемент группы G. Тот факт* что a&G обладает свойством Ej,
мы обозначим через Ej{a).
Лемма 2. Предположим, что Ej(a) не имеет места, и
Ь, c&G таковы, что gi(b) и g\(c), (£2(6) и g2{c)) отличаются
только на тех входах, бт которых Oj не зависит; тогда
аф gp(b • с~х)'(аф gp (/г1 • с)). Здесь g\ и g2 — те же, что в
определении 3.
Доказательство. Мы докажем только половину
утверждения, ибо вторая половина доказывается аналогично. По
предположению для любого элемента хеС имеем
= hj(c-x)
(поскольку Oj не зависит от входных линий, на которых g\(b)
и g\(c) отличаются). Таким образом,
£,-((6.с-1) .х)=к)(Ь-((г1-х))*=11}(с: {c-x-x))=hj(x)
для всех х е G. Полагая х = е, получаем hj(b-c-l)=hj(e);
полагая х~Ь-с~\ получаем hj(e) = /ij(&- c~l) = /tj((6 • с1)2);
полагая x=(b-c~l)s для всех целых: s, находим, что Ej(b-c~l)
выполняется. Однако если бы aggp(b-c~l), то тогда Ej(a) также
выполнялось бы, следовательно, a^gp(b - с~х).
Определение 6. Пусть еф as Я ^ G1); будем говорить, что
имеет место свойство Р (а, Я), тогда и только тогда, когда
{е} ф Hi с Hz^'a е Яь Будем говорить, что свойство Я (Я)
имеет место для Я с= G, если либо Я = [ё], либо существует
элемент а, еФа^Н, такой, что Р(а,Н) имеет место.
Лемма 3. Пусть С есть d-значная логическая схема,
вычисляющая ф: G X,G-*G. Пусть а и Я (е Ф as Я s G) таковы,
что имеет место Р(а,Н), и пусть Oj— такой выход, что к^(а)Ф
= hj(e)\ тогда ojt зависит не менее чем от ]\ogd\H\[ входных
линий из каждого класса входов схемы С (|Я| обозначает
порядок Н).
Доказательство. Допустим, что Oj зависит только от
<7<]l°gdl^|[ входных линий первого класса; тогда найдутся
Ь, с^Н, таки^, что g\(b) и g\(c) отличаются только на тех
входных линиях, от которых Oj не зависит. По лемме 2
a^gp{b - с~]), т. е. имеем противоречие. Подобными же
рассуждениями устанавливается этот результат для второго класса
входных линий.
1) Я, Н\, Н2 — группы. — Прим. перев.
46
С. Виноград
Пусть a(G) = тах{|Я| \Н е G и Р(Н)}. Заметим, что в
случае G = {е} имеем <x(G) > 1, так как если ефas G, то, приняв
порядок а равным plq (где q взаимно просто с р), найдем, что
P(api~lcft gpiai)) выполняется и что \gp(a<i) | =р* > 1.
Теорема 1. Пусть С есть d-значная логическая схема,
каждый из элементов которой имеет не более г входных линий,
и пусть С вычисляет ф: G X G-+G за* время т; тогда если
вф{е1 то T>]logr2]logda(G)[[.
Доказательство. Пусть #^G-r такая подгруппа,
что Р(Н) выполняется и |#|~a(G). Пусть asfl такой, что
Р(а,Н) выполняется. Тогда существует выход Oj, такой, что
hj(a) 4=hj(e), и, следовательно, по лемме 3 Oj зависит не
менее чем от 2]log<*|#|[ = 2]log<*a(G)[ входных линий схемы С.
Применяя лемму 1, получаем T>]logr2]log<ja(G)[[.
Мы видели в теореме 1, что нижняя оценка времени,
требуемого для вычисления ср: G X G-+G логической схемой,
зависит от a(G). Может представить интерес дальнейшее
исследование a(G) и подгруппы Я, для которой Р(Н) выполняется.
Замечание 1. Если Я такова, что Р(Я) выполняется, и
Ь, с^Н имеют порядки р\ q* соответственно (где р и q
—.простые числа), то p=pq, потому что если а, ефа^Н, такой, что
Р(а,Н) выполняется, то порядок а делит рх и qK
Следовательно, если Р(Н) выполняется, то Я обязана быть р-группой,
т. е. порядок Я, так же как и порядок каждого элемента из Я,
есть степень р для некоторого простого числа р.
Замечание 2. Если Н = Н\Х Я2, то Р(Н) не может иметь
места, так как Р(Н) имеет место тогда и только тогда,-когда
f\ Я' = {е}, а Я = Н\ X Я справедливо тогда и только
{е} фН'^Н
тогда, когда Н\ Л Я2 =* {е}.
Замечание 3. Если Я — абелева группа, то Р{Н)
выполняется тогда и только тогда, когда Я — циклическая группа
порядка р* для некоторого простого числа р.
Поскольку любая абелева группа может быть представлена
единственным образом в виде произведения циклических
р-групп, мы приходим к выводу, что в случае, когда G
—абелева группа, a(G) есть порядок наибольшей циклической р-под-
группы группы G.
В частности, если G = Z^={0, 1, 2, ..., fx — 1 >, причем
групповая операция ср определена посредством равенства^ (2Ь г2) —
= Zi-hz2mod[xy мы получаем a(G)=a(^i), где а(ц)
определяется как a {\i) = max {р£ | pt простое, n натуральное и р*|ц}-
О времени, требующемся для выполнения сложения 47
Прежде чем закончить раздел, мы приведем два
непосредственных следствия теоремы 1.
Следствие 1. Пусть С есть d-значная логическая схема,
каждый из элементов которой имеет не более г входных линий,
и пусть С вычисляет q/: GXG-+G за время т, где ср'(а, 6) =
= a-b~l\ тогда x>]logr2]logda(G)[[.
Доказательство. Пусть gu g2 и h — кодирующие и
декодирующая функции. Рассмотрим функции g\ = gv g£(a)=»
*=g2{a~1)H h'=h. Ясно, что при таких функциях С будет
вычислять ф: GXG—>G, где ср(а, b)=a-b, за время т;
следовательно, t>]logr2]logda(G)[[.
Следствие 2. ПусГь С есть d-значная логическая схема,
каждый из элементов которой имеет не более г входных линий,
и пусть С вычисляет
yh: GX GX~...XG-^G,
где ф(яь #2, •••» 0¾) =01-02 ••• 0¾1)^ за время т; тогда
T>]\ogrk]\ogda{G)[l
Доказательство. В случае & = 2 мы имеем
утверждение теоремы 1. Ясно, что леммы 2 и 3 верны также и для схем,
вычисляющих щ. Поэтому теми же рассуждениями, что
использовались при доказательстве теоремы 1, получается
утверждение следствия.
4. ВЫЧИСЛИТЕЛЬНАЯ СХЕМА ДЛЯ АБЕЛЕВЫХ ГРУПП
В этом разделе, мы опишем схему вычисления групповой
операции для абелевых групп. Эта схема требует времени,
которое близко к нижней оценке, полученной в предыдущем
разделе, и в действительности приближается к нижне- оценке,
если число входов элементов, образующих схему, увеличивается.
Сначала мы опишем схему вычисления для циклических
групп порядка р* в предположении, что используются d-знач-
ные логические схемы, а в заключение мы рассмотрим общий
случай произвольной конечной абелевой группы в
предположении, что используется d-значная логическая схема.
При рассмотрении циклических групп порядка р, будет
удобно называть групповую операцию сложением по модулю \i
1) Определения, связанные с функцией ерь, совершенно аналогичны
соответствующим определениям, относящимся к функции (р. При переводе разд. 2
их пришлось опустить в связи со сделанными там изменениями (см.
примечание ца стр. 42). — Прим. перев,
48
С. Виногрйд
и использовать такие термины, как «перенос». В случае
циклических Групп мы будем «кодировать» и «декодировать»
элементы группы, испольауя обычное представление натуральных
чисел в позиционной системе счисления с основанием d.
Прежде чем описать схему (Вычисления, мц несколько
уклонимся в сторону с тем, чтобы показать, что если для
вычисления ф в циклической труппе порядка р1 используются р-значные
логические схемы, то тогда представление с основанием р обоих
аргументов и результата дает настолько малую зависимость
выходных линий от входных, насколько это возможно. Говоря
0 циклических группах порядка рп, мы будем рассматривать
Zp/i = {0, 1, ...,р — 1} как множество элементов вместе со
сложением по модулю.рп в качестве групповой операции. Если
мы используем представление с основанием р обоих слагаемых
и результата, то одна выходная линия зависит от п входов
каждого слагаемого, два выхода зависят по крайней мере от
п—1 входов каждого слагаемого я в общем случае k выходов
зависят по крайней мере от'гс — k+l входов каждого
слагаемого.
Следующее утверждение показывает минимальность этой
зависимости.
Утверждение. Пусть С есть р-значная логическая схема,
вычисляющая Zpn + Zpn mod рп\ тогда для каждого /г,
1 ■<&< просуществует не менее k выходов, которые зависят не
менее чем от п — k + 1 входов каждого класса.
Доказательство. Рассмотрим множество выходов
0* = {о/|3'- Pn~k^Zpt, такое, что Ау(/ • рп~к)ф Л/(О)}. Ясно,
что, поскольку в Zpn имеется рк — 1 элементов вида / • рп~к,
мощность Ok не меньше k. Мы покажем, что каждый выход
из Ok зависит не менее, чем от п — k + 1 входных линий
каждого класса, и тем самым докажем сформулированное выше
утверждение. Рассмотрим множество Qh =* {0, 1,2,..., pn~k+l—l}. Если
бы выход jQ$ е Ok зависел только от q < п — k + 1 входных
линий первого класса, то тогда нашлись бы два элемента а,
b 6Е Qk, такие, что g\ (а) и g\ (Ь) отличались бы только на тех
входных линиях, от которых Oj не зависит. Но, поскольку
t-pn-h^gp(a — 6), мы получаем противоречие лемме 2.
Подобные, же рассуждения справедливы и для второго
слагаемого.
Лемма 4. Для каждого г^Ъ существует d-значная
логическая схема из элементов, имеющих не более г входных линий,
О времени, требующемся для выполнения сложения 49
которая вычисляет Zdt + Zdtmodd\ где <= -~ r , за
время t=s+l (здесь [х] обозначает целую часть х).
Доказательство.- Мы докажем лемму индукцией по 5.
При доказательстве слагаемые так же, как и сумма,
представляются в позиционной системе счисления с основанием d.
В случае 5 = 0 мы можем представить любое число из
Zdt посредством 4г Цифр и, таким образом, мы можем
вычислить сумму за время т=1, используя логические элементы
с не бодее, чем г входами (фактически на каждую цифру
выхода требуется только один такой элемент). Более того, за
время t~ 1 мы можем для любых двух элементов Ь, с е Zdt
определить, выполняется ли b + c^df или нет, т. е. мы можем
также образовать и перенос. Заметим еще, что в этом случае
мы могли бы вычислить и 1 +Zdt + Zdt,mod d* с образованием
переноса за время т=1.
Предположим, что для s — m мы можем вычислить
Zat-^ Zdt mod d* я 1 +Zdt + Zdtmod d*9 а также образовать
переносы в обоих случаях за время т=т+1. Положим s = m+l.
Мы можем Построить желаемую схему из 2 г 2 — 1 схем,
каждая яз которых вычисляет a + Zd* + Zdt mod d* для s = m
(а = 0 или 1), Затратив на объединение выходов этих схем одну
единицу времена; таким образом, мы можем получить
результат за время т=т+1+1 =m4-2 = s + l.
Обозначим "J г^21 чеРез ''•■-Пользуясь представлением
с основанием d элементов из Zdt (для s = m+l), мы можем
считать, что совокупность цифр этого представления разбита
на |-^2j КУСК0В> каждый, из которых состоит из f цифр:
первый — из V младших цифр, второй — из цифр разрядов с весами
от d2t'~l дб dv, и т. д. Пусть С, С, ..., С \г-п —такие
[г + 1 Т L 2 J
-у- — 1 схем, что Су вычисляет Zdt' + Zdt> mod dv с
образованием переноса, если / четно, и С/ вычисляет 1 + Zd? +
-f Zdt> mod dr с образованием переноса, если j нечетно. На входы
схемы С/ поступает k-й кусок каждого из, слагаемых, где
k = 1^+1- Ясно, что схема C2k складывает (& + 1)-е куски,
как если бы никакого переноса „справа не приходило", в то
время как схема C2k-\ складывает (k+ 1)-е куски, как если бы
всегда „справа приходил" перенос.
50
С. Виноград
Пусть c°k обозначает перенос, образованный схемой С2й,
а с\ обозначает перенос, образованный схемой C2k-i- Ясно, что
со> cv cv •••» с/* с) однозначно определяют, имеем ли мы при
сложении (/ + 2)-х кусков (если мы хотим получить правильный
результат сложения по модулю dl) перенос «пришедший справа»
или нет. Таким образом, число входных линий, необходимое для
получения правильного результата, а также переноса, не
превосходит 2 у——I— 1 ^г, и, следовательно, требуется
дополнительно только одна единица времени. Поэтому время, требующееся
для вычисления Zdt + Zjmodd', а также для образования
переноса, равно т + 2. Видоизменяя доказательство требованием, что
Со вычисляет 1 + Zdt> + Zdt> mod df\ мы получаем, что как 1 + Zdt +
-f Zdt mod d\ так и перенос в этом случае тоже могут быть
вычислены за время т=т + 2. Схема доказательства леммы 4
основана на схеме, изложенной в [2]; она иллюстрируется на рис. 1.
/'
г
г
Рис. 1.
/ — первое слагаемое; 2 — второе слагаемое; 3 — перенос; 4 — результат.
Следующие два утверждения получаются как простые
следствия леммы 4.
Следствие 3. Для каждого г!>3 существует d-значная
логическая схема из элементов с не более, чем г входными
линиями, которая вычисляет Zdn + Zdnmoddn за время т=1 +
О времени, требующемся для выполнения сложения 51
Следствие 4. Для каждого г > 3 и каждого а е Zd«
существует d-значная логическая схема из элементов с не
более, чем г входными линиями, которая вычисляет a + Zan +
+ Zdnmoddn за время х
1+]"*тщ[-
Лемма 5. Для каждого г > 3 существует d-значная
логическая схема из элементов с не более, чем г входными
линиями, которая может вычислить Zpn + Zpn mod рп за время
logfr+r
2
т = 2 +
"1 logr^+j, —i— ]logd ря [ Г.
Доказательство. Пусть s=]logdPn[. Заметим, что
если а + Ь<рп, то a + b mod pn = a + b modd8, а если а + 6>/?п,
то a + b+ (ds — рп) modd8 = a + b modpn\ более того, a + 6>pw
тогда, и только тогда, когда а +b+ (ds — pn)^ds. Таким
образом, мы сначала конструируем два сумматора, один из
которых складывает а + bmodd8, другой складывает а + Ь +
+ (ds — pw) modd8. Согласно следствию 4, оба таких сумматора
MojyT вычислить соответствующие функции за время т = 1 +
Выбирая выход подходящего сумматора в
log
i-i ш
соответствии с тем, имеется ли перенос на выходе второго из
них, мы получаем a + b mod рп. Заметим, что выбор
подходящего выхода можно сделать за одну единицу времени, так как
r>3. Таким образом, полное время вычисления a + b mod рп
равно
т = 2 +
|08тщ[-2+]|08тШ
]logdp"t
Теорема 2. Пусть G — конечная абелева группа. Для
каждого г > 3 существует d-значная логическая схема из
элементов с не более, чем г входными линиями, которая
вычисляет ф: G X G -+G за время
т = 2 + | logrr+i 1
I 2
Щ
]log„a(G)[
Доказательство. Поскольку G — конечная абелева
группа, G может быть разложена в произведение вида
G = G\ X G2 X ... XGm, где каждое G* есть циклическая
группа, порядок которой равен степени простого. Таким образом
52
С. Виноград
мы можем построить т схем, каждая из которых вычисляет
фг-: GiXGi-+Gi и требует количество времени' ^-==2 +
+
logrr+ii 77Т 11о&*1 G* II Для вычисления этой функции.
12 J Ы L
зычислить свою
Так что вся схема, может вычислить свою функцию за время
т= тахт; = 2+ logrr+i1TTT]Iogda(G)[
(Идея доказательства здесь та же, что в [3].)
Сравнение теоремы. 2 е теоремой 1 показывает, что с ростом
г время, требующееся для вычисления ср: GXG-+G, для ко:
нечной абелевой группы приближается к нижней оценке. Более
точно, пусть Tact обозначает время, полученное в теореме 2,
a tmin обозначает нижнюю оценку, полученную в теореме 1;
тогда
1 ]log*a(G)[|
Tact = 2 +
,ogm|ij
~ 2 + 1(^+11—r]logda(G)[
~ 2 - logr^-, Щ +1 l0«r log,a (G)[ logj^, j r.
Итак, для достаточно больших г, таких, что bgr_MrM у ^ *
и logrr+n г « 1, мы получаем ract «* тт|П + 1.
5. ОБСУЖДЕНИЕ
В разд. 3 мы видели, что нижняя оценка времени,
требуемого для вычисления групповой операции, для конечной
группы G зависит от логарифма логарифма порядка некоторой
р-подгруппы' группы G. В случае, когда G — абелева группа
(и, в частности, если G есть Z^, где групповой операцией
является сложение по модулю |л), эта р-подгрупиа представляет
собой наибольшую циклическую подгруппу, порядок которой
есть степень простого. В разд. 4 мы видели, что к этой нижней
оценке можно приблизиться, если число входных.линий
логических элементов, используемых для построения схемы,
увеличивается.
Эти результаты зависят от конкретного определения
понятия «логическая схема С способна вычислить функцию ср»,
О времени, требующемся для выполнения сложения 53
В нашем определении мы потребовали, чтобы входы схемы
были разделены на классы и каждый класс соответствовал
одному аргументу вычисляемой функции. Это было сделано для
того, чтобы функция ф действительно вычислялась схемой, а
для этого входы должны нести информацию только об
аргументах, но не о способе их комбичирования для получения
результата. Читатель легко убедится в том, что если бы мы
заменили требование, наложенное на gj в определении 3,
требованием существования gff: I'cicilci ->Л7,то мы прлучили
бы эквивалентное определение.
Требование существования функции h: Y-+Oc эквивалентно
требованию существования h': Ос^2 Oe-lli+ у. Целью
требования 1 : 1 для h! было устранить возможность того, чтобы
выходы несли в точности ту же самую информацию, что и
входы, и чтобы функция W «действительно» выполняла
вычисление. Разумеется, возможны и другие определения понятия
вычисления, которые еще соответствуют нашим интуитавным
представлениям. В [4] описана схема сложения, в которой
требование, наложенное на h'y ослаблено, а именно взамен
потребовано, чтобы один и тот же код использовался как для
кодирования каждого из слагаемых, так и для кодирования
результата.
Другой чертой определения 3 является фиксированное
время т, через которое обследуется выход. Другой подход состоит
в том, чтобы рассматривать время «установления» схем,
которое, конечно, зависит от конкретных значений, принимаемых
аргументами, и затем считать среднее время «установления»
схемы временем вычисления (см. [5]). Предполагается, что
это среднее время имеет тот же самый порядок, что и
нижняя "оценка, однако доказать это предположение нам не
удалось.
Другое направление исследования состоит в рассмотрении
обоих параметров — и времени вычисления и числа логических
элементов, требующиеся для построения схемы (см. [1]). Этот
подход можно даже соединить с ослаблением допущения о том,
что входы несут всю информацию об аргументах в момент
времени т=0, разрешив подавать входы в схему
«последовательно».
Благодарности. Автор благодарен М. О. Рабину за
предложение задачи о времени вычисления сложения при
ограничении, что компоненты имеют г входов, а также за
постановку вопроса о том, может ли быть это время улучшено,
если не пользоваться позиционным представлением чисел.
64
€. Виноград
Необходимо также выразить благодарность К. К. Элготу за его
помощь в прояснении многих положений и Дж. Б. Райту за его
поучительные комментарии.
ЛИТЕРАТУРА
1. Офман Ю. П., Об алгоритмической сложности дискретных функций,
ДЛЯ, 145, № 1 (1962),48-51.
2. М а с S о г 1 е у О. L., High-speed arithmetic in binary computers, Proc.
IRE, 49, № 1 (1961), 67—91.
3. Garner H. L., The residue number system, IRE Trans., EC-8, № 2
(June 1959), 140—147.
4. Avi^ienis A., Signed-digit number representations for fast parallel
arithmetic, IRE Trans., EC-10, № 3 (Sept. 1961), 389—400.
5. Gilchrist В., Pomerene J. H., Wong S. Y., Fast carry logic for
digital computers, IRE Trans., EC-4, № 4 (Dec. 1955), 133—136.
6. Sklansky J., An evaluation of several two-summand binary adders, IRE
Trans., EC-9, № 2 (June 1960), 213—226.
О времени, требующемся
для выполнения умножения1
С. Виноград
Исследуется время, требующееся для выполнения умножения. Находится
нижняя оценка времени, требующегося для выполнения умножения, а также
для выполнения умножения по модулю N, и показывается, что к этим нижним
оценкам можно приблизиться. Затем находится нижняя оценка времени,
требующегося для вычисления старших цифр произведения I -~- I.
1. Введение
Целью данной статьи является исследование количества
времени, требующегося для перемножения двух целых чисел
с помощью логической схемы в случае, когда оба сомножителя
пробегают множество значений UN={0, 1, 2, ..., N—1}. Эта
задача рассматривалась Тоомом [1] для случая N=2n при
представлении множимого, множителя и произведения сигналами
в соответствии с представлением целых чисел в позиционной
системе счисления с основанием 2. В этих условиях Тоом
исследовал скорость роста обеих величин: и числа элементов, и
количества времени, требующегося для выполнения умножения,
при увеличении 2П. В данной статье мы продолжаем
исследование, начатое в [2], т. е. мы найдем нижнюю оценку времени,
требующегося для выполнения умножения при произвольном N
и произвольном представлении множимого, множителя и
произведения; при этом не обращается внимания на то, какое
число элементов необходимо для приближения к этой нижней
оценке.
Точная формулировка задачи дается в разд. 22); в разд. 3
мы получаем нижние оценки времени, требующегося для
выполнения полного сложения и для выполнения полного
умножения, и показываем, что к этим оценкам можно приблизиться.
Раздел 4 посвящен получению нижней оценки времени,
требующегося для выполнения умножения по модулю N, а
!)Winograd S., On the time required to perform multiplication,
J. ACM, 14, № 4 (1967), 793—802.
2) Перевод разд. 2 приведен в предыдущей статье автора (см. стр. 42—43
настоящего сборника и примечание на стр. 42). — Прим. перев.
56 С. Виноград
в разд. 5 мы описываем схему вычисления для умножения
по модулю Л/, которая требует времени-, приближающегося
к нижней оценке из разд. 4.; В разд. 6 мы получаем нижнюю
оценку времени, требующегося для нахождения старших цифр
произведения, т.е. для вычисления 4т-|, где [х] обозначает
целую часть х.
Многие из результатов данной хтатьи связаны с
результатами статьи [2], поэтому предполагается знакомство читателя
с [2],
3. Нижняя оценка для умножения
Цель данного р.аздела состоит в получении нижней оценки
времени, требующегося для выполнения умножения, т. е. для
вычисления функции ц>(х,у)=ху1 где х и у пробегают
множество чисел {1, 2, ..., N), а результат, разумеется, может
достигать ./V2. Прежде чем получить эту оценку для умножения,
мы получим оценку времени, требующегося для выполнения
сложения, т. е. для вычисления функции у'(х>у)=х+у, где х
и у пробегают множество {0, 1, 2, ..., N—1}, а результат1—
множество {0, 1, 2, ..., 2N — 2}.
Для изложения этих результатов нам понадобятся
определение и лемма (которая приводится без доказательства) из [2].
Пусть С — логическая схемя. Будем использовать Cj(s> t, т)
для обозначения /-й компоненты c(s-, f, т), т. е." состояния
выхода Oj в момент времени т, если в момент времени 0 схема
находилась в состоянии 5 и был приложен вход *'.
Определение 4. Говорят, что выходная линия Oj s-незави-
сима (seSc) от входной линии tk в момент времени т, если
для всех i'i, i*2 е/с, отличающихся только состоянием 4, имеет
место равенство Cj(s, iu т) —Cj(s, fe, т). Если выходная линия
не является s-независимой от линии /* в момент времени т, то
говорят, что она s-зависима от lk в момент времени т.
Лемма 1. Пусть С — логическая схема, каждый из
элементов которой имеет не более г (г > 1) входных линий. Для
всех линий Oj из С справедливо утверждение: если Oj So-зави-
сима от k входных линий в момент времени т, то T^]logrA[
(где ]х[ обозначает наименьшее целое, не меньшее х).
Лемма 2. Пусть С — логическая схема, вычисляющая q/
(см. выше). Пусть Ь, £е{0, 1, ..., N—1} (Ь > с) такие, что
g\(b) и gi(c) (gz(b) и g2(c)) отличаются только на тех
входах, от которых Oj не зависит. Тогда hj(t(b — с)) есть кон-
О" времени, требующемся для выполнения умножения 57
стантапри ]у^[<*<[-£-:
+ 1 (где hj (х) есть j-я компо-
с
нента h(x)y а [х]-^ целая часть х)
Доказательство. Мы докажем только половину
утверждения, ибо вторая половина доказывается аналогично.
По условию леммы для каждого jce{0, 1, ..., iV — 1}
имеем ^(6+^)=^(50,^1^)^2(^)),^=^(50, {gi(t), Ы*)), т) =
~tij(c+x). Следовательно; для каждого, х^ с м& получаем
hj(b — c+x)=hj(b+(x — с))—Aj.(£+(*_ c))^hj(x). В
частности, полагая #=/(&— с), где /> , с_ 1 , мы получаем
hj(t(b — с)) =hj((t+\) (b — с)). Это равенство выполняется
при * = ]yz7[> JT^Tl"^"1, "" [ 6~c ]у чт0 Д°казывает
лемму.
Для каждого целого пг мы определим Qrh как наименьшее
общее кратное чисел 1, 2, ..., т. Для каждого. целого п мы
определим у(п) как наименьшее т, такое, что Qm^ п (т. е.
Qn>-i<n<.Qm)1). .
Теорема 1. Пусть С есть d-значная логическая схема,
каждый из элементов которой имеет не более г входов, и
С вычисляет ф' за время т; тогда т^ log, 2 log^yl nr ).| | •
Доказательство. Пусть m = y( -тН ) и, следовательно,
Qm-i< ] х [ и ^Qm-xKN. Пусть выход о5 таков, что
кз(С1гп-\)ФAj(2Qm-i). Мы покажем, что Oj зависит не м^нее,
чем-от ]log<fm[ входных линий, которые определяют /с, ь и не
менее, чём от ]logdm[ входных л^ний, которые определяют
/с>2, и тем самым с помощью леммы 1 докажем теорему.
Допустим, что #j -зависит от q <]log<f m[ входных линий,
определяющих 1с, и тогда найдутся два числа 6, се {1,2, ..., т},
такие, чтр g\(b) и g\(c) отличаются только на тех входных
линиях, от которых Oj не зависит. Без ограничения
общности допустим, что b > с. Поскольку b — с < т, мы
находим, что Ь — с делит Qm-X и 2Qm-i; так что пусть Qm-i =
==*i • (Ь — с). Поскольку c<.Qm_i (с делит Qm-i), мы
получаем *i=~y?~r> ]у^с(» а П0СК0ЛЬКУ 20m-i <W— 1, мы
получаем 2tx gg , ~ [+ 1; следовательно, по лемме 2 hj(2Qm^) =
■=Aj(Qm-i)i т-е- имеем противоречие. Аналогичным образом
1) Из теории чисел известно, что у(п) ~ In я.— Прим. перев.
58
С. Виноград
мы можем доказать, что о;- зависит не менее, чем от
h°gdY( |у| )| входные линий, определяющих /с,2, и, таким
образом, доказать теорему.
Для того чтобы показать, что к этой нижней оценке можно
приблизиться, нам потребуется по-другому охарактеризовать
у(п). Как и в [2], мы положим а(п) = тах{рг'|рг* делит /г}. После
этого положим y'{ri) =mfn{a(JV) |Л^> п).
Лемма- 3. у(п) = у'{п).
Доказательство. в Пусть у(п) = т\ тогда, поскольку
Qm^=Qm-\ (Qm^n, в то время как Qm-\ < п), мы находим,
что т = /я для некоторого простого числа р. Далее, поскольку
Qm^IIP/^ гДе Рз пробегает все простые числа, не
превосходящие т, и <x/^[logp т], мы видим, что <x{Qm)—m\
следовательно, у'{п) <Ст—у(п).
Пусть N — такое число, что a{N) — y'(n). Мы можем написать
N = Ц p®L Поскольку a(JV)<I т, ни одно из р/ не превосходит т;
таким образом, мы можем принять, что N = Ц Ру/, где все р/
не больше, чем т. Более того, поскольку a{N)^mt мы
находим, что Py<[logP/m], и, таким ббразом, рЬ<^т. Пусть
р —показатель степени числа р Гв произведении Ц Р/71 (гАе
т = р'); если р = /, то а (АО = a (Qm) = m и утверждение верно.
Если же р</, то P/<[logp/(m—1)], и, следовательно, N делит
Qm-u и, таким образом, N^Qm-i<nt т. е. имеем противоречие.
Теорема 2. Для каждого г > 3 и для каждого d > 1
существует схема, которая вычисляет q/ за время
т<2 +
^[Г±1Щ]^МШ)[
Доказательство. Мы можем выполнить сложение х с у,
где х и у пробегают множество {0, 1, 2, ..., JV—1},
складывая х и у по модулю Qm, где m = y (2iV - 1). По теореме 2 из [2]
это можно сделать за время т = 2+ 1°£Гг+п jj-T]logdm [ •
Пусть m' = y (] у [), т. е. Qm' > ] у [ > и> следовательно,
О времени, требующемся для выполнения умножения 59
6- Qm>>2JV— 1. Однако m-y(2N- 1) = Y'(2W- l)<a(6Qm')<
<3a(Qm') = 3Y( 1-|*[), что доказывает теорему.
Теперь мы можем получить нижнюю оценку времени,
требующегося для вычисления ф(х, у) ~ху, где х и у пробегают
множество {1, 2, ..., N}.
Теорема 3. Пусть С есть d-значная логическая схема,
каждый из элементов которой имеет не более г входных линий,
и пусть С вычисляет <р(х,у) за время т; тогда
%>
]log,2],og,V(]™[)[[.
Доказательство. Ограничимся рассмотрением ф в
случае, когда х и у являются степенями 2. При этом схему,
вычисляющую ф, можно рассматривать как схему,
выполняющую сложение (показателей степени х и у), при котором
каждое слагаемое пробегает множество {0, 1, >.., [log2Af|}.
Применяя теорему 1, мы получаем утверждение теоремы.
Теорема 4. Для каждого г !> 3 и для каждого d > 1
существует схема, которая вычисляет ф за время
т<2+р08т_±.]1огЛ(]Ю[)[
Доказательство. Пусть Р^ = {рь Р2> .. •} — множество
всех простых чисел, не превосходящих N. Если п — мощность
PN, то мы можем представить каждое число х из {1, 2, ..., Л/}
л-кой (ось Я2> ..., an), где a* — степень pi в разложении х на
простые множители. В таком случае умножение сводится
к сложениям соответствующих показателей степени (которые
могут выполняться параллельно),и поэтому время, требующееся
для работы схемы, равно
T<maxJ2+1log^i^
-*+]4m^].og.3V(]^[)[
Код, использованный для приближения к нижней оценке
времени умножения, сам по себе не приводит к простому
получению младших или старших цифр произведения. В последующих
разделах мы получим нижние оценки времени, требующегося для
вычисления ху цо модули) N (младшие цифры произведения)
60
С. Виноград
и для вычисления -jgM (старшие цифры произведения). Эти
нижние оценки будут значительно больше времени,
требующегося для выполнения полного умножения. Это показывает, что
наша неспособность извлечь простым способом эти функции из
результата, полученного на вкходе «быстрой» схемы,
выполняющей умножение, не является особенностью^ выбранного кода,
а является свойством, присущим всем кодам, которые
позволяют выполнить полное умножение за время, близкое к нижней
оценке теоремы 3. .
4. Нижняя оценка для умножения по модулю N
В этом разделе мы получим нижнюю оценку времени, тре*
бующегося для выполнения умножения., по модулю N в случае,
когда оба- сомножителя-пробегают множество UN — {0, 1, ...
..., ./V—1}. Нижняя оценка получается путем ограничения
множества значений аргументов таким образом, что
получающаяся операция становится групповой, и последующего
применения теоремы 1 из [2].
Лемма 4. Пусть <р: Х{ X X2-+.Y и ф: X[XX'2->Y' -
конечные функции, такие, что существуют три функции fx: X[->XV
f2: Х2->Х2 и f3: Y' -i-i* F, удовлетворяющие условию: для всех
хх е Х[у х2 е Х2 имеет место равенство ф (fx {х{\ f2 (х2)) =
= /3(^(^1» х2))> тогда если С способна вычислить ср за время т,
то С способна также вычислить «ф за время т.-
Доказательство. Пусть s0, g\> §2 и Л такие, как это
требуется, согласно определению 3,- для того, чтобы С была
способна вычислять <р за время ъ. Положим s'0=s0i g'l?ssgl*fl,
g2 = g2;f2 и ^'==/г-/3; тогда для каждой пары *, е Х{, х2^Х2
мы имеем c(s'0, (#(*,), eJW> *) = c(s09 (^(^(^)), g2(f2(x2)))> т) =
■= A(<P(/i(*i)» /2(^2)))^=^(^(^, ^2))» что доказывает лемму.
Пользуясь леммой 4, мы видим, что вместо того, чтобы
рассматривать умножение по модулю N, при котором
множимое и множитель пробегают множество UN = {0, 1,2, ..., N— 1},
Мы можем рассматривать умножение по модулю ./V только в
множестве А^={хе Un\ наибольший общий.делитель (x,N)=*
= 1}. Используя в качестве /i, /2 и /з из леммы 4 отображения,
переводящие каждый элемент в себя, мы находим, что любая
нижняя оценка для выполнения умножения по модулю N в
множестве AN оказывается апостериори нижней оценкой для
умножения по модулю N, рассматриваемому в множестве 1/#.
О времени, требующемся для выполнения умножения 61
Преимущество рассмотрения умножения в множестве AN
состоит в том, что AN вместе е операцией умножения по модулю N
образует абелеву группу, и поэтому непосредственно приложимы
результаты из [2]. (Мы будем использовать символ AN не
только для обозначения множества, но и для обозначения
группы, описанной выше.) В соответствии с терминологией
статьи [2] мы обозначим через a{AN) наибольший порядок
циклической р-группы, содержащейся в ANy и как
непосредственное следствие теоремы 1 из [2] мы получим следующую теорему.
Теорема 5. Пусть С ебть d-значная логическая схема,
каждый из элементов которой имеет не более г входных линий, и
пусть С способна выполнить умножение по модулю- N за
время т; тогда т >]logr2]logd a(AN)[[.
Оставшаяся часть этого раздела посвящена тому, чтобы
найти разложение AN и, таким образом, получить более
простой способ вычисления значения a(AN).
Пользуясь китайской теоремой об остатках [3], мы
получаем лемму.
Лемма 5. Если N'« р"1 • р22 ... ра/, то AN = А <*, X
X А а0 X ... X А а •
Следующие две леммы показывают, как разлагается Ара.
Лемма 6. Пусть JV=2n {п > 2), тогда AN = Z2ft_2 X Z2,
где Zm обозначает циклическую группу из m элементов.
Доказательство. Для случая я = 2 (т. е. Aj = Z2) лемма
легко может быть проверена прямым .вычислением. Для того
чтобы доказать ее для произвольного я, мы сначала докажем
индукцией по п^2, что 52rt~"2 *= (2^ + 1) 271 + 1 для некоторого
целого /. Это верно для п = 2, поскольку 51 = 5 = 1 • 4 + 1.
Допустим, что мы уже знаем, что 52Гг~2 = (2/ +_1У2" +1; тогда
52»-i в 52"-2 . 52*"~2 з (2/ + I)2. 2п~2 • 2 • 2rt+1 + (2/ + 1) 2*+1 + 1 ==
= [2 ((2/ + 1)2 • 2ft"2 + /)+1] 2rt+1 + 1. Следовательно, подгруппа
группы ANf порожденная, элементом 5, имеет лорядок 2s для
некоторого s^.n — 2, так как 52Г1~"2== 1 mod2/z. Однако 52*~3 =
«(2//+1)2я"1 + 1-//-2й + 2я'"1 + 1 Ф lmod2", так что
подгруппа, порожденная элементом 5, имеет порядок 2"~2. Таким
образом, мы получили, что либо А2п~ Z2fl-u либо A2n=Z2n-2XZ2
(поскольку мы указали элемент из А2пу порядок которого
равен 2*~2). Мы покажем, что А%п Ф Z%n-u и, таким образом,
установим лемму.
62
С. Виноград
= Zr>n-\<
Допустим, что A2n — Z2n-\) поскольку порядок числа 5
равен 2П_2, мы приходим к выводу, что сравнение x2=5rriod2n
имеет решение, т. е. i2=5 + *«2n. Однако в таком случае,
поскольку правая часть нечетна, мы получаем х=2и+1. Делая
подстановку, мы имеем 4u2+4u+l=5 + t • 2П. Вычитая 1 из
обеих частей и деля на 4, мы получаем и2 + и= l+t • 2П_2;
однако правая часть этого равенства нечетна (п>-3), в то время
как левая четна. Это противоречит предположению, что А2П =
= Z2n-\ и, следовательно, А2П = Z2„-2 X Zr
Лемма 7. Пусть рФ2 простое и N—pn\ тогда AN =
Доказательство. Как и в лемме 6, мы скачала
установим индукцией по п, что {p + l)pn =(pt+l)pn+l. Для
п=1 мы получаем (р+1)1 = 1 • р+1. Допустим, что
утверждение верно для п\ тогда
о? + i)pM(p+i)p"^p=( (р'+о р"+ор ==
= 2 cp(Pt + if pnl = р • (pt + i)p p(p-1)n-y+1 +
/=0
+ Pn+l"'£ciP{l+tp)iPii~l)n~l+(pt + \)pn+l + L
/=2
что имеет желаемый вид, поскольку Ср делится на р при
1 = 2, 3, ..., р—1. Следовательно, порядок подгруппы группы
ANf порожденной элементом р+1, равен р71-1. Пусть а —
первообразный корень числа р, т. е. a8=lmodp тогда и только
тогда, когда s = k(p—1) для некоторого целого £. Поскольку
из a8=lmodpn вытекает, что as=lmodp, мы находим, что
порядок элемента а из AN равен k(p—1), а поскольку
порядок AN равен рп~1(р—1), мы находим, что k=pi для некото-
торого /. Но тогда порядок элемента a(p+l)modpn есть
наименьшее-общее кратное чисел р*(р—1) и pn_1, т. е. он равен
рп-Цр—\)у ЧТо доказывает лемму.
Результаты, изложенные в виде лемм 6 и 7, можно найти
также в другой форме в разд. 29—35 из [4].
Принимая во внимание леммы 5—7, мы определим для
каждого натурального N число P(iV) следующим образом:
(i) р(2)= 1, Э(4) = 2.
(И) Если #=2», п>3, то P(iV)=2*-2.
(iii) Если N = рп, р Ф 2 — простое число, то р(^) =
«=max(pn-1, а (р—1)), где #(р—1) определяется посредством
равенства а (p.— 1),= тах{<^'|<7 простое и q* делит р— 1}.
О времени, требующемся для выполнения умножения 63
(iv) p(N) = max{p(/?j) \р простое и pi делит NJ.
Из определения (J(iV) ясно, что а(Л^)=р(М), поэтому мы
можем переформулировать теорему 5 следующим образом.
Теорема 5'. Пусть С есть 4-значная логическая схема,
каждый из элементов которой имеет не более г входных линий,
и пусть С способна выполнить умножение по модулю N за
время т; тогда T>]logr2]logdP(N)[[.
5. Реализация умножения по модулю N
В этом разделе мы опишем схему вычисления для
умножения по модулю N, которая требует времени, близкого к
нижней оценке, установленной в разд. 4. После того как будет
описана общая схема, она будет модифицирована для частного
случая, когда для выполнения умножения по модулю,
являющемуся степенью 2, используются двоичные схемы.
Если N=Ni'N2i где N\ и N2 взаимно просты, то умножение
по модулро N может быть осуществлено путем выполнения
умножения по модулю N{ и умножения по модулю N2\ поэтому
мы будем рассматривать только тот случай, когда N есть
степень простого.
Поскольку разложение А2п несколько отличается от
разложения АрП, рф2, мы сначала будем предполагать, что рФ2,
а потом модифицируем нашу схему для случая р = 2.
Каждый х^ЦрП может быть записан в виде х=у*р\ где
у^АрП и O^jKn (мы пишем рп вместо 0). В таком случае
умножение может быть выполнено путем перемножения всех у
и сложения показателей степени у- рК Поскольку из равенства
х=у«р' вытекает, что у < pn~i (разумеется, если исключить рп,
для которого у равен 1=р°), мы должны при умножении
х=у'рэ на х'=у' * pi' обеспечить такую модификацию
результата умножения у на у', чтобы он стал меньше рп~1-1''. В
некоторых особых случаях/например при умножении по модулю,
являющемуся степенью 2, с использованием двоичных схем, это
нетрудно сделать.
В общем,случае может использоваться следующая
модификация. С каждым числом x~y»pi ассоциируются л+1 чисел
(*о, хи х2,..., хп-и j)> где **=»1, / = 0, 1, 2, ..., /-1, и
Х1 = уто&рп~1, i^j. Если х = у.р/, x' — у''р1', то с х" =*
= х • х' mod рп ассоциируется (п + 1)-ка (лс^, х", ..., х"_{9 /"),
где /" »/ + /', х" = 1 при / = 0, 1, .. ., /" — 1 и х" — xt • х\modрп"'\
i^J". В случае j + j'^n мы полагаем \"*=п и A:i = 1 при
64
С. Виноград
0</^п— 1. Поскольку Ai.s^n-^r 0<i<«-l, умножение
по модулю рп сводится к одновременному выполнению п + 1
групповой операции (т.е. / + /' и xt< х\ mod рп~1) и
„исправлению" х" на 1 при i<j + j\ ,
Как было показано в разд. 4, АрП~1рП~\ X Zp_x и для кале-
дого у&АрП величина ytnodp однозначно определяет его
Zp_rKoMnoHeHTy. Поскольку для (п+ 1)-ки (х0, хь ..., л:Л_ь Д
представляющей число ч х = у • р', имеют место соотношения
*/mod/? ==*/+!mod/?= ... = x„_imod р« ^.^), мы можем
представить любое чцело x = y'pi (п+1)-кой {j/0, z/b ..., уп-и j\
где ^ = ^ при i<jy y^i^Xn-i2) и у£«сть Zp^i-гкомпонента ^
при j^i<n — 1.
Схема умножения по модулю рпу которая базируется на
предыдущих рассуждениях, состоит из трех частей.
I. Сумматоры. Эта часть состоит из п + 1 сумматоров
Л°, Л1, ..., Л71-1, Лп. Сумматор А{ складывает компоненты у%
по модулю рп~{-~\ О <^ i < я — 1; Л71""1 складывает
компоненты yn_i по модулю р— 1; Лп складывает компоненты / по
модулю п+1.
II. Сравнение, Эта часть сострит из я схем сравнения
С0, С1, ..., О-1, где Ck проверяет, не превосходит ли сумма
компонент / числа к. (Поскольку /+/' > k. тогда и только тогда,
когда {п — ft)+/+/'>n, это можно сделать, проверяя наличие
переполнения в схеме, вычисляющей (/г — k) + / + /'.)
III. Коррекция. Эта часть устанавливает выход Ak в О,
если сумма компонент / превосходит k. В случае, когда сумма
компонент / превосходит п— 1, выход А71 устанавливается в п.
Схемы частей I и II могут начать работать одновременно.
Ясно, что наибольшее время ,для выподнения операции
требуется схеме Л°; таким образом (по теореме 2 из [2]),
части I и II могут выполнить .свои операции за время т=2 +
log гг+i if-pj ] Iog^P(pft)[| > и, поскольку для части III требу-
ь Ы L
*) И, таким образом, все я*, /<1^я—1, имеют одну и ту же Zp-f-
компоненту, если рассматривать Хг как элемент группы Ая_/ —Z n_i_lX
XZV-X. — Прим. tie pes.
2) Здесь правильнее было бы вместо xn-i поставить его
Zp_i-компоненту, т. е. элемент группы Zp_b соответствующий хп-\, ибо в дальнейшем
Zp~i рассматривается как группа по сложению. — Прим. перев.
О времени, требующемся для выполнения умножения 65
ется только одйа единица времени, множительное
устройство в целом выполнит .свою операцию за время т=3 +
^glL±1]J-r}logMPn)[
1 2 UTj
В случае умножения по модулю 2П, ввиду того что
А2п = Z2n-2 X Z2, мы можем воспользоваться числом —1 "для
порождения Z2 и числом 5 для порождения Z2rt-2. Таким
образом, если мы повторим предыдущий анализ, то получим
xn-i = 1 и найдем, что г данном случае хп~2 определяет
Z2-KoMnoHeHTy всех хи 0</<п — 2. Пользуясь этой
информацией, мы- можем каждое число х=у*2э представить п-кой
{Уо> У и ...» f/n-2» /Ь что является, как и в случае умножения
по модулю рпу р Ф 2, основой для построения множительного
устройства. Таким образом, нами доказана следующая теорема.
Теорема 6. Для каждого г>3 существует d-значная
логическая схема из элементов с не более, чем г входными
линиями, которая вычисляет х • у mod N за время
^- 3 +] logr г±1} j+j ] log,p(A0[[.
12' ы
В особом случае умножения по модулю 2Л с
использованием двоичных схем возможно дальнейшее упрощение схемы,
выполняющей умножение.. Пусть <=^-2п~3+/2, такое, что
5'=*#mod2n; тогда, поскольку 5 " = 1 mod~2rt~\ мы получаем
5*г=*ххпо<12п~1. Следовательно, если х—у*2э ассоциируется
с л-кой ((/о,уи ••«> Уп-2,/), то для каждого /<л<п-—3 имеет
место равенство у1+\*=Угто&2п~{~х, т. е. z/*+i можно получить
из уь обращая в 0 i+l старших цифр в двоичном
представлении у*. В доказательстве теоремы 2 из [2] представление чисел
с основанием 2 использовалось для того, чтобы приблизиться
к нижней оценке в случае сложения по модулю 2k с
использованием двоичных схем; следовательно, мы можем представить
х = у • 2* тройкой (уъ, у и /), где у\ есть 22-компонента у е Л2« *
8=5 Z2rt-2 X Z2, а у0 получается из Z2n-r компоненты у путем
принудительной установки в 0 / старших цифр в ее представлении
•с основанием 2. При этом схема, выполняющая умножение,
модифицируется таким образом, что часть I содержит только
три сумматора, а часть, вносящая исправление (часть III),
вместо всех выходрв сумматоров устанавливает в 0 только
некоторые из них.
С. Виноград
6. Нижняя оценка для -^н
В этом разделе мы получим нижнюю оценку времени,
требующегося для вычисления старших цифр произведения; иными
словами, если ^е[/^ и y^Uny то мы интересуемся оценкой
для ф (лс, у) = ~г- . Мы получим также нижнюю оценку
времени, требующегося для выполнения «сравнения» (теорема 8)
и для «определения переполнения» (теорема 9).
Теорема 7. Пусть ср: Un X UN-* UN определяется
посредством равенства ф(лг, #)— -4т- . Если С есть d-значная
логическая схема из элементов с не более, чем г входами,
вычисляющая ф за время т, ror^J logr 2jlogrfL^2JLL'
Доказательство. Пусть BN=*\ 1, 2, ..., [Л^Л- Для
у I = — + L- Тогда N <
^** Ух^М + х* fx<2N, в то время как (х—1)ух = хух — ух =
Пусть; выход о/ такой, что Л(0) и Л (Г) отличаются
состоянием о/ мы утверждаем, что о/ 50-зависим не менее, чем
от 2« J log^LA^2 J [входных линий, половина которых является
линиями, определяющими 1е% ь а половина — линиями,
определяющими /Л2> где so — то же, что в определении 3. Как только
это будет установлено, теорема будет следовать из леммы 1.
Допустим, что Oj зависит только от q линий,
определяющих /с, ь где <7<Jlogdl_N2J[. В этом случае существует не
менее двух чисел хи x2^BNy таких, что g\(x\) и g\(x2)
совпадают на q линиях, от которых зависит Oj. Без ограничения
общности допустим, что Х\>х2 и, следовательно, X\^BN — {1}.
В силу выбора у мы имеем —j^11 = 1, в то время как
1 *N* J ^0, и' слеД°вательно» сИ5о, (gi(*i)> g2{yXl))> т) Ф
фсз(з0, (gi(x2), g2(yXl))> т), что противоречит допущению о
том, что Oj зависит только от q линий, определяющих /с, ь
Теперь утверждение вытекает из симметрии.
Доказательства двух следующих теорем весьма похожи на
доказательства теорем 1 и 5 (а также теоремы 1 из [2]), и,
хотя они даже не касаются умножения, они здесь приводятся
О времени, требующемся для выполнения умножения 67
как дальнейшая иллюстрация избранного подхода к
получению нижней оценки времени, требующегося для вычисления
функции.
Теорема 8. Пусть q>: UN X £^v—*{0, 1} определяется
равенствами: (р(хуу) = 1, если х^-у, и у(х,у) = О, если х<у. Пусть
С есть d-значная логическая схема, каждый из элементов
которой имеет не более г входных линий, и пусть С вычисляет ф за
время т; тогда т > ]logr2]logdN[[.
Доказательство. Пусть Oj — выходная линия,
отличающая друг от друга два возможных выхода. Если бы Oj зависела
от q<]\ogdN[ входных линий, определяющих /0, ь то нашлись
бы хих2& UNy такие, что g[(x\) и £1(^2) совпадали бы на
этих q линиях. Пусть у *= т&х(хих2)\ тогда Cj(s0, (£i(*i)>
&{У))> т)« с,-(50,(6*1 (x2),g2(y)), т), в то время как <р(хиу)Ф
*£ф(*2, */); т. е. имеем противоречие. Из соображений
симметрии мы видим, что Oj зависит также не менее, чем от ]\ogdN[
входных линий, определяющих /с,г; в силу леммы 1 теорема
установлена.
Теорема 9. Пусть <р': UN X UN -► {0,1} определяется
равенствами: q/(*, у) = 1, если х + # > N, и ф'(л:, у) « 0, если
х + у < N. Пусть С есть d-значная логическая схема, каждый
из элементов которой имеет не более г входов, и пусть С
вычисляет ф' за время т; тогда т ^ ]logr2]logdA/r[[.
Доказательство. Теорема может быть доказана так же,
как теорема 8. Мы ее, однако, докажем с помощью замечания
о том, что x + y^-N тогда и только тогда, когда *>N — у.
Таким образом, если схема вычисляет ф', то она также может
вычислить ф из теоремы 8, и, следовательно (по лемме 4),
t>]logr2]log^{[.
В [2] было показано, что ф' может быть вычислена за время
т=*1+ |logrr+i_i77Tl^°Srf^f I ,таким образом, оценка теоре-
J Ь]Ы L
мы 9 является довольно точной. Пользуясь тем, что х^у тогда
и только тогда, когда х + (N — у) > N, мы видим, что оценка
теоремы 8 также близка к окончательной.
Автору не удалось построить схему вычисления для 4/"],
которая по времени была бы близка к нижней оценке
теоремы 7; наилучшее время, полученное автором, примерно вдвое
больше нижней оценки теоремы 7, поэтому, насколько точна
эта нижняя оценка, не установлено.
68
С. Виноград
7. Обсуждение
В разд. 4 мы получили нижнюю оценку времени,
требующегося для. выполнения умножения по модулю N, которая мало
отличается от нижней оценки времени, требующегося для
выполнения сложения по модулю N [2], а в разд. 5 мы показали,
что к этой нижней оценке можно приблизиться при увеличении
сложности используемых логических элементов. Код,
использованный для того, чтобы показать, что к нижней оценке разд. 4
можно приблизиться, совсем не такой, как код, использов.анный
в [2] для получения сходного результата. Более того, схема,
которая преобразует один код в другой, по-видимому, является
довольно сложной. Это приводит к предположению о том, что
если один и тот же код используется и для умножения по
модулю N и для сложения по модулю N, то хотя бы одна из этих
схем будет требовать для своей работы значительно больше
времени, чем это указывается нижней оценкой.
При получении нижних оценок для сложения и умножения
по модулю N мы встретились с числами a{N) и P(iV), которые
естественным образом приводят к системе счисления в
остаточных классах [5]. У разработчиков логических схем имеется опыт,
свидетельствующий о том, что использование «системы
остаточных классов» делает схемы сравнения и «определения
переполнения» весьма сложными и требующими довольно большого
времени для вычисления этих функций. В разд. 6 мы показали,
что как раз те функции, которые сложно реализовать при
использовании «системы остаточных классов», являются одними
из тех, что вызывают появление в своей нижней оценке N (или
№*), а не а(М) или P(N). Более того, результаты разд. 6
показывают, что если одновременно с выполнением сложения или
вычитания необходимо «определение переполнения» (а это
необходимо почти при всех применениях вычислительных машин),
то в целом никакого выигрыша времени от использования
«системы остаточных классов» не будет. Определение времени,
требующегося для вычисления этих функций в «системе
остаточных классов», до сих пор остается открытой проблемой:
Имеется подозрение, что причина неудачи подхода данной
статьи и статьи [2] к решению вышеупомянутых открытых
проблем (а также, возможно, к получению более точной оценки
для \Чг\$ поскольку мы не показали, что к полученной нижней
оценке можно приблизиться) лежит в ограничениях леммы I
(леммы 1 из [2]), которая является основной леммой избран*
ного подхода. Можно легко показать (сравнивая (яК) г~~х • пгЯ —
О времени, требующемся для выполнения умножения 69
число возможных деревьев-схем глубины q из элементов с г
входами, вычисляющих функции от п переменных, с ddtl—числом
d-значных функций от п переменных), что почти все функции
от п переменных требуют для своего вычисления времени,
которое, грубо говоря, растет, как n*logrd; однако у нас нет
критерия для того, чтобы по виду функции определить, требует ли
она этого, времени для своего вычисления. Можно также легко
проверить, что, пользуясь дизъюнктивной нормальной формой
функции, ее можно вычислить за время, не превосходящее
]nlogr<i[+]logrtt[. Самое большее, что нам дает лемма 1, это
критерий для определения того, что время, требующееся для
вычисления функции-от п переменных, не меньше, чем ]logrn[. По:
этому самое большее, что может дать подход данной статьи, это
то, что время, требующееся для вычисления функции ф: Х\ X
X Х2 -> У, должно превосходить величину т = ]logr(]logd Хх[+
+]logd Х<$)[, которая может не быть точной оценкой для многих
функций ф.
В разд. 3 мы показали, что при отсутствии ограничений
сложение и умножение могут быть выполнены, значительно
быстрее, чем сложение и умножение по модулю N. Это результат
того понимания термина «вычисление», которое использовалось
в данной статье. Задача схемы, вычисляющей функцию
<р:Х{ X Х2 —► У у состоит в разбиении X 4 X Х2 на эквивалентные
классы, определяемом следующим образом: (xv *2)~(*р*2)
тогда и только тогда, когда ф(д:1, #2) = ф(яр xQ, (См. также
обсуждение понимания термина «вычисление» в [6].) Таким
образом, две функции, алгебраическое описание которых весьма
похоже, могут, однако, привести к совершенно различным
разбиениям и, следовательно, могут требовать разного времени для
своего вычисления.
Благодарности. Автор хочет выразить свою благодарность
М. О. Рабину за предложение задачи о вычислении старших
цифр произведения. Необходимо также поблагодарить?. Е.
Миллера за многочисленные полезные обсуждения и за
внимательное прочтение рукописи.
ЛИТЕРАТУРА
1. То ом А. Л., О сложности схем из функциональных элементов,
реализующих умножение целых чисел, ДАН, 150, № 3 (1963)» 496—498.
2. Winograd S., On the time required to perform addition, /. ACM, 12,
№ 2 (1965), 277—285. (Русский перевод: см. настоящий сборник, стр. 41—54.)
3. р i с k s о n L. Е., Introduction to the theory of numbers, Dover
publications; New York, 1957.
4. Shanks D., Solved and unsolved problems in number theory, Spartan
books, Washington, 1962,
70
С. Виноград
5. Garner Н. L., The residue number system, IRE Trans,, EC-8, № 2 (1959),
140—147.
6. Winograd S., Cowan J. D., Reliable computation in the presence of
noise, MIT Press, Cambridge, Mass., 1963. (Русский перевод: Виноград С,
Коуэн Дж. Д., Надежные вычисления при наличии шумов, «Наука»,
М., 1968.)
ПРИЛОЖЕНИЕ
НЕКОТОРЫЕ АСИМПТОТИЧЕСКИЕ ФОРМУЛЫ ДЛЯ ВРЕМЕНИ
СЛОЖЕНИЯ И УМНОЖЕНИЯ
Лемму 4 из статьи С. Винограда «О времени, требующемся
для выполнения сложения» (см. стр. 48 настоящего сборника)
можно усилить (по крайней мере,начиная с некоторого s)
следующим образом.
Лемма. Для любого г!>2 существует d-значная логине-
екая схема из элементов с не более, чем г входами, которая
вычисляет Zdt + Zdt mod d\ где t = ~\rs, за времят<s + |/2s" + 4.
Эта лемма, доказательство которой почти дословно
совпадает с доказательством теоремы 1 из статьи «Об
асимптотической оценке времени сложения параллельного сумматора» (сб.
«Проблемы кибернетики», вып. 19, «Наука», At, 1967,
стр. 107—122), позволяет получить верхние оценки, которые
в большинстве случаев асимптотически совпадают с
соответствующими нижними оценками С. Винограда. Таким образом,
попарное объединение верхних и нижних оценок дает ряд
окончательных результатов. Эти результаты сформулированы ниже
в виде теорем.
Теорема I. Пусть т — минимальное время, за которое
d-значная логическая схема из элементов с не более, чем г
входами, способна вычислить ср: GxG->G, где G — абелева группа.
Пусть также a(G)->oo. Тогда при любых г>2 и d>2
т ~ logrloga(G).
Теорема Г. Пусть т — минимальное время, за которое
d-значная логическая схема из элементов с не более, чем г
входами, способна вычислить х + у mod N, где х, у е {0,1,..., N—1}.
Тогда при любых г>2 и d>2(« N-+00)
т ~ logrloga(#).
Теорема II. Пусть т — минимальное время, за которое
d-значная логическая схема из элементов с не более, чем г вхо-
О времени, требующемся для выполнения умножения 71
дами, способна вычислить х + у, где х, j/e{0,1, ..., N— 1}.
Тогда при любых г>2 и d>2(a N-+00)
t~logr log log Af.
Теорема III. Пусть х— минимальное время, за которое
d-значная логическая схема из элементов с не более, чем г
входами, способна вычислить ху, где х,#е{0,1,..., N—1}. Тогда
при любых г > 2 w d > 2 (и N -> оо)
т ~ logr log log log N.
Теорема IV. Пусть х — минимальное время, за которое
d-значная логическая схема из элементов с не более, чем г
входами, способна вычислить ху mod N,гдех, уе{0,1, ..., N— 1}.
Тогда при любых г>2 и d>2 {и N->oo)
т~ logrlogp(W).
Теорема V. Пусть х — минимальное время, за которое
d-значная логическая схема из элементов с не более, чем г
входами, способна вычислить хNy (признак переполнения), где
х,.у&{0, 1,...,N— 1}. Тогда при любых г > 2 и d>2 (ы N->oo)
х ~ logrlogN.
Следствие. Пусть х— минимальное время, за которое
d-значная логическая схема из элементов с не более, чем г
входами, способна вычислить
если х^у,
если х < у,
где х, j/g{0, 1, ..., N — 1}. Тогда при любых г > 2 и
d>2 {uN-+oo)
х ~ logr log N.
В заключение отметим, что число элементов в схемах, на
которых достигается асимптотически минимальное время
выполнения операций: GXG-+G, х+у mod N, х+у, [^тА и
ф<*.*)-{ 0;
_, если х^у,
Ф(*.!/)Н п есшх<у,
I О,
может быть сделанб жlogN (здесь \G\ = N).
В. М. Храпченко
Нижняя оценка числа
пороговых функций0
С. Яджима, Т. Ибараки
ВВЕДЕНИЕ
Пороговые функции —это класс булевых функций, которые
ранее изучались под разными названиями, такими, как
мажоритарные функции, линейно разделяемые функции и линейные
функции входов. Среди нерешенных задач в пороговой' логике
число пороговых функций особенно важно как мера сложности
схем из пороговых элементов. Точное число пороговых функций
известно лишь для пороговых функций самое большее
шести.переменных2). Оно получено при помощи методов линейного
программирования [1].
Пусть число пороговых функций не более, чем от п
переменных, есть N(n). Верхняя и нижняя оценки N(n) были получены
и затем улучшены многими авторами. Наилучшие известные
сейчас оценки таковы:
f"w<Af(«)<2|^.1< 2п\ (1)
где верхняя оценка была независимо получена несколькими
авторами, например в [2], а нижняя получена в [3].
В этой статье будет доказана новая нижняя оценка3)
N(n)>2{n{n~m+* (n>6) (2)
или
й*6о *2 ^ 2
ОПРЕДЕЛЕНИЯ
Пусть f(X)—булева функция, определенная на булевом
векторе Х=(Хи Х2, ..., хп), каждая компонента которого есть
1) Yajima S., Ibaraki Т., A lower bound of the number of
threshold functions, Trans. IEEE, EC-14, № 6 (1965), 926—929.
2) P. Минник сообщил авторам после просмотра рукописи, что пороговые
функции семи переменных были сосчитаны Р. О. Уайндером.
3) В статье М. Блоха и Я. Моравека (см. стр. 82--87 настоящего
сборника) устанавливается (наряду с другими результатами) аналогичная оценка
более эффективным способом. — Прим. ред%
Нижняя оценка числа пороговых функций 73
1 или 0, и пусть
Xf, = {X|/(X) = l},
Хр-{Х|/(Х)-0}. (3)
Определение. Говорят, что f(X) есть пороговая функция
(п. ф.) тогда и только тогда, когда существуют весовой вектор
W ±=(w\,W2, .... wn), каждая компонента которого есть
действительное число, и действительное число Г, называемое
порогом, такие, что
f WX^T для X^Xfu
[WX<T для X&Xfo, (4)
где WX — скалярное произведение.
Обратно, если W и Т заданы, то п. ф. определена
единственным образом. Обозначим эту функцию, через [W\ Т\:
Непосредственно из определения следует, что [W\ Т] и
\cW\cT\ где с — положительное действительное число,
выражают одну и ту же функцию, и, следовательно, такие величины,
как
min WX- max WX
X&Xfi X&Xfo
или
21о>д (5)
могут быть произвольными. Отсюда следует, что система
неравенств (4) эквивалентна с точки зрения совместности
некоторой системе вида
WX>T для Х€Е^>,
WX'KT-l для Xefr (6)
Пусть
(*,в1)-Г,
(IP, -Г)-А
I>-{K|X€5Xf}f
Yto~{Y\X€=Xfo}; (7)
тогда система неравенств (6) переписывается так:
f AY>0 для ГеГр,
I ЛУ<~1 для Y<=Yfo. (&)
В дальнейшем, однако, будет использоваться определение
весового вектора и порога при помощи неравенств (4), пока не
будет оговорено противное,
74
С. Яджима, Т. Ибараки
НИЖНЯЯ ОЦЕНКА N(n)
Здесь мы построим функции (п + I) переменных из
функций п переменных следующим методом:
h(X)-f(X)xn+xV g(X)Sn+i. (9)
Здесь X в h(X) имеет п + 1 компонент.
Функция h(X) есть п.ф. тогда и только тогда, когда f(X) и
g(X) суть п.ф., имеющие один и тот же весовой вектор. В силу
того что f{X) =J№; Tf] и ?(Х) = [W- ТХ функция Л(Х)
реализуется посредством [W, Tg — 77; Tg]. Обратно, в силу того что
h(X) = [wuW2y ..., wnt wn+u Г], функция f(X) реализуется
посредством [wu w2y ..., wn\ Т — wn+i] и g(X) — посредством
[wu w2, ..., wn\ T\.
Предположим, что другая функция h'(X) построена
аналогично:
h'(X) = f'(X)xn+lVg'(X)xn+l. (10)
В этом случае h(X) и W(X) различны тогда и только тогда,
когда
НХ)ФГ(Х) *™g{X)*g'{X). (11)
Следовательно, если число п. ф. не более, чем от п
переменных (п. ф. не более, чем от п переменных, будем обозначать
п-п. ф.), которые имеют одинаковый весовой вектор с данной
f{X)y есть sn(f)y то
N(n)
N(n+ 1)= S sa(ft), (12)
где fi пробегает все я-п. ф. При вычислении sn(f) если f(X)
«сть п.ф в точности / переменных, j<nt то f(X) можно
реализовать при помощи n-мерного весового вектора, добавив (п — /)
несущественных переменных.
В дальнейшем наши основные рассмотрения будут
посвящены получению нижних оценок для sn(f). Мы начнем со
следующей леммы.
Лемма 1. Существует весовой вектор W и порог Т,
которые реализуют данную п. ф., такие, что все скалярные
произведения WX принимают различные значения,
Д о к аз а те л ьст во. Согласно определению (4)
просуществует весовой вектор W и порог Г, которые реализуют данную
п. ф. Используя этот вектор Wt вычисляем все скалярные
произведения и, если есть скалярные произведения, имеющие
одинаковую величину, выбираем из них одну пару и изменяем одно
нз скалярных произведений пары, увеличивая Wj на е, где
Нижняя оценка числа пороговых функций 75
0< е < fi и 6 — минимальная разность величин всех скалярных
произведений и Т. После замены Wj на Wj + е значения величин
из упомянутой выше пары станут различными. Однако
невозможно, чтобы скалярные произведения, которые имеют уже
различные значения-, принимали одинаковые значения или чтобы
скалярные произведения, которые были меньше, чем 7,
превзошли 7, потому что 8 выбрано меньше, чем б. С этим новым
весовым вектором повторяем ту же процедуру; тогда в конечное
число шагов будет получен нужный весовой вектор.
Доказательство будет закончено, если обозначить полученный вектор
через W.
Лемма 2. Для всякой п-п. ф. f(X)
sn(f)>2n + 1, л = 0, 1,2, ... .
Доказательство. Для данной f(X) примем в качестве
весового вектор W, полученный по лемме 1, и будем менять
непрерывно порог от —оо до +оо. Тогда построим (2n + 1)
различных n-п. ф., и они по построению будут иметь те же самые
веса, что и f{X). При п = 0 всегда есть две константы 0 и 1.
Доказательство закончено.
Используя эту лемму и (12), мы можем получить
непосредственно следующую теорему.
Теорема 1.
N(n+ 1)>(2*+ l)N(n) (п>0).
Теорема 2.
JV(h)> 2^-^)+8 (л>6).
Доказательство. Согласно теореме 1,
N(n)> 2n~[N(n-l) =
^2n-l2n-2 26JV(6)>
>2«-l2«-2 _ 26223e
_n(n(rt-l)/2)+8
поскольку JV(6)>223 [1].
Это есть улучшение оценки Муроги [3], хотя наше
доказательство в отличие от его не конструктивно. Интересно
отметить, что N(n) лежит между 2п и 2ft2/2, если оценивать грубо.
Следующие результаты приводят к дальнейшему усилению
теоремы 1, хотя они существенно усиливают теорему 1 лишь
для малых п.
76 С. Яджима, Т. Ибараки
Лемма 3. Для всякой п-п.ф. f(x)
2((»+i)»+i {п четно)>
2^ + 2^2 (л нечетно)
(П>\2»-п-2 + \^„ , %П (">0).
Доказательство: Предположим, что весовой вектор* и
порог функции f(X), т. е. вектор Л, могут быть вычислены при
помощи системы линейных неравенств (8); Из теории линейных
неравенств известно, что множество решений (8) образует
выпуклое множество. Рассмотрим некоторую вершину этого
выпуклого множества. Это — экстремальные точки множества.
Тогда мы получим следующие (n^-l) линейно независимых
уравнений путем изменения подходящего множества (п + 1)
неравенств на равенства, поскольку число неизвестных равно
(п+ 1) [41, т. е.
ЛУ/ = 0, /=1, 2, ..., т,
AYk*=-\, £ = т + 1, т + 2, ..., л + 1, (13)
A-(W, -Т),
где векторы Yj и Yh линейно независимы.
Поэтому для достаточно малого действительного числа е и
всякого q векторы К/ из т векторов Yj могут быть сделаны
такими, чтобы удовлетворять соотношениям
A'Yf =е, е>0, /e = mp т2, ..., т^<={1, ..., т},
лтуе=о, /<£{/J,
ЛТ*=-1,
Л' = (№ +Д№,Г +ДГ), 04)
а Д№ и Д7* удовлетворяют неравенству
п
2lAw,l + |Ar|<-i. (15)
Тогда очевидно, что № + Д№; Г — чН выражает исходную
функцию /(X) и [W + AW\ Т + AT + е] представляет такую п. ф.,
которая равна 1 только для У/е исходного вектора Y5. Эти две
п. ф. имеют одинаковый весовой вектор. Справедливо равенство
m
2<Я»-2т,- (16)
«-о
где
Нижняя оценка числа пороговых функций 77
а приведенные выше рассуждения применимы к Yk следующим
образом:
Л'%=0,
Л"К*е= -1 -fe, kB = mum2, ..., m^e{m+l,m + 2, .. .,n+l}, (17)
Л'%=-1, k&{k&).
Следовательно, есть по крайней мере
>[(/г+1)/2] + 1
mm
т
г « »+1 m if 2[(n+,)/2,+l - 1 (я нечетно), 1
[2+2 -Н-Ч^»-. <,,,е™>} (18)
различных п. ф., которые могут иметь один и тот же весовой
вектор с f(X). Так как две функции: одна, полученная
посредством {/в } = {1, 2, .... /и}, и другая — посредством {ke} = 0 —
могут совпадать, то из общего вычитается 1.
Этот результат получен при помощи рассмотрения только
(п + 1) входных векторов Y$ и Yh. Следовательно, леммы 1 и 2
могут быть применены еще к оставшимся входным векторам.
Поэтому можно добавить (2П + 1) п. ф., полученных по лемме
2, вычтя число, функций, которые могут встретиться среди
функций, строящихся согласно (14) и (17). Число этих функций не
больше, чем (п + 1) + 1.
Следовательно, мы имеем
Sn(f)>
Г 2»»+1>«+1-1(п нечетно), И
(2П+1)-{(" + 1)+1} + |2- + 2^-1(„ четно)}]'
(19)
что заканчивает доказательство этой леммы.
Лемма 4. Пусть f(X) есть i-n. ф., тогда
Sn{f)>{SiQ)-\){N{n — i)-\)+ 1 (n>i>0).
Доказательство. Пусть структура функции f(X) =*
= /(*ь*2, ... f Xi) такова:
[wu w2, ..., wrt Tf]. (20)
Построим новую функцию
е(Х) = е{хих2 ..., Xi)=z[wuw2> :.., wt; Те] (21)
варьированием порога f(X)t где
i i
Tf = min 2 WtX] и Te= min 2 ДО/*/.
Эти две функции имеют одинаковый весовой вектор.
Предположим, что этот весовой вектор определен так, чтобы удовлетво-
78
С. Яджима, Т. Ибараки
рять лемме 1. Предположим далее, что минимальная разность
скалярных произведений WX есть у (у>0)-
Теперь реализуем (п — /)-п. ф.
t{X) = t(xi+b xt+2, ..., *fi)-[«>i+b Wi+«. ...» u>n> Tt] (22)
с весовым вектором и порогом, такими, что
n—i n—i
У|а>1+/К-5к ^= mfn У ш,+/**+/> (23)
используя свойство (5).
Затем построим другую /i-п. ф. следующим образом:
d(x) = [wu w2 «v, r, + rj-
-*(*ь ** .... **)'(**+i, ^+2,..., xn)\/e'(xu ^2,..., *,), (24)
где e'(X)—та же п. ф., что и е(Х), за исключением того, что
среди входных векторов Х&Хе\ входной вектор,
удовлетворяющий равенству
имеет выход 0. Эта d(X) может иметь тот же весовой вектор,
что и f(X), потому что функция
f(X)-[wu »2, .... и>»; ?>-|] (25)
получена при помощи (20) и ограничения (23) в
предположениях (UI). Кроме того, легко показать, исходя из (24), что если
брать в качестве е(Х) и ((X) различные пары функций,
отличных от константы 0, то получающиеся d(X) все различны. Так
как число различных е(Х), за исключением 0, есть ($*(/) — 1)
и число различных (n—t)-n. ф., кроме 0, есть (N(n — i) — l),
утверждение этой леммы доказано. Последняя единица
добавляется для того, чтобы учесть еще и константу d(X) = 0.
Лемма 5. Пусть f(x) есть п. ф., состоящая только из одной
положительной конъюнкции
f (X) = xklXk2 ... xk. (п > i > 1),
или константа 0 или 1. Пусть число различных положительных
i-п.ф. есть P(i). Тогда
М/) -*('")•
Нижняя оценка числа пороговых функций
79
Доказательство. Если некоторую заданную
положительную /-п. ф. р{Х). реализовать с положительными весами
W = {wkx> wk%>...% Wkt), WkjX), /=1, 2, .,., /,
то
К?Л<]
выражает f(X). Кроме того, п. ф. реализуется с
положительными весами тогда и только тогда, когда она есть
положительная п.ф.
Эта Лемма справедлива и в слегка измененном виде, когда
в конъюнкцию входят либо несколько переменных с
отрицаниями, либо сама функция берется с отрицанием. Обозначим
класс функций такого типа через R. Число n-п. ф. в R есть
(2.2^ (1+1),
\2п (/=1),
так как все функции в R суть п. ф. Случай i = 1 рассмотрен
отдельно, потому что отрицание переменной и функции дают одну
и ту же функцию.
Суммируя полученные результаты и введя обозначения:
T(i)—число п.ф. в точности от i переменных,
| г"'*'""*' « нечетно),
получим следующую теорему.
Теорема 3.
N(n+l)>t{cllT(i)-rn{i)}{(U(i)--\)(N(n-i)-l)+l} +
+ £r„(0{(/>W-l)(JV(n-/)-0+1} (п>0).
Доказательство.
N(n)
№+1Н2м//)>
>%CnT{l){(st{f)-l)(N(n-1)-1) + 1) (по лемме 4). (*)
80
С. Яджимй, Т. Ибараки
Теперь рассмотрим отдельно функции f(X)^R и f(X)^Rt
тогда
(*)= 2 |-с£Г(0-г*(0}(5,(f)- 1)(ЛГ(л-0-D+D +
+ S гл<0{(«, (П - 1) (АА (л - 0 - 1) + 1} >
> 2 {с£г(/) - гл(*)} {(¢/ (0 - 1)(ЛГ (л - /) - 1) + 1} +
п
+ Згя(0{(Р(0-1)(Л^(л-0-D+1) (по леммам 3 и 5).
*-0
Теорема доказана.
Если мы хотим вычислить N(n), используя эту теорему, то
необходимо получить нижние оценки для Т(1) иР{1), Они
получаются следующим образом:
i-\
T{i)>N{i)-^C\T(j),
/-о
Р (*)> U(/)- 2 /-,(/) W + 2 /-,(/)/2^.
I /-0 Г /-о
(28)
Вторая половина (28) рассмотрена отдельно, так как все
функции в R всегда получаются уже описанным методом.
Таблица 1
Нижняя оценка N(n)
п
1
2
3
4
5
6
N (п>
4
14
104
1882
94 572
15 028 134
Нижняя оценка N {п)
4
14
104
1690
51692
2 684 646
В табл. 1 приведены нижние оценки N(n) до п = 6, исходя
из Л/(0) = Р(0) = г0(0) = 2, полученные с использованием
теоремы 3 и (28). Точные значения }Цп) взяты из работы [1]%
Нижняя оценка числа пороговых функций
81
Л ИТЕРАТУРА
1. Muroga S., Toda 1., Takasu S., Theory of majoritv decision
elements, J. Franklin Inst., 271 (May 1961), 376—418; J. Inst. Elect. Commun.
Engrs Japan (October — December 1960).
2. Winder R. 0., Single stage threshold logic, Switching circuit theory and
logical design, AIEE Special Publ., S-134 (October 1960), 321—332.
3. M u г о g a §., Lower bounds of the number of threshold functions and a
maximum weight, Trans. IEEE, EC-14 (April 1965), 136—148 (AIEE 3-rd
Annual Symp. on Switching Circuit Theory and Logical Design, Chicago,
1962).
4. С h a r n e s А., С о о p e r W. W., An introduction to linear programming,
N. Y., Wiley, 1960.
Оценка числа пороговых функций')
М. Блох, #. Моравек
ВВЕДЕНИЕ
Пороговый элемент есть схема с п входами Х\, лг2, ..., хп и
одним выходом у (рис. 1), поведение которой может быть
описано следующими соотношениями:
где
y = F(xu лг2, ..., хп),
#«=1, если S = IJjWiXi^t,
п
у = 0, если S = 2 wixi < t-
(l)
<-i
Переменные х* могут принимать значение 0 или 12), а
параметры Wi и / суть действительные числа; до* называются <?е-
саж^ at — порогом. Можно изобразить пороговый элемент
следующим образом (рис. 2).
*/
д*
*л
F
Рис. 1.
Рис. 2.
Будем рассматривать выход у как булеву функцию входов я*.
Назовем пороговыми функциями булевы, функции, которые
реализуемы пороговым элементом. Необходимым и достаточным
условием того, чтобы булева функция была пороговой, является
1) Bloch М., Moravek Ja., Bounds of the number of threshold
functions, Information Processing Machines, Prague, № 13 (1967), 67—73.
2) В определении порогового элемента можно предположить вообще, что
xi принимает два произвольно выбранных значения. Ясно, что этот выбор
не играет роли.
Оценка числа пороговых функций
83
существование чисел w{ и f, таких, что соотношения (1)
справедливы. Веса Wi и порог t в соотношениях (1) определяют
гиперплоскость в м-мерном евклидовом пространстве, которая
делит множество вершин я-мерного единичного куба на две
части. Вершинам, расположенным в одной части, приписывается
значение у = 1, а вершинам, лежащим в другой, — значение
0-0').
Структура пороговых функций еще недостаточно хорошо
известна. С этой задачей связан вопрос о числе пороговых
функций. Задача о числе пороговых функций возникает в
теоретических вопросах синтеза схем из пороговых элементов (см.,
например, [1, 2, 5]).
Верхняя оценка числа порогрвых функций п переменных
содержится в статьях Камерона [2], Нечипорука [5] и Уайнде-
ра [I]2). Наилучшая нижняя оценка, известная авторам,
принадлежит Муроге [3], хотя его результат справедлив для класса
более узкого, чем самодвойственные пороговые функции. В
нашей статье дается лучшая нижняя оценка, полученная
построением некоторого класса пороговых функций8).
Всякий весовой вектор w «* (w\, а>2» • • •, и>п) определяет
квазиупорядочение всех входных векторов х в соответствии со
значением S. В нашей статье дается оценка числа различных
упорядочений такого таща.
На некоторое возможное расширение результатов этой статьи
указано в заключении.
1. Пусть через Еп обозначено /i-мерное евклидово
пространство, МсЕп — конечное подмножество, содержащее т
различных элементов. Пусть w • х = t — уравнение гиперплоскости в
Еп, причем
Q+ = {x|w.x>/}
есть соответствующее положительное подпространство,
Q-={x|w.x<*}
есть соответствующее отрицательное подпространство.
Введем обозначения
1) Вот почему пороговые функции называются иногда линейно
разделимыми функциями.
2) Верхние оценки справедливы для более общих объектов, ч*ем пороге*
вые функции. По этому поводу см., например, работу Уайндера [1] или
теорему 1 настоящей работы.
3) После того как рукопись была отослана, авторы узнали о работе [6],
которая содержит ту же самую асимптотическую нижнюю оценку, что и
теорема 1.
84 Л1 Влох, Я. Моравек
Упорядоченную пару (М+, М~) назовем линейным
разбиением множества М. Из статьи Уайндера [1] немедленно следует
теорема.
Теорема 1. Если т>3я +2, м>2, то число всех
линейных разбиений меньше, чем тпХ).
2. Обозначим через В„ множество всех булевых векторов
размерности п и через N{n) число пороговых функций п
переменных.
Теорема 2. Если п ^>2, то
0,5(/2- I)2 < log2A^(Az)< лг2 2).
Доказательство, а) Верхняя оценка, следует из
теоремы 1 и из того факта, что N(2) = 14, N(3) = 104/[4].
Ъ) Нижняя оценка. Для каждого п мы можем построить
некоторый класс Рп, содержащий N(n) пороговых функций,
зависящих от п переменных (N(n) будет определено в
нижеприведенном доказательстве). Мы положим / = 1 в выражении (1).
Тогда класс Рп определится как множество я-мерных векторов
»%i={w(U) 1/=1,2,... ,#(*)}.
Для п = 1 положим w(l, 1) = 1, w(2, 1) == — 1
(соответствующие функции суть Х\ и константа 0),
Предположим, что класс Рп построен и всякий вектор w(/,n)
из Wn удовлетворяет следующим условиям.
Если
X! ф х2, х, е= В„, х2 €= ВПУ
то
w (/, п) • X! Ф w (/, п) • х2 (2)
(для п — 1 соотношения (2) справедливы).
Далее 2П чисел r(i,/t,x) = 1 — w(i,n)*x могут бы^ь
упорядочены по величине следующим образом:
r{(i, n)<r2{i, п)< ... </yi(/, п).
Положим
rQ{i, я) = - оо, r2n+l = + оо,
тогда
r0{i, n)<r{(it п)< ... </yi+1(/, п). (3)
х) Уайндер формулирует следующую лемму: если m гиперплоскостей
проходят через начало координат (m-fl)-мерного евклидова пространства, то
п
пространство делится самое большее на 2 2 Cm-i областей.
j-o
2) Нижняя оценка в [3] есть 0,33048 /г2.
Оценка числа пороговых функций 85
Теперь мы можем выбрать числа p(if n, /), /-1, 2, ..., 2^+1,
так, что
ri-\{U п)<р{1, я,/)<**(', я) (4)
и
р (/, п, I) ф гг (/, п) - гг (/, л), (5)
если
1</'<2"+1, 1</"<2Л+1.
Множество Т^пл.\ будет построено следующим образом: ^n+i
содержит все (ai+ 1)-мерные векторы вида
(w(*, п), р(/, /г, 0).
Число векторов множества 7t°n+l есть
ЛГ(Аг + 1) = (2Л+1)ЛГ(п). (6)
Пусть Рп-н — соответствующий класс пороговых функций от
{п + 1) переменных. Из (4) следует, что функции класса Рп-и
попарно различны. Условие (2) необходимо для того, чтобы
индуктивное^ доказательство следовало из (5). Соотношение (6)
вместе с W(l) = 2 дает нижнюю оценку.
3. Каждому вектору weEn будет приписано отношениеква-
зйупорядочения l) ^C(w) множества Вп
{X! < (w) х2} ФФ {w . х{ < w . х2}, (7)
если
Xi, X2 е Вп.
Если вектор w удовлетворяет (2), то, согласно (7),
упорядочение < (w) множества Вп определено так:
{х{ < (w) х2} 4Ф {w • хх < w • х2}, (8)
если
Хь х2 е Вп.
Пусть через М(п) обозначено число всех квазиупорядочений (7),
Теорема 3.
a) N(n)<{2" + 1)М(п).
b) log2N(n)<Z.\og2M(n)2).
1) Квазйупорядочение множества А есть бинарное отношение R,
удовлетворяющее следующим условиям: а) для каждой пары элементов а, Ь е А
справедливо либо uRb, либо bRa; Ъ) если справедливы" aRb и bRc, то
справедливо aRc для любых а, Ь, с&А; с) для всякого элемента аеЛ
справедливо aRa.
2) Символ ^ означает асимптотическое неравенство.. Если Ьп>0, то
выражения ап ^ Ьп и lim sup (an/bn) < 1 эквивалентны.
86
М. Блох, Я. Моравек
Доказательство, а) Всякая пороговая функция (1)
определена посредством некоторого квазиупорядочения (7) и
посредством сечения порогом L Очевидно, что максимальное
число различных сечений есть 2п + 1.
Утверждение Ь) следует из а) и теоремы 1.
Теорема 4. Если п > 2, то
0,5 log2 3 (п — 1)2 < log2 М (п) < log2 Зл2.
Доказательство. Пусть Тп с: Еп — множество всех
я-мерных векторов, координаты которых принимают значения
1, 0 или —1. Число векторов в Тп есть Зп.
a) Верхняя оценка. Если v — вектор, определенный
квазиупорядочением (7), то гиперплоскость v • х = 0 в Еп определяет
линейное разбиение множества Тп. Различным
квазиупорядочениям (7) соответствуют различные линейные разбиения
множества Тп. Верхняя оценка тогда следует из теоремы 1.
b) Нижняя оценка. Множество всех векторов v е Еп,
определенное упорядочением (8), является открытым. Поэтому
вектор v всегда может быть выбран так, что
v-Xi = v.x2 для Xi=£x2,XbX2eTn. (9)
Построим для каждого п некоторое множество Un,
содержащее М(п) различных упорядочений (8). Множество Un будет
определено через множество я-мерных векторов Vn в смысле
отношения (8)
V„={v(i\/0ji'=l, 2, ..., М(п)). (10)
Для п = 1 положим v(l, 1) = l,v(2, 1) = —1, т. е. М{\) = 2.
Предположим, что мы уже построили пару множеств (Un, Vn),
и введем обозначения
s(х, /, п) = V(/, п)• X, ХЕ Тп.
Мы можем предположить, что (8) выполнено, и упорядочить
числа s(x, i,n) по их величине
sx{i, n)<s2(iy п)< ... <s3n(i, п).
Положим
s0(i, л)- - оо, 53«+1(/, л)= + оо.
Тогда справедливы отношения
50(/, nXs^i, п)< ... <5зЛ+1(/, п). (11)
Оценка числа пороговых функций
67
Построим последовательность действительных чисел t(i\ n, j),
где j в 0, 1, ..., Зп, так что
Sj (/, п) < t (f, л, /) < si+i (/, n). (12)
Пусть Vn+1 содержит все (п + 1)-мерные векторы вида
(v(/,n), /(/,/1,/)),
т. е.
М(п+ 1) » (3* + \)М(п) (13)
векторов. Соотношения (10) и (13) дают нижнюю оценку.
ЗАКЛЮЧЕНИЕ
Покажем, что характер полученных результатов не зависит
полностью от двузначности логики. Рассмотрим класс функций
f(x) = f(x\,X2 ..., хп), зависящих от п р-значных переменных
хи х2, ..., хп (лгг = 0, 1, ..., р—1); функции же принимают
только значения 0 и 1. Функцию f будем называть р-значной
пороговой функцией, если существует гиперплоскость W • х = t,
такая, что
f(х)= 1, если>у«х>/, ПА.
f(x) = 0, если wx< t. <14>
Обозначим через N(p,ri) число всех р-значных пороговых
функций (14), зависящих от п переменных.
Определим квазиупорядочение ^(w) множества всех р-знач-
ных векторов х — (х\, х2, ..., хп) по вектору wgE„
следующим образом:
{xj <(w)x2} 4$ {w • X! < w • x2}. (15)
Пусть M(p,n) —число всех квазиупорядочений (15). Используя
методы доказательства теорем 1—4, получим следующую
теорему.
Теорема 5. Если р — константа, п -> со, то
a) log2iV(p, n)^log2M (р, п\
b) 0,5 fog2 р-п2^. log2 N (р, п) ^ log2 Р • п2,
c) 0,51og2(2p~l).rt2^:iog2M(p, n)^log2N(2p-l, п)^
^log2(2p-1)-^).
1) Фактически во всех случаях можно заменить асимптотические
неравенства некоторыми точными неравенствами. Однако точное асимптотическое
поведение логарифмов исследуемых функций до сих пор еще не, найдено, так
что, по мнению авторов, затраченные усилия не слишком полезны.
88
М. Блох, Я. Моравек
Л ИТЕРАТУРА
1. Winder R. О., Bounds of threshold date realizability, Trans. IEEE,
EC-12, №5 (1963).
2. С a m e г о n S. H., An estimate of the complexity requisite in a
universal decision network, Wright Air Development Division Rept 60—600, Aug.
1960, 197-212.
3. Muroga S., Lower bounds of the number of threshold functions, and a
maximum weight, Trans. IEEE, EC-14, № 2 (1965).
4. W i n d e r R. 0., Trans. IEEE, EC-14, № 3 (1965).
5. Нечипорук Э. И., О синтезе схем из пороговых элементов, сб.
Проблемы кибернетики, вып. 11, Физматгиз, М., 1964.
6 Y a j i m a S% I b a r a k i Т., A lower bound of the number of treshold
functions, Trans. IEEE, EC-14, № 6 (1965). (Русский перевод: см. стр. 72—81
настоящего сборника.)
Алгебра пар
и ее применение к теории автоматов1)
Дж. Хартманис, Р. Стирнз
1. ВВЕДЕНИЕ
В этой, статье мы определяем алгебру пар как абстрактную
математическую систему и излагаем ее формальные свойства.
У алгебры пар потенциально широкая область приложений, и
особенно она пригодна для изучения природы функциональных
отображений. В этом исследовании мы применяем алгебру пар
к структурным проблемам з теории автоматов (или последова-
тёльностных машин).
В, разд. 2 мы определяем алгебру пар и формулируем
некоторые ее свойства. Абстрактный подход выбран в целях
достижения единства и сжатости описания, По мере развертывания
изложения, когда будут обрисовываться применения множества
различных алгебр пар, читатель сможет оценить значение
этого подхода и единую основу всех результатов. В перрон
части разд. 3 мы даем основные определения разложения
машин и суммируем результаты, полученные при анализе пар
разбиений [3, 5, 8]. В дополнение к некоторым результатам,
которые будут необходимы в дальнейшем, мы надеемся установить
родство между новыми и старыми результатами,
устанавливаемое посредством метода алгебры пар. В последней части разд. 3
мы определяем системы множеств (set systems) и некоторые
алгебры пар, образуемые системами множеств, которые исполь*
зуются при изучении структуры машин.
Системы множеств отличаются от разбиений тем, что они
могут иметь пересекающиеся блоки (или подмножества). Это
обобщение дает систематический метод расширения машины при
введений избыточных состояний (расщепления состояний) с
целью получить разложение или другие желаемые реализации,
которые не могут быть обнаружены при разбиении в алгебре
пар. Последний раздел показывает, что все результаты,
полученные посредством системы множеств, в равной степени
применимы к не полностью определенном машинам (т. е. к машинам
с условием „don't cafe").
!) Hartmanis J., Stearns R. EM Pair algebra and its application to
automata theory, Information and Control, 7 (1964), 485—507.
90
Дж. Хартманис, Р. Стирнз
2. АЛГЕБРА ПАР
Задача данного раздела состоит в том, чтобы раз и навсегда
установить математические основы, которые были бы
применимы к множеству отдельных ситуаций. Когда в последнем
разделе будут даны разные интерпретации алгебры пар,
абстрактные теоремы данного раздела приведут к практическим
результатам, не требующим дальнейшего доказательства. Таким
образом, первоначальный абстрактный подход оправдывается
впоследствии и вносит единые принципы в область различных
результатов.
Наши исходные определения и результаты даются в терминах
конечных структур, хотя все эти результаты легко
распространяются на бесконечные полные структуры, которые
удовлетворяют условию цепей. Теоретико-структурные операции взятия
наибольшей нижней грани {н. н. г.) и наименьшей верхней
грани (н. в. г.) обозначаются через- «•» и « + » соответственно, а
нулевой и единичный элементы — через «О» и «/».
Определение 1. Пусть L\ <и £2—конечные структуры. Тогда
подмножество Д прямого произведения L\ X L2 является
алгеброй пар на L\ XL2 тогда и только тогда, когда выполнены два
следующих постулата:
Рь Если (хиух) и (х2,у2) принадлежат Д, то {xx*x2i У\*Уг)
и (х\ + Хг, у\ + у2) принадлежат Д.
Р2. Для каждого х из L\ и у из L2 имеем, что (ху I) и (О, у)
принадлежат Д.
Таким образом, алгебра пар — это бинарное отношение на
L[ X L2, которое замкнуто относительно покомпонентных
операций Pi и содержит все элементы, указанные в Р2.
Читатель, знакомый с работами [5, 8], вспомнит, что
множество пар разбиений на полностью определенной последователь-
ностной машине М образует алгебру пар, для которой
структуры Lx и L2 обе совпадают со структурой разбиений на
множестве состояний М. Читатель должен также иметь в виду, что
множество / — S пар, множество S — 0 пар и множество / — О
пар также являются алгебрами пар.
Лемма 1. Если Д — алгебра пар на Li X £? и (х,у)
принадлежит Д, то х' < х и у < у' влечет за собой, что (х\ у),
(ху у') и (х\ у') принадлежат Д.
Доказательство. Согласно Рг, имеем (*',/) е Д.
Согласно Рь из того, что (*',/) и (л:, у) принадлежат Д, следует,
что
(х' • х, I • у) - (х\ у) €= Д.
Алгебра пар и ее применение к теории автоматов 91
Другие два случая разбираются аналогично.
Таким образом, если некоторая пара лежит в алгебре пар Л
на L\ X £2, то можно получить другую пару, заменяя первую
компоненту на меньший элемент и (или) вторую компоненту на
больший элемент. Следующее определение характеризует
наибольшую из возможных первых компонент пар в Д и
наименьшую из возможных вторых компонент.
Определение 2. Пусть Д есть алгебра пар на L\XL2. Для
xeLi мы определим
m(x) =Tl{yi\(x9yi) е=Д}.
Для y^L2 определим
Af (0)-2 {**!(*!. 0)€=Д}.
Определение 3. Для (дс, у) и (*', у') из L, х L2 определим
(*,*/)<(*', У')
тогда и только тогда, когда
х < х' в L\ и у < у' в L2.
Определение 4. Элемент (ху у) в алгебре пар А называется
Mm парой тогда и только тогда, когда
у = т(х) и х*= М(у).
Теорема 1. Если Д — алгебра пар, то
(i) [М(у\ у] и [х, т{х)\ принадлежат Д;
(И) Х\^х2 влечет m{xi)^m(x2)]
(iii) m {хх + х2) = m (х,) + m (*2){
(iv) m (*i • дг2Х m (xi) • m (#2);
(v) y^m(x) тогда и только тогда, когда (х, j/)gA;
(vi) У\>у2 влечет М{у1)>М(у2);
(vii) M(yl + y2)>M(yl) + M{y2)\
(viii) М (ух • */2) - М (f/0 • М (у2);
(ix) лг<;М(*/) гогда и только тогда, когда (х, //)еД;
(х) М[ш(х)]>х;
(xi) m[M (*,)]<*/;
(xli)Af{m[Af(if)]}-M(y);
(xili) m{M[m{x)]) = m{x)\
(xiv) {M (*/), m [M {у)]} и {M [m {x)]t m (x)} являются Mm
парами в Д;
92
Дж. Хартманис, Р, Стирнз
(xv) если (xu yi) и (x2t у2) являются Mm парами в Д, то
*1^лг2 эквивалентно ух^у2\
(xvi) множество Mm пар в Д образует структуру, в которой
н. н. г. {{хи ух\ (хь у2)} - [(xi • х2\ m (хх • х2)],
н. в. г. {(хи ух), (лг2, у2)}~[М{ух + у2), ух + у2].
Доказательство.
(i). Утверждение следует непосредственно из определений
1 и 2.
(И). Согласно (i), имеем, что [хи т(хх)] лежит в Д, а,
следовательно, х\ > х2 влечет (лемма 1) [x2i т{хх)] g Д. Поэтому
(определение 2)
т(хх) >т(лг2).
(Ш). Поскольку
Х\ + х2 > хх и х{ + х2 > x2t
то из (и), следует, что
т(хх + х2)>т(хх) и т(хх + х2)>т(х2),
и, таким образом,
т (хх + х2) > т (хх) + т (х2).
Из (i) известно, что
[хит(хх)1 [дс2, т(д:2)]еД.
Поэтому (Pi)
[хх + х2, т(хх) + т(х2)]& Д
и, следовательно (определение 2),
т(хх + х2)^т(хх) + т(х2).
Комбинируя эти два неравенства, получаем
т(хх + х2) — т(хх) + т(х2).
(iv). Поскольку
хх • х2 К хх и хх • х2 << х2,
из (ii) следует, что
т(хх >х2) ^т(хх) и т(хх*х2) *&т(х2).
Поэтому
т(хх*х2) <Ст(хх) *т(х^).
(v). Поскольку, согласно (i), имеем [х, т (х)] & Д, то (/>
>т(х) по лемме 1 влечет (*,*/)еД. Если (х,у)еД, то по
определению 2 имеем у^.т(х).
Алгебра пар и ее применение к теории автоматов. 93
(vi) — (ix). Следуют из аналогичных рассуждений.
(х) — (xiv). Доказываются прямыми рассуждениями.
(xv). Условие х\ •< х2 влечет m(x\) ^т(х2), согласно (ii), а,
следовательно, Ух^У2, так как у\ — т(х\), а у2 = т(х2).
Аналогично у\ 4^у2 влечет Х\ 4^х2.
(xvi). Если {хиу\) и (х2,у2) суть Mm пары, то, согласно (Hi),
Щ{ух + у2),ух +½] = {М[т(хх + х2)Ът{хх + х2)}
тоже есть Mm пара. Поскольку у\ + у2 есть н. в. г. у\ и у2, а по
(xv) каждая компонента определяет порядок для Mm пар, мы
получаем
н. в. г. {(*i,j/i), (x2ty2)} = [М(ух + у2)+ух + у2].
Аналогично, используя (viii), мы заключаем, что
н. н. г. {(хиух), (x2ly2)} = [x{-x2im(xx-x2)].
Следствие 1. Если Д — алгебра пар на L X L, то
множество I = {лге= L\m(x) *Сх<*СМ(х)} является подструктурой L.
Д о к а з а те л ь ств о.. Пусть хх и х2 таковы, что т(х\) К
*Cxi^CM(xi) и-т(х2)<Сх24^М(х2). Тогда
т {хх) + т (х2) < Хх + х2 < М (xt) + М (х2)
и
т (хх) • т (х2) < Хх • х2 < М (х{) • М (хг).
Отсюда по теореме 1, согласно (Hi), (iv), (vii), (viii), получаем
т{хх +х2) <*! + х2*СМ(хх + х2)
и
т (хх • х2) К лгх • х2 < М {хх • х2).
Это показывает, что множество / замкнуто относительно
операций н. в. г. и н. н. г. и является, следовательно, подструктурой L.
Если Д — алгебра пар всех пар разбиений на последователь-
ностной машине М, структура / содержит все разбиения со
свойством подстановки (substitution property), которое связано
с гомоморфизмом и играет важную роль в теории разложения
последовательностных машин [3].
Если Д определена на LXL; положим
т> (х) = т[х) и* mh(х) = m[mh~l (х)] для k > 1.
Аналогично определим степени М(у).
Следствие 2. Если Д — алгебра пар на Lx L, то mh(х) =а
=0 тогда и только тогда, когда х < Л1Й(0),
94
Дж. Хартмание, Р. Стирнз
Доказательство. Если mh(x) = О, то, применяя
отношение (теорема 1, (х)) М[т(л;)]>л;, получаем
Л!*(0) = Mk[mh (х)] > Mh-i[mb-i (х)] >...>х.
Обратно, из лг<М(ь>(0) аналогичными рассуждениями
выводим, применяя теорему 1, (xi),
mk(x)<mh[M*(0)]<01
что и завершает доказательство
3. ПРИМЕНЕНИЕ К ПОСЛЕДОВАТЕЛЬНОСТНЫМ МАШИНАМ
А. Предварительные замечания
В этом разделе мы исследуем некоторые применения
алгебры пар к последовательностным машинам.
Напомним определение последовательностной машины.
Определение 5. Последовательностной машиной М (типа
Мили) называется набор из 5 объектов
M**(S,I, О, К Р),
где (i) S — конечное непустое множество состояний;
(ii) / — конечное непустое множество входов;
(ш) О — конечное непустое Множество выходов;
(iv) X' I X S-+S есть функция переходов состояний;
(V) р: /X S-+0 есть функция выходов.
Все результаты этой статьи в полной мере применимы к ма*
шинам типа Мура, однако мы в дальнейшем не будем на это
ссылаться.
Определение б. Машина
M'~(S'f /', 0\ V, р')
является подмашиной машины
М - (S, /, О, К Р)
тогда и только тогда, когда
S'cSJ'c/, О's О,
V « Я, рассматриваемой только на Y X S',
Р' » р, рассматриваемой только на /' X S'.
Определение 7. Машина
М - (S', /', О', X', Ю
Алгебра пар и ее применение к теории автоматов 95
называется гомоморфным образом машины
М = (S, /, О, X, р)
тогда и только тогда, когда существуют три однозначных
отображения:
//,: S-+SA, Н2: 1-*1\ Я3: 0-+0\
такие, что
tfi[Ma,s)] = A'[//2(a), Hi(s)l
/Ша,*)] = р'[#2(а), Hx(s)l
Определение 8. Будем говорить, что4^ реализует поведение
состояний М2 тогда и только, тогда, когда машина М2
изоморфна подмашине М\.
Определение 9. Будем говорить, что М\ реализует М2 тогда
и только тогда, когда приведенная форма М2 является
гомоморфным образом подмашины М\.
Различие между этими двумя типами реализации уже
обсуждалось (см. [4]), и было показано, что реализация поведения
состояний может быть ограниченной и что наиболее экономные
реализации машины не обяза¥ельно будут реализациями
поведения состояний. Далее в этой статье мы используем новую
алгебру пар, которая дает возможность найти некоторые из этих
других реализаций.
В. Пары разбиений
В этой части мы даем основные определения для
разложения машин и суммируем результаты [5, 8]. Мы приводим
некоторые результаты, которые потребуются в дальнейшем, а кроме
того, мы надеемся вывести аналогию между новыми и старыми
результатами с помощью метода алгебры пар.
Определение 10. Последовательным соединением двух машин
Mi - iSu Л, О и Хи Pi) и М2 ш* (52, /2, 02, Х2> р2),
для которых 0\ = /2, называется машина
M=(SiXS2, /ьО,Д, р),
где
Я [a, (s, *)]-{М«. *)>ЫМа, s), *]},
р[а, (s, /)]-fc[M*. s), /].
Определение 11. Параллельным соединением двух машин
Мх = (Sb /ь Оь Ль Pi) и Af2 - (S2. /я, О* ta fe)
96 Дж. Хартманис, Р. Сгирнэ
называется машина
М = (S, X S2, 7, X /2, О, X 02, К р),
где
РК*. 6),(5. *)]-[pi(a, s)..fc(M)L
Определение 12. Упорядоченная пара разбиений (я, т),
определенная на множестве состояний М =(5, /, О, X, Р), есть пара
разбиений на М тогда и только тогда, когда
влечет для всех а в /
X{a,s) ===X(a,t)(x}
[$ = /(я) означает, что s и / входят в одно и то же множество
(block) разбиения я].
Теорема 2. Множество всех пар разбиений на М =
*= (S, /, О, А,, р) образует а. п. (алгебру пар) Q на L х L, где
L — структура всех разбиений на множестве S.
Следствие 3. Множество всех разбиений на множестве S
состояний машины М
I = {я | m (я) < я}
образует подструктуру структуры всех разбиений на S.
Отметим, что такие разбиения были сначала определены на
последовательностных машинах [2] ~и назывались разбиениями
со свойством подстановки (с. п.). Поли называет эти разбиения
«допустимыми разбиениями» в своей статье о разложении
машин [9]. Как показывает следующая теорема, они
играют-главную роль в изучении разложения машин.
Теорема 3. Поведение состояний машины М может быть
реализовано последовательным соединением двух меньших
машин Мх и М2 тогда и только тогда, когда существует
нетривиальное с. п. разбиение я на множестве состояний S
машины М. {Под нётривиальностью разбиения я мы подразумеваем,
что О Ф я ф I.)
Теорема 4. Поведение состояний машины М может быть
реализовано параллельным соединением двух меньших машин
М\ и М2 тогда и только тогда, когда существуют два
нетривиальных с. п. разбиения п\ ик я2 на множестве 5 машины М,
такие, что
Я1 • Я2 =?= 0.
Алгебра пар и ее применение к теории автоматов 97
Доказательство этих теорем дано в статье [3].
Применение пар разбиений в изучении последовательностных
машин используется в работах [3, 5, 8].
С. Системы множеств
В этой части мы определим системы множеств и применим
их к изучению последовательностных машин. Системы множеств
отличаются от разбиений тем, что они могут содержать
перекрывающиеся множества (blocks). В анализе машин эти
перекрывающиеся множества системы множеств будут использованы
для систематического увеличения машин (путем расщепления
состояний) в целях получения желательной реализации, которая
не может быть достигнута с помощью алгебры пар разбиений.
Определение 13. Совокупность различных подмножеств
ф — {^а} множества 5 называется системой множеств тогда и
только тогда, когда
(i) U5a = 5;
(ii) Sa ^ 5p влечет a = p.
Таким образом, система множеств ф подразделяет 5 на
подмножества, такие, что каждый элемент 5 принадлежит по
крайней мере одному множеству, т. е. блоку ф, и между блоками
системы ф не имеет места отношение включения. Если {Si} —
любая совокупность подмножеств конечного множества 5, то
через Max {5¾} мы обозначим класс множеств, содержащий те
множества из {5г}, которые не являются собственной частью других
множеств из {Si}.
Определение 14. Если ф1 и ф2 — системы множеств на 5, то
положим ф1^ф2 тогда и только тогда, когда каждый блок ф1
содержится в некотором блоке ф2.
Лемма 2. Множество L всех систем множеств на
множестве S образует дистрибутивную структуру относительно
порядка, введенного в определении 14.
Доказательство. Легко видеть, что
<p.q>' = Мах{ВП ВЧВеф и В' е= ф'},
Ф + ф' = Мах {В \В е <р или В е ф'}
и что эти операции дистрибутивны.
Мы определим теперь алгебру пар (а. п.) на структуре
систем множеств, связанных с последовательностной машиной М.
Определение 15. Пара (ф, ф') систем множеств на множестве
состояний машины М = (S, /, О, Я, Р) называется парой систем
98
Дж. Хартмйнис, Р. Стирнз
на М (systems pair on М) тогда и только тогда, когда Sg<p
влечет
А, (а, В) = {s | s = Л, (а, 0,'еВ}дВ/
для некоторого В' из ф'.
Теорема 5. Множество Д вседг пар систем на S машины М
является алгеброй пар на LxL (где L — структура из леммы 2).
Доказательство. Пусть (фр ф[) и (ф2, ф2) принадлежат
множеству Д. Если В ^ ф! • ф2, то В ^ Bi е ф1 и В ^ В2& ф2-
Но тогда для всех а из / имеем
Л(а, B)sA(a, В1)ПЯ(а, В2)дВ'ЕФ;.ф;.
Таким образом, (ф, • ф2, ф[ • ф2) е Д. Если ВеФ1 + ф2, то
В sBi е ф1 или ВсВ2е ф2. Поэтому
X(atB) <^%(а,Вх) или Х(а,В2)
и
А(а, BJsfl'eqpJ + qpJ.
Следовательно,
(Ф1 + Ф2» ф[ + Фг)еД.
Наконец, (ф,/) и (О, ф), очевидно, принадлежат Д, поскольку
они тривиально удовлетворяют условиям пар. Следовательно, Д
является алгеброй пар.
Из приведенной теоремы немедленно следует, что все ранее
полученные результаты для алгебр пар (теорема 1, лемма 1 и
следствия 1 и 2) остаются в силе для пар систем на любой
машине М. Наша следующая теорема показывает, как некоторые
элементы множества Д могут быть использованы для решения
задачи разбиения машин путем, подобным тому, который при*
менялся для с. п. разбиений. Метод систем множеств, однако,
является более сильным, чем метод разбиений, так как он
указывает, как расширить машину, 4jo6bi достигнуть нетривиаль*
ного разложения ее, которое нельзя получить с помощью
разбиений на М.
Замечание. Вычисление т(ф) можно провести следующим
образом:
1. Для каждого множества В* из ф и каждого входа а из I
вычисляем
A (a, B^-^a-foeSI^-Afa, 0. tsBt}9
Алгебра пар и ее применение к теории автоматов 99
т. е. В\ а является множеством, на которое отображается В*
посредством входа а.
2. m(qp) = Max{fi; fl}.
Если ф — система множеств (с. м.) на множестве 5
состояний машины М, то пусть
|ф| обозначает число блоков в ф,
а
#|ф| обозначает число состояний в наибольшем блоке ф.
Теорема 6. Пусть М — последовательностная машина, а ф
есть с. м. на S, такая, что
т(ф)^ф.
Тогда М можно реализовать как последовательное соединение
двух машин М{ и М2, где Мх имеет |ф| состояний, а М2 имеет
#|ф| состояний.
Доказательство. Из условия т(ф)^лр вытекает, что
состояния, содержащиеся в одном и том же блоке, будут
отображены снова в общий блок (не обязательно единственный, как
в случае с. п. разбиений, когда блоки не пересекаются). Таким
образом, систему множеств можно применить для определения
машины Ми состояния которой являются блоками ф, а
переходы определяются переходами состояний машины М (если они
не единственны, можно выбрать кацой-ммбудь из возможных
вариантов).
Машина М2 строится для того, чтобы различать состояния в
блоке ф, используя /2 = / X S\ в качестве входов. Такую
машину всегда можно построить, если использовать для
различения состояний М в каждом блоке ф (состояний М{) один из
#|ф1 элементов, а затем подходящим образом определить
переход для каждого входа в /2 = / X 5Ь Для нахождения нужного
перехода смотрим настоящее состояние М\ (которое является
частью входа), определяем настоящее состояние М, следующие
состояния М и Mi и затем выбираем переход М2 в такое
состояние, которое позволяет отличить следующее состояние М среди
тех состояний машины (М), которые попадают в следующее
состояние М\ (блок ф). Последовательное соединение М\ и М2,
очевидно, реализует М\ доказательство завершено. Более
короткое доказательство может быть проведено позднее с использо*
ванием теорем 3 и 7.
Родственные результаты о расщеплении состояний получены
в статье [6] с применением техники графов. См. также статью [1],
где имеются другие результаты.
100
Дж. Хартманис, Р. Стирнз
Пример. Рассмотрим машину А (рис. 1). Легко проверяется,
что у этой машины с. п. система множеств (т.е. т(ф)^ф)
Ф = {0, 1,2, 3; 3, 4, 5, 6}.
Найдем последовательное разложение машины Л, основанное на
этой системе множеств ф.
Сначала построим первую машину А\ с состояниями {А, В},
соответствующими блокам ф. В этом частном случае А{
определяется однозначно и приводится на рис. 2.
0 I
2
3
0
1
0
3
2
5
6
4
3
2
3
2
Рис. 1. Машина Л. Р-и с. 2. Машина А\,
Состояние Л={0, 1, 2, 3},
состояние В = {3,4, 5, 6}.
Построим «хвостовую» (tail) машину А2. Мы знаем, что
потребуется ф|ф| = 4 состояния, поэтому выберем 52 = {я, Ъ, cxd).
Далее для каждого состояния 5 из А и каждого блока ф
(состояния i4i), содержащего 5, нам нужен по крайней мере один
элемент 52, чтобы отличать 5. Это легко сделать, написав
таблицу, в которой каждая строка обозначает блок ф, каждый
столбец представляет состояние А2 и на каждом месте
находится состояние А в соответствующем блоке ф, которое
различается соответствующим столбцом. Наша таблица имеет вид
abed
Л 0 1 2 3
В 6 5 4 3
Переходы для А2 можно найти способом, указанным в
последнем доказательстве, а результат показан на рис. 3.
Машины А{ и Л2 вместе определяют машину А' (рис. 4). Машина А'
является «расщепленным» (split) вариантом машины Л, и
система множеств ф теперь соответствует с. п. разбиению
я = {0, 1, 2, 3; 3', 4, 5, 6}.
Заметим, что таблицу, которую мы написали для
различения состояний, можно теперь использовать для нахождения со-
Алгебра пар и ее применение к теории автоматов 101
стояния в Л, являющегося образом данной пары состояний Л\
и А2. Если бы блоки ф были различной мощности, некоторые
места в таблице повторялись бы или оставались пустыми.
Покажем теперь непосредственно, как минимально
расширить машину М, для которой т(ф)^ф, так, чтобы у
расширенной машины М' было с. п. разбиение, которое переходит в ф при
сведении состояний М' к М.
о i
0
b
с
d
0,А
С
d
0
ь
I.A
b
0
С
d
о.в
С
d
0
b
l.B
С
d
с
d
(A.a)
(A,b)
(A.C)
(A,d)
(B,d)
(B,c)
(B,b)
(B,0)
2
3
0
1
1
0
3
2
5
6
4
3
3 1
2
3
2 j
Рис. 3.Машина A2.
Рис. 4. Машина A'.
Определение 16. Пусть Ян отображает 5 на 5', т. е.
nR\ S-+S'. Тогда образом системы ф на 5 является система ф'
на S', определенная посредством
Ф'= Мах {В; | £{ = Яд (В,), В, €= ф}.
В наших приложениях ян будет разбиением 5, а S' будет
состоять из блоков ян. Таким образом, ян будет отображать S
на множества классов эквивалентности относительно ян.
Определение 17. Если ф — система на 5 = {su s2i ..., sn}, то
кратность (multiplicity) элемента s* в ф на единицу меньше
числа блоков ф, содержащих $;. Обозначим кратность 5г- в ф
через ki.
Теорема 7. Пусть М — машина с п состояниями, а ф —
система множеств (см.) на S, такая, что т(ф)<^ф. Тогда
существует машина М' с
N = п + kx + k2 + ... + kn
состояниями, обладающая с. п. разбиениями я и яд, такими, что
Ян отображает М' на М, а тс отображает М' на ф.
Доказательство. Заменим состояние Si (i= 1,2,..., п)
В тех блоках ер, в которых оно встречается, на sf\ $(Д
102
Дж. Хартманис, Р. Стирнз
соответственно. Каждому блоку В из ф теперь соответствует
блок В' разбиения я на множестве
S'«{s<*>|l<i</i, 0<£<*,}.
Чтобы найти переходы состояниймашины М', мы поступим так.
Для В из ф выберем в ф такой блЬк С, что
Я (a, B)sC.
Для s\l) в В' положим
где
Наконец, пусть
Очевидно, разбиение я^ на S' таково, что
обладает с. п. на М' и отображает М' на М.
Разбиение тс также имеет с. п. на ЛГ, а ян отображает я на
ф-систему множеств на М, что и надо было установить.
о I о I
2
2
2'
3
3 1
2'1
2
1 |
Рис. 5. Р и с. 6. Два ф-образа Рис. 7. Машины
Машина В. машины В. Состояние В и В'.
Л = {1, 2} и состояние
В -{2, 3}.
Наш следующий пример проиллюстрирует неединственность
ф-образа М, как это обсуждалось в теореме 6. Рассмотрим
машину В (рис. 5). Система множеств ф = {1, 2; 2, 3} такова, что
т(ф)-<ф, и можно применить теорему 6. Заметим, что
множество {1, 2} отображается входом «0» на множество {2}, которое
входит в каждый блок ф, и, следовательно, ф-образ В
неединствен..На ряс. 6 показаны эти два ф-образа В.
Для машины В' получаем
S'«{1, 2, 2', 3} и {1, 2}-*{1, 2}, {2, 3}-{2', 3}.
Мож1Но выбрать
V(0,1) = Я'(0,2) = 2 или V(0, 1) = Я'(0,2) = 2'.
1
?
3
0
2
?
3
i
3
?
i
А
В
0
А
А
1
6
А
А
В
0
В
В
1
В
А
1
2
2
3
Алгебра пар и ее применение к теории автоматов 103
Две машины, получающиеся в результате, показаны на рис. 7.
Применением теорем 4 и 7 или прямым доказательством,
аналогичным доказательству теоремы 6, можно установить
следующую теорему.
Теорема 8. Пусть q>\ и ц>2 — системы множеств на М, та-
кие, что
т(ф1)<фЬ т(ф2)<ф2 и ф1-ф2 = 0.
Тогда машина М может быть реализована посредством
параллельного соединения двух машин Мх и М2, где Мх является
ух-образом, а М2 является ф2-образом М, содержащими
соответственно \(р\\ и |ф2| состояний.
Пример. Рассмотрим машину С (рис. 8).
Для этой машины две системы множеств
ф1 - {1, 2, 3; 3, 4, 5}, ф2 - {175; 271; 3)
удовлетворяют теореме 8.
о ь с
Q О С
5
4
3
2
: 1
3
2
3
4
3
4
4
5 1
4 1
4
Рис. 8. Машина С. Рис. 9. Машина С.
Расширенная машина описана таблицей на рис. 9. Для этой
машины разбиения
^«{ТТгТз; а^ЛТб} и я2 = {Т75; 2Л; зГз7}
являются с. п. разбиениями и, согласно теореме 4, ведут к
параллельному разложению С.
Необходимо заметить, что теорема 8 не сильнее, чем
соответствующая теорема о реализации поведения состояний
машины М. Специально можно построить машину М с с. п.
системами множеств фь ф2, такими, что ф1 • ф2 > 0; но затем
состояния машины М расщепляются, соответствующие разбиения jti и
я2 таковы, что Я1 • я2 = 0 и, следовательно, приводят к
параллельному разложению машины М'.
Когда посредством отображения nR мы перейдем от М' к М,
разбиение п на М' может дать в результате тривиальную
систему ф или систему ф, содержащую меньше блоков, чем л;,
5
1 4
1 3'
1 3
2
1
3
2
3
3 .
4
3
4
4
5
5
4
4 !
104
Дж Карт мание, Р. Стирнз
поскольку мы применяли операцию Мах при образовании ср.
Кроме того, в этом случае в теорему можно ввести условие
«тогда и только тогда», коль скоро мы ограничим число
состояний в компонентах машины.
Следствие 4. Пусть М — (приведенная) машина с п
состояниями. Тогда ее можно реализовать последовательным
соединением двух машин Мх и М2, каждая из которых содержит
меньше, чем п состояний, тогда и только тогда, когда
существует нетривиальная система множеств ф, такая, что
т(ф)^ф и |ф|^л.
Доказательство. Если дана нетривиальная система
множеств ф, такая, что т(ф)<!ф и |ф| < я, то, согласно теореме 7,
существует последовательное разложение машины М на двема*
шины, каждая из которых имеет меньше, чем п состояний.
Обратно. Если М' реализует МиМг является
последовательным соединением двух машин, каждая из которых имеет
меньше состояний, чем М, то по теореме 3 существует с. п.
разбиение я на М\ такое, что |я|, #|я| < м, а разбиение тсп тогда
приводит М.' к, М. Поскольку ни один блок я не содержит п
состояний, nR отображает я на ф Ф /. Так как л содержит
меньше; чем п блоков, tcr отображает я на ф Ф 0, и, стало быть,
Ф нетривиально. Ясно, что т(ф)^ф, и наше доказательство
завершено.
Теперь мы применим развитые ранее идеи к изучению
обратной связи и канонических форм последовательностных машин.
Сначала введем новую алгебру пар Д/, которая будет играть
важную роль в этом вопросе.
Определение 18. Для машины М = (S, /, О, А,, р) и
функции f,
f: /XS-I/,
положим, что пара систем множеств (ф, ф') принадлежит Д,
тогда и только тогда, когда
С ^ В, Веф и f(a,s) = f (а, /) для всех s и t в С
влечет
Я (а, С)^В' для некоторого В' из ф'.
Лемма 3. Множество Д/ является алгеброй пар.
Доказательство. Элементы Д/ удовлетворяют условиям
Pi и Рг определения 1.
Алгебра пар и ее применение к теории автоматов 105
Снова операторам m и М в А/ на М можно дать простое
интуитивное истолкование, и эти операторы будут использованы
для формулировки и решения ряда задач. Для данной системы
множеств ф оператор т(ф) дает наименьшую систему
(наибольшее количество информации), которую можно получить
относительно состояния машины М после одного такта работы М,
если нам известен лишь некоторый блок ф, который содержал
прежнее состояние машины М, вход и значение f.
Аналогично оператор М для данной системы ф дает
наибольшую систему Л1(ф) (наименьшее количество информации),
с помощью которой можно определить блок ф, содержащий
текущее состояние М, если мы знаем блок М(ф), содержащий
состояние М, вход и значение f.
Лемма 4. Пусть М — приведенная машина. Тогда
состояние М является функцией только последних п входов и
последних п значений f тогда и только тогда, когда
(i) mn(/) « 0 в Д/
или
(ii) Af»(0) =/бД/.
Доказательство. Условия (i) и (ii) эквивалентны для
любой алгебры пар, согласно следствию 2, и, следовательно,
нам нужно показать только, что выполняется {\). По
определению если шп([) = 0, то по всякой последовательности входов
длины п и соответствующим п значениям f можно определить
состояние машины М. Если
mn(I) = ф> 0,
то найдутся два состояния s и t и последовательность входов
хи лг2, ..., хп, такие, что данная последовательность переводит
состояние s в s\ а / в /' и s' Ф /', а соответствующие
последовательности значений / одинаковы для этих переходов. Таким
образом, состояние машины М не является функцией только от
последних п входов и значений f.
Следующее утверждение является незначительным
обобщением леммы 4.
Лемма 5. Пусть М — приведенная машина. Тогда mn(I) = ф
в А/ тогда и только тогда, когда существует функция
последних п входов и последних п значений f, выделяющая то
множество из ф, которое содержит состояние машины М.
Доказательство утверждения аналогично предыдущему.
Определение 19. Приведенная машина М имеет реализацию,
использующую f, f: I X 5 —> U в качестве обратной связи, тогда
106
Дж, Хартмание, Р. Стирнэ
и только тогда, когда для некоторого п состояние машины М
является функцией последних п входов и значений / (рис. 10
и 11).
1
. J—1 ,
|." ■ »
1 " ■" »
Т 1 1 "1 1] | 1 »
' ' ' ' ■ »1
2
.
i » 3
j
4
Рис. 10. Канонический вид реализации машины М с использованием / для
обратной связи.
/ — вход; 2 —комбинаторная логика, <? — выход; 4 —единичная задержка.
С
1 »-
л
Рис. 11. Схематическое представление реализации машины М с
использованием / для обратной связи.
/ — вход; 2 — выход.
Теорема 9. Для приведенной последовательностей маши*
ны М эквивалентны следующие три утверждения:
1) машина М может быть реализована с применением f для
обратной связи-;
2) пгп(1) = 0 в А/;
3) М"(0) =/e Af.
Доказательство. Машину М можно реализовать,
используя f для обратной связи, тогда и только тогда, когда
состояние М есть функция последних п входов и последних п
значений / для некоторого фиксированного п. Это, согласно
лемме 4, эквивалентно условию
пгп (/) = 0 в А/.
Согласно следствию 2, условие 2 эквивалентно условию 3.
Алгебра пар и ее применение к теории автоматов 107
Если обратной связи нет (/«const), то Д/ является
алгеброй Д пар систем множеств на Му и мы получаем следствие.
Следствие 5. Следующие три условия являются
эквивалентными для всякой приведенной машины Men состояниями:
1) машина М может быть реализована без обратных связей;
2) mn(I) « 0 в Д;
3) Мп(0) = I в Д.
Поскольку Mk(0) в Д таково же, как Mk(0) в Q, то
следствие 5 останется справедливым, если заменить Д на Q. В такой
форме это следствие фактически совпадает с следствием 3 из
статьи [б].
Пример. Рассмотрим машину D (рис. 12). В этом случае
положим f = р. Тогда
m(/)-{1727¾ ЗДГб}>пг2(1)- {3~4; ТЛГЗ; ЗГб}>т3(/)-
«{2Л; ЗГ4; 1ТЗ; 5}>т4(/)-{2ГЗ;Т; 4; 5}>т5(/Н0,
из чего мы заключаем, что машина D может быть реализована
посредством схемы глубины 5 с использованием ее выхода для
обратной связи.
о i о i
5
! 3
3
2
1
3
4
А
5
3
[ 1
0
0
0
1 °
0
0
1
0
0
Рис. 12. Машина D.
Если машина М не мозк-ет быть реализована без обратной
связи, то иногда нужно бывает определить, какую машину М2
с наименьшим числом состояний нужно соединить
последовательно с машиной Mi без обратной связи, чтобы реализовать
машину М. Можно себе представить это, как
запоминание.последних k входов (скажем, в регистре сдвига) с целью
уменьшения числа состояний в машине М2, которая содержит все
обратные связи системы.
Задачи такого типа с использованием поведения состояний
машины М рассматривались в статье [5]. Следующая теорема
является обобщением следствия 4 из упомянутой статьи. В
статье [7] дается другой подход к этим задачам, не использующий
понятия алгебры пар.
108
Дж. Хартманис, Р. Стирнз
Теорема 10. Пусть М — приведенная машина, для которой
I>m(I) >m2(I) >...>mk(I) =mh+l(I) =q>
в А. Тогда M может быть представлена в виде соединения
машины М\ (глубины k) без обратных связей и машины М2 с
=14= | ф | состояниями; не существуют машины М'2 с меньшим
числом состояний, которая могла бы в соединении с какой-нибудь
машиной М[ (без обратных связей) реализовать М.
Доказательство. Так как система ф такова, что
т(ф)^Сф, то она определяет ф-образ М, скажем Мф. Для Мф
имеем
тА(/) = ф(=0 на S' машины Мф),
и, следовательно, Мф не содержит обратных связей.
Наибольший блок ф содержит #|ф| состояний, а следовательно,
существует машина М2 с #|ф| состояниями, которая требуется в
теореме (см. теорему 6). Для доказательства того, что нельзя
взять машину с меньшим числом состояний, заметим, что если
Вбф и |В| =ф|ф|, то по определению mk(I) существует
входная последовательность произвольной длины, которая
отображает #|ф| различных начальных состояний М на
состояния В. Ввиду того что М — приведенная машина, никакие два
ее состояния не эквивалентны, и, следовательно, необходима
машина с #|ф| состояниями для различения состояний из В.
м,
Рис. 13. Реализация машины М из теоремы 11.
Теорема 11. Приведенная машина М, для которой
/>m(/)>...>mfe(/) = mh+l(I) = ф в Ар,
может быть реализована с помощью машины М2 с #|ф|
состояниями, входами которой являются последние k входов и
последние k выходов этой машины; никакая машина с меньшим
числом состояний не подходит для такой реализации
(схематически эта реализация изображена на рис. 13).
Алгебра пар и ее применение к теории автоматов 109
Доказательство проводится аналогично доказательству
теоремы 10.
Из последней теоремы можно получить следствие для
специального случая.
Следствие 6. Для приведенной машины М следующие
три условия эквивалентны:
(i) состояние машины является функцией только последних
k входов и выходов;
(И) mk(I) = 0 в А3;
(Hi) Af* (0)=/ в Др.
В соответствующей реализации этой машины машина М2 на
рис. 13 имеет только одно состояние и, стало быть, является
комбинаторной схемой.
4. ПРИМЕНЕНИЯ К НЕПОЛНОСТЬЮ ОПРЕДЕЛЕННЫМ МАШИНАМ
Посмотрим теперь, как применять алгебры пар к машинам с
«don't care» условиями1). Под этими условиями
подразумевается, что некоторые переходы или выходы машины не
определены и могут быть выбраны произвольно по усмотрению
конструктора устройства. Отметим, что определение 15 обобщается
на случай «d. с», и в этом смысле было дано обобщение пар
разбиений [8]. Более точно следующее определение:
Определение 20. Пара (ф, ср') систем множеств на
множестве состояний машины М = (5,/, ОД, р) с «d. с» условиями
является слабой парой систем на М тогда и только тогда, когда
ЙЕф влечет
Я(а, В) ={s|s = A,(a, t) для некоторого t из В} s В'
для некоторого В' е q/.
Данное обобщение пар разбиений [8] было несколько
неудовлетворительным, поскольку обобщенные пары не
удовлетворяли закону суммы и не образовывали поэтому алгебру пар.
Это вызывало некоторый пессимизм относительно таких
обобщений, но в рассматриваемом здесь случае нас ждет приятный
сюрприз.
Теорема 12. Множество А' всех слабых пар систем
множеств для машины с условиями «d. с.» является алгеброй пар.
Доказательство проверяется очень легко.
1) То есть к последовательностным машинам, определенным не на всех
входных последовательностях. — Прим, перев.
110
Дж. Хартманис, Р. Стирнз
Таким образом, мы видим, что со слабыми парами систем
можно так же легко обращаться, как с парами систем.
Нетрудно видеть, что все приведенные здесь результаты сохраняют
силу для случая «d. с». Доказательства совершенно
аналогичны. На этом пути можно получить редуцированные
зависимости и перекрестные разложения. Поэтому такие методы без
дополнительных усилий переносятся на случай «d. с».
5. ЗАКЛЮЧЕНИЕ
Метод алгебры пар является очень гибким и более
глубоким, чем метод пар разбиений, который рассматривался
вначале. Чтобы подчеркнуть это обстоятельство, мы применили
этот метод для довольно легкого решения различных задач.
Некоторые из этих задач и соотношений встречаются в
литературе, но со значительно более длинными выводами.
Авторам известны также другие опубликованные решения задач,
которые можно просто сформулировать и решать в терминах
соответствующей алгебры пар, но перечисление их немного
добавит к сказанному выше. Главная цель состоит в том, что
алгебры пар потенциально могут иметь применения к будущим
задачам. Поэтому если у читателя есть задача, которая, как он
интуитивно чувствует, может быть решена с рассмотрением
вперед и наблюдением за тем, как распространяется
«информация», тогда налицо потенциальное применение алгебры пар.
Мы надеемся, что он вернется к содержанию данной статьи и
поставит три вопроса:
1. Можно ли привести «информацию», о которой мы
упомянули, к форме структур (разбиений, систем множеств и т. д.)?
2. Можно ли «распространение» или «поток» информации
описать на языке информационных пар?
3. Удовлетворяют ли эти пары двум условиям алгебры пар?
Если ответы на эти вопросы положительны, то
правдоподобно, что можно получить простое алгебраическое решение.
ЛИТЕРАТУРА
1. Ginzburg A., Yoeli М., Products of automata and the problem of
covering, Techn. Rept., № 15, 1963.
2. H a r t m a n i s J., Symbolic analysis of a decomposition of information
processing machines, Inform. Control, 3 (1960), 154—178.
3. Hartmanis J., Loop-free structure of sequential machines, Inform.
Control, 5 (1962), 25—43.
4. H a r t m a n i s J., Stearns R. E., Some dangers in state reduction of
sequential machines, Inform. Control, 5 (1962), 252—260.
Алгебра пар и ее применение к теории автоматов 111
5. Н а г t m a n i s J., Stearns R. E., A study of feedback and errors in
sequential machines, IRE Trans., Electron. Computers, EC-12 (1963), 223—
232.
6. Kohavi Zvi. Secondary state assignment for sequential machines, IRE
Trans., Electron. Computers (1964).
7. M с С 1 u s к e у E. J., Reduction of feedback loops in sequential circuits and
carry leads in iterative networks, Inform. Control, 6 (1963), 99—118.
8. S t e a r n s R. E., H a r t m a n i s J., On the state assignment problem for
sequential machines, II, IRE Trans., Electron. Computers, EC-10 (1961),
593—603.
9. Y о e 1 i M., The cascade decomposition of sequential machines, IRE Trans.,
Electron. Computers, EC-10 (1961), 587—592.
Обобщенная теория конечных автоматов
и ее приложения к проблемам
разрешения в логике второго
порядка1)
Дж. В. Тэтчер, Дж. Б. Райт
Развито обобщение многих важных понятий и результатов обычной
теории автоматов на случай, когда вместо конечных автоматов рассматриваются
конечные алгебры. Доказаны стандартные теоремы о замыкании для класса
множеств, «распознаваемых» конечными алгебрами, и дано обобщение
теории регулярных событий Клини. Теоремы обобщенной теории применяются
затем для получения положительного решения проблемы разрешения в логике
второго порядка.
1. ВВЕДЕНИЕ
Предположим сначала, что читателю известно понятие
«обобщенного конечного автомата». При этом предположении
излагаемые .здесь результаты можно легко резюмировать [19],
сказав, что обычная теория автоматов поддается обобщению,
причем довольно естественным путем! От нашего
предположения также легко избавиться: обобщенный конечный автомат
есть конечная абстрактная алгебра в смысле Биркгофа [1]; это
есть конечное множество Л вместе с операциями fu ..., fn на Л.
(Алгебры, рассматриваемые здесь, не являются столь же
общими, как алгебры, рассматриваемые Биркгофом [1]. Мы
допускаем только конечное число операций (случай бесконечного
числа операций будет рассмотрен в последующих работах), и
каждая операция есть функция из Аш в А при некотором т.
Биркгоф требовал только, чтобы некоторое подмножество
множества \JA{ было областью определения каждой из операций—
i
обобщение, которого не было в его предисловии к Алгебре в
работе [2].)
Наиболее широко используемое определение [14] описывает
конечный автомат с входным алфавитом 21 как четверку Ж =
= (Л, М, а0, AF), где А — конечное множество, множество
состояний; М — функция из ИХ Л в Л, функция непосредственных
переходов; а0 е Л0 — начальное состояние; AF^ А —
множество заключительных состояний. Функция непосредственных
переходов расширяется до функции из множества 2* (множества
l) Thatcher J. W., Wright J. В., Generalised Finite Automata
Theory with an Application to a Decision Problem of Second-Order Logic,
Mathematical Systems Theory, 2, № 1 (1968), 57—81.
Обобщенная теория конечных автоматов и ее приложения 113
конечных цепочек на 2, включая рустую цепочку Л) в А
посредством равенств М(А) = а0 и М(ах) = М(в, М(х)) для всех
аб2 l).Доведение Л, или множество цепочек, допускаемых^,
есть {х\М(х)<= AF}.
Строение автомата Л напоминает алгебру2), если
игнорировать заключительные состояния, а также тот факт, что
функция переходов определяется на 2X^4, где 2 не является частью
множества элементов алгебры. Так как множество 2 конечно,
мы можем получить алгебру, рассматривая вместо двуместной
функции М монарную функцию аа:Л->Л для каждого
ае2, где а0 (а) = М(в, а)3). Таким образом, структура
автомата дописывается как монарная алгебра с^ = (Л, aaj ,..,aart> a0)
(2={ai, ..., On})- Тогда ^функция Ж_определяется в
сущности таким же образом: М(Л) = ao, М(ах) = аа {М(х)) для
всех aeS и xgS*. Отбросив заключительные состояния из
описания автомата, мы получим поведение как функцию от
заключительных состояний. В соответствующих обозначениях мц
пишем bhjt(AF)=z{x\M(x)eAF}.
Переходя теперь к обобщению, предположим, что 2 есть
алфавит, состоящий из двух символов: 2 = {g, f}. Каждый
конечный автомат с входным алфавитом 2 есть алгебра с двумя мо-
нарными функциями и с константой (начальное состояние).
Если мы рассматриваем /, g е 2 как символы монарных
функций (синтаксические объекты), то мы можем определить
множество Ts константных термов (используя Л в качестве
индивидного символа) как наименьший класс, содержащий
символ Л и такой, что если t& Ts, , то ft и gt содержатся в Г2.
Таким образом, константные термы суть цепочки в алфавите
1) Чтобы сделать обобщение более аккуратным, мы используем функцию
М(ах) вместо М(хо)\ это соответствует автомату, работающему на входной
ленте справа налево.
2) Сходство отчасти неясно, хотя в современной литературе мы
находим доказательства того, что каждый автомат обладает группой
автоморфизмов; ср. работу [1], в которой утверждается: «Не имеет смысла
доказывать детально всем известный факт, что каждая алгебра имеет группу».
3) Эта формулировка для конечных автоматов была предложена в
Мичиганском университете на семинаре, которым руководили Бюхи и Райт,
осенью 1960 г. (см. работы [5, 6, 17]). Известно, какое влияние оказал Бюхи
на алгебраическую интерпретацию автоматов и использование
алгебраических понятий для решения основных задач теории. Возможность обобщения
на произвольные алгебры неявно подразумевалась в работах Бюхи и Райта.
В некотором смысле настоящая работа есть изложение, которое делает эти
идеи явными. В качестве исторического комментария интересно заметить, что
первое определение конечного автомата как алгебры с монарными
операциями принадлежит Медведеву [12]. И поэтому те ссылки их работы,
которые касаются полугрупп и автоматов, должны отметить также и эту статью.
114
Дж. В. Тэтчер, Дж. Б. Райт
{/, gt Л}, включая, например, объекты Л, fggfA, fffAt gA и т. д.
Очевидно, что множество 2* цепбчек можно взаимно
однозначно поставить в соответствие множеству Г2 термов: Л (пустая
цепочка) соответствует Л (индивидному символу), а для
о>еЕ* — {Л} цепочка w соответствует терму wA.
В силу этого1 соответствия мы можем считать, что входы
автомата представляют собой константные термы в языке
термов, который соответствует алгебраическому классу подобия
автомата. С алгебраической же точки зрения это множество Tz
константных термов можно взять в качестве области определен
ния абсолютно свободной или порождающей [generic] алгебры,
^2= (7^2, f, g, Л), где f(t) = ft и g.(t) = gt. Итак, если задан
произвольный автомат А = (Л, а/, а* а0), то существует
единственный гомоморфизм А*, переводящий o^s в^и заданный
равенствами А^(Л)=ао и_й*(/ОвМА«*(0)- Легко заметить, что
h,#{t) есть в точности M(t)t так что поведение автомата Л с
множеством AF заключительных состояний есть просто h^(Ap)**
= {t\hAt)<~AF).
В этом направлении й возникает обобщение: обычные
конечные автоматы имеют дело с монарными алгебрами; наши
обобщенные автоматы имеют дело с конечными алгебрами.
Таким образом, при этом обобщении (и в согласии со
сказанным выше) автомат есть конечная алгебра, входными
символами автомата являются функциональные символы
определенного ранга, а «входные цепочки» суть константные термы в
соответствующем языке термов. В разд. 2 мы проведем
формальные определения указанных понятий и перейдем к
доказательству стандартных теорем о замыкании для класса множеств,
распознаваемых конечными автоматами1).
Другая характеристика класса распознаваемых множеств
в обычной теории автоматов получена с помощью введенного
Клини понятия регулярного множества (см. [11, 7]). Класс
регулярных множеств в алфавите 2 = {/, g} есть наименьший
класс подмножеств, содержащий конечные множества и
замкнутый относительно операций U» • и *> гДе
а • р = [t?t21 *i е а и U е р}
и где а* есть наименьшее подмножество р множества 2*,
содержащее а и обладающее свойством Р'р = р. Эти регулярные
операции — сложное произведение и замыкание — на подмно-
1) В разд. 2 в основном содержится изложение теории конечных
автоматов. Доказательства обобщенных теорем соответствуют доказательствам
теории в обычной теории конечных автоматов, < и поэтому читатель,
знакомый с последней, может не читать эти доказательства.
Обобщенная теория конечных автоматов и ее приложения 115.
жествах из 2* зависят явно от операции сочленения
[concatenation] (t?t^) в 2 . Попытка обобщить теорию регулярности таким
же образом, как мы обобщили теорию распознаваемости,
вынуждает нас внимательнее исследовать природу сочленения,
когда объекты из 2* рассматриваются как термы, например
fgfAngA = fgfgA, [fgf (xf g (x) = fgfg (x)].
Эта иллюстрация может подсказать читателю — и,
действительно, подсказка оказывается полезной, — что сочленение
цепочек соответствует замещению (или подстановке в данном
случае) для термов. В разд. 3 мы разовьем теорию
регулярности, основанную на отношении замещения, и докажем важную
теорему об эквивалентности распознаваемости и регулярности.
Последний раздел содержит приложение обобщенной теории
конечных автоматов. В нем доказано существование
разрешающей процедуры для слабой одноместной теории второго порядка
со многими операторами следования.
2. ОСНОВАНИЯ ОБЩЕЙ ТЕОРИИ РАСПОЗНАВАЕМОСТИ
Специя определяется как упорядоченная пара ^^==(2, а),
где 2 — множество функциональных символов из £f, а а —
отображение из 2 в N (неотрицательное целое число). Для /е2
величина a(f) есть ранг f. Ради удобства введем обозначения
для множества функциональных символов ранга г, 2г = а^1(г);
2о есть, множество констант или индивидных символов из 2, и
во всех случаях мы предполагаем, что 2О=£0. Специя- (2, о)
конечна, если 2 конечно; мы будем иметь дело только с
конечными специями.
Алгебра специи (2, а), или короче 2-алгебра, есть пара
Л = (Л, а), где А — множество, называемое носителем Ж, и
а — функция, отображающая 2 в' класс операторов над
множеством Л, таким, что а(/) = а/ есть а(/)-местная функция
a(f)^ AA°{f\ Константами называются 0-местные функции
(а(Х) для Я,е20).
Недетерминированная алгебра (за неимением лучшего
термина) специи (2, о) есть система отношений для специи
(2, а + 1), т. е. пара Ш = (/?, р), где p(/)s #a(f)+1. Снова R
называется носителем М, и Si конечно, если R конечно.
Специя (2, а) однозначно определяет множество Тъ
(константных) термов, определяемое как наименьшее
подмножество из 2* (множество всех слов над 2)/ удовлетворяющее
следующим соотношениям:
(О 20 <= ТУ,
(и) если [ei и tu ..., ^е^, то ft{ ... /л <= Г2.
116
Дж. В. Тэтчер, Дж. Б. Райт
Одна алгебра специи (S, о) возникает немедленно, если
использовать Ге в качестве носителя; порождающая (абсолютно
свободная) алгебра <&~ъ есть S-алгебра (Гг, i), где
(i) для AeS0 имеем 4 = А;
(ii) для f<=S„ и tu ..., tne=Tz имеем if{tu ..., tn) = ft{ ... *л.
При таких определениях мы в действительности
отождествляем специю с некоторым выбором языка термов, который
часто называют алгебраическим классом подобия. Различный
выбор символов для языка термов класса подобия приводит к
различным специям, например множества So == {A), Si ={1,2,...
...,&} и S = So (J Si приводят к специи для «инициальных
£-монарных алгебр». Алгебру Л = (Л, а) этой специи можно
записать в виде Ж = (А, ао, аь ..., а&), где а0 = а(А,) и а*:
Л-*Л есть a(i). Если S' = {0, s0, ..., s^-i}, то мы получаем
другую специю по существу для того же самого класса алгебр.
Смысл термина «класс подобия» при использовании в
предыдущем абзаце не уточнялся; его можно сделать более
точным, если ввести канонические специи. Однако для настоящего
изложения такого рода уточнений не требуется.
Мы значительно отклонимся от обычного курса
алгебраических исследований, рассматривая алгебры заданной специи
как характеризацию или распознавание некоторых
подмножеств множества термов. Это различие усиливается нашихМ
интересом к операциям над специями (наиболее интересным
примером является проекция) и к замыканию распознаваемых
множеств- относительно таких операций. Наше исследование
оправдано тем, что оно в действительности является прямым
обобщением обычной теории конечных автоматов. Чтобы
облегчить сравнение с этой теорией, мы будем применять ее
терминологию к рассматриваемым структурам.
Если задана специя (S, а), то S есть множество входных
(функциональных) символов, а Т% —пространство допустимых
входных термов (цепочек). Автомат (недетерминированный)
специи (S, а) есть конечная (недетерминированная) алгебра
этой специи; если JL = {А9 а), то А — множество состояний, a
для каждого X е S0, ах есть начальное состояние и для / е Sn,
а/ есть функция (непосредственных) переходов для входного
символа f. Для недетерминированных автоматов терминология
сходна: рх есть множество' начальных состояний,
соответствующих индивидному символу Я, и р/ есть отношение перехода для
входа /.
Таким образом, входы S-автомата Л = (Л, а) суть термы
из множества 72, и каждый вход / порождает выходное
состояние hrf(t) g/I, определяемое следующим образом:
Обобщенная теория конечных автоматов и ее приложения 117
(i) для ЯеИ0 имеем h^{k) = ak;
(ii) для [gE„ и t\9 ..., tn<=Tz имеем
hA№ ...V„H af(M'i). ..., h*(tn)).
Символ h^(t) используется здесь потому, что это состояние
есть не что иное, как образ / при естественном гомоморфизме
из £Гъ в А> индуцируемом при продолжении отображения
а|2о.
Для недетерминированного автомата <£? = (R, р)
определение отличается лишь слегка. В этом случае входной терм
порождает множество выходных состояний:
(i) для А,е=20имеем hm(K) = p^
(ii) для fe2„ и tu ..., tn^Tv имеем
hm{ftx ••• ^) = ^13^...3^^(^, ..., ап% а)Л/\а.еЛЛ(/.)]|.
Индуктивное предположение в определении hm можно
переписать таким образом, что оно будет выглядеть в точности так
же, как в случае детерминированных автоматов. Для этого
надо использовать понятие я-местной функции множеств г),
индуцируемой (п + 1) -местным отношением г\. Функция fj
определяется следующим образом:
*1(Рь ...» Р«) — {* 13*i ... ЗЬп[Фи .... ЬЯ9 ft) Л AftiSftJJ.
Тогда, очевидно, (ii) можно записать в виде*
(ii)' для /е2„ и t\t ..., tn^Tz имеем
Это сходство между детерминированными и
недетерминированными автоматами предсказывает теорему об
эквивалентности, которую мы докажем ниже. Прежде чем доказать ее, мы,
однако, должны определить понятие поведения или множества
термов, распознаваемого автоматом.
Для детерминированного автомата Л = (Л, а) и
выбранных заключительных состояний AF^A поведение Л
относительно AF задается равенством
bhA(AP) = {t\hA(t)*=AP}.
Аналогично, если <0l = (R, р) есть недетерминированный
автомат и RF^R, то
bh*{RF) = {t\h»{t)(\MP^ 0).
118
Дж. В. Тэтчер, Дж. Б. Райт
Множество U s Т% распознаваемо, если существует 2-авто-
мат Л (детерминированный или недетерминированный) и
множество AF заключительных состояний для JL, такие, что
Ыгл{АР) = и.
Теорема 1. (Эквивалентность недетерминированного и
детерминированного автоматов: конструкция подмножеств.)
Множество U <=,Тъ распознаваемо детерминированным
^-автоматом тогда и только тогда, когда оно распознаваемо
недетерминированным Ъ-автоматом.
Доказательство. В одну сторону эквивалентность
тривиальна, поскольку любой детерминированный автомат <А = (Л, а)
соответствует недетерминированному автомату JLr = (Л, а'),
где а£ есть график функции af (т. е. o!f(av ..., ап,а)<-*>
4->af(au ..., ап) = а). Для любого AF^A имеем 6/г^(Л/?)==
*=bh*>(AP), так как h*>(t) = {h*(t)}.
Для доказательства в другую сторону (в этом случае
эквивалентность также очевидна интуитивно, если исходить из
обычной теории конечных автоматов) предположим, что задан
недетерминированный автомат М = (/?, р), такой, что U = hhm (RF).
Тогда из Si мы построим «автомат подмножеств» ut = (2R, р).
(Обозначение р не совсем аккуратно, мы подразумеваем, что
Р (/)= Р/) Простое доказательство по индукции (которое мы
предоставляем проделать читателю) показывает, что в
действительности МиА имеют одинаковые выходные функции: кл (t) =
= Л*(0- Заключительные состояния автомата Л выбираются
следующим образом:
АР = {и | и £ R и и П RF Ф 0}.
Таким образом,
t е= bh*(AF)+-+h*(t)е= AP+-+hm(t){]Rf¥= 0 ++t<==:bhm (RF).
Следовательно, Ыгл{АР)=* bh*{RF\ и теорема эквивалентности
установлена. ^
Так как мы доказали эквивалентность детерминированных
и недетерминированных автоматов, то мы будем пользоваться
термином «распознаваемый» без ссылок на род автомата. Как
известно из обычной теории конечных автоматов, для
некоторых целей необходимы недетерминированные автоматы; в
других случаях требуется использовать детерминированные
автоматы. Доказательство следующей теоремы о замыкании
относится к последней категории автоматов; теоремы о замыкании
распознаваемых множеств относительно проекции и регуляр-
Обобщенная теория конечных автоматов и ее приложения 119
ных операций требуют использования недетерминированных
автоматов.
Теорема 2. (Замкнутость распознаваемых множеств
относительно булевых операций.) Если U и V суть
распознаваемые подмножества множества 7s, то U0V и Тъ — U
распознаваемы.
Доказательство. Пусть Л и 35 суть 2-автоматы,
такие, что bh^(Ap)^U и 6А^(Й^)=7. Тогда
(1) bhAA-AF) = Tz-Uy
(И) Ыихл(АРХВР)-иПУ9
где otX Я? — прямое произведение алгебр Л и &. В силу
сходства с обычной теорией мы опускаем подробности
доказательств равенств (i) и (и).
Теорема о булевом замыкании имеет дело с операциями
над подмножествами термов одной специи; напротив, теорема
о проекции, которую мы теперь рассмотрим, имеет дело с
распознаваемыми подмножествами, возможно, различных специй.
Действие проекции состоит просто в замене символов (иногда
многих одним) в термах. В этом случае нетрудно установить,
что класс всех распознаваемых множеств замкнут относительно
проекции.
Чтобы уточнить понятия, изложенные выше, возьмем две
специи (2, а) и (Q, со). Отображение я: 2-+Q, которое
удовлетворяет условию a(f) = (d7t(f) для всех fe2, может быть
продолжено до отображения я: Тъ-+Та следующим образом:
(i) для ^eS0 имеем я(А,) = л{Х);
(ii) для feSrt и <i /йбГх
я(#1 ... 'n)e«(/)«('i) .- «('«)•
Таким образом, мы рассматриваем соответствия между
двумя множествами функциональных символов; расширение до
термов делается естественным образом. Любое отображение,
полученное так, называется проекцией. Следующие две
теоремы показывают, что распознаваемые множества замкнуты как
относительно проекций, так и относительно обратных проекций.
Теорема 3. (Замкнутость распознаваемых множеств
относительно проекций.) Если U есть распознаваемое
подмножество множества^ Тъ и если й есть проекция Тг в Tq, то
я (U)~ распознаваемое подмножество множества Та.
Доказательство. Пусть s& = (Л, а) есть 2*автомат с
поведением 6/г«*(Л/?) — U. Мы построим недетерминированный
Я-автомат 91 = (Л, р) с отношениями перехода
120
Дж. В. Тэтчер, Дж, Б. Райт
(i) р\ = {аб | б е 20 и я (б) = Я) для А, е Q0;
(ii) для /eflnHCj ап, CGi4 имеем р/ (аь ..., ап> а) «-►
<->ag(ai, ..., ап) = а для некоторого g, такого, что n(g) = f.
Доказательство требуемого свойства поведения, а именно
(I) n[bhjt(AP)] = bh.(AP),
зависит от следующих двух свойств:
(II) й«с(0^А*(я;(0) для всех /е=7У,
(III) для всех ГеГд имеем а£АЛ(Г)->А^(;) = а для
некоторого f, такого, что я (/) = /'.
Из (II) мы получаем, что если t^bh^(AF)t то h^(t)^ha (n(t))
и, следовательно, Л* (я (f)) f| AF ф 0 и я(/) е &Л* (Л/?);
я [bh^(Ap)] s &Л* (/?f). Обратное включение следует из (III).
Доказательства (II) и (III) проводятся по индукции одинаковым
образом; мы докажем только (III).
Для f = ^GQ0, если а£рА, то из (i) получаем, что a = a6
для некоторого б, такого, что я(б) = А,. Таким образом, при
выводе (III) положим t равным б: /^(0-°¾ и я(/) = А,. Теперь
пусть / есть n-местный функциональный символ из Q и
предположим, что (III) верно для термов t'v ..., ?п. Рассмотрим
терм V==ft[ ... t'n. Если oGft^ (t')t то по определению h9
существуют av ..., ая, где а.еАД^), такие, что pf(ap ..., ап, а).
Это означает (в силу (ii)), что существует функциональный
символ geS, такой, что n(g) = f и ag(au ..., aj = a.
Применяя теперь предположение индукции к t'v мы видим,
что существуют 2-термы tu ..., /„, такие, что n{ti)==t\ и
h^(t.)= аг Таким образом, t надо взять равным g/, ... tn, и
мы получаем (по определению я и Л«Д что я(/) = V и
/и(0 = <%(0 = %(/u(*i), ..., h^(tn)) = a. Следовательно, по
индукции мы установили свойство (III); утверждение (II)
доказывается подобно (III), как уже отмечалось.
Теорема 4. (Замкнутость распознаваемых множеств
относительно обратной проекции.) Если U ^Тъ распознаваемо и
если л —проекция множества Та в jTz, то h~~l(U) является
распознаваемым подмножеством множества jTq.
Доказательство. Пусть <Л = (А,а) есть. 2-автомат,
такой, что Ыгл{Ар) = и. Построим Q-автомат SS = (A9 р), где
Pf ^ аШ) Для всех символов / е Q. По индукции мы докажем, что
а)
М') = М*(')).
Обобщенная теория конечных автоматов и ее приложения 121
Для / = Аей0 это верно в силу определения р: йЛ(Я) = РЛ =
^ ал (К) = ^л (я М )• Предполагая, что (I) верно для термов
/i, , <„, рассмотрим ^ = /^1 ... tn. Тогда
M'HMM'i). .... M'«))-<WM*('i)). .... МЙШ-
Но правая часть этого равенства есть прос.то h,#(n>(t)).
Теперь, если t^A~l(U)f то существует некоторое ?, такое,
что Ал (?) е Л/? и я (*)=-=/'. Но в силу (I) кл{?) = h^(t)^ AF и,
таким образом, t^bh^(AF). Поэтому мы имеем A~l.(U)sbh#{Л/?).
Для обратного включения предположим, что t^bh^iAp). Тогда
^(я(())е^ и, следовательно, n(t)^U\ это убеждает нас
в том, что t^n~*l(U). Таким образом, по нашему построению
автомат ^ распознает я-1([7), и теорема 4 доказана.
В приложении обобщенной распознаваемости к решению
проблемы разрешения (разд. 4) мы будем интерпретировать
подмножества множества Т% (с соответствующим выбором 2)
как определимые отношения ограниченной теории второго
порядка. При такой интерпретации мы можем говорить, что то или
иное отношение распознаваемо. Необходимо будет доказать, что
определенные отношения распознаваемы, и потом показать, что
распознаваемые отношения замкнуты относительно пропози-
ционных связок и квантификации. Эта последняя задача
выполнена с помощью применения теорем о замыкании, которые мы
доказали; мы могли бы доказать распознаваемость
примитивных отношений действительным построением работающего
автомата. Однако лучше использовать теорию регулярности,
которая интересна независимо от приложений и которую мы
изложим в следующем разделе.
Приложение к проблеме разрешения было бы бесплодным,
если бы не тот факт, что определенные вопросы, касающиеся
обобщенных автоматов, могут быть решены эффективно.
Как и в случае обычной теории конечных автоматов, мы
могли бы относительно большого числа утверждений показать,
что все задачи можно решить эффективно. Однако наше
приложение требует только одного доказательства; мы покажем,
что существует эффективная процедура для ответа на вопрос:
«Ыгл(АР)=* 0?».
Эффективное решение вопроса «Ыгл(Ар)=* 0?» для обычных
конечных автоматов зависит от проверки всех входных цепочек,
длина которых не превосходит числа состояний автомата $£ и
которые порождают выходные состояния из AF\ более
длинный вход w приводит к повторению промежуточных состояний,
и, таким образом, удаление «куска» w позволяет построить
более короткую цепочку с тем же выходом. То же самое можно
122
Дж. В. Тэтчер, Дж. Б. Райт
сказать в обобщенном случае, хотя мы должны быть более
точны в отношении «длины» и «удаления куска». Так как
каждый Е-терм / в действительности есть цепочка (/g2*), то мы
хотим .сохранить понятие длины l(t) в том виде, как это и
подразумевалось здесь, — как число символов в t\ вместо этого мы
будем говорить о глубине терма (что интуитивно более
содержательно) и определим ее рекурсивно следующим образом:
(i) d (X) = 1 для к <= 20;
(И) dUU ... fj-max {dfo)}+l.
i
Процесс преобразования входа при условии, что получается
то же самое выходное состояние, приводит в общем случае к
известному понятию замены. Нам Нужно ввести понятие
подтерма: V есть подтерм терма t, если существует терм /", такой, что
/ есть результат замещения некоторого вхождения индивидного
символа в t" на t\ Используя обозначение t >> V для случая,
когда «t имеет V в качестве подтерма», мы дадим формальное
определение следующим образом:
(i) для Ле20 X^tf тогда и только тогда, когда А = /';
(И) для /е2«, /ь ...» tn^Tv и t = ft{ ... tny t^f тогда
и только тогда, когда t=*tf либо t^t' для некоторого /,
\<i<n.
Важное свойство замены, относящееся к конечным
автоматам, состоит в том, что если подтерм t\ терма / заменить
термом h, который вырабатывает то же самое выходное состояние,
что и tu то результат замещения вырабатывает то же самое
выходное состояние, что и /. Этот факт, аналогичный леммам о
замене в логике, будет доказан ниже.
Лемма 5. (Лемма о замене.) Если Л есть ^-автомат и
tb t2i t, f суть t-термы, такие, что ? получается из t заменой
вхождения t2 на tu и если /u(/i) = /u(*2), то hA(t)**h*(?).
Доказательство. По индукции по построению термов,
если' t = Я, то h = t и V « t\\ кл(t) = кл (*2) =5 Ьл {U) = кл (*')• Для
t — ft\ ... t'n если замена появляется в одном из термов fp то
по индуктивному предположению h^(t)*=h^t'). Если t2^tff
(для удобства пусть t\), то V'«/VJ ... t'n, а так как А^(*,) =
eM'i)« то ясно, что h^(t)^h^{f).
Повторным применением леммы о замене к
неперекрывающимся или несравнимым вхождениям подтермов в терме / мы
получаем следствие, которое нам понадобится в разд. 3.
Обобщенная теория конечных автомате и ее приложения 123
Следствие. Пусть заданы несравнимые
(неперекрывающиеся) вхождения подтермов tb ..., ts терма t. Если V
получается путем замещения t. на t\ и если ^(^)=/^(^)
(/-1,..., s), токЛЦ) = кЛ(Г).
Теперь мы можем доказать свойство, с помощью которого
получим эффективное решение проблемы пустоты.
Лемма 6. Пусть Ж есть ^-автомат с п состояниями. Если
существует терм t, такой, что h^(t)=^a^ А, то существует
терм t\ такой, что d{t')^n и h^(t') = a.
Доказательстве^. Мы имеем h*(t)=*a. Если d(t)^n, то
лемма выполняется. Если d(t)>n9 то существует по крайней мере
одна последовательность подтермов / = t0 > t{ > ... > td {t) e 20
(t )> t' тогда и только тогда, когда t^tf и t Ф V). Как известно
из обычной теории, соответствующая последовательность
состояний ^=^(^.) должна содержать повторение, например
а^ = а/ для /</. Тогда по лемме о замене, если V получается
из t заменой tf на th то Л^(0=*^(Г). Теперь d(t')^l(t')<l(t),
и, таким образом, если d(tf) все еще больше, чем п> то мы
повторяем описанный процесс до тех пор, пока не получим
приведенный терм, который имеет глубину, не превосходящую п,
и вырабатывает выходное состояние а.
Теорема 7. (Эффективное решение проблемы пустоты.)
Пусть задан ^-автомат s&. Тогда существует эффективная
процедура для выяснения, имеет ли место равенство Ыгл(Ар) = 0.
Доказательство. Из предыдущей леммы очевидно, что
такая процедура состоит просто в проверке всех термов t, для
которых d(t)4^.n, где п — число состояний автомата зФ. Если
хотя бы один такой терм имеет выходное состояние из AF, то
bhst{AF)¥= 0; в противном случае &Л^(Л^)==0.
3. ОСНОВАНИЯ ОБОБЩЕННОЙ ТЕОРИИ РЕГУЛЯРНОСТИ
В этом разделе мы опишем алгебраические характеристики
распознаваемых множеств, аналогичные тому, что может быть
названо теорией Клини для обычных конечных автоматов.
Исследования в этом направлении мы начнем с введения понятия
сложного произведения и операций замыкания на множествах
термов. Пусть (2, а) есть специя; для каждого Хе2р
существует произведение и операция замыкания, обозначаемые и • %V
и Uk (аналогично U-V и £/*). Для множеств £/, V s Гх
множество U-уУ есть множество всех термов fe 7s, для которых
124
Дж. В. Тэтчер, Дж. Б. Райт
существует f е U, такое, что t получается замещением каждого
вхождения X в V некоторым элементом из V. Заметим, что
различные вхождения X могут быть заменены различными термами
из V.
Следующие примеры сложного произведения иллюстрируют
некоторые важные случаи:
(a) f/.,{^} = [/, {X}.KU = U;
(b) U *^0 есть множество термов из С/, которые не
содержат X;
(c) если СЛ £ С/2 и У, s V2, то С/,. ^ s U2 • KV2.
Операция замыкания определяется так же, как в обычной
теории, сначала описанием последовательности множеств:
Х° = {К},
Xn+l = Xn[}U-j,X\
а затем
оо
и*= \3хп.
п=0
Так как X1 = U [}{Х}У имеем U s Uh и легко проверить, что
U • jJJx ^ Ux. Приведем следующие примеры использования
операций замыкания.
(d) Пусть A^ = {fX\ ... Xn\Xi е2о, f^^nY, множество Ле есть
множество атомных (не индивидных) термов. Если 20 = {А,}, то
Л|=Г2. Если 20 = {Я, б}, то Ш6 = {АъУ = Тъ.
Последний пример наводит на мысль о возможности
(которая была бы желательна) коммутирования различных операций
замыкания; это опровергается следующим рядом примеров
(2 = {£, Я, б}, 20 = {Я, б}, 21 = {£}):
(e) {gM6 = {6, Я*};
(О {gttk = {K gK ggK gggK ..Л;
(g) ({^)б)" = {б, gXf-Tr,
(h) ({gtf)6 = {W{gtf¥*Tx.
По аналогии с теорией конечных автоматов эти операторы
подсказывают естественное определение регулярности. Класс
^-регулярных подмножеств множества Тъ есть наименьший
класс подмножеств множества Ге, который содержит конечные
подмножества и замкнут относительно U, ч и А для всех X из
S0. И тогда желаемая теорема имела бы вид: множество термов
2-регулярно тогда и только тогда, когда оно распознаваемо
Обобщенная теория конечных автоматов и ее приложения 125
2-автоматом. К сожалению, это неверно. Например, возьмем
2г = Щ и определим V индуктивно следующим образом:
(i) Л €5 У;
(И) если t<=V, то Ш е V.
При этом V распознаваемо, но не регулярно (в предположении,
что 2 = {ЛД}). Если мы добавим другой индивидный символ, а
именно б, то
К = {Ш^.б{Л}.
Таким образом, V является- ^/-регулярным для множества
символов 2', которое является расширением 2. Это приводит нас
ко второму определению: U ^Т^ регулярно, если существует
специя (2', о'), такая, что 2^ = 2„для п> 1 и U является 2'-ре~
гулярным. Таким образом, в соответствии с данным
определением множество V в приведенном выше примере регулярно.
Этот пример иллюстрирует важную черту определения
регулярности. Для того чтобы получить все распознаваемые
подмножества множества Is, нам потребуется расширить
множество символов 2 до множества, содержащего новые индивидные
символы, а также и правило произведения
«незаключительный —► заключительный»; последнее из приведенных выше
равенств замещает дополнительные индивидные символы
индивидными символами из S.
Теперь мы докажем основную теорему этого раздела.
Теорема 8. (Эквивалентность распознаваемости и
регулярности.) Множество U <^Тъ распознаваемо тогда и только
тогда, когда оно регулярно.
Доказательство этой эквивалентности состоит из двух
основных частей: теорема анализа показывает, что каждое
распознаваемое множество регулярно; теорема синтеза в свою очередь
состоит из четырех частей: мы должны доказать, что все
конечные подмножества распознаваемы и что все распознаваемые
множества замкнуты относительно U (теорема 2), -х и \ а это
означает, что каждое регулярное множество распознаваемо.
Теорема 9. (Теорема анализа.) Каждое распознаваемое
подмножество множества Ts регулярно.
Доказательство. Пусть s4 есть автомат с состояниями
А = {аи . •., #т} и заключительными состояниями AF,
распознающий подмножество U ^ Ts. Мы построим новое
множество символов 2' = (2 — So) U {h, ..., hm} и 2'-автомат зФ',
который в точности совпадает с s£} за исключением того, что
126
Дж. В. Тэтчер, Дж. Б. Райт
а'к — а( -для i = 1, ..., m. Сначала проанализируем поведение
автомата s/>' и из этого анализа получим регулярное
множество, которое является поведением автомата $Ф. Значение
добавленных Kj показывает следующее. Пусть t — произвольный
2'-терм, такой, что Л^(/)=аеА Если hjc(t') = ajt то из
леммы о замене следует, что кл (tf/) ~ а для любого t'\
получаемого замещением kj на f в /. Таким образом, Kj играет роль
некоторого рода пунктуации (подобно нетерминальному символу
в определении языка с помощью формальной грамматики), и
оно может быть замещено любым термом, который переводит
автомат в состояние ау, результат замещения будет переводить
автомат в то же самое состояние, что и исходный терм.
Чтобы проанализировать $£■\ мы определим последователь*
ность недетерминированных автоматов JLX, ..., JLm = <А'. В
каждом случае множество состояний есть Л, а переходы являются
функциями (очень удобно сохранить функциональные
обозначения), но определенные не на всем множестве А. В частности
akf(ab , ап) определено для /eSn тогда и только тогда,
когда а/(аь ..., ап) е {аь ..., ак}, и в том случае, когда оно
определено, имеем ajf(a,, ..., ап) = af(a1? ..., аД Для
индивидных символов и для всех & имеем a£ = а.. Конструкция
вполне ясна; зФк совпадает с s£', за исключением того, что
неинициальные переходы разрешаются только для множества
{аь ..., ан} S А. Мы рассмотрим последовательность автоматов,
используя регулярные множества, полученные при анализе s&h,
для анализа поведения s£h+l. С этой целью определим для
каждого k и i
Действительно, Т\ =? Ыгль ([а{]). Заметим, что , мы должны
были записать h^k(t)=^[at)9 но так как все переходы
функциональны, то все такие множества либо состоят из одного
элемента, либо пусты, поэтому мы можем обойтись без обозначения
множеств.
Теперь мы можем дать индуктивное доказательство того, что
Т\ регулярно для i = 1, ..., m. Для k = 1 и i Ф 1 множество
Т\ = {А,*}, очевидно, регулярно; для i=l мы утверждаем, что
(I) П - Ufr
где £/* в общем случае определяется так:
Обобщенная теория конечных автоматов и ее приложения 127
Подробное доказательство равенства (I) мы предоставляем
провести читателю. Существенно, что включение Т\ ^ £/?"
доказывается индукцией по построению термов, а включение
U\x S Т\ доказывается индукцией по последовательности,
используемой в определении и\\
Основное предположение индукции состоит в том, что т\
регулярно для i = 1, ..., m, и'мы хотим показать, что Т\+х
также регулярно. Мы получаем Г?+1 с помощью следующих опре-
делений: ^.(.^((^.^.^...).^
Теперь мы хотим доказать, что
(И) Tki+l = Tkt.h+1W, *-1, ..., ft+1.
Очевидно, что т)+х Аля i>k + l просто равно {Aj.
Для t = fkt ... Я^ е(/Н1 имеем hAb+\(t) = ak^x по
определению Uk+X. Следовательно, по лемме о замене (если
V е {t} • Л/Гь то h& (f) = кЛ' (t)) мы получаем, что каждый
терм из V также будет вырабатывать выходное состояние ak+\.
Идентичными рассуждениями мы устанавливаем, что если
/ef, то h^k+i (t) = ak+v Наконец, если / е= Т\ • к W, то
снова из леммы о замене следует, что h^+\{f) — ar Мы имеем
Для равенства (II) включение в другую сторону
доказывается труднее. Мы ^должны доказать для этого, используя
индукцию по л, следующее утверждение.
(III) Если h^k+iit)**^ и существует в точности п
вхождений неинициальных переходов в щ+{ при вычислении h^k+i(t),
Т0 ШТК^ где *0=S{V.} и Xn+i = Xn\)V-4+X\
Если не существует неинициальных переходов в ak+u то
/е Г? = Г* • jtft+1{A*+i}. Предположим, что (III) верно для л,
и рассмотрим терм /, такой, что A^+iW — flj и вычисление
A^*+i(0 имеет в точности п + 1 переходов в ал+1. В этом случае
существуют термы tu t2, такие, что (1) A^fc+i^)88" ^ и имеется
в точности п переходов в ak+{ в вычислении A^+i^,);
(2) A^+i(/2)= afe+1 и (3) t получается путем замены одного
вхождения kk+i в t{ на t2 (а всех остальных на Я^+i).
128
Дж. В. Тэтчер, Дж. Б. Райт
Из (2) следует, что t2 = ft{ ... tn, и при соответствующем
выборе Xij имеем Д/} ... ^e(/Hi. В вычислении каждого
из h^k+iit.} не может быть неинициальных переходов в ak+x
(так как в t2 имеется только один) и, следов ательдо, каждое
tj^Tt, поэтому t2^V. Согласно (1) и индуктивному
предположению, имеем t\^Tkt • xk+iXn, что ввиду (3) дает
t<=(Tki -ц+1Хп)- ik+lV. Легко проверить, что
(тк Vn\ Л Г I— т& vti+1
It -bk + iX )'Ч+1У-11 * *>k+lX •
Таким образом, по индукции мы установили (III). Так как
У Tki-h+iXn = Tki-h+lWH, как мы показали, т\+х czjj Г?.Хл+1Г.
то равенство (II) справедливо.
Этим заканчивается доказательство основного индуктивного
предложения о том, что. Т\ регулярно. Теперь мы хотим
связать эти результаты с поведением исходного автомата s&.
Мы показали, что каждое из множеств Т? регулярно и что
ТТ есть множество всех 2'-термов, которые вырабатывают
состояние а\ в автомате s£'. Если бы нас интересовал только
автомат s&\ то
bhA>(AP)~ U ТТ.
at<=Ap
В действительности мы имеем поведение автомата <5$, за
исключением начальных состояний. Если мы определим
то
ЪкЛ {AF) = ЪкЛ> {Ар) - a,,Ai . ^A2 • ... • xmAm.
Это верно потому, что (1) если а$ не есть начальное состояние,
то Aj = 0 и все термы, содержащие Jtj, исчезают в
произведении, и (2) если <2j есть начальное состояние, то Aj есть
множество индивидных символов, значением которых является ajy и в
произведении Xj может быть замещено на любой из индивидных
символов из Aj. Мы показали, что Т? регулярно.
Следовательно, Ькл'{Аг) регулярно, и, наконец, последнее равенство
приводит нас к желаемому результату: bh^{Ap) регулярно.
Как было уже сказано, теорема синтеза состоит из четырех
частей, первую из которых мы приведем без доказательства.
Лемма 10. Все конечные подмножества множества Тх
распознаваемы.
Обобщенная теория конечных автоматов и ее приложения 129
Простейшее доказательство этой леммы состоит в
индуктивном построении автомата, распознающего одноэлементные
множества; тогда в силу теоремы 2 будут получены все конечные
множества.
Мы уже доказали замкнутость распознаваемых множедтв
относительно операции объединения множеств; следующие две
леммы показывают их замкнутость относительно сложного
произведения и операций замыкания.
Лемма Н. (Замкнутость распознаваемых множеств
относительно • 6.) Если U и V суть распознаваемые подмножеств/г
множества Тг,, то U • bV есть распознаваемое множество для
любого 6 е So-
Доказательство. Пусть заданы автоматы Л и <$ (с
множествами заключительных состояний AF и Вр), которые
распознают U и V соответственно; мы построим
недетерминированный автомат Ж = (/?, р), где R = A U В, а отношения перехода
определяются следующим образом:
(i) для X & Sq
[ {аб, ръ ал>, если XфЬ и feefl^,
л _ (ая> РлК если Я, =^ б и рЛ <£ В/,,
Р я — »
К, fle>, если А, = б и %e=:'BF\
. ( (PeK если X = 6 и $ьфВр\
(н) для /sJ„, а^еЛ, ft,е= В и Ig/?
pf(ab ..., ая, X)^->af(ab ..., aft) = X,
pf(&„ ..., 6Я> J)^pf(6„ ..., Ьп) = Х
или
0,(6,, ..., bn)^BF и X = ad.
Мы утверждаем, что bh*(Ap)~ U * 6V. Этот факт вытекает
из следующих двух предложений:
(I) aeMO^anfesfrbeK и /и(П = я],
(II) freMO^MO-k
Если t € 6А* (Л/?), то А# (ОП ^f =j£ 0. Таким образом,
существует некоторое абА# (i£ которое также является
заключительным состоянием автомата <4- Но, согласно (I), существует
V & U, такое, что t е {*'} • 6V и, следовательно, t <= £/ • bV.
Обратное, т. е. V • 6V & bit* (Ар\ также немедленно следует
из (I). В действительности мы должны использовать (II) для
130
Дж. В. Тэтчер, Дж. В. Райт
проведения индуктивного доказательства (I), к которому мы
сейчас переходим.
Для /eS0 сначала рассмотрим случай t = k=£6. Если
a g fts (Д то из (I) либо (а) а==ах, либо (Ь) а = а6 и fa^BF.
В случае (а) в качестве V возьмем А,. Тогда X е {л} • 6V и
h^(l)==ak. В случае (Ь) положим f = б. Так как ЯеК, мы
имеем X = {6}-6V и, кроме того, Л^(б) = а6. Теперь, если £ = 6,
то ag/i< (0 тогда и только тогда, когда а = аб и р6 е Б/?. Но
при этих условиях 5е|/ и, таким образом, при /' = 6 имеем
t^{6}-bV и Л^(б) = а6. Все это дает доказательство базисного
случая (t е 20) соотношения (I) в одном направлении; назовем
его (1->). Доказательство (I<—) мы предоставляем сделать
читателю, так как оно проводится аналогично путем разбора
отдельных случаев. Для базисного случая соотношения (II)
мы заметим, что, согласно (i), Ъ е= h* (Л)«-> Ъ = ^ (независимо
от того, выполняется ли равенство Л = 6) и й#(^) = Рл» поэтому
(II) легко проверяется.
В индуктивной части доказательства предположим, что
(I) и (II) выполняются для термов tb ..., tn9 и пусть / есть
символ п-местной функции, такой, что t = ft{ ... tn. Рассмотрим
соотношение (I-*). Если a s А« (/)» то в силу (И) нужно
рассмотреть два случая. Либо (а) существуют ^ е Ал (^-), такие,
что af(ab ..., ап) = ау либо (Ь) существуют 6f- е Ал (У, такие,
что Pf(6i, ..., bn)^BF и а = а6. В последнем случае
индуктивное предположение (II) дает нам, что h$(ti)=bi и,
следовательно, h<$(t)^BF, t^V. Таким образом, для (Ь) мы можем
положить /' = б; t^{6}-6V и Л^(б) = аб = а.
В случае (а) из индуктивного предположения (I) следует
существование термов t\, таких, что /Je/J-eV и h^(t') = ar
Таким образом, мы можем взять tf = ft[ ... t'n; tf^t'-6V и
ЫП-чЫЪ .... Л-сЮ)-«,К .... «„)=«•
Мы доказали переход по индукции для (1->), а
доказательство случая (I*-) снова предоставим сделать читателю. Для
(II), как и в случае базы индукции, мы видим, что b^h*(t)
тогда и только тогда, когда существует bi е h» (tt) и
Р/(61, ..., bn)*=b. Но по предположению индукции мы знаем,
что это эквивалентно тому, что h$(t)**b.
Мы установили предложения (I) и (II) по индукции;
согласно приведенным выше соображениям о связи (I) и (II) с
требуемым результатом, доказательство леммы II завершено.
Лемма 12. (Замкнутость распознаваемых множеств
относительно б.) Если U^Tz — распознаваемое множество, то U6
также распознаваемо.
Обобщенная теория конечных автоматов и ее приложения 131
Доказательство. Пусть si> — автомат, у которого
Ъкл (AF) = £/. Мы построим недетерминированный автомат
52 = (Л,р), имеющий следующие отношения перехода:
(О 9х = Ю для А е 20;
(и) pf(au ...,ая, *)«r*af(a,, ..., an) = * илиа/(а1, ..., an)e=
e AF и x = a6 для /е2п и аг-, л: е Л.
Доказательство того, что эта конструкция приводит нас к
требуемому результату, т. е. что ЬНЛ (AF)='U6, аналогично
доказательству леммы И, поэтому подробности мы опускаем.
Леммы 10—12 вместе с теоремой 2 из разд. 2 дают нам
теорему синтеза, а именно что каждое регулярное множество
распознаваемо. Вместе с теоремой анализа эти результаты
завершают доказательство основного утверждения этого
раздела, т. е. эквивалентности распознаваемости и регулярности
(теорема 9).
Мы закончим этот раздел об обобщенной регулярности
введением еще одной операции над множествами термов, которая
сохраняет регулярность: некоторого рода обращения 6-сложного
произведения
U/6V = {t\({t}^V)OU^0}.
Эта операция, называемая иногда сокращением [truncation]
или правым делением, может быть описана как операция над £/;
процесс состоит в том, чтобы взять каждый терм /gJ/и
отнести к U/6V любой терм t', который может быть получен
одновременным удалением (замещением на б) непересекающихся
подтермов терма t, принадлежащих V, при условии, что
каждое вхождение б должно содержаться в некотором
замещаемом подтерме, хотя могут замещаться и подтермы, не
содержащие б.
Лемма 13. (Замкнутость распознаваемого множества
относительно деления.) Если U^Tz распознаваемо и V есть
произвольное подмножество Тъ, то U/^V распознаваемо.
Доказательство. Предположим, что автомат JL = (А, а)
распознает С/; bh^(AF)=U. Пусть Av =(/^(/) 1*е V}', мы
построим недетерминированный автомат <^ = (Л, р) следующим
образом:
(0 Рь = {а?Д и Рб = Ау для А,€=20 и К Ф б;
(ii) pf есть график а{ для f eSft.
132
Дж. В. Тэтчер, Дж. Б. Райт
Таким образом, автомат Si является недетерминированным
автоматом только за счет множества его начальных состояний
для индивидного символа б; в остальном он в точности
совпадает с з4>. Мы докажем, что bhm {Af)~ U/bV, путем
установления следующих двух утверждений:
(I) Ге=*.вУ-*й<с(ОеМ*),
(II) a<=h*(t)-*Btl[h.*(t') = a и t'e=t-6V].
Утверждение (I) дает нам включение UjbV s bfix (Af)
следующим образом. Если t е U/bV, то по определению операции
деления существует некоторое V щ U f| / • б1Л Следовательно,
h^{tf)^AF, и, согласноШ, hjt(t')&hm(t). Поэтому ft* (О Л А?Ф<£
и /еМ,(Л/?). Из утверждения (II) мы получаем обратное
включение* Ыг* (Af) £ U/bV: если t & bh& (Af), то существует
некоторое og Ap(]hm(t). Из (II) следует также, что
существует /', такое, что h*(t'y***a& Af и /'e/^I/. Таким
образом, t^V(]U^09 и по определению операции /6, t&U/6V.
Теперь мы продолжим доказательство утверждений (I) и (II)
индукцией по определению термов.
Доказательство утверждения (I). Индукция по t.
Если t = X Ф 6, то V должно быть равно X и ' кл (tf) =
==- аЛ^ ft* (/)=*{%}. Если /=*$, то V может быть любым
элементом из V, и /u(V)es Av=** ft* (f). Предполагая,
что-утверждение (I) верно для термов ^,..., tn, рассмотрим терм
t*=fti ... tn. Для tf &t * 6V должны существовать термы tt
(/=1, ..., п\ такие, что / — //...** и /Je^-бК. Из
предположения индукции /u(*9^ft*(*i) и из того, что по
определению Л* (О = $f(h* (t[\ ..., ft* (/„)), мы получаем, что
h*{t) = *f{h*(ti)9 ..., h*(ta))ehmit').
Доказательство соотношения (II). Так как из
t шв А ^ б, а е A* (f) следует, что а = аъ то, взяв /' = А, мы
получим, что кл(f) -= а и /' е * • 6V. Если / = 6, тоизаеА^ (/)
следует, что Нл(У) = а для некоторого ГеУ. Но мы имеем
также t'&t-6V, что завершает доказательство для индивидных
символов. Пусть теперь t**fti...tn, и предположим, что
свойство (II) имеет место для 4tt (/==1,/.., п). Выражение
аЫкя (0 означает, что существуют a* е ft* (/,), такие, что
Pf(au ..., aft, а). По индукции существуют //, такие, что
Нл 09 ^cii и t't^ti- bV'. Ясно, что / = //1... /¾ удовлетворяет
утверждению (II).
Обобщенная теория конечных автоматов и ее приложения 183
4. ПРИЛОЖЕНИЕ ОБОБЩЕННОЙ ТЕОРИИ АВТОМАТОВ
К ПРОБЛЕМЕ РАЗРЕШЕНИЯ ОГРАНИЧЕННОЙ
ИНТЕРПРЕТИРОВАННОЙ ТЕОРИИ ВТОРОГО ПОРЯДКА
Мы будем использовать стандартный алфавит Ak = {I,
2, ..., k) для множества Nk цепочек Jfe-символов; Nh содержит
пустую цепочку Л. Арифметические теории со многими опера*
циями следования используют множество Л/* (при некотором k)
и k (правых) функций следования гь ..., гЛ, где ra(w)~wo
(Ла = а) для всех w е Nki а также отношения и функции,
которые могут быть рекурсивно определены с помощью функций
следования. Здесь мы коснемся слабой одноместной теории
второго порядки для Nkck функциями следования.
Соответствующий язык 2% ест*> прикладной одноместный
язык второго порядка, содержащий следующие компоненты:
(i) индивидные переменные х9 yf г, хи ..., принимающие
значения из Nh\
(И) множественные переменные а, р, аь'- • •» принимающие в
качестве значений конечные подмножества множества Л^р^ДО*);
(Ш) константы =,е в их обычной интерпретации;
(iv) символы двуместных предикатов Ra (а е Ah),
интерпретируемых как графики k функций следования
Ro(u, v)+~+ra(u)**v;
(v) пропозициональные связки, индивядные кванторы и
кванторы по множествам, пунктуация и скобки, какие требуются для
прикладного языка.
Правила образования для формул в яз|аке 2^ обычные;
атомарными формулами являются выражения вида х = у,х&а или
Ra(x>y)i и если F и G СУТЬ формулы, toF A G, ПЛ Э*/7, Эа^
(х — любая индивидная переменная, а — любая множественная
переменная) также являются формулами. Предложениями в
языке 3?ъ. называются такие формулы, в которых utj свободных
переменных.
Теория, которую мы. здесь рассматриваем, называется слабой
одноместной теорией второго порядка со многими операциями
следования и состоит из всех предложений в языке 24,
истинных относительно указанной интерпретации. Формальное
определение языка и его интерпретации опущены, так как мы
надеемся, что природа языка ясна из данного описания, и большая
формализация только осложнит дело.
Выразительная способность элементарного языка со многими
операциями следования (т. е. языка, описанного выше без
множественных переменных или кванторов по ним) весьма
ограничена; единственными определимыми множествами являются
134
Дж. В. Тэтчер, Дж. Б. Райт
дефинитные множества, а, например, отношение префикса
u<v*-*3wy w = v, не является определимым [18]. Добавление
конечного множества переменных и кванторов усиливает
выразительную способность языка; Райт показал, что все
регулярные подмножества множества Nh определимы, и для того,
чтобы привести пример определения, укажем, что следующая
формула определяет отношение префикса в 2V
Va[y <s AA4z4w[z^aA(Ri(w, z)VR2(w> z))-+w еа]->л:еа]#
Эта формула (обозначим ее F(xyy)) определяет отношение
префикса в том смысле, что F(uy v) истинно тогда и только
тогда, когда и есть префикс для v для всех и, v ^ N2. Формула
F(xyy) требует, чтобы каждое конечное множество,
содержащее у и замкнутое относительно предшествования (если wo е ос,
тошба), также содержало и х.
Слабая одноместная теория второго порядка с одной
операцией следования (случай k = 1) разрешима. История этого
результата, как это показывает Донер [8], такова: доказательство
впервые было найдено Эренфойхтом, но не было им
опубликовано (смЛ16, 10]). Последующие доказательства были найдены
независимо Бюхи и Элготом [3] и опубликованы ими в
работах [4, 9].
Вопрос о разрешимости слабой одноместной теории второго
порядка со многими операциями следования впервые был
поставлен Бюхи [4]. Донер [8] получил положительный результат,
используя понятие обобщенного конечного автомата, которое
сходно с приведенным здесь и было сформулировано
независимо. Метод применения этих понятий аналогичен методу Бюхи
и Элгота для случая одного следования.
Теорема 14. (Донер.) Слабая одноместная теория второго
порядка со многими следованиями разрешима.
Далее мы будем говорить только о случае k = 2; обобщение
на случай более чем двух функций следования не представляет
трудности. Процедура доказательства состоит в следующем:
(I) Найти язык =2*2, эквивалентный языку &%> который не
содержит индивидных переменных или кванторов.
(II) Закодировать д-ки конечных подмножеств множества М2
термами специи 2", где Й={Л} и 22=(0, If; 2* = 2SU22*.
(III) Показать, что каждое определимое отношение для J?2
распознаваемо, если его интерпретировать относительно
кодирования (II).
В процессе выполнения шагов (I) — (III) мы должны убедить
читателя в том» что существует эффективная процедура пере-
Обобщенная теория конечных автоматов и ее приложения 135
хода от формулы в JS?2 к формуле -2*2 и потом к автомату,
который распознает соответствующее (по (II)) множество
термов. После этого процедура разрешения в j?2 будет состоять в
следующем: пусть задано предложение S в j?2, находим
эквивалентное предложение S* в -¾ S* имеет вид либо (а) ЗаГ(а),
либо (Ь) УаГ(а), причем Т (а) определяет множество конечных
подмножеств N2\ находим автомат, который распознает
соответствующее множество термов, — пусть, например, 6Л^(Л/?) есть
такое множество термов. Тогда, если 5* имеет вид (а), то S
истинно тогда и только тогда, когда Ъкл{АР)Ф 0, а если S*
имеет вид (Ь), то S истинно тогда и только тогда, когда
bh*{A-AP)=0.
Так как для обобщенною конечного автомата вопрос
пустоты может быть эффективно выяснен (теорема 7), то тем самым
нами описана эффективная процедура для определения
истинности предложений в &2- Этот набросок станет более ясным
после того, как мы продолжим описание эквивалентного языка
-2*2 и кодирования я-ок конечных множеств.
Индивидные переменные могут быть исключены из &2 путем
простого замещения их множественными переменными, которые
при переводе с J£% na_J2?2 будут представлять собой
одноэлементные множества. В последующем описании языка J?2 мы
введем множественные переменные, поставленные во взаимно
однозначное соответствие с индивидными переменными; это не
является необходимым, но облегчает перевод.
] принимают
(i) Множественные перемен- в качестве зна*
ные а*, ау, аг, а*,, ... | чений конечные
(И) Множественные переменные а, р, аь ... подмножества
) множества N2.
(Hi) Константа £ с ее обычной интерпретацией. _
(iv) Символы постоянных двуместных предикатов Ra (а е Ak),
интерпретируемых как график функций следования на
одноэлементных подмножествах: /?а(а, Р)«->а, р —
одноэлементные множества и /*а(а)-=Р (/а есть функция
множеств, индуцируемая га).
(v) Пропозициональные связки, кванторы по множествам
и т. д.
Правила образования для J2*2 те же, что и для -2*2, за
исключением того, что не включаются индивидные переменные.
Теперь мы определим перевод * с .2^ на .2*2 со следующими
свойствами:
136
Дж. В. Тэтчер, Дж. В. Райт
(A) Если (v, U) удовлетворяет F(x, a), tq ({v}, U)
удовлетворяет F* (а*, а).
(B) Если (V, U) удовлетворяет F*'(a*, а), то V = {v} для
некоторого v и {v, U) удовлетворяет F(x, а).
Конечно, (А) и (В> должны быть в общем случае
установлены для формулы F(хи ..., хя, оь ..., о™), но процесс легко
Просматривается и без введения этого сложного обозначения.
Мы вйедем предикат Sing (а), который представляет собой
множество одноэлементных подмножеств; предикат Sing
определяйся в о2^:
Sittg(tf>^MWf &<* ~* fasp V VPi№cp,))l Л Эр! la ер,.
Тогда период.MMMf следующий вид:
0) Для атомарных формул
(|**^*«^6ауЛ Sing(ах)Л Sing(оД
(*«ft)*ш^ваЛ Sing(«Д
(#а (*•#))* «#<*(**> ау).
(2) * расширяется на-все формулы с помощью соотношений
(IjtF)* * 3¾ fSiftg (aj Л Л,
Так как перевод весьма прост^ то мы опустим детали
доказательства того, что выполняются соотношения (А) и (В).
Также должно быть ясным, что если S есть любое предложение
в 9?ь то S истинно тогда и только тогда, когда истинно S*.
Кодирование конечных подмножеств множества N2
основано на тесном соответствий между строением любого терма
в бинарной специи |г*де неиндивидные символы имеют ранг 2) и
конечного префяксйб замкнутого подмножества множества N2.
Действительно, вместо определения термов как цепочек
(следовательно, функций из конечных отрезков множества N в 2) мы
магЛй бы предпочесть определение термов как функций из
конечных отрезков (конечных префиксно замкнутых подмножеств)
множества N2 в 2. Например, терм /, изображенный графически
на рис. 1, соответствует функции из #$ в 2, определенной
благодаря соответствию между вершянами графов, например/(Л) == /,
/(11) =М(21>~£.
Теперь, еоШ вш обратим это соответствие и посмотрим на
прообраз некоторого функционального символа, то мы сможем
связать произвольное конечное подмножество множества N2 с
Обобщенная теория конечных автоматов и ее приложения 137
термом; действительно (обозначения будут уточнены ниже),
М(£)-0.21} (см. рис. 1) и <-!tf)-{A,2>.
, Обращаясь теперь к специи; с которрй будем иметь дело, мы
можем рассматривать терм из 7V в онисаннрм выше смысле
как характеристическую функцию конзчцого подмножества
множества N2; множество, связанное с таким термом /,
представляет собой в интуитивном обозначении, использованном выше,
/_1(1). Вместо того чтобы формально описывать процесс
отождествления термов с функциями на замкнутых подмножествах
2П 212 х .
12 У 2) 22
Л 1
Рис. i.
множества N2y мы прямо дадим индуктивное определение
отображения с/которое каждому /еГх» приписывает конечное
подмножество c(t) 9% Имеем
0) с(К)=0;
(И) c{mxt2)^Uc{tx)\]J2c{t2Y
c(ltlt2) = ric(tl)(jl2c(t2)U{Al
где la есть левое следование с помощью символа а: /0 (w) = ow.
Функция с есть отображение на ртМ2. Это будет индуктивно
доказано в предположении, что если а имеет длину -^л
(длина а равна длине самого длинного члена), то а принадлежит
области значения с. Тогда любое множество длины п + 1 может
быть представлено в виде a = 1^1)^2 или a = lxax [) 1^ [) {Л},
где длина oti -^ пу и то же самое верно для 0¾. Предположение
индукции дает существование /1,/2,~где c(t\) *= аи а в силу
указанной выше альтернативы a = ¢(0/1/2) или 1а = c(lt\tz)
соответственно.
Отображение с не является взаимно однозначном, как
показывают примеры на рис. 2. Очевидно, что если c(t) = ее и
Г'€={/}• ь{0М}\ то с(/') = а. Или, иначе, c(t)= £(/') тогда и
только тогда, когда / и /' различаются только подтермами g
функциональным символом 0.
138 Дж. В. Тэтчер, Дж. Б. Райт
Таким образом, чтобы получить кодирование конечных мтю*
жеств, мы должны выбрать представителя с-1 (а); назовем его
е(а) (для кодирования). Естественно выбрать наименьший терм
в с-1 (а); кроме того, интуитивно ясно, что мы можем
формализовать цонятие «наименьший» несколькими эквивалентными
способами. Как указано выше, термы можно рассматривать как
а А А А А А
\ v V 7°
X У0
1 1
Рис. 2.
А А
А
Л А
V
1
О
Рис. 3.
функции префиксно замкнутых подмножеств множества Л^2.
При этой интерпретации имеем е(а) = (]с~1(а). Иначе мы
можем определить отношение частичного порядка =^, обобщая
отношение префикса для цепочек следующим образом:
Тогда е(а) есть наибольшая нижняя граница для с1 (а) в
соответствии с этим обобщенным отношением префикса:
В другом описании е(а) есть такой терм из с-1 (а), в к@то-
ром нет подтерма ОАЛ. Из рис. 2 мы видим, что е{Л, И} = tu
а на рис. 3 приведены еще два примера кодирования е.
Мы занимались описанием кодирования конечных множеств
в надежде, что читатель получит достаточно хорошее представ-
\
Обобщенная теория конечных автоматов -и ее приложения 139
ление об этой технике. Это необходимо, так как мы будем
полагаться на такое представление при доказательстве некоторых
утверждений в дальнейшем, по возможности опуская
подробные выкладки и громоздкие доказательства.
Прежде чем перейти к расширению отображения е до
кодирования п-ок конечных множеств, мы детально докажем
следующую лемму в качестве образца результатов, которые нам
потребуются.
Лемма 15. Множество кодов конечных подмножеств
множества N2, U\ = e(p{dN2), распознаваемо.
Доказательство. На самом деле мы докажем, что U\
регулярно, а поэтому по теореме 3 U\ распознаваемо. Для этого
обозначим
Щ = {Ш, 06А,, 066, Ш, Ш,, Ш, 266},
U\ = (U'{f.
Теперь мы утверждаем, что
Как было отмечено при определении сложного
произведения *6, выражение U\ • б0 обозначает просто множество таких
термов из (Ур которые не содержат индивидного символа 6.
Таким образом, если <g(/J-60, то (g[/J и 6 не входит в t.
По определению U[ все атомарные подтермы из t должны
иметь вид Ш,; 0 не является функциональным символом
никакого атомарного подтерма из t, поэтому /g[/i (см. третье
описание е(а)). В обратную сторону мы докажем по индукции
следующее утверждение.
Если /g Uи где 1 ^глубина (t)^.nt то /е/, где X ={6},
Хп+1 = Хп[) С/Г-бХ". Так как U'i=[)Xn, это немедленно дает
нам, что U\ s U\ (за исключением А,), но так как 6 не входит
ни в один терм из £/ь то мы знаем также, что U\ г и\ • б 0 U {к}.
Для лг == 1 терм t=\XX является единственным возможным
термом, и Ш, gZ' = {6} U {]". Если t^Ux имеет глубину п + 1,
то терм / должен иметь один из следующих видов: t = tlt?y
t = fXt2 или t = ftiX, где /=0 или /=1_, причем 1 < глубина (tL) <п
и ti^Ui. По предположению индукции tt^Xn, и,
следовательно, учитывая, что Xn+l = £/f = £/Г • ьХп [) Хп> получаем, что
<Gf+1.
140, Дж. В. Тэтчер, Дж. Б. Райт
Продолжая кодирование для (pJV2)n, мы будем иметь
дело со специей 2n={A)U{0, J}n. Определим отображение
Щ\ {0J}n-40,]} (**1, ..., п) fan: щ{Ьи ..., бЛ> **&,<. Потом,
как и в разд. 2, мы расширим я* до проекции ht: Тъп-^Т1\щ
Продолжая кодирование конечных множеств, мы сначала
определим отображение сп множества Т%п на множество (р(йМ2)п
следующим образом:
cnt**(chit, ..., chnt).
Графический пример дан на рис. 4.
Снова кодирование /г-ки й = (аь *..» <хп) выбирается как
наименьший терм в c~l(a): e(a) = t *->cn(t)=* а Л V/' [^Ю*5*
Другая характеристика е(а) снова ясна: е(а) есть такой
терм ъ с~1(а), в KOtopoM нет подтерма 0 ... 0ХХ. Если в
примере на рис. 4 обведенный кружком подтерм 00М, заменить
на Я, то в результате получаем терм е({1,2, 112}, {Л, 2, 11, 112,
21}). Обобщение леммы 15 доказывается почти идентично.
Лемма 16. Множество кодов п-ок конечных подмножеств
множества N2> Un=e(p&N2)nt распознаваемо.
Определим, что означает, что отношение конечных подмно?
жеств из pJV2 распознаваемо. По определению R^ (pa>N2)n
распознаваемо тогда и только тогда, когда eR распознаваемо.
Теорема, которая нам нужна Для получения разрешающей
процедуры, описанной ь общих чертах в начале этого раздела,
состоит в следующем.
Обобщенная теория конечных автоматов и ее приложения 141
Теорема 17. Если R есть отношение, определимое в <2?2>
то R распознаваемо.
Как и следовало ожидать, мы разделим доказательство
теоремы 17 на две части: сначала покажем, что отношения,
определяемые атомарными формулами, распознаваемы, а затем
покажем, что распознаваемые множества замкнуты
относительно пропозициональных операций (Л, "1) и квантификации
(За).
Лемма 18. Отношения Ни p(dN2, определяемые
атомарными формулами в .2*2, распознаваемы.
Доказательство. Мы должны показать, что s и
Л0(аеЕ2) распознаваемы. Рассмотрим следующие
регулярные множества:
(A) Ss « {ИМ, 01М, 0Ш}\ Ss = Ss П U2;
(B) V - {ОШ, 0Ш}6, S, = V • 6{Ш 01Ш),
S2~V -6{lQk 01U}.
Мы утверждаем, что £s = Ss и eRa — S0. Это дает
требуемый результат), так как Ss, Si и S2 регулярны и,
следовательно, по теореме 8 распознаваемы; множество- Ss также
распознаваемо (лемма 16, теорема 2).
(А). Что такое ё^ с неформальной точки зрений?
Читателю будет нетрудно самому убедиться в том, ч?о ё^ есть в
точности множество таких термов из £/2, которые не содержат
функционального символа Ш. Но Se есть множество всех
термов, не содержащих ]0, поэтому Sffi = Ss П &2 = ^ ~<
(В). Сначала мы докажем индукцией по построению Si,
что c2Si ш R\. Легко проверить (поскольку операций сложных
произведений вполне дистрибутивны), что
Si-LHiVeOo ojm}),
если Уо={6} и КП+1={00Я6,00бЯ}-бУл. Для м=0 выражение
/е К0'б{И)0_1 Ш) означает, что /=]0 01 Ш, и с2/^
*= ({А}, {1}) s Ль Теперь, если / es Ул+1 • дЦО 01 т}, то
/ е {00Я6, 006А} • б (У,, • в (10 ШШ,}.
(Заметим, что операции сложного умножения ассоциативны,
(U;bV).J=U.6(V.J), но, например, '{/}-({«}• xWKW*
*={6} x(W-e{Q)4«.)
142
Дж. В. Тэтчер, Дж. Б. Райт
Следовательно, существует /'еУп*6{10 01Ш), где / = 0Ш'
или / = 00/% и по индукции получаем, что c2t'=*{{w}, {w\}) e^i.
Но по определению с2, ^/= ({2ш}, {2wl})^R\ или с2/ =
= {{\w}y {lw\})^Ri соответственно в двух случаях. По
индукции мы получаем c2Si ^ R. Легко видеть, что S\ cz U\,. таким
образом, мы показали, что S\^eR\. Доказательство обратного
утверждения также весьма громоздко, и мы предлагаем
читателю выполнить его самостоятельно.
Последнее свойство, которое нам нужно, это замкнутость
множества распознаваемых отношений относительно
логических операций. Наши рассуждения тесно связаны с
доказательством Ричи [15] для регулярных отношений. Поэтому мы
опишем конструкцию и опустим подробности.
Лемма 19. (Замкнутость множества распознаваемых
отношений относительно логических операций.) Если R(au ..<
.. •, am, pi, ..., рп) и S(pb ...f pn, Yi. •••» Yp) —
распознаваемые отношения, то
(1) /?(a, jJ)_AS(jJ, у) распознаваемо,
(2) ~l/?(a, jj) распознаваемо,
(3) Эа1#(аь a2, ..., am, (5) распознаваемо.
Доказательство. Без ограничения общности мы
можем рассмотреть только случай m = n = p=l. Обобщение на
другие значения индексов совершенно ясно.
(1) Сначала мы заметим, что отношения R'(a, р, y)<->R(a, р)
и S7(a, р, у)Чг^5(р, у) распознаваемы. Рассмотрим
отображение я: 23-*22, где п{о\, 02, аз) = (<Ji, аг). Тогда очевидно, что
n~leRf]U3 = eR/. По предположению е/? распознаваемо, и в силу
теорем 4 и 2 мы получаем, что eRf распознаваемо. Таким
образом, R' распознаваемо. Аналогично S' распознаваемо. Поэтому
e(RAS) есть просто eR'CieS' и, таким образом, RAS
распознаваемо.
(2) Отношение 7V — eR распознаваемо по предположению
и вследствие теоремы 2. Однако это не есть в точности £("!/?),
так как оно содержит термы не из области е. Но это легко
устранимо, поскольку е(~1/?) = (Tz* — eR)f\U2 и, следовательно,
П/? распознаваемо.
(3) Пусть нам дано, что /?(а, р) распознаваемо. Мы снова
придем к требуемому результату, если рассмотрим
отображение я: S2-*^1, определяемое равенством n(ot> 02) = 02. Тогда
U'=heR почти совпадает с £(Эа#)> за исключением того, что
мы выходим за область значений ё. В действительности такие
термы из V должны быть подправлены путем исключения
подтермов, содержащих 0. Это выполняется с помощью операции
Обобщенная теория конечных автоматов и ее приложения 143
деления из разд. 3
e(3aR) = (ASRk{0kk^{]Ux).
Леммы 18 и 19 завершают доказательство теоремы 17. За
исключением начала этого раздела, мы ничего не сказали об
эффективности. Мы опирались на то, что читатель должен
быть убежден в возможности эффективного построения
автомата, распознающего множество термов, соответствующих
любой заданной формуле. Процесс, построения действительно
эффективен, как легко можно проверить, поскольку каждая из
лемм о замыкании из разд. 2 описывает эффективную процедуру
построения результирующего автомата из заданных автоматов.
Л ИТЕРАТУРА
1. Birkhoff G., On the structure of abstract algebras, Procs Cambridge
Phil. Soc, 31 (1938), 433-t454.
2. Б и p к г о ф Г., Теория структур, ИЛ, М., 1952.
3. В и с h i J. R., E 1 g о t С. C., Decision problems of weak second-order
arithmetics and finite automata, Abstract 553-112, Notices Amer. Math. Soc,
5 (1958),834.
4. Buchi J. R., Weak second-order arithmetic and finite automata,
University1 of Michigan, Logic of Computers Group Technical Report, September
1959; Z. Math. Logik Grundlagen Math., 6 (I960), 66—92.
5. Buchi J. RM Wright J. В , Mathematical Theory of Automata, Notes
on material presented by J. R. Buchi and J. B. Wright, Communication
Sciences 403, FalL1960, The University of Michigan.
6. Buchi J. R, Mathtmatische Theorie des Verhaltens endlicher Automaten,
Z. Angevandte Math, und Mech., 42 (1962), 9—16.
7. Copi I. M., El got С ¢., Wright J. В., Realization of events by
logical nets, J. Assoc. Сотр. Mach., 5 ^958), 181—196. (Also in Moore
[13].) (Русский перевод: Копи И. M., Элгот К. С, Райт Д. Б.,
Реализация событий логическими сетями, Кибернетический сборник, № 3,
ИЛ, М., 1961, стр. 147—166.)
8_. D о n е г J. Е., Decidability of the weak second-order 'theory of two succes-
' sors, Abstract 65T-468, Notices Amer. Math. Soc, 12 (1965), 819; 13 (1966),
513.
9. E1 g о t С. C, Decision problems of finite automaton design and related
arithmetics, University of Michigan, Department of Mathematics and
Logic of Computers Group, Technical Report, June 1959, Trans.'Amer. Math.
Soc, 98 (1961), 21—51.
10. Feferman S., Vaught R. L., The first-order properties of products
of algebraic systems, Fund. Math., 47 (1959), 57—103.
11. Kleene S. C, Representation of events in nerve nets and finite
automata, Automata Studies, pp. 3—42, Annals of Math. Studies, № 34,
Princeton University Press, Princeton, N. J., 1956. (Русский перевод: Кли-
н и С. К-, Представление событий в нервных сетях и конечных
автоматах. Сб. «Автоматы», ИЛ, М., 1956, стр. 15—67.)
12. Медведев Ю. Т., О классе событий, допускающих представление
в конечном автомате, Сб. «Автоматы», ИЛ, М., 1956, стр. 385—401.
13. М о о г е Е. F., Sequential Machines, Selected Papers, Addison-Wesley,
Reading, Mass., 1904,
144
Дж. В. Тэтчер, Дж. Б. Райт
14. R a b i п М. О., S с о 11 D., Finite automata :and their decision problems,
IBM J. Res. Develop., 3 (1959), 114—125. (Русский перевод: РабинМ. О.,
Скотт Д., , Конечные автоматы и задачи их разрешения,
Кибернетический сборник, № 4, ИЛ, М., 1962, стр. 58—91.)
15. Ritchie R. W., Classes of predictably computable functions, Trans. Amer.
Math. Soc, 100 (1963), 139—173.
16. Robinson R. M.f Restricted set-theoretic definitions in arithmetic, Proc.
Amer. Math. Soc, 9 (1958), 238—242.
17. Thatcher J. W., Notes on Mathematical Automata Theory, University
of Michigan Technical Note, December, 1963.
18. Thatcher J. W.f Decision Problems and Definability for Generalized
Arithmetic, Doctoral Dissertation, The University of Michigan; IBM
Research Report RC 1316, November, 1964.
19. Thatcher J. w., Wright J. В., Generalized finite automata, Abstract
65T-469, Notices Amer. Math. Soc, 12 (1965), 820.
Теория языков1)
Л. В. Ахоу, Дж. Д. Улман
1. КОНЕЧНЫЕ ОПИСАНИЯ: ГРАММАТИКИ Ц АВТОМАТЫ
1.1. Введение
Пусть 2 — конечное множество символов, или алфавит.
Обозначим через 2* множество всех строчек (strings) конечной
длины, составленных из символов множества 2, включая е—
строчку длины 0. Языком называется подмножество множества
2* для некоторого алфавита 2. Ясно, что естественные языки
и программистские языки являются языками также и в
формальном смысле.
Теория языков занимается описанием языкбв, их
распознаванием и переработкой. Язык может содержать бесконечное
множество строчек, так что необходимо иметь по крайней мере
конечное описание языка. Отдельные типы конечных описаний
будут давать полезные свойства языков, которые они
определяют, в особенности если класс языков, определяемый ими,
является «узким» (т, е. не каждый представляющий интерес язык
может быть описан). Если .С есть цласс языков, определимый
некоторым типом описания, то желательно знать, сохраняются
ли члены класса С темк или иными операциями. Хотелось бы
знать, могут ли языки из класса С распознаваться быстро и
просто, в особенности если пытаются строить компилирующие
системы для языка или языков из С. Также полезны те
описания языков из С, которые позволяют легко определить,
принадлежит ли данный язык классу С. Наконец, желательно иметь
алгоритмы, если они существуют, дакшше ответы на
определенные вопросы о языках из С, такие, как: «принадлежит ли
строчка w языку L?»
В этой статье мы дадим основные методы описания языков
и главные результаты, касающиеся этих методов.
1.2. Иерархия грамматик Хомского
Первыми формальными методами, развитыми для описания
языков, были четыре типа грамматик, определенные Хомским
l) Ah о A. VM Ullman J. D., The theory of languages, Mathetwtigal
Systems Theory, 2, № 2 (1968), 97—125.
146
А. В. Ахоу, Дж. Д. Улман
[8, 9]. Эти классы грамматик до сих пор остаются образцом, по
которому оцениваются возможности других способов описания.
Грамматикой, часто называемой грамматикой типа 0,
является совокупность G=(Af, Г, Р, S), где N и Т —
непересекающиеся конечные множества нетерминалов (синоним:
переменные) и терминалов соответственно; 5 из N является начальным
символом (синоним: символ предложения), а Р есть множество
продукций. Продукции имеют вид а-*р, где р принадлежит
(ЛШГ)*, а а принадлежит (N\JT)*N(N[)T)*, т. е. а является
строчкой терминалов и нетерминалов, содержащей по крайней
мере один нетерминал, а р — произвольная строчка терминалов
и нетерминалов.
Определим =#> как отношение на (N[)T)*t такое, что У1=#^2
Q G
тогда и только тогда, когда yi = 610^62, Y2=6iPS2 и а-*р
является продукцией из Р. Содержательно, =Ф соотносит ук и Y2,
о
если мы можем'найти среди символов yi левую часть
некоторой продукции и, заменив ее на правую часть этой
продукции, получим у2.
Вообще если R есть отношение1) на множестве S, то R'
является рефлексивным транзитивным замыканием R тогда и
только тогда, когда
(1) sR's для всех s из 5;
(2) если s{Rfs2 и s2Rsz, то siR's3',
(3) si/?^ только тогда, когда это следует из (1) и (2).
•
Обозначим через =Ф рефлексивное транзитивное замыкание
G
*
отношения =Ф, т. е. Yo^Y* тогда и только тогда, когда не-
о о
которая последовательность (возможно, пустая) замен левых
частей продукций из Р_их правыми частями переводит строчку
«Yo в Yn- Последовательность строчек у0, уь •, уп, такая, что
^,=^у/ Для 1^*^я, называется выводом уп из у0 в G.
о
Язык, порожденный грамматикой G, есть
L(G) = ( x\S^x и хеГ|.
Пример 1.1. Пусть G = (N, Т, Р, S), где N = {5}, Т = {0,1} и
P = {S->0S1, S->01}. Тогда L(G) = {0n ln \n> 1}. (Если ay-
строчка, то до" есть до, написанная /г раз. Заметим, что до0 есть е).
2) Имеется в виду бинарное отношение. — Прим. перев,
Теория языков
147
*
Легко видеть, что 5=фОл1л, согласно выводу
G
S#0S1=#00S11=# ... фО^Г"1 =#0*1*.
G G G О О
Продукция S->0S1 использовалась п — 1 раз, а продукция
S —>► 01 использовалась последний раз. Нетрудно показать, что
если w не имеет вида 0П1П, то w не принадлежит L(G).
Заметим, что хотя каждая продукция из Р имеет слева один
символ, не требуется, чтобы это выполнялось в общем случае.
Пусть G = (Ny 7, Р, S), и предположим, что если а-*р
принадлежит Р, то |р|>|а|. (Здесь \х\ есть длина х или число
символов в строчке х.) Тогда G является контекстной (context-
sensitive) (синоним: типа I)1) грамматикой.
Пример 1.2. Пусть G = (N, T,P,S)9N = {S, Я, Q, Т = {а, 6, с}
и пусть Р состоит из S->aSBC, S-+aBC, СВ-+ВС, аВ-+аЬ,
ЬВ-*ЬЬ, ЬС->Ьс, сС-+сс. Тогда LG={anbncn\n > 1}. Чтобы
вывести апЬпсп, надо использовать п—1 раз продукцию
$-+aS.BC и один раз S-+aBC для получения S =Ф ал (ВС)\
Затем, используя (1/2)п(п—1) раз продукцию СВ-+ВС, полу-
*
чаем S=^anBnCn. Тогда остальные четыре продукции дают
G
*
S=$anbncn. Труднее показать, что никакие другие строчки не
G
могут быть порождены, однако сделать это можно.
Пусть G= (N, Tt Р, S). Предположим, что каждая
продукция из Р имеет вид А -*р, где А € N и ре (NU^)*. Тогда G —
бесконтекстная грамматика (синонимы: грамматика типа 2,
грамматика непосредственных составляющих
(phrase-structure), бэкусовская нормальная форма или Бэкусй— Наура
форма) 2).
Грамматика в примере 1.1 является бесконтекстной.
Хорошим источником информации о бесконтекстных грамматиках
является работа [17].
Предположим, что каждая продукция из Р имеет вид
А-+аВ или А-*а, где Л, BeJV, а е rU{e}, Тогда G назы-
1) Часто употребляется другой синоним: контекстно-чувствительная
грамматика. — Прим. перев.
2) Еще один синоним — контекстно-свободная. Следует отметить, что в
русской литературе термины «грамматика непосредственных составляющих»
и «грамматика» употребляются обычно как синонимы термина «контекстная
грамматика». — Прим. перев.
148
А. В. Ахоц, Дж. Д. Улман
вается регулярной (синоним: типа 3) или праволинейной
грамматикой {).
Как общее правило мы будем называть язык, порожденный
«такой-то» грамматикой, «таким-то» языком. Язык,
распознаваемый «таким-то» устройством (устройства будут определены
позднее), является «таким-то» языком. Языки типа 0
называются также рекурсивно-перечислимыми множествами.
По определению- контекстный язцк является языком типа 0;
регулярный язык является бесконтекстным ^языком. Однако
бесконтекстный язык может содержать строчку е, в то время
как контекстный не может. Тем не менее мы рассматриваем
типы 0, 1, 2 и 3 как образующие иерархию в следующем смысле.
Теорема 1.1. (а) Если язык L peгyляpныйi то он
бесконтекстный. (Ь) Если язык L бесконтекстный, то L —{е}
контекстный, (с) Если язык L контекстный, то он типа 0.
1.3. Некоторые распознающие устройства
Другой метод финитного определения языка основан на
использовании множества строчек, приемлемых некоторым
распознающим устройством.
Автомат, или распознающее устройство в его наиболее об-
щей форме, показан на рис. 1.1. Он содержит входную ленту
< °1 а2
2
m
Конечное
управление
Рис, 1.1. Распознающее устройство.
с отметками концов, на которой записана строчка. Входная
головка считывает по одному входному символу. Имеется
конечное управление, которое может находиться в конечном числе
состояний. Имеется бесконечная память, возможно, с некото-
■) Обычно праволинейными называют грамматики более общего типа, а
именно когда Р состоит из продукций вида А -> &В или А -> Р, где
р е Г*. - Прим. перев.
Теория языков
149
рой структурой. Автомат делает элементарные шаги,
зависящие от состояния конечного управления, символа,
считываемого входной головкой, и конечного объема информации из
бесконечной памяти. За один шаг он может:
1) изменить состояние конечного управления,
2) передвинуть входную головку на одну клетку в любом
направлении или оставить ее на месте и
3) изменить бесконечную память некоторым конечно опи-
суемым способом.
Устройство может иметь не более одного допустимого
элементарного шага в каждой ситуаций, тогда оно является
детерминированным. Оно может иметь произвольное конечное
множество допустимых шагов в некоторых ситуациях, и тогда оно
является недетерминированным. Если нет ограничений на
движение входной головки, то устройство называется
двусторонним. Можно не позволять передвигать его головку влево, и
тогда оно будет односторонним. Конечно, одностороннее
устройство тривиально является двусторонним, а также
детерминированное устройство является недетерминированным.
В начале конечное, управление автомата находится в
некотором начальном состоянии при некотором начальном
содержании бесконечной памяти и с входной головкой у метки левого
конца.
По соглашению знаки Ф и % будут всегда обозначать
левую и правую метки концов соответственно и будет
предполагаться, что они не содержатся ни в каком алфавите, если явно
не указано противное.
По существу множество автоматов с «одинаковой»
структурой бесконечной памяти образует семейство автоматов.
Семейство имеет четыре класса автоматов: двусторонних
недетерминированных, двусторонних • детерминированных, односторон*
них недетерминированных и одосторонних детерминированных.
Мы будем сокращенно обозначать эти классы 2N, 2Z), IN и ID
соответственно. Формализация понятия класса автоматов
появилась в работах [44, 45], но здесь дана не будет. Класс IN
формализован также в работе [18].
Мы, однако, опишем классы автоматов, которые естественно
связаны с типами грамматик в иерархии Хомского.
Машина Тьюринга [74], изображенная на рис. 1.2,
представляет собой устройство, бесконечной памятью которого является
линейная лента клеток со считывающей и записывающей
ленточной головкой. За один шаг, зависящий от ее состояния и
символов, считываемых входной и лентрчной головками,
машина Тьюринга может:
1) изменить состояние,
150
А. В. Ахоу, Дж. Д. Улман
2) изменить символ, считываемый ленточной головкой, и
3) передвинуть входную и ленточную головки на одну
клетку независимо в любом направлении.
Формально двусторонняя недетерминированная машина
Тьюринга (или просто машина Тьюринга) обозначается так:
^=(5,2,1^,6,^0,5,^), где 5, 2, Г и F суть конечные
множества состояний, входных символов, ленточных символов и
заключительных состояний соответственно; F ^ S; qo из 5 —
начальное состояние; В из Г — пустой символ; 6— это
отображение S X (2U{<£, $}) X Г в класс подмножеств множества
S Х(Г —{В})Х {—1,0, +1} X {—1,0, +1}. Интерпретацией того
|ф|а,|а2| ... \а{\ ... |ап| ||
г>
Конечное .
управление
lw-
V
А,|А2|._.. |Aj| ...
Рис. 1.2. Машина Тьюринга
факта, что (p,Y,dud2)&8(q,a,X)y является следующее: если
машина Тьюринга М находится в состоянии q, считывает а на
входе и X на ленте, то она имеет право перейти в состояние рг
напечатать непустой символ Y вместо X и передвинуть свои
входную и ленточную головки в направлениях dx и d2
соответственно (—1 обозначает сдвиг влево, 0 — отсутствие движения,
+ 1—сдвиг вправо).
Конфигурация машинн Тьюринга М будет обозначаться
(q, аха2 ... &х ... ап, ХХХ2 ... Xj ... Xm). Здесь q есть
состояние (*! = #, ап = $и а2аг ... аи-\ — вход, где каждое ak, 2<&<
•<п—1, принадлежит 2. Символы Х\ и Хт пустые, а Х2Хг ...
... Хт-\ — непустая часть ленты машины М. Входная и
ленточная головки считывают а* и Xj соответственно, что обозначено
«крышками».
Отношение \-м определяется следующим образом.
Предположим, что b(q,ahXj) содержит {p,Y,dud2) и KWi<n.
Мы можем написать
(q, аха2 ... й{ ... ап, Х{Х2 ... X/ ... Хт) \~м
Ьм(р, а\а2 ... di+di ... аПу YqY\Y2 ... Yj+a2 ... YmYm+i)>
Теория языков
151
где Yk=Xh для l^Ck^m и кФ\\ У; = У. Если /=1, то У0=В,
а если / = /л, то Ут+1—В. В противном случае Уо и Ут+1 суть е.
(Таким образом, строчка на ленте продолжается, будучи
окружена пустыми символами.)
Через Ь-^ будем обозначать рефлексивное транзитивное
замыкание отношения bjvf. Строчка w из 2* приемлема (is
accepted) машиной Af, если (q0i фхю%, ВВ) \-*м(р, 0w$, Yi^) Для
некоторых р из F, X из Г и \ь Y2 из Г*. Введем обозначение:
T(M)={w\w приемлемо'машиной Af}.
Пример 1.3. Пусть М =({</,, </2}, {0,1}, {X, В}, б, ?ь В, Ы).
Отображение б определено следующим образом:
1) 6(quC,B) = {(quX9090)9 (<7ь *ь+1,0)};
2) 6(qu09X)={(q2,X9+U+l)}\
3) б(?2, 1\В)={(<72,*>+1,-1)};
4) для остальных аргументов б имеет значение 0.
Если машина М начинает работу с конфигурации(qu (£01$,
ВВ), то, согласно (1), следующей конфигурацией может быть
(<7ь <?01$, ВХВ) или (ql9 ¢01 $, ВХВ). Так как 6(?1, ¢, Х)-0,
то Af не имеет движений из первой конфигурации. Однако по
правилу (2)
(<7„ (?01$, BXB)\-M(q29 СОЦ; ВХВ).
По правилу (3)
(</2> ДО1$, ВХВ) \-M(q29 т% ВХХВ).
Таким образом, (q0i ¢01 $, ВВ) Ь^ (q29 ¢01^, ВХХВ), т. е.
строчка 01 приемлема машиной Af.
Если М = (S, 2, Г, б, </о, В, F) и для любых q из S, а из
2U{<£, $} и! из Г множество b{q,a,X) содержит не более
одного элемента, то Af является детерминированной. Если ни для
каких q, а и X множество б(#, а, X) не содержит элемент вида
(р, У,—l,d), то М является односторонней. Таким образом,
определены четыре класса машин Тьюринга: 2Л/, 2D, IN и ID.
Два* класса автоматов называются эквивалентными,^ если
они распознают одинаковые языкр.
Теорема 1.2. Четыре класса машин Тьюринга (2N, 2D,
1JV, ID) попарно эквивалентны, и каждый распознает в
точности все языки типа 0.
Существуют также другие модели машин Тьюринга. Одна из
них введена в разд. 5.1 настоящего обзора. Однако все модели
машин Тьюринга эквивалентны относительно их способности
152
А. В. Ахоу, Дж. Д. Улман
распознавания. Хорошее описание машин Тьюринга
содержится в работе [59].
Пусть M = (S, 2, Г, б, q0t В, F) есть 2#-машина Тьюринга.
Предположим, что существует константа fe, такая, что если
weS* и (ш( = л, то из (q0, $»8, ВВ) \-*M(qw{aw2, \\Ху2)
следует, что \y\Xyz\-*Сkn. Тогда М называется линейно
ограниченным автоматом [54, 56, 62]. Классы 2N, 2D, \N и ID
линейно ограниченных автоматов -определяются в точности так
же, как и для машин Тьюринга.
Теорема 1.3. (1) Классы 2N и IN линейно ограниченных
автоматов эквивалентны, и каждый распознает язык L тогда
и только тогда, когда язык L — {е} является контекстным.
(2) Классы 2D и ID линейно ограниченных автоматов
эквивалентны.
Вопрос об эквивалентности классов 2N и 2D линейно
ограниченных автоматов остается открытым.
[TT^F
IH
к*
конечное
управление
Рис. 1.3. Магазинный автомат.
Устройством, которое моделирует процедуру
грамматического анализа многими* компиляторами, является магазинный
автомат1), показанный на рис. 1.3. Бесконечной памятью
является магазинный2) список. За один шаг, зависящий от
состояния, символа под входной головкой' и верхнего символа
магазинного списка, магазинный автомат может изменить
состояние, передвинуть свою входную головку и заменить верх-
1) Синонимы: пушдаун- автомат, автомат С магазинной памятью. — Прим.
персе
2) В подлиннике last-in, first-out list. — Прим. перев.
Теория языков
153
ний символ магазинного списка произвольной строчкой
конечной длины, включая е *).
Формально двусторонним недетерминированным магазинным
автоматом (просто магазинным автоматом обычно называют
таковрй из IN класса) называется совокупность P=(S, 2, Г, б,
qo,Z0/F), где S, 2, Г и F — конечные множества состояний,
входных символов, магазинных символов и заключительных
состояний соответственно; F^S\ qo из S является начальным
состоянием и Zq из Г — начальный символ. Здесь б — отображение
S X (2 U {¢, $}) X Г в множество конечных подмножеств
произведения S X Г* X {—1, 0, +1}.
Конфигурацией магазинного автомата Р называется
(q, аха2 ... й{ ... а„, ХХХ2 ... Хт)> где ах*=*$, а„ = $ и flj-eS,
2j£j-*Cn—1. Через аг- обозначен символ, считываемый
входной головкой, через ХхХ2...Хт— содержание магазинного
списка, причем символ Хт является верхним в списке.
Предположим, что 6(q,aiyXm) содержит (р, y,d), где P&S, у & Г*,
d**—1, 0 или +1 и 1 4^i+d-£r£ Тогда мы можем написать
(q, аха2 ... dt ... ani ХХХ2 ... Хт) \-р
Ьр(р, аха2 ... di+d ... аП9 ХХХ2 ... Хт_ху).
Заметим, что у может быть пустой строчкой е, и в этом случае
символ Хт в верхней части магазинного списка просто
стирается. Определим \-*р как рефлексивное транзитивное
замыкание Ь-р. Тогда Т(Р)—язык, распознаваемый или
приемлемый2) автоматом Р, есть {до |иуе2* и (q0i $w$, Zq)\-*p(p,@w$, у)
для некоторых р из F и y из Г*}.
Если ни для каких q из S, а из 2(J{#, $} и X из Г
множество б(<7, а, X) не содержит б9лее одного элемента, то
автомат Р является детерминированным. Если ни для каких q, а
и X множество 6(q,a,X) не содержит элемента вида (/?, у,—1),
то Р является односторонним.
Теорема 1.4. Язык приемлем \N магазинным автоматом
тогда и только тогда, когда он является бесконтекстным языком.
Магазинные автоматы класса \N и. их связь с
бесконтекстными языками впервые появились в работах [5, 11]. Класс ID
был рассмотрен в [19, 39, 52], а классы 2N и 2D — в [2, 32, 39].
1) Существует несколько вариантов эквивалентных определений
магазинных автоматов. Одной из последних работ, посвященных этим автоматам,
является статья: Глушков В. М., Кибернетика, № 5 (1968). —- Прим. пе*
рев.
2) Второй термин добавлен при переводе, поскольку он используется
авторами в дальнейшем. — Прим. перев.
154
А. В. Ахоу, Дж. Д. Улман
Метки концов входа для классов IN и Ш не существенны, и в
литературе они обычно отсутствуют.
Пример 1.4. Мы построим автомат Р, являющийся IN
магазинным автоматом, распознающим язык {wwR\w е {а, &}*—
— {е}}, где wR есть обращение т. Говоря содержательно, Р
хранит входные символы в своем списке до тех пор, пока
«считает», что он видит строчку т. Затем он стирает
магазинный список символ за символом, проверяя, является ли он
обращением w на входе.
Пусть Р = ({qu q2, q3}> {а, J?}, {Z, Л, В}, б, qu Z, {q3})t a
б определено следующим образом:
(1) 6(<7i, Фу Z) = {(qu Z, +1)}{Р движется вправо от ф);
(2) б for,, a, X)={(qu ХА, +1), (%, X, 0)};
б fa,, 6, X) = {(</„ ХВ, +1), (flf2f X, 0)}
для любого X из Г. (Автомат Р может хранить входной символ
в верху своего магазинного списка. Кроме того, имеется
возможность перейти в состояние ^2, соответствующее
предположению о том, что уже достигнута середина входа.)
(3) 6(<72,М)Ч(<72,е, +1)}, б(?2ЛВ)={(<72,е, +1)}.
(Автомат Р сравнивает входной символ с верхним магазинным
символом, стирает магазинный символ и остается в
состоянии q2.)
(4) б(</2, $, Z)-{(<73, 2, 0)}.
(5) В остальных случаях значением б является 0.
Автомат Р принимает abba последовательностью
конфигураций
{qu фаЬЬа%, Z) \-P(qu фйЬЬа$, Z) \-P(qu ФаЬЬа%, ZA) Ь-Р
\-P(qu фаЬЪа%, ZAB)\-P{q2, ФаЬЬа%, ZAB)\-P
hP(q2, ФаЬЬй$, ZA) Y-P{qb фаЬЬа% Z) ЬР
Ь>(<7з, ФаЬЬа% Z).
Так как автомат Р недетерминированный, он имеет другие
последовательности движений для того же самого входа, но
оказывается, что никакая другая последовательность не
приводит к заключительной конфигурации.
Конечный автомат — это просто устройство, не имеющее
бесконечной памяти вообще. Исходя из состояния конечного
управления и считываемого символа, автомат может изменять
состояние и передвигать входную головку в произвольном
направлении.
Теория языков
155
Мы не -будем определять конечный автомат формально.
Формальное определение имеется в работе [66]. Однако мы
приведем одну теорему.
Теорема 1.5. Четыре класса конечных автоматов
(2Л/, 2D, IN, ID) эквивалентны, и каждый распознает в
точности регулярные языки.
2. НОРМАЛЬНЫЕ ФОРМЫ И ХАРАКТЕРИСТИКИ
2.1. Нормальная форма для контекстных грамматик
Имеются некоторые очевидные ограничения на
бесконтекстные грамматики, которые не изменяют классы порождаемых
языков. Две грамматики эквивалентны, если они порождают
один и тот же язык.
Теорема 2.1. Если G — контекстная грамматика, то су-
ществует грамматика G\= {N,T, P,S), эквивалентная G и та-
кая, что каждая продукция из Р имеет вид
аЛр->ауР; а,реГ, ЛеЛ/, y ^ (N U Т) *— {е}.
Теорема 2.1 оправдывает наименование «контекстная».
Символ А может быть заменен строчкой y в подходящем
«контексте» (аир).
2.2. Нормальные формы для бесконтекстных грамматик
Теорема 2.2. Если G — бесконтекстная грамматика и
L(G)—бесконечное множество, то существует грамматика
G\ = (N,T,P,S), эквивалентная G и обладающая следующими
свойствами:
(1) Если А е N — {S}, то А -* е не содержится в Р.
(2) Для всякого А из N существует бесконечное множество
*
строчек х из Т*, таких, что А =ф х.
(3) Для всякого А из N существуют строчки у и z из Т*, та-
*
кие, что S^yAz.
о,
Свойства (2) и (3) гарантируют, что каждый нетерминал
используется в бесконечном множестве выводов.
Теорема 2.3. Каждая бесконтекстная грамматика G
эквивалентна грамматике Oi= {N,T, Р, S), обладающей свойствами
теоремы 2.2 и такой, что любая продукция из Р либо есть S -> е,
либо имеет вид А =+ ВС или А-+аг еде Л, 5, С е N, аеГ,
156
А. В. Ахоу, Дж. Д. Улман
Теорема 2.4. Каждая бесконтексШая грамматика G
эквивалентна грамматике G^ = (N, Г, P,S), обладающей свойствами
теоремы 2.2 и такой, что'любая продукция из Р либо есть S—*е,
либо имеет вид А-+а,А-+аВ или А -* аВС, где А, В, С е N,
аеГ.
Теоремы 2.3 и 2.4 опубликованы в работах [8 и 33]
соответственно. Простое доказательство теоремы 2.4 и некоторые
другие нормальные формы бесконтекстных грамматик содержатся в
работе [67].
2.3. Характеристики бесконтекстных языков
Язык Дика — это язык, порождённый грамматикой Gfe =
= ({S}, 7\ Р, S), где k > О, Т « {а,, а2, ..., аЛ, 6,, ft2, ■ ■., Ч и Р
состоит из продукций S-*SS, S —► е, S —► а^Ь^ 1 ^i^k. Пусть
1¾ = L(Gk). Ясно, что язык Дика бесконтекстный. Можно
считать, что язык Дика — это- множество всех строчек
уравновешенных скобок k различных типов, где аг- и Ъх суть левая и
правая скобки соответственно для каждого /. Язык Дика образует
«основу» любого бесконтекстного языка, что выражено в
теореме 2.5.
Гомоморфизмом конечного алфавита 2 называется
отображение элементов 2 в строчки из А*, где Д — некоторый
алфавит. Если h — гомоморфизм 2, то он распространяется на
2*: А(е)*=е и h(wa) —h(w)h(a) для любых а из 2 и w
из 2*. Если L — язык, то h(L) = {x\h(w) = х для некоторого w
из!}.
Теорема 2.5. Если £ — бесконтекстный язык, LgS* и S
содержит s элементов, то существуют гомоморфизм h и
регулярный язык /?, такие, что L = h(Lkf] Р), где А = 4(s + 1).
Доказательства теоремы 2.5 или близкого результата
опубликованы в работах [5, 17, 72].
Имеются два необходимых условия для того, чтобы язык
был бесконтекстным. Ясно, что они полезны для доказательства
того, что конкретный язык не является бесконтекстным.
Теорема 2.6. Пусть L — бесконтекстный язык. Тогда
существует константа р, такая, что если z^L и |г|>р, то z
может быть записано в виде uvwxy, где \vwx\ <р, v и х не
могут быть оба е, и для всех натуральных i: uvlwxly е £.
Используя теорему 2.6, легко показать, что такие языки, как
{апЬпсп\п> 1} или {О?!/? — простое число], не являются
бесконтекстными.
Теория языков
157
Определим для наших целей л-вектор как n-ку
неотрицательных целых чисел. Если с ^неотрицательное целое число и
V7 = (м, £2, ..., in) — я-вектор, то cV обозначает n-вектор (ciu
ci2,... ,c/n). Также имеем
(i\y h,... э f») + (/it J2> • • • ♦ In) = (A + /ь fe + /2, • • •, *n + /n).
Множество S я-векторов называется линейным множеством,
если существуют л-векторы С, Рь Рг. • • •, Рл Для некоторого
конечного &, такие, что все элементы S, и только они, суть
С + а\Р\ + а2Рг + ... + uhPk для некоторых неотрицательных
целых чисед! а\, а^ ..., я^. Здесь С называется константой, а
Рь Р2, ..., Pfe — периодами. Полулинейным множеством
называется конечная сумма линейных множеств.
Пусть 2={аьа2,..., ап}, и лустья>^2*. Для К/<л
определим #j(t#) как число вхождений а^ в строчку до. Если £ —
язык, 1е=Е* и 2 *» {audi,.. .,ап}, то имеется множество, S(L)
я-векторов, естественно ассоциированное с Z,, такое, что (fb t2. .*..
..., /n) eS(I) тогда и только тогда, когда существует до из L,
такое, что для всех /, 1^/^п, Фз(®>)~1у
Теорема 2.7. £г./ш L—бесконтекстный язык, то S(L) —
полулинейное множество.
Обращение теоремы 2.7 ложно. Например, если L =
={апЬпсп\п > 1}, то 5(1)—линейное множеством константой
(1, 1, 1) и с одним периодом также (1, 1, 1). Однако язык L не
является бесконтекстным. Теорема 2.7 имеется в работе [63].
Один интересный результат следует из теоремы 2.7.
Теорема 2.8. Если L е {а}* для произвольного символа а,
то следующие три утверждения эквивалентны:
(1) S{L) — полулинейное множество;
(2) L — регулярный язык;
(3) L — бесконтекстный язык.
Таким образом, не существует нерегулярных бесконтекстных
языков над однобуквенным алфавитом.
3. ОГРАНИЧЕННЫЕ БЕСКОНТЕКСТНЫЕ ЯЗЫКИ
3.1. Общие ограничения
В этом разделе мы дадим некоторые определения ограничен*
ных форм бесконтекстных языков, которые рассматривались в
литературе. Основанием для рассмотрения таких классов
158
А. В. Ахоу, Дж. Д. Улман
является обычно то, что они содержат некоторые языки,
представляющие практический интерес, поскольку вводимые
ограничения облегчают задачу грамматического анализа или
распознавания. Ни один из этих классов не эквивалентен классу всех
бесконтекстных языков.
Пусть G = (N, 7, Р, А\) — бесконтекстная грамматика
Предположим, что N = {Ль Л2,..., Ап} и что если Л*-* а
принадлежит Р, то а е (Г U {Лг-, Лг+ь ..., Лп})* для каждого i между
1 и п. Тогда G называется последовательностной грамматикой
[24, 25. 71]. По нашему соглашению L(G) — последовательности
ный язык.
Пример 3.1. Язык! = {04j|/> * > 1} — последовательностный
язык, L = L(G), где G = ({Ль Л2, Л3},{0, 1}, Р, Ах) и Р состоит
из Л х -+ 0Л2Л3, Л2 -* 0Л2Л3, Л2 -+ е, Л3 -» Л3Л3 и Л3 — 1.
Пусть G — (N, 7\ Р, S) -бесконтекстная грамматика.
Предположим, что если Л -* а содержится в Р, то а есть строчка из
Т*ЛТ* или из Г*. Тогда G — линейная грамматика [35, 37,38].
Заметим, что S=#>y означает, что у содержит самое большее
о
один нетерминал.
Пример 3.2. Грамматика из примера 1.1—линейная
грамматика; {0п1п|я> 1} — линейный язык.
Пусть L — бесконтекстный язык. Предположим, что
существуют строчки Wu v»2,..., Wk, такие, что каждая строчка w из L
имеет вид w = ю\1хю122... w*kk для неотрицательных целых чисел
*ь i2. . *'*. Тогда L — ограниченный язык. Ограниченные языки
изучались очень детально. Их свойства и характеристики в
терминах полулинейных множеств описаны в работах [17,27].
Пример 3.3. Пусть G—({5,Л}, {а,Ь},Р,Б), где Р состоит из
S-±aSby S->A, A-+Aab, Л-ve. Тогда L(G) = [а*{аЬ)Щ1>0.
/>()}. Язык L(G) удовлетворяет определению ограниченного
языка при k = 3, W\ = a, w2 — ab и w3 = 6. Заметим, что L(G)
является также последовательностным и линейным языком.
Предположим, что Р= (S, 2, Г, б, <7o,Zo, Р) есть Ш
магазинный автомат. Предположим, что Г состоит из двух символов:
первый Z0, а Другой обозначим X. Если для всех ^ из S и а из
2U{#, $} множество 6(^, a,Z0) содержит только элементы вида
(р, Z0X% d), а 6(^, a, X) содержит только элементы вида (p,X\d),
где />0 в обоих случаях, то Р называется машиной со
счётчиком [60, 70]. Если Р может иметь конфигурацию с
магазинным списком у» то y = Z0X* для некоторого i ^ О,
Теория языков
159
Пусть опять Р = (5,2,^6,(70,^0./7) есть IN магазинный
автомат. Пусть
fai. о>ь Yi) Нр(%. ^2» Y2) f-p... ЬР((7т, wm, Ym)
есть последовательность конфигураций P, где ^i =» <70 и Yi = £o«
(Заметим, что wuW2>... ,a;m одинаковы, за исключением
позиции входной головки.) Предположим, что lv<-i|<lYil Для не"
которого i и |уг| = iУш| = ... Hy*I и Iy*I > "lYft+il Для нексн
торого k^CL Тогда мы назовем конфигурацию (quWuyi)
возвратом (turn). Возврат по существу означает максимум длины
магазинного списка. Если существует константа с, такая, что ни
для какого входа швРне существует последовательности
конфигураций
(qo, $w$9 Z0) \-P(qu wu Yi) f-P(<72, w* Y2) bP(?m, wmt ym)
с более чем с возвратами, то Р называется конечно-возвратным
магазинным автоматом [28].
Пример 3.4. Очевидно, что \N магазинный автомат Р из
примера 1.4 является конечно-возвратным с константой 1.
Автомат Р распознает язык L = {wwR\w е {а, &}*— {е}}; Р может
увеличивать длину своего списка до тех пор, пока он не придет
в состояние q2. Тогда он делает «возврат» и длина .магазинного
списка больше не может расти. Заметим, что L — линейный
язык и что вообще бесконтекстный язык является линейным
тогда и только тогда, когда он распознаваем одновозвратным
\N магазинным автоматом.
Мы также должны включить W магазинные автоматные
языки в качестве подкласса бесконтекстных языков. Некоторые
результаты об этих языках имеются в работах [19,39,52,53].
3.2. Неоднозначность
Пусть G = (N, Т, Р, 5) — бесконтекстная грамматика и
S = a0=^ai^a2=^ ...=фал = ш— вывод в О. Мы будем назы-
G Q G Q
вать этот вывод левым (leftmost), если для каждого /, Q*Ci<n,
мы можем записать а* в виде а>И<Рь где w{&T* и А{ s N.
Кроме того, Ai-+yi — продукция из Р, используемая при
переходе от а; к а<+ь и a«+i = tWfY<P<« Содержательно вывод является
левым, если на каждом шаге замещается самая левая
переменная.
Теорема ЗА.-Если w&L(G), то существует левый
вывод w в G.
160
А. В. Ахоу, Дж. Д. Улман
Мы можем сопоставить каждому выводу вида 5*=а0=фа|=#
о G
=Ф ... =Ф «л в оконечное корневое дерево, называемое деревом
Q Q
вывода (сийоним: диаграмма анализа (parsing diagram)).
Вершинами дерева вывода являются наборы целых положительных
чисел вида (lu ..., ir), где г > 1. Ориентированными дугами
дерева являются упорядоченные пары ((i\,..., ir), (ib ..., iri /r+1)).
Каждая вершина отмечена нетерминальным или терминальным
символом грамматики G. Мы можем ассоциировать отмеченную
вершину € некоторым символом строчки вывода. Корнем дерева
вывода является отмеченная вершина S(l). Если аг= рЛу,
аг-н = РХ\Х2... Хту и Л -* XjXa ... Xm — продукция из Р,
использованная при выводе оьг+ь.и если это конкретное А
ассоциировано с отмеченной вершиной A (£ь - - -, h), то Xj ассоциируете^
с отмеченной вершиной Xj(iu ... JnJ) для 1 </<m. Символы
из р и у в <*г+1 ассоциируются с теми же самыми вершинами,
ЧТО HB«f
Пример 3.5. Пусть G — грамматика примера 1.1. Дерево вы-
вода для вывода S=# 000111 показано на рис. 3.1.
G
0(1.2,2.1)4 у 1(1.2,2,2)
0(1,2,1)ч S(?,2,2) /1(1.2,3)
0(1.1)ч NS(1,2)' /Н1.3)
S(l)
Рис, 3.1. Дерево вывода для «S =ф 000111.
О
Бесконтекстная грамматика G = (Af, 7, Р, S) называется
неоднозначной, если существует строчка w из L(G) с двумя
различными левыми выводами. Иначе трамматика неоднозначна,
если некоторое слово w из L(G) имеет два различных дерева
вывода, ассоциированных с выводом w из S в G.
Бесконтекстный язык L называется существенно
неоднозначным, если любая бесконтекстная грамматика,
порождающая L, неоднозначна.
Теорема 3.2. Существуют существенно неоднозначные
бесконтекстные языки, например {04*0* |i = / или / = k}.
Теория языков
161
Неоднозначность является важным понятием теории языков.
Существенно, например, что грамматика, служащая для
порождения языка программирования, неоднозначна; иначе говоря,
программа в этом языке может иметь более чем одну
возможную интерпретацию.
Результаты, касающиеся неоднозначности и существенной
неоднозначности, можно найти в работах [4, 14,30, 31, 42, 63].
4. КЛАССЫ, ПРОМЕЖУТОЧНЫЕ МЕЖДУ БЕСКОНТЕКСТНЫМИ
И КОНТЕКСТНЫМИ
4.1. Программные грамматики
Давно существует мнение, что для полного описания
естественных или программистских языков необходима более тонкая
структура, чем та, которую дают бесконтекстные грамматики.
Однако контекстные языки слишком сложны, чтобы быть
полезным описанием. Необходим компромисс. Недавно* появились
два обобщения- бесконтекстных грамматик. Мы опишем здесь
программные грамматики [68], а в следующем разделе —
индексные грамматики [1].
' Программной (programmed) грамматикой является G = (N,
Г,/, Р, S), где N,T и Р — конечные множества нетерминалов,
терминалов и .продукций соответственно; S — начальный символ
из N; /—множество меток продукций. Продукция из Р имеет
вид
(r)A-+aS(V)F(W),
где Л~>а называется ядром (core); оно имеет бесконтекстную
форму; A &N\ a^(N [} Г)*; (г) является меткой; re/.
Никакие две продукции из Р не могут иметь одну и ту же метку.
Далее V называется областью удачи, W — областью неудачи;
V и W — подмножества множества /. Содержательно, если
пытаются применить продукцию г к строчке у и если имеется
вхождение А в у, то самое левое А заменяется на а, а следующая
используемая продукция должна иметь метку из V. Если у не
содержит Л, то y не меняется и следующая используемая
продукция должна иметь метку из W.
Формально отношение =Ф определено для пар вида (а, г), где
о
ae(iV I) Г)* и re/. Предположим, что продукция с меткой г
есть A-+yS{V)F(W). Если а = аИа2, ai€=(Af U Т—{А})* и s —
произвольная метка из V, то мы можем написать (а, г) ^(а^а , s).
G
Если же aG(iVl) Г —{Л})* и S — метка из W, то. мы можем
162
А. В. Ахоу, Дж. Д. Улман
написать (a, г)=#>(а, 5). Пусть =Ф есть рефлексивное транзи-
G G
тивное замыкание =Ф. Тогда порожденный грамматикой G язык
G
L(G) ееть (г/|*/еГ* и для некоторого г из J имеет место
(5, 1)#(у, г)}.
G
Пример 4.1. Пусть G = ({S, Л, 5, С}, {а, 6, с}, {1, 2,..., 8}, Р, S),
где Р состоит из следующих продукций:
Удача Неудача
етка
(0
(2)
(3)
(4)
(5)
(6)
(7)
(8)
Ядро
S-+ABC
А -> аА
В->ЬВ
С->сС
А->а
В->Ь
С->с
S->S
S({2,5})
S ({3})
S({4})
S ({2,5})
S ({6})
5 ({7})
S({8»
S(0)
F(0)
F(0)
F(0)
F(0)
F(0)
F(0)
F{0)
F{0)
Тогда имеем L(G) ={anbncn\n > 1}. Заметим, что язык L(G)
не является бесконтекстным. С помощью продукции (1) мы
имеем (S, 1)=#>(Л£С, 2) и (S, 1) =#>(ЛВС, 5). В последнем
G G
случае можно использовать только продукции (5) — (7) и тогда
закончить вывод.
В этом случае мы имеем
{ABC, 5) ^(аВСу 6) =$>{аЬС, 7) =#>(afec, 8).
G Q G
К паре (ЛВС, 2), как легко видеть, можно применять цикл
продукций (3), (4) и (2) до тех пор, пока после (4) будет выбра-*
на (5). Таким образом, имеем
(5, \)1${ап-1АЬп-хВ<Г-хС% 5)
G
для всех п ^ 1. Далее легко видеть, что
{сГ^АЬ^Вс^С, 5) i(aW, 8).
G
С другой стороны, нужно показать, что никакие другие
терминальные строчки не порождаются, однако здесь мы этого
делать не будем.
Теорема 4.1. Любой язык типа О порождается
программной грамматикой.
Теория языков 168
- -'- *- - -
Бесконтекстной программной грамматикой G называется
программная грамматика (N, Г, /, Р, 5), в которой никакая
продукция из Р не имеет ядра вида А -* е.
Теорема 4.2. Если L = L(G) для бесконтекстной
программной грамматики G, то L является контекстным языком.
Многие другие результаты, касающиеся программных
грамматик, содержатся в работе [68].
4.2. Индексные грамматики
Индексной грамматикой [1] называется грамматика G= (Л/, Г,
F.P.S), где N, Г, F и Р — конечные множества нетерминалов,
терминалов, указателей (flags) и продукций соответственно;
S из N — начальный символ. Указатели из F суть конечные
множества индексных продукций вида А -> а, где А ^ N и
ae(Af U Г)*. Продукции из Р имеют вид
где Хи X2i..., A'm принадлежат W или Г, а г|)ь^2,..., ipm
принадлежат F*. Если Хг е Г, то г|)г = е.
Содержательно, за нетерминалами в строчке могут следовать
произвольные списки указателей. Если нетерминал, за которым
следуют указатели, заменяется одним или более нетерминалами,
то возникают указатели, следующие за каждым нетерминалом.
Если нетерминал замещается терминалом, то указатели
исчезают. Если за нетерминалом А следуют указатели f\f2---fn и
fi содержит индексную продукцию вида А -+ а, то мы можем
убрать /ь заменить А на а и написать вслед за каждым
нетерминалом из а список указателей /2/3... fn-
Формально пусть G= (jV, Г, У7, Р, S)—индексная
грамматика. Определим отношение =ф на строчках из (NF* U Г)*
следующим образом.
(1) Если аЛбр — строчка, такая, что айв принадлежат
(NF*[) Г)*, Ле=#, e'esf* и
Л-> Х{ЬХ2Ь • • • ХпЛт ^ Р*
где Xi е N U Т и г|)г ^ F* для всех i, то мы можем написать
аЛ9р ^аХ^ХгФз ... Ятфшр.
Здесь фг есть е, если -^ е Г, и фг = гМ, если Х{ е N. Заметим,
"то если ^г е Г, то г|)г = 8 по определению.
(2) Если аЛ/ер — строчка, такая, что аир принадлежат
(NF* ur)*,AeJV,feF, ВеР, а Л -* ХХХ2 ... Хт является
!64
А. В. Ахоу, Дж Д. Улман
индексной продукцией из /, то мы можем написать
а Л/Эр фаЯ^Хгфг ... XM<fnfi,
G
где фг = 8, если Х{ еЕ_7\ и ф* = Э, если Xi е N.
*
Пусть =Ф есть рефлексивное транзитивное замыкание =Ф.
G G
Язык, порожденный грамматикой G, обозначается L(G) и есть
[у\уе=Г и S^y].
Пример 4.2. Пусть G - ({S, Г, Л, В, Q, {а, 6, с}, tf, #}, Р, S), где
Р состоит из продукций 6' -► Tg, Т -* Г/, Г -* ЛВС, где / = [Л -*
->аЛ, В~>ЬВУ С-»сС] и £ = И->а, В->6, С->с].
Имеем L(G) = {anbncn\n^ 1}. Применяя первую продукцию
один раз, затем вторую продукцию л — 1 раз и наконец третью
продукцию, находим
s^Tg^Tfg=$... =½ Tfn~lg # ArlgBrlgcrlg.
G G Q Q G
Затем, используя указатели, получаем
АГ'ё =$аАГ2§=$ ... =$an-lAg =Фа".
G G G G
Аналогично
Bfn-lg^bn и crlg^f-
Таким образом, S =$anbncn.
G
Многие свойства индексных- грамматик и ограниченных ин«
дексных грамматик имеются в работе [1]. Мы приведем здесь
только два результата.
Теорема 4.3. Любой индексный язык L порождается
индексной грамматикой G=(N, 7\ Fy Р, S), обладающей
следующими свойствами:
(1) Индексные продукции из F имеют вид А -*В, где А и В
из 7V, В Ф S.
(2) Если А Ф S, tg А-+г не принадлежит Р.
(3) Продукции из Р (отличные от S -* е, если такая
продукция содержится в Р) имеют вид А —► ВС, А-+ Bf или А-+а для
AtB^CezNifesF и аеГ.
Теорема 4.4. Ясли L — индексный язык, то L —
контекстный язык.
Теория языков
165
Существует устройство, называемое «гнездовым стэковым
автоматом», которое распознает в точности языки, порождаемые
индексными грамматиками [1].
5. МЕРЫ СЛОЖНОСТИ
5.1. Определения*
Предпринимались попытки оценивать «сложность» языка L
с помощью числа ячеек ленты, используемых машиной
Тьюринга, распознающей язык L («ленточная сложность»1) языка /-),
или же с помощью числа элементарных шагов, выполняемых
машиной Тьюринга, распознающей L («временная сложность»
языка L), Меры сложности обычно являются функциями п —
длины входа.
Ленточная сложность легко может быть формализована в
терминах машины Тьюринга из разд. 1.3. Пусть М « (S, 2,Г, б,
Конечное
управление
... |о,|о,|../ ^...Щ ...-
Рис. 5.1. Многоленточная машина Тьюринга.
q0,B,F)—такая машина Тьюринга и L(n)—функция от
потакая, что если ayeS*, | w \ = п и (q0, #о>$, ВВ) \-*M{q, wxdw2y ахАа^,
то |аИсб2| ^L(n). Тогда М является L(n) ленточно-ограничен-
ной машиной Тьюринга.
Чтобы определить надлежащим образом временную
сложность, нам потребуется более общая модель машины
Тьюринга — детерминированная многоленточная машина
Тьюринга, изображенная на рис. 5.1. За один элементарный шаг,
зависящий от состояния конечного управления и символа,
*) В русской литературе часто употребляется другой термин: «емкостная
сложность». — Прим. перев.
166
А. В. Ахоц, Дж. Д. Улман
считываемого каждой ленточной головкой, многоленточная
машина Тьюринга может изменить состояние, напечатать новые
символы в каждой из ячеек, воспринимаемых головками, и
каждую головку передвинуть независимо влево, вправо или
оставить на месте.
Вначале вход конечной длины записан на первой ленте,
причем остальная часть ленты пуста. Другие ленты полностью
пусты. Головка первой ленты находится в левом конце входа,
а конечное управление — в начальном состоянии. Приемлемость,
как обычно, определяется заключительным состоянием.
Мы не будем определять конфигурацию или отношение \—м
формально, так как соответствующие выражения весьма
сложны. Читатель без труда может получить их из определений для
машины Тьюринга из разд. 1.3. Будем говорить, что устройство
останавливается, если оно достигает конфигурации, из которой
устройство не может сделать элементарного шага.
Детерминированная многоленточная машина Тьюринга
имеет временную сложность Т(п), если для любого входа длины п
машина М не может сделать более чем Т(п) элементарных
шагов до ее остановки.
Сделаем несколько пояснений относительно выбора моделей
для временной и ленточной сложности. Детерминированная
многоленточная машина Тьюринга эквивалентна
первоначальной модели машины Тьюринга. (Первоначальная модель,
определенная в разд. 1.3, во избежание недоразумений будет
называться машиной Тьюринга с входной лентой (сокращенно —
в. л. машина Тьюринга).) Однако некоторые языки могут быть
распознаны многоленточной машиной Тьюринга быстрее, чем
в. л. машиной Тьюринга.
Дополнительные ленты машины Тьюринга не уменьшают
числа ячеек, необходимых для распознавания языка. Если мы
желаем пожертвовать скоростью, то одну ленту можно
использовать для того, чтобы смоделировать любое конечное число лент
путем разбиения единственной ленты на «дорожки» (tracks).
Одноленточная машина Тьюринга (многоленточная машина
Тьюринга с одной лентой) не является подходящей моделью
для измерения ленточной сложности. Так как вход должен
находиться на ленте, такая машина Тьюринга не может иметь
ленточную сложность, меньшую, чем L(n) = п.
Машина Тьюринга для измерения временной сложности
должна быть детерминированной, так как невозможно
воспроизвести недетерминированное устройство временной сложности
Т(п) за Т(п) элементарных шагов вычислительной машины.
Если язык L распознаваем детерминированной
многоленточной машиной Тьюринга временнбй сложности Т(п), то L имеет
Теория языков
167
временную сложность Т(п). Если L распознаваем
детерминированной в. л. машиной Тьюринга ленточной сложности L(n),
то L имеет ленточную сложность L(n). Если L распознаваем
недетерминированной в. л. машиной Тьюринга ленточной
сложности L{n), то L имеет недетерминированную ленточную
сложность L(n).
Понятие временной сложности впервые было формализовано
в работе [40]. Классы ленточной сложности впервые появились
в [39, 57] и были обобщены для недетерминированных классов
в [49]. Если не указано особо, приводимые ниже результаты о
ленточной сложности взяты из [39], а о временной сложности —
из [40].
5.2. Теоремы о «повышении скорости» и иерархии
Как общее правило, когда имеют дело с категорией
сложности, константные множители в оценке сложности
несущественны.
Если f(n)—функция от д, то мы используем supn^oof(n)
для обозначения предела при п-+оо верхней грани f(n),
f(n+ 1), /(д+72), .... Аналогично этому inf n^f (п) есть
предел при п -> оо нижней грани / (п), / (п + 1), / (п + 2),... .
Теорема 5.1. Если L — язык временной сложности Т(п) и
Шп-+ооТ(п)/п = оо, то для любого с > 0 язык L имеет
временную сложность [сТ(п)]+ {[х]+ — наименьшее целое число ^-х).
Теорема 5.2. Если L — язык (недетерминированной)
ленточной сложности L (п), то для любого с > 0 язык L имеет
(недетерминированную) ленточную сложность [cL(n)]+.
Таким образом, величина сложности п2 не отличается от
сложности 2п2 или д2/10. Однако если две сложности относятся
не как константа, то может существовать язык, имеющий
большую сложность, но не меньшую.
Функция L(n) ленточной сложности называется
конструируемой (constructible), если существует детерминированная в. л.
машина Тьюринга, которая имеет ленточную сложность L(n),
но не L\(n)t где L\(n) < L(n) для всех п.
Теорема 5.3. Если Lx(n) и L2(n) —конструируемые, и
L2 (п)
sup г) : = oot
то существует язык ленточной сложности L2(n), tie являющийся
языком ленточной сложности L\(ri).
led
А. В. А ход, Дж. Д. Улман
Теорема 5.4 [49]. Если L} (п) и L2 (п) — конструируемые,
L2(n)
a L\(n) и L2(n) каждая ^\ogn, то существует язык
недетерминированной ленточной сложности L2(n), не являющийся языком
недетерминированной ленточной сложности L\(n).
Строго возрастающая функция f(n) называется функцией,
вычислимой в реальное время [75], если существует
детерминированная многоленточная машина Тьюринга, которая, начав
работу с пустыми лентами, переходит в заключительные
состояния тогда и только тогда, когда она выполнит/(1),/(2),/(3),...
элементарных шагов.
Теорема 5.5. Если Тх(п) и Т2(п) — функции, вычислимые
в реальное время и
то существует язык временной сложности Т2(п) log Т2(п)9 не
являющийся языком временной сложности Т\ (п).
5.3. Соотношения между мерами сложности языков
Мы отмечали, что дополнительные ленты не уменьшают
сложности языка. Однако число имеющихся лент может влиять
на временную сложность языков. (Этот вопрос, по крайней мере
частично, открыт. См., например, [65].) Мы знаем, что
уменьшение числа лент не влияет на временную сложность «очень
сильно»; это выражено в следующих теоремах.
Теорема 5.6. Если L — язык временной сложности Т(п)
и infrt->00 Т {п)/п= оо, то L распознаваем детерминированной од-
ноленточной машиной Тьюринга временной сложности Т2(п).
Теорема 5.7 [41]. Если L — язык временной сложности
Т(п), то L распознаваем детерминированной многоленточной
машиной Тьюринга с двумя лентами временной сложности
T(n)\ogT(n).
Еще один результат устанавливает интересную связь между
временной и ленточной сложностями.
Теорема 5.8 [50]. Если язык L распознаваем
детерминированной одноленточной машиной Тьюринга временной
сложности Т(п), то L имеет ленточную сложность Тх12(п).
Теория языков
169
в. СТЭКОВЫЕ АВТОМАТЫ
6.1. Определения
Стэковый автомат — это по существу магазинный автомат
с возможностью просматривания своего магазинного списка
без -изменения его символов. Эти устройства были впервые
описаны в [21,22].
Формально двусторонний недетерминированный стэковый
автомат — это А= (S, 2, Г, б, бь, <7о, Z0, F), где S, 2, Г и F — ко<
нечные множества состояний, входных символов, стэковых
символов и заключительных состояний соответственно; F ^ 5;
q0— начальное состояние и Zo— начальный символ.
Отображение бь определяет следующий шаг автомата Л, если стэковая
головка находится в верху стэка; 6Ь отображает S X (2 U
U{#, $}) X Г в конечные подмножества множества S X Г* X
Х{—1,0,+1}. Отображение б определяет следующий шаг,
когда стэковая головка находится внутри стэка; б отображает
SX(2U{<?, $}) X Г в подмножества множества SX{— 1, 0, + 1}Х
Х{—1,0, +1}.
Конфигурация автомата А есть (q, аха2 ... а* • • • ап, £\%2 ...
... Zj ... Zm), где q е S, ах = <£, ап = % и ^eS, 2<i<n~l;
символы Zi, Z2, • ••> 2тЕГ. Входная и стэковая головки
воспринимают а\ и Zj соответственно; Zm является «верхним
символом стэка».
Отношение \-А определяется следующим образом.
(1) Предположим, что / = га и бь(#, a*, Z™) содержит
(ptytd). Кроме того, I ^i + d^n. Тогда
(q, аха2... а{... ап, Z\Z2 ... Zm) \-А
,h-A(p, аха2... ai+d ... ani YXY2 ... Уг),
где Yk = Zh для 1<&^т—1 и YmYm+\ ... Уг=у- Заметим, что
V может быть е, и в этом, случае r = m— 1. (Когда стэковая
головка находится у верхнего стэкового символа, автомат А можег
выбирать действие подобно магазинному автомату.)
(2) Для любого / межд)г 1 и /п„ если b{q,aiyZj) содержит
(р, dbd2), l<i + di<n и I ^Cj+d2*Cmi то
(q, а{а2 ... аь ... am Zx Z2 ... Zy ... Zm) h-A
Ьл (p, ai<x2 ... a*+d, ... a„, ZXZ2 ... Z/+d2 ... Zm).
(Автомат А всегда имеет возможность передвигать свою
стэковую головку вверх и вниз по стэку, но только в режиме
считывания.)
170
А. В. Ахоу, Дж. Д. Улман,
Пусть \-*А есть рефлексивное транзитивное замыкание
отношения Ь-л. Обозначим через Т(А) множество лент,
приемлемых автоматом А, т. е.T{A) = {w \{q0y Cw%, Z0)\~-*A{p,Cw$y y\Zy2)
для некоторого р из F и у\ и Y2 из Г*}.
Мы будем называть стэковый автомат A = (S^ 2, Г, б, бь, <7о,
Zo,/7) детерминированным, если ни для каких q из S, а из 2_
и Z- из Г множество 6(<7, a, Z) 11бб(<7, а, Z) не содержит более
одного элемента. Автомат А является односторонним, если
6(q,a,Z) не содержит элементов вида (р,—l,d), и бь не
содержит элементов вида (р, у,—1). Автомат А является нести-
рающим, если 6b(q,a,Z) не содержит элементов вида {р,г,й).
Таким образом, стэк нестирающего стэкового автомата не
может уменьшать длину.
Мы можем также добавить, что если 8(q,a, Z)=0 для всех
q, a, Z, то А является магазинным автоматом.
Пример 6.1. Мы построим автомат М= (S, 2, Г, б, бь, q<>, Z0, F),
распознающий {wcw\w е {а, 6}*}, где S={q0, <7ь ?2, <7з}, 2 =
= {а, 6, с}, r = {Z0, Л, В, ZJ, F={<73}. Определим б и бь
следующим образом:
(1) 6а(<7о, ¢. Z0) = {(9o> Z0, +1)} (М движется вправо от ¢),
(2)6,(90, а, X) ={(<7о, ХЛ, +1)},
М<7о, 6, X) ={(?о, ХВ, +1)},
где X = Zq, А' или В. (В состоянии ^0 автомат М запоминает
свой вход в верху стэка, подобно магазинному автомату.)
(3) б6(<7о, с, X) = {(<7i, XZb 0)},
где X = Zq, А или В. (Когда автомат М видит символ с, он
помещает Zi в верх стэка, переходя в состояние q\.)
(4) Ъ(Яи с, X) = {(</„ 0, -1)},
6(^, с, Zo) = {(?2, +1, +1)},
где Х=Л, В или Zj. (Автомат М движется вниз по стэку до
тех пор, пока не дойдет до Zo, который означает самый низ
стэка.)
(5) Ь(Яъ a,. A) = {(q2, +1, +1)},
6(q2, Ъ, B) = {(q2, +1, +1)}.
(Автомат М сравнивает свой вход со стэком.)
(6) 6(<fc, $, Z0 = {(^ 0, 0)}.
Теория языков
171
Если автомат М достигает верха стэка и правого граничного
маркера входа одновременно, то все символы выдержали
сравнение, и М принимает входную строчку.
Заметим, что М является детерминированным
односторонним и нестирающим автоматом.
6.2. Соотношения между стэковыми автоматами
и классами ленточной сложности
Имеется большое количество результатов, касающихся
сравнительной мощности классов временной и ленточной сложности
и различных классов стэковых автоматов, нестирающих стэко-
вых автоматов и магазинных автоматов. Мы приведем здесь
основные результаты.
Теорема 6.1. Класс 2D нестирающих стэковых автоматов
эквивалентен классу детерминированных в. л. машин Тьюринга
ленточной сложности п log п.
Теорема 6.2. Класс 2N нестирающих стэковых автоматов
эквивалентен классу недетерминированных в. л. машин
Тьюринга ленточной сложности п2.
Теорема 6.3. Если язык L приемлем недетерминированной
в. л. машиной Тьюринга ленточной сложности п log п, то L
приемлем 2D стэковым автоматом.
Заметим, что 2N линейно-ограниченные автоматы
эквивалентны недетерминированным в. л. машинам Тьюринга
ленточной сложности п. Таким образом, каждый контекстный язык
распознаваем 2D стэковым автоматом.
Теоремы 6.1 и 6.2 взяты из [47]. Несколько ослабленный ва^
риант теоремы 6.3 имеется в [22].
Теорема 6.4 [48]. Если язык L приемлем IN стэковым
автоматом, то L имеет ленточную сложность п.
Теорема 6.5 [57]. Если L приемлем \N магазинным
автоматом (L — бесконтекстный), то L имеет ленточную сложность
log2 п.
Теорема 6.6 [39]. Если L приемлем 2D магазинным
автоматом, то L имеет ленточную сложность п.
Теорема 6.7 [2]. Если L приемлем 2N магазинным
автоматом, то L имеет ленточную сложность п2.
Изложенные выше результаты представлены на рис. 6.1,
который подобен таблице из работы [22].
172
А. В. Axon, Дж. Д. Улман
Пояснения к рис. 6.1:
LBA— недетерминированный
линейно-ограниченный автомат,
5Л = стэковый автомат,
NESA = нестирающий стэковый автомат,
PDA = магазинный автомат,
Df(n) = детерминированная в. л. машина Тьюринга
ленточной сложности f(n),
Mf(n) = недетерминированная в. л. машина Тьюринга лен«
точной сложности f(n)t
FA = конечный автомат.
Рис. 6.1. Иерархия устройств.
Верхние классы иерархии содержат более низкие. Заметим*
что здесь выражено много тривиальных соотношений, таких, как
Nf(n) sDf(n), 2NSA a 2NNESA и т. д.
6.3. Соотношения между магазинными автоматами
и классами временной сложности
Теорема 6.8 [76]. Если L приемлем IN магазинным
автоматом (L — бесконтекстный), то L имеет временную
сложность я3.
Теорема 6.9. Если L приемлем 2D магазинным автоматом,
то L имеет временную сложность п2 log п.
Теорема 6.10. Если L приемлем 2N магазинным
автоматом, то L имеет временную сложность п*.
Последние два результата имеются в работе [2].
Теория языков
173
7. СВОЙСТВА ЗАМКНУТОСТИ
7.1. Абстрактные семейства языков
Многие из определенных выше классов языков замкнуты
относительно различных операций. Наилучшим подходом для
обобщения таких результатов являются, по-видимому, «абстракт*
ные семейства языков» [18]. Показано, что семейства языков,
замкнутые относительно различных простых операций, должны
быть замкнуты и относительно некоторых более сложных опе^
раций.
Пусть L\ и L2 — языки. Объединением L\ и L2,
обозначаемым L\ U L2, является {w\w^Lx или w е L2}.
Произведением1) (concatenation) L\ и L2, обозначаемым LxL2t является
{w | w = xy, x e Lb у e L2}.
Замыканием языка Lb обозначаемым Li+> является
L{ U LjLi U LiLiLi U ... .
Гомоморфизмом алфавита 2 в алфавит Д является отожде*
ствление символов из. 2 со строчками из Д*. Если h —
гомоморфизм, то h может быть расширен на область 2* так: Л(е) =8
и h{wa) = h{w)h(a) для а из 2 и w из 2*.
Конечно, гомоморфизм h не определен вне 2*. Если L —
язык, то h(L) ={y\h(w) =у для некоторого w из 1} и h~l(L) =
*= {w\h(w) е L}. Если h(a) Фе для всех а из 2, то /г
называется г-свободным.
Пусть о2* — множество языков. Предположим, что для
любых L\ и L2 из -2*, гомоморфизма fti, е-свободного
гомоморфизма h2 и регулярного языка R следующие языки
принадлежат &\
(1) LX\}L2 (объединение),
(2) L\L2 (произведение),
(3) L\ (замыкание),
(4) /гГ (L\) (инверсия гомоморфизма),
(5) h2(L{) (е-свободный гомоморфизм),
(6) L\ П R (пересечение с регулярным языком).
Тогда J2* называется абстрактным семейством языков, для
краткости (AFL).
Если AFL J? замкнуто относительно произвольного
гомоморфизма, то -2* называется полным AFL. Если е не принадлежит
ни одному из языков семейства ^, то J? называется е-сво-
бодным.
11 Синонимы: сцепление^ конкатенация, соединение, — Прим. перев.
174
А. В. Ахоу, Дж. Д. Улман
Обобщенная последовательностная машина с
заключительными состояниями (сокращенно —о. п. м.) [16] — это конечный
автомат с выходом. Она обозначается так: (/=(5,2^,6,^0,^),
где S, 2, А и F — конечные множества состояний, входных
символов, выходных символов и заключительных состояний
соответственно; F ^ S; q0 из S — начальное состояние. Отображение б
отображает S X (2 U {г}) в класс конечных подмножеств
множества S X А*. Мы расширим б до 5 с областью определения
S X 2* следующим образом:
(1) 5(9, е) содержит (9, е);
(2) если b{q,w) содержит (/?, у) и б(р, а) содержит (syx),
то 5(<7, wa) содержит (s, ух) для w из 2* и а из 2и{е}.
Если L — язык, то G(L) = {у \ 6(q0iw) содержит (р, у) для
некоторых р из F и w из L}\ положим также G-1(L) ={w\6(qo, w)
содержит (/?, у) для некоторых р из У7 и у из L}.
Если существует константа с > 0, такая, что |yl^[c|t»|]
.для всех (руу) из 8(?,ш), то мы будем называть машину G
о. п. м. с г-ограниченным выходом; здесь ([х] есть целая часть
от х).
Теорема 7.1. £слм j? есть AFL, Lei?, Gj— о. п. м. и
G2 — о. п. м. с г-ограниченным выходом, то G\l {L) и G2(L)
принадлежат 2?.
Если язык R регулярный, а язык L произвольный, то L/R =
={ш|ще! для некоторого х из /?}; /?\L = {oy|л:до е L для
некоторого X из /?}.
Теорема 7.2. Пусть 2? — полное AFL, и nr/сть L^g,
R — регулярный язык, G — о. п. м. Тогда G"1 (L), G (L), L/R,
R\L принадлежат J2*.
Шесть аксиом в определении AFL не являются
независимыми. В работе [36] показано следующее.
Теорема 7.3. Если множество языков 9? замкнуто
относительно объединения, замыкания, инверсии гомоморфизма,
г-свободного гомоморфизма и пересечения с регулярным
языком, то 3? замкнуто относительно произведения. Следовательно,
S есть AFL.
Теорема 7.4. Если множество языков 3? г-свободно и
замкнуто относительно произведения, замыкания, инверсии
гомоморфизма и г-свободного гомоморфизма, то 9? замкнуто
относительно объединения и замкнуто относительно пересечения с
регулярным языком. Следовательно, 9? есть AFL.
Теория языков
175
7.2. Примеры AFL
Теорема 7.5. Следующие классы языков являются
полными AFL: (1) языки типа 0; (2) бесконтекстные языки; (3)
конечно-возвратные языки; (4) счетчиковые языки1); (5)
регулярные языки; (6) индексные языки; (7) IN стэковые языки; (8) IN
нестирающие стэковые языки.
Теорема 7.6. Следующие классы языков являются AFL:
(1) контекстные языки;
(2) языки ленточной сложности L(n) для любой монотонной
функции L(n), такой, что L(n)^-п, и для которой существует
константа k, такая, что L(2ri)<CkL(n) (т. е. L(n) по порядку
не превосходит п);
(3) языки недетерминированной ленточной сложности L(n)
для любой функции L(n), удовлетворяющей условиям,
сформулированным в (2);
(4) 2N стэковые языки;
(5) 2D стэковые языки.
Заметим, что, согласно (2) и (3) и теоремам 6.1 и 6.2,
каждый из классов 2N и 2D нестирающих стэковых автоматов
определяет AFL.
Некоторые из свойств, выраженных в теоремах 7.5 и 7.6,
недостаточно обоснованы. Тем не .менее приведены даже те из них,
которые не совсем тривиальны и сформулированы без
доказательств. Многие свойства замкнутости бесконтекстных языков
даны в [17, 25, 29, 69]. Свойства регулярных языков даны в [25,
51, 66]. Об индексных языках см. работу [1]. Некоторые
результаты об односторонних стэковых автоматах даны в [21]. О
контекстных языках см. [20, 56]. Некоторые свойства классов
ленточной сложности опубликованы в [49], а свойства
двусторонних стэковых автоматов описаны в [23].
7.3. Другие свойства классов языков
Многие классы языков не образуют AFL, хотя обладают
некоторыми из шести свойств, определяющих AFL. Кроме того,
существуют другие свойства, которыми иногда обладают
классы языков, такие, как замкнутость относительно дополнения,
пересечения, обращения и подстановки. Будем называть
множество S7 языков замкнутым относительно подстановки, если для
всех L из J? L^S*, верно следующее. Для каждого а из 2
пусть La обозначает некоторый язык из 2. Тогда {w\w =
1) То есть распознаваемые машинами со счетчиком (см. разд. 3.1).—
Прим. nepeQ,
175
А. В. Ахоу, Дж. Д. УлМан
=,w\W2 ... wk и для каждого 19 1<л<£, существует а{ из Б,
такое, что wt е Lai и аха2 ... ak^ L} является языком из i?.
Содержательно, вместо каждого символа в строчки языка L
подставляется целый язык. Если & обладает указанным выше
свойством при условии, что в не принадлежит La для любого а
из 2, то множество $£ замкнуто относительно г-свободной
подстановки.
Теорема 7.7. Следующие классы языков замкнуты
относительно подстановки: (1) языки типа 0; (2) бесконтекстные
языки; (3) регулярные языки; (4) индексные языки.
Теорема 7.8. Следующие классы языков замкнуты
относительно г-свободной подстановки: (1) контекстные языки; (2) 2N
стэковые языки; (3) 2D стэковые языки; (4) языки ленточной
сложности L(n)y если L(n) монотонна и L(n)^n\ (5) языки
недетерминированной ленточной сложности L(n), если L(n)
монотонна и L(n)^ п\ (6) бесконтекстные программные языки.
Из (4) и (5) следует, что классы 2N и 2D нестирающих
стэковых языков замкнуты относительно е-свободной подстановки.
Некоторые свойства замкнутости программных языков даны
в [68], 2N и 2D магазинных языков — в [32], Ш магазинных
языков — в [19], ID стэковых языков — в [46], ограниченных
языков — в [17,27], последовательностных языков — в [25; 71].
8. РАЗРЕШИМЫЕ И НЕРАЗРЕШИМЫЕ ПРОБЛЕМЫ
8.1. Проблемы
Для каждого класса языков, описанного в этой статье, либо
существуют алгоритмы для решения определенных проблем,
либо должно быть показано, что проблемы являются
неразрешимыми. Формально проблема (question) — это логический
предикат, по крайней мере с одной свободной переменной,
способной принимать бесконечное множество значений. В теории
языков свободной переменной обычно является грамматика,
устройство некоторого типа или строчка в некотором алфавите.
Проблема называется разрешимой (solvable, decidable), если
существует машина Тьюринга, которая принимает «разумно
закодированные» свободные переменные, служащие входом, когда
проблема истинна для данных значений переменных, и
останавливается без принятия, когда проблема ложна. В противном
случае проблема неразрешима.
Мы определим обозначение, используемое при описании
каждой конструкции в данной статье (например, G= (N, Г, Я, S)
Теория языков
177
для грамматик и т. п.), как «разудоно'е». Однако, так как
машина Тьюринга имеет конечное число ленточных символов, а
такие множества, как N и Т, могут быть сколь угодно
большими, мы будем представлять элементы конечного множества
Е = {аь а2, ..., ап} двоичными числами 1, 2, ...; п. Мы увидим,
что истинность или ложность каждой рассматриваемой
проблемы инвариантна относительно переименования символов.
Обозначение также будет «разумным», если существует машина
Тьюринга, которая всегда останавливается и которая может
перевести его в обозначение, имеющееся в настоящей статье.
Мы надеемся, что это" определение «разумности» не
произвольно. Если пользоваться «неразумным» обозначением, скажем
«грамматика», то в действительности получается другой объект,
относительно которого ничего не известно. Можно доказывать
теоремы о таком объекте, но не следует удивляться, если
полученные результаты' не будут согласовываться с результатами,
данными здесь.
Примеры проблем:
(1) Проблема принадлежности. «Принадлежит ли w языку
L?» Здесь w может быть произвольной строчкой в
произвольном конечном алфавите, a L — любой язык какого-либо класса
(бесконтекстный, IN стэковый и т. п.). Если проблема
принадлежности разрешима для класса языков, то кл-асс называется
рекурсивным.
(2) Проблема пустоты. «Существует ли в L тю крайней мере
одна строчка?» Здесь опять L — любой язык какого-либо типа.
(3) Проблема эквивалентности. «Справедливо ли L(G\) =
= Ь((32)Ъ или «Справедливо ли Т(А\) =Т(А2)Ъ> Здесь Gj и
G2 — грамматики одинакового типа и Л! и А2 — автоматы
одинакового типа.
В литературе рассматривались и другие проблемы, но мы
для простоты ограничимся этими тремя.
8.2. Разрешимость принадлежности, пустоты и эквивалентности
Важным результатом для машин Тьюринга является
неразрешимость вопроса, останавливается ли машина Тьюринга при
данном входе [74]. Таким образом, мы имеем теорему.
Теорема 8.1. (1) Проблема принадлежности неразрешима
для языков (типа 0), распознаваемых машинами Тьюринга.
(2) Для всех других классов языков, упоминаемых в этой
статье, проблема принадлежности разрешима.
Относительно утверждения (2) см. работы [1, 22, 68].
178
А. В. Ахоу, Дж. Д. Улман
Теорема 8.2. Проблема пустоты разрешима для (1) IN и
W стэковых языков и нестирающих стэковых языков [21];
(2) бесконтекстных языков; (3) индексных языков; (4)
регулярных языков. Она неразрешима для (5) языков типа 0;
(6) контекстных языков; (7) двусторонних магазинных
стэковых и нестирающих стэковых языков; (8) языков временной
сложности Т(п) для любой Т(п); (9) языков ленточной
сложности или недетерминированной ленточной сложности L(n),
такой, что supn^ooL(n) = оо; (10) бесконтекстных программных
языков.
Некоторые из этих результатов полностью не доказаны, но
их доказательства несложны. Заметим, что не все утверждения
теоремы 8.2 независимы, но были включены в теорему для
четкости. (Например, так как магазинные автоматы являются
ограниченными стэковыми автоматами, то (1) влечет (2).)
Будем называть Ш магазинный автомат простым, если он
имеет одно состояние и на каждом шаге передвигает входную
головку вправо. Простой магазинный автомат принимает те
слова, для которых магазинный список становится пустым.
Бесконтекстная грамматика G = (А', Г, Р, S) называется
скобочной грамматикой, если Т содержит [и], и каждая продукция
из Р имеет вид А ->[а], где А е N и aE(JV U Т — {[,]}) *.
Теорема 8.3. Проблема эквивалентности разрешима для
(1) конечных автоматов [61, 66]; (2) простых магазинных
автоматов [53]: (3) скобочных грамматик [58]; (4) ограниченных
языков [17, 27].
Эта проблема неразрешима для остальных классов языков,
упомянутых в этой статье, исключая, возможно, Ш магазинные
автоматы, стэковые автоматы и нестирающие стэковые
автоматы. Вопрос о разрешимости проблемы эквивалентности для
последних трех классов остается открытым.
Опять заметим, что некоторые из этих результатов не
доказаны.
Первые результаты о неразрешимых проблемах для
бесконтекстных языков появились в [3]. Другие результаты о
разрешимости встречаются в [4, 10, 14, 26, 30, 34, 35, 37]. Результаты
о разрешимости для Ш магазинных автоматов имеются в [19,
73], для двусторонних магазинных автоматов — в [32], для
односторонних стэковых автоматов — в [21], для индексных
языков—в [1] и для программных языков — в [68]. Некоторые
общие результаты, касающиеся разрешимости проблем
принадлежности и пустоты для 2N, 2D, IN и Ш устройств одного типа
имеются в [45].
Теория языков
179
Многие из теорем, утверждающих, что проблема
неразрешима, доказаны с использованием неразрешимости «проблемы
соответствия Поста» (Post's Correspondence Problem) {) [64].
Простое доказательство неразрешимости этой проблемы появилось
в [13].
9. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
9.1. Другие обзоры
Несколько других обзоров по теории языков и автоматов
находятся в печати. Среди них [6, 7, 15, 43]. Работа [12]
является обзором по теории автоматов, а [55] — по проблемам
разрешения 2).
9.2. Некоторые нерешенные задачи
В теории языков имеется много интересных открытых
вопросов. Мы перечислим здесь некоторые из них. Следующий
список вопросов содержит как трудные, так и фактически
неразрешимые вопросы. К сожалению, авторы не могут указать
принадлежность их к той или иной группе.
(1) Существуют ли контекстные языки, которые не
приемлемы любыми детерминированными линейно ограниченными
автоматами?
(2) Разрешима ли задача эквивалентности для
односторонних детерминированных
(a) магазинных автоматов;
(b) стэковых автоматов;
(c) нестирающих стэковых автоматов?
(3) Распознаваем ли каждый бесконтекстный язык
двусторонним детерминированным магазинным автоматом?
(4) Является ли условие supn.+<x>f (n)/g(n) = со достаточным
для того, чтобы существовал язык
(a) временной сложности f(n), но не g(n);
(b) недетерминированной ленточной сложности f{n), но не
g(n)} (Ответ для (Ь) положителен, если /(/г)-^ log /г, согласно
теореме 5,5.)
(5) Если supn-+ooL(n)/logп = 0, то существует ли язык L
ленточной сложности L(n), который не приемлем любой в. л.
1) В русской литературе эта проблема обычно называется
комбинаторной проблемой Поста. — Прим. перед.
2) См. также Гусев Л. А., С ми р н о в а И. М., Языки грамматики и
абстрактные модели, Автоматика и телемеханика, № 4 (1968), 72—94; N« 5
(1968), 73-94. - Прим. перев.
180
А. В. Ахоу, Дж. Л. Улман
машиной Тьюринга ленточной сложности L(n), для которой
гарантирована остановка при любом входе, принадлежащем или
не принадлежащем L? (Ответ отрицателен, если L(rt)>logn.)
(6) Существует ли бесконтекстный язык временной
сложности п3, но не меньшей?
(7) Существует ли бесконтекстный язык ленточной
сложности log2 п, но не меньшей?
Л ИТЕРАТУРА
1. Ah о А. V., Indexed grammars, an extension of context free grammars,
Princeton Univ. Doct. Thesis, 1967. См. также: IEEE Conf. Record of
Eighth -Annual Symp. on Switching and Automata Theory, Austin, Tex.,
October, 1967.
2. A h о A. V., H о p с г о f t J. E., U 11 m a n J. D., Tape and time
complexity of pushdown automaton languages, Information and Control. (В
печати.)
3. Bar-Hi 1 lei Y., Perles M., Shamir E., On formal properties of
simple phrase structure grammars, Z. Phonetik Sprachwiss. Rommunikat.,
14 (1961), 143—172.
4. Cantor D. C, On the ambiguity problem of Backus systems, /. Assoc.
Comput. Mach., 9 (1962), 477—479.
5. Chomsky N., Context-free grammars and pushdown storage, Quart.
Prog. Dept. № 65, M. I. T. Res. Lab. Elect., 1962, pp. 187—194.
6. Chomsky N., Formal properties of grammars, Handbook of Math.
Psych., v. 2, Wiley, New York, 1963, pp. 323—418. (Русский перевод:
X о м с к и й Н., Формальные свойства грамматик, Кибернетический
сборник (новая серия), вып. 2, изд-во «Мир», 1966, стр. 121—230.)
7. С h о m s к у N., Miller G. A., Introduction to the formal analysis of
natural languages, Handbook of Math. Psych., v. 2, Wiley, New York, 1963,
pp. 269—321. (Русский перевод: Хомский H., Миллер Дж.,
Введение в формальный анализ естественных языков, Кибернетический
сборник (новая серия), вып. 1, изд-во «Мир», 1965, стр. 229—290.)
8. С h о m s к у N., On certain formal properties of grammars, Information
and Control, 2 (1959), 137—167. (Русский перевод: Хомский H.,
О некоторых формальных свойствах грамматик, Кибернетический
сборник, вып. 5, ИЛ, М., 1962, стр. 279—311.)
9. Chomsky N.. Three models for the description of language, IRE
Transactions, IT-2 (1956), 113—124. (Русский перевод: Хомский H.,
Три модели описания языка, Кибернетический сборник, Вып. 2, ИЛ, М„
1961, стр. 237—266.)
10. Chomsky N., Schutzenberger М. P., The algebraic theory of
context free languages, Computer programming and formal systems, North
Holland, Amsterdam, 1963, pp. 118—161. (Русский перевод: ХомскийЕ,
Шютценберже М. П.. Алгебраическая теория контекстно-свободных
языков, Кибернетический сборник (новая серия), вып. 3, изд-во «Мир»,
1966, стр. 195—242.)
И. Evey J., The theory and application of pushdown store machines., Har.
vard Univ. Doct. Thesis,4963.
12. Fiscjier P. C, Multi-tape and infinite state automata — a survey, Commu-
nic. Assoc. Comput. Mach., 8; № \2 (1965), 799—805. (Русский перевод:
Фи шep П., Многоклеточные и бесконечные автоматы, Обзор,
Кибернетический сборник (новая серия), вып. 5, изд-во «Мир», 1968, стр. 64—
80.)
Теория языков
181
13. Floyd R. W., New proofs and old theorems in logic and formal
linguistics, Computer Associates Inc., Wakefield, Mass., 1964.
14. Floyd R. W., On ambiguity in phrase structure languages, Communic.
Assoc. Comput Mach., 5 (1962), 526—534.
15. Floyd R. W., The syntax of programming languages — a survey, IEEE
Transactions, EC-13, № 4 (1964), 346—353.
16. Ginsburg S., Examples of abstract machines, IRE Transactions, EC-11
(1962), 132—135.
17. Ginsburg S., The mathematical theory of context-free languages,
McGraw-Hill, New York, 1966.
18. Ginsburg S., Greibach S. A., Abstract families of languages, IEEE
Conf. Record of Eighth Annual Symp. on Switching and Aautomata Theory,
Austin, Tex., October, 1967.
19. Ginsburg S., Greibach S. A., Deterministic context-free languages,
Information and Control, 9 (1966), 620—648.
20. Ginsburg S., Greibach S. A., Mappings which preserve context
sensitive languages, Information and Control, 9, № 6 (1966), 563—582.
(Русский перевод: Гинзбург Г. С, Грейбах Ш., Об инвариантности
класса НС-языков относительно некоторых преобразований,
Кибернетический сборник (новая серия), вып. 5, изд-во «Мир», 1968, стр. 167—188.)
21. Ginsburg S., Greibach S. А., Н а г г i so n М. A., One-way stack
automata, J. Assoc. Comput. Mach., 14 (1967), 389—418.
22. Ginsburg S., Greibach S. A., H a r r i so n M. A., Stack automata
and compiling, J Assoc. Comput. Mach., 14 (1967), 172—201.
23. Ginsburg S., Hopcroft J. E., Two-way balloon automata and
AFL's, System Develop. Corp. Santa Monica, Calif. (В печати.)
24. Ginsburg S., Rise H. G., Two families of languages related to
ALGOL, Л Assoc. Comput. Mach., 9 (1962), 350—371. (Русский перевод:
см. настоящий сборник, стр. 184.)
25. G i n s b u г g S., Rose G. F., Operations which preserve definability in
languages, 7. Assoc. Comput. Mach., 10 (1963), 175—195.
26. G i n s b u r g S , Rose G. F., Some recursively unsolvable problems in
ALGOL-like languages, I. Assoc. Comput, Mach.y 10 (1963), 29—47.
27. G i n s b u r g S., Spanier E. H., Bounded ALGOL-like languages,
Trans. Amer. Math. Soc, 113 (964), 333—368.
28. Ginsburg S., Spanier E. H., Finite turn pushdown automata, J.
SI AM Control, 4 (1966), 429—453.
29. G i n s b u г g S , Spanier E. H., Quotiets of context-free languages, /.
Assoc. Comput. Mach., 10 (1963), 487—492.
30. Ginsburg S., Ullman J., Ambiguity in context-free languages, J.
Assoc. Comput. Mach., 13 (1966), 62—68.
31. Ginsburg S., Ullman J., Preservation of unambiguity and inherent
ambiguity in context-free languages, J. Assoc. Comput. Mach., 13 (1966),
364—368.
32. G г а у J. N.. H a r r i s о n M. A., I b а г r a 0., Two-way pushdown
automata, Information and Control, 11 (1967), 30—70.
33. G r e i b а с h S. A., A new normal form theorem for context-iree phrase
structure grammars, J. Assoc. Comput. Mach., 12 (1965), 42—52.
34. G г e i b а с h S. A., The undecidability of the ambiguity problem for
minimal linear grammars, Information and Control, 6 (1963), 117—125.
35. Greibach S. A., The unsolvability of the recongnition of linear context-
free languages, I. Assoc. Comput. Mach., 13 (1966), 582—587.
36. Greibach S. A., Hopcroft J. E., Independence of AFL operations,
Systems Develop. Corp. Santa Monica, Calif. (В печати.)
37. Gross M., Inherent ambiguity of minimal linear grammars, Information
and Control, 7, (1964), 366—368.
182
А. В. Ахоу, Дж. Д. Улман
38. Н a i п в з L. Н., Note on the complement of a (minimal) linear language,
Information and Control, 7 (1964), 307—314.
39. Hartmanis J., L^wis P. M., Stearns R. E., Hierarchies of
memory limited computations, IEEE Conf. Record on Switching Circuit
Theory and Logical Design, Ann. Arbor, Mich., October, 1965, pp. 179—190.
40. Hartmanis J., Stearns R. E., On the computational complexity of
algorithms, Trans. Amer. Math. Soc, 117 (1965), 285—306. (Русский
перевод: Хартманис Дж., "С т и р н з Р. Е., О вычислительной сложности
алгоритмов, Кибернетический сборник (новая серия), вып. 4, изд-во
«Мир», 1967, стр. 57—85.) N
41. Hennie F. С, Stearns R. E., Two tape simulation of multitape
Turing machines, J. Assoc. Comput. Mach., 13 (1966), 533—546.
42. H iD b a r d Т., U 11 m a n J., The independence of inherent ambiguity from
complementedness among context-free languages, J. Assoc. Comput. Mach.,
13 (1966), 588—593.
43. H о p с г о f t J. E., U 11 m a n J. D., A survey of formal language theory,
Proc. First Annual Princeton Conf. on Inf. Sciences and Systems,
Princeton, N. J., March, 1967, pp. 68—75.
44. H о p с г о f t J. E., U 11 m a n J. D., An approach to a unified theory of,
automata, Bell. System Techn. J., 46 (1967), 1793—1827. См. также: IEEE
Conf. Record of Eighth Annual Symp. on Switching and Automata Theory,
Austin, Tex., October, 1967.
45. H о p с г о f t J. E., U 11 m a n J. D., Decidable and undecidable questions
about automata, J. Assoc. Comput. Mach., 15 (1968).
46. H о p с г о f t J. E., U 11 m a n J. D., Deterministic stack automata and the
quotient operator, JCSS, 1 № 4 (1968). См. также: IEEE Conf. Record of
Eighth Annual Symp. on Switching and Automata Thtory, Austin, Tex.,
October, 1967.
47. H о p с г о f t J. E., U 11 m a n J. D., Nonerasing stack automata, JCSS,
1, № 2 (1967), 166—186.
48. H о p с г о f t J. E., U 11 m a n J. D., Sets accepted by one-way stack
automata are context-sensitive. (Представлено в Information and Control). См.
также: Two results on one-way stack automata, IEEE Conf. Record of
Eighth Annual Symp. on Switching and Automata Theory, Austin, Tex.
October, 1967.
49. H о p с г о f t J. E., U 11 m a n J. D., Some results on tape bounded Turing
machines. (Представлено в J. Assoc. Comput. Mach.)
50. H о p с г о f t J. E., U11 m a n J. D., Relations between time and tape
complexity, J. Assoc> Comput. Mach. (В печати.)
51. К lee ne S. C, Representation of events in nerve nets and finite
automata, Automata Studies, Princeton Univ. Press, Princeton, N. J., 1956, 3—
42. (Русский перевод: К л и н и С. К., Представление событий в нервных
сетях и конечных автоматах, Сб. «Автоматы», ИЛ, М., 1956, стр. 15-—
67.)
52. Knuth D. Е., On the translation of languages from left to right,
Information and Control, 8 (1965), 607—639.
53. Korenjak A. J., Hop его ft J. E„ Simple deterministic languages,
IEEE Conf. Record of Seventh Annual Symp. on Switching and Automata
Theory, Berkeley, Calif. October, 1966, pp. 36—46.
54. Kuroda S. Y., Classes of languages and linear-bounded^automata,
Information and Control, 7 (1964), 207—223.
55. L a n d w e b e r P. S., Decision problems of phnase structure grammars,
IRE Trans., EC-13 (1964), 354—362. (Русский перевод: Ландвебер П.,
Проблемы разрешения в грамматиках непосредственных составляющих,
Кибернетический сборник (новая серия), вып. 5, изд-во «Мир», 1968,
стр. 103—127.)
Теория языков
183
56. Landweber P. S., Three theorems on phrase structure grammars of
type 1, Information and Control, 6 (1963), 131—136.
57. L e w i s P. M., S t e a r n s R. E., H a r t m a n i s J., Memory bounds for
recongnition of context free and context sensitive languages, IEEEf Conf.
Record on Switching Circuit Theory and Logical Design, Ann. Arbor, Mich.
October, 1965, pp. 191-202.
58. McN au gh to n R., Parenthesis grammars, J. Assoc. Comput. Mach., 14
(1967), 490—500.
59. M i n s к у M. L., Computation: finite and infinite machines, Prentice-Hall,
Inc. Englewood Cliffs, N. J., 1967.
60. M i n s к у ML., Recursive unsolvability of Post's problem of «tag» and
other topics in the theory of Turing machines, Ann. of Math. (2), 74
(1961), 437—455.
61. Moore E. F., Gedanken experiments on sequential machines, Automata
Studies, Princeton Univ. Press, Princeton, N. J., 1956. (Русский перевод:
M у p Э. Ф., Умозрительные эксперименты с последовательностными
машинами, Сб. «Автоматы», ИЛ, М., стр. 179—210.)
62. Myhill J., Linear bounded automata, WADD Tech. Note, № 60—165,
Wright Patterson Air Force Base, Ohio, 1960.
63. P a r i k h R. J., Language generating devices, Quart. Prog. Rept. № 60,
M. I. T. Res. Lab. Elect., 1961, pp. 199—212. Эта статья была
перепечатана под другим названием: On context-free languages, J. Assoc. Comput.
Mach., 13 (1966), 570—581.
64. P о s t E., A variant of a recursively unsolvable problem, Bull. Amer. Math..
Soc, 52 (1946), 264—268.
65. Rabin M 0., Real-time computation, Israel. /» Math., 1 (1963), 203—211.
66. R a b i n M. 0., S с о 11 D., Finite automata and their decision problems,
IBM J. Res. Develop., 3 (1959), 115—155. См. также в сб. «Sequential
Machines: Selected papers (Moore E. F. ed.), Addison—.Wesley, Reading,
Mayss., 1964, 63—91. (Русский перевод: Рабин M. О., Скотт Д.,
Конечные автоматы и задачи их разрешения, Кибернетический сборник, вып.
4, ИЛ, М., 1962, стр. 58—91.)
67 Rosen krantz D. J., Matrix equations and normal forms for context-
free grammars, J. Assoc. Comput. Mach., 14 (1967), 501—507.
68 R о s e n k r a n t z D. J., Programmed grammars — a new device for
generating formal languages, Columbia Univ. Doct. Thesis, 1967. См. также IEEE
Conf. Record of Eighth Annual Symp. on Switching and Automata
Theory, Austin. Tex., October, 1967.
69 S с h e i n b e r g S., Note on the Boolean properties of context free langua*
ges, Information and Control, 3 (1960), 372—375.
70 Schutzenburger M P., Finite counting automata, Information and
Control, 5 (1962), 91—107.
71 Shamir E., On sequential languages, Z. Phonetik Spracnwiss. Kommu-
nikat, 18 (1965), 61—69.
72 S t a n 1 e у R. J., Finite state representations of context free languages,
Quart. Prog. Rept., № 76, M. I. Т., Res. Lab. Elect., 1965, pp. 276—279.
73 Stearns R. E., A regularity test for pushdown machines, Information
and Control (В печати.)
74. T u r i n g A. M., On computable numbers with an application to the Ent-
scheidungsproblem, Proc. London Math. Soc, (2), 42 (1936), 230—265;
Исправление: ibid, (2), 43 (1937), 544—546.
75. Y a m a d a H., Real-time computation and recursive functions not real-time
computable, IRE Trans., EC-11 (1962), 753—760.
76. Younger D H., Recongnition and parsing of context-free languages in
timen3, Information and Control, 10, (1967), 189—208,
Два класса языков типа АЛГОЛ1)
С. Гинзбург, X. Райе
ВВЕДЕНИЕ
Использование современных информационных систем в
значительной степени затрудняется высокой стоимостью
программирования и необходимостью тратить на него много времени.
Задачи, которые ставятся заказчиками, и решения этих задач
формулируются на некотором естественном языке, например на
английском. Чтобы воспользоваться услугами вычислительной
машины, необходимо перевести это описание на машинный
язык, другими словами, запрограммировать задачу. В
последнее время стали предприниматься попытки йерекинуть мост
между этими двумя типами языков. Используемый при этом метод
состоит в построении языков (называемых проблемно
ориентированными языками или ПО-языками), таких, что они
(i) достаточно. полны для описания множества задач и их
решений;
(и) в разумных пределах близки к языку, обычно
используемому заказчиком при формулировке и решении задач;
(iii) формализованы в такой степени, чтобы допускать
автоматический перевод на машинный язык.
Примерами ПО-языков могут служить КОБОЛ и АЛГОЛ.
Цель настоящего исследования — составить некоторое
представление о синтаксисе ПО-языков, в частности АЛГОЛа [1].
Именно кратко излагается метод нахождения составных частей
языка АЛГОЛ-60, позволяющий выделять некоторое семейство
множеств цепочек и доказать ряд математических утверждений
об этом множестве. Теперь определяемый язык типа АЛГОЛ
(мы не уверены, можно ли применить к этому понятию термин
«ПО-язык») может рассматриваться как одно из таких
множеств (множество предложений) или как конечная
совокупность таких множеств, одно из которых есть множество
предложений, а остальные являются составными частями языка и
используются для построения предложений. Такой подход
подобен одной распространенной точке зрения на естественные
языки [4—6]. Определяющая схема АЛГОЛа оказывается экви-
*) Ginsburg S., Rice Н. G., Two families of languages related to
ALGOL, Journal of the Association for Computing Machinery, 9, № 2 (1962),
350—371.
Два класса языков типа АЛГОЛ
185
валентной одной из нескольких схем, описанных Хомским [6]
при попытке исследовать синтаксис естественных языков.
Несомненно, что ПО-языки, являясь некоторым специальным типом
языков, должны вписываться в общую теорию языков. Однако
естественно предполагать, что ПО-языки, будучи
искусственными языками, специально построенными так, чтобы допускать
автоматический перевод на машинные языки, имеют более
простой синтаксис по сравнению с естественными языками.
В настоящей работе получены следующие формальные
результаты. Описываются два семейства множеств цепочек:
семейство определимых множеств и семейство последовательностно
определимых множеств. Определимые множества получаются из
систем уравнений некоторого специального вида. Эти системы
являются формализацией способа описания, принятого в АЛГОЛе.
Определимые множества оказываются тождественными
введенным Хомским [6] обобщенным (т. е. содержащим .пустую
цепочку) языкам типа 21). Последовательностно определимые
множества получаются из систем уравнений, решаемых
последовательно, т. е, одно за другим. Системы второго типа
представляют собой частный случай систем первого типа — именно
тот случай, когда возможно исключение неизвестных.
Полученные таким образом два семейства множеств не совпадают
(разд. 4). Известно, что если а — определимое множество и (3 —
регулярное множество, то множество а—р определимо.
Доказано, что аналогичный факт не имеет места для
последовательностно определимого множества а. Однако если а
последовательностно определимо и р конечно, то а — р последовательностно
определимо (теорема 3). Наконец, если в системе уравнений,
из которой получено определимое множество, каждое уравнение
линейно или коэффициенты во всех уравнениях перестановочны,
то данное множество является последовательностно
определимым (разд. 5).
1. ОПРЕДЕЛИМЫЕ И ПОСЛЕДОВАТЕЛЬНОСТНО ОПРЕДЕЛИМЫЕ
МНОЖЕСТВА
Рассмотрим следующие три металингвистические формулы
из АЛГОЛа:
(идентификатор): : =
== (буква)((идентификатор) '(буква)|(идентификатор)(цифра),
(целое без знака): : = (цифра)|(целое без знака)(цифра), (1)
(метка): : = (идентификатор)!(целое без знака).
1) В более современной терминологии — обобщенным контекстно-свобод*
ным языкам. — Прим. ред.
186
С. Гинзбург, X. Райе
Это типичный пример формул, используемых для определения
различных составных частей АЛГОЛа. Перепишем (1)
следующим образом. Пусть 1\ — множество идентификаторов, т. е.
1\ — (идентификатор); L\ — (конечное) множество букв; Dx —
(конечное) множество цифр; U\ — множество целых без знака
и Lb — множество меток. Заменим знак : : = на знак ==, а знак
| заменим на +. Тогда система (1) примет более компактный
вид
Ii^Li + IxLx + IxDu
U^Dx + UxDu (2)
L6 = /, + £/!.
Из системы (1) и, следовательно, из системы (2) видно, что
множества Л, U\ и L5 порождаются множествами L\ и D\.
С точностью до конечных множеств система (2) может быть
представлена в функциональном виде следующим образом:
Л-МЛ, Uи 1б),
f/i = /2(/1, Ult L5), (3)
£5-/3(/1. U и Ц)
или
/1-/4(/1).
£/1 = /5(/1, f/i), (4)
/«-МЛ, Uи Ц).
Однако в АЛГОЛе имеются системы формул, имеющие вид
(3), а не (4), например те, которые используются при
определении арифметических выражений. В этой статье изучаются оба
вида систем — вид (3) из-за его общности и вид (4) из-за его
внутренней простоты.
Остальная часть настоящего раздела посвящена
формализации понятий, о которых шла речь выше, с целью получить
возможность исследовать эти понятия точными методами.
Обозначение. Пусть 2 = {а, &,...} — непустой конечный
алфавит (конечное множество элементарных символов или букв).
Пусть 0(2) (сокращенно в) обозначает множество всех слов,
т. е. цепочек, в алфавите 2, включая пустую цепочку е.
Рассмотрим функции /(£(1), ..., £(п)), полученные из конечного
числа М-переменных (переменных, значениями которых
являются множества) |W ..., #п\ где каждая £<*> пробегает
множество всех подмножеств множества в, и конечного числа
подмножеств множества 0 (называемых коэффициентами) в
результате конечного числа применений операций „ + " (сложение или
Два класса языков типа АЛГОЛ
187
объединение множеств) и „•" (прямое умножение множеств1)).
Поскольку умножение дистрибутивно по отношению к
сложению, каждая из этих функций может рассматриваться как поли-
ном, т. е. f = 2 Пь где каждое Пг есть произведение М-пере-
менных и констант.
Каждая «з описанных в предыдущем абзаце функций
является неубывающей, т. е. если 2) (#1\ ..., £<n)) s {v<l\ ..., v(n)),
то f{#l\ ..., |(n)) s/(vW ..., v<n>). Более общо, предположим,
что fu • •., fn — последовательность описанных выше функций
от переменных $1\ ..., |<Ч Пусть 2е — семейство всех
подмножеств множества 6. Пусть / =* (/ь • • •» fn)—отображение f
множества (2е)п (декартова произведения множества 2е на себя
п раз) во множество (2е)п, определенное следующим образом:
/(6<!>, ..., £(П)) = (Ы£(1), •••, $(я)), .... Ы6(1), .... 1(п))).
Каждая из функций / = (/ь ..., fn) является неубывающей в
том смысле, что если £ = (Ц{\ ..., £<п>) г v = (v^>, ..., v<n>), то
/(6)S/(V).
Однако функции (2) и вообще определяющие функции
АЛГОЛа удовлетворяют еще некоторому дополнительному
ограничению, а именно все коэффициенты являются конечными
множествами.
Определение. Функция / (описанного выше типа) называется
стандартной функцией, если каждый ее коэффициент —
конечное множество.
Из соображений удобства мы будем рассматривать систему
функций /ь • • •, fn как одну функцию / =* (/ь ..., /п).
Определение. Пусть /ь ..., fn — последовательность,
состоящая из п стандартных функций от переменной g =» (#1\ ..., £(*))
каждая. Тогда функция /(g) = (/ь ..., /п) называется п-компо-
нентной стандартной функцией.
х) Пусть Ли ..., Am — последовательность множеств цепочек. Прямым
произведением А\> А2-... • Аш (сокращенно А\ ...Ат) называется множество
цепочек {хх... хт\ для каждого /, ^еЛг}; xi...xm — цепочка, полученная из
цепочек х\ (взятых в данном порядке) с помощью операции конкатенации.
Если одно или несколько из множеств Аи скажем Л^о, ..., Ацг), состоят
каждое из единственной цепочки, скажем flj(i), ..., flj(r> соответственно, то
вместо каждого вхождения Aj(i) записывается цепочка аму Например,
будем писать АЬ вместо А{Ь) и е вместо {с}.
2) Пусть (|(1), ..., £(w))—множество л-ок {(хи ..., *n)l*<GgWt
l^^n}. Тогда (1^\ .... £(п)) будет называться n-кой множеств. Каждое
£(<) будем называть координатой. Заметим, что (JO), ..., g<n>) &
s(v(1), ..., v<n>) тогда и только тогда, когда (OsSv* для каждого L
188
С. Гинзбург, X. Райе
Тецерь мы можем рассмотреть решение системы формул
вида (2). Мы увидим (см. ниже теорему 1), что понятие, фор*
мальным определением которого мы сейчас займемся, адекватно
смыслу, вкладываемому в такие системы в АЛГОЛе.
Определение. Подмножество у множества 9 называется оя-
ределимым, если (Существует я-компонентная стандартная
функция /, такая, что одной из координат наименьшей неподвижной
точки 1) функции f является множество у.
Изредка мы будем для наглядности записывать равенство
f(£(l), ..., 1{п)) = (£(1), ..., Е(п)) как систему из п уравнений
i(1) = Ui(1), ..., i(n)),
i(2> = /2(S(1), ....ew),
tin)=fn(t(l\ ...,|(П)).
Предыдущие рассуждения относятся к системам типа (3).
Теперь нетрудно исследовать системы типа (4).
Определение, я-компонентная стандартная функция f($l\ ...
...» Е(п)) = (/ь ..-, М называется п- компонентной последова-
тельностно стандартной функцией (л-компонентной П-стандарт-
ной функцией), если /г = MS(1), ..., £(г))> l-^i-^n. Множество
называется последовательности определимым
(П-определимым), если оно определимо с помощью некоторой д-компонент*
ной П-стандартной функции.
Пусть Т0 — множество всех конечных подмножеств
множества 0. Для п ^- 0 пусть Гп+1 — семейство множеств, каждое из
которых является наименьшей неподвижной точкой хотя бы
одного полинома от одной М-переменной с коэффициентами из
множества Тп. Множество у является П-определимым тогда и
только тогда, когда оно совпадает с некоторым
семейством 2) Тп.
После того как определены два семейства множеств, а
именно семейство определимых множеств и семейство П-определи«
мых множеств, естественно возникает вопрос, эквивалентны ли
эти два семейства. Было бы полезно, если бы эти семейства
оказались эквивалентными, ибо структура множеств последнего
*) Точка а=(а<1>, ..., а(п>) называется неподвижной точкой функции
f(5(1>. .♦•» l(n))*=(fu •••♦ /п), если f(a)«=a. Кроме того, если asp для
всех п-ок множеств Р= (Р(1), .... Р(п)), таких, что /(0)*=?, то а называется
наименьшей неподвижной точкой. Очевидно, что существует не более одной
наименьшей неподвижной точки.
2) См. лемму 6 из разд. 4.
Два класса языков типа АЛГОЛ
189
семейства интуитивно кажется проще структуры множеств
первого. Однако, как отмечено во введении, в разд. 4 будет
показано, что существуют определимые множества, не являющиеся
П-определимыми.
Известно, что каждая я-компонентная (последовательности©)
стандартная функция имеет наименьшую неподвижную точку
[10]. Сейчас будет показано, что наименьшая неподвижная точка
л-компонентной (последовательностно) стандартной функции
может быть найдена с помощью имеющейся в АЛГОЛе [1, стр.301]
рекуррентной процедуры для вычисления значений переменных
в системах формул вида (3) или (4). Это показывает, что
«-компонентные стандартные функции и их наименьшие
неподвижные точки могут служить моделью для определяющих
систем формул в АЛГОЛе.
Обозначение. <р будет обозначать пустое множество.
Теорема 1. Пусть для каждого i9 1 ^ / ^ n, ft — полином
от переменных f\ ..., |(n); f(f\ ..., g(rt)) = (/i, .... М и <*0-
= (^, ..., а§1)) = /(ф, ..., ф). Пусть далее для каждого i
имеем ai+x«(<x(/jif ..,, а£>,) *= f(a{) и а= (а(*>, ..., а^) есть
наименьшая неподвижная точка функции /. Тогда для каждого j имеет
оо оо
место а(/) = (J а ^ и а = (J ak.
Доказательство. Индукцией по k легко доказывается,
что aft£aHi для каждого k. Пусть р = (р(1), ..., р(л)), где р(У) =
оо
= [Jctjp для каждого /. Покажем, что a = p = Uafc-
Пусть х — (хи ..., хп) — элемент множества р. Для каждого
натурального числа I существует натуральное число k(i)9
такое, что ^saj|j0. Пусть k = max {k{i)}. Тогда x^ak. Поскольку
aftcafc+iaB/(aft)sf(p), то xe=f(p), т. е. psf(p). Аналогично
Р sfjajfe. Поскольку ak s р для каждого k, то (J ak s р. Следо-
* /is
вательцо, р = (J afe г / (р).
k
Пусть лс = (^1, ..., хп) — элемент 'множества f(p) и | = (|а>, ...
..., 1(п)). Для каждого натурального числа /полагаем М£) =
si
= S^.r©» гДе Ri.riX) есть произведение коэффициентов и
М-переменных £(У). Поскольку л^2П<>г(р), то ^еПЬг (р)
г
для некоторого г*. Пусть П/, г/ (§) =y*. i • • • Уи «о» гДе каждое
190
С. Гинзбург, X. Райе
Yt,и(1) есть либо коэффициент, либо одна из переменных gw>.
Тогда существуют элементы yit и из множества yi, u(P), такие,
что Xi = xjiy i, ..., \jiy t(i). Следовательно, x{ e Щ Г/ (a^)) для
некоторого достаточно большого числа k(i). Тогда х = f(а&), где
ft = max {&(/)}. Из того что f (%) = аь+i ^ р, следует, что
f (Р) е р всякий раз, когда f (Р) = р. Следовательно, р есть
неподвижная точка функции /. Остается показать, что р является
наименьшей неподвижной точкой функции f.
Доказательство проведем по индукции. Заметим, что ао =
= f (ф, ..., ф) £f(a) = а. Предположим, что аи ^ а. Тогда
aft+i = f (<%k) ^ f (a) =^= a. Следовательно, P==(Ja^ s a. Посколь-
ку a — наименьшая неподвижная точка функции /, то р = а.
Обозначения. Пусть f(g(l>, ..., £<*>) = (/ь ..., /п), где каждое
fi является полиномом от переменных £0>, ..., g(n>, и пусть
a = (aW, ..., а(я)) — наименьшая неподвижная точка функции /.
Будем сокращенно записывать это так: «Пусть f(Q = (fu ..., fn),
каждое fi— полином от переменных £<l>, ..., g(n>, и пусть a —
наименьшая неподвижная точка функции f». Всюду в
дальнейшем мы будем считать, что a0 = (aW, ..., 0^) = /(9, ..., ф) и
a*+ieK+p •••• aikli) = f(ak) для всех k>°-
За исключением наиболее простых случаев, множества afp
становятся сложными достаточно быстро. Для иллюстрации
рассмотрим систему двух уравнений
gu> = £а>с+ £(2>d + a,
Здесь c#>«{a}, a(02) = {6}, «^-{a, ac, bd}, a<2> = {&, ad, be}, a<J)-
= {a, ac, fed, ac2, &dc, ad2, 6cd} и т. д.
Как отмечено во введении, п-я координата a(n) наименьшей
неподвижной точки я-компонентной стандартной функции f(|) =
= (fu • • •» fn) может рассматриваться как язык, при этом a(n) —
множество «предложений», а другие координаты — множество
составных частей этого языка. Эти составные части
соответствуют множествам глаголов, групп существительных и т. дмчто
согласуется с современной точкой зрения на язык [4—6].
Действительно, в теореме 2 показано, что определимые множества
эквивалентны описанному в [6] семейству обобщенных
контекстно-свободных языков.
Следуя [2], назовем контекстно-свободной (КС-) системой
упорядоченную пару (V,P), где V— конечный алфавит, Р —
конечное множество правил вида
X-+x{X&Vt JC€=8(V)).
Два класса языков типа АЛГОЛ
191
Будем писать у =ф г, если у = uXv, z = uxv и Х~>л;—
правило из Р. Будем писать yt—^z, если либо у = z, либо
существует последовательность г0, ..., zry такая, что у = 20, гг = 2 и
z,- =фгг+1 для каждого /. Обобщенной контекстно-свободной
(КС-) грамматикой называется упорядоченная четверка (У, Р,
2,5), где (У, Р)—КС-система; 2— подмножество
множества V, ни один из элементов которого не встречается в левых
частях правил из Р; S — выделенный элемент множества V — 2.
Если G = (V, Р, 2, S)—обобщенная КС-грамматика, то множе*
ство
L(G) ={*1*е= 0(2), S*->x}
называется обобщенным КС-языком.
Теорема 2.Семейство определимых множеств совпадает с
семейством обобщенных КС-языков.
Доказательство. Пусть /(g) = (/i, ..., fn) есть я-компо.
нентная стандартная функция и а— ее наименьшая неподвижная
точка. Пусть V = 2 U {£(1), ..., |(/г)}. Поскольку умножение
дистрибутивно по отношению к сложению, каждая стандартная
функция ft может быть представлена в виде ft= 2lL /(£), где
i
п/. / (£) = Y/, i ••• У),та,1) и кажДое y[k есть либо переменная,
либо цепочка. Для любых / и / имеется правило l{i) —>П/§ 7(£);
пусть Р — множество всех таких правил. Пусть G = (V, Р, 2, g<*>).
Покажем, что l{t) ь—>* до для всех / и всех цепочек до е aj>'>.
Это, очевидно, верно при & = 0. Допустим, что это верно для
некоторого &, и пусть до — цепочка из а£|г Тогда дое/,(аЛ),
следовательно, доеП/§/(аЛ) для некоторого /. Тогда ^ = ^ ... xmiitf),
где для каждого а имеет место ха=*у^а, если Y/ а — цепочка,
и имеет место xflEa[v(fl^, если v/,fl— переменная'g<v(a)). В
последнем случае g(v(a))i—>лгЛ по индукции. Поскольку £((/)ь->
^П/, /(|)-правило из Р, имеем |(/) ь-> ^ ... *m а, л = до. Итак,
5(|)н-»ш для всех ffiiGa(/), Полагая / = я, получаем L(G) Эа(,1).
Чтобы убедиться, что L(G)Sa(tt) и, следовательно, L(G) = a(w),
достаточно показать, что
если хх и ^ — произвольные цепочки из Q(V) и #i—>x2i
го *i(a) = х2(а) + g(a) для некоторого множества g(a). (5)
Пусть а;—произвольная цепочка из L(G), тогда ^п)ь->^.
Отсюда a<n> = до + g(a), гак что до = а<4 Рассмотрим такие
цепочки #! и х2 из 0_(Ю, для которых имеет место ххь->хг. Для
192
С. Гинзбург» X. Райе
любых таких цепочек хх и х2 рассмотрим ^последовательность
z0, ..., zr, такую, что хх = г0, х2 = zr и 24=ф zi+i для всех /.
Предположим, что г= 1. Тогда для хх и л:2 существуют цепочки
и>ь ^2, яуз и до4 из 8(У), такие, что хх = о^ади^» *2 = wxwkw2 и
до3 —► wk е Р. Поскольку х$)ъ-+х$)к<=: Р, то а;3(a) = wk(а) + gi(а).
Тогда *i (a) = wx (а) ш3 (а)ш2 (а) = wx (а) ку4 (а) w2 (а) + а^ (а) •
'gi(a)w2{a)= х2{а) +g(a), где g(a) = wx(a)gx(a)w2(a).
Продолжая индукцию, предположим, что (5) -имеет место для всех
цепочек хх и х2 при условии, что г К к. Пусть хх и лт2 —две
цепочки, при которых г = k + 1. Тогда хх = z0-^zh и zh-+zk+x =
= #2. По предположению индукции Zk (а) = #i (а) + gx (а) и
Л'2(а)= zk(a) + g2(a). Тогда x2*(a) = хх{а) + g(a), где g(a) =
= gi(a) + #2 (а). Итак, (5) справедливо в общем случае, и
L(G) = а<4 Следовательно, каждое определимое множество
является обобщенным КС-языком.
Наконец, пусть G =(У,Р, 2,S) — обобщенная
КС-грамматика. Обозначим элементы множества V — 2 через £(l>, ..., Qn\
где £(n> = S. Для каждого l{i) пусть £(/)->до|, ..., g<'> -+w\^ —
все правила из Р с левой частью g(i). Рассмотрим л-компонент-
ную стандартную функцию / = (/ь ..., fn), где //= 2W- Пусть
/-1
G = (У, Р, 2, S)— обобщенная КС-грамматика, получаемая с
помощью процедуры, описанной в предыдущем абзаце. Итак,
L(G) = a(n), где (а(1), ..., а^)— наименьшая неподвижная
точка функции /, т. е. каждый обобщенный КС-язык является
определимым множеством. Доказательство теоремы 2
закончено.
Пусть G = (1/, Р,2, g(w>)—обобщенная КС-грамматика и
V — 2 = {|<#| 1 "Ci^Cri}. Предположим, что для всякого £<*> и
всякого правила |<*> -> w каждая переменная g<j), встречающаяся
в цепочке w, такова, что j^L Тогда L(G) является П-опреде-
лимым множеством. Более того, каждое П-определимое
множество может быть порождено таким образом.
Из теоремы 2 и только что сделанного замечания следует,
что при рассмотрении определимых и. П-определимых множеств
выбор между использованием систем уравнений или систем
правил связан лишь с соображениями удобства.
2. ПАРАЛЛЕЛЬНЫЕ РЕЗУЛЬТАТЫ
Многие известные факты, касающиеся определимых
множеств, имеют место также и для П-определимых множеств.
Здесь мы приведем некоторые из них.
Два,класса языков типа АЛГОЛ
193
Известно, что семейство определимых мнржеств замкнута
относительно операций +, • и * [2]1). Семейство П-определимых
множеств замкнуто относительно тех же операций. Именно
предположим, что у[Ь\— П-определимое множество,
являющееся m-й [n-й] координатой наименьшей неподвижной точки
m-компонентной [л-компонентной] П-стандартной функции
f(t) = (fu •--, fm)[g(vV\ ..., v^) = (gu .., gn)l Тогда
множества уЬ, у + б и y* являются (ш -f- п + 1)-и координатами
наименьших неподвижных точек функций (fb ..., /m, gh ..., gny
gn + \), (fb ..., fm, g\> ..., gn> gn+2) И (fi, ..., /m, g\, ..., gn,
gn+з) соответственно, где gn^\ = £<mMn>, gn+2 = £(m) + v(n> и
£.+3 = g<» + 3>g<"» + 8.
К настоящему времени широко изучены два важных
семейства множеств — регулярные множества2), связанные с
конечными автоматами3), и рекурсивно перечислимые множества [7],
связанные с машинами Тьюринга [7]. Хомский [6] заметил, что
семейство определимых множеств строго содержит семейство
регулярных множеств и строго содержится в семействе
рекурсивно перечислимых множеств. Это справедливо и для
семейства П-определимых множеств. Свойство П-определимости
регулярных множеств следует из свойств замкнутости
семейства регулярных множеств. С другой стороны, множества
{апсап/п > 0} является П-определимым, поскольку оно является
наименьшей неподвижной точкой функции а\а 4- с и, как
известно, не является регулярным [8]. Другой пример можно
привести из языка АЛГОЛ.
Пусть Pi — переменная, пробегающая множество чистых
строк, и 02 — переменная, пробегающая множество открытых
строк. Тогда р[ = PiH + H
00
1) Операция «*» определяется как Л* = МЛг* для каждого множества Аг
i = 0
где Л°=е и Ai+i=A'A для i>0.
2) Семейство регулярных множеств — это наименьшее семейство
множеств, содержащее конечные множества и замкнутое относительно операций
+ , • и * [8].
. 3) Конечным автоматом называется упорядоченная пятерка (/С, 2, 6, q0,
F), где К — конечное непустое множество (множество состояний), 2 —
непустое конечное множество (множество входных символов), 6 — функция
(функция переходов), отображающая множество /СХ2 во множество /С, q0 —
элемент К (начальное состояние), F — подмножество множества К
(множество заключительных состояний) [8]. Говорят, что цепочка
(последовательность входных символов) допускается конечным автоматом, если существует
такое вычисление автомата с этой цепочкой на входе, которое переводит
автомат из состояния q0 в некоторое состояние из множества F. Известно, что
множество является регулярным тогда и только тогда, когда оно состоит
в точности из тех цепочек, которые допускаются подходящим конечным
автоматом [8].
194
С. Гинзбург, X. Райе
где Н — конечное множество, не содержащее ни одного из двух
символов V. Методом, близким к использованному в [8]/ можно
показать, что если (PJ, 00 — наименьшая неподвижная точка,
то 0'2 не регулярно! Из этото следует, что 0'2 не допускается
никаким конечным автоматом, т. е. не существует конечного
автомата, определяющего, принадлежит ли произвольная
цепочка из 9 множеству Огг
Известно, что семейство определимых множеств не замкнуто
относительно операции пересечения (следовательно, и
относительно операции взятия дополнения) [2, 9]. Семейство П-опреде-
лимых множеств также не замкнуто относительно операции
пересечения (следовательно, и относительно операции взятия
дополнения). Действительно, пример, приведенный в [9], подходит
и для данного случая. Пусть он = {ап/п > 1} и а2 = {Ьпап/п > 1}.
Здесь он и ос2 — наименьшие неподвижные точки функций
ag + а и fega + Ьа соответственно. Следовательно, ai и аг —
П-определимые множества. Далее доказательство в точности
совпадает с приведенным в [9].
Следующий результат, известный в несколько иной форме
для определимых множеств [9, лемма 3], справедлив вместе с
доказательством для П-определимых множеств.
Теорема А. Если а! — бесконечное П-определимое
множество, то существуют П-определимые множества б, Р, у, [l и v,
такие, что
(1) 6 есть бесконечное множество;
(2) либо (л, либо v не пусто;
(3) (i6v^6;
(4) р6у<=а'.
На П-определимые множества можно перенести вместе с
доказательством еще один результат, известный для определимых
множеств [2, теорема 3.3]. Он заключается в следующем.
Теорема В. Пусть а есть П-определимое множество. Если
h(x) есть П-определимое множество для каждого х е 2, то
[J h(x\) .. Л(хг) — также П-определимое множество.
Ввиду теоремы 2 можно дать следующую эквивалентную
формулировку теоремы В.
Теорема С. Пусть /(gO), ..., £(*)) = (fb ..., fn), где каждое
fi — полином от переменных I*1); ..., g(n> и каждый
коэффициент есть П-определимое множество. Тогда каждая координа-
Два класса языков типа АЛГОЛ
195
та а(г) наименьшей неподвижной точки a =(0^, ..., а^)
является U-определимым множеством. Более того, пусть
Ль ..., As — все попарно \ различные коэффициенты и
аь ..., as — абстрактные символы, такие, что ft(flj) = Aj для
каждого j. Пусть через g = (gu ..., gn) обозначена п-компо-
нентная П-стандартная функция, полученная заменой каждого
Aj на aj. Пусть р = (£<*), ..., р<л>) — наименьшая неподвижная
точка функции g. Тогда для каждого i имеем а^> =
U ft(*i) ••• *(*r).
(w^i})(w = xy..xr)
3. ВЫЧИТАНИЕ
Предыдущий раздел был посвящен результатам, одинакова
справедливым для определимых и П-определимых множеств.
Покажем теперь, что аналогичные результаты не могут быть
перенесены на вычитание,
В работе [2, теорема 8.1] было показано, что если о! —
определимое множество и В — регулярное множество, то множества
а/ — В определимо. Для П-определимых множеств
соответствующий факт не имеет места.
Пример. Пусть т\' — множество, состоящее из всех
симметричных слов вида
an*b-idbn**-*dan*-*d ... dbn4an^can^dbn4 .:. da^-i,
где ft, ni,..., nab-i — натуральные числа. В разд.-4 будет
показано, что г]' — определимое, но не П-определимое множество.
Пусть М = ец'е. Пользуясь теоремой В, легко проверить, что М
не есть П-определимое (хотя и определимое) множество. Пусть
о!— множество симметричных слов вида
exfy .. .xfixfictfixfr ... x\ke,
где A, /ii,..., /I* — натуральные числа Х\ = xk — а, Х{ =* а,Ь или
d и хшфх{. Пусть /а(Ч£<2и(3)) = (Ы2,Ы, где fx = а$»а +
+ bl^b + dgO>d + аса, fe = а|(% + al&a и /3 = е^ё. Множество
а' является-третьей координатой наименьшей неподвижной
точки /. Поэтому о! есть П-определимое множество.
Пусть А = (/С, 2, б, ри {Р\})—конечный автомат1),
определенный следующим образом: К = {pi\l KiK6) и 2 = {а, 6, с, d, г};
функция б определяется так: 6(pi,e) = p2, 6(р2,6) = р6, 8(р2,^) =
= Рз, 6(р2,е) = Рь б(р3, a) = 6(p3,d) = p6, б(р3, *) = Л, 6(р4, а) =
= Ре, б (р4, d) = р5, б (р5, л) = Р2, б (р5, Ь) = б (р5, d) = Ре и
8(pJ) =р для всех остальных р и /. Множество Я цепочек,
допускаемых автоматом Л, регулярно1). Легко видеть, что для
]) См. примечание 3 на стр. 193.
196
С. Гинзбург, X. Райе
каждой цепочки X из множества о! имеет место 6(р\,Х) = ри
если X принадлежит множеству М, и имеет место 6(/?i,X) = /?6,
если X не принадлежит множеству М. Итак, а' П Я = iM. Пусть
i? — дополнение множества Н. Поскольку Н — регулярное
множество, В также регулярно. Однако о! — В = М. Итак, а' есть
П-определимое множество, В — регулярное, и а' — В не
является П-определимым множеством.
Ниже, в теореме 3, мы дадим некоторые условия, которым
должно удовлетворять множество В, чтобы множество а! — В
было П-определимо, если о! является таковым. Предварительно
докажем две леммы.
Лемма 1. Пусть А—множество, такое, что для каждой
стандартной функции g{Qx\ ..., Qn)) и каждой
последовательности v(1), ..., v<n> П-определимых множеств все множества
(v<*> О А) и g(vQ) ПА, ..., v<*> П Л) —(v<*> П А) являются П-
определимыми. Пусть, кроме того, А таково, что для любых
цепочек х, у и z если xyz^A, то у^А. Тогда для каждого П-
определимого множества о! множество а —А также
П-определимо.
Доказательство. Пусть а' — произвольное
П-определимое множество, f(l) = (fu •••, fn)—я-компонентная П-стан-
.дартная функция, а — наименьшая неподвижная точка и a(n> =
= а'. Для 1 < i < п положим F{ = А П а<*>, Gi = fi (Fh ... ,Fi) и
Di = Gi — Fi. По условию леммы все множества Fi и D{
являются П-определимыми. Для каждого / будем записывать М£(,) +
+ Fu . .. ,£<*> + Fi) в виде gi(Ql\..., £<*>) + Gu где gt — полином
от переменных |^), ..., gw без свободного члена. Для каждого /
полином hi = gi + Di содержит в качестве коэффициентов
только множества Fx,.. . ,FuDi и конечные множества. Пусть р =
= (Р(1),... ,р(п)) — наименьшая неподвижная точка функции
ft(6<!>,...,6<*>) = (hu...,hn). Тогда р = ирл, где ро-(ft0, ...
..., 6Г) = /*(Ф> --..Ф). и кажД<* P*+i = (Pi% .... РЙОвА(Р*)-
Согласно теореме С, каждое р(/) есть П-определимое множество.
Покажем, что для каждого i имеет место р^ = а^> — Fi = а<*> —
— А. Поскольку р(п> есть П-определимое множество,
доказательство леммы будет на этом закончено.
Очевидно, что Р^0 = Dt s oSl) — Fr Предположим, что pj£> s
s a(l) — Fi9 так что поскольку F{ e a(/), то PJJ + /^ sa^ для
каждого i. Тогда
Два класса Языков типа АЛГОЛ
197
Допустим, что множество Р$+1Г|Л не пусто, т. е. содержит
некоторую цепочку v. Поскольку pw+1 S Ф\ "цепочка v
принадлежит множеству а(/) О А. Тогда v & Dh так как £>, =»
= G, - (а<*> П Л). Поскольку pg>+1 - ft (p<J>, ..., pg>) + Di9 цепочка о
принадлежит множеству gt(^> ..., Р$). Из определения
функции gi следует, что gt (pi*, ..., pm) есть объединение
произведений, каждое из которых содержит в качестве множителя
хотя бы одно из множеств ^. Следовательно, v = xyz, где
у — цепочка, принадлежащая одному из множеств pW, ..., р<£,
скажем множеству р$. По предположению индукции цепочка у
принадлежит множеству Л, так что оеА, Следовательно,
y&Qf£()A. Однако
p$n4s(aWT-F/)fM-<p.
Из полученного противоречия следует, что множество Р^+1 П Д
пусто. Итак, р^+1 sa<*> — A *=а<'>~- Fit Следовательно, по
индукции flS?=.a(,)-F/ для всех / и т. Итак, f} = []$} ^a>{i) - Ft
m
для всех /.
Что касается обратного включения, то для каждого I имеет
место
Предположим теперь, что а.% — F{^ p<f). Отсюда а<£ s pw + Fr
Тогда
s/дГ + Л. ....(^ + ^)-^1-
-ЫР(1). ..., p<'>)+G,W,£
= ft№(1),..., ^) + (01-^)-^.
Итак, a^ — Fi^P(i) для всех m, так что a<*> —Z7* s=p(<).
Следовательно, а<г> — F{ = р(г>.
Лемма 2. Пусть а' есть П-определимое множество и 22 —
подмножество основного алфавита 2ь Тогда о! П 0(¾) ^сть П-
определимое множество.
Доказательство. Для каждого ^6¾ полагаем f(#) =*
=={*}, и для каждого #e2i—22 пусть f(x) =0. Пусть р'=
= U /(*,) ...f(Xr). Очевидно, что а!Г1 8(22) = р'.
Согласно теореме В, множество р' является П-определимым.
198
С. Гинзбург, X. Райе
Теорема 3. Пусть В — либо конечное множество, либо
П-определимое множество цепочек, являющихся степенями
некоторого данного символа. Тогда о! — В есть П-определимое
множество для каждого П-определимого множества а'.
Доказательство. Предположим сначала, что В —
конечное множество, состоящее из цепочек wu ... ,шг. Для каждой
цепочки хев через L(x) обозначим длину цепочки х. (В
частности, L(e) = 0.) Пусть h = max{L(^t) |1 -4^'^г} и A = {x\x&Q,
L(x) ^h\. Очевидно, что А удовлетворяет условию леммы 1.
Следовательно, множество о! — А является П-определимым.
Поскольку множества о! П А и В конечны, множество (а' Г\ А) — В
будет П-определимым. Тогда о! — В = (а' — А) + [(а' П А) — В]
есть П-определимое множество.
Допустим теперь, что В есть П-определимое множество
цепочек, являющихся степенями одного символа, скажем символа а.
Тогда В = {as\s е^}, где, как будет показано (следствие 2 из
теоремы 4), Л — периодическое множество неотрицательных
целых чисел 1). Пусть А = {а'|/^0}, где а0 = е. Согласно лемме 2,
если у есть П-определимое множество, то и множество у П А
является таковым. Согласно следствию 2 из теоремы 4, семейство
всех П-определимых множеств цепочек, являющихся степенями
одного символа, совпадает с семейством регулярных множеств
в алфавите, состоящем из одного этого символа. Пусть g(£(1), ...
• • •, £(п))—произврльная стандартная функция. Через v Г1 Л
обозначим п-ку (v(1) Г1 Л, ..., v<n> Г1 А). Каждое v(*> П А есть
регулярное множество. Тогда g(v(]A) представляет собой
объединение произведений регулярных множеств. Поскольку
семейство регулярных множеств замкнуто относительно операций
произведения, объединения и вычитания, то множество g(v Л
П А) — (v(*> Л А) регулярно и тем более П-определимо.
Следовательно, А удовлетворяет условиям леммы 1. Тогда of — А
является П-определимым. Кроме того, (а'Л Л) —В есть
П-определимое множество, поскольку а' Л Л и В — регулярные
множества. Тогда а' — В= (а' — Л) +[(а'(]А)— В] есть
П-определимое множество. Теорема доказана.
4. ПРИМЕР
Возникает вопрос: совпадает ли семейство определимых
множеств с семейством П-определимых множеств? Ответ на этот
*) Множество неотрицательных целых чисел X называется
периодическим, если существуют такие натуральные числа По и р, что для всякого
n^riQ из п е % следует п+р е А.
Два класса языков типа АЛГОЛ
199
вопрос отрицательный. Мы приведем пример определимого
множества т|', не являющегося П-определихМым.
Предварительно докажем несколько лемм.
Лемма 3. Пусть f(g) = (/i, ..., fn) есть п-компонентная
П-стандартная функция, а — ее наименьшая неподвижная
точка и и(\),,.. 9u(s) — подпоследовательность
последовательности 1,..., п. Для каждого i пусть gt(g(u(1)), ...,
g<u<s»)—функция fu в которой каждая переменная gW) (/ не совпадает ни
с одним u{k)) заменена.на Ф\ Тогда наименьшей неподвижной
точкой функции g(g<u<1», ..., #иЩ ={gu(\), ..., gu(s)) будет у =
= (^^)),...,^^))).
Доказательство. Поскольку а — неподвижная точка
функции f, то cx<j) = f j (а) для каждого /. Поэтому а^г)) = fu«)(a) =
= gu(i)(y)- Следовательно, у — неподвижная точка функции g.
Осталось показать, что у — наименьшая неподвижная точка
функции g.
Пусть р = (р("(1)), ..., р<и(*») — наименьшая неподвижная точка
оо
функции g. Согласно теореме 1, р = (J Р*, где ро = (Ро"(1)), .. .
. .., РГ5))) = £(Ф> •••> Ф) и Р,+1-(Р^)0), .... РШ-«(Р*) для
каждого k. Тогда для каждого u(j) имеет место
«*,W)-/.0)(f) = U(vi v«) = ^'
где Vi = ф, если / = и(х) для некоторого х9 и v* = a<*> в
противном случае. Для каждого i4in и каждого k положим
v<p = p(p, если i = u(x) для некоторого xt v^) = a(/) в противном
случае и v^ = (v^), ..., vj^)). Продолжая индукцию,
предположим, что (<4"(1)), ..., a%{s)))^$k^fi. Тогда для каждого u(j)
имеем
-Pftp> =
£Р<«</».
оо
Итак, (J а^^)> = Ф </» г р<"(»), следовательно, Y ~ Р- Из того, что
неподвижная точка р является наименьшей, следует, что v = Р-
Таким образом, у — наименьшая неподвижная точка функции^.
В качестве следствия получаются следующие леммы.
Лемма 4. Пусть /(g) = (fu... ,fn) есть п-компонентная
П-стандартная функция и a—ее наименьшая неподвижная точка.
200
С. Гинзбург, X. Райе
Предположим, что для некоторого целого числа i
множество оь<*> конечно. Пусть g = (gu...,gi-u £«+ь .. ..gn). где для
каждого целого числа j Ф i через g$ обозначена функция вида
= MS(1) ф~1\ ф,\{М) , &(л)).
Тогда g есть \п — 1) -компонентная U-стандартная функция и
у = (а*1),..., а**-1*, a(f+1),..., а(п>) — ее наименьшая
^неподвижная точка.
Лемма 5. Пусть /(g) ~ (fь..., fn) есть п-компонентная
П-стандартная функция и а — ее наименьшая неподвижная
точка. Для некоторого целого числа i полагаем fi(Q =* g<*) + A(g).
Тогда функция g(g)'= (gu...,gn), где g,(g) = ft(g) и ft(|) a,
ЯЫ£) для] Фь, является п-компонентной П.-стандартной
функцией, а и — ее нйименьшей неподвижной точкой.
Доказательство леммы 5 следует из теоремы 2 и того факта,
что всегда можно обойтись без правил вида £W —*|W.
Приведем £ще одно следствие леммы 3.
Лемма 6. Пусть (а^>,..., а<п>) — наименьшая неподвижная
точка п-компонентной П-стандартной функции (fb..., fn). Тогда
а<*> яв-ляется наименьшей неподвижной точкой функции f^aP*,...
...,а<-4|«>).
Пусть 2 = {a, 6,c,d} и g(v,T)) = (gug*), где gi = 6v6 +
+ bdx\db и g2 = tfdvda + аца + аса. Обозначим через (v', t|')
наименьшую неподвижную точку функции (gug%). Легко
проверяется, что r\f — множество симметричных цепочек вида
[пи ..., /itf-d-a11*-^ ... dbn*dan*can*dbn*d ... b**-*da**-i9
где ft, sii, . . . , n2ft-i — натуральные числа. Следовательно, tj' —
определимое множество.
Предположим, что т)' есть П-определцмое множество.' Пусть
f (£<*>, ..., £(n))e(fi» -..» /п) есть /г-компонентная П-стандартная
функция, наименьшая неподвижная точка (а*1*,..., а<п>)
которой такова, что a<n> = tj'. Согласно лемме 4, можно допустить,
что каждое a(i> бесконечно. Пусть m — наименьшее натуральное
числи, удовлетворяющее следующим двум условиям:
(a) существует пара {uyv) цепочек, таких, что uaSm)v —
подмножество множества a<n);
(b) множество ua(m)v содержит бесконечное число цепочек
[rii, ...,nj, таких, что, каковы бы ни были числа l,...,s— 1,
для них имеет место пх < ... < п8-г. Поскольку п удовлетворяет
условиям (а) и (Ь), такое число m существует. Докажем, что
Два класса языков типа АЛГОЛ
201
множество х\' не является П-определимым. Для этого покажем,
что существование числа m приводит к противоречию.
Предварительно докажем, что
для произвольного а^> если W и У — такие два
множества, что Wa^Y ^ т]', то каждое из мно- .
жеств W и Y содержит в точности одну цепочку, w
скажем w и у соответственно,
Чтобц это показать, положим, что тку — произвольные
цепочки из множеств W и Y соответственно. Пусть хх и *2 — две
цепочки из бесконечного множества а^\ Допустим, что w
содержит символ с. Рассмотрим две цепочки из ц'\ тх\у и wx2y,
где с е до. Очевидно, что обе эти цепочки не могут быть
одновременно симметричными. Однако это противоречит тому, что
каждая цепочка из множества г)* симметрична. Итак, цепочка w
не содержит символа с» Аналогично доказывается, чго цепочка у
не содержит символа с. Следовательно, каждая цепочка из мно*
жества а^ содержит символ с. Предположим, что W содержит
вторую цепочку W\. Рассмотрим две цепочки из г)': W\Xxy и wxxyy
где с s.wu Обе эти цепочки одновременно не могут быть сим^
метричными, что опять-таки противоречит симметричности
каждой цепочки из г\'. Итак, множество W состоит в точности из
одной цепочки. Аналогично доказывается, что. множество Y
состоит в точности из одной цепочки. Утверждение (6) доказано.
Рассмотрим множество а<т). По предположению (а(1), ...
...,а<п)) — неподвижная точка функции f. Таким образом,
a<m> = fm(a({\..., a<w>). Так как fm— полином от переменных
|(1>*.. • ,|(т), мы можем записать fm в виде
М£(1),•.. &т)) - А^Вг + ... + A&WBt + К,
где /C=fm (£(1),..., S(m~4 0) и для каждого / имеем» At = А{(Ц1\...
. ..,g<m>) и Вг =*В{($1\... , £<т>). В силу леммы 5 можно
считать, что £(т> не совпадает ни с одним из слагаемых Л*|(т)23*.
Пусть /С' — fm(a(I)....» о&ш~1\ 0) и для каждого I полагаем
А\-Аг{<*1\ ..., a<W) и В'й-Вл(а<1\ ..., а<™>). Таким образом,
а(т)efm(а(!)э ^% a(«)j.A[cfi^B[ +...+ A'taMB't + К\
Поскольку uA'flWB'iVSuaWvsrf, то, согласно (6), каждое из
множеств иА\ и В'р состоит в точности из одной цепочки.
Теперь мы можем показать, что существование числа т при*
водит к противоречию. Чтобы сделать это, рассмотрим
множество К'. Именно мы установим, что К' должно удовлетворять
одному из двух взаимоисключающих условий и что выбор каж*
дого из этих условий приводит к противоречию,
202
С. Гинзбург, X. Райе
Случай 1. Предположим, что множество uK'v содержит
бесконечное число цепочек [tt\ , ns], таких, что, каковы бы ни
были числа l,./.,s—1, для них имеет место rt\ <....< п8-\.
Запишем функцию К = fm(i{l\..., l(m~l\ 0) в виде
К = П2 (|<Ч..., Б<*-1>) + ... + Щ (1(1)...., 6<"-i>),
где каждое Пг- — произведение конечных множеств и
переменных |(,),.... S(w"!). Заменяя каждое gO) на a<j), получаем
где каждое Рг = Ui(aV\..., а^"1)). Множество А'' есть
объединение конечного числа множеств Рг. Следовательно, для
одного из этих множеств — назовем его Р\ — множество uP\V со*
держит бесконечное число цепочек [пи ..., п8], таких, что,
каковы бы ни были числа 1, ..., 5— 1, для них имеет место п\ <
< ... < ns_i. Множество Р\ представляет собой произведение
конечных множеств и множеств а(1),..., а^т"х\ В числе
сомножителей множества Р\ должно быть одно из множеств а(1), ...
...,alm~l\ скажем а^\ Если бы это Выло не так, то
множество Pi представляло бы собой произведение конечных
множеств и, таким образом, само было бы конечно, а это
противоречит тому, что множество uPxv бесконечно. Таким образом,
множество Р{ может быть записано в виде Q\a^p)Q2- Поскольку
uQia^Q2v £ г)', то, согласно (6), каждое из множеств uQx и
Q2v состоит в точности из одной цепочки, скажем w и у
соответственно. Отсюда wa^y = uP\V. Тогда р есть число,
меньшее т и удовлетворяющее условиям (а) и (Ь). Это
противоречит минимальности числа т. Следовательно, случай 1
невозможен.
Случай 2. Предположим, что множество uK'v содержит в
точности конечное число цепочек [пи ..., ns], таких, что, каковы бы ни
были числа 1,...,5—1,для них имеет место пх<.. .<п&-\.
Согласно лемме 6, а<т*> есть наименьшая неподвижная точка функции
fm(«(1), ..., <x(m~])> tm))=HA'itm)B'i + K'. Уже было показано,
i
что для каждого i существуют цепочки w{ и yh такие, что
/1J= juyl и B,i^{yi), Итак, а<т) есть наименьшая неподвижная
точка функции 2 *^6(т)у* + #'• Тогда а{т) есть объединение всех
множеств вида zq ... Z\K'z\Z2 ... zq*, a ua(m)v — объединение всех
множеств вида uzq ... zxK'z\z'2 ...z'v, где q — переменная; для
каяедого l через г[ обозначена одна из цепочек wJf через z\ —
Два класса языков типа АЛГОЛ
203
соответствующая цепочка #/. Однако множество uK'v состоит
в точности из конечного числа цепочек [пи ..., ns], таких, что,
каковы бы ни были числа 1, ..., 5—1, для них имеет место
п\ < ... < fi5_i; множество же ua^v состоит из бесконечного числа
цепочек. Итак, цепочки вида uzq ... z{ могут содержать в
качестве подцепочек сколь угодно длинные цепочки, являющиеся
степенями либо символа а, либо символа Ь. Таким образом,
одна из цепочек wh скажем wb имеет вид ае для некоторого
£>0. Точно так же одна из цепочек wit скажем w2y имеет вид
Ье\ е'>0. Пусть х0 — цепочка из множества К'. Тогда
цепочка uw2wlXoyiy2v принадлежит множеству tj' и содержит
подцепочку Ьа> а этого не может быть. Следовательно, случай 2
невозможен.
Поскольку для множества К' должен иметь место один из
случаев 1 или 2 и оба случая приводят к противоречию, то
множество К' не может существовать. Следовательно, число m
также не существует. Итак, определимое множество т\' не является
П-определимым.
Было бы интересно для некоторого определимого множества,
встречающегося в АЛГОЛе, показать, что оно не является
П-определимым. Ввиду громоздкости АЛГОЛа мы не знаем,
существует ли такое множество. Есть основания подозревать, что
множество арифметических выражений в АЛГОЛе не является
П-определимым. Поскольку для описания множества
арифметических выражений требуется более 15 формул, мы не в
состоянии явно определить это множество, чтобы показать, что оно не
является П-определимым.
5. ФУНКЦИИ, ПОРОЖДАЮЩИЕ П-ОПРЕДЕЛИМЫЕ МНОЖЕСТВА
Только что мы доказали, что существуют определимые
множества, не являющиеся П-определимыми. Ниже (теорема 4) мы
покажем, что если все коэффициенты л-компонентной стандарт-*
ной функции f перестановочны, то каждая координата
наименьшей неподвижной точки функции / является П-определимым
множеством. Для доказательства этого факта предварительно
покажем, что мы можем (i) ограничиться переменными,
пробегающими некоторое семейство множеств, для которого
коммутативность имеет место; (ii) заменить некоторую функцию другой
функцией, у которой одна из переменных линейна; (iii) «решить»
функцию, полученную в. д. (ii), т. е. выразить одну из
переменных через остальные; (iv) заменить одну из переменных в
каждой из оставшихся функций «решением», полученным в (iii)
(при этом и число функций и число переменных уменьшится на
единицу); (v) повторять (i) — (iv) до тех пор, пока останется
204
С. Гинзбург, X. Райе
в точности одна функция и одна переменная; (vi) решить эту
последнюю функцию (при этом получится последняя
координата наименьшей неподвижной точки исходной л-компонентной
функции); (vri) вычислить каждую из оставшихся координат
исходной л-компонентной функции с помощью повторной
подстановки.
Для выполнения этих семи шагов программы нам
необходимы некоторые вспомогательные понятия и результаты.
Обозначение. Как и в примечании на стр. 193, для каждого
оо
множества Л полагаем Л* = LM'*
Определение. Полиномом с итерацией, (И-полиномом) f (|(1),...
...,g<n>) называется функция, построенная из конечного числа
М-переменных Ql\ ..., Qn\ каждое gw пробегает множество всех
подмножеств множества 8, и являющаяся объединением конеч-
ного числа членов f = 2 П*> каждое П* имеет вид П* = 6i... бг -
(г — переменная). Здесь каждое 6; есть либо П-определимое
множество, либо одна из переменных gW,..., Qn\ либо 6* = т*,
где т имеет вид х — y\...yt С — переменная), каждое yj есть
либо П-определимое множество, либо одна из переменных
6(1),. • • • 6(п)- Каждое 6¾ или у$, являющееся П-определимым,
называется коэффициентом функции /.
Например, / = Л(5<,>5|<2>)* + Л есть И-полином, но
/ = A[($l)B)*#2)]* + В не является таковым (Л и В есть П-опре-
делимые множества).
Определение. Семейство Д подмножеств множества 0
называется базисом, если
(i) ееД;
(ii) для каждой пары множеств Л и В из Д имеем АВ е Д
и АВ = ВА;
(Hi) для каждой последовательности {Л*} множеств из Д
множество \J.Ai также принадлежит Д.
i
Из (iii) и (ii) следует, что для каждой пары множеств Л, В
из Д множества Л + В и Л* также принадлежат Д.
Впоследствии через Д будем обозначать фиксированный
базис.
Определение. Функция /(£(1),..., £(п)) называется базисным
полиномом, определенным на множестве Д (базисным
полиномом на Д), если (i) f есть И-полином, в котором область
изменения каждой переменной £<*> ограничена множеством Д, и (ii)
каждый коэффициент функции / содержится в Д,
Два класса языков типа АЛГОЛ
205
Лемма 7. Пусть J (£0),..., g<n>) — функция, полученная из
Ni-переменных #1\ ..., |(п>, области изменения которых
ограничены множеством А, и констант из А, являющихся П-определи-
мыми множествами, в результате конечного числа применений
операций + , • и *. Тогда
№i\...., i(n)) = «1 а(,),..., £(п)н(1) + Ы1<2>, -.., £(w)),
где gi м #2— базисные полиномы на множестве Д. Более того,
коэффициенты функций g{ и g2 получены из коэффициентов
функций f и из г в результате конечного числа применений
операций + , • и *.
Доказательство. Сначала преобразуем f в базисный
полином /t(£(1),... ,£(п>) на множестве А с помощью следующих
тождеств:
(1) (Л*> = (Л*)*=Л*,
(2) (А + В)* = Л*В*,
(3) (Л*В)* - е + л*вв*,
где Л и В — множества из А. .Эти тождества легко вывести из
оо
определения /4* = |Ji4f' и свойства перестановочности мно-
1-0
жеств Л и В.
Первый шаг преобразования f в h заключается в применении
тождества (2) до тех пор, пока не исчезнет операция + в
области действия операции *. результат представляет собой
объединение членов, каждый из которых содержит только операции
• и •.
Введем следующие понятия: «гнездо», его «глубина» и
«ширина». Итерация прямого произведения переменных и констант
определяется как гнездо глубины 0 и ширины 0. Выражение
(|ii ... |xiv) *, где все \\j — гнезда, a v — прямое произведение
(возможно, пустое) констант и переменных, определяется как
гнездо ширины / и глубины 1 + max {глубина |ij}. Очевидно, что
ширина гнезда равна 0 тогда и только тогда, когда его глубина
равна 0.
Затем если некоторое слагаемое суммы содержит в
качестве сомножителя гнездо ширины > 1 или гнездо ширины 1 и
с непустым v, то мы применяем тождество (3) и заменяем
слагаемое (|ii... Hiv)*Y на У + 1М ••• Н-Мн*- •• Mav)*Y> т- е- на Два
слагаемых, каждое из которых есть прямое произведение гнезд,
имеющих (за исключением у) либо меньшую глубину, либо ту
же глубину, но меньшую ширину, чем исходный сомножитель.
Если ни одно слагаемое не содержит в качестве сомножителя
гнезда ширины >1 ис непустым v, то мы применяем тождество
206
С. Гинзбург, X. Райе
(I) ко всем гнездам ширины 1 и с пустымv, уменьшая их
глубину до 1. Когда таких гнезд не останется, повторим
процедуру, описанную в предыдущем абзаце. Чередование этих
процедур должно окончиться, когда не останется ни одного гнезда,
ширина или глубина которого больше 0. Таким образом мы
получим базисный полином ft(£(1),..., ^п>) на Д.
Образуем теперь из ft два базисных полинома g\ и g2.
Поскольку множества, принадлежащие семейству А,
перестановочны, мы можем записать каждое слагаемое полинома ft,
содержащее gw в качестве сомножителя, в виде у£(1)- Для каждого
такого слагаемого отнесем соответствующее у к g{. Каждое
слагаемое полинома ft, в котором gw не встречается, отнесем к g2.
Останутся только те слагаемые полинома ft, в которых gW
встречается только внутри гнезд (являющихся сомножителями).
Пользуясь тождеством
{АВ...У = е + (ЛЯ...)(ЛВ...)*,
мы очевидным образом получим из каждого такого слагаемого
два новых слагаемых. Одно из них имеет вид у$1\ и мы
помещаем у в gu второе (полученное из ё) имеет на 1 меньше гнезд,
являющихся сомножителями и содержащих £0), чем исходное
слагаемое. Этот процесс продолжается до тех пор, пока не
останется гнезд. Полученный остаток мы поместим в g2. Из
построения ясно, что ft = gigw + |Ы£(2)» • • • t 1{п))» гДе ё\ и ё2 — базисные
полиномы, определенные на Л. Из способа построения ясно
также, что коэффициенты полиномов gx и g2 обладают
свойством, указанным в формулировке леммы. Лемма доказана.
Для иллюстрации процедуры, предложенной в лемме 7,
положим f = [(At*)* + (Вг\)*1* + т]*}*, где I и т) есть g(» и |(2)
соответственно. Применив дважды тождество (2), мы получим
/ = №*у + (ВлГ ГГ (лТ = РГ)Т [(ВЦ)* ?]* WY.
Здесь [(Вт) )*£*]*— единственное гнездо ширины больше 1; при
этом нет ни одного гнезда ширины 1 и с непустым v. Пользуясь
тождеством (3), мы получим
[(Вп)Т]* = е+(Вг])Т(Г)*,
откуда
f ШУТ (л7 + №7Y (л7 W V (67.
Здесь не существует слагаемого, содержащего в качестве
сомножителя либо гнездо ширины больше 1, либо гнездо ширины 1
и с репустым v. Применив тождество (1) ко всем гнездам
ширины 1 и с пустым v, мы получим
/=(Л6ТгГ + М67»Г(ВлПТ.
Два класса языков типа АЛГОЛ
207
Здесь имеется только одно гнездо ширины 1 и с непустым v,
а именно (Л£*)* (входящее дважды). Перепишем (Л|*)* в виде
(£М)*. Согласно тождеству (3),
(БМ)* = е + i*aa:
Тогда
/ - V + VAA'rf + ч (Вт,)* IX + Л* (ВчУ ПГАА\
Это и есть базисный полином h.
Определим теперь gx и g2. Поместим rf в g2. Используя
тождество £* = e + gg*, заменим %*АА*ч на ЛЛ*т]* + Й*^^*Л*-
Поместим АА*ч\ в g2 к 1*АА*г) в g{. Заменим ц (ВчУ 1*1* на
г)ЦВг))* £ +г) (Вг))* 1*11*. Поместим ч* (ВчУ IX в gx. Заменим
Л*(£л)Ч* на л*(Вл)* + Л*(Ял)ЧБ*. Поместим Ч*(ВчУ в g2 и
г\\ (Ву))*1* в gx. Точно так же последнее слагаемое полинома А,
а именно ч*(Вч)*£1ХАА*, в конечном счете заменяется на
Ч*(Вч)ЧХ&АА* + ч* (ВЦ)* 1*11* АА*+ ч* (ВцУ & A A*+ rf(BriyAA*.
Это приводит к следующим выражениям для gi и g2:
gl = €ААV + лЧВлГ 6Т + V W Г + ч (ВчУ 1*аа* +
+ Ч (ВчУ 1ГАА* + ч (ВчУ IXVAA*
g2 = ч* + АА*ч* + Ч* (ВчУ + Л* (ВчУ АА*.
Это не самые „простые" выражения для gx и g2. Например,
заметив, что П*8*5!*» мы получим
и - ллг л* + (ВлГ 6V + ^^ (ВлГ Г л*
g2 = л* + лл V + W л* + /i/i* (ВчУ л*.
Если бы мы это заметили несколько раньше, мы бы значительно
сократили вычисления.
Пусть fu ..., fn есть п функций, каждая из которых
получена из множеств, принадлежащих Д, и переменных £(1\...,£(л)
(каждое £<*> пробегает множество всех подмножеств
множества 0) в результате конечного числа применений операций +,•
и *. Легко видеть, что теорема 1 остается в силе и в этом
случае. Более того, каждое af принадлежит множеству Д,
следовательно, каждое a^^JJa^ также принадлежит множеству Д.
k
Итак, поскольку речь идет о нахождении наименьшей непддвиж-
ной точки, область изменения каждой М-переменной может быть
ограничена множеством Д. Далее это будет сделано. Это
позволит нам использовать лемму 7 и считать все рассматриваемые
множества перестановочными.
206
С. Гинзбург, X Райе
Л е м м а 8. Пусть а — наименьшая неподвижная точка
функции / (Б(1)1 • • •»£(п)) *= (/ь . • •,/п), гдя каждое U — базисный
полином на Д. Предоположим, что /i » Ы6(^ • •• »£(n))i(1) + &г(£(2)»
. ..,£(п)), *<?* gi « gz —базисные полиномы на Д. Я^/сть h\($x\
..., £л>) - gifesU<2),..., &<n)) ,6«...., «(1) + ^2 (£<2>,..., Vn)), a
для * 5> 2 пусть hi = /i. Тогда a — наименьшая неподвижная
точка функции h = (ftb..., йп).
Доказательство. Пусть p = (pw... ,ptn>) —
наименьшая неподвижная точка функции ft. Положим а = (а(1),.. . ,а(п)).
Пусть, кроме того, аА = (а^Ч ..., а^) и pfe = (р<|>,... ,pj^) имеют
тот же смысл, что и раньше. Для доказательства леммы
достаточно показать, что a(i)sp(i) и р<*>£а<*> для каждого t.
Доказательство второго включения ввиду простоты предоставляется
сделать читателю. Доказательство первого достаточно тонко.
Приведем его.
Очевидно, что a(/; = Р^} s pw для каждого /. Пусть D =
= ¾^2^ •••» P<w))# ТогЛа «о)==£)- Поскольку р — неподвижная
точка функции Л, имеет место равенство Р(1) = gfi [D, Р(2), .. .
..., p(n)]pa) + D и, следовательно, £>^р(1). Предположим, что
а£>£р<*> для каждого / и что aj^pMsDp(1). Для />2 имеем
ai+i = // (¾) s /* №)в Р(0- Остается показать, что а^+1 г р(1)
(поскольку тогда a(1)»Uafsp(1)) и что аЙ-,р(1) <= Dp(1).
Пусть 61(^, ..., £(n)), ..., 6^(^),^.., g<w)) — произвольная
конечная последовательность, где каждое 6¾ (|(1), ..., £<Л)) — либо
константа из А, либо одна из переменных Ql\ ..., g<n>,
пробегающих множество Д. Определим т (Ц1\ ..., £(Л>) как произведение
т (б*1),...,*™) -fii... б/. Тогда
/«*o /-о
Для каждого I определим Yi как множество бг(аь), если 6i(|}^
Ф £W, и как D, если 6* (6) = 6(/)* Ввиду перестановочности
двукратным применением индуктивного предположения получаем
U 6i Ы • • • б<Ы'Р(,) - Uv{... yF}=*(D> <2) «№
/-о /-о
Таким образом,
т(<х<», ..., <>)'р<'> £ t(Z), of, ..., а<«>)'рЧ (7)
Два класса языков типа АЛГОЛ
Й09
Рассмотрим функцию g\ (£(*>,..., £<п>). Поскольку gx — базис-
S
ный полином на А, имеем gi(S(1), ..., 6(я))-2 П,^1), ..., £<">),
где П,- (£<*>,*.., |(Л)) = vi... vr (г — переменная). Здесь каждое, Vj
есть либо константа из Д, либо одна из переменных gw ... ,g<n>,
пробегающих множество А, либо функция t(£<*>,..., g(n>)*, где
т^1*, ...,£<п)) определена, как в предыдущем абзаце. Тогда из
(7) и свойства перестановочности множеств путем двойного
применения предположения индукции а* У0 s D$(1) получим
* № .... аЙ°) Р(,) - 2 П, (а1", ... ,а£") р(1) s 2 П, (d, <#, ...
.... <t>)p<'>.
Таким образом,
Я.М" aj*)pfl> £*,(/>, af, .... ajp»)pOs
= *,(Я, p», .... p(«))pa)^P(1).
Рассмотрим ai+i. Из предыдущего следует
£Ы«*)Р(1) + ЫР(2)..... P(n))^
= p<» + po>-p<»
а это одно из искомых включений.
Наконец,
^#^a*)P(I) + g2(P(2)> ..., p<A>)pO>s
^Dp(1) + Dp(1) = Z)p(1).
Л e м м а 9. Пусть а — наименьшая неподвижная точка
функции f (£<Ч ..., £<п)) = (/1,..., fп), где каждое f * — базисный
полином на А. Предположим далее, что f\ =^(^), ..., g(n))gO) +
+ g2(§(2\..., §(п)). где gi и g2 — базисные полиномы на Д. Пусть
Ai (£(2),...»£(п)) « ft*;. Для i > 2 полагаем A, = f< (ftlf 6«,..., #»>).
Гогда а еггь наименьшая неподвижная точка функции (hu...
..., An).
Лемма, доказывается путем уже привычных нам
рассуждений. Поэтому мы опустим доказательство.
Теорема 4. Пусть f = (fi,..., fn), где каждое f{ Ф f;(£(1), ...
...»£(п)) есть полином. Предположим, что все коэффициенты есть
П-определимые множества, удовлетворяющие условию переста-
210
С. Гинзбург, X. Райе
новочности. Тогда каждая координата наименьшей неподвижной
точки функции f есть Неопределимое множество и, более того,
может быть получена из коэффициентов функции f и из г в
результате конечного числа применений операций + ,-«*.
Доказательство. Пусть Д — наименьшее семейство
множеств, содержащее все коэффициенты функции /, а также е
и замкнутое относительно операций'умножения и счетного объе«
динения. Поскольку операции умножения и счетного объединен
ния сохраняют перестановочность, легко доказать с помощью
трансфинитной индукции, что каждые два множества из Д пере-*
становочны, т. е. Д есть базис.
Обозначим через а = (а(1),..., а(п)) наименьшую
неподвижную точку функции f. Рассуждения, предшествующие лемме 8,
позволяют считать, что каждое fi— базисный полином на Д.
Рассмотрим следующее утверждение:
Пусть /« (/ь ..., fnl где каждое /< - М6(,\ •••»
^-базисный полином на А. Тогда каждая координата наименьшей
неподвижной точки а=(а<1>, .... а<п>) функции / есть П-определи- /р ч
мое множество и, более того, может быть получена из ко- * п)
эффициентов функции f и из е в результате конечного числа
применений операций + , • и *.
Для доказательства теоремы достаточно показать, что
утверждение (Рп) справедливо для всех п.-Утверждение (Рп) мы
докажем по индукции.
Пусть п = 1, т. е. f(6(1)) = (fi). Согласно лемме 7, fi(6(1)) =
=gi(6(1))6(1) + К. гДе £i(6(I)) — базисный полином на Д; /Си
коэффициенты функции g\ получены из коэффициентов
функции fi и из е в результате конечного числа применений операций
+ , • и *. Согласно лемме 8, а*1*—наименьшая неподвижная
точка функции hx (£0>), где hx (£0)) = gx (К) 6(1) + /С. Тогда
сс(1) = gx (К) *К. Поскольку семейство П-определимых множеств
замкнуто относительно операций +, • и *, множество а<!)
является П-определимым. Более того, а*1* построено из
коэффициентов функции f\ нужным способом. Следовательно, утвер-»
ждение (Pi) истинно.
Продолжая индукцию, предположим, что (Рп) истинно для
всех чисел, меньших г. Рассмотрим случай п = г. Согласно
лемме 7, существуют базисные полиномы gi(6(1), ..., 6(п)) и
Ы6(2)> •> Ъ{п))> такие, что
М6(1), .... 6(П))=Ы6(|\ ..., 6(П))6(1) + Ы6(2), ... 6(п)).
Более того, коэффициенты функций gx и gz получены из
коэффициентов функции / и из е в результате конечного числа
применений операций +, • и *, Согласно лемме 8, а есть наимень-
Два класса языков типа АЛГОЛ
211
шая неподвижная точка функции (fn+u /2, •. •, /п), где
fn+i(t(l) б^ныйй00. ■■■. п i(2\ ..>, vn)n(l) +
+£2а(2),..., i(n)).
Согласно лемме 7, можно считать, что (i) gi(#2, £(2)» • • •> £(n))
есть базисный полином gz(l(2\ ••-, S(n)) и (ii) коэффициенты
функции £з получены из коэффициентов функций gu gi и,
следовательно, из коэффициентов функции f\ нужным способом.
Тогда
f„+i(E(1), ..., lM)-gAlw, ..., lin))l(1) + g2(l(2\ .... S(n)).
Согласно лемме 9, а есть наименьшая неподвижная точка
функции (Ль ..., Ап), где hx = g*3g2 и ^ = /,(^, £(2), ..., £(Л)) для
/i>2. Согласно лемме 7, можно считать, что каждое Лг(£(2), ...
..., £(п>) есть базисный полином, коэффициенты которого
получены из коэффициентов функций fiy g2, gz и, следовательно, из
коэффициентов функции f нужным образом.
Рассмотрим наименьшую неподвижную точку р = (р<2\ ...
..., р<п>) функции А(6<2), Л., &<Г|>)= (Л2, .-., Ап). Из того, что а
есть наименьшее решение уравнения
[А,(6(2). •-.. 6(я)). М£(2). ..., g<*>), ..., Ая(6<2>, .... £(»))] =
следует, что (i) а<!> = Ai(a<2>, ..., а<п>) и (ii) (а<2\ ..,, а<п>)~-
неподвижная точка функции A(g<2>, ..., £(п)). Следовательно,
(р, .. ., р<">) s (а<2>, ..., а<п>). Поскольку А,(р<2>, ..., р<»>) =
= р«) для />2, то (МР(2)> • ••, Р(п)), Р(2)> •••> P(n)) -1
неподвижная точка функции (Ад, ..., Ап). Итак, a^ £ ¢^, следовательно,
a(f) — р(г) для />2. Другими словами, (а<2), ..., а<п>)—
наименьшая неподвижная точка функции (h2y ..., hn).
Теперь h(Q2\ ..., £(")) содержит менее г функций, каждая из
которых представляет собой базисный полином на А. По
индуктивному предположению (Рп) справедливо для п < г.
Следовательно, для / > 2 каждое а(г) является П-определимым
множеством и получается из коэффициентов функции ft и из е,
следовательно, из коэффициентов функции f и из е нужным образом.
Поскольку aW = Ai(a<2>, ..., a(7?))> то же самое справедливо и
для а*1). Следовательно, (Рг) истинно, и теорема доказана.
Если коэффициенты функции / являются степенями одного и
того же множества, то они перестановочны. Получаем
следствие.
Следствие 1. Если / = (/ь ..., /п) есть п-компонентная
стандартная функция, все коэффициенты которой являются
степенями одного и того же множества, скажем множества Л, то
212
С, Гинзбург, X. Райе
каждая координата наименьшей неподвижной точки функции f
является П-определимым множеством и получается из А и из г
в результате конечного числа применений операций + , • и *.
Итак, каждая координата наименьшей неподвижной точки
является регулярным множеством.
Условие следствия 1, очевидно, выполняется в случае, когда
алфавит 2,состоит в точности из одного символа.
Следовательно, в этом случае каждое определимое множество регулярно.
Обратное, разумеется, также верно. Известно, что множество
А ={ап|яе^} регулярно тогда и только тогда, когда К —
периодическое множество неотрицательных целых чисел *).
Поэтому имеет место следствие.
Следствие 2. Если алфавит 2 состоит в точности из одного
символа, то (П-) определимые множества эквивалентны
регулярным множествам, т. е. множество {а71 \п е X} есть (П-)
определимое множество тогда и только тогда, когда К —
периодическое множество неотрицательных целых чисел.
Замечание. При внимательном изучении теоремы 4 и
относящихся к ней лемм обнаруживается, что координаты наименьшей
неподвижной точки строятся только по отличным от е
коэффициентам функции f. Действительно, все результаты настоящей
статьи могли бы быть получены без введения пустой цепочки е.
Это означало бы, конечно, что ни одно (П-) определимое
множество не могло бы содержать пустой цепочки е и поэтому
необходимо было бы сделать некоторые незначительные измене-
оо
ния, например определить Л* как (J А1.
Для иллюстрации теоремы 4 положим
fi hs Л2£2 + A*%v + А* и /2 ■■. А% + A*%v + A2v +Л\
где А — некоторое конечное множество цепочек; ^ и v
представляют собой 5(1) и £Р> соответственно. Определим наименьшую
неподвижную точку (|, v) функции / в (fi, /2).
Теперь fi приобретает вид
(A*t + A\)t + A*. (8)
Функцию (8) можно преобразовать $ такую:
[ЛМ* + A3v]g + Л4. (9)
1) Доказательство этого факта непосредственно получается из последнего
предложения примечания 3 на стр. 193.
Два класса языков типа АЛГОЛ
213
Тогда (|, v) есть наименьшая неподвижная точка функции
(/«, h)> где
/в (5, у)-(ЛЧ + Л*)М«
f4(v) н Л4(Л*у + Л6)М4 + j4*v(i4»v + Л6)М4 + i4*v + Л2.
Тогда V—наименьшая неподвижная точка функции Mv).
Переписав f4(v) в виде g\(v)v + К, получим
U = Л8 (АЧ? (А*? + Л7 (4«v + Л6)Ч + Л2v + Л2 -
= Л8 (Л6)* + Л8 (Л6)* Л^ (Л^)* + Л7 (A*v + Лб)\ + A2v + А2 -
= [Л11 (Л6)* (ЛЧ)* + Л7 (i4«v + Л6)* + Л2] v + Л8 (Л6)* + Л2. (10)
Функция из (10) преобразуется в следующую:
/5 - #v + К,
где
# - Л11 (Л6)* (Л3 [Л*(А*)* + Л2])* + Л7 (Л3 [Л8 (Л6)* + Л2] + Л6)* + Л2
/С«Л8(Л6Г + Л2.
Тогда v = Я*ТС и |« (Л3Я*/С + Л6)*Л4. При желании можно
применить лемму 7 для уменьшения глубины и ширины ънезд,
появляющихся в vh | (разумеется, при этом степени множества
Л рассматриваются как переменные).
Имеется другая система функций, представляющая интерес и
порождающая П-определимые множества, тогда как их форма
предполагает определимые множества. Это тот случай, когда
/(1^), ..., £<">) = (/ь ..., /п), где каждая функция U в правой
п
части линейна, т. е. /*= 2 Л/,/£(У) +Л/, и все коэффициенты
есть П-определимые множества. Можно показать, что каждая
координата наименьшей неподвижной точки а = (а*1), .. „ а(п>)
функции f есть П-определимое множество и, более того,
получается из коэффициентов функции f в результате конечного
числа применений операций +, -и *. Этот факт можно доказать,
пользуясь понятием самовложения, определенного в [6]. Может
быть дано также другое доказательство, зависящее от
результата, полученного в [3]. Приведем набросок еще одного
доказательства, основанного на последовательном исключении
переменных. Из fi получаем
|(1) - Ли, (i Л, £<'> + Л, ) = S А\.,Л, ,f Ч AltAu
\/-2 / /-2
214 С. Гинзбург, X. Райе
Заменив £(1) на 2 Ai,\A\tjlu) + A*t\А\ в функциях /2, ..., /п,
получим (л—1) функцию £2(£(2), ..- 1(п)), .... £n(l(2>, ..., £(п)),
где каждая функция gi в правой части линейна и содержит в
качестве коэффициентов только П-определимые множества.
Наименьшей неподвижной точкой функции (g2> ..., gn) является
(а(2), ..., a<n>). Таким способом исключается одна из
переменных и одна из функций. Процедура продолжается до тех пор,
пока не останется одна переменная и одна функция. Тогда а<п>
определена. Повторной подстановкой получаются а^-1*, ..., а*1*.
Результат и схема доказательства, описанного в
предыдущем абзаце, очевидно, сохраняются также (конечно, с
небольшими изменениями), если в f = (/ь ..., fn) каждое fa в правой
п
части линейно, т. е. ft = 2 |(^Л / + At.
В АЛГОЛе нет функций, которые иллюстрировали бы либо
теорему 4, либо ситуации, рассмотренные в двух предыдущих
абзацах.
Л ИТЕРАТУРА
1. Naur P. (ed.), Report on the algorithmic language Algol 60, Coram.
ACM, 3 (May, 1960), 299—314.
2. В а г - H i 11 e 1, P e г 1 i s, Shamir, On formal properties of simple
phrase structure grammars, Tech.,Rep. № 4 (July 1960), Applied Logic Branch,
The Hebrew University of Jerusalem.
3. Buche J.., Regular canonical stems and finite automata, Department of
Philosophy, Technical Report, December 1959, University of Michigan, Ann.
Arbor, Michigan.
4. С h о m s k у N.f Three models for the description of language, IRE Trans.
Inf. Theory, 2 (1956), 113—124. (Русский перевод: Хомский H., Три
модели для описания языка, Кибернетический сборник, вып. 2, ИЛ, М.,
1961, стр. 237—266.)
5. С h о m s к у N., Miller G., Finite state languages, Information and
Control, 1 (1958), 91—112. (Русский перевод: Хомский H.,
Миллер Дж., Языки с конечным числом состояний, Кибернетический сборник,
вып. 4, ИЛ, М., 1962, стр. 231—255.)
6. Chomsky N., On certain formal properties of grammars, Information
and Control, 2 (1959), 137—167. (Русский перевод: Хомский H.,
О некоторых формальных свойствах грамматик, Кибернетический
сборник, вып. 5, ИЛ, М., 1962, стр. 279—319.)
7. D a v i s М., Computability and unsolvability, McGraw Hill, New York,
1958.
8. R a b i n, Scott, Finite automata and their decision problems, IBM /.
Res. Dev., 3 (1959), 114—125. (Русский перевод: Рабин M, Скотт Д.,
Конечные автоматы и задачи их разрешения, Кибернетический сборник,
вып. 4, ИЛ, М., 1962,'стр. 58—91.)
9. Scheinberg S., Note on the Boolean properties of context free
languages, Information and Control, 3 (1960), 372—375.
10. Tar ski .A., A lattice-theoretical fixpoint theorem and its applications,
Pacific J. Math., 5 (1955), 285—309.
Математическая
экономика
Аддитивный алгоритм для решения
задач линейного программирования
с переменными, принимающими
значения 0 или 1**
Э. Балаш
Предлагается алгоритм для решения линейных задач с переменными,
принимающими значения 0 или 1. Алгоритм начинается с того, что все п
переменных полагаются равными нулю, а затем с помощью некоторой
систематической процедуры отдельным переменным последовательно приписывается
значение 1 таким образом, что после испытания (малой) части имеющихся
2п комбинаций или получается оптимальное решение, или устанавливается
факт, что в задаче нет допустимого решения. В алгоритме используются
лишь операции сложения и вычитания; таким образом, исключаются ошибки
округления. Задачи с 15 переменными с помощью этого алгоритма могут
быть решены вручную не более, чем за 3—4 часа. Возможно
распространение алгоритма на линейные целочисленные задачи и на нелинейные задачи,
но в настоящей статье этот вопрос не затрагивается.
Известно, что важные классы экономических (и не только
экономических) задач имеют своей математической моделью
задачу линейного программирования с целыми переменными.
Среди таких задач можно выделить задачи, которым
соответствуют линейные задачи с переменными, принимающими одно
из значений 0 или 1. В литературе описано очень большое число
практических задач этого типа (см. [1—4], [5, стр. 650—656;
695—700], [6], [7, стр. 194—202], [8, стр. 535—550], [9—11]).
В настоящее время имеется ряд методов для решения задач
рассматриваемого здесь вида (см. [12—27], [5, стр. 700—712], [7,
стр. 160—194], [8, стр. 514—535], [28, стр. 190—205]). Наиболее
известны алгоритмы Гомори [13, 14] для решения
целочисленных задач линейного программирования. Эти алгоритмы
используют двойственный симплекс-метод и автоматически
получаемые новые ограничения, которые добавляются к исходному
множеству ограничений. Эти ограничения удовлетворяют Любым
целочисленным решениям задачи и исключают нецелочисленное
решение, полученное в момент их введения. Метод сечений
применялся также Билом [17] и Гомори [14] при разработке алгчь
ритма для решения частично целочисленных задач, т. е. задач,
в которых требуется целочисленность не всех, а только части
переменных. Методы для решения таких задач имеются также
в работах [6, 24].
*) В а 1 a s Е., An additive algorithm for solving linear programs with
zero-one variables, Operations Research, 13, № 4 (1965), 517—546.
218
9. Валаш
Другой тип алгоритма для решения полностью и частично
целочисленных задач предложили Лэнд и Дойг [18]. Этот
алгоритм также исходит иа оптимального нецелочисленного
решения. Оптимальное целочисленное (или частично целочисленное)
решение находится путем систематических параллельных
сдвигов гиперплоскости, соответствующей целевой функции.
Аналогичные методы можно также найти в работах [21, 22, 25, 26].
Другой подход к задаче, основанный на применении методов
булевой алгебры, был предложен Фортетом [29] и подробно
исследован Сэмионом [30] путем введения полей Галуа.
Используя аналогичные идеи, Иванеску [23] развил метод для решения
дискретных полиномиальных задач программирования.
Алгоритм, излагаемый в данной статье*), использует
комбинаторный подход к проблеме решения задач линейного
программирования с дискретными переменными, в частности с
переменными, принимающими лишь значения 0 или 1. Алгоритм
представляет собой сокращенный перебор, и в этом отношении
он примыкает к комбинаторным методам, применяемым в
смежных областях (см., например, [33, 34]). Этот алгоритм является
прежде всего прямым методом решения задач линейного
программирования с переменными 0 или 1, и для этого частного
типа задач он кажется нам очень эффективным. Алгоритм
может быть распространен [32] на задачи линейного
программирования с целыми переменными и как приближенный метод на
линейные задачи более общего типа, чем те, с которыми обычно
имеют дело.
1. Основные идеи и описание аддитивного алгоритма
Задача линейного программирования с переменными,
принимающими лишь значения 0 или 1, в общем виде может быть
записана следующим образом.
Найти х', минимизирующий (максимизирующий)
с'х', (10
при условиях
A'x'Sb', (20
*; = 0 или 1, (/€=#), (30
где х' = (xj) — /г-мерный вектор-столбец, с' = (с,) — заданный /г-
мерный вектор-строка, А' — (я*/) — заданная матрица размером
*) Начальный вариант аддитивного алгоритма см. в [9]; краткие
замечания по этому алгоритму опубликованы в [31] и далее — в [32]. Интересную
интерпретацию аддитивного алгоритма с использованием теории графов и
сравнение с некоторыми современными результатами см. в [35].
Аддитивный алгоритм для решения задач линейного программирования 219
qXn и Ь'= (&у)—заданный ^-мерный вектор-столбец; {1,...,^1=3
-Q, {1, ..., n} = N.
Однако для наших целей сформулированную задачу удобнее
рассматривать в несколько иной форме, а именно: все
ограничения имеют один и тот же вид ^=, а все коэффициенты целевой
функции (которая минимизируется) неотрицательны. Любая
задача типа (1'), (20, (30 может быть сведена к такой форме
посредством следующих операций:
(a) замена всех равенств двумя неравенствами;
(b) умножение на —1 всех неравенств вида ^;
(c) подстановка
f x'i для c'i 2£ 0 в случае минимизации; для с'} ^ 0
_ 1в случае максимизации;
! \\ — x'i для с|<0 в случае минимизации; для с^>0
[в случае максимизации.
Вводя, кроме этого, вспомогательные переменные (т-мерный
нeoтpицafeльный вектор у), мы получим следующую задачу.
Найти х, такой, что
^ = ex = min^ (1)
Ах +'у - Ь, (2)
*y = 0 или 1, j&N, (3)
У ^ 0, (4)
где с^О, ах, с, АиЬ получаются из х', с', А' и Ь' с помощью
описанных выше операций. Размерность х и с осталась равной п.
Пусть b — m-мерный вектор и {1, ..., m} = М, m>q.
Задачу (1), (2), (3) и (4) обозначим через Р; пусть aj —/-й
столбец матрицы А.
Будем называть (п + ш) -(мерный вектор u = (х, у) решением,
если он удовлетворяет (2) и (3); допустимым решением, ес;ли
он удовлетворяет (2), (3) и (4); оптимальным (допустимым)
решением, если он удовлетворяет (1), (2), (3) и (4).
Пусть Ps — задача линейного программирования,
определяемая (1), (2), (4) и ограничениями
Xj Ш 0, / €= N9 (За)
Xj = 1, /€Е/„ (ЗЬ,)
где Js — подмножество мнржества N. Пусть /0 = 0 и Р° —
задача, определяемая (1), (2), (За) и (4).
Основная идея, используемая в нашем алгоритме,
следующая. Мы исходим из обычной задачи линейного
программирования Р° с решением и0 = (х°, у0) = (0, b) t которое, очевидно,
220
Э. Валаш
двойственно допустимо для Р° (так как с^О).
Соответствующий базис состоит из единичной матрицы \т = (е*), / = 1, ..., т%
где ti — t-й орт. Для некоторых /, таких, что и] < 0, мы
выбираем в соответствии с некоторыми правилами вектор а/, (такой,
что ацх < 0), подлежащий введению в базис. Но вместо того,
чтобы вводить а/, -в базис вместо вектора ег-, как это делается
в двойственном симплекс-методе, мы добавляем к задаче Р°
ограничение дг/, = 1 в несколько модифицированной ^форме:
—xix + Ут+\ — —1» где ym+i — вспомогательная переменная.
Таким образом, мы получаем задачу Р1 с J\ = {/i}, т. е. задачу,
определяемую (1), (2), (За), (4) и дополнительным
ограничением
*/, - 1. (зьо
Отсюда, полагая Xj = 0 (/ е N), ух = bi (i е Af), ym+i = —1,
мы получаем двойственно допустимое решение для Р1. В
расширенном базисе 1т-н = (ei), i= 1, ..., т + 1, имеем, что(т+1)-й
единичный вектор ew+i соответствует ym+i. Если вместо этого
единичного вектора ет+\ мы введем a/j и переменная Xjt
примет, таким образом, в новом решении значение 1, то новое
решение для Р1, очевидно, окажется двойственно допустимым. Так
как вспомогательная переменная #т+ь принявшая теперь
значение 0, в дальнейшем не играет никакой роли, то она может
быть исключена, и новое решение может быть записано в виде
и' = (х>, у') = (*!,..., х1у\,...,у1).
Ввиду очень простого дополнительного ограничения
(направляющий элемент равен —1) новое двойственно допустимое
решение и1 (х1, у1) для Р1 равно
Так как операции, которые необходимо выполнять на каждой
такой итерации, исчерпываются лишь сложением и вычитанием,
то мы назовем алгоритм аддитивным.
Если решение и1 все еще содержит отрицательные
компоненты, то в соответствии с вышеуказанным правилом мы выбираем
другой вектор а/2 и добавляем к Р1 новое ограничение х/2 = 1 в
форме — Xf2 + ym+2 = — 1, где ym+2 — новая вспомогательная
переменная. Это даёт нам задачу Р2, определяемую (1), (2),
(За) и (4) и дополнительным множествам ограничений (ЗЬ2),
требующим, чтобы ^= 1, */2= 1. Множество xfl = 1, Xj =
*» 0[/е= {N — {/]})], yi^bi-ацх(isAf), ym+2 = -1- двойствен-
Аддитивный алгоритм для решения задач линейного программирования 221
но допустимое решение для Р2. Теперь вводим а/, в базис
вместо ет+2; в новом решении для Р2 переменная х^ принимает
значение 1, и это решение двойственно допустимое.
Вспомогательная переменная ут+2 в дальнейшем никакой
роли не играет (оставаясь все время равной 0) л может быть
исключена из вычислений, (так же как в случае ym+i)- Новым
двойственно допустимым решением для Р2 является и2 = (х2, у2),
где
Описанная процедура повторяется до тех пор, пока или не
будет получено решение и8 с неотрицательными компонентами,
или не станет очевидным, что такое решение задачи Р8 не
существует. ■
Если получен неотрицательный вектор u8 = (х8, у8), то он
является оптимальным (допустимым) решением^ для Ps. Такое
решение может и не быть оптимальным для задачи Р, но оно
всегда является допустимым для этой задачи.
Затем процедура повторяется. При этом исходят из
некоторого решения up (/?<s), выбранного в соответствии е
некоторым правилом. Для выбора векторов, вводимых в базис, здесь
используют другие правила. 3 результате либо получают другое
допустимое решение и*, такое, что zt < zs (zp — значение z для
up, р = 0, 1, ...), либо убеждаются в том, что такого решения
не существует.
Последовательность u? (q = 0, 1, ...) сходится к
оптимальному решению.
Описываемый алгоритм можно было бы назвать
псевдодвойственным алгоритмом, так как здесь, как и в двойственном
симплекс-методе, исходят из двойственно допустимого решения и
затем, постоянйо сохраняя эту двойственную допустимость,
последовательно приближаются к «области», допустимой в пря*
мом смысле. Однако итерации в нашем алгоритме
существенным образом отличаются от итераций двойственного симплекс-
метода; здесь не используется критерий двойственного симплекс-
метода для выбора вектора, вводимого в базис, и ни один из
векторов *i (/= 1, ..., т) не исключается из базиса, т. е. не
заменяется другим вектором. Все изменения в базисе
осуществляются посредством добавления новых единичных строк и
единичных столбцов или отбрасывания их. При этом, что наиболее
важно, коэффициенты матрицы А остаются неизменными.
Единичные строка и столбец, введенные.на некоторой итерации, не
играют никакой роли в последующих итерациях, и поэтому
сохранять их не нужно.
222
Э. Балаш
Особенности аддитивного алгоритма можно легко понять,
если сравнить его с полным перебором всех имеющихся
решений. Так как переменные задачи Р могут принимать лишь
значения 0 и 1, то множество U = {и} всех решений (2) и (3)
конечно и содержит 2П элементов, где п — число переменных ху
Xjs0{j'l ,5)
Процесс проверки всех 2п возможных решений
проиллюстрирован на рис. 1 для задачи с 5 переменными. На рисунке имеется
5 «уровней». Начиная от вершины, на каждом «уровне» мы
приписываем поочередно значения 0 и 1 той переменной, номер
которой совпадает с номером уровня. Все точки, лежащие на
отрезках, идущих вниз налево, соответствуют одному и тому же
решению, а точки, лежащие на отрезках, идущих вниз
направо, — различным решениям. Продолжив этот процесс до тех пор,
пока всем переменным не будут приписаны значения 0 и 1, мы
получим все множество, состоящее из 25 = 32 решений.
Наш аддитивный алгоритм отличается от полного перебора
тем, что он дает возможность получить оптимальное решение
(если такое существует), исследовав лишь некоторые из ветвей
дерева рис. 1, отбросив большинство из них. Исходя из
вершины, в которой все п переменных равны 0, аддитивный алгоритм
Аддитивный алгоритм для решения задач линейного программирования 223
систематическим образом приписывает значение 1 некоторым из
переменных, при этом после проверки лишь малой части всех 2П
возможных решений либо достигается оптимальное решение,
либо становится очевидным, что не существует допустимого
решения. Это обеспечивается благодаря некоторому множеству
правил, определяемых на каждой итерадии. На каждой
итерации в аддитивном алгоритме определены:
a) множество переменных, которым можно было бы
приписать значение 1, — множество улучшающих векторов;
b) правило выбора из этого множества.
На некотором этапе алгоритма становится ясным, что либо
можно получить оптимальное решение со значениями 1 для всех
переменных, которым это значение приписано, либо это
невозможно. Во втором случае вычисления прекращаются и
начинаются вновь с предыдущего этапа. Другими словами, правила
алгоритма позволяют отбрасывать те ветви дерева решений,
которые не могут привести к допустимому решению, лучшему, чем
уже полученное. На рис. 1 проиллюстрировано решение первого
из числовых примеров, рассмотренных в последнем разделе.
Исследованным решениям соответствуют жирные линии рис. 1.
Таким образом, в этом примере вместо 25 = 32 возможных
решений оказалось необходимым испытать лишь следующие 3:
и°: - *° = 0 (/=1, ..., 5),
' ' \0 (/=1,2,4,5),
и, „ П (/ = 2,3),
' / \0 (/=1,4,5).
Последнее решение оказалось оптимальным. «Стоп-сигналы»
алгоритма (на рис. 1 они показаны кружочками в конце
жирных линий) гарантируют, что ниже их не существует ни одного
допустимого решения, лучшего, чем уже имеющееся1) *).
Конечно, при таких обстоятельствах эффективность
алгоритма сильно зависит от эффективности этих «стоп-сигналов» на
множестве ветвей, которые не нужно продолжать. Позже будет
показано, что во многих случаях алгоритм дает значительное
уменьшение числа решений, которые нужно проверить.
*) Примечания редактора перевода снабжены сквозной нумерацией и
помещены в приложении к статье. — Прим. перев.
234
Э. Балаш
2. Некоторые определения и замечания
Рассмотрим задачу Р.
Так как каждое ограничение . из (2) содержит в точности
одну компоненту у, решение и? = (х*\ ур) единственным
образом определяется множеством /р= (/ |/еЛГ, х?~ 1}.
Действительно, если
хр-[1 (/'е/р)'
ТО
0?-**-2а« (teM). (6)
Как уже показано, аддитивный алгоритм порождает
некоторую последовательность решений; s-й член этой
последовательности мы будем обозначать через
ue-u(/lf ..., /г)* (Xе, у), (7)
где
{Л..... /Л-7.-{Я/елг. xj-i}, (8)
а через г5 — значение линейной формы (1) для и8.
Последовательность начинается с и0, для которого /о = 0,
т. е. х° = 0, у8 = Ь и г0 = 0. Ясно, что /0 е: /р для любого р Ф 0.
Множество значений, принимаемых целевой функцией при
допустимых решениях, полученных при s итерациях, обозначим
Za = {zp\p<~sy up>Q}. (9)
Если это множество не пусто, то его наименьший элемент
будем называть предельным значением для решения и*. Если
оно пусто, то роль предельного значения будет играть оо. Таким
образом, предельным для и* будем называть
г*<*> («>> еслиг,= 0,
IminZp, если Zs^0.
1 zs
На каждой (s + 1)-й итерации новый вектор, вводимый в базис,
выбирается из некоторого подмножества {8ij\j^N}t
называемого множеством улучшающих векторов для решения и8.
Соответствующее множество индексов / обозначим через N8 (конечно,
JVesJV). Точнее это множество будет определено ниже*).
*) Повсюду в статье символ s обозначает включение, ас —строгое
включение.
Аддитивный алгоритм для решения задач линейного программирования 225
Теперь мы определим некоторые величины, которые будут
служить критерием для выбора вектора, вводимого в базис.
Итак, для каждого us и каждого / е N8 мы определим величины
vr
где
О (je=Ns; Мр = 0), (И)
Af;-={/|yf-a//<0). (12)
Значение этой величины очевидно: vfc равна сумме
отрицательных компонент решения us+!, которое может быть получено
из решения и8, если положить /s+i = Js U {/*}•
Как уже было сказано, величины Vs служат критерием2) при
выборе нового вектора, вводимого в базис. Этот критерий
оказался довольно эффективным; однако необходимо подчеркнуть,
что он выбран эмпирически и не является ни обязательным, ни
существенным для аддитивного алгоритма, для которого воз*
можны и другие критерии. Выбор критерия для введения нового
вектора в базис, разумеется, влияет на эффективность
алгоритма, но никак Н£ сказывается на конечности работы алгоритма.
В аддитивном алгоритме величины v*j> связанные с некоторым
решением и*, последовательно аннулируются в следующих
итерациях в соответствии с некоторыми правилами. Пусть Cl(k^.s)
есть множество тех /, для которых величины v*, связанные с
решением и*, были аннулированы до того, как было получено
решение us (cl =0 по определению).
Множество тех /, для которых величины v?jt связанные с
решениями и*\ такими, что р < s и /р с: /* были аннулированы
до получения u*f обозначим
С*« U С%. (13)
Теперь мы определим для решения и* множество D8 тех
/ е(#— С*), что если ъ$ ввести в базис (это дает J8+i «ДО {/}),
то значение целевой функции достигло бы предельного значения
при ue:
А~ [I\IMn-С% cf^:z*{s)-zs). (14)
Далее определим множество Е8 тех / &[N — (С8 U А,)], что
если а^ ввести в базис (это дает 1Ш±\ » J9 U {/}), то ни одно
226
9. Балаш
отрицательное yf не увеличивается:
£,-{Л/е[ЛГ-С'иЯ,], Щ<0^аи^0). (15)
Теперь мы можем дать определение множества улучшающих
векторов для решения us. Это множество тех Ej, для которых /
принадлежат3) множеству
NS = N-(C*[)D8[)E8). (16)
Очевидно, Ns = 0 для любого допустимого решения us.
Аналогично определению Ds мы для пары решений uh и и* (к < 5)
определим множество D% тех / е (Nk — Cl), что если а; вводится
в базис (/s+i = Д U {/}), то 2s+i будет достигать предельного
значения при us:
Dj-f/l/eto-Cft */25 2^-2.}. (17)
Наконец, если дана пара решений us и uh, такая, что
us = u(/i, ..., /r), u*«u(/b ..., /r-л), l^h<r; JkaJs,
то мы определим множество улучшающих векторов для
решения uft, остающихся после итерации s. Это множество тех г.^
для которых / принадлежит множеству
NSk = Nk-{Csk\}Dt). (18)
Множества, определяемые (16) и (18), будут играть
основную роль в нашем алгоритме. Всякий раз, когда получено ре*
шение и8, для введения в базис будут рассматриваться лишь
улучшающие для этого решения вектора. Всякий раз, когда
множество улучшающих векторов для решения us оказывается
пустым, это интерпретируется как «стоп-сигнал», который
означает, что не существует допустимого решения и*, такого, что
J$a Jt и Zt< z*(s\ В таких случаях мы возвращаемся к
предыдущему решению uft, определяемому согласно некоторым
правилам, и для любого такого решения для введения в базис
должны рассматриваться только векторы из множества улучшающих
векторов для решения и\ оставшихся после итерации s.
3. Описание аддитивного алгоритма
Мы начинаем с двойственно допустимого решения и0, для
которого
хо^О, у°~Ь и го = 0, (19)
Аддитивный алгоритм для решения задач линейного программирования 227
Предположим, что после s итераций мы получили решение
us = u(/i, ..., /г), для которого
( 1, /е/„
*|-\0, /«(ЛГ-/А (20)
z5 = 2 ch (21)
Тогда можно принять следующую процедуру (см. рис. 2).
Шаг 1. Просматриваем */f (/еМ),
1а. Если j/^0(i'eM), то полагаем zs = г*К Образуем
множества £>|э согласно (17), для всех k<s, вычеркиваем
(аннулируем) все У/, для которых / е D|, & < s, и переходим
к шагу 5. Если это произошло в случае и0, то и0 — оптимальное
решение, и вычисления заканчиваются.
lb. Если существует iu такое, что yslx < 0, переходим к
шагу 2.
Шаг 2. Определяем улучшающие векторы для решения и3,
образуя множество N8, как это определяется в (16).
2а. Если Ns = 0, т. е. для us нет улучшающих векторо-в, то
переходим к шагу 5.
2Ь. Если Ns ф 0, то переходим к шагу 3.
Шаг 3. Проверяем соотношения
ga-rgy? (*1#<0), (22)
где aZ — отрицательные элементы А.
За. Если найдется i\ е М9 для которого (22) не выполняется,
то переходим к шагу 5.
ЗЬ. Если все соотношения (22) выполняются как строгие
неравенства, то вычисляем величины vsr согласно (11) и (12), для
всех / е Ns и выбираем /s+i так, что
Vs, « max Vs. *), (23)
вычеркиваем vj и переходим к шагу 8.
*) Если (23) или (28) выполняются более чем для одного /=/«+1 (пусть
^тах — множество тех /, для которых это выполняется), то выбираем /e+i
так, что cyj+1~ min Cj. Если же и это соотношение выполняется более
*'е/тах
чем для одного /*=/•+!, то выбираем любое из них в качестве j9+i>
1 Аннулируем-v/Jcf
[Вычисляем zt.t t.
у*"(Ш)(но-
doe решение)
r lar^e)
'1" '
1«
r tttaet л
\ нет Ob)
r Шаг2 ]
* нет (2b)
ШагЗ ' 1
1 da (3d или
\ нет (3 c)
\ иет(Щ
Аннулируем v} для ]Щ
\ Аннулируем Vj',](f;a
{вычисляем zt.,uy?'\
(ИМ)
| (ноНое решение) |
, f
* \
да (5a)
да (Га)
ЯМ/fltf Г
Образуем D% (к <s) 1
Аннулируем Vj(JiDl)\
—ч
fatfty
V
^/77 (За)
Зс) 1
идо; 1
Вычисляем Vj'tjtNs
Выбираем js.t
Аннулируем vf,..
V
S |
/ 1
/ 3
Шаг 8
а 3s.,*Jsu{Js+tL,
вычисляем zM и и?
jwfte решение)
« VU
Шаг 5
\ нет, для к
\ да, Зля к-кя
V ' J
i нет (6с)
Шаг 7
\нет(П)
1 УК
! Существует ли
K<Kfi(J„CJs)?
V. и - ■-*
Ь*ЮТ
*№
нет (6а) ^
(бьилиба
да (66) t
t
{повторяем шаг5 для
\к<кл, заменив к+но
1 к+^бшагахбиб
\да
ГАннулируем tfrfawl
Существует fa "*
дыВираем j$.j
Аннулируем vj*,
ч
Xtem
J
У
1 -
J
да
1 Повторяем шаг 5 для
J н <кД, заменив кр на
j л>и в шагал бив
U—^
■
/««•
Рис. 2.
Аддитивный алгоритм для решения задач линейного программирования 229
Зс. Если все соотношения (22) выполняются и существует
подмножество Ms множества М, такое, что для i^Ms
соотношения (22) выполняются как равенства, то переходим к шагу 4.
Шаг 4. Проверяем соотношение
2 cf<z*^-zsy (24)
где 4) Fs— множество тех /е Ns, для которых ац < 0 по
крайней мере для одного i е Ms.
4а. Если (24) выполнено, вычеркиваем (аннулируем) Vs. для
всех /е/\ч-(не вычисляя их численных значений). Полагаем
Д+i = Д U F8, вычисляем значение целевой функции
zs+l = zs + S ¢/ (25)
и слабых переменных
уГ] = У1~ S- *// (<е^ (26)
/^
для нового решения us+l и переходим к следующей итерации
(т. е. опять начинаем с шага 1).
4Ь. Если (24) не выполняется, вычеркиваем vsf для всех
/ е Ns (не вычисляя их значений) и переходим к шагу 5.
Шаг 5. Определяем улучшающие векторы для решений
uh(k\Jk a /s), оставшиеся после итераций 5, т. е. проверяем
множества Nsk(k\ Jka Д), определенные согласно (18), в
порядке уменьшения номеров k до тех пор, пока или не будет найден
номер ku такой, что Jki cz Д и N*k Ф 0, или окажется, что Nl
пусто для любого &, такого, что Д с Д.
5а. Если Wl = 0 для всех ft, таких, что Д с: Д, т. е. нет
улучшающих векторов для иЛ(Л|Дс:Д), то работа алгоритма
заканчивается. В этом случае если Zs = 0, то задача Р не
имеет допустимого решения. Если Zs Ф 0, то и?, для которого
гд = 2*<8>, является оптимальным решением, a £*<s> — минимумом
для целевой функции этого рршения.
5Ь. Если Nsk ф 0 или k = kv ДсгД, то переходим к шагу 6.
Я/аг 6. Проверяем соотношения
2*Г/^# (*1#<0) (27)
для Л = Аь
230
Э. Балаш
6а. Если какое-либо из соотношений (27) не выполняется
(для k = &0, то вычеркиваем vf для всех j^N8kl и повторяем
шаг 5 для k < k\f записывая k2 вместо k* в шагах 5 и 6. Каждый
раз, когда шаг 5 повторяется для k < kat записываем fta+i
вместо ka в шагах 5 и 6.
Если (27) не выполняется ни для какого k, такого, что
Л/1=т*=0, алгоритм заканчивается с тем же заключением, что
и в 5а.
6Ь. Если для k = k$ все соотношения (27) выполняются как
строгие неравенства, то выбираем /s+i так, что
vf = max аД (28)
Js+i
fetf'
вычеркиваем vf и переходим к шагу 8.
6с. Если для k: = k$ все соотношения (27) выполняются и
существует подмножество ML множества М, такое, что соотно*
шения (27) выполняется как равенства для leAff, то
переходим к шагу 7.
Шаг 7. Проверяем соотношение
2 Cj<sfW-zku, (29)
где FL — множество тех / е JVjL для которых а*/ < 0 по
крайней мере для одного I е ML-
7а. Если (29) выполняется, то вычеркиваем v^p для всех
j&Fsk . Полагаем Js+{ = Jk U Fsk , вычисляем значение целевой
функции
^+1 = ^+ 2 с/ (30)
и слабых переменных
tf+l-#- 2 а|; (ШМ) (31)
для нового решения us+1 и переходим к следующей итерации
(т. е. опять "начинаем с шага 1).
7Ь. Если (29) не выполняются, вычеркиваем величины vkf
для всех j €= Ns и повторяем шаг 5 для k < k$. Если не суще*
Аддитивный алгоритм для решения задач линейного программирования 231
ствует k < A3, т. е. если ftp = 0, то алгоритм заканчивается с
тем же заключением, что и в 5а.
Шаг 8. Полагаем /s+i = Jp V {j&+\} и вычисляем значение
целевой функции и слабых переменных для нового решения u8+1 в
соответствии с формулами
*,+i = *p + <?/j+1- 2 ch (32)
0?+,e0f-a» = *,- 2 fl„ (/€=М), (33)
где р определяется последней вычеркнутой величиной v^j .
Переходим к следующей итерации-(к шагу 1).
Алгоритм заканчивается, если получено решение и*, для
которого: (1) выполняется ситуация 5а или (2) имеется ситуация
6а, причем (27) не выполняется ни для какого ft, такого, что
N1=7^0, или (3) имеет место ситуация 7Ь и ftp ="0.
Замечание 1. Описанный аддитивный (алгоритм дает одно
оптимальное решение (если такое существует). Но если мы
поставим знак > вместо ^ в (14) и (17) и знак ^ вместо < в
(24) и (29)-, то получим новый вариант того же алгоритма,
дающий все существующие оптимальные решения задачи.
Замечание 2. С другой стороны, число решений,
проверяемых алгоритмом, может быть уменьшено за счет относительно
небольших дополнительных вычислений в каждой итерации,
изменив следующим образом шаги 3t>, Зс и 6Ь, 6с.
ЗЬ. Если все соотношения (22) выполнены, то проверяем
соотношения
2«Г/-*Г/.^Я (*1#<0), (22а)
' N S
где ат, = max атл если все соотношения (22а) выполнены, то
вычисляем величины gj для всех / е Na, выбираем /5+i так, что
v* =m*xv°r (23)
вычеркиваем vsf и переходим к шагу 8.
Зс. Если все соотношения (22) выполнены и существует
подмножество Ms множества М, такое, что соотношения (22а) не
выполняются для /е Afs, то переходим к шагу 4.
Совершенно аналогичные изменения следует сделать в шагах
6Ь и 6с.
232
Э. Балаш
Практическое применение алгоритма облегчается, если
использовать таблицы, подобные полученным в последнем разделе
при решении численных примеров.
4. Доказательство конечности алгоритма
Аддитивный алгоритм порождает последовательность
решений и0, и1, ... . Будем говорить, что решение и* является
отброшенным, если, руководствуясь алгоритмом, мы либо должны
проверить Nsp (0 ^ р < k ^ s), либо должны остановиться.
Основная особенность нашего алгоритма, которая в то же
время способствует доказательству его сходимости, может быть
выражена теоремой 1.
Теорема 1. Если решение ик является отброшенным при
аддитивном алгоритме, то не существует такого допустимого
решения и*, что Jkcz Jt и zt< z*(k\
Решение может оказаться отброшенным в результате одного
из следующих шагов алгоритма: 1а, 2а, За, 4Ь, 5, 6а, 7Ь. Для
того чтобы доказать, что сформулированная теорема имеет
место для всех этих ситуаций, нам потребуются две леммы.
Во-первых, рассмотрим множество Ср. Согласно правилам
нашего алгоритма, существуют три обстоятельства, в силу
которых величина У/*, приписываемая решению и*\ может
оказаться аннулированной до итерации s, т. е. имеются три
причины для /* принадлежать множеству Csp:
a) Соотношение (27) не выполняется для k = р (т. е. vJj*
вычеркивается на шаге 6а).
b) Решение и? (р < q ^s) было получено из и? введением
а, в базис (т. е. v? было вычеркнуто на одном из шагов ЗЬ,
4а*, 6Ь, 7а).
c) Если а/* должен быть введен в базис, но z достигает пре^
дельного значения для us (т. е. v^ вычеркнуто на одном из
шагов la, 4Ь или 7Ь).
Обозначим через Csp(a), Csp(b) и Csp(c) подмножество
индексов /, отвечающих тем £>/» которые вычеркиваются до
итерации 5 по причинам а), Ь), с) соответственно, так что
Csp = CSp(a)l)Cp(b)[)Csp(c)^ и, кроме того, через О (а), С*(Ь) и
Cs(c) —соответствующие подмножества Cs, такие, что
С* = С*{а) U 0{b) U С* (с).
Аддитивный алгоритм для решения задач линейного программирования 233
Лемма 1. Если для данного решения и* существует такое
допустимое решение и', что J8czJt и zt < г*(*), то
(Jt-Js) ПО = 0. (34)
Доказательство. Соотношение (34), очевидно,
выполняется для любого решения us, такого, что С8 = /s, и в любом
случае оно имеет место для и0, так как /0 = С0 = 0. Мы можем
предположить, что (34) выполняется для некоторой
последовательности решений и? (р = 0, 1, ...), состоящей по крайней
мере из одного члена.
Мы докажем, что если (34) имеет место для up (/? = 0; 1, ...
..., п), то qho имеет место также для un+1. Обозначим un =
= и (/ь..., /V). Возможны два случая
(1) /л^Ли-ь
В этом случае либо Jn+\ = Jp U {/n+i} и 0+1 = Cn U {/n+i},
либо /n+i ^/nUFn и Cn+* = Cn U Fn. В обоих случаях (34),
очевидно, имеет место для un+1.
(2) JP<£Jn+i-
Обозначим через Д = {/ь • • ♦» /V^/i}, где А — наименьшее
число (1 ^ А^ г), для которого Jk <= /n+i.
Согласно определению Cn+1,
c»+ie (J ^ = Г (J (сГ-'-С*)1иС\ (35)
P\Jp^Jk [pUpsfk J
Так как для u* соотношение (34) предполагается выполненным
и так как 4 с /rt+I и z*{k) *z z*{n+l), то мы имеем
У*-/л+1)ПС*-0 (36)
для любого и' ^ 0, такого, что /rt+ic:/, и zt<z*(n+l).
С другой стороны, поскольку Jk с: /п+1, мы имеем
С(а)-0(р1/р = /4) и ^+,(6)-Cj(&)(p|/pc/A),
так что
C;+,-C* = ^+l(c)-Cj(C)(p|/pc:/c/ft) (37)
и
СГ1 - Cj ~ СГ1 = СГ* (с) U СГ1 (ft). (38)
Далее по определению Ср+](с)
(W«+i)nf U IC'(c)-c;ic)]\-0. (39)
234
Э. Балаш
Таким образом, из приведенных соотношений следует, что
('* - '„+.) П Сп+{ = (/, - Jn+1) П Cnk+i (b). (40)
Теперь имеются две возможности: либо Jn+\ = /feU{b+i}, либо
^+1 = ^11^. Предположим, что имеет место первая из этих
двух возможностей, и поэтому C£+I(6) = C^(6)U {in+\}
(совершенно аналогичные рассуждения справедливы для второй
ситуации).
Мы имеем
(/,- /.+1) П Cn+l - (/,- Jk) П(/, - {/.+I}) fl [Cnk(b)U {/n+I}] (41)
или, так как
(/*-{/»+!» П {/»+!>-0. (42)
имеем
С, - Л+i) П Ся+' = (/, - /0 П (/, - {/„+,}) П Cl (b). (43)
Теперь мы покажем, что
(Jt - '*) Л Cnk (6)=0. (44)
Предположим противное, т. е. что существует /fi, такое, что
и обозначим Jq *= Jk^iJf}-
Очевидно, Jt не совпадает с /^, так как из /^GCj(fi)
следует, что q\<ny т. е. 2*(<?i) ^ г*(л), в то время как z*{t)<z*(n).
Таким образом, если (45) выполняется, то должен
существовать /^, такой, что
/^[(WjnC-W]. (46)
В противном случае должно иметь место
(У, - J J =[N- Cl (b)] - С* U Л„ U *„ U К - С; (b)\. (47)
Но, так как k<q^<n и jf^Cnk(b) влечет ]q<£Jn+v мы
имеем JV = C*+I и C"+I(&) = C" (ft). Таким образом,
^-^(««Cj^eJUCW. (48)
С другой стороны, из определения Dqi, Cnq* (а) и С^+ (с) и
из того факта, что (34) предполагается выполненным для t/b
так как ц^<п и / с: /№, следует, что
С* - ' J П [С' U />„ U C;+l (a)U С (с)] - 0, (49)
Аддитивный алгоритм для решения задач линейного программирования 235
и по определению Eq.
W„S*„- (5°)
Следовательно, (47) невозможно, т. е. (46) должно иметь место,
если выполняется (45).
Теперь если С",(6)=0, то мы получаем противоречие, и
справедливость (44) доказана. Если же это не так, то
рассуждения, совершенно аналогичные приведенным, показывают,
что если существует
^{(''-''Л^-гЧ (51)
то
in+^le-wzM (52)
также должен существовать (i = 2, 3, ...); J'q и Jq
определяются аналогично / .
Так как число множеств СЯ1{Ь)ф 0 конечно, эта
последовательность импликаций, очевидно, приводит в конце концов к
противоречию, что и доказывает справедливость (44).
Таким же образом показывается, что соотношение (34)
имеет место также и в случае (2), и это завершает
доказательство леммы 1.
Лемма 2. Даны два решения u5~u(j{9 ..., jr) и uk =
= u(/j. • •.. /,^)(1 =A=r' h^s)* такие> что Np = cT (k<P^s)-
Если существует допустимое решение и*, такое% что Jk a Jt
и zt<z*(*\ то
(Л-/*)ПС^-0. (53)
Доказательство. Соотношение Jk a Js гарантирует, что
С1(а)=0, в то время как соотношение
(/,-^)Пед=0 (54)
следует из определения Ct(c). Таким образом, (53) сводится
к соотношению
(Л-^ПС; (6)=0. (55)
которое может быть доказано точно так же, как (44).
Доказательство теоремы 1. Для решений,
отброшенных на одном из шагов la, 4Ь или 7Ь, теорема очевидна.
Мы докажем теперь ее для других случаев.
236
Э. Валаш
2а. В этой ситуации, так как Nh = 0, существование
допустимого решения и*, такого, что Jkcz Ju zt<z*(k\ повлекло бы
соотношение
Jt-JhsN-Nk~Cb\)Dh\)Ek, (56)
которое невозможно ввиду леммы 2 и определений Dh и Еъ..
За. Если (?2) не имеет места, то ввиду определения Ек
допустимое решение и* с требуемыми свойствами могло бы суще-
хтвовать,.только в том случае, если
(Jt-h)r\(Ch\)Dk)*0, (57)
чего не может быть, согласно лемме 1 и определению Dh.
5. Если' Nl = 0 для некоторого k, то существование
решения и* с требуемыми -свойствами влекло бы
Jt-Jk<=N-Nsk. (58)
Но ввиду определений D*, Dl и'СЦс) ни один элемент любого
из этих множеств не может содержаться в Jt — Д. Далее,
d(a)—0 вследствие того, что проверка Nl для некоторого kt
определенного на шаге 5, всегда предшествует возможному
вычеркиванию величин v*j для того же самого k на шаге 6а.
С другой стороны, проверка Nl для ky определенное на
шаге 5, никогда не может иметь места прежде, чем не будет
установлено равенство Л/р = С£+ для всех р, таких, что k<p^s.
Следовательно, согласно лемме 2, (/* — /*) ПС* также пусто и
(58) сводится к
J}-JksEk, (59)
что, очевидно, невозможно.
6а. Если (27) не выполняется для определенного k, то
решение и', какое требуется в теореме, могло бы существовать
только в том случае, если
(W*)n[tf-(^U<>]#0. (60)
Но это, как было показано в предыдущем пункте, невозможно.
Таким образом, теорема 1 доказана. Теперь мы можем
сформулировать следующую теорему.
Теорема 2 (теорема о сходимости алгоритма). За
конечное число итераций аддитивный алгоритм приводит либо к
оптимальному решению, либо к заключению, что задача не имеет
допустимых решений.
Доказательство. Из теоремы 1 следует, что
завершение работы алгоритма (которое означает, что все испытанные
Аддитивный алгоритм для решения задач линейного программирования 237
алгоритмом решения оказались отброшенными) приводит либо
к оптимальному допустимому решению, либо к заключению, что
допустимых решений задачи не существует. Мы докажем, что
аддитивный алгоритм завершает работу за конечное число
шагов.
a) За конечное число шагов каждая итерация выдает новое
решение или же алгоритм заканчивается. Повторение некоторых
шагов в течение одной и той же итерации может появиться в
одной из ситуаций 6а или 7Ь. В обоих случаях шаг 5, который
требует проверки Nsk (k \ Jk cz /s), должен повторяться для k < ka%
где ka есть некоторое число, для которого эта проверка была
уже сделана. Таким образом, возможно только конечное число
таких повторений.
b) Никакое решение не может быть получено аддитивным
алгоритмом дважды. Предположим противное, т. е.. пусты
us = u (ju ... , /г) и u' = u(fti,. <., kr) — два решения,
полученные аддитивным алгоритмом, такие, что us = u' (t>$). Мы не
можем иметь /* = &г (* = 1> • • • > г)> так как в этом случае
/геС^! (где q определяется либо из соотношения ^ — ^U {/г}>
либо из соотношения ^ = ^11^^), и это исключает jr^Jr
Пусть (/а, ka) есть первая пара индексов Qh kt), тикая, что
)ьфк{, и обозначим up = u (/,, ...,/ы). Тогда ja&C*~l о С*"1
и, таким образом, /а^/*.
Этим завершается доказательство теоремы о сходимости.
5. Некоторые замечания об эффективности алгоритма5)
В отличие от большинства известных алгоритмов для
решения задач линейного программирования с целыми переменными
аддитивный алгоритм решает непосредственно задачу
линейного программирования с переменными, принимающими
значения 0 или 1; для его применения не требуется предварительного
решения соответствующей обычной задачи линейного
программирования.
Как уже указывалось, единственными операциями,
используемыми в аддитивном алгоритме, являются сложение <и
вычитание. Это исключает возможность ошибок округления.
Аддитивный алгоритм не налагает тяжелых требований на
память вычислительной машины. Большинство промежуточных
результатов может быть опущено вскоре после их пЪлучения.
В настоящее время эксперименты с аддитивным алгоритмом
лишь начинаются. До сих пор решено вручную около дюжина
задач не более, чем с 15-ю переменными, и одна задача ббльшего
размера (тоже вручную). Результаты очень обнадеживающие,
238,
Э. Балаш
однако этих экспериментов, конечно, недостаточно, чтобы
сделать окончательный вывод об эффективности алгоритма
особенно для задач большого размера. Ниже мы прокомментируем
упомянутые выше эксперименты, однако все наши выводы в
этом разделе следует рассматривать как предположительные
ввиду скудности экспериментального материала.,
Данные об 11 .задачах, решенных вручную аддитивным
алгоритмом, приведены в табл. 1.
Таблица 1
Номер
задачи
1
2<а)
3
4(а). <Ь>
5
6<а)
7
8
д(а), (О
10
11
Число переменных
со значениями 0 или 1
5
5
7
9
10
10
11
11
12
14
15
Число ограничений
(неравенств)
2
3
5
4
4
7
6
7
6
9
12
Число
итераций
6
3
11
31
12
5
21
8
39
23
22
Задача решена в качестве примера в последнем разделе.
Задача не имеет допустимых решений.
Задача с одним-единственным допустимым решением *).
*) Замечено, что эта задача имеет несколько допустимых решений
[36*] -Прим перев.
При решении этих задач в среднем затрачивалось 7 мин на
одну итерацию. Задачи 3—5, 7, 8, 10 и 11 были решены за
1—з час, задачи 1, 2, и 6—менее чем за 1 час, а на задачу 9
было затрачено более 4 час.
Каждый, кто пытался решить вручную задачу того же типа
и размера с помощью методов отсечений, знает, что это
требовало в несколько раз большего времени, не говоря уже об
ошибках округления. Более того, решение обычных задач линейного
программирования без введения ограничений 0 и 1,
соответствующих указанным выше задачам, требует значительно
большего времени, чем решение исходных задачч с помощью
аддитивного алгоритма.
Единственной задачей большого размера, которую пытались
решить с помощью аддитивного алгоритма, была задача об
управлении лесопосадками [10]. Целевая функция задачи
линейна, а возможные значения переменных — 0 и 1. Помимо
Аддитивный алгоритм для решения задач линейного программирования 239
обычных ограничений, в этой задаче необходимо было учесть
ряд дополнительных («логических») условий. Для этого в
исходную задачу были введены дополнительные переменные со
значениями 0 и 1, и в результате была получена задача
линейного программирования, все переменные которой могут
принимать лишь значения 0 или 1 и которая содержала 40
переменных и 22 ограничения.
Число ненулевых элементов в матрице полученной задачи
было равно 140, из которых Д15 равны 1 или —1. Эта задача
была выбрана специально для изучения применимости
алгоритма к определенному типу задач управления. Специальная
структура задачи позволила заранее определить ее оптимальное
решение. После 35 итераций, сделанных вручную (в среднем на
каждую итерацию затрачивалось 20 мин), было получено
приближенное решение, отличающееся от оптимального на 1,4%.
Однако ввиду специальной структуры матрицы, в частности
плохой ее заполненности, мы не склонны из этого эксперимента
делать вывод о быстрой сходимости алгоритма.
Проведенный вычислительный эксперимент подтвердил
преимущества аддитивного характера алгоритма. Например,
ошибка, обнаруженная на 19-й итерации, возвращала вычисления к
З-ji итерации, и на ее исправление затрачивалось около 2 час.
Дальнейшее изложение касается зависимости объема
вычислений от размера задачи и других ее характеристик и
основывается частично на умозрительном анализе механизма
алгоритма, частично на проведенных вычислительных экспериментах.
Пусть п — число переменных задачи, a m — число ограничений.
(a) Объем вычислений на одной итерации. Число операцай,
необходимых для проверки соотношений (22) и (27) (шаги 3 и
6 соответственно) и для вычислений величин vsf (шаг ЗЬ),
линейно зависит от m X п. Число операций, необходимых для
построения или проверки множеств Ns и N% (шаги 2 и 5),
линейно зависит от п, а число операций, необходимых для
вычисления и проверки нового решения (шаги 8, 4а, 7а и 1а),
линейно зависит от т. Таким образом, весь объем
вычислений на одной итерации линейно зависит от величины \х
min[myn]K\iKmX п.
(b) Число итераций, необходимых для решения задачи.
Очевидно, что число итераций в первую очередь зависит от п. Что
касается га, то его увеличение повышает эффективность
некоторых «стоп-сигналов» (шаги За и 6а) и, таким образом,
уменьшает число итераций. (Это важное преимущество алгоритма.)
Основным в вопросе об эффективности алгоритма является
характер зависимости числа итераций от п. Из комбинаторной
природы алгоритма вовсе не обязательно следует, что эта
240
Э. Балаш
зависимость экспоненциальная. Хотя множеств?) всех решений,
из которых выбирается оптимальное, увеличивается с ростом п
экспоненциально, эффективность некоторых «стоп-сигналов»,
возможно, увеличивается быстрее. Проведенные эксперименты
не выявили экспоненциальной зависимости. В трех задачах
небольшого размера (задачи 1, 2 и 3; см. табл. 1) число итераций
изменялось от 0,6 п до 1,6 лг, в двух больших задачах (10 и
11) —от 1,5я до 1,6я. В самой большой из решенных до сих пор
задач (11) было исследовано 22 решения из общего числа 215 =
= 32 768. Разумеется, этих экспериментов недостаточно; только
машинные эксперименты с большим числом задач большого
размера помогут выяснить вопрос об эффективности алгоритма.
Число итераций зависит также и от других характеристик
задачи. В случаях, когда существует оптимальное решение, в
котором лишь немногие переменные имеют значения 1,
относительно большой размер множеств Ds делает «стоп-сигналы»
особенно эффективными, и. это обеспечивает быструю
сходимость алгоритма (см., например, задачу 6 табл. 1 (пример 2 из
последнего раздела), где было исследовано лишь 5 решений из
210 — 1024). С другой стороны, если задача не имеет
^допустимого решения, то все множества Ds пусты и эффективность
«стоп-сигналов» уменьшается. То же самое верно, однако в
меньшей степени для задач с очень большим числом
допустимых решений. Но все же следует отметить, что даже в этих
случаях «вырожденных» задач число итераций не становится
необозримо большим. Так, задача 4 табл. 1 (пример 3
последнего раздела) с 9 переменными и 4 ограничениями, не имеющая
ни одного допустимого решения, была «решена» (т. е. было
установлено отсутствие допустимых решений) за 31 итерацию.
Задача же 9 табл. 1 (пример 4 последнего раздела) с 12
переменными и 6 ограничениями, имеющая лишь одно допустимое
решение, была решена после испытания 39 решений из 212 =
- 4096.
6. Численные примеры
Пример 1 (задача 2 табл. 1).
Рассмотрим задачу
-5*{ + 74+104-3*;+ 4aminf
- 4""34+ 5хз~ К-4х'в>°>
-24-64+ 34-24--24^-4,
-4*)+ 2*з+ <~ 4>2>
4 = 0 или 1 (/= 1, ..., 5).
*) В оригинале опечатка, там стоит ^2х2. — Прим. перев.
Аддитивный алгоритм для решения задач линейного программирования 241
Умножая на —1 первое и третье неравенства и полагая
хг
х] (/ = 2, 3, 5),
1-х] (/=1, 4),
мы приведем задачу к стандартной форме (см. задачу Р в
разд. 2):
5*1 + 7*2+ 10*3 + Злг4+ *5 =mln,
— *1 + 3*2 — 5*з ~ *4 + 4*5 + #i = —2,
2*i — 6*2 + 3*з + 2*4 — 2*5 + у2 =0,
*2- 2*з+ *4+ *5 +уг=* -1,
Xj = 0 или 1 (/=1,...,5).
Для дальнейших вычислений ^удобнее иметь дело с матрицей
Ат вместо матрицы А (индекс f означает операцию
транспонирования)
Аг =
-1
г
-5
-1
4
2
-6
3
2
г-2
0
1
-2
1
1
решения и0 = (0, Ь). Все необходимые данные
(я /о-0, z0 = 0, г/? = &!-= —2, ^=62«0, */° =
Мы начнем с
для этого решения
= &3= — .1 помещены в левую часть 1-й строки табл. 2.
В табл. 2, чтобы сделать иллюстрацию решения задачи
более ясной, аннулирование величин v* показано не
вычеркиванием, а нумерацией их в порядке аннулирования.
Ход решения задачи показан также на рис. 1.
Итерация 1.
Шаг 1. г/}<0 для /=1, 3; имеет место ситуация lb.
Шаг 2. No = N-(C*VD0{)Eq); С°-0, 2)о=0. £о = {2, 5}
(см. строку 1 табл. 2).
#0в{1, 2, 3, 4, 5} —{2, 5} = {1, 3, 4}; таким образом, имеет
место случай 2Ь,
242
Э..Балаш
Таблица 2
Номер
строки
1
2
3
4
5
6
7
8
9
10
11
12
s
0
1
2
Js
|0
' 3
3,2
zs
0
10
17*
Ns
1
3
4
2
5
1 rf
/ejv„
! »i
2 ай
У\ ~ al2
! • й
/
1
-2
-7
-1
-1
5
-1
0
-2
2
0
-2
-3
-2j
-3
-8**)
-1
3
-2
3
-1
-2
-1
-2
1
0
0
"5
-44
-31
-55
02
-23
cs
0
3
^
! 0
0
£s
2,5
1,4
F
rs
0
0
0
**) В оригинале опечатка, там стоит - 2. — Прим. перев.
Шаг 3. Проверяем соотношения (22) для *=1, 3 (см. строку 2
табл. 2)
Ц а~ ==а~ + а.^ + а-= ~1--5--1 =-7< z/J== ~-2,
/€=#„ '
Все соотношения выполнены как строгие неравенства,
поэтому имеет место случай ЗЬ,
Аддитивный алгоритм для решения задач линейного программирования 243
Вычисление величины о°, согласно (11) и (12), для j^N0,
т. е. для / = 1, 3, 4, показано в строках 3, 4 и 5 табл. 2:
t>?= 2-(»?-fln)-(-2+1) + (0-2) + (-1-0)--4,
'«<
v»= 2 (f/?-ai4) = (-2 + l) + (0-2) + (-l-l)=-5.
Таким образом, у°, = max {v^} = у° = —3. Мы аннулируем о°
и переходим к шагу 8.
Шаг 8. /, = /0U{3} = {3},
г, = 20 + с3 = 0 + 10=10,
у\ = у0-а13= -2 + 5 = 3,
^-^-^,-0-3--3,
^ = ^-^33=-^2 = 1
(см. строку 6 табл. 2).
Итерация 2.
ZZ/аг 1. #! < 0 для / = 2, так что имеет место ситуация lb.
Шаг 2. JV, — JV — (С1 U i>i U £"i); С'={3}, /),-0, £,={1, 4}
(см. строку 6 табл. 2).
JV, = {1, 2, 3, 4, 5}-({3}(J{l, 4}) = {2, 5}, так что имеет место
случай 2Ь.
Шаг 3. Проверяем соотношения (22) для / = 2 (см. строку 7
табл. 2):
2 а~--6-2--8 < у'--3*).
Таким образом, имеет место случай ЗЬ. Вычисление v' для
/еЛГ, показано в строках 8 и 9 табл. 2:
t>2 = 0 (М2" = 0),
*J- 2 ДО-ай)-(3-4) + (-3 + 2) + (1-1)--2.
*) В оригинале опечатка, там стоит —2. — Прим. перев.
244
Э: Балаш
Таким образом, v) = max \v\) =*vl2 — Q. Мы аннулируем v\ и
11 /eJV, l /J
переходим к шагу 8.
Шаг 8.
/a-/iU{2}-{3, 2},
^2 = ^1 + ^2= 10 + 7= 17,
^ = ^-^ = 3-3 = 0,
*/2 = */'-а22 = -3 + 6 = 3,
^в»3"а32в1-1в0
(см. строку 10 табл. 2).
Итерация 3.
Шаг 1. j/f>0 для всех /sM; мы имеем случай 1а.
Полагаем г2=17 = ;г*<2) и образуем множества Z)|, согласно (17),
для k= 1, 0:
iV, = {2, 5}; С2 = {2}; ^~С2 = {5}; с5=1< 17-10, так что
ЛГ0-{1, 3, 4}, С2 = {3}; ЛГ0-С*-{1, 4}; с, - б < 17-0; с4 -
= 3 < 17 — 0, так что Dg=®.
Переходим к шагу 5.
Шаг 5. Проверяем множество Л/|, определяемое по (18),
для & = 1:
N2{^N{- (С? U Р?) = {2, 5} - {2} = {5}, т. е. имеет место
ситуация 5Ь.
Шаг 6. Проверяем соотношения (27) для t = 2 (строка 11
табл. 2):
S а2-у=-2<^=-3.
Так как (27) не выполняется, то имеет место случай 6а.
Мы аннулируем и* для /еД[^'т. е. v\, и возвращаемся
к шагу 5.
Шаг 5. Проверяем множество N\ для & = 0:
^0 = ^0-(^^0)==(^ 3> 4}-{3} = {1, 4}, т. е. опять имеет
место случай 5Ь.
Аддитивный алгоритм для решения задач линейного программирования 245
Шаг 6. Проверяем (27) для f = 1, 3 (строка 12 табл. 2):
2 a;;--l-l--2-tf--2,
2 oj-o^-i.
Так как (27) не выполняется для / = 3, то опять имеет место
случай 6а, и мы аннулируем v® для / е N\, т. е. v\ и v\.
Так как (27) не выполняется ни для какого &, для
которого Р/\ф09 то вычисления закончены. Оптимальным решэ-
нием приведенной задачи (оно помечено звездочкой в табл. 2)
является u2 = u (3,2), для которого
х\ = х\=\, 4 = 4 = 4 = °. 01=0. #! = 3> %2 = ° и ^2=17-
Соответствующее оптимальное решение исходной задачи
есть
Л/1 """■ Лл """"" Ли\ "" Лд """" 1 f Ике "Т-' V/.
Значение целевой функции с'х' = 9.
Пример 2 (задача 6 табл. 1).
Рассмотрим задачу
10л:;— 7х'2+ х'3-12х'4 + 2х'5+8х'й-3х1т- х'&+ 5л^ + 3д^0«=шах,
34+124" 8х'3 - х\ - 7^+2^(,^-8,
4+Ю4 +54~ 4+7л7+ хв ^13»
— ОХ. оХп~т~ Хо ^*^8 ^1()1^ *
- 44+ 24 -54- 4 + 9*8- 2*9 = ~8>
- 94 +124-74+64 -24-154-340^-12,
84 + 54- 24- 74+ 4 -54 +Ю4 ^16-
4 = 0 или 1 (/=1, ..., 10).
После замены равенства в ограничениях задачи двумя
неравенствами, умножения на —1 целевой функции задачи и всех
неравенств вида =а и подстановки
J 4 0 = 2,4,7,8),
Xj=\ I-4 (/=1. 3, 5, 6, 9, 10)
CO
о
*
3
**
^
а
^
*> 1
«9
«0
«0 ->
г*.
<Г>
ю
-
л
OJ
-
5:
«0.
«0
to
<и
1 I
1
IS
Q
Q
1
1
со
1
-
т
т
<N
1
о •«
О
Q
О
~
§
ю сч таг» оо
1 1 1 ' ' 1 1 1 ' 1
*
» со со — -* —<
oo II III
1
^N-COt^ «SO) "4f
7 ' 7 ' 7 ' ' '
oi со со —'CO ^p *—'CO
^11 II 1 II
1 1
COCO _ ^ _ .^ — <N
II 1 1 «1 1 II
Ю — <N — <N 00 <N -< —
"J 1 1 1 1 1 1 1 1
t^m со oj oj oj см rf
7 1 1 1 1 1 1 1
Q 0* о* «Г cT o" o* q° 0* cT 0*
^¾ l 1 I I I l I l l l
— счсо^юсо^ооо^о
CM С0ТГ*ЮС01>»00ОО*-СМ
0
0
G5
G5
00
T
-
T
T
Ю
~=sT
Ю
G>
~
со
S>
со 0
1
7
*
* —
0 1
<N 1
1
1
CO
1
Ю <N
7 '
1 £Г <N 00
<N CO
Tf Ю CO
17
18
19
20
21
22
23
24
25
26
27
28
29
2
3
4
9,3
5
5,3
6*
2
3
4
5
6
8
0
3
8
0
y\~ai4 ,
#,2 J
2 «&
yf
2 «Г/
/estf,
y\
2 аГ/
2 аГ/
13
-8-
-2
-8
-2
6
-8
-1
-2**)
-2
9
-35
4
14
-10
-1
-1
-1
0
-3
-1
-3
0
-2
-3
-1 \
0
1
-1
0
-1
-1 j
3 i
-13
-3
-13**)
1
-9
-13
8
-10
0
—2
0
-3
7
-6
0
-2
-2
-5
-28
-29
310 **\
'-311
-213
-514
1
1,2,4,
5,6,9
1,2,3,
14,5,6,9
l
0
7,10
\
7,10
8
0
*) В оригинале допущены опечатки, которые здесь исправлены. — Прим. перев.
248
Э. Балаш
мы получим стандартную форму задачи, где
c = (q, ..., ^10)==(10, 7, 1, 12, 2, 8, 3, 1, 5, 3),
Аг =
3
-12
-8
1
-7
2
1
-10
-5
1
7
1
5
-3
-1
-2
1
-5
3
1
2
-1
-4
-2
-5
1
-9
-2
9
-12
-7
6
2
-15
-3
-8
5
2
-7
-1
-5
-10
b =
-2
-1
-1
1
.-3
-7
-1
Применение алгоритма к этой задаче можно проследить по
табл. 3. Нумерация величин vf здесь также соответствует
порядку их вычеркивания.
Оптимальным решением (оно помечено звездочкой в табл. 3)
является u2 = и (9,3), для которого
г2 _ г2 — 1 г2 _ у.2 _ г2 _ у-2 _ г2 _ „2 _ г2 _ г2 _ Л
Ад Ад I, Aj А2 — А^ Ад Ag Л? — Ag A|Q — U,
1/2=13, ^ = 9, ^ = ^-0, 0|-3f #2 = 8, */72 = 7 и z2 = 6.
Для соответствующего оптимального решения исходной задачи
значения переменных таковы:
лj — Х^ == Xq == Л jq ==s 1» «*2 == «*д X^ == Л^ л^ *— Лд == U.
Значение целевой функции равно с'х' = 23.
Пример 3 (задача 4 табл. 1).
Следующая задача представляет собой крайний случай —
она не имеет ни одного допустимого решения:
4х{ + 2х2 + х3 + 5лг4 + 3*5 + 6л;б + х7 + 2xQ + Злг9 = min>
3^ + 5^2-2^- хА — лгб — 4лг8 + 2л:9^ — 1,
6*1 - 2х2 - 2лг4 + 2х5 - 4х6 + Зх7 ^ - 3,
5½ + Злг4 — Зл:5 + 6лгб — х7 — 2лг9=^2,
--5^-4^ + лг3 +5а:$ —2х7+ лга— Ar9Si-8.
Таблица 4
Последовательность
s
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
решений
's
0
4
4,9
4, 9, 8
4, 9, 8, 7
4, 9, 8, 7, 2
4, 9, 8, 7, 2, 3, 5,6
4, 9, 8, 2
4, 9, 3
4, 9, 3, 7 ,
4, 9, 3, 7, 6
4, 9, 3, 2
4, 7
4, 7, 6
4, 1
3
Последователь-
шагов
А
А
А
А
А
В
СО)
С(1)
А
А
С(\)
С (2)
А
С(\)
С(\)
А
S
16
17
18
19
20
21
22
23
24
25
23
27
28
29
30
31
Последовательность
решений
Js
3, 9
3, 9, 6
3, 9, 6, 7
3, 9, 6, 7, 2
3, 9, 6, 1
3, 7
3, 7, 2, 6
3, 1, 2
7
7, 2,6
8
8, 6
8, 6, 9
8, 6, 9, 1
6
6, 9
Последователь-
шагов
А
А
В
С(0)
С (2)
В
С(0)
С(0)
в
С(0)
А
А
А
cm
А
D(2)
Конец
Таблица б
Последовательность
решений
s
0
1
2
3
4
5*
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
}s
0
3
3, 4
3, 4, 8
3, 4, 8, 10
3, 4, 8, 10, 12
3, 4, 8, 10, 2
3, 4, 8, 10, 6
3, 4, 12
3, 4, 6
3, 4, 6, 10
3, 4, 6, 10, 11
3, 4, 2
t 3, 4, 2, 10
3, 4, 2, 10, 1
3, 4, 2, 5
3, 4, 1
3, 8
3, 7
12
12, 4
Последователь-
шагов
А
А
А
А
А
Е(0)
F(0)
F(D
С(0)
А
А
^(1)
Л
А
F(0)
^(0
^(0)
0(0)
С(1)
Л
А
Последовательность
решений
s
21
22
23
24
! 25
26
27
28
29
30
31
32
33
34
35
36
37
38 -
39
Js
12, 4, 8
12, 4, 8, 2, 11
12, 4, 8, 2, 11, 10
12, 4, 11
12, 8
12, 8, 9
12, 7
8
8, 4
8, 4, 7
8, 4,6
8, 4, 1, 2
8, 7
8, 2
8, 9
8, 9, 6
4
4, 6
7
Последователь-
шагов
В
А
f(0)
С(1)
А
С(\)
F(D
А
А
С(0)
Я(0)
С(1)
С(0)
С(0)
А
С (2)
А
С(1)
D(0)
Конец
250
Э. Балаш
Не останавливаясь подробно на решении этой задачи,
в табл. 4 мы приводим последовательность решений и
выполненные шаги на каждой итерации.
Обозначения в табл. 4 соответствуют следующим
последовательностям шагов:
Л=1Ь, 2Ь, ЗЬ, 8,
fi = lb, 2Ь, Зс, 4а,
С(&)= lb, 2b, За, 5b, 6а, ..., 5b, 6а, 5b, 6b, 8,
2k ""
£>(&)= lb, 2b, 3a, 5b, 6a, ..., 5b, 6a, 5a.
2k ""
Пример 4 (задача 9 табл. 1).
Следующая задача имеет единственное допустимое решение:
6*1+ *2 + 3*3 + 2*4+ 6*5 + 4*6 + 7*7 + 2*8+4*9+ *ю+ *n+5*i2=min,
— *i + 3*2— 12*з — *5 + 7*6— *7 +3*ю—5*п— *i2^—6,
3*1-7*2 + *4+ 6*5 ^1,
11*1 + *з —7*4 — *б + 2*7+ *8-5*9 +9*ц ^—4,
5*2+ 6*3 —12*5 + 7*б +3*8+ *9-8*ю +5*12^8,
-7*!- *2— 5*3 + 3*4+ *5-8*б -2*8+7*9+ Хм -7*12^-7,
— 2*1 —4*4 —3*7-б*8— Хд + *ц+ *12^—4.
В табл. 5 приведены последовательность решений и шагов,
выполненных на каждой итерации.
Символы Л, В, C(k) nD(k) имеют тот же смысл, что и в
табл. 4. Смысл остальных обозначений следующий:
£(&)=1а, 5Ь, 6а, ..., 5Ь, 6а, 5b, 6Ь, 8,
F(£)=lb, 2а, 5Ь, 6а, ..., 5Ь, 6а, 5b, 6Ь, 8,
2k "
G(£) = lb, 2b, Зс, 4b, 5b, 6a, ..., 5b, 6a, 5b, 6b, 8,
4 2k -"
#(&)=lb, 2b, 3a, 5b, 6a, ..., 5b, 6a, 5b, 6c, 7a,
Аддитивный алгоритм для решения задач линейного программирования 251
Оптимальное решение задачи отмечено в табл. 5 звездочкой
(в данном случае оно единственное допустимое решение):
f 1 (/ = 3, 4, 8, 10, 12),
*> 10 (/=1, 2, 5, 6, 7, 9, 11).
Благодарности. Автор многим обязан проф. В. В. Куперу, а
также Ф. Гловеру' и С. Зайонцу за комментарии и советы,
которые способствовали улучшению данной статьи. Автор такжз
выражает признательность за помощь Э. Маринеску, которая
провела, вычислительную работу для задачи об управлении
лесопосадками, обсуждавшейся в разд. 6.
Л ИТЕРАТУРА
i. Dantzig G. В., Discrete variable extremum problem, Operations Re-
search, 5 (1957), 266—277.
2. Markowitz H. M., Manne A. S., On the solution of discrete
programming problems, Econometrica, 25 (1957), 84—110.
3. Eisemann K., The trim problem, Management ScL, 3 (1957), 279—284.
4. D a n t z i g G. В., On the significance of solving linear programming
problems with some integer variables, Econometrica, 28 (1§60), 30—44.
5. Charnes A., Cooper W. W., Management models and industrial
applications of linear programming, Wiley, New York, 1961.
6. В e n -1 s r a e 1 А., С h a r n e s A., On some problems of diophantine
programming, Cahiers du Centre d'Etudes de Recherche Operationnelle (Bru-
xelles), 4 (1962), 215—280.
7. Simonnard M., Programmation linealre, Dunod, Paris, 1962.
8. D a n t z i g G. В., Linear programming and extensions, Princeton
,University Press, 1963.
9. В a 1 a s E., Linear programming with zero-one variables (на румынском
языке), Proceedings of the Third Scientific Session on Statistics,
Bucharest, December 5—7, 1963*.
10. В a 1 a s E., Mathematical programming in forest management (на
румынском языке), Proceedings of the Third Scientific Session on Statistics,
Bucharest, Dezember 5—7, 1963.
11. Mi hoc Gh., В alas E., The problem of optimal timetables, Revue de
Mathemetiques Pures et Appliquees, 10 (1965).
12. Go mo г у R. E., Outline of an algorithm for integer solutions to linear
programs, Bull. Am. Math. Soc, 64 № 3 (1958).
13. G ото г у R. E., An all-integer programming algorithm, in J. R. Muth,
G. L. Thompson (eds.), Industrial Scheduling, Chap. 13, Prentice-Hall, 1963.
14. Gomory R E., An algorithm for integer solutions to linear programs,
in R. L Graves., Ph. Wolfe (eds), Recent Advances in Mathematical
Programming, pp. 269—302, McGraw-Hill, New York, 1963.
15. Dantzig G. В., Note on solving linear programs in integer, Naval. Res.
Log. Quart., 6 (1959), 75—76.
16. Gomory R. E., Hoffman А. Т., On the convergence of an integer-
p/ogramming process, Naval Res. Log. Quart., 10 (1963), 121—124.
17. В e a 1 e E M. L., A method of solving linear programming problems
when some but not all of the variables must take integer values,
Statistical Techniques Research Group, Technical Report № 19, Princeton
University, 195&,
252
Э. Балаш
18. L a n d А. Н., D о i g A. G., An automatic method of solving discrete
programming problems, Econometrica, 28 (1960), 497—520.
19. В e a d e r s J.% F., С a t с h p о 1 e A. R., К u i к e n L. C, Discrete-variable
optimization problems, Paper presented to the Rand Symposium on
Mathematical Programming, Santa Monica, 1959.
20. H а г r i s P.M. J., The solution of mixed integer linear programs, OpnL
Res. Quart, 15 (1964), 117—133.
21. Thompson G. L., The stopped simplex method, Part I, Revue Francaise
de Recherche Operationnelle, 8 (1964), 159—182.
22. Thompson G. L., The stopped simplex method, Part II, Revue
Francaise de Recherche Operationnelle, 9 (1965).
23. I v a n e s с u P. L., Programmation polynomial en nombers entiers, Comp-
tes Rendus de VAcademic des Sciences (Paris), 257 (1963), 424—427.
24. Glover F., A bound escalation method for the solution of integer
programs, Cahiers du Centre d'Etudes de Recherche Operationnelle (Bruxel-
les), 6 (1964).
25. E lma ghraby S. E., An algorithm for the solutkfn of the «Zero-One»
problem of integer linear programming, Department of Industrial
Administration, Yale University, May, 1963.
26. S z w a г с W., The mixed integer linear programming problem when the
variables are zero or one, Carnegie Institute of Technology, Graduate
School of Industrial Administration, May, 1963.
27. Lambert F., Programmes lineaires mixtes, Cahiers du Centre dy Etudes
de Recherche Operationnelle (Bruxelles), 2 (1960), 47—126.
28. Vajda S., Mathematical programming, Addison-Wesley, 1961,
29. Forte t R., Applications de Talgebre de Boole en recherche
operationnelle, Revue Francaise de Recherche Operationnelle, 4 (1960), 17—25.
30. Camion P., Une methode de resolution par l'algebre de Boole des prob-
lemes combinatoires ou interviennent des entiers, Cahiers du Centre dyEtudes
de Recherche Operationnelle (Bruxelles), 2 (1960), 234—289.
31. В a las E., Un algorithme additif pour la resolution des programmes
lineaires en variables bivalentes, Comptes Rendus de VAcademic des
Sciences (Paris), 258 (1964), 3817—3820.-
32. В a 1 a s E., Extension de Talgorithme additif a la programmation en norn-
bres entiers et a la programmation nonlineaire, Comptes Rendus (Paris),
258 (1964), 5136-5139.
33. R a d б F., Linear programming with logical conditions (на румынском
языке), Comunicarile Academiei RPR, 13 (1963), 1039—1041.
34. Little J. D. C, Murty K. G., Sweeney D. W., Karel C, An
algorithm for the traveling* salesman problem, Operations Res., 11 (1963),
972—989.
35. Berth ier P., Nghien Ph. Т., Resolution de problemes en variables
bivalentes (Algorithme de Balas et procedure S. E. P.). Note de travai]
№ 33, Sosiete d'Economie et de Mathematique Appliquees, Paris, 1965.
36*. Glover F., A multiphase-dual algorithm for the zero-one integer
programming problem, Operation Research, 13 (1965), 879—913.
37*. Geoff roin A., A reformulation of Balas' algorithm for integer linear
programming, The Rand Corporation, RM-4783-PR, September 1965.
38*. Balas E., An additive algorithm for solving linear programs with zero-
one variables, Research Memorandum, Mathematical Programming Group,
Centre of Mathematical Statistics, Bucharest Revised Release, February
1965.
Приложение*)
1. ПРИМЕЧАНИЯ
1) (к стр. 223). Нам кажется полезным следующее описание
алгоритма. Рассмотрим множество £<п> вершин л-мерного
единичного куба, т. е. множество точек х = (хи ..., хп), таких, что
#*е{0,1}, /е N = {1,... ,м}. Отождествим с £<п> граф,
вершинами которого являются элементы £(п>, а ребра соединяют все
пары вершин, находящиеся друг от друга на расстоянии,
равном единице. В качестве примера см. граф Е^ ira рис. 1. Будем
говорить, что вершина х1 = («*}, ..., х1п)
лежит «выше» вершины x2 = (jc^, ..., л;2),если
для всех / е N имеем х\ :> х\
(соответственно вершина х2 лежит «ниже» вершины х1).
Решениями Балаш называет вершины
графа №>, допустимыми решениями —
вершины, удовлетворяющие системе неравенств.
Если мы находимся в какой-то вершине
графа №>, т. е. рассматриваем некоторое
решение, то основным множеством для
алгоритма Палаша является множество
ребер, идущих из одной вершины вверх.
Например, для точки (\00) е£<3> такими ребрами будут ((100),
(ПО)), ((100), (101)). Эти ребра по определенным
правилам могут стать запрещенными для движения, а из незапре-
щенных ребер снова по определенным правилам выбирается, то
по которому наДо перейти к следующему решению. Если же
запрещены все ребра, идущие вверх, то мы возвращаемся к
решению, лежащему ниже, точнее к тому, из которого мы пришли
в данное. Алгоритм естественно заканчивает работу, когда мы
находимся в вершине (0, ..., 0), и все ребра, идущие вверх,
запрещены. Последующие замечания будут опираться на данное
описание алгоритма.
2) (к стр. 225). Критерием выбора ребра для движения
вверх является maxaj. Более удобным (для сокращения числа
(000)
Рис. 1.
*) Написано редактором перевода В. К. Коробковым. — Прим. перев.
264
Э. Балаш
шагов) критерием для выбора ребра был бы следующий:
выбирать такое ребро, что при движении по нему мы ближе всего
подходим к допустимой области. Определение v) в некотором
приближении дает этот эффект.
3) (к стр. 226). Отметим прежде всего, что после движения?
по ребру мы обязательно его запрещаем (см. описание
алгоритма в разд. 3); поэтому соотношение (13) дает следующее:
множество EW(xiv ..., xik) можно представить в виде Е' U Е" (см.
рис. 2), где
£'= {*!*€=£„, х^ = 0}, E" = {x\xc=Ekt xik=l}.
Если мы от (0,...,0,0) перейдем к (0,...,0,1), то в силу (13)
для любой вершины из Е' будет запрещен переход в вершину
(О
(0"А0) (0,...ду
Рис. 2.
из Е". Поэтому, находясь в вершине Xs и выбрав для движения
вверх некоторое ребро, ведущее в xs+l, мы разбиваем все
вершины, лежащие выше Xs, на два непересекающихся множества
и одно множество исследуем, исходя из Xs, а другое — исходя из
х&+1. Из (13) следует, что алгоритм не попадает дважды в
одну и ту же вершину, а так как число вершин конечно, то
отсюда и следует конечность работы алгоритма.
Смысл Ds очевиден: так как все сг ^ 0, то функционал не
убывает при движении вверх, поэтому можно запретить все
ребра, идущие вверх, концы которых принадлежат
полупространству сх > z*(s\ так как все решения в этом
полупространстве имеют худшие значения функционала. Отметим, что (13)
после получения Ds позволяет сократить вычислений для
решений, лежащих выше Xs.
4) (к стр. 229). Рассмотрим случай, когда только для
одного to имеет место равенство 2 ягу = ysh. Так как у*о < 0, то
из приведенного равенства следует, что yph^0, где J8czJp,
Аддитивный алгоритм для решения задач линейного программирования 255
только при условии Js U Fs a Jv. Поэтому в качестве решения
us+1 рассматриваем то, которому соответствует /s+i =/e U/v
5) (к стр. 237). Замечания об эффективности алгоритма
изложены в п. 2 приложения.
2. КОНТРПРИМЕРЫДЛЯ ОЦЕНОК ЭФФЕКТИВНОСТИ АЛГОРИТМА
БАЛАША
В работах [1—3] содержится описание алгоритма Балаша и
ряд предложений для увеличения эффективности этого
алгоритма. В этих работах имеются также некоторые результаты
о численных экспериментах с алгоритмом. Целью настоящей
заметки является указание области применимости данного
алгоритма. Ниже мы будем пользоваться обозначениями,
введенными в [1], а также в п. 1 приложения.
Основой для дальнейших рассуждений является следующая
теорема.
Теорема 1. Для любого k е N = {1,..., п} существует
задача, для которой число итераций (число решений) по методу
k-i
Балаша не менее 2 Сп-
/=о
Доказательство. Пусть k <=JV. Рассмотрим задачу
Imin (xi+ ... + хп)9
хг+ ... +*„>&,
*,е={0, 1}, iezN,
или в приведенной форме
min(*,+ ... +хп),
-хх- ... -хп + у= - ky
(О,
*, = < j /€=#.
Пусть получено s решений х1 ,..., Xs. Рассмотрим решение
п
x* = (*f, ..., хр), такое, что 2*?<&-2. Тогда Dsp = 0, так
как z*{s)^k> a zp + Cf^.k — 1. Рассматривая решение Xs, ВИ-
дим, что если 2 *f <& -2, то аналогично Ds = 0, Es = 0.
Отметим также, что (22) из [1] выполняется для любого решения
как строгое неравенство,
256
Э. Балаш
Оценим теперь число итераций. Рассмотрим первый шаг
алгоритма и0 = (0,..., 0, — k). Так как v°. = 1 — k, с(=-1 для всех
/ и /, то мы можем выбирать любое ребро, например последнее;
тогда получим и1 = (0,..., 0, 1, — k + 1), причем Nl = N \ {я},
Nl0 = N\ {п}. Из вышесказанного следует, что, начиная с
решения и1, мы будем решать задачу
тш(л:1+ ... +*„-i),
- х{- ... -*n-i + */=-£+l,
а вернувшись в u°, мы будем решать задачу
| min(A;i+ ... +*n_i),
1 -*!-...- xn_i + у = - k.
k-2 # k-\ k~\
Так как 2 Cn-i + 2 Cn-i = 2 Cn, то индукцией по n легко
i=0 i~0 *=0
получить утверждение теоремы.
Непосредственно проверяется, что для п = 2 число итераций
(2, &=1,
L»<*>-{!f 1-2 L3^)= 5, *-2,
Можно построить примеры, которые не будут отличаться
простотой примеров теоремы 1, но которые требуют такого же
числа итераций, что и примеры теоремы 1.
В самом деле, рассмотрим задачу
min {сххх + ... + спхп),
п
^cLifXf^bi (/=1, ..., m),
/=i
*,е{0,1} (i<=N),
{ с,>(), ац >0, b(>0 для всех / и j
(M)
и условия на элементы матрицы
(1) CLu^hi для всех / и /,
max Ci
(2)
min ci
<
k-l
[ —j- < atj < '. для всех / и /'.
(2a>
(26)
Аддитивный алгоритм для решения задач линейного программирования 257
Назовем задачу (М) с условием (1) задачей Ми а (М) с
условиями (2) — задачей Mk(k = 2,..., я). Справедлива теорема.
Теорема 2. Для любого k^N алгоритм Балаша при ре-
k-\
шении задачи Mh делает не менее 2 Cfn итераций.
/«о
Доказательство. Используя рассуждения теоремы 1,
достаточно заметить, что из условий (2а) следует, что Dsp = 0
п
(р = О, 1,..., s) для всех решений х*\ таких, что 2 *? ^ k — 2,
а из условий (26) следует, что множества допустимых решений
задач Ak и Mk совпадают.
Замечание 1. Несмотря на простоту указанных примеров,
следует отметить, что если с,-, Ь\, ац выбираются, например, из
множества Q = {1,2,..., rfi/г}, т. е. из множества задач,
имеющего мощность (di^)wm4m+n, то мощность множества задач Mk
имеет порядок (d2n)nm (здесь db d2 — константы). Для этого
заметим, что теорема 2 остается верной и в том случае, когда
условие (26) выполняется для одного неравенства, а для
остальных неравенств выполняются условия
bi<al}- (2в)
Замечание 2. В работе [4] задача М сводилась к задаче
расшифровки монотонной функции алгебры логики. Там же
указывалось, что задача М естественным образом разбивает
множество £(n) на два непересекающихся множества: Е°— множество
недопустимых решений и Е1 — множество допустимых решений
задачи М. Если алгоритм Балаша не «углубляется» в
множество Ех ( в силу, например, определения множеств Ds), то, как
показывают теоремы 1 и 2, он может перебрать все решения,
принадлежащие Е°. Желание не «углубляться» в множество Е°
привело к созданию алгоритмов расшифровки монотонных
функций алгебры логики. Оценки для этих алгоритмов высоки из-за
большого числа монотонных функций. Если рассматривать
подклассы монотонных функций, то можно существенным образом
понизить и оценку числа шагов алгоритмов расшифровки. £)дна^
ко и в узких подклассах монотонных функций оценки числа
шагов алгоритмов расшифровки могут быть неприемлемыми,
например, для решения на ЭВМ. Это следует из того, что
алгоритмы расшифровки по существу находят всю границу между
множествами Е° и ЕК
258
Э. Балаш
Поэтому при создании прямых методов решения
целочисленных задач с переменными, принимающими значения 0 и 1,
нужно четко выделять несколько моментов.
1. Будет ли предлагаемый алгоритм для задач типа М искать
всю границу между Е° и Е1? Если да, то неизбежны случаи,
когда для сравнительно небольших п алгоритм практически не
сможет получить оптимального решения (даже на самых
быстродействующих ЭВМ).
2. В силу доказанного выше «углубление» в множества Е°
и Е1 только может ухудшить положение.
3. Любой предлагаемый алгоритм должен поэтому
позволять оценивать «долю» границы между Е° и Е\ которая будет
просматриваться в ходе работы алгоритма.
4. Алгоритм Балаша, видимо, будет неплохо работать, когда
разброс Ci велик, а число переменных, разных единице в
допустимых решениях, мало по сравнению с п.
5. Алгоритмы расшифровки монотонных функций алгебры
логики легко распространяются на многозначную логику,
поэтому все вышеизложенные замечания остаются верными,
если, например, переменные могут принимать значения из
Р = {0,1, ..., Р).
Л ИТЕРАТУРА
1. В alas Е, An additive algorithm for solving linear programs with zero-
one variables, Operations Res., 13, № 4 (1965), 517—546. См. стр. 217
настоящего сборника.
2. G 1 о v е г F., Z i о n t s S., A note on the additive algorithm of Balas, Ope-
ration Res., 13, № 4 (1965), 546—549. См. следующую статью настоящего
сборника.
3. Р е t е г s е п С. С, Computational experience with variants of the Balas
algorithm applied to the selection of R&D projects, Management Sci., 13,
№ 9 (1967), 736—750.
4. Коробков В К, О некоторых целочисленных задачах линейного
программирования, Сб. «Проблемы кибернетики», вып. 14 (1965), стр. 297—
299.
Замечание об аддитивном алгоритме
Балаша1)
Ф. Гловер, С. Зайонц2)
В предшествующей статье Балаша изложен интересный
комбинаторный метод для решения задач линейного
программирования с переменными, принимающими значения 0 или 1. Этот
метод по существу является алгоритмом исследования дерева,
который использует информацию, получаемую в ходе
исследований, для исключения части дерева из рассмотрения. Целью
данной заметки является: (1) предложить дополнительные
правила3), предназначенные для увеличения эффективности
алгоритма Балаша путем сокращения числа возможных решений,
просматриваемых в ходе вычислений, и (2) указать приложение,
в котором применение этого алгоритма особенно полезно. В
последующем изложении предполагается знакомство с алгоритмом
Балаша.
Сначала рассмотрим пути сокращения числа решений,
рассматриваемых методом Балаша. Заметим, что в своем методе
Балаш определяет множество Ds (здесь используются его
обозначения и сохраняется нумерация уравнений), состоящее из
/e(W —Cs), таких, что если a.j вводится в базис, то значение
целевой функции будет не меньше лучшего значения (z*(s>),
полученного ранее. Отсюда непосредственно следует, что
переменные, связанные с элементами множества Ds, могут не
рассматриваться при попытке улучшить решение вдоль текущей ветви
дерева решений. Однако множество Ds может быть расширено
благодаря использованию почти непосредственного критерия для
включения, который определяется следующим образом. Сначала
рассматривается каждое / из Ms (в любой желаемой
последовательности) и выясняется, дает ли /s U {/} допустимое решение.
^Glover F., Z i о n t s S., A note on the additive algorithm of Balas,
Operation Research, 13, № 4 (1965), 546—549.
2) Авторы реферировали статью Балаша [1] для Operation Research.
Вместе с отзывом они представили данную статью, обобщающую некоторые
результаты Балаша.
3) Дополнительные правила, предлагаемые в данной заметке, уменьшают
число решний за счет увеличения объема вычислений на каждой итерации.
Хотя мы предполагаем целесообразность введения этих правил, в
действительности это должно решаться на основе вычислительного эксперимента.
260
Ф. Гловер, С. Зайонц
(Это необходимо сделать когда-нибудь для некоторых / в
любом случае.) Если устанавливается допустимость для
некоторого /s U {/}, то получается новое улучшающее решение, которое
может быть найдено обычным способом при помощи алгоритма
Балаша. Но более вероятен случай, когда /s U {/} не
удовлетворяет одному из ограничений, скажем ограничению ' (#*/>#!)•
Тогда рассмотрим коэффициенты целевой функции
ch = min [ср | р е= (Ns - {/}) и aip< 0].
Учитывая определение N8, данное Балашем, легко увидеть, что
Ds может быть расширено за счет включения тех /, для которых
сумма Ch + Cj при прибавлении к текущему значению целевой
функции zs будет не меньше, чем z*(s>1).
Аналогично этому мы можем соответствующим образом
расширить множество Dk, чтобы сократить число переменных,
которые должны просматриваться в алгоритме после возвращения
к решению uk.
Другим средством, которое может быть применено для
увеличения эффективности алгоритма, является включение
дополнительных ограничений в шагах 3 и 6 алгоритма. Чтобы понять
значение предлагаемых соотношений, необходимо рассмотреть
соотношения (22) и (27), которые Балаш включает в эти
шаги [1]. Для любого неудовлетворенного ограничения (ys( или
у\ < 0) аддитивный алгоритм предлагает посредством (22) и
(27) определять, может ли быть удовлетворено ограничение
путем присвоения всем допустимым переменным с
отрицательными коэффициентами значения 1. Если нет, то, так как
ограничения представляют отношения-< (меньше или равно),
совершенно очевидно, что не имеется улучшающего решения,
которое было бы допустимым по данной ветви дерева, и
алгоритм соответственно возвращается назад.
Однако заметим, что для правил, заключенных в (22) и (27),
вполне возможно продвижение по ветви дерева только за счет
достаточно большого увеличения значения целевой функции.
Ограничиваясь шагом 3, мы определяем достаточное (но не
необходимое) условие для обнаружения подобной ситуации. Если
1) Если Ch не определено, то это эквивалентно тому, что не
удовлетворяется соотношение (22) (из [1]) в шаге 3 аддитивного алгоритма. Шаг 3
алгоритма мы обсудим ниже. Более широкий критерий для включения в DB
может быть обоснован при рассмотрении, является ли /8 U {/} U {Л}
допустимым решением; однако при этом необходимо учитывать увеличение объема
вычислений на каждой интерации. С целью сокращения объема вычислений
с* заменяется на 1 (при условии, что ср — положительные целые числа),
Замечание об аддитивном алгоритме Балаша
261
существует /, такое, что
у\ < О и у\ (cfla~) > z* <*> - zs для всех / е= Ns (а~ < 0),
то не найдется допустимого решения по текущей ветви дерева,
которое будет лучше уже полученного.
Чтобы доказать это, мы предположим, что улучшающее
решение существует. Тогда для любого такого решения мы имеем
2#7}^*/ргДе сумма берется по таким отрицательным а^, что
/ е Nsy и aj содержится в базисе для удовлетворенного решения.
Тогда если 2Cj ограничивается теми же самыми /, то значение
целевой функции zs плюс Scj даст более низкую оценку
значения целевой функции улучшающего решения. Но благодаря
вышесказанному мы имеем
zs + 2 с, = zs + S aTj (С//аГ/) > zs + 2 ац (z*<*> - z,)/# > z*<*>,
и утверждение доказывается от противного.
Подобные же выводы могут быть сделаны относительно
условий, встречающихся в шаге 6. Формулировка расширенного
правила для этого шага может быть дополнена следующим
образом: «Для /, таких, что у] < 0, проверяем соотношение
yki(cilau)>zHs)-zk (27а)
для всех /^Af| и для k = k\. Если (27а) справедливо для
любых- /, то, когда (27) не являются справедливым для
некоторых /, проводим указанную процедуру»1).
Теперь вернемся к вопросу образования и исследования
дерева решений.
Во-первых, отметим, что для многих задач допустимое
решение известно заранее. Это решение может быть использовано
для того, чтобы установить начальное значение 3*(s> (отличное
от бесконечности) и тем самым ускорить сходимость к
оптимуму. Такое решение может быть также использовано и для
других целей. Если предположить, что значения большей части
переменных в допустимом решении и в некотором оптимальном
решении совпадают, то это может быть использовано для того,
чтобы применить двухстадииныи алгоритм, который по-разному
обрабатывает (главное) множество переменных, равных 1 в
допустимом решении, и (второстепенное) множество переменных,
равных 0. В частности, было бы желательным для такого алго-
1) Общие» правила, которые становятся более сильными в некоторых
комбинаторных методах, см. в [5]. О применении правила исключения
несвязанных ограничений и посторонних переменных в математическом
программировании вообще см. [6].
262
Ф. Гловер, С. Зайонц
ритма предусмотреть быстрое изменение различных
определений 0 или 1 главных переменных на первой стадии и затем
применять аддитивный алгоритм к переменным на второй стадии.
Хотя описание такой процедуры в деталях и выходит за
пределы данной заметки, отметим, что возможно использовать
упрощенную расчетную схему на первой стадии (использующей
единичный вектор, компоненты которого принимают только три
значения), так, что при незначительной модификации правил,
описанных выше, могут быть применены ограничения 0—1,
необходимые для алгоритма Балаша (см. [5]).
Интересным приложением для алгоритма Балаша является
его возможное соединение с методом Гилмори — Гомори для
решения задачи об оптимальных запасах [3,4]. Хотя эта задача
и может быть дана в терминах целочисленного
программирования, но число переменных даже' для задач умеренных
размеров так велико, что практически обычный метод
целочисленного программирования является бесполезным. Не подходят
даже обычные методы линейного программирования. Метод
Гилмори—Гцмори обходит эту трудность, ограничиваясь
рассмотрением очень малого подмножества переменных для
получения начального решения методом линейного программирования.
Если полученное решение допустимо, то используется решение
задачи о рюкзаке для основных переменных данной задачи 1).
Затем процесс решения чередуется с введением новых
переменных и решением задачи линейного программирования, чтобы
увидеть, какая из вновь образованных переменных должна быть
включена в решение. Когда улучшающие переменные не могут
быть найдены, алгоритм прекращает работу.
В данном приложении полезно использовать три следующие
особенности алгоритма Балаша. Во-первых, метод Гилмори —
Гомори не обеспечивает целочисленность решения — алгоритм
Балаша дает его. Во-вторых, кроме первого решения
целочисленной подзадачи имеется начальное значение z*(s), полученное
из решения предыдущей задачи. Такие решения могут быть
использованы, как предлагалось выше. В-третьих, на любой
стадии метода Гилмори — Гомори необходимо рассматривать
только те решения, которые включают по крайней мере одну из
вновь образованных переменных, — ситуация, с которой метод
Балаша справляется довольно хорошо.
Известно, что значительная часть задач о распределении
запасов может быть представлена в виде, использующем переменные,
1) В первой формулировке своего метода Гилмори и Гомори решают
задачу о рюкзаке методом динамического программирования, во второй они
предлагают специальный алгоритм для задачи о рюкзаке и доказывают его
превосходство над методом динамического программирования.
Замечание об аддитивном алгоритме Балаша
263
принимающие значения 0 или 1, а переменные,
принимающие большие значения, представляются в виде суммы
переменных с двумя возможными значениями. Применение аддитивного
алгоритма Балаша к задачам линейного программирования [2]
показало улучшение эффективности такого представления, что
делает метод еще более привлекательным.
Л ИТЕРАТУРА
1. В а 1 a s Е., An additive algorithm for solving linear programs with zero-
one variables, Operations Res., 13, 517—546 (1965). См. стр. 217 настоящего
сборника.
2. В а 1 a s Е., Extension de l'algorithme additif a la programmation en nomb-
res entiers et a la programmation nonlineaire, Comptes Rendus (Paris), 258
(1964), 5136—5139.
3. Gilmore P. C, Gomory R. E., A linear programming approach to
ihe cutting-stock problem, Operations Res., 9 (1961), 849—859
4 Gilmore P. C, Gomory R. E., A linear programming approach to the
cutting-stock problem, part II, Operations Res., 11 (1963), 863—888.
5. G1 о v e г P., A multiphase-dual algorithm for the zero-one integer
programming problem, Operations Research, 13 (1965), 879—913.
6. Z i о n t s S., Thompson G. L., T о n g e F. M., Techniques for
removing nonbinding constraints and extraneous variables from linear
programming problems, Carnegie Institute of Technology, Graduate School of
Industrial Administration, Pittsburgh, Pennsylvania, November, 1964.
СОДЕРЖАНИЕ
Математические вопросы
Ж.-М. Гёталс, Ф. Дейзарт. Один класс циклических кодов с
мажоритарным декодированием. Перевод И. И. Грушко . .... 7
Д. Колабро, Дж. Паольело. Синтез циклически ортогональных
двоичных последовательностей одного и того же наименьшего периода.
Перевод И. И. Грушко 24
Н. Г. д е Б р ё й н. Одна комбинаторная задача. Перевод А. А. Евдокимова 33
С. Виноград. О времени, требующемся для выполнения сложения.
Перевод В. М. Храпченко 41
С. В и н о г р,а д. О времени, требующемся для выполнения умножения.
Перевод В. М. Храпченко . ., 55
С. Яджима, Т. Ибараки. Нижняя оценка числа пороговых функций.
Перевод Н. А. Карповой 72
М. Блох, Я. М о р а в е к. Оценка числа пороговых функций. Перевод
Н. А. Карповой 82
Дж. Хартманис, Р. Стирнз. Алгебра пар и ее применение к теории
автоматов, Перевод А. А. Мучника 89
Д ж. В. Тэтчер, Дж. Б. Райт. Обобщенная теория конечных автоматов
и ее приложения к проблемам разрешения в логике второго порядка.
Перевод Е. Ю. Захаровой 112
А. В. А х о у, Д ж. Д. У л м а н. Теория языков. Перевод Ю. И. Янова . . 145
С. Гинзбург, X. Райе. Два класса языков типа АЛГОЛ. Перевод
Л. С. Модиной 184
Математическая экономика
Э. Б а л а ш. Аддитивный алгоритм для решения задач линейного
программирования с переменными, принимающими значения 0 или 1. Перевод
Ю. И. Волкова, С В. Жака и Н. К. Марцинкевич 217
Ф. Гловер, С. 3 а й о н ц. Замечание об аддитивном алгоритме Балаша.
Перевод 3. В. Коробковой 259
КИБЕРНЕТИЧЕСКИЙ СБОРНИК
Новая серия
Выпуск 6
Редакторы Г. М. Ильичева и А. С. Попов Художник Я. К> Сапожников
Художественный редактор В. И Шаповалов
Технический редактор Я. Д. Толстякова Корректор Я. А. Матюхина
Сдано в производство 14/V-G9 г. Подписано к печати 16/Х-69 г.
Бумага тип № 3 60х901/16=8,25 бум. л. Усл. печ. л. 16,50 Уч.-изд. л. 14,22.Изд. № 1/5312.
Цена 1 руб. 26 коп. Зак. 179
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2
Ленинградская типография №2 имени Евгении Соколовой Главполиграфпрома
Комитета по печати при Совете Министров СССР. Измайловский проспект, 29.