Текст
Кибернетический
сборник
НОВАЯ СЕРИЯ
ВЫПУСК
Сборник переводов
Под редакцией
А. А. ЛЯПУНОВА и О. Б. ЛУПАНОВА
ИЗДАТЕЛЬСТВО «МИР»
Москва 1968
УДК 519.95
Научный совет по кибернетике
Академии наук СССР
Пятый выпуск новой серии кибернетических сборников
состоит из двух разделов: математические, вопросы w некоторые
технические реализации. В первом разделе представлены работы
по теории кодирования, теории автоматов и статьи * (С.
Гинзбурга и др.) по математической лингвистике, также тесно
связанные с теорией автоматов. Во втором разделе помещена
оригинальная статья Ван Хао, посвященная некоторым проблемам
неразрешимости.
Сборник рассчитан на научных работников, инженеров,
аспирантов и студентов различных специальностей, интересующихся
кибернетикой в ее математическом аспекте.
Редакция литературы по математическим наукам
Инд. 2-2-3
математические вопросы
Анализ рекуррентных кодов1}
Э. Вайнер и Р. Эш
I. Введение
Двоичный корректирующий^ блоковый код может быть
определен как множество двоичных n-мерных векторов-столбцов Х\
называемых «кодовыми словами» и удовлетворяющих
множеству т проверочных уравнений
А'Х' = 0 (mod 2), (1)
где А— бинарная (тХп)-матрица. Предполагая, что
уравнения (1) независимы, можно произвольно выбрать k = n— т
символов X' (в качестве «информационных» символов); тогда
остальные т символов (называемые «проверочными») будут
определяться уравнениями (1).
Если последовательность передаваемых информационных
символов очень велика, кодовое слово можно рассматривать
как полубесконечный вектор (последовательность) Ху
удовлетворяющий проверочным уравнениям
А 0 0 0
0 А 0 0
0 0 А 0
АХ-.
Х = 0,
(2)
где А' есть (тХп)-матрица из (1). Следовательно,
закодированное сообщение можно рассматривать как последовательность
блоков из п символов, в которой символы различных блоков
полностью независимы.
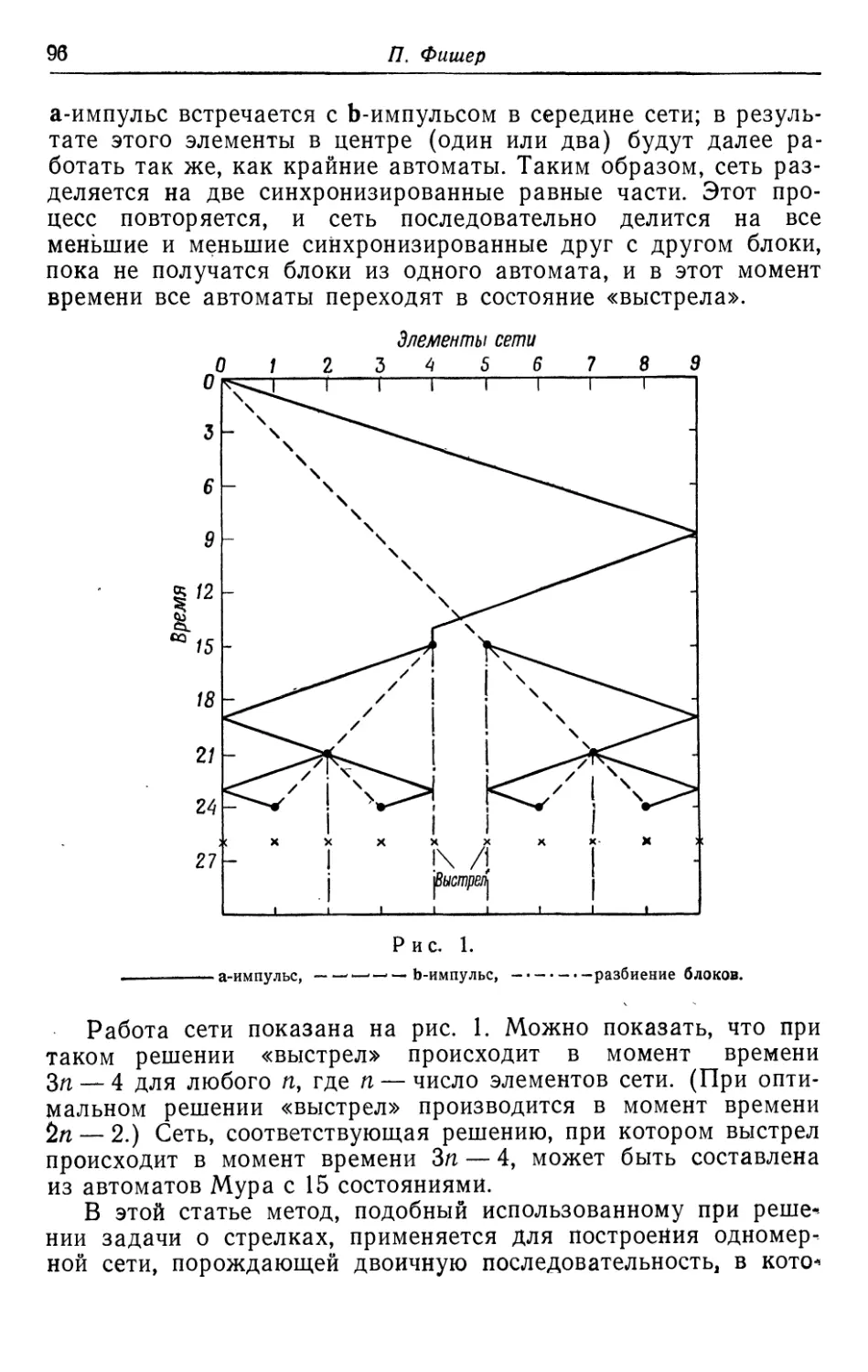
На рис. 1 приведена блок-схема системы связи, в которой
можно использовать такие коды. Передаваемая информация
кодируется по k символов одновременно в блоки из п символов.
l) Wyner A. D., Ash R. В., Analysis of recurrent codes, IEEE Trans,
on Inf. Theory, IT-9, № 3 (1963), 143—156. Перевод статьи публикуется без
приложений; в текст статьи внесены соответствующие изменения и
замечания. — Прим. ред.
б
Э. Вайнер, Р. Эш
Избыточность, включенная в передаваемое сообщение,
используется в декодирующем устройстве для того, чтобы исправить
ошибки, которые могли произойти из-за шума в канале.
Выходом декодирующего устройства является последовательность
исправленных информационных символов.
В 1955 г. Элайес [1] предложил один тип корректирующего
кода, названного им «сверточным» кодом, в котором кодовыми
словами являются полубесконечные двоичные векторы. Эти
коды отличаются от кодов (2) тем, что их матрицы не могут
быть разбиты на блоки. Сверточные коды были переоткрыты в
Информация
Кодирующее
устройство
Закодированное
сообщение
Канал
Полученное
сообщение
(У=Х+Е)
Декодирующее
устройство
Исправленная
информация
Шум (£)
Рис. 1. Система связи.
1959 г. Хегельбергером [3], который использовал их для
исправления пакетов ошибок и назвал их «рекуррентными» кодами.
Эти коды изучались также Возенкрафтом [9], Рейффеном [7] и
Зпстейном [2] в связи с независимыми ошибками и Килмером
[4, 5] в связи с пакетами ошибок и независимыми ошибками.
Особым достоинством рекуррентных кодов, в частности кодов
Хегельбергера, является то, что часто они имеют очень легкую
реализацию.
Основной трудностью в анализе рекуррентных кодов
является отсутствие рабочей математической модели, в терминах
которой можно было бы ответить на такие вопросы, как:
1) Каким необходимым и достаточным условиям
должна удовлетворять проверочная матрица для того, чтобы
исправлять ошибки данного типа?
2) Какие существуют соотношения между избыточ*
ностью рекуррентных кодов и их корректирующими воз«
можностями? (Например, таким соотношением для
блоковых кодов 1) является «граница Хэмминга».)
В разд. II настоящей работы мы предлагаем такую модель
и отвечаем на первый вопрос. В разд. III мы выводим границы
для рекуррентных кодов, исправляющих пакеты ошибок, и на-
*) См. [6], стр. ,68.
Анализ рекуррентных кодов
7
ходим максимальную корректирующую способность кода при
заданной избыточности. Кроме того, строится общий класс ре-»
куррентных кодов, исправляющих пакеты ошибок. В разд. IV
получены граниды для кодов, исправляющих независимые
ошибки.
II. Предварительные замечания
А. Определение рекуррентного кода
Определим рекуррентные или сверточные коды как
множество двоичных последовательностей, удовлетворяющих набору
проверочных уравнений, причем проверочная матрица имеет
следующий вид.
п
j
Рис. 2. Схематическое изображение полубесконечной проверочной матрицы
Л. Ненулевые элементы находятся в заштрихованных участках.
Пусть Во — полубесконечная матрица из Ь столбцов и
бесконечного числа строк. Предположим, что В0 содержит только
конечное число ненулевых элементов. Пусть В{ — матрица той же
рьазмерности, что и В0, образованная из В0 «сдвигом» строк на i
шагов вниз, т. е. пусть &-я строка В* будет нулевой для
6=1, 2, ..., i и (/+/)-я строка Bt будет /-й строкой В0 для
/ = I, Z, , .» •
8
Э. Вайнер, Р. Эш
Проверочной матрицей А кода является
А = [В0ВтВ2тВгт ... ],
где т — фиксированное положительное число. Матрица А схе-
матически приведена на рис. 2.
Кодовыми словами являются такие последовательности X
(полубесконечные векторы-столбцы), что
АХ = 0 (mod 2).
(3)
(В данной работе арифметические операции над векторами и
столбцами производятся по mod 2 и под словом «вектор» всегда
понимается «вектор-столбец».)
Пример 1:
в0=
1 о о
0 1 о
О 0 1
1 1 1
0 0 0
/ге = 2;
А = [В0В2В,В6...]:
в0 в2 в4
100 000 000
010 000 000
0 0 1 10 0 0 0 0
111 0 10 0 0 0
0 0 0 0 0 1 10 0
... 111 010
... 000 001
. . . ... 111
0 0 0
и т. д.
Анализ рекуррентных кодов
9
Пример 2:
#0 =
1 1
1 О
О О
/и = 1;
: [50fii52
В0 В,
110 0
10 11
0 0 10
..00
. . . '.
в2
0 0 1
0 0
1 1
ю и т- Д'
0 0
Пусть Xi будет i-й позицией кодового слова X. Можно считать,
что первые га строк А задают га уравнений относительно b
неизвестных Хи х2, ..., Хъ. Предполагая первые га строк А линейно
независимыми, b — га позициям X среди первых b позиций
можно придавать произвольные значения. Если уже выбраны
Хи Хъ . •., Хъ, удовлетворяющие первым га уравнениям, то
следующие га строк А определяют еще га уравнений от b
неизвестных Хь+и Хь+2, • •., Хчъ< Среди них опять b — га могут быть
выбраны произвольным образом. Эта процедура может быть
повторена для каждого блока из b позиций; b — га элементов в
каждом блоке могут быть выбраны произвольно, а остальные га
будут определяться проверочными соотношениями. Таким
образом, среди каждых b позиций га являются проверочными и
избыточность равна mjb.
Проиллюстрируем процедуру кодирования на примере 2.
Пусть информационная последовательность имеет вид: 1 1 0
1 0 0.... Первым проверочным уравнением является a:i+x2=0.
Предполагая, что xu х3, x5i ..., х2и+и -.. являются
информационными символами, имеем #1=1 и х2 =—#1=1. При так
выбранных Xi и хг вторым уравнением будет l+#3+X4=0. Так как
#з —второй информационный символ — равен 1, то л:4=1+л:з = 0.
Продолжая этот процесс, находим, что закодированное
сообщение имеет вид: 111001110100
10
Э. Вайнер, Р. Эш
В. Процедура декодирования
Декодирование полученного сообщения производится на
основе синдрома, который строится по обычным правилам
построения синдрома для корректирующих кодов. А именно
если Е — «вектор ошибки» ..(полубесконечный вектор с ненуле^
выми элементами на искаженных позициях) и Y=X+E — по^
лученное сообщение, то синдром S равен
5 = AY = А {Х + Е) = АХ + АЕ = АЕ. (4)
Таким образом, S является полубесконечным вектором-^
столбцом, представляющим собой сумму по модулю два тех
столбцов Л, которые соответствуют искаженным позициям.
Мы будем предполагать, что полученное сообщение
декодируется по Ъ символов одновременно. При этом для
декодирования блока из Ъ символов мы не можем ожидать, пока будет
вычислен весь синдром, так как это приводит к требованию бес*
конечной задержки во времени. Соответственно сделаем
следующее допущение: для декодирования первого блока из Ь
символов используются только первые N позиций синдрома, где
N — фиксированное положительное число. Второй блок
декодируется на основе первых N+m позиций S, третий блок — на
основе первых N+2m позиций и т. д.
Для ясности вернемся к примеру 2 разд. Н-А:
1 Г
Я0 =
1 0
0 0
т= 1.
Мы утверждаем, что этот код может исправлять любой, вектор
ошибки, такой, что искаженные позиции разделены по меньшей
мере тремя правильными позициями (т. е. что единицы в Е
разделены по меньшей мере тремя нулями).
Для проверки утверждения положим N=2. При этом мы
декодируем позиции 1 и 2 на основе первых двух символов
синдрома S. Эти символы образуют двумерные векторы,
представляющие собой линейные комбинации столбцов матрицы,
построенной из первых двух строк матрицы А:
Г1 1 00 00 00 ... 1
[l 0 1 1 0 0 0 0 ... J'
Если теперь первая или вторая позиция (но не обе
одновременно) искажены, то в первой позиции S будет стоять 1. Так
Анализ рекуррентных кодов
И
как (согласно сделанной выше оговорке) за ошибкой должны
следовать три правильные позиции, то, в частности, позиции 3
и 4 должны быть правильными. Таким образом, первые два эле-
П1 г
мента S образуют вектор , если искажена первая позиция,
и вектор , если искажена вторая позиция. После этого на
основе третьего и четвертого символов S мы можем
декодировать 5 и 6 позиции принятого вектора (3 и 4 позиции являются
правильными).
Если позиции 1 и 2 не искажены, то первый символ S
является нулевым и мы исследуем второй и третий символы S для
декодирования второго блока по описанному правилу.
С. Различные типы ошибок, исправляемых рекуррентными
кодами
1) Коды типа А (предназначенные для независимых оши*
бок).
Коды типа А исправляют любой вектор ошибки £, такой,
что никакое множество из п последовательных элементов Е не
содержит более чем е единиц. Код, приведенный в примере 2
разд. II-А, является кодом типа А с м=4, е=1. -
2) Коды типа В (предназначенные для пакетов ошибок).
а) Коды типа В\ — коды типа В\ исправляют любой вектор
ошибки £, такой, что ненулевые элементы любых «л» последов
вательных позиций ограничены пакетом из «/» последователь-*
ных позиций. (Предполагается, что / кратно длине блока Ь.)
Это эквивалентно требованию о том, что пакеты ограничены
безошибочными «защитными интервалами» из (п—1) позиций.
б) Коды типа В2 — коды типа В2, так же как и коды типа В1,
исправляют пакеты длины / с тем дополнительным требованием,
что пакет ограничен г=//6 последовательными блоками. (Опять
предполагается, что Ь делит /.) .
Например, если 6 = 4, /=8, то накладываемое ограничение
состоит в том, что пакет концентрируется в пределах //6 = 2чбло-
ков. Возможно, однако, расположение пакета длины 8 и в
пределах трех блоков. Например, ошибки в позициях 3, 4, 5, 6, 7,
8, 9, 10 образуют пакет длины 8, распространяющийся на
блоки 1, 2, 3.
Целесообразность рассмотрения кодов типа В2 состоит в
том, что они допускают упрощение анализа, приводящее к
возможности получения интересных результатов, которые частично
применимы и к кодам типа BL
12
Э. Вайнер, Р. Эш
ST
to
Т =
0 0 0
о о
10
0.
N<
Отметим, что при //&'2>1 корректирующие возможности
кодов типа В2 приближаются к корректирующим возможностям
кодов типа 51 с теми же / и Ъ. Например, если 6 = 3 и /=15,
коды типа В\ исправляют все пакеты длины не более 15, а коды
типа В2 исправляют все
пакеты длины не более 13 и неко«
торые пакеты длин 14 и 15.
Заметим, наконец, что ко-»
ды типа, 52 можно
рассматривать как коды, исправляющие
все пакеты в / последователь^
ных позициях, при условии, что
пакеты разделены
безошибочными защитными интервала-*
ми из g= (nib) — 1 блоков.
Изучать, как оказалось, более
удобно л, а не g.
D. Некоторые дальнейшие
определения
1) Мы предположили, что
первый блок декодируется
после анализа первых N
элементов синдрома S. Для данного
вектора ошибки первые N
элементов S определяются
первыми N строками А. Если, кроме
того, предположить, что га
делит Af„ то все ненулевые эле^
менты первых N строк А бу*
дут расположены в первых
(N/m) • Ь столбцах. Это
определяет матрицу AN, состоящую
из первых N строк и первых
(Nlm)'b столбцов матрицы А.
Матрица AN изображена
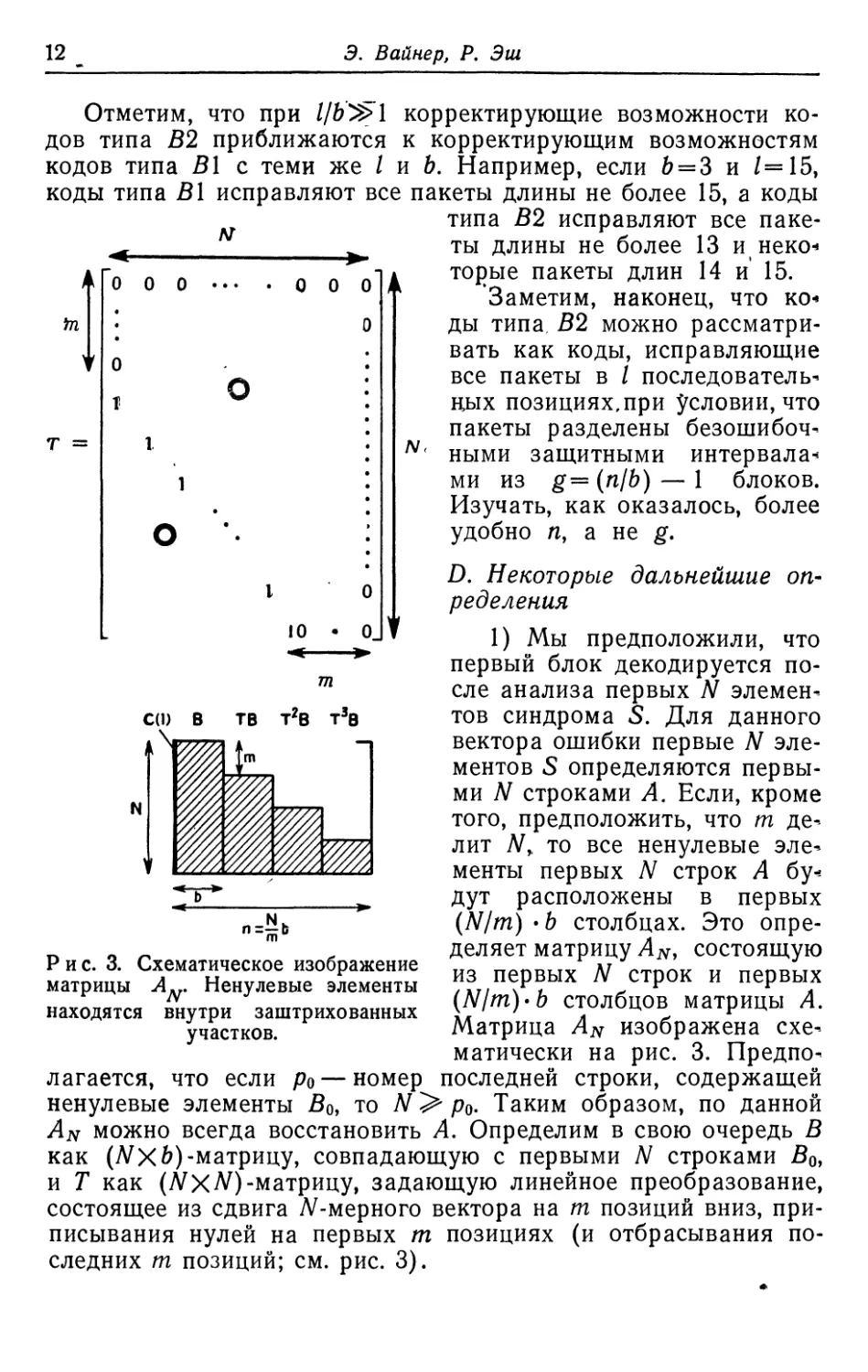
схематически на рис. 3.
Предполагается, что если ро — номер последней строки, содержащей
ненулевые элементы 50, то iV> р0. Таким образом, по данной
AN можно всегда восстановить Л. Определим в свою очередь В
как (А^Х6)-матрицу, совпадающую с первыми N строками 50,
и Т как (NXN)-матрицу, задающую линейное преобразование,
состоящее из сдвига Af-мерного вектора на m позиций вниз,
приписывания нулей на первых m позициях (и отбрасывания
последних m позиций; см. рис. 3).
«=£ь
Рис. 3. Схематическое изображение
матрицы AN. Ненулевые элементы
находятся внутри заштрихованных
участков.
Анализ рекуррентных кодов
13
Тогда AN=[B, ТВ, Т2В TW™)-lB].
Пример:
[\ о]' m=h
ГО 01
0 01
1 1
так что
Аы —
4V
110 0
10 11
2) Обозначим через С(1) i-й столбец AN. Предположим, что
первый элемент некоторого столбца в AN, скажем С(1),
равен 1.
3) Для вектора X определим 5-мерный вектор [X]s, компо^
нентами которого являются s первых позиций X. Например,
если Х-
^о[Х}2=[1].
'4) /Сг={1, 2,.. J) — множество, состоящее из чисел 1,2,..., L
5) Множество чисел / называется исправляемым типа Г
(для Г = Д, Bl, В2), если / соответствует исправляемой ошибке
типа Г (с уже определенными n, /, b и т. д.). Например, если
м = 5 и е = 2, то /={1, 5} — исправляемое множество типа Л,
а //=={1, 4, 5} — неисправляемое множество, так как мы можем
исправить ошибку в 1 и 5 позициях, но не в позициях 1, 4 и 5.
Наконец, сумма 2 С (;') столбцов матрицы AN, соответ*
ствующих /, называется исправляемой линейной комбинацией
типа Г, если множество / является исправляемым типа Г.
Е. Сводка терминологии и допущений
Прежде чем переходить к анализу рекуррентных кодов, под*
ведем для удобства итог принятой терминологии и предполо^
жений.
1) Проверочная матрица А имеет вид A = [B0BmB2m - • •], где
В0 — полубесконечная матрица из b столбцов и Bkm получается
14 Э. ВайЯер, Р. Эш
из Во сдвигом строк матрицы В0 на km позиций вниз. Первые т
строк А предполагаются линейно независимыми.
2) Первый блок из Ь позиций декодируется на основании
первых N позиций синдрома, где N — фиксированное
положительное число (выбранное таким образом, что т делит N).
Вообще, первые k блоков декодируются на основе первых
N + (k— \)т позиций синдрома (А~1, 2, Г..).
3) Матрица AN состоит из первых N строк и (N/m) • b
столбцов матрицы А. Иначе,
AN=[B, ТВ, Т2В, ..., т<"М-1в\,
где В состоит из первых W строк В0 и Т определяется так:
N
m
▼
Т =
t
пг
В теореме 1 будет показано, что свойства рекуррентного кода
данного типа могут быть установлены путем исследования
матрицы ANf где л= (Nlm) -6.
F. Необходимые и достаточные условия на AN для исправления
ошибок типов А и В
Начнем анализ рекуррентных кодов. Ответом на вопрос 1
разд. I является следующая теорема:
Теорема 1. Матрица AN с числом столбцов n=(NJm) *b
определяет код типа Г (Г=Л, fil, В2) тогда и только тогда, когда
выполняются следующие условия*
ооо
о
1
О О ^0
10
N.
Анализ рекуррентных кодов
15
Пусть Z, = 2 С (/) и Z2 =■ 2 С (У) — исправляемые линей-
ные комбинации столбцов AN типа Г. Тогда Zi=Z2 влечет за
собой равенство I Г\Кь = 1 П К& (где /(ь={1, 2, ..., 6} г/ П
означает пересечение множеств). Иными словами, исправляемые
векторы ошибок, не совпадающие в первом блоке, не
могут приводить к одному и тому же усеченному синдрому
[S]w.
Доказательств р. а) Необходимость. Пусть уже
построен код типа Г с n=(Nlm) *Ь. Предположим, что 1^=1г и
/ [\КъФ1 П/Сб- Пусть, например, 1ПКь не пусто. Тогда Zt
является усеченным синдромам [S]N, соответствующим
исправляемой, ошибке типа Г, содержащей ненулевые элементы в
позициях первого блока (т. е. в тех позициях, которые принадлежат
/П/Сь).
Так как Zi = Z2 и I Г\КъФ1 ПКъ, то Zt является также
усеченным синдромом, соответствующим исправляемой ошибке типа Г,
отличающейся от первой ошибки множеством ненулевых эле^
ментов в первом блоке.
Таким образом, по [S]N нельзя декодировать блок 1. Это
противоречит предположению 2 разд. П-Е. Следовательно, / П /Сь =
= /П/(б, если Zi=Z2.
b) Достаточность. Пусть AN удовлетворяет,
сформулированным условиям. Если произошла исправляемая ошибка типа Г,
включающая позиции блока 1, то, согласно предположению,
можно по [S]N определить ошибку в блоке 1 (так как, согласно
предположению, любой [%=IjC(/) соответствует однознач-
ному пересечению / П Къ).
Таким образом, анализируя [S]N, можно точно указать
искаженные позиции блока 1 и вычесть из S столбцы. Л,
соответствующие искаженным позициям в блоке 1 (устранив этим их
отрицательное воздействие на S). После этого можно
переходить к декодированию блока 2 по тем же правилам, по которым
декодировался блок 1 и т. д.
Замечания. 1) Z*=^C(i) является исправляемой
комбине/
нацией типа А тогда и только тогда, когда / состоит из е или
меньшего числа членов. Для кодов типа" Л условия теоремы 1
могут быть переформулированы так: любая линейная
комбинация не более чем 2е столбцов матрицы ANi включающая в
себя по крайней мере один столбец из первых Ьг отлична от
нуля.
16
Э. Вайнер, Р. Эш
2) Z= 2 C(t) является исправляемой комбинацией типа В\
тогда и только тогда, когда / соответствует пакету длины, не
превосходящей /. Аналогично для кодов типа 52.
G. Примеры
Следующие примеры проиллюстрируют применение
теоремы 1: ■
1) Коды типа Л:
а) В примере 2 разд. П-Л имеем
Г1 1] Г1 1 О о
в = [\ oj' л"-[1 О' 1 1
7V = 2, л == 4.
Очевидно, что AN удовлетворяет условиям теоремы 1 и, еле-*
довательно, описывает код типа А.
Ь) Предположим, что в только что рассмотренном примере
е = 2 вместо 1. Пусть Zi = C(l), Z2=C(2)+С(3). Тогда /={1},
/ = {2, 3}. Но Z{=Z2 и / П Кгф1 Л К2- Условия теоремы 1
нарушаются, и, следовательно, код не может исправлять двойные
ошибки.
В-
2, /л=1, е = 2 (N = 6),
с) Г1 1
О О
0 О
1 О
0 1
.1 о_
1 2 3 4 5 6 7 8 9 10 И 12
1 1000000000 0
001100000000
000011000000
1000 0 0110000
011000001100
_1 0011000001 1_
Можно проверить, что условия теоремы 1 удовлетворяются
и, следовательно, код исправляет любой вектор ошибки £, у
которого никакие 12 последовательных позиций не содержат более
двух единиц.
Ам —
лы
Анализ рекуррентных кодов
17
2) Коды типа В2:
В:
Г1
0
0
Li
°1
1
1 1
oj
AN —
В
~ 1 0
0 1
0 1
1 0
ТВ
0 0
1 0
0 1
0 1
гв
0 0
0 0
1 0
0 1
т*в
0 0
0 0
0 0
1 0
/ = 6 = 2,
llb = r=l,
'm=l, N=4,
л = 8.
Прежде всего убедимся, что AN удовлетворяет условиям
теоремы 1. Единственно допустимыми пакетами ошибок являются
такие, которые содержат не более двух ошибок в одном и том
же блоке. Таким образом, надо проверить, что любая линейная
комбинация столбцов блока 1 отлична от любой линейной
комбинации столбцов внутри других блоков.
Это сразу видно, если заметить, что любая линейная
комбинация в блоке 1 симметрична относительно пунктирной линии,
проведенной посредине матрицы AN, и что никакая линейная
комбинация столбцов другого блока не обладает этим
свойством.
Проиллюстрируем теперь процедуру декодирования для
этого примера. Матрица А имеет вид
1 2 3 4 5 6 7 8 9 10 И 12
10
0 110
010110
10010110.. . .
001-0010110. .
А = \ ..0010010110
....00100101
.... 0 0 1 0 0 1
.... 0 0 1 о
.... о о
Допустим, что позиции 3, 4 и 11 искажены. Тогда
транспонированный синдром имеет вид
18
Э. Вайнер, Р. Эш
ST = [0 111110 0 10 0...].
1) Рассмотрим [5]^ = [0 1 1 1]. Так как он не имеет
отмеченной выше симметрии, то мы заключаем, что в блоке 1 нет
ошибок.
2) Анализируем следующий отрезок синдрома из четырех
позиций (т. е. позиции 2—5) [1 1 1 1]. Он указывает на ошибку
в третьей и четвертой позициях. Следовательно, надо вычесть из
S эти столбцы А (т. е. 3-й и 4-й столбцы) и положить
[5]/Г=[0 111110 0 10 0 ...] — [0 11110 0 0 0] =
= [00000100100...].
3) Рассматриваем позиции 3—6 вектора S'r = [0 0 0 1].
Заключаем, что в блоке 3 нет ошибок. (Их, конечно, и не должно
было быть, так как произошла ошибка во втором блоке.)
Повторяем до тех пор, пока не дойдем до позиций 6—9 вектора S/T —
= [100 1], соответствующих ошибке в одиннадцатой позиции
принятого вектора.
III. Коды типа В
Одна из задач теории кодирования состоит в максимизации
корректирующей способности кода при минимизации
избыточности. Для кодов типа В эта задача ставится следующим
образом: каково минимально возможное n=(N/m) *b при
фиксированных ft, т и /? Иначе говоря, мы должны минимизировать
защитный интервал g при фиксированных длине блока,
избыточности и длине пакета.
Начнем с вывода нижней границы для N в случае кодов
типа В2 и затем построим некоторые коды, которые достигают
этой нижней границы. После этого приведем общий метод
построения кодов типа 52, достаточно близких к оптимальным.
Наконец, обсудим коды типа В\ и сравним построенные нами
коды с кодами Хегельбергера [3].
А. Вывод для нижней границы для N при произвольном г и
Предположим, что уже построены коды типа В2 с /п=1.
Дадим следующие определения:
1) В' есть ([N + r — l]Xb)-матрица, состоящая из первых
N + r—1 строк В0. Заметим, что последние г—\ строк Bh
являются нулевыми.
Анализ рекуррентных кодов
19
2) V есть (N+r—l)X(N + r—1)-матрица вида
Г' =
о о
1
1
О
о
1 о
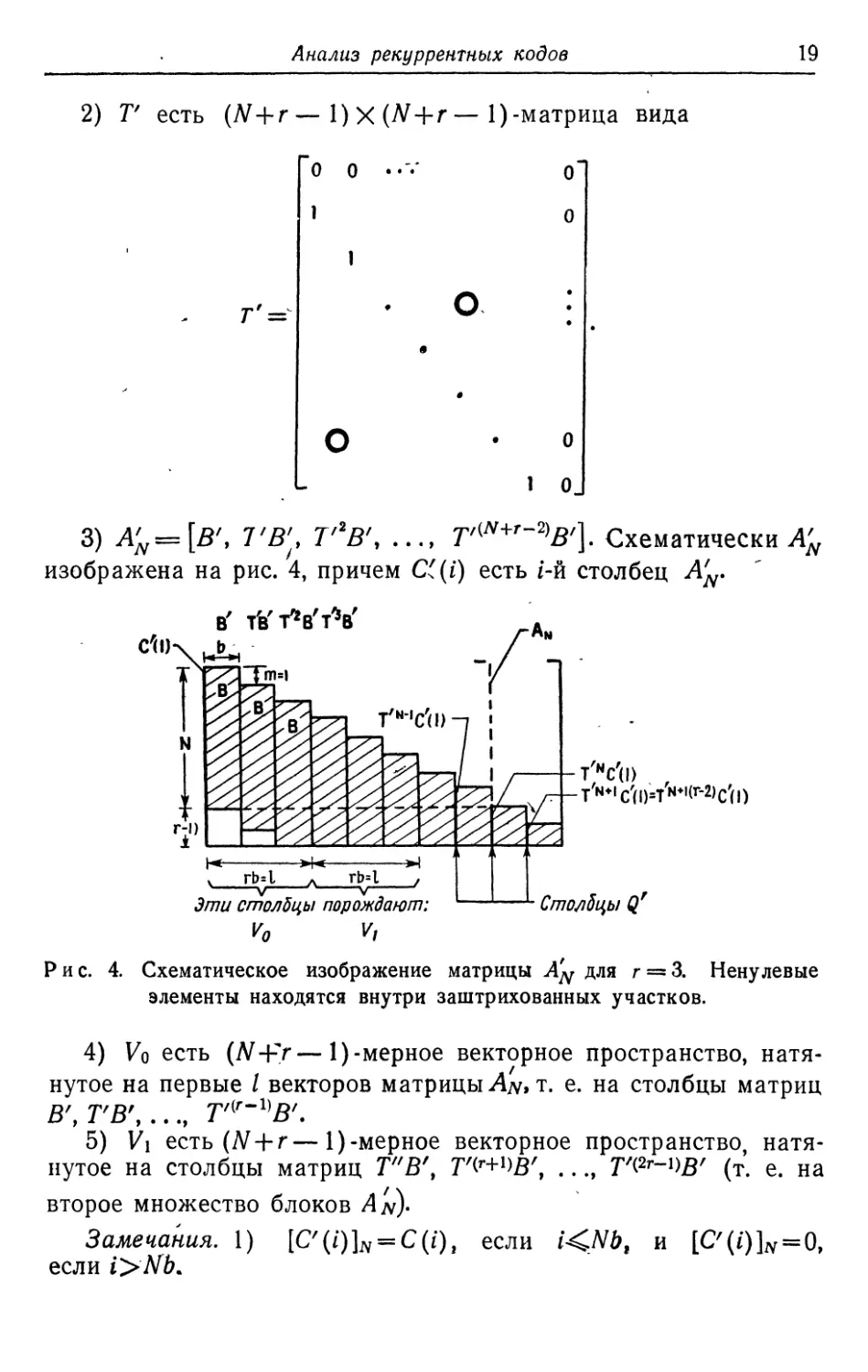
3) A'N=\B\ VB'I% Т'2В\ ..., т'^+'-^В']. Схематически A'N
изображена на рис. 4, причем C((i) есть /-й столбец A'N.
в' t'b'tVtV
T'N+.c'(|)=TW.(r-2)c'(|)
Эти столбцы порождают: ' ' L Столбцы Qr
Vq V,
Рис. 4. Схематическое изображение матрицы A'N для г = 3. Ненулевые
элементы находятся внутри заштрихованных участков.
4) Vq есть (N-fr—1)-мерное векторное пространство,
натянутое на первые / векторов матрицы An* т. е. на столбцы матриц
В', Т'В\ ..., Т*~1)В'.
5) V\ есть (N + r—1)-мерное векторное пространство,
натянутое на столбцы матриц Т"В\ Г^В', ..., T'(2r-lW (т. е. на
второе множество блоков An)-
Замечания. 1) [С'(i)]N = С (i) t если /<#*, и [С'(/)]# = О,
если i>Nb*
20
Э. Вайнер, Я. Эш
2) Если ЛГ=2С'(/), то
является линейной комбинацией столбцов AN. Передокажем те-*
перь необходимое условие теоремы 1 применительно к
матрице An»
Теорема 2. Если X == 2 С7(/) a K=2jC'(у) — испра-
вляемые линейные комбинации столбцов An типа В2, то
X = Y влечет ir\Ki=J{\Ki.
Доказательство. Доказательство аналогично
доказательству теоремы 1. Если 1=7 и /П Ki4=l Л/Q, то X и У по
усеченному синдрому [S]iv+r-i соответствуют двум различным мно^
жествам ошибок в первых г блоках. Таким образом, по [S]A4-r-i
нельзя декодировать первые г блоков. Это противоречит
предположению 2 разд. 11-Е. Следовательно, X = Y влечет равенство
inKi=Jr\Ki.
Нетрудно показать, что условие теоремы 2 не только
необходимо, но и достаточно. Заметим также, что если г=1, то
An = An и теорема 2 превращается в «необходимую» часть
теоремы 1.
Докажем последовательность лемм, которые совместно с
теоремой 2 приведут к нижней границе для N.
Лемма 1. N>r.
Доказательство1). Согласно определению, г==у<"г»
где п = —• й. Поэтому N > rm^-г, что и требовалось доказать,
Лемма 2. Если X — нетривиальная линейная комбинация
векторов, порождающих V0 (т. е. первых I столбцов An), то
Доказательство. Предположим, что лемма не верна,
так что [X]N-i = 0. Рассмотрим матрицу
Q/=[7v("-i>C'(l)f Г"С'(1), ..., Г("+Г-2)С'(1)].
*) Приведенное очень простое доказательство предложено
переводчиком. — Прим. ред.
Анализ рекуррентных кодов
21
Столбцы Q' являются первыми столбцами последних г блоков
в Ду Из определения V следует, 4to4[Q/]jv-i = 0. Кроме того,
так как мы предположили, что верхний элемент С(1) [и,
следовательно, С'(1)] равен 1, то последние г строк Q' образуют
треугольную и, следовательно, невырожденную матрицу. Отсюда
следует, что столбцы Q' являются (N+r—1)-мерными
векторами, первые N— 1 координат которых равны нулю. Таким
образом, если [X]N-i = 0, то X можно записать в виде линейной
комбинации столбцов Q', или эквивалентно
Х = %С'{1), (5)
где / ограничено последними г блоками матрицы An, т. е. />
>(W—1)6+1 для всех i£I. Заметим, что / является
исправляемым множеством типа В2, так как столбцы Q'
ограничены г последовательными блоками AN. Теперь, согласно
предположению, X € Vq и, следовательно,
* = 2С'(А • (6)
где / является ненулевым подмножеством Ki и, следовательно,
исправляемым типа В2. Приравнивая (5) и (6), находим
2 с (О =2 с (т); ^ . (7)
где / П /Сг=^= ^>. Мы же утверждаем, что /П/Сг=^>, и тем самым
получаем противоречие с теоремой 2, доказывающее лемму.
Для доказательства этого утверждения заметим, что из леммы 1
следует неравенство i> (г— 1)6+ 1, так как i>(N— 1)6+1 для
всех i€/. И так как каждое i соответствует первому столбцу
блока, то />r6+1=/+1 и, следовательно, /П/(/ = ^, ч. т. д.
Следствие 1. Размерность пространства V0 равна I:
DimV0 = /.
Доказательство. Если / порождающих V0 не
независимы, то существует нетривиальная линейная комбинация X
этих порождающих, равная нулю. Таким*образом, в
противоречие с леммой 2 получаем [X]N-i = 0.
Следствие 2. Dim Vi = /.
Доказательство. Пусть Т0 — линейное преобразование
из V0 в пространство всех (N + r — 1)-мерных двоичных
векторов, определяемое равенством TQ(X)=T'X (Х£ VQ). Так как
22
Э. Вайнер, Р. Эш
Vi — множество всех векторов Т^Х), X £Vo, то можно
записать 1Л = Го(1/о). Если мы сможем доказать, что Тг0 является
невырожденным (т. е. изоморфизмом) и сохраняет, таким
образом, размерность, то dim Vi = dim Vq = L Для этого достаточно
показать, что ядро Го состоит только из нулевого вектора.
Предположим, что X принадлежит ядру То, т. е. X£Vo и ТГ0(Х) —
= (Т')Г X = 0. Из определения V следует, что если (T')hY=Oy то
верхние N+r—1—k элементов У являются нулевыми.
Следовательно, верхние N + r—1 — г=Л^—1 элементов X должны
быть нулевыми, т. е. [Xhv-i = 0. Но так как Х£ V0t то в силу
леммы 2 Х = 0, что и завершает доказательство.
Лемма 3. У0П Vi={0}.
Доказательство. Если Х£ V0, то можно записать Х =
— 2 С (О» гДе 1 — подмножество Кь Если X 6 Vif то можно за*
писать Х= ]£С' (у), где / — подмножество К&\Кь Таким об*
разом, /П/С/=у. Так как / и / — исправляемые множества
типа 52, то по теореме 2 /П /(/=<£. Так как /с/С/, то /= ^ и,
следовательно, Х = 0.
Теорема 3. Любой код типа 52 с т=\ удовлетворяет
условию N > 2/ — г +1.
Доказательство. Пусть Vo+Vi—сумма подпространств
V0 и Vu т. е.
V0+Vl = {aX+bY: X£V0; Y£VX\- a,b = 0 или 1}.
Типичная теорема теории векторных пространств утверждает,
что
dim(K04-Vr1) = diml/r0 + dimK1 —dim(K0nl/i).
Так как Vo+Vi является пространством (N+r— 1)-мерных
векторов, то dim(V0+Vi)KN + r — 1. В силу леммы 3 и следствий
из леммы 2 N+r — 1 >/+/ —0 = 2/, ч.т.д.
Частный случай. Если*//6 = 1, то Af> 2/==26.
Пример. Рассмотренный в п. 2 разд. II-G код является ко*
дом типа В2 с N = 2b=2l. Следовательно, код достигает
нижней границы.
Анализ рекуррентных кодов
23
В. Построение оптимальных и почти оптимальных кодов
Определение. Код типа В2 с т=1 называется
оптимальным, если
N = 2l — r+l.
Хотелось бы построить оптимальные коды для всех возможных
b и /. Следующая теорема упрощает поиск.
Теорема 4. Для произвольного положительного числа г и
заданного кода типа В2 с m=l, b = b0, l/b = l и N = N0 возможно
построить код типа В2 с т=1, b = b0, l/b = r и N=(N0— 1)г+1.
В частности, если N0 — 2b, то (N0—l)r+l=2rb — r+l =
= 2/— г+1, так что построение кода с г=1 и N~2b влечет за
собой построение кода для произвольного г, достигающего
нижней границы теоремы 3.
Доказательство1),
кода с г=1 строим [(No-
г— 1 нулевых строчек
ными строчками В.
По заданной (N0Xb)-матрице В
- 1)г+1]Х&-матрицу Б*, вставляя
между каждыми двумя последователь-
Пример:
В.
Г1
0
0
1 1
о-
1
1
0 1
N = N0 = 4, l = b = 2;
В*--
Г\
0
0
0
0
0
1
°1
0
1
0
1
0
0 1
г = 2. 7V = (7V0— 1)г4-1=7.
') Доказательство основано на переплетающейся схеме, рассмотренной
24
Э. Вайнер, Р. Эш
Aisi —
w
\N — матрицы, ассоциированные с В и 5*, имеют вид
•10 0 0 0 0 0 0
0 1 10 0 0 0 0
0 10 110 0 0
J00101 1 0_
■1000000000000 0
00100000000000
01001000000000
AN = i 00010010000000
01000100100000
00010001001000
„1 000010001001 0_
Так как декодирование первого блока осуществляется на основе
позиций синдрома, соответствующих ненулевым строкам В* (в
данном примере нечетные строки), то можно видеть, что, как
и утверждалось, В* задает код типа В2.
Ниже приводятся примеры оптимальных кодов для г=1,
т=1, 6 = 2, 3 и 4:
1)й = 2,Г1 0"| 2) й = 3,Г1 1 01 3) й = 4,Г1 0 0 0
0 10 0
В =I 0 1 I• I 0 0 0 I I 1 0 0 0
0 0 0 0
В= I 0 0 1 о
0 0 0 1
0 0 0 1
_0 0 1 0__
Наилучшее, что мы умеем строить для произвольных
блоковых длин к настоящему времени, являются коды, достаточно
близкие к оптимальным1), определяемые матрицей В,
изображенной на стр. 27 при N = 2(b— l)+b = 3b — 2, m = l.
l) E. Берлекамп и Ф. Препарата одновременно и независимо построили
оптимальные коды типа В2 для произвольных b и т, а следовательно, и г
(см. теоремы 4 и 4' данной статьи). Таким образом, первый знак
неравенства в (8), (9), (10), (11) надо заменить на знак равенства. Подробности
см. в работах.
В е г 1 е с a m р Е. R., Note on Recurrent Codes, IEEE Trans, on Inf.
Theory, IT-10, 3 (1964), 257—259;
Preparata F., Systematic construction of optimal linear recurrent
codes for burst error correction, Calcolo, 2 (1964), 1—7.- Прим. ред.
г\
0
0
Li
°1
1
1
oj
= 3,
B =
"1 1 0"
0 0 1
0 0 0
10 0
0 10
10 0 1
Анализ рекуррентных кодов
25
В п. 2 разд. II-G
(иллюстрирующем теорему 1) приведен такой код с
b = 2 (Af = 4). Это единственный
случай, когда код оптимален. Доказатель-.
ство того, что матрица В определяет
код типа £2, полностью аналогично
доказательству, проведенному в п. 2
разд. II-G.
Результаты, полученные для кодов
типа В2, можно подытожить в виде.в
для г=1
26<7V<3fi — 2, (8)
для произвольного г (из теорем 3 и 4)
2/-r+l<W<3/ —Зг+1. (9)
Так как n = Nb, то
Ь{21 — г+1)<я<й(3/ — Зг+1). (10)
С. Обобщение нижней границы на случай произвольного m
С помощью процедуры, аналогичной использованной ранее,
можно доказать следующее обобщение теоремы 3.
Теорема 3'. Любой код типа В2 должен удовлетворять
неравенству
N>2l—(r — \)m. . (11)
о/./
Соответственно п = (N/m) • b > (г — 1) b.
Как и для случая т=1, построение оптимальных кодов [т, е.
кодов, для которых в (11) достигается равенство] упрощается
следующим обобщением теоремы 4:
Теорема 4'. Для произвольного положительного числа г и
заданного кода типа В2 с m = m0, b = bQl //& = 1 и N = N0
возможно построить код типа В2 с m = m0, b = b0, l/b = r и Л/ =
~ (N0— m)r + m.
Оптимальный код с m = 2, 6 = 3 и г=1 задается матрицей
В =
Г1 0 0 1
0 10
0 0 1
0 0 0
0 0 1
!_0 0 1 J
N=6,
tt = (Nlm)-b:
:9.
26
Э. Вайнер, Р. Эш
D. Коды типа В\ —коды Хегельбергера
Так как коды типа В\ являются одновременно и кодами
типа В2, то к ним приложимы все полученные выше результаты.
Усиления нижней границы для л, однако, пока получить не
удается (если, конечно, оно в принципе возможно). Оптималь*
ный код типа В\ для / = 6 = 2 и т=1 определяется матрицей
1 1
В =
О 1
О 1
О О
N = 2b = 4.
Необходимо указать, что коды, построенные Хегельберге*
ром [3], являются кодами типа В\ с т= 1 и
п = ЫЬ(Ь)-\-Ь — 19 (12)
где L(b) —наименьшее число >log26 + l. Для того чтобы по-*
казать, что коды Хегельбергера могут быть улучшены,
рассмотрим код Хегельбергера для 6 = 3 и /=12. В силу (12) для этого
кода п=99. Сравним его с оптимальным кодом типа 52 с 6 = 3
и /=15 (приведенным в разд. III-B). Последний код исправляет
все пакеты длины, не превосходящей 13, и некоторые пакеты
длин 14 и 15. Для него в силу теоремы 4 n = b\2l — y-f-l) =
= 78. Таким образом, при той же самой избыточности мы
получаем код с несколько меньшим защитным интервалом, чем
у кода Хегельбергера.
IV. Коды типа А
Как и для кодов типа В, попытаемся максимизировать кор*
ректирующие возможности кода при минимизации его избыточ-*
ности. Для кодов типа А эта задача формулируется так:
каково минимально возможное n=(N/m) -b при фиксированных
6, m и е>
Наше обсуждение кодов типа А ограничивается случаем
т=1. Мы начнем с вывода нижней границы для Af (и,
следовательно, для п) в частном случае, когда е=1. Затем мы покажем,
что эта нижняя граница всегда реализуема, так что
оптимальный код с исправлением одиночных ошибок может быть
построен для произвольного Ь. Затем находится нижняя граница
для N при произвольном е. Наконец, так как известны *) только
1) Одновременно с данной работой была выполнена работа Дж. Л. Мес-
си «Пороговое декодирование» (изд-во «Мир»4 1966), в которой автор
приводит широкий класс кодов типа Л,
Анализ рекуррентных кодов
27
некоторые специфические коды типа Л, мы для случая 6 = 2 при
произвольном е выводим верхнюю границу для N посредством
построения, аналогичного описанному в [8].
А. Коды с исправлением одиночной ошибки (е=1)
Переформулируем прежде всего теорему 1 на случай кодов
типа А с е=1: матрица AN определяет код типа А с е = 1 тогда
и только тогда, когда для всех положительных чисел t, /, таких,
что i^Cb и i^=/, справедливо C(i)=C(j). Другими словами, ни
один столбец первого блока в AN не равен другому столбцу
матрицы AN. Иначе говоря, если СИ) и С(/) — два столбца
первого блока матрицы AN (%ф\\ i, j-^b), то ТкС(1)ФСЦ) для k =
= 0, 1,..., TV—1.
Выпишем теперь реализуемую нижнюю границу для N.
Теорема 5. 1) Любой код типа А с m = e=l должен
удовлетворять неравенству N > log2 b + l.
2) Для произвольных положительных чисел N0 и 60, таких,
что Afo^>log2 bo+U существует код типа А с b = b0f m=e=l и
N=-NQ.~~
Доказательство. 1) Определим следующее отношение
эквивалентности на множестве ненулевых Af-мерных векторов:
Xc^Y тогда и только тогда, когда либо ThX = Y для некоторого
й = 0, 1, ..., N—1 и k нижних элементов X равны нулю, либо
ThY=X для некоторого й = 0, 1, ..., N— 1 и k нижних
элементов У равны нулю. (Условие, накладываемое на нижние
элементы, обеспечивает транзитивность отношения.)
Если X и У —два различных Af-мерных вектора с единицей
в первой позиции, то X и У лежат в разных классах
эквивалентности. Более того, никакие два столбца первого блока матрицы
AN не могут лежать в одном классе эквивалентности, так как
если C(i)c~C(j) (1Ф1\ i, /<&), то или ThC(i)=C(j), или
ThC(j)=C(i), что противоречит сделанной выше
переформулировке теоремы 1.
Отсюда следует, что b не может быть больше числа классов
эквивалентности в множестве ненулевых ЛЛмерных векторов.
Мы утверждаем, что существует 2N~l классов
эквивалентности. Так как никакие два различных вектора с единицей в
первой позиции не эквивалентны, то число классов эквивалентности
по меньшей мере равно 2N~l. Далее, число классов
эквивалентности не может превышать 2N~l, так как любой ненулевой
ЛЛмерный вектор эквивалентен вектору с единичным первым
элементом.
28
Э. Вайнер, Р. Эш
г°~
0
1
i 1
—
~i_
1
0
0
Например, если TV = 4, то
Таким образом, всего существует 2^-1 классов эквивалентно-»
сти, так что
й<2
Д-1
или 7V>log26 + l.
2) Утверждение легко следует из того, что в качестве
столбцов матрицы В (первого блока AN) можно выбрать столбцы из
множества всех 2^-1 различных Xf-мерных векторов с единицей
в первой позиции. Такой выбор В удовлетворяет условию
теоремы 1, так как ThC(i) (k>0) имеет в первой позиции нуль и,
следовательно, не может быть равен ни одному столбцу
матрицы В.
В. Нижняя граница для N при произвольном е>\ (т = 1)
Предположим, что мы построили код типа Л. Если а — число
различных исправляемых линейных комбинаций столбцов AN
типа Л, то а^2^, так как каждый столбец матрицы AN является
yV-мерным вектором. Если мы сможем найти нижнюю границу
для а, то этим мы получим нижнюю границу для N. Разобьем
исправляемые линейные комбинации типа Л следующим
образом на подклассы Hs (s = 0, 1, ..., е): X = 2 С (/) принадлежит
К*
классу #s, если множество I Г\Къ содержит точно 5 членов (т. е.
X имеет точно 5 «представителей» в первом блоке). Из
теоремы 1 вытекает, что Hs не пересекаются, и, следовательно, если
через n(Hs) обозначить число элементов в Hs, то.
= 2 я (я,).
5 = 0
(13)
Найдем теперь нижнюю границу для n(Hs). Согласно
теореме 1, если X и У принадлежат Hs и имеют различные
представители в первом блоке, то ХФУ.
Для всякого X£HS в первом блоке можно выбрать 5
представителей
^ъ— s!(6__s)1
способами (Сь по определению равно нулю для s>b). Таким
образом, если через F(p) обозначить число различных векторов,
являющихся линейной комбинацией не более р столбцов ма-<
Анализ рекуррентных кодов
29
трицы AN, исключая первый блок, то получим
n(Hs) = CtF(e-s). (14)
Подставляя (14) в (13), имеем
2^>a=SCjF(^-s). (15)
5 = 0
Выведем теперь нижнюю границу для F(p), используя
следующую теорему:
Теорема 6. Пусть X = 2 С(/) и Y= 2^(/)- линей-
яые комбинации не более t столбцов матрицы AN(t*Ce). Тогда
из равенства X=Y следует, что I ПК[2(е_()+ць = / nK[2(e_t)+l]b.
Теорема 6 является распространением теоремы 1 на коды
типа Л; йри t = e теорема сводится к «необходимой» части
теоремы 1.
Определим теперь матрицу M(t) как матрицу AN с
вычеркнутыми первыми 2(e — t)—l блоками (/=1, 2, ..., е—1). Из
теоремы 6 вытекает, что любые две равные линейные
комбинации не более t столбцов матрицы M(t) должны иметь одних и
тех же представителей в первых двух блоках M(t). Точно мы
сформулируем это следующим образом:
Следствие из теоремы 6. Если X=^C(i) и Y =
= 2 С (у)— две линейные комбинации не более t столбцов
матрицы М(/), то
X = r=$lnK' = Jf)K'.
где K'={[2(e-f)-i]b+l\ [2(e-t)-l]b + 2\ ..., [2(e-t) + l]b].
[Соответствует первым 2b столбцам матрицы M(t)\ см. рис. 5.]
Доказательство. Следствие вытекает непосредственно
из теоремы 6, так как К'^Кр^-ф+ц ь-
Мы определили F(p) как множество различных векторов,
являющихся линейными комбинациями не более р столбцов
матрицы ANi исключая блок 1. Таким образом, если мы
определим Ф(р, /) как множество различных линейных комбинаций
не более р столбцов матрицы M(t), то, очевидно, будет
выполняться равенство F(p)=(b(p, е—1).
Мы установим нижнюю границу для F(p) с помощью
рекуррентных соотношений. Для р</, проводя вывод,
аналогичный выводу соотношения (15), с использованием матрицы M(t)
30
Э. Вайнер, Р. Эш
вместо AN и сформулированного выше следствия вместо
теоремы 1, получаем
р Г число способов,выбора s^
ф(л, t) = 2 \ представителей в первых ХФ(/?~5, t — 1),
5-о1 двух блоках М (t) )
ИЛИ
Ф(/>, t)=%CS2bO(p-s,t-\).
5 = 0
{С1ь полагается равным нулю при s>2b).
(16)
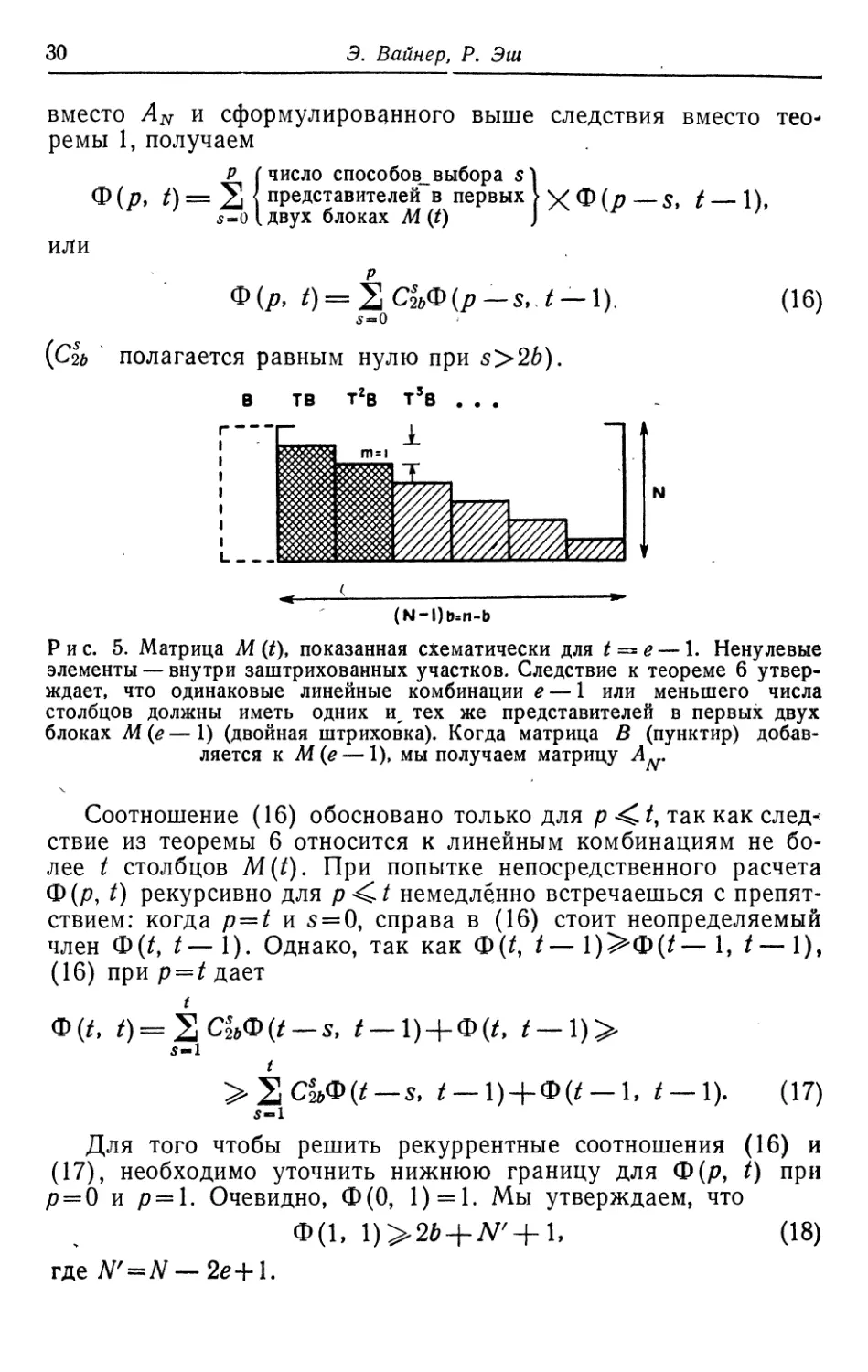
(N-l)tbn-b
Рис. 5. Матрица М (t), показанная схематически для t = е — 1. Ненулевые
элементы — внутри заштрихованных участков. Следствие к теореме 6
утверждает, что одинаковые линейные комбинации е — 1 или меньшего числа
столбцов должны иметь одних и^ тех же представителей в первых двух
блоках М (е — 1) (двойная штриховка). Когда матрица В (пунктир)
добавляется к М(е — 1), мы получаем матрицу Ам.
Соотношение (16) обосновано только для р ^t, так как
следствие из теоремы 6 относится к линейным комбинациям не
более t столбцов M(t). При попытке непосредственного расчета
Ф(р, t) рекурсивно для р<С/ немедленно встречаешься с
препятствием: когда p — t и 5 = 0, справа в (16) стоит неопределяемый
член Ф(/, t— 1). Однако, так как Ф(/, t— 1)>Ф(/ — 1, t — 1),
(16) при p = t дает
Ф(/, t)=^Cs2b®(t — s, t — \)-\-<S>{t, t — \)>
t
>2С^Ф(/— s, t — 1) + Ф(/ — 1, /-1). (17)
Для того чтобы решить рекуррентные соотношения (16) и
(17), необходимо уточнить нижнюю границу для Ф(р, t) при
р = 0 и р = 1. Очевидно, Ф(0, 1) = 1. Мы утверждаем, что
Ф(1, 1)>26 + ЛГ+1, (18)
где N'~N — 2e+\.
Анализ рекуррентных кодов
31
Доказывается это следующим образом: рассмотрим М(1).
В силу следствия из теоремы 6 первые 26 столбца Л1(1), как
линейные комбинации первого столбца М(1) и различных
«представителей» в первых двух блоках М(1), различны.
Далее, первые столбцы каждого из оставшихся N' блоков
матрицьгМ(1), т. е. столбцы
С[(2г —1)6 + 1], С[2*6 + 1], ..., C[(N — 1)6+1],
образуют множество S (мощности N') линейно независимых и,
следовательно, различных столбцов М(1). [Незадисимость
следует из тогр, что первым элементом С(1) является 1.] В силу
следствия й5 теоремы 6 S не пересекается с первыми 26
столбцами М(1). Таким образом, включая нулевой вектор, мы
получаем по меньшей мере 26 + W+1 различных линейных
комбинаций не более одного столбца М(1).
Теперь мы доожем установить нижнюю границу для N. Так
как F(p)=<b(p, €—1) и F(e)=Q>(e, е— 1)>Ф(е— 1, е— 1),
из (15) получаем следующий результат:
2">2С2Ф(*—s, е — 1) + Ф(г — 1, е — 1). (19)
5 = 1
Наименьшее значение ^удовлетворяющее (19), и является
искомой нижней границей. Ф(р, t) отыскивается, рекурсивно из
<16), (17), (18).
Примеры:
1) Пусть 6 = 2; £? = 3. Тогда
Ф(1,1)>2(6 — e) + N + 2 = N,
ф(1,2) = Ф(1, 1) + 4Ф(0, l)>7V + 4,
Ф(2,2) = Ф(2, 1) + 4Ф(1, 1) + 6Ф(0, 1)>5Ф(1, 1) + 6Ф(0, 1)>
>5Лг + 6.
Таким образом, из (19)
2" > 2Ф (2, 2) + Ф (1, 2) + Ф (2, 2),
или
2^>167V + 22. (20)
Наименьшим значением Л/", удовлетворяющим (20), является
N = 8. Следовательно, любой код типа А с т=1, 6 = 2, е = 3
должен удовлетворять условию iV=8.
2) Пусть е = 2. Тогда из (19)
2"<6Ф(1, 1) + С*Ф 0, 1) + Ф(1, 1) = (6 + 1)Ф(1, 1) + С|.
32
Э. Вайнер, Р. Эш
.Из (18)
Ф(1, 1)>2(й — 2) + 7V + 2 = JV + 2fi — 2t
Следовательно,
2N<{b+\)(N + 2b — 2) + Cl (21)
При 6 = 2 наименьшим числом, удовлетворяющим (21), является
N = 5. В разд. II был приведен код типа А с m=l, Ь=е = 2 и
N = 6.
Нижние границы для N (и п) для кодов типа А, т =* 1
и различных значений £ и <?
6
2
3
4
5
е
2
3
4
2
3
2
3
2
N
5
8
10
6
9
7
л = М>
10
16
20
18
27
28
40
35
ь
6
7
8
9
10
е
2
2
2
2
2
N
8
8
8
9
9
n=Nb
48
56
64
81
90
В таблице приведены наименьшие значения Л/, удовлетво-*
ряющие (19) для различных значений Ь и е.
С. Верхняя граница N при 6 = 2 и произвольном е>\ (т=\)
Нами показано, что для любого е>\ существует код типа А
с 6 = 2, т=1 и N, равным наименьшему числу,
удовлетворяющему неравенству
2"-1 > 5 CLv-з. (22)
/-о
Аналогичная, хотя и более слабая граница, получена другим
методом Возенкрафтом и Рейффеном [9]. К сожалению, способ,
используемый для вывода (22), не имеет простого обобщения
на случай произвольного б1). Полученные границы являются
очень громоздкими и поэтому не приводятся.
1) Для произвольных bum очень легко может быть
получена следующая граница для N, обеспечивающая существование кода:
S CbN-ь < 2m(N~l\ где d0 — минимальное расстояние наилучшего
*-°
(b, b • т) линейного кода. Эта граница эквивалентна границе Варшамо-
ва — Гилберта для блоковых кодов. — Прим. ред*
Анализ рекуррентных кодов
33
Можно показать, что для больших е (и соответственно боль:
ших п и N) отношение е/п стремится к константе. В этом
смысле рекуррентные коды ведут себя так же, как блоковые1).
V. Заключение и открытые проблемы
Результатом разд. III и IV является вывод количественного
критерия, позволяющего судить о качестве рекуррентного кода,
а именно о близости N к его нижней границе. Основной
нерешенной проблемой является отыскание методов синтеза
«хороших» кодов. Результаты разд. III наводят на мысль, что можно
отыскать оптимальный код типа 52 общего вида2).
Для реализации рекуррентных кодов можно использовать
простые методы, предложенные Хегельбергером [3] и Питерсо-
ном3). Возможно, что существуют более тонкие методы
технической реализации, позволяющие значительно сэкономить
оборудование. Другой требующей рассмотрения практической
проблемой применения рекуррентных кодов являются задачи
синхронизации и предотвращения размножения ошибок.
ЛИТЕРАТУРА
1. Eli as P., Coding for noisy channels, IRE International Convention
Record, 4 (1955), 37—46.
2. E p s t e i n M. A., Construction of convolution codes by suboptimalization,
M. I. T. Research Lab. of Electronics, Cambridge, Mass., Tech. Rept.
№ 341, 1959.
3. Hagelbarger D. W., Recurrent codes: easily mechanized,
burst-correcting binary codes, Bell. Sys. Tech. /., 38 (1959), 969—984.
4. Kilmer W. L., Some results on best recurrent-type binary-error-correcting
codes, IRE International Convention Record, 4 (1960), 135—147.
5. К i 1 m er W. L., Linear recurrent binary error-correcting codes for memory-
less channels, IRE Trans. Information Theory, IT-7 (1961), 7—13.
6. Peterson W. W., Error-correcting codes, The M. I. T. Press, Cambridge,
Mass., and John Wiley and Sons, Inc., New York, 1961. (Русский
перевод: Питерсон У., Коды, исправляющие ошибки, «Мир», М., 1964.)
7. R е i f f е п В., Sequential encoding and decoding for the discrete memoryless
channel, Ph. D. dissertation, Dept. of Elec. Engrg., M. I. Т., Cambridge,
Mass., 1960.
8. S а с k s G. E., Multiple error correction by means of parity checks, IRE
Trans. Information Theory, IT-4 (1958), 145—147.
9. Wozencraft J. M., Reiffen В., Sequential decoding, The M. I. T.
Press, Cambridge, Mass., and John Wiley and Sons, Inc., New York,
1961, 47—55s (Русский перевод: Возеккрафт Дж,, Рейффен Б.,
Последовательное декодирование, ИЛ, М., 1963.)
1) См. [6].
2) Такие линейные коды найдены (см. примечание на стр. 24). — Прим.
ред.
3) См. [6], гл. 13, в которой обсуждаются коды Хегельбергера.
Коды без запятой, исправляющие
ошибки 1}
Дж. Дж. Штифлер
I. Введение
Известны многочисленные классы кодовых словарей,
обладающих способностью исправления или обнаружения
аддитивных ошибок. Так как использование таких кодов предполагает
синхронизацию между, передатчиком и приемником, то в
большинстве случаев бывает удобно предусмотреть некоторый метод
получения ее из полученной последовательности кодовых слов.
Один подход к решению этой проблемы состоит в
добавлении специальной синхронизующей последовательности,
предшествующей каждому кодовому слову. Этот метод исследован при
различных ограничениях в [1] и [2]. К сожалению, избыточность,
добавляемая к этим кодам для получения синхронизации, не
увеличивает их способность исправлять ошибки (во всяком
случае, когда это относится к аддитивным ошибкам). Второй
подход состоит в построении кодовых словарей без запятой [3], [4],
[5]. Однако обычно эти словари либо не обладают свойством
исправления ошибок, либо об этом- ничего не известно. Кроме
того, эти коды обычно не обладают алгебраическими
свойствами, которые давали бы возможность эффективного
декодирования; например, они не образуют группу или смежные
классы группы. В настоящей статье показано, что, беря один из
смежных классов группы, а не саму группу в качестве
кодового словаря, можно обеспечить самосинхронизационные
свойства, не жертвуя интересами декодирования, не добавляя
избыточности и не теряя свойств исправления ошибок по сравнению
с исходным кодом. В разд. II дается условие, которому должен
удовлетворять смежный класс группы, чтобы он являлся кодом
без запятой. В разд. III показано, что существует смежный
класс любого (л, k) циклического группового кода,
удовлетворяющий этому условию по крайней мере для некоторых из
возможных перекрытий, и что, кроме того, если k*C(n—1)/2, то
смежный класс образует кодовый словарь без запятой. Нако-
*) Stiffler J. J., Comma-free error-correcting codes, IEEE Transactions
on Information Theory, ITrll, № l (1965), 107—112.
Коды без запятой 35
нец, в разд. IV указано, что не существует кодов Хэмминга без
запятой [отличных от (3, 1)], независимо от того, получены ли
они из циклического группового кода или нет.
II. Уравнение отсутствия запятой
Кодовый словарь называется поддающимся синхронизации
в позиции г, если последовательность
аг+1аг+2 ... апЬф2 ... Ь, (1)
не является кодовым словом, где а^ а%... ап и bi b2... bn суть
любые два (не обязательно различные) слова из словаря. Если
словарь является поддающимся синхронизации во всех позициях
г(г=1, 2, ..., п—1), то он называется словарем без запятой.
Если слова из словаря образуют двоичную1) группу
размерности &, ясно, что словарь не может быть поддающимся
синхронизации ни в какой позиции, так как слово 00 ... О есть элемент
группы. Однако может оказаться, что к каждому элементу
группы возможно прибавить двоичный вектор с, в результате
чего получается смежный класс, поддающийся синхронизации
по крайней мере в некоторых позициях. Смежный класс
обладает теми же свойствами исправления ошибок, что и группа,
так как он имеет те же свойства расстояний. Будем считать,
что групповой кодовый словарь обладает теми же свойствами
поддаваться синхронизации, что и лучший из его смежных
классов.
Пусть G— матрица порядка nXk, столбцы которой
являются образующими группы, т. е. допустим, что G обладает тем
свойством, что любой элемент | группы может быть записан
в виде
l = Qx, (2)
где х есть двоичный столбец из k компонент. Если кодовый
словарь является смежным классом группы, порожденной G,
то любое кодовое слово а может быть выражено как
a = Gx © с
для некоторого вектора х. (Символ © обозначает сложение по
mod 2.) Пусть G разделена на G{ и G2порядка mXk и (п—m)Xk
соответственно:
а-\а] <3>
1) Мы ограничимся здесь рассмотрением двоичных групповых кодов.
Однако излагаемый метод легко распространяется на линейные коды,
заданные над произвольным конечным полем,
3*
36
Дж. Штифлер
и аналогично пусть с разделен на векторы й и с2 из m и п — m
компонент каждый:
с —
L^2
Если векторы аир определены как
а = Огг®с19 Р = <32*/фс2,
(4)
(5)
где__г/ и z — два двоичных столбца из k компонент, то вектор
(Р, а) может быть использован как обозначение любого
перекрытия вида (1). Число несовпадающих координат у любого
кодового слова а и любого такого перекрытия может быть
определено путем подсчета числа единиц в векторе wt
определенном следующим образом:
w = a-\-\ _
_ , _
р
L °т
+
-.
Оп-т
а
—
^2 "п-щ
О
- от ог 1
1 х
У
L z J
Фс0
•-1 -!
• (6)
Векторы бт имеют т компонент, каждая из которых равна
нулю, матрицы От имеют порядок mXk, и все их элементы
также равны нулю. Если смежный класс, который должен быть
использован в качестве словаря, не поддается синхронизации
в позиции т, то существует двоичный вектор v размерности 3fe,
такой, что
Mv = b,
(7)
где
М =
О
&2 ^п-т
От Ог
С®
1 J
Для доказательства того, что код поддается синхронизации
в позиции т, достаточно показать, что не существует вектора v,
для которого уравнение, написанное выше, имеет решение. Но
Коды без запятой
37
хорошо известно, что (7) обладает решением тогда и только
тогда, когда
р(М) = р(М, Ь),
где р(Л) обозначает ранг матрицы А и М, Ъ есть матрица
порядка яХ(3£+1), полученная добавлением столбца Ъ к
матрице М. Очевидно, что p(Af) << р(М, Ь). Следовательно,
групповой код поддается синхронизации в позиции m тогда и только
тогда, когда р(М)<р(М, &), где М и b определены
соотношением (7).
Ранг матрицы можно рассматривать как число линейно
независимых строк. Полезное свойство матриц состоит в том, что
ее ранг не изменяется при прибавлении кратного одной строки
к любой (другой) строке. Предположим, что существует
линейно зависимое множество Sj строк fhi матрицы М. Так как
все операции рассматриваются над двоичным полем, имеем
и для любого i0£ Sj
2 /И/ = е
its,
(8)
При последовательном прибавлении всех строк из Sj (кроме
/о) к t0 ранг матрицы М становится равным рангу матрицы М\
где
М' =
О
/Л/о + 1,1
. nii0-it и
.. О
• л&г0+1, 3ft
тх
Л, 1
т
п, 3& -I
(9а)
Далее, та же последовательность операций, произведенных
над матрицей М, Ъ дает матрицу (М, Б)', у которой первые
3k столбцов совпадают с аналогичными столбцами матрицы М\
38
Дж. Штифлер
a (3k + 1)-й столбец имеет вид
*2
2 *i
/€5,
Если 2 ^ = Ь то *о-я строка матрицы (М,Ь)' может быть
its j
добавлена к любой другой строке, для которой 6,-=1, при этом
мы получим матрицу
/7Z19 . . . /И,оь 0~
(Ж, *)" =
w.
12
1, ЗЛ
^/0-1, 1
0
^/о+1. 1
. .. tfZ/0-i, зл 0
... 0 1
• • • /И/о+1, зй 0
(9b)
Ясно, что никакая линейная комбинация строк матрицы
(Af, Ъ)" не равна ее /0-й строке. Так как для каждого линейно
зависимого множества строк матрицы (М, Ъ)" существует
соответствующее линейно зависимое множество в матрице М\ то
р((М, b)") = p(M, Ь)>р(М) = р(М'),
если
2*, = ь
Если, с другой стороны, не существует линейно зависимого
множества S;-, такого, что 2 6/ = 1 »■ то р(М, 5)=р(М) и код
itsj
#е поддается синхронизации в заданной позиции»
Коды без запятой
39
Остается, такцм образом, определить множества S,-.
Заметим, что каждомЁу линейно зависимому множеству строк S$
матрицы М соответствует линейно зависимое множество строк
Sj матрицы G (начало строк матрицы М длины k). Множество
всех линейно зависимых множеств строк матрицы G есть
просто нулевое пространство группы, порожденной G, т. е. для
каждого группового кода существует соответствующее нулевое
пространство, такое, что если д\ есть i-я строка в G и Й есть
вектор нулевого пространства, то
■£а,?£ = 0, (10)
где hi есть /-я компонента h. Все векторы й, удовлетворяющие
(10), составляют нулевое пространство Ш кода. Таким
образом, Sj есть множество, для которого
2?*=о (П)
тогда и только тогда, когда существует вектор h из $0 с
компонентами
Г 1 для всех ^, .
{ О в остальных случаях.
Векторы h нулевого пространства, вообще говоря, легко
определяются из описания кода; в действительности часто код
задается при помощи своего нулевого пространства. Можно
показать [6], что если код имеет размерность k (gi имеет k
компонент), то существует в точности 2n_ft различных векторов /г,
удовлетворяющих соотношению (10). Нулев.ое пространство
имеет поэтому размерность п — k и может быть порождено
линейными комбинациями строк некоторой матрицы Н
порядка (п — k)Xn. Матрица Н часто называется проверочной
матрицей, так как ее строки характеризуют независимые проверки
четности, которым удовлетворяет каждое кодовое слово.
В предыдущих абзацах было установлено, что соотношение
(8) может иметь решение только для подмножества множеств
Sj, определенных в (12). Отсюда следует, что если
соотношение (8) выполнено, то в &€ существует вектор й, такой, что
n-m т __ п-т
g М = 2 hl+n_mg(p = g нф=о, (13)
40
Дж. Штифлер
где g{}] и gf) обозначают i-e строки в Gi и G2
соответственно. Но
m m
s^-^-Sv.-^. (14)
и
n — m п
2W2)=(2Ur as)
Следовательно, доказана
Теорема 1.1) Если (л, k) групповой код имеет смежный
класс, поддающийся синхронизации в позиции т, то его _нуле*
вое пространство <§£ должно содержать три вектора 7г, Ы^
и Ы2\ такие, что
1, 2, ..., ш,
■tn-\-1, ..., п -
и
,(2) f 0 /=1, 2, ..., пг,
.(1) | hi+n~m * —
~~ \ 0 1 = 1
2) Если условие 1 выполняется для некоторого вектора й,
то все смежные классы группы, для которых
/==1
поддаются синхронизации в позиции т. Вектор 5 задается
соотношением (7).
Таким образом, вопрос о возможности сделать групповой
код поддающимся синхронизации в любой позиции m можно
решить с помощью простого исследования, содержит ли его
нулевое пространство три вектора, удовлетворяющих описанным
выше условиям. Это сильно сокращает объем работы,
необходимой для обнаружения свойства отсутствия запятой у
группового кода. Кроме того, в некоторых специальных случаях
возможно найти более простые необходимые и достаточные
условия существования смежных классов без запятой. Этот вопрос
исследуется в следующем разделе.
[II. Циклические коды без запятой
Циклический групповой код обладает тем свойством, что
все циклические перестановки любого его кодового слова также
являются кодовыми словами и, следовательно, входят в группу.
Если G порождает некоторый (л, k) циклический групповой
Коды без запятой
41
код, то его нулевое пространство Фв также циклично. Кроме
того [6], базис Я нулевого пространства может быть записан
в виде
Ьх б2 ... бА+1 0 0...0 0 0 ...о
Н--
0 6, б2 ... 6к 6к+1 о ... о о о
о
0 0 0
О 0 0...0¾
Jk + l _L
(16)
где ни бь ни бл+i не равны нулю, причем число столбцор
равно п. Сопоставляя этот факт с результатами, полученными
в предыдущем разделе, мы можем доказать следующую
теорему:
Теорема 2. Любой (n, k) двоичный циклический код
может быть сделан поддающимся синхронизации во всех
позициях г, где |г|<^м — k—1, простым дополнением первой
координаты каждого кодового слова.
Доказательство. Прежде всего заметим, что если
m'^n — k — 1, то £Ш удовлетворяет условию 1) теоремы 1.
Пусть h есть первая строка матрицы Я из (16), тогда вектор
hi , определенный в условиях теоремы 1, тождественно равен
нулю и вектор hf] есть просто (т + 1)-я строка матрицы Я.
Остается проверить, что
2*А = 1
для всех m ^Сп — k — 1. Но так как
Ь = с +
L*l J
о
то
*/ =
1 / = 1, п — гпА-\.
[0 в остальных случаях.
(17)
(18)
(19)
(20)
42
Дж. Штифлер
Отсюда следует, что
п k+l
2Jaa = Зал=^-=1, (21)
£-1 /-1
если k+\<n — m+1, т.е. если m^Cn — k— 1.
Повторяя эти рассуждения для последней строки
матрицы Н вместо первой, можно установить, что та же ситуация
получается, если
п — яг<# — k — 1.
Следовательно, соотношение (7) не будет иметь решения, если
Ъ определено так, как выше, для всех т, таких, что
ftfi|<# — k — 1,
что доказывает теорему.
Нужно заметить, что смежные классы, отличные от тех,
которые получаются дополнением первого столбца, также могут
обладать требуемыми свойствами. Например, легко видно, что
дополнение последнего столбца дает тот же самый эффект.
Можно доказать также и обратное утверждение к теореме 2.
Теорема 3. Все смежные классы любого (п, k)
двоичного циклического кода не поддаются синхронизации во всех
позициях г, где п — k ^ г ^L k.
Доказательство. По определению ЗЮ содержит строки,
характеризующие все линейно зависимые строки G. Легко
показать, что если первая единица в строке из е%? встречается
в 1-й позиции, то последняя единица не может появиться до
(/ + &)-й позиции. Это следует из того факта, что все строки Ъ
в е%? являются линейными комбинациями строк матрицы Н
из (16). Действительно, предположим, что 1-я строка матрицы
Н является первой, входящей в такую линейную комбинацию.
Тогда, очевидно, 1-я координата h равна единице. Аналогично
если последняя строка матрицы Я, которая входит в линейную
комбинацию, имеет номер (/+v), то (1+ч+к)-я координата Ъ
также равна единице. Так как очевидно, что v > 0, то
утверждение имеет место. Но тогда по теореме 1, если код поддается
синхронизации в позиции т, то матрица <$№ должна содержать
векторы й, W"> и W\ Разделение между первой и последней
ненулевыми компонентами в М1) и /г<2) не может превосходить
m—1 и п — m—1 соответственно, тогда как разделение
между первой и последней ненулевыми компонентами _во всех
векторах &6 должно быть не меньше, чем k. Так как /г*1) и й<2)
Коды без запятой
43
не могут быть оба тождественно равны нулю (иначе h было бы
тождественно равно нулю), теорема 1 не может иметь места,
если и m— 1, и п^-пг— 1 меньше k. Это доказывает теорему.
В действительности теорема может быть доказана для более
широкого класса кодов, а именно для любого группового кода,
у которого первые k координат линейно независимы.
Доказательство этого утверждения следует из замечания, что никакое
множество из первых п — m4^k строк G и, следовательно, М
не может быть линейно зависимым, так как первые k строк G
независимы. Но, кроме того, никакие из последних m^Ck строк
М не могут быть включены в линейно зависимую комбинацию,
так как строки d линейно независимы. Следовательно, р(М) =
= п и условия теоремы 1 не выполняются.
Следствие 1. Если k<C(n—1)/2, то (n,k) циклический
код может быть сделан кодом без запятой. Если k> (/1-1)/2,
то никакой смежный класс никакого (я, k) циклического кода
не является кодом без запятой.
Доказательство. Это следует из факта, что, если
Гтах^- (п— 1)/2, где гтах есть максимальное значение г в
теореме 2, все возможные позиции поддаются синхронизации. Но
и 1 \ п — 1
имеет место лишь при
£<^. (22)
Из теоремы 2 следует, что если k>(n—1)/2, все значения
r>n — k—1 не поддаются синхронизации независимо от
выбора смежного класса.
Интересно сравнить этот результат с верхней оценкой числа
кодовых слов, если требуется только отсутствие запятой. Эта
оценка [4] устанавливает, что *)
k^n — log2 п, (23)
и, как можно ожидать, она гораздо выше полученной здесь
оценки при больших значениях п. (Заметим, что (3,1) код
достигает этой оценки, но что [n — log2n]> (п—1)/2 для всех
я>3.) С другой стороны, коды, исследуемые здесь, могут
исправлять е=п/9 ошибок при больших п [4].
1) В [4] доказана в действительности немного более низкая верхняя
оценка, но данное приближение для нас достаточно.
44
Дж. Штифлер
IV. Несуществование кодов Хэмминга без запятой
Возникает вопрос, обладают ли нециклические групповые
коды, исправляющие ошибки, смежными классами без
запятой и, в частности, существуют ли такие смежные классы при
k>(n—1)/2. Интуитивно можно предположить, что тот факт,
что нулевое пространство группового кода без запятой должно
удовлетворять условиям теоремы 1, дает преимущество цик*
лическим кодам перед нециклическими, когда речь идет об
отсутствии запятой. Представляется сложным доказать общее
утверждение относительно свойства отсутствия запятой у
смежных классов нециклических кодов, хотя иногда легко исследо^
вать некоторые специальные коды, используя метод,
изложенный выше.
Рассмотрим, например, смежный класс группы, полученной
некоторой произвольной перестановкой координат в коде
Хэмминга, исправляющем одну ошибку. Эти коды обладают тем
свойством, что
Т$^ = 2*- '(24)
Можно показать, что каждый групповой код, исправляющий
одну ошибку и удовлетворяющий соотношению (24), является
некоторой перестановкой кода Хэмминга. Поэтому все такие
коды и их смежные классы мы будем называть здесь кодами
Хэмминга.
Сразу проверяется, что k>(n—1)/2 для всех кодов
Хэмминга, за исключением (3,1) кода. [То, что (3,1) код Хэмминга
без запятой существует, видно из исследования любого из ко-
001 100
довых словарей: или .] Для доказательства того, что
никакой код Хэмминга не есть код без запятой при й>1, снова
достаточно показать, что р(М)=п для некоторой позиции т,
в которой код не поддается синхронизации. Легко показать,
что каждая строка матрицы нулевого пространства &в содержит
в точности (я+1)/2 единиц. Рассмотрим матрицу Му где пг =
= (п—1)/2. Так как в точности (п+1)/2 строк в G должны
быть включены в любую проверку четности и так как Gi в
данном случае содержит только (п—1)/2 строк, то никакое
подмножество нижних (п— 1)/2 строк М не является линейно
зависимым. Единственная оставшаяся возможность состоит в том,
что верхние (/1+1)/2 строк М линейно зависимы. Из этого
немедленно следует условие, что
(л + 1)/2_ п _
2 *,=о, 2 gi = o.
l-l / = (/7 + 1)/2
Коды без запятой
45
где снова д% представляет собой i-ю строку порождающей мат-»
рицы G. Это в свою очередь требует, чтобы
1=1
^ (я+ 1)/2
т.е., чтобы линейная комбинация п—1 строк из G была
тождественно равна нулю. Это противоречит условию, что в точ^
ности (п+1)/2 строк должны входить в любую такую
комбинацию, если только не выполнено равенство п—1 = (л+1)/2,
т.е. если пфЪ. Следовательно, (3,1) код есть единственный
двоичный код Хэмминга без запятой. Подобным же образом
можно установить, что если ослабить условие отсутствия
запятой и потребовать только, чтобы любая ошибка в
синхронизации могла быть определена в не более чем 5 словах (отсутствие
запятой влечет, что 5 = 2), то даже этому условию не может
удовлетворять никакой код Хэмминга (кроме (3,1)) для любого
конечного 5.
V. Заключение
Изложен метод для определения того, может ли быть
какой-нибудь смежный класс заданного группового кода сделан
поддающимся синхронизации в некоторой позиции /п. Кроме
того, предложен простой метод переделки л'юбого
циклического группового кода в код, поддающийся синхронизации во
всех позициях в пределах расстояния tn^n — k—1 от,
правильной позиции. Как следствие имеем, что если k^C (п— 1)/2,
то любой (n, k) циклический код может быть сделан при
помощи этого метода ^одом без запятой.
Значение кодов без запятой, исправляющих ошибки, состоит
в том, что они могут быть использованы в каналах с шумом
без необходимости добавления дополнительной избыточности
для получения синхронизации слов. Следует признать, что нз-за
наличия аддитивных ошибок не всегда оказывается
возможным различить немедленно синхронные и асинхронные позиции.
Однако, исследуя некоторые полученные слова, мы видим, что
благодаря отсутствию запятой среднее число ошибок в одной
позиции оказывается меньше, чем среднее число ошибок во
всех других позициях, что позволяет с возрастающей
надежностью устанавливать правильную синхронизацию. Для
каналов с сильным шумом это различие может стать менее
заметным. Для этих каналов, однако, желательно использовать коды
с большей избыточностью, т. е. коды, для которых отношение
kjn мало. В этом случае возможно наложить более сильное
46
Дж. Штифлер
условие, чем условие отсутствия запятой. Можно найти коды,
для которых каждое перекрытие отличается от любого
истинного кодового слова по крайней мере в d позициях [7], в
результате чего синхронная и асинхронная операции легко
различимы даже в каналах с шумом. Наконец, если k>(n—1)/2,
то метод, изложенный здесь, не позволяет устанавливать
синхронизацию во всех ошибочных позициях, по крайней мере
если используются циклические коды. Однако даже здесь
первые п—k— 1 позиций с обеих сторон от правильной позиции
защищены и вставка или выпадение .п — k — 1 символов могут
быть обнаружены.
ЛИТЕРАТУРА
1. Barker R. Н., Group synchronization of binary digital systems, in
Communications theory, (T) W. Jackson, ed. London, 1953, 273—287.
2. G i 1 b e r t E. N., Synchronization of binary messages, IRE Trans.
Information Theory, IT-6 (1960), 470—477. (Русский перевод:
Гилберт Э. Н., Синхронизация двоичных сообщений, Кибернетический
сборник, вып. 5, ИЛ, М., Г962.)
3. Sellers F. F., Jr., Bit loss and gain correction code, IRE Trans.
Information Theory, IT-8 (1962), 35—38. '
4. G о 1 о m b S. W., Gordon В., Welch L. R., Comma-free codes,
Canadian J. Math., 10 (1958), 202—209. (Русский перевод: Голом б С. У.,
Гордон Б. и В е л ч Л. Р., Коды без запятой, Кибернетический
сборник, вып. 5, ИЛ, М, 1262.)
5. Kendall W. В., Reed I. S., Path invariant comma-free codes, IRE Trans.
Information Theory, IT-8 (1962), 350—355.
6. Peterson W. W.. Error-correcting codes, The M. I. T. Press, Cambridge,
Mass., and John Wiley and Sons, Inc., New York, 1961. (Русский
перевод: Питерсон У., Коды, исправляющие ошибки, «Мир», М., 1964.)
7. Stiffler J. J., Synchronization of telemetry codes, IRE Trans, on Space
Electronics and Telemetry, SET-8 (1962), 112—117.
Минимальное число замыкающих
контактов, достаточное для реализации
одной симметрической булевой
функции п переменных1}
Жорж Апсель
Введение
Рассмотрим симметрическую булеву функцию п переменных
i<j
Лупанов [1] показал, что для минимального числа Ап
замыкающих контактов, достаточного для построения двухполюсной
схемы [состоящей только из замыкающих контактов]2),
реализующей эту функцию, справедливы неравенства
Ci и С2 суть константы. Цель настоящей работы — получение
следующих более точных неравенств [см. п. 1, 2, 3
дополнений]:
п log2 п < Ап < п (1+ 1-'°^^'°^) log2 „. w
Этот результат показывает, что Ап — бесконечно большая
величина порядка п log2 п.
1. Доказательство неравенства Лл>я \ogztt
Приведение схем. Можно показать, что каждая схема,
реализующая функцию Fnt может быть преобразована без
увеличения числа контактов в ней в схему, удовлетворяющую двум
следующим условиям:
1) каждая вершина, отличная от полюсор (/ и Г), связана
по крайней мере одним контактом с полюсом / и с полюсом Г;
2) когда контакт некоторой переменной х{ связывает полюс
(/ или Т) с какой-то другой вершиной, никакой другой контакт
1) Hansel G., Nombre minimal de contacts de fermeture necessaires
pour realiser une fonction booleenne symetrique de n variables, C. R. Acad.
Sci. Paris, 258, № 26 (1964), 6037—6040.
2) В квадратных скобках э данной ц последующих двух статьях
помещены примечания редактора перевода. — Прим. ред,
48 Ж. Апсель
той же самой переменной Х\ не связывает этой вершины с
третьей [см. п. 4 дополнений].
Впоследствии мы можем ограничиться только изучением
схем, удовлетворяющих этим двум свойствам [такие схемы
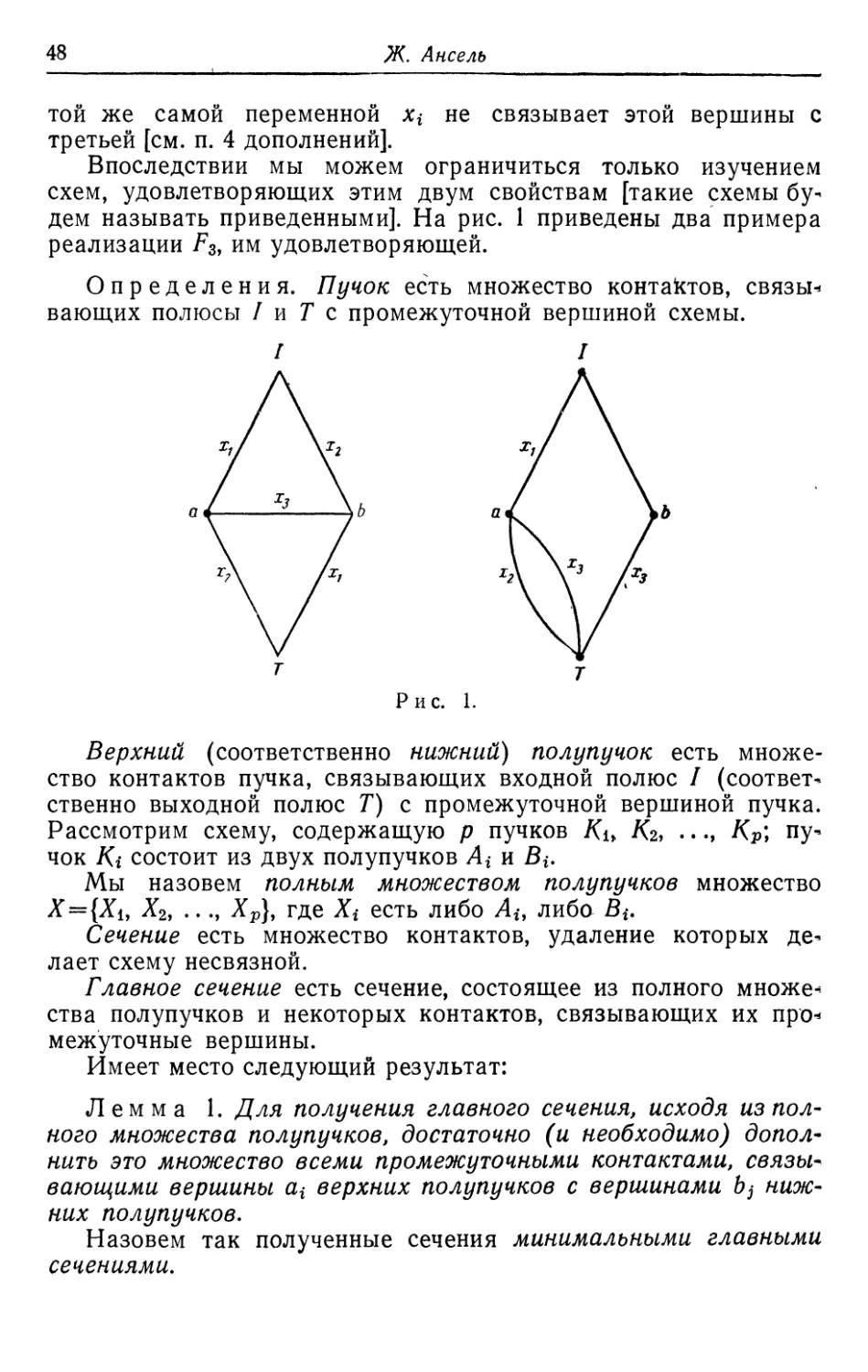
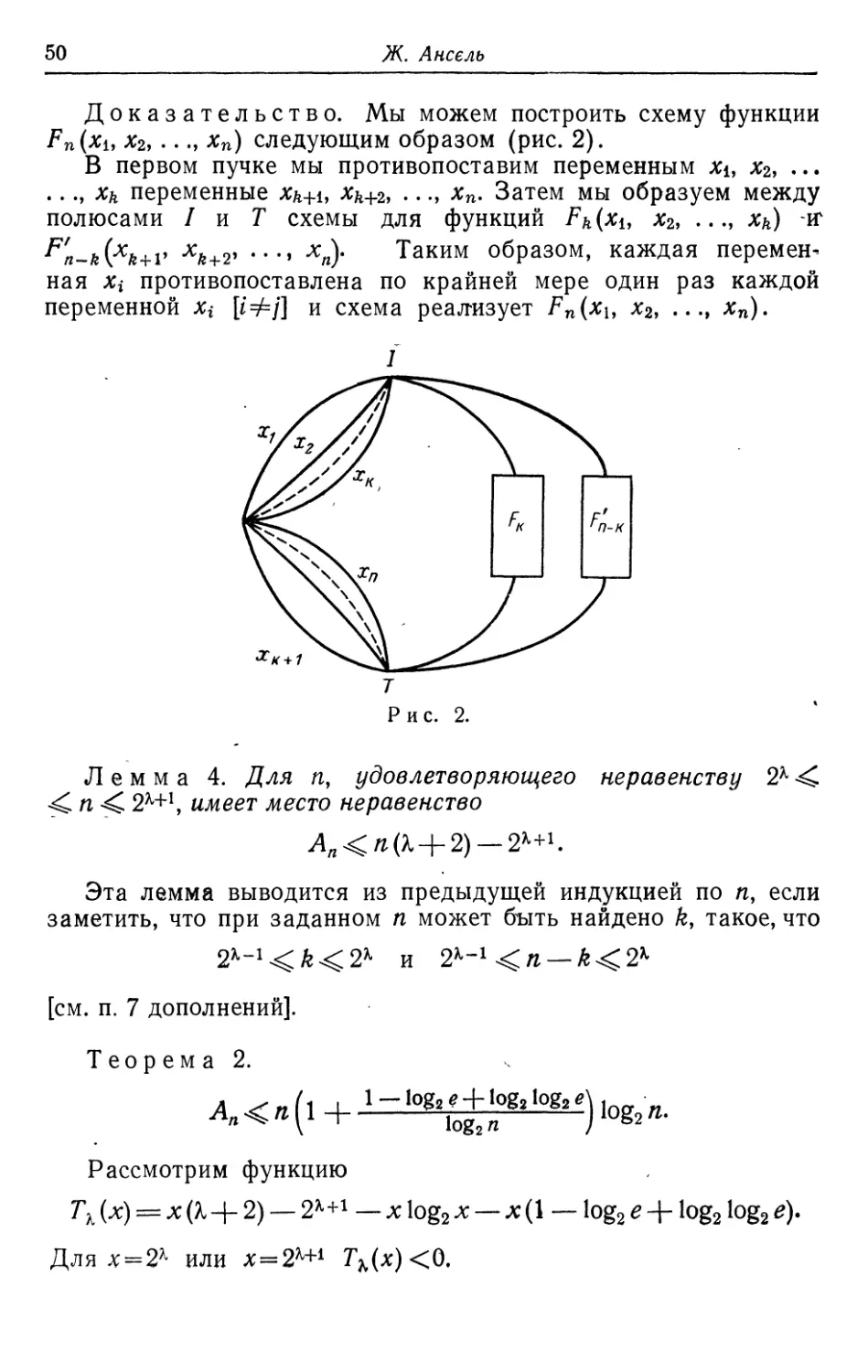
будем называть приведенными]. На рис. 1 приведены два примера
реализации F3, им удовлетворяющей.
Определения. Пучок есть множество контактов, связью
вающих полюсы / и Т с промежуточной вершиной схемы.
Рис. 1.
Верхний (соответственно нижний) полупучок есть
множество контактов пучка, связывающих входной полюс /
(соответственно выходной полюс Т) с промежуточной вершиной пучка.
Рассмотрим схему, содержащую р пучков Ки -Кг, ..., Кр\
пучок К% состоит из двух полупучков Ai и В*.
Мы назовем полным множеством полупучков множество
X = {Xi, Х2, ..., Хр}, где Х{ есть либо Лг-, либо Вг-.
Сечение есть множество контактов, удаление которых
делает схему несвязной.
Главное сечение есть сечение, состоящее из полного
множества полупучков и некоторых контактов, связывающих их про*
межуточные вершины.
Имеет место следующий результат:
Лемма 1. Для получения главного сечения, исходя из
полного множества полупучков, достаточно (и необходимо)
дополнить это множество всеми промежуточными контактами,
связывающими вершины ai верхних полупучков с вершинами bj
нижних полупучков.
Назовем так полученные сечения минимальными главными
сечениями.
Минимальное число замыкающих контактов
49
Схема из р пучков содержит ровно 2Р полных множеств
полупучков и 2Р различных главных минимальных сечений
Обозначим через
р число пучков схемы;
pi число пучков, не содержащих контактов
переменной Хи
а{ число контактов переменной xit связывающих
промежуточные вершины.
Тогда можно доказать следующую лемму:
Лемма 2. В приведенной схеме, реализующей Fn,
существует 2Рга'1 минимальных главных сечений, не содержащих
п
переменной xit и, таким образом, по меньшей мере 2 2Pi~ui
1-1
различных минимальных главных сечений [см. п. 5
дополнений].
Теорема 1. Ап k>п log2 п.
Сохраняя те же самые определения чисел р, рь я*,
получаем, что число Ап контактов схемы равно [см. п.- 6 дополнений]
п п
Ап = пр—21р1+21а1.
i-i , /-1
Схема содержит (в силу леммы 2) по меньшей мере
п
22р'~а' различных минимальных главных сечений и, следо-
i-i
вательно,
Числа 2pt~ai положительны, поэтому
п
\^2pi-ai>[2^prai)} ", откуда An>nlog2n.
1-1
2. Доказательство неравенства
Лемма 3. Для всякого k, заключенного между 0 и п,
числа Ап, Ak, An-h удовлетворяют неравенству
50
Ж. Лисель
Доказательство. Мы можем построить схему функции
Fn(xu x2l ..., хп) следующим образом (рис. 2).
В первом пучке мы противопоставим переменным xt, х2у ...
..., хк переменные Xh+u xk+2, ..., хп. Затем мы образуем между
полюсами / и Т схемы для функций Fk(xu х2, ..., Хь) -и1
F'n-k(xk+v xk+v •••> хпУ Таким образом, каждая
переменная Xi противопоставлена по крайней мере один раз каждой
переменной х% [i=f=f\ и схема реализует Fn(xu х2, ..., хп).
Лемма 4. Для п, удовлетворяющего неравенству 2Л <!
< п К 2Я+1, имеет место неравенство
Ап^п(1 + 2) — 2к+1.
Эта лемма выводится из предыдущей индукцией по я, если
заметить, что при заданном п может быть найдено k, такое, что
2^-1<fe<2^ и 2^-1 </г — £<2*
[см. п. 7 дополнений].
Т е о р е м а 2.
Рассмотрим функцию
7\ (л:) = х {% + 2) — 2Х+1 — х log2 х — х (1 — log2 е + log2 log2 е).
Для х = 2* или х=2^ Th(x)<0.
Минимальное число замыкающих контактов
51
Максимум Тх(х) при х в пределах от 2К до 2^-+1 равен нулю.
Следовательно, если 2x<a:<2x+1, то
В силу леммы 4 теорема выводится из этого неравенства.
Дополнения редактора перевода
1) Верхняя оценка указанного автором вида фактически
была установлена ранее В. К. Коробковым [2]. Р. Е.
Кричевским было показано [3], что Ап !> -^ п log2 п, и тем самым
установлен порядок роста функции Ап.
[Рис. 3.]
2) Оценки, найденные автором, дают асимптотику функции Ап
Ап — п log2 /г.
Нижняя оценка в (*) достигается для последовательности
я = 2т, т.е. A2m = m2rn (см. ниже), т.е. известная схема для
функции Fn при п = 2т является минимальной.
3) Впоследствии независимо и почти одновременно
автором этой работы и Р. Е. Кричевским было показано" [4, 5], что
верхняя оценка, приведенная в лемме 4 этой работы, является
точной.
4) Если некоторая вершина а соединена контактом Х\ с
полюсом / и с другой вершиной р, то «перебросим» конец а
контакта (оф) в / (рис. 3). После конечного числа таких
преобразований получится схема, обладающая свойством 2 относи^
тельно полюса /.
Если некоторая вершина не соединена контактом с /,
отождествим ее с Г. В результате таких преобразований (и
отбрасывания лишних контактов, если такие появятся) получится
схема, реализующая F и обладающая свойством 1..
52
Ж. Апсель
Наконец, к полученной схеме применим преобразования
первого типа, но относительно полюса Т.
5) Разобьем пучки, не содержащие контактов переменной
%и на подмножества, отнеся в одно подмножество пучки, вну^
тренние вершины которых можно соединить цепочкой из
промежуточных контактов переменной Х{. Число этих подмножеств
равно Pi — щ (если аг = 0, то каждое подмножество состоит из
одного пучка; добавление одного промежуточного контакта
переменной Х{ уменьшает число подмножеств на единицу —
объединяет два подмножества в одно). При образовании
рассматриваемых сечений в каждом подмножестве (независимо) можно
включать в сечение (все) верхние или нижние полупучки.
6) В минимальной схеме число контактов переменной х{
в пучках равно числу пучков, содержащих контакты
переменной Хи т. е. равно р — pi.
7) При к=1 (2-<я<^4) неравенства леммы очевидны:
Л2<2, Л3<5, Л4<8.
Л ИТЕРАТУРА
1. Лупанов О. Б., О сравнении сложности реализации монотонных
функций контактными схемами, содержащими лишь замыкающие контакты,
и произвольными контактными схемами, ДАН СССР, 144, № 6 (1962),
1245—1248.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
2. Коробков В. К., Реализация симметрических функций в классе П-схем,
ДАН СССР, 109, № 2 (1966).
3. К р и ч е в с к и й Р. Е., О сложности параллельно-последовательных
контактных схем, реализующих одну последовательность булевых
функций, сб. Проблемы кибернетики, вып. 12, Физматгиз, М., 1964.
4. Hansel G., Nombre des lettres necessaires pour ecrire une fonction syme-
trique de n variable, C. R. Acad. Sci. Paris, 261, № 21 (1965), 1297—1300.
5. Кричевский P. E., Минимальная схема из замыкающих контактов для
одной булевой функции от п аргументов, сб. Дискретный анализ,
вып. 5, Новосибирск, 1965.
О числе монотонных булевых функций
п переменных1*
Жорж Апсель
Задача определения числа г|?(п) элементов дистрибутивной
свободной структуры с п образующими (равного числу
монотонных2) булевых функций п переменных) была поставлена
Дедекиндом в 1897 i\ [1]. Она была решена этим автором
для п = 4.
Р. Черч решил ее в 1940 г. [2] для л = 5.
М. Уорд сделал то же самое для п = 6 в 1946 г. [3].
В 1954 г. [4] Э. Н. Гилберт показал, что ty(n) удовлетворяет
неравенствам
сЖ c[f]
2 п <г|)(/г)</г п + 2,
где [п/2] — наибольшее целое число, меньшее или равное л/2.
В серии публикаций В. К. Коробкова с 1962 по 1965 г.
получены результаты [5]
[-1 [-1
2 п <г|)(#)<2 п \ п) (еЛ->0 при #->оо);
ATI srW
2 п <Ф(/г)<25С« .
Тот же автор показал, что минимальное число ср(я)
операций наилучшего алгоритма распознавания одной произвольной
монотонной булевой функции удовлетворяет неравенствам 3)
с1Т^с1Т^1<Ф(/г)<5сИ(1 + еЛ),
1) Hansel G., Sur le nombre des fonctions booleennes monotones de n
variables, С R. Acad. Sci. Paris, 262, № 20 (1966), 1088—1090.
2) У автора monotones croissantes. Булева функция f(xu ..., xn)
называется монотонной, если f(alt . a., an) </(pi, ..., Pn) для всяких двух
наборов (аь ..., ап) и (рь ..., Рп), таких, что ai<|3j, ..., ап< fin. —Прим.
ред.
3) Определение функции ср(/г) см. в [5], стр. 7, — Прим. ред.
54
Ж. Апсель
где
Цель настоящей работы — установить следующие
результаты:
2 я <Ф(л)<3 л
Ф(«)=#'+сИ+1.'
Лемма. Единичный n-мерный куб Вп, наделенный
обычным отношением порядка (ср. [4] или "[5]), может быть покрыт
множеством из С„ попарно непересекающихся цепей*),
обладающих следующими свойствами:
a) число цепей длины п — 2р+1 равно Срп — С%~г(0^р^
<; [/г/2]) [минимальный элемент каждой такой цепи есть
набор с р единицами и п — р нулями, максимальный — с р нулями
и п — р единицами];
b) если заданы три элемента <х\ < аг < аз, образующие цепь
и принадлежащие одной и той же цепи длины п — 2/7 + 1, то
относительное дополнение а2 на интервале [аь а3]2)
принадлежит цепи длины п — 2р— 1.
Доказательство. Доказательство проводится по
индукции. Для п = 1, 2 лемма верна.
1) Куб Вп делится на два подмножества Вп-\ и Вп-\
[минимальное и максимальное], изоморфные кубу fin-i и полученные
соответственно присоединением 0 или 1 слева к координатам
куба Bn-i- В предположении, что лемма верна для куба Вп-ь
мы покроем Вп множеством цепей [определяемых следующим
образом]:
Г Пусть Z?i-i и 5л_л покрыты каждое множеством CiJiT1)/21
цепей, обладающих свойствами, указанными в формулировке
леммы [вторая часть свойства а) — без учета добавления раз-*
ряда]. Пусть d — одна из цепей Вп-ъ и пусть уу—ее
наибольший элемент.
1) Цепь —это последовательность Р(1), Р(2), ..., Р(ф
элементов из Вп, такая, что Р^ ; получается из
заменой одного нуля (в наборе координат) на единицу.—
Прим. ред.
2) То есть четвертый элемент р, образующий вместе с
аи (%2 и а3 квадрат (рис. 1). — Прим. ред.
&ъ
Р
*»
[Рис. 1.]
О числе монотонных булевых функций п переменных 55
2° Мы продолжим Си добавив к ней наибольший элемент
у2 цепи С2, изоморфной С\ в Вп-\ [см. рис. 2].
3° Отнимем у С2 ее наибольший элемент у2. [После
осуществления преобразований 2° и 3° для новых цепей будет
выполнена вторая часть свойства а).]
0/7-/
[Рис. 2.]
4° Произведем те же самые операции со всеми цепями из
Вп-ъ
Тогда цепи, покрывающие Вп, не будут пересекаться и
число цепей длины п — 2р+1 будет равно
{CU - с>:1)+(cs:l - с*:?) = с»п- Сп-\
2) Свойство Ь) леммы является непосредственным
следствием вышеприведенной конструкции [см. дополнение
редактора перевода].
Теорема 1. Минимальное число операций ф (п)
наилучшего алгоритма распознавания произвольной монотонной
булевой функции f(xit х2, ..., хп) есть
ф(Я)=с[*'+с1*1+1.
Доказательство. Из [5] мы уже знаем, что
Ф(/0>с[тЧс« \
56
Ж. Апсель
С другой стороны, свойство Ь) вышеупомянутой леммы и
монотонный характер функции f(xi, х2, ..., хп) позволяют
сделать следующий вывод: если значение f(xit х2, ..., хп) известно
во всех вершинах цепей длины п — 2р—1, то в каждой цепи
длины п — 2р + 1 существуют самое большее две (соседние)
вершины, где значения f(xi, х2, ..., хп) остаются
неопределенными. В результате получаем, что 1)
ф(«)<сИ+сИ+1.
Теорема 2. Число г|)(л) монотонных булевых функций п
переменных удовлетворяет неравенствам 2)
сШ с!т1
2 я <*(")< 3 п .
Доказательство. Нижняя оценка \|)(/г) уже доказана в [4].
Пусть cti и а2 (cti<a2) —две соседние вершины, оставшиеся
неопределенными в цепи из Вп. Функция f(xi, х2, ..., хп)
может принимать в этих вершинах лишь следующие наборы
значений: (0, 0) или (0, 1), или (1, 1). В результате получаем, что
г|)(/г)<3Ся .
Следствие. Число функциональных элементов
(конъюнкций, дизъюнкций, отрицаний), достаточное для реализации
произвольной монотонной булевой функции [п переменных],
оценивается сверху величиной
(log2 3) Y~ J* П +8 (*)]•е (») -+ ° "Р*
>оо.
Это следствие получается применением метода локального
кодирования, описанного в [5]3) (для теоремы 4а), с
использованием приведенной выше верхней оценки.
1) Ф(я)^ (число цепей длины 1)+2(число цепей длины !> 2).— Прим.
ред.
2) Если п — четное, то можно записать
СШ сИ_с[тН с[тЬ
3) Более подробно о принципе локального кодирования см. в [6]. —
Прим. ред.
О числе монотонных булевых функций п переменных 57
Дополнение редактора перевода
Цепи в Вп — двух сортов: «удлиненные», возникшие из
цепей в 5/г-ь и «укороченные», возникшие из цепей в Bn^v
Рассмотрим несколько случаев для трех последовательных
элементов ai<a2<a3, лежащих на построенной цепи С в Вп
(длины п — 2р+1).
I. С — удлиненная цепь, и а3 не есть ее максимальный
элемент. В этом случае ot±, а2, а3 лежат на некоторой «старой»
цепи в Bln^\ (длины п — 2р). Относительное дополнение
элемента а2 находится на некоторой цепи С (длины п — 2р — 2)
в Вп-ъ которая будет продолжена при переходе к Вп до цепи
длины п — 2р — 1.
II. С — удлиненная цепь, и а3—ее максимальный элемент.
Пусть С = С\ (рис. 2) возникла в результате удлинения цепи
С4 из Вгп-г; С2 — цепь в Вп-\> изоморфная С4;
С?—укороченная цепь, возникшая из С2 \С2 имеет длину п — 2р—1).
Тогда относительное дополнение элемента а2 есть
максимальный элемент цепи С2.
III. С — укороченная цепь. Пусть С = С<2 возникла из
цепи С2 (длины п — 2р + 2) в Вп^\. Тогда, во-первых, а3—не
максимальный элемент цепи С2 и, во-вторых, в силу второй
части свойства а) максимальный элемент а цепи С2 имеет р—1
нулей. В силу свойства Ь) относительное дополнение р
элемента а2 принадлежит некоторой цепи С длины п — 2р в В2п^\\
максимальный элемент этой цепи имеет р нулей. Так как
Р<а3<а, то р имеет не менее р+\ нулей и поэтому не является
максимальным элементом цепи С. Следовательно, р
принадлежит укороченной цепи длины п — 2р—1, получающейся из С.
ЛИТЕРАТУРА
1. Dedekind R., Ueber Zerlegungen von Zahlen durch ihre grossten ge-
meinsamen Teiler, Festschrift Hoch. Braunschweig, 1897 u. ges. Werke, II,
103—148.
2. Church R., Numerical analysis of certain free distributive structure, Duke
Math. /., 6 (1940), 732—734.
3. Ward M., Abstract 52-5-135, Bull. Amer. Math. Soc.t 1946.
4. Gilbert E. N., Lattice theoretic properties of frontal switching functions,
J. Math. Phys., 33, № 1 (1954), 57—67. (Русский перевод:
Гилберт Э. Н., Теоретико-структурные свойства замыкающих
переключательных функций, Кибернетический сборник, вып. 1, ИЛ, М., 1960.)
5. К о р о б к о в В. К., О монотонных функциях алгебры логики, сб.
Проблемы кибернетики, вып. 13, изд-во «Наука», М., 1965.
6*. Лупанов О. Б., Об одном подходе к синтезу управляющих систем —
принципе локального кодирования, сб. Проблемы кибернетики, вып. 14,
изд-во «Наука», М., 1965, 31—110.
Построение двухполюсной контактной
схемы для произвольной монотонной
булевой функции п переменных1)
Жорж Апсель
Введение. Обозначим через:
<£Гп (соответственно &п) множество булевых функций
(соответственно монотонных булевых функций) п переменных;
L(n) (соответственно £/(я)) минимальное число контактов,
достаточное для реализации двухполюсной схемой произвольной
функции из <£Гп (соответственно &п)2)\
Fh(n) (соответственно 1н{п)) число функций из &'п
(соответственно из Зп), каждую из которых можно реализовать
h контактами.
2п
Шеннон [1] показал, что для всякого е>0 при А = —'(1 —е)
Используя тот же метод и результаты Э. Н._Гилберта [2],
/2~ 2п
7=^(1 —е)
я пуп
С другой стороны, Лупанов [3] показал, что
Цель настоящей работы — доказательство неравенства3)
п }^ пУш \ ^ \\og2nj)
1) Hansel G., Construction d'un schema de contacts bipolafre pour une
fonction booleenne isotone arbitraire de n variable, С R. Acad. Sci. Paris, 263,
№ 19 (1966), 651—654.
2) Допускаются размыкающие контакты. — Прим. ред.
3) Аналогичный результат для контактно-вентильных схем получен
Э. И. Нечипоруком (Э. И. Н е ч и п о р у к, «О вентильных схемах», Тезисы
докладов Международного симпозиума по теории релейных устройств и
конечных автоматов, 24 сентября — 2 октября 1962 г., М., 1962, 42—43) как
следствие его результата о реализации булевых матриц вентильными
схемами. — Прим. ред.
Построение двухполюсной контактной схемы 59
1. Обозначения. Пусть Вп— единичный я-мерный куб,
наделенный обычным отношением порядка.
Полагая X=(xif ..., хп), мы обозначим через Ка(Х)
характеристическую функцию множества АаВп. Пусть g(X) €<^п.
Обозначим через g+(X) функцию, определенную следующим
образом:
J-/W И» если существует а<ЛГ с g(p) = l,
g+ (X) = < *
[ 0 в противном случае.
Наконец, мы обозначим через [х] целую часть х.
2. Разложение монотонной булевой функции. Пусть f(X) =
=f(xu х2, •.., хп)—монотонная булева функция.
Разобьем переменные из X на два множества
X1 = (xv ..., xk) и Л2 = (^+1, ..., хп).
ГА]
Мы показали [4], что Bh может быть разбит на С\2 J цепей;
пусть это Jv J2, ..., Jm% ..., J r*i,
42j
Мы разобьем цепи на q подмножеств вида х)
Ч
Li={JJai-i+l (1<1<Ч> ао = 0)»
ы\
таких, что для всех i пусть справедливы неравенства
5 — функция я, которая будет уточнена позднее.
Простые алгебраические вычисления тогда показывают,
что 2)
с14Чй+')
"< s-bsJ+V +'■ <2>
!) Цепи рассматриваются как множества элементов. — Прим. ред.
2) В силу (1) для каждого подмножества Li
тт 2s 2s
11(|/(т^1+г| + 1)> max|/m| + i ^т+т-
С другой стороны, поскольку число цепей длины k — 2p+\ равно С%—С%~\
60
Ж. Апсель
Множества Li представляют собой разбиение куба В*.
Лупанов [3] показал, что если г есть целая степень двойки,
то множество Вт может быть разделено на 2г/г сфер (§,), 1 <
</<2'/г.
Предположим, что r-<n — kt и положим Cj = S>jXBn~k~r.
Множества (Cj), 14^j^2r/r, представляют собой
разбиение Bn~h.
Пусть fij{X)—булева функция, совпадающая с f(X) на
LiXCj и равная нулю вне LiXCj.
Расположим элементы Li в определенном порядке; пусть
^i = {ai» а2> •••» amf •••' a\L.\)' Обозначим через f*j(X)
отображение Cj в В\1^» определенное как
* = flj(V)={fu(av Р). М^ Р). •••• M<*«. Р). •••• fiji^L^Y
Отображение /*;-(Р) индуцирует разбиение Cj. Обозначим через
С) множество элементов Q, образ которых при отображении
fij есть f.
имеем
Поэтому
Но
[-1
Q sl L 2 J ср_ср-\
ПП(|-Ч 1+г|+1)=-П ^-2^+2)й * •
[4]
2 (С* - Cg"1) log2 (ft-2р +2)
^ ~ s-log2(ft + 2) +ь
l
[т] \ ' [4]
П(й-2р + 2)С'-С'_1) •< * t (*-^ + 3)(С«-СП
С
и
L 2 J ш
2(^-2^ + 2)(^-^)-(^-2^ + 2)4^ +
р-0
+ 2 J] Cf = 2ft + 42J-
Из трех последних соотношений получаем (2).—Прим, ред.
Построение двухполюсной контактной схемы
61
Кроме того, всякий раз t=(tu t2i ..., tm, ..., t\Lt\)-
Сопоставим каждому множеству Li его подмножество L%
определенное так:
Мы можем тогда сформулировать
Предложение 1. Всякая монотонная булева функция
f(X) имеет разложение вида
/(*)=2 2 2 К^(Хг)КсЛХ^
3. Пусть S — контактная схема типа (/, т), т. е. имеющая
/ входных полюсов /ь /2, ...,// и m выходных полюсов Pi, Р2,
..., Pw. Обозначим через fab функцию, реализованную между
полюсами а и Ь. Мы говорим, что S разделительная, если для
всяких /, fe, г, 5 (гФ$) справедливы соотношения
f'jPs>f'jPkfprPs и fp/s>fpjIJIrIs:
Тогда имеет место
Предложение 2. Пусть даны две разделительные
контактные схемы: Si типа (1,т), имеющая один входной полюс
/ и т выходных полюсов Ри Р2, ..., Рт, и S2 типа (т, 1),
имеющая входные полюсы /4, /2, ..., /т и выходной полюс Р. Если
соединить выходные полюсы Si с соответствующими входными
полюсами S2, то реализуемая функция такова:
m
у-1 "V ЛГ
(fab — функция, реализованная между а и Ь в Si.)
4. Предложение 3. Двухполюсная схема функции
может быть реализована посредством r2 + 2n-ft-r+1+r2n_ft-r-f
L+2s£s контактов, где г — целая степень двойки и r^Cn — k.
62
Ж. Апсель
Доказательство. Лупанов [3] показал, что
разделительная схема типа (1, |/*ДСу)|)> реализующая все функции
К t(X^t t^Fijipj)* может быть построена из г -f-2
/z-fc-r+l
+
+ 2Л k тг контактов.
Положим L\ t == L\ П Ja +l> и пусть m\ t— наименьший
элемент L\,i. Имеем
Ki
и, следовательно,
"^№=2 2 ка{хх)
K^X^^K^JX,).
(3)
Из неравенства (1) легко вывести s^s (1 •</-</?) и
f]j (Су) | < 2s к так как fa(X) монотонна на L^XQ.
Используя (3), можно, следовательно, построить
разделительную схему типа (|ПДС/)|» 1), реализующую множество
функций K*t{X^t t£f*ij{p)) посредством 2sks контактов.
Применяя предложение 2, получаем искомый результат.
5. Теор е м а.
M*)<y+,^"h +о(-Ч1-
М ;^ лГяп L V log2 /г; J
Доказательство. Используя предложения 1 и 3, так же
как и неравенство (2), можно построить для произвольной
монотонной функции !{Х)£&п схему, число S(n) контактов
которой удовлетворяет неравенству
S(*)<T
-Ш
log2
2*
.[т]
s — log2(£ + 2)
+ 1
(г2+2л-
ft-r+1
Ч-
4-r2"-*--r+ 2s ks).
Положим
Ji
log2/i
r = 2La "4 s = [| —/й], * = [|-31og2«].
Тогда легко получим основной результат.
Построение двухполюсной контактной схемы 63
ЛИТЕРАТУРА
1* S h a n п о п С. Е., The synthesis of two-terminal switching circuits, BSTJ,
28, № 1 (1949), 59—98. (Русский перевод: Шеннон К., Работы
по теории информации и кибернетике, ИЛ, М., 1963.)
2. Gilbert Е. N., Lattice theoretic properties of frontal switching functions,
J. Math. Phys., 33, № 1 (1954), 57—67. (Русский перевод:
Гилберт Э. Н., Теоретико-структурные свойства замыкающих
переключательных функций, Кибернетический сборник, вып. 1, ИЛ, М., 1960.)
3. Л у п а н о в О. Б., О синтезе некоторых классов управляющих систем, сб.
Проблемы кибернетики, вып. 10, Физматгиз, М., 1963.
4. Hansel G., Sur le nombre des fonctions booleennes monotones de n
variables, C. R. Acad. ScL Paris, 262, serie A (1966), 1088. (Русский перевод:
см. настоящий сборник, стр. 55—59).
Многоленточные и бесконечные
автоматы. Обзор 1}
Патрик Фишер
Обзор посвящен машинам, более мощным, чем автоматы,
но с меньшими возможностями, чем общие машины Тьюринга.
По-видимому, машины этого типа также тесно связаны с
такими цифровыми вычислительными устройствами, как
конечные автоматы и неограниченные машины Тьюринга.
Промежуточные машины могут порождаться при
добавлении бесконечной памяти к машине с конечным числом
состояний, когда выполняется по крайней мере одно из условий:
1) ограничивается способ поступления неограниченных порций
памяти; 2) ограничивается число шагов для вычисления
некоторой возрастающей рекурсивной функции от длины входа;
3) ограничивается общий объем памяти, доступный в этом
смысле. Рассматриваются примеры из этих трех классов и
обсуждаются их свойства.
1. Введение
В последние годы возрос интерес к абстрактным машинам
с большей вычислительной способностью, чем конечные
автоматы, но с меньшей потенциальной сложностью, чем машины
Тьюринга. Хотя вычислительное устройство без
вспомогательной ленты может рассматриваться как конечный автомат,
а устройство с неограниченной вспомогательной лентой — как
машина Тьюринга (см. Ван [65]), ни тот, ни другой подход не
позволяют проникнуть в суть природы вычислений настолько
глубоко, как этого хотелось бы.
Регулярные множества Клини [36], распознаваемые одно-
ленточными автоматами с конечным числом состояний,
составляют очень небольшой подкласс класса рекурсивных множеств.
Последние могут быть распознаны машинами Тьюринга [64], но,
вообще говоря, не могут быть распознаны машинами с меньшей
вычислительной способностью. Между регулярными множе-
l) F i s с h е г Р. С, Multi-tape and infinite-state automata, A survey, Com-
тип. ACM., 8, № 12 (1965), 799-805.
Многоленточные и бесконечные автоматы
65
ствами и рекурсивными множествами лежит бесчисленная
совокупность классов множеств неотрицательных целых чисел1).
Такими классами являются детерминированные (pushdown)
языки [26], контекстно-свободные языки [8], языки, зависящие от
контекста [8], элементарные множества [28],
примитивно-рекурсивные множества [35], доказуемо-рекурсивные множества [20]
и многие другие.
Любой из вышеперечисленных классов может оказаться
более тесно связанным с реальным вычислением, чем регулярные
множества и рекурсивные множества. Таким образом, во
многих случаях машины с промежуточной вычислительной
способностью служат лучшей моделью для реальных вычислительных
устройств, чем более изученные конечные автоматы и машины
Тьюринга.
В этой статье делается попытка дать список невероятности
ных промежуточных машин. Конечные автоматы и
неограниченные машины Тьюринга обсуждаться не будут, но
предполагается знакомство с [51] и первой частью [13]. Термины машина
и автомат оба употребляются для обозначения полностью
определенной дискретной системы, определяющей класс множеств,
лежащей между регулярными и рекурсивными множествами.
Термины акцептор (допускатель), генератор и преобразователь
обозначают соответственно машины, которые не имеют иных
выходов, кроме «допускаю» или «отвергаю»,, машины, не
имеющие входа, кроме единственного начального сигнала, и машины
с входами и выходами.
2. Многоленточные автоматы с конечным числом состояний
Простейшим обобщением одноленточных машин с конечным
числом состояний являются я-ленточные односторонние
акцепторы, которые ввели Рабин и Скотт. Эти устройства
распознают множества я-наборов строчек, причем в ходе вычисления
на каждом шаге одна из входных лент продвигается на один
квадрат и машина переходит в новое состояние. Сдвигаемая
лента зависит от текущего состояния машины, и м-набор
допускается или отвергается в зависимости от того, приходит ли
машина в заключительное состояние после прочтения всех
символов со всех я,лент или нет. Допускаются специальные
символы на концах лент.
1) Часто предпочитают иметь дело со строчками символов, а не с
числами. Обычная процедура связывает с числом строчку, представляющую его
я-значное выражение для некоторого nt взятого за основание (без потери
общности можно считать, что л=2)»
66
П. Фишер
Детерминированный и недетерминированный варианты этих
машин порождают для каждого п классы множеств я-наборов,
обозначаемые через Dn и Nn соответственно. Для м>1 класс
Dn замкнут относительно взятия дополнения, но Рабин и Скотт
показали, что он не замкнут относительно объединения или
пересечения [51]. Розенберг показал, что Dn не замкнут
относительно обращения входных слов, сцепления слов (т. ё.
умножения) и оператора замыкания (звездочки) Клини [54] *).
В отличие от случая п=\ для п>\ детерминированный
я-ленточный автомат- существенно отличается от
недетерминированного. Пример множества из N2— D2l данный Розенбер-
гом, есть множество всех пар строк, в которых второй элемент
пары равен некоторому отрезку конца первого элемента (т. е.
вида (ху, у)). Элгот и Мезей установили, что Nn замкнут
относительно объединения, сцепления, звездочки и обращения
входов [15]. Поскольку Nn в действительности является
наименьшим классом, содержащим все конечные множества я-наборов
и замкнутым относительно объединения, сцепления и звездочки,
для Nn имеет место аналог теоремы Клини о регулярных
событиях. Однако для я>1 класс Nn не замкнут относительно
дополнения и пересечения.
В дополнение к тому, что классы Dn и Nn замкнуты
относительно меньшего числа операций, эти классы в некотором
смысле более сложны, чем D{ = N{ (регулярные множества).
Проблемы, разрешимые для Du ^часто оказываются
неразрешимыми для Dn (п>1). Одной из таких проблем является
проблема пересечения: определить, непусто ли пересечение двух
элементов класса множеств (см. Рабин и Скотт [51]). Проблема,
разрешимая для Du но открытая для £>п, состоит в определении
того, допускают ли две данные машины в классе одинаковые
множества я-наборов строк. Класс D2 содержит в качестве
собственного подкласса класс всех отношений, определимых
посредством «обобщенных последовательностных машин»
Гинзбурга [25].
Гинзбург и Спеньер .рассмотрели многоленточные
преобразователи с конечным числом состояний как расширение
обобщенных последовательностных машин [27]. Для машин с конечным
числом состояний с двумя входными лентами и одной
выходной они устанавливают, что если языки, допускаемые на двух
лентах из трех, регулярны, то таков же и третий язык; если
один регулярен, а другой контекстно-свободен, то и третий
1) Обращением строки GiG2... on-\On является строка Gnon-i •.. о^Оь
где Oi может быть любым символом входного алфавита. Обращение л-на-
бора производится покомпонентно,
Многоленточные и бесконечные автоматы
67
контекстно-свободен; но если два языка контекстно-свободны,
то третий не обязательно будет контекстно-свободным. Фишер
и Розенберг дали обобщение этих результатов: для я-ленточ-
ного акцептора, если п — 2 ленты ограничены регулярными
языками, а одна контекстно-свободным, то язык на последней
ленте будет контекстно-свободным и т. д. [24].
Элгот и Рутледж рассматривали детерминированные я-лен-
точные автоматы с лентами, пустыми всюду, за исключением
единственного символа на конце [17]. В отличие от общего
случая Dn проблема пересечения для класса множеств,
определенных этими машинами, разрешима. Это следует из
существования эффективного отображения таких множеств в класс
формул Пресбургера (теория сложения неотрицательных целых
чисел первого порядка), для которых проблема выполнимости
разрешима. Если допускается более чем одна головка на ленте,
то получаются все отношения Пресбургера. Были также
исследованы свойства машин, когда одна или более лент замкнуты
в кольца, а не являются прямыми лентами. Проблема,
допускает ли машина с двумя кольцевыми лентами (или с одной
лентой и двумя головками) непустое множество, неразрешима.
Для машин с одной кольцевой лентой (с одной головкой) и
п прямыми лентами проблема пересечения остается открытой.
Она разрешима, если разрешима десятая проблема Гильберта.
3. Машины с ограниченным доступом к памяти
Если обратиться к устройствам с бесконечным числом
состояний, то станет ясно, что в общем случае они обладают
вычислительными возможностями машины Тьюринга. Можно,
однако, получить промежуточные классы, накладывая ограничения
на доступ устройства к его памяти (т. е. на переходы
состояний) и (или) путем запрещения вычислений, при которых
данная мера сложности (например, число «шагов») превышает
некоторую величину (обычно функцию входа). Первый из этих
подходов обсуждается в этом разделе.
Известным примером ограничения доступа к памяти является
память типа pushdown (магазинная память), в кот9рой лишь
последний символ информации, помещенной в память,
непосредственно доступен считывающей головке. Одноленточные машины
Тьюринга, в которых лента применяется лишь как память
pushdown, называются pushdown-store машинами (машинами с
магазинной памятью). Такие машины представляют интерес для
теории автоматов и математической лингвистики, так как Хом-
ским обнаружена важная связь между двумя областями: язык
является контекстно-свободным тогда и только тогда, когда он
Ь*
68
П. Фишер
распознаваем некоторым pushdown-store акцептором [9]. Таким
образом, результаты лингвистики могут быть использованы для
доказательства теорем о pushdown-store автоматах и обратно.
Другим примером ограничений доступа к памяти является
счетчик (counter). Значение счетчика есть любое
неотрицательное целое число, и на одном шаге работы машины значение
счетчика может увеличиться на единицу, уменьшиться на
единицу или выясняется, что значение счетчика равно 0 !). Счетчик
можно также рассматривать как память pushdown с
односимвольным алфавитом.
Эви [18] и Фишер [21] исследовали детерминированные и
недетерминированные машины с одной или более pushdown-
stores и (или) счетчиками. Были исследованы отношения между
акцепторами, генераторами и преобразователями и показано,
что множество, допускаемое недетерминированным вариантом
одной из рассматриваемых машин, могло бы также быть
определено как выход детерминированного преобразователя того же
типа, и обратно. Например, класс всех множеств, являющихся
выходами детерминированных машин с одним счетчиком, класс
всех множеств, являющихся выходами недетерминированных
машин с одним счетчиком, и класс всех множеств, являющихся
областью (входа) недетерминированной машины с одним счет*
чиком, совпадают с классом С, описываемым ниже.
Согласно результату Минского [44], машины с двумя
счетчиками (а следовательно, машины с двумя pushdown-store)
обладают возможностями машины Тьюринга. Таким образом,
результат Эви и Фишера дает в точности четыре различных
промежуточных класса, которые могут быть представлены как мно«
жества, распознаваемые детерминированными и
недетерминированными акцепторами с одним счетчиком (С и С) или как
распознаваемые детерминированными или
недетерминированными pushdown акцепторами (Р и Р'). Класс Р' это, конечно,
класс контекстно-свободных языков и замкнут относительно
объединения, сцепления и звездочки, но не дополнения и
пересечения (см. Шейнберг [55] и Бар-Хилел, Перлес и Шамир [5]),
а Р является интересным собственным подклассом Р' и замкнут
относительно дополнения, но не объединения или пересечения.
Классы С и С не представляют интереса с лингвистической
точки зрения и не привлекли к себе большого внимания.
Ранние работы по pushdown-store машинам описаны Этин-
гером [47]. Шютценберже [60] дает несколько усложненное
алгебраическое определение детерминированных pushdown-store
f) Способности машин остаются неизменными, если допускать счетчики,
принимающие любые целые значения.
Многоленточные и бесконечные автоматы
69
машин и доказывает некоторые основные свойства, из которых
тривиально следует замкнутость Р относительно дополнения.
Недавно Гинзбург и Грейбах исследовали Р. За исключением
[26], большая часть их результатов еще не опубликована1).
Р и Рг и связанные с ними машины недавно были
исследованы Хэйнсом [29]. Тот факт, что языки в Р всегда
недвусмысленны (unambiguous), независимо установлен в [26] и [29].
Другие виды автоматов с ограниченным доступом к памяти
обсуждаются в некоторых статьях Шютценберже. В [56] он
рассматривает класс конечных преобразователей со способностями,
большими, чем у обобщенных последовательностных машин, но
меньшими, чем у недетерминированных конечных
преобразователей с одним входом и одним выходом. Регулярность множеств
при таких преобразованиях сохраняется.
В [57] вводятся акцепторы с бесконечнозначными
счетчиками. В отличие от вышеописанных машин со счетчиками
состояние части машины с конечной памятью2) (контрольного
органа) не зависит от содержания счетчиков (итак, машины с
двумя или более счетчиками не обладают вычислительными
возможностями машин Тьюринга). Для каждой комбинации
состояния контрольного устройства и входного символа машина
осуществляет преобразование в области ее счетчиков таким
образом, что новое значение каждого счетчика могло бы быть
вычислено конечной вычисляющей программой" (у машины есть
временная память, достаточная для того, чтобы содержать
промежуточные результаты) с применением лишь следующих
операций: 1) сложение или вычитание двух целых чисел, 2)
умножение целых чисел на ограниченную целую константу, 3)
приведение целых чисел по модулю (ограниченной) целой
константы. Машина допускает входную ленту, если я-набор,
представляющий значение счетчика после переработки всего входа,
не принадлежит данному подпространству в я-мерном
векторном пространстве над целыми числами, где выбранное
подпространство зависит от конечного состояния контрольного
устройства машины.
Шютценберже показывает, что его машины могут быть
определены в терминах конечных множеств целочисленных пХп
матриц, где п зависит от машины. Машина является таким го<
моморфным отображением моноида входов в кольцо матриц,
что входное слово допускается тогда и только тогда, когда
верхний правый вход в матрицу, связанную со словом, не равен
!) В настоящее время опубликованы работы по этой теме. См. список
дополнительной литературы [6*], [7*]. — Прим. перев.
*) Здесь говорится о конечной памяти части машины; память всей
машины бесконечна. — Прим. перев*
70
/7. Фишер
нулю. Установив эквивалентность, Шютценберже показал
алгебраическими методами, что класс, определенный целым
семейством его машин, замкнут относительно объединения,
пересечения, сцепления и звездочки, но не дополнения. Аналог
теоремы Клини, однако, не получается, потому что неизвестен
подходящий базис для индукции (для регулярных событий
базисом является класс конечных множеств).
В [58] вышеуказанные машины ограничены требованиехМ,
чтобы отношение количества информации, заключенной в
памяти машины, к длине входного слова стремилось к нулю с
ростом длины входного слова. Получается менее обширный класс,
который замкнут относительно объединения, пересечения и
сцепления, но не дополнения и звездочки. Результаты в [59] и [10]
и результаты Хомского связаны с проблемами разрешения
некоторых типов автоматов с ограниченным доступом к памяти,
включая pushdown-store машины и порождаемые языковые
грамматики с подходящей алгебраической структурой.
Центральным понятием в этом исследовании является понятие
о формальных степенных рядах.
4. Машины Тьюринга, ограниченные во времени
Время вычисления у некоторых машин обязательно должно
быть ограничено рекурсивной функцией длины входа; для
конечных автоматов из [51] таковой является тождественная
функция. С другой стороны, в общем случае для машин Тьюринга
не имеется эффективной a priori границы для времени
вычисления, иначе можно было бы разрешить проблему останова
для машин Тьюринга.
Первым, кто рассмотрел ограниченные во времени
вычисления на машине Тьюринга, был Ямада [66, 67]. Ямада особенно
интересовался строго возрастающими функциями,
определенными на неотрицательных целых числах со значениями из этой
же области и вычислимыми в реальное время согласно его
терминологии. Пусть характеристической последовательностью
множества А неотрицательных целых чисел будет двоичная
последовательность a=aoaia2, • • •» такая, что ап = 1 тогда и
только тогда, когда п£ А. Тогда монотонная функция вычислима
в реальное время, если некоторая многоленточная машина
Тьюринга может породить характеристическую последовательность
области значений f, т. е. число ап может быть порождено за
время п. Было доказано, что класс вычислимых в реальное
время функций замкнут относительно сложения, умножения,
суперпозиции, экспонирования и содержит все полиномы одного
Переменного. Зигель доказал, что существуют непримитивно-ре-
Многоленточные и бесконечные автоматы
71
курсивные функции, вычислимые в реальное время, и
монотонно возрастающие примитивно-рекурсивные функции, не
вычислимые в реальное время [62].
Хартманис и Стирнс изучали в более общей постановке
ограничения на время работы машин Тьюринга [31]. Для любой
монотонно возрастающей функции Т обозначим через SlT рласс
всех бесконечных двоичных последовательностей a=a0aia2...,
таких, что существует многоленточная машина Тьюринга,
которая порождает ап за время Т(п) для всех я. Такой класс ST
называется классом сложности. Легко показать, что для всякой
монотонной рекурсивной функции Т класс сложности ST
является рекурсивно-перечислимым множеством. Поскольку
каждая вычислимая последовательность содержится в Su для
некоторой рекурсивной функции £/, отсюда немедленно следует,
что существует бесконечно много классов сложности и что класс
всех классов сложности не может быть эффективно
перенумерован. В случае вычисления в реальное время класс Sn (т. е.
ST, где Т(п) =п) является минимальным.
Хартманис и Стирнс установили, что умножение временной
функции на константу не изменяет класса сложности, т. е.
ScT = ST для всех монотонных функций Т и констант с. Классы
сложности также не изменятся, если допустить более чем одну
считывающую и записывающую головку на ленте. Если a€ST,
то существует одноленточная машина Тьюринга, порождающая
ап за время (Т(п))2 для всех п. Тот же «закон квадрата»
появляется при переходе от многомерных лент к линейным лентам.
Хенни и Стирнс доказали, что в частично упорядоченном
множестве классов имеется плотное подмножество [34]. Они
показали, что если a€ST и функция Т вычислима в реальное
время, то существует двуленточная машина Тьюринга, которая
порождает ап за время Т(п) log (Т(п)). Это позволяет,
применяя диагональный метод, доказать, что если Т вычислима в
реальное время и
то Su содержит ST как собственный подкласс. Поскольку
функции п и [п1+е] удовлетворяют условиям теоремы, из этого
следует существование подмножества классов с порядковым
типом рациональных чисел.
Хенни также занимался проблемами распознавания с
ограничением во времени. В [33] он полагает, что вход помещен
на одной из рабочих лент машины Тьюринга (где он при
желании может быть позднее записан). Для этой модели он
72
П. Фишер
показывает, что упомянутый выше «закон квадрата» не может
быть улучшен. Для одноленточной машины он также показывает,
что если 2>р>9>1, то Snp содержит Snq как собственный
подкласс. Хотя «offline» акцепторы Хенни внешне лишь
немного отличаются от «online» варианта, в котором вход помещается
на специальной односторонней ленте, не входящей в число
рабочих лент машины, эти две модели обладают совершенно
различными свойствами.
Работа Хартманиса, Хенни и Стирнса поднимает много ин^
тересных проблем. Верно ли, что при lim п\ \ = 0 ST Ф 5^?
_ Л->оо и \п)
Двоичное представление У"2 лежит в Sn*- Является ли этот
класс наименьшим? Можно ли поручить соотношения,
аналогичные тем, которые устанавливаются в [18] и [21] и охваты^
вают генераторы, акцепторы и преобразователи, с одной
стороны, и online и offline машины — с другой? В отличие от
порождения для распознавания равенство ST = ScT заменяется на
ST(n) = SC(T(n)-n)+n, поскольку считывание входных символов не
может быть ускорено. Как относится специальный случай
Т(п) =п к случаю Т(п) > (1 +е)п для е>0?
Рабин дает ответ на вопрос, поставленный в обзоре Мак^
Нотона по теории автоматов в 1961 г. [42]: может ли двулен-
точная машина Тьюринга делать в реальное время больше, чем
одноленточная? Для online акцептора он показывает, что две
ленты лучше, чем одна, если потребовать, чтобы машина
запоминала две последовательности и по требованию обращала
одну из них без задержки [50]. Заслуживающий внимания ас-:
пект этой проблемы состоит в том, что утверждение, которое
сначала кажется совсем простым, требует весьма тщательного
и сложного доказательства. Далее, никому еще не удалось
доказать на такой же модели, что три ленты лучше, чем две.
Блюм развил абстрактный подход к вычислительной
сложности [7]. Все, что он требует от меры сложности, состоит
в том, что она должна быть определена всякий раз, когда
определена частично-рекурсивная функция, с которой связана
мера сложности1), и можно эффективно определить, когда
данная граница сложности окажется превзойденной временем
вычисления (которое может завершиться или не. завершиться).
Примерами допустимых мер сложности является число шагов
в вычислении на машине Тьюринга, число квадратов ленты,
использованных при вычислении, максимальное число последова-
1) Предполагается, что мера сложности характеризует данный способ
вычисления частично-рекурсивной функции, а для другого способа
вычисления этой же функции мера сложности может быть иной. — Прим. перев.
Многоленточные и бесконечные автоматы
73
тельных единиц, появившихся на ленте в процессе вычисления,
и т.д.
Блюм доказывает, что для любой меры вычислительной
сложности, удовлетворяющей вышеуказанным требованиям, и
для всякой рекурсивной функции g(x) существует рекурсивная
характеристическая функция f(x), вычисление которой может
быть «ускорено» («speed up») в следующем смысле. Для
всякого способа вычисления f(x) существует другой способ
вычисления f(x) так, что если F(x) обозначает меру сложности
первого способа, a F'(x) —второго способа, то F(x) ^-g(F'(х))
для всех, кроме конечного числа значений х. (С другой
стороны, из работ [31] и [34] можно вывести, что существуют
также функции с мерой сложности F(x), вычисление которых не
может быть «ускорено» посредством g(x) = л;1+е.)
5. Машины Тьюринга с ограничениями длины ленты
Хорошо известным примером машин с ограниченной лентой
является линейно-ограниченный автомат Майхилла [46].
Линейно-ограниченный автомат является машиной Тьюринга,
которая работает только с лентой, занятой входным словом.
Поскольку алфавит машины может быть больше входного
алфавита, это эквивалентно высказыванию, что обмен допустимой
информационной памяти является линейной -функцией длины
входа.
Курода показал, что контекстно-зависящие (контекстные)
языки (типа 1) Хомского являются в точности теми
множествами, которые могут быть распознаны недетерминированными
линейно-ограниченными автоматами [39]. С другой стороны,
множества, распознаваемые детерминированными
линейно-ограниченными автоматами, образуют булеву алгебру [39, 40]. Вопрос
о том, совпадают ли классы, определенные
детерминированными и недетерминированными линейно-ограниченными
автоматами, остается открытым. Если да, то класс
контекстно-зависящих языков, очевидно, замкнут относительно дополнения.
Р. В. Ричи занимается изучением иерархии функций,
основанной на вычислениях с ограниченной лентой [53]. Он
определяет Fq как класс функций, вычислимых конечными
автоматами. Для каждого i>0 F* определяется как класс всех
функций, которые могут быть вычислены на машине Тьюринга,
когда объем используемой ленты ограничен некоторой функцией
из Fi-i от длины входа1). Получается иерархия типа со, а
*) Натуральные числа кодируются при этом /г-ичными слозами, где
п>\. — Прим. перевг
74
П. Фишер
объединение всех F* дает функции, элементарные по Кальмару.
Классы Fi не замкнуты относительно композиции, но замкнуты
относительно некоторых ограниченных операций. Если вместо
конечных автоматов начать с линейно-ограниченных автоматов,
получится подобная же иерархия, которая переплетается с
первой и опять-таки дает все элементарные функции.
В [37] подход [53] релятивизируется с применением
функционалов, вычисления которых связаны с ограниченной
лентой. В [38] Крайдер и Р. В. Ричи рассматривают подкласс трех-
символьных детерминированных линейно-ограниченных
автоматов. Подкласс содержит «универсальную» машину, но не
замкнут относительно подстановки и отождествления
переменных.
Совсем недавно Хартманис, Льюис и Стирнс выполнили
работу о вычислениях с ограниченной лентой [30]. Offline модель
Хенни модифицирована таким образом, что она содержит
машину Тьюринга с двусторонней лентой, на которой ничего не
пишется, и рабочей лентой. Длина используемой рабочей ленты
определяет сложность в этой классификации. Также изучаются
и online машины, и в каждом случае рабочая лента может
быть ограничена или не ограничена pushdown-store операцией.
Приведена иерархия, аналогичная той, что получается для
классов сложности с ограничениями на время.
Несмотря на название работы [30], насколько известно
автору, еще никто детально не исследовал соотношение между
ограничениями на память и время. Было бы приятно, если бы
существовал разумный эквивалент времени для памяти и
обратно, такой, что мера вычислительной сложности могла бы
учитывать оба фактора в содержательном смысле.
6. Итеративные сети в реальное время
Итеративная n-мерная сеть конечных автоматов состоит из
идентичных конечных автоматов, нумеруемых м-наборами
неотрицательных целых чисел [32]. Два автомата называются
соседними, если их индексы совпадают везде, кроме одной ком^
поненты, в которой они отличаются на единицу. Входы и
выходы сети связаны с автоматом с номером (0, 0, ..., 0): За
исключением начального момента времени, состояние всякой
машины сети в момент /+1 зависит только от состояний ее и ее
соседей в момент /, а ее состояние в момент 0 есть специальное
состояние покоя.
Можно показать, что некоторые изменения в определении
итеративной сети не меняют ее свойств. Начальный автомат
можно сделать отличным от всех остальных; определения со-
Многоленточные и бесконечные автоматы
75
седства можно несколько ослабить, условия начала работы
машин могут отличаться от указанных выше.
Легко видеть, что одномерная итеративная сеть без труда
моделирует машину Тьюринга, потому что такая сеть может
моделировать любое конечное число pushdown лент. Таким
образом, для итеративных сетей должны иметь место другие
ограничения, чтобы получались промежуточные классы множеств
слов1). Общие ограничения на время, подобные тем, что
сделаны для машин Тьюринга у Хартманиса и Стирнса, еще не
исследованы. Однако специальный случай вычислений в^
реальное время на детерминированных итеративных сетях конечных
автоматов изучался несколькими авторами. Наиболее
исчерпывающее исследование принадлежит Коулу [12]. . *
Одномерные итеративные сети могут совершать много
неожиданных операций. Коул показал, что они могут распознавать в
реальное время множество всех симметричных слов и
множество всех слов вида хх. Первое из этих множеств по pushdown-
store подходу является существенно недетерминированным,
а второе даже не является контекстно-свободным. Фишер
показал, что одномерные сети могут порождать
характеристическую последовательность множества всех простых чисел, т. е.
машина выдаст 1 в момент t, если t—простое число, и 0 в
противном случае [22]2). Атрубин доказал, что одномерные
итеративные сети могут производить в реальное время умножение,
если входы записаны в двоичной системе и подаются справа
налево [1].
Коул установил, что класс множеств, распознаваемых
n-мерными итеративными сетями, является булевой алгеброй, но не
замкнут относительно обращения и сцепления. Так, он
доказал, что множество всех слов с непустым концом вида хх
нераспознаваемо на м-мерных итеративных сетях. Это множество
является, однако, сцеплением множества всех слов и множества
слов вида хх, и оба эти множества распознаваемы на
итеративных сетях. Далее, обращение этого множества опять-таки
распознаваемо на итеративной сети.
Метод Коула можно также применить к множеству всех
слов с непустым концом, который является симметричным
словом. Этот язык является контекстно-свободным, но не
1) Рассматривая преобразования входных слов в выходные, мы можем
ограничивать длину итеративной сети (длиной слова или как-нибудь еще).—
Прим. перев.
2) Другие интересные примеры последовательностей, порождаемых на
итеративных сетях в реальное время, получены Ю. А. Бухштабом, который
установил некоторые свойства замкнутости этого класса
последовательностей [1**]. — Прим. перев.
76
П. Фишер
распознаваем никакой n-мерной итеративной сетью. Далее, для
каждого п существует контекстно-свободный язык, распознаваем
мый в реальное время (п+1)-мерной сетью и не
распознаваемый никакой n-мерной сетью. Таким образом, итеративные сети
в реальном времени и контекстно-свободные языки несравнимы
в очень сильном смысле.
7. Разные результаты
Другие работы, относящиеся к вычислительной сложности,
упоминаются здесь вкратце. Перлес, Рабин и Шамир [49], Эг^
ган [14], Пэйперт и Мак-Нотон [48] изучали подклассы
регулярных множеств и отношения между их лингвистическими и
машинными свойствами.
Ли [41] и Фишер [23] рассматривали минимальные
множества операций машины Тьюринга и исследовали универсальность
различных ограниченных машин Тьк1ринга. Шепердсон и Стур-
гис [61], Элгот и Робинсон [16] рассматривали вычисления на
машинах, у которых вместо лент имеется конечное число
регистров, каждый из которых может, содержать произвольное
целое число. Такие машины с условным переходом и
сложением двух чисел эквивалентны машине Тьюринга.
Акст изучает иерархию рекурсивных функций, построенную
из примитивно-рекурсивных функций как исходных
порождением новых классов посредством униформных диагональных ые--
тодов[2]. Близка к этому и работа Фабиена [19]. В другой работе
Акста [3], в работах Клива [11], Мейера [43] и Д. Ричи [52]
показывается, что несколько различных методов классификации
примитивно-рекурсивных функций дают иерархии, тесно
связанные с иерархией Гжегорчика [28] *).
Скоро должен появиться интересный обзор Бечваржа [6]. Он
дает классификацию многих моделей вычислительных устройств,
используемую при исследовании вычислительной сложности, и
рассматривает общие вопросы связи .некоторых из этих
моделей с реальными вычислениями. Хорошо известны работы
советских ученых по вычислительной сложности2), в особенности
статья Трахтенброта [5].
Наконец, автор хотел бы пожелать, чтобы следующие
библиографические обзоры содержали статьи, не цитированные
1) Я. Б. Казанович предложил классификацию примитивно-рекурсивных
функций по типу (о2, основанную на ограничении используемой при
вычислении ленты машины Тьюринга, являющуюся распространением классификации
Р. В. Ричи элементарных функций на другие классы Гжегорчика [6**]. —
Прим. перев.
2) См, список дополнительной литературы [2**=—17**]. — Прим. перев,
Многоленточные и бесконечные автоматы
77
выше и относящиеся к рассматриваемой здесь области,
особенно статьи по математической лингвистике и проблемам
разрешения для автоматов. Библиографии в [4, 6, 9, 10, 13, 35, 42, 45]
рекомендуются тем читателям, которые ищут дополнительную
литературу.
Л ИТЕРАТУРА
1. At rub in A, J., An iterative one-dimensional real-time multiplier, Paper
for Appl. Math., Harvard U., Cambridge, Mass. (1962).
2. A x t P., On a subrecurcive hierarchy and primitive recursive degrees, Trans.
Amer. Math. Soc, 92 (1959), 85—105.
3. A x t P., Enumeration and Grzegorczyk hierarchy, Z. Math. Logik Grund-
lagen Math., 9 (1963), 53—65.
4. В a r - H i 11 e 1 Y., Language and information, John Wiley, New York, 1964,
5. Bar-Hillel Y., Perles M., Shamir E., On formal properties of
simple phase structure grammars, Z. Phonetik, Sprachwiss., Kommunika-
tionsforsch., 14 (1961), 143—172.
6. Becvaf J., Real-time and complexity problems in automata theory,
Submitted for publication.
7. Blum M., A machine-independent theory of recursive functions, Doctoral
thesis, Massachusetts Institute of Technology, Cambridge, Mass., 1964.
8. Chomsky N., On certan formal properties of grammars, Inform. Control,
2 (1959), 137—167. (Русский перевод: Хомский H., О некоторых
формальных свойствах грамматик, Кибернетический сборник, вып. 5,
ИЛ, М., 1962, 279—312.)
9. Chomsky N., Formal properties of grammars, Handbook of
Mathematical Psychology, v. 2, John Wiley, New York, 1963, 323—418. (Русский
перевод: Хомский H., Формальные свойства грамматик,
Кибернетический сборник, нов. серия, вып. 2, изд-во «Мир», М., 1966.)
10. Chomsky N., Schutzenberger М. P., The algebraic theory of
context-free languages, Computer Programming and Formal Systems, North-
Holland, Amsterdam, 1963, 118—161.-(Русский перевод: Хомский H.,
Шютценберже М., Алгебраическая теория контекстно-свободных
языков, Кибернетический ёборник, нов. серия, вып. 3, изд-во «Мир»,
М., 1966.)
И. Cleave J. P., A hierarchy of primitive recursive functions, Z. Math.
Logik Grundlagen Math., 9 (1963), 331—345.
12., Cole S. N., Real-time computation by iterative arrays of finite-state
machines, Doctoral thesis, Rep. BL-36, Harvard U., Cambridge, Mass., 1964.
13. Djavis M., Computability and Unsolvability, McGraw-Hill, New York, 1958.
14. E g g a n L. C, Transition graphs and the star-height of regular events,
Mich. Math. J., 10 (1963), 385—397.
15. E 1 g о t С. С, M e z e i J. E., On finite relations defined by generalized
automata, IBM J. Res. Develop., 9 (1965), 47—68.
16. El got С. С, Robinson A., Random-access stored-programm machines
an approach to programming languages, J. ACM, 11 (1964), 365—399.
17. El got С. С, Rut ledge J. D., RS-machines with almost blank tape,
J. ACM, 11 (1964), 313—337.
18. E v e у J. The theory and applications of pushdown-store machines,
Doctoral thesis, Rep. NSF-10, Harvard U., Cambridge, Mass., 1963.
19. F a b i a n R. J., Hierarchies of general recursive functions and ordinal
recursion, Tech. Rep., Case Institute of Technology, Cleveland, Ohio, 1964.
20. Fischer P. C, Theory of provable recursive functions, Trans. Amer. Math,
Soctt 117 (1965), 494—520.
78
П. Фишер
21. Fischer Р. С, On computability by certain classes of restricted Turing
machines, Proc. Fourth Ann. Symp. Switching Circuit Theory and
Logical Design, Chicago, 1963, 23—32.
22. Fischer P. C, Generation of primes by a one-dimensional real-time
iteration array, I. ACM, 12 (1965), 388—394. (Русский перевод: см.
настоящий выпуск, стр. 95—102.)
23. Fischer Р. С, On formalisms for Turing machines, I. ACM, 12 (1965),
570—580.
24. Fischer P. C, Rosenberg A. L., Further results on nondeterministic
«-tape automata, Abstr. 65T-48, Amer. Math. Soc. Notices, 12 (1965),
139, 140.
25. Ginsburg S., An introduction to mathematical machine theory,
Addison— Wesley, Reading, Mass., 1962.
26. G i n s b u r g S., G r e i b а с h S., Deterministic context-free languages,
Abstr. 65T-155, Amer. Math. Soc. Notices, 12 (1965), 246.
27. G i n s b u r g S., S p a n i e r E. H., Mappings of languages by two-type
devices, Proc. Fifth Ann. Symp. Switching Circuit Theory and Logical
Design, Princeton, 1964, 57—67.
28. G r z e g о г с z у k A., Some classes of recursive functions, Rozprawy
Mathematcyzne, Warsaw, 1953, 1—45.
29. H a i n e s L.. Generation and recegnition of formal languages, Doctoral
thesis, Massachusetts Institute of Technology, Cambridge, Mass., 1965.
30. Hartmanis J., "Lewis P. M., Stearns R. E., Classifications of
computations by time and memory requirements, Proc. IFIP Int. Congr.,
v. 1, 1965, 31—36.
31. Hartmanis J., Stearns R. E., On the computational complexity of
algorithms, Trans. Amer. Math. Soc, 117 (1965), 285—306. (Русский
перевод: Хартманис Дж., С т и р н з Р., О вычислительной сложности
алгоритмов, Кибернетический сборник, нов. серия, вып. 4, изд-во «Мир»,
1967.)
32. Hennie F. С, Iterative arrays of logical circuit, MIT Press, 1961.
33. Hennie F. C„ One-type off-line Turing machine computations, Submitted
for publication.
34. H e n n i e F. C, Stearns R. E., Two-tape simulation of multitape Turing
machines. Submitted for publication.
35. Kleene S. C, Introduction to Metamathematics, Van Nostrand,
Princeton N. J., 1952. (Русский перевод: К л и н и С. К., Введение в
метаматематику, ИЛ, М., 1957.)
36. Kleene S. С, Representation of events in nerve nets and finite automata,
Automata Studies, Princeton, 1956, 3—41. (Русский перевод: Кли-
н и С. К., Представление событий в нервных сетях и конечных
автоматах, сб. «Автоматы», ИЛ, 1956, 15—67.) ,
37. К г е i d е г D. L., Ritchie R. W., Predictable computable f unctionals and
definition by recursion, Z. Math. Loglk Grundlagen Math., 10 (1964),65-80.
38. К r e i d e r D. L., Ritchie R. W., A universal two-way automaton, Sub-
emitted for publication.
39. К u г о d a S. Y., Classes of languages and linear bounded automata,
Informal Contr., 7 (1964), 207—223.
40. L a n d w e b e r P. S., Three theorems on phase structure grammars of
Type I, Informal Contr., 6 (1963), 131—137.
41. Lee С Y., Categorizing automata by W-machine programs, L ACM, 8
(1961), 384—399.
42. M с N a u g h t о n R., The theory of automata, a survey. In Advances in
Computers., v. 2, Acad. Press, New York, 1961, 379—421.
43. Meyer A. M., Depth of nesting and the Grzegorczyk hierarchy, Abstr.
622-656, Amer. Math. Soc. Noticest 13 (1965), 342,
Многоленточные и бесконечные автоматы
79
44. М i n s к у М. L., Recursive unsolvability of Post's problem of tag and
other topics in theory of Turing machines, Ann. Math., 74 (1961),
437—455.
45. Moore E. F., Sequential machines: selected papers, Addison — Wesley,
Reading, Mass., 1964.
46. My hi 11 J., Linear bounded automata, Wadd Tech. Note 60-165, Wright-
Patterson AFB, Ohio, 1960.
47. Oetttnger A. G., Automatic syntactic analysis and the pushdown store,
Proc. Symp. Appl. Math., v. 12, Amer. Math. Soc, Providence, R. I.,
1961.
48. Papert S., McNaughton R., On topological events, Submitted for
publication.
49. P e r 1 e s M., Rabin M. 0., Shamir E., Theory of definite automata,
IEEE Trans., EC-12 (1963), 233—243.
50. Rabin M. 0., Real-time computation, Israel I. Math., 1 (1963), 203—
211.
51. Rabin M. 0., Scott D., Finite automata and their decision problems,
IBM J. Res. Develop., 3 (1959), 115—125.
52. Ritchie D. M., Complexity classification of primitive recursive functions
by their machine programs, Abstr. 622-659, Amer. Math. Soc. Notices,
13 (1965), 343.
53. Ritchie R. W., Classes of predictably computable functions, Trans. Amer.
Math. Soc, 106 (1963), 139—173.
54. Rosenberg A. L., On «-tape finite-state acceptors, Proc. Fifth Ann.
Symp. Switching Circuit theory and Logical Design, Princeton, 1964,
76—81.
55. Scheinberg S., Note on the Boolean properties of context-free langua-
* ges, Inform. Contr., 3 (1960), 372—375.
56. Schutzenberger M. P., A remark on finite transducers, Inform.
Contr., 4 (1961), 185—196.
57. Schutzenberger M. P., On the definition of a family of automata,
Inform. Contr., 4 (1961), 245—270.
58. S с h u t z e n b ej g e r M. P., Finite counting " automata, Inform. Contr.,
5 (1962), 91—107.
59. Schutzenberger M. P., Certain elementary families of automata, Proc.
Symp. Mathematical Theory of automata, Polytech. Inst, of Brooklyn,
1962, 139—154.
60. S с h u t z e n b e r g e r M. P., On context-free languages and pushdown
automata, Inform. Contr., 6 (1963), 246—264.
61. Shepherdson J. C, Sturgis H. E., Computability of recursive
functions, J.'ACM, 10 (1963), 217—255.
62. S i e g e 1 J., Some theorems about Yamada's restricted class of recursive
functions, IBM Res. Pap. RC-510, T. J. Watson Res. Ctr., Yorktown Hts.,
N. Y., 1961.
63. T p a x т e н б p о т Б. А., Тюринговы вычисления с логарифмическим
замедлением, Алгебра и логика, Семинар, вып. 3 (1964), 33—48.
64. Т u г i n g А. М., On computable numbers, with an application to the
Entscheidungsproblem, Proc. London Math. Soc, Ser. 2-42, 1936,
230—265.
65. Wang H., A variant to Turing's theory of computing machines, J. ACM,
4 (1957), 63—92.
66. Y a m a d a H., Counting by a class of growing automata, Doctoral thesis,
U. of Pennsylvania, Philadelphia, Pa., 1960.
67. Y a m a d a H., Real-time computation and recursive functions not real-time
computable. IRE Trans. EC-11 (1962), 753—760.
80
П. Фишер
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Atrubin A. J., A one-dimensional real-time iterative multiplier, IEEE
Transactions on Electronic Computers, EC-14 (1965), 394. (Русский
перевод: см. настоящий выпуск.)
2. А х t P., Iteration of Relative Primitive Recursion, Mathematische Annalen,
167, № l (1966), 53—55.
3. A x t P., Iterations of primitive recursion (Forthcoming).
4. В1 u m M., A machine-independent theory of the complexity of recursive
functions, J. ACM, № 2, 14 (1967).
5. F i s h e r P. C, Turing machines with restricted memory, Inf. and Contr.,
9 (1966), 364—380.
iinsouri
6. Ginsburg S., Greibach S., Deterministic context-free languages, Inf.
and Contr., 9 (1966), 620—648.
7. Ginsburg S., Greibach S., Harrison M., Stack automata and
compiling, J.\ACM, 14 (1967), 172—201.
ЛИТЕРАТУРА НА РУССКОМ ЯЗЫКЕ
1. Б a p д s и н ь Я. M., Емкость среды и поведение автомата, ДАН СССР,
163, № 2 (1965).
2. Б ар дз инь Я. М., Проблемы универсальности в теории растущих
автоматов, ДАН СССР, 157, № 3 (1964).
3. Бардзинь Я. М., Универсальные пульсирующие элементы, ДАН СССР,
157, № 2 (1964).
4. Б у х ш т а б Ю. А., Реализуемость функций на одномерных сетях в
реальное время, Проблемы кибернетики, вып. 22, изд-во «Наука», М, 1968.
5. К а з а н о в и ч Я. Б., О классификации примитивных рекурсивных
функций при помощи машин Тьюринга, Проблемы кибернетики, вып. 22,
изд-во «Наука», М., 1968.
6. К о з м и д и а д и В. А., О бесконечных автоматах, Проблемы кибернетики,
вып. 22, изд-во «Наука-», М, 1968.
7. Козмидиади В. А., Марченков С. С, О многоголовых автоматах,
Проблемы кибернетики, вып. 21, изд-во «Наука», М., 1968.
8. Кратко М. И., Регулярные и стабильные итеративные системы,
Проблемы кибернетики, вып. 19, изд-во «Наука», М., 1967.
9. Матвеева С. Г., К теореме Рабина о сложности вычислимых функций,
Сиб. матем. журнал, 6, № 3 (1965), 546—555.
10. Мучник А. А., Об общих линейных автоматах, Проблемы кибернетики,
вып. 22, изд-во «Наука», М., 1968.
11. Непомнящий В. А., Об алгоритмах, осуществляемых повторяющимся
применением конечных автоматов, сб. Дискретный анализ, вып. 5,
Новосибирск, 1965.
12. Плесневич Г. С, О событиях, связанных с семейством автоматов,
сб. Вычислительные системы, Новосибирск, 1963, 44—67.
13. Т р а х т ен б р о т Б. А., Оптимальные вычисления и частотное явление
Яблонского, Алгебра и логика, Семинар, 4, № 5 (1965), 79—97.
14. Т р а х т е н б р о т Б. А., О нормированных сигнализирующих для тьюрин-
говых вычислений, Алгебра и логика, Семинар, 5, № 6 (1966),
61—70.
15. Ф р е й в а л д Р. В., О порядке роста точных временных
сигнализирующих для тьюринговых вычислений, Алгебра и логика, Семинар, 5, № 6
(1966).
16. Ф рейва лд Р. В., Сложность распознавания симметрии на машинах
Тьюринга со входом, Алгебра и логика, Семинар, 4, Nfe \ (1965).
Одномерное итеративное умножающее
устройство, работающее в реальное
время1}
А. Д. А7рубин
I. Введение
Каждое из двух сколь угодно больших целых чисел
выражается в двоичной записи последовательностью 0 и 1, причем
низший разряд соответствует начальному моменту времени и
п-й разряд следует за (п—1)-м разрядом через одну единицу
времени. Будет описано устройство с дискретными
состояниями (синхронизированное на входе). На входы подаются две
двоичные последовательности, а именно в каждый момент
времени подаются соответствующие разряды, и с выхода снимается
двоичная последовательность, соответствующая произведению
двух целых чисел, поданных на вход, причем первым выдается
низший разряд.
Мак-Нотон [1], рассматривая машины с дискретными
состояниями, заметил, что сложение двух сколь угодно больших
двоичных чисел (записанных как и ранее в виде
последовательностей) может быть осуществлено на конечном автомате. Этому
автомату достаточно иметь в точности два состояния.
Мак-Нотон также заметил, что умножение таких последовательностей
не может быть выполнено на конечном автомате. Произведение
двух достаточно больших целых чисел может иметь насколько
угодно больше разрядов, чем имеется у большего из них,
следовательно, автомат должен после прекращения подачи
информации на вход печатать ни выходе сколь угодно долго цифры-
произведения. Непосредственно видно, что такой автомат не
может иметь только конечное число состояний. Будет построена
машина с бесконечным числом состояний, производящая
умножение.
Мак-Нотон также рассматривал проблемы, относящиеся
к машинам с дискретными состояниями, работающим в
«реальное время». Предположим, что на вход машины подается
последовательность i'o, iu /2, •.. и с выхода снимается
последовательность и0, Uи U2,..., где Un есть функция от входных
символов до in включительно. Вычисление называется выполняемым
l) Atrubin A. J., A one-dimensional real-time iterative multiplier, IEEE
Trans, on EL Computers, EC-14, № 3 (1966), 394—399«
$ Зак. )904
82
A. At рубин
в реальное время, если машина вычисляет Un в течение
фиксированного промежутка времени (не зависящего от п),
прошедшего после поступления in на вход. Однако в том случае,
когда задержка между поступлением in и вычислением Un
становится сколь угодно большой для достаточно больших я,
вычисление назовем «обычным» в отличие от вычисления в
«реальное время». Кроме того, заметим, что каждая операция,
реализуемая на конечном автомате, может быть также
произведена на конечном автомате в реальное время. Например,
в двоичном сумматоре выход организуется в тот же момент
времени, в какой воспринимается вход (или, быть может,
задерживается на единицу времени). Мак-Нотон сформулировал
задачу об осуществимости умножения двух сколь угодно
больших чисел в реальное время. Умножающее устройство,
описываемое в этой статье, работает в реальное время. Ниже
указываются некоторые дальнейшие ограничения, накладываемые на
это устройство.
Хенни [2] рассматривал итеративные сети логических схем.
Этот класс машин описывается в настоящей статье, но нами
допускаются бесконечные сети, тогда как Хенни использовал
только конечные. Характер поставленной задачи таков, что
нам, вероятно, было бы более удобно строить двумерную сеть.
Разряды множителя могли тогда распространяться в
направлении оси х, а разряды множимого — в направлении оси у.
Каждый двоичный разряд произведения мог бы быть тогда
образован в узле решетки сети, затем производилось бы
суммирование и возвращение назад к начальному узлу решетки, где
печатался бы выход. Другая возможность заключается в
построении нашего устройства как одномерной сети. Цель этой
работы заключается в построении именно такой одномерной
сети.
При описании работы сколь угодно длинных сетей из
конечных устройств должно быть учтено следующее явление.
Несущие информацию сигналы перемещаются с конечной скоростью
(верхней границей является скорость света). Такие сигналы
в течение конечного интервала времени не могут передаваться
из одной точки сети в другую точку сети, находящуюся сколь
угодно далеко. При построении рассматриваемого устройства
учитывается, что в течение одного такта времени сигналы из
некоторой ячейки сети могут передаваться не далее чем в
смежные ячейки.
Таким образом, наше устройство будет итеративной
одномерной двухсторонней сетью ячеек с конечным числом
состояний и с единичной задержкой при обмене информацией между
смежными ячейками (все это употреблялось и Хенни, за исклю-
Одномерное итеративное умножающее устройство ; 83
чением допускаемой нами бесконечности числа ячеек в сети).
Таким образом (рис. 1), каждая ячейка в сети имеет только
конечное число состояний. Состояние каждой ячейки в сети
в момент времени t есть функция ее собственного состояния
в момент времени t — 1 и состояний двух соседних ячеек в
момент времени t—1. Исключая начальную ячейку, все ячейки
(они обозначены буквой С) одинаковы. Таким образом,
состояние каждой ячейки зависит от ее предыдущего состояния и
предыдущих состояний соседних ячеек. Структура начальной
ячейки будет несколько иная, чем у других ячеек, ввиду того
что в ее функции входят восприятие входа и печать выхода.
Начальная
ячейка Ячейка Ячейка
Произведение
Рис. 1. Структура устройства с двухсторонней связью ячеек.
Нами будут построены два различных устройства. Первое
из них выдает свою выходную последовательность с задержкой
на одну единицу времени по отношению к входной
последовательности. Следовательно, п-и разряд произведения выдается
через одну единицу времени (один такт времени) после
восприятия п-х разрядов множимого и множителя. Начальная
ячейка этого устройства не отличается от остальных ячеек, хотя,
конечно, она имеет головку, которая печатает выходную
последовательность. Второе устройство образует /i-й разряд
произведения в течение того же момента времени, в который
воспринимаются п-е разряды множимого и множителя. Точнее, может
иметься небольшая задержка, соответствующая
характеристикам элементов первой ячейки, но эта задержка будет мала по
сравнению с тактом времени работы сети. Такие задержки,
связанные с характеристиками элементов, не будут
приниматься нами во внимание, и мы будем говорить, что выход
выдается одновременно с восприятием входа. Структура
начальной ячейки этого второго устройства иная, чем у других
ячеек, начальная ячейка имеет два дополнительных состояния,
но тем не менее в основном она работает так же, как и другие
ячейки. Вообще говоря, оба рассматриваемых устройства мало
отличаются друг от друга. Будет дано детальное описание
только второго из них, а первое мы рассмотрим очень кратко.
Множитель
Множимое
6*
84
A. Atрубин
Наше устройство удобно будет конструировать, как
показано на рис. 2, из двух отдельных блоков, которые затем
объединяются. Первый блок односторонний, причем информация
в нем передается по сети, исходя из начальной ячейки. Работа
этого блока не зависит от второго блока. Сначала независимо
от второго будет построен первый блок. Второй блок также
Г~
1
1 *
1
L-
Г"
1
1
1
1
1
1
ll
'
'
h
,
1
Первый
односторонний ёлок
Bttil
сгпор
с,
1
г-
с2
?рой 0
онний
дно-
Sjjok
Ci
'
1 ,
с2
Рис. 2. Блоки устройства.
односторонний, однако информация в нем передается в
обратную сторону, т. е. по направлению к начальной ячейке. Работа
второго блока зависит от состояния первого.
II. Алгоритм умножения
Предположим, что перемножаемые два целых числа имеют
вид
где
a (/) = 0 или 1 при 0</'</га,
где
B=^b(i)2\
/-о
b (1) = 0 или 1 при 0<1<я;
без ограничения общности предположим, что я>т и, таким
образом»
п
Л=2а(г)21,
Одномерное итеративное умножающее устройстве 85
где
а (/) = 0 для m < / < п.
Рис. 3 дает пример применения двоичного аналога обычного
алгоритма умножения, причем переносы записаны внизу. В
пересечении 1-й строки и /-го столбца стоит произведение
a(i)Xb(j — i).
Строки
Номер разряда
Множимое (В)
Множитель (А)
11 110 | 9 | 8 | 7 [б ] 5 | 4 | 3 | 2 | 1 | 0
1
0
1
0
0
0
1
1
0
0
0
1
1
1
1
1
1
1
0
1
1
0
1
1
дона
переноса
Произведение
Столдць/
—
|о
0
22
Таблица
произведения
0
0
0
21
0
0
0
1
1
20
1
0
0
0
1
0
19
0
1
0
0
0
1
0
18
1
0
0
0
0
0
1
1
1
17
1
1
0
1
0
0
0
1
1
1
16
1
1
0
0
0
0
0
0
1
1
1
1
15
1
1
0
1
0
0
0
0
0
1
1
1
0
14
1
1
0
1
0
0
1
0
0
0
1
1
1
1
13
0
1
0
1
0
0
0
1
0
0
0
1
1
1
1
1
12
1
0
0
1
0
0
1
0
1
0
0
0
1
1
1
1
0
11
1
0
1
0
0
1
1
0
0
0
0
1
1
1
1
0
10
0
0
0
0
1
1
1
0
1
0
1
1
1
1
0
9
1
0
0
1
1
1
0
0
1
1
1
1
0
8
0
0
1
1
1
0
1
0
1
J
1
1
,7
0
0
1
1
0
1
1
1
1
1
1
6
1
0
1
0
1
1
1
1
0
5
1
0
0
1
1
1
0
4
1
0
1
1
1
3
0
0
1
1
2
1
0
-4
1
1
]
1
0
Рис. 3. Двоичное умножение,
Цифра / произведения /?(/) является суммой по mod 2
нулей и единиц, записанных в столбце / (суммируются все цифры,
записанные как в таблице произведения, так и в зоне
переноса). Число единиц переноса, стоящих в (/+1)-м столбце,
выражается через [s(/)], сумму единиц в /-столбце
<ЧУ+1):
[s (У)] -[s (у)] mod 2
2
при у>0
и
¢(0) = 0.
86
A. At рубин
Этим способом и будут образовываться разряды произведения.
Для вычисления разрядов /?(/) суммируются по mod 2 все
произведения
a(i)Xb(j — i), где 0</</,
и переносы, образованные при вычислении p(j—1). Каждая
пара единиц, являющихся слагаемыми суммы, формирующей
/?(/), образует отдельную единицу переноса, передающуюся для
вычисления р(/+1).
III. Построение умножающего устройства
Устройство будет работать следующим образом. Каждое
g(i)=[b(i), a{i)] будет запоминаться в некоторой ячейке сети.
Пусть в момент времени i на вход подается g(0- Это g(i) будет
затем перемещаться вдоль цепочки' ячеек по направлению к
соответствующей ячейке. Когда оно проходит через ячейки, в
которых уже запомнились #(/), где 0-</<О', то будут
образовываться произведения a(i)Xb(j) и a(j)Xb(i). Когда g(i) дойдет
до соответствующей ей ячейки памяти (первой пустой ячейки),
формируется произведение a(i)Xb(i). По мере образования
каждого произведения видоизменяется соответствующее p(k),
которое перемещается к начальной ячейке. В каждую единицу
времени запоминаются соответствующие переносы, ожидая
прохождение следующего p(k).
Если g(j) хранится на расстоянии примерно //2 ячеек от
начальной ячейки, то тогда после подачи на вход g(i) (в
момент времени i, где />/) для распространения
соответствующего сигнала от начальной ячейки до g(j) и обратно к
начальной ячейке требуется / единиц времени, т. е. именно этим
сигналом определяется выход в момент времени j + L Хранение
g(j) на большем расстоянии от начальной ячейки не
допускается. Следовательно, по крайней мере два g должны
храниться в одной ячейке. Предположим теперь, что в начальной
ячейке будут храниться g(0) и g(l), в следующей ячейке будут
храниться g(2) и g(3) и т.д. Первый блок каждой ячейки
будет состоять из следующих трех частей: 1) ВСП — верхняя
секция памяти, предназначенная для g с большими номерами;
2) НСП — нижняя секция йамяти для g с меньшими
номерами; 3) ПСП — переходная секция памяти, предназначенная
для перемещения g". На рис. 4 изображено несколько первых
шагов процесса, а также несколько шагов после момента
времени /=12. Состояния этого блока устройства будут изобра*
жаться тройкой (до, х, у), где w, х и у могут быть Q, (0, 0),
(0, 1), (1,0) или (1, 1). Последняя четверка представляет собой
Одномерное итеративное умножающее устройство 87
возможные значения g(i)=[b(i), a(i)]. Состояние Q — это
начальное состояние, или состояние покоя. Таблица дает краткое
описание работы первого блока устройства, иллюстрируя
пример, заданный на рис. 4. Эта таблица определяет последующее
псп
всп
нсп
t«o
t=i
t«2
t=3
t«4
1 Q
Q
1 Q 1
T]
Q
Q
ol
Q
Q
1 й(6) 1
Q
1 Q 1
Q
Q
Q
Q
Q
Q
|g(D
Q
|g(0)
Q
Q
Q
Q
Q
Q
-
|g(2)
|g(l)
|g(0)
0
Q
4
Q
Q
1 Q
|g(3)
1 g (1)
1 g(6)
|g(2)
Q
Q
Q
Q
Q
|g(4)
g(D
|g(0)
g(3)
Q
|g(2)
Q
Q 1
1 Q
t=5
t = 12
t=13
t=14
t=15
t=16
g(5)
g(D
g(0)
g(4)
g(3)
g(2)
Q
Q
Q
jg(12)
g(l)
|g(0)
g(ll)
g(3)
g(2)
iooj"
g(5)
g(4)
g(9)
g(7)
g(6)
g(8)
Q
Q
Q
Q
Q
"Q 1
Q
Q
|g(13)
g(D
1 g(0)
g(!2)
g(3)
g(2)
g(11)
g(5)
g(4)
g(10)
g(7)
g(6)
6(9)
Q
6(8)
Q
Q
Q
Q
Q
Q
|g(H)
g(D
g(0)
g(13)
g(3)
g(2)
g(12)
g(5)
g(4)
g(H)
g(7)
g(6)
g(10)
g(9)
g(8)
Q
Q
Q
Q
Q 1
Q
|g(1S)
g(D
g(0)
g(H)
g(3)
g(2)
g(13)
g(5)
g(4)
g(12)
g(7)
g(6)
g(ll)
g(9)
g(8)
g(10)
Q
Q
Q
Q
Q
lg(16)
go)
[g(0)
g(15)
g(3)
|g(2)
g(H)
g(5)
g(4)
g(13)
g<7)
g(6)
g(12)
g(9)
g(8)
g(H)
Q
g(10)
Q
Q
Q 1
P и с 4. Заполнение ячеек памяти.
состояние ячейки как функцию ее настоящего состояния и
настоящего состояния ячейки, находящейся слева от нее. В
таблице последующих состояний символы g, hy /, k и m могут
принимать значения (0, 0), (0, 1), (1, 0) или (1, 1). Пробелы
Таблица последующих состояний
Имеющееся
(Q. Q. Q)
(g. Q, Q)
U. Q, g)
(m, f, g)
Имеющееся состояние
ячейки слева
(-. Q. -)
(Q. Q. Q)
(Л, к, -)
(Л, Q. Q)
(Л. Q, g)
(Л, У, g)
(Л. ;\ ir)
88
Л. Лтрубин
«не принимаются во внимание». На место черточек могут быть
поставлены любые используемые буквы. Все ячейки сначала
находятся в состоянии (Q, Q, Q). Этим завершается описание
первого блока.
Рис. 5 изображает две ячейки, в которые уже включены
вторые блоки. Второй блок состоит из следующих двух частей:
1) регистр частичного произведения и 2) память переноса.
Для наглядности эти ячейки показаны в конкретный мо-
Ячейка Ячейка ™ент вРемени lt=s.U> см' Рис' 4>'
j 4 Состояния секции, которым на
рис. 5 соответствуют пустые
клетки, не интересуют нас в этом
примере. Заметим, что в
рассматриваемый момент времени g(ll)
и g(6), взаимодействуя,
будут образовывать произведения
а(11)Хб(6) иа(6)Х&(11). Также
Р и с. 5. Структура ячейки. ^-(12) и g(5), взаимодействуя,
будут образовывать a(\2)Xb(5)
и а(5)Х&(12). Кроме того, заметим, что в этот момент времени
другие ячейки сети не будут непосредственно участвовать в
формировании 17-го разряда произведения.
Такие произведения двоичных цифр формируются в каждый
момент времени и образуют разряды полного произведения,
перемещающиеся к начальной ячейке в регистр частичного
произведения. Говоря точнее, состояние регистра частичного
произведения и памяти переноса в ячейке i в момент времени /
являются функциями состояний ПСП, ВСП и памяти переноса
ячейки i в момент времени t— 1, а также ПСП, НСП и
частичного произведения ячейки i+l в момент времени /—1. В
примере, изображенном на рис. 5 в рассматриваемый момент
времени (/=14), регистр РР будет содержать частично
сформированный 17-й разряд произведения. Частичное формирование
означает суммирование по mod 2 всех произведений двоичных
цифр, соответствующих только тем g(0, У которых 6<0'<11,т. е.
[a(7)Xb(l0) + b(7)Xa(l0) + a(8)Xb(9) + a(9)Xb(8)] mod2.
Также в момент времени /==14 в регистре Р частично
формируется 16-й разряд произведения. В процессе образования этого
16-го разряда произведения в регистре К формируется
некоторый перенос. Новые значения частично сформированного 17-го
разряда будут вычислены и помещены в Р, а получающийся
при этом результирующий перенос будет помещен в К. Эти
новые значения будут определять состояния регистров частичного
псп
всп
нсп
Частичное
произведение
Память переноси
8(12)
8(5)
Р
К
6(11)
8(6)
РР
Одномерное итеративное умножающее устройство 89
произведения и памяти переноса ячейки 3 в момент времени
^= 15. Пусть
£ = а(11)Х*(6) + а(6)Х*(Н) + л(12)Х*(б) +
+ а(5)Хй(12) + ЯЯ + /С
где РР и К изображают числа, хранящиеся в этих регистрах
в момент времени /=14. Тогда новый, частично
сформированный 17-й разряд произведения как раз равен
Е mod 2,
а новый перенос равен
£ — £mod2
2
Частично сформированный 17-й разряд произведения сдвигается
на ячейку ближе к начальной ячейке и накапливает новые
вносимые в него двоичные знаки. Можно ли сделать это,
учитывая, что память переноса ячеек имеет лишь конечное число
состояний? Заметим, что при образовании суммы Е в нее за
счет соответствующих g вносится максимум четыре единицы,
а за счет частично сформированного ранее разряда может быть
внесено самое большее одна единица. Предположим, что
существует некоторое максимальное значение переноса С. Тогда
наибольшее значение нового переноса С должно удовлетворять
соотношению
С = (5 + Q--(5 + C)mod2 <с.
минимальное положительное целое С, удовлетворяющее этому
соотношению, равно 4. Таким образом, память переноса может
иметь в точности пять состояний, соответствующих переносам
О, 1,2,3 и 4.
Наконец, дальнейшие соображения касаются g(k) в ПСП
той ячейки, в которой только ВСП находится в состоянии Q
либо и ВСП, и НСП находятся в состоянии Q. В этом случае
g(k) как раз достигает ячейки, в которой она запоминается,
и в этот момент времени образуется произведение a(k)Xb(k),
входящее в соответствующую сумму. Таблица переходов,
которую мы здесь не будем приводить, должна соответствовать
этому. В приведенном ниже числовом примере будут употреби
ляться некоторые специальные обозначения, а именно когда
g(k) прибывает в ячейку, в которой только ВСП находится
в состоянии Q, то это состояние ВСП будет изображаться не
символом Q, a g(k), заключенным в кружок. Аналогично, когда
g(k) прибывает в ячейку, в которой и ВСП, и НСП находятся
90
A. Atрубин
в состоянии Q, состояние НСП будет изображаться в виде#(&),
заключенного в кружок; эти обозначения дают возможность
применять обычные методы вычисления hob^ix значений
частичных произведений и переносов, употребляя их с одной
поправкой. Именно, все произведения, формируемые с использованием
записи, заключенной в кружок, прежде чем они войдут в
соответствующую сумму, должны быть разделены на 2
[произведение, сформированное обычным образом с использованием g(k),
заключенного в кружок, будет 2Х#(&) Xb(k)]. Этим
завершается построение нашего устройства, за исключением
начальной ячейки.
Начальная ячейка несколько отличается от других ячеек; это
различие необходимо только для того чтобы избежать задержки
на один такт времени между входом и выходом. Если начальная
ячейка не будет отличаться от других, то значение £,
вычисляемое в ней в момент времени t = i, будет равно
а(/-1)Х*(1) + а(1)Х*('-1) + а(/-2)Х*(2) +
+ а(2)Х*('-2) + РРН
с соответствующими значениями РР и /(. Однако необходимо
в момент времени / использовать g(i) для образования выхода.
Таким образом, значение Е в начальной ячейке должно быть
пополнено произведением a(i)Xb(0)+a(0)Xb(i). Используя те
же соображений, что и ранее, мы видим, что начальная ячейка
должна запоминать переносы, достигающие значения 6, т. е. ее
память переноса должна иметь не пять, а семь состояний.
Цифра произведения, выдаваемая на выход, должна в точности
совпадать со значением Р в начальной ячейке. Этим
завершается построение умножающего устройства.
Подобным образом строится умножающее устройство с
единичной задержкой. Тем же способом вычисляется £, а также
Р и /С; однако значения, запоминаемые в регистрах Р и /С,
смещены на одну ячейку вправо по отношению к тому, что
было в ранее рассмотренном умножающем устройстве. Точнее,
состояния регистров частичного произведения и памяти
переноса ячейки / в момент времени t являются функциями
состояний ПСП и ВСП ячейки i— 1 в момент времени t—
^состояний ПСП, НСП и памяти переноса ячейки / в момент
времени /—1, а также состояния регистра частичного произведения
ячейки /+1 в момент времени /—1. Это означает, что
второй блок устройства является скорее двухсторонним, чем
односторонним, так как при вычислении Р и К нужно
обращаться к некоторым g, находящимся слева, и к
предшествующему значению Р направо. Выход есть в точности значение Р
Одномерное итеративное умножающее устройство 91
W
в начальной ячейке, которая не отличается от других ячеек.
Состояния всех ячеек в умножающем устройстве с
единичной задержкой и в умножающем устройстве без задержки
будут изображаться в виде столбца, представленного правее и ниже.
1) w, х, у могут принимать значения Q, (0, 0),
(0, 1), (1,0) или (1, 1), 2) Р может принимать
значение 0 или 1 (частично сформированный разряд
произведения) и С может принимать значения 0, 1, 2, 3 или
4 (для начальной ячейки в случае когда задержки
нет, значение переноса может быть равно 6).
Вход представляет собой пару двоичных чисел,
записываемых в секцию w начальной ячейки. -Выходом
является значение Р начальной ячейки. Верхней
гранью числа состояний в ячейке является число
5x5x5x2x5=1250. В случае когда нет задержки,
границей числа состояний начальной ячейки будет
5X5X5X2X7 = 1750. Все ячейки первоначально
находятся в состоянии, представленном на столбце
слева внизу.
Рис. 6 дает описание сети без задержки,
причем используемые числа те же, что и
в примере, изображенном на рис. 3. Рис. 7
дает то же самое для сети с единичной задержкой.
В обоих случаях для облегчения вычислений в
соответствующих ячейках Q заменяются на ^,
заключенные в кружок. В качестве примера подсчитаем
значение частичного произведения и памяти переноса
во второй ячейке в момент времени /=10 на рис. 6.
Эти числа являются функциями состояний в момент
времени / = 9. Перемножая значения ПСП и ВСП
второй ячейки в момент времени / = 9 и суммируя, мы
получим 2, а ПСП и НСП третьей ячейки в момент
/ = 9 дают 0. В памяти переноса второй ячейки в
момент / = 9 содержится 2, а частичное произведение
из третьей ячейки есть 1. Подводя итог, получаем
число 5, т. е. окончательно значение нового
частичного произведения есть 1, а значение переноса равно 2. Теперь
вычислим значения в регистрах третьей ячейки в момент / = 7
на рис. 7. В момент / = 6 ПСП и ВСП второй ячейки дают 2,
ПСП и НСП третьей ячейки дают 1 (так как соответствующий
символ заключен в кружок), перенос дает 1, регистр
частичного произведения четвертой ячейки дает 0, таким образом,
окончательно получаем число 4, т. е. в регистр частичного про-*
изведения вносится 0, а в регистр переноса 2.
И Q
О Q
© Q
1 0
0 0
Q
Q
Q
0
0
01
10
11
1
3
11
11
01
0
\
11 Q
Q Q
© Q
0 0
0 0
00
10
11
1
1
10 10
11 11
01 11
1 0
1 1
00
00
01
0
0
и Q
Q Q
© Q
0 0
0 0
00 00
10 11
11 01
0 0
0 о
00 00 00 00
11 00 00 10
11 01 11 10
1 0 0 0
0 0 0 0
t*0
t=6
t=12
t*!8
10
©
11
1
0
Q
Q
Q
0
0
Q
Q
Q
0
0
00
10
11
1
2
01
11
01
0
2
11
©
11
0
0
Q
Q
Q
0
0
00
10
11
1
I
00
11
01
1
1
10
11
11
0
1
10
00
01
1
0
00
©
11
0
0
Q
Q
Q
0
0
t*l'
t*7
t=13
00 00 00 00 00 00
10 11 11 00 00 10
11 01 11 01 11 10
0 10 0 0 0
0 ooooo
t»19
01
10
11
1
0
Q
Q
Q
0
0
Q
Q
Q
0
0
11
10
11
0
2
00
11
01
1
2
01
11
11
1
0
Q
Q
Q
0
0
00
10
11
0
1
00
11
01
0
1
00
11
11
0
2
10
00
01
0
0
10
00
11
0
0
Q
Q
Q
0
0
t-2
t=8
t=14
00 00 00 00 00 00
10 11 11 00 00 10
11 01 11 01 11 10
1 ooooo
0 0 0 00 о 0
t=20
11 01
10 о
11 ©
1 0
1 0
t=3
11 11
10 ©
11 01
0 0
2 0
Q
Q
Q
0
0
Q
Q
Q
0
0
00
10
и
0
2
10
10
11
0
2
11
11
01
0
2
t=9
00
11
01
1
2
00
11
11
1
0
11
11
11
0
0
01
Q
©
0
0
00
®
01
0
0
00
10
11
1
0
00
10
11
1
0
00
11
01
1
0
00
11
01
1
0
00
11
11
1
1
oo
00
01
1
0
t«l$
00
11
11
0
1
00
00
01
1
0
10
00
11
0
0
00
00
11
0
0
10
Q
©
0
0
10
©
10
0
0
00 00 00 00 00 00
10 11 11 00 00 10
11 01 11 01 11 10
о ooooo
о ooooo
t=21
00 00 00 00 00 00
10 11 11 00 00 10
11 01 11 01 11 10
о ooooo
о ooooo
t*4
t»10
t*16
t«22
11
10
11
0
8
11
11
01
1
0
Q
Q
Q
0
0
10
10
u
0
2
10
11
01
0
2
00
11
11
0
1
11
00
01
0
0
00
10
11
1
0
00
11
01
0
0
00
11
11
0
1
00
00
01
0
0
00
00
11
0
0
00
10
10
0
0
t=5
t=ll
t=17
Рис. 6. Пример работы сети без задержки.
11 Q
¾Q
Q
о 0
о 0
t=0
0
Q
Q
0
0
01
10
11
0
2
11
11
01
0
2
11
Q
©
0
1
Q
Q
Q
0
0
00
10
11
0
1
10 10
11 11
01 u
0 1
1 1
00
00
01
0
1
11 Q
О Q
© Q
0 0
0 0
t»6
t=12
00 00 00 00 00
10 11 11 00 00
11 01 11 01 11
10 0 10
0 0 0 0 0
t=18
10
©
11
1
0
Q
Q
Q
0
0
Q
Q
Q
0
0
00
10
11
1
1
01
11
01
0
2
11 Q
© Q
11 Q
0 0
2 0
00
10
11
1
0
00
11
01
1
1
10
11
11
1
1
10
00
01
0
1
00
©
11
1
0
Q
Q
Q
0
0
t=l
t=7
t=13
00 00 00 00 00
10 11 11 00 00
11 01 11 01 11
0 0 10 0
0 0 0 0 0
t*19
01
10
11
1
0
Q
Q
Q
0
0
Q
Q
Q
0
0
li
10
11
1
0
00
11
01
0
1
01
11
11
1
2
Q
Q
Q
l
0
00
10
11
1
0
00
11
01
0
1
00
11
11
0
1
10
00
01
0
2
10
00
11
0
0
Q
Q
Q
0
0
t=2
t*8
t=14
00 00 00 00 00
10 11 11 00 00
11 01 11 01 11
0 10 0 0
0 0 0 0 0
t=20
11 01
10 Q
11 @
1 1
0 0
t=3
Q
Q
Q
0
0
00
10
u
0
1
11
11
01
1
1
t=9
00
11
11
0
2
01
X
©
1
0
00
10
11
0
0
00
11
01
1
0
00 00
11 00
11 01
1 1
0 1
t*15
10
00
11
1
0
10
я
©
0
0
, 00
10
11
1
0
00
11
01
0
0
00 00
11 00
11 01
0 0
0 0
t=2l
00
00
11
0
0
11
10
11
1
1
11 Q
© Q
01 Q
1 0
0 0
10
10
11
1 0
1
00
11
01
0
1
11
11
11
1
2
00
®
01
0
0
t«4
t=10
00 00 00 00 00 10
10 11 11 00 00 @
11 01 11 01 11 10
1110 10
0 0 0 10 0
t=ie
00 00 00 00 00
10 11 11 00 00
11 01 11 01 11
0 0 0 0 0
0 0 0 0 0
t=22
11
10
11
0
2
11
11
01
0
1
Q
Q
Q
l
0
10
10
11
0
1
10
11
01
0
1
00
11
11
0
2
11
00
01
0
1
00
10
11
1
0
00
11
01
1
0
00
11
11
0
0
00
00
01
0
1
00
00
11
0
0
00
10
10
0
1
1*5
t-11
t»17
Рис. 7. Пример работы сети с единичной задержкой. \
94
А. Атрубин
Могут быть сделаны некоторые дополнительные замечания.
Например, сигнал, отмечающий завершение выхода, легко
реализуется, когда мы имеем сигнал, указывающий на окончание
подачи информации йа вход. Напомним, 4to трудности,
связанные с построением, были вызваны тем, что рассматриваемые
числа могут быть сколь угодно велики. Для практических
целей при-перемножении чисел ограниченной величины можно
использовать конечную часть нашего устройства, причем число
ячеек в сети будет приблизительно равно половине числа
разрядов входного числа. Запоминающему устройству достаточно
иметь объем в 11 битов, так как 2П>1250. Особенно просто
построить устройство, запоминающее*^, х, у, Р и С в
отдельности, используя один бит для Р и по три бита для каждого из
других; в итоге нам потребуется 13 битов для ячейки.
Конструкции такого рода могут применяться в различных
вычислительных машинах. Такое умножающее устройство может
быть или смонтировано в виде сети, или если это нужно,
представлено программой в управляющей системе.
IV. Заключение
В этой статье доказывается существование итеративной
одномерной двухсторонней сети из ячеек с конечным числом
состояний и с единичной задержкой между смежными
ячейками, осуществляющей умножение двух двоичных целых чисел
в реальное время, причем низший разряд подается на вход
первым. Требуемый объем памяти (в расчете на один разряд
множимого и множителя) достаточно мал для возможных
приложений в технике.
Вопрос о существовании устройства, описываемого в этой
статье, был предложен автору проф. Э. Ф. Муром. Работа была
выполнена в Гарвардском университете на семинаре по теории
автоматов, руководимом проф. Э. Ф. Муром в течение
весеннего семестра 1962 г.
Л ИТЕРАТУРА
[l]McNaughton R., The theory of automata, a survey, in Advances in
Computers, v. 2, New York, Academic Press, 1961, 379—421.
[2] H e n n l e F. C, Iterative Arrays of Logical Circuits, M. I. T. Press,
Cambridge, Mass., 1961,
Порождение простых чисел
на одномерной итеративной сети
в реальное время1}
Патрик Фишер
1. Введение
Одномерные итеративные сети конечных автоматов
неожиданно оказались весьма эффективными при работе в реальное
время. Выяснилось, что они могут перерабатывать многие
последовательности таким образом, что при поступлении на вход
последовательности "длины k выход формируется в течение k
единиц времени после восприятия первого члена
последовательности. А. Атрубин показал, что умножение сколь угодно
больших целых двоичных чисел может быть осуществлено в
реальное время [1]. Один из результатов С. Коула заключается в том,
что множество всех симметричных слов четной длины
распознается в реальное время [2].
Интересная задача, связанная с итеративными сетями, —
это «задача о стрелках», в которой рассматриваются конечные
(хотя и сколь угодно длинные) сети. Как указывает Э. Мур [7],
задача была поставлена Д. Майхилом в 1957 г. и впервые
решена Д. Маккарти и М. Минским. Минимальное решение было
позднее дано Э. Гото [4], а более простая конструкция сети
недавно предложена А. Ваксманом [8]. В задаче требуется
построить одномерную итеративную сеть конечных одинаковых
(кроме крайних) автоматов («солдат»), находящихся в начале
в состоянии покоя, таким образом, что после подачи на вход
крайнего левого автомата одиночного возбуждающего сигнала
все автоматы через некоторое время должны одновременно
(и впервые) перейти в отмеченное состояние «выстрела».
Конструкция элементов сети не должна зависеть от ее длины.
Решение задачи о стрелках удобно излагать, вводя понятие
импульсов различного вида, перемещающихся вдоль сети с раз^
ными скоростями. В приводимом решении задачи о стрелках
крайний левый автомат посылает направо а-импульс,
перемещающийся вдоль сети со скоростью 1 и отражающийся от
крайнего правого автомата, кроме того, он же посылает также Ь-им-
пульс, который перемещается со скоростью -тт. Возвращаясь,
l) Fischer Р. С, Generation of primes by a one-dimensional real-time
iterative array, /, ACM, 12, № 3 (1965), 388—394,
96
П. Фишер
а-импульс встречается с b-импульсом в середине сети; в
результате этого элементы в центре (один или два) будут далее
работать так же, как крайние автоматы. Таким образом, сеть
разделяется на две синхронизированные равные части. Этот
процесс повторяется, и сеть последовательно делится на все
меньшие и меньшие синхронизированные друг с другом блоки,
пока не получатся блоки из одного автомата, и в этот момент
времени все автоматы переходят в состояние «выстрела».
а-импульс, —-—-— b-импульс, — • "—разбиение блоков.
Работа сети показана на рис. 1. Можно показать, что при
таком решении «выстрел» происходит в момент времени
Зд — 4 для любого п, где п — число элементов сети. (При
оптимальном решении «выстрел» производится в момент времени
йп — 2.) Сеть, соответствующая решению, при котором выстрел
происходит в момент времени Ъп — 4, может быть составлена
из автоматов Мура с 15 состояниями.
В этой статье метод, подобный использованному при
решении задачи о стрелках, применяется для построения
одномерной сети, порождающей двоичную последовательность, в кото«
Порождение простых чисел на одномерной сети 97
рой Y-й член печатается в момент времени t и равен 1 тогда
и только тогда, когда t простое число. (В отличии от задачи
о стрелках сеть, так же как у Атрубина и Коула, должна быть
бесконечной, так как иначе на выходе в конце концов будет
печататься периодическая последовательность.) Задача о
простых числах была поставлена Т. Кроули и решена им с
использованием двухмерных сетей.
2. Предварительные замечания
Определение. Бесконечной одномерной итеративной
сетью называется множество конечных автоматов (см. [3] и [6]),
поставленное во взаимно однозначное соответствие с
неотрицательными целыми числами, так что.
1) состояние автомата Mni соответствующего п, в момент
времени t зависит только от состояний Мп_ь Мп и Mn+i в
момент времени t— 1 для всех п>0;
2) все автоматы, исключая М0, одинаковы и в момент
времени ^ = 0 находятся в состоянии покоя;
3) вход и выход итеративной сети связан с автоматом М0, и
состояние М0 в момент времени t определяется только входом
и состоянием автомата Mi в момент времени t—-1. (Более
подробное описание может быть найдено в [2] и [5].)
Будет построена .одномерная бесконечная сеть конечных
автоматов М0, Ми М2, ..., которая будет печатать на выходе 1
в момент времени 3^+1, если на вход в момент времени 3t
подается 1 и t есть простое число или если в момент времени 3^
на входе подается 0 и t не является простым числом. Во всех
остальных случаях на выходе в момент времени ЗЛ-1
печатается 0. Можно объединить автоматы в группы по три
автомата и построить новую сеть из более сложных автоматов
Жо, М\9 Мъ ..., которая будет давать тот же результат, но без
множителя 3, т. е. новая сеть будет распознавать входные
последовательности, в которых t-й член есть 1 тогда и только
тогда, когда t — простое число. (Подробное описание метода,
при котором работа одномерной итеративной сети ускоряется в
некоторое число раз, приведено в [2].) Далее можно
рассматривать сеть как устройство порождающее, а не распознающее
простые числа, т. е. можно модифицировать крайний автомат
(Mo) так, что начальный входной сигнал просто служит для
возбуждения сети, которая затем начинает выдавать на выход 1
в моменты времени f+1, если i простое число, и 0, если / не
является простым числом. Наконец, легко модифицировать
крайний автомат так, что соответствующий символ будет выда*
ваться -на выход в момент времени if, а не в момент t+l%
7 Зак. 1204
98
Я. Фишер
3. Конструкция элементов сети
Приведенное ниже построение легче понять, если условиться
игнорировать структуру автоматов в, сети и рассматривать их
как устройство, передающее импульсы с различными
внутренними задержками. Ясно, что если такие конечные устройства
существуют, то их синтез легко осуществить. Автор построил
решение этой задачи, используя автоматы Мура Af< (*>0)
с 37 состояниями и автомат М0 с 11 состояниями.
Входными и выходными символами сети являются 0 и 1, на
выходе печатается 0, когда /^"l(mod3), а когда feEl(mod3),
на выходе может быть напечатано либо 0, либо 1.
Имеются три вида импульсов, перемещающихся вдоль сети;
обозначим их a, b и с. В каждый момент времени t данный ав^
томат может передавать двум смежным автоматам один им*
пульс, несколько импульсов или ни одного импульса. Крайний
автомат отличается от остальных. Остальные автоматы могут
быть двух видов: N- (разбиваемые) и Р- (разбивающие)
автоматы^ Все автоматы (кроме М0) в начальный момент вре*
мени являются Af-автоматами. В дальнейшем они могут
становиться и оставаться Р-автоматами или могут сколь угодно долго
оставаться ЛЛ-автоматами.
Поведение элемента сети
Строка
1
2
3
4
5
6
7
8
9
10
11
12
13
Тип
автомата
N
N
N
N
N -
N
N
Р
t
Р
Р
Р
Р
Р
Входной
импульс
в момент
времени t
а и b
а, но не b
а
Ь, но не а
b
е
с
а
а
b
b
с
с
Откуда
прибывает
л l
л
п
л
п
л
п
л
(
п
л
п
л
п 1
Выходной
импульс
а
b
а
а
b
b
с
с "
а
&
с
b
b
с
с
b
Куда
посылается
л
п
п
л
п
л
п
л
п
п
п
л
Время
t-
t-
t-
t-
t-
t-
t-
t-
t-
t-
t-
-2
r-2
-lv
-1
-3
-3
-2
-1
-1
-1
-2
-3
Невозможно
л
л
П
1 л
t-
t-
t-
t-
h3
-1
-2
И
Новый
тип
автомата
i '
N
N
N
N
N
N
P
1
1p
P
' P
I -
Порождение простых чисел на одномерной сети
99
Крайний автомат М0 ведет себя следующим образом.
1) Подача на вход первого 0 или 1 означает начало отсчета
времени, т. е. момент /=0.
2) В момент времени ^= 1 направо посылаются а-импульс и
Ь-импульс.
3) В момент времени t=4 направо посылается а-импульс.
4) В моменты времени t=\ и /=4 на выходе печатается 1,
если на вход в момент времени t — 1 подавался 0.
5) При любом £>6, где /~0 (mod 3), на выходе в момент
времени t+\ печатается 1, если на М0 в момент t поступил
b-импульс, а на входе в момент t был 0 или если на М0 в
момент t не поступал b-импульс и на входе в момент /была 1.
6) Во всех других случаях на выходе сети печатается 0 и
автомат М0 не посылает направо никаких импульсов.
Работа других элементов сети иллюстрируется таблицей. За
исключением случаев, соответствующих 1-й, 2-й и 4-й строкам
таблицы, при одновременном поступлении на автомат двух и
более импульсов их воздействие будет эквивалентно объединению
действий соответствующих одиночных импульсов.
4. Функционирование сети
Сеть отмечает пррстые числа, используя модификацию эра-
тосфенова решета. Рассматривается последовательность
положительных целых чисел, больших 1. Левый член этой
последовательности, равный 2, объявляется простым числом, и каждый
второй из остальных членов вычеркивается. Теперь первый не-
вычеркнутый член последовательности, равный 3, есть простое
число и каждый третий член, больший чем 3, вычеркивается.
(Разумеется, некоторые члены вычеркиваются более одного
раза.) При использовании метода эратосфенова решета процесс
продолжается, давая последовательно числа 5, 7, 11 ... . Нами
будет использован менее эффективный метод. После шага,
соответствующего числу 2, вычёркивается каждый -третий член
последовательности, начиная с 9. Далее вычеркивается каждый
четвертый член последовательности, начиная с 16 (этот шаг,
также как и все шаги, не соответствующие простым числам,
будет, очевидно, излишним). Вообще при выполнении шага,
соответствующего числу й, вычеркивается каждый k-й член
последовательности, начиная с kK Числа, которые при этом остаются
невычеркнутыми, представляют собой простые числа.
Для разбиения сети на состоящие из Af-автоматов блоки,
ограниченные с каждой стороны Р-автоматами, используются
а-импульс и идущий направо b-импульс. Если определить длину
блока как расстояние между ограничивающими его двумй
100
П. Фишер
Р-автоматами, то для каждого k >- 2 существует блок
длины k. В соответствующий момент времени с-импульс начинает
колебаться внутри блока и период колебания равняется
утроенной длине блока. Каждый раз, когда с-импульс поступает на
автомат, ограничивающий блок слева, налево посылается Ь-им-
пульс, перемещающийся к началу сети со скоростью 7з- Если
b-импульс совпадает с идущими из других блоков Ь-импуль-
сами, то он просто продолжает двигаться дальше как
одиночный b-импульс. Первый b-импульс, образованный в блоке
длины й, достигает автомата М0 в момент времени Зй2, а
последующие b-импульсы, образованные в этом блоке, будут поступать
на М0 в моменты времени, равные 3(й2+й), 3(k2 + 2k),
3(k2 + 3k), ... . Таким образом, поступление на крайний
автомат b-импульса в момент времени 3^ эквивалентно
вычеркиванию t в последовательности натуральных чисел, так как
в этом случае t имеет некоторый собственный делитель.
5. Подробный анализ сети
Лемма I. Для каждого &>1 автомат Mh(h+i)/2
становится Р-автоматом, что обусловлено одновременным приходом
слева в момент времени (3k2 + k)l2— 1 &-импульса и Ъ-импуль-
са, затем &-импульс в момент времени (3k2 + 3k) /2 возвращается
к M(h-\)h/2- Более того, только автоматы с индексами вида
k(k +1)/2 становятся Р-автоматами.
Доказательство. Докажем это индукцией по k. Пусть
k = 2. При таком k утверждение справедливо, так как в этом
случае а- и b-импульсы достигают автомата М3 в момент
времени 6, а-импульс возвращается к автомату Mi в момент
времени 9, а на автомат М2 а-импульс и b-импульс не поступают
одновременно.
Предположим теперь, что лемма верна для k -< п. Тогда
b-импульс, посланный направо автоматом Mn(n+i)/2 в момент
времени (Зп2 + п)/2+1, достигает автомата Мх в момент
времени
/==3(;t —(/z2+/i)/2 —1) + (3/г2 + /г)/2+1.
Точно так же а-импульс, посланный направо автоматом
М{п-1)п/2 в момент времени (Зп2 + Зп)/2+1, достигает Мх в
момент времени
t = (х — (п2 — я)/2 — 1) + (3/г2 + 3/г)/2 +1.
Таким образом, а-импульс и b-импульс встретятся, когда
t = Зх — (Зп2 + Зп)12+{3п2+п)12-2=х—(#2-/г)/2+(3/*2+3/г)/2,
Порождение простых чисел на одномерной сети
101
т. е. на автомате с номером
* = (л2 + Зл + 2)/2 = (л+1)(/1 +2)/2
в момент времени
^=(лг24-3/г-Ь 2)/2 — (п2 — л)/2 + (3/г2 + Зл)/2 =
= (3/г2 + 7/г+ 2)/2 = (3 (/г+1)2 +(/г +1))/2-1.
Отсюда следует, что никакой автомат между Afn(n+i)/2 и
Л[(П+1)(п+2)/2 не станет Р-автоматом. Наконец, а-импульс,
посланный автоматом Af(n+i)(n+2V2 в момент времени t + 2, достигает
автомата Afn(n+i)/2 в момент времени
t + 1+/г + 1=(3/г2 + 9/г + 6)/2 = (3(/г+1)2 + 3(/г + 1))/2.
Это полностью завершает индукцию, и таким образом лемма
доказана.
Лемма 2. Для каждого k >- 2 Ъ-импульсы посылаются
налево автоматом M(k-i)h/2 и достигают автомата М0 в моменты
времени t = 3k2+3ck, где сХ) — произвольное целое.
Доказательство. Когда с-импульсы образуются, они
начинают колебаться с периодом 3k между автоматами М{к-т/2
и Mh(k+i)/2- Каждый раз, когда с-импульс посылается направо
автоматом М^-фп, на одну единицу времени позже налево
посылается b-импульс. Первый такой b-импульс посылается в
момент времени (3&2+3fe)/2 + 3 (лемма 1 и 9-я строка таблицы)
и достигает автомата М0в момент времени
(3£2 + 3£)/2 + 3 + 3((£— 1)Л/2 —1) = 3#.
Теорема. Рассмотренная выше сеть может при любом х
распознавать множество всех слов вида aoOi... о3х, таких, что
для п-*Сх азп = 1, если п простое число, и азп = 0, если п не про-
стое число.
Доказательство. Автомат М0 обеспечивает работу сети,
в случае когда п<2. Для п > 2 лемма 2 показывает, что Ь-им-
пульс достигает автомат М0 в момент времени t тогда и только
тогда, когда t имеет вид 3k(k + c), где k и с положительные
целые числа (k > 2, с>0). Таким образом, прибытие Ь-им-
пульса на автомат М0 в момент времени Зп означает, что п
имеет собственный делитель и, следовательно, не является
простым числом. Автомат М0 тогда действует как сравнивающее
устройство, дающее требуемый выход.
102
П. Фишер
Следствие. Mootcei быть построена бесконечная сеть
конечных автоматов Мо, Ми Мъ ..., которая будет для
любого х распознавать множество всех сло0 вида ооО\ ... ах,
таких, что для п*Сх (Хп = 1 тогда и только тогда, когда п —
простое число.
Доказательство предоставляется читателю в качестве
упражнения.
Для любого автомата Mi достаточно иметь число
состояний, не большее чем 373 = 50 653.v Используя тот факт, что
только один из автоматов M3h M$i+u M3i+2 может быть Р-ав-
томатом, можно уменьшить число состояний в Mi до
величины порядка 30 ОбО. Дальнейшие уточнения могут быть
получены на основании других свойств сети.
ЛИТЕРАТУРА
1. Atrubin A. J., An iterative one-dimensional real-time multiplier, Term
paper for Appl. Math., Harvard University, 1962. '
2. С о 1 e S. N:, Real-time computation by iterative arrays of finite-state
machines, Doctoral Thesis, Report BL-36, Harvard University, 1964.
3. Ginsburg S., An introduction to mathematical machine theory, Addison-
Wesley, 1962.
4. Goto*" E., A minimum time solution of the firing:squad problem, Course
notes for Appl. Math., Harvard University, 1962, 52—59.
5. Hennie F. С., Iterative arrays of logical circuits, M. I. T. Press, 1962.
6. Moore E. F., Gedanken-experiment's on sequential machines, Automata
Studies, Princeton, 1956, 129—153. (Русский перевод: Мур Э.т
Умозрительные эксперименты с последоватёльностными машинами, сб.
«Автоматы», ИЛ, М., 1956Г)
7. М о о г е Е. F., The firing squad synchronization problem, in Sequential
Machines: Selected Papers, Addispn-Wesley, 1964, 213—214. (Русский
перевод: Мур Э., Задача о синхронизации цепи стрелков,
Кибернетический сборник, новая серия, вып. 1, изд-во «Мир», М., 1965.)
8. W a k s m a n A., An optimum solution to the firing squad synchronization
problem, Inf. and Contr., 9, № 1 (1966), 66—78.
Проблемы разрешения в грамматиках
непосредственных составляющих^
Питер С. Ландвебер
Введение
Грамматики непосредственных составляющих были введены
и впервые изучены Н. Хомским [1, 2] как механизмы для
порождения предложений языка. С помощью ограничений
возрастающей строгости, налагаемых на правила грамматики, Хомский
выделил четыре типа грамматик: грамматики типа 0 (самые
общие), типа 1 (контекстные, или контекстно-связанные), типа 2
(бесконтекстные, или контекстно-свободные) и типа 3
(грамматики с конечным числом состояний). В данной работе рассма^
триваются и решаются (в основном в отрицательном смысле)
некоторые проблемы разрешимости для этих классов
грамматик и порождаемых ими языков.
Как показали Рабин и Скотт [3], все раосматриваемые здесь
проблемы для грамматик типа 3 являются разрешимыми.
(Грамматики типа 3 эквивалентны конечным автоматам.) Для
грамматик типа 0 почти все эти проблемы неразрешимы; это
следует из результатов теории рекурсивных функций
(грамматики типа 0 эквивалентны полусистемам Туэ; см. Дэвис [4])2).
В данной работе будет показано, что, большинство этих проблем
неразрешимо уже для грамматик типов 1 и 2.
Из результатов, ранее получ.енных в этой области, следует
отметить работы Кантора [5] и Бар-Хиллела, Перлса и Шамира
[6]; в частности, последняя работа содержит все излагаемые
здесь результаты, относящиеся к грамматикам тип^ 2.
Представленные здесь доказательства и способ изложения, хотя и
сходные с доказательствами Бар-Хиллела и др., были получены
независимо3) и в том, что касается грамматик типа 0 и 1,
представляют собой существенное расширение работы [6].
В качестве примера неразрешимых проблем можно привести
следующие: не существует алгоритма, который. бы узнавал
1) является ли грамматика типа 2 неоднозначной;
^Landweber P., Decision problems of phrase-structure grammars,
IEEE Trans. Electronic Compute 13, № 4 (1964), 354—362.
2) См. также К лини С. К., Введение в метаматематику, § 71, ИЛ, М.,
1957 [13]. — Прим. перев.
3) Рецензентами была обнаружена ошибка в доказательствах теорем 7,
10 и 13. При исправлении были использованы доказательства аналогичных
теорем из работы [6].
104
П. Ландвебер
2) порождают ли две грамматики типа 2 один и тот же
язык;
3) является ли язык, порождаемый грамматикой типа 1, пу*
стым (или бесконечным);
4) является ли язык, порождаемый грамматикой типа i9
языком типа j(j>i; i = 0, 1, 2; / = 2, 3);
5) порождает ли грамматика типа 2 язык типа 3.
Последняя проблема есть, очевидно, частный случай четвер--
той; предварительный результат в ее решении имеется у Хом-
ского[1,2].
После вступительного раздела, посвященного
предварительным определениям, рассматриваются разрешимые проблемы для
грамматик типов 2 и 3. Следующий раздел посвящен
неразрешимым проблемам грамматик типа 2 и грамматикам типа 1.
В заключительном разделе рассматриваются проблемы,
касающиеся грамматик различных типов4 одновременно. Сводка
результатов, относящихся к проблемам разрешения для
грамматик всех типов, представлена в таблице, где указано, для каких
проблем доказана их разрешимость или неразрешимость.
Таблица {)
Проблема
Пуст ли язык, порождаемый данной
грамматикой? (LQ = 0)
Бесконечен ли язык, порождаемый данной
грамматикой? (Z,Q бесконечен)
Состоит ли язык, порождаемый данной
грамматикой, из всех слов в терминальном словаре?
{LQ = V*T)
Порождают ли две грамматики один и тот же
язык? (LQ = LQ\
Составляет ли язык, порождаемый одной
грамматикой, подмножество языка,
порождаемого другой? (LG с Lg\
Тип 3
Р
Р
Р
Р
Р
Классы
Тип 2
Р
Р
н
н
н
грамматик
Тип 1
н
н
н
н
н
Тип 0
н
н
н
н
н
Проблемы разрешения в грамматиках
105
Продолжение
Проблема
Пусто ли пересечение языков, порождаемых
двумя данными грамматиками? (LQ [\ LQ = Ф\
Является ли пересечение языков,
порождаемых данными грамматиками, языком того же
типа? (LQ П Lq язык того же типа")
Является ли дополнение языка,
порождаемого данной грамматикой, языком того же типа?
(VT\LQ язык того же типа)
Для любых слов ф, ф, выводимо ли ф ИЗ ф
в данной грамматике? (ф =ф я|)) '
Для любых ф, г|?, выводимо ли слово,
содержащее ¢, из ф в данной грамматике? (ф=ф>а|))
Есть ли в языке грамматики предложение,
выводимое более чем одним способом? (<7
неоднозначна)
Есть ли однозначная грамматика того же
типа, порождающая тот же язык?
Тип 3
Р
Да
Да
Р
Р
Р
Да
Классы
Тип 2
н
н
н
р
р
н
?»)
грамматик
Тип 1
н
Да
?
Р
Н
Н
?
Тип 0
Н
Да
Н
Н
Н
Н
Да
1) Обозначения к таблице: Р—проблема разрешима (т. е. существует
алгоритм, дающий ответ на данный вопрос для любых грамматик данного
типа), Н — проблема неразрешима (такого алгоритма не существует),? — не
известно, Существует ли' разрешающий алгоритм для данной проблемы,
Да — ответ на вопрос будет «да» для любых грамматик данного типа.
Отметим, что если вопрос касается пары грамматик, то обе они относятся к
одному и тому же типу.
2) Отрицательное решение этой проблемы получено А. В. Гладким
в работе «Алгоритмическая нераспознаваемость существенной
неоднозначности контекстно-свободных языков», Алгебра и логика, Семинар, 4, № 4
(1965). — Прим. ред.
106
П. Ландвебер
Предварительные определения ч
Предполагается, что читатель знаком с первой половиной
основополагающей работы Хомского [1], а также с основными
результатами и методами теории рекурсивных функций так, как
они представлены, например, в книге Дэвиса [4]. Кроме того,
бчень полезно знакомство с работой Рабина и Скотт [3].
Читатель может захотеть сравнить настоящую работу с работой Бар-
Хиллела и др. [6], в которой содержатся сходные результаты. '
Однако для полноты ниже кратко излагаются основные
понятия и определения, относящиеся к грамматикам
непосредственных составляющих.
Определение 1. Алфавит представляет собой конечное
непустое множество. Множество всех непустых конечных слов в
алфавите 2 обозначим 2*. (Пустое слово не вводится в
рассмотрение, за исключением тех случаев, когда это специально
оговорено; это позволяет упростить изложение.) Любое
подмножество множества 2* называется^язш;ож над алфавитом 2.
Определение 2. Грамматика непосредственных
составляющих— это упорядоченная четверка G = {VNl VT, Р, 5), где
1) V.N и VT — непересекающиеся алфавиты, называемые
словарями грамматики G, соответственно нетерминальным и
терминальным. (V=VN\JVT называется объединенным словарем
грамматики G.)
2) Р — это конечное множество упорядоченных пар (ф, ty),
где ф и г|> — слова в объединенном словаре t и где ф содержит
по меньшей мере один символ из W (Эти пары суть
подстановки или правила грамматики,G.)
3) S — выделенный символ словаря VN, играющий роль
аксиомы (начальный символ или символ предложения).
В дальнейщем, говоря о грамматиках непосредственных
составляющих, будем называть их просто грамматиками; G
является грамматикой над алфавитом 2, если Vr = 2.
Следуя Хомскому, принимаем, что заглавные латинские
буквы будут использоваться для обозначения слов в VN,
строчные латинские буквы — для слов в VT, греческие буквы — для
слов в V, начальные буквй всех алфавитов — для обозначения
отдельных символов (элементов словарей).
Определение 3. Определим теперь, каким образом
грамматика порождает язык. Дана грамматика G = (VN, VT, Р, S).
Запись
Проблемы разрешения в грамматиках
107
означает, что \|)i — 0)1ф0)2, ip2=o)i\|)(Og, где оь 0)2—слова
(возможно, пустые) в словаре V, а пара (ф, \|)) 6 Я. Далее, пишем
Ф=#Ф>
если существует последовательность (называемая выводом \|)
ИЗ ф) ф0, фь ..., фп (^>0), Такая, ЧТО фо = ф, фп=,ф И ф,г-1—*фг
(**=1, ..., ft). Язык, порождаемый грамматикой G, определяется
тогда как множество
10 = {х\хеУт и S=^x}.
Определение 4. Пусть G— грамматика и ф, г|) — слова
в словаре У. Запись
ф4>Ф (ф-^)
означает, что существует вывод
Ф=^01<ф02 (ф->о>1^02),
где о)1 и о)2 — слова ;в V, возможно, пустые. Это определение бу*
дет использоваться в следующем разделе.
Определение 5. Грамматики Gi и G2 называются
эквивалентными, если Lq{ = Lq2.
Определение 5а. Пусть 5->Ф1->Ф2-* ••• ->фл
—вывод в грамматике G типа 2 (см. ниже, определение 9). Пусть
Г/, п2, ...,Г;л—последовательность правил, применявшихся в
этом выводе, a Nif N2, ..., Nn — последовательность
натуральных чисел, таких, что переход
*фу_1->фу (/=1,..., п) (5 = ф0)
получен заменой Nj-ro символа ф^Гпо правилу Гц. (Отметим,
что если задан только вывод и грамматика, последовательность
правил г/, и последовательность чисел Nj определяются не
однозначным образом; для каждого вывода существует
конечное число пар таких последовательностей, и для каждой такой
пары может быть построено дерево.)
Сопоставим каждому правилу (Л, c&i ... ak) грамматики G
размеченное дерево такого вида, как показано на рис. 1. Тогда
соответствующее выводу S-^ф!—►.... —►фп и двум
последовательностям Гф Nj дерево вывода может быть получено следующим
образом: начинаем с дерева, сопоставленного правилу S—>ф1.
Это дерево представлено на рис. 2 при ф1 = aia2... 0¾. Далее,
беря по порядку каждое из деревьев, сопоставленных правилам
108
П. Ландвебер
ri , Г[ , ..., ri , «приклеиваем» самый верхний узел дерева
г/, к Nj-щ из самых нижних узлов уже частично
построенного дерева. Самые нижние узлы — это узлы, из которых не
исходит больше ни одного ребра; если прочитать слева направо
А А
Рис. 1. Дерево, соот- Р и с. 2. Дерево, соответ-
ветствующее правилу. v ствующее правилу (S.cpi).
символы, стоящие в этих узлах, то получится слово, стоящее в
последней строке вывода.
Пример. G = {VN, VT,.P, 5), где VT={a, 6}, VN={S}, S = Sf
а множество правил P={(S, ab),(S, ba),(S, aSb),(S, bSa),(S,SS)}.
Единственное дерево, соответствующее выводу S-^aSb-^abab,
S 5
^ A
Рис. 3. Дерево вывода Рис. 4. Дерево вывода
5 -> aSb -> abab. S -> SS -> a#S -> a#a#.
4
показано на рис. 3. Кроме того, слово abab имеет и другой
вывод с существенно отличным деревом вывода, изображенным
на рис. 4.
Определение 6. Грамматика G называется однозначной,
если для каждого слова x€.LG все его выводы имеют одно и то
же дерево. (Два дерева тождественны друг другу, если они
имеют одинаковую структуру и если соответствующие узлы
помечены одинаковыми символами.) В вышеприведенном примере
грамматика G была неоднозначной,,
Проблемы разрешения в грамматиках
109
Определение 7. Грамматика G называется приведенной,
если любой ее нетерминальный символ А удовлетворяет
следующим двум условиям: (1) S=$>A, (2) Зх{А=фх).
Определение 8. Для любого слова х в некотором
алфавите его длина Х(х) определяется как число символов,
входящих ва:1).
Теперь уже можно определить грамматики и языки типов 0,
1,'2 и 3. Далее последует несколько замечаний о грамматиках
типа 1 и грамматиках, использующих граничный символ.
Определение 9. Определяются грамматики и языки*
типов 0, 1, 2 и 3:
0) любая грамматика G есть грамматика типа 0;
1) грамматика G является грамматикой типа 1, если для
каждого правила (ф, г|?) выполняется Я(ф)<1Я(^);
2) грамматика G является грамматикой типа 2, если все
ее правила имеют вид (Л, ф), где А € VV,
3) грамматика G является грамматикой типа 3, если все ее
правила имеют вид (Л, аВ) или вид (Л, а).
Язык LGi порождаемый грамматикой типа i, будем также
называть языком типа и
Между данным здесь определением грамматики типа 1 и
первоначальным определением Хомского [1] имеются два
различия. Во-первых, Хомский выделяет особый символ ф € Vt в
качестве граничного символа и считает, что грамматика G
порождает язык LQ={x\ # S # =Ф # х #}. Автором данной
статьи показано [8], что при использовании граничного символа
класс языков типа 1 остается прежним. Во-вторых, в
определении Хомского требуется, чтобы правила грамматики типа I
имели вид (о)Иа)2, о)1фсо2), т. е. заменялся бы. только один
символ. Но, по утверждению самого Хомского [1, стр. 286—
287 русск. перевода], языки, порождаемые грамматиками типа 1,
на правила которых наложено такое ограничение, — это просто
языки типа 1 в нашем смысле; доказательство этого не пред*
ставляет затруднений.
Основные свойства языков этих четырех типов подробно
рассмотрены Хомским [1] и Шейнбергом [9]. Приведем наиболее
важные из этих свойств:
1) как для грамматик, так и для языков тип 0 г> тип 1 г>
zd тип 2 :э тип 3; более того, во всех случаях имеет место
строгое включение;
1) Точнее, как число вхождений символов в х. — Прим. перев.
110
П. Ландвебер
~ 2) языки типа 0 над алфавитом 2 — это в точности
рекурсивно-перечислимые множества слов в 2;
3) языки типа 1 (а также языки типа 2 и языки типа 3)
равномерно примитивно-рекурсивны. Последовательность множеств
(£i, £2, •. •) является равномерно примитивно-рекурсивной, если
существует примитивно-рекурсивный предикат /?(л;, i), такой,
что xdEiz^R(xi i); очевидно, каждое из множеств Е{ само
является примитивно^рекурсивным;
4) языки типа 3 суть- регулярные события, т. е. множества
слов, представимые в конечных автоматах; "^
5) множество языков типа 3 над алфавитом 2 образует
булеву алгебру. Множество языков каждого типа замкнуто
относительно объединения в конечном числе. Класс языков типа 2
не замкнут ни относительно пересечения, ни относительно
дополнения. Классы языков типа 3 и типа 1 замкнуты
относительно пересечения (результат, касающийся типа 1, был
получен автором данной статьи [8]). Дополнение языка типа 0 не
всегда будет языком типа 0; 'относительно языка типа 1 этот
вопрос остается открытым.
Разрешимые проблемы (грамматики типов 2 и 3)
Пусть даны G, G\ й G2 — грамматики типа 3 (или, что то же,
конечные автоматы1)). Рабин и Скотт [3] показали, что можно
эффективно определить, имеет ли место следующее2):
1) LG пуст;
2) LG бесконечен;
3) Lqx = Lq2. ~~
Мы будем интересоваться рекурсивной разрешимостью или
неразрешимостью подобных проблем для грамматик типов 0,
1 и 2.
Но вначале докажем разрешимость «проблемы
неоднозначности» для грамматик типа 3, т. е. покажем, что по любой
грамматике типа 3 можно эффективно решить, является ли она
неоднозначной или нет. Далее будет показано, что можно узнать
по данной грамматике типа 2, верно ли, что:
1) LG пуст;
2) LG бесконечен;
3) G является грамматикой с самовставлением (определение
см. ниже).
Теорема 1. Для грамматик типа 3 разрешима проблема
неоднозначности. А именно, если в грамматике G имеется п не-
1) Об этой эквивалентности см. [7].
2) Рецензентами было указано, что это следует уже из работы Мура [10].
Проблемы разрешения в грамматиках
111
терминальных символов, то G неоднозначна тогда и только
тогда, когда для некоторого x^LG длины не более п2+2п
существуют два неэквивалентных вывода 5=фх.
*
Доказательство. (Приводится не полностью; некоторые
детали предоставляется восполнить читателю; доказательство
ведется на языке конечных ориентированных графов.)
Доказательство начинается с замены G приведенной
грамматикой G' типа 3. Эта грамматика получается из G
выбрасыванием каждого нетерминального символа Л, который не удо-
*
влетворяет хотя бы одному из следующих двух условий: Б=фА
и Зх(А=^х), равно как и всех правил, содержащих
выбрасываемые символы. Грамматика G' может быть эффективно
получена из G./Важно, что грамматика G' тогда и только тогда
неоднозначна, когда неоднозначна G; выводы вида S=#>x
будут одними и теми же для G и для G' и LG = Lo'.
' Допустим теперь, что G неоднозначна; в этом случае G'
также будет неоднозначной. Покажем, что существует слово
z(LLG'> по длине не превосходящее /г2 + 2м, которое, имеет два
неэквивалентных вывода S=#z.
Для этого достаточно найти в грамматике G' два вывода
вида Л=фл:а, где Х(х)<^п2 и а — либо нетерминальный
символ грамматики G', либо пустое слово; поскольку, если A=f=S,
существует вывод 5=фгхЛ, где Zi — некоторое слово в
терминальном словаре, а кроме того, если а не пусто, существует
вывод афг2 с некоторым терминальным z2. Это верно даже в
предположении, что длина zu как и длина z2, не превосходит п.
Тогда мы получим два неэквивалентных вывода S=^ZiXZ2
слова z (z = ZiXz2), длина которого не превышает п2 + 2п.
Согласно нашему предположению, G' неоднозначна. Это означает,
что в грамматике G' существует два неэквивалентных вывода
Л=# ха, где а — или нетерминальный символ, или пустое слово.
Пусть х — слово наименьшей длины, допускающее такие два
вывода Афха {с одними и теми же Л и а). Если длина х
равна т, эти выводы имеют следующий вид: l .
А = А0->ахАх -> ... ->аг ... ат_1Лт^1 ->аг ... ama = ха,
A = BQ -> а1В1 -> ... -> аг ... ат-\Вт_х ->аг ... ата = ха.
Из предположения о минимальности длины х следует, что
Ai=j=B.i для 0<i<m. Если же т>п2у то обязательно найдутся
тадие i и / {0<i<j<m), что А^А) ц В^В^ поскольку
112
П Ландвебер
существует лишь п2 различных пар (Л, В), а тогда мы можем
получить два неэквивалентных вывода
А0—> ... —> #] ... а^/1^ —> aj . . . CLiCL]+\A]+i—> ...
... ->#! ... Я/Яу-н ... ата,
В0-> ... ->#! ... aiBi->ax ... Я/а;+15у+1-> ...
... ->ах ... ataJ+l ... ата
вида Л=Фуа, где г/ короче, чем я, что по предположению
невозможно. Следовательно, длина h(x)=m не может превосходить
п2 и теорема доказана.
Далее до конца этого раздела мы будем заниматься
исключительно грамматиками типа 2. Сначала определим понятие
грамматики с самовставлением.
Определение 10. Пусть G = {VN, VTi Р, S) — грамматика
типа 2. Если для некоторого А € VN ^-
Л=ФфА|),
где ф и г|) — непустые слова в V, то О называется грамматикой
с самовставлением.
Важность этого понятия явствует из следующей теоремы
Хомского [1, 2]: язык L типа 2 тогда и только тогда не является
языком типа 3, когда все грамматики типа 2, порождающие L,
являются грамматиками с самовставлением.
Введем еще два определения, которые понадобятся в
дальнейшем: понятие высоты вывода и понятие вывода с повторением.
►фп — вывод в
Определение 11.
амматике типа 2, где
%. ф/==а^Ц^ ...
ПуСТЬ фо~*ф1-> . •
а<?> (a</>6V; / = 0
., /г).
Определим функцию h(i, j) по индукции следующим образом:
1) /1(0,/)=0 (К/А);
2) Если функция h(i, /) определена для некоторого i и для
К/4^ и если переход <рг-—>*фж происходит путем замены
аФ на а^+1>... а</+1), положим
fh(t9j) 0<J<J\)>
A(/+l, j) = { A (/, jx)+l {j\<J <Л)>
I h {/, у + у*! — y2) (y2 < у < Ai+1).
Теперь определим высоту вывода как
щахh(п, J) il<j<kn)<
Проблемы разрешения в грамматиках
113
Иначе говоря, высота вывода — это длина самой длинной ветви
дерева, соответствующего этому выводу, а функция /i(/, /)
равна числу подстановок, которые приводят к появлению /-го
символа в слове фг-. (Для .наглядности читатель может разобрать
несколько примеров.)
Определение 12. Сохраним обозначения предыдущего
определения: Для некоторого 0-</<п обозначение
аф^а(т) (;,<;< Л)
указывает на то, что а(?+1) есть один из новых символов, воз-
никающих при подстановке вместо символа а(Я. Если
говорим, что а^ подчиняет oSl.+s\ Если какой-либо символ в
выводе подчиняет самого себя, вывод называется выводом с
повторением.
Лемма 1. Если ф0—►... -*фт — вывод без повторения в
грамматике G типа 2 и если G имеет п нетерминальных
символов, то высота этого вывода не превышает п.
.Доказательство. (Дается лишь набросок.) В
бесповторном выводе каждый символ из G, поскольку он не может
подчинять самого себя, может подчинять только п — 1
нетерминальных символов. Если символ уже подчинен г
нетерминальным символам, он может подчинять не более п — г — 1
нетерминальных символов. Поэтому очевидно, что длина любой ветви
дерева не может превышать п, а следовательно, и высота
вывода не может быть больше, чем п, и лемма доказана.
Лемма 2. Пусть G — грамматика типа 2 и LG не пуст;
тогда существует х £ LG, обладающее бесповторным выводом
Доказательство. Поскольку LG не пуст, выберем слово
из LCri обладающее таким выводом
который имеет наименьшую длину m среди всевозможных
выводов элементов из LG. Если бы теперь этот вывод оказался
выводом с повторением, т. е. если бы сцмвол а<р подчинял
114
П. Ландвебер
символа^,'*, где / < /' и aip = aip,TO ясно, что можно было бы
свернуть его и получить новый вывод
S = %-> ... ->ф/->фг+1-> ... ->Фт = й .
где х также является терминальным словом, причем новый
вывод оказался бы короче прежнего, что противоречит нашему
допущению о выборе первоначального вывода. Следовательно,
первоначальный вывод является бесповтарным, что и
доказывает лемму.
Теорема 2. Поскольку в грамматике G может
существовать только конечное число выводов ограниченной высоты, мы
доказали следующую теорему: можно эффективно узнать, будет
ли язык LG, порождаемый грамматикой G типа 2, пустым или
непустым. А именно, если G имеет п нетерминальных символов,
язык LG непуст в том и только в том случае, когда существует
вывод S^x, высота которого меньше или равна п и где х —
терминальное слово.
Лемма 3. Пусть G — грамматика типа 2 и ф, \|) —► слова в
ее объединенном словаре V. Существует метод, позволяющий
узнать, верно ли, что ффф.
Доказательство. Пусть m — большая из длин слов ф
и гЬ. Тогда рассмотрим все слова в V длиной не больше m и от-
берем те пары слов (coi, <ог), для которых o)i—ко2. Получаем
конечный ориентированный граф, который, разумеется, может
#
быть построен эффективно. Далее, легко видеть, что ф=фг|?
тогда и только тогда, когда существует вывод
Ф = Фо--^1-^ ••• -**Ф/г = ^>
где X(q>i)*Cm при i = 0, 1, ..., п. Тогда по полученному графу
можно определить, существует ли путь из узла ф в узел \|) и,
*
следовательно, имеет ли место ф=фг|) или нет, что и
требовалось доказать.
Теорема 3. Можно эффективно определить, является ли
язык LG, порождаемый грамматикой типа 2, бесконечным. (См.
статью Шейнберга [9].)
Доказательство. Пусть G={VNl VT, Я, S)—грамма-
^\\щ щщ £. В силу теоремы 2 и лщмц 3 мы мо>#?м? так ще ц$ц
Проблемы разрешения в грамматиках 115
это делалось в доказательстве теоремы 1, построить
эквивалентную ей приведенную грамматику Q' ={V'N, VT, P't S). Теперь
воспользуемся следующим результатом Шейнберга [9]: для
приведенной грамматики G' типа 2 язык Lq> тогда й только тогда
бесконечен, когда существует такой символ A£Vjv, что Л=Ф
=^фАф, где хотя бы одно из -слов ф, \|) непусто. Разрешимость
этого свойства грамматики G' следует опять-таки из леммы 3.
Следовательно, мы можем решить проблему бесконечности для
LG, что и требовалось доказать.
Теорема 4. Последняя теорема этого раздела
вытекающая непосредственно из леммы 3, формулируется следующим
образом: можно эффективно распознать, является ли данная
грамматика типа 2 грамматикой с самовставлением.
Д о к аз ател ьство. Чтобы решить эту проблему, нужно
*
просто определить, имеет ли место Л=ФаЛр для какого-либо
Л€У*иа, Р€ V.
Неразрешимые проблемы для грамматик типа 2
В этом разделе доказывается неразрешимость следующих
проблем для грамматик типа 2:
1) пусто ли пересечение Lqx[\Lq^
2) является ли G однозначной;
3) является ли пересечение Lgx П Lq2 языком типа 2;
4) является ли LG «полным» языком VT\
5) верно ли, что Lqx = Lq2;
6) верно ли, что Lqx с Lq2; -
7) является ли дополнение Vt\Lq языком типа 2.
Можно заметить,- что все эти проблемы неразрешимы уже
для подкласса грамматик типа 2, который соответствует
наборам п стандартных последовательностных функций,
определенным Гинзбургом и Райсом [11]. Для этого надо только
убедиться, что все языки типа 2, которые встречаются в этом раз*
деле, являются последовательностно определимыми
множествами.
Доказательство будет вестись таким образом, что
неразрешимость проблемы 1 будет использована при доказательстве
неразрешимости остальных проблем. Ответ на вопрос 2 был
дан Кантором [5], на большинство остальных вопросов ответили
Бар-Хиллел, Перле и Шамир [6]. Приводимое здесь
доказательство неразрешимости проблемы 2 более симметрично, чем
116
П. Ландвебер
канторовское, а использование комбинаторной проблемы Поста
проще, чем у Бар-Хиллела и др. Некоторые другие проблемы,
касающиеся и языков типа 3, также должны быть рассмотрены,
но откладываются до следующего раздела; простейший пример
подобной проблемы: «Является ли язык LG (G — грамматика
типа 2) языком типа 3?» Прежде всего рассмотрим теорему
Поста [12] о неразрешимости комбинаторной проблемы. Из этой
теоремы будет выведена неразрешимость проблемы 1, а отсюда
легко получается неразрешимость проблем 2 и 3. Следующий
шаг состоит в том, чтобы показать, как из неразрешимости
проблемы 1 следует неразрешимость проблемы 4; на этом шаге
будет показано, что дополнения к элементам некоторого класса
языков типа 2 будут снова языками типа 2. -После этого
неразрешимость остальных трех проблем получается очень просто.
Комбинаторная проблема Поста для алфавита 2 и целого
положительного п формулируется следующим образом: по
данным двум спискам х=(хи ..., хп) и у=(Уи • • •, Уп) слов в
алфавите 2 решить, существует ли последовательность индексов
i'i, ..., ir (г> 1), где 1 ^ij^Cn, такая, что
X, X, ... х, = у, у, ... у, .
Пост [12] *) доказал, что, каков бы ни был алфавит 2 более
чем из одной буквы, существует такое целое положительное
число п, что комбинаторная проблема для 2 и п алгоритмически
неразрешима. (Эта формулировка представляет собой некоторое
усиление результата Поста, неявно содержащееся в его
доказательстве.) v
Сведем теперь комбинаторную проблему к некоторой
проблеме, касающейся грамматик типа 2. С этой целью
зафиксируем алфавит 2 и число п, для которых комбинаторная
проблема неразрешима. Введем алфавит 2o = {6t, ..., bn], каждая
буква которого отлична от остальных и от букв алфавита 2, и
пусть 2i = 2U20. Если х=(хи ..., хп) —список п слов в
алфавите 2, то обозначим через Q(x) множество всех слов вида
для всех последовательностей iu ..., in У которых г>1 и
l^Y<7z. Ниже следуют две леммы, относящиеся к этим языкам;
доказательство первой из них очевидно.
Лемма 4. Если х=(хи .. ., хп) и y—iyu • • •, Уп)—два
списка, содержащие по п слов в алфавите 2, то комбинаторная
1) См. также Марков [14, гл. VI, § 9].— Прим. ред..
Проблемы разрешения в грамматиках
117
проблема для этих списков имеет решение тогда и только тогда,
когда
Q(x){]Q(y)^0.
Лемма 5. Для каждого списка х = (хи ..., хп) из п слов в
2 множество Q(x) является языком типа 2 над 2i.
Доказательство. Построим грамматику G типа 2 над
алфавитом Si, такую, что LG = Q(x). Для этого возьмем Vn = {S}>
1/T = 2i и следующие правила: (S, &л), (5, biSxi) для каждого
i'=l, ..., п. Проверку того, что эта грамматика порождает язык
Q(x), можно предоставить читателю.
Теорема 5. Не существует алгоритма, который по двум
грамматикам Gi и G2 типа 2 определял бы, пусто ли
пересечение языков Lqx П £о2-
Доказательство. Если бы можно было эффективно
определить, пусто ли пересечение Lq{ П Lg2> то можно было бы
узнать, пусто ли Q{x) П Q (г/), поскольку грамматика,
порождающая Q(x), строится эффективно по х=(хи ..., хп). По лемме 4
отсюда следовала бы разрешимость комбинаторной проблемы,
а это приводит нас к противоречию, чем и доказана
неразрешимость.
Нужно заметить, что комбинаторная проблема Поста
используется весьма аналогично тому, как использовали ее Рабин и
Скотт [3].
Теорема 6. Не существует эффективного метода,
позволяющего решить, является ли данная грамматика типа 2
неоднозначной или нет. (См. статью Кантора [5].)
Доказательство. Из леммы 5 очевидно, что языки Q(x)
порождаются однозначными грамматиками. Язык Q(x) UQ(y)
порождается грамматикой G со словарями Vjv = {S, А, В}, VT =
= 2i и правилами
5->Л, A->btxit A->biAxi \
5->5, B->btyh B-^bfiy,] (' = Ь.... л).
[В дальнейшем мы предпочитаем записывать правила в виде
(p-*\|>, а не (ф, г|)), если это не приведет к недоразумению.] Эта
грамматика неоднозначна в том и только в том случае, когда
Q(x)0Q(y) непусто, а это последнее свойство неразрешимо.
Следовательно, неразрешима и проблема неоднозначности для
грамматик типа 2, что и требовалось доказать.
118
П. Ландвебер
Теорема 7. (Приводимое ниже доказательство
принадлежит Бар-Хиллелу и др. [6] и кратко излагается здесь для
полноты картины.) Не существует алгоритма, который бы решал,
является ли пересечение Lg1(]Lg2 языков, порождаемых двумя
грамматиками типа 2, сноЪа языком типа 2 или нет.
Для доказательства необходимо заменить языки Q(x) и
Q(y) языками Q(x, у) и Q', определяемыми так:
Q(x, y)={<tc$\4>eQ(x)W£Q(y)} =.
= {bt/ . .*,д.. .xlrcyJs.. ГУ]Ь.Г .bjs) (1</,<л, 1 <;,<*)
и
(?'={г<£|г€Я},
где с — новый терминальный символ, а:, у и Si имеют то же
значение, что и в предыдущих доказательствах, a z обозначает
отражение слова г.
Легко видеть, что пересечение Q(x, у) flQ' непусто (и
бесконечно) тогда и только тогда, когда существует положительное
решение"комбинаторной проблемы Поста для списков х и у.
Можно показать, что языки Q(x, у) и Q' также являются язы*
ками тцпа 2. Тогда для них справедливы утверждения, анало*
гичные лемме 4 и лемме 5. Но аналог леммы 4 может быть зна*
чительно усилен, так что имеем следующий результат:
Лемма 4а. (Бар-Хиллел и др., см. приложение I.) Пересе-
чение Q(x, у) flQ' непусто тогда и только тогда, когда
комбинаторная проблема Поста для списков х и у имеет
положительное решение. Более того, когда Q(x, у) DQ' непусто, оно не
является языком типа 2.
Лемма 5а. Множества Q(x, у) и Q' являются языками
типа 2; грамматика G(x, у), порождающая язык Q(x, у),
может быть получена эффективно по х и у.
Опираясь на эти леммы, мы можем теперь приступить
непосредственно к доказательству теоремы 7.
Доказательство теоремы 7. Предположим, что
существует алгоритм, определяющий, является ли языком типа 2
пересечение Lqx[\Lg2 языков, порождаемых грамматиками G4
и G2 типа 2. Пусть G(x, у) и G'—грамматики, порождающие
языки Q (а:, у) и Q'; эти грамматики могут быть построены
эффективно по спискам х и у. Тогда можно эффективно
определить, является ли пересечение Q(x, у) flQ' языком типа 2. Но по
Проблемы разрешения в грамматиках
119
лемме 4а это пересечение является языком типа 2 тогда и только
тогда, когда оно пусто и, следовательно, когда комбинаторная
проблема имеет для списков хну отрицательное решение. Тогда
мы получили бы алгоритм для решения проблемы Поста, что не«
возможно.
Теперь мы можем приступить к решению проблемы 4. Пусть
Si и Q(x) имеют то же значение, что и выше. Мы знаем, что не
существует алгоритма, определяющего, пусто ли пересечение
Q(x)()Q(y). Но пустота пересечения эквивалентна равенству
(S\QW)u(St\Q(t/)) = 2l.
Если удастся показать, что Si\Q(x) всегда является
языком типа 2, то получим неразрешимость равенства Lqx U £g2 = Si
для грамматик Glt G2 типа 2 над Si. Отсюда мы сможем
заключить, что невозможно эффективно определить, имеет ли место
равенство Z,q==Si для грамматик G типа 2 над Si, поскольку
грамматика, порождающая объединение Lgx\}Lg^ получается
эффективно по Gi и G2.
Лемма 6. В предыдущих обозначениях языки 2* \ Q (х)
все являются языками типа 2.
Доказательство. Пусть М — {ху\x£2q, */£S*}
(напоминаем соглашение о том,, что пустое слово не принадлежит
S* ил и S*). Тогда Q (х) ^М и
Zl\Q(x) = &\M)[}(MrQ(x)).
Ясно, что М — язык типа 3, так что его дополнение Si\M
есть также язык типа 3, а следовательно, и. язык типа 2.
Остается показать, что M\Q(x) есть язык типа 2, т. е, мы
должны найти грамматику типа 2, которая порождает все слова
множества Af, не принадлежащие языку Q(x).
Читателю предоставляется убедиться в том, что следующая
грамматика типа 2 порождает язык M\Q(x): возьмем
VN={S, A, Bv В2, £3> Сг Ся, Dx Dn), КГ = 2Х
и следующие правила:
1. S-+BJ 2. S->B2; 3. S->£3; 4- -A-*Mrf
5. A->blAxi(i = l, ...,й); 6. B1^blA; 7. B1-^biB1(i = l> ...,/*);
8. В2->Аар 9. B2->B2aj (aygS); 10. B^bfit 11. Bb-+btACt
12. B3->biBz (/=1, ..., n)\
13. Ct->x [для всех x, таких, что X(x) < X(xt), / = 1 n)\
14. Dt->x [для всех хФх1г X(x) — X(xl), /==1, ..., /г];
1§. D(~>D^; 16. C{->Dt (/,/=1, ...,*; ay^S). *
120
П. Ландвебер
Идея, лежащая в основе этой грамматики, состоит в
следующем: чтобы порождалось слово из M\Q(x), начнем строить
слово из Q(x) и затем как-нибудь «испортим» это построение.
(Более подробное доказательство см. в приложении П.)
Лемма 6а. Языки 22 \ Q (х, у) и 1>1\ Q' порождаются
грамматиками типа 2, которые могут быть эффективно
построены по х и у. Здесь через 22 обозначено объединение
2iU{c}.
Теорема 8. Предыдущая лемма и рассуждения,
предваряющие лемму 6, дают нам возможность заключить следующее:
не существует алгоритма, который по грамматике G типа 2
с терминальным словарем VT определял бы, справедливо ли
равенство Lg = Vt-
Перейдем к доказательству неразрешимости проблемы
эквивалентности и проблемы включения для грамматик типа 2.
Вначале покажем, что для грамматик одного и того же типа эти
две проблемы равносильны, т. е. сводятся друг к другу.
Лемма 7. Для грамматик одного и того же типа i (/ = 0, 1,
2 или 3) разрешающий алгоритм для проблемы эквивалентности
(Lg1 = Lg2) существует в том и только в том случае, когда
существует разрешающий алгоритм для проблемы включения
(LGx с LG?).
Доказательство. Доказательство непосредственно
вытекает из соотношений
LGl = LGi ^ {LGl S LGi и Lq2 с Lg),
LGl с LGi ^(LGlU Lq2) = Lg*
Теорема 9. Проблема эквивалентности для грамматик
типа 2 неразрешима.
Доказательство. Если бы можно было эффективно
определить, когда имеет место LGi = Lg2, то, в частности, можно
было бы определить, в каких случаях справедливо равенство
Lqz^Vt* где VT — терминальный словарь грамматики G. Но
это противоречило бы теореме 8, и наша теорема доказана.
Следствие. Проблема включения для грамматик типа 2
неразрешима.
Проблемы разрешения в грамматиках
121
Теорема 10. По грамматике G типа 2 невозможно
эффективно определить, является ли Vt\Lg языком типа 2.
Доказательство. Предположим, что существует
алгоритм, позволяющий узнать, является ли Vt\Lg языком
типа 2. Тогда, в частности, мы могли бы узнать, является ли
языком типа 2 язык
L = l.l\[(2l\Q(x, y))u&\Q')}, ,
применив лемму 6а и тот факт, что грамматика, порождающая
объединение Lgx U £о2> определяется эффективно по Gi и G2. Но
язык L равен Q(x, у) Г1 Q' и, следовательно, мы могли бы
эффективно определить, является ли Q(x, у) П Q' языком типа 2.
А это в силу леммы 4 дало бы возможность решить комбинат
торную проблему Поста.
Неразрешимые проблемы (грамматика типа 1)
Основным результатом этого раздела является
доказательство неразрешимости проблем пустоты и бесконечности для
грамматик типа 1. Кроме того, будет показано, что предикат
* *
фгфг|) для грамматик типа 1 неразрешим. (Предикат ф=фг|)
зависит, кроме ф и г|?, также от грамматики G.)
Покажем вначале, что все пересечения Q(x) flQ(y) языков,
определенных в предыдущем разделе, представляют собой языки
типа 1. Это следует из теоремы о пересечении (контекстных
языков), принадлежащей автору [8], но применительно к данному
случаю будет дано специальное более изящное доказательство.
Поскольку не существует алгоритма, определяющего, пусто ли
пересечение Q(x) {)Q(y), проблема пустоты для грамматик
типа 1 должна быть неразрешима. Очевидно, что, когда
множество Q(x) f\Q(y) не пусто, оно бесконечно; следовательно,
проблема бесконечности для грамматик типа 1 также неразрешима.
Таким Образом, осталось доказать нижеследующую лемму:
Лемма 8. Все пересечения Q(x) flQ(y) являются языками
типа 1.
Доказательство. Продолжаем использовать
обозначения предыдущего раздела. Так, х=(хи ..., хп) и у=(уи ...
. •., Уп) — Два списка по п слов в алфавите 2, a 20={&i, ...
..., bn) — алфавит из п новых, отличных друг от друга букв.
Допустим, 2 = {ai, ..., ар}. Введем пр новых символов следующего
вида:
C=[CtJ\i = l9 ,.., п\ у=1, ..., р\.
122
П. Ландвебер
Если Xi начинается с буквы а^ то обозначим через х\ слово,
полученное из х\ заменой первой буквы на символ Сц\ точно так
же через у\ обозначим слово, полученное из \ji заменой первой
буквы символом Cij, если а,-— первая буква у\. Например, если
#2*=#3#7#i, то x'2 = C2da7av Кроме того, пусть 6,-(/=1, ..., р) —
еще р новых букв, образующих алфавит 2. Для любого слова и
в алфавите 2 U С обозначим через й слово, полученное из и
заменой каждой буквы а,- на а,. Например,, если и — а^С^а^ то
й^йзСма^а. если, как в предыдущем примере, х2=а3а7аи то
х^^С^а^- Теперь определим грамматику G как грамматику
над алфавитом 2i = 2U20 с нетерминальным словарем VN =
=2 U С U {S} и правилами
Cijak->ajClJt
akCij -* С/л#/
#/-*#/ (/=1, ..., /г; A= 1, ..., p).
Так определенная грамматика G типа 1 порождает язык
Q(x) OQ(y). Грамматика сперва подражает грамматике,
порождающей слова bi :..biXi ... xi языка Q(x), а затем
перебрасывает маркеры Cik через буквы S,- до тех пор, пока
не станет возможно привести полученное слово к виду
Ь, ... Ь, у. ... у, . Лемма доказана.
1г l\ li v
Лемма 8а. Для каждой пары х, у пересечение Q(x, у) flQ'
порождается грамматикой типа 1, которая может быть
построена эффективно по х и у.
*
Теорема 11. Предикат ф =#> ф неразрешим для грамма-
G
тик G типа 1.
Доказательство. Теорема будет доказана для
грамматик типа 1, использующих граничный символ. Если задана (7 =
— {Vnj У Ту S, #, Р)—грамматика с граничным символом, то
добавим два новых символа e4 и е2 и построим грамматику О, =
MVV утг> Sv #• Л) типа 1. где VNx = VN U VT U {^}. ^,=
^=(^), Si=S, a Pi — множество, включающее следующие правила:
Проблемы разрешения в грамматиках
123
1) каждое правило грамматики G;
2) для каждого а £ VT правила # а -> # ех и еха -> ехег\
3) правило ^itt->^2#-
Легко видеть, что язык LG непуст тогда и только тогда,
#
когда S^e2. Поскольку проблема пустоты для грамматик типа 1
*
неразрешима, неразрешим и предикат S=^e2 (для G[ типа 1).
о
*
А тогда предикат ф=ф\|) (G типа 1) также неразрешим и тео-
G
рема доказана.
Из доказательства теоремы И дополнительно следует, что
невозможен эффективный метод, позволяющий узнать,
применяется ли данное правило грамматики типа 1 хотя бы в одном
выводе из начального символа.
Языки различных типов
В данном разделе рассматриваются проблемы разрешения,
связывающие между собой яйыки различных типов.
Грамматики типа I будут обозначатьсй G^\ В основном нас интересуют
следующие проблемы:
1) можно ли по данным i и / решить, совпадает ли язык
LGa) с языком LGu),
2) можно ли по данным i и / решить, является ли язык L^
языком типа /'.
Проблема 1) есть не что иное, как расширение проблемы
эквивалентности; проблема 2) представляет интерес, только
если /</.
Теорема 12. Для данных /, /, 0 •< i < 3, 0 < /<3, не
существует алгоритма, определяющего, справедливо ли равенство
Доказательство. Возьмем пару (/, /),
удовлетворяющую условию теоремы, и зафиксируем грамматику #<*),
порождающую язык Vt. Поскольку для / = 0, 1, 2 невозможно
узнать, равен ли язык LGU) языку VT — LH(i)> расширенная
проблема эквивалентности LG(i) = LG(j) неразрешима.
Теорема 13. Для 1 = 0, 1, 2, / = 2, 3 и i<j невозможно
эффективно определить, является ли язык L ^ языком типа /.
124 П. Ландвебер
Доказательство. Рассмотрим случаи i = 2, / = 3 и .1=1,
/==2; остальные случаи с очевидностью вытекают из них,
поскольку для k<i грамматика G<2'> является и грамматикой GW.
В случае / = 2, / = 3 предположим, что существует алгоритм для
определения того, является ли L (2) языком типа 3. Тогда
можно узнать, является ли языком типа 3 язык
(2S\Q(^y))u(2S\Q0
(сохраняя обозначения предыдущего раздела). Поскольку
дополнение языка типа 3 также есть язык типа 3, мы сможем
узнать, является ли языком типа 3 язык Q(x, у) П Q'. Но это
приводит нас к противоречию в силу леммы 4а: если язык
Q(x, у) flQ' непуст, он не является языком типа 2 и тем более
не является языком типа 3.
Пусть теперь /=1, / = 2. Если бы мы имели алгоритм,
определяющий, когда L (4) является языком типа 2, то по лемме 8а
мы могли бы определить, является ли язык Q(x, у) П Q' языком
типа 2V Как и выше, используем лемму 4а и приходим к
противоречию, которое и доказывает теорему.
Приложение 1 1)
Доказательство того, что какой-либо язык не является
языком типа 2, опирается на основное свойство языка типа 2,
сформулированное и доказанное Бар-Хиллелом и др. [6, разд. 4].
Ниже следует изложение этого основного свойства, слегка
модифицированное в расчете на читателя данной статьи.
Теорема. Пусть G={VN, VT, S, Р) — грамматика типа 2.
Можно определить такие два натуральных числа р и q, что
каждое слово г языка LG длиной X(z)>p может быть
представлено в виде z = xuwvy, где ифА2) или и=£Л, X(uwv)Kq, причем
все слова вида Zk=xuhwvky(k=l, 2, ...) также принадлежат
языку LG.
Доказательство. Вначале построим грамматику G',
эквивалентную G и не содержащую правил вида (Л, В), где В —
единственный нетерминальный символ. (Такая грамматика
может быть построена эффективно по G.) Затем построим
приведенную грамматику G", эквивалентную G', и заметим, что по
построению грамматика G" также не будет содержать правил
вида (Л, В). Пусть п — число нетерминальных символов грам-
1) Приложения добавлены при переводе. — Прим. ред-
2) Здесь Л обозначает пустое слово.—Прим. ред.
Проблемы разрешения в грамматиках
125
матики G". Как уже говорилось в данной статье, в
грамматике G" существует лишь конечное число деревьев вывода
с вершиной S, высота которых не превышает п. Число слов,
выводимых при помощи таких деревьев, также конечно;
обозначим через р максимум длин таких слов. Тогда слово z языка
Lq", длина которого больше р, должно порождаться деревом
высоты >п. Пусть (Аи Аъ ..., Аг) (г>п) — самая длинная ветвь
этого дерева, а (Аг-п, ..., Аг) — ее конец длины п+1. Этот
конец будет самой длинной ветвью поддерева с вершиной Лг_п;
следовательно, высота этого поддерева равна п+1.
По лемме 1 это дерево должно соответствовать выводу с
повторением, а именно среди символов Лг_п, ..., Аг хотя бы один
должен повториться, т.е. Ai=Aj = W (г — n^.i<jО).
Рассмотрим поддерево с вершиной А\. Этому поддереву соответствует
вывод в грамматике G" вида W =$>cpWy\)=^uwv (иФК или
v=t=A), поскольку грамматика G" приведенная и не
содержит правил (А, В). Кроме того, слово uwv, как нетрудно
видеть, будет подсловом слова z\ следовательно, z может быть
представлено в виде z—xuwvy.
Заметим теперь, что выводы W =^yW^, Ф=ф#, \\)=$>v
могут быть повторены k раз (£=1, 2, ...). Таким образом, в
грамматике G" для любого k могут быть получены выводы
W=$ykW^k, S=$xWy=$x(pkWy\)ky, и любое, слово zh =
= xuhwvky принадлежит языку ZG» = Z,G.
Наконец, из того, что узел Лг- принадлежит поддереву с
вершиной Аг-п, вытекает, что высота поддерева с вершиной Лг- не
превосходит п+1. Тогда можно указать такое число q, что
K(uwv) <! q. Доказательство теоремы закончено.
Следствие. Язык Q(x,y) flQ' не является языком типа 2,
если он не пуст.
Доказательство. Вопреки предположению допустим,
что язык Q(x,y) nQ' не пуст и является все же языком типа 2.
Тогда язык Q(x,y) П Q' содержит сколь угодно длинные слова
вида z = $tct$u где р— слово в алфавите So, t — слово в
алфавите S, a Pi и ti представляют собой отражения соответственно
слов р и /. Очевидно, по любой из частей р, Pi можно
однозначно восстановить все слово z.
Пусть теперь z— слово языка Q(x, y)r\Q', для которого
ЦР) и X(t) больше, чем р и чем q. По основному свойству
языка типа 2 z = xuwvy, X(uwv) <! q и любое слово zk = xuhwvhy
должно принадлежать языку Q{x^y) П Q'. Но из четырех частей
р, t, tu Pi подслово uwv может захватить одну или две
соседние; остальные две или три останутся нетронутыми при изме-
126
П. Ландвебер
нении k. Тогда очевидно, что ни при каком кФ\ слово Zh не
может принадлежать языку Q(x,y) f\Q\ Это противоречие и
доказывает наше следствие.
Приложение II
Докажем, что грамматика с правилами 1—16,
представленными на стр. 119, действительно порождает язык M\Q(x).
Доказательство будет опираться на следующие утверждения:
1) слово z выводимо из S (т.е. порождается данной
грамматикой) тогда и только тогда, когда z выводимо либо из Вь
либо из В2, либо из В3 (правила 1—3);
2) слово z выводимо из А тогда и только тогда, когда
z€Q(x) (правила 4, 5);
3) слово z выводимо из Bi (соответственно из В2) тогда и
только тогда, когда z = tw (z = wt), где w£Q(x) и t —
произвольное непустое слово в алфавите 20(2) {правила 6—9);
4) слово z выводимо из Di тогда и только тогда, когда г-—
лроизвольное слово в алфавите 2, такое, что X(z) !> Х(х{) и z
не начинается словом Х\ (/=1, 2, ..., п) (правила 14, 15);
5) слово z выводимо из С{ тогда и только тогда, когда либо
z выводимо из Di, либо z — произвольное слово в алфавите 2,
для которого X(z)<X(Xi) (i=l, 2, ..., п) (правила 13, 16);
6) Из [4] и [5] следует, что z выводимо из Cd тогда и только
тогда, когда z — произвольное непустое слово в алфавите 2, не
начинающееся с х{ (i=l, 2, ..., п)\
7) теперь уже очевидно, что никакое слово, порождаемое
этой грамматикой, не принадлежит Q(x) и принадлежит М, т. е.
принадлежит M\Q(x\;
8) покажем, что любое слово языка M\Q(x) порождается
этой грамматикой. Если слово z£M\Q(x) начинается или
кончается словом из Q(x), то оно, очевидно, выводится из Bi или
из В2 и порождается нашей грамматикой. Пусть слово z£M\
\Q(x) не начинается и не кончается словом из Q(x).
Поскольку z принадлежит М, имеем: 2=И1>, и — слово в
алфавите So, v — слово в алфавите 2. Возможны два случая: либо
у слова z есть подслово из Q(x), либо нет. В последнем случае,
если обозначить через Ь{ последнюю букву слова и, то ясно,
что v не должно начинаться словом Х{. Но тогда v выводимо
из С{ и все слово z может быть получено из В3 по правилам 10
и 12. В случае же когда z имеет одно или несколько подслов
из Q(а:), ясно, что все эти подслова вложены друг в друга и
являются подсловами одного максимального подслова из Q(x).
Обозначим последнюю букву левого крыла вхождения этого
Проблемы разрешения в грамматиках
127
максимального подслова через Ь{ и заметим, что правое крыло
этого вхождения представляет собой непустое слово, не
начинающееся словом Xi. Тогда оно выводится из Ciy а все словом
получается из В3 по правилам И и 12 (плюс правила для
вывода из Л и из Сг). Доказательство закончено.
Л ИТЕРАТУРА
1. Chomsky N., On certain formal properties of grammars, Information
_ and Control, 2, № 2 (1959), 137—167. (Русский перевод: Хомский H.,
О некоторых формальных свойствах грамматик, Кибернетический
сборник, вып. 5, ИЛ, 1962, 279—311.)
2. С h о m s к у N., A note on phrase-structure grammars, Information and
Control, 2, 393—395, 1959. (Русский перевод: Хомский H., Заметка
о грамматиках непосредственных составляющих, Кибернетический
сборник, вып. 5, ИЛ, 1962, 312—315.)
3. R a b i n М., Scott D., Finite automata and their decision problems,
IBMJ, 3, 114—125, 1959. (Русский перевод: Рабин M. О., Скотт Д.,
Конечные автоматы и задачи их разрешения, Кибернетический сборник,
вып. 4, ИЛ, 1962, 58—91.)
4. Davis М., Computability and Unsolvability, McGraw-Hill Book Co.,
№ 4, 1958.
5. Cantor D., On. the ambiguity problems of Backus systems, J. ACM, 9
(1962), 477—479.
6. В a r - H i 11 e 1 Y., P e r 1 e s M., Shamir E., On formal properties of
simple phrase structure grammars, Zeitschrift fur Phonetik, Sprachwissen-
schaft und Kommunikationsforschung, 14 (1961), Г43—172.
7. Chomsky N., Miller G., Finite state languages', Information and
Control, 1 (1958), 91—112. (Русский перевод: Хомский H.,
Миллер Дж., Языки с конечным числом состояний, Кибернетический
сборник, вып. 4, ИЛ, 1962, 231—255.)
8. L a n d w е b е г P., Three theorems on phrase structure grammars of type
1, Information and Control, 6 (1963), 131—136.
9. Scheinberg S., Note on the Boolean properties of context free
languages, Information and Control, 3 (1960), 372—375.
10. Moore E. F., Gedanken-experiments on sequential machines, Automata
Studies, 1956, 129—153. (Русский перевод: Мур Э. Ф.,
Умозрительные эксперименты с последовательностными машинами, сб. «Автоматы»,
ИЛ, М., 1956.)
11. Ginsburg S., Rice Н., Two families of languages related to ALGOL,
J. ACM, 9 (1962), 350—371.
12. Post E., A variant of a recursively unsolvable problem, Bull. Am. Math.
Soc, 52 (1946), 264—268.
13. Kleene S. C. Introduction to Metamatematics, Van Nostrand Company,
. N. Y., 1952. (Русский перевод: Клини С. К., Введение в
метаматематику, ИЛ, М., 1957.)
14. Марков А. А., Теория алгорифмов, Труды МИАН, т. 42.
Характеристика машинных
отображений1}
С. Гинзбург, Дж. Роуз
Введение. Обобщенной последовательностной машиной
(сокращенно ОПМ) называется шестерка (/(, 2, А, б, 1, /?i), где
/С, 2, А — конечные непустые множества («состояний», «входов»
и «выходов» соответственно), б (функция
переходов)—отображение КХ% в К, К (функция выходов)—отображение ДХ2
в A*2), a pi (начальное состояние) —выделенный элемент в К.
(Для множеств слов X и Y
со
XY^\xy\x£X,y£Y\, X*=\JXl,
где Х°={е}, е — пустое слово. Таким образом, для
произвольного множества Е £* — свободная полугруппа, порожденная Е.)
Функции б и Я распространяются на /СХ2* по определению
6(/7, е) = /?, 6(р, ххх2 ... xk) = 6[6(p, хг ... **_!), jcJ,
Х(р, е) = г
и
для каждого р из Д" и каждой последовательности .^, ..., xk
элементов 2. Функция /, отображающая 2* в А*, называется
машинным отображением3) или отображением, реализуемым
ОПМ, если f(x)=K(pux) для всех х из 2* для некоторой
ОПМ S. Машинное отображение, реализуемое ОПМ S, обозна^
чается также через S.
Цель настоящей заметки доказать, что функция /,
отображающая 2* в А*, реализуется ОПМ тогда и только тогда, когда
выполняются следующие условия:
(О f(e)=e;
l) GinsburgS. and Rose G., A characterisation of machine mappings,
Canad. J. of Math., XVIII, № 2 (1966), 381—388.
2) Через А* обозначается множество всех слов в алфавите А.
3) В отечественной литература более распространен термин «автомагное
отображение», — Прим. nepee\
Характеристика машинных отображений
129
(ii) / сохраняет начальные подслова, т.е. если и —
начальное подслово vt то f(u) является начальным подсловом f(v);
(iii) выход f ограничен, т. е. существует число М, такое, что
\f(ua)\-\f(a)\<M
для всех и в Е* и а в 2 (\и\ обозначает длину слова и);
(iv) f~l сохраняет свойство регулярности множеств, т. е. для
каждого регулярного множества Y^A* множество f~l(Y) =
= {xlf(x) 6 У} регулярно. Автоматом называется пятерка А =
= (/С, 2, б, ри F), где К и 2 — конечные непустые множества,
б — отображение /(Х2 в /С, pi— выделенный элемент /Си/7 —
подмножество К (быть может, пустое); б распространяется на
/(Х2*, как в ОПМ. Множество U регулярно, если существует
автомат Л, такой, что
U=[w£ir\b(pv w)£F).
Из условий (i) — (iv) вытекает, что отображение /
реализуемо ОПМ, откуда, согласно [5], следует, что
(v) / сохраняет свойство регулярности множеств.
Статья состоит из трех разделов. Доказательство основного
результата образует разд. 1. Контрпримеры, показывающие
независимость условий (i) — (iv), даже при наличии (v)
составляют содержание разд. 2. В разд. 3 приводятся два следствия.
1. Доказательство. Если / реализуемо в ОПМ, то
выполнение условий (i), (ii) и (iii) очевидно, a (iv) доказано в
работе [5].
Предположим, что / удовлетворяет (i) — (iv). Согласно
(iii), существует целое число М, такое, что
\f(wa)\-\f(w)\^M (1)
для каждого w из 2* и а из 2. Пусть
U (a, w) = [ujf (иа) = / (и) w]
м
для каждого w из (JA^ и кажД°Г0 о. из 2. Во-первых, дока*
У-о
жем, что
U{a> w) есть регулярное множество. (2)
Пусть ga(X) ={и/иа€Х} для каждого а из 2 и Х^2*. По
работе [5, теорема 2.2] ga(X) регулярно, если X регулярно. Пусть
д/== (Дм+1) *д* для каждого 0<^Ми
м
V{a, w)=\Jga\r\btw)\[\rl{bt)
/-0
130
С. Гинзбург, Дж. Роуз
для каждого а £ 2 и
м
we (J д;
Поскольку Д/ОУ — регулярное множество, согласно (iv)
регулярно и множество f~l(Atw). (Класс регулярных множеств
является наименьшим из классов множеств, содержащих все
конечные множества и замкнутых относительно объединения,
произведения и *. Кроме того, класс регулярных множеств
замкнут относительно вычитания и пересечения [3].) Таким
образом, множество ga[f~l(^tw)] регулярно. Так как А* регулярно,
то регулярно и /_1(Д/). Поэтому множество V(a,w) регулярно.
Рассмотрим произвольное слово и£ U(ayw). Так как
м
существует целое число t, такое, что f(u) £Д*, т.е. i/6f_1(A/).
Так как
f (иа) = f(u)w£ \w, ua^f1 (ktw)
и и €ga\f'*(&№)]- Таким образом, £/(а, w)<=:V(a, w). Теперь
возьмем любое слово u(i V(a,w). Тогда для некоторого t и
принадлежит каждому из множеств ga(f-l(Atw)) и f-{(At). Таким
образом, ua(zf-l(Atw)„ т.е. f(ua)£ktw и f(u)£kt. Тогда для
некоторых целых чисел Ли/
\f(ua)\ = h(M+l) + t + \w\, (3)
\f(u)\ = i(M+\) + t. (4)
Согласно (ii) и (1), f(ua)=f(u)v для некоторого слова vt
\v\^CM. Отсюда
\f(ua)\ = t(M + l) + t + \v\. (5)
Поскольку |и|, \w\ -<М, из выражений (3) и (5) следует, что
|ш| = |и|. Следовательно, w = v,< так что f(ua)=f(u)w. Таким
образом, u£U(a, w). Тогда £/(а, w) = V(a, w) и имеет место
утверждение (2). Рассмотрим конечное множество всех
гомоморфизмов т полугруппы 2* в А*, таких, что
м
t(a)6UA'
J-о
для каждого а из 2. Для каждого такого т положим
U(х)= [и£И*\f (иа) = f (и)%(а) для всех a£2}.
Характеристика машинных отображений
131
Поскольку
£/(т)=Р|£/(а, т(а)),
множество £/(т) регулярно согласно (2). Множества £/(т) по*
парно не пересекаются, а их объединение есть 2*. Для ка-*
ждого т пусть Лг обозначает автомат (Кх, 2, Зт, рт, /^), такой,
что U(x) ={u\6t (рт, и) 6 Fx}. Пусть п, ..., тг — различные
отображения т. Рассмотрим конструкцию Л=(/(, 2, бА, Ра, Яь ...
..., Яг), где
Рл = (Рхх'~-Рхг)' К^КХХ ... X*t/
»д = ((Л. ..- Рг)> a) = (\(Pl> а)' — 6tr(/V ^))
для каждого набора (рь ..., рг) € /С и а£ 2 и для каждого /
Hij^Ktj — Fxj или Hij = FXj1
если /=£/ или / = / соответственно, и Яг = ЯиХ... ХЯ^Г. Тогда
{Яг/1 ^/^ г) является семейством непересекающихся
подмножеств К ([3], стр. 109) и слово х входит в £/(тг), тогда и только
тогда, когда 6а(Ра> х) 6Яг-. Наконец, пусть S является ОПМ
(К, 2, Аг6а, Я», Ра), где для каждого р£К и а£2 ^(р, а) =
=Тг(а), если Яг- содержит р, и Д,(р,а)=е, если
p£K-()Ht.
Для завершения доказательства достаточно установить, что
к(рл, x)=f(x) для всех слов х. Име?м Х(рА, е) =/(е) =е.
Предположим ^(Ра, а:) =/(д:) для всех слов a:, |*| ^5. Для а£2
рассмотрим Х(рА,л:а). Тогда
ЧРа> ха) = %{рА, х)К\ЬА(рА, х), a] = f(x)X[bA(pA, х), а].
Для некоторого i х£ U(xi). Тогда 6а(Ра, х) £ Н{. По
определению %t %i(a) =Ц6а(Ра, а:), а]. Поскольку х£ £/(тг),
/ (ха) = / (х) т, (а) = / (х) X, [6А (рл, л:), а] = Я, (рд, ха),
что завершает доказательство.
Замечание. Доказательство показывает, что условие (iv)
можно ослабить, требуя лишь, чтобы f~l(Y) было регулярным
для всех множеств У= (Дм+1)А*оу, где 0-^.t^M и
м
w 6 (J А'.
132
С. Гинзбург, Дж. Роуз
2. Контрпримеры. Покажем теперь, что ни одно из условий
(i) — (iv) нельзя исключить даже при наличии (v). Функции
/ и /_1 сохраняют свойство языков быть контекстно-свободными
для каждой из таких функций /, хотя этот факт мы не
доказываем.
Пример 1. Пусть 2 = Д={а, Ъ). Для каждого слова адб2*
положим f(w)=aw. Тогда очевидно, что f удовлетворяет (ii) —
(v), но не (i).
Пример 2. Пусть 2 = Д = {а, Ь). Положим f(a)=b, f(b)=a и
f(x)=x в остальных случаях. Очевидно, что / удовлетворяет (i),
(iii) — (v), но не (ii).
Пример 3. Положим 2={а, Ь) и Д={а}. Положим f(ai)—ai и
f(aibu)=azi для г> 0 и и£2*. Очевидно, что f удовлетворяет
(i), (ii), но не удовлетворяет (iii). Рассмотрим (iv). Пусть S
является ОПМ ({ри р2}, {а}, {а}, 6S, A,s, Pi), где
65 (pv a) = pv Ь$ (pv а) = pv %s (pv a) = е, Xs (р2, а) = а.
Для каждого У^а*
rl(V) = V[i[S(Yn(a^)]b2\
Таким образом, f~l сохраняет свойство регулярности множеств.
Рассмотрим (v). Пусть Т обозначает ОПМ
({?i> ЯгЬ 2>Л> 5г» *т> Я\)'
где
bT(qv a) = qv bT = q2 в остальных случаях;
hT(qv а) = а2, Хт = е в остальных случаях.
Для каждого события ХсЕ*
f (X) = (X[\cf)\}T (XJ) а*ЬЪ*).
Таким образом, f сохраняет свойство регулярности множеств.
Пример 4. Пусть 2 = Д = {а, Ь). Положим f(aibvw)=a2i+xb^w\
если |и| =/^0, и f(x)=alx] в противном случае. Ясно, что
функция / сохраняет длину слов и удовлетворяет (i), (ii) и
(iii). Для установления того факта, что / не удовлетворяет (iv),
достаточно показать, принимая во внимание основную теорему,
что отображение / не реализуется никакой ОПМ.
Предположим, что существует ОПМ S=(/C, 2, Д, б, X, pi),
такая, что f(x)=S(x) для всех #€2*. Пусть pit .,,, pt будут
Характеристика машинных отображений 133
различные элементы К- Тогда найдутся целые числа i и /,
1 Ki<i+j К t+.l, такие что Ь(р\, а{) ~6(ри ai+i). Имеем
„"^/(a'+V^H^ a'+1*'+2) =
= X(pv al+})K[b(pv ai+>), a'+1-'-V+2] =
= ai+}%[b{Pv at+i), at+1-'-}bt+\
так что
X[b(pv at+J)> а'+1-1-}Ь^) = а2(+3-1-К
Далее,
X(pv at+1-Jbt+2) = X(pv a%[b(pv a% at+1-l-Jbt+2} =
= а'ф(А, ai+)), a'+1"'-V+2] =
= aW**-'-* = a2t+*-j Ф f (a'+1-V+2),
т. е. получаем противоречие.
Рассмотрим (v). Пусть g обозначает отображение А* в Д*,
определенное посредством g(ai)=ai и g(aibw)^=aib^+l9 £>0.
Тогда g реализуется ОПМ
£/ = ({/у г2}, {а, Ь), {а, Ь), Ьа, Ха, гг),
где 6w(ri, а) =Гь 6и = г2 в остальных случаях, %и{риа) = а и
Хп = 6 в остальных случаях. Заметим, что /(*)==/£(*) длявсехл:
из 2*. Если х=а\ то !(а1)=1£(а{). Если x = a{bw, \w\>i, то
f(jc)=aW*f(a*66H)=fe(x).
Если x = a{bw, \w\ >t, то
Для доказательства того, что / сохраняет свойство
регулярности множеств, возьмем произвольное регулярное множество R.
Поскольку g реализуется ОПМ, g сохраняет регулярность
множеств. Таким образом, g(R) сЛ* — регулярное множество.
Множества слов {^b^/jKi+l} и {а{ЬЦ]>1+1} являются
контекстно-свободными языками. [Грамматикой называется четверо
ка (Vt 2, Р, а), где V—конечное множество, 2 —
подмножество V, а — элемент V—-2, а Р — конечное множество правил
l + w с IZV — X и w€V*.
Для слов х, y€V* записываем х^у, если х=у или
существует натуральное число k и слова
XsssX-^f Ху •••» Xfc = yt tl-j^t • ••> 11^—1$ *0\* ...» TJ£_j>
f/j» • • •» Ун-v zv • • •» г*-1»
134
С. Гинзбург, Дж. Роуз
такие, что Xi = uiyiVii xi+i = UiZiVi и правила у{-+г{ содержатся
в Р для 1 <л-<й— 1. Подмножество L слов из 2* называется
контекстно-свободным языком, если существует грамматика
*
(V, 2, Р, а), такая, что L = {w£ 2*/а фш}.] Поскольку
пересечение контекстно-свободного языка и регулярного множества
является контекстно-свободным языком [1], множества
R2 = g(R)nWbilj>i±\)
являются контекстно-свободными языками. Возьмем
гомоморфизм т множества 2* "в а*, заданный посредством равенств
х(а)=х(Ь)=а. Будучи гомоморфизмом, т сохраняет
регулярные множества и контекстно-свободные языки [1]. Поэтому
f(Ri)=x(Ri)^a* является контекстно-свободным языком.
Согласно [4] (теорема 4, следствие 2), каждый
контекстно-свободный язык в а* является регулярным. Поэтому событие f(R\)
регулярно.
Так как g(R) = /¾ U R2 и
f (/?) =, fg (R) = f (/¾ U /¾) = f (/¾) U f (/¾).
достаточно доказать, что множество слов /(/¾) регулярно. Для
этого нам нужна следующая лемма.
Лемма. Для каждого регулярного множества В
существуют регулярные множества Uh ..., Ur, Vu • • •> Vr со
следующими свойствами:
1) ()и№ = в.
i=\
2) Для всех слов и, и, таких, что uv € В, существует
натуральное число k, такое, что и£ Uk и v£ Vh.
Доказательство. Пусть А=(К, 2, б, ри F) — автомат,
такой, что
B=[w\b(pv w)£F].
Пусть ри ..., рг — элементы К. Для каждого i пусть
Ui = {u£V\b{pvu)=pi}
Vt = [u£V\b(pita)tF\.
Очевидно, что U\b ,.., Ur, Vu ..., Vr удовлетворяют заключению
леммы.
Характеристика машинных отображений
135
Теперь рассмотрим f(/?2)~. Поскольку g(R) — регулярное
множество, согласно лемме существуют регулярные множества
Uи ..., Ur и V[, ..., Vr, такие, что
а) [)UiVi=g(R) и
б) для всех и и у, таких, что uv£g(R), существует
натуральное число /, такое, что и^{]\ и v6 V\-. Для каждого k
положим
U'kb = Uk(){albi+2li>0}-
Очевидно, что
R2=(j U'kbVk.
Поскольку множество 1/Л регулярно, и'ф является
контекстно-свободным языком [1]; тогда Uk также является
контекстно-свободным языком [5]. Для каждого й, 1 ^ k 4i г,
f{UfkbVk) = x{Ur^)\i(bVk)* где \i есть гомоморфизм,
определенный посредством \i(a) =\i(b)=b. Тогда т((/[)са является
контекстно-свободным языком и потому регулярным
множеством [4]. Ввиду регулярности \k{bVh), множества f{U'kbVk),
г
а следовательно, / (/¾) = (J / (UkbVk) регулярны.
3. Следствия. Если f—отображение, сохраняющее длину
слов, то мы получаем следующий результат, впервые
доказанный (неопубликованный) Дж. Родсом и Е. Шамиром:
Следствие 1. Пусть / отображение 2* в Д*, сохраняющее
длину и начальные подслова, такое, что f"1 сохраняет свойство
регулярности множеств. Тогда f реализуется полной
последовательностей машиной, т. е. ОПМ, в которой X отображает
КХ2вД.
Замечания. (1) Известны другие характеристические свой-*
ства отображений, реализуемых полными последовательностны-
ми машинами (см. [2, 7]).
*(2) Нам неизвестны способы доказательства основного ре-*
зультата, использующие следствие 1.
Возникает вопрос, при каких условиях частичное
отображение / можно доопределить до отображения, реализуемого ОПМ.
Здесь дается один список условий. (Список условий на / для
полных последовательностных машин дан в работе [6].)
136
С. Гинзбург, Дж. Роуз
Следствие 2. Пусть XsS*-, а / — отображение X в А*,
удовлетворяющее следующим условиям:
(i) если е 6 X, то /(e) = е;
(ii) если и < о и i>6X, то f{u)Kf(v). (Отношение <^ на
множестве 2* является частичным упорядочением: u-^Cv тогда и
только тогда, когда и является начальным отрезком v.)
(Hi) Существует натуральное число М со следующим свой-^
ством: если и и v — элементы множества X, u<v, ни для какого
хб X не имеет места u<x<v, то
\f(v)\-\fW<M.
(iv) /-1 сохраняет свойство регулярности множеств.
Тогда f можно доопределить до отображения g моноида 2*,
реализуемого ОПМ.
Доказательство. Определим g следующим образом.
Для хб X положим g{x)=f(x). Если и^-х не имеет места ни
для какого х£Х, положим g(u)=e. Если х^Х, и>х и не
существует у€Х, такого, что х<у*Си, положим g{u)=g(x). Ясно,
что отображение g является продолжением / на 2*, которое
удовлетворяет условиям (i), (ii) и (iii) из введения. Для
доказательства реализуемости g на ОПМ достаточно установить, что
g~l сохраняет свойство регулярности множеств.
Пусть Z^A* является регулярным множеством. По пред-*
положению f~l{Z) и Х=/_1(Д*) —регулярные множества. Тогда
Hi=f-l(Z), Н2 = Х — f~l{Z) и #3=2* — X являются
непересекающимися регулярными множествами, объединение которых
есть 2*. Тогда существует конструкция
(/С, 2, 6, pv Fv F2, /¾
з
и F{ не пересекаются, \jFt =К, так что
Hi = {w^\b{pv~w)^Fi) для / = 1,2,3 (см. [3]).
Для всякого рб К введем абстрактные символы р' и р". Для
каждого а 62 введем абстрактные символы а! и а". Пусть 2' =
= {^^62}, 21=(0/, a"ja6 2}, и пусть s0 — символ, не
содержащийся в {//, р"|/?6/(}. Пусть т—гомоморфизм 2i в 2 ,
определенный посредством т(а') =х(а") =а для всяких а! и а" в 2i.
Сконструируем ОПМ S= (Ks, 2, 2i, 6s, Яв, 50)t где
Ks=[s0)U[pf.^\peK).
такую, что для Z) = t[S(2*)n 2^2'] либо
D\]{z) = g^{Z), - (*)
либо D = g-1(Z), (**)
и тем самым мы докажем, что множество g~l (Z) регулярно.
Характеристика машинных отображений
137
(a) e£Z. Пусть а принадлежит 2. Если 6(^, a)£Fv
положим bs(s0, a) = b(pv а)" и Xs\s0, а) = а". В остальных
случаях пусть bs (s0, а) = 6 (/jp а)' и Я,5 (s0, а) — а'. Если 6 (/?, а) £ г2,
пусть &s(p', а) = 6(р, а)" и Я,$(р', а) = а"; в остальных случаях
6^(/7^, а) = 6 (/?, а)' и А^(р', ^ = ^/.
Если 6 (/?, a)£Fv положим 6S {р"\ а) == 6 (/?, а)' и Xs (рР, а) = а'\
в остальных случаях пусть Ъ8\р", а) = Ь(р, а)" и Я5(р", ^ = ^.
Имеем e£Du{e} и eg^'^Z). Если ни для какого х£Х
не имеет места и > х, и Ф е, то # £ D и, ввиду того что g* (и) = е,
u£g"1(Z). Если #=£е принадлежит f_1(Z), то #£#-^^)11 £>•
Если x^/'^Z) и и>х и не существует у£Х такого, что
х <у<Си> то
Если иеХ — Г1 (Z), то а лежит в 2*-[D и {е}] и в S*-^-1 (Z).
Если х£ X — f"~l{Z)> а > х и не существует такого у£Х, что
х<у^Си, то # лежит в 2* —^(Z) и в 2* —[Dll {е}]..
Следовательно, выполняется соотношение (*).
(р) e(£Z. Пусть a £2. Если 6(^, a)£Fv положим 65(s0, а) =
М% а) = а\
В остальных случаях положим 65(s0, a) = b(pv а)" и
^s(5o> а) = а"; определим^ (У, а), 65(/Л а), ^5(р', а) и %s(pP, а)
так же, как и в (а). Соотношение (**) имеет место в силу тех
же аргументов, что и в случае (а).
ЛИТЕРАТУРА
1. Bar-Hell el Y., Perles М.,ч Shamir E., On formal properties of
simple phrase structure grammars, Z. Phonetik, Sprachwiss. und Kom-
munikationsforsch., Ц (1961), 143—172.
2. E 1 g о t C, Decision problems of finite automata design and related
arithmetics, Trans. Amer. Math. Soc, 98 (1961), 21—51.
3. G i n s b u r g S., An introduction to mathematical machine theory, Reading,
Mass., 1962.
4. G i n s b u r g S., R i с e H. G., Two families of languages related to ALGOL,
J. Assoc. Comput. Mach., 9 (1962), 350—371.
5. G i n s b u r g S., Rose G. F., Operations wich preserve definability in
languages, J. Assoc. Comput. Mach., 19 (1963), 175—195.
6. Л e т и ч e в ск и й А. А., Автоматные разложения отображений свободных
полугрупп, Журнал вычислительной математики и математической
физики, 2, № 3 (1962), 467—474.
7. Raney G„ Sequential functions, J. Assoc. Comput. Mach., 5 (1958), 177—
180. (Русский пеоевод: Кибернетический сборник, вып. 3, ИЛ, 1961,
142—145.)
Об инвариантности классов языков
относительно некоторых
преобразований1)
С. Гинзбург и Дж. Роуз
Линейно-ограниченный преобразователь (преобразователь с магазинной
памятью) есть линейно-ограниченный автомат (автомат с магазинной
памятью), снабженный выходной лентой. В работе дается ответ на следующие
два вопроса: 1) Является ли множество S(L) языком некоторого известного
класса, если S есть линейно-ограниченный преобразователь, или
преобразователь с магазинной памятью, a L есть НС-язык, КС-язык, регулярное
множество? 2) Можно ли по произвольным двум НС- или КС-языкам L\ и L2
эффективно определить, существует ли линейно-ограниченный преобразователь
(преобразователь с магазинной памятью), осуществляющий а) отображение
L\ на L2 или б) нетривиальное отображение L\ в L2?
Введение
Если на каждом такте работы линейно-ограниченный
автомат (автомат с магазинной памятью) осуществляет запись на
выходе, то соответствующее устройство называется «линейно-
ограниченным преобразователем» — сокращенно «ЛО-преобра-
зователем» («преобразователем с магазинной памятью» —
сокращенно «МП-преобразователем»). В настоящей работе дан
ответ на следующие два вопроса:
1) Является ли множество S(L) языком некоторого
известного класса, если S есть ЛО-преобразователь или
МП-преобразователь, a L — НС-, .КС-язык или регулярное
множество?
2) Существует ли эффективная процедура, позволяющая по
произвольным двум НС- или КС-языкам Li и L2 определить,
найдется ли ЛО-преобразователь (МП-преобразователь),
осуществляющий а) отображение Li на L2 или б) нетривиальное
отображение Li в L2?
Работа состоит из трех разделов. В разд. 1 дан обзор
основных понятий, некоторые из них до сих пор не излагались в до-
^Ginsburg S. and Rose G. F., Preservation of Languages by
Transducers, Information and Control, 9, № 2 (1966), 153—176. Эта работа
частично финансировалась Кембриджскими исследовательскими
лабораториями ВВС США.
Об инвариантности классов языков
139
статочно явной форме. Особый интерес представляет
теорема 1.1, в которой утверждается, что граничный маркер в
линейно-ограниченном автомате может быть элиминирован.
В разд. II рассматриваются ЛО-преобразователи. Если L
пробегает всевозможные регулярные множества, a S —
всевозможные ЛО-преобразователи, то S(L) пробегает всевозможные
рекурсивно-перечислимые множества. Если на каждом такте
работы ЛО-преобразователь осуществляет на выходе запись
некоторой непустой цепочки и L — НС-язык, то S(L)—также
НС-язык. Если L пробегает всевозможные конечные множества,
a S — всевозможные ЛО-преобразователи, то S(L) пробегает
всевозможные регулярные множества. Что касается вопроса 2),
то существует алгоритм, позволяющий по произвольным
регулярным множествам Li и L2 определить, найдется ли
ЛО-преобразователь, осуществляющий отображение Li на L2
(нетривиальное отображение LA в L2). В то же время не существует
алгоритма, позволяющего по произвольным КС- (и,
следовательно, НС-) языкам Li и L2 определить, найдется ли
ЛО-преобразователь, осуществляющий отображение Li на L2
(нетривиальное отображение LA в L2).
Разд.. III посвящен изучению МП-преобразователей. Для
подходящего КС-языка L и подходящего МП-преобразователя S
язык S(L) может быть произвольным
рекурсивно-перечислимым множеством. Если L пробегает произвольные регулярные
множества, з S — произвольные МП-преобразователи, то S(L)
пробегает всевозможные КС-языки. Если на каждом такте
работы МП-преобразователь осуществляет запись на выходе
непустой цепочки, то S(L) есть НС-язык для каждого НС-
(следовательно, для каждого КС-) языка L. Что касается
вопроса 2), то существует алгоритм, позволяющий по произвольным
двум КС-языкам Li и L2, не содержащим пустой цепочки,
определить, найдется ли МП-преобразователь, осуществляющий
отображение Li на L2 (нетривиальное отображение Li в L2).
В случае же когда Li и L2 могут содержать пустую цепочку,
такого алгоритма не существует.
I. Языки и автоматы
Напомним определения некоторых известных понятий.
Определение. Порождающей грамматикой называется
упорядоченная четверка G=(V, S„ Р, а), где
1) V — конечное непустое множество.
2) 2 — непустое подмножество V,
140
С. Гинзбург, Дж. Роуз
3) Р— непустое конечное множество пар вида (и, v),
и€(У-2)* — {е}и и€ У*1)-
4) a£V — 22).
Элементы множества К — S называются вспомогательными
символами.
Элементы множества 2 называются основными
(терминальными) символами.
Каждый элемент (и, v) множества Р называется правилом
и обычно записывается и-* v.
Обозначение. Пусть G=(V, 2, Р, а) — порождающая
грамматика и wit w2d V*. Тогда ^4% если существуют-#,
и, 2, у, такие, что wx=yuz, w2 = yvz и и-*у6 Р. Далее, о>==>**ь
если либо ay=x, либо существует последовательность цепочек
Wo = w, wu ..., wh = x, такая, что ^=#^+1 для каждого /.
Последовательность цепочек w0, ..., ш^, такая, что w^Wi+i
для каждого i, называется выводом цепочки wh (из цепочки w0).
Используя введенное выше обозначение, определим понятие
языка, порождаемого грамматикой. v
Определение. LcJ* называется языком, порождаемым
грамматикой, если существует порождающая грамматика G =
= (У, 2, Р, а), такая, что L = L(G) ={ш 62*/о=Ф *ш}.
Пусть G — некоторая порождающая грамматика. Будем го*
ворить, что язык L порождается грамматикой G или что
грамматика/б порождает язык L, если L = L(G).
Множество цепочек является языком, порождаемым
грамматикой, тогда и только тогда, когда оно рекурсцвно-перечис-
лимо (Chomsky, 1959).
Мы будем рассматривать несколько типов языков, порож-
даемых грамматиками.
Определение. Порождающая грамматика 0 = {]/,Ъ,Р,о)
называется грамматикой непосредственно составляющих
(сокращенно НС-грамматикой), если либо 1) каждое правило
имеет вид y\z-+ywzy где £€ V — 2 и w=f=z, либо 2) о-*г£Р^ и
1) Если X и У — некоторые множества цепочек и XY={xy/x£X, y£Y}t
где ху — конкатенация цепочек х и у, то Х°={е} (8 — пустая цепочка),
оо
Таким образом, для произвольного множества
символов £ £* есть свободная полугруппа, порожденная множеством Е.
2) Это определение порождающей грамматики отличается от
определения Хомского (1959) тем, что: а) мы не вводим граничный символ; б) мы
требуем, чтобы в правиле u->v цепочка и удовлетворяла условию u£(V —
—2)* — {е}, тогда как в определении Хомского требуется только u£V*—{е}.
Однако это видоизменение несущественно.
Об инвариантности классов языков
141
все остальные правила имеют вид y^z-^ywz, где £ £ V — Е и
w(L(V — {(?})* — {е}. Язык LgS* называется НС-языком, если
L порождается некоторой НС-грамматикой1).
Множество L является НС-языком тогда и только тогда,
когда оно порождается некоторой грамматикой G = (V, 2, Р, а),
такой, что либо 1) для каждого правила и —>v £ Р имеет место
\и\ •< |v\ 2), либо 2) а —> е € Р и для всех других правил и —► v
в Р имеет место |^| -< \v\ и у не содержит вхождений
символа о (Chomsky, 1959, Kuroda, 1964) 3).
Определение. Порождающая грамматика G = {V, 2, Р, а)
называется контекстно-свободной (сокращенно
КС-грамматикой), если каждое правило имеет вид | -> v, где
£—вспомогательный символ. L ^ 2* называется КС-язы/ссш, если L
порождается некоторой КС-грамматикой.
Каждый КС-язык является НС-языком (Bar-Hillel et al,
1961).
При рассмотрении НС-языков зачастую оказывается удоб--
ным использование так называемого «граничного маркера».
Определение. НС-грамматикой с граничным маркером
называется упорядоченная пятерка (V,- 2, Р, а, ф), где
(1) #62.
(2) {V, 2U{#}, Р, а) есть НС-грамматика.
(3) В каждом правиле u->v либо 1) u = wv v = w2\ либо
2) u=#wv v=#w2\ либо 3) u = w1#t v = w2#, где зд>,,
Определение. Пусть G есть НС-грамматика с
граничным маркером. Множество
#L#^L(Q) = {#w#£#2*#l#o#^>*#w#}
называется языком, порождаемым грамматикой G.
Z,£|2* является НС-языком тогда и только тогда, когда
# L # порождается некоторой НС-грамматикой с граничным
маркером (Landweder, 1963) 4).
1) В определении, предложенном Хомским (Chomsky, 1959)
НС-грамматика удовлетворяет лишь условию 1). Очевидно, что L С 2* является
НС-языком в сортветствии с приведенным выше определением тогда и только
тогда, когда L=L' или L=L'U{e}, где V — некоторый НС-язык в
определении Хомского.
2) \х\ обозначает длину цепочки х.
8) Это утверждение является незначительным видоизменением результата,
полученного Куродой (Kuroda, 1964), а именно распространением этого
результата на языки, содержащие пустую цепочку е.
4) Несмотря на то, что доказательство Ландвебера (Landweber, 1963)
проводится для НС-языков, не содержащих пустой цепочки 8, утверждение
имеет место также и для НС-языков, содержащих е.
142
С. Гинзбург, Дж. Роуз
С классом всех языков (соответственно НС- и КС-языков)
ассоциируется устройство, которое в некотором смысле
характеризует этот класс. Хорошо известно (Davis, 1958), что
машины Тьюринга позволяют получать рекурсивно-перечислимые
множества (или языки, порождаемые грамматиками)
различными способами. Наиболее интересующие нас классы языков,
а именно НС- и КС-языки, характеризуются соответственно
«линейно-ограниченными автоматами» и «автоматами с
магазинной памятью», определения которых приводятся ниже.
Определение. Линейно-ограниченным автоматом
(сокращенно ЛО-автоматом) называется упорядоченная пятерка В =
= (/(,2, б, q0, F), где
(1) К — конечное непустое множество (множество
состояний).
(2) 2 — конечное непустое множество (множество входных
символов), /(Л 2 = ф.
(3) б — отображение множества /(Х2 во множество всех
подмножеств множества /(Х2Х{—1, 0, 1}.
(4) q0 £ К (начальное состояние).
(5) Р<=:К (множество заключительных состояний).
Приведем формальное описание способа функционирования
линейно-ограниченного автомата.
Определение. Цепочка из множества 2*/(2* называется
конфигурацией ЛО-автомата В = {К, 2, б, qo, F).
(Конфигурация tfi ... а{-1ра{ ... aw, где 1-^ /-< т, для
каждого / я* 6 2, p(LK интерпретируется как указание на то, что
ЛО-автомат, находясь в состоянии р, обозревает /-й символ
цепочки ai ... am.)
Определение. Пусть B = (V, 2, б, <7о, F) есть ЛО-автомат
и \-*в (или \— *, если В подразумевается) — отношение на мно*
жестве 2*/С2*, определенное следующим образом: если и, v £'2*,
с £2, то (1) ucpav\- uqcbv, если (#, ft,—1) 6 б(р, я); (2) upav (—
\-uqbv, если (#, 6,0) £б(р, а); (3) г/раи |— ubqv, если (#, 6, 1) 6
6б(р, а). Для каждого аб2*/(2* полагаем а Ь*а. Для
а, р£2*/(2* полагаем а |—*Р> если существуют а = а0, ..., а* =
= р, такие, что а* |— o&i+i для каждого i<k.
а\— Р означает, что ЛО-автомат переходит из
конфигурации а в конфигурацию р за один такт работы. Так, например,
при условии (#, 6,— 1) £ 6(р, а) запись исряо f- uqcbv означает,
что ЛО-автомат обозревает символ а в состоянии р, переходит в
состояние q, заменяет а на 6 и сдвигает ленту на одну ячейку
вправо. 2) и 3) интерпретируются аналогично, а I— *р означает,
Об инвариантности классов языков
143
что ЛО-автомат переходит из конфигурации а в конфигурацию р
за несколько тактов работы.
Заключительные состояния используются для «допускания»
множеств цепочек.
On р ед ел ение. Цепочка шб2* допускается ЛО-автома-
том В = {К, 2, б, q0, F), если ^0^Ь*Р для некоторого р из 2*F.
Множество цепочек, допускаемых ЛО-автоматом В, обозначим
через Т(В).
Заметим, что е€Г(В) тогда и только тогда, когда qo£F.
Следующий результат был известен только для ЛО-автома-
тов с граничным маркером ф.
Теорема 1.1. Множество X является НС-языком тогда и
только тогда, когда существует ЛО-автомат В, такой, что
Х^Т(В).
Доказательство. Известно [Kuroda (1964), теорема 1 и
сноска 3], что X является НС-языком тогда и только тогда,
когда существует ЛО-автомат £ = (/G 2U {#}, &> 4о> F),
удовлетворяющий следующим условиям:
(1) Хс?;-"
(2) # £ 2;
(3) если (q, b, п)£Ь(р9 «:), то Ь=#;
(4)Т(В) = Х#.
Это утверждение распространяется на НС-языки, содержащие
пустую цепочку.
Чтобы доказать нашу теорему, достаточно показать, что ЛО-
автомат В, удовлетворяющий условиям (1) — (4), существует
тогда и только тогда, когда существует ЛО-автомат С, такой,
ЧТо Х = Т(С) 1).
Предположим, что существует ЛО-автомат С = (/Сс, 2С, 6С,
9с> Fc)> такой, что Х = Т(С). Пусть /, #g/CcU2. Рассмотрим
ЛО-автомат B = (KcU[f]. 2CU {#}> 6, qc, {/}), где b(q, а) =
= 6С(<7, а), если q£Kc> #£2С, и М#> #)={(/» #> 1)Ь если
q£Fc2). Очевидно, В удовлетворяет условиям (1) — (4).
Предположим, что В = {К, 2U{#}, б, <7о> F) — ЛО-автомат,
удовлетворяющий условиям (1) — (4). Определим ЛО-автомат
С--=(Кс> 2С, 6с, <7с, Fc) следующим образом. Для всех q€K к
аб 2 1)(^} введем новые символы q, а', а и а (а означает, что
1) Эта эквивалентность противоречит замечанию Куроды [Kuroda 0964),
сноска 3] о необходимости правого граничного маркера.
2) Если при задании функции f{x), значениями которой являются
множества, для некоторого х значение не указывается, то имеется в виду, что
144
С. Гинзбург, Дж. Роуз
в В справа от обозреваемого символа а записан символ #;
->
а означает, что в В слева от обозреваемого символа # записан
символ а).
Пусть qc, R, L и # — абстрактные символы. Пусть
Kc=K\}{qlq£K)\}{qc. R. Ц
и
2c = Su{#}U{a/, a, а/аб2и{#}}-
Пусть Fc = {qlq£F)\}[qc), если ебХ и Fc = {qlq£F\
в противном случае. Пусть
(5) М#с, я) = (/?, а', 1), если а^Е1);
(6) ftc(/?, а) ={(L, а, —1), (/?, а, 1)}, если а£Ъ\
(7) 6C(Z,, а) ={(L а, —1)}, если а6¾
(8) 6C(Z,, а') = {(?0> ^, 0)}, если а 6¾
(9) 6С(/?, а) =6(/?, а), если /?6ЛГ и а62и{#};
10) 6с(/>, а) = {(?, X-\)l(q, b, -1)6^(^, а)} U
U[(q.t0)l(q, b, 0)£?>(p, a)}\J
\}{q, t 0)l(q, b, 1)66(/?, a)},
если /?£# и а£2и{#};
(11) 6c(/>, a) = {(?, a,0)l(q, #, -1)6» (A #)1 U
U{(q> a. 0)l(q, #, 0)6&(/?, #)} U
U{(£a. l)/fo, #, 1)6 * (P. #)b
если /?6^ и a6Su{#}-
Покажем, что ХсГ(С). Определим отображение g
следующим образом. Пусть и, v6(SU {#})*> #6SU{#}> ?6АГ;
тогда g{aqva^) = aqva, g{uaq#) = uqa, g{ua#q) = uaq.
(В остальных случаях отображение не определено, ср. со
сноской 2 на стр. 143.) Нетрудно видеть, что для всех цепочек
л: 6 2*— {е} и всех 5-конфигураций р из q0x#\—*B$ следует
qc*\-c8$)- Итак> XsT(C).
Предположим, что х£Т(С). Если х = г, то, очевидно, х£Х.
Пусть х Фе. Тогда, как нетрудно видеть, х£%* и для
x = tia{ti£??t а£Ц имеет место qcaa\— *cq0ua\~~*c vbq, где
^6 (2 U {#})*> #62U{#} и q£F. Индукцией доказывается, что
если q0ua\-*cy, то существует р, такое, что q0tia#\—*B$
1) В оригинале, (б) 6с(<7с a) ={(<7о, a,0), (Я, а'у 1)}, что усложняет
конструкцию, не меняя результата. — Прим, перев.
Об инвариантности классов языков
145
и у = g (р). Отсюда q0ua # \—*в vb # q. Следовательно, х # £ Т (В),
откуда х£Х. Итак, Т(С)еХ, так что Т(С) = Х.
Перейдем к рассмотрению «автоматов с магазинной
памятью».
Определение. Автоматом с магазинной памятью
(сокращенно МП-автоматом) называется упорядоченная семерка М==
= (/(, S, Г, 6,Z0, <7о, Р),где
(1) К — непустое конечное множество (множество
состояний).
(2) Е — непустое конечное множество (множество входных
символов).
(3) Г — непустое конечное множество (множество
вспомогательных символов).
(4) б — отображение множества /СХ(211{е})ХГ во
множество всех конечных подмножеств множества /<"ХГ*.
(5) Z06r.
(6) qo£K (начальное состояние).
(7) F—.подмножество множества К (множество
заключительных состояний) !).
Обозначение. Пусть дан МП-автомат
М = (К, 2, Г, 6, Z0, q0, F). .
Отношение \—*м (или |—*, если М подразумевается) есть
отношение на множестве /СХ2*ХГ*, определенное следующим
образом. Если Z£I\ л;£2и{е} и (q, y)£b{p, xt Z), то
положим (р, xw, aZ)f-(q, w, ay). Кроме того, будем считать
(р, wt а) |—* (/?, w, а) для всех /?, w, а. Для a, р £ Г* и xt £ 2 U {е}
(1 <[/<;&) в случае, когда существуют последовательность
состояний Pi=p, ..., Pk+i = 4 и последовательность цепочек
a1 = a, ..., ak+1 = $ над Г, такие, что
[Pi> xt ... xkw, щ)\-(рц.х, xl+1 ... xkw, a,+1),
где 1 <i / «<£, положим (p, Xi.. .XkW, a)|— *(<7> a;, P).
Содержательно это означает, что МП-автомат имеет
входную ленту, множество состояний и ленту магазинной памяти
(на которую записываются вспомогательные символы). (/?, xw,
aZ) \— (q, w, ay) означает, что, находясь в состоянии р и обо*
зревая на входной ленте символ х (возможно, x = e2)), а на
*) Эта концепция МП-автомата несколько отличается от общепринятой
(Chomsky, 1962) наличием множества заключительных состояний.
2) Содержательно, х = е означает, что на данном такте работы
МП-автомат не читает на входе. — Прим. перев.
146
С. Гинзбург, Дж. Роуз
ленте магазинной памяти крайний правый символ Z,
МП-автомат переходит в состояние q, записывает цепочку у вместо Z
и стирает к.
Определение. Цепочка w допускается МП-автоматом
М = (К, 2, Г, б, Z0, q0, F), если (q0, w, Z0) \-*{q, e, а) для
некоторых q<i F и a 6 Г* !). Множество всех цепочек, допускаемых
МП-автоматом М, обозначим Г(М).
Множество цепочек является КС-языком тогда ни только
тогда, когда оно допускается некоторым МП-автоматом
(Chomsky, 1962; Evey, 1963; Ginsburg, 1966).
Мы будем изучать также регулярные множества,
называемые иногда «языками с конечным числом состояний».
On р еде лени е. Множество Х^2* называется
регулярным, если X может быть получено из конечных множеств
конечным числом применений операции объединения, умножения
и итерации (операция итерации обозначается звездочкой*).
Определение. Конечным автоматом2) называется
упорядоченная пятерка А = {К, 2, б, S0, F), где
(1) /С, 2 и F означают то же, что и прежде.
(2) S0<=:K (множество начальных состояний).
(3) б — отображение множества /Cx2U{e} во множество
всех подмножеств множества /С, причем б (q, e)={q} для всех
q£K.
Если S0 и каждое из множеств 6(q, х) состоят из одного
элемента, то А называется детерминированным конечным
автоматом 3).
Определение. Пусть дан конечный автомат А = (К, 2, б,
So, F). Будем говорить, что цепочка w = Wi... wh, ^£2,
допускается конечным автоматом Л, если существует
последовательность состояний s0, • •., $k в /С, 506S0 и sk£F, такая, что
Si£6(Si-u Wi) для каждого и Множество всех цепочек,
допускаемых конечным автоматом Л, будем обозначать Т(А).
Следующие три утверждения эквивалентны (Rabin and
Scott, 1959): 1) X — регулярное множество; 2) Х = Т(А) для не-
*) В определении МП-автомата, в форме Хомского (1962) цепочка w
считается допускаемой, если (q0,w,Z0) h*(q, е, в) для некоторого q € К.
2) В подлиннике употребляется термин ncndeterministic automaton. Мы
использовали здесь, так же как и в некоторых других случаях (см. ниже),
термин, более употребительный в советской литературе. — Прим. перев.
3) В подлиннике — automaton. — Прим. перев.
Об инвариантности классов языков
. 147
которого конечного автомата А\ 3) Х = Т(А) для некоторого
детерминированного конечного автомата А.
Каждое регулярное множество является КС-языком, а
именно Х^2* является регулярным множеством тогда и только
тогда, когда существует КС-грамматика G = (V, 2, Р, о),
порождающая X и такая, что каждое правило из Р имеет вид l~>wv
или g—>ш, где оу£2*, v€ V — 2 (Chomsky, 1959).
II. Линейно-ограниченные преобразователи
Перейдем к рассмотрению линейно-ограниченных
преобразователей. Содержательно линейно-ограниченный преобразователь
есть не что иное, как линейно-ограниченный автомат,
снабженный выходной лентой, на которой он может писать на каждом
такте работы. Приведем формальное определение
линейно-ограниченного преобразователя.
Определение. Линейно-ограниченным преобразователем
(сокращенно, ЛО-преобразователем) называется упорядоченная
пятерка S = (/(, 2, A, (i, q0), где
(1) К, 2 и-<7<) имеют тот же смысл, что и в определении
ЛО-автомата;
(2) А — непустое конечное множество (множество выходных
символов);
(3) \х — отображение множества /(Х2 во множество всех
конечных подмножеств множества /СХ2ХА*Х{— 1, 0, 1}.
Изучая ЛО-преобразователи, мы будем использовать
следующие обозначения (при этом соблюдается аналогия с
обозначениями для ЛО-автоматов).
Обозначение. Пусть S = (/C, 2, А, ц, q0) — ЛО-преобра-
зователь. На множестве 2*/С2*ХА* определим отношение |—*
следующим образом: если и£2*, v6 2*, с 62, ау£Д*, то
(1) {ucpav, w) h (uqcbv, wy), если (q, b, y, —l)6|x(P, a)\
(2) (upav, w)\- (uqbv, wy), если (q, b, у, 0)€ц(р, а), и
(3) (tfpay, w)h(ubqv, wy), если (¢, Ь, у, l)£\i{p, a). Далее
полагаем (и, a>) |—*(и', о;'), если либо и = и' и ay = a/, либо
существуют последовательности и = и0, ии ..., uk = u', w0 = w,
wu •••> Wh = w\ такие, что (и*, a>*) h (и+ь wi+l), 0<t<A— 1.
Обозначение. Пусть S=(K, 2, A, jx, 90) — ЛО-преобразо-
ватель иш^*; тогда S(w) = {yl(qQw, е)(-*(р, у), где р£2*К}.
Если А* с 2*, положим S (JQ == [J 5 (х).
В частности, 5(e) =е.
148
С. Гинзбург, Дою. Роуз
Если S — ЛО-преобразователь, то отображение S(x) множе-*
ства 2* во множество всех подмножеств множества А* назы«
вается ЛО-отображением.
Известно, что каждый детерминированный конечный
преобразователь !) отображает регулярное множество на регулярное
множество (Ginsburg and Rose, 1963b). Естественно возникает
вопрос, какова природа языка, являющегося образом НС-языка
при ЛО-отображении.
Теорема 2.1. Если S содержит по крайней мере два
символа, то класс НС-языков не замкнут относительно операции
гомоморфизма.
Доказательство. Пусть а — выделенный элемент
множества 2, S/ = S-r{a} и G = (V> 2', Р, а) —произвольная
порождающая грамматика, такая, что язык L(G) не является
НС-языком. Мы можем считать, что а £ V. Поскольку все
НС-языки рекурсивны, такая грамматика G существует. Пусть
ga£ V и G' = (V", 2, Р\ о)—порождающая грамматика, где
V = V\J{a, la} и Р' состоит из следующих правил:
(1) w->y, где w->y£P и |ш|<|г/|;
(2) w->ytlw^yl> где w->y£P и \y\<\w\;
(3) Ы~*11а Для каждого ££ V — 2;
(4) 6«=*av
Поскольку |и|^|и| для каждого u-+v£P\ L(G') является
НС-языком. Пусть h — гомоморфное отображение множества 2*
во множество 2*, определенное следующим образом: h(x)=x,
если а:6 2 — {а} и h{a)=z. Тогда h(L(G'))=L(G).
Замечание. Если L — НС-язык и h — гомоморфизм,
такой, что к(х)Фг для каждого xd 2, то h(L) —НС-язык.
Поскольку всякое гомоморфное отображение может быть
осуществлено подходящим детерминированным конечным
преобразователем, а следовательно, ЛО-преобразователем, то
справедливо такое следствие:
1) Детерминированным конечным преобразователем (в подлиннике —
generalized sequential machine; сокращенно gsm) называется упорядоченная
шестерка S= (К, 2, А, б, Я, So), где 1) /С, 2 и s0 имеют обычный смысл;
2) Д — непустое конечное множество (множество выходных символов);
3) 6 — отоображение множества КХ2 во множество К\ 4) Я — отображение
множества /СХ2 во множество А*. Отображения 6 и Я могут быть
продолжены на множество /СХ2* следующим образом: 6(q, e)=q, 6(q, wx) =
= 6 [6(q, w)% x], k(qt e)==e и Я (q, wx) = X(q, w)X[b(q, w), x] для всех
q^K, и; £2* и x ¢2. Итак, детерминированный конечный преобразователь
есть детерминированный конечный автомат с «детерминированным» выходом.
Об инвариантности классов языков
149
Следствие. Образ НС-языка при ЛО-отображении в
общем случае не является НС-языком. Для каждого рекурсивно-
перечислимого множества Y существуют НС-язык X и
ЛО-преобразователь S, такие, что S(X) = Y.
В третьем разделе будут рассмотрены два случая, в которых
преобразователи с магазинной памятью порождают КС-языки.
Покажем, что в аналогичных ситуациях ЛО-преобразователи не
всегда порождают НС-языки.
Определение. ЛО-автомат В = (К, 2, б, 9о> F) и
ЛО-преобразователь S = (K, 2, А, |л, <7о) называются согласованными,
если б(р, #)={(?, by m)l(q, Ъ, у, пг)£\\(р, а) для некоторого
j/6 А*} для всех (р, а) £ /(Х2.
Другими словами, ЛО-автомат и ЛО-преобразователь
являются согласованными, если ЛО-преобразователь получен из
ЛО-автомата добавлением выходной ленты.
Теорема 2.2. Для каждого рекурсивно-перечислимого
множества Y существуют ЛО-преобразователь S, ЛО-автомат В,
согласованный с S, и регулярное множество X, такие, что S(X) =
=S(T(B))=Y.
Доказательство. Из доказательства теоремы 2.1 видно,
что существуют НС-язык W и гомоморфизм А, такие, что
Y = h(W). Пусть BW = (KW, Hw, bw, qw, Z7^) —ЛО-автомат,
такой, что W'=Т'{Bw). Определим ЛО-автомат./? == (/^2,6, q0,F)
и ЛО-преобразователь S = (/C Е, A, \х, q0) следующим образом.
Для каждого q£Kw, q—абстрактный символ. qQ, R, Z,, d —
также абстрактные символы, не принадлежащие множеству
fa Я\я£К*У Далее, K={q, qlq£Kw}U{<lo> Я Ц, Z = Zw\]{d]
и F={qlq£Fw). Все символы, входящие в цепочки из
множества A(2V), образуют множество А. Для каждого a£%w,
b(q0,d) = {(R,d,l)}, 5(/¾ а) = {(/?, a, 1)}, в(/?, d) = {(L d, -1)),
b(L, a) = {L, a, —1% Ц1, d) = [(qw, d, 1)}, 6(q, a) = bw (q, а) для
q£Kw, b{q,d) — {(qyd, 1)} для q£Fw, [i(R, a) = {(R, a, h(a), 1))
и \x(p, *) = {(q,,b, e, m)l(q, b, ^)6б(/?, x)}, если p Ф R или x 5 2^.
Очевидно, что ShS являются согласованными, dWd=T(B),
множество aSW регулярно и 5 (rfS*wd) = S (dWd) = Y.
Замечание. Если алфавит, над которым определено множен
ство У, содержит не менее двух символов, то (при подходящем
кодировании) множества X и Т(В) могут быть выбраны над
этим алфавитом.
150
С. Гинзбург, Дою. Роуз
Однако при некотором ограничении на ЛО-преобразователь
множество S(L) будет НС-языком, если L есть НС-язык.
Теорема 2.3. Для каждого ЛО-преобразователя S,
непрерывно пишущего на выходе1), и каждого НС-языка X
множество S (X) является НС-языком.
Доказательство. Пусть #X#=L(G), где 0 =
= (V, Slf Я, а, #-) — НС-грамматика с граничным маркером.
Без потери общности можно считать, что если #а#=Ф*а, то
а имеет вид Др#, где р£ (V — {#})*. Пусть S = {K, 2, A, \i9q0).
Поскольку S — ЛО-преобразователь, непрерывно пишущий
на выходе, можно предположить, что у принадлежит
множеству А (а не множеству А*—(е)), если (q, ft, у, m)(zii(p, а)>
Мы можем также предположить, что множества V — 2Р /С, 2
и А попарно не пересекаются. Определим НС-грамматику
с граничным маркером, порождающую язык #S(X)#. Для
каждых у£А, а £2 и q£K пусть Еу, (q, а, —) и (—, а, у) —
абстрактные символы [(q, а, —) означает, что в состоянии q
ЛО-преобразователь обозревает символ а]. Пусть V
содержит Vj А, все символы (q, а, —), (—, а, у) и Еу2). Пусть
G' = (V, А, Р\ а, #), где Р' содержит Р и все правила вида
(q, a, а', у, у' обозначают элементы множеств /С, 2, 2, А и А
соответственно):
(1) # а -*#(%. а, —);
(2) (q, а, —)->у (р, ft, —), если (р, ft, у, 0) £ \i (q, а);
(3) (q, а, —)а'->(—, ft, у)(р, а', —), если (р, ft, у, 1)6М-(?» а)\
(4) (—, а', #')(?» а, —)->у'у(р, а', —)ft, если (р, ft, у, —1)£
€ М- (?> «);
(5) (—, а, у)у'->у{—, а, у7);
(6) (?, а, —)#->Еу#, если (/?, ft, у, l)6|i(?, а) для
некоторых р и ft;
{ уЕу'->Еуу'\
(8) #^->#у.
Покажем теперь, что L(G') = #S(X) #. Пусть g- и А
—гомоморфизмы, определенные на множестве К следующим
образом: g((q, a, —)) = qa, g(a) = g{{—, а, у)) = а, в
остальных случаях # = е; h(y) = h({—,a,y)) = h(Ey) = y и А = е
в остальных случаях.
*) ЛО-преобразователь (X, 2, Д, \i, qo) непрерывно пишет на выходе,
если из того, что (q,b,y,m) £\i(p,a), следует, что уфъ для всех р и а.
2) В оригинале неточность: «...l/' содержит V и все символы (q, а,—),
(—га, у) и Еу». — Прим. перев.
Об инвариантности классов языков
151
Предположим, что w£S(x) для некоторого х£Х. Если
до = е, tox = evl#w#£L (О7). Предположим, что х Ф е. Тогда
для некоторого r>lf = j/1.,,j/r и каждое У/£Л. Отсюда
#a#=#>*G,#x# и
(ft*, e)|-(alf ух)\- ... f-(arf ^ ... уг)
для некоторых ар ..., аг, аг£2*/С Индукцией по /(1</<г)
можно доказать [с учетом правил (1) — (6)], что существуют
рр — р,, такие, что
(9) #х##*0, # р1 # =Ф', ... #*G, # р. #;
(10) если ai=pavt где /7 ^ АГ и a ¢2, то,р* = #(/7, a, — )v,
где #6:д*> т>£Е*, £(р,) = а, и к(Ь) = уг ... #,;■
(11) если а; = ираю, где # =£е, р£К, а £ 2,то р^ = и (р, а, —) г;,
где я£Л*[{(- й, У)/^2, t,£A}*_{e}], ^£2*, £(&) = <** и
h{$i) = Dx ... yt\ и
(12) pr£A*{(-, 6, 0)/6 6¾ */6A№r и Л ¢,) = ^ ... уг
Более того, из (7) и (8) следует, что #p#=^,#A(p)#
для всех РбД*{(-^^)/^^^6дГ{^/Убд}д*-
Следовательно, из (9) и (11) вытекает
#а##*0, #*##*, #pr#=^, #^ ... уг#.
Итак, #S(*)# с £(<?')•
Предположим теперь, что # до # 61 (О7)- Если w = z, то
# е # 6 Z, (О) и, следовательно, # е # 6 # 5 (АГ) #. Пусть w Ф е.
Поскольку множества (К —2г), 2, /? и Л попарно не
пересекаются, то существует вывод цепочки #w#, в котором
все применения правил из Р предшествуют применениям
правил из Р'—Р. Итак, существует цепочка #х# £L(Q),
т. е. х£Х, такая, что
#G#^*G#X#=$*G,#W#.
Пусть x = xl... xk и каждое ^¢2^. Нетрудно видеть, что
если #*#=#£, # w #, то существуют рг = (q0, xv —)х2 ... хк,
р2, ..., рг, тр ..., т5, такие, что
(13) #X#=$G, #рг#=ф0, ...=ф0, # Рг # =^ог # Т! # #0, .. .
(14) всякий раз, когда #р. # =#>0, #р.+1 #, применяется
одно из- правил типа (2), (3), (4) или (5);
(15) всякий раз, когда #tj#=$>g,#xj+1#j применяется
некоторое правило типа (7);
152
С. Гинзбург, Дж. Роуз
(16) в -случае когда #xs #=#>G, #^ #> применяется
некоторое правило типа (8);
(17) в случае когда #рг #=ф0, #-^ #, применяется
некоторое правило типа (6).
Итак, h(x1) = w. Пусть далее Yi» •••» Y/ —
последовательность, полученная удалением повторений из
(У (Pi). A (Pi)). •••• (*(РгМ(Рг))-
Тогда Yi(— • •• h-yth-ivp* w) Для некоторых ^£2* и р£К-
Следовательно, w£S(X), т. е. Z(G')£ #S{X) #.
Рассмотрим теперь образ конечного множества при ЛО-ото-
бражении.
Теорема 2.4. (а) Если S — ЛО-преобразователь и X —
конечное множество, то S(X) — регулярное множество.
(б) Для каждого регулярного множества №^2* и каждой
непустой цепочки w£%i существует ЛО-преобразователь S,
такой, что S(w) = W.
Доказательство, (а) Пусть S = (K, 2, А, ц, ^о). Без
потери общности можно считать, что y£AU{e} всякий раз, когда
(q, Ь, у, ш) £ [х(р, а). Достаточно показать, что S(x)
—регулярное множество для каждой цепочки х длины т>0.
Пусть А = (КА, Дл, б, {#0-*}» /^ — конечный автомат, где
m
КА = и21К2т-1,Р=1тК, АЛ=Д U К), яе-абстрактный символ,
не принадлежащий множеству А, 6 (а, а) = {р^/Сл/(а, е)|—(р, а)}
для всех (а, а)£КАХ& и б (а, ае) = {Р£ЛГл/(а, е)|— (р, г)} для
всех а^/Сд. Пусть А— гомоморфное отображение Ал в А,
определенное следующим образом: h(a) = a для всех а£А
и Л(ае) = е. Индукцией по d можно доказать, что если
(Ро> e)K(Pi- ^i)K • • • К (IV »1 ' • • ^>
где р0, ..., Р<*£ЛГЛ и r/j, ..., ^6ди{е), то для всех / (l</<d)
P/66(P/-i» У*)' где ^* обозначает ае, если yt = e, или уг если
y-i 6 А. Обратно, если P/66(P/-i» ^/)-(/ = 1, ..., d\ р0, ..., §d£KA\
гр ..., г^^Ал), то
(Ро> e)b(lV A(«i))K ' •' Ы**> А(г1 ''' z<t)>
Следовательно,
S(x) = {yfcqQx, е)(—*(р, у) для некоторого Р6/7} = h(T(A)).
Об инвариантности классов языков
153
Поскольку Т(А)—регулярное множество, то h(T(A))=S(x)
также регулярно. \
(б) Пусть Л = (К, 2, б, Ри ^—детерминированный
конечный автомат, такой, что W = T(A).. Положим w = wit. .wk, где
fe>l и wu • •., Wft б Si. Пусть, кроме того, /?2, ..., Pk+i — символы,
не содержащиеся в /С, и /Cs=/CU{Pi/2 *Ci^Ck +1}. Рассмотрим
ЛО-преобразователь S = (/Cs, Si, S, ц, pi), где
\i(p, wx)=r= \(b(p, x), wv x, 0)/х£Ц U {(pv wv e, l)lp£F)
для p€K и
М-(Л. ^/)={(Л+1» «>„ е' 1)1
для 2<л-0.
Нетрудно видеть, что S(w) = T(A) = W.
Замечания. (1) Пусть S = {{pu р2> рз}, [а, Ъ, с\ (л:, j/,z}, ц, pi)—
ЛО-преобразователь, где ц(рь a)={(pi, а, х, 1)}, |л(рь 6) =
= {(Pl, 6, А:, 1)}, |Х(Р1, С) ={(р2, С, У, —1)}, |i(P2, ^) ={(Р2, ft, У, —1)},
ц(р2, а)={(р3, а, г, 1)} и (х(р3, м)={(Рз, ", 2, 1)}, где и = а, 6
или с. Тогда S(ab*c)={xnynzn+l/n^'l} и язык в правой части
равенства не является КС-языком. Итак, образ регулярного
множества при отображении, осуществляемом ЛО-преобразова-
телем, непрерывно пишущим на выходе, в общем случае не
является КС-языком и тем более регулярным множеством.
(2) Согласно теореме 2.4 (б), существуют
ЛО-преобразователь Si и символы а, 6, с, такие, что Si(a)=ab*c. Пусть S —
ЛО-преобразователь, описанный в замечании (1). Тогда
SSi(a)={xnynzn+llr£t?;l}, т. е. SSi не является ЛО-отображе-
нием. Следовательно, суперпозиция ЛО-отображений не обяза-*
тельно является ЛО-отображением.
В работах (Ginsburg and Rose, 1963а) и (Ginsburg and Hib-
bard, 1964) рассматривались следующие алгоритмические
проблемы. Существуют ли алгоритмы, позволяющие по
произвольным КС-языкам X и У и по произвольным регулярным множен
ствам X и У узнавать:
(1) Существует ли детерминированный конечный
преобразователь S, такой, что S(X) = У?
(2) Существует ли детерминированный конечный
преобразователь^, такой, что S(X)^Y и S(X) бесконечно, если X беско-*
нечно?
Рассмотрим аналогичные вопросы для ЛО-преобразователей,
Из теоремы 2.4 (б) и из распознаваемости свойства регулярных
множеств быть бесконечными (Rabin and Scott, 1959) следует,
что для регулярных множеств и ЛО-преобразователей
проблемы (1) и (2) алгоритмически разрешимы. В случае, же когда X
154
С. Гинзбург, Дж. Роуз
и У суть КС- (и, следовательно, НС-) языки, имеет место
следующая теорема:
Теорема 2.5. Не существует алгоритма, позволяющего для
произвольных двух КС- (и, следовательно, НС-) языков X и Y
узнавать:
(а) Существует ли Л О-преобразователь S, такой, что
S(X) = Y?
(б) Существует ли ЛО-преобразователь S, такой, что
S(X)<=:Y и S(X) бесконечно, если X бесконечно?
Доказательство, (а) Пусть X состоит из одного
символа. Согласно теореме 2.4, ответ на вопрос (а) положителен
тогда и только тогда, когда У — регулярное множество.
Поскольку не существует алгоритма определения по
произвольному КС-языку, является ли он регулярным множеством (Ваг-
Hillel et al., 1961) *), проблема (а) алгоритмически
неразрешима.
(б) Пусть 2 = {а, 6, с} и Х = а* — {е}. Для каждой м-ки
w=(wu ..., wn) непустых цепочек из множества {а, &}*
рассмотрим КС-язык
L(w)=labtl ... ab^cw. ... w. /£> 1, 1 </lf ..., //|</гi.
Далее, для каждых двух п-ок х=(хи ..., хп) и у=(уи •••
.. .„ уп) непустых слов из множества {а, &}* рассмотрим КС-язык
L(x,y)=()lcL(x)}"[cL(yT.
- Покажем, что ЛО-преобразователь S, такой, что S(X)^
^.L(x, у) и S(X) бесконечно, существует тогда и только тогда,
когда существует последовательность натуральных чисел 14, ...
..., /л, такая, что х. ... х. ==у1 ... yt. Поскольку
последнее есть не что иное, как алгоритмически неразрешимая
проблема соответствий (Post, 1946), то проблема (б) алгоритмы*
чески неразрешима.
1) Сходные вопросы рассматриваются в работе Ландвебера «Проблемы
разрешения в грамматиках непосредственных составляющих», перевод
которой напечатан в настоящем сборнике, стр. 103—127. В частности,
нераспознаваемость регулярности КС-языка доказана в теореме 13 (стр. 123).
Распознаваемость пустоты и бесконечности КС-языка, на которые опирается
доказательство теоремы 3.5, доказаны у Ландвебера в теоремах соответственно 2 и 3.
В доказательстве теоремы 3.6 используется построение, отличное от работы
Ландвебера, но нераспознаваемость «полноты» КС-языка доказана в
теореме 8. — Прим. ред.
Об инвариантности классов языков
155
Предположим, что существуют натуральные числа iu ..., ih,
такие, что' х. ... х. =у. ... у. . Пусть S — ЛО-преобразо-
ватель с одним состоянием ({/?}, {а}, {а, 6, с}, \\, р), гле\х<{р, а) =
= (р, а, (сай'* ... аЬ^сх1{ ... xtJ, l). Тогда
S (*) = {( со*'* ... аь\хь ... JtJm|/rc>l}
есть бесконечное подмножество множества L(x, у).
Допустим теперь, что S — ЛО-преобразователь, такой, что
S(X)^L(x, у) и S(X) бесконечно. Возможны следующие два
случая.
(a) S(as) бесконечно для некоторого s>l. Согласно
теореме 2.4, множество S(as) регулярно. Таким образом,
множество S(as) является бесконечным регулярным подмножеством
множества L(x, у). Однако, как было отмечено при
доказательстве леммы 3.2 (Ginsburg and Rose, 1963а), множество L(x, у)
содержит бесконечное регулярное множество тогда и только
тогда, когда существует последовательность натуральных чисел
/i, ..., ik, такая, что xt ... Xik = УЬ ... у%.
(Р) S(as) конечно для всех s>l. Поскольку множество S(X)
бесконечно, a S(a) конечно, то существует />1, такое, что
S(a')—8(а)фф. Пусть w^Sfa*)—S(a). Существуют u£S(a)
и v4=г, такие, что w = uv. Поскольку и и w принадлежат
множеству L(x, у), то существуют г и s (r<s), такие, что
u(i [cL(x)]r[cL(y)]r и w£. [cL(x)]s[cL(y)]s. Тогда и имеет вид
cpi ... ср2г, где pi€ L(x) для 1<л<г ир^ L(y) для г+Кл'.<2г.
Аналогично w имеет вид cq^ ... cq2s, где qi^L(x) для 1<л<$ и
qidL(y) для 5 + 1^/^25. Поскольку w = uv, то pi = qi для
\*Ci4i2r. Тогда pr+i€ L(x) f\L(y). Следовательно, существуют
натуральные числа it, ..., ^, такие, что
рг,Л ==abk ... ab lcx, ... х, = ab к ... ab хсу. ... у, ,
так что xix ...xik = yix . ..yik.
Замечание. Подходящим кодированием можно добиться,
чтобы язык У содержался во множестве {а, &}*.
III. Преобразователи с магазинной памятью
Данный раздел посвящен изучению устройства, которое на*
ходится в том же отношении к МП-автомату, в котором
ЛО-преобразователь находится к ЛО-автомату.
156
С. Гинзбург, Дж. Роуз
Определение. Преобразователем с магазинной памятью
(сокращенно МП-преобразователем) называется упорядоченная
семерка S={K, 2, Г, А, |л, Z0, q0), где
(1) /С, 2, Г, Z0 и q0 имеют тот же смысл, что и в
определении МП-автомата;
(2) Д — конечное множество (множество выходных
символов);
(3) \х— отображение множества /(Х(2и{е})ХГ во
множество всех конечных подмножеств множества Л'ХГ^ХД*.
Приведем формальное описание способа функционирования
МП-преобразователя. Это описание аналогично
соответствующему описанию МП-автомата.
Обозначение. Пусть S = (/С, 2, Г, Д, ц, Z0,
^—МП-преобразователь. Определим отношение |—* на множестве /СХ2*Х
ХГ*ХД* следующим образом: для произвольных Z£T и
л;£Еи{е} имеет место (р, xw, aZ, y)\~(q, w, ay, ууг)9 если
(q> Y> Уг) 6 М- (Р> х> z)- Пусть, кроме того, [р, w, а, у) |—* (р, w, а, у)
для всех р, w, а и у. Для a,p£F*, «/,«/'£ Д* и лг;£2и{е}
(1 <;/•< А) полагаем (/?, ^ ... л^яе;, a, у)\—*(q, w, р, у*), если
существуют последовательность состояний/?!=/?, . ., Pk+i = 9>
последовательность 04 = 01, ..., ал+1 = р элементов множества Г*
и последовательность y = yv...t yk+1 = y' элементов
множества Д*, такие, что
(pl9 хь ... xkw, ait yi)\-(pnv xin ... xkw, ai+1, yi+1)
для l^i^Ck.
Обозначение. Пусть S = (AT, 2, Г, Д, \\, Z0,q0) —
МП-преобразователь. Для каждого x£l?S(x) есть множество цепочек
у£Д*, таких, что (q0, х, Z0, е)|—*(q, е, а, у) для некоторого
(4, а)6/СХГ*. Если ХсГ, то S(X)=\JS(x).
Отображение # в S(x) для каждого х£2* называется
МП-отображением.
Теорема 3.1. Для произвольного
рекурсивно-перечислимого множества Y существуют КС-язык X и
МП-преобразователь S, такие, что S (X) = У.
Доказательство. Поскольку Y — рекурсивно-перечис-
димое множество, существует порождающая грамматика
Об инвариантности классов языков
157
G = {V, 2, Р, а), такая, что L(G) = Y. Пусть / и я — абстрактные
символы, не принадлежащие множеству V. Пусть
A = {uldfi*u*dlu€V*,l-+fiGP}1) и X = {od$*dlo-+$€P}A*t.
Легко видеть, что X есть КС-язык. Пусть S = (Kj__ VU{d},
VU{Z0}, 2, |л, Z0, 9о) —МП-преобразователь, где Z0€ V, К=
= {qo> qu 02, 0з} и отображение |х определено следующим
образом:
(1) \x{q0, a, Z0)={(qv Z0, е)};
(2) \x(qv х, x) = [(qv е, е)} для x£V\
(3) |л(^, d, x)={(q2, х, г)} для *€ VU {Z0};
(4) ц(02, х Z)={(q2, Zx, г)} для x^V и Z£V\]{Z0)\
(5) ц(02, rf^Z) ={(^, Z, е), (03, Z, e)} для Z£VU{Z0};
(6) ц(03, e, £) = {(03, e, Z)} для Z£2;
(7) \x{qz, tt Zo)={(03, e, e)}.
Покажем, что S(X) = Y. Пусть w£Y. Тогда существуют
£>0, w0, ..., wk+v ut, |/f ^, fy (0</<£), такие, что a = -a;0,
^fi = ^ и для всех./<A fwi = aili'vii wl+l = ufiivi и^->р^Р.
Нетрудно видеть, что для каждого /
(<70> №W#9 • • • №*№0' zo> е)К(?2> d> zo^f+vе>
Следовательно, (0О, (u^d^ugd) ... (uklkd$*u*d), Z0, е)|—*
|—* (0з» е, Zq^^, е) f—* (03, е> Z0, <я>) |— (qs, е, е, яу), так что w £ S (X).
Предположим теперь, что w£S(х) для некоторого х£Х.
Тогда х имеет вид (u0l0df>*u*d) ... (uklk d^a^dy где £>0,
#0 = е и lo = a» и (#о> ■*» ^о> е)Ь-*(#» е> е» ^) Для некотррого q.
Тогда
(0О, л:, Z0, z)\—*(q', е, Z0, w)|—(0, е, е, w)
для некоторого 0'. Очевидно, что 0 = 03 и q'=q2. Тогда
(0О, я, Z0, е)Ь-*(02, d> Zq®r> с) I—(03, e, Zq^, e)f—*(03, e, e, яу).
Как следует из определения отображения |л, для'некоторых
vo> •••> ^*+i имеет место 0 = ^0=^^=^ ... ^>wk+1 = w, где
wt = #^^ и vin = afiiVi для / < k. Итак, до £,К, т. е. S (X) = Y.
Замечания. (1) Если 2 содержит по крайней мере два
символа, то VU{d} может быть так закодировано элементами
множества 2*, что для каждого рекурсивно-перечислимого
1) Для каждой цепочки w wR = w, если ш = 8, и щп=хц ... х^ есл,и
W=%i ... Хц\ для каждого i Xi — символ.
158
С. Гинзбург, Дж. Роуз
множества У^2* можно подобрать КС-язык X^S* и
МП-преобразователь S, такие, что S(X) =Y. Однако это не имеет места,
если 2 состоит в точности из одного элемента, скажем а.
Каждый КС-язык Х^а* является регулярным множеством (Ginsburg
and Rice, 1962). Согласно теореме 3.3 (см. ниже), множество
S(X) является КС-языком. Однако существуют
рекурсивно-перечислимые множества Y<^a*, не являющиеся регулярными,
например, {ап2/п>1}.
(2) Если L — КС-язык и S — МП-преобразователь,
непрерывно пишущий на выходе1), то S(L) не обязательно является
КС-языком. В самом деле, пусть 5 = (/С 2, Г, А, \х, Z0, q0) —
МП-преобразователь, где K={q0> qv q2> #зЬ 2 = (a, b, с],
Г = {а, b, Z0}, Д = {а, Ь, с} и отображение \х определено
следующим образом: \\(q0, a, Z0)=={(qv Z0, a)}, \x(qv a, Z0) =
= {(qv Z0af a)), \x(qv b, Z0)= {(qz,Z0,b)}, \x(qv a, a) = {(qv aa,a)},
\x(qv b, a)={(q2> e, 6)}, \x(q2> b, a)={(q2, e, b)}, \\(q2, b, Z0) =
= {(q?, Z0, b)} и \x(q3, c, Z0)={(qs, Z0, с)}. Тогда если Z,=
= {a^V//,y>l}, то S(Z,) = {aW//> lj. Итак, L является
КС-языком, a S(L) — нет.
Эви (Evey, 1963) указал условия, которым должны
удовлетворять S и L, чтобы язык S(L) был КС-языком, если L
является таковым. Для полноты изложения приведем новое
короткое доказательство этого факта.
Определение. МП-автомат М = (К, 2, Г, б, Z0, q0, F)
и МП-преобразователь S = (K, 2, Г, А, ц, Z0, q0) называются
согласованными, если для каждого (q, х, Z) £КХ (2 U |е|) ХГ
6(9, х, Z)={(p, а)/(р, а, */)€ \x{q, х, Z) для некоторого */€Д*}.
Теорема 3.2. [Evey, (1963), теорема 2.6.6.] Если
МП-автомат М и МП-преобразователь S являются согласованными и
L = T(M), toS(L) —КС-язык.
Доказательство. Пусть М = (К, 2, Г, 6, Z0, q0, F) и
S = (K, 2, Г, А, \\, Z0, q0). Пусть 2' —множество
упорядоченных пар (х, у) £(2 и {е})Хд*> Для которых существует (q, Z, р, а),
такое, что (/?, a, y)£\x(q, х, Z). Очевидно, 2х конечно. Пусть
ЛГ = (/С, 2', Г, bM>, Z0, #0, /^ — МП-автомат, где
Ъм> (q> (*> У)* Z)={(p, а)!(р, a, y)£\k{q, х, Z)}
1) МП-преобразователь (К, 2, Г, Л, [i, Z0, q0) непрерывно пишет на
выходе, если из {q,y,y)€ №(р, x,Z) следует, что уф г для всех Р^ К,
х£ 2 U {е} и Z € Г.
Об инвариантности классов языков
159
для каждого (q, (х, y)t Z) £/Сх2'ХГ. Определим гомоморфное
отображение / множества 2'* во множество А* следующим
образом: !((х,у))=улля каждого (х, у) £2'.
Поскольку класс КС-языков замкнут относительно
гомоморфизмов (1), достаточно показать, что f ]7"(Л^г)] = *S (Z,).
Пусть (xv уг) ... (xk, yk) £ Т {М'). Поскольку для всех q и Z
имеет место bMr (q, е, Z) = <j>, существуют qv ..., qk(zK> где
qk£F, и аг ... ай£Г*, такие, что
(<7о> (*i> Ух)--- (■**• Уи)> ZoKr(?i> (½ ^)---
.. • (xk, yk), аг)\-м, ...\-M. (qk-v {*k> </*> ^_i)b' (<7*> *> <**)•
Из определения отображения ЬМ' и того факта, что М и S
являются согласованными, следует, что
(<70, хг... хЛ, Z0, e)h-s(qv х2 ... xk, av yx)[-s ...
• • • К(<7*_1> *k. <Vr уг... Ук_г)\-8(як, e, a,, yx ... yk)
И (^0, *l...*ft, Zq) j—m . . . <|— M(Qk-U Xk, CLh-i) У-м(с/к, 8, ttfc).
Итак, Xi...xk£L и yi...yk = f i(xu 0i).. .(*л, #*Ж S(L), т. e.
f[7,.(M/)]s5(L). Аналогично можно показать, что S(L)^f[r(M')],
следовательно, S(L) =/[Г(М')].
Рассмотрим теперь образ регулярного множества при МП-
отображении.
Теорема 3.3. Для произвольного МП-преобразователя S и
произвольного регулярного множества L множество S(L)
является КС-языком.
Доказательство. Пусть S = (K> 2, Г, А, \х, Z0, qQ).
Поскольку L — регулярное множество, существует конечный
автомат А = (КА, 2, бл, р0, FA), такой, что L = T(A). Пусть
S' = (KXKA, 2, Г, А, \х\ Z0, (q0fP0)) — МП-преобразователь, где
li'((q9 р), х, Z)=^{((q', ЬА(р, х)), a, y)l(q'9 a, y)£ii(q, х, Z))
для всех ((</, р), х, Z) 6 (КХКА) X (2 и{е}ХГ. Пусть, далее,
М' = {КХКа>Ъ> г> Ьм<, Z0, (q0, р0), KXFA)— МП-автомат,
согласованный с S', с множеством заключительных состояний
KXFA, и М = {К, 2, Г, б, Z0, q0, К) —МП-автомат,
согласованный с S, с множеством заключительных состояний /(. Тогда
S(T(A))=S(T(M)(]T(A))=S'(T(M')). Согласно теореме 3.2,
S'(T(M')) —КС-язык.
Замечания. (1) Эви [Evey, (1963)., теорема 2.6.3] показал, что
регулярное множество 2*с, где с — символ, не принадлежащий
160
С. Гинзбург, Дж. Роуз
2, обладает следующим свойством: каков бы ни был КС-язык
L^2*, найдется МП-преобразователь S, такой, что S(2*c)=L.
(Нетрудно показать, что при подходящем кодировании для
произвольного КС-языка L существует МП-преобразователь S,
такой, что S({a, &}*c)=L, где а, Ь и с — различные символы.)
Имеет место также следующее утверждение (его
доказательство мы опускаем): «для каждого регулярного множества R су*
ществует детерминированный конечный преобразователь S,
такой, что S({a, b}*c)=R, где а, b и с — различные символы».
(2) Пусть 2 = {а, Ь, с, d) и Ь={а}ЬчЦ{, />1}. Согласно
замечанию (1), существует МП-преобразователь Si, такой, что
Si ({a, 6, c}*d) = L. Пусть S2 — МП-преобразователь, построенный
в замечании (2) к теореме 3.1. Тогда S2(L) ={а{Ь*с{/1 <> 1}. По-^
скольку S2Si({a, 6, c}*d) = {а1Ь1с1\1^ 1} не есть' КС-язык,
согласно теореме 3.3, S2Si не является МП-отображением. Итак,
суперпозиция МП-отображений в общем случае не является
МП-отображением.
(3) Существует МП-отображение, не являющееся ЛО-ото-
бражением. Рассмотрим МП-преобразователь S = ({/?, q}, {а},
{Zo, а, 6}, {а, 6}, , Z0, р), где ц(р, е, Z) ={(/?, Za, а), (?, Z, а)}
для Z£{Zo, а}, \i(q, е, а)={(<7> е, 6)} и ц(<7, а, Z0)={(<7, е, &)}.
Очевидно, S(a) ={anbn/n^l} не есть регулярное множество.
Согласно теореме 2.4, не существует ЛО-преобразователя Si, та-*
кого, что Si (a) =S(a).
(4) Существует ЛО-отображение, не являющееся
МП-отображением. Пусть У={аг"&г'сг7*>1}- Тогда множество У рекурсивно
перечислимо, но оно не является КС-языком. Согласно
теореме 2.2, существуют ЛО-преобразователь S и регулярное мно*
жество X, такие, что S(X) = Y. Согласно теореме 3.3, не суще^
ствует МП-преобразователя Si, Такого, что Si(X)=Y.
В замечании (2) к теореме 3.1 мы отметили тот факт, что
если S — МП-преобразователь, непрерывно пишущий на выходе,
и L — КС-язык, то множество S(L) не обязательно является
КС-языком. Следующая теорема, аналогичная теореме 2.3,
показывает, что множество S(L) должно быть НС-языком, если
L — НС-язык и S — МП-преобразователь, непрерывно пишущий
на выходе.
Теорема 3.4. Пусть S = (/(, 2, Г, Д, jm, Z0i q0)
—МП-преобразователь, непрерывно пишущий на выходе, и L — НС-язык,
тогда S(L) также есть НС-язык,
Доказательство. Пусть G=(V, 2, Р, а, #) — НС«грам*
матика с граничным маркером, порождающая язык #L#.
Без потери общности мы можем считать, что множества 2, А и
Об инвариантности классов языков
161
V — 2 попарно не пересекаются. Мы можем также считать, что
е 5 L. [В самом деле, если e€L, то S(L) = S(e) [}S(L — {е}),
S(e)—КС-язык, a L — {г} — НС-язык.] Построим
НС-грамматику с граничным маркером, G/ = (V/, Д, Р', а, #),
порождающую язык #5 (£)#.
Пусть /г1 = тах{ \y\l(q, Y> ^бМ/7» •*» -2) Для некоторых /?,
х, Z, q, w) и /z2 = max {\w\l(q, yt w)£\x(pt х, Z) для некоторых
pt х, Z, q, у]. Всем л;£2и {е}\ q£K, у£Г* длины </гх и яу£А*
длины <^/г2 сопоставим абстрактные символы (х, q, у, w),
(—, ?, Y» ^)» (—. —. Y» ^)» £«, и Fw. Пусть, далее, V
содержит как все элементы множества V U А, так и все символы
(х, ?, Y> «О, (—. ?> Y. ^). (—» —» Y» w), £«, и /v> Я' содержит
все правила из Я и все следующие правила [символы х> у,
w, v, Z, y (возможно, с индексами) обозначают элементы
множеств 2, 2и{е}, А*— {е}, А*—(е), Г и Г* соответственно]:
(1) #х->#(х, q0, Z0, е);
#x->#(et qQ9 Z0, г)х\
(2) (yt q, Z, е)->(—, р, у, w)9 если (pt у, w)£\\(q, у, Z);
(3) (—, q, yZ, w)->(—9 —, Y> *a;) (е. <7> 2. e);
(—, #, y^» «;).*-*(—, —, y» w)(a;, ?, Z, e);
(4) (—, —, e, w)->Ew\
(5) (—, —, yZ, w^)Ew->EWl(—> —, y^» w); -
(6) (—> —, Y^> w)(—, ?, e, ^)-^(-, —, Y> ^)(- ?> Z> Щ)\
(7) (—, q* Y. ^)#->^#;
(—, —, Y» w)FWl-^Fww1;
#Fw->#w.
Покажем, что L(Gr)= # S (L) #. Определим гомоморфные
отображения gv g2> g$ и gA на множестве V следующим
образом: gi((y, q, у, w)) = g1((—, q, у, w)) = q, в остальных
случаях £х = е; £2((у, ?, Y> ^)) = ^0/) = ^ в остальных
случаях £2=е; £3 ((</> Я* Y> w) )=g3 ((—, q* Y> tw) )=£8 ((—, —, Y> w) )=
= Y; gA((y* Я> Y. w)) = £4((—. ?. Y. w)) = £4((—, — Y. w)) =
= g4(w) = g4Ww) = g4(Fw) = w> в остальных случаях g4 = e.
Пусть g = (gv g2> g^ &)•
Предположим, что v£S(u) для некоторого #£Z,. Тогда
#а#=Ф^#гг# и существуют v0 = e, ^ ^бА*-(е),
uv ..., %62U{e}, ^, ..., qk£K. y0 = Z0, yv ..., Y*€r*> такие,
что и = иг . . . Uk, V = ^1 ... vk и
(%» «i • • • «*» Yo> -»o) I— (^1» «2 • • • я*» Yp ^i)h- ...
• • • Ь (^. e» Y*. ^1 • • • *>*).
11 Зак. 1204
162
С. Гинзбург, Дж. Роуз
Индукцией по / можно доказать [с учетом (1) — (7)], что
для всех i^k существуют р0, ..., fy, такие, что
(9) # и # =>*G, # р0# =>*0, ... #*0, # р, #;
(10) если/< А, то существуют0 <y</,Yy+i» •••» Y-бГ*—{е}
и Z.£T, такие, что Y/ = Yy+1 ••• y'iZl и
¢.=^ ... eVj(-9 -,. y;+1, vO • • •
(И) P,=*v..^y(-.-.Y',+1. v)-h-ti'Vi)^
где 0</</ и yV+1» • ••> Y*_i€r*—(еЬ Следовательно,
согласно (8), # a # #*G, # и # =^*G, # £k # =ф*0, # v #. Итак,
#S(i)#s£(O0-
Предположим теперь, что # i; # £ Z, (G'). Поскольку V—2,
S и А попарно не пересекаются, существует вывод цепочки
#^#, в котором все применения правил из Р предшествуют
применениям правил из Р/~Р. Итак, существует цепочка
#и# £L(Q), т. е. u£L, такая, что,
Нетрудно видеть, что если # и # =Ф^, #^#, то существуют
uv ..., ^£2и{е}, Pi = (^, ?0> zo» е)я2... ик, Р2, ..., Pf, tp ..., т^
такие, что
(12) и = иг ... ял;
(13) # а # =#0, # Рх # =#0, ... =#0, # рг # =Ф0, # тх # =#0. • ••
... =ф0, #t5#^>g, #тг#;
(14) всякий раз, когда # р£ # =Ф0, # р£+1 #, применяется
одно из правил типа (2), (3), (4), (5) или (6);
(15) всякий раз, когда # xj # =Ф0, # xj+1 #, применяется
одно из правил типа (8);
(16) в случае когда # xs # =Ф0, # v #, применяется одно
из правил вида # Fw -> # w,
s (17) в случае когда # рг # =Ф0, # т1 #, применяется одно
из правил типа (7).
Тогда g4(pr) = g4(хг) = v. Пусть av ..., щ —
последовательность, полученная удалением повторений из
£(Pi). ..-. £Фг)-
Тогда а2 = (#0, иг ... uk, Z0, е) |— ... f- а, = (q, е, y» ^) Для
некоторых #£ЛТ и y€T*. Следовательно, ^¢5(/,), т. е. £(<?')£
с#5(1)#.
Об инвариантности классов языков
163
Прежде чем заняться проблемами разрешимости для МП-
отображений, докажем следующую лемму:
Лемма 3.1. Пусть У^2* — КС-язык и тфг — элемент
множества Si. Тогда существует МП-преобразователь S, такой,
что S(w)=Y.
Доказательство. Пусть Q = (V, S, Я, а) —
КС-грамматика, порождающая язык У, и w==wx ... wk, для каждого /
wte^v Пусть, далее, S = (K, 2,, 1/U{Z0}, S, ц, Z0, q0) — МП-
преобразователь, где/С = {^/0</<£ + 1}, 2о£У*р(Яо' е» ^о)=
= {(?, Zno, е)}, |л(^, е, х)= {(qv е, л:)} для всех x^S, |xfalf е, |)=
= {{qv Р*. е)/6->р G Я} для g 6 1/-Е и jx (qit wit Z0) = {(?£+1, Z0, e)}
для 1<*<&. Непосредственно проверяется, что S(w) = Y.
Теорема 3.5. Следующие проблемы алгоритмически
разрешимы для произвольных КС-языков (и, следовательно,
регулярных множеств) X cr S* — {е} и Кс S2:
(а) Существует ли МП-преобразователь S, такой, что
S(X)=Y?
(б) Существует ли МП-преобразователь S, такой, что
S(X)^Y и S(X) бесконечно, если X бесконечно?
Доказательство, (а) Если Х=ф, то
МП-преобразователь S, такой, что S(X)=Y, существует тогда и только тогда,
когда У= ф, а свойство КС-языка быть пустым алгоритмически
распознаваемо (Bar-Hillel et al., 1961). Предположим, что
Хфф. Пусть w — цепочка наименьшей длины, принадлежащая
множеству X. Согласно условию теоремы, хюФг. Пусть S —
построенный в лемме 3.1 МП-преобразователь, отображающий
цепочку w на множество У. Из способа построения S и того
факта, что w имеет наименьшую длину, следует, что если x = w,
то S(x) = Y\ в противном случае S(#)=^- Итак, S(X)=Y.
б) Доказательство аналогично доказательству в случае (а),
поскольку свойство КС-языка быть бесконечным
алгоритмически распознаваемо (Bar-Hillel et al., 1961).
В случае когда е£Х, проблемы (а) и (б) алгоритмически
неразрешимы.
Теорема 3.6. 'Для произвольных КС-языков X и У каждая
из следующих проблем алгоритмически неразрешима:
(а) Существует ли МП-преобразователь S, такой, что
S(X) = Y?
(б) Существует ли МП-преобразователь S, такой, что S(X)^
£У и S(X) бесконечног если X бесконечно?
и*
164
С. Гинзбург, Дж. Роуз
Доказательство, (а) Пусть а, Ь и с — различные сим-*
волы. Для произвольных я-ок у=(уи • •., Уп) и 2:=(2:1, ..., zn)
непустых цепочек над алфавитом {а, 6}* существует
бесконечный КС-язык W(y, z)^{a, 6}*, эффективно строящийся по у и г
и такой, что W(y, z) ={а, 6}* тогда и только тогда, когда не
существует последовательности натуральных чисел ч, ..., 1к,
такой, что yt ... f/,. =z£ ... z. (Bar-Hillel et al., 1961) l). Пусть
Г (у, z)=[a, b}*[) W(y, z)c[a> b}*[}[a, b}*cW(y, z)c
Ввиду алгоритмической неразрешимости проблемы
существования натуральных чисел i\, ..., ^, таких, что Угх---У1к =
= zti ... Zi (Post, 1946), достаточно доказать, что W(y, z)~
={а, &}* тогда и только тогда, когда существует
МП-преобразователь S, такой, что S(e) = y(#, z).
Предположим, что W (у, г) = {а, Ь}*. Пусть S = ({q0 ,qx},
{a}, {Z0}, (а, й, с], |л, Z0, <70)— МП-преобразователь, где
\x(q0, е, Z0)={(?0, Z0, а), (?0, Z0, й), (q0, Z0, с)} и |A(ft. е, Z0) =
= ((^, Z0, а), (qv Z0, й), (^, е, с)}. Тогда
5(е) = Г(г/, *)={а, й}*и{а, Ь)*с{а, Ь}*\}{а> Ь)*с{а, Ь}*с.
Предположим* теперь, что S=(K, 2, Г, А, ц, Z0,
^—МП-преобразователь, такой, что S(e) = Y(y, z). Пусть
т = max {\и \l(q, у, u)£ \x (p, e, Z) для некоторых p, q(zKf
Поскольку множество W(y, z) бесконечно, существует цепочка
v£W(y, г), такая, что m-<|i>|. Пусть w — произвольная
цепочка, принадлежащая множеству {а, 6}*. Тогда wcvcd Y(y,z) =
=S(e). Согласно определению числа т, существуют v'=f=e, v",
a, Z, у, р, 9» такие, что vc = v"v' и
(<70, е, Z0, е) (—*(/?, е, aZ, wcv")\—s(qt е, ay, ^i/V).
Тогда wcv" 6 5(e) = У (у, z). Следовательно, ayct/'б V(y, z)c{a, 6}*
и йу£ IF (у, z). Поскольку w — произвольная цепочка, W(y, z) =
(б) Пусть a, 6 и с — различные символы и множества L(x),
L(y) и L(x, у) определены так же, как в п. (б) теоремы 2.5.
Пусть Х=а* и Y(xy y)=L(x, у) U{e}. Предположим, что
существует последовательность натуральных чисел iu ..., ik, такая, что
хь ... xt =yt ... yt . Пусть z = (cabik ... abl^cxt ... x. \2.
l) Теорема 6.2 (а), — Прим. перевг
Об инвариантности классов языков 165
Тогда множество z* есть некоторое бесконечное подмножество
множества Y(x, у). Пусть S~{{p}, {a}, {Z0}, {а, 6, с}, ц, 20, р) —
МП-преобразователь с одним состоянием, где \\(р, a, Z0) «=
= (р, Z0, г). Тогда множество S(X)=z* является бесконечным
подмножеством множества Y(x, у).
Предположим теперь, что S=(/C, 2!, Г, А, ц, Z0, <7о) —
МП-преобразователь, такой, что S(X)^Y(x, у) и S(X)
бесконечно. Пусть
яг = max {\г' \j(q, у, z')£[i(p9 t, Z) для некоторых pt q£K>
<6SU{e}, Z£Y и Y€H-
Пусть г — цепочка из множества S(X), такая, что \z\>m.
Тогда существуют i, /, ифе, v=f=e, а, р, такие, что 2 = ии и
(qQt а\ Z0, е) (—*(/?, а;', a, u)\—{q, е, р, яг>).
Итак, цепочка ифе принадлежит множеству Y(x, у) и мфи.
Нетрудно видеть, что отсюда следует существование
натуральных чисел ii9 ..., i^ таких, что х. ... х. =у. ... у. .
Итак, S(X)^Y(x, у), где S(X) бесконечно, имеет место тогда
и только тогда, когда существует последовательность
натуральных чисел iu • • -, h> такая, что х. ... х. = у. ... у. , а эта
проблема алгоритмически неразрешима.
Замечание. При подходящем кодировании множества У
можно считать, что Уе{а, &}*.
В заключение отметим, что проблемы, касающиеся
МП-отображений, алгоритмически неразрешимы для двух
произвольных НС-языков X и У, даже если каждый из них не содержит
пустую цепочку. В самом деле, рассмотрим проблему,
относящуюся к отображению X на У. Пусть у=(уи • •., Уп) и г=*
= (zu • •., zn), y=t=z, — произвольные м-ки непустых цепочек над
алфавитом {а, &}*, и пусть L(y) и L(^) определены, как в
теореме 2.5. Пусть, далее, М(у, z)=L(y) flL(z). Тогда множество
М(у, z) не содержит пустую цепочку е и М(у, z) есть НС-язык
(Landweber, 1963), не являющийся КС-языком (Bar-Hillel et al.,
1961) *), если только он не пуст. Тогда МП-преобразователь S,
такой, что S(a)=M(y, z) существует тогда и только тогда,
когда М(у, z)= ф, & это алгоритмически нераспознаваемо.
Рассмотрим проблему, относящуюся к отображению X в У.
со
Пусть-/V(г/, z) = \J [L (у) () L (z)]J. Очевидно, что N(y, z) есть
У-1
1) См. приложение I к статье Ландвебера в настоящем сборнике.—
Прим. ред.
166 С. Гинзбург, Дж. Роуз
НС-язык, не содержащий пустую цепочку в. Пусть Х = аа*. Тогда
МП-преобразователь S, такой, что S(X) ^N{y,z) и S(X)
бесконечно, существует тогда и только тогда, когда L(y) [\Ь(г)Ф
Ф Ф, а это алгоритмически нераспознаваемо.
Л ИТЕРАТУРА
В а г - Н i 11 е 1 Y., Р е г 1 е s М., Shamir Е., On formal properties of simple
phrase structure grammars, Z. Phonetik, Sprachwiss. Kommunikations-
forsch, 14 (1961), 143—172.
Chomsky N., On certain formal properties of grammars, Inform. Control, 2
(1959), 137—167. (Русский перевод: Хомский H., О некоторых
формальных свойствах грамматик, Кибернетический сборник, вып. 5, ИЛ,
М., 1962.)
Chomsky N., Context-Free Grammars and Pushdown Storage, Quarterly
Progress Report № 65, Research Laboratory of Electronics, MIT, 1962.
Davis M., Computability and Unsolvability, McGraw-Hill, New York, 1958.
Evey J., The Theory and Applications of Pushdown Store Machines, PhD
Thesis, Harvard University, 1963.
Q i n s b u r g S., The Mathematical Theory of Context Free Languages, McGraw-
Hill, New York, 1966 (в изд-ве «Мир» готовится к печати русский
перевод) .
Ginsburg S., Hibbard Т. N., Solvability of machine mappings of
regular sets to regular sets, J. Assoc. Comput. Mach., 11 (1964), 302—312.
Ginsburg S., Rice H. G., Two families of languages related to ALGOL,
J. Assoc. Comput. Mach., 9 (1962), 350—371.
Ginsburg S., Rose G. F., Some recursively unsolvable problems in ALGOL-
like languages, J. Assoc. Comput. Mach., 10 (1963a), 29—47.
Ginsburg S., Rose G. F., Operations which preserve definability in
languages, J. Assoc. Comput. Mach., 10 (1963 b), 175—195.
К u г о d a S. Y., Classes of languages and linear-bounded automata, Inform.
Control, 7 (1964), 207—223.
L a n d w e b e r P. S., Three theorems on phrase structure grammars of Type
I, Inform. Control, 6 (1963), 131—136.
Post E., A variant of a recursively unsolvable problem, Bull. Am. Math. Soc,
52 (1946), 264—268.
Rabin M., Scott D., Finite automata and their decision problems, IBM
J. Res. Develop., 3 (1959), 114—125. (Русский перевод: Рабин M. О.,
Скотт Д., Конечные автоматы и задачи их разрешения,
Кибернетический сборник, вып. 4, ИЛ, М., 1962.)
Об- инвариантности класса НС-языков
относительно некоторых отображений^
С. Гинзбург и Ш. Грейбах
В работе доказана теорема, определяющая условие, при котором класс
языков непосредственных составляющих (НС-языков) замкнут относительно
гомоморфизмов (в том числе и некоторых укорачивающих гомоморфизмов).
С помощью этой теоремы получаются, следующие основные результаты:
указываются условия, при которых преобразователи с магазинной памятью и
линейно-ограниченные преобразователи переводят НС-языки в НС-языки;
доказывается, что грамматики некоторого специального вида порождают
НС-языки, а не произвольные рекурсивно перечислимые множества; особый
интерес представляет тот факт, что если правая часть каждого правила
грамматики содержит хотя бы один основной символ, то язык,
порождаемый такой грамматикой, является контекстно-свободным.
Введение
В теории контекстно-свободных языков (КС-языков) одним
из важных методов является преобразование данного
КС-языка в другой КС-язык с помощью какого-либо оператора,
относительно которого класс КС-языков замкнут. Представляется
правдоподобным, что этот метод может оказаться полезным
также и в теории НС-языков. В настоящее время известно
несколько общих операций, относительно которых класс
НС-языков инвариантен. Сюда относятся пересечение с другим НС-
языком (Landweber, 1963) 2), отображение, осуществляемое
преобразователем с магазинной памятью (Ginsburg and Rose,
1966), и отображение, осуществляемое линейно-ограниченным
преобразователем (Ginsburg and Rose, 1966). Однако класс
НС-языков замкнут относительно последних двух
отображений только при условии, что соответствующие преобразователи
*) Ginsburg S. and G г е i b а с h Sh., Mappings which Preserve
Context Sensitive Languages, Information and Control, 9, № 6 (1966). Эта работа
финансировалась согласно программе независимых исследований SDC
(System Development Corporation). Контракт .AF—19/628/5166, Кембриджская
исследовательская лаборатория, программа алгоритмических языков,
проект № 5632, задание № 563 205.
2) См. также Гладкий (1963) и Kuroda (1964). — Пдищ ред%
168
С. Гинзбург, Ш. Грейбах
пишут на выходе непустую цепочку на каждом такте работы.
Цель настоящей работы — указать ситуацию, в которой данное
ограничение может быть ослаблено. Это достигается путем
введения некоторого общего условия, гарантирующего
замкнутость класса НС-языков относительно гомоморфизмов одного
простого типа. [Грубо говоря, это условие состоит в том, что
длина цепочки х ограничена сверху линейной функцией от
длины цепочки h (х).]
Работа состоит из четырех разделов. В разд. I приводятся
необходимые предварительные сведения и вспомогательные
утверждения; здесь же доказывается, что класс НС-языков
замкнут относительно гомоморфизмов некоторого специального
вида. [После того как работа была сдана в печать, мы
обнаружили результат Гладкого (1963), из которого как следствие
может быть получена теорема 1.3. С другой стороны, результат
Гладкого может быть легко доказан с помощью теоремы 1.3 и
некоторого видоизменения доказательства теоремы З.1.] В разд. II
рассматриваются приложения основного результата первого
раздела к различным отображениям, таким, как отображение,
осуществляемое преобразователем с магазинной памятью, и
отображение, осуществляемое линейно-ограниченным
преобразователем. В разд. III используется основной результат первого
раздела для доказательства того, что грамматики некоторого
специального вида порождают НС-языки, а не произвольные
рекурсивно перечислимые множества. Разд. IV посвящен
доказательству того, что если каждое правило грамматики имеет
вид u-+v, где и — непустая цепочка вспомогательных символов
и v содержит по крайней мере один основной символ, то такая
грамматика порождает КС-язык.
Надо заметить, что некоторые теоремы разд. II становятся
более очевидными, если использовать хорошо известный факт,
что множество цепочек тогда и только тогда является
НС-языком, когда оно допускается некоторым линейно-ограниченным
автоматом (Kuroda, 1964). Однако доказательство того, что
некоторый линейно-ограниченный автомат допускает в точности
то или иное множество цепочек, значительно сложнее
рассуждений, приводимых в работе.
I. Основной результат
Прежде всего напомним определения необходимых
основных понятий, относящихся к грамматикам и языкам. Затем
будет доказано, что класс НС-языков замкнут относительно
гомоморфизмов (в том числе и некоторых укорачивающих
гомоморфизмов), удовлетворяющих приведенному ниже условию.
Об инвариантности класса НС-языков
169
Определение. Порождающей грамматикой
(грамматикой) *) называется упорядоченная четверка G = (V, 2, Р, а), где
(1) V — конечное непустое множество.
(2) 2 — непустое подмножество множества V.
(3) а 6 V —2.
(4) Р — конечное множество правил вида (и, у), где
и£ (V —2)* —(е}и i>6V*2).
Элементы множества V — 2 называются вспомогательными
символами (variables). Элементы множества 2 называются
основными символами (terminals). Элементы множества Р
записываются обычно в виде «и—*и»«
Обозначение. Пусть G = (V, 2, Р, сг)—порождающая
грамматика. Если w^ w2 € V* и г/—*и 6 Р, то полагаем w^uw^ =½
=4 WiVWz. Кроме того, х =Ф *у, если либо х = у, либо существуют
Хи ..., #п, такие, что Xi=a;, хп = г/ и Хг=#> xi+i, 1 <л<Х
Последовательность цепочек до0, -. •> ^ь> такая, что wx =#> ш^+i, 0 ^ i<kf
называется выводом цепочки wk из цепочки w0.
Теперь мы можем определить НС-языки.
Определение. Грамматика G = (V, 2, Р, а)
называется монотонной, если для каждого правила u-^v^P либо
(1) |и|<И3) и и£ (V — {а})* — {е}*; либо (2) и = а и и 6 V*.
Множество L^2* называется языком непосредственных
составляющих (сокращенно НС-языком), если существует
монотонная грамматика G=(V, 2, Р, а), такая, что L = L(G), 'где
£(£)={до £2*Дт =ф *оу}. Будем говорить, что грамматика G яо
рождает язык L 4).
!) Это определение несколько отличается от определения порождающей
грамматики в форме Хомского. Его цепочка и из п. (4) может быть
произвольным элементом множества V* — {б}. Однако порождающая сила
грамматики при настоящем определении та же, что при определении Хомского.
2) Если X и У— множества цепочек, то по определению XY={xyjx£Xf
у £ У} где ху обозначает конкатенацию цепочек х к у. Полагаем также
оо
Х°={е}, где е —пустая цепочка, Xi+1 = Х1Х и X* = (J X1. Таким обра-
t=o
зом, для произвольного множества символов Е множество Е* есть
свободная полугруппа с единицей, порожденная множеством Е.
3) Для каждой цепочки х \х\ означает длину этой цепочки.
4) НС-языки обычно определяются как языки, порождаемые
грамматиками, правила которых имеют вид xZy->xwy, где Z6 V — 2 и М!>1.
Однако нет существенного различия в порождающей силе грамматик в этих
двух определениях. Множество L является НС-языком в соответствии с
приведенным здесь определением тогда и только тогда, когда множество
L — {&} является НС-языком в смысле Хомского.
170
С. Гинзбург, Ш. Грейбах
Каждый НС-язык является рекурсивным множеством, но
существуют рекурсивные множества, не являющиеся НС-язьн
ками.
При изучении НС-языков одним из важных вопросов
является вопрос о том, относительно каких отображений замкнут
класс НС-языков. Следующий общеизвестный результат до сих
пор нигде не был изложен в явной форме.
Теорема 1.1. Если f — подстановка, определенная на
множестве 2* 1) и такая, что для каждого а€2 множество f(a)
является НС-языком и не содержит пустой цепочки е, и L—
некоторый НС-язык, то множество f(L) также является НС-
языком.
Доказательство. Пусть L = L(G), где G = (V, 2,Р,а) —
некоторая монотонная грамматика. Без потери общности мы
можем считать, что L^2* —{е}. Можно, как заметил Курода
(Kuroda, 1964), допустить, что Р состоит из правил следующих
видов ($ — некоторый выделенный элемент множества V —
(1) а-+$аиа-*$.
(2) SiS2->£3JB4 Для некоторых Ви Я2, Я3, B^V — 2 — {а}.
(3) В—>а для некоторых В £V — 2 и а€2.
Пусть для каждого а£2 Ga = (Va, 2а, Ра, аа) — монотонная
грамматика, порождающая множество f(a). Можно
предполагать, что (Уа-2а)П (V-2) = Ф И (Уа-2а)П(УЬ-2ь)=0,
где а, 66 2 и афЬ. Пусть G' = {V'f[J 2а, Р', а)—монотонная
а
грамматика, где
P'=\J PaU(P-[B-+alB£V-2, аеЩ)[)[В-+оа1В->а£Р}.
Очевидно, L(G') =f(L).
Условие, что каждое из множеств f(a) не содержит пустой
цепочки е, является существенным. Например, в работах
(Evey, 1963; Ginsburg and Rose, 1966) был. получен следующий
результат:
*) Пусть для каждого а £ 2 2а — конечное непустое множество и f(a) C2fl.
Пусть /(e) = {е} и f(xx... x^ — fC^i) ... f (хг)\ для каждого /' х/£2*
Тогда отображение / называется подстановкой. В случае когда для каждого
a £2 множество f(a) состоит из одной цепочки wa, принадлежащей
множеству 2а, отображение / называется гомоморфизмом и рассматривается
как отображение множества 2* во множество
m
Об инвариантности класса НС-языков
171
Теорема 1.2. Пусть L ^ 2^ — рекурсивно-перечислимое
множество, символ с £ 2 и |лс — гомоморфное отображение,
определенное следующим образом: \хс(а)=а для а£2 и \хс(с) =
= 8. Тогда может быть эффективно построен НС-язык U ^ 2*с*,
такой, что \\C(L')=L.
Класс НС-языков не замкнут относительно произвольных
гомоморфизмов, поскольку они могут «стирать». Однако класс
НС-языков замкнут относительно гомоморфизмов с «линейным»
укорачиванием («стиранием»). Это понятие будет разъяснено
ниже.
Обозначение. Пусть 2— произвольный алфавит,
символ £^2 и 2с = 21){с}. Тогда \хс— гомоморфное отображение,
определенное на множестве 2* следующим образом: |лс(а)=а
для а 6 2 и \хс(с) =8.
Лемма 1.1. Пусть L <= 2*(с22*)* — НС-язык, где с 6 2.
Тогда множество \ie(L) также является НС-языком.
Доказательство. Пусть L = L(G), где G = (V,2C, Р, о)—
монотонная грамматика. Пусть
Le = [wjw £L — цепочка четной длины}
и
L0— {wjw^L — цепочка нечетной длины}.
Множества {w £ 2^ — цепочка четной длины} и [w £ 2^ —
цепочка нечетной длины} являются НС-языками. Поскольку
пересечение НС-языков есть НС-язык (Landweber, 1963),
множества Le и LQ являются НС-языками. Так как объединение
НС-языков есть НС-язык и L = Le\JL0, достаточно доказать
утверждение для L = Le и L = L0.
Пусть L = Le, доказательство для множества L0 аналогично.
Очевидно, мы можем предположить, что е 6 Le. Мы можем также
считать, что множество Р состоит из правил следующих видов
($—некоторый элемент множества V—2С—{а}):
(1) а->$а и а-»$.
(2) В^-^ВгВ^ для некоторых Bt, Въ Bz, £4€ V— 2С — {а}.
(3) £—>Ь для некоторых £€ V — 2С и 6 6 2с.
Пусть G'={V, 2, Р', а) — монотонная грамматика, опреде*
ленная следующим о0разом: V'^ojU (VxV) U2. Множество
Pf содержит следующие правила:
(1) Начальные правила: а->($, $)о и о->($, $).
172
С. Гинзбург, Ш. Грейбах
(2) Промежуточные правила: (Ви B2)->{B3l В4) и
(Д, Si) (52> D2) -+ (Д, Ba) (S4, D2) для всех ВхВ2-+Вф&
6 Р и всех Д,Д £ V — 2С — {а}.
(3) Терминальные правила: (В, D) -* (b, D) и (Д В) —►
—* (Д 6) для всех В —► 6 6 Р и каждого D 6 V— {а}.
(4) Заключительные правила: (а,&)—*а&, (а, с)-* а и
(с, а)-* а для всех а, 6 62. Поскольку грамматика G'
монотонна, множество L(G') является НС-языком.
Очевидно, мы можем считать, что в выводе произвольной
цепочки из языка L(G') все правила типа (1)
применяются раньше правил типа (2), (3) и (4); все
правила типа (2)—раньше правил типа (3) и (4); все
правила типа (3) —раньше правил типа (4).
Содержательно, правила типа (1), (2) и (3) «имитируют»
правила грамматики G. Индукцией по длине вывода можно
показать, что о=ф* Д ... A2k (для каждого i А& V —
— {а}) имеет место тогда и только тогда, когда
<?=#>£, (Аи А2) ... {A2h-u A2h). В случае когда для
каждого / А{= $, это очевидно. Индукционный шаг
нетрудно провести после внимательного рассмотрения
правил типа (2) и (3). В частности, ai...a2n6i(G) тогда
и только тогда, когда о=ф*0,(а19 а2) .. . (а2п-\> а2п)> для
каждого / (a2/-1, а2/)€(2с Х2,.)— {(с, с)}. Согласно (4),
o=$*G,(av а2) ... {a2n_v а2п), для каждого / (a2i_v a2t)£
¢(2, Х^с)—{{с, с)} имеет место тогда и только
тогда, когда а =>*0, {av а2) ... (a2n_v a2n)^*Q, tic(ax ... a2fl)
Итак, L(Q') = \]lc(L) и множество \ic(L) есть НС-язык.
Следующая лемма позволит нам заменить условие
смежности другим, более слабым условием:
Лемма 1.2. Пусть символ с£% и 1с2с — НС-язык. Если
\w|^С 2\\\c(w) | для каждой цепочки w£Ly то множество \\,C{L)
является НС-языком.
Доказательство. Для каждого а С 2С введем абстракт*
ный символ а, положим 2с = {а/а^2с} и L = L(G), где G =
= (V, 2с, Р, а) — монотонная грамматика. Пусть, кроме тога,
/—гомоморфное отображение, определенное на множестве!/*
следующим образом: f(a)=a для каждого а£2с и f(A)=A для
каждого AZV— 2С. Пусть G' = (VU2C, 2С, Р', а), где
pf = {f(u)->f(<v)lu->v£P} U {аг->га, са->ас, а->а, с->с/а^1}.
Об инвариантности класса НС-языков
173
Рассмотрим множество Li=^L(Gf) П2*(с22*)*. Поскольку
пересечение НС-языков является НС-языком, множество Li есть
НС-язык. Согласно лемме 1.1, множество \ic(Li) также есть
НС-язык. Кроме того, для каждой цепочки w 6 L, |[хс(ш)|>
^>-k\w\. Итак, w(LL тогда и только тогда, когда существует
некоторая цепочка w'£Li, представляющая собой перестановку
цепочки w и такая, что \ic{w)—\xc{wr). Следовательно, [xc(£i) =
= \ic(L) и множество \ic{L) есть НС-язык.
Теперь мы можем доказать, что класс НС-языков замкнут
относительно гомоморфизмов, удовлетворяющих некоторому
общему условию.
Теорема 1.3. Пусть символ с£1, и L cSc — НС-язык.
Если существует натуральное число k, такое, что \w\ ^k\\xc{w)\
для каждой цепочки w£L, то множество \xc(L) является
НС-языком.
Доказательство. Согласно лемме 1.2, утверждение
истинно для k=l и k = 2. Предположим, что утверждение
справедливо для всех k<m, m>3. Пусть k = m. Введем
абстрактный символ d,. не принадлежащий множеству 2С. Определим
подстановку / следующим образом: f(a)={a} для всех а £2 и
f(c)={c, d). По теореме 1.1 множество f(L) есть НС-язык. Пусть
Lx = f(L)n 2* (1>*с1*с1)* (2* и 2*с2*).~
Тогда множество Li является НС-языком и
№* (Li) = №d (f Щ) = Vc (£)•
Теперь половина всех вхождений символа с в каждую
цепочку из множества L заменилась вхождениями символа d в
цепочки из Li. Итак, \w\ -*C2\\bd{w)\ для каждой цепочки w^L{.
Согласно лемме 1.2, множество \\d(Li) есть НС-язык. Нетрудно
видеть, что, поскольку m> 3,| \id(w) |<(m— 1) \\xc\id(w) |для
каждой цепочки w^L{. Следовательно, множество \xc(L) =
= HcM-<*(£i) есть НС-язык и теорема доказана.
Следствие. Пусть символ с £ 2 и L^2>*c — НС-язык. Если
существует натуральное число k, такое, что каждая цепочка из
языка L содержит не больше k вхождений символа с, то
множество \ic(L) является НС-языком.
II. Приложения к преобразователям
Воспользовавшись теоремой 1.3, мы докажем теперь, что
класс НС-языков инвариантен относительно отображений,
осуществляемых преобразователями, удовлетворяющими некоторым
174
С. Гинзбург, Ш. Грейбах
слабым допущениям. Мы будем рассматривать
детерминированные конечные преобразователи, преобразователи с
магазинной памятью и линейно-ограниченные преобразователи. В
работе (Ginsburg and Rose, 1966) было отмечено, что 1) класс
НС-языков инвариантен относительно отображений,
осуществляемых каждым из этих устройств, если эти устройства
являются непрерывно пишущими на выходе; 2) если же эти
устройства не являются непрерывно пишущими на выходе, то
класс НС-языков не замкнут относительно осуществляемых
ими отображений. Это требование будет здесь несколько
ослаблено.
Приведем определения преобразователей, изучением
которых мы будем заниматься. Определения и обозначения
заимствованы из работы (Ginsburg and Rose, 1966), где они объяс*
нены более подробно.
Определение. Детерминированным конечным
преобразователем (сокращенно ЦК-преобразователем) называется
упорядоченная шестерка S = {K, 2, Д, б, Я, q0), где
(1) К — непустое конечное множество (множество
состояний).
(2) 2—непустое конечное множество (множество входных
символов).
(3) Д — непустое конечное множество (множество выход-
ных символов).
(4) б — отображение множества /(Х2 во множество К
(функция переходов).
(5) А,— отображение множества /СХ2 во множество Д*
(функция выходов).
(6) <7о € К (начальное состояние).
Отображения б и % могут быть продолжены на множество
/СХ2* следующим образом: 6(q,e)=q, 6{q,wx)=6[6(q,w),x],
k(q,e)=e и X(q, wx) =X(q, w)k[6(q, w),x] для всех q€ К, ш(:2*
и х€2.
Обозначение. Если S = (/(, 2, Д, б, Я, <7о) — ДК-преобра-
зователь, то
S(L)={X(q0, w)lw£L}.
Определение. Преобразователем с магазинной памятью
(сокращенно МП-преобразователем) называется упорядоченная
семерка 5 = (/(, 2, Г, Д, 6, Z0, qo), где
(1) /О 2, Г и Д — конечные непустые множества (множества
состояний, входных символов, вспомогательных символов и
выходных символов соответственно).
Об инвариантности класса НС-языков
175
(2) 6 — отображение множества /СХ(^и {е} X Г во
множество всех конечных подмножеств множества АГХГ*хА*.
(3) q0£K (начальное состояние).
Обозначение. Пусть М = (/С, 2, Г, Д, 6, Z0, q0) —
МП-преобразователь. Полагаем (/?, xw, aZ, t/)|—-(#, до, ay, у^) (назовем
это тактом работы МП-преобразователя), если (q, у, ух) 6
6 6 (/?, л:, Z), до 6 2*, a £ Г* и у 6 А*. Пусть (р, до, а, у) \—* (р, до, а, у)
для всех (/?, до, a, #) 6 /С X 2* X г* X А*. Полагаем (/?, до, а, у) р*
|—*(//, до', а', у'), если существуют pit wit al9 yt, 1</<я,
такие, что (/?, до, a, y) = (pv wv av уг), (/?', до', а', у*) =
= (Рп> ™п> <*я, Уп) и
(Л> W/. a,, yt)\-(Pi+v Wi+v ai+1> у£+1)
для всех /. Пусть Z,c:2*, тогда
M(L)={y£/±*l(q0> х, Z0, е)|—*(q9 е, а, у) для некоторых x£L>
Аналогично определяется линейно-ограниченный
преобразователь.
Определение. Линейно-ограниченным
преобразователем (сокращенно ЛО-преобразователем) называется
упорядоченная пятерка 5 = (/С, 2, А, 6, qQ)9 где
(1) К, 2 и А— конечные непустые множества (множества
состояний, входных символов и выходных символов
соответственно).
(2) 6—отображение множества ЛГХ^ во множество всех
конечных подмножеств множества ЛГХ2ХА*Х{—Ь 0, 1}.
(3) q0€K {начальное состояние).
Обозначение. Пусть S — (К, 2, А, 6, q0) — ЛО-преобра-
зователь. Определим отношение f—* следующим образом:,для
и, v£l*> ¢¢2 и до 6 А* полагаем
(lT (ucpav. w)\-(uqcb<v, wy), если (q, b, y,—l)£b(p, a). .
(2) (upav, w)\—(uqbv, wy), если (q9 b, y, 0)65(/1, a), и
(3) (upav, w)\-{ubqv9 wy), если (q, b, y, l)6M/>> #)•
(Каждый из этих переходов называется тактом работы
ЛО-преобразователя.) Пусть и, и'£Ъ*ЮГ и до, до'6 А*; тогда
полагаем (и, до)Ь~*(#', до')> если либо (и, w) = (u', до'), либа
существуют ut, wt (1</<я), такие, что (uv wx) = (u, w),
(ип, wn) = (u', w') и (ul9 wi)}--(ui+v wux) для всех i < п. Если
L с 2*, то полагаем
S(L)={y£k*l(q0w, е)|-*(Р> 1/) Для некоторых до6^> Рб^Ь
176
С. Гинзбург, Ш. Грейбах
Поскольку класс НС-языков не замкнут относительно
гомоморфизмов, он не замкнут также относительно
отображений, осуществляемых ДК-преобразователями,
МП-преобразователями и ЛО-преобразователями. Мы наложим на ДК-пре-
образователь ограничение, при котором множество S(L) есть
НС-язык, если L является таковым. Соответствующие
ограничения для МП- и ЛО-преобразователей будут приведены
ниже.
Теорема 2.1. Пусть S — ДК-преобразователь {непрерывно
читающий на входе МП-преобразователь1) и L — НС-язык.
Если существует натуральное яисло k, такое, что \w\^k\ у\
для всех w£L и всех y£S(w), то множество S(L) является
НС-языком.
Доказательство. Пусть 5 = (К> 2, А, 6, А,, ^ —
ДК-преобразователь и символ £gA. Пусть Sc — ДК-преобразователь,
отличающийся от S только тем, что Sc пишет на выходе
символ cf когда S ничего не пишет на выходе. Формально пусть
SC=(K, 2, A (J {¢), Ь, К* Яо)> гДе Для всех Я и а имеет место
Xc(q, a) = 'k(q, а), если X(q, а)фе, и Xc(q, а) = с, если X(q, а) = е.
Тогда S€ есть непрерывно пишущий на выходе
ДК-преобразователь2). Итак, множество SC(L) является НС-языком (Gins-
burg and Rose, 1966). Пусть r = max { \X(q, a) \/q£K, a£2).
Тогда
|5(^)|<г|^| и \Sc(w)\^r\w\.
Очевидно, \xc(Sc(w)) = S(w) для всех w£L. Тогда для всех
w£ L
\\xc(SeM)\ = \S(w)\>^\w\>^\Sc(w)\9
т. е. \Sc{w) |<Уй| \xc(Sc(w))\. Согласно теореме 1.3, множество
VC(SC(L)) = S(L) есть НС-язык.
Предположим, что 5 —непрерывно читающий на входе
МП-преобразователь. В этом случае доказательство
аналогично доказательству для ДК-преобразователя. Различие
состоит в том, что вместо S(w) может быть записана любая
цепочка у из множества S(w).
!) МП-преобразователь 5= (/С, 2, Г, А, б, Z0j q0) непрерывно читает на
входе, если 6(q, е, Z) = Ф для всех q £ К и Z £ Г.
2) ДК-преобразователь (К, 2, А, б, Я, qQ) непрерывно пишет на выходе,
если М<7, а)фе Для всех q£K и a ¢2. МП-преобразователь (/С, 2, Г, А, б,
Zq, Яо) непрерывно пишет на выходе, если у #= е всякий раз, когда
{Я, а>> У) (: й^. а> z)- ЛО-преобразователь (К, 2, А, а, Яо) непрерывно пишет
на выходе, если */4=е всякий раз, когда (яу Ьу уу d) ¢6 (р, а).
Об инвариантности класса НС-языков 177
Замечание. Пусть S — ЛО-преобразователь, L — НС-язык
и существует натуральное число k, такое, что |^|<£|y| Для
всех w£L и y£S(w). Тогда способом, существенно отличным
от предложенного в теореме 2.1, можно доказать, что
множество S(L) является НС-языком.
Следствие. Пусть JL — НС-язык и т, п —
положительные числа. Тогда множества
[w | wx £L и n\w\ — m\x\ для некоторого х],
{w\yw£L и n\w\ = m\y\ для некоторого у)
и
{w\xtts:y^L и n\w\ = m(\x\-\-\y\) для некоторых х, у]
являются НС-языками.
Доказательство. Пусть 1с? и символ £¢2.
Определим подстановку т следующим образом: т(а)={а, с] для
всех a ¢2 и Lc = x(L). Итак, Lc есть НС-язык. Пусть Cmt„ =
= {wxlw£%*, х£с*, n\w\ = m\x\}. Тогда множество Ст%п
является НС-языком (на самом деле, КС-языком).
Следовательно, множество
\ic(LcnCmtn)=[wlwx£L и n\w\ = m\x\ для некоторого w)
является НС-языком. Для остальных множеств доказательство
аналогично.
Определим теперь „последовательность k реализуемых
тактов работы*4 ДК-преобразователя, МП-преобразователя и
ЛО-преобразователя соответственно.
Определение. Пусть ах ... ak (&>1; для каждого/,
а££2)— некоторая цепочка входных символов;
последовательность b(qv al) = q2, 6(q2, a2) = qz, ..., b(qk, ak) = qk¥l называется
последовательностью k реализуемых тактов работы
ДК-преобразователя {/С, 2, Д, 6, X, q0), если b(q0, w) = qx для
некоторого w. k(qv ах ... ak) называется выходной цепочкой этой
последовательности. Последовательностью k реализуемых
тактов работы МП-прёобразователя {К, 2, Г, Д, Z0, qQ)
называется последовательность
(4v <*р Yi» У)\- ••• Ь («W а*+1» Y*+i» УУг ••• Jk).
в которой (q0, w, Z0, e)\—*(qv av yv уг) для некоторого w.
Цепочка У\ ... yk называется вьрсодной цепочкой этой
последовательности. Последовательностью к реализуемых тактов
178
С. Гинзбург, Ш. Грейбах
работы ЛО-преобразователя {К, 2, Л, 6, qQ) называется
последовательность
(alf р)Ь ... ЬК+р Pf/i ... */*),
в которой (дае>, e)f—"(с^, р) для некоторого до. Цепочка
уг ... ук называется выходной цепочкой этой
последовательности.
Теорема 2.2. Пусть S — ДК-преобразователь,
МП-преобразователь или ЛО-преобразователь, L — НС-язык и k —
натуральное число, такое, что выходная цепочка каждой
последовательности k реализуемых тактов , работы
преобразователя S непуста всякий раз, когда на вход
преобразователю S подается цепочка из множества L. Тогда
множество S (L) является НС-языком.
Доказательство. Пусть S(Z,)S=A*, символ £^Д и
преобразователь Sc определен как в доказательстве теоремы 2.1.
Тогда \xc(Sc(L)) = S(L). Поскольку Sc непрерывно пишет на
выходе, множество SC(L) является НС-языком (Qinsburg and
Rose, 1966). Так как выходная цепочка каждой
последовательности k реализуемых тактов работы преобразователя 5
непуста всякий раз, когда на вход преобразователь S
подается цепочка из множества L, то эта выходная цепочка
содержит — при том же условии — вхождение элемента
множества А. Пусть Н—(конечное) множество тех цепочек
из множества SC(L), которые получены в результате
применений последовательностей реализуемых тактов работы
преобразователя Sc, состоящих менее чем из k тактов каждая.
Тогда Sc(w) — H есть НС-язык и \Se(w)- #|<(£— 1) X
X | Цс ($с (w) ~~ Н) I *)• Итак, множество [ic (Sc (L) — Н) является
НС-языком. Следовательно, множество
S{L) = \Lc{Sc{L)) = »c{S^L)-H)\)\ic{H)
также является НС-языком.
Рассмотрим теперь вопрос об инвариантности класса
НС-языков относительно отображений, осуществляемых
обращенными ДК-преобразователями.
Лемма 2.1. Для каждого ДК-преобразователя S =
= (К, 2, А, б, К q0) существуют положительное число k и
МП-преобразователь S' — (К, А, Г, 2, 6', Z0, q0), такие, что
*) В оригинале неточность „ | у 1 < 2k \ \хс (Sc (w)) | для каждого w £ L
и каждого y£Sc(w) — Hu. Вместо Sc(w)—H может быть записана любая
цепочка из Sc (w) — Н. — Прим. перге.
Об инвариантности класса НС-языков 179
(1) S'(w) = S~l(w)1) для всех w£k* и
(2) выходная цепочка каждой последовательности k
реализуемых тактов работы МП-преобразователя S' непуста.
Доказательство. Пусть £=тах {1, | X(q, a)\lq£K> a¢2}.
Для каждого а£Д введем новый символ а и для каждого
а£2--новый символ а. Пусть символ^ ^0€(а» a\a^ts]\}
U {а, а\а £2} и Г = {Z0} и {а, а/а £ A) U {а, а/а £ 2}. Определим
отображение б7 следующим образом (?^/( и а£2):
(1) Если ^ (^, #) = #! ... £г, г> 1, для каждого / #/бЛ, то
(б (#, a), Z0abr ... £2, е) £ б" (#, fi2; Z0).
(2) Если A, (<?, а) = е,_то (б (q, а), Z0, a)£b'(q, е, Z0).
(3) (?, е, е) £ б7 (<7, ft, й) для всех й £ А. -
(4) (?, е> а) 6 б7 (#, е, а).
Непосредственно проверяется, что k к S' удовлетворяют
условиям (1) и (2) леммы.
Из леммы 2.1 и теоремы 2.2 непосредственно получается
следующая теорема:
Теорема 2.3. Множество S~l (L) является НС-языком
для каждого ДК-преобразователя S и каждого НС-языка L.
Аналогичный результат для МП-преобразователей не имеет
места.
Теорема 2.4. Существуют непрерывно пишущий^ на
выходе МП-преобразователь S и НС-язык L', такие, что
множество 5~г{Ь') ) не есть НС-язык.
Доказательство. Пусть Lc — нерекурсивное
рекурсивно перечислимое множество, такое, что IcS* и символ
¢¢2. Согласно теореме 1.2, существует НС-язык L'ci Led*,
символ d£2u {с}, такой, что \id(L') = Lc. Пусть S = ({cj0, q\),
2и{^Ь {^оЬ 2U{£> d\, б, Z0, <70) — непрерывно пишущий на
1) Пусть 5 — ДК-преобразователь. Для каждой цепочки w и каждого
множества цепочек L полагаем S*"1 (w) — {x/S (х) = w} и S~l (L) =
= \Js~l(w):
2) Пусть 5 — МП- или ЛО-преобразователь. Для каждой цепочки w и
каждого множества цепочек Е мы будем полагатьS~1(w)={x/S (х)[\{т}фФ}
hS-1(£)«(J S~\w).
12*
180
С. Гинзбург, Ш. Грейбах
выходе МП-преобразователь и отображение 6 определено
следующим образом:
(1) 6(#0, a, Z0)={(<7o> %о> я)} Для всех #€s-
(2) b{qQtctZ0)={{qvZ0,c)\.
(3) b{qvzt Z0)={(^,Z0, rf)}.
Очевидно, S(Lc) = Lcd* и 5 ^) = 1^(^) Для всех w£l>*cd*.
Тогда множество U является НС-языком, а множество
S~l(//) = \kd{L') = Lc не есть НС-язык.
Замечания. (1) Мы можем выбрать язык L'zzLcd* таким
образом, что множества L' и /У = (2и [ct d})* — U являются
НС-языками. Тогда множество
[w/S (w) s L'} = [w/S (w) fU' = <£} =
= [wjw 6 (2 U И)* - 2V} U (Е* — £) с
не является рекурсивным и, следовательно, не является
НС-языком.
(2) Различными способами можно показать, что если S есть
1) непрерывно пишущий на выходе МП-преобразователь или
2) ЛО-преобразователь, такой, что для некоторого £>0
имеет место |я>|<;Л|л;| для всех х и всех w£S(x), то класс
НС-языков замкнут относительно отображений,
осуществляемых преобразователем 5"1.
III. Приложения к грамматикам
Укажем теперь, пользуясь теоремой 1.3, некоторые
условия, при выполнении которых грамматика может содержать
укорачивающие правила, т. е. правила u->v, где | v | < | и |,
и тем не менее порождать НС-язык.
Определение. Пусть 0 = (1Л 2, Р, а) —
порождающая грамматика. Числом укорачиваний Е(х) в выводе
т: ^4...4¾ называется мощность множества [il\ui+1\< \ut\}.
Таким образом, число укорачиваний в выводе есть число
применений в этом выводе укорачивающих правил.
Теорема 3.1. Пусть G = (V, 2, Я, а) — порождающая
грамматика. Тогда для каждого натурального числа k
множество Lk(Q)={w^2*/Е(т) < k \w | для некоторого вывода
т: а=Ф ... =#«>} является НС-языком. В частности, L(Q)
есть НС-язык, если L(0) = Lk(G) для некоторого k.
Доказательство. Без потери общности мы можем
считать, что каждое правило грамматики С? имеет вид u-+v> где
Об инвариантности класса НС-языков
181
v£(V — 2)* или v£I>*. [В противном случае мы можем
заменить грамматику О грамматикой Q' = (y', 2, Я', а),
определенной следующим образом: пусть l/' = V U {a'la£Z>}, каждое
а! — новый символ, не принадлежащий множеству V.
Определим гомоморфное отображение г|) следующим образом:
г|>(а) = а' для a£2 и $(А) = А для A£V — 2. Пусть Я' =
= {u->ty(v)lu->v£P}[}{a'-+ala£Z}. Тогда Lk(Q') = Lk(Q) и
каждое правило грамматики 0/ имеет вид а —> v, где я £ (V'—2)*
или ^£2*.]
Пусть ¢, ¢, а? и я?— новые символы, не принадлежащие
множеству V, и G = (V\]{c, с, d, d}', 2и{^, d), Я, а), где Я
определено следующим образом:
(1) Если u->v£P и I^KI^I» то u->v£P.
(2) Если u->v£P и \v\<\u\, то u^vcd^1'^1'1 ^Р.
(3) сА->Аси dA->Ad принадлежат множеству Р для всех
AGV — 2
(4) dc->cd, с->с и а?->а? принадлежат множеству Я.
Очевидно, множество L (G) является НС-языком и
ixjia(L(0)) = L (О). Пусть
Nk=[wcrdnlw^\ r^k\w\].
Нетрудно видеть, что Л/^ есть НС-язык. (На самом деле Nk
есть даже КС-язык.) Итак, множество 1(6) []Nk является
НС-языком.
Покажем теперь, что Lk (О) = \xc\id (L (О) Г) Nk). Пусть
t = max{l, \и\ — \v\ — \ju->v^P).
В этом доказательстве w всегда обозначает элемент
множества 2*. Предположим, что wcrdn£L(G)[\Nk. Тогда w£L(G)
и г = Е(х) для некоторого вывода т: а=Ф> ... =^w в
грамматике О. Поскольку wcrdn также принадлежит множеству Nk,
E(x) = r^k\w\. Следовательно, w£Lk(G). Обратно, пусть
w£Lk(G). Тогда существует вывод т: а=Ф> ... =^w в
грамматике О, такой, что E(x)^k\w\. Очевидно, существует /г, такое,
что wcrdn£L(G)rtNk, где г = Е(х). Итак, w6мЛг(£(О)ПNk),
так что
4(0) = tW£(6)n;vft).
Пусть Л — гомоморфное отображение, определенное
следующим образом: h(d) = c и h(x) = x для x£%U{c]. Тогда
множество h(L(G)(]Nk) является НС-языком и
Lk (О) = jyi, (I (б) П Лд = М (I (5) П NJ.
182
С. Гинзбург, Ш. Грейбах
Для цепочки wcrdn £ L (G) (] Nk имеет место
\&crdn\^(t+l)k\w\ + \w\^[(t + l)k-t-l]\w\.
Тогда wcg £ h (L (О) Г) Nk) тогда и только тогда, когда wcrdn£
£L(G)[\Nk для некоторых г, п, таких, что g = r-±n. Итак,
для цепочки wcg 6 h (L (О) Г) Nk) имеет место
\wcg\^[(t + \)k + \]\w\.
Согласно теореме 1.3, множество Lk (О) = \ic \h (б) П Nk)\
является НС-языком.
Следствие. Если каждое удлиняющее правило u->vl)
грамматики G = (V, 2, Я, о) таково, что v£V*%V*, то
L {О) —НС-язык.
Доказательство. Числом удлинений I(т) в выводе т
назовем число применений в этом выводе удлиняющих правил.
Очевидно, существует kv такое, что E(x)^kl[(x). По условию
из того, что правило u->v, \u\<\v\, принадлежит
множеству Я, следует, что v£V*l>V*. 44так, существует k2, такое,
что для каждого вывода т: оф ... ^w цепочки из
множества L(Q) имеет место / (т) < k2 \ w |2). Таким образом, Я(тХ
^kxk2\w\. Согласно теореме 3.1, множество L(Q) является
НС-языком.
Ниже будет показано, что если условие изменить следую-1
щим образом: из того, что | и | > | v |, следует, что v£V*2V*,
то такая грамматика также порождает НС-язык.
Определение. Пусть т: их=^> ... =Фип — вывод в
грамматике Q = (V, 2, Я, о). Пусть для любых /, г, xltf: #/=ф ...
...фи[+г есть часть вывода т. Характеристическим
числом D(x) вывода х называется максимальное число из
множества
{А/для некоторых /, г; E(xltr) = k и цепочка uUr содержит не
больше вхождений основных символов, чем иь).
Грубо говоря^ D(x) есть максимальное число применений
укорачивающих правил между двумя появлениями основных
символов в цепочке.
1) Правило u~>v называется удлиняющим, если |ы(<М.
2) Более того, легко видеть, что &2 можно считать равным \. — Прим.
ред.
Об инвариантности класса НС-языков 183
,, ,
Теорема 3.2. Для каждой порождающей грамматики
G = {Vt S, р, о) и каждого натурального числа &>0
множество
Lk(Q)= {w£2*lD(x)^k для некоторого вывода т: а=Ф ... =Фяу}
является НС-языком. В частности, L(G) есть НС-язык,
если 1(0) = Lk(0) для некоторого kl).
Следствие 1. Если каждое укорачивающее правило
грамматики О = (V, 2, Р, а) имеет вид и —> v9 где v £ К*2У*,
то множество 1(0) есть НС-язык.
Доказательство. Поскольку L(G) = L0(G), множество
L(G) является НС-языком. В частном случае мы получаем
Следствие 2. Если каждое правило грамматики О
имеет вид u->v, где v£V*IV*> то L(G) есть НС-язык.
IV. Специальный результат
.Следствие 2 из теоремы 3.2 утверждает, что если каждое
правило грамматики 0 = (1Л 2, Я, о) имеет вид u->v, где
v£V*2V*9 то множество L(G) является НС-языком. В настоя*
щем разделе мы усилим этот результат, а именно, покажем,
что L(G) есть КС-язык2). Для доказательства* нам
понадобится ряд лемм различной сложности. -
Лемма 4.1. Пусть G = (V, 2, Я, о) — порождающая
грамматика, все правила которой имеют вид u->v, где
v £ V*2V*. Тогда существует грамматика G' = (!/', 2', РГУ а),
все правила которой имеют вид u->v, где | и |<2 и
v £ (V)* 2' (V')*, и гомоморфизм h, такой, что L(G) = h (L (G')).
') Доказательство теоремы 3.2, занимающее более двух страниц, в
переводе опущено, поскольку эта теорема просто получается из предыдущей.
Именно, назовем правило u->v сильным, если р€У*2У*. Число s(t)
применений сильных правил в выводе т цепочки до 6 2* не превосходит,
очевидно, числа \w\. Число применений укорачивающих правил между двумя
соседними применениями сильных правил (а также перед первым
применением сильного правила и после последнего) не превосходит Ь(т) [по
определению числа D(t)]. Поэтому число применений в выводе т укорачивающих
правил, не являющихся сильными, не превосходит^ D(r) (s(t) + 1), а общее
число применений укорачивающих правил £(*т) < D(t)(s(t) + 1) +s(t) <
<£(М+1)+М < (2k+\)\w\. Остается применить теорему ЗЛ. — Прим. ред.
2) Порождающая грамматика G= (V, 2, R, а) называется контекстно-
свободной (КС-грамматикой), если каждое ее правило имеет вид u-^v, где
и€ V — 2. Множество L С 2* называется контекстно-свободным языком
(сокращенно КС-языком), если L = L(G), где G — некоторая
КС-грамматика.
184
С. Гинзбург, Ш. Грейбах
Доказательство. Пусть rv ,,.,гя- различные правила
грамматики О. Если правило rt имеет вид u->v, где |# |<2,
то u->v£P'. Пусть правило rt имеет вид Ах ...Ak~>yaz,
где k>2, для каждого у Aj£V — 2, у, г£1/* и а£2. Пусть
^л» •••• Yik* aiv •••• а*(л-о ~~новые символы и AxA2->yanYiv
YnA3->ai2Yl2, ..., ^(^-.2)^-^^(^-1)^(^-1) и Уць-.1)->аг —
элементы множества Я'. Пусть 2'=2и {я^у/все а£у} и V' =
= Ъ'U [Yulвсе Yu). Очевидно, L(G) = h(L(G')), где Л
—гомоморфное отображение, определенное на множестве (2')*
следующим образом: h(a) = a для всех а £ 2 и h (atj) = е для всех atj.
Лемма 4.2. Пусть О = (К, 2, Я, а) — грамматика, все
правила которой имеют вид u->v, где \ и |< 2 # я £ V*2 V*.
Тогда существуют грамматика Gr = (V 2', Я', а) # ДК-пре-
образователь S, удовлетворяющие следующим условиям:
(1) 2' = {аг а^/1 <7-</г} — множество, состоящее из 2п
элементов, где п— число правил грамматики О'.
(2) Каждое правило грамматики G' имеет вид u->yaia[zi
где | и |<2, у, г £ (!/' —2')* и каждая цепочка аьа\ появляется
в точности в одном правиле из Я'.
(3)5(1(00) = ^(0)-
Доказательство. Без потери общности мы можем
считать, что каждое правило грамматики G имеет вид u->yaz,
где a¢2 и у, z£(V — 2)*. Пусть rv ..., гп — правила
грамматики О, 2' = {а£, а£/1 < /</г} — множество из 2п элементов
и V" = 2'U(V—2). Если правило rt имеет вид Ui-^yfi-z^
где bt £ 2 и f/p г£ £ (I/—2)*, то введем новое правило ut -> yfi^z..
Множество всех таких правил обозначим через Я'. Пусть
S — ДК-преобразователь с двумя состояниями, отображающий
каждую цепочку аьа\ в символ bt. Очевидно, G' и 5
удовлетворяют условию леммы.
Следующая лемма послужит основой для доказательства
главного результата этого раздела.
Лемма 4.3. Пусть G = (V, 2, Я, а) — порождающая
грамматика, где 2 = [а£> а£'/1 < / >< /г} — множество из 2п
элементов (п —число правил грамматики О). Пусть для каждого
/ (1 <; / < п) i-e правило из множества Я имеет вид
и.->yiaia\zv где |иь|<2 а ^£(V — 2)*. Тогда множество L (G)
является КС-языком.
Об инвариантности класса НС-языков
185
Доказательство. Мы можем считать, что для 1 </<;m
/-е правило имеет вид
(1) А^у.а^г^
а для m-^-l^i^n i-e правило имеет вид
(2) В.С1->у1а.а'1гг где В., С£ £1/-2.
Пусть G'==(l/',2, Я', а) — КС-грамматика, где множество Р'
определено следующим образом:
(3) Каждое правило типа (1) принадлежит множеству Я'.
(4) Если 5£С£->г/£а^г££Я, то
(а) Bi-^yiai
и
(б) C^a'ft
принадлежат множеству Р.
Пусть /?={а£а;/1</<л}* и R=(R[)(V— Ъ))\ Поскольку
пересечение КС-языка и регулярного множества есть КС-язык
(Bar-Hillel et al., 1961)х), множество L(Q')(\R является
КС-языком. Для завершения доказательства леммы достаточно
показать, что L (С) t\R=L (О). Очевидно, L(0)sL (G') П Я
Чтобы доказать обратное включение, достаточно установить,
что
(5) если #=Ф0, ...=^Qlv (u£R и v£ R) — вывод длины р,
то существует вывод #=ф0 ... =¥0^ длины ^р.
Доказательство проведем индукцией по длине вывода
#=Ф0, ... #0,tf. Пусть длина равна единице, т. е. #=Ф0д>.
Тогда и = и'Хи", v = u'wu", где a', #"£/? и X->w£P'.
Очевидно, что X->w — правило типа (3), т. е. X — At и
w = ata[ для некоторого и Поскольку Ai->aia\ также
принадлежит множеству Я, u=$Qv. Пусть (5) имеет место для
всех выводов длины меньше р и # = #0=>o, ... =^G,up = <v —
вывод длины р. Тогда u = tY1 ... Ydtr и v = tv4rt где t, t',
v'£R> Yv Yd£V — S и для каждого j Yj£V. Мы можем
считать, что t = t' — e. Итак, v = v'< Пусть k — наименьшее
натуральное число такое, что первое правило, примененное
к символу Yk, не есть правило типа (4а). Поскольку правило
типа (4а) не применяется к символу Yd (в противном' случае tf
будет оканчиваться некоторым символом at), такое k
существует. Возможны три случая.
!) См. также статью Н. Хомского «Формальные свойства грамматик»
р Киб. сб., вып. 2 (новая серия), стр» 200, теорема 32.— Прим. ред.
186
С. Гинзбург, Ш. Грейбах
(а) К символу Yk применяется правило типа (46). Тогда
k> 1 и
Y1...Yk...Yd=BJi...BhjjYk+l...Yd^Gf
Поскольку <££/?, jk_x = jk. Итак,
Ki ... Yk ... Yd = BJi .... BJk_Bjk_Cjk_Yk+l ... K*=^,
G h ib-2 h-\ h-i h-i h-i k+1 d
Тогда v = vxaj a'j v2, где vv v2 £ /?. Поскольку
0/—КС-грамматика, В, ... В, у, =^*rtv,—вывод длины не больше рл
h Jk-2 Jk-\ и l / l
и zj ^k+i • • • ^й^*о' ^2 — вывод Длины не больше р2, где
Рг+Р2+2 = Р- Очевидно, 5. ... Вj у, и z, Yk+1... Krf при-
1 Л —"2 к — I к — 1
надлежат множеству /?. По индукции В.... В j уj =¾^ —
вывод длины не больше рг и z} Yk+1 ... Yd =Ф*0 v2 — вывод
длины не больше рт Итак,
y,...yd = Bli...B/tcujM...y^0v
— вывод длины не больше /vb/b+l <Р-
(Р) К* = ^ 6 S, Тогда £>1, поскольку Кх £1/-2. Кроме
того,
^...^-=^....^^^...^^.
для подходящих индексов. Тогда £ = a', . Это противоречит
___ Jk-i
тому, что Yx ... Yd£R.
(Y) К символу Yk применяется правило типа (3). Тогда
Yl.,.Yk...Yd^Bh...Bh_A]Yk+l...Yd^0>
для некоторых vv v2£R. Тогда Л. ->#. aj a/jzj ^Р и
Yi...Yd = BJi...BJk_A)Yk+1...Yd^Q
^о Bh--- Bh_ »)haika')uzJkY*+i — Y*'
i Об инвариантности класса НС-языков 187
Поскольку G' — КС-грамматика, В....В. у =ф* v — вывод
yi Jk-\ Jk и L
длины не больше рг и zj Yk+1 ... К^=Ф^,^2 —вывод длины не
больше р2, где /7=/^ + /^+1- Очевидно, что Bj ... В} у
и zy КЛ+1 ... Y d принадлежат множеству 7?. По индукции
Вj ... Вj уj =¾¾¾ — вывод длины не больше рг и zj Yk+1 .. .
. .. Yd^>*Qv2 — вывод длины не больше /?2, где /7=/^+/^ + 1.
Итак, Кх ... yd=¥o^j a'j v2 — вывод длины не больше /?.
Таким образом, индукция проведена для каждого из трех
случаев. Отсюда сразу следует результат.
Теперь мы можем доказать основной результат этого
раздела.
Теорема 4.1. Если G = (V\ 2, Я, о) — порождающая
грамматика, все правила которой имеют вид u—>v, где
v£V*W*> то множество L(G) является КС-языком.
Доказательство. Согласно леммам 4.1 и 4.2,
существуют грамматика G' и ДК-преобразователь S, такие, что Qf
удовлетворяет условиям леммы 4.3 и S(L(G')) = L(G)./
Согласно лемме 4.3, множество L(G') является КС-языком.
Поскольку класс КС-языков замкнут относительно отображений,
осуществляемых ДК-преобразователями (Ginsburg and Rose,
1963), 1(0) есть КС-язык.
Пользуясь теоремой 4.1, мы получим как следствие
результат, сформулированный Метьюзом на Международном
коллоквиуме ^о алгебраической лингвистике и теории
автоматов в Израиле в 1964 г. (До сих пор в печати не
появилось доказательство этого факта.)
Определение. Пусть G = {V, 2, Я, о) — порождающая
грамматика. Для всех u->v£P, а £2* и y£V* полагаем
аиу=Фьаъу и yua=^R yva. Если uv ..., ип — последовательность,
такая, что для каждого / ut=^Lul+1 или ut=^Rui+1, то
полагаем ux^LR*un.
Следствие. Пусть G = (V\ 2, Р, о)— произвольная
грамматика. Тогда множество {w£%*lo^LR*w} является
КС-языком.
Доказательство. Без потери общности мы можем
считать, что каждое правило из Р имеет вид u->v, где v£(V~ 2)*
или v £2* — (е}. Пусть a', L, R, с — символы, не принадлежащие
188 С. Гинзбург, Ш. Грейбах
множеству V, и G' = (Vu{a'> L R, с], 2[}{с], Р', а'>, где
Pf определено следующим образом:
(1) о' ->LoR, L->c и R->c принадлежат множеству Р'.
(2) Если u->v£P, где v£(V — 2)*, то Lu-+cLv и uR->vRc
принадлежат множеству Я'.
(3) Если u->v£P, где ^^2*—{е}, то Lu->vL и uR->Rv
принадлежат Я'.
Очевидно, что ixc(Z,(G')) = {w£I>*lo=$>if*w\. Согласно
теореме 4.1, множество Z (О') является КС-языком. Поскольку класс
КС-языков замкнут относительно гомоморфизмов (Bar-Hillel et
al., 1961), множество \xc(L(G')) также является КС-языком.
Л ИТЕРАТУРА
Bar-Hillel Y., Р е г 1 е s М., Shamir Ем On formal properties of simple
phrase structure grammars, Z. Phonetik, Sprachwissen. Kommunikations-
forsch., 14 (1961), 143—172.
Chomsky N., On certain formal properties of grammars, Inform. Control, 2
(1959), 137—167. (Русский перевод: Хомский H., О некоторых
формальных свойствах грамматик, Кибернетический сборник, вып. 5, ИЛ,
М., 1962, стр. 279—312.)
Evey R. J., The Theory and Application of Pushdown Store Machines,
Mathematical Linguistics and Automatic Translation, Report № NSF-10, The
Computation Laboratory of Harvard University, 1963.
G i n s b u r g S., Rose G. F., Operations which preserve definability in
languages. J. Assoc. Comput. Mack., 10 (1963), 175—195.
G i n s b u r g S., Rose G. F., Preservation of languages by transducers, Inform.
Control, 9 (1966), 153—176.
Гладкий А. В., Грамматики с линейной памятью, Алгебра и логика,
Семинар, 2 (1963), стр. 43—55.
К и г о d a S., Classes of languages and linear-bounded automata, Inform.
Control, 7 (1964), 207—223.
Landweber P., Three theorems on phrase structure grammars of type I,
Inform. Control, 6 (1963), 131—136.
Кратчайший путь через сеть
с переменным временем пробега
по дугам1}
/С Л. Кук, Э. Холсей
1. Введение
Рассмотрим множество N городов, каждые два из которых
связаны дорогой. Если города можно нумеровать в
произвольном порядке, то мы обозначим место' назначения номером N.
Пусть нам дана матричная функция G(t) = (ga(t))9 которая не
обязательно является симметричной. Здесь ga(t)—время,
необходимое для проезда из города i в город / и представляющее
собой функцию от времени t отправления из пункта и Мы хотим
найти путь, который минимизирует время пробега из пункта I
в пункт N для случая, когда наше путешествие начинается в
момент t = t0. Постановка задачи не меняется, если города i и j
либо не связаны вообще никаким путем, либо связаны лишь
в одном направлении. В этих случаях полагаем соответствую^
щее время переезда ga(t) равным очень большому числу или
же бесконечности. Кроме того, времена gij(t) могут зависеть от
t произвольным образом.
Для случая, когда все gu(t) суть константы tih Беллман
ввел в рассмотрение числа /.*, где fi— длины оптимальных пу-<
тей из i в N для i = l, ..., N— 1 и fN = 0 [1]. Он доказал
существование и единственность чисел fi и, используя принцип опти^
мальности [2], показал, что они удовлетворяют равенствам
ft = min (*„ + /,), / = 1, 2, ..., TV—1,
fN=o.
Эти числа были найдены с помощью итерационной схемы
ft*> = min(itJ + f(/-D), i = l, 2, .... N-l,
ДО-оГ
где f\k) сходятся к fi не более чем за Af—1 итерационных
шагов при условии, что начальные приближения для ^0) были
выбраны достаточно корректно.
l) Cooke К. L. and Halsey Е., The shortest route through a network
with time-dependent internodal transit times, Journal of Mathematical Analysis
and Applications, 14, № 3 (1966), 493—498.
190
К. Кук, Э. Холсей
Для того чтобы упростить решение вопроса о существовав
нии и обеспечить удобную схему для вычислений, мы выберем
дискретную временную шкалу /0, t0+l, U + 2, ....
Соответственно мы будем предполагать, что все ga(t) определены и
принимают положительные целые значения для t£S = {t0, t0+lt
t0 + 2t ...} и 1Ф\ (в самом деле, мы могли также предположить,
что все gij{t) являются кратными некоторой величины А, и
использовать другую временную шкалу {/0, 4+А, 4+2Д, ...}).
Обозначим теперь через Ei(t) множество всех путей *), которые
выходят из i в момент t и достигают N за конечное время после
конечного числа шагов. Так как время для каждого пути "из
Ei(t) есть положительное целое -число, то существует минимум
по этим временам. Теперь для всех t(zS мы определим fi(t) —
минимальное время для пути из Ei(t), /=1, 2, ..., N—1,
fN(t)=0, где минимальное время fi(t) достигается по меньшей
мере на одном пути из / в N, имеющем конечное число звеньев.
Исходя из принципа оптимальности [2], мы устанавливаем,
что для /£ S
ft(t) =mln(gu(t) + fj(t + gu(t)))9 /=1, 2, .,., N-l,
ЫО=о. - .(1)
2. Итерационный процесс
Мы хотим теперь определить последовательность итераций,
которая будет сходиться к числу. /г(^о) для каждого /, 1<л<Ж
Для удобства вычислений мы будем действовать таким обра-*
зом, что нам потребуются значения, полученные с помощью
итераций только для фиксированного конечного множества
моментов времени ST={4, U+l, U+2, ..., U+T}, где целое Т
выбирается так, чтобы все числа, входящие в нашу итерацию, были
однозначно определяемыми для /€ST. Как мы в дальнейшем
увидим, наиболее удобно выбирать Г = М, где М удовлетворяет
для всех f= 1, 2, ..., N неравенству
КУетСоК^Г- (2)
Поэтому всегда возможно выйти из i в момент U и достичь N
не позднее момента t0+M.
Перейдем теперь к заданию итерационного процесса. Мы на*
чинаем с выбора Г = М, удовлетворяющего (2), и потом моди*
фицируем числа gij(t) следующим образом: для /£ ST и
1) В предположении Ei (t) Ф Ф.
Кратчайший путь через сеть
191
i, j— 1, ...%N положим
gu (*), если t + gu (t) <t0-)~T,
^W-| oo, если t + gu(t)>t0 + T. (3)
Другими словами, мы выбрасываем любой участок пути, если
время прибытия на конец этого участка не лежит в ST. Теперь
мы определим для t€S
ДО (0 = 0.
№(*) = ёшЮ- '=Ь 2, .... N-1. (4)
Таким образом, ff^t) есть время переезда по однозвенному
пути из / в W с началом движения в момент t при условии, что
N достигается не позднее момента U+T. В противном случае
f<l»(t) = оо. В частности, ff)(t) = oo для t>t0 + T и ft°>(<) =
= 8ш(*) для ' = '<)•
Обозначим теперь через E^\t) множество всех путей,
состоящих из одного или двух звеньев, выходящих из i в момент t
и достигающих N не позднее tQ + Т. Потом определим для 16 S
минимальному времени для пути из Ef\t), если
оо, если Ei?){t) = 4>, 1 = 1, 2, ..., 7V— 1.
Из принципа оптимальности следует, что
!?(*)={
^)(0 = mln(^(<) + ^[< + i,yW]). / = 1. 2 JV-1. (5)
Чтобы доказать (5), заметим, что, если- E{?)(t) = ff
однозвенный путь из i в W, выходящий из i в момент t, должен
достичь N после момента t0 + T, так что JfiN(t)=* оо.
Следовательно, ни один двухзвенный путь из i в / и из / в N не может
достичь N к моменту tQ + T, так что ни один однозвенный путь,
исходящий из / в момент t+pij(t), не может достичь N к
моменту to+T. Следовательно, или §i)(t) =оо, или /^(^+^^(0)=00
и правая часть в (5) есть оо, что в свою очередь является
значением, приписываемым f\l)(t) по определению. Если, с
другой стороны, Е{Р (t) не пусто, тогда существует по крайней
мере один путь, состоящий из одного или двух звеньев,
исходящих из / в момент t и достигающий N к моменту t0+t, причём
192
/С. Кук, Э. Холсей
существует минимальный подобный путь. Этот минимальный
путь идет из i к некоторому /, а затем следует однозвенный путь
из / к N, который имеет наименьшее время прохождения, если
/ покидается в момент t+gij(t)=t+gij(t) *).
В общем случае обозначим через E?tk)(t) множество всех
путей, состоящих не более чем из k звеньев, покидающих i в,
момент t и достигающих N не позднее tQ + T, и положим для
| минимальному времени для пути из E^f*X)(t),
fl*>(*) = | если &?+Х)Ц)Фф,
' оо, если Мй+1) (t) = ф,
i = \, 2, .... N—l, k=l, 2, 3
Мы утверждаем, что для <€ 5
$49 = 0,
ft«(0 = min(£iyW + f(*-»>[* + £<y(*)])f /=1, 2 N-1. (6)
j ф I
Справедливость (6) устанавливается аналогично (5).
Теперь предположим, что Т выбирается удовлетворяющим
(2). Так как оптимальный путь из i в N, выходящий из i в
момент /о, достигает N в момент (to+fi(tQ))^tQ+T и этот путь
реализуется за определенное конечное число шагов k0+l, то
этот путь принадлежит £/ (^о). Отсюда следует, что мы
должны доказать сходимость (6) за конечное число итераций,
т. е. что для k^-ko выполняется равенство
/F4'o) = /i('o>
В самом деле, всякий раз, как t+fi(t)<Ct0 + T, существует
минимальный путь из i, достигающий N к моменту t0 + T и имеющий^
конечное число звеньев. Следовательно, существует целое k0,
зависящее от / и t и такое, что2)
ffit)^!^) для k^k0, если *+/,(*) «о+Г.
*) Если только минимальный путь не реализуется при ]=*N. В этом
случае справедливость (5) очевидна.
2) При определении ff](t) мы установили, что f\k) (t) < ffel) (*)< ...
... < ff} (*). 1 < i< N. ' £ S- В частности, тогда f[k) (i0) < /JP> (t0) =
= ^/лг (¾ < М = 7\ Следовательно, мы уверены, что *0 + /(/° (*0) < *0 + ^ и»
наконец, что *0 + ft (*о) < *о + Т.
F
Рис. 1 !). Проблема домино состоит в том, чтобы из трех разноцветных
костей построить блок, который может быть продолжен до бесконечности
таким образом, чтобы все прилегающие друг к другу края были одинакового
цвета (см. рис. 3). Предполагается, что игрок имеет бесконечное число
костей каждого типа и что кость нельзя поворачивать в двух измерениях.
Проблема решается нахождением прямоугольного блока, в котором
последовательность цветов на верхнем основании такая же, как на нижнем, а на
правой боковой стороне такая же, как на левой. Такой блок можно
повторять во всех направлениях, заполняя им бесконечную плоскость (см. рис. 3).
1) Рисунки, помещенные на этой вклейке, относятся к статье Ван Хао
„Игры, логика и вычислительные машины" (стр. 195—207). — Прим. ред.
■'^щ^'
tiw-iT^wrt-'''
' костей построить блок, который может быть продолжен до
таким образом, чтобы все прилегающие друг к другу края были одинакового
цвета (ем. рис. 3). Предполагается, что игрок имеет бесконечное число
костей каждого типа и что кость нельзя поворачивать в двух измерениях.
Проблема решается нахождением прямоугольного блока, в котором
последовательность цветов на верхнем основании такая же. как на нижнем, а на
• правой боковой стороне такая же. как на левой. Такой блок можно
повторять «О всех направлениях, заполняя им бесконечную плоскость (см. рис. 3).
„Игры, логика и
на этой вклейке, относятся к статье Ван Хао
(стр. 195—207). — Прим. ред.
(Аух а Вух'МВукл Сух')у(СухлАух')
-{Аухл Вху)у~(8хулСху)у~(СхулАху)
Рис. 2. Правила игры в доыиио могут быть
изложены с помощью символики, употребляемой
в математической логике (см. словарь в правом
верхнем углу рисунка). Сверху в середине —
набор костей: А, В и С. Выражение / гласит, что
должны совпадать цвета у левого и правого
края; выражение 2 — что должны' совпадать
цвета верхнего и нижнего края. Третье правило
состоит в том, что кости нельзя располагать одну
над другой. .Выражение 4, которое представляет
собой типичный пример ограничения,
используемого для усложнения игр с целью приблизить их
к трудным вычислительным проблемам, означает,
что иа главной диагонали плоскости может
находиться только кость А. Расположение иа
плоскости описывается с помощью декартовой
системы координат. В обозначениях типа *Аух*
первая переменная у выражает положение кости
относительно горизонтальной оси, вторая —
положение относительно вертикальной оси.
:т7¥^( * '•Ф*Г№1@Ц
if
if
►
Ш
1
►
►
Wr
Рис. 3.
Кратчайший путь через сеть
193
3. Вычисления
Подобно другим итерационным схемам, предназначаются ли
они для вычисления кратчайшего пути или нет, эта схема
хорошо приспособлена для реализации на ЭВМ. На практике,
если мы хотим вычислить fi(t0) для КйС/V, то мы начинаем
с выбора достаточно большого числа Г, удовлетворяющего (2);
или же, если мы хотим вычислить /г-(^) одновременно для t = t0,
t0+l, ..., t0+x, мы можем выбрать
/=1, 2, ..., N;
T>max(glN(t)), (7)
i, t t — to» *отЬ."» *от>'
В некоторых случаях каждое из этих определений Т должно
допускать Т= оо (или же «Г равно очень большому числу»). Так
как это оказывается нежелательным при практических расчетах,
реальное переменное значение Т получается заменой giN(to)
в (2) [или giN{t) в (7)] на «путь, начинающийся в i в момент t0
[или «во время t» в (7)], содержащий наименьшее возможное
число звеньев, но, однако, еще достигающий N в приемлемо
короткое время». Мы находим такой путь первой проверкой всех
двузвениых путей из I в N, потом всех трехзвенных путей и т. д.,
пока не найдем приемлемый k\ -звенный путь. «Приемлемо
малое время» зависит от памяти ЭВМ, ограничения на время счета
или же от требований, предъявляемых к скорости1). Если же
теперь (2) используется для выбора Г, то мы можем лишь
заметить, что t0 -f- /^) (/0) <; t0 -)- 7\ если £>&' — 1, где
^ = max(A;), 1</<7V.
Теперь gtj{t) заменяются на gij(t), определяемые с помощью
формул (3), а с помощью формул (4) вычисляется матрица М0) (/)
«начальных приближений», которая содержит значения ff^t)
для 1</<!7V, t£ST2). Затем, используя (5), вычисляем матрицу
F(P (0 = (fi, t)> r^e ft, t = f(P (0- Если gu (t) = оо для всех у, то
. 1) Наш метод требует хранения значений gij(t) и fi (t) для 1 </, ./< N,
^Sr —всего (N2 + N)(T-\-l) значений.
Если минимальный путь из / в N, начинающийся в момент t0, лежит
в £(*°+1)(*0), но не в £}Л)(*0) Для 1<£<£0, тогда fi(t0)>kQ + l, так как
glj (0 > 1 Для * 6 S. Но мы знаем, что // (t0) < Т. Поэтому k0^T — 1 и
сходимость имеет место за самое большее k04^T—1 итераций.
-Могут быть развиты различные методы сокращения объема хранимой
информации и ускорения сходимости, но изложение их не является целью
данной статьи.
2) Нет необходимости хранить значения ff) (0 для t £ ST.
13 Зак. 1204
194
К. Кук, Э. Холсей
/(1)(/) = оо. Если же /-f gtj{t) £ ST Для любого у, то тогда
из (4) и (3) следует, что /^(/ + #/у(/)) = оо, и вследствие (5)
справедливо равенство /^>(/)==ро. Когда оба числа gtj{t) и
/^(^ + ^//(0) конечны для некоторого у, мы вычисляем первую
величину непосредственно, а последнюю находим с помощью
/^(/). Затем ищем минимум их сумм по всем у для
отыскания /Ф(/). Тем же самым путем, используя (6), мы
последовательно вычисляем матрицы М2)(0» • • •» rtk)(t), ... для 1 </<7V,
t£ST. В конечном счете векторы
fft)).'(/fw) <те>-
обязательно сходятся к вектору кратчайшего пути (fi(t0)).
Самый кратчайший путь получается нахождением
последовательности индексов, для которых переменные достигают минимума.
Если требуется большая точность задания функции gij(t),
нежели точность до целого значения, то вместо целых чисел в
качестве масштаба точности должна использоваться величина А,
упомянутая нами выше.
Заключение
Задачи о кратчайшем пути, изучавшиеся до сих пор, были
далеки от реальности. Везде предполагалось, что время
пробега между двумя вершинами (узлами) постоянно. Это
предположение, очевидно, не выполняется для большинства
физических и биологических задач. Проведенный нами анализ
демонстрирует, как можно осуществить поиск кратчайшего пути в
более реалистическом случае, когда время передвижения
является переменным.
В статье используется модифицированная итерационная
схема Беллмана [1] для отыскания кратчайшего пути между
любыми двумя вершинами сети. Она сходится за конечное
число шагов к кратчайшему пути между двумя любыми
вершинами, причем для любого начального момента времени в случае
выполнения некоторых начальных условий. Одна из основных
особенностей этого подхода заключается в такой организации
работы, что вычисление новой итерации не требует повторения
вычислений предыдущих итераций.
ЛИТЕРАТУРА
1, Bellman R., On a routing problem, Quart. Appt. Math., 16 (1958), 57—90.
2 Bellman R., Dynamic programming, Princeton University Press,
Princeton, New Jersey, 1957. (Русский перевод: Беллман P., Динамическое
программирование, ИЛ, М., 1960.)
Некоторые технические реализации
Игры, логика и вычислительные
машины1}
Ван Хао
Немалая часть работы, которую раньше способны были
выполнить только человеческие мускулы и человеческий мозг, в
настоящее время выполняется машинами. Поэтому люди часто
задают такого рода вопросы: «Какие из человеческих
способностей не могут быть воспроизведены машиной?», «Чего машины
не могут сделать?» Читателя, быть может, удивит, что в то
время как на первый вопрос никакого определенного ответа
дать нельзя, для второго вопроса имеется прямое
математическое решение.
Еще раньше, чем была построена первая современная
вычислительная машина, ныне покойный английский логик Алан
Тьюринг поставил именно такой вопрос: «Чего машины не
могут сделать?» Исследуя, что может быть вычислено на машине,
а что нет, Тьюринг описал простую и медленно действующую
врображаемую вычислительную .машину (машину Тьюринга), и
доказал, что она теоретически способна выполнять любые
операции любой вычислительной машины. С помощью своей машины
он продемонстрировал тесное родство между теорией
вычислительных машин и логикой — двумя областями математики,
которые обе связаны с математическими доказательствами и со
способами записи, позволяющими точно выражать наши мысли.
Задача этой статьи — пояснить некоторые фундаментальные^
понятия из области, пограничной между теорией вычислительных
машин и логикой, с помощью некоторых видов игр.
Человеческий ум может воспринимать лишь относительно
малые вдела и количества. А^ежду тем математика имеет дело
прежде всего с бесконечностью. Конечность математических
операций и бесконечность математических сущностей
удивительным образом контрастируют друг е другом. Плавный переход от
интуитивно понятных частных случаев к неограниченно общим
ситуациям — это замечательное достижение человеческого
интеллекта. Абстрактные соображения, касающиеся игр, могут
послужить естественным введением в изучение этого явления.
l) Нао .Wang, Games, logic and computers, Scientific american, 213,
№ 5 (1965), 98—100.
13*
196
Ван Хао
Нахождение последовательности ходов, обеспечивающей
победу в такой игре, как «крестики — нолики», — это логическая
проблема, в точности аналогичная проблеме нахождения
последовательности шагов, обеспечивающей решение произвольной
математической проблемы из заданного класса. Для некоторых
игр нет оптимальной стратегии, которая могла бы
гарантировать победу; аналогично для некоторых классов проблем не
существует алгоритма решения, т. е. не существует общего
метода, который давал бы возможность выбрать
последовательность шагов, приводящую к решению. Поскольку машинная
программа есть просто алгоритм, приспособленный для
реализации на машине, то отсюда следует, что имеются классы
проблем, которые машина не может решить. Прежде чем говорить
о трудностях, возникающих при построении алгоритмов для
решения математических проблем (а также при создании
программ для выработки оптимальной стратегии ведения игры),
попытаемся понять, почему разработка таких алгоритмов и
программ не только полезна, но и составляет конечную цель
математики.
Очевидно, что на запоминание таблицы умножения должно
было бы уйти бесконечное количество времени и энергии,
если бы эта таблица включала не только произведения всех
возможных пар однозначных чисел, но и произведения всех
многозначных чисел. Человек сделал так, что эту бесконечную
таблицу умножения запоминать не требуется: таблица
умножения для одозначных чисел и последовательность шагов, вклкн
чающая «сдвиг» (на разряд) и сложение частичных произведем
ний, дают возможность перемножать произвольные
многозначные числа.
Как известно, операции элементарной арифметики основаны
на формальных правилах, а многие, наверное, помнят, что и
некоторые другие операции, такие, как извлечение квадратного
корня, также могут быть представлены как строго определенная
последовательность шагов. Имеются, однако, более сложные
проблемы, про которые уже менее очевидно, что они могут быть
решены с помощью алгоритма. Рассмотрим, например, такую
проблему: «даны два положительных числа 6 и 9; найти их
наибольший общий делитель». Читатель тотчас же находит ответ: 3.
Если задать числа 68 и 153, то читатель, который имеет
склонность к терпеливому перебору различных возможностей, найдет
ответ и в этом случае: 17. Однако, если бы удалось показать,
что общая проблема — «даны два положительных числа а и Ь\
найти их наибольший общий делитель» — может быть решена
с помощью алгоритма, то любой человек и любая машина,
способные выполнять заданный набор операций, могли бы ре-
Игры, логика и вычислительные машины
197
шить эту проблему для произвольных а и Ь. Такой алгоритм
существует; он был построен Евклидом (рис. 4—6).
Польза алгоритмов столь же очевидна и в области игр: здесь
алгоритм дает инструкцию относительно наиболее выгодных
ходов. Математик, разумеется, заинтересован' не столько в том,
чтобы выиграть игру, сколько в том, чтобы понять абстрактную
структуру данного класса игр. Выяснить существование или
несуществование выигрышной стратегии — это и значит
проникнуть в абстрактную структуру данной игры и других игр того
же типа.
Возьмем в качестве примера так называемую игру «ним».
Произвольное число предметов, например шесть спичек, делится
на три кучки. Игроки А к В берут поочередно любое число
спичек из любой кучки (но каждый раз только из одной).
Побеждает тот, кто берет последнюю спичку. Число спичек
конечно, и когда-нибудь спички заведомо кончатся, так что в
этой игре нет ничьих. Существенно то, что только один из
игроков располагает выигрышной стратегией; кто именно — зависит
от того, как разделены предметы и чей первый ход. В частности,
в игре, где кучки состоят соответственно из одной, двух и трех
спичек, беспроигрышную стратегию имеет игрок В, т. е. тот, кто
ходит вторым. Это можно доказать с помощью схематического
дерева, где вершины изображают положение на
соответствующем этапе игры, а ветви, отходящие от вершины, — возможные
ходы, которые игрок может сделать в данной ситуации (рис.7).
Допустим, что мы играем в эту игру, начиная с кучек,
содержащих первая 10 млн. спичек, вторая — 234 спички и третья —
2729. Теоретически можно и для этого случая затабулировать
все возможные последовательности ходов и понять, имеется ли
у А или у В выигрышная стратегия. Однако построить такую
таблицу ни один человек не захочет и не сможет. Математик
прежде всего начнет систематический поиск сокращенных пу*
тей, ведущих к упрощению операций и к экономии мысли.
Поиски такого рода для игры в «ним» действительно
предпринимались, и был выработан простой рецепт для определения того,
какой из игроков имеет выигрышную стратегию. Этот рецепт
состоит в том, что игрок А всегда может выиграть, если при
представлении числа предметов в каждой из трех кучек в
двоичной системе получившиеся двоичные разложения содержат
нечетное число единиц хотя бы в одном разряде. Нахождение
такого рецепта может не означать ничего, кроме блистательного
окончания работы, но может также привести к важному
математическому осмыслению каких-то явлений — это зависит от
природы игры и от того, насколько непосредственно она связана
с большими математическими и логическими проблемами.
tR
GCO * THIS ROUTINE C0MPUTES THE GREATEST C0MM0N
$ DIVIS0R 0F Ш INTEGERS A AND B.
|R
EXTERNAL FUNCTION (A,B)
NORMAL №Oe IS INTEGER
ENTRY T0 GCO.
L00P REMAIN = В - A*(B/A)
WHENEVER REMAIN.E.O.FUNCTION RETURN .ABS.(A)
Ь t A
A = REMAIN
TRANSFER.T0 L00P
ENO 0F FUNCTION
TYPE INPUT TYPE INPUT
A=8,B:12* A = 12W678,B = 8765<*321*
THE GCO 0F A AND В IS THE GCO 0F A AND В IS
«♦ 9
Рис. 4. Алгоритм, записанный на машинном языке, задает
последовательность шагов, с помощью которых может быть найден наибольший общий
делитель прозвольных двух чисел. Внизу — полученные рзшзн!я для двух
пар чисел. Операции записаны на языке, называемом MAD (Michigan
algorithm decoder — Мичиганский декодировщик алгоритмов). Буква О
перечеркивается при печати косой чертой, чтобы отличать ее от нуля.
;- рМШ^тРи dQ(* положит ель-
нбщ числа а и b . Н$рШи
v к Следующей инструкции.
2. Сравни два рассматриваемых
чи§/1а (определи, ра&щли они,
4 если нет, то которое больше).
Перейди к следующей
инструкции
3. Если числа равны, любое из них
является ответом; остановись
Если нет} перейди к
следующей инструкции.
4.Вычти меньшее число из
большего и замени два
рассматриваемых числа на вычитаемое
v и остаток. Перейди к
инструкции 2.
Рис. 5. Тот же алгоритм, записанный на обычном языке. Процесс деления
ааменяется повторным вычитанием. Эта последовательность операций
известна под названием алгоритма Евклида.
Внутренняя ( ^ \
память V* г)
(Считывающее
устройство
Устройство
для сдвига
ленты
Логический
блок
Стирающее
и записывающее
устройство
Устройство
для сдвига
ленты
I hlililikhlihhlihl I I 1 1 11 hlihiii*iiiu 1 1 I и I ia|ai«|b!b| I I I
1 hhhlA|»|B|ll»|»h|.-| I Mill l«hlA|A|»|BlB| 1 I I I I I i.i.i*I 1 1 1 1 I
1 |A|A[AlAl»lBlBlB|B|lHl 1 1 1 | 1 1 l.ll|*Hlll 1 | 1 I I 1 I 1 ТТГ. hi 1 1 1 I I
Рис. 6. Машина Тьюринга, предназначенная для. осуществления алгоритма Евклида, в этом схематическом
изображении содержит на ленте числа 4 и 6. (Каждая единица представлена штрихом; звездочка отделяет одно число
от другого.) Логический блок машины содержит инструкции, определяемые отметкой на обозреваемой ячейке
ленты и состоянием внутренней памяти. Осуществление шагов алгоритма ведет к изменениям на ленте, как
показано внизу. Вначале машина определяет, какое число длиннее, с помощью «цикла сравнения»: штрихи,справа
и слева от звездочки заменяются символами (слева ставится символ А, справа — В). Когда один набор
штрихов подойдет к концу, машина начинает «цикл вычитания», т. е. стирает символы меньшего числа, а символы
большего числа обращает снова в штрихи. Этот набор отделяется от штрихов, соответствующих остатку от
вычитания, с помощью звездочки. Процесс сравнения и вычитания повторяется после того, как на ленте
остаются числа 4 и 2, а затем 2 и 2; в конце-концов на ленте появляются 2 и 0. Когда начинается цикл
сравнения, пустая ячейка с одной стороны от звездочки вызывает из логического блока сигнал остановки (!), и
машина останавливается, когда на ее ленте записан ответ (2). Машина Тьюринга является идеализированной
машиной, поскольку ее лента потенциально бесконечна.
200
Ван Хао
Такие игры, как «ним», считаются «нечестными», поскольку
один игрок всегда имеет выигрышную стратегию. Игры вроде
«крестиков — ноликов» считаются «безрезультатными»,
поскольку оба игрока имеют беспроигрышную стратегию, так что
в ней невозможно выиграть. Эти характеристики могут- быть
б ооо ооо
001 от
А
6
3
А
2
В
1
А
Начало
он то он ооо ооо ооо ооо ооо
Рис. 7. Дерево игры в «ним» показывает, что игрок, который ходит
вторым (В), имеет выигрышную стратегию. В начале игры (см. кореш дерева)
имеются кучки из одной, двух и трех спичек (цифры при каждой вершине
дерева показывают число спичек, остающихся в кучках). Игроки забирают
одну или несколько спичек из одной кучки, пока кто-нибудь не выиграет,
забрав последнюю спичку. Ребра дерева показывают все возможные ходы
для А и ведущий к выигрышу ответ В на каждый из них.
сформулированы в виде теоремы: всякая игра является либо
безрезультатной, либо нечестной, если в ее дереве имеется
фиксированная верхняя граница длины всякого пути и если при
этом от каждой вершины отходит конечное число ребер. Эта
теорема верна потому, что если игра конечна и если на каждом
этапе имеется конечное число разрешенных ходов, то общее
число возможных последовательностей ходов тоже конечно.
Теперь, представив в виде дерева все разрешенные варианты игры,
ыЫ увидим, что если ни один из игроков не имеет выигрышной
стратегии, то обязательно каждый из игроков имеет беспроиг^
рышную.
Игры, логика и вычислительные машины
201
Эта теорема неприложима к игре в шахматы, до тех пор
пока не существует гочных правил для предотвращения
бесконечных партий. Предположим, однако, что мы ввели правила,
i
i
i
i
Рис. 8. Лемма о бесконечности подсказывается деревом, растущим вверх.
Эта лемма есть утверждение о том, что если в дереве имеется бесконечное
число связанных вершин, но от каждой вершины отходит лишь конечное
число ребер, то на каждом уровне дерева должна существовать вершина,
от которой отходит вверх бесконечное число ребер. Эти два обстоятельства,
взятые вместе, дают бесконечный путь. Эта лемма может быть
перефразирована следующим образом: «Если род человеческий никогда не исчезнет,
то сейчас существует человек, потомок которого будет жив в произвольно
далеком будущем».
которые исключают бесконечные партии, но не тем, что
накладывают какие-то ограничения на абсолютное число ходов в
партии, а как-то иначе. Тогда мы могли бы применить к шахматам
утверждение, известное как лемма о бесконечности, которое
гласит, что если в дереве игры имеется бесконечно много вер*
шин, связанных ребрами, но от каждой вершины отходит
конечное число ребер, то в этом дереве имеется бесконечный путь.
Если даны лемма о бесконечности и допущение о том, что
новые правила игры исключают возможность бесконечных
партий, то отсюда следует, что дерево, представляющее игру в
202
Ван Хао
шахматы, содержит конечное число ребер. В противном случае,
поскольку от каждой вершины отходит лишь конечное число
ребер, были бы бесконечные пути (т. е. бесконечные партии). Сле^
довательно, имеется лишь конечное число возможных
последовательностей ходов, а значит, как мы показали ранее, игра в
шахматы является либо нечестной, либо безрезультатной.
Доказательство леммы о бесконечности почти очевидно.
Возьмем вершину, образующую корень дерева. Поскольку мы
допустили бесконечное число ребер, но конечное число ребер,
отходящих от одной вершины, то по крайней мере одна из
вершин следующего уровня должна быть корнем поддерева с
бесконечным числом ребер. Назовем эту вершину X. Наша
гипотеза состоит в том, что непосредственно от X отходит лишь
конечное число ребер. Следовательно, одна из вершин на том
уровне, который следует за X, должна быть корнем
бесконечного поддерева. Повторяя это же рассуждение, мы увидим., что
на каждом уровне имеется по крайней мере одна вершина,
которая является корнем бесконечного поддерева; а вместе эти
вершины определяют в дереве некоторый бесконечный путь.
Между прочим, применяя лемму о бесконечности
«антропоморфически», мы должны заключить, что если род человеческий
никогда не исчезнет, то сейчас существует человек, потомок которого
будет жив в произвольйо далеком будущем (рис. 8).
Разумеется, исследование игры представляет интерес в
зависимости от того, насколько важные математические вопросы
она затрагивает. В 1960 г., когда я работал, в лаборатории
компании «Бэлл телефон», я придумал игру для одного 'человека,
похожую на домино с раскрашенными костями. Позднее в
Лаборатории вычислительных машин Гарвардского университета я и
мои коллеги нашли некоторые неожиданные и важные
применения этой игры. Некоторые проблемы, возникающие при игре в
это домино, являются точными аналогами задач, для решения
которых предназначалась машина Тьюринга. Условия,
которыми задается эта игра в домино, могуу быть поставлены в
соответствие с вычислениями, осуществляемыми на машине
Тьюринга, так что анализ этой игры может послужить основой для
новых подходов — иногда чрезвычайно плодотворных — к неко*
торым математическим проблемам.
При этой игре в домино игрокам дается конечное число
квадратных костей; все кости одинакового размера, но каждый
из краев имеет некоторый определенный цвет, и цвета
комбинируются несколькими способами. Предполагается, что имеется
бесконечное число экземпляров каждой кости и что нельзя
поворачивать кость в двух измерениях. Цель игры — покрыть
костями бесконечную плоскость так, чтобы края костей, прилегаю-
Игры, логика и вычислительные машины, 203
щие друг к другу, были одинакового цвета. Ебли плоскость
может быть покрыта данным множеством костей, то это множество
называется разрешимым.
Рассмотрим набор из трех костей на рис. 1. Этот набор
разрешим^ потому что из него можно построить блок в 9 костей,
который удовлетворяет указанному выше условию и может
быть повторен в любом направлении. Если имеется решение для
всей плоскости, то очевидно, что можно обрубить три квадранта
и получить решение для одного квадранта. Обратное менее
очевидно, но здесь мы можем использовать лемму о бесконечности.
Покрыть секцию декартовой плоскости
белыми и черными костями таким
образом, чтобы не получилось ни одного-
блока (того размера, который показан
на рисунке справа, или большего) с
совпадающими краями-правыми и левыми
или верхними и нижними. Можно ли
заполнить блоками такого вида
бесконечную плоскость ?
п
г т
i 1
п
i. 1
! Т
i 4
1 1
П
П
Рис. 9. Автор предлагает читателю четыре проблемы. Только для этай
первой и для четвертой проблемы решения известны. Решение первой
проблемы см. на рис. 12.
Поскольку существует решение для бесконечного квадранта, то
существуют частные решения для квадрантов этого квадранта,
т. е. решения для любого квадрата размером п на п. Из таких
частных решений мы можем построить бесконечное дерево и
показать с помощью леммы о бесконечности, что в этом дереве
существует бесконечный путь, который дает решение для всей
плоскости. Таким образом, если можно заполнить квадрант
бесконечной плоскости, то можно заполнить и всю плоскость.
Игрой в домино можно имитировать различные машины
Тьюринга и строить эквиваленты для важной тьюринговской
«проблемы остановки». Будет проще, если считать известным,
какая кость находится в исходной точке плоскости, т. е. какая
кость была выставлена первой. С некоторым усилием можно
добиться того же, если ввести условие о том, что некоторые
кости лежат на главной диагонали, или даже если опустить все
условия, кроме тех, которые были упомянуты ранее.
Рассмотрим эквивалентность проблемы остановки игре в домино более
подробно. -
Тьюринг имел в виду, что его простая вычислительная
машина будет соперничать с вычислителем. Человек, решающий
математическую задачу, скорее всего, пользуется
карандашом и бумагой, т. е. пишет и стирает числа; он может также
204
Ван Хао
иметь под рукой запас математических фактов — в виде
таблиц— и содержащийся либо в уме, либо на бумаге набор
инструкций для выполнения нужных шагов в нужной
последовательности. Воображаемая машина Тьюринга также имеет
устройство, позволяющее делать пометки, и стирающее устройство,
которые вместе позволяют. записывать числа в соответствии
с инструкциями, посылаемыми логическим блоком, который
действует в соответствии с заранее написанной таблицей команд.
Можно договориться, что цепочка
из нулей и единиц дает „потомство"
по следующим правилам:
1. Если в цепочке менее чем 3
символа, остановиться^
2. Если цепочка начинается с нуля,
стереть три символа слева
и добавить справа 00*
3. Если цепочка начинается с
единицы, стереть три символа слева
и добавить справа 1101*
Существует ли алгоритм,
позволяющий определить, является ли
одна из двух цепочек потомком
друёой?
011010001001
01000100100
0010010000
001000000
00000000
0000000
000000
00000
0000
000
00
(stop)
101110110011
1101100111101
11001111011101
011110111011101
11011101110100
111011101001101
0111010011011101
101001101110100
0011011101001101
10110100110100
1101001101001101
(progeny continue)
Рис. 10. Вторая проблема — найти алгоритм, который определяет,
являются ли две цепочки из нулей и единиц связанными друг с другом.
Проблема усложняется тем, что некоторые цепочки могут давать бесконечное
потомство. Другое решение состоит в том, чтобы доказать, что такого
алгоритма не существует. [Stop (англ.) — остановка, progeny continue —
порождение потомства продолжается.]
Числа записываются в виде штрихов в квадратных ячейках
бесконечно длинной ленты, служащей в качестве памяти.
(Поскольку никакая действительная машина не может иметь
бесконечной памяти, машина Тьюринга является идеализированным
устройством.)
Считывающая головка рассматривает ячейки ленты, по
одной в каждый момент времени, и передает символ в ячейке в
логический блок (рис. 6). Логический блок обращается к своим
внутренним инструкциям с помощью указателя, который
направлен на участок, называемый «Текущая инструкция». В
зависимости от того, что находится на ленте, вырабатывается
одна из следующих четырех команд: (1) напечатать некоторый
символ в ячейке, стерев предварительно ее содержимое, если
это потребуется; (2) передвинуть ленту на одну ячейку вправо;
(3) передвинуть ленту на одну ячейку влево; (4) остановиться.
Кроме того, инструкция указывает, где хранится следующая
Игры, логика и вычислительные машины 205
команда. В машину Тьюринга можно заложить столько
инструкций и команд, сколько потребуется, а лента может содержать
бесконечное число ячеек; это дает возможность решить на
машине Тьюринга любую заданную ей математическую проблему
(если эта проблема относится к числу разрешимых с помощью
алгоритмов).
Тьюринг выдвинул проблему остановки в качестве примера
проблемы, для которой никакая программа не может дать всех
Существует ли алгоритм, а для уравнений такого вида
позволяющий определить имеет желаемый алгоритм известен
ли полином с целочисленными I Найти все делители ап
коэффициентами целочисленные 2.Подставить каждый из них
корни ? на место х и вычислить значение
оят уравнения _ значение 0, то он является корнем
и х -4X + J-U уравнения; если такого нет, то
q2+ Ьг- с2=0 уравнение не имеет целочислен-
В первом уравнении имеется НЬ1Х к0Рнеи
только одно неизвестное х. Следо- Проблема состоит в том, чтобы
вательнОу оно может быть при- построить такой алгоритм
ведено к виду для уравнений второго типаtт.е.
для уравнений с более чем одним
неизвестным.
апхп + ап.1хп~'1 +....+ajX+ao=0,
Рис. 11. Третья проблема известна как «10-я проблема Гильберта» с тех
пор, как немецкий математик Давид Гильберт включил ее в 1900 г. в число
выдающихся проблем математики.
правильных решений. Он превысил возможности всякой
единичной машины Тьюринга, поставив вопрос, касающийся всех
машин. Он показал, что хотя всякая машина в зависимости от
содержимого ее ленты либо остановится, либо будет
продолжать работать до бесконечности, тем не менее здесь не суще-»
ствует алгоритма, который мог бы определить поведение ма^
шины, т. е. для этой проблемы не существует общего рецепта,
похожего на рецепт определения победителя в игре «ним».
Оказывается, однако, что для всякой машины Тьюринга можно
найти такой набор костей домино, что машина останавливается
в том и только в том случае, когда этот набор не является
разрешимым. Прямым следствием этого факта является
неразрешимость проблемы домино: если бы мы могли решить проблему
домино, то мы могли бы решить и проблему остановки; мы не
можем решить проблему остановки, а следовательно, не можем
решить и проблему домино. Иными словами, не существует
общего метода получения ответа на вопрос, является ли данный
набор костей домино разрешимым.
206
Ван Хао
Проблема домино является примером бесконечной проблемы
такого тииа, который часто возникает в логике, в теории
вычислительных машин и вообще в математике. Эта проблема
является бесконечной в следующем смысле слова. Всякое решение
проблемы домино должно представлять собой единый метод
получения правильного ответа на бесконечное число вопросов
а
db
а Ь Ьа
abbabaab
ab bab аа b baa bab ba..
Рис. 12. Решение первой проблемы (см. рис. 9). Для того чтобы провести
это построение, обозначим черную кость через а, белую—через Ь (см. левую
часть рисунка). Напишем а и заменим его на аЬ. Затем заменим Ь на Ьа и
далее будем заменять а и Ь таким же образом. Запишем эту
последовательность в верхнем ряду и повторим каждый символ вдоль всей диагонали,
идущей от правого верхнего угла к левому нижнему.
вида: «Можно ли с помощью данного набора костей домино
покрыть плоскость?». Хотя каждый конкретный набор типов
костей конечен, таких наборов, разумеется, бесконечное число, и
потому число вопросов также бесконечно.
Таким образом, мы свели проблемы, касающиеся наборов
костей домино, к проблемам, касающимся машин, и установили
некоторые факты относительно игры в домино, апеллируя к
результатам, известным для машин. Следующий этап — это
сведение проблемы интерпретации формулы в логике к проблеме
разрешимости набора костей домино. Поскольку условие о том,
что набор костей домино разрешим, может быть выражено в
виде простой логической формулы, то такое сведение решает
проблему разрешения — важнейшую из проблем логики.
Если мы хотим выразить условие о том, что набор из трех
типов костей домино имеет решение в первом квадранте
бесконечной плоскости, то прежде всего приходит в голову записать
положение кости в декартовой системе координат и представить
каждую кость в виде предиката; например, Аху будет означать,
что кость А занимает положение (ху у). Если обозначить х+1
через х\ то требуемое условие может быть сформулировано в
Рис. 13. Четвертая проблема (проблема
домино с десятью костями) состоит в том,
чтобы построить из этих косгей блок, в
котором схема распределения цветов
одинакова для верхнего и нижнего края с одной
стороны и для левого и правого края —
с другой. Решение см. на рис. 14.
Г^Щ#Т."Л
Рис' 13. Четвертая проблема (проблема
домино с десятью костями) состоит в том,
чтобы построить.из этих костей блок, в
котором схема распределения цветов
одинакова для верхнего и нижнего края с одной
стороны и для левого и правого края —
с другой. Решение см. иа рис. 14.
Рис. 14. Решением проблемы
с 10 костями является прямоугольный блок
из 36 костей. На рисунке изображены два
таких блока, разделенные жирной линией,
проходящей через центр рисунка. Это
решение не является единственным, т. е.
существуют другие в равной мере
приемлемые конфигурации, построенные из
указанного набора костей.
Рис. 14. Решением проблемы домино
с 10 костями является прямоугольный блок
из 36 костей. На рисунке изображены два
таких блока, разделенные жирной линией,
проходящей через центр рисунка. Это
решение не является единственным, т. е.
существуют другие в равной мере
приемлемые конфигурации, построенные из
указанного набора костей.
Игры, логика и вычислительные машины
207
виде нескольких предложений с очень небольшим числом
кванторов (т. е. конструкций с оборотами «для всякого» и
«существует»). Кроме того, из конечных операций формальной логики
мы расщедримся только на «не», «и» и «или» (рис. 2). Мы
можем заключить, что для любого заданного набора костей можно
-найти соответствующую АЕА-формулу (т. е. предложение,
начинающееся словами: «Для всякого X существует У, такое, что
для всякого Z», после чего следует комбинация логических
связок и предикатов, уже без кванторов), такую, что набор
является разрешимым тогда и только тогда, когда формула не
является противоречивой. Иными словами, мы можем перевести
проблему домино в логическую формулу, введя некоторые
ограничения, а затем устанавливать разрешимость проблемы домино
по тому, является ли противоречивой соответствующая формула.
Следовательно, раз общая проблема домино неразрешима, то не
существует общего метода для решения вопроса о том, является
ли противоречивой произвольная Л£Л-формула.
Этот результат весьма полезен, поскольку сложность
формулы в логике в значительной мере определяется числом и
порядком кванторов и логические формулы часто относятся
к различным классам в зависимости от структуры кванторных
оборотов. Тот факт, что такой простой класс формул, как
Л£Л-формулы (всего с тремя кванторами), неразрешим, весьма
удивителен. Действительно, имея этот результат, мы можем
решить проблему разрешения для всех классов формул с данным
набором кванторов. Если дана произвольная цепочка
кванторов, мы можем сказать, является ли класс определяемых ею
формул разрешимым.
Логическая проблема разрешения имеет большое значение
потому, что все математические теоремы могут быть
сформулированы в рамках элементарной логики. Вопрос о том, может ли
формула F быть выведена из системы аксиом Л, сводится
к тому, чтобы решить, является ли логическая формула «Л, но
не.-F» противоречивой. В этом смысле вся математика сводится
к логике. Действительно, одна из мер сложности
математической проблемы задается структурой соответствующей ей
логической формулы. Тем самым определение сложности различных
классов логических формул является важной задачей.
Можно с полным основанием утверждать, что ,вся
математика может быть сведена через посредство машины Тьюринга
к игре в домино (для одного человека). В большинстве случаев
это сведение не облегчает решения проблемы. Однако
доказательство того, что некоторые проблемы неразрешимы с помощью
вычислительной машины, часто упрощается при сведении их к
проблемам домино.
СОДЕРЖАНИЕ
Математические вопросы 5
Э. В а й н е р, Р. Э ш. Анализ рекуррентных кодов. Перевод И. И. Грушко 5
Дж. Штифлер. Коды без запятой, исправляющие ошибки. Перевод
Е. /О. Захаровой .34
Ж. А н с е л ь. Минимальное число замыкающих контактов, достаточное
для реализации одной симметрической булевой функции п
переменных. Перевод Н. А. Карповой 47
Ж. А н с е л ь. О числе монотонных булевых функций п переменных.
Перевод Н. А. Карповой 53
Ж. Ане ель. Построение двухполюсной контактной схемы для
произвольной монотонной булевой функции п переменных. Перевод
Н. А. Карповой 58
П. Фишер. Многоленточные и бесконечные автоматы. Обзора Перевод
А. А. Мучника 64
А. Атрубин. Одномерное итеративное умножающее устройство,
работающее в реальное время. Перевод Ю. А. Бухштаба 81
П. Фишер. Порождение простых чисел на одномерной итеративной
сети в реальное время. Перевод Ю. А. Бухштаба 95
П. Ландвебер. Проблемы разрешения в грамматиках
непосредственных составляющих. Перевод М. В. Ломковской 103
С. Гинзбург, Дж. Роуз. Характеристика машинных отображений.
. Перевод А А. Мучника 128
С. Гинзбург, Д ж. Р о у з. Об инвариантности классов языков
относительно некоторых преобразований. Перевод Л. С. Модиной .... 138
С. Гинзбург, Ш. Грей б ах. Об инвариантности класса НС-языков
относительно некоторых отображений. Перевод Л. С. Модиной . . 167
К. Кук, Э. X о л с е й. Кратчайший путь через сеть с переменным
временем пробега по дугам. Перевод В. А. Евстигнеева 189
Некоторые технические реализации 195
Ван Ха.о. Игры, логика и вычислительные машины. Перевод Е. В. Па-
дучевой 195
КИБЕРНЕТИЧЕСКИЙ СБОРНИК
Новая серия
Выпуск 5
Редактор А. Г. Крылов. Художник Я. К. Сапожников
Художественный редактор В. И. Шаповалов
Технический редактор Т. В. Чечик. Корректор И. С, Цвет/сова
дано в производство I2/IV 1968 г. Подписано к печати 25/Х 1968 г. Бумага тип. № 3 60X90Vi6=6,6
бум. л. 13.38 печ. л., в т/ч 3 вкл. Уч.-изд. л. 12,16. Изд. № 1/4732. Цена 1 р. 03 к. Зак. 1204-
Темплан изд-ва «Мир» 1968г.,пор,№ 10
ИЗДАТЕЛЬСТВО „МИР*
Москва, 1 й Рижский пер., 2
Ленинградская типография № 2 имени Евгении Соколовой Главполиграфпрома
Комитета по печати при Совете Иинистров СССР, Измайловский проспект, 29,