ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЕ
В. П. ГРИГОРЬЕВ, Ю. А. ДУБИНСКИЙ
ЭЛЕМЕНТЫ ВЫСШЕЙ
МАТЕМАТИКИ
Допущено
Министерством образования Российской Федерации
в качестве учебника для студентов образовательных учреждений
среднего профессионального образования, обучающихся
по группе специальностей 2200
«Информатика и вычислительная техника»
10-е издание, стереотипное
ACADEM*A
Москва
Издательский центр «Академия»
2014
УДК 51(075.32)
ББК 22.1я723
Г834
Рецензенты:
доцент кафедры высшей математики Московского государственного института стали и
сплавов (ТУ) Т. Н. Сабурова (зав. кафедрой — проф. Б. Г. Разумейко);
преподаватель Московского государственного колледжа информационных технологий
5.77. Родичев
Григорьев В.П.
Г834 Элементы высшей математики : учебник для студ. учрежде-
ний сред. проф. образования / В. П. Григорьев, Ю. А. Дубинский. —
10-е изд., стер. — М. : Издательский центр «Академия», 2014. —
320 с.
ISBN 978-5-4468-0784-0
В учебнике представлены все основные разделы высшей математики: эле-
менты теории множеств, линейной алгебры, аналитической геометрии, диффе-
ренциального и интегрального исчисления; числовые последовательности; обык-
новенные дифференциальные уравнения.
Теоретическую часть учебника дополняет большое количество практических
задач; в приложении дано краткое описание пакета прикладных программ по
математике MAPLE.
Учебник может быть использован при изучении дисциплины в естественно-
научном цикле в соответствии с требованиями ФГОС СПО для укрупненной
группы специальностей 230000 «Информационная и вычислительная техника».
Для студентов технических специальностей учреждений среднего професси-
онального образования.
УДК 51(075.32)
ББК 22.1я723
Оригинал-макет данного издания является собственностью Издательского центра
«Академия», и его воспроизведение любым способом без согласия правообладателя запрещается
Учебное издание
Григорьев Валерий Петрович, Дубинский Юлий Андреевич
Элементы высшей математики
Учебник
Редактор Л. В. Честная. Технический редактор Е.Ф. Коржуева.
Компьютерная верстка: Д. В. Федотов. Корректоры Г. И. Петрова, В.А.Жилкина
Изд. № 110106426. Подписано в печать 10.02.2014. Формат 60x90/16. Гарнитура «Таймс».
Бумага офсетная № 1. Печать офсетная. Усл. печ. л. 20,0. Тираж 2 500 экз. Заказ №
ООО «Издательский центр «Академия», www.academia-moscow.ru
129085, Москва, пр-т Мира, 101В, стр. 1.
Тел./факс: (495) 648-0507, 616-00-29.
Санитарно-эпидемиологическое заключение № РОСС RU. АЕ51. И 16476 от 05.04.2013.
Отпечатано с электронных носителей, предоставленных издательством,
в ОАО «Саратовский пол и граф ком бин ат», www.sarpk.ru
410004, г. Саратов, ул. Чернышевского, 59.
© Григорьев В.П., Дубинский Ю.А., 2011
© Образовательно-издательский центр «Академия», 2011
ISBN 978-5-4468-0784-0	© Оформление. Издательский центр «Академия», 2011
ПРЕДИСЛОВИЕ
Содержание учебника соответствует требованиям Государствен-
ного образовательного стандарта для специальностей техническо-
го профиля среднего профессионального образования, таких, как
«Вычислительные машины, комплексы, системы и сети» (2201),
«Автоматизированные системы обработки информации и управ-
ления» (2202), «Программное обеспечение вычислительной тех-
ники и автоматизированных систем» (2203).
Авторы надеются, что книга будет востребована при реализа-
ции учебных программ по математике и для других специальностей.
Дело в том, что учебный материал, представленный в книге,
соответствует той базовой части математического образования,
которая для всех специальностей является основой как дальней-
шего математического образования, так и приложений к реше-
нию технических задач, отвечающих конкретным проблемам.
Что касается методики изложения, то авторы стремились до-
биться максимального уровня математической строгости и безус-
ловно исключить какие-либо недоговоренности научного характе-
ра. В тех же местах, где по каким-либо причинам полного обосно-
вания теорем дать невозможно, приводятся «неформальные» разъяс-
нения существа сформулированных утверждений, а также поясня-
ющие рисунки и конкретные примеры.
Такому подходу изложения материала способствует и современ-
ная тенденция широкого использования различных обучающих
прикладных пакетов в процессе математического образования. Ра-
зумеется, даже самые лучшие пакеты обучающих программ не могут
заменить вдумчивого изучения теоретических основ математики.
Однако в самом процессе освоения учебных программ их сбалан-
сированное использование весьма полезно и существенно. Поэто-
му в дополнение к основному тексту книги дано приложение —
краткое описание математического пакета MAPLE, применимое к
любой его версии. Авторы надеются, что этот пакет будет исполь-
зован читателями при решении практических задач, соответству-
ющих основному теоретическому материалу книги.
Для того чтобы помочь читателю лучше ориентироваться в тексте,
а также в структуре и в логике доказательства, использован специ-
альный знак ▲, означающий окончание доказательства.
Авторы будут благодарны всем читателям, которые сообщат свои
замечания и пожелания по адресу: 111250, Москва, Красноказар-
менная ул., 14, МЭИ (ТУ), кафедра математического моделиро-
вания.
3
ГЛАВА 1
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
1.1. Понятие множества. Операции над множествами
Многие фундаментальные понятия в математике базируются на
наших интуитивных представлениях об объектах и их свойствах. Од-
ним из таких фундаментальных понятий является понятие множе-
ства. Множество нельзя определить через какие-то уже известные
понятия, это возможно только благодаря интуитивным, т.е. полу-
ченным из опыта, представлениям. Слово «множество» использу-
ется и в быту. Соответствующее ему математическое понятие по
смыслу почти ничем не отличается от «бытового» понятия. Дей-
ствительно, при рассмотрении нескольких объектов, объединяе-
мых по какому-то признаку, употребляется слово «множество». На-
пример, множество студентов в группе; множество автомобилей,
выпущенных заводом за год; множество грибов в данном лесу. Эти
примеры показывают, что в одних случаях множество может быть
легко охарактеризовано некоторым числом, а в других — это сде-
лать значительно труднее, хотя, в принципе, — всегда возможно.
Но встречаются такие множества, для которых возможность «пе-
ресчета» всех их элементов неочевидна. Например, множество це-
лых простых чисел. Оказывается, что элементы этого множества
нельзя сосчитать, т.е. охарактеризовать каким-либо числом. Если
начать этот пересчет, то он никогда не закончится. Существует
прием, позволяющий набор из любого конечного числа простых
чисел увеличить еще на единицу. Поэтому никакое число не го-
дится для того, чтобы охарактеризовать множество простых чисел.
Их количество бесконечно.
Множество, состоящее из некоторого натурального числа эле-
ментов, называется конечным множеством. Если не существует та-
кого числа, определяющего количество элементов в множестве,
то такое множество называется бесконечным. Так, множество авто-
мобилей, выпущенных заводом, — конечное множество, а мно-
жество всех простых чисел — бесконечное множество.
К числу множеств оказывается удобным отнести и пустое мно-
жество, т.е. множество, не содержащее ни одного элемента. Его
роль аналогична роли нуля в арифметике чисел.
4
Множества обычно обозначаются большими латинскими буква-
ми: А, Д С, а их элементы — малыми буквами: а, й, с. Принадлеж-
ность элемента данному множеству обозначается так: а е А. Эта за-
пись означает, что а является элементом множества А. Если же а не
принадлежит множеству Л, то пишут a е А. Другие обозначения: А с
В — все множество А содержится в множестве В (в этом случае гово-
рят, что А является подмножеством множества В); А = В — любой
элемент множества А является элементом множества В и наоборот,
любой элемент множества В является элементом множества А.
Существуют различные способы задания множеств. Кроме опи-
сательных способов, которые были упомянуты выше, когда опре-
делялись свойства элементов, по которым они объединялись в одно
множество, можно, например, перечислить все элементы множе-
ства. Например, множество городов, входящих в маршрут «Золо-
тое кольцо России», состоит из Сергиева Посада, Переславля-За-
лесского, Ростова, Ярославля, Костромы, Суздаля и Владимира.
Можно задать множество с помощью следующей записи: А = {1, 4,
..., л2, ...}. Используется также способ, когда указываются свойства
элементов с помощью математических символов. Например, А =
= {х: х2 + Зх - 2 > 0} есть множество всех х, для которых выполняет-
ся указанное неравенство.
Наиболее важные операции, которые можно производить с дву-
мя множествами А и Д — объединение двух множеств и построе-
ние их пересечения.
Объединение двух множеств — новое множество, состоящее из
элементов как множества Л, так и множества В. Это множество
обозначается через A U В.
Пересечением двух множеств называется множество, в которое
входят только те элементы, которые одновременно принадлежат
обоим множествам А и В. Обозначается это множество через А П В.
Например, пусть А = {х: х2 - Зх + 2 = 0}, В = {1, 3, 5, 7}. Тогда,
поскольку уравнение х2 - Зх + 2 = 0 имеет два корня: х, = 1 и х2 = 2,
A U В= {1, 2, 3, 5, 7}, А П В= {1}.
Операции объединения и пересечения можно производить с
любым конечным числом множеств, а также — и с бесконечным
числом. Например, пусть Ан = {л}, где п — целое положительное
число. Тогда множество всех натуральных чисел, обозначаемое обыч-
но через N, будет совпадать с объединением всех множеств А„ для
л=1,2,.... Этот факт можно записать в такой форме:
N = U4-
«=1
Когда объединяется конечное число множеств Д, Л2, ..., А„,
fl
объединение обозначается как (J Ак. Аналогично обозначают пере-
Л *=1
сечения множеств: либо [ ] Ак — в случае конечного числа «пере-
а-=]
5
секающихся» множеств, либо Q Ак — если их число бесконечно.
а-=]
Пустое множество, обозначаемое обычно через 0, при объедине-
нии играет роль нуля при сложении чисел: для любого множества
А имеет место равенство A U 0 = А.
1.2.	Конечные и бесконечные, счетные
и несчетные множества
Если конечные множества характеризуются количеством своих
элементов, выражаемым конечным числом, то для бесконечных
множеств такой характеристики не существует. Употребляется сим-
вол о®, который указывает на то, что множество является беско-
нечным, но этот символ не так хорошо характеризует множество,
как конечное число. Если множество конечно и известно число его
элементов, то это число говорит не только о конечности множе-
ства, но и о том, например, на сколько равных групп его можно
разбить. Более того, все конечные множества с одинаковым чис-
лом элементов обладают одними и теми же свойствами, между
любыми двумя такими множествами можно установить взаимно
однозначное соответствие, когда каждому элементу одного мно-
жества ставится в соответствие один элемент другого множества и
при этом любому элементу второго множества поставлен в соот-
ветствие только один элемент из первого множества. Например,
пусть А = {1, 3, 5, 7} и В= {2, 6, 10, 14}. Тогда, ставя в соответствие
каждому числу X из множества А то число из множества В, кото-
рое равно 2Х, получим взаимно однозначное соответствие между
множествами А и В.
С бесконечными множествами дело обстоит сложнее: между
некоторыми бесконечными множествами можно установить вза-
имно однозначное соответствие, а между некоторыми — нельзя.
Наиболее привычное нам бесконечное множество — это множе-
ство натуральных чисел N = {1, 2, 3, ..., л, ...}. Другие бесконечные
множества, наиболее часто используемые в математике, это:
•	Z — множество целых чисел (включая 0, положительные и
отрицательные целые числа);
•	R1 — множество действительных чисел (все обычные числа,
называемые еще вещественными);
•	Q — множество рациональных чисел (чисел, которые можно
т
представить в виде дроби —, где т и п e Z, п * 0);
п
•	[а, />], где а < b — два действительных числа; это множество,
называемое отрезком, состоит из всех действительных чисел X,
удовлетворяющих условиям:
6
л/З; 0), (—; 4; -1,5) явля-
a<X<b;
•	Rn = {x: x = (xl,x2,...,xf), Xj g R',y = 1, 2, ..., n}, n g N. Это
множество состоит из упорядоченных наборов из п действитель-
ных чисел. Например, наборы чисел (-5;
ются элементами множества R3.
Важную роль в теории бесконечных множеств играют счетные
множества. Это такие бесконечные множества, все элементы кото-
рых можно занумеровать, т.е. установить взаимно однозначное со-
ответствие между ними и множеством натуральных чисел N = {1,
2, ..., л, ...}.
Например, множество натуральных четных чисел N2 = {2, 4,
2л, ...} будет счетным. Его легко занумеровать, т.е. каждому эле-
менту множества дать свой номер: числу 2 дадим номер 1, следую-
щему числу 4 — номер 2 и вообще, числу 2л — номер п. Таким
образом каждое четное натуральное число получило свой номер.
Например, число 100 будет иметь номер 50. Здесь мы сталкиваемся
с удивительным фактом: четные числа, составляющие половину
всех натуральных чисел, содержат такое же «количество» чисел,
как и множество всех натуральных чисел. Слово «количество» здесь
уже неуместно, и поэтому говорят иначе: множества N2 и N имеют
одинаковую мощность. Таким образом, счетные множества — это
такие множества, которые имеют одинаковую мощность с множе-
ством N. Таких множеств довольно много. Но не всегда бывает про-
сто доказать, что множество является счетным. Так, например,
множество Q — множество рациональных чисел — будет счетным.
Однако доказательство этого факта несколько тяжеловесно, по-
этому здесь не приводится. Счетное множество можно представить
как «минимальное» бесконечное множество: легко доказать, что
любое бесконечное множество содержит подмножество, являю-
щееся счетным. Поэтому не существует бесконечного множества,
которое не содержало бы счетного подмножества, т.е. не суще-
ствует бесконечного множества, которое было бы в этом смысле
«меньше», чем счетное множество.
С другой стороны, любое бесконечное подмножество счетного
множества является счетным. Этот и еще несколько фактов приве-
дем без доказательства:
•	объединение двух и более (в конечном числе) счетных мно-
жеств — счетно;
•	объединение счетного числа счетных множеств — счетно;
•	существуют несчетные бесконечные множества, примерами
которых могут служить такие множества, как [«,/»], R1, R".
Из приведенных примеров видно, что множество всех действи-
тельных чисел не является счетным, у него другая и, естественно,
большая мощность. Эту мощность обычно называют мощностью
континуума. Мощностью континуума обладают многие числовые
7
множества: кроме всех действительных чисел R1, это всевозмож-
ные отрезки [а,д], конечные интервалы (a,b) = {X \ а < X < />},
полуинтервалы [а,Ь) = {А| а < Х< Ь}, (а,Ь] = {Х\ а < Х< Ь}; бесконеч-
ные полуинтервалы [£,+<*>) = {Х \ а < Х\, (-<*>, я] = {А | Х< а}\ беско-
нечные интервалы (а,+«») = {X | а < А}, (~^,а) = {А | X < а} и,
наконец, R1 также может быть представлено в виде бесконечного
интервала (-оо,+оо).
1.3.	Числовые множества. Действительные числа
Теория действительных чисел необходима для обоснованного
использования их свойств при различных математических рассуж-
дениях и выкладках. Свойства чисел достаточно хорошо известны
из школьного курса математики, и все вышеприведенные упоми-
нания о них базировались именно на этих представлениях, в зна-
чительной степени интуитивных. Но во многих доказательствах,
где суть дела порой просматривается с трудом, четкая аргумента-
ция и ссылки на конкретные факты становятся необходимыми не
только для успешного проведения доказательства, но и для его
восприятия и понимания. В данном курсе нецелесообразно изла-
гать теорию действительных чисел в полном объеме, как это обычно
делается в курсах математического анализа. Здесь будет дан набор
аксиом, фиксирующих все фундаментальные свойства чисел, и
точное определение действительных чисел, пригодное для всех
последующих применений в математических рассуждениях. Это
делается на основе аксиоматики.
Определение 1,1, Множество R1 называется множеством действи-
тельных чисел, а его элементы — действительными числами, если и
только если выполняются следующие условия, называемые акси-
омами действительных чисел.
Аксиомы сложения
На множестве R1 определена операция сложения, когда каж-
дой упорядоченной паре (х,у) элементов х, у из R1 ставится в
соответствие некоторый элемент х + у е R1, называемый суммой х и
у. При этом выполнены следующие условия:
1)	существует нейтральный элемент 0 (называемый нулем} та-
кой, что для любого хе R'x + 0 = 0 + x = x;
2)	для любого элемента хе R1 найдется в R1 элемент -х (называ-
емый противоположным к х) такой, что х + (-х) = (-х) + х = 0;
3)	операция сложения коммутативна, что означает, что для
любых элементов х и у из R1 выполняется равенство х + у = у + х;
4)	операция сложения ассоциативна, что означает, что для
любых элементов х, у и z из R1 выполняется равенство (х + у) + z =
= х + (у + z).
8
Аксиомы умножения
На множестве R1 определена операция умножения, когда каж-
дой упорядоченной паре (х.г) элементов х, у из R1 ставится в
соответствие некоторый элемент ху е R1, называемый произведе-
нием х и у. При этом выполнены следующие условия:
1)	существует нейтральный элемент 1 (называемый единицей)
такой, что для любого элемента х е R1 выполняется равенство
х  1 = 1  X = х;
2)	для любого элемента х е {R1 \ 0} найдется в {R1 \ 0} элемент
х-1 (называемый обратным к х) такой, что хх-1 = х“'х = 1;
3)	операция умножения коммутативна, что означает, что для
любых элементов х и у из R1 выполняется равенство ху = ух;
4)	операция умножения ассоциативна, что означает, что для
любых элементов х, у и z из R1 выполняется равенство (xy)z =
= x(yz);
5)	операция умножения дистрибутивна по отношению к опе-
рации сложения, что означает, что для любых элементов х. у и z
из R1 выполняется равенство (х + y)z = xz + yz.
Аксиомы порядка
Для любых двух элементов х, у из R1 установлено, выполняется
соотношение х < у или нет. При этом выполняются условия:
1)	для любого х из R1 х < х;
2)	если х < у и у < х, то х = у;
3)	если х < у и у < z, то х < z;
4)	для любых х и у из R1 либо х < у, либо у < х;
5)	для любых элементов х, у и z из R1 справедливо утвержде-
ние: если х < у, то х + z < у + z;
6)	для любых элементов х и у из R1 справедливо утверждение:
если 0 < х и 0 < у, то 0 < ху.
Аксиома полноты
Если Е и Y — два непустых числовых множества, обладающих
тем свойством, что для любых х из Е и у из Y справедливо соотно-
шение х < у, то существует р е R1 такое, что для любых двух эле-
ментов х из Е и у из Y справедливо соотношение х < |3 < у.
Замечание, Если для любых хе Е и у е Y выполняется неравен-
ство х < у, то говорят, что Е < Y. Аксиома полноты требует, чтобы
для любой пары множеств £ и Y, т. е. таких, что Е < Y, существова-
ло бы действительное число |3 такое, что для любых хе Е и у е Y
выполнялись бы неравенства х < р < у.
Приведенная система аксиом, являясь непротиворечивой, од-
нозначно определяет такой математический объект, как действи-
тельное число. Из аксиом могут быть выведены все алгебраические
свойства чисел, а также свойства их непрерывности (между любы-
ми двумя числами всегда есть другие числа).
9
Многие из этих аксиом, согласуясь с нашей интуицией, кажут-
ся настолько «естественными», что вызывают недоумение. Но для
четко аргументированной теории они необходимы, все свойства
действительных чисел должны вытекать из этих аксиом. Некото-
рые из этих аксиом наоборот, кажутся непонятными. Например,
аксиома полноты, ее называют еще аксиомой непрерывности.
Целесообразность этой аксиомы легче понять, если проанали-
зировать ее в действии. Для дальнейшего оказывается важной сле-
дующая теорема о так называемой верхней грани множества. Дока-
жем эту теорему, опираясь на аксиому полноты, предварительно
дав несколько определений.
Определение 1.2, Множество X называется ограниченным сверху
(снизу), если существует число М такое, что для любого х е X вы-
полняется неравенство х < М (х > М).
Определение 1.3. Множество X называется ограниченным, если оно
является одновременно ограниченным снизу и ограниченным сверху.
Определение 1,4, Число М, фигурирующее в определении 1.2,
называется верхней (нижней) границей множества X.
В некоторых книгах можно встретить термин: М — мажоранта
(миноранта) множества X.
Определение 1.5. Наименьшая из верхних границ множества X
называется верхней гранью (или точной верхней границей) множе-
ства X и обозначается sup X (читается «супремум А»).
Определение 1.6. Наибольшая из нижних границ множества X
называется нижней гранью (или точной нижней границей) множе-
ства X и обозначается inf X (читается «инфимум А»).
Данные определения требуют уточнения: ведь не каждое число-
вое множество содержит наибольший и наименьший элемент. На-
пример, множество Х= (0,1] содержит наибольший элемент х = 1,
но не содержит наименьшего элемента, так как 0 g А. Этот вопрос
решает следующая теорема.
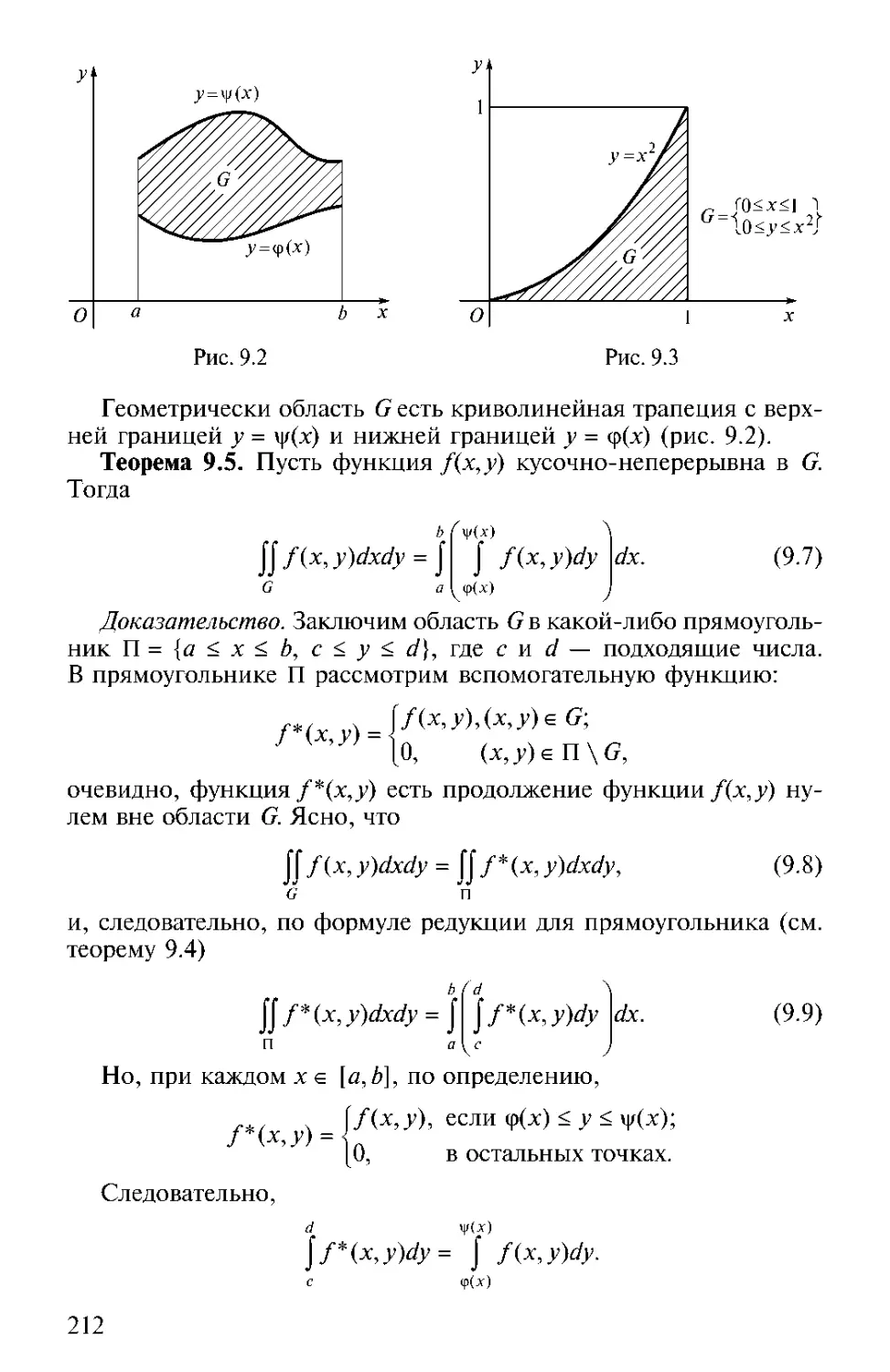
Теорема. Если непустое числовое множество А ограничено сверху,
то у него существует верхняя грань, т.е. sup А, и притом един-
ственная.
Доказательство. Докажем сначала единственность sup А. Пред-
положим противное: существуют две верхних грани А = sup Аи В =
= sup А. Тогда, по определению sup А, так как А и В являются
наименьшими верхними границами множества А, то А < В и В < А.
Это возможно только в случае, когда А = В, т. е. sup А, если она
существует, то она единственна.
Докажем теперь существование sup А. Рассмотрим множество
Y, элементами которого являются всевозможные верхние границы
множества А. По условию теоремы А — непустое числовое множе-
ство так же, как и У. Очевидно, что А < У.
В силу аксиомы полноты существует число р такое, что для любых
х е А и у е У выполняются неравенства х < |3 < у. По определению
10
верхней границы множества Л, число р является таковым (х < р).
Вторая часть неравенства |3 < у показывает, что р является наи-
меньшей из всех верхних границ множества Л, т.е.
Р = sup X. ▲
Следствие. У непустого множества £, ограниченного снизу,
существует и притом единственная нижняя грань inf Е.
Доказательство. Если множество Е ограничено снизу, то мно-
жество G, состоящее из чисел (-х), где х е £, будет множеством,
ограниченным сверху. Действительно, если число М ограничивает
множество £ снизу (М < х), то число (-М) ограничивает множе-
ство G сверху (—х < -М). Поэтому, в силу теоремы, существует и
притом единственная верхняя грань sup G. Отсюда следует, что
существует и притом единственная inf £ = -sup G. ▲
Замечание. Сами числа sup X и inf X могут как принадлежать
самому множеству Л, так и не принадлежать. Например, если X =
= (0,1], то sup X = 1, a inf X = 0. В данном случае sup X е X. а
inf X e X. Для множества Y = [0,1), наоборот, sup У g У, a inf Y е Y.
Для множества £= (0,1) ни верхняя, ни нижняя грани не принад-
лежат множеству.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1.	Пусть А и В — два подмножества множества С, т.е. А cz С и В cz С.
Дополнением подмножества А до множества С называется множество тех
элементов множества С, которые не принадлежат множеству А Обознача-
ется это множество через А. Аналогично определяется множество В —
дополнение множества В. Разумеется, Л с Си 5 с С, т.е. и А, и В
являются подмножествами множества С. _ _
Докажите равенство множеств A U В = А П В.
2.	Пусть множество £2 — множество диагоналей в правильном шести-
угольнике ABCDEF. Опишите множество £2, перечислив все его элементы.
3.	Докажите, что объединение двух счетных множеств является счет-
ным множеством.
4.	Известно, что если между элементами двух бесконечных множеств
можно установить взаимно однозначное соответствие, то эти множества
имеют одинаковую мощность. Докажите, что любые два конечных отрез-
ка [а, />] и [с, d] (а < b, с < d), рассматриваемые как множества чисел х и у,
удовлетворяющих неравенствам а < х < Ь, с < у < d, имеют одинаковую
мощность.
5.	Пусть £2 — множество чисел отрезка [-5,2]. Найдите sup £2 и inf £2.
6.	Пусть £2 — множество чисел интервала (1,4). Найдите sup £2 и inf £2.
(-1)"
7.	Пусть £2 — множество чисел вида 3 + (-1)л + -—— , где п g N.
п
Найдите sup £2 и inf £2.
8.	Пусть £2 — множество значений функции у =-Докажите, что
это множество ограничено.	+ л
ГЛАВА 2
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
2.1. Матрицы и действия над ними
В математике при решении ряда задач, например при решении
систем линейных алгебраических уравнений, оказывается полез-
ным такое понятие, как матрица. Под матрицей понимают табли-
цу прямоугольной формы, заполненную числами или символами,
их обозначающими. Обозначают эти объекты большими латински-
ми буквами, а саму таблицу заключают в скобки — круглые, квад-
ратные или другой формы. Например,
LX«J
Числа или символы, заполняющие таблицу, называются эле-
ментами матрицы. Множество элементов матрицы, расположен-
ных в одной строке, естественно называть строкой матрицы. Ана-
логично понятие столбца матрицы. Если в матрице содержится т
строк и п столбцов, то говорят, что матрица имеет размеры т х п.
Если т = «, то матрица называется квадратной, а если т # /?, то —
прямоугольной. Строки и столбцы удобно занумеровать: сверху вниз
и слева направо соответственно. Тогда каждый элемент матрицы
получает два номера: i — номер строки и у — номер столбца, в
которых этот элемент расположен.
Если матрица заполнена символами, то их снабжают двойным
индексом, например, ад. Первый индекс является номером строки,
а второй — номером столбца, в которых расположен элемент мат-
рицы. Так, матрица А с элементами ад может быть записана в виде
f «И «12	••• «1»^
_ «21	«22	••• «2«
4«wl «m2	••• атп j
Если из контекста ясно, каковы размеры матрицы, и важно
обозначить только общий вид элемента матрицы, то матрицу зада-
12
ют в более компактной форме: А = ||я/7||, по умолчанию полагая,
что / и j изменяются в пределах: 1 < i < т, 1 < j < п. В дальнейшем
будем записывать матрицу в развернутом виде, используя круглые
скобки, а для краткой записи — двойные прямые скобки, т.е.
й]2
_ й2]	й22
а]п У
а2” , или А =||й/7||.
^ат\ ат2
@тп ।
Определим основные действия с матрицами. Для этого прежде
всего необходимо ответить на вопрос: что означает равенство двух
матриц между собой.
Определение 2.1. Матрицы А и В называются равными, если они
имеют одинаковые размеры и элементы, стоящие на одинаковых
местах, равны между собой.
Определение 2.2. Суммой двух матриц А = || ай| и В = || Ьу\\ одинако-
вого размера т х п называется матрица С = ||с^-|| тех же размеров,
элементы которой равны суммам соответствующих элементов мат-
риц А и В:
С = А + В означает, что сц = а у + by для всех / и j (i = 1, 2, ..., т;
j= 1, 2, ..., «).
Операция нахождения суммы двух матриц называется сложени-
ем матриц.	/	2	1 \ Г 0 1 —2 Л
Пример 2.1. Пусть А = I	, В = I	I. Тогда
При сложении матриц роль нуля при сложении чисел играет
нулевая матрица 0 = ||0|| соответствующего размера, т.е. матрица,
все элементы которой равны нулю. Действительно, для любой мат-
рицы А имеет место равенство А + О = А.
Нетрудно доказать, что операция сложения матриц обладает
всеми свойствами, присущими операции сложения чисел:
Г) А + В= В + А — коммутативность сложения;
2) (Л + 7?) + С = А + (В + С) — ассоциативность сложения;
3) для любой матрицы А найдется единственная матрица В та-
кая, что А + В = О.
Очевидно, что если А = ||я/7|| и В = \\Ьу ||, то by = -ay для всех i и у.
В обоснование приведенных свойств операции сложения матриц
заметим, что операция сложения матриц сводится к обычному сло-
жению чисел для элементов матриц. Для обычных чисел эти свойст-
ва имеют место. Поэтому, согласно определению 2.2, свойства 1 — 3
могут быть легко выведены. Например, возьмем свойство 1. Имеем:
А + В = ||ау + Ьу\\ = ||by +	= В + А. ▲
13
Определение 2.3. Произведением матрицы А = ||^|| на действи-
тельное число 1 называется матрица В = ||/?(у||, элементы которой
получаются из соответствующих элементов матрицы А умножением
их на число л: /? = л/1 означает, что by = 'kaij для всех значений i и у.
Операция нахождения матрицы В называется умножением мат-
рицы А на число 1.
Пример 2.2. Пусть А =
5 8-13	.
0 7	4 и 1 = -2. Тогда
U / —о
(-2)Л =
-10 -16 2 3
О -14 12 /
В частности, при умножении матрицы А на (-1) получится мат-
рица, которая в сумме с матрицей А дает нулевую матрицу: А +
+ (-1)А = О. Эту матрицу обозначают как (-Л), определяя операцию
вычитания для матриц по формуле
А-В = А + (-1)5.
Полученная таким образом матрица называется разностью мат-
риц А и В.
Таким образом, если имеется несколько матриц А,, Л2, Ак,
то можно, применяя несколько раз операцию сложения и умно-
жения матриц на число, получить матрицу С = A,p4] + л2/12 + ... +
+ ХкАк. Такая матрица называется линейной комбинацией матриц Ah
А2, ..., А, а про матрицу С говорят, что она линейно выражается
через матрицы А}, Аъ Ак.
Умножение матрицы на число и операция сложения матриц
при совместном применении, как нетрудно доказать, обладают
следующими свойствами:
1)	Х(А + 5) = ХА + ХВ;
2)	(1 + pH = ХА + рА;
3)	(Ад) А = А(цЛ) = ц(АЛ).
Определение 2.4. Произведением двух матриц
а]2 ... а}п
й22 ... а2п
ат2 ... @тп
Ь2\
Ьп\
/?]2	...	ь}ру
/?22	•••	Ь2р
^12	...	bnp J
называется матрица
%	С}2	...
С2]	с22	...	с2р
Сщ\	Cm2	• • •	Стр ,
14
имеющая столько же строк, сколько их имеет матрица А, и столько
же столбцов, сколько их имеет матрица Д и элементы которой
находятся по формулам
Су = ^aikbkj, i = 1, 2,..., m; j = 1, 2,..., p.
*=i
Операция нахождения произведения матриц А и В называется
умножением матриц, и его результат записывается так: С = АВ.
Как следует из определения произведения двух матриц А и В.
операция умножения возможна лишь при условии, что число столб-
цов у матрицы А равно числу строк у матрицы В. При этом матри-
цы А и В не обязаны иметь одинаковые размеры. Отсюда следует,
что не всегда произведения АВ и ВА существуют одновременно, а
если существуют, то не всегда совпадают. Это видно из следующих
примеров.
(2 -3 4
Пример 2,3, А =	j
( 5 3>
I, В= 4 О
-1 2
_ Г2 • 5-3 • 4 +4 • (-1) 2• 3 + (-3)• 0 + 4• 23 Г-6 143
С = АВ= 3.5 + 4.4 + 1.(.j)	3-3 + 4 0 + 1-2	= I 30 И /
D = ВА =
5-2 + 3-3
4-2 + 0-3
(—1)-2 + 2 • 3
5-(-3) + 3-4
4-(-3) + 0-4 4-4 + 01
1-3 + 2-4 (-1)-4 + 2-1
5-4 + 31
'19
8
4
-3
-12
И
23Л
16 ,
-2
откуда видно, что АВ и ВА совершенно различные матрицы.
fV
х2
Пример 2.4. А = ||йу||, i = 1, 2, ..., m'. j= 1, 2, ..., п, Х =
«цХ| +й|2Х2 +... + «|Яхй
й2 । X] + й22х2 +... + а2лх,
£7mjX| + йт2Х2 + ... +
Если ввести в рассмотрение матрицу В =
, тогда
Ь]
, то матричное
)
соотношение АХ = В будет эквивалентно, как следует из определе-
ния равенства двух матриц, следующей системе соотношений:
15
ацХ| + а}2х2+... + а}пхп = b};
а2]Х] + а22х2 +... + а2„хп = Ь2;
Gm]X] + От2Х2 +    + атпхп — Ьт.
Если считать числа и Ь, известными, а хь х2, ..., хп — неизве-
стными, то система соотношений превращается в систему линей-
ных алгебраических уравнений. Следовательно, любую такую си-
стему можно записать в виде матричного уравнения (неизвестной
является матрица X) АХ = В.
Такая форма записи системы линейных алгебраических уравне-
ний называется матричной формой.
Пример 2,5, Рассмотрим еще один случай, когда матрица А яв-
ляется квадратной (размером т х т) матрицей специального вида
Г1 О
ООО
о >
о
1
а В= || bjj\\ — произвольная матрица, имеющая т строк. Тогда
т.е. получилось, что АВ= В. Если теперь умножить произвольную
матрицу С, имеющую т столбцов, на матрицу А, то получится
%	с12 .	••	^1т	ч	0	0 ..	.. (р		р]|	с12 .	-- с\т
С21	с22 .	• -	^2т	0	1	0 ..	.. 0	=		с22 .	• • ^2т
/«1	сл2	• • Спт	0	0	0 ..	.. 1			^п2	• • спт j
т.е. опять имеем, что СА = С. Можно показать, что матрица А
ведет себя как единица при умножении чисел: 1-5 = 51=5. По-
этому эту матрицу называют единичной матрицей порядка т и обо-
значают Ет.
Итак, Ет — это квадратная матрица размером т х т (употреб-
ляют также термин «квадратная матрица порядка /и»), имеющая
вид:
16
10	0	...	о>
0 1	о	...	о
О 0	0	...	1
По диагонали, идущей слева вниз направо, именуемой главной
диагональю, стоят единицы, а все остальные элементы матрицы
равны нулю.
Для любой квадратной матрицы /’порядка т будет справедли-
вым равенство EmF = FEm = F.
Пример 2,6, В этом примере покажем, что даже тогда, когда
существуют матрицы АВ и ВА, они, как правило, различны. Быва-
ют случаи, когда они совпадают, и в этом случае говорят, что
матрицы А и В перестановочны. Это бывает довольно редко. Возьмем
в качестве матриц А и В следующие матрицы:
, (3 2] п (5 1
' -1 0	41 4
_ Г21 1П	(14 15Э
Тогда АВ =	, а ВА =	.
I -5 —11	15 6 1
Свойства операции умножения матриц отличаются от анало-
гичных свойств операции умножения чисел именно тем, что ре-
зультат умножения матриц зависит от того, в каком порядке они
умножаются:
1)	АВ # ВА (вообще говоря, не равны);
2)	А(В + С) = АВ + АСи(В+ С)А = ВА + СА;
3)	(АВ) С = А(ВС).
Справедливость свойства 1 видна из примера 2.6. Свойства 2 и 3
могут быть без особых затруднений доказаны исходя из определе-
ний равенства двух матриц и произведения матриц. Докажем, на-
пример, свойство 2:
Аналогично доказывается, что (В + С)А = ВА + СА, а также
свойство 3.
2.2. Определители матриц
2.2.1.	Основные определения
Если А — квадратная матрица порядка п, то с ней можно свя-
зать число, называемое определителем матрицы А и обозначаемое
через |Л|. В некоторых учебниках можно встретить другой термин:
17
детерминант матрицы А и соответствующее ему обозначение clcl(/l).
Естественно, что определитель матрицы зависит от всех ее эле-
ментов, и если какой-то элемент изменить, то определитель, во-
обще говоря, изменится. Таким образом, определитель представ-
ляет собой функцию от п2 аргументов. Эта функция, записанная в
виде формулы, уже при п > 3 представляет собой очень громоздкое
выражение. Поэтому ее использование для вычисления определи-
теля нерационально. Это можно сделать гораздо успешнее, если
изучить его свойства.
Если А = ||й,у||, (/ = 1, 2, п; j = 1, 2,	я), то определитель
матрицы А обозначают как матрицу, взятую в прямые скобки:
йи я]2 ... а[ц
|^| _ Й21	а22	••• а2п
Й„1 ац1 ... а,
При п = 1, А = (яп) и по определению полагаем |Л| = ян; при
п = 2 — \А\ = йи
Й21
= йнй22 “ Й12Й2Ь При П = 3 — |Л| =
Й11
Й21
Й31
й12 й13
й22 й23
й32 й33
“ ЙНЙ22Й33 + й12й23й31 + й13й21й32 “ й13й22й31 “ й12й2]й33 “ ЙНЙ23Й32-
Как видим, с ростом п громоздкость формул, дающих выраже-
ние определителя через элементы матрицы Л, возрастает.
Для того чтобы понять, что из себя представляет определитель
/i-го порядка (так называют определитель, матрица которого име-
ет порядок л), необходимо познакомиться с таким понятием, как
перестановка.
Если имеется множество из п элементов, то его всегда можно
сделать упорядоченным, или, как еще говорят, ввести отношение
порядка, когда про любые два элемента однозначно решается воп-
рос, какой из них первый, а какой второй. Этот факт можно обо-
значить так: если из двух элементов <хи]3 первым является а, то
пишут а -< р. Например, если это множество п различных чисел, то
естественным отношением порядка будет сравнение их по величи-
не. Первым считается то из двух чисел, которое меньше.
Но возможны и другие способы введения отношения порядка.
Эти способы должны подчиняться некоторым правилам, на кото-
рых не будем останавливаться. Если имеется множество М из п
различных элементов, то будем считать его упорядоченным следу-
ющим способом: все элементы записаны в виде последовательно-
сти /], /2, 4, ..., 4, которая и определяет, какой элемент из двух — 4
или I/ — первый. Если к< /, то первым является ik. Если /ь /2, /3,..., /н —
действительные числа, будем считать, что эта последовательность
выбрана так, чтобы при k < I выполнялось неравенство 4 < О, т.е.
18
набор из п различных чисел упорядочен естественным способом:
с помощью сравнения по величине (а -< р тогда и только тогда,
когда ос < 3).
Теперь запишем последовательность из п различных элементов
не в правильном, а в произвольном порядке /а(, /И1,	. Напри-
мер, при п = 5, вместо последовательности i}, i2, /3, /4, i5 рассмотрим
последовательность /3,	/5, /2, /4. Она состоит из тех же элементов,
что и «правильная» последовательность, но записанных в «непра-
вильном» порядке.
Определение 2.5. Множество всевозможных последовательностей
из п различных фиксированных элементов /ь /2, /3, i„ называется
множеством перестановок из этих п элементов, а элементы этого
множества — перестановками.
Пример 2.7. Пусть п = 3; /, = 1; /2 = 5; /3 = 7. Множество пере-
становок из этих трех чисел состоит из шести элементов: (1,5, 7),
(1, 7, 5), (5, 1, 7), (5, 7, 1), (7, 1, 5), (7, 5, 1).
Количество перестановок с увеличением числа п довольно бы-
стро возрастает. Можно подсчитать, что число всех перестановок
из п элементов равно п\ = 1 -2-3... (п - 2)(л - 1)л (читается «эн
факториал»). Например, если п = 5, то 5! = 1 • 2 • 3 • 4 • 5 = 120, при
л=10: 10! = 3 628 800. Рассмотрим произольную перестановку, на-
пример, при п = 3 (7, 1, 5). Если взять в ней произвольную пару
чисел, например, 7 и 5, то эти числа стоят в неправильном поряд-
ке: число 5 меньше чем 7, а стоит правее него. Этот «беспорядок»
называется инверсией, которую образует пара чисел 7 и 5. Еще одну
инверсию образует пара 7 и 1, а пара 1 и 5 инверсии не образует.
Таким образом, в приведенном примере перестановка (7, 1, 5)
содержит две инверсии. Если сосчитать число инверсий в другой
перестановке, например, в (5, 1, 7), то окажется, что это число
равно единице. Следовательно, в разных перестановках число ин-
версий может быть различным.
Определение 2.6. Перестановка называется четной, если она
содержит четное число инверсий, и нечетной — в противном случае.
Утверждение. Если в перестановке поменять местами два эле-
мента, то четность перестановки изменится: если она была чет-
ной, то станет нечетной, и наоборот, если она была нечетной, то
станет четной.
Доказательство. Рассмотрим сначала случай, когда переставля-
емые элементы расположены рядом. Тогда, если они образовыва-
ли инверсию, то после перестановки эта инверсия исчезнет, а если
не образовывали инверсии, то теперь она появится. Инверсии,
которые образуют эти два элемента с другими элементами, при
такой перестановке не пострадают, их число останется прежним.
Следовательно, общее число инверсий либо уменьшится на еди-
ницу, либо увеличится. А это означает, что четность числа инвер-
сии в любом случае изменится.
19
Значит, в случае перестановки соседних элементов утвержде-
ние доказано.
Перестановку не соседних элементов, а таких, между которы-
ми имеется еще к элементов, осуществляют с помощью последова-
тельных перестановок соседних элементов. Действительно, элемент,
расположенный левее, можно последовательно переставлять с со-
седствующими справа элементами и переместить его на нужную
позицию с помощью к + 1 таких перестановок. При этом второй
переставляемый элемент окажется смещенным на одну позицию
влево. Последовательно переставляя его с элементами, стоящими
слева, можно за к перестановок перевести его на требуемую пози-
цию, для чего понадобится 2к + 1 перестановок соседних элемен-
тов. При каждой такой перестановке четность меняется, а поскольку
число 2к + 1 нечетно, четность изменится нечетное число раз. Сле-
довательно, окончательная четность перестановки изменится. ▲
Определение 2.7. Определителем квадратной матрицы А = ||afy||
порядка п называется сумма
/ .xSfcq.R,.а„)
>, (-1)
(а,,
где 5((Х], а2, , ан) — число инверсий в перестановке («], <х2,  , ан)
из п номеров столбцов матрицы А. Сумма берется по всем таким
перестановкам.
Нетрудно убедиться в том, что ранее введенные определители
первого, второго и третьего порядков удовлетворяют этому опре-
делению.
Рассматривая приведенную в определении сумму, заметим, что
ее слагаемые, называемые членами определителя, строятся по сле-
дующему правилу: все элементы произведения стоят в разных стро-
ках и в разных столбцах матрицы А, причем каждая строка и каж-
дый столбец имеют одного и только одного представителя в каж-
дом члене определителя. Общее число слагаемых в сумме равно
числу перестановок из п номеров столбцов матрицы А, т.е. пере-
становок (1, 2, ..., я), (2, 1, ..., п), ..., (п, п - 1, ..., 1). Их число
равно п\, т.е. при больших п весьма велико. Например, при п = 10
оно равно, как было указано выше, 3 628 800. Поэтому формула,
фигурирующая в определении, как правило, мало пригодна для
вычисления определителей. Но она позволяет доказать ряд свойств
определителя, использование которых приводит к более простым
приемам его вычисления.
2.2.2.	Свойства определителя
Пусть А = ||а,7|| — квадратная матрица порядка п. Рассмотрим
матрицу В = || bjj\\ порядка п такую, что для всех значений / и j имеют
место равенства by = а^-. Эти равенства означают, что элемент мат-
20
рицы В, стоящий в /-й строке и ву-м столбце, совпадает с элемен-
том матрицы Л, стоящим в у-й строке и в /-м столбце. Например,
А (°	-2
если А =
3
I „ ГО 33
, то В =	, матрица А как бы поворачивает-
ся вокруг главной диагонали. Матрица В называется транспониро-
ванной по отношению к матрице А и обозначается через АТ.
73
Пример 2,8, А = -1 2 1
, Ат =
\	7 V.
Переход от матрицы А к матрице А1
-1
2
1
(Р
4
5
называется транспонирова-
нием матрицы А. Из примера видно, что при транспонировании
строки матрицы А становятся столбцами матрицы АТ, а столбцы —
3
8
О
4
5
3
8
7
строками.
Иногда бывает так, что при транспонировании матрица не из-
меняется, т. е. Ат = А. Тогда матрица А называется симметрической
матрицей. Например, матрица
-1 7Л
-2 5
5 8
7
является симметрической матрицей. Нетрудно убедиться в том, что
матрица будет симметрической тогда и только тогда, когда ее эле-
менты, симметрично расположенные относительно главной диа-
гонали, совпадают, т.е. а^ = а^ для всех значений / и у. Теперь можно
сформулировать первое свойство определителя.
Свойство 1, Определитель матрицы А не меняется при транспо-
нировании матрицы, или |Л| = |ЛТ|.
Доказательство. Из определения 2.7 имеем
И1 = у	..
(а,,а,.а„)
Каждое произведение а1аа2а,... an<t можно переписать, переста-
вив множители так, чтобы на первом месте стоял представитель
первого столбца дР|1, на втором месте — представитель второго
столбца а^2 и т.д.
Общее произведение будет иметь вид лР)1^Р)2... а^, т.е. все мно-
жители расположены в порядке номеров столбцов, из которых они
берутся. Напомним, что второй индекс у элемента а^ — это номер
столбца, в котором он находится.
Теперь заметим, что при упорядочивании в естественное распо-
ложение вторых индексов (аь а2, , ал), мы производим из чисел
1, 2, ..., п (первых индексов) новую перестановку (рь р2, •••> 3«)-
При этом, если два числа а5 и а, не образовывали инверсию, то их
21
перестановка в правильное расположение (а, раньше, чем (/.J при-
ведет к перестановке чисел .ии. нарушающей их естественный
порядок, т.е. к образованию инверсии. Таким образом, после уст-
ранения всех инверсий в перестановке (аь а2, ..., ай) она превра-
тится в перестановку (1, 2, ..., л), а итоговая перестановка из
вторых индексов (рь р2, •••> Р«) будет иметь столько же инверсий,
сколько их имела перестановка (аь а2,  , «й).
В транспонированной матрице рассматриваемое произведение
примет вид	а его знак будет определяться числом
инверсий в перестановке (рь 02, —, Р»), которое, как мы убеди-
лись, совпадает с числом инверсий в перестановке (ос,, а2, ..., <х„),
т.е. с числом 5((Х], а2, •••> «„). Следовательно, произведение
a1pi<72p входит в сумму членов определителя |ЛТ| с тем же
знаком, что и произведение а1аа2а.... ап„п в сумму членов опреде-
лителя |Л|. Поэтому будем иметь
И = v	..“•> =
(Р,,|32....,Р„)
Замечание, Полученный результат позволяет сделать вывод о
том, что любое свойство определителя, справедливое для его строк,
будет справедливым применительно к его столбцам, и наоборот,
любое свойство, справедливое для столбцов, будет справедливым
и для его строк. Действительно, поскольку при транспонировании
матрицы определитель остается постоянным, а строки и столбцы
меняются ролями, то любое утверждение, касающееся строк, дол-
жно быть справедливым и для столбцов, и наоборот. Поэтому в
дальнейшем, учитывая это замечание, можно доказывать свойства
определителя либо только для строк, либо только для столбцов, а
справедливы они будут как для тех, так и для других.
Свойство 2, При перестановке двух строк или двух столбцов
определитель меняет знак.
Доказательство. Если переставлены /-я и у-я строки (/ < у), то в
новом определителе каждый член может быть получен из соот-
ветствующего члена старого определителя: например, в члене
alraa2c(,... ajn ...aja ... а,,,. следует переставить сомножители а,п и aja .
Таким образом, члены нового определителя с точностью до знака
совпадают с членами старого. Выясним, как обстоит дело со зна-
ками. Перестановка (аь а2, •••> %> •••>	•••> определяющая
знак при члене старого определителя, отличается от перестановки
(«I, а2, ..., ау, а,, ..., ай), определяющей знак при члене нового
определителя, тем, что в последней переставлены два элемента: а,-
и ctj. Таким образом, эти две перестановки имеют разную четность.
22
Это приводит к тому, что знаки при рассматриваемых членах оп-
ределителя в старом и новом определителе будут различными, что
и доказывает изменение знака у всего определителя. Доказатель-
ство проведено для случая, когда переставляются две строки. В силу
сделанного выше замечания результат будет справедлив и для двух
столбцов. ▲
Свойство 3, Если в матрице определителя содержится две оди-
наковые строки, то такой определитель равен нулю. Аналогичный
результат верен и для столбцов.
Доказательство. Если переставить две одинаковые строки, то с
одной стороны, поскольку матрица определителя останется неиз-
менной, определитель не изменится, а с другой, в силу свойства
2, он должен изменить знак. Это означает, что |Д| = -|Л|. Такое
возможно только при |Л| = 0. ▲
Свойство 4, Если в матрице определителя содержится строка,
состоящая из одних нулей, то такой определитель равен нулю. Ана-
логичный результат верен и для столбцов.
Замечание, Строка, состоящая из одних нулей, называется ну-
левой строкой. Аналогично именуется нулевым столбец, состоя-
щий из одних нулей.
Доказательство. Исходя из определения 2.7, представим его в
виде суммы:
И1 = х	.
..а„)
Теперь замечаем, что в каждом слагаемом один из множите-
лей — представитель нулевой строки, равен нулю. Следовательно,
все слагаемые рассматриваемой суммы равны нулю. Поэтому равна
нулю и вся сумма, т.е. |Л| = 0. ▲
Свойство 5, Если какая-нибудь строка или столбец содержат
общий множитель, то его можно вынести за знак определителя.
2
Например, 3
0
3	7	2	3	7
21	6	=3	1	7	2
5	3	0	5	3
Доказательство. Пусть /-я строка матрицы определителя имеет
вид («;1 «/2 ••• ain) = C-Ci ^а'/2	Исходя из определения
определителя, представим его в виде суммы:
И = V й|„]й2а1...а„г (-!)«“'“.........“•) =
(И1,«2.П„)
V"1	1	'	i	..«„)
— (— 1)
(а,,
23
Вынося общий множитель X из-под знака суммы, получим
И = х X	..
..«„)
где |Л'| — определитель, матрица которого отличается от матрицы
А тем, что /-я ее строка имеет вид: (я'[ а'2 ... а'п). ▲
Свойство 6. Если в матрице определителя содержатся две про-
порциональные строки или два пропорциональных столбца, то
такой определитель равен нулю.
Пропорциональность двух строк означает, что одна из них по-
лучается из другой путем умножения ее на некоторое число. На-
пример, строки (1 3 5 7) и (-3 -9 -15 -21) пропорциональны, так
как вторая из них получается из первой путем умножения всех ее
элементов на число (-3), а первая получается из второй путем ум-
ножения на число (”^)« Аналогично понимается пропорциональ-
ность двух столбцов.
Доказательство. Пусть /-я строка матрицы получается из у-й стро-
ки путем умножения последней на некоторое число 1. Тогда, пользу-
ясь свойством 5, можно вынести за знак определителя общий мно-
житель из /-й строки: число 1. Матрица оставшегося определителя
|Л'| будет иметь две одинаковые строки. По свойству 3 такой опре-
делитель равен нулю. Следовательно,
H = zH = o. ▲
Свойство 7. Если в матрице определителя А какая-либо строка
представлена как сумма двух строк:
(ап ai2 ... аД = (a'i} + а”}, a'i2 + а"2,	<4 + «") =
= (а<| а'2 ... a'fl) + (а'] а'2 ... а"),
то определитель этой матрицы может быть представлен в виде сум-
мы двух определителей, у каждого из которых в матрице А эта
строка заменена одной из слагаемых строк. Аналогичный результат
справедлив и для столбцов.
Доказательство. Из определения определителя получается ра-
венство
И= ±	..“> =
(ге1,«2.а„)
= Z a]na2ni...(a'Cii + а-а)...апПп	..=
(otj.Иг])
V'’	/	/ 1 \S(a., а,,...,а..)
~	   Qa,    ^па„ (“V	+
((Л.ос,,
+ Ц	  а'П1 ...апПп	= |х'| + |А"\,
..«„)
24
где |Л'| и |Л"| — определители, матрицы которых получены из мат-
рицы А заменой /-й строки строками (а'п а'2 ... а'„) и (а"} а”2 ... a"f!)
соответственно. ▲
Свойство 8, Определитель не изменится, если в его матрице к
какой-либо строке прибавить другую строку, умноженную на лю-
бое число. Аналогичный результат справедлив и для столбцов.
Доказательство. Пусть в матрице определителя А к /-й строке
прибавляется у-я строка, умноженная на число X. Эта преобразо-
ванная /-я строка будет иметь следующий вид: (й(1 + kaj}, ai2 +
..., ain + ‘кцД, т.е. будет суммой двух строк. Используя свойство 7,
определитель можно представить в виде суммы двух определителей.
Первый из них равен |Л|, второй — нулю как определитель, в
матрице которого две строки пропорциональны: /-я и у-я строки.
Следовательно, определитель преобразованной матрицы равен |Л|,
т.е. исходному. ▲
Рассмотрим далее некоторую систему строк Вь В2, Вк, где
В, — строки, которые можно рассматривать как матрицы, состоя-
щие из одной строки и п столбцов, i = 1, 2, ..., к. Пользуясь опера-
циями сложения матриц и умножения их на число, можно пост-
роить новую матрицу-строку по формуле С = k\Bl + /_2/?2 + ... +
+ kkBk, где 1], 12, ..., кк — произвольные числа.
Эта строка С называется линейной комбинацией строк В\, В2, ..., Вк.
Свойство 9, Определитель матрицы не изменится, если к ка-
кой-либо ее строке прибавить линейную комбинацию других ее
строк. Аналогичный результат справедлив и для столбцов.
Доказательство. Получить матрицу с прибавленной к какой-то
строке линейной комбинацией других строк к}В} + f.2B, + ... + ккВк
можно, последовательно прибавляя сначала к\В{, затем к2В2 и т.д.
Последней будет прибавлена строка ккВк. На каждом шаге опреде-
литель не меняется в силу свойства 8.Следовательно, он не изме-
нится, когда будет закончено прибавление всех слагаемых, т. е. всей
линейной комбинации + f.2B, + ... + ккВк. ▲
Свойство 10. Если какая-либо строка матрицы определителя
может быть представлена как линейная комбинация остальных
строк, то в этом случае определитель равен нулю. Аналогичный
результат справедлив и для ее столбцов.
Доказательство. Если какая-то строка представляется как ли-
нейная комбинация других строк, то, не изменяя величины оп-
ределителя, можно вычесть (прибавить, умножив на -1) эту ли-
нейную комбинацию из этой строки. В результате проведенной
операции строка станет нулевой и, в силу свойства 4, определи-
тель равен нулю. Следовательно, и исходный определитель равен
нулю. ▲
Прежде чем рассматривать очередное свойство определителя,
введем некоторые новые понятия. Представим определитель в сле-
дующем виде:
25
и= \	....“> =
(r,.r,,..,r„)
= &]l	7,	^2a,_^3as    ^na„ (— Q	+
(r,, «з.re„)
/ 1,5i'fil.l,iL.r)
** &2]	7 , ^la,^3rei    &па.„ (—0	+
(r, , Rj.«„)
+.................................................+
/ 1 \ ‘>’(«1 , «5, ..., R,,_,J)
**^«]	/ ,	^la,^3«i  ^(л-1)а„ (—1)
(r, , R j.
Поясним это представление. Формула
/ i45(r,.R,.R„)
>, a{na2a,...an(tis (-1)
(а,, R;,...,a,.)
по которой находят величину определителя, представляет собой
сумму слагаемых, каждое из которых определяется перестановкой
(«I, «2, •—> «л), образованной из чисел 1, 2, п. Число 1 в пере-
становке может находиться как на первом месте, так и на любом
другом.
Первая группа слагаемых, отщепленная от всей суммы,
V’’	/ <45(1, а„я, а,,)
«Л X	(“I)
(r,,R3..Rrl)
— слагаемые, которые порождаются перестановками вида (1, а2,
«з, ..., <х„), т.е. перестановками, у которых число 1 стоит на первой
позиции. Поскольку <Х] = 1 у всех членов определителя этой груп-
пы, число а} [ оказывается общим множителем, и его можно выне-
сти за знак суммы (или, как говорят, вынести за скобки).
Аналогично строится вторая группа слагаемых: это те слагае-
мые в общей сумме, которые порождаются перестановками вида
(«I, 1, аз, ..., а,(), т.е. перестановками, у которых число 1 стоит на
второй позиции. Ясно, что ни одно слагаемое этой части суммы не
входит в первую группу, поскольку число 1 не может находиться
одновременно и на первой, и на второй позициях в перестановке
(oti, «2, •—> осл) (напомним, что эта перестановка представляет со-
бой поставленные в некотором порядке числа 1, 2, ..., л, и одно и
то же число дважды присутствовать в ней не может). Таким образом,
во второй группе слагаемых выполняется равенство а2 = 1  Поэтому
все члены определителя этой группы содержат общий множитель
«21, который можно вынести за знак суммы. Последующие слагае-
мые группируются по такому же принципу: к-я группа слагаемых
представляет собой объединение тех членов определителя, кото-
рые находятся перестановками с числом 1 на к-й позиции. Анало-
26
гично тому, как это было в случае, когда к= 1 и 2, у всех слагаемых
возникает общий множитель яА1, который выносится за знак суммы.
Рассмотрим первую группу слагаемых:
..«„)
«11 X	«№„ (-1)
«з.иг1)
Эта сумма напоминает выражение для определителя порядка
(«- 1)
«22	«23	•••	«2»
Л/,, =	Й32	й33	-	йз",
««2	«нЗ	•••	«ня
умноженного на йи.
Действительно, все слагаемые с точностью до знака совпадают
с членами этого определителя. Остается пока неясным вопрос, с
правильным ли знаком входят в первую группу слагаемых
V’’	/ i\5(l, а„ «з.а,.)
X «2а2«3гп «»«„ (-1)	’
(«,, Г<з.«„)
произведения а2а,а3ах... а„ап. В определитель
«22	«23	•••	«2н
«32	«33	•••	«Зя
«я2 «яЗ ••• «ля
эти слагаемые входят со знаком (-1)5, где Л”7 — число инверсий в
перестановке (а2, <Хз, ан). Но это число инверсий совпадает с
числом инверсий в перестановке (1, а2, а3, ..., а„), так как число
1 никаких новых инверсий по сравнению с перестановкой (а2, а3,
..., оу) не образует. Поэтому для первой группы слагаемых У =
= 5(1, ос2, «з, ..., а„) и, следовательно, знаки у всех слагаемых
совпадают со знаками членов определителя Мп .Таким образом,
для первой группы слагаемых оказывается справедливым равенство
«И X «2а2«Заз---^„(-1)
«22	«23	••• «2я
«я2 «яЗ • • • апп
27
При аналогичном анализе второй группы слагаемых
Х’’	/ < x-STct, ,1,«з.а,.)
«2] L а\па^...апП:1 (-1)
(«I , R3.«„)
выясняется, что перестановки (осн <х3, ..., ая) и (а], 1, а3,	<х„)
имеют разную четность (если одна из них четна, то другая — не-
четна). Действительно, по сравнению с перестановкой (oq, «з,
ал) перестановка (осн 1, <х3, ..., а„) имеет на одну инверсию боль-
ше: пара oq, 1 образует дополнительную инверсию. Следователь-
но, сумма
Л й1г<]й3из...<7„Ии (-1)
(а,, «з.иг])
и определитель
«|2	«13 ... «ь,
°32	й33	•••
Яп1 ... £1цц
отличаются между собой знаком. Поэтому для второй группы сла-
гаемых будет выполняться равенство
При рассмотрении третьей группы слагаемых обнаруживается,
что перестановки (oq, а2, oq, ..., (/.,.) и (oq, oq, L ос4, •••, «л) отли-
чаются на две инверсии: пары oq, 1 и oq, 1 образуют две дополни-
тельные инверсии по сравнению с первой перестановкой. Поэтому
для третьей группы слагаемых имеем
28
Нетрудно убедиться в том, что в дальнейшем при рассмотре-
нии последующих слагаемых чередование знаков сохранится, а все
определители МА1 вычисляются по следующему правилу: их мат-
рицы получаются из матрицы определителя |Л| вычеркиванием пер-
вого столбца и строки с номером к. Таким образом, |Л| = ах-
- я21Л/2| + «з]^3] - ••• + й«1(_ 1)"+1Мн- Определители Мк}, к= 1, 2, ..., /?,
называются минорами. Все они имеют порядок на одну единицу
меньше, чем порядок определителя |Л|, т.е. (п - 1). Если миноры
Мк] домножить на (-1)А+1, то получатся числа = (-1 )к+]Мк], на-
зываемые алгебраическими дополнениями к элементам матрицы
ак1. Таким образом, пришли к очередному свойству определителя.
fl
Свойство 11, |Л| = ак ]ЛА-|. Это представление называется разло-
*=i
жением определителя по первому столбцу. С помощью этого разложе-
ния вычисление определителя и-го порядка сводится к вычислению
п определителей порядка (п- 1). Например, имея формулы для на-
хождения определителей третьего порядка, можно получить опре-
делители четвертого порядка. А умея вычислять определители чет-
вертого порядка, можем получить определитель пятого и т.д.
Пример 2,9, Пусть требуется вычислить определитель
10 0 0
UI- 0100
11 0 0 10'
0 0 0 1
Разложив его по первому столбцу, получим
	1 0 0		0 0 0		0 0 0		0 0 0		1 0 0	
и = 1	0 1 0	-0	0 1 0	+ 0	1 0 0	-0	1 0 0	=	0 1 0	= 1
	0 0 1		0 0 1		0 0 1		0 1 0		0 0 1	
Приведенное выше преобразование определителя единичной
матрицы четвертого порядка в определитель единичной матрицы
третьего порядка, показывает, что такое преобразование можно
провести с определителем единичной матрицы любого порядка.
Поэтому для любого п будет выполняться равенство |£л| = | Еп_\ | =
= |£л_2| = ... = |£2| = 1-Е]I = 1- Таким образом, определитель единичной
матрицы любого порядка равен 1.
В силу замечания к свойству 1 имеет место аналогичное разло-
п
жение определителя по первой строке: |Л| = ^а]кА1к, где А]к =
к=]
= (-1 )*+|М]к, а М1к - миноры, т.е. определители порядка (п - 1),
матрицы которых получаются по тому же правилу: из матрицы
определителя |Л| вычеркивается первая строка и £-й столбец.
29
Пусть теперь в матрице определителя |Л| выбран произволь-
ный столбец с номером у, (J — любое число от 2 до п). Тогда
можно последовательной перестановкой соседних столбцов поста-
вить его на первое место. Таких перестановок, называемых смеж-
ными, придется сделать (у - 1). Поэтому преобразованный опреде-
литель |Л| будет отличаться от исходного множителем (-I)7-1, т.е.
|Л| = (-1)7-||Л|. Разложив определитель | А\ по первому столбцу, по-
лучим
Ml = (-1)>-'| А\ = (-I)'-' f akJ AtJ, где AkJ =
k=l
В данном случае числа Mkj- равны определителям (п - 1)-го по-
рядка, матрицы которых получаются из матрицы определителя |Л|
вычеркиванием к-й строки и у-го столбца.
Определители Мц называются дополнительными минорами к эле-
ментам матрицы определителя |Л| ац, а числа Ац =	—
алгебраическими дополнениями к элементам ац. Тогда рассмот-
ренное выше равенство можно записать в такой форме: |Л| = QkjAkj 
к=\
Оно вполне аналогично разложению по первому столбцу с той
только разницей, что здесь у — любое число. Естественно называть
это представление разложением определителя по у-му столбцу.
В силу замечания к свойству 1 аналогичное разложение спра-
ведливо и для любой /-й строки:
М| = 2>д4ь	(2.1)
к=\
называемое разложением определителя |Л| по /-й строке (/ — любое
число от 1 до п). Таким образом, определитель может быть разло-
жен по любому столбцу или по любой строке матрицы А. Это свой-
ство определителя позволяет более рационально организовать его
вычисление.
Пример 2,10. Пусть требуется вычислить определитель
12 3 4
2 3 5 6
3 5 8 2’
-13 5 1
Прежде чем раскладывать определитель по какой-либо строке
или столбцу, преобразуем его, пользуясь свойством 9, в частности
тем, что можно к любой строке прибавить другую строку, умно-
женную на число, не изменив при этом величины исходного
30
определителя. Прибавим ко второй строке первую строку, умно-
женную на (-2). Получим
12	3	4
О -1	-1	-2
3 5	8	2
-13	5	1
Далее прибавим к третьей строке первую, умноженную на (-3).
Получим
12	3	4
\А\ =	°	-1	-2	.
11	0-1-1	-10
-13	5	1
Еще один шаг: прибавление к последней строке первой дает
12 3	4
0 -1 -1 -2
0 -1 -1 -И
0 5 8	5
После таких преобразований разложение определителя по пер-
вому столбцу будет содержать только одно слагаемое (все осталь-
ные равны нулю). Получим
И = 1-(-1Г
-1 -1 -2
-1 -1 -10
5 8	5
-1 -1 -2
-1 -1 -10
5 8	5
Этот определитель уже можно вычислить, пользуясь формулой
для определителя третьего порядка. Имеется другой путь — про-
должить преобразование его матрицы по той же схеме: делая нуля-
ми элементы первого столбца. Вычитая первую строку из второй,
получим
и=
-1 -1 -2
0 0-8
5 8 5
Прибавляя к последней строке первую, умноженную на 5, по-
лучим, снова разлагая по первому столбцу,
31

-1
о
о
-1
о
3
-8 =(-l)(-l)l+l
-8
5
= -24.
Замечание. Метод вычисления определителей, проиллюстри-
рованный приведенным примером, называется методом Гаусса.
Существуют и другие методы, основанные на использовании рас-
смотренных выше свойств определителя. Некоторые из них могут
оказаться более эффективными, чем метод Гаусса, в каких-то ча-
стных случаях. Но в отличие от них метод Гаусса универсален и,
будучи несколько модифицирован, дает хорошие результаты. По-
этому он находит широкое применение в вычислительной практике.
Рассмотрим еще один пример, который окажется полезным в
дальнейшем.
Пример 2.11. Квадратная матрица называется треугольной, если
все ее элементы, расположенные либо выше, либо ниже главной
диагонали, равны нулю. Вычислим определитель такой матрицы. Имеем
	«и	ап 	«!<«-])	«1л
	0	«22	..	«2(л-])	
				
	0	0 .	«(л-1)(л-])	а(п-\)п
	0	0 .	0	апп
Разложив этот определитель по первому столбцу, получим
	«22	«23		«2<л-])	«2»
	0	«33		«3(л-1)	«Зл
И = «и				
	0	0 .	••	«(Л-1)(Л-])	«(л-])л
	0	0 .	0	«лл
Далее, разложив определитель (/? - 1)-го порядка по первому
столбцу, получим
	«33	«34	«3(л-1)	«Зл
	0	«44	..	«4(л-])	«4 л
|Л| - й[]П22				
	0	0 .	«(«-])(/?-])	«(л-])л
	0	0 .	0	«лл
Продолжая эти действия, в итоге получим
32
|Л| - й[]«22---
т.е. определитель треугольной матрицы равен произведению эле-
ментов матрицы, стоящих на главной диагонали. Или еще говорят
так: определитель равен произведению диагональных элементов.
Если матрица такова, что все ее элементы, стоящие выше главной
диагонали, равны нулю, то транспонирование матрицы приводит
этот случай к рассмотренному выше.
Еще одно свойство определителя, которое важно отметить, по
содержанию близко к свойству 11. Предположим, что в матрице
определителя какую-либо строку, например строку с номером /,
заменили другой строкой с номером у. Тогда в матрице нового оп-
ределителя будут две одинаковые строки. В этом случае, согласно
свойству 3, определитель будет равен нулю. Разложив его по /-й
строке, получим равенство
у1, ajk-^-ik = О,
Хг=1
которое составляет содержание очередного свойства определителя.
Свойство 12. Сумма произведений элементов строки матрицы
определителя на алгебраические дополнения к элементам другой
строки равна нулю. Аналогичный результат верен и для столбцов.
Свойство 13. Если матрица С является произведением двух квад-
ратных матриц А и В, то ее определитель равен произведению
определителей этих матриц, т.е., если С = АВ, то |С| = |Л||5|.
Доказательство этого свойства несколько громоздко и поэтому
здесь не приводится.
2.3. Обратная матрица
Для дальнейшего потребуется такое понятие, как присоединен-
ная матрица.
Определение 2.8. Пусть А — квадратная матрица порядка п. Мат-
рица А*, получающаяся из матрицы А заменой всех ее элементов
на алгебраические дополнения к этим элементам, называется при-
соединенной матрицей по отношению к матрице А.
Таким образом, А* = || Ду||, где Ау — алгебраические дополнения
к соответствующим элементам ау матрицы А.
Определение 2.9. Квадратная матрица А называется невырожден-
ной, если |Л| не равен нулю. В противном случае матрица называет-
ся вырожденной.
Определение 2.10. Матрица А 1 называется обратной по отноше-
нию к квадратной матрице А, если и только если выполняются
равенства A~lA = AA~l = Е, где Е — единичная матрица.
33
Теорема 2.1. Если существует обратная матрица Л-1, то она един-
ственна.
Доказательство. Предположим противное, что существует еще
одна матрица В такая, что ВА = АВ = Е. Тогда, пользуясь тем, что
при умножении матриц единичная матрица ведет себя как едини-
ца при умножении чисел, получим В = ЕВ = (А 'А)В = А~1(АВ) =
= А-'Е = А-'. А
Теорема 2.2. Для того чтобы существовала матрица А~' — обрат-
ная по отношению к матрице Л, необходимо и достаточно, чтобы
матрица Л была невырожденной, т. е. чтобы |Л| # 0.
Доказательство. Докажем сначала необходимость. Если Л-1 су-
ществует, то пользуясь свойством 13 (определитель произведения
матриц равен произведению их определителей), получим 1 = \Е\ =
= |ЛЛ-1| = |Л||Л-’|. Из этого равенства следует, что |Л| # 0, иначе
справа стояло бы число, равное нулю, а слева — единице. Необхо-
димость условия | Л | 0 доказана.
Для доказательства достаточности условия | Л| # 0 для существо-
вания обратной матрицы произведем умножение матрицы Л на
матрицу (Л*)т, где
матрица Л* — присоединенная по отношению к Л:
	ап •	.. а}пу		Л2]	Ди	.. ЛР		Ди	С12 .	„ А •  е]п
а2\	«22 .	• • ®Лп	л12	Л22	Дз2 •	• • Д;2	=	С21	«22	•	«2/7
	«л2	• • @пп 1		А1п				Д"1	сп2	спп 2
Пусть i # /, тогда с^ = У, aikAjk = 0, в силу свойства 12 определи-
*=1 п
теля. Если же i = j, то с/7 = ^aikAik = |Л|, согласно формуле (2.1).
Хг=1
Таким образом, матрица С = Цс^Ц имеет диагональный вид:
'|л|	0	0	...	0
с= о	|л|	о	...	о
о	о	...	|л|;
т.е. все элементы матрицы, расположенные вне главной диагона-
ли, равны нулю. Нетрудно проверить, что умножение матриц (Л*)т
и Л в другом порядке также дает диагональную матрицу С. Следо-
♦ т	1
вательно, если матрицу (Л ) умножить на число то будут спра-
ведливыми равенства:
34
Это означает, что матрица | Дт(Л*)т | является обратной по
Ijni )
отношению к матрице А. Таким образом доказана и достаточ-
ность. ▲
Замечание, При доказательстве достаточности условия |Л| #= О
было не только доказано существование обратной матрицы, но и
фактически указан способ ее построения. Этот способ называется
методом присоединенной матрицы.
Пример 2.12. Найдем указанным способом обратную матрицу к
матрице А:
	44	13
А =	41	40
	28	27
12>
41
27
/
Сначала вычисляем определитель матрицы А. Имеем
14 13
41 40
28 27
12
41
27
Вычтем из третьей строки первую, умноженную на 2, а из вто-
рой — первую, умноженную на 3. Получим
14
И= -1
о
13 12
1 5
1 3
Теперь к первой строке прибавим вторую, умноженную на 14.
Получим
о
-1
о
27 82
1	5
1	3
Разложив определитель по первому столбцу, найдем
H = (-i)(-i)2+1
27 82
1	3
27 82
1	3
и=
и=
Второй этап — это вычисление элементов присоединенной мат-
рицы. Имеем
35
Л] 2
40
27
41
27
= 27
40
1
41
1
= 27(40-41) = -27;
= (-D
41
28
41
27
= 41
1
28
1
27
= 41(27-28) = -41;
Лз -
41
28
40
27
40
27
= (27-40) = -13;
Л. = (-1)
13
27
12
27
= -27
13 12
1 1
= -27(13- 12) = -27;
Л22 -
14
28
12
27
12
27
= (54-12) = 42;
Л2з = (-D
14
28
13
27
13
27
= -(27-13) = -14;
^31 -
13
40
12
41
1
-1
12
41
= (41+ 12) = 53;
Л32=(-1)
^зз -
14
41
14
41
12
41
14 12
1 1
= -41(14-12) = -82;
13
40
13
40
= (40-13) = 27.
A
1
1
2
1
1
1
Определители второго порядка были вычислены путем предва-
рительного вычитания второго столбца из первого.
Таким образом, присоединенная матрица имеет вид:
А
"-27
-27
53
41
42
-82
-13>
-14
27
Разделив ее элементы на |Л| = -1 и
ние, находим обратную матрицу:
произведя транспонирова-
А~] =
27
-41
13
27
-42
14
82
-27
36
2.4. Системы линейных алгебраических уравнений
2.4.1. Основные понятия
Системами линейных алгебраических уравнений называются
системы уравнений следующего вида:
ЯцХ] +я12х2 + ... + я1„х„ =ь}-
а2]Х[ + й22х2 +... + а2пхп = />2;	п
йт]Х[ + йи2а'2 +... + атпхп — Ьт,
где X], х2, х„ — неизвестные величины, а числа а у и bh 1 < i < т,
1 < j < и заданы. Матрица А = ||а^|| называется матрицей системы
(2.2), а матрица
pi
)
— матрицей правых частей системы (2.2). В примере 2.4 (см. 2.1)
было показано, что если ввести в рассмотрение матрицу
то матричное уравнение АХ = В оказывается эквивалентным систе-
ме (2.2).
Определение 2,11. Система (2.2) называется совместной, если у
нее есть хотя бы одно решение, и несовместной, если решений
нет.
Простейшие примеры показывают, что существуют как совме-
стные, так и несовместные системы линейных уравнений.
Пример 2.13. Система
X] + х2 =1
Зх[ + 2х2 = 4
совместна, поскольку у нее есть решение: X] = 2, х2 = -1.
Пример 2.14. Система
Х[ + х2 = 1
Х| + х2 = О
несовместна, так как не существует таких чисел Х[ и х2, которые в
сумме давали бы одновременно и 0, и 1.
37
2.4.2. Правило Крамера
Рассмотрим частный случай системы (2.2): систему, у которой
число уравнений т равно числу неизвестных п. Тогда матрица си-
стемы А будет квадратной. Пусть определитель этой матрицы, на-
зываемый определителем системы, отличен от нуля. Покажем, что
такая система всегда совместна, какие бы правые части у нее ни
были. А именно, докажем следующую теорему.
Теорема 2.3. Если |Л| О, (А = ||Лу||), то система
+й|2х2+ +	= Ь{;
а21х\ + а22х2 + ••• + а2пхп ~
<Wi + ап2х2 + ... + аппхп =ЬЦ
при любых значениях Ь2, ..., Ь„ совместна, и ее решение един-
ственно.
Это решение может быть найдено по правилу Крамера:
х, = i= 1, 2, ..., п,
А
где А = |Л|; а А( равно определителю, который получается после
замены в матрице А /-го столбца столбцом из правых частей

Доказательство. Поскольку |Л| =# 0, то у матрицы А существует
обратная матрица А~]. Умножим матричное уравнение АХ = В слева
на матрицу Л-1. Получим А~'АХ= А~'В, или ЕХ=А~] В, или Х=А~1В.
Это равенство показывает, что если решение X существует, то оно
обязано быть равным А~] В. Следовательно, решение А единствен-
но. С другой стороны, подстановка Х= А~'Вв матричное уравнение
обращает его в тождество. Значит, X = А~]В является решением, т. е.
матричное уравнение имеет решение. Поэтому система (2.3), эк-
вивалентная матричному уравнению АХ = В, также имеет решение
и оно единственно. Пользуясь выражением А~[ через присоединен-
ную матрицу, столбец из неизвестных х2, ..., х„, с использова-
нием формулы Х= А~]В, можно представить в следующем виде:
Л2] Л31
л22 л32
Дэл
Ап]
А„ 2 b2
38
^Л|]6] + A2]b2 + A3]b3 + ... + A„{b„
A\ib\ + A22b2 + A3 2 b3 + ... + An2b„
...................................
A Ahb] + A2ib2 + A3jb3 +... + A,,^
^ A[ftbi + Л2я/ъ + A3nb3 +... + A„„blt
Теперь, если определитель Af разложить по /-му столбцу, то
получится /-я строка этой матрицы. Действительно, имеем
ЙИ	й12	•••	й1{(-1)	^1	й1((+1)	•••	а]п
i?2i	й22	...	«2(/-в	Ь2	й2((+])	...	a2ll
а„\	ап2	...	йя(/_| )	b„	CLn(i+\)	• • •	апп
= Afr-bf + A2ib2 + A3lb3 + ... + Anib„.
Таким образом,
или х. = — , i = 1, 2, ..., п. ▲
А
Пример 2.15. Пусть дана система линейных алгебраических урав-
нений
Эх, - 2х2 + А'з = -11;
2х] + Зх2 - 5х3 = 0;
Х| - х2 + 6х3 = 1,
которую требуется решить, используя правило Крамера.
Решение. Чтобы применить правило Крамера, сначала следует
вычислить определитель системы и убедиться в том, что он отли-
чен от нуля. Имеем
А = |Л| =
3 -2 1
2 3-5
1 -1 6
= 54 + 10 - 2 - 3 + 24 - 15 = 68 ^0.
39
Затем вычисляются определители Л], А2 и А3:
-11-2 1
Л, = 0	3 -5 = -198 + 10 + 0- 3- 0 + 55 = -136;
1	-1 6
3-11 1
А2 = 2 0 -5 = 0 + 55 + 2 - 0 + 132 + 15 = 204;
1	1	6
3-2-11
А3 = 2 3	0 =9 + 0 + 22 + 33 + 4 + 0 = 68.
1 -1 1
В итоге имеем:
X] =
А( _ 136
Л " 68
а2
Л
204	А3 68
~68=3’ "3 = Т = бГк

Замечание, Доказанная теорема дает достаточное условие со-
вместности системы. Это условие не является необходимым. Равен-
ство определителя системы нулю не означает, что система несов-
местна. Бывают системы, которые совместны несмотря на то, что
их определитель равен нулю.
Пример 2,16, Пусть дана система уравнений
( X, + хг = 1;
|2х[ + 2х2 = 2.
Ее определитель
1 1
2 2
= 0,
но она имеет решение, например X] = 0, х2 = 1.
Пример несовместной системы с определителем, равным нулю,
был приведен выше (см. пример 2.14). Таким образом, если опре-
делитель системы равен нулю, то про совместность системы ниче-
го сказать нельзя, требуется дополнительное исследование этого
вопроса.
2.4.3. Метод Гаусса исследования и решения
систем линейных уравнений
Переходим к рассмотрению систем линейных алгебраических
уравнений общего вида, когда число уравнений, вообще говоря,
не равно числу неизвестных.
40
Напомним одно определение, известное из курса математики
средней школы.
Определение 2.12. Две системы линейных алгебраических урав-
нений относителвно неизвестных хь х2, хп называются эквива-
лентными тогда и только тогда, когда любое решение первой си-
стемы является решением второй и, наоборот, любое решение вто-
рой системы является решением первой.
В случае, когда не применимо правило Крамера, оказывается
целесообразным преобразование системы к некоторому специаль-
ному виду. При этом преобразованная система оказывается экви-
валентной исходной. Основанием для преобразований системы слу-
жит следующая теорема.
Теорема 2.4. Если в системе линейных алгебраических уравнений
йцх1 + апхг+... + а[пх„ = /?,;
й21Х| + я22х2 + ... + а2пх„ = Ь2;
Дт1Х\ + ат2Х2 + • •. + ИтпХп — Ьт
к одному из уравнений прибавить другое, умноженное на любое
число, то полученная таким образом новая система будет эквива-
лентна исходной.
Доказательство. ПустьХ], х2,..., хп — решение исходной системы.
Это означает, что все уравнения системы при подстановке в
них этих чисел обращаются в тождества. При умножении тожде-
ства (его левой и правой части) на число оно остается тождеством.
При сложении двух тождеств также получается тождество. Поэтому
числа х2, •••> будут удовлетворять всем уравнениям новой
системы, поскольку преобразованное уравнение, в силу сказан-
ного выше, при подстановке в него этих чисел также будет тожде-
ством. Следовательно, любое решение исходной системы является
решением преобразованной. Чтобы убедиться в этом, достаточно
заметить, что последняя может быть получена из преобразованной
с помощью тех же операций: надо умножить ранее прибавленное
уравнение на то же самое число, но со знаком минус, и снова
прибавить его к преобразованному ранее уравнению. В итоге послед-
нее уравнение превратится в исходное, как и вся система. Следо-
вательно, и к исходной системе применимы использованные выше
доводы, что позволяет сделать вывод о том, что любое решение
преобразованной системы является решением исходной. Если ис-
ходная система несовместна, то будет несовместной и преобразо-
ванная система, как это следует из последнего рассуждения. ▲
Доказанная теорема дает возможность преобразовать исходную
систему таким образом, чтобы вопрос о ее совместности легко
разрешался и просто находились сами решения. Заметим только,
что в число действий по преобразованию системы можно вклю-
41
чить такие, как перестановка уравнений и перенумерация неизве-
стных. Эти действия также приводят к системе, которая будет эк-
вивалентна исходной. Например, очевидно, что системы
Z = 1
z + у = 2
z + у + х = 3
х + у + z = 3
у + z = 2
2 = 1
и
эквивалентны.
Рассмотрим случай, когда преобразованная система имеет сле-
дующий вид:
ЙИХ| + й12Х2 + ... + й1йхй =Ьу
а22х2 +... +а2„х„ = Ь2;
(2.4)
аппхп Ьп,
где йи * 0; й22 * 0;...; апп * 0. Решение этой системы легко находится.
Действительно, из последнего уравнения сразу получается:
Ь„
В предпоследнем уравнении
которое также сразу находится:
1
неизвестным остается только х,
(^-i - й(1
Й(Я-1)(Л-])
Далее, переходя к предыдущему уравнению, имеем ту же ситу-
ацию: все неизвестные кроме одного уже найдены, а коэффици-
ент при ненайденном х„_2 отличен от нуля. Поэтому х;; 2 находится
по аналогичной формуле:
(^«-2 ~	“ а(н-2)пХп )
й(«-2)(«-2)
Таким образом, все неизвестные хь х2, ..., хй однозначно опре-
деляются. Система оказалась однозначно разрешимой (решение су-
ществует и оно единственно).
Возможен случай, когда преобразованная система имеет следу-
ющую, так называемую верхнюю трапециевидную форму:
й22х2 + ... + а2гхг + а2(г+])хг+] + ... + й2йх„ = by,
где й] । #=0; й22 * 0; ...; агг ф 0.
42
Систему можно переписать в виде
«h*i + anx2+... + a}rxr =-а^}хг+{-...-а}пхп+Ь{\
а21х2+... +а2гхг = -a2(r+i)xr+l -...-а2пх„ + Ь2;
arrxr = -аг^+[)Хг+] -... - а!1Их„ + bn.
Неизвестные хь х2, ..., хг называются базисными, a хг+н хг+ъ ...,
хп — свободными. После такого преобразования системы видно, что
она совместна и решений у нее бесконечно много. Действительно,
какие бы значения ни были даны свободным неизвестным xr+h
хг+2,	х„, базисные неизвестные хь х2, ..., хг однозначно нахо-
дятся, поскольку относительно них система имеет форму, к кото-
рой применимо правило Крамера:
«и	«12		«Кг-D	в\г		
0	«22	..	a2(r_i)	«2г	~ а\\а21 •	.. ап. ф 0.
0	0 .	..	«(r-l)(r-l)	a(r-\)r		
0	0 .	0	агг		
В этом случае, как известно, решение хь х2, ..., хг существует и
единственно.
Таким образом, давая различные произвольные значения сво-
бодным неизвестным хг+1, хг+2, ..., х„ и однозначно находя значения
соответствующих базисных неизвестных хн х2, ..., хг, можно убе-
диться, что решений у преобразованной системы бесконечно много.
Выражение базисных неизвестных через свободные можно полу-
чить с помощью того же правила Крамера. Обозначая величину опре-
делителя матрицы при базисных неизвестных через Л, получим
А = <7|}а22 ...агг * О,
	«н 0	«12	••• «22	...	«](/-!) «2(/-])	4 di	«](/+!) «2(/+1)	«!(/-]) «2(r-l)	«Ц «2r
А/ =	0	0 ...	«(/-!)(/-])	d,-y	«0-l)(/+l)	«(/-D(r-I)	«(/-l)r
	0	0 ...	0	di	«/(/+])	«/(r-l)	«/r
	0	0 ...	0	df+]	«(/+])(/+!)	«o+])(r-l)	«(/+l)r
	0	0 ...	0	d..	0	0	«ГГ
где dj = -aj{r+V}xr+{ - aj{r+2}xr+2 - ... - ajnxn + fy, j = 1, 2, ..., r.
43
Записывая /-й столбец в развернутом виде, получим
			-й1(г+2)Х/-+2 ~	.. -щпхп + Ь}
di	=	-й2(г+1)Л'г+1	-й2(г+2)Л'г+2 “	.. -л2Л + Ь2
^dr ,		-й7-(/-+])Хг+1	~^r(r+2)Xr+2 ~	.. -arnx„ + Ьг /
откуда видно, что он представляет собой сумму (п - r+ 1) столб-
цов. Используя свойство 7 определителя, можно разложить А, в
сумму таких определителей:
«11 0		«12 ... «22 ...	«](/-]) «2(7-1)	~а\(г+к)Хг+к	«1(7+1) ~a2(r+k)Xr+k	a2(i+l)	«l(r-l) •••	«2Ц-1)	й2г	
0		0 ...	«(/-])(/-!)	~a(i-])(r+k)xr+k	a(i~])(/+!)	••• «(7-l)(/-l) a		i-])r
0		0 ...	0	~ai(r+k)Xr+k	ai(i+])	... Яцг-])	1	^ir
0		0 ...	0	~a(i+\)(r+k)xr+k a(i+])(7+l)	••• «(7+l)(r-]) «	0+1)/-	
0		0 ...	0	~ar(r+k)xr+k	0	0	(	
	«и	«12 ...	«1(7-1)	~a](r+k)	«1(7+1)	«1(г-1)	в\г		
	0	«22 ...	«2(7-1)	~a2(r+k)	a2(i+l)	а2{г-\)	а2г		
	0	0 ...	«(/—1)(7—1)	~a(i-l)(r+k) «(7-l)(/+l) •••	«(/-1)(г-1) а(/-])г		xr+k
	0	0 ...	0	~ai(r+k)	ai(i+])	air		
	0	0 ...	0	~a(i+])(r+k) «(7+l)(7+l) •••	й(/+1 )(г-1) й(/+])г		
	0	0 ...	0	~@r(r+k)	0	0	агг		
- ^ikxr+k,
где к = 1, 2, п - и еще одного
	«и	<7|2	...	^10-1)	b}		Я](г-])	17],
	0	й22 ...	a2{i-])	/>2	a2(i+i)	й2(г-1)	a2r
A/o =	0 0	0	... 0	...	a(i-W-V) 0	b/-i bi	Я(;-1)(/+1) •••	ai(r-l)	^ir
	0	0 ...	0	b/+]	a(i+W+i) •••		a(j+\)r
	0	0 ...	0	br	0	0	arr
44
Таким образом, формулы
xi
А/ _ А/]
А ~ А
А;2	,	, А/«-г)
—— Хг+2 + ... +-------
А	А
А/0
А ’
где i = 1, 2, г дают выражение базисных неизвестных через
свободные неизвестные. Задавая значения свободных неизвестных
хг+1 = С[, хг+2 = с2, х„ = сп_г и вычисляя по полученным формулам
базисные неизвестные:
X/
получим
форме
(
А/]	А;2	А/^„_
= 44 + 44 +-'- + ^Г
А	А	А
решение системы. Запишем это
— , / = 1, 2, ..
Л
решение
в матричной
X! >		4И		412		п-г)		
х2		«21		«22		®2(n-r)		«20
хг		«И		«,2		п-г)		«г0
С+1	= С]	1	+ с2	0	+... + с„_г	0	+	0
С+2		0		1		0		0
х„		0		0		1		0
(2.7)
Здесь обозначены «,5/ =	, 5=1,2, ..., г; t = 0, 1, ..., (л - г).
Теперь, какие бы числа сь с2, с„_г мы ни подставляли в эти
формулы, всякий раз будет получаться решение системы. Возни-
кает естественный вопрос: все ли решения системы охвачены эти-
ми формулами? Утвердительный ответ получается следующим об-
разом: если р|, р2, ...,	— какое-либо решение системы, то поло-
жив С] = f\.+], с2 = |Зг+2,	получим, ЧТО X] = р], Х2 = р2, —,
хг= В противном случае система (2.6) при одинаковых значени-
ях правых частей уравнений имеет два различных решения, что
невозможно в силу теоремы о правиле Крамера.
Таким образом, полученные выше формулы при любых значе-
ниях чисел С], с2, ..., с„_г дают решение системы, и любое реше-
ние системы может быть получено по этим формулам за счет соот-
ветствующего выбора этих чисел, т.е. формулы позволяют найти
общее решение системы (2.5).
Замечание. Если система такова, что все правые части в ее урав-
нениях равны нулю, то система называется однородной. Система
(2.5), у которой правые части заменены нулями, является одно-
родной, соответствующей исходной неоднородной системе. Она
имеет следующий вид:
45
йцХ1 + а12х2 +... + a]rxr +al(r+l)*r+1 + --- + «iA =0;
a22x2 + ... + a2rxr + a2(r+v>xr^ + ... + a2„x„ = 0;
arrxr + ar(r+])Xr+l +  + a„nx„ = 0.
(2.8)
Поскольку столбец правых частей состоит из нулей, то опреде-
литель А/о = 0 для / = 1, 2, г. Это обстоятельство приводит к
тому, что общее решение однородной системы будет иметь вид
' X, >		'(Х][ >		'а12 '		О^Цп-г)
х2		«21		«22		«2 («-/)
X/.				«г2		«г( И—г)
А'г+1	= <Л	1	+ С2	0		0
Хг+2		0		1		0
х„		0		0		1
		V	7		\ /		
Поскольку числа С\, с2, G произвольны, то выбрав С| = 1,
с2 = 0, с„_г = 0, получим, что первый столбец дает решение
однородной системы; при с} = 0, с2 = 1, с3 = 0, сп_г = 0 — то же,
для второго столбца и т.д. Эта система решений
однородной системы называется фундаментальной.
Если система не является однородной (не все правые части в ее
уравнениях равны нулю), то, положив в формулах (2.7) с} = 0, с2 = 1,
с3 = 0, ..., с,: , = 0, получим, что столбец
'(Хю
«20
(Хг0
0
о
о
46
будет давать одно из решений неоднородной системы. Поскольку
это решение лишь одно из бесконечного множества решений, про
него говорят, что оно является частным решением неоднородной
системы.
Таким образом, общее решение неоднородной системы пред-
ставляет собой сумму с произвольными числовыми коэффициен-
тами решений, входящих в фундаментальную систему решений
соответствующей однородной системы и еще одного частного ре-
шения неоднородной системы. Если система изначально однород-
на, то в общем решении присутствуют лишь слагаемые из реше-
ний, входящие в фундаментальную систему решений.
Теперь рассмотрим еще один вариант преобразованной систе-
мы — вариант, когда в процессе преобразования возникают урав-
нения, не имеющие решений. Это говорит о том, что вся преобра-
зованная система несовместна, а следовательно, несовместной
является и исходная система. Ответим на вопрос: какие уравнения
не имеют ни одного решения? Одно линейное уравнение всегда
имеет решение, если хотя бы один из коэффициентов при неизве-
стных отличен от нуля. Поэтому несовместным одно уравнение
может быть только тогда, когда коэффициенты при всех неизвест-
ных равны нулю, а правая часть нулю не равна. Например, не су-
ществует таких х, у, 2, чтобы удовлетворялось уравнение
0x + 0y+0z=l.
Такие уравнения могут возникать в процессе преобразования
исходной системы. Например, преобразовывая систему
|х + у + z = 1;
[х + у + z = О,
можно вычесть из первого уравнения второе. При этом появляется
уравнение, приведенное выше, которое не имеет ни одного реше-
ния. Следовательно, рассматриваемая система несовместна.
Таким образом, возникновение в процессе преобразования ис-
ходной системы несовместного уравнения, у которого левая часть
всегда равна нулю, а правая — не является нулем, дает основание
для вывода: исходная система несовместна.
Перейдем к изложению алгоритма метода Гаусса, который по-
зволяет всегда привести преобразованную систему к одному из
рассмотренных выше случаев: либо к виду (2.4), либо к виду (2.5),
либо к одному из них с несовместными уравнениями. Приведение
произвольной системы к одному из указанных видов позволяет
довести до конца и исследование системы на совместность, и ее
решение.
Итак, пусть имеется произвольная система линейных алгебраи-
ческих уравнений:
47
аих}+апх2+... + а}пхп =
а2\Х] + а22х2 +... + а2пх„ = Ь2;
(2.9)
cim]X] + ат2х2 +... + атпхп — Ьт.
Перестановкой уравнений всегда можно добиться, чтобы ко-
эффициент при в первом уравнении был отличен от нуля. По-
этому можно считать, что =#0. Найдем числа ц,] = —, /= 1, 2,
йп
..., т. Вычтем последовательно из второго, третьего, m-го урав-
нений системы (2.9) первое уравнение, умноженное соответственно
на Ц21, Изи  , Ишь В результате этих преобразований во всех урав-
нениях, кроме первого, неизвестное jq исчезнет. Полученная си-
стема будет иметь следующий вид:
йиХ| + а}2х2+... + а}„хп = Ь};
а22х2 + ... + a2f1x„ = Ь2,
‘	— Ь^,
где = ay - b] = b, - pzl/?|, /, j = 2, 3, m.
Далее рассматриваем систему без первого уравнения:
а\1х2+а\3х2+... + а\пхп = Ь\',
а\2х2 + а\2х3 +... + а2пх п = />];
а}т2х2 + бД3х3 +... + а}тпхп = Ь}т.
Если в этой системе имеются уравнения, у которых все коэф-
фициенты при неизвестных равны нулю, то в случае, когда соот-
ветствующая правая часть не равна нулю, процесс заканчивается
выводом: система несовместна.
Если же соответствующая правая часть также равна нулю, то
уравнение удовлетворяется при любых значениях неизвестных, и
его можно в дальнейшем не учитывать, т.е. просто отбросить.
Может оказаться, что в результате таких действий от системы
(2.10) не останется ни одного уравнения. Тогда процесс преобра-
зования также следует считать законченным. Оставшееся первое
уравнение всегда имеет вид либо системы (2.4), либо системы (2.5).
Если же матрица системы (2.10) не является нулевой, то к систе-
ме можно снова применить преобразование, которое было исполь-
зовано для исходной системы. Для этого, возможно, понадобятся
такие действия, как перестановка уравнений и перенумерация
48
неизвестных, для того чтобы обеспечить выполнение условия
«22 * 0, необходимого для следующего шага метода Гаусса.
Тем же приемом, что был использован выше, система (2.10)
приводится к виду
а^х2 + а^3х3 + ... + а^х„ = Ь{2,
a33x3 + ... + alnxn = bl\
«,2„3х3+ ... + <Ос«
а исходная система примет вид
«ИХ| +fl]2*2 + а13х3 + ... + а]пхп =
а]22х2 + а'23х3 + ... + а'2пх„ = Ь±;
<	al3x3 + ... + alnxn = b3;
+ ... +	= Ь}п.
Дальнейшее исследование и преобразование системы продол-
жается по уже описанной выше схеме. В любом случае система бу-
дет преобразована либо к виду (2.4), либо к виду (2.5), либо будет
обнаружена ее несовместность.
Число г, характеризующее преобразованную систему [как сис-
тему (2.4), так и систему (2.5)] и определяющее структуру ее об-
щего решения, называется рангом матрицы А = ||«^||, т.е. матрицы
системы.
Можно доказать, что это число, а следовательно, и структура
общего решения, не зависят от способа, которым исходная систе-
ма была приведена к эквивалентной ей системе вида либо (2.4),
либо (2.5).
Вычисление ранга матрицы возможно несколькими способа-
ми, но наиболее рационально поступать с матрицей так же, как с
уравнениями при применении метода Гаусса.
В результате матрица превратится в матрицу системы вида (2.4)
или вида (2.5). Количество ненулевых элементов на главной диаго-
нали преобразованной матрицы и даст ранг исходной матрицы.
Пример 2,17. Найти ранг матрицы Л, где
3	2	1	4^
А =	-1	0	1	3
4	2	0	1
49
Решение. Поменяв местами первую и вторую строки, получим
'-1 0 1 3^
3 2 14.
4 2 0 1
Далее первую строку, умноженную на 3, прибавим ко второй
строке. Имеем
^-10 1 3'
0 2 4 13 .
4 2 0 1
\ /
Затем первую строку, умноженную на 4, прибавим к третьей
строке. Получим
^-10 1 3'
0 2 4 13 .
0 2 4 13
\ /
И наконец, из третьей строки вычитаем вторую и в результате
имеем
^-10 1 3'
0 2 4 13 .
0 0 0 0
\ /
Матрица А преобразована в верхнюю трапециевидную форму.
Ее ранг равен 2, так как на главной диагонали находятся только
два числа, отличных от нуля.
Для однородных систем оказывается важным вопрос существо-
вания для них ненулевых решений. Если такое решение есть, то
система называется нетривиально совместной. Например, система
J х + у = 0;
[2х + 2у = 0
будет нетривиально совместной потому, что имеет наряду с триви-
альным решением х = 0, у = 0 нетривиальные решения х = с, у = -с,
где с — любое число.
В терминах ранга матрицы ответ на поставленный вопрос весь-
ма прост: однородная система нетривиально совместна тогда и
только тогда, когда ранг матрицы системы меньше, чем число
неизвестных. В используемых выше обозначениях это условие вы-
глядит так: г < п. Обоснование этого факта вытекает из формулы
общего решения однородной системы.
Для неоднородных систем важен вопрос их совместности, ко-
торый также может быть решен в терминах ранга матрицы исход-
50
ной системы А = |Д,|| и ранга так называемой расширенной матрицы
системы Л, которая получается из матрицы А добавлением одного
столбца: столбца из правв1х частей уравнений системы. При этом
справедлива следующая теорема.
Теорема 2.4 (Кронекера —Капелли). Система линейных алгеб-
раических уравнений совместна тогда и только тогда, когда ранги
матрицы системы А и расширенной матрицы системы А совпадают.
Доказательство этой теоремы здесь не приводим не столько из-
за сложности, сколько из-за ее ограниченной важности. Дело в
том, что для проверки выполнения условия теоремы — равенства
рангов — требуется вычислить ранги матриц А и Л, что по трудо-
емкости эквивалентно исследованию и решению системы мето-
дом Гаусса. Отсюда следует, что практическое значение этой тео-
ремы невелико.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Пусть
, (-2 -5 73	Г-3 8 43
Д-З 1 0} Д 4 0 5 J*
Найдите матрицу С = ЗА + 5 В.
2. Пусть
Найдите
3. Пусть
матрицу
Найдите матрицу С = АВ и ее определитель | С|.
4. Вычислите определитель четвертого порядка
-19 14
4! -5
2 15 8
5.	Найдите матрицу, обратную к матрице А, если
(8 7
А = 13 12
11 10
3
10
7
51
6.	Решите систему линейных алгебраических уравнений, используя
правило Крамера:
2х + 5 у + 6z = 74;
9х + 2у - 3z = -60;
7x + 5y + 3z = 22.
7.	Методом Гаусса найдите общее решение однородной системы ли-
нейных алгебраических уравнений:
2х+ у- z - 1 би =0;
12х + 4у + 6z + 8г 4- 20г = 0;
38х 4-11у 4- 23z 4-64г 4-68г = 0;
4x4- у 4- 3z 4-12и 4- 8г = 0.
Примечание. Поскольку фундаментальная система решений определе-
на неоднозначно, то окончательный ответ может не совпасть с ответом,
данным в конце книги. Но количество базисных и свободных (параметри-
ческих) неизвестных должно совпадать.
8.	Методом Гаусса исследуйте на совместность неоднородную линей-
ную систему алгебраических уравнений и в случае наличия совместности
найдите общее решение:
2х 4- Зу 4- 9г- 5г =-17;
9х-6у- 5z4- Зи = -51;
3x4- у 4- 3z 4- Зи = -8;
4х 4- бу 4- 4z =18;
7x-7y-21z + 35r = 26.
ГЛАВА 3
ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
3.1.	Геометрические векторы и действия над ними
Если какая-то величина характеризуется только своим числовым
значением, то она называется скалярной величиной или скаляром.
Примеры физических скалярных величин: масса тела, температу-
ра, потенциал электростатического поля и др. Но среди физиче-
ских величин можно встретить такие, которые характеризуются не
только числовым значением, но и направлением, например, сила,
скорость, напряженность электростатического поля. Эти величи-
ны называются векторными или векторами, их можно изображать
в виде направленного отрезка прямой, т.е. такого отрезка, на ко-
тором указано (обычно стрелкой), где у него начало, а где — ко-
нец. При этом длина отрезка равна числовому значению величины
(например, величине скорости), а направление отрезка совпадает
с направлением вектора (например, направлением скорости).
Оказывается, что все действия с векторными величинами произ-
водятся совершенно аналогично тому, как это делается с направлен-
ными отрезками. Поэтому достаточно изучить только действия с
последними, которые будем называть геометрическими векторами
(или просто векторами). Они обозначаются буквами полужирного
шрифта прямого начертания, например, а. Иногда бывает удобно
задавать вектор как упорядоченную пару точек, например, АВ. При
этом буква, обозначающая начало вектора, ставится первой.
К векторам относят также и нулевой вектор. Это такой отрезок,
у которого начало и конец совпадают. Обозначать его будем буквой 0.
Расстояние от начала до конца вектора называется его длиной (или
модулем). Длина вектора обозначается |а| или |АВ|. Вектор имеет
длину, равную нулю, тогда и только тогда, когда он нулевой.
Векторы называются коллинеарными, если они расположены на
одной или на параллельных прямых. Векторы называются компла-
нарными, если они расположены на одной или на параллельных
плоскостях. Относительно нулевого вектора удобно принять услов-
ное соглашение: считать, что он коллинеарен любому вектору.
Определение 3,1. Два вектора а и b называются равными, если
они коллинеарны, одинаково направлены и равны по длине.
53
Если геометрически не различать равные векторы, то возникает
понятие свободного вектора — вектора, который можно перемещать
параллельно самому себе, помещая его начало в любую точку. В час-
тности, если имеется несколько векторов, то их всегда можно приве-
сти к одному началу, т. е. поместить начала всех векторов в одну точку.
Первое из рассматриваемых действий над векторами — это ум-
ножение вектора на число (на скаляр).
Определение 3.2. Произведением вектора а на число X называ-
ется вектор Ь, который обозначается / а. удовлетворяющий следу-
ющим условиям:
1)	|b| = |Z||a|;
2)	вектор b коллинеарен вектору а (векторы а и b коллинеарны);
3)	векторы а и b сонаправлены (имеют одинаковое направле-
ние), если X > 0, и противонаправлены (имеют противоположное
направление), если X < 0.
Замечание. Если X = 0, то из условия 1 следует, что |Ь| = 0, а это
означает, что b = 0, т.е. является нулевым вектором. Итак, для лю-
бого вектора а имеет место равенство 0а = 0.
Вторая операция над векторами — это сложение векторов.
Определение 3.3. Суммой двух векторов а и b называется вектор
с, который обозначается а + Ь, удовлетворяющий условию: если
начало вектора b перенести в точку, являющуюся концом вектора
а, начало вектора с совпадет с началом вектора а, а конец — с
концом вектора Ь.
Например, если а = АВ, а b = ВС, то с = а + b = АС. Геометри-
ческое построение вектора с = а + b осуществляется построением
треугольника АВС и поэтому называется правилом треугольника.
Можно построить вектор с = а + b другим способом. Поместим
начала векторов а и b в одну точку А и пусть а = АВ, a b = AD. Через
точку В проведем прямую, параллельную вектору Ь, а через точку
D — прямую, параллельную вектору а. В получившемся паралле-
лограмме ABCD диагональ АС даст вектор с = а + Ь. Этот способ
называется правилом параллелограмма.
Нетрудно убедиться в том, что оба способа построения суммы
двух векторов эквивалентны.
Действия над геометрическими векторами обладают следующими
свойствами, которые могут быть доказаны с помощью определе-
ний и теорем элементарной геометрии:
1)	для любого вектора а и любых чисел X и и справедливо ра-
венство Х(ца) = (Хц)а;
2)	если вектор а * 0, то для любого вектора Ь, коллинеарного
вектору а, найдется и притом единственное число X такое, что
b = Ха;
3)	для любых двух векторов справедливо равенство а + b = b + а;
4)	для любых трех векторов справедливо равенство (а + Ь) + с =
= а + (Ь + с);
54
5)	для любых двух векторов а и b и любого числа X справедливо
равенство Х(а + b) = Ха + ХЬ;
6)	для любых двух чисел Хирн любого вектора а справедливо
равенство (X + р) а = Ха + ра;
7)	для любого вектора а справедливо равенство а + 9 = а.
Для дальнейшего введем такое понятие, как базис. Если рас-
сматривать геометрические векторы на прямой, т.е. множество век-
торов, начала и концы которых находятся на одной и той же пря-
мой, то базисом здесь назовем любой ненулевой вектор е, принад-
лежащий этому множеству. Как следует из свойства 2, любой век-
тор х из этого множества единственным образом представим в виде
х = Хе. В этом случае говорят, что вектор х линейно выражается
через вектор е. Число X называется координатой вектора х в базисе е.
Если рассмотреть множество векторов на плоскости, т.е. мно-
жество таких векторов, которые параллельны некоторой фиксиро-
ванной плоскости, то базисом здесь назовем любые два неколлине-
арных вектора е и f, взятых в фиксированном порядке. Покажем,
что и в этом случае базис обладает свойством, аналогичным случаю
векторов на прямой: любой вектор х из этого множества единст-
венным образом представим в виде х = Хе + pf. В этом случае также
говорят, что вектор х линейно выражается через векторы е и f.
Для доказательства заметим, что ни один из векторов е и f не
может быть нулевым вектором (иначе векторы е и f будут коллине-
арными). Случай, когда вектор х коллинеарен одному из векторов
е или f, сводится к свойству 2. Пусть теперь вектор х не коллинеа-
рен ни одному из векторов е и f. Поместим начала всех трех векто-
ров х, е и f в одну точку О. Конец вектора х обозначим буквой А,
т. е. х = ОА. Через точки О и А проведем прямые, параллельные
векторам е и f, которые пересекутся соответственно в точках В и С.
Векторы ОВ и ОС по правилу параллелограмма в сумме дадут век-
тор х. С другой стороны, векторы ОВ и ОС коллинеарны векторам е
и f соответственно и согласно свойству 2 найдутся единственные
числа X и и такие, что ОВ = Хе и ОС = pf. Следовательно, х = ОВ +
+ ОС = Хе + pf . А
Аналогично можно рассмотреть случай векторов в простран-
стве (векторы не подчинены никаким условиям). В этом случае ба-
зисом назовем любые три некомпланарных вектора е, f и g, взятых
в фиксированном порядке.
Справедливо аналогичное случаю векторов на прямой и на плос-
кости утверждение: любой вектор х единственным образом пред-
ставим в виде х = Хе + pf + vg. В этом случае также говорят, что
вектор х линейно выражается через векторы е, f и g, а числа X, р
и v называются координатами вектора х в базисе е, f и g. Доказыва-
ется это свойство таким же способом, как и в случае плоскости:
делается аналогичное построение в пространстве. При этом оказы-
вается, что сумма трех векторов, начала которых помещены в одну
55
общую точку О, является диагональю параллелепипеда, постро-
енного на этих векторах.
Введение базиса позволяет производить действия над вектора-
ми аналитически, сводя геометрические построения к вычислени-
ям. Это возможно на основе следующих утверждений.
Утверждение 3.1. Пусть е, f, g — базис в пространстве и числа
X, ц, v — координаты вектора х в этом базисе. При умножении
вектора х на число а его координаты умножаются на это число.
Доказательство. Имеем: х = Хе + uf + vg. Тогда ах = а(Хе + uf + vg) =
= (аХ)е + (ocp)f + (<xv)g. ▲
Утверждение 3,2. Пусть е, f, g — базис в пространстве и числа
X. li. v — координаты вектора х, а X, р, v — координаты вектора у в
этом базисе. При сложении двух векторов х и у координаты вектора
z = х + у равны суммам соответствующих координат векторов х и у.
Доказательство. Имеем: х = Хе + pf + vg, у = Хе +jlf + vg.
Тогда z = х + у = Хе + pf + vg + Хе + pf + vg = (X + Х)е + (р + p)f +
+ (v + v)g. ▲
Утверждение 3.3. Два ненулевых вектора, имеющих разложе-
ние по базису е, f, g: х = Хе + pf + vg, у = Хе + pf + vg, коллинеарны
тогда и только тогда, когда их координаты пропорциональны, т.е.
X р v
найдется число t такое, что — = — = — = t, где система равенств
X р v
понимается в расширенном смысле: если знаменатель дроби равен
нулю, то обязательно равен нулю и числитель.
Доказательство. Пусть ненулевые векторы х и у коллинеарны. В
силу свойства 2, найдется число t такое, что х = /у. Равенство двух
векторов влечет равенство их координат X = ZX, р = Zp, v = Zv, откуда
X р v t „г
следуют равенства — = — = — = /. Обратно, если эта система ра-
X р v _
венств выполняется, то X = /X, р = Гр, v = Zv, откуда следует, что
х = ty. По определению умножения вектора на число получаем,
что векторы х и у коллинеарны. ▲
Замечание, Если один из векторов, например, х = 0, то все его
координаты равны нулю, и поэтому для любого вектора у будут
иметь место равенства X = /X, р = /р, v = Zv, где t = 0. Поэтому слу-
чай нулевого вектора (с учетом соглашения: нулевой вектор кол-
линеарен любому вектору) включается как частный случай в ут-
верждение 3.3.
3.2. Системы координат на прямой, на плоскости
и в пространстве
Определение 3.4, Системой координат на прямой называется
совокупность фиксированной точки О и фиксированного ненуле-
вого вектора е, принадлежащих этой прямой.
56
Точка О называется началом координат, а вектор е образует ба-
зис на этой прямой. Если точка М лежит на этой прямой, то мож-
но рассмотреть вектор ОМ. Он называется радиусом-вектором точ-
ки М.
Определение 3.5. Координатой точки М на прямой называется
координата радиуса-вектора этой точки ОМ в базисе е.
Таким образом, каждая точка прямой имеет свою координату,
т.е. между всеми точками прямой и числовой осью установлено
взаимно однозначное соответствие. Это имеют в виду, когда гово-
рят, что прямая превращается в ось.
Обычно вектор е выбирают таким, чтобы |е| = 1. Тогда коорди-
ната точки по модулю всегда равна расстоянию от этой точки до
начала координат.
Определение 3.6. Системой координат на плоскости называется
совокупность фиксированной точки плоскости О и фиксирован-
ного базиса еь е2 на этой плоскости.
Точка О называется началом координат. Если точка М принад-
лежит этой плоскости, то вектор ОМ называется радиусом-векто-
ром этой точки.
Определение 3.7. Координатами точки М на плоскости называ-
ются координаты радиуса-вектора этой точки ОМ в базисе ен е2.
Таким образом, каждой точке плоскости М поставлена в соот-
ветствие упорядоченная пара чисел: координаты вектора ОМ в
базисе в], е2. Координаты точки обычно записывают в круглых скоб-
ках после буквы, обозначающей точку. Так запись М(а, р) означа-
ет, что ОМ = осе1 + ре2. На плоскости также оказывается удобнее
использовать не произвольный базис в], е2, а так называемый ор-
тонорм ированный базис i, J, который характеризуется следующи-
ми свойствами:
i)|i| = |j| = i;
2) векторы i и j взаимно перпендикулярны (или, иначе, орто-
гональны)',
3) кратчайший поворот вектора i к вектору j осуществим как
поворот против движения часовой стрелки.
Определение 3.8. Система координат, в основе которой лежит
ортонормированный базис i, j, называется прямоугольной декарто-
вой системой координат на плоскости.
Прямая, проходящая через точку О и параллельная вектору i,
обычно называется координатной осью Ох, а соответствующая
координата точки, обозначаемая через х, называется абсциссой
точки М. Вторая, перпендикулярная первой, прямая, параллель-
ная вектору], называется осью Оу, а соответствующая координата
точки, обозначаемая через у, называется ординатой точки М.
Определение 3.9. Системой координат в пространстве называет-
ся совокупность фиксированной точки О и фиксированного бази-
са ен е2, е; в пространстве.
57
Точка О называется началом координат, вектор ОМ, как бьыо
указано выше, называется радиусом-вектором точки М.
Определение 3.10. Координатами точки М в пространстве назы-
ваются координаты радиуса-вектора ОМ в базисе е(, е2, е3-
Таким образом, каждой точке пространства М поставлена в соот-
ветствие упорядоченная тройка чисел: координаты вектора ОМ в ба-
зисе еь е2, ез. Координаты точки в пространстве также записывают в
круглых скобках после буквы, обозначающей точку. Так запись А/(а, |3, у)
означает, что ОМ = осе] + |3е2 + уе3. В пространстве также оказывается
удобнее использовать не произвольный базис eh е2, ез, а ортонорми-
рованный базис i, j, к, который обладает следующими свойствами:
1)	|i| = 1Л = |k| = 1;
2)	векторы i, j и к взаимно перпендикулярны (ортогональны}',
3)	кратчайший поворот вектора i к вектору j должен наблю-
даться с конца вектора к как поворот против направления движе-
ния часовой стрелки. В последнем случае говорят, что тройка век-
торов i, j, к является правой тройкой. Порождаемая ими система
координат также носит название правой системы координат.
Определение 3.11. Система координат, в основе которой лежит
ортонормированный базис i, j, к, называется прямоугольной декар-
товой системой координат в пространстве.
Прямая, проходящая через точку О и параллельная вектору i,
обычно называется координатной осью Ох, а соответствующая
координата точки, обозначаемая через х, называется абсциссой
точки М. Вторая, перпендикулярная первой, прямая, параллель-
ная вектору], называется осью Оу, а соответствующая координата
точки, обозначаемая через у, называется ординатой точки М. Тре-
тья прямая, проходящая через точку О и параллельная вектору к,
называется осью Oz, а соответствующая координата точки, обо-
значаемая через z, называется аппликатой точки М. Таким обра-
зом, каждой точке пространства М ставится в соответствие упоря-
доченная тройка чисел: М(х,у, z).Последняя запись означает, что
имеет место следующее разложение вектора ОМ:
ОМ = xi + yj + zk.
Очевидно, что своими координатами точка М однозначно оп-
ределяется.
Рассмотрим несколько вспомогательных задач, связанных с
системами координат.
Задача 1. По известным координатам точек А и В найти коор-
динаты вектора АВ.
Координатами вектора АВ являются числа хАВ, уАВ, zAB, удов-
летворяющие равенству АВ = xABi + yABj + zABk, которое удобно
записывать в более компактной форме: АВ = {хАВ, уАВ, zAB}.
Пусть Л(хА,уА, zA) и В(хв,ув, zB). Тогда имеем: ОВ = О А + АВ. Это
векторное равенство эквивалентно трем скалярным соотношени-
58
ям: хв = хА + хАВ; ув = уА + уАВ, zB = zA + zAB, из которых получается,
что
АВ = {xfi - хА, ув - уА, zB - zA}.
Таким образом, чтобы найти координаты вектора, следует из
координат его конца вычесть координаты начала.
Задача 2. Найти координаты середины отрезка прямой, соеди-
няющего точки А и В, если известны координаты этих точек.
Обозначим через С точку, являющуюся серединой отрезка АВ,
а ее координаты — через хс, ус, Zc- Тогда ОС = xci + y(j + Zck. Но
вектор ОС можно представить так:
ОС = ОА + |аВ.
Это равенство означает, что
хс = хА + |(хв - хф; ус = уА + ±(ув - уА); zc = zA + ±(zB - zA).
Следовательно,
1,	s	1,	s	1,	ч
xc =	+ Ус = ^(Ув + Ул); *c = ~^(zB + zA),
т. e. координаты середины отрезка равны средним арифметическим
значениям от координат его концов.
Задача J. Найти расстояния между двумя данными точками. Для
решения этой задачи заметим, что расстояние между точками А и
В равно длине вектора АВ, т.е. величине |АВ|. Поскольку система
координат является прямоугольной декартовой системой, то из
разложения вектора
АВ = {xs - хА, ув - уА, zB - zA} = (хв - x4)i + (ув - yA)j + (zB- zA)k
следует, что вектор АВ, являясь суммой трех взаимно перпенди-
кулярных векторов, геометрически изображается диагональю
прямоугольного параллелепипеда, длины сторон которого равны
|х5 - *л1, |Уя - Ул1, I %в - zAi- Следовательно,
| АВ|2 = (хв - хА)2 + (у в - уА)2 + (zB - zA)2.
Таким образом, расстояние между точками А и В может быть най-
дено по формуле
IАВ| = ^(хв - хА }2 + (ув - уА }2 + (zB - zrf.
На плоскости это расстояние будет находиться по формуле
|АВ| = J(xs -xj2 + (ys - Ул)2, а на прямой — |АВ| = |xfi - хф
В заключение приведем без доказательства условие ортогональ-
ности двух векторов', векторы а = x,i + yj + Z]k и b = x2i + y2j + z2k
59
ортогональны (с учетом соглашения: нулевой вектор ортогонален
любому вектору) тогда и только тогда, когда х(х2 + У1У2 + -ч А = О-
Для векторов на плоскости хОу это условие имеет вид Х]Х2 +
+ КС = О-
3.3.	Понятие уравнения линии и уравнения
поверхности
Пусть на плоскости введена прямоугольная декартова система
координат. И пусть имеется уравнение, связывающее две перемен-
ные х и у, F(x,y) = 0 и некоторая линия на плоскости L. Например,
х2 + у 2 - 1 = 0 — уравнение и L — окружность с центром в точке О
и радиусом, равным единице.
Определение 3,12. Уравнение F(x,y) = 0 называется уравнением
линии L в данной системе координат, если координаты любой точ-
ки М(х,у), лежащей на /., удовлетворяют этому уравнению, и на-
оборот, если координаты какой-либо точки удовлетворяют этому
уравнению, то точка лежит на линии L.
Пример 3.1. Приведенное выше уравнение х2 + у2 - 1 = 0 является
уравнением окружности с центром в точке О и радиусом, равным
единице. Действительно, уравнение, переписанное в виде х2 + у2 = 1,
может быть истолковано так: уравнению удовлетворяют те и только
те точки плоскости, для которых величина х2 + у2, равная квадрату
расстояния от точки до точки 0(0,0), постоянна и равна единице.
Очевидно, что этим свойством обладают только точки, лежащие
на окружности с центром в точке О и радиусом, равным единице.
Замечание. Рассуждения, аналогичные тем, что были приведены
выше, позволяют сделать вывод о том, что уравнение х2 + у2 = R2
является уравнением окружности с центром в точке О и радиу-
сом, равным R.
Если рассмотреть уравнение (х - хА)2 + (у - уА)2 = R2, то без
особого труда аналогичными рассуждениями удастся доказать, что
оно является уравнением окружности с центром в точке Л(хА,уА)
и радиусом, равным R.
В пространстве уравнение F(x,y,z) = 0 является, как правило,
уравнением поверхности. Соответствующее этому случаю опреде-
ление вполне аналогично определению уравнения линии.
Определение 3.13. Уравнение F(x,y, z) = О называется уравнени-
ем поверхности S в данной системе координат, если координаты
любой точки Mix.y. z), лежащей на 5, удовлетворяют этому урав-
нению, и наоборот, если координаты какой-либо точки удовлет-
воряют уравнению, то эта точка лежит на 5.
Пример 3.2. Рассмотрим уравнение (х - хА)2 + (у - уА)2 + (z - zA)2 =
= R2. Аналогично случаю плоскости легко устанавливается, что этому
60
уравнению удовлетворяют координаты тех и только тех точек, ко-
торые находятся на расстоянии R от точки А(хА,уА, zA). Следова-
тельно, рассматриваемое уравнение является уравнением сферы с
центром в точке Л(хА.уА. zA), имеющей радиус, равный R.
В дальнейшем будут рассмотрены другие примеры уравнений
линий на плоскости и поверхностей в пространстве.
3.4.	Различные виды уравнения прямой на плоскости
3.4.1.	Общее уравнение прямой
Пусть на плоскости введена прямоугольная декартова система
координат с началом в точке О и с базисными векторами i и j.
В дальнейшем такую плоскость будем называть координатной плос-
костью хОу. точка М на этой плоскости имеет координаты хну.
Рассмотрим уравнение первой степени, связывающее эти коорди-
наты: Ах + Ry + С = 0, где А, В, С — заданные числа такие, что
А2 + В1 * 0, х, у — координаты точки на плоскости. Для одних
точек их координаты удовлетворяют этому уравнению, для дру-
гих — нет. Координаты х, у, входящие в уравнение, называют те-
кущими координатами точки.
Теорема 3.1. Уравнение Ах + By + С = О, (А2 + В2* 0), рассмот-
ренное на плоскости хОу, является уравнением прямой линии.
Доказательство. Поскольку А2 + В2 # 0, то найдется точка
Л/о(хо,уо), координаты которой удовлетворяют уравнению, т.е. Ах0 +
+ Вуо + С = 0. Введем вектор и = {А, В} и рассмотрим на плоскости
хОу прямую, проходящую через точку и перпендикулярную
вектору и. Заметим, что точка Mix. у) принадлежит этой прямой
тогда и только тогда, когда вектор М0М перпендикулярен (орто-
гонален) вектору и. Вектор М0М имеет координаты: М0М = {х- х0,
у - уо). Используя необходимое и достаточное условие ортогональ-
ности двух векторов, получим, что А(х - х0) + В(у - у0) = 0. Но Лх0 +
+ Ву0 + С = 0. Поэтому равенство Ах + By + С = 0 является необходи-
мым и достаточным условием того, чтобы точка М(х.у) принадле-
жала прямой. Следовательно, уравнение Ах + By + С = 0 действи-
тельно является уравнением этой прямой. ▲
Следствие. Если прямая на плоскости хОу задана уравнением
Ах + By + С = 0, то вектор и = {А, В} перпендикулярен этой прямой.
Этот вектор называется вектором нормали к прямой, или нор-
мальным вектором к данной прямой.
Определение 3.14. Уравнение прямой Ах + By + С= 0 называется
общим уравнением прямой.
Замечание 1. Нетрудно доказать, что для любой прямой ли-
нии, проведенной на плоскости хОу, существует уравнение Ах +
+ By + С = 0, которое является уравнением этой линии.
61
Замечание 2. Как следует из теории систем линейных уравне-
ний, уравнение Ах + By + С = 0 после умножения на любое число,
отличное от нуля, переходит в уравнение, эквивалентное исход-
ному. Поэтому уравнение прямой линии при умножении на такое
число останется уравнением той же прямой.
3.4.2.	Уравнение прямой с угловым коэффициентом
Если в общем уравнении прямой Ах + By + С = 0 коэффициент
при у отличен от нуля, то уравнение можно переписать в следую-
щей форме:
у = кх + Ь,
где к~-
— число, называемое угловым коэффициентом, b =
f-1
Определение 3.15. Уравнение прямой линии, записанное в форме
у = кх + Ь, называется уравнением прямой с угловым коэффициентом.
Определение 3.16. Пусть прямая на плоскости хОу пересекает
ось Ох в точке F. Наименьший угол, на который следует повернуть
против часовой стрелки вокруг точки /’ось Ох так, чтобы она со-
впала с прямой, называется углом наклона (р прямой. Если прямая
параллельна или совпадает с осью Ох, то угол наклона считается
равным нулю.
Таким образом, измеренный в радианах угол наклона <р удов-
летворяет неравенствам 0 < <р < л.
Чтобы пояснить геометрический смысл углового коэффициен-
та, возьмем на прямой две точки Л/|(хьу]), Л/2(х2,у2), (х, < х2).
Тогда у2 = kx2 + b и у\ = kxt + b. Вычитая из первого равенства
второе и разделив левую и правую части на (х2 - х,), получим
- X,
Если через точку М} провести прямую, параллельную оси Ох, а
через точку М2 — прямую, параллельную оси Оу, то эти прямые
пересекутся в точке М3(х2,у]). При этом |М[М3| = |х2 -хф а |М2М3| =
= 1/2 - /| I- Поэтому |£| = tga, где а — угол при вершине в тре-
угольнике A/[A/24/3. Теперь заметим, что поскольку Х] < х2 и поэто-
му |х2 - X] | = х2 - xb то знак коэффициента к определяется знаком
разности у2 - у].Нетрудно убедиться в том, что, если угол наклона
прямой удовлетворяет неравенствам 0 < <р < у, то у2 - у1 > 0, а
значит, и к > 0. При этом оказывается, что угол а равен углу <р.
Следовательно, угловой коэффициент к = tgtp. Если же у < <р < л,
то у2 - у, < 0, и поэтому к < 0. При этом оказывается, что угол a
равен л - (р, и в этом случае получаем
62
к = -tga = -tg(я - (p) = tg(p.
Таким образом, в любом случае оказывается, что угловой ко-
эффициент равен тангенсу угла наклона прямой. Полученный ре-
зулвтат оказывается полезным при решении такой задачи, как на-
хождение угла между двумя прямыми. Действителвно, один из уг-
лов между прямыми всегда равен разности углов наклона этих пря-
mbix. Обозначая этот угол через р, а углв! наклона прямых — через
cpj и ф2 соответственно, получим
tgp = tg(ф2 - ф1) = tg(P2 ~tg(P1 = f2 к' ,
1 + tg<p! tg ср2	1 + к}кг
т. е. тангенс угла между прямыми выражен через их угловые коэф-
фициенты.
В частном случае, когда угол р = 90° (прямые взаимно перпен-
дикулярны) tg р не существует. Из полученной формулы видно,
что это бывает тогда и только тогда, когда знаменатель дроби ра-
вен нулю, т.е. выполняется равенство 1 + к}кг = 0. Или
Это условие является необходимым и достаточным для взаим-
ной перпендикулярности двух прямых.
3.4.3.	Уравнение прямой «в отрезках»
Если в общем уравнении прямой Ах + By + С = 0 все коэффици-
енты отличны от нуля, то уравнение можно преобразовать к сле-
дующему виду:
* + >_
_С _С
L А) I В)
Обозначая	получим уравнение
*+i=l
а b
называемое уравнением прямой «в отрезках».Числа а и b имеют сле-
дующий геометрический смысл: если прямая пересекает ось Ох в
точке А, а ось Оу — в точке 5, то А(а,0), В(0,Ь) и |СМ| = |п|, \ОВ\ =
= \Ь\, т.е. модули чисел а и b равны длинам отрезков ОА и ОВ,
отсекаемых прямой от осей координат.
63
3.5.	Различные виды уравнения плоскости в пространстве
3.5.1.	Общее уравнение плоскости
Пусть в пространстве введена прямоугольная декартова система
координат с началом координат в точке О и с базисными вектора-
ми i, j и к. Каждая точка М этого пространства имеет координаты
х, у, z. Рассмотрим уравнение первой степени, связывающее эти
координаты: Ах + By + Cz + D = 0, где коэффициенты подчинены
условию А2 + В2 + С2 * 0.
Теорема 3.2. Уравнение Ах + By + Cz + D = 0 (А2 + В2 + С2 * 0),
является уравнением плоскости.
Доказательство. Условие Л2 + В2 + С2 * 0 позволяет утверждать,
что найдется точка М^{х^у^ zb), координаты которой удовлетво-
ряют данному уравнению, т. е. Ах0 + Ву0 + Czv + D = 0. Рассмотрим
вектор и = {А, В,С} и плоскость, которая проходит через точку Л/о
и перпендикулярна этому вектору. Точка Mix. у, z) будет лежать в
этой плоскости тогда и только тогда, когда вектор М0М будет пер-
пендикулярен вектору п. Далее, п = {Л,ДС} и М0М = {х - х0, у - у0,
z - Zob Используя необходимое и достаточное условие перпенди-
кулярности двух векторов в координатной форме, получим, что
А(х - х0) + В(у - у0) + C(z - Zq) = 0. Поскольку Ах0 + Ву0 + Czq = -D,
окончательно получим: Ах + By + Cz + D = 0. Итак, точка М(х,у, z)
будет тогда и только тогда принадлежать плоскости, когда ее ко-
ординаты удовлетворяют данному уравнению. Следовательно, это
уравнение является уравнением плоскости. ▲
Следствие. Если плоскость задана уравнением Ах + By + Cz + D =
= 0, то вектор и = {А, В,С} перпендикулярен этой плоскости.
Этот вектор называется вектором нормали к плоскости, или
нормальным вектором к данной плоскости.
Определение 3.17. Уравнение плоскости Ах + By - Cz + D б
называется общим уравнением плоскости.
Замечание 1. Нетрудно доказать, что для любой плоскости су-
ществует уравнение Ах + By + Cz + D = 0, которое является уравне-
нием этой поверхности.
Замечание 2. Как следует из теории систем линейных уравне-
ний, уравнение Ах + By + Cz + D = Q после умножения на любое
число, отличное от нуля, переходит в уравнение, эквивалентное
исходному. Поэтому уравнение плоскости при умножении на та-
кое число останется уравнением той же плоскости.
3.5.2.	Уравнение плоскости «в отрезках»
Если все коэффициенты в уравнении плоскости Ах + By + Cz +
+ D = 0 отличны от нуля, то уравнение можно привести к следую-
щему виду:
64
( D\	( D\ .( D\
ИЛИ, обозначив 7 =Й? __7Г =^ _77 =С,
А)	\ В)	\ С )
*+^=1.
а b с
Это уравнение носит название уравнения плоскости «в отрезках».
Геометрический смысл чисел а, b и с аналогичен геометрическо-
му смыслу таких чисел в уравнении прямой «в отрезках»: точки
с координатами Л(а,0,0), В(0, 6,0) и С(0,0,с) являются точками
пересечения плоскости с осями координат. Поэтому \ОА\ = |й|,
|ОР| = |6|, |ОС| = |с|, или модули чисел а, b и с равны длинам
отрезков, отсекаемв1х плоскостью от осей координат.
3.5.3.	Нормированное уравнение плоскости
Если в уравнении плоскости Ах + By + Cz + D = О (А2 + В1 + С2 * 0),
коэффициент D ф 0, то уравнение можно преобразовать следую-
щим образом. Вычислим коэффициент
±1
>М2 + Р2 + С2
и выберем у него знак таким образом, чтобы выполнялось нера-
венство < 0, и умножим уравнение на ц. Получившееся уравне-
ние (цЛ)х + (цР)у + (p.C)z + (цР) = 0 называется нормированным
(или нормальным) уравнением плоскости. Оно обладает полезным
при решении ряда задач основным свойством. При подстановке в
это уравнение координат любой точки Р(а, 0, у) в левой части урав-
нения получится число 5, называемое уклонением точки Рот плос-
кости. Если точка Р и точка О (начало координат) лежат по одну
сторону от данной плоскости, то 5 будет равно расстоянию от точ-
ки Р до плоскости, взятому со знаком минус. Если же точки Ри О
лежат по разные стороны плоскости, то 5 будет равно расстоянию
от точки Р до плоскости. В любом случае расположения точки Р
модуль числа 5 будет равен расстоянию от точки Рдо плоскости.
Доказательство этого свойства здесь не приводим.
Пример 3.3. Пусть требуется найти расстояние отточки Р(3,-9,3)
до плоскости, заданной уравнением 2x-y-2z + 6 = 0. Воспользуем-
ся нормированным уравнением плоскости. Найдем коэффициент
+ 1	±1 _ ±1
ц ~ у1л2 + В2 + С2 ~ V4 + 1 + 4 ~ 3 '
65
Учитывая, что знак у числа D = 6 положителен, выбираем знак
минус. Таким образом, ц = - i. Нормированное уравнение плоско-
сти имеет вид:
— х + — у + -Lz-2 = 0.
I 3J	Ш
Подставляя в левую часть координаты точки Р, получим 5 = -5.
Следовательно, точка Р и точка О лежат по одну сторону от плос-
кости и расстояние от точки Рдо этой плоскости равно 5.
3.6. Уравнения прямой в пространстве
3.6.1. Общие уравнения прямой
В пространстве прямая обычно задается как линия пересечения
двух плоскостей. Для этого уравнения этих плоскостей рассматри-
ваются совместно в виде системы уравнений
Дх + В{у + C]Z + Р[ - 0;
А2х + В2у + C2z + D2 = 0.
При этом важно, чтобы плоскости, задаваемые этими уравне-
ниями, пересекались, а не были параллельными или совпадаю-
щими. Две плоскости будут пересекаться по прямой тогда и только
тогда, когда их векторы нормали П] и п2 не коллинеарны. Учитывая
условие коллинеарности двух векторов, получим, что плоскости
будут пересекаться по прямой линии тогда и только тогда, когда
координаты векторов П] = {А\,В\, СД и п2 = {А2,В2,С2} не будут про-
порциональны. (Напомним, что пропорциональность означает
4	С' А Ы
выполнение равенств — = — = —.) Итак, если коэффициенты в
а2 в2 с2
уравнениях двух плоскостей при переменных х, у и z не будут
пропорциональны, то эти уравнения, рассмотренные совместно,
определяют прямую в пространстве.
Определение 3,18, Уравнения (3.1) при выполнении указанных
условий называются общими уравнениями прямой в пространстве.
Заметим, что одновременно обоим уравнениям удовлетворяют
координаты тех и только тех точек, которые одновременно при-
надлежат как одной, так и другой плоскости, т.е. лежат на их ли-
нии пересечения, на прямой. Очевидно, что плоскостей, проходя-
щих через фиксированную прямую, бесконечно много. Поэтому и
общие уравнения прямой могут быть сформированы бесконечным
числом способов: достаточно взять уравнения любых двух различ-
ных плоскостей, проходящих через эту прямую.
66
Рассмотрим такое понятие, как пучок плоскостей. Это множе-
ство всех плоскостей, проходящих через одну фиксированную пря-
мую. Оказывается, что любая плоскость из этого множества может
быть получена из общей формулы
а(Л[Х + By + С[2 + /)[) + р(Л2х + By + C2z + /X) = 0 (3.2)
за счет выбора соответствующих значений параметров аир. Поэто-
му уравнение (3.2) называется уравнением пучка плоскостей. При
любых значениях аир, одновременно не равных нулю, уравнение
(3.2) дает уравнение плоскости, проходящей через фиксирован-
ную прямую, но для каждой такой плоскости соответствующие
значения параметров аир определяются неоднозначно. Если пред-
положить, что р * 0, то вводя новый параметр X = —, уравнению
(3.2) можно придать следующий вид:
Л(Л|Х + By - Су - Д) + (Л2х + By + C2z + Z>2) = 0	(3.3)
В этой форме уравнение пучка зависит от одного параметра Л,
что оказывается более удобным при решении задач, но из всего
пучка выпадает одна плоскость, имеющая уравнение Ay + By +
+ Q z + D} = 0 (это соответствует случаю р = 0). Если про это обсто-
ятельство не забывать, то можно пользоваться уравнением пучка
плоскостей в форме (3.3).
Пример 3,4. Через прямую, заданную общими уравнениями
J х - Зу + 5z - 3 = 0;
[2х + y-3z-5 = 0,
надо провести плоскость, проходящую через точку М(2,1,1).
Решение. Искомая плоскость принадлежит пучку плоскостей,
проходящих через данную прямую. Запишем уравнение пучка в
форме (3.3):
Х(х - Зу + 5z - 3) + (2х + у - 3z - 5) = 0.
Проверим, что плоскость, заданная уравнением х - Зу + 5 z - 3 0.
не дает решения задачи. Действительно, подстановка координат
точки Л/(2,1,1) в это уравнение показывает, что оно не удовлет-
воряется, и, следовательно, данная плоскость не проходит через
точку М, т. е. не является решением поставленной задачи. Подста-
вив координаты точки М в уравнение пучка, получим
а + 2)2 + (1 - Х)1 + (5Х - 3)1 - ЗХ - 5 = 0.
Решая уравнение относительно неизвестного значения парамет-
ра Л, находим X = 3. Следовательно, искомую плоскость можно
определить из уравнения пучка, если параметру X придать значе-
ние X = 3. В итоге уравнение искомой плоскости имеет вид
5х-8у+ 12г- 14 = 0.
67
3.6.2. Канонические уравнения прямой в пространстве
Определение 3.19. Ненулевой вектор а = {р, q, г}, коллинеар-
ный прямой /., называется направляющим вектором этой прямой.
Как следует из определения, у прямой существует бесконечно
много направляющих векторов. Например, если имеется один на-
правляющий вектор, то умножив его на число, отличное от нуля,
получим снова направляющий вектор этой прямой. Поскольку раз-
личных чисел бесконечно много, то и направляющих векторов тоже
будет бесконечно много. С другой стороны, все направляющие век-
торы коллинеарны прямой L, а следовательно, коллинеарны друг
другу. Откуда следует, что для любых двух направляющих векторов
а и а найдется число ц (р * 0) такое, что а = ца.
Пусть а = {/?,<?, г} — направляющий вектор прямой £, а
Л/0(х0,у0, 2о) — точка на этой прямой. Рассмотрим произвольную
точку А/(х.г. z). Точка Л/(х,г. г) будет лежать на прямой L тогда и
только тогда, когда вектор М0М будет коллинеарен этой прямой
или, что то же, коллинеарен направляющему вектору а = {р, г}.
Вектор М0М = {х - х0, у - у0, z - 2q}, и условие его коллинеарности
вектору а = {р, q, г} можно записать в виде
= Т~Уо = z-zQ	(3 4)
р я г '
Таким образом, точка М(х,у, z) будет лежать на прямой L тогда
и только тогда, когда ее координаты удовлетворяют уравнениям
(3.4). Поэтому естественно назвать эти уравнения уравнениями
прямой L.
Определение 3.20. Уравнения (3.4) называются каноническими
уравнениями прямой L.
Если известны канонические уравнения прямой, то из них сра-
зу можно получить направляющий вектор прямой и координаты
точки Мй, принадлежащей этой прямой. Эта информация часто
оказывается полезной при решении задач. В отличие от каноничес-
ких уравнений прямой, общие уравнения не содержат явно этой
информации. Поэтому при решении ряда задач приходится допол-
нительно затрачивать усилия на ее получение из общих уравнений.
Это можно сделать, например, по следующей схеме. Поскольку в
общих уравнениях прямой, как было показано, коэффициенты при
переменных х, у, z не пропорциональны, т.е. не все отношения
коэффициентов — , —, — равны между собой, то найдется пара
Л-2 В2 С2	АВ
неравных отношений. Пусть, например, —- #= —Тогда систему
Л2 В2
уравнений (3.1) можно переписать в следующем виде:
А[Х + В}у = - C[Z - Д;
А2х + В2у = - C2z - D2.
68
Дадим z какое-либо значение z = Z\. Тогда правая часть системы
будет иметь конкретные значения, и относительно переменных х и
у получится система двух уравнений с двумя неизвестными с оп-
А В
ределителем, не равным нулю (Л,7?2 -	* 0, так как ~г * дг-)-
Аг В2
По правилу Крамера однозначно находятся координаты X] и yh
соответствующие значению z= z{. Тем самым оказалось найден-
ным одно из решений системы (3.1), т.е. координаты точки
М\ (Х| ,у(, Z]), лежащей на прямой L. Если теперь дать переменному
z другое значение z = z2, z2 / zh то будет найдена тем же способом
вторая точка на прямой М2(х2,у2, z?). Зная две точки на прямой,
находим направляющий вектор прямой:
а = М]М2 = {х2 - X], у2 - у\, z2 - Z]}.
Таким образом, задача нахождения координат точки на прямой
и ее направляющего вектора решена.
Пример 3.5. Прямая L задана общими уравнениями
х- у + z -10 = 0;
2х - 8у - z - 23 = О,
и пусть требуется написать канонические уравнения этой прямой.
Решение. Поскольку определитель
преобразуем систему к виду
x-y = -z + 10;
2х - 8у = z + 23.
Задаем значение z = 1 и решаем получающуюся систему по пра-
вилу Крамера. Имеем
Таким образом, х( = 8, у, = -1, Z| = 1 и Л/|(8,—1,1).
Теперь задаем другое значение: z = 5 и снова решаем получаю-
щуюся систему, которая имеет вид
х - у - 5;
2х-8у = 28.
Имеем
д¥
5 -1
28 -8
= -12; АЛ.
1 5
2 28
= 18; А = -6.
69
В итоге получается вторая точка Л/2(2,-3,5). Зная координаты
двух точек на прямой, находим направляющий вектор:
М)М2 = {2 - 8, -3 + 1, 5 - 1} = {-6,-2,4}.
Теперь, зная координаты направляющего вектора и одной из
точек, пишем канонические уравнения прямой
х-8_у + 1_2-1
-6
Канонические уравнения прямой, проходящей через две задан-
ные точки, Л/](х],у], 2[) и М2(х2,у2,z2), исходя из разобранного
примера, могут быть написаны для любых двух точек. Очевидно,
что они имеют следующий вид:
*~*1 = У~У1 = z-z{	(3
X2-Xj	у2-у1	z2-z{'
Если в знаменателе какой-либо дроби оказалось число, равное
нулю, то в соответствии с соглашением о пропорциональности
координат векторов считаем, что соответствующий числитель тоже
равен нулю. Например, если х2 = хь то канонические уравнения
прямой будут иметь вид
. . 3^-Ji	2- z{
Л — Л [ , -- — -----.
У1 -л z2-z{
Если же выполняются два равенства: х2 = jq и у2 = , то канони-
ческие уравнения прямой будут иметь вид
* = у = у}
(z принимает любые значения, а это означает, что прямая парал-
лельна оси Oz).
3.6.3.	Параметрические уравнения прямой в пространстве
Если, имея канонические уравнения прямой, ввести в рассмот-
рение параметр t следующим образом:
= У~3;о = z-z^ = t
р q г
то текущие координаты точки на прямой становятся функциями
этого параметра:
х = х0 + pt; у = yQ + qt; z = Zq + rt; -со < t < +oo. (3.6)
Если имеются координаты какой-либо точки на прямой, то из
уравнений (3.6) однозначно находится соответствующее этой точ-
ке значение параметра t. И наоборот, зная значение параметра Z,
70
по уравнениям (3.6) однозначно находятся координаты точки. Та-
ким образом, каждой точке на прямой соответствует единствен-
ное значение параметра t, и каждому значению параметра t соот-
ветствует единственная точка на прямой.
Определение 3.21. Уравнения (3.6) называются параметрическими
уравнениями прямой.
Очевидно, что переход от параметрических уравнений прямой
к каноническим и наоборот не представляет никаких трудностей.
По сравнению с каноническими параметрические уравнения при
решении ряда задач имеют преимущества, продемонстрируем это
на примере.
Пример 3.6. В пространстве две прямые, если они не параллель-
ны, не обязаны пересекаться. Они могут, как говорится, скрещи-
ваться, т. е. лежать в двух параллельных плоскостях и не быть друг
другу параллельными. В этом случае существует прямая, которая
перпендикулярна этим двум плоскостям и пересекает обе прямые.
Эта прямая называется общим перпендикуляром к двум скрещиваю-
щимся прямым. Пусть первая прямая £, имеет канонические урав-
нения
x-l_y-5_z-l
2
а вторая прямая /_2 —
х - 8 у - 2 z-5
3 = 4 = 1 *
Необходимо написать канонические уравнения общего перпен-
дикуляра к этим двум прямым.
Решение. Перейдем к параметрическим уравнениям этих пря-
мых. Для прямой £[ получим
х = 1 + 2t; у = 5 + 2t; z = 1 - t.
Параметр для прямой /_2 обозначим буквой а. Тогда параметри-
ческие уравнения прямой Л2 будут иметь вид
х = 8 + 3s; у = 2 + 4s; z = 5 + s.
Пусть точка Л/ находится на прямой L}, и ей соответствует зна-
чение параметра /, а точка N находится на прямой £2, и ей соот-
ветствует значение параметра s. Рассмотрим вектор
MN = {7 + 3s - 2t, -3 + 4s - 2t, 4 + s + r}.
Этот вектор будет коллинеарен общему перпендикуляру к обе-
им прямым тогда и только тогда, когда он будет перпендикулярен
каждой из прямых и /_2 или, что то же самое, — направляющим
векторам этих прямых. Используя условия перпендикулярности
векторов, получим два уравнения
71
(7 + 35 - 2r) (2) + (-3 + 4a - 20 (2) + (4 + 5 + г) (-1) = 0,
(7 + 35 - 2r) (3) + (-3 + 45 - 2r) (4) + (4 + 5 + /) (1) = 0.
Преобразуя их, получим систему двух уравнений
Г135- 9/=-4;
[265 - 13/ = -13,
единственное решение которой имеет вид: 5 = -1; / = -1. Зная значе-
ния параметров, находим координаты точек: М(-\, 3,2) и Л(5,-2,4).
По формулам (3.5) получаем уравнения общего перпендикуляра:
x+l_y-3_z-2
~6~~ -5 ” 2 *
3.7.	Кривые второго порядка на плоскости
3.7.1.	Понятие кривой второго порядка
Уравнение прямой на плоскости содержит только первые сте-
пени переменных х и у. Если же рассматривать уравнения, в кото-
рые входят такие слагаемые, как х2, ху, у2, то оказывается, что
многообразие соответствующих этим уравнениям геометрических
объектов на плоскости увеличивается. Появляются кривые, отлич-
ные от прямой линии. Кроме того, если рассматривать общее урав-
нение, содержащее вторые степени переменных х и у, а также их
произведение:
Ах2 + Вху + Су2 + Dx+ Еу+ 6=0,	(3.7)
где А2 + В2 + С2 * 0, то среди этих уравнений могут встретиться
такие, которые не определяют на плоскости никакой кривой. На-
пример, уравнение х2 + у2 + 1 = 0 не может быть удовлетворено
никакими значениями х и у, и, следовательно, на плоскости нет
ни одной точки, координаты которой удовлетворяли бы этому
уравнению. Таким образом, уравнение х2 + у2 + 1 = 0 не определяет
никакой кривой.
Но большая часть уравнений, имеющих вид (3.7), все-таки оп-
ределяет некоторые линии на плоскости, которые называются кри-
выми второго порядка. Уравнение (3.7) называется общим уравнени-
ем кривой второго порядка. Из всего множества кривых второго по-
рядка наиболее важными его представителями являются три кри-
вые: эллипс, гипербола и парабола. При первоначальном знакомстве
с ними ограничимся следующими фактами: геометрическая ха-
рактеристика, каноническое уравнение, каноническая система
координат и форма кривых.
72
3.7.2.	Эллипс
Определение 3,22, Эллипсом называется геометрическое место
точек плоскости, для которых сумма расстояний до двух фиксиро-
ванных точек F\ и F2 этой плоскости, называемых фокусами, есть
величина постоянная и большая, чем расстояние между фокусами.
Если выбрать систему прямоугольных декартовых координат на
плоскости так, чтобы ось Ох проходила через фокусы эллипса,
начало координат находилось посередине между ними, то в этой
системе координат уравнение эллипса будет выглядеть так:
а1 Ь1
Замечание, Отметим, что в определении не предполагается, что
фокусы F} и F2 обязательно различны, не исключается и их совпа-
дение. В последнем случае построение канонической системы ко-
ординат сводится только к тому, что начало координат помещает-
ся в точку, совпадающую с фокусами, а направление координат-
ных осей берется произвольно.
(3-8)
Анализируя уравнение (3.8), прежде всего замечаем, что пере-
менные х и у входят в уравнение во второй степени. Следователь-
но, эллипс — это кривая второго порядка. Величина а равна полу-
сумме расстояний от точки эллипса до фокусов, b - у/а2 - с2, где
с — половина расстояния между фокусами. Если а = Ь, то с = 0 и,
следовательно, оба фокуса сливаются в один. Уравнение (3.8) мо-
жет быть переписано в виде х2 + у2 = а2, в котором нетрудно узнать
известное уравнение окружности с центром в точке О и радиусом а.
Форма, которую имеет кривая в общем случае, показана на рис. 3.1.
3.7.3.	Гипербола
Определение 3,23, Гиперболой называется геометрическое место
точек на плоскости, для которых модуль разности расстояний до
двух фиксированных различных точек F} и F2 этой плоскости, на-
73
зываемых фокусами, есть величи-
на постоянная, положительная и
меньшая, чем расстояние между
фокусами.
Если выбрать систему прямо-
угольных декартовых координат
на плоскости так, чтобы ось Ох
проходила через фокусы F{ и Fi,
а начало координат находилось по-
середине между ними, то в этой
системе координат уравнение ги-
перболы будет выглядеть так:
£i_Z = i
а2 Ь2
(3.9)
Это уравнение называется каноническим уравнением гиперболы.
Если взять другую систему координат, уравнение будет более слож-
ным. Поэтому выбранная система координат также называется ка-
нонической. Гипербола так же, как и эллипс, является кривой вто-
рого порядка. Величина а равна модулю полуразности расстояний
от точки гиперболы до фокусов, b = л/с2 - а2, где с — половина
расстояния между фокусами. Форма кривой показана на рис. 3.2.
3.7.4.	Парабола
Определение 3.24, Параболой называется геометрическое место
точек на плоскости, для которых расстояние до некоторой фиксиро-
ванной точки /'этой плоскости, называемой фокусом, равно рассто-
янию до некоторой прямой, лежащей в этой плоскости и не прохо-
дящей через фокус F. называемой директрисой. Если выбрать систему
координат таким образом, чтобы начало О находилось посередине
между фокусом /и точкой D^-у,	, являющейся основанием пер-
пендикуляра, опущенного из точки /на директрису, а ось Ох имела
направление вектора DF, то уравнение параболы будет иметь вид
у2 = 2рх. (3.10)
Рис. 3.3
Это уравнение называется ка-
ноническим уравнением парабо-
лы, а описанная выше система
координат — канонической си-
стемой координат для данной
параболы. Параметр р имеет про-
стой геометрический смысл: он
равен расстоянию от фокуса па-
74
раболы до директрисы. Из вышесказанного следует, что фокус па-
раболы имеет координаты Ду, 0), а директриса — уравнение х = - -у
Эта кривая также является кривой второго порядка, поскольку в
ее уравнении присутствует слагаемое у2, степень которого (в дан-
ном случае вторая) определяет порядок кривой. Эта кривая более
известна из курса средней школы (как график функции, являю-
щейся квадратным трехчленом: у = ах2 + Ьх + с). Как выглядит эта
кривая в канонической системе координат, показано на рис. 3.3.
3.8.	Поверхности второго порядка
3.8.1.	Общее уравнение поверхности второго порядка
Аналогично случаю плоскости в пространстве также рассмат-
риваются геометрические объекты, определяемые уравнениями,
содержащими вторые степени переменных х, у и z, а также их
попарные произведения. Эти объекты, как правило, являются по-
верхностями и поэтому называются поверхностями второго поряд-
ка. Общий вид уравнения, описывающего такие объекты, можно
представить следующим образом:
Ах2 + By2 + Cz2 - Dxy + Exz + Fyz + Gx + Hy + Kz + L = 0, (3.11)
где /I2 + В2 + С2 + D2 + E2 + F2 * 0. Многообразие форм поверхно-
стей в пространстве значительно увеличивается по сравнению с кри-
выми второго порядка. Поэтому имеет смысл при первоначальном
знакомстве с ними ограничиться описанием их канонических урав-
нений, формы и расположения относительно координатных осей.
3.8.2.	Эллипсоид
Каноническое уравнение эллипсоида имеет вид
из которого можно сделать вывод о том, что эта поверхность сим-
метрична относительно всех координатных плоскостей: хОу, xOz
и yOz. Действительно, если точка Mix. у. z) принадлежит поверх-
ности, то это означает, что ее координаты удовлетворяют уравне-
нию (3.12). Тогда симметричная ей относительно координатной
плоскости хОу точка M'(x,y,-z), очевидно, также удовлетворяет
этому уравнению и, значит, принадлежит поверхности. Аналогич-
но убеждаемся в симметрии поверхности относительно других ко-
ординатных плоскостей. Рассуждая подобным образом, нетрудно
убедиться в том, что координатные оси Ох, Оу и Oz являются
75
осями симметрии, а начало ко-
ординат — центром симметрии
этой поверхности. Подробный
анализ поверхности показывает,
что эллипсоид можно получить
путем вращения эллипса вокруг
одной из его осей и последую-
щего сжатия. Он представляет
собой ограниченную овальную
поверхность. В частности, если
а = b = с, то уравнение (3.12)
можно записать в виде
х2 + у2 + z2 = а2,
в котором нетрудно узнать известное уравнение сферы с центром
в начале координат радиусом а. Таким образом, сфера является
частным случаем эллипсоида. Форма и расположение эллипсоида
относительно осей координат изображены на рис. 3.4.
3.8.3.	Гиперболоиды
Каноническое уравнение однополостного гиперболоида имеет вид
X2 у2 Z2
а2 + Ь2 с2
(3.13)
и, как в случае эллипсоида, нетрудно убедиться в том, что поверх-
ность симметрична относительно координатных плоскостей хОу.
xOz и yOz, оси координат являются для нее осями симметрии, а
Рис. 3.5
начало координат — центром
симметрии. Если а = й, то гипер-
болоид называется гиперболои-
дом вращения, поверхность мо-
жет быть получена вращением ги-
X2 Z2
перболы —-----2" = 1, располо-
женной в координатной плоско-
сти xOz вокруг оси Oz. В общем
случае, если а Ь, то поверх-
ность, полученная вращением,
должна быть подвергнута сжатию
в направлении одной из осей: Ох
или Оу. В результате в сечении
плоскостями, перпендикулярны-
ми оси Oz, будут получаться не
окружности, а эллипсы. Форма
поверхности и ее расположение
76
Рис. 3.6
по отношению к осям координат
изображены на рис. 3.5.
Каноническое уравнение дву-
полостного гиперболоида имеет
вид
(з.14)
а1 Ь1 с1
Название двуполостный ги-
перболоид объясняется тем, что
вся поверхность состоит из двух
не связанных друг с другом час-
тей (или, как говорят, полостей).
Чтобы представить, как устрое-
на эта поверхность, достаточно
взять гиперболу в координатной
z^ х^
плоскости xOz —:---т = 1 и ее вращение вокруг оси Oz приведет к
с2 а1
двуполостному гиперболоиду вращения. Если подвергнуть его сжа-
тию в направлении одной из осей Ох или Оу, то получится повер-
хность, описываемая уравнением (3.14). Все свойства симметрии,
присущие однополостному гиперболоиду, сохраняются и для дву-
полостного гиперболоида.
Форма поверхности и ее расположение по отношению к осям
координат изображены на рис. 3.6.
3.8.4.	Конус
Каноническое уравнение конуса имеет вид
4+4-4=°- <з-15)
a1 tr с2
Эта поверхность второго по-
рядка может быть получена пу-
тем вращения в пространстве
вокруг оси Oz прямой, перво-
начально расположенной в плос-
кости xOz и имеющей уравне-
с
ние z = — х. В этом случае полу-
а
чится так называемый круговой
конус (в сечении которого ок-
ружности), а если его подверг-
нуть сжатию в направлении од-
ной из осей Ох или Оу, то полу-
чится поверхность, описываемая
77
уравнением (3.15) (в сечении плоскостью, параллельной плоско-
сти хОу. — эллипсы). Ось Oz обычно называют осью конуса.
Форма поверхности и ее расположение по отношению к осям
координат изображены на рис. 3.7.
3.8.5.	Эллиптический параболоид
Каноническое уравнение эллиптического параболоида имеет вид
X2 у2
Z~l2+~b2'
(3.16)
Исходя из вида уравнения по аналогии с предыдущими случа-
ями, можно сделать вывод о том, что поверхность симметрична
относительно координатных плоскостей xOz, yOz и относительно
оси Oz. Если а = 6, то поверхность является поверхностью враще-
ния (она может быть получена вращением параболы, расположен-
ной в плоскости xOz и имеющей уравнение х2 = a2z, вокруг оси
Oz). Если а ф Ь, то поверхность, полученная вращением, должна
быть подвергнута сжатию. Форма поверхности и ее расположение
по отношению к осям координат изображены на рис. 3.8.
3.8.6.	Гиперболический параболоид
Каноническое уравнение гиперболического параболоида имеет вид
По аналогии с предыдущими случаями делаем вывод о том,
что поверхность симметрична относительно координатных плос-
костей xOz, yOz и относительно оси Oz. Форма поверхности и ее
78
расположение по отношению к осям координат изображены на
рис. 3.9.
3.8.7.	Цилиндры
Цилиндры — это поверхности второго порядка, получающиеся
следующим способом. В плоскости хОу через каждую точку эллип-
са (3.8) проводится прямая, параллельная оси Oz. Получается бес-
конечная труба с поперечным сечением в форме этого эллипса.
Поверхность, построенная таким способом, называется эллипти-
ческим цилиндром. Оказывается, что уравнением этой поверхности
будет
^+^=1
я2 Ь2 ’
но рассматриваемое в пространстве. Действительно, если точка
Л/о(х,у,О), лежащая в плоскости хОу, находится на эллипсе, то ее
координаты удовлетворяют этому уравнению. Любая точка М', ле-
жащая на одной прямой, параллельной оси Oz, с точкой Л/о, име-
ет первые две координаты такие же, как и точка Л/о, а поскольку
координата z в уравнение (3.8) не входит, координаты точки М’
будут удовлетворять этому уравнению. Таким образом, этому урав-
нению будут удовлетворять координаты всех точек эллиптического
цилиндра. Форма поверхности и ее расположение по отношению к
осям координат изображены на рис. 3.10.
Аналогично уравнение (3.9), известное как уравнение гипербо-
лы на плоскости, рассмотренное в пространстве, оказывается урав-
нением поверхности (также построенной описанным выше спосо-
бом), называемой гиперболическим цилиндром. Форма поверхности
и ее расположение по отношению к осям координат изображены
на рис. 3.11.
Каноническим уравнением
параболического цилиндра будет
уравнение параболы (3.10), рас-
смотренное как уравнение по-
верхности в пространстве. Сама
поверхность строится по пара-
боле тем же способом: проведе-
нием через все точки параболы
прямых, параллельных оси Oz.
Форма поверхности и ее распо-
ложение по отношению к осям
координат изображены на рис.
3.12.
Рассмотренные поверхности
второго порядка являются ос-
79
новными представителями множества таких поверхностей. Кроме
них есть различные вырожденные случаи поверхностей, как пра-
вило, представляющие второстепенный интерес. Например, урав-
нение —г + Дг- = 0 является уравнением не поверхности в обыч-
СГ Ь1
ном понимании, а прямой: оси Oz. Уравнение второй степени вида
(Л]Х + В}у + С] 2 + D])G42x + В2у + С22 + D2) = О
определяет в пространстве пару плоскостей:
А[X + В}у + С] z +	= 0 и А2х + В2У + C2z + D2 = 0.
Если уравнение поверхности второго порядка не имеет канони-
ческого вида, то существуют способы, позволяющие распознать
тип этой поверхности и указать каноническую систему координат,
т.е. такую, в которой данная поверхность будет иметь канониче-
ское уравнение. В данном курсе эти способы не рассматриваются.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1.	Выясните, какие из векторов образуют пары коллинеарных векто-
ров, если а - {-3,6,21}, b - {2,-1,1}, с - {1,-2,-7}, d - {-6,3,-3}, е - {0,0,0}.
2.	Выясните, является ли тройка векторов компланарной, если а =
- {5,-1,3}, b - {4,-5,1}, с - {1,4,2}.
3.	Выясните, образуют ли базис в пространстве три вектора: а = {1,-2,4},
b - {3,-1,5}, с - {6,0,'1}.
4.	Пусть даны координаты векторов а и Ь: а = {7,-4,2}, b = {-5,6,1}.
Найдите координаты векторов с - За. d - 2а i 4Ь и е - 9b - 2d i с.
5.	В треугольнике АВС даны координаты вершин: А(-3,7,4), 5(1,-5,0);
С(—2,6,9). Найдите координаты векторов АВ, АС и СВ.
6.	В треугольнике АВС даны координаты вершин: А(-12, 7,5);
5(-12,19,21); С(15,-17,-3). Найдите площадь треугольника.
7.	Напишите уравнение окружности радиусом 5 = 5, центр которой
находится в точке С(-1,3).
80
8.	Напишите уравнение сферы радиусом R = 3, центр которой нахо-
дится в точке С(2,-3,0).
9.	Напишите уравнение плоскости, проходящей через три заданные
точки: >4(14,3,-6), R(l,l,l), С(4,-2,-2).
10.	Найдите канонические уравнения прямой в пространстве, если
дано, что эта прямая перпендикулярна плоскости Зх - 2у + 7z - 8 = 0 и
проходит через точку >4(7,-5,3).
11.	Уравнение кривой второго порядка 16х2 - 9г - 144 = 0 приведите к
каноническому виду, определите тип кривой, ее полуоси и фокусы.
12.	Определите по уравнениям тип поверхностей второго порядка:
а)	х2 + у2 + z2 - 1 = 0;
б)	х2 + у2 - z2 - 1 = 0;
в)	х2 + у2 - z2 = 0;
г)	х2 - у2 - z2 - 1 = 0;
д)	4х2 + у2 + 9z2 -1=0;
е)	х2 + у2 - z = 0;
ж)	х2 - у2 - z = 0;
з)	х2 - z = 0.
ГЛАВА 4
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ИХ ПРЕДЕЛЫ
4.1. Ограниченные и неограниченные
последовательности
Пусть задан занумерованный бесконечный набор чисел хь х2,
хн, ... . Это значит, что всякому натуральному числу п = 1, 2, ...
поставлено в соответствие по определенному закону веществен-
ное число хп.
Примерами таких наборов являются наборы чисел:
1	1	1
X] =1, х2 =-,..., х„ =-,...;
2	п
X] = arctgl, х2 = arctg2, ..., хп = arctg/7, ... .
Определение 4.1. Всякий занумерованный бесконечный набор
чисел Х|, х2, ..., хн ... называется числовой последовательностью.
Для краткости числовая последовательность обычно обозначается
символами х„, п = 1, 2, ..., или {хД (без указания, что п = 1, 2, ...),
а х„ называется общим членом последовательности.
Введенное понятие числовой последовательности имеет про-
стую геометрическую иллюстрацию. Именно, отметим на веще-
ственной оси R1 значения хь х2, .... Тогда получим множество то-
чек Е, соответствующее данной последовательности (рис. 4.1).
В предыдущих примерах эти множества суть
Е = |1,^,-р..J, Е =	’"Т1	= {агс^Гarctg2,arctg3,...}.
Очевидно, во всех этих примерах разным значениям /7=1,2, ...
соответствуют разные точки множества £, и поэтому последова-
тельности {хД можно представить как множество соответствующих
точек на прямой R1. В общем слу-
—--------*—♦—---------------х чае это не так- Например, число-
вая последовательность х, = (-1
Рис. 4.1	п = 1, 2, ... принимает на веще-
82
ственной оси только два значения, а именно, хп = 1, когда п четно,
и х„ = -1, когда и нечетно. Это говорит о том, что каждая из точек
х = 1 «накрывается» значениями общего члена последовательности
хп бесконечно много раз. Поэтому в данном случае последователь-
ность х„, /7=1,2, ... не следует отождествлять ее геометрическим
образом на вещественной оси, т. е. с множеством £={-1,1}, состо-
ящим из двух точек.
Тем не менее приведенная геометрическая иллюстрация спо-
собствует пониманию различных свойств последовательностей и,
в частности, свойства ограниченности.
Определение 4.2. Числовая последовательность х„, п = 1, 2, ...
называется ограниченной, если найдется число М> 0 такое, что для
всех номеров /7=1,2,... выполнено неравенство |хл| < М, или, что
то же, двустороннее неравенство -М < хп < М.
В соответствии с геометрической иллюстрацией последователь-
ности ее ограниченность означает, что все точки хп, /7=1,2, ...
расположены на некотором отрезке [~М,М] и, следовательно,
образуют ограниченное множество.
Пример 4.1. х„ = —, /7 = 1, 2, ... — ограниченная последователь-
/7	1
ность, так как для всех /7=1,2,... Ixd = — < 1.
п
Таким образом, в качестве числа М > 0, ограничивающего пос-
ледовательность, можно взять число М> 1.
Пример 4.2. хп = (-1)" -—-, п = 1, 2, ... .
п
Покажем, что и для этой последовательности в качестве числа
М можно взять любое число, больше или равное единице. Дей-
ствительно, при всех п
это и требуется.
Может случиться, что вещественное множество £ = {хл, /7=1,
2, ...}, соответствующее последовательности х„, п = 1, 2, ..., явля-
ется неограниченным. Это значит, что общий член х,; в процессе
неограниченного возрастания номера п может принимать по мо-
дулю сколь угодно большие значения. Такие последовательности
называются неограниченными.
Точно это выражается следующим определением.
Определение 4.3. Последовательность х„, п = 1, 2, ... называется
неограниченной, если какое бы большое число М > 0 ни взять, все-
гда найдется номер п такой, что |хн| > М.
Пример 4.3. Установим, что последовательность хн = (-1 )"/72, /7=1,
2, ... неограничена. Действительно, так как |хл| = п2, то какое бы
М > 0 ни взять, ясно, что при п > 4М выполняется неравенство
83
и2 > М. Таким образом, в качестве номера и можно взять какое-
либо целое число, больше -Л/.
Пример 4.4. Дана последовательность
fl, если п нечетно;
*»=	<4-0
[2fl, если п четно.
Ясно, что все х„ с нечетными номерами не могут принять зна-
чений, больших единицы, сколь бы далекими эти номера ни брать.
Напротив, если номера п четны, т.е. п = 2т, т = 1, 2, ..., то для
любого выбранного М > 0 всегда найдутся достаточно большие
номера п = 2т, для которых |хл| > М, т.е. 2п > М.
Чтобы найти такие номера, достаточно решить неравенство
2п > М, или, что то же, неравенство 22т > М.
Имеем 22т = 4"': > М. Следовательно, логарифмируя это неравен-
ство, находим, что в качестве п можно взять любое четное число
п = 2т, для которого т > log44/.
Тем самым установлено, что последовательность (4.1) неогра-
ниченна.
Замечание, Подчеркнем принципиальную разницу между нео-
граниченными последовательностями, данными в примерах 4.3 и
4.4. Именно, если в примере 4.3 неравенство |хл| > М выполняется
сразу для всех номеров п, лишь бы п > ТлГ, то в примере 4.4 —
только для четных номеров п > log_,W. т. е. только для части номеров.
Неограниченные последовательности, для которых неравенство
|хл| > М выполняется сплошь для всех п, больших некоторого номе-
ра, зависящего от М, называются бесконечно большими.
Определение 4,4, Последовательность хл, w = 1, 2, ... называется
бесконечно большой, если для любого сколь угодно большого числа
М > 0 найдется номер N (вообще говоря, зависящий от М) такой,
что для всех номеров п > N выполняется неравенство | хн| > М.
В примере 4.3 неограниченная последовательность хп = (~1)пп2,
/7=1,2,... является бесконечно большой, в примере 4.4 — после-
довательность (4.1) не ограничена, но не является бесконечно
большой.
4.2. Бесконечно малые последовательности
Среди всевозможных последовательностей особую роль играют
последовательности ан, п = 1, 2, ... которые стремятся к нулю при
п —> <», т. е. в процессе неограниченного возрастания номера обще-
го члена ан. Такие последовательности называются бесконечно ма-
лыми.
Определение 4,5, Числовая последовательность ан, п = 1, 2, ...
называется бесконечно малой, если она удовлетворяет следующему
84
условию: каково бы ни было сколь угодно малое число е > 0, все-
гда найдется номер N (зависящий от выбранного е > 0) такой, что
для всех номеров п > N справедливо неравенство |ая| < е.
Пример 4.5. Последовательность ая = —, п = 1, 2, ... является
п
бесконечно малой. В самом деле, пусть е > 0 — произвольное сколь
угодно малое число. Покажем, что найдется номер N такой, что
для всех номеров п, больших N, будет справедливо неравенство
|ай| < е. В нашем случае = —, поэтому номер 7V должен быть та-
п 1
ким, чтобы для всех п > N выполнялось неравенство — < е. Это
1 п
возможно, очевидно, если N > -.
е ГМ
Пример 4.6. Последовательность ая = sin L п = 1, 2, ... также
\п )
является бесконечно малой. Действительно, так как для любого
положительного х справедливо неравенство si их < х, то, полагая
1	I I  f 1 1 1	Г
х = получаем, что ая = sin —7 1< — < г. как только п > .
п2	М ) п1
Поэтому в качестве JV(e) можно взять целую часть числа J-, т.е.
Чй
Пример 4.7. Рассмотрим последовательность aH = qn, п = 1, 2, ...,
где |^| < 1, и установим, что эта последовательность бесконечно
малая. Действительно, взяв е > 0 сколь угодно малым и логарифми-
руя неравенство |ая| = \q\” < е по основанию |^|, получаем, что
п > log|^|E. Таким образом, неравенство |ая| < е будет выполняться
для всех п > logi^e. Поэтому можно положить N = [log^e] — целая
часть log। |g. Это и требуется.
Обратимся к основным свойствам бесконечно малых последо-
вательностей, которые выражаются в следующих теоремах.
Теорема 4.1. Пусть aH, п = 1, 2, ... — бесконечно малая последо-
вательность. Тогда для любого числа М произведение Маю /7=1,
2, ..., есть также бесконечно малая последовательность.
Доказательство. Возможны два случая: Л/ = 0 и М =# 0. В первом
случае утверждение теоремы очевидно. Рассмотрим случай М # 0.
Пусть е > 0 — произвольное сколь угодно малое положительное
число. Положим Е] = щр Поскольку ая, /7 = 1,2, ... — бесконечно
малая последовательность, то для выбранного Е] найдется номер
JV] такой, что для всех номеров п > выполнено неравенство
IaJ < Ei. Следовательно, |MxJ < \М\ led < Me, = М— = е также для
М
всех номеров п > N. Это и значит, что последовательность Мап —
бесконечно малая. ▲
85
Теорема 4.2 (о произведении бесконечно малой последователь-
ности на ограниченную). Пусть ая, п = 1, 2, ... — бесконечно малая
последовательность, а х„, п = 1, 2, ... — ограниченная последова-
тельность. Тогда произведение апхп, п = 1, 2, ... есть бесконечно
малая последовательность.
Доказывается аналогично теореме 4.1.
Теорема 4.3. Пусть а„ и р„, л = 1, 2, ... — две бесконечно малые
последовательности. Тогда их сумма или разность н,; ± является
также бесконечно малой последовательностью.
Доказательство. Действительно, пусть е > 0 — произвольно ма-
£
лое число. Положим Е] = — и заметим, что е( также произвольно
малое число. Поскольку ая, л = 1, 2, ... — бесконечно малая после-
довательность, то для выбранного 6] найдется номер 7V) такой, что
при всех п > N] будет выполнено неравенство
Ы < £]
(4-2)
Точно так же для бесконечно малой последовательности п =
= 1, 2, ... найдется номер М такой, что при всех л > N2 будет
выполнено неравенство
Ш<е,.	(4.3)
Положим теперь А = тах(7У[,Л2)- Тогда для всех л, удовлетворя-
ющих неравенству п > N, будут выполнены неравенства (4.2) и
(4.3). Следовательно, для всех п > N будет выполнено неравенство
|а„ ± ря| < |а„| + |ря| < £[ + £[ = | +1 = е.
Так как е > 0 — любое число, это и значит, что последователь-
ность ± ря является бесконечно малой. ▲
Следующая теорема гласит о том, что всякая последователь-
ность, «зажатая» между двумя бесконечно малыми последователь-
ностями, является также бесконечно малой.
Теорема 4.4 (о промежуточной бесконечно малой последова-
тельности). Пусть даны три последовательности ан, х,; и рл, п = 1,
2, ... такие, что:
1) для всех /7=1,2, ... удовлетворяются неравенства ан < х„ < ря;
2) ан и рп, я = 1, 2, ... — бесконечно малые последователь-
ности.
Тогда и промежуточная последовательность х„, п = 1, 2, ... яв-
ляется бесконечно малой.
Доказательство. При доказательстве теоремы 4.3 было установ-
лено, что если с/.,; и рн — две бесконечно малые последовательно-
сти, то для любого е > 0 найдется номер N такой, что при всех
номерах п > N одновременно выполняются неравенства
|а«1 < е, 13d < е,
86
или, что то же,
-е < ап < е, -е < ря < е.	(4.4)
Учитывая подчеркнутые неравенства в (4.4), из условия 1 не-
медленно получаем, что для тех же номеров п > N все члены про-
межуточной последовательности х„, п = 1, 2, ... удовлетворяют
двусторонним неравенствам
-е < ал < хп <	< е.
Отсюда, очевидно, следует, что при п > N
-г < х„ < е, т.е. |хй| < е.
Это и значит, что хн, п = 1, 2, ... — бесконечно малая последо-
вательность. ▲
Пример 4.8, В качестве примера рассмотрим частный случай тео-
ремы, часто встречающийся на практике. Именно, пусть хп > О,
п = 1, 2, ... — последовательность неотрицательных чисел (корот-
ко — неотрицательная последовательность). Допустим, что эта нео-
трицательная последовательность не превосходит какой-либо бес-
конечно малой последовательности рн, п = 1, 2, ..., т.е. для всех п
О < х„ <	(4.5)
Мы утверждаем, что тогда последовательность х„, п = 1, 2, ...,
сама является бесконечно малой.
Это утверждение немедленно следует из теоремы 4.4. В самом
деле, последовательность хн, удовлетворяющая неравенствам (4.4),
может трактоваться как промежуточная последовательность между
тривиальной последовательностью ая = 0, л = 1, 2, ... и последова-
тельностью ан, /7=1,2, ..., и нам остается только применить тео-
рему 4.4.
Наконец, установим связь между бесконечно большими и бес-
конечно малыми последовательностями.
Теорема 4.5. Пусть хн, /7=1,2,... — бесконечно большая после-
довательность. Тогда последовательность обратных величиной = —,
/7=1,2,... является бесконечно малой последовательностью.
И обратно, если а„, п = 1, 2, ... — бесконечно малая последова-
тельность, причем ан # 0, то последовательность х„ = —, /7=1,2, ...
является бесконечно большой.
Доказательство. Действительно, пусть х„ — бесконечно боль-
шая последовательность. Покажем, что в этом случае последова-
тельность =—,/7 = 1,2,... есть бесконечно малая последователь-
ность. Для этого выберем любое е > 0 и положим М = -. Тогда
е
87
в соответствии с определением 4.4 найдется номер N такой, что
при п > N справедливо неравенство
kl >м.
Тогда при тех же номерах п > N будем иметь lad = J-r < — = е.
1 1 |х„| М
Это означает, что ан — бесконечно малая последовательность.
Докажем обратное утверждение. Пусть последовательность ая,
п = 1, 2, ... — бесконечно мала. Докажем, что последовательность
х„ = —, /7 = 1,2,... бесконечно велика. Действительно, пусть М> 0 —
сколь угодно большое число. Положим е = — и найдем номер N
М
такой, что | ан| < е для всех п > N. Но тогда при тех же п > N будем
иметь
|х„| = Дт > - = d/ , т.е. |х„| > М. ▲
|«„| е
4.3. Предел числовой последовательности
Данный подраздел является основным в этой главе. Здесь вво-
дится понятие предела последовательности и изучаются сходящиеся
последовательности.
4.3.1. Основные определения
Определение 4.6. Число а называется пределом числовой последо-
вательности хн, п = 1, 2, ..., если разность с/.,; = хп - а является
бесконечно малой последовательностью.
Обозначается предел символом а = lim х„.
Последовательности, имеющие предел, называются сходящимися.
Факт сходимости последовательности хп, п = 1, 2, ... к своему
пределу а принято обозначать так: х„ —> а (п —> ©о), или хп —> а.
Используя определение 4.5 бесконечно малой последователь-
ности, нетрудно сформулировать понятие предела на так называе-
мом «е - П» языке.
Определение 4.7, Число а называется пределом последовательно-
сти х„, если для любого е > 0 найдется номер N (зависящий, вооб-
ще говоря, от е) такой, что для всех номеров п > N справедливо
неравенство |хн - й| < е.
Пример 4.9. Прежде всего заметим, что в рамках определения
4.6 бесконечно малые последовательности — это те и только те
последовательности, предел которых равен нулю. Таким образом,
88
сказать, что а„, п = 1, 2, ... — бесконечно малая последователь-
ность или сказать, что Нт а„ = 0 — одно и то же.
-
/7 + 1
Пример 4,10. Покажем, что lim----= 1.
Действительно,
поскольку----> 0 при п —> +оо.
п
Пример 4.11. Вычислим сумму всех членов бесконечно убываю-
щей геометрической прогрессии 1, q, q2, ..., q”, ..., где |#| < 1.
Именно, пусть Sn = 1 + q + q2 + ... + qn, n = 0, 1,2, ... — последо-
вательность сумм первых п слагаемых.
Покажем, что lim S„ = —-—.
1 — q
Действительно, как известно
qn+{ — 1
1 + q + q2 + ... + qn =-----,
tf-l
и, следовательно,
с _ q,l+l -1 _ яп+] 1
‘ г ,
q-\	q-\ q-\
или, иначе
Поскольку |c/| < 1, то последовательность qn —> 0 при п —> (см.
пример 4.7), т.е. является бесконечно малой. По теореме 4.1 после-
довательность $ qn также является бесконечно малой, и из (4.6)
?-1
получаем, что последовательность 5Н, п = 0, 1, 2, ... сходится к
числу —!—, т. е. lim Sn = —!—. Найденный предел и принимается в
I - с/	\-q
качестве суммы бесконечно убывающей геометрической прогрес-
сии, т.е.
\ + q + q2 +... + qn + ... = ——.
1-?
Выясним геометрический смысл предела последовательности.
Как известно, совокупность всех точек хе R1, удовлетворяющих
неравенству |х - а\ < е, является интервалом радиусом е с центром
в точке х = а. Такой интервал называется е-окрестностью точки а и
89
U г.	обозначается Uу Следовательно,
।	f--“----, фигурирующее в определении
“OJ * £	’	* 4-6 неравенство |хл - й| < е, п
n>N	> N, геометрически выражает тот
рис 4 2	факт, что для всех номеров, на-
чиная с номера N + 1, члены
последовательности хн, п = 1, 2, ... попадают в е-окрестность точ-
ки х = а.
В итоге в геометрической интерпретации определение предела
а = lim xt, выглядит следующим образом: число а является преде-
лом последовательности х„, п = 1, 2, ..., если сколь бы малую
окрестность U* ни взять, всегда найдется номер N такой, что все
члены хп с номерами большими, чем N, попадают в эту е-окрест-
ность точки а, т.е. х,; е п > N. Вне же окрестности U* остается
не более чем конечное множество элементов последовательности
(рис. 4.2).
С уменьшением е > 0 номер N становится, вообще говоря, все
больше и больше, однако всякий раз весь «хвост» x?v+], xjV+2, ...
последовательности хь х2, ... попадает в выбранную окрестность
U* предельной точки а.
4.3.2. Свойства сходящихся последовательностей
Нижеследующие теоремы составляют основу для практическо-
го нахождения пределов числовых последовательностей.
Прежде всего отметим так называемые «арифметические» свой-
ства пределов. Эти свойства заключены в следующей теореме.
Теорема 4.6. Пусть хп и у„, п = 1, 2, ... — сходящиеся последова-
тельности, т.е.
lim хп = а , lim у„ = b.
fl—
Тогда справедливы следующие утверждения:
1)	для любого числа М последовательность Мх„ также сходится,
причем
lim (Мх„) = М lim хп = Ма;
2)	сумма (разность) хн ± у„ также сходится, причем
lim(хл ±уп) = limх„ ± limу„ =а±Ь;
ft—>^	н—п—
3)	произведение хпуп также сходится, причем
lim (х„уп) = lim х lim у„ = ab;
ft—>^	п—
4)	при дополнительном условии b # 0 частное — также сходит-
ся, причем
90
Доказательство. Все четыре утверждения доказываются одно-
типно, поэтому дадим строгое доказательство, например, для про-
изведения последовательностей, т.е. для утверждения 3.
Действительно, в соответствии с определением предела после-
довательности х„ и у„ представляются в виде х„ = а + ай, у„ = b + ря,
/7=1,2, ..., где ай и рй — бесконечно малые последовательности.
Следовательно,
х„у„ = (а + ай) + (Ь + рй) = ab + у„,	(4.7)
где
уп = а(5„ + Ьа„ + аД.
Так как а и b — числа, то произведения а$п и Ьа,: суть бесконеч-
но малые последовательности (см. теорему 4.1). Произведение же
двух бесконечно малых последовательностей тем более является
бесконечно малой. Таким образом, у„ также является бесконечно
малой последовательностью и запись (4.7) по определению преде-
ла означает, что ab есть предел последовательности х„у„. ▲
Как уже отмечалось, эти свойства являются основным инстру-
ментом нахождения конкретных пределов. Рассмотрим несколько
примеров использования теоремы 4.6.
ц- — 2п — 1
Пример 4,12. Найти предел lim------=--.
,,	3/72
Имеем
v л?2-2л?-1 ,	э	1,. /72—2/7 —1 1 .. Л 2 П
lim----г— = {утверждение 1) = — hm----5----= —lim 1------т =
3/72	3«-“	/72	3«^™( п rr J
^утверждение 2) = -f liml-lim — -lim-O=-(1-0-0) = -.
Пример 4.13. Найти предел 1 Имеем	г‘ lim n^yjn2 + 1 - V/72 - 1) ,.	2п = lim —.		,	: f fi 1 I1	1 /7 ,11 4	у -f- .11	7 1 v	n1	V	n1 1 L 1	.	L	1 так как JI + -^5- —> 1 и JI —7 —> V/72	V /?	/^00	ri	1	J	J im n[\ln2 + 1 - V/72 - 1). i-	2 = lim n .	.	= V/72 + 1 + V/72 - 1 = 2 lim	,	= 1, «—f L 1 L 1 ) Jl + — + JI — 1 V /72 V /7 1 1 при /7 —> OO.
91
Замечание, Отметим, что непосредственное (т.е. без предвари-
тельных преобразований) применение теоремы 4.6 ни в первом
(см. пример 4.12), ни во втором (см. пример 4.13) случае невоз-
можно, поскольку это приводит к неопределенностям. Неопреде-
ленности бывают разных типов, их условно можно представить в
оо	О
виде—,	, О-*». Ниже познакомимся с одной неопределен-
ен	О
ностью типа 1" (неопределенность типа «е»). Раскрытие этих нео-
пределенностей и составляет содержание практики нахождения
пределов.
Следующий вопрос, который рассмотрим, касается предельно-
го перехода в неравенствах.
Теорема 4.7 (теорема о пределе промежуточной последователь-
ности). Пусть имеются три последовательности х„, у„ и zH, п = 1, 2,
..., причем:
1) хп < у,: < zH, /7=1,2, ...,
2) lim х,; = lim zn = а.
Тогда промежуточная последовательность уп также сходится,
причем к тому же пределу й, т. е. lim у„ = а.
Доказательство. Из условия 2 следует, что х„ и у„ представляют-
ся в виде х„ = а + а„, z„ = а + где ая, рн, п = 1, 2, ... — бесконечно
малые последовательности. В таком случае неравенства 1 суть
а +	< хп < а +
или, иначе
а„ < х„ - а < п = 1, 2, ... .
Следовательно, согласно теореме 4.4, разность хп - а —> 0 при
п —> оо. А
Заключительная теорема указывает на то, что в числовых нера-
венствах можно переходить к пределу, при этом предельное нера-
венство имеет тот же знак.
Теорема 4.8. Пусть х„, у„, /7=1,2, ... — сходящиеся последова-
тельности, причем
< у„.	(4.8)
Тогда и lim х„ < lim у„.
fl—>00
Доказательство. Пусть limxfl=£Z, limyw = />. Необходимо ус-
тановить, что а< Ь. Допустим противное, т. е. а > Ь, или, что то же,
а - b = е0 > 0, п = 1, 2, ... .
Имеем хп = а + ап, у„ = b + рд, где а„ и п = 1, 2, ... —
бесконечно малые последовательности. В силу (4.8),
а + ап < b + п = 1, 2, ...,
92
откуда
а - b < а„ -
или, что то же,
а„ -	> е0, п = 1, 2, ... .
Но это несовместимо с тем, что и — бесконечно малые
последовательности, а значит, и разность £„ - ап также бесконеч-
но малая последовательность (см. теорему 4.3). Полученное проти-
воречие доказывает теорему. ▲
4.4. Монотонные последовательности. Число «е»
Пусть хп, п = 1, 2, ... — числовая последовательность. По опре-
делению, она монотонно возрастающая, если для всех номеров
/7=1,2,... справедливо неравенство х„ < х„+\.
В случае строгого неравенства х,; < х,:..} последовательность на-
зывается строго монотонно возрастающей.
Примерами монотонно возрастающих последовательностей яв-
ляются последовательности х„ = 1 —, х„ = arctg/7, х„ = n2 и т.д.
n
Интересно отметить, что в первых двух случаях последователь-
ности сходятся, а именно
В то же время последовательность х„ = п2 конечного предела,
очевидно, не имеет. И это не случайно. Дело в том, что последова-
, 1
тельности хп = 1---и х„ = arctg/7 ограничены, а последователь-
72
ность хп = п2 — нет.
Общий результат о сходимости монотонно возрастающей после-
довательности устанавливается в следующей теореме.
Теорема 4.9. Всякая монотонно возрастающая и ограниченная
сверху последовательность имеет конечный предел.
Доказательство. Действительно, пусть последовательность х„,
/7 = 1, 2, ... удовлетворяет условиям теоремы, т.е.
1) x„+h п = 1, 2, ...;
2) существует число М такое, что для всех п справедлива оцен-
ка х„ < М.
Покажем, что существует число а такое, что х„ —> а.
Для этого рассмотрим множество значений последовательно-
сти х„, /7=1,2, ... и обозначим его через Е. В соответствии с усло-
вием 2 множество Е ограничено сверху некоторым числом М. По-
этому, как всякое ограниченное множество, оно имеет точную
93
верхнюю грань а = sup£. Покажем, что это число и есть искомый
предел последовательности х„, п = 1, 2, ... .
В самом деле, в соответствии с определением точной верхней
грани множества, число а обладает двумя свойствами:
1) х„ < а для всех номеров /7=1,2, ...;
2) каково бы ни было е > О, найдется номер N такой, что xN > а - е.
Ясно, что ввиду монотонности последовательности из свойства 2
следует, что при любом п = N + 1, N + 2, ... тем более хп > а - е.
С учетом свойства 1, это дает двустороннее неравенство
а - е < хп < й, п = N + 1, N + 2, ...
и, как следствие, неравенство
а-г<х„<а + г, п = N + 1, 7V + 2, ... .
Таким образом, для любого е > 0 нашелся номер JV, начиная с
которого |х„ - й| < е. Это и значит, что а = lim х„. ▲
Примером использования доказанной теоремы является стро-
гое введение одного из самых известных и важных иррациональ-
ных чисел, а именно числа е = 2,718281828... .
( 1Y
Рассмотрим последовательность х„ = 1 + — , п = 1, 2, ... и по-
I /7 I
кажем, что она имеет конечный предел, который по определению
и есть число е.
Для этого установим, во-первых, что последовательность х„
монотонна.	, у
Утверждение 4,1, Последовательность хй=1 + — ,л = 1,2,...
/7
монотонно возрастает.	V /
Доказательство. Согласно формуле бинома Ньютона,
" п(п—1)...(/7 —к + 1) 1
х„ = 1 +	-------L —
к=\
или после преобразования
п(п- 1)...(/7 — & + 1) _ п п - 1
пк	п п
то же самое, что
к\	пк
п - к + 1 _ ] С 1 А С к -1
п I	/7 J I п
Ясно, что при замене п на п + 1 значение каждой скобки увели-
1	к-\
чится, ибо из единицы будут вычитаться вместо чисел —,----
1	к-\	п п
меньшие числа-----,...,---.
/7 + 1	/7 + 1
94
Кроме того, и число слагаемых станет больше на единицу. Та-
ким образом, для любого п имеем х„ < х„+1. ▲
( 1Y
Утверждение 4.2. Последовательность хп = 1 + — , п = 1, 2, ...
I п J
ограничена сверху числом М= 3.
Доказательство. Обратимся вновь к формуле (4.9). Заменив в
ней каждую скобку единицей, получим оценку сверху
—।—— + • • • н-
2 22	2"
и тем более оценку хп < 1 + У где 5 — сумма бесконечно убываю-
1 т
щей геометрической прогрессии со знаменателем q = —. Так как
1
5 =----, то 5 = 2, и тем самым хп < 3 для всех п = 1, 2, ... . ▲
1-<7
В результате приходим к следующему выводу. Последователь-
ность хп = 1 + — удовлетворяет условиям теоремы 4.9 и, следова-
I nJ
тельно, имеет предел. Этот предел и есть по определению число е.
Тем самым мы установили один из так называемых замечательных
пределов
= е.
Вычисления показывают, что е = 2,718281828... .
Отметим также, что число е является основанием логарифма,
получившего название «натурального логарифма». Натуральные
логарифмы наиболее часто употребляются на практике.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1.	Докажите, что всякая сходящаяся последовательность ограничена.
2.	Назовем последовательность х„, п = 1, 2, ..., ограниченной сверху,
если найдется число Л/такое, что для всех номеров п = 1, 2, ... выполня-
ется неравенство хп < М.
Аналогично назовем последовательность п = 1, 2, ..., ограниченной
снизу, если найдется число т такое, что для всех п = 1, 2, ... выполняется
неравенство т < хп.
Докажите, что последовательность хп, п = 1, 2, ..., ограничена (см.
определение 4.2) тогда и только тогда, когда она ограничена сверху и
снизу одновременно.
3.	Докажите, что последовательность
п +1
----при п четном,
и
п2 при п нечетном
ограничена снизу, но не ограничена сверху.
95
4.	Пусть последовательность хп = 1,2,... сходится к числу а, т.е. Нт х„ = а.
Докажите, что тогда последовательность уп = |х„|, п = 1, 2, ... сходится к
|д|,т.е. lim|xd = |a|.
5.	Пусть х„, п = 1, 2, ... — числовая последовательность. Рассмотрим
произвольный бесконечный набор возрастающих номеров щ < п2 с ... <
< пк < ... . Тогда последовательность чисел у] = хН|, у2 = х„2,..., ук = хнр ...
называется подпоследовательностью исходной последовательности х„, п =
= 1, 2, ... .
Докажите, что если последовательность хп сходится, то любая ее под-
последовательность также сходится, причем к тому же самому пределу.
Иначе, если lim х„ = а, то и lim ук = а.
6.	Вычислите следующие пределы:
п2	2"	.. ,	---7 ч (2а + 1)!+ (2л + 2)!
lim------;---7, lim------, 1ип(-$/л + 2л -1 - л), нт -----—--------.
^«(2 + л)2+л2 »^Зл + 1’	7	(2л+ 3)!
ГЛАВА 5
ПРЕДЕЛ ФУНКЦИИ ОДНОЙ ВЕЩЕСТВЕННОЙ
ПЕРЕМЕННОЙ. НЕПРЕРЫВНОСТЬ
5.	1. Определение функции
Пусть X — некоторое множество вещественных чисел. Допус-
тим, что каждому значению х е X по какому-либо закону постав-
лено в соответствие вещественное число у. Это сопоставление опре-
деляет однозначное отображение и называется функцией одной
вещественной переменной х с областью определения X. Множество
всех значений у обозначается через Yи называется областью значе-
ний этой функции.
Общепринято функции обозначать буквой /, а более точно
у = Дх), подчеркивая, что значение у е Y определяется по зна-
чению х е X. При этом переменная величина х называется
аргументом.
Заметим, что закон, определяющий функцию у = f(x), может
задаваться различными способами, в том числе словесно, табли-
цей значений и т.д. Но чаще всего функция у = /(х) задается
какой-либо формулой, т. е. аналитически, поскольку этот вид за-
писи наиболее удобен для исследования различных свойств фун-
кции.
Пример 5.1. Простейшими функциями, определенными на всей
вещественной оси, являются многочлены степени п > 1
у = а„хц + а„_{хц~} + ... + й|Х + «0,
где ап, ап_\, at, aQ — коэффициенты многочлена.
Многочлены первой степени у = арс, + ай являются линейными
функциями, их графики — прямые.
Многочлены второй степени у = а-2х2 + а{х + «0 являются квад-
ратными трехчленами, их графики — различного вида параболы.
Пример 5.2. Важнейшими элементарными функциями являют-
ся тригонометрические функции
у = sinx, у = cosx
и обратные к ним функции
у = arcsinx, у = arccosx.
97
Функции sin.Y и cosx являются периодическими функциями с пе-
риодом 2л и определены на всей вещественной оси (рис. 5.1, 5.2).
Напротив, функции arcsinx и arccosx определены только на отрез-
ке [-1,1] (рис. 5.3, 5.4).
Пример 5.3. Показательная и логарифмическая функции также
относятся к элементарным функциям
у = ах и у = log0x,
98
Рис. 5.7
Рис. 5.8
а > 0, а * 1 — фиксированное число. Показательная функция у = ах
определена для всех х е R1 и принимает только положительные
значения (рис. 5.5). Напротив, логарифмическая функция у = log^x
определена только для х > 0, но принимает всевозможные значе-
ния, как положительные, так и отрицательные (рис. 5.6).
Пример 5,4, Определим две функции, не являющиеся элемен-
тарными, а именно функцию у = [х], называемую целой частью
вещественного числа х, и функцию у = {х}, называемую дробной
частью числа х.
Как известно, любое вещественное число х однозначно пред-
ставляется в виде х = п + а, где п — целое число, а число а удовлет-
воряет неравенству 0 < <х < 1. По определению полагаем [х] = н,
{х} = а. Ясно, что числа и и а зависят от х и являются функциями,
определенными на всей вещественной оси (рис. 5.7, 5.8).
5.	2. Предел функции
5.	2.1. Определение. Таблица замечательных пределов
Нижеследующее определение предела является центральным
определением в теории функций одной вещественной перемен-
ной, оно характеризует поведение функции у = f(x) в процессе
стремления ее аргумента х к фиксированной точке а е R1.
Итак, пусть функция у = /(х) определена в некоторой окрест-
ности какой-либо фиксированной точки й, исключая, быть мо-
жет, только саму точку а.
Определение 5.1. Число b называется пределом функции /(х) при
х —> й, если для любой последовательности аргументов хь х2,
х„, ... (хн * а), сходящейся к й, соответствующая последователь-
ность значений функции /(х,), /(х2), ...,	... сходится к Ь.
Предел функции обозначают символом lim f(x) и пишут
99
b = lim f(x).
В логических символах это определение записывается в виде
b = lim f(x): {Vx„ -> а(х„ * а) Дх„) Ь}.
Предел имеет простой геометрический смысл, если обратиться
к графику функции (рис. 5.9).
Он состоит в том, что при любом выборе последовательности
хп -ь а соответствующая последовательность у„ —> Ь(ул = /(хй)) на
оси Оу. Это значит, что последовательность точек Л/й(хй, распо-
ложенных на графике функции у = /(х), устремляется к точке (а, Ь).
Подчеркнем, что в самой точке х = а функция у = /(х) может
быть не определена, что на графике отмечено стрелками и круж-
ком с пустотой.
Замечание. Часто удобно пользоваться определением предела
функции в следующей эквивалентной форме. Именно, b = lim f (х),
если при любом выборе последовательности
(хл # й) последовательность b - f(x„) -ь 0, т.е.
Пример 5.5. Первый замечательный предел
.	sin х „	,
Рассмотрим функцию у =------. Эта функция определена всюду
кроме точки х = 0. В самой же этой точке при подстановке х = 0
0 п
получается, как принято говорить, неопределенность вида —. По-
sin х	0
этому найти предел функции-----при х —> 0 фактически означает
х
раскрыть эту неопределенность.
г sinx .	_
Итак докажем, что lim-----= 1, т.е. докажем, что для любой
х—>0 х
последовательности аргументов хп 0 (хй * 0) соответствующая
аргументов x„ —> a
бесконечно мала.
,. sin x
lim-----= 1.
л-^0 x
100
sin x„ .	~
последовательность y„ =------ 1 при n —>	С этой целью прежде
.	sin X
всего заметим, что ввиду четности функции-----достаточно огра-
х
ничиться рассмотрением только положительных значений аргу-
мента х. В таком случае воспользуемся известным двусторонним
неравенством
sinx < х < tgx, хе
(5-1)
при 0 < х < у, выражающим геометрически тот факт, что радиан-
ная мера х угла, опирающегося на дугу окружности единичного
радиуса (ОВ = 1), равна длине этой дуги (х = ВС) и, очевидно,
больше катета АС = sinx, но меньше катета ВО = tgx (рис. 5.10).
Опираясь на неравенство (5.1), сравним теперь значения функ-
sin X .	Л —
ции у =-----с 1 в процессе х 0. Так как sinx < х, то
х
0<	(5.2)
х
С другой стороны, так как х < tgx, то
1 sin х 1 sin х i
1--------< 1------= 1 - COS X.
X	tgx
Поскольку
1	3 • 2 *
1 - cosx = 2 sin2	,
2
то, вновь используя неравенство sinx < x (x > 0), получаем из (5.2),
что
 2
2
. sin x _ . 2 x _ ( x A2
1------< 2 sin2 — < 2 —
x 2 У 2 J
С учетом неравенства (5.2) имеем
0 < 1 sinx х2
х < 2
Отсюда ясно, что какова бы ни была последовательность аргу-
л	1 sin
ментов хн —> 0, последовательность I-------- удовлетворяет дву-
стороннему неравенству
0 < j sin <а!
xfl 2 ’
101
т.е. зажата между двумя бесконечно малыми последовательностя-
ми, одна из которых тождественно равна нулю, а вторая равна -у-,
sin _Y
Значит, и последовательность------ является бесконечно малой
sin х Xfl
(см. теорему 4.4), т.е. 1--- —> 0 . Это значит, что lim-= 1. ▲
Х„	X
Этот, а также другие замечательные пределы приведем без до-
казательства в виде таблицы (табл. 5.1).
Таблица 5.1
Таблица замечательных пределов
. .. sinx , 1. lim	= 1 -Y^O X	8.1im'og°(1 + x)=_L a-^o x	In a
_ .. arcsinx . 2. lim	= 1 -Y^O	X	n .. (l+x)rt-1 9. lim 				= a x->0	x
3.	= i _Y^0 X . .. arctgx . 4. lim	— = 1 _Y^0	X	(a — вещественный параметр) .. 1 -cosx 1 10. lim		— = — x2	2
Cl- eY-1 1 5. lim	= 1 A^O	1	11. lim(l + x)~ = e x->0
ln(l+x) . 6. lim —-		 = 1 _Y^0	X	.. sh x , 12. lim	= 1 A->0 X
_ .. ax -1 . 7. lim	= In a x	.. thx , 13 lim	= 1 •л-^0 X
Таблица замечательных пределов используется для вычисления
пределов на практике.
5.	2.2. Основные свойства пределов функции
Основные свойства пределов функции изложим в виде следую-
щих теорем.
Теорема 5.1. Пусть существует lim f(x) = b. Тогда для любого
А—
числа а е R1 функция а/(х) также имеет предел, причем
lim(o/(x)) = a lim f(x) = ab.
Теорема 5.2. Пусть существуют lim f(x) = b и limg(x) = c.
102
Тогда:
1)	функция f(x) ± g(x) также имеет предел при х —> а, причем
lim[/(x) ± g(x)] = lim /(х) ± lim g(x) = b±c,
т.е. предел суммы (разности) двух функций равен сумме (разно-
сти) пределов этих функций;
2)	функция f(x)g(x) также имеет предел, причем
lim[/(x) • g(x)] = lim /(х) • lim g(x) = b e,
x—?a	x—
т.е. предел произведения двух функций равен произведению пре-
делов функций;	г/ .
3)	при дополнительном условии с * 0 функция J ' имеет пре-
дел, причем
х^а g(x) с
т.е. предел частного равен частному пределов.
Доказательство всех перечисленных утверждений проводится
одинаково и является прямым следствием аналогичных свойств
пределов числовых последовательностей, доказанных в 4.3.
Проведем доказательство, например, для случая 2 теоремы 5.2.
Доказательство. Действительно, пусть х„ —> а (хп * а) — произ-
вольная последовательность аргументов, стремящихся к а. Тогда
по условию /(хн) -» b, a g(xn} —> с. Следовательно, по теореме 4.6,
произведение f(x„)g(xn) —> be. Это значит, что существует
lim/(x)g(x), причем справедлива формула
х-ьа
lim f(x)g(x) = lim f(x) lim g(x) = be. ▲
Пример 5.6. Найти предел
.. ( , sin2x
hm x1 +-------
A-^0	X
Имеем
.. ( sin 2x i ..	? .. sin2x sin2x ~
lim х2 н----------= hm х2 + hm------------= 2 hm---------= 2
X	x-—>0 X -^0 2x
(здесь использован первый замечательный предел).
Пример 5.7. Найти предел lim 5111 А' . Имеем
r1
.. sin x
НтЛЛХ= ™ x
*->o еЛ -1	.. еЛ -1
hm-----
x->0 x
(здесь вновь использованы замечательные пределы из табл. 5.1).
103
5.	3. Бесконечно малые функции. Метод эквивалентных
бесконечно малых величин
Определение 5.2, Функция сх.(х) называется бесконечно малой при
х —> а (или в точке а), если она имеет предел при х —> а, причем
этот предел равен нулю.
Кратко: а(х) — бесконечно малая при х 0. если lim а(х) = 0.
А—
Например, функции х, sinx, х2, 1 - cosx и другие являются бес-
конечно малыми при х 0. Функция sinx является бесконечно
малой и в процессе х —> ±л, ±2л, поскольку
lim sin х = sin = 0 при к = ±1, ±2, ... .
х—
Аналогично функция 1 - cosx является бесконечно малой при
х —> 2кк, к = ±1, ±2, ... .
Ясно, что бесконечно малые функции могут стремиться к нулю
по-разному или, как говорят, с разной скоростью. Поэтому беско-
нечно малые функции принято сравнивать между собой в зависи-
мости от того, как ведет себя их отношение.
Пусть ос(х) и р(х) — две бесконечно малые функции в процессе
х —> й, причем р(х) 0 при х*а.
Определение 5.3, Бесконечно малые с/.(х) и р(х) называются бес-
конечно малыми одного порядка малости, если существует предел
1-	^(Х) А	Л п
пт = А, причем А # 0.
р(х)
Пример 5.8. Сравним две бесконечно малые функции о.(х) =
= 1 - cos2x и р(х) = х2 при х —> 0.
Имеем
а(х) _ 1 - cos 2х _ sin2 х _ sin х sin х
р(х) х2	х2 х х 1
откуда, используя первый замечательный предел, получаем, что
.. а(х) ... sinx .. sinx Л
lim —— = 2 lim------lim = 2^0.
л-^0 p(x)	X—>0 x л-^0 х
В соответствии с определением 5.3 это означает, что бесконеч-
но малые х2 и 1 - cos2x имеют один порядок малости.
Особенно важен случай А = 1, который постоянно используется
при практическом нахождении пределов.
Определение 5,4, Две бесконечно малые функции а(х) и р(х)
г а(х) .
называются эквивалентными при х —> а, если lim---= 1.
х~>а Р(Х)
Примерами эквивалентных бесконечно малых функций (табл.
5.2) являются пары функций, приводящих к замечательным пре-
делам (см. табл. 5.1).
104
Таблица 5.2
Таблица эквивалентных величин (всюду х -> 0)
1. sinx - x	7. aA'-1 -xlna, a # 1, a > 0
2. arcsinx- х	8. log^l +x) - x/lna, a 1, a > 0
3. tgx - х	9. (1 + х)и - 1 - ax, a g R1
4. arctgx - x	10. 1 — cosx - x2/2
5. eA - 1 - x	11. shx- x
6. ln(l + x) - X	12. thx - x
Примечание. Эквивалентность бесконечно малых величин обозначается, как
обычно, знаком
(5-3)
Практическое значение таблицы эквивалентных величин опре-
деляется нижеследующей теоремой, дающей один из важнейших
методов нахождения пределов вида
lim Ж
х^а Р(х)
где <х(х) и р(х) — бесконечно малые при х -ь а.	п <х\
Теорема 5.3. Пусть а(х) - офх), р(х) - р[(х) и существует lim—-.
р,(х)
Тогда существует и предел (5.3), причем справедлива формула
х^а Р(х) х^а р](х) •
Доказательство. Очевидно имеем
<х(х) = а(х) а1(х)р1(х)
р(х) <Х|(х) р](х) р(х) ‘
Тогда по теореме о пределе произведения (см. теорему 5.1)
.. ос(х) ..	<х(х) .. айх).. р.(х) . .. а.(х) . г <х,(х) .
lim —— = lim у 7 lim 7 lim 7 = l lim 7 • 1 = lim 7. ▲
х-мг р(х) х->а (Х[(х) х->а р[(х) х->а р(х) х->а р[(х) х->а р[(х)
Пример 5.9. Найти предел lim Sm .
*->o sin 4х
Так как при х —> 0 sin3x - Зх, a sin4x - 4х, то
.. sin3x .. Зх 3
lim------= lim — = —.
х^о sin4x х->о 4х 4
ех_е3х
Пример 5.10. Найти Нт--------.
1	1	>--о tg х
Так как tgx - хв процессе х —> 0, то заменим вначале в знамена-
теле tgx эквивалентной ему величиной х. Тогда получим
105
ех-_е3л-	ех_е3х	ех _ j _ /е3х _
lim-------= hm---------= lim--------1------- =
*-><• tgx	X х^О	X
= limе ~ 1 - lim-—— = 1 -lim— = -2
х-0 х х^О X	x^Q X
(в заключительных выкладках воспользовались тем, что с '' - I - Зх
при х —> 0).
Пример 5.11. Найти предел lim х(л / 2 - arctg х).
Прежде всего заметим, что при х —> +« функция arctgx -ь л/2,
так что в данном примере имеем неопределенность типа <*> • 0. Сле-
довательно, для использования метода эквивалентных бесконечно
малых величин надо преобразовать произведение х(л/2 - arctgx) к
виду, приводящему к неопределенности 0/0.
Это удобно сделать с помощью замены t = (л/2 - arctgx), при
которой, очевидно, процесс х ^ +«-> заменяется процессом t —> 0.
Далее arctgx = л/2 - t, откуда х = tg(ic/2 - t) = ctgZ. Таким образом,
получаем, что
lim х(л / 2 - arctg х) = lim t ctg t = lim 11 tg t = 1,
Г->0	/->0
ибо tgr - t при t —> 0.
5.4.	Непрерывные функции
До сих пор теория пределов функций /(х) изучалась вне связи с
их значениями /(л) в предельной точке х= а. Это объясняется прежде
всего тем (и мы это подчеркиваем!), что при определении предела
используются только значения /(х) при х * а, а в самой точке х = а
функция может быть и не определена. Однако теория пределов имеет
содержательный интерес и для функций, определенных в полной
окрестности точки й, т.е. и в точке х = а. Именно для таких функ-
ций вводится понятие непрерывности.
5.4.1.	Основные определения
Итак, пусть функция у = f(x) определена в некоторой окрест-
ности точки а, включая саму точку а.
Определение 5.5. Функция у =f(x) называется непрерывной в точке
а, если она имеет предел lim /(х) и этот предел равен значению
функции в точке а, т.е. ''i!
Yvmf(x) = f(a).	(5.4)
Говорят также, что в этом случае точка х = а является точкой
непрерывности функции у = /(х).
106
Дадим эквивалентные определения непрерывности функции.
Обозначим аа(х) = /(х) - f(a). Ясно, что равенство (5.4) экви-
валентно тому, что limafl(x) = 0 и понятие непрерывности f(x) в
точке а можно переформулировать следующим образом.
Определение 5.6. Функция у = /(х) непрерывна в точке а, если
разность осд(х) = /(х) - f(a) является бесконечно малой при х —> а.
Можно сказать и иначе: функция у = /(х) называется непре-
рывной в точке а, если она (функция) представима в виде
/(х) = f(a) + ая(х),	(5.5)
где ай(х) — бесконечно малая при х —> а.
Замечание. С вычислительной точки зрения равенство (5.5) озна-
чает, что в точке х, близкой к точке а, значение непрерывной
функции /(х) приближенно равно ее значению f(a), причем абсо-
лютная погрешность приближения
А = |/(х) -/(а)| = |офс)| -> 0 (х -> а),
т.е. будет сколь угодно мала, если х достаточно близко к точке а.
Наконец, весьма удобно для практической работы определение
непрерывности в терминах приращения функции. Именно, дадим
точке а приращение Ап, т. е. перейдем от точки а к точке х = а + Да.
Тогда функция у = /(х) получит приращение Аг = /(х) - f(a), или,
что то же, Ay = f(a + Да) - /(а).
Ясно, что непрерывность функции у = /(х) в точке а означает,
что Аг —> 0 при Да —> 0.
В таком варианте определения непрерывности обычно принято
точку а заменять на произвольную фиксированную точку х.
Тогда Аг = f(x + Ах) - /(х), где Ах — приращение аргумента х и
строгое определение непрерывности функции у = /(х) в точке х
звучит следующим образом.
Определение 5.7. Функция у = /(х) непрерывна в точке х, если
из условия Ах 0 следует, что и Ау —> 0.
Пример 5.12. Покажем, что в любой точке х вещественной оси
функция у = sinx непрерывна. Действительно,
Ду = sin(x + Ax) - sin x = 2 cos
I . Ax
sin —.
I 2
, имеем
Отсюда, используя неравенство | sinx | <
I Л..1 п Ах п Ах _ |
Т “I
при Ах —> 0. Следовательно, в этом процессе и Ау —> 0. Это значит,
что у = sinx — непрерывная функция в точке х. Так как х было
выбрано произвольно, то непрерывность функции sinx на оси х
установлена.
2
107
Аналогично доказывается, что и cosx — непрерывная функция
на всей вещественной оси.
Пример 5.13, Покажем, что функция у = — непрерывна при
х
любом х * 0, т.е. непрерывна всюду, где она определена.
В самом деле, если х # О,
л 1	1	-Л*
Ау =---------=----------,
х + Ах х (х + Ах)х
откуда при Ах —> 0 и
। । |Ах| о
Ау = ।—!—L-i	= 0.
1	|х + Ах||х|	|х21
Это и требовалосв.
У читателя возникает естественный вопрос: каково положение
с непрерывноствю других элементарных функций — степенных,
показательнв1х, логарифмических и т.д. Ответом является следую-
щее утверждение.
Утверждение. Элементарные функции непрерв1вны всюду, где
они определены.
Например, функция у = tgx определена всюду на вещественной
оси, кроме точек хп = ±л/2 + ял, п = 0, ±1, ... . Таким образом, в
любой точке х е R, отличной от указанных точек х,„ функция tgx
непрерывна.
Однако элементарные функции встречаются в практических
задачах не толвко «в чистом виде», но и в различных комбинаци-
ях, например, у = sinx+ cosx, у = e*cosx, у = х2/1пх и т.д.
Спрашивается, будут ли такие комбинации непрерывнв1х фун-
кций также непрервшными функциями? Ответ положительный и
вытекает из нижеследующих теорем.
5.4.2.	«Арифметические» свойства непрерывных функций
Теорема 5.4. Пусть функция /(х) непрерывна в точке а. Тогда
функция с/(х), где с — любое число, также непрерывна в точке а.
Теорема 5.5. Пусть функции /(х) и д(х) непрерывны в точке а.
Тогда:
1)	сумма или разность /(х) ± д(х) также непрерывны в точке а\
2)	произведение f(x)g(x) также непрерывно в точке а;
f(x)
3)	при дополнительном условии g(a) * 0 частное J ’ также
непрерывно в точке a.	'
Доказательство. Все утверждения обеих теорем немедленно вы-
текают из аналогичных арифметических свойств пределов функ-
ций (см. 5.2). Установим, например, свойство 2. Действительно, из
условия непрерывности /(х) и g(x) в точке а следует, что
108
lim f(x) = f(a), lim g(x) = g(a).
Тогда по теореме о пределе произведения
lim/(x)g(x) = lim f(x) lim g(x) = f(a)g(a).
Это значит, что произведение /(x)g(x) непрерывно в точке а. ▲
Доказанные теоремы существенно расширяют множество изве-
стных нам непрерывных функций. Однако наиболее общей теоре-
мой, позволяющей утверждать непрерывность произвольных ком-
позиций непрерывных функций, является теорема о непрерывно-
сти сложной функции.
5.4.3.	Непрерывность сложной функции
Пусть у = ф(х): X —> У — функция одной вещественной перемен-
ной с областью определения X и областью значений У. Пусть далее
имеется вторая функция z = f(y): У—> R1, определенная на области
значений первой функции у = <р(х) и принимающая вещественные
значения.
Определение 5.8. Функция z = /|<р(_х) |: X —> R1 называется слож-
ной функцией, образованной функциями у = <р(х) и z = /(у).
Отметим, что сложная функция z = /| <р(_х) | является функцией
переменного х с областью определения X. Геометрически сложная
функция есть сквозное отображение z = z(x): X -ь R1, образован-
ное композицией отображений у = <р(х): X -ь У и z = f(y): У —> R1
(рис. 5.11).
Теорема 5.6 (о непрерывности сложной функции). Пусть функ-
ция у = <р(х) непрерывна в точке х = а, а функция z = f(y) непре-
рывна (как функция переменной у) в точке b = <р(й). Тогда сложная
функция z = /[ср(х)] непрерывна в точке х = а.
Доказательство. Пусть хн -» а (п —> ©о) — произвольная последо-
вательность, сходящаяся к а. Покажем, что соответствующая чис-
ловая последовательность /[ <р(.х,) | сходится к /[ ф(а) ] при п —> ©©.
Действительно, так как функция у = ср(х) непрерывна в точке
х = а, то ун = <р(х„) —> <р(й), т.е. у„ —> Ь, где b = <р(«). Но тогда в силу
непрерывности функции /(у) в точке b будем иметь /(ун) —> /(/>)
или, что то же,/[<р(хД] —>/[ср(я)]. Это значит, что функция /[<р(х)]
непрерывна в точке х = а. ▲
Рис. 5.11
109
Пример 5,14. Рассмотрим функцию z = In sinx. Это сложная фун-
кция, так как она является композицией двух функций у = sinx и
z = 1пу. Область определения этой функции — те значения, в кото-
рых у = sinx > 0. Это есть набор интервалов 2лп < х < (2м + 1 )л, п = 0,
±1, ... . По теореме 5.6 функция z = Insinx непрерывна на этом
множестве.
Замечание. Ясно, что доказанная теорема имеет место и для
сложных функций, являющихся композицией не только двух, но
и трех и более непрерывных функций. В частности, можно утверж-
дать, что любая композиция элементарных функций непрерывна
всюду в своей области определения.
5.5.	Свойства функций, непрерывных на отрезке
В предыдущем подразделе изучены свойства функций в отдель-
ной точке х = а, при этом значения самих функций используются
только в некоторой окрестности Ua (пусть даже весьма малой) этой
точки. Такие свойства функции называются локальными, так как
они не зависят от значений /(х), удаленных от точки а.
В данном подразделе, напротив, исследованы те свойства не-
прерывных функций, которые определяются ее значениями в пол-
ной области определения, а именно на отрезке. Такие свойства
называются глобальными, они характеризуют функцию в целом.
К ним относятся: ограниченность функции, максимальные и ми-
нимальные значения и др.
5.5.1.	Теорема о нуле непрерывной функции
Рассмотрим теорему о нуле непрерывной функции, играющей
важную роль в численных методах.
Теорема 5.7. Пусть функция
У = f(x) определена на отрезке
[а, Л| и удовлетворяет следующим
условиям:
1) /(х) непрерывна на отрез-
ке [а,б], т.е. непрерывна в каж-
дой точке отрезка [а, б] ;
2) в концевых точках отрезка
[а, б] /(х) принимает значения
разных знаков (например, f(d) <
< 0, a /(d) > 0, или наоборот).
Тогда существует по крайней
мере одна точка е (а, б) такая,
что Ж) = о (рис. 5.12).
110
Доказательство. Доказательство проведем известным методом
деления отрезка пополам. Именно, обозначим через Ао = [я0,60]
исходный отрезок [а,/?], т.е. а0 = a, bQ = b. По условию 2 f(aQ} < О,
й0 + ^0 D
-----. Возможны
2
а/(^о) > 0- Разделим отрезок пополам точкой с =
два варианта: либо /(с) = 0, либо /(с) * 0. В первом случае поиск
точки с;:, закончен.
Во втором случае на концах хотя бы одной из половин, кото-
рую обозначим через Л] = [«],/?]], функция /(х) имеет разные зна-
ки, причем /(й[) < 0, а /(£>[) > 0.
Для отрезка А, = [й,, dj проведем то же самое рассуждение. Тог-
да (отбросив тривиальный случай /(с) = 0) найдем отрезок А2 =
= (это одна из четвертей исходного отрезка Ао) такой, что
/(й2) < 0, а /(62) > 0. И так далее. На п-м шаге получим отрезок
Ая = [а„, Ь,.\ длиной Ьн - ан = такой, что f(af!) < 0, а /(/>„) > 0.
В результате проведенного построения получаем последователь-
ность вложенных отрезков Ао =э А( z>...	А,,. ] =>... или, что то же,
[а0Л1 => [^Л] => - \ап,Ьп] =) [а„+1Л+|] о ...,
обладающих двумя свойствами:
1) длина А/г = Ьп - ап 0 при п —>
2) f(an) < 0, f(bn} > 0 для любого п = 0, 1, 2, ... .
Теперь поиск точки <;0, в которой /(^0) = 0, завершают следую-
щие рассуждения.
Очевидно, последовательность левых концов ап есть монотонно
возрастающая и ограниченная сверху последовательность. Следова-
тельно, по теореме о существовании предела монотонной ограни-
ченной последовательности она сходится к некоторому пределу,
который обозначим через т.е. а„ —> Точно так же последова-
тельность правых концов Ьп, будучи монотонно убывающей и ог-
раниченной снизу, сходится к некоторому пределу т.е. b„ —> %ь.
Ясно, что < %ь, но так как bn - at, —> 0, то на самом деле = ^ь.
Обозначим их общее значение через 2,о и покажем, что это и есть
искомая точка, т.е. корень уравнения f(x) = 0.
Действительно, так как f(an} < 0 для всех и. по теореме о пере-
ходе к пределу в неравенствах
Нт/(й„)<0.	(5.6)
fl —
Но по условию 1 функция непрерывна на отрезке [а, Ь] и, в
частности, непрерывна в точке £0, к которой стремится последо-
вательность ап. Это значит, что lim f(a„) = /(£0) и> следовательно,
в силу (5.6) /(^о) - 0. С другой стороны, так как f(bfl) > 0 и Ьп Сц
при п -ь «о, то точно так же получаем, что /(^0) > 0. Таким обра-
зом, получим /(^) = 0. ▲
111
Замечание. Отметим, что про-
веденный метод доказательства
является реальным численным
методом нахождения решений
уравнения /(х) = 0. И хотя этот
метод отнюдь не самый быстросхо-
дящийся, он сохраняет свое зна-
чение ввиду очевидной простоты
алгоритма.
Следствием доказанной теоре-
мы является теорема Коши о про-
межуточном значении непрерыв-
ной функции.
Теорема 5.8. Пусть /(х) — не-
прерывная функция на отрезке [а,Ь]. Пусть далее f(x) принимает
на концах различные значения, т.е. f(a) * f(b). Тогда, каково бы
ни было число с, промежуточное между f(a) и f(b), найдется хотя
бы одно значение аргумента х = £с, такое, что /(^.) = с. (Иными
словами, непрерывная функция /(х) при изменении аргумента х
от а до b принимает все значения между /(«) и /(/?) хотя бы один
раз (рис. 5.13).)
Доказательство. Рассмотрим вспомогательную функцию <р(х) =
= /(х) - с. Это, очевидно, непрерывная функция на отрезке [а,Ь].
Далее, так как число с промежуточно между f(d) и f(b), то значе-
ния ф(д) и <р(Л) имеют разные знаки. Следовательно, согласно
теореме 5.7, найдется точка <;0 е («,/»), в которой <р(^0) = 0- Но эт0
означает, что /(^0) = с- т е- и есть искомая точка ▲
5.5.2. Теоремы Вейерштрасса
Обратимся теперь к свойствам непрерывных функций, извест-
ных под общим названием первой и второй теорем Вейерштрасса.
Определение 5.9. Функция у = /(х), определенная на отрезке
[а, Ь\. называется ограниченной на этом отрезке, если найдется число
М > 0 такое, что для любого х е 1а,Ь] выполняется неравенство
|/(х)|<М
Теорема 5.9 (первая теорема Вейерштрасса). Если функция /(х)
непрерывна на отрезке [а,Ь], то она ограничена на этом отрезке.
Содержание этой теоремы геометрически проиллюстрировано
на рис. 5.14 и означает, что график функции, непрерывной на от-
резке [а, /?|, обязательно располагается в ограниченной по у полосе
—М < у < М. где М — некоторое число (разумеется, для каждой
функции свое).
Подчеркнем, что на полуинтервале или интервале утверждение
п	д.	1
теоремы неверно. Примером может служить функция у = —, рас-
х
112
0<л-<1
Рис. 5.15
смотренная на полуинтервале (0,1] (рис. 5.15). Эта функция непре-
рывна в каждой точке полуинтервала (0,1], но не является, очевид-
1	п
но, ограниченной на этом полуинтервале, так как---> при х —> 0.
х
Определение 5.10. Значение/(х0), где х0 g [я,6], называется наи-
большим значением функции f(x) на отрезке [а, б], если для любой
точки х g [а,б\ справедливо неравенство /(х) < /(х0).
Таким образом, значение /(х0) является максимальным среди
всех значений/(х) на отрезке [а, /ф Поэтому часто точку х0 обозна-
чают как хтах, а наибольшее значение как /(хтах) = max f(x).
Аналогично определяются точки xmin и j(xmin).
Теорема 5.10 (вторая теорема Вейерштрасса). Если функция f(x)
непрерывна на отрезке [а, б], то она принимает на этом отрезке
как свое максимальное, так и свое минимальное значения.
Иначе говоря, какова бы ни была непрерывная на отрезке [а, б]
функция /(х), всегда найдутся точки х0 g [а, б] и X] g [а, б] такие,
что для всех точек х из отрезка [а, Л| справедливо двустороннее
неравенство
/0ч) < /(х) < /(х0).
Это значит, что
*0 = Хтах, а /(х0) = max /(х),
и точно так же
*] = *min, а/(Х]) = min /(х).
ле[М1
Ясно, что значение /(хтах) ограничивает все значения функции
/(х), х g [а,б], сверху, a /(xmjn) — снизу, причем эти границы
точные (рис. 5.16).
Отметим, что и во второй теореме Вейерштрасса условие не-
прерывности функции /(х) именно на отрезке существенно и за-
113
менить отрезок интервалом или полуинтервалом нельзя. Например
(рис. 5.17), функция f(x) = х2, рассмотренная на интервале (0,1),
является непрерывной на этом интервале, но ни в одной точке
х0 g (0,1) ее значение f(xQ) не является максимальным среди всех
ее значений. Действительно, для любой точки х0 < 1 всегда найдется
точка х* такая, что х0 < х* < 1 и, следовательно, /(х0) < /(х*).
В заключение приведем следствие из второй теоремы Вейершт-
расса и теоремы Коши, которое будет использовано далее.
Следствие. Пусть/(х) — непрерывная функция на отрезке [а, Ь\ и
т = min /(х), М = max /(х) — ее минимальное и максимальное
ле	Хе[<7,/>]
значения. Тогда для любого числа с, удовлетворяющего неравен-
ствам т < с < М, найдется по крайней мере одна точка е [а, й]
такая, что /(£) = с.
Из этого следствия вытекает, что всякая функция, непрерыв-
ная на отрезке [а,Ь], принимает любое значение, промежуточное
между своими минимумом и максимумом, хотя бы один раз.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Назовем число b левосторонним пределом (или пределом слева)
функции у = f(x) в точке а, если для любой последовательности хп а, и
такой, что х„ < а, последовательность значений /(х„) -> b при п
Обозначается предел слева символом b_ = Нт /(х).
1.	Определите аналогично правосторонний предел b+ = lim /(х).
2.	Докажите, что число b является пределом функции f(x) при х„ -> а
(см. определение 5.1) тогда и только тогда, когда существует левосторон-
ний и правосторонний пределы Ь_ и Ь+, причем b = Ь_ = Ь+, т.е.
lim/(x)= lim /(х) = lim /(х).
X^a	.¥-><7-0	.Y —>(7-1-0
2.	Вычислите односторонние пределы при х —» 0 следующих функций:
. fx2 +1, при х < 0;	.. .	|е¥,прих<0;
/00 =	3	А	А	А
[xJ, при х > 0;	(0, при х > 0.
Укажите на графиках этих функций числа Ь_ и Ь+.
114
3.	Пусть функция f(x) ограничена в некоторой окрестности Ua точки
а, т.е. для всех точек х, принадлежащих окрестности Ua, справедливо не-
равенство
1Ж)|йХ
где М > 0 — некоторая постоянная.
Докажите, что произведение /(х)а(х), где а(х) — бесконечно малая
функция при х а, есть также бесконечно малая функция при х а.
Рассмотрите пример <х(х) = х, /(х) = sin— при х -» 0.
4.	Бесконечно малая функция а(х) называется бесконечно малой бо-
лее высокого порядка малости по сравнению с бесконечно малой функ-
цией р(х), если
lim^ = 0.
р(х)
Докажите, что две бесконечно малые <х(х) и oq(x) эквивалентны в том
и только в том случае, если их разность у(х) = а(х) - ai(x) является бес-
конечно малой более высокого порядка малости, чем каждая из них, т.е.
|imV«=o, lim_*XL = o.
а(х) <Xi(x)
5.	Установите, в каком отношении друг к другу находятся бесконечно
малые функции
х2, sinx, 1 - cosx, ln(l + 2х), е2х- 1
(всюду х —> 0): одного порядка, эквивалентны или разного порядка малости.
6.	Докажите, что если функция /(х) непрерывна в точке х = а, то и
функция |/(х) | также непрерывна в точке х= а.
7.	Вычислите пределы:
lim
х2 + 2х — 3
х2 — 1
птД^,
л-^-2 х + 2
.. sinx-tgx
lim------,
л-^о	x3
ГЛАВА 6
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
ОДНОЙ ВЕЩЕСТВЕННОЙ ПЕРЕМЕННОЙ
6.1.	Производная функции. Основные правила
дифференцирования
6.1.1.	Определение. Таблица производных
Пусть у = f(x) — функция вещественной переменной, опреде-
ленная на некотором интервале (а, Ь). Рассмотрим отношение при-
ращения функции
Ду = fix + Ax) -f(x)
к приращению аргумента, т.е.
Ay _ fix + Ах) - /(х)
Ах	Ах
Определение 6.1. Пусть существует конечный предел отноше-
ния (6.1) в процессе Ах —> 0. Тогда функция у = /(х) называется
дифференцируемой в точке хе (а,/?), а сам предел
Um s lim
Дх->0 AX Ay—0	Дх
называется производной функции у = f(x) в точке х.
Обозначается производная функции у = /(х) либо у', либо/'(х).
Итак, кратко
, г Ау
у = игл —,
ay—о Дх
или, что то же,
у'= lim +
Да-->о Ах
Ясно, что в каждой конкретной точке х е (а, Ь) производная у'
есть число, поэтому, если функция дифференцируема в каждой
точке интервала (а,Ь), то ее производная является также функци-
ей на интервале (а, Ь).
Пример 6.1. у = с, где с — постоянная. Ясно, что для постоян-
ной функции Ау = 0 при любом Ах. Следовательно (с)' = 0, т.е.
производная постоянной равна тождественно нулю.
Пример 6.2. Покажем, что при любом /7=1,2, ... производная
(хпУ = пхл~[.
116
Действительно:
Ду = (х + Лх)п - хп =
= Хп + /7Х"-1АХ +	1) х"~2(Ах)2 +... + nx(Ax)n~l + (Ax)n - хп =
= пхх~}кх +	1) х"~2(Ах)2 + ... + (Ах)".
Следовательно,
(x"Y = lim — = lim | пхп~[ + ——— х"“2Ах +... + (Ах)"-1 | = пхп~
хх->о Ах дх—>о 12!	J
Это и требовалось.
Пример 6.3, Найдем производную функции у = sinx.
Имеем
л  / лл • n f Ах А . (Ах А
Ay = sin(x + Ах) - sin х = 2 cos х + — sin — .
Следовательно,
откуда, используя свойство непрерывности функции cosx и пер-
вый замечательный предел, находим, что
г ДУ
lim — = cos х.
дх->о Ах
Итак, (sinx)' = cosx.
Можно показать, что все элементарные функции дифферен-
цируемы во всех точках, где они определены. Приведем форму-
лы дифференцирования элементарных функций в виде таблицы
(табл. 6.1).
При нахождении производных более сложных функций исполь-
зуется ряд правил, которые сформулируем в виде теорем.
Однако вначале докажем лемму, имеющую и самостоятельный
интерес.
Лемма 6.1. Если функция /(х) дифференцируема в точке х, то
она непрерывна в этой точке.
Доказательство. По условию леммы существует конечный предел
lim — = у'(х).
дх—о Ах
Это то же самое, что функция а(х, Ах) = — - у'(х) — бесконеч-
Ах
но малая при Ах —> 0, т.е. а(х. Ах) 0.
117
Таблица 6.1
Таблица производных элементарных функций
1. с' = 0 2. (хк)' = ах™-1, а е R1 (^Х )	X 4'(7;)'=2^ 5.	(sinx)' = cosx 6.	(cosx)' = -sinx 7.	(tgx)' = — COS2 X 8.	(ctgx)' = —Д— sin2 X 9.	(e*)' = eA 10.	(ax)' = a'Ina, a > 0	11.	(lnx)' = i 12.	(log„x)' = —— x In a 13.	(arcsinx)'= 1 14.	(arccosx)' =	2 15.	(arctgx)' =	1 1 + X2 16.	(arcctgx)' =	U 1 + x2 17.	(shx)' = chx 18.	(chx)' = shx 19.	(thx)' = —1- ch2 x 20.	(cthx)'=—-1— sh2 x
Легко видеть, что
Ау = у'(х)Дх + а(х, Ах) Ах.	(6.2)
Поскольку х — фиксированная точка, то у'(х) есть некоторое
число, и, значит, при Ах -ь 0 в правой части равенства (6.2) как
первое, так и (тем более) второе слагаемое стремятся к нулю. Та-
ким образом, при Ах -ь 0 и приращение функции Ау —> 0. Это
значит, что функция у = /(х) непрерывна в точке х. ▲
6.1.2.	«Арифметические» свойства производной
Теорема 6.1. Пусть /(х) — дифференцируемая функция. Тогда
при любой постоянной с функция с/(х) — также дифференцируе-
мая функция, при этом
(с/(х))' = cf'(x).
Теорема 6.2. ПустьДх) и g(x)— дифференцируемые функции.
118
Тогда:
1)	сумма или разность f(x) ± g(x) также дифференцируемая
функция, при этом
(f(x) ± g(x))' = f'(x) ± g'(x);
2)	произведение f(x)g(x) — также дифференцируемая функ-
ция, при этом
(/(x)g(x))' = f'(x)g(x) + f(x)g'(x);
3)	при дополнительном условии g(x) * 0 частное ——— также
дифференцируемая функция, при этом
(= f'(x)g(x) - f(x)g'(x)
|^(х) J g2(x)
Доказательства всех утверждений, приведенных в теоремах 6.1
и 6.2, проводятся по одной схеме. Остановимся для определенно-
сти на формуле для производной произведения функций.
Обозначим у = f(x)g(x) и рассмотрим приращение
Ду =/(х + Ax)g(x + Дх) -f(x)g(x).
Очевидно, Ду можно представить в виде
Ду = [Дх + Дх) -/(x)]g(x + Дх) +/(x)[g(x + Дх) - g(x)].
Следовательно,
Ду _ Д/(х)
Дх Дх
g(x + Дх) + /(х)
Ag(x)
Дх
Отсюда, учитывая, что по лемме 6.1 g(x + Дх) —> g(x) при Дх —> О,
немедленно получим, что
lim= f'(x)g(x) + /(x)g'(x),
Av—О Дх
т.е.
y' = (fgy=f'g+fg'- ±
Приведенные правила дифференцирования существенно рас-
ширяют возможности практического нахождения производных.
Однако наиболее мощным средством вычисления производных
является правило дифференцирования сложных функций.
6.1.3.	Производная сложной функции
Пусть z = /(<р(х)) — сложная функция, т.е. композиция двух
функций у = <р(х) и z = /(у) (см. определение 5.8). Допустим, что
функция ф(х) имеет производную, которую обозначим через <р'(х),
а функция /(у) имеет производную fy(y). Спрашивается, будет ли
иметь производную по х сложная функция /(<р(х))?
119
Утвердительный ответ на поставленный вопрос дает следую-
щая теорема.
Теорема 6.3. Если функция у = ф(х) дифференцируема по х, а
функция Ду) дифференцируема по у, то сложная функция z = /(ф(х))
дифференцируема по х, причем ее производная вычисляется по
формуле
(/(ф(х))' =//(ф(х))ф'(х)
или, что то же,
(/(ф(х))К =/ф'(ф(х))ф;(х).	(6.3)
Доказательство. Вывод формулы (6.3) приведем (ради просто-
ты) при дополнительном условии строгой монотонности функ-
ции у = ф(х).
С этой целью дадим х приращение Ах. Тогда функция у = ф(х)
получит приращение Ду = Аф(х), где Аф(х) = ф(х + Ах) - ф(х).
Следом и функция z = Ду) получит приращение Az = АДу), где
А/(у) = ЯУ + Ау) - Ду) = /(ф(х + Ах)) - /(ф(х)).
Заметим теперь, что в силу условия монотонности функции у =
= ф(х), если Ах # 0, то и Ау * 0. (Кроме того, при Ах —> 0 и прираще-
нии Ау —> 0, см. лемму 6.1.) Следовательно, можно записать
Az _ Az Аф
Ах Аф Ах
или, что то же,
А/(ф(х)) _ А/(у) Аф
Ах Ау Ах
Отсюда, устремляя Ах к нулю, приходим к формуле
(/(ф(х))' =/;(у)ф;.(х),
где, очевидно, у = ф(х). Таким образом,
(/(ф(х)));=4(ф(х))ф'.(х). ▲
Пример 6.4, Приведем примеры использования доказанных пра-
вил дифференцирования:
a)	(Vx + Inx)'= (Vx)'+ (1пх)'= —!= + —;
2ух х
б)	(2' tgх)' = (2х)' tgx + 2х(tgх)' = 2х In2 tgх + 2х —;
COS2 X
. ( х3 (х3)' sinx - (sinх)'х3 Зх2 sinx -х3 cosx
в)	-— = —---------------------— =-------—---------;
I sinx I	sin X	sin X
г)	(ех’)' = (ех2 )^-з (х2)' = е*’2х;
д)	(arctg Vx)' = (arctg Vxi^iVx)7 =-=— —= =  -------=.
120
6.1.4.	Геометрический смысл производной
В заключение остановимся на геометрическом смысле производ-
ной f'(x) в фиксированной точке х= а. Для этого рассмотрим зада-
чу о проведении касательной прямой к графику функции у = Дх)
в точке Ма(а, Да)). Дадим значению а приращение Аа и проведем
секущую	через точки Ма(а, Да)) и Мй+Дй(а + Аа, Да + Ла))
(рис. 6.1).
Как известно, уравнение прямой 7л<,л/и+Ли имеет вид
у - Да) = ка, а+Аа(х - а),	(6.4)
где ка, а+Аа — угловой коэффициент секущей. Очевидно,
_Ау _ Да + Аа) - Да)
К,а,а+/\а Л	.
Аа	Аа
Устремим теперь Аа —> 0. Тогда точка Ма+Аа, скользя по графику
функции у = Дх), будет стремиться к точке Ма, а секущая	—
к некоторой предельной прямой ТМа, которую естественно назы-
вать касательной прямой к графику функции у = Дх) в точке Ма.
Переходя к пределу при Аа —> 0 в уравнении (6.4), получим уравне-
ние касательной прямой ТМа. Именно, при Аа —> 0 угловой коэф-
фициент секущей
^=/(а+АЛа)-/(а) -/'(«),
Аа
поэтому уравнением касательной ТМи будет уравнение
у-Да) = Д(а)(х- а).
Это и есть уравнение прямой, проходящей через точку Ма(а,Да))
с угловым коэффициентом kMa = f'(a).
В итоге получаем, что значение производной f'(a) является уг-
ловым коэффициентом касательной прямой, проведенной в точке
Ма(а, Да)) к графику функции у = Дх).
В этом и состоит геометрический смысл производной.
121
Замечание. Как известно из аналитической геометрии, прямая
N м , перпендикулярная к Д , имеет угловой коэффициент
. “ 1 , 1
k,vi; =	, т.е. k;V; = -, и, следовательно, ее уравнение есть
у-Да) = -—!—(х-д)	(6.5)
/(л)
(разумеется, мы должны предположить, что Д(а) # 0).
Прямая NМа называется нормалью, проведенной к графику фун-
кции у = Дх) в точке Ма, а уравнение (6.5) — уравнением нормали.
6.2.	Теоремы о среднем для дифференцируемых
функций
Теоремами о среднем для дифференцируемых функций назы-
ваются теоремы, в которых значения функций на концах отрезка
[а, Л| связываются с производными этих функций в некоторых сред-
них точках интервала (а,Ь).
Предварительно, однако, установим лемму Ферма, которая
известна как необходимое условие локального экстремума функ-
ции и будет изложена ниже (теория экстремума функций будет
приведена в 6.7).
Определение 6.2. Скажем, что функция у = Дх) имеет в точке
х = а локальный максимум, если найдется окрестность Ua этой точ-
ки (хотя бы и малая), такая, что для любой точки х g Ua справедли-
во неравенство Дх) < Да).
Аналогично определяется локальный минимум.
Геометрическая иллюстрация этого определения приведена на
рис. 6.2.
Отметим, что точка х = а, в которой имеется локальный макси-
мум, не обязательно является точкой, где функция достигает наи-
122
большего значения, поэтому при
исследовании функции на отрез-
ке [а, /?| (например, при построе-
нии ее графика) следует разли-
чать точки, в которых достигает-
ся локальный максимум (или
минимум) функции, и точки, где
значение этой функции на отрез-
ке [а, й] максимально (минималь-
но). (Отсюда происходит и назва-
ние «локальный» максимум, т.е.
вблизи точки а.)
Лемма 6.2 (лемма Ферма). Пусть в некоторой точке х = а функ-
ция у = f(x) имеет локальный максимум (минимум) и дифферен-
цируема в этой точке. Тогда
f'(a) = 0.
Иначе говоря, в точках локального максимума и минимума
производная функции у = f(x) обязательно равна нулю.
Геометрически утверждение Ферма вполне прозрачно, если
учесть, что значение f'(d) есть угловой коэффициент касательной
прямой к графику функции у = f(x) в точке М(а, f(a)). Именно в
точке локального максимума или минимума касательная к графи-
ку функции горизонтальна (рис. 6.3).
Доказательство. По определению
/(а) = lim
До-0
А/(а)
Ла
(6.6)
где Ла — приращение аргумента при переходе от точки х = а к точке
х = а + Ла, а Л/(а) = /(а + Ла) - /(а) — соответствующее прираще-
ние функции. Отметим при этом, что Ла может стремиться к нулю
любым способом, т.е. формула (6.6) справедлива при том, что
Ла —> 0 по любому закону. Этим и воспользуемся для доказатель-
ства того, что в точке локального максимума /'(а) = 0. Устремим
вначале Ла —> 0, оставляя его положительным, т.е. Ла > 0. Тогда
отношение
А/(Д) < 0
Ла
ибо вблизи точек локального максимума всегда /(а + Ла) < /(а) и,
следовательно, Л/(а) < 0. Но в таком случае (теорема о переходе к
пределу в неравенствах)
Ш =
lim
До—+0 Дй
<0.
(6-7)
Теперь устремим Ла 0, оставляя его отрицательным, т.е. Ла < 0.
123
Тогда
А/(а) Q
V/
и, следовательно,
f'ia) = lim < 0.	(6.8)
До—-0 Дй
Очевидно, неравенства (6.7) и (6.8) совместимы, если только
Л°) = 0. ▲
Обратимся теперь непосредственно к теоремам о среднем.
Теорема 6.4 (теорема Ролля о нуле производной). Пусть функ-
ция у = fix) определена на отрезке [а,/>] и удовлетворяет следую-
щим условиям:
1)	fix) непрерывна на отрезке [а, 6];
2)	fix) дифференцируема по крайней мере на интервале (а,Ь);
3)	f(a) = fib).
Тогда существует хотя бы одна точка е (а, Ь) такая, что = 0-
Геометрический смысл теоремы Ролля таков же, что и леммы
Ферма: в условиях теоремы найдется внутри отрезка [а, й] хотя бы
одна точка для которой касательная прямая к графику функции
горизонтальна (рис. 6.4).
Строгое доказательство, которое в деталях не приводим, опи-
рается на лемму Ферма. Именно, логически возможны два случая:
1) f(x) = с, где с — постоянная, и, напротив, 2) fix) # с на от-
резке [а,Ь\ тождественно.
В первом случае очевидно, f'(x) = 0 на [а, /?| и в качестве точки
£ можно взять любую точку из интервала (а, Ь).
Во втором случае в силу условия fia) = fib) найдется хотя бы
одна внутренняя точка х = £ локального максимума или минимума
функции у = fix). По лемме Ферма, в этой точке f'it) = 0. Таким
образом, £ — искомая точка.
Теорема 6.5 (теорема Лагранжа о среднем значении). Пусть фун-
кция у =fix) определена на отрезке [а, Л| и удовлетворяет условиям:
1) fix) непрерывна на отрезке
к, ь\-,
2) fix) дифференцируема по
крайней мере на интервале ia,b).
Тогда найдется хотя бы одна
точка с g i&,b) такая, что
/(*)	/'(!;) =	(6.9)
Ь - а
х Доказательство. Геометриче-
ский смысл формулы (6.9) виден
из рис. 6.5.
124
Ясно, что правая часть формулы (6.9) есть угловой коэффици-
ент хорды АВ. Вспоминая, что значение Д(£>) равно угловому ко-
эффициенту касательной Тм, приходим к выводу: в условиях тео-
ремы всегда существует хотя бы одна точка £ е (а,Ь) такая, что
касательная Тм к графику функции у = f(x) параллельна хорде АВ.
Утверждение теоремы Лагранжа легко вытекает из теоремы Ролля.
Действительно, рассмотрим вспомогательную функцию
р(х) = Дх) - [/(й) +	~	(х - «)],
о - а
где р(х) — «расстояние» между графиком функции у = /(х) и гра-
фиком хорды
ч ДЬ) - Да) z .
у = Да) +	' (х - а).
Ь-а
Очевидно, что р(а) = р(6) = 0. Следовательно, по теореме Рол-
ля, существует точка се (а, Ь), в которой р'(£) = 0. Так как
,, X Ч ДЬ)-Да)
р (х) = / (х) -	\
b - а
то равенство р'(^) = 0 и означает, что
b - а
Замечание. Очевидно, формулу (6.9) можно записать в виде
ДЬ)-Да)=Д^)(Ь- а).	(6.10)
Именно в таком виде она чаще всего и применяется.
В заключение сформулируем наиболее общую теорему Коши.
Теорема 6.6 (теорема Коши). Пусть функции f(x) и g(x) опре-
делены на отрезке [а, Ь] и удовлетворяют условиям:
1)	/(х), g(x) непрерывны на отрезке [а,Ь];
125
2)	f(x) и Дх) дифференцируемы по меньшей мере на интерва-
ле (а, й);
3)	Д(х) * 0 на интервале (а, Ь).
Тогда существует хотя бы одна точка е (а, Ь) такая, что
ДЬ)-Да)_Д(&
g(b) - g(a) g'(t)'
Замечание., Читатель, наверное, заметил, что все три теоремы о
среднем носят характер так называемых теорем существования: в
них утверждается существование точек £ е (а, Ь), для которых име-
ют место соответствующие равенства, но ничего не предлагается
для их конструктивного нахождения. Тем не менее и при таком
«недостатке» теоремы о среднем находят самые разные примене-
ния. В следующем подразделе исследуем свойства монотонности
функции и установим знаменитое правило Лопиталя с помощью
этих теорем.
6.3.	Следствия из теорем о среднем
(монотонность, правило Лопиталя)
6.3.1.	Критерий монотонности
Исследуем вначале свойство монотонности функции Дх), оп-
ределенной на отрезке \а,Ь\ [или на интервале (а,/»)].
Определение 6.3. Функция у =f(x) называется монотонно возра-
стающей на множестве £, если для любых точек х( и х2 этого мно-
жества из условия Х[ < х2 следует, что и Дх,) <Дх2). В случае строгих
неравенств х, < х2 и Дх,) < Дх2), функция называется строго
монотонной.
Аналогично определяются монотонно убывающие и строго мо-
нотонно убывающие функции.
В дальнейшем в качестве Е будем выбирать отрезок или интервал.
Пример 6.5. Функция у = ev строго монотонно возрастает на всей
вещественной оси (см. рис. 5.5).
Пример 6.6. Функция у = arccosx монотонно убывает на отрезке
[-1,1] (см. рис. 5.4).
Пример 6.7. Функция у = |х| (см. рис. 6.8) монотонно убывает на
полуоси (-оо, 0] и, напротив, монотонно возрастает на полуоси
[0, +<*>).
Участки монотонности функции Дх) однозначно определяют-
ся знаком производной Д(х), что следует из следующей теоремы.
Теорема 6.7 (критерий монотонности). Дифференцируемая фун-
кция монотонно возрастает на интервале (а, Ь) в том и только в
том случае, когда Д(х) > 0 в любой точке этого интервала.
126
Доказательство. Пусть f'(x) > 0 на интервале (а, Ь). Покажем, что
для любых точек Х] < х2 справедливо неравенство f(x{) < f(x2) или,
что то же, f(x2) - f(x}) > 0.
Действительно, применяя теорему о среднем Лагранжа [см. фор-
мулу (6.10)] на отрезке [Х],х2], получаем, что
(6.11)
где £ g (jcl3x2) — некоторая средняя точка.
Поскольку по условию f'(x) > 0 в любой точке хе (а, Ь). то и в
точке £ значение > 0. Отсюда немедленно следует, что правая
часть формулы (6.11) неотрицательна. Следовательно, и левая часть
f(x2) -/(х,) > 0. А
Напротив, пусть f(x) монотонно возрастает. Покажем, что в
любой точке х е (а, Ь) производная f'(x) > 0.
Действительно, дадим х приращение Дх и рассмотрим отношение
А/(х) = Дх + Дх) - /(х)	12)
Дх	Дх ’
Так как функция монотонно возрастает, то f(x + Дх) - /(х) > 0
при Дх > 0 и, наоборот, f(x + Дх) - f(x) < 0 при Дх < 0. Следователь-
но, во всех случаях
А/(х) >р
Дх
Переходя к пределу при Дх —> 0, немедленно получаем, что и
/(х) = lim
Ay-О
А/(х)
Дх
>0. А
6.3.2.	Правило Лопиталя
Под правилом Лопиталя понимается прием раскрытия неопреде-
„	0 со	,
ленностеи вида—,—, использующии производные функции, на-
0 °°
холящихся в числителе и знаменателе этих неопределенностей. Более
точно, пусть, например, а(х) и р(х) — бесконечно малые функ-
ции в процессе х —> а. Рассмотрим вопрос о нахождении предела
г <х(х)	„	О
lim----, который, очевидно, отвечает неопределенности вида —
х^а р(х)	О
Теорема 6.8 (правило Лопиталя). Допустим, что выполнены сле-
дующие два условия:
1)	а(х) и р(х) дифференцируемы в некоторой окрестности Ua
точки а, исключая, быть может, саму точку а\
2)	существует предел отношения производных а'(х) и р'(х), т.е.
lim^
х^а Р (х) 
127
Тогда существует и предел отношения самих функций <х(х) и
р(х), причем
lim^ = Um = ^.
х~а |3(х) х^а |У(х)
(6.13)
Доказательство. Прежде всего заметим, что по условию 1 фун-
кции а(х) и р(х) дифференцируемы при х * а, а значит, согласно
лемме 6.1, и непрерывны при х*а.
Доопределим функции а(х) и р(х) нулем в точке х = а, т.е.
будем считать, что а(й) = 0, |3(й) = 0. Так как <х(х) —> 0, р(х) —> 0 при
х —> а, то доопределенные таким образом функции ос(х) и р(х)
становятся непрерывными и в точке х= а, т.е. в полной окрестно-
сти Ua.
Теперь, опираясь на теорему о среднем Коши, можно устано-
вить формулу (6.13). Имеем при х * а
а(х) _ а(х) - а(й) _ а'(^)
р(х) Р(х) - Р(а) р'(£,) ’
где £ g (й,х) — некоторая средняя точка. Ясно, что при х а и
£ —> а. В силу условия 2 предел правой части при £ —> а существует.
Следовательно, существует и предел левой части, причем
.. а(х) ..
hm —— = hm -Д-^-
X- 3(Х)	№)
или, что то же,
lima« = iimaW А
х^а р(х) р (X)
Замечание. Теорема 6.8 устанавливает правило Лопиталя для слу-
0
чая неопределенности — в процессе х а, где а — конечная точка.
Можно показать, что правило Лопиталя справедливо и для случая
неопределенности при х —> +оо или х —> -«о. Оно верно и для
неопределенностей вида — как при х —> й, так и при х —> ± <».
ГТ	z o I I I- sin X - X
Пример 6.8. Наити lim---;---.
х3
Очевидно, здесь а(х) = sinx - х, р(х) = х3 — бесконечно малые
дифференцируемые функции при х -ь 0. Следовательно, по прави-
лу Лопиталя,
.. sinx-x .. cosx-1
lim-------= lim------—
X3 х—Л Зх2
lim
х-0
-х2/2 _ -1
Зх2 6
(здесь использована «эквивалентность» 1 - cosx - х2/2).
128
Пример 6.9, Найти lim —. Имеем
х->4-= ех
2х 2
lim — = lim — = lim — = О,
x-^4-o e* x—eA х^-н» ел
так как еА —> +=>-' при x —> +=« (здесь применено правило Лопиталя
дважды).
Пример 6,10. Найти предел lim(xlnx).
А'—>0
Заметим, что при х > 0 и х -> 0 функция 1плг —> -«о, поэтому
данный предел имеет неопределенность типа 0 •<» и о формальном
применении правила Лопиталя речи нет. Однако эта неопределен-
ность легко сводится к неопределенности типа —, к которой пра-
вило Лопиталя уже применимо.	°°
Действительно,
lim(x In х) = lim = lim = - lim х = 0.
х^О	х—>0 X/х -Х/х1
тт £ 11 и г (1п(1+х))2 ..
Пример 6,11. Наити lim-------------. Имеем
Х-->4-=	X
(ln(l + x))2	21n(l + х)	1(1	)
lim -------— = lim-------------= 2 lim —------------- =
X	1	1 + X
1
= lim * + х = lim —— = 0
х—1	1 + X
(здесь вновь дважды применено правило Лопиталя).
В заключение приведем в виде леммы утверждение, которое
понадобится нам в следующей главе.
Лемма 6.3. Пусть f'(x) = 0 на интервале (а,Ь). Тогда функция
/(х) является постоянной на этом интервале, т.е.
/(х) = С, хе (й,/>),
где С — постоянная.
Доказательство. Действительно, выберем на интервале (й, Ь)
какие угодно точки X] и х2. Тогда по теореме о среднем Лагранжа
f(x2) “Ж)	- х(),
где g (Х[ ,х2) — некоторая «средняя» точка, находящаяся между Х|
и х2. По условию f'(x) = 0 в любой точке интервала (й, Ь) и, в
частности, = О- Это означает тогда, что
Ж) =/(х2).	(6.14)
Так как выбранные точки X] и х2 — любые, то равенство (6.14)
говорит о том, что на интервале (а,Ь) все значения функции /(х)
129
совпадают друг с другом. Это возможно лишь в том случае, если f(x)
постоянна на этом интервале, т.е. f(x) — некоторая константа. ▲
Замечание., Поскольку для любой постоянной функции f(x) = С,
очевидно, f'(x) = 0 на («,/»), то в результате получили утвержде-
ние: функция f(x) постоянна на интервале (й, Ь) в том и только в
том случае, если ее производная тождественно равна нулю.
6.4.	Первый дифференциал функции,
связь с приращением функции
Пусть функция у =f(x) имеет производную в каждой точке х, в
которой она определена. Такую функцию мы назвали дифферен-
цируемой.
Определение 6.4. Выражение
dy = f'(x)Ax
или, что то же,
df(x) = f'(x)6x
называется первым дифференциалом функции у = f(x) в точке х.
Пример 6.12. а) у = хп, тогда dy = пх”~]Ах;
2
б)	у = tg 2х, тогда dy =-=-Ах .
cos2 2х
Как видно, дифференциал функции у = f(x) зависит не только от
точки х, в которой он вычисляется, но и от приращения аргумента
Ах. Важно отметить, что первый дифференциал зависит от Ах линей-
но (этого, конечно, не скажешь относительно его зависимости от х).
Если вспомнить, что значение производной f'(x) равно угло-
вому коэффициенту касательной Тм (см. рис. 6.1), то становится
ясен и геометрический смысл дифференциала. Именно, значение
дифференциала dy в заданной точке х при выбранном приращении
Ах равно приращению ординаты касательной ТМк при переходе от
точки х к точке х + Ах (рис. 6.6).
Интересно сравнить значения дифференциала dy и полного
приращения функции Аг = /(х + Ах) - /(х).
Из рисунка видно, что при малых значениях Ах приращение
функции Аг и дифференциала dy весьма мало отличаются друг от
друга, что наводит на мысль о том, что вблизи х полное прираще-
ние функции и ее полный дифференциал приближенно равны.
Точно эта близость выражается следующей теоремой.
Теорема 6.9. Пусть функция у =/(х) дифференцируема в точке х.
Тогда справедлива формула
Ay = dy + а(х, Ах) Ах,
где величина <х(х,Ах) 0 при Ах —> 0.
130
Доказательство (фактически оно уже было проведено при обо-
сновании леммы 5.1). Действительно, дифференцируемость функ-
ции у = f(x) в точке х означает, что существует предел
В соответствии с определением предела это значит, что разность
= а(х,Дх)
Ах
есть бесконечно малая величина в процессе Ах —> 0.
Отсюда и получаем, что
Ау = /'(х)Ах + ос(х, Ах)Ах,
т.е.
Ay = dy + <х(х, Ах)Ах. ▲	(6.15)
Анализ формулы (6.15) позволяет сделать выводы о том, что
приращение функции Ау приближенно равно ее дифференциалу
dy, при этом абсолютная погрешность приближения определяется
бесконечно малой величиной а(х, Ах)Ах. Эта погрешность есть про-
изведение двух бесконечно малых величин а(х, Ах) и Ах и ее
обозначают о(Ах) (читается «о» малое от Ах), подчеркивая, что
о(Ах) = а(х, Ах)Ах стремится к нулю быстрее, чем Ах в том смысле,
что имеет более высокий порядок малости, чем Ах. Поэтому фор-
мула (6.15) часто представляется в виде
/(х + Ах) - /(х) = /'(х)Ах + о(Ах),	(6.16)
а дифференциал dy = /'(х)Ах называется главной линейной частью
полного приращения функции Ау = /(х + Ах) - /(х).
В заключение покажем, как применяется формула (6.16) для
вычисления приближенных значений функций.
Пусть х0 — фиксированная точка, х = х0 + Ах0 — значения аргу-
мента, близкие к Xq (рис. 6.7).
131
Допустим, что в точке х0 известны значения f(xQ) и f'(xQ). Тог-
да, согласно (6.16),
f(xQ + Ах0) - Дх0) = f'(x0)Ax0 + о(Ах0)
или, что то же,
f(x) = f(x0) +f'(x0)(x - х0) + o(x - x0).
Следовательно, можно считать, что
f(x) = Дх0) +/'(х0)(х-х0),	(6.17)
при этом значение Дх) будет найдено тем точнее, чем меньше
разность аргументов х - х0.
Пример 6.13. Вычислим значения функции /(х) = 4х в точках
х= 1,2; х= 1,1; х= 1,05.
Решение. Так как данные точки близки к единице, то положим
Xq = 1 и воспользуемся приближенной формулой (6.17).
Имеем
Ж) = 1, Жо)=Д= =1-
Следовательно, получаем приближенную формулу
Vx = 1 +1(х-1),
откуда при х = 1,2; х = 1,1; х = 1,05 будем последовательно иметь
= 1,100;	1,050; Д05 - 1,025.
Можно показать, что абсолютные погрешности соответствую-
щих вычислений равны Л] = 0,010; Л2 = 0,002; А3 = 0,001. Как видно,
эти погрешности монотонно убывают.
6.5.	Производные и дифференциалы высших порядков
Пусть у = Дх) — дифференцируемая функция на интервале (а, Ь).
Тогда производная у' = f'(x) является функцией, определенной
также на интервале (а, Ь), и, следовательно, можно поставить воп-
рос о существовании производной от производной исходной фун-
кции. Она называется второй производной от функции у = Дх). Далее
естественно возникает третья производная, четвертая и т.д.
Определение 6.5. Пусть п = 2, 3, ... — натуральное число. Тогда
производная порядка п от функции у=Дх) определяется по формуле
Ул>(х) = (Ул-1)(х))'.
Ясно, что, исходя из первой производной у'(х), последователь-
но можно найти производные любого порядка:
132
У'(х) = (./(х))', /"(*) = (У'(х))' и т.д.
Если существуют производные функции у = f(x) до какого-
нибудь п = 2, 3, то говорят, что функция у = f(x) дифференци-
руема и раз. Если, дополнительно, н-я производная Ул)(х) непре-
рывна на интервале (а, Ь), то функция у = f(x) называется «-раз
непрерывно дифференцируемой на интервале (а,Ь).
Если функция у = f(x) имеет производные любого порядка, то
такая функция называется бесконечно дифференцируемой. Далее уви-
дим, что все элементарные функции бесконечно дифференцируе-
мы всюду, где они определены.
Пример 6,14. у = хт, т — натуральное число. Имеем у' = (хт)' =
= тхт~], у" = т(т - 1)х": 2. ..., у{т) = т\ Ясно, что все производные
(хт)(/?) = о, если п > т + 1. В общем виде любую производную от хт
можно записать в виде
(х'”)(л) = т(т _ ] )	_ /; + И = 1, 2, ... .
Пример 6.15. у = sinx. Имеем у' = cosx, у” = -sinx, у”' = -cosx,
rlv = sinx. Очевидно, что все последующие вычисления производ-
ных пятого, шестого и других порядков будут повторяться. Нетрудно
убедиться, что производную w-го порядка можно представить в виде
Аналогично
(cosx)(fl) = cos^x + /7 у п = 1, 2, ... .
Пример 6.16. у = ах. Имеем у' = йа1пй, у” = я*1п2«, ... . Общая
формула = «А1п"«.
Пример 6.17. у = 1пх, у' = — = х-1, у" = (—1 )х-2, ут = (—1)(—2)х-3, ...
X
Общая формула (lnx)(fl) = (—1)(—2)... (-« + 1)х_", или, что то же,
(lnx)w = (-1)"-’(/7 - 1)!х".
С помощью производных высших порядков вводятся дифферен-
циалы высших порядков. Как и производные, они определяются
последовательно.
Именно, второй дифференциал d2y есть дифференциал от пер-
вого дифференциала, dy = /'(х)Дх, при том же самом приращении
Ах. Таким образом, d2y = d(dy) или, подробнее
d2y = d(f'(x)Ax) = d(f'(x)Y\x = /"(х)АхАх = /"(х)(Ах)2.
Аналогично
d3y = /"'(х)(Ах)3 и т.д.
133
Определение 6,6, Дифференциалом п-го порядка от функции
у = f(x) называется первый дифференциал от дифференциала по-
рядка п - 1, т.е.
dny = d(d”~ly)
или, что то же,
dy = /(/?)(х)(Ах)".
Еще раз отметим, что все дифференциалы, начиная с первого,
определяются при одном и том же приращении Ах.
Пример 6.18, Воспользуемся только что вычисленными произ-
водными «-го порядка. Получим следующие дифференциалы «-го
порядка:
a)	dn(xm) = т(т -	- п + 1)х"мЧАх)'г;
б)	dn(sinx) = sin^х + «у^(Ах)л;
в)	d”(cos х) = cos^x + «^(Ах)";
г)	dn(ax) = ях1п"я(Ах)л;
д)	бР(1пх) = (-1)"“'(« - 1)! х_/?(Ах)/?.
При вычислении дифференциалов общепринято приращение Ах
независимого аргумента х обозначать dx, т. е. по определению пола-
гать Ах = dx. Тогда дифференциалы запишутся в виде
dy = f'(x)dx; d2y = f"(x)(dx)2; ...; dny = fM(x)(dx)”.
Эта форма записи дифференциалов особенно полезна в теории
обыкновенных дифференциальных уравнений, которые будут рас-
смотрены в гл. 11.
6.6.	Формула Тейлора
Пусть /(х) — функция, определенная в некоторой окрестности
UXf) фиксированной точки х0. Формула Тейлора приближенно вы-
ражает значения /(х) при х #= х0 через значения функции и ее про-
изводных в точке х0, т.е. через значения /(х0), /'(х0), ••• •
С таким приближенным представлением функции f(x) мы уже
сталкивались, сравнивая дифференциал функции с ее полным
приращением, а именно [см. формулу (6.17)]
/(х) =/(х0) + /'(х0)(х - х0) + о(х - х0).	(6.18)
Здесь о(х - х0) — погрешность приближения
/(х) = /(х0) +/'(х0)(х- х0),	(6.19)
134
являющаяся бесконечно малой величиной более высокого поряд-
ка малости, чем приращение аргумента Ах0 = х - х0.
Формула (6.18) и тем самым приближение (6.19) справедливы
для любой функции, имеющей в точке х0 первую производную
Д(х0). Возникает естественный вопрос: если функция имеет не толь-
ко первую производную Д(х0), но и высшие производные /"(х0),
..., ДДхо) до порядка п > 2, то нельзя ли формулы (6.18), (6.19)
уточнить и получить приближение функции более высокой точно-
сти. Ответ заключается в следующей теореме.
Теорема 6.10. Пусть функция у = f(x) определена в некоторой
окрестности UXo и имеет в этой окрестности производные Д(х),
f"(x), ..., /(,,)(х) до порядка п > 1, причем непрерывна в
точке х0. Тогда для любой точки х е U справедлива формула
/(х) = /(х0) + ^*°\х-х0) + ^ ^°\х-х0)2 + ...
...+	)^°\х-х0)я +о((х-х0)Л).	(6.20)
п\
Формула (6.20) носит название формулы Тейлора порядка п и
является основной формулой дифференциального исчисления.
Поэтому прежде чем дать доказательство этой формулы, скажем
несколько слов о ее содержании.
Выражение
Тп = /(х0) +	(х - х0) + ... +	Yo) (х - х0)"
1!	п\
есть, очевидно, многочлен степени п, который называется много-
членом Тейлора функции Дх) в точке х0. Таким образом, из фор-
мулы (6.20) следует, что функция Дх) приближенно равна своему
многочлену Тейлора Т„(х), при этом абсолютная погрешность при-
ближения Дх) = Д(х), х g есть о((х - х0)л), т.е. бесконечно
малая более высокого порядка малости, чем старшая степень од-
ночлена х - х0, входящая в Д(х).
Можно показать, что никакой другой многочлен степени л, кроме
многочлена Тейлора, не дает приближения функции Дх) с точ-
ностью о((х - х0)"). В этом смысле многочлен Тейлора является
многочленом наилучшего приближения функции Дх) вблизи точ-
ки х0.
Доказательство. Обозначим а„(х0, х - х0) = Дх) - Д(х) и пока-
жем, что при х —> Хо величина ая(х0, х - х0) есть бесконечно малая
более высокого порядка, чем (х - х0)л, т.е.
.. ал(хо,х-хо) п
1Ш1 —Ш = 0.
(х - х0)"
135
Действительно, применяя п раз правило Лопиталя, имеем
п (х y	/(х)-/(х0)-/ (х0 )(х-х0° (х—х0 )п
(х-х0)л	А^((	(х-х0)/7
/'(х) - /'(х0) - ^7 /Дх0 )2(х - х0	(х0 )я(х - х0)-’
= lim--------------—-------------------------------------------=
/Дх) - /Дх0) -... -^-/<fl)(x0)«(« - 1)(х -хо)"-2
____________________nl________________________
п(п- l)(x-Xo)fl“2
п!
так как по условию /(л)(х) непрерывна в точке х0. А
Замечание., Особенно просто выглядит формула Тейлора в слу-
чае х0 = О, а именно
/(х) = /(0) +	х +... + ^)(0)х" + о(х").
1!	п\
Приведем представления основных элементарных функций по
формуле Тейлора в окрестности точки х0 = 0.
Пример 6.19. Пусть /(х) = еА. Тогда ,/':';,(х) = (с\)(';) = ех и, следо-
вательно, коэффициенты многочлена Тейлора
7	W=—,Д=0, 1, ....
п' п\
Таким образом,
ех = 1 + х + — + ... + — + о(х").
2 п\
Пример 6.20. Пусть /(х) = sinx. Тогда
/(и)(х) = (sinx)(w) = sin
Следовательно, коэффициенты Тейлора
0, есл, п =2 щ
sm[п
п\ п\
(-1)т
—-—-—, есл, п =2 т +1, т =0,1, ....
(2m +1)!
Таким образом,
г3	/_ 1W
sinx = х-----+	——-—x2m+l +o(x2m+1).
3!	(2m+ 1)!
136
Пример 6.21. Пусть f(x) = cosx. Имеем
у2	t_ |\m
cosx = 1-----+ ... + -—— x2m + o(x2m).
21	(2m) 1
Пример 6.22. Пусть f(x) = ln(l + x). Тогда
f“\x) = (-\)n~](n - 1)1(1 + x)-,!
и, следовательно,
Л>(0) = (-!)"-’(« - 1)’-
Отсюда получаем, что
у 2 у 3	/_1 \ я—]
1п(1 + х) = X ——— + -— + ••• + ----Х>1 + о(х").
2	3	п
Пример 6.23. Пусть f(x) = (1 + х)и, где а — вещественное число.
Тогда
/(fl)(x) = ос((х - 1)... (а - п + 1)(1 + х)а-"
и, следовательно,
/(/?)(0) = ос((х - 1)... (ос - п + 1).
Таким образом,
(1 + ху = 1 + ах + у +... + а(а-1)...(а-» + 1) х„ + 0(хП)
21	nl
Представление функций по формуле Тейлора имеет разнооб-
разные приложения, с которыми будем неоднократно встречаться
далее, а здесь покажем на примере, как можно использовать эту
формулу при нахождении пределов.
Пример 6.24. Найти lim Sin * Х . Используя формулу Тейлора
л-^0 XJ
X3
sinx = х- — + о(х3),
будем иметь
XJ /
х-----+ o(xJ)-x
,. Sin X - X ,.	f. у 7
hm--------— = hm-----------------
A-^0 X3	X3
-у + 0(*3) f 1 0(*3)А	1
,	= lim|__ + _L_2 =__
= lim
х-эО
х-эО
137
6.7. Экстремумы функций
Теория экстремумов посвящена задаче нахождения тех точек, в
которых значения функции у = f(x) являются наибольшими или
наименьшими среди всех значений этой функции в близлежащих
точках. Такие точки мы назвали в 6.2 точками локального максимума
или локального минимума функции у = f(x). Теория локального
экстремума функции у = f(x) позволяет «видеть» поведение функ-
ции при изменении аргумента и, в частности, строить ее график.
6.7.1. Необходимое условие экстремума
Определение 6.7Точки локального максимума и локального
минимума функции у = f(x) называются ее экстремальными точ-
ками.
Пример 6.25. Точка х = О является точкой локального минимума
функции у = |х| (рис. 6.8).
Пример 6.26. На рис. 6.2 точка х = b является точкой локального
максимума функции /(х), а точка х = а — точкой локального мини-
мума.
Зададимся вопросом: как найти экстремальные точки заданной
функции у = /(х)? К сожалению, универсального ответа на этот
вопрос нет и решать его следует всякий раз индивидуально для
каждой конкретно заданной функции. Однако, если ограничиться
рассмотрением дифференцируемых функций, то здесь имеется ряд
результатов, носящих общий характер.
Прежде всего вспомним лемму Ферма (см. лемму 6.2), приводя-
щую к необходимому условию локального экстремума.
Если у = Дх) — дифференцируемая функция и х0 — экстремаль-
ная точка этой функции, то
138
Из этого утверждения следует, что все точки локального экст-
ремума дифференцируемой функции у = f(x) обязательно являют-
ся корнями уравнения (6.21). Тем самым условие (6.21) является
необходимым условием экстремума.
Обратное, однако, неверно, т.е. точка х0 может быть решением
уравнения (6.21), но не являться экстремальной точкой функции
у = f(x). Примером такой точки может служить точка х = О для
функции у = х3. Действительно, х = О удовлетворяет уравнению
у' = 0, но в то же время не является ни точкой локального макси-
мума, ни точкой локального минимума (рис. 6.9).
Чтобы различить корни уравнения (6.21) и точки локального
экстремума, введем определение.
Определение 6.8, Точки х, удовлетворяющие уравнению f'(x) = О,
называются стационарными точками функции у = /(х).
Из определения ясно, что стационарных точек, вообще гово-
ря, больше, чем точек экстремума. В связи с этим возникает воп-
рос о том, каким способом выделить среди стационарных точек
те, которые действительно являются экстремальными точками
функции у = /(х).
Сформулируем две теоремы, дающие достаточные условия эк-
стремума.
6.7.2. Достаточные условия экстремума
Теорема 6.11 (достаточное условие экстремума по знаку первой
производной). Пусть выполнены следующие условия:
1) х0 е (а,Ь) — стационарная точка дифференцируемой на (а,Ь)
функции/(х), т.е./'(х0) = 0;
2) при переходе аргумента х через точку Хц производная /'(х)
меняет знак.
Тогда точка х0 является точкой локального экстремума функ-
ции /(х), причем:
а)	если f'(x) < 0 при х < х0 и /'(х) > 0 при х > х0, то х0 — точка
локального минимума;
б)	если, напротив, f'(x) > 0 при х < х0 и /'(х) < 0 при х > х0, то
х0 — точка локального максимума.
Замечание. Отметим, что, говоря о смене знака производной
/'(х) при переходе через точку х0, подразумеваем, что условия
/'(х) > 0 или f'(x) < 0 имеют место вблизи точки х0, поскольку
речь идет о нахождении локальных экстремумов. Ясно, что в этом
случае значения функции или ее производной в точках, далеких
от х0, роли не играют.
Доказательство. Пусть интервал (х0 - 6, х0 + S), (5 > 0 — некоторое
число) есть та окрестность, в которой выполнены условия теоре-
мы, например, условия а), т.е. f'(x) < 0 для всех хе (х0 - 5, х0) и
/'(х) > 0 для всех х е (х0, х0 + 5).
139
Покажем, что в точке х0 функция f(x) имеет локальный минимум.
Действительно, так как х0 — стационарная точка функции f(x),
т.е. /'(xq) = 0, то в левом полу отрезке (х0 - 5. xj производная f'(x) <
< 0, а в правом полуотрезке [х0, х0 + 5) производная f'(x) > 0.
Согласно критерию монотонности (см. теорему 6.7) это означает, что
на левом полуотрезке (х0 - S. х0] функция f(x) убывает и, следова-
тельно, f(x) > Дх0) для всех хе (х0 - 5- х0]. На правом же полуотрез-
ке [х0, х0 + 5), напротив, Дх) монотонно возрастает и, следователь-
но, Дх0) < Дх) для всех хе [х0, х0 + 5). В итоге для любой точки из
полной окрестности (х0 - 5, х0 + 5) справедливо неравенство Дх0) <
< Дх).Тем самым установлено, что х0 — локальный минимум.
Аналогично рассматривается и случай б. ▲.
Пример 6,27. Рассмотрим функцию у = х(х - 2). Имеем у'(х) =
= 2х - 2 = 0 в точке х = 1. Значит, точка х0 = 1 — стационарная точка
функции у = х(х - 2). Замечаем теперь, что при х < 1 производная
у' < 0, а при х > 1 производная у' > 0. Следовательно, точка х0 = 1 —
точка локального минимума функции у = х(х - 2).
Теорема 6.12 (достаточное условие экстремума в терминах вто-
рой производной). Пусть выполнены следующие условия:
1)	точка х0 — стационарная точка, т.е. Д(х0) = 0;
2)	функция у = Дх) дважды дифференцируема в точке х0, при-
чем /"(х) непрерывна в этой точке;
3)	Д'(*о) * 0-
Тогда х0 есть точка локального экстремума функции Дх), причем:
а) если Д'(х0) > 0, то точка х0 — точка локального минимума;
б) если /"(х0) < 0, то точка х0 — точка локального максимума.
Доказательство. По формуле Тейлора для любой точки х имеем
/(х) = /(х0) + ^у^(х-х0)+ -^^^(х-Хо)2 + о((х-х0)2),
где о((х - х0)2) — бесконечно малая более высокого порядка мало-
сти, чем (х - х0)2, т. е.	—> 0 при х х0. Так как f'(xQ) = 0,
(х-х0)2
то эта формула может быть записана в виде
Лх')-дх<>)= Д^+о0)
(6.22)
(*-*о)2,
где о(1) —> 0 при х х0. Ясно, что при х, достаточно близких к х0,
знак квадратной скобки будет тем же самым, что и знак числа
Д'(х0). Поэтому, если /"(х0) > 0, то из (6.22) немедленно получа-
ем, что в достаточно малой окрестности точки х0
Дх) - Дх0) > 0.
Это означает, что в точке х0 функция Дх) имеет локальный
минимум. Аналогично, если Д'(х0) < 0, то в точке х0 функция Дх)
имеет локальный максимум. ▲
140
Пример 6.28. Рассмотрим функцию у = х4 + х2 + 1. Имеем у' = 4л:3 +
+ 2х = 2х(2х2 + 1), откуда из уравнения у' = 0 получаем, что х0 = 0 —
стационарная точка. Далее у" = 12х2 + 2 и, следовательно, у"(0) =
= 2 > 0. Таким образом, точка х0 = 0 является точкой экстремума
функции у = х4 + х2 + 1, а более точно, точкой минимума.
6.8.	Выпуклые функции. Точки перегиба
Свойство выпуклости функции есть одна из наиболее тонких ее
характеристик. Знание участков выпуклости и точек, в которых
направление выпуклости меняется, особенно существенно при
построении графика функции.
6.8.1.	Определение. Критерий выпуклости
Пусть у = /(х) — дифференцируемая на интервале (й, Ь) функ-
ция. Как известно, в любой точке М^х^у^) графика этой функции
имеется касательная прямая Тм, уравнение которой определяется
формулой
ТМй : у = у0 + f'(x0 )(x - х0)
или, что то же,
TM(i 'У = /(х0) + //(х0)(х-х0).
(6.23)
Определение 6.9. Функция у = Дх) называется выпуклой вниз на
интервале (а,Ь), если, какова бы ни была точка х0 е (а,Ь), график
этой функции целиком находится над графиком касательной Тм
(рис. 6.10).
Аналогично определяется выпуклость вверх с заменой слов «над
графиком» на слова «под графиком».
Замечание. Анализируя рис. 6.10, можно понять математический
смысл понятия выпуклости вниз. Именно, в любой точке отрезка
х е (й, Ь) величина /(х), равная разности ординат графиков функ-
ции у = Дх) и касательной пря-
мой Гд/о, неотрицательна, т.е.
/(х) = Дх) - /(х0) -
-Г(хо)(х-х0)>О. (6.24)
Для выпуклых вверх функ-
ций, очевидно, 1(х) < 0.
Как оказывается, свойство
выпуклости тесно связано со
знаком второй производной
Г(х).
141
Теорема 6.13. Пусть Дх) — дважды дифференцируемая функ-
ция на интервале (й, Ь), причем вторая производная f"(x) непре-
рывна на интервале (а, Ь). Тогда нижеследующие утверждения А и
Б равносильны:
А) функция Дх) выпукла вниз на интервале (а, 6);
Б) в любой точке х е (а,Ь) вторая производная f"(x) > 0.
Доказательство [импликация А => Б]. Пусть Дх) выпукла вниз
на (а, Ь). Тогда, согласно формуле (6.24), при любой фиксирован-
ной точке х0 g (й, Ь)
Цх) = Дх) - f(xQ) - f'(x0)(x - х0) > 0	(6.25)
для всех х е (й, Ь). В соответствии с формулой Тейлора,
f (х) - f (х0) - f\xQ)(x - х0) = ? ^Х°\х-х0)2 + о((х-х0)2).
Следовательно, в силу (6.25) и
f ^°\х-х0)2 + о((х-х0)2) >0
или, что то же,
Д\хД о((х-х0)2) п
(х-х^ ги'	(6.26)
Переходя к пределу в неравенстве (6.26) при х х0, немедлен-
но получаем, что /"(х0) - 0-
Так как х0 выбрана произвольно, это значит, что f"(x) > 0 на
интервале (й, Ь).
Обратно [импликация А <= Б]. Пусть Д'(х) > 0 всюду на интерва-
ле (й, Ь). Покажем, что /(х) > 0 на (а,Ь). Действительно, очевидно,
что /(х0) = 0. В то же время /'(х) = Д(х) - /'(х0), а Г'(х) = f"(x) > 0.
Второе неравенство означает, что функция /'(х) монотонно воз-
растает, обращаясь, очевидно, в нуль в точке х0. Это значит, что
производная /'(х) при переходе через точку х0 меняет знак с «ми-
нуса» на «плюс». Тем самым в точке х0 функция /(х) имеет мини-
мум. Поскольку /(х0) = 0, то для х * х0 функция /(х) > 0. Это и
означает, что функция у =/(х) выпукла вниз на интервале (й, Ь). ▲
Обратимся к точкам перегиба функции у = Дх).
6.8.2.	Исследование точек перегиба
Определение 6,10. Точка х0 е (й, Ь) называется точкой перегиба гра-
фика функции у = Дх) [или функции /(х)], если при переходе через
эту точку у графика функции меняется направление выпуклости.
Пример 6.29. Функция у = х3 (см. рис. 6.9) имеет в точке х = 0
перегиб, так как слева от нуля ее график является выпуклым вверх,
а справа — вниз.
142
Пример 6.30, Функция у = cosx имеет на интервале (0,2л) две
точки перегиба х = и х = у (см. рис. 5.2).
Для фактического нахождения точек перегиба функции f(x)
используется теорема о необходимом условии перегиба.
Теорема 6.14. Пусть f(x) дважды дифференцируема на интерва-
ле (а,Ь), причем f"(x) непрерывна. Пусть далее х0 е (а,Ь) — точка
перегиба f(x). Тогда
Г(х) = 0.
(6.27)
Доказательство. Пусть (для определенности) при переходе че-
рез точку х0 график функции f(x) меняет выпуклость вниз на вы-
пуклость вверх.
В соответствии с критерием выпуклости (см. теорему 6.13) это
значит, что при х < х0 справедливо неравенство f"(x) > 0, а при
х > х0, напротив, f"(x) < 0. Поскольку по предположению f"(x)
непрерывна на (а,Ь), то она непрерывна и в точке х0, т.е. f"(x) —>
—> /''(xq) в процессе х —> х0.
Очевидно, что переходя в неравенстве f"(x) > 0 к пределу х х0
слева, а затем в неравенстве f"(x) < 0 — справа, получаем, что
предельное значение f"(xQ) удовлетворяет неравенствам f"(xQ) > 0
и /"(xq) < 0. Это значит, что f"(xQ) = 0, что и требуется. ▲
Замечание. Из доказанного ясно, что для дважды дифференци-
руемых функций уравнение (6.27) является необходимым услови-
ем перегиба функции в точке х0. Это не значит, однако, что всякая
точка xq е (д, Z>), в которой/"(xq) = 0, обязана быть точкой перегиба.
Пример 6.31. Рассмотрим функцию у = х4. Очевидно, что в точ-
ке х0 = 0 производная у" = 12х2 обращается в нуль, но точка х0 = 0
является точкой минимума, а не точкой перегиба функции у = х4
(рис. 6.11).
Простым достаточным условием, обеспечивающим перегиб гра-
фика /(х) в точке х0 е (а,Ь), является следующая теорема.
Теорема 6.15. Пусть точка х0 является корнем уравнения f"(x) = 0,
т.е./"(х0) = 0. Если при переходе через точку х0 вторая производ-
ная /"(х) меняет знак, то х,( — точка пере-
гиба функции /(х), при этом:
а)	если при х < х0 f"(x) > 0, а при х > х0
f"(x) < 0, то выпуклость вниз меняется на
выпуклость вверх;
б)	если при х < х0 f"(x) < 0, а при х > х0
f"(x) > 0, то выпуклость вверх меняется на
выпуклость вниз.
Доказательство теоремы немедленно
следует из теоремы 6.13. При этом ясно,
что х0 — изолированная точка перегиба,
т. е. вблизи других точек перегиба нет.
143
Пример 6.32, Найдем точки
перегиба функции у = In (1 + л:2).
Имеем
, = 2х „ = 2(1-х2)
1 + X2 '	(1 + X2)2 ’
Следовательно, уравнение у" = О
имеет два решения х0 = 1, х, = -1.
Выясним, используя теорему 6.15,
являются ли эти точки действитель-
но точками перегиба.
Очевидно, знак второй производной определяется знаком чис-
лителя, т.е. величиной (1 - х2) = (1 - х)(1 + х). Ясно, что вблизи
точки х = 1 второй множитель (1 + х) положителен и, следователь-
но, знак произведения определяет первый множитель 1 - х, кото-
рый отрицателен при х > 1 и, напротив, положителен при х < 1.
Таким образом, х0 = 1 является изолированной точкой перегиба
(см. п. б) теоремы 6.15). Аналогично получаем, что точка X] = -1
также является точкой перегиба функции у = In (1 + х2). График ее
представлен на рис. 6.12.
6.9.	Асимптоты. Общая схема построения графиков
Основная цель подраздела — дать общую схему построения гра-
фиков функций. Большая часть элементов этой схемы уже подго-
товлена, в частности, теория экстремумов, определение интерва-
лов выпуклости, монотонности графика, точек перегиба и т.д. Не
менее важными элементами построения графиков являются асим-
птоты графика (говорят также асимптоты функции). Асимптоты
бывают разными. Здесь изучим только прямолинейные асимпто-
ты, которые разделяются на три типа: горизонтальные, вертикаль-
ные и наклонные.
Определение 6.11. Прямая у = b называется горизонтальной асим-
птотой функции /(х) при х +оо, если lim f(x) = b (или, что то
же, lim (b - /(х)) = 0).
Аналогично определяется горизонтальная асимптота в процес-
се х —> -оо.
Определение 6.12. Прямая х = а называется вертикальной асимп-
тотой функции у = /(х), если
lim /(х) = оо.
Если/(х) —> «о при х а справа (т.е. при х > я), то говорят, что
прямая х = а является вертикальной асимптотой «справа». Анало-
гично для предела слева.
144
Пример 6.33. Пусть у =---. Очевидно lim _г(х) = 1. Следовательно,
х - 1
прямая у = 1 является горизонтальной асимтотой как при х —> +<*>,
так и при х —> -оо. Далее, точка х = 1 является нулем знаменателя,
при этом limy(x) = <*>. Следовательно, прямая х= 1 является верти-
кальной асимптотой функции у (рис. 6.13).
Определение 6.13. Прямая у = кх + b называется наклонной асим-
птотой функции у = f(x) при х —> <х>, если
lim [/(х) - кх - />] = 0.	(6.28)
Геометрически это означает, что в процессе х <*> график функ-
ции у = Дх) сколь угодно близко приближается к прямой у = кх + Ь.
Отметим, что на практике полезно различать наклонные асим-
птоты функции у = Дх) в процессе х -> +%> и в процессе х —» -<*>, так
как они могут быть различными.
Из определения наклонной асимптоты, а точнее из условия
(6.28), вытекают весьма простые формулы для нахождения угло-
вого коэффициента к и свободного члена Ь.
Действительно, если Дх) - кх - b -ь 0, то и
f(x)-kx-b Л
----------> 0 ПРИ X -> оо.
X
Отсюда
.	.. ( f(x) b} .. /(х) .. b	.. /(х)
к = lim -------= hm 2-L2. - hm — = lim 22—'.
Л--Ц X	X )	X	X x^°° X
145
Итак,
£ = lim2M.	(6.29)
х—X
После того, как найдено число к, вновь из (6.28) немедленно
получим, что
b = lim [/(х) - кх].	(6.30)
Формулы (6.29) и (6.30) суть искомые формулы нахождения
параметров к и b наклонной асимптоты.	i
Пример 6.34. Найдем наклонную асимптоту функции у = (х - 2)е
Имеем
]
(х-2)е * r х-2	-1
к = пт--------= пт----lim е х = 1.
х	х—х
Значит, возможная наклонная асимптота имеет вид у = х + Ь.
Далее,
b = lim (х - 2)е А - х = lim х(е А - 1) - 2е А =
1
р х __1	1	__1	_/
= lim — -----2 = (замена t = —) = lim---------2 = lim----2 = -3.
х-»	1	X f-0	/	?-0 t
Следовательно, можно сделать вывод о том, что прямая у = х - 3
является наклонной асимптотой графика функции у = (х - 2)е А
(рис. 6.14).
В заключение на конкретном
примере дадим общую схему по-
строения графика функции.
Именно, построим график
функции у = (х-2)е А, изобра-
женный на рис. 6.14. При пост-
роении графика желательно (но
вовсе не обязательно) соблюдать
следующий порядок.
1. Область определения. Оче-
видно, функцияу = (х - 2)е А оп-
ределена всюду, кроме х= 0, по-
этому область определения D есть
вся ось R* 1, кроме нуля, или, что
то же, D = (-оо,0) U (0,+оо) —
объединение двух открытых по-
луосей (-оо,0), (0,+оо).
146
2.	Характерные точки. Обычно это точки пересечения графика
с осями координат, точки разрыва, отдельные (легко вычисляе-
мые) значения функции и др.
В нашем случае х = 2 — точка пересечения с осью Ох. С осью Оу
график не пересекается, так как х = 0 не входит в область опреде-
ления функции у = (х- 2)е х.
Полезно отметить, однако, что при х -ь 0 справа
i	]
lim (х - 2)е А = lim е Л = О,
Х-+0	А-^+0
а при х —> 0 слева
]
lim (х - 2)е х = -оо.
Следовательно, прямая х = 0 является вертикальной асимптотой
графика слева.
3.	Поведение на бесконечности. Наклонные асимптоты. Легко
видеть, что
]
lim у(х) = lim (х - 2)е х = ±<х> ,
что приводит к мысли о возможном существовании наклонных
асимптот. И это так. Как было ранее установлено (см. пример 6.34)
прямая у = х - 3 есть наклонная асимптота графика функции
у = (х-2)е““.
4.	Экстремумы и интервалы монотонности. На эти вопросы от-
вет содержится в исследовании первой производной функции
у = (х - 2)е Y. Как показывают вычисления,
Следовательно, у' = 0 в тех точках, где х2 + х - 2 = 0, т. е. в точках
х = 1 и х = 2. Поскольку при переходе через точку х = 1 производная
у' меняет знак с «-» на «+», то точка х = 1 — точка минимума (при
этом у(1) = -—). Напротив, при переходе через точку х = -2 произ-
водная у' меняет знак с «+» на «-», поэтому точка х = -2 — точка
максимума (при этом у(-2) = -4>/ё).
Поскольку ни в каких других точках, кроме х = -2 и х = 1, про-
изводная у'(х) не обращается в нуль, то автоматически получим
интервалы монотонности:
-о® < х < -2 — интервал возрастания;
-2 < х < 0 — интервал убывания;
О < х < 1 — интервал убывания;
1 < х < +оо — интервал возрастания.
147
5.	Точки перегиба и интервалы выпуклости. Эти вопросы иссле-
дуются с помощью второй производной. Имеем в нашем случае
„ 5х-2 4
У =——е
X4
2
Следовательно, точка х = —, возможно, точка перегиба. Это дей-
5	2
ствительно так, поскольку у" < 0 при х < — и, наоборот, у" > О
2	5
при х > —. (Разумеется, точка х = 0 исключается, так как она не
5	2
входит в область определения.) Итак, точка х = — является точ-
кой перегиба, причем слева от этой точки график функции имеет
выпуклость вверх, а справа — вниз.
Теперь, имея достаточно информации, можно построить гра-
фик функции у = (х - 2)е х, последовательно отметив на рисунке
характерные точки графика, наметив его отдельные фрагменты и
плавно соединив. Получим график, изображенный на рис. 6.14.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1.	Пусть
f 1, если х > О
SSnX= I	А
[-1,если х < О
(читается «знак х» или «сигнум х»). Установите следующие формулы:
|х|' = sgnx (х * 0),
(x2sgnx)' = 2|х|, -оо < х < +<».
При этом докажите, исходя из определения производной, что функ-
ция |х| в точке х = 0 недифференцируема и, напротив, производная фун-
кции x2sgn х в точке х = 0 существует и равна нулю.
2.	Функция, определенная на интервале (-а, а), называется нечетной,
если для любой точки х из интервала (-а, а) справедливо равенство
/(-х) = -f(x).
Если же для любой точки х из интервала (-а, а) имеет место равенство
/(-х) = /(х), то функция называется четной.
Докажите, что производная нечетной функции есть четная функция,
а производная четной функции есть нечетная функция.
3.	Функция Дх), определенная на всей вещественной оси, называется
периодической функцией с периодом Т, если для всех вещественных х
справедливо равенство
/(х+П = Дх).
Докажите, что производная периодической функции есть также перио-
дическая функция с тем же периодом Т.
148
4.	Известно (см. лемму 6.3), что если на интервале (а,Ь) производная
f'(x) = 0, то функция f(x) постоянна на (а, Ь), т.е. Дх) s const, х е (й,/>).
Пусть теперь функция Дх) определена на множестве Е = (a,b) U
являющимся объединением двух непересекающихся интервалов. Верно ли
утверждение: если Д(х) s 0 на множестве Е, то Дх) постоянна на множе-
стве Е?
5.	Докажите, что прямая
Ж. = 1
а1 2 ь2
является касательной прямой, проведенной к графику эллипса
в точке х0, у0.
6.	Запишите многочлен
Р(х) = Зх4 + 5х3 - х2 + Зх - 7
по степеням двучлена х - 1.
7.	Докажите, что на отрезке [аД] всякая линейная функция принима-
ет наибольшее и наименьшее значения в конечных точках а и Ь.
8.	Пусть дифференцируемая функция Дх) определена на всей веще-
ственной оси и монотонна. Рассмотрим функцию ф(х) = Дах + р), где а и
р — произвольно взятые числа. Опираясь на критерий монотонности, до-
кажите, что функция <р(х) также монотонна.
9.	Найдите асимптоты функций:
1) У = ~г-р 2) у = ^-, 3) у = xarctgx.
х2 - 1	х + 2
ГЛАВА 7
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ
ВЕЩЕСТВЕННОЙ ПЕРЕМЕННОЙ
7.1. Первообразная и неопределенный интеграл
7.1.1. Первообразная. «Почти единственность» первообразной
Пусть Дх) — некоторая функция, заданная на интервале (а,Ь).
По этой функции определяется вторая функция Дх), также задан-
ная на интервале (а,Ь), называемая первообразной функции Дх).
Определение 7.1. Дифференцируемая функция Дх) называется
первообразной функции Дх), если в каждой точке интервала (а, б)
справедливо равенство
F'(x) = Дх).
Пример 7.1. Пусть Дх) = 1. Тогда в качестве первообразной этой
функции можно взять Дх) = х, так как х' = 1.
Пример 7.2. Пусть Дх) = cosx. Тогда в качестве первообразной
этой функции можно взять Дх) = sinx, так как (sinx)7 = cosx.
Читатель, вспомнив таблицу производных, без труда приведет
дополнительные примеры различных первообразных.
Теперь обратим внимание на то, что первообразная заданной
функции Дх) определяется неоднозначно. Действительно, если
функция Дх) = х является первообразной функции Дх) = 1, то и
функция 6)х) = х + с, где с — произвольная постоянная, также
является первообразной той же функции Дх) = 1. Это немедленно
следует из того, что при любом выборе с производная (х + с)' =
= х' + с' = 1, поскольку с' = 0.
То же самое можно сказать и о том, что для функции Дх) =
= cosx, наряду с Дх) = sinx, ее первообразной является и любая
функция G(x) = sinx + с, где с — любая постоянная.
Это наблюдение не случайно: оказывается, отмеченная неодно-
значность первообразной Дх) имеет место для любой функции Дх).
Более того, указанная неоднозначность (в виде аддитивной посто-
янной с) полностью исчерпывает произвол, возникающий при
определении первообразной.
Теорема 7.1 (о «почти единственности» первообразной). Пусть
Дх) и G(x) — две первообразные одной и той же функции Дх).
Тогда найдется постоянная с такая, что 6'(х) = Дх) + с для всех
хе ДД).
150
Доказательство. Действительно, в соответствии с определением
7.1 в любой точке х е (а, Ь) справедливы равенства
F'(x) = f(x) и G'(x) = f(x).	(7.1)
Обозначим и(х) = G(x) - F(x). Тогда из (7.1) немедленно следу-
ет, что и'(х) = 0 на интервале (а,Ь). Следовательно (см. лемму 6.3,
п. 6.3.2), функция и(х) постоянна на интервале (а,й), т.е. и(х) = с,
где с — некоторая постоянная. Это и значит, что G(x) - F(x) = с,
т. е. G(x) = F(x) + с. ▲
Из теоремы следует, что множество всех первообразных задан-
ной функции f(x) может быть получено из какой-либо конкрет-
ной первообразной F(x) путем добавления произвольной посто-
янной. Именно так и было сделано в предыдущих примерах.
7.1.2. Таблица неопределенных интегралов
Определение 7.2. Множество всех первообразных функции /(х)
называется неопределенным интегралом от этой функции и обозна-
чается символом
J f(x)dx.
Иначе, по определению,
\f(x)dx=F(x) + С,
где F(x) — какая-либо первообразная функции /(х); С — произ-
вольная постоянная.
Из определения ясно, что
-^-jf(x)dx = f(x),
т. е. операция неопределенного интегрирования является обратной
по отношению к операции дифференцирования. Это дает возмож-
ность «прочитать» известную таблицу производных «справа —на-
лево» и получить таблицу основных неопределенных интегралов
(табл. 7.1).
Кроме того, на практике часто встречаются неопределенные
интегралы (табл. 7.2), существенно дополняющие основные.
Разумеется, далеко не всякий неопределенный интеграл может
быть найден исходя из приведенных табличных интегралов. Более
того, весьма простые на вид неопределенные интегралы вообще
не вычисляются через элементарные функции. К таким интегра-
лам относятся, например, такие:
f с '- dx. Г и др.
J J Inx
151
Таблица 7.1
Таблица основных неопределенных интегралов
1 .jW = C	8. f , dX = arcsin x 4- C J Vl-x2
2. f xndx = —J— xra+l 4- C, J	a 4-1 где a Ф -1 любое конечное число	A г dx	„ 9. 	v = arctg x 4- C J 1 4-X2 10. fe*£/x= e*4- C
3. [— = ln|x| + C	j 11. [a^dx = — + C
4. Jcosxt/x= sinx4- C	J	In a 12. jchxt/x= shx4- C
5. JsinX£&=-COSX4- C	13. jshxt/x= chx4- C
г dx *	„ 6. 	— = tg X 4- C J COS2 X	. . r dx	.	„ 14.	—-— = th x 4- C J ch2 x
7.	= -ctgx + C J sin2 X	15. f-=-cthx + C J sh2 x
Таблица 7.2
Таблица неопределенных интегралов
. г dx	1	.X	Л
1.	—:-------- = — arctg — + С, а * О
J а2- + х2	а	а
2.	Г Х = — In ——- + С, а ф 0 («высокий» логарифм)
1 х -а 2а |х 4- а\
3.	J .	= In |х 4- yjx2 ± а21 4- С («длинный» логарифм)
J dx2 ± а2
4J^TLT = ±5lnla2±x2l + c
J а1 ± х2 2
5.	f .	= arcsin — 4- С, а > О
J 44^44
6.	=	+ с
7.	fc'a' - x2dx = — ^a2 - x2 + — arcsin — + C, a > 0
J	2	2 a
8.	J Vx2 ± a2dx = у Vx2 ± a2 ± In |x + Vx2 ± a21 + C
152
Наша ближайшая цель — выяснить основные правила неопре-
деленного интегрирования и на их основе исследовать некоторые
классы элементарных функций, для которых первообразные явля-
ются конечными комбинациями также элементарных функций.
7.2. Основные правила неопределенного интегрирования
Прежде всего отметим связь между неопределенным интегра-
лом и первым дифференциалом, которая выражается формулами:
1) J dF(x) = F(x) + С или, что то же, JF'CvWv = F(x) + С;
2) d\f(x)dx=f(x)dx или, что то же, -^-jf(x)dx = f(x).
Обе формулы являются непосредственными следствиями поня-
тий неопределенного интеграла и первого дифференциала (напом-
ним, что dy = y'(x)dx).
Правило 1 (вынесение константы за знак интеграла):
Ja/(x)d5c = af/(x)d5c, a — любое число.	(7.2)
Правило 2 (интеграл от суммы равен сумме интегралов):
J [/(*) +	= f/Wdbc + Jg(x)d5c. (7-3)
Правило 3 (интегрирование по частям). Пусть f(x) и g(x) — диф-
ференцируемые функции. Тогда
j f(x)g'(x)dx = -j f'(x)g(x)dx +f(x)g(x)	(7.4)
или в дифференциалах
J7(x)dg(x) = -jg(x)4f(x) + f(x)g(x).
Правило 4 (замена переменной). Пусть х = <p(Z), где <p(Z) - диф-
ференцируемая функция переменного t. Тогда
//(х)Л = ]7[<Р(Г)]<Р'«Л,	(7.5)
при этом в правой части формулы (7.5) переменная / должна быть
выражена через х, исходя из замены х = <р(/).
Замечание, Отметим, что в каждом из равенств (7.2) —(7.5) речь
идет о равенстве множеств функций, а именно множеств первооб-
разных, отличающихся друг от друга на постоянную величину.
Поэтому для проверки формул (7.2) —(7.5) достаточно убедиться
в том, что производные от левой и правой частей этих формул
тождественно равны между собой на интервале (а, Ь).
153
После этого наблюдения легко видеть, что сформулированные
правила интегрирования являются следствиями известных правил
дифференцирования.
Рассмотрим, например, формулу (7.2). Имеем
1) — (J<x/(x)Jx) = af(x) — производная левой части.
С другой стороны, учитывая, что константа выносится за знак
производной, получим
2) — f(x)dx} = a^“(J f(x^x} =	— производная пра-
вой части. Производные левой и правой частей, очевидно, равны,
и формула (7.2) доказана, т.е. константу можно выносить за знак
интеграла.
Из формулы (7.3) (она доказывается аналогично) следует, что
интеграл от суммы функций равен сумме интегралов от каждого
слагаемого.
Наконец, формула интегрирования (7.4) отражает правило диф-
ференцирования произведения функций, а формула (7.5) — пра-
вило дифференцирования сложной функции (см. 6.1).
Пример 7.3.
= 18j4xdx = 18jx}!2dx = 18-|x3/2 +C = 12xVx + C.
Пример 7.4.
[f 2 sin x-b/x = Г 2 sin xdx - [ —dx = 2 [ sin xdx - — Г=
2Vx) J	J2V^ J 2J
= 2 J sinxdx-^jx~^2dx =- 2 cosx - -Jx + C.
Пример 7.5. Интеграл j"xcosx6tx вычислим, используя формулу
интегрирования по частям (7.4). Для этого заметим, что cosx = (sinx)'
и, следовательно, интеграл можно записать в виде
Jx cos х dx = Jx (sinx)'<iY.
Очевидно, полагая /(х) = х, g(x) = sinx, по формуле (7.4) будем
иметь
Jxcosx dx = Jx(sinx)7/x = -J sinx dx + x sinx
и дело свелось к табличному интегралу от функции sinx. Оконча-
тельно
JxcosxJx = cosx + х sinx + С.
154
Формула замены переменной (7.5) является одним из наиболее
сильных инструментов вычисления неопределенных интегралов.
Рассмотрим несколько примеров.
Пример 7,6, Получим вначале простое обобщение табличной
формулы
[ xadx = —?—xa+l + С, а ф -1,
J а + 1
а именно докажем, что при любых а * 0 и произвольных b
\(ax + by~dx =-!---(ах + b)a+l + С.	(7.6)
J	й(а + 1)
Для этого сделаем замену ах + b = Г, или, что то же самое,
х = — (Z - /?). Тогда, учитывая, что при такой замене dx = — dt, из
а	я
формулы (7.5) получаем, что
[(йх + by-dx =	— dt = — \tadt =-!---Za+1 + C.
J	J a a J a(a +1)
Возвращаясь от переменной t к исходной переменной х, полу-
чаем искомую формулу.
Пример 7.7. Вычислим интеграл 1-^=--. Сделаем замену х = t2
J у/х -1
(избавляемся от кубического корня). Тогда dx = 3t2dt, a 1/х = t. По
формуле (7.5) имеем
г 3t2dt
J t-\
г dx
J у/х - 1
t-}
(7.7)
Последний интеграл также вычисляется с помощью замены
и = t — 1. Тогда du = dt и, значит,
с dt г du , . , „ . ,	,, „
[---= [ — = In | и | + С = In 11 - 11 + C.
i t - 1 i и
Тем самым из (7.7) находим
= 3(r2 + t + In | /- 1|) + С,
J ч/X - 1
откуда, возвращаясь к переменной х по формуле Цх = t, получаем
окончательный ответ:
J ^.Х 1 = 3(\/х^ + 3/х + In | ч/х - 11) + С.
155
В заключение отметим, что при нахождении неопределенных
интегралов от более сложных функций полезно использовать со-
временные математические пакеты, в частности пакет MAPLE (см.
прил.), с помощью которых находятся первообразные рациональ-
ных функций, тригонометрических выражений, биномиальных
дифференциалов Чебышева.
7.3. Задача нахождения площади криволинейной
трапеции. Определенный интеграл
В этом подразделе вводится основное понятие интегрального
исчисления функции одной вещественной переменной, а именно
понятие определенного интеграла.
Рассмотрим вначале задачу о нахождении площади криволи-
нейной трапеции.
Пусть у = f(x) — функция, определенная на некотором отрезке
[й,Ь]. Пусть, кроме того, функция f(x) неотрицательна, т.е./(х) > О
на отрезке [й, /?|. Тогда ее график определяет плоскую фигуру 5, изо-
браженную на рис. 7.1, которая называется криволинейной трапецией.
Поставим перед собой задачу найти площадь этой фигуры.
Эта задача распадается на две. Именно, необходимо, во-пер-
вых, выяснить, что называть площадью 5, и, во-вторых, указать
способ вычисления этой площади. Обе эти задачи решаются одно-
временно с помощью процесса «бесконечно малых разбиений»,
называемого процессом интегрирования функции f(x) на отрезке [й, Ь]
и состоящего в следующем (рис. 7.2).
Пусть п — натуральное число и
а = х0 < X] < ... < Х/_[ < х( < ... < хп = Ь,
(7.8)
(/</<«) — произвольно взятый набор точек на отрезке [а,Ь].
Очевидно, точки х0, хь ..., х„ определяют разбиение отрезка [й, Ь]
на п частей [х0,X]], [хнх2], ..., [xw_|,xj. Выберем на каждом «малом»
отрезке [х(_],х;] произвольную
точку (т. е. е [х,_],х(], / = 1, ...,
п) и составим сумму
(7.9)
/=1
где f(^j) — значения Дх) в вы-
бранных «средних» точках
AX/ = X/ - х(_] — длины отрезков
[х(_],х(]. Сумма (7.9) называется
интегральной суммой для фун-
кции Дх).
156
Поскольку произведение /(^)Axz равно площади прямоугольни-
ка с основанием [xz_|,xz] и высотой h, = /(^,) > 0, то интегральная
сумма <?„ равна площади ступенчатой трапеции, образованной эти-
ми прямоугольниками (см. рис. 7.2).
Из рисунка видно, что при достаточно мелком разбиении (7.8)
площадь этой ступенчатой трапеции можно принять в качестве
приближенного значения площади исходной криволинейной тра-
пеции 5, причем точность приближения будет тем лучше, чем мель-
че будет разбиение отрезка [а,Ь] точками х0, хь ..., х„. Поэтому,
если в процессе неограниченного измельчения разбиений отрезка
[а, /?| последовательность он будет стремиться к некоторому пре-
дельному значению о, то это число естественно назвать площадью
криволинейной трапеции 5, т. е. по определению положить пл. S = о
или, что то же, пл. 5 =
Тем самым получен ответ на поставленный в начале задачи воп-
рос о том, что называется площадью криволинейной трапеции S.
Замечание, Отметим, что хотя приведенное определение пло-
щади S интуитивно ясно, оно является еще недостаточно строгим.
Это объясняется тем, что интегральные суммы зависят не толь-
ко от номера п, но и от выбора точек разбиения х0, хн ... хн, а
также от выбора средних точек е [х(_],х(]. Поэтому заранее неяс-
но, получится ли значение площади S одним тем же числом при
различных разбиениях отрезка [а, Ь] и выборе точек £z, /= 1, ..., п.
Требуют математического пояснения и слова «в процессе нео-
граниченного измельчения разбиений отрезка [я, &]».
Чтобы исключить неопределенности, дадим строгое определе-
ние площади криволинейной трапеции S. Для этого введем число
X,. - max Ах.-,
i</<«
которое, очевидно, равно максимальной длине отрезков разбие-
ния ДХ], ..., Дхн.
157
Определение 7,3. Площадью криволинейной трапеции 5 на-
зывается число <т > О, удовлетворяющее следующему условию:
для любого сколь угодно малого е > 0 найдется число 3 (зависящее
от е) такое, что при любом выборе разбиения отрезка [я, 6], лишь
бы оно удовлетворяло неравенству < 3, и любом выборе точек
е [%/_[, х,-], / = 1, л, выполняется неравенство
а-^№)Лх(-
/=]
< £.
Это число о и принимается в качестве площади криволинейной
трапеции 5, т.е.
пл. S - lim ^/(^Дх,.	(7.10)
/-1
С другой стороны, предел интегральных сумм, стоящий в пра-
вой части формулы (7.10), называется определенным интегралом от
ь
функции/(х) по отрезку [а,Ь\ и обозначается символом j/(x)dx,
т. е. по определению	а
\f(x)dx= limf/W	(7.11)
а	""	' = 1
и тем самым
ь
пл.5 = ^f(x)dx	(7.12)
(не забываем, что здесь /(х) > 0).
Ясно, что, отвлекаясь теперь от исходной задачи нахождения
площади криволинейной трапеции 5 (тем самым от условия /(х) > 0),
можно принять формулу (7.11) в качестве формулы для вычисле-
ния определенного интеграла в случае произвольной функции Дх).
Именно, фактически повторяя определение 7.3, приведем другое
определение.
Определение 7.4. Определенным интегралом от функции Дх) по
ь
отрезку \а,Ь\ называется число, обозначаемое символом j/(x)dx,
которое удовлетворяет условию:	а
для любого сколь угодно малого е > 0 найдется число 3 > 0 (за-
висящее от е) такое, что при любом выборе разбиения отрезка
[а,Ь], лишь бы оно удовлетворяло неравенству < 3, и любом
выборе точек € [x/-i,x;], / = 1, ..., л, выполняется неравенство
УДх^-^/^Дх,.
а	>= I
158
Важность понятия определенного интеграла (и, в частности,
его связь с неопределенным интегралом) будет раскрыта в следу-
ющих подразделах, а сейчас на некоторое время вернемся к задаче
нахождения площади криволинейной трапеции S и заметим сле-
дующее.
С помощью формулы (7.10) [или, что то же, формула (7.12)]
можно вычислить площадь 5, однако непосредственное вычисле-
ние значения как самих интегральных сумм
/=1
так и их предела весьма затруднительно и на практике возможно
только в условиях проведения вычислительного процесса на ком-
пьютере. Поэтому одной из целей интегрального исчисления явля-
ется разработка простых методов вычисления определенных ин-
тегралов, минуя их прямое определение. В дальнейшем это будет
сделано и тем самым формулы (7.10), (7.12) наполнятся практи-
ческим содержанием.
В заключение сделаем еще одно замечание.
Замечание, До настоящего момента всюду предполагалось, что
а < Ь. В дальнейшем полезно использовать определенный интеграл
и при а> Ь, полагая в этом случае по определению
f/(x)</x = -j/(x)</x.
a	h
7.4. Основные свойства определенного интеграла.
Теорема о среднем
В этом подразделе рассмотрим некоторые классы функций, от
которых существует определенный интеграл, и установим ряд ос-
новных свойств, включая теорему о среднем.
Начнем с простых наблюдений о том, что далеко не от каждой
функции существует определенный интеграл или, что то же, да-
леко не каждая функция интегрируема на отрезке [а,Ь].
Прежде всего заметим, что неограниченная на отрезке [а,Ь]
функция f(x) не может быть интегрируемой на этом отрезке.
Действительно, если функция f(x) не ограничена на отрезке
[а,Ь], то при любом разбиении отрезка [а,Ь]
а = х0 < X] < ... < х,_1 < х„ = b
она будет неограниченной хотя бы на одном из отрезков разбие-
ния [х0,Х]], ..., [xfl_|,xj. Пусть (для определенности) она не огра-
ничена на первом отрезке [х0,Х]], т.е. принимает на [х0,Х]] сколь
159
угодно большие значения. Тогда ясно, что и интегральная сумма
а„, которую запишем в виде
= Ж1)ЛХ] + £/(^.)Дх(-,
i=2
также может принимать сколь угодно большие значения за счет
выбора точки в первом слагаемом.
Это означает, что последовательность пй не может иметь какое-
либо число о своим пределом в смысле определения 7.4 (т.е. неза-
висимо от выбора средних точек £z), что и означает неинтегрируе-
мость функции f(x).
Таким образом, установлено, что ограниченность функции f(x)
на отрезке [й, Ь] является необходимым условием ее интегрируемо-
сти по этому отрезку. Иначе доказано следующее утверждение.
Утверждение 7.1. Если функция f(x) интегрируема на отрезке
[й,Ь\, то она ограничена на этом отрезке.
Однако, как показывает нижеследующий пример функции Ди-
рихле, условие ограниченности функции отнюдь не является до-
статочным для ее интегрируемости.
Пример 7.8. Рассмотрим функцию Дирихле:

если х е [а, /?| рационально;
если х 6 [й, /?| иррационально.
Эта функция, будучи, очевидно, ограниченной на отрезке [й, д],
не интегрируема.
Действительно, пусть
= ^Р^ДДх;, п = 1, 2,...
;=]
— последовательность интегральных сумм этой функции. Очевид-
но, что на любом отрезке [х(_|,х(] имеются как рациональные, так
и иррациональные точки. Поэтому, если все точки £,= [x^^xj взять
рациональными, то получится пй = b - й. Если же, напротив, взять
все точки иррациональными, то получится = 0. Видим, что
при одном выборе средних точек сумма c„ = b-a—> b - а, а при
другом — пй = 0 —> 0 при 1Й —> 0. Это и значит, что функция D(x)
неинтегрируема на отрезке [й,6].
Замечание. Понятно, что определенный интеграл от функции
D(x) не существует по той причине, что она слишком разрывна,
более точно — разрывна в каждой точке отрезка [й,6].
В результате возникает естественный вопрос о выявлении усло-
вий, достаточных для существования определенного интеграла.
Сформулируем на этот счет ряд утверждений.
Утверждение 7.2. Пусть функция /(х) непрерывна на отрезке
[й,/?]. Тогда она интегрируема на этом отрезке.
160
Утверждение 7,3. Пусть функция f(x) монотонна на отрезке
[а,Ь]. Тогда она интегрируема на этом отрезке.
Утверждение 7.4. Пусть функция f(x) ограничена на отрезке
[й, и непрерывна на нем за исключением конечного числа точек
разрыва первого рода аь a.v, находящихся на этом отрезке.
Тогда f(x) интегрируема как на всем отрезке [а, д], так и на каждом
подотрезке [й,Н|], [а^аг], —, причем
J/(x)6bc = ^f(x)dx + f(x)dx + ...+ | f(x)dx+ J f(x)dx.
a	a	a,	aiV_|	a,v
Перейдем теперь к основным свойствам определенных интег-
ралов.
Свойство 1. ПустьДх) интегрируема на отрезке [й, 6]. Тогда при
любом числе ос функция а/(х) также интегрируема на отрезке [й, Ь\,
причем
ь	ь
\<xf(x)dx = v]j\x)dx
а	а
(постоянный множитель выносится за знак интеграла).
Свойство 2. Пусть функции Дх) и g(x) интегрируемы на отрез-
ке [а,Ь]. Тогда сумма (или разность) Дх) ± у(х) также интегриру-
ема на отрезке [а,Ь], причем
j[/(x)±g(x)]rfx = J7(x)dx± J#(x)£Zx	(7.13)
а	а	а
(интеграл от алгебраической суммы равен алгебраической сумме
интегралов).
Свойство 3 (интегрирование неравенств).
Если функции Дх) и g(x) интегрируемы на отрезке и,
кроме этого, связаны неравенством f(x) < g(x) для любого х из
[й,6], то
b	ь
\f(x)dx < jg(x)dx.
а	а
Свойство 4. Пусть функция Дх) интегрируема на [й, Ь]. Тогда
функция |Дх)| тоже интегрируема на [а,Ь], причем
j/(x)^</|/(х)|Л	(7.14)
а	а
(модуль интеграла не превосходит интеграла от модуля).
Свойства 1 — 3, а также сама формула (7.14) легко вытекают из
аналогичных свойств интегральных сумм. Остановимся, например,
на доказательстве свойства 2.
161
Доказательство. Действительно, пусть
a,(/±g) = i[/(t)±gfe)]Ax,.
/=1
— интегральная сумма для функции f(x) ± g(x). Очевидно, что
=	(7.15)
По условию, при стремлении параметра разбиения к нулю
ь	ь
<3„(g)^\g(x)dx и ой(/)-> J/(x)dx.
а	а
Следовательно, из (7.15) немедленно получаем существование
предела lima„(/±g), который по определению равен опреде-
h
ленному интегралу j/(x) ± g(x)dx . Переходя к пределу в равенстве
(7.15), получаем требуемую формулу. ▲
Свойство 5. Пусть f(x) интегрируема на [а, д], тогда для любого
значения с из этого отрезка функция f(x) будет интегрируема на
[а,с] и [с,Ь\, причем
J/(x)dx = j/(x)dx + j/(x)dx.	(7.16)
И наоборот, если f(x) интегрируема на отрезках [а,с] и [с,/>],
то она интегрируема по отрезку [а,Ь], причем справедлива форму-
ла (7.16).
Замечание, Формула (7.16) в случае f(x) > 0 выражает геомет-
рически очевидный факт: площадь криволинейной трапеции S1’ равна
сумме площадей <5£и S}. (рис. 7.3).
В заключение установим одно из самых значительных свойств
определенного интеграла, называемое теоремой о среднем.
Теорема 7.2. Пусть/(х) — непрерывная функция на отрезке [й, Ь].
Тогда найдется хотя бы одна точка £ из отрезка [а, Ь] такая, что
= f(Q(b-a).	(7.17)
а
Доказательство. Поскольку /(х) непрерывна на отрезке [й, д],
то по второй теореме Вейерштрасса она принимает на этом отрез-
ке свои максимальное и минимальное значения (М и т соответ-
ственно). Поэтому для любой точки х из отрезка [а; Ь] можно запи-
сать двустороннее неравенство
т < f(x) < М.
Интегрируя это неравенство (см. свойство 3), получаем, что
162
b	b	b
mjXdx < J f(x)dx < Л/JXdx
a	a	a
или, что то же,
b
m(b - a) < J/(x)dx < M(b - a),
a
b
ибо очевидно, что J Xdx = b - а (площадь прямоугольника с осно-
ванием (b — а) и высотой 1).
Запишем последнее неравенство в виде
1
т < ----^f(x)dx<M	(7-18)
а
1
и заметим, что число и =--| f(x)dx в силу (7.18) является про-
b - a J
а
межуточным значением между максимальным и минимальным
значениями функции f(x) на отрезке [а,Ь]. По теореме Коши о
промежуточном значении непрерывной функции найдется хотя бы
одна точка £ из отрезка [а,Ь], в которой f(x) примет значение ц,
т. е. хотя бы в одной точке £ из [а, Ь]
f(Q = -^—\f(x)dx.
b-aJ
а
Это и есть искомая формула (7.17). ▲
Замечание, В случае f(x) > 0 теорема о среднем, а точнее форму-
ла (7.17) имеет простой геометрический смысл (рис. 7.4): площадь
криволинейной трапеции, ограниченной прямыми х = анх = Ьи
функцией Дх), равна площади некоторого прямоугольника с вы-
сотой /(^) и основанием (Ь - а).
163
7.5. Формула Ньютона—Лейбница
В этом подразделе доказывается основная формула интеграль-
ного исчисления — формула Ньютона —Лейбница, являющаяся
главным инструментом для нахождения определенных интегралов.
Выводу этой формулы предшествует изучение свойств специаль-
ной первообразной функции f(x).
7.5.1. Определенный интеграл как функция верхнего предела
Пусть f(x) — интегрируемая на [а, Ь] функция. Выберем произ-
вольную точку t из [а,Ь\ и рассмотрим интеграл
]7(хЖ
а
Геометрически, как нам известно из 7.1, в случае неотрица-
тельной функции это — площадь криволинейной трапеции, обра-
зованной функцией f(x) на участке [я,/] (рис. 7.5).
Ясно, что при изменении точки t меняется и интеграл, т.е. он
определяет функцию точки верхнего предела. Обозначим ее через
S(f) = J7(X) dx.
а
Поскольку для аргумента, меняющегося на вещественной оси,
принято обозначение х, то заменим / на х. а переменную интегриро-
вания х на любую другую букву, например вновь на t. Тогда имеем
а
Оказывается, что для непрерывной функции Дх) функция 5(х)
является ее первообразной. Именно, справедлива следующая тео-
рема.
164
Теорема 7.3. Пусть функция f(x) непрерывна на отрезке [а,Ь].
Тогда функция 5(х) дифференцируема на этом отрезке, причем
У(х) = f(x).
Доказательство. Прежде всего заметим, что всякая непрерыв-
ная функция на отрезке [а, /?| является интегрируемой, поэтому
5(х) определена на всем [а,Ь]. Покажем, что в каждой точке из
[а,Ь] функция 5(х) имеет производную.
Действительно, пусть
Л.$'(х) = 5(х + Ах) - S(x)
— приращение функции 5(х) при приращении аргумента Ах. Оче-
видно (рис. 7.6), что
A5(x) = "f	= А +f f(f)dt.	(7.19)
a	a	x
Поскольку функция f(x) непрерывна на [a, Z>], то по теореме о
среднем (см. теорему 7.2) найдется точка £ е [х, х + Ах], такая, что
х+Дх
А5(х)= J f(t)dt =/(^)(х + Ах-х) = /(^)Ах.
Отсюда следует, что
=	+	(7.20)
Ах
Так как /(х) непрерывна в точке х, то при Ах —> 0 будем иметь
/(£) —>Дх) (ясно, что при Ах —> 0 средние точки £ —> х). Тем самым
из (7.20) немедленно получаем, что и------» /(х). Это по опре-
Ах
делению и значит, что функция 5(х) дифференцируема в точке х,
причем ее производная в этой точке равна /(х). Поскольку точка х
выбрана произвольным образом из отрезка [а, Z>], то теорема дока-
зана. ▲
Замечание, Формулу А'(х) = Дх) часто записывают в виде
А |=/(х)
I a J
и читают: «производная интеграла по верхнему пределу равна зна-
чению подынтегральной функции в точке верхнего предела».
Этот результат имеет большое значение в теории интегрирова-
ния — он показывает, что любая непрерывная функция имеет пер-
вообразную (хотя эту первообразную часто невозможно выразить в
элементарных функциях).
165
7.5.2. Вывод формулы Ньютона—Лейбница
Теорема 7.4 (Формула Ньютона—Лейбница). Пусть f(x) непре-
рывна на отрезке [й, /?| и F(x) — какая-либо ее первообразная фун-
кция. Тогда
f/(x)dx = F(b)-F(a).	(7.21)
Доказательство. Пусть Fix} — первообразная функции f(x). Так
как 5(х) — тоже первообразная Дх), то найдется константа С та-
кая, что Дх) + С= S(x) для всех х из [а, /ф Поскольку это равенство
справедливо в любой точке отрезка, то возьмем в качестве х точку
а. Если учесть, что S(a) = 0, то можно получить, что С = -F(a). Тем
самым это равенство записывается в виде
Дх) = F(x) - F(a),
или, учитывая определение Дх), в виде
]f(t)dt = F(x)-F(a).
Теперь осталось только положить х, равным Ь. ▲
Замечание, При практических вычислениях разность F(b) - F(a)
обычно записывают короче, как Дх)|£.
Формула (7.21) является основным инструментом, позволя-
ющим находить значения определенных интегралов, минуя непо-
средственное суммирование интегральных сумм, поскольку дело
сводится к отысканию первообразных, т.е. к неопределенному ин-
тегрированию.
Пример 7.9. Вычислить площадь криволинейной трапеции, об-
разованной функцией у = х3 на участке от 0 до 2 (рис. 7.7).
166
Имеем
Пример 7.10. Найти площадь эллипса — + 2-r- = 1 (рис. 7.8).
а1 Ь2
Очевидно, искомая площадь 5 является удвоенной площадью
криволинейной трапеции 5+, образованной верхним контуром эл-
липса, который задается уравнением у = — -Ja2 - х2 .
Имеем (см. табл. 7.2)	а
1 а	1 Г	2	Iй
е тс	f Г~2----2 -Д X Г~2------X а1 . X
S = 25+ = 2—1 yja1 - х1 =2— — Va - х1 н-arcsin— =
a J	а 2	2 а
-a	L	J _д
~Ь а2 . , а2 - /
= 2 — — arcsin 1-----arcsin(-1)
а 2	2
= ab - 2 arcsin 1 = ab • 2 — = itab.
Отметим, что при а = b = R имеем площадь окружности kR2.
7.6.	Интегрирование по частям и замена переменных
в определенном интеграле
Теорема 7.5. Пусть f(x) и g(x) — непрерывно дифференцируе-
мые функции на отрезке [а,Ь]. Тогда справедлива формула
j/(x)g'(x)Jx = /(x)g(x)|* - J/'(x)g(x)afx. (7.22)
а	а
Доказательство. Формула дифференцирования произведения
(/(x)g(x))' = f'(x)g(x) + f(x)g\x)
означает, что функция f(x)g(x) является первообразной функции
f'(x)g(x) + g'(x)f(x), следовательно, по формуле (7.21) — формуле
Ньютона—Лейбница
J [/'(х)£(х) + g'(x)f(x)]dx = f(x)g(x)\ha
а
или, что то же,
b	ь
j f(x)g'(x)dx + j f'(x)g(x)dx = /(х)^(х)|* . А
а	а
Замечание. Формула (7.22) записывается также в дифференциа-
лах, а именно в виде
167
J f(x)dg(x) = -Jg(x)df(x) + $(x)/(x)|*.
fl	fl
Обратимся к формуле замены переменной.
Теорема 7.6. Пусть выполнены условия:
1)	функция f(x) определена и непрерывна на отрезке [д,6];
2)	функция х = <р(7) непрерывно дифференцируема, определе-
на на отрезке [c,d] и принимает значения из [й, £>];
3)	<р(с) = й, <р((7) = Ь.
Тогда справедлива формула
b	d
J f(x}dx = j/[(?'(/) ]q>'(r )dt.	(7.23)
fl	c
Доказательство. Пусть Fix) — какая-либо первообразная функ-
ции f(x), т.е. F'(x) = f(x), тогда по формуле Ньютона—Лейбница
= 7^'[<р(/)]ф'(Г) = /[<р(Г)]<р'(О? * е
Это означает, что функция F[q>(/)] как функция переменной t
является первообразной функции/[<р(/)]ф'(О на отрезке [с, d]. Сле-
довательно, вновь по формуле Ньютона —Лейбница
j/Wz)]9W/ = m)]|" =f №)]-?[<№] = F(b)-F(a), (7.24)
ибо по условию g>(d) = b, <р(с) = а. Сравнивая (7.24) и (7.21),
очевидно получаем формулу (7.23). ▲
Пример 7.11. Вычислить J xln xdx.
i
По формуле интегрирования по частям
С	/	7 \	С	2 1	fl J Х	f Х J Х 1 хшхах= шхй — =- — dx + — 1г । 1 2 ) । 2 2 тг/4 Пример 7.12. Вычислить j IgAv/.v. 0 Имеем %4	{	х = tg х dx = замена t = cos x,	 о	x = = -1п|/||® = -1пЛи	ix =-— +O,5e2 = —(e2 + 1). !	4, Oof = 1 1 A/2 ( ж a _ i^t = d2/2j	•[ ( t J = 1п(Д) = 11п2.
168
7.7.	Приложения определенного интеграла
В этом подразделе приведен ряд приложений определенного
интеграла к различным геометрическим задачам.
7.7.1.	Вычисление площади плоской фигуры
Как известно из 7.3, в случае неотрицательной функции f(x)
определенный интеграл равен площади криволинейной трапеции,
образованной графиком функции у = f(x) на отрезке [а, Ь].
Рассмотрим теперь более общий случай трапеции, образован-
ной двумя функциями у = ф(х) и у = v(x), причем <р(х) < ф(х) при
а<х< Ь (рис. 7.9).
Очевидно, в этом случае
h
пл. S = j [\|/(х) - ф(х)]г7х.
а
(7-25)
Пример 7.13. Вычислить площадь фигуры 5, образованной пе-
ресечением параболы у = х2 и прямой у = 2х.
Очевидно, парабола у = х2 и прямая у = 2х пересекаются в точ-
ках х = 0 и х = 2. Следовательно, искомая фигура есть криволиней-
ная трапеция 5 = {0 < х < 2, х2 < у < 2х}.
Используем формулу (7.25), полагая ф(х) = х2, ф(х) = 2х,
2	/
пл. .S' = J(2х - x2)dx = х2
о	I
= 4-*
3
4
3‘
Весьма удобно вычислять площадь плоских фигур, заданных в
полярных координатах г, ф.
Пусть плоская фигура S задана системой полярных неравенств, а
именно 5 есть совокупность точек плоскости, полярные координа-
ты которых удовлетворяют неравенствам <х < ф < 0, г0(ф) - г - П(ф),
где а, 0 — неотрицательные числа; Го(ф), Л(ф) — непрерывные,
или, более обще, интегрируемые, функции переменного ф (рис. 7.10).
169
Рис. 7.11
В этом случае площадь S вычис-
ляется по формуле
пл.5 = | |[г12(ф)-г02(ф)]г7ф. (7.26)
а
Пример 7.14, Вычислить площадь
кардиоиды, полярные уравнения
которой имеют вид г = а(1 + со5ф),
О < ф < 2л (рис. 7.11).
Применяем формулу (7.26) [здесь
а = 0, |3 = 2л, Г[(ф) = й(1 + со5ф),
г0(ф) = 0]:
пл. S = — J (1 + cosф)2(7ф = — J (1 + 2cosф + cos2 ф)</ф =
о	о
й	1	3
= — 2л + 2л(вш 2л - sin 0) + л + — (sin 2л - sin 0) = —й2.
4
2
7.7.2.	Вычисление длины кривой
Пусть Г — кривая, являющаяся графиком функции у = /(х),
а < х < b (рис. 7.12).
Пусть функция /(х) непрерывно дифференцируема на отрезке
[й,Ь\, т.е. она имеет производную /'(х), которая непрерывна на
[й,/ф В этом случае длина кривой Г (обозначим ее /) вычисляется
по формуле
h
1 = \Ф + Г2Мдх.	(7.27)
а
Выведем эту формулу методом
бесконечно малых разбиений ана-
логично тому, как вычисляли пло-
щадь криволинейной трапеции
(см. 7.3).
Пусть й = Xq < X] < ... < Х„_| < хп =
= b — произвольное разбиение от-
резка [а, Ь],	= тахЛх. 1= 1, ..., п.
Заменим приближенно кривую Г
кусочно-линейной кривой, состо-
ящей из малых хорд, соединяющих
170
точки (хьу^ € Г, где у,- = f(Xj), 1= 0, 1, ..., п - 1. Тогда длина кривой
Г приближенно равна длине построенной таким образом кусочно-
п-]
линейной кривой, т.е. I ~ где /,• — длина хорды на участке [х„
/=о
Хн_[].Очевидно, по теореме Пифагора
6 = д/ах/ + Ду/ = ^Дх/ + [/(х/+|)-/(х/)]2.	(7.28)
Поскольку функция Дх) имеет непрерывную производную, по
теореме о среднем Лагранжа (см. теорему 6.5)
/(х/+1) -Дх,) =/'(U(^i - */)
где — некоторые точки, находящиеся на отрезках [х/,х/+1].
Тогда из (7.28) получаем, что /z = у'1 + /'2(^)ДХ; и, следова-
тельно,
/ = ХУ + /'2(5,Ж-	(7.29)
(=0
Очевидно, правая часть формулы (7.29) есть интегральная сум-
ма для функции ^1 + Д2(х) на отрезке [а, Ь]. Так как по предполо-
жению функция f'(x) непрерывна на [а,Ь], то и функция + f'2(x)
также непрерывна на отрезке [а,Ь\ и, значит, интегрируема.
Тем самым при Хй —> 0 в формуле (7.29) правая часть имеет
ь
предел, равный определенному интегралу j+ f'2(x)dx. Это и
а
приводит к формуле (7.27). Вывод завершен.
Если кривая Г задана в параметрической форме, т. е.
Г = {(х,у): х = <р(0, у = у(0, 0 < t < Т},
то ее длина вычисляется по формуле
/ = j 7<Р'2(О +У2(0^-	(7.30)
о
Если кривая Г задана полярным уравнением г= г(<р), ос < <р < р, то
ее длина вычисляется по формуле
Р ____________
/ = j у1г2(($ + r'2((p)d(p.
а
Пример 7,15, Вычислить длину астроиды х2' + у22 = а2-' (рис. 7.13).
Запишем уравнение астроиды в параметрической форме
х = a cos\ у= a sin3f, 0 < t< 2л
(параметр t играет роль угла, образованного радиусом-вектором
г= {х,у} с осью Ох).
171
Тогда по формуле (7.30)
/ = J ylx'2(t) + y'2(t)dt =
о
2 л:
= j" ^9tf2(cos4 / sin2 Z + sin4 / cos2 f)dt =
0
2 it __________ 2tc
= 3a j cos21 sin2 tdt = 3a ||cosZsinz|zfr =
о	0
2it
=J|sin2z|(7r. (7.31)
о
Очевидно, функция у = |sin2z| является периодической с пери-
л
ОДОМ —, поэтому
2л:	тг/2	тг/2
J|sin 2t\dt = 4 j |sin2/|dt = 4 | sin2tdt = -2(cos2 • — - cosO) = 4.
0	0	0	2
Таким образом, из (7.31) следует, что длина астроиды / = 6а.
7.7.3.	Вычисление объема и площади поверхности тел вращения
Рассмотрим тело, полученное вращением криволинейной тра-
пеции S = {(х,у): а< х< b, G <у < f(x)} вокруг оси Ох (рис. 7.14).
Объем V полученного тела вращения определяется формулой
ь
V = л j f2(x)dxy	(7.32)
а
а поверхность вращения о по формуле
ь
о = 2л| f (х)^1 + f'2(x) dx.	(7.33)
а
Обе формулы выводятся также методом бесконечно малых раз-
биений. Получим, например, формулу (7.32) для объема.
Пусть а = х0 <	< ... < х,. । < х„ = b — произвольное разбиение
отрезка [а,Ь]. Рассечем объем /набором плоскостей x = x;(/ = 0, 1,...,
л), перпендикулярных оси Ох. Если разбиение достаточно мелкое,
т.е. А,л = шах Ах. достаточно мало, то в получившейся «нарезке»
1
малый слой можно считать лежащим горизонтально цилиндром
высотой й/ = Ах, и радиусом = /(£,), где е [х,-, х... ।] — некоторая
средняя точка. Тогда объем данного слоя равен
Vt = кг-2 =к/2(^)Ах;,
172
а полный объем тела вращения
И = ^тг/ЛУМ-.
/=0
Ясно, что величина справа
есть интегральная сумма для
функции л/2(х) на отрезке [а,Ь].
Поэтому при —> 0 получаем
искомую формулу
V = я[/2(хЖ.
а
Пример 7.16. Вычислить объем тела, полученного вращением
криволинейной трапеции 0 < у < sinx, 0 < х < л.
Имеем
V = kJ sin2 xdx = л • - J (1 - cos 2a)J.y = —.
о	J	2
7.8. Несобственные интегралы
До сих пор рассматривались определенные интегралы по ко-
нечному промежутку [а,6]. На практике, однако, часто необходи-
мо интегрировать функции, заданные на бесконечном промежут-
ке [я,+<*>). Такие интегралы называются несобственными интеграла-
ми и обозначаются символом J f(x)dx. Дадим строгое определе-
а
ние несобственного интеграла.
7.8.1. Определение несобственного интеграла
Пусть f(x) — непрерывная функция, определенная на полуоси
[я,+<*>), где а — некоторое число (рис. 7.15).
Рассмотрим определенный интеграл
= J/(x)iZx
а
как функцию верхнего предела Ь> а (см. рис. 7.15) (геометрически
функция Ф(Ь) выражает заштрихованную площадь криволиней-
ной трапеции на участке [а, />]). Устремим теперь b к -к». Очевидно,
возможны два варианта: функция Ф(Ь) либо имеет конечный пре-
дел, либо не имеет.
173
Определение 7,5, Если функция Ф( /?) имеет при b —> ©о конеч-
ный предел, то этот предел называется несобственным интегралом
от функции f(x) по промежутку [д,+©о). Коротко
|/(х)й(х= Um
а	а
В этом случае говорят также, что функция f(x) интегрируема на
полуоси [а,+оо) в несобственном смвюле, а несобственнвш интег-
рал j f(x)dx называют сходящимся.
Если же предел функции Ф(6) не существует или он бесконе-
чен, то функцию f(x) называют неинтегрируемой на полуоси
[я,+<*>), а сам несобственный интеграл — расходящимся.
Пример 7.17. Ввыснить, сходится или расходится несобствен-
нвш интеграл 1 = j e~xdx.
о
По определению,
Г t~xdx = lim f z~xdx = lim (—(e-z> - e0)) = lim (1 - e~b) = 1,
так как e_/>	0 при b —> +«->.
Значит, интеграл / существует, причем 1= 1. Геометрически это
означает, что площадв бесконечной трапеции, расположенной под
графиком экспонентв! у = с". х > О, равна единице.
Пример 7.18. Ввыснить, при каких значениях а > 0 несобствен-
+™ ।
нвш интеграл У(х) = | —dx сходится, а при каких — расходится.
j
Имеем (вначале при
X * 1)
г dx ,. r dx
— = lim I —
j Г5	Ys
lim---------
1 _ 5 x
1
5-1
i .. г i
=------lim —r - 1
bS~'
174
Таким образом, исходный интеграл /(а) сходится при 5 > 1 и
расходится при 5 < 1.
Остается рассмотреть случай 5 = 1. В этом случае
Г — = lim f — = lim (In b - In 1) = lim In b = +<*>,
J X	J X b—
т. e. интеграл расходится. Итак,
f dx ,	1	..
— = (сходится, если 5 > 1; расходится, если s < 1}.
Заметим, что полученный результат будет использован далее
при изучении числовых рядов.
Переходим к некоторым общим вопросам теории несобствен-
ных интегралов, первоочередным из которых является вопрос схо-
димости или расходимости несобственного интеграла.
В рассмотренных примерах нам удалось ответить на этот вопрос
прямыми вычислениями, при этом сделать даже больше — точно
вычислить значение несобственного интеграла. Часто, однако, точ-
ное значение несобственного интеграла вычислять нет необходи-
мости, а нужен только сам факт сходимости или расходимости
несобственного интеграла. При ответе на этот вопрос важную роль
играют теоремы, называемые теоремами сравнения.
7.8.2. Теоремы сравнения
Теорема 7.7 (первая теорема сравнения). Пусть даны две неотри-
цательные функции f(x) и g(x), определенные на полуоси
причем выполнены два условия:
О f(x)<g(x), при х>а;
2) j g(x)dx сходится,
л	+”
Тогда интеграл I f(x)dx также сходится.
а
Теорема 7.8 (вторая теорема сравнения). Пусть Дх), g(x) — две
неотрицательные функции на полуоси причем выполнены
два условия:
1) /(х) < g(x), при х > а;
2) j f(x)dx расходится.
а 4Т
Тогда I g(x)dx также расходится.
а
175
Замечание, Коротко приведенные теоремы сравнения гласят: если
несобственный интеграл от большей функции g(x) сходится, то и
от меньшей функции f(x) интеграл также сходится. И наоборот,
если интеграл от меньшей функции расходится, то интеграл и от
большей функции также расходится.
Подчеркнем, что в теоремах сравнения речь ведется только
о неотрицательных функциях, т.е. f(x) > 0 и g(x) > 0. (Для функ-
ций любого знака теоремы сравнения, вообще говоря, не имеют
смысла.)
Ограничимся интуитивным геометрическим доказательством
(рис. 7.16) сформулированных теорем.
Как известно, величина
Ф(6) = |/(х)б6с
а
равна площади криволинейной трапеции Sb(f), образованной фун-
кцией f(x) > 0 на отрезке [«,/»]. Поэтому несобственный интеграл,
если он существует, естественно считать площадью бесконечной
трапеции на участке [0,+<*>), т.е.
5„(/)= Пт5Д/)	(7.34)
>4оо
или, что то же,
Если же предел (7.34) бесконечен, т.е. несобственный интег-
рал расходится, то площадь соответствующей криволинейной тра-
пеции бесконечна.
Ясно, что если f(x) < g(x) для всех х > й, то график функции
у = f(x) лежит ниже графика функции у = g(x) и поэтому площади
соответствующих трапеций связаны неравенством 5Д/) < 5TO(g).
176
Поэтому если площадь Sm(g) конечна, т.е. интеграл Г g(x)dx
сходится, то и площадь 5ТО(/) также конечна, т.е. интеграл J f(x)dx
а
также сходится. Напротив, если 5Д/) = +<*>, т.е. интеграл j f(x)dx
а
расходится, то и площадь S„(g) = +<», т.е. интеграл I g(x)dx также
расходится. ▲	а
Пример 7,19, Выяснить, сходится или расходится интеграл
/ = Je х arctg xdx.
о
Применим первую теорему сравнения. Для этого прежде всего
отметим, что при х > О функция /(х) = с 'arctgx неотрицательна,
так как е' > 0 при всех х, a arctgx > 0 при х > 0. Далее, поскольку
arctg х с — при всех х > 0, то е А arctg х < — е
и можно применить
первую теорему сравнения, полагая Дх) = e_*arctgx, g(x) = е'.
Поскольку функция g(x) = е' интегрируема на [0,+«>] (см. пример
7.17), то интегрируема и функцияДх), т.е. исследуемый интеграл
/сходится.
П	-7 ЧЛ Г>	I Г 2 + Sil1 * Л ГА
Пример 7,20. Рассмотрим интеграл / =	----=—dx. Очевидно,
[ VX
.	2 + sin х
что подынтегральная функция -------—— положительная, так как
|sinx| < 1.
Более того,
2 + sinx > 2 — |sinх| > 1
>/х Vx V*
Как известно (см. пример 7.18), интеграл расходится.
По второй теореме сравнения получаем, что и исходный не-
собственный интеграл также расходится.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1.	Зная, что (arcsin х)' = .	, докажите, что (arccosx)' = - .	.
VI-х2	VI -х2
Аналогично поставьте и решите задачу для функций arctgx и arcctgx.
2.	Пусть Дх) — первообразнаяДх), т.е. для неопределенного интегра-
ла имеет место формула
]7(х)Л=£(х)+ С,
где С — произвольная постоянная.
177
Рассмотрим функцию f(ax + />), где а и b — произвольные числа, при-
чем а * 0.
Докажите справедливость формулы
J f (ах + b)dx = — F(ax + b) + C.
3.	(Это задача-шутка.) Студенту требуется найти неопределенный ин-
теграл
Он заглядывает в ответ и делает замену и = ответ. (Такую замену сту-
денты зовут «универсальной».) К чему сведется решение задачи?
4.	Формула Ньютона—Лейбница
]f(x)ilx=F(b)-F(a),
а
где F(x) — какая-нибудь первообразная функции f(x), не конкретизирует
выбор этой первообразной.
Объясните, почему при выборе различных конкретных первообразных
функции f(x) результат всегда будет один и тот же.
5.	Рассмотрим определенный интеграл с переменным верхним преде-
лом
F(x) =
о
где <р(х) — дифференцируемая функция, а /(/) — непрерывная функция.
Выведите формулу
F'(x) = f [<р(х)]<р'(х).
Рассмотрите пример функции
F (х) = J e“r Jx.
о
6.	Пусть функция f(x) четна, т.е. для любого хе R1 справедливо равен-
ство/(-х) = /(х).
Докажите, что при любом а > 0
j f(x)dx = 2ff(x)dx.
-а	0
7.	Пусть функция f(x) нечетна, т.е. для любого х g R1 справедливо
равенство f(-x) = -f(x).
Докажите, что при любом а > 0
j f(x)dx = 0.
-а
8.	Вычислите площадь плоских фигур, образованных пересечением па-
раболы и прямой:
178
1) у = х(2 - х), у = х;
2) у= (х- 2)1 2, у = 4х - 8.
9.	Вычислите длину дуги следующих кривых:
1)	параболы у = —х2, 0 < х < 2;
2)	цепной линии у = chx, -1 < х < 1;
3)	циклоиды (заданной в параметрической форме)
х = / - sin/, у = 1 - cos/, 0 < / < 2л.
10.	Вычислите, исходя из определения, сходятся или расходятся не-
собственные интегралы:
1)	2) 1-^; 3) Jxe-Wx; 4) j-Д
Jx2+4 Jxlnx J	J J2^
6)Jctgx*.
ГЛАВА 8
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
8.1.	Функции нескольких переменных. Предел
и непрерывность
В случае одной вещественной переменной изучалисв функции,
определеннвк на интервале или отрезке. В случае многих перемен-
hbix множество областей определения функций гораздо богаче,
поэтому начнем с рассмотрения примеров основных областей. При
этом в основном будем рассматривать двумерный и трехмерный
случаи, поскольку они весьма наглядны.
Пусть R2 — плоскость переменных х. у, т. е. множество всех точек
А/(х.у) с двумя координатами. Примерами областей на плоскости
являются следующие множества.
Пример 8.1, Множество
UR = {M(x,y) е R2 у таких, что х2 + у2 < R2}
называется кругом радиусом R > 0 с центром в начале координат.
Обратим внимание на то, что граница круга, т. е. окружность ради-
усом R, не включается в круг. Такой круг называется открытым.
Открытые круги UR при разных R > 0 называются окрестностями
точки (0,0).
Ясно, что аналогичным образом можно определить окрестно-
сти любой точки A/o(jcq,Jo) как множества
UR = {М(х,у) е R2y таких, что (х - х0)2 + (у - уо)2 < 7?2}.
Пример 8.2, Открытым прямоугольником (или прямоугольником
без границы) называется множество В = {М(х,у): а <х < Ь, с < у < d},
где a<bnc<d— некоторые числа.
В трехмерном пространстве R3 переменных х, у, z аналогичными
областями являются:
а)	шар
UR(MQ) = {М(х,у, z) е Rly s: (х - х0)2 + (у - у0)2 + (z - Zq)2 < R2}
радиусом R > 0 и центром в точке Mq(xq, у0, zq);
б)	параллелепипед
В = {Л/(х,у, z) е R^y,z’. а < х < b, с < у < d, / < z < т},
где а < Ь, с < d, I < т — некоторые числа.
180
Читатель без труда самостоятельно приведет примеры других
областей G как в у, так и в
Переходим к функциям двух переменных х, у.
Определение 8.1, Функцией двух переменных с областью опре-
деления G называется отображение /, сопоставляющее каждой
точке М g G число w, и которое обозначается и = f(M).
Подчеркнем, что рассматриваются только однозначные отобра-
жения /, т.е. отображения, сопоставляющее каждой точке Мтоль-
ко одно значение и = f(M).
Далее, поскольку каждая точка М на плоскости определяется
двумя координатами (х,у), то функцию и = f(M) чаще обозначают
как и =f(x,y), подчеркивая ее зависимость от двух переменных х, у.
Аналогично определяется функция трех переменных (х,у, z).
Пусть Mq = Л/0(х0,у0) — фиксированная точка G, а Мп = Л/(хл,ун),
л=1,2,	— последовательность точек в области G. Будем гово-
рить, что последовательность Мп стремится к при л —> <х>
(и обозначать М„ -ь Л/о), если х„ -ь х0, a у„ —> у0. Будем писать также
(хл,ун) —> (х0,у0). Следующие два определения аналогичны тем, что
были даны в случае одного переменного.
Пусть функция и = f(x,y) определена в некоторой окрестности
точки Af0(x0,y0), исключая, быть может, саму точку Л/0(х0,у0).
Определение 8,2. Число b называется пределом функции и = fix, у)
при (х.г) —> (х0,у0), если для любой последовательности (хл,ун)
—> (х0,у0), п = 1,2,... (х„ #=х0, у,. *у0 одновременно), соответствующая
числовая последовательность ип = f(x„,yn) —> b.
В соответствии с этим определением принято обозначать
b = lim /(х,у) или b = lim f(M).
х,Л’->х0,>’0
Ясно, что для введенного понятия предела функции двух пере-
менных справедливы те же свойства, что и для одномерного слу-
чая, названные «арифметическими» свойствами пределов (см. тео-
рему 5.1). Приведем эти свойства в виде формул, оставляя читате-
лю строгие формулировки и доказательства по аналогии с одно-
мерным случаем.
Теорема 8.1. Имеют место формулы:
1)	lim [С/(х,у)] = С lim /(х,у), С — постоянная;
2)	lim [/(x,y)±g(x,y)] = lim /(х,у)± lim g(x,y);
XjV^XojJ-’d	XjJ-’^XojJ-’d
3)	lim [/(x,y)g(x,y)] = lim /(x,y) lim g(x,y);
XjV^Xojl'n	X,	x,y—
4)
lim
g(x,y)
lim /(x,y)
_ x-,y^x-(),ytl_______
lim g(x, y)'
181
х2 у2
Пример 8.3, Покажем, что lim —, ' .г = 0.
л-,у^ох2+у2
Действительно, пусть х,; —> 0 и у„ —> 0 произвольным образом,
лишь бы хп * 0 и уп * 0 одновременно. Так как при любых значениях
х и у справедливо неравенство
|ху|<|(х2+у2)1
х2 у2
то функция f(x,y) =2^2 удовлетворяет двустороннему нера-
венству	х + У
х2у2 < 1 (х2 + у2)2
х2 + у2 ~ 4 х2 + у2
= i(x2+y2)
и, следовательно,
0 < /(хй,уй) < |(х2 + у2).
Отсюда немедленно следует при хн —> 0 и у„ —> 0 и функция
/(хя,ул) —> 0. Это и требовалось.
Пример 8.4. Выясним, существует ли lim ?.
x.v-О х2 + у1
Очевидно, функция /(х, у) =	определена всюду, кроме
х2 + у2
точки х0 = 0, у0 = 0. Согласно определению предела, последователь-
ность ип = /(хн,ул) должна стремиться к одному и тому же пределу
b при любом стремлении к нулю последовательностей хп и ун. Однако
в данном примере это не так. Действительно, если выбрать после-
довательность хн —> 0 (х„ * 0) и у„ = 0, п = 1, 2, ..., то
=f(x„, 0) = 0
и, следовательно, «вдоль оси Ох» значения f(xn, у„) —> 0. С другой
стороны, если взять последовательность х„ -ь 0 и уп = х„, то
«« =/(^,К) =	= |
2х2	2
и, значит, вдоль прямой у = х функция f(xn,yn) —>
Это указывает на то, что для рассматриваемой функции на-
шлись по крайней мере две различные последовательности хп —> 0
и ун —> 0, для которых последовательности значений /(х,„ ул) стре-
мятся к различным пределам. Таким образом, lim . —т не су-
%, V—>0
шествует.	л -
Обратимся к понятию непрерывной функции двух переменных.
Оно в точности такое же, что и для случая одной переменной.
182
Определение 8.3. Функция и = f(x, у) называется непрерывной в
точке Мй(хй,уо), если она имеет предел при х. у —> х0, у0 и этот
предел равен значению функции в этой точке.
Коротко, функция f(x,y) непрерывна в точке Мо(хо,уо), если
lim f(x, у) = f(xQ, yQ).
>X'O,J-’o
Для непрерывных функций нескольких переменных справедли-
вы многие теоремы, которые были доказаны для случая одной
переменной. К таким теоремам относятся, например, теоремы,
выражающие «арифметические» свойства непрерывных функций,
непрерывность сложной функции и другие результаты. Их форму-
лировки дословно повторяют одномерный случай и поэтому не
приводятся.
Остановимся на формулировках первой и второй теорем Вей-
ерштрасса, которые понадобятся в дальнейшем. _
Теорема 8.2 (первая теорема Вейерштрасса). Пусть G — ограни-
ченная область в Rl у вместе со своей границей (G называется ком-
пактом в Rl vY Если функция /(х,у) непрерывна на компакте G,
то она ограничена на нем, т. е. существует постоянная С > 0 такая,
что |/(х, у) | < С для любой точки (х,у) g G.
Теорема 8.3 (вторая теорема Вейерштрасса). Пусть/(х,у) — не-
прерывная функция на компакте G. Тогда она достигает на нем
своих максимального и минимального значений.
Последнее означает, что найдется точка (х0,у0) е G [точка абсо-
лютного максимума /(х.у)| такая, что для всякой точки (х,у) е G
справедливо неравенство /(х,у) < /(х0, у0). (Аналогично для наи-
меньшего значения.)
В заключение отметим, что всякая точка, в которой функция
и = f(x, у) не является непрерывной, есть, по определению, точка
разрыва этой функции. У функции двух переменных х, у множе-
ство точек разрыва бывает самым разнообразным. Например, фун-
кция
имеет единственную точку разрыва х = 0, у = 0. Функция
1
и =----
х-у
разрывна на всей прямой у = х.
Двумерная функция Хевисайда
(1, для х > 0, у > 0,
0(^,У)= ’
[0, для всех остальных точек
разрывна, очевидно, на полуосях х > 0, у > 0.
183
8.2. Частные производные. Дифференциал функции
нескольких переменных
8.2.1. Частное дифференцирование.
Понятие непрерывно дифференцируемой функции
Пусть и = f(x, у) — функция двух переменных, определенная в
некоторой области G с R~v. Пусть также (х,у) — фиксированная
точка в этой области.
Дадим аргументу х приращение Дх, оставляя значение у неизмен-
ным. Иными словами, перейдем от точки (х,у) к точке (х + Ах,у).
Тогда функция /(х,у) получит приращение
Aj(x,y) =f(x + Ах,у) -/(х,у),
называемое частным приращением функции f(x, у) по переменной х.
Определение 8.4. Пусть существует предел
lim Аа-Жт) _ lim Я* + Ах, у)-/(х,у)
Av—О	АХ	Ay—О	Дх
Тогда этот предел называется частной производной функции f(x,y)
/	\	к	Э/(х,у)
в точке (х, у) и обозначается символом .
Коротко	^х
ЭЯ^Т) = Ит Я* + Ах,у)-/(х,у)
дх Ay-О	Ах
Аналогично определяется частная производная по у:
ЗЯ^Т) = Ит f(x,y + by)~ f(x,y)
Эу	аг-о	Ду
а	Э/(х, у)
Ясно, что частная производная —-— есть обычная производ-
Эх
ная функции /(х,у) по х при фиксированном аргументе у, а част-
Э/(л:,у)
ная производная---------обычная производная по у при фикси-
Эу
рованном аргументе х.
Ввиду этого, практическое нахождение частных производных
сводится к обычному дифференцированию по какой-либо пере-
менной при условии, что все остальные переменные фиксирован-
ны, т.е. постоянны.
Пример 8.5. Вычислить частные производные функции /(х,у) =
= х2у - у3 + 1.
Имеем
^ЬУ1 = 2ху, =
дх	Эу	Л
184
Пример 8.6. Вычислить частные производные функции и = In г.
где г = ^х2 + у2.
По правилу дифференцирования сложной функции имеем
ди Z1 ч, Эг 1	1 Э z 2	1 ~ л
— = (In г), — =---.—(х2 + у2) = —-2х = —.
Эл дх г 2^х2 + у2 дх	2г2 г2
Аналогично
ди _ у
ду г2 '
Замечание. Ясно, что значения частных производных функции
/(х,у) меняются от точки к точке, т.е. частные производные сами
являются функциями переменных х, у.
От свойств частных производных (как функций х, у) существен-
но зависят и свойства самой функции/(х, у).
В дальнейшем будем предполагать, что частные производные
df /	\ df z ч	г-
— (х, у) и — (х, у) существуют в каждой точке области G и, кро-
Эх Эу
ме того, непрерывны.
Определение 8.5. Функция и = fix,у) называется непрерывно диф-
ференцируемой в области G, если выполнены два условия:
1) в каждой точке (х,у) g G существуют частные производные
df { х df, ,
v-(x,y) и тМх,у);
Эх Эу
2) эти частные производные непрерывны в области G.
В приведенных выше примерах 8.5 и 8.6 функции и = х2у - у3 + 1
и и = Inу/х2 + у2, очевидно, являются непрерывно дифференци-
руемыми каждая в своей области определения.
8.2.2. Дифференциал и его связь с приращением функции
Пусть функция и = f(x,y) имеет в каждой точке области Gnpo-
df df
изводные — и —.
Эх Эу
Определение 8.6. Дифференциалом функции и =/(х,у) в точке (х,у) g
g G называется выражение
, Э/ z ч. df ,
аи = — (х, у)Ах + — (х, у)Ау,
Эх	Эу
где Ах и Ау — произвольные приращения х и у.
Ясно, что дифференциал функции и = /(х,у) зависит не только
от точки (х,у) g G, но и от приращений Ах, Ау, которые придают-
ся аргументам х и у (для краткости обозначений все эти величины
не указываются).
185
Пример 8.7. Найти дифферен-
циал функции и = С, где С —
постоянная. Очевидно, что du = О,
т.е. дифференциал постоянной
тождественно равен нулю в об-
ласти G. Нетрудно показать и об-
ратное: если дифференциал
функции и = f(x, у) равен нулю
в каждой точке области G, то
и = const.
Пример 8,8. Найти диффе-
ренциал функции и = In г, где
г = ^х2 + у2 в точке х = 1, у = 2 при приращениях Ах = 0,1; Ау = 0,5.
Имеем (см. пример 8.6)
du = Д- Ах + -Д- Ау.
г1 г1
Следовательно,
1	2
du = - • 0,1 + — • 0,5 = 0,22 при х = 1, у = 2, Ах = 0,1 и Ау = 0,5.
Первостепенное значение понятия дифференциала связано с
оценкой полного приращения функции и =f(x,y). Именно, пусть
М(х,у) е G — фиксированная точка. Дадим ей произвольное при-
ращение (Ах,Ау), т.е. перейдем к точке Л'(х + Ах, у + Ау) (рис. 8.1).
Определение 8.7. Полным приращением функции и = J\x.y) при
переходе от точки А/(х.у) к точке N(x + Ах, у + Ау) называется
разность
Ап = /(х + Ах, у + Ау) - /(х,у).
Связь полного приращения функции с ее дифференциалом
определяется следующей теоремой.
Теорема 8.4. Если функция и = f(x,y) непрерывно дифференци-
руема в области G, то для любой точки (х,у) е G справедлива
формула
Au = du + о(р),	(8.1)
где р = д/(Ах)2 + (Ау)2 — расстояние между точками ,V(x + Ах, у + Ау)
и М(х,у). (Напомним, что через о(р) обозначается величина более
о(р) Л	А \
высокого порядка малости, чем р, т.е. ——	0 при р 0.)
Р
Доказательство. Запишем равенство (8.1) в развернутом виде
Дх + Ах, у+ Ау)~ Дх, у) =	(х, у)Ах +	(х, у)Ау + о(р)
Эх	Эу
186
и рассмотрим более детально ее левую часть. Имеем
Aw = Дх + Дх, у + Ду) - /(х, у) =
= [/(х + Дх, у + Ду) - /(х, у + Ду)] + [/(х, у + Ду) - /(х, у)]. (8.2)
Очевидно, разность, стоящая в первой квадратной скобке, есть
частное приращение по х, так как вторая переменная равна у + Ду
в обоих слагаемых. Поэтому по теореме Лагранжа о среднем значе-
нии (см. теорему 6.5),
Дх + Дх, у + Ду) - /(х, у + Ду) = <а,у + Ду)Дх, (8.3)
дх
где £ е (х, х + Дх) — некоторая средняя точка. Далее, поскольку по
определению непрерывно дифференцируемой функции частная
df
производная — (х, у) непрерывна в области G [и, в частности, в
дх
рассматриваемой точке (х,у)], то
<(^ + Ду)-> |^-(х,у)
дх	дх
при р = 7(Ах)2 + (Ду)2 -> 0, так как в этом процессе, очевидно,
средняя точка £ -> х. Следовательно, разность
а(Дх, Ду) = — (^,у + Ду) - — (х,у)	(8.4)
дх	дх
есть бесконечно малая величина в процессе р -> О, т.е. а(Дх,Ду) -> О
при р -> 0.
В таком случае из (8.4) и (8.3) получаем
df
Дх + Дх, у + Ду) - /(х,у + Ду) = — (х, у)Дх + а(Дх, Ду),
дх
где также а(Дх, Ду) -> 0 при р -> 0.
Аналогично находим, что
Дх, у + Ду) - /(х, у) =	(х, у)Ду + р(Дх, Ду),
dy
где р(Дх,Ду) -> 0 при р -> 0.
Подставляя полученные выражения в равенство (8.2), имеем
Аи = — (х, у)Дх + — (%, у)Ду + а(Дх, Ду)Дх + Р(Дх, Ду)Ду,
дх	ду
т.е.
Ди = du + у(Дх, Ду),	(8.5)
где у(Дх,Ду) = а(Дх,Ду)Дх + р(Дх,Ду)Ду.
187
Очевидно,
lim v(Ду) = цт	дх, Ду)	+ р(дх, Ду) — =0,
р^° р	р-*° |_	р	р
так как величины а(Дх, Ду) и Р(Дх, Ду) суть бесконечно малые, а
величины — и — ограничены единицей. Это означает, что у(Дх, Ду) =
Р Р
= о(р). Тем самым формула (8.5) и дает искомое соотношение (8.1). ▲
Таким образом, установили, что полное приращение всякой
непрерывно дифференцируемой функции и = /(х,у) отличается от
ее дифференциала du на бесконечно малую величину о(р) более
высокого порядка малости, чем р = -У(Дх)2 + (Ду)2. Поскольку диф-
ференциал du есть линейная функция по переменным Дх и Ду, это
указание существенно, ибо иначе сравнивать бесконечно малые
величины, которыми являются сами Дй и du, не имеет смысла.
Формулу (8.1), как и в одномерном случае, можно рассматри-
вать как формулу приближенного вычисления значений функции
/(х,у) в точке 7У(х + Дх, у + Ду), а именно
/(х + Дх, у + Ду) /(х, у) +	(х, у)Дх + Ц- (х, у)Ду. (8.6)
йх	бу
Поэтому, если в некоторой «опорной» точке Л/(х,у) известны
значения функции и ее частных производных, то формула (8.6)
позволяет найти значение функции в точке 7V(x + Дх, у + Ду), при-
чем приближение будет тем качественнее, чем ближе смещенная
точка к опорной, т. е. чем меньше р = 7(Дх)2 +(ду)2.
8.2.3. Правила частного дифференцирования
Частное дифференцирование производится по тем же форму-
лам, что использовались для функций одной переменной (диффе-
ренцирование сумм, произведения и частного). Что же касается
формул дифференцирования сложной функции, то здесь правила
похожие, но иные.
Рассмотрим сложную функцию
w(0 =/[х(Г),у(/)],
где /(х,у) — заданная функция двух переменных х и у, которые в
свою очередь являются функциями переменного t. В итоге сложная
функция (8.6) есть функция одного переменного /.
Теорема 8.5. Пусть функция /(х,у) является непрерывно диф-
ференцируемой как функция двух независимых переменных х и у,
а функции х(/) и у(Г) дифференцируемы по Л Тогда функция «(/)
дифференцируема по t и ее производная вычисляется по формуле
188
u'(t) = [x(0, XO] *'(O +	[*(O, y(O] y'(f)-	C8-7)
Пример 8.9. Найти производную функции u(f) = ev cosy, где x =
= 1 - t3, у = t2. Очевидно, функция u(f) является сложной функци-
ей вида (8.6), где f(x,y) = exl cosy .
Имеем
— (x,y)-2xev cosy, — (x,y)--ev smy.
ЙХ	dy
Следовательно, по формуле (8.7),
u'(f) = (2xeЛ’2 cosy- C) -(e*2 siny)(z2) =
= (2xe ¥2 cosy)(-3/2)-(e ¥2 sin у j It
(здесь x = 1 - t\ у = t2Y
Столь же часто приходится сталкиваться со сложными функци-
ями вида
д(Г,т) = /(х,у), где х = x(t,x), у = у(бт).
В этом случае частные производные и(/,т) по / и т вычисляются
по формулам
ди _ of дх + df ду ди _ df дх df ду
dt дх dt ду dt ’ дт дх дт ду дт
Доказательство этих формул здесь не приводим.
8.3. Касательная плоскость и нормаль к поверхности
Пусть F(x,y, z) — непрерывно дифференцируемая функция трех
переменных, т.е. функция, имеющая непрерывные частные про-
dF ,	. dF . dF	п _	_
изводные —(х, у, z), —(x,y,z) и —(х,у, z). Для удобства обо-
дх	ду	dz
значим эти производные символами /Дх,у, z), Ffwy. z) и Ffx,y, z).
Как известно, уравнение
F(x,y,z) = 0	(8.8)
описывает в трехмерном пространстве R3,v.z некоторую поверх-
ность S (рис. 8.2).
Ставится задача — определить и написать уравнение плоско-
сти, касающейся поверхности 5 в заданной точке Л/о(хо,уо, Zb).
Прежде всего определим, какую плоскость естественно назвать
касательной плоскостью к поверхности 5 в точке Л/0(х0,у0, z0).
189
n={F;(M0),F^M0),F^M0)}
Рис. 8.2
Для этого выберем произвольную кривую L, лежащую на по-
верхности 5 и проходящую через точку Л/о.
Пусть кривая L описывается параметрическими уравнениями
L = {(х,у, z): х = x(f), у = y(t), z = z(t)},
где t — вещественный параметр.
Поскольку кривая L целиком находится на поверхности 5, опре-
деляемой уравнением (8.8), то при всех значениях t
F[x(t),y(t),z(t)\ - 0.	(8.9)
[В частности, при некотором значении t = /0 точка кривой
(x(/0),y(r0), 4W является точкой Л/0(х0,у0, Zq), т. е. х0 = х(Г0), Уо = уОо),
Zq = zOo)L Дифференцируя тождество (8.9) по t [см. формулу (8.7)],
получаем
Ф(0,И0, z(r)]x'(r) + £;[x(r),y(r), z(z)]y'(r) + Ф(0,Х0, z(/)]z'(r) = 0.
В частности, при t = /0 имеем
/ДЛ/0Мг0) + ^W)y'(k) + ВДНо) = 0.	(8.10)
Это равенство можно, очевидно, записать в виде скалярного
произведения векторов
(п,1) = 0,	(8.11)
где и = {Fx(Mq), Fy(Mo), F^(MQ)} — вектор, называемый градиентом
функции F(x,y, z), 1 = {х'(/0),у'(/0), z'(/0)} — вектор, касательный к
кривой L в точке Л/о.
Из равенства (8.11) следует, что касательный вектор 1 ортого-
нален вектору-градиенту п.
Заметим теперь, что кривая L была выбрана совершенно произ-
вольно, поэтому касательные векторы ко всевозможным кривым
190
на 5, проходящим через точку ортогональны одному и тому же
вектору-градиенту и тем самым лежат в одной плоскости. Ее-то и
примем (по определению) в качестве касательной плоскости Р.
Итак, касательной плоскостью к поверхности 5 в точке на-
зывается плоскость, проходящая через точку Л/о и ортогональная
вектору
п={да0),да,ВД)}.
Остается заметить следующее: из аналитической геометрии из-
вестно, что указанная плоскость Р описывается уравнением
Р: Fx(Mq)(x - х0) + Fj(M0)(y - у0) + F^MQ)(z - Zp) = 0.
Уравнение соответствующей нормальной прямой N
N. х - х0 у-у0 z-z0
 F^Mt>)	F'Z(MO)
(естественно, в обоих случаях требуется, чтобы хотя бы одно из
чисел Fx(Mq), Fy(Mo), /^(Л/р) было отлично от нуля).
Замечание, Выпишем уравнения касательной плоскости и нор-
мали к поверхности 5, заданной явным уравнением z = f(x,y),
(х,у) е G.
Ясно, что это частный случай рассмотренного общего уравне-
ния F(x.y. z) = 0, если положить F(x.y. z) = f(x,y) - z. Тогда
п = Ж(х0,у0),^(хр,у0),-11	(8.12)
(бх dy	J
и, следовательно,
Р: z-z0 = |£(хр,уо)(х-х0) + |£(хо,у0)(у-у0);
X — Хр = У-Уо = Z-ZQ
df {	. df, ч -1
dxv	dy
Пример 8,10, Написать уравнение касательной плоскости Р и
нормали N к поверхности эллипсоида
X2 у2 Z2 .
а1 Ь2 с2
в точке Л/р(хр,у0, zp), лежащей на эллипсоиде.
Решение. Запишем уравнение (8.12) в виде
г X2 у2 Z2
^ = — + -77 + — -1-0.
а1 Ь1 с2
(8.13)
191
Вычислим нормальный вектор п, т.е. вектор-градиент функции
F(x,y,z) в точке Л/0(х0,у0, z0):
[2*0 2у0 2z0 ]
I а2 ’ Ь2 ’ с2 J*
Следовательно, уравнение Р имеет вид
^(х-Х0) + ^(у-у0) + ^у-(2-20) = 0,
а2	а2	с2
или, что то же,
УоУ ZqZ (х02 Уо лП _ fi
а2 Ь2	с2 ^а2 Ь2 с2)	'
Так как точка Л/о(хо,Уо, 2b) лежит на поверхности эллипсоида,
то в силу уравнения (8.13) выражение в скобках равно единице, и
уравнения касательной плоскости и нормали N принимают вид:
р. хдх yQy zQz
а2	Ь2	с2	’
7V: й2 *~*о = b2 Т-То = с2 z-zQ .
*о	То
8.4.	Частные производные и дифференциалы
высших порядков. Формула Тейлора
8.4.1.	Частные производные высших порядков
До сих пор рассматривались частные производные первого по-
рядка. Поскольку они также являются функциями многих пере-
менных, то от первых частных производных можно еще раз найти
частные производные. Получим частные производные второго по-
рядка, которые обозначаются
d2/ / ч d2f , ч d2f , А d2f , ч
^y(x,y), ——(x,y), -^-(x,y), -4(x,y).
dx2 дхду дудх  ду1
Продолжая этот процесс, можно получить частные производ-
ные любого порядка.
Пример 8.11. Найти частные производные второго порядка от
функции /(х,у) = excosy.
Имеем
df	л- df
— - еЛ cosy, — - -е¥ sin у.
dx	ду
192
Вычисляя от полученных выражений еще раз частные произ-
водные по х и по у, находим
б2/	х	d2f х .	d2f х .	d2f	х
—-	еА cos у,	——	- -еА sin у,	—— - -еА sin у,	—- -еА	cos у.
СХ~	дудх	дхбу	СУ
Обратим внимание на то, что смешанные производные второго
б2/ d2f
порядка —— и —— тождественно равны, т.е. их значения оказа-
дхду дудх
лись одинаковыми независимо от того, дифференцируем мы фун-
кцию f(x,y) сначала по х, а затем по у, или наоборот. Это не слу-
чайно. Имеет место следующая теорема.
Теорема 8.6. Пусть функция /(х,у) имеет в области G смешан-
б2/ / ч d2f z ч
ные производные —— (х,у) и —— (х,у), причем они непрерыв-
дхду дудх
ны. Тогда
б2/ z ч d2f (	\ г
—— (х, у) = —— (х, у) в области G.
дхду дудх
Не останавливаясь на доказательстве этой теоремы, заметим,
что аналогичные равенства имеют место и для производных любо-
го порядка. Например,
б3/	б3/	б3/
—=-----------=----т— и т. д.
дхду дудхду ду дх
8.4.2.	Дифференциалы высших порядков
Согласно определению первого дифференциала функции и = f(x,y),
х, у) = ^-(х, у) Ах + у-(х,у)Ау,
при этом дифференциал является функцией точки (х,у), в кото-
рой он вычисляется, и приращений Ах и Ду, выбираемых произ-
вольно. Если приращения Ах и Ау не менять, то дифференциал
df(x,y) становится функцией только переменных х, у и от него
можно вычислить вновь первый дифференциал при тех же Ах и Ау.
Определение 8,8, Дифференциалом второго порядка d2f(x,y) на-
зывается дифференциал от первого дифференциала df(x,y), т.е.
d2f(x,y) = d(df(x,y)).
Далее
^3/(x,y) = r/(J2/(x,y)) и т.д.
193
Вычислим второй дифференциал подробнее. Согласно опреде-
лению,
Sf 3
d2f (х,у) = di ^(х,у) Ах +
Так как Ах и Ау постоянны, то
d
д2 f	д2 f
—Ax + —— Ay Ax +
_дх2	дудх
d2f	d2f	"I
—— Ax + —Av Av =
дхду	dy2
= —C(x, y) Ax2 + 2	(x, y) AxAy + —v(x, y) Ay2, (8-14)
dx2	дхду	ду2
d2f	d2f
поскольку —— (x,y) = —— (x,y).
дхду	дудх
Символически первый и второй дифференциалы можно запи-
сать в виде:
#(x,y) = f^-Ax + ^-AyV(x,y),
1^(5х	ду	)
( д	д	V
d2f(x,y)= — Ах + — Ау /(х,у).
х ^<3х ду)
Для придания смысла этим равенствам в первом случае надо
Q
просто после символа — поставить /(х,у), во втором случае —
бх
возвести выражение в скобке в квадрат, считая по определению
f д У _ д2 д д _ д д _ д2 ( д У _ д2
^6х J дх2 ’ дх ду ду дх дхду ’ ^5у )	ду2 ’
и затем опять поставить /(х,у).
Нетрудно проверить, что для любого п
dl1f{x,y) = (^Ax + ^Ay} f(x,y).
\дх ду)
Пример 8.12. Вычислить дифференциал второго порядка от фун-
кции /(х,у) = х3у4 в точке х = 1, у = -1.
Имеем
— = Зх2у4, — = 4х3у3, ——= бху4, = 12х2у3, ^^ = 12х3у2.
дх	ду	дх2	дхду	ду2
194
В частности, в точке х = 1, у = -1
з7 . з2/	п 57 п
дх2 дхду ду2
Следовательно,
d2/(l,-l) = бАх2 - 24АхАу + 12Ду2.
Отметим, что если первый дифференциал df(x,y) есть линей-
ная форма относительно приращений аргументов Дх и Ду, то вто-
рой дифференциал — квадратичная форма по Дх, Ду. Нетрудно
видеть, что дифференциал /7-го порядка есть полилинейная фор-
ма по Дх, Ду порядка п.
Аналогично вводятся дифференциалы для функций трех и бо-
лее переменных.
8.4.3.	Формула Тейлора
Вспомним вначале формулу Тейлора для функции одной веще-
ственной переменной t в точке t = О
w(z) = w(0) + ^yw'(O)/ + уу w"(O)C + ... +	(0)C + f'n (8-15)
и запишем ее в дифференциалах
w(z) = w (/) + Yydu(O) +	(®) + ••• + —yd"w(O) + r„.
(Здесь r„ — остаточный член формулы Тейлора, который, как мы
доказали, есть o(tn).)
Именно в последней форме получим многомерную формулу
Тейлора.
Теорема 8.7. Пусть функция f(x,y) имеет в области G непре-
рывные частные производные до порядка п + 1 включительно. Тог-
да для любой точки (х,у) е G справедлива формула
/(х+Дх,у +Ду) =
= /77 + ]т7(ат) + ^7(ау) + -.. + ^777 + 0(р'')’
где р = ^/дх2 + Ду2. (Разумеется, приращения Дх и Ду таковы, что
точки х + Дх и х + Ау находятся в области G, а точнее в некоторой
окрестности точки (х,у), находящейся в области G.)
Доказательство. Зафиксируем точку (х,у) е G. а также прира-
щения Дх и Ду и рассмотрим функцию одной переменной t g [0,1 ]
w(0 = f(x + t&x, У + d\y).
195
Очевидно,
w(l) = f(x + Дх, у + Ду), «(0) = f(x,y).
Далее нетрудно видеть, что функция u(f) имеет п + 1 непре-
рывную производную на отрезке [0,1]. Действительно, по формуле
(8.7), имеем
w'(/) =	+ /Дх, у + /Ау) Ах + ^~(х + 1Лх,У + /Ау)
и, в частности,
U> = fa	+	Л>’ =
Точно так же вычисляем, что
д2 f	д2f
u"(t) = —А-(х + /Ах, у + /Ду) Дх2 + 2—— (х + /Ах, у + /Ау)АхАу +
дх2	дхду
^2 f
+ ^-у(х + /Ах, у + /Ау) Ау2
и, следовательно, w"(0) = d2f(x,y).
И так далее, на л-м шаге получим, что w(fl)(0) = dnf(x,y).
Подставляя эти выражения в формулу (8.15), находим, что для
любого / е [0,1]
и (/) = f (х, у) +1 df (х, у) / + ^-yd2f (х, у)/2 +... + A-d V (х, у) tn + г„
В частности, при / = 1 получаем искомую формулу Тейлора
/(х + Ах,у + Ау) =
= f (*, + уу df (х, у) + ^d2f (X, у) +... + dnf (х, у) + г„, (8.16)
где гп — остаточный член. Можно показать, что
/ \«+1
= — Ах + — Ду f (х+ тДх, у + тАу)
(сХ ду )
при некотором т е (0,1).
Так как исходная функция /(х,у) по предположению имеет не-
прерывные частные производные до порядка п + 1, существует
постоянная М > 0 такая, что
|г„| < ЛГ(|Дх| +1Ау|Г+1,
или (что эквивалентно)
196
|r„| < Л/р"+',
где р = у1&х2 + Ду2. Это неравенство указывает на то, что остаточ-
ный член есть бесконечно малая величина более высокого поряд-
ка, чем pfl, т.е. rH = o(pfl). А
Пример 8.13. Представить функцию /(х,у) = с'cosx в окрестно-
сти начала координат по формуле Тейлора второго порядка.
Имеем (с учетом того, что х = Дх, у = Ду)
/(0,0) = 1, #(0,0) = (eAcosy)0j0x + (exsiny)0i0y = х;
#/(0,0) = (eAcosy)0i0x2 + 2(eA'(-siny))0i0xy + (-eAcosy)0i0y2 = x1 - у1.
Таким образом,
еА cos у = 1 + х + (х2 - у2) + о(р2).
Замечание. Как и в одномерном случае, значение многомерной
формулы Тейлора состоит в том, что функция /(х,у) произволь-
ной структуры приближенно представляется в виде простой эле-
ментарной функции, а именно многочлена, который называется
многочленом Тейлора.
8.5.	Экстремумы функции. Задача о наибольшем
и наименьшем значениях
В этом подразделе изучим теорию экстремальных точек функ-
ции двух переменных, т.е. теорию локальных максимумов и мини-
мумов, а также задачу о наибольшем и наименьшем значениях
функции на компакте. В последнем случае предварительно необхо-
димо исследовать задачу так называемого условного экстремума.
8.5.1.	Необходимые условия экстремума
Начнем с определения точек экстремума функции и выясне-
ния необходимых условий экстремума. Пусть функция и = f(x,y)
определена в некоторой области G.
Определение 8.9. Точка (х0,у0) € G называется точкой локально-
го максимума функции /(х,у), если найдется окрестность U точки
(х0,у0) такая, что для любой точки (х,у) е U справедливо нера-
венство
fix, у) </(х0,у0)-
Аналогично определяется точка локального минимума.
Определение 8.10. Точки локального максимума и точки локаль-
ного минимума функции fix,у) называются ее экстремальными
точками, или точками локального экстремума.
197
Наша основная цель — нахождение и исследование экстремаль-
ных точек заданной функции f(x,y). Это и составляет содержание
теории безусловного экстремума (или «просто экстремума»).
Теорема 8.8. (Необходимые условия экстремума.) Пусть (хо,уо) е
€ G — точка локального экстремума функции /(х,у). Если /(x,j)
имеет в этой точке частные производные — (х,у) и — (х,у), то
дх	dv
они равны нулю, т.е.	•
= 0, |^(хо,у0) = 0.	(8.17)
дх	ду
Эти равенства и составляют необходимые условия экстремума
дифференцируемой функции.
Доказательство. Рассмотрим функции одной переменной х, а
именно функцию <р(х) = /(х,у0), где у0 — вторая координата точки
локального экстремума (х0,у0). Очевидно, точка х = х0 является эк-
стремальной точкой функции (р(х), причем точкой локального
максимума или минимума в точном соответствии с тем, каков
экстремум функции f(x,y) в точке (х0,у0), как функции двух пере-
менных.
Следовательно, в соответствии с необходимым условием экстре-
мума функции одной вещественной переменной <р'(х)|X=X|) = 0, т.е.
(р'(х0) = 0. Но это значит, что — (х, у)|д.=х v=v = 0, т.е. — (х0,у0) = 0.
дх 1	дх
Аналогично устанавливается и второе равенство — (х0, у0) = 0. ▲
ду
Итак, координаты всякой точки экстремума дифференцируе-
мой функции обязаны удовлетворять системе уравнений (8.17).
Однако (как и в одномерном случае) может получиться, что не
все корни системы (8.17) будут точками локального максимума
или локального минимума данной функции.
Пример 8.14. Рассмотрим функцию z = -х2 + у2, которая в про-
странстве трех переменных х, у, z образует гиперболический пара-
болоид (рис. 8.3).
Действительно, в этом случае
— =-2х, — = 2у
дх	ду
и, следовательно, точка (0,0)
удовлетворяет необходимым усло-
виям экстремума. Однако ясно,
что в начале координат у функ-
ции z = у2 - х2 нет ни локального
минимума, ни локального макси-
мума — это так называемая сед-
ловая точка.
198
В связи с этим вводится дополнительное понятие стационарных
точек функции f(x,y).
Определение 8.IL Точка (х0,у0) называется стационарной точкой
дифференцируемой функции f(x,y), если ее координаты удовлетво-
ряют системе (8.16), т.е.
|^(х0,уо) = О, |^(хо,уо) = О.
дх	ду
Отсюда следует, что всякая экстремальная точка является ста-
ционарной, но, вообще говоря, не наоборот.
8.5.2.	Достаточные условия экстремума
Вопрос о том, как выяснить, является ли стационарная точка
экстремальной или нет, решается с помощью вторых частных про-
изводных функции f(x,y).
Для удобства формулировки основной теоремы этого подразде-
ла введем обозначения
о2/ z , d2f ,	, d2f z ,
=—<*0’To), й12	ап =——(xQ,yQ).
дх	дхду	ду
Теорема 8.9. Пусть (х0,уо) — стационарная точка дважды непре-
рывно дифференцируемой функцииf(x,y). Тогда:
1)	если й1]а22 ~ ап > О, то точка (х0,у0) является экстремальной
точкой функции /(х,у), при этом:
а)	если ЙЦ >0, то (х0,у0) — точка локального минимума,
б)	если <0, то (х0,у0) — точка локального максимума;
2)	если Ццй22 -	< 0, то в точке (хо,уо) экстремума нет;
3)	если лпа22 - й?2 = то требуется дальнейшее исследование.
Доказательство. Сравним значения /(х0,у0) со значениями
/(х0 + Ах, у0 + Ду), используя формулу Тейлора. Имеем
/(х0 + Ах, у0 + Ау) -/(х0,у0) = #(х0,уо) + |^2/(х0,Уо) + »(р2),
где р2 = (Ах)2 + (Ау)2.
Поскольку (х0,у0) — стационарная точка, то б(Дх0,у0) = 0 и,
следовательно, приращение А/(хо,уо) записывается в виде
VWo) = |i/2/(x0,y0) + »(р2),
или, что то же,
А/(х0,у0) = |ки(Ах)2+ 2а]2АхАу + й22(Ау)2] + о(р2).
Вначале покажем, что в условиях 1 приращение А/(х0,у0) > 0
или, наоборот, Д/(х0,Уо) < 0 (в зависимости от знака аи), т.е.
199
Л-0,7о Д*
Xg+Дх, >’о+Л7
ДУ t глх = р cos <р
х t Ду = р sin ip
Рис. 8.4
в точке (хо,уо) имеется экстремум.
Для этого удобно записать прираще-
ния Дх и Ду в полярных координатах
(рис. 8.4), а именно
Дх= pcoscp, Ду= psintp, р = -у/дх2 + Ду2.
Имеем
Д/(х0,у0) =	[(й, | COS2<p + 2«|2COS(psin<p + i722sin2(p) +	) ],
2	р2
где (р меняется на отрезке [0,2л], р > 0.
Заметим, что если функция
Л(ф) = й| j cos2tp + 2a12cos<p sin<p + rz22sin2(p (8.18)
окажется на отрезке [0,2л] строго положительной, то, согласно
второй теореме Вейерштрасса, она достигает в некоторой точке
(р0 е [0,2л] своего минимального значения т = min Д(<р) = /(ф0) > 0.
0<(р< 2к
Тем самым при достаточно малых р > 0 (например, с того мо-
мента, когда
о(р2)
Р2
< —) будем иметь
. „ х Р2 f л/ \ о2 m А
Д/(х0,у0)> у I Дф)- — >	— >0
при р * 0 и любом <р е [0,2л]. Это и будет означать, что в точке
(х0,у0) функция /(х,у) имеет локальный минимум.
Совершенно аналогично рассматривается случай Л(ф) < 0, ф е
€ [0,2л], который приводит к локальному максимуму функции/(х,у).
Итак, дело свелось к исследованию знака функции Д(ф) в усло-
виях 1.
Нетрудно видеть, что при йий22 - й122 > 0 значение Оц*0и
функцию Л(ф) можно представить в виде
Л(ф) = —[(йисо5ф + й]28Шф)2 + (й|[й22 - «22)8т2ф],	(8.19)
йн
где оба слагаемых неотрицательны.
Более того, поскольку зшф и сойф одновременно в нуль не об-
ращаются, то при любом ф е [0,2л] выражение в квадратных скоб-
ках строго положительно.
В итоге получаем, что если при этом >0, то Л(ф) > 0, а если
йн <0, то Л(ф) < 0 при всех ф е [0,2л]. Это и требуется.
Обратимся теперь к условию 2, т. е. к случаю, когда а} ]й22 - й22 < 0,
и покажем, что в точке (х0,у0) экстремума нет. Для этого, очевид-
но, достаточно указать два угловых направления ф = ф] и ф = ф2,
вдоль которых функция Л(ф) будет иметь разные знаки при любых
достаточно малых р > 0.
200
Эти направления нетрудно увидеть. Именно, если * О, то из
(8.19) получаем, что при cpj = 0 значения Л(ср[) = ян, а при (р2 =
— значение Л((р2) =-----------sin2tp2.
an)	&ii
Поскольку ПО условию 2 «]|й22 - й12 < 0, то, каков бы ни был
знак числа йи, значения Л(ср]) и Л(<р2) имеют разные знаки. Так
как при этом р > 0 может быть сколь угодно малым, это и значит,
что в точке (х0,уо) экстремума нет.
Если «ц =0, то функция Л((р) принимает вид
Л((р) = (2«]2COS(p + t?22 sin <р) sin ср
(заметим при этом, что в случае =0 из условия 2 следует, что
ап * 0).
Ясно, что при достаточно малых ср функция в скобках имеет тот
же знак, что и число л12. В то же время sin ср изменяет знак при пере-
ходе через точку (р = 0. Следовательно, при достаточно малых о / 0
форма Л((р) меняет знак. Это указывает на то, что экстремума нет.
Что же касается вырожденного случая йцй22 - ап = 0 (условие 3),
то, как показывают конкретные примеры, в этих точках возмож-
ны как экстремумы, так и их отсутствие. ▲
Пример 8.15. Исследовать на экстремум функцию
Дх,у) = х4 + у4 - 4х + 32 у - 7.
Вначале ищем стационарные точки этой функции, т. е. находим
корни системы уравнений
= 4л3 - 4 = 0,	= 4у3 + 32 = 0.
дх	ду '
Очевидно, единственной стационарной точкой будет точка
Ж 1,-2).
Теперь выясним, применяя теорему 8.9, является ли эта точка
экстремальной. Имеем
^н
дх1
|4(М0) = 12х2	=12, а22 = у-у-(Л/0) = 12_у2 Ai
дх	у.-2	ду	у
=48,
>=-2
d2f
Й12=4т- = 0-
дхду
Таким образом, а1} > 0, япй22 _ ап > 0, т.е. условие 1а. Следова-
тельно, в точке Л/0(1,-2) функция имеет локальный минимум.
Пример 8.16. Исследовать на экстремум функцию/(х,у) у2 - х2.
Имеем
— = -2х,	= 2у.
дх , ду 7
201
Следовательно, начало координат Л/о(О,0) является стационар-
ной точкой этой функции. Далее
=^4(л/„) = -г, я22 =-|Дл/0) = 2, й,2 = Дчм0) = о.
дх1	ду1	дхду
Таким образом, flnfl22 _ ап = _4 (условие 2). Следовательно, в
стационарной точке экстремума нет (см. рис. 8.3).
8.5.3.	Условный экстремум. Метод множителя Лагранжа
На практике часто приходится иметь дело с экстремальными
задачами для функций многих переменных при различных ограни-
чениях, связывающих независимые переменные. Такие задачи на-
зываются экстремальными задачами с ограничениями или задача-
ми условного экстремума.
Классической задачей условного экстремума является следующая.
Пусть z = Дх,у) — функция, определенная в некоторой облас-
ти G Rl v. Пусть, далее, Г — некоторая кривая, лежащая в обла-
сти G и характеризуемая уравнением <р(х,у) = 0, где <р(х,у) —
некоторая функция.
Требуется найти экстремальные значения функции z = f(x,y)
при условии, что точки (х,у) находятся на кривой Г (или, что то
же, удовлетворяют уравнению <р(х,у) = 0), рис. 8.5.
Символически эту задачу записывают так:
z = f(x,y) -> extr, (р(х,у) = 0,	(8.20)
причем соотношение <р(х,у) = 0 называют условием, или уравне-
нием связи.
Переходим к строгим формулировкам.
Пусть А/0(х0,у0) € Г — некоторая точка. Это означает, что ее
координаты удовлетворяют уравнению связи, т.е. (р(хо,уо) = 0.
Определение 8.12. Точка MQ е I
ловного максимума задачи (8.20),
называется точкой локального ус-
если найдется такая окрестность
С(хО,Уо) точки Мй, что для лю-
бой точки из этой окрестности,
лежащей на кривой Г, справед-
ливо неравенство Дх,у) < Дх0,уо).
Аналогично определяется
точка локального условного ми-
нимума.
Замечание. Очевидно, что глав-
ное отличие определения 8.11 от
определения точки безусловного
локального максимума (см. опреде-
ление 8.9) в том, что со значени-
ем Дхо,уо) сравниваются значения
202
f(x,y) не для всех близких значений (х,у) е l/(xb,jb), а только для тех,
которые дополнительно удовлетворяют уравнению связи ср(х,у) = 0.
Ясно, что точка условного локального максимума или миниму-
ма вовсе не обязана быть соответствующей точкой безусловного
экстремума функции f(x,y).
Точки локального условного максимума и точки локального
условного минимума называются экстремальными точками задачи
условного экстремума.
Задача условного экстремума значительно сложнее задачи бе-
зусловного экстремума, поэтому здесь остановимся только на не-
обходимых условиях, которые приводят к практическому методу
нахождения точек условного экстремума задачи (8.20).
Теорема 8.10. Пусть точка Л/0(х0,уо) есть точка условного экст-
ремума задачи (8.20). Тогда существует число /ч) (называемое мно-
жителем Лагранжа) такое, что трехмерная точка (х0,у0Д0) являет-
ся стационарной точкой безусловного экстремума функции
£(х,у,Х) = /(х,у) + Хф(х,у).
Таким образом, теорема утверждает, что какова бы ни была
экстремальная точка Л/0(х0,у0) задачи (8.20), ее координаты (х0,у0)
необходимо являются (вместе с множителем Лагранжа) решени-
ем системы уравнений
—	= 0, — = 0, — = 0,
дх ду 5л
т.е. системы
—	(х,у) + X — (х,у) = 0;
дх 	7 дх 	7
<	^(Х,3,) + ^(Х,3,) = О;	<8-21>
бу 5у
ср(х,у) = 0.
Отсюда вытекает и практический алгоритм решения задачи ус-
ловного экстремума (8.20), называемый методом множителя Лаг-
ранжа'.
1)	составление функции Лагранжа £(х,у,Х);
2)	решение системы (8.21);
3)	отбор среди всевозможных решений (xo,yo,Zo) системы (8.21)
тех пар (х0,у0), которые являются решением исходной задачи (8.20).
Это осуществляется с привлечением дополнительных соображе-
ний геометрического, физического характера и др.
Пример 8.17. Решить задачу
f/(x, у) = у2 — х2 -> extr;
203
Геометрически эта задача заключается, очевидно, в нахожде-
нии экстремальных точек функции f(x.y) при рассмотрении ее
значений только на единичной окружности с центром в начале
координат.
Запишем уравнение связи в виде
tp(x,y) = х2 + у2 - 1 = О
и составим функцию Лагранжа
Цх,у,Х) = у2 - х2 + Z(x2 + у2 - 1).
Ищем теперь стационарные точки функции Лагранжа как ре-
шение системы (8.21):
-2х + 2л_х = О	Г х(-1 + X) = О
2у + 2ку = 0 о < у(1 + X) = 0
х2 + у2 -1 = 0 х2 + у2 - 1 = 0.
Решением этой системы являются четыре точки (x,y,Z):
(±1,0,1), (0,±1,-1).
Следовательно, точки (±1,0), (0,±1), лежащие на окружности
х2 + у2 = 1, могут быть экстремальными точками задачи (8.22).
Все они, действительно, являются таковыми, при этом из вида
функции f(x,y) = у2 - х2 очевидно, что в точках (0,±1) имеется
максимум функции /(x,j), равный /(0, ±1) = 1, а в точке (±1,0) —
минимум, равный /(±1,0) = -1.
8.5.4. Задача о наибольшем и наименьшем значениях
В заключение рассмотрим задачу о наибольшем и наименьшем
значениях функции /(х, j), заданной в ограниченной области вместе
с границей. Именно, пусть f(x,y) определена в замыкании области
G, т.е. на компакте G = G U Г, и эта функция непрерывна в G.
Тогда, согласно второй теореме Вейерштрасса, она достигает в G
своих наибольшего и наименьшего значений. Это значит, что су-
ществует хотя бы одна точка (х0,у0) е G такая, что
ЖУо) = П1ах/(х,у), (х,у) € G,
и хотя бы одна точка (хь jj) е G такая, что
/(Х],У|) = min/(x,j), (x,j) е G.
Эти точки (х'. у) е G называются точками абсолютного максимума
и абсолютного минимума функции f(x,у) на компакте G, или, что
то же, точками наибольшего и наименьшего значений.
Наша цель — указать метод практического отыскания точек наи-
большего и наименьшего значений /(х,у) в G.
204
Для этого заметим, что каждая из точек (хр,уо), (X|,yi) может
оказаться либо внутренней точкой компакта G = GUT, т.е. при-
надлежать области G, либо находиться на границе Г.
Рассмотрим, например, точку (х0,уо)- В первом случае она, оче-
видно, окажется и точкой локального максимума функции f(x,y).
Следовательно, она может быть найдена с помощью теоремы 8.9 о
безусловном экстремуме. Во втором случае точка (х0,уо) е Г будет,
очевидно, точкой условного максимума задачи
f(x,y) -> extr, (х,у) е Г.	(8.20)
То же можно сказать и о точке абсолютного минимума.
Из изложенного вытекает и метод решения задачи о наиболь-
шем и наименьшем значениях. Он состоит из трех этапов:
1)	находятся возможные точки локального безусловного экст-
ремума функции /(х,у) в области G;
2)	определяются точки условного экстремума задачи (8.20), т.е.
точки экстремума функции /(х,у), когда (х,у) е Г;
3)	сравниваются значения функции f(x,y) во всех точках, най-
денных на предыдущих этапах, и среди них выбираются наиболь-
шее и наименьшее значения.
Пример 8.18. Найти наибольшее и наименьшее значения функ-
ции z = у2 3 4 5 - х2 в единичном замкнутом круге х2 + у2 < 1. Эта задача
была фактически решена в примерах 8.15 и 8.17. Из примера 8.15
следует, что внутри единичного круга точек безусловного экстре-
мума у функции z = у2 - х2 нет. Напротив, на единичной окружно-
сти х2 + у2 = 1 имеются две точки (0,±1) условного максимума и
две точки (±1,0) условного минимума. В этих точках и достигаются
абсолютные максимум и минимум функции z = у2 - х2 в замкну-
том круге х2 + у2 < 1.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Пусть м(х, у) = eYcosy, v(x,y) = evsinx. Убедитесь в том, что имеют
место тождества
ди _ dv ди _ dv
дх ду ’бу дх'
2. Пусть и(х,у, z) = .	1 Покажите, что в любой точке (х,у, z)
д/х2 + у2 + z2
не расположенной в начале координат,
д2и д2и д2и „
дх2 ду2 dz2
3. Представьте многочлен Р(х,у) = х2 - ху + у2 по степеням х - 1, у + 1.
4. Найдите экстремальные точки функции /(х,у) = х2 - ху + у2.
5. Найдите наибольшее и наименьшее значения функции z = х - 2у - 3
в области, определенной неравенствами х > 0, у > 0, х + у < 1.
ГЛАВА 9
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
9.1. Объем цилиндрического бруса. Определение
двойного интеграла
9.1.1. Основные определения
Пусть z = f(x,y) > 0 — непрерывная функция двух переменных,
определенная в области G с R^ v. Графиком этой функции явля-
ется некоторая поверхность 5, ограничивающая цилиндрический
брус с основанием G (рис. 9.1).
Поставим задачу: определить объем Vцилиндрического бруса и
найти способ вычисления этого объема.
С этой целью разобьем область G гладкими линиями на конеч-
ное число подобластей G}, G2, GN, т.е. представим область Gb
виде объединения |J G,.
Ясно, что каждая подобласть G, определяет находящийся над
ней маленький брус объемом Vh являющийся частью исходного
бруса.
Поскольку подобласть G, мала, то соответствующий малень-
кий брус можно считать минипризмой высотой г,- =	где
(£,,т|,) е G, — некоторая средняя
Рис. 9.1
точка.
Положим приблизительно =
=f(^i,T\i)Gh где а(- — площадь по-
добласти G,. Тогда получим, что
полный объем
И = Х V,= f Ж, Л,Ж
/=1	/=1
При этом интуитивно ясно,
что чем мельче разбиение облас-
ти G, тем приближение будет
точнее, и в конечном итоге в
процессе неограниченного из-
мельчения разбиения области G
получим истинное значение И
Теперь перейдем к строгому
изложению.
206
Пусть d, — диаметр области Gh т.е. верхняя грань расстояний
между всевозможными точками области бу. Обозначим через Z,v
максимальный диаметр среди d\, d2. ..., 4й назовем это число диа-
метром разбиения б], б2,..., GN.
Определение 9.1. Число К назовем объемом криволинейного цилиндри-
ческого бруса, образованного графиком функции z=/(x,y), (х г) g G,
если для любого сколь угодно малого е > 0 найдется число 5 = 5(e) > О,
такое, что при любом разбиении б = [J6,. для которого Z;V < 5,
выполняется неравенство	»=]
/=1
< е.
Коротко можно записать:
(=1
Читатель, конечно, обратил внимание на то, что идеи нахож-
дения объема цилиндрического бруса точно такие же, как при
определении площади криволинейной трапеции и определенного
интеграла от функции одной вещественной переменной.
Здесь аналогично приходим к понятию двойного интеграла от
любой функции /(х,у) по области б, а именно
Я Ж, y)dxdy = lim £ Ж, йЖ	(9-1)
G	' = 1
Строгое определение повторяет определение 9.1, поэтому его
не приводим. Подчеркнем лишь, что и здесь существенным является
требование, чтобы предел не зависел от конкретного выбора раз-
биения области G и выбора средних точек (^,т|() g G„ i = 1, ..., N.
Можно показать, что для функции /(х,у), непрерывной в облас-
ти G вместе с границей, т.е. в замыкании области G, предел (9.1)
существует и не зависит от выбора разбиения и средних точек. Та-
ким образом, для непрерывной в замыкании G функции двойной
интеграл существует, т.е. она интегрируема по области G.
Далее, пусть область G разделяется гладкой (или кусочно-глад-
кой) кривой на две подобласти G} и б2. Предположим, что функ-
ция f(x,y) кусочно-непрерывна в области G, т.е. она непрерывна
как в б|, так и в замыкании б2, и на линии раздела имеет разрывы
первого рода.
Примерами кусочно-непрерывных функций могут быть функции:
1, х > 0, у > 0;
0, при других значениях х и у
или
1) Дх,у) =
207
2) Дх,у) =
х2 - у2, верхняя половина круга х2 + у2 < 1;
О, нижняя половина круга.
Первая функция (она называется двумерной функцией Хевисайда)
имеет разрывы первого рода на полуосях х> 0 и j > 0, а вторая —
на отрезке [-1,1].
9.1.2. Свойства двойных интегралов. Теорема о среднем
Имеет место следующая теорема, играющая важную роль в
приложениях.
Теорема 9.1. Если функция/(х,у) кусочно-непрерывна в области
G = G{ U G2, то она интегрируема в области G, причем
Д Дх, y)dxdy = Д Дх, y)dxdy + Д Дх, y)dxdy .
G	6\	G,
В случае Дх,у) > 0 формула (8.19) имеет простой геометриче-
ский смысл: объем цилиндрического бруса с основанием G равен
сумме объемов цилиндрических брусов с основаниями G{ и
Уместно заметить, что на самой линии разрыва, разделяющей
области G] и (?2, значения кусочно-непрерывной функции роли
не играют и формула (8.19) от этих значений не зависит. Таким
образом, двойной интеграл обладает следующим замечательным
свойством: если значения функции Дх, у) изменить на конечном
числе кривых, находящихся в области G, то двойной интеграл не
изменится.
Сформулируем ряд свойств двойных интегралов в виде общей
теоремы.
Теорема 9.2. Пусть в нижеследующих формулах Дх,у) и yCv.y) —
интегрируемые функции в области G.
Тогда:
1)	для любой постоянной с функция сДх,у) также интегриру-
ема в G, причем
Д сДх, y)dxdy = сД Дх, y)dxdy;
G	G
2)	сумма (разность) Дх,у) ±g(x,y) также интегрируема в обла-
сти G, причем
Д [Я*, Т) ± g(x, у)] dxdy = Д Дх, y)dxdy ± Д g(x, y)dxdy,
G	G	G
3)	если Дх,у) < g(x.y) для всех (х,у) g G, то
Д Дх, y)dxdy < Д g(x, y)dxdy;
G	G
4)	функция |/(x,y) | также интегрируема в области G, при этом
208
Д f(x, y)dxdy < Д |/(x, y)| dxdy.
В заключение установим теорему о среднем для двойных интег-
ралов.
Теорема 9.3. Пусть f(x,у) непрерывна в замыкании области G,
которое_обозначим через G. Тогда найдется хотя бы одна точка
(^,т|) g G такая, что
Д fix, у) dxdy = Ж т|) mes G,
G
где символом mes G обозначена площадь области G.
Доказательство. Как неоднократно отмечалось, непрерывная на
компакте функция f(x,y) достигает своих минимального и макси-
мального значений и, следовательно, для любой точки (х,у) е G
справедливо двустороннее неравенство
т <f(x,y) < М,	(9.2)
где т = min fix,у), М = max fix,у) т в области G.
Интегрируя неравенство (9.2), получаем
тД dxdy < Д fix, y)dxdy < М Д dxdy.
G	G	G
Учитывая, что Д dxdy = mes G, запишем последнее неравенство
в виде	g
т • mes G < Д fix, y)dxdy < М • mes G
G
и заметим, что число ц = —!— ff fix,y')dxdy является промежу-
mes G ”
точным между минимумом и максимумом непрерывной функции
f(x,y). Следовательно, найдется хотя бы одна точка (ф,т|) е G, в
которой fif,, т|) = ц. Это и есть искомая формула. ▲
9.2. Вычисление двойного интеграла с помощью
повторного интегрирования (формула редукции)
Вычислять двойные интегралы как пределы интегральных сумм
весьма затруднительно, поэтому возникает естественная задача о
разработке техники двойного интегрирования, минуя непосред-
ственное суммирование и предельный переход в формуле (9.1).
Важнейшим результатом в этом направлении является формула
сведения двойного интегрирования к двум последовательным ин-
тегрированиям по каждой переменной х и у в отдельности.
209
Эта формула носит название формулы редукции и выглядит наи-
более просто для области G. являющейся прямоугольником. С это-
го случая начнем строгое изложение.
Теорема 9.4. Пусть функция f(x,y) непрерывна в замкнутом пря-
моугольнике
[а < х < b
П = 1
[с < у < d
Тогда
b/d	\
JJ Дх, y)dxdy = J J f(x, y)dy dx.
П	a I c	>
(9-3)
Доказательство. Прежде всего заметим, что ввиду непрерывно-
сти функции f(x,y) оба интеграла в формуле (9.3) существуют, и
обоснования требует лишь само равенство.
Пусть
а = х,, < *i <	< xi <	< хп = b
— произвольное разбиение отрезка [а,Ь]. Введем обозначение
g(x) = |/(х,уф/у.
Тогда правая часть формулы (9.3) запишется в виде
j J Дх,уДу dx = jg(x)dx = £ j g(x)dx.
a с	j a	'=0 x.
По теореме о среднем,
J g(x)dx =
Поэтому из (9.4) получим
j Дх, y)dy
dx = Y gCCd^x, =Y f Ж, y)dy.
i=0	i=0 c
(9-4)
(9.5)
Теперь разобьем отрезок [c,d] на т частей
с =	< У| < ... <	< ... < ут = b
и аналогично, применяя теорему о среднем по у, находим
d	т-]	т-1
\f(^hy)dy=Y ( f(^,y)dx= ^Ж,т1У/)Луу,
с	У=о у,	7=0
где т|(у е 1УрУ/+ 1] при всех /= 1, ..., л; j = 1, ..., т.
210
В итоге из (9.5) получаем, что повторный интеграл
(d	\	п.т
J \f(x,y)dy А= £	(9.6)
а ус	J	i,J=®
Полученная формула указывает на то, что повторный интеграл
представлен в виде двойной интегральной суммы для функции
/(х,у), которая отвечает произвольным разбиениям отрезков [а,д]
и [c,d], а тем самым и прямоугольника. Поскольку выбор средних
точек (^(,т|д) может быть любым, то при стремлении длин разбие-
ний к нулю из (9.6) немедленно получаем, что
b	3
J J Дх, уМу \dx = JJ Дх, y)dxdy. A
Дс	J	П
Замечание, В формуле редукции (9.3) переменные х и у можно
поменять ролями, т.е. наряду с формулой (9.3) справедлива и фор-
мула
d / b	\
JJ /(х, y)dxdy = J J Дх, y)dx \dy.
П	с уст	J
Особенно просто формула редукции выглядит для функций с
разделенными переменными, т. е. для функций вида f(x,y) = Х(х) ¥(у).
В этом случае
JJ X(x)Y(y)dxdy =J X(x)dx J Y(y)dy.
П	ст	c
Пример 9.1. Вычислить двойной интеграл по прямоугольнику
П = {(х,у), 0<х<1,2<у<3}от функции f(x,y) = х2 - у.
Имеем по формуле редукции
1/3	\
JJ (х2 - y}dxdy =J J (х2 - y)dy \dx =
П	0 \ 2	J
Замечание. С небольшими дополнениями формула редукции (9.3)
доказывается и для кусочно-непрерывных функций. Примем этот
факт без описания соответствующих дополнений.
Обратимся к случаю произвольной области. Точнее, пусть об-
ласть G задана в виде неравенств
G = {(х,у): а < х< Ь, ф(х) < у < ф(х)}.
211
Геометрически область Сесть криволинейная трапеция с верх-
ней границей у = ф(х) и нижней границей у = ф(х) (рис. 9.2).
Теорема 9.5. Пусть функция f(x,y) кусочно-неперерывна в G.
Тогда
ь (у(А-)	А
jjДх, y)dxdy = j j f(x,y)dy \dx.	(9.7)
G	a ^ip(x)	J
Доказательство. Заключим область Св какой-либо прямоуголь-
ник П = {а < х < />, с < у < d}, где с и d — подходящие числа.
В прямоугольнике П рассмотрим вспомогательную функцию:
|0, (х,у)е П\С,
очевидно, функция/*(х,у) есть продолжение функции /(х,у) ну-
лем вне области G. Ясно, что
Л fix, y)dxdy = Л/*(х, у )dxdy,	(9.8)
G	П
и, следовательно, по формуле редукции для прямоугольника (см.
теорему 9.4)
Л /* (*> tWt = j J/*(x,y)zZy |dx.
П	a	)
Но, при каждом x e [a,b], по определению,
f*(x = А если ф(х) < у < ф(х);
[О, в остальных точках.
Следовательно,
d	V(x)
J/*(x, y)dy= J f(x,y)dy.
c
(9-9)
212
Подставляя это выражение в
формулу (9.9), а затем в форму-
лу (9.8), получаем искомую фор-
мулу (9.7). ▲
Формула (9.7) является важ-
нейшим инструментом вычисле-
ния двойных интегралов.
Пример 9.2. Вычислить двой-
ной интеграл
Д _\;е '''dxdy.
G
где G — криволинейная трапеция, образованная графиком пара-
болы на отрезке [0,1] (рис. 9.3).
Очевидно, область G записывается в виде неравенств
Г(х,у): 0 < х < 1,
[О < у < х2
поэтому по формуле (9.7)
У	]
x3cxydy \dx = J(x2eX7)^ * dx =
J	о	y~
Дх3еXydxdy = J J
G	(ЦО
= Jx2(e*3 -l)<fr =	=|(e-2).
о	^33 Jx=l) 3
x2 у2
Пример 9.3. Пусть G — внутренность эллипса -у- + уу = 1
й2 о2
(рис. 9.4).
Записать двойной интеграл Д f (х, y}dxdy в виде повторных ин-
тегралов.	G
Очевидно,
G = |(х,у): ^у +
I а
Эту область можно представить в виде неравенств двумя спосо-
бами:
1) G = J(x,y): -а < х < й,-/ь/1 -^у < у < bjl -^у
V й2 V а1
2) G = j (х, у): —Ь < у < Ь, -й^1-^у - Л' -
213
Следовательно,
9.3. Вычисление двойного интеграла
в полярных координатах
Как известно, ряд областей на плоскости удобно описы-
вать в полярных координатах (р,ф). Полярные координаты связаны
с декартовыми координатами формулами
х = pcoscp, у = р sintp.
Переменная р есть расстояние от начала координат О до точки
М(х,у), а <р — угол, образованный вектором ОМ с положитель-
ным направлением оси Ох. Полярный угол ср изменяется либо в
пределах 0 < <р < 2л, либо в пределах -л < <р < л (рис. 9.5).
Линии р = R (R > 0) и ф = фо (0 < <р0 < 2л) называются коорди-
натными линиями и образуют на плоскости (х,у) так называемую
полярную сетку — семейство окружностей и лучей. Именно облас-
ти, ограниченные (хотя бы частично) координатными линиями,
являются наиболее удобными для вычисления двойных интегра-
лов в полярных координатах. Такими областями являются области,
приведенные в табл. 9.1.
Заметим важное общее обстоятельство, присущее перечислен-
ным областям: все эти области в полярных координатах описыва-
ются неравенствами, причем в случае р0(<р) = const, р|(ф) = const
область G в полярных координатах есть обычный прямоугольник.
Это существенно упрощает вычисление двойных интегралов.
Ясно также, что таблица характерных областей составлена по
принципу «от простого к сложному» и последняя область является
наиболее общей в том смысле, что при различных значениях пара-
метров ос и р, а также функций р0(ф) и
Л	р । (<р) можно получить все предыдущие
) области (читатель легко убедится в этом
.л ’ самостоятельно). Поэтому, если установить
y=pcos(p формулу перехода в двойных интегралах
от декартовых координат к полярным для
C) .v=pSin(|1 2 случая криволинейного кольцевого секто-
ра, то тем самым будут охвачены и все
Рис. 9.5	остальные области.
214
Таблица 9.1
Области вычисления двойных интегралов в полярных координатах
Область G	Чертеж на плоскости R;,,			Задание в полярных координатах
Круг радиусом R с центром в начале координат	У‘		/G/\	G= {(р, ф): 0 < ф < 2л, 0 < р < R}
	\/°			
Кольцо	У			G = {(р, <р): 0 < ф < 2л, г < р < R}
			VZ4A’ х // ту	
Круговой сектор				G = {(р,<р): а < ф < р, р < R}
	О	х			
Кольцевой сектор	1					G = {(р,ф): сс<ф<р, г < р < 7?}
	О	х			
Звездная область	/\\	Р=Р|<<Р> ) х			G= {(р,ф): 0 < ф < 2л, р < р](ф)} р|(ф) > 0 — некоторая функция угла ф, описывающая границу
Криволи- нейное кольцо	LJ р=	/\р=р](ф) ро(<р)		G = {(р,ф): 0 < ф < 2л, р0(ф) < р < р|(ф)} ро(ф) и р|(ф) — некоторые фун- кции угла ф, описывающие гра- ницу кольца
	(1 С	 /1 *		
215
Окончание табл. 9.1
Область G	Чертеж на плоскости R2y	Задание в полярных координатах
Криволи- нейный сектор	/1Р=Р|(<Р)	G= {(р,Ф>: a < (р < р, 0 < р <
Криволи- нейный кольцевой сектор	^z4P=Pi(<p) р=ро(ф)/С^К_ г_	G= {(р,ф): a < <р < р, Ро(<Р> < Р < Р|(Ф)}
Итак, пусть требуется вычислить двойной интеграл
I = Д/(х,у)йМу,
G
где G = {(р,ср): а < <р < р, ро(ср) < р < р1(<р)} и — непрерыв-
ная в G функция.
Теорема 9.6. Пусть fix. у) — непрерывная в G функция. Тогда
имеет место формула
Р ( р,<ф)
Jj f(x,y)dxdy = J j /[pcos<p,psinq)]p£/p tZ<p.
(9.10)
Доказательство формулы (9.10) можно провести строго по той
же схеме, что и доказательство формулы редукции (9.5), но мы
предложим хотя и нестрогое, но геометрически ясное рассужде-
ние, которое к тому же проливает свет на появление и роль мно-
жителя р в правой части.
По определению, двойной интеграл есть предел интегральных
сумм [см. формулу (9.1)], причем разбиение области G и выбор
средних точек в каждой подобласти разбиения могут быть произ-
вольными.
Запишем двойной интеграл по области G в виде
§f(x,y)dxdy = Д/(х,у)<УС,	(9.11)
G	G
подразумевая под символом dG площадь «бесконечно малых» по-
добластей, участвующих в определении двойного интеграла.
Далее, учитывая свободу выбора подобластей разбиения, раз-
делим область G полярной сеткой на элементарные площадки,
ограниченные окружностями радиусами р и р + ф и лучами,
образующими с осью Ох углы <р и <р + d<y (рис. 9.6).
216
Очевидно, площадь dG такой
подобласти вычисляется по фор-
муле dG= рфбЛр. Следовательно,
заменяя в правой части равенст-
ва (9.11) х на р cos<р и у на р sin<p,
a dG на рфф, получаем, что
JJ/(x,y)rfG =
G
= JJ /[pcoscp,psin ср] рг/рг/ф. (9.12)
G
Остается заметить, что в полярных координатах область G за-
писывается в виде
G = {(р,ср): а < ф < р, р0(ф) < р < р](ф)}
и, следовательно, по формуле редукции (9.5) приходим к иско-
мой формуле (9.10). ▲
Замечание. Попутно обратим внимание на геометрический смысл
множителя р в формуле (9.12). Он виден из полученного соотно-
шения dG = pdpdtp и является коэффициентом растяжения при
сравнении бесконечно малой области G на плоскости хОу и ее
образа на декартовой плоскости полярных координат (рОф).
Пример 9.4. Вычислить двойной интеграл
JJ(x2 - y2)dxdy,
G
где G — сектор, ограниченный прямой у = х, положительной по-
луосью х и окружностью х2 + у2 = 1.
Легко видеть, что G есть круговой сектор
G = {(р,<р): 0 < <р< р0 < р < Ц .
Следовательно,
о	о
4 ( 1	\	4	1	|
JJ(x2-y2)dxJy=J Jp2(cos2 ф-sin2 ф)рфэ <7ф=J cos 2фг7ф Jp3t/p = -.
G	0^0	J	°	0
Пример 9.5. Вычислить интеграл
JJ у/х2 + у2 dxdy,
G
где G — область, ограниченная кривой х2 + у2 = 2ах. Очевидно, что
это кривая может быть представлена в виде (х - а)2 + у2 = а2 и,
следовательно, это окружность радиусом а и центром в точке (я, 0)
(рис. 9.7).
217
Рис. 9.7
В полярных координатах уравнение
этой окружности есть р = 2acos<p, при
7Г	ТС г-р
этом угол <р меняется от — до —. Та-
ким образом,
G= {(р, <р):	< р < 2acos<p}
и, значит,
гс/2 /2л cos (р ___ \
/Jv'-V2 +y2dxdy = | J	^9 =
G	-л/21	0	J
k/2 з p=2<rcos(p	3 k/2	о з л/2
J	d($ = —— j cos3<p//<p = —— j (1 -sin2<p)//sin<p =
-it/2 3 p=0	-ir/2	3 -it/2
= (замена
.	. ч 8й3	,2ч .	32 з
Z = smq>) = — J	- t2)dt = — a?.
9.4. Приложения двойного интеграла
В этом подразделе даны некоторые приложения двойного ин-
теграла к геометрическим задачам, а также к задачам механики.
9.4.1. Вычисление объемов
Вопрос об определении объема криволинейного бруса был рас-
смотрен в подразделе 9.1. Тот факт, что объем криволинейного
Рис. 9.8
бруса выражается формулой
V = || f(х, y)dxdy, (9.13)
G
принято считать геометрическим
смыслом двойного интеграла от
неотрицательной функции /(х,у).
Простым следствием форму-
лы (9.13) является более общая
формула вычисления объема,
заключенного между двумя по-
верхностями, определенными в
области G с R2 .
Именно, пусть z = /(х,у) и
z = g(x,y) — две функции, оп-
218
ределенные в одной и той же области Сна плоскости (л,у). Пусть,
кроме того, fix. у) < g(x,y) на данной области. Графики этих фун-
кций в трехмерном пространстве (х, у, z) определяют поверхности
5Г= {(x,y,z): (х,у) е G, z=/(x,y)}
и
= {(х,у, z): (х,у) g G, z = g(x,у)},
между которыми заключен объем, имеющий торцевые поверхности
5/И 5Дрис. 9.8).
Ясно, что объем V этого тела вычисляется по формуле
V = Jj[g(x, j) - /(х, y)\dxdy.
G
9.4.2. Площадь криволинейной поверхности
Пусть Л = {(х,у, z): (х,у) е С, z=/(x,y)} — поверхность, являю-
щаяся графиком непрерывно дифференцируемой функции z =
= /(х,у), определенной в области G (рис. 9.9).
Наша задача — найти площадь поверхности 5, т.е. определить
ее и указать способ вычисления.
Для этого разобьем поверхность 5 гладкими линиями на N час-
тей ..., 5дг, т.е. представим 5 в виде объединения 5 =	.
]<<<Х
Этому разбиению соответствует разбиение области G на подобла-
сти (?,, ..., Gv, каждая из которых является проекцией на плос-
кость (хОу) «малых» поверхностей »
Как известно, при проекти-
ровании плоских фигур их пло-
щади связаны проекционным 2
множителем cosv, где v — угол
между нормалью к 5 и направ-
лением проектирования. Поэто-
му, если разбиение 5), ..., ^до-
статочно мелкое, то можно при-
ближенно считать, что
пл. G, = пл. cosv(,
где v( — острый угол, образован-
ный нормалью и к 5. и положи-
тельным направлением оси Oz 0
(индекс / означает, что вектор
нормали п вычисляется в сред-
ней точке М, = (^j,r\hZj), где
(^Л,.) G Gh
ъ Sv-
Рис. 9.9
219
Таким образом, приближенно полагаем, что
пл. 5 = У пл. Sj ~ У —!— пл. G..	(9.14)
м	/ZfcosV;
Выразим теперь cos v как функцию точки поверхности 5 через
функцию z= f(x,у). Действительно, как известно из 8.3 [см. замеча-
ние и формулу (8.12)], вектор нормали к поверхности 5, заданной
явным уравнением, имеет вид
п = ±Ж(х,у),|^ (х,у),-11.
[Эх ду J
Следовательно, косинус нормали, образующей острый угол с
осью Oz, вычисляется по формуле
1
cos V = .	= .
1 Р/,	A?	aY
J1+ -Чх,у) + f (x,y)
У [Эх	J I dy j
Подставляя это выражение в формулу (9.14), находим, что
пл.5 = У 1+ -2-(^.,т](-) + М-(^,т]/) пл.С/.
/=] у Эх J Эр J
Очевидно, правая часть есть интегральная сумма для функции
—-— по области G. Следовательно, при	—> 0 приходим к формуле
cos v
Пример 9.6. Найти площадь части поверхности эллиптического
параболоида z = х2 + у2, отсекаемой плоскостью z = 1 (рис. 9.10).
Имеем
УТУ — Рис. 9.10	пл. 5 = JJyjl + (2х)2 + (2y)2dxdy, G где G — единичный круг. Перехо- дя к полярным координатам х = = р coscp, у = р sintp, получаем, что 2тг Л ] 	 \ пл. 5 = j Jх/1 + 4p2pt/p ю<р = (До	J = 2тг|71 + 4р2 |<Д1 +4р2) = о	°
220
5	7	Н=5
= (замена t = 1 + 4р2) = — f 4tdt = — — Jt*\ = — (5>/5 - 1).
4 '	4 3 lr=] 6
В заключение укажем некоторые формулы использования двой-
ных интегралов в механике.
Пусть плоская пластинка с плотностью p(.v.v) > 0 занимает не-
которую область G в плоскости R2 тогда координаты х0, у0 ее
центра тяжести вычисляются по формулам
Л" = 77 Я -У)^У- Уо = -77 Д У№“*У,
М G	М G
где М = [J р(х, y)dxdy — масса пластинки.
G
Далее пусть dx и Iv — моменты инерции той же пластинки отно-
сительно осей Ох и Оу соответственно.
Тогда
= Д }’2р(х.г) Jay/v\ Ц = Дх2р(х,у)аЬа/у.
G	G
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1.	Пусть область G на плоскости х, у определяется неравенствами
а<х< Ь, 0 < у < f(x),
где f(x) — непрерывная на отрезке [а, Л| функция.
Докажите, что
JJ dxdy = mesG,
G
где mes G — площадь криволинейной трапеции, образованной графиком
функции у = Дх).
2.	Пусть G — треугольник на плоскости хОу с вершинами в точках
(0,0), (1,0) и (0,1). Запишите (двумя способами) двойной интеграл
JJ f(x>y}dxdy в виде повторных интегралов.
G
3.	Пусть ик(х$,уУ} — круг радиусом R > 0 с центром в точке (х0,у0), т.е.
^ШьТо) = {(*,/): (* - *о)2 + О' - То)2 М
По определению, величина
/(х0,у0,/?) =-^ Jj f(x,y)dxdy
называется круговым средним функции f(x,y) в точке (х0, у0) радиусом R.
Докажите, что если f(x,y) — непрерывная функция, то
*ini/(x0,y0,/?) = /(х0,у0).
221
4.	Вычислите следующие двойные интегралы:
1)	jj^x2 + у2 dxdy, где G — единичный круг с центром в начале коор-
G
динат;
2)	jjdxdy, где G — четверть единичного круга, расположенная
G
в первом квадранте плоскости хОу;
3)	jj е*4-*"dxdy, где G — часть кругового сектора 1 < х2 + у2 < 4, распо-
G
ложенная в первом квадранте плоскости хОу.
5.	Пусть функция f(x,y) непрерывна в круге х2 + у2 < R радиусом R за
исключением начала координат, в котором она имеет неограниченную
особенность.
Определим несобственный интеграл от функции f(x,y) по формуле
jj /(x,y)tta/y = Hm jj f(x,y)dxdy
x:+y-<R-	e<x2 у y2<R-
и назовем его сходящимся, если этот предел существует и конечен, и
расходящимся — в противном случае.
Докажите следующее утверждение: несобственный интеграл
Я ,	, , , , [сходится, если -2 < X < 0;
(х2+у2)А^у =	э
y.+ ,.<д:	( расходится, если X < -2.
6.	Пусть S — плоская пластинка, ограниченная линиями у = 2-ч/х, у = 0,
х = 1. Найдите:
1) массу пластинки 5, если ее поверхностная плотность р = х + Зу2;
2) координаты центра тяжести пластинки.
ГЛАВА 10
ОСНОВЫ ТЕОРИИ РЯДОВ
10.1. Числовые ряды
10.1.1. Ряды сходящиеся и расходящиеся
Бесконечная последовательность чисел, соединенных знаком
сложения,
it] + и2 + w3 + ... + ип + ...	(10.1)
называется числовым рядом.
Выражение
»„=/(«),	(10.2)
где f(n) — функция натурального аргумента, называется общим
членом ряда.
Часто употребляют более короткую запись для ряда: У, ип.
л=]
Пусть дан ряд (10.1). Будем последовательно складывать его члены:
5] = И,,
S2 = «I + «2,
= u} + w2 + «з,	(10. 3)
Sfl = щ + u2 + u3 + ... +
Эти суммы называются частичными суммами ряда (10.1). Таким
образом, получается бесконечная числовая последовательность
частичных сумм:
S|, s2, s3, ..., s„, ...	(10.4)
Рассмотрим ее предел lims,r Он может существовать или не
существовать.	н->“
Определение 10,1. Если этот предел существует и, значит, коне-
чен, т.е. lim .s,, = s, то ряд (10.1) называется сходящимся, а число
s — его суммой.
Если же этот предел бесконечен или вовсе не существует, то
ряд (10.1) называется расходящимся.
223
В первом случае, т.е. когда ряд сходится, этот факт записывают
в такой форме:
=5.
«=1
Во втором случае, если предел является бесконечностью опре-
деленного знака, то пишут 5 = +<« и s = -оо, или выражают этот
факт в такой форме:
=4-00 И ^ип =-оо.
Л=]	ff=l
Пример 10.1.
1 । 1 । 1 ।	।	1	। -У 1
1 -2 + 2-3 + 3-4 + “’+ п(п + 1) + ‘"“^/7(/7 + 1)-
Общий член ряда имеет вид:
_ 1
и" п(п + 1) 
Необходимо исследовать ряд на сходимость, для чего найдем
его сумму, исходя из определения.
Имеем
111 1
S.. =--1---1---h ... Н------.
" 1 2 2-3 3-4 п(п + \)
Каждое слагаемое этой суммы преобразуем по формуле
1	_ 1 1
к(к +1) " к (к + 1) ‘
Получим
Л 1W1	1W1	1 3	fl	1 W1 1 3	, 1
2	J ^2	3J ^3	4 J	^/7-1	п J ^/7	/7+1 J /7+1
поскольку после раскрытия скобок обнаруживается, что все слага-
емые, кроме первого и последнего, взаимно уничтожаются. Пере-
ход к пределу при п <*> дает
lim sn = lim | 1-J— | = 1 - lim —i— = 1.
л—I /7 + 1 J	/7 + 1
Таким образом, ряд сходится и его сумма 5=1. Этот факт мож-
но записать в виде
1	1	1	1	у 1
1 • 2 + 2 • 3 + 3 • 4 +	+ п(п + 1) +//(/7 + 1)
224
Пример 10.2. Рассмотрим числовой ряд, называемый геометри-
ческой прогрессией,
а + aq + aq2 + aq2 + ... + aq"-' + ... = ^a qn 1, a # 0.
я=]
Для этого ряда общий член имеет вид: и,, = aqn~}. Для частичной
суммы
sn = а + aq + aq2 + aq2 + ... + aqn~}
можно, пользуясв формулой для суммы членов геометрической
прогрессии, получить следующее выражение (при q # 1):
а
sn
(\-qn
= а ---—
1-<7
aqn
Теперь следует рассмотреть отдельно четыре случая:	а
a)	\q\ < 1, тогда qn —> 0 при п —> ©о и поэтому lim sn =-, т.е.
а	1 - q
ряд сходится и его сумма 5 =---;
1-4
б)	\q\ > 1, тогда q,! при п —> °© и поэтому lim s„ не существу-
ет, т.е. ряд расходится;	"
в)	q = -1, тогда s„ = у(1 - (-l)wj; эта последовательность такова:
а, 0, а, 0, ... и, поскольку а # 0, предела не имеет; это означает,
lim sn не существует и ряд расходится;
fl —
г) q = 1, в этом случае ряд имеет вид: а + а + а + ... и s„ = па,
откуда следует, что lim s„ не существует и ряд расходится.
Таким образом, геометрическая прогрессия, т.е. ряд ^aq”~l
сходится, если |^| < 1, и расходится, если 1^1 > 1.	«=i
Пример 10.3. Исследуем на сходимость числовой ряд, называе-
мый гармоническим'.
,111	1	1
2 3 4	п	п^п 
Данный ряд расходится. Убедимся в этом. Возьмем частичную
сумму ряда с номером п = 2к, где к — натуральное число, и разобь-
ем ее на к групп, следующим образом:
1W1 1 (1 1 1 и
2 J 1^3 4 J 1^5 6 7 8 J
1 1 1
2k~l +1 + 2к~' + 2+ ‘+ 2k~l +2к~1
Каждое из выражений, взятых в скобки, имеет одинаковую
структуру, и все они, начиная со второго, могут быть представле-
ны формулой
225
1 1 1
/и-] । ।	2m-' । 2	। 2w-‘
где m = 1, 2, ..., к - 1. Заменяя знаменатель каждой дроби, кроме
последней, большим числом, получим неравенство
1 1 1
т-1 । 1 'Jm-l । 9	9/И-] । 9/И-]
п	fl И 1
Для первого слагаемого также верно это неравенство 1 + — > —.
Таким образом, учитывая, что число всех групп равно к, полу-
чаем неравенство
5 >кХ-
"	2 ’
откуда следует, что при п —> <х> s„ неограниченно возрастает, т.е.
sn —> ©о. Следовательно, limsH не существует и ряд расходится.
Я—>оо
10.1.2.	Необходимое условие сходимости ряда
Теорема 10.1. Если числовой ряд У и„ сходится, то lim/г, = 0.
Л=1
Доказательство. Если ряд сходится, то lim s„ =s и	=5,
откуда получается и„ = s„ - s„_[ и
lim и„ = lim(is,, - 5W_]) = lim sn - lim 5„_[ =5-5 = 0. ▲
fl—H—fl—
Замечание. Условие lim = 0 называется необходимым услови-
ем сходимости ряда. Но на практике используется эквивалентное
этому достаточное условие расходимости ряда: если lim ип # 0 (или
вовсе не существует), то ряд 2^ип расходится.
«=1
Пример 10.4. Рассмотрим ряд
У п	1	+ 2	+
^10000/7 + 1 “ 10001 + 20001 +” ‘
Общий член ряда
п	1	1
и” ~ 10000/7 + 1 " 10000 + 1 юооо при п
п
следовательно, рассматриваемый ряд расходится (не выполнено
необходимое условие сходимости).
226
10.1.3.	Критерий Коши сходимости ряда
Теорема 10.2. Для того чтобы ряд (10.1) сходился, необходимо
и достаточно, чтобы для любого е > 0 нашелся номер N = _/V(e)
такой, что
I U/l+2 + • •• + «„+/,1<е	(Ю-5)
для всякого п > N и для всех значений р = 1, 2, ... .
Доказательство. Пусть s„ = и} + и2 + и3 + ... + uf! — частичная
сумма ряда (10.1). Составим последовательность частичных сумм
5[, s2, 53,	$л, ... . Она сходится или не сходится одновременно с
рядом (10.1).
Но для сходимости числовой последовательности s„ необходимо
и достаточно, в силу критерия Коши, чтобы для любого е > 0 нашелся
номер N = 7V(e) такой, что \sfl+p - sH| < е, как только п > N и для всех
значений р = 1, 2, ... . Но sn+p - s„ = и„+] + и„+2 + uf!+3 + ... + ufl+p, и
условие \s„+p - s„| < е принимает вид (10.5). ▲
10.1.4.	Свойства рядов
Свойство 1. Первое из свойств рядов можно сформулировать в
виде теоремы.
Теорема 10.3. Пусть дан ряд (10.1); его сходимость или расходи-
мость не изменятся, если к нему прибавить или от него отнять
конечное число членов, может измениться только его сумма.
Доказательство. Рассмотрим ряд (10.1). Выделим первые к членов
U] + U2 + U3 + ... + Uk + Uk+\ + Uk+2	+ ...
и обозначим и} + и2 + и3 + ... + ик = А. Если отбросить первые к
членов, то получится ряд
ик+{ + ик+2 + ... + ип + ... .	(10.6)
Пусть = «/с+1 + ик+2 + ... + tik+f! — частичная сумма ряда (10.6), а
s„+k = и\ + и2 + и3 + ... + ик + ик+] + ик+2 + ... + и„ — частичная сумма ря-
да (10.1). Тогда очевидно, что s,:..k = А + или = sn+k - А.
Пусть теперь ряд (10.1) сходится. Тогда —> 5 при п —> и,
следовательно, -ь s - А = о, т.е. ряд (10.6) тоже сходится. Его
сумма о отличается от суммы ряда (10.1) 5 на величину А.
Пусть теперь ряд (10.1) расходится, т.е. limsfl+jt либо бесконечен,
либо вовсе не существует. Тогда в силу соотношения sn+k = А + а,..
lim ст,; не может существовать. Иначе, по теореме о пределе суммы
fl —
двух числовых последовательностей, получилось бы, что lim у,./
fl~
существует. Следовательно, ряд (10.6) тоже расходится. Таким обра-
зом, доказано, что если два ряда отличаются друг от друга на конеч-
ное число членов, то они сходятся либо расходятся одновременно. ▲
227
Свойство 2, Пусть дано, что ряд (10.1) сходится. Рассмотрим
новый ряд:
ww+] + и„+2 + ... .	(10.7)
В силу свойства 1 этот ряд также сходится. Обозначим его сумму
через гп. Таким образом, гп = иц+} + z/,,.2 + •••  Сумма этого ряда
называется остатком ряда (10.1). Очевидно, что s = s,. + гп, откуда
следует, что г„ —> 0 при п —> <». Кроме того, величина |гл| является
абсолютной погрешностью приближенного значения суммы ряда,
получаемого по формуле 5 = s„.
Свойство 3. Это свойство также сформулируем в виде теоремы.
Теорема 10.4. Пусть даны два сходящихся ряда:
s' =	+ w2 + «3 + ... + ип + ...	(10.8)
s" = Vt + v2 + Vj + ... + v„ + ...	(10.9)
Тогда ряд
(и, + г,) + (и2 + v2) + («з + v3) + ... + (и„ + v„) + ..., (10.10)
полученный из рядов (10.8) и (10.9) их почленным сложением,
также сходится и его сумма s = s' + s".
Доказательство. Для частичной суммы ряда (10.10) sn = (щ +
+ V]) + (и2 + v2) + (w3 + v3) + ... + (и„ + v„) имеем очевидное
равенство: s„ = s'„ + s", переход к пределу при п <*> в котором
доказывает и сходимость ряда (10.10), и равенство 5 = 5' + s". ▲
Замечание. Очевидно, что аналогичный результат будет спра-
ведливым и для разности двух сходящихся рядов. Общий итог можно
представить в такой форме: если ряды (10.8) и (10.9) сходятся, то
Л = ]	?1=1	?1=1
Свойство 4. Свойство сформулируем в виде теоремы.
Теорема 10.5. Пусть имеется сходящийся ряд
5 = W| + U2 + W3 +	.	(10.11)
Тогда для любого числа X ряд
ХМ] + Xw2 + Xw3 + ... + XuH + ...	(10.12)
сходится и его сумма равна Xs.
Доказательство. Очевидно, что частичная сумма ряда (10.12)
an = Xsn, где s„ — частичная сумма ряда (10.11). Переходя к пределу
в этом равенстве при п —> <*>, получим, что Ит<тя существует и
fl —
равен Xlimsw = Xs. Следовательно, ряд (10.12) сходится и его сум-
п—
ма равна Xs. ▲
228
Замечание, Полученный результат можно представить в такой
форме: если ряд (10.11) сходится, то ряд (10.12) тоже сходится, и
общий множитель у всех членов ряда можно выносить за знак сум-
мы, т.е.
п=1	п=1
10.1.5.	Ряды с положительными членами
Пусть дан ряд
U] + ^2 + ^3 + ••• +	+  ,	(10.13)
члены которого положительны: и„ > 0. Тогда частичная сумма этого
ряда
S„ = и{ + «2 + w3 +
с увеличением п может только возрастать:
^?1+] =	> $п-
Здесь возможны два случая:
а)	если sn растет неограниченно, то sn —> +<*>, и ряд расходится;
б)	если sn остается ограниченной, т.е. s„ < В, то ряд сходится
потому, что ограниченная сверху монотонно возрастающая после-
довательность s„ имеет предел. С другой стороны, если последова-
тельность s„ имеет предел, то она ограничена. Следовательно, спра-
ведлива следующая теорема.
Теорема 10.6. Для того чтобы ряд с положительными членами
сходился, необходимо и достаточно, чтобы последовательность его
частичных сумм была ограниченной последовательностью.
Замечание, Следует отметить, что одной из основных задач,
связанных с рядами, является задача исследования ряда на сходи-
мость. Теорема 10.6, хотя и дает критерий сходимости ряда, имеет
узкое применение, поскольку проверка ее условия (ограниченность
последовательности sfl) не всегда возможна. Поэтому более эф-
фективными оказываются так называемые признаки сходимости
ряда, которые представляют собой только достаточные, но зато
более легко проверяемые условия сходимости ряда. Эти признаки
дополняются признаками расходимости ряда.
10.1.6.	Теоремы сравнения для рядов с положительными членами
Теорема 10.7 (первая теорема сравнения). Пусть даны два ряда с
положительными членами
«] + w2 + w3 + ••• + ин + •••>	(10.14)
+ v2 + v3 + ... + vn + ... .	(10.15)
229
И пусть для всех значений к = 1, 2, ... выполняются неравенства
ик < vk. Тогда:
а)	если ряд (10.15) сходится, то сходится и ряд (10.14);
б)	если ряд (10.14) расходится, то расходится и ряд (10.15).
Доказательство. Пусть
S'„ = W| + и2 + «з + ... + и„,
s" = V) + v2 + v2 + ... + vf!.
Тогда, в силу условия ик < vk, будет справедливым неравенство
Докажем вначале случай а). Допустим, что ряд (10.15) сходится
и его сумма равна s". Тогда при любом п выполняется неравенство
s„ < s" (поскольку s" — часть суммы положительных слагаемых,
равной s"). Откуда следует, что
S'n < S" < S".
Таким образом, доказано, что частичные суммы ряда s'„ ограниче-
ны. Применяя доказанное выше необходимое и достаточное усло-
вие сходимости ряда, получим, что ряд (10.14) сходится.
Перейдем теперь к случаю б). Допустим, что ряд (10.14) расхо-
дится. Тогда ряд (10.15) не может сходиться, так как из этого в
силу только что доказанного случая а), сразу следовало бы, что
ряд (10.14) сходится. А поскольку это не так, то ряд (10.15) расхо-
дится. ▲
Замечание. Требование о том, чтобы неравенства ик < vk выпол-
нялись при всех значениях к = 1, 2, ..., можно ослабить и допус-
тить, чтобы эти неравенства имели место при всех значениях к,
начиная с некоторого номера (к + 1). При этом утверждения теоре-
мы останутся в силе. Действительно, этот случай может быть све-
ден к предыдущему путем отбрасывания первых к членов у обоих
рядов. При этом сходимость или расходимость исходных и преоб-
разованных рядов не изменится. Применяя к рядам с отброшен-
ными членами теорему 10.7, возвращаемся к исходным рядам,
добавляя те члены, которые были отброшены, и получаем, что
результат верен и в рассматриваемом случае.
Пример 10.5. Дан ряд
]_
Д ’
Исследуем вопрос о его сходимости с помощью первой теоре-
мы сравнения. Для этого воспользуемся сходящимся рядом из при-
мера 10.1:
— + — + — + +----------!---+ ... = У--!---.	(10.16)
1-2 2-3 3-4 л(л + 1) и(и + 1)
230
У рассматриваемого ряда г отбросим первый член. Новый
ряд будет выглядеть так 1 п
1	1	1	1	1 /щ п\
2-2 3-3 4-4 (л + 1)(л + 1)	^(л + 1)2 7	7
Его члены меньше соответствующих членов ряда (10.16). По
первой теореме сравнения ряд (10.17) сходится. Добавляя к нему
отброшенный первый член, получаем ряд > —который также
обязан сходиться. Найти сумму этого ряда значительно труднее,
у-1	1 г	cz	V 1
чем у ряда У ------. Без доказательства сообщим, что > — = —,
+	6
где л = 3,14159265... — отношение длины окружности к длине ее
диаметра.
Пример 10.6. Рассмотрим еще один ряд
™	1
2~г-
n=i
Этот ряд расходится по первой теореме сравнения. Чтобы убе-
диться в этом, надо сравнить этот ряд с расходящимся рядом
,111	1	1
234	п
(гармонический ряд, см. пример 10.3). Действительно, при всех п
имеет место неравенство
1 > 1
у[Й~ п’
из которого следует, что данный ряд расходится.
Теорема 10.8 (вторая теорема сравнения). Пусть имеются два
ряда с положительными членами
U[ + U-2 + W3 + ... + ип + ...,	(10.18)
ц +	+ v3 + ••• +	•	(10.19)
И пусть существует конечный предел
lim —=
vn
где К > 0. Тогда оба ряда либо одновременно сходятся, либо одно-
временно расходятся.
Доказательство. Поскольку lim — = К. пользуясь определени-
ям v„	к
ем предела числовой последовательности, выбираем е = — > 0, для
231
которого найдется N = Л(с) такое, что при всех п> N будет выпол-
няться неравенство
^-К < е.
vfl
Это неравенство эквивалентно двойному неравенству
K-v< — < К + г,
vfl
К
из которого следует (с учетом того, что е = — > 0), что для всех
п > N будут выполняться такие неравенства:
ч ЗК	2и„
а) и„ <—vn-, б) vn
2.	л
Теперь, если сходится ряд (10.18), то из неравенства б) и первой
теоремы сравнения (см. теорему 10.7) следует, что сходится ряд
(10.19). Если же сходится ряд (10.19), то ряд (10.18) будет также
сходиться, что следует из неравенства а) и первой теоремы срав-
нения. Таким образом, ряды (10.18) сходятся (а значит, и расхо-
дятся) одновременно. ▲
Замечание., Нетрудно доказать, что если К = 0, то из сходимости
ряда (10.19) следует сходимость ряда (10.18), а обратное неверно.
Меняя ролями ряды (10.18) и (10.19), получим, что если К= +<*>,
то из сходимости ряда (10.18) следует сходимость ряда (10.19), а
обратное неверно.
Пример 10.7. Дан ряд
Исследуем его на сходимость с помощью второй теоремы срав-
нения. Для этого вспомним, что если с/.,; — бесконечно малая пос-
ледовательность, то 1п(1 + ая) также будет бесконечно малой пос-
ледовательностью, причем эквивалентной ая. Следовательно,
In ( 1 + Д |
и2-
lim	= 1 > 0
1
п1
и рассматриваемый ряд сходится, поскольку (как нам уже извест-
но) СХОДИТСЯ ряд
Л=1
Пример 10,8. Анализируя ряд
Ё1п(1+-М
л=]	VW )
232
аналогично предыдущему, сравниваем его с рядом У —j=. Поскольку
Л=1
этот ряд расходится (см. пример 10.6), то, по второй теореме срав-
нения, получим, что и исследуемый ряд расходится.
10.1.7.	Признаки Даламбера и Коши
Достаточные условия сходимости ряда обычно называют при-
знаками сходимости. Иногда объединяют в одну группу как доста-
точные условия сходимости, так и достаточные условия расходи-
мости ряда. Для рядов с положительными членами признаков схо-
димости довольно много. Ниже будут рассмотрены наиболее упот-
ребительные из них.
Теорема 10.9 (признак Даламбера). Пусть дан ряд с положи-
тельными членами
U[ +	+ иу + ... + ип + ...	(10.20)
и пусть существует конечный предел
lim^i±L = р
Тогда:
а)	если р < 1, то ряд (10.20) сходится;
б)	если р > 1, то ряд (10.20) расходится;
в)	если р = 1, то вопрос о сходимости ряда (10.20) остается
открытым.
Доказательство. Пусть имеет место случай а), т.е. р < 1. Между
.	р + 1 п „
числами р и 1 находится число q =	. Действительно, имеем
Р	Р	Р	1	Р+1 Р	1	1	1	1
н 2	2	2	2	2	4 2	2	2	2
Следовательно, выполняются неравенства р < q < 1. Возьмем
положительное число е = q - р. Для этого е найдется номер N = 7V(e)
такой, что для любого п > N будет выполняться неравенство
^±L_p
< е,
которое эквивалентно двойному неравенству (с учетом того, что
е = Q - Р)
Из неравенства
ип+\
ип
< Q-
^п+\
ип
233
следует, что при п > N будет выполняться неравенство
ww+i < qun.
Разделим правую и левую части этого неравенства на С'1- Получим
> ^п+\
qn q"+] ’
т.е. последовательность
монотонно убывает с ростом п и при этом ограничена снизу (//,, > 0).
Следовательно, существует предел
>0.
По второй теореме сравнения для рядов с положительными чле-
нами получаем, что ряд (10.20) сходится, если сходится ряд ^qn.
л=1
Но этот ряд был рассмотрен в примере 10.2. Там было установле-
но, что он сходится при условии, что |(?| < 1. Поскольку в нашем
случае 0 < q < 1, то ряд ^qn сходится, а с ним — и ряд (10.20).
л=1
Рассмотрим теперь случай б):
lini^±L = p > 1.
п^°° ип
Здесь имеем 1 < q < р. В качестве е > 0 возьмем число р - q. Для
него найдется номер N' = N'(e) такой, что для всех п > N' будет
выполняться неравенство
—-Р <е,
«„
эквивалентное двойному неравенству, в котором заменим е через
Р - Q,
q <	< 2р - q.
ип
Пользуясь первой частью этого неравенства, получим
поскольку q > 1. Из этого неравенства следует, что последователь-
ность ип > 0 и монотонно возрастает. Следовательно, ип не стре-
мится к нулю при п —> ©о, т. е. не выполняется необходимое условие
сходимости ряда. Отсюда следует, что ряд (10.20) расходится.
234
Чтобы доказать, что в случае в), когда
JJ	’
из этого факта нельзя сделать никакого вывода о сходимости ряда,
достаточно предъявить два ряда, для которых р = 1, один из кото-
рых сходится, а другой — расходится. Пример сходящегося ряда
дает ряд У —7, рассмотренный в примере 10.5. Действительно,
Zt	j
п2
= lim-------у = 1.
Нт-—т-
1
п2
Таким образом, р = 1 и ряд сходится. Другой пример расходящего-
ся ряда дает ряд рассмотренный в примере 10.6. Для него
имеем	W=1
1
. yl(n + 1)	.	.
р = lim —— ----= lim .	= lim
+ 1)
4n
Таким образом, p = 1 и ряд расходится. ▲
Замечание. Нетрудно распространить применение признака Да-
ламбера и на тот случай, когда
lim^^- =
В этом случае ряд (1.19) расходится. Для доказательства заме-
тим, что начиная с некоторого номера будет выполняться нера-
венство —— > 1, из которого следует, что ип+} > и„. Следовательно,
и„ не стремится к нулю и ряд расходится.
Пример 10.9. Пусть требуется исследовать на сходимость ряд
У — ,
э/?
и=1 2
Применим признак Даламбера, для чего вычислим предел
п +1
..	Э«+1	/7 + 1	1
р = игл —---= lim---= —.
п 2п 2
2"
Поскольку р < 1, то, по признаку Даламбера, ряд jTсходится.
„=1 2
235
Пример 10.10, Исследуем на сходимость ряд
f)=l J
Применим признак Даламбера, для чего вычислим предел
(/7 + 1)!
V'+1	1-	/7 + 1
р = lim J ,— = lim-------= +оо.
F
v-i /7 '
В силу замечания к признаку Даламбера ряд 2^—- расходится.
п=]
Теорема 10.10 (признак Коши). Пусть дан ряд с положительны-
ми членами
U[ + ih + Uy + ... + ип + ...	(10.21)
и пусть существует конечный предел lim^wfl = р. Тогда:
а)	если р < 1, то ряд (10.21) сходится;
б)	если р > 1, то ряд (10.21) расходится;
в)	если р = 1, то вопрос о сходимости ряда (10.21) остается
открытым.
Доказательство. Пусть имеет место случай а), т.е. р <
выше, берем число q =
, которое оказывается между
1. Как и
числами
Р + 1
2
р и 1: справедливы неравенства р < q < 1. Возьмем положительное
число е = q - р. Для этого е найдется номер TV = JV(e) такой, что для
любого п > N будет выполняться неравенство
|^-Р|< е,
которое эквивалентно двойному неравенству (с учетом того, что
е = Q- Р):
2р <	< q.
Из неравенства
д/ < Q
следует, что при п > N будет выполняться неравенство
ип < qn.
Поскольку q < 1, то ряд сходится. По первой теореме сравне-
Я=]
ния, сходится и ряд (10.21).
Рассмотрим теперь случай б): lim = р > 1. В этом случае име-
ем 1 < q < р. В качестве е > 0 возьмем число р - q. Для него найдется
236
номер N' = N'(p) такой, что для всех п > N' будет выполняться
неравенство
эквивалентное двойному неравенству, в котором заменим е через
Р -
q <	< 2р - q.
Пользуясь первой частью этого неравенства, получим, что
> qn.
Поскольку q > 1, то ряд ^\q,: расходится. По первой теореме срав-
?i=i
нения расходится и ряд (10.21).
В случае в), т. е. когда р = lim у'У = 1, достаточно предъявить два
ряда, удовлетворяющих этому условию, из которых один сходит-
ся, а другой расходится. Если вспомнить, что lim tfn = 1, то станет
очевидным, что в качестве двух искомых рядов можно взять ряды
У — (сходится) и расходящийся гармонический ряд У—. Для
обоих рядов р = lim = 1. ▲
Замечание., Аналогично тому, как это делалось применительно
к признаку Даламбера, можно показать, что в случае, когда р =
= lim = +<*>, ряд (10.21) расходится.
Общее замечание, касающееся как признака Даламбера, так и
признака Коши, состоит в том, что если р > 1 или р = +о°, то, как
было видно из доказательств, общий член ряда не стремится к
нулю (не выполняется необходимое условие сходимости).
[ч п
----- с по-
Зл + 1)
мощью признака Коши. Имеем
г ( п 1	.. п 1 .
р = пт «  ------ = lim ------ = - < 1 .
«^“^3/7 + 1 J 3/7 + 1	3
По признаку Коши, ряд сходится.	«>
Пример 10,13. Исследуем на сходимость ряд У,— с помощью
признака Коши. Имеем	«=1 п
р = lim = lim —Д— = 2 > 1
Здесь было учтено, что lim tfn = 1.
Л—
По признаку Коши, ряд расходится.
237
10.1.8.	Интегральный признак сходимости
Теорема 10.11. Пусть у = f(x) — функция, определенная при
х > 1, непрерывная, положительная и монотонно убывающая. Рас-
смотрим ряд
и} + и2 + и3 + ... + и„ +	(10.22)
где и„ = f(n), п = 1, 2, ..., и несобственный интеграл
//(х)Л.	(10.23)
]
Тогда ряд (10.22) и интеграл (10.23) сходятся или расходятся
одновременно.
Доказательство. Представим J f(x)dx как сумму интегралов по
]
отрезкам [1; 2], [2; 3], [3; 4],	[п; п + 1]. Получаем равенство
j f(x)dx = £ f f(x)dx.
i	£=i k
jt+]
Каждый из интегралов j" f(x)dx представляет число, равное
k
площади криволинейной трапеции ££1)£(рис. 10.1).
Поскольку функция f(x) монотонно убывает, то площадь ука-
занной трапеции оказывается меньше, чем площадь прямоуголь-
ника EBCF, и больше, чем площадь прямоугольника EADF. Пло-
щадь первого из них численно равна его высоте (так как длина
основания равна единице), т.е. /(£). Аналогично площадь второго
прямоугольника равна f(k+ 1). Таким образом, имеем
Ж + 1) < J f(x)dx <f(k), k=\,2, .... п.
Складывая эти неравенства, по-
лучим
±fik + \)<± \f(x)dx<±f(k),
k=l	k=] /с	k=l
причем
±f(k + \) = S„+l-Ul.
k=]
Сумма интегралов преобразуется в
интеграл по формуле
и Zr+1	я+]
X J f(x)dx = J f(x)dx,
Zr=l к	]
Я
а последняя сумма ^/W = s„, где s„ — л-я частичная сумма pac-
*=j
сматриваемого ряда. Итак, для любого п получены следующие не-
равенства:
Л+1
^+1 - «I < f f(x)dx < s„.	(10.24)
1
Теперь заметим, что из сходимости интеграла J f(x)dx вытека-
]
ет, что при п —> оо существует предел числовой последователь-
ности
сп = J7(x)dx,
i
равный о, который, в силу монотонного возрастания этой после-
довательности, больше, чем любой член о,;. Поэтому если | f(x)dx
сходится, то для любого п справедливо неравенство 1
]/(х)ббс < ст.
]
Используя первое из неравенств (10.24), получим
л+1
s„+1 < и} + j f(x)dx <	+ (J.
i
Это неравенство показывает, что частичные суммы ряда (10.22)
ограничены (справа стоит число, которое не зависит от п). Для
рядов с положительными членами это условие является необходи-
мым и достаточным для их сходимости. Следовательно, если ин-
теграл (10.23) сходится, то сходится и ряд (10.22).
Пусть теперь дано, что ряд (10.22) сходится. Тогда любая
частичная сумма s,; меньше, чем сумма всего ряда s, т.е. для любо-
го п имеет место неравенство s„ < s. Из второй части неравенства
п
(10.24)	следует, что последовательность = \f(x)dx ограничена,
л+1	*
(ай+] = j f(x)dx < s„< s'). Но монотонная и ограниченная последо-
вательность является сходящейся. Следовательно, при п —> суще-
п
ствует предел числовой последовательности пн = |/(х)</х. Отсюда
следует, что интеграл (10.23) сходится. ▲	1
239
Пример 10,14. Рассмотрим ряд У, —, где а > 0. Этот ряд удов-
«=]"
летворяет условиям интегралвного признака сходимости. Соответ-
..	..	7 dx „
ствующии несобственный интеграл имеет вид:	—. Про него из-
вестно, что он сходится, если а > 1, и расходится, если а < 1. Сле-
V 1
дователвно, то же самое можно сказать про ряд > —: ряд сходит-
ся при а > 1 и расходится при а < 1. В частности, при а = 1 получается
другое доказательство расходимости гармонического ряда .
«=]п
10.1.9.	Знакочередующиеся ряды
Определение 10.2, Рассмотрим ряд, у которого члены ряда по
очереди меняют знак:
и} - w2 + «3 - «4 + ... + (-1)/?+1«„ +	(10.25)
где все и„ > 0. Такой ряд называется знакочередующимся рядом.
Пример 10.14.
(-1Г1	Illi	(-1Г1
L^ = 1-T + T-T + T-- + L^ + --	<10-26>
и	2 3 4 5 п
Для знакочередующихся рядов имеет место достаточный при-
знак сходимости, который выражается в следующей теореме.
Теорема 10.12 (признак Лейбница). Пусть дан ряд (10.25), удов-
летворяющий следующим требованиям:
1)	члены ряда по абсолютному значению монотонно убывают,
т.е.
> и2 > «з > и4 > ... > ufl > ...;
2)	общий член ряда при п —> <х> стремится к нулю, т.е.
Нт ип = 0.
fl —
Тогда ряд (10.25) сходится.
Доказательство. Возьмем частичную сумму ряда (10.25), содер-
жащую четное число слагаемых, т.е. частичную сумму
s2m =и\~ и1+	w4 +  + и2/и-1 “ и2т= (и] ~ и1) + (w3“	+ •• + ( H2ffJ_] - W2m).
Поскольку все слагаемые, заключенные в скобки, положитель-
ны (в силу монотонного убывания последовательности «„), то с
ростом т последовательность s2m монотонно возрастает: с увеличе-
нием т добавляются новые положительные слагаемые. Теперь пере-
пишем в другом виде выражение для s2m:
240
s2m - U] - U2 + U3 - U4 + ... - U2m_2 + u2m~] ~ li2m ~
= U}- (U2 - W3) - (W4 - W5) - ... - (U2m_2 - U2m_}) - U2m.
Все слагаемые, заключенные в скобки, положительны, как и
последнее слагаемое. Поэтому
< W|.
Итак, получено, что последовательность s2m монотонно возрас-
тает и ограничена сверху. Следовательно, существует предел
lim s2m = s.
Теперь рассмотрим частичную сумму ряда (10.25), содержащую
нечетное число слагаемых,
52m+l = s2m + w2m+l-
Для нее имеем
lim s2m+l = lim s2m + lim u2m+i = s,
так как lim u2m+1 = 0 (по условию теоремы, последовательность un
m—
имеет предел, равный нулю, тогда любая ее подпоследователь-
ность, в частности и2т+1, имеет тот же предел). Таким образом, две
подпоследовательности последовательности s„: s2m и s2m+i имеют
общий предел, равный 5. Этого достаточно, чтобы утверждать, что
lim^ =s. Действительно, если имеется произвольное е > 0, для
fl —>00
него найдутся номера jVj = 7У](е) и N2 = TV2(e) такие, что при выпол-
нении условий 2т > N\ и 2т + 1 > N2 будут верными неравенства:
|s2m - s| < е и |s2m+i - s| < е.
Если обозначить через
N= 7V(e) = max{JV],JV2},
т.е. наибольшее из чисел jV] и N2, то при выполнении условия
п > N = 7V(e) будет верным неравенство |sfl - s| < е независимо от
того, является ли п четным или нечетным. Следовательно,
lim sn = s.
п—
Это означает, что ряд (10.25) сходится. ▲
Пример 10,15. Рассмотрим ряд (10.26)
п 2 3 4 5 п
Для него ип = —. Эта последовательность, монотонно убывая,
п
стремится к нулю, т. е. выполнены оба условия признака Лейбница.
Следовательно, ряд (10.26) сходится.
241
10.1.10.	Знакопеременные ряды
Пусть дан ряд
= й] + «2 + w3 +  +	• ••>	(10.27)
л=]
удовлетворяющий условию: его члены ип * 0 и имеют произволь-
ные знаки.
Тогда ряд
Ёы = |«]| + |«2| + |«з1 + - + 1"«1 + -	(10.28)
?i=i
будет рядом с положительными членами, и к нему применимы те
подходы, которые были разобраны выше. На вопрос о связи меж-
ду сходимостью ряда (10.27) и ряда (10.28) дает ответ следующая
теорема.
Теорема 10.13. Из сходимости ряда £|ин| вытекает сходимость
т-i	fl=i
ряда 2Л"-
Л=1
Доказательство. По критерию Коши сходимости рядов, для схо-
димости ряда ^и>: достаточно, чтобы для любого е > 0 нашелся
«=1
номер N = 7У(е) такой, что при любом п > N и любом р выполня-
лось бы неравенство
I ^я+]	^п+2	«л+р|<е.	(10.29)
Поскольку ряд £|«я| сходится, то, по тому же критерию Коши
?i=i
(имея в виду, что его условие является и необходимым), получим,
что для выбранного выше е > 0 найдется номер N = 7V(e) такой,
что при при любом п > N и любом р будет выполняться неравен-
ство
I I I ^«+2| + ••• + I Чц+р\ < £•
Из этого неравенства следует, что при любом п > N и любом р
будет выполняться достаточное для сходимости ряда £ ип условие
(10.29). Действительно, имеем
I ^п+1 + ^п+2 + • • - + ^n+p I — I I + I «й+2| + +! Uft+P I
Здесь использовано известное из курса математики средней шко-
лы неравенство \а + b\ < |а| + |6|, т.е. модуль суммы не превосходит
суммы модулей каждого из слагаемых. Таким образом, ряд
сходится по критерию Коши. ▲	w=l
242
Замечание. Из сходимости ряда не вытекает сходимость
«=i
- (-1)"41
ряда У |wfl|. Действительно, ряд У -—-—, как было показано выше,
«=]	Я = ]	п < |
сходится, а ряд из модулей его членов У — (гармонический ряд)
Zi 11
расходится.
Пример 10.16. Рассмотрим ряд
у 5Н1(/7л/2)
Zf «2
Этот ряд сходится, так как сходится ряд, составленный из мо-
I sin(/b/2) I
дулей его членов: 5 1--------1 (по первой теореме сравнения для
Zt
рядов с положительными членами в силу неравенства
| sin(/?V2) | < 1
п2 п2
случае, когда
что ряд У ип
ряд Уд; сходится, ряд
Л=]
сходится условно.
V 1 \
и сходимости ряда У
7^"
Определение 10,3. В том
У|мЛ| расходится, говорят,
//=1	Г1— I
Определение 10.4. В том случае, когда ряд У ип сходится вместе
ОО	00/7=]
с рядом У |ыя|, говорят, что ряд У и„ сходится абсолютно.
?i=l	л=]
Например, рассмотренный выше ряд
у '
Z1 «
V 1 D
сходится условно, так как расходится ряд У—. Ряд
_	«=] w
у sin(wV2)
Zf «2
Л	I sin(/iV2) I
сходится абсолютно, потому что ряд У J----------1 сходится.
Zf п2
10.1.11.	Признаки абсолютной сходимости рядов
Поскольку ряд, составленный из модулей членов ряда У и„,
т.е. ряд У|ил|, является рядом с положительными членами, то к
243
нему применимы некоторые из признаков сходимости для таких
рядов. Если будет установлена сходимость ряда £ | ип |, то по теореме
=	л=1
10.13 будет сходиться и ряд Поэтому достаточные условия
=	«=i
сходимости ряда являются достаточными условиями сходи-
ло	Я=]
мости ряда uH. С другой стороны, достаточные условия расхо-
Л=1 со
димости ряда не являются, вообще говоря, условиями рас-
«=]
ходимости ряда 51 и„, так как последний ряд может сходиться ус-
«=1
ловно. Тем не менее признаки Даламбера и Коши удается исполь-
зовать и в случае, когда в силу этих признаков ряд 511 ип | расходится.
л=1
Теорема 10.14 (признак абсолютной сходимости Даламбера).
Пусть дан ряд У, ип, члены которого имеют произвольные знаки.
Н = ]
Рассмотрим ряд УЦмй|, и пусть существует конечный предел
«=]
lim^±J = p.
|«„|
Тогда, если р < 1, то ряд 51 ип сходится абсолютно; если р > 1,
то ряд 51w« расходится; если р = 1, то про сходимость ряда 51
Л=]	Л=]
ничего сказать нельзя.
Доказательство. В случае, когда р < 1, по признаку Даламбера для
рядов с положительными членами, ряд 51lw«l сходится и, по теореме
™	я=]	™
10.13, сходится ряд 51 ип. Поскольку ряд сходится вместе с рядом JJhh|,
Н = ]	?1=1
то сходимость его будет абсолютной. В случае, когда р > 1, ряд
511 и„ | будет расходиться по признаку Даламбера, при этом, как видно
?i=i
из доказательства этого случая, ряд расходится по той причине, что
общий член ряда не стремится к нулю (не выполняется необходимое
условие сходимости). Следовательно, в случае, когда р > 1, получит-
ся, что lim I //,, | #0. Но из этого следует, что lim ип * 0, и необходимое
И—>ео	Я—>оо	оо
условие сходимости не выполняется уже для ряда 51 и- СЛеДОВа-
нН
тельно, он расходится. При р = 1, как это делалось при доказатель-
стве признака Даламбера, можно рассмотреть два ряда:
244
Первый их них, как было показано выше, сходится, а второй —
расходится, так как общий член ряда не стремится к нулю. Для
обоих рядов р = 1:
lim—= 1 иит(« + 1)<« + 1) =1. а
п + 1	п(п + 2)
Теорема 10.15 (признак абсолютной сходимости Коши). Пусть
дан ряд члены которого имеют произвольные знаки. Рас-
л=]	“
смотрим ряд	и пусть существует конечный предел
lim I = p. Тогда, если p < 1, то ряд У сходится абсолютно;
w=l
если р > 1, то ряд расходится; если р = 1, то про сходимость
ряда У ип ничего сказать нельзя.
л=]
Доказательство. Рассуждения в случае признака Коши вполне
аналогичны тем, что были изложены при доказательстве признака
абсолютной сходимости Даламбера, включая примеры для случая
" (-i)H+1
р = 1. Действительно, для сходящегося ряда У -—-—
Zt «
р = lim ЛЛ = lim » — = 1.
Я—™ V	ft
п+} ( п А
Для расходящегося ряда у (-1)	----
/7=1	у w + 1 J
р = lim = lim « —= 1 . ▲
я—у fl + ]
10.2.	Функциональные ряды
10.2.1.	Область сходимости функционального ряда
Определение 10,5, Пусть имеется бесконечная последовательность
функций
ZW, Л(*)>/з(*)>	(10.30)
где все функции определены на общем множестве G с R1.
245
Тогда ряд
£/„(*) = /,(х) + /2(х) + /3(х) + ...+ fn(x) + ...	(10.31)
n=l
называется функциональным рядом.	~
Положим х = х0. Получим числовой ряд 2^fn(xo\ который мо-
жет сходиться или расходиться.	1
Определение 10.6, Если этот ряд сходится, то точка х = х0 назы-
вается точкой сходимости ряда (10.31), а если расходится — точ-
кой расходимости.
Определение 10.7. Совокупность всех точек сходимости ряда
(10.31) называется областью сходимости ряда (10.31).
Область сходимости ряда (10.31) будем обозначать через Q.
Пример 10.17. Пусть требуется найти область сходимости ряда
еА + 2е2* +Зе3х + 4е4х +... + ле"А' +... = ^лепх. (10.32)
Я = ]
Поскольку при любом х леА > 0, то ряд (10.32) является рядом с
положительными членами и можно применить признак Даламбе-
ра. Имеем
„х г ип+\ г (п + 1)е(л+1)А	(л +1)
и„ = пепх, р = lim —— = lim -------= lim еА ----- = еА.
Un	MQflx	п
Таким образом, р = е\ т.е. является функцией от х. Множество
тех значений х, для которых р < 1 (обозначим его через Q[), по
признаку Даламбера, содержится в области сходимости ряда, т.е.
Qi с Q. Чтобы определить это множество, следует решить неравен-
ство еА < 1. Очевидно, что для х должно выполняться неравенство
х < 0. Таким образом, Q] = {х | х< 0}. Множество тех значений х, для
которых р > 1 (обозначим его через Q2), по признаку Даламбера,
не содержится в области сходимости ряда, т. е. Q2 <z О. Чтобы опре-
делить это множество, следует решить неравенство е' > I. Очевид-
но, что для х должно выполняться неравенство х > 0. Таким обра-
зом, О2 = {х | х > 0}, и для всех х, кроме х = 0, решен вопрос о
принадлежности к области сходимости ряда. При х = 0 имеем: и„ = и
и видно, что при и —> оо общий член ряда не стремится к нулю, что
влечет расходимость ряда. Следовательно, точка х = 0 и не принад-
лежит области сходимости. Итак, Q = {х | х < 0}.
10.2.2.	Равномерная сходимость функционального ряда
Пусть имеется функциональный ряд
^Л(х) = /](х) + /2(х) + /з(х) + ... +Л(х) + ...,
w=l
246
для которого областью сходимости является отрезок [а,Ь]. Это оз-
начает, что ряд сходится в каждой точке этого отрезка.
Таким образом, сумма этого ряда, определена в каждой точке
отрезка и представляет собой функцию от х, заданную на этом
отрезке. Обозначим ее через s(x). Следовательно, по определению
суммы ряда, для любого е > 0 и для любого х е [а, Л| найдется
номер N = А'Ц'.х) такой, что при п > N будет выполняться нера-
венство |$(х) - 5я(х)| < е. Эту обычную сходимость функционально-
го ряда иногда называют поточечной сходимостью, или сходимо-
стью в каждой точке. Она не очень удобна, поскольку не всегда
позволяет производить с рядами и их суммами операции, исполь-
зуемые в математическом анализе. Например, менять порядок опе-
раций таких, как переход к пределу и суммирование ряда.
Если ряд сходится в каждой точке отрезка [а,Ь], то без допол-
нительных условий не всегда будет выполняться равенство
lim £ f„(x) = £ lim f„(x).
x^Xa n=l	n=]
Аналогично обстоит дело и с другими операциями математи-
ческого анализа. Дополнительные условия на сходимость ряда ока-
залось эффективным формулировать в терминах так называемой
равномерной сходимости ряда.
Определение 10.8. Ряд £/й(х) называется равномерно сходящим-
п=\
ся на [«,/>], если и только если он сходится в каждой точке отрезка
[а,Ь\ к сумме s(x) и для любого е > 0 найдется номер N = А(е),
зависящий от е и не зависящий от х, такой, что при п > N для
любого х е [а,Ь\ выполняется неравенство
|5(х) - 5й(х)| < е.
Термин «равномерная сходимость» вполне соответствует по
смыслу характеру сходимости ряда на отрезке: ряд сходится таким
образом, что во всех точках отрезка приближение с ростом п после-
довательности sn(x) к своему пределу s(x) происходит равномер-
но, т.е. для получения приближения частичной суммы ряда 5я(х)
к сумме ряда .six) с точностью до е > 0 во всех точках отрезка
достаточно одинаковой величины п: п > А(е).
10.2.3.	Критерий Коши равномерной сходимости ряда
Этот критерий, как и критерий сходимости числового ряда, ос-
нован на критерии Коши сходимости числовых последовательностей.
Теорема 10.16 (критерий Коши равномерной сходимости). Ряд
£/я(х) сходится равномерно на отрезке [а,Ь] тогда и только тог-
л=1
247
да, когда для любого е > 0 найдется номер N = N(e), зависящий от
е и не зависящий от х, такой, что при п > N и любом натуральном
р для всех А' е [а, /?| выполняется неравенство
|sw(x) - 5й(х)| < е.
Доказательство. Докажем сначала необходимость. Пусть ряд
£/л(х) сходится равномерно на отрезке [а,Ь]. Надо доказать, что
Л=1
для любого е > 0 найдется номер N = N(e), зависящий от е и не
зависящий от х, такой, что при п > N и любом натуральном р для
всех хе [а,Ь\ выполняется неравенство
|sw(x) - 5й(х)| < е.
Пусть задано е > 0. Из равномерной сходимости ряда следует,
е
ЧТО ДЛЯ £] = —
и для всех х е
> 0 найдется номер /V =	— j
[а, /?| выполняется неравенство
такой, что при п
> N
|s(x) - 5й(х)| <
Поскольку п + р > N, то
|s(x) - 5„+/?(х)| < |
для всех х е [а, />]. Пользуясь этими неравенствами, получаем
|^+/х) - S„(X)| = |5Й+/Х) - 5(Х) + 5(Х) - 5й(х)| <
1МХ) -	+15<*) -	< f+ f = е
для всех х е [а, д], что и требовалось доказать.
Теперь доказываем достаточность. Дано, что условия критерия
Коши выполнены. Надо доказать, что ряд сходится равномерно.
Из критерия Коши для числовых последовательностей следует,
что ряд ^/я(х) сходится в каждой точке х е [«,/>]. Обозначим его
Я=1	g
сумму через s(x). Пусть е > 0 задано. Возьмем Е] = — > 0. По условию
теоремы найдется номер JV = JV(e), зависящий от е и не зависящий
от х, такой, что при п > N и любом натуральном р для всех х е [а, Ь]
выполняется неравенство
IM*) -	< f •
В этом неравенстве перейдем к пределу при р —> «->. Получим,
что
248
lim|5fl+(x) - s„(x)| = l*(x) - 5„(x)| < ^ < e, т.е. при n > JV(e)
p^°°	2
и любом A' e [a,b\ выполняется неравенство
|s(x) - 5„(x)| < e.
Это, по определению, означает, что ряд ^/я(х) сходится равно-
мерно на отрезке [«,/>]. ▲	"=l
10.2.4.	Признак Вейерштрасса равномерной сходимости ряда
Выяснение вопроса о равномерной сходимости ряда часто ока-
зывается более простым, чем на основе определения, если пользо-
ваться достаточными условиями равномерной сходимости ряда
У, /я(х), называемыми признаками равномерной сходимости. Наи-
л=1
более употребительным из них является признак Вейерштрасса.
Теорема 10.17 (признак Вейерштрасса). Пусть для ряда У/я(х),
?i=i
рассматриваемого на отрезке [«,/>], существует сходящийся число-
вой ряд ^с,: такой, что для всех п = 1, 2, 3, ... и любого х е [«,/»]
я=]
выполняются неравенства
1Л(*)1 с„.
Тогда ряд £Л(х) сходится равномерно на отрезке [я, 6].
?i=i
Доказательство. По первой теореме сравнения для рядов с по-
ложительными членами получается, что в каждой точке отрезка
[а,Ь\ сходится ряд У|/Я(х) |, откуда следует, что в каждой точке
л=1	™
этого отрезка сходится ряд У/Н(х) (по теореме 10.13). Обозначим
«=] ™
его сумму через s(x), сумму ряда 2_Д,: — через о, а его п-ю частич-
«=]
ную сумму — через ап. Тогда
(J — Оя — Ся+] + Сп+2 +	+ ... —
— остаток числового ряда Он стремится к нулю при п —>
л=1
Это означает, что для любого е > 0 найдется номер N= 7V(e) такой,
что при п > N будет выполняться неравенство |гя| < е. Но из нера-
венств |/,(х)| < с,; следует, что все сн > 0. Поэтому |гя| = гн.
Таким образом, при п > N
Гп ~	+ Сп+2 +	+ ... < Е.
249
Теперь имеем для любого х g [л, /?|
|5(х) - 5я(х)| = |/я+1(х) + /,+2(х) + f„+3(x) + ... | <
|/1+](х)| + iTLOOl + 1Л+з(х)| + ... .
Это неравенство получается предельным переходом в неравен-
стве для частичных сумм сходящихся рядов У А(х)и У |/Не-
действительно,	к=”+] k=n+l
l/,+i(*) +/,+2<Н + - +Л+т(*)1 1Л+|(*)1 + 1Л+2(*) I + - + 1Л+ИН1
и предельный переход при т —> приводит к приведенному выше
неравенству.
Теперь, пользуясь неравенствами |/(х)| < с„, получаем
|s(x) - 5й(х)| < |/,+i(x)| + |/fl+2(x)| + |/+3(х)| + ... < с„+] + с„+2 + с„+3 + ... < е.
Здесь также применяется предельный переход в неравенстве
|/н-1(-0| + |/г+2(Т) I + l/i+зСО I + ••• + |/н-т(/) I — Сг+1 + ^"я+2 + *-т?+3 +  + ^п+т
при т —> оо. Итак, для заданного е > 0 найден номер N = JV(e)
такой, что при п> N для любого х g [а, /?| будет выполняться нера-
венство
|5(х) - 5„(х)| < е.
Это означает, что ряд У/„(х) сходится равномерно на отрезке
[л, £]. А	"=’
Замечание., Для ряда У /,(х) сходящийся ряд У/',,. для которо-
го справедливы неравенства
|/Дх)| < cfl, д = 1, 2, 3, ...,
называется мажорирующим рядом. Теперь можно кратко сформу-
лировать признак Вейерштрасса так: если на отрезке [а,Ь\ у ряда
существует мажорирующий ряд, то ряд сходится равномерно на
этом отрезке.
Пример 10.18. Рассмотрим на произвольном отрезке [а, /?| функ-
sin (дх) .,	г
циональныи ряд 5------—- . Нетрудно убедиться в том, что у этого
Zt «	» j
ряда мажорирующим будет ряд 51 “. Действительно, ряд этот схо-
Л=1 п
дится. При всех х g [а,Л| и при всех п = 1, 2, 3, ... имеют место
I sin (дх) Llj-.	_ ..
неравенства ----=— < —г. Применяя признак Вейерштрасса, полу-
| п1 | д2
sin (дх)	г	, „
чаем, что ряд > --—- сходится равномерно на любом отрезке | <7. Ь\.
250
10.2.5.	Общие свойства функциональных рядов
Свойства функциональных рядов выражаются в следующих
теоремах.
Теорема 10.18 (о непрерывности суммы ряда). Если функцио-
нальный ряд £/я(х) сходится равномерно на отрезке [а,/>], при-
?i=i
чем все члены ряда непрерывны на этом отрезке, то и сумма ряда
непрерывна на этом отрезке.
Доказательство. Пусть задано е > 0. В силу равномерной сходи-
мости ряда найдется номер N = _/V(e) такой, что при п > N для
любого х е [й, /?| будет выполняться неравенство
|s(x) - s„(x)| < |.
Пусть х = х,| произвольная фиксированная точка отрезка [а, Ь].
Тогда при п > N будут выполняться неравенства:
|s(x0) - s„(xo)| < | И |s(x0 + Ах) - 5я(х0 + Ах)| < |.
Рассмотрим
|s(x0 + Ах) - 5(х0) I =
= |[s(x0 + Ах) - S„(Xo + Ах)] + [5„(х0 + Ах) - 5„(х0)] + [5„(х0) - s(x0)] <
< |s(x0 + Ах) - s„(x0 + Ах)| + |ля(х0 + Ах) - s„(x0)| + |s„(x0) - s(x0) |.
Поскольку члены ряда непрерывны в точке х0, то будет непре-
рывной и конечная сумма непрерывных слагаемых: функция $я(х).
Поэтому найдется 5 > 0 такое, что при |Ах| < 5 будет выполняться
неравенство
|5я(х0+Лх)-5„(х0)|<|.
Таким образом, для заданного е > 0 найдено S > 0 такое, что
при |Ах| < 5 имеем
|5(х0 + Ах) - s(x0)| < |s(x0 + Ах) - <Цх0 + Ах)| +
+ |5fl(X() + Ах) - S„(Xq) | + |5я(х0) - 5(х0) l<f + f + | = £-
Это означает, что функция а(х) непрерывна в точке х0. ▲
Теорема 10.19 (о почленном интегрировании ряда). Если функ-
циональный ряд ^/н(х) сходится равномерно на отрезке [а,Ь],
Я = ]
причем все члены ряда непрерывны на этом отрезке, то
/Ё fn(x)dx = £ |/л(х)<Ух.
а »=1	л=1а
251
Доказательство. Прежде всего заметим, что сумма ряда s(x) по
теореме о непрерывности суммы равномерно сходящегося ряда
является непрерывной и поэтому
b	ь „
п = р(х)й6с =
а	а ,,=1
существует, так как непрерывная функция является интегрируемой.
Теперь рассмотрим ряд
YjfMdx.
«=1 а
п
Пусть = ^^fk(x)dx — его частичная сумма. Оценим величину
£=1 й
|о - оя|. Имеем
|о - oj =
а ^=1	^=1 а
f X fk (x)dx - J £ fk (x) dx
a k=\	a k=\
£ fk(x)dx <] £ Л(х) dx-
k=n+\	a k=n+{
Пусть теперь задано e > 0. В силу равномерной сходимости ряда
найдется номер N = 7V(e) такой, что при п> N для любого х е [а, Ь]
будет выполняться неравенство
|5(х) - 5„(х)| =
£ aw
£=/?+!
е
(Ь-а\
Таким образом, если п > N, то
Это означает, что последовательность частичных сумм <зп ряда
со Ь
£j/„(x)dx сходится к
л=1 а
Ь	Ь оо
0 = 1 s(x)dx = Л (x)dx,
а	а я=1
т. е. о является суммой этого ряда. Поэтому
b со	QO Ь
= £]7„(х)г&. А
а л=1	»=1а
252
Теорема 10.20 (о почленном дифференцировании ряда). Пусть
имеется ряд ^fn(x), члены которого f„(x) определены и непре-
«=i	df
рывны вместе со своими производными -^-(х) на интервале (а,Ь),
dx
причем сам ряд сходится в некоторой точке х0 е (а, Ь). Пусть, кроме
того, ряд У (х) сходится равномерно на каждом [а, В] с (а.Ь).
Zt
Тогда ряд У сходится на всем интервале (а,Ь), его сумма
Л = ]
дифференцируема на («,/>) и
^^Zt J ^dx
Доказательство этой теоремы здесь не приводим.
Замечание., Можно доказать, что при выполнении условий тео-
ремы сам ряд У fn(x) не только сходится в каждой точке интерва-
«=]
ла (а, Ь), но и сходится равномерно на любом отрезке [ос, [3] с (а, Ь).
10.3.	Степенные ряды
Определение 10.9. Степенным рядом называется ряд следующего
вида:
с0 + С[Х+ срС + срС + ... + с„х" + ... = У сцхп.	(10.33)
«=0
Эти ряды являются частным, но очень важным случаем функ-
циональных рядов. Общий член ряда (10.33) имеет вид
fM = спхп, п = 0, 1, ... .
Числа сп называются коэффициентами степенного ряда. Рассмат-
риваются также ряды
У с^х-хф” = Са+с](х-хф + с2(х-хф2 + су(х-хф2+... + сп(х-х())п+...,
п=0
называемые степенными рядами в точке х0. Эти ряды сводятся к
предыдущим заменой z = (х - х0).
Ряд (10.33) всегда сходится в точке х= 0. Возникает вопрос: есть
ли у этого ряда другие точки сходимости?
Теорема 10.21 (теорема Абеля). Если степенной ряд (10.33) сходит-
ся при некотором значении х = X] # 0, то этот ряд сходится и при
том абсолютно при каждом значении х = х2 таком, что |х2| < |xj.
253
Доказательство. Поскольку ряд У с„х^ сходится, то общий член
ряда должен стремиться к нулю при п «о, т.е. последовательность
{c^xf} является сходящейся. А так как всякая сходящаяся последо-
вательность является ограниченной, то найдется положительное
число М такое, что для всех п будет выполняться неравенство
Пусть теперь х = х2 таково, что |х2| < |X]|. Тогда
|сЛ”| = |сХ||^| .
Обозначив q =
*2
Х1
, получим, что для q справедливы неравен-
ства: 0 < q < 1. Таким образом, имеет место оценка | с„х21 < Mqn при
любых значениях п, из которой следует (по первой теореме срав-
нения), что ряд X|с„х21 сходится, поскольку сходится ряд ^Mqn
п=0	п=0
(геометрическая прогрессия со знаменателем 0 < q < 1). По теореме
10.13	получаем, что сходится и притом абсолютно ряд У с„Х2. ▲
“	«=0
Следствие. Если ряд 2^ct,x!: расходится при х = х0, то он будет
«=0
расходиться при любом х таком, что |х| > |х0|.
Доказательство. Действительно, если бы при хтаком, что |х| > |х0|,
ряд ^спхп сходился, то по теореме Абеля должен был бы схо-
«=0	°°
диться ряд У cwXq , что противоречит данному условию. ▲
я=0
10.3.1.	Радиус сходимости степенного ряда
Изучая область сходимости степенного ряда, следует обратить
внимание на тот факт, что если он сходится в какой-то точке х0 # 0,
то, по теореме Абеля, весь интервал (—|х0|, |х0|) содержится в обла-
сти сходимости этого ряда.
Действительно, любая точка х е (-|х0|,|х0|) удовлетворяет нера-
венству |х| < |х0|. По теореме Абеля, ряд в этой точке сходится, т.е.
хе Q. Если |х0| может быть сколь угодно большим, то в этом случае
ряд будет сходиться при всех значениях х. Такие ряды существуют.
™ XfI
Например, ряд У —-, (0!, по определению, считаем равным 1)
«=о
является таким рядом.
Покажем это. Рассмотрим ряд из модулей его членов
Пусть х?* 0.
254
Тогда этот ряд является рядом с положительными членами.
Применим признак Даламбера для решения вопроса о его сходи-
мости. Имеем
г И+1«! г И а 1
lim —°------- = lim ——— = 0 < 1.
|х|"(л + 1)! (п + 1)
Таким образом, при любом х ряд сходится, поскольку сходится
ряд из его модулей (по теореме 10.13).
Рассмотрим теперь другой пример, в котором степенной ряд
сходится только в одной точке х = 0. Это ряд X и! хл. Действитель-
но	оо
но, рассматривая ряд, составленный из модулей его членов X
и применяя к нему признак Даламбера, получим	"=0
г (и +1)!|x|fl+1	.. ,	।
р = hm------1— = lim(/7 + 1)!|х| = +<>о.
п! |х|"
В силу замечания к признаку Даламбера для случая, когда р = +<»,
и замечания к теореме 10.13 ряд X 11 •х” расходится при любом х * 0.
л=0 °°
Пусть теперь у степенного ряда ^с„х" есть как точка сходимо-
и=0
сти Х[, отличная от точки х = 0, так и точка расходимости х2. По
теореме Абеля для всех х таких, что |х| > |х2|, ряд расходится. Следо-
вательно, множество точек сходимости ряда ограничено, а зна-
чит, является ограниченным множество чисел |х|, представляю-
щих расстояния точек сходимости до начала координат. Всякое
ограниченное сверху множество имеет верхнюю грань. Поэтому
существует конечное число R = sup {|х|}, где хе Q.
Определение 10,10, Число R называется радиусом сходимости сте-
пенного ряда £Сих", если оно равно sup {|х|}, где хе Q, когда Q
н=0
отлично от одной точки или всей числовой оси. Если Q = {0}, т.е.
ряд сходится только при х = 0, то, по определению, полагается
R = 0. В случае, когда ряд сходится при любом х, по определению,
полагается R = <».
10.3.2.	Интервал сходимости степенного ряда
Определение 10,11. Интервалом сходимости ряда Xc«xo называ-
ло
ется интервал (~R,R), где R — радиус сходимости ряда.
Прежде всего покажем, что в любой точке этого интервала ряд
сходится.
255
Пусть /г > 0 и точка х0 е (-7?, А). Это значит, что |х0| < R. Возьмем
е = —-—. Тогда, по определению радиуса сходимости и по свой-
ству верхней грани множества в интервале (R - е, R), найдется
число IxJ такое, что ряд £с„х[' будет сходиться. Но
«=о
|у d Р_ * + 1*о| . |х0| + |х0| । ,
|Х]| > л - е - —-— >---------- |х0|.
По теореме Абеля, ряд ^с„х^ сходится и притом абсолютно.
Итак, если |х| < R, то степенной ряд в точке хсходится. С другой
стороны, из определения верхней грани следует, что не существу-
ет точек сходимости ряда, для которых выполняется неравенство
|х| > R. Это означает, что, если выполняется это неравенство, то
ряд расходится. Остается неизученным случай, когда |х| = R, или
х = ±R. Здесь общая закономерность отсутствует: существуют ряды,
у которых имеет место сходимость в обеих точках x = ±R: существу-
ют такие, у которых имеет место сходимость только в одной из
этих точек; и наконец, есть такие ряды, которые расходятся в обе-
их точках. Приведенные ниже примеры демонстрируют эти случаи.
Но прежде чем мы обратимся к этим примерам, необходимо обсу-
дить вопрос о том, как находить радиус сходимости.
Один из способов связан с применением признака Даламбера к
ряду, составленному из модулей членов степенного ряда:
п	»=0
В результате получим
р(х) = lim^l^r1 = limlc^IM= |Х| limKill < 1,
ЫМ" ™ |сй|	|с„|
если
и р(х) > 1, если
lx I > lim-^L
— kU-
В силу замечания к признаку Даламбера для случая р > 1 и в силу
I с I
теоремы 10.13 получаем, что если существует lim . то он и
равен радиусу сходимости ряда. Итак,
R= lim-l^L,	(10.34)
K+il
256
если этот предел существует. Если он бесконечен, то следует счи-
тать, что 7? = оо.
Аналогично, используя признак сходимости Коши, можно по-
лучить для радиуса сходимости такую формулу:
R =-----!•
(10.35)
если этот предел существует. При этом считаем, что если lim = 0,
I-----------------------	fl-
то R = оо, а если Нтм\сп\ = <*>, то R = 0.
/7^00
Пример 10,19. Рассмотрим ряд У —. Найдем его радиус сходи-
и=1
мости по формуле (10.34). В нашем случае
1	п2
=1С"1 = ТТ’ 7f=lim-------у = 1.
И	(п + I)2
Теперь рассмотрим ряд в граничных точках интервала сходимо-
сти (-1,1), т.е. при х = ±1. При х = 1 получается сходящийся ряд
У — (по интегральному признаку сходимости), а при х = -1 име-
и=1 п ™ (—1)"
ем ряд У —=—, который сходится в силу теоремы 10.13. Таким
Zi п
Л~1	” хп
образом, ряд У -г- сходится на обоих концах своего интервала
Zt
сходимости. Его областью сходимости будет [-1,1], т.е. интервал
сходимости не совпадает с областью сходимости.
” хл
Пример 10.20. Рассмотрим ряд У —. Для него находим
11=1 П
R = lim—2— = 1.
(п + 1)
Исследование вопроса о сходимости ряда на концах интервала
сходимости (-1,1) приводит к двум рядам: У -—— и У —. Пер-
Zt "	»=] «
выи из них был рассмотрен выше и является сходящимся. Второй,
известный под названием гармонического ряда, расходится. Таким
образом, область сходимости ряда у — представляет собой по-
луинтервал [-1,1).	оо	П = ] п
Пример 10.21. Дан ряд ^хл. Для него сн = |cj = 1. Найдем его
«=о
радиус сходимости по формуле (10.35). Имеем
R = —= 1.
257
Следовательно интервал (-1,1) будет для этого ряда интерва-
лом сходимости. Исследование граничных точек интервала сходи-
мости приводит к рядам X (+1)" и £ (-1)", которые являются рас-
я=0	л=0
холящимися (общий член ряда не стремится к нулю, не выполне-
но необходимое условие сходимости ряда). Поэтому для ряда £ хп
«=0
область сходимости совпадает с интервалом сходимости: (-1,1).
Таким образом, разобранные примеры показывают, что область
сходимости степенного ряда может отличаться от интервала схо-
димости не более чем двумя точками х = ±7?, которые не входят в
интервал сходимости, но могут входить в область сходимости.
10.3.3.	Равномерная сходимость и непрерывность суммы
степенного ряда
Теорема 10.22 (о равномерной сходимости степенного ряда).
Пусть дан ряд спхп с радиусом сходимости 7? # 0. В таком случае
на всяком отрезке [-г, г] с (-7?, 7?), (г> 0) ряд сходится равномерно.
Доказательство. Из включения [-г, г] с (-7?, 7?) следует, что г < R.
Тогда х = г принадлежит интервалу сходимости и поэтому сходит-
ся ряд | с„гп|. Он является мажорирующим рядом для ряда ^c„xfl
п=0	п=0
на отрезке [-г, г], так как для любого х g [-г, г] выполняются нера-
венства |cwx"| < |cwr"|. По признаку Вейерштрасса равномерной схо-
димости, получаем, что на отрезке [-г, г] ряд ^слх" сходится рав-
номерно. ▲	л=0
Следствие. При выполнении условий теоремы ряд ^с„хц схо-
дится равномерно на любом отрезке [ос, р] с (-7?, 7i). л-°
Доказательство. Для любого отрезка [ос, р] с (-7?, 7?) можно
найти отрезок [-г, г] такой, что [а, |3| с [-г, г] с (—7?,7?). Из равно-
мерной сходимости ряда на отрезке [-г, г] следует равномерная
сходимость ряда на отрезке [ос, [3]. ▲
Теорема 10.23 (о непрерывности суммы степенного ряда). Пусть
дан ряд ^спхп с радиусом сходимости 7? # 0. В таком случае его
«=о
сумма Л'(х) непрерывна в любой точке интервала сходимости.
Доказательство. Пусть х g (-7?, 7i). Тогда можно найти такой ин-
тервал (—г, г), 0 < г < 7?, что х g (-г, г). На любом отрезке [-г, г] cz
cz (-7?, 7?) ряд сходится равномерно и члены его непрерывны на
этом отрезке. По теореме о непрерывности суммы функционального
ряда, получим, что его сумма непрерывна на всем отрезке [-г, г]
и, следовательно, в точке х. ▲
258
10.3.4.	Почленное дифференцирование и интегрирование
степенных рядов
Теорема 10.24. Пусть дан ряд ^спх” с радиусом сходимости
п=0
R * 0. В таком случае его сумма s(x) дифференцируема в любой
точке интервала сходимости, причем
аХ	л=1
т.е. ряд можно почленно дифференцировать. Кроме того, для лю-
бой такой точки х имеет место равенство
У	" Г v/?+l
5	».о л + 1
т.е. ряд можно почленно интегрировать. При этом радиусы сходи-
мости рядов X nc„xfl~l и ------- будут равны R.
n=l	Zo « +1
Доказательство этой теоремы здесь не приводим. Отметим толь-
ко, что оно опирается на теоремы о почленном интегрировании и
дифференцировании функциональных рядов.
Следствие. Поскольку почленно продифференцированный ряд
снова имеет радиус сходимости, равный R, то он также удовлет-
воряет условиям теоремы и его можно почленно продифференци-
ровать еще раз. Отсюда следует, что сумма степенного ряда имеет
производные любого порядка, а ряд можно дифференцировать
почленно любое число раз.
10.3.5.	Ряды Тейлора
Определение 10.12. Если функция у = fix) в некоторой окрест-
ности точки Xq имеет производные любого порядка, то для нее
можно построить ряд
/(x0)+^^/Vo)+^^^n^o)+...+^^=^/(”l(x0)+..., (10.36)
1!	2!	п\
который называется рядом Тейлора в точке х0 этой функции. Если
л;, = 0, то этот ряд носит название ряда Макларена.
Для функции у = f(x) справедлива при любом п и формула
Тейлора:
/W=/(*o)+^^/Vo)+(Z?)2 Г(*о)+-+(*~*о)" /1,,)(^о)+Дд,
1!	2!	п'.
где Rn — остаточный член формулы Тейлора, который можно пред-
ставить в разных формах. Например, в форме Лагранжа
259
R" =	Х°1Г'	+ 9(* - *o)),
(/7 + 1)!
где 0 < 9 < 1. Поэтому между значением функции f(x), частичной
суммой ^(х) ряда Тейлора и остаточным членом формулы Тей-
лора имеется связь:
f(x) = sfl+l(x) + R„,
из которой видно, что если остаточный член формулы Тейлора
стремится к нулю в некоторой окрестности точки xQ при п —> «о, то
ряд Тейлора будет сходиться и его суммой будет f(x). В этом случае
говорят, что функция у = f(x) разлагается в ряд Тейлора в окрест-
ности точки х0.
Итак, если R„ —> 0 при п -ь ©о, то
(0! = ]).
«=0	«!
Очевидно, что верно и обратное утверждение: из разложимости
функции в ряд Тейлора следует, что R„ -ь 0 при п <*>.
Таким образом, стремление к нулю остаточного члена форму-
лы Тейлора в некоторой окрестности точки л~,( является необходи-
мым и достаточным условием разложимости функции в данной
окрестности в ряд Тейлора.
Теорема 10.25 (теорема единственности). Если функция у = f(x)
является суммой степенного ряда в точке х0, т.е.
f(x) = ^сЛх-ХоУ
н=0
в некоторой окрестности точки х0, то этот ряд является для нее
рядом Тейлора, т.е.
Ся=£2М„ = о,1,....
п\
Доказательство здесь не приводим.
Замечание., Сформулированная теорема имеет большое практи-
ческое значение: она утверждает, что найденное любым способом
разложение функции в степенной ряд дает разложение функции в
ряд Тейлора.
10.3.6.	Разложение функции в степенной ряд
В различных вопросах математического анализа и его приложе-
ний возникает потребность в представлении функции в виде сум-
мы степенного ряда, т. е. в разложении ее в ряд Тейлора. Но приме-
нять для этого определение не всегда удобно. В силу теоремы един-
260
ственности можно использовать другие приемы, в частности уже
найденные разложения других функций. Поясним сказанное на
примере.
Пример 10.22. Пусть требуется разложить в ряд Маклорена фун-
кцию у = In(1 - х). Замечаем, что
— In (1 -х) = ( 1) = (—1)(1 + х + х2 + ... + хп + ...) = -У хп.
dx	(1-х)
Интегрируя это тождество от 0 до х, получим
°О у/?+1
1п(1 - х) = -£ ------.
Zo (я + 1)
Здесь в правой части тождества проинтегрировали ряд почлен-
но. То, что сумма бесконечно убывающей прогресии
равна----, нам известно из примера 10.2.
1 - х
В приведенном примере ключевую роль играло так называемое
готовое разложение
1
Практика разложения функций в ряды Тейлора базируется на
некотором запасе таких готовых разложений.
Приведем без вывода наиболее важные из них:
v2 v3 v4	vn
1)
е
R =
nl
COS X = 1 —
sin х = х -
2! 3! 4!
X2 + X4 ~2! + ~4!	X6 ”бГ + "	 + (-1)"	х2"	п 	+..., 7? = (2«)!	’
X3 X5 	1		X7 	h .,	 + (-1)"	у 2«+] —	+ ..., R =
3! 5!	7!		(2д + 1)!
2)
3)
4)
5)
•у.2	Y3	v4	у.п
1п(1 + х) = X---------+ --------+ ... + (-1)л+1------+ ..., X (
2	3	4	п
(1 + ХГ = 1 + тх +	+ '"С'” - 1)(т - 2)
т(т - 1)(т - 2) •... • (т - п + 1) ч
3!
.., x g (-1,1], m > -1. При m це-
п\
лом и положительном ряд превращается в конечную сумму (фор-
мула бинома Ньютона).
Пример 10.23. Покажем, как используются ряды Тейлора для
приближенного интегрирования. Допустим, что требуется найти
261
r	f sinx ,	_
приближенно J dx. Этот интеграл не выражается через конеч-
ное число элементарных функций. Поэтому найти точное его зна-
чение не удастся. Применим разложение подынтегральной функ-
ции в ряд по степеням х. Имеем
sinx if X3 X5 х7 z 1Ч„ х2л+|	(-1)"
'[^ЦЛ='[у (-Р" x2..dT-y (-»)" Ь^_у_______________________
J„ *	Jo^(2«+D! h (2«+l)iJ0	Й(2»+1)! (2л+1)’
Пользуясь приближенным равенством
г sinx = у (-1)"
Jo * Х Го(2« + 1)! (2/7 + 1)’
за счет выбора N можно добиться любой требуемой точности.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1.	Пользуясь определением суммы ряда и его сходимости, выясните,
сходится ли ряд У In 1 + — .
Zf I
2.	Используя теоремы сравнения, исследуйте на сходимость ряд
А 2 + sin п
Ь «2 + 1 ‘
3. С помощью признака Даламбера исследуйте на сходимость ряд
“ у
Sw-
4.	С помощью радикального признака Коши исследуйте на сходимость
( п -1 Y п
ряд§Ы +
5.	С помощью интегрального признака Коши выясните, сходится или
расходится ряд	,
S (л + 1) з/1п(л + 1)
6.	Применив признак Лейбница, докажите сходимость ряда
П = 1	“	л(х-1)"
7.	Найдите область сходимости ряда ^(-1) --
Л=1 п 2"
8.	Применяя почленное дифференцирование, найдите сумму ряда
^(л + Пх-1.
9.	Разложите в ряд Тейлора по степеням х функцию у = sin3x.
i
10.	Найти приближенную формулу для вычисления интеграла je-v t/x.
ГЛАВА 11
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
11.1.	Введение
11.1.1.	Основные понятия
Дифференциальные уравнения принадлежат классу функцио-
нальных уравнений, когда неизвестной является функция. Мы уже
имели дело с функциональным уравнением F(x,y) = 0 при изуче-
нии неявных функций. Требовалось выяснить, когда она существу-
ет, и найти функцию у = <р(х), которая при подстановке ее в урав-
нение обращает его в тождество, т.е. /’(х,<р(х)) = 0. Это имеют в
виду, когда говорят, что функция у = <р(х) является решением
функционального уравнения F(x,y) = 0.
Дифференциальные уравнения — более сложные объекты: под
знаком функции F находятся не только х, у, но и производные
неизвестной функции.
Обыкновенными дифференциальными уравнениями называются
уравнения, когда неизвестная функция зависит только от одного
аргумента — х. Уравнения, неизвестными в которых являются фун-
кции нескольких переменных, называются уравнениями с частны-
ми производными. Здесь будем рассматривать только обыкновенные
дифференциальные уравнения.
Общий вид такого уравнения можно представить в следующей
форме:
Г(х,у,у,У',...,У'Д = 0.	(11.1)
Максимальный порядок входящих в уравнение производных
называется порядком дифференциального уравнения. Таким обра-
зом, уравнение (11.1) является уравнением /?-го порядка. Решить
это уравнение — значит найти функцию у = <р(х), которая при
подстановке ее в уравнение обращает его в тождество на некото-
ром интервале (а,д). Естественно эту функцию называть решением
дифференциального уравнения (11.1).
Задача нахождения решения или всех решений для уравнения
(11.1) является основной задачей, которой занимается теория диф-
ференциальных уравнений. Эта теория содержит не только методы
нахождения решений, но и методы анализа уравнений, позволя-
ющие изучить вопрос о разрешимости задачи нахождения реше-
263
ний. Уже первые примеры дифференциальных уравнений показы-
вают, что решений у дифференциальных уравнений бывает беско-
нечно много.
Пример 11.1. Рассмотрим дифференциальное уравнение, имеющее
следующий вид: cosx - у' = 0. Его можно записать иначе: у' = cosx.
Теперь видно, что задача нахождения решения дифференциаль-
ного уравнения в данном случае является задачей отыскания пер-
вообразной функции для cosx, т.е. задачей интегрального исчис-
ления. Множество всех первообразных — это неопределенный ин-
теграл от cosx, т.е.
j cosx dx = sinx + С,
где С — произвольная постоянная. Видим, что множество всех ре-
шений этого дифференциального уравнения является бесконечным.
В данном случае ответ можно представить в виде простой формулы:
у = sinx + С.
Как известно, решая дифференциальное уравнение
У =Ж>,
мы придем к необходимости вычислить интеграл
J/Wx,
который, во-первых, не всегда выражается через конечное число
элементарных функций, а во-вторых, когда такое выражение мо-
жет быть получено, нахождение его в некоторых случаях может
быть очень сложным.
Эти соображения показывают, что уже в простейшем случае,
коим является дифференциальное уравнение у' =/(х), нахождение
явного выражения у через х может быть сложным и громоздким, а
.sinx _
в некоторых случаях, например при j (х) =-, вообще невоз-
можным.
Пример 11.1 заставляет задуматься над постановкой задачи,
которая была дана выше: определить функцию у = <р(х), обращаю-
щую дифференциальное уравнение в тождество, т.е. найти реше-
ние дифференциального уравнения. В такой постановке задача смо-
жет быть доведена до ответа в очень небольшом наборе дифферен-
циальных уравнений. Поэтому необходимо расширить класс урав-
нений, для которых можно найти решение. Первый шаг в этом
направлении — считать, что дифференциальное уравнение реше-
но, если решение, т.е. функция, представлено с помощью интег-
рала, возможно не выражающегося через элементарные функции.
Второй шаг — допускать ответ в такой форме, когда решение зада-
ется неявно с помощью функционального уравнения, не содер-
264
жащего производных, но, возможно, содержащего неберущиеся
интегралы от известных функций. И наконец, допускать, чтобы
решение уравнения было представлено в виде суммы функцио-
нального ряда. Если можно найти решение дифференциального
уравнения, удовлетворяющее первым двум правилам, то говорят,
что уравнение интегрируется в квадратурах.
В некоторых случаях для нахождения всех решений уравнения
нет необходимости вычислять интегралы. Тем не менее процесс
нахождения решений называется интегрированием дифференциаль-
ного уравнения.
11.1.2.	Понятие общего и частного решений. Задача Коши
Дифференциальные уравнения, как правило, имеют бесконеч-
ное множество решений, которое может зависеть от произвольных
постоянных. Так, в примере 11.1 множество всех решений диффе-
ренциального уравнения
cosx - у = О
описывается формулой
у = sinx + С,
содержащей одну произвольную постоянную С. Множество реше-
ний уравнения
У' = о
может быть получено двумя последовательными интегрированиями:
у' = С[ и у = С[Х + С2.
Как видим, это множество зависит от двух произвольных по-
стоянных: С] и С2. Количество произвольных постоянных в свою
очередь зависит от порядка дифференциального уравнения. В слу-
чае дифференциального уравнения первого порядка произвольная
постоянная — одна, для дифференциального уравнения второго
порядка
У' = о
— две. Обычно, как правило, так и бывает — количество произ-
вольных постоянных в формуле, описывающей все решения урав-
нения /?-го порядка, равно /?, т.е. порядку этого дифференциаль-
ного уравнения. Такую функцию
у = <p(x,C„C2,...,Q,
обладающую тем свойством, что, с одной стороны, при любых зна-
чениях Q, С2, ..., С„ (каждое из них может иметь свой интервал
изменения: pj < С, < qh i = 1, 2, ..., w) из нее получается некоторое
265
решение дифференциального уравнения, а с другой стороны, для
любого, наперед заданного, решения уравнения у(х) найдутся един-
ственные значения констант С], С2, ..., С„ такие, что при подста-
новке их в качестве аргументов в эту функцию будет получено
решение у(х), называют общим решением дифференциального урав-
нения. Бывает так, что эта функция оказывается заданной неявно
уравнением
Ф^лСнС,,...,^) = 0.
Такое представление общего решения называется общим интегралом
дифференциального уравнения. Для дифференциальных уравнений
первого порядка общее решение и общий интеграл имеют вид
у = <р(х,С) и Ф(х,у, С) = 0.
Иногда общий интеграл представляют в виде
<р(х,у) = С.
Если взять какое-то решение дифференциального уравнения
у = /г(х), то оно может быть получено из формулы для общего ре-
шения путем придания константам С], С2, ..., С„ каких-то конк-
ретных частных значений.
Поэтому решение у = h(x) называют частным решением диффе-
ренциального уравнения. Если же это решение получается из об-
щего интеграла путем фиксирования значений произвольных по-
стоянных как функция, заданная неявно уравнением
Я(х,у) = 0,
то это уравнение называется частным интегралом.
Частное решение, как и частный интеграл, уже не зависит от
произвольных постоянных, а зависит только от х.
Как будет видно из дальнейшего, только одно решение из бес-
конечного множества всех решений интересует исследователя,
применяющего для моделирования изучаемого процесса диффе-
ренциальное уравнение: именно то, которое описывает этот про-
цесс. Поэтому дополнительно к проблеме нахождения всех реше-
ний дифференциального уравнения возникает задача выделения
этого решения из бесконечного множества всех решений. Это можно
сделать только при наличии какого-то дополнительного условия,
выделяющего искомое решение из множества всех решений. В за-
висимости от вида этих условий различают задачу для дифферен-
циального уравнения: найти решение, удовлетворяющее заданным
условиям. Как правило, эти условия таковы, что определяемое ими
решение существует и единственно. Про такую задачу говорят, что
она поставлена корректно.
Для уравнений первого порядка наиболее важной задачей явля-
ется задача Коши. Она состоит в том, чтобы из всего множества
266
решений дифференциального уравнения найти то, которое в дан-
ной точке А' = х0 принимает заданное значение у = у0. При изучении
с помощью дифференциальных уравнений процессов, изменяю-
щихся с течением времени (например, движения материальной
точки), роль независимой переменной играет время. Тогда, опре-
делив значения xQ и г,, можно узнать состояние системы в момент
времени х0, характеризуемое значением г,, (известна координата,
а значит, и положение точки).
Пришедшая из механики терминология укоренилась в теории
дифференциальных уравнений, и значения х0 и у0 называют на-
чальными данными задачи Коши, а условия у = у0 при х = xQ —
начальными условиями.
Пример 11,2, Поставим задачу Коши для рассмотренного выше
дифференциального уравнения cosx - у' = 0: найти решение урав-
нения, удовлетворяющее условию у = 1 при х = 0. Для решения
задачи Коши воспользуемся общим решением, которое имеет вид
у = sinx + С. Подставляя в левую часть формулы у = 1, а в правую
х = 0, находим, что С = 1. Таким образом, решением задачи Коши
будет частное решение у = sinx + 1.
В случае, когда уравнение имеет порядок выше первого, рав-
ный п, в формулу общего решения входит п произвольных посто-
янных С], С2, ..., Cfl, для однозначного определения которых тре-
буется уже не одно, а п условий.
Задача Коши состоит в том, чтобы найти частное решение урав-
нения, удовлетворяющее условиям:
У(*о) = То, /(*о) = Тн Т"(*о) = У1,	T(/?“l)W = Уп-\-
Пример 11.3. Решим задачу Коши: для уравнения у" = 0 найти
частное решение, удовлетворяющее условиям у(0) = 1, у'(0) = 3.
Воспользуемся формулой для общего решения у = С]Х+ С2. Диффе-
ренцируя ее, найдем, что у' = Ch Подставляя начальные условия в
эти два соотношения, получим систему уравнений относительно
костант С] и С2: 1 = С2 и 3 = С(. Откуда получаем искомое решение
у = Зх + 1.
11.1.3.	Геометрический смысл уравнения и его решений
Если ввести на плоскости прямоугольные декартовы координа-
ты х и у, то решению у = ср(х) на этой плоскости будет соответ-
ствовать кривая: график этой функции. Такая кривая называется
интегральной кривой данного дифференциального уравнения (на-
звание сохраняется и в том случае, когда решение задается неявно).
Если рассмотреть дифференциальное уравнение первого порядка
# = f(x,y),	(11.2)
267
то интегральные кривые этого уравнения характеризуются тем,
что тангенс угла наклона касательной (в этом состоит геометри-
ческии смысл —) равен в каждой точке области, в которой опре-
dx
делена функция /(х,у), ее значению в этой точке. Поскольку фун-
кция f(x,y) задана, можно, не имея самой интегральной кривой,
найти уравнение и построить касательную к ней в каждой точке
области (х0,у0):
У = То + ЖьТо)(* - *о)-
Таким образом, в каждой точке области, где определена функция
f(x,y), можно провести прямую. Хотя эта прямая определяет на-
правление на плоскости с точностью до знака, тем не менее гово-
рят, что дифференциальное уравнение (11.2) определяет в облас-
ти на плоскости поле направлений.
Если рассмотреть множество точек, в которых выполняется ра-
венство /(х,у) = к, то эти точки образуют на плоскости, вообще
говоря, некоторую кривую, во всех точках которой касательные к
интегральным кривым будут иметь одинаковый тангенс угла на-
клона, равный /г, а значит, и одинаковый угол наклона, т.е. будут
все параллельны. По этой причине кривая, определяемая уравне-
нием
Жт) = к,
называется изоклиной — линией равного наклона. Эти кривые на-
ходят применение при геометрическом приближенном построе-
нии множества интегральных кривых для уравнения (11.2).
Задачу Коши для уравнения (11.2) в геометрических терминах
можно сформулировать так: среди всего множества интегральных
кривых данного дифференциального уравнения найти такую, ко-
торая проходит через заданную точку с координатами (х0,у0)-
11.1.4. Разрешимость задачи Коши
Пусть Пу — множество точек (х,у) на плоскости, удовлетворя-
ющих условию х0 < х < X -оо < у < +оо; это множество назовем
полосой.
Теорема 11.1. Пусть функция /(х,у) определена и непрерывна в
полосе Пу и удовлетворяет условию Липшица', существует постоян-
ная L такая, что для любого х е [х0, Т| и любых У] и у2 выполняется
неравенство
1Ж^) -/ОЖ! Ж -^1-	(И.З)
Тогда для любого начального значения у0 решение задачи Коши
найти решение уравнения
268
^ = Дх,у),
dx
удовлетворяющее условию у(х0) = Ж существует и единственно
на всем отрезке [хо,А].
Доказательство этой теоремы здесь не приводим.
Замечание, Если функция f(x,y) имеет в полосе Пу частную
производную — (х, у) такую, что существует постоянная L такая,
Эу
что для любого х g | а;,. АД и любого у выполняется неравенство
|^(х,у) <£,
Эу
то условие Липшица выполнено.
Пример 11.4. Рассмотрим уравнение
dy / л
— = cos(x + у).
dx
Здесь /(х,у) = cos(x + у). Функция /(х,у) имеет
|^(х,у) =-sin(х+ у) и ~~(х, у)
Эу	Эу
< 1.
Следовательно, при любых х0, у0 и X задача Коши имеет един-
ственное решение на отрезке [хо,А].
11.2.	Уравнения первого порядка,
интегрируемые в квадратурах
dy
11.2.1.	Уравнения вида — = f(х)
dx
Пусть функция f(x) непрерывна на интервале (а, Ь). Тогда, как
известно из курса интегрального исчисления, если х0 и х принадле-
жат этому интервалу, то одним из решений рассматриваемого диф-
,	dy ч ,
ференциального уравнения — = / (х) будет функция
dx
у(х) = \f(t)dt.
Все другие решения отличаются от него на постоянное слагае-
мое. Поэтому общим решением будет функция
у(х) = J f(t)dt + С.
269
Пример 11.5. Найти общее решение уравнения
Имеем
у(х) = I е dt + С = ef + С = ел - е*0 + С = ел + С],
J	1хй
где Q = С — ел° будет произвольной константой, поскольку тако-
вой является С.
dy
11.2.2.	Уравнения вида -^- = f(y)
dx
Это уравнение в том случае, когда f(y) непрерывна и не обра-
щается в нуль на интервале (а,Ь), можно переписать в форме (по-
меняв ролями х и у)
dx _ 1
"/(у)’
что позволяет свести это уравнение к виду, рассмотренному выше
(см. п. 11.2.1). Его общий интеграл будет иметь вид
[уо и у принадлежат интервалу (а, /?)]. Если же в какой-либо одной
точке У[ этого интервала окажется, что/(у[) = 0, то интервал (а,Ь)
распадется на два интервала (я, у,) и (у1ч Z>), на каждом из которых
может быть найден общий интеграл и, кроме того, возникает еще
одно решение у = У].
Пример 11.6. Найти общий интеграл уравнения
Переписываем уравнение в виде
dx 1	dx	„
— = —,	или	—	= е	-1.
dy еу	dy
Откуда получаем
у
х = f с 'dt + С = - е-г|Л + С = -е-Л’ + С + е“1'° = -е-Л’ + С,,
J	Ч’о
где С[ = С + с-1 — произвольная константа.
270
11.2.3.	Уравнения с разделенными переменными
Уравнение первого порядка вида
можно умножить на dx и записать в виде
dy-f(x,y)dx = $,
или, как говорят, в дифференциальной форме.
В более общем случае уравнения представляются в следующем
виде:
P{x,y)dx + Q{x,y)dy = Q,	(11.4)
где переменные х и у входят симметрично (равноправно). Это об-
стоятельство приводит к тому, что представлению решения в виде
у = <р(х) не отдается предпочтения по сравнению с представлени-
ем либо х = /(у), либо F(x,y) = 0. Интегрирование дифференциаль-
ных уравнений, т.е. процесс нахождения решений, не подразуме-
вает обязательного представления решения в виде у = <р(х), что
соответствует тем правилам, которые были изложены выше. То же
самое можно сказать относительно общего решения: уравнение
считается решенным, если найден его общий интеграл.
Уравнением с разделенными переменными называется уравнение вида:
f(x)dx + g(y)dy = Q,	(11.5)
где коэффициент f зависит только от х, a g — только от у, т.е.
переменные разделены.
Очевидно, что это уравнение является частным случаем урав-
нения (11.4). Будем считать, что функции /(х) и g(y) непрерывны
на интервалах (а, Ь) и (с, d) соответственно. Его можно переписать
в следующем виде:
j f(t)dt + J g(s)ds
= 0,
(11.6)
т. e. как дифференциал от функции двух переменных: хну. Здесь х0
и х принадлежат интервалу (а, й), а у0 и у — интервалу (с, d). Таким
образом, функция, стоящая под знаком дифференциала, опреде-
лена и дифференцируема внутри прямоугольника а<х< Ь, с< у < d.
Функция, имеющая первый дифференциал, тождественно равный
нулю в прямоугольнике, является в этом прямоугольнике кон-
стантой. Поэтому тождество (11.6) эквивалентно тождеству
(11.7)
271
Поскольку оно не содержит производных, то представляет со-
бой общий интеграл уравнения (11.5). Его можно записать в виде
F(x,y) = С. Произвольность постоянной С ограничивается интер-
валом изменения функции F(x,y).
Пример 11.7. Рассмотрим дифференциальное уравнение
2xdx + 2 ydу = 0.
Применяя формулу (11.7), получаем
х2 + у2 = С.
Это общий интеграл уравнения. Семейство интегральных кри-
вых представляет собой семейство окружностей с центром в нача-
ле координат. Произвольная постоянная С может принимать толь-
ко положительные значения: С > 0.
11.2.4.	Уравнения с разделяющимися переменными
К уравнениям с разделенными переменными легко сводятся
уравнения вида
F(x)F(y)dx + G(x)H(y)dy = 0,	(11.8)
называемые уравнениями с разделяющимися переменными. Достаточно
умножить уравнение на функцию -------и оно приобретает вид
(11.5):
7ГЗЛ+ ^T3dy = 0-	(1L9)
ед F(y)
Общий интеграл этого уравнения имеет вид S(x,y) = С, где
cz .	г£(х),	У(Н(у).
ЖЬ =	+ I -^ydy-
1	G(x) 1 F(y)
Однако при умножении уравнения (11.8) на множитель (11.9)
возможна потеря некоторых решений. Если у, таково, что F(y}) = 0,
то у уравнения (11.8) существует решение у = которого нет у
уравнения (11.9). Кроме того, у уравнения, записанного в дифферен-
циальной форме, возможны решения вида х = jq. И такое решение
будет, в отличие от уравнения (11.9), если G(x}) = 0. В итоге име-
ем, что эти дополнительные решения должны быть присоединены
к тем решениям, которые определяются выражением 5(х,у) = С.
Пример 11.8. Пусть требуется решить дифференциальное урав-
нение
Зх2(1 + y3)dx - Зу2( 1 + x3)dy = 0.
Без труда распознаем в нем уравнение с разделяющимися пере-
менными и производим их разделение. Получим
272
3x2dx 3y2dy _ g
1+X3	1 +v3
В качестве точки (xo,jo) берем точку (0,0). Интегрируя, получим
1п| 1 + х3| - 1п| 1 +у3| = 1пС.
Потенцируя, получим
(1 + х3) = (1 + у3)С.
Здесь константа была записана в виде In С для удобства записи
окончательного результата; при потенцировании модули опущены
за счет того, что постоянной С, которая стояла под знаком лога-
рифма и была обязана быть положительной, теперь разрешается
принимать любые значения. При этом решение х = -1 получается
при С = 0, а решение у = -1 не получается ни при каком значении
С. Поэтому его следует учитывать дополнительно.
11	.2.5. Однородные уравнения
Многие дифференциальные уравнения, не являясь уравнения-
ми с разделяющимися переменными, приводятся к ним с помо-
щью замены переменных. К таким уравнениям относятся однород-
ные уравнения, общий вид которых
— =	(И.10)
dx	\х )
При решении таких уравнений делается замена переменной у
по формуле у = и(х)х, где и — новая переменная. Тогда
dy du	у
— = —х + и, а — = и.
dx dx	х
Подставляя эти выражения в уравнение (11.10), получим
— х + и = Ди),
dx
т. е. уравнение с разделяющимися переменными. Разделяя перемен-
ные, получаем
du =—. (11.11)
/(w) - и х
Интегрирование дает
Ф(«) - 1п|х| = С,
где Ф(у) — одна из первообразных функций функции —— -----.
□	у	f(u) - и
Заменяя и = —, получаем
х
273
ф(—'I - ln|x| = С.
Iх /
Множество решений, даваемых этой формулой, должно быть до-
полнено решениями вида и = и$, если /(д0) - «о = 0, или у = uQx.
Пример 11.9. Найдем все решения дифференциального уравнения
dy _ 2ху
dx х2 + у2
Это уравнение после деления в правой части числителя и зна-
менателя на х2 принимает вид
dy
dx
Положив — = w, получим
х
или
du 2и и - w3
___ у =__________/7 = ______
dx 1 + и2 1 + и2 ’
Далее
u?(\ + t2)dt
1
если в качестве //,, взять //,, =
интеграл имеет вид
. Следовательно, для и общий
In |	] | - ln|x| = In С.
о	У
Заменив и = —, получаем
у= (у2 - х2)С.
Опускание модулей компенсируется, как и выше, разрешени-
ем для С принимать любые значения, отличные от нуля. Рассмот-
рим теперь вопрос о дополнительных решениях, связанных с ре-
шениями уравнения f(u) - и = 0. В нашем случае имеем
2и п Л и-и3 п
----7 -2 = 0, или 	= = 0.
1 + w2	1 + w2
Решение уравнения uQ = 0 дает решение у = 0. Это решение будет
содержаться в формуле у = (у2 - х2) С, если С разрешить принимать
значение С = 0. Два других решения = -1 и и2 = 1 порождают
дополнительные решения у = -х и у = х.
274
11.2.6. Линейные уравнения
Линейным дифференциальным уравнением первого порядка на-
зывается уравнение вида
= р(х)у + q(x),	(11.12)
dx
где функции р(х) и q(x) непрерывны на интервале (а,Ь). Если q(x) = О
на интервале (а,Ь), то уравнение называется линейным однородным
и имеет вид
%- = Р<х)у,	(11.13)
ах
являясь уравнением с разделяющимися переменными. Его общее
решение может быть представлено в виде
у = Се?(л),
где Р(х) — первообразная функция по отношению к р(х) на ин-
тервале (а,Ь), т.е.
Р(х) = \Pdx.
Если q(x) не является функцией, тождественно равной нулю
на (й,/>), то уравнение (11.12) называется линейным неоднородным
уравнением, а уравнение (11.13) — линейным однородным, соот-
ветствующим уравнению (11.12). Общее решение неоднородного
уравнения обычно находят с помощью приема, называемого вари-
ацией постоянной. (Можно встретить такой термин «метод вариа-
ции постоянной».) В чем заключается этот метод? Общее решение
неоднородного уравнения ищут в виде у = С(х)е?(А), т. е. в той фор-
ме, которую имеет общее решение соответствующего однородно-
го уравнения, но с той разницей, что здесь С = С(х) и является
неизвестной функцией. Замена произвольной постоянной С в вы-
ражении для общего решения однородного уравнения у = Ce?w
на функцию С(х) и объясняет название метода. Для того чтобы
найти С(х), надо подставить выражение у = С(х)е?(л) в неоднород-
ное уравнение (11.12). Получим
— е™ + С(х)е/,(«	= р(х)С(х)еРЫ
ах	ах
Поскольку Р(х) — первообразная для /Дх). то
уравнение упрощается:
(И.14)
р(х), и
dP(x)
dx
— еР(А) = q(x), или — = q(x)c~P(x).
dx	dx
Если Н(х) — первообразная по отношению к функции q(x)e~PM,
то С(х) = -Н(х) + Сн где С, — произвольная постоянная. Таким
275
образом, общее решение неоднородного линейного уравнения
имеет вид
у(*) = Ш + Ci)e?w,
где Р(х) — первообразная по отношению к р(х); Н(х) — первооб-
разная по отношению к функции q(x)c р" '.
Пример 11.10. Рассмотрим линейное неоднородное уравнение
dy
— = -2ху + хе А .
ах
Здесь р(х) = -2х. В качестве Р(х) возьмем Р(х) = -х2. Тогда
q(x)e~PM = х и Н(х) =
Следовательно, общее решение имеет вид
у = (с, +^е-<
11.2.7. Уравнения Бернулли
Уравнением Бернулли называется уравнение вида
= p(x)y + q(x)y\	(11.15)
ах
где а — произвольное число, не равное 0 и 1. Это уравнение сво-
дится к линейному уравнению с помощью замены z = у1-". Дей-
ствительно, делением уравнения (11.15) на у" приводим его к виду:
у-а — = /jC'OJ’1-” + Q(x)-	(11.16)
dx
Теперь замечаем, что левая часть уравнения в точности равна
1 dz
;-----После умножения уравнения на (1 - а) получаем линей-
1 - a dx
ное уравнение:
d z
^ = (l-aW)2 + (l-ak(x),	(11.17)
dx
которое может быть решено по схеме, приведенной в п. 11.2.6.
Замечание., Если а > 0, то при делении уравнения на у'; происхо-
дит потеря решения у = 0, которое следует также учесть.
Пример 11.11. Решим уравнение Бернулли:
— = -2ху + 2х3у3.
dx
276
Здесь a = 3. Делаем замену z = Д-. Уравнение после умножения
f-2^	У
на I -р- I и замены переменного примет вид
dz л л з
— = 4x2 - 4xJ
dx
Решаем его с помощью вариации постоянной: р(х) = 4х, откуда
Р(х) = 2х2; q(x)e~P{x) = -4х3е_2л\
,	1 + 2х2 _2х2
Н(х) = —-—е 2А ,
откуда
1 + 2х2 Я 2 2
z - С, +--------е 2А е2А .
2
О	1	Л
Заменяя z на — после несложных преобразовании, придем к
формуле	У
Л-Сс2^ + х2 + |,
Г	2
охватывающей все решения уравнения, кроме одного: у = 0, кото-
рое следует также учесть, так как a = 3 > 0.
11.2.8. Уравнения в полных дифференциалах
Уравнением в полных дифференциалах называется дифференци-
альное уравнение первого порядка следующего вида:
P(x,y)dx + Q(x,y)dy = ^	(11.18)
если его левая часть представляет собой полный дифференциал
функции двух переменных. Если функции Р(х,у) и (?(х,у) имеют
непрерывные частные производные, то для того, чтобы уравнение
(11.18) было уравнением в полных дифференциалах, необходимо
и достаточно, чтобы выполнялось тождество
Это условие легко проверяется, и если оно выполнено, то сущест-
вует функция t/(x,y) такая, что dU P(x,y)dx+ Q(x,y)dy. Следователь-
но, уравнение имеет вид dU(x,y) = 0, и его общий интеграл будет
£/(х,у) = С,
где С — произвольная постоянная. Остается невыясненным воп-
рос, как найти функцию t/(x,y)? Это можно сделать несколькими
способами. Один из них приводит к следующей формуле:
277
U(x,y)= XjP(t,yQ)dt+ \Q(x,s)ds,
X(I	VO
где произвольная точка (хо,Уо) принадлежит области, в которой
выполняются указанные выше условия для функции Р(х,у) и Q(x,y).
Доказательство здесь не приводим. Итак, общий интеграл уравне-
ния (11.18) при выполнении условия (11.19) имеет следующий
вид:
J P(t,yQ)dt + j Q(x,s)ds = С,	(11.20)
л
где С — произвольная константа.
Пример 11.12, Рассмотрим уравнение
(2х + 3y)dx + (Зх + Зу2)г7у = 0.
Здесь
Р(х,у) = (2х + Зу), (?(л:,у) = (Зх + Зу2).
Проверим выполнение условия (11.19). Имеем
— = 3 ^- = 3
ду ’ дх
т. е. условие 11.19 выполняется. Находим функцию
X	у
U(x,y) = ^2tdt + j(3x + 3s2)ds = x2 + Зху + y3
о	0
[в качестве точки (x0,y0) взяли точку (0,0)]. Общий интеграл имеет
вид
х2 + Злу + у3 = С.
Замечания. 1) Естественно, что, зная частные производные,
можно восстановить функцию U(x.y) только с точностью до по-
стоянного слагаемого. Внешне выражения для общего интеграла
могут быть разными, но множество решений при этом не изме-
нится.
2) Произвольность постоянной С, стоящей в правой части об-
щего интеграла, ограничивается интервалом изменения значений
функции U(x,y). Например, если общий интеграл имеет вид
со5(л:2 + у2) = С,
то С может принимать любые значения только из отрезка [-1,1],
поскольку
I cos (х2 + у2) | < 1.
278
11.3. Уравнения высших порядков, их общие решения
сГу
11.3.1 .Уравнения вида —— = f(х)
dxn
Х7	Г/ X
Уравнения вида —— - f(x) легко интегрируются в квадратурах.
dx”
Последовательными интеграциями получим:
^4= ]/«Л + С,;
d х” 1 J
х0
d”~2y
d х”~2
f f(s)ds
Л'()
dt + С\(х - х0) + С2;
d”~3y
d х”~3
h
и наконец,
У = Н j J'“	ds\dt +
(д-1)!
СДх-Хр)"-1 , С2(х-х0)'
(д-2)!
• • + Cfi-i (х ~ хо) + С
где интегрирование произведено п раз. Точка х0 выбирается произ-
вольно из интервала, на котором рассматривается данное уравне-
ние. Эта формула дает общее решение. Проиллюстрируем ее при-
менение на примере.
Пример 11.13, Найти общее решение дифференциального уравнения
d3y
—v = cosx.
dx3
Имеем
---Y = SinX + С]
dx2
(в качестве точки х0 взяли точку х = 0). Далее
— = -cosx + Qx + С2
dx
и наконец,
х2
у = -sinx + С| — + С2х + С3.
Это и есть общее решение рассматриваемого уравнения.
279
11.3.2. Уравнения, допускающие понижение порядка
Дифференциальные уравнения, порядок которых выше, чем
единица, носят название уравнений высших порядков. Построить
общее решение или, как говорят, проинтегрировать такое уравне-
ние — задача, по сравнению с уравнениями первого порядка, го-
раздо более сложная. Поэтому те случаи, когда это можно сделать,
представляют особый интерес. Бывает так, что уравнение проин-
тегрировать не удается, но можно понизить его порядок. Это, как
правило, существенно помогает и исследовать уравнение, и, если
требуется, найти решение численно, т.е. вычислить значения ре-
шения в некотором наборе точек, получив решение в виде табли-
цы. Поэтому уравнения, порядок которых может быть понижен за
счет соответствующей замены переменных, представляют собой
важный класс уравнений высших порядков. Уравнение вида
очевидно, принадлежит этому классу. Для него удается предста-
вить общее решение в квадратурах.
Рассмотрим еще несколько случаев, когда возможно пониже-
ние порядка дифференциального уравнения.
1. Уравнения, имеющие вид
F(x,y^k\y(k+]\ ...,y(w)) = О,
классифицируются как уравнения, не содержащие явно искомой
функции у(л') и ее младших производных до порядка (к - 1) вклю-
чительно. Их порядок может быть понижен на к единиц. Для этого
вводится в рассмотрение новая неизвестная функция
Z(x) = у{к}(х\
Тогда z' = у(А+1), z” = у(А+2), ..., z{n~k} = ум. И заменяя у(/;+1), ...,
у(л) соответственно на z, z', z", ..., z(/?-A), получим относительно
функции z(x) дифференциальное уравнение порядка (п - к):
F(x, z,z',..., z{n~k}) = 0.
Если для него удастся найти общее решение
z = <р(х, С|, С2,..., С„_к),
то общее решение исходного уравнения может быть найдено как
общее решение уравнения типа, рассмотренного в п. 11.3.1:
т.е. последовательными интеграциями.
Пример 11.14. Рассмотрим дифференциальное уравнение тре-
тьего порядка:
280
У'" = (У")3-
Порядок этого уравнения может быть понижен на две единицы
заменой z = у". Тогда
У”' = Z'.
Относительно z уравнение примет вид
z' = Z3.
Уравнения такого типа были рассмотрены в п. 11.2.2. Его общий
интеграл представляется в виде
где 2о можно взять равным 1. Тогда имеем
Обозначив 2С + 1 = С] и умножив все соотношение на 2, найдем
общее решение для функции z:
z = (Q -2хр.
Теперь для искомой функции г(л') получаем уравнение
y" = (C,-2x)~i
Последовательными интеграциями находим:
1 1 3
у =-(G -2х)2 + С2 и У = |(С] -2х)2 + С2х + С3.
Эта формула должна быть дополнена (см. п. 11.2.2) решениями,
которые получаются при z = 0, или у" = 0. Интегрирование этого
уравнения дает
Итак, все решения данного уравнения найдены.
2. Рассмотрим дифференциальные уравнения, имеющие следу-
ющий вид:
Г(у,у',у") = 0.
Это дифференциальное уравнение второго порядка классифи-
цируется как уравнение, не содержащее независимого перемен-
ного, т.е. х Порядок такого уравнения может быть понижен на
одну единицу. Это делается путем введения новой неизвестной
функции q = q(y) такой, что q = у'. Тогда
281
„ dq dy
у = угуг = чч-
dy dx
Поэтому уравнение принимает вид
= О,
т. е. превращается в дифференциальное уравнение первого порядка.
Если удастся найти его общее решение
q = <р(у,С]),
то для искомого решения исходного уравнения получится уравнение
у' = ф(у,С]),
которое рассмотрено в и. 11.2.2. Его общий интеграл дается формулой
с учетом решений, которые могут получаться из уравнения
Ф^С,) = О
(см. п. 11.2.2).
Пример 11,15, Рассмотрим уравнение
уу" + (У)2 = 1-
Оно не содержит переменного х Сделаем замену у' = q (у). Урав-
нение примет вид
y<fq + (q)2 = 1.
Это уравнение является уравнением с разделяющимися пере-
менными, его общий интеграл имеет вид
или
In (у2) + ln| 1 - <?2| = In С,.
Потенцируя и разрешая соотношение относительно q, получим
У
Заменяя q на у' и интегрируя получающееся дифференциаль-
ное уравнение, получим
±д/у 2 — С] — х + С2 
282
Возведя в квадрат, преобразуем ответ к виду
(х + С2)2 - _и2 = С,.
Дополнительных решений здесь нет, поскольку у = у0 не удов-
летворяет исходному уравнению.
В заключение обсудим методику решения задачи Коши для урав-
нений высшего порядка, допускающих понижение порядка. На-
хождение решения, удовлетворяющего начальным условиям, в
рассматриваемом случае целесообразно осуществлять не исходя из
формулы для общего решения, что приводит, порой, к непрео-
долимым трудностям, а последовательно находя значения произ-
вольных постоянных С|, С2, ... по мере их появления в процессе
последовательных интеграций. Проиллюстрируем эту идею на при-
мере.
Пример 11,16, Решить задачу Коши: найти решение уравнения
Ь" = 3Z
удовлетворяющее начальным условиям у(-2) = 1, у'(-2) = -1.
Решение. Делая замену у' = q(y), приводим уравнение к виду
2qq' = Зу2.
Интегрируя, получим
или
(У)2 =/ + С|.
При х = -2, как следует из начальных условий, у = 1, а у' = -1.
Подставляя эти значения в полученное уравнение, имеем
1 = 1 + С],
откуда следует, что
з
С] = 0 и у' = ±у2 .
При х = -2 это равенство также должно иметь место. Поскольку
з
у' = -1, а у = 1, то у' = -у2 .
Теперь интегрируем это уравнение. Имеем
У _3	X
-р 2dt = jds + C2,
I	-2
или
-2 1—=(х + 2) + С2.
283
Полагая здесь х = -2 и учитывая, что при этом у = 1, найдем,
что С2 = 0. Теперь, выражая у через х, получим
4
У (х + 4)2 *
Это и есть искомое решение задачи Коши.
11.4.	Уравнения высших порядков. Задача Коши
11.4.1.	Постановка задачи Коши
Среди уравнений высших порядков выделим такие, которые
можно записать в следующем виде:
(11.21)
а хп
т.е. в разрешенном относительно старшей производной. Напом-
ним, что задачей Коши для уравнения (11.21) называется задача
нахождения частного решения этого уравнения у(х), удовлетворя-
ющего условиям:
Лк) = То, У(хо) = К, Т"(хо) = Т2,	T(w“l)(x0) = K-i,
где Xq, То, Ti, •••> К-] — заданные числа.
Вопрос о разрешимости задачи Коши на отрезке [x0,2f] реша-
ется в терминах, аналогичных случаю уравнений первого порядка.
11.4.2.	Разрешимость задачи Коши
Пусть
z = (zl,z2,z3,...,z„)
— упорядоченный набор действительных чисел. Обозначим через
llzll = yjzf +zl + zj + ... + Z2 .
Множество точек в (/?+1)-мерном пространстве
(x,Z) = (x,Z|,Z2,Z3,...,Zw),
для которых х е [x0,2f], a z}, z2, z3, ..., zn принимают любые зна-
чения, называется слоем и обозначается как Щ. Функцию, сто-
ящую в правой части уравнения (11.21), будем рассматривать как
функцию (п + 1) переменных: Дх, z2, z3,..., z„).
Теорема 11.2. Пусть функция Дх, Z|, z2, z3,..., z„) определена и
непрерывна в слое Пу и пусть она удовлетворяет условию Липшица
в следующей форме: существует положительная константа L та-
284
кая, что для любых х е [ х,,, Л|. и произвольных и = (w(, w2, w3,..., )
и v = (V], г2, v3,..., vn) выполняется
|/(x,W|,w2,w3,...,H„) -/(х,ц,г2,п3,...,г„)| < L ||й-й||,
где w - v = (W| - V\, w2 - r2, w3 - z>3,	- z>„).
Тогда для любого набора начальных значений: j0, у},	у„_)
существует и притом единственное решение задачи Коши для урав-
нения (11.21) на отрезке [xq,^].
Следствие. Если уравнение (11.21) имеет вид
^-^=а}(х)у(п-" + й2(х)У«-2) + ... + а„(х)у + /(х), (11.22)
а х"
где й[(х), й2(х), ..., дй(х),/(х) — функции, непрерывные на (а,Ь),
то при любом х0 е (а, Ь) и любых начальных данных решение зада-
чи Коши существует и единственно на всем интервале (а, Ь).
Доказательства теоремы о разрешимости задачи Коши и ее след-
ствия здесь не приводим.
11.5.	Линейные уравнения высших порядков
11.5.1.	Основные понятия
Линейным уравнением порядка п называется уравнение следую-
щего вида:
й0(х)у(,,) + я1(х)У',-]> + й2(х)у("-2) + ... + а„(х)у = /(х), (11.23)
где ац(х), й|(х), а2(х), ..., а„(х),/(х) — функции, непрерывные на
некотором интервале (а,Ь) [этот интервал может быть (-<»,+<*>)],
причем на этом интервале функция я0(х) # 0 ни в какой точке.
Как вытекает из следствия из теоремы о разрешимости задачи
Коши, уравнение (11.23) при любых начальных данных имеет един-
ственное решение, удовлетворяющее начальным условиям. Чтобы
описать структуру формулы, дающей общее решение такого урав-
нения, необходимо ввести некоторые понятия.
Определение 11.1. Уравнение (11.23) при условии, что /(х) = О
на (а, Ь), называется линейным однородным уравнением п-го порядка.
Определение 11.2. Соответствие L, когда по заданной функции
/Дх) однозначно находится другая функция g(x), называется опе-
ратором L. При этом используется запись
Ш(х)] = g(x).
Пример 11.17. Пусть оператор L ставит в соответствие каждой
функции /Дх) ее производную
L[/2(X)] = h'(x).
285
Такой оператор называется оператором дифференцирования,
его обозначают через —. Это удобно, поскольку запись
dx
ЦЛ(х)] = h(x) = h'(x)
dx
хорошо согласуется с обозначением производной — = п .
dx
Определение 11,3. Оператор L называется линейным оператором,
если он удовлетворяет двум условиям:
а)	для любой функции /?(х) любого числа X справедливо равенство
L[XA(x)] = Щй(х)];
б)	для любых двух функций Л(х) и фх) справедливо равенство
Ш(х)+фх)]=Ш(х)] + Щ(х)].
Пример 11.18. Опереатор дифференцирования
очевидно, является линейным оператором, поскольку константу
всегда можно выносить за знак дифференцирования:
£(W))j=^(W
а производная суммы равна сумме производных
(Мх) + g(x)) =	(Л(х)) +	(g(x)).
Пример 11.19. Более сложным примером линейного оператора
является оператор вида
L[/z(x)] = й0(х)Л(л) + а [ (х) h{n~1 > + а2(х}й(п~1} + ... + an(x)h,
называемый линейным дифференциальным оператором порядка п.
Здесь функции «о(х), Я|(х), «2(х),	а„(х) подчинены тем же усло-
виям, что и в уравнении (11.23). Как и в примере 11.18, легко
устанавливается, что оператор L является линейным оператором,
если учесть, что
(h + g)w = h(k} + и (X/z(x))w = Х(Л(х))(А)
при любом натуральном к.
Замечание. Используя линейный оператор, рассмотренный в
примере 11.19, дифференциальное уравнение (11.23) можно за-
писать в операторной форме'.
L[y(x)] = /(х).	(11.24)
286
Определение 11.4, Система функций <р|(х), ф2(х), Фз(х), , <pm(x),
определенных на интервале (а, />), называется линейно зависимой на
этом интервале, если и только если существуют числа
не все равные нулю, и такие, что
Х]ф|(х) + Z2(p2(X> + ^3ф3(х) + ... +	= О
на интервале (а,Ь).
Замечание. Поскольку определение линейной зависимости си-
стемы функций совершенно аналогично определению линейной
зависимости системы строк или системы столбцов матрицы, то
это приводит к тому, что критерий линейной зависимости систе-
мы строк: система строк линейно зависима тогда и только тогда,
когда найдется строка, которая линейно выражается через осталь-
ные, оказывается справедливым и для системы функций: система
функций линейно зависима тогда и только тогда, когда хотя бы
одна из функций системы линейно выражается через остальные
функции, т.е. при некотором j
ф/х) = £«*фДх),
к=\
где с/.А — некоторые числа.
11.5.2.	Линейные однородные уравнения
Линейное однородное дифференциальное уравнение имеет вид
<70(x)y(w) + а।	1 > + а2(х)у{п~1} + ... + ап(х)у = 0, (11.25)
где ац(х), й|(х), a^fx), ап(х) — функции, непрерывные на неко-
тором интервале (а,Ь), причем я0(х) # 0 ни в одной точке этого
интервала. С помощью линейного оператора L, определенного фор-
мулой
ОДх)] = Oo(x)y(w) + я,(х)у<"-1) + a2(x)y<w-2) + ... + а„(х)у,
уравнение (11.25) можно записать как
ОД = 0.
Пользуясь линейностью оператора L, легко доказать следующие
свойства решений уравнения (11.25).
Теорема 11.3. Пусть и(х) и v(x) — два решения уравнения Цг| = 0.
Тогда:
а)	функция w(x) = и(х) + v(x) также будет решением этого
уравнения;
б)	для любого действительного числа 1 функция z(x) = /.и(х)
будет решением уравнения L[y] = 0.
287
Доказательство. Поскольку н(х) и v(x) — решения уравнения,
то Ци] = 0 и L[r] = 0. Для функции w(x} = и(х) + v(x) имеем
L[w] = L[w + v] = L[w] + L[f] =0 + 0 = 0,
т.е. w(x) является решением.
Для функции z(x) = /.и(х) имеем
L[z] =L[M =1ОД =1-0 = 0,
т.е. z(x) является решением. ▲
Следствие. Если функции yi(x), yiW, УзСО,  Ут(х) являются
решениями уравнения L[y] = 0, то будет решением этого уравне-
ния любая линейная комбинация этих решений, т.е. функция
у(х) = £а*уДх),
k=l
где ak — некоторые числа.
Определение 11.5. Любая линейно независимая система из п
решений линейного однородного уравнения (11.25) называется
фундаментальной системой решений этого уравнения.
Теорема 11.4. Для любого линейного однородного уравнения
(11.25) существует фундаментальная система решений.
Доказательство. Поставим для уравнения (11.25) п задач Коши:
1)	уЫ	=	1,	У(х„)	=	О,	у"Ы)	=	О,	....	У"~Щ0)	=	о;
2)	уЫ	=	0,	У(х0)	=	1,	У'(х0)	=	0,	....	y-'U)	=	0;
3)	у(х0)	=	0,	У(х„)	=	0,	У'(х„)	=	1,	....	У"~Щ0)	=	0; (11.26)
«) Дх»)	=	0,	/(хо)	=	0,	у"(хо)	=	0,	/""'’(хо)	=	1-
Все эти задачи однозначно разрешимы по теореме о существова-
нии и единственности решения задачи Коши. Пусть это будут функ-
ции yi(x), у2(х),  , уДх). Если бы они образовывали линейно зави-
симую систему, то существовали бы постоянные	•••> К,
не все равные нулю, и такие, что
Х]У](х) + ^2У2(х) + ... + МлО) = 0
на интервале (а, Ь). Дифференцируя это тождество (п - 1) раз, по-
лучим вместе с исходным систему тождеств на интервале (а, Ь):
^уфх) + Z2y2(x) + ... + Х„у„(х) = 0;
Х]У{(х) + Z2y2(x) + ... + Хяу'(х) = 0;
Xjyftx) + Х2у2(х) + ... + А.ду"(х) = 0;
+ - + M£”l)C0 = о,
которая обязана выполняться и в точке х = х0. Подставляя это зна-
чение в первое тождество и учитывая равенства (11.26), получим
288
1| = 0. Аналогично из второго тождества имеем, что Z2 = 0, и т.д. Из
последнего тождества вытекает, что = 0. Полученное противоре-
чие заставляет признать линейную независимость системы функ-
ций _У|(х), у2(х), •••> Л(х)- Следовательно, эти решения образуют
фундаментальную систему решений. ▲
Следующая теорема приближает нас к формуле для общего ре-
шения уравнения (11.25).
Теорема 11.5. Любые (п + 1) решений уравнения Цу] = 0 образу-
ют линейно зависимую систему.
Доказательство. Пусть функции _У|(х), у2(х),	К+Фх') являются
решениями уравнения L[y] = 0. Составим определитель
T]	У2	Тз •	•• Тл+I	
y']	У2	Уз 	•• K+i	
У]	У2	Уз 	•• Уп+\	(11.27)
	У(21}	У? 	•• тХ!	
Из уравнения Цу] = 0 или
й0(х)у(,,) + tf1(x)y(fl“1) + <з2(*)Х"”2) + ... + а„(х)у = 0
следует, что у'!П может быть представлена как линейная комбина-
ция функций yw-l)(x), У':’~'(х). ..., у'(х), у(х). Действительно, по-
скольку а0(х) # 0, то
ум(х) =------}—(ai(x)y<fl-l) + а2(х)у<"~2) + ... + ап(х)у),
й0(х)
и, следовательно, при каждом фиксированном л: последняя строка
определителя линейно выражается через остальные его строки. Как
известно из теории определителей, в этом случае определитель
равен нулю. Следовательно, рассматриваемый определитель равен
нулю при любом х е (а, Ь). Теперь попробуем из функций j](x),
у2(х), ..., yfl+](x) построить как линейную комбинацию такое ре-
шение уравнения
X*) = С|У|(х) + С2у2(х) + С3уз(х) + ... + Cw+iyfl+1(x),
которое удовлетворяло бы условиям Х*о) = Ф Х(*о) = Ф у"(*о) = Ф
..., Xw)(xo) = 0- Это означает, что должны выполняться следующие
соотношения:
С[У[(х0) + С2у2(х0) + С3уз(х0) + ... + С„+] y,j+i(xo) = 0;
GXGo) + C2y'2(xQ) + C3y'3(xQ) + ... + C„+1X+i(*o) = 0;
Gy"(x0) + C2y2(*o) + Сзу3(х0) + ... + C„+iX+i(xo) = 0;	(11.28)
GX^o) + c2X"U) + c3X"Vo) + - + G+Iy<;^(xo) o.
289
Относительно величин Сь С2, С3, Ся+1 эта система равенств
представляет систему из (п+ 1)-го уравнения с определителем, рав-
ным нулю. Из теории однородных линейных систем алгебраичес-
ких уравнений следует, что она имеет ненулевое решение, т.е. най-
дутся Ch С2, С3, ..., Cfl+], не все равные нулю, и такие, что будут
выполняться все равенства (11.28). Решение уравнения, получен-
ное с помощью этих Сн С2, С3, ..., Ся+1 по формуле
/(X = С,у,(х) + С2у2(х) + ... + Cw+lyfl+](x),
удовлетворяет условиям j(xq) = 0, Х(х0) = 0, ..., г(';’<Лэ) = 0, и
поэтому является решением следующей задачи Коши: найти ре-
шение уравнения L|r| = 0, удовлетворяющее условиям у(х0) = О,
у'(хо) = 0, ..., Х"’1^) = 0. Но решением этой задачи Коши явля-
ется функция, тождественно равная нулю. В силу единственности
решения задачи Коши, построенное решение у(х) = 0 на интер-
вале (й, Ь). Или
C]j](x) + С2у2(х) + ... + C„+iy„+](x) = 0,
что означает линейную зависимость системы функций У[(х), у2(х),
..., л+1(х) на (a,by ▲
Следствие 1. Если решения уравнения L|r| = 0 у((х), у2(х), ...,
уя(х) образуют фундаментальную систему решений, то любое ре-
шение уравнения линейно выражается через решения, входящие в
фундаментальную систему.
Доказательство. Пусть XX — произвольное решение уравне-
ния L[y] = 0. Составим новую систему из (и + 1)-го решения, при-
соединив X*) к фундаментальной системе решений. По теореме
11.5 она является линейно зависимой, т.е. найдутся числа Zo,
X, ..., 1Я, не все равные нулю, и такие, что
XXX + Хи(Х + Xz>(X + , + Хл(Х = °
на интервале (а, Ь). Заметим, что Ху не может быть равным нулю.
В этом случае получилось бы, что система функций У](х), у2(х),
..., уя(х) является линейно зависимой, что невозможно, так как
эта система — фундаментальная. Пользуясь тем, что * 0, имеем
XX = С,у,(х) + С2у2(х) + ... + С„у„(х),
где С\ =	£=1,2, ..., п. ▲
X
Следствие 2. Если решения уравнения L| r| = 0 У[(х), у2(х), ...,
уя(х) образуют фундаментальную систему решений, то общее ре-
шение этого уравнения может быть представлено в следующей
форме:
XX = CiJ](X + С2у2(х) + ... + С„у„(х),	(11.30)
где С], С2, С3, ..., Сп — произвольные постоянные.
290
Доказательство. Для доказательства надо проверить выполне-
ние двух условий: 1) при любых значениях Сь С2, С3, Сп фор-
мула (11.30) дает решение уравнения L[y] = 0; 2) для любого,
наперед заданного решения уравнения у(х) найдется единствен-
ный набор констант С\, С2,..., Сп такой, что
у(х) = С} (х) + С2у2(х) +... + Спу,, (х).
Первое условие, очевидно, выполняется, так как любая линей-
ная комбинация решений уравнения, как было показано выше,
снова является решением уравнения. Второе условие вытекает из
следствия 1, но требуется доказать единственность набора кон-
стант Си С2,..., С„. Если предположить, что имеется другой набор
Д, Д,..., Д, обеспечивающий равенство
Я*) = Ду,(х) +Ду2(х) + ... +ДуЛ(х),
то, вычитая левые и правые части первого и второго представле-
ний функции у(х), получим
(G - Д) У|(х) + (С2 - Д) у2(х) +... + (С„ - Д) Л(х) = 0
на интервале (а, Ь). Такое равенство возможно только тогда, когда
выражения во всех скобках равны нулю, иначе получилось бы, что
система уДх). у2(х), ..., у„(х) линейно зависима. Таким образом,
другого набора констант не существует. ▲
11.5.3. Линейные неоднородные уравнения
Теорема 11.6. Общее решение линейного неоднородного урав-
нения (11.23)
й0(х)у(,,) + «[(х)у(й-1) + а2(х)у(,,~2) + ... + af!(x)y = f(x)
может быть представлено в следующем виде
у(х) = Ду^х) + С2у2(х) + ... + С„у„(х) + Дх), (11.30)
где У](х), у2(х), ..., _г,;(х) образуют фундаментальную систему ре-
шений соответствующего однородного уравнения, а и(х) — неко-
торое фиксированное частное решение неоднородного уравнения.
Доказательство. Пусть г(х) — произвольное решение уравне-
ния (11.23), т.е.
ЦДх)] = /(х).
Тогда функция /Дх) = v(x) - Дх) будет решением соответству-
ющего однородного уравнения. Действительно,
Ц/Дх)] = Ь[Дх) - Дх)] = Ь[Дх)] - Ь[Дх)] =/(х) - f(x) = 0.
Поэтому найдутся единственные константы Сь С2,..., Сп такие,
что
w(x) = Cly1(x) + C2y2(x) + ... + Cflyfl(x),
291
или
v(x) = Clyl(x) + C2y2(x) + ... + С„у„(х) + и(х),
т.е. любое решение неоднородного уравнения L[r(x)] = f(x) при
единственном наборе произвольных постоянных получается из
формулы (11.30). С другой стороны, при любых значениях Сь С2,
С3,..., Сп формула (11.30) дает решение уравнения L|r(x)l = f(x).
Действительно,
L[C,y,(x) + С2у2(х) + ... + С„у„(х) + м(х)] =
= C.LLMx)] + C2L[y2(x)] + ... + CflL[b(*)] + U«(x)] = f(x),
поскольку ЦуДх)] = 0, к = 1, 2, ..., /?, a L[w(x)] = f(x). Следователь-
но, формула (11.30) дает общее решение линейного неоднород-
ного уравнения L|r(x)| =f(x). ▲
11.5.4. Линейные однородные уравнения
с постоянными коэффициентами
Функции я0(х), 0|(х), л2(х), ..., я„(х), фигурирующие в уравне-
нии (11.23), т.е.
й0(х)у(л) + й](х)У',-]> + a2(x)y(fl~2) + ... + a„(x)y=f(x)
называются коэффициентами этого уравнения. До сих пор предпола-
галось, что эти коэффициенты — непрерывные на (я, Ь) функции.
В этом подразделе рассмотрим частный, но весьма важный, слу-
чай линейных уравнений: случай, когда коэффициенты не зависят
от х, т.е. постоянны.
Итак, будем изучать линейные дифференциальные уравнения
вида
у{п} +	+ «2y(fl“2) + ... + а „у = Дх), (11.31)
где «], а2, ап — действительные числа (я0 — коэффициент при
Ул) без ограничения общности можно считать равным единице).
Естественно, что все результаты, полученные для уравнений с
переменными коэффициентами, остаются справедливыми и для
этих уравнений. В поисках частных решений, необходимых для по-
строения фундаментальной системы решений и формулы общего
решения, обычно обращаются к функциям вида у = е*\ Если под-
ставить эту функцию в однородное уравнение
ум + й]У(/?“1) + «2y(fl_2) + ... + а„у = 0,	(11.32)
то с учетом формулы
Лтркх
-----= kmekx, т = \, 2,...,
dxm
292
получим
F(k)ekx = (к" + а[к"~] + a2kn~2 + ... + an_}k + af!)ekx = 0.
Многочлен
F(k) = kn + a\kl!~l + a2kn~2 + ... + an_\k + an
называется характеристическим многочленом уравнения или диф-
ференциального оператора L, который можно представить как
линейную комбинацию операторов дифференцирования разных
порядков:
_ d”	dn~]	dn~2
L — —---1- Й] —-г +	—T + ... + .
dx”	dx”~l	dx”~2
Полученное в результате подстановки функции у = сАл уравнение
имеет вид
F(k)ekx = 0.
Если к — действительное число, то екх # 0. Сокращая на еА\ полу-
чим уравнение относительно к‘.
F(k) = 0.
Это алгебраическое уравнение степени п называется характе-
ристическим уравнением, а его корни — характеристическими кор-
нями уравнения (11.32) или соответствующего дифференциально-
го оператора.
Если к таково, что F(k) = 0, то функция у = екх будет решением
однородного уравнения. Поэтому нахождение характеристических
корней уравнения приводит к нахождению частных решений од-
нородного уравнения.
На этом пути появляется возможность найти п частных реше-
ний, которые могли бы составить фундаментальную систему ре-
шений. Дело в том, что по основной теореме алгебры алгебраиче-
ское уравнение и-й степени имеет ровно п корней, если каждый
корень считать столько раз, какова его кратность. Поэтому первый
случай, когда имеется п различных решений, просматривается сразу:
это случай, когда все корни действительны и различны: к}, к2, к3,
..., кп, ks * к{ при .s' * t. Тогда получаем п различных частных реше-
ний: e*lA,e*2X,e*3X,.
Убедимся в том, что эта система решений линейно независима.
Для этого рассмотрим линейную комбинацию этих решений
Ge*'* + С2е^ + С3е^' + ... + С„е*"х.
Пусть она тождественно равна нулю. Выберем из чисел к{, к2,
к3, ..., кп наибольшее (пусть это будет к}) и разделим равенство
С,е^А' + С2е^' + С3е^ +... + Cfle^ = 0
293
на е*|Х. Получим
С, + С2е(к^х + С3е<^')А' + ...+ Спе{к”-^х = 0.
При увеличении х все слагаемые, начиная со второго, имея от-
рицательное число при х в показателе степени, стремятся к нулю.
Отсюда следует, что С, = 0.
Рассуждая аналогично, получим, что все числа Сь С2, С3, ...,
С„ должны быть равными нулю. Следовательно, система решений
eA|Jf, e*jX, еА)Х,..., ек"х линейно независима, т.е. образует фундамен-
тальную систему решений. Поэтому общее решение однородного
уравнения в этом случае будет иметь вид
у = С}ек1Х + C2eKv + С3ек1Х С„ек*х.	(11.33)
Пример 11,20, Пусть требуется найти общее решение дифферен-
циального уравнения
у'" + у" - 2у' = 0.
Составляем характеристическое уравнение
А3 + к2 - 2к = 0.
Решая его, находим характеристические корни: к\ = -2, к2 = 0,
к3 = 1. Функции е“2л, 1, ех образуют фундаментальную систему ре-
шений. Общее решение имеет вид
у(х) = С[е“2л' + С2 + С3еЛ'.
В рассмотренном случае характеристический многочлен раскла-
дывается на линейные множители:
F(k) = (к- к})(к - к2)...(к - к„),
где все кь к2, ..., к„ различны. По образцу этого разложения можно
разложить и дифференциальный оператор
< dn	dn~2 ( d . Y d , \ ( d . \
dxn dxn~l 2 dxn~2	J	J
Допустим теперь, что два корня совпадают, например, к„ = к„_[.
Тогда оператор можно записать в виде
( d V
Если найти функцию у(х) такую, что------к„ у(х) = Q, то,
очевидно, и L[y(*)l = 0, т.е. у(х) будет решением исходного одно-
родного уравнения.
294
Рассмотрим подробнее уравнение
у(х) = 0,
ах J
или
у(х) - 2к„ у(х) + к^у(х) = 0.
ах	ах
Введем в рассмотрение новую неизвестную функцию
z(x) = е~к”х у (х)
или
у(х) = ek“x z(x)
и подставим ее в это уравнение. Имеем:
№
—7 у(х) = k„QknXz(x) + 2kfleknXz'(x) + eki]Xz>'(x);
dx1
-2kn^~ y(x) = -2k„(knz(x) + z'(x))ek°x = -2k^z(x)ek'‘x - 2kf!zXx)ek'-x',
dx
k^y(x)= kfck"xz(x).
Складывая левые и правые части последних трех равенств, по-
лучим, что функция z(x) является решением уравнения
О = ek"xz"(x).
Сокращая на множитель еА’х, в итоге имеем уравнение
z"(x) = 0.
Его общее решение легко находится двумя последовательными
интеграциями:
z(x) = С] + С2х.
Следовательно, общее решение уравнения
у(х) - 2к„ у(х) + к„у(х) = 0
dx1	dx
имеет вид
у(л) = С]е*пА' + С2ХскпХ,
откуда видно, что функции eA;v и хек*х будут решениями этого
уравнения. Таким образом, в случае совпадения двух корней (крат-
ность корня к = кп равна двум) им соответствует два решения: еАлЛ
и хекпХ.
Аналогично можно показать, что при совпадении 5 корней:
295
им будет соответствовать 5 решений е*л, ле*’х, х2ел”х,..., х5-|еАл,
которые, как нетрудно доказать, образуют линейно независимую
подсистему всей системы решений однородного уравнения. Эти
рассуждения помогают получить результат о формуле общего ре-
шения однородного уравнения в случае, когда все характеристи-
ческие корни являются действительными числами.
Приведем без вывода описание фундаментальной системы ре-
шений. Итак, в фундаментальную систему решений каждый дей-
ствительный характеристический корень к = к$ вводит своего пред-
ставителя с/ч', а если этот корень имеет кратность .v. где а > 1, то
дополнительно включаются решения хе*°\ х2е*°х,..., а '. В n roic
набирается п решений, которые и составляют фундаментальную
систему решений.
Пример 11,21, Пусть требуется найти общее решение уравнения
yIV - 2у"' - Зу" + 8/ - 4г = 0.
Характеристическое уравнение имеет вид
Л4-2С-3^ + 8Л;-4 = 0.
Разлагая характеристический многочлен на множители, полу-
чим
(к-2)(к + 2)(к- I)2 = 0,
откуда к] = -2, к2 = ку = 1, /с4 = 2. Фундаментальная система реше-
ний имеет вид: е-2л, е\ хе', е2л. Следовательно, общее решение
дается формулой
у = Cft~2* + С ft* + С3хе* + С4еЧ
В интегральном исчислении обычно используется разложение
многочлена на множители (без использования комплексных чи-
сел). Многочлен с действительными коэффициентами всегда мо-
жет быть разложен на множители также с действительными коэф-
фициентами. Эти множители могут быть линейными, как, напри-
мер, в приведенном примере, или квадратичными, т.е. иметь вид
(к1 + рк+ д),
где р1 < 4q. В этом случае выделением полного квадрата можно
преобразовать множитель:
z	ч2
(к1 + рк + q) = I к + у I + г2,
где г2 = -^(4д - р2). Соответствующий дифференциальный опера-
тор имеет вид
т +	+г
ах 2 )
296
и, решая дифференциальное уравнение
[4" + ^ Хх) + '*2Хх) = 0,
IXх 2)
найдем частные решения однородного уравнения, порождаемые
множителем (к2 + рк + q). Решение этого уравнения проводится по
той же схеме, что и выше: вводится неизвестная функция
ра
z(x) = е2 у(х)
и в уравнении производится замена Xх) на Xх)- Для функции z(x)
уравнение упрощается и имеет следующий вид:
z"(x) + r2z(x) = 0.
Это уравнение не содержит переменного х, и можно понизить его
порядок, а затем — проинтегрировать. Получим, что общее реше-
ние этого уравнения представляется в виде
z(x) = C[Sin(nc) + C2cos(rx).
Возвращаясь к функции Xх), получим
_д¥	_д¥
Xх) = С(е 2 sin(rx) + С2е 2 cos(rx).
Таким образом, множитель (к2 + рк + q) в характеристическом
многочлене порождает пару решений однородного уравнения:
_дА.	_р_х
е 2 sin(rx) и е 2 cos(rx),
которые должны быть включены в фундаментальную систему ре-
шений.
Подробное доказательство этого факта технически громоздко и
малопоучительно с идейной точки зрения. Поэтому здесь его не
приводим.
Рассмотренный случай разобран при молчаливом предположе-
нии, что все квадратичные множители различны. Но может ока-
заться, что среди них попадутся одинаковые. Тогда эти одинако-
вые множители можно собрать в один, записав его в виде
(к2 + рк+ q)s,
где 5 > 1, и доказать, что этому множителю характеристического
многочлена в фундаментальной системе решений соответствует
следующая группа частных решений:
_д¥	_Р¥	_р_х	_р_х	JLX
е 2 sin(rx), е 2 cos(rx), хе 2 sin(rx), хе 2 cos(rx), х2е 2 sin(rx),
_дА	_дА	_р¥
х2е 2 cos(rx), ..., х'1 е 2 sin(rx), х'1 е 2 cos(rx).
297
Пример 11.22, Пусть требуется найти общее решение следующе-
го дифференциального уравнения:
yIV - 8 у"' + 26у" - 40у' + 25у = 0.
Характеристический многочлен
к* - $к3 + 26А2 - 40Аг + 25
можно представить в виде
(к2 - 4к + 5)2 = [(к - 2)2 + I]2.
Выписывая фундаментальную систему решений, найдем общее
решение:
Их) = KG + С2х) sinx + (С3 + С4х) cosx|e2'.
Таким образом, на основе вышеизложенного можно сделать
вывод, что решение линейного однородного дифференциального
уравнения с постоянными коэффициентами всегда доводится до
общего решения, если удается разложить характеристический мно-
гочлен на линейные и квадратичные множители. Эта последняя
задача относится к алгебре, и здесь ее обсуждать не будем.
11.5.5. Линейные неоднородные уравнения. Метод вариации
постоянных
Для нахождения общего решения линейного неоднородного
уравнения следует сначала найти общее решение соответствующе-
го однородного уравнения, а затем — какое-нибудь частное реше-
ние неоднородного уравнения. Если первая часть задачи у нас уже
не вызывает принципиальных трудностей, то вторая — как найти
частное решение неоднородного уравнения, пока неизвестна.
Существует несколько способов нахождения частного решения
неоднородного уравнения.
Один из них, называемый методом подбора, продемонстриру-
ем на примере.
Пример 11.23. Пусть требуется найти общее решение уравнения
у" + 9у = х2.
Общее решение однородного уравнения у" + 9у = 0:
X*) = С, sin Зх + С2 cos Зх.
Попытаемся найти частное решение неоднородного уравнения
в виде многочлена той же второй степени, т. е. будем искать реше-
ние в виде
у = Ах2 + Вх+ С.
298
Подставив в уравнение вместо у(х) функцию Ах2 + Вх + С, по-
лучим
2А + 9Ах2 + 9Вх + 9С = х2.
Два многочлена тождественно равны тогда и только тогда, ког-
да у них совпадают коэффициенты при одинаковых степенях. При-
равняв эти коэффициенты, получаем систему линейных алгебраи-
ческих уравнений
9 А = 1;
< 9В = 0;
2А + 9С = 0.
Неизвестные Л, В и С однозначно определяются, таким обра-
зом, требуемое частное решение:
1 2 2
у = —X----.
•	9	81
Теперь имеем возможность написать общее решение неодно-
родного уравнения:
у(х) = G sin Зх + С2 cos Зх + i х2
2
8Г
Метод подбора прост в употреблении, но имеет и ряд недостат-
ков. Прежде всего, он не универсален, т.е. применим не всегда, а
только для некоторого, хотя и важного, набора правых частей в
неоднородном уравнении. Кроме того, употребление его в общем
случае (когда он применим) связано с непростым сопоставлени-
ем набора корней характеристического уравнения и правой части
уравнения, от которого зависит, в какой форме ищется частное
решение, т.е. технология его применения не так проста, как мо-
жет показаться после рассмотрения примера. Тем не менее репута-
ция этого метода такова: когда он применим, его использование
предпочтительно.
Другой метод, называемый методом вариации произвольных по-
стоянных, в отличие от предыдущего универсален и алгоритми-
чески прост. Он применим и к уравнениям с переменными коэф-
фициентами. Поэтому изложим его как основной метод решения
неоднородного уравнения.
Метод вариации произвольных постоянных также предполагает
решение соответствующего однородного уравнения. Будем считать,
что функции q>[(x), <р2(х), ф3(х), ..., <рн(х) образуют фундаменталь-
ную систему решений для однородного уравнения. Тогда общее
решение однородного уравнения будет иметь вид
у(х) = С]ф|(х) + С2ф2(х) + С3фз(х) + ... + Сйф„(х).
299
Теперь будем искать частное решение неоднородного уравне-
ния в таком же виде с той разницей, что постоянные Сь С2, С3,
Сп теперь считаем неизвестными функциями от х, т.е.
у(х) = С](х)ср](х) + С2(х)ф2(х) + С3(х)ф3(х) + ... + СДх)фДх).
Для их нахождения требуется решить следующую систему урав-
нений:
С[(х)ф|(х) + СДх)ф2(х) + СДх)ф3(х) + ... + СДх)фДх) = 0;
< С[(х)ф!(х) + СДх)фДх) + СДх)фДх) + ... + СДх)фДх) = 0;
ОДф^Чх) + СДх)фГ '>(х) + ОДфГ’(*) + - + ВДфГ >(*) = f(x),
где f(x) — правая часть неоднородного уравнения.
Можно доказать, что эта система всегда однозначно разрешима
и ее решение можно найти, например, по правилу Крамера. В ре-
зультате решения системы получится п соотношений
Cj(x) = АДх), Q(x) = А2(х), С3(х) = А3(х), ..., СДх) = АДх),
где функции hj(x),j= 1, 2, ..., п — известны. В качестве функций
Cj(x) берем jгде х0 — произвольная точка. В итоге оказы-
вается найденным частное решение неоднородного уравнения и
теперь можно написать общее решение
у(х) = С^Дх) + С2ф2(х) + С3фз(х) + ... + СйфДх) +
+ С|(х)ф](х) + С2(х)ф2(х) + С3(х)ф3(х) + ... + СДх)фДх).
Замечание. В случае неоднородного уравнения с переменными
коэффициентами эффективность метода несколько падает, по-
скольку в этом случае нет общего метода построения фундамен-
тальной системы решений.
Пример 11.24. Пусть требуется найти общее решение линейного
неоднородного дифференциального уравнения
у” + 2у = 4х2е-Л\
Решаем сначала однородное уравнение
у” + 2у = 0.
Его характеристическое уравнение имеет вид
к2 + 2 = 0.
В соответствии с теорией получаем, что общее решение одно-
родного уравнения дается формулой
у(х) = Q sin (V2x) + С2 cos (>/2х).
Теперь ищем частное решение неоднородного уравнения в виде
300
у(х) = C|(x)sin (V2x) + C2(x)cos (>/2x).
Составляем систему уравнений по предписанному выше правилу:
C[(x)sin(>/2 х) + C2(x)cos(V2 х) - 0;
C[(x)cos(V2 х)-С2(х) sin(V2 х) = -у=4х2е“А'2
(11.34)
и решаем ее по правилу Крамера. Определитель системы Л = -1.
Находим определители
	=	0 —^4х2е“л2 V2		cos (>/2x) - sin(V2x)	= —^=4х2е х'~ cos (л/2х) V2
и	Д2 =		sin(V2x) cos(V2x)	0 -^4х2е“л2 V2	= —J=4x2e-A’ sin(V2x), V2
откуда получим
С[(х) = — = -Д[ = -^4х2е-Л'2 cos (>/2х);
Л <2
С2(х) = — = -Д2 = --i=4x2e“A'2 sin(V2x).
Д	V2
Интегрирование по частям позволяет вычислить интегралы от
этих функций. Имеем
С|(х) = е-А'2 (sin(V2x) - V2xcos(V2x));
С2(х) = e“¥? (cos(V2x) + V2xsin(V2x)),
откуда получаем частное решение неоднородного уравнения
у(х) = е-А'2 (sin(V2x) - V2xcos(V2x))sin(V2x) +
+ е-А'2 (cos(V2x) - л/2хsin(V2x))cos(V2x) =
= е“А'2 (cos2G/2x) + sin2(V2x)) = e-*2.
Таким образом, общее решение уравнения у” + 2у = 4х2е“А' име-
ет вид
у(х) = С{ sin(T2x) + С2 cos(V2x) + е-А'2.
301
1.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Найдите общий интеграл дифференциального уравнения
v dy
2.
3.
4.
5.
Найдите общее решение дифференциального уравнения
dx \х)
Найдите общий интеграл дифференциального уравнения
— + 2ху = 2х3у3.
dx
Найдите общее решение дифференциального уравнения
J2y
--v = X + Sinx.
dx2
Найдите общее решение дифференциального уравнения
d2y . х [ dy
dx2 dx '
Решите следующую задачу Коши: найти решение дифференциал ь-
6.
ного уравнения
2^ = 3Л
удовлетворящее начальным условиям у(—2) = 1, —(-2) = -1.
dx
7.	Найдите общее решение дифференциального уравнения
Д+4-2,=0.
dx1 dx
8.	Найдите общее решение дифференциального уравнения
^+4+13^=°-
dx1 dx
9.	Найдите общее решение дифференциального уравнения
J2y
—Уу + У = COSX.
dx2
10.	Найдите частное решение дифференциального уравнения
dx1 dx
удовлетворяющее начальным условиям: у(0) = 1, -у-(О) =
ПРИЛОЖЕНИЕ
Введение в математический пакет MAPLE
Многие практические задачи, связанные с использованием данного
курса математики, можно решить с помощью компьютера. В настоящее
время имеется несколько мощных математических пакетов, позволяющих
решать такие задачи быстро и эффективно. Одному из них, а именно па-
кету MAPLE, посвящена эта небольшая справка.
Математический пакет MAPLE имеет несколько версий, называемых ре-
ализациями. Наибольшее распространение имеют реализации MAPLE V R5,
MAPLE VI и MAPLE VII. Для начинающего пользователя эти реализации
практически неразличимы. Поэтому то, что будет дано в качестве руковод-
ства к использованию пакета, применимо к любой из этих реализаций.
Наиболее простой режим работы пакета — диалоговый. Приглашение
к диалогу пакет осуществляет путем высвечивания на экране в начале
строки знака > . Пользователь набирает вопрос и нажимает клавишу Enter
(Ввод). В ответ компьютер выводит на экран монитора соответствующую
информацию.
Например:
>	13 + 5- 4;
14
>	sin (1.0);
.841470985
Знак (;) после введенного вопроса обеспечивает выдачу ответа неза-
медлительно. В приведенных примерах числа 14 и .841470985 это реакция
пакета на введенные вопросы. Бывает так, что вопрос состоит из несколь-
ких пунктов. Например, пусть требуется решить уравнение х2 - Зх + 2 = 0.
Можно поступить так: сначала определить функцию f(x) = х2 - Зх + 2, а
затем решить уравнение Дх) = 0. Это делается так:
>	f := хл2 - 3*х + 2 : g := solve (f = 0, х);
В ответ на этот вопрос на экране появятся корни уравнения:
g := 2, 1
Из этого примера видно, что вводимые вопросы задаются по прави-
лам, принятым для всех компьютерных строчных редакторов. Запись f :=
при задании вопроса означает, что выражение, стоящее справа, обозна-
чается через f. После введения обозначения поставлен знак (:), а не (;).
Поэтому на экране никакой реакции на этот вопрос не последовало. Если
бы был поставлен знак (;), то на экране был бы такой ответ:
f := х2 - Зх + 2
g := 2, 1
После того как компьютер «отчитался» по заданному вопросу, на эк-
ране вновь появляется приглашение к диалогу, т.е. в начале строки высве-
303
чивается знак >. Если же отчет не удался по причине некорректного воп-
роса, выдается указание об ошибке (а иногда и подсказка об исправле-
нии).
Например,
> sin (1,0);
Error, (in sin) expecting 1 argument, got 2
Здесь пользователь число 1 записал не с точкой, а с запятой. Пакет вос-
принял число 1,0 как два числа 1 и 0, что недопустимо при использовании
встроенной функции sin(x). Ошибка фиксируется и дается подсказка, прав-
да, на английском языке. Если пользователь не знает английского языка и не
понял, чем «не доволен» пакет, то следует внимательно проанализировать
введенное выражение вопроса, соблюдены ли все «правила игры», памятуя
о том, что компьютер всегда прав. После исправления текста вопроса следует
поставить курсор в любое место текста вопроса и нажать клавишу Enter.
Важным свойством пакета является способность к символьному ис-
числению, т.е. преобразование и работа с буквенными выражениями. На-
пример, могут быть решены в буквенной форме:
• квадратное уравнение
> f := solve (а*хЛ2 + b*x + с = 0, х);
Р 1 -b + Vb2 - 4ас 1 —b - Vb2 - 4ас .
2 а ’2 а
• производная от функции sin (Зх)
> f := sin (3*х): g: = diff (f, x);
g := 3 cos (3x);
• неопределенный интеграл Jcos5xdx:
> f := cos (5*x): g := int (f, x);
g := | sin (5x);
• сумма числового ряда У Дг:
> g := sum (1/пЛ2, n = 1 .. infinity);
g: = |PP.
Здесь Pi означает число л = 3.14159265....
Систематическое описание математического пакета MAPLE в рамках
этого приложения невозможно. Поэтому целесообразно рассмотреть толь-
ко те задачи, которые возникают при изучении курса высшей математи-
ки, изложенного в данном учебнике. Это проще сделать, демонстрируя на
примерах решения типовых задач.
1) В этом пункте рассматриваются задачи, связанные с разделом «Эле-
менты линейной алгебры». Для решения таких задач следует предвари-
тельно загрузить пакет расширения linalg. Это делается следующим обра-
зом: вводится команда
> with (linalg):
304
После этого можно пользоваться функциями этого пакета расшире-
ния. Первое, чему здесь необходимо научиться, — это введению в ком-
пьютер матрицы, что выполняется следующим образом. Пусть требуется
ввести матрицу
р	1	3 7 43
3-5-631
А~ -4 0 -7 8 1 '
5 -4 -3 10 5
\	J
Ввод происходит построчно слева направо. В скобках, содержащих ин-
формацию о вводимой матрице, стоят прежде всего два числа: число строк
и число столбцов в вводимой матрице, затем в квадратных скобках пере-
числяются последовательно, через запятую, все ее элементы.
> А := matrix (4, 5, [2, 1, 3, 7, 4, 3,-5,-6, 3, 1,-4, 0,-7, 8, 1,5,-4,-3, 10, 5]);
После нажатия клавиши Enter на экране появится матрица А. Точку с
запятой ставить не обязательно, можно поставить и двоеточие. Тогда мат-
рица А на экране не появится и не будет возможности проверить визуаль-
но правильность ввода матрицы. Если матрица введена, то теперь можно
производить с ней различные операции:
• нахождение ранга матрицы
> г := rank (А);
г := 3
• вычисление определителя матрицы
>	В := matrix (3, 3, [-1, 2, 3, 4, 5, 6, 7, 8, 9]);
(-1 2 33
В := 4 5 6
7 8 9
\	7
>	s := det (В);
s := 6
• нахождение обратной матрицы
>	Т := inverse (В);
	Л2 1	1 2
Т :=	1 -5	3
	1 11	13
	2 3	6
• нахождение произведения матриц
> С := matrix (3, 3, [0, 1, 1, 1, 0, 1, 1, 1, 0]);
305
F := multiply (В, С);
F:= И
17
2 1 >
10 9
16 15
7
(здесь матрица F равна произведению матриц: F = ВС),
• сложение двух матриц; например, если матрица Р = F + С, то
> Р := evalm (F + С);
Р: =
5
12
18
3 2 >
10 10
17 15
7
Следующая важная операция — это введение координат вектора в виде
строки. Например, требуется ввести четырехмерный вектор Н= (-3, 2, 1, 5).
Это делается так:
> Н := vector (4, [-3, 2, 1, 5]);
Н := [-3, 2, 1,5]
Теперь мы готовы к тому, чтобы решать системы линейных алгебраи-
ческих уравнений. Пусть имеется система трех уравнений с тремя неизве-
стными
х - 2у - 3z = -10;
5x + 3y + 3z = 27;
х + у + z = 7.
Вводим матрицу системы Q = 5
S = (-10, 27, 7). '	!
-2 -3
3
> Q: = matrix (3, 3, [1, -2, -3, 5, 3, 3, 1,
Э -2
Q: = 5 3
и вектор из правых частей
1, 1]); S: = vector (3, [-10, 27, 7]);
-3>
3
1
5
3
S: = [-10, 27, 7]
Теперь запускаем решение системы:
> X: = linsolve (Q, S);
X: = [3, -1, 5]
Выданный результат надо истолковывать так: решение найдено и
х = 3; у = -1; z = 5.
Если введены координаты двух геометрических векторов а = {-4, 2, 1}
и b = {1, -5, 3}, то можно определить их скалярное и векторное произве-
дения. Это делается следующим образом:
306
а Ь'\
. Имеем:
с d
d
ad - be
с
ad - be
>	L: = vector (3, [-4, 2, 1]): V: = vector (3, [1, -5, 3]): sc: = dotprod (U,V);
W: = crossprod (LJ,V);
sc: = -11
W: = [11, 13, 18]
Полученный результат означает, что (а, b) = -И, [а, Ь] = {И, 13, 18].
В заключение этого пункта полезно отметить, что многие матричные
функции способны производить вычисления и выдавать результаты в сим-
вольном виде.
Например, найдем обратную матрицу к матрице А =
>	А := matrix (2, 2, [a,b,c,d]): В: = inverse (А);
Получим:
b
ad - be
а
ad - be
т.е. обратную матрицу к матрице А в символьном (буквенном) виде.
2)	В числе пакетов расширений MAPLE содержится пакет геометри-
ческих расчетов, подключаемый с помощью команды
> with (geometry):
Он позволяет решать некоторые типовые задачи по аналитической гео-
метрии на плоскости. Ио эффективность его невелика главным образом
потому, что применение его к сложным задачам требует более высокой
степени освоения системы MAPLE, а несложные задачи по аналитиче-
ской геометрии на плоскости проще решать без использования пакета,
особенно для начинающих пользователей.
3)	В этом пункте рассматриваются задачи, относящиеся к разделу «Ос-
новы математического анализа». Прежде всего следует ознакомиться с
встроенными элементарными функциями и встроенными константами.
Начнем с констант.
Для решения задач этого раздела из всего набора встроенных констант
могут оказаться полезными только две: число л, обозначаемое в пакете
как Pi, и мнимая единица i = лДТ, обозначаемая как I. Число е среди
встроенных констант отсутствует, в качестве него рекомендуется исполь-
зовать exp (1). Если требуется получить численное значение какой-либо
величины, представленной в виде некоторого выражения F, содержаще-
го известные на данном этапе вычислений переменные и функции, то
это можно сделать с помощью команды evalf (F,n), где п — количество
требуемых цифр после десятичной точки. Например,
>	evalf (sin (1), 5);
.84147
Число п можно не указывать. В этом случае по умолчанию считается,
что п = 10.
Эта команда бывает необходима, когда аргументом у элементарной
функции является фундаментальная константа, целое или рациональное
307
число. В этом случае пакет выводит не численное значение функции, а
обозначение этой функции со значением аргумента. Например,
>	In (2);
In (2)
>	evalf (In (2));
.6931471806
Теперь познакомимся со встроенными функциями. Их очень много,
но нам интересны только элементарные функции. MAPLE имеет полный
набор таких функций. Их обозначения в основном совпадают с теми обо-
значениями, которые приняты в математической литературе. Но есть и
некоторые отличия. Прежде всего степенная и показательная функции
вводятся в соответствии с правилами строчных редакторов: вместо x'z и ах
следует писать хЛа и алх. Для функции ех имеется специальное обозначе-
ние: ехр (х), как и для квадратного корня 7х, который обозначается как
sqrt (х). В тригонометрических функциях по-другому обозначаются тан-
генс и котангенс: tan (х) и cot (х), так же как и обратные к ним: arctan (х)
и arccot (х). Натуральный логарифм не отличается обозначением от общепри-
нятого, а для десятичного логарифма используется обозначение log 10 (х).
Произведение двух величин обозначается знаком *. Например, 3sin(2x)
следует записать так: 3*sin(2*x). Деление обозначается знаком /. Напри-
t£ X
мер, функцию следует записать так: tan (х) / (1 + хЛ2).
1 + х2
Рассмотрим теперь задачу нахождения предела последовательности.
Пусть требуется найти lim где sn — некоторое выражение, заданное
как функция от п. Тогда результат может быть получен с помощью команды:
>	f: = 5П: L: = limit (f,n = infinity);
+ 1 + rtV
Например, пусть требуется найти предел lim-—. Имеем:
у/76 + 1
> f: = ((sqrt (пЛ2 + 1) + п)л2)/ ((пл6 + 1)л(1/3)): L: = limit (f, n = infinity);
L: =4
Вычисление предела функции непрерывного аргумента осуществляет-
ся по этой же схеме. Например, lim
разом:
вычисляется следующим об-
> f := (хЛ2 - sqrt (x))/(sqrt (х) - 1): L: = limit (f, х = 1);
L := 3
Рассмотрим задачу нахождения производной функции у = F(x). Эта
задача решается символьно с помощью команды:
> f := F (х): g: = diff (f, х);
Например, пусть требуется продифференцировать функцию у = Jx.
Имеем:
308
f := sqrt (x): g: = diff (f, x);
1
g: = 2Vx
Чтобы вычислить производную высокого порядка, используется опе-
ратор $.
Например, чтобы найти четвертую производную от Vx, следует ввести
команду
>	f := sqrt (х): g: = diff (f, x$4);
Часто бывает необходимо найти производную в заданной точке х = х0.
Для этого используется функция subs. Например, для нахождения значе-
ния второй производной от функции е' в точке х = 0 следует ввести
команды:
>	f := exp (-хЛ2): g: = diff (f, x$2): h: = subs (x = 0, g); k: = value (h);
h: = -2 e°
k: =-2
Без каких-либо усложнений находятся частные производные. Напри-
;--------------- Э42
мер, если z = ^х2 + у2 и нас интересует четвертая производная , то
результат получается с помощью команды:
> z := sqrt (хЛ2 + ул2): g: = diff (z, х, у$3);
g = -15—5X_ + _2i>L__
(х2+у2)2 (х2+у2)2
Переходим к задачам интегрального исчисления. Неопределенные ин-
тегралы j/(x)i/x вычисляются с помощью следующей команды:
>	f: = f(x): g: = int (f, x);
Например, пусть требуется вычислить Jх cos х dx. Имеем:
>	f: = х * cos (x): g: = int (f,x);
g: = x sin(x) + cos(x)
Бывает так, что MAPLE не может вычислить интеграл. Тогда возвра-
щается исходная запись интеграла.
Часто при вычислении неопределенного интеграла возникает задача
Р(х)
разложения рациональной функции на простые дроби. Здесь Р(х) и
v (А)
(Дх) — многочлены. Для решения этой задачи необходимо разложить зна-
менатель (Дх) на множители с вещественными коэффициентами. Эта за-
дача может быть решена командой:
>	f := factor (Q(x));
Например, пусть (Дх) = х4 + х3 + 2х2 + х + 1. Имеем:
309
>	f := factor (хл4 + хл3 + 2*хл2 + х + 1);
f := (х2 + х + 1)(х2 + 1)
ь
Вычисление определенных интегралов j f(x)dx осуществляется командой
>	f := int (f(x), х = а .. b);
Например, вычислим интеграл I'L dx. Имеем:
4 dx + 1
>	f := int ((х - 1)/ (sqrt (x) + 1), x = 4 .. 9);
-4
В том случае, когда предел интегрирования бесконечен, вместо числа
ставится infinity в случае +«> и -infinity в случае -«>. Например, при вычис-
лении интеграла j е~2х cos 6х dx следует ввести команду:
о
>	f := int (ехр(- 2 * х) * cos(6 * х), х = 0 .. infinity);
Вычисление кратных интегралов возможно только после того, как
интеграл записан как повторный, т.е. в нем произведена расстановка пре-
делов.
Например, тройной интеграл JJJ (х2 + y2)zdxdydz вычисляется ко-
мандой:
>	f := int (int (int ((хЛ2 + уЛ2) * z, х = 0 .. а) у = 0 .. a) z = 0 .. а);
а двойной интеграл j j (2 - х - у) dxdy — командой
>	f := int (int (2 - х - у, х = sqrt (у) .. уЛ2) у = 0 .. 1);
Кратко перечислим некоторые другие возможности пакета MAPLE:
•	построение графика функции у = f(x) на интервале (отрезке) осуще-
ствляется командой plot (f(x), х = а .. b);
•	нахождение максимумов и минимумов функции у = f(x) осуществля-
ется командами maximize (f(x), х = а .. b, location); и minimize (f(x), х = а .. b,
location);
•	эти же команды применимы и к функциям нескольких переменных,
например,
310
minimize (хл2 - 3*x + ул2 + 3*y + 3, location);
3 [ГГ 3	31
2’1 И" 2’Х“2Г
t 3
(в приведенном примере число равно минимуму функции; параметр
location обеспечивает выдачу координат точки минимума и значения фун-
кции в точке минимума; если его опустить, то в ответе будет выдано
3
только значение минимума функции, т.е. число -—);
•	исследовать числовой ряд на сходимость программе, как правило, не
удается; имеется возможность суммировать ряды в том случае, когда ответ
может быть выражен как значение элементарной функции в некоторой
м	I
точке; например, ряд У (-1)Л,+1— сходится и его сумма равна In (2); по-
Zi	"
этому его сходимость и сумма могут быть обнаружены командой:
> sum (((—1)Л(п + 1)) * (1/п), п = 1.. infinity);
In (2)
другой сходящийся ряд У------— имеет сумму, не выражающуюся через
Zl^ln^w
значения элементарных функций; программа ничего с этим рядом сделать
не может: ни обнаружить его сходимость, ни найти его сумму; в некото-
рых случаях программе удается обнаружить расходимость ряда; например,
в случае гармонического ряда У — на команду sum (1/п, n = 1 .. infinity);
“f и
пакет выдает ответ:
• решение дифференциальных уравнений первого порядка осуществля-
ется с помощью команды dsolve (ODE, у(х)); где ODE означает дифферен-
циальное уравнение, в котором производная записана как diff (у(х), х);
например,
> dsolve (diff (у(х), х) - у(х) = ехр (-х), у(х));
у(х) = ^-|е^2х)+С1 je-¥;
• решение дифференциального уравнения второго порядка у" - у' =
= sinx показано в следующем примере:
> dsolve (diff (у(х), х$2) - diff (у(х),х) = sin(x), у(х));
Я*) = -|sin(x) + ^cos(x) + еЛС| + С2.
В заключение следует отметить, что поддержка, даваемая пакетом
MAPLE, не может заменить знаний, необходимых для решения задач курса
высшей математики. Его применение вслепую очень ограничено и прино-
сит мало пользы обучающемуся. Поэтому следует стремиться к понима-
нию того, что делает компьютер. Это позволит лучше использовать воз-
можности пакета не только как вычислительного, но и как аналитическо-
го средства решения задач.
311
ОТВЕТЫ И УКАЗАНИЯ К ЗАДАЧАМ
ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
ГЛАВА 1
1.	Пусть х является элементом множества A U 5, т\е. х g В. Тогда
х g A U В. Следовательно, х А и х g В. Но тогда хе /I их. В , а значит,
хе А П В, что и требовалось доказать. Пусть теперь, наоборот, х g А П В.
Тогда х g А и х g В, откуда следует, что х g Аи х<£ В, а значит, xt AIJ В,
т.е. хе A U В.
2.	£2 = {AC; AD; АЕ; BD; BE; BF; СЕ; CF; DF}.
3.	Пусть £2, = {х^ х2; х3; ...;х„;...} и £22 =	...;у„;...}. Для элементов
z множества £2 = £2, U £22 можно использовать такую нумерацию: z, = х(;
z2 =х; z3 = х2; z4 = у2;...; z2„_| =х„; z2ll = yn; .... Таким образом, все элементы
множества £2 оказываются занумерованными. Это означает, что это мно-
жество счетно.	. , _ .
4.	Пусть х g [а, 6]. Поставим ему в соответствие у = --(х - а) + с. Это
(Z>-a)
соответствие взаимно однозначно, поскольку х однозначно выражается
через у: х = ——— (у - с) + а. Если хе [а, 6], т.е. а<х< Ь, то для у получает-
(fif-c) z, ,
(Ь-аС ч
ся неравенство а < —-----(У-с) + а < Ь. Используя левую часть неравен-
- с)
ства, получим 0 < (у - с) или у > с. Правая часть неравенства дает (у - с) <
< ( d - е) или у < d. Итак, при любом х g [а, Ь] соответствующее значение у
принадлежит отрезку [c,d] и, как нетрудно проверить, меняя ролями х и
у, наоборот: для любого у g [e,d] соответствующее ему значение х при-
надлежит отрезку [а,Ь]. Следовательно, построенное соответствие будет
взаимно однозначным соответствием между элементами рассматривае-
мых множеств. Поэтому их мощности одинаковы.
5.	sup £2 = 2 и inf £2 = -2.
6.	sup £2 = 4 и inf £2 = 1.
7.	sup £2 = 4,5 и inf £2 = 1.
8.	Имеем: |у| = —. Пусть | х | < 1. Тогда , заменяя в
| 1 + х2 I 1 + х1 1 +|х|“
знаменателе 1 + |х|2 на 1 (уменьшая знаменатель), получим, что
|у| = ] р < -yl = |х| < 1. Пусть теперь |х| > 1. Тогда, заменяя в знамена-
теле 1 + |х|2 на |х|2 (снова уменьшаем знаменатель), получим, что
Iу| = —< И = I х I < 1. Таким образом, при любых х |у| < 1, а это озна-
1+И2	1	х	х
чает, что множество значении функции У = ограничено.
ГЛАВА 2
„J-21 25 413
р 3 25/
312
6
-5
2
-3
2
10
31
5
4. |Д| = -40.
z 16
-19
2
-2>
-2 , |С| = 0.
6
5. A~l =
19 -34
-23	41
3 -5
7
7
6.	Д = -12; Дх = 60; Дд, = -72; Дг = -108; х = -5; у = 6; z = 9.
7.	Х= 2Сц Y= 4G, - 2С2; 7= -8С, - 2С2; U= С,; V= С2.
8.
Система уравнений несовместна (т.е. не имеет решений).
1.
2.
3.
ГЛАВА 3
Пары векторов: {а, с}, {b, d{, {а, е}, {b, е{, {с, е}, {d, е}.
Векторы компланарны.
Да, образуют.
4.	с = {21; -12; 6}, d = {-6; 16; 8}, е = {-12; 10; -1{.
5.	АВ = {4; -12; -4{, АС = {1; -1; 5}, СВ = {3; -И; -9}.
6.	5= 306. Указание: найти длины сторон и воспользоваться формулой
Герона.
7.	(х + I)2 + (у - З)2 = 25.
8.	(х- 2)2 + (у + 3)2+ z2 = 9.
9.	3x-2y+5z-6 = 0.
10,£zZ = £±5=£-3
3	-2	7
х2 г2
11. —	1 — гипербола; полуоси: а = 3, b = 4; фокусы: F{(-5;0),
^2(5; 0).
12. а) сфера; б) однополостный гиперболоид; в) конус; г) двуполост-
ный гиперболоид; д) эллипсоид; е) эллиптический параболоид; ж) ги-
перболический параболоид; з) параболический цилиндр.
ГЛАВА 4
1. Указание: воспользоваться определением предела последовательно-
сти, взяв, например, е = 1.
4. Указание: воспользоваться неравенством ||х| + |у || < |х - у|.
6. |, 0, 1, +оо.
ГЛАВА 5
4. Указание: воспользоваться теоремой 4.2 (о произведении бесконеч-
но малой последовательности на ограниченную).
6. Указание: воспользоваться результатом задачи 4 (см. гл. 4).
313
ГЛАВА 6
Л*) = I
4. Неверно. Указание: рассмотреть функцию
1 при х е (0,1);
-1 при X G (-1,0).
6. 3(х- I)4 + 17(х- I)3 + 32(х- I)2 + 28(х- 1) + 3. Указание: использовать
формулу Тейлора в окрестности точки х0 = 1.
9. 1) у = х — наклонная асимптота, у = ±1 — вертикальные асимптоты;
2) у = х + 2 — наклонная асимптота, у = -2 — вертикальная асимптота.
3) у =	- 1 — наклонные асимптоты (при х -> ±«>).
Указание: в последнем случае использовать пример 5.11.
ГЛАВА 7
1.	Указание: воспользоваться формулами
л	л
arcsinx + arccosx= —, arctgx + arcctgx = .
2.	Указание: сделать замену t= ах+ b (см. также пример 7.6).
3.	Очевидно, при замене и = ответ получится формула
J/(x)iZx = du
и дело сводится к табличному интегралу
^du = и + С.
4.	Указание: использовать теорему 7.1 (о «почти единственности» пер-
вообразной).
5.	F'(x) = 2хе“<4. Указание: использовать теорему 7.3 и правило диффе-
ренцирования сложной функции (см. теорему 6.3).
1	32
8.	1) ~6, 2)
9.	1) V5+^ln(2 + V5); 2) 2sh 1; 3) 8.
10.	1) сходится; 2) расходится; 3) сходится; 4) сходится; 5) расходит-
ся; 6) расходится.
ГЛАВА 8
3.	Р = (х — I)2 - (х — 1)0 + 1) + (у + I)2 + 2(х-1) - 2(у+ 1) + 3.
Указание: воспользоваться формулой Тейлора в точке х0 = 1, у0 = -1.
4.	х = 0, у = 0 — точка минимума.
5.	Наибольшее значение достигается в точке х = 1, у = 0 и равно -2.
Наименьшее значение достигается в точке х = 0, у = 1 и равно -5.
ГЛАВА 9
1. Указание: воспользоваться теоремой 9.5 и геометрическим смыслом
одномерного интеграла (см. и. 7.3).
314
2.	JJ f(x, y)dxdy = j J j f(x, y)dy Idx = N j f(x, y)dx dy.
G	0 [.0	J 0 [j-	J
3.	Указание: использовать теорему о среднем для двойного интеграла.
4.	1) — ; 2) — |	3) — (е4-е). Указание: перейти к полярным ко-
3	2 е)	4
ординатам и использовать пример 7.18.
6. 1) т = 4; 2) Ч =~^-, Уо =-р
ГЛАВА 10
1.
2.
3.
4.
5.
сходится.
сходится.
сходится,
расходится.
Ряд расходится (5= +<»).
Ряд
Ряд
Ряд
Ряд
6. Указание: монотонность убывания модулей членов ряда вытекает из
следующего неравенства: sin
0.
 2«+l
2 — х
8.Ях) = ^, |х|<1.
«	т2«+1
9. sin3x=Z<-D”^—[уу
10. Г и ' dx » У (-1)"----, ошибка (абсолютная погрешность)
J	(2/7 + 1)77!
£< (2У + 3)(У + 1)!'
ГЛАВА 11
1.	у + С|Ху -1=0.
2.	у = хе|+С|¥.
3.	у = С, е2*: + х2+ -.
4.	у = — sin х + С|% + С2.
6
х2
5.	у=	С2-х- —.
6'^(7Т4Р-
7.	у= С,еЧ С2е-2х.
8.	у= e-3x(C1cos2x+ C2sin2x).
9.	у = С( cosx+ C2sinx+ ^xsin х.
10.	у = е х+ х2.
ОГЛАВЛЕНИЕ
Предисловие................................................... 3
Глава 1. Элементы теории множеств............................. 4
1.1.	Понятие множества. Операции над множествами........... 4
1.2.	Конечные и бесконечные, счетные и несчетные множества.. 6
1.3.	Числовые множества. Действительные числа.............. 8
Глава 2. Элементы линейной алгебры............................12
2.1.	Матрицы и действия над ними...........................12
2.2.	Определители матриц...................................17
2.2.1.	Основные определения.............................17
2.2.2.	Свойства определителя............................20
2.3.	Обратная матрица......................................33
2.4.	Системы линейных алгебраических уравнений.............37
2.4.1.	Основные понятия.................................37
2.4.2.	Правило Крамера..................................38
2.4.3.	Метод Гаусса исследования и решения систем линейных
уравнений...............................................40
Глава 3. Элементы аналитической геометрии.....................53
3.1.	Геометрические векторы и действия над ними............53
3.2.	Системы координат на прямой, на плоскости и в пространстве.... 56
3.3.	Понятие уравнения линии и уравнения поверхности.......60
3.4.	Различные виды уравнения прямой на плоскости..........61
3.4.1.	Общее уравнение прямой............................61
3.4.2.	Уравнение прямой с угловым коэффициентом.........62
3.4.3.	Уравнение прямой «в отрезках».....................63
3.5.	Различные виды уравнения плоскости в пространстве.....64
3.5.1.	Общее уравнение плоскости........................64
3.5.2.	Уравнение плоскости «в отрезках».................64
3.5.3.	Нормированное уравнение плоскости................65
3.6.	Уравнения прямой в пространстве ......................66
3.6.1.	Общие уравнения прямой...........................66
3.6.2.	Канонические уравнения прямой в пространстве.....68
3.6.3.	Параметрические уравнения прямой в пространстве...70
3.7.	Кривые второго порядка на плоскости...................72
3.7.1.	Понятие кривой второго порядка...................72
3.7.2.	Эллипс...........................................73
3.7.3.	Гипербола........................................73
3.7.4.	Парабола.........................................74
3.8.	Поверхности второго порядка...........................75
3.8.1.	Общее уравнение поверхности второго порядка......75
3.8.2.	Эллипсоид........................................75
3.8.3.	Гиперболоиды.....................................76
3.8.4.	Конус............................................77
316
3.8.5.	Эллиптический параболоид.......................78
3.8.6.	Гиперболический параболоид.....................78
3.8.7.	Цилиндры.......................................79
Глава 4. Числовые последовательности и их пределы...........82
4.1.	Ограниченные и неограниченные последовательности....82
4.2.	Бесконечно малые последовательности.................84
4.3.	Предел числовой последовательности..................88
4.3.1.	Основные определения...........................88
4.3.2.	Свойства сходящихся последовательностей........90
4.4.	Монотонные последовательности. Число «е» ...........93
Глава 5. Предел функции одной вещественной переменной.
Непрерывность...............................................97
5.1.	Определение функции.................................97
5.2.	Предел функции......................................99
5.2.1.	Определение. Таблица замечательных пределов....99
5.2.2.	Основные свойства пределов функции............102
5.3.	Бесконечно малые функции. Метод эквивалентных бесконечно
малых величин............................................104
5.4.	Непрерывные функции................................106
5.4.1.	Основные определения..........................106
5.4.2.	«Арифметические» свойства непрерывных функций..108
5.4.3.	Непрерывность сложной функции ................109
5.5.	Свойства функций, непрерывных на отрезке............ПО
5.5.1.	Теорема о нуле непрерывной функции.............ПО
5.5.2.	Теоремы Вейерштрасса..........................112
Глава 6. Дифференциальное исчисление функций одной вещественной
переменной.................................................116
6.1.	Производная функции. Основные правила дифференцирования ... 116
6.1.1.	Определение. Таблица производных..............116
6.1.2.	«Арифметические» свойства производной.........118
6.1.3.	Производная сложной функции...................119
6.1.4.	Геометрический смысл производной..............121
6.2.	Теоремы о среднем для дифференцируемых функций ....122
6.3.	Следствия из теорем о среднем (монотонность, правило
Лопиталя)................................................126
6.3.1.	Критерий монотонности.........................126
6.3.2.	Правило Лопиталя..............................127
6.4.	Первый дифференциал функции, связь с приращением
функции..................................................130
6.5.	Производные и дифференциалы высших порядков........132
6.6.	Формула Тейлора....................................134
6.7.	Экстремумы функций ................................138
6.7.1.	Необходимое условие экстремума................138
6.7.2.	Достаточные условия экстремума................139
6.8.	Выпуклые функции. Точки перегиба...................141
6.8.1.	Определение. Критерий выпуклости..............141
6.8.2.	Исследование точек перегиба ..................142
6.9.	Асимптоты. Общая схема построения графиков.........144
317
Глава 7. Интегральное исчисление функций одной вещественной
переменной.................................................150
7.1.	Первообразная и неопределенный интеграл............150
7.1.1.	Первообразная. «Почти единственность» первообразной .... 150
7.1.2.	Таблица неопределенных интегралов............151
7.2.	Основные правила неопределенного интегрирования.....153
7.3.	Задача нахождения площади криволинейной трапеции.
Определенный интеграл...................................156
7.4.	Основные свойства определенного интеграла. Теорема
о среднем...............................................159
7.5.	Формула Ньютона—Лейбница..........................164
7.5.1.	Определенный интеграл как функция верхнего предела ... 164
7.5.2.	Вывод формулы Ньютона—Лейбница...............166
7.6.	Интегрирование по частям и замена переменных
в определенном интеграле................................167
7.7.	Приложения определенного интеграла.................169
7.7.1.	Вычисление площади плоской фигуры............169
7.7.2.	Вычисление длины кривой......................170
7.7.3.	Вычисление объема и площади поверхности тел
вращения............................................172
7.8.	Несобственные интегралы............................173
7.8.1.	Определение несобственного интеграла.........173
7.8.2.	Теоремы сравнения............................175
Глава 8. Дифференциальное исчисление функций нескольких
переменных.................................................180
8.1.	Функции нескольких переменных. Предел и непрерывность.... 180
8.2.	Частные производные. Дифференциал функции нескольких
переменных..............................................184
8.2.1.	Частное дифференцирование. Понятие непрерывно
дифференцируемой функции............................184
8.2.2.	Дифференциал и его связь с приращением функции.185
8.2.3.	Правила частного дифференцирования...........188
8.3.	Касательная плоскость и нормаль к поверхности......189
8.4.	Частные производные и дифференциалы высших порядков.
Формула Тейлора.........................................192
8.4.1.	Частные производные высших порядков..........192
8.4.2.	Дифференциалы высших порядков................193
8.4.3.	Формула Тейлора .............................195
8.5.	Экстремумы функции. Задача о наибольшем и наименьшем
значениях...............................................197
8.5.1.	Необходимые условия экстремума ..............197
8.5.2.	Достаточные условия экстремума...............199
8.5.3.	Условный экстремум. Метод множителя Лагранжа.202
8.5.4.	Задача о наибольшем и наименьшем значениях...204
Глава 9. Интегральное исчисление функций нескольких переменных ...206
9.1.	Объем цилиндрического бруса. Определение двойного
интеграла...............................................206
9.1.1.	Основные определения.........................206
318
9.1.2.	Свойства двойных интегралов. Теорема о среднем..208
9.2.	Вычисление двойного интеграла с помощью повторного
интегрирования (формула редукции)........................209
9.3.	Вычисление двойного интеграла в полярных координатах.214
9.4.	Приложения двойного интеграла.......................218
9.4.1.	Вычисление объемов.............................218
9.4.2.	Площадь криволинейной поверхности..............219
Глава 10. Основы теории рядов.............................223
10.1.	Числовые ряды....................................223
10.1.1.	Ряды сходящиеся и расходящиеся.............223
10.1.2.	Необходимое условие сходимости ряда........226
10.1.3.	Критерий Коши сходимости ряда .............227
10.1.4.	Свойства рядов.............................227
10.1.5.	Ряды с положительными членами..............229
10.1.6.	Теоремы сравнения для рядов с положительными
членами............................................229
10.1.7.	Признаки Даламбера и Коши..................233
10.1.8.	Интегральный признак сходимости ...........238
10.1.9.	Знакочередующиеся ряды.....................240
10.1.10.	Знакопеременные ряды......................242
10.1.11.	Признаки абсолютной сходимости рядов......243
10.2.	Функциональные ряды..............................245
10.2.1.	Область сходимости функционального ряда....245
10.2.2.	Равномерная сходимость функционального ряда.246
10.2.3.	Критерий Коши равномерной сходимости ряда...247
10.2.4.	Признак Вейерштрасса равномерной сходимости ряда ... 249
10.2.5.	Общие свойства функциональных рядов........251
10.3.	Степенные ряды...................................253
10.3.1.	Радиус сходимости степенного ряда..........254
10.3.2.	Интервал сходимости степенного ряда........255
10.3.3.	Равномерная сходимость и непрерывность суммы
степенного ряда..............................258
10.3.4. Почленное дифференцирование и интегрирование
степенных рядов..................................259
10.3.5.	Ряды Тейлора...................................259
10.3.6.	Разложение функции в степенной	ряд.............260
Глава 11. Обыкновенные дифференциальные	уравнения..............263
11.1. Введение.............................................263
11.1.1.	Основные понятия..............................263
11.1.2.	Понятие общего и частного решений. Задача Коши.265
11.1.3.	Геометрический смысл уравнения и его решений .267
11.1.4.	Разрешимость задачи Коши......................268
11.2. Уравнения первого порядка, интегрируемые в квадратурах ... 269
11.2.1. Уравнения вида — = f(x) ...................269
11.2.2.	Уравнения вида — = f(y) ...................270
dx
11.2.3.	Уравнения с разделенными переменными.......271
319
272
273
275
276
277
279
279
280
284
284
11.2.4.	Уравнения с разделяющимися переменными.....
11.2.5.	Однородные уравнения.......................
11.2.6.	Линейные уравнения.........................
11.2.7.	Уравнения Бернулли.........................
11.2.8.	Уравнения в полных дифференциалах..........
11.3. Уравнения высших порядков, их общие решения......
б/ у
11.3.1.Уравнения вида —— = f(x)
dx'1
11.3.2. Уравнения, допускающие понижение порядка....
11.4. Уравнения высших порядков. Задача Коши............
11.4.1. Постановка задачи Коши .....................
11.4.2.	Разрешимость задачи Коши..................284
11.5. Линейные уравнения высших порядков................285
11.5.1.	Основные понятия...........................285
11.5.2.	Линейные однородные уравнения..............287
11.5.3.	Линейные неоднородные уравнения...........291
11.5.4.	Линейные однородные уравнения с постоянными
коэффициентами....................................292
11.5.5.	Линейные неоднородные уравнения. Метод вариации
постоянных........................................298
Приложение.................................................303
Введение в математический пакет MAPLE......................303
Ответы и указания к задачам для самостоятельной работы.....312