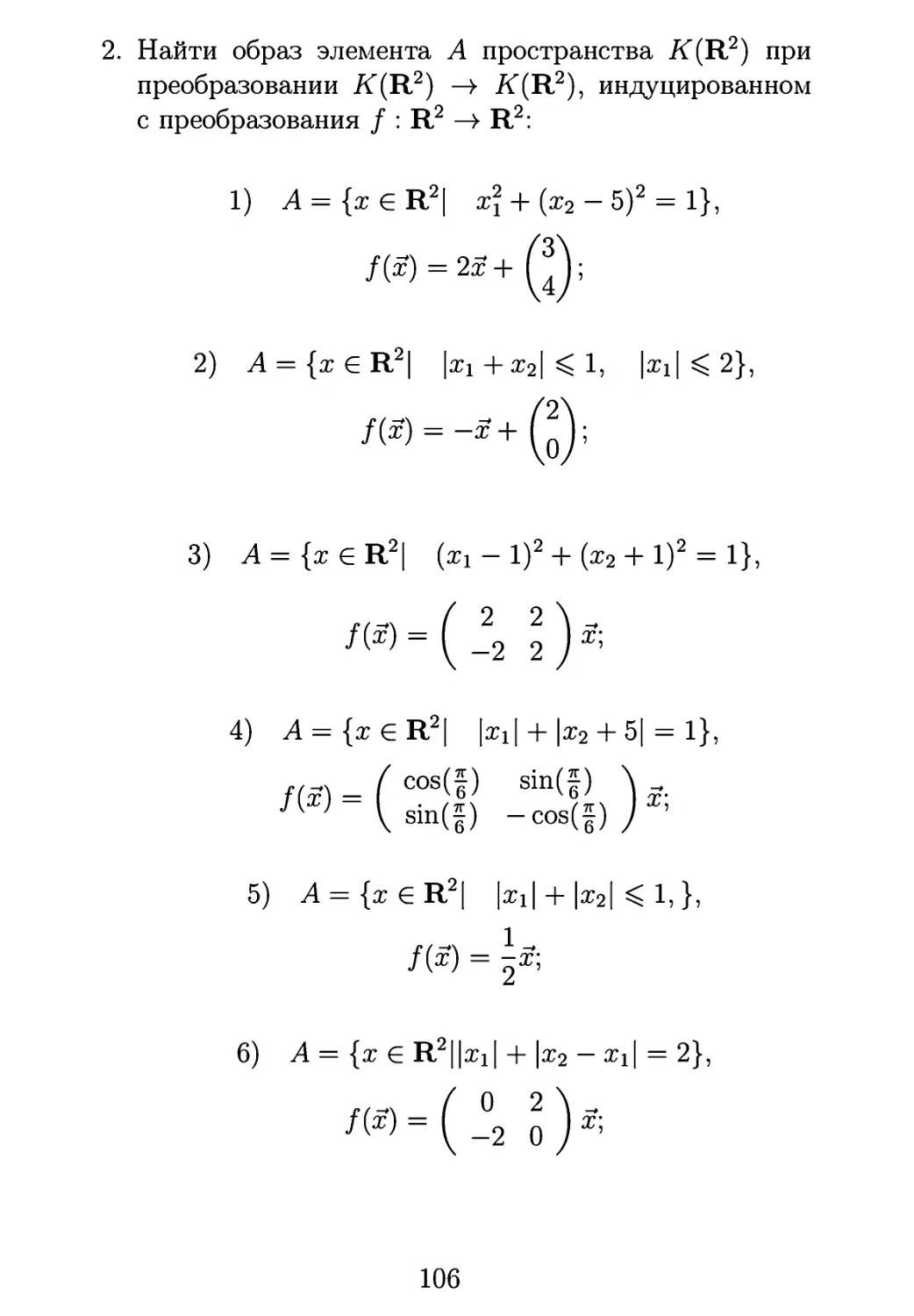Фрактальная геометрия. Детерминированные фракталы - Шихеева В.В.

Глава 1. Примеры детерминированных фракталов
Глава 5. Аффинные преобразования плоскости
Глава 7. Некоторые свойства детерминированных фракталов
Автор: Шихеева В.В.
Теги: программотехника разработка вычислительных систем геометрия фрактальная геометрия
ISBN: 978-5-906953-91-9
Год: 2019
Похожие
Фрактальная геометрия природы
Методы современной теории автоматического управления. Том 3
Фрактальная физика
Фрактальная геометрия природы
Текст
                    В.В. ШИХЕЕВА
ФРАКТАЛЬНАЯ
детерминированные
ГЕОМЕТРИЯ
аттракторы

№2949 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ «МИСиС»
ИНСТИТУТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
И АВТОМАТИЗИРОВАННЫХ СИСТЕМ УПРАВЛЕНИЯ
Кафедра инженерной кибернетики
В.В. Шихеева
ФРАКТАЛЬНАЯ ГЕОМЕТРИЯ
ДЕТЕРМИНИРОВАННЫЕ АТТРАКТОРЫ
Учебник
Рекомендовано редакционно-издательским
советом университета
МИСиС
Москва 2019

УДК УДК 004.41
Ш65
Рецензент
д-р физ.-мат.наук проф. СМ. Хорошкин
Шихеева В.В.
Ш65 Фрактальная геометрия. Детерминированные
фракталы: учебник / В.В. Шихеева. - М. : Изд. Дом НИТУ
«МИСиС», 2019. - 270 с.
ISBN 978-5-906953-91-9
Учебник представляет собой изложение курса «Фрактальная
геометрия», преподаваемого студентам третьего курса бакалавриата.
Курс посвящен системам итерированных преобразований и понятию
детерминированного аттрактора. В учебнике изложены базовые
понятия, основные определения и теоремы. Приведены
доказательства основных теорем. Введено понятие динамической системы на
аттракторе и приведены алгоритмы построения детерминированных
фракталов с помощью как детерминированного, так и
стохастического алгоритмов. Завершает изложение курса знакомство с понятием
фрактальной размерности и различными методами ее вычисления.
В конце каждой главы приведены упражнения. Изложение
дополняют многочисленные примеры.
Учебник предназначен для студентов, обучающихся в
бакалавриате по направлению подготовки 01.03.04.
УДК УДК 004.41
© В.В. Шихеева, 2019
ISBN 978-5-906953-91-9 © НИТУ «МИСиС», 2019

Содержание
Введение 4
Глава 1. Примеры детерминированных
фракталов 7
Глава 2. Некоторые элементы топологии 36
Глава 3. Множество К(Х) всех компактных
множеств метрического пространства X 64
Глава 4. Преобразования пространства К(Х) и
системы итерированных функций (СИФ) 82
Глава 5. Аффинные преобразования плоскости 121
Глава 6. Множества накопления 135
Глава 7. Некоторые свойства
детерминированных фракталов 152
Глава 8. Кодовое пространство СИФ 166
Глава 9. Адресная функция СИФ 183
Глава 10. Динамические системы 202
Глава 11. Динамика на фракталах 221
Глава 12. Хаотическая динамика 235
Глава 13. Фрактальная размерность 252
Список литературы 266
Предметный указатель 267
3

Введение
Этот курс посвящен фрактальной геометрии, науке
новой, не устоявшейся и продолжающей развиваться. Слово
fractal по-английски означает дробный. Объекты,
изучаемые фрактальной геометрией, давно известны в
математике, однако только во второй половине XX в. их стали
систематически изучать именно с точки зрения их
фрактальной природы. В 1977 г. Бенуа Мандельброт (Benoit В.
Mandelbrot) выпустил работу «Фракталы», где
сформулировал понятие фрактала и фрактальной размерности.
Начиная с этого момента фракталы вошли в моду и
появилось множество работ, им посвященных. Фракталы
исследовались как сами по себе, так и в качестве
инструмента для решения прикладных задач в различных областях
человеческой деятельности, например, таких, как
медицина, экономика, биология, химия, геология, вплоть до
кинематографии. Математические методы при исследовании
фрактальных объектов также весьма различны. Это и
топология, и комбинаторика, и линейная алгебра, и теория
вероятностей, и теория чисел, и теория функций
комплексного переменного, и теория динамических систем.
Предлагаемый курс затронет только некоторые вопросы
фрактальной геометрии, рассмотрит весьма небольшой класс
объектов фрактальной природы и привлечет
ограниченный математический аппарат для их изучения. Основная
литература, которая будет использоваться:
Ричард М. Кроновер. Фракталы и хаос в динамических
системах (М.: Постмаркет, 2000)
Michael Barnsley. Fractals everywhere (Boston: Academic
Press, 1988).
Дополнительная литература в огромном количестве
имеется в интернете как в виде монографий, так и в виде ста-
4

тей и заметок.
Курс построен следующим образом.
Сначала рассмотрено несколько примеров классических
детерминированных фракталов, обладающих свойством
самоподобия и введено понятие размерности подобия. После
краткого экскурса в топологию, введено понятие
детерминированного фрактала как аттрактора — неподвижной
точки специально построенного сжимающего
преобразования метрического пространства. Рассмотрен алгоритм
построения фракталов, основанный на этом определении.
Далее определена динамическая система на аттракторе,
исследованы ее свойства и предложен алгоритм
построения фракталов, использующий рассмотренные свойства.
Завершает курс знакомство с понятием фрактальной
размерности и различными методами ее вычисления.
При составлении иллюстраций были использованы
материалы [5,6].
Автор выражает глубокую признательность С.К.Ландо
за помощь при оформлении курса и С.М.Хорошкину за
терпение и поддержку.
Прежде чем начать курс, имеет смысл сказать
несколько слов о причинах популярности фрактальной теории.
Математики прошлого старались свести геометрию к
простым геометрическим фигурам, а при анализе
окружающего мира опирались на мощный аппарат
математического анализа, дифференциальное и интегральное
исчисления, методы теории функций и решения
дифференциальных уравнений. Фрактальные объекты, появлявшиеся
в работах известных математиков XIX и начала XX в.,
как-то: множества Кантора, кривые Пеано, функции Вей-
ерштрасса, множества Жюлиа, — рассматривались как па-
тал огии и назывались монстрами. Однако в природе
существует множество сложно устроенных объектов, для
которых аппроксимация их гладкими функциями приводит
5

к неизбежным и, главное, колоссальным потерям,
качественно искажая особенности их природы. При
ближайшем рассмотрении оказалось, что именно фракталы
соответствуют наиболее часто встречающимся реальным
объектам в самых разных природных и человеческих
системах. Обратитесь ли вы к географии — вы увидите горы,
побережья, водные системы, имеющие ярко выраженный
фрактальный характер, посмотрите на человеческий
организм — устройство кровеносной системы, системы
дыхания и мочеиспускания напоминают деревья с ветвистой
кроной, у которых каждая ветка подобна всему дереву, а
значит — это тоже фрактальные объекты. Даже
экономические и социологические кривые, отражающие поведение
валют на биржевых торгах или состояние общественного
мнения, являются кривыми фрактального типа. Таким
образом, фракталы, будучи абстрактными математическими
объектами, являются весьма удобным аппаратом для
исследования окружающего нас мира.
6

Глава 1. Примеры
детерминированных фракталов
Рассмотрим несколько конкретных фракталов, давно
известных в математике и являющихся, с одной стороны,
классикой жанра, а с другой — основой всей дальнейшей
теории.
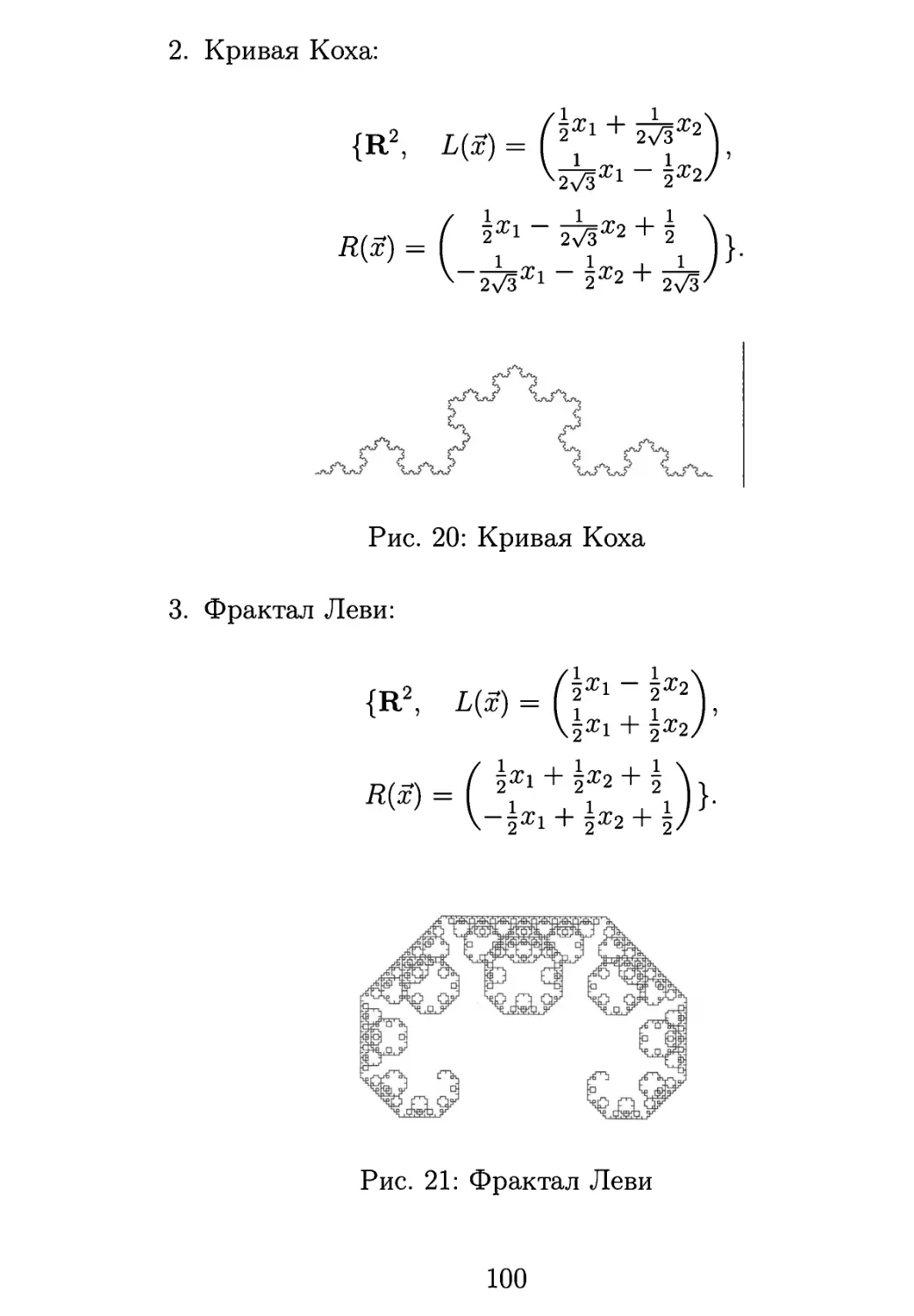
Пример первый. Канторово множество
Рассмотрим отрезок [0,1]. Выбросим из него среднюю
треть — интервал (|, |). Из двух оставшихся отрезков [0, \]
и [|, 1] выбросим их средние трети: (§,§) и (|, §),
соответственно. С оставшимися четырьмя отрезками [0, |], [|,|],
[§, |] и [|, 1] проделаем аналогичную операцию. В
результате получим восемь отрезков, с которыми можно
проделать то же самое. Если продолжить эту процедуру до
бесконечности, что получится в пределе? Давайте назовем
предельное множество Канторовым множеством и
обозначим его буквой К.
Рис. 1: Итерации Канторова множества
Какими свойствами обладает множество К?
1. Множество К не пусто, поскольку оно содержит все
концы выброшенных интервалов, а также точки 0 и
7

1. Более того, оно несчетно, т.е. его мощность равна
континууму.
2. Мера множества К равна нулю.
3. Если рассмотреть любой сколь угодно малый отрезок
[а, Ь] на отрезке [0,1], то пересечение [а, Ь] П К будет
подобно множеству К.
Докажем утверждения, сформулированные выше.
Утверждение 1. Множество К несчетно.
Доказательство этого факта состоит из двух
утверждений:
1) каждому элементу х множества К можно
однозначно сопоставить бесконечную последовательность из нулей
и двоек, являющуюся представлением числа х в троичной
системе счисления;
2) множество бесконечных последовательностей из двух
элементов несчетно.
Докажем сначала второе утверждение: множество
бесконечных последовательностей из двух элементов
несчетно.
Предположим, что это не так, пересчитаны все
последовательности и каждая получила свой порядковый
номер. Построим новую последовательность по следующему
правилу: на первом месте у нее стоит не та цифра, что у
последовательности под номером один, на втором месте —
не та цифра, что у последовательности под номером два,
на десятом месте — не та цифра, что у последовательности
под номером десять. И так для любого знака : у новой
последовательности он не совпадает с тем знаком, что стоит
под этим номером у последовательности, номер которой
8

равен номеру этого знака. Это всегда возможно.
Например, если последовательности состоят из нулей и двоек и
если у к-й последовательности на к-м месте стоит ноль,
то у новой последовательности на к-е место ставим два,
и наоборот, если у к-й последовательности на к-м месте
стоит два, то у новой на к-е место ставим ноль. На каком
месте при пересчете окажется вновь построенная
последовательность? Она не может быть на первом, поскольку ее
первая цифра не совпадает с первой цифрой первой
последовательности, она не может быть на втором, так как
ее вторая цифра не совпадает со второй цифрой второй
последовательности, она не может быть на десятом,
поскольку ее десятая цифра не совпадает с десятой цифрой
десятой последовательности, и так для любого числа к.
Эту последовательность некуда поставить, ее нельзя
сосчитать, откуда следует, что множество бесконечных
последовательностей из двух элементов несчетно.
Теперь вернемся к первому утверждению.
Каждому элементу х множества К можно однозначно
сопоставить бесконечную последовательность из нулей и
двоек, являющуюся представлением числа х в троичной
системе счисления.
Правило, по которому элементу х Канторова
множества сопоставляется последовательность, следующее: на
первом месте последовательности стоит 0, если х
принадлежит отрезку [0, |], и 2, если х принадлежит отрезку
[§, 1]. На втором месте стоит 0, если х принадлежит
первой трети одного из отрезков [0, \] и [|,1], т.е. отрезкам
[О, |] и [|, |], и 2, если х принадлежит последней трети
одного из отрезков [0, |] и [|,1], т.е. отрезкам [|,|] и [|,1].
Дальнейшие 0 и 2 расставляются по тому же принципу:
если на г-м шаге, т.е. после того как г — 1 раз поделили
все оставшиеся отрезки на три части и выбросили внут-
9

ренность второй трети у каждого, точка х принадлежит
первой трети одного из оставшихся отрезков, на г-е место
последовательности ставится цифра 0, если х
принадлежит третьей трети — цифра 2. Второй трети точка х
принадлежать не может, иначе она будет выброшена на г-м
шаге и не будет принадлежать множеству К.
Например, рассмотрим х = ^ и получим его троичное
Поскольку 0 ^ х ^ 1, нас интересует
последовательность цифр после запятой. В нашем примере х ^ |,
значит, на первом месте последовательности стоит 0. Дальше
нужно рассмотреть расположение х в первой трети
отрезка [0,1], или, что тоже самое, расположение Зх в самом
отрезке [0,1]. Поскольку Зх = ^ ^ | — это то же самое,
что х ^ |, на втором месте последовательности тоже стоит
0. Рассуждая аналогично, получаем 9х = уу ^ |, значит,
на третьем месте последовательности стоит цифра 2.
Последнее неравенство означает, что точка х принадлежит
третьей трети на третьем шаге процедуры, или что точка
х принадлежит отрезку [^, |].
Для дальнейшего деления надо рассмотреть отрезок
[^, |] как аналог исходного отрезка [0,1].
Отображение у = 27'х — 2 переводит отрезок [^,|] в
отрезок [0,1]. Рассмотрим расположение (21 х — 2) в отрезке
[0,1]:
21х - 2 = ^-.
Поскольку | ^ уу ^ |, на четвертом месте
последовательности стоит цифра 1. Расположение (3(27х — 2) — 1) на
отрезке [0,1] аналогично расположению точки х в
соответствующем отрезке на пятом шаге процедуры.
(3(27x-2)-l) = i-,
10

значит, следующая цифра последовательности равна 1, так
как з ^ ТТ ^ з-
Продолжив рассуждения, получим
(3(3(27* - 2) - 1) - 1) = -р
а значит последовательность начала повторяться, тем
самым троичное представление числа yj- равно 0.(00211), где
скобки означают бесконечно повторяющийся участок
последовательности. Троичное представление точки х = у^
показывает, что эта точка не лежит в Канторовом
множестве. Но на этом примере видно, как устроен механизм
перевода числа из отрезка [0,1] из одной системы счисления
в другую: на г-м шаге смотрим, в какой из третей отрезка
[0,1] лежит число а?;, первой трети соответствует цифра 0,
второй 1, третьей 2; соответствующая цифра к{ ставится
на г-е место троичного представления, а Х{ вычисляется по
формулам
Xq == Х^ Xi+\ == oXi — rCj, 2^U,1,^,....
Особенно просто этот механизм работает в случае,
когда х является рациональным числом £. Будем считать,
что р и q — взаимно просты, причем р < q. Тогда для того
чтобы узнать, в какой трети лежит х, надо разделить Зр
на q с остатком. Частное являет собой к\, а остаток,
поделенный на q, даст новое число х\. Аналогично, Xi = —,
где 3r;_i = kiq + г* — деление числа Зг^_1 на q с
остатком. Для конкретной дроби это представление получается
следующим образом:
3 3
Ж=13=*Жо=13'
9
3 • 3 = 0 • 13 + 9 => кг = 0, гх = 9 => хх = —,
11

3 • 9 = 2 • 13 + 1 => к2 = 2, r2 = 1 => х2 = —,
lo
3
3 ■ 1 = 0 ■ 13 + 3 => к3 = О, г3 = 3 => х3 = —.
В результате х% = xq, поэтому троичная запись числа ^
будет равна 0.(020), где в скобках стоит бесконечно
повторяющийся набор цифр. В отличие от числа ^ число ^
принадлежит Канторову множеству, ибо в его троичном
представлении цифра единица отсутствует.
Утверждение 2. Мера множества К равна нулю.
Прежде чем доказывать это утверждение, подсчитаем
длину интервалов, выброшенных из отрезка [0,1] при
построении Канторова множества:
Определение множества меры нуль требует
выполнения следующего: существует последовательность
открытых множеств Mj, мера которых стремится к нулю при
г —> со и каждое из которых содержит исходное
множество К.
Построим эти открытые множества М; следующим
образом. Для получения Канторова множества из отрезка
[0,1] на первом шаге выбросили интервал (|, |), на втором
— два интервала (§, |) и (|, §), и т.д.
Рассмотрим в качестве множества Si объединение всех
интервалов, выброшенных из отрезка [0,1] к г-му шагу.
Затем для каждого из интервалов, входящих в объединение
Si рассмотрим отрезок, лежащий внутри этого
интервала, длина которого отличается от длины
соответствующего интервала не больше чем на ^т+т- Обозначим буквами
Gi объединение всех таких отрезков.
12

Мера множества Gi будет отличаться от меры Si не
больше чем на величину ^т+т? умноженную на число всех
отрезков во множестве Gi или, что тоже самое, число
выкинутых интервалов к г-му шагу. Это число равно 1 + 2 +
4 + 8 + • ■ • + Т — 2г+1 и, следовательно, мера множества
Gi отличается от меры множества Si не больше чем на
ог+1 1 _ J_
^ ' 22г+1 — 21'
Выберем в качестве Mi разность между отрезком [0,1] и
множеством Gi, объединенную с двумя полуинтервалами
(-5Йт,0]и[1,1 + 5Йт):
Каждое из множеств Mi открыто, поскольку получено как
разность между интервалом (—^ттД + 2Ш") и
объединением конечного числа лежащих в этом интервале
непересекающихся отрезков. Каждое из множеств Mi содержит
Канторово множество по построению.
Мера множества Mi равна разности между длиной
отрезка [— 2ят, 1 + 27тт] и меР0И множества Gi, т.е. будет
отличаться от разности между числом (1 + ^) и мерой
множества S{ меньше чем на ^. Разность между числом (1 + ^)
и мерой множества Si равна
I + 1_I_2.I_4.I...2-.i =
2« 3 9 З3 3*
1,1/24 2i_1\
= * + 1-3(1 + 3 + 9 + - + f0 =
*+1 з Vi-iy
Таким образом, мера множества Mi не превосходит вели-
13

чины А, которая равна
1 1 1 /l — |^\ _ 1 1 2*
~ % + 2* + 1 ~ 3 \1-|/ ~ 21 + 2* + #'
Величина А стремится к нулю при г —> оо, что и
доказывает исходное утверждение.
3. Самоподобие.
Рассмотрим произвольный отрезок Т = [р,^г], где
г = 0,1,2,...,3*-1.
Предположим, что у него есть непустое пересечение с
Канторовым множеством: А = Т П К.
Функция у = Зкх — г задает отображение этого отрезка
в отрезок [0,1], причем точки Канторова множества
отразятся в точки Канторова множества, и наоборот, образы
точек отрезка Т, не лежащих в Канторовом множестве,
не будут лежать в Канторовом множестве. Таким
образом, Канторово множество является самоподобной
структурой. Отрезки Канторова множества длины 3_г подобны
всему множеству с коэффициентом подобия 3_г, причем
для составления исходного Канторова множества
требуется 2г таких отрезков.
Определение 1.1. Размерностью подобия
называется показатель степени D в формуле
N = LD,
где число L показывает, во сколько раз уменьшился
линейный размер множества, а число N — количество
подобных исходному множеству множеств в L раз
меньшего размера, необходимых для составления исходного
множества.
Например, требуется ровно два отрезка вдвое меньшей
14

длины для составления исходного отрезка, отсюда N = L]
ровно четыре маленьких треугольника, подобных
данному и со стороной вдвое меньшей длины, чтобы составить
исходный треугольник, т.е. в этом случае N = L2; ровно
27 кубиков со стороной втрое меньшей стороны исходного
куба, чтобы его составить, поэтому для куба N = L3.
Размерность подобия отрезка равна 1, треугольника —
2, куба — 3. Из этих же соображений получаем для Кан-
торова множества 2г = (Зг)°, где 3~г —длина отрезка, а их
количество равно 2г, откуда размерность подобия Канто-
рова множества равна
In 2
пТз'
Канторово множество — фрактал, который будет часто
обсуждаться в течение этого курса. Иногда это множество
еще называют пылью Кантора. Это название отсылает к
еще одному свойству Канторова множества — оно вполне
несвязно. Это значит, что любое замкнутое подмножество
Канторова множества, состоящее более чем из одной
точки, может быть представлено как объединение двух
непустых непересекающихся замкнутых подмножеств. Иначе
говоря, связной компонентой Канторова множества могут
быть только точки. При этом ни одна точка Канторова
множества не является изолированной, все его точки
являются предельными.
Что же получено в итоге? Удивительное множество
меры нуль, которое больше, чем счетное множество
изолированных точек, но меньше, чем прямая, связными
компонентами которого являются точки, но оно не содержит ни
одной изолированной точки, да к тому же еще и себепо-
добное, а это значит, что сколько ни смотри на это
множество, увеличивая масштаб, его вид не изменится.
Рассмотрим еще несколько примеров подобных множеств, чтобы
увидеть, что их существует довольно много.
15

Пример второй. Треугольник Серпинского
Рассмотрим произвольный треугольник ABC и
проведем все три его средние линии A\Bi, B\C\, С\А\. Эти
средние линии делят треугольник ABC на четыре одинаковых
треугольника АВ\С\, ВА\С\, СА\В\, AiB\C\, подобных
исходному с коэффициентом подобия, равным 2.
Рассмотрим процедуру, аналогичную той, с помощью которой
было получено Канторово множество. А именно, выбросим
внутренность среднего маленького треугольника AiB\C\ и
рассмотрим объединение трех оставшихся. На следующем
шаге с каждым из трех оставшихся маленьких
треугольников AB\Ci,BA\C\,CA\Bi проделаем аналогичную
процедуру, в результате чего останется объединение девяти еще
меньших треугольников, подобных исходному
треугольнику ABC с коэфициентом подобия, равным 4.
Этот процесс можно продолжить до бесконечности.
Множество, которое получается в пределе, называется
треугольником Серпинского. Если начнать изображать
процесс на бумаге или на экране компьютера, то уже через
пять итераций картинки становятся неразличимы,
поскольку на взгляд человека объединение З5 маленьких
треугольников и объединение З6 треугольников, еще меньших,
неразличимы.
Какими свойствами обладает подобный объект?
Обозначим его для простоты буквой Т.
Множество Т больше, чем просто линия, поскольку его
граница бесконечна. Граница множества Т содержит в
себе все границы всех маленьких треугольников. Сумма длин
всех этих отрезов равна
где L — длина периметра исходного треугольника ABC.
Этот ряд расходится, так как является суммой геометри-
16

ческой прогрессии со знаменателем, равным |, который
больше 1.
Множество Т меньше, чем плоскость, поскольку его
площадь равна нулю. Это легко показать, сосчитав
суммарную площадь всех выкинутых треугольников:
где S — площадь исходного треугольника ABC.
И наконец, если рассмотреть произвольный маленький
треугольник t на произвольном шаге процедуры, который
остался невыкинутым, то его пересечение с треугольником
Серпинского Т будет точной уменьшенной копией
множества Т, причем коэффициентом подобия будет
коэффициент подобия между треугольниками Т и t. Размерность
же подобия треугольника Серпинского Т будет равна |^|,
поскольку при уменьшении линейных размеров объекта
вдвое количество, которое требуется для замощения
большого объекта малыми, равно трем.
Рис. 2: треугольник Серпинского
При рассмотрении треугольника Серпинского видим те
же фрактальные свойства: объект самоподобен и пред-
17

ставляет собой что-то промежуточное между двумя
привычными геометрическими объектами, в первом случае —
между точкой и линией, во втором — между линией и
плоскостью. Рассмотрим еще пару-тройку подобных
фрактальных объектов, просто предложив их конструкции и не
обсуждая свойства.
Пример третий. Кривая Коха
Отрезок длины один делим на три равные части; на
средней части, как на основании строим равносторонний
треугольник, а затем внутренность основания его
выбрасываем. Получаем ломаную, составленную из четырех
отрезков длиной одна треть. Для каждого из этих отрезков
процедуру повторяем, и так до бесконечности. В
результате получаем самоподобную ломаную бесконечной
длины, называемую кривой Коха. Иногда эту кривую
называют «колбаска Коха» или «сосиска Коха», поскольку на
ограниченной части плоскости она располагается
довольно плотно.
(в) (г)
Рис. 3: Итерации кривой Коха
18

Рис. 4: Кривая Коха
Пример четвертый. Бинарное дерево
Рассмотрим букву Г и ее вдвое уменьшенную копию.
Пририсуем по такой копии к исходной букве с двух
сторон так, чтобы горизонтальные палочки всех трех букв
были параллельны, а нижние концы вертикальных
палочек двух маленьких букв совпадали с концами
горизонтали большой. Продолжив этот процесс до бесконечности,
получим бинарное дерево.
^^^
Рис. 5: Бинарное дерево
19

Рис. 6: Бинарное дерево из буквы "Y"
Рис. 7: Н-фрактал — бинарное дерево из буквы "Н"
20

Пример пятый. Дерево Пифагора
На верхней стороне квадрата как на гипотенузе
построим вне квадрата прямоугольный треугольник. На его
катетах построим вне треугольника два новых квадрата. На
стороне каждого нового квадрата, противоположной
соответствующему катету, построим вне него прямоугольный
треугольник, подобный первому. Продолжив процесс до
бесконечности, получим дерево Пифагора.
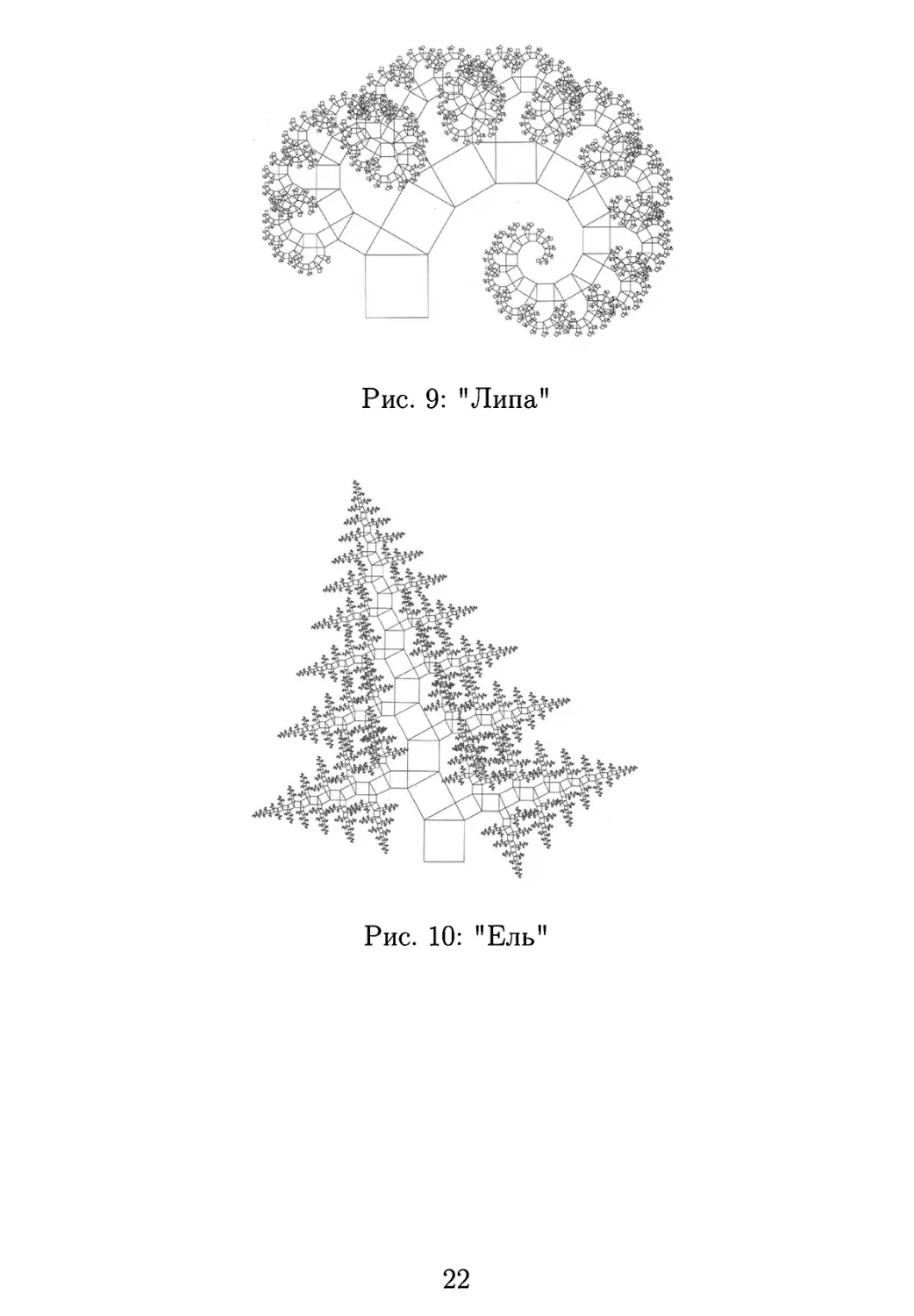
Рис. 8: Симметричное дерево Пифагора
Небольшое замечание: два равных или подобных
треугольника могут быть одинаково или противоположно
ориентированы на плоскости. Если при построении
ориентация треугольников сохраняется, то в результате дерево
Пифагора будет напоминать дуб или липу, если же на
каждой итерации менять ориентацию на
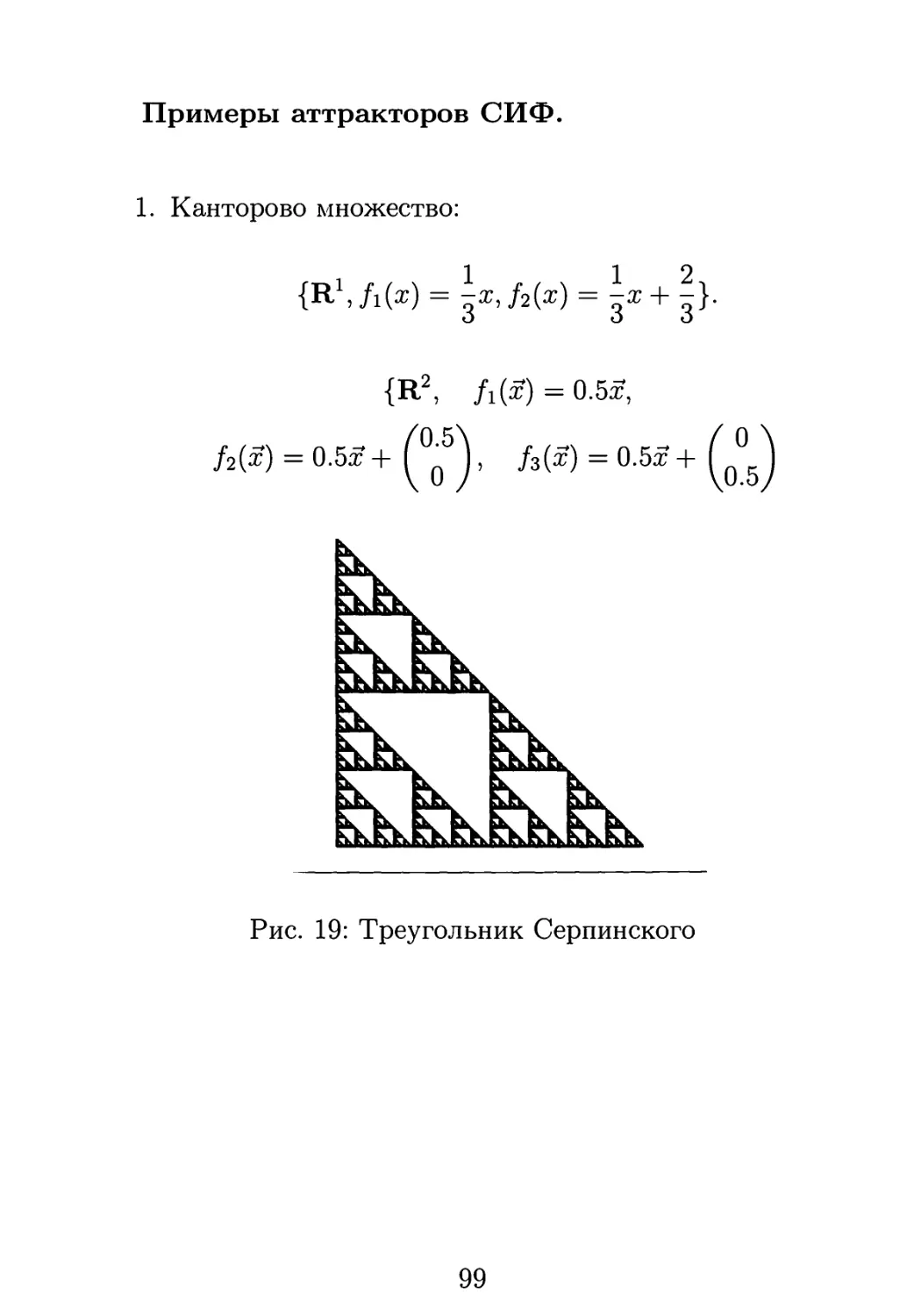
противоположную, то ель или лист папоротника. Если менять
ориентацию треугольников хаотично, то и дерево можно получить
в результате весьма «лохматое».
21

Рис. 9: "Липа"
Рис. 10: "Ель"
22

Рис. 11: "Лохматое" (со случайной ориентацией) дерево
Пифагора
23

Пример шестой. Фрактал Леей
Фрактал Леви строится аналогично дереву Пифагора,
только без квадратов. На единичном отрезке как на
гипотенузе строим равнобедреный прямоугольный
треугольник и гипотенузу выбрасываем. На его катетах как на
новых гипотенузах строим два новых равнобедреных
прямоугольных треугольника, и так до бесконечности. Фрактал
Леви напоминает симметричное дерево Пифагора, но без
ствола, что-то вроде «куста Пифагора».
Рис. 12: итерации фрактала Леви
24

Рис. 13: Фрактал Леви
Все предложенные на рассмотрение объекты самопо-
добны и все они, кроме дерева Пифагора и бинарного
дерева, строятся по одинаковому принципу:
1. Выбирается геометрический объект, так называемая
база.
2. Выбирается правило замены «базы» на объединение
нескольких объектов, подобных базе, но меньших по
своим линейным размерам, — так называемый
«мотив».
Иногда, слова «база» и «мотив» заменяются словами
«аксиома» (или инициатор) и «порождающее
правило».
Для треугольника Серпинского базой является
треугольник, а для Канторова множества, кривой Коха
и фрактала Леви — единичный отрезок.
Рассмотрим еще одно свойство всех представленных
объектов, кроме деревьев. Мотив представляет собой
объединение нескольких маленьких подобий базы. Можно
рассмотреть набор отображений всего пространства в себя,
каждое из которых отображает базу в точности в одно из
25

этих подобий. Например, для Канторова множества это
отображения плоскости вида
U)i(x) = -X, U2{X) = -Ж + -,
переводящие отрезок [0,1] в его первую и последнюю треть,
соответственно.
Рис. 14: Итерации треугольника Серпинского
Для треугольника Серпинского таким будет набор из
трех отображений плоскости, являющихся сжатием
плоскости в два раза с последующим сдвигом на вектор.
Вектор сдвига равен половине вектора, соответствующего
вершине исходного треугольника. Эти три отображения
переводят треугольник в три подобных ему треугольника,
каждый из которых образован двумя сторонами и
средней линией.
Для кривой Коха и фрактала Леви существуют
соответствующие им наборы преобразований плоскости.
Возьмем такой набор преобразований для выбранного
фрактала и произвольный отрезок, или произвольную
точку или даже произвольную «кляксу», единственным
требованием к которой является ее ограниченность.
Применим к этому начальному множеству все преобразования из
набора, а затем объединим все образы в новое множество.
Повторим процедуру много раз. Довольно скоро резуль-
26

тат очередного применения этой процедуры начнет
напоминать выбранный фрактал, которому соответствовал
исходный набор преобразований.
Этот факт пока можно проверить только эксперемен-
тально. Одной из целей курса является теоретическое
обоснование этого свойства фракталов. Тот факт, что фрактал
можно построить, зная только несколько преобразований
плоскости, дает возможность кодировать картинку
(фрактал) набором преобразований, а точнее, их общим видом
и небольшим числом параметров, что сильно сокращает
объем информации. На этом основаны принципы
фрактального сжатия изображений.
27

Упражнения
1. Записать в троичной системе счисления числа
7 2 11 7 34
8' 9' 13' 10' 81'
2. Записать в двоичной системе счисления числа
? I А А ?5
8'9' 13' 10'64'
3. Записать в виде обыкновенной дроби число, запись
которого в семеричной системе счисления есть
бесконечная периодическая дробь с периодом 12:
а; = 0.(12).
4. Доказать, что последовательность
на отрезке [0,1] имеет меру 0.
Считается, что множества М С Rn имеет меру 0,
если оно может быть покрыто семейством открытых
множеств {Ua,k,OL Е Д к Е Z} таких,что выполнено:
М С Ua€AUa,k, lim V 5(C/Q,fc) = 0,
аеА
где s(G) — площадь множества G в пространстве
Rn. На прямой простейшим открытым множеством
является интервал, площадь интервала в R1 — его
длина.
28

5. Доказать, что множество целых чисел Z на прямой
R1 имеет меру 0.
6. Доказать, что окружность и отрезок на плоскости
R2 имеют меру 0.
7. Доказать, что множество рациональных чисел
счетно.
8. Доказать, что множество точек пересечения Канто-
рова множества и отрезка [§, §] несчетно.
9. Доказать, что множество точек отрезка [0.1], в
десятичном представлении которых отсутствуют цифры
3,5 и 7, несчетно.
10. Доказать, что множество точек отрезка [2,3],
десятичное представление которых составлено только из
цифр 2 и 8, несчетно.
11. Доказать, что множество М, являющееся
объединением девяти последовательностей М = U?=1{ik,k =
1,2,...}, — счетное множество.
12. Доказать, что множество М, являющееся
объединением счетного числа последовательностей
M = U1~1{i*,A=l,2,...})
— счетное множество.
13. Найти размерность подобия треугольника Серпин-
ского, бинарного дерева, кривой Коха, фрактала Ле-
ви.
14. Найти размерность подобия предельных множеств,
полученных следующим образом:
29

1) квадрат делим на 9 одинаковых квадратов и 5 из
них выбрасываем; с каждым из четырех оставшихся
повторяем процедуру;
2) куб делим на 27 одинаковых кубиков и
выбрасываем центральный и восемь угловых; с каждым из
восемнадцати оставшихся кубиков повторяем
процедуру; фрактал, полученный в пределе называют
губкой Менгера;
3) отрезок [(0,0),(1,0)] на плоскости R2 заменим на
ломаную
[(0,0),(^0)]и[(^0),(|,^)]и
и[ф^),ф°)]и[ф°м|-^)]и
u[(|-^),(|o)]u[(|o),(i,o)],
состоящую из шести отрезков, вчетверо меньшей
длины; каждый из этих отрезков заменим на
аналогично построенную ломаную: отрезок делится на четыре
равных отрезка и на двух средних строятся
равносторонние треугольники, после чего отрезки, на
которых треугольники были построены, выбрасываются;
процедуру продолжим до бесконечности.
15. Найти размерность подобия фрактала на плоскости,
состоящего из точек (х,у), где х,у Е [0,1], причем
в пятеричной системе счисления в записи числа х
отсутствуют цифры 1 и 2, а в записи числа у
отсутствуют цифры 0 и 3.
16. Описать фрактал из задачи 14(2) с помощью
троичной системы счисления.
30

17. Рассмотрим фрактал /Q, построенный с помощью
следующей процедуры.
К концам отрезка длины 1 пристроим
перпендикулярно расположенные и касающиеся его в своей
середине отрезки длины а. К их концам пристроим
перпендикулярно к ним расположенные и
касающиеся их в своей середине отрезки длины о?. К
концам последних отрезков пристроим
перпендикулярно к ним расположенные и касающиеся их в своей
середине отрезки длины а3. Этот процесс продолжим
до бесконечности. Предельное множество назовем 1а-
фрактал.
Докажите, что если \ < а < -4, то /а-фрактал
компактен, а сумма длин отрезков, из которых он
составлен, бесконечна.
Примеры решения некоторых задач
1. Записать в семеричной системе счисления число |.
Процесс перевода из десятичной системы в троичную
подробно описан в главе 1, данная задача решается
аналогично:
Число 2 при делении на 9 с остатком дает 0 и 2 в
остатке. Ноль пишем первой цифрой
последовательности, остаток умножаем на 7 — основание системы
счисления.
Полученный результат 14 делим с остатком на 9,
получаем 1 и 5 в остатке, 1 — вторая цифра
последовательности (первая после запятой).
Цифру 5 умножаем на 7, полученный результат 35
делим с остатком на 9, получаем 3 и 8 в остатке,
31

цифра 3 — третья цифра последовательности (
вторая после запятой).
Цифру 8 умножаем на 7, полученный результат 56
делим с остатком на 9, получаем 6 и 2 в остатке,
повторяем процесс, получаем число 14, которое при
делении на 9 дает 1 и 5 в остатке, т.е. началось
повторение процесса.
В результате получаем периодическую
последовательность 0.136136136... или 0.(136), которая и
является записью исходной дроби | в семеричной системе
счисления.
2. Записать в виде обыкновенной дроби число, запись
которого в пятеричной системе счисления есть
бесконечная периодическая дробь с периодом 23:
х = 0.(23).
Пятеричная система имеет основание 5, это значит,
что сразу после запятой стоят пятые доли единицы,
затем — двадцать пятые, затем — сто двадцать
пятые, и т.д. Значит, число х равно сумме всех
нечетных степеней одной пятой с коэффициентом 2 и всех
четных степеней одной пятой с коэффициентом 3:
оо у л ч 2г-1 оо / л\2г
*-»Е( +'Е()
г=1 N ' г=1 х '
Используя формулу для суммы бесконечной
убывающей геометрической прогрессии, получим
окончательный результат:
*=2(й)+3й) = ё-
32

Доказать, что граница квадрата на плоскости имеет
меру нуль.
Определение множества меры нуль дано в задаче 3.
Построим семейство открытых множеств
{Uaik,a€A,ke Z}
на плоскости R2 таких,что выполнено
М С UaGAUa,k, lim V s(Ua,k) = О,
к->оо *-^
аеА
где s(G) — площадь множества G в пространстве R2
и М — квадрат без внутренности, т.е.
М = {xeR2: \хг\ = \х2\ = 1}.
В качестве открытого множества Uk выберем
открытую «рамку»:
Uk = {х е R2: (1 - ±) < \Xl\, \х2\ < (1 + 1)}.
Площадь множества Uk равна разности между
площадями квадратов Ак и В^:
Ak = {xeR2:\x1\,\x2\<(l + ^)},
Bfc = {ж е R2 : W, Ы < (1 - i)}.
Таким образом,
S(Uk) = (2(1 + l)f - (2(1 - ^))2 = 16(1 + i)i
следовательно, S(Uk) —> 0 при к —> со.
33

4. Доказать, что множество пар рациональных чисел
счетно.
Множество рациональных чисел счетно. Это
отдельная задача, которую считаем уже решенной. Это
значит, что каждому рациональному числу поставлен
в соответствие порядковый номер. Расположим
пары рациональных чисел в виде матрицы Л, поставив
на место в г-й строке и j-м столбце пару, у которой
первое число имеет номер г, а второе j.
Получается бесконечная матрица со столбцами j = 1,2,...,
и строками г = 1,2,.... Пересчитаем элементы этой
матрицы следующим способом: на первое место
поставим элемент a^i, на второе и третье место
поставим элементы а\^ и <22,ь соответственно, на
четвертое, пятое и шестое места — элементы ^1,3,^2,2,^3,1,
соответственно, на
(0.5гг(гг-1) + 1), (0.5гг(гг-1) + 2),..., (0.5гг(гг-1) + гг)
места — элементы
<2l,n, ^2,n-l, • • • Яп-1,2, апд.
Таким образом, двигаясь от левого верхнего угла
матрицы, пересчитаем все ее элементы.
5. Найти размерность подобия фрактала F,
полученного следующим образом: ему принадлежат все точки
на плоскости, у которых координаты лежат между
О и 1, а в десятичном представлении имеют только
цифры 1 и 7.
Фрактал F лежит в квадрате с вершинами
(1,1),(1,0),(0,0),(0,1). Сторона этого квадрата равна
1. Если разделить сторону этого квадрата на десять,
то он окажется составленным из ста маленьких квад-
34

ратов со стороной 0.1. Точки фрактала F
расположены внутри пересечений второй или восьмой
горизонтальной полосы маленьких квадратов, если считать
от оси абсцисс вверх, и второй или восьмой
вертикальной полосы маленьких квадратов, если считать
от оси ординат вправо, поскольку именно там лежат
точки с координатами, у которых первая цифра
после запятой равна 1 или 7. Таких пересечений
четыре, и каждое из них есть квадрат со стороной,
равной 0.1, содержащее внутри уменьшенную в десять
раз копию фрактала F. Это означает, что фрактал F
может быть составлен из четырех уменьшенных в 10
раз (с точки зрения линейных размеров) фракталов
F. Таким образом, размерность подобия фрактала F
равна j^Q.
6. Построить фрактал на плоскости, размерность
подобия которого была бы равна |^|.
Рассмотрим квадрат на плоскости и разобьем его
стороны на семь равных частей каждую. Тогда квадрат
разбивается на 49 одинаковых квадратиков, сторона
которых в семь раз меньше стороны исходного
квадрата. Выберем четыре из этих 49 квадратов,
например все угловые. Все остальные квадраты выбросим,
а в этих четырех повторим процедуру. Предельное
множество будет фракталом с размерностью
подобия щ.
In 7
35

Глава 2. Некоторые элементы
топологии
В этой главе приведем краткий обзор основных
сведений из топологии, которые понадобятся в дальнейшем.
Самый простой и основополагающий математический
объект — множество, то есть то, что имеет элементы.
Вводя дополнительные структуры на множестве, можно
получать различные пространства. Например, введя операции
сложения и умножения на число, удовлетворяющие
линейному закону, получим линейное пространство. Выбрав
на исходном множестве семейство открытых подмножеств,
получим топологическое пространство. Задав на исходном
множестве метрику, получим метрическое пространство.
Определим понятия метрики и метрического
пространства.
Определение 2.1. Говорят, что на множестве X
задана метрика, если задана функция из прямого
произведения X х X в неотрицательные действительные числа
р : X х X -► R?0,
обладающая следующими свойствами:
для Ух,y,z e X всегда выполнено:
1) р(х,у) = 0<^=)> х = у,
2) р(х,у) = р(у,х),
3) р{х,у) ^ p{x,z) + p(z,y).
Определение 2.2. Множество с введенной на нем
метрикой {X, р) называется метрическим
пространством. Значение р(х,у) называют расстоянием
между х и у.
36

Примеры метрических пространств
1. Пространство вершин тетраэдра. Множество X в этом
случае имеет четыре элемента, расстояния между
любыми несовпадающими элементами равны единице.
2. Плоскость R2 с евклидовой метрикой на ней:
р(х,у) = (\xi - yi\2 + \х2 - Ы2)^.
3. Плоскость R2 с р-метрикой на ней:
Рр(х,у) = (\xi - yi\p + \х2 - у2\р)*•
4. Плоскость R2 с оо-метрикой на ней:
Роо(х,у) = max(|xi -yi\,\x2 -y2\).
5. Плоскость R2 со следующей метрикой на ней:
рассмотрим сферу S2 радиуса один в трехмерном
пространстве R3, касающуюся плоскости R2. Соединим
все точки плоскости прямыми с полюсом А сферы,
противоположным точке касания. Каждая прямая
пересекает сферу еще в одной точке, кроме этого
полюса. Поставим каждой точке плоскости
соответствующую точку на сфере. Таким образом мы
получили отображение
а : R2 -> S2\{A}.
Определим расстояние между точками плоскости как
евклидово расстояние между их образами при
отображении а:
Р(х,у) = (\<*(x)i -а(у)х\2 + \a(x)2-a(y)2\2+
37

+ \a(x)3-a{y)3\2)i.
6. Сфера в трехмерном пространстве. Расстояния
между точками совпадают с евклидовыми расстояниями
между ними.
7. Сфера в трехмерном пространстве. Расстояния
между точками совпадают с длиной меньшей дуги
геодезической между ними.
В приведенных примерах расстояния могут быть
ограниченными, как в случаях 1, 5, б, 7, и неограниченными,
как в случаях 2, 3, 4.
Дадим основные определения понятий топологии,
которые потребуются в дальнейшем.
Определение 2.3. Две метрики р и а на множестве
X называются эквивалентными, если существуют два
положительных числа С\, c<i > 0 такие, что для любых
элементов х, у Е X выполнено неравенство
cip(x,y) < <г(х,у) < с2р{х,у).
В приведенных выше примерах метрики на плоскости
R2 для случаев 2,3,4 эквивалентны, а случай 5 определяет
метрику, не эквивалентную случаям 2, 3, 4. Случай 6 и
случай 7 задают эквивалентные метрики на сфере.
Приведем еще один пример двух неэквивалентных
метрик на прямой R: обычное расстояние р(х,у) = \х — у\
и о~(х,у) = \х3 — у3\. Не существует такого с\ > 0, что
р{х,у) > С\сг(х,у) для любых х и у, поскольку
х3 -у3 = (х- у)(х2 + ху + у2).
Второй сомножитель может быть сколь угодно велик.
38

Определение 2.4. Метрика т на множестве Y
называется индуцированной с метрического пространства
{X, р) с помощью взаимно однозначного отображения
р : X -> У,
если каждая точка х еУ имеет прообраз
д~\х)ех
и расстояние для любых точек х,у £ Y определены по
формуле
т{х,у) = р(д~1(х),д~1{у)).
Пример 5 (из приведенных выше) определяет на
плоскости метрику, индуцированную со сферы.
Другой пример индуцированной метрики. Рассмотрим
интервал (0,1) на прямой и отобразим его в прямую R с
помощью следующей формулы:
y = tg(ir(x--)).
В качестве расстояния на прямой возьмем расстояние
между прообразами:
a(x,y) = \&VCtg{x)-&VCtg{y)\.
7Г 7Г
Легко показать, что функция а(х, у) является метрикой и
что она не эквивалентна евклидовой метрике на прямой.
Второе утверждение следует из того, что значения а(х,у)
не превосходят единицы.
Определение 2.5. Два метрических пространства
{X, р} и {У, о-} называются эквивалентными, если
существует взаимно однозначное соответствие между точ-
39

ками такое, что исходная метрика а и
индуцированная из X с помощью g на множестве Y
эквивалентны.
В качестве примера эквивалентных метрических
пространств можно привести две концентрические сферы,
метрики на которых индуцированы с евклидовой метрики
пространства R3, в котором они лежат, или рассмотреть
равносторонний треугольник и описанную вокруг него
окружность с расстояниями на них, индуцированными с
плоскости. В обоих случаях соответствие g между точками двух
множеств может быть получено с помощью лучей,
выходящих из центра сфер в первом случае и центра описанной
окружности — во втором.
Определение 2.6. Фундаментальной
последовательностью точек метрического пространства {X, р)
называется такая последовательность {xi,i = 1,2,...}; что
для любого положительного числа £ > О найдется
целое число N такое, что для любых п,т > N выполнено
Примером фундаментальной последовательности на
комплексной плоскости может быть последовательность
Jexp(m) \
а не фундаментальной — последовательность
{(-1)»,п = 1,2)...}.
Определение 2.7. Последовательность
{xi,i = 1,2,...}
точек метрического пространства {X, р} называется
сходящейся или имеющей предельную точку, если существу-
АО

em точка а метрического пространства {X, р) такая,
что для любого положительного числа е > 0 найдется
целое число N такое, что для любого п > N выполнено
р(хп, а) < е. Точка a G X называется пределом
последовательности {xi, г = 1,2,... }.
Последовательность {exp^m) ? n = 1,2,...} имеет
пределом точку 0, а последовательность {(—1)п,гг = 1,2,...}
предела не имеет.
Определение 2.8. Метрическое пространство
называется полным, если любая его фундаментальная
последовательность сходится, т.е. имеет предел.
В приведенных выше примерах метрических
пространств все они являются полными, кроме случая 5. В
этом случае будем считать, что исходная плоскость — это
координатная плоскость х% = О, а точка касания — точка
(0,0,0). Последовательность точек плоскости {(п, 0,0),п =
1,2,...} является фундаментальной, но предела не имеет.
Это легко показать следующим образом. Пусть точка А с
координатами (0,0,d) — точка на сфере, противоположная
точке касания (0,0,0), d — диаметр окружности 52.
Евклидово расстояние в трехмерном пространстве от точки А до
образа точки {(п, 0,0)} при отображении а : R2 —>> 52\{А}
меньше, чем ^-, Этот факт следует из теорем
планиметрии при рассмотрении сечения сферы плоскостью,
проходящей через точку Л, центр сферы и точку (гс, 0,0).
Значит, расстояние между хп и хт, которое равно евклидову
расстоянию между а(хп) и а(хт), не превосходит суммы
их расстояний до Д т.е. не больше, чем 2тах(^-, ^).
Таким образом, последовательность фундаментальна и ее
образы на сфере сходятся к точке А. Но точка А не имеет
прообраза при отображении а : R2 —> 52\{А}, поэтому
исходная последовательность предела не имеет.
Еще одним примером неполного метрического
пространства является интервал (0,1) с евклидовой метрикой на
41

нем. Последовательность {-,п=1,2,...}
фундаментальна, но ее пределом является 0, который не принадлежит
интервалу (0,1). Пространство рациональных чисел также
не является полным метрическим пространством.
Определение 2.9. Открытый шар радиуса г с
центром в точке х0 Е X:
В(х0,г) = {х : р(х,х0) <r,x G X}
— множество точек х из множества X, расстояние от
которых до точки х0 Е X меньше г. Такой шар также
называют г-окрестностью точки Хо Е X.
Определение 2.10. Замкнутый шар радиуса г с
центром в точке Хо Е X:
В(х0, г) = {х : р(х, хо) <г,хе X}
— множество точек х из множества X, расстояние от
которых до точки х0 G X не больше г.
Иногда замкнутый шар радиуса г с центром в точке
хо е X обозначают следующим образом: Б[х0,г].
Определение 2.11. Открытое множество М в
метрическом пространстве X — это множество, для
каждой точки х которого существует число е(х) > 0 такое,
что В{х,е{х)) С М. Иначе говоря, каждая точка
открытого множества входит в него со своей окрестностью.
Примеры открытых множеств в R — интервал (0,2),
луч (0, оо), объединение интервалов (7,8) U (9,100); в R2
— внутренность круга; точки плоскости, удовлетворяющие
неравенству х\ + Ъх\ > 9, полоса \х\ + 5| < 2.
Определение 2.12. Точка х называется внутренней
точкой множества М, если она входит в это
множество с некоторой своей окрестностью, то есть
существует число е(х) > 0 такое, что В(х,е(х)) С М.
Определение 2.13. Внутренностью множества М
42

называется совокупность всех его внутренних точек. По-
другому можно определить внутренность М как
объединение всех открытых множеств, содержащихся в М.
Внутренность М обозначается как М0 и является
открытым множеством.
Внутренностью отрезка [0,1] на прямой R является
интервал (0,1), а на плоскости R2 у отрезка внутренние
точки отсутствуют.
Определение 2.14. Предельной точкой множества
М в метрическом пространстве X называется точка
пространства X, в любой окрестности которой
находится по крайней мере одна точка из множества М, не
совпадающая с ней самой. Предельная точка множества М
не обязана принадлежать множеству М.
Предельными точками внутренности круга являются
все точки круга.
Заметим, что если рассмотреть последовательность
{xui = 1,2,...}
точек метрического пространства {X, р} как множество в
этом пространстве, то оно может иметь несколько
предельных точек, в то же время предел любой
последовательности либо не существует, либо единственен. Примером
может служить последовательность {(—1)п + -, п = 1,2,...}
на прямой R, которая расходится ( то есть не имеет
предела) как последовательность, но имеет две предельные
точки {1} и {—1} как множество.
Определение 2.15. Множество, содержащее все
свои предельные точки, называется замкнутым.
Отрезок — замкнутое множество, интервал — нет.
Множество целых чисел замкнуто, а множество рациональных
чисел — нет. Единственными множествами, которые
одновременно и замкнуты, и открыты, являются все простран-
43

ство и пустое множество.
Определение 2.16. Замыканием множества М
называется множество, состоящее из точек множества
М и всех его предельных точек. Оно обозначается М и
получается присоединением к множеству М предельных
точек, ему не принадлежащих. Другим способом
можно определить замыкание М как пересечение всех
замкнутых множеств, его содержащих. Замыкание М
замкнуто.
Замыканием интервала является отрезок, замыканием
сферы с выколотой точкой — вся сфера.
Определение 2.17. Точка х множества М
называется изолированной, если существует ее окрестность
В(х,г) такая, что В(х,г)Г)М = {х}, то есть точка х —
единственная точка в этой окрестности из множества
М.
Канторово множество не содержит ни одной
изолированной точки, отрезок не содержит ни одной
изолированной точки, во множестве {^,тг= 1,2,...} все точки
изолированные, во множестве {0,^,п = 1,2,...} изолированные
все точки, кроме точки 0.
Определение 2.18. Множество называется
совершенным, если оно замкнуто и не содержит
изолированные точки.
Канторово множество — совершенное множество,
отрезок — совершенное множество, шар — совершенное
множество. Последовательность {^,гг = 1,2,...} не является
совершенным множеством.
Определение 2.19. Граничной точкой множества
М в метрическом пространстве X называется точка
пространства X, в любой окрестности которой
находится по крайней мере одна точка из множества М и по
крайней мере одна точка, множеству М не
принадлежащая. Совокупность граничных точек множества М на-
44

зывается границей множества М. Границу множества
М можно получить как разность между замыканием и
внутренностью множества М:
ГМ = М\М0.
Границей интервала (1,4) на прямой является пара
точек {1,4}, на плоскости — отрезок [0,1], границей круга на
плоскости — окружность, границей множества {0, ^,га =
1,2,...} — само это множество.
Определение 2.20. Множество А называется всюду
плотным во множестве В, если
АС В С А.
Множество рациональных чисел всюду плотно во
множестве действительных чисел. Интервал (0,1) всюду
плотен в отрезке [0,1].
Определение 2.21. Множество М называется
связным, если его нельзя представить в виде объединения двух
непустых множеств А и В таких, что пересечение
каждого из этих множеств с замыканием другого есть
пустое множество: А П В = 0 и А П В = 0.
Компонентой множества М называется его связное
подмножество, которое не содержится ни в каком другом связном
подмножестве М.
Окружность — связное множество, множество
рациональных чисел — нет, Канторово множество — нет,
треугольник Серпинского — связное множество. Связная
компонента множества целых чисел — точка, связная
компонента множества решений уравнения Х\Хч = 1 — одна из
ветвей гиперболы.
Определение 2.22. Множество М называется вполне
45

разрывным ( вполне несвязным), если все его связные
компоненты — точки.
Канторово множество, множество целых чисел,
множество рациональных чисел вполне разрывны.
Определение 2.23. Множество М называется
ограниченным, если существует замкнутый шар В(х,г),
целиком содержащий М: М С В(х,г).
Треугольник, отрезок, эллипсоид — ограниченные
множества, луч, гиперболлоид, бесконечный цилиндр — нет.
Определение 2.24. Диаметром множества М
называется наибольшая верхняя грань всех расстояний
между парами точек из множества М:
DM = sup{p(x,y),Vx,y G М}.
Диамером равностороннего треугольника является
длина его стороны, круга — его диаметр, куба со стороной
единица — у/3.
Диаметр множества М не превосходит диаметр
минимального шара, содержащего М.
Определение 2.25. Семейство множеств
{Bui el],
где I — некоторое множество индексов, называется
покрытием множества М, если выполнено
М С UieIBi.
Определение 2.26. Семейство множеств {B^i £
70}, где Io Q I — некоторое подмножество множества
индексов I, называется подпокрытием множества М, ес-
46

ли {B{,i G /} — покрытие М и выполнено
М С UieIoBu
то есть {Bi,i G /0} также покрытие М.
Множество всех возможных открытых шаров радиуса
1 с центрами в точках отрезка [0,1] образует его покрытие.
Два шара £?(0,1) и Б(1,1) образуют конечное
подпокрытие этого покрытия.
Другой пример — покрытие интервала (0,1)
открытыми множествами (0,1 — ^),п = 1,2,..., — у этого покрытия
нет конечного подпокрытия.
Определение 2.27. Множество М называется
компактным, если из любого его покрытия открытыми
множествами можно выбрать конечное подпокрытие.
Это означает, что для любого покрытия {Б;, г G /}
множества М, у которого все Б;, г G I — открытые множества,
можно выбрать конечное число таких
{Bik,k = 1,2,...,К},
объединение которых будет содержать М:
м с uf=1Bit.
Заметим, что в евклидовом пространстве Rn понятия
«компактное множество» и «компакт» совпадают.
Компактными множествами (компактами) на
плоскости являются круг, квадрат, отрезок, треугольник Сер-
пинского, в пространстве — сфера, шар, поверхность тора,
эллипсоид. Компактами не являются луч, интервал,
внутренность круга, гипербол л оид, бесконечный цилиндр.
Важное замечание: в евклидовом пространстве Rn
компактность эквивалентна замкнутости и ограниченности,
47

то есть множество компактно тогда и только тогда, когда
оно замкнуто и ограниченно.
Определение 2.28. Отображение метрического
пространства X в метрическое пространство Y называется
непрерывным, если прообраз любого открытого
множества в Y есть открытое множество в X.
Еще одно замечание: последние четыре определения
имеют смысл не только в метрическом, но и в
топологическом пространстве, то есть в пространстве без заданной
метрики, но с заданными открытыми множествами.
Определения при этом не теряют смысла.
Сформулируем основные утверждения, касающиеся
введенных выше понятий.
Теорема 2.1. Пересечение любого числа и
объединение любого конечного числа замкнутых множеств есть
замкнутое множество.
Теорема 2.2. Пересечение любого конечного числа и
объединение любого числа открытых множеств есть
открытое множество.
Теорема 2.3. Дополнение к открытому множеству
есть замкнутое множество.
Важное замечание: для того, чтобы ввести на
множестве структуру топологического пространства, необходимо
и достаточно определить на множестве систему открытых
множеств так, чтобы выполнялись вышесформулирован-
ные теоремы.
Теорема 2.4. Всякое открытое множество на
числовой прямой есть объединение конечного или счетного
числа попарно непересекающихся интервалов.
Теорема 2.5 (о вложенных шарах). Для того,чтобы
метрическое пространство было полным, необходимо и
достаточно, чтобы любая последовательность вложен-
48

них друг в друга замкнутых шаров, радиусы которых
стремятся к О, имела непустое пересечение.
Теорема 2.6 (Гейне — Бореля). Из любого
покрытия отрезка интервалами можно выбрать конечное
подпокрытие.
Теорем 2.7. Замкнутое подмножество компактного
множества в Rn компактно.
Теорема 2.8. Любое бесконечное подмножество
компакта имеет предельную точку, лежащую в этом
компакте.
Теорема 2.9. Непрерывный образ компакта есть
компакт.
Теорема 2.10. Непрерывная функция ограничена на
компакте и достигает на нем свои верхнюю и нижнюю
грани.
Рассмотрим, например, непрерывное отображение
плоскости R2 на прямую R, заданное формулой
у(хъх2) = х\ + х\.
Рассмотрим компакт К на плоскости, заданный
уравнениями
К = {х = (хих2) : \xi\ + \х2\ = 1}.
Это квадрат с вершинами в точках
{{1,0)}, {(0,1)}, {(-1,0)}, {(0,-1)}.
Множество К компактно. Его образом будет отрезок [|, 1]
на прямой. Это также компакт. Максимальное значение
функции у(х) на компакте К равно единице, минимальное
— |, они достигаются в точках {(1,0)} и {(§,|)},
соответственно.
49

Упражнения
1. Покажите, что каждая из нижеследующих формул
определяет метрику в соответствующем пространстве:
1) Манхэттенское расстояние в пространстве Rn:
п
Р(Я,У) = ^2\Х{-Уг\;
t=l
2) р-метрика в пространстве Rn:
п
р{х,у) = (^2 \xi ~ ^1Р)*> Р= 1,2,...;
г=1
3) оо — метрика в пространстве Rn:
р(х,у) = max{|zi — г/г | г = 1,...,п};
4) метрика в пространстве R1:
р{х,у) = \х3-у3\;
5) метрика на сфере S2 С R3:
з
Р&у) = ^2\xi-yi\;
г=1
50

6) метрика на сфере 52 С R3 с диаметром d:
7) метрика на множестве вершин куба, заданного
неравенствами {0^#г^1,г = 1,2,3}в пространстве R3:
р(х,у) = ^2i\xi-yi\;
8) метрика на множестве вершин куба, заданного
неравенствами {0 ^ Xi ^ 1, г = 1,2,3} в пространстве R3:
р{х,у) = maxflzi-s/il};
i=L,2,o
9) метрика на множестве вершин куба, заданного
неравенствами {0^Жг^1,г = 1,2,3}в пространстве R3,
определенная по правилу: если вершины соединены
ребром, то расстояние между ними равно 1; если они
лежат на одной грани, но не соединены ребром, то
расстояние между ними равно 2; а если они не лежат
на одной грани, то расстояние между ними равно 3;
10) метрика в пространстве R2:
Р(х,у) = \x\-yl\ + \х2-У2\\
11) метрика в пространстве R2:
р(х,у) =4|si — s/xI + 5|:г2 - у2\;
51
d arcsin

12) метрика в пространстве R3:
р(х,у) = max{(2|xi - уг\ + \х2 -у2\),3\х3 -у3\}-
2. Разбейте приведенные выше метрики на классы
эквивалентности .
3. Опишите, какой вид имеет окружность ГВ(хо, 1) для
каждой из этих метрик. Точку xq выберите
произвольным образом.
4. Докажите теоремы №2.7—2.10.
5. Докажите, что формула
/:R2->S2 VfeR2
f[X) ~ \d2 + x2 + x2' d2 + x2 + x2' d2 + x2 + x2)
задает отображение плоскости R2 = {x G R3|^3 = 0}
в сферу S2 С R3 с диаметром d, касающуюся этой
плоскости в начале координат.
Замечание: эту задачу можно решить либо с
помощью непосредственной подстановки, либо используя
аппарат школьной геометрии.
6. Выведите формулу, задающую метрику на сфере S2 С
R3 с диаметром d, индуцированную с плоскости R2 =
{х Е R3|£3 = 0}, касающейся сферы в точке (0,0,0),
с помощью отображения / из предыдущей задачи.
7. Какие из приведенных ниже последовательностей на
плоскости R2 фундаментальны?
1) {£;, г = 1,2,... \xiA = 2~\ х{,2 = 5 - 3*} С R2;
52

2) {xi,i = 1,2,... |хгд = 2sinz,Xj)2 = cos г} С R2;
3) {x*i,i = 1,2,... \xiti = 2sin(z-1),:ri,2 = cos(z-1)}
CR2;
2 1
4) {x*i,i = 1,2,... \хц = -smi,xi2 = tCOsz}
г ' г
CR2;
5) {Xi, l = 1, 2, . . . |£i,i = Sin —, Яг>2 = C0S "г}
CR2;
ч г _* , Sill 7 COS 7 , 0
6) {£*, г = 1,2,... жм = -т±, *i|2 = -т^} С R2;
г г
7) {fi? г = 1,2,... |х0д = а, х0,2 = Ь, а2 + Ъ2 ф О,
_ ffj-1,1 _ #1-1,2 л
xi,l — / ? xi,2 — / J
yXi-l,l + Жг-1,2 у Хг-1,1 + Хг-1,2
CR2;
8) {£*, г = 1,2,... |ж0,1 = а, #о,2 = b, a2 + b2 ф 0,
53

Хц — —5 ; 5 J Хг,2 — ~~о \ о / <- **- 5
хг-1,1 ^ хг-1,2 хг-1,1 ^ хг-1,2
9) {£*, г = 1,2,... |х0д = а, х0,2 = Ь, а2 + б2 ^ О,
_ ^г-1,1 _ Д^г-1,2 -,
2*№-1,1 + Хг-1,2) ^(З^^д + ^j_1)2)
CR2.
8. Какие из перечисленных ниже пространств
являются полными метрическими пространствами:
1) пространство всех иррациональных чисел на
отрезке [0,1] с обычным расстоянием р(х,у) = \х — у\\
2) пространство точек на двумерной сфере в R3 с
расстоянием, индуцированным из R3;
3) пространство точек на двумерной сфере в R3 с
выколотой точкой и расстоянием, индуцированным
изЯ3;
4) пространство точек на двумерной сфере в R3 с
выколотой точкой и расстоянием, индуцированным
из R2 с помощью отображения / из задачи 5;
5) пространство вершин куба с метрикой из задачи
1(8).
9. Ниже перечислены множества в метрических
пространствах. Определите, является ли каждое из
перечисленных множеств в соответствующем
метрическом пространстве открытым, замкнутым,
компактным, связным, совершенным, ограниченным, всюду
плотным. Найдите границу и внутренность каждого
множества. Если множество ограничено, найдите его
диаметр.
54

Если не оговорено противное, на прямой и плоскости
задана евклидова метрика.
1) множество рациональных чисел на отрезке [0,1];
2) множество иррациональных чисел на отрезке [0,1];
3) множество точек на плоскости с иррациональными
координатами;
4) множество точек на плоскости с координатами (х\, х2)
для которых выполнены условия:
1) х\ + х\ ^ 4;
2) 0 < х\ + х\ ^ 4;
3) 0 ^ х\ + х\ ^ 4;
4) {4 $С х\ + х\ ^ 9} П {К (X! - 4)2 + (х2 - З)2 ^ 4};
5) {4 ^ (Х1 - I)2 + х\ ^ 9} U {К х\ + (х2 - З)2 ^ 4};
6) {4 ^ х\ + х\ ^ 9} U {1 ^ (Xl - 4)2 + (х2 - З)2 ^ 4};
7) {4 ^ х\ + х\ < 9} П {К х\ + х| < 8};
8) {4 ^ х2 + х\ < 9} П {1 < х\ + z2, ^ 4};
9) х\ - Ъх\ = 5;
10) {х\ + я2 = 9} П {К х\ - х\ ^ 8};
11) {4 ^ х2 - х\ < 9} П {К -х\ + х2 < 8};
5) Канторово множество на отрезке [0,1];
6) треугольник Серпинского на плоскости;
7) отрезок [0,1] на прямой;
8) отрезок [0,1] на плоскости;
9) множество точек последовательности
{exp(in), n = l,2,..., i2 = — 1}
55

на единичной окружности на комплексной
плоскости, расстояние на окружности индуцировано с
плоскости;
10) множество точек последовательности
{exp(in), n = l,2,..., i2 = —1}
на комплексной плоскости;
11) множество точек последовательности
{ехр(-п), п= 1,2,...}
на отрезке [0,1];
12) множество точек
{0,ехр(-тг), п= 1,2,...}
на отрезке [0,1].
10. Найдите точки множества В в метрическом
пространстве {X, р}, находящиеся на кратчайшем расстоянии
до точки А в нижеследующих случаях:
1)
X = R2, р(х,у) = \xi — 2/i I + \х2 — 2/21,
А = {(1,1)}, В = {х G R2|xi = -х2}\
2)
X = R2, р(х,у) = max{|zi -уг\,\х2 — 2/21},
А = {(1,1)}, B = {xeR2\x1 = -x2}]
3)
X = R2, р(х,у) = у/\хг -2/i|2 + \x2 — 2/212,
56

А = {(1,1)}, В = {х е К2\х1 + х2 = 9};
5)
X = R2, р(х,у) = у/\х\ -у\\2 + \х2 — 2/212,
А = {(1,5)}, В = {х е К2\х2 + x22 = 1};
6)
X = R2, р(х,у) = у/\хх ~У\\2 + \х2 — 2/212,
А = {(1,1)}, В — треугольник Серпинского с
вершинами в точках {(0,0)}, {(1,0)}, {(0,1)};
7)
X = R2, р(х,у) = y/\xi -yi\2 + \x2 — 2/212,
А = {(0.9,0.1)}, В — треугольник Серпинского с
вершинами в точках {(0,0)}, {(1,0)}, {(0,1)};
8)
X = R\ p(x,y) = \x-y\, Л = ф,
В — Канторово множество на отрезке [0,1].
Примеры решения некоторых задач
1. Докажите, что формула р\(х,у) = \хъ — уъ\ задает
метрику в пространстве R1, не эквивалентную
метрике р(х,у) = \х-у\.
57

Решение.
Если равны пятые степени двух действительных
чисел, то равны и эти числа, поэтому выполнено
первое свойство метрики. Второе следует из
симметричности формулы и четности функции модуля. Третье
свойство — правило треугольника — следует из того,
что модуль суммы не превосходит суммы модулей.
Поэтому р\ задает метрику. Для любых двух чисел
х и у верно
pi(x, у) = р(х, у){хА + х3у + х2у2 + ху3 + у4).
Второй сомножитель правой части при больших
положительных х и у может принимать любые сколь
угодно большие значения, поэтому нельзя подобрать
такое с > О, чтобы для Ух, у е R1 всегда было
выполнено: р\(х,у) < ср(х,у). Таким образом, метрики
Pi(x,y) и р(х,у) не эквивалентны.
2. Докажите, что формула р2{х, у) = \х2 — у2\ не задает
метрику в пространстве R1.
Решение.
Приведенная формула имеет ноль в правой части в
тех случаях, когда \х\ = \у\, например, х = 5, у = —5.
Это значит, что из равенства р2(х,у) = 0 не следует
равенство х = у, что противоречит первому свойству
метрики.
3. Докажите, что метрика в пространстве R2:
Pi(x,y) = y/\xi - yi\2 + 3\х2 - у2\2
эквивалентна метрике
р2(х,у) = Mxi — 2/11 + 5|х2 -у2\
58

в пространстве R2.
Решение.
Для любых точек х, у Е R2 верно
max{|xi -уг\,\х2 — 2/21> < Pi(x,y) =
= V\xi -2/i|2 + 3|x2 -y2\2 < 2max{\x1-y1\,\x2-y2\}
и одновременно
4max{|a:i -yil\x2 — Уг|} < P2{x,y) =
= A\xi -2/11 + 5|z2 -2/21 < 9max{|xi -yil\x2 — 2/21}-
Отсюда следует, что для любых точек ж, у Е R2 верно
Pi (ж, 2/) < 02 (я, 2/) < 9pi(x,y),
что и доказывает эквивалентность метрик pi (ж, 2/) и
р2(х,у) на плоскости R2.
4. Опишите, какой вид имеет окружность ГБ((0,1), 1)
на плоскости R2 с метрикой
р2{х,у) = 2\хх -2/1I + |s2 — 2/21 -
Решение.
Точки этой окружности (х\,х2) удовлетворяют
равенству
2|х1-0| + |х2-1| = 1
Рассмотрев это равенство как уравнение, получим,
что в евклидовой метрике точки этой окружности
59

образуют ромб с вершинами в точках
(0,0),ф1),(0,2),(-|,1),
составленный из четырех отрезков прямых
х2 = 2-2жь 0<rci^-,
х2 = 2хг, О ^ xi ^ -,
х2 = 2 + 2^1, -- ^ xi ^ О,
х2 = -2хъ -- < xi < О,
являющихся решениями уравнения при раскрытии
модуля.
5. Фундаментальна ли последовательность
{x*i,i = 1,2,... \xi}i = 2cosz,^,2 = cos2z} C R2?
Решение.
Рассмотрим расстояние между двумя членами этой
последовательности:
p{Xi,Xj) = у/\х^1 - Xj^\2 + \xii2 ~ Xj,2\2 =
= -у/4 (cos г — cos j)2 + (cos2z — cos2j)2 =
+(2 sin—-—sin —)2) =
60

= 2у 4(sin L-1 Sm £±2)2 + (sin(j _ i) sin(j + г))2.
Если взять г = j + 2, то
p(xi,Xj) = 2v^sin 1 sin(z + l)2 + (sin2sin(2z + 2)2 ^
^ 4|sin(z + 1)| sin 1.
Поскольку г натуральное число и | > 1, то всегда
можно подобрать сколь угодно большое г, такое, что
для некоторого п
7Г 37Г
2тгп + - < г + 1 < 2ттп + —,
4 4
при этом выполнено sin (г + 1) > ^, и тогда
p(xi,Xj) ^ 4|sin(i + l)|sinl > 4 ( — I > 2,
следовательно, последовательность не
фундаментальна.
6. Является ли полным пространство всех чисел на
полуинтервале (0,1] с обычным расстоянием р(х,у) =
\х-у\.
Решение.
Рассмотрим последовательность {^, п = 1,2,... }
точек на этом полуинтервале. Эта последовательность
фундаментальна и стремится к 0 при п —> сю. Но
точка 0 пространству не принадлежит, значит, оно
не является полным метрическим пространством.
7. Является ли полным метрическим пространством
пространство Q вершин правильного тетраэдра с ребром
61

длины 1 в R3 с евклидовым расстоянием?
Решение.
Поскольку все пространство Q состоит из
изолированных точек, то любая фундаментальная
последовательность в нем постоянна, а значит, сходится к
точке этого пространства. Следовательно,
пространство Q полное.
8. Определите, является ли множество
M = {xl + xl<9}n{l<xl-xl< 4}
в пространстве R2 открытым, замкнутым,
компактным, связным, совершенным, ограниченным, всюду
плотным. Найдите границу и внутренность
множества М. Если множество М ограничено, найдите его
диаметр.
Решение.
Множество М есть пересечение открытого круга с
центром в начале координат и радиусом 3 и
открытого множества, лежащего между ветвями гипербол.
Это пересечение открыто, поэтому не замкнуто, не
совершенно и не компактно, состоит из двух
компонент связности, то есть несвязно, не содержит
изолированных точек, ограничено, поскольку лежит в
круге радиуса 3, по этой же причине не является всюду
плотным на плоскости. Его внутренностью является
оно само, а его граница состоит из кусков
окружности {х\ + х\ = 9} и гипербол {х\ — х\ = 1} и
{х\ — х\ = 4}. Диаметр d множества М равен б,
поскольку d(M) = supx eM p(x, у) достигается на
точках границы множества М, а конкретно — на точках
окружности с центром в начале координат радиуса
62

3, симметричных относительно центра, и равен
диаметру этой окружности.
9. Найдите все точки множества
В = {х е R2|xi = х2}
на плоскости с манхэттенским расстоянием
2
р(х,у) = ^2\х{-у{1
г=1
находящиеся на кратчайшем расстоянии от точки
А(1,2).
Решение.
Ответом задачи является отрезок / = [(1,1), (2,2)] на
множестве В. Расстояние от точки А до любой точки
этого отрезка будет равно 1, до всех остальных точек
множества В расстояние от точки А будет больше 1.
Действительно, если х Е /, то его координаты лежат
в отрезке [1,2], причем \х\ — 1| + \х2 — 2| = Х\ — 1 +
2 — х2 = 1. Если х ф I, то обе его координаты либо
больше 2, либо меньше 1. Тогда либо
|xi-l| + |x2-2| =xi-l-\-x2-2 = 2xi-3 >4-3 = 1,
либо
|х1-1| + |х2-2| = 1-х1 + 2-х2 = 3-2zi > 3-2 = 1.
63

Глава 3. Множество К(Х) всех
компактных множеств метрического
пространства X
Рассмотрим фракталы, определенные в предыдущих
лекциях. Это Канторово множество, треугольник Серпин-
ского, фрактал Леви, бинарное дерево и дерево Пифагора.
Все эти множества замкнуты и ограничены. Поскольку все
они лежат в евклидовом пространстве, то они компактны.
Рассмотрим новое множество — множество всех непустых
компактных множеств на метрическом пространстве X.
Обозначим его К(Х). Если X — плоскость, то К(Х) —
множество всех компактов на плоскости, если прямая, то
на прямой. Поставим задачу определить метрику на этом
множестве, чтобы оно стало метрическим пространством.
Определение 3.1. Введем на множестве К(Х) всех
компактных множеств на X, где X — метрическое
пространство {X, р}, метрику, которую обозначим той же
буквой р, с помощью следующей формулы:
для любых двух компактов А,В£ К(Х)
р(А, В) = max ( sup inf p(a, 6), sup inf р(а, b) 1 ,
\aeA b£B ьев a^A J
где р(а, b) — расстояние между точками a ub
пространства X.
Докажем, что эта формула корректно задает метрику
на множестве К(Х), то есть докажем, что выполнены все
три свойства метрики.
1. Первое свойство требует доказательства в обе
стороны:
64

a) Если р(А, В) = О, то
sup inf р(а, b) = sup inf p(a, b) = 0.
a(=A b€B beB a^A
( \/ae A inf6€5 p(a, b) = 0 => a G В
^ [VbeB infa€Ap(a,b) = 0 ^bGi
Вышеприведенные выводы верны, поскольку
множества А и В компактны, а значит замкнуты, то есть
содержат все свои предельные точки. Из этого
следует, что если infb€# р(а, Ь) = 0, то a G В.
( АСВ
^{в1а
=ф А = В.
Мы доказали, что
р(А,В) = 0=>А = В.
b) Если множества А и В совпадают, то есть А = В,
то верно, что
{Уа Е А а Е В => infb6jB p(a, b) = p(a, a) = 0
V6 G Б be A => infa6A p(a, 6) = p(b, b) = 0
=>> max ( sup inf p(a, 6), sup inf p(a, b) ) = 0.
\а€Л feeB beB aEA J
Следовательно,
A = B^ p(A,B) = 0.
65

Первое свойство метрики выполнено.
2. Второе свойство — симметрия — автоматически
следует из определения.
3. Третье свойство — неравенство треугольника.
Докажем, что оно также выполнено.
Сначала введем вспомогательное обозначение:
Ро(а,В) = inf р(а, b).
b£B
Это число, которое в школьной геометрии
соответствовало расстоянию от точки до множества. Оно не
является расстоянием в смысле метрики, например
потому, что если a Е Б, то ро(а, В) = О, хотя аф В.
Рис. 15: Примеры ро(а,В)
Очевидно, что
Г Vae А р0(а,В)^р(А,В) (3.1)
^ \ \/Ъ е В р0(а, В) ^ р(а, Ъ). (3.2)
66

Рис. 16: Примеры ро(а,В)
Пусть А, В, С G К(Х), тогда для любых трех точек
а £ A, b £ В, с £ С выполнено неравенство
треугольника в метрическом пространстве X
р{а,с) ^p(a,b) + p{b,c).
Учитывая (3.2), получаем, что для любых трех точек
а е A, b e В, с G С выполнено неравенство
Ро{а,С) ^ р(а,Ъ) + р{Ъ,с).
Поскольку С — компакт, для каждой точки b G В
найдется такая точка с0 G С, что р0(Ь,С) = р(Ь,с0).
Отсюда следует, что для любых точек а Е A, b G В
выполнено
А)(а,С) К:Р{а,Ь) + ро(Ь,С).
Учитывая (3.1), получаем, что для любых точек a G
A, b G В выполнено
pQ(a,C)^p{a,b) + p(B,C).
67

Поскольку В — компакт, то для каждой точки a Е А
найдется такая точка &о € В, что Ро{а,В) = р(а,Ьо).
Отсюда следует, что для любой точки а £ А
выполнено
Ро(а,С)^ро(а,В)+р(В,С),
Учитывая (3.1), получаем, что для любой точки a Е
А выполнено
Ро(а,С)^р{А,В) + р{В,С).
Последнее неравенство верно для всех точек А,
значит, и для той, на которой ро(а, С) принимает
максимальное значение. Такая точка существует, так как
А — компакт. Итак, получаем неравенство
supр0(а, С) ^ р(А, В) + р(В, С),
а€А
иначе говоря
sup inf р(а, с) < р(А, В) + р(В, С).
а<ЕА С^С
Если поменять местами а и с и повторить все
рассуждения сначала, можно получить неравенство
sup inf р(а, с) < р(А, В) + р(В, С),
сес а^А
Отсюда следует, что для любых компактов А, В и С
из К(Х) выполнено неравенство
р(А,С)^р(А,В) + р(В,С),
что завершает доказательство корректности
определения метрики на К(Х).
Таким образом, метрика на К(Х) задана корректно и
68

получено метрическое пространство {К(Х), р}. Эта
метрика называется метрикой Хаусдорфа.
Теорема 3.1. Если метрическое пространство {X, р)
полное, то метрическое пространство {К(Х),р} также
полное.
Доказывать эту теорему не будем, примем на веру. В
дальнейшем, если не оговорено противное, предполагаем,
что имеем дело только с полными метрическими
пространствами.
Рассмотрим на примерах, как вычисляется расстояние
в пространстве всех компактов на плоскости — в if (R2).
Примеры
1. Расстояние между точкой а и компактным
множеством В.
В метрике K(R2) расстояние от точки а до
множества В равно sup6GB p(a, Ь).
Замечание. При вычислении расстояния между
двумя множествами понадобится величина т^ьев р(а, 6),
которая всем знакома из школьной геометрии, где ее
называли расстоянием от точки а до множества В и
обозначали ро(а, В). Видим, что в метрическом
смысле эта величина расстоянием не является. Тем не
менее для простоты изложения будем употреблять этот
термин в случае, если в контексте не возникает
путаницы с расстоянием между точкой и множеством
в метрическом смысле.
69

Расстояние между двумя замкнутыми кругами.
Пусть есть два круга, для которых известны их
радиусы и расстояние между их центрами. Обозначим
круги буквами А и В, радиусы г и R соответственно,
г ^ R, расстояние между центрами d.
Рис. 17: Два круга, случай б
Взаимное расположение кругов может быть
следующим:
1) А С В, центры совпадают;
2) А С Б, центры не совпадают;
3) А С Б, А и В касаются;
4) АП В т^ 0, В ^ Л, круги не касаются;
5) В ^ А, А и В касаются;
6) АПВ = 0.
Рассмотрим каждый случай отдельно.
1) А С В, центры совпадают. В этом случае А С В,
следовательно
sup inf p(a, b) = 0.
aeAb^B
Число
sup inf p(a, b)
70

достигается на точках граничной окружности круга
В. Отсюда следует, что
sup inf р(а, b) = R — г.
ьегва^А
2) А С В, центры не совпадают. В этом случае также
А с Б,
следовательно, supaGj4 inheB p(a, b) = 0, а
sup inf p(a, b)
ьев a^A
достигается на точке граничной окружности
круга В, лежащей на прямой, соединяющей центры,
поэтому
sup inf p(a, b) = R — г + d.
bGB a^A
3) А С Б, А и В касаются. Рассуждение аналогично
предыдущему случаю, результат такой же.
4) А Г) В Ф 0, Б ^ А, круги не касаются. В этом
случае каждое из чисел
sup inf p(a, b) и sup inf p(a, b)
a€A b€B bEB a^A
достигается на точках граничных окружностей
кругов А и В соответственно, лежащих на прямой,
соединяющей их центры, при этом
sup inf p(a, b) = г — R + d,
aerAbeB^K
sup inf p(a, b) = R — r + d,
ьегва^А
71

поэтому
р{А,В) = R-r + d.
5) В jb Д А и В касаются. И в этом случае каждое из
чисел из supa€A inf6G£ p(a, 6) и supbeB infaGj4 p(a, 6)
достигается на точках граничных окружностей кругов
А и В соответственно, лежащих на прямой,
соединяющей их центры, при этом
R + г = d,
sup inf p(a, b) = 2r,
а£ГАь^в
sup inf p(a, 6) = 2i?,
поэтому
p(A,B) = 2R = R-r + d.
6) AnB = 0. Рассуждая по аналогии, получаем, что
в этом случае искомое расстояние есть расстояние
между точками граничных окружностей, лежащих
на прямой, соединяющей центры, причем у круга А
это самая близкая к центру круга В точка на этой
прямой, а у круга В — самая далекая от центра круга
А, и расстояние это равно R + d — г.
Таким образом, получили общую формулу, не
зависящую от взаимного расположения кругов:
р(А,В) = R-r + d.
В самом первом случае концентрических кругов эта
формула также верна, поскольку в этом случае
расстояние d равно 0.
3. Расстояние между квадратом, заданным на двумер-
72

ной плоскости уравнением \х + у\ = 1, и отрезком с
концами А(0, —2) и В(2,0) на этой же плоскости.
Вершины квадрата лежат в точках
C(1,0),D{0,1),E(-1,0),F{Q,-1).
Обозначим квадрат буквой А, а отрезок — буквой /.
Тогда
sup inf р(а, b) = p(A, F) = 1,
bei а^л
a
/9
supinf р(а,Ь) = sup inf р(а, b) = p(E,G) = 1 + —,
5€д ael bGED o^eAB 2
где точка G(|,^) — основание перпендикуляра из
точки Е на прямую АВ.
Следовательно, р(/, А) = 1 + Щ-.
4. Расстояние между Канторовым множеством и
отрезком [0,1], на котором оно построено.
Канторово множество принадлежит отрезку [0,1],
поэтому задача состоит в поиске точки на этом отрезке,
наиболее удаленной от самой близкой к ней точки
Канторова множества. Эта точка {|} и расстояние
от нее до точек Канторова множества минимально
в точке {|} или в точке {|}, значит, расстояние от
Канторова множества до отрезка [0,1] равно |.
5. Расстояние между треугольником Серпинского и
треугольником ABC, на котором он построен.
Можно рассмотреть два случая:
1) треугольник ABC рассматривается с внутренними
точками;
73

2) рассматривается только граница треугольника ABC.
В первом случае треугольник Серпинского
содержится в ААВС, поэтому надо искать точку внутри
ААВС, наиболее удаленную от треугольника
Серпинского. Этой точкой является точка пересечения
биссектрис треугольника, вершинами которого
являются середины сторон ААВС — первого
треугольника, выброшенного при построении треугольника
Серпинского. Расстояние от этой точки до
треугольника Серпинского равно радиусу вписанной в этот
выброшенный треугольник окружности.
Выброшенный треугольник подобен исходному с
коэффициентом подобия равным |, поэтому расстояние от
треугольника Серпинского до ААВС равно половине
радиуса окружности, вписанной в ААВС.
Во втором случае граница ААВС содержится в
треугольнике Серпинского, поэтому надо искать точку
треугольника Серпинского, наиболее удаленную от
границы ААВС. Это будет одна из трех точек
пересечения средних линий ААВС с
соответствующими биссектрисами ААВС. Расстояния до границы
ААВС от этих трех точек ровно вдвое меньше
расстояний от оснований биссектрис ААВС до двух
других сторон этого треугольника. Максимальное из этих
трех расстояний и будет расстоянием от
треугольника Серпинского до границы ААВС, на котором он
был построен.
Например, если ААВС имеет вершины
(0,0), (1,0), (0,1),
то максимальное расстояние равно половине
расстояния от середины гипотенузы до любого катета, то
есть равно \. Следовательно, расстояние от треуголь-
74

ника Серпинского, построенного на треугольнике с
вершинами (0,0), (1,0), (0,1), до границы этого
треугольника равно \.
6. Расстояние между отрезком [0,1] и
последовательностью точек
{0,-^, п = 1,2,...}.
1 '2n J
Последовательность лежит внутри отрезка, поэтому
расстояния от ее точек до отрезка равны нулю.
Среди расстояний от точек отрезка до
последовательности максимум достигается в точке 1 и он равен \.
Следовательно, расстояние от точки до
последовательности равно |.
Если рассмотреть расстояние между отрезком [0,1]
и последовательностью точек
{0,^, п = 0,1,2,...},
то соответствующий максимум будет достигаться в
точке |, поскольку в этом случае точка 1 будет
принадлежать последовательности, самой удаленной от
последовательности точкой будет |, а расстояние от
этой точки до последовательности будет равно \.
При вычислении расстояний между множествами
удобно воспользоваться следующей теоремой.
Теорема 3.2. В случае, если А и В — выпуклые
компактные множества, supaGA т£ьев p(a, b) достигается на
точках границ множеств А и В.
75

Упражнения
Найдите расстояния между точками А и В в простране
К(Х), где пространство X и точки А, В и следующие:
1. R, [0,1], [\,6].
2- R, [0,1], [\,\\.
3. R, [0,1], [-2,6].
4. R, [0,1], [2,6].
5. R2,
6. R2,
7. R2,
8. R2,
9. R2,
10. R2,
1—1 Т—1
о о
1 1
1 1
i—I 1—I
О О
i i
Л Hi
i 1
о о
1-4 1—1
О О
1 1
1—1 1—1
о о
1 1
■ ш-
«•(->
[СУ-СУ]-
\(2) ( 3 ^1
, {х\х\ + х\ = А}.
76

11. R2,
, {ж||ж,| + |а;2|=4}
12. R2, {x\\xl\ + \x2\=2},
{£!(*!-2)2 + (ж2)2 = 16}.
13. R2, {ж||ж1 + 2| + |ж2| = 2},
{f|(a:,-2)2 + (*2)2 = 16}.
14. R2, {x\\Xl-2\ + \x2 + l\ = 2},
{x\(Xl-2)2 + (x2)2 = 16}.
15. R2, {x\\x1\2+\x2\2 = 25},
{x\(Xl-2)2 + (x2 + 3)2 = 16}.
16. R2, {ж||ж1| + |ж2К2},
{£!(*,-2)2 + Ы2 = 1}.
17. R2, {x\\Xl-3\ + \x2 + l\^2},
{x\(Xl - 2)2 + (Ж2)2 ^ 4}.
18. R2, {ж||ж1+3| + |ж2 + 1К2},
77

{2\\xi-2\ + \x2\^4}.
19. R2, треугольник Серпинского, построенный в
отрезок [Q,©].
20. R2, треугольник Серпинского, построенный в
ЧО-М-
отрезок [Q,(})].
21. R2, треугольник Серпинского, построенный в
Ч(о)-С).©)-
отрезок [Q,(!)].
2
22. R, Канторово множество на отрезке [0,1],
отрезок [—|, |].
23. R, Канторово множество на отрезке [0,1],
отрезок [-£,£].
24. R2, бинарное дерево со стволом [Q, (J)].
отрезок [Q,©],
25. R2, бинарное дерево со стволом [Q, (J)],
отрезок [Q,Q].
78

26. R, две последовательности точек на прямой {ап =
n}?S=i' и {bn = ^r}^Li5 взятые вместе со своим пределом
каждая,
27. R3, {£||:г1 + 2| + |:г2| + |:гз|=2},
{£\(х1-2)2 + (х2)2 + (х3)2 = 16}.
Примеры решения задач
1. Найдите расстояние между точками А и В в
пространстве if(R2), где
А = {х\\хг - 3| + \х2 + 1| < 2}, Б =
Решение.
Множество А на плоскости есть квадрат с вершина-
ми в точках ШДМДМД).
Самый короткий путь от произвольной точки
плоскости до заданного отрезка лежит либо на
перпендикуляре из этой точки к отрезку, если основание
перпендикуляра попадает на отрезок, либо это путь
к ближайшему к точке концу отрезка, если
перпендикуляр из точки на прямую, на которой лежит
отрезок, не пересекает отрезок.
Множество А лежит вне перпендикуляров,
восстановленных из точек отрезка В к отрезку В, поэтому
самый короткий путь от любой точки а квадрата А
до отрезка В = [(~q), (J)] — это путь от точки а до
точки (0).
о'
79

Максимальный из всех самых коротких путей от
точки до выпуклого множества заканчивается на
границе этого множества, поэтому самый длинный из этих
самых коротких путей — это путь от точки (_3) до
точки (J). Длина этого пути равна \/13-
Самый короткий путь от точки плоскости до
квадрата — это либо путь по перпендикуляру к стороне
квадрата, либо путь по прямой к вершине
квадрата, в зависимости от взаимного расположения
точки и квадрата. В нашем конкретном случае для
точек отрезка [(0), (J)] — это путь по перпендикуляру
к стороне [(_\), (I)] квадрата А, а для точек отрезка
[("g1), Q] — это путь по прямой к точке (Д).
Самый длинный из этих самых коротких путей —
путь между точками (~х) и (_\), длина этого пути
равна у/Е.
Так как \/13> у/Ь, то
р(А, В) = л/13.
Задача решена, и ответ равен л/13.
2. Найдите расстояние между точками А и В в
пространстве AT(R), где А и В — последовательности
точек на прямой {ап = 1 - ±}£°=1 и {Ъп = (-|)n}£°=i,
взятые вместе со своим пределом каждая,
соответственно.
Решение.
Последовательность А монотонно возрастает от
точки 0 до точки 1. Последовательность В расположена
между точками Ъ\ = — | и Ьч = |. Поэтому самый
короткий путь от любой точки последовательности В
до последовательности А не превосходит |, а самый
80

длинный из самых коротких путей от точек
последовательности А до последовательности В — это путь
из точки 1 до последовательности В, то есть путь от
точки 1 до точки |, который равен |. Таким
образом, получили р(А, В) = |, что и является ответом
на вопрос задачи.
81

Глава 4. Преобразования
пространства К(Х) и системы
итерированных функций (СИФ)
В предыдущей главе было рассмотрено множество всех
компактов в полном метрическом пространстве X и
введена метрика на нем, то есть расстояние между двумя
компактами. Таким образом, было получено новое
метрическое пространство К(Х) всех компактных множеств на
пространстве X.
Рассмотрим теорему, которая в дальнейшем поможет
оценить расстояние между компактами.
Теорема 4.1 (о расстоянии между
объединениями компактов). Для любых четырех компактов
A,B,C,DeK(X)
выполнено следующее неравенство:
р(А U Б, С U D) < тах(р(Д С), р(В, £>)).
Докажем это утверждение.
По определению
p(AuB,CUD) =
= max( sup inf p(a,7), sup inf p(a,^/)).
aeAuB-veCuDHK U\ecuD^eAuBHK
Предположим без ограничения общности, что этот
максимум достигается на первом числе, то есть
p(AuB,CUD) = sup inf p(a,7).
a^AuB^CuD
82

Поскольку a Е A U В — компакт, то супремум
достигается на конкретном а0, иначе говоря, существует некоторая
точка ао Е A U В такая, что
p(Al)B,CUD) = sup inf p(a,7)= inf p(ao,7)-
а€Ли£7€Си£> 7€CUD
Нижняя грань функции по множеству всегда не
превосходит ее нижнюю грань по подмножеству, поэтому
выполнены следующие неравенства:
infрКл) < inf р(а0,7) (4.1)
7GCU£> 7€С
i^f,n^a°'7) - inj>(«o,7) (4.2).
Если а0 е А выберем неравенство (4.1), если а0 Е Б, то
неравенство (4.2). В первом случае получаем неравенство
p(AuB,CUD) = inf p(a0,7)<
7GCU£)
< inf р(а0,7) < sup inf p(a, 7) < p(A, C).
Во втором случае получаем неравенство
p(AuB,CUD) = inf p(a0,7)<
7GCLID
< inf p(a0,7) < sup inf р(а,^) < p(B,D).
В любом случае выполнено неравенство
р(А U Б, С U L>) < тах(р(Д С), р(Б, £>))
и теорема доказана.
83

Примеры преобразований пространства К(Х)
1. Преобразования К(Х), индуцированные с X.
Рассмотрим непрерывное преобразование
пространства X:
/ : X -> X.
Образ компакта при непрерывном преобразовании
является компактом, поэтому преобразование
f-.x^x
индуцирует преобразование пространства К(Х),
которое будем обозначать той же буквой:
/ : К{Х) -»• К(Х),
f-.в*f(B) = {}{х)\хев} \/век(Х).
Примеры преобразований К(Х), индуцированных с
X:
1) пусть
Х = К\ f(x) = ±x, В = [4,7] U [8,10],
тогда /(Б) = [2,3.5] U [4,5];
2) пусть
X = R2, f{xux2)= (^-хъ3х2\в = [2,8} х [3,9],
тогда ДБ) = [1,4] х [9,27];
84

3) пусть
X = R2, f(xux2) = (x1 + x2ll),B = [4,1\x[8,10],
тогда ДБ) = [12,17] х {1}.
2. Постоянное преобразование пространства К(Х).
Выберем какой-нибудь элемент С пространства К(Х)
и зададим преобразование (рс пространства К(Х),
которое любому элементу из К(Х) ставит в
соответствие элемент С, то есть
увек(х) <рс(в) = с.
Например, выберем в качестве С круг радиуса 1 с
центром в точке (0,0) на плоскости. Тогда образ
любого компакта на плоскости будет этот круг.
Постоянное преобразование К(Х) в общем случае не
является преобразованием, индуцированным с
пространства X, за одним исключением. Это случай,
когда компакт С является точкой пространства С.
В этом случае постоянное преобразование
пространства К(Х) является индуцированным с постоянного
преобразования пространства X.
3. Преобразование компакта в его границу.
Граница ГВ любого компактного множества В Е
К(Х) также является компактным множеством. Тем
самым задано отображение
<рг : К(Х) -> К(Х), ipr{B) = ГВ.
При таком отображении образом отрезка на прямой
будут две его граничные точки, а на плоскости — он
85

сам будет своим образом. Образом Канторова
множества и на плоскости, и на прямой будет само Канто-
рово множество. Образом круга на плоскости будет
его граничная окружность. Образом шара в
трехмерном пространстве будет сфера. Слова «на прямой, на
плоскости, в трехмерном пространстве» показывают,
какое пространство X выбираем изначально.
4. Преобразования К(Х), заданные с использованием
операций над множествами.
Пусть определены два преобразования пространства
К(Х) в себя:
£,и:К(Х)^К{Х).
Тогда каждому элементу В Е К(Х) можно
поставить в соответствие элемент
«и«/)(В)€/фО.
определенный по формуле
(£Ui/)(B) = e(B)U«/(B).
Мы получили новое преобразование пространства
К(Х), которое можно называть объединением двух
исходных.
В обычном метрическом пространстве такая
конструкция невозможна, но в пространстве К(Х), в
котором каждая точка является одновременно
компактным множеством в пространстве X, такое возможно,
поскольку объединение двух компактов так же
компакт. Точно также можно строить преобразования
86

пространства К(Х) с использованием других
операций над множествами, но в этом курсе они нам не
понадобятся, и мы этого делать не будем.
Примером такого преобразования является
отображение \х U (\х + \) на if (R1). Образом отрезка [0,4]
при таком преобразовании является отрезок [0,2|],
отрезка [0, \] — объединение отрезков [0, \] U [|, 1], а
отрезка [0,1] — сам отрезок [0,1].
Определение 4.1. Неподвижной точкой Xf
преобразования f : X —»• X называется точка множества X,
образом которой является она сама, то есть выполнено
f{xf)=xf.
Примеры неподвижных точек для различных
преобразований
1. Рассмотрим преобразование пространства
X = R1: f{x) = \x + \.
У него существует ровно одна неподвижная точка
Xf = \- Проверить, что это неподвижная точка
можно, решив уравнение f(x) = х.
2. У преобразования пространства
X = R2: f(x) = \x+(^j
также существует ровно одна неподвижная точка
^4>
xf
87
-©■

3. У любого постоянного преобразования fc
пространства существует ровно одна неподвижная точка —
точка С — образ любой точки при этом
преобразовании.
4. Отображение компакта в его границу пространства
К(Х) имеет бесконечно много неподвижных точек.
Любой компакт без внутренних точек, а таких
бесконечное множество, является неподвижной точкой
этого преобразования пространства К(Х). Такими
являются окружность, сфера, треугольник без
внутренности, поверхность куба, поверхность тора, Кан-
торово множество, треугольник Серпинского, кривая
Коха, фрактал Леви, бинарное дерево. Дерево
Пифагора будет неподвижной точкой для этого
преобразования в том случае, если при его построении берем
только границы квадратов и треугольников без их
внутренних точек.
5. Рассмотрим преобразование W пространства if (R2) :
УВ е K{R2)
W(B) = 0.5В U (0.55 + rQ5 )) U (0.5Б + ( °J).
Единственной неподвижной точкой этого
преобразования является треугольник Серпинского.
6. Единственной неподвижной точкой преобразования
W пространства К(R1), полученного как
объединение двух преобразований этого пространства,
индуцированных с пространства R1,
vse^R1) w4B) = 1buQb + |V
88

является Канторово множество.
Рассмотрим два отображения плоскости R2 в себя:
Цх)
002.
Эти отображения задают преобразование L U R на
пространстве if (R2). Единственной неподвижной
точкой этого преобразования будет кривая Коха.
Во всех приведенных выше примерах мы предъявляли
неподвижную точку преобразования и в некоторых случаях
утверждали, что она единственная. Для конкретной
точки несложно выяснить, является ли она неподвижной для
данного преобразования. Гораздо сложнее найти
неподвижную точку, не зная ее заранее, и доказать, что она
единственная. Выделим такой класс преобразований, для
которых всегда существует и притом единственная
неподвижная точка, и поиск этой точки может быть осуществлен по
заданному алгоритму.
Определение 4.2. Сжимающим преобразованием
(сжатием) метрического пространства X с коэффициентом
сжатия к, где О ^ к < 1, называется такое
отображение f : X —> X пространства X в себя, при котором для
Ух, у Е X выполнено неравенство
P(f(x),f(y)) ^kp(x,y).

Замечания.
1. Если число к является коэффициентом сжатия для
некоторого преобразования /, то все числа, лежащие
в интервале (/с, 1), также являются коэффициентами
сжатия для этого преобразования.
2. Точная нижняя грань всех коэффициентов сжатия
отображения / : X —» X также является его
коэффициентом сжатия.
Определение 4.3. Рассмотрим отображение
f-X^Y
метрического пространства {X, р) в метрическое
пространство {У,pi}, для которого найдется число к, где
О ^ к < 1 такое, что для Ух, у Е X выполнено
неравенство
Pi(f(x)J(y)) ^kp(x,y).
Такое отображение называется сжимающим
отображением метрических пространств с коэффициентом
сжатия к.
Теоремы о сжимающих отображениях
Теорема 4.2. Сжимающее отображение
пространства непрерывно.
Теорема 4.3. Композиция сжимающих
преобразований метрического пространства есть сжимающее
преобразование, причем его коэффициент сжатия равен
произведению коэффициентов сжатия компонент.
Теорема 4.4. Преобразование пространства К(Х),
индуцированное с сжимающего преобразования пространства
90

X, является сжатием с тем же коэффициентом
сжатия, что и у исходного преобразования.
Теорема 4.5. Преобразование пространства К(Х),
являющееся объединением конечного числа сжимающих
отображений, является сжатием с коэффициентом сжатия,
равным максимальному из коэффициентов сжатия
компонент.
Докажем две последние теоремы.
Доказательство теоремы 4-4
Рассмотим сжимающее преобразование / : X —> X
пространства X в себя с коэффициентом сжатия к.
Для УД В Е К(Х) существуют точки а0 Е А и b0 Е В
такие, что
p(f(A)J(B)) = p(f(a0)J(b0)).
Будем для определенности считать, что
p(f(A), /(B)) = sup mfp(/(a), /(b)).
Тогда верно, что
p(f(A), /(B)) = p(f(a0), f(b0)) < p(/(a0), f(b)) Vb в В.
Учитывая, что преобразование / сжимающее, получаем
p(f(A), /(B)) < p(f(a0), /(b)) < kp(a0, b) V6 e B.
Последнее неравенство верно для всех 6 G 5, а значит,
верно следующее неравенство:
p(f(A),f(B)) ^ inf kp(a0,b) ^ ksup inf p(a,b) ^ kp(A,B),
b€B aeA b£B
91

что и доказывает теорему.
Доказательство теоремы 4-5
Докажем сначала, что объединение двух сжимающих
преобразований /ид пространства К(Х) в себя с
коэффициентами сжатия kf и kg соответственно, является
сжатием с коэффициентом сжатия, равным тах(А;/, А^).
Для доказательства воспользуемся теоремой 4.1 о
расстоянии между объединениями компактов. По этой
теореме выполнено следующее:
VA, В е К{Х) p(f(A) U д(А), f(B) U д(В)) ^
^ maX(p(f(A),f(B)),p(g(A),g(B))).
Учитывая теорему 4.4, получаем
VA, В е К{Х) p(f(A) U g(A), f(B) U д(В)) ^
^ rrmx(kfp(A, В), кдр(А, Б)),
тах(А;/р(Д В), кдр(А, В)) = тах(&/, кд)р(А, Б),
откуда получаем окончательный результат
VA, В е К{Х) p(f(A) U g(A), f(B) U д(В)) ^
^ max(A:/, кд)р(А, В).
Для объединения N сжимающих преобразований на К(Х)
достаточно применить метод математической индукции.
Для двух преобразований теорему 4.5 мы только что
доказали.
Предположим, что для (N — 1)-го преобразования
теорема 4.5 доказана, то есть объединение (N — 1)-го сжатия
92

есть сжатие с коэффициентом равным максимуму
коэффициентов сжатия компонент:
fc/iu/a-u/jv-i = max{kfl ... к/м_г}.
Тогда объединение N сжатий есть объединение двух
сжатий: объединения первых (N — 1)-го сжатия и
последнего iV-ro сжатия, причем
^Ли/а-и/дг.хи/дг = max{max{kfl ... fc/^.J, kfN} =
= max{kfl...kfN_1,kfN},
что и завершает доказательство теоремы 4.5.
Теоремы, которые были доказаны, позволяют
конструировать различные сжимающие преобразования
пространства К(Х) всех компактных множеств на пространстве X,
используя сжимающие преобразования самого
пространства X. Чем же так интересны сжимающие
преобразования? Для того чтобы это понять, докажем основную
теорему о сжимающих преобразованиях.
Теорема 4.6 (о сжимающих преобразованиях).
Пусть f : X —)> X — сжатие полного метрического
пространства X. Тогда для этого преобразования
существует ровно одна неподвижная точка Xf Е X : f(xf) = Xf,
и для любой другой точки х Е X последовательность ее
образов {fn(x),n = 1,2,...} сходится к этой точке Xf,
иначе говоря,
УхеХ lim fn(x) = xf.
п—>оо
Доказательство будет состоять из нескольких этапов.
93

1. Поскольку / — сжимающее преобразование X, то
для любой точки х Е X и любых натуральных чисел
n, m выполнено неравенство
р(Г(х),Г(х)) < (/с,)min<"-TOV(z,/'"""'(ж)),
где kf G [0,1) — коэффициент сжатия
преобразования /.
2. Оценим расстояние между точкой а: и ее образом
fn(x) с помощью неравенства треугольника:
р(х, /»(*)) < р(х, /(*)) + />(/(*), /2(ж)) + • • • +
+р(Г1(1),/"(1)).
Учтем неравенство предыдущего пункта:
р(х, /»(i)) < p(i, /(i)) + %>(*, /(*)) + • • • +
+(kf)n-1p(xj(x)) =
= (1 + fc, + (fc/)2 + ' •' + (fc/)n"1)p(a:, f(x)) <
^(l-^-V^/W).
3. Докажем, что последовательность /п(х)
фундаментальна.
Выберем натуральное число N(e) так, чтобы
(l-fc/)-V(x,/(x))(fc/)JVW<e.
Это всегда можно сделать, поскольку величина (1 —
hf)~lp(x, f(x)) постоянна для фиксированного х, а
О < kf < 1.
94

Тогда для любых натуральных чисел т,п > N(e)
выполнено
Р(Г(х),г(х)) ^ (^П"<"-™>(1 - к,)~1р{х,Пх)) <
<(l-kf)-lp(x,f(x))(kf)N^<e.
Это означает, что последовательность fn(x)
фундаментальна, а значит, имеет предел
х0 = lim fn(x).
4. Покажем, что хо — неподвижная точка
преобразования /:
/Ы = /(Нт/»).
п—»оо
Преобразование / сжимающее, а значит, оно
непрерывное и перестановочно с операцией предельного
перехода. Поэтому верно равенство
/Ы = /( Нт /»(*)) = lim /(/**(*)) =
п—>оо п—>оо
= lim /n+1(z)= Hm /n(x) = x0.
n—too n—>oo
5. Покажем, что неподвижная точка х0 единственная и
не зависит от выбора исходной точки х.
Предположим, что есть две различные неподвижные
точки преобразования /:
а,ЪеХ f(a) = a, f(b) = b, афЬ.
Тогда
p(a,b)=p(f(a),f(b))<kfp(a,b),
95

откуда следует, что
(l-kf)p(a,b) <0.
Но поскольку (1 — kf) > 0 и расстояние между
точками неотрицательное, неравенство (1 — kf)p(a,b) < О
выполнено только если р(а, Ь) = 0, что
противоречит предположению о существовании двух
различных неподвижных точках преобразования /.
Теорема о неподвижной точке сжимающего
преобразования полного метрического пространства
доказана. Заметим, что в ходе доказательства был получен
конструктивный алгоритм поиска неподвижной
точки.
Паутинные диаграммы. Для случая, когда X = [а, 6],
поиск неподвижной точки можно наблюдать графически с
помощью паутинной диаграммы. Если нарисовать квадрат
[а, Ь] х [а, 6], то преобразование / : [а, Ь] —> [а, Ь]
отобразится на нем в виде графика функции /. Точки пересечения
этого графика с диагональю [(а, а), (6, Ь)] квадрата будут
иметь координатами неподвижные точки преобразования
/•
Паутинная диаграмма строится следующим образом.
Через произвольную точку X на оси абсцисс проведем
вертикаль до пересечения с графиком функции /. Через
точку пересечения проводим горизонталь до пересечения с
диагональю [(а, а), (6, Ь)] квадрата. Через полученную
точку диагонали проводим вертикаль до пересечения с
графиком функции /, и т.д. Точки на графике будут иметь
координаты
(х, /(*)), (/(*), /V)), • • • (Пх), fn+1 И)
96

а точки на диагонали
(/(*), /(*)), (f(x), f(x)),... (/»(*), Г(х))....
Последовательность fn(x),n = 1,2,... будет сходиться к
неподвижной точке Xf преобразования /, поэтому
последовательность точек на диагонали
(Г(х),Г(х)),п = 1,2,...
и последовательность точек на графике
(f(i),r+1W),n=l,2,...
будут сходиться к точке (xf,Xf) — точке пересечения
диагонали и графика.
Рис. 18: Примеры паутинных диаграмм
Определение 4.4. Системой гиперболических
итерированных функций (СИФ) называют полное
метрическое пространство X с заданным на нем конечным
набором сжимающих преобразований /1? /2, • • • In с
коэффициентами сжатия О < &i, k2,..., k^ < 1 соответственно:
{X,fi,f2,...fN:X^X}.
97

@С Коэффициентом сжатия такой системы является
max{ki,k2,.. .,kN}.
Иногда систему итерированных функций называют
системой итерированных преобразований (СИП).
Если задана система итерированных функций, то
можно рассмотреть преобразование W пространства К(Х),
полученное как объединение всех преобразований К(Х),
индуцированных с пространства X с помощью
преобразований fuf2,...fN'.
VB€K(X) W(B) = U>Lji(B).
Преобразования /i, /г, • • • /jv являются сжимающими
преобразованиями исходного пространства. Учитывая
теоремы 4.4 и 4.5, получаем, что преобразование
W : К{Х) -+ К(Х)
является сжимающим преобразованием пространства К(Х)
Следовательно, у такого преобразования пространства К(Х
будет существовать ровно одна неподвижная точка
Aw е К(Х).
Определение 4.5. Аттрактором ( или
детерминированным фракталом) системы итерированных функций
{X, /ь /2,... /n ' X —у X} называется неподвижная
точка Aw G К(Х) преобразования W : К(Х) —»• К(Х),
заданного формулой
vb е К(Х) W(B) = uUm.
98

Примеры аттракторов СИФ.
1. Канторово множество:
{R1,f1(x) = ^x,Mx) = ^x+^}.
{R2, f1(x) = 0.5x,
f2(x) = 0.5* + (°05), /3(f) = 0.5f + (J^j
ГК кк кк кК
Рис. 19: Треугольник Серпинского
99

2. Кривая Коха:
{R2, L(f)=(j + ^3
V2v/3Xl 2
2уД^1 2^2 "Г 2v^/
Рис. 20: Кривая Коха
3. Фрактал Леви:
т = (j
{R2, L{x)=[f\f2
\хх + \х2
\х2 + \
Xi
ад=(л;'л;+г|(-
Рис. 21: Фрактал Леви
100

4. Лист:
V 9Я1 + 5^2 + 10 /
5. Папоротник:
{R2,
V б^1 + 4X2 + 7/ \з^2 + goo/
101

6. Симметричное «сухое» дерево Пифагора:
{R2, L{x)=L*X)^X2
\\Xi + p2 + 1
т = { **. + §*. у
V-^l + ^2 + 1/
Рис. 22: Сухое дерево Пифагора
102

7. Ковер:
Рис. 23: Ковер
Для получения аттрактора на плоскости достаточно
взять набор из нескольких сжимающих преобразований
плоскости и применить эти преобразования к произвольно
выбранному компактному множеству В. Образы
объединить и к полученному объединению применить все
исходные сжимающие преобразования. Повторив эту
процедуру несколько раз, можно получить множество, весьма
похожее на аттрактор, который возникает при применении
этой процедуры бесконечное число раз. Итак, получаем
алгоритм построения детерминированного фрактала.
103

Детерминированный алгоритм построения
фрактала.
Пусть задана система гиперболических итерированных
функций
{X,h,f2,...fN:X^X}.
1. Выберем произвольный компакт A Е К(Х).
Обозначим А0 = А.
2. Найдем А{ по формуле
Ai = U%ssJn{Ai-1) t = l,2,....
3. Проделаем процедуру до тех пор, пока не будет
выполнено неравенство
p(Ai,Ai+i) < e,
где е — заданная точность.
Точность изображения можно оценивать и «на
глазок», все зависит от поставленных требований.
Процесс сходящийся, как было доказано ранее.
Множества Ai сходятся к неподвижной точке Aw
преобразования W(-) = U^=1/n(-) пространства К(Х).
Замечание. Следует отметить, что аттрактор СИФ
может оказаться любым компактным множеством,
например, отрезком или квадратом. Он обладает свойством
самоподобия, характерным для фракталов, но не всегда
устроен столь же причудливо, как Канторово множество или
кривая Коха. Тем не менее в дальнейшем под понятием
«детерминированный фрактал» будем понимать именно
аттрактор некоторой СИФ.
104

Рис. 24: Итерации треугольника Серпинского
Упражнения
1. Найти расстояния р(А U Б,С U D),p(A,C),p(B,D)
между элементами пространства К(И2) и сравнить
эти расстояния:
1) A = {xeR2\ х\ + {х2-Ь)2 = 1),
£ = {:reR2| \xl+x2\^l, |zi|<2},
D = {xeR2\ (a;1-l)2 + (a;2 + l)2 = l};
2) A = {xeR2\ |si| + |s2 + 5| = l},
B = {xeR2\ \x!\ + \x2\ < 1,}
C={N + l*2-*i|=2},
D = {xe R2| (хг + l)2 + (x2 + l)2 = 1}.
105

2. Найти образ элемента А пространства K(R2) при
преобразовании K(R2) -*■ A"(R2), индуцированном
с преобразования / : R2 —»• R2:
1) А = {хеК2\ х\ + (х2 - 5)2 = 1}
№ = &+(%
2) А = {х€В?\ \Xl+x2\^l, |a;i|<2},
f(S) = -x+(2\,
3) A = {xeR2\ (xi - l)2 + (x2 + l)2 = 1},
/(f)=(-2 \)S>
4) A = {xeR2\ \Xl\ + \x2 + 5\ = l},
H* _ ( cosd) sind) V
/W-l,sin(|) -008(|)J'
I X\
5) A = {^R2| laril + lxaKl,},
f(x) = -x-
6) A = {xe R2||:ri| + |x2 - Xi\ = 2},
/(f)=(-2 o)f;
106

7) A = {xeK2\ (zi + l)2 + (x2 + l)2 = 1},
3. Найти образ элемента А пространства К{К2) при
преобразовании Г : К (Л2) —> if(R2), ставящим в
соответствие множеству А его границу:
1) A = {xeR2\ х2 + [х2 - 5)2 = 1};
2) A = {xeR2| |xi + x2|<l, |a;i|<2};
3) i = {xGR2| (х!- I)2 + (х2 + I)2 = 1};
4) i = {xGR2| |a:i|+ 1x2 + 51 = 1};
5) A = {xeR2\ l^l + l^l^l,};
6) A = {x e П2\Ы + \x2 - Xi\ = 2};
7) A = {xeK2\ (^ + l)2 + (x2 + l)2 = l}.
107

4. Найти образ элемента А пространства K(R2) при
преобразовании (g\J /) : K(R2) —> if (R2), где
#(f) = ( -2 2 ) f' ^ = 2f'
а множество А задано формулами:
1) A = {xeR2\ х\ + (х2 - 5)2 = 1};
2) A = {xeR2| |xi + x2|^l, |xi|^2};
3) A = {xeR2\ (ж!-1)2 + (я;2 + 1)2 = 1};
4) A = {xeR2\ |ж1| + |ж2 + 5| = 1};
5) A = {xeR2\ \Xl\ + \x2\Kl,}\
6) A = {xe R2\\xi\ + \x2 - xx\ = 2};
7) A = {xeR2\ (an + l)2 + (x2 + l)2 = 1}.
5. Найти неподвижные точки преобразования
/ : R2 -> R2
в следующих случаях:
108

i) /(*) = ( о * )*+(});
2 3
2» ««-5*- (Т>
6. Найти неподвижные точки преобразования
/ : K(R2) -»• K(R2)
в следующих случаях:
1) /(B) = {ia?|a?6B}ujia?+Q|*€B
2) /(B) = |lf+^i1)|f€B}u|^+Q|f€B
и||ж|же в|;
\хеВ
7. Определить, являются ли нижеперечисленные
преобразования плоскости сжимающими:
109

1) /:R2^R2 /(5D=(_22 l^jS;
2)
/:R2^R2 /W=(_°^
5 0.5 N ^ /2
5 0.5 )X+[2
3) /:R2^R2 f(x) =
0.7 0.8 \ _ /0.1
-0.8 0.7 J X+ \0.2У'
4) /:R2^R2 /(5)=(_°1 £)*;
5)/:R2.R2 /(,)=(_S,°08)-(S
6) /:R2^R2 /(*)=(l7^);
7)
/:R2^R2 /(f) = lf^ ^
.2 _ „2\ ^
8. Найти предел последовательности на плоскости:
1) {Г * }£*, /(*) =
0 0.7\^_/7>
-0.8 0 'Х
110

Ч ((/,)•(?>- '« = (-о'з и)*"©'
#(£) = -£;
9. Построить паутинную диаграмму и найти
последовательность точек
{хп = /»(*)}» 0 :
1) /:R-»R, /(ж) = ж2 - Зж, ж0 = 1;
2) /:R-^R, /(ж) = х2 - Зж, ж0 =-1;
3) /:R->R, f(x) = x2-3, х0 = 1;
4) / : R ->■ R, f(x) = sin(x) ж0 = 10.
10. Построить первые к итераций детерминированного
алгоритма построения аттрактора СИФ. В качестве
исходного компакта взять многоугольник с
вершинами в неподвижных точках преобразований СИФ:
111

1) {R; /i(f) = 0.5£, f2(x) = -0.5x + 3}, к = 3;
2) {R2;/1(f) = 0.5f,/2(f) = -0.5f+ }, fc = 3:
ЗУ
2У
3) {R2; /j (£) = 0.5f, /2(£) = -0.5f +
/s(5)=0.5f+r005)}, fc = 3;
4) {R2; h{x) = -0.5f, /2(£) = 0.5f +
/з(ж) = 0.5ж+(1)}, fc = 3;
5) {R2;/i(f) = 0.(3)£,/2(£) = 0.(3)£ + Q,
/3(f)=0.(3)f+f]}, fc = 2;
6) {R2;/1(f) = 0.5f,/2(f)=(_°5 °Q5y+Q,
h(x) = 0.5x+(^}, k = 3;
112

2. ,/гЛ „rr, ,/гЛ / О 0.5Ь, /^
7) {R2; /,(<?) = -0.5af, /2(f) = (^ _q 5 q J f+ yQ
/3(f) = 0.5f+^o°5)}, fc = 3.
Примеры решения задач
1. Найти образ элемента
A = {x\\Xl + l\ + \x2\ = l}
пространства К(И2) при преобразовании
K(R2) -+ K{R2),
индуцированном с преобразования
/:R^R2, /(*)=(_°Б °Л^,0
Решение
Компакт А представляет собой квадрат с вершинами
в точках
/(Л
W
преобразование / является композицией поворота на
90° по часовой стрелке вокруг точки (°), сжатия в
два раза и сдвига на вектор (J), поэтому образ f(A)
представляет собой квадрат с вершинами в точках
ГМоМ::)'
1\ /0.5
0740.5
©■а-
113

2. Найти образ элемента
A = {x\\Xl + l\ + \x2\ = l}
пространства K(R?) при преобразовании (д U /) :
К (Л2) —» if (R2), где преобразования # и / задаются
формулами
f,g:R2^R-
2 v D2
Решение
Компакт А представляет собой квадрат с вершинами
в точках
(oHij'UH-i,
преобразование / является композицией поворота на
90° по часовой стрелке вокруг точки (0), сжатия в
два раза и сдвига на вектор (J), преобразование д
является композицией поворота на 90° против
часовой стрелки вокруг точки (°), растяжения в два раза
и сдвига на вектор Q), поэтому образ f(A)
представляет собой квадрат с вершинами в точках
W'UsHO'W'
образ д(А) представляет собой квадрат с вершинами
в точках
\o)'\V'\ о
-.)■
114

Объединение этих образов будет двумя квадратами
с параллельными сторонами, один внутри другого.
3. Найти образ элемента
А = {х\\х! + 1\ + \х2\^1}
пространства К(И2) при преобразовании (д U /) :
if (R2) —>• К (R2), где преобразования д и / задаются
формулами
Решение
Компакт А представляет собой квадрат с
внутренностью с вершинами в точках
преобразование / является композицией поворота на
90° по часовой стрелке вокруг точки (0), сжатия в
два раза и сдвига на вектор (J), преобразование д
является композицией поворота на 90° против
часовой стрелки вокруг точки (°), растяжения в два раза
и сдвига на вектор Q), поэтому образ f(A)
представляет собой квадрат с внутренностью с вершинами в
точках
(oKo.sKiJ'Us)'
115

образ д(Л) представляет собой квадрат с
внутренностью с вершинами в точках
'UH0M-2}
Объединением этих образов будет квадрат с
внутренностью с вершинами в точках
'UH0M-2}
4. Найти неподвижные точки преобразования
/ : R2 -> R2,
'«-U")*+G)-
Решение
Решим систему уравнений
/(£) = х
и получим
-(A)-
5. Определить, является ли преобразование плоскости
сжимающим:
/:R2^R2, f(x)=[_06 09)x.
116

Решение
Рассмотрим расстояние между образами точек хну
при линейном преобразовании плоскости
Представим коэффициенты матрицы преобразования
в виде
а = ricostp, b = risintp, r2 = a2 + b2,
c = r2cos0, d = r2sin</>, rl = c2 + d2.
Обозначим px = \xi-yi\, p2 = \x2 — 2/21-
Расстояние между образами равно
p(m,f(y}) = V(m + bP2)2 + (m + dP2y.
Расстояние между прообразами равно
р(х,у) = yjpf+pl
Сравним эти расстояния:
(api + bp2)2 = т\ (cos2 ippl + 2 cos ip sin (ppip2 + sin2 cpp2,),
(cpi + dp2)2 = r|(cos2 </>p2 + 2 cos 0 sin фр\р2 + sin2 </>p2).
Сравним величины (cos2 tpp\+2 cos 99 sin i^pip2-\-sw? да>2)
npj+pl
Для этого рассмотрим разность этих величин и
разделим ее на р\. Если р2 = О, то р\ ф О, и делить
117

можно на р2. Обозначим D = —. Имеем
р\+р\ — (cos2 ipp\ + 2 cos if sin <^piP2 + sin2 ipp\)
A =
= D2 + 1 - (cos2 ipD2 + 2 cos <p sin (pD + sin2 <p) =
= sin2 ipD2 + 2(р sin <pD + cos2 (p =
= cos2 <p(tg2 (pD2 + 2tgtpD + l) =
= cos2y>(tgipD + l)2 ^ 0.
Отсюда следует, что
p(/(£), /(у)) = v^Pi + to)2 + (cpi+dP2)2 ^
^ max (n,r2)ypi + p2 = max (n,r2)p(f, #).
Это значит, что для того чтобы аффинное
преобразование плоскости было сжатием, достаточно,
чтобы сумма квадратов матричных элементов по
каждой строке матрицы линейного оператора была бы
меньше единицы. Несложно показать, что это
условие является и необходимым. В данной задаче сумма
матричных элементов по второй строке равна
(-0.6)2 + 0.92 = 1.17,
то есть преобразование не является сжатием.
6. Найти предел последовательности на плоскости:
118

Решение
Преобразование / — сжимающее. Легко показать,
что аффинное преобразование плоскости является
сжимающим, если для коэффициентов матрицы,
задающей это преобразование, сумма квадратов
матричных элементов по каждой строке меньше
единицы. В нашем случае
0.42 + 0.72 = 0.65 < 1 и (-0.5)2 + 0.32 = 0.34 < 1.
У любого сжимающего преобразования есть ровно
одна неподвижная точка, которая является пределом
последовательности {fn(x)}^=1 для любого х, в том
числе и для последовательности
к»:-
Поэтому можно найти предел этой
последовательности, решив уравнение f(x) = х. Подставив в это
уравнение условия задачи, получаем систему
линейных уравнений
Г {0.4xi + 0.7х2 - 15 = xi
\ —0.5Xi + 0.3X2 — 6 = Х2 '
решив которую находим предел исходной
последовательности, равный
119

7. Найти неподвижные точки преобразования F : К (И?) —>>
К(И2) , заданное формулой
Идея решения
Неподвижной точкой этого сжимающего
преобразования / : К(И2) —>• K(R?) является аттрактор СИФ
{R2; /x(f) = -\х+ Q , /2(аф+ ("*) , /3(f) = \S).
Чтобы его найти, надо применить преобразование F
несколько раз к произвольному компакту В на
плоскости. Удобно в качестве В выбрать треугольник с
вершинами в неподвижных точках преобразований
/15/25/з-
120

Глава 5. Аффинные
преобразования плоскости
В предыдущей главе был рассмотрен способ
построения фрактала с помощью набора сжимающих
преобразований полного метрического пространства — так
называемой системы итерированных функций (преобразований).
В дальнейшем разумно пользоваться довольно узким
классом таких преобразований, разнообразие получаемых
фракталов при этом достаточно широко. В качестве такого
класса на плоскости имеет смысл взять группу аффинных
преобразований, а в большинстве случаев хватает даже ее
подгруппы, состоящей из преобразований подобия.
Посвятим несколько слов этой группе преобразований
плоскости.
Общий вид аффинного преобразования пространства
Rn дает следующая формула:
/:Rn->Rn V£eRn f(x) = Ax + b,
6eRn, ,4eRnxRn.
Аффинные преобразования переводят прямые в прямые,
а отрезки в отрезки.
Аффинные преобразования отрезка [0,1]
В случае пространства R1 преобразование принимает
вид скалярной функции f(x) = ах + 6, поэтому для того
чтобы понять, является ли преобразование прямой R1
преобразованием отрезка [0,1] в себя, надо посмотреть, куда
переходят при этом преобразовании точки 0 и 1. Отсюда
следует вывод: аффинное преобразование f(x) = ах + Ъ
переводит отрезок [0,1] в себя в случае, если выполнены
121

следующие условия:
((а + Ь)в [0,1],
I ье [0,1].
Аффинные преобразования пространства R2
Рассматривая дальше аффинные преобразования
плоскости, опустим преобразование сдвига, которое хотя и не
перестановочно с преобразованиями плоскости, не
меняет матрицу А. Фактически сейчас рассмотрим возможные
представления линейной части аффинного
преобразования.
Матрица A Е R2 x R2 может иметь различные
представления. Общий вид ее записи следующий:
Аффинное преобразование плоскости можно
представить следующим образом:
1) ось абсцисс поворачивается на угол в\ и
растягивается в 7*1 раз;
2) ось ординат поворачивается на угол в2 и
растягивается в г2 раза.
При таком представлении матрица А может быть
записана следующим образом:
л — ( ri cos ^i —r2 sin ^2 \ _
у 7*1 Sin в\ 7*2 COS #2 /
_ / cos#i — sin #2 \ ( т\ 0 \
у sin^i cos в2 / \ 0 7*2 ) '
Порядок множителей существен! Углы поворотов и
коэффициенты растяжения можно получить из исходной мат-
122

рице по формулам
= л/о^Т
а . л с
Г\ = Vflr + (Г, COSt/i = , Sill 01 =
-6
r2 = \/62 + d2, cos ^2 = / ) sin ^2 =
л/62 + <22' x/PTd2'
Определение 5.1. Преобразованием подобия
называется такое аффинное преобразование плоскости, при
котором коэффициенты растяжения по координатным осям
совпадают, а углы поворота осей отличаются на число,
кратное 7г.
Аффинное преобразование плоскости можно также
представить и по-другому:
1) сначала производим растяжения по осям с
коэффициентами 7*1, Г 2 5
2) затем производим поворот всей плоскости на угол 6;
3) производим растяжения по новым осям с
коэффициентами Гз,Г4-
При таком представлении считаем, что коэффициент
растяжения может принимать отрицательные значения в
том случае, когда ось меняет ориентацию.
Матрица А в этом случае может быть записана
следующим образом:
/ г3 0 \ / cos(9 -sin0 \ /
\ 0 r4 J \ sin<9 cos(9 J \
7*1 О
О г2
Коэффициенты нетрудно вычислить, перемножив
матрицы последнего представления и приравняв матричные
элементы произведения соответствующим матричным
элементам исходной матрицы.
123

При таком представлении аффинного преобразования
у преобразования подобия все коэффициенты Г1,Г2,гз,Г4
должны иметь одинаковую абсолютную величину.
Преобразование подобия может быть получено как
произведение преобразования поворота вокруг некоторой
точки и скалярного растяжения либо как произведение
отражения относительно какой-нибудь прямой и
скалярного растяжения, плюс всевозможные сдвиги плоскости.
Запись преобразования подобия имеет следующий вид:
и(х) = Ах + Ь.
Матрица А имеет вид
л _ ( г ° \ ( cos0 -sin0 \
\ ° г / \ sin<9 cos^ /
в случае поворота относительно некоторой точки
плоскости на угол в против часовой стрелки.
Матрица А имеет вид
А-(г 0\/cos<9 -sin(9\/l 0 \_
\ 0 г J \ sin<9 cos<9 J \ О -1 /
_( г 0 \ / cos<9 sin(9 \
~ V 0 г )\ sin в -cos<9 )
в случае отражения относительно некоторой прямой
плоскости, образующей с осью абсцисс угол |.
Проверить эти формулы можно непосредственно,
подставив в качестве аргумента вектора базиса на плоскости
GMD-
124

Определение 5.2. Назовем коэффициентом подобия
число г, равное отношению длин вектора и его образа при
подобии, взятое со знаком плюс, если подобие не
меняет ориентацию пространства, и со знаком минус, если
меняет.
Сформулируем теоремы, которые в дальнейшем
помогут при работе с аффинными преобразованиями Rn.
Теорема 5.1 (о построении аффинного
преобразования на плоскости). Любые три точки общего
положения на плоскости можно перевести в любые три
точки плоскости с помощью аффинного преобразования.
Заметим, что от второй тройки точек — образов
преобразования, — общего положения не требуется.
Доказательство
Надо по двум тройкам точек {х1, х2, х3} и {у1, у1, у3} на
плоскости, из которых первые три — общего положения,
найти аффинное преобразование у = Ах + b такое, что для
г = 1,2,3 выполнено
у1 = Ах1 + Ъ.
Матричные элементы матрицы А и координаты
вектора b неизвестны. Зато известны координаты заданных
шести точек. Составим систему уравнений, в которых
координаты точек будут представлять коэффициенты, а
матричные элементы матрицы А и координаты вектора Ъ —
искомые неизвестные. Система уравнений будет иметь
следующий вид:
125

f Q>\,\x\ +«1,2^2 + &i =
а2Лх\ + a2,2^2 + &2 =
ai,i#i + aii2xl + h =
&%\x\ + a2,2x\ + b2 =
auxj + ai)2^2 + &i =
а2Лх\ + a2,2^2 + &2 =
vl
vl
vl
vl
vl
Эта система из шести уравнений с шестью
неизвестными разбивается на две независимые системы, в каждой из
которых по три уравнения с тремя неизвестными:
{ai.is} + ah2x\ + bi = у\,
а1Лх\ + awxl + bi = у\,
^1,1^1+^1,2^2 + ^1 = 2/1 >
а2Лх\ + a2)2:r2 + b2 = у\,
а2Лх\ + а2,2х\ + Ь2 = 2/|,
a2,i#? + a2,2^2 + &2 = у\
и одинаковыми невырожденными матрицами,
задающими систему
Невырожденность этой матрицы следует из
предположения, что все три точки а*1, х2, х3 являются точками общего
положения, то есть не лежат на одной прямой.
Теорема доказана.
Посмотрим, как изменится запись аффинного
преобразования при замене системы координат.
126

Теорема 5.2 (о записи преобразования при
замене координат). Пусть дано преобразование
f : Rn -> Rn,
которое в заданной системе координат имеет запись
и пусть дана замена координат
х* = Q(x).
Обратная замена координат задается в виде
x = Q-\x*).
Тогда запись этого преобразования в новой системе
координат будет иметь вид
yt = Q(f(Q-1(S*))).
Доказательство очевидно.
Из предыдущей теоремы очевидным образом вытекает
следующая теорема.
Теорема 5.3. Б случае, когда
f : Rn -> Rn
— аффинное преобразование, заданное в виде
у = Ах + Ь,
127

и аффинное преобразование координат имеет вид
х* = Мх + q,
где М — невырожденная матрица, запись в новой
системе координат имеет следующий вид:
у* = МАМ^х* - MAM~lq + Mb + q.
Иначе говоря, преобразование в новой системе координат
имеет вид:
у* = А*х* + Ь*,
где
А* = МАМ'1, b* = -MAM~lq + Mb + q.
Эту теорему бывает удобно использовать при записи
преобразований.
Примеры
1. Получить вид преобразования поворота вокруг
точки А(3,4) на угол | против часовой стрелки.
Для этого надо:
1) перенести начало координат в точку Л(3,4) с
помощью сдвига на вектор q = — (4);
2) повернуть в новых координатах плоскость вокруг
точки (0,0) с помощью матрицы поворота
cos и — sin с
sin в cos в
HU)-
128

3) вернуть старые координаты с помощью обратного
сдвига на вектор q = Q).
Окончательный вид преобразования будет
следующий:
/(Hf ?Mf ?)©+
2. Найти вид преобразования отражения плоскости
относительно прямой, заданной уравнением
х2 = 3xi + 2.
Эта прямая образует с осью абсцисс угол в.
Для решения задачи надо:
1) перенести начало координат в точку А(1,5), через
которую проходит данная прямая, с помощью сдвига
на вектор q = — Q);
2) отразить в новых координатах плоскость
относительно прямой, заданной уравнением х2 = Sxi с
помощью матрицы
/ cos 2(9
V sin 2(9
_ / cos(2arctan3)
у sin(2 arctan 3)
3) вернуть старые координаты с помощью обратного
сдвига на вектор q = (*).
Окончательный вид преобразования будет следую-
sin2<9 \ _
-cos2(9 ) ~
sin (2 arctan 3)
— cos (2 arctan 3)
129

щий:
п/-\ _ ( cos(2arctan3) sin(2arctan3) \ _>
Кх>-\ sin(2 arctan 3) -cos(2arctan3) ) Х+
(1 — cos(2 arctan 3) — sin(2arctan3) \ /1\
— sin(2arctan3) 1 + cos(2 arctan 3) J \5/
В данном случае можно привести
тригонометрические формулы к числовым результатам.
Действительно,
1-а2
cos(2 arctan а)
1 + а2'
1-а2
sin(2 arctan а) = \ll — ( г)2.
V 1 + аг
Для данного конкретного примера получаем
ч 1-а2 1-9 4
cos(2arctana) = TT^ = —= -,
sin(2 arctan a) = x/l- ([^J)2 = ^1 - ф2 = |
Окончательно
4 3 \ / I _|\ Л>
5 5 / \ 5 5 / \5>
/(£) = I *4 *+' 5" "5
130

Упражнения
1. Найти параметры аффинного преобразования
плоскости, переводящего квадрат с вершинами
Л(0,0),В(1,0),С(1,1),£(0,1)
в прямоугольник с вершинами
P(0,2),Q(5,2),i?(5,4),S(0,4).
2. Найти параметры аффинного преобразования
плоскости, переводящего квадрат с вершинами
A(0,0),B(1,0),C(1,1),D(0,1)
в прямоугольник с вершинами
Р(3,5), Q{\, -5), Д(-4, -4), 5(-2,6).
3. Найти параметры поворота плоскости вокруг точки
А(1, —3) на угол | .
4. Найти параметры поворота плоскости вокруг точки
А(—2,4) на угол -§7г .
5. Найти параметры отражения плоскости
относительно прямой, заданной уравнением х2 = 4^i + 3.
6. Найти параметры отражения плоскости
относительно прямой, заданной уравнением 2х2 = Х\ + 6.
7. Найти параметры отражения плоскости
относительно прямой, заданной уравнением ?>х2 + Ъх\ = 16.
8. Найти параметры отражения плоскости
относительно прямой, заданной уравнением 2х2 + 4^i + 34 = 0.
9. Найти параметры аффинного преобразования
плоскости, переводящего треугольник с вершинами
Л(0,0),В(1,0),С(1,1)
131

в треугольник с вершинами
0(3,2)^(5,4), 5(0,-1).
10. Найти параметры аффинного преобразования
плоскости, переводящего треугольник с вершинами
у4(0,0),В(1,0),С(1,1)
в треугольник с вершинами
0(1,2), Л(1,4), 5(0,-1).
11. Найти параметры аффинного преобразования
плоскости, переводящего треугольник с вершинами
А(2,0),Б(1,0),С(1,1)
в треугольник с вершинами
0(3,1),й(1,4), 5(0,-1).
12. Найти параметры аффинного преобразования
плоскости, переводящего треугольник с вершинами
А(0,2),Б(1,0),С(1,1)
в треугольник с вершинами
Q(1,2),#(2,4),S(0,0).
13. Определить, является ли преобразование
плоскости, переводящее треугольник с вершинами
Л(0,2),В(1,0),С(1,1)
132

в треугольник с вершинами
Q(0,0),fl(-3,0),S(-6,-3),
преобразованием подобия. Если да, найти его
коэффициент подобия.
14. Определить, является ли преобразование
плоскости, заданное формулой
/«=(1 а1 )»--(<>
преобразованием подобия. Если да, найти его
коэффициент подобия.
Примеры решения задач
Примеры решения задач №1—12 приведены в данной
главе. Ниже дано решение задачи, аналогичной задаче 14.
Определить, является ли преобразование плоскости,
заданное формулой
преобразованием подобия. Если да, найти его
коэффициент подобия.
Преобразование подобия изменяет длины всех
векторов одинаково, поэтому если данное преобразование
является преобразованием подобия, то длина базисных
векторов (J) и (J) изменится одинаково. Это значит, что сумма
квадратов элементов матрицы преобразования по
столбцам постоянна. В данном конкретном случае она равна
числу 2,5 для обоих столбцов. Вторым условием подобия
является сохранение углов; это означает, что образы
базисных векторов образуют угол |. Иначе говоря, косинус
133

угла между образами базисных векторов должен быть
равен 0. Угол if между двумя векторами (£) и (^)
является разностью между углами а и /3, образованными этими
векторами с осью абсцисс. Тригонометрические функции
этих углов легко считаются по их координатам:
a b
а , то > sin а = ,
а2 + о2 а2 + о2
с • я- d
с2 + ^2' Sm^-c2 + rf2-
Косинус угла ip между двумя векторами (£) и Q) может
быть вычислен по формуле
cos у = cos(a — /3) = cos a cos /3 + sin a sin /3 =
а с b d
= a2 + 62 ' с2-Ы2 + a2 + fc2 ' c2 + d2'
Как было показано только что, длина образов базисных
векторов одинакова, поэтому значение косинуса угла
между ними с точностью до множителя равно сумме попарных
произведений их координат:
3 11 3_3
2 ' 2 + 2 ' 2 ~ 2'
которая отлична от нуля. Это означает, что исходное
преобразование не является преобразованием подобия.
cos a =
cos/3 =
134

Глава 6. Множества накопления
Определение 6.1. Рассмотрим систему
гиперболических итерированных преобразований
{X;fi,fa,...,fN:X^X}
с коэффициентом сжатия к. Добавим к имеющимся
постоянное преобразование /0 пространства К(Х) всех
компактных множеств пространства X :
\/веК(Х), МВ) = с, СеК(Х).
Назовем множество С множеством накопления ( или
конденсации), а совокупность
{Х\ /о, /ь /г, • • •, In ' X ->• X}
— системой гиперболических итерированных
преобразований с накоплением ( системой итерированных функций
с конденсацией) с коэффициентом сжатия к.
Теорема 6.1. Пусть дана система гиперболических
итерированных преобразований с накоплением
{Х\ /о, /ъ Л? • • • ? In '■ X -> X}
с коэффициентом сжатия к. Тогда преобразование
Wq : К(Х) -> К(Х),
заданное формулой
мв е К{Х) w0(B) = и10МВ),
является сжимающим преобразованием пространства К(Х)
с коэффициентом сжатия к.
135

Теорема эта следует из соображения, что постоянное
преообразование пространства есть сжатие с
коэффициентом 0.
Следствием этой теоремы является наличие
неподвижной точки А у преобразования W0(B) = \jfL0fi(B),
пространства К(Х), которую можно найти как предел
бесконечного числа итераций этого преобразования:
А = lim W£(B), УВ е К(Х).
п—ьоо
Такая неподвижная точка так же, как и в СИФ без
конденсации, называется аттрактором СИФ с конденсацией
или детерминированным фракталом.
Примеры аттракторов СИФ с накоплением
1. Бинарное дерево
{R ;/о»/ь/2}
/о : K{R2) -> #(R2), \/B e К(К2)
где компакт
С =
-/MDHCMS)
fo(B) = С,
е K(R2),
/,:R2^R2, /,(£) = -£ +
/2:R2^R2, /2(f) = if +
Аттрактором этой системы будет бинарное дерево.
136

2. Дерево Пифагора.
{R ;/о5/ъ/2}
/о : K(R2) -> tf(R2), V£etf(R2) Л(В) = С
где компакт С Е -ftT(R2) — квадрат со стороной 1 с
вершинами в точках
'W'U'U'
Л : R2 -> R2,
<• /• -л /т Z' cos 0 - sin 0 \ ^ /0\
/1И= coeW^^ cose J*+(J-
/2 : R2 -> R2,
//■-N • /ЧЛ ( Sin^ COS0 \ ^ , / COS26> \
f2(x) = sm(e)^_cose siae)z+{1 + cosesine)-
Аттрактором этой системы будет дерево Пифагора,
у которого угол наклона левой ветки равен в против
часовой стрелки, а угол наклона правой ветки равен
(| — в) по часовой стрелке. Для симметричного
дерева Пифагора матрицы преобразований примут вид
/i:R2^R2, /,(£)=( 1 ~} )х +
/2:R2^R2, /2(f)=(A |)f+(l)
'•
137

Рис. 25: Симметричное дерево Пифагора
Рис. 26: Несимметричное дерево Пифагора
138

3. Логарифмическая спираль
{R2;/o,/i},
/о : K(R2) -> K(R2), \/BeK(R2) f0(B) = C,
где компакт С € K(R2) — отрезок [(J), (Jj's)]-
Л : R2 -»• R2, /,(*) = (j 7 ) f.
Аттрактором этой системы будет ломаная
логарифмическая спираль.
Рис. 27: Ломаная логарифмическая спираль
139

Рис. 28: Логарифмическая спираль с окружностью в
качестве множества накопления
Рассмотрим логарифмическую спираль чуть
подробнее
Рассмотрим уравнение на плоскости R2, записанное
в полярных координатах (г, у?):
г = ехр(а<р).
Точки плоскости, удовлетворяющие этому уравнению,
образуют спираль на плоскости, которая
«скручивается» к нулю при if —> со в случае а < О
«раскручивается» при if —> со в случае а > О и вырождается в
окружность в случае а = 0.
Обозначим начало координат буквой О и возьмем
три точки Pi, Р2, Рз на спирали так, чтобы углы
между лучами из начала координат в эти точки были бы
равны: /-РхОР2 = ^Р2ОР3 = а.
Тогда выполнено
Pi(rb ф), Р2(г2, у> + а), Рз(?"з, if + 2а),
140

Рис. 29: Логарифмическая спираль
И = ехр(а</?), г2 = ехр(а(у? + а)), г3 = ехр(а(<^ + 2а)),
откуда
т\ = пгз,
из чего следует подобие треугольников:
АРгР20 ~ АР2Р30,
по одному углу и двум парам пропорциональных
сторон.
Отсюда следует, что
А.ОРхР2 = А.ОР2Ръ, ZOP2P1 = ZOP3P2.
Это значит, что если откладывать равные углы с
вершиной в начале координат, то точки пересечения
сторон этих углов с логарифмической спиралью
образуют узлы ломаной линии, угол между соседними
звеньями которой и отношение длин этих звеньев
постоянны. Отношения длин соседних звеньев равны
141

Рис. 30: Участок логарифмической спирали
(1 : ехр(аа)), а углы между ними (7Г — а), где а —
угол, образованный лучами, соединяющими начало
координат с соседними узлами ломаной
логарифмической спирали.
Рис. 31: Логарифмическая спираль с касательной
142

У ломаной спирали, являющейся аттрактором
приведенной выше системы итерированных
преобразований с накоплением, отношение длин соседних
звеньев равно ^, а угол между ними ^f. Если менять
угол поворота и коэффициент сжатия
преобразования /i, то можно получать всевозможные ломаные
логарифмические спирали. Отрезок, задающий
преобразование /о 5 надо выбирать равным
[ъ,мь]уъеп2.
Например, приведенная ниже СИФ с накоплением
будет иметь аттрактором ломаную логарифмическую
спираль с отношением длин соседних звеньев 1 : 3 и
углом ^ между ними:
{R2;/o,/!},
/о : K(R2) -> K(R2), VBetf(R2) f0(B)=C,
где компакт С G A"(R2) — отрезок [(J), (T)],
h : R2 -► R2, h(S) =(f ~j)x.
Если в качестве компакта С взять не отрезок, а круг,
квадрат, треугольник или просто кляксу, то
аттрактором такой системы с накоплением будет спираль,
составленная из все более уменьшающихся исходных
множеств С. Полученный аттрактор может быть как
связным, так и несвязным множеством; это зависит
от соотношения коэффициентов и множества С.
Например, если в качестве множества С в
приведенной выше СИФ взять отрезок [(J), (})], то аттракто-
143

ром будет несвязное множество уменьшающихся
отрезков, расположенных по спирали.
Если же в этой СИФ в качестве множества С взять
отрезок [(J), ( 3i )], то аттрактором будет ломаная
спираль с «торчащими» из нее отрезками —
«веточками».
Заметим также, что ветки дерева Пифагора
устроены как логарифмические спирали.
Рис. 32: Ветка дерева Пифагора
Логарифмические спирали возникают при решении
задачи из школьной геометрии. Рассмотрим
квадратный двор, по четырем углам которого стоят четыре
собаки. Одновременно все четыре начинают бежать
по прямой, каждая в направлении ближайшей к ней
собаке по часовой стрелке. Время от времени они
обнаруживают, что их цель сместилась, и
одновременно корректируют направление. Каковы траектории
их движения? Оказывается, что этими
траекториями будут четыре ломаные логарифмические
спирали, сходящиеся в центре квадрата. При
непрерывной коррекции траектории становятся гладкими
логарифмическими спиралями.
144

Рис. 33: "Четыре собаки"
4. Звездчатый фрактал
{R- ;/о5/ь/2,/з}5
/о : K(R2) -+ K(R2), \/BeK(R2) f0(B) = C,
где компакт С Е K(R?) — равносторонний
треугольник со стороной 1 с вершинами в точках
©■©•$■
/i:R2^R2, /.(f) =-If,
/2:R2^R2, /2(f) = -If+^,
/3:R2^R2, /з(2) = -^+(м)-
145

Теорема 6.2. Аттрактор А системы итерированных
преобразований с накоплением
{X;f0:K(X)^K(X),
(\/ВеК(Х) fo(B) = C),
fi-.X->X,i = l,2,...,N}
равен пределу
А= lim С U W[C) U W2{C) • ■ • U Wn{C) =
п—*оо
= lim UUWk(C)
п—>оо
объединения множества накопления С и его образов при
применении всевозможных степеней Wn(C), п = 1, 2,3,...
преобразования
w(C) = и^мс)
пространства К(Х), полученного с помощью
преобразований /j,2 = l,2,...,iV исходного пространства X.
Доказательство
Рассмотрим систему итерированных преобразований с
накоплением:
{^;/о,/ь/2, • • • >/n}5
где
/о : К(Х) -> К(Х)
задано формулой
VBeK(X), fQ(B) = c, СеК(Х),
а преобразования
hif2,---ifN'-X->X
146

сжимающие.
По теореме о неподвижной точке сжимающего
преобразования метрического пространства аттрактор этой
системы равен пределу
lim W£(B), УВ Е К{Х).
п—>оо
Выберем в качестве В множество С — образ
преобразования /о : К{Х) ~^ К{Х)- Тогда выполнены следующие
равенства:
W0(C) = С U Л (С) U f2{C) U ... U fN(C) = С U W(C),
w*(C) = с и мо и мо и • • • и мо и Л2(С)и
иЛ(/2(С)) и... Л(Л(С))... /£(С) = с и w(0 и J^2(C),
W0n(C) = С U W(C) U W2(C) U ... U Wn(C).
Мы получили возрастающую последовательность
вложенных компактных множеств, имеющую пределом
аттрактор исходной СИФ:
С С W0(O Q W$(0 Я W*(0 £ • • • С W£(0 Я • • • •
Теорема доказана.
Этой формулой удобно пользоваться при построении
аттрактора СИФ с накоплением: взять исходное
множество накопления С, добавить к нему его образ W(C), к
полученному объединению добавить VK2(C), затем VF3(C),
и т.д., пока точность изображения не начнет нас
устраивать.
147

Пример
Рассмотрим СИФ с накоплением
{R- ;/о,/ь/2},
f0:K(X)^K(X) VBeK(X), f0(B) = C, С G K(X)
В качестве множества С выберем «галочку» —
объединение двух отрезков:
К'1)
.и/
/оу
W.
и
уо\
АО/
HI
W.
Достаточно взять объединение
С U W{C) U 1У2(С) U Т¥3(С) U W\C),
чтобы увидеть аттрактор этой системы.
Рис. 34: У-множество
Это будет так называемое У-множество, которое пред-
148

ставляет собой две боковые стороны равнобедренного
треугольника с вершинами в точках
/-2N /0\ /2\
с добавленными средними линиями
[(-.')■ G)]
5
Ш
к основанию
КГЮ1-
которые образуют с половинками боковых сторон два
новых маленьких равнобедренных треугольника с
вершинами в точках
(7М7)-0
■0-0-
с которыми проделана та же операция добавления средних
линий, и так до бесконечности. В пределе весь аттрактор
расположен внутри исходного равнобедренного
треугольника, и точки аттрактора, лежащие на основании этого
треугольника образуют множество всех точек с
абсциссами вида
к_
2п
для всевозможных целых к и натуральных п таких, что
к
-2 < — < 2.
2П
149

Упражнения
Описать систему итерированных функций с накоплением,
аттрактором которой является компактное множество А
на плоскости:
1) А — ломаная логарифмическая спираль с центром в
нуле, отношения соседних звеньев которой равно 0.5;
2) А — ломаная логарифмическая спираль с первым
звеном {х\ 0 ^ х\ + Х2 ^ 3}, отношения соседних звеньев
которой равно 3, а угол между звеньями равен |7г;
3) А — бинарное дерево со стволом длины 2 и
отношениями ветвей соседних порядков как 1:3;
4) А — дерево Пифагора с несимметричной кроной,
прямоугольным стволом и углами между стволом и
ветками первого порядка равными ^7г и — |7г;
5) А — дерево Пифагора с несимметричной кроной,
прямоугольным стволом и углами между ветками n-го и
п + 1-го порядка равными (—1)П|7Г и (—1)п+1|7г;
6) А — ветвящаяся структура, напоминающая реальное
дерево с прямоугольным стволом и тремя отростками в
местах ветвления.
Пример решения задачи
Описать систему итерированных функций с
накоплением, аттрактором которой является компактное
множество А на плоскости, где множество А является ломаной
логарифмической спиралью с центром в начале координат
и углом между соседними звеньями, равным 0.757г.
Решение
Центр спирали находится в начале координат,
поэтому она преобразуется в себя с помощью преобразования
/i плоскости, которое является композицией поворота на
угол 0.257Г и сжатия с коэффициентом ехр(0.25а7г). Выбрав
150

в качестве множества накопления отрезок
в = [(1,ош(1,о))],
получаем СИФ с накоплением:
{R- 5/о,Л},
где
/о : ^(R2) -+ K(R2)
определено по формуле
VCe/f(R2) Л(С) = В,
/1(f)=exp(0.25a7r)[ ^ ^ 1 х.
151

Глава 7. Некоторые свойства
детерминированных фракталов
Еще одним вспомогательным инструментом при
построении аттрактора является теорема коллажа, которую
сформулировал М.Барнсли в 1985 году.
Теорема 7.1 (коллажа). Рассмотрим систему
итерированных функций с коэффициентом сжатия к : О ^
к < 1 на метрическом пространстве X (можно с
конденсацией). Пусть А — аттрактор этой системы, а В —
произвольное компактное множество пространства X.
Тогда выполнено следующее неравенство:
р(А,В)^^р(В,Ш(В)),
а для системы с накоплением р(А, В) ^ Y^p(B, Wo(B)),
где р — расстояние в пространстве К(Х).
Для доказательства теоремы воспользуемся
неравенством, выведенным в главе 4 при доказательстве теоремы
4.6 о неподвижной точке сжимающего отображения:
если / : X —> X — сжатие с коэффициентом к, то для
любой точки пространства X выполнено
Из этого неравенства следует неравенство
р(ж, lim fn(x)) ^ -p(x,f(x)).
п—>оо 1 — К
152

Взяв в качестве сжимающего отображения
отображение W : К(Х) ->• К(Х) (или W0 для СИФ с
накоплением), а в качестве х компакт Б, получим
доказательство теоремы.
Эта теорема позволяет получать системы
итерированных преобразований, для которых аттрактором является
заданное изображение. Достаточно подобрать такой
набор сжимающих преобразований, для которых
объединение образов этого изображения будет мало ( не более чем
на е) отличаться от исходного изображения. Тогда
аттрактор такой системы будет отличаться от исходного
изображения не более, чем на yz*;£, где к — коэффициент
сжатия этого набора, то есть максимальный из
коэффициентов сжатия этих преобразований.
Теорема 7.2. Даны два метрических пространства
{X, р) и {Р,а}, причем пространство X — полное.
Рассмотрим отображение
F:PxX -+Х
такое, что при каждом фиксированном р Е Р
отображение
F(p,-):X^X
является преобразованием сжатия с коэффициентом к,
а при каждом фиксированном х Е X отображение
F{-,x) :P^X
непрерывно на Р.
Рассмотрим отображение
Ф : Р -> X,
153

которое каждому р Е Р ставит в соответствие
неподвижную точку хр Е X сжимающего отображения
F(p,-):X^X.
Тогда отображение Ф : Р —> X непрерывно.
Доказательство. Рассмотрим расстояние р(хр, xq)
между неподвижными точками
хр Е X и xq Е X отображений F(p, •) : X —>• X и
F(q, •) : X -+ X.
Поскольку Хр = F(p,xp) и xq = F(q,xq), то
р{хр, xq) = p(F{p, хр), F{q, xq)).
По правилу треугольника
p{F(p, хр), F(q, xq)) < p{F(p, xp), F(q, xp))+p(F(q, xp), F(q, xq
Учитывая, что отображения F(p, •), F(q, •) —
сжимающие, получаем
p(F(q,xp),F(q,xq)) < kp(xp,xq),
откуда следует
p{F(p, xp), F(q, хд)) < p{F(p, xp), F(q, xp)) + kp(xp, xq),
и, подставив в последнее неравенство равенство
р(хр, xq) = p(F(p, хр), F(q, xq)),
имеем:
р(хр,xq) ^ p{F(p,xp), F(q, xp)) + kp(xp,xq).
154

В итоге получаем
(1 - к)р(хр, xq) ^ p(F(p, хр), F{q, xp)).
Отображение F(-, хр) : Р —» X непрерывно на Р,
поэтому для любого е найдется 6 такое, что как только сг(р, q) <
5, так
—-p(F(p,xp),F(q,xp)) < e,
что и доказывает непрерывность отображения Ф : Р —>
X.
Теорема доказана.
Теорема 7.3. Даны два метрических пространства
{X, р) и {Р,а}, причем пространство X — полное, а
пространство Р — компактное.
Рассмотрим отображение
F-.PxX^X
такое, что при каждом фиксированном р G Р
отображение
F(p,-):X^X
является преобразованием сжатия с коэффициентом к,
а при каждом фиксированном х £ X отображение
F(-,x) :P^X
непрерывно на Р.
Можно рассмотреть индуцированное сХ на К(Х) отоб
ражение
F:Px К(Х) -> К(Х)
и отображение
F{-,B) :P^K(X)
155

при каждом фиксированном В Е К(Х).
Тогда теорема утверждает, что отображение F(-, В)
Р —> К(Х) непрерывно на Р при каждом фиксированном
В е К{Х).
Доказательство. Рассмотрим расстояние
p(F(p,B),F(q,B)).
Без ограничения общности верно неравенство
p(F(p, Б), F(q, В)) = sup inf p(F(p, х), F(q, у)).
хеВ уев
По правилу треугольника
p(F(p, х), F(q, у)) < p(F(p, x), F(q, x)) + p(F(q, x), F(q, у)),
откуда
p(F(p,B),F(q,B))^
< sup inf (p(F(p, x), F(q, x)) + p(F(q, x), F(q, y))).
хевуев
Прямое произведение Р х В компактов есть компакт, а
значит сходимость F(q, х) к F(p, х) на Р х В равномерна,
то есть для любого числа е существует число 5 такое, что
как только o-(p,q) < 5, так p(F(p,x),F(q,x)) < e для всех
хе В.
Отсюда следует, что как только cr(p, q) < 5, так
p(F(p, Б), F{q, В)) < sup inf (e + p{F(q, x), F(q, у))) =
хевуев
= е + sup inf p(F(q, х), F{q, у)).
хев уев
Второе слагаемое этой суммы
sup inf p(F(q,x),F{q,y))
хев уев
156

равно 0, поэтому получаем, что как только сг(р, q) < <5,
так
p(F(p,B),F(q,B))^e.
Теорема доказана.
Теорема 7.4. Даны два метрических пространства
{Х,р}и{Р,а},
причем пространство X — полное, а пространство Р —
компактное.
Рассмотрим отображения
Fi-.Px К(Х) -> К(Х), % = 1,2,... N
такие, что при каждом фиксированном р Е Р каждое
отображение
Fi{p,-):K{X)^K{X), г = 1,2,... TV
является преобразованием сжатия с коэффициентом
ki, а при каждом фиксированном В Е К(Х) каждое
отображение
Fi(-,B) :Р-+К(Х), г = 1,2, ...ЛГ
непрерывно на Р.
Тогда отображение
F = Ui=1,2 NFi : Р х К{Х) -> К(Х)
при каждом фиксированном В Е К(Х) непрерывно на Р.
Доказательство этой теоремы можно получить, исполь-
157

зуя неравенство
VA B,c,De K(X)
р{А UB,CUD)^ тах{р(Д С), р(В, D)}
и метод математической индукции.
Действительно, для N = 2 теорема следует из
приведенного неравенства и предыдущей теоремы.
При N > 2 объединение (N + 1)-го отображения предста-
вимо как двойное последовательное объединение N
отображений с еще одним. Объединение N отображений
непрерывно по предположению индукции, а его объединение с
последним отображением есть объединение двух
отображений, непрерывность которого только что была
доказана.
Из приведенных теорем следует очень важная теорема.
Теорема 7.5. Даны два метрических пространства
{Х,р}и{Р,а},
причем пространство X — полное, а пространство Р —
компактное.
Рассмотрим отображения
Fi-.PxX ->*, г = 1,2,... TV
такие, что при каждом фиксированном р Е Р каждое
отображение
Ъ(рг):Х^Х, z = l,2,...7V
является преобразованием сжатия с коэффициентом
ki, а при каждом фиксированном х £ X каждое отобра-
158

жение
Fi(;x):P^X, i = l,2,...iV
непрерывно на P.
Тогда отображение Р —» К(Х), ставящее каждому
р £ Р аттрактор системы итерированных
преобразований
{Х;Ъ(р,-):Х^Х, i = l,2 JV},
непрерывно на пространстве Р.
Замечание. Сформулированная теорема остается
верной и для системы итерированных преобразований с
накоплением.
Примеры
1. Рассмотрим систему итерированных преобразований
с накоплением, аттрактором которой будет дерево
Пифагора.
{R- ;/о,/ь/2},
/о : K(R2) -> K(R2), VBeK(R2) f0(B) = C,
где компакт С Е K(R?) — квадрат со стороной 1 с
вершинами в точках
Л : R2 -> R2,
/1(x) = cosW^s.ne cos0 Jx+y,
/2 : R2 -► R2,
159

/2(o:) = Slll(0) Q • /1 # + 1 - л • л 1
w w V -cos<9 sin<9 / \l-\-cosOsmOJ
В качестве пространства параметров Р возьмем
отрезок прямой [|,|]. Меняя параметр в внутри
этого отрезка, получаем непрерывное изменение дерева
Пифагора.
2. Рассмотрим следующую систему итерированных
преобразований:
Если выбрать в качестве параметра а Е Р = [0,27г],
то получим аттрактором отрезок, один конец
которого лежит в начале координат, а второй в зависимости
от параметра перемещается по единичной
окружности с центром в нуле, то есть является чем-то вроде
стрелки секундомера.
Упражнения
В сформулированных далее задачах предполагается, что
знак угла указывает направление его отсчета:
положительный — против часовой стрелки, отрицательный — по
часовой стрелке.
1. Описать систему итерированных преобразований,
аттрактором которой является компактное множество А на
плоскости:
а) А — параллелограмм, заданный условием
А = {х\0 < хх ^ 2,0 ^ хх + х2 ^ 1};
160

b) A — треугольник с вершинами в точках
P(l,-l),Q(l,2),5(-2,3);
c) А — правильный шестиугольник с центром в точке
0(0,0) и вершиной в точке #(1,0);
d) A — разность двух параллелограммов, заданная
условием:
А = {ж||ж1| ^ 3, |2m + rr2| <5}\{£||a;i| < 1,\2хх+х2\ < 3};
e) А — квадрат без верхнего угла:
А = {х\\хг\ < 1, \х2\ < 1} \ {х\0 < X! ^ 1,0 < х2 < 1};
/) А — треугольник Серпинского с вершинами в
точках Р(2, -1), 0(1,0), 5(-2, -2);
д) А — последовательность на плоскости вида:
h) A — объединение двух отрезков:
A = {f||a;i| < 1, х2 = 0} U {х\хх+х2 = 0,0^£2 < 1}.
2. Оценить расстояние между заданным компактом В
на плоскости и аттрактором А заданной системы S
итерированных преобразований:
а) В = {х| - 1 < xi < 0, xi + х2 = 1}U
U{£|0 ^ xi < 1, -xi + х2 = 1}U
U{x|0 ^ж2 < l,xi = 0},
£ = {R 5/05/15/2}?
161

где
/о : K(R2) -»• К(R2)
такая, что
VC e K{R2) /о(С) = {х|0 ^ я2 < 1, а* = 0},
/ъ /2' R —)• R ,
/i(f)=(! 1)f+(?)' №)=(-I1)4?
b) В = {х| - 1 ^ xi ^ 0, хг + х2 = 1}U
U{x|0 ^ Ж1 ^ 1, -xi + х2 = 1}U
U{f| - 1 ^ хх ^ 1,х2 = 2},
где
/о : i^(R2) -> ^ (R2)
такая, что
VC e A-(R2) /„(С) = {ж|0 ^ х2 < 1, ж! = 0},
/i(S) = ( I ~j)f+(~j)' b(f)=(_j |)f+(
3. Описать систему итерированных преобразований с
параметром р, аттрактором которой является компактное
множество А(р) на плоскости:
а) А(р) — объединение двух отрезков:
А(р) = {х\0 ^ х\ ^ cos(p),x2 = л/1 - a^}U
162

U{£|0 ^ Xl ^ 0.5cos(^),a:2 = 0.50. - ж?};
b) A(p) — треугольник на плоскости с вершинами в
точках
Примеры решения некоторых задач
1. Описать систему итерированных преобразований,
аттрактором которой является компактное множество А на
плоскости, где множество А есть трапеция с
внутренностью и вершинами в точках Б(2,0), С(—2,0), D(—l, 2), Е(1,2).
Решение
Представим исходную трапецию А как объединение
пяти трапеций с вершинами в точках:
Ах : В1(1,2),С1(0,2),А(-0.5,1),^1(1.5,1),
А2 : Б2(-1,2), С2(0,2), £>2(0.5,1), £2(-1.5,1),
А3 : В3(1,0), С3(-1,0), D3(-0.5,1), £3(0.5,1),
А4 : Б4(-2,0), С4(0,0), £>4(-0.5,1), £4(-1.5,1),
А5 : Б5(2,0), С5(0,0), Д>(0.5,1), Д5(1.5,1),
Л = i4i U A2 U А3 U A4 U Аь.
Каждая из маленьких трапеций является образом
большой при преобразовании подобия с коэффициентом
сжатия 0.5 и сдвигом:
Ai = fi(A), ft :R2->R2, fi(x) = 0.Ьх+ъ, г = 1,2...,5,
Окончательно система итерируемых преобразований име-
163

ет вид
{R2Jt(x) = 0.52+t*, i = 1,2,... ,5},
где
2. Оценить расстояние между заданным компактом
В =[(1,0), (1,1)]
на плоскости и аттрактором А заданной системы S
итерированных преобразований,
S = {R2,/i(f) = 0.2x,f2(x) = 0.5£ + ( J )}•
Решение
Вычислим расстояние между множеством В и его
образом при преобразовании W = /i U f2'
p(B,W(B)) = 0.8.
Отсюда следует, что расстояние между А и В не
превышает отношения (0.8 : (1 — /с)), где к — коэффициент сжатия
СИФ:
Р(А, в) ^ Y^PiB, w(B)) = y^o.s = | = i.e.
3. Описать систему итерированных преобразований с
параметром р, аттрактором которой является компактное
164

множество А(р) на плоскости. Рассмотрим в качестве А(р)
параллелограмм
А(р) = {х\ 0^x1^2p,\-x1 + x2\*ip, 0.5 ^р^1}.
Решение
Параллелограмм А(р) можно представить как
объединение четырех ему подобных:
А[р) = Ах[р) U A2[p) U A3(p) U Л4(р),
где
Up) = fi(A(p)l fi'.R2^ R2,
fi{x,p) = 0.5£ + й5(р), i = 1,2..., 4,
поэтому СИФ с параметром будет иметь следующий
вид:
{R2,fi(x,p) = 0.5£ + Vi(p), г = 1,2,3,4,},
где
Vl(p) = ( -0.5р ) ' V"2{p] = ( 0.5р ) '
*<"> = ( 1.5р ) • *<"> = ( 0.5р ) •
165

Глава 8. Кодовое пространство
СИФ
Рассмотрим несколько примеров детерминированных
аттракторов.
Канторово множество К. Оно сохраняется при
применении к нему объединения двух преобразований
1 12
к = мк)имк).
При этом образы f\{K) и ^{К) не пересекаются:
fi(K)nf2(K) = 0.
Каждая точка Канторова множества попадает ровно в
одно из множеств fi(K) или /2 (if)- Таким образом,
каждой точке х G К можно поставить в соответствие число
1 или 2 в зависимости от того, в каком из множеств она
лежит.
Для каждого образа f\(K) и /2 (if) существует
обратное взаимно-однозначное отображение этого образа в
Канторово множество if:
/Г1 : h{K) -► К, /f1(a;) = 3x,
/2-1 : ЫК) -»• К, /2"1(х)=Зх-2.
Если точке х Е К соответствовало число г, равное 1 или
2, тоу = /Г1(х)€К
Точке у Е if также можно поставить в соответствие
одно из чисел 1 или 2 в зависимости от того, в образе
какого преобразования /i(if) или /2(if) она лежит.
166

Этот процесс можно продолжать до бесконечности. В
результате получится бесконечная последовательность,
составленная из чисел 1 и 2. По этой последовательности
можно восстановить исходную точку х.
Действительно, если на первом месте
последовательности стоит цифра 1, точка X принадлежит первой трети
отрезка [0,1], если 2 — третьей трети отрезка [0,1]. Если на
первых двух местах стоит 11, точка X принадлежит
первой девятой части отрезка [0,1], если 12 — третьей девятой
части отрезка [0,1], если 21 — седьмой девятой части
отрезка [0,1], если 22 — девятой девятой, если на первых трех
местах последовательности стоит 111 — первой двадцать
седьмой части и т.д. Можно интерпретировать
полученную последовательность единиц и двоек как троичную
запись числа X после запятой, в которой все нули заменены
единицами.
Троичная запись для действительного числа не всегда
единственна. Две записи соответствуют одному числу X в
том случае, если в первой записи на каком-то месте
стоит 1, а дальше одни нули, а у второй на этом месте стоит
0, все цифры перед этим местом совпали с цифрами
первой записи, а все цифры после этого места равны 2. Это
легко объяснить. Если 0,2i,Z2,... троичная запись числа
х G [0,1], то
Ч . г2 г3
Ж=3 + 9+27 + ---
и если выполнено:
к = Зк, 0 <к < М, гм = 0, jM = 1,
Ч = 2, Зк = 0, к > М,
ii + ^ + ^ + .
3 9 27
167

Ч , г2 , г3 , , ъм-1
fc=M+l
*1 г2 ^3 ^м-1
3 9 27 3м"1 Зм+11-|
= !l + !^ + il + ^м-1 1 =
3 9 27 3м"1 3м
= Zi + -Ь. _l ^i , Зм-i Зм _
3 9 27 3м"1 3м
_ Ji Зг ,3з Зм-\ ,3м» ST х
"з"+9" + 27+ +1мЗГ + ^7+их ^ з*-
к=М+1
По построению Канторова множества все его точки
имеют троичную запись, в которой отсутствует цифра 1. Для
тех точек отрезка, которые лежат в Канторовом
множестве и имеют неоднозначное троичное представление,
можно игнорировать неоднозначность, поскольку лишь одна
из троичных записей не содержит цифры 1. При этом
любое число отрезка, которое имеет троичную запись без
цифры 1, лежит в Канторовом множестве. Таким образом,
существует взаимно-однозначное соответствие между
бесконечными последовательностями из нулей и двоек и
точками Канторова множества. Если в таких
последовательностях все нули заменить единицами, то получится
взаимнооднозначное соответствие между точками Канторова
множества и последовательностями из единиц и двоек.
Геометрический смысл такого соответствия был разобран выше.
В результате получаем кодирование точек Канторова
множества последовательностями из единиц и двоек.
Треугольник Серпинского. Каждая точка X
треугольника Серпинского Т лежит в образе треугольника
Серпинского при одном из преобразований системы
итерированных функций, для которой треугольник Серпин-
168

ского является аттрактором:
Г = /1(Г)и/2(Г)и/з(Г),
^\/xeT:3i:xe fi(T).
Однако в отличие от случая Канторова множества в
треугольнике Серпинского есть точки, которые лежат в
образах сразу двух различных преобразований:
Q.o) e/i(T)n/2(T), Q,0 €/3(Г)п/2(Т),
О,0€/1(Г)П/3(Г).
Аналогично случаю Канторова множества для каждой
точки треугольника Серпинского можно построить
бесконечную последовательность чисел 1,2,3, по которой можно
будет найти исходную точку. Отличие от случая Канторова
множества состоит в том, что для некоторых точек
треугольника Серпинского можно построить сразу несколько
таких кодирующих точку последовательностей.
Рис. 35: адреса на уровне 2 в треугольнике Серпинского
Например, точке (0.5,0) соответствуют последователь-
169

ности 1,(2) и 2,(1),где в скобке выделен период. Точке (0.5,0.5)
соответствуют последовательности 2,(3) и 3,(2), точке (^, Ц)
соответствуют последовательности 2,1,1,1,2,(3) и 2,1,1,1,3,(2),
а точке (|, §) — ровно одна последовательность (3,2).
В дальнейшем, если в последовательности участвуют
только однозначные числа, будем опускать запятые.
В рассмотренных выше примерах каждой точке
аттрактора системы итерированных функций ставилась в
соответствие одна или несколько последовательностей чисел
— номеров преобразований СИФ, по которой можно
найти эту точку аттрактора. Остановимся на этом подробнее.
Пусть дана система итерированных преобразований
{Х;/{:Х^Х,г = 1,2,...,Щ
с коэффициентом сжатия к и аттрактором Л.
Определение 8.1. Кодовым (адресным, символьным)
пространством системы итерированных преобразований,
состоящей из N преобразований, называется множество
Е бесконечных последовательностей чисел от 1 до N,
являющихся номерами преобразований СИФ, с метрикой
d(s,o~), определенной по формуле
\fc, а е Е : <; = <^2<;з • • •, сг = о-^сгз • • •,
г=1 v '
Корректность заданной метрики легко проверяется: ряд
всегда сходится, сумма его равна нулю тогда и только
тогда, когда все слагаемые равны нулю, то есть когда
последовательности совпадают, ряд симметричен относительно
^ и а, и, наконец, правило треугольника выполнено, по-
170

скольку сумма модулей двух чисел всегда не меньше, чем
модуль их суммы.
8.1. Свойства метрического пространства {Е, d}
1. Ограниченность.
N -1
Va,s e Е d(s,a) ^ .
Действительно, расстояние между двумя
последовательностями из N символов максимально, если
модуль разности между каждыми соответствующими
членами этих последовательностей равен N — 1. В
этом случае сумма соответствующего ряда равна
^ (N + IV ~ N + 1 ^ (N + IV-1 ~
г=1 v ' г=1 v '
_JV-lA 1 _ N-lN + l _ N-l
~ N + 1^(N + 1Y~ N + l N ~ N '
г=0 v '
Отсюда следует, что
At \ ^ N~1 N~1
maxdk, a) = > ————т = ———.
^aeE ~i {N + iy N
2. Несчетность. Легко показать, что пространство Е
из двух и более символов несчетно. Доказательство
аналогично доказательству несчетности Канторова
множества, приведенному в г.1. Предположим, что
Е счетно и пересчитаны все его элементы, то есть
каждому присвоен порядковый номер. Рассмотрим
бесконечную последовательность, у которой на
первом месте стоит не то, что у последовательности №1,
171

на втором — не то, что на втором месте у
последовательности №2 и т.д. Мы можем построить такую
последовательность, поскольку символов больше, чем
один. Эта последовательность не может иметь
никакого порядкового номера, поскольку на каждом г-м
месте у нее не то, что стоит на г-м месте у
последовательности №г. Следовательно, Е несчетно.
3. Замкнутость и совершенность (отсутствие
изолированных точек). Рассмотрим, как устроено
расстояние между точками Е.
Пусть для двух элементов
Я = ^1^2^з • • • , ст = СГ1СГ2СГ3 •••ЕГ
выполнено
0i = Si Vi = 1,2, ...га-1, (Упф^п,
тогда
1 N-1
Первая часть неравенства следует из неравенства
а вторая доказывается так же, как и ограниченность
пространства Е.
Из оценок расстояния на Е следует, что в этом
пространстве нет изолированных точек, поскольку для
любой его точки а можно постоить
последовательность точек {хк Е Е}™=1, к ней сходящуюся. Для
этого достаточно в качестве последовательности хк
выбирать последовательность, у которой первые к
172

элементов совпадают с первыми к элементами
последовательности а. Из этих же оценок следует полнота
пространства Z\ поскольку у членов любой
фундаментальной последовательности, начиная с
некоторого номера, будут совпадать первые п элементов.
4. Компактность. Предположим, что множество Е не
является компактом. Тогда существует его
бесконечное покрытие открытыми множествами
Ua: ГС \jUa,
у которого нет конечного подпокрытия.
Рассмотрим семейство преобразований множества Е:
\/а = cricr20"3 •••€£, ол(сг) = гсг1сг2сг3 • • • G Г,
i=l,2,...,j\r.
Множество Е является объединением своих образов
при преобразованиях cuf.
Е = ul^iS),
Покрытие {Ua} : EC uUa бесконечно и не может
быть заменено конечным подпокрытием хотя бы на
одном из образов и^(Е). Диаметр множества ио^(Е)
в N + 1 раз меньше диаметра пространства Е. Этот
образ можно представить как объединение
<*, (Г) = u£lWil (<*(£)),
причем хотя бы на одной из компонент ш^ш^Е))
этого объединения покрытие Ua бесконечно и не
может быть заменено конечным подпокрытием.
Диаметр этой компоненты и)^(и)^(Е)) меньше диаметра
173

Е в (N + I)2 раз. Этот процесс можно продолжить
до бесконечности. В пределе получим
последовательность множеств, диаметр которых стремится к нулю,
Е D co^E) D uh(uji2(E)) D • • • D
Dujil(ui2(...ujin...(E)...),
которая сходится к некоторой точке
С = «1*2*3 • ■ • € Е,
причем каждое из этих множеств не может быть
покрыто конечным подпокрытием покрытия {UQ}. Но
точка С лежит внутри одного из открытых множеств
Uai покрытия {Ua}, а значит, при достаточно
большом М множество ш^ (uji2 (... ujihI (Е)...) лежит
внутри Uai. Получилось противоречие, что доказывает
неверность предположения.
Следовательно, Е является компактом.
5. Вполне несвязность. Рассмотрим любое
подмножество М С Е. Если это подмножество не состоит
из одной точки, то у него существуют по крайней
мере две точки с самой короткой цепочкой первых
совпадающих элементов:
Я = 9К2<й • • •, сг = (У\(У2(Уъ • • • G М,
т.е. выполнено
(?i = Я Vz = 1,2,... п — 1, ап ф яп,
причем п минимально по всем а, я Е М. Определим
множества Mi и М^ как подмножества множества
М, в первом из которых лежат точки М с первыми
174

п элементами, совпадающими с элементами а, а во
втором — точки, у которых хотя бы один из первых
п элементов не такой, как соответствующий элемент
у а. Оба эти множества не пусты, в первом лежит а,
а во втором я. При этом М = М\ U М2.
Любая точка множества М\ отдалена от точки а не
далее чем на щщгр^- Это значит, что
Любая точка множества М2 отдалена от точки а не
менее чем на (Nl1\n- Это значит, что
М2СМ\ Б(сг, ———).
v (N + l)nJ
Очевидно, что
В{а' N(N + 1)»> - В{а' N(N + l)n> g
= , TV-0.5 . „, 1
gg(g'iV(Ar + i)^)gg((T'(jvTIF)-
Следовательно, Mi П М2 = 0.
Таким образом, доказано, что для VM С Е,
состоящего более чем из одной точки, найдутся такие
множества Mi и М2, что выполнено
Mi П М2 = 0, М = Mi U М2.
Следовательно, 27 вполне несвязно.
Мы показали, что кодовое пространство замкнуто,
ограничено, компактно, совершенно и вполне несвязно. Теми
175

же свойствами обладает Канторово множество. Давайте
покажем, что кодовое пространство метрически
эквивалентно Канторову множеству. Но сначала несколько
обобщим понятие Канторова множества.
Определение 8.2. Обобщенным Канторовым
множеством называется аттрактор системы итерированных
преобразований следующего вида:
Обобщенное Канторово множество представляет собой
множество точек на отрезке [0,1], у которых в записи (N+ 1)-
ричного представления отсутствует цифра 0. Это значит,
что точка обобщенного Канторова множества имеет
следующий вид
#1 #2 #3
х = 0,Х1Х2Хз... = -— + —_ + __ + ...,
где
^G{l,2,...,iV}; г=1,2,3,...
Обозначим обобщенное Канторово множество той же
буквой К и далее слово «обобщенное» будем опускать.
Поскольку Канторово множество принадлежит
отрезку [0,1], то на нем есть обычное расстояние на прямой, то
есть выполнено
оо оо
Vx.i/eR1 p(x,y) = \x-y\ = \Y ,*1 -У\>г№ I.
г=1 v ' г=1 v '
Теорема 8.1. Кодовое пространство метрически
эквивалентно Канторову множеству.
Доказательство. Точка х Канторова множества одно-
176

значно определена своей (iV + 1)-ричной записью, которая
является последовательностью символов {1,2,..., N},
поставленных после нуля и запятой. Убрав ноль и запятую,
получаем элемент а = ф(х) кодового пространства. Это
отображение ф взаимно однозначно. Для доказательства
теоремы достаточно найти два таких положительных
числа С\ И С2, ЧТО
Ух,уеК СкЦф(х),ф(у)) ^ р(х,у) ^ С2(1(ф(х),ф(у)).
Иначе говоря, надо найти такие С\,Съ > 0, что для всех
х,у Е К выполнено
ОО , , ОО ОО
%i yi\ ^ \ I I \~^ "^ \~^ У* I ^
Ci Е ш+иг < \х - у\ -1E ш+л» - Е
г(Лг + 1)^' »■ 'tr^ + iy t!(N + iy
c2j:
\Xi-Vi\
^(N + iy
Поскольку сумма модулей всегда не меньше чем модуль
суммы двух чисел, то для всех х,у Е К верно
ОО ОО ОО | |
ЕХг у> Уг | < V^ \Xi-yi\
г=1 (ЛГ+1)^ ^^+1) ^^(^+1)*'
откуда получаем С2 = 1.
Пусть гг — наименьшее значение индекса г, для
которого Xi ф yi.
Учитывая, что для любых чисел а и b всегда верно
Н-|&К|а + &К|а| + |&|,
177

получаем
г=1 ч ' г=1 ч '
%i V-^ Vi
12^ i n ■+■ i v 2^
^(Лг + 1)г ^(ЛГ + iy1
^ \^п Уп\ I V-"4 хг Уг i ^
^ (N + l)n ~ ' .f^ (iV + 1)*' "
> Fn -2/n| _ v^ Fi -У»| >
" (N + l)n .2-" (N + 1Y "
v ' г=п+1 v '
> \хп-Уп\ _ v^ N -1 =
^ (JV + l)n ^ (iV + lV
v ' г=п+1 v '
\хп-Уп\ N-l 1
(JV + l)n N (JV + 1)
= (|жп-2/п| гт—)7
TV J(N + l)n'
Для любого N > 0 выполнено (N — l)2 ^ 0, откуда
непосредственной проверкой можно доказать, что верно
1 7V-1 1 ч
Из последнего неравенства и того, что
1 < \хп - уп\ < N,
следует
1 ч N-\, 1 ч
kn-^|(l-^)>^r(l + ^).
178

Отсюда получаем
, N-1 1 „ . N-1,
F„ - Уп\ д^— > Д^(К - Уп\ + —^—),
откуда следует
, /, , N-1, 1
k-!/l^(kn-yn|--^r)(iV + 1)n^
_1_ (. _ , iV-1 1
^ N2(\Xn Уп\+ N )(Д^+1)п-
= J_ (\хп-Уп\ N-l \ =
N2 \(N + l)n N(N + l)n)
= J_ (\ХП-Уп\ V2^ ^-1 , >
N2 \ (N + l)n ^ (N + 1Y "
>
1 / |ж„-2/„| , v^ \xi-y,
^+E
ЛГ2КЛГ + 1)п i^W + ty
= ^(g|f^)=j>(^))-
Для доказательства теоремы достаточно взять
1
Cl~ N2'
Теорема доказана.
Замечание. Можно было сразу доказать последнюю
теорему, и тогда все свойства пространства U, которые нам
пришлось доказывать, следовали бы из наличия этих свойств
у Канторова множества и эквивалентности метрических
пространств.
179

Упражнения
1. Найдите коэффициенты с\, с^ > 0 такие, что для любых
двух бесконечных последовательностей
а = {<*}£, и и = {щ)Г=1,
состоящих из чисел 1 и 2, выполнено неравенство
ci (21^—^—) ^ IZ^^^^I ^с- (21^—^—)
\г=1 / г=1 \г=1 /
2. Найдите коэффициенты ci, C2 > 0 такие, что для
любых двух бесконечных последовательностей а = {cri}^ и
v = {^i}£i, состоящих из чисел 1,2 и 3, выполнено
неравенство:
CML^^ ^ 12l^ —^—I ^c2 Z^^i^
\г=1 / г=1 \г=1 /
3. Найдите расстояние между двумя бесконечными
последовательностями
состоящими из чисел 1 и 2, где
а) сг = (12), v =122(12);
b) а = (1122), v = 122(12);
c) сг = (121), i/ = 122(12).
В круглых скобках стоят цифры периода — бесконечно
180

повторяющиеся в исходной последовательности, то есть
(21) = 212121....
4. Найдите образ пространства Е всех бесконечных
последовательностей
° = Ыёх-
состоящих из чисел 1,2 и 3, при преобразовании
(р : £ -> Г,
где
а) (р(а)) = fi(a) = {г, сть сг2, а3 ... }, г = 1,2,3;
6) <р(*)) =/Ш*));
с) ^)) = /1(/2(/зИ));
d) <р(<т)) = {а2,сг3...}.
Пример решения задачи 3
Найдите расстояние между двумя бесконечными
последовательностями
а = {*}£, и i/ = {«/,}&,
состоящими из чисел 1,2 и 3, где
сг = (123), v = 21(32)
Решетке
Последовательность а можно записать в виде
а = 12(312) = 12(312312),
181

а последовательность v в виде
г/ = 21(323232).
Тогда выполнены следующие равенства:
1,г = 1,
1,г = 2,
0, г = 3 + 6fc, fc = 0,1
1,г = 4 + 6/с,/с = 0,1
1,г = 5 + 6/с,/с = 0,1
1, г = 6 Н- 6Ас, А; = 0,1
2, г = 7 + 6fc, к = 0,1
О, г = 8 + 6fc, А; = 0,1
■<* =<
Отсюда следует
' + £;
_i _i_ y-_L_ y-_L_ v_L
_ 4 16 ^-^ 44+6/г ^-^ 45+6/г ^-^ 46+6fc ' ^-^ 47+6к
к=0 к=0 к=0 к=0
_1 J_ (l_ 1_ 1_ 2\(^J_^
~ 4 + 16 + V44 + 45 + 4б + 47/ \f^Q 46fcy
~4 + 16+\44 + 45 + 4ё + ;
_ 1 \_
~ 4 + 16
_L _L _L —
44 + 45+ 46+ 47
1
Оставим результат в виде конечной суммы, упрощать
ответ не будем.
Решение задач 1 и 2 можно найти в изложенной главе,
решение задачи 4 разобрано не будет как элементарное.
182

Глава 9. Адресная функция СИФ
Рассмотрим кодовое пространство системы
итерированных функций (СИФ) и покажем, как в общем случае
кодируются точки аттрактора СИФ.
Компактность исходного пространства
Всякий раз, когда рассматривалась какая-нибудь
система итерированных функций, за основу выбиралось
метрическое пространство X, вообще говоря, не
ограниченное. В конкретных примерах это было пространство Rn, n =
1,2. Аттрактор любой СИФ есть, наоборот, множество
компактное и потому ограниченное. Возникает вопрос:
можно ли получить такой же аттрактор, если в качестве
исходного пространства в СИФ выбирать что-то
ограниченное? И как выбрать такое ограниченное метрическое
пространство, что преобразования исходной СИФ
определены на нем и аттрактором будет то же множество, что
и для неограниченного исходного метрического
пространства? Ответ на эти вопросы дает следующая теорема.
Теорема 9.1. Рассмотрим СИФ на полном
метрическом пространстве X:
{X; fnX-^X, i = l,2,...,N}
с коэффициентом сжатия к и аттрактором А и некое
произвольное компактное множество Н Е К(Х).
Тогда существует такое компактное множество
н е к(Х),
содержащее Н: Н С Н, для которого определена СИФ:
{Я; Д:Я->Я, t = l,2,...,W},
183

причем аттрактор новой СИФ совпадет с аттрактором
исходной.
Доказательство. Метрика на компакте Я Е К(Х)
индуцируется с пространства X. Для того чтобы система
итерированных преобразований была определена на
метрическом пространстве компакта Я, необходимо и
достаточно, чтобы преобразования /j, г = 1,2,..., N
отображали компакт Я в себя. Следовательно, перед нами стоит
следующая задача: по заданному компактному множеству
Я Е К(Х) и заданному набору сжимающих
преобразований пространства {/* : X —> X, г = 1,2,..., iV}
построить компактное множество Я такое, что выполнено
ЯСЯ, /ДЯ)СЯ,г = 1,2,...,т¥.
Рассмотрим СИФ с накоплением на исходном
пространстве X, выбрав Я в качестве множества накопления:
{Х- f0:K{X)->K(X), \IBeK{X) f0(B) = H,
ff.X-tX, t = l,2 TV}.
Эта система имеет аттрактором компактное множество
Я = lim (Я U W(H) U W2{H) U • • • U Wn{H)),
п—>оо
где
W(-) = и?=1Ш W : К(X) ->■ К(Х).
По построению для множества Н выполнено
НСН, ft(H)CH,i = l,2,...,N.
Это значит, что система
{Я; fi-.H-tH, i = l,2,...,N}
184

корректно определена. Ее аттрактор А есть неподвижная
точка преобразования
W(-) = U?=1M-), W : К(Н) -»■ К[Н),
в пространстве К(Н):
W(A) =А, Ае К(Н) С К(Х),
а значит и в пространстве К(Х). Но аттрактор А исходной
СИФ
{Х- fnX^X, * = 1,2 JV}
также является неподвижной точкой этого отображения в
пространстве К(Х) :
W{A) = А, Ае К(Х).
Поскольку у сжимающего преобразования может быть
ровно одна неподвижная точка,
А = А.
Теорема доказана.
Доказанная теорема позволяет считать, что любая
интересующая нас СИФ определена на компактном
метрическом пространстве.
Адресная функция
Рассмотрим систему итерируемых преобразований
{Х- fi-.X-tX, i = l,2,...,N}
с коэффициентом сжатия к, аттрактором А и кодовым
пространством Е.
185

Определим отображение
Ф-.ExNxX ^Х
с помощью следующей формулы:
Ф(а, п, х) = fai(fa2{... {fan(х)...),
где
а = а\<72 ... 0"п • • • Е 27, n G N, х £ X.
Теорема 9.2. Для построенного выше отображения,
Ф:Ех^хХ ^Х
с помощью следующей формулы:
Ф(<7,п,а;) = /„,(/„(... (/„п(а;)...),
где
а = о~\0~2 . •. сгп • • • G 27, n G N, xGl
существует предел
lim Ф((7,п,д;),
п—>оо
который не зависит от исходной точки х £ X и лежит в
аттракторе А. При этом на любом компакте Н G К(Х)
сходимость последовательности {Ф(а, п, х)}™=1 к этому
пределу равномерна.
Доказательство. Рассмотрим две произвольные
точки ж,г/ G H G К(Х). Пусть Н G АГ(Х) — компактное
множество пространства X, содержащее Н, СИФ на
котором
{Я; Ь:Н->Н, i = 1,2,..., Я}
186

корректно определена, то есть fi(H) С Я, г = 1,2,..., N,
а это значит, что аттрактор этой СИФ совпадает с
аттрактором СИФ на пространстве X:
{Х- ff.X^X, t = l,2,...,#}.
Пусть D — диаметр множества Я,
D = sup p(a, b).
а,Ь€Н
Тогда верно неравенство
р(ф(а,п,х),ф(а,т,у)) < kmin^D.
Действительно, предположим для определенности,
что т < п. Тогда
ф(а, п, х) = ф(а, га, ф(я, п — т, х)),
Я = СГт+1(7т+2СГт+з • • • Е Е.
Обозначим z = ф(я, п — га, х), тогда ф(а, п, х) = ф(а, га, z).
Из
X,yeHCH,Z = fam+1 {fam+2(fam+3(- ..fffn(x)...)
И
Л(Я)СЯ, z = l,2,...,iV
следует z G Я, откуда вытекает, что p(z,y) ^ Д а это
значит, что
р(ф(<т,п,х), ф(<т, га,у)) = р(ф(<т,га, z), </>(а, ш,у)) <
^kmp(z,y)^kmD.
Из этого неравенства следует, что любая из перечисленных
187

ниже последовательностей фундаментальна:
{ап = ф((т,п,х)}™=1, {Ьп = ф(а,п,у)}™=1,
\C2n-l = ап,С2п = ^тг}п=1-
Пространство X полное, поэтому все три эти
последовательности имеют предел, а поскольку первые две
являются подпоследовательностями третьей, то предел у всех
трех один и тот же, а значит, не зависит от точек х и у.
Из доказанного выше неравенства также следует
равномерная сходимость по всему компакту Н.
Осталось доказать, что предел последовательности
{ап = ф((т,п,х)}™=1
лежит в аттракторе А.
Каждый член последовательности ап = ф(а,п,х)
принадлежит (U^1/i)n(if), поэтому ее предел лежит в
lim (и^ПН).
п—>оо
При этом по теореме о сжимающем отображении
А = lim (и^ДНЯ) УН е К(Х),
п—>оо
поэтому
lim ап = lim ф(а, п, х) Е А.
п—>оо п—too
Теорема доказана.
Мы получили отображение кодового пространства в
аттрактор СИФ. Докажем сюрьективность и непрерывность
этого отображения.
188

Теорема 9.3. Отображение ф : Е —>■ А, заданное
формулой
\/а = G\o~2 .. .сгп- - • е Е
ф(а) = lim 1аЛ1<т2(1аЛ- • • Un{x)...),
п—>оо
сюрьективно и непрерывно.
Доказательство
1. Непрерывность.
Надо показать, что для
Ve>0 36 >0:
V(T,seE: d(a, я) < 6 => р(0(<т), </>(<)) < е.
Расстояние между образами р(ф(сг), ф(я)) равно
р( lim /„,(... /.„(ж)...), Нт /«(...Д,(а:)...) =
п—>оо п—юо
= lim р(/„,(/„,(.../„„(*). ..)>/«(/«(• • •/«.(*) •••))•
п—>оо
Если J < тдщйг, то первые п компонент у
последовательностей а и я одинаковы:
с\ = Si, сг2 = $2, • • • crn = яп,
поэтому для М > п верно неравенство
Р(Л, (fa, (■■■ fa,, (*) . . . ), /« (/«(••• Л* (I)•••)) *S
< fc"p(/«r.+, (• • • Л« (*) • • •), Лп+1 (• • • /«, (ж) • • • ))•
Учитывая предыдущую теорему, имеем
p(fan+1 (• ■ • U, (Х)-.. ), Л.+1 (. • • UU (*)•■•))< D.
189

Отсюда
P(l/m /*„+! (• • • fvM (X) ■ • • )> l/m Л„+1 (• • • Лл/ (*) • • • )) <
Обозначим
У = lim fan+1(fan+2{- • • /<rM(s) • . . ),
M—>oo
z= Hm Лп+1(Лп+2(---Лм (*)•••)•
Тогда
МИ, *(?)) =
= P( lim /<т, (• • • /a„ (ж)...), lim /n (... /,„(ж)...)) <
M—юо M—юо
< A;np( lim /ffn+1 (... /ffJW (x)...), lim /<n+1 (... f,M (x)...
M—>oo M—>-oo
Выбирая n таким, что knD < e, получаем
р(ф{а),ф{я)) <е,
как только
с?(сг, <г) < 5 <
Непрерывность отображения ф доказана.
2. Сюрьективность.
Рассмотрим произвольную точку а € А. Всякая
точка аттрактора является предельной точкой для
некоторой фундаментальной последовательности образов:
а = Пт /a(n)i(/a(n)2(/<r(n)3(- • • f<r(n)n(x) ...),
п—>оо
190

/a(n)1(/a(n)a(/a(n)3(---/a(n)n(a:)...) G ^П(Я)
Ухен е к(Х).
Продолжим произвольным образом конечные
последовательности индексов
{a(n)i,a(n)2, сг(п)з,..., а(п)п}
до бесконечности. Получим последовательность
элементов кодового пространства {сг(п)}^=1 таких, что
а = lim ф(а(п),п,х).
П—¥00
Поскольку пространство Е компактно, то у
последовательности {а(п)}™=1 должна быть сходящаяся
подпоследовательность .
Без ограничения общности можно считать, что
последовательность {<т(п)}™=1 сходится.
В силу специфики пространства Е любая его
сходящаяся подпоследовательность устроена следующим
образом: для Уп существует номер М такой, что как
только номера членов этой последовательности
элементов Е больше чем М, так все первые п компонент
этих элементов совпадают.
Иначе говоря, если у последовательности {^(i)}^
есть предел a Е Е, то из г > М следует
a(i)r = аг, г = 1,2,... , п.
Отсюда следует
а = lim ф(а, п,х),
п—*оо
что и требовалось доказать.
191

Теорема доказана.
Определение 9.1. Отображение ф : Е —> А, заданное
формулой
Vcr = 0~\О2 .. .ап- ■ ■ Е Е
ф(а) = lim Л1(/а2(/а3(- • • f*n(x) • • •),
п—>оо
называется адресной функцией системы итерированных
преобразований.
Дадим еще несколько определений.
Определение 9.2. Адресом точки а аттрактора А
системы гиперболических итерируемых функций
называется любой элемент прообраза точки а при отображении
ф : Е —> А кодового пространства в аттрактор этой
СИФ.
Определение 9.3. Система гиперболических
итерируемых функций называется вполне несвязной, если
каждая точка ее аттрактора имеет единственный адрес.
Определение 9.4. Система гиперболических
итерируемых функций называется системой с касанием, если
число тех точек ее аттрактора, которые имеют больше
одного адреса, счетно.
Замечание. В книге М.Барнсли дается другое
определение системы с касанием, на наш взгляд, неудачное,
поскольку треугольник Серпинского, который обладает
всеми свойствами системы с касанием, под определение
Барнсли не попадает.
По Барнсли, СИФ является системой с касанием, если
существует открытое множество Q С А такое, что
выполнены следующие два условия:
vljmcn, /<(rt)n/i(rt) = 0,
Vt#j, t,i = l,2 ЛГ.
192

Примером СИФ с касанием по определению Барнсли
является следующая СИФ:
{R;-*,-* + -}.
Аттрактором А этой СИФ является отрезок [0,1]. Все
рациональные точки аттрактора,представимые в виде
несократимой дроби со степенью числа 2 в знаменателе, имеют
по два адреса. Все остальные точки этого аттрактора
имеют по одному адресу. Таким образом, число точек этого
аттрактора, имеющих больше одного адреса, счетно.
Если в качестве множества Q С. А выбрать интервал
(0,1), то условие Барнсли будет выполнено.
Определение 9.5. Системой с перекрытием
называется СИФ, не удовлетворяющая первым двум
определениям, то есть не являющаяся ни системой вполне
несвязной, ни системой с касанием.
9.3. Примеры различных типов СИФ
Перечислим системы итерированных функций разного
типа.
1) Канторово множество — вполне несвязно;
2) кривая Коха — с касанием;
3) фрактал Леви — с перекрытием;
4) {R; |х, \х + |} — вполне несвязно;
5) {R; |х, |х + |} — с перекрытием;
6) {R; |ж, \х + |} — с касанием;
7) {R; \х, \х + |} — с перекрытием;
8) {R; |х, \х + |} — вполне несвязно.
Теорема 9.4. Рассмотрим СИФ {X, /i} г = 1,2,..., TV}
с инъективными преобразованиями fi,i = 1,2, ...,iV и
аттрактором А. Эта система вполне несвязна тогда и
193

только тогда, когда образы аттрактора при этих
преобразованиях не пересекаются:
MA)nfj(A) = 0 Vi,j €{1,2,...,N},i?j.
Доказательство. Пусть существует непустое
пересечение /^ П fj = Б, В^0, be В, тогда точка
6 = /«(c) = /j(d)
и имеет по крайней мере два адреса
а = гф~1(с) и я = зФ~1{о1).
Наоборот, если точка b имееет хотя бы два различных
адреса а ф с, то у этих адресов первые (/с — 1) индексов
совпадут, а на А;-том месте будут разные индексы.
Возможно, к = 1. Преобразования /$, г = 1,2,. ..,7V инъективны
на аттракторе, то есть имеют обратные преобразования из
соответствующего образа в аттрактор:
fi1 : fi(A) ^ A, i = l,2,...,N.
Точка
/.-'(/^(•••(/i.w---)
будет принадлежать аттрактору и иметь два разных
адреса, у которых различаются уже первые компоненты. Но
мы знаем, что первая компонента адреса указывает на
принадлежность точки образу соответствующего
преобразования. Значит, в этом случае точка
лежит в пересечении образов двух разных преобразова-
194

НИИ.
Теорема доказана.
Теорема 9.5. Рассмотрим СИФ {X, /», г = 1,2,..., N}
с преобразованиями fi,i = 1,2,..., N и аттрактором А.
Если система вполне несвязна, то преобразования
fi,i = l,2,...,N
взаимно-однозначны на аттракторе А.
Доказательство. Предположим, что это не так и
существует /г, 1 ^ г ^ N и две разные точки аттрактора
а\,а2 G Л, а\ ф а2 такие, что fi(a\) = fi(a2) = a G А.
Поскольку точки а\ и а2 различны, то и адреса их о\а2 • • •
и QiQ2... различны, а это значит, что точка а
аттрактора имеет два различных адреса га\и2 ... и^^..., что
противоречит тому, что система вполне несвязна.
Теорема доказана.
Упражнения
1. Найдите на Канторовом множестве координаты точек с
адресами (12),122(211).
2. Найдите на треугольнике Серпинского координаты
точек с адресами (32),312(213).
3. Найдите на кривой Коха координаты точек с
адресами 211(12),122(121).
4. Найдите на аттракторе СИФ
{R1, h{x) = 0.25ж, f2(x) = 0.75ж + 0.25}
координаты точек с адресами (122),22(221).
5. Найдите адреса точек х = 0.9 и у = | Канторова
множества.
195

6. Найдите адреса точек х = Щ и у = ^ аттрактора
СИФ
{R1, /г(х) = 0.25z, f2(x) = 0.75z + 0.25}.
7. Найдите адреса точек х = (§, *§) и у = (|, ||)
кривой Коха.
8. Найдите адреса точек ж = (|,|)и^=(|,^|)
треугольника Серпинского.
9. Определить тип СИФ:
a) кривая Коха;
b) фрактал Леви;
c) {R1, h(x) = 0.25x, f2(x) = 0.75х + 0.25};
d) {R1, fi(x) = 0.5s, f2[x) = 0.75x + 0.25};
e) {R1, /i(z) = 0.25x, f2{x) = O.bx + 0.25};
/) {R1, fi(x) = 0.25:r, f2(x) = 0.25* + 0.75};
д) {R2, /i(f) = 0.25£, f2[x) = 0.5£ + (0.5,0),
/3(£) = 0.25£+ (0,0.75)};
/i) {R2,/i(f) = 0.75f,/2(f) = 0.752 + (0.25,0),
/3(£) = 0.252 + (0,0.75)};
г) {R2,/i(f) = 0.252,/2(2) = 0.52+ (0.5,0),
/з(2) = 0.252 + (0,0.75)}.
196

Примеры решения задач
1. Найдите на кривой Коха координаты точки с
адресом 21(112).
Решение
Искомая точка х является пределом
последовательности:
х= lim /а1(/^(Лз(...(/(7„(у)...)>
п—>-оо
где а = {cri,cr2,cr3,...} = 21(112),
а преобразования fi = L,f2 = R определяют СИФ:
{R2,
аттрактором которой является кривая Коха.
Рассмотрим предел последовательности
z= lim /а3(/а4Utb(• • • (/*»(#) • • • )•
п—юо
Поскольку выполнено: сг^ = cri+3, при г > 2, то в
приведенной последовательности есть подпоследовательность вида
{(/i(/i(/a(2)))n}SLi,
которая сходится к неподвижной точке сжимающего
преобразования /i(/i(/2(-))) плоскости. Эту точку можно
найти, решив уравнение
197

Подставим вместо /i и /2 выражения для L и R и получим:
^=, Ь + 275^'
V = I *Zl~ *%** + 2
1 1 у 1~ I 1
=21 — ~Z2
2>/3A1 2^ "Г 2уд/
Окончательный вид у системы линейных уравнений
следующий:
{ Zl = ^Z\~ ёТз^2 + б' i
^ Z2 = ~e7sZl~ 6^ + ^75 '
Решением этой системы уравнений является вектор
37
Точка z является пределом последовательности
{ап_2 = Д,(/„4(Л»(-.. (Л,® ... )}~=3,
поэтому предел последовательности
х = lim f^if^ifasi- ■ ■ (f*n(y) • • •)
п—>-оо
может быть найден, если к вектору z применить
преобразования fa2 и fai:
£=/<Tl(/<72(2)),
198

откуда получаем
62
in
16
Это и будет искомая точка кривой Коха с адресом 21(112).
2. Найдите адрес точки х = | аттрактора СИФ
{R1, /г(х) = 0.25z, f2(x) = 0.75z + 0.25}.
Решение
Аттрактором исходной СИФ является отрезок [0,1]:
[0,1] = /1([0,1])U/2([0,1])
°4
V
Точка х = | лежит в отрезке [|, 1], значит первая
компонента ее адреса равна 2.
Точка х\ = /^(х) = |(| — \) = | лежит в отрезке [0, |],
значит вторая компонента адреса х равна 1.
Точка Х2 = f\l(x\) = | лежит в отрезке [|, 1], значит
третья компонента адреса х равна 2.
Точка х3 = /2_1(^2) = §(§ — \) = ^ лежит в отрезке
[|, 1], значит четвертая компонента адреса х равна 2.
Точка Х4 = /г"1^) = f (^ — \) = £i лежит в отрезке
[0, |], значит пятая компонента адреса х равна 1.
Аналогичным способом получим точки
_ 4 _ 16 _ 64
*5~81,Я;6~81,Я;7~81
и шестую, седьмую и восьмую компоненты адреса: 1,1,2.
Степень числа 3 в знаменателе дроби все время
растет, поэтому адрес не будет периодической или «в
конце концов» периодической последовательностью, и можно
просто считать, что нас интересует несколько знаков этой
199

1
0.7
4
и
1
т,1
4'
последовательности, например, семь. Тогда адрес равен:
2122111 плюс неизвестный нам хвост.
Если нас интересуют восемь компонент, то это 21221112..
3. Найдите адрес точки х = ^ аттрактора СИФ
{R1, /г(х) = 0.25z, f2(x) = 0.75х + 0.25}.
Решение
Аттрактором исходной СИФ является отрезок [0,1]:
[0,1] = /,([0,1])U/2([0,1]) =
Точка х = y|g лежит в отрезке [0, |], значит первая
компонента ее адреса равна 1.
Точка Х\ = /^(х) = -^ лежит в отрезке [0, |], значит
вторая компонента адреса х равна 1.
Точка х2 = /i_1(^i) = js лежит в отрезке [0, |], значит
третья компонента адреса х равна 1.
Точка £3 = Л-1 (х2) = з| лежит в отрезке [|, 1], значит
четвертая компонента адреса х равна 2.
Точка х4 = 12~1(хз) = f(i| ~ \) = и = Х2 лежит в
отрезке [0, |], значит пятая компонента адреса х равна 1.
Поскольку х4 = х2, постольку хъ = хб, то есть дальше
адрес будет циклично повторяться. Следовательно, адрес
точки х = j^g аттрактора СИФ
{R1, h(x) = 0.25х, f2(x) = 0.75х + 0.25}
равен 11(12).
4. Определить тип СИФ:
{R2,/i(f) = 0.5f,/2(x) = 0.75£ + (0.25,0.25),
200

f3(x) = 0.5x + (0,0.5)}.
Решение
Аттрактором А исходной СИФ является структура,
похожая на треугольник Серпинского, но более «плотно»
устроенная, поскольку образы аттрактора при
преобразованиях СИФ пересекаются по целым отрезкам:
fi(A)nf2(A) dB, В = {х\0.5^х1 ^ 0.75,z2 = 0}.
Следовательно, это система с перекрытием.
201

Глава 10. Динамические системы
Определение 10.1. Динамической системой на
множестве X (топологическом или метрическом
пространстве) называется это множество X (топологическое или
метрическое пространство) и его преобразование
f : X -> X.
Обозначается динамическая система в виде пары {X, /}.
Примеры динамических систем
1) {R,f(x) = x2};
2) {R2,f(x) = Ax + b};
3) {R,/(aO = sin(;c)};
4) {*,/(*)= (4>
5) {Г, /i(a) = 1сг1сг2 ... }, а = ага2 • • • G Е.
Определение 10.2. Орбитой точки х динамической
системы {X, /} называется последовательность точек
{Xi = f(x)}Z0
пространства X, где
/*(*) = /(/(•••/(*)•••), f(x)=x.
г
202

Примеры орбит точек динамических систем
1. Динамическая система {R, f(x) = х2}, х = 2. Орбита
этой точки
{2,4,16,256,...,(...(22)2)2...)2,...}.
2. Динамическая система
{R2J(x) = Ax + b},
Орбита точки х — это последовательность
И1) (3) и f*-1) }
IW'w'w'"Л о )■■■)'
что легко вычислить непосредственно.
Для этой же динамической системы орбита х = (°)
— это последовательность
нО'У'U'lsJ'-i * )■■■}•
что также легко вычислить непосредственно.
Для этой же динамической системы орбита х = (~х)
— это постоянная последовательность
{(оМо)-(о)-}'
203

что следует из равенства
4-.') ♦'-Г.1)-
3. Динамическая система
{R2,f(x) = Ax + b},
-(_»;)• '-©• *■©■
Орбита точки х — это последовательность,
состоящая из четырех точек
W'V-J'V-J'W'-J'
что легко вычислить непосредственно.
Для этой же динамической системы орбита точки
х = (J) — это также последовательность, состоящая
из четырех точек
{ШоМ-2М::)-1
что также легко вычислить непосредственно.
Для этой же динамической системы орбита точки
х = (_2i) — это постоянная последовательность
204

что следует из равенства
А(4)+Ч-\>
4. Динамическая система
{R,f(x) = sin(a;)},
х = 0, у = 1, z = 10.
Орбитой точки х будет постоянная
последовательность {х{ = 0}г^0,
Орбитой точки у будет последовательность
{lft = sm(...(sml)...)}eo,
г
причем
sin 1 < 1, sin(sin 1) < sin 1,...,
sin(... (sin 1). •.) < sin(... (sin 1)... )•
4 v ' Ч v '
i i—\
Эта последовательность монотонна и сходится к 0.
Обитой точки z будет последовательность
{2i = sin(...(SinlO)...)}£o.
г
причем
sin 10 < 1, sin(sin 10) < sin 10 < 1,...,
sin(... (sin 10)...) < sin(... (sin 10)...).
4 v ' ^^ v '
г г—1
И эта последовательность монотонно сходится к 0.
205

5. Динамическая система
{Ra'/(f)=Cfi>'
Орбита точки х = Q) — это постоянная
последовательность
{*=(;)}£..
орбитой точки х = (2) будет неограниченно
возрастающая последовательность
^Xi = \2i+1 Jj^0'
орбита точки х = (~ ) — это последовательность
{«•ш -(',)-•}:•
постоянная начиная со второго ее члена.
6. Динамическая система
{Г, /i(cr) = l<7icr2... }, а = gig2 • • • € Е.
Орбитой точки а = а\а2- • • € Е будет
последовательность последовательностей
{cricr2...; l<7i<72...; 1,1,(7! 0-2. ••;
...1,!,...,! crio-2...}~05
которая сходится к постоянной последовательности
{1,1,1,...}.
206

Замечание. На приведенных примерах можно увидеть
совершенно разное поведение орбит даже в пределах одной
динамической системы. Некоторые орбиты ограниченны,
некоторые стремятся к бесконечности. Какие-то орбиты
состоят из конечного числа точек, какие-то — из
бесконечного, какие-то орбиты возвращаются в исходную
точку, какае-то — нет. Наибольший интерес для нашего
изучения представляет поведение орбит точек динамических
систем.
Определение неподвижной точки преобразования было
дано раньше.
Определение 10.3. Неподвижной точкой
динамической системы будем считать неподвижную точку
соответствующего преобразования, задающего эту систему.
Преобразование произвольно, поэтому неподвижных
точек может быть несколько, а может и вовсе не
существовать. Например, для динамической системы
{R2,/(£) = Аг + 6},
существует только одна неподвижная точка (_2i),
2
для динамической системы
{B?,f(x) = Ax},
существует бесконечно много неподвижных точек — это
все точки с совпадающими координатами;
207

для динамической системы
{R2,/(£) = x+Q}
неподвижные точки отсутствуют.
Определение 10.4. Неподвижная точка х
преобразования f называется притягивающей неподвижной
точкой, если существует такой шар В(х,е) радиуса е с
центром в точке х, что
f{B(x,e)) С В(х,е),
и преобразование f является сжатием на В(х,е).
Определение 10.5. Неподвижная точка х
преобразования f называется отталкивающей неподвижной
точкой, если существуют такой шар В(х,е) радиуса е с
центром в точке х и положительное число с > 1, такие,
что для любой точки у Е В(х,е), у Ф х выполнено
неравенство
p(f(x),f(y)) >cp(x,y).
Определение 10.6. Точка х пространства X
называется периодической (циклической) точкой
преобразования f ( динамической системы) с периодом п, если
существует такое п > 0, для которого выполнено равенство
fn(x) = х. Наименьшее из таких чисел п называется
наименьшим периодом точки х. Орбита периодической
точки х называется периодической, или циклом.
Минимальный период точки — число различных точек ее орбиты.
Замечание. Обычно, если не оговорено противное, под
периодом понимают минимальный период, а слово
«минимальный» опускают.
Определение 10.7. Орбита точки х называется «в
208

конечном итоге периодической», если существуют такие
натуральные числа п и т, п ф т, что fn(x) = fm{x).
Определение 10.8. Периодическая точка х
преобразования f периода п называется притягивающей, если
она притягивающая неподвижная точка для
преобразования fn.
Определение 10.9. Периодическая точка х
преобразования f периода п называется отталкивающей, если
она отталкивающая неподвижная точка для
преобразования fn.
Определение 10.10. Периодическая орбита
преобразования f называется притягивающей, если она
содержит хотя бы одну притягивающую периодическую
точку преобразования f.
Определение 10.11. Периодическая орбита
преобразования f называется отталкивающей, если она
содержит хотя бы одну отталкивающую периодическую
точку преобразования f.
Примеры неподвижных точек и циклов
1. Динамическая система {R, f(x) = х2} имеет две
неподвижные точки 0 и 1. Точка 0 — притягивающая,
точка 1 — отталкивающая. Периодические орбиты
минимального периода больше 1 отсутствуют. В
конечном итоге периодической является орбита точки
-1.
2. Динамическая система
{R2J(x) = Ax + £},
-(s ;)■'-©■
209

У этой динамической системы есть ровно одна
отталкивающая неподвижная точка (~х), периодические и
в конечном итоге периодические орбиты
отсутствуют.
3. Динамическая система
{R2J(x) = Ax + b},
_ *-(il)-'-0-
Точка (_\) — неподвижная, при этом она не является
2
ни отталкивающей, ни притягивающей. Все
остальные орбиты этой динамической системы —
периодические, состоящие из четырех точек.
4. Динамическая система
{R,/(aO = sin(a:)}.
У этой динамической системы есть ровно одна
неподвижная точка 0, она является притягивающей.
Циклы и в конечном итоге периодические орбиты
отсутствуют.
5. Динамическая система
<*•'»-(£)>•
Эта динамическая система имеет бесконечное
множество неподвижных точек. Это точка (°) и все точки,
у которых первая координата равна 1. Точка (°) -
притягивающая, это нетрудно показать. Остальные
точки не являются ни притягивающими, ни оттал-
210

кивающими, поскольку образуют прямую на
плоскости, а это значит, что в окрестности каждой из них
найдутся точки, расстояние между которыми
неизменно. В конечном итоге периодическими являются
точки с первой координатой равной — 1, их орбита на
первом шаге попадает в неподвижную точку.
6. Динамическая система
{Г, /i(a) = 1ctiCt2 ... }, а = аха2 • • • G Г.
Отображение /i — сжатие, поэтому имеет ровно одну
неподвижную точку. Она притягивающая, никаких
циклов и в конечном итоге периодических орбит у
этой динамической системы нет.
7. Динамическая система
{£, Т{а) = а2а3 ... }, а = аха2 • • • G Г.
Неподвижными точками этой динамической системы
являются все постоянные последовательности. Их
столько, сколько символов. Все эти неподвижные
точки — отталкивающие. Периодическими являются
орбиты периодических последовательностей, все они —
отталкивающие циклы. В конечном итоге
периодическими являются последовательности, у которых
периодичное повторение символов наличествует, но
начинается не с первой компоненты.
8. Динамическая система
{R,/(*)},
„. . I х + 1, если х < 0;
№ = 1 ,i ^ п
I —х + I, если х ^ 0.
211

Для исследования этой системы полезно
воспользоваться паутинной диаграммой.
Рис. 36: Паутинная диаграмма: Xq = 1.75
У этой динамической системы ровно одна
неподвижная точка |, бесконечное число циклов периода 2 —
это орбиты точек отрезка [0,1], исключая точку \.
Все остальные орбиты этой системы — в конечном
итоге периодические.
Определение 10.12. Гомеоморфизмом топологических
пространствX иУ называется взаимно-однозначное сюръ-
ективное (то есть у каждого элемента есть и притом
ровно один прообраз) непрерывное отображение
пространства X в пространство Y такое, что обратное
отображение, ставящее каждому элементу пространства Y
его прообраз в пространстве X, также непрерывно.
212

Определение 10.13. Два метрических пространства
называются топологически эквивалентными, если
существует гомеоморфизм этих пространств, а именно
существует взаимно-однозначное, сюрьективное и
непрерывное отбраоюение в : X —»• Y такое, что обратное
отображение 0_1 :Y ^ X также непрерывно.
Замечание. Определение метрически эквивалентных
метрических пространств было дано в г. 2. Для метрической
эквивалентности необходимо и достаточно существование
взаимно-однозначного соответствия между множествами
X и У такого, что выполнена эквивалентность
собственной метрики и индуцированной с другого пространства.
Эквивалентность метрик есть требование более сильное,
чем непрерывность отображений.
Если взаимно-однозначное сюръективное отображение в :
X —> Y индуцирует на пространстве X метрику,
эквивалентную собственной метрике пространства X, то это
отображение непрерывно и обратное к нему отображение
также непрерывно.
Примеры эквивалентных и неэквивалентных
пространств
1. Отрезок [0,1] с евклидовой метрикой,
индуцированной с прямой, эквивалентен отрезку [5,120] с
аналогичной метрикой и топологически, и метрически.
Отображение в определено по формуле
(9(х) = 115х + 5.
Индуцированное расстояние р* между двумя
точками х и у отрезка [0,1] равно
р*(х,у) = р(0(х),0(у)) = 1115*+ 5- (115?/+ 5)| =
213

= 115|х -у\ = 115р(ж, у) =4> р * (х, у) ^ р(ж, у),
то есть собственное и индуцированное расстояния
эквивалентны.
2. Интервал (0,1) и прямая R с евклидовой метрикой
эквивалентны топологически, но не эквивалентны
метрически.
Взаимно-однозначное сюръективное непрерывное в
обе стороны отображение интервала в прямую
задает формула
в{х) = tg(7TX - J).
Но построить отображение, при котором собственное
и индуцированное расстояния были бы
эквивалентны, невозможно, поскольку расстояния на интервале
ограниченны, а на прямой можно найти точки,
между которыми расстояние будет сколь угодно
большим.
3. Интервал (0,1) и отрезок [0,1] неэквивалентны ни
топологически, ни метрически, поскольку нельзя
построить непрерывное в обе стороны
взаимнооднозначное сюръективное отображение из
интервала в отрезок.
Это легко объяснить. На отрезке всякая
бесконечная последовательность имеет предельную точку.
Если бы желаемое отображение существовало, то
любая последовательность на интервале вела бы себя
так же, как последовательность образов на отрезке,
то есть имела бы предельную точку. Но на
интервале есть последовательности, не имеющие предельных
точек, например
яг
Ып=1
214

I »» Jn=l
Определение 10.14. Две динамические системы
{XJ}u{Y,g}
эквивалентны, если существует такой гомеоморфизм в :
X —>• У пространств, что для любого х е X и любого
у еУ выполнены следующие равенства:
}{х) = в-\д{в{х))) и д{у) = ви{в-\у))).
Иначе говоря, коммутативна диаграмма:
X —в-+ У
Л 4
X —?-> У
Диаграмму можно нарисовать немного по-другому,
второй вариант тоже должен быть коммутативен:
X —^ X
У > У
9
215

Примеры эквивалентных динамических систем
1. Динамические системы
{(0,1),/(*) = ±*}
{{1,оо),д(х) = 2х}
эквивалентны.
Гомеоморфизм в задает формула в(х) = К
Легко проверить, что
Уже (0,1) в-1(д(в(х))) = /(х)
И
Vj,e(l,oo) e(f(e-1(y))) = g(y);
поэтому
в 1 д 2 е-1 х
хх 2
2. Рассмотрим две динамические системы:
{Канторово множество, f(x) = -х}
о
{Е = {бесконечные последовательности из 1 и 2},
s(a1a2cr3 ...) = lcricr2cr3 ... }.
Эти динамические системы эквивалентны,
эквивалентность задают троичное представление элемента
216

Канторова множества и замена в дробной части
этого представления всех нулей на единицы.
Теорема 10.1. Даны две эквивалентные
динамические системы
{X,f}~{Y,g},
эквивалентность определяется гомеоморфизмом в : X —>•
Y.
Тогда верны следующие утверждения:
10.1.1. Если х — неподвижная точка преобразования
f, то 6(х) — неподвижная точка преобразования д.
10.1.2. Если {xi, х2,..., хп} — цикл минимального
периода п динамической системы {X, /}, то
{в(х1),в(х2),в(х3),...,в(хп)}
— цикл минимального периода п динамической системы
{Y,g},
причем если {xi, х2,..., хп} — отталкивающий цикл, то
и
{е(х1),0(х2)10(х3)1...10(хп)}
— отталкивающий цикл.
10.1.3. Если
{Г(*)}~о
— в конечном итоге периодическая орбита динамической
системы {X,f}, то
{дп(в(х))}^0
— в конечном итоге периодическая орбита динамической
системы {Y,g}.
217

Замечание. Свойство цикла быть притягивающим при
эквивалентности динамических систем не сохраняется.
Упражнения
1. Найдите первые шесть элементов орбиты точки Хо для
следующих динамических систем:
1) {R, f{x) = х2 - 1}, х0 = -2;
2) {R, f(x)=x2-l}, x0 = ^;
3) {R2, /(S)=(| ~j)f}> fo=(l);
4) {R2, f{x) = ( -_\ ~\)S}, *o=(j).
2. Есть ли у вышеприведенных динамических систем
неподвижные точки и периодические орбиты? Если «да»,
то найдите все периодические орбиты вышеприведенных
систем периода не выше трех.
Примеры решения задач
Найдите для динамической системы
{[-2,2], /(*) = х2- 2}
все периодические орбиты, периода не выше 2. Сколько
эта система имеет периодических орбит периодов 3 и 4 ?
Решение.
Рассмотрим паутинную диаграмму для этой
динамической системы. На отрезке [—2,2] парабола у = х2 — 2
218

монотонно убывает от 2 до —2 на промежутке [—2,0] и
монотонно возростает от —2 до 2 на промежутке [0,2]. На
промежутке [—2,2] эта парабола пересекает прямую у = х
дважды: в точке х = — 1 и в точке х = 2. Это две
неподвижные точки данной динамической системы. Найдем
периодические орбиты этой системы периода 2.
Рассмотрим уравнение:
{х2-2)2-2 = х <^х4-4х2-х + 2 = 0.
Многочлен х4 — 4х2 — х + 2 поделим на произведение
(х + 1){х - 2),
поскольку в точках х = -1их = 2 выполнено равенство
f(x) = х, а значит, и равенство f(f(x)) = x. Частное будет
равно х2 + х — 1.
Отсюда получаем, что многочлен хА — Ах2 — х + 2 имеет
четыре корня, а именно:
_1 о -i-v^ -1 + л/5
Х' А 2 ' 2 '
причем первые два корня являются неподвижными
точками динамической системы, а два другие образуют цикл
периода 2. Это легко увидеть и на паутинной диаграмме.
При применении функции f(x) = х2 — 2 дважды на
промежутке от —2 до 0, график такой композиции сначала
убывает от 2 до —2 при изменении а; от —2 до — у/2, потом
растет от —2 до 2 при изменении х от — л/2 до 0, пере-
-1-л/5
секая при этом график у = х дважды: в точке
и в точке -1. Аналогично, на промежутке [0,-2] график
функции f(f(x)) пересекает прямую у = х дважды в точ-
-1 + У5
ках и 2.
2
219

Если продолжить рассуждения, то при третьем
применении функции f(x) возникнет график, который будет
иметь восемь промежутков монотонности с изменением
значений от —2 до 2 или наоборот, и будет восемь раз
пересекать прямую у = х, при этом две точки пересечения
будут при х = — 1 и х = 2, т. е. соответствовать
неподвижным точкам, а шесть других будут образовывать две
орбиты периода 3.
Аналогично, при четвертом применении функции f(x)
возникнет график, который будет иметь шестнадцать
промежутков монотонности с изменением значений от —2 до 2
или, наоборот, от 2 до —2 и будет шестнадцать раз
пересекать прямую у = х, при этом две точки пересечения будут
при х = — 1 и х = 2, то есть соответствовать неподвижным
— 1 - л/5 —1 + л/5 ,
точкам, две точки и образуют цикл
периода 2, а оставшиеся двенадцать будут образовывать три
орбиты периода 4.
Рис. 37: Графики /, /<2>, /<3)
220

Глава 11. Динамика на фракталах
Определение 11.1. Рассмотрим вполне несвязную
систему итерированных функций
{X, /ь/г,.. • ,/лг}
с аттрактором А. Определим преобразование S на
аттракторе А по формуле
\/аеА S(a) = fr1(a),
для такого преобразования fi, что a Е fi(A).
Поскольку система вполне несвязна, преобразования
/ъ /г, • • •, /лг инъективны, их образы на аттракторе А
не пересекаются, а объединение этих образов образует
в точности аттрактор А, постольку преобразование S
определено корректно.
Преобразование S называется преобразованием
(обратного) сдвига на аттракторе А, а динамическая система
{A, S} называется системой (обратного) сдвига.
Теорема 11.1. Рассмотрим вполне несвязную
систему итерированных функций
{^?/ь/2, • • • ,/лг}
с аттрактором А. Пусть Е — кодовое пространство
данной СИФ, определенное на N символах. На кодовом
пространстве Е задана динамическая система с помощью
отображения Т, стирающего первый элемент
последовательности:
{Z1, Т}, Т(а) = сг2<7з ..., а = o\G<i • • • Е Е.
221

Тогда динамическая система на кодовом пространстве
{Е,Т}
эквивалентна динамической системе сдвига на
аттракторе
{A,S}.
Доказательство. Гомеоморфизмом, задающим
эквивалентность динамических систем является адресная
функция ф : Е -> А.
Можно ли построить динамическую систему на
аттракторе в случае, если СИФ, задающая этот аттрактор, не
является вполне несвязной? Эта задача разрешима при
некоторых дополнительных предположениях.
Рассмотрим систему итерированных функций
{^/ьЛ, • • • ,In}
с аттрактором А.
Предположим, что преобразования {/i, /2, • • •, In}
взаимнооднозначны, но система не является вполне несвязной.
Наша задача — построить аналог динамической системы
сдвига на аттракторе. Если для каждой точки х Е А искать
образ S(x) = f^l(x) при условии х Е fi(A), то
отображение S : А —> А будет неоднозначным, поскольку некоторые
точки аттрактора лежат в образах fi(A) аттрактора при
разных г. Тем не менее можно рассмотреть
последовательности
{xJ-\x)J-\}-\x)),f-\f-\f-\x))),...}
при предположении, что все обратные отображения имеют
222

смысл. Такие последовательности напоминают орбиты, но
ввиду неоднозначности S орбитами не являются. В любой
динамической системе если две орбиты имеют одинаковый
элемент, то и все остальные элементы этих орбит,
следующие за ним, у них совпадают. В последовательностях
это свойство не выполняется. Говоря бытовым языком,
орбита задана своим начальным элементом однозначно, в
то время как построенные последовательности могут
сходиться и расходиться, как пересекающиеся тропинки.
Определение 11.2. Назовем последовательность
при предположении, что все обратные отображения
имеют смысл, орбитой случайного сдвига точки х.
Пример. Рассмотрим СИФ
{[0,1]; h(x) = 0.5rr, f2(x) = 0.5* + 0.5}.
Для всех точек х Е [0,1], кроме точки 0.5, отображение
S(x) задано на отрезке [0,1] однозначно. Если точка х при
применении к ней произвольное число раз отображений
/i и /2 в произвольном порядке не попадет в точку 0.5, то
последовательность
совпадет с орбитой отображения S(x), где S(x) = f~l(x)
при условии х Е /г ([0,1]).
Если точка х = -^ G [0,1], то возможны две последова-
223

тельности вида
одинаковые в своей первой части до тех пор, пока не
появится член последовательности, равный 0.5, а затем все
члены первой последовательности станут равны нулю, а
второй — единице.
Вернемся к такой системе итерированных функций
{X,fUf2,...,M,
что преобразования {/i, /2, • • •, In} взаимно-однозначны,
но система не является вполне несвязной. Построим
новую вполне несвязную СИФ такую, что ее аттрактор
может быть спроецирован на аттрактор исходной СИФ. При
этом орбиты динамической системы сдвига построенной
СИФ проецируются на орбиты случайного сдвига
исходной СИФ.
Определение 11.3. Поднятой системой
итерированных функций для
"№ /i 5 /2, • • • ,/n}
с взаимно-однозначными преобразованиями
{/ъ/2? • • • 5/лг}
и адресным пространством Е называется следующая
система итерированных функций:
{XxZJ*(x,a) = (fi(x),ia1a2...),i = l,...N}.
224

Легко показать, что аттрактором поднятой системы
будет множество пар (х, а) таких, у которых первая
компонента лежит в аттракторе исходной СИФ, а вторая
является адресом первой компоненты в исходной СИФ.
Одновременно, вторая компонента является адресом пары в
поднятой СИФ. Из последнего следует, что поднятая система
вполне несвязна, поскольку разные адреса соответствуют
разным точкам аттрактора. Таким образом, у поднятой
СИФ существует динамическая система сдвига.
Рис. 38: Динамика поднятой СИФ
Теорема 11.2. Возьмем произвольную орбиту
случайного сдвига для СИФ
{^, /ъЛ, • • • ,/n}
с взаимно-однозначными преобразованиями
{/ь/г, • • • ,/#}•
Тогда существует такая орбита динамической системы
225

сдвига поднятой СИФ
{X х Г, f*(x, a) = {fi{x), гаха2 ...), г = 1,... N},
что последовательность первых компонент элементов
этой орбиты составляет исходную орбиту случайного
сдвига.
Более того, последовательность первых компонент
элементов любой орбиты динамической системы сдвига
поднятой СИФ всегда является орбитой случайного сдвига
исходной СИФ.
Пример. Рассмотрим СИФ
Адресное пространство этой системы — все
последовательности, составленные из 1 и 2. Любую такую
последовательность можно интерпретировать как троичную запись
после запятой такой точки отрезка [0,1], у которой в этой
записи отсутствует цифра 0. Таким образом, адресное
пространство можно представить как подмножество отрезка
[0,1]. Если приписывать к последовательности слева
единицу (или двойку), то соответствующая точка отрезка
делится на 3 и складывается с | (соответственно |).
Поднятая СИФ имеет вид
{[0,l]x[0)l];/1'(i)«7)=Qi,iff + i
Проекции орбит динамической системы сдвига поднятой
СИФ на первую компоненту дают орбиты случайного
сдвига исходной СИФ.
■
226

Рассмотрим, к примеру, точку х = ^ Е [0,1].
Построим для нее орбиты случайного сдвига. Первый элемент
xq любой такой орбиты будет сама точка х = ^ Е [0,1].
Эта точка лежит только в образе /i([0,1]), поэтому
следующий элемент орбиты случайного сдвига Х\ будет точка
f\l{xo) = I' Аналогично, последующие элементы любой
орбиты случайного сдвига точки х = ^ равны
3 1
Точка хз = \ лежит в пересечении образов /i([0,1]) П
/2([0,1]), поэтому следующий элемент орбиты
случайного сдвига Х4 не определен однозначно и орбит случайного
сдвига может быть две: х± = /Г1^) = 1 и 14 = ./^(^з) =
0. Дальше для каждой орбиты случайного сдвига все
однозначно, у первой все последующие элементы равны 1, у
второй — 0. Получили две орбиты случайного сдвига
-ZLI з 1 1
16'8'4'2' ' ''-'J
— I - Inn
16'8'4'2' ' '•
Точка х = yq Е [0,1] имеет два адреса 1221222... и
1222111....
Аттрактор поднятой СИФ состоит из пар (точка
аттрактора исходной СИФ, ее адрес), поэтому есть две точки
аттрактора поднятой СИФ с первой компонентой х = ^,
а именно:
у= (^,1221222.
227

= (1,1222111...)
Орбиты динамической системы сдвига точки у и точки
z определены однозначно:
{2/о = 2/= (j£, 1221222.. Л , у, = Q, 221222 .
2/2= Q,21222... ),2/3=Q, 1222... Vy4 = (1,222..
г/5 = (1,222...) = у6 = у7 = ... }
и
{г°=2=(hi222in • • •)'zi=(Ь2221п • • •
z2 = f ?, 22111... V*3 = Q,2111...V^ = (0,lll...)i
z5 = (0,111...) = z6 = z7 = ...}.
Первые компоненты этих орбит составляют орбиты
случайного сдвига точки х = ^ G [0,1].
Мы вычисляли орбиты точно. Возникает вопрос: если
при вычислениях на каждом шаге допускается
незначительная ошибка, как совокупность этих ошибок влияет на
результат? Оценить это помогает следующая теорема.
Теорема 11.3 (о вычислении орбит с ошибками
— теорема затенения). Рассмотрим вполне несвязную
систему итерированных функций
{X, /i, /2, • • • ,/n}
228

с аттрактором А и коэффициентом сжатия к. На ней
определена динамическая система сдвига с помощью
преобразования S(x) = ^_1(х), при условии, что х Е fi(A).
Рассмотрим последовательность точек аттрактора
{х*}^о шакую, что для некоторого заданного
положительного числа е и всех п от 1 до оо выполнено
неравенство p«,S«_i)) <e.
Тогда существует орбита динамической системы
сдвига {хп = 5n(xo)}^L0 такая, что для всех п от 0 до оо
выполнено неравенство
( * \ ^ ке
Комментарий. Название (теорема затенения) говорит
о том, что орбита, вычисленная с ошибками, находится в
окрестности (в тени) некоторой настоящей орбиты.
Однако надо помнить, что первоначальная орбита с ошибками
подразумевает, что все точки {х*п}^0 лежат в аттракторе
А, в противном случае теорема не работает. Это значит,
что просто округлять вычисления не всегда возможно, ибо
округленное значение может не лежать в аттракторе.
Доказательство. Преобразование сдвига S для
каждой точки аттрактора совпадает с обратным
преобразованием ровно одного из преобразований СИФ
{/ъ/г, • • • ,/лг},
поэтому для каждого элемента последовательности {x*n}™=i
существует свое число гп от 1 до N такое, что
Построим последовательность {i0iiz2 ... }. Эта последова-
229

тельность является элементом кодового пространства, а
значит, адресом некоторой точки х аттрактора А.
Выберем в качестве искомой орбиты орбиту этой
точки:
{х0 = x,xi = S(x0) = fr1(x),...
xn = Sn(xQ) = fr\fr\i(...f-i(x)...),...}.
Сравним попарные расстояния между членами двух
последовательностей: {#*}5JL0 и ixn}™=o-
Выберем достаточно большое число М ^> 0.
Поскольку точки обеих последовательностей лежат в аттракторе,
выполнено неравенство
p№m_iW/) ^ DA <оо,
где DA — диаметр аттрактора.
Следовательно, учитывая, что хм = S(xm-i),
получаем
p(S(x*M_1),S(xM.1)) < DA < со.
Точка х была выбрана таким образом, что для любого п
выполнено
Ь(хп) — Jin \xn)i
а это значит, что верно неравенство
Сй-А^Ы) ^DA<oo.
Преобразование f^[x — сжимающее с коэфициентом
сжатия к, поэтому верно неравенство
P^Jf-i^M-i) ^ kDA,
которое можно переписать в следующем виде:
p(x*M_vS(xM-2)) ^kDA.
230

Воспользуемся правилом треугольника:
p{S(x*M_2),S{xM-2)) ^
хМ-2)'ХМ-1 ) + р{х*м-ъ S(xM-2)) < £ + /с£>А
Повторяя предыдущие рассуждения, получаем
P(X*M-2i ХМ-2) ^ fc(£ + fcDA).
Проделав такие рассуждения большое число раз,
получаем, что для любого п : 0 < п ^ М верно равенство:
р{х*м_п, хм-п) ^ ке + к2е + к3е + • • • + kn~le + knDA.
Заменив обозначения I = М — п, получаем, что для любого
I : 0 ^ I < М верно равенство
p{x*t, xi) ^ ке + к2е + к3е + • • • + kM~l~le + kM~lDA.
Устремив М к бесконечности, получим неравенство,
верное для любого / ^ 0:
ке
р(х%xt) ^ ке+к2е+к3е+- • • = ек(1+к+к2+к3+. ..) = - -.
I — А;
Теорема доказана.
Пример
Рассмотрим пространство последовательностей из двух
элементов — адресное пространство СИФ с двумя
преобразованиями. Введем на нем преобразования,
приписывающие последовательности слева цифры 1 или 2, то есть
построим такую СИФ:
{Г, /i(cr) = 1<710-2сгз ..., f2(a) = 2ага2а3 ....}.
Динамическая система сдвига на пространстве Е осуществ-
231

ляется преобразованием Т, стирающим первую
компоненту последовательности. Рассмотрим постоянную
последовательность элементов U, то есть последовательность
одинаковых последовательностей:
{< = (12)}^ ,.
Орбитой первого элемента этой последовательности будет
последовательность
{й»-1 = (12),1йп = (21)}^.1.
Расстояние между соответствующими элементами
исходной последовательности и орбиты ее первого элемента
достигает, но не превосходит |. Можно ли найти орбиту
динамической системы сдвига, элементы которой ближе к
элементам исходной последовательности?
Воспользуемся только что доказанной теоремой.
Преобразование Т у каждого элемента исходной
последовательности стирает первый элемент, в данном случае это
всегда 1. Это значит, что в данном случае всегда
Т«) = /Г1«) = (21),
значит начальная точка орбиты будет иметь адрес (1), то
есть в данном случае xq = (1). В результате получаем
постоянную орбиту {хп = (l)}JJLi, расстояние между
элементами которой и элементами исходной
последовательности не превосходит |. По оценкам теоремы эта разница
не должна превосходить ^. В данном случае к = |, а
е = р(х*п, Т{х*п_1)) = р((12), (21)) = |, то есть должна быть
не больше |, а значит, в данном примере оценка даже с
большим запасом.
232

Упражнения
1. Найдите первые шесть элементов орбиты
динамической системы сдвига точки Xq на аттракторе для
следующих систем итерированных функций:
a) {R, /х(д;) = |ж, /2(ж) = |ж + §}, х0 = 0.25;
b) {R, fi(x) = \x,f2(x) = lx + l}, х0 = ±;
c) {R, f1{x) = lx,f2{x) = lx + j}, xQ = ^-
d) {Н2,Л(£) = if, /2(f) = И+ (о)' /a(f) =
e) {Н2,Л(£) = |f, /2(f) = 5*+ ( § ) » ЛИ =
2. Для СИФ {R, fx{x) = \xj2{x) = \x + \) и точки
£o = y§ вычислить все возможные орбиты
случайного сдвига.
3. Найти точки СИФ
{В?,Ш) = \х, f2(x) = !*+(!), h{x) = \$ ( 2 )}
имеющие несколько орбит случайного сдвига.
4. Найти вид преобразования динамической системы
сдвига для поднятой СИФ
{R2,/i(*) = \i, /2(f) = f*+( g ) . /з(*) = \*( | )}
233

вточке(х0,а) = {( \ J, 2(3)).
Пример реп1ения задач
Найдите для динамической системы сдвига на
аттракторе СИФ {R, fi(x) = |х, /г(^) = \х + |} орбиту точки
хо = \-
Решение
Точка х0 = \ лежит в образе первого
преобразования, поскольку \ < \- Следовательно, следующей точкой
орбиты будет точка х\ = /f1^) = f' К0Т0Рая Уже ле_
жит в образе второго преобразования. Поэтому
следующей точкой орбиты динамической системы сдвига будет
точка х2 = J2l{xi) = 3| — 2, которая совпадает с точкой
х0. Таким образом, орбита точки х0 = \ является циклом
с периодом 2.
234

Глава 12. Хаотическая динамика
Определение 12.1. Подмножество В С X
называется всюду плотным подмножеством метрического
пространства X, если его замыкание совпадает с X:
~В = Х.
Замечание. Если множество точек орбиты Я/
динамической системы на X всюду плотно в X, то для любой
точки a Е X существует подпоследовательность этой
орбиты, имеющая своим пределом точку а.
Примеры всюду плотных множеств
1. Рациональные числа всюду плотны во множестве всех
действительных чисел R.
2. Множество всех периодических последовательностей
всюду плотно в адресном пространстве Е.
3. Рассмотрим все конечные последовательности из двух
символов 1 и 2. Таких последовательностей счетное
число. Пересчитать их можно следующим образом:
упорядочим все последовательности из п элементов,
принимающих значения 1 или 2 лексико-графическим
способом. Это значит, что если у
последовательностей а и /3 первые к элементов одинаковы, а на к + 1
месте у а стоит 1, а у /3 — 2, то а < /3. Кроме
того, будем считать, что любая более короткая
последовательность меньше любой более длинной. Таким
235

образом, упорядочено все множество Т конечных
последовательностей из двух символов 1 и 2.
Поставленные по порядку без пробелов и запятых эти
последовательности образуют новую бесконечную
последовательность Т, являющуюся элементом
кодового пространства Е бесконечных
последовательностей из двух символов 1 и 2. Орбита точки Т
динамической системы {Е, Т}, в которой преобразование
Т стирает первую компоненту последовательности,
будет всюду плотной в Е.
4. Рассмотрим динамическую систему на окружности,
удваивающую угол в полярных координатах точки.
Орбина точки, чей угол несоизмерим с 7г, будет всюду
плотна на окружности.
Замечание. Свойство подмножества быть всюду
плотным сохраняется при гомеоморфизме пространств. Это
означает, что верна следующая теорема.
Теорема 12.1. Подмножество В метрического
пространства X всюду плотно в X, гомеоморфному
некоторому метрическому пространству Y = О(Х), тогда и
только тогда, когда образ 0(B) всюду плотен в Y. Если
на X задана динамическая система{Х, /}, а на Y
задана эквивалентная система {Y,g}, то орбита Ох точки
х Е X всюду плотна в X тогда и только тогда, когда
орбита О у точки у = О(х) Е Y всюду плотна в Y.
Определение 12.2. Динамическая система {X, /}
называется транзитивной, если для любых открытых
множеств U и V метрического пространства X найдется
такое целое число п ^ 0, что выполнено
fn(U)HV^0.
236

Примеры транзитивных и нетранзитивных
динамических систем
1) {[0,1]; f(x) = min{2x, 2 — 2х}} — транзитивна;
2) {[0,1]; f(x) = 2x(modl)} — транзитивна;
3) {[0,1]; f(x) = 0.5х} — не транзитивна;
4) {R; f(x) = 2х} — не транзитивна;
5) {R2; f(x) = Ах + 6}, где А — матрица поворота, —
не транзитивна.
Теорема 12.2. Эквивалентные динамические
системы транзитивны или нетранзитивны одновременно.
Иначе говоря, динамическая система {Y,g}, эквивалентная
динамической системе {X, /}, транзитивна тогда и
только тогда, когда транзитивна {X,f}.
Доказательство несложно и может быть предложено в
качестве упражнения.
Определение 12.3. Динамическая система {X, /}
называется чувствительной к начальным условиям, если
существует 5 > О такое, что для любого х Е X и любого
шара В(х, е) существуют точка у Е В(х, е) и целое число
п > 0, такие, что выполнено неравенство
p(F(x)Jn(y))>S-
Иногда, вместо «чувствительна к начальным
условиям» говорят «существенно зависит от начальных условий».
237

Примеры существенной зависимости от
начальных условий и ее отсутствия
1) {[0,1]; f(x) = min{2x, 2 — 2х}} — чувствительна к
начальным условиям;
2) {[0,1]; f(x) = 2x(modl)} — чувствительна к
начальным условиям;
3) {[0,1];/(ж) = 0.5а;} — нечувствительна к
начальным условиям;
4) {R; f(x) = 2х} — чувствительна к начальным
условиям;
5) {R2; f(x) = Ах + &}, где А — матрица поворота, —
чувствительна к начальным условиям.
Рассмотрим две динамические системы
{(0,1); f{x) = 0.5а;} и {В?1; f(x) = 2х}.
Эти системы эквивалентны, эквивалентность
устанавливается с помощью гомеоморфизма 9 : R>: —> [0,1),
заданного формулой в(х) = х-1. При этом первая система
нечувствительна к начальным условиям, а вторая —
чувствительна.
Приведенный пример означает, что чувствительность
к начальным условиям не есть одновременно выполненое
(или невыполненое) свойство эквивалентных динамических
систем. Однако такой пример возможен только у
динамических систем, заданных на некомпактном пространстве.
Теорема 12.3 ( без доказательства). Пусть
метрические пространства X и Y компактны и
динамическая система {У, д} эквивалентна динамической системе
{X, /}. Тогда динамическая система {У, д}
чувствительна к начальным условиям тогда и только тогда, когда
динамическая система {X,f} чувствительна к
начальным условиям.
238

Определение 12.4. Динамическая система {X, /}
называется хаотичной, если:
1) она транзитивна;
2) она чувствительна к начальным условиям;
3) множество точек ее периодических орбит всюду
плотно в X.
Замечание. В действительности из первого и
третьего свойств приведенного выше определения обычно
следует его второе свойство. Этот факт доказывает следующая
теорема.
Теорема 12.4. Если динамическая система {X, /},
заданная на бесконечном метрическом пространстве {X, р)
с помощью непрерывного преобразования f : X —> X,
транзитивна, а множество точек ее периодических орбит
всюду плотно в X, то она чувствительна к начальным
условиям.
Доказательство. Введем обозначения:
1) точки х обозначим Ох = {х, /(ж), /2(ж),... };
2) если x,q е X, то d(x, Oq) = infy€oq р(х,у);
3) если p,qeX, то d(Op, Oq) = mixe0p,yeoq р(х,у).
Выберем две произвольные периодические точки
P,qtX,
имеющие непересекающиеся орбиты. Такие точки
существуют, поскольку множество точек периодических орбит
всюду плотно в X и множество X бесконечно. Пусть
A = d(Op,Oq).
Покажем, что в качестве 8 в условии чувствительности к
начальным условиям можно выбрать 6 = ^.
239

Орбиты Ор и Oq конечны и не пересекаются, поэтому
А > 0 и для любого х £ X выполнено либо d(x, Op) ^ у,
либо d(x,Oq) ^ у. Без ограничения общности, считаем
далее, что выполнено d(x, Oq) ^ у = 45.
Возьмем произвольную точку х Е X и открытое
множество [/CI, содержащее точку х. Пусть В(х,6) — шар
с центром в точке х радиуса 6 и пусть W = В(х, 6) П U.
Множество W открыто и содержит точку х, поэтому
существует шар В(х,г) С W. Поскольку множество точек
периодических орбит всюду плотно в X, существует
периодическая точка h с ненулевым периодом, лежащая в
В(х, г) С W. Пусть период точки h равен некоторому
числу п. Положим
v = nuf{-ii(B(fi(q),s)).
Множество V непусто, поскольку q Е V, и открыто, так
как преобразование / непрерывно и прообразы открытых
множеств при непрерывных преобразованиях открыты.
Динамическая система {X, /} транзитивна, поэтому
существует такое целое к ^ О, что fk(W) ПУ / 0, иначе
говоря, существуют такие к > 0 и у Е W, что fk(y) Е V.
Рассмотрим представление числа к при делении его на
п:
к = jn + r,
где j — частное от деления к на п, а г — остаток. Числа п
и к неотрицательные, поэтому 0^jn0^r<n.
Следовательно, выполнено неравенство п ^ n(j + 1) — к > 0.
По построению
fn{i+1\y) = fn{j+1)-k(fk(y))e
€ fnU+i)-k(y) с B(fn{j+1)-k(q),6).
Оценим расстояние p(fn^+1^(h), fn^+1\y)). Период точ-
240

ки h равен гг, поэтому
fnV+V(h) = h.
Обозначим а = fn{j+1){y) и Ъ = fn(j+1">-k(q).
Точка a Е В(Ь,8), поэтому р(а, b) < 8.
Применим неравенство треугольника к треугольникам
с вершинами /i, a, b и х, /г, <?:
р(М) ^ p(h,a) + p(a,b),
р(х, 6) ^ р(х, /i) + p(h, b).
Тогда
р(я, Ъ) ^ р(ж, /i) + p(h, a) + р(а, 6)
или
p(h, а) ^ р(я, Ь) - р(х, К) - р{а, Ь).
По построению
p(x,b)=p(x,r^-k(q))>
^ d{x, Од) ^ 48.
Так как h Е В{х,8), то р(х, К) < 8, поэтому
p(h,a)> 48-8-6 = 25,
то есть
p(/n0+1)(ft),/n(j+1)(2/))>25.
Применим неравенство треугольника к треугольнику с
вершинами
fn{j+1\h), fn{j+l\x), fn{j+1){y).
241

Сторона fn(j+1\h), fn(j+1\y) больше 2<5, поэтому одна
из двух его оставшихся сторон больше 5:
либо
р(/п0+1)(Л),/п0+1)(*))>*,
либо
p(fnU+1Kv),fnU+lKx))>6.
В любом случае в открытом множестве U существует
точка (у или К) такая, что ее образ при преобразовании
fn(J+1) находится от соответствующего образа точки х на
расстоянии, большем 6.
Мы доказали, что для непрерывного отображения / и
бесконечного пространства X динамическая система {X, /}
чувствительна к начальным условиям всегда, когда она
транзитивна и множество ее периодических точек всюду
плотно.
Примеры хаотичных динамических систем
1. Функция /(егв) = е2гв на окружности 51, где в —
полярная координата на окружности, задает на S1
хаотичную динамическую систему.
2. Функция
Х) ~ \ 3 - Зх, х > \ '
называемая тентообразным отображением, задает на
Канторовом множестве хаотичную динамическую
систему.
Предлагается доказать хаотичность приведенных
примеров в качестве упражнений.
242

Теорема 12.5. Рассмотрим динамическую систему
на кодовом пространстве Е бесконечных
последовательностей из N символов, ставящую каждой
последовательности а последовательность о, начинающуюся со
второго элемента а, причем каждый элемент
последовательности q равен следующему по номеру элементу
последовательности а:
{Г,Г}, V<r G Е : T{a)i = ai+llг = 1,2,...
Эта динамическая система хаотична.
Доказательство. Докажем по очереди наличие у этой
системы каждого из свойств хаотичной динамической
системы.
1. Транзитивность. Пусть U и V — произвольные
открытые множества из Е. Без ограничения
общности можем считать множество U шаром радиуса г
с центром в некоторой точке а. Рассмотрим
натуральное число к такое, что выполнено неравенство:
(N+iy~k < г. Любая последовательность, у которой
первые к компонент совпадут с соответствующими
компонентами последовательности а будет
принадлежать множеству U. Это значит, что
Tk(U) = Е.
Следовательно,
Tk(U)HV^0.
Мы доказали транзитивность динамической системы
{Г,Т}, V<7 € Е : T{a)t = ai+ui= 1,2,...
2. Чувствительность к начальным условиям.
Возьмем 8 = 2(n+i) - В любой окрестности любого a Е Е
243

найдется последовательность д : д ф а, д Е Е.
Поскольку выполнено д ф а, существует натуральное
п > О такое, что дпф сгп. Из последнего неравенства
следует
откуда
1
p{Tn-\g),Tn-\a)>{N + iyl>
2(iV + l)
Тем самым доказана чувствительность к начальным
условиям.
3. Всюду плотность множества точек
периодических орбит. Для произвольной последовательности
a Е Е последовательность периодических
последовательностей
{e' = («riff2...ff0}£i
будет иметь а своим пределом. Это доказывает, что
точки периодических орбит преобразования Т всюду
плотны в Е и завершает доказательство хаотичности
динамической системы
{Г, Г}, V<7 Е Е : T{a)i = <ri+u i = 1,2,...
Теорема доказана.
Рассмотрим вполне несвязную систему итерированных
функций и ассоциированную с ней динамическую систему
сдвига. В предыдущей главе было доказано, что
динамическая система сдвига на аттракторе эквивалентна
динамической системе
{Г, Г}, VaeE: T(a)i = ai+1,i = 1,2,...
244

на соответствующем кодовом пространстве Е. Свойства
транзитивности и всюду плотности множества точек
периодических орбит сохраняются при переходе к
эквивалентной системе, а свойство чувствительности к
начальным условиям также сохраняется при условии, что
исходные пространства динамических систем компактны. Эти
соображения приводят к следующей теореме.
Теорема 12.6. Динамическая система сдвига,
заданная на аттракторе вполне несвязной системы
итерированных преобразований, хаотична.
Аналогично верна также следующая теорема
Теорема 12.7. Поднятая динамическая система
сдвига системы итерированных преобразований хаотична.
На хаотичной динамике динамической системы сдвига
Д51 на аттракторе А вполне несвязной системы
итерированных преобразований основан алгоритм построения
фракталов с помощью генератора случайных чисел. Сам
алгоритм приведен в книге M.Barnsley «Fractals everywhere»
(Academic Press, Boston, MA: Academic Press, 1988, p.91,
programm3.8.2).
Идея построения аттрактора с помощью
генератора случайных чисел(ГСС)
Динамическая система сдвига на аттракторе
хаотична, а значит, взятая случайным образом произвольная
орбита с большим периодом в общем случае будет плотно
заполнять аттрактор. Если отметить на аттракторе все
точки этой орбиты, то получим изображение, близкое к
изображению самого аттрактора. Но при построении
орбиты требуется на каждом шаге проверить, в образе какого
преобразования исходная точка находится, и лишь потом
245

применить к ней обратное преобразование. Не зная
заранее аттрактор, провести такую проверку довольно
сложно. Поэтому будем действовать противоположным
образом. Вместо того чтобы двигаться по орбите от точки х к
точке S(x), будем двигаться от точки S(x) к точке х.
Преобразованию 5-1 соответствует одно из преобразований
системы итерированных преобразований, которое
определено не только на аттракторе, но и на всем исходном
пространстве X. Какое именно преобразование СИФ брать в
каждом случае, нам не очень важно, поскольку нас
интересует произвольная орбита системы сдвига, лишь бы ее
период был не слишком мал. Поясним сказанное на
конкретном примере.
Пусть {R2, /1? /2} — вполне несвязная СИФ на
плоскости с аттрактором А и точкой a Е А. Пусть Е — кодовое
пространство СИФ, a Е Е — адрес точки а: Ф(сг) = а.
С помощью генератора случайных чисел получим
последовательность единиц и двоек большой конечной
длины, например миллион:
2211112...221
всего миллион символов
Обозначим элементы этой последовательности
^,г = 1,...106,
то есть
fll = 2, fl2 = 2, fl3 = 1, . . . , /^999998 = 2, Д999999 = 2, /^ЮООООО = 1
Каждому символу соответствует преобразование СИФ,
246

откуда:
а = Ф(<т),
Л (а) = Ф(1(т),
/2(Л(а)) = Ф(21(т),
//ife (//xfc+i (• • • /дюооооо (а) • • • ) = Ф(Цк^к+1 • • • MlOOOOOO^),
Ui(U2(- • • /мюооооо(а) • • • ) = Ф(/^1М2 • • • /^ЮОООООО-)-
Обозначим
^ = JV4 WA»2\* • • / AUoooooo W • • • J =
= ЫШШШШ- • • /2(/2(/i(a)...),
5(6) = (/w(. • • /Mlo0oooo(a) • • • ) =
= (/2(/.(/i(/i(/.(/2(.../2(/2(/.(a)...),
^(Ь) = (/w(- • • /Woooooo(a) • • • ) =
= (/i(/i(/i(/i(/2(-../2(/2(/i(a)...),
5юооооо(ь) = a
Получаем орбиту (точнее, первый миллион ее точек)
некоторой точки b динамической системы сдвига СИФ.
Нанесенные на плоскость точки этой орбиты дадут
приближенное изображение аттрактора СИФ. Если
изначально точка а не принадлежала аттрактору, то мы получим
последовательность точек, приближающих некоторую
орбиту СИФ. Это следует из теоремы затенения.
247

Рис. 39: Треугольник Серпинского, построенный с
помощью ГСС, 10000 точек
Остается вопрос: если построенная орбита будет иметь
маленький период, то она будет плохо приближать
аттрактор. Какова вероятность того, что построенная
последовательность из миллиона точек будет непериодичной или
периодичной с большим периодом? Ответ на этот вопрос
дает следующая теорема.
Теорема 12.8. Число А(р) различных периодических
последовательностей из N элементов минимального
периода р определяется по формуле
NP _ £P-i Nk
Л(р) = ^^ .
Р
Идея доказательства. Цикл длины р задается Np
различными способами, причем этот цикл может быть
задан своими р различными точками. Кроме того, надо
отбросить все циклы неминимальной длины р, длины
которых будут делителями числа р.
Число Л(р) очень быстро растет с ростом р. Это хорошо
248

видно даже на примере N = 2:
Л(1) = 2, Л(2) = 1, Л(3) = 2, Л(4) = 3, Л(5) = 6,
Л(6) = 9, Л(7) = 18, Л(8) = 30,..., Л(20) = 52377.
Как видно из приведенного примера, рост Л(р) с ростом
р происходит почти экспоненциальный, в частности 99.8%
циклов периода 20 имеют его своим минимальным
периодом. Орбита с большим периодом с большой вероятностью
является орбитой с большим минимальным периодом, что
и завершает обоснование алгоритма построения
аттрактора с использованием генератора случайных чисел.
Упражнения
1. Являются ли транзитивными следующие
динамической системы:
(a) {R, /(*) = И>
(b) {R, f(x) = Зх},
(c) {[-2,2], /(z) = |2*|-2},
(d) {R2,/(£) = -£+(j)}.
2. Будет ли множество периодических точек
динамической системы {[—2,2], f(x) = х2 — 2} всюду
плотным на отрезке [—2,2]?
3. Будет ли динамическая система
{R2, /(*)=(| "|)f+("|)>
249

чувствительной к начальным условиям?
4. Хаотична ли динамическая система
<*' '<*> = (! 1)f+("5)}?
Пример решения задач
Является ли транзитивной динамическая система
{[0,1], f(x) = {2x}},
где {х} означает дробную часть х?
Решение
1. Можно показать, что орбита любого
рационального числа, имеющего нечетный знаменатель, является
периодической. Поэтому множество точек
периодических орбит всюду плотно на отрезке [0,1].
2. Какой бы маленький интервал 8 ни возьмем,
применяя к нему функцию f(x) = {2a;}, получаем
либо интервал вдвое большей длины, либо
объединение двух интервалов, чья длина в сумме либо вдвое
больше длины исходного интервала, либо равна
единице. Отсюда следует, что после нескольких
применений функции f(x) = {2x}получаем полуинтервал
[0,1), который пересекается с любым открытым
множеством в [0,1]. Это значит, что исходная система
транзитивна.
3. Используя предыдущее рассуждение, получаем, что
после нескольких применений функции f(x) = {2х}
250

к любому маленькому интервалу 5 получаем
полуинтервал [0,1), то есть в любой окрестности любой
точки х исходного интервала [0,1] найдется точка у,
образ которой после нескольких применений
функции f(x) = {2х} будет находиться от образа точки х
на расстоянии, не меньшем |. Это значит, что
исходная система чувствительна к начальным условиям.
Итак, доказано наличие у исходной системы всех свойств
хаотичной динамической системы.
251

Глава 13. Фрактальная размерность
Рассмотрим компактное множество А в некотором
метрическом пространстве X. Выберем поизвольное число е >
О и покроем множество А замкнутыми шарами радиуса е.
Поскольку множество А компактно, это можно сделать с
помощью конечного числа таких шаров. Существует
самое маленькое число шаров радиуса £, которыми можно
покрыть множество А. Обозначим это число N(A,e).
Рис. 40: Покрытие компактного множества шарами
Определение 13.1. Если существует предел
е->о — In e
то такой предел называется фрактальной размерностью
компакта А и обозначается как D(A).
Существование такого предела означает, что при
малых е число шаров N(A, е) ведет себя как степень е:
N{As) « CeD(A),
где С — некоторый конечный коэффициент.
252

Рассмотрим несколько примеров.
1. А = {ai}f=l — множество А состоит из одной или
нескольких изолированных точек. При достаточно
малых е необходимо ровно К шаров радиуса е, чтобы
покрыть множество А. Отсюда
N(A, е) = К, => lim )—L-L = lim —— = 0.
2. A = [0,1] — отрезок. Тогда
Отсюда получаем
1=цт^м^ит1плг^£^ит1п^;'+1^
e->0 — In £ e^O — In £ e->0 — In £
<]im-b(g) + m(i + g)=]jmZb(g) = L
e->0 — In £ e->0 — In £
Следовательно,
d(a) = i.
Теорема 13.1. Рассмотрим последовательность
{en = CV"}~=1
для некоторых произвольных 0<г<1иС>0.
Тогда для произвольного компакта А на метрическом
пространстве X верно
lim Ь^») = Я(Л),
п-юо — In Sn
253

если этот предел существует.
Доказательство. Введем обозначение
7(e) = max{sn = Crn : еп < s}.
Без ограничения общности можно считать, что j(e) < г
Тогда выполнено
7(e) < е ^ ^£) < 1,
Г
откуда
N(A, 7(e)) > N(A, e) > N(A, ^) ^ 1.
г
Следовательно,
J In N(A, 7(e)) S* In iV(A, е) ^ In iV(A, ^) ^ 0,
\ ln7(e)<lne^ln^ <0.
Меняем знаки во втором неравенстве:
' In N(A, 7(e)) > In iV(A, e) ^ IniV(A, ^) ^ 0,
-ln7(e) > -InO -ln^ >0.
Окончательно получаем
lnJV(A7(g)) lniV(A,g) lnJV(A^)
_ln 2i£l ^ -lne ^ -In 7(e) '
г
Разложим логарифм произведения на слагаемые:
In Af(A, 7(e)) ^ЫЩА,е)^ 1п7У(А,2Ы)
-ln7(e) + lnr^ -lne ^ -1п^ - lnr'
254

При е —>• 0 выполнено j(e) —> О, поэтому имеем
е->0 —In 7(e) +ЬГ е->0 -lne e^O _ Jn 7(£) _ ln r '
г
1п7У(Л7(£)) r In N(A,en)
lim— ——-— = lim ,
e->o — In 7(e) + lnr п-юо — lnen
Um lniV(A^) Um ]nN(A,en)
е-ю _inii£l -lnr n^°° -lnen
г
следовательно, если предел
1;„ ЪЩА,£п)
п—too
-\li£n
существует, то существует предел
и эти пределы равны,
Теорема доказана.
lim
£->0
]nN(A,e)
— lll£
Замечание. С помощью этой теоремы легко вычислить
размерность Канторова множества. Действительно, выбрав
С = 1,г = |, получим, что для покрытия Канторова
множества замкнутыми шарами радиуса ^г (на прямой
замкнутый шар — это отрезок длиной в диаметр шара)
требуется ровно 2П шаров. Отсюда следует, что фрактальная
размерность Канторова множества равна
In 2
ЬЗ*
Теорема 13.2. Пусть A Е Rm — компактное
множество в евклидовом га-мерном пространстве и пусть
255

все пространство Rm покрыто замкнутой квадратной
решеткой. Иначе говоря, каждая точка пространства
попадает в какой-либо т-мерный кубик со стороной а,
причем два кубика могут либо не пересекаться, либо
совпадают по к-мерной грани, где к < т. Пусть
Q
а = —, С > О, г > 1.
Обозначим Nn(A) — минимальное число граней решетки,
объединение которых содержит множество А.
Тогда, если предел
п->оо — П 1П Г
существует, то он равен фрактальной размерности
множества А.
Доказательство. Если множество А покрыто N(A, |)
шарами диаметра d, то оно содержится в объединении не
более чем 2mN(A, |) клеток со стороной d, поскольку
каждый шар может пересечь не более 2т клеток со стороной,
равной его диаметру. Отсюда следует неравенство
С другой стороны, каждая клетка со стороной а может
быть покрыта шаром радиуса у/т^ — это следует из
теоремы Пифагора. Отсюда следует неравенство
Nn(A)>N(A,^).
256

Совместно оба неравенства показывают, что пределы
п->оо — П In Г
е->0 — In £
существуют одновременно и равны.
Теорема доказана.
Замечание. Этот способ вычисления фрактальной
размерности называется подсчетом с помощью коробок и очень
удобен, например, в случае треугольника Серпинского.
Действительно, выбирая С = 1,г = 2, получим,что
Nn(A) = 3",
откуда получаем фрактальную размерность треугольника
Серпинского равную
1пЗ
1п2'
Теорема 13.3. Пусть {X, р} и {У, д} — метрически
эквивалентные метрические пространства. Тогда
соответствующие компактные множества А и О(А), где О
— гомеоморфизм, устанавливающий эквивалентность
пространств, имеют одинаковую фрактальную размерность.
Доказательство не приводится ввиду очевидности.
Замечание. Из сформулированной теоремы следует, что
треугольник Серпинского, построенный с вершинами в трех
произвольных точках плоскости общего положения, будет
257

иметь фрактальную размерность
1пЗ
Немного подкорректируем определение фрактальной
размерности таким образом, чтобы для любого компакта она
была определена.
Определение 13.2. Рассмотрим компактное
множество А в некотором метрическом пространстве X.
Выберем произвольное число е > 0 и покроем множество
А замкнутыми шарами радиуса е. Пусть, как и раньше,
N(A,e) обозначает наименьшее число шаров радиуса е,
которыми можно покрыть А. Тогда существует предел
\nN{A,e)
lim sup ;
v^oQ<£<v -те
такой предел называется фрактальной размерностью
компакта А и обозначается как D(A).
Замечание. Очевидно, что последнее определение не
противоречит первому, и когда оба предела
е^О — In £
.. mN(A,e)
lim sup
*7->°o<e<77 -me
существуют, то они совпадают.
В последнем определении постулировалось существо-
258

вание предела. Докажем, что если X = Rm, то предел
1пЛГ(Л,е)
lim sup
т1^° 0<е<77 - In €
всегда существует.
Теорема 13.4. Пусть А,В — компакты в Ит, причем
А^ В. Тогда фрактальные размерности D(A) и D(B)
существуют, причем выполнено неравенство: О ^ D(B) ^
D(A) ^ т.
Доказательство. Без ограничения общности можно
считать, что А С G, где G — куб в Rm с ребром единичной
длины. Если разбить G замкнутой квадратной решеткой
с ребром длины ^г, то верно неравенство:
1 < Nn(B) < Nn(A) < Nn(G) = 2тп.
Следовательно, для любого п верно
п ^ lnNn(B) ^ In Nn(A) ^ lnJVn(G) In У"
U ^ ^ ^ = = 771.
1п2п 1п2п 1п2п 1п2п
Если функция f{x) определена и ограничена на интервале
(О, а), то функция ф(г)) = sup0<£<7? f(e) определена,
монотонна и не убывает на интервале (0, а). Поэтому
существует предел
lim ф(г)) = lim sup f(e).
77^-0+ 77^-0+ 0<£<77
Рассмотрим ft(x) = ^^ для х = £ и f2(x) = 1-^^
для х = ^-. Из предыдущих рассуждений следует, что
D(A) и D(B) существуют, причем
0 ^ D(B) ^ D(A) ^ га.
259

Теорема доказана.
Теорема 13.5. Пусть А,В — компакты в Ит, причем
верно D(B) ^ D(A). Тогда D(A U В) = D(A).
Доказательство. Очевидно, что Уе > О выполнено
N(A,е) + N{B,е) ^ N(A UB,e)^ N(A,е) ^ N(B,е).
Следовательно,
lim sup ^
^^°о<в<г7 -те
^ lim sup ^ lim sup .
*7->°о<£<77 —те v^o0<e<TI —те
Отсюда
шМА,е) ,. mN(AuB,e)
lim sup ^ lim sup ^
v^o0<£<v -ine v^o0<£<v -Ine
lniV(A,s) + ln(™ + l)
^ lim sup —— .
v^o0<£<v -Ine
Поскольку (NfA,e£l ^ 1, первый и третий пределы равны, а
значит, они равны второму пределу:
шМА,е) Л. \nN(A\JB,e)
lim sup = lim sup
*7->°o<e<77 -\ne v^0q<£<t1 — Ine
откуда
D(A) = D(A\JB).
Теорема 13.6. Пусть дана СИФ вполне несвязная или
с касанием
260

с аттрактором А, причем преобразования /i,..., /jv
являются подобиями с коэффициентами подобия
ки ..., kN : 1 > \ki\ > 0,..., 1 > \kN\ > О
соответственно.
Тогда фрактальная размерность D(A) аттрактора А
является единственным решением уравнения
N
^|/сп|* = 1, ж€[0,т].
п=1
Если СИФ является системой с перекрытием, то
выполнено D(A) ^ х, где х -решение уравнения
N
J2\kn\X = h *€[0,m].
n=l
План доказательства. Преобразования подобия
переводят шары в шары, изменяя их радиус. Поэтому
fn(B(x,r)) = B(fn(x),\kn\r).
Отсюда
f-l(B(x,r)) = B(f-1(x),\kn\-lr).
И далее
N(A,s) = N(fn(A),\kn\e)
ИЛИ
N(fn(A),e) = N(A,\kn\-1).
Если система вполне несвязна, то при достаточно малом
261

радиусе шара можно предположить, что шары,
покрывающие разные компоненты fn(A) аттрактора А, не
пересекаются. А это значит, что при достаточно малом е выполнено
равенство
N(A,e) = N(Ji(A),e) + ■■■ + N(fN(A),e) =
= N(A, Ih^e) + ■■■ + N(A, M"1*).
Если фрактальная размерность D(A) существует, то
N(A,e)~Ce-D{A).
Тогда верно
Ce~D^ « Clfcxl^'e-^) + • • • + C\kN\D^e-D^A\
и, сократив выражение, получаем
что и доказывает теорему.
Замечание. Из сформулированной теоремы следует, что
кривая Коха будет иметь фрактальную размерность
In 4
1пЗ"
Экспериментальное вычисление фрактальной раз
мерности
При вычислении фрактальной размерности реальных
объектов, например облаков или кровеносной системы,
объект сохраняет свойство самоподобия только в
ограниченных пределах, и устремить радиус покрывающих шаров к
262

О становится затруднительно. Поэтому вычисляют
количество покрывающих шаров (или кубов) для нескольких
значений радиуса, затем строят график зависимости числа
шаров от радиуса в двойных логарифмических
координатах, после чего график аппроксимируется прямой, тангенс
угла наклона которой, взятый с обратным знаком, и будет
значением искомой фрактальной размерности.
Рис. 41: Экспериментальное вычисление фрактальной
размерности
263

Рис. 42: Эксперимент Ричардсона: вычисление
фрактальных размерностей береговых линий
Упражнения
Вычислите фрактальную размерность аттрактора для
следующих систем итерированных функций:
1. {R, h{x) = \x,h{x) = \x+\).
2. {R, fl(x) = lxj2(x) = lx+l}.
3. {R, /i(a0 = |a:,/2(a0 = !*+!}.
4. {R2,h(x) = if, h(x) = H?+( | ) , /з(5) = §*( | )}•
5. {R2,/,(-g) = \x, f2{x) = £*+( | ) • f3(x) = i* ( J )}•
Пример решения задач
Вычислите фрактальную размерность аттрактора СИФ
{11аЛ(х) = h, f2(x) = iX+ ( 2 ) , f3(x) = 5* ( I )}•
264

Решение:
Данная СИФ является системой с касанием, все
преобразования которой являются преобразованиями подобия
с коэффициентами |, | и | . Отсюда следует, что можно
вычислить фрактальную размерность D аттрактора,
используя уравнение
Введем обозначение
-О'-
Получаем уравнение:
х2 + 2х - 1 = О,
единственным положительным решением которого будет
число л/2 — 1, откуда следует, что
1п(л/2-1)
In 2
265

Список литературы
1. Barnsley M. Fractals everywhere. Boston : Academic
Press, 1988.
2. Божокин СВ., Паршин Д.А. Фракталы и мульти-
фракталы. - Ижевск: НИЦ «Регулярная и хаотическая
динамика», 2001.
3. Ильяшенко Ю.С. Аттракторы и их фрактальная
размерность. М.: МЦНМО, 2005.
4. Кириллов А.А. Повесть о двух фракталах. М.:
МЦНМО, 2009.
5. Кроновер P.M. Фракталы и хаос в динамических
системах. М.: Постмаркет, 2000.
6. Lauwerier H. Fractals. Princeton: Princeton University
Press, 1991.
7. Мандельброт Б.Б. Фрактальная геометрия природы.
М.: Институт компьютерных исследований, 2002.
8. Пайнтген Х.-О., Рихтер П.Х. Красота фракталов. М.:
Мир, 1993.
9. Рудин У. Основы математического анализа. М.: Мир,
1976.
10. Федер Е. Фракталы. М.: Мир, 1991.
11. Шредер М. Фракталы, хаос, степенные законы.
Ижевск: Изд. дом «Удмурдский университет», 2000.
266

Предметный указатель
аттрактор, 98
динамическая система,
202
сдвига, 221, 225
5
чувствительность
к начальным
условиям, 237
эквивалентность,
215
, хаотичность,
239, 243
, на кодовом
пространстве, 222
, неподвижная
точка, 207
, орбита, 203
, отталкивающая
неподвижная
точка, 208
, отталкивающая
периодическая
орбита, 209
, отталкивающая
периодическая
точка, 209
, периодическая
орбита(цикл), 208
, периодическая
точка, 208
, притягивающая
неподвижная
точка, 208
, притягивающая
периодическая
орбита, 209
, притягивающая
периодическая
точка, 209
, транзитивность,
237
, в конечном
итоге
периодическая
орбита, 209
Канторово множество, 7
, СИФ, 99
, кодирование,
168
, обобщенное, 176
, размерность,
255
, размерность
подобия, 15
, свойства, 7, 89,
166, 176
, троичное
представление, 11
Коха кривая, 18, 89
, СИФ, 100
, размерность,
262
коммутативная
267

диаграмма, 215
логарифмическая
спираль, 139
метрическое
пространство
эквивалентность,
40
—, полное, 41
метрика, 36
оо-метрика, 50
—, р-метрика, 50
—, Хаусдорфа, 64
—, эквивалентность,
38
—, индуцированная,
39
—, манхэтенская, 50
множество
— меры нуль, 8, 12, 28
— накопления, 135
—, диаметр, 46
—, граница, 45
—, граничная точка,
44
—, изолированная
точка, 44
—, компактное, 47
—, ограниченное, 46
—, открытое, 28, 42
—, покрытие, 46
—, предельная точка,
43
—, самоподобие, 14
—, совершенное, 44
—, связное, 45
—, внутренность, 43
—, внутренняя точка,
42
—, вполне несвязное,
46
—, всюду плотное, 45
—, замыкание, 44
—, замкнутое, 43
паутинная диаграмма, 96
Пифагора дерево, 21
, СИФ, 102
, СИФ с
накоплением, 137
последовательность
—, фундаментальная,
40
—, сходящаяся, 41
преобразование
—, аффинное, 121
—, индуцированное,
84
—, использующее
операции над
множествами, 86
—, неподвижная
точка, 87
—, подобия, 123
—, сжимающее, 89
пространство
—, гомеоморфизм,
212
—, кодовое, 170
268

—, метрическое, 36
—, топологическое,
212
Серпинского
треугольник, 16
, кодирование,
169
, размерность,
257
, размерность
подобия,17
, свойства, 17
СИФ, 98
— с касанием, 192
— с накоплением, 136
— с параметром, 159
— с перекрытием, 193
— вполне несвязная,
192
—, адрес точки
аттрактора, 192
—, адресная
функция, 192, 222
—, орбита случайного
сдвига, 223
—, поднятая, 224
фрактал
- Леви, 24, 100
—, алгоритм
построения, 103,
245
—,
детерминированный, 98,
136
—, размерность, 252,
258, 261
—, звездчатый, 145
269

Учебное издание
Шихеева Валерия Владимировна
ФРАКТАЛЬНАЯ ГЕОМЕТРИЯ
Детерминированные аттракторы
Учебник
Редактор Л.М. Цесарская
Компьютерная верстка В.В. Шихеева
Подписано в печать 23.09.19 Уч.-изд. л. 16,9
Формат 60 х 90 1/16 Электронная версия
Национальный исследовательский
технологический университет «МИСиС»,
119049, Москва, Ленинский пр-т, 4
Издательский Дом НИТУ «МИСиС»,
119049, Москва, Ленинский пр-т, 4
Тел. 8 (495) 638-44-06
Отпечатано в типографии
Издательского Дома НИТУ «МИСиС»,
119049, Москва, Ленинский пр-т, 4
Тел. 8 (495) 638-44-16, 8 (495) 638-44-43